В. ЗАЛИЗНЯК
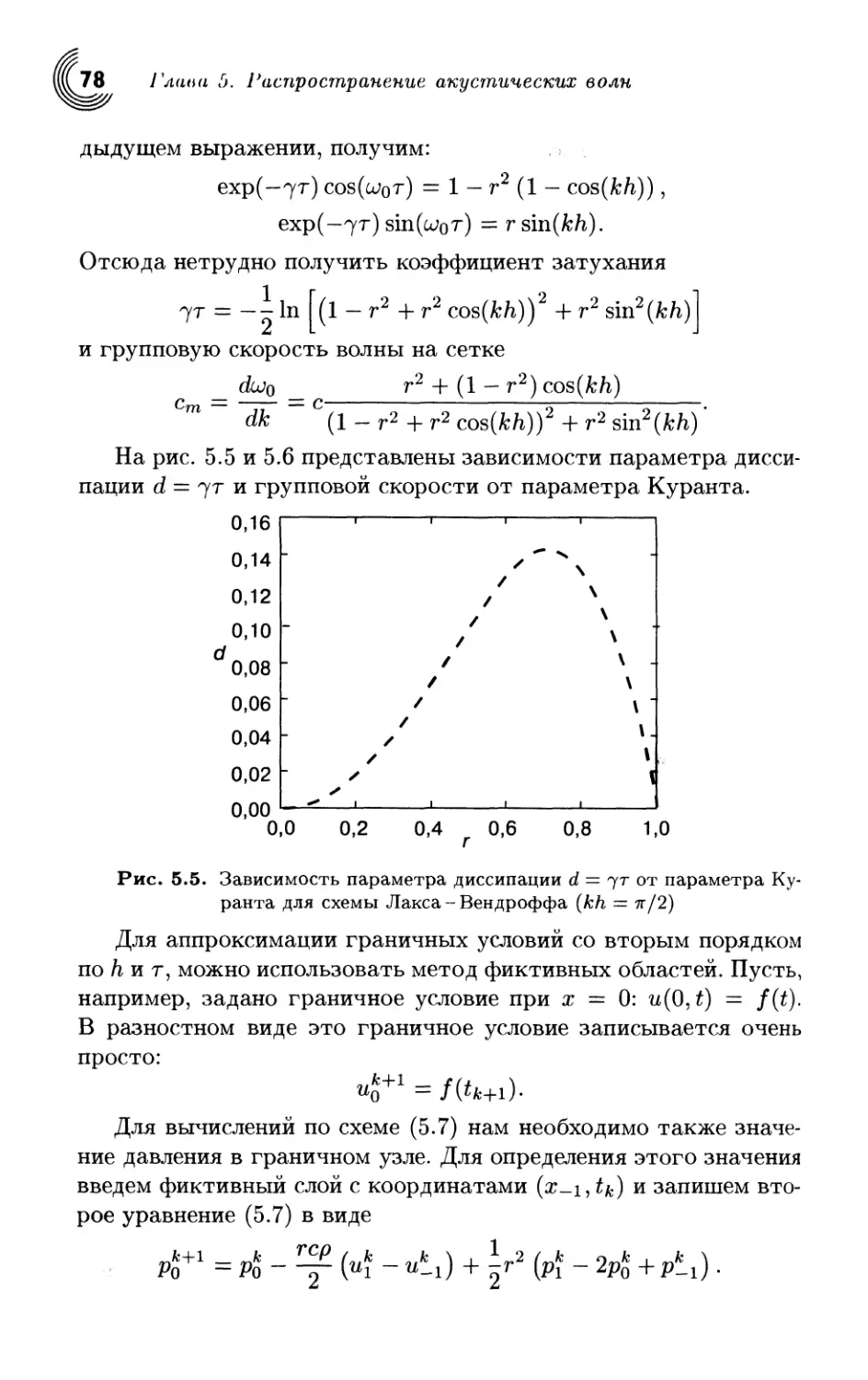
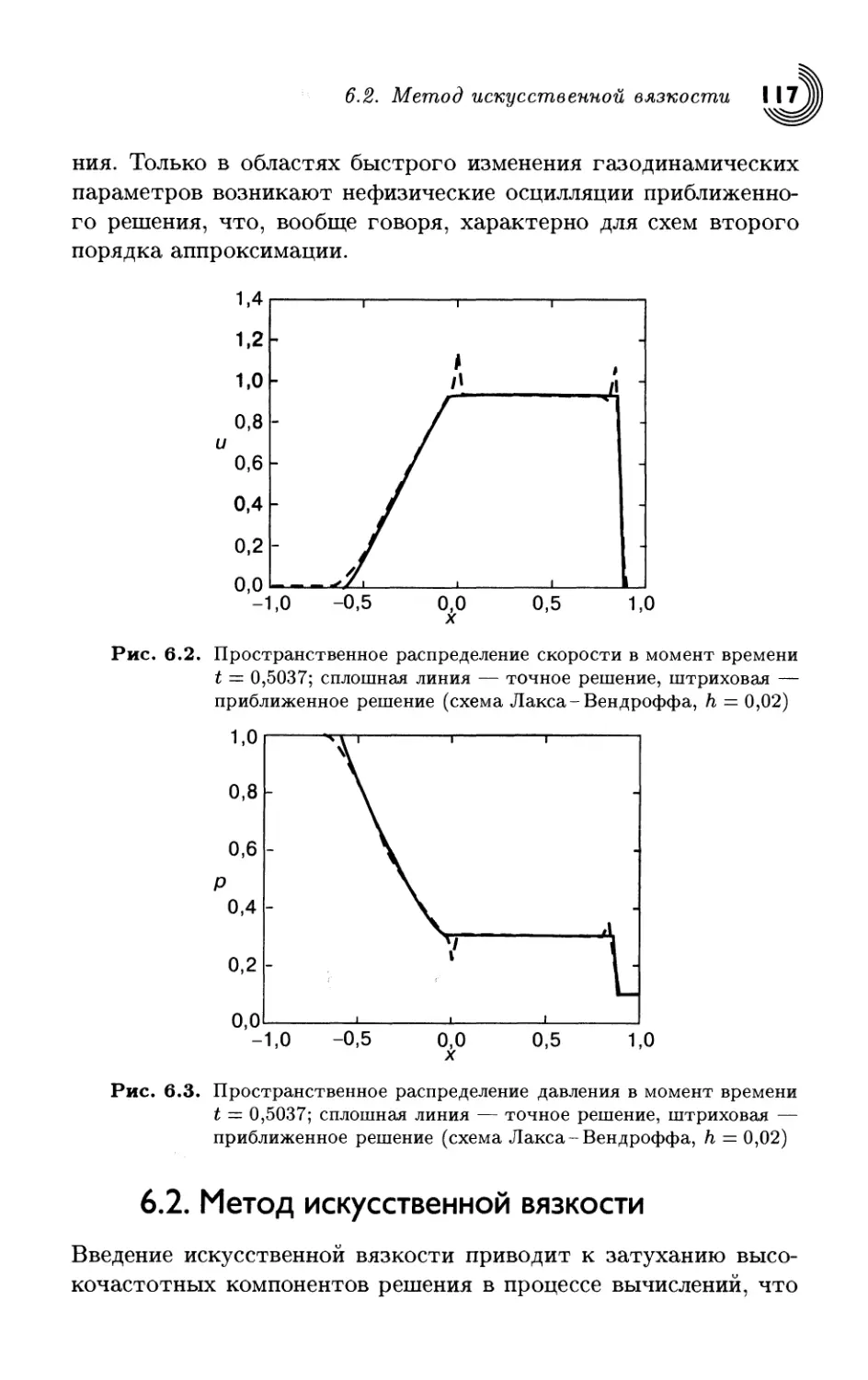
Основы
вычислительной
физики
Часть I
1 И Р
изики и техники
В. ЗАЛИЗНЯК
Основы
вычислительной
физики
Часть I. Введение
в конечно-
разностные методы
Рекомендовано УМО по образованию в об-
ласти прикладных математики и физики в
качестве учебного пособия для студентов
вузов по направлению 511600 «Прикладные
математика и физика»
ТЕХНОСФЕРА
Москва
2008
Рецензенты:
И.О. Вогульский, д.ф.-м.н., профессор, ведущий научный сотрудник
Института Вычислительного моделирования СО РАН, г. Красноярск
А.И. Лобанов, д.ф.-м.н., профессор кафедры вычислительной
математики МФТИ, зам. декана ФУПМ по научной работе
Зализняк В.Е.
Основы вычислительной физики
Часть 1. Введение в конечно-разностные методы
Москва:
Техносфера, 2008. - 224с. ISBN 978-5-94836-132-1
Предлагаемая книга является первой частью курса «Основы вы-
числительной физики» и рассматривает методы решения уравнений
математической физики.
Описывается построение вычислительных моделей для исследований
таких явлений, как теплопроводность, распространение акустических
волн, движение сжимаемой среды и движение вязкой несжимаемой
жидкости. Приводятся методы решения стационарных уравнений.
Материал излагается в простой и доступной форме, содержит мно-
жество примеров, демонстрирующих применение рассматриваемых
методов.
Книга дополняется пакетом программ, реализующим большинство
изложенных методов. Этот пакет представляет собой набор функций
для среды MATLAB и может быть использован как для практических
занятий, так и при выполнении курсовых и дипломных проектов.
Книга предназначена для студентов старших курсов, магистрантов и
аспирантов физических и инженерных специальностей.
© 2007, В.Е. Зализняк
© 2008, ЗАО «РИЦ «Техносфера»,
оригинал-макет, оформление
ISBN 978-5-94836-132-1
Содержание
Предисловие.................................. 6
Глава 1
Вычислительный эксперимент................... 7
1.1. Роль вычислительного эксперимента....... 7
1.2. Постановка вычислительного эксперимента. 9
Глава 2
Основные уравнения математической физики 12
2.1.	Распространение малых возмущений и колебания... 12
2.2.	Уравнение теплопроводности (диффузии)......... 13
2.3.	Уравнения Максвелла........................... 13
2.4.	Уравнение Шредингера.......................... 14
2.5.	Уравнения газо-гидродинамики.................. 14
2.6.	Уравнения Навье-Стокса........................ 15
2.7.	Стационарные уравнения........................ 16
2.8.	Постановка основных задач для уравнений	матема-
тической физики	 17
2.8.1.	Задача Коши.............................. 18
2.8.2.	Краевая задача для стационарных уравнений. 19
2.8.3.	Смешанная краевая задача................. 20
Глава 3
Основные методы построения и анализа раз-
ностных схем....................................... 21
3.1.	Обсуждение основных понятий на примере разност-
ных схем для уравнения переноса.................... 22
3.2.	Основные свойства разностных схем: аппроксимация
и устойчивость............................... 26
3.3.	Анализ аппроксимации.......................... 29
3.4.	Критерий фон Неймана для анализа устойчивости
разностных схем.............................. 32
3.5.	Принцип замороженных коэффициентов............ 35
3.6.	Шаблон разностной схемы....................... 37
Содержание
Глава 4
Распространение тепла (диффузия)................. 39
4.1.	Разностная схема для одномерного уравнения тепло-
проводности с постоянными коэффициентами.......... 39
4.2.	Построение разностных схем для одномерного урав-
нения теплопроводности с переменными коэффици-
ентами............................................ 47
4.3.	Метод расщепления по пространственным переменным 52
4.4.	Разностные схемы для решения многомерного урав-
нения теплопроводности............................ 54
4.5.	Численное решение задачи Стефана............ 64
Глава 5
Распространение акустических волн................ 68
5.1.	Разностная схема для уравнения колебаний.... 68
5.2.	Диссипация и дисперсия сеточного волнового решения 71
5.3.	Схема Лакса-Вендроффа....................... 74
5.4.	Характеристическая форма уравнений акустики.. 80
5.5.	Недиссипативная схема Ф. Роу................ 82
5.6.	Метод С. К. Годунова........................ 85
5.6.1.	Схема первого порядка................... 86
5.6.2.	Схема второго порядка................... 91
5.7.	Кусочно-экспоненциальный метод.............. 92
5.8.	Разностные схемы для решения многомерных задач .. 98
5.9.	Заключительные замечания................... 109
Глава 6
Движение сжимаемой жидкости (газа)................ 111
6.1.	Схема Лакса-Вендроффа для одномерных задач... 112
6.2.	Метод искусственной вязкости............... 117
6.3.	Задача о распаде разрыва................... 120
6.4.	Схема С. К. Годунова....................... 123
6.5.	Метод взвешенного усредненного потока...... 127
6.6.	Метод уменьшения суммарного отклонения (TVD).... 132
6.6.1.	Концепция TVD и ограничители потоков..... 133
6.6.2.	Ограничение потоков в схеме метода WAF... 138
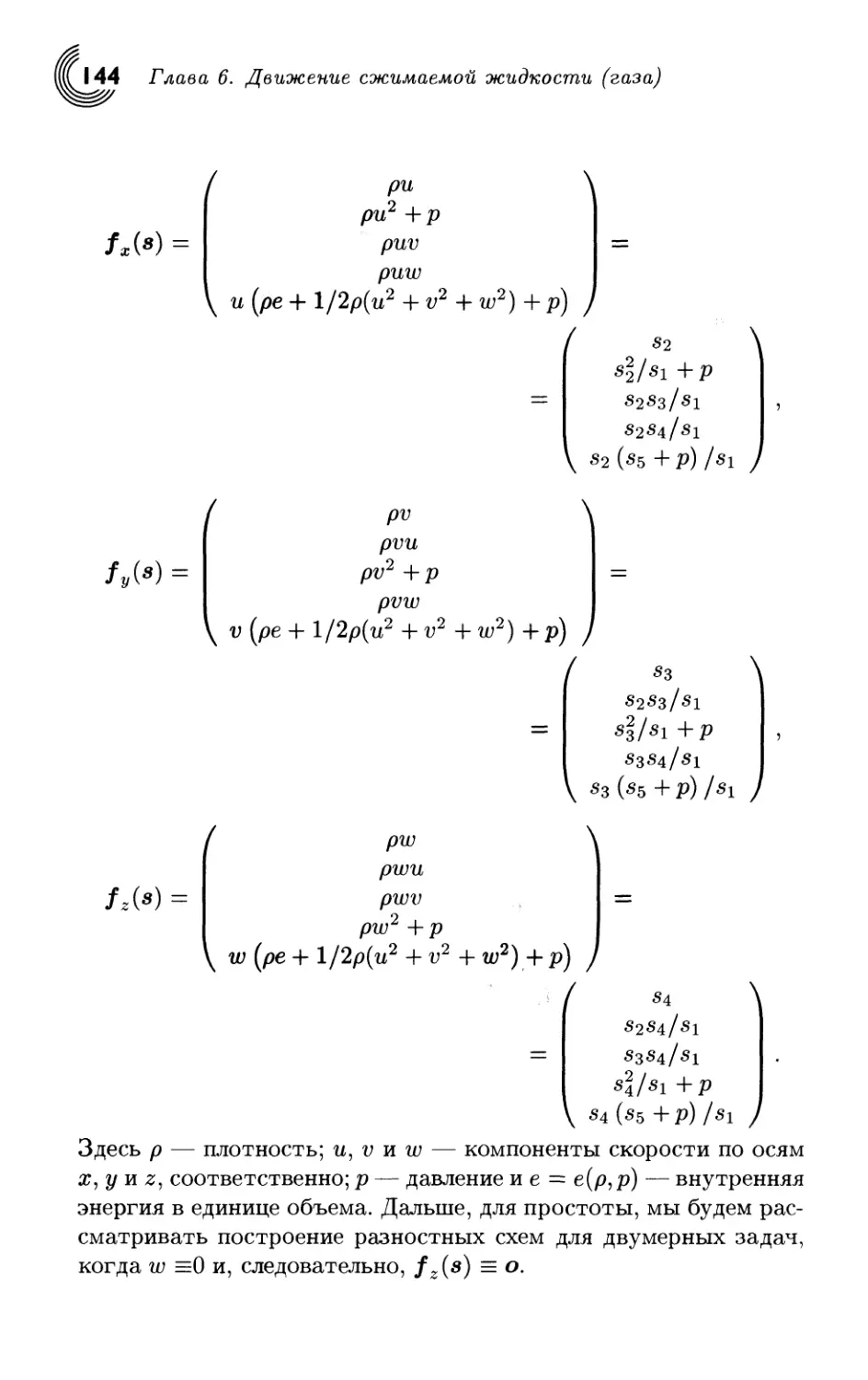
6.7.	Численное решение многомерных задач........ 140
6.8.	Заключительные замечания................... 151
Содержание 5
Глава 7
Стационарные уравнения...................... 153
7.1.	Выбор метода........................... 154
7.2.	Формулировка разностных уравнений	в виде
системы уравнений...................... 155
7.3.	Применение быстрого преобразования	Фурье. 164
7.4.	Метод Конкуса и Голуба................. 168
7.5.	Метод установления..................... 171
7.6.	Заключительные замечания............... 178
Глава 8
Движение несжимаемой вязкой жидкости.......... 180
8.1.	Введение............................... 180
8.2.	Разностные схемы в переменных функции
тока-завихренность..................... 184
8.3.	Метод маркеров и ячеек................. 192
Приложение А
Параметры и дисперсионное соотношение
для схемы РЕМ................................201
Приложение Б
Решение задачи о распаде разрыва
для идеального газа..........................203
Б.1.	Конфигурация	1......................... 206
Б.2.	Конфигурация	2......................... 206
Б.З.	Конфигурация	3......................... 207
Б.4.	Конфигурация	4......................... 207
Б.5. Определение решения в точке х = 0...... 208
Приложение В
Краткое описание прилагаемых программ .... 209
Литература...................................223
Посвящается моим родителям
Предисловие
Вычислительная физика является одним из методов физического ис-
следования, который использует численное моделирование. При этом
компьютер играет роль прибора, который дает новые возможности
для изучения свойств различных физических моделей. Компьютер, как
и любой другой прибор, бесполезен без соответствующих методик его
использования. Роль вычислительной физики и состоит в примене-
нии и развитии вычислительных методик, использующих компьютер,
для того, чтобы получить как можно более полное представление о
реальных физических процессах. Развитие компьютерной техники и
численных методов дает нам возможность не только работать со все
более сложными моделями, но и применять различные методы визуали-
зации, которые позволяют лучше понять природу исследуемых явлений
и открывают перед нами всю красоту этих явлений.
С математической точки зрения многие физические явления опи-
сываются уравнениями в частных производных. Поэтому численные
методы решения этих уравнений составляют одну из основных частей
вычислительной физики. Наиболее простыми и наглядными являют-
ся конечно-разностные методы. Применению этих методов к решению
уравнений математической физики и посвящена эта книга.
Прежде всего книга предназначена для студентов старших курсов
физических и инженерных специальностей. Уровень изложения мате-
риала предполагает, что читатель освоил курсы уравнений матема-
тической физики и методов вычислений. Относительно курса методов
вычислений, следующая книга часто цитируется в тексте, поэтому для
нее введена специальная аббревиатура: ОНВ — Зализняк В. Е., Осно-
вы научных вычислений. Введение в численные методы для физиков и
инженеров, РХД, Москва-Ижевск, 2006.
Книга дополняется небольшим пакетом программ, реализующим
большинство изложенных методов. Этот пакет представляет собой на-
бор функций для среды MATLAB и может быть использован как для
практических занятий, так и при выполнении курсовых и дипломных
проектов.
В. Е. Зализняк,
Сибирский Федеральный Университет, 2007
ГЛАВА I
ВЫЧИСЛИТЕЛЬНЫЙ
ЭКСПЕРИМЕНТ
В этой книге мы обсудим область научного исследования, в ко-
торой компьютер играет центральную роль. Рассматриваемые
нами темы часто называют «численным моделированием» или
«вычислительной наукой».
В научном исследовании основой вычислительной науки служит
математическая модель интересующего нас физического явле-
ния. Уравнения математической модели переводятся в дискрет-
ную алгебраическую форму, поддающуюся численному решению.
Дискретные алгебраические уравнения описывают вычислитель-
ную модель, которая, если перевести ее в последовательность ко-
манд на каком-нибудь языке программирования, дает программу
моделирования для компьютера. После этого компьютер и про-
грамма позволяют исследовать эволюцию модельной физической
системы в вычислительных экспериментах. Методы дискретиза-
ции, используемые при создании численных моделей, включают
в себя конечно-разностные методы, методы конечных и гранич-
ных элементов и методы частиц. В этой книге мы будем иметь
дело с первым подходом к построению вычислительных моделей.
1.1.	Роль вычислительного эксперимента
В научном исследовании численное моделирование становится воз-
можным благодаря быстродействующим компьютерам. Однако
сам факт возможности исследования с помощью моделирования
не всегда означает, что это наилучший метод. Как и при теоре-
тическом и экспериментальном исследованиях, необходимо вы-
яснить, каковы ограничения и преимущества вычислительного
эксперимента. Для того чтобы получить представление о значе-
нии моделирования, рассмотрим традиционную картину разви-
Глава 1. Вычислительный эксперимент
тия науки и возможные применения вычислительного экспери-
мента в этом развитии.
Экспериментальная работа связана в основном с накоплени-
ем опытных данных. Теоретическая работа направлена, главным
образом, на приведение такой информации в логически последо-
вательную систему для того, чтобы вывести законы описываю-
щие то или иное явление. В своем развитии как теория, так и
эксперимент проверяют и обогащают друг друга. В непосред-
ственном воздействии теории на эксперимент можно выделить
три момента. Теория ведет к экспериментам с целью:
-	определить те факты, которые, согласно математической
модели, основанной на некоторой системе принципов, су-
щественны для описания конкретных явлений;
-	проверить теоретические предсказания и предположения, и
- определить эмпирические величины, которых требует тео-
рия.
Точно также и экспериментальная работа оказывает воздей-
ствие на теорию: ее модифицируют в соответствии с экспери-
ментом, и используют для предсказания наиболее существенных
опытных данных. Обычная практика науки состоит в сопоста-
влении теории с опытом. Существенные различия оказываются
в центре внимания как теории, так и эксперимента, и их разре-
шение приводит либо к обобщению существующих теорий, либо
к пересмотру основных принципов с целью построения более со-
вершенных теорий.
Потребности технологии послужили дополнительным стиму-
лом перейти к исследованию задач, для которых невозможно пост-
роить аналитическое решение, а постановка прямых экспериментов
вызывает большие трудности. Чтобы преодолеть возникающие
затруднения, широко используются компьютеры как новое сред-
ство проведения экспериментов, вычислительных экспериментов,
которые ликвидируют разрыв между теорией и опытом.
Вычислительные эксперименты можно грубо подразделить на
три категории. К первой относятся эксперименты, предназначен-
ные для моделирования работы сложных устройств с тем, чтобы
оценить большое количество вариантов, прежде чем создавать
оптимальную модель с применением дорогостоящей технологии.
Вторая группа вычислительных экспериментов направлена на по-
1.2. Постановка вычислительного эксперимента
лучение информации в ситуациях, когда имеется большой раз-
рыв между возможностями теории и эксперимента. Лаборатор-
ные эксперименты сталкиваются со всей сложностью природы:
условия могут с трудом поддаваться контролю, измерения не
всегда можно легко осуществить, и, как следствие, результаты
зачастую трудно интерпретировать однозначно. Например, так
обстоит дело при моделировании галактик, землетрясений или
субмикронных электронных приборов, когда рассматриваются
очень большие или очень малые пространственные и временные
масштабы. И наконец, имеется группа вычислительных экспе-
риментов, «теоретические эксперименты», которые дают ценные
рекомендации для развития теории.
Объединение вычислительного эксперимента, теории и натур-
ного эксперимента оказывается гораздо более эффективным для
получения полезных результатов, чем любой из этих методов по
отдельности или сочетание любых двух из них. Недостатки ка-
ждого метода исследования компенсируются достоинствами дру-
гих методов. Роль вычислительного эксперимента определяется
его сильными сторонами: возможностью дополнить теоретиче-
ские исследования, когда математическая модель очень сложна и
нелинейна, а также дополнить экспериментальные исследования,
когда приборы дороги, данные недоступны для непосредственно-
го измерения или явления очень сложны.
1.2.	Постановка вычислительного
эксперимента
Отправным пунктом всех вычислительных экспериментов явля-
ется некоторое физическое явление, и цель этих экспериментов
состоит в получении физически полезных результатов. Между
этими двумя пунктами можно выделить ряд этапов, показанных
на рис. 1.1.
Каждый этап вносит свои ограничения. Как всегда, мате-
матическая формулировка представляет собой лишь приближен-
ное описание физического явления. Поэтому ученый-вычислитель
должен знать, какие упрощающие предположения сделаны, что-
бы определить те случаи, когда справедливы эти уравнения, а
следовательно, — и его вычислительная модель.
Глава 1. Вычислительный эксперимент
Более строгие ограничения возникают на этапе перехода к
дискретной алгебраической аппроксимации, на котором непре-
рывные дифференциальные или интегральные уравнения мате-
матической модели заменяются алгебраическими аппроксимаци-
ями для того, чтобы сделать возможным численное решение на
компьютере. На этом этапе возникают вопросы о влиянии ко-
нечного временного шага, дискретных пространственных сеток
и, в случае моделей частиц, конечного числа частиц. Метод дис-
кретизации зависит от каждой конкретной задачи. Он должен
учитывать все основные особенности точного решения матема-
тической модели при минимальных вычислительных затратах.
Рис. 1.1. Постановка вычислительного эксперимента
В результате дискретизации возникают алгебраические сис-
темы уравнений (линейные или нелинейные), вид которых зави-
сит от способа дискретизации. Хотя объем информации, кото-
рый можно обработать с помощью компьютеров, велик, он тем
не менее ограничен. Поэтому этот фактор должен всегда учиты-
ваться при построении вычислительных моделей. В настоящее
время существует множество надежных численных алгоритмов
1.2. Постановка вычислительного эксперимента
для решения систем уравнений. Во многих случаях можно вос-
пользоваться библиотеками стандартных программ. Необходимо
только выбрать соответствующую процедуру с учетом свойств и
структуры решаемой системы.
После того, как все вопросы, связанные с построением алго-
ритма, решены, можно строить «прибор» — программу модели-
рования. При этом необходимо уделить достаточно внимания со-
зданию правильно функционирующей программы. Качественно
разработанная программа должна быть удобочитаемой, неслож-
ной в использовании и легко модифицируемой. Она должна иметь
модульную структуру и встроенную диагностику и должна соби-
раться только из проверенных программных компонентов. Пол-
ная программа должна быть испытана на известных задачах как
для проверки алгоритма и кода, так и для определения параме-
тров дискретизации, которые обеспечивают компромисс между
качеством численного решения и вычислительными затратами.
Только когда испытания и «калибровка» завершены, «уста-
новку» можно считать готовой для проведения вычислительных
экспериментов.
ГЛАВА 2
ОСНОВНЫЕ
УРАВНЕНИЯ
МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Математическое описание многих физических процессов приво-
дит к дифференциальным, интегральным или к интегро-диффе-
ренциальным уравнениям. В этой главе мы рассмотрим харак-
терные физические процессы, которые приводят к различным
краевым задачам для дифференциальных уравнений.
2.1.	Распространение малых возмущений и
колебания
Многие физические процессы (например, колебания струн, стерж-
ней, мембран и трехмерных объемов) описываются волновым урав-
нением вида
~ div(6(a?)grad(u)) - с(ж)и + /(ж, t),	(2.1)
где неизвестная функция u(x,t) зависит от п (п = 1,2,3) про-
странственных координат х = (^i,^2,^з) и времени t; коэффици-
енты а(ж), Ь(х) и с(х) определяются свойствами среды; функция
f(x,t) выражает интенсивность внешнего воздействия. Напри-
мер, трехмерное волновое уравнение в декартовой системе коор-
динат
д2и 2 /д2и д2и д2и\
dt2	\ дх2 дх^ дх^)

(2-2)
описывает процесс распространения звуковой волны в однород-
ной среде. Этому уравнению удовлетворяют давление газа и по-
тенциал скоростей. Часто задачи на распространение волн удоб-
2.2.	Уравнение теплопроводности (диффузии)
нее формулировать в виде системы дифференциальных уравне-
ний первого порядка. Так, вместо предыдущего уравнения, про-
цесс распространения звуковой волны в однородной среде можно
описать следующей системой уравнений:
др 9 ( ди dv dw
+ pc2 — + — + —
ot \oxi д x2 дхз
д / и \	/ др/дх\ \	/ 0 \
r + I dp/dx2 =	°	,
\ w у у др/дхз у \ О У
где р — давление газа; и, и, w — компоненты скорости частиц
газа; р — плотность газа; с — скорость звука.
2.2.	Уравнение теплопроводности
(диффузии)
Процессы распространения тепла или диффузии частиц в среде
описывается следующим общим уравнением:
ди
а(х) — = div(b(a?)grad(u)) — с(х)и + /(ж, t).	(2-3)
В случае тепловых процессов u(x,t) обозначает температу-
ру среды в точке х = (#1,#25яз) в момент времени t; а(ж) есть
произведение плотности среды на теплоемкость; 6(ж) — коэффи-
циент теплопроводности, a f(x,t) описывает внешние источни-
ки тепла. Для процессов диффузии и(ж,£) обозначает плотность
частиц в точке х = (xi,x2, хз) в момент времени t; а(х) — по-
ристость; Ь(х) — коэффициент диффузии и с(ж) характеризует
поглощение среды. Например, распространение тепла в однород-
ной среде без источников тепла описывается уравнением
«Эи х Л
рс—- = АДи,
dt
где Д — оператор Лапласа.
2.3.	Уравнения Максвелла
Пусть в некоторой среде имеется переменное электромагнитное
поле. Введем обозначения: E(x,t) — (Е^ Е2,	— напряжен-
ность электрического поля;	— (Н^Н^Нз) — напряжен-
Глава 2. Основные уравнения математической физики
ность магнитного поля; р(х) — плотность зарядов; £ — диэлек-
трическая постоянная среды; р — магнитная проницаемость сре-
ды; /(ж, t) = (Zi, Z2 Дз) — ток проводимости. Тогда эти величины
удовлетворяют линейной системе дифференциальных уравнений,
называемых уравнениями Максвелла:
div(£l?) = 4тгр(ж),
div(/zH) = О,
=-сгоЦЕ),	<24>
= с  rat(jr) - -4 т/
где с— скорость света в пустоте. Например, если р = 0, е — const,
р — const и I — сгЕ (закон Ома, ст = const), то уравнения Макс-
велла преобразуются в так называемые телеграфные уравнения:
д2Е _ с2	4тгсг д Е
=	е	дГ
д2Н _	_ 47ГСГ дН
dt2 ец	е dt
2.4.	Уравнение Шредингера
Пусть квантовая частица массы т движется во внешнем силовом
поле с потенциалом U(x). Состояние этой частицы описывается
волновой функцией Ф(ж,£), так что |Ф(ж, £)|2 Дг(ж) есть вероят-
ность того, что частица будет находиться в окрестности г (ж)
точки ж в момент времени ti здесь Д — объем г (ж). Тогда функ-
ция Ф(ж,£) удовлетворяет уравнению Шредингера
дФ И2
= (2-5>
где h — постоянная Планка, деленная на 2тг.
2.5.	Уравнения газо-гидродинамики
Рассмотрим движение сжимаемой жидкости (газа), в которой
отсутствуют силы вязкости. Пусть ж = (ж1,Ж2,ж3) — декарто-
ва система координат, и(ж,£) = (щ, 112,^3) — вектор скорости
2.6. Уравнения Навье-Стокса
движения частиц жидкости, p(x,t) — ее плотность, p(x,t) —
давление, е(ж, t) — внутренняя энергия отнесенная к единице мас-
сы. Эти величины удовлетворяют следующей (нелинейной) систе-
ме уравнений, называемых уравнениями гидродинамики (газовой
динамики) в форме Эйлера:
1)	уравнение неразрывности
др Л д(рик) =
& дхк
2)	уравнение движения
д(рип) Ду д
—х,	+ 22 л— ^Рикип + р$пк) = о,
к=\ UXk
п = 1,2,3,
здесь 6пт — символ Кронекера:
&пт
1, п = т,
О, п^т,
3)	уравнение энергии
О	3	ГЛ	3 Q
de	5—>	de _ р у-л duk
dt + Uk дхк	р dxk
fc=i К	r k=i К
Для замыкания этой системы уравнений необходимо еще за-
дать уравнение состояния вида е = е(р,р). Например, для иде-
ального политропного газа это уравнение имеет вид
Р	-7
е = —-----— и рр r = const,
Р<7 “ 1)
где 7 = cp/cv — показатель адиабаты, а ср и cv — удельные те-
плоемкости среды при постоянном давлении и постоянном объеме
соответственно.
2.6.	Уравнения Навье-Стокса
Рассмотрим теперь движение вязкой жидкости (газа). В рам-
ках введенных в предыдущем пункте обозначений, это движение
описывается следующей системой уравнений (уравнения Навье-
Стокса):
Глава 2. Основные уравнения математической физики
1)	уравнение неразрывности
, v д(Ри^ = о
dt	дхк
к=\
2)	уравнение движения
д{рип)
dt
3 д
у.	Р$пк &пк) = О,
“ дхк
к=1
3
( дип	дик \	£	duk
&пк — Р I “7	И “7 )	4"	ЛОпк	/	"7	5
\ охк	дхп J	дхк
к=1
п = 1,2,3,
3) уравнение энергии
дТ
~адГк~
з
2 Un&nk — О,
где д — первый коэффициент вязкости; А — второй коэффици-
ент вязкости, который имеет отношение к внутренним силам при
сжатии (для элементарной модели одноатомного газа А = —2д/3);
а — коэффициент теплопроводности и Т — температура. Как и
прежде, чтобы замкнуть эту систему уравнений, необходимо за-
дать уравнение состояния. Часто предполагается, что жидкость
несжимаема, то есть р — const. Тогда предыдущие уравнения не-
сколько упрощаются, так как
1.	/ ч	дик
'MU>=Efe=°
к — \
и отпадает необходимость в уравнении энергии.
2.7.	Стационарные уравнения
Для стационарных процессов, когда решение не зависит от вре-
мени, уравнения колебания (2.1) и диффузии (2.3) принимают вид
div(6(a?)grad(u)) — с(х)и = —f(x).	(2.6)
2.8. Постановка основных задач
При 6(ж) = const и с(ж) = 0 уравнение (2.6) называется урав-
нением Пуассона
Ди =	(2.7)
а при f = 0 уравнение (2.7) называется уравнением Лапласа
Ди = 0.
Пусть в волновом уравнении (2.2) внешнее возмущение f(x,t)
есть периодическая функция с частотой f(x^ t) — /о(ж) exp(zutf).
Если искать периодическое возмущение и(ж, t) с той же частотой
и неизвестной амплитудой uq(x): u(x,t) = uq(x) ехр(гсЛ), то для
функции uq(x) получим стационарное уравнение
(2.8)
С2	с2
называемое уравнением Гельмгольца.
Уравнения Максвелла (2.4), в случае стационарного процесса,
превращаются в уравнения электростатики
div(s2?) = 4тгр(ж), rot(£?) = 0,
и в уравнения магнитостатики
4л
div(/z/f) = 0, rot(K) = —I.
с
Если энергия Е квантовой частицы имеет определенное зна-
чение, то такое ее состояние называется стационарным. В этом
случае волновая функция Ф(ж,£) имеет вид
Ф(ж, t) = exp (—iEt/h) </?(ж),
где волновая функция у>(х) в силу (2.5) удовлетворяет стационар-
ному уравнению Шредингера
+ U(x)p = Е<р.	(2.9)
При U(ж) = 0 (свободная частица) уравнение (2.9) превраща-
ется в однородное уравнение Гельмгольца (2.8).
2.8.	Постановка основных задач для
уравнений математической физики
В этом параграфе мы рассмотрим математические модели для
ряда характерных физических процессов, которые сводятся к
Глава 2. Основные уравнения математической физики
различным краевым задачам для дифференциальных уравнений.
Пусть D е Rn — область, где происходит процесс, и S — ее
граница, которая представляет собой кусочно-гладкую поверх-
ность. Таким образом, D есть область изменения аргумента х
для стационарных уравнений (область задания). Областью за-
дания для нестационарных уравнений будем считать цилиндр
D х{0 ^t^T} высоты Т с основанием D.
Для полного описания того или иного физического процесса
необходимо, кроме самого уравнения, описывающего этот про-
цесс, задать начальное состояние системы (начальные условия) и
режим на границе той области, в которой происходит этот про-
цесс (граничные условия). Задача с начальными и граничными
условиями называется краевой задачей. Различают три основных
типа краевых задач для дифференциальных уравнений:
1)	задача Коши для нестационарных уравнений: задаются на-
чальные условия, область D совпадает со всем простран-
ством Вп, граничные условия отсутствуют;
2)	краевая задача для стационарных уравнений: задаются гра-
ничные условия на границе S, начальные условия, естествен-
но, отсутствуют;
3)	смешанная задача для нестационарных уравнений: задают-
ся и начальные, и граничные условия.
Рассмотрим подробнее постановку каждой из перечисленных
краевых задач.
2.8.1.	Задача Коши
Для волнового уравнения второго порядка (2.1) задача Коши
ставится следующим образом: найти функцию и (ж, £), удовлетво-
ряющую соответствующему уравнению в полупространстве t > О
и начальным условиям при t = О
ди
и(ж,0) = fo(x), —(x,0) = fi(x).	(2.10)
Для уравнений диффузии и Шредингера задача Коши ставит-
ся так: найти функцию и (ж, £), удовлетворяющую этим уравнени-
ям в полупространстве t > 0 и начальному условию при t — О
и(ж,0) - /о(ж).	(2-И)
2.8. Постановка основных задач
Для систем уравнений первого порядка задача Коши формули-
руется аналогично: найти функцию u(x,t) = (иДх, f), • • •, ип(х, £)),
удовлетворяющую данной системе в полупространстве t > 0 и на-
чальным условиям при t = О
и(ж,0) = £0(ж).
(2.12)
2.8.2.	Краевая задача
для стационарных уравнений
Краевая задача для уравнения (2.6) состоит в нахождении функ-
ции и (ж), удовлетворяющей в области D уравнению (2.6) и гра-
ничному условию вида
ди
аи + р —
дп
= 0о,
s
(2.13)
где п — нормаль к S; а, /3 и до — заданные кусочно-непрерывные
функции на S, причем а О, /3	0, а + (3 > 0. Часто встречаются
следующие типы граничных условий (2.13):
1)	граничные условия первого рода (а = 1, {3 = 0)
u\s =9о,
2)	граничные условия второго рода (а = 0, (3 = 1)
ди
дп s
3)	граничные условия третьего рода (а 0, Д — 1)
ди
+аи
дп
= 0о-
S
Краевая задача для уравнений Лапласа и Пуассона с гранич-
ными условиями 1-го рода называется задачей Дирихле, а с гра-
ничными условиями 2-го рода — задачей Неймана.
Аналогично ставятся краевые задачи для уравнения (2.6) и во
внешности ограниченной области D (внешние краевые задачи).
Отличие состоит в том, что помимо граничного условия (2.13)
на S, задаются еще условия на бесконечности. Такими условия-
ми, например, могут быть условия излучения Зоммерфельда при
Глава 2. Основные уравнения математической физики
оо для уравнений Гельмгольца или Шредингера:
f \ г, ( 1 \	ди I. ( 1
«(®) = О — ,	—— - tku = о 7—7 .
\ж/ ож	\х/
2.8.3.	Смешанная краевая задача
Для нестационарных уравнений второго порядка смешанная за-
дача ставится так: найти функцию и(х, t), удовлетворяющую со-
ответствующему уравнению в цилиндре D х{0СН Т}. началь-
ным условиям (2.10) или (2.11) и граничному условию (2.13). При
этом должно быть выполнено условие согласованности
t=0
I а/о 4- Р~^— )	=
\ dnj s
Для систем уравнений первого порядка смешанная задача ста-
вится так: найти функцию u(x,t) = (щ(х,1),... ,un(x,t)), удо-
влетворяющую данной системе в цилиндре D х {0 t Т},
начальным условиям (2.12) и граничному условию
k=l
= 00,
S
где и до — заданные кусочно-непрерывные функции на S,
причем ctfc 0, Qfc > 0.
k=l
ГЛАВА 3
ОСНОВНЫЕ
МЕТОДЫ
ПОСТРОЕНИЯ
И АНАЛИЗА
РАЗНОСТНЫХ
СХЕМ
Математические модели различных физических явлений часто
формулируются в виде краевых задач для дифференциальных
уравнений в частных производных, и изучение таких моделей
требует решения этих уравнений. В некоторых случаях их ре-
шение может быть выражено через известные функции. Однако,
как правило, это невозможно, поэтому получение решения в виде
явных выражений нельзя рассматривать как стандартный ме-
тод решения дифференциальных уравнений. Нельзя сказать, что
аналитические методы потеряли свое значение. Они остаются
необходимым инструментом для решения упрощенных, так на-
зываемых, модельных задач. Исследование модельных задач по-
зволяет получить важную информацию о решении более сложных
задач.
Наряду с аналитическими методами широко используются раз-
личные численные методы для решения дифференциальных урав-
нений. Мы рассмотрим методы, основанные на конечных раз-
ностях. Основная идея этих методов состоит в том, что при-
ближенное решение определяется на некотором множестве точек
обычно называемом сеткой. Для вычисления этого приближен-
ного решения используются конечноразностные уравнения, ко-
торые приближают и заменяют дифференциальное уравнение.
При численном решении краевых задач возникают вопросы о по-
строении конечноразностных уравнений, о методах их решения,
Глава 3. Основные методы построения разностных схем
об устойчивости численных процедур их решения и точности
приближенного решения. В нескольких ближайших параграфах
настоящей главы эти вопросы будут рассмотрены на примере
простейшей задачи распространения одномерной волны.
3.1.	Обсуждение основных понятий
на примере разностных схем
для уравнения переноса
В этой главе основные идеи иллюстрируются на примере числен-
ного решения задачи Коши для уравнения переноса. Если и(х, t)
обозначает амплитуду малого возмущения в точке х в момент
времени £, то распространение этого возмущения в бесконечной
среде описывается следующим уравнением:
ди ди
— + с— = 0,	—оо < х оо, t О,
dt дх	(3.1)
и(х,0) = д(х), —оо < х < оо,
где с = const — скорость волны, которую для определенности мы
будем считать положительной. Эта задача является линейной и
имеет решение u(x,t) = g(x — ct), t > 0, т.е. начальное состояние
просто переносится вправо со скоростью с. Предположим, что
функция д(х) равна нулю при х < 0, и мы будем рассматривать
решение при х > 0.
Вначале мы должны задать разностную сетку. Для одномер-
ных нестационарных уравнений она определяется узлами (жп, ^)
как показано на рис. 3.1, где хп = nh, п = 0,1,... и tk — кг,
к — 0,1,... Параметры h = хп+1 — хп и т = tk+i — tfc называют-
ся, соответственно, шагами по пространству и времени.
Приближенное решение уравнения (3.1) определяется в узлах
сетки, т. е. оно представляет собой множество значений
ик = {и^ = u(a\xn.tk)}, n = 0,1,...; к = 0,1,....
Такое множество часто называют сеточной функцией. Теперь
нам нужно заменить производные некоторыми разностными от-
ношениями, определенными на сетке. В дальнейшем мы будем
использовать, в основном, следующие приближения для диффе-
ренциальных операторов:
3.1. Обсуждение основных понятий на примере
du, х и^х^ 4- /z)	Un-Y-i Un
—lxn) «-------------------=----------- — разность вперед,
dx	h	h
du.	. u(xn)	- u(xn	- h)	Un-Un-x
— Ы ~------------z--------=------z---- — разность назад,
dx	h	h
du . . u(xn + h) — u(xn — h)
"----------2h----------=
^П-f-l	^n — 1	zo n\
_----------------центральная разность, (3.2)
2h
d?u u(xn + h) - 2u(xn) + u(xn - h) _ un+i - 2un + un_i
d^-n)~	Л2	/i2
Рис. 3.1. Разностная сетка на плоскости (x,t)
Применяя разность вперед для приближения производной по
времени в точке хп и разность назад для приближения производ-
ной по пространству в момент времени мы получим вместо
дифференциального уравнения (3.1) разностное уравнение в ка-
ждом узле сетки:
Un = g(xn), п = о, 1,....
„ (3‘3)
Набор разностных уравнений, определенных на некоторой сет-
ке, называется конечно-разностной схемой (или просто разност-
ной схемой). Для вычисления приближенного решения, перепи-
Глава 3. Основные методы построения разностных схем
71 = 0,1,...; fe = 0,1,...
(3.4)
шем разностную схему (3.3) в виде
ик+1 = ик - — (ик - ик
Un = g(xn), 77 = 0,1,....
Из начального условия гл(ж, 0) = д(х) следует, что значения
U°n = д(хп),
известны для каждого п — 0,1,.... Поэтому, из формулы (3.4)
можно вычислить значения для каждого п = 0,1,.... Повто-
ряя эту процедуру, после того как значение и1 определено, можно
последовательно вычислить значения и2, и3,.... Разностные схе-
мы, которые позволяют непосредственно вычислять решение в
момент времени через известное решение в момент време-
ни tk, называются явными (схема (3.3) является примером такой
схемы).
Вообще говоря, можно построить бесконечное количество раз-
ностных схем для данного дифференциального уравнения. На-
пример, модифицируем схему (3.3), приближая производную по
пространству не в момент времени tк, а в момент времени ^+1 •
В результате мы получим следующую разностную схему для урав-
нения (3.1):
__ о,к
_П-------”+с_^-----= о, п = 0,1,...; А; = 0,1,...
т	h	(3.5)
Un = g(xn), 77 = 0,1,....
Это выражение является примером неявной схемы. В общем слу-
чае такие схемы не позволяют непосредственно вычислить реше-
ние в момент времени через известное решение в момент
времени так как они образуют некоторую систему уравнений
(для данной задачи мы предположили, что д(х) = 0 при х 0,
поэтому
«t1! = 0
и вычисления могут быть организованы явным образом). Приме-
няя разность вперед для приближения производной по простран-
ству в момент времени £&, мы получим еще одну схему:
__/цк	л,к ___л,к
-----^+С^-----------^ = 0, 7г = 0,1,...; fe = 0,l,...
г	h	(3.6)
Un=9(xn), 77 = 0,1,....
3.1. Обсуждение основных понятий на примере
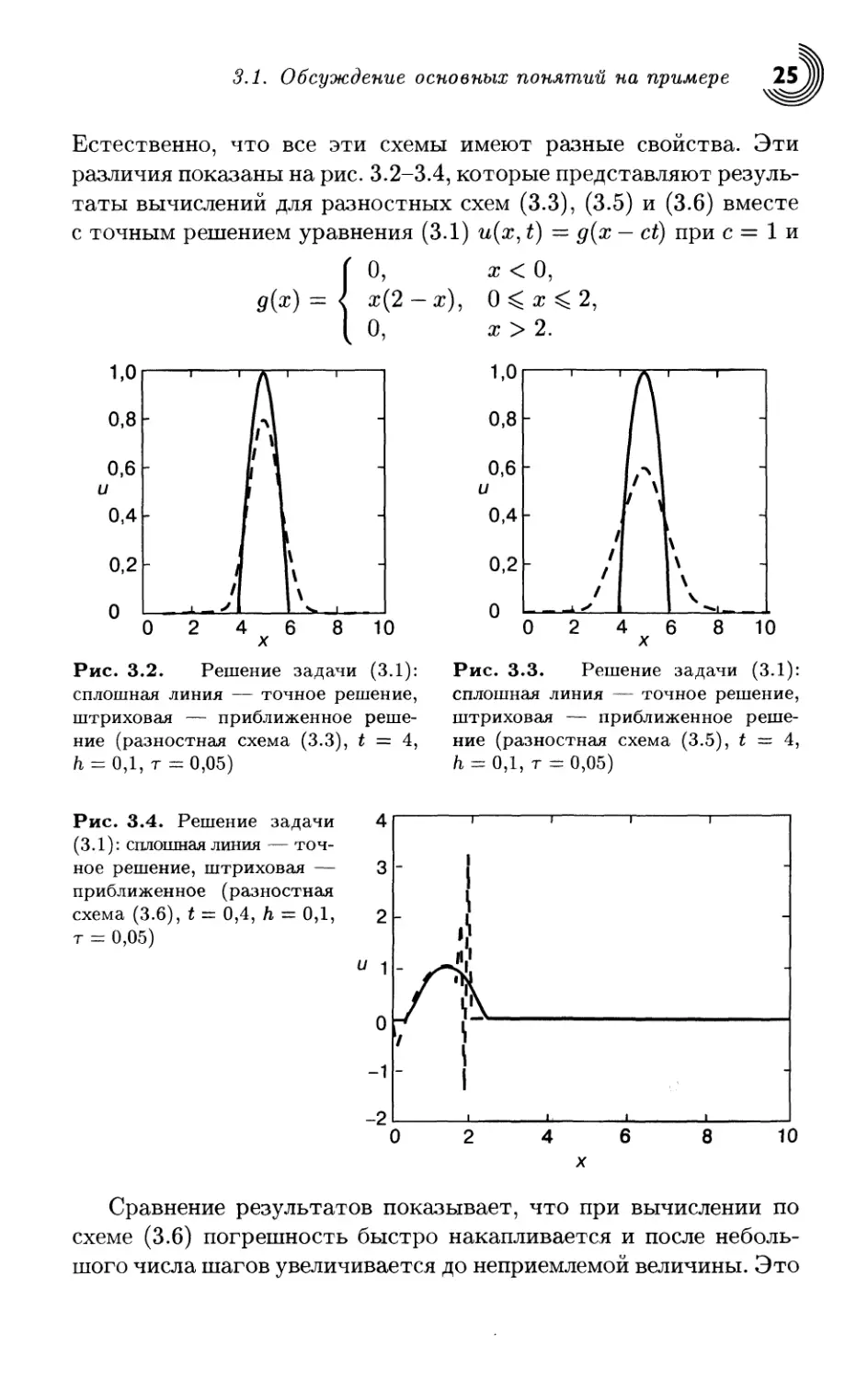
Естественно, что все эти схемы имеют разные свойства. Эти
различия показаны на рис. 3.2-3.4, которые представляют резуль-
таты вычислений для разностных схем (3.3), (3.5) и (3.6) вместе
с точным решением уравнения (3.1) и(х, t) = g(x — ct) при с = 1 и
Рис. 3.2. Решение задачи (3.1):
сплошная линия — точное решение,
штриховая — приближенное реше-
ние (разностная схема (3.3), t = 4,
h = 0,1, т = 0,05)
Рис. 3.4. Решение задачи
(3.1): сплошная линия — точ-
ное решение, штриховая —
приближенное (разностная
схема (3.6), t = 0,4, h = 0,1,
т = 0,05)
Рис. 3.3. Решение задачи (3.1):
сплошная линия — точное решение,
штриховая — приближенное реше-
ние (разностная схема (3.5), t = 4,
h = 0,1, т = 0,05)
Сравнение результатов показывает, что при вычислении по
схеме (3.6) погрешность быстро накапливается и после неболь-
шого числа шагов увеличивается до неприемлемой величины. Это
Глава 3. Основные методы построения разностных схем
явление называется неустойчивостью и является внутренним свой-
ством самой системы разностных уравнений (3.6).
Этот пример демонстрирует, что построение разностных схем
и решение дифференциальных уравнений с помощью этих схем
не совсем простая задача. Часто возникают ситуации когда, ка-
залось бы, схема должна давать достоверный результат, а мы
получаем приближенное решение, которое не имеет ничего об-
щего с точным решением. Поэтому, прежде чем рассматривать
методы построения разностных схем, мы должны познакомить-
ся с требованиями, выполнение которых обязательно для любой
практически пригодной схемы.
3.2.	Основные свойства разностных схем:
аппроксимация и устойчивость
В этом параграфе мы рассмотрим определения аппроксимации,
устойчивости и сходимости разностной схемы. Для простоты мы
дадим основные определения в случае одномерных нестационар-
ных задач. Предположим, что дифференциальная задача опреде-
лена в некоторой области S. Это значит, что требуется найти ре-
шение дифференциального уравнения (или системы уравнений)
u(x,t) в области S при дополнительных начальных и граничных
условиях, налагаемых на и(ж, t). Далее мы будем записывать диф-
ференциальную задачу в символической форме:
Du = f,	(3.7)
где D — дифференциальный оператор и f — правая часть. На-
пример, чтобы записать задачу (3.1) в форме (3.7), мы определим
C^L	( 0, —ос х оо, t 0,
Du = dt дх" f = \
^0,
Другой пример: краевая задача для уравнения теплопроводности
ди д2и
~dt=K~d^ 0
u(O,t) = t^O,
u(7,£) =/2(t),
3.2. Основные свойства разностных схем
может быть представлена в виде (3.7), если записать
Du ~ <
ди _ „ д2и
dt ™дх2 ’
и(х, о),
w(0, t),
u(l, f),
0,
P(*),
Ш,
О	х	I, t О,
О < х	Z,
t > О,
t 0.
Предположим, что решение u(x,t) задачи (3.7) существует
в области S. Для того чтобы вычислить это решение методом
конечных разностей вводится конечное число точек (узлов) в
области S. Это множество точек называется сеткой, и будет обо-
значаться как Sh — {жп, th}- Теперь мы будем искать не решение
u(x,t) задачи (3.7), а сеточную функцию и^е\ которая предста-
вляет собой множество значений решения в узлах Sh'-
и(е} = {йп = U.(xn,tk)}.
Сетка Sh зависит от положительных параметров h = xn+i —хп
и г — tk^-i —tk, которые могут быть выбраны сколь угодно малы-
ми. По мере увеличения количества узлов сетки h 0 и т 0 и
сеточная функция будет давать все более полное представле-
ние решения. Тогда, используя интерполяцию, можно получить
решение в любой точке области S. Однако точно вычислить
невозможно. Вместо сеточной функции мы можем вычислить
другую сеточную функцию
“(a) = {un = и(О)(®пЛ)} ,
которая стремится к , когда число узлов сетки увеличивается.
Для вычисления этого приближенного решения и О) используют-
ся разностные схемы. По аналогии с выражением (3.7), разност-
ную схему можно записать в символическом виде:
Dhu^ =fW.	(3.8)
Например, разностная схема (3.3), может быть представлена
в виде (3.8), если записать
0,
р(^п),
п = 0,1,...; к = 0,1,....
Прежде чем продолжить наше обсуждение, нам нужно опре-
делить способ измерения сеточных функций. В дальнейшем мы
Глава 3. Основные методы построения разностных схем
будем использовать следующую норму:
l|u(a) II = max(max |и*|).
к п
Если подставить в разностную схему (3.8), то мы не по-
лучим точного равенства, т. е. возникает некоторый вектор не-
вязки:
Dhu^ = /(а) +6f(a\
Мы будем говорить, что разностная схема	ап-
проксимирует дифференциальную задачу Du = f на решении
u(x,t) если	—> 0, когда Л—>0ит—>0. В дополнение, если
выполняется неравенство
||<5/(а)|| ^(W + Czro,	(3.9)
где константы С± > 0, С72 > 0, р > 0, q > 0, тогда мы будем гово-
рить, что имеет место аппроксимация порядка р по h и порядка
q по г.
Как было показано выше, приближенное решение и^а\ полу-
ченное с помощью разностной схемы (3.6), не отображает точно-
го решения, хотя эта схема аппроксимирует задачу (3.1) с первым
порядком по h и т. Разностная схема должна обладать не только
свойством аппроксимации, но также быть устойчивой.
Рассмотрим возмущенную разностную схему
Dhz^ = f(a) +Е<а),	(3.10)
которая получается из разностной схемы (3.8) путем добавления
в правую часть возмущения . Мы будем называть разностную
схему (3.8) устойчивой, если существуют числа ть > 0 и <5 > 0 та-
кие, что для любого т < 7о и ||е(а)|| < <5 разностная задача (3.10)
имеет единственное решение z^ и это решение отличается от
на сеточную функцию z^ — которая удовлетворяет
оценке	С	где константа С не зависит от
h и т. Это неравенство означает, что малое возмущение правой
части разностной схемы (3.8) приводит к малому возмущению
решения.
В случае линейной дифференциальной задачи (3.7) следую-
щее определение эквивалентно данному выше определению. Мы
будем называть разностную схему (3.7) устойчивой, если для лю-
бой правой части разностная задача	имеет
3.3. Анализ аппроксимации
единственное решение и выполняется оценка
||и(а)||^С||/й)||,	(3.11)
где константа С не зависит от h и т.
Основной вопрос, который возникает при практических вы-
числениях, — насколько полученное приближенное решение от-
личается от точного решения и как сделать это отклонение до-
статочно малым.
Предположим, что разностная схема (3.8) аппроксимирует за-
дачу (3.7) на решении u(x,t) и устойчива. Тогда приближенное
решение сходится к точному решению и^е\ т.е.
||г/е) _	—> 0, когда /г —> 0 и т —> 0.
Если при этом выполняется неравенство (3.9), то в этом слу-
чае мы будем говорить, что имеет место сходимость порядка
O(hp + rq) или что разностная схема (3.8) имеет точность поряд-
ка р по h и порядка q по т. Понятно, что чем больше значения
р и q (выше порядок аппроксимации), тем быстрее приближен-
ное решение стремится к точному решению по мере уменьшения
шагов сетки. Однако сравнение схем по порядку точности имеет
смысл проводить лишь при достаточно малых шагах расчетной
сетки h и т, при этом главный член ошибки аппроксимации за-
висит не только от шагов сетки, но и от производных решения
(см. параграф 3.3). Практически же используются достаточно
крупные расчетные сетки, на которых асимптотические оценки
могут быть несостоятельны. Таким образом, может оказаться,
что схема первого порядка точности на реальных сетках точ-
нее схемы второго порядка точности и т. д. Наличие сходимости
является основным требованием, предъявляемым к разностным
схемам, так как только в этом случае мы можем аппроксими-
ровать точное решение с любой точностью, в пределах ма-
шинной арифметики, выбирая шаги по пространству и времени
достаточно малыми.
3.3.	Анализ аппроксимации
Так как точное решение исходной задачи нам неизвестно, мы
можем сделать только оценку невязки. Далее мы рассмотрим при-
мер, который демонстрирует общепринятый метод исследования
аппроксимации.
Глава 3. Основные методы построения разностных схем
Рассмотрим разностную схему (3.3) для задачи (3.1). Если
вместо сеточной функции подставить точное решение и(х, £),
то выражение (3.8) примет вид:
u(xn,	) и(хп, tk)	и(хп, tk) и(хп-1, tk)   р
г	С	h	~ ’	(3.12)
71=1,2,...; к = 0,1,...
Исследуем аппроксимацию в точке (жп, £&). Предположим, что
все частные производные функции гл(ж, £), до второго порядка
включительно, непрерывны и ограничены. Тогда мы можем раз-
ложить
u(xn-lytk) = и(хп - h,tk) И u(xn,tk+i) - u(xn,tk + т)
в окрестности точки (xn,tk) по степеням Лит, используя фор-
мулу Тейлора:
ди	1 д2 и
u{xn Л, tk) = ^(#n? tk) h-^{xn^ tk) Я- 2^ ^.2	^ь)	)
и
Эи. ч 1 9д2и,	, x ъ
~g^(Xn,tk) + —T ~g^(xn,tk) + О(Т ).
Подставляя эти разложения в (3.12), получим
ди, . ди	1 д2и, ч
tk) +	tk) = ~ 2T~dt^^Xni +
1	д^ и
+ -ch—(xn.tk)+C)(h2+r2). (3.13)
2	oxz
п = 1,2,...; к = 0,1,... Выражения такого вида называются
дифференциальными приближениями разностного уравнения. По
своей сути они занимают промежуточное место между исходным
дифференциальным уравнением и аппроксимирующей его раз-
ностной схемой. Дифференциальное приближение имеет струк-
туру дифференциального уравнения, но его коэффициенты зави-
сят от параметров рассматриваемой схемы, что облегчает ана-
литическое исследование ее свойств.
Выражение в правой части (3.13) представляет собой невязку,
так как начальное условие задается точно. Оценка нормы невяз-
ки дает
|	11 = max ( max
к \ п
1 д2и	1 д2и \
Г1йГХп'Лк) + rhd^Xn,tk^)
3.3. Анализ аппроксимации
1
- max
2 k
max
g^.2
4- h
C /
- max max
2 к \ n
d2u /
дх2(ж”’ fc)
= Ci/i + C2t,
т.е. разностная схема (3.3), в общем случае, аппроксимирует за-
дачу (3.1) с первым порядком по h и т. Анализ аппроксима-
ции иногда позволяет получить условия на параметры сетки, при
которых сходимость разностной схемы значительно ускоряется.
В случае разностной схемы (3.12) для задачи (3.1) такая возмож-
ность существует. Из уравнения (3.1) следует, что
д2и	Зд3и
dt2 дх2 ’ dt3 дх3 ’
Тогда выражение (3.13) можно записать в виде
ди. х ди z х
4" (xnytk) —
dt	дх
1 z_ хд2и/ ' х 1 /7‘2	2 2ч дги ,	± х
= --с(Л-ст) —(жп,^) - ^(/Г - с r2)-^(xn,tk) 4- •••
п = 1,2,...; fc = 0,1,...
Если мы выберем т — h/c, то невязка будет равна нулю и
разностная схема будет давать точное решение в пределах по-
грешности вычислений.
Погрешность аппроксимации разностной схемы возникает, в
основном, при замене дифференциальных операторов на разност-
ные операторы. Применяя рассмотренный выше подход, получим
следующие выражения для главного члена ошибки аппроксима-
ции часто используемых разностных отношений:
и(зп 4- As) - u(sn) ди, х 1. д2и, х _ (. Л х2\
(3.14а)
u(sn) - u(sn - As) ди 1лвд'и1с.1,п11\^-\
-------Ts-------=	~ 2+ ° ((Д5) ) ’
(3.146)
Глава 3. Основные методы построения разностных схем
u(sn 4- As) — u(sn — As) ди. .
---------as----------=	+
1 д^ ? /
+ _(A.s.)2_(.Sn) + O((A,)4), (3.14в)
u(sn + As) - 2u(sn) + u(sn - As) _ d2u ( A
(M)2	“ d^[Sn) +
1	11
+ ^(As)2^(sn) + O((As)4), (3.14г)
где s обозначает пространственные переменные или время и,
соответственно, As обозначает шаг по пространству или по вре-
мени. В дальнейшем мы будем использовать эти готовые выраже-
ния для анализа различных разностных схем. При этом мы будем
подразумевать, что решение обладает достаточной гладкостью
и все необходимые нам для анализа производные существуют и
ограничены.
3.4.	Критерий фон Неймана для анализа
устойчивости разностных схем
В этом параграфе мы рассмотрим критерий фон Неймана, кото-
рый широко используется для анализа устойчивости разностных
схем. Он применим для исследования устойчивости разностных
схем в случае однородной задачи Коши. Вначале мы ограничимся
случаем задачи с постоянными коэффициентами, а в следующем
параграфе расширим наши результаты на случай переменных ко-
эффициентов.
Выведем критерий фон Неймана на примере разностной схе-
мы (3.3) для задачи (3.1). Для разностной схемы, записанной в
виде (3.8), мы имеем следующий критерий устойчивости:
Учитывая, что в нашем случае
и определяя нормы как
Н«(а)Н = max(max|u*|), ||/(а)|| = max|p(a:n)|,
кп	п
3-4- Критерий фон Неймана для анализа устойчивости
условие устойчивости примет вид
max(max |w{4)	С max |д(яп)| = Стах|г^|.
к п	п	п
Тогда, если будет выполняться условие
max \икп\ Стах \и„\, к = 0,1,	(3.15)
го приведенное выше условие также выполнится. Для анализа
устойчивости выберем
uQn — exptjwxn) = exp^icunh) = ехр(гап), (3.16)
где а — вещественный параметр. Тогда сеточное решение, опре-
деляемое разностной схемой (3.3), имеет вид (смысл параметра
А мы обсудим ниже):
ип — А^(а) ехр(гап), 0 а 2л,	(3.17)
где А (а) в общем случае — комплексный параметр. Тогда условие
устойчивости (3.15) принимает вид
max \и„\ = |А*(а)| - max | ехр(гап)| Стах | ехр(шп)|, к = 0,1,...
п	п	п
и окончательно
|А(а)|*^С, к = 0,1,...
Это условие выполнится для любых значений /с, если
|А(а)|	1, 0^а^2л.	(3.18)
Это и есть спектральный критерий устойчивости фон Неймана.
Обсудим теперь возникновение и смысл параметра А. Запишем
разностную схему (3.3) для одного шага по времени и подставим
туда начальное условие вида (3.16). В результате получим
— ехр(гап) ехр(гап) — ехр(га(п — 1)) _
т	h
Выразим из этого соотношения:
и\ = ех^(1ап) —	(1 — ехр(—га)) ехр(гап) =
= (1 —	(1 — ехр(—га))) ехр(гап) = А(а) ехр(гап) = А(а)гг^.
Таким образом, А представляет собой собственное значение
оператора перехода на один шаг по времени (в данном случае
собственное значение совпадает с оператором перехода, в общем
же случае он представляет собой некоторую матрицу). Когда а
Глава 3. Основные методы построения разностных схем
изменяется от 0 до 2тг, значения Л (а) образуют спектр оператора
перехода. Тогда необходимое условие устойчивости можно сфор-
мулировать следующим образом: спектр оператора перехода на
один шаг по времени должен лежать внутри единичного круга на
комплексной плоскости. Если оператор перехода S является нор-
мальной матрицей (SSH — SHS = 0, где символ «Н» обозначает
последовательное применение двух операций: комплексного со-
пряжения и транспонирования), то критерий фон Неймана (3.18)
является также и достаточным условием устойчивости. В слу-
чае одного уравнения, выражение для Л (а) можно получить, если
подставить (3.17) непосредственно в разностную схему; это даст
некоторое уравнение на А(а).
Рассмотрим теперь устойчивость построенных выше схем.
Параметр А(а) для схемы (3.3) мы уже определили:
А(а) = 1 — г (1 — ехр(—га)) = 1 — г 4- г cos(a) — ir sin(a),
где г = ст/h. Тогда
|А(а)| = \/(1 — г)2 4- 2г(1 — г) cos(a) 4- г2.
Когда а изменяется от 0 до 2тг, |А(а)| пробегает значения от 1
до |1 — 2г|. Следовательно, по критерию устойчивости (3.18) эта
схема будет устойчива, если
ст
г С 1 или — < 1.
h
Схема (3.3) является примером условно устойчивой схемы.
Это условие совпадает с условием Куранта-Фридрикса-Леви
h
— с,
записанного для случая гиперболических уравнений. Это усло-
вие имеет простое физическое объяснение. Предположим, что
начальное условие гг(ж,О) равно 0 во всех точках пространствен-
ной сетки, кроме одной. Тогда решение в узле сетки, удаленном
от этой точки на п пространственных шагов, должно оставаться
нулевым, по крайней мере, в течение п временных шагов. Это
эквивалентно условию, что шаг по времени т должен быть мень-
ше того промежутка времени, в течение которого волна прохо-
дит расстояние, равное пространственному шагу Л, или что ско-
рость распространения информации на сетке h/т должна быть
больше скорости волны.
3.5.	Принцип замороженных коэффициентов
Если мы подставим разностное решение вида (3.17) в схе-
му (3.5), то получим
Д&+1 ехр(гст) — Xk exp^ian)
г
+ cAfe+i ехр(шп) - ехр(ш(п - 1)) = Q
h
Далее, разделим это выражение на Xk exp(ian) и получим следу-
ющее уравнение для Л:
Л-1 + еА1 — ехр(—ш) = 0,
т	h
из которого нетрудно получить, что
|Л(а)| =  г-	.....
>/(1 4- г)2 — 2г(1 4- г) cos(a) 4- г2
Так как г 0, то |А(а)| будет всегда меньше единицы. Это го-
ворит о том, что разностная схема (3.5) устойчива при любых
значениях параметров Лит (безусловно устойчива). Обратим-
ся теперь к схеме (3.6). Применяя использованный выше подход,
получим следующее уравнение
Л-1 + еАехр(ш) - 1 =
т	h
из которого следует, что
|А(а)| = у/(1 4- г)2 — 2r (1 4- г) cos(a) 4- г2.
Когда а изменяется от 0 до 2тг, |А(а)| пробегает значения
от 1 до 1 4- 2г. Так как г >0, то |А(а)| будет всегда больше
единицы. Это говорит о том, что разностная схема (3.6) неустой-
чива. Неустойчивые разностные схемы обычно дают осциллиру-
ющие решения возрастающей амплитуды, подобные показанному
на рис. 3.5, и, естественно, такие схемы не имеют никакого прак-
тического значения.
3.5.	Принцип замороженных коэффициентов
Теперь мы рассмотрим простой метод, который расширяет об-
ласть применения критерия фон Неймана и дает возможность
использовать его для анализа разностных схем в случае задач
с переменными коэффициентами. В качестве примера выберем
Глава 3. Основные методы построения разностных схем
следующее нелинейное уравнение переноса:
ди	ди
— 4- и— — 0,	— ос х оо, 0 t tjy,
dt	дх
u(x,0)=g(x),	— ос х < оо.
По аналогии с (3.3) мы можем построить следующую схему:
«п+1 - «п , к ип - Un-1
Т + ” h
= о,
n = o,i,•••; k = о,1,...
(3.19)
Un = g(xn), п = о, 1,....
Для проведения вычислений по этой формуле, нам необходимо
выбрать шаг по времени, а это требует анализа-устойчивости.
Непосредственно применить критерий фон Неймана мы не мо-
жем. Поэтому сначала применим следующий подход: «заморо-
зим» переменный коэффициент в некоторой точке ж*, области
определения задачи. В результате мы получим набор разностных
схем:
7/&+1 __ „.к	л.к — л.к
Тк	h
= 0,
n = 0,1,...; fc = 0,1,...,
(3.20)
u°n = g(xn), n = o, i,...,
где и(х*, £*) — некоторый постоянный коэффициент. Принцип за-
мороженных коэффициентов можно сформулировать следующим
образом: разностная схема (3.19) будет устойчива, если схема
(3.20) будет устойчива для всех значений ж*, Г из области опре-
деления задачи. Для с = и(ж*,£*) = const условие устойчивости
нам известно:
Учтем теперь, что
1)	в исходной задаче скорость распространения волны зависит
от самого решения;
2)	для обеспечения устойчивости решения во всех точках, нам
следует ориентироваться на максимальное значение сеточ-
ного решения в каждый момент времени.
3.6. Шаблон разностной схемы
В результате мы приходим к следующему условию:
rftmaxu*	,
-----	 < 1 ИЛИ Тк < -г.
h------------------------------max и*
п п
3.6.	Шаблон разностной схемы
Для более наглядного представления разностной схемы мы бу-
дем иногда использовать мнемонические диаграммы, называе-
мые шаблоном. Шаблон указывает способ образования разност-
ной схемы, показывая точки разностной сетки, используемые при
применении формулы. В случае одномерной нестационарной за-
дачи, ось t будет направлена вверх, а ось х — горизонтально
вправо. Если два узла связаны вертикальной или горизонтальной
прямой, то они используются для аппроксимации первой произ-
водной по времени или по пространству. Если три узла связаны
вертикальной или горизонтальной прямой, то они используются
для аппроксимации второй производной по времени или по про-
странству. Например, разностные схемы (3.3), (3.5) и (3.6) имеют
следующие шаблоны, показанные на рис. 3.5:
Рис. 3.5. Шаблоны для схем (3.3), (3.5) и (3.6), соответственно.
Если для аппроксимации пространственных производных ис-
пользуется комбинация разностных отношений в различные мо-
менты времени, то соответствующие весовые коэффициенты будут
указываться справа. Например, шаблон, показанный на рис. 3.6,
соответствует разностной схеме
7/^+1 _	Г ?Л+1 _ ?/*+1	_ „.к
Un-----+	™n-l
r	h	h
= 0,
(3-21)
0^/3 ^1,
Глава 3. Основные методы построения разностных схем
которая переходит в схему (3.3) при /3 = 0 и в схему (3.5) при
/3=1.
к+1, л-1	к+1, л
к, л-1 к, л
Рис. 3.6. Шаблон для схемы (3.21).
ГЛАВА 4
РАСПРОСТРАНЕНИЕ
ТЕПЛА
(ДИФФУЗИЯ)
В качестве примера диффузионного процесса мы рассмотрим
распространение тепла в неподвижной среде. Эта задача формули-
руется следующим образом: заданы начальное распределение тем-
пературы, граничные условия, источники тепла и требуется най-
ти распределение температуры в последующие моменты времени.
Уравнение теплопроводности в декартовой системе коорди-
нат имеет вид
ди д ( . хди\	д / z х ди\
c(x,t)p(x,t) — = -— a(x,t)-— + д— a(x,t) —— +
dt	dxi \ dxij	дх2 \ dx^J
д ( , ч ди \	. . х
+ — ( а(ж> о— ) + fs(x, О?
дхз \ дхз )
где и (ж, t) — температура среды в точке х — (#i, х^ х%) в момент
времени £, р(х, t) — плотность, с(х, t) — теплоемкость, а(х, t) —
коэффициент теплопроводности и /s(x,£) — источник тепла. Вна-
чале мы рассмотрим основные идеи построения разностных схем
для задач теплопроводности на примере простого одномерного
уравнения с постоянными коэффициентами.
4.1. Разностная схема для одномерного
уравнения теплопроводности с
постоянными коэффициентами
В случае одномерной однородной среды предыдущее уравнение
принимает вид
=	0^;,	(4.1)
Глава 4- Распространение тепла (диффузия)
где к = а/ср — коэффициент температуропроводности. Кон-
кретная физическая задача определяется начальным условием
(начальным распределением температуры) w(#,0) = g(x) и гра-
ничными условиями, которые мы запишем в общем виде:
ди	ди
aiu(0,f)+ «2^-(0,f) = /1(0, O!3u(Z,t) + о!4 —(Z,t) = /2(0,
OX	ox
где g(x), /i(£), /2 (О — заданные функции.
Введем разностную сетку с узлами (xn,tk) и шагами /гит.
Аппроксимируем производную по времени разностью вперед от-
носительно точки (#n, tk), а производную д2и/дх2 — трехто-
чечным разностным оператором в момент времени (см. (3.2)).
В результате дифференциальное уравнение (4.1) заменяется раз-
ностной схемой:
“n+1 - Un _	«п+1 - 2un +
Г ~	&
fc = 0,l,...; n = l,...,N -1,
Un = g(xn), n = 0,...,N,
+ разностная форма граничных условий.
Так как эта схема явная, то процесс вычислений организуется
очень просто. Запишем предыдущее выражение в виде
(4.2а)
(4.26)
(4.2в)
•2г)
к = 0,1,...; п = 1,..., TV — 1.
Так как распределение температуры в момент времени всегда
известно, то мы получили формулу для расчета распределения
температуры в момент времени ^4-1. Рассмотренный нами при-
мер является частным случаем более общей схемы вида
/	- 2u£+1 +	ч u*+1 - 2ик + икп_, \
\	h.	№	)
(4.3а)
0 ^7^1, fc = 0,1,...; n = l,...,N -1,	(4.36)
которая включает в себя все возможные двухслойные схемы. Ша-
блон этой схемы показан на рис. 4.1.
4.1. Схема для одномерного уравнения теплопроводности
Введение дополнительного па- к+1, п-1	к+1,п	к+1, п+1
раметра позволяет управлять свой- •----------t---------•
ствами разностной схемы, но это
приводит к неявным разностным
уравнениям. Решение таких урав-
нений мы обсудим ниже.	•--------•---------•
Рассмотрим погрешность аппрок- к' п~^ к,п к' п+^
симации схемы (4.3). Подставляя Рис 4л Шаблон схемы (4 3)
точное решение в (4.3) и используя
соотношения (3.14), получим
= К у
ди. х .	1 д'2и.	2	2ч
-^(xn,tk) + 2T^^Xn’tk^ + 0{т ) =
1 т 2^и
12h lh+
+ О(/14).
Проведем исследование аппроксимации в точке (жп, £&). Тогда ве-
личины, определенные в точке (жп,^+1), необходимо разложить
в ряд Тейлора в точке tk по степеням т. Окончательно мы при-
ходим к следующему дифференциальному приближению
ди, \	1 д2и. х z ох д2и
-Q^xn, h) + 2T^"^n’ tk> +	) ==: ^дх2^’ tk> +
33u	кЬ2 д4и
+ '‘тгалй(а?"’ +	+ (>{h ’
из которого следует, что в общем случае схема (4.3) аппроксими-
рует уравнение (4.1) с точностью до членов О(т + Л2). Выбирая
параметр 7 определенным образом, можно повысить порядок
аппроксимации схемы (4.3). Действительно, из уравнения (4.1)
следует, что
д2и _ 2^4п
dt2 & дх^И dx2dt Кдх4
Тогда дифференциальное приближение можно записать в виде
<Эи . д2и
^т(^п, tk) - K-^(Xn,tk)
dt	dxz
= К
1	h2
--^т + ^7^+
Za	jl^
+ /i4)-
Глава 4- Распространение тепла (диффузия)
Отсюда следует, что при
1	(А
7 = 2 ~ ISP	(44)
выражение в квадратных скобках равно нулю и разностная схе-
ма (4.3) аппроксимирует уравнение (4.1) с точностью до величин
О(т2 + /г4).
Для анализа устойчивости схемы (4.3) подставим в нее реше-
ние вида (3.17) и получим
А-1	, ,	.	.. ехр(га) - 2 + ехр(-га)
-----= к (7А + (1 - 7)) -^-1----------
h2
= -4^sin2^a) (?А + 1 - 7),
и окончательное выражение для собственного значения операто-
ра перехода принимает вид
1 -4(1 — 7)/?sin2(|a)	кг
v '	1 + 47/3sin2(|a)	/12
В данном случае А (о) принимает вещественные значения в ин-
тервале
1-4(1-?)й < Л(«) « 1.
1+47/? v '
Из спектрального критерия устойчивости необходимо, чтобы
1 — 4(1 — 7)/3	.
1 + 47/З
и мы приходим к условию
- = в^-д—
h2 Р^2-47’
/3 — любое >0, 1/2	7	1.
(4-5)
В частности, для явной схемы (4.2) (7 = 0) условие устойчи-
вости приобретает вид (3	0,5. Как следует из выражения (4.4),
эта схема будет иметь четвертый порядок аппроксимации при
еще более строгом ограничении {3 = 1/6. Напротив, схема (4.3)
будет устойчива при любом значении /3, если 7 определяется вы-
ражением (4.4).
Перейдем теперь к обсуждению важного вопроса, связанно-
го с аппроксимацией граничных условий. В случае граничных
условий первого рода, когда на границе задается значение тем-
пературы, представление этих условий в разностной форме не
4.1. Схема для одномерного уравнения теплопроводности
представляет особого труда. Например, заданное при х = 0 усло-
вие гл(О, t) = f(t), записывается как
uk0+1 = f(tk+1).	(4.6)
Граничные условия второго и третьего рода определяют значе-
ния теплового потока в граничных точках. В качестве примера
можно привести следующие физические процессы, приводящие к
условиям такого рода:
1)	воздействие теплового потока на вещество
a^(0,*) = fW,	(4.7)
2)	конвективный теплообмен
ди
а—(О, t) = ко (u(0, t) — ис),
их
где ис — температура окружающей среды, ко — коэффици-
ент теплоотдачи
3)	тепловое излучение
а|^(0,£) = сг(м(0,£))4,
где а — коэффициент излучения.
Для простоты рассмотрим граничное условие (4.7). Очевид-
ное представление этого условия в разностной форме
_?Л+1
« 1 h ° = f(h+1)
непригодно, так как оно имеет первый порядок аппроксимации
по h, что значительно снижает точность приближенного реше-
ния (см., например, ОНВ, пример 6.11). Для построения более
точной аппроксимации, второго порядка по h, применим метод
фиктивных областей. Для этого введем фиктивный слой с узла-
ми (x_i,tk). Тогда, используя центральную разность, граничное
условие (4.7) можно записать в виде
« ~9,  1 =	к = 0,1,...
2ri
Значения температуры в граничном узле вычисляется из раз-
ностного уравнения (4.3) при п = 0:
Глава 4- Распространение тепла (диффузия)
*4+1-«о	( uf+1 - 2uo+1 + «-t1 Z1 Л1 -2u§ + «-i\
“ (j ~ё--------------+(1 -1) 
Исключение из этих двух выражений, фиктивных значений с но-
мером п = — 1 дает разностную форму граничного условия (4.7),
которую мы запишем в виде
(1 + 2^7) u*+1 - (2/?7) u*+1 = (1 - 2/?(1 - 7)) и* +
+ (2£(1 - 7)) <4 - — (7/(^+1) + (1 - ?)Ш) • (4-8)
а
В случае явной схемы (7 = 0) это выражение непосредственно
дает формулу для вычисления температуры в граничном узле.
В общем случае, когда 7	0, разностная схема (4.3) является
неявной, так как при каждом значении п разностное уравнение
включает в себя неизвестные в момент времени tk+i значения
температуры в трех узлах сетки. Для того чтобы вычислить ре-
шение в момент времени tk+i, необходимо рассмотреть совокуп-
ность всех разностных уравнений. Перепишем выражение (4.3),
группируя неизвестные величины в левой части, а известные в
правой:
- (^7) u*tXi + (1 + 2/?7) "Т - (£7) <1 =
= (1 - 2^(1 - 7)) < + /?(1 - 7) (uLi + <1) = dn, (4.9)
п = 1,...,7V- 1.
Введем обозначения
w = (u*+1,...,4+1)T, d = (do,...,dNf .
Тогда предыдущее выражение представляет собой систему ли-
нейных уравнений вида
Aw = d,	(4.10)
с трехдиагональной матрицей
/ «о г0	\
Pi Si	Г1	0
А=
Рп	f п
о ...
\	PN	3N	/
4.1. Схема для одномерного уравнения теплопроводности
Коэффициенты этой матрицы следуют из (4.9) и равны
рп = -/?7, зп = 1 + 2/37, rn = -/3'f, n = l,...,N-l,
а коэффициенты первого и последнего уравнений определяются
граничными условиями. Например, для граничного условия (4.6)
s0 = 1, го — 0, do = /(ifc+i), а для граничного условия (4.8)
So = 1 + 2/З7, Го = -2^7,
do = (1 - 2/3(1 - 7)) и* + (2/3(1 - 7)) и* -
-^(7Ж+1) + (1-7)Ж))-
Так как элементы матрицы А удовлетворяют условию |sn| >
> \Рп\ + |гп|, то для решения системы уравнений можно при-
менить метод прогонки (см., например, ОНВ, п. 2.6.1). Таким
образом, для выполнения одного шага по времени в схеме (4.3)
требуется большее количество операций по сравнению с явной
схемой (4.2). С другой стороны, в неявной схеме мы можем вы-
брать больший шаг по времени, поэтому при заданной длитель-
ности процесса потребуется меньшее число шагов и общее коли-
чество операций будет сравнимо или даже меньше, чем для явной
схемы. Для вычисления одного временного шага по явной схеме
(4.2) необходимо 47V операций. Для вычислений по неявной схеме
(4.3) сначала необходимо определить вектор d (47V операций), а
затем решить систему уравнений (~ 87V операций), что в сум-
ме дает приблизительно 127V операций на один шаг по времени.
Поэтому, если в неявной схеме шаг по времени выбрать из соот-
ношения Д « 1,5, то общее количество операций будет сравнимо с
количеством операций, требуемых для вычисления по явной схе-
ме.
Пример 4.1 (остывание бесконечной пластины). Рассмотрим
бесконечную пластину толщины I. Пусть в момент времени t = О
она имеет температуру ио, а температура окружающей среды
поддерживается равной нулю. Тогда распределение температуры
в пластине описывается уравнением (4.1) с условиями:
7i(x,0) = ио	— начальное условие,
n(0, t) = п(/, 7) = О — граничные условия.
Точное решение этой задачи имеет вид	.,,
Глава 4- Распространение тепла (диффузия)
,	. 4uo ехр (~ктг2(2т + 1)2<//2) . /тг(2т + 1)х\
и(х, t) = -- > -----*------------------- Sin ----;---- .
тг '	2m+ 1	\ I )
т=0
(4-12)
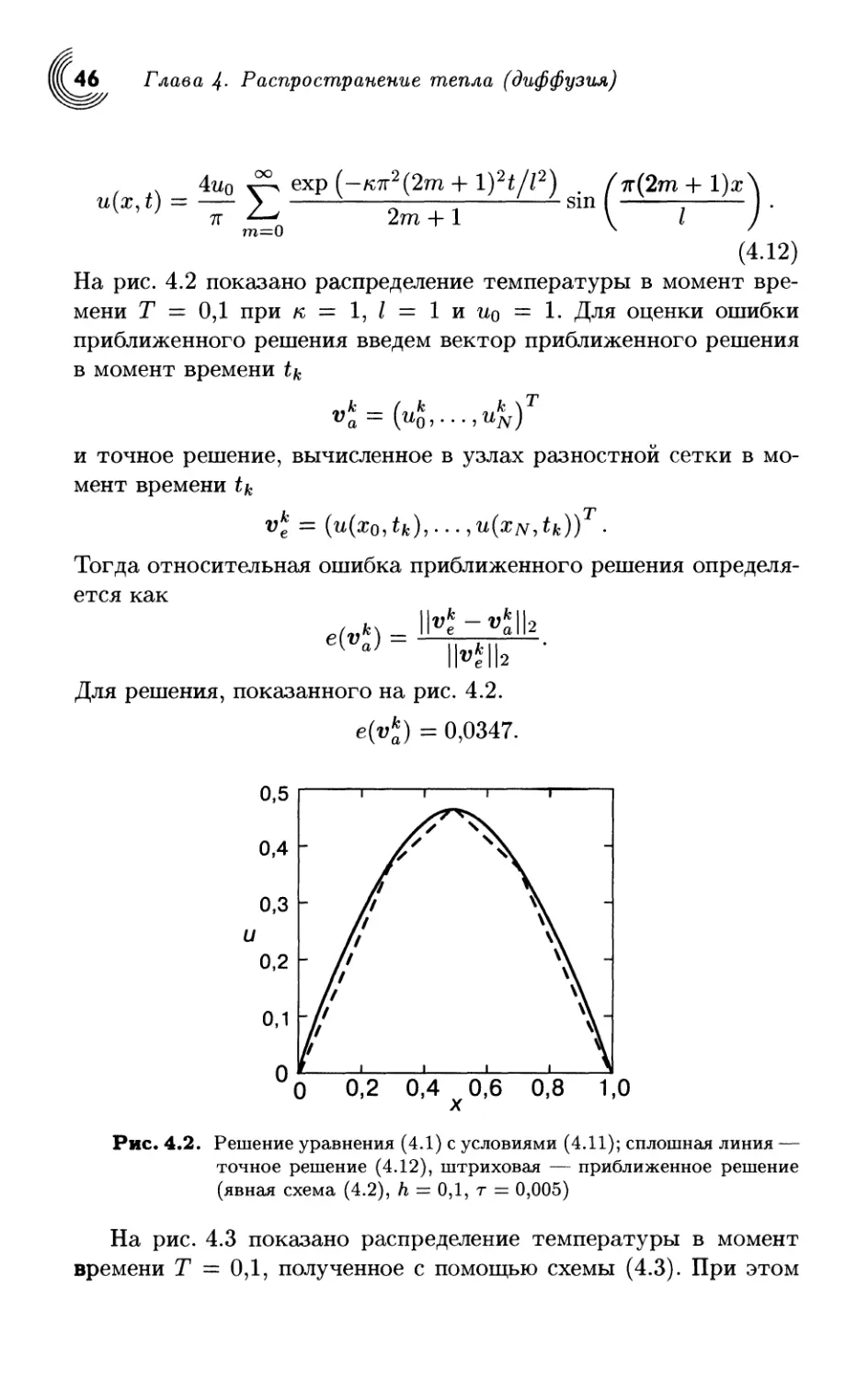
На рис. 4.2 показано распределение температуры в момент вре-
мени Т = 0,1 при к = 1J = 1 и но = 1. Для оценки ошибки
приближенного решения введем вектор приближенного решения
в момент времени
«а = (u^,...,UkN)T
и точное решение, вычисленное в узлах разностной сетки в мо-
мент времени tk
vk = (u(x0,4),..., и(ядг, tk))T 
Тогда относительная ошибка приближенного решения определя-
ется как
Для решения, показанного на рис. 4.2.
е(г>*) = 0,0347.
Рис. 4.2. Решение уравнения (4.1) с условиями (4.11); сплошная линия —
точное решение (4.12), штриховая — приближенное решение
(явная схема (4.2), h = 0,1, т = 0,005)
На рис. 4.3 показано распределение температуры в момент
времени Т = 0,1, полученное с помощью схемы (4.3). При этом
1^.2. Построение разностных схем для одномерного уравнения
значение 7 выбиралось из условия (4.4), а шаг по времени выби-
рался из условия
Р —	= 1,66666.
п/
Для этого решения
e(v*) = 0,0136,
что демонстрирует эффективность применения неявной схемы
для решения такого типа задач.
Рис. 4.3. Решение уравнения (4.1) с условиями (4.11); сплошная линия —
точное решение (4.12), штриховая — приближенное решение
(схема (4.3), h = 0,1, г = 1,66666 • 10"2, 7 = 0,45)
4.2. Построение разностных схем для
одномерного уравнения
теплопроводности с переменными
коэффициентами.
Предположение о постоянстве теплофизических свойств среды
далеко не всегда приемлемо. На практике мы часто имеем дело с
материалами с неоднородными физическими свойствами. Более
того, теплофизические свойства большинства материалов зави-
сят от температуры. Поэтому встает необходимость решения
уравнения теплопроводности с переменными коэффициентами.
Вначале мы рассмотрим распространение тепла в одномерной не-
Глава 4- Распространение тепла (диффузия)
однородной среде, которое описывается уравнением
• °«(< г'°«*«'
Введем обозначение для теплового потока
q = а
тогда предыдущее уравнение примет вид
(4.13)
ди
=&' ,4Л4)
Введем две сетки: Sm с узлами (жп,^) (основная сетка) и Sa
с узлами (#n+i/2^fc) (вспомогательная сетка), как показано на
рис. 4.4. Далее температура будет определяться в узлах основной
сетки, а потоки в узлах вспомогательной сетки.
Рис. 4.4. Основная сетка — сплошная линия; вспомогательная сетка —
штриховая
Проинтегрируем уравнение (4.14) по разностной ячейке Sa:
tk + l xn + l/2
/ /
tk хп —1/2
Вычисление интегралов дает
хп +1/2
У р(х)с(х) (u(a;,ifc+i) - и(х, tk))dx =
хп — 1/2
tk + 1
= У (g(xn+i/2,t) - 9(жп-1/2,^) dt. (4.15)
4.2. Построение разностных схем для одномерного уравнения
Это выражение представляет собой закон сохранения энергии,
записанный для разностной ячейки. Такая форма записи являет-
ся более универсальной, так как, например, если функция а(х)
разрывна в некоторых точках отрезка 0 х Z, то уравне-
ние (4.13) в этих точках смысла не имеет. Для того чтобы по-
строить разностную схему, необходимо сделать некоторые пред-
положения о распределении п(ж,на отрезке [xn-i/2,#n+i/2]
и Q(^n-i/2^) на отрезке [£&, ^+i]- Пусть u(x,tk) на каждом от-
резке [^п-1/2^п+1/2] принимает постоянное значение, которое
мы обозначим а значение потока д(жп+1/2Д) постоянно на
каждом интервале [^,^+1] и равно
q(xn+l/2,e) « 79(ж„+1/2,4+1) + (1 - 7)9(arn+i/2,ift) =
= 79^1/2+ (1-7)9п+1/2-
Введем обозначения
7 X	1
(pc)n = -
тогда выражение (4.15) принимает вид
(pc)n(«n+1 ~un)h =
= (7(9X2 -9П-1/2) + -
Нам осталось выразить тепловой поток через температуру. Ап-
проксимируя выражение для теплового потока центральной раз-
ностью относительно точки хп+1/2, получим
пк _п ип+1 - ип
Qn+1/2 — ап+1/2 д
Подстановка этого соотношения в предыдущее выражение дает
нам разностную схему
7/	— 7 А
(рс)х—=
/	?Л+1 _ ? fc+i
_ л (	ап+1 ип
-7lttn+l/2
—1/2
- ик„
~ ап-1/2
I (Л Ч (	Un+1
+ (1 “ 7) I ап+1/2---^2
77^ + 1   + 1
ип_____ип-1
h2
ук — „.к
ln un
h2
Глава 4- Распространение тепла (диффузия)
Легко показать, что когда р, с и а постоянны, эта схема пе-
реходит в схему (4.3).
В случае уравнения с переменными коэффициентами анали-
тическое исследование аппроксимации не всегда возможно. До-
пустим, что а(х) является дважды непрерывно дифференцируе-
мой функцией. Тогда можно показать, что, в общем случае, раз-
ностная схема (4.16) аппроксимирует дифференциальное урав-
нение (4.13) с точностью до членов О (г + Zi2), а если положить
7 = 1/2 — то с точностью до членов О (г2 + h2). В случае кусочно-
непрерывной функции а (ж) о порядке аппроксимации нельзя ни-
чего сказать заранее, так как он будет зависеть от решения
конкретной задачи.
Для анализа устойчивости применим принцип замороженных
коэффициентов. Заменим переменные параметры (pc)n, an-i/2
и an+i/2 в схеме (4.16) на некоторые константы ci, С2 и сз соот-
ветственно. Далее исследуем полученную схему на устойчивость.
В результате мы придем к условию (4.5), где = (с2 + сз)/(2с1).
Учитывая, что значения коэффициентов зависят от номера сеточ-
ного узла, мы окончательно получим следующее условие устой-
чивости схемы (4.16):
Д = — max
hz п
О 7 < 1/2.
( Qn~1/2 + QM-l/2\	1
\ (Pc)n /	1 - 27’
Д — любое > 0, 1/2 ^7^1.
(4-17)
Для неявной схемы (7	0) вычисления производятся так же, как
и для схемы (4.3), только коэффициенты матрицы А из (4.10)
определяются как
ап-1/2т	. ,
= '” = 1 + т
(pc)n/i2
(РЧпЬ
Для нелинейной задачи
/ / х&А
— (p(u)c(w) • и)
д
дх

разностная схема строится аналогичным образом. Только для
данной задачи следует использовать явную аппроксимацию с пе-
ременным шагом по времени, так как неявная схема требует
4-2. Построение разностных схем для одномерного уравнения
решения системы нелинейных уравнений на каждом временном
шаге, что может потребовать неоправданно большого объема вы-
числений. Учитывая это замечание, преобразуем схему (4.16) к
следующему виду:
к к ип ип _ пк ап+1 ап
Рпсп	an+l/2 L2
/	II
?Л+1 _
— пк	Un	ап-1 /Д-|О\
ап-1/2	^2	’ \*-1о)
где
Рп = Х“п), сп = с(ипк 4+1/2 =
— а ^2 (^n+i 4“	•
Условие устойчивости для данной схемы следует из условия
(4.17) при 7 = 0:
ЛЬ (ап-1/2 + ап+1/‘2\ Л
Т? ШаХ ------ к~к----- L
h2 п \ р*Ск I
Пример 4.2 (распределение температуры в неоднородной сре-
де при воздействии теплового потока). Рассмотрим задачу о
воздействии теплового потока на границу неоднородного полу-
пространства. Тогда при х > 0 распределение температуры будет
описываться уравнением (4.13). Начальные и граничные условия
зададим в виде
и(ж,0) =0, х > 0,
a(0)^(0,Z) = -/o, t > 0,	(4.19)
OX
lim u(x, t) = 0.
x—>oo
Пусть зависимость теплофизических параметров от координаты
имеет следующий вид:
р(х)с(х) = РоСо(1 + х), а(х) = а0(1 + х).	(4.20)
Такая зависимость характерна, например, для грунтов.
Для численного решения рассматриваемой задачи применим
явную схему (4.16), где
(рс)п = роСо(1 + Хп), ап+1/2 = а0(1 + хп + 0.5Л).
Легко проверить, что в данном случае условие устойчивости (4.17)
совпадает с условием устойчивости для однородного уравнения:
/3 1/2.
Глава 4- Распространение тепла (диффузия)
Применяя преобразование Лапласа по времени, можно полу-
чить точное решение рассматриваемой задачи:
w(a;, s) =---- z ________<----,
s3/2Ki (/s/к)
где к — ао/(росо)5 s — переменная преобразования Лапласа, Kq и
Ку — модифицированные функции Бесселя второго рода (функ-
ции Макдональда) порядка 0 и 1 соответственно. Обращение это-
го выражения дает точное решение задачи u(x,f).
На рис. 4.5 показано распределение температуры в момент
времени Т — 0,5, полученное с помощью схемы (4.16), вместе
с точным решением при = 1, по = 1, /о — 1-
х
Рис. 4.5. Решение уравнения (4.13) с условиями (4.19) и (4.20); сплош-
ная линия — точное решение, штриховая — приближенное
решение (явная схема (4.16), h = 0,25, т = 0,0278)
4.3. Метод расщепления по
пространственным переменным
Метод расщепления является одним из важнейших инструмен-
тов для построения разностных схем для многомерных задач
математической физики. Мы обсудим основные идеи этого ме-
тода на примере двумерного уравнения теплопроводности, но
аналогичные рассуждения справедливы и для других типов за-
дач, например, для уравнений акустики и газовой динамики.
4.3. Метод расщепления по пространственным переменным
Рассмотрим следующую задачу
ди _
dt
д2и д2и\
дх2 + ду2 J 1
О < t С Т, О С х С 1Х, О С у 1У.
и(х,у,0) = д(х,у),
ди
biu(O,y,t) + b2 — (0,y,t) =
OX
ди
b3u(lx,y,t) + b4 — (lx,y,t) = f2(y,t),
du
b5u(x,0, t) + 66 —(ж,0, Z) = f3(x,t),
dy
du
b7u(x,ly,t) + b9 — (x,ly,t) = fi(x,t).
(4.21a)
(4.216)
(4.21b)
(4.21r)
(4.21Д)
(4.21e)
(4.21ж)
Запишем дифференциальное уравнение этой задачи в опера-
торном виде:
ди	д2и д2и
— = Du = dxu + Dyu =	+ «7-5-.
dt	v дх2 ду2
Пусть решение в некоторый момент времени tk известно. Тог-
да решение в момент времени tk + т можно выразить через это
известное решение, используя разложение в ряд Тейлора:
ы(т, у, + г) = и(х, y,tk) + т~д^х> У у f'k) + О(т2) =
= (I + TD)u(x,y,tk) + О(т2), (4.22)
здесь I — единичный оператор (1и — и). Расщепим исходную
задачу (4.21) на две одномерные задачи:
dv
— = Dxv,	(4.23а)
dt
tk tk 4- r, 0 x lx, Q ^y	(4.236)
v(x, y, tk) = u(x, y, tk),	(4.23b)
dv
biv(O,y,t) + b2—(0,y,t) = fi(y,t),	(4.23r)
OX
dv
b3v(lx,y,t) + b4^-(Jx,y,t) = fafat}, (4.23д)
OX
Глава 4. Распространение тепла (диффузия)
dw
~dt -
tk 'С "С tk ~Ь х, 0 х 1 О 'С У 1у ,
w(x,y,tk) = v(x,y,tk + г),
b5w(x,0,t) + b6^(x,0,t) = fs(x,t),
7	/	7	\ T	f .	.	Л/	\
b7w(x,ly,t) 4- 68 — (x,ly,t) = n(x,t).
(4.24а)
(4.246)
(4.24b)
(4.24r)
(4.24д)
Последовательное решение этих задач дает решение w(x, ?/, tk 4-т)
и, естественно, это решение должно совпадать с u(x,y,tk 4- г).
По аналогии с (4.22) можно показать, что
v(x, у, tk + r) = (I + tDx) v(x, у, tk) + О(т2)
w(x, У, tk + г) = (J + TDy) w(x’ V,tk) + O(r2).
Тогда из (4.22), (4.23) и (4.24) следует, что
w(x, У, tk+r) = (I + rDy) v(x, у, tk+r) + О(т2) =
= (/ + rDy) (I + tDx) v(x, y,tk) + O(r2) =
= (/ + r(Dx + Dy)) u(x, y, tk) + O(r2) =
= (/ + tD) u(x, y, tk) + O(r2) = u(x, y, tk+r) + O(r2).
Таким образом, мы показали, что решение, полученное после
последовательного решения задач (4.23) и (4.24) совпадает с точ-
ностью до членов О (г2) с решением задачи (4.21). Это дает воз-
можность заменить многомерную задачу последовательностью
более простых одномерных задач.
4.4. Разностные схемы для решения
многомерного уравнения
теплопроводности.
Мы рассмотрим основные методы решения многомерных задач
на примере построения разностных схем для двумерного уравне-
Разностные схемы для решения многомерного уравнения
ния теплопроводности
ди (д2и д2и\ . . ч
~dt =К\д^ + д^) +
О Т, О С х 1Х, О С у С 1У,
и(х,у,0) = д(х,у),
+ граничные условия.
(4.25а)
(4.256)
(4.25в)
(4.25г)
Чтобы применить метод конечных разностей в этой ситу-
ации, поступим совершенно так же, как и в одномерном слу-
чае. С этой целью построим множество равноотстоящих точек
хп (п = О, ...,7V) на отрезке 0 С х С lx с xq = 0, xn = lx,
#n+i — хп = h, а также — множество равноотстоящих точек ут
(т = 0,..., М) на отрезке 0 у 1У с уо - 0, ум = 1У, Ут+i ~
— Ут — h. После этого область, где ищется решение, покрывает-
ся прямоугольной пространственной сеткой: через каждую точку
хп проводятся прямые параллельные оси у, а через каждую точ-
ку Ут — прямые параллельные оси х (рис. 4.6). В дополнение
введем множество точек по времени tk (к = 0,1...) с t^+i —
-tk = т. Тогда типичная точка разностной сетки имеет коорди-
наты вида (xn,ym,tk)' После этого входящие в уравнение (4.25)
частные производные заменяются соответствующими конечно-
разностными аппроксимациями (см. (3.2)).
Рис. 4.6. Двумерная пространственная сетка
Глава 4. Распространение тепла (диффузия)
Для более компактной записи разностных схем примем следу-
ющие обозначения для разностных операторов, аппроксимирую-
щих вторые производные по х ну:
^2 (^п-Ь1,т ^ип,т 4" ип—1,т) ?
^Уип,т = д2 (Mn,m+1 ~ ^ип,т + ип,т-1) •
Тогда двумерный аналог схемы (4.3) записывается как
— „.к
= Ку (Д^Д + Д^) +
+ к(1 - 7)	+ ^Уип,т) + Л(Жп, Ут, tk) (4-26)
* = 0,1,...; n = l,...,N-1; т = 1,...,М - 1.
Шаблон, схематически представляющий эту схему, показан на
рис. 4.7.
Рис. 4.7. Шаблон для схемы (4.26)
Если 7 > 0, то схема (4.26) неявная; для каждого значения к
необходимо решать разностное уравнение вида
+ ^УНп(т) ~ dn,m
относительно неизвестных значений в момент времени ^+1- Эф-
фективное решение такого уравнения возможно только для до-
вольно узкого класса задач (см. гл. 7). С другой стороны, яв-
ная схема (4.26) имеет довольно сильное ограничение на шаг по
времени (для квадратной сетки /3 < 1/4), что также может по-
требовать большого объема вычислений. Поэтому мы не будем
4-4’ Разностные схемы для решения многомерного уравнения
останавливаться на подробном анализе этой схемы, а перейдем
к рассмотрению более экономичных разностных схем, построен-
ных на основе метода расщепления.
Существуют различные способы построения разностных схем,
основанных на уравнениях (4.23) и (4.24). Мы рассмотрим лишь
несколько примеров. Если использовать явную схему (4.2) для ре-
шения задач (4.23) и (4.24), то получим явную схему расщепления
k
у _____________
----— = кДхи* + fs(xn,ym,tk),	(4.27а)
Г
n = 1,... ,JV — 1; m = ms,...,me,	(4.276)
(4.27в)
т
п = ns,... , тп = 1,..., М — 1,	(4.27г)
ип,т =9(хП,Ут},	(4.27Д)
+ разностная форма граничных условий,	(4.27е)
которая представляется в виде шаблона, показанного на рис. 4.8.
Рис. 4.8. Шаблон для схемы (4.27)
При записи этой схемы мы ввели обозначения
wn,m = Vn,m И
Параметры ns, пе, ms, тпе зависят от типа граничных условий:
_ ( 1, для граничных условий 1-го рода при х = О,
8	[0, для граничных условий 2-го рода при х = 0;
_ ( N — 1, для граничных условий 1-го рода при х = 1Х,
е [ N, для граничных условий 2-го рода при х = 1Х;
{1, для граничных условий 1-го рода при у — О,
О, для граничных условий 2-го рода при у = 0;
Глава 4- Распространение тепла (диффузия)
_ ( М — 1, для граничных условий 1-го рода при у = 1У,
е [ 7И, для граничных условий 2-го рода при у = 1У.
Вычисления по схеме (4.27) производятся следующим образом.
На первом шаге, при каждом значении т, решаются одномерные
задачи по ж, что дает промежуточное решение v =	За-
тем, решая, при каждом значении п, одномерные задачи по у, мы
получаем сеточную функцию ufc+1, которая и считается прибли-
женным решением в момент времени ^+1-
Для анализа аппроксимации запишем сначала схему (4.27) в
виде одного уравнения. Для этого выразим vn,rn из первого урав-
нения и подставим это выражение во второе уравнение. В резуль-
тате получим
= к т +	+ г«2 *Д,Дх^>т +
4~ T^yfs(xn, Уту ^/с) 4“ fs (^п, Ут у tk) • (4.28)
Подставляя в это выражение точное решение и учитывая, что
операторы Ахип,т и Ауип,т аппроксимируют вторые производ-
ные по х и у (см. (3.14)), приходим к дифференциальному при-
ближению в точке (xn,ym,tk)
ди.	.1 д2и .	.	2.
Уту tk) + 2^	tk) О\Т ) —
(/	х д2и.	А _ ,	ч
— К (	tk) 4“ ^^2	Ут ’tk) 1 4“ fs\%ny Уту tk) 4”
ft/z2 / д4и	д4и	\
4 12“ I	(Хп у Ут у tk ) 4"	(%пу Уту tk) J 4"
д^и	д2 fs
+ Т^2 Qx2Qy2 (Хп> Ут’ tk) 4" т-д^2~(^пуУту tk) + 0(h4).
Поэтому схема (4.27) аппроксимирует дифференциальную задачу
(4.25) с первым порядком по т и со вторым порядком по h.
Процедура исследования устойчивости схемы (4.27) аналогич-
на процедуре, которую мы использовали для анализа одномерных
задач. Только в двумерном случае мы зададим решение в виде
Un,m — ехР (га1^ 4"	•	(4.29)
Подставим это решение в (4.28) и получим (функция
при этом не учитывается, так как она не влияет на устойчи-
Разностные схемы для решения многомерного уравнения
вость):
А — 1 4к . 2 /1 А 4к . 2 (1 \
16к2Т2 . 2 / 1	\ • 2	\
+ ——— sin I -Qi 1 sin I -а2 1 •
Решение этого уравнения относительно А дает выражение для
собственного значения оператора перехода на один шаг по вре-
мени:
1 -4/3 sin2	(1-4/3
/3 =	0	«1,0:2	2?Г,
поэтому
0^ |A(ai,a2)|	(1-4/3)2
. 2 (1
sin I -а2
\
и для выполнения критерия фон Неймана необходимо 11 — 4/?| ^1,
откуда следует условие устойчивости (3 < 1/2. Это говорит о
том, что мы можем выбрать вдвое больший шаг по времени по
сравнению с явной схемой (4.26).
Если мы используем для решения задач (4.23) и (4.24) неявную
схему (4.3) с 7 = 1, то получим неявную схему расщепления
—	"Ь f8(xn, Ут->	(4.30а)
Т
п = 1,..., N — 1; т — ms,..., те, (4.306)
.fc+l — л.
п-^т~ -п'т =	(4-ЗОв)
п = ns,..., пе;	т = 1,..., М — 1,	(4.30г)
ип,т = 9&п,Ут),	(4.30д)
+ разностная форма граничных условий,	(4.30е)
которая представляется в виде шаблона, показанного на рис. 4.9.
Для последовательного вычисления решения по схеме (4.30) на
первом шаге, при каждом значении т, решаются системы урав-
нений вида (4.10), где
~ (^0,т? • • • j VN,rri) ?
d = (u0,m + Tfs(x0, Ут, tk),---, ^N,m + rfs(xN, Ут, tk))T 
Глава 4- Распространение тепла (диффузия)
Затем, при каждом значении п, решаются системы уравнений
вида (4.10), где
w = (unV’--->unjw) > d = (vnfi,...,vn,M)T.
Рис. 4.9. Шаблон для схемы (4.30)
В результате мы получаем требуемое решение в момент вре-
мени ffc+i.
Для нахождения порядка аппроксимации выразим vnjn из вто-
рого уравнения и подставим результат в первое уравнение. Это
дает следующее разностное уравнение:
г
=	+ Ьуик+') +тк2Л.у^хи1^ + fs(xn,ym,tk). (4.31)
Анализ этого уравнения показывает, что схема расщепления
(4.30) аппроксимирует дифференциальную задачу (4.25) с точно-
стью до членов O(r-|-/i2). Подстановка решения (4.29) в уравнение
(4.31) дает следующее выражение для собственных значений опе-
ратора перехода:
А( i,«2) +4Дбш2 (jcti)) (1 H-4/3sin2 (|а2))
Тогда |A(qi,Q2)|	1 для всех значений «1, а2 и значит схема
(4.30) устойчива при любых значениях /3 > 0.
Вообще говоря, рассмотренный нами способ расщепления не
является единственно возможным. Например, уравнение (4.21)
можно представить в следующей форме:
ди _ к /д2и д2и\ к /д2и д2и\
dt	2	ду2 ) + 2 \Эж2 + ду2 )
4-4- Разностные схемы для решения многомерного уравнения
На основе такого расщепления можно записать следующую схему
v —	к	1
п’т Т п,т = 2 (^xVn,m + ДзХ.т) +	ут, tk), (4.32а)
п = 1,..., N — 1; гп = ms,..., me, (4.326)
q.k+l _	-1
----— = - (b.xvn,m + Дуи„^) + ~fs(xn, ym, tk), (4.32b)
T---Zt	Lt
n = ns,...,ne-, m = 1,... ,M - 1, u^m = g(xn,ym'), (4.32r)
4- разностная форма граничных условий,	(4.32д)
которая имеет шаблон, показанный на рис. 4.10.
Рис. 4.10. Шаблон для схемы (4.32)
Эта схема получила название «метод переменных направле-
ний» (ADI, Alternating Direction Implicit). Так как эта схема явля-
ется неявной, то процедура расчета по этой схеме аналогична
процедуре расчета по неявной схеме расщепления (4.30). Более
подробная запись, анализ аппроксимации и устойчивости схе-
мы (4.32) оставляется читателю в качестве упражнения.
В заключение, обсудим расчет граничных условий. Разност-
ная форма граничных условий первого рода практически оди-
накова для всех рассмотренных нами схем. Например, условие
и(0, у, t) = t) в случае явной схемы (4.26) записывается как
«о^г1 =	т = 1,...,М - 1.
В случае схем расщепления (4.27) и (4.30) граничное условие име-
ет вид
Й),т — f (.Уту £&+1)>	~ !>•••> Af 1*
Так как на втором шаге расчета по этим схемам это значение не
изменяется, то можно положить
U0/m = v0,m-
Глава 4- Распространение тепла (диффузия)
В случае граничных условий второго рода их разностная фор-
ма зависит от вида основной разностной схемы. В качестве при-
мера рассмотрим граничное условие
a^Q,y,t^ =
Для явной схемы (4.26) применение метода фиктивных облас-
тей дает следующую разностную форму этого граничного условия
= (1 - 2^)	+ 2/М,т + (3 («U+1 - 2ио,т + <т-1) +
2/ЗЛ	х г ,	х
4 /\УтЛк) "Ь Утч tk),
а
т = 1,...,7И —1.
Представление граничных условий для схем расщепления (4.27)
и (4.30) непосредственно следует из выражения (4.8). Поэтому
для схемы (4.27) можно записать
Vo,m ~ (1 ~ 2/?) izo?w +	4	—— f (Ут, tk) 4“ Т fs{xO, У mi tk),
т = ms,..., те.
Аналогично, для схемы (4.30) получим
(1 4- 2/3) Vo?m — 2/3?;i?m = и^ т 4 — f {Ут, tk) 4- т fs(xQ,ym,tk),
т = ms,..., те.
Пример 4.3 (нагрев пластины при воздействии на нее теплового
потока). Рассмотрим квадратную пластину размером I и толщи-
ной d. Пусть при z — 0 она теплоизолирована, а при z — d на нее
воздействует распределенный тепловой поток вида
9<x,y,t) = 16/оу (1 - у) у (1 - у) exp(-ct).
В начальный момент времени t = 0 пластина имеет температу-
ру uq. Края пластины теплоизолированы. Тогда распределение тем-
пературы в пластине подчиняется уравнению (4.25) с fs(x, у, t) =
— y(xi У 3) и условиям
и(х,у,&) = и0,	^(O,y,t) = <^(l,y,t) =0,
tz«X>	(zvt/
^(a:,O,t) =	= 0.
ду	dy
(4.33a)
(4.336)
44- Разностные схемы для решения многомерного уравнения
Здесь под и(х,у,Р) понимается средняя по толщине пластины
температура.
На рис. 4.11 показана зависимость температуры в центре пла-
стины от времени, при лс = 1, Z ~ 1, Уо = 1 ? с = Ю и = 0- Точное
решение этой задачи имеет вид
сю сю
и(х, у, t) = /о 52 52 ип^1п,т (г) Sin
п=0 т=0
где
Un,m
— ——о (1 + cos(7rm)),	п — 0, т ± О,
Зтг2т2
---	 (1 4- cos(?m)),	п 0, т = О,
ЗтГ2П2
64
..9—- (1 4- cos(?rn)) (1 4- cos(?rm)), п / 0, т / О,
7г4п2т2
/.ч exp(-6n,mt) -ехр(-с£)	ктг2 z 2	2.
7n,m W =-----------—------------, bn,TO = — (nz + пГ).
C On,m	*
Приближенное решение вычисляется с помощью явной схемы рас-
щепления (4.27).
Рис. 4.11. Решение уравнения (4.25) с условиями (4.28); сплошная ли-
ния — точное решение, штриховая — приближенное решение
(h = 0,1, т = 0,005)
Глава 4. Распространение тепла (диффузия)
4.5. Численное решение задачи Стефана
Фазовые изменения возникают в различных физических процес-
сах. Одним из примеров такого рода процессов является распро-
странение тепла, включающее затвердевание (плавление) среды.
Классическая математическая модель, применяемая для описа-
ния этого явления, называется задачей Стефана. Основная труд-
ность при решении этой задачи возникает из-за присутствия дви-
жущегося фазового фронта, который в трехмерном случае пред-
ставляет собой некоторую поверхность. Тепловой поток терпит
разрыв на этой поверхности, поэтому уравнение теплопровод-
ности на ней заменяется условием, которое связывает скорость
движения фазового фронта и величину изменения теплового по-
тока при переходе через этот фронт. Аналитическое решение
задачи Стефана не всегда возможно, поэтому встает вопрос о
ее численном решении.
Мы обсудим основные идеи построения вычислительного ал-
горитма на примере решения одномерной задачи. Рассмотрим
среду, которая в начальный момент времени находится в жид-
ком состоянии при температуре и(х, 0) > ир, где ир — темпе-
ратура плавления. Поверхность среды при х = 0 поддержива-
ется при температуре iz(O,f) < ир, а при х = I температура
u(l,t) > ир. Предполагая, что плотность среды не меняется при
фазовом превращении, процесс затвердевания описывается сле-
дующими уравнениями:
ди д2и „	, .	z, Л.
pcs—=	—,	0^x<y(t),	(4.34а)
ди д2и , ч	Л.
pc/—= —,	y(f)<x^l,	(4.346)
где y(t] — положение фазового фронта (в данном случае фронта
затведевания). Индекс s обозначает твердую фазу, а I — жидкую
фазу. Эти уравнения дополняются начальными и граничными
условиями г/(х,0) = д(х), 0 х I, u(0,t) = /i(£), u(l,t) = Л(^) и
условием Стефана на фазовом фронте
+ (4'35>
где L — скрытая теплота плавления (затвердевания). Это усло-
вие следует из условия баланса энергии при движении фазового
фронта.
4.5. Численное решение задачи Стефана
Наиболее удобной для решения задачи Стефана представляется
энтальпийная формулировка, которая позволяет избежать необ-
ходимости явно учитывать движение фазового фронта. Опреде-
лим энтальпию как функцию температуры следующим образом:
ТТ(и\ _ Г С8иУ	U < UP,
[ ciu — (ci — cs)up 4- L, и Up. \ • )
Энтальпия H пропорциональна температуре, исключая область
фазового фронта, где она скачкообразно изменяется. Тогда вме-
сто уравнений (4.34) и условия (4.35) можно записать следующее
эквивалентное уравнение:
= 1Г (а(х’	’ 0 х	(4-37)
at дх\ дх)
где зависимость температуры от энтальпии следует из (4.36) и
имеет вид
{H/cs,	Н csUp,
Up,	csup < Н < csup 4- L,
(Я - L)/ci - up(ci - Cs)/ci, H csUp 4- L.
Когда температура в некоторой точке принимает значение ир,
начинается фазовое превращение. Так как оно происходит не
мгновенно, то в этой точке в течение некоторого времени од-
новременно существуют твердая и жидкая фазы. Так локальная
доля твердой фазы определяется следующим образом:
{1,	H(x,t)^csUp,
1 — (Н — csUp)/L, csup < Н(х, t) < csup 4- L,
О,	H(х, t) csup 4- L.
Тогда коэффициент теплопроводности можно задать как
Разностная схема для уравнения (4.37) аналогична схеме (4.18):
Я*+1 - Я* _ к Ц*+1 - U* _ к Ukn-ukn
Р т	ап+1/2	^2	°п-1/2	^2
А; = 0,1,...; П = 1,..., Я — 1,
u°=ui, Н° = С1Щ - (ct - cs)up +L, n = Q,...,N,
(4.38a)
(4.386)
(4.38b)
Глава 4- Распространение тепла (диффузия)
Uq = us, Hq = csus,	(4.38г)
их = ui, Hx = ciui - (ci - cs)up + L,	(4.38д)
гдеи*=и(Я*),
an+l/2 ~ a ( 2 (S(a'»i+1 >	4“ s(xn> tk))
= aQ(s(H*+i)+ *(#*))}•
Вычисления по схеме (4.38) производятся следующим образом:
1) по заданному в начальный момент времени распределению
температуры вычисляются энтальпия и коэффициент те-
плопроводности;
2) для каждого последующего момента времени =tk + т,
к — 0,1,... сначала вычисляется энтальпия Н^1, п = 0,..., 7V,
а затем температура, коэффициент теплопроводности и ло-
кальная доля твердой фазы:
«п+1/2 = а (Яп+1 ’ Нп+1) }> n = 0,...,N.
4+1 = s (н*+1)	)
Условие устойчивости для схемы (4.38) непосредственно сле-
дует из условия (4.17) при 7 = 0:
т	( as ai\	1
— max —, — <
h2	\pcs pci J	2
Исходя из определения локальной доли твердой фазы, поло-
жение фазового фронта в момент времени tk, для данной задачи,
можно вычислить следующим образом:
N
п=0
о
Пример 4.4 (замерзание водоема). Рассмотрим задачу об обра-
зовании ледяного покрова на водоеме. Предположим, что обра-
зование льда происходит равномерно по всей площади водоема.
Тогда можно применить одномерную модель (4.34), где х = 0
будет соответствовать поверхности водоема, а х = I — дну во-
4-5. Численное решение задачи Стефана
доема. Выберем следующие параметры задачи:
g(x) = 7х/7 + 273 К,
f^t) = 273 - 13(1 - ехр(—0,0001 * t)) К,
/2(£) = 280 К, ( = 1м.
Теплофизические параметры представлены в табл. 4.1.
Таблица 4.1. Теплофизические параметры задачи
	Вода	Лед
Плотность, кг/м3	1000	1000
Теплоемкость, Дж/(кг-К)	4200	2100
Коэффициент теплопроводности, Вт/(м-К)	0,56	2,25
Коэффициент температуропроводности, м2/с	1,33  10“7	1,08  10~6
Удельная теплота плавления, Дж/кг	3,3 • 105	
Температура плавления, К	273	
На рис. 4.12 и 4.13 показано приближенное решение, получен-
ное с помощью схемы (4.38).
Рис. 4.12. Распределение темпера-
туры по толщине водоема; сплош-
ная линия — в момент времени t =
= 106 с (Л = 0,05 м, т = 1166,66 с),
штриховая — начальное распреде-
ление при t — 0
Рис. 4.13. Положение фазового
фронта (толщина ледяного покро-
ва) в зависимости от времени
ГЛАВА 5
РАСПРОСТРАНЕНИЕ
АКУСТИЧЕСКИХ
ВОЛН
В этой главе мы обсудим численные методы решения задач рас-
пространения волн малой амплитуды. Необходимость решения
таких задач возникает в самых различных областях, например:
-	аэроакустика (снижение шума);
-	распространение электромагнитных волн (микроэлектроника);
-	волны в твердых телах (методы неразрушающего контроля,
динамика конструкций, сейсморазведка);
-	методы медицинской диагностики;
-	предсказание прихода волны цунами.
Мы начнем наше обсуждение с простейшего уравнения колебаний.
5.1.	Разностная схема
для уравнения колебаний
В одномерном случае колебания однородной среды в отсутствии
внешнего воздействия описываются уравнением
(5.1)
dt2 дх2
с начальными условиями
ди
и(ж,0) = gi(x), — (x,0)=g2(x)
и граничными условиями
di /	di 1
Q1U(0,f) + a2^-(0,t) = /1(0, «зЦМ) +	= А(0-
ОХ	ох
Здесь и обозначает либо скорость частиц среды, либо давление,
с — скорость звука. Введем разностную сетку с шагами т и
5.1. Разностная схема для уравнения колебаний
h = l/(N — 1), где N — количество узлов разностной сетки. Ис-
пользуем разностное выражение для второй производной, опре-
деленное в (3.2), и применим его для аппроксимации производной
по времени в точке хп и производной по пространству в момент
времени t^. В результате получим разностную схему
un+1 - 2мп + «п-1 _ 2 Un+1 - 2un + «£-1
г2	~	А2 ’	(5.2)
n= 1,.. .,N - 1; k = 1,2,...,
которая приводит к вычислительной формуле
м„+1 = 2ukn - u*-1 + r2(u*+1 - 2ukn 4- икп_г),
n = l,...,N-1; k = l,2,...,
где r = ст/h — безразмерный параметр, называемый параметром
Куранта. Шаблон для схемы (5.2) показан на рис. 5.1, поэтому ее
часто называют схемой «крест».
Рис. 5.1. Шаблон схемы «крест»
к+ 1, п
к,п-1>--------------• к, п + 1
к- 1, п
Значения приближенного решения при к = 0 и к — 1 вычи-
сляются из начальных условий, а значения при п — 0 и п = N
вычисляются из граничных условий. В случае граничных усло-
вий первого рода (аг = Щ = 0, ori = аз — 1) формулы имеют
простой вид:
«о=/1(^)> ukN^h(tk), к = 1,2,....
Для аппроксимации граничных условий второго рода (аг =
=	= 1, Qi = аз = 0) следует использовать метод фиктив-
ных областей. Рассмотрим эту процедуру на примере граничного
условия, заданного в точке х = 0. Введем фиктивный слой с коор-
динатами (a?-i, ffc), тогда можно аппроксимировать производную
Глава 5. Распространение акустических волн
в граничной точке со вторым порядком по Л, используя централь-
ную разность
= Ж), fc=l,2,....
В дополнение, запишем схему (5.2) при п — 0:
ug+1 - 2wfj + uk~4 _ 2«1 - 2ug + U* !	_
~2	~С &	’	^-1,2,....
Исключая фиктивное значение из последнего выражения, мы по-
лучим формулу для вычисления приближенного решения в гра-
ничной точке
uk+1 = 2ик - и*-1 + 2r2(uk -uk- hf(tk)), к =1,2,....
Исследуем свойства схемы «крест». Используя последнее соот-
ношение из (3.14), получим следующее выражение:
<Э2и,	.	2^2и/	* \ _
^2(хп4к) С g^2(xn,tk) -
= Л	+ c2h2^~(xn,tk)\ +0 (h4 + т4).
Это значит, что разностная схема (5.2) аппроксимирует диффе-
ренциальную задачу (5.1) со вторым порядком по h и т. Далее,
подставляя в разностную схему решение в виде (3.17), получим
уравнение для собственных значений оператора перехода
А2 — 2А + 1 = г2 (ехр(ш) — 2 4- ехр(—ia)) — —4r2 sin2(a/2).
Решение этого уравнения имеет вид:
А(а) = 1 — 2г2 sin2(a/2) ± ^/(1 — 2r2 sin2(a/2))2 — 1,
и, согласно критерию фон Неймана, схема «крест» будет устой-
чива при г < 1.
Пример 5.1 (схема «крест»). Рассмотрим задачу (5.1) с нулевы-
ми начальными условиями и граничными условиями
u(0,f) = |	u(l,t) = 0,	(5.3)
((1 I п) \ n
-------) , n — 10. Решение, полученное с ломо-
ть J
щью схемы (5.2), показано на рис. 5.2.
5.2. Диссипация и дисперсия сеточного волнового решения
Как показывают эти результаты, данная схема сохраняет ам-
плитуду, но искажает форму волны. Более того, появляются вы-
сокочастотные осцилляции, отсутствующие в точном решении.
Рис. 5.2. Решение уравнения (5.1) с граничными условиями (5.3) в
момент времени t = l(Z==l, с=1); сплошная линия — точ-
ное решение, штриховая — приближенное решение (Д = 0,05,
т = 0,0333, г = 2/3)
Понятно, что в пределе ft, г —> 0 приближенное решение бу-
дет стремиться к точному, но реально мы работаем с конечными
шагами по пространству и времени. В этом случае анализ ап-
проксимации не позволяет получить более полную информацию
о свойствах разностной схемы, таких как, например, диссипа-
ция и дисперсия. Далее мы обсудим метод анализа этих важных
свойств.
5.2.	Диссипация и дисперсия
сеточного волнового решения
Прежде чем рассматривать диссипацию и дисперсию разностно-
го решения, мы должны определить эти свойства для дифферен-
циального волнового уравнения. Для этого возьмем решение в
виде
и(х, t) = uq exp(z(otf — кх\),
где cj =	— круговая частота, к = 2л/Л — волновое чис-
ло. Если мы подставим это решение в какое-нибудь линейное
Глава 5. Распространение акустических волн
волновое уравнение, то получим зависимость ш = cu(fc), кото-
рая называется дисперсионным соотношением. Если ш принимает
вещественные значения, то амплитуды гармоник не изменяют-
ся со временем. В противном случае, когда ш принимает ком-
плексные значения, волна будет затухать (диссипировать) как
ехр(—= ехр(—yt). Отношение
Recj
-JT=cf
называется фазовой скоростью, т.е. скоростью, с которой дви-
жется фаза или узел отдельной гармоники. Величина
d
—Rew = cq
dk у
называется групповой скоростью. Она может интерпретировать-
ся как скорость волнового пакета, состоящего из гармонических
волн с близкими волновыми числами. Передача энергии в волне
осуществляется с групповой скоростью. Если фазовая (группо-
вая) скорость зависит от к, то гармоники с разными волновыми
числами распространяются с разными скоростями. Это явление
называется дисперсией. Для уравнения (5.1) нетрудно получить,
что си = ск и, следовательно, Cf = сд = с. Это значит, что точное
решение уравнения (5.1) представляет собой волну, которая рас-
пространяется без затухания и дисперГии. Другой пример: для
линеаризованного уравнения Бюргерса
ди ди	д2и
dt + Сдх	дх2 '
зависимость имеет вид
cu(fc) = ск + ipbk2.
Это соотношение описывает затухающую недиспергирующую
волну. В частности, при ц = 0 мы получаем уравнение перено-
са (3.1), для которого справедливо соотношение с/ = сд — с и
коэффициент затухания равен нулю.
При численном решении волновых задач возникает затухание
и дисперсия сеточного решения, что связано с формой разност-
ных уравнений. Сильное затухание приводит к тому, что через
некоторое число шагов по времени волна просто исчезает (при-
мер такого решения показан на рис. 3.3). Дисперсия, хотя и не
влияет на амплитуду волны, но искажает ее форму. Дисперсия
5.2. Диссипация и дисперсия сеточного волнового решения
также приводит к возникновению ошибки при расчете отраже-
ния и интерференции волн.
Анализ диссипации и дисперсии сеточного решения мы будем
проводить на решении
икп = и* exp - кхп)).	(5.4)
Если подставить это решение в разностную схему, то мы по-
лучим некоторое соотношение вида cj = cj(A;, т, h). Сравнивая это
соотношение с соответствующим дисперсионным соотношением
для дифференциального уравнения, которое эта схема аппрокси-
мирует, мы можем анализировать свойства данной схемы. В ка-
честве примера рассмотрим свойства схемы «крест». Подставим
приведенное выше решение в схему (5.2) и получим выражение
exp(zcjr) — 2 + exp (—гейт) = r2(exp(—ikh) — 2 + exp(ifch)),
из которого следует, что
sin(cjr/2) — г • sin(A;/i/2).
В данном случае со принимает вещественные значения, и зна-
чит, сеточное волновое решение не затухает со временем. Выра-
жая си из предыдущего выражения, мы приходим к следующему
дисперсионному соотношению:
2 • ( •
со = - arcsin г sin ~kh
Г \	\2 JJ
Тогда групповая скорость волны, распространяющейся на сетке,
определяется как
_ dco _ cos(^kh)
7 1	Г ..........  >
yjl — r2 sin2 (|А;Л)
т.е., в отличии от уравнения (5.1), возникает дисперсия. Только
когда г — 1, групповая скорость приближенного решения совпа-
дает с групповой скоростью точного решения.
Минимальная длина волны, которая может быть представлена
на сетке, составляет Л = 4h (kh = я/2). Понятно, что гармоники
с такой длиной волны сильнее всего подвержены влиянию дис-
персии. Для этого случая зависимость безразмерного параметра
а — Ст/с от параметра Куранта показана на рис. 5.3.
Зависимость, показанная на этом рисунке, представляет наи-
худшую ситуацию. Для длин волн много больших пространствен-
Глава 5. Распространение акустических волн
ного шага, дисперсия приближенного решения уменьшается (убе-
дитесь в этом с помощью программы properties).
,0	0,2	0,4	0,6	0,8	1,
1,10
1,05
1,00
0,95
a 0,90
0,85
0,80
0,75
0,70
0,0	0,2	0,4 r 0,6	0,8	1,0
Рис. 5.3. Зависимость параметра а — ст/с от параметра Куранта для
схемы «крест»; сплошная линия — безразмерная групповая
скорость волны Сд/с — 1 для дифференциального уравнения;
штриховая — параметр а при Л:Л — тг/2
Теперь мы можем объяснить возникновение осцилляций в при-
ближенном решении, представленном на рис. 5.1. Любое гладкое
решение можно представить в виде ряда Фурье по простран-
ственным гармоникам:
2тгпх \	, . / 2тгпж \\
Так так вычисления проводились при г — 2/3, то возника-
ет дисперсия приближенного решения и гармоники с разными
значениями п распространяются с разными скоростями. Через
некоторое время возникает пространственное разделение этих
гармоник, и появляются осцилляции, отсутствующие в точном
решении.
N /
и(х, t) — и\(fyuz(х) ~ ui (f)	( ап cos
5.3.	Схема Лакса-Вендроффа
Часто задачи на распространение волн удобно формулировать
в виде системы дифференциальных уравнений первого порядка.
Так распространение одномерной акустической волны в однород-
5.3. Схема Лакса-Вендроффа
ной среде описывается следующей системой:
где
дз дз
dt + А дх °’
О я Z,
(5.5)
О
рс2
Up А
0 / ’
Здесь и — скорость частиц среды, р — давление, р — плотность
среды, ис — скорость звука. Уравнения (5.5) дополняются на-
чальными условиями
и(х,0) = 9i(x), р(ж,0) = д2(х)
и граничными условиями
Qi w(0, t) + «2Р(О, t) = /i (Z), a3w(Z, Z) + сцЖ t) = f2(t).
В дальнейшем мы будем рассматривать построение разност-
ных схем для системы (5.5).
Предположим, что решение в момент времени t известно. Тог-
да решение в следующий момент времени t + At можно получить
с помощью разложения функции s(x, Z+At) в ряд Тейлора в точке
(ж, t) по степеням At, т. е.
/ а \	/ х А дз z .	1 , А ч9 д2з z
s(x,t + Ai) = s(x,t) + &t—(x,t) + -(Af) —(ж,<) + •••
C/C	&	Gru
Производные no t заменяются производными по x путем ис-
пользования системы (5.5):
дз	дз	д2з	д	дз	2д2з
dt	дх	dt2	dt	дх дх2
Подставим эти выражения в наше разложение и получим
/9 ч	1	д2 я
s(x,t + At) = s(+, <)-A^A — (z, <) + -(Дг)2Д2—-(+,<) н-(5.6)
их	2	oxz
Теперь введем разностную сетку с узлами (xn,tk) и шага-
ми h и т. Затем построим разностную аппроксимацию выраже-
ния (5.6) на этой сетке, используя приближения второго порядка
для производных по х (см. (3.2)) и полагая т = At. Это приводит
к схеме Лакса-Вендроффа
«п+1 = 4 -	(4+i - 4-1) +
+ |(02а2С4+1-24 + 4-1), (5-7)
Глава 5. Распространение акустических волн
п = 1,..., N — 1; к — 0,1,..., или в развернутом виде —
«п+1 = ип -	(Рп+1 -Рп-1) +	(«п+1 - 2ип + «п-1) ,
Рп+1 = Рп -	(икп+1 -	+ |г2 (ркп+1 - 2ркп +р*-1) .
n = l,...,N-1; fc = 0,l,....
Из процедуры построения следует, что схема (5.7) имеет вто-
рой порядок по h и т. Рассмотренная нами схема удобна, ко-
гда матрица А постоянна. В случае переменной матрицы про-
ще использовать другой подход, который исключает вычисление
производных от матрицы А- Сначала в центрах прямоугольных
ячеек на плоскости (ж, Z) вычисляются промежуточные значения
(рис. 5.4):
*+1/2 _ 1 ( k	, Ц _ т ( .k k _ .k к\
n+1/2	2 V n+1	2h '^п+!г’п+1	^-П^п) 4	(5 g)
n = 1,...,7V — 1; к = 0,1,...,
где
Л   f	0	1 /Р^пч^к) А
п “ \ p(xn,tk)c2(xn,tk) О у*
к+1------
к+1/2
к -----
Л-1	л	л+1
Рис. 5.4. Вспомогательные узлы
«х» для вычисления промежуточно-
го решения
л-1/2
л+1/2
Окончательные значения получается затем из уравнения
чАН-1 _ Л _ I /лА:+1/2 А:+1/2 _ АН-1/2 АН-1/2 \
П	П	h vWl/2 ™+1/2	^n-1/2%-1/2J '
п = 1,...,7V- 1; к = 0,1,...
(5.9)
Выражения (5.8) и (5.9) называются двухшаговой схемой Лак-
са -Вендроффа. Легко проверить, что в частном случае, когда
матрица А постоянна, эта схема переходит в схему (5.7).
5.3. Схема Лакса-Вендроффа
Перейдем к анализу устойчивости схемы (5.7). Только теперь
мы имеем систему уравнений, поэтому вместо (3.17) зададим ре-
шение в виде
= Xk(a) exp(ian)s*,
где s* — некоторый постоянный вектор. Подстановка этого ре-
шения в разностную схему (5.7) дает следующее выражение:
As* = s* — — (ехр(ш) — ехр(—ш)) As* +
2h
1 / Т \ 2
+ х(т) (ехр(га) - 2 + ехр(-га)) А2»*.
2 \п/
После некоторых преобразований, мы получим стандартную
задачу на собственное значение:
I- (i^sin(a)) А - (l-cos(a))A2
з* = Вз* = Аз*.
Решение характеристического уравнения det (В — А/) = 0 да-
ет следующее выражение для собственного значения оператора
перехода:
А(о) = 1 — r2(l — cos(q)) ± ir sin(o).
Тогда из критерия фон Неймана следует, что разностная схема
(5.7) будет устойчива при г 1.
Анализ диссипативных и дисперсионных свойств разностных
схем для системы уравнений (5.5) мы будем проводить на решении
8^ = s* exp (i(wtk - kxn)).
Если подставить это решение в разностную схему (5.7), то мы
получим систему уравнений
^ехр(гсит) - 1)/ - sin(ATi)) А +
+ (0 (1 — cos(A;h)) = Ds* = о.
Из условия det (В) = 0 следует дисперсионное соотношение
exp(zcjr) — 1 — г2 (1 — cos(khY) + zrsin(fch),
и, следовательно, ш принимает комплексные значения, что гово-
рит о диссипации сеточного решения. Введем обозначение и =
= cjq + г’7, и, приравнивая вещественные и мнимые части в пре-
J'лава 5. Распространение акустических волн
дыдущем выражении, получим:
ехр(—7т) cos(cjqt) = 1 — г2 (1 — cos(khY),
ехр(—yr) sin(cjo7") — т sin(fcfo).
Отсюда нетрудно получить коэффициент затухания
7т — — In £(1 — г2 + г2 cos(A;h))2 + г2 sin2(fc/z)]
и групповую скорость волны на сетке
_	_	г2 + (1 - г2) cos(kh)
т dk (1 — г2 + г2 cos(A;h))2 + г2 sin2(kh)
На рис. 5.5 и 5.6 представлены зависимости параметра дисси-
пации d = 7т и групповой скорости от параметра Куранта.
0,16
0,14
0,12
0,10
d
0,08
0,06
0,04
0,02
0,00
0	0
Рис. 5.5. Зависимость параметра диссипации d = ут от параметра Ку-
ранта для схемы Лакса-Вендроффа (kh ~ тг/2)
Для аппроксимации граничных условий со вторым порядком
по h и т, можно использовать метод фиктивных областей. Пусть,
например, задано граничное условие при х = 0: u(0,£) = f(t).
В разностном виде это граничное условие записывается очень
просто:
«0*+1 = Ж+0-
Для вычислений по схеме (5.7) нам необходимо также значе-
ние давления в граничном узле. Для определения этого значения
введем фиктивный слой с координатами (ж-i, tk) и запишем вто-
рое уравнение (5.7) в виде
р£+1 =	~	- И-1) + |г2 (р? - 2р* + р* 1).
5.3. Схема Лакса-Вендроффа 79
1,0
0,8
0,6
а
0,4
0,2
0,0
0,0	0,2	0,4 г 0,6	0,8	1,0
Рис. 5.6. Зависимость параметра а = Ст/с от параметра Куранта для
схемы Лакса-Вендроффа; сплошная линия — безразмерная
групповая скорость волны cg/c = 1 для дифференциального
уравнения; штриховая — параметр а при kh = тг/2
Для исключения фиктивных значений ик_х и рк_г используем
очевидное приближение
оЖ + u-i) = «£ = №)•
Тогда первое уравнение из (5.7) примет вид:
~ № - р-0 = «о - 4+1 = Ш - f(tk+1).
После несложных преобразований, мы получим формулу для
вычисления второго граничного условия
Ро+1 = Ро - Рс  r (ui - Ж+0) + г2 (Р1 - Ро) •
В случае, когда на границе задано давление, аналогичная про-
цедура применяется для определения скорости в граничной точке.
Пример 5.2 (схема Лакса-Вендроффа). Рассмотрим задачу
(5.5) (которая эквивалентна задаче (5.1)) с нулевыми начальными
условиями и граничными условиями (5.3). Приближенное реше-
ние, полученное с помощью схемы Лакса-Вендроффа (5.7), по-
казано на рис. 5.7.
Это решение подтверждает результаты проведенного выше
теоретического анализа: амплитуда волны уменьшается (схема
(5.7) диссипативна) и происходит запаздывание волны, так как
скорость распространения всех гармоник меньше, чем групповая
скорость, определяемая системой уравнений (5.5) (см. рис. 5.6).
Глава 5. Распространение акустических волн
Рис. 5.7. Решение уравнений (5.5) с граничными условиями (5.3) в
момент времени t — 1 (Z — 1, с = 1, р = 1); сплошная ли-
ния — точное решение, штриховая — приближенное решение
(h = 0,05, г = 0,0333, г = 2/3)
5.4.	Характеристическая форма
уравнений акустики
Прежде чем продолжить наше обсуждение, нам необходимо рас-
смотреть одно важное свойство уравнений акустики. Запишем
уравнения (5.5) в развернутом виде:
ди	1 др	др	2ди
	777 Н— я~ ~	“ 0-
dt	р ox	ot	ох
Умножим первое уравнение на ср, а затем получим два новых
уравнения путем сложения этих уравнений и вычитания первого
уравнения из второго:
д .	. д . х
-	(р + ср-и) + с— (р + ср • и) = 0,
д	д
—	(р-ср-и)- с-^ (р-ср-и) = 0.
В результате мы получим характеристическую форму урав-
нений (5.5). Она представляет собой два уравнения переноса для
величин R = p + cp-unS — р — ср • и, которые называются инва-
риантами Римана. Решение исходной системы может быть легко
(5.10)
5.4- Характеристическая форма уравнений акустики
выражено через эти инварианты:
u=2-(R-S), P=±(R + S).
2ср	2
Решение этой системы можно записать в виде R(x,t) = R(x — ct)
и S(x,f) — S(x + ct). Решение такого вида говорит о том, что
инвариант R сохраняется вдоль характеристики dx/dt — с, т.е.
R = const при х — ct — const, и, соответственно, инвариант S
сохраняется вдоль характеристики dx/dt = —с: S — const при
х -Ь ct = const.
Используя эти свойства инвариантов Римана, построим ре-
шение задачи о распаде разрыва. Пусть начальное условие для
задачи (5.5) имеет следующий вид:
.	( щ,	ж 0,	z ( pi,	х О,
u(x,G) = \	р(я,0) = {	’
4	7	[ иг,	х > О,	v	7	[ рг,	х > 0.
При t > 0, эта конфигурация распадается на две волны, распро-
страняющиеся влево и вправо от точки х = 0 (рис. 5.8).
Рис. 5.8. Задача о распаде раз-
рыва; штриховая линия — началь-
ное состояние; сплошная — со-
стояние в некоторый момент вре-
мени t > 0
-ct 0 ct х
Обозначим решение в точке х = 0 как ио и ро- Тогда, учитывая
свойства инвариантов Римана, в точке х — 0 можно записать:
р0 + ср • и0 = R(-ct) = pi + ср- щ,
Ро — ср  ио = S(ct) — рг ~ ^Р' Ur-
ns результате, мы приходим к решению:
1 / ч 1 z
Ро = 2 to + Рг) + 2 СР (Ul “ Ur>'
1 /	X	1 2	7
Uo = 77 (ui +ur) + — (р/ - Pr) -
2	2cp
(5.11)
Глава 5. Распространение акустических волн
5.5. Недиссипативная схема Ф. Роу
Схема, предложенная Ф. Роу, основывается на характеристиче-
ской форме (5.10). Так как эта форма представляет собой сис-
тему из двух уравнений переноса, то имеет смысл рассмотреть
сначала построение схемы для уравнения
ди ди
-^7 + с— = 0.
dt дх
Как обычно, введем разностную сетку с узлами (жп,^) и ша-
гами h и т. Основная особенность этой схемы состоит в методе
аппроксимации производной по времени: приближение для du/dt
задается как полусумма разности вперед по времени в точке хп
и разности назад по времени в точке xn_i. Производная по х
аппроксимируется разностью назад относительно точки хп. Ша-
блон этой схемы имеет вид, показанный на рис. 5.9, и разностная
схема записывается как
1 Г?4+1 - ик	икп_г - икп_\ 1 ик - uk_j _
2 г + г +С h “°’	(5.12)
n = l,...,N -1; к =
<► л, к+1 Рис. 5.9. Шаблон схемы (5.12)
л-1, к
п, к
п-1, к-1
В отличие от рассмотренных нами схем, схема (5.12) явля-
ется трехслойной (разностное уравнение связывает три момента
времени).
Разностная схема для одномерного уравнения акустики стро-
ится на основе характеристической формы (5.10). Для аппрок-
симации первого уравнения применяется схема (5.12). Аппрокси-
5.5. Недиссипативная схема Ф. Роу
мация второго уравнения производится с помощью аналогичной
схемы, учитывающей, что это уравнение описывает волну, рас-
пространяющуюся влево. В результате мы получим следующую
разностную схему:
1	Rk+1-Rk Rk,-Rk-\	Rk-Rk 1	(5.13a)
2	т	т	+ с п , п 1 = 0, h	
1	с/с+1 _ ак	ак _ ак-1 	'п । °п-Н ° п+1 т	т	ак _ ак _ r_Zl±L—_П. — о	(5.136)
2		h	
	Rn=Pn+cP-	1	Sk=pk-cp.ukn,	(5.13b)
	ukn = 0,5(Rk-Sk)/cp, рк	= 0,5(Rkn + Sk).	(5.13r)
Для анализа свойств этой схемы, достаточно рассмотреть схе-
му (5.12), так как разностные уравнения в (5.13) непосредственно
не связаны друг с другом. Подставляя точное решение в (5.12) и
используя выражения (3.14), получим
к	X LZ СС ,	V
i?^fc) — ог'Б72’(Жп-1 ’
1	\ди, ч 1 д2 *и .	.
2	[di (Xn’tk) + 2T'di^^Xn,t^ +
314/	.	1 д2и	1
4“	\хп — 11^к) ~~ п.э \хп—1^к) 4"
ot	2 ot2
ди f .	1 д2и, J Л / л 9Ч
4-	С —(Xmtk) - -h^^Xn.tk) +0 (h2 4-т2) = 0.
дх	2 дх2	4 * *	7
Так как мы проводим анализ аппроксимации в точке (жп,^),
то нам еще необходимо разложить величины, определенные в точ-
ке (xn-i,tk) в ряд Тейлора в точке хп по степеням h. Тогда мы
приходим к следующему дифференциальному приближению:
диz	ч ди . ч 1_ д2и . ч
— (xn,tk) + c—(xn,tk) = 2hd^dt +
1	/9^7/
4- ~ch — (xn, tk) + О (h2 + г2) .
2 дх2	v 7
Из уравнения переноса следует, что d2u/dxdt = —сд2и/дх2.
Тогда два первых слагаемых в правой части предыдущего выра-
жения сокращаются и, следовательно, схема (5.13) имеет второй
порядок аппроксимации по h и г. Анализ устойчивости схемы
(5.13) оставляется читателю в качестве упражнения.
Глава 5. Распространение акустических волн
Для анализа диссипации и дисперсии применим подход, рас-
мотренный в пункте 5.3. В результате получим следующее дис-
персионное соотношение:
sin (сит — ^:kh ) = (1 “ 2r) sin ( ^-kh ] .
\	Z J	\Z J
Так как cu принимает только вещественные значения, то дис-
сипация отсутствует. Групповая скорость волны, распространя-
ющейся на сетке, определяется как
dw с
Ст dk 2г
(1 - 2г) cos (^kh)
^/1 — (1 — 2r)2 sin2
На рис. 5.10 показана зависимость безразмерного параметра
а — ст/с от параметра Куранта.
2’°Г
1,8"
1,2
1,6
а
1,4
1,0
0,8
0,0	0,2	0,4 г 0,6	0,8	1,0
Рис. 5.10. Зависимость параметра а = Ст/с от параметра Куранта для
схемы Ф. Роу; сплошная линия — безразмерная групповая
скорость волны сд/с = 1 для дифференциального уравнения;
штриховая — параметр а при kh = л/2
Рассмотрим теперь расчет граничных условий. Пусть, напри-
мер, задано граничное условие при х = 0: u(0, t) = f(t). Вычисле-
ние этого условия не представляет особого труда:
nofc+1 = /(4+1).
Для вычисления давления в граничной точке мы используем
схему (5.13). Так как состояние в точке х — 0 определяется вол-
ной, распространяющейся влево, то следует взять второе уравне-
5.6. Метод С. К. Годунова
ние при п = 0:
1 (р*+1 - ср  uk+l - Sq + Sf - S*-1) - С- (S* - Sofc) = 0.
Z /	n
Тогда второе граничное условие вычисляется по формуле
р*+1 = ср • u*+1 + (1 - 2r)S£ - (1 - 2r)Sk + S{=-’.
Для вычисления граничных условий, заданных на правой гра-
нице при х — Z, применяется аналогичный подход. Только в этом
случае, следует использовать уравнение для R инварианта при
n = N.
Пример 5.3 (схема Ф. Роу). Как и прежде, рассмотрим зада-
чу (5.5) с нулевыми начальными условиями и граничными услови-
ями (5.3). Приближенное решение, полученное с помощью схемы
(5.13), показано на рис. 5.9.
Рис. 5.11. Решение уравнений (5.5) с граничными условиями (5.3) в
момент времени t = 1 (Z = 1, с = 1, р = 1); сплошная линия —
точное решение, штриховая — приближенное решение (h =
= 0,05, т = 0,0333, г = 2/3)
5.6.	Метод С. К. Годунова
До сих пор мы представляли приближенное решение как набор
значений в узлах разностной сетки. Другой способ представления
приближенного решения состоит в том, что распределение вели-
чин аппроксимируется ступенчатыми функциями, такими, что
Глава 5. Распространение акустических волн
эти величины имеют постоянные значения на каждом интервале
[хп, xn+i], как показано на рис. 5.12. Значение некоторой величи-
ны на интервале [xn,xn-i-i] будет обозначаться как и, для
определенности, мы будем относить это значение к середине ин-
тервала. Далее мы рассмотрим построение разностных схем на
основе такого представления приближенного решения.
Рис. 5.12. Представление приближен-
ного решения в виде кусочно-постоян-
ной функции
5.6.1.	Схема первого порядка
Для того чтобы построить основную схему, проинтегрируем урав-
нения (5.5) по площади разностной ячейки {хп < х < xn+i,tk
^Л+1}:
Жп4-1 ^fc + 1	tk + i
У у ^dldx + A / /	=
Хп. tk	tk Хп
Вычисляя интегралы от производных, получим
Жп + 1	^4-1
У (s(x,tk+1) - s(x,tk)) dx + А У (s(xn+1,t) - s(xn,ty) dt = 0.
Xn	tk
Введем следующие обозначения: £ J s(x,tk)dx = sn+i/2 —
Хп
среднее значение величины з на интервале [жп,ггп+1]>
t к 4-1	rj-i
f 3(xn,t)dt = fn(s) = fntpY) — поток величины s че-
tk
рез узел xn за время от tk до tk+i-
С учетом этих обозначений, предыдущее соотношение прини-
мает вид:
(SX2-Sn+l/2),l + A(^+l(S)-^(a)) =°	<5’14)
5.6. Метод С. К. Годунова
Самый простой способ вычисления потоков основывается на
предположении, что величина s(xn,t) постоянна на каждом ин-
тервале [tk, tjfe+i], и мы обозначим ее значение как s\. Тогда схема
(5.14) записывается как
n+i/2-. n+1/2 + А°п+1Г- = 0,	(5.15)
t	h
или в развернутом виде —
лЛ+1 ___	k	k
тг+1/2 n -1-1/2 i Рп+1 Рп   Q
Т	ph
+ 1	Ь	k
Рп+1/2 Рп+1/2	2ип+1 ~ ип _ п
т	Р h
n = l,...,N-1; k = 0,l,...
Для того чтобы производить вычисления по схеме (5.15), нам
необходимо иметь некоторый алгоритм вычисления значений ве-
личин в узлах хп,через средние значения этих величин в соседних
ячейках. С. К. Годунов предложил использовать для этой цели
решение задачи о распаде разрыва. Действительно, в некоторый
момент времени tk приближенное решение имеет вид ступенча-
той функции, как показано на рис. 5.12. При t > tk каждый
разрыв распадается на две волны. Одна из этих волн движется
в направлении возрастания координаты х, а вторая — в сторону
ее убывания. Между волнами, скажем в точке хп, и и р постоян-
ны по времени до тех пор, пока волны от соседних разрывов не
пройдут расстояние h, т. е. в течении времени т h/с (это и есть
физическое обоснование устойчивости данной схемы). Поэтому,
при tk С t tk + т можно использовать решение задачи о распаде
разрыва (5.11). Если обозначить
(	и1 \	( Un-l/2	|	Tjr	(	иг А _ ( Un+l/2	|
I I ----- I Ь	|	И	I I — li*	5
\Р1 )	р£_1/2 )	\Рт )	\ Рп+1/2 J
то значения величин и и р в узле хп вычисляются по формулам:
ип — 2 (wn-i/2 4- ^+1/2) 4- 2^ [Рп-1/2 ~~Ркп+1/2^ ,	(5.16а)
Рп ~ 2 (^п-1/2 4"Рп4-1/2^ 4- — ('Un-1/2 — ^+1/2) •	(5.166)
Подставляя эти выражения в (5.15) мы получим схему С. К. Го-
Глава 5. Распространение акустических волн
дунова для уравнений акустики:
Цп+1/2 ~ Цп+1/2 __	Рп+3/2 ~ ^п-1/2
Т	2ph
+ 2д (ип+з/2 ~ ^wn+i/2 + ип-1/2^ > (5.17а)
Рп+1/2	Рп+1/2 _ _^2 Цп+3/2 Цп-1/2
Т ~ С Р 2h
+ 2Д (Рп+З/2	%Рп+1/2 + Рп-1/2^ , (5.176)
п = 1,... ,N - 1; к = 0,1,...
Анализ аппроксимации проведем в точке (жп+1/2,^). Подста-
вляя точное решение в (5.17) и используя выражения (3.14), по-
лучим
ди	1 др	1 д2и
~0^\хп+1/2-)^к) "И р£^(Хп+1/2’^) ~ — 2Г 9^" Жп+1//2’	+
1 _ С? 71 z	ч хл/19	9 \
+ ^h—{xn+1/2,tk) + 0 (А2 +т2).
Приводится только первое уравнение из (5.17), так как для
второго уравнения получается аналогичное выражение. Из урав-
нения (5.5) следует, что d2u/dt2 = с?д2и/дх2. Тогда предыдущее
выражение преобразуется в
ди	1 др
~0^\хп+1/2^к) "И ~ 7^(#п+1/2? *к) —
= |c/i(1-r)|^(a;n+i/2,4) + (9(/i2 + T2),
и это говорит о том, что схема (5.17) имеет только первый по-
рядок по h и т. Качественный анализ этого выражения пока-
зывает, что схема (5.17) диссипативна. Действительно, члены
вида рд2и/дх2 представляют собой вязкие силы, поэтому с точ-
ностью до величин второго порядка малости можно сказать, что
схема (5.17) добавляет к исходному уравнению (5.5) «вязкость»
0,5с/г(1 — г)д2и/дх2. Такая «вязкость» (называемая аппроксимаци-
онной вязкостью) приводит к тому, что амплитуда волны умень-
шается со временем при г < 1.
5.6. Метод С. К. Годунова 89
Разностную схему (5.17) можно записать в виде
Sn+l/2 = Sn+l/2 ~	(Sn+3/2 - Sn-l/2) +
+ 2^^ (sn+3/2 - 2s„+1/2 + в„_1/2) •
Тогда для анализа свойств этой схемы можно непосредственно
применить методику, рассмотренную в параграфе 5.3. В резуль-
тате мы получим следующее выражение для собственных значе-
ний оператора перехода:
А (а) = 1 - 2r sin2(a:/2) ±zrsin(a).
Тогда из критерия фон Неймана (3.18) следует, что схема (5.17)
будет устойчива при г ^1. Коэффициент затухания и групповая
скорость сеточного решения удовлетворяют соотношениям:
7т = — In ^(1 — г + г cos(A:7z))2 + г2 sin2 (A:7i)] ,
_ du0 _ г + (1 — г) cos (кН)
Ст dk С (1 - г)2 + г2 4- 2г(1 — г) cos (kh) ’
На рис. 5.13 и 5.14 представлены зависимости параметра дис-
сипации d = 7т и групповой скорости от параметра Куранта.
0,35-------1------1—।-----------1-------
0,30 -	/	\
0,25-	/	\
0,20	/	\	-
d	/	\
°’5- /
0,10- /	\ -
0,05 /	\-
I	\
0 00 к-----1------1--------1----1-------2I
0,0	0,2	0,4 г 0,6	0,8	1,0
Рис. 5.13. Зависимость параметра диссипации d = ут от параме-
тра Куранта для схемы С. К. Годунова первого порядка
(kh — 7г/2)
Схема С. К. Годунова выгодно отличается от других схем про-
стотой расчета граничных условий. Например, если в точке х = 0
задано условие tz(O, t) = f(t), то скорость в граничном узле вы-
Глава 5. Распространение акустических волн
числяется как
— f
и нам еще необходимо определить давление в этом узле. Состоя-
ние в точке х — 0 определяется волной, движущейся в направле-
нии убывания координаты ж, и зависит от значений и и р в ячейке
примыкающей к границе. Тогда в течение времени tk С t tk +1
условие сохранения инварианта S примет вид
k	k k	k
Po - CpUo = Pl/2 - 4^1/2 >
откуда следует формула для вычисления давления в граничном
узле. Другие типы граничных условий вычисляются аналогично.
1,4
а
1,2
1,0
0,6
0,4
0,2
0,8
0,0
0,0	0,2	0,4 _ 0,6	0,8	1,0
Рис. 5.14. Зависимость параметра а = ст/с от параметра Куранта для
схемы С. К. Годунова первого порядка; сплошная линия
безразмерная групповая скорость волны с5/с = 1 для диф-
ференциального уравнения; штриховая — параметр а при
kh — 7г/2
Пример 5.4 (схема С.К. Годунова первого порядка). Приме-
ним рассмотренную схему для решения задачи (5.5) с нулевыми
начальными условиями и граничными условиями (5.3). Прибли-
женное решение, полученное с помощью схемы (5.17) показано
на рис. 5.15.
Этот результат показывает, что амплитуда приближенного
решения значительно отличается от точного решения. Это объ
ясняется тем, что схема С. К. Годунова приводит к сильной дис
сипации сеточного решения. К тому же для г — 2/3, групповая
скорость ст > с (см. рис. 5.14) и при t = 1 приближенное решение
5.6. Метод С. К. Годунова
включает в себя отраженную от жесткой стенки волну. В точном
же решении отражение происходит при t > 1.
Рис. 5.15. Решение уравнений (5.5) с граничными условиями (5.3) в
момент времени t=l(/ = l,c=l,p=l); сплошная линия —
точное решение, штриховая — приближенное решение (А =
= 0,05, т = 0,0333, г = 2/3)
5.6.2.	Схема второго порядка
Разработаны различные методы повышения точности схемы
С. К. Годунова. Мы рассмотрим один из подходов, основанный
на коррекции величин, полученных после решения задачи о рас-
паде разрыва. На рис. 5.16 схематически показано распределение
и или р в момент времени t = tk+т/Ъ, возникающее после распада
разрыва.
Рис. 5.16. Схематическое распре-
деление скорости и давления на от-
резке [xn-i, Яп+i] в момент времени
tk + т/2 (xw = ст/2)
В схеме С. К. Годунова первого порядка используется только
значение в узле хп, а остальные характеристики решения не учи-
Глава 5. Распространение акустических волн
тываются. Более полное использование информации достигается,
если вычислять значение в узле хп следующим образом:
xn+h/2
sn+1/2 - У 8(х,	+ т/2) dx,
хп — h/2
где функция $(#,£& +т/2) имеет вид распределения, показанного
на рис. 5.16. Вычисление интеграла дает
4+1/2 = ^(1 - H«n-l/2 + Г8п + |(! - Ф£+1/2>
где есть значения в узле хп, полученное из решения задачи о
распаде разрыва (см. рис. 5.16). Если теперь в схеме (5.17) зна-
k	k+l/2
чения з^ заменить на зп , то мы получим разностную схему,
которая формально совпадает со схемой Лакса-Вендроффа.
Хотя в случае уравнений акустики рассмотренный подход не
дал ничего нового, тем не менее он нам понадобится при постро-
ении разностной схемы для уравнений газовой динамики.
5.7.	Кусочно-экспоненциальный метод
Для построения более точного приближенного решения автором
была предложена модификация схемы С. К. Годунова. Основная
идея предложенного метода состоит в том, что вместо распреде-
ления в виде кусочно-постоянной функции приближенное реше-
ние на каждом разностном интервале задается в виде экспонен-
циальной функции
u(x,tk) \ = / п(х) \
p(x,tk) J \ 9г,п(®) /
^2,п
+
®п+1 X \
h ) ’
(5.18)
Таким образом, приближенное решение представляет собой
кусочно-экспоненциальную функцию, причем в каждом узле сет-
ки это решение непрерывно. Поэтому этот метод получил на-
звание РЕМ (Piecewise Exponential Method, кусочно-экспоненци-
5.7. Кусочно-экспоненциальный метод
альный метод). Для того чтобы построить такое представле-
ние решения, т.е. определить шесть неизвестных параметров,
нам необходимо шесть условий. Поэтому, наряду со средними
на интервале значениями, мы также будем вычислять значения
приближенного решения в узлах сетки. Тогда параметры dm,n,
т = 1,..., 6 определяются из следующей системы уравнений:
91,nW) = < = di,n + dkn + d^nZ!,	(5.19а)
%п 4-1
У 9i*,n W = Un+l/2 = dl,n + (d2,n + d3,n) *2,	(5.196)
91,nW+l) = Un+1 = di,n + d2,n^l + d3,n>	(5.19в)
92,nW) = Pn = d4,n + d5,n +	(5.19r)
•En 4-1
/ Q2,n^)dx =р£+1/2 = d4,n + (d5,n + d6,n)z2,	(5.19д)
X n
9*,nW+i) = Pkn+1 = dk,n + <nZ1 + 4	(5.19e)
где z\ — exp(—1) и = 1 — Z\. Значения и потоки величин в
узлах разностной сетки находятся из решения задачи о распаде
разрыва с начальными условиями вида (5.18). Таким образом,
для определения приближенного решения в узле хп необходимо
решить систему (5.5) с начальными условиями
w(x,0) =	( 91,п-1(®)> I 91,„(^,	X хП1 X > Xfi ч	(5.20а)
р(ж,0) — <	92,п-1(®)> ( 92,nW,	X > хп.	(5.206)
Используя свойства инвариантов Римана, получим:
U W, tk+r) = u*+1 = W - ст) + qkn (хп + ст))/2 +
+ (92,п-1 W - ст) - q^n (ж0 + ст))/(2ср),
Р(xn,tk + т) = pk+1 = (g2,n-i (хп - ст) + qk п W + ст))/2 +
+ (91,п-1 (хп - СТ) - 91,П («О + ст)) ср/2,
n = l,...,N-1,
а также выражения для потоков величин в узле хп:
Глава 5. Распространение акустических волн
tk+i
fn(u) = У (91,п-1 (®п - Ct) + 91,п (®П + Ct)) dt +
tk
tk + 1
У (92,n-1 (хп ~ Ct) - q^n (ж0 + Ct)) dt,
tk
i (xn - Ct) + 92,„ <Xn + Ct)) dt +
£fc+l
/£(p) = l1 (92V
tk
tk+1
+ y У (91,п-I (г« - ct~) - 91, n {x0 + ct)) dt,
tk
n = 1,... ,N- 1.
Полученные выше значения зависят от параметров dmtn, т =
=	Выражая эти параметры через значения сеточной
функции из соотношений (5.19), окончательно получим:
wn+1 - а1ип + у (*4-1/2 + *4+1/2 ) + 2^ (рп-1/2 “Pn+l/2) +
+ у «I +<i) + (Pn-i -Pkn+J , (5.21а)
z	£ср
ft(u) = b1Ukn +	(<1/2 + <1/2) + h- (pti/2 - Pt-1/2) +
+ у «1 +<i) + (pLi -Pn+1) > (5-216)
Pn+1 = atPn + yep (u‘.1/2 - <+l/2) + у (Pn-l/2 +РП+1/2) +
+ УCP (Un-1 - ukn+i} + у (Pn-1 + Pn+1), (5.21b)
4b	4b
fn (p) = 51Pn + yep (“Ll/2 - «‘+1/2) + у (Pn-1/2 + Pn+1/2) +
+ ycP («n-1 - Wn+1) + у (Pn-1 +Pn+1), (5.21r)
n =	1.	(5.21Д)
5.7. Ку сочно-экспоненциальный метод
Значения параметров ат, bm (т — 1,..., 3) приведены в при-
ложении А. Перейдем теперь к построению разностной схемы
для системы уравнений (5.5). Как и прежде, основная схема бу-
дет иметь вид (5.14), мы только запишем ее в форме, пригодной
для вычислений:
s
*+1 _ -
п+1/2 ~ *
k
п+1/2
(5.22)
или
„*+1 _	/п+1 (р) - /п (р)
Un+l/2 - “п+1/2	ph
„*+1	_ vk	2 /п+1(Ц) ~ /nW
^п+1/2 “ ^п+1/2 С Р
Рассмотрим теперь расчет граничных условий. В ограничен-
ной области, в граничных точках задаются зависимости скоро-
сти или давления от времени (и от координат для многомерных
задач). Состояние в точке х — 0 определяется волной, движу-
щейся влево, и зависит от значений и и р в ячейке примыкающей
к границе. Тогда в течение времени tk С t < tk + т из условия
сохранения инварианта S следует:
Ро+1 - сРио+1 - “1 (ро - сР«о) +
+ “2 (pJ/2 - cpw?/2) + a3 (р* - срик), (5.23а)
/о (Р) - cPfo (и) = bi (Ро - сРио) +
+ b2 (pi/2 - cpw?/2) + b3 (jPr - сри1)  (5.236)
Поэтому значения и потоки величин в граничном узле вычи-
сляются из соотношений (5.23) и следующих соотношений:
ifc4-l
aiu£+1 +a2p§+1 = fi (ife+i), ai/o (u) + «2/0 (p) = f
tk
Аналогично состояние в точке х = I определяется волной, дви-
жущейся вправо, и условие сохранения инварианта R дает
p^+1 + сри1^1 = ai (pkN + pukN) + a2 (рдг_1/2 + cpukN_1/2j +
+ «3 (pn-i + cpu^-i) ,
Глава 5. Распространение акустических волн
/лг (р) + cpfN (u) — &1 (Pn + Pun) + ^2 (pn- 1/2 + CPUN-1/2)
+ &3 (рдг-l +
и граничные условия записываются как
«3Uw+1+O!4P^+1 =/2 (tfc+1), аз/дг(и) + а4/лг(р) = У /2 (t) dt.
th
Дифференциальное приближение схемы РЕМ по своей струк-
туре совпадает с дифференциальным приближением для схемы
С. К. Годунова:
fljT (®п+1/2,М +	(^п+1/2,4) =
= |с/1-5(г)|^(Жп+1/2,4)+О(/12+т2),
(?(г) = 1 - г + ——
z%r
т.е. схема кусочно-экспоненциального метода имеет первый по
рядок по h и т. Однако коэффициент аппроксимационной вязко
сти для этой схемы очень мал и
max^(r) ~ 6 • 10~3,
поэтому следует ожидать слабого затухания разностного реше-
ния. Более того, на реальных сетках эта схема может давать
меньшую ошибку аппроксимации по сравнению со схемами бо-
лее высокого порядка, когда решение в некоторых точках имеет
большой градиент.
Для анализа устойчивости схемы представим решение в с.
дующем виде:
(Jfe \	/	\
“n+ip j	= Xk	/ и	\	ехр (п +	,
Рп+1/2 /	\	Ра	/
/ цк	\	.	/ 11г	\
Подставляя эти выражения в разностную схему, получим одно
родную систему уравнений для неизвестных постоянных (иа, р(1
Ub, ръ)- Из равенства нулю определителя матрицы этой системы
следует уравнение на собственные значения оператора перехо-
да А(а). Анализ этих значений показывает, что схема устойчива
при г <1.
Дисперсионное выражение для схемы РЕМ имеет довольно
громоздкий вид и приведено в приложении А. На рис. 5.17 и 5.18
представлены зависимости параметра диссипации d = "ут и груп-
повой скорости от параметра Куранта.
Эти результаты показывают, что схема РЕМ
1) хотя и обладает диссипативными свойствами, но коэффи-
циент затухания приближенного решения для этой схемы
гораздо меньше чем для схем Лакса-Венд роффа и С. К. Го-
дунова;
2) имеет наилучшие дисперсионные свойства из всех рассмо-
тренных нами схем.
0,05
0,04
0,03
d
0,02
0,01
0,0
0	0
Рис. 5.17. Зависимость параметра диссипации d = 7т от параметра
Куранта для схемы РЕМ (Л;7гтг/2)
Пример 5.5 (схема РЕМ). Применим рассмотренную схему для
решения задачи (5.5) с нулевыми начальными условиями и гра-
ничными условиями (5.3). Приближенное решение, полученное с
помощью схемы (5.21), (5.22) показано на рис. 5.19.
Этот результат показывает, что схема РЕМ дает наилучшее
приближенное решение из всех рассмотренных нами схем. Данная
точность достигается благодаря тому, что эффекты диссипации
Глава 5. Распространение акустических волн
и дисперсии, производимые этой схемой, незначительно искажа-
ют сеточное решение при выбранном параметре Куранта.
1,05
1,00
0,95
0,90
a
0,85
0,80
0,75
0,70
0,65
0,0	0,2	0,4 г 0,6	0,8	1,0
Рис. 5.18. Зависимость параметра а = Cmjc от параметра Курант.1
для схемы РЕМ; сплошная линия — безразмерная групповая
скорость волны сд/с — 1 для дифференциального уравнения,
штриховая — параметр а при khn/2
Рис. 5.19. Решение уравнений (5.5) с граничными условиями (5.3) в
момент времени t = 1 (Z = 1, с — 1, р = 1); сплошная линия —
точное решение, штриховая — приближенное решение (h =
= 0,05, г = 0,0333, г = 2/3)
5.8. Разностные схемы для решения
многомерных задач
Построение разностных схем для волновых уравнений с двумя
и тремя пространственными переменными — более сложная за
5.8. Разностные схемы для решения многомерных задач
дача, однако используемые принципы идентичны применяемым
в одномерном случае. Рассмотрим вначале двумерное уравнение
колебаний в прямоугольной области
<Э* 2и _ 2 /92и	д2и\
dt2 С \дх2 + ду2) ’	(5.24)
О ж	O^t^T
с некоторыми начальными и граничными условиями. Чтобы по-
строить разностную схему для этого уравнения, поступим так
же, как в одномерном случае. С этой целью построим разностную
сетку с узлами (хп, ут, tk), и шаги этой сетки равны xn+i —хп —
hx, Ут+i ~Ут — hy и tk+i —tk — т. После этого входящие в уравне-
ние (5.24) частные производные заменяются соответствующими
конечно-разностными соотношениями. В результате мы получим
схему
tfm ~ ^п,т +
Г2
2 t ^п+1,т 2ип,т 4” ^п—1,т
с	h2
. Un,m+1 ~	+ ип,т—1
Ь2
Пу
п =	— 1; m =	1; к = 1,2,...,
(5.25)
которая является непосредственным обобщением схемы (5.2). Ис-
следование аппроксимации производится так же, как и в одно-
мерном случае. В результате мы получим, что схема (5.25) ап-
проксимирует уравнение (5.24) с точностью до членов О(г2 +
+ (hx)2 + (hy)2). Процедура исследования устойчивости анало-
гична процедуре, которая использовалась в одномерном случае.
Только в двумерном случае решение задается в виде
ип,т — ехР + Ш2Тп) .	(5.26)
Подстановка этого решения в схему (5.25) дает уравнение
2 2	2 2
А — 2А + 1 = -4А^- sin2 (а/21) - 4А^- sin2 (а/2э) •
fly
Решив это уравнение, мы найдем A(oi, «2)- Тогда из критерия
фон Неймана следует, что
100 Глава 5. Распространение акустических волн
2 2 /	। 1
с Т \h?x + h?
\ it	у
(5-27)
В частности, для квадратной сетки hx — hy = h это условие
принимает вид
и это говорит о том, что в случае двумерной задачи мы имеем
более сильное ограничение на шаг по времени по сравнению с
одномерной схемой. Такая ситуация характерна для большинства
разностных схем.
Перейдем к построению разностных схем для волновых задач,
сформулированных в виде системы дифференциальных уравне-
ний. В качестве примера возьмем двумерное уравнение акустики
ds ds ds
777 + А 77-----h В~^~
dt Эх dy
/гч 0 у 1у.
= о,
(5.28)
0
где
/ и \	/00 1/р \
s = I v I , А = [ 0 0 0 I,
\ р /	\ рс2 0	0/
/ 0	0	0 \	/ 0 \
В = о 0	1/р	, 0=0.
\ 0 рс2	0 /	\ 0 /
По аналогии с одномерным случаем построение схемы Лак-
са- Вендроффа для уравнения (5.28) осуществляется на основе
разложения
/	ч / ч ds	1 2d2s
s(x, у, t + т) = S{x,y,t) + r—(x,y,t) + -т -^(x,y,t) + •••
Используя уравнение (5.28) и полученное на его основе соот-
ношение
d2s
dt2
d2 я
=	+ (AB + BA)
dx2
d2s
dxdy
+ B2
d2s
dy2'
мы придем к двумерному аналогу выражения (5.6):
5.8. Разностные схемы для решения многомерных задач 101
1 2 / 2 d2S .	.
+ Г и +
^2 g
+ (АВ + В А)	- (х, у, t) + В
охду
Замена производных по х и у на соответствующие разност-
ные отношения второго порядка точности дает схему Лакса-
Вендроффа для системы (5.28):
в&+1 _ к _	(д Sn-\-l,m 8п-1,т gn,m+l gn,m-l \
n’m (	2/z,.	+ B 2hy J
_2 ( ok	_ ‘у nk I nk
। ‘ I Л2°п+1,т £On.m '	.
T (л-----------------------------+
qk	_ о qk	I Q,k	\
( „2 dn,m+l ^dn,m ' ъп,т — 1 | ,
+ B	V	+
ny	)
r2
+ д (-A-S + BA)(s„+lim+1 - 4-i,m+i -
______________________________	I
&п+1,т — 1 ' sn — l,m — l
n = 1,... ,N - 1; m =	- 1; к = 1,2,....
(5.29)
Из процедуры построения следует, что эта схема аппроксими-
рует уравнение (5.28) со вторым порядком по h и т. Устойчивость
схемы определяется условием (5.27).
Для вычисления граничных условий можно использовать ме-
тод фиктивных областей, вводя дополнительные (фиктивные) уз-
лы с координатами (ж_1, ут, tk\ (^tv+i, ут, tk\ (хп, у_ъ tk) и
2/М+1? ^)- Процедура вычисления решения в граничных точ-
ках аналогична рассмотренной нами процедуре для одномерных
уравнений (параграф 5.3).
В параграфе 5.5 мы рассмотрели одномерную схему Ф. Роу,
которая основана на характеристической форме волнового урав-
Глава 5. Распространение акустических волн
нения. В многомерном случае такая форма имеет несколько более
сложный вид. Рассмотрим систему волновых уравнений вида
дз	дз
dt + “ дхр
— °,
где (#i, #2, #з) — (%, У, z) и АР — некоторые постоянные матрицы
размером J х J. Умножим эту систему на lj, левый собственный
вектор матрицы Ai, которому соответствуют собственные зна-
чения Xj. В результате получим систему уравнений
3(1,*)
dt
3(Ls) Л, ds
р=2

которая описывает распространение волн в направлении оси xi.
Для волн, распространяющихся в других направлениях, получа-
ются аналогичные системы. Построим характеристическую фор-
му двумерных уравнений акустики (5.28), учитывая, что Ai = А
и А2 — В- Собственные значения матрицы А определяются как
А = ±с,0. Собственный вектор, соответствующий Аз = 0, не дает
ничего полезного, а два других вектора Zi?2 = (рс, 0,±1). Тогда
для волн, распространяющихся в направлении оси ±ж, получим
следующие характеристические уравнения:
д ,	д	2 dv
s(p + c^U) + cs(p + <:/>.«) = -c
д .	. д .	2 dv
(5.30а)
(5.306)
Аналогично, для волн, распространяющихся в направлении оси ±у,
характеристические уравнения имеют вид:
d .	d	.	2 du
-(p + cp-vl+^tp + epy)^^ p-,
д ,	ч д ,	ч 2 ди
^р-ср-р)-е^р-ср-«) = -р Р~.
(5.31а)
(5.316)
Для обобщения схемы (5.13) на случай двумерных уравнений
требуется две сетки (рис. 5.18). Для аппроксимации уравнений
(5.30) введем сетку с узлами (хп, ym^i/2, tk), где
хп = п • hx, п = 0,..., N,	(5.32а)
5.8. Разностные схемы для решения многомерных задач 103
Ут+1/2 = (т + 1/2) • hy, т - 0,..., М - 1,	(5.326)
tk = k-r, к = 0,1,...,	(5.32в)
а для аппроксимации уравнений (5.31) — сетку с узлами (жп+1/2,
Ут, tk), где
^п+1/2 =	(п + 1/2) • hx,	п = 0,... ,7V — 1,	(5.33а)
ут = т • hy,	т = 0,..., 7И,	(5.336)
tk = к • т,	к = 0,1,...	(5.33в)
Такие сетки называются смещенными. Они возникают, когда
различные величины или группы величин вычисляются в различ-
ных узлах.
т+1
т+1/2
т
т-1/2
т-1
п-1	п-1/2 п п+1/2	п+1
Рис. 5.20. Пространственная сетка для аппроксимации уравнений (5.30)
и (5.31); в узлах «•» определяются и и р; в узлах «х» опреде-
ляются v и р
Рассмотрим сначала построение разностной схемы для урав-
нений (5.30). Эти уравнения, при каждом значении у, представ-
ляют собой два уравнения переноса с отличной от нуля правой
частью. Поэтому левая часть уравнений (5.30) аппроксимируется
так же, как в схеме (5.13) на сетке (5.32), а правая часть — на
сетке (5.33). Тогда разностная схема примет следующий вид:
104 Глава 5. Распространение акустических волн
"	__ /?fc	/?fc	__ z?fc—1
п,тп+1/2 XLn,m+1/2	£Ъп-1,т-\-1/2	п-1,тп+1/2
27	+	27
/?fc _ г>к
£Ъп,т+1/2	1Ьп-1,т+1/2
hx
„к	_ „.к
*2 ип—1/2,тп+1	ип—1/2,тп
hy
" ofc+1 _ ак
°п,тп+1/2	°п,тп+1/2
27
ак	_ ofc—1
°п+1,т+1/2	°п+1,т+1/2
27
ofc	_ ofc	«.fc	_ Q.k
С’п+1,ТП + 1/2	°72,772 + 1/2 _	2 ™+1/2,т+1	72+1/2,ГП
'	~hx	~ ~рс	hy
^п,т+1/2 ~ Рп,т+1/2 + СР ' Un,m+l/2>
^72,772+1/2 Рп,772+1/2 ^Р ’ ^72,772+1/2 ’
7Z = 1,...,TV — 1; т = 1,...,М - 1; к = 1,2,....
Выражая из этих соотношений неизвестные величины в мо-
мент времени i^+i, мы получим расчетные формулы. Оконча-
тельно, скорость и давление вычисляются как
7/fc+i _____ 1 (z?fc+i _ cfc+i 'I
а72,772+1/2 2ср \ П’Ш+1/2	П,772+1/2,/’
nfc+l —If	+-
Tn,772+1/2	2 \ ьп,тп+1/2 ' с’п,тп+1/2 J ’
Разностная схема для уравнений (5.31) строится аналогичным
образом:
"/9/г+1	_ nfc
п+1/2,тп	п+1/2,тп
27
Г)к — ок~1
^п+1/2,тп —1	^п+1/2,тп —1
27
п+1 /2,тп	^п+1/2,тп —1
hy
2 Un+l,m-l/2 Un,m-l/2
к-х
Тк	_ тк	„.к	_ „k
^п+1/2,пг+1	^п+1/2,пг __	2 ип+1,тп+1/2	и'п,тп+1/2
hy	~ ~РС	hx
5.8. Разностные схемы для решения многомерных задач
Q п+1/2,т	Рп+1/2,т	СР ’ ^n+l/2,m’
^n+l/2,m	Рп+1/2,т	’ ^n+l/2,m’
п = 1,... ,N — 1; m = 1,..., М — 1; fc = 1,2,....
7Л+1	= 1 (Ок+1 — ТА;+1
n+l/2,m 2ср \ *n+l/2,m J’n+l/2,my ’
/г+1	_ 1 (П^1	4- Т*^1 А
Рп,т+1/2	2 \ *n’т+1/2 ' ± n,m-\-l/2j *
Из построения этой схемы следует, что она аппроксимирует
двумерные уравнения акустики со вторым порядком по h и т. Ис-
следование устойчивости этой схемы приводит к очень громозд-
кому уравнению четвертого порядка для собственных значений
оператора перехода. Анализ этого уравнения дает необходимое
условие устойчивости рассматриваемой схемы:
( 1 1 \ .
CT\hx + hy)^ ’
а в случае квадратной сетки hx = hy — h —
ст < 1
~h 2
Для построения разностных схем для многомерных задач мож-
но использовать метод расщепления. Рассмотрим этот подход на
примере схемы С. К. Годунова. Следуя процедуре, представлен-
ной в параграфе 4.3, вычисление решения в момент времени i^+i
по известному решению в момент времени tk производится в два
этапа. На первом этапе вычислим промежуточные значения, ре-
шая одномерные задачи по х с использованием схемы (5.17):
Jfe+i/2	_ k
8n+l/2,m+l/2	* * Sn+l/2,m+l/2
T
к	к
Sn+3/2,m+l/2 — Sn-l/2,m+l/2
+ A	2hx
~	(Sn+3/2,m+l/2 - 2sn+l/2,m+l/2 +
+	1/2,т+1/г) = 0, (5.34)
n = 1,..., N — 2; m = 0,...,M-1.
Глава 5. Распространение акустических волн
Расчет значений в ячейках, примыкающих к границам, которые
имеют индексы (1/2, m +- 1/2) и (N — 1/2, m + 1/2), производятся
с учетом граничных условий. На втором этапе решаются одно-
мерные задачи по у, используя аналогичную схему, основанную
на уже вычисленном промежуточном решении:
Q^+l	_ Q^+l/2
п+1/2,m+1/2	n+1/2,m+1/2 ।
*+1/2	_ fc+1/2
( n n+l/2,m+3/2	n+1/2,m-1/2
+ B
_____J_R2f fc+1/2	_ ?ЛИ/2
2chy \ n+l/2,m+3/2	^dn+l/2,m+1/2
+ ^//L-i^) = 0, (5.35)
n = 0,	— 1; m — 1,..., M — 2,
+- расчетные формулы для ячеек примыкающих к границам.
В результате мы получим требуемое решение в момент вре-
мени ifc+i-
Исследуем устойчивость этой схемы. Для этого зададим ре-
шение в виде
(\ k	/ * \
и \	/ и \
v I	= | v* I ехр (Ш1П +- ia2m).
Р / n+1/2,m+1/2	\ Р /
Подстановка этого решения в схему (5.34) дает следующее выра-
жение для промежуточного решения:
(\ ^+1/2	/ X 7 X * \
и \	/ Ai(ai)iz* \
v I	= I v* I ехр (Ш1П+-ш2т),
/ п+1/2,m+1/2	\ ^(а1)Р /
где Л1 (се 1) — собственные значения оператора перехода для одно-
мерной задачи (см. параграф 5.6). Далее, подставляя полученное
промежуточное решение в схему (5.35), мы получим
(\ *+1
и \
7; I	—
V I
Р / n+1/2,m+1/2
5.8. Разностные схемы для решения многомерных задач
/	Ai(ai)u*	\
=	I	^2(02)^*	I	ехр(гсцп + iazm).
\	Ai(ai)A2(a2)p*	/
Тогда для устойчивости необходимо выполнение условий:
|А1 (П1)| 1,	|Л2 («2)|	1,
|А1(СЕ1)Л1(О!1)| = |А1 («1)1 • |А2(«2)|	15
для всех 0	«1, «2 2тг. Таким образом, устойчивость двумер-
ной схемы определяется устойчивостью одномерных схем. В свою
очередь, одномерные схемы будут устойчивы, если
ст	ст
~hx^ “ h~y^ ’
и, следовательно, двумерная схема будет устойчива при условии
min (Лж, hy)
Процедура расщепления, которую мы рассматривали до сих
пор, имеет первый порядок аппроксимации по т. Это можно уви-
деть, например, из соотношения (4.31), где предпоследнее слага-
емое в правой части возникает в результате расщепления. Для
того чтобы построить схему расщепления второго порядка ап-
проксимации, рассмотрим эту процедуру в более общем виде.
Пусть
С™ = Dx «1,т, 8кп,т, 8кп+1>т, Т, hx) (5.36)
представляет собой некоторую схему для решения системы
ds ds
dt + Адх ~ °’
а
Cm = Dy «т-1, С»> sn,m+l’ г> М (5-37)
есть схема для решения системы
ds ds
’dt+Bdy=o'
В этих обозначениях схема расщепления (5.34), (5.35) выгля-
дит следующим образом:
Cm/2 = D* «-l,m,Cn>Cl,m’T’M ’	(5’38а)
n=l,...,N -1; т = 0,...,М,	(5.386)
sk+l — П (e^+V2	е/г+1/2	Л+1/2	7 \	/г og ч
ьп,т “ I ьп,тп-1’> ьп,т -> Йп,т+П 7 ’ 11У J •>
n = 0,...,7V; т = 1,...,М - 1.	(5.38г)
Построение более точной схемы расщепления требует, в об-
щем случае, большего объема вычислений. Наиболее эффектив-
ной представляется следующая процедура:
9n,m = °х	зкп m, s^+l m, |т, hx^ ,	(5.39a)
n=l,...,N -1; m = Q,...,M,	(5.396)
= Dy (<Li,<L<m+i^A) ,	(5.39b)
n = Q,...,N; m =	-1,	(5.39r)
= Dx ^221>m, <m, Q^m, jr, hx^ ,	(5.39д)
n = l,...,N -1; m = 0,...,M.	(5.39e)
При вычислении по этой схеме число операций возрастает
приблизительно в полтора по сравнению со схемой (5.38). Данная
процедура может также применяться и для решения нелинейных
задач, когда шаг по времени зависит от к. В случае линейных
задач, когда шаг по времени может быть выбран постоянным,
можно построить еще более эффективную схему расщепления.
Приведем один из вариантов такой схемы:
— (sn-l,m> Sn,m’	Т’> hx) ,	(5.40а)
n = l,...,N -1; m = 0,...,M,	(5.406)
Ck = Dy	, T, hy) ,	(5.40b)
n = 0,..., N; m — 1,..., Л/ — 1,	(5.40r)
q(3) — jj fq(2)	q(2) q(2)	t \	/г лл \
чп,тп — ^У \ 4n,m-l)4n,mi4n,m+liTi Г1УJ •>	^О.чид;
n = 0,...^; m = 1,...,M - 1,	(5.40e)
= Dx	,	(5.40ж)
n=l,...,N -1; т = 0,...,7И.	(5.40з)
Исходя из известного решения в момент времени , вычисле
ния по этой схеме дают решение в момент времени t^i + 2т, т. е
через два шага по времени. Поэтому в расчете на один шаг по
5.9. Заключительные замечания 109
времени требуется приблизительно такой же объем вычислений,
что и для схемы (5.38).
Если одномерные схемы (5.36) и (5.37) имеют второй порядок ап-
проксимации по h и т, то и схемы расщепления (5.39) и (5.40) ап-
проксимируют уравнения акустики со вторым порядком по h и т.
Подводя итог нашему обсуждению, можно выделить следую-
щие преимущества схем расщепления:
1)	шаг по времени обусловливается устойчивостью одномер-
ных схем и не зависит от размерности задачи;
2)	упрощается построение разностной формы граничных условий;
3)	упрощается программирование многомерных задач, т. к. ре-
шение одномерных задач (5.36) и (5.37) можно оформить в
виде одной процедуры.
5.9. Заключительные замечания
В этой главе мы рассмотрели некоторые методы построения раз-
ностных схем для численного решения задач распространения
акустических волн. Однако аналогичные подходы могут исполь-
зоваться и для других типов задач, таких как, например, рас-
пространение волн в твердых телах, распространение электро-
магнитных волн, теория глубокой воды и волновые модели рас-
пространения тепла.
Очевидно, что в одной главе невозможно охватить все су-
ществующие методы. Мы обсудили лишь некоторые подходы, а
именно:
1)	конечно-разностная аппроксимация волнового уравнения вто-
рого порядка;
2)	схема Лакса-Вендроффа;
3)	методы, основанные на характеристической форме волно-
вого уравнения;
4)	методы, использующие решение задачи о распаде разрыва.
В качестве примера мы рассмотрели распространение одно-
мерной волны в однородной среде. В этом случае рассмотренные
схемы дают точное решение, когда параметр Куранта равен еди-
нице. В реальности мы часто имеем дело с неоднородными или
Гно
Глава 5. Распространение акустических волн
нелинейными средами. Тогда скорость распространения возму-
щений будет переменной и вычисления с параметром Куранта
близким к единице в каждом узле разностной сетки станет невоз-
можным. Следовательно, качество приближенного решения будет
в значительной мере зависеть от того, как свойства диссипации
и дисперсии той или иной схемы зависят от параметра Куранта.
Вот почему мы уделили большое внимание анализу этих свойств и
привели зависимости коэффициента диссипации и сеточной груп-
повой скорости от параметра Куранта для всех рассмотренных
нами разностных схем.
Некоторые методы построения и анализа разностных схем
для уравнений акустики пригодятся нам в следующей главе, где
мы обсудим построение разностных схем для нелинейных урав-
нений газовой динамики.
ГЛАВА 6
ДВИЖЕНИЕ
СЖИМАЕМОЙ
ЖИДКОСТИ
(ГАЗА)
Различные научные и практические задачи выдвигают для ис-
следований целый ряд проблем гидродинамики. К ним относят-
ся, например, аэродинамика летательных аппаратов, изучение и
предсказание атмосферных явлений, поверхностных волн в океане.
Трудности аналитического исследования определяются слож-
ной математической постановкой: в общем случае — это краевые
задачи для нестационарных нелинейных уравнений, описываю-
щие вихревые течения сжимаемой жидкости (газа). Течение жид-
кости (газа) часто характеризуется внутренними разрывами, та-
кими как, например, ударные волны, на которых требуется ста-
вить специальные условия. Эти условия описываются известными
уравнениями Ренкина-Гюгонио, но их применение на практи-
ке затруднено тем, что поверхности разрывов перемещаются по
жидкости, и это движение не известно заранее, а определяется из
самих дифференциальных уравнений и условий на разрыве. По-
этому, как правило, лишь численное моделирование и довольно
сложные физические эксперименты позволяют определить необ-
ходимые характеристики течения.
Для расчета задач газодинамики существуют два основных
подхода: методы выделения разрывов и однородные схемы сквоз-
ного счета. Выделение разрывов позволяет строить хорошие при-
ближенные решения для некоторых типов задач, но в общем слу-
чае это неудобно из-за сложного программирования. Поэтому мы
сосредоточим наше внимание на схемах сквозного счета, позво-
ляющих проводить вычисления без предварительного выделения
особенностей.
Глава 6. Движение сжимаемой жидкости (газа)
6.1. Схема Лакса-Вендроффа
для одномерных задач
Сначала запишем уравнения гидродинамики (см. параграф 2.5)
в дивергентной форме, т.е. в виде законов сохранения. Введем
новые зависимые переменные ри и р(е + 1/2и2). Тогда уравнения
гидродинамики в одномерном случае примут вид
дз 9f(s) =
dt дх
где s и /(з) — векторы определенные равенствами
(6.1)
р
ри
р(е + и2/2)
(Ji \	/	Ри	\
h I = I ри2 +р	I =	С6-2)
/з /	\ и(ре +ри2/2+р) /
8'2
82/Sl +Р
82(53 +p)/si
Мы будем рассматривать движение идеального газа с урав-
нением состояния
е = —Р—
Р (7 - 1)
Тогда давление и температура определяются как
(2 \
«3 -А), Т=ТБ^
2si у	pH
где R — газовая постоянная. Поэтому действительно, явля-
ется функцией от s. Система (6.1) называется дивергентной фор-
мой уравнений гидродинамики. Физическая интерпретация этого
определения состоит в следующем: если проинтегрировать урав-
нения (6.1) по некоторому объему, то мы получим законы сохра-
нения величины s для этого объема.
Введем разностную сетку с узлами (а?п, ^), где хп = nh, п =
= 0,1,... и tk+i — tk Tk. Для аппроксимации уравнений (6.1)
удобнее использовать двухшаговую схему Лакса-Вендроффа,
аналогичную схеме (5.8) и (5.9). Сначала в центрах прямоуголь-
6.1. Схема Лакса-Вендроффа для одномерных задач I 13
ных ячеек на плоскости (г, t) (рис. 5.3) вычисляются промежу-
точные значения:
ЛсЧ-1/2 _ 1 (sk	— I1L (fk _ fk\
%+i/2 - 2 V n+1 + bn) 2h V n+1	* n) ’
n = 1,...,7V- 1,
где
fn = f (4) 
Окончательное решение вычисляется затем по схеме
е&+1 _	/ cfc+1/2 _ nfc+1/2 \	„к
Sn Sn	n+1/2 J n-l/2j •
Так же как и в случае уравнений акустики, эта схема имеет
второй порядок аппроксимации по h и т.
Непосредственное исследование устойчивости схемы (6.3) не-
возможно, из-за нелинейности системы (6.1) которую эта схе-
ма аппроксимирует. Поэтому применим принцип замороженных
коэффициентов. Сначала линеаризуем систему (6.1). Для этого
представим решение в виде s = s0 + w, где з0 — постоянный
вектор вида
/	Ро	\
5о —	I	Ро^о	I	,
\	Ро (ео + х/2“о)	/
а вектор w — малое возмущение. Тогда
/(«) = /(so + w) « /(s0) + A(s0)w + • • • ,
где
A(s0) = {aij (s0)} =	(so)} •
Подставляя это разложение в (6.1), мы получим линейную систе-
му уравнений с постоянной матрицей Ао — А(^о) вида
Эш	dw
~г~ + Ао-тг“ = о.	(6.4)
dt	дх
Тогда схема (6.3) переходит в схему (5.7) с матрицей А = До, а
для анализа этой схемы уже можно применить критерий фон Ней-
мана. Следуя процедуре, рассмотренной в параграфе 5.3, можно
получить следующее выражение для собственных значений опе-
ратора перехода:
Xj(a) = 1 - i sin (а) -	(1 - cos (а)), j — 1,2, 3,
\ fL /	\ fl /
где (jjj есть собственные значения матрицы Ао, которые равны
uq, ио±Со, здесь cq = (7Po/po)lyZ2 — скорость звука. Из критерия
фон Неймана следует, что схема для линеаризованного уравнения
(6.4) будет устойчива, если
тк max ЦI _ Tfcmax(|Mo|)|Mo + Co|)|Mo co[)
h ~	h
Тогда шаг по времени выбирается из условия
Тк Л/(|«о| + со).
Это условие можно использовать для вывода условия устой-
чивости схемы (6.3). Учитывая, что при течении газа скорость
среды и скорость звука являются функциями координаты и вре-
мени, мы приходим к условию устойчивости схемы (6.3):
к " шах(Н| +с£) тах’ п ^/Рп)	'
п
или в терминах компонент вектора s
h
Тк	/	Г	7	2\ -1 1/2\ '
max М 4-	)
п l|(*l)n|	7 у(«1)п	2	yj j
Величина
max (|u£| + с*)	(6.5)
оценивает наибольшую скорость волны в заданной области в мо-
мент времени t = tk- Данная оценка получена из анализа устой-
чивости линеаризованной системы (6.4), поэтому в некоторых
случаях величина (6.5) будет давать заниженное значение наи-
большей скорости волны. Тогда вычисления с шагом по времени
Tk близким к ттах могут быть неустойчивыми. Поэтому шаг по
времени задается как
Tk=rrmaxj	(6.6)
где г — параметр Куранта (0 < г < 1), и на практике часто
выбирается г = 0,9. Для более надежного достижения устой-
чивости можно использовать следующий подход. Расчет первых
нескольких временных шагов производить с малым параметром
Куранта. Это позволит течению сформироваться, и оценка (6.5)
станет более надежной. Тогда последующие вычисления можно
производить с большим параметром Куранта.
6.1. Схема Лакса-Вендроффа для одномерных задач
Для расчета граничных условий вводятся фиктивные слои,
что позволяет не нарушать единообразия вычислений для гранич-
ных ячеек. Мы рассмотрим два вида граничных условий: твердая
стенка (или ось симметрии) и открытая граница расчетной обла-
сти. В качестве примера рассмотрим расчет этих условий на
левой границе расчетной области. Пусть граничным точкам от-
вечают индексы (О, А;), а соответствующим фиктивным узлам —
индексы (—1, А?). Тогда граничное условие на твердой стенке
iz(0, t) = о, t > о
запишется как
0,5 («* х + 7Z*) =	= 0, A=pt
или
)к
1
(\ *
82 I =
*3 / -1
Далее рассчитываются величины
S-l/2 И S0
по приведенным выше формулам. Через открытые границы газ
(жидкость) может втекать или вытекать из области, и здесь
должны быть обеспечены условия непрерывности движения. Пусть,
например, газ (жидкость) втекает в область с левой стороны.
Тогда в фиктивных узлах задаются параметры набегающего по-
тока (помечены знаком «оо»):
р\	I	р	\
и I = I	и	I
р /	-	\	р	I
г /	— 1	\	г	' оо
В случае, когда вытекает слева из области, наиболее естествен-
но представить вытекающий поток однородным. В простейшем
случае значения параметров потока в фиктивных узлах (—1,А?)
должны быть такими же, как и в узлах (0, А?):
(\ к / х к
81 \ I 81 \
82 I	— I 82 I
83 / _х \ $3 /
Глава 6. Движение сжимаемой жидкости (газа)
Пример 6.1 (схема Лакса-Вендроффа). В качестве тестово-
го примера рассмотрим задачу об ударной трубе (задача Сода).
Пусть бесконечная труба, заполненная воздухом (7 = 1,4), в точ-
ке х = 0 разделена перегородкой. При t — 0 состояние газа
описывается кусочно-постоянной функцией:
(р^Орд),
(рлОрл), х > 0.
В момент времени t = 0 перегородка мгновенно убирается, и эта
конфигурация распадается на две волны, распространяющиеся
влево и вправо от точки х = 0. Например, если
/ pL \ /1\ f pR\ f 0125 \
I UL I = I 0 I	И I Ur I = I 0 I ,	(6.7)
\ PL /	\ 1 /	\ PR /	\ 0.1 /
то влево распространяется волна разрежения, а вправо — кон-
тактный разрыв и ударная волна. На рис. 6.1-6.4 показано при-
ближенное решение уравнений (6.1) с начальными условиями (6.7),
полученное с помощью схемы Лакса-Вендроффа, а также точное
решение этой задачи.
Рис. 6.1. Пространственное распределение плотности в момент вре-
мени t = 0,5037; сплошная линия — точное решение, штри-
ховая — приближенное решение (схема Лакса-Вендроффа,
h = 0,02)
Эти результаты показывают, что схема Лакса-Вендроффа
хорошо передает все основные характеристики точного реше-
6.2. Метод искусственной вязкости
ния. Только в областях быстрого изменения газодинамических
параметров возникают нефизические осцилляции приближенно-
го решения, что, вообще говоря, характерно для схем второго
порядка аппроксимации.
х
Рис. 6.2. Пространственное распределение скорости в момент времени
t = 0,5037; сплошная линия — точное решение, штриховая —
приближенное решение (схема Лакса-Вендроффа, h — 0,02)
х
Рис. 6.3. Пространственное распределение давления в момент времени
t = 0,5037; сплошная линия — точное решение, штриховая —
приближенное решение (схема Лакса-Вендроффа, h = 0,02)
6.2.	Метод искусственной вязкости
Введение искусственной вязкости приводит к затуханию высо-
кочастотных компонентов решения в процессе вычислений, что
Г| 18 Глава 6. Движение сжимаемой жидкости (газа)
можно использовать для подавления нефизических осцилляций
разностного решения. Включение вязкости можно осуществить
с помощью специальных членов, которые добавляются к системе
уравнений. Так если (6.1) есть исходная система уравнений, то
модифицированную систему можно записать в виде
дз df(s) д (	( хдз\
+ 4г2 = V ’	6’8
dt дх ох \ дх )
где В(з) — квадратная матрица; р — коэффициент искусствен-
ной вязкости. Матрица В(з) должна быть подобрана таким обра-
зом, чтобы решение s(x,t) системы (6.8) обладало достаточной
гладкостью и при р —> 0 приближалось к решению исходной
системы (6.1). Аппроксимируя систему (6.8) соответствующей
разностной схемой, мы получим разностные уравнения с дисси-
пативными членами, которые и определяют вязкостные эффекты
схемы. Следует отметить, что введение искусственной вязкости
имеет смысл только для схем второго и выше порядков аппрок-
симации. Схемы первого порядка обладают аппроксимационной
вязкостью, которая порождается самой структурой разностной
схемы.
Рис. 6.4. Пространственное распределение удельной внутренней энер-
гии в момент времени t = 0,5037 ; сплошная линия — точное
решение, штриховая — приближенное решение (схема Лакса-
Вендроффа, h = 0,02)
Рассмотрим включение искусственной вязкости в схему Лак-
са-Вендроффа. В простейшем случае можно положить B(s) = I
и для сохранения второго порядка аппроксимации р = pa(i)h2.
6.2. Метод искусственной вязкости
Тогда вязкостный член примет вид
/,А,
дх2.
Аналогичные выражения описывают вязкие силы при дви-
жении вязкой жидкости, но в отличии от реальной вязкости,
искусственная вязкость исчезает при /г —> 0. Аппроксимируя вто-
рую производную в момент времени получим схему Лакса-
Вендроффа для системы (6.8):
<,*+1 _ як _ 21 / ^+1/2 _ -fc+1/2 \
%	~	^^/n+1/2 J 71-1/2)^
+ Р-аП («п+1 - 2sn + <1) ,	(6’9)
71 = 1,.
где v — p^Tk — постоянный малый параметр. Величина пара-
метра и подбирается экспериментально, так как она зависит от
конкретной задачи и шага разностной сетки.
Введение искусственной вязкости иногда бывает необходи-
мым для получения устойчивого процесса вычислений. Дело в
том, что анализ устойчивости схемы (6.3) проводился для урав-
нений линеаризованных в окрестности течения с постоянными
параметрами и не учитывал нелинейных эффектов, которые в
ряде случаев являются источником неустойчивости. Такая не-
устойчивость называется нелинейной. Для предотвращения этого
явления в некоторых задачах оказалось необходимым введение
в разностную схему дополнительных слагаемых, определяющих
искусственную вязкость. Так нетрудно получить, что схема (6.9)
требует более строгого ограничения на шаг по времени:
Тк TmaxV^l — 2f.
Вообще говоря, включение искусственной вязкости в неустойчи-
вую схему может сделать эту схему устойчивой.
Пример 6.2 (схема Лакса-Вендроффа с искусственной вязко-
стью). Рассмотрим задачу Сода с начальными условиями (6.7).
Только теперь для решения этой задачи применим схему (6.9).
Результаты расчетов показаны на рис. 6.5-6.8.
Эти результаты показывают, что введение искусственной вяз-
кости позволяет подавлять нефизические осцилляции приближен-
120 Глава 6. Движение сжимаемой жидкости (газа)
ного решения, хотя это достигается за счет некоторого разма-
зывания разрывов.
Рис. 6.5. Пространственное распределение плотности в момент вре-
мени t = 0,5046; сплошная линия — точное решение, штри-
ховая — приближенное решение (схема Лакса-Вендроффа,
h = 0,02, и = 0,06)
Рис. 6.6. Пространственное распределение скорости в момент времени
t = 0,5046; сплошная линия — точное решение, штриховая —
приближенное решение (схема Лакса-Вендроффа, h = 0,02,
v = 0,06)
6.3.	Задача о распаде разрыва
В гл. 5 мы рассмотрели задачу о распаде разрыва для уравнений
акустики, которая имеет довольно простое решение. Аналогии-
6.3.	Задача о распаде разрыва
ная задача может быть сформулирована и для уравнений газовой
динамики. Однако даже в случае простейшего уравнения состо-
яния идеального газа (который мы рассмотрим) аналитическое
решение не всегда может быть получено.
Рис. 6.7. Пространственное распределение давления в момент времени
t = 0,5046; сплошная линия — точное решение, штриховая —
приближенное решение (схема Лакса-Вендроффа, h, = 0,02,
I/ = 0,06)
х
Рис. 6.8. Пространственное распределение удельной внутренней энер-
гии в момент времени t = 0,5046 ; сплошная линия — точное
решение, штриховая — приближенное решение (схема Лакса-
Вендроффа, h = 0,02, I/ = 0,06)
Течение газа определяется тремя независимыми переменными
Глава 6. Движение сжимаемой жидкости (газа)
и постоянной 7, которая характеризует конкретный газ. Тог-
да задачу о распаде разрыва можно сформулировать следующим
образом: пусть в момент времени t = 0 распределение газодина-
мических величин имеет вид
/ Г X О,
w (я,0) = <	,'
[ WR> X > О,
где
(Pl \	/ PR \
UL I и Wr - \ Ur I —
PL /	\ PR /
постоянные векторы. При t > 0 это состояние распадается на
две волны, которые разделены контактной поверхностью. В за-
висимости от начальных данных могут возникать либо ударные
волны, либо волны разрежения. Возможные комбинации пока-
заны на рис. 6.9, где отмечены положения фронта волны или
контактного разрыва на (ж, f) диаграмме. Задача Сода, рассмо-
тренная в примере 6.1, является примером конфигурации 2, и
на рис. 6.1-6.4 показано распределение газодинамических вели-
чин при распространении волны разрежения, ударной волны и
контактного разрыва. Следует заметить, что конфигурация 5 те-
оретически возможна для идеального газа, но в такой ситуации
сама модель идеального газа не применима. Поэтому в реально-
сти такая конфигурация осуществиться не может.
Для решения задачи о распаде разрыва необходимо опреде-
лить шесть неизвестных величин
(POL \	/ POR \
UOL I И WOR = UqR I
POL /	\ POR /
по обе стороны от контактного разрыва. Эти величины выража-
ются через известные состояния и Wr либо через соотноше-
ния Ренкина-Тюгонио для ударной волны, либо через изэнтро-
пические характеристические уравнения для волны разрежения.
Учитывая, что только плотность претерпевает разрыв на кон-
тактной поверхности, а скорость и давление непрерывны, т.е.
uol = uor = ио и pol — Por — Po, уравнения, описывающие
решение задачи о распаде разрыва, сводятся к одному нелиней-
ному алгебраическому уравнению. В общем случае это уравнение
может быть решено итерационным методом. Только в случае од-
6.4- Схема С. К. Годунова
покомпонентной среды конфигурация 4 допускает аналитическое
решение. Более подробное описание процедуры решения задачи
о распаде разрыва приведено в приложении Б.
Рис. 6.9. Пять возможных конфигураций решения задачи о распаде
разрыва; S — обозначает ударную волну; R — волну разре-
жения; С — контактный разрыв
В последующих параграфах решение задачи о распаде разры-
ва будет использоваться для построения численных схем расчета
газодинамических течений. Так в схеме С. К. Годунова исполь-
зуется только решение в точке х = 0. В методе взвешенного
усредненного потока используется также информация и о струк-
туре течения, возникающего после распада разрыва.
6.4.	Схема С. К. Годунова
В параграфе 5.6 мы рассмотрели схему С. К. Годунова для урав-
нений акустики. Аналогичные принципы могут быть использо-
ваны и для построения разностной схемы для уравнений газовой
динамики.
Введем разностную сетку с узлами (xn,tfc), где хп — nh,
= 0,1,... и = tk + Интегрирование уравнений (6.1)
Глава 6. Движение сжимаемой жидкости (газа)
по разностной ячейке дает следующую схему:
Snti/2 - <1/2 , f «1) - f „
й + h ~ °’	(6.Ю)
n = 0,...,N -1.
Полуцелые индексы обозначают средние на интервале значе-
ния, которые определяют приближенное решение в виде кусоч-
но-постоянной функции (рис. 5.10). В момент времени tk такая
функция известна. За время порядка Tk < ттах поведение этой
системы также известно: каждый разрыв немедленно распада
ется с образованием ударных волн или волн разрежения, как
показано на рис. 6.9. Тогда, полагая
®£=<1/2 И W«=Wn+l/2>
из решения задачи о распаде разрыва, мы получим
w* = w(0,rk)
в каждом узле хп. Так как s выражается через w, то величины
/«, n = 0,...,N	(6.11)
определяются из соотношений (6.2). Вычисление одного шага по
времени завершается определением решения в момент времени
tfc+i из схемы (6.10). Анализ аппроксимации показывает, что эта
схема аппроксимирует уравнения (6.1) с первым порядком по h
и г. Шаг по времени задается соотношением (6.6).
Граничные условия учитываются при расчете величин (6.11)
при п = 0 и п = N. Мы рассмотрим два типа граничных усло-
вий: твердая стенка (или ось симметрии) и открытая граница
расчетной области. В качестве примера рассмотрим расчет этих
условий на левой границе расчетной области при х — 0. Для это-
го введем фиктивный слой с некоторым состоянием	Для
граничного условия на твердой стенке u(0,t) = 0 это фиктив-
ное состояние определяется из известного состояния в соседней
правой ячейке следующим образом:
(\ *
Р 1
U I
/ -1/2
Р1/2
—Ul/2
\ Р1/2 /
А: = 0,1,...
После решения задачи о распаде разрыва с Wj — w-i/2 и Wr ~
6.4- Схема С. К. Годунова 125
= МЫ получим решение в граничном узле. В случае откры-
той границы, когда газ истекает из области, можно положить
w^/2 = wi/2, чт0 Дает тривиальное решение и никаких волн,
которые могли бы исказить решение внутри области, не возни-
кает.
Пример 6.3 (схема С. К. Годунова). Применим схему (6.10) к
задаче Сода с начальными условиями (6.7). Результаты расчета
показаны на рис. 6.10-6.13.
Рис. 6.10. Пространственное распределение плотности в момент времени
t = 0,5027; сплошная линия — точное решение, штриховая —
приближенное решение (схема С. К. Годунова, h — 0,02)
Рис. 6.11. Пространственное распределение скорости в момент времени
t = 0,5027; сплошная линия — точное решение, штриховая —
приближенное решение (схема С. К. Годунова, h, = 0,02)
Глава 6. Движение сжимаемой жидкости (газа)
Рис. 6.12. Пространственное распределение давления в момент времени
t = 0,5027; сплошная линия — точное решение, штриховая —
приближенное решение (схема С. К. Годунова, h — 0,02)
3,0
2,8
2,6
2,4
е
2,2
2,0
1,8
1,6
-1,0	-0,5	0,0	0,5	1,0
х
Рис. 6.13. Пространственное распределение удельной внутренней энер-
гии в момент времени t = 0,5027; сплошная линия —
точное решение, штриховая — приближенное решение (схе-
ма С. К. Годунова, h, = 0,02)
Так как схема С. К. Годунова является схемой первого поряд-
ка аппроксимации, то в областях непрерывного течения она дает
менее точное решение по сравнению, например, со схемой Лакса-
Вендроффа. В области ударного скачка решение имеет довольно
крутой профиль и колебаний за фронтом скачка не возникает,
поэтому этот метод успешно применяется для расчета сильных
ударных волн.
6.5. Метод взвешенного усредненного потока
6.5.	Метод взвешенного
усредненного потока
Метод взвешенного усредненного потока (WAF, Weighted Av-
erage Flux) представляет собой один из способов модификации
метода С. К. Годунова для того, чтобы получит схему второго
порядка точности. Основная идея этого метода, по сути дела,
была рассмотрена в пункте 5.6.2 применительно к уравнениям
акустики. Рассмотрим теперь реализацию этого подхода в слу-
чае уравнений газовой динамики. Основная схема метода WAF
по своей структуре совпадает со схемой (6.10):
<^1/2 - Sn+l/2 М+1) - /(8*) _
rk	h ~°’	(6-12)
n = 0,...,N-l,
где
Xn+h/2
8п = 8(™п),	= У w(x,tk+0,5rk)dx.	(6.13)
хп -h/2
Здесь	обозначает решение задачи о распаде разрыва с
начальными данными
(Wn-l/2>Wn+l/2) ’
Так как при распаде разрыва образуется одна из четырех кон-
фигураций течения, то вычисления интеграла (6.13) имеет ряд
особенностей для каждой из этих конфигураций. Поэтому мы
рассмотрим подробно два случая, а затем получим общую фор-
мулу.
В случае конфигурации 1 (две ударные волны) решение имеет
вид, показанный на рис. 6.14 (здесь и далее используются обо-
значения, введенные в приложении Б) и интеграл (6.13) легко
вычисляется:
= ^(Mi - «kiwi + \di~d3\wOL + |с?з -di\wOR + |d4
где координаты dp (р = 1,..., 5) отсчитываются от точки хп и
равны
л Ч /	1 я 1 я - 1 Л Ч
di =	(i2 — -С\Тк, = дСзТь, «4 — xc5Tk, ds = -h.
Z	Z	Z	z	z
Глава 6. Движение сжимаемой жидкости (газа)
Рис. 6.14. Схематическое представление решения задачи о распаде раз-
рыва в случае конфигурации 1; а, С5 — скорости ударных
волн, сз — скорость контактного разрыва
Для более компактной записи введем следующие обозначения:
= Wl,	= WOLi	= 'WOR,	— WR
и запишем предыдущую формулу в виде
где коэффициенты ар выражаются следующим образом:
«1 = 1 + ^ = 1 + Л,	(6.15а)
а2 = ^-(с3-ci) =-Л,	(6.156)
п
«3 =	(С5 - Сз) = /?3 -(6.15в)
Г1
«4 = 1-	= 1-^3.	(6.15г)
Для конфигурации 2 (волна разрежения — ударная волна) ре-
шение имеет вид, показанный на рис. 6.15. Вычисление интеграла
(6.13) в этом случае требует интегрирования решения вдоль вол-
ны разрежения. В принципе, это можно сделать точно, так как
решение Wpi(x,t) известно (см. (Б.8) в приложении Б).
6.5. Метод взвешенного усредненного потока
Рис. 6.15. Схематическое представление решения задачи о распаде раз-
рыва в случае конфигурации 2
Для упрощения вычислений и уменьшения числа операций обыч-
но прибегают к приближенной оценке интеграла по области, со-
держащей волну разрежения. Так интеграл по отрезку [с/2, t/з]
вычисляется следующим образом:
ds
fw(x,tk+0,5rk)dX=\d2^d3\^ Z°FLLb,t),
d2
Вычисление остальных частей интеграла (6.13) производится так-
же, как и в предыдущем случае, и окончательный результат мож-
но представить в виде (5.18), где
w(2) = Г wol, с2 < О
( ^рь(ОД), с2 > 0.
Общая формула для вычисления усредненного значения имеет
вид (5.18), только компоненты определяются в зависимости
от конфигурации решения. Компоненты и одинаковы
для всех конфигураций:
— WL,	= WR,
а компоненты и w® определяются следующим образом:
Глава 6. Движение сжимаемой жидкости (газа)
1) конфигурация 1
w(2) = wol, w<:!) = wOr;
2) конфигурация 2 w(2) = Г WL,	С2 < [ Wz,(0,t), с2 > 3) конфигурация 3	0’	= WOR.
— wol.	—	f WOR.	C4 > 0, [ wfr(^ £)> c4 < 0;
4) конфигурация 4
(2) = ( WOL, С2 < 0,	(3) = ( WOR, С4 > О,
[ l«FL(0,^), С2 > 0,	1 ™Ffl(0,i), с4 < 0.
Коэффициенты ар (р — 1,...,4) определяются выражениями
(6.15), только скорости ci и С5 имеют разный смысл для различ-
ных конфигураций (см. приложение Б).
Представленная схема метода WAF аппроксимирует уравне-
ния (6.1) со вторым порядком по h и г. Шаг по времени выбирает-
ся из условия (6.6). Для расчета граничных условий применяется
такой же подход, что и в схеме С. К. Годунова.
Пример 6.4 (схема метода WAF). Применим схему (6.12) к за-
даче Сода с начальными условиями (6.7). Результаты расчета
показаны на рис. 6.16-6.19.
Как и следовало ожидать, эти результаты напоминают при-
ближенное решение, полученное с помощью схемы Лакса-Вен-
дроффа. Обе схемы имеют второй порядок аппроксимации, по-
этому в областях, где точное решение изменяется непрерывным
образом, приближенное решение вычисляется достаточно точно.
В областях, где точное решение изменяется резко, приближенное
решение проявляет осциллирующий характер.
Флуктуации приближенного решения в методе WAF не только
ухудшают качество этого решения, но могут приводить к более
серьезным последствиям. Например, на каком-то этапе вычисле-
ний может возникнуть такая комбинация газодинамических ве-
личин, при которой решение задачи о распаде разрыва не будет
иметь физического смысла. Это приводит к остановке вычисли-
тельного процесса. Поэтому подавление нефизических осцилля-
6.5. Метод взвешенного усредненного потока
ций в методе WAF имеет первостепенное значение. В простей-
шем случае можно применить метод искусственной вязкости, как
в схеме (6.9), но эта процедура требует настройки алгоритма
для каждой конкретной задачи. Существует более универсаль-
ный способ уменьшения амплитуды осцилляций, основанный на
применении специальных параметров (ограничителей), завися-
щих от изменения приближенного решения.
Рис. 6.16. Пространственное распределение плотности в момент вре-
мени t = 0,501; сплошная линия — точное решение, штрихо-
вая — приближенное решение (схема метода WAF, h = 0,02)
х
Рис. 6.17. Пространственное распределение скорости в момент време-
ни t = 0,501; сплошная линия — точное решение, штрихо-
вая — приближенное решение (схема метода WAF, h = 0,02)
Глава 6. Движение сжимаемой жидкости (газа)
х
Рис. 6.18. Пространственное распределение давления в момент време-
ни t = 0,501; сплошная линия — точное решение, штрихо-
вая — приближенное решение (схема метода WAF, h == 0,02)
Рис. 6.19. Пространственное распределение удельной внутренней энер-
гии в момент времени t — 0,501; сплошная линия — точное
решение, штриховая — приближенное решение (схема мето-
да WAF, h = 0,02)
6.6.	Метод уменьшения суммарного
отклонения (TVD)
Метод уменьшения суммарного отклонения (TVD, Total Varia-
tion Diminishing) является эффективным подходом для предот-
6.6. Метод уменьшения суммарного отклонения (TVD) 133
вращения возникновения нефизических осцилляций. Вначале мы
рассмотрим основные идеи этого метода и его реализацию для
уравнения переноса:
ди ди	.	.
— + с— — 0, —сю х сю, t 0,	(6.16а)
dt дх
и(х,0) = д(х), — сю х < сю.	(6.166)
Затем мы обсудим построение TVD версии метода WAF для
уравнений газовой динамики.
6.6.1.	Концепция TVD и ограничители
потоков
Рассмотрим некоторую разностную схему для уравнения (6.16),
записанную в виде
где uk = {wn+i/2} — сеточная функция, определяющая прибли-
женное решение в момент времени Суммарное отклонение
сеточной функции ик определяется как
'	оо
TV(t?)= £ |<1/2-<1/2|.
п= — оо
Схема (6.17) называется TVD-схемой, если
TV(i?+1) sj TV(u*).	(6.18)
Схемы удовлетворяющие этому свойству сохраняют монотон-
ность приближенного решения. Это значит, что если функция ик
монотонна, то функция также монотонна. Далее мы будем
рассматривать следующую форму схемы (6.17):
«п+1/2 ~ «п+1/2 икп+1-икп_п
г + С h--------------- °’	(6.19)
п = — оо,..., сю; к = 0,1,...,
где значения в узлах определяются как
ип = ^ (ип-1/2 + «п+1/2) + |sign(c)9Pn (u*_1/2 - w*+1/2) • (6.20)
Здесь <рп — некоторый параметр, который позволяет управлять
свойствами схемы. Например, если <рп — 1, то схема (6.19) пере-
134 Глава 6. Движение сжимаемой жидкости (газа)
ходит в схему (3.3); при
мы получим схему Лакса-Вендроффа, а выбор ipn = — 1 дает
схему (3.6), которая является неустойчивой. Поэтому, на основа-
нии крайних случаев срп = 1 и tpn = —1, параметр <рп должен
удовлетворять ограничению
1 Р’п 1
(6.21)
для всех значений п. В рассмотренных выше примерах параметр
<рп был постоянным. В общем случае, для построения TVD-схем
с порядком аппроксимации выше первого необходимо, чтобы па-
раметр (pn был переменным, что и будет предполагаться в даль-
нейшем.
Воспользоваться определением (6.18) для построения TVD-схе-
мы весьма затруднительно, поэтому для схемы (6.19) часто ис-
пользуется следующее условие:
__ о» &
о < ,"+1-------ny-1Z— < 1,	(6.22)
Ып+1/2-р - <+1/2
где р = sign (с). Схемы удовлетворяющие этому условию являются
также и TVD-схемами. Рассмотрим сначала случай с > 0 (р = 1).
Подставим выражение (6.20) в схему (6.19) и после некоторых
преобразований получим
Wn+l/2 Wn+l/2 Г 1 -
--------k----“ й ----------+ 9?n + 1 ,
Un-l/2 Un+l/2 L 4W1
6.6. Метод уменьшения суммарного отклонения
где
<+1/2 Un-l/2
Уп+1 =	----г-2-.
<+3/2 ” <+1/2
Тогда условие (6.22) принимает вид
,	1-¥>п+1 ,	2 —г
— 1	---------1- рп ------
<7п+1	Г
(6.23)
Когда с < 0, можно получить аналогичное неравенство
где
_ <+3/2 “ <+1/2
Qn — ~~й	Е •
<+1/2 - <-1/2
Дальнейшие рассуждения будут проводиться для неравенства
(6.23), но они также справедливы и для приведенного выше нера-
венства, если заменить срп и 9?n+i в (6.23) на </>n+i и <рп соответ-
ственно.
Неравенство (6.23) все еще не удобно на практике, так как со-
держит два независимых параметра. Поэтому необходимо ввести
дополнительные ограничения. Для этого мы зададим два отдель-
ных неравенства:
-1 срп 1,	-1 Уп+- < 2^~г).	(6.24)
Qn+i	г
Из выполнения этих неравенств следует выполнение неравен-
ства (6.23). Теперь мы можем получить область задания пара-
метра рп+1- При < 0 из неравенств (6.21) и (6.24) следует,
что (рп+1 = 1- При gn+i 0 неравенства (6.21) и (6.24) можно
переписать в виде:
1 /	2(!-г)~
1 Рп 1?	9-^n+l	1	^п+1-
г
Все эти неравенства и определяют область задания параметра <рп,
которая показана на рис. 6.20.
Конкретные значения параметра рп определяются как (/?п =
—	г), где (/>(<7, г) — некоторая произвольная функция (функ-
ция-ограничитель) , область значений которой принадлежит ТVD-
области. Любая функция, удовлетворяющая этому условию, будет
136 Глава 6. Движение сжимаемой жидкости (газа)
давать TVD-схему, которая не производит нефизических осцил-
ляций.
Рис. 6.20. Область задания параметра
<рп для TVD-схемы (6.19), (6.20)
Кратко обсудим механизм работы ограничителей. Для пра-
вильного моделирования распространения волн TVD-схема долж-
на корректно работать как в областях быстрого изменения ре-
шения, так и в областях медленного изменения решения. Оценка
поведения приближенного решения осуществляется с помощью
параметра qni который представляет собой относительное изме-
нение решения для трех соседних ячеек. Любое фиксированное
значения параметра срп дает схему с аппроксимационной вязко-
стью. При г < срп 1 эта вязкость будет положительна, что
приводит к размазыванию разрывов и затуханию высокочастот-
ных осцилляций. При — 1 tpn < г аппроксимационная вязкость
будет отрицательна, и это приведет к увеличению градиента при-
ближенного решения. Случай qn < 0 означает возникновение ло-
кального экстремума, что требует срп ~ 1. Другие ситуации мы
разберем на примере решения, показанного на рис. 6.21.
I_____
л-1/2 л+1/2 п+3/2 п+5/2
Рис. 6.21. Схематическое представление приближенного решения в
области контактного разрыва или ударной волны
6.6. Метод уменьшения суммарного отклонения (TVD) 137
Рассмотрим ячейку с номером п + 1/2, где 0 < ^n+i 1. При
использовании схем высокого порядка точности в таких областях
возникают нефизические осцилляции, поэтому лучше применить
схему первого порядка с параметром близким к единице.
Для ячейки с номером п+3/2, которая находится сразу перед раз-
рывом, ^n+2	1. В этом случае следует задать — 1 рп+2 < г,
чтобы предотвратить излишнее размазывание разрыва. Когда из-
менение приближенного решения меняется незначительно (gn « 1),
следует выбирать ipn = г, что соответствует более точной схе-
ме второго порядка аппроксимации. Поэтому функция-ограни-
читель часто удовлетворяет дополнительному условию
99(1, г) — г.
Приведенный качественный анализ определяет характер по-
ведения функции г). На практике часто используются следу-
ющие ограничители:
1) функция ultraa
</’(?,’’) = vua(q,r) = <
1,
1-^9,
-1,
Q < О,
q > r/(l - г);
2) функция super а
У>(9,г) = Vsa(q,r) =
1,
1-2(1 — r)q,
г,
1-(1-г),
2г- 1,
<7^2,
3) функция ван Леера
1
<p(<7,r) = <pvi(q,r) = <
1,
1-Ц^<7,
1+? 41
q < о,
q > 0;
4)	функция ван Албады
<p(.q,r) = <pva(q,r) = < 1
1, q < о,
5)	функция mina
Глава 6. Движение сжимаемой жидкости (газа)
6)	функция Лина
<^(Q,r) = <Р1п(?,г) =
'	1,	«<о,
= <	1 —2(1 —r)g	0^9^ 1/2,
г,	l/2<q^l,
-1 + (1 + г) ехр (-50(1 - r)(q - 1)), q > 1;
Суммируя все, изложенное выше, вычисления по TVD-схеме
проводятся следующим образом:
1)	по известному в момент времени tk решению вычисляется
параметр qn:
Un-l/2 “ Un-3/2	п
=	<+1/2 - <-1/2
<+3/2“ <+1/2
п+3/2	п+1/2	~
ь	ь , С <. U,
<+1/2 ~<-1/2
2)	используя какую-нибудь функцию-ограничитель, вычисля-
ются параметры <рп: <рп — (p(qn^)i
3)	значения в узлах вычисляются по формуле (6.20);
4)	окончательно решение в момент времени tk+i определяется
по схеме (6.19).
Так как параметр <^п зависит от qn, а значит от решения
задачи, то приведенная схема является нелинейной даже для ли-
нейного уравнения. Поэтому методы анализа свойств разностной
схемы, которые мы постоянно используем, в данном случае не-
применимы. Можно только сказать, что порядок точности рас-
смотренной схемы больше единицы, но меньше двух и зависит от
конкретной задачи.
6.6.2. Ограничение потоков
в схеме метода WAF
Рассмотрим теперь приложение концепции TVD к схеме метода
WAF. В случае линейного уравнения переноса возможно стро-
гое обоснование TVD-свойства разностной схемы. Для одномер-
ных уравнений газовой динамики приложение концепции TVD
носит несколько эмпирический характер. В отличие от скаляр-
6.6. Метод уменьшения суммарного отклонения (TVD)
ного уравнения переноса мы теперь имеем три независимые пере-
менные. К тому же, при распаде разрыва образуется три волны.
Поэтому возникает необходимость отслеживать изменение трех
величин для трех типов волн. Тогда вместо скалярного параме-
тра qn введем векторный параметр
(<71,п \
(?2,n I •
Q3,n /
Здесь qi,n определяется изменением р, q^n — изменением и, а
Q3,n — изменением р.
Значение решения в узлах разностной сетки, определяемое вы-
ражением (5.18), можно записать в виде
йп = 5 (Wn }	+ | EX’” (W"P> ~ wn+1))’
Р=1
где (р = 1,  • •, 4) и /Зр1П = (cp,nTk)!h (р = 1,..., 3), описывают
решение задачи о распаде разрыва с начальными данными
(Wn-l/2,Wn+l/2) ’
Тогда по аналогии с (6.20) можно записать:
= 5 («’п^ + «’п 9 +
1 3
+ ^52 signup,п)
Р=1
(p)
l,n
(p)
2,n
(p)
3,n
- w(p+1)
-w^11
(6.25)

w
w
w
\
/
где	(qm^n, |/3P,n|) и q>(q,r) — одна из функций-ограни-
чителей. Напомним, что
Параметры Qm?n (т = 1,..., 3) определяется следующим образом:
Глава 6. Движение сжимаемой жидкости (газа)
«(₽) =
Чт,п
w(p+1) _w(p)
w(p+1) _ w(p)
шт,п шт,п
J./P+1) _№(р)
шт,п+1 шт,п4-1
(р+1)	(р)
w£,n - w^;n
£р,П
> О,
£p,n < О.
(6.26)
Вычисление одного шага по времени в TVD-версии метода
WAF может быть организовано следующим образом:
1)	по известному решению в момент времени tk вычисляется
шаг по времени Tk из соотношения (6.6);
2)	для каждого значения п решить задачу о распаде разрыва
с начальными данными
(W„-l/2,^+1/2) .
В результате мы получим:
W”P)’ 1 П = 1,...Л_1;
Ср,П, Р -- 1, • • • 9 J
3)	параметры q$n (т = 1,..., 3; р = 1,..., 3) для каждого
значения п вычисляются согласно (6.26);
4)	значения в узлах сетки вычисляются по формуле (6.25);
5)	окончательно решение в момент времени tk+i вычисляется
по схеме (6.12).
Пример 6.5 (TVD-версия схемы метода WAF). Применим рас-
смотренную схему к задаче Сода с начальными условиями (6.7).
Результаты расчета показаны на рис. 6.22-6.25. Сравните эти
результаты с расчетами из примера 6.4.
6.7. Численное решение многомерных задач
В многомерных течениях возникает целый ряд различных осо-
бенностей, разрывов, их пересечений и взаимодействий, что час-
то создает очень сложную физическую картину. В качестве при-
мера рассмотрим явление маховского отражения, которое пока-
зано на рис. 6.26.
6.7. Численное решение многомерных задач 141
х
Рис. 6.22. Пространственное распределение плотности в момент вре-
мени t = 0,5048; сплошная линия — точное решение, штри-
ховая — приближенное решение (TVD-схема метода WAF,
функция-ограничитель supera, h — 0,02)
х
Рис. 6.23. Пространственное распределение скорости в момент време-
ни t = 0,5048; сплошная линия — точное решение, штри-
ховая — приближенное решение (TVD-схема метода WAF,
функция-ограничитель supera, h = 0,02)
Плоская ударная волна, движущаяся слева направо вдоль удар-
ной трубы, встречает жесткий клин на нижней стенке ударной
трубы. Возмущение течения начинается от острия клина в мо-
мент, когда ударная волна касается его. Это приводит к возник-
новению отраженной волны, которая имеет искривленный фронт.
При определенных условиях, налагаемых на угол клина и пара-
метры основной ударной волны, первичная и отраженная волны
Глава 6. Движение сжимаемой жидкости (газа)
х
Рис. 6.24. Пространственное распределение давления в момент време-
ни t — 0,5048; сплошная линия — точное решение, штри-
ховая — приближенное решение (TVD-схема метода WAF,
функция-ограничитель supera, h — 0,02)
Рис. 6.25. Пространственное распределение удельной внутренней энер-
гии в момент времени t = 0,5048; сплошная линия — точное
решение, штриховая — приближенное решение (TVD-схема
метода WAF, функция-ограничитель supera, h = 0,02)
6.7. Численное решение многомерных задач 143
встречаются в некоторой точке, называемой тройной точкой и
расположенной выше клина. Между этой точкой и клином две
волны сливаются в единственную волну, называемую маховской
конфигурацией. Вниз по течению от тройной точки образует-
ся поверхность скольжения, на которой давление и нормальная
компонента скорости остаются непрерывными, а плотность и ка-
сательная компонента скорости имеют разрывы. Этот пример
показывает, что многомерные течения представляют собой до-
вольно сложную проблему для численного моделирования.
Рис. 6.26. Образование маховского отражения
Дивергентная форма многомерных уравнений газовой дина-
мики в переменных Эйлера аналогична уравнениям (6.1) и (6.2).
Для случая декартовых координат она имеет вид
дз ЭЛ(3) dfy(s) ЭД(а) _
dt дх ду dz
где з, fx(s), f (в), и fz(s) — векторы, определенные равенствами
8 —
( р \
ри
ри
pw
\ р(е + 1/2(м2 + v2 + w2)) /
< «1 >
«2
«з
«4
\ /
Глава 6. Движение сжимаемой жидкости (газа)
ри	\
ри2 +р
puv
puw
и (ре 4- 1/2р(и2 + v2 + w2) + р) )
'	82
82/81 +Р
8283/81
8281/81
\ 82 (з5 +Р) /81
pv	\
pvu
pv2 +p
pvw
v (pe + l/2p{u2 + v2 + w2) + p) J
83
8283/81
«з/«1 + Р
«3 («5 + р) /81
pw
pwu
pwv
pw2 +p
w (pe + 1 /2p(u2 + v2 + w2) + p)
84
S2S4/81
8^84/Si
84/81 + Р
84 ($5 + р) /Si
Здесь р — плотность; и, v и w — компоненты скорости по осям
х, у и г, соответственно; р — давление и е = е(р,р) — внутренняя
энергия в единице объема. Дальше, для простоты, мы будем рас-
сматривать построение разностных схем для двумерных задач,
когда w =0 и, следовательно, fz(s) = о.
6.7. Численное решение многомерных
Введем разностную сетку с узлами (жп, ym,tk), где xn+i —хп —
- hx, ут+\ -ym = hy и tk+1 - tk =тк. При обобщении схемы (6.3)
на многомерный случай удобно изменить обозначения: дробные
индексы можно устранить, предполагая, что элементарная ячей-
ка сетки имеет размеры 2ЛЖ, 2hy и тк + в направлениях х,
у и t. Сначала найдем промежуточные значения при t = tk+i из
соотношения
^n,m ($n+l,m + &п — 1,т + &п,т+1 Sn,m — 1) —
- 2^ (Л (®U+1) - fy >
n=l,...,N-1; m =	- 1.
Затем окончательное решение при t = tk+2 вычисляется из
уравнения
Л+2 _ „fe+1 Tk + Тк+1 / , / fc+l \ _ f ( k+1
°п,т °n,m 2ft,	\J х \ n+1,mJ J x \ n — l,mj J
- ++ v, -1,««_.)). <6-28)
n = 1,...,7V-1; m = 1,...,M-1.
Как и в случае одной пространственной переменной, эта раз-
ностная схема на гладком решении аппроксимирует уравнения
(6.27) со вторым порядком по h и т, а конечно-разностные ана-
логи интегральных законов сохранения выполняются точно.
Устойчивость линеаризованной схемы (6.28) определяется усло-
вием (5.27). Тогда, объединяя этот результат с условием (6.6),
шаг по времени для случая hx = hy = h выбирается из соотношения
Тк —	/—Гтах,
V "
h
Гт ах —	/	-----------------
Шах ( Сп т -|- л/(ип т) Т (^п,т)
п,т \	’ у v ’ 7	’
4,т=(7РкП,т/ркп,т)1/2-
Дополнительное затруднение, возникающее при численном ре-
шении многомерных задач газовой динамики, обусловливается
тем, что влияние нелинейной неустойчивости проявляется в боль-
шей степени, чем в одномерном случае. Так в некоторых задачах
такая неустойчивость возникает в областях быстрого изменения
решения и искажает все решение, если не ввести в разностную
схему дополнительное слагаемое, соответствующее искусствен-
ной вязкости. В простейшем случае, по аналогии с (6.9), это сла-
гаемое будет иметь вид (двумерная схема):
V	~ ^^71,771 Sn—l,m) +	~~	Sn,m — 1) •
Обобщение разностных схем С. К. Годунова и метода WAF на
многомерный случай можно естественным образом осуществить
на основе метода расщепления. Следуя этой процедуре, в дву-
мерном случае мы должны последовательно решать одномерные
системы
/	Р
д	ри
dt р {е -I- |(?z2 -I- г2))
\ pv
(	ри
О	ри2 + р
+ дх и {ре -I- |p(u2 -I- v2) -I- р)
\	puv
(6.29)
и
/	Р	\
д	pv
dt р(е+ |(u2 +v2))
\	Ри	/
/	pv
pv2 +р
v {ре + ^р(и2 -I- v2) -I- р)
у	pvu
(6.30)
Здесь для удобства дальнейшего изложения мы изменили порядок
переменных. Рассмотрим сначала уравнения (6.29). В этом случае
и есть нормальная компонента скорости, a v — тангенциальная.
Первые три уравнения системы (6.29) очень похожи на одномер-
ные уравнения (6.1). Единственное отличие состоит в том, что
появляется вклад компоненты v в кинетическую энергию. Ис-
пользуя первое уравнение системы (6.29), последнее уравнение
этой системы можно преобразовать к виду
dv	dv
— + u— = 0.
dt	дх
Это говорит о том, что компонента v просто переносится со
скоростью и. Рассмотрим теперь задачу о распаде разрыва с на-
чальными условиями
UL,
aR-
О,
где вектор а определяется как
и
р
а =
«2
«3
а4 /
будет точно таким же как и в
Тогда решение для р, и и р
одномерном случае (см. параграф 6.3), а решение для компоненты
v будет иметь следующий вид:
VL,
VR,
uot > х,
not < х,
здесь uq — скорость контактного разрыва. Аналогичные рассу-
ждения справедливы и для системы (6.30), только теперь v будет
нормальной компонентой, а и — тангенциальной. Тогда решение
задачи о распаде разрыва с начальными условиями
У о,
У > о,
bi-
bR)
где вектор Ъ определяется как
V
р
Ъ =
Ьг
Ъз
bi
u(y,t) =
для р, v и р будет точно таким же, как и в одномерном случае, а
решение для компоненты и будет иметь вид:
ul, vot > у,
ur, vot < У-
Рассмотрим теперь построение схемы С. К. Годунова для дву-
мерных задач. На первом этапе при каждом значении т = 0, ...,
М — 1 решаются задачи о распаде разрыва с начальными условиями
sk
n,m
(an-l/2,m+l/2’an+l/2,m+l/2) 5	П — 1, . . . , TV 1.
В результате мы получим значения:
an,m+l/2 Sn,m+l/2> П = 0, . . . , TV, ГП = 1, . . . , М - 1
в граничных точках разностных ячеек, которые обозначены сим-
волом «х» на рис. 6.27. Здесь и далее символ —> обозначает пре-
образование вектора з в векторы а или Ъ и наоборот. Применяя
схему (6.10) к уравнениям (6.29), вычислим промежуточное ре-
шение
* + 1/2	_
п+1/2,т+1/2 —
= Sn+l/2,т+1/2 — (f х (Sn+l,m+l/2z	//и
п = 0,..., TV — 1, т = 0,..., ТИ — 1.
На втором этапе при каждом значении п = 0,..., TV — 1 реша-
ются задачи о распаде разрыва с начальными условиями
f » *+1/2	j fc+1/2	\	и д г -|
y^n+l/2,m —1/2’ ^n+l/2,m+l/2 J ’ Ш — 1, . . . , ТИ - 1.
В результате мы получим значения:
^в^/2ГО> га = о, - 1, т = 0,...,М.
n+1/2, т	n+1/2,т’	’	’	‘	‘	7
в граничных точках разностных ячеек, которые обозначены сим-
волом «•» на рис. 6.27.
'X
т+1
/77+1/2 :i-
m L
n
n+1/2
n+1
Рис. 6.27. Разностная ячейка для двумерной задачи
6.7. Численное решение многрмерных задач 149
Далее, применяя схему (6.10) к уравнениям (6.30), вычислим
требуемое решение в момент времени tk+i
n+1/2,m+1/2
_ fc+1/2	/ fc+1/2	/ fc+1/2	\\ П
~ n+1/2,m+1/2	У n+1/2,m+1 J	J У n+1/2,m) )
n = 0,..., N — 1, m = 0,..., M — 1.
Прежде чем перейти к формулировке схемы метода WAF для
многомерных уравнений, нам необходимо получить формулы для
расчета значений решения в граничных точках разностных яче-
ек. Рассмотрим сначала уравнения (6.29). По аналогии с выраже-
нием (6.25) для узла с номером (n,m + 1/2) можно записать:
пк	= -(п^	+л(4)	4-
п,m+1/2	2 \ n,m+1/2	Un,m+1/2 J '
1 3 4“ 2	sign(cp,n,m+l/2) р=1	(Ар)	1 Sri,n,m+1/2 1 ,Др)	। ^2,n,m+1/2 1	(Ар) lul,n,m+1/2 la(p) I u2,n,m+1/2	- a(p+1) ul,n,m+1/2 J - a(p+1) u2,n,m+1/2 1	A
	(р) ^3,n,m+1/2 1	[a(p) (a3,n,m+1/2	- a(p+1)	’ a3,n,m+1/2 j	
	,Др)	,	( n(P)	_ z7(p+1)	<	
	у^4,п,m+1/2	^a4,n, m+1/2	a4,n,m+1/2 j	4
(6.31)
ГДе m+1/2 = ^(Й>т+1/2,1+п,т+1/2|)> ф(?,г) - ОДНИ ИЗ
функций-ограничителей, а а^+1/2 (р = 1,• • • ,4) и +,n,m+i/2 =
(cp,n,m+i/2TA:)/^ (р = 1, • • •, 3) описывают решение задачи о рас-
паде разрыва с начальными данными
(к	к	\
an-l/2,m+l/2’an+l/2,m+l/2 J •
Параметры ^,n,m+i/2 G =	определяются следующим
образом:	r a(₽+1)	_ a(p) az,n-l,m+1/2	uz,n-l,m+1/2	n „(Р+1)	_ „(Р)	’ CP.".™+l/2 > U>
0(p) - < m+1/2	Ui,n, m+1/2 ai,n,m+1/2 „(Р+1)	_ fl(p) ai,n+l, m+1/2 az,n+l,m+1/2	n (p+l)	_ (p)	’	CP>«,m+1/2 < U- <	ai,n, m+1/2 ai,n, m+1/2 (6.32)
Глава 6. Движение сжимаемой жидкости (газа)
Вычисление значений решения в узле с номером (п + 1/2, т)
осуществляется аналогичным образом.
Для построения двумерной TVD-схемы метода WAF лучше
использовать более точную процедуру расщепления (5.39). Пусть
^n,m+l/2 = 9 (а1/2,т+1/2>	aN-l/2,m+l/2’ Т)
обозначает процедуру вычисления значения в узле разностной
сетки в TVD-версии метода WAF, которая определяется выра-
жениями (6.31) и (6.32). Тогда аналог схемы расщепления (5.39)
выглядит следующим образом:
1)	на первом этапе вычисляется промежуточное решение
з(1)
°n+l/2,m+l/2
— Sn+l/2,m+l/2 — х ^n+l,m+l/2^ ~ f х ^n,m+l/2^) 2^ ’
п = 0,..., TV — 1, ш = 0,..., М — 1,
гДе Sn+l/2,m+l/2	an+l/2,m+l/2’
^n,m+l/2 — 9	,
^n,m+l/2	^n,m+l/2>	= 0, . . . , TV, ГП = 0, . . . , M — 1;
2)	на втором этапе вычисляется промежуточное решение
' я(2)
°n+l/2,m+l/2
-з(1)	- (f fs(1)	- f fs(1)
“ n+l/2,m+l/2 У yn+l/2,m+l J h\n+l2jn)j^‘
п = 0,..., N — 1, т = 0,..., М — 1,
М	-4
п+1/2,т+1/2	°n+l/2,m+l/2’
Ъп+1/2,т — 9 (&п-|-1/2,1/2’ * * * ’ ^n+l/2,M-l/2’ Тк’ ^У’^ ’
Ьп+1/2,т ~> ^n+l/2,m’	= 0, • • • 5	— 1, Ш = 0, . . . , М;
3)	и окончательно на третьем этапе вычисляется требуемое
решение в момент времени tk+i
Л+1	_
°п+1/2,т+1/2
= s(2)	-(f (s(2) Vf (s(2)
°n+l/2,m+l/2 \J x \jn+l,m+l/2) J x \Jn,m+l/2J J 2/j,
6.8. Заключительные замечания 151
п = 0,..., N — 1, т = О,..., М — 1,
s(2)	а(2)
n+1/2,m+l/2	п+1/2,т+1/2’
-(2)	( (2)	(2)	1	, А
ап,т+1/2 — 9 ^а1/2,т+1/2’ * * ’ ’ a7V-l/2,т+1/2 ’ 2 Т/г ’	'
«J/L 1 i /9 i 1 /95 П — О, • • • , N, ТП — О, . . . , М - 1.
п, т+1/2	м,т<+1/2’	’	’	’	’	’
Как было показано на примере схем расщепления для урав-
нений акустики, устойчивость многомерной схемы определяется
устойчивостью одномерных схем. Тогда, учитывая (6.6), получим
условие устойчивости рассмотренных двумерных схем:
Tk = г • min <
Ьх
+ах(Н+1/2,т+1/2|+<
__________________hy_________________
(lUn+l/2,n»+l/2l + Сп+1/2,т+1/2
/	k	\	1/2
k	  I	^n+1/2,m+l/2	|
Cn+l/2,m+l/2 — I y~k	J
\	^n+1/2,771+1/2	/
6.8. Заключительные замечания
В этой главе мы рассмотрели некоторые методы решения неста-
ционарных уравнений гидродинамики. Разностные схемы, при-
меняемые для решения этих уравнений можно приближенно раз-
делить на два типа:
1) схемы, непосредственно аппроксимирующие дивергентную
форму уравнений гидродинамики;
2) методы, использующие решение задачи о распаде разрыва.
Схема Лакса-Вендроффа является примером метода первого
типа, а схема С. К. Годунова и схема метода WAF — примерами
методов второго типа.
В настоящее время разработано множество методов для рас-
чета газодинамических течений и, естественно, в одной главе
Глава 6. Движение сжимаемой жидкости (газа)
невозможно рассмотреть, даже кратко, все основные подходы.
Наряду с рассмотренными нами схемами, популярными являются
такие методы как PPM (Р. Colella and Р. R. Woodward, J. Comput.
Phys., 54,174-201,1984), различные модификации метода MUSCL
(В. van Leer, J. Comput. Phys., 14, 361-370, 1974; P. Colella, SIAM
J. Sci. Stat. Comput., 6, 104-117, 1985; M. Ben-Artzi, J. Comput.
Phys., 65, 170-178, 1986), схемы ENO/UNO (A. Harten and S. Os-
her, SIAM J. Numer. Anal., 24, 279-309, 1987).
Основной объем вычислений в схемах второго типа прихо-
дится на решение задачи о распаде разрыва. Мы рассмотрели
точное решение этой задачи, которое требует итерационного ре-
шения нелинейного уравнения. Существуют приближенные ме-
тоды решения задачи о распаде разрыва, позволяющие избежать
итераций, хотя они и дают менее точное решение. К наиболее
популярным методам этого типа относятся процедура Ф. Роу
(Р. L. Roe, J. Comput. Phys., 43, 357-372, 1981) и метод HLLE
(В. Einfeldt, SIAM J. Num. Anal., 25, 294-318, 1988).
Рассмотренные в этой главе методы могут применяться для
решения различных задач механики сплошной среды. В качестве
примеров можно привести такие проблемы, как
1)	уравнения мелкой воды;
2)	стационарные сверхзвуковые течения;
3)	уравнения Навье-Стокса для сжимаемой жидкости;
4)	волны детонации;
5)	уравнения магнитной гидродинамики;
6)	нелинейные волны в твердых телах.
ГЛАВА 7
СТАЦИОНАРНЫЕ
УРАВНЕНИЯ
Одним из наиболее часто встречающимся стационарным урав-
нением является уравнение Гельмгольца (и его частный случай
уравнение Пуассона), которое представляет собой математиче-
скую модель различных физических явлений. Некоторые приме-
ры таких явлений мы рассмотрели в параграфе 2.7. Часто эти
уравнения возникают как промежуточный этап в некоторых вы-
числительных моделях. Например, моделирование поведения сис-
темы заряженных частиц и движения несжимаемой жидкости
требует многократного решения уравнения Пуассона для опре-
деления электрического поля и поля давления соответственно.
Поэтому методы решения этих уравнений, как правило, числен-
ные, являются важной частью вычислительной физики.
В этой главе мы обсудим некоторые основные идеи, на кото-
рых основаны методы решения стационарных уравнений. В ка-
честве примеров мы рассмотрим следующие уравнения:
1)	неоднородное уравнение Гельмгольца с переменными коэф-
фициентами
3 С\ /	г\ \
охк \	охк J
здесь х = (^1,а;2,^з) —
2)	нелинейное уравнение вида
з
(7-2)
Пусть G есть граница области Z), тогда уравнения дополня-
ются граничными условиями
ди
= 9&).
XEG
6jL54 Глава 7. Стационарные уравнения
7.1.	Выбор метода
Какой из методов решения эллиптических уравнений следует при-
менять? сильно зависит от вида уравнений, и не существует уни-
версального и наилучшего для всех случаев метода. Выбор мето-
да определяется следующими характеристиками задачи:
1)	видом уравнений, т. е. линейностью, размерностью, наличи-
ем переменных или постоянных коэффициентов;
2)	свойствами области и граничных условий.
На рис. 7.1 приведена примерная диаграмма для выбора мето-
да. Эта диаграмма не является исчерпывающей. Она, в основном,
касается методов, которые будут обсуждаться в этой главе.
Рис. 7.1. Примерная диаграмма для выбора методов решения стацио-
нарных уравнений
Первым возникает вопрос о линейности рассматриваемого урав-
нения. Если уравнение нелинейно, то его разностную форму мож-
1.2. Формулировка разностных уравнений в виде системы
но свести к системе нелинейных уравнений, а затем применить
какой-нибудь метод для решения таких систем. Для некоторых
уравнений можно также применить метод установления. Для ли-
нейных уравнений выбор метода определяется формой области,
в которой ищется решение, видом коэффициентов и граничны-
ми условиями. Если область определения задачи является прямо-
угольником или параллелепипедом, а граничные условия имеют
специальный вид, то можно использовать методы, основанные на
быстром преобразовании Фурье (FFT, Fast Fourier Transform).
Рассмотрим, например, двумерную область {0 < х < О < у 1У}.
Под специальными граничными условиями мы будем понимать
одно из следующих условий:
1) и(0,т/) = и(1х,у) — периодическое условие,	(7.3)
w(0, У) = 91 (.У) и и(1х, у) = дз(у) — условие Дирихле, (7.4)
ди .	. ди,,	.	, .	тт „
= 9х\У) и э^"х’У) = 9з(У) — условие Неймана,
(7-5)
2)
и(х, 0) = и(х,1у),
и(х,0) = р2(ж) и и(х,1у) = 94(х),
^(ж,0) = д2(х) и ^(х,1у)=д4
ду	ду
(7-6)
(7-7)
(7-8)
В случае трехмерных уравнений специальные граничные усло-
вия определяются аналогичным образом.
Если область определения задачи имеет сложную форму, то
разностная форма исходного уравнения представляется в виде
системы линейных уравнений, и затем применяется тот или иной
метод для решения полученной системы.
Перейдем теперь к более подробному обсуждению методов ре-
шения стационарных уравнений. Для простоты мы будем рассма-
тривать двумерные задачи. Методы решения трехмерных задач
строятся аналогичным образом.
7.2.	Формулировка разностных уравнений
в виде системы уравнений
Мы начнем наше обсуждение с линейного уравнения (7.1), задан-
ного в прямоугольнике. Тогда задача принимает вид
156 Глава 7- Стационарные уравнения
&	+’М+4 (г’“='(1'’’’
D = {0 < х 1Х, О 1У},
(7-9)
4- некоторые граничные условия на G. , z
Введем разностную сетку с узлами хп — ппх пут = mrty (п =
О,..., N; т — 0,..., М), где шаги сетки hx = lx/N, hy = ly/M.
Полученная сетка показана на рис. 4.5. Для построения разност-
ной аппроксимации уравнения (7.9) применим подход, рассмо-
тренный в параграфе 4.2. В результате получим следующее раз-
ностное уравнение:
^п+1 /2,т — ®	4" 2	>	(7.106)
^n,m+l/2 ~	Ут 4" ^У^ ’ ^п,т ~ (^nj Ут) у	(7.10в)
n=l,...,N -1; m = 1,...,М-1.	(7.10г)
После приведения подобных слагаемых это уравнение примет вид:
I ^(2)	__ (з)	.
сп,т-1ип,т-1 Т-	сп,тагь,т
4" Cn\iun+l,m 4~ Сп,т^^^+1 = /п,7П>	(7.И)
п = 1,..., N — 1, т = 1,..., М — 1, где
(1) _ ®п,т+1/2 (2) _ ап+1/2,т
Сп,т ~ ^2 ’ Сп,т ~ ^2 ’
У
(3) __ ^п+1/2,т 4~ (^п—1/2,т ^п,т+1/2 4~ ^п,т—1/2	,
Сп,т ~~	^2	'	Д2	Оп,т-
х	у
Если функция а(х,у) достаточно гладкая, то разностная схе-
ма (7.10) аппроксимирует дифференциальное уравнение (7.9) с
точностью до членов O((hx)2 + (hy)2). В дополнение к разност-
ным уравнениям (7.10), которые справедливы для внутренних
1.2. Формулировка разностных уравнений в виде системы 157
точек области, необходимо также записать граничные условия
в разностном виде. Рассмотрим, например, аппроксимацию гра-
ничных условий при х = 0. Разностная форма условия Дирихле
^(0,?/) = 91(у) имеет простой вид: w0,m = 91(Ут), т = 0,... ,М.
Для условия Неймана |^(0,т/) =д1(у), как обычно, можно при-
менить метод фиктивных областей, вводя дополнительные узлы с
координатами (х_1,ут). Тогда производная в граничных точках
аппроксимируется как
----2^-----= 91{Ут), т =	- 1.
В дополнение запишем уравнение (7.11) при п = 0:
С1)	। (2)	(3)	. (2)
4"	4" C0,m^l,rn 4"
4"	~ /o,m*
Исключая из этих двух уравнений величину и полагая
(2)	(2)
c-i m “ сот, окончательно получим
(1)	I о (2)	(3)	.	(1)
С0,т-1и0,т-1 4- 2cO mUi^m c0,mU°,m 4~ Со,ш?1о,т+1 —
— fo,m 4- 2cQ^mhxgi(ym)j
m = 1,...,М- 1.
Преобразуем сеточные функции ип,т и в вектора v = {'Ср}
и d = {dp}, соответственно, применяя следующее преобразование:
Up —	dp — fn^mi Р — m(N 4” 1) 4- п 4~ 1,
п = 0,..., 7V; т — 0,..., М.
Тогда разностное уравнение (7.11) и граничные условия можно
представить в виде системы линейных уравнений
Fv = d,	(7.12)
где матрица F является блочно-трехдиагональной:

См-1
В*м /
Глава 1. Стационарные уравнения
В свою очередь Ат, Вт и Ст представляют собой квадрат-
ные матрицы размером N х N:
Д)
W— 1,т—1
0^2,т-1 /
У2,т
Коэффициенты матриц, помеченных звездочкой, определяют-
ся граничными условиями при у = 0 и у = ly, а коэффициенты
а, 0 и 7 в матрицах Ат, Вт и Ст определяются граничными
условиями при х = 0 и х — 1Х. Например, если во всех точках
границы задано условие Дирихле, то
Во — Вм ~ I
Cl = А*М = О,
^l,m—1 ~ ^2,m —1 — О,
02,т — 03,т ~ О,
т — 0,..., М.
(1 — единичная матрица),
(О — нулевая матрица),
01,т ~ 04,т — 1,
71,т ~ 'У2,т — О?
Таким образом, матрица F представляет собой ленточную пя-
тидиагональную матрицу и ширина ленты равна 27V4-1. Наиболее
универсальным методом для решения системы (7.12) является ме-
тод LU-разложения (см., например, ОНВ, п. 2.6). Он применим
1.2. Формулировка разностных уравнений в виде системы
для различных граничных условий и произвольных коэффици-
ентов а(х,у) и Ь(хуу). Однако объем вычислений в этом методе
сильно возрастает с увеличением числа сеточных узлов. Так в
двумерном случае число операций Nops ~ (^)3/2, где Ns = N •
М — число сеточных узлов. Поэтому метод LU-разложения обыч-
но применяется для малых систем с Ns ~ 1000. Если коэффициен-
ты уравнения остаются неизменными для большого количества
правых частей, то требуется только одно разложение, и этот ме-
тод будет вполне приемлем для решения систем из нескольких
тысяч уравнений.
Если коэффициенты уравнения меняются для каждой правой
части или количество сеточных узлов превосходит 10000, то ис-
пользуются итерационные методы решения систем уравнений.
Одним из популярных методов является метод последователь-
ной верхней релаксации (SOR) (см., например, ОНВ, п. 2.7.4).
Можно непосредственно применить метод SOR к системе (7.12),
но лучше использовать эквивалентную форму, основанную на се-
точных уравнениях (7.11). Пусть на границе задано граничное
условие Дирихле. Тогда итерационная схема SOR для сеточных
уравнений (7.11) может быть записана в следующем виде:
ио^т1) = 91(Ут),	= дз(ут), т = 0,...,М, (7.13а)
ип,о1} = 92(хп),	= д4(хп), n = 0,...,N,	(7.136)
,.(*+1) = fr(l) ,.(*+D +г(2) ,.(*+!) .
un,m	(з) I ^п,т — 1 ^ПуГп — 1 ~ сп — 1,тип—1,т '
cn,m
+ Сп,тип+1,т + cn,mwn,m+l — fn,m^ + (1 — Wk) ищт (7.13в)
п= 1,...,ДГ-1; т = 1,...,М-1; к = 0,1,...	(7.13г)
Итерации начинаются с некоторого начального решения
и продолжаются до тех пор, пока не выполнится условие
l|u(*+i) _u(fc)||
1И+1)112
ЙГде в — заданная точность. Напомним, что сходимость итера-
ционного процесса определяется максимальным по модулю соб-
ственным значением (спектральным радиусом) итерационной ма-
трицы s(B) = max |АР(В)| • При этом относительная ошибка
1к-цШИ2
lk-«(0)ll2

(7-14)
где и* обозначает точное решение системы уравнений. Отсюда
следует, что для сходимости необходимо s(B) < 1- Чем меньше
значение $(В), тем быстрее сходимость и, следовательно, требу-
ется меньше итераций, чтобы вычислить приближенное решение
с заданной точностью. В методе SOR, з(В) зависит от параме-
тра который называется параметром релаксации. Если метод
сходится, то существует такое значение ш — шор1, при котором
s(cu) имеет минимум. В нашем случае мы решаем систему с ма-
трицей F- Если она симметричная и положительно определенная,
то для матриц такого типа
2
где Bj = I — В-1 F — матрица Якоби матрицы F и D есть
диагональ матрицы F. Тогда s(Bsor) = ^opt — 1-
Рассмотрим свойства метода SOR на примере модельной за-
дачи (7.9) с а(х,у) = const, b(x,y) — 0 в квадрате {0 < х < 1,
О у 1} и граничными условиями тх(О,т/) = и(1,у) — и(х,0) =
— и(х, 1) = 0. В этом случае s(Bj) — cos(tt/N). Тогда параметр
релаксации в схеме (7.13) задается как
2
— ^opt —	: т ., n
l + sin(7r/TV)
и спектральный радиус —
,	.	1—sin(7rW)
s(Bsor) -	--. ~T~ /Г7Т-
1 + Sin(7r/7v)
Это выражение показывает, что при увеличении N сходимость
метода замедляется, так как s(Bsor) приближается к единице.
Оценим число итераций fc, необходимое для уменьшения ошибки
начального приближения в 10р раз. Из соотношения (7.14) полу-
чим
Тогда
Ю р — sk(BsOR) =
1 — sin(7r/TV)\ к
1 -h sin(7r/7V) /
р • 1п(10)
In (1 — sin(7r/TV)) — In (1 + sin(7r/JV))
1.2. Формулировка разностных уравнений в виде системы
При больших значениях N, когда тг/N С 1,
= FpJnllO) 1 гр ,
27Г	L3 J
Таким образом, если требуется точность 10~3 (р = 3), то чис-
ло итераций приближенно равно количеству сеточных узлов в
каждом направлении. Для достижения точности 10~6 необходи-
мо удвоить это число итераций. Из соотношения (7.13) следует,
что для выполнения одного шага итерационного процесса тре-
буется 117VS операций. Тогда общее количество операций будет
~ 11(7V5)3/2 для двумерных задач и ~ 11(7V^)4/3 для трехмерных
задач.
Применять метод SOR для решения задач, подобных рассмо-
тренной нами модельной задачи, не имеет смысла, так как для
Ьгакого сорта задач существуют более эффективные методы. Ите-
рационные методы обычно применяются для решения уравнений
с переменными коэффициентами в областях сложной формы. Од-
нако в этом случае получить аналитические выражение для спек-
трального радиуса матрицы Якоби невозможно. Тогда можно
начать вычисления с некоторым значением со, скажем co — 1, и
одновременно с вычислением приближенного решения, уточнять
это значение, используя степенной метод для определения спек-
трального радиуса матрицы Якоби. Для задачи (7.13) степенной
метод можно записать следующим образом:
1) начиная с некоторого начального приближения , после-
дующие приближения к собственному вектору вычисляются по
формуле
UJr> т
w(k+l) _ (k) ш0,т — uO,nV w(*+l) _ AV Wn,0 — Vn,0’ (!) (*)	W(*+D _ AV	0 WN,m ~ VN,m’ ТП — \J,. w(*+i) _ AV	Q шп,М — IJn,M' Il — V,-  lc(2) w(fc) +c(2) AV "cn-l,mun-l,m^cn,mUn+l,rl	.,N, n	JV un,m-hl
	AV Cn,m		
n = 1,...,7V — 1;	m = 1,..., M — 1; k =	0,1,...	
2) приближение к спектральному радиусу матрицы Якоби опре-
деляется как отношение Рэлея вектора
162 Глава 7. Стационарные уравнения
N М	(и I 1 \
V V	w(fc+1)
/ j / j Un,mWn,m
(fc) _ n=C) m=0________
S ~ N M z ... \2 ’
E E (<™)
n=C) m—0 '	'
3) и окончательно, после нормализации, получим
(fc+l)
?.(fc+i) _ Wn^m
Тогда параметр релаксации на А;-том шаге итерационного про-
цесса вычисляется как
2
=-------/....... Т
1 + у 1 -
Таким образом, по мере увеличения к, —> s(JBj) и wOpt-
Метод SOR можно применять только для решения определенного
типа задач, для которых известно, что метод сходится и можно
определить оптимальное значение параметра релаксации. Таким
типом, например, являются уравнения вида (7.1) с граничными
условиями Дирихле при Ь(х) 0. При &(ж) > 0 матрица Г пере-
стает быть положительно определенной.
В случае нелинейных задач разностная аппроксимация при-
водит к системе нелинейных уравнений. Рассмотрим, например,
построение такой системы для уравнения (7.2) с граничными
условиями Дирихле. Для построения разностной схемы исполь-
зуем соотношение для аппроксимации д(а(и)ди/дх)/дх, которое
мы применили при выводе схемы (4.18). В результате получим
ио,т = 91(.Ут), UN,m = дз(ут), т = 0,...,М,	(7.15а)
Wn,o = 52(жп), ип,м = У4(хп), n=0,...,N,	(7.156)
~	^п — 1,т j
^n-|-l/2,m	^2	1/2,m	'
! _	^n,m	^n,m	—1 _
' ^n,m-|-l/2	T~2	0"n,m —1/2	T~2
Пу	Hy
-f(.xn,ym), (7.15b)
n=l,...,N-1; m =	- 1; к = 0,1,...
1.2. Формулировка разностных уравнений в виде системы
Здесь
Оп-\-1/2,т — О
ttn,m+l/2 — О
После несложных преобразований приведем схему к виду
^2 (ип,т, Un,m_ 1 ^Un,m — 1 ~Ь С1 (ип,тч On — iym)un — iym
п^тч Оп — 1,т
п,т ч Оп+1,т ) + с2(и.
п,т
+ cz(un ,тч Un,m+l))Unim ~b Ci (^п,Ш5	+
T C2(un,m,	i)^,m+1 — f (хпчУт) = 0»
n = 1,..., N — 1; m = 1,..., M — 1, где
i	\	1
Cl уЦ'плпч ^n+l,m) —
1
C2 \^п,тч^п,т+1) — ~К2^
Пу
При каждом фиксированном значении п и т мы получаем одно
уравнение из системы. Далее эта система решается каким-нибудь
итерационным методом (см., например, ОНВ гл. 4).
Пример 7.1 (метод SOR). Рассмотрим уравнение (7.1) при а = 1,
Ъ = 0 в квадрате {0 х 1,0 т/ 1} с граничными условиями
и (0,т/) = и (1,1/) = 0, и (х, 0) = 0, и (х, 1) = я(1 — х) • 1п(2). (7.16)
Правая часть уравнения
/М = -ц^-2-1п(1+г/)-
Зададим разностную сетку с N = М — 16. При начальном
приближении tzn°m = 0, (п = 0,..., N; т = 0,..., М) и е — 10"5
итерационный процесс сходится за 40 итераций. Приближенное
решение показано на рис. 7.2.
Точное решение этой задачи — ^(ж,т/) = ж(1 — ж) • 1п(1 + т/).
Для оценки ошибки приближенного решения введем обозначения:
= {и(хп, ут)} — точное решение, вычисленное в узлах сет-
ки, и и = {'Un,m} — приближенное решение задачи. Тогда для
164 Глава 7. Стационарные уравнения
решения, показанного на рис. 7.2,
Рис. 7.2. Приближен-
ное решение уравне-
ния (7.1) с граничными
условиями (7.16), ме-
тод SOR (а = 1, b — О,
N = М = 16, е = 10-5)
7.3. Применение быстрого
преобразования Фурье
Если область определения задачи представляет прямоугольную
односвязную область, коэффициенты уравнения (7.1) постоянны
и граничные условия в одном из направлений имеют специальный
вид, то можно применить метод, основанный на преобразовании
Фурье. Мы рассмотрим основные идеи этого метода на примере
одной задачи, а затем обсудим все остальные случаи, в которых
этот метод можно применять.
Пусть коэффициенты уравнения (7.9) постоянны: а(х,у) — а
и Ъ(х,у) — Ь, область определения — прямоугольник {0 х 1Х,
О у 1у}, а граничные условия имеют вид
и(0,у) = и(1х,у) = О,
ди	ди
aiu(x,O) + а2^(ж,0) = 5г(а:), а3и(х, ly) + а4 — (x,ly) = gt(x).
Тогда разностная схема (7.11) примет вид
Cl	—1 “Ь C2Un — 1 ,т	“И ^2^n-|-l,т Н- ^1 l^n,m+l — fn,m> (7-17)
п - 1,..., N — 1; т = 1,..., М — 1,
llO,m = UN,m = О, ГЛ = 0, . . . , М,	(7-18)
1.3. Применение быстрого преобразования Фурье
( 2c1a1hy\
С2^п-1,0 — I СЗ---------^п,0 + С2^п+1,0 + ^CiUn \Unд =
\ а2 /
/п,о + 2с^у д^п),
^п,0 — ~.92(«^п),
«2 7^ О
а2 = О,
(7.19)
п =	— 1,
дд&п), од о
ОД = О,
(7.20)
о	।	(	. 2CiCt3/i^\
£ClUn,M-l + С2^П-1,М — С3 Ч-----------Un,M + С2^п+1,м —
\	ОД
{£	‘lexh
JTI^M
Un,M = ^54(®n),
m = 1,..., M — 1. Здесь
Ci =	c3 = 2(ci +c2) — b
и для вывода граничных условий при у = 0 и у — 1У применялся
метод фиктивных областей.
Для этого типа граничных условий решение можно предста-
вить в виде конечного ряда Фурье:
1 7V"1
Un,m -	52 Vk'm sin^kn/N), m = 0,...,M.	(7.21)
к=1
Правую часть уравнения также можно представить в виде
2 TV—1
fn,m - 5L dk’m sin^kn/N), m = 0,...,M,	(7.22)
V k=i
и коэффициенты с/^?т вычисляются по формуле
7V-1
dk,m = 52 sin(7rbi/]V), ш = 0,..., М. (7.23)
П=1
В дальнейшем операцию вида (7.23) мы будем обозначать как
dk,m — Fn (fn,rn)> где п указывает на параметр, по которому про-
исходит суммирование.
Подстановка выражений (7.21) и (7.22) в уравнения (7.17) и
граничные условия (7.19) и (7.20) дает следующую систему урав-
нений:
7fc1)Ufe,o + 7fc2) * * * * * ВUk,i = 4,о,	(7.24а)
civk,m-i - (с3 - 2с2 cos (кк/N)) vk,m + civfc,m+i = 4;ТП, (7.246)
166 Глава 7. Стационарные уравнения
т=1,...,М -1,	(7.24в)
7fe3)^fe,M-i +7*4)^,м = dk,M,	(7.24г)
где
_ ( (ff2 (хп)) ,	«2=0,
к’° ~ | Fn (уП)0 + ^^-д2 (Жп)} , «2 / о,
_ Г (54 fan)) >	«4=0,
yfn,M £/4 (хп)j , «4 ф О*
Параметры 7^,...,7^ определяются как
(1) _fl’	«2=0,
^к ~ [ — сз + 2с2 cos(tfA;/W) + 2c\OL\hy/a2, о2 / О,
(2) _ Г 0,	«2=0,	(з) _ Г 0,	«4 = о,
2ci, (*2 7^ 0, ^к [ 2ci, «4 О,
(4) _ ( 1,	«4=0,
~ | —сз + 2с2 cosfjrk/N) — 2ciashy/a4, сц 0.
Система (7.24) представляет собой систему уравнений с трех-
диагональной матрицей. При 6^0 эта матрица будет иметь
свойства диагонального преобладания, и для решения этой сис-
темы можно применить метод прогонки (см., например, ОНВ
п. 2.6.1).
Эффективность данного метода определяется эффективно-
стью вычисления преобразования Fn(...). Рассматриваемый на-
ми метод имеет широкое применение благодаря тому, что при
N = 2Р существует алгоритм, который позволяет вычислить пре-
образование Fn(...) за O(log2(TV)) операций. Этот алгоритм но-
сит название «быстрое преобразование Фурье» (FFT, Fast Fourier
Transform). В настоящее время процедура вычисления FFT явля-
ется стандартной и входит в состав всех инструментальных сред
и библиотек программ.
Суммируя изложенное выше, процедура решения уравнения
(7.17) состоит в следующем:
1)	проводят дискретное преобразование Фурье (7.23) правой
части, используя FFT;
2)	для каждого значения к = 1,..., N решают системы (7.24)
И НаХОДЯТ
1.3. Применение быстрого преобразования Фурье 167
3)	используя FFT, проводят обратное преобразование (7.21)
сеточной функции Vk,m для получения решения ип,т.
Полное число операций, необходимое для выполнения этой
процедуры составляет 7VS(2,5 log2(2Vs) +8), что значительно мень-
ше чем, например, в методе SOR.
Мы рассмотрели построение алгоритма, когда в граничных
точках при х = 0 и х = 1Х решение равно нулю. Можно легко
обобщить данный метод и для граничных условий (7.4). Запишем
уравнение (7.17) при п — 1:
+ (^Щ),т) ~ Сз^1,т + ^2^2,m + С1^1,»п+1 = fl,m-
Согласно граничному условию (7.18) слагаемое в скобках рав-
но нулю. Если задано граничное условие	то мы
можем перенести слагаемое с<2и$,т в правую часть, и при этом
левая часть уравнения будет такой же, как и для условия (7.18).
Таким образом, применяя рассмотренный выше алгоритм с мо-
дифицированными правыми частями
/1,т	~ с2У\.(Ут) •>	—	> Z/V — 1,т — ^29з{Ут)
мы получим решение уравнения с граничными условиями (7.4).
Естественно, что в конце вычислений мы должны положить и^т =
= gi(ym) и uN,m = дз(ут).
Построение метода для других типов специальных граничных
условий производится аналогичным образом. Дискретное пре-
образование Фурье в общем виде можно представить в следу-
ющей форме:
1 N
~	7ZZ — 0, . . . , Л/,
' к=0
где
срк п = sin — Для граничных условий (7.4),
(лкп\ ( 1/2, к = 0, к = N,
Рк^п - cos	о < к < N
— для граничных условий (7.5),
срк п = ехр	— для граничных условий (7.3).
Все эти преобразования вычисляются с использованием алгорит-
ма FFT.
168 Глава 7. Стационарные уравнения
Для граничных условий Неймана (7.5) правая часть должна
быть модифицирована следующим образом:
fo.m * fo,m ^^хУ^Ут), fN,m * fN,m ‘^СъЬхУЗ^Ут') •
Таким образом, мы полностью обсудили методы решения уравне-
ния (7.1) с постоянными коэффициентами, граничными услови-
ями (7.3)-(7.5) по х и граничными условиями общего вида по у.
Решение уравнения с граничными условиями (7.6)-(7.8) по у и
граничными условиями общего вида по х осуществляется совер-
шенно аналогичным образом.
Рассмотренный метод можно использовать для задачи с по-
стоянными коэффициентами и в трехмерном случае, выполняя
двойное преобразование Фурье по тем координатам, для кото-
рых заданы граничные условия специального вида.
Пример 7.2 (метод FFT). Применим метод FFT к задаче из
примера 7.1. Тогда система (7.24) примет вид:
h2
Vk,0 — 0,	1	2 (2 COs(7r/b/TV)) Vfc m ~Ь Vk m+1 ~
a
m = 1,..., M - 1, vk,M = dk,M-
На сетке N = M = 16 ошибка полученного решения
а время вычислений примерно в 10 раз меньше по сравнению с
методом SOR.
7.4.	Метод Конкуса и Голуба
Метод преобразования Фурье можно использовать и для реше-
ния стационарного уравнения более общего вида. При условиях,
допускающих применение этого метода, Конкус и Голуб предло-
жили итерационный алгоритм для решения уравнения (7.1) при
а(х) > 0 и 6(ж)	0. Рассмотрим кратко этот результат.
Если а(ж) имеет вторые производные, то можно ввести замену
переменных
v = иу/а(х).
7-4- Метод Конкуса и Голуба 169
Тогда уравнение (7.1) преобразуется к виду
з /9^
^d^~h{x}v = h (ж) ’	(7-25)
п=1 п
где
Граничные условия для v получаются из граничных условий
для и. Таким образом, замена переменной преобразует диффе-
ренциальную часть оператора в оператор Лапласа. Далее, для
решения уравнения (7.25) строится следующая итерационная схема:
3 Д2 (fc+l)
52 я 2-------cw(fc+1) - (А (®) - a) + /2 (®),	(7.26)
дх-
к = 0,1,... и 1/°)(ж) — некоторое начальное приближение, удо-
влетворяющее граничным условиям. Здесь а — параметр, кото-
рый можно менять для улучшения сходимости. При этом наилуч-
шая сходимость достигается когда
а =	( max (а(ж)) + min (а(х\)
2
Построим разностную аппроксимацию уравнения (7.26) на не-
которой сетке. В результате получим следующую итерационную
схему:
Aft^fc+1) - av<*+1) =	- а) + /2Л,	(7.27)
к — 0,1,..., где	д, /2 h — сеточные функции и	—
разностная форма оператора Лапласа.
Например, для двумерной задачи (7.9) эта схема записывается
как
С1 Vn,m-1 + c^vn-l,m VC3 + a)vn,m + c2^n+l,m + C1 un,m+l ~
= (fi(xn,ym) -	+ f2(xn,ym),
Общая структура метода выглядит следующим образом:
1)	задать начальное приближение и определить параметр а;
Глава 1. Стационарные уравнения
2)	для каждого значения к = 0,1,-.. решить уравнение (7.27)
относительно v^k+1\ используя FFT. Это становится воз-
можным, так как уравнение (7.26) представляет собой за-
дачу с постоянными коэффициентами;
3)	если при каком-то значении к
1и+,,и
где е — заданная точность, то v^k+i^ есть приближенное
решение уравнения (7.25);
4)	приближенное решение исходной задачи вычисляется как
Uh = V(hk+1)/y/^xj.
Если коэффициент а (ж) является относительно гладкой функ-
цией, то метод сходится за несколько итераций и это число ите-
раций слабо зависит от числа сеточных узлов.
Пример 7.3 (Метод Конкуса и Голуба). Рассмотрим уравнение
(7.9) при
1	х2 + у2
а(х,у) =—Ь(х,у) =--------------—-	и /(ж,?/) = 0
cos2 (ж?/)	cos2(;n/)
в области {0^ж^1,0^?/^1}и граничными условиями
1/(0, У) — 0, 1/(1, У) — sin(i/), и(х, 0) = 0, и(х, 1) = sin (ж).
Для этой задачи уравнение (7.25) имеет вид
d2v d2v 2 (ж2 + у2)
2	Л-2-------77 = 0-
ох1	иу-	cos2(#i/)
Введем равномерную разностную сетку с hx = hy = h. Тогда
итерационная схема для этой задачи записывается как
(fc+l) (к+1) _/4. аД2у (к+1) .	(к+1)	(к+1) =
^п,т~1	^п—1,т	гп,т ' ^n+l,m ' ^п,т+1
_ . 2 / %(хп + Ут) _ \ (*)
П \сО8ЦхпУт) J Vn’m’
п=	-1; т = 1,...,М -1; fc = 0,l,...,
v0,m] = U7V,m ’ =	т = 0,...,М,
7.5. Метод установления
vnfi1} = Vn,N1} = tgC^n), п = 0,..., N.
Параметр а вычисляется как
а= | (1/cos2 (1) + 1) «2,213.
£
При начальном приближении ип,т = 0 (п = 0,..., N; т = 0,..., М)
и е = 10“ 5 итерационный процесс сходится за 5 итераций. При-
ближенное решение показано на рис. 7.3. Точное решение этой
задачи — и(х, у) = sin(xy).
Рис. 7.3. Приближенное
решение уравнения (7.9),
метод Конкуса и Голуба
(TV = М = 16, г = 10~5)
Ошибка приближенного решения
= ||ц-ц(е)||2
||«(е)||2
«6,7- 10'5.
7.5.	Метод установления
Решение стационарной задачи можно рассматривать как равно-
весное состояние, к которому приближается решение некоторой
нестационарной задачи. Поэтому иногда удобнее и эффективнее,
с вычислительной точки зрения, решать такую нестационарную
задачу, чем непосредственно искать решение исходной стацио-
нарной задачи. Такой подход называется методом установления.
Мы обсудим основные идеи этого подхода на примере модельной
задачи
д2и д2и\
дх2 ду2 )
=	у),
(7.28а)
Глава 7. Стационарные уравнения
{Q^x^lx,Q^y ^1у},	(7.286)
«(О, у) = 91 (у) и и(1х,у) = д3(у),	(7.28в)
и(х, 0) = д3(х) и u(x,lv) = gi(x).	(7.28г)
Вначале мы должны сформулировать соответствующую не-
стационарную задачу. В нашем случае она может быть записана
в следующей форме:
dv (d2v d2v\	\	Zr_ х
а=°(а? + а?)“/(1'9)'	1 1
{0 х 1Х, 0 у ly}. v(x, у. 0) = д(х, у).	(7.296)
^(0,т/) = 9i(y)	и v(lx,y) = д3(у),	(7.29в)
v(x,ty=g2(x) и v(x,ly) = #4(я0-	(7.29г)
где функция д(х, у) задает произвольные начальные условия. Так
как граничные условия не зависят от времени, то естественно
ожидать, что решение v(x, у, t) с течением времени будет менять-
ся все медленнее и медленнее. Поэтому в пределе при £ —> оо это
решение будет стремиться к решению задачи (7.28), т.е.
lim v(x,y,t) = и(х,у).
Следовательно, вместо стационарной задачи (7.28) можно решать
нестационарную задачу (7.29) до некоторого момента времени
когда решение v(x, у, t) перестанет изменяться в пределах задан-
ной точности. Это и есть основная идея метода установления.
В соответствии с нашим рассмотрением теперь нужно постро-
ить разностную схему для задачи (7.29). Решение такого типа
задач мы обсуждали в гл. 4. Вначале рассмотрим явную схему
(4.26), которая применительно к нашей задаче имеет вид
.Л+1 — ук
’Jn,m п.т
---------------= а
n = 1,...,7V- 1;
r0,m — 91(Ут\
Vnfi1 =92(Хп),
(Axvn,m + AyV1^^ f(xn,ym),
m =	- 1; A: = 0,1,...,
vn,m = 9(xn,ym),
vN\m=93(ym), m = 0,...,M,
Vn+M = 9t(xn), n = 0,...,N.
Здесь и далее используются следующие обозначения:
^х^п,т ^2 G’n+l.m — 2Уп>т + ^п—1,ш) >
(7.30а)
(7.306)
(7.30в)
(7.30г)
(7.30д)
7.5. Метод установления
^yVn,m то (^n,m+l	+ vn,m — l) ’
ПУ
Тогда разностную схему для уравнения (7.28) можно записать в
виде
о (Ахипт + AyUn,m ) — f (хп 1 Ут),	(7.31а)
n = 1,...,2V—1; т = 1,...,М-1; А: = 0,1,...,	(7.316)
Uo,mffi(Um), u^mg3(t/m), т = 0,..., М,	(7.31в)
ип,оУ2(яп), и=мд4(хп), n = 0,...,N.	(7.31г)
Решая задачу (7.30), мы будем последовательно вычислять се-
точную функцию
«‘ = 0 * = 0,1,....
Когда эта функция уже не изменяется в пределах заданной точ-
ности, т. е.
||vfe+1 — vk\\
И+111
процесс установления завершается, и есть приближенное
решение стационарной задачи. Естественно, возникает вопрос:
всегда ли сеточная функция vk+1 будет приближаться к решению
стационарной задачи? Для того чтобы ответить на этот вопрос,
нам необходимо провести анализ поведения разности
еп,т = vn,m — un,mi	(7.32)
при к —> оо. Задачу (7.31) можно записать в следующей эквива-
лентной форме:
ип.т / Л	. л	\	£(	\
—	— О, у^.хип^т +	J \Хп, Ут) •>
'U"n,m ~ ^п,т>
п = 1,... ,Л7 — 1; т = 1,...,М-1; к = 0,1,...,
+ граничные условия.
Вычитая эти уравнения из (7.31), получим
рк+1 _ „к
~ а \^х^п,т + ^Уеп,т) ’	(7.33а)
en,m ~ vn,m ~ ип,т — 9(хп^Ут) ~	(7.336)
п = 1,...Л -1; m = 1,...,М-1; к = 0,1,...,	(7.33в)
Глава 1. Стационарные уравнения
=4+^=0, т = 0,..., М,	(7.33г)
<о1=<Л=0, n = 0,...,N.	(7.33д)
Для дальнейших оценок будем полагать, что N = М. Предпо-
ложим, что функция д(х,у) удовлетворяет граничным условиям
задачи (7.28). Тогда начальную ошибку можно представить в ви-
де конечного ряда Фурье:
7V-1 TV—1
еп,т ~ У? У2 sin(7rrn/^ sin(7rsm/JV).
s—1 r=l
Подставляя это выражение в уравнение (7.33), можно получить,
что
7V-1 7V-1
- Е Y. (ХГу8)к Qr,s sin(7rrn/TV) sin(jpism/N),
S=1 Г=1
где
Ar,s = 1 -	sin2(7rr/2./V).	(7.34)
Тогда относительную величину ошибки можно оценить как
\\ек\\	( \к
= а^	(7.35)
Поэтому, для того чтобы |\ек 11/1 |е° 11 стремилось к нулю, ко-
гда к —> оо, необходимо чтобы а < 1. Так как а = ск(т), то
при некотором значении т величина а будет наименьшей и зна-
чит будет наблюдаться самое быстрое уменьшение ошибки. Из
соотношения (7.34) видно, что Xieft Ans Xright, где
Xieft = 1 - 2 (Л + /32) cos2(7t/2A9	1,
Xright = 1 - 2 (ft + /32) sin2(7r/2W)	1,
hi	hi.
у
Увеличение г, начиная с т — 0, приводит к тому, что эти
крайние значения сдвигаются влево на числовой оси. При неко-
тором значении т — т* возникает ситуация, когда Xieft и Xright
располагаются симметрично относительно нуля, т.е.
Xieft - Xright.	(7.36)
При этом ск(т*) = |Xieft | = Xright- Это и есть наименьшее из всех
возможных значений ск, так как при дальнейшем увеличении г,
7.5. Метод установления
Xright будет Приближаться К нулю, a Xleft — удаляться от нуля
и а (г) — |А/ер| > а(т*). Таким образом, оптимальное значение т
определяется из условия (7.36) и равно
__	(^ж hy}
Т~ 2а (hl + h?y) •
Тогда
о = 1 — 2sin2(7r/2TV).
Количество шагов по времени к, необходимое для того, чтобы
ошибка начального приближения уменьшилась в 10р раз, можно
оценить из соотношения а — 10-р. Тогда
к = - р' 1п(10)
|_ln(l -2sin2(7r/2A0)
и для больших значений N
к
9
~^р • 1п(10) • N2
7Г2
•
Для расчета одного шага по времени по схеме (7.30) требуется
(?(№) операций. Тогда общее число операций будет 0(pN4/2) =
- O((7VS)2).
Можно построить более эффективный метод, используя схему
переменных направлений (4.32). Для уравнения (7.29) она запи-
сывается следующим образом:
Wn,m vn,m а / л	। д k \ г/	\	/^7 0^7 \
— g	^у^п.т) л!\хП)УтЬ (7.37а)
ТА	Zi
п = 1,..., N — 1;	m=l,...,M-l;	А: = 0,1,...,	(7.376)
vn,m = a	^Wn m + Д^+J)	_ 1/(ж„,ут),	(7.37в)
n=l,...,N -1;	т= 1, —1;	к = 0,1,...,	(7.37г)
^п,т= 9(хп,ут),	(7.37д)
u0,m =51(Ут),	дз(ут), т = 0,...,М,	(7.37е)
Со'=32(0’	v^M=9dxn), n = 0,...,7V.	(7.37ж)
Поведение ошибки (7.32) для этой схемы также описывается
выражением (7.35), только
176 Глава 7. Стационарные уравнения
(1-/31 sin2(7rr/2?/)) (1 - /?2 sin2(7rs/2/V))
r,s (1 + Д sin2(7r?727V)) (1 + /32 sin2(7rs/27V))
Минимальное значение а достигается при
__	hxhy	Nhxhy
2а • sin(7r/2TV) cos(tt/27V) атг
и для больших значений N равно
(7.38)
а = 1- —/— +	~ 1 - —
N \hy hx) ~ ЛГ
Количество шагов по времени к, необходимое для того, чтобы
ошибка начального приближения уменьшилась в 10р раз, оцени-
вается как
р • 1п(10)
7
N.
к ~
Тогда общее число операций будет O((7VS)3/2), что примерно со-
ответствует вычислительным затратам итерационного метода SOR.
Дальнейшее ускорение сходимости можно достигнуть прово-
дя вычисления со специальным образом подобранным набором
переменных шагов по времени {т>}. Однако построение тако-
го набора возможно только для задач, допускающих разделение
переменных, а в этом случае методы на основе FFT являются
более эффективными. Поэтому метод установления обычно при-
меняется для решения задач с переменными коэффициентами в
областях сложной формы, а также для некоторых нелинейных
задач. Естественно, что для таких задач невозможно получить
аналитические выражения для оптимального шага по времени,
но все же полученные нами соотношения можно использовать как
руководство для выбора т.
В качестве примера рассмотрим построение разностной схе-
мы для уравнения (7.2) при а (и) > 0 и граничными условиями
Дирихле. По аналогии с (7.15) схему переменных направлений в
этом случае можно записать в следующем виде:
к	к
^п,т	°п+1/2,тп ,
—	(^n+l,m — Шп,т
Тк
п
ип —1/2,m
2h2x
ак
г	\ , ип,тп+1/2 / к
\™п,т — W-l,m) Н 2^2	(Гп,т+1
1.5. Метод установления
ak
n,m-l/2 , k
2h2 \Vn,m

n = l,...,N -1- т = 1,...,М-1; * = 0,1,...,
\т wn,m	_	°n+l/2,m	,	A
—	(^n+l,m	— ^n,m)	“
7>	2hx
2/^2	\ШП,ТП	Wn-l,m)	-r	2^2	\vn,m+1 vn,m)
x	у
-I
п = 1,... ,7V- 1; т = 1,...,7И- 1; к = 0,1,...,
— Ут) •>
«О,™ =Л(Ут), vkN,m = 9з(Ут), ТП = 0,...,М,
4м)1 =g-2(xn), V^ = g4(xn), n = 0,...,N,
где
^п+1/2,т

к
ап,т+1/2 ~ а
Л
п,т+1
Здесь для приближения нелинейных членов мы использовали яв-
ную аппроксимацию, поэтому вычисления по этой схеме произво-
дятся так же, как и для линейной схемы (7.37). Для выбора шага
по времени используем соотношение (7.38), учитывая, что теперь
параметр а зависит от решения задачи:
(N 4- М) hx^y
?к =
7г ( шаха (v* ) 4- min а
\ г». т '	’	' п т
Пример 7.4 (метод установления). Рассмотрим уравнение (7.2)
при а(и) — ехр(—и) в квадрате {0 х 1,0 у 1} с гранич-
ными условиями
zz(0,2/)=0, zz(l, 2/) = 1п(1 + 2/),
(7.39а)
Глава 7. Стационарные уравнения
и(ж, 0) — 0, и(х, 1) = 1п(1 + х).
(7.396)
Правая часть уравнения
(1+эт/)3
Зададим разностную сетку с N — М = 10. При начальном условии
v$n = 0, (та = 0,...,TV; m = 0,...,M)
и е = 10~5 процесс установления сходится за 14 шагов. При-
ближенное решение показано на рис. 7.4. Точное решение этой
задачи — и(х,у) — 1п(1 + ху). Ошибка приближенного решения
1И4)-ц(е)112
||^)||2
«3-10“4.
Рис. 7.4. Приближенное решение уравнения (7.2) с граничными усло-
виями (7.39), метод установления (IV = М — 10, е = 10~5)
еа
7.6.	Заключительные замечания
В этой главе мы кратко обсудили вопросы, связанные с выбором
методов для решения наиболее часто встречающихся в физиче-
ских приложениях стационарных уравнений. Мы также рассмо-
трели основные особенности некоторых наиболее важных мето-
дов. Из методов, которые мы не рассматривали, следует упомя-
нуть метод циклической редукции, алгоритм FACR, основанный
на циклической редукции и FFT, и многосеточные методы. Все
7.6. Заключительные замечания
они имеют довольно громоздкое обоснование, сложность кото-
рого выходит за рамки этой книги. Описание методов цикличе-
ской редукции и FACR читатель может найти в книге Р. Хокни,
Дж. Иствуд «Численное моделирование методом частиц», Мир,
1987, а описание многосеточных методов — в книге Н. С. Бахва-
лов, Н. Н. Жидков, Г. М. Кобельков «Численные методы», Лабо-
ратория базовых знаний, 2000.
ГЛАВА 8
ДВИЖЕНИЕ
НЕСЖИМАЕМОЙ
ВЯЗКОЙ
ЖИДКОСТИ
Модель несжимаемой вязкой жидкости описывает самые разно-
образные явления, такие как, например, волны в океане, движе-
ние атмосферы, обтекание тел при малых скоростях набегающе-
го потока и т. д. Широкое применение эта модель имеет и в раз-
личных инженерных приложениях. Движение несжимаемой вяз-
кой жидкости описывается уравнениями Навье-Стокса в пред-
положении, что плотность жидкости постоянна. Это предполо-
жение, с одной стороны, упрощает уравнения, а с другой сто-
роны, создает некоторые новые особенности, которые затрудня-
ют решение этих уравнений. Вначале мы рассмотрим различные
формы уравнений Навье-Стокса, на основе которых мы в даль-
нейшем будем строить численные схемы.
8.1. Введение
Уравнения Навье - Стокса для несжимаемой жидкости имеют вид:
1) уравнение неразрывности
div(u) - О,
2) уравнение движения
ди
р— +p(U’V)u = -Vp + z/Ди + fe(x^ (8.1)
x e D, t o,
u(x,0) = go(®) + граничные условия.
8.1. Введение
или в разверну том виде:
£^ = о,
^1дхк
дип . V' dUn др V'd2un _1_ t (	t\
^+^Eu^ = -^;+^E
k=l	k=l	K
n — 1,2,3. Здесь
(и	\	/ tzi	\
V I — I U2 I -
W	У	\ Us	/
скорость частиц жидкости в точке х = (a?i, #2, #з) в момент
времени t, р — плотность жидкости, р — р(х, t) — давление,
и — коэффициент вязкости и f e(x,t) — внешние силы.
Запишем уравнения (8.1) в безразмерном виде. Для этого вве-
дем новые переменные и*, р*, х* и t*:
и = и* • ис, р — р* • ри^, Х = Х* - I,
t = t*-l/uc, fe=re-pu2Jl,,
где I и ис представляют некоторые характерные параметры за-
дачи. После этого уравнения (8.1) принимают вид:
div(u*) = 0,	(8.2а)
^ + («’  V) и* = -Vp* +	Г),	(8.26)
(Jlf	led
здесь Re = pucl/v — число Рейнольдса. В дальнейшем мы будем
использовать безразмерные уравнения. При этом знак «*» мы бу-
дем опускать. Характер течения определяется величиной числа
Рейнольдса. Можно выделить три основных режима течения:
Re 1. В этом случае вязкие силы значительно меньше инер-
ционных сил, что приводит к очень сложной картине течения
из-за возникновения турбулентности.
Re — 0(1). В этом режиме вязкие силы сравнимы с инерци-
альными.
Re 1. Этот режим характерен для течения очень вязких
жидкостей. В этом случае уравнения (8.2) можно заменить ли-
нейным стационарным уравнением.
Мы будем рассматривать методы решения задач, для которых
реализуются первый и второй режимы течения.
Глава 8. Движение несжимаемой вязкой жидкости
Одной из трудностей в решении уравнений (8.2) является то,
что отсутствует эволюционное уравнение для давления. Для не-
сжимаемой жидкости давление не имеет своего обычного термо-
динамического смысла, а является следствием несжимаемости.
Обычно мы сталкиваемся с задачами о течении жидкости в
некоторых замкнутых областях или с задачами об обтекании тел.
В этом случае возникает вопрос о постановке условий на гра-
ницах области или поверхности тела. Из вида уравнений (8.2)
следует, что удобнее всего формулировать граничные условия
для скорости. Разберем, например, постановку граничных усло-
вий в двумерном случае. Пусть п есть единичный вектор нормали
к границе в точке (ж, у), a fc — вектор касательной в той же точ-
ке. Часто на практике задаются следующие условия:
1)	для нормальной скорости —
(u,n) = gn(x,y,t),	(8.3)
здесь (•, •) — скалярное произведение,
2)	для касательной скорости —
(u,fc) - gk(x,y,t),	(8.4)
или условие свободного проскальзывания
^l^ = (V(u,fe),n) = 0,	(8.5)
on
3)	равенство нулю нормального и касательного напряжения
на свободной поверхности (более подробно этот случай мы
рассмотрим позже).
Мы рассмотрим два подхода к решению уравнений Навье-
Стокса. Первый из них основан на уравнениях (8.2), где кон-
вективный член записывается в дивергентной форме, что дает
следующие уравнения:
div(u) = О,
ди dfx(u) dfy(u) dfz(u)	.
= -Vp+ -Г^и + fe(x,t),
rte
8.1. Введение 183
Здесь
(и2 \	/ v-u \	/ w • и \
и • V , f у (и) = I V2 , f z (u) = W  V .
и • W J	у V • W У	у w2 У
Если течение не содержит свободных поверхностей, то мож-
но исключить давление, взяв операцию rot от уравнения движе-
ния (8.2). Учитывая, что rot(grad(p)) — 0, можно получить
1
— + (и • V) ш - (ш • V) и = — Ди + rot (f е(х, t)),	(8.7)
ut	ne
w(x, 0) = rot (go(x)), x e D, 0,
где w = rot(u) — завихренность. Левая часть уравнения опи-
сывает перенос завихренности вместе с жидкостью. Определим
скорость через функцию тока гр следующим образом:
и = rot (гр).	(8.8)
Так как div (rot (гр)) — 0, то условие неразрывности выпол-
няется. Для того чтобы замкнуть уравнения, нам необходимо
соотношение между завихренностью и функцией тока. Для этого
возьмем операцию rot от (8.8) и получим
rot (и) — щ = rot (rot (и)) = —Агр + grad (div (гр)).
Функция тока определяется из уравнения (8.8) неединствен-
ным образом, поэтому нам необходимо некоторое дополнитель-
ное условие. Удобнее всего положить div(t/?) = 0. Тогда связь
между щ и гр выражается уравнением Пуассона
Д-0 = -щ.	(8.9)
Таким образом, мы получили замкнутый набор уравнений для
описания движения несжимаемой жидкости: эволюционное урав-
нение для завихренности, уравнение Пуассона (8.9) для функции
тока, из которой определяется поле скоростей согласно уравне-
нию (8.8). Граничные условия для о? и гр следуют из граничных
условий для и. Уравнения (8.7)-(8.9) называются уравнениями
Навье-Стокса в переменных функция тока-завихренность. Эта
форма особенно удобна в случае двумерных задач, когда
(u(x,y,t) \	/ feyl(x,y,t) \
v(x,y,t) И fe = fey2(x,y,t) .
о /	\	0	/
Глава 8. Движение несжимаемой вязкой жидкости
Тогда нетрудно получить, что
/ ° \	/ 0 \
ы = I О I и -0 = I О I .
\ ш /	\ Ф /
Система уравнений (8.7)-(8.9) при этом значительно упроща-
ется и принимает вид
доз доз доз 1 / д2оз д2сз\	.
~dt+ud^ + vd^~ Re \д^ + fa?) + Mx>y’f)’ (8-10)
/	(^90,2	ддо 1
а2)/; а2)/;
а^ + а? = ~“(
(х,у) е D, t о,
(8.11)
(8-12)
где
fs(x,y,t) =
:,е
Обычно граничные условия задаются на и и v. Тогда из урав-
нения (8.8) мы получим граничные условия для которые ис-
пользуются при решении уравнения (8.9).
8.2. Разностные схемы в переменных
функции тока-завихренность
Перейдем к построению разностных схем для уравнений (8.10)—
(8.12) в прямоугольной области {0 < х < 1Х, 0 < у < 1У}. Предпо-
ложим, что fe= const. Граничные условия примем в следующем
виде:
°
91 (У, 0 / ’
ЫМ) \
0 / ’
0
9s(y,t)
34(2^, 0
0
которые, согласно (8.12), преобразуются в
8.2. Схемы в переменных функция тока-завихренность
ф \ дф/дх J	(о,у)	(	0 -л (у, 0
Ф \		0
дф/дх J		. -5з(уЛ)
Ф \		'	0
, дф/ду )	(ж,0)	< 92 (ж, <)
Ф \		( °
дф/ду J	(ж,/у )	54 СМ)
Введем разностную сетку с узлами (хп, ут, tk) и шагами hx =
г = lx/N, hy — ly/M и Tk. Для построения разностной схемы
для уравнения (8.10) применим метод расщепления. Производная
по времени аппроксимируется разностью вперед, первые про-
изводные по пространству — центральной разностью и вторые
Производные — обычным трехточечным разностным отношени-
ем. В результате получим:
, Л+1/2 / л
Тк
_ к	^п—1,т
“ ~Un’m 2hx
п = 1,... ,N — 1;
k’n+l.m	m	/о i о \
Re -Л2	’ (	'
т = 1,..., М — 1,
o.fc+1 _ Шк+Ф2
Тк
, Л+1/2 _ ( к+1/2	* *+1/2	9 к+1/2	*+1/2
к Шп,т-Ы шп,т-1	шп,т+1	£Шп,тп	’ ^n,m—1
Vn’m 2hy	Re • h2
*	У
(8.136)
n=	1; m = 1,...,M- 1, к = 0,1,...
Уравнение (8.11) представляет собой уравнение Пуассона с по-
стоянными коэффициентами. Поэтому для аппроксимации этого
уравнения можно использовать схему (7.17) с а = 1 и Ь — 0, ле-
вую часть которой мы обозначим как P(ttn>m). Тогда разностная
схема для определения ф в момент времени имеет вид
186 Глава 8. Движение несжимаемой вязкой жидкости
P«ro1) = -W^,	(8.14а)
n = l,...,7V -1; m = 1,...,М-1.	(8.146)
Аппроксимируя уравнения (8.12), мы получим формулы для
вычисления скоростей в момент времени tfc+r.
_________________________________гЬк+г
fc+1 _ ^n,m+l
(8.15а)
2hy
□/Л+1	—	+ 1
2hx
m = 1,...,M- 1.
= —
vn,m
(8.156)
п =	— 1;
(8.15b)
Нам осталось сформулировать граничные условия для уравне-
ний (8.10) и (8.11). Для примера рассмотрим граничные условия при
х = 0. Первое условие в разностной форме имеет простой вид:
^,„=0, т = 0,...,М.	(8.16)
Для аппроксимации второго условия применим метод фиктив-
ных областей и получим
?/Л+1 _ ?/Л+1
-----= -91(ym,tk+l)-
Как обычно, запишем уравнения (8.14) при п — 0:
(*К - 2«ii‘++ ц №ii+, - 2*й»‘+=
= -4S-
Далее выражая фиктивное значение из предыдущего соотноше-
ния и учитывая условие (8.16), окончательно получим
~ д2 (^l,m Ьх91(Ут, ^/г+1)) ?
m = 1,...,М - 1.
(8-17)
Это соотношение определяет граничное условие для завихренно-
сти при х = 0, так как в момент времени tk+i нам известно
из решения уравнения (8.14). Вычисление граничных условий на
других границах осуществляется совершенно аналогичным спо-
собом.
8.2. Схемы в переменных функция тока-завихренность
Так как схема (8.13) является явной, то возникает вопрос об
устойчивости этой схемы и выборе шага по времени. В схемах
расщепления устойчивость всей схемы обусловливается устойчи-
востью одномерных схем. Поэтому, применяя принцип «заморо-
женных» коэффициентов, мы должны сначала исследовать на ус-
тойчивость схему (8.13) для уравнения
дш дш 1 д2ш
dt С дх + Re дх2 ’
где с — const. Из критерия фон Неймана можно получить огра-
ничение на шаг по времени
т min
4Re-/>2	1	2
4 + c2Re2/»2 ’ 2Re' x
Распространение этого результата на схему (8.13) приводит
с следующему условию:
Tk min (и, т2),
(8.18)
где
Т1 < min
4Re •/»2	1	,,
----------Ч--------, 2^  hx
max(u* )2 ) Re2/»2
п,т ’ J
4Re  /г2	1	„
—7---------\------->2^-^ •
4 + I max(u* )2 Re2/»2
\ п,т	/	/
Это условие показывает, что при больших числах Рейнольдса
возникает сильное ограничение на шаг по времени. Применение
неявной схемы не решает этой проблемы, так как в этом случае
уравнения (8.13) и (8.14) становятся связанными через граничное
условие (8.17), что приводит к крайне неэффективному алгорит-
му для нахождения (a/+1, ^+1). Решение этой проблемы требует
изменения процедуры интегрирования по времени. Схему рас-
щепления можно представить в следующем виде:
^0,т __ р	_
dt ~ ’ dt ’
(8.19а)
188 Глава 8. Движение несжимаемой вязкой жидкости
&8п,т
dt
= —и
к
п,т
gn+l,m gn—l,m
2hx
3n+l,m %$п,т 4" ^n—l,m
Re • h2 ’
(8.196)
tk^t^tk + тк'. n - 1,... .N - 1;	(8.19b)
m =	1, sn,m (tk) = Wn>TO,	(8.19r)
dqnfi = 0 d^M = 0,
dt	dt
d([n,m _ к Qn,m+1 Qn,m — 1 j Qn,m+1 ^Qn,m 4“ Qn,m—1
dt ~ ~Vn'm 2hv +	Re-h%	’
(8.206)
tk tk 4- Tk'. n - 1,.... N - 1;	(8.20b)
ТП — 1. M 1; Q.n,m (tk) — Qn,m (tk 4“ ^k) •	(8.20r)
To есть мы аппроксимировали разностными отношениями только
производные по пространству и получили при каждом значе-
нии (п.т) системы обыкновенных дифференциальных уравне-
ний. Последовательное решение этих систем дает нам
^гуп = Яп,т (tk 4“ Tk) •
Схемы (8.19), (8.20) можно записать в матричном виде:
dsm ___
~Т7~ — Ат^гп',
dt
sm(tk) — задано,
tk t tk 4“ Tk.
т — 1,...,М- 1,
(8.21)
dQn
j, — Bn<ln, tk t tk 4~ Tk.
dt
Qn(tk) — задано, n — 1,..., N — 1,
(8.22)
где
sm — {s0,m, • • • 5 sN,m} ? Qn ~ {#п,0> • • • •> Яп,м} •
и Am, Вп — трехдиагональные матрицы. Устойчивость того или
иного метода решения систем обыкновенных дифференциальных
уравнений вида ds/dt — Аз зависит от собственных значений
матрицы А. а именно: параметр р — Tk\j(A) должен принад-
лежать некоторой области на комплексной плоскости для всех
8.2. Схемы в переменных функция тока-завихренности
j — 1,..., J, где J — число уравнений. Форма области зависит
от метода. Оценим собственные значения матриц Ат и Вп- Эти
матрицы не являются постоянными, поэтому на основе принципа
«замороженных» коэффициентов мы будем работать с некоторой
постоянной матрицей До, которая имеет такую же структуру
как матрицы Ат и Вп- Нас интересует случай больших чисел
Рейнольдса. Поэтому в пределе Re —> оо матрица До будет иметь
вид
где h принимает значение либо hx, либо hy и с = const. Собствен-
ные значения этой матрицы равны
Ay (Ao) =-^sin(7rj/L), j =
т.е. все собственные значения принадлежат отрезку [О, —г • c/h],
здесь i — мнимая единица. Возвращаясь к матрицам Ат и ВП1
можно заключить, что при Re —> оо собственные значения ма-
трицы Ат в момент времени tk принадлежат отрезку
Aj (Дт) £
г
— — шах
hx п,т
2 I k
— шах \и
1гх п,т 1	’
(8.23)
Кт|

и аналогично для матрицы Вп
Xj (Вп) G
г
— — шах
Пу п,т
(8.24)
j = 1,...,М.
Эти результаты говорят о том, что для интегрирования си-
стем (8.21) и (8.22) необходимо применять метод, область устой-
чивости которого включает мнимую ось. Наиболее подходящими
являются методы Рунге-Кутта порядка выше второго (см. ОНВ,
рис. 6.4). Возьмем трехстадийный метод третьего порядка. На
рис. 8.1 показана часть области устойчивости этого метода вбли-
зи мнимой оси. Схема Рунге-Кутта 3-го порядка будет устой-
190 Глава 8. Движение несжимаемой вязкой жидкости
чива для систем (8.21) и (8.22), если параметр р для собственных
значений (8.23) и (8.24) будет принадлежать отрезку [—г • a, i • а],
где а & 1,6. Учитывая, что при конечном значении числа Рей-
нольдса члены со второй пространственной производной также
влияют на устойчивость, мы приходим к условию Tk min (ti , Т2),
где
1,6 mm(hx,hy)	1	.	2
И =------т2 =	,
max ( max |u*,m|, max |v* |)
\ n,m 1	’ 1 n,m 1	’
которое накладывает более слабое ограничение на шаг по време-
ни, чем условие (8.18) при том же шаге по пространству.
Рис. 8.1. Область устой-
чивости метода Рунге -
Кутта 3-го порядка вбли-
зи мнимой оси. Область
устойчивости находится
слева от кривой
В качестве примера можно привести схему Рунге - Кутта 3-го
порядка, которая задается следующей таблицей Бучера:
Таблица 8.1. Параметры схемы Рунге-Кутта 3-го порядка
О
1/2
3/4
1/2
О 3/4
2/9 1/3 4/9
Тогда процедура решения системы (8.21) строится следующим
образом:
0^4” 1  	1
—---------- = т (2di + 3d2 + 4d3),
Тк	У
8.2. Схемы в переменных функция тока-завихренность
где
/	1	\	/ з \
dl — Am^rn,-) d2 — Ат ( $т ~^~kdl ) > с/з — Ат ( $т ~^J~kd2 ) •
Аналогичная процедура применяется затем к системе (8.22).
Суммируя изложенное выше, процедура вычисления одного
шага по времени организуется следующим образом:
1)
2)
3)
4)
по известному в момент времени tk полю скоростей вычи-
сляется шаг по времени т&;
во всех внутренних точках области вычисляется завихрен-
ность в момент времени tk+i- Для этого используется либо
схема (8.13), либо схема (8.21), (8.22);
функция тока в момент времени tk+i определяется из реше-
ния уравнения (8.14) с граничными условиями вида (8.16).
Так как коэффициенты этого уравнения постоянны, то мож-
но применить методы на основе FFT;
по известной функции тока вычисляется завихренность в
граничных узлах и поле скоростей в момент времени tk+i
по формулам (8.15).
Пример 8.1 (движение жидкости в полости). Рассмотрим дви-
жение жидкости в квадратной полости {0^ж^1,0^?/^1}.
Пусть в момент времени t = 0 жидкость покоится:
и(х,у,(У) = v(#,?/,0) — 0.
Нормальные к поверхности полости компоненты скорости равны
нулю:
ti(0, у, t) = w(l, у, t) = 0, v(x, 0, t) — v(x, 1, t) — 0.
На верхней границе полости задается касательная скорость
и(х, 1, t) — Uq • Sm(0,17F • t),
что приводит к возникновению вихревого движения внутри по-
лости. На остальных границах задается условие свободного про-
скальзывания:
= |^(0, у, i) = о,	= 0.
дх	дх	ду
На рис. 8.2 показано решение этой задачи в момент времени t = 15.
Течение жидкости происходит вдоль изолиний функции тока.
192 Глава 8. Движение несжимаемой вязкой жидкости
Рис. 8.2. Изолинии функ-
ции тока для течения в по-
лости (Re = 103, N = М =
= 32)
8.3. Метод маркеров и ячеек
Применение переменных функция тока-завихренность бывает не
всегда удобно для решения задач о течении вязкой несжимаемой
жидкости. Так в течениях со свободными поверхностями исполь-
зование этих переменных сильно затрудняет постановку гранич-
ных условий. Использование в качестве неизвестных функций
давления и компонент скорости позволяет избежать многих слож-
ностей, особенно в трехмерных задачах. Поэтому в дальнейшем
мы будем работать с уравнениями (8.6). Одним из часто исполь-
зуемых методов является метод маркеров и ячеек (MAC, Marker
and Cell). Первоначальная идея была предложена Харлоу и Уэл-
чем, которая затем получила дальнейшее развитие в различных
модификациях метода МАС. В этом методе производится инте-
грирование уравнений движения несжимаемой вязкой жидкости
с одновременным рассмотрением маркеров-частиц, перемещаю-
щихся со скоростью жидкости. Мы обсудим основные особен-
ности этого подхода на примере решения двумерных задач в
прямоугольной области.
Введем разностную сетку с шагами hx = xn±i — хп и hy =
= Ут+i — Ут- Параметры жидкости будут определяться в «сме-
щенных» точках, как показано на рис. 8.3.
Предполагая, что давление в момент времени tk известно, на
первом этапе вычисляется промежуточное поле скоростей на осно-
ве следующей аппроксимации уравнений (8.6):
8.3. Метод маркеров и ячеек
Рис. 8.3. Расчетная ячейка в методе МАС. л?+1
В точках «•» вычисляется компонента ско-
рости щ в точках «х» — компонента v;
давление вычисляется в точках «□»
Л7+1/2
т
п	л+1/2	л+1
Un,т+1/2 Un,т+1/2	\U ) п+1/2,т+1/2	\U /п-1/2,m+1/2
~	‘ V^n,m _	Рп+1/2,т+1/2 ~ Рп-1/2,т+1/2
hy	hx
+ jife (+un,m+1/2 + +un,m+1/2) + fe,l(Xn,ym+l/2itl+ (8.25)
n = 1,... ,N - 1; m =	— 1,
(U • U)n+l,m - (Ц • v/jm
hx
Pn+l/2,m+l/2 Pn+l/2,m-l/2
hy
+	+ ^yVn+l/2,m} + fe,2^n+l/2тУт^к) i (8.26)
n	1; m =	- 1,
где
)n+1/2,m+1/2 ~~ Un+l,m+l/2 * Un,m+l/2^
)n+l/2,m+1/2 ~~ Vn+l/2,m+l ’ Vn+1/2,mi
* ^)n,m	^n,m+1/2	Un,m —1/2^ ^n+l/2,m + ^n—1/2,m^ >
194 Глава 8. Движение несжимаемой вязкой жидкости
(7/
an,m+1/2
ип+1/2,т
л I m+1/2
I 1)к
\ ^71+1/2,m
_ 1 ( Un+1,m+1/2	2wn,m+1/2 4" wn-l,m+1/2
\ Vn+3/2,m “ 2rn+l/2,m 4" Vn-l/2,m
_ J_ f Un,m+3/2 ~ 4,m+1/2 + Un,m-l/2
h2y \ Vn+l/2,m+l — 2rn+l/2,m 4" Vn+l/2,m-l y
Соотношения (8.25) и (8.26) необходимо еще дополнить гра-
ничными условиями, записанными в разностной форме. Рассмо-
трим, например, расчет граничных условий, заданных на верти-
кальной границе х — 0. Тогда вектор нормали п = (1,0), вектор
касательной k = (0,1) и условия (8.3)-(8.5) принимают вид
u(0,y) -gn(y,t),	(8-27)
f(0,y) - ffk(y,t),	(8.28)
или
(8.29)
g(0.») = °.
Разностная форма условия (8.27) записывается очень просто:
U0,m+1/2 = Sn(ym+l/2,tk+l), m = 0,...,M -1.
Условие (8.28) или (8.29) используется для определения скорости
v в точке (1/2, т) через расчет величин (и • т и Дж^/2,т-
Эти величины включают в себя мнимое значение v_1/2,m- Для
исключения этого значения в случае условия (8.28) можно поло-
жить
V-l/2,m ~~ ^9k{ym^k) ^1/2,m’
2 (4/2,m + v-l/2,m) = 9k(Vr
а в случае условия (8.29) —
k	k
Vl/2,m - ^-1/2,m _	к _ k
— U	r-l/2,m — rl/2,m-
Расчет условий на других границах производится аналогичным
образом.
Исследование устойчивости схем (8.25), (8.26) проводится так
же, как и для схемы (8.13). В результате мы получим следующее
условие:
1
4(7з +74)
Tk min I ------------~------------7, —------т I ,
\4 (7з + 74) + (71 4- 72)	2 (7з + 74) I
8.3. Метод маркеров и ячеек
где
7! = —max|u* I, 72 = — max|t£ |,
flx п,т ’	fly п,т ’
73 = Re-h2x’	74 = Re №'
л	у
Вычисленные промежуточные значения скорости могут не удо-
влетворять условию неразрывности, записанному для каждой рас-
четной ячейки, т. е.
л^+1/2
n+l/2,m+l/2 —
fc+1/2	_ £+1/2	£+1/2	_ £+1/2
_ Wn+l,m+l/2 Un,m+l/2 Vn+l/2,m+l Vn+l/2,m ,
hx	+	hy	* ’
n — 1,..., N — 1; m — 1,..., M — 1.
Поэтому эти промежуточные значения необходимо скорректи-
ровать для того, чтобы условие неразрывности выполнялось для
каждой расчетной ячейки. Для этого введем некоторую потенци-
альную функцию 92, и окончательные значения скоростей будем
вычислять по формулам:
£+1	_ £+1/2	_ ^n+l/2,m+l/2	^n-l/2,m+l/2
^n,m+l/2	^n,m+l/2	L	’
fc+1 _ k+l	(8-30)
£+1	_ £+1/2	_ ^n+l/2,m+l/2	^n+l/2,m-l/2
^n+l/2,m	^n+l/2,m
Тогда
л£+1	—	_
n+l/2,m+l/2	n+l/2,m+l/2
^n+3/2,m+l/2	^n+l/2,m+l/2	Yn-l/2,m+l/2
h2x
£+1	_ n Aj+1	I Aj+1
^n+l/2,m+3/2	^^n+l/2,m+l/2	^n+l/2,m-l/2
h2y
Из требования m+1/2 — 0 следует разностное уравнение
Пуассона для вычисления функции (р:
Р (^n+l/2,m+l/2) “ ^n+l/2,m+l/2‘	(8.31)
ижение несжимаемой вязкой жидкости
Граничные условия для этого уравнения следуют из гранич-
ных условий для нормальной к границе компоненты скорости.
Так как промежуточные и окончательные значения скоростей
удовлетворяют граничным условиям, то из (8.30) следует, что
(V/^n) = 0 во всех точках границы, здесь — разностная
форма оператора V.
Давление в момент времени tk+i вычисляется по известным
значениям функции <р. Так соотношение (8.25) можно предста-
вить в виде
/ q \ к
к+1/2	_ к ,	/ \ I dP\
Un,т+1/2 “	т+1/2 + Тк (• • •) тк I о I
\ОХ/ п,т+1/2
Корректировку (8.30) можно трактовать как введение неко-
торого дополнительного поля давления, т. е.
/Л \ к + 1
?Л+1	_ ?/+1/2	_
%,т+1/2 — ап,т+1/2
— Un,m+1/2 + Тк (• • •) rk
п,т+1/2
(др\к +(др^к+1
^дх)п,т+1/2	\дх
п, т+1/2
Тогда
/ dp \	/ dp \	* р
- +-	= -П	=> р* = —
\ОХ)	\ ОХ )	Tk
и давление в момент времени tk+i вычисляется как
„А;+1	_ к	, ^n+1/2,m+1/2
^n+1/2,m+1/2	"n+1/2,т+1/2
п = 1,... ,7V — 1; т = 1,..., TVf — 1.
Если в задаче отсутствуют свободные поверхности, то вы-
числительный процесс на этом заканчивается, в противном слу-
чае вводятся частицы-маркеры. Эти частицы не участвуют в
вычислении движения жидкости непосредственным образом, а
служат для выделения свободной поверхности и визуализации
течения. В начальный момент времени предполагается, что по-
ложение маркеров известно. Дальнейшее их перемещение опреде-
ляется движением жидкости и описывается уравнениями:
= u(xp,yp,t),	= V (xp,yp,t), p—l,...,Np, (8.32а)
8.3. Метод маркеров и ячеек
Хр (0), ур (0) — заданы,	(8.326)
где (хр,ур) — координаты маркера в декартовой системе коор-
динат.
Для получения разностной формы уравнений (8.32) исполь-
зуется линейная интерполяция скорости как по пространству,
так и по времени для каждой разностной ячейки. Пусть, напри-
мер, маркер с номером р находится в момент времени tk в ячейке
{хп С х < хп+1,ут < у Ут+1}> и значения скорости в узлах
(n, m + 1/2), (n +1, т +1/2), (n + l/2,m) и (n + l/2,m + l) извест-
ны как в момент времени £&, так и в момент времени tfc+i. Тогда
положение этого маркера в момент времени вычисляется по
формулам:
Л+1 _ Л
р	*Ьр
Un^m+l/2 + Un, m+1/2
Un+1,m+1/2 + Wn+1,m+1/2/ (Хр Хп
Ур+1 +	1/2,m + *4+1/2,m) (^+1 ~ Ур) +
+ (Vn+l/2,m+l + Гп+1/2,т+1) (Ур “ ?/m)] •
Положение жидкости определяется распределением маркеров
по ячейкам разностной сетки. При этом выделяется три типа
ячеек: пустая ячейка (Е), которая не содержит маркеров, поверх-
ностная ячейка (S), которая содержит частицы-маркеры и гра-
ничит с пустыми ячейками и ячейки жидкости (F) (см. рис. 8.4).
Давление в пустых ячейках равно рвнеш, которое для просто-
ты мы будем считать равным нулю, так как мы всегда можем
этого добиться путем замены р —> р — рвнеш- Тогда граничным
условием на свободной поверхности будет отсутствие нормаль-
ного и касательного напряжений. Если п = (пх,Пу) есть вектор
нормали к свободной поверхности в некоторой точке, то эти усло-
вия имеют вид:
(8.33)
Глава 8. Движение несжимаемой вязкой жидкости
Расчет давления и компонент скорости в поверхностных ячей-
ках осуществляется специальным образом и основывается на гра-
ничных условиях (8.33) и условии неразрывности. При этом вы-
деляется четыре типа поверхностных ячеек, а именно:
1)	ячейки, граничащие с одной пустой ячейкой;
2)	ячейки, граничащие с двумя пустыми ячейками;
3)	ячейки, граничащие с тремя пустыми ячейками;
4)	ячейки, окруженные пустыми ячейками и представляющие
собой изолированные капли.
Рис. 8.4. Частицы-маркеры определяют ячейки, занятые жидкостью
Наличие свободной поверхности вносит свои коррективы и в
вычисление потенциальной функции ср. Для ячеек, занятых жид-
костью, справедливо уравнение (8.31) с граничным условием ср — О
в поверхностных ячейках. При этом область определения урав-
нений (8.31) задается положением частиц жидкости, а значит
зависит от времени. Если эти уравнения дополнить соотноше-
нием ср — 0 в пустых ячейках, то мы получим систему уравнений
с переменными коэффициентами и с постоянной областью опре-
деления, которая совпадает с областью определения задачи. Для
решения полученных уравнений обычно применяются итераци-
онные методы. Так как поле скоростей меняется незначительно
8.3. Метод маркеров и ячеек
в течение одного шага по времени, то в качестве хорошего на-
чального условия для вычисления ср в момент времени t^i можно
взять значение этой функции в момент времени
Суммируя все изложенное выше, расчет одного шага по вре-
мени для течения со свободными границами производится следу-
ющим образом:
1)	по известному в момент времени tk полю скоростей опреде-
ляется шаг по времени т&;
2)	по известным в момент времени tk координатам маркеров
выделяются ячейки жидкости (F) и поверхностные ячейки (S);
3)	вычисляются промежуточные скорости в ячейках F;
4)	решается уравнение Пуассона для определения функции <р;
5)	в ячейках F вычисляются скорости и давление в момент
времени ffe+1;
6)	вычисляются скорости и давление в ячейках S;
7)	определяются новые положения маркеров в момент времени
Пример 8.2 (взаимодействие струи вязкой жидкости с жест-
кой стенкой). Рассмотрим задачу о столкновении тонкой струи
жидкости с жесткой стенкой. Пусть жидкость выдавливается в
верхней части полости через щель шириной d со скоростью vq и
движется вниз под действием силы тяжести. Возникающее тече-
ние можно описать двумерными уравнениями (8.6) при
Л,1 - 0,	fe,2 = -gd/v^,
в прямоугольной области {0 С х С /<т,0 С у С 1У} с начальными
условиями
и(х,у,0) — v(x,y,0) = О
и граничными условиями
и(х, 0, t) — v(x, 0, t) = 0, и(х, ly, t) — О,
v(x,ly,t) — —vo, —d/2 ОС d/2,
здесь g — ускорение свободного падения. На рис. 8.5 показана
динамика течения при следующих параметрах
d = 0,005 м, vo — 0,5 м/с, и/р — 0,01 м2/с,
так что число Рейнольдса, основанное на d, vq и v/р, равно Re =
= 0,25.
Глава 8. Движение несжимаемой вязкой жидкости
Рис. 8.5. Визуализация течения в различные моменты времени: а) —
t = 0,125 с; б) — t = 0,2375 с; в) — t = 0,3 с; г) — t =
= 0,425 с; д) — t — 0,4875 с (из статьи М. F. Tome et al.,
«А finite difference technique for simulating unsteady viscoelastic
free surface flows», J. Non-Newtonian Fluid Meeh., 106 (2002),
pp. 61-106, с разрешения Elsevier)
ПРИЛОЖЕНИЕ А
ПАРАМЕТРЫ
И ДИСПЕРСИОННОЕ
СООТНОШЕНИЕ
ДЛЯ СХЕМЫ РЕМ
Параметры ат, bm (m = 1,2,3) в выражениях (5.21) и (5.22) опре-
деляются следующим образом:
611 = —То-1—77 (-г2 + г1(! - ^з) + (1 - 2zi)(2:i + z4)),
Z2VOZ1 — 1)
г3 - z4
612 = 3^1’
аз = ~ 7ч1—77 (-22 + (1 - 2zj)(l - Z3) + Zi(zi + z4)),
^{OZ! - 1)
h
b2 = (5^wl + 21b23-’4)-
>2 = а(зЛ ik (212, + (1~ 221)22 ~22Г)-
где параметры zm (m = 1,..., 4) равны
zi = exp(-l), z2 = 1 - z3 = 1 - exp(-r),
z4 = Zi(exp(r) - 1), r = y.
Для линейных (однородных и неоднородных) задач все эти
параметры не зависят от времени и поэтому могут быть заданы
перед началом основного вычислительного процесса.
Приложение А. Параметры для схемы РЕМ
Дисперсионное соотношение для схемы РЕМ имеет вид:
7т = - jin (gl(kh) + g%(kh)),
_ dw0 _ gi(kh)g1(kh) - g3(kh)g2(kh)
Cm dk C r (gi(kh) + gl(kh)) ’
где
51(a) = 1 - ^sin2(a/2) (b2 + 2b3cos(a/2)),
2c
92(a) = — sin(a/2) (b2 cos(a/2) + b3 cos(a) +bi),
2c
5з(а) = sin(a/2) [i>2 cos(a/2) + b3 (2 - 3sin2(a/2))] ,
94(a) =
= [cos(a) (b2 + b3 cos(a/2)) + cos(a/2) (bi - 3b3 sin2(a/2))] .
ПРИЛОЖЕНИЕ Б
РЕШЕНИЕ ЗАДАЧИ
О РАСПАДЕ РАЗРЫВА
ДЛЯ ИДЕАЛЬНОГО ГАЗА
В общем виде структура течения, возникающего после распада
разрыва, может быть представлена в виде следующей диаграммы:
Рис. Б.1. Структура течения после распада разрыва
Здесь W£, Wr определяют начальное состояние, Wq£, wqr —
параметры постоянного течения слева и справа от контактного
разрыва, a = wp^t) vlwfr =	— распределение
газодинамических величин в волне разрежения. Параметры с*
(fc = 1,2,4,5) обозначают скорости движения волновых фронтов,
а сз есть скорость движения контактного разрыва, которая равна
ио = иоl — uor- Смысл параметров Ck зависит от конкретной
ситуации, а именно:
конфигурация 1)
сх = с*2 — скорость левой ударной волны (w^ отсутствует),
с4 = С5 — скорость правой ударной волны (wfr отсутствует),
конфигурация 2)
ci — скорость головы левой волны разрежения,
Б. Решение задачи о распаде разрыва
С2 — скорость хвоста левой волны разрежения,
С4 = С5 — скорость правой ударной волны (wfr отсутствует),
конфигурация 3)
Ci = С2 — скорость левой ударной волны (Wfl отсутствует),
С4 — скорость головы правой волны разрежения,
С5 — скорость хвоста правой волны разрежения,
конфигурация 4)
ci — скорость головы левой волны разрежения,
С2 — скорость хвоста левой волны разрежения,
С4 — скорость головы правой волны разрежения,
с5 — скорость хвоста правой волны разрежения.
Существует множество методов для решения задачи о распа-
де разрыва. Это объясняется тем, что нелинейное уравнение для
ио или ро можно представить в различных формах. В дополне-
ние, для решения этого уравнения можно использовать различ-
ные итерационные процедуры с различными начальными прибли-
жениями. Мы рассмотрим подход, предложенный С. К. Годуно-
вым, в котором давление ро вычисляется как решение уравнения
f (р) = /ь (р) + Jr (р) + ur - иь = 0.	(Б.1)
Функции Д (р) и /ц (р) определяются как
fb (р) = <
Р ^PL,
fR (Р) = <
(р Pl) ^pb((7+i)p_|_(7_i)pL)
(Р Pr) у
Р > PL]
Р P-R,
Р > PR-
Здесь cL = {^Pl/plY/2 и cr = (^Pr/Pr)1/2 . Для решения уравне-
ния (Б.1) можно применить метод Ньютона (см., например, ОНВ
п. 1.2.1), который представляется в виде следующей итерацион-
ной схемы:
р(*+1)
/ (pw)
Итерации выполняются до тех пор, пока не выполнится условие:
p(fe+l) _ р(*)
р(/г+1)	р(^)
= pW_
fc = 0,1,...
2

Приложение Б. Решение задачи о распаде разрыва
где е — заданная точность. Тогда значение выбирается
в качестве ро — Pol — Por- Как обычно, для инициализации
итерационного процесса нам необходимо задать начальное при-
ближение р(°к Выбор хорошего начального приближения имеет
важное значение, так как это позволяет значительно уменьшить
число итераций и повысить надежность итерационной схемы. По-
этому выбор начального приближения основывается на прибли-
женных решениях уравнения (Б.1). Первое приближение следует
из решения задачи о распаде разрыва для уравнений акустики
(смотри (5.11)):
РА = (PL + PR) + | (uL - Ur) (pL + Pr) (cL + Cr) .
Z	о
Второе приближение следует из предположения, что образу-
ется конфигурация 4 (две волны разрежения). Тогда точное ре-
шение уравнения (Б.1) имеет вид
Ptr —
cl+cr- 0.5 (7 - 1) (Ur - uL)
И наконец, третье приближение следует из предположения,
что образуется конфигурация 1 (две ударные волны). Тогда при-
ближенное решение уравнения (Б.1) можно задать в виде
9(pa,Pl,Pl)Pl + 9(pa,Pr,Pr)pr + ul -ur
9 (Ра, Pl,Pl) + 9(pa,Pr,Pr)
где
1/2
9 (P, Pi,Pi) =
Pi((7 + l)p+(7-l)pi)
2
Какое из приближений следует выбрать зависит от начально-
го состояния. Можно применить, например, следующую процедуру:
р(0) =
тах(ртд,5),
тах(рд,<5),
max(prs,5),
рл/тт(р£,рд) < 1,
1 РА/тт(р£,рд) 2,
РА/min(pl,Pr) > 2,
здесь 6 — некоторое малое положительное число, которое вводит-
ся для того, чтобы исключить появление отрицательного значе-
ния для давления.
Приложение Б. Решение задачи о распаде разрыва
После того как давление ро вычислено, скорость контактного
разрыва определяется по формуле
ио = 0,5 (uL + uR + fR (ро) - h (ро)) 
Остальные параметры течения определяются в зависимости
от возникающей конфигурации течения.
Б. I. Конфигурация I
Эта конфигурация возникает когда ро > Pl Ро > Pr- Плот-
ность по обе стороны от контактного разрыва вычисляется как
_ Ро (7 + 1)+ PL (у - 1)
P°L PLpo (7 - 1) + Pl (7 + 1) ’
Ро (7 + 1) + PR (7 - 1)
POR — PR--7---77“-----—77.
PO (7 - 1) + PR (7 + 1)
Скорости ударных волн —
Cl - UL - CL
'y + lpo
PL
Cb=UR + CR
7 + 1 Po
27 pR
(Б.2)
(Б.З)
(Б.4)
(Б.5)
здесь cl и Cr — начальные скорости звука.
Б.2. Конфигурация 2
Эта конфигурация возникает, когда pr < ро Pl- Плотность
слева от контактного разрыва следует из соотношения на адиа-
бате:
/	\ 1/т
POL = PL\ --	,	(Б.6)
\PL J
a Por определяется из соотношения (Б.З). Скорости волны раз-
режения —
/ро\(7“1)/27
ci = ul — сь, с? = ио — cl \ —	,	(Б.7)
\PlJ
а скорость ударной волны определяется из соотношения (Б.5).
Б.З. Конфигурация 3 207
Течение в волне разрёжения находится методом характеристик:
PL [7Т1 + (7+1)cl	~
[с£ + ^UL + x/t]
[4т + <44? (ul - */*)]71 )
(Б.8)
Б.З. Конфигурация 3
Эта конфигурация возникает когда рь < Ро Pr- Плотность
справа от контактного разрыва следует из соотношения на адиа-
бате:
(\ 1/7
— )	,	(Б.9)
PR/
а роь определяется из соотношения (Б.2). Скорости волны раз-
режения —
С5 — Ul — Cl ,
= ио — cl
po\h~1)/2y
Pl)
(Б.10)
а скорость ударной волны а определяется из соотношения (В.4).
Течение в волне разрежения —
/ Р \
wfr (М) = I и I
\ V / FR
PR [7+I	(7+1)сД ^UL
^4 [—CR +	+ x/t]
к Р* [4т - 777	- */*)]7-1 >
(Б.11)
Б.4. Конфигурация 4
Эта конфигурация возникает когда ро < Pl Ро < Pr- Плот-
ности роь и por определяются из соотношений (Б.6) и (Б.9).
Скорости волн разрежения определяются из соотношений (Б.7)
и (Б.10), а течение в волнах разрежения — из соотношений (Б.8)
и (Б.11).
Приложение Б. Решение задачи о распаде разрыва
Б.5. Определение решения в точке х=0
Информация о структуре течения, возникающего после распада
разрыва, используется в схеме метода WAF. При вычислениях по
схеме С. К. Годунова нам необходимо только значение решения
в точке х — 0, которое далее обозначается как ш. Это решение
определяется следующим образом:
1) при ио > О
2) при ио < О
ПРИЛОЖЕНИЕ В
КРАТКОЕ
ОПИСАНИЕ
ПРИЛАГАЕМЫХ
ПРОГРАММ
Это приложение содержит краткое описание прилагаемых про-
грамм (www.technosphera.ru/software/132), которые могут быть
использованы как для практических занятий, так и при выполне-
нии курсовых и дипломных проектов. Дополнительную информа-
цию об использовании программ можно найти в примерах. Хотя
автор приложил все усилия для того, чтобы программы работали
без ошибок, ни автор, ни издатель не несут никакой ответствен-
ности за последствия применения этих программ.
Ниже приводится список прилагаемых программ и краткое
описание основных функций.
Таблица В.1. Список прилагаемых программ
Основная функция	Примеры и вспомогательные функции
1	2
heat_ld_un	example4_l, fl_e41, f2_e41, fs_e41
heat_ld_nun	example4_2, fl_e42, f2_e42, fs_e42
heat_2d_es	example4_3, gl_e43, g2_e43, g3_e43, g4_e43, fs_e43
stefan_ld	example4_4, fl_e44, f2_e44, fs_e44
properties	
cross	example5_l, fl_e51, f2_e51
lw_acoustics	example5_2, fl_e51, f2_e51
Таблица В.1 (окончание).
1	2
roe	example5_3, fl_e51, f2_e51
godunov_ acoustics	example5_4, fl_e51, f2_e51
pern	example5_5, fl_e51, f2_e51
Iw-gasdynamics	example6_l, example6_2
godunov.gasdynami c s	example6_3
waf -gasdynami c s	example6_4
waf _t vd-gasdynami c s	example6_5, limiter_mina, limiter_supera, limit er _ultraa, limit er _vanAlbada, limiter.vanLeer, limiter_Lin
riemann	
helmgotz_2d_lu	
helmgotz_2d_sor	example7_l, gl_e71, g2_e71, g3_e71, g4_e71, a_e71, b_e71, f_e71
he Img о t z _2d_f f t	example7_2, gl_e71, g2_e71, g3_e71, g4_e71, f_e71
helmgotz_2d_cg	example7_3, gl_e73, g2_e73, g3_e73, g4_e73, a_e73, b_e73, f_e73
poisson_2d_td	example7_4, gl_e74, g2_e74, g3_e74, g4_e74, a_e74, f_e74
ns_2d_vsf	example8_l, gl_e81, g2_e81, g3_e81, g4_e81
Таблица В.2. function [uu]=heat_ld_un
(ud,kappa,a,nx,h, t ime,t au,b,gamma,bl,br,fbl,fbr,f s)
Назначение		Вычисление одного шага по времени по схеме (4.3)
1	2	3
Входные параметры	ud	Температура в момент времени tk
	kappa	Коэффициент температуропроводности (к)
	a	Коэффициент теплопроводности
	nx	Число сеточных узлов
Приложение В. Краткое описание прилагаемых программ
Таблица В.2 (окончание).
1	2	3
	h	Шаг по пространству
	time	Момент времени tfc+i
	tau	Шаг по времени
	b	Параметр кт/h2
	gamma	Параметр 7 = 0 — явная схема >0 — неявная схема
	bl, br	Тип граничного условия при х = 0 и х = 1 соответственно. =0 — граничное условие первого рода, = 1 — граничное условие второго рода
	fbl, fbr	Имена m-файлов, в которых задается зависимость температуры или теплового потока от времени при х = 0 и х = 1 соответственно.
	f s	Имя m-файла в котором задается функция внешнего источника тепла в зависимости от координаты и времени
Выходные параметры	uu	Температура в момент времени tk + l
Таблица В.З. function [uu]=heat_ld_nun
(ud,roc,а,nx,h,t ime,tau,b,gamma,bl,br,fbl,fbr,f s)
Назначение		Вычисление одного шага по времени по схеме (4.16)
1	2	3
Входные параметры	ud	Температура в момент времени tk
	гос	Массив значений рс в узлах основной разностной сетки
	а	Массив значений коэффициента теплопроводности в узлах вспомогательной сетки
	пх	Число сеточных узлов
	h	Шаг по пространству
	time	Момент времени
	tau	Шаг по времени
	gamma	Параметр 7: = 0 — явная схема, >0 — неявная схема
•е описание прилагаемых программ
Таблица В.З (окончание).
1	2	3
	bl, br	Тип граничного условия при х = 0 и х = 1 соответственно. = 0 — граничное условие 1-го рода, — 1 — граничное условие 2-го рода
	fbl, fbr	Имена m-файлов, в которых задается зависимость температуры или теплового потока от времени при х = 0 и х = 1 соответственно.
	f s	Имя m-файла, в котором задается функция внешнего источника тепла в зависимости от х и t
Выходные параметры	uu	Температура в момент времени tk + l
Примечание. Эту функцию можно использовать для решения нелинейного
уравнения (схема (4.18)). Необходимо только на каждом шаге по времени
пересчитывать значения гос, а и tau.
Таблица В.4. function [uu]=heat_2d_es(ud,kappa,a,nx,ny,hx,hy,tau,
t ime,bxl,bxr,fbxl,fbxr,byl,byr,fbyl,fbyr,f s)
Назначение		Вычисление одного шага по времени по схеме (4.27)
1	2	3
Входные параметры	ud	Температура в момент времени
	kappa	Коэффициент температуропроводности (к)
	а	Коэффициент теплопроводности
	пх, пу	Число сеточных узлов по х и у соответственно
	hx, hy	Шаги по пространству по х и у соответственно
	time	Момент времени tk+i
	tau	Шаг по времени
	bxl, bxr	Тип граничного условия при х = 0 и х = 1х соответственно. =0 — граничное условие 1-го рода, = 1 — граничное условие 2-го рода
	fbxl, fbxr	Имена m-файлов, в которых задается зависимость температуры или теплового потока от у и t при х = 0 и х = 1х соответственно
Приложение В. Краткое описание прилагаемых программ
Таблица В.4 (окончание).
1	2	3
	byl, byr	Тип граничного условия при у = 0 и у = 1у, соответственно. = 0 — граничное условие 1-го рода, = 1 — граничное условие 2-го рода.
	fbyl, fbyr	Имена m-файлов, в которых задается зависимость температуры или теплового потока от х и t при у = 0 и у = 1у, соответственно.
	f s	Имя m-файла, в котором задается функция внешнего источника тепла в зависимости от х, у и t
Выходные параметры	uu	Температура в момент времени ^fc+i
Таблица В.5. function [entu,uu,sf]=stefan_ld(entd,ud,ro,cs,cl,as,
al,lh,up,nx,h,tau,time,bl,br,fbl,fbr,fs)
Назначение		Вычисление одного шага по времени по схеме (4.38)
1	2	3
Входные параметры	ud, entd	Температура и энтальпия в момент времени
	го	Плотность среды
	cs, cl	Теплоемкость твердой и жидкой фазы соответственно.
	as, al	Коэффициент теплопроводности твердой и жидкой фазы соответственно.
	Ih	Скрытая теплота плавления
	up	Температура плавления
	nx	Число сеточных узлов
	h	Шаг по пространству
	time	Момент времени ^+1
	tau	Шаг по времени
	bl, br	Тип граничного условия при х — 0 и х — 1 соответственно. =0 — граничное условие 1-го рода, = 1 — граничное условие 2-го рода.
	fbl, fbr	Имена m-файлов, в которых задается зависимость температуры или теплового потока от времени при х = 0 и х = 1 соответственно.
Таблица В.5 (окончание).
1	2	3
	f s	Имя m-файла, в котором задается функция внешнего источника тепла в зависимости от координаты и времени.
Выходные параметры	uu, entu	Температура и энтальпия в момент времени 4+1
	sf	Локальная доля твердой фазы в момент времени 4+1
Таблица В.6. function [dis,cg]=properties(kh,r,method)
Назначение		Вычисление коэффициента затухания и безразмерной групповой скорости сеточного решения вида (5.3) для различных схем
Входные параметры	kh	Волновое число, умноженное на шаг по пространству
	г	Параметр Куранта
	method	Метод решения «сгз» — схема «крест» «Ixw» — схема Лакса-Вендроффа «гое» — схема Ф. Роу «god» — схема С. К. Годунова «реш» — схема РЕМ
Выходные параметры	dis	Коэффициент затухания
	eg	Безразмерная групповая скорость
Таблица В.7. function [uu]=cross
(ud,um,с,ro,nx,h,time,tau,bl,br,fbl,fbr)
Назначение		Вычисление одного шага по времени по схеме (5.2)
1	2	3
Входные параметры	ud, urn	Решение в момент времени 4-1 и 4 соответственно.
	с	Скорость распространения волны
	го	Плотность среды
	пх	Число сеточных узлов
	h	Шаг по пространству
	time	Момент времени 4+1
	tau	Шаг по времени
Приложение В. Краткое описание прилагаемых программ
Таблица В.7 (окончание).
1	2	3
	bl, br	Тип граничного условия при х = 0 и х = 1 соответственно. =0 — граничное условие 1-го рода, = 1 — граничное условие 2-го рода.
	fbl, fbr	Имена m-файлов, в которых задается зависимость решения или производной решения от времени при х = 0 и х — 1 соответственно.
Выходные параметры	uu	Решение в момент времени
Таблица В.8. function [uu,pu]=lw_acoustics
(ud,pd,imp,nx,time,r,bl,br,fbl,fbr)
Назначение		Вычисление одного шага по времени по схеме Лакса-Вендроффа (5.7)
Входные параметры	ud, pd	Скорость и давление в момент времени
	imp	Значение рс
	nx	Число сеточных узлов
	time	Момент времени tk+i
	r	Параметр Куранта
	bl, br	Тип граничного условия при х = 0 и х = 1 соответственно. =0 — граничное условие на и, = 1 — граничное условие на р
	fbl, fbr	Имена m-файлов, в которых задается зависимость скорости или давления от времени при х = 0 и х = 1 соответственно.
Выходные параметры	uu, pu	Скорость и давление в момент времени
Таблица В.9. function [uu,pu]=roe
(ud,pd,um,pm,imp, nx, t ime,r,bl,br,fbl,fbr)
Назначение		Вычисление одного шага по времени по схеме Ф. Роу (5.13)
1	2	3
Входные параметры	ud, pd	Скорость и давление в момент времени tk-i
	um, pm	Скорость и давление в момент времени
	imp	Значение рс
	nx	Число сеточных узлов
	time	Момент времени
Приложение В. Краткое описание прилагаемых программ
Таблица В.9 (окончание).
1	2	3
	г	Параметр Куранта
	bl, br	Тип граничного условия при х = 0 и х = 1 соответственно. =0 — граничное условие на и, = 1 — граничное условие на р
	fbl, fbr	Имена m-файлов, в которых задается зависимость скорости или давления от времени при х = 0 и х — 1 соответственно.
Выходные параметры	uu, pu	Скорость и давление в момент времени tk+i
Таблица В.10. function [uu,pu]=godunov_acoustics
(ud,pd,imp,nx,time, r,bl,br,fbl,fbr)
Назначение		Вычисление одного шага по времени по схеме С. К. Годунова (5.17)
Входные параметры	ud, pd	Скорость и давление в момент времени tk
	imp	Значение рс
	nx	Число сеточных узлов
	time	Момент времени
	r	Параметр Куранта
	bl, br	Тип граничного условия при х = 0 и х = 1, соответственно. =0 — граничное условие на и, = 1 — граничное условие на р
	fbl, fbr	Имена m-файлов, в которых задается зависимость скорости или давления от времени при х = 0 и х — 1 соответственно
Выходные параметры	uu, pu	Скорость и давление в момент времени
Таблица B.ll. function [ub,pb,uu,pu]=pem(ua,pa,ud,pd,imp,nx,r,
time,tau,al,a2,a3,bl,b2,b3,bl,br,fbl,fbr)
Назначение		Вычисление одного шага по времени по схеме РЕМ (5.23)
1	2	3
Входные параметры	иа, ра	Средние на разностном интервале скорость и давление в момент времени tk
	ud, pd	Скорость и давление в узлах разностной сетки в момент времени tk
	imp	Значение рс
	nx	Число сеточных узлов
Приложение В. Краткое описание прилагаемых программ
Таблица В. 11 (окончание).
1	2	3
	г	Параметр Куранта
	time	Момент времени
	tau	Шаг по времени
	al, a2, a3, bl, Ь2, b3	Параметры схемы РЕМ (приведены в приложении А)
	bl, br	Тип граничного условия при х — 0 и х = 1 соответственно. =0 — граничное условие на и, = 1 — граничное условие на р
	fbl, fbr	Имена m-файлов, в которых задается зависимость скорости или давления от времени при х = 0 и х = 1 соответственно
Выходные параметры	ub, pb	Средние на разностном интервале ско- рость и давление в момент времени tk+i
	uu, pu	Скорость и давление в узлах разностной сетки в момент времени tk+i
Таблица В. 12. function [rf ,uf ,pf]=riemann
(x,t,rl,ul,pl,r2,u2,p2,gamma)
Назначение		Вычисление точного решения задачи о распаде разрыва для идеального газа
Входные параметры	X	Координата
	t	Время
	rl, ul, pl	Начальные значения плотности, скорости и давления при х < 0
	г2, и2, р2	Начальные значения плотности, скорости и давления при х > 0
	gamma	Показатель адиабаты
Выходные параметры	rf, uf, pf	Значение плотности, скорости и давления в точке х в момент времени t
Таблица В.13. function [d,u,p,e,time]=lw_gasdynamics
(dd,ud,pd,h,nx,r,cad,tp,gamma,bcl,bcr)
Назначение		Расчет одномерного течения идеального газа по схеме Лакса-Вендроффа (6.3)
Входные параметры	dd, ud, pd	Распределение плотности, скорости и давления в момент времени t = 0
	h	Шаг по пространству
	nx	Число сеточных узлов
	r	Параметр Куранта
	cad	Коэффициент искусственной вязкости
	tp	Длительность процесса (приближенная)
	gamma	Показатель адиабаты
	bcl, bcr	Тип граничного условия при х — 0 и х=1 соответственно. =0 — жесткая стенка, = 1 — открытая граница
Выходные параметры	time	Реальная длительность процесса
	d, u, p, e	Распределение плотности, скорости, давления и внутренней энергии в момент времени time
Таблица В.14. function [d,u,p,e,time]=godunov_gasdynamics
(dd,ud,pd,h,nx,r,tp,gamma, bcl,bcr)
Назначение		Расчет одномерного течения идеального газа по схеме С. К. Годунова (6.10)
Входные параметры	dd, ud, pd	Распределение плотности, скорости и давления в момент времени t = 0
	h	Шаг по пространству
	nx	Число сеточных узлов
	r	Параметр Куранта
	tp	Длительность процесса (приближенная)
	gamma	Показатель адиабаты
	bcl, bcr	Тип граничного условия при х = 0 и х — 1 соответственно. =0 — жесткая стенка, = 1 — открытая граница
Выходные параметры	time	Реальная длительность процесса
	d, u, p, e	Распределение плотности, скорости, давления и внутренней энергии в момент времени time
Таблица В.15. function [d,u,p,e,time]=waf_gasdynamics
(dd,ud,pd,h,nx,r,cad,tp,gamma,bcl,bcr)
Назначение		Расчет одномерного течения идеального газа по схеме метода WAF (6.12)
Параметры имеют тот же смысл, что и для функции lw_gasdynamics		
Приложение В. Краткое описание прилагаемых программ
Таблица В.16. function [d,u,p,e,time]=waf_tvd_gasdynamics
(dd,ud,pd,h,nx,r,tp,gamma,bcl,bcr,limiter)
Назначение		Расчет одномерного течения идеального газа по TVD версии схемы метода WAF
Входные параметры	dd, ud, pd	Распределение плотности, скорости и давления в момент времени t = 0
	h	Шаг по пространству
	nx	Число сеточных узлов
	r	Параметр Куранта
	tp	Длительность процесса (приближенная)
	gamma	Показатель адиабаты
	bcl, bcr	Тип граничного условия при х = 0 и х = 1 соответственно. =0 — жесткая стенка, = 1 — открытая граница
	limiter	Имя m-файла, в котором задается функция-ограничитель. Приведенные в книге ограничители прилагаются
Выходные параметры	time	Реальная длительность процесса
	d, u, p, e	Распределение плотности, скорости, давления и внутренней энергии в момент времени time
Таблица В.17. function [u,k]=helmgoltz_2d_sor
(f,ac,be,lx,ly,nx,ny,gl,g2,g3,g4)
Назначение		Решение уравнения (7.9) с граничными условиями Дирихле. Метод SOR
Входные параметры	f	Имя m-файла в котором задается функция правой части f(x,y)
	ас	Имя m-файла в котором задается коэффициент а(ж,?/)
	Ьс	Имя m-файла в котором задается коэффициент Ь(х,у)
	1х, 1у	Размер области по х и у соответственно
	пх, пу	Число сеточных узлов по х и у соответственно
	gl. g3	Имена m-файлов, в которых задается зависимость решения от у при х = 0 и х = 1х соответственно
	g2. g4	Имена m-файлов в которых задается зависимость решения от х при у = 0 и у = 1у соответственно
Выходные параметры	u	Решение в узлах разностной сетки
	k	Число итераций
Примечание. Итерационный процесс завершается, когда либо относитель-
ная ошибка приближенного решения становится меньше чем 10“5, либо
число итераций достигает значения 3 • max(nx,ny).
Приложение В. Краткое описание прилагаемых программ
Таблица В.18. function [u]=helmgoltz_2d_fft
(f,a,b,lx,ly,nx,ny,gl,g2,g3,g4)
Назначение		Решение уравнения (7.9) с постоянными коэффициентами и граничными условиями Дирихле. Метод на основе FFT
Входные параметры	f	Имя m-файла, в котором задается функция правой части f(x,y)
	а	Значение коэффициента а
	b	Значение коэффициента b
	1х, 1у	Размер области по х и у соответственно
	пх, пу	Число сеточных узлов по х и у соответственно
	gl. g3	Имена m-файлов, в которых задается зависимость решения от у при х = 0 и х = 1х соответственно
	g2. g4	Имена m-файлов, в которых задается зависимость решения от х при у = 0 и у = 1у соответственно
Выходные параметры	u	Решение в узлах разностной сетки
Примечание. FFT применяется по координате х, поэтому для эффективно-
го решения следует задавать пх = 2Р + 1.
Таблица В.19. function [u,it]=helmgoltz_2d_cg
(up,f,a,b,lx,ly,nx,ny,gl,g2,g3,g4)
Назначение		Решение уравнения (7.9) с граничными условиями Дирихле. Метод Конкуса и Голуба на основе FFT
Входные параметры	up	Начальное приближение
	f	Имя m-файла, в котором задается функция правой части f(x,y)
	а	Имя m-файла, в котором задается коэффициент а(х,у)
	b	Имя m-файла, в котором задается коэффициент Ь(х, у)
	1х, 1у	Размер области по х и у соответственно
	пх, пу	Число сеточных узлов по х и у соответственно
	gl. g3	Имена m-файлов, в которых задается зависимость решения от у при х = 0 и х = 1х соответственно
	g2, g4	Имена m-файлов, в которых задается зависимость решения от х при у = 0 и у = 1у соответственно
Выходные параметры	u	Решение в узлах разностной сетки
	it	Число итераций
Примечание. Итерационный процесс завершается, когда относительная
ошибка приближенного решения становится меньше чем 10-5. FFT при-
меняется по координате х, поэтому для эффективного решения следует
задавать пх = 2Р + 1.
Приложение В. Краткое описание прилагаемых программ
Таблица В.20. function [и,к] =poisson_2d_td
(up,f,a,lx,ly,nx,ny,gl,g2,g3,g4)
Назначение		Решение двумерного нелинейного уравнение (7.2) с граничными условиями Дирихле методом установления
Входные параметры	up	Начальное приближение
	f	Имя m-файла, в котором задается функция правой части f(x,y)
	а	Имя m-файла, в котором задается коэффициент а(и,х,у)
	1х, 1у	Размер области по х и у соответственно
	пх, пу	Число сеточных узлов по х и у соответственно
	gb g3	Имена m-файлов, в которых задается зависимость решения от у при х = 0 и х — 1х соответственно
	g2, g4	Имена m-файлов, в которых задается зависимость решения от х при у — 0 и у — 1у соответственно
Выходные параметры	u	Решение в узлах разностной сетки
	k	Число итераций
Примечание. Процесс установления завершается, когда относительная
ошибка приближенного решения становится меньше чем 10~5.
Приложение В. Краткое описание прилагаемых программ
Таблица В.21. [u,v,w,ps i,time] =ns_2d_vsf (u,v,w,Re,tp,lx,ly,nx,ny,
bxl,bxr,byl,byr, gl, g2, g3, g4)
Назначение		Решение двумерного уравнения Навье-Стокса в переменных функция тока-завихренность
Входные параметры	U, V,W	Значение компонент скорости и завихренности в момент времени t = 0
	Re	Число Рейнольдса
	tp	Длительность процесса (приближенная)
	lx, ly	Размер области по х и у соответственно
	nx, ny	Число сеточных узлов по х и у соответственно
	bxl, bxr	Тип граничного условия на v при х — 0 и х — 1х соответственно. = 0 — задается значение скорости, = 1 — условие свободного проскальзывания
	byl, byr	Тип граничного условия на и при у — 0 и у — 1у соответственно. = 0 — задается значение скорости, — 1 — условие свободного проскальзывания.
	gl. g3	Имена m-файлов, в которых задается зависимость v от у и t при х = 0 и х = 1х соответственно
	g2> g4	Имена m-файлов, в которых задается зависимость и от х и t при у = 0 и у = 1у соответственно
Выходные параметры	time	Реальная длительность процесса
	u, V, w	Значение компонент скорости и завихренности в момент времени time
	psi	Функция тока в момент времени time
Примечание. Для нормальных к границе компонент скорости приняты сле-
дующие граничные условия: и — 0 при x = 0jix = Ix,v = 0 при у — 0 и
У = 1у.
1
Литература
1.	Белоцерковский О. М., Давыдов Ю. М. Метод крупных ча-
стиц в газовой динамике, М: Наука, 1982.
2.	Владимиров В. С., Жаринов В. В. Уравнения математиче-
ской физики, М: Физматлит, 2000.
3.	Годунов С. К., Рябенький В. С. Разностные схемы, М: Нау-
ка, 1976.
4.	Зализняк В.Е., Основы научных вычислений. Введение в
численные методы для физиков и инженеров, РХД, Москва-
Ижевск, 2006.
5.	Зализняк В. Е., Кусочно-экспоненциальный метод для моде-
лирования распространения волн, Вычислительные методы
и программирование, т. 7, с. 266-272 (2006)
(http://num-meth.srcc.msu.su).
6.	Поттер Д. Вычислительные методы в физике, М: Мир.
1974.
7.	Рихтмайер Р., Мортон К. Разностные методы решения
краевых задач, М: Мир, 1972.
8.	Хокни Р., Иствуд Дж. Численное моделирование методом
частиц, М: Мир, 1987.
9.	Численное решение многомерных задач газовой динамики.
Под ред. Годунова С. К., М: Наука, 1976.
10.	Concus Р. and Golub G. Н. Use of fast direct methods for the
efficient numerical solution of non-separable elliptic equations,
SIAM J. Num. Anal., v. 10, pp. 1103-1120 (1973).
11.	Harlow F.H. and Welch J.E. Numerical calculation of time-
dependent viscous incompressible flow, Physics of fluids, v. 8,
p. 2182 (1965).
12.	Roe P. Linear bicharacteristic scheme without dissipation, SIAM
J. Sci. Comput., v. 19, № 5, pp. 1405-1427 (1998).
13.	Toro E. F. Riemann solvers and numerical methods for fluid
dynamics, Springer-Verlag, 1997.
Заявки на книги присылайте по адресу:
125319 Москва, а/я 91
Издательство «Техносфера»
e-mail: knigi@technosphera.ru
sales@technosphera.ru
Факс:(495) 956 33 46
В заявке обязательно указывайте
свой почтовый адрес!
Подробная информация о книгах на сайте
http://www.technosphera.ru
Зализняк Виктор Евгеньевич
Основы вычислительной физики
Часть 1. Введение в конечно-разностные методы
Компьютерная верстка — С.А. Кулешов
Корректор — Е.М. Конова
Дизайн книжных серий — С.Ю. Биричев
Дизайн — И.А. Куколева
Выпускающий редактор — О.Н. Кулешова
Ответственный за выпуск — О.А. Казанцева
Формат 84 х 108/32. Печать офсетная.
Гарнитура Computer modern LaTeX.
Печ. л. 7. Тираж 2000 экз. Зак. № 201.
Бумага офсет № 1, плотность 65 г/м2.
Издательство «Техносфера»
Москва, ул. Краснопролетарская, д.16, стр.2
Диапозитивы изготовлены ООО «Европолиграфик»
Отпечатано в ППП «Типография «Наука»
Академиздатцентра «Наука» РАН
121099 Москва, Шубинский пер., 6
lr3N
14836-132-1
785948'
361321
ПРИМЕНЕНИЕ ЧИСЛЕННЫХ
МЕТОДОВ К РЕШЕНИЮ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ,
ПАКЕТ ПРОГРАММ
ТЕХНОСФЕРА
ЗАЛИЗНЯК ВИКТОР ЕВГЕНЬЕВИЧ -
PhD (МЕЛЬБУРНСКИЙ КОРОЛЕВСКИЙ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ),
АВТОР НЕСКОЛЬКИХ КНИГ
И МНОГОЧИСЛЕННЫХ ПУБЛИКАЦИЙ
В РОССИЙСКИХ И ЗАРУБЕЖНЫХ
ЖУРНАЛАХ

физики и техники
В. ЗАЛИЗНЯК
Основы
вычислительной
физики
Часть I. Введение в конечно-
разностные методы