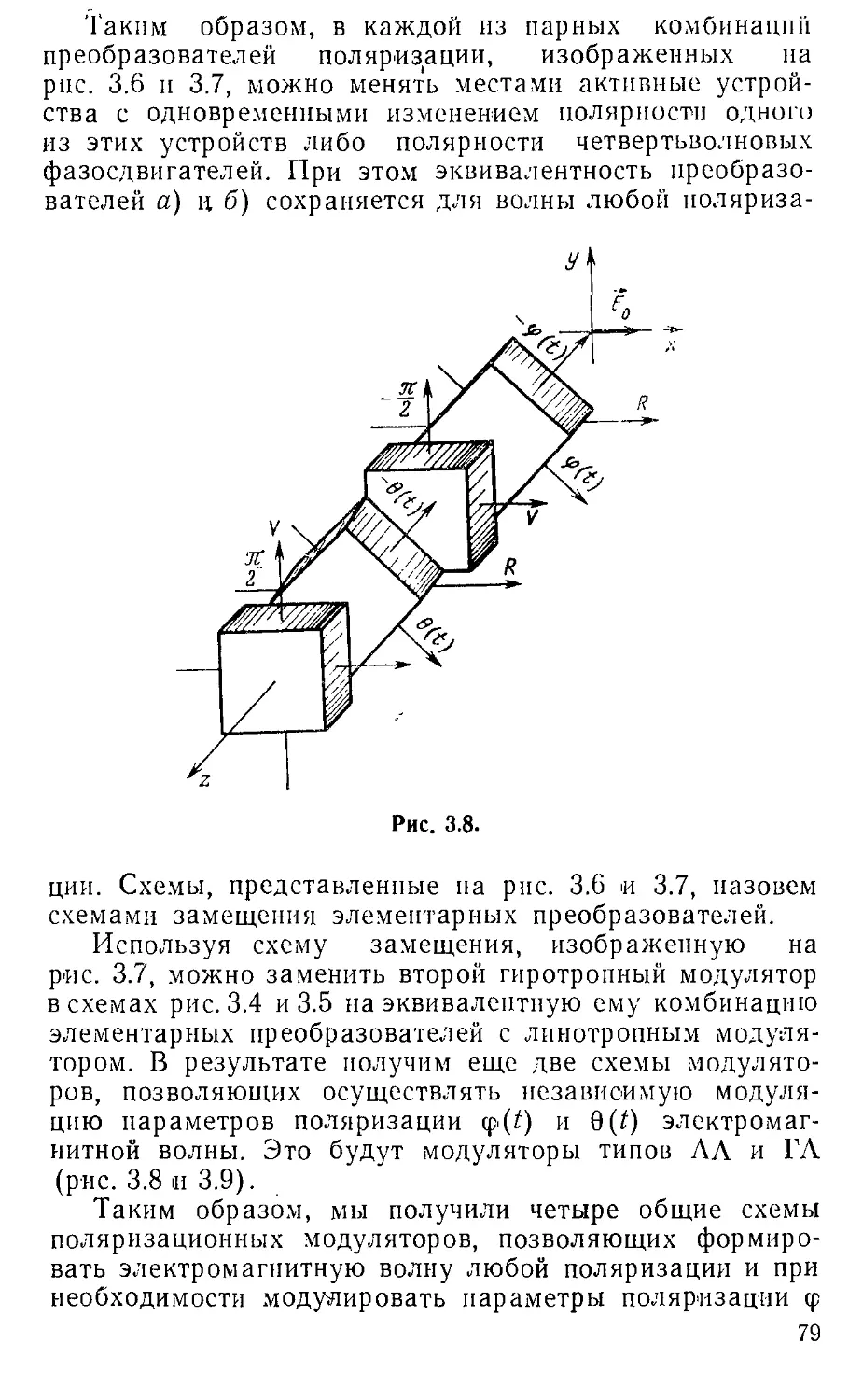
Text
К.Г.ГУСЕВ.А.ДФИПАТОВ.А.П.СОПОЛЕВ
ПОЛЯРИЗАЦИОННАЯ МОДУЛЯЦИЯ
К. г. ГУСЕВ, А. Д. ФИЛАТОВ, А. П. СОПОЛЕВ
поляризационная модуляция
МОСКВА «СОВЕТСКОЕ РАДИО» 1974
УДК 621.3.096.1
Гусев К. Г., Филатов А. Д., Сополев А. П. Поляризационная
модуляция. М., «Сов. радио», 1974, 288 с.
Монография посвящена вопросам передачи сообщений
модуляцией параметров поляризации электромагнитной волны.
Рассматриваются различные виды поляризационной модуля-
ции, некоторые схемы поляризационных модуляторов. Для
описания поляризационпо модулированных (ПМ) сигналов
введена форма их представления в виде экспоненциальной
функции от комплексного аргумента с двумя мнимыми едини-
цами, облегчающая анализ и синтез таких сигналов. Приво-
дятся полные (амплитудные, фазовые и поляризационные)
спектры некоторых видов ПМ сигналов, практические схемы
приема и обработки таких сигналов. Анализируются оптималь-
ные методы обработки ПМ сигналов, оценивается нх потен-
циальная помехоустойчивость.
Книга предназначена для научных работников, радио-
инженеров и студентов старших курсов радиотехнических
специальностей.
Рис. 59, табл. 1, библ. пазв. 48.
Редакция литературы по вопросам
космической радиоэлектроники
30401-066
046(01)-74
(g) Издательство «Советское радио», 1974 г.
ПРЕДИСЛОВИЕ
Возможность использования параметров поляриза-
ции электромагнитных волн в целях повышения эффек-
тивности радиолокационных систем и радиотехнических
систем передачи информации в настоящее время не вы-
зывает сомнений. Использование в радиолиниях сигна-
лов с поляризационной модуляцией позволяет улучшить
такие параметры этих линий, как скорость передачи
информации и помехоустойчивость. Особо важное зна-
чение поляризационная модуляция приобретает в связи
с освоением миллиметрового, субмиллиметрового и опти-
ческого диапазонов волн, где она позволяет снять ряд
принципиальных и конструктивных трудностей.
Однако до последнего времени проблема управления
параметрами поляризации волн, анализ способов пере-
дачи сообщений поляризационно-модулированными сиг-
налами, а также вопросы синтеза и анализа приемных
систем таких сигналов остаются еще мало изученными.
В данной работе сделана попытка несколько сократить
этот пробел. Основным содержанием работы является
изложение общих вопросов формирования и приема
поляризациоино-модулированных (ПМ) сигналов, оцен-
ка помехоустойчивости линий связи с такими сигналами
и анализ оптимальных методов приема таких сигналов.
В гл. 1 и 2 подробно рассматриваются вопросы пред-
ставления поляризационпо-модулированных сигналов
в комплексной форме. Причем, для описания ПМ. сигна-
лов вводится две совмещенные комплексные плоскости:
обычная временная 1, / и пространственная 1, I, соот-
ветствующая двумерному пространству, в котором су-
ществуют ПМ сигналы. Представление ПМ сигналов
функциями комплексной переменной с двумя мнимыми
единицами (t и /) дает возможность сократить многие
математические выкладки и сделать изложение многих
вопросов анализа и синтеза ПМ сигналов более четким.
3
Гл. 3 посвящена вопросам синтеза модуляторов поля-
ризации электромагнитных волн. В гл. 4 и 5 анализи-
руется поляризационно-спектральная структура ПМ сиг-
налов с непрерывной и дискретной модуляцией поляри-
зационных параметров. Гл. 5—9 посвящены вопросам
приема ПМ сигналов, разработке оптимальных способов
приема, оценке потенциальной помехоустойчивости ПМ
сигналов.
Материал книги носит общий характер в том смысле,
что не привязывается к какой-либо конкретной линии
связи, поэтому книга может быть полезной широкому
кругу специалистов.
Авторы выражают глубокую благодарность докто-
рам технических наук, профессорам В. А. Потехину,
С. И. Поздняку, взявшим на себя труд по рецензиро-
ванию рукописи и за ряд ценных советов и пожеланий,
способствовавших улучшению изложения материала
книги.
ВВЕДЕНИЕ
Долгое время при передаче информации по радио
использовались радиоволны с неизменными во времени
параметрами поляризации. Поляризация их была, как
правило, линейной или плоской. Необходимость под-
держания устойчивой связи со спутниками, недостаточ-
но жестко стабилизированными в пространстве, заста-
вила применять в таких радиолиниях волны с круговой
или эллиптической поляризацией. Однако н в этом слу-
чае параметры поляризации волны оставались неизмен-
ными и не использовались для улучшения информатив-
ности, помехоустойчивости и других качеств радиолинии.
Лишь сравнительно недавно стали появляться рабо-
ты, в которых, главным образом в теоретическом плане,
исследовались некоторые вопросы передачи информации
модуляцией тех или иных параметров поляризации
электромагнитной волны, а также вопросы использова-
ния поляризационной структуры электромагнитного по-
ля для многих других практических приложений. В на-
стоящее время можно указать на следующие основные
направления теоретических и экспериментальных иссле-
дований в области использования поляризации радио-
волн:
— поляризационная селекция радиолокационных сиг-
налов точечных п распределенных объектов обнаружения
[12, 15, 16];
— передача сообщений модуляцией параметров по-
ляризации электромагнитного поля [13, 14];
— поляризационное разделение каналов связи [13,
20, 30];
— поляризационно-разнесенный прием [24];
— изучение свойств среды дальнего космоса [14, 10];
— изучение электрических характеристик различных
материальных сред [10, 16], в том числе и характери-
стик поверхности Луны и других планет.
5
Проблемам поляризационной селекции сигналов нФ
священы работы В. Е. Дулевича, Д. Б. Канарейкина,
В. А. Потехина, Н. Ф. Павлова, С. И. Поздника,
Г. С. Сафронова, Ю. А. Митягина, В. А. Мелитицкого
и других авторов. Вопросы передачи информации моду-
ляцией параметров поляризации исследуются в работах
Н. Т. Петровича, Е. Ф. Камнева, В. С. Стригина,
А. В. Кондрашкова, А. П. Родимова. В 1962 г. Н. Т. Пет-
рович и Е. Ф. Камнев предложили способ передачи
дискретной информации путем изменения направления
вращения вектора напряженности электрического поля
с круговой поляризацией. В. С. Стрпгин одним из пер-
вых исследовал вопрос модуляции угла ориентации век-
тора напряженности электрического поля линейно-поля-
ризованной волны. Возможности использования поля-
ризационных параметров частично поляризованных
волн для целей связи рассматриваются в работах
А. П. Родимова. Ряд работ Ю. И. Давпдчевского и
В. В. Кирдеева посвящены изучению поляризационных
спектров электромагнитной волны с вращающейся по-
ляризацией.
Применению поляризационных свойств радиоволн
для передачи информации посвящены многие работы
зарубежных авторов. В работах [42, 44] описываются
системы лазерной связи с передачей сообщений измене-
нием видов поляризации волны. В монографии У. Шер-
клиффа [40] упоминается о создании в США системы
секретной связи, использующей модуляцию параметров
поляризаций электромагнитной волны.
В последнее время появились работы [2, 20, 30, 33]
и монографии [3, 26, 27], в которых излагаются теория
и принципы действия различных поляризационных мо-
дуляторов применительно к конкретным диапазонам
волн. В исследованиях поляризационных устройств опти-
ческого диапазона следует отметить большие заслуги
коллективов советских ученых, руководимых И. А. Де-
рюгиным и Р. В. Хохловым.
Электромагнитная волна с вращающейся поляриза-
цией позволяет применить качественно новые способы
передачи сообщений модуляцией параметров поляриза-
ционной структуры. Использование в радиолиниях поля-
ризационной модуляции дает возможность получить ряд
новых полезных функций, а именно: передавать на од-
ной несущей частоте два независимых сообщения с од-
6
повременной модуляцией двух параметров поляриза-
ционной структуры; осуществлять сопряжение различ-
ных видов поляризационной модуляции с известными
видами модуляции; использовать для передачи инфор-
мации шумоподобные по поляризации сигналы; сокра-
тить эффективную ширину спектра сигнала без сниже-
ния скорости передачи информации.
В книге освещаются такие, еще недостаточно полно
изученные вопросы, как возможности управления пара-
метрами поляризации радиоволн или совокупностью
этих параметров, анализ и синтез поляризационно-мо-
дулированных (ПМ) сигналов, а также ПМ сигналов,
сопряженных с другими видами модуляции, прием и
обработка таких сигналов, оценка помехоустойчивости
и эффективности каналов связи с поляризационной
модуляцией. Под каналом связи понимается линия свя-
зи, командная линия, канал системы управления лета-
тельным аппаратом, линия телеметрии, капал связи
внешнетраекторпых измерений и т. и. Однако особенно-
сти работы конкретных линий связи при использовании
поляризационной модуляции в настоящей работе пе рас-
сматриваются.
При изложении большинства вопросов в книге ис-
пользуется комплексная форма представления ПМ сиг-
налов на двойной комплексной плоскости, одиа.'из кото-
рых является обычной, временной с осями 1, /, а вторая
(с осями 1, I) соответствует двумерному пространству,
в котором существуют ПМ сигналы.
Представление ПМ сигналов функциями комплекс-
ной переменной с двумя мнимыми единицами (/’ и i)
позволило значительно сократить многие математиче-
ские выкладки и, кроме того, дало возможность изло-
жить многие вопросы более четко и наглядно. Основы
такой формы представления ПМ сигналов и правила, по
которым производятся математические операции с чис-
лами па двойной комплексной плоскости, объяснены
в гл. 1. Знакомство с этой главой облегчает понимание
материала последующих разделов книги.
ГЛАВА 1
ПАРАМЕТРЫ ПОЛЯРИЗАЦИИ
МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ
В КОМПЛЕКСНОМ ПРЕДСТАВЛЕНИИ
Поляризацию электромагнитных воли чаще всего характеризуют
двумя основными параметрами: углом ориентации (6) одной из по-
луосей эллипса поляризации и отношением малой полуоси эллипса
поляризации к большой (коэффициентом эллиптичности К). При
этом направление вращения вектора поля задается знаком коэффи-
циента эллиптичности. Угол эллиптичности <p = arctgK используется
как параметр поляризации реже. И почти никогда не учитывается
фаза эллиптически-поляризованной волны.
При передаче информации модуляцией параметров поляризации
волны основными параметрами, изменяющимися в соответствии
с передаваемым сообщением, являются углы <р и 0. Фаза ф эллип-
тически-поляризованной волны может служить еще одним парамет-
ром, содержащим полезную информацию, или использоваться для
однозначного определения величин <р и 0. Необходимо в связи
с этим уточнить пределы однозначного измерения параметров ср, 0,
а также само определение фазы эллиптически-поляризованной вол-
ны. Этим вопросам и посвящаются первые параграфы данной
1лавы. Остальные параграфы главы посвящены вопросам представле-
ния эллиптически-поляризованного поля на двойной комплексной
плоскости.
1.1. ПОЛЯРИЗАЦИОННАЯ ДИАГРАММА
СистОхМа уравнений Максвелла
. Л dFt l с 1
rot Н = еа -дГ , rot Е = —
(1.1.1)
для плоской однородной электромагнитной волны, рас-
пространяющейся в непроводящей однородной изотроп-
ной среде вдоль оси ог декартовой системы координат
oxyz, приводится к четырем скалярным уравнениям
дНу__ дЕх dz ‘ Sa dt ’ 0Ех дг дНу 1X0 dt ’ (1.1.2а)
дНх =Sa^t dz а * дЕу - dz -и — dt ’ (1.1.26)
8
относительно неизвестных проекций векторов электриче-
ского Е и магнитного Н полей на оси ох и оу. Эти урав-
нения образуют две независимые системы (1.1.2а) и
(1.1.26), возможными решениями которых являются две
плоские однородные гармонические электромагнитные
волны:
р ___% / («>П-*,г+ф.)
£-1 --А'0£-'7П1с >
(1.1.3а)
~р "Т. р ^2? + фз)
^2--- Уоь,Ш2^ ♦
я2=— хонту , (1.1.зб)
векторы Е,_2 и Я12 которых попарно ортогональны. Не-
зависимость систем уравнений (1.1.2а) и (1.1.26) имеет
следствием независимость решений (1.1.3а) и (1.1.36), в
то время как решения для магнитного //, и электриче-
ского Е, (соответственно Н2 и Ё2) полей не независимы:
зная Ё„ из уравнений (1.1.2а) можно однозначно опреде-
лить Н„ и наоборот. Поэтому для полной характеристики
таких волн достаточно задать, например, только их элек-
трические составляющие Е, и Е2. Поскольку эти векторы
не меняют своей ориентации в пространстве, то такие
волны называют плоско- или линейно-поляризованными; за
плоскость поляризации принимается плоскость*, в кото-
рой лежит вектор напряженности электрическогоJ поля
Е и вектор Пойнтинга: П = [£'•//].
Если, однако, в решениях (1.1.3а) и (1.1.36) поло-
жить одинаковыми частоты колебаний гармонических
векторов, т. е.
cot = 2л/1 = со2 = 2 л/2 = со
и ___ _________________ ’ щгН
k, — <в, V8ар,0 — k2 = Ш2 Уеаца = k,
где еа, уа — диэлектрическая и магнитная проницаемо-
сти среды, в которой распространяется электромагнит-
* В некоторых работах, особенно в работах по оптике, под
плоскостью поляризации понимают плоскость, в которой лежит век-
тор И и вектор Пойнтинга.
9
мая волна, то оба решения (1.1.3а) и (1.1.36) следует
рассматривать как единую плоскую гармоническую
электромагнитную волну, вектор Е которой в процессе
распространения вдоль оси oz меняет не только свою
величину, но и ориентацию. Конец вектора Е в неподвиж-
ной плоскости, перпендикулярной направлению распро-
странения, описывает замкнутую фигуру, представляю-
щую собой эллипс, который в частном случае равенства
фаз ф1 и ф2 вырождается в прямую линию, а в случае
равенств амплитуд Emi = Em2 и фазово.м сдвиге А =
= ф1—ф2, равном л/2,— в окружность. Направление
вращения вектора Е во всех случаях определяется вели-
чиной разности фаз А. На фигуре, являющейся годо-
графом вектора Е, направление вращения указывается
стрелкой, и эта фигура называется поляризационной
диаграммой, поляризационным эллипсом или эллипсом
поляризации электромагнитной волны. Направление
вращения считается правым, если для наблюдателя,
смотрящего навстречу движению волны, вектор Е вра-
щается против * часовой стрелки.
Параметры, характеризующие поляризационную диа-
грамму (или просто параметры поляризации), можно
ввести различными способами. Для гармонических воли
чаще других употребляются параметры, характеризую-
щие эллиптичность и ориентацию поляризационной диа-
граммы. Как уже было сказано в начале главы, при
рассмотрении вопросов передачи поляризациопно-моду-
лированпых сигналов предпочтительнее оперировать
с угловыми величинами, характеризующими параметры
поляризации. Соответствующие углы отсчитываются от
одной из полуосей эллипса поляризации. Эту полуось
будем называть основной или главной. От того, какая
из четырех полуосей эллипса поляризации гринимается
за главную, зависят пределы однозначного определения
параметров поляризации. Мы будем одинаково часто
использовать следующие два понятия главной полуоси
поляризационного эллипса.
Главная полуось поляризационного эллипса есть:
1) большая его полуось, ближайшая к положительной
* В некоторых работах, особенно опубликованных 10—15 лет
назад, правым называется вращение, противоположное принятому
в дайной работе (см., например, [40]).
10
полуоси ox; 2) большая или малая полуось, ближайшая
к положительной полуоси ох.
При этом для параметров поляризации и фазы
эллиптически поляризованной электромагнитной волны
и в первом и во втором
случае справедливы сле-
дующие определения:
0 — угол ориентации
поляризационной диа-
граммы (эллипса поляри-
зации)—угол между осью
ох и главной полуосью эл-
липса поляризации;
ф — угол эллиптично-
сти поляризационной диа-
граммы (или просто угол
эллиптичности) — угол
между главной полуосью
эллипса поляризации и ближайшей к пей диагональю
прямоугольника, описанного вокруг поляризационного
эллипса так, что его стороны параллельны большой и
малой осям эллипса (рис. 1.1). Угол <р отсчитывается
в сторону вращения ноля и имеет знак плюс, если вра-
щение правое, и минус, если вращение левое;
ф— фаза эллиптически-полярпзованного поля —фа-
зовый угол проекции вращающегося вектора E(t) на
направление главной полуоси эллипса поляризации.
Таким образом, эллиптически-поляризоваииая волна бу-
дет иметь нулевую фазу, если в моменты времени, крат-
ные периоду высокочастотного колебания, направление
вектора Е электромагнитной волны совпадает с направ-
лением главной полуоси поляризационного эллипса.
Можно ввести и полную фазу ф(/) эллиптическн-поля-
ризованной волны:
ф (/) =(|^+ф. (1-1.4)
Полная фаза в некотором (не постоянном в течение
одного периода колебания) масштабе определяет угол
&(/) между главной полуосью поляризационного эллип-
са и мгновенным положением вектора Е. ф(^) и -&(1)
не равны по величине, так как вектор поля эллипти-
чески-поляризоваппой волны вращается с разной ско-
ростью на протяжении одного периода, Только в те
П
моменты времени, когда E(t) совпадает с полуосями
поляризационного эллипса, имеет место равенство ф = 0.
В остальные же моменты времени величина угла # на-
ходится из соотношения
tgo(o =tg ф tgt|? (/),
(1.1.5)
откуда
& (/) = arctg[tg?tg {>(/)] +
Ч—тг S!’gn {sin<f> sinф(/)}[ 1 —sign {cos? cos <[>(/)}], (1.1.6)
где символ sign {а} означает „знак a“, т. e.
1
— 1
sign {a} =
при a > 0,
при 0.
(1.1.7)
На поляризационной диаграмме кроме направления
главной полуоси поляризационного эллипса и направ-
ления вращения вектора поля будем изображать мгно-
венное положение вектора Е в момент времени / = 0.
Тогда угол между вектором Е и главной полуосью будет
приближенно определять фазу ф эллиптически-полярп-
зованной волны. Положительные значения ф отклады-
ваются в сторону вращения поля.
В дальнейшем угол б будем называть фазой поля-
ризационной диаграммы в отличие от фазы ф волны.
На рис. 1.1 изображена поляризационная диаграмма
эллиптически-поляризованной волны правого вращения,
распространяющейся в направлении оси oz. Параметры
этой поляризационной диаграммы следующие: угол
эллиптичности ф = 27°; угол ориентации 0 = 30°; фаза
0 = 52°.
Из рассмотрения рис. 1.1 следует, что в случае пер-
вого определения главной полуоси эллипса поляризации
значения угла ориентации лежат в пределах —л/2^
^0^л/2, угла эллиптичности — в пределах —л/4<^ф<^
s^n/4, а фазы — в пределах —л^ф^л. Для второго
определения главной полуоси эллипса поляризации зна-
чения угла ориентации лежат в пределах —л/4=С?0:£Дп/4,
а угла эллиптичности — в пределах —л/2^ф^л/2. Зна-
чения фазы ф лежат в тех же пределах, что и в преды-
дущем случае.
В дальнейшем мы получим общее выражение для
поляризационной диаграммы, позволяющее формально
12
задавать <р и 0 в больших пределах, причем это общее
выражение всегда может быть приведено в соответствие
с первым или вторым определением параметров <р и 0.
Следует отметить, что если в последующем при за-
писи электромагнитной волны угол эллиптичности при-
нимает значение |ср| л/4, угол 0 будет заключен между
осью ох и большой полуосью эллипса поляризации, ко-
торая в этом случае принимается за главную.
1.2. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
ЭЛЛИПТИЧЕСКИ-ПОЛЯРИЗОВАННО1Т волны
Для четкого понимания последовательности преобразования
поляризации электромагнитной волны различными устройствами ча-
сто желательно графически представить поляризационную структуру
волны в различных точках этого устройства. Вычислять каждый раз
параметры поляризации и строить поляризационную диаграмму не
совсем удобно, так как эти операции связаны с большими затратами
времени. Однако вид поляризационной диаграммы можно прибли-
женно оцепить и без построения годографа вектора Е, если изве-
стны соотношения между амплитудами и фазами двух ортогональ-
пых линейно-поляризованных составляющих вектора Е и их ори-
ентация в пространстве. При этом графическое представление ука-
занных компонент в пространстве играет не последнюю роль при
формировании в сознании пространственно-временного представ-
ления эллиптически-ноляризованной волны. Возникает вопрос, с ка-
кой подробностью нужно графически изображать каждую из со-
ставляющих вектора Е, чтобы достаточно точно и правильно пред-
ставить себе вид поляризационной диаграммы этой волны?
Гармоническая линейно-поляризованная волна, распространяю-
щаяся вдоль оси oz и имеющая в качестве плоскости поляризации
плоскость хог, полностью определяется законом изменения вектора £
этой волны:
£(/, г) =- x0£mcos [со^ — k (г — zmax)j, (1.2.1)
где zmax — координата ближайшей к началу координат точки, в ко-
юрой вектор E(t, г) в момент времени f=0 достигает максималь-
ного положительного значения. На рис. 1.2,а условно изображено
распределение мгновенных значений вектора E(t, г) в дискретных
точках оси ог в начальный момент времени. Распространение волны
можно представить как перемещение такого изображения волны
вдоль оси ог с фазовой скоростью Гф.
Для представления линейно-поляризованной волны пет необхо-
димости изображать все распределения вектора Е. Достаточно
изобразить только лишь положение и длину вектора Е в момеиг
Еремени / = 0 в точке z = zmux.
Величина гтах определяет положение ближайшего к началу
координат положительного максимума волны и, таким образом,
13
определяет фазу волны; длина вектора в точке z—zmnx характе-
ризует амплитуду волны, а положение вектора определяет ориен-
тацию его в пространстве. Остальную картину распределения век-
тора Е можно без особого труда представить и без графического
построения.
Таким образом, гармоническую линейно-поляризованную
можно графически характеризовать только положением и
одного вектора Е=Етах в системе координат xyz (рис.
волну
длиной
1.2,6).
волна может быть пред-
Тогда любая эллиптически-поляризованная
ставлена в пространстве двумя линейными векторами, сдвинутыми
относительно начала координат на расстояния
г!=ф1Л/2л и г2 = ф2А./2л,
где ф1 и фг — фазы векторов; X — длина волны в среде, в которой
она распространяется ' ” "'
(рис. 1.3). В дальнейшем масштаб оси ог
умножаем па 2л/Х, так что вдоль этой
осн будем откладывать собственно фа-
зы векторов.
Наблюдатель, который смотрит на-
встречу движению волны, представлен-
ной своими максимальными значениями
£i и Ez на рнс. 1.3, сначала как бы ви-
дит максимальное значение максимума
Ег волны, поляризованной параллельно
оси оу, а затем, по мере распростране-
ния волны вдоль оси ог, видит макси-
мум Ei волны, поляризованной в пло-
скости хог. Результирующий вектор
этих двух волн представляется вращаю-
щимся по часовой стрелке, а поляриза-
ционная диаграмма имеет вид эллипса, ориентация и форма которого
зависят как от амплитуд Ei и Ег, так и от значения фазового сдвига
Ф1+Ф2-
И
Векторы Et и Е2 могут быть и не взаимно перпендикулярными
(не ортогональными). Кроме того, в общем случае осям ох и оу
можно сопоставить не только линейные орты, по и ортогональные орты
произвольной эллиптической поляризации. Тогда рис. 1.3 будет гра-
фически отображать представление эллиптически-поляризованной
волны в произвольном ортогонально-эллиптическом базисе разло-
жения. Соответственно в этом базисе можно построить и свою
полиризациопную диаграмму поля. Как известно [15], такое пере-
строение поляризационной диаграммы соответствует смещению точ-
ки отсчета па сфере Пуанкаре в точку, соответствующую одному
из ортогональных ортов, по. которым раскладывается эллиптически-
поляризовапная волна.
1.3. ПРЕДСТАВЛЕНИЕ ЭЛЛИПТИЧЕСКИ-ПОЛЯРИЗОВАННОЙ
ВОЛНЫ НА ДВОЙНОЙ КОМПЛЕКСНОЙ ПЛОСКОСТИ
Эллиптически-поляризовапная гармоническая волна
в ортогонально-линейном базисе разложения в ком-
плексной форме может быть записана в виде
§ (() = (7хЕхе'Ф* +7уЕуе'Фу) ez , (1.3.1)
где ix, iy — единичные орты осей ох и оу, Ех, Еу—амп-
литуды; фу — фазы проекций гармонического вектора
Е на оси ох и оу соответственно. В последующих записях
множитель е' опускаем.
Пусть интенсивность электрического поля волны
(1.3.1) равна единице, т. е.
х ‘ V
Тогда выражение (1.3.1) можно представить в виде
<S’(0 = k’xCos<p+ty sin<pe“/4 ] еФ* , (1.3.2)
где А = фж— фу; coscp = £x; sin(p = Ey.
Как известно, при А = л/2 выражение (1.3.2) опре-
деляет эллиптически-поляризованпую волну, поляриза-
ционная диаграмма которой представляет собой эллипс
с углом эллиптичности <р и углом ориентации 0 = 0.
Величина фх есть не что иное, как фаза этой волны,
поэтому индекс «х» можно опустить.
Поставим в соответствие плоскости хоу комплексную
плоскость, мнимая ось i которой совпадает с осью оу,
а действительная ось — с осью ох. Тогда выражение
(1.3.2) для этой комплексной плоскости запишется
в виде
S' (0 = (cos <р + i sin <ре~7Л;/2) е'ф
15
или
g(t) =-(cos? — ij sin?) е;ф. (1.3.3)
Выражение (1.3.3) есть форма записи эллиптически-
поляризованного поля на двойной комплексной плоско-
сти: временной (1, /) и пространственной (1, Г).
Представляя произведение ij как совмещенную мни-
мую единицу, получаем
^(/)-=е“1/1₽е/ф. (1.3.4)
Всякий поворот линейного вектора Е, лежащего в
плоскости хоу, на угол 6 в положительном направлении,
т. е. против движения часовой стрелки, если смотреть
со стороны, в которую направлена ось ог, соответствует
умножению комплексного изображения Е вектора Е на
комплексной плоскости (1, i) на экспоненциальный мно-
житель е'6. Поэтому запись на двойной комплексной
плоскости поляризационного эллипса с углом эллиптич-
ности ср, но повернутого па угол 0 относительно оси ох
примет вид
= (1.3.5)
Здесь для полноты записи учтен и временной множи-
тель е'ш‘, который в предыдущих выражениях опущен.
В дальнейшем мы также будем опускать множитель
e'“z, если это ие будет приводить к недоразумениям.
Фактически это соответствует замене неподвижной ком-
плексной плоскости (1, /), на которую трансформиру-
ется форма представления гармонической величины,
соответствующей электрическому полю линейно-поля-
ризованной волны, вращающейся с частотой ы, ком-
плексной плоскостью. Поскольку выражение
£ = e“'7V9ert (1.3.6)
определяет все параметры поляризационной диаграммы,
то комплексное число (1.3.6) можно считать формой
записи поляризационной диаграммы или просто поляри-
зационной диаграммой. Это же число, умноженное на
л . и О
е , представляет гармонический вращающийся вектор
£(/) в плоскости хоу.
16
Форма представления эллпптически-полярпзбваппой
волны в виде (1.3.5) ие только дает компактную ее
запись, но позволяет в сокращенном виде производить
многие математические выкладки при преобразовании
поляризации волны, при представлении ее в различных
базисах, сокращает расчеты при нахождении спектров
эллиптпчески-поляризованных и поляризациоино-моду-
лированиых сигналов, делает многие расчеты четкими
и наглядными. Все эти качества формы представления
поляризационной диаграммы электромагнитной волны
в виде (1.3.5) пли (1.3.6) мы проиллюстрируем в даль-
нейшем па примерах. Сейчас же определим алгебраи-
ческие операции над числами типа (1.3.6), которые мы
будем использовать в дальнейшем.
Множество К чисел типа
£ = £е~;/1₽е;9е'ф, (1.3.7)
где Е— действительное число, вместе с полем М ком-
плексных чисел типа
j_I I J arg Л
<xj = | a I е
и полем J комплексных чисел типа
pr- = j p|eiarg?,
где индекс I и / у изображения комплексного числа
означает соответствующую мнимую единицу, т. е. числа
с индексом j принадлежат к комплексной плоскости
(1, /), а числа с индексом i — к комплексной плоско-
сти (1, i) образуют комплексное линейное пространство,
для которого справедливы следующие линейные опе-
рации.
1. Для любых а, Б из К
а + Б = Б + а.
2. Для любых а, Б, с из К
(а+Б)+с=а+(Б+с) =а+Б+с.
3. й + 0 = а, где 0 — нулевой элемент множества К.
4. Для любого элемента а из К существует противо-
положный элемент Б=—а такой, что а + Б = 0.
5. 1 • а = а.
6. а3 (р3 а) = (я3 р3) а = а(а3р3'),
aS (р« а) — (aS рг) а = а (aS рг’),
аг' (р3 а) = рз (ага) = а (аг' рз) = а (р3 аг).
2—667
17
Свойство (6) коротко можно записать в виде
a(iv/) [p<'v'»a] = [a(iv/) p(‘v/)J а = a
где a(‘V;) — комплексное число а комплексной плоскости
(1, /) или комплексной плоскости (1, /).
7. [a('v/> + p(;v/)] a=+fla"v/) + a3(,'v/).
8. a,iv;)(a-|-'i)=a(‘v')a4-a('v;)fr=aa1'v;)4-i&a(iv') .
Все эти восемь линейных аксиом являются необходи-
мыми, чтобы множество J\ чисел типа (1.3.7) представ-
ляло линейное пространство.
Первые пять линейных операций пояснений не тре-
буют. Остановимся подробнее на свойстве (6).
Выражение (1.3.7), умноженное на гармонический мно-
житель е'описывает гармоническую волну эл-
липтической поляризации. Квадрат модуля этой вели-
чины Е2 есть интенсивность этой волны, Е — приведен-
ная амплитуда этой волны. Множитель (1.3.6) опи-
сывает поляризационную диаграмму этой волны, а этот
же множитель, домноженный на e/ (cuZ“fa), описывает эл-
липтически-поляризованную волну с интенсивностью, рав-
ной единице (с единичной амплитудой). Умножение (1.3.6)
на комплексное число е‘0° означает разворот поляриза-
ционной диаграммы этой волны на угол 0О, а умноже-
ние на множитель е^“— изменение фазы этой волцы на
угол фо- Эти две операции могут быть выполнены одно-
временно или последовательно и независимо друг от
друга. Такова физическая интерпретация свойства (6)
комплексных чисел типа (1.3.6), (1.3.7), когда они
используются для описания волн с вращающейся поля-
ризацией.
Для того чтобы множество чисел К составляло коль-
цо, необходимо определить для этих чисел операции
сложения и умножения [22]. Определим сначала вторую
операцию, т. е. умножение, причем определим ее так,
чтобы при умножении двух чисел <§i и <§2 типа (1.3.7)
показатели степеней при одинаковых мнимых единицах
складывались. Комбинацию из двух мнимых единиц (//)
назовем совмещенной мнимой единицей и будем заклю-
18
чать ее в круглые скобки в отличие от простого умноже-
ния i на /.
Основное определение: произведение двух комплекс-
ных чисел
0„ ф.) = ^е^’е/в,е/ф|
и
^2(Уа. 62> ф2) = £2е-"'^е'9’еж "
есть комплексное число
Ъ р р a—ii (91 + <Ра) (01 + 02) J (Ф1 + Ф2)
G> 12 2^ С С •
Приняв такое определение произведения комплекс-
ных чисел, представленных на двойной комплексной
плоскости, мы можем вывести как следствие правила
перемножения мнимых единиц i, j и (ij). Для этого
каждый из сомножителей с разными мнимыми едини-
цами в выражениях для чисел <§i, <§2 представим через
тригонометрические функции по формулам Эйлера, про-
изведем почленное перемножение этих чисел по прави-
лам обычной алгебры и сгруппируем члены с одинако-
выми комбинациями мнимых единиц. При этом совме-
щенные мнимые единицы, стоящие в показателях
степени перед <pi и ср2, необходимо обязательно взять
в круглые скобки. Затем проделаем аналогичную опе-
рацию с комплексным числом <§i2 и приравняем полу-
ченные числа. Чтобы равенство соблюдалось, необхо-
димо принять следующие правила перемножения мни-
мых единиц:
= /./ = -1; ((•/) .((;)= —1. (1.3.8)
Покажем это на примере перемножения чисел ij>, и ij>2 при
Ф, = ф2 = 0:
= £’,е+1/ч,> е/в* =
= Et [cosf, cos0, + i (ч) sin ф, sin 0! -ф i cos<?i sin 0, -ф
ф (ij) sin cos0,|.
Для числа <f2 развернутая форма записи такая же,
нужно только 1 заменить на 2. Почленное перемножение
выражений в квадратных скобках приводит к равенству
§, — £Д {[cos ф, cos <f2 4- (ij) (ij) sin <p, sin ®2] X
Г 19
X (cos 6, cos б2 + ii sin б, sin б2) Ц-
+ G7) sin (?, + ?2)-(cos6, cos 6,4“ sin 6, sin б2) Ц-
+ i [cos ?, cos ?„ + (ij) (if) sin sin ?2] sin (б, Ц- 62) +
4- i (ij) sin (<p. + ?2) sin (0, + 62)}.
Развернутая форма числа ^,2 имеет вид
^<2 = Ei [ cos (?, 4- ?2) cos (б, 4- б2) 4-
4- (ij) sin (?, 4- ?2) cos (б, 4- б2) 4- i cos (?, 4-'?г) sin (б, 4- б2) 4-
4 i (ij) sin (ср, 4- ср,) sin (б, 4- б2)].
Очевидно, что ^’,<?2=<?12, если равны действительные
коэффициенты при одинаковых комбинациях мнимых
единиц. Отсюда и следует выражение (1.3.8). Учитывая
это правило перемножения мнимых единиц, можно по-
казать справедливость основного определения для про-
изведения двух и более комплексных чисел вида (1.3.7)
и при ф1=^=ф2=^0.
Из (1.3.8) следует и еще один важный вывод: совме-
щенную мнимую единицу (ij) можно раскрыть, но при
этом необходимо изменить на противоположный знак
у остальных сомножителей с совмещенной мнимой еди-
ницей.
Если остается только один сомножитель с совмещен-
ной мнимой единицей, то его можно раскрывать без
всяких последствий и полученные самостоятельные мни-
мые единицы перемножать согласно (1.3.8).
Это правило можно проиллюстрировать следующими
примерами:
(Ч) (Ч') = Ч (— Ч) = —г • г •/•/ = — 1;
'('/)=—/; /('7)=—G
(ij) = j/e'7* = eiy<₽ е‘Е/2 е;”/2
и т. д.
Справедливо и обратное: свертывание произведения
двух мнимых единиц i j в совмещенную мнимую еди-
ницу (ij) сопровождается изменением на противополож-
ный знака перед совмещенной мнимой единицей у осталь-
ных сомножителей.
Введенное выше правило перемножения комплекс-
ных чисел с двумя мнимыми единицами коммутативно.
20
Можно также ввести правило деления таких комплекс-
ных чисел на комплексное число, не равное нулю, по
обычным правилам для комплексных чисел, т. е.
а” е--е2' *-*=)•
<?2 (?2. 02’ Фг)
Эта алгебраическая операция совместно с операция-
ми суммирования и вычитания превращает пространство
комплексных чисел типа (1.3.7) в поле.
Дальнейшее исследование этого вопроса увело бы
нас в сторону от основной темы, поэтому рассмотрение
комплексных чисел с двумя мнимыми единицами мы
закончим определением суммы таких чисел, полагая,
что вычитание, как операция, обратная суммированию,
не требует особого определения.
Сумма двух (и более) комплексных чисел б,, ?i)
и <?Д?2, ®2> ф2) равна комплексному числу, которое полу-
чается при суммировании действительных коэффициен-
тов при одинаковых мнимых единицах в развернутой
форме записи этих комплексных чисел.
1.4. НЕКОТОРЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ
ЭЛЛИПТИЧЕСКИ-ПОЛЯРИЗОВАННОЙ ВОЛНЫ
Запись поляризационной диаграммы эллиптически-
поляризованной волны в виде (1.3.6), т. е. числом на
двойной комплексной плоскости, позволяет сравнительно
просто получить многие интересные формы представле-
ния этой волны в различных базисах разложения. Неко-
торые из этих форм представления нам понадобятся
в дальнейшем. Они позволяют лучше понять структуру
эллиптически-поляризованной волны, наглядно демонст-
рируют многообразие форм ее представления. Наконец,
приведенные ниже преобразования помогут лучше осво-
иться с правилами оперирования над комплексными чис-
лами вида (1.3.5), (1.3.6).
1. Представление эллиптически-поляризованной вол-
ны в виде суммы двух линейных векторов. Если в выра-
жении (1.3.6) раскрыть показательные формы по триго-
нометрическим функциям, то после несложных преобра-
зований мы получИхМ хорошо известное разложение
эллиптически-поляризованной волны по координатным
21
осям ох и оу.
е-»/<₽ е»е __ (cos jp cos g sjn p sjn g) _|_
-ф- i (cos <p sin 9 — / sin p cos 9).
(1.4.1)
Поскольку мнимой оси i на комплексной плоскости
соответствует ось оу, то в выражении (1.4.1) действи-
тельная по i часть есть составляющая Ех, а мнимая
по i часть — Еу.
Таким образом, проекции эллиптически-поляризован-
ной волны иа координатные оси определяются как дей-
ствительная и мнимая по i части комплексного числа
вида (1.3.5):
£\ = Re, {’<Г(0}; Ду=1шг-{/(/)},
где символы Re,, Im,- означают вещественную и мнимую
части по комплексной плоскости (1, /).
Действительные выражения компонент волны, совпа-
дающих с осями ох и оу, найдем -из условия
Ех = Re,j (/), Еу — Im, Re,- {<§ (/)}.
Представим теперь поляризационную диаграмму
эллиптическп-поляризованной волны нулевой фазы
в виде
— e-l/'₽e'9 = (cosp — ij sin р) е19. (1-4.2)
Скобки около совмещенной мнимой единицы ij опу-
щены, так как в выражении (1.4.2) нет других сомно-
жителей с совмещенной мнимой единицей, кроме одного,
и, следовательно, раскрытие (ij) или свертывание ij не
сопровождается никакими изменениями этого выра-
жения.
Разлагая далее cos ср и sin ср по формулам Эйлера и
группируя соответствующие члены, получаем две фор-
мы представления поляризационной диаграммы (1.4.2)
в зависимости от того, какую мнимую единицу брать
в формулах Эйлера — i или /:
(е^е-^ + е^е''"74) е;е, (1.4.3)
е-‘"е1'9 = (e‘ VM/4 + e~t,fein/i) е1'9. (1.4.4)
22
Очевидно, эти выражения равнозначны, так как они, во-
первых, описывают одну и ту же эллиптически-поляри-
зованную волну (при J умножении их на и, во-
вторых, эти выражения переходят одно в другое путем
простой замены i на j и наоборот в круглых скобках,
что согласно (1.4.2) не приводит к изменению комплекс-
ного числа (§. Очевидно также, что равнозначны все
выражения (1.4.1) — (1.4.4).
Физическая же интерпретация этих выражений раз-
лична. А именно, эллиптически-поляризованная волна
Рис. 1.4.
может быть представлена в соответствии с (1.4.1) —
(1.4.4) в виде:
— двух линейно-поляризованных гармонических век-
торов с определенными амплитудами и фазами и ориен-
тированных вдоль осей прямоугольной системы коорди-
нат, т. е. находящихся в пространственной квадратуре;
— двух гармонических векторов с амплитудами
costp и sin ср, находящихся одновременно в пространст-
венной и временной квадратуре и ориентированных
вдоль осей поляризационного эллипса (рис. 1.4,а);
— двух одинаковых по амплитуде векторов с фазами
+ ф и —q>, развернутых на —л/4 и л/4 относительно
главной полуоси эллипса поляризации (т. е. находя-
щихся в пространственной квадратуре) (рис. 1.4,6);
— двух одинаковых по амплитуде векторов, находя-
щихся во временной квадратуре и развернутых в про-
странстве на угол —ф и ф относительно главной полуоси
поляризационного эллипса (рис. 1.4,в).
23
Эллиптическп-поляризоваппую волну формально
можно представить и в виде двух линейных гармони-
ческих векторов, не находящихся ни в пространственной,
ни во временной квадратуре, однако физически осуще-
ствить такое разложение не представляется возможным.
2. Представление эллиптически-поляризованной вол-
ны в произвольном ортогонально-эллиптическом базисе.
Перепишем выражение (1.3.6) в виде
g = (ф‘+<₽а) е'9 е/ф = е“,7ф1 е~'7(₽’е;ве/ф, (1.4.5)
где ?i+<Р2 = <Р. Далее показательную форму е~,?*'можно
представить в виде комплексного числа через тригоно-
метрические функции но формулам Эйлера: е-‘УФ'=
= cos<p!—(i/)sin<pi. Раскрывая затем совмещенную .мни-
мую единицу (ij) согласно правилу (1.3.8), получаем
следующее выражение для эллиптически-поляризовап-
ной волны с параметрами поляризации <р=<рi + <р2 и 0:
g = [cos<Pie~',y<₽a — ij sin <?! е,у<₽а] e19 еуф
или
g — [cos tp1e~‘yi₽Je19 — j sin^e'^'e' <9+’t/2)] еуф. (1.4.6)
Выражение (1.4.6) есть не что иное, как разложение
поляризационной диаграммы (1.3.6) по ортогональным
эллиптическим ортам
Э1 = Э(<р2, 0) и Э2 = Э(—<Р2, 0-Н/2),
причем
Э.(<р2, 0) = e'~iy>Jei9,
Э2(— <р2, 0 + 1t/2) = ei/%ei (9+п/2).
Орты 3t и Э2 ортогональны, так как они имеют одинако-
вую эллиптичность (одинаковая абсолютная величина
угла эллиптичности), противоположное направление
вращения и их главные полуоси развернуты на л/2.
Кроме того, эти орты сипфазны и имеют нулевую фазу.
Такие два орта называют базисными или просто
базисом.
Выражение (1.4.5) можно представить и в несколько
ином виде, если в последующих выкладках не раскры-
вать совмещенную мнимую единицу—(ij), а предста-
вить ее каке-"771' . Тогда вместо соотношения (1.4.6)
24
(1-4.7)
получим
= [cos ?1е-;/ф’ e‘9 + Sin ?2e~I; <ф’+к/2) ei9] е/ф. (1.4.8)
Соотношение (1.4.8) есть разложение волны (1.3.6) по
двум ортам, у которых углы эллиптичности отличаются
на л/2. Поскольку справедливо равенство
е— ч <<рз+«/2) е<9__уе‘,ф2 е‘ <9+и/2) (1 4.9)
то орты 9) и Э2 9^ также поляризационно
ортогональны и, кроме того, сдвинуты по фазе па л/2,
т. е. находятся в пространственной и временной квадра-
турах.
В дальнейшем два орта, находящихся в пространст-
венной и временной квадратурах, будем называть для
краткости квадратурными в отличие от ортогональных
ортов, которые поляризационно ортогональны, но син-
фазны. Кроме того, базис будем обозначать только пер-
вым ортом Э1 = Э(ср, 0), подразумевая при этом, что вто-
рой орт ортогонального базиса есть орт Э(—<р, 9 + л/2),
а второй орт квадратурного базиса — Э(ф + л/2, 9).
В следующем параграфе покажем связь представле-
ния эллиптически-поляризованной волны в В'иде ком-
плексных чисел двойной комплексной плоскости с дру-
гими формами ее представления, в частности, с формой
представления в виде комплексных векторов, а также
докажем соответствие ортогональных и квадратурных
ортов двумерного векторного пространства и комплекс-
ных чисел (1.4.7) с совмещенной мнимой единицей. Пока
же огарничимся лишь тем замечанием, что если орты
выражения (1.4.7) представляют поляризационные диа-
граммы двух когерентных волн одинаковой амплитуды,
то эти две волны поляризационно ортогональны и могут
быть приняты за орты при разложении эллпптически-
поляризованных волн. Это справедливо и для квадра-
турных ортов.
Выражения (1.4.6) и (1.4.8) представляют эллипти-
чески-поляризованную волну в ортогонально-эллиптиче-
ском базисе, у которого угол ориентации первого орта
равен углу ориентации поляризационного эллипса самой
волны (см. выражение (1.4.5)). Найдем теперь выраже-
ние для разложения волны в любом ортогонально-
эллиптическом базисе Э1(ф0, 0О). Для этого запишем
25
поляризационную диаграмму волны в виде
£ = е“‘7фе''е°егА9, (1.4.10)
где Д0 = 0—0О.
Представив е‘А9 в тригонометрической форме, перепи-
шем (1.4.10) в виде
(f = (cos AG + i sin ДО) е~‘7ф е100.
Теперь умножим sin ДО одновременно на —j и j
и свернем произведение i (— /) в совмещенную мнимую
единицу
—[cos Дбе~1у9— j (ij) sin Абеt/<₽] e10°.
Далее выносим e~'1/9° из каждого слагаемого в квадрат-
ных скобках и представляем оставшиеся показательные
формы в тригонометрической форме:
'/§— {cos Дб [cos Д'? — (ij) sin A1?] — j (ij) sin ДО [cos (<? 4~ <?„) 4-
+ (ij) sin ('? + '?„)]}
Д? = ? — ?0-
Раскрывая прямоугольные и фигурные скобки, полу-
чаем окончательно
& — [cos Д'? • cos Дб -j- j sin (<? ?0) sin Дб] е “1/ч’°е19° 4~
4- [sin Д<? • cos Дб 4- j cos (у 4- То) sin ДО] X
X е-‘7 (9°+к/2) eie°. (1.4.11)
Выражение (1.4.11) представляет собой разложение
эллиптически-поляризованной волны в квадратурно-
эллиптическом базисе. Переход к ортогонально-эллип-
тическому базису осуществляется преобразованием вто-
рого орта согласно равенству (1.4.9).
Можно подобрать ортогонально-эллиптический базис
так, чтобы амплитуды обеих компонент волны в этом
базисе были однаковы. Соответствующее разложение
получается следующим:
Х> е~ »/<₽ е'в_е-‘/*/4е—И (Ч>—*/4) е>6 1 е-«7 (<₽—«/4>е*в _|_
ИГ
+y=e“‘7(9+,t/4)eie, (1.4.12)
26
Это и есть разложение эллиптически-поляризованной
волны в квадратурном базисе Э1 = Э(|р— -гс/4, 9), Э2 =
= 3(?4-it/4, 0). Проекции вектора вращающегося поля
на эти орты одинаковы по амплитуде и фазе. Преобра-
зование выражения (1.4.12) к ортогонально-эллиптиче-
скому базису дает
о-- 1 (Ч>-ч/4) ie 1 ;1/ (Ч>-«/4) i (в + ч/2) _
б-р-е е -уу/е е -
==_^ е—<ч’+’с/4) e!'94--L/е'7 (<₽+’t,M) е; (9+’t/2). (1.4.13)
И 2 ~ И 2 1 К ’
3. Представление эллиптически-поляризованной вол-
ны в ортогонально-круговом базисе. Угол эллиптичности
кругополяризованной волны правого направления вра-
щения равен л/4, левого —л/4, поляризационная диа-
грамма
<^ = e“,>/4ei9, (?д = е‘7“/4е‘9. (1.4.14)
Можно доказать, что
iQ ±i/tc/4 т/9
е = е е ,
(1.4.15)
т. е. изменение ориентации главного радиуса поляриза-
ционной диаграммы кругополяризованной волны равно-
сильно изменению фазы этой волны, что, впрочем, ясно
и из физических соображений.
Получим теперь формулы для представления эллип-
тически-поляризованной волны в ортогонально-круговом
базисе:
е-б'ф^е19__ е‘/’'/4 Ч (ф + г.М) е1в
Представляя (чы-я/п по тригонометрическим функ-
циям, получаем
е-7’ е19 = sin (? + те/4) e">/4 е'9 +
4-cos(?-H/4)e~‘7,tMe''9 (1.4.16)
или с учетом (1.4.15)
е-‘,,р е19 = sin (f> 4- it/4) е'9 р+,/“/4 -f-
4-cos(?4-r/4)e-/9e1>/4. (1.4.17)
Таким образом, проекции эллиптически-поляризованной
волны па круговые квадратурные орты нулевой ориента-
27
цйй правого и Левого направлений вращений равны
соответственно
О) = Sin (<ртг/4) е' (ш<+9), |
^L(i) = cos(t>+1Г/4)е'(ш<-6). J
(1.4.18)
1.5. КОМПЛЕКСНЫЕ ЧИСЛА ДВОЙНОЙ
комплексной ПЛОСКОСТИ И КОМПЛЕКСНЫЕ ВЕКТОРЫ
Итак, состояние поляризации монохроматической
электромагнитной волны вполне описывается числами
двойной комплексной плоскости:
£ = £е~''фе''9е/ф (1.5.1)
или
§ = Е[а +jb + ic-[-(ij)d\, (1.5.2)
где а, Ь, с, d — действительные числа, связанные про-
стыми соотношениями с параметрами поляризации ср, 0
и фазой ф волны; Е — приведенная амплитуда электри-
ческого поля волны.
Обозначим
ga=§IE (1.5.3)
нормированное значение комплексного числа g.
Тогда
а — RejRe^o, b = Im jRe/d?».
с = Rejlm, <£0, а = Imjlm, §0.
Форма (1.5.2) представления эллиптической поляри-
зованной волны тесно связана с ее представлением в ви-
де комплексного вектора. Чтобы показать эту связь,
запишем эллиптически-поляризованпую волну в виде
суммы ее проекций на осп ох и оу координатной пло-
скости хоу:
% = хаЕх&*х + уаЕу ,
или в развернутом виде
ё = х0 (Ех cos + jEx sin фх) + у0 (Еу cos фу + jEy sin <ру).
(1.5.4)
28
Сгруппируем в (1.5.4)
отдельно действитель-
ные и мнимые части.
Тогда комплексный
вектор <§ будет опреде-
лен как сумма двух
действительных векто-
ров, находящихся во
временной квадратуре,
= + (1.5.5)
где Er = .r0£xcos^x-(-
4- i/Xcos^;
Рис. 1.5.
~Ei = хаЕх sin + *уаЕу sin <ру.
Векторы Ег и Ei не обязательно ортогональные. Домно-
женные на гармонический множитель e/W, они в сумме
образуют вращающийся вектор, конец которого описы-
вает эллипс, являющийся поляризационным эллипсом
для рассматриваемой волны, и, таким образом, сами
являются сопряженными полудиаметрами этого эллипса
(рис. 1.5).
Любой действительный вектор Е мо кет быть пред-
ставлен комплексным числом Ё, действительная и мни-
мая части которого равны соответственно проекциям
___
вектора Е на оси ох и оу системы координат хоу. При
этом мнимая ось комплексной плоскости должна соот-
ветствовать оси оу координатной плоскости хоу. В ма-
тричной форме вектор Е обычно записывается в виде
матрицы-столбца
Е =
Еу
или в виде матрицы-строки, и тогда сам вектор пазы-
вается транспонированным Е = |! ДДу ||.
Соответствие вектора Е комплексному числу Е:
Е*—>Ё, есть соответствие
|| ЕХЕУ || — Ех 4- iEy.
29
Имеет место точно такое же соответствие комплексного
вектора S — Er-}-jEi комплексному числу S двойной
Комплексной плоскости. Комплексный вектор <S предста-
вим в виде матрицы S'-
ЕХг + ]Ext
f’-yr + jEyi
а соответствующее ему комплексное число — в виде
(1.5.2):
S = А + jB + /С + (ij)D.
Соответствие и S имеет место, если
А = Е„, В — ЕХг,
C = Eyr, D = Eyi.
Таким образом, комплексный вектор <§ и комплекс-
ное число двойной комплексной плоскости описывают
одну и ту же эллиптически-поляризованную волну, если
равны матрицы, составленные из координатных проек-
ций комплексного вектора и элементов комплексного
числа, т. е.
S--------►<£,
если
II ЕХг + 1Ехг
II Eyr + jEvi
А+/В
C+iD
(1.5.6)
Условие (1.5.6) сокращенно будем записывать так:
(1.5.6а)
т. е. матрица комплексного вектора S равна матрице
комплексного числа S.
Для комплексных векторов имеет место скалярное
и векторое произведение. По определению, скалярное
произведение комплексных векторов М и N есть скаляр,
определяемый следующим соотношением:
M-У* — MT-N*,
(1.5.7)
30
где Л4Г — транспонированная матрица вектора М;
N* — комплексно-сопряженная матрица вектора N.
Векторное произведение комплексных векторов М
и N есть комплексный вектор, совпадающий с нормалью
к плоскости, в которой лежат М и N, а длина его равна
комплексному числу, которое получается при скалярном
умножении вектора М на вектор N, повернутый на 90°
по часовой стрелке. Мы будем описывать векторное про-
изведение комплексных векторов только скаляром, тогда
M\N — Мт
0 1
-1 0
N.
(1.5.8)
Соотношения (1.5.7) и (1.5.8) позволяют определить
условия поляризационной ортогональности и поляриза-
ционной коллинеарности электромагнитных воли. Оче-
видно, что скалярное произведение двух параллельных
комплексных векторов равно единице, а векторное—
пулю.
Определим соотношения между параметрами поляри-
зации параллельных и ортогональных комплексных век-
торов. Для этого представим поляризационные диаграм-
мы двух эллиптически-поляризовапиых волн с ампли-
тудами, равными единице, в виде комплексных чисел
61 И Qz:
В соответствии с условиями (1.5.6) и (1.5.6а) комплекс-
ные векторы этих волн будут иметь матрицу
g _______________ cos ?! cos 9, + / sin sin 9,
cos <p, sin 9,—/ sin cos 9i
для первого вектора и точно такую же матрицу, ио
с индексами «2» — для второго.
Применяя формулы (1.5.7) и (1.5.8), получаем сле-
дующие выражения для скалярного и векторного про-
изведений:
£1 = cos (<?, — <р2) cos (6, — б2) Д- / sin (<р,+<рг) sin (6,—02),
(1.5.9)
31
£.Х <?2 = - [cos (<р, + ?!) sin (6, - 92) -
— /sin(<р, — <р2) cos(9, — 92)]. (1.5.10)
Из полученных соотношений следует, что векторы
<9, и параллельны (две волны с поляризационными диа-
грамамми и имеют одинаковую поляризацию), если
(р1=<Р2, 01 = 02, и эти же векторы ортогональны (две
волны поляризационно ортогональны), если <р2=—ФИ
02 = 01 + л/2, так как у поляризационно-ортогональных
векторов скалярное произведение равно нулю, а вектор-
ное произведение равно единице.
Таким образом, две волны с поляризационными диа-
граммами
^ = e-0>.eze и <?2=хе;/фе;(9+я/2)
поляризационо-ортогональны, а описывающие их поля-
ризацию векторы образуют базис. Для базисных век-
торов примем обозначения
Э(<?, 0) и Э(— ?, бД-эт/2), (1.5.11)
а для их отображения на двойную комплексную пло-
скость —
Э(<?, 6) и Э(—<?, 9 +«/2). (1.5.11а)
Последние два числа следует считать ортогональными
ортами двойной комплексной плоскости.
Мы будем применять и другие обозначения для
ортов, например, § и ц, особенно в тех случаях, когда
не задаются их параметры поляризации. Это вызывается
лишь необходимостью более компактной з1.ппси различ-
ных соотношений н не должно приводить к недоразуме-
ниям.
Орт Э(<? -\-т./2, 9) согласно (1.4.9), приводится к сле-
дующему виду:
е—;/ (ф+п/2) е;в . ^ij<f (в+п/2)
Таким образом, ортЭ(<рД-л/2, 9) находится во вре-
менной квадратуре по отношению к орту Э(—<р, 9Д-л/2)
и одновременно во временной и пространственной квад-
32
ратуре к орту Э(<р, 6). Матрица этого орта получается
из матрицы орта Э(<р, 6) следующим образом:
||Э(? + ^/2, 6)Ц = — /
II Э(?, 6)||Ч
а базис Э(<р, 6) и Э(«р -J-Tt/2, 6) называется квадратурным
эллиптически-поляризованным базисом.
Очевидно, что для определения двумерного базиса
достаточно задать лишь один из его ортов. Поэтому
в дальнейшем будем определять базис его первым ортом
Э1(<р, 0) или Э1( <р, 0).
Векторное произведение ортогональных ортов равно
единице, векторное произведение квадратурных ортов
равно /, скалярное произведение в обоих случаях равно
нулю.
Совокупность проекций некоторого вектора (<Pi, 61),
заданного в ортогонально-линейном базисе (т. е. в си-
стеме координат хоу}, на оси ортогонально-эллиптического
базиса Э, (<р2, 62) образует по отношению к осям нового
базиса некоторый вектор U.
Преобразование § в U осуществляется умножением
матрицы исходного вектора § на оператор, описывающий
такой переход. Для двумерных векторов таким операто-
ром является комплексная матрица размером 2X2.
Для комплексных чисел такое преобразование назы-
вается ортогональным преобразованием комплексного
пространства или унитарным преобразованием. Основ-
ное условие этого преобразования — неизменность мо-
дуля комплексного числа (неизменность длины вектора).
Для осуществления такого преобразования в рамках
поля К комплексных чисел Q введем операторное или
направленное произведение исходного комплексного
числа на комплексное число, описывающее первый орт
нового базиса. Это произведение будем обозначать
следующим образом:
= (1.5.12)
3-607
33
где индекс «*/» означает комплексное сопряжение по
мнимой единице t.
Произведение (1.5.12) осуществляется в следующей
последовательности:
и = § (<?„ 0,) X Э*г’ (?2, 02) = [£e'i/,₽1ei9‘] X 3c‘03I =
= Е[е-^'е‘л~м\Хе‘!'ъ =
= Е [cos (Oj — 02) е~11 <ч:,~ч’2> -ф. I sin (Gj — 02) е—
(1.5.13)
Обращаем внимание читателей на особенность опе-
раторного произведения комплексных чисел двойной
комплексной плоскости. Эта особенность, как это видно
из (1.5.13), состоит в том, что
Ле_''/¥1Хе±1/92~Ле“';/ф'-е±;/92==Ле“;н‘,’,Т1?2), (1.5.14)
где А — любое комплексное число, не содержащее мни-
мой единицы I. Но
щ X e±i/<₽2= ie_‘yIf>1 = Ze"0’(ф,±Ч (1.5.15)
Справедливость соотношения (1.5.15) доказывается сле-
дующим образом. Представим ie-44’' в виде
j-g-O'T. _- у у
Согласно свойству (1.4.8), ij можно объединить в совме-
щенную мнимую единицу, изменив знак в показателе сте-
пени е, т. е.
/е-б4. = _ у (//) е«7Ф. = _ yei/ (<₽. + к/2).
Далее согласно (1.5.14) получаем
— /е"’ (l₽1+,c/2) X е±;/92 = - / (ij) е“’ <ф,±1₽а) = 1е~“ (ъ±^\
что п доказывает справедливость (1.5.15).
Дальнейшее преобразование выражения (1.5.13) осу-
ществляется по обычным правилам, изложенным в пре-
дыдущем параграфе. Окончательное выражение для
произведения <§ ХЭ/ будет иметь вид
оо.) хэ;‘(?2, е2)=
= Е {cos Д<р cos Д0 -ф- / sin (<р, -ф- <р2) sin Д0 -ф-
34
—pi Icos (<Pi —|—<p2) sin ДО — j sinA<p-cos ДО]},
(1.5.16)
где A(p = (pi—фг; A0 = 0i—'02.
Нетрудно видеть, что реальная по мнимой единице i
часть числа U равна скалярному произведению^3 на Э,:
Re^q.-^/.Э*,, (1.5.17)
а мнимая по i часть этого же числа равна векторному
произведению § на Эи взятому с обратным знаком, или
скалярному произведению § на ортогональный к Э! орт:
1шг- ](/] = - g X Э, § • Э* (- <?г, 62 + т./2) = S Э*2,
(1.5.18)
т. е.
О^^ХЭ^/’Э^ + г/.Э*,. (1.5.19)
В матричной форме соотношение (1.5.19) будет иметь
следующий вид:
U = L+<?, (1.5.20)
где L — матрица размером 2X2, столбцы которой явля-
ются матрицами ортов Э] и Э2, a L+—эрмитово сопря-
женная матрица.
В рассматриваемом случае, когда параметры поляри-
зации орта Э! есть <р2, 62, матрица L+ имеет вид1
cos <f2 cos 92 — j sin <j>2 sin 02
L+= cos <f2 cos (92 + л/2) — j sin (—у2) sin(92+’t/2)
. (1.5.21)
cos <f2 sin 92 + / sin <f2 cos 92 I
cos 92ein (92'+ st/2) -J- j sin (— y2) cos (9] st/2) ]
Операторное произведение комплексных чисел двойной
комплексной плоскости не выводит эти числа за рамки
поля комплексных чисел К и поэтому может существо-
вать наряду с обычным произведением, введенным
в§ 1.3.
3* 35
Преобразование вида (1.5.16) пли (1.5.20) является
унитарным, так как не приводит к изменению модуля
исходного вектора <§. Такие преобразования поляриза-
ции волны осуществляются в различных преобразовате-
лях поляризации без потерь энергии электромагнитной
волны, если пренебречь одновременным изменением
фазы преобразуемой волны, которое можно учесть в по-
следующем фазовым множителем е\ Взаимодействие
падающей волны с реальными физическими устрой-
ствами, в которых наряду с преобразованием поляриза-
ции происходит изменение амплитуды и фазы волны,
будет описываться соотношением
£7 = £е/ф(£ХЭД (1.5.22)
в котором коэффициент k учитывает энергетические по-
тери, а е/ф— фазовый набег.
Определив соотношением (1.5.16) операторное произ-
ведение комплексных чисел, мы можем теперь показать,
что числа Э(?, 6) и Э(—<р, представляют поляри-
зационно-ортогональные орты, а числа Э(<р, 6) и Э(<р-|~
-pit/2, 0)--квадратурные орты. Операторное произведение
первых двух чисел дает
Э(<р, 0) ХЭ*г'(-?, 6 + и/2) =
= [e~‘/t₽e‘e] X [е‘/ч>ег (e+K/2)]*z = — ie-i/l₽e+;/l₽ = — i,
т. e. их скалярное произведение равно нулю, а вектор-
ное— единице, а операторное произведение квадратур-
ных ортов
[е-//фе''вПХ К'' <ф+л/2>ei0]** = ij
дает число ij, т. е. согласно (1.5.17) и (1.5.18) скаляр-
ное произведение этих комплексных чисел также равно
нулю, а векторное произведение равно —/.
1.6. ПАРАМЕТРЫ ПОЛЯРИЗАЦИИ ЭЛЕКТРОМАГНИТНОЙ
ВОЛНЫ В ПРОИЗВОЛЬНОМ БАЗИСЕ
Представление поляризационных параметров элек-
тромагнитной волны как параметров <р и 0 поляриза-
ционной диаграммы этой волны при разложении ее на
ортогонально-линейные компоненты в прямоугольной
36
системе координат пе является единственно возможным.
Это утверждение справедливо не только в отношении
угла эллиптичности ср и угла ориентации 0 поляриза-
ционного эллипса, но и в отношении других количествен-
ных характеристик поляризации волны.
В [15], например, введено понятие параметров Стокса
при представлении электромагнитной волны в произ-
вольном ортогонально-эллиптическом базисе. Точно так
же можно ввести и понятие поляризационной диаграммы
волны или поляризационного эллипса в ортогонально-
эллиптическом базисе. Но поскольку паши представле-
ния связаны в основном с линейным пространством, то
при изображении поляризационной диаграммы волны
в таком базисе ортогонально-эллиптическим ортам ста-
вятся в соответствие орты прямоугольной системы коор-
динат, проекции вектора Е на эллиптические орты пред-
ставляются как ортогонально-линейные компоненты по-
ля, и дальнейшее построение поляризационного эллипса
ничем не отличается от построения поляризационной
диаграммы волны по ее проекциям на оси прямоуголь-
ной системы координат. Построенный таким образом
эллипс следует считать поляризационным эллипсом илй
поляризационной диаграммой волны в ортогонально-
эллиптическом базисе, а угол эллиптичности <р и угол
ориентации 0 этого эллипса — параметрами поляриза-
ции волны в ортогонально-эллиптическом базисе.
Целесообразность введения понятия поляризационной
диаграммы и ее параметров (параметров поляризации)
в произвольном ортогонально-эллиптическом базисе вид-
на из следующих соображений.
При прохождении волны через преобразователь по-
ляризации ортогонально-линейные компоненты поля на
выходе этого преобразователя могут рассматриваться
как проекции входного вектора <§ на орты ортогонально-
эллиптического базиса, первый базисный орт которого
описывается той же функцией Э (срп, 0п), что и сам пре-
образователь. Поле па выходе преобразователя в общем
случае также эллиптически поляризовано, для него мо-
жет быть построена поляризационная диаграмма и опре-
делены параметры поляризации <р, 0 и фаза ф. Ясно,
что по отношению к полю <§ на входе преобразователя
37
параметры <р, 0, ф могут рассматриваться как парамет-
ры поляризации и фаза ф этого поля в базисе Э((рп, 0П).
Установим зависимость между параметрами поляриза-
ции %, 0О исходного поля $ (<р0, 0о) — £'oe_!'If°e!0°, парамет-
рами поляризации <pu, 0и базиса и параметрами поляриза-
ции преобразованного поля U(<р, 0), т. е. параметрами по-
ляризации поля £ (?0, М в базисе Э(<ри, 0и).
Исходными для определения этих зависимостей явля-
ются соотношения (1.5.16) или (1.5.20), которые позволя-
ют найти проекции £, и Ё2 волны $ (%, 0О) па оси базиса
Э (?!!, 0П) как проекции преобразованной волны U на вы-
ходе преобразователя па оси ох и оу прямоугольной си-
стемы координат хоу. Представив [7 в виде
V^E^iE,- (1.6.1)
можно затем перейти к показательной форме записи ком-
плексного вектора U:
U = Е9е~‘^е1ве^. (1.6.2)
Приравняв правые части (1.6.1) и (1.6.2), получим
исходное уравнение для определения неизвестных пара-
метров ср, 0, ф. При этом полагаем, что преобразователь
поляризации волны унитарен, и пренебрегаем постоян-
ной фазовой задержкой волны в этом преобразователе.
В противном случае в (1.5.16) и (1.5.20) необходимо
ввести переходный множитель ke,a, который будет при-
сутствовать одновременно в (1.6.1) и в (1.6.2), и, сле^
довательно, уравнение для определения ф, 0, ф можно
сократить па этот множитель. Поэтому и в случае пре-
образователя поляризации с потерями параметры поля-
ризации преобразованной волны находятся из урав-
нения
S (<Ро, 0о) X Э*!' (?u, 0и)=£ое "‘V9е/ф, (1.6.3)
а множитель £е;а учитывается в окончательной записи
преобразованной волны:
^/X'Xe^'VV.
Осуществим операторное умножение в (1.6.3). В ре-
зультате получим
38
Z?o[cos(0o — 0„) e,/l₽nЦ- isin(O0—0„) e 1Jl₽n] e 'J’’0 —
= £oe~‘’'W< (1.6.4)
Уравнение (1.6.4) относительно параметров ф, 0 и ф
решается неоднозначно. Решения зависят от того, в ка-
ких пределах однозначности мы будем определять вели-
чины ср и 0, т. е. в конечном счете оттого, какую полу-
ось поляризационного эллипса принимаем за главную.
В соответствии с двумя определениями главной полуоси
получим две системы формул для определения ф, >и 0.
В пределах каждой из этих систем величины ф и 0 опре-
деляются однозначно.
Если ф и 0 определять так, что больший из этих
углов не будет превышать л/2 по абсолютной величине,
то фаза ф может принимать значения в пределах
—л ... л. Поэтому для однозначного определения фазы
необходимо определить отдельно созф и зшф.
Для этого необходимо так преобразовать уравнение
(1.6.4), чтобы справа оставался только один фазовый мно-
житель е,ф. Такое преобразование осуществляется путем
приведения анализируемой волны к базису Э(ф, 0), т. е.
в результате операторного умножения левой и правой ча-
сти уравнения (1.6.4) на Э(ф, 0). Осуществив такое ум-
ножение, получим
е/ф = cos Д0 (cos 0et/<₽ — i sin 0е—1/4>) е l₽I|)
sin Д0 (sin Qetiv i cos Oe~‘l,f)e (<₽o+<₽«) ; (1.6.5)
где Д0==0О —0n.
Представив правую часть выражения (1.6.5) в виде
a + jb + ic+ (ij)d и приравняв коэффициенты при одина-
ковых мнимых единицах слева и справа, получим сле-
дующие соотношения:
cos ф = а = cos Д0 cos 0 cos (фо—фп—ф) +
+ sin Л0 sin 0 соз(фо+фп—Ф), (1.6.6)
sin Ф = 0 = 5Ш Д0 COS 0 sin (фо + фп + ф) —
—cos Д0 sin 0 sin (фо—фп + ф), (1.6.7)
C==sin Л0 COS 0 COS (фо + фц + ф)—
—cos ДО sin 0 cos (фо—фц + ф) = 0, (1.6.8)
39
—d=cos AB cos 0 sin (фо—фп—ф) +
+sin AB sin 0 з!п(фо+фп—ф) =0. (1.6.9)
Уравнения (1.6.6) и (1.6.7) являются конечными для
определения фазы ф. В них кроме ф0, фгг и Во, 0п необ-
ходимо подставить значения ф и 0, которые получаются
из совместного решения уравнений (1.6.8) и (1.6.9).
Решения системы уравнений (1.6.8) и (1.6.9) также
зависят от того, в каких пределах однозначности мы
будем определять ф. и 0. Если —л/4^ф^л/4, то
—л/2^0^л/2 и угол 0 есть угол между горизонталь-
ной осью системы координат хоу и большой полуосью
поляризационного эллипса, которая и принимается
в данном случае за главную полуось. Формулы для
определения <р и 0 в этом случае следующие:
sin 2<р = sin 2ф>0 cos 2<рп — cos 2<р0 sin 2<f>n cos 2Д9,
, a ______sin 2<pn-cos 2y0-sin 2Д9
S sin 2<f>0 + sin 2 (<pn— <p0)‘
(1.6.10)
Если в качестве главной осп поляризационного эллип-
са взять ближайшую к положительному направлению
оси ох полуось (большую или малую), то пределы одно-
значного определения параметровф и 0 будут —л/2... л/2
и —л/4... л/4 соответственно, а формулы для определе-
ния ф и 0 будут иметь вид
sin 2Д9
cos 2Д9 cos 2?n-|-sin 2?n tg 2<p0’
_ cos 29 (sin 2?0 cos 2yn — cos 2<p„ sin 2y„ cos 2Д9)
g ' cos 29 + (sin 2?0 sin 2<pn cos 2<p0 cos 2<pn cos 2Д9)'
(1.6.11)
Если электромагнитная волна в произвольном орто-
гонально-эллиптическом базисе Э(фп, 0П) задана своими
проекциями па орты этого базиса в виде
U^E^' + iE^,
то параметры поляризации этой волны находятся ана-
логично предыдущему из уравнения
40
или из равносильного ему уравнения
cos уе/ф1 -ф- i sin уе/фа— е-ч,,е'ве/ф, (1.6.12)
где Y = arctg(£2/£I).
Для решения уравнения (1.6.12) относительно <р, 0
и гр его следует сначала преобразовать к виду
_ZA. i (*-Я
cosye 2 ф- i sin уе 2 =e_,/lfe,ee ' 2 , (1.6.13)
где
Д=ф1—грг; а = г|и—грг.
Левая часть выражения (1.6.13) путем замены три-
гонометрических функций показательными с мнимой
единицей i и показательных функций—тригонометри-
ческими преобразуется в форму
cos(A/2) е‘тф- j sin (Д/2) е“п,
после чего путем приведения (1.6.13) к базису e“1JI₽e'6
получим уравнение с комплексными членами
cos cos (y — 6) ф- j sin cos (y ф- 6) j e4lf-|-
ф- i ^cos sin (y — 6) — / sin —2 sin (y ф- 6)j e-i/lf= eJ (ф-о/2),
(1.6.14)
из которого путем приравнивания коэффициентов при
одинаковых мнимых единицах слева и справа и решения
полученной системы уравнений находим, как и в пре-
дыдущем случае, два вида соотношений для определе-
ния параметров поляризации:
sin 2<р— sin 2y sin A,
Е Q _ , sin 2-fCos A
° cos 2y + cos 2y ’
tg26 —tg 2y cos A,
______Г sin 2-f sin A cos 20
g cos 2y cos 20
(1.6.15)
(1.6.16)
Из выражений (1.6.15) получаем однозначные значения
<р в пределах —л/4... л/4 и однозначные значения 0
в пределах —л/2... л/2. Из (1.6.16), наоборот, — одно-
41
злачные значения 0 в пределах —л/4 ... л/4 и однознач-
ные значения <р в пределах —л/2 ... л/2.
Уравнения для определения фазы ф—-ог/2 общие как
для системы (1.6.15), так и для системы (1.6.16) и
имеют следующий вид:
cos — cos cos cos (0 — у) -ф-
-ф- sin <р sin sin (9 -ф- у),
д (1-6-17)
sin (ф----) = cos<psin-^- cos (О ф- у) —
— sin <р cos sin (9 — д).
Однако выражения (1.6.15), (1.6.16) позволяют опре-
делять значения ф, 0 и в пределах, больших пределов
однозначности функций tg(-) и sin( •). Расширение
пределов определения ф и О скажется на определении
главной оси поляризационного эллипса, до которой от-
считывается угол 0, и, в конечном счете, на изменении
фазы ф. Форма и ориентация поляризационной диаграм-
мы при этом не изменяется. При вычислениях важно
лишь, чтобы для определения <р и 0 использовались либо
совместно уравнения (1.6.15), либо уравнения (1.6.16).
Заметим, что во всех известных авторам работах,
посвященных изучению поляризационных свойств элек-
тромагнитных воли, приводятся лишь первые из (1.6.15)
и (1.6.16) соотношения для определения параметров
поляризации волны по ее проекциям на ортогональные
орты, т. е.
tg 20~=tg 2у cos Д, sin 2cp = sin 2у sin Д. (1.6.18)
Ясно, что соотношения (1.6.18) позволяют однознач-
но определить ф и 0 лишь ь пределах —л/4... л/4.
Соотношения для определения общей фазы эллпптн-
чески-поляризованной волны вообще не приводятся.
Из формы представления поляризационной диаграммы
эллиптически-поляризованной волны в виде (1.4.1) следу-
ет, что функция = e-l/l,leI0e'4' периодична с периодом
2л по каждому из параметров ф, 0 и ф. Следовательно,
оперируя с числами типа (1.5.1), мы можем не забо-
титься об ограничениях, накладываемых на величины ф,
42
0, ф. Однако при окончательных выводах о форме поля-
ризационной диаграммы необходимо привести конечные
выражения к форме, в которой <р и 0 находились бы
в определенных выше пределах однозначности.
1.7. ПАРАМЕТРЫ СТОКСА И МАТРИЦА КОГЕРЕНТНОСТИ
Параметры электромагнитного излучения, носящие
теперь имя Стокса, были введены Стоксом [39] в 1852 г.
для описания поляризационных свойств частично поля-
ризованного ноля, т. е. такого поля, которое можно, как
это показал Стокс, представить в виде суммы полностью
поляризованной составляющей и составляющей, в кото-
рой невозможно выделить даже в среднем какой-либо
преимущественный вид поляризации, называемой неполя-
ризованной составляющей излучения. Параметры Стокса
тесно связаны с представлением эллиптически-поляризо-
ванной волны точкой на сфере Пуанкаре и являются
фактически координатами этой точки в прямоугольной
системе координат. Подробно такое представление пол-
ностью поляризованной волны описано, например, в ра-
ботах [15, 40].
Для описания свойств радиосигналов с изменяющи-
мися параметрами поляризации сфера Пуанкаре особо-
го значения не имеет и может найти лишь частичное
применение для лучшего физического представления
происходящих процессов. Поэтому мы определим пара-
метры Стокса электромагнитной волны не как коорди-
наты точки на сфере Пуанкаре, а так, как принято сей-
час в литературе, посвященной поляризационным свой-
ствам электромагнитного поля. Будем рассматривать
монохроматическую волну единичной амплитуды с поля-
ризационной диаграммой
Тогда все параметры Стокса, полученные для этой вол-
ны, будут нормированными. Ненормированные же пара-
метры получаются умножением нормированных на
интенсивность волны, т. е. на Ео2.
Итак, первым параметром Стокса является интенсив-
ность волны /. В нашем случае этот параметр равен 1.
Второй параметр носит название «преимущественность
волны горизонтальной поляризации» и обозначается
Р = ]£Э*(0, 0)|2 —|£3*(0,it/2)|2 = £* — Е2. (1.7.1)
43
Остальные параметры — преимущественность колеба-
ния под углом 45° U и преимущественность круглополя-
ризованной волны правого направления вращения V —
определяются аналогичным образом:
и = I g Э*(0, тг/4) I2-1 g Э* (0, - тг/4) |2=£~,- Ё2У„ (1.7.2)
V = |d? Э* (ти/4, 0) I2 - I s Э* (—чг/4, 0) |2 = 4 - < -
(1.7.3)
Вычисления по вышеприведенным формулам дают:
Q = cos 2<р cos 20, {7=cos2<psin20,
V=sin2<p. (1-7.4)
Из приведенных соотношений следует, что параметры
Стокса являются энергетическими параметрами волны.
Они применялись Стоксом для описания частично и пол-
ностью поляризованного квазимонохроматического излу-
чения оптического диапазона. В этом диапазоне волн
в то время можно было регистрировать только средние
по времени от квадрата компонент поля значения, т. е.
интенсивность волны. Поэтому собственно параметрами
Стокса являются усредненное по времени величины
(1.7.1) — (1.7.3), т. е. О, U, V и средняя интенсивность/.
Для частичного поляризованных волн интенсивность /
состоит из интенсивности неполяризованной части излу-
чения /Сл и интенсивности полностью поляризованной
части излучения /п. Отношение 1п/1 называется степенью
поляризации электромагнитной волны.
Параметры Стокса тесно связаны с часто применяе-
мой при описании частично и полностью поляризованно-
го излучения матрицей когерентности. Матрица коге-
рентности определяется соотношением
7=^+, (1.7.5)
где —матрица-столбец вектора волны, а — эрми-
тово сопряженная матрица.
Для частично и полностью поляризованных квазимо-
нохроматических излучений матрица когерентности полу-
чается усреднением (1.7.5) по времени, т. е.
7=^+.
•14
Определим вид матрицы когерентности для пол-
ностью поляризованной волны.
Для этого подставим в (1.7.5) выражение матрицы
<g волны с параметрами поляризации q?, 0:
g,__£ II cos <р cos 9 -|- j sin <f sin 9
° И cos <p sin 9 — j sin <p cos 9
После перемножения матриц £ и получим
2
1 cos 2<f cos 9
cos 2u sin 29 — j sin 2<f>
cos 2<p sin 29 + / sin 2<p
1 — cos 2(p cos 9
(1.7.6)
След этой матрицы Тг/ равен интенсивности волны Ео.
Нетрудно видеть, что матрицу J можно разложить по
спиновым матрицам Паули, как это сделано для аналогич-
ного случая в [46]:
(1.7.7)
где
— спиновые матрицы Паули, а коэффициенты Sk
в выражении (1.7.7) есть не что иное, как параметры
Стокса волны <§:
S0 = I=E20; S, =Q = Е2 cos 2<р cos 20;
S2 = IJ = E2 cos2<p sin 20; S3 = V = E20 sin 2<p.
Фактически для монохроматической волны достаточ-
но знать только параметры Q, U, V. Интенсивность /
определяется из соотношения
Iz=qz+uz+V2.
Зная Q, U, V, можно определить геометрические пара-
метры поляризационной диаграммы волны:
sin2<p = V//, tg20 = U IQ. (1.7.8)
45
Выражение (1.7.8) позволяет определить параметры
поляризации волны через ее параметры Стокса в том
случае, когда волна задана своими проекциями на оси
прямоугольной системы координат:
£ (/) = (Е^1 -ф/£2е/ф2)е/ш/. (1.7.9)
При этом параметры Стокса определяются подстановкой
(1.7.9) в (1.7.1) — (1.7.3). В результате осуществления
математических преобразований получим выражения па-
раметров Стокса через амплитуды и фазы ортогонально-
линейных компонент поля:
/ = е* + е22, Q — E^ — E^,
t/ = 2fi1E2cos(<}1—ф2), V = 2E1E2 sin (ф,— ф). (1.7.10)
Формулы (1.7.10) позволяют определить параметры
Стокса волны в любом базисе, если в форме (1.7.9) за-
даны проекции этой волны на орты g, т] этого базиса,
а соотношения (1.7.8) дают возможность определить па-
раметры поляризации волны <§ в базисе g, т]. Однако
это соотношение однозначно определяет <р и 0 лишь
в интервале — л/4 ... л/4. Кроме того, параметры Стокса
не позволяют определить общую фазу волны.
Наконец, получим соотношения для определения пара-
метров Стокса в произвольном базисе i, tj, если известны
параметры Стокса волны, например, в ортогонально-ли-
нейном базисе оху. Для этого разложим исходную волну
б(<ро, 0») по ортам базиса t т). Если положить, что этот
базис квадратурный, т. е.
т1 = е-‘7(‘₽,ь’‘/2,е;в1,
то разложение запишется в виде
S (?о, 0») = Ео {[cos Д<? cos ДО -ф / sin (% -ф ?,) sin ДО] 5 -ф
+ [sin Д? cos ДО-}-/cos (<р0-ф sin Д0] -tj}, (1.7.11)
где Д? = ?о —ДО = 0о — О,,
Аналогично получаем разложение волны £ (фо, 0о) по
ортам базиса т/, повернутого относительно g, т] на
л/4, а также по ортам Ir, t]l, отличающимся от g, т] на
л/4 по эллиптичности. Тогда параметры Стокса волны
ё (фо, Оо) В базисе т] можно определить через ее про-
46
бкцйи на осп базиса g, т], базиса rf и базиса gn, цщ
(1.7.12)
П ~ I I I е-г-,1. I •
Вычисления по формулам (1.7.12) позволяют получить
следующее соотношение:
’i
qZ ^.y
($ Я R Vе я
*x,y l'x,y v x,y
Qx.y
Ux.y ’
Vx.y
где Q*y, (/ , V*y — параметры Стокса орта $ нового ба-
зиса в ортогонально-линейном базисе оху; эти же симво-
лы, но с индексом — параметры Стокса орта раз-
вернутого на it/4, т. е. параметры Стокса орта
=Э(<Р1, 0,-1—-те/4) в базисе oxy; Q*R, V'xR — параметры
Стокса орта =Э (?,-]-it/4, 0j) в базисе оху.
Соответственно, если известны параметры Стокса
Qa. ?’ Цх Кх з волны в базисе а, р, то параметры Сток-
са этой волны в квадратурном базисе £, т] можно опре-
делить из соотношения
Q-.
Ql? <A,? vt?
Q\’.3 Сз
OiR U'R vVR
Чх,? «,(* vcx.p
<?x.
a,
(1.7.13)
и
a
3 I
Элементы матрицы 3X3 в выражении (1.7.13) явля-
ются параметрами Стокса ортов g, g' и в базисе а, 0.
Очевидно, что четвертый параметр Стокса—-интенсив-
ность волны—инвариантен относительно изменения ба-
зиса.
Зная параметры Стокса волны в любом базисе, мож-
но всегда определить матрицу когерентности волны из
соотношения (1.7.7).
В заключение отметим, что существует ряд других
параметров, характеризующих поляризационные свойст-
ва волны, и разработаны различные графики и иомо-
47
граммы для перехода от одних парамотроп к другим.
Подробно с этипи вопросами можно ознамомиться по
работам (2, 15, 40]. В рамках данной работы вполне до-
статочно лишь тех параметров поляризации, которые
описаны в этой главе.
ГЛАВА 2
МГНОВЕННЫЕ ПАРАМЕТРЫ ПОЛЯРИЗАЦИИ
ДВУМЕРНЫХ СИГНАЛОВ
Параметры поляризации <р и 0 применялись, как пра-
вило, для характеристики электромагнитных колебаний
неизменной поляризации. Электромагнитная волна с пе-
ременными параметрами поляризации представляется
обычно в виде суммы полностью поляризованной и не-
поляризованной составляющих. При этом неполяризо-
ванная составляющая волны характеризуется только
своей интенсивностью. Такое представление электромаг-
нитной волны не применимо в случае поляризационно-
модулированных сигналов. В этом случае должны быть
известны значения параметров ср и в как функции вре-
мени и передаваемого сообщения. Описание электромаг-
нитной волны комплексными числами двойной комплекс-
ной плоскости позволяет найти эти функции практи-
чески для всех возможных сигналов.
Вопросам определения параметров <р(/), 9(0 и ф(/)
по заданным проекциям электромагнитной волны на ко-
ординатные оси и посвящена данная глава.
2.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Монохроматическая волна, параметры поляризации
которой были рассмотрены в гл. 1, является идеализа-
цией электромагнитного колебания, так как, по опреде-
лению, монохроматическое колебание должно быть неиз-
менным и непрерывным в течение неограниченного вре-
мени. Используемые на практике радиосигналы имеют
конечную длительность и, согласно преобразованию
Фурье, должны иметь бесконечно широкий частотный
спектр. Однако чаще всего характер изменения реаль-
ных сигналов таков, что за пределами сравнительно
узкой полосы частот амплитуды спектральных состав-
ляющих настолько малы, что общая энергия их состав-
ляет лишь незначительную часть энергии сигнала. По-
48
этому составляющими спектра вне пределов узкой поло-
сы частот можно пренебречь. Такие сигналы называют
узкополосными, что означает, что спектральные состав-
ляющие сигнала группируются в относительно узкой по
сравнению с некоторой центральной частотой со0 спектра
полосе. Электромагнитную волну, образующуюся при
излучении такого сигнала, называют квазимонохрома-
тической, тем самым подчеркивая сосредоточенность ее
энергии около монохроматической линии спектра, соот-
ветствующей частоте й0.
Математическая запись такого радиосигнала имеет
вид:
S(t) =А (/) cos[tt»o/ + i|)(0], (2.1.1)
где A(t) и ф(/)—медленно меняющиеся по сравнению
с coscoo/ функции. В частном случае A(t) и (или) ф(/)
изменяются по закону передаваемого сообщения, и тог-
да сигнал называется амплитудно- и (или) фазомодули-
рованным сигналом.
Квазимонохроматическая волна может быть пред-
ставлена совокупностью своих проекций на оси ортого-
нального базиса, т. е. совокупностью двух радиосигна-
лов Si(/) и Sz(i):
§{t) =ГЭД + ^2(0, (2.1.2)
причем комплексному представлению ортов ?, т; базиса
должно соответствовать комплексное представление си-
гналов Sj (/), S2 (/). Если эти сигналы заданы в виде
(2.1.1), от комплексное их представление есть
Sft(/)= Лй(0е/[^+Ф',Ю1> /fe = 1, 2. (2.1.3)
Средние или, как их еще называют, несущие частоты
этих сигналов не обязательно одинаковые, но, по край-
ней мере, близки друг к другу настолько, что спектры
сигналов Si(i) и Sz(t) перекрываются на большей части
занимаемой ими полосы частот.
В противном случае сигналы S, (/) и S2 (/) должны рас-
сматриваться как проекции на оси £ и т; базиса двух не
связанных между собой квазимонохроматических волн, па-
раметры поляризации которых совпадают с параметрами
поляризации ортов 5, ц, и нет смысла рассматривать $ (^
4—667 49
как одну квазимонохро^атическую волну. 11оэтому в 6оЛьй
шинстве случаев мы будем полагать в (2.1.3)
Помехи в радиолинии могут быть как узкополосны-
ми, например помехи от соседних станций, работающих
на близкой к wo частоте, так и широкополосными. Одна-
ко при приеме спектр широкополосной помехи ограничи-
вается по верхней и нижней частоте в силу конечной
полосы пропускания приемного устройства. Поэтому по-
меху также можно считать квазимонохроматической
волной вида (2.1.2), причем Ah(l), для помехи —
случайные функции. Строго говоря, и в случае сигнала
функции фй (/) являются случайными, так как за-
ранее известная функция информации не несет. Однако
для уяснения многих существенных свойств сигнала
вполне допустимо считать его амплитуду Ah(t) и фазу
ф/г(О детерминированными функциями. В частности, это
условие принимается при анализе поляризационной
структуры радиосигналов.
Говоря о поляризационной структуре сигнала, сле-
дует помнить, что поляризационными свойствами обла-
дает электромагнитная волна, распространяющаяся
в свободном пространстве или в специальных направ-
ляющих системах типа волноводов. Бессмысленно гово-
рить о поляризации сигнала на выходе, например, сме-
сителя. Однако поляризационные параметры волны
определяются исключительно амплитудно-фазовыми
соотношениями ее компонент. Эти соотношения сохра-
няются и в сигналах, которые образуются на выходах
приемной антенны при приеме волны.
Обычные антенны, в том числе и эллиптической по-
ляризации, принимают только ту компоненту волны, па-
раметры поляризации которой совпадают с поляриза-
ционными параметрами самой антенны. Компонента
ортогональной поляризации при этом отражается. Что-
бы принимать полностью энергию волны любой поляри-
зации, в конструкции приемной ?.нтенны должна быть
предусмотрена возможность разложения принимаемой
волны на две поляризационно-ортогональные компонен-
ты с последующим усилением п преобразованием каждой
из этих компонент в своем канале.
Такую антенну, совмещающую в себе фактически
две антенны ортогональной поляризации, будем назы-
вать двухкомпонентной антенной эллиптической поляри-
зации. Если предусмотрены специальные меры против
50
амплитудных и фазовых искажений в двух каналах
приемного устройства, то по амплитудно-фазовым соот-
ношениям принятых сигналов можно оценить поляри-
зационную структуру той волны, которая порождает эти
сигналы. В этом смысле можно говорить о поляриза-
ционной структуре самих сигналов, а также и помех.
При этом оба сигнала Si(t) и Sz(t) мы должны рассма-
тривать как две компоненты единого сигнала, сущест-
вующего в двух каналах общего приемного устройства,
и поэтому, так же как и принимаемую плоскую волну,
этот сигнал будем называть двумерным, а его состав-
ляющие Si(/) и Зг(0 —проекциями двумерного сигнала
на оси базиса, в котором рассматривается этот сигнал.
Фактически базис сигнала задается поляризационными
параметрами двухкомпонентной приемной антенны.
Однако, как будет показано в дальнейшем, некоторые
линейные преобразования над двумерным сигналом
в самом приемном устройстве равносильны изменению
параметров поляризации (или базиса) приемной антен-
ны. Поэтому, говоря о базисе, в котором представляется
двумерный сигнал, нет необходимости подчеркивать,
определяется ли он антенной или структурой двухка-
нального приемника.
Таким образом, выражение (2.1.2) при ортогонально-
линейных ортах £ и т] является комплексной формой пред-
ставления двумерного сигнала, который можно интер-
претировать либо как проекцию плоской квазимонохро-
матической волны на неподвижную плоскость, перпен-
дикулярную вектору Пойнтинга этой волны, либо как
совокупность двух сигналов St(t) и Зг(0, существующих
одновременно в двух каналах устройства формирования
или обработки этих сигналов. Комплексное представле-
ние двумерного сигнала на двойной комплексной плоско-
сти получается из комплексной формы представления
компонент этого сигнала Si(i) и Зг(/) при одновремен-
ной замене неподвижной плоскости, на которую проек-
тируется волна, либо воображаемого двумерного прост-
ранства, в котором существуют сигналы Si(t) и 5г(0,
комплексной плоскостью с мнимой единицей i. В ре-
зультате двумерный сигнал в ортогонально-линейном
базисе принимает вид
S (0 = ^(0+^(0. (2.1-4)
4* 51
а в ортогонально-эллиптическом базисе
S (/)= ! S. (О 4-71\(0. (2.1.5)
Поляризационную структуру двумерного сигнала
можно определить, указав поляризационные параметры
каждой гармоники спектра этого сигнала. Но сам спектр
Фурье можно определить лишь для периодических сигна-
лов. Для непериодических сигналов можно определить
лишь спектральную функцию, а для случайных сигналов
и помех-—энергетический спектр, который не несет
информации о фазах спектральных составляющих и,
следовательно, о поляризационных параметрах прини-
маемой волны. Тем не менее можно определить некото-
рые энергетические характеристики случайных сигналов
и помех, которые будут достаточно полно описывать
поляризационные свойства принимаемой волны. Для де-
терминированных сигналов можно определить функции,
описывающие процесс изменения состояния поляризации
принимаемой волны во времени. Определению и описа-
нию этих параметров и будет посвящена данная глава.
2.2. ПОЛЯРИЗАЦИОННАЯ ДИАГРАММА СУММЫ
ДВУХ МОНОХРОМАТИЧЕСКИХ ВОЛН
Простейшей квазимонохроматической волной является волна,
состоящая из двух монохроматических волн, распространяющихся
з одном и том же направлении и имеющих частоты о>1 и <т>2, незна-
чительно отличающиеся между собой: разностная частота А<т> =
= (i>i—м2 должна быть гораздо меньше любой из основных частот.
Положим, что обе эти монохроматические волны имеют одинаковые
параметры поляризации и, следовательно, одну и ту же поляризаци-
онную диаграмму е~'‘-/,₽е19, но разные амплитуды и фазы. Суммар-
ная волна
ё (/) = е~‘;ч> е‘® [£1е/(Ш1'+ф') +£2e'w+w ] (2.2.1)
может быть представлена как колебани„ частоты о>о= (o>i + со2)/2,
у которого с течением времени меняется амплитуда и фаза:
ё (/) ei9E (/) е/г<0°*+ф(0 +*°J, (2.2.2)
где /;'(/) ~ [£2 + А2 + 2£,£2 cos (Дсо£ + Дф)]1^2—огибающая квази-
монохроматической волны ё(С),
Фо = (Ф1 + Фа) /2- ДФ ~ Ф1 — Фг. Дсо = C0j — сог,
. ... f Et — £г Ди/ + ДФ \
ф (0 arctg tg----j---) +
52
. л Г Дсо/ -I- Дф
+ ~2~ sign (£1 — Zi'2)sin--------------g------
cos
Дм/ + ДФ
2 Jf
(2.2.3)
sign [aj =
при a > 0,
при a < 0.
Из соотношения (2.2.2) следует, что конец результирующего
вектора <g (/) описывает кривые линии, тем меньше отличающиеся
от эллипса с параметрами <р, 0, чем медленнее изменяется огибаю-
щая £(/) или чем медленнее меняется cos Д<о/ по сравнению
с cos aot. Размеры этого эллипса изменяются с течением времени,
по форма и ориентация остаются неизменными. Поэтому такая
квазимонохроматическая волна считается полностью поляризован-
ной с неизменными параметрами поляризации.
Не трудно видеть, что если квазимонохроматическая волна пред-
ставляет собой целую совокупность незначительно удаленных друг
от друга по частоте гармоник одинаковой поляризации, то сово-
купная волна имеет те же параметры поляризации, что и каждая
гармоника в отдельности, а ее поляризационная диаграмма опи-
сывается комплексным числом е~49 е‘9. Поляризационная диаграм-
ма такой волны не совпадает с годографом электрического вектора,
а представляет собой эллине единичной амплитуды, только по фор-
ме и ориентации совпадающий с годографом вектора Е любой
спектральной составляющей волны. Годограф суммарного вектора
Е, наблюдаемый в течение нескольких периодов центральной ча-
стоты спектра квазимонохроматической волны, по форме и ориента-
ции весьма незначительно отличается от поляризационной диаграм-
мы волны.
Рассмотрим теперь случай, когда квазимонохроматическая
волна представлена суммой двух волн разной частоты и разной
поляризации, т. е.
^ (/) =е-^ + е-^’ е^Е2е>^‘+^ (2.2.4)
при условии
а=--Л/Е(1,); b=B/E(tl)-, c=C/E(tt)-t d=D{E(tl). (2.2.5)
Перепишем выражение (2.2.4) в виде
£(/) — [Е,е/(4ш/+4Ф,/2 e-'W91 +
। Е2е~И4ш7+4Ф)/2 е-‘/ч>2 e‘0q е/(“о7+Фо). (2.2.G)
При условии (2.2.5) выражение, стоящее в (2.2;6) и квадратных
скобках, в течение короткого (в несколько периодов частоты
f—<0о/2л) промежутка времени Д/ можно считать постоянным и
равным значению, которое оно принимает при t=it, где /1 — момент
времени, совпадающий со срединой интервала АЛ Эту постоянную
величину можно представить в виде
. Дю^ + Дф . Дш^Ц-Дф
Е,е ‘ ~+ Е,е ~ е‘'9> =
53
— Л ф- /В ф- iC + (ij) D - E (/,) frt + jb + ic + (<•/) d], (2.2.7)
где E (/,) = КЛ2^+В2’+Т?“2 фТО2; (2.2.8)
a=A/E(ft); Ь = В/Е(/,); c^C/E^); d=D/E(it). (2.2,9)
Коэффициенты А, В, C, D и a, b, c, d зависят от параметра
и постоянны на интервале Д/.
Преобразуя левую часть выражения (2.2.7), получаем следую-
щие значения для коэффициентов А, В, С и D:
Д<о/, ф- Дф
А = (£) cos cos 9i ф- Е2 cos ?2 cos 92) cos ----------
Д со/, ф- Д ф
— (£, sin ?! sin 9! — Е2 sin ?2 sin 92) sin->
Дсо/,4- Дф
В — (Е, sin ?, sin 9! ф- £2 sin ?2 sin 92) cos ----Н
Дсо/, ф-Дф
ф- (Е, cos ?! cos 9! — /:2 cos ?2 cos 92) sin-%-- 1
Дсо/, ф-Дф
С = (£, cos ?! sin 9, ф- Е2 cos ?2 sin 92) cos -<,-Н
Дсо/, ф-Дф
ф- (£, sin ?! cos 9, — /:2 sin ?2 cos 92)sin--;
Дай, ф-Д?
D -- — (Ег sin ?! cos 9! ф- £2 sin ?2 cos 92) cos-------Н
Дай, ф-Дф
ф- (£, cos ?! sin 9, — £2 cos ?2 sin 92) sin-----• (2.2.10)
Из (2.2.8) и (2.2.9) следует, что a2 + b2 + c2 + d2 = 1, и, следова-
тельно, выражение, стоящее в (2.2.7) в квадратных скобках, можно
представить на двойной комплексной плоскости комплексным чис-
лом, модуль которого равен единице, т. е.
Е (tt) \а ф- jb ф- ic ф- (i/) dj ----- Е (/,) е~‘^А егв(/1) е/ф(/1) . (2.2.11)
Таким образом, квазимонохроматическая волна (2.2.4) на ин-
тервале времени
2л 2тг
— < Д/<т— (2.2.12)
со0 Дсо ' '
может быть представлена как электромагнитная волна с постоян-
ной амплитудой, с постоянными параметрами поляризации и с не-
сущей частотой <г>о=0,5(<г>1 + <о2):
& (f) = £(/,) a-EfttA е‘Ж) е'Ф(£) e;W+4o) (2.2.13)
, Д/ Д/
при if 2 Л И- 2 *
Амплитуда £(/i) этой волны находится из выражения (2.2.8), кото-
рое после подстановки в пего значений коэффициентов А, В, С и D
из (2.2.10) преобразуется к виду
£2(Л) =£(2+£22 +2£!£2[cos(cpi—cp2)cos(0i—02)со5(Дй)/!+Дф)—
—sin(tp14-<p2)sin(01—02)sin(Aco/i4-A4")]. (2.2.14)
И
Выражение (2.2.14) подтверждает известный из [6] факт, что
поляризационно-ортогональные полны не интерферируют. Действи-
тельно, при поляризационной ортогональности двух рассматривае-
мых волн, когда <pi=—ф2, O2=0i + n:/2 либо 0i = 02, <pi—ф2=±л/2,
выражение, стоящее в (2.2.14) в квадратных скобках, обращается
в ноль и амплитуда Е квазимонохроматической волны становится
постоянной величиной, не зависящей от времени. Амплитуды поля-
ризационно-ортогональных компонент могут при этом меняться во
времени, что находит свое отражение в изменении параметров по-
ляризации суммарной волны. Однако сумма их квадратов должна
быть постоянной. Иначе будет меняться и приведенная амплитуда
результирующей волны с переменными параметрами поляризации.
Параметры поляризации <p(^i), 0(/i) и фаза ф(/1) этой волны
находятся из равенства
а +/6 + “'+('/) d _• e~,Jlf(Z1) e‘0(Z1) e,‘f'(Z,). (2.2.15)
Как и в случае, рассмотренном в § 1.6, комплексное уравнение
(2.2.15) относительно параметров tp(/i), 0(li) и ф(Н) решается не-
однозначно.
Решения зависят от того, в каких пределах однозначности мы
будем определять каждый из этих параметров. Если пределы одно-
значного определения фазы ф(/,) выбрать в интервале —л ... л,
то необходимо получить из (2.2.15) раздельные выражения для опре-
деления созф(/1) и з1пф|(/|). Для этого правую часть выражения
(2.2.Г5) приводим к виду е‘*^0 путем операторного умножения
левой и правой части уравнения (2.2.15) на e‘,lf(Z‘) :
е/4(6) ,= + jb + ic + d] X [e+‘z9(Z1) e~z0(Z1)j. (2.2.16)
Осуществив операторное умножение в (2.2.16) и приравняв коэф-
фициенты при одинаковых мнимых единицах слева и справа, по-
лучим систему уравнений
cos ф = cos 0 (а cos ф—d sin q>) + sin 0 (c cos <p+b sin q>),
sin ф = соз 0(6 cos (p+c sin cp) +sin 0(d cos ф—a sin ф), (2.2.17)
из которой можно найти ф, определив предварительно ф и 0.
Здесь для сокращения записи опущены обозначения зависимости
величин от параметра
Значения ф и 0 находятся путем решения системы еще двух
уравнений, получаемых из (2.2.16):
cos 0(с cos ф—b sin ф)—sin 0(а cos ф+d sin ф) =0,
cos 0 (d cos ф-' a sin q.) —sin 0(6 cos ф—c sin ф) =0. (2.2.18)
Решение системы двух последних уравнений дает, как и в аналогич-
ном случае, рассмотренном в § 1.6, две системы формул для опре-
деления ф и 0:
sin 2у = 2 (сб — ad) / (а2 + Ь2 + с2 + d2),
n п (ас — bd) — (ab — cd) sin 2у
tg 9 = 2 (а2 — b2)(c2 — d2j+(a2^62+c2—d2) cos 2?+ 2(ad + be) sin 2?
(2.2.19)
55
ta 2й - 2 (<?C +
Tg ° ~ (a2 + 62) — (c2 + d2) ’
(ac — bd) cos 29 — -^г (a2 — b2 — c2 -ф d2) sin 29
(лб -ф cd) -ф (ab — cd) cos 29 -ф (ad -ф be) sin 29
(2.2.20)
Системы формул (2.2.19) и (2.2.20) равнозначны. Для опреде-
ления параметров <р и О можно воспользоваться как той, так и
другой системой. Но из (2.2.19) угол эллиптичности определяется
однозначно в интервале —л/4 ... л/4 и угол ориентации — в ин-
тервале — л/2 ... л/2, а из (2.2.20), наоборот, угол ориентации поля-
ризационной диаграммы однозначно определяется в пределах
—л/4 ... л/4, а угол эллиптичности — в пределах —л/2 ... л/2. Об-
щая фаза ф колебания определяется однозначно в пределах
—л... л из уравнений (2.2.17). В эти уравнения следует, кроме из-
вестных величин а, Ь, с н d, подставить значения cos <р, sin ср, cos 0,
sin 0, полученные из (2.2.19) или (2.2.20).
Заметим, что поскольку коэффициенты а, Ь, с и d в (2.2.19) и
(2.2.20) входят в квадрате или в виде попарных произведений, то
при использовании этих выражений можно подставлять ненорми-
рованные значения коэффициентов А, В, С и D. В общем случае
такая подстановка дает слишком громоздкие выражения. Приведем
их лишь для величии — sin 2ср и tg 20:
tg 20 (ti) = {£i2 cos 2<pi sin 20i+E22 cos 2<p2 sin 202+
+ 2£i£jJ[cos (<pi+<p2) sin (0c+02) cos (Ди/1+Дф) +
+ sin (cpi—<p2)cos (0i + O2)sin (Дй/1 + Дф)]}/{Е12соз2ф1СО5201 +
+E22cos2<p2cos202+2EiE2'[cos (cpi + cp2) cos (0i + 0г) cos (Дев 11 + Дф) —
—sin (cpi—<p2)sin (01 + 02)sin (Дйф+Дй)]}; (2.2.21)
sin 2y (ф) = —{^i sin 29i -ф E\ sin 2?2'-ф
4-2Z-, E2[sin (у, 4- y2) cos (6j — 62) cos (Ди/, -ф Дф) —
— cos (?! — y2) sin (6) — 92) sin (Дйф -ф Дф)]}. (2.2.22)
Разобьем теперь отрезок времени, на котором определена
квазимонохроматическая волна (2.2.4), на прилегающие друг к дру-
гу элементарные отрезки ДФ, средина каждою из которых есть мо-
мент времени ti. На каждом из этих отрезков можно согласно
предыдущему определить амплитуду, фазу и параметры поляризации
волны из соотношения (2.2.11) и вытекающих из него последующих
выражений. Если уменьшать длину элементарных отрезков Дф, то
в пределе можно заменить фиксированные моменты времени Ф па
текущее время t и представить квазимонохроматическую волну
(2.2.4) в виде электромагнитной волны с непрерывно изменяющими-
ся амплитудой, фазой и параметрами поляризации:
ff(t) = E(t)
56
Параметры <р(0. &(0 назовем текущими или мгновенными парамет-
рами поляризации. Соответственно E(t) и ф(0—мгновенные ампли-
туда и фаза квазимонохроматического колебания.
Рассуждения, аналогичные приведенным выше, позволяют опре-
делить мгновенные параметры поляризации для квазимонохромати-
ческой волны, представляющей конечную сумму близко располо-
женных на оси частот монохроматических волн. Для частного слу-
чая суммы двух монохроматических волн с известными параметра-
ми поляризации мгновенные параметры поляризации суммарной
квазимонохроматической волны определяются выражениями (2.2.19)
и (2.2.20), в которые вместо фиксированного параметра следует
подставить текущее время /.
2.3. ПОЛЯРИЗАЦИОННЫЕ ПАРАМЕТРЫ
ДВУМЕРНЫХ СИГНАЛОВ
Рассмотрение квазимонохроматической волны, со-
стоящей из двух монохроматических волн эллиптической
поляризации, позволило нам определить понятие мгно-
венных параметров поляризации квазимонохроматичес-
кой волны. Это понятие можно распространить и на
более общий случай квазимонохроматической волны —
такой волны, проекции которой на поляризационно-орто-
гональные оси произвольного базиса представляют со-
бой либо два полностью независимых сигнала, либо два
сигнала, между которыми существует определенная
функциональная связь. Необходимо по этим двум
проекциям определить параметры поляризации самой
волны. Причем нас интересуют не усредненные за дли-
тельный промежуток времени параметры поляризации,
которые определяются параметрами Стокса или матри-
цей когерентности, а параметры поляризации как функ-
ции времени, в законе изменения которых может быть
заложено передаваемое сообщение.
Будем полагать, что проекции квазимонохроматичес-
кой волны на оси ортогонального базиса представлены
в виде
s1(o=x1(o cos^+taoi,
Хг(/) =Лг(0 cos(0], (2.3.1)
гдеА(0, ф(0—медленно меняющиеся по сравнению
с (tit функции времени.
Вначале рассмотрим частный случай, когда Si(t) и
Хг(t) являются проекциями поля квазимонохроматичес-
кой волны в некоторой точке пространства на ортого-
нальные оси Ох и Оу, перпендикулярные к направлению
распространения волны, и coi = со2 = оз.
57
Если При ЭТОМ ВЫПОЛНЯЮТСЯ условия Л1(0 — kiAzit),
^j(/)—ф2(0 = const, то квазимонохроматическая волна,
заданная в данной точке пространства вектором
S (/) (/) +4$, (0, (2.3.2)
будет обладать постоянными параметрами поляризации.
Строго говоря, конец вектора S(/) будет описывать
в плоскости хоу медленно меняющуюся по форме фигуру,
близкую к эллипсу. Однако если положить, что функции
Ai (/) и Л2(/) меняются настолько медленно, что в тече-
ние отрезка времени в несколько высокочастотных
периодов их можно считать постоянными, то поляриза-
ционная диаграмма вектора S(t) будет представлять со-
бой эллипс с постоянными параметрами ф и 0, у которо-
го с течением времени медленно меняется только фаза
и размеры.
Это самый обычный случай радиосигнала с постоян-
ной поляризацией. Подбором пассивного преобразовате-
ля поляризации его всегда можно превратить в линейно-
поляризованную волну определенной ориентации и при-
нять полностью обычной антенной. В этом смысле
такой сигнал можно считать одномерным.
Мы будем рассматривать более общий случай, когда
функции А(0, и ф1 (/), фг(О попарно связаны не-
линейной зависимостью, и, по существу, в этой зависи-
мости и заложено передаваемое сообщение.
В этом случае волна, представляемая вектором S(t),
будет обладать переменными параметрами поляризации,
и прием поля такой волны без потерь энергии возможен
только на антенну, два выхода которой эквивалентны
двум антеннам ортогональной поляризации. Такую
антенну будем называть двухкомпонентной антенной,
а саму радиоволну или совокупность двух порождаемых
ею радиосигналов — двумерным сигналом. Полезная
информация, переносимая таким сигналом, выделяется
путем совместной обработки в двухкаиальном приемни-
ке сигналов с выходов двухкомпонентной антенны.
На двойной комплексной плоскости сигнал (2.3.2)
представляется в виде
S (t) = [А, (0е'ф‘(/) -f 1А2 (/) е/ф2 (/)] е'ш/. (2.3.3)
58
Множитель e'wt для сокращения записи обычно опускает-
ся. Итак, мы имеем сумму двух компонент сигнала, на-
ходящихся в пространственной квадратуре. Будем рас-
сматривать нормированные сигналы, т. е. сигналы вида
S (/) = а. (О е/ф1 (0 + ш2 (0 е/фа (0, (2.3.4)
где
а (t) —____л' • a (t) =------------.
Дальнейшее преобразование выражения (2.3.4) в це-
лях получения удобного для решения уравнения, опреде-
ляющего неизвестные параметры <р(/), 0(0 и фазу ф(0
эллиптически поляризованной волны (2.3.4) с перемен-
ными параметрами поляризации, можно осуществить
различными путями. Первый путь — это повторить вы-
вод, проделанный в § 1.6 для определения неизвестных
параметров поляризации монохроматической волны.
В этом случае выражение (2.3.4) переписываем в виде
S J) = cos у (h е/ф‘{t) -|- i sin у (t) е®*(2.3.5)
где
KO^arctg^-. (2.3.6)
Такая форма записи выражения для нормированного
сигнала (2.3.4) справедлива, поскольку
Я12(0+О22(0 = 1-
Мгновенные параметры поляризации квазимопохромати-
ческой волны, соответствующей сигналу (2.3.5), опреде-
ляются тождеством
e-i/9 (Пе*е (Ое/Ф (0 = cosy (Qe'*‘(Z) Д-i sin у (О е'ф1 (Z),
(2.3.7)
которое можно переписать в виде
. A (Z) __ . Af . g (f)
е-4/ф(М(<)е;ф(О = [со8у(0е ~ + isiny(Oe '2Je 2 ,
(2.3.8)
где
Д(0=ф1(0—ф2(/); о (О =Ф1(0 +Фг(О-
Тождество (2.3.6) по своему виду совпадает с урав-
нением (1.6.12) и решается оно тем же путем, что и
59
уравнение (1.6.12). Решения его относительно парамет-
ров <р(0, 0(0 получаются неоднозначными. Они зависят
от того, в каких пределах однозначности мы будем опре-
делять текущие параметры поляризации <р(0, 0(0 и
фазу эллиптически-поляризованной волны ф(0. Точнее,
при решении получаются выражения для определения
разности фаз ф(0—о (0/2, из которых при известной
функции о(0 не представляет труда получить функцию
ф(0. Однако при таком решении выражения для опреде-
ления параметров <р(0, 0(0 зависят только от отноше-
ния амплитуд 01(0/02(0 компонент волны и от разности
их фаз А(0.
Если необходимо фазовый угол ф(0—ст(0/2 опреде-
лять однозначно в интервале — л ... л, т. е. искать от-
дельно выражения для соз(ф(0—о (0/2] и sin[t|) (0 —
—о (0/2], то формулы для определения всех искомых па-
раметров совпадают с выражениями (1.6.15) — (1.6.17),
если в последние подставить зависимые от времени аргу-
менты у(0, А(0 и ст(0. При этом система формул
(1.6.15) определяет однозначно 0(0 в пределах — л/2 ...
... л/2, <р(0 —в пределах — л/4 ... л/4, и главной полу-
осью поляризационного эллипса считается его большая
полуось, ближайшая к положительной полуоси ох, а си-
стема формул (1.6.16), наоборот, определяет однозначно
гр(0 в пределах — л/2 ... л/2, 0(0 —в пределах — л/4 ...
... л/4, и главной полуосью поляризационного эллипса,
от которой отсчитывается и фазовый угол ф(0, и угол
эллиптичности ф(0, считается любая ближайшая к по-
ложительной полуоси ох полуось поляризационного
эллипса, большая или малая.
Можно, однако, и не вводить параметр у(0 и не пре-
образовывать выражение (2.3.4) к виду (2.3.8), а вос-
пользоваться для нахождения параметров <р(0, 0(0 и
ф(0 тем фактором, что и выражение (2.3.4), и выра-
жение
$' (0 = е-;/¥(Ое'9(Се/ф(О
при правильно выбранных функциях <р(0, 0(0, ф(0
представляют собой только разные формы записи одного
и того же комплексного числа, модуль которого равен
единице. Умножив оба этих выражения операторно на
е‘/ч> (О, получим тождество
ef ф (,) = [a, (!) е'ф*(<) + ia2 (t) е/фа (,)] e~i9 (0 X е‘/<₽ (С, (2.3.9)
60
из которого можно определить искомые параметры.
Тождество (2.3.9) будет выполняться тогда и только тог-
да, когда тождественно равны коэффициенты при одина-
ковых мнимых единицах слева и справа. С учетом этого
условия из (2.3.9) после соответствующих преобразова-
ний получаем
sin 2<р(/) =2ai(/)a2(0 sin[-ф±(^) — ф2(01,
tgO(Z) =[(а12соз2ф1—а22соз2ф2) sin 2<р +
4-2а1а2 sin (ф1 + ф2)]Д (а^ sin 2ф!—а22 sin 2ф2) +
+ (at2 sin 2ф 1 + а22 sin 2ф2) cos 2<р—
—cos (ф1 + ф2) sin 2q>]; (2.3.10)
(2.3.11)
tg 26 (t) = —2д‘(1)дН0СО5[Ф1(0 —Фг(О]
a2 (t) cos 2Ф1 (t) — д| (/) cos 2ф2 (t)
, (al — д?) sin 20 +
tg <₽(/)==________—-___-______-___________►
(д2 sin _2ф, + д| sin 2ф2) + (a2 sin 2Ф2 —
______+ 2д!Дг cos (Ф) + Ф2) cos 20_‘
— д2 sin 2ф2) cos 20 -|- 2д!Д2 sin (Ф>+Ф8) sin 20
Как и в предыдущем, может быть использована либо
система формул (2.3.10), либо (2.3.11) в зависимости от
требуемых пределов однозначного определения параме-
тров.
Формулы для определения мгновенной фазы ф(/)
эллиптически-поляризованной волны получаются из
(2.3.9) в виде
cos ф (/) = (ai cos ф! cos 0+a2 cos ф2 sin 0) cos ф +
+ (at sin ф1 sin 0—a2 sin ф2 cos 0) sin <p;
sin ф (t) ~ (ai sin ф1 cos 0+a2 sin ф2 sin 0) cos <p—
— (at cos ф! sin 0—а2созф2соз0) sin<p. (2.3.12)
В этом и в выше приведенных соотношениях для со-
кращения записи опущено обозначение зависимости всех
аргументов от времени.
Как видно из (2.3.12), фаза ф определяется только
после вычисления и подстановки в это соотношение зна-
чений параметров <р(0 и 0(О> полученных либо из
(2.3.10), либо из (2.3.11).
61
Можно заметить, что амплитудные коэффициенты
ai(t) и a2(t) в (2.3.10) и (2.3.11) входят в числитель и
знаменатель в квадрате или в виде попарных произведе-
ний. Поэтому при вычислениях по этим формулам вмес-
то нормированных амплитуд можно подставлять истин-
ные значения амплитуд Л1(/) и Л2(/) компонент.
Таким образом, мы нашли выражения для определе-
ния текущих параметров поляризации и фазы квазимо-
нохроматической эллиптически-полярнзованной волны
с переменными параметрами поляризации, когда эта
волна задана своими проекциями на оси ортогонально-
линейного базиса. Если волна задана своими проекция-
ми Si(/) и S2(t) на оси эллиптически-поляризованного
базиса, то аналогичным образом можно определить ее
параметры поляризации в этом базисе, а затем перейти
при необходимости к ортогонально-линейному базису,
воспользовавшись формулами преобразования парамет-
ров поляризации волны при переходе от одного базиса
к другому, полученными в § 1.6, либо сначала предста-
вить волну в виде
5 (0 - S, а,?5, 05Х+ iS2 (t, 05), (2.3.13)
в котором учтена зависимость ортогонально-линейных
компонент от параметров исходного базиса, а затем
воспользоваться выше приведенными соотношениями для
определения текущих параметров поляризации.
В тех случаях, когда сигналы St(t) и S2(t) заданы
в форме, отличной от (2.3.1), т. е. в записи этих сигна-
лов не выражены отдельно огибающие н фазы либо
не определены их несущие частоты ои и т2, то для
определения поляризационных свойств двумерного сиг-
нала можно воспользоваться комплексным представле-
нием сигналов Si(/) и S2(t) в виде аналитических сиг-
налов
S,(0 = $. (0 + /S.(0. (2.3.14)
в которых функции S^t), St(t) и S2(t), S2 (t) попарно свя-
заны преобразованием Гильберта. Если сигналы Si(/) и
S2(/) узкополосные в том смысле, что их комплексные
спектральные функции, соответствующие положитель-
ным и отрицательным частотам, не имеют перекрываю-
щихся областей, т. е. положительная ветвь спектральной
функции не заходит в область отрицательных частот, и
наоборот, то формы (2.3.1) и (2.3.14) представления сиг-
62
налов Si(0 и S2(0 идентичны. Выражение
+ (2.3.15)
при St(0 и S2(0 из (2.3.14) есть не что иное, как форма
представления аналитического двумерного сигнала на
двойной комплексной плоскости. Из (2.3.15) можно пе-
рейти к показательной форме представления двумерного
сигнала:
S(0 = Е (0 е“'/ч> (/)е'9 юе/ф (<). (2.3.16)
Неизвестные мгновенные параметры поляризации
ф(0> 0(0, полную фазу ф(/) и приведенную амплитуду
E(t) находим из условия, что правые части выражений
(2.3.15) и (2.3.16) тождественно равны. При этом
Е(0 = S* (о + S, (0 + s[ (t) + s:2 (/), (2.3.17)
a cp(/), 0(/), ф(0 можно получить пз соотношений
(2.2.17), (2.2.19) и (2.2.20), в которые вместо коэффи-
циентов а, Ь, с и d следует подставить нормированные
значения функций S^t), S2(0 и их гильбертовских пре-
образований, т. е. положить
a = St (t)/E(t), b=--St(t)/E (/),
c = S2 (/)/£(/), r/ = S2(/)/£(0-
Выражение (2.2.17) в этом случае определяет полную
фазу ф(0 двумерного сигнала. Производная от этой
фазы по времени есть мгновенная частота двумерного
сигнала.
ГЛАВА 3
ПРИНЦИПЫ ПОСТРОЕНИЯ ПОЛЯРИЗАЦИОННЫХ
ПРЕОБРАЗОВАТЕЛЕЙ И МОДУЛЯТОРОВ
Поляризационные свойства присущи электромагнитному полю
любой частоты. Однако возможность практического использования
этих свойств для улучшения качественных показателей радиотехни-
ческих систем в сильной степени зависит от длины волны, па ко-
торой работает передатчик данной системы. Эта зависимость обус-
ловлена как техническими трудностями построения устройств фор-
мирования и излучения радиоволн заданной поляризации, так и
влиянием окружающей среды на степень изменения параметров по-
ляризации волны при ее распространении от передающей до при-
63
емкой антенны. Известно, что в диапазоне длинных и средних
волн влияние поверхности Земли, ионосферы и протяженных неодно-
родностей атмосферы приводит к весьма существенным искажениям
параметров поляризации волны. Причем эти искажения носят, как
правило, случайный характер. Поэтому использование изменения
параметров поляризации волны, например, для передачи информа-
ции в этом диапазоне воли весьма затруднено, если не невозможно.
Наиболее подходящим в этом отношении является диапазон
дециметровых н более коротких волн, вплоть до ультрафиолетового
диапазона, т. е. диапазон от сверхвысоких до оптических частот
включительно. Распространение электромагнитного поля этих частот
носит лучевой характер, причем лучевые свойства поля тем больше
проявляются, чем выше частота излучения. Формирователи полярн-
зацяи волны и излучатели ее лосят приемлемые размеры. Лучевые
свойства поля, т. е. способность двух рядом расположенных лучей
с размерами поперечного сечения в несколько десятков длин волн
распространяться почти независимо друг от друга, а также приме-
нение для преобразования поляризации волны устройств с распре-
деленными параметрами позволяют формировать излучение не толь-
ко с переменными во времени поляризационными параметрами, но
и с зависимостью этих параметров от пространственных координат.
Эти качества полей сверхвысоких частот обусловливают повышен-
ный интерес к изучению возможностей использования их парамет-
ров поляризации в целях получения определенного положительного
эффекта. Поэтому и в данной работе основное внимание будет
обращено на принципы построения поляризационных преобразова-
телей и модуляторов сверхвысоких и оптических частот. Тем не ме-
нее рассматриваемые ниже принципы могут быть трансформированы
и применительно к устройствам, рассчитанным на преобразование
поляризации полей более низких частот. Хотя рассматриваемые
в настоящей главе схемы построения преобразователей поляризации
и не претендуют на всеобщность, тем не менее они вполне удов-
летворительно описывают весьма широкий класс преобразователей
и модуляторов поляризационных параметров поля сверхвысоких и
оптических частот.
3.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Известно довольно большое число различных
устройств, предназначенных для преобразования пара-
метров поляризации электромагнитной волны. В основу
работы большинства из них положен принцип изменения
поляризации электромагнитной волны за счет изменения
относительного фазового сдвига между поляризационно
ортогональными компонентами волны.
В зависимости от динамических свойств эти устройст-
ва делятся на две большие группы:
1. Пассивные преобразователи поляризации, параме-
тры которых не изменяются с течение,м времени либо
изменяются с небольшой скоростью (например, преобра-
зователи поляризации с механической перестройкой па-
раметров за счет линейного перемещения или вращения
64
их элементов). В литературе их называют преобразова-
телями поляризации в отличие от поляризационных мо-
дуляторов.
2. Активные преобразователи поляризации или поля-
ризационные модуляторы. Параметры последних изме-
няются под действием внешних управляющих напряже-
ний или токов с частотой от десятков килогерц до сотен
мегагерц.
Основные требования, которые предъявляются к пас-
сивным преобразователям поляризации, — это малые
потери энергии преобразуемой волны, широкополос-
ность, стабильность параметров преобразователя во вре-
мени, технологичность и удобства эксплуатации и высо-
кая эксплуатационная надежность.
Поляризационные модуляторы должны удовлетво-
рять как требованиям, предъявляемым к преобразовате-
лям поляризации, так и специфическим требованиям,
таким, как высокое быстродействие, широкий динами-
ческий диапазон, линейность модуляционной характе-
ристики, высокая чувствительность по отношению
к управляющему воздействию, приемлемые энергетичес-
кие характеристики и др.
В качестве пассивных преобразователей поляризации
в оптическом диапазоне используют определенным обра-
зом ориентированные пластинки с разными коэффициен-
тами преломления для волн ортогональной поляризации.
По типу поляризации различно преломляемых волн эти
пластинки называют линейными, циркулярными или
эллиптическими фазовыми пластинками. В СВЧ диапа-
зоне для этих же целей используют волноводы эллипти-
ческого сечения, круглые или квадратные волноводы
с тонкой диэлектрической пластиной вдоль продольной
оси волновода или более сложные устройства, которые
в большинстве случаев можно представить состоящими
из расщепителя исходной волны на две ортогонально-
поляризованные компоненты, фазосдвигающих устройств
и сумматора ортогональных компонент (рис. 3.1).
Наибольшее распространение получили устройства,
создающие относительный фазовый сдвиг между ортого-
нально-линейными компонентами волны и между круго-
поляризоваиными компонентами противоположного на-
правления вращения, т. е. между ортогонально-круговы-
ми компонентами. Этот фазовый сдвиг создается за счет
разной скорости распространения воли противоположной
5—0(57 65
поляризации в данном устройстве. Среды, в которых
с разной скоростью распространяются волны ортого-
нально-круговой поляризации, называют гиротрапными.
Поэтому устройства, в которых ортогонально-круговые
Рис. 3.1.
компоненты электромагнитной волны получают одина-
ковый по абсолютной величине и противоположный по
знаку фазовый сдвиг, будем называть:
— гиротропным фазосдвигателем, если это устройст-
во создает строго постоянный фазовый сдвиг;
— гиротропным фазовращателем, если в данном
устройстве предусмотрена возможность изменения вели-
чины фазового сдвига;
— гиротропным модулятором, если данное устройст-
во предназначено для модуляции относительного фазо-
вого сдвига между ортогонально-круговыми компонен-
тами.
Аналогично, устройства, создающие фазовый сдвиг
между ортогонально-линейными компонентами волны,
будем называть л инотропными фазосдвпгателямп, фазо-
вращателями либо модуляторами.
Гиротропные устройства инвариантны относительно
поворота их вокруг продольной оси, поэтому основными
параметрами, характеризующими такие устройства,
являются величина относительного фазового сдвига,
возможные пределы регулирования этой величины, а для
модулятора — крутизна модуляционной характеристики,
пределы ее линейности и остальные из перечисленных
выше параметров.
Для липотропных устройств необходимо, кроме того,
знать их ориентацию относительно ориентации поляри-
зационной диаграммы падающей волны либо относи-
тельно той системы координат, в которой задается поля-
ризационная диаграмма. Ориентацию таких устройств
определяют по ориентации оси наибольшей скорости,
66
Т. е. по ориентации той линейно-поляризованной компо-
ненты электромагнитной волны, которая получает в дан-
ном устройстве наименьшую фазовую задержку. Эту ось
обозначим буквой V. Перпендикулярную ей ось назовем
осью Н. Иногда удобнее задавать ориентацию оси, раз-
вернутой на угол л/4 относительно оси V. Эту ось будем
обозначать буквой R.
На рис. 3.2,а, б представлены условные изображения
липотропных устройств. Если ориентация устройства за-
Рис. 3.2.
дается осью V, то около оси Н такого устройства указы-
вается фазовый сдвиг, который получает //-поляризо-
ванная компонента относительно У-поляризованной
(рис. 3.2,а). Очевидно, что этот фазовый сдвиг будет
всегда отрицательным, так как, по определению, ось V
есть ось наибольшей скорости распространения волны.
Фазовый сдвиг, получаемый У-поляризованпой компо-
нентой, в рассматриваемом случае не существен, так как
он не влияет на поляризацию волны. В основном
в таком виде представляют только- те лпнотропные
устройства, которые создают относительный фазовый
сдвиг л/2 и л. Эти устройства называют четвертьволно-
выми и полуволновыми фазосдвигателями.
В остальных же случаях полагают, что У-поляризо-
ванная компонента в липотропном устройстве получает
фазовый сдвиг а, а //-поляризованная компонента одно-
временно получает фазовый сдвиг —а, и ориентацию
этого устройства определяют по ориентации оси /?
(рис. 3.2,6).
В липотропных модуляторах а пропорциональна ве-
личине управляющего сигнала, т. е. является функцией
времени: а —а(/). При этом а может быть как больше
5* 67
пуля, так и меньше нуля. При изменении знака а
ориентация оси У? в данном случае не меняется.
Четвертьволновый фазосдвигатель, изображенный на
рис. 3,2,а, можно представить и в виде липотропного
фазосдвигателя, аналогичного изображенному на
рис. 3.2,6. Для этого достаточно определить угол ориен-
тации оси Д этого устройства Р«=Ру + л/4 и положить
а = л/4. При этом как для Н- так и для ^-поляризован-
ной компоненты добавлен
у л постоянный фазовый сдвиг
л/4; это всегда можно учесть
/^4 "Ч/ в конечных результатах ли-
\ б° вовсе не учитывать, если
----1 \ /----постоянный фазовый сдвиг
I / }/ * всей волны несуществен.
У Гиротропный фазосдвига-
тель будем изображать в ви-
У де, представленном на рис.
3.3, где € — половина отно-
рис зз \штелыго фазового сдвига
между кругополяризованны-
ми компонентами, создаваемого данным устройством. Из-
вестно, что при прохождении такого фазосдвигателя по-
ляризационная диаграмма волны поворачивается на
угол 'О без изменения своей формы.
Гиротропный фазосдвигатель может быть взаимным
или невзаимным. Для невзаимного гиротропного фазо-
сдвигателя необходимо указать направление распростра-
нения волны, при котором фазовый сдвиг между правой
круговой и левой круговой компонентами будет равен 2'0'.
На рисунке это направление обозначается стрелкой.
Тогда для волны, распространяющейся в противополож-
ном направлении, этот сдвиг будет равен —201. Для
взаимного гиротропного фазосдвигателя фазовый сдвиг
не зависит от направления распространения волны.
Типичным представителем невзаимного гиротропного
фазосдвигателя является продольно намагниченный
феррит, типичным представителем взаимного гиротроп-
ного фазосдвигателя — определенным образом вырезан-
ная из монокристалла кварца пластинка.
Взаимное гидротропное устройство может быть созда-
но из комбинации липотропных устройств. Невзаимное
устройство построить так нельзя, так как не существует
певзаимных липотропных устройств и сред.
68
Эффект воздействия как лийОтрбпного, так и nipd-
тропного устройства (под устройством здесь и далее
подразумевается фазосдвигатель, фазовращатель либо
модулятор) на электромагнитную волну математически
можно представить в виде оператора, на который необ-
ходимо умножить входной сигнал, чтобы определить ко-
нечный результат.
Обычно эти операторы выражают в виде матриц
Мюллера или векторов Джонса [40] или матриц разме-
ром 2x2, используемых в работе [46]. При отображении
эллиптически поляризованной волны на двойной ком-
плексной плоскости эти операторы также выражаются
комплексным числом на этой плоскости и принимают
весьма простой вид. В следующем параграфе мы найдем
эти операторы. Сейчас же заметим, что комбинируя
различным образом ориентированные гиротропные и ли-
потропные устройства, можно создать самые разнообраз-
ные преобразователи и модуляторы параметров поляри-
зации электромагнитной волны. Поэтому липотропное и
гиротропное устройства можно назвать элементарными
преобразателями поляризации, из которых строятся
более сложные поляризационные модуляторы и преоб-
разователи.
3.2. ОПЕРАТОРЫ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
ПОЛЯРИЗАЦИИ
1. Л инотропное устройство. Оператор А (а) преобра-
зования волны этим устройством зависит от его ориента-
ции. При нулевой ориентации, т. е. когда фв = 0
(рис. 3.2), линейно-поляризованные компоненты прохо-
дящей через устройство волны, ориентированные вдоль
осей V и Н липотропного устройства, получают одинако-
вый по абсолютной величине и противоположный по зна-
ку фазовый сдвиг. Следовательно, линейно-поляризован-
ная волна горизонтальной поляризации (ёвх=1) преоб-
разуется этим устройством следующим образом:
ввых = евхА (а) = -4= (е1’74 + е“"'/4) А (а) =
т
(e'”/4e"/a + е-"'/4е'а), (3.2.1)
г 2
где А (а)—оператор преобразования волны липотроп-
ным устройством. Согласно равенству (1.4.3), выражение
69
(3.2.1) можно записать в виде
е;ых==е-;'“,
следовательно, оператор липотропного устройства равен
А(а) = е~‘;“. (3.2.2)
Этот оператор справедлив не только по отношению к ли-
нейно-поляризованной волне, но и по отношению к вол-
не любой поляризации. Если же рл=#0, то при исполь-
зовании оператора (3.2.2) необходимо исходную волну
записать в системе координат, ось ох которой совпадает
с осью R, умножить выражение волны на Л (а) и при-
вести полученный результат к исходной системе коорди-
нат. То есть, если исходное поле
евх = е е ,
то результат его преобразования липотропным устройст-
вом получается следующим образом:
ёВЫх = {ёвхе“Ф/г х Л (а)} еЧ (3.2.3)
Умножать на оператор Л(а) необходимо по правилам
операторного умножения, изложенным в § 1.5 [см. вы-
ражения (1.5.14), (1.5.15)]. В результате перемножения
из (3.2.3) получим
[е-%г (9-^Xe-,7a]e/?/? =
= [cos (0 - рЛ) е-// (l₽+a) + i sin (0 - рЛ) е"'7 (1₽~а) ] е'Ч
Для волны, распространяющейся в обратном направ-
лении, оператор Л(а) не изменится. Однако если волна
распространяется в сторону отрицательных значений z
системы координат xyz, изображенной на рис. 3.2,6, то
эту волну и ее поляризационную диаграмму целесооб-
разнее рассматривать в системе координат ХоУо^о, кото-
рая получается из системы xyz путем разворота послед-
ней на 180° вокруг оси оу. В новой системе координат
будет другим и оператор Л (а). Из рассмотрения
рис. 3.2,6 можно заключить, что при переходе к системе
координат xoyoZo необходимо поменять знаки на обрат-
ные у величин а и рл.
70
2. Гиротропное устройство. Известно, что гиротропное
устройство, создающее относительный фазовый сдвиг 2$
между кругополяризованными компонентами правого и
левого вращения, поворачивает поляризационную диа-
грамму проходящей через это устройство волны на угол
О' (эффект Фарадея). Поворот на угол ft на двойной
комплексной плоскости равносилен умножению ком-
плексного числа на множитель е‘а- Следовательно, опе-
ратор преобразования волны гиротропным устройством
имеет следующий вад:
r(») = eia. (3.2.4)
Если гиротропное устройство взаимное, то относитель-
ный фазовый сдвиг ортогонально-круговых компонент
остается одним и тем же как для волны, распространяю-
щейся в направлении оси z (рис. 3.3), так и для волны,
распространяющейся в обратном направлении. Если пи-
ротропное устройство невзаимное, то при изменении на-
правления распространения волны меняется знак ft.
Поэтому для волны, распространяющейся вдоль оси
о?о системы координат oxoz/oZo, оператор взаимного гиро-
тропного устройства останется без изменения, а для не-
взаимного гиротропного устройства при переходе к си-
стеме Xo*/oZo необходимо поменять знак перед ft.
3. Четвертьволновый фазосдвигатель. Оператор чет-
вертьволнового фазосдвигателя, изображенного на
рис. 3.2,а, можно представить в форме (3.2.3), положив
Ря=л/4 + Ру и а = л/4, добавив фазовый множитель
е 4. Однако в большинстве случаев удобнее исполь-
зовать тот факт, что четвертьволновый фазосдвигатель
в системе координат xyz, ось ох которой совпадает
с осью V, задерживает у-ую компоненту по фазе на л/2.
Поскольку с осью оу совмещена мнимая ось I, то в вы-
ражении для электромагнитной волны достаточно i до-
множить на —/.
Таким образом, если в системе координат xyz
(рис. 3.2,а) вдоль оси oz распространяется эллиптичес-
ки-поляризованная волна
ёвх = е-%‘'9,
которая в системе координат, повернутой вокруг оси oz
на угол Ру, запишется в виде
_i/(p £ (0—₽у) . .... . . £ (9 —
ек = е е = [cos<p — (tj)sin<p]e ,
71
то на выходе четвертьволнового фазосдвигателя в этой
же системе координат получим
г — ч (в—
ввых = [cos? —/(—г/) sin <р]е =
-ij (9_₽у) . . iS <e—pV)
= cos?e —rsin?e
(3.2.5)
t. e. волна (3.2.5) на выходе четвертьволнового фазо-
сдвигателя представляет собой сумму двух поляриза-
ционно-ортогональных эллиптически-поляризованных
волн с амплитудами cos (р и sincp.
Для записи волны в исходной системе координат еле-
дует выражение (3.2.5) умножить на е . Таким обра-
зом, если обозначить А(—/) оператор четвертьволнового
фазосдвигателя, то его воздействие на проходящую вол-
ну математически можно записать в виде
ёвых = {[eBXe’'£₽v] А (- /)} Л. (3.2.6)
Иногда удобнее считать, что одна из ортогонально-
линейных компонент в четвертьволновом фазосдвигателе
получает положительный сдвиг фазы на л/2, а вторая
распространяется с неизменной скоростью. В этом слу-
чае задается угол [Зи ориентации еси Н, и оператор та-
кого фазосдвигателя будет А(/).
4. Полуволновый фазосдвигатель. Полуволновый фа-
зосдвигатель с нулевой ориентацией задерживает у-ю со-
ставляющую волны на л, что равносильно изменению
знака перед мнимой единицей i в форме представления
волны комплексными числами на двойной комплексной
плоскости. Оператор такого фазосдвигателя обозначим
А(—1). Таким образом, если исходная волна эллиптиче-
ски поляризована, то на выходе полуволнового фазо-
сдвигателя получим
= {[S.Z’ПА (- I)} е‘,и = X
X А(- I» е*= {e«V "-’0 )
(3.2.7)
Из (3.2.7) следует, что оператор полуволнового фазо-
сдвигателя, ориентированного под углом будет равен
A?^4) = A(-l),e‘W’ (3.2.8)
72
причем при умножении волны на этот оператор необхо-
димо выражение волны умножить сначала на Л(—1),
т. е. поменять знаки перед i, а затем результат умно-
жить на е
При переходе к системе координат xoyoz() операторы
Л(—/), Л(/), A(Z/2) не меняются, меняется лишь знак .
В следующих параграфах мы покажем, как можно
найти результат преобразования поляризации волны
различными комбинациями элементарных преобразова-
телей поляризации, используя операторы этих преобра-
зователей. При преобразовании выражений, которые бу-
дут получаться при перемножении исходной волны и
операторов, мы будем пользоваться тождествами, дока-
зательство которых дано в приложении 1.
3.3. ПРЕОБРАЗОВАНИЕ ПОЛЯРИЗАЦИИ ЛИНЕИНО-
ПОЛЯРИЗОВАННОИ ВОЛНЫ
Определенный интерес представляет собой случай, когда ис-
ходная линейно-поляризованная волна горизонтальной поляризации
проходит через ориентированные под различными углами липотроп-
ные фазосдвигатели с различными относительными фазовыми сдви-
гами. Поскольку на двойной комплексной плоскости рассматриваемая
здесь волна ёвх=1, то суммарный эффект воздействия последо-
вательно включенных липотропных фазосдвигателей будет опре-
деляться произведением операторов отдельных устройств с учетом
их ориентации и последовательности включения. Рассмотрим наи-
более интересные преобразователи, часто используемые на прак-
тике.
1. Вращающийся четвертьволновый фазосдвигатель. Оператор
фазосдвигателя А(—/), угол ориентации оси V |Зу = Ш. Волна на
выходе фазосдвигателя имеет вид:
^=[e“i?lZA(-/)]e^ = e^eiG< (3.3.1)
Таким образом, параметры поляризации электромагнитной волны
на выходе такого фазосдвигателя линейно меняются во времени:
<р=—Ш; 0 = Ш;
причем ориентация главной оси эллипса поляризации все время со-
впадает с осью V фазосдвигателя.
2. Вращающийся полуволновый фазосдвигатель. Оператор фа-
зосдвигателя А(Х/2), угол ориентации оси V |Зу = Ш,
^Hz=l'A?l/(X/2) = eI'2tV = ei2az,
т. е. такой фазосдвигатель вращает линейно-поляризованную волну
с удвоенной частотой.
3. Два скрещенных четвертьволновых фазосдвигателя. Обозна-
чим их углы ориентации и Линейно-поляризованная волна
73
Этими фазосдвигателями преобразуется к виду
ётх-- {[е-^А(-/)]е‘^^> Л (
= [cos (?Ki - + i sin (?Ki - ?K>) elJ-%J A (- /) e‘^ -
== [cos (?K1 —e‘?v'* —j/sin(?Ki — ^)e el?v\ (3.3.2)
Рассмотрим некоторые частные случаи.
а) — л/4. После подстановки в (3.3.2) находим
«вых - lc°s (?/а — л/4) е'л/4 + ij sin (fKj— л/4) e-*’t/4] е'^’-
Далее выносим е‘г’/4 за квадратные скобки и окончательно получаем
«вых-е^^’е7^-^4’. (3.3.3)
Следовательно, если вращать второй четвертьволновый фазо-
сдвигатель, оставляя неподвижным первый, то на такой же угол бу-
дет поворачиваться ориентация и фаза линейно-поляризованной
волны на выходе этого устройства.
б) = л/4. После подстановки в (3.3.2) получим
«,ых = (е;^ + ,7е-^)е;?Ч (3.3.4)
Воспользуемся тождеством (П.1.3):
«вых - [cos Р^е''тс/4 + ё sin ?/ic^i'r-/4 J е'?и’. (3.3.5)
Выносим в (3.3.5) за квадратные скобки е1,:/4. Тогда с учетом тож-
деств (П.1.5) и (П.1.7) и условия — ру + л/4 получим
«вых- [cos^e^^^e-'^ + sin^e-W4 е'^4] е;(^+“/2) =
= [cos?v,ie'>/4 + sin?l/e-;/’!/4 ] ei(i4+x/2) е'х/4 =
(3.3.6)
Этот же результат можно получить и более коротким способом.
На выходе первого фазосдвигателя согласно (3.3.1) имеем волну
ё\ =ег'>> е‘Ч (3.3.7)
Второй фазосдвигатель представляем как липотропный фазосдвигатель
с оператором А (л/4) =- е~‘;г’/4 е—JX/4 и ориентацией оси R под углом
₽Я= Ру, + ’'/4- Тогда волна (3.3.7) после прохождения второго фа-
зосдвигателя преобразуется к виду
«вых = [О‘(л/4)] е^*'4’. (3.3.8)
Положив [!у — = л/4, из (2.3.8) получим выражение
О" (?U, + n/4) фу _Гтс/4
«вых =е V1 е е (3.3.9)
которое можно свести к (3.3.6).
74
Отметим, что если принять —^а = п/4, то из (3.3.8) найдем
; Ли. .-/«/4
6ВЫХ —с е е
т. е. получим волну, находящуюся в пространственно-временной
квадратуре с (2.3.9).
4. Скрещенные четвертьволновый и полуволновый фазосдигате-
ли. Волна преобразуется к виду
ё.их Л (- 1)] = c~ii?v‘ ei(2^ (3.3.10)
т. е. два таких фазосдвигателя путем определенной их ориентации
позволяют получить волну с любыми параметрами поляризации,
причем параметры поляризации связаны с углами поворота весьма
простыми соотношениями.
5. Полуволновый фазосдвигатель с произвольной ориента-
цией р, расположенный между двумя четвертьволновыми фазосдвига-
телями с ориентацией [^-=’’/4.
Волна на выходе первого четвертьволнового фазосдвигателя
ё, = е е^4 ---= е'^-'4 <ё*14.
Волна па выходе полуволнового фазосдвигателя
ё2 = е«'(2?-х/4).
Волна па выходе второго четвертьволнового фазосдвигателя
ёг - [е~‘‘*14 е^-^А (- /)] ei,l/4 -
= [е~‘М4 е/<23-’1/2>л(_ j)] е^/4 = (3.3.Ц)
Таким образом, такая комбинация фазосдвигателей представляет
собой фазовращатель линейно-поляризованпой волны, не изменяю-
щий ее ориентацию.
Аналогичным образом можно найти результат преобразования
линейно-поляризованной волны и другими комбинациями элемен-
тарных преобразователен поляризации.
3.4. СХЕМЫ ПОЛЯРИЗАЦИОННЫХ МОДУЛЯТОРОВ
Задача ставится следующим образом: используя эле-
ментарные преобразователи поляризации — гиротропные
и липотропные устройства — сформировать из линейно-
поляризованной волны волну эллиптической поляриза-
ции с изменяемыми в соответствии с модулирующими
сигналами S^t) и SQ (f) параметрами поляризации.
Амплитуду исходной волны полагаем равной единице,
поляризацию — горизонтальной.
Схема поляризационного модулятора первого типа
получается элементарно. Из вида операторов А (ср) и
Г(0) сразу следует, что последовательно включенные ли-
75
нотропный и гиротропный модуляторы (рис. 3.4) преоб-
разуют горизонтально поляризованную волну в эллнптп-
чески-поляризованную:
ёвых-е-‘7?(/)е'9(<). (3.4.1)
Такой модулятор будем называть модулятором типа
АГ — по начальным буквам используемых элементарных
преобразователей поляризации.
Столь же просто получается и другая схема модуля-
тора— модулятора типа ГТ. Действительно, если линей^
по-поляризованную волну еY с выхода первого ги-
ротропного модулятора пропустить через четвертьволно-
Рис. 3.4. Рис. 3.5.
вый фазосдвигатель с нулевой ориентацией, то на выхо-
де его получим эллиптически-поляризованную волну
—I!ф (t) и ъ
е с нулевой ориентацией эллипса поляризации.
Второй гиротропный модулятор развернет ее поляриза-
ционную диаграмму на угол 0(0- В результате на вы-
ходе такой комбинации преобразователей получим волну
(3.4.1). Схема модулятора типа ГГ изображена на
рис. 3.5.
Из сравнения рис. 3.4 и 3.5 видно, что липотропный
модулятор с оператором А[<р(^)] по отношению к гори-
зонтально поляризованной волне линейной поляризации
эквивалентен последовательному соединению гиротроп-
ного модулятора и четвертьволнового фазосдвигателя
с нулевой ориентацией оси V. Эта эквивалентность
76
объясняется тем, что горизонтально поляризованную
волну можно представить как в виде суммы линейно-
поляризованных компонент, развернутых на угол ±л/4
относительно оси
V
так и в виде крутополяризованных компонент противо-
положного направления вращения такой же амплитуды:
Кругополяризованные компоненты в гиротропном моду-
ляторе получают такой же фазовый сдвиг, как и линей-
но-поляризованные ориентированные под углом ±л/4
относительно оси R компоненты в линотропном модуля-
торе,
? =-J= [e^V9 (Z) + e-w4e'9 (Z)],
r 2
а четвертьволновый фазосдвигатель после гиротропного
модулятора превращает кругополяризованные компонен-
ты в линейно-поляризованные с ориентацией ±л/4:
?Л(-/)=:-1= [еь/4е~/9 (/) + е~;л/4е/9 (<)] =
v 2
Однако эквивалентность липотропного модулятора
в первых двух преобразователях в схеме рис. 3.5 нару-
шается, если входная волна будет иметь поляризацию,
отличную от линейной.
Если же перед гиротропным модулятором поставить
четвертьволновый фазосдвигатель, преобразующий ли-
нейно-поляризованную компоненту с ориентацией л/4
в круг левого вращения е,/"',2> а линейно-поляризован-
ную компоненту с ориентацией —л/4 — в круг правого
вращения е-1'1^4 т. е. поставить фазосдвигатель с опе-
ратором Л(/‘), то комбинация элементарных преобразо-
вателей с операторами Л (/), Г(ср(£)], Л(—/) по отноше-
нию к волне любой поляризации, распространяющейся
в направлении оси oz или в обратном направлении, бу-
дет эквивалентна липотропному модулятору с операто-
ром Л[<р(/)].
Следовательно, операторы преобразования электро-
магнитной волны для двух схем, изображенных на
77
рис. 3.6,а, б, тождественны п равны Л[ср(/)]. При этом
полагаем, что гиротроппый модулятор взаимен.
В случае, если гиротроппый модулятор невзаимен, то
тождественность операторов обеих схем сохраняется
только для волны, распространяющейся в положитель-
ном направлении оси oz. Для волны противоположного
направления распространения операторы этих схем бу-
дут Л[—ср (/)] и Л[ф'(01 соответственно.
Аналогичным образом можно доказать, что операто-
ры двух преобразователей поляризации, изображенных
на рис. 3.7,а, б, также тождественны по отношению
к волне любой поляризации и равные
Рис. 3.7.
78
Таким образом, в каждой из парных комбинации
преобразователей поляризации, изображенных иа
рис. 3.6 и 3.7, можно менять местами активные устрой-
ства с одновременными изменением полярности одного
из этих устройств либо полярности четвертьволновых
фазосдвигателей. При этом эквивалентность преобразо-
вателей а) ц б) сохраняется для волны любой поляриза-
Рис. 3.8.
ции. Схемы, представленные па рис. 3.6 и 3.7, назовем
схемами замещения элементарных преобразователей.
Используя схему замещения, изображенную на
рис. 3.7, можно заменить второй гиротропный модулятор
в схемах рис. 3.4 и 3.5 на эквивалентную ему комбинацию
элементарных преобразователей с липотропным модуля-
тором. В результате получим еще две схемы модулято-
ров, позволяющих осуществлять независимую модуля-
цию параметров поляризации ф(^) и Q(t) электромаг-
нитной волны. Это будут модуляторы типов ДА и ГА
(рис. 3.8 и 3.9).
Таким образом, мы получили четыре общие схемы
поляризационных модуляторов, позволяющих формиро-
вать электромагнитную волну любой поляризации и при
необходимости модулировать параметры поляризации ф
79
и 6 независимо Друг от друга. Эти схемы являются
общими для любого диапазона волн, хотя в конструк-
тивном отношении элементы модуляторов весьма раз-
личны для различных диапазонов.
Рис. 3.9.
Отметим особенности и наиболее рациональные обла-
сти применения этих модуляторов.
1. Модулятор типа ГГ (см. рис. 3.5). Этот модулятор
может быть выполнен целиком на невзаимных гиротроп-
ных средах — ферритах. Основным его достоинством
является крайняя простота. Разработанные в настоящее
время типы ферритов позволяют использовать его в диа-
пазоне от дециметровых до субмиллиметровых волн.
Кроме того, как сообщается в работе (48], монокристал-
лы ферритграната можно использовать для модуляции
поля дальнего инфракрасного участка спектра.
Недостатком такого модулятора является не очень вы-
сокая частота модуляции — единицы мегагерц на некри-
сталлических ферритах и десятки мегагерц на монокри-
сталлах.
2. Модулятор типа АЛ (рис. 3.8). Модулятор выпол-
нен полностью на анизотропных средах. Наиболее целе-
сообразная область применения — инфракрасный и све-
80
товой диапазоны. Это объясняется тем, что в основном
лишь для этих диапазонов разработаны достаточно на-
дежные и экономичные липотропные управляющие
устройства на монокристаллах. Этот тип модулятора по-
зволяет осуществлять модуляцию сразу двух парамет-
ров поляризации с весьма высокими частотами.
3. Модуляторы типов ЛГ и ГЛ являются комбиниро-
ванными и могут быть использованы в специфических
схемах. Например, основное достоинство модулятора
типа ЛГ — наличие всего лишь двух элементов. Он мо-
жет быть использован в тех случаях, когда необходимо
с большой скоростью менять эллиптичность поля и с ма-
лой скоростью — угол ориентации.
Рассмотренные выше схемы поляризационных моду-
ляторов могут быть использованы и как элементы антен-
ных устройств с перестраиваемыми электрическим путем
параметрами поляризации.
3.5. КЛАССИФИКАЦИЯ СПОСОБОВ ПОЛЯРИЗАЦИОННОЙ
МОДУЛЯЦИИ
В предыдущем параграфе мы рассмотрели возмож-
ные схемы поляризационных модуляторов, позволяющих
модулировать непрерывными сигналами параметры по-
ляризации электромагнитной волны.
Отличительной чертой поляризационной модуляции
является то, что при этом виде модуляции интенсивность
радиосигнала (сумма квадратов огибающих поляриза-
ционно-ортогональных компонент) остается постоянной,
так же как и его общая фаза и частота, тогда как
амплитуда и фазы поляризационно-ортогональных со-
ставляющих являются функциями модулирующего сооб-
щения.
Приведенные схемы модуляторов могут быть исполь-
зованы не только для непрерывной, но и для дискретной
модуляции параметров поляризации. Для дискретной
поляризационной модуляции можно сконструировать и
специфичные модуляторы, основанные на переключении
энергии генератора высокочастотных колебаний от одно-
го преобразователя поляризации к другому.
Таким образом, как и другие виды модуляции, поля-
ризационная модуляция может быть непрерывной или
дискретной.
Непрерывная поляризационная модуляция (ПМ)
различается параметрами, которые модулируются пере-
6—667 81
Даваемыми сообщениями, а также глубиной модуляции
или величиной девиации параметров поляризации. В за-
висимости от величины девиации угла эллиптичности и
угла ориентации меняется эффективная ширина спектра
ПМ радиосигнала.
Как будет показано ниже, если девиация угла эллип-
тичности или (и) угла ориентации не превышает л/4, то
эффективная полоса ПМ сигнала равна полосе AM сиг-
нала, и такая ПМ называется узкополосной. При боль-
ших значениях девиации параметров поляризации
спектр ПМ сигнала существенно расширяется, и такая
ПМ называется широкополосной. Это определение широ-
кополосное™ и узкополосности ПМ относится не только
к непрерывной, но и к дискретной ПМ.
В зависимости от вида модулированного параметра
поляризационной диаграммы различают модуляцию:
— угла эллиптичности; в этом случае поляризацион-
ная модуляция обозначается ПМ ;
— утла ориентации поляризационного эллипса—ПМ0;
— одновременную модуляцию углов эллиптичности
и ориентации ПМ^ 0, или совмещенную ПМ.
В последнем случае параметры ср и 0 могут модули-
роваться либо двумя независимыми сообщениями Si(/)
и S2(/), либо одним и тем же сообщением S(t) (напри-
мер, для повышения достоверности передачи сообще-
ния) .
Модулируемое излучение может быть как непрерыв-
ным, так и прерывистым, импульсным. В последнем слу-
чае говорят о поляризационной модуляции импульсов
(ПМИ) непрерывным процессом.
В тех случаях, когда состояние поляризации волны
может в процессе модуляции принимать только дискрет-
ные значения, модуляцию называют поляризационно-им-
пульсной (ПИМ) или дискретной поляризационной мо-
дуляцией. При этом в обозначении излучаемого сигнала
первые индексы относятся к модулирующему процессу
(АИМ, ВИМ, ШИМ, КИМ), а последние два означают
вид собственно поляризационной модуляции: ПМ^ ПМ0,
ПМ
<р, о
Классификация видов поляризационной модуляции
представлена в табл. 3.1.
Табл. 3.1 не исчерпывает все возможные виды поля-
ризационной модуляции. В частности, в нее не включены
82
Таблица 3.1
Непрерыв- ная ПМ Дискретная ПМ Непрерыв- ная ИМ Дискретная ПМ
пм9 АИМ-ПМ9 ВИМ-ПМ^ ШИМ-ПМ^ КИМ-ПМ^ ИМ „с Ч>.5 АИМ-ПМЧ,_ 8 ВИМ-ПМ9’ 8 ШИМ-ПМ,,’ 9 КИМ-ПМ9_ о
пм8 АИМ-ПМд ВИМ-ПМд ШИМ-ПМ9 КИМ-ПМ„ □ ПМИ¥ пми0 пми9в Квантованная ПИМ^ ПИМ8 ПИМФ. 9
виды поляризационной модуляции в сопряжении с моду-
ляцией других параметров электромагнитной волны, на-
пример частоты или фазы. Некоторые из этих видов мо-
дуляции будут рассмотрены в последующих главах.
ГЛАВА 4
СИГНАЛЫ С НЕПРЕРЫВНОЙ ПОЛЯРИЗАЦИОННОЙ
МОДУЛЯЦИЕЙ
В настоящее время информация в аналоговом виде передается
по линиям радиосвязи сравнительно редко. В большинстве случаев
ее сначала преобразуют в дискретную форму, кодируют, а затем
уже полученным в результате этих преобразований сигналом моду-
лируют несущую частоту. Таким образом, даже при передаче
аналоговой информации применяется дискретная модуляция. Однако
для анализа спектральной структуры ПМ сигналов целесообразно
предварительно рассмотреть модуляцию параметров поляризации
непрерывными, гармоническими колебаниями. Анализ спектров ПМ
сигналов с непрерывной модуляцией позволит в дальнейшем без
лишних затруднений получить и проанализировать спектры дискрет-
ной ПМ.
4.1. МОДУЛЯЦИЯ УГЛА ЭЛЛИПТИЧНОСТИ
Введем обозначения: S(f)—-передаваемое (модули-
рующее) сообщение; Atp — девиация угла эллиптичности;
<ро, 0о — параметры поляризации немодулированной гар-
монической несущей.
6* 83
Интенсивность гармонической несущей полагаем рав-
ной единице, передаваемое сообщение — нормирован-
ным, без постоянной составляющей, т. е. —1 S (t) 1,
S(0=0, гДе черта сверху означает усреднение по вре-
мени.
При этих условиях ПМф электромагнитная волна на
двойной комплексной плоскости запишется в виде
е- ‘i (/)] (ut-kz) (4 । р
Сигнал вида (4.1.1) можно сформировать из эллиптически-
и — i/Фо iOo / (<ot—kz)
поляризованной волны е е °е' , если пропустить
последнюю, например, через линотропный модулятор,
ось R которого ориентирована под углом 60 (рис. 4.1).
Поляризационные диаграммы сигнала (4.1.1) для ди-
скретных значений S(t) изображены на том же рис. 4.1.
В выражении (4.1.1) величину можно отнести к по-
стоянной составляющей модулирующей функции. Если
же рассматривать случай, когда постоянная составляю-
84
щая модулирующей функции равна нулю, то следует по-
ложить <ро = 0. Не нарушая общности рассуждения, мож-
но положить 9и = 0. И, таким образом, ПМ сигнал будет
иметь вид
£(/)==е“‘74‘₽5(')е/ю/. (4.1.2)
Рассмотрим вид поляризационной диаграммы волны
(4.1.2) для дискретных значений угла эллиптичности
Ф=.Дф5(/) при изменении его в интервале —л.. . л. Со-
ответствующие поляризационные диаграммы для поло-
жительных и отрицательных значений ср изображены на
рис. 4.2,а, б. Верхний рисунок соответствует положитель-
ным дискретным значениям <р, равным 6<л/4; л/4; л/2—
6; л/2; л/2+б; л/2—б, нижний — тем же самым величи-
нам, но взятым с отрицательным знаком. Такие формы
поляризационной диаграммы м'ожно наблюдать у ПМф
волны при дискретных значениях модулирующей функ-
ции S(t), если Дф=л.
На поляризационных диаграммах рис. 4.2,я, б пока-
заны также мгновенные положения вектора Е для мо-
ментов времени t=&7'о(7'о = 2л/<п)—сплошные векторы,
и для моментов времени tl = kT()+ Тй/4, k = 0, 1, 2...—
пунктирные векторы. Из рассмотрения рис. 4.2 можно
сделать вывод, что форма поляризационной диаграммы
и направление вращения вектора Е определяют одно-
значно угол эллиптичности только в интервале —л/4,^
^Ф^л/4, т. е. при главных значениях угла эллиптично-
85
сти. При |ф| >л/4 для однозначного определения значе-
ния ф необходимо учитывать не только форму поляриза-
ционной диаграммы и направление вращения вектора
поля, пои ориентацию поляризационной диаграммы. Так,
при двух значениях ср, равных 6 и л/2—б, форма поля-
ризационной диаграммы одинакова и определяется ве-
личиной 6, однако поляризационная диаграмма волны
при ф=б отличается от поляризационной диаграммы
волны при ф = л/2—б ориентацией и фазой волны:
е- ;/(п/2-&)= _ (е//5== е- ЦЪ &i*/2
Начиная с величины угла ф=л/2, поляризационная
диаграмма волны при ф = л/2±б отличается от поляри-
зационной диаграммы волны при ф =— (л/2+б) только
значением фазы волны, т. е.
е— Ц (я/2±5) еП (*/2 + 5) (4 13
Следовательно, если анализатор поляризации будет
фиксировать не только параметры, определяющие фор-
му, направление вращения и ориентацию, по и общую
фазу эллиптически-поляризованной волны, то с помощью
такого анализатора поляризации можно различить ср
в пределах — л<Сср<г:л. Этот вывод следует и из того
факта, что функция g (ф, 6, ф) периодична с периодом
2л по любому из трех параметров, если два другие счи-
тать фиксированными.
4.2. СПЕКТРЫ *ПМ.? СИГНАЛОВ
Определим сначала спектр сигнала (4.1.2) при моду-
ляции угла эллиптичности-гармоническпм колебанием,
т. е. положим
S(/)=sinQ^, Q<^co.
Как известно, для любой комплексной функции z име-
ет место соотношение
4p(Z—1/z) оо
е - S /п(Д?)г", (4.2.1)
п=—ОО
где А(Д?) — функция Бесселя /z-го порядка.
Подставив в (4.2.1) z = eT‘ist, получим
e-^sinS/= £ 7п(д?)е-(7^ =
П=—00
86
1. (Л?) +S Л. (ДТ) |е“ (- 1)" е"“'| =
п-=\
= Jo (Д<Р) + 2 S [Лп (д?) cos 2яй/ —
/1 = 1
- (zj)Zn _ДД<Р) sin (2/г - 1)Йф (4.2.2)
Разложив тригонометрические функции по формулам
Эйлера с мнимой единицей j и умножив левую и правую
часть выражения (4.2.2) па е’Ш{, получим спектр ПМ9
сигнала в комплексной форме в ортогонально-линейном
базисе:
е = е~i/A<₽ sin st = Jv (Д?) e'w Д-
оо
+S {/„ (Л?) е' , (Д-р) |е''-+ |2“-'1' -
Л=1
_е/[Ю-(2П-1)а]/ц> (4.2.3)
Как следует из (4.2.3), амплитуды гармонических со-
ставляющих ПМ.^ сигнала являются бесселевыми функ-
циями от девиации угла эллиптичности. Нулевая гармо-
ника (т. е. в данном случае гармоника несущей частоты
и) и четные боковые гармоники частоты й (т. е. гармо-
ники с частотами <о±2пй) линейно поляризованы, син-
фазны, и ориентация их совпадает с ориентацией исход-
ного немодулированного колебания. Гармоники <o+(2/i—
— 1)й и и—(2п—1)й также линейно поляризованы, ио
поляризационно ортогональны четным гармоникам. Кро-
ме того, нечетные гармоники попарно противофазны.
На рис. 4.3 изображен графически спектр ПМ.^ сиг-
нала вида (4.2.3) для некоторых дискретных значений
Дер. Амплитуды спектральных составляющих нечетных
гармоник, поляризация которых совпадает с осью оу,
изображены на рис. 4.3 без изменения масштаба.
Есть определенная аналогия между спектром ПМф
и спектром ФМ сигнала. Действительно, ФМ сигнал име-
ет вид
ефм(0 =COs[<oZ—ДФ81ПЙ/] =
= cos (at cos[A<Dsiпй/] + siп (at зт[ДФзтй(|. (4.2.4)
Если взять Rej от левой части выражения (4.2.3), то
87
получим
еПМф (О = COS со/ cos[A(psinQ/] + i‘ sin и/ sin[A<psinQ/]. (4.2.5)
Таким образом, если в спектре ФМ сигнала с девиацией
фазы АФ=Д<р развернуть все нечетные гармоники в про-
странстве на л/2, то получим
х“ спектр ПМф сигнала. Поэто-
Ду-30°
Рис. 4.3.
му и ширину спектра ПМф
колебания можно опреде-
лить так же, как и ширину
спектра ФМ колебания:
Д/=₽Д<рЙ. (4.2.6)
Величина р определяется
из графика рис. 4.4, если
не учитывать гармоники,
амплитуда которых меньше
0,01.
Практически при Д<р,<л/4
второй и более высокими
Рис. 4.4.
гармониками частоты Q можно пренебречь, и, следова-
тельно, спектр узкополосной ПМ будет представлять
собой несущую горизонтальной поляризации (ось ох —
горизонтальная ось) и две боковых вертикальной поля-
ризации. ПМф колебание может быть превращено в при-
емном устройстве в ФМ сигнал. Для этого достаточно
сложить с учетом фаз составляющие ex(t) и ey(t) с вы-
ходов двухканального приемного устройства либо свести
в одну плоскость и просуммировать высокочастотные
—► —►
Ех и Еу составляющие в антенно-фидерном тракте. .
88
Рассмотрим спектр ПМф сигнала при сро=И=.'О, 0о=#О.
Представим (4.1.1) в ортогонально-эллиптическом ба-
зисе:
е (0 = cos [Дф5 (0] е- ‘'м е1'9’ем +
+ sin [Ат • S (OJ е'^’е'<9о+к/2) е;' (ш/~к/2), (4.2.7)
и сравним (4.2.7) с (4.2.5). Из сравнения видим, что
энергетический спектр ПМф колебания в этом случае
остается тем же самым, но теперь четные и нулевая гар-
моники частоты Q имеют эллиптическую поляризацию
с параметрами ф0, 0о, а нечетные гармоники — ортого-
нальную эллиптическую поляризацию. Обозначим орт
с параметрами поляризации <ро, 0о как Э(фо, 0о), а орто-
гональный орт —Э(—фо, 0о+л/2). Реальную часть
(4.2.7) запишем в виде
е (0 =Э (ф0, 6о) cos cos [ДфЗ (f)[
4-Э (—фо, 6о +тг) sin sin 1Л<р5 (*)!• (4-2.8)
Ортам Э(Ф0, 60) и Э(—ф0, г60-|-тс/2) соответствуют
поляризационно-ортогональные выходы двухкомпонент-
ной эллиптически- поляризованной антенны, а сигналы
с этих выходов есть проекции па ортогональные орты
принимаемой электромагнитной волны.
Если эти сигналы просуммировать (уже как скаляр-
ные величины), то получим фазомодулированный сиг-
нал.
Часто для приема ПМф сигнала используют кругопо-
ляризованные антенны противоположного направления
вращения либо линейно-поляризованные антенны, ори-
ентированные под углом ±л/4 по отношению ориентации
большой полуоси поляризационного эллипса немодули-
рованной несущей. Рассмотрим спектр составляющих
ПМ сигнала на выходах таких антенн.
Если сигнал (4.1.1) принимается на двух компонент-
ную кругополяризованную антенну, то согласно (1.4.14)
на двух ее выходах получим сигналы
eR it) = sin [То + «/4 + ДфЗ (0] е' (ш/+9о),
eL (t) = cos [Фо + it/4 + Дф5 (01 e' (ш/'9о).
(4.2.9)
§9
Эти сигналы содержат как четные, так и нечетные
гармоники частоты Й, расположенные симметрично от-
носительно составляющей с частотой со, и саму эту со-
ставляющую, т. е. составляющую несущей частоты.
При <р0 = 0 составляющие спектров сигналов eR (t) и
eL(t) отличаются только фазами. Ширина спектров этих
сигналов определяется соотношением (4.2.6).
Сигналы на выходах линейно-поляризованных антенн
с ориентацией ±л/4 относительно ориентации поляриза-
ционного эллипса иемодулированиой несущей, согласно
выражению (1.4.3) будет иметь вид
(л__ 1 J (О— <Ро1
11
(4.2.10)
е 1 eJ 1ш(+Д(₽5 (О+то1
и представляют собой обычные фазомодулировапные
сигналы с отрицательной и положительной девиацией.
При S(/)=sinQ/ и фо = 0 спектральные составляющие
сигнала £i(/) с частотами ®±nQ, где п=1, 3.5..., отли-
чаются по фазе на л от таких же спектральных состав-
ляющих сигнала . Поэтому сумма сигналов £а(0 и
не содержит нечетных гармоник частоты Q, т. е.
представляет балаиспо модулированное функцией
cos(A<psin Qt) колебание частоты ю, а разность не содер-
жит четных гармоник частоты й, т. е. является колеба-
нием частоты и, балансно модулированным функцией
sin(A<psinQ0. Это ясно и из (4.2.10), откуда непосредст-
венно следует
es (0 + К (0 = 2 cos [Д?• S (0 + ?0] е/шг, (4.2.11)
е2 (0— ei (0 = 2 sin [Д<р • S (0 -ф- <р0] е1ш‘. (4-2.12)
4.3. ПМе СИГНАЛЫ И ИХ СПЕКТРЫ
Используя те же обозначения, которые были приня-
ты при рассмотрении ПМ^ сигналов, сигнал при моду-
ляции сообщением S(0 угла ориентации поляризацион-
ной диаграммы волны (ПМ0 сигнал) запишем в виде
ф(/) = е-г/ч>|>е;9<,е;д0”'$(Ое/ф(. (4.3.1)
90
Такой сигнал получается на выходе гиротропного мо-
дулятора или эквивалентного ему устройства, если ис-
ходная вемодулированная волна эллиптически поляризо-
вана с параметрами поляризации цл,, Оо (рис. 4.5). Поля-
ризационные диаграммы сигнала (4.3.1) для дискретных
значений S(/) и сро<л/4 изображены на рис. 4.5 после
гиротропного модулятора.
Исследуем поляризационно-спектральную структуру
сигнала (4.3.1) при модуляции гармоническим колебани-
ем, т. е. при S(/)=sinQ/.
В случае, если сро=0, 0о=О, то сигнал (4.3.1) прини-
мает вид
е (/) = e'A0sinSZe'“z (4.3.2)
и его можно превратить в ПМ^ сигнал, сдвинув i-ю со-
ставляющую волны (4.3.2) на —л/2.
Следовательно, спектр ПМ0 сигнала при нулевых
параметрах поляризации немодулированной несущей от-
личается от спектра ПМф сигнала только фазовым сдви-
гом на +л/2 вертикально поляризованных (вдоль оси оу)
спектральных составляющих. Все остальные выводы от-
носительно ПМ? сигналов при q\> = 0o = O справедливы и
для ПМ( сигналов при тех же условиях.
91
Рассмотрим Тейерь сйектр Г1М9 сигнала При фпХД
0о=#О и S(/) = sin Q/.
Представим множитель е,495!ПЯ' в выражении (4.3.1)
в виде комплексного ряда Фурье:
е'Л9 sin я/ = 70 (ДО) 4- 2 2 [J2n (ДО) cos 2/zQ/ +
л=1
(ДО) sin (2/г — 1) Q£] =
00
= /о (ДО) +2 {-4п (ДО) [е/2/!й/ 4-е-/2'!й/] -
Л = 1
— г-//2„_ж(Д0)[е/(2"-1)я#—e-z й/]}.
(4.3.3)
Подставим (4.3.3) в (4.3.1). При этом необходимо учесть,
что в выражении (4.3.3) ij есть независимое произведе-
ние мнимых единиц, а не совмещенная мнимая единица
(i/). Это существенно, потому что в (4.3.1) множителю
е предшествует множитель е . После соответ-
ствующих преобразований получим
ё (/) = е-‘/<₽ое‘9°
ПМд ' '
1„ (Д0) ем 4- f Лп (Д0) [е' <ш+2"Я) * +
. Л—1
‘ 9о+ -4 -/-4
4-e/<“-2"8MJ j4-e-‘me ' 'е X
Х£ 72П_1(Д9{е/(ш+<2п“')я' — e/fw-(2"-,)81<}. (4.3.4)
л=Н
Для дальнейшего сравнения запишем здесь же спектр
ПМ* сигнала при аналогичных условиях. Спектр ПМ*
сигнала можно получить из выражения
ёпМ1? (0 =е“ ,7’’.е-
подставив в него вместо множителя е- ‘J'44>sinSi' его раз.
ложение в ряд Фурье (4.2.2). После соответствующих
92
йреобразовании получим
еа^ Ю = е 'мe'e°U (Дб) e/m/ +S /2П (Дб) |е' (ш+2лй) 1 +
I Л=1
о , 1 ‘ (е» +4) 00
+ е, (-2лй) /j + eiM е ( ч е-/к£ Лп _ > (дб) х
J п — \
Х {е/[“ + (2л- 1) Я] (2п- 1) 2]/у (4 2
Спектры ПМ? и ПМ0 сигналов при Дф=Д0 = 6О° и ср0<
<л/4 представлены на рис. 4.6,а, б.
Из сравнения выражении (4.3.4) и (4.3.5) следует су-
щественное различие поляризационно-спектральной
структуры П и ПМ9 сигналов при эллиптически-по-
ляризованной несущей.
Спектральные компоненты с частотами a>±2k Q
(& = 0, 1, 2, 3, ...) у ПМ^ и ПМ9 сигналов идентичны.
Спектральные компоненты с частотами ю± (2& +1)й
93
у ПМ^ сигнала поляризационно-ортогональны спек-
тральным компонентам с частотами w±2/jQ. Поэтому
эти спектральные компоненты можно разделить с по-
мощью поляризационных фильтров. У ПМ0 сигналов
эти компоненты не ортогональны, и с помощью поляри-
зационных фильтров их разделить невозможно. Поэто-
му ПМ0 сигнал при сро=/='О нельзя превратить в ФМ
сигнал так же просто, как ПМ.^ сигнал.
Рассмотрим ПМ0 сигнал в ортогонально-круговом
базисе.
В ортогонально-круговом базисе выражение (4.3.1)
согласно (1.4.13) запишется в виде
е- ‘/Ч>ое«’ [во+Ш («)] е/®« __ е- sjn я е/(®«+Де5(О+во) +
+ е"*/4 cos (? + -гс/4) е' (^~ies (<) ~Ч (4.3.6)
Сигналы на выходах двухкомпонентной кругополяри-
зованной антенны будут
^ (/) = sin + -^ ) cos [со/ -ф- Д 0S (/) + 0О],
eL (t) = cos f¥0 + cos [со/ — Д05 (/)—0O],
(4.3.7)
t. e. представляет собой фазомодулированные сигналы
с различными амплитудами и девиацией фазы Д0 и
—А0. В двухканальном приемном устройстве подбором
коэффициентов усиления К в каналах можно выравнять
амплитуды сигналов (4.3.7), если только амплитуда
одного из сигналов не равна нулю. Тогда, суммируя
ед(/) п eL(t), можно получить балансную модуляцию
K,eL (/) K2eR (/) = к {cos [со/ + Д0 • S (/) + 0О]
cos [со/ — Д0 • S (/) — 0О]} =
__2^. icos[A0S (/)-[-0OJ cosco/ (438)
(sin [ДOS (/) -[- 0О] sin со/.
Фазы 0о при необходимости можно скомпенсировать
в антенно-фидерном устройстве или в трактах усилите-
лей промежуточной частоты.
В частном случае, когда пемодулировапная волна
кругополяризована, т. е. сро=л/4, ПМ0 сигнал является
94
ФМ сигналом круговой поляризации, так как
. . Я .. я
„ 4 [So + A9S (/)] М _ J М + ASS (0 + So)
С С с —~ с с
4.4. ОДНОВРЕМЕННАЯ МОДУЛЯЦИЯ УГЛА
ЭЛЛИПТИЧНОСТИ И УГЛА ОРИЕНТАЦИИ
ПОЛЯРИЗАЦИОННОЙ ДИАГРАММЫ
В § 3.5 было показано, что можно построить такой
модулятор, который позволит одновременно и независи-
мо модулировать оба параметра поляризации: <р и 0.
Модуляция двух параметров поляризации может
быть использована в системах передачи информации.
. Для этого параметры ср и 0 модулируются либо двумя
различными сообщениями, и в этом случае достигается
уплотнение капала связи за счет использования его по-
ляризационных свойств, либо одним и тем же сообще-
нием в целях получения сигнала, обладающего опреде-
ленными качествами.
Рассмотрим последний случай, т. е. положим, что па-
раметры tp и 0 модулируются одним и тем же сообще-
нием S(t). Используя те же обозначения, как и в пре-
дыдущих параграфах, запишем П Мф 0 сигнал в виде
.е-</14=0+^5(01 ei [So+ A0S (О] е/<0«( (4.4.1)
т. е. будем рассматривать случай, когда ср и 0 модули-
руются одним и тем же сигналом, но с различной девиа-
цией.
В выражении (4.4.1) ПМ^сигнал записан через свои
мгновенные параметры поляризации. Для анализа тако-
го сигнала удобнее иная форма представления — в виде
двух качающихся векторов одинаковой амплитуды. Для
такого представления воспользуемся выражением
(1.4.4). Получим
"е (/) = —1— {ег [4>о+Аф-5 (01_^ Je- I [Фо+АфЗ (01} [So+ASS (0]\^
. ft__
£ \ 4 /|9o+t?o+ (Л9 + Лф) 5 (/)] j
/
j jel l0°—<ро+(д0—А<р) s (<)]} е \ 4/. (4.4.2)
95
yi Два линейно-поляризованных
. вектора, входящие в выражение
/ (4.4.6), не перпендикулярны друг
х/2 11 другу в пространстве (рис. 4.7).
Угол между этими векторами ра-
х вен двойному углу эллиптичности
____волны (4.4.1). Однако эти два век-
f / У Тора находятся во временной
/ квадратуре, поэтому их нельзя
суммировать как обычные век-
Рис. 4.7. торы.
Найдем спектр сигнала (4.4.1)
при модуляции параметров поляризации гармоническим
колебанием, т. е. при S(/)=sinQl.
В выражении (4.4.2) сомножители е‘ (9<’±ч>°) представим
в тринонометрической форме, а сомножители е‘ (Д9±дч>)5(<)>
определяющие угловую ориентацию линейно-поляризо-
ванных векторов, разложим в ряд Фурье по формуле
е± м sin = Jo (Д) + 2 f [Jan (Д) cos 2/zQf zb
л=1
zb Цгп _, (Д) sin (2п — 1) Qt ].
В результате поляризационно-спектральная структура
ПМ^ в сигнала с гармонической модуляцией параметров
<р и 0 будет определяться выражением
00
'е^. тг "(в0 + 901 /о (Д0+}+2 S[Лп (Д0+
-ф- Д?) cos2/iQZ -HAni-i (Д9 + Д'?) sin (2п — l)Qm -j-
ef ,9-^ Ja (ДО - Д?) + 2 £ [У2П (ДО -
п=\
— A‘P)cos2/z£y-|-iJ2n_1 (ДО— Д'?) sin (2п — l)Q^]|e'“z.
(4.4.3)
Из (4.4.3) следует, что поляризация и амплитуда гар-
моник с частотами co±2^Q при k=0, 1, 2, 3, ... опреде-
ли
ляются из уравнения
Д2А,е ‘/1радeS'2Rе'*ад =у=-[(<V + /М+1 (<^+/Ч0|.
(4.4.4)
а поляризация и амплитуды гармоник с частотами
dz(2&4*l)^ — из выражения
е" i/t₽2'l+, е;в2'1+1 К«2*+1 +
+ /^2й+1) + г (С2й+1 + /Чл+i)]’ (4.4.5)
где
a, = cos (Оо + фо)/;(АО + Аф);
bt = cos (0о—сро)/г (А0—Аф);
(4.4.6)
c; = sin (0о+сро)Л(АО+Аф);
dt = sin (9о—фо)Л(А0—Аф)
и
/ал+1 (—А) = —/гл+1(А); /гл (—А) = /гл (А).
Из (4.4.4) и (4.4.5) следует, что амплитуды At гармони-
ческих компонент ПМ^ е сигнала определяются выра-
жением
= /;(Д6 + Д?)+/;(ДО-Д¥). (4.4.7)
Выражения для фаз ф, и углов эллиптичности и углов
ориентации гармонических компонент ИМ е сигнала мож-
но получить, решив уравнение
Аейе/ф = [(а + jb) A-i(c + jd}\ (4.4.8)
относительно параметров ф, 0, ф.
Преобразуем выражение (4.4.8) так, чтобы слева
осталось комплексное число е/ф. Далее приравняем ко-
эффициенты при одинаковых мнимых единицах слева и
справа. В результате получим исходные уравнения, из
7—667 97
которых путем несложных преобразований получаются
следующие системы формул для определения интере-
сующих нас величин:
sin 2<р = 2 (cb — ad)la2 -j- 62 -|-с2 -|-о!2;
(ad + cb) [(д2 ~ с2) — — d2)j s'n
® (ab—cd)-(-(ab+cd) cos 2<p + (bd — ac) sin 2<p ’
tg 26 = 2 (ac -|- bd)l(a2 — c2) (b2 — d2)\
1
(ac — bd) cos 29 — [(a2—c2)-(&2—d2)J sin29
tg (ab — cd) cos 29 + (ab + cd) -|- (ad 4- be) sin 26 ’
cos <[> -j-p—[cos 0 (a cos <p — a! sin <?)-[-
-[- sin 6 (c cos <p sin <?)];
sin [cos 6 (b cos <p) -|- c sin <p) + J
-|- sin 6 (d cos <p — a sin <p)].
(4.4.9)
(4.4.10)
(4.4.11)
Значение А в выражении (4.4.11) определяется соотно-
шением (4.4.7). Системы формул (4.4.9) и (4.4.10) рав-
нозначны. При определении параметров ср и 0 можно
использовать как соотношения (4.4.9), так и (4.4.10), при
этом уравнения (4.4.11), определяющие фазу эллиитиче-
ски-поляризовапной гармоники, справедливы как для си-
стемы (4.4.9), так и для системы (4.4.10).
Таким образом, подставляя значения а; ... di из
(4.4.6) в выражения (4.4.9) ... (4.4.11), и учитывая со-
отношения (4.4.4) ... (4.4.7), можно определить полную
поляризационно-фазовую спектральную структуру ПМф 9
сигнала при синхронное! модуляции параметров ср и 0
одним и тем же гармоническим колебанием.
Выражения (4.4.9) ... (4.4.11) являются общими вы-
ражениями для определения мгновенных параметров по-
ляризации сигнала, представленного в виде (4.4.8).
В рассматриваемом нами случае анализа поляризацион-
но-спектральной структуры ПМ всигпала эти выражения
можно значительно упростить. Для этого положим
в (4.4.6) 0о = О и подставим эти коэффициенты в (4.4.9).
Получим следующие соотношения;
98
sin 2=pz- = 2 sin 2?0
/f (Д8 + Ду)/, (Д8 — Д?)
J-(Д?+Д9) + / (Д8 — Д?) ’
tg 0» =
sin 2?0
cos 2<p0 + cos 2yt
Дт) .
/*(Д9+Д¥)+^(Д0-Д?) ’ |
)
(4.4.12)
tg 20г- tg 2?0
J? (Д9 + Ду) — /(Д9 — Д?)
Jp (ДО + Ду) + /• (Д9 — Ay) ’
_-t? (Л9+Д<?) sin 2 (<?0—9t)+Z? (Д9—Д?) sin 2 (<f0+9t) _
?г ~~ Л (^9 + Д?) Л (49 — ДУ) cos (9t + Vo) cos (y0 — 9t) ’
(4.4.13)
COS фг- = Ji (Д0 A?) COS <?i COS (0г —
— Vo) + Л (AO — A?) sin ?г sin (0г + Vo);
sin фг = Ji (Д0 4- A?) sin <fi sin (?0—0г)
+ Ji (Д0 — A?) COS ?г COS (0г + ?0).
(4.4.14)
Из соотношений (4.4.12) ... (4.4.14) следует, что при
одновременной модуляции параметров ср и 0 исходной
эллиптически - поляризован-
ной волны поляризационно-
спектральная структура
ПМф 8 сигнала даже при
модуляции гармоническим
сигналом становится доволь-
но сложной. При этом не
только параметры поляриза-
ции гармоник, но и их фазы
у разных гармоник различ-
ны и зависят от девиации
параметров поляризации.
Несколько проще поляризационно-спектральная
структура у ПМф 0 сигнала при модуляции ср и 0 с оди-
наковой девиацией, т. е. при Аср=Л0. В этом случае вы-
ражение (4.4.2) принимает вид
"е (0 = [/ е“ /ф°-|-е‘ <ф°+24в sin st) ] ei0° е~/п/4, (4.4.15)
т. е. ПМ^ 0 сигнал представляет собой сумму двух волн:
линейно-поляризованной гармонической волны, ориенти-
рованной под углом (0о—сро) по отношению к оси ох, и
7* 99
Лиис“шо-полярнзопанпой ПМе полны (рис. 4.S), находя-
щейся во временной квадратуре к первой. В соответст-
вии с этим спектр такого сигнала такой же, как и
у ПМ0 сигнала:
1 /2Д9 s:n 2/
е —-v--e ,
"ч6 |/-2
с той лишь разницей, что нулевая гармоника имеет
эллиптическую поляризацию с поляоизацпопнымп па-
Рис. 4.9.
раметрами, которые можно определить из соотношений
От_о оИ, m о (249)
ЫП SIU -----5----•,
1 + /о(2Д9)
sin 2<р0 7о (246)—1
cos 2<р0 + cos 2? ’ j* (249) + 1 ’
6 = 6o + arctg
и амплитуду
= 1 + /о(2Д6) ’
т. е. всегда больше половины общей энергии волны при-
ходится на несущую.
На рис. 4.9 изображена поляризационно-спектраль-
ная структура ПМф в сигнала при Аср=А0 = 6О°.
4.5. ПОЛЯРИЗАЦИОННО-СПЕКТРАЛЬНАЯ СТРУКТУРА ПМ^
СИГНАЛА ПРИ МОДУЛЯЦИИ ПАРАМЕТРОВ <р и 0
РАЗЛИЧНЫМИ СООБЩЕНИЯМИ
При модуляции параметров <р и 9 гармонической
волны двумя различными сообщениями в спектре сигна-
ла присутствуют гармоники как от первого, так и от
второго сообщения, причем поляризация у этих гармоник
100
будет различная. Рассмотрим спектр ПМф в сигнала
в случае модуляции параметров поляризации двумя гар-
моническими колебаниями с частотами Ц, и Ц.
Общее выражение для сигнала имеет вид
e(/) = e e e(4.5.1)
Постоянный угол ориентации 0o можно при анализе
не учитывать, так как мы его всегда можем компенси-
ровать соответствующим выбором системы координат,
либо можно учесть в окончательном выражении. Поэто-
му в дальнейшем полагаем 0о=0.
Представим в выражении (4.5.1) сомножители
— sin .
е и е их комплексными рядами Фурье:
00
— i/&4> sin Яфг . тл ( , , z260»' -/W\ |
е 9 =A(Af)+VUn(A?)(e 9 —е 9 ) +
71=1
+ Й) -р.»-. (if) |е'- е" ' “И ); (4.5.2)
е‘“1. (Ы)+ £ (У,,(ДИ) (е'"» ‘ - е~ 12"‘‘ ’) +
и=1 4
I i , /А0\ Г ' (2»-1) < -J (2n-l) Eg f ~|
+—Лп-1(Д9)[е — е . (4.5.3)
Подставим (4.5.2) и (4.5.3) в (4.5.1) и произведем
перемножение с учетом правил умножения на совмещен-
ную мнимую единицу. В результате получим следующее
выражение для спектраПМ^ сигнала, у которого пара-
метры ф и 9 модулированы гармоническими колебаниями
различной частоты:
3(f.A)U(W.(M) +
+1. (дв)^/,,^* +
+ Л(Д?)^Лп(Д9)едавЧ
п=1
101
Рис. 4.10.
+£ J* (Д?) Лп (ДО) [е* 72 (^+nSe)' +
+ е ! ' 41 е> 1 +/Э(— <р0,6о)^4к_1(Д?)Х
6=1
п=1 I
_е±/[(2*-1)еф+(2П-2)2е]< |+(^ j) § (?0,90 + 4г) X
Хро(Д?)£ Л„-,(Д0)е* (2n~,)Set +
+ J J2ft (Д?) /2П_, (Д?) [е*712fe‘" + (2"-1) Ей 1 ‘ -
_e±/[^_(2n_1)20H]j+(qp)^_?oieo +
+1) (л (Д0) Е Л.-1 (Д?) е* +
’ *=1
102
± 1 [2nS0 + (2fe—I) Вф] t
У Afc-iWg hn (АО) Iе
ft=l n—l
± / [2/is?e — (2fe—1) ev] t
iwi
e •
(4.5.4)
Спектр сигнала (4.5.2) при Дср=Л0 = 0,8 рад и Д<р =
= Д0=1,8 рад изображен па рис. 4.10,а, б.
4.6. ПОЛЯРИЗАЦИОННАЯ МОДУЛЯЦИЯ
ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
РАДИОИМПУЛЬСОВ
Исходная электромагнитная волна, параметры поля-
ризации которой модулируются, может быть не только
монохроматической, как это рассматривалось в преды-
дущих параграфах, но может представлять собой целый
спектр частот, общая ширина которого должна удовле-
творять условию квазимонохроматичности. В частности,
в качестве модулируемого излучения может быть перио-
дическая последовательность радиоимпульсов треуголь-
ной, экспоненциальной, колоколообразной или какой-ли-
бо другой формы.
Будем пропускать такую последовательность радио-
импульсов через поляризационный модулятор с линейной
модуляционной характеристикой. Если при этом модули-
рующий сигнал имеет вид реализации непрерывного
процесса, то таким образом получим непрерывную поля-
ризационную модуляцию периодической последователь-
ности радиоимпульсов (ПМИ, см. § 3.6).
Действительно, так как периодическая последователь-
ность радиоимпульсов всегда содержит гармоническую
составляющую несущей частоты к>о, то, по крайней мере,
поляризация электромагнитной волны этой частоты бу-
дет модулирована в соответствии с управляющим воз-
действием. Если поляризационный модулятор широкопо-
лосный, то по такому же закону будет промодулирована
поляризация всех гармоник последовательности радио-
импульсов. В результате такой модуляции каждая спек-
тральная составляющая превратится в некоторый спектр,
структура которого зависит от вида поляризационной
модуляции и вида модулирующей функции.
В соответствии с рассмотренными ранее видамц по-
ляризационной модуляции можно представить себе сиг-
103
налы ПМИф, ПМИ9 и ПМИф 9 Кроме того, каждый
из этих способов модуляции может быть разбит на два
вида по тем же принципам, что и для АИМ. Именно,
если модулирующий сигнал изменяется в течение дли-
тельности радиоимпульса в соответствии с передаваемым
сообщением, то такая ИМИ называется поляризацион-
ное модуляцией радиоимпульсов первого рода (ПМИ-1).
В случае поляризационной модуляции радиоимпульсов
W)
Рис. 4.11.
второго рода (ПМИ-2) поляризация радиоимпульса
определяется мгновенными значениями модулирующей
функции S(t), взятыми в дискретные моменты времени.
Интервал дискретизации берется обычно равным или
кратным периоду Тп следования радиоимпульсов, а не-
прерывная модулирующая функция S(t) заменяется
ломаной огибающей.
В качестве примера на рис. 4.11 изображен случай,
когда моменты выборки мгновенных значений функции
совпадают со срединой радиоимпульсов с прямоугольной
огибающей. Непрерывная модулирующая функция за-
меняется в данном случае ее прямоугольной аппрокси-
мацией, изображенной на рис. 4.11,а пунктиром. При
девиации угла эллиптичности Д<р=л/3 поляризационные
104
диаграммы радиоимпульсов на выходе поляризационно-
го модулятора будут иметь вид, представленный на
рис. 4.11,в жирными линиями. У немодулированной
последовательности радиоимпульсов поляризация приня-
та линейной с ориентацией вектора Е под углом л/4
к горизонтальной оси.
Практически для получения ПМИ-1 достаточно на
модулятор, предназначенный для непрерывной модуля-
ции параметров поляризации, подать управляющий сиг-
Рис. 4.12.
нал, соответствующий передаваемому сообщению, а мо-
дулируемое электромагнитное поле можно получить от
высокочастотного генератора, работающего в импульс-
ном режиме и синхронизированного периодической по-
следовательностью видеоимпульсов (рис. 4,12,а).
Для получения ПМИ-2 необходимо ту же самую по-
следовательность видеоимпульсов, которая используется
для синхронизации генератора несущей, преобразовать
в АИМ-2 последовательность, модулированную переда-
ваемым сообщением, а АИМ-2 сигнал подать на поля-
ризационный модулятор. При этом модулирующие им-
пульсы должны быть шире радиоимпульсов, чтобы к мо-
менту появления радиоимпульса в поляризационном
модуляторе закончились переходные процессы.
При длительностях импульсов, гораздо меньших пе-
риода гармоники сообщения S(t) с наибольшей часто-
той, ПМИ-1 и ПМИ-2 практически совпадают.
Рассмотрим спектр ПМИ-1 сигнала при модуляции
угла эллиптичности волны.
Если обозначить через /о(0 смодулированную по-
следовательность видеоимпульсов, то последовательность
когерентных радиоимпульсов в комплексной форме мож-
но записать в виде
^(0=^о/о(0е/(ш°' + фо). (4.6.1)
105
Вектор Ёа определяет амплитуду и поляризацию радиоим-
пульсов. У нсмодулированных по поляризации радиоим-
пульсов все гармонические составляющие поляризованы
одинаково.
Если последовательность радиоимпульсов (4.6.1) мо-
дулируется по поляризации, тоПМИф-1 сигнал можно
представить в виде
£(0 = Еое~ ‘‘ [<₽o+A’'fS <Ш°(+Фо) ei0°. (4.6.2)
Положим, что модуляция осуществляется гармоническим
колебанием S(t) =sin Последовательность видеоим-
пульсов единичной амплитуды /о(О с периодом следова-
ния 7'п=2л/Йп и длительностью импульсов т представим
в виде ряда Фурье:
/о(0 =
(4.6.3)
а модулирующую по поляризации функцию согласно
(4.2.2) — в виде
е-чФ. е.е.е- sin 2о<== е- а*, Ь (Д(р) 2
XS (Д?) cos 2 W — (ijjJzk-! (Д?) sin (2&-— l)Qcf] .
й=1
.(4.6.4)
Подставляя (4.6.3) и (4.6.4) в (4.6.2), после соответст-
вующих преобразований получим разложение колебания
(4.6.2) в комплексный ряд Фурье, который и будет опре-
делять спектр ПМ.Иф-1 сигнала,
пмИ,-,(О=Э(?..0.)Е.^( £
71=—00
00
I Г /А V / I —/2*V <
+у]44Д?)(е ‘ 4-е 0 )
106
00
% ^e'“VX
'«=—00
X S (e'(2ft-” V-e-1'(2k-^ ) b< (4.6.5)
fe=i '
где
хп = плт/Тп.
Из (4.6.5) можно видеть все особенности спектра
ПМИ^-1 сигнала, а именно: каждая гармоническая со-
ставляющая спектра периодической последовательности
немодулировапных радиоимпульсов в результате поляри-
зационной модуляции этой последовательности умень-
шается до величины /о(А’ф) (sin Хп)/ха. Поляризация этих
гармонических составляющих не изменяется по сравне-
нию с исходной.
Вокруг каждой из этих гармонических составляющих
образуется спектр, аналогичный спектру ПМф сигнала.
На рис. 4.13 изображен спектр ПМИ^-1 сигнала при
Фп=Оо = О и Лер = 60°. Пунктирная огибающая есть оги-
бающая спектра немодулировапной последовательности
радиосигналов. Из этого рисунка можно видеть, что если
составляющие спектра, поляризованные вдоль оси оу,
развернуть в пространстве на —90°, т. е. совместить ось
оу с осью ох, то ПМИ^-1 сигнал превратится в после-
107
довательность радиоимпульсов, несущая которых моду-
лирована по фазе гармонической функцией sinQct а де-
виация фазы ДФ =—Аф.
Если исходные параметры поляризации немодулиро-
ванной несущей не равны нулю, т. е. фот^О, 0о#=О, то
х-поляризованные составляющие в спектре ПМИ^-1 сиг-
нала будут иметь те же самые параметры поляризации
фо, 0о, а //-поляризованные составляющие будут иметь
ортогональную эллиптическую поляризацию.
Спектр ПМИ9 и ПМИ^ 9 сигналов можно найти точно
так же, как и спектр МПИ9 сигнала. Для этого доста-
точно спектр ПМ9 или ПМ9 9 сигнала умножить на спектр
периодической последовательности видеимпульсов. Отли-
чия в спектрах сигналов ПМИ? и ПМИ9 точно такие же,
как и у спектров сигналов ПМ9 и ПМ9. Именно, если
у ПМИ9 сигнала четные и нечетные по модулирующей
частоте гармоники поляризационио ортогональны, то
в спектре ПМИ9 сигнала поляризационно-ортогональных
гармоник нет.
ПМИ9 сигнал довольно легко превращается в ПМИ9
сигнал. Для этого достаточно пропустить его через чет-
вертьволновое устройство А(—/) с ориентацией оси V
под углом 0о. В соответствии с ранее приведенными пра-
вилами умножения исходного поля
§т (0 = Eof„ (0 е‘ [9о+Д95 е'4' (4.6.6)
на оператор А(—/) на выходе преобразователя получим
£вых (0 Eofo (0 е- ‘ws е‘9° е/ф< (4.6.7)
Столь же просто осуществляется и обратное преобразо-
вание ПМИф сигнала в ПМИ9 сигнал. Однако при пра-
ктической реализации такого преобразователя необходи-
мо учитывать, что преобразуемый сигнал занимает опре-
деленную полосу, и в пределах этой полосы преобразо-
ватель должен сохранять свои свойства.
10S
ГЛАВА 5
СИГНАЛЫ С ДИСКРЕТНОЙ
ПОЛЯРИЗАЦИОННОЙ МОДУЛЯЦИЕЙ
Дискретной, пли импульсной, будем называть такую поляри-
зационную модуляцию, при которой параметры поляризации моду-
лируемого излучения могут принимать значения из некоторого
дискретного множества. Само излучение может быть как непрерыв-
ным, так и импульсным, т. е. представлять собой дискретную по-
следовательность радиоимпульсов.
Системы связи, в которых непрерывное радиоизлучение модули-
руется таким импульсным процессом, у которого моменты начала
или (и) окончания импульсов могут принимать любое значение из
некоторого непрерывного множества, называются системами связи
с непрерывной импульсной модуляцией. К ним относятся системы
связи с амплитудно-импульсной (АИМ), время-импульсной (ВИМ)
и широтно-импульсной (ШИМ) модуляцией, т. е. определяющим
в названии сигнала является вид модулирующей функции. Второй
индекс в названии сигнала определяет тот параметр радиоволны, на
который воздействует модулирующая функция (ВИМ-ЧМ, АИМ-ЧМ,
ШИМ-ЧМ — для частотной модуляции, АИМ-ФМ, ВИМ-ФМ,
ШИМ-ФМ — для фазовой модуляции). Точно так же сигналы в си-
стеме связи с непрерывной поляризационно-импульсной модуляцией
будем обозначать как ВИМ-ПМ, ШИМ-ПМ, АИМ-ПМ или общим
названием «сигналы поляризационно-импульсной модуляции» (ПИМ
сигналы).
Другую разновидность систем связи с дискретной модуляцией
составляют так называемые смешанные системы. В смешанных си-
стемах связи дискретны и моменты появления (окончания) сигнала,
и те значения, которые они могут принимать. К числу таких систем
при использовании поляризационной модуляции можно отнести, на-
пример, системы с КИМ-ПМ, дельта-модуляцию с ПМ несущей
и др.
Дискретное изменение состояния поляризации может быть ис-
пользовано и в случае передачи дискретной информации при не-
прерывном сигнале, когда сообщение может принимать два или
несколько дискретных значений в случайные моменты времени.
Дискретная ПМ может применяться и в различных других
случаях и системах, когда необходимо скачкообразно менять па-
раметры сигнала без изменения общей его энергии.
Скачкообразное изменение поляризации может быть бинарным,
когда поляризация волны меняется от исходного состояния поля-
ризации в ортогональное, либо п-кратпым, когда поляризация волны
может принимать одно из п значений. Рассмотрим ПМ сигналы при
некоторых простейших законах дискретного изменения состояния
поляризации электромагнитной волны.
5.1. МОДУЛЯЦИЯ ПАРАМЕТРОВ ПОЛЯРИЗАЦИИ
ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ
ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
Сигнал, представляющий собой электромагнитную
волну, модулированную по параметрам поляризации
периодической последовательностью импульсов, может
109
быть исходным сигналом для его последующей модуля-
ции сообщением, но может иметь и самостоятельное зна-
чение. Анализ поляризационно-спектральной структуры
такого сигнала позволит легче представить структуру бо-
лее сложных сигналов с дискретной поляризационной
модуляцией. Определим полный (т. е. частотный, ампли-
тудный, фазовый и поляризационный) спектр такого сиг-
нала.
Пусть модулирующая функция представляет собой
периодическую с периодом Т последовательность импуль-
сов длительностью т (рис. 5.1). Модулированный этой
функцией' по параметрам поляризации сигнал запишем
в виде
при----<t — kT
Эо(?2,02)е/ш»'
при -L-<f — kT<Т----
(5.1.1)
где k — 0, 1,2,...; Эо(?!, О,), Э0(<р2, 02)—эллиптические орты,
определяющие состояние поляризации волны в соответ-
ствующий интервал времени. Эти орты на двойной ком-
плексной плоскости запишутся соответственно в виде
е-о<р.е^ и
ПО
Амплитуду электромагнитной волны полагаем равной
единице.
Модуляцию электромагнитной волны по закону
(5.1.1) можно осуществить обычными модуляторами,
предназначенными для
непрерывной модуляции
параметров поляризации,
либо импульсными моду-
ляторами поляризации,
предназначенными только
для дискретного измене-
ния поляризации на опре-
деленную величину.
Для первого случая
структурная схема пере-
дающего устройства при-
Рис. 5.2.
менительно к СВЧ диапазону
изображена на рис. 5.2.
СВЧ генератор работает в непрерывном режиме и
вместе с модуляторами и антенно-волноводной систе-
мой формирует электромагнитную волну с парамет-
рами поляризации фг, 02. Модулирующая последователь-
ность импульсов S(t) через блоки нормирования с коэф-
фициентами передачиk* и ke подается одновременно па
модуляторы двух параметров поляризации. В результате
параметры поляризации поля скачком изменяются до
значений ерь 01 и остаются постоянными на время дли-
тельности импульса.
Упрощенная функциональная схема передатчика
с импульсной модуляцией поляризации дискретным мо-
Рис. 5.3.
дулятором с бинарным изменением параметров поляри-
зации представлена на рис. 5.3. Основу дискретного мо-
дулятора поляризации составляет переключатель СВЧ
111
энергии из верхнего капала 1 в нижний 2 и формирова-
тель/5 параметров поляризации электромагнитной волны.
Работой переключателя управляет модулирующая после-
довательность импульсов •$(/). Формирователь поляриза-
ции устроен так, что если электромагнитная энергия
поступает на пего по каналу 1, то излучаемая волна
будет иметь параметры поляризации <₽ь 0ь в противном
случае — параметры <р2, Оа. Преимуществом такого моду-
лятора по сравнению с обычным линейным поляризаци-
онным модулятором является то, что значения парамет-
ров поляризаций электромагнитной волны в каждом из
двух положений переключателя определяются только
параметрами формирователя поляризации и не зависят
от незначительных изменений управляющего сигнала
S(/).
Для нахождения спектра сигнала (5.1.1) достаточно
разложить функцию
е 1/91 е'61 при — — kT< т/2,
|е“ е10’ при т/2 < t — kT < Т — т/2
в спектр Фурье по функциям е/пй/при Й=2тг/Г, т. е. пред-
ставить ее в виде
00
7(/)=С0+ X Cnelnst (5.1.2)
Л=—00
Л76О
и результат разложения умножить на е'ш°7 В резуль-
тате спектральное разложение сигнала (5.1.1) в ком-
плексной форме запишется в виде
00
е (/) =С0 е'ш°' + £ Сп е' (“о+пй) (5.1.3)
00
п^О
Для представления спектра сигнала (5.1.1) в действи-
тельной форме необходимо найти Re; от (5.1.3).
Коэффициенты ряда Фурье получаются из следую-
щих соотношений:
г/9“еге*е/"Е7л
112
___ * sin nnt/T , _ i/ф, /в,_ — i/<p, ie2i
r twi/T Iе
(5.1.4)
7, t
Co-----у-ё
e'S'+^l--^ е-'^е'Л
(5.1.5a)
Из (5.1.4) следует, что все спектральные составляющие
сигнала . (5.1.1), за исключением составляющей с несу-
щей частотой ыо, поляризованы одинаково и синфазны
(в пределах постоянного знака функции (sinxn)/xn).
Огибающая спектра совпадает с огибающей спектра пе-
риодической последовательности радиоимпульсов. Поля-
ризация гармоник зависит только от состояния поляриза-
ции волны во время первой и второй части периода
импульсной последовательности.
Поляризация компоненты несущей частоты зависит
не только от дискретных значений параметров поляри-
зации волны, но и от соотношения между длительностью
импульса т и паузы Т—т модулирующей функции.
Амплитуда несущей также зависит от соотношения меж-
ду т и Т. Но как и амплитуды остальных гармоник, она
также определяется значениями параметров q>i, 04 и срг,
02, точнее, величиной относительного изменения парамет-
ров поляризации.
Рассмотрим некоторые частные случаи.
1. Манипуляции направлением вращения кругополяри-
зованной волны.
В этом случае в выражении (5.1.1) следует поло-
жить
ф1=л/4; ф2=—Ф1=—л/4; 0i = 02=0o.
Положим, кроме того, 0о=О. Тогда выражения (5.1.4) и
(5.1.5а) преобразуются к виду
. ___ т ein (/глт/ту г _ 1/х/4
n Т nm/T 1е e
_ ij /Г4- -51п-^-е"/2е- ^2, (5.1.56)
1 r T rmz/T ' '
C ‘7K/4 I f i__Ji*/4
0 ——- y, v ” 1 “ ij4 j C
= Ь/Г + 07)(1-т/Г)]е-г^4.
(5.1.6)
113
8—667
Обозначим в (5.1.6)
До = ]/(т/7')2 + (1 — -//Т — амплитуда несущей спектра
радиосигнала;
t/7\40 = cosa; (1—т/Г)/Д0 = sin а. (5.1.7)
С учетом этих обозначений (5.1.6) преобразуется к виду
Со = Дое-1; W4~a), (5.1.8)
где
1 Г—т
a=arctg—
Таким образом, в случае манипуляции направлением
вращения кругополяризоваппой волны спектр резуль-
тирующего сигнала содержит эллиптически-поляризован-
ную с углом эллиптичности л/4—а и амплитудой До ком-
поненту несущей частоты ®о и вертикально поляризо-
ванные п задержанные по фазе па —л/2 относительно
исходной волны компоненты с частотами coo±nQ, ампли-
туды которых равны
Сп =У2 Ап = У2 ~ —п{^) • (5.1.9)
1 I1TVt/ 1
На рис. 5.4 показан графический способ нахождения а
и До по заданному значению отношения т/Т. Соответст-
вующие графики зависимостей До(т/Т) и а(х/Т) изобра-
жены на рис. 5.5.
Как видно из рис. 5.5, компонента несущей частоты
при любом соотношении т/Т несет больше половины всей
энергии сигнала. Остальная часть энергии приходится на
спектр боковых гармоник сигнала. Только при манипу-
114
ляции меандром, т. е. при т/7’=1/2, энергия несущей рав-
на суммарной энергии боковых гармоник. При этом а=
^л/4 и несущая становится горизонтально поляризован-
ной. Все боковые гармоники спектра сигнала оказыва-
ются вертикально поляризованными. Спектр такого сиг-
нала представлен па рис. 5.6.
2. Манипуляция ортогонально-поляризованными эл-
липсами.
В этом случае между параметрами <рь 0! и <рг, 02 бу-
дут иметь место соотношения ф2=—cpi=—фо, 02=01+
+л/2 = 0о + л/2.
Соответственно для коэффициентов (5.1.4) и (5.1.5а) ря-
да Фурье (5.1.3) получим выражения
Сп =^- Sin^r) (e-ii,₽»—iei/'₽0)eie°, (5.1.10а)
С; = |\Ге-^» + г(1—т/Г)ег/9°] еге°. (5.1.11а)
Преобразуем выражение, стоящее в (5.1.10а) в скобках:
(е- г-еч'90) = уу (cos-?- е-i/9° - i sin -J-e"^ =
= j/2 (cosrp0e~ ‘“/4^—ij sin'Pq e,’'/4)=J/2 е,т°е-1л/4,
(5.1.12)
откуда
C„ = /2 4- sin (П4/Г) емег <9’~“/4). (5.1.106)
115
8‘
Таким образом, все боковые гармоники спектра радио-
сигнала, полученного манипуляцией эллиптически-поля-
ризованной электромагнитной волны от исходных пара-
метров поляризации к ортогональным, являются линей-
но-поляризованными с ориентацией под углом —л/4
относительно главной полуоси эллипса поляризации не-
модулированной несущей и имеют фазовый сдвиг, рав-
ный углу эллиптичности несущей во время импульса мо-
дулирующей функции.
Несущая компонента спектра радиосигнала имеет
эллиптическую поляризацию, параметры которой найдем
следующим образом.
Преобразуем выражение (5.1.11а), положив в нем
0о=О, к виду
С„ = (2 ~ — 1) е'9” + i е“ 1 е",ч'4 =
= Дое~г/9ег(8'-"/4). (5.1.13)
Из (5.1.13) следует выражение для амплитуды Ло несу-
щей компоненты спектра модулированного сигнала:
д0=гт2+(1-<о2-
т. е. то же самое значение (5.1.7), которое было получе-
но для случая манипуляции направлением вращения.
Обозначив далее
cos y = (2t/7’— l)/j/2 Ао, sin у=1/|/2 Л„, Д=2?о
и воспользовавшись выражениями (1.6.13) и (1.6.15),
для определения параметров ср и 0' получим следующие
соотношения:
2т/7'
sin 2<р = sin 2^0 sin 2y =----------— sin 2?0,
, g, _. tg f cos y„ cos — sin <Po sin <p
° COS PoCOS <f — tg f’sin O0 sin <f ’
(5.1.14)
где tgY = T/(2T — T).
Если выражение для Co представить в виде
Со = a -J- jb i (с -f- jd),
то, подставив значения коэффициентов a, b, с, d в соот-
ношения (2.2.19) и (2.2.20), получим следующие выра-
116
жения для вычисления параметров поляризации несу-
щей спектра:
. „ (т/Г)2 — (1 — т/Г)2 . „
sin 2Т — (т./т’р _|_ ц _ т/2р stn2<p0,
tK 29 =______^(i-vr)_________
S [(Т’/т)2 — (1 — т/Г)2] cos 2
(5.1.15)
Между 0', фигурирующим в выражении (5.1.13), и 0 —
в выражении (5.1.15) существует очевидное соответ-
ствие:
0 = 0'—п/4.
Из (5.1.13) следует, что при х/Т = 0,5, т. е. при мани-
пуляции параметров поляризации меандром, несущая
компонента спектра, так же как и в предыдущем слу-
чае, будет линейно поляризована. Угол ориентации этой
компоненты равен л/4, т. е. она будет поляризационно
ортогональна всем боковым составляющим спектра.
3. Квадратурная манипуляция поляризации. При
квадратурной манипуляции поляризации (КМП) элек-
тромагнитные волны, соответствующие импульсу и паузе,
находятся не только в пространственной, но и во времен-
ной квадратуре, т. е. они поляризационно ортогональны
и сдвинуты на —л/2 по фазе. Математическая запись та-
кого сигнала следующая:
е— </9о е1'®»
при----у <t —kT
^кмп—
е
ei%e'4f при + 4- < t - kT< Т- .
Таким образом, квадратурная манипуляция поляризации
соответствует изменению параметра ср на л/2 от импуль-
са к паузе.
Соответственно для коэффициентов (5.1.4) и (5.1.5)
ряда Фурье (5.1.3) получим следующие выражения:
т sin (ллт/Л г - i/% „—>/(’Ро+”/2) 1 +i60
C”==’F—wr— |е —е Iе —
_т/2~ т s'nlnnt/T') с- ц (ф°-к/4)е<е0. ?5 j ig\
’ Т ntm/T ’ ' ‘ '
= (5.1.17)
117
где аи Ло определяются из соотношений (5.1.8) и (5.1.7)
соответственно. Следовательно, в случае квадратурной
манипуляции поляризации как боковые гармоники, так и
несущая спектра разложения поляризованы эллиптиче-
ски. Однако и в этом случае поляризация боковых со-
ставляющих спектра не зависит от соотношения т/Т.
Можно отметить большое сходство между квадратур-
ной поляризационной манипуляцией и манипуляцией на-
правлением вращения кругополяризовапной волны: при
(р0=л/4 первая переходит во вторую. Следовательно, ма-
нипуляция направлением вращения кругополяризован-
пой волны есть частный случай квадратурной поляриза-
ционной манипуляции.
4. Манипуляция угла ориентации эллиптически-поля-
ризованной волны. При модуляции данного типа имеем
ср2 = Ср1 = Сро, 01 = 00, 02 = 0о+л/2.
Комплексные амплитуды боковых гармоник спектра
радиосигнала имеют вид
СП^'ЛП(1 — (5.1.18
(51
п Т пп-./Т ’ '
Комплексная амплитуда несущей спектра
Со = Ло [cos a -|- i sin a] е- Аое~ (во+«), (5.1.20)
где а и Ло определяются из выражений (5.1.8) и (5.1.7).
Если в выражениях (5.1.18) и (5.1.20) положить ср0=
= 0, то получим спектр сигнала при манипуляции на л/2
угла ориентации линейно-поляризованной волны.
5. Манипуляция направлением вращения эллиптиче-
ски-поляризованной волны. Для модуляции этого типа
имеем:
?2 = —?! = — ?о- 61 = 62 = 0о,
Сп = Ап (е”[г/<₽0— ег/ф”) е‘9° = — г/2Лп sin?0 eZ9°, (5.1.21)
Со = (1 — sin ?0) е+ г/? е,Г)о, (5.1.22)
где
п cos Фо . п . 1 — sin
cos В =--------------- sm В — 1----------5—12-------
1—-у— sin f о 1—-у— sin у о
(5.1.23)
Отметим некоторые интересные особенности радио-
сигнала, полученного путем манипуляции направления
вращения эллиптически-поляризованной волны. Как сле-
дует из (5.1.21), амплитуды боковых гармоник зависят
от угла эллиптичности волны во время действия неиз-
меняемой части модулирующей функции — во время
плоской вершины импульса. При '(ро=0, когда немодули-
рованная несущая линейно поляризована и, следователь-
но, поле невращающееся, а поэтому нет смены направле-
ния вращения от импульса к паузе и наоборот, то, есте-
ственно, нет и боковых гармоник в спектре радиосиг-
нала:
|cn|=o,ii;co 1=1.
Если же <р0=л/2, то манипуляция направления вра-
щения переходит в манипуляцию фазы линейно-поляри-
зованной волны от значения л/2 до —л/2:
е- о-/2 ei0" е/ш°'= - j е‘ (e“+,l/2) e'w при —t/2 < t -
— kT<z/T,
, ;(e°+vl ,
е ' ef9°e;w°' = je k 1 e'““z при т/Г<t — kT<T—z]T.
В этом случае амплитуды боковых гармоник спектра
принимают максимальные значения из значений при
всех рассмотренных видах поляризационной манипуля-
ции. Несущая спектра такого сигнала поляризована ли-
нейно, амплитуда несущей зависит только от отношения
т/Г и обращается в нуль при модуляции меандром (т. е.
при т/Г=0,5).
При <ро=л/4 манипуляция направлением вращения
эллиптически-поляризованной волны переходит в мани-
пуляцию направлением вращения кругополяризованной
волны, рассмотренную ранее (§ 5.1, п. 1).
Сравним спектры сигналов при различных видах по-
ляризационной манипуляции со спектром амплитудной
и фазовой манипуляции. Среднюю энергию сигнала AM
положим равной средней энергии поляризационно-мани-
пулированного сигнала, т. е. если амплитуда 6/Пм немо-
дулированной несущей при ПМ равна 1, то амплитуда
несущей при AM будет равна
119
Выпишем выражения для спектров соответствующих сиг-
налов.
1) Спектр сигнала при амплитудной манипуляции
эллиптически-поляризованной волны
(5.1.24)
2) Спектр сигнала при фазовой манипуляции эллип-
тически-поляризованной волны (при ф=0 во время им-
пульса и ф = л во время паузы)
Д / (0>0±«S) t
/1П V
ч'ч>о„*ео •
С С •
(5.1.25)
3) Спектр сигнала при квадратурной манипуляции
поляризации (К.МП) эллиптически-поляризованной
волны
ёкмп(0> Де-^е^+е- i/,t/2|/2 X
xf Ane/(“0± nS)t ] е~‘,ч>0 eie° ,
n=l
где а и Ао определяются выражениями (5.1.8) и (5.1.7).
4) Спектр сигнала при поляризационно-ортогональ-
ной модуляции эллиптически-поляризованной волны
(ПОМ)
+ е',,е'<1/2 S Л„е'Че*
П=1 J
где ср, 0 определяются из (5.1.15).
5) Спектр сигнала при манипуляции угла ориентации
эллиптически-поляризованной волны при поляризацион-
ной импульсной модуляции угла 0 (ПИ Мв)
120
|Ае е ° +
+ X Апе' (“0±лй) '1 e-i/%eZ9°.
n=l J
6) Спектр сигнала при манипуляции направления
вращения эллиптически-поляризованной волны (ПИМ^,):
епимф = [(1 - sin ?«) е"?е'4' -
- (г/) 2 sin % Jj Апе'' (w’±nS)S'l е‘\
п=1
где 3 определяется из (5.1.23).
Как видно из приведенных выражений, при всех этих
видах модуляции в спектре радиосигнала содержатся
компоненты одних и тех же частот. Однако эти спектры
отличаются друг от друга как своей поляризационно-фа-
зовой структурой, так и распределением энергии между
несущей и боковыми компонентами.
Величины, определяющие энергию несущей при AM,
ФМ и всех видах ПИМ (за исключением п. 6) находят-
ся в таких же отношениях, как (т/Т)2, [(Т/т)—2]2 и 1 +
+[(7'/т)—2]2 соответственно. Следовательно, при малой
скважности импульсов модулирующей последовательно-
сти (Т/т~2) наибольшее содержание энергии в несу-
щей спектра имеет место при амплитудной манипуляции
и наименьшее (~0) при фазовой манипуляции. Поляри-
зационная манипуляция занимает промежуточное поло-
жение.
При 7'/т^>2 в отношении распределения энергии по
спектру все эти виды манипуляции приблизительно оди-
наковы.
5.2. ПОЛЯРИЗАЦИОННО-ФАЗОВАЯ МАНИПУЛЯЦИЯ (ПФМ)
На практике может иметь место случай, когда одно-
временно с дискретным изменением параметров поляри-
зации изменяется и фаза несущего колебания. Это мо-
жет быть, например когда манипуляция поляризации
осуществляется путем коммутации энергии ВЧ генерато-
ра в соответствии с импульсной программой из одного
' 121
ВЧ тракта с устройством формирования поляризацион-
ной диаграммы в другой (рис. 5.3). Если при этом трак-
ты 1 и 2 не сфазированы, то наряду с поляризационной
модуляцией будет наблюдаться фазовая модуляция. Из-
лучаемый сигнал в принятой форме записи может быть
представлен в виде
ё(0 = ^(0е/ш< (5.2.1)
где A(f)— модулирующая функция, имеющая вид
__(е <;1₽’е‘9'е/9> при —т/2<7— kT <^т/2,
(е-‘/ч,ае‘9ае;фа при -фт/2<7 —<Т — т/2.
(5.2.2)
Дополнительная фазовая модуляция ПИМ сигнала
может быть неконтролируемой, паразитной, но может
быть и специально предусмотренной, предназначенной
для получения сигнала с определенными свойствами.
Рассмотрим поляризационно-спектральную структуру
сигнала при такой модуляции.
Обозначим:
Фо= (<Р1 + фг)/2; Дф= (фг—ф1)/2;
ео=(е!+е2)/2; до=(О2-01)/2;
Фо = (ф1+фг)/2; Дф= (ф2—ф1)/2.
В дальнейшем без ущерба для общности рассужде-
ния можно положить 9о = О, фо —0. Тогда модулирующая
функция A(t) примет вид
' —</ (ф0—Аф) —(Д9 ~/Аф
с ее
<
ц—«7 (фо + дф)е<Д0е/Аф
Д(0 =
при — т/2 <Z t — kT < т/2,
при т/2 < t — kT < Т — т/2.
Спектр сигнала (5.2.1), как и в предыдущих случаях,
находится путем разложения модулирующей функции
A(t) в комплексный спектр Фурье
00
Л(О = С;+ 2 Cne‘nst (5.2.3)
Л=—00
п,40
и последующего умножения ряда (5.2.3) на е7”0'".
В результате соответствующих преобразований для
коэффициентов ряда (5.2.3) получаем следующие выра-
жения:
122
f' ____ * „—«7 (фр—Аф) iA9„—/Аф , ( ,
*->0---p C cc l~ I 1
Lj g—7 (Фо+ А1₽)е1'Д9е/Аф
(5.2.4)
T
sin Лп-у-
7> X 1 r„—ii (Фо—Дф) — iA0 — /Дф —Ij (Фо+4Ф) (Д0 /Дф-
V/ fl -q> IV V v ----" V V V
ПП ~qT
(5.25)
Из этих соотношений следует, что огибающая спек-
тра, как и в случае обычной манипуляции поляризации,
есть функция (sinx)/x. Однако из-за наличия разности
фаз 2Дф между колебаниями в момент «импульса» т и
«паузы» Т—т происходит изменение не только параме-
тров поляризации спектральных составляющих сигнала,
но и перераспределение энергии между несущей и боко-
выми составляющими.
Чтобы определить параметры поляризации и ампли-
туды пулевой и всех боковых гармоник спектра ПФМ
сигнала, представим выражения (5.2.4) и (5.2.3) в виде
Со = At<r‘W = (ав + jb„) + i (ев + jd0), (5.2.6)
С __ " sin(«ret/7’) . -lit, 19, _
П ~~~' 'ji , zp J* t V V V "*
T
T
sin (nn z/T)
nn z/T
[(a. +/M + i (О + /Ч)],
(5.2.7)
Амплитуды компонент спектра Ao и At получаются
из соотношения
Ai = 4-1 = 0, 1.
а их параметры поляризации п фазы можно получить,
если подставить коэффициенты a,-, b{, с,, d, в соотноше-
ния (2.2.19), (2.2.20).
Формулы для этих коэффициентов следующие:
а0 = cos Д9 cos Дф Г-^- cos (<р0 — Д?) -|-
+(1 — cos (?о + Д?)
— sinAQsinA^ sin(<p0 — Д?)4-
sin (<р0 4- Д?)
123
60 — cos Дб sin Дф —cos (ф0 — Дф)-|-
+ (1 — cos(<p0 -ф-Дф) +
>8Дф[—sin (/fa’— Дф) + ^1-sin('
c0 = sin Д9 cos Дф [ —cos (ф0 — Дф) -|-
-[-cos Д6 sin Дф
~ sin (ф0 — Дф) -Ц1 — —j sin (ф0-|-Дф) j;
d0 — sin Д6 sin Дф |y-cos(ф0 — Дф) -|-
+ f 1 — COS (ф0-i- Дф) 1—
—соэДОсоэДф ~ sin(<?0 — Д<р) ~j sin (^0-4-Д'р) j;
ai = 2[cos Д9 cos Aip sin фо + sin Д9 sin Дф cos cpo]sin Дер;
bt = 2[—cos Д9 sin Дф cos фо—sin Д9 cos Дф зтфо]соз Дф;
ct = 2[—sinA9 cos Дф соэфо—cos Д9 sin Дор sin qxjcos Дф;
6/t = 2[sin Д9 sin Дф sin фо+cos Д9 cos Дф cos фо]в!п Дф.
5.3. СОПРЯЖЕНИЕ ПОЛЯРИЗАЦИОННОЙ МАНИПУЛЯЦИИ
И МАНИПУЛЯЦИИ ПО ФАЗЕ
Сопряжение поляризационной манипуляции и мани-
пуляции по фазе может выполняться при передаче двух
независимых дискретных сообщений на одной несущей
частоте или при передаче одного дискретного сообщения
с манипуляцией двух параметров сигнала с целью повы-
шения достоверности передачи сообщений и помехоза-
щищенности радиолинии.
Манипулированное колебание по поляризации и фазе
в круговом базисе разложения может быть представлено
в следующем виде:
eR(t) =Е0 со5[ф(0— л/4] cos[wi + a(0 +9(t)],
eL(t) =Ео соэ[ф(/) +n/4)cos[<o^ + a(0—9(/)].
Введем обозначения: a(i)+9(i) =2(0! «(О—9(/)=Д(/).
124
Пусть осуществляется манипуляция поляризации и фазы
двумя независимыми дискретными сообщениями. Период
повторения последовательности импульсов первого сооб-
щения обозначим через Л, а период повторения после-
довательности импульсов второго сообщения — через
Т2. Для простоты анализа положим, что начало следова-
ния первых импульсов обеих программ совпадает и про-
исходит в момент времени ti — О. Тогда
Т(0 =
Д(0 =
Д.
д2
при + +
при (67\ + Q<Xft + (& + 1)7\];
при (пТ2 + Q < t < (/, + пТ2),
при (пТ2 +12) < t < ft + (п + 1) 7’Д;
(5.3.1)
при
при (rtT2 + ^)<^< ft+ («+1)Л1,
где /2—7i = Ti — длительность импульса первой програм-
мы дискретных сообщений; t3—— длительность им-
пульса второй программы дискретных сообщений.
В результате суперпозиции двух процессов манипуля-
ции видим, что манипуляции по поляризации и фазе
будут перекрываться, что не нарушит качества передачи
независимых сообщений, так как спектры манипулиро-
ванных колебаний различны.
Используя спектральное разложение Фурье, манипу-
лированные колебания представим в виде*:
е . (t) — E (/) cos + >
где EaR (/) = Ео cos [<р (t) — it/4] или
= £ Гcos ^cos (2Ы/7\) +
+aMsin4/?sin(2W/r’) ] (5-3-2)
и
EnL (t) = До cos [<р (t) + it/4]
* Двухъярусная запись относится к полю правого (/?) и ле-
вого (L) направлений вращения.
125
или
об
EnL (0=аоп1 + X К/.cos 'Jwcos <2М^.) 4-
fe=i
+ <W sMftnL sin^W/T,)].
Рассмотрим спектральный состав манипулированных
колебаний раздельно.
1. Манипуляция поляризации:
____1_
а0п|^— J-j
т, Л
cos^j ^=тс/4)Л + Jcos(4>2=Hit/4)df
о х.
„ , 2
а*и|/гcos ~ т\
cos (<р, -+- it/4) cos (2W/ Tt) dt 4-
Ti
-J- J cos (?, ч= it/4) cos (2Ы/Г,) dt];
j* cos (<p, 7— it/4) sin (2W/7\) dt -|-
b
• । 2
akuiRs,n V*ni/e y
li. It
Л
-j- Г c os (<p2 th it/ 4) sin (2 W/ T^dt
или
an|R = T“ cos (?• ’'Z4) + (! — ^i/A) COS (<P2 it/4);
126
Таким образом, поляризационно-манипулированное
колебание может быть представлено следующим выра-
жением:
|s=77cos + — cos
+ 2 sin sta £ Щ- Х
' *=1 L
v . . 2km, 2knt . „ 1 . „ km, . 2knt 1
X sin cos -y—-4-2—sin2-y2-sin-y— . (5.3.3)
2. Манипуляция фаз.
Рассмотрим процесс манипуляции фазы компоненты
правого направления вращения, т. е. процесс изменения
ЭД.
Так как
cos [ш/ + S (О] = cos S (/) cos wt — sin S (/) sin wt, (5.3.4)
разложим в ряд cosS(Z) и sinS(Z).
Для cosS(0
a'0(j> — cos S( -f- ( 1----£-) cos S2 =
‘г у Г2 J
V1 I 2т2 • S, -I- So " ^2 - ^*1
= cos -4- sin Д - 2 sin —Цт——,
2 1 Тг 2 2
, . 2 2nm2 . S, 4- S, . S2 — S,
a пФ cos Ф„ф= — sin -y-1 sin * sin ,
. • । 4 • л /27CTo • “4“ io • io
a пФ sin Ф„ф = — Sin2 -y- sin sin .
Для sinS(0
a' '«j, = sin S, -f- ( 1 — -Д-) sin 22 =
*2 \ * 2 J
__ • « 2^2 “Ь ^2 ’ ^2 2|
= sin S2 — cos — ‘ 2 sin 2 o ,
2 T2 2 2
а''ПфСО5 Хф^-Lsin ^p-[sinS,~ sinS2] =
/In 1 2
4 S, 4- S2 . S2 — S, . nm, nm„
= ------COS—’X' sin —1- sin cos
rm 2 2 T2 T2 -
а"пф sin фПф — sin2 [sin S, — sin S2] =
4 S, -4- S, . S2 — S, . 2 nm,
— — cos —— sin 2 9 —• sin2-yA.
2 2 /2
127
Таким образом,
00
cos 2 (t) = а'оф + yj £ а'пф cos фпф cos
n=l
00
, , . . . 2nntl . . VI f f2nnt , '
+ а'пф sin фпф sin -у-1 = а Оф + V а'пф cos I-у-— ф„ф
n=l
где
, 4 . S, 4- . S« — S, лпт2
a'„. =- — sin—- sin ——— sin
пф nit 2 2 J г
, tint, . , nr.t2 , nnt,
COS ф„ф = COS-у-Ц 51Пфлф = ^-ИЛИ фпф = -у-Д.,
Следовательно,
cos 2 (/) = cos 22 + sin -— у — - sin —2-^—t-
00
1 4 • nnz2 . S, 4- S2 . S2 — S. /2nr.l nm2\
+ >! — sin sin sin - - -o— - cos f --- )
1 ZJ rm T2 2 2 \ T2 T2 J
n=l
ИЛИ
cos 2 (/) = cos S2 + sin S| j? sin —"2 Z"-1—|-
/ 2 2 2
00
... S, 4- S2 X, - X, r, 1 , .
+ 4s,n—-X
n=l
Xsin-^- cos (5.3.5)
^2 ^^2 ^2/
Аналогично получим
sin 2 (0 = sin 22 - cos -‘-t-2 - sin -^-^+
1 2
00
+ cos-^sinsin^X
n—\
n = l
(5.3.6)
128
Таким образом, сделав подстановку полученных выраже-
ний в (5.3.4), будем иметь
‘ COS СОТ—
у]
sin wt =
cos [<W + S(/)] —
a'ai
а'пфсо5
2 nr. I
~rT
00
,, , VI П /2rvni
a пф+У a n*cosf-y--
n~~2
£ ___E
— а'Оф cos wt — а' 'Оф sin ш/ -|- 4 sin ' 1
2 Li
n-1
Xcos(^ - ^WsinA±^Cos^ +
\ 7 2 1 2 J \ .
+ cos --—sin ш/ Y (5.3.7)
Определим общие коэффициенты разложения:
йоф = а'оф COS Ш/ — а"Оф>!П <в/ =-. у + а'ф2 sin («>/+6,),
где
tg8,=
д'Оф .
д"оф
или
1/<+<2-1/1 + I , 2^У-^1 sin2-^- .
г оф 1 оф I/ I \ ^2 ) T\ J 2
Произведя подстановки, получим
/. . » / 2-са X2 4тг | . о / S2 — S, \
1 [ \Т\ J 7\ j Sln 2 у X
00
X sin (^ + 5.) + 4 sin -Ъ-^- _L sin X
Xcosf-^ -^sin S‘t—Y (5-3-8)
\ 7 2 1 2 J \ J
9—667 129
Не повторяя аналогичных выводов, идентично можно
получить выражение для фазоманипулированпого коле-
бания компоненты с левым направлением вращения:
cos [«7 -|- Д (/)] =
СО
х sin (wt + 52) + 4 sin У sin X
X /А fl Т* J 2
П = 1
Xcosp^--!p-)sin^ + --'+-2-), (5.3.9)
где tg8a = — я'Оф1£/а"оф1£ .
Далее необходимо определить аналитическое выра-
жение поляризационпо-фазоманнпулированпого колеба-
ния.
Решение этой задачи в соответствии с [9] возможно
путем перемножения спектров поляризационно-манипу-
лировапного и фазоманипулированпого колебаний. Для
удобства перемножения представим раздельно спектры
колебаний несколько в иной форме:
cos |j (0-j = cos (j2 — sin -2^'- X
Xsin --+4sin*?1 J?2 X
“ sin~n^~
Xsin S eos -X).
4 7 A=1 4 7
cos [?(0+-r]=cos + x~) + 77sin •2~' x
X sin ( -+-^+4sin
X/ oln / ?1 + ?2_sinfa^/Z, /2kr.t km, \
X Sin I 2 4 J Zj kit 5 11 I 7, T, J ’
COS + S (0] = COS (at + S2) + sin X
Xsin (wt-Y ’J H-4sm 2 2 --X
130
об
х si„ + А + А) £ ALSAA cos
n—1
cos [irf + Д (/)] = cos (wt -|- Д2) -]- A sin As~ A1 X
X sin (wt + A+A/j+4 sin AjzA_ x
X sin +A±A) £ cos
Выполнив перемножение спектров, получим выраже-
ния поляризационно-фазоманипулированпого колебания
в спектральном представлении:
ек (О = Е« {c°s [<Р (0-4~ ] cos [a>f X S (/)] | =
00
= E0JaaT sin(iu^X§i) + «o^v V --n -A x
U | 4>o ~o 4 1 v 1 *?o - / J ПП zs
n~ 1
ч у f2nnt П7ГТ2 \ . I + So \ f
Xcos sin ^-\---v I +
k 1 2 * 2 J X. J
(5.3.10)
9*
131
. . s2 —s,
a.. ~ 4 sin o
L z
2^ f S2 — S, \ / S2 +
—'sin S2 + y" sin I-2--I COs I-2
CtgS.^---------- V 7 V
cos S2
2т2 ^2 —* S2 4“
-у- sin------g' sin--------2
составляющей спектра с левым на-
будем иметь
Аналогично для
правлением вращения
e, (t) = Ea {cos cos[co/ + A(0] }
132
Рассмотрим частный случай:
I ?0 при </<(/2 + ^Г1),
?(0= при (kT\ + t2) </<[Л + (.^4-1) Т,].
Угол пространственной ориентации осей эллипса по-
ляризации оставим без изменений, т. е. 0(/) =0о= const,
а'фазу колебания будет манипулировать следующим об-
разом:
а0 при (я7’24-Л)<Х(/,4-яГ2),
а0 + z при (пТ2 +13) < / < [/, + (п + 1) Т2\.
[ ли
В этом случае будем иметь a(?Q— cos +
-{--yr-^sinfo, &% = COS^>o--------—^y-COSfo;
<7ф = 2 У2 sin <р0, = (Г—г^а/Га), Дг = 4, 8, = а0 + <2 + 0О,
b<f = 2 У2 cos ?«; &д0 = (I — 2т1/7’1); &д = 4; «2 = а„ + <2 —9„.
Тогда eR(t) = E9 ((1 - 77J [cos (?»+ “I")+
4-2^2tsin <р0] cos (со/ + а0 4- 0о)4-
4-4£0[cos (?0 4--J-) 4--^ sin ?0]х
sin
х S • т^2-cos (4?— -тг)cos +а»+м+
о . ^ят1
о sin~ *
+ 2Ш1-^уГ8щ% ^2-Х
4 ‘ А=1
х cos cos (mt 4- а0 4- 90) 4-
“ sin
4- £08 V‘2 sin % 2 cos X
A=1 \ 1 ’ /
“sin^
2j J COS i cos и + а, + 9,).
(5.3.12)
133
Аналогично,
... п ( . 2т, \ Г ( и \ . Кг t, 1 v
eL (t)~E Д 1 -— cos (jo----4-J 4—7^ cos ?0J A
[/ n \ H2~ t 1
COS ^>0----4- ) + '~ 7\ ~ COS'foj X
00 sin —
VI ?2 / 2mtt mn, \ , , . csi
X /J — cos (~t2--------------cos+ a“ — б») +
x '
X COS J cos (wt + a0 — 60) 4-
; 00 sin^
4- 8 |/2 Ea cos % yj ——cos X
k=l s 1 1 J
“ sin'-^-
X 7j — cosf^- -^cosH4-ae-0()). (5.3.13)
n=l ' '
Представляет интерес случай стопроцентной модуля-
ции, т. е. случай, когда нулевая гармоника модулирован-
ного колебания несущей частоты обращается в нуль.
Необходимым и достаточным условием реализации та-
кого способа модуляции является выполнение равенства
1—2т2/7’2=0 или Tz=2tz. В этом случае выражения поля-
ризационно-ортогональных составляющих колебания мо-
гут быть представлены в следующем виде:
(0 = 4А0 [cos 4- -J-) 4-sin %] X
“ sin-^r-
х Ij cos (— ?) cos (<"Z+a°+0O> +
n=l
21 sin-^
4-8/2 Aosin?o V -—cos —
i t iTC К 1 2 “ z
и — 1 X /
134
~ knz,
2® sin -y—
X\ 1 11 / 2k~t k~z, \ , , , , л
cos ( -y-------у— j cos Ч- “I- So)- (5.3.14)
*=i ' 1 1 '
Аналогично,
• eL(t) = 4E0 cos ( ?o —
— COS
Mt
sin —
2nnt n~
~T. 2
OCo
со
+ 8/2 £0 cos <?о
nit
sin “x-
1 ( 2nitt nit
------- COS I ------------FT
mz \ T2 2
ktvz,
sin —
/. —z------cos (-у—— у—cos («>/-|-oc0— 90)- (5.3.15)
Выполним сравнительный анализ полученных ранее
выражений поляризационно-манипулированного колеба-
ния и поляризационно-фазоманипулированного колеба-
ния.
Сравнивая спектры, можно видеть, что в случае со-
пряжения поляризационной манипуляции с манипуляци-
ей фазы волны нулевая гармоника поляризационно-мани-
пулированного колебания оказывается дополнительно
промодулировапной по фазе, вследствие чего грамоники,
стоящие под знаком одинарной суммы, образуют спектр
фазоманипулированного сигнала. Каждая боковая гар-
моника спектра поляризационно-манипулированного ко-
лебания представляется двумя одинаковыми симметрич-
ными и равными по амплитуде гармониками. Таким
образом, при дополнительной фазовой манипуляции
спектр поляризационно-манипулированного колебания
трансформировался в более широкий спектр за счет гар-
монических составляющих, стоящих под знаками двой-
ных сумм.
Ранее сформулированные выводы по результатам
анализа поляризационно-манипулированного колебания
полностью справедливы и для этого сопряженного вида
манипуляции.
135
При меандровой модулирующей функции (7'2=2т2)
гармоники спектра сопряженной манипуляции, стоящие
под знаком двойных сумм, ортогонально поляризованы
с гармониками, определяемыми одинарными суммами.
При рассмотрении способов передачи непрерывных и
дискретных сообщений путем модуляции параметров по-
ляризационной структуры пространственно-двумерных
сигналов,-а также возможных путей уплотнения каналов
связи с поляризационной модуляцией (манипуляцией)
была показана необходимость анализа поляризационно-
го спектра колебания. Состав поляризационного спектра
и вес отдельных гармоник в передаче сообщений для
различных способов модуляции (манипуляции) разли-
чен. Без выяснения возможностей выделения в приемном
устройстве нужных гармонических составляющих спектра
анализ способов поляризационной модуляции был бы не
полным. Поэтому представляет теоретический и практи-
ческий интерес выяснить возможности поляризационной
селекции.
ГЛАВА 6
НЕКОТОРЫЕ СПОСОБЫ ПРИЕМА ПМ СИГНАЛОВ
Несмотря на то что имеются работы, в которых рассмотрены
способы приема простейших ПМ сигналов (см. введение), в целом
этот вопрос изучен очень слабо, так же как и сама поляризацион-
ная модуляция. В настоящей главе описываются только простейшие
методы приема непрерывных поляризационно-модулиронаниых сиг-
налов. Некоторые из описываемых устройств исследовались авто-
рами экспериментально, измерялись, в частности, искажения сигна-
лов при различной глубине модуляции параметров поляризации.
В результате теоретических и экспериментальных исследований
были сформулированы практические рекомендации по применению
тех или иных схем.
6.1. ПОЛЯРИЗАЦИОННЫЕ ПАРАМЕТРЫ
АНТЕННЫ ЭЛЛИПТИЧЕСКОП ПОЛЯРИЗАЦИИ
Сигналы с поляризационной модуляцией являются
переменными векторами в двумерном пространстве. В ка-
честве такого пространства может рассматриваться пло-
скость, перпендикулярная направлению распространения
электромагнитной волны, если последняя является фи-
зическим носителем сигнала, либо это пространство
отождествляется с двумя каналами устройства, в кото-
ром существуют электрические сигналы — компоненты
136
общего сигнала, который поэтому называется двумер-
ным.
Вектор в двумерном пространстве определяется дву-
мя своими проекциями на оси ортогонального базиса.
Электромагнитная волна с переменными параметрами
поляризации определяется двумя своими проекциями на
оси поляризационно-ортогонального базиса. В частном
случае, когда рассматривается прием электромагнитной
волны, то в качестве базиса разложения электромагнит-
ной волны используется базис приемной антенны. Этот
базис определяется параметрами поляризации приемной
антенны. В качестве этих параметров принимаются угол
эллиптичности гр и угол ориентации 0 поляризационной
диаграммы такой волны, которую данная антенна прини-
мает полностью, без поляризационных потерь.
Принято считать, что если какая-то антенна в режи-
ме передачи излучает волну с параметрами поляризации
Ф, 0, то в режиме приема она полностью принимает вол-
ну с точно такими же параметрами поляризации. В дей-
ствительности же этот принцип применим не во всех
случаях. Определим условия, при которых он справед-
лив.
Пусть в передающей антенне излучателю предшеству-
ет преобразователь поляризации, который формирует
волну заданной поляризации, а сам излучатель поляри-
зацию волны не преобразует. Преобразователь можно
представить себе состоящим из двух последовательно
включенных устройств: первое устройство задает необ-
ходимую форму поляризационного эллипса, а второе —
заданный угол его ориентации. Операторы этих
устройств описываются выражениями
Лц(?) = е-;/1р, Гц(?) = ег9 (6.1.1)
Исходная волна горизонтальной поляризации после про-
хождения этих двух устройств преобразуется к виду
ёвых (0 - Лц (?) Гп (9) = (6.1.2)
При этом волна рассматривается в правой системе ко-
ординат, ось oz которой совпадает с направлением рас-
пространения волны, ось ох — горизонтальная, оу — вер-
тикальная ось.
Принимаемую волну удобнее рассматривать в системе
координат охоУо^о, ось ог0 которой совпадает с направле-
137
кием распространения волны, т. е. направлена в сторону
приемной антенны, ось оуо параллельна оси оу, ось охо
противоположна но направлению оси охо, т. е. система
координат oxayoZo получается из системы координат oxyz
разворотом последней на 180° вокруг оси оу. И наоборот,
система координат oxyz получается путем такого же раз-
ворота системы координат охйуага.
Разворот системы координат вокруг оси оу па 180°
можно заменить разворотом на 180° вокруг осн oz и по-
следующей сменой направлений осей оу и oz на противо-
положные. Такая замена позволяет весьма просто перей-
ти от комплексного представления эллиптически-поляри-
зованной волны в системе координат oxyz к такому же
представлению ее в системе координат oxoyaz0. Так, если
излучаемая антенной волна в системе координат oxyz
описывается выражением (1.6.2), то в системе координат
ox0yoZo выражение для этой же волны примет вид
§(/) = 50e‘7<fe_‘ (8+к)е/ (ш</+*2°+ф), (6.1,3)
где аргумент л учитывает разворот системы координат
на 180° вокруг оси oz, а смена знаков перед I и k учиты-
вает изменения направления осей оу и oz на противопо-
138
ложные (рис. 6.1). Из (6.1.3) следует, что для волны
правого направления вращения, распространяющейся
в направлении, противоположном направлению оси oz,
показатель экспоненты с совмещенной мнимой единицей
будет положительным (в системе координат oxyz).
Опишем теперь преобразование поляризации волны
приемной антенной эллиптической поляризации. Пусть
в качестве приемной используется такая же антенна, как
и для формирования волны (6.1.1).
Преобразователь поляризации выполняет теперь функ-
цию селекции волны по поляризации, поэтому мы его
будем называть поляризационным селектором. Прини-
маемая антенной волна
£пр (t) = е-'W (Юо<~Аго+ф> (6.1.4)
проходит сначала устройство поворота поляризационной
диаграммы с оператором Гс(0), а затем устройство пре-
образования формы поляризационной диаграммы с опе-
ратором Лс(ф). В результате на выходе поляризацион-
ного селектора мы получим электромагнитную волну,
описываемую выражением
£вых (0 = [£цр (0 Ге (6)] X Ас (?), (6.1.5)
причем умножение в (6.1.5) должно быть операторным.
Обычная антенна эллиптической поляризации преоб-
разует в электрический сигнал только ту компоненту из
(6.1.5), которая имеет горизонтальную поляризацию, т. е.
сигнал на выходе такой антенны описывается выраже-
нием
S(0 = Rez[>BbIX(01- (6.1.6)
Поэтому волна (6.1.4) будет принята без поляризацион-
ных потерь только в том случае, если операторы Лс(ф)
и Гс(0) поляризационного селектора будут соответствен-
но равны следующим величинам:
Ac(?) = e+iX Гс(9) = е“Л (6.1.7)
т. е. операторы преобразователя поляризации в режиме
поляризационной селекции должны быть комплексно со-
пряженными по i операторам (6.1.1).
Если поляризационный преобразователь (в режиме
излучения) и поляризационный селектор — одно и то
139
же устройство, то условие (6.1.7) будет выполнено лишь
в том случае, если операторы (6.1.1) при замене систе-
мы координат oxyz на систему охо^о^о и при одновремен-
ном изменении направления распространения волны пре-
вращаются в операторы (6.1.7).
Проанализируем, какие из рассмотренных ранее
(гл. 3) устройств обладают такими свойствами. Назовем
волну, распространяющуюся вдоль оси oz системы коор-
динат oxyz, прямой волной, а волну, распространяющую-
ся вдоль оси oz0 системы координат oxaijoZo (рис. 6.1),—
обратной волной. Запишем операторы преобразования
прямой и обратной волн элементарными преобразовате-
лями.
1. Гиротропное устройство, выполненное в виде про-
дольно намагниченного феррита. Оператор для прямой
волны Гп = е‘9, для обратной волны
Гс ~ е~‘9, (6.1.8)
так как продольно намагниченный феррит—певзаимный
элемент.
2. Волноводная скрутка на угол 9 (рис. 6.1). Скрутка
разворачивает и прямую, и обратную волну, распростра-
няющуюся вдоль продольной оси волновода, на один и
тот же угол 9, если он отсчитывается в прямой и обрат-
ной системе координат. Поэтому и для прямой, и для
обратной волн оператор скрутки будет одинаков:
Гп = Гс = е19. (6.1.9)
Но его следует по-разному применять для скрутки в ви-
де квадратного или прямоугольного волноводов. В квад-
ратном волноводе распространяется волна любой поля-
ризации, поэтому для скрутки из квадратного волновода
оператор (6.1.9) применим к волне любой поляризации.
В прямоугольном волноводе с волной ТЕю распростра-
няется только линейно-поляризованная волна. Поэтому
такая скрутка выполняет две операции: выделение ком-
поненты, поляризованной параллельно узкой стенке вол-
новода, и поворот плоскости поляризации этой компо-
ненты на угол 9. С учетом этого, прямая волна <?пр(0
преобразуется скруткой, изображенной на рис. 6.1, к виду
^«xn^{Re4<rnP(0]}eie, (6.1.10)
140
а обратная волна преобразуется в обратной последова-
тельности:
^Bbxxo = Ref[<?o(0e,e]. (6.1.11)
3. Линотропное устройство (рис. 3.6,а). Оператор для
прямой волны
Ап = е-г/1₽,
а для обратной волны
Ac = ei/?. (6.1.12)
4. Четвертьволновое устройство (рис. 3.2,а). Это уст-
ройство инвариантно относительно разворота системы
координат вокруг оси оу, если его собственные оси па-
раллельны осям ох и оу. Поэтому
Чп=Чс. (6.1.13)
Операторы (6.1.8) — (6.1.13) позволяют определить вы-
ражения для прямой волны на выходе преобразователя
поляризации и для обратной волны на выходе поляриза-
ционного селектора, если задана исходная волна, а сам
преобразователь (селектор) состоит из рассмотренных
выше элементарных преобразователей.
Положим, что исходная волна в режиме излучения
горизонтально поляризована, а в режиме приема в сиг-
нал преобразуется также только горизонтально-поляри-
зованная компонента волны на выходе селектора. В этом
случае все пять типов преобразователей поляризации,
изображенных на рис. 3.4—3.7 и 6.1 формируют волну
йизл (0 = E.e^W
В режиме поляризационной селекции только один из
этих преобразователей — преобразователь типа АГ
(рис. 3.4) —принимает без поляризационных потерь вол-
ну точно такой же поляризации, что и излучаемая вол-
на. Остальные четыре типа преобразователей в режиме
поляризационной селекции дают на выходе горизонталь-
но-поляризованную волну, если поляризационная диа-
грамма принимаемой волны описывается выражением:
— для преобразователя типа ГА (рис. 3.9) е0 = е'^е-10,
— для преобразователя типа АА (рис. 3.8)1 ё0 =
= е-^е-‘»,
141
— для преобразователя типа IT (рис. 3.5)
— для преобразователя типа «скрутка — четвертьвол-
новое устройство» (рис. 6.1)
eo = e-;/Vi0.
Заметим, что в тех случаях, когда преобразователь
не содержит певзаимных элементов (типа ЛА и типа
«скрутка — четвертьволновое устройство»), поляризаци-
онная диаграмма излучаемой и принимаемой воли
в одной и той же системе координат (oxyz или oxayoZa)
описывается одним и тем же числом.
6.2. ПРИЕМ ПМ СИГНАЛА НА ДВУХКОМПОНЕНТНУЮ
АНТЕННУ
Чтобы электромагнитная волна любой поляризации
принималась антенной полностью, без поляризационных
потерь, необходимо обеспечить преобразование в элек-
трический сигнал сразу двух компонент волны на выхо-
де поляризационного селектора: вертикальной и гори-
Рис. 6.2.
зонтальной. Такая антенна называется двухкомпонент-
ной антенной эллиптической поляризации. В дальнейшем
будем рассматривать только такую двухкомпопентную
антенну, операторы поляризационного селектора которой
являются комплексно сопряженными по i от операторов
поляризационного преобразователя. Тогда параметры
поляризации такой антенны, и в режиме приема, и в ре-
жиме передачи будут одни и те же: <рд, 9д.
Эквивалентная схема двухкомпопентной приемной
антенны эллиптической поляризации изображена на
рис. 6.2. Антенна состоит из устройств 1, 2 компенсации
углов ориентации и эллиптичности поляризационной ди-
аграммы принимаемого сигнала. Операторы преобразо-
142
вания этими устройствами поляризации прямой электро-
магнитной волны, т. е. в режиме излучения, можно за-
писать как операторы гиротропного и липотропного
устройств, т. е.
Г, = Г (6А) = е‘0А, (6.2.1)
Л;=Л(?А) = е~/,1?А. (6.2.2)
Преобразование эллиптически-поляризоваиного сиг-
нала этими устройствами в режиме селекции математи-
чески представляется как умножение выражения для
сигнала <§с(0 на комплексно сопряженные по i опера-
торы Г1 и А2.
Таким образом, последовательность преобразования
сигнала <?C(Q—е се ceJmZ устройствами 1 и 2 двухком-
понентной антенны может быть записана в виде следую-
щего выражения:
<?,ыИо=Нсг;;1хл;/. (6.2.3)
Оконечное устройство 3 приемной двухкомпонентной
антенны эллиптической поляризации разделяет линейно-
поляризовапные компоненты сигнала (6.2.3), ориентиро-
ванные вдоль осей ох и оу этого устройства, на два
выхода двухкомпоиеитной приемной антенны. Если дей-
ствительная и мнимая оси комплексной плоскости (1,0
совпадают с осями ох и оу оконченного устройства, то
на выходах х в у двухкомпоиеитной антенны получим
следующие сигналы:
ex(0 = Re^:[<?вых(0], (6.2.4)
Су (0 == Inil вых (01 >
где сигнал <fBbIX(0 определяется выражением (6.2.3).
Проделав соответствующие преобразования, получим
ех (0 = [cos (?с — ?А) cos (0С — 0Д) +
+ / sin (?с + срА) sin (0С — 0А)] е/ш"^
(6.2.5)
ёу (0 = [cos (?0 + ?А) sin (0С — 0А) —
— / sin (?с — ?д) cos (0С — 0А)[ е/ш<
143
Скалярные функции ex(t) и ey(t) являются проекциями
двумерного сигнала на базис двухкомпонентной антенны
с параметрами поляризации <рл, 0д.
В дальнейшем удобно обозначить эллиптический по-
ляризованный базис двухкомпонентной антенны ком-
плексными векторами g и -г), каждый из которых на двой-
ной комплексной плоскости можно представить в виде
Е = ЗДД: в4) = о и’4е"л.
Ч = Э.(-<Р4;. «+«/2) = е1'’ле‘"4"'”. (6.2.6)
Тогда проекции комплексного вектора сигнала sc на комп-
лексные векторы £ и т] будут равны
(П = Rez [есё**] — ех (/),
(6-2.7)
(t) = Rez- [ест]*»] = еу (/).
Положим теперь, что сигнал (/), снимаемый с вы-
хода у двухкомпонентной антенны, получает дополни-
тельный фазовый сдвиг л/2 относительно сигнала (Г)
(например, за счет разной длины волноводных линий).
Тогда будем иметь
е\ (0 (0 = {sin (<рс — ?А) cos (9С — 0А) +
+ i cos (?с + ?А) sin (0с - 0Д)} =
= | CoS [?0 (<рА -]---2~ ' j COS (0О — 0д) -ф-
+ j sin + [ ?А + ] sin (0С - 0А) | е'“< (6.2.8)
Сравнивая (6.2.8) с выражением для ex(t) в (6.2.5),
видим, что сигнал е'г (/) есть не что иное, как проек-
ция того же сигнала <?с(0 на комплексный вектор т],
равный
V = Э0(?а + ^/2, 0а), (6.2.9)
144
Таким образом, в качестве базиса двухкомпонентной
приемной антенны можно принять как векторы
т), определяемые выражением (6.2.6), так и векторы Е, тд',
где т/ определяется выражением (6.2.9).
В любом случае сигналы на выходах двухкомпонент-
ной антенны определяются из соотношения (6.2.7), в ко-
торое следует подставить выбранный базис приемной
антенны.
Из (6.2.5) следует, что только при <р0 = <рА и 90 —
= Од получаем е^(/) — е'ш‘, = 0, т. е. вся энергия
сигнала поступит на Е-й выход двухкомпонентной антенны.
И наоборот, при ортогональных параметрах поляризации
сигнала, т. е. при <р0 = — <рА, 90 = 0А Ц--л/2 либо при
?с-?д+т./2, 9С = 9А, вся энергия этого сигнала будет
поступать па г]-й выход двухкомпо.нентной антенны. В об-
щем же случае, т. е. при параметрах поляризации сигна-
ла, не совпадающих с параметрами поляризации при-
емной антенны, энергия сигнала будет распределяться
между первым и вторым выходами двухкомпонентной
антенны пропорционально значениям поляризационных
коэффициентов приема yi и уг, которые вычисляются как
| ех |2 и | еу |2 соответственно. Из (6.2.5) получаем:
yi=0,5[l +sin 2срс sin 2cpA + cos 2срс cos 2cpAcos 2 (9C—9д)],
(6.2.19)
yi = 0,5 [ 1 -4-sin 2cpc sin 2<pA + cos 2<pc cos 2cpA cos 2(9C—9д].
Формулы (6.2.10) позволяют оценить селектирующие
свойства эллиптически поляризованной антенны по па-
раметрам поляризации.
Если мощность сигнала Рс, то в результате несовпа-
дения параметров поляризации антенны и параметров
поляризации сигнала па один выход двухкомпонентной
антенны поступит только часть мощности сигнала, рав-
ная yiPc, а на другой, поляризационно-ортогональный
выход — уг/’с-
Если две поляризационно-ортогональные компоненты
электромагнитной волны несут различные сообщения и
часть сигнала S2, попадающая в первый канал из-за
отклонения параметров поляризации сигнала от параме-
тров поляризации антенны, является помехой в этом
10—667 145
Канале, то отношение с=у2/у1 характеризует степень раз-
вязки между поляризационно-ортогональными каналами.
На рис. 6.3 приведены графики зависимости величины с
от поляризационных расстроек Аф = фс—фа и А9 = 9с—9а
Рис. 6.3.
для четырех значений угла эллиптичности антенны фА.
При малых поляризационных расстройках можно поло-
жить, что с не зависит от знака Аф и А9. Из рис. 6.3
видно, что при приближении формы поляризационной
диаграммы сигнала и антенны к линии влияние поляри-
зационных расстроек на степень развязки увеличивается.
146
Для антенн круговой поляризации коэффициент с не
зависит от ДО, так как изменение угла ориентации поля-
ризационной диаграммы антенны или сигнала приводит
лишь к изменению фазовых соотношений между сигнала-
ми в ортогональных каналах.
Из (6.2.10) и (6.2.5) следует, что при приеме поляри-
зационного модулированного сигнала на двухкомпонент-
ную антенну сигналы e^(t) и е (t) на ее выходах будут
в общем случае модулированы как по амплитуде, так и
по фазе. В этом смысле поляризационную модуляцию
можно характеризовать как амплитудно-фазовую моду-
ляцию ортогонально-поляризованных компонент единой
электромагнитной волны.
Кроме того, из (6.2.10) видно, что если интенсивность
сигнала на одном из выходов приемной антенны увели-
чивается, то на другом ее выходе она будет одновре-
менно на столько же уменьшаться. Аналогичным обра-
зом ведут себя и фазы сигналов (/) и ег< (/). Поэтому
поляризованная модуляция является, по существу, моду-
ляцией относительных фаз и амплитуд ортогонально-
поляризованных компонент электромагнитной волны.
Анализируя сигнал с одного выхода антенны эллипти-
ческой поляризации, мы в принципе можем выделить
ту информацию, которая была заложена в этот сигнал
при поляризационной модуляции волны. Однако такой
анализ сопряжен с определенными трудностями. Кроме
того, ни сигнал e^(t), ни (t) в отдельности не позво-
ляют однозначно определить сразу два параметра: <рс
и Ос, если эти параметры могут принимать значения,
большие л/4. Поэтому приемное устройство, позволяю-
щее однозначно определить информацию, представлен-
ную параметрами поляризации принимаемой волны, прин-
ципиально должно быть двухканальным и осуществлять
совместную обработку сигналов (t) и е (t). Только
в простейших случаях узкополосной поляризационной
модуляции можно ограничиться одпокапальным прием-
ником, заранее смирившись с тем, что часть энергии
сигнала будет безвозвратно потеряна.
При использовании двухканального приемника к его
каналам, усиливающим и преобразующим сигналы, по-
лученные с выходов двухкомпонентной антенны, предъ-
являются следующие требования:
W* |4?
1) Каналы должны иметь идентичные амплитудные
и фазовые частотные характеристики в полосе прини-
маемого сигнала.
2) Каналы должны быть линейны.
Практически к этим требованиям можно приблизить-
ся путем соответствующей калибровки обоих каналов
приемного устройства, а также применением для двух
каналов единой системы автоматической регулировки
усиления (АРУ) и общего гетеродина для супергетеро-
динного приемника.
Таким образом, функциональная схема двухканаль-
ного приемника поляризационно-модулированных сигна-
лов должна иметь вид, изображенный на рис. 6.4. Верх-
ний (с индексом 1) и нижний (с индексом 2) каналы
усиления и преобразования частоты сигналов (t) и (t)
имеют коэффициенты передачи Ki(«>) и Кг(<1>). Для иде-
ального приемника выполняется тождество
(6.2.11)
в полосе принимаемого сигнала. Реально же тождество
(6.2.11) обеспечить невозможно. Отличия КДю) от А2(®)
приведут к некоторому искажению информации на вы-
ходе приемного устройства. Эти искажения будут зави-
сеть как от степени различия между Ki и Кг, так и от
вида поляризационной модуляции и от принципа работы
устройства выделения информации. Однако следует стре-
миться к выполнению условия (6.2.11). Поэтому при
дальнейшем рассмотрении вопросов приема поляризаци-
148
опно-модулпрованных сигналов будем считать, что
A'i (ш) = Кг (<“) = е 1ШГ‘ ’
где шг — частота гетеродина. Тогда напряжения u,_(t) и
(f) па выходах верхнего и нижнего каналов усиления
и преобразования частоты сигналов (f) и (t), посту-
пающих с выходов двухкомпонентной эллиптически-поля-
ризованной антенны, будут описываться выражением
(6.2.5), в которое вместо несущей частоты ш0 следует
подставить промежуточную частоту ш = — «>г Такая
идеализация позволяет найти алгоритмы, по которым сле-
дует создавать устройства выделения информации из
сигналов (t) и ет (t) для различных видов ПМ сигналов.
Для каждого такого случая впоследствии можно будет
оценить влияние несоблюдения тождества (6.2.11) на
степень искажения информации.
Рассмотрим наиболее простые способы обработки ПМ
сигналов.
6.3. ОБРАБОТКА СИГНАЛОВ С НЕПРЕРЫВНОЙ ПМф
Пусть ПМф сигнал принимается на двухкомпонентную
приемную антенну, базис которой 6, т; определяется со-
отношениями Ё = Э (?А , 9а), т) = Э(?А -4-ти/2, 9А) и <рА=
= ?с, 9а =0с. Тогда, подставляя выражение для ПМф сиг-
нала (4.1.1) в (6.2.7), получаем следующие скалярные
сигналы па выходах g и г] двухканального приемника:
(0 ~ cos (0) cos wt> ит (0 = s,n (0] cos mt.
(6.3.1)
Сигналы (t) и (t) оказываются балансно модули-
рованными. Для раздельной демодуляции этих сигналов
необходимо иметь опорное напряжение, синхронное и
синфазное с несущей. Получение такого напряжения
является не простой задачей. Совместная же обработка
сигналов (0 и (t) позволяет довольно просто осу-
ществить их демодуляцию. Действительно, перемножим
эти сигналы. В результате получим
(0 (t) — 0,25 sin [2A<pS (<)][! -ф- cos 2a>(f)].
149
Низкочастотная фильтрация этого напряжения позво-
ляет выделить составляющую
ич (0 = 0,25sin[2A?S(0|. (6.3.2)
При достаточно малой величине Аф можно положить
sin[2A<pS(7)]~2A'(pS(7).
Модулирующая функция, как это было обусловлено
выше, по абсолютной величине не превосходит единицы:
| S (/) | 1 • Следовательно, на
выходе фильтра низкой ча-
стоты получим напряжение,
пропорциональное переда-
ваемому сообщению. Функ-
циональная схема демодуля-
тора ПМ сигнала, построеп-
AyS(t)
Рис. 6.6.
Рис. 6.5.
пого по принципу перемножения сигналов щ (/) и (/),
изображена на рис. 6.5, а на рис. 6.6 показана переда-
точная функция (характеристика) такого демодулятора.
Из рис. 6.6 видно, что характеристика демодулятора
линейна только при небольшой глубине модуляции угла
эллиптичности. Степень искажения сигнала S(t) в за-
висимости от величины девиации Аф угла эллиптичности
можно оценить по коэффициенту К гармоник выходного
напряжения (t) при модуляции угла эллиптичности
гармоническим колебанием.
Положим в (6.3.2) S(7) = sinQZ. Функция
sin(2A<p sin Qt) содержит только нечетные гармоники ча-
стоты Q, амплитуды которых равны
а{ = 2Л(2Аф), i = l,3, 5,... (6.3.3)
Ограничиваясь учетом только первых двух гармоник, для
коэффициента (А?) получим следующее выражение:
(А?) = Л (2Д?)/J, (2Дф). (6.3.4)
График зависимости 7^ (А?) изображен на рис. 6.7.
150
Если S(t) — не гармонический сигнал, а такой, что его
можно представить в виде некоторой суммы гармониче-
ских составляющих различных, в общем случае не крат-
ных частот, то в спектре функции (6.3.2) будут содер-
жаться не только основные компоненты сигнала S(t) и
их гармоники, но и комбинационные частоты. Поэтому
при оценке степени искаже-
’ния сложного сигнала следует
учитывать не только гармони-
ки его спектра, но и ком-
Рис. 6.8.
бинациоппые гармоники, а также и изменение соотно-
шения между амплитудами основных спектральных со-
ставляющих. Практически искажения сигнала почти не
заметны при Дф<25°.
Из приведенного анализа следует, что демодулятор
ПМф ’сигнала, изображенный на рис. 6.5, хотя и прост
в отношении его технической реализации, однако вносит
большие искажения в принимаемое сообщение при боль-
шой девиации угла эллиптичности. Достоинством этого
демодулятора является то, что различия в коэффициен-
тах передачи каналов 1 и 2 приемника (рис. 6.4) при-
водят лишь к изменению уровня сигнала на выходе де-
модулятора, т. е. коэффициенты передачи КДы) и Kz(a>)
не обязательно должны быть равны по величине.
В том случае, когда перемпожитель в схеме демоду-
лятора по каким-либо соображениям использовать не-
желательно, можно вместо схемы рис. 6.5 использовать
схему демодулятора, изображенную па рис. 6.8. Эта
схема состоит из двух квадратичных детекторов (Дь Д2)
и вычитающего устройства (S-). На выходе квадратич-
ных детекторов имеем следующие напряжения:
“д = Kdi cos2 [A<pS(О) = 0,5K5i {1 + cos [2A?S (f)]}, g
«a. = sin2 (01 = °»5Kdi {! — COS [2A=pS(01}, ’ ' >
151
Где Kdt и Кд—коэффициенты передачи детекторов ZZ,
и Д2. Напряжение на выходе вычитающего устройства
будет равно
- 0,5 (Kdt - Kda) + 0,5 (Kdi + Kdi)cos [2A<pS (/)].
Если коэффициенты передачи детекторов сделать оди-
наковыми, то напряжение на выходе демодулятора будет
равно Кд соз[2Л'ср5(7Л- Эта функция не может быть при-
нята за сигнал S(t), так как косинус является четной
функцией. Поэтому в данном случае необходимо так
перестроить параметры поляризации приемной антенны,
чтобы сигналы u^(t) и u.r(t) имели огибающие
cos[A<pS(7)—л/4] и sin[A<pS(7)—л/4]. Этого можно до-
стичь, если угол эллиптичности модулированной электро-
магнитной волны будет отличаться на л/4 от угла эл-
липтичности антенны.
Сигнал (?с (0 = е“ 41,15 (Z)I е,9»е^^ преобразуется та-
кой антенной к виду
^11P(0 = e-‘7149-s’l°-,t/'" е/ш<
и на двух выходах приемника получим сигналы
(/) = cos [A'pS (t"' — тг/4] cos wt, 1
(t) = sin [A'f’S (t) — it/4] coswZ. j ( )
В результате на выходе вычитающего устройства
в схеме рис. 6.8 будем иметь напряжение
(0 = 0,5 (Kdt - кд1) + 0,5 (Кд1 + K(lj) Sin [2Д?Э (/)]. (6.3.7)
Постоянную составляющую Ио = О,5 (Кд — Кд^) можно ли-
бо отфильтровать, либо свести к нулю выравниванием
коэффициентов передачи детекторов и коэффициентов
усиления каналов приемника. Передаточная функция
рассматриваемого демодулятора такая же, как и у демо-
дулятора, выполненного по схеме рис. 6.5. Отличитель-
ной особенностью его является то, что он не чувствите-
лен ни к фазовым сдвигам сигналов u^(t) и ur< (t) в двух
каналах приемника, пи к различию коэффициентов уси-
ления этих каналов, чего нельзя сказать о демодуляторе
первого типа. Однако нелинейные искажения и в данном
случае остаются весьма большими при А<р>25°.
152
Гораздо лучшие результаты можно получить, если
в схеме демодулятора, изображенной на рис. 6.8, вместо
квадратичных детекторов использовать линейные. Как
и в случае демодулятора с квадратичными детекторами,
входные сигналы должны определяться соотношением
(6.3.6). Тогда на выходе вычитающего устройства полу-
чим напряжение
% (0 = к<> I cos [Д?5 (0 — г/4] | — । s’n (/) — г/4]
(6.3.8)
Нормированные характеристики такого демодулятора при
= 0,7/С К = Kd и Кд — 0,7К? изображены на
рис. 6.9. Эти характеристики почти линейны в пределах
изменения Лер от —л/4 до л/4. Однако такой демодулятор
критичен к изменению ко-
эффициентов передачи
обоих каналов приемника.
Если эти коэффициенты
не одинаковы, то характе-
ристика становится несим-
метричной относительно
начала координат. Одна-
ко и в этом случае хоро-
шая линейность характе-
ристики сохраняется. По-
скольку балансировкой
каналов всегда можно
добиться равенства коэф-
фициентов усиления кана-
лов приемника, то практически можно положить Кд =Кд_
К фазовым сдвигам в каналах схема не чувствительна.
Поэтому схему демодулятора ПМ9 сигнала с линейными
детекторами можно рекомендовать к применению при
Дф<л/4.
Коэффициент нелинейных искажений сигнала на вы-
ходе демодулятора с линейными детекторами при моду-
ляции угла эллиптичности гармоническим колебанием
S (t) = sin (Ш) можно вычислить следующим образом.
Положим = ^=1 и Дф<л/4. Тогда выражение
(6.3.8) запишется в виде
и? (t) [Д<р sinQ/]. (6.3.9)
Разлагая sin[.Acp sin в спектр и учитывая только пер-
153
вые две гармоники спектра, получим следующее выра-
жение для коэффициента гармоник выходного сигнала:
/с9(д?)-Л(д?)М(д?). (6.3.Ю)
Сравнивая (6.3.10) с (6.3.4), видим, что в случае ли-
нейного балансного детектора ПМф сигнала амплитуды
гармоник спектра колебания (I) равны бесселевым
функциям от аргумента, равного девиации угла эллип-
тичности. Для приближенной оценки можно восполь-
Рис. 6.10.
выполняется условие Дф<л/4
циент нелинейных искажений
зоваться графиком рис.
6.7, увеличив на нем мас-
штаб горизонтальной оси
в два раза. Однако пра-
вильная оценка коэффи-
циента нелинейных иска-
жений по графику рис. 6.7
возможна лишь при Дф<
<л/4, так как при боль-
ших значениях Дф стано-
вится несправедливым вы-
ражение (6.3.9). Если же
и Кда = Кд , то коэффи-
налряжения на выходе
линейного балансного детектора не будет превосхо-
дить 1,5%'.
Рассмотренные выше способы обработки ПМф сиг-
нала являются некогерептными. Однако можно осуще-
ствить и когерентную обработку ПМф сигнала. Как из-
вестно, когерентные методы обработки повышают поме-
хоустойчивость приема. Применительно к ПМ^ сигналам
когерентная обработка позволяет осуществлять прием
пм9 сигналов при девиации Дф>л/4 с небольшими иска-
жениями принимаемой информации. Одна из возможных
схем когерентной обработки ПМф сигнала представлена
на рис. '6.10. Когерентное с несущей частотой напряже-
ние выделяется одним из известных способов из сигна-
ла, снимаемого с одного из выходов приемника. Целе-
сообразнее выделять его из колебания Ц), так как
согласно (6.3.1) этот сигнал содержит достаточно боль-
шую составляющую несущей частоты даже при больших
значениях девиации угла эллиптичности. Сигнал, подле-
жащий когерентной обработке, получаем путем сумми-
154
рования (в противофазе сигналов ut(7) и и.,. (t). В ре-
зультате такого суммирования получаем фазомодулиро-
ванное колебание, если только коэффициенты передачи
обоих каналов, приемника одинаковы. Действительно, в
этом случае на выходе сумматора (2S-) имеем
ws (t) — cos [W -|- Д?5 (/)]. (6.3.11)
Дальнейшая обработка сигнала (6.3.11) осуществля-
ется обычным фазовым детектором. При амплитуде ко-
герентного опорного напряжения, равной амплитуде сиг-
нала (6.3.11), выходное напряжение фазового детектора
будет определяться выражением
(0 = Kdsin[A<?S(0/21. (6.3.12)
Сравнивая (6.3.12) с (6.3.7) и (6.3.8), видим, что за-
метные искажения принимаемой информации S(l) из-за
нелинейности демодулятора в случае когерентной обра-
ботки по схеме рис. 6.10 будут наступать при девиации
Дф, в два раза большей, чем для схемы с линейными
детекторами, и в четыре раза большей, чем для схемы
с квадратичными детекторами (рис. 6.8) или для схемы,
построенной по принципу перемножения сигналов (0
и (0 (рис. 6.5). Однако схема когерентной обработки,
изображенная на рис. 6.10, критична к относительному
изменению как амплитудных, так и фазовых характери-
стик каналов приемника.
6.4. ОБРАБОТКА СИГНАЛОВ С НЕПРЕРЫВНОЙ ПМ9
Сигнал, полученный путем модуляции сообщением
S(t) угла ориентации поляризационной диаграммы вол-
ны, определяется выражением (4.3.1). При приеме этого
сигнала на двухкомпонентную антенну с базисом (6.2.6)
напряжения (t) и (/) на двух выходах приемного
устройства, изображенного на рис. 6.4, будут равны
(0 = cos (<р0 — <РА) cos [A0S (0 4- 90 — 9Д] 4-
4- j sin (<?„ 4- <рА) sin [ Д 9S (0 4- 90 — 9J,
(0 = cos (?„ 4- <рА) sin [Д95 (0 4- 9о—9а] —
— j sin (<р0 — <?А) cos [Д95 (0 4- 90 — 9J. (6.4.1)
155
Рассмотрим сначала некоторые частные случаи.
1. Модуляция угла ориентации плоскости поляризации
линейно-поляризованной волны. В этом случае фо—О и
выражения (6.4.1) примут следующий вид:
(/) = cos <рА cos [AOS (t) 4- 01О— 0А] +
+ / sin<pA sin [A0S(O + 0o — 0a],
(0 = cos Vin [AOS (0 4- 0o — 0A] 4-
4-/ s'n=pAcos[AOS(/)4-00— OJ. (6.4.2)
Если положить теперь ?A = 0, то напряжения (t) и
(/) на выходе усилителей промежуточной частоты
двухканального приемного устройства будут соответст-
венно равны
(0 = cos [AOS (/) 4- 0о OJ cos ш/,
(/)sin [AOS (/) 4- 0о — OJcosatf,
т. е. представляют собой балансно модулированные ко-
лебания. Эти напряжения выбором величины 0А всегда
можно привести к виду (6.3.1) или (6.3.6). Дальнейшая
обработка этих сигналов может осуществляться одной из
схем, изображенных па рис. (6.5, 6.8 и 6.10). Поэтому
в особом рассмотрении этот случай не нуждается.
Если <?а^А0, то, взяв сумму и разность сигналов
(/) и (/) из (6.4.2), получим
е/?л sin [A9S (/) Д- 0О — 0А 4- ^/4],
= (0 —«ч(0] =
= е-;<РА cos [A9S (/) 4-90 — 9А4-^/4]. (6.4.4)
Сдвинув по фазе иг на угол — <рА, а иъ — на <рА, по-
лучим для суммарного и разностного сигнала выражения,
аналогичные (6.3.6), если 9А = 9Э. Однако такой фазовый
сдвиг не обязателен, если осуществляется раздельное
детектирование этих сигналов. Если, например, обработ-
ка сигнала осуществляется по схеме с линейными детек-
торами (рис. 6.8), то общая схема двухканального при-
156
емника сигнала с Модуляцией угла Ориентации плоскости
поляризации линейно-поляризованной волны будет иметь
вид, показанный на рис. 6.11.
Суммирование и вычитание сигналов (6.4.2) можно
осуществить не только на промежуточной, но и на вы-
сокой частоте. Этим удается свести к минимуму влияние
Рис. 6.1 1.
несоблюдения равенства коэффициентов усиления и фа-
зовых сдвигов в каналах приемного устройства.
2. Фазовая модуляция кругополяризованной волны.
В этом случае гр0=л/4. Принимаемый сигнал имеет вид
£ __ е—Чтс/4 цА®о/+во+дв5(0]
Такой сигнал можно принимать на однокомпонентную
кругополяризованную антенну, и приемник может быть
обычным приемником фазомодулированных сигналов.
3. Модуляция угла ориентации эллиптически поляри-
зованной волны. В этом случае <роУ=О, <роУ=л/4.
Прием сигнала целесообразно осуществлять на круго-
поляризованную антенну, базис $, т; который имеет вид
? = Э(я/4, 0О), т] = Э(— it/4, 60). (6.4.5)
Подставим значения <ра = л/4, а 0д = 0о в (6.4.1). Тог-
да для сигналов на выходах двухканального приемника
получим следующие выражения:
(t) = sin (<р0 4-it/4) cos [<о/ -J- A0S (/)],
un (0 — cos (?o + ’>'/4) sin [<o/ — A0S(/)]. (
Таким образом, щ (f), (t) представляют собой фазомо-
дулированные колебания в общем случае неодинаковой
амплитуды, причем, если фаза первого из этих сигналов
157
увеличивается, то одновременно фаза второго сигнала
уменьшается на такую же величину.
Сигналы (6.4.6) можно подвергнуть обработке по спо-
собу перемножения и последующей фильтрации по низ-
кой частоте. На выходе такого демодулятора получим
напряжение
(t) = 0,25 cos 2<р0 sin [2ASS (/)]. (6.4.7)
Этот способ обработки аналогичен способу обработки
пм9 сигнала по схеме рис. 6.5. Сравнивая (6.4.7) с вы-
ражением (6.3.2), описывающим выходное напряжение
Рис. 6.12.
приемника ПМ^ сигнала, видим, что отличие этих соот-
ношений состоит только в зависимости напряжения us(t)
от угла эллиптичности фо модулированной волны. При
Фо->л/4 амплитуда сигнала (t) стремится к нулю. Как
и в случае приема ПМ^ сигнала, такая обработка свя-
зана с большими нелинейными искажениями сообще-
ния S(t).
Рассмотрим другой способ обработки сигналов
(6.4.6) —с использованием в качестве демодулятора фа-
зового детектора. Подадим па сигнальный вход баланс-
ного фазового детектора колебание (t), а на вход,
опорного напряжения — колебание (t). Амплитуды сиг-
налов на вторичных обмотках трансформаторов
(рис. 6.12) обозначим и^т и и^т.
Соответствующие напряжения запишутся в виде
и' (t) = — и” (/) = и^т sin (<р0 -J- it/4) cos Н + (0]>
«о (0 = u^mcos (<р0 + ’l/4) sin [arf — ASS (/)]. (6.4.8)
158
Амплитуда выходного напряжения детектора определя-
ется следующим выражением:
V {[sin2 (?<> + т*cos2 + -т)+
1
4-m cos 2<р0 sin 2Д9 J 2 — sin2 (<р0 +
i
-pm2 cos2 Г<Ро — т cos 2<р0 sin 2Д9 j 2 I, (6.4.9)
где tn — и /и^ Кд — коэффициент передачи детектора,
зависящий от сопротивления нагрузки и прямого сопро-
тивления диодов.
Зависимость амплитуды выходного напряжения от
девиации АО угла ориентации поляризационного эллипса
Рис. 6.14.
Рис. 6.13.
при различных значениях угла эллиптичности фо и при
/72 = 1, т. е. характеристика балансного детек-
тора ПМ0 сигнала, изображена па рис. 6.13.
Из рисунка видно, что только при фо=О характери-
стика детектора приближается к линейной. Уравнение
этой характеристики можно получить, подставив т = \
и фо = О в выражение (6.4.9):
U0m = 1^2 11 Sin (Д0 + ’V4) । ~ CC0S <Л0 + ’V4) 11’
(6.4.10)
159
Выражение (6.4.10) преобразуется к виду
и. = il К, (I sin Дб 4-cos Дб I— 1 sin Дб — соэДб!)
или
Uim = 2%пКд sin Дб ПРИ |Д61<Г/4’
иВт =- 2и^кд COS Дб при it/4< Дб<1г/2. (6.4.11)
Следовательно, при т=1 и сро=0 характеристика де-
тектора представляет собой отрезок синусоиды па наи-
более линейном его участке. При увеличении угла эл-
липтичности величина напряжения uo(t), подаваемого на
вход опорного напряжения фазового детектора, умень-
шается. И хотя при этом одновременно увеличивается
напряжение и'(1) на сигнальном входе, амплитуда на-
пряжения на выходе детектора уменьшается, а сама
характеристика детектора становится нелинейной.
Наиболее линейной характеристика детектора полу-
чается при выполнении равенства
t\m sin (То + */4) = и^т cos (<?0 + z/4) (6.4.12)
или
sin(qio+n/4) =m cos (ф0 +л/4). (6.4.13)
Значение коэффициента т зависит от отношения ко-
эффициентов усиления принимаемого сигнала в каналах
£ и т] двухканального приемника и поэтому может быть
как больше, так и меньше единицы. При увеличении пг
растет амплитуда выходного напряжения детектора. Для
значения А0 = л/4 максимум значения амплитуды вы-
ходного напряжения также получается при выполнении
условия (6.4.13). Поэтому характеристика детектора,
получаемая при выполнении этого условия, т. е. при ра-
венстве амплитуд фазомодулированных колебаний в ка-
налах g и т], является оптимальной. Таким образом, оп-
тимальное соотношение между коэффициентами передачи
сигналов в канале g и -q определяется из выражения
/Поит = (®) /\ (®) = 1g (?0 + */4). (6.4.14)
При увеличении пг выше оптимального значения ве-
личина максимума характеристики детектора не меняет-
ся, однако нелинейность характеристики становится весь-
ма заметной. Это хорошо видно из рис. 6.15, на котором
изображены характеристики балансного детектора ПМе
сигнала при <ро = ЗО° и различных значениях т.
160
Таким образом, работа балансного детектора ПМ9
сигнала при больших т, т. е. в переключательном ре-
жиме по входу опорного напряжения, допустима только
при передаче и приеме дискретных сообщений типа «1»,
«О».
Если условие (6.4.13) выполняется, то, произведя под-
- СТЗНОВКу ЗНаЧСНИЯ WIght из (6.4.14) в (6.4.9), после пре-
образований получим следующее выражение для харак-
теристики детектора ПМд сигнала при сро=>—0:
Ц,, =2L\inK() /2“sin (?0 + т/4) sin Д0. (6.4.15)
Таким образом, и в этом случае оптимальная в смыс-
ле линейности характеристика детектора представляет
участок синусоиды для значений аргумента —л/4<с/Л0<г;
<' л/4.
6.5. ОБРАБОТКА СИГНАЛОВ С НЕПРЕРЫВНОЙ ПМ^ 9
При одновременной модуляции параметров ср и 0
двумя различными сообщениями 5ф(/) и S9 (t) поляри-
зационная диаграмма принимаемой электромагнитной
волны определяется выражением
«> (01 Ц9о+М59(/)1 jmot
й(/) —е е е . (6.5.1)
При приеме этой волны на двухкомпонентную антенну
с произвольными параметрами поляризации 0Д сигналы
(/) и и (/) на выходах двухканального приемника будут
модулированы как по амплитуде, так и по фазе одно-
временно обоими сообщениями. Поэтому разделение
сообщений (t) и S9 (t) в этом случае невозможно.
Если же положить <рд—. т:/4, т. е. осуществлять прием
электромагнитного поля на антенну круговой поляризации,
то, как это следует из (6.2.5), (2.6.10), амплитуды сигналов
(0 и мт (/) будет зависеть только от (/), а фазы — от
S9 (/). Выражения для этих сигналов будут следующие:
(0 = cos (0 -Ь?о — т/4] cos [ш/Д- Д059 (/) + (0О—0А)].
(0 = sin (0 + - и/4] cos Н—Д039 (/) — (0О — Од)].
(6.5.2)
Выделение из сигналов (6.5.2) сообщения S^t) не
вызывает трудностей. Достаточно использовать одну из
схем обработки, описанных в § 6.3. Например, можно ис-
11—667 161
пользовать схему с квадратичными или с линейными де-
текторами (рис. 6.8). В этом случае необходимо поло-
жить ?о = 0, т. е. не модулированная по углу эллиптич-
ности волна должна быть линейно поляризована.
Для выделения сообщения Se (t) можно воспользо-
ваться одной из схем, приведенных в § 6.4. Однако во
всех случаях при этом необходимо предварительно
обеспечить постоянство амплитуд сигналов (t) и (t).
При неглубокой модуляции угла эллиптичности, точнее
при Д?<С^/4, мешающую выделению сообщения Se (/)
амплитудную модуляцию сигналов (/) и (t) сообще-
нием (;) можно устранить простым ограничением этих
сигналов по амплитуде. Полученные путем ограничения
сигналы постоянной амплитуды можно подать, например,
на фазовый детектор, на выходе которого получим напря-
жение, пропорциональное sin [A6S0 (/)], если только
Дд и/4.
Общая схема приемника ; ПМ^ сигнала для такой
простейшей обработки показана на рис. 6.15. Достоин-
Рис. 6.15,
162
СТвоМ её является простота технической реализаций,
а существенный недостаток схемы состоит в том, что она
не позволяет применять достаточно глубокую модуляцию
по ф из-за трудностей хорошего ограничения сигнала при
глубокой модуляции по амплитуде. Практически величи-
на девиации угла эллиптичности Дф не должна превос-
ходить (20 ... 25)°, что энергетически невыгодно, так
как при этом снижается эффективность использования
мощности сигнала и ухудшается помехоустойчивость ка-
нала передачи сообщения
Обеспечить постоянство амплитуды сигнала, модули-
рованного по фазе сообщением Se (t), можно не только
путем амплитудного ограничения. Поскольку амплитуды
сигналов (I) и (t) пропорциональны величинам
cos (£)— it/4] и sin [Д?5, (t) — тс/4], то сумма квад-
ратов их будет постоянной величиной, если только оди-
наковы коэффициенты передачи каналов S и 7] приемника.
Этот факт использован в схеме выделения сообщения
Se (£) из ПМ^ в сигнала, изображенной на рис. 6.16.
Сигналы с выходов УПЧ1 и УПЧ2 подаются на умно-
жители частоты на два, построенные в виде устройств
с квадратичной характеристикой, и на схему выделения
когерентного опорного напряжения (ВОН). На выходе
удвоителей частоты после фильтрации получим сигналы
(0 = К’ц cos2 [А^ (t) — тс/4] cos 2 [<dZ -ф-
+ 10Se(O + Oo-0A],
11*
163
u'Ti (0 = /Сц sin2 [A<?S9 (t) — T./4] cos 2 [<uf —
-A9S0(/)-0o + 0a]. (6.5.3)
Эти сигналы подаются далее на преобразователи часто-
ты СМ1 и СМ2 с нижней и верхней настройкой частоты
гетеродина. Как видно из рис. 6.16, в качестве гетеро-
динного используются когерентное с обрабатываемыми
сигналами напряжение промежуточной частоты и на-
пряжение утроенной частоты. Преобразование частоты
с верхней и нижней настройкой гетеродина позволяет
получить сигналы на выходе каналов Н и т] с одинаковым
знаком фазы:
и'\ (0 = cos2 [A?S9 (0 - r/4] cos +
+ 2ДЦ (0 + 2 (0О - 0Л)|,
(0 (0 — */41 c°s [да/ +
+ 2Д05в (О + 2(09-0л)|.
Если общие коэффициенты передачи удвоителя частоты
и смесителя каналов £ и т; одинаковы, т. е. если К Д —
= КцК2^=:К, то на выходе сумматора (S) получим фазо-
модулировапное напряжение постоянной амплитуды
(0 = и (0 + и' r = К cos [orf + 2A0S0 (Z) +2 (0О— 0Л)|.
Фазовое детектирование этого напряжения позволяет вы-
делить сигнал S6(t). Напряжение на выходе фазового
детектора при равенстве амплитуд опорного и сигналь-
ного напряжений будет описываться выражением «0(О =
= KK5sin[A0S0 (t)], если обеспечить сдвиг фаз опорного
и сигнального напряжения в статическом режиме 90°.
Линейный участок фазового детектора в этом случае со-
ответствует А0^л/4.
ГЛАВА 7
ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ ТЕОРИИ
ОПТИМАЛЬНОГО ПРИЕМА ПМ СИГНАЛОВ
В процессе приема поляризациоцно-модулировапных сигналов
в приемную систему поступает либо смесь поляризационно-модулп-
ровапного сигнала с помехами, либо одни помехи, если нет по-
пала.
164
Принятую смесь ПМ сигнала с помехой приемная система Долж-
на подвергнуть анализу и вынести конкретное решение о сигнале,
г. е. определить наличие или отсутствие сигнала, наличие какого-
либо определенного типа сигнала, отличающегося от других ПМ
сигналов, или оценить какой-либо поляризационный параметр ПМ
сигнала.
Система принимает решение на основе анализа поляризацион-
ной структуры смеси сигнала с помехой по определенному правилу.
Правило принятия решения указывает методику обработки при-
нимаемой смеси, приводящую к решению. Основными задачами
теории оптимального приема поляризацпонно-модулированных коле-
баний являются:
— отыскание путей реализации систем, работающих с ПМ сиг-
налами по оптимальным правилам решения;
— определение минимальных ПМ сигналов, которые еще могут
быть приняты с допустимым риском ошибки;
— оценка реальных приемных систем ПМ сигналов путем
сравнения их с оптимальными.
7.1. СТАТИСТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ СВЯЗИ
С ПМ СИГНАЛАМИ
Статистические модели радиолиний, встречающиеся
в литературе [25, 36] по статистическому моделированию
систем передачи сообщений, можно распространить и на
радиолинии, использующие ПМ сигналы. Спецификой
таких радиолиний является использование в качестве
переносчиков сообщений поляризационных параметров
электромагнитной волны.
Пространство сообщений Е состоит из множества воз-
можных значений, передаваемых по п каналам сообще-
ний е,. Его можно разделить па несколько подпро-
странств Et, Е2, ..., Еп в соответствии с используемыми
каналами. В общем случае подпространства Е, могут
б/ять перекрывающимися и неперекрывающимися, функ-
ционально зависимыми и независимыми между собой.
Сообщения, заключенные в подпространствах Е}-, также
могут быть функционально зависимыми или независимы-
ми. Сообщения ehj, где А— номер сообщения в/-м канале,
могут иметь различный смысл в зависимости от назначе-
ния системы связи. Они представляют собой значения не-
которого измеряемого параметра или совокупности изме-
ряемых параметров. Параметры могут передаваться по ка-
налам как в аналоговом, так и в дискретном виде. Сообще-
ния ehj могут, наконец, представлять некоторые временные
процессы или даже совокупности временных процессов.
165
Все эти сообщения отображаются на ПМ сигнале
S(t; Л) посредством некоторого оператора Тр по закону
S(f; Л) = rp||efcj||, (7.1.1)
где Uefejll — матрица передаваемых сообщений; Тр— опе-
ратор, включающий в себя операторы независимых ка-
налов; Х= НМА.2 ... М — параметры ПМ сигнала S(t-, 2).
Способ формирования сигнала S(t', Л), из сообщений
ekj, осуществляемый оператором Тр, определяет выбор
параметров сигнала, которые будут переносчиками ин-
формации для каждого канала и способ кодирования.
Каждую из величин еь, можно представить точкой в про-
странстве соответствующей мерности, причем появ-
ление определенных значений сообщений происходит
в каждом случае с определенной плотностью вероятно-
сти f(ek)j. Если известны или некоторым образом опре-
делены плотности вероятностей f (&h) то различным под-
пространствам Ej и элементам этих подпространств
поставлены в однозначное соответствие вероятности. Эти
плотности вероятностей многомерные, и их следует счи-
тать дискретными или непрерывными в зависимости от
дискретного или непрерывного характера подпро-
странств Ej. Пространству сообщений Е ставится в одно-
значное соответствие пространство ПМ сигналов <§ с по-
мощью поляризационной модуляции. Сведения о ПМ
сигнале и его статистике могут задаваться двойным спо-
собом: сигнал может быть задан непосредственно как
случайный процесс, т. е. плотность вероятности /'(<§) =
= считается известной априори, или же, как чаще
всего бывает, сигнал S(t; X) может быть известной
функцией одного или нескольких случайных параметров
из совокупности параметров iT = ||Xi; Х2; 23, ..., Лщ|| и
задается плотностью вероятности /(X) этих параметров.
Поэтому часто задачей приема и обработки являются
решения относительно параметров, а не сигнала.
Устройство Тр должно осуществлять операцию нало-
жения передаваемой по каналам информации на пере-
носчики сообщений — параметры поляризации высокоча-
стотного электромагнитного поля, т. е. преобразовать по-
ле сигнала в соответствии с передаваемой информацией.
166
Множество всех сигналов S (/; 2), различающихся
значениями параметра 2, заполняет пространство сигналов
Далее ПМ сигналы S(t; 2) передаются по каналу
связи, в котором действуют помехи. Если пересчитать
помехи, действующие в устройствах формирования ПМ
сигналов и в устройствах селекции и обработки, на вход
приемной системы, то совместно с внешними помехами
случайные и регулярные помехи по способу их воздей-
ствия на ПМ сигнал можно подвергнуть традиционному
делению на аддитивные n(t) и мультипликативные ц.(/).
Воздействие этих помех может быть отображено в виде
оператора J, так что па вход приемного устройства бу-
дет поступать колебание u(Z; 2):
п (t) — вектор-столбец аддитивной
S, (/; 2)
и (t; 2) — ,/{S (/; 2); я (/); (a(/)}=S(/; 2) (а (/) 4- п (/), (7.1.2)
где (A (t) — вектор-столбец мультипликативной помехи;
помехи;
О
S2(Z; 2)
S(/; 2) =
О
— диагональная матрица ПМ сигнала без помех; и (t-, 2) —
вектор-столбец колебаний на входе приемной системы.
Пространство U представляет собой множество всех
возможных значений принимаемых электромагнитных коле-
баний и(/; 2) и называется пространством колебаний
на входе приемной системы. Статистические характе-
ристики помех и оператора TPJ, определяющего работу
линии связи с ПМ сигналами, считаются известными.
Это значит, что определены двумерные плотности ве-
роятностей принимаемых колебаний и (t; 2) при каж-
дом данном ПМ сигнале S(Z; 2).
Можно еще более усложнить задачу приема и рас-
сматривать случай, когда частично или полностью не-
известны априорные плотности вероятностей помех
/[«(/)] и f[ц(0], однако это сильно усложняет задачи
синтеза и анализа приемных систем и нами рассматри-
ваться не будет.
167
Приемная система ПМ сигналов производит над
принятыми электромагнитными колебаниями u(Z; Л)
операции Тп или Тп', включающие в себя кроме обычных
операций операции разделения сообщений по соответ-
ствующим каналам передачи информации, в результате
чего на ее выходе формируются решения относительно
ПМ сигналов £*(/; Л) или оценки Кг* поляризационных
параметров К, этих сигналов, воспроизводящие передан-
ные сообщения ejk.
Таким образом, последовательность формирования оце-
нок сообщений e*kj и решений S* (tf, 2) будет следующей;
TnU К*—> Е*,
(7.1-3)
7''nt/(2) = S*(/z;
где §* —• пространство принятых решений; Е* — прост-
ранство оценок сообщений.
Иначе говоря, приемная система осуществляет пре-
образование пространства принимаемых колебаний
U в пространства решений &* или оценок Е* посредством
операторов Тп или Т’п.
Структуры пространств решений или оценок Е*
должны совпадать со структурой пространства передан-
ных ПМ сигналов Q и сообщений Е. Обратное утвержде-
ние, вообще говоря, неверно, так как каждой точке
или Е* соответствует определенная область из прост-
ранства принимаемых колебаний U.
В таком изложении проблемы решений и оценок
предполагалось, что выборки производятся дискретно и
что интервал выборок задан и конечен. Однако ни пер-
вое, ни второе из этих допущений, предположенные для
удобства описания, не являются совершенно необходи-
мыми. Процесс выбора может быть и непрерывным, что
не вызовет недоразумений и не нарушит общности рас-
суждений.
Предложенное описание системы связи с ПМ сигна-
лами носит общий характер и его можно отнести прак-
тически к любой системе передачи информации, в част-
ном случае, и к системам, использующим обычные
сигналы. Статистическая модель системы передачи ин-
16
формации в соответствии с вышеизложенными рассужде-
ниями может быть представлена в виде, изображенном
на рис. 7.1. К специфике радиоканалов с ПМ сигналами
можно отнести то, что преобразование временных про-
цессов в пространственно-временные происходит в поля-
ризационных модуляторах, в передающих и приемных
Рис. 7.1.
антеннах, в то время как в радиолиниях с обычными
сигналами эти преобразования осуществляются только
в антенно-фидерных устройствах. Поэтому для более
полного учета реальных условий работы радиолинии
с ПМ сигналами необходимо отнести передающую
антенну к системе, осуществляющей операции Тр, а при-
емную — Тп или Т,/.
Работа статистической модели, изображенной на
рис. 7.1, будет описываться выражениями
ЩЦеМ); ц(/)]-Л*-£*. 1
rn/[7'p(eft)j}x(/); /z(0|-S(4-; Z)-*£*. J
Это выражение моделирует работу систем радиотеле-
метрии, радиосвязи, траекторных измерений и др. си-
стем, которые используют ПМ сигналы. В частном слу-
чае они будут справедливы и для радиолиний с обыч-
ными сигналами.
Опираясь па рассмотренную статистическую модель,
можно сформулировать в общих чертах задачу синтеза
приемных систем ПМ сигналов следующим образом.
169
Пусть заданы семейство функций распределений
вероятностей f [u(f; Z)/S (f; Z)|, f [S(/; Z)], область воз-
можных решений (или £*) и функция потерь
E{S(t; Z); у [и (f;£Z]}, где у \и (f; Z)] есть функция, опре-
деляющая закон, по которому принимаются решения
приемной системой. Требуется определить оптимальное
правило выбора решений, т. е. оптимальный вид функ-
ции у [и (/; Z)]. Такая формулировка справедлива как
для системы обнаружения ПМ сигналов, так и для си-
стем оценки параметров этих сигналов, однако в каж-
дом конкретном случае необходимо взять соответствую-
щие функции и область возможных решений или оценок.
Полученные понятия могут быть использованы для
постановки задачи оценки качества оптимальных п суб-
оптимальных систем с ПМ сигналами. В общей теории
синтеза оптимальных систем, как правило, используют
методы оценки приемных систем, позволяющие затем
определить критерии качества систем, относительно ко-
торых определяется оптимальность.
При заданном ПМ сигнале S (/; Z) априорный риск
[19] L{S, Р [у («)/«]} определяется как условное матема-
тическое ожидание функции потерь:
L {S; Р [у («)/«]} = J dt f d и f f (uJS)X
т d
X F [S; Y(«)]f[Y («)/«] <Ш (7.1.5)
где f[y(u)/u]— плотность вероятности, определяющая,
правило использования данных для выбора решений
у (и); Р [у («)/«] — вероятность, определяющая правило
использования данных для выбора решений.
При таких обозначениях охватываются как дискрет-
ные, так и непрерывные пространства решений <§*; для
дискретного пространства интеграл по <g* необходимо
заменить на сумму.
Средняя оценка потерь SC{f(s); Р [Y (“)/«]} при выборе
правила решений Р [у («)/«] определяется как безусловное
170
математическое ожидание потери:
{f (?); f [Y («)/«]} = J dt J ds $duf (ufs) X
f g и
XfCs)P{s^WU(d)lu\dX^ (7.1.6)
Необходимо отметить, что функция потерь может
приписывать каждой комбинации ПМ. сигнала и реше-
ния (оценки) некоторую стоимость С, не зависящую от
правила выбора решения Р[у(и)/и],
MS; y(«)1=c[(S;y[(«)].
(7.1.7)
Однако с точки зрения теории информации часто
пользуются более общей функцией
Р* f»/Y Й1 = - log Р ]S/Y («)]- (7-1 -7а)
где P[S/y(u)] — апостериорная вероятность наличия ПМ
сигнала S(t; 1), если известно решение Y [u(Z; Z)].
В этом случае средняя оценка потерь представляет
собой известное выражение неопределенности (ненадеж-
ности) из теории информации.
Выражение оценок (7.1.5) и (7.1.6) можно предста-
вить в виде, при котором четко определяются вероят-
ности ошибок, соответствующие различным решениям.
Обозначив через Pt [y’(u)/S] условную вероятность то-
го, что приемное устройство ПМ сигналов выдает реше-
ние y[«(^; *)], если принят ПМ сигнал S(/; Z) и принято
правило выбора решений Р [y (u)/u], мы можем написать
Л IY («)/S] = ,f dt J f («/S)f [Y («)/«] d«. (7.1.8)
В этом случае выражение условного риска примет вид
г {S;P[y (ЭД} =
= j dt[ f[Y («)/«] du j C [S; Y («)] f (S) dY («)• (7-1.9)
171
Далее можно сравнивать решающие системы ПМ сиг-
налов, определив для каждой из них средние оценки по-
терь Р [!(.«)/«]} или значения средних рисков
R {f (S); Р [Y («)/«]} = .( Л J г {S, Р [г («)/«[} f (S) dS.
(7.1.10)
ТакихМ образом, сформулирован количественный ме-
тод различения как оптимальных, в смысле выбранных
критериев, систем, использующих ПМ сигналы, так и
квазиоптпмальных, причем сравнение выполнено на ос-
нове общего критерия, а имеющуюся информацию
можно учесть способом, наиболее полно соответствую-
щим той или иной используемой системе с ПМ сигна-
лами.
Статистическое моделирование систем связи с ПМ
сигналами и синтез таких систем требуют учета некото-
рых/ особенностей обнаружения и оценки параметров
ПМ сигналов. Поэтому необходимо более подробно
остановиться на этих вопросах, чтобы конкретизировать
некоторые аспекты основных задач.
7.2. ЗАДАЧА ОБНАРУЖЕНИЯ ПМ СИГНАЛОВ,
ЯВЛЯЮЩИХСЯ ЗАДАННЫМИ ФУНКЦИЯМИ
ПОЛЯРИЗАЦИОННЫХ ПАРАМЕТРОВ
В общей постановке, которая дана в § 7.1, задача синтеза опти-
мальной системы связи с ПМ сигналами в настоящее время прак-
тически не разрешима. Это объясняется тем, что трудно определить
статистические характеристики пространства U, включающие в себя
как статистику аддитивных и мультипликативных помех, так и ста-
тистику сообщений и ПМ сигналов. Поэтому общую задачу опре-
деления оптимальной системы связи с ПМ сигналами необходимо
разделить на две части и раздельно оптимизировать задачу фор-
мирования ПМ сигналов из сообщений, т. е. оптимизировать опера-
тор Гр, и задачу оптимизации приема ПМ сигналов, т. е. оптимизи-
ровать Тп при заданной статистике Тр и определенном критерии
качества.
В настоящей работе мы остановимся па второй задаче и анализе
количественных оценок потенциальной возможности системы связи
с ПМ сигналами при наличии помех.
Для рассмотрения общего решения задачи определения опти-
мальной приемной системы ПМ сигналов положим, что ПМ сигнал
на выходе системы Тр представляет собой детерминированную
функцию S(t\ А) времени и передаваемого сообщения, которое
заложено в поляризационной структуре сигнала, а также задана
172
статистика помех n(t) и [t(Z), способ J их комбинирования с сиг-
налом, т. с. статистика пространства U.
Однако математический аппарат теории синтеза и анализа
систем связи с учетом мультипликативных помех получается слож-
ным, требующий особого рассмотрения. Поэтому мы воспользуемся
здесь традиционной идеализацией — делением па быстрые и медлен-
ные флюктуации параметров канала связи с ПМ сигналами, кото-
-рая в большинстве случаев отвечает реальным условиям работы
радиолиний связи.
При медленных флюктуациях будем считать, что время соб-
ственной и взаимной корреляции функций pi(Z), рг(0 значительно
больше длительности ПМ сигнала S(t; 1), поэтому на интервалах
наблюдения можно считать p(/)=const, и тогда сигнал на входе
приемной системы будет иметь вид
и (/; 1)- Re {S(/;X) ?}+«(/). (7.2.1)
где —
р.
P-i exp (/>,)
Р-г exp (/<f2)
В случае быстрых флюктуаций, когда время собственной и
взаимной корреляции параметров канала связи меньше интервала
повторения, но значительно больше длительности элементарных ПМ
сигналов на каждом периоде повторения, случайный процесс рг(/)
можно заменить статистически независимыми векторами ,и(/) =
= Ц1, Ц2,..., Цп и принимаемый ПМ сигнал представить в виде
«(/; X) - Re {£ + «(/), (7.2.2)
где п — число повторений сигнала; ti — временной сдвиг до i-ro
элементарного сигнала
So £).
Эти идеализации позволяют представить ПМ сигнал на фоне
аддитивных и мультипликативных помех в виде
и (/; X) — S (/; X,; Х2) + п (t).
(7.2.3)
где в Х2 объединены параметры ПМ сигнала, которые стали слу-
чайными, но независящими от времени величинами, учитывающими
воздействие мультипликативных помех.
Задача обнаружения ПМ сигнала эквивалентна задаче про-
верки гипотез На и Hi. После приема некоторой реализации и из
пространства U наблюдатель должен принять решение относительно
пулевой гипотезы Но, соответствующей отсутствию ПМ сигнала, или
альтернативной Hit соответствующей присутствию ПМ сигнала. Вы-
173
бор одной из гипотез при наблюдении каждой из возможных реа-
лизаций и эквивалентен разделению пространства U на два подпро-
странства Uo и U\. Основная задача заключается в том, как опти-
мальным образом разделить пространство U, при этом сразу воз-
никает вопрос о критерии оптимальности.
Подход к задаче обнаружения на основе теории статистических
решений был предложен в известных работах [23, 25, 35, 36, 41],
где указывается, что приемная система в этом случае должна либо
выносить некоторое суждение о неизвестной величине, т. е. быть ре-
шающей, либо давать наблюдателю апостериорные вероятности на-
личия и отсутствия сигнала, на основании которых наблюдатель
должен принимать решения. Естественно, что в последнем случае
неизбежна зависимость качества решений от субъективных качеств
наблюдателя, которые трудно оценить. Так как при обнаружении
ПМ сигнала пространство решений <§* состоит только из двух зна-
чений у(^*)=0, y(S*)=fl и наблюдателю безразлично, какие зна-
чения принял ПМ сигнал, то функция потерь r(S; у) не зависит от
конкретных значений S(t; к), а зависит только от событий S(t; К) =
= 0 и S(t; X) =И=0. Значит, величины Гц определяют матрицу потерь
IMI
r(S=0; 0)
г (5 ф 0; 0)
r(S = 0; 1)
r(S/ 0; 1)
(7-2.4)
Потерям гц можно приписать стоимости эксперимента, стоимость
действий предпринятых после принятия решений, а также стоимость
последствий этих действий. Поэтому естественно положить, что
г (S = 0; 1) = r01 > г (S = 0; 0) =>00.
г (S^0; 0)-rlo>HS^0; i) = rn.
(7.2.5)
Выбирая различные значения для элементов ri} матрицы потерь,
мы будем получать различные критерии оптимальности обнаруже-
ния. Используя выражение '(7.2.5), требование среднего риска соглас-
но (7.1.10) можно записать как
м [г (S; Y)] = 7 {гооР- [Y = 0] + rolP_ [у = 1]} +
5=0 5 = 0
+ Р{г10Р^ [Г = 0]+г„Р^ [r=lj} = min, (7.2.6)
s^o
где Р . [у = 0] —вероятность принятия правильного решения, если
5=0
отсутствует ПМ сигнал; Р_> [у = 1 ] — вероятность принятия lipa-
se о
вильного решения, если имеется ПМ сигнал;
Р-> [у = 1] = 1-Р^ [у = 0];
5=0 5 = 0
Р- [y = 0J = 1—Р_ [Y = l]; <7.2.7)
5=^0 5ч«
М( ] — знак математического ожидания.
174
Решение «Г1М сигнал есть», когда он на самом деле отсутствуй Г',
называется ошибкой первого рода или «ложной тревогой», решение
«ПМ сигнала нет», когда он на самом деле есть, называется ошиб-
кой второго рода или «пропуском сигнала».
Таким образом, Р^, [у = 1 ]—вероятность ложной тревоги, а
s •= о
Р.» [у = 0] — вероятность пропуска ПМ сигнала.
5э40
Используя равенства (7.2.7), требование минимума среднего
риска (7.2.6) преобразуем к виду
Af[r(S; у)] [Y = И + pRiP-* [у = 0] +
5 = 0 5=^0
+ qroo + рГи = min, (7.2.8)
где в соответствии с (7.2.5)
/?о=Го1—гоо>0, Ri—ria—Гц>0. (7.2.9)
Из (7.2.8) видно, что качество системы обнаружения ПМ сигналов
можно характеризовать вероятностью ложной тревоги и вероятно-
стью пропуска сигнала, зависящими от правила решения, так как
величина qroo+PHi фиксирована при заданной функции потерь и
не зависит от правила решения. Многие критерии можно определять
исходя из выражения (7.2.8), изменяя только коэффициенты qRa
и pRi в линейной комбинации вероятностей ошибок первого и вто-
рого рода. Согласно критерию идеального наблюдателя оптимальной
системой обнаружения считается система, минимизирующая полную
вероятность неправильного решения:
qP-* [у = II + рР-+ [y = 0]=min.
5 = 0 5»М)
(7.2.10)
Сравнивая выражение (7.2.10) с (7.2.8), находим, что критерий
идеального наблюдателя относится к критерию минимума среднего
риска с матрицей потерь.
(7.2.11)
Следовательно, при критерии идеального наблюдателя правильным
решениям сопоставляются нулевые потери, а ошибочным — одинако-
вые потери. При критерии Неймана — Пирсона минимизируется
оптимальной системой обнаружения вероятность пропуска сигнала
[у = 0] = min
5^0
(7.2.12)
при заданном значении вероятности ложной тревоги
P?=ofY=1]=a-
(7.2.13)
175
Метод неопределенных множителей Лагранжа позволяет сфор-
мулировать эту задачу как отыскание минимума величины
[у 0] -ф 1УР_+ [у = 1] = min (7.2.14)
s^o s = 1
или
IqP^ [y-1] + /?P_* [Y-0j-min, (7.2.15)
.S -?3 5V0
где l = ltp!q—неопределенный множитель.
Сравнивая выражение (7.2.15) с 1(7.2.8), находим, что критерий
Неймана — Пирсона можно рассматривать как критерий минимума
среднего риска с матрицей потерь
0 I
I 0
(7.2.16)
где неопределенный множитель I находится из условия (7.2.15).
При критерии взвешенных комбинаций оптимальной считается си-
стема обнаружения, максимизирующая величину
Р.+ [Y--1]—wP.+ [y — I]-=max, w > 0, (7.2.17)
S-^0 S = 0
T. e. система обнаружения, дающая максимальную вероятность пра-
вильного обнаружения при минимальной вероятности ложной, тре-
воги. С учетом равенств (7.2.7) находим, что условие (.7.2.17) экви-
валентно условию
Р_> [у=0] + игР_ [у = 1] =П11П, (7.2.18)
3^0 s = о
а это значит, что критерий взвешенных стн к критерию минимума среднего риска комбинаций с матрицей можно отне- потерь
1 0 Т
— 0 я (7.2.19)
Из рассмотренных критериев можно придти к общему выводу, что
требование(7.2.18)можно представить в виде
а„Р_, [у = И + aiP-> [Y--OJ = min (а0, ai>0), (7.2.20)
3 = 0 3=^0
где ио и at могут быть заданы, а неизвестными являются вероят-
ности ошибок первого и второго рода, что соответствует фиксиро-
ванным значениям функции потерь, либо может быть задана одна
из вероятностей, а коэффициент при ней является неизвестным и
находится из условия заданного значения вероятности. Если пра-
вило решений Р[у/и] рандомизированное, то вероятность ложной
тревоги равна
Р_ [у = 1 ] =- С («) P]l/a] dx, (7.2.21)
з=о Д з=о
и
176
а вероятность пропуска I IM Сигнала равна
[у 0] . С f (S) П (7/S) Р [0/7] du -=
S=?=j J J
e U
= P [0/ul dll j f (S) f (a/S) dS, (7.2.22)
U s’
где (a)—плотность вероятности и при условии, что S 0.
s лэ
Учитывая, что
Р [ 1 .7] =- 1 — Р [0/ui • (7.2.23)
и подставляя (7.2.21) и (7.2.22) в выражение (7.2.20), находим
«о + «1 f Р [0/7] [f_» (а) —(a0.'“i) («)] d« = min. (7.2.24)
5#Э 5=0
и
Минимизация выражения (7.2.24) эквивалентна минимизации интег-
рала второго слагаемого. Поскольку 0 < Р [0/и] < 1, то интеграл в
(7.2.24) будет минимальным; если Р [0/и] = 0 для всех и, при кото-
рых (и) — (a0'“i)f-» (и) > 0, и Р[0,ц| = 1 для всех и, при ко-
5^=0 5=0
торых (и)— (а0/а,) ('')</0. Следовательно,
5/--0 5=0
Р [0/7] -= 0, Р[1/7] = 1,
если
f-> (7)/f_* (7) >«»/«,. (7.2.25)
'S^’l / 5=0
И
p [0/7] = i, p [/7] = о,
. если
U (7)/U (а)<«о/«1. (7.2.26)
5=/=') 5=0
Величина
A (7)=^ (u)/f^ (7), (7.2.27)
стоящая в левых частях неравенств (7.2.25) и (7.2.26), называется
отношением правдоподобия. Заметим, что в аргументах плотностей
вероятностей наблюдаемого сигнала при условии, что он содержит и
не содержит ПМ сигнала, стоят выборочные значения и, измерен-
ные в результате приема U(t; Л).
12—667 177
Такйм образом, правило реШеййя, ойтимальное согласий кри-
терию (7.2.24), заключается в следующем: при приеме какого-либо
сигнала и вычисляется отношение правдоподобия Л(ы) и сравни-
вается с порогом
x = ao/«i. (7.2.28)
Если Л(ы)>х, принимается решение «ПМ сигнал есть», если
Л(«)<х, принимается решение «ПМ сигнала нет». Так как и пред-
ставляет собой точку пространства колебаний U, то уравнение
Л(и)=х (7.2.29)
представляет собой уравнение гиперповерхности, разделяющей
пространство U на две неперекрывающяеся области: Uo и Ui. Так
как все рассмотренные критерии могут быть сведены к требованию
(7.2.24), то оптимальная операция для них заключается в вычис-
лении отношения правдоподобия,' которое сравнивается с порогом
данного критерия. Из выражений (7.2.8), (7.2.20) следует, что в слу-
чае матрицы потерь общего вида (7.2.4) порог сравнения
В практических исследованиях систем обнаружения наибольшее рас-
пространение нашли критерий идеального наблюдателя, для кото-
рого с учетом (7.2.11)
x~q!p, (7.2.31)
и критерий Неймана-Пирсона, для которого с учетом (7.2.16)
x=?//?=Zi. (7.2.32)
Критерий взвешенных комбинаций в соответствии с матрицей по-
терь (7.2.19) имеет порог ограничения
х=а>. (7.2.33)
Поскольку для апостериорных вероятностей наличия и отсутствия
ПМ сигнала имеют место соотношения
Р (u/S ф 0) = р\_* (u)/f (и),
s^o
(7.2.34)
Р (u/S = 0) = (u)/f (и),
5=0
то, используя (7.2.27), получаем
До (u) = qp &S ./• 0)/pP (u/S = 0). (7.2.35)
Из сопоставления (7.2.35) и (7.2.27) находим, что новый порог Xi,
с которым сравнивается отношение апостериорных вероятностей,
выражается через порог х, с которым сравнивается Л(и), по фор-
муле
Х1=рх/<7. (7.2.36)
178
Эта формула позволяет определить пороги для всех вышерассмот-
ренных критериев.
В заключение заметим, что во всех предыдущих рассуждениях
мы считали, что наблюдаемые сигналы являются случайными век-
торами, и пользовались плотностями вероятностей векторов. Однако
можно прийти к соотношению (7.2.35), когда u(f; Л) представляет
собой случайный векторный процесс, так как существуют апостериор-
• ные вероятности P(u(f; X)/S(f; X) =И=0] н \)/S(Z; Х)=0].
Чтобы апостериорный риск в этом случае был минимальным, не-
обходимо принимать решение
Р[и(<; X)/S(f; X) УгО] у — 0, если < Р [и (f; X)/S(f; X) =0] „ ^01 — ^00 ' Go —Gi ’ (7.2.37)
, P[u(f; X)/S(f; Х) = 0] , Gi—Go (7.2.38)
P[u(t- X) 5=0] Go —Gi ’
Выражения (7.2.37) и (7.2.38) означают, что задача оптимального
обнаружения считается решенной, если известны апостериорные
вероятности наличия и отсутствия ПМ сигнала.
Пусть входной сигнал u(t; X) с вероятностями р и q может быть
двух видов;
1) w(f; X) =S (f; X)+ «(/),
(7.2.39)
2) «(f; X) = n(t), t е [0; Г],
где Х=Хо, Xi..... Х„—случайные параметры S(f; X). Придадим
дополнительно параметру Хо значение интенсивности, принимающей
значения 1 и 0 соответственно с вероятностями р и q.
Тогда плотность вероятности параметра Хо запишется как
f(Xo)=76(X0)+p6(Xo—I), (7.2.40)
а сигнал (7.2.3) можно заменить выражением
и (Г; Х)=Х05 (f; X)4-n(/). (7.2.41)
Если параметр Хо независим по отношению к остальным случайным
параметрам ПМ сигнала Xi, Х2,..., Х„, то плотность вероятности
совместного распределения этих параметров будет определяться
выражениями
f (Хо, X,.. X„)=f(X0)f(X,, Х2... Х„) =
Г (7.2.42)
!=f(Xi, Х2, .. ., Хп) [?б.(Х0) 4-рб(Хо—1)].
Тогда для решения задачи обнаружения достаточно найти апо-
стериорные вероятности Р(и/Хо), т. е. вероятности наличия и отсут-
12* 179
ствия ПМ сигнала:
1 +д ОО 00 п
Р (и/1) j d\0 - | f (Хо, Л,, .... Ц, и) ЭД <А;.
I—Д —00 - 00 i = I
(7.2.43)
+ д 00 00 п
P(«/l)-J d/,0 f,.. f/(X0. Л........... М)Плр
—Д —00 — 00 / = 1
где Л — произвольная положительная малая величина. Отсюда вид-
но, насколько бывает важно в задаче обнаружения знать методы
определения апостериорных плотностей вероятностен параметров
поляризации ПМ сигналов, рассмотренные в работах [15, 30].
7.3. ЗАДАЧА ОЦЕНКИ ПАРАМЕТРОВ ПОЛЯРИЗАЦИИ ПМ
СИГНАЛОВ
Рассмотренная в предыдущем параграфе задача обнаружения
ПМ сигнала должна предшествовать задаче оценки его параметров
поляризации в тех случаях, когда возможно отсутствие ПМ сигнала
на входе приемной системы. Эти задачи имеют между собой орга-
ническое сходство в определении среднего и условного рисков,
однако в каждой из них необходимо учитывать свою специфику,
которая раскрывается в постановке задачи.
При оценке параметров поляризации ПМ сигнала в общем слу-
чае каждой точке пространства Л* посредством оператора Тп приво-
дится в соответствие некоторая область пространства U. В этом
смысле это преобразование является необратимым. Кроме того,
в задачах оценки параметров наблюдателю не просто необходимо
определить, отличен ли сигнал от нуля или нет, а узнать с наиболь-
шей точностью значения параметров принятого сигнала. Следова-
тельно, здесь мы имеем не две точки, а целое пространство решений,
и приходим к необходимости разделения пространства U па обла-
сти, которым соответствуют различные решения.
Если параметры поляризации ПМ сигнала принимают дискрет-
ные значения Лц Ха,..., лш, то пространство U делится па m не-
перекрывающихся областей. Определение оптимальной системы оцен-
ки параметров поляризации сводится в таком случае к оптималь-
ному разделению пространства U па неперекрывающнеся области
и1л иг... Um различных решений, которое обеспечивает минимум
среднего риска
<7=М[г(Л; Л*)], (7.3.1)
где г(Л; Л*) —некоторая функция потерь.
Функция потерь может однозначно определяться заданием
пары значений параметров поляризации X и X*. В этом случае
средний риск (7.3.1) находится, по формуле
= (Xi X*i) Р(Ь)Р(К*Л). (7.3.2)
Д Л*
180
Однако могут быть случаи, когда при заданных X и X* значения
функции потерь зависят еще от того, по какому правилу выбора
решения Р[\/и] была принята оценка X*. В этом случае средний
риск (7.3.2) определяется по формуле
,=sss г fa tj) Р (С) р (Х%/Х() Р [Y/U].- (7.3.3)
Р — вероятность того, что при передаче ПМ сигнала с пара-
метрами поляризации Х; будет принято решение Х*?, равна вероят-
ности того, что при передаче ПМ сигнала с параметрами поляри-
зации X, колебание и попадет в область Uj. Следовательно, выра-
жения для средних рисков (7.3.2) и (7.3.3) можно переписать
в виде
<7=2 S' Х*5)Р(Х;)Р(^), (7.3.4)
А А*
q - S S S г (xf; X*,) Р (Х4) Р Р [Y/^J• (7.3.5)
Таким образом, при оценке параметров поляризационной струк-
туры необходимо каждой возможной реализации и на входе опти-
мального приемника ПМ сигналов поставить в однозначное соот-
ветствие некоторое значение вектора X из области А, т. е. сформиро-
вать некоторый функционал (p=<pfu (/,; X)], называемый оценкой.
Из-за наличия помех неизбежны ошибочные оценки параметров
поляризационной структуры. Каждое такое ошибочное решение со-
провождается некоторыми потерями, которые, в свою очередь
характеризуются соответствующими функциями стоимости. В си-
стемах связи с дискретными сообщениями или параметрами наи-
большее распространение получила простоя функция стоимости. Под
простой функцией стоимости понимается такая функция, когда стои-
мость правильной оценки параметра принимается равной гп, а стои-
мость всех ошибочных оценок имеет одно и то же значение Гц>гп
.независимо от величины ошибки. В этом случае функция стоимости
г(Х; X*) может быть представлена в виде
т
г (X; X*) - S [Гн — (гн— гп)3) ], (7.3.6)
я • я
k=l
где
( 1, при Х„ =
О-ч „ - “ <
'к 1к I 0, при Хк ф Yk-
Таким образом, согласно (7.3.6) определяется штраф гн за каж-
дый неверно оцененный параметр Хь(&=1, 2,..., т) и меньший
штраф гд, если дана правильная оценка \k = \k. Подставляя полу-
181
ченное выражение (7.3.6) в (7.3.5), получим
т
q=mrs- (,в - гп) S S S S \ т Р W Р («А) Р (Т/«) (7.3.7)
Я я
4=1 Л Д’
где и т. д. обозначают, что суммирование производится по
л
всем допустимым значениям каждого из поляризационных парамет-
ров X*.
Из выражения (7.3.7) следует, что для минимизации риска надо
так выбрать правило выбора решений Р(у/ц), чтобы максимизиро-
вать
= S S \ Th Р А) Р («А) Р (г А) =
= S P(fK) РМ^М,
(7.3.8)
А\
где
Р(М = S РА).
А~АЬ
р (ufa = S р («А).
о-дЛ
р (YiA) = S Р (Ч/“)
А#-А\
В принятых обозначениях
вить в более сжатой форме:
— частные вероятности.
(7.3.9)
средний риск (7.3.7) можно предста-
q = тгп — (ги — гп) S Qk (и; Р).
4=1 £>
(7.3.10)
Далее оптимизация осуществляется путем соответствующего
выбора т правил выбора решений
Р(Ть/и). 6=1.2......... т. (7.3.11)
Этот риск будет наименьшим, если каждое Qk имеет наибольшее
значение, так как при
Р(«/Ть)<1. Р(Тч)<1, P(W«)>0.
Максимизация Qk получается, если положить
Р (Т»/«) = 8 - = 0 при ф у*,
(7.3.12)
(7.3.12а)
182
где ул = [Xft] — безусловная оцёйка максимального правдоподобий flfl*
раметра Хк, определяемая выражением
Р (Х„) р («Ан) > р (Х„) Р {Ц/Ю (7.3.13)
при всех значениях Ха из области Ль
Таким образом, мы пришли к выражению байесова риска:
Я = <7min = wrK — (Гн - rD)S S Р Ал) Р ЩК) (7.3.14)
Необходимо отметить, что для принятой функция стоимости
оценки параметров поляризационной структуры ПМ сигнала Xi*,
• •» * представляют безусловные оценки максимального прав-
доподобия ун=Х* каждого нз параметров X* в отдельности. Пара-
метры поляризационной структуры сигнала статистически связаны
между собой, что определяется Р(и/Х), прячем каждая из веро-
ятностей Р(Хн) и Р(«/Х*) содержит такие связи, но безусловные
оценки максимального правдоподобия определяются независимо
друг от друга. Следовательно, при простой функции цены опти-
мальным является решение, принимаемое по максимуму правдопо-
добня, а оптимальный оператор системы имеет вид u^Uj (или
Х*=Х/), когда удовлетворяется система неравенств
Р > Р (и/\к) при i#-j. (7.3.15)
Если пространство принимаемых колебаний U параметров Л
и решений Л* непрерывно, то простую функцию цены можно пред-
ставить в виде
г (X; Х*)=г,2 К-ЙСГЛ-Х*)], (7.3.16)
fe=l
где
п=гн—гп; гл=г'лгн/(гн—гп);
— постоянные, положительные, имеющие размерность дельта-
функции (т. е. | X* |-1), выбранные таким образом, что средний риск,
соответствующий каждому поляризационному параметру сигнала
Xs, был равен нулю нлн больше его.
В соответствия с вышеизложенным средний риск
й=1
Гл-J , (7-3.17)
где
Qa («; f) = f f (Yh) f (u/fk) f (Ys/«) dfK. (7.3.18)
183
Оптимизация будет достигаться путем выбора правила решений
f (Yh и), чтобы величина Qh (и, f) принимала максимальное значение.
По аналогии е выражением (7.3.12а)
Hy*/«)(7.3.18а)
где Yh = представляет безусловную оценку параметра поляриза-
ционной структуры, определяемую выражением максимального прав-
доподобия
/ (7.з.19)
при всех значениях 7.л по области Л.
Таким образом, оптимальной оценкой параметра поляризацион-
ной структуры можно считать величину Хл, при которой безусловная
функция правдоподобия F(U-, X) достигает наибольшего значения,
т. е. оптимальная оценка является корнем системы уравнений
-^-ЛД(В)(^; Л) — О,
д -*
ТГ-(„)((/; Д) = О,
г)Х1 (7.3.20)
Fд vh) (77; Л) - •• 0,
где FД (U-, Л) = Р (X) Р (ц/Х); Fн (U-, Л) = f (X) f (а/Л).
Для оптимальной оценки параметров поляризационной струк-
туры при передаче дискретных (или непрерывных) сообщений опти-
мальная система должна формировать по принятому колебанию и
и априорной статистике безусловную функцию правдоподобия Дд
(пли Fu) для множества возможных значений сообщений Л и вы-
бирать значение Х* = Х, соответствующее максимуму этой функции.
Характер оптимальности оценок поляризационных параметров за-
ключается в том, что минимизируется средняя вероятность оши-
бочных решений.
Простую функцию стоимости желательно применять в системах
с ПМ сигналами, в которых нет оснований различать стоимости,
связанные с различными ошибками. Однако в системах передачи
количественной информации стоимость ошибки возрастает по мере
увеличения абсолютной величины ошибки. Поэтому величина функ-
ции стоимости r(X; X*) также должна возрастать по мере увели-
чения ошибки, допускаемой системой с ПМ сигналами.
При оценке векторного параметра X можно пользоваться в прак-
тике инженерных расчетов квадратичной функцией стоимости,
которую можно представить в виде
т
г (X;X*)=7„S П,к(Х(-Х\) (Хл-Х*„), (7.3.21)
i, k=l
184
где ||г;,л|| — некоторая симметричная неособенная матрица, г0>0.
Эта функция стоимости равна квадрату расстояния оценки от
истинного значения параметра. Широкое применение ее обусловле-
но тем, что она удобна с математической точки зрения, достаточно
хорошо учитывает большие значения ошибок по сравнению с ма-
лыми и, кроме того, в некоторых случаях приводит к методам, ос-
нованным на критерии минимума средпеквадратической ошибки для
линейных систем с ПМ сигналами.
Средний риск определяется в этом случае выражением
т
rtA\tdu\cKi--K\')(Xk-W)f^fiu3.)dK. (7.3.22)
Если функция стоимости дифференцируема по отношению к опе-
рации оценки, то получается следующее условие минимума среднего
риска:
-> -> -- dr (X; X*) -> Л
^min = I du V (М f ("А) ----------=3---dX °-
J J дХ*
(7.3.23)
Условие экстремума, т. е. минимума функции стоимости
, dr (X; X*)
W (X) f («А)-------
J дХ*
Л
dX = 0.
(7.3.24)
Минимизация среднего риска (7.3.22) приводит к минимизации
эллипсоида рассеяния совместных оценок параметров поляриза-
ционной структуры, который определяется матрицей II<7min II с эле-
ментами (7.3.23). Для практики определения качественных харак-
теристик радиолинии с ПМ сигналами наибольший интерес пред-
ставляют диагональные элементы матрицы ||*7min г,л!1, которые
определяют дисперсии различных параметров поляризации, образую-
щих X*. При допущении некоррелированности параметров поляри-
зационной структуры матрица ||</min т,а|| вырождается в диагональ-
ную и оптимизация заключается в минимизации дисперсий ошибок
по каждому из параметров.
Подставляя в (7.3.24) квадратичную функцию стоимости
(7.3.21), получаем
Xf (и, X) dX
f Xf (Х/и) dX = £—_> _ > (7.3.25)
д j f (и, X) dX
д
где f (и, X)—совместная плотность вероятности входных колебаний
ц и параметров X,
185
Таким образом, независимо от вида матрицы ||Ггл11 оптимальная
оценка определяется из системы уравнений
J (A,-A*I0«)f (A/«)dl = 0,
А
f (Аг А*гоп1) f (A/И) d\ = О,
v (i
А
J(An-A*„onI)f (A/«)dA = O,
Л
аналогичной {36].
Мы рассмотрели решения по оценке поляризационных парамет-
ров, получаемые при использовании двух наиболее распространенных
функций стоимости: простой и квадратичной. Хотя число возможных
функций стоимости в теории ие ограничивается, в практике оно огра-
ничивается реально существующими способами передачи информации,
видом сигналов и т. д. Поэтому применения других разумных функ-
ций стоимости может привести к получению новых оптимальных
операторов оценки параметров поляризационной структуры. Однако
оператор оптимальной приемной системы в очень многих, практи-
чески важных случаях остается некритичным к виду априорного
распределения, к выбору критерия качества системы. Это объясняет-
ся тем, что оценка параметров поляризационной структуры ПМ
сигнала необходима тогда, когда априорное распределение вероят-
ности f(A), существенно шире апостериорного f(A/«), а следователь-
но, и функции правдоподобия f(«/A);
Поэтому f(A) в окрестностях максимума функции правдоподо-
бия можно считать постоянной f(A) = const, и тогда
f (и/А), ХеСт±Д- (7.3.27)
Кроме того, в реальных условиях работы системы функция апо-
стериорного распределения вероятности f(A/«) практически имеет
нормальный закон распределения. Чтобы конкретизировать задачу
синтеза оптимальных структурных схем приемных систем ПМ сигна-
лов, остановимся несколько подробней па анализе аддитивных и
мультипликативных помех и механизме их воздействия на параметры
поляризации сигнала.
7.4. ВОЗДЕЙСТВИЕ АДДИТИВНЫХ ПОМЕХ НА ПМ СИГНАЛ
На двухкомпонентную антенну приемной системы
ПМ сигналов кроме полезного сигнала, несущего инфор-
мацию о переданном сообщении в поляризационной
структуре, поступают аддитивные помехи, которые,
складываясь с собственными шумами антенны и прием-
186
йбго тракта, снижают или полностью исключают воз-
можность обнаружения, различения, а также оценки
параметров поляризации ПМ сигналов. Чувствитель-
ность современных приемных систем, использующих
малошумящие СВЧ усилители, определяется в основном
помехами, действующими непосредственно на входе
приемного устройства [36, 37, 38]. В радиолиниях связи,
использующих ПМ сигналы, применение которых осо-
бенно перспективно в сантиметровом, миллиметровом
и более коротких диапазонах волн [12, 13], естественные
помехи, действующие на входе приемной системы, со-
здаются излучением окружающей среды и космическим
излучением. Будем представлять их в виде вектора
По(/), компоненты которого считаем стационарными и
стационарно связанными нормальными процессами (с ну-
левыми средними <n0t>=0, i=l, 2) и корреляционной
матрицей
RAWt) = <па (/,) «г(/2)>. (7.4.1)
где [ ]т — индекс транспонирования.
Кроме перечисленных помех, в СВЧ диапазонах волн
имеют место хаотические отражения, которые возникают
в силу различного рода обстоятельств [5, 15]. Помеху,
обусловленную хаотическим отражением ПМ сигнала,
можно описать вектором случайных импульсных харак-
теристик h(t; т), компоненты которого имеют нулевые
средние </ггД/; т)>=0, i, j=l, 2, и корреляционную
матрицу
Rh*2; ъ; ъ)=<h а>;ъ)>• (7.4.2)
-Тогда помеха, вызванная хаотическими отражениями,
пересчитанная на вход двухкомпонентной антенны, опре-
деляется из выражения
(0 = J hT (t; т) S (т; Л) t/т:,
—00
(7 4.3)
где
5(т; Л) =
S, (т; К) О
О S2 (т; К)
187
Корреляционная матрица компонент «<-,(/) определяет-
ся как
Re (tt; Q = J J s1 (x,; X) Rh (tt; t2; т,; x2) S (т2,1) d^d^.
—00
(7.4.4)
При условии независимости векторов n0(t} и ne(t) ком-
поненты суммарного вектора аддитивной помехи
п (/) = п0 (/) + пе (/) (7.4.5)
будут также нормальными случайными процессами с пу-
левыми средними </ii(/)>=0 и корреляционной мат-
рицей
Rn (Л; Q = <П (/.) пт (t2)> =RB (Л; Q + Re (/.; /3).
(7-4.6)
Аналогичные рассуждения можно распространить и на
помехи, возникающие в антенно-волноводных системах.
Поэтому в дальнейшем используется суммарный вектор
n(t) аддитивной помехи, которая считается стационар-
ным процессом, т. е. ее ортогональные компоненты rii(t)
стационарны и стационарно связаны. В очень многих
практически важных приложениях аддитивную помеху
можно считать широкополосной в том смысле, что ши-
рина энергетического спектра значительно больше ши-
рины спектра ПМ сигнала. В то же время ее можно
считать узкополосной в том смысле, что ширина энерге-
тического спектра помехи во много раз меньше цен-
тральной частоты спектра <о0. Компоненты такой помехи
в ортогонально-круговом базисе в точке приема можно
представить в виде
Пг(/)=«,(/)cos[<о/—фг(/)], 1 = 1, 2, (7.4.7)
где а,(/) и <р,(/)—соответственно амплитуды и фазы
компонент, представляющие собой медленно меняющие-
ся случайные функции по сравнению с at.
Вводя в рассмотрение квадратуры аддитивной по-
мехи, (7.4.7) можно записать как
tii(l) —nci (/)cos <0^4- nSI (/)sin at, (7.4.8)
188
где
nci(t) = at (/)cos <р, (/), nei(/) =at(t)sin <pf (Z).
Как правило, квадратуры аддитивной помехи nCi(t)
и rtSi(Z) являются нормальными независимыми случай-
ными процессами. Следовательно, для нормальной адди-
тивной помехи n(t) с пулевым средним плотность ве-
роятности
ИМ/)]——=j==x
2л V det Rn (/,; /2)
Хехр [-4- nT(Q (/,; /2) п (Z2)J, (7.4.9)
где
det/?„(/,;/2) — определитель корреляционной матрицы
Rn (/, — /2) = <п (/,) п (/2)> — RnQ (/, — /2) cos ю (/,— /2);
Rnc (/. - 4) -<«с (/.) пТс (Q> = <ns (/,) nTs (/2)>;
4 (/) || /гс_ (/) /zCi(/) ||, ? (/,) = |1Ч (/) /zs2 (/) ||;
/?’(/,;/2) — матрица, обратная /?„(/,; /2).
Если среднее значение векторного случайного про-
цесса /?(/) не равно нулю, то в (7.4.9) необходимо
вместо п(/) подставить центрированный векторный про-
цесс
/?0 (/) = /? (/') — //„, (7.4.10)
где «„ — </? (/)>^0.
Известно, что строго монохроматическая аддитивная
помеха всегда полностью поляризована [7]. Неполяризо-
ванная помеха характеризуется тем, что конец электри-
ческого (магнитного) вектора движется совершенно не-
регулярно. В общем случае изменение векторов поля
помехи не является пи вполне регулярным, ни вполне
нерегулярным. Поэтому в большинстве практических
задач мы встречаемся с квазимонохроматической поме-
хой, обладающей частичной поляризацией. К частично
поляризованным помеха.м относятся электромагнитные
поля с функциональной поляризацией, когда параметры
поляризации изменяются во времени по произвольному,
189
йо йпоЛне определенному Закону, а таюке Поля с флюк-
туационной поляризацией, когда параметры поляриза-
ции изменяются по случайному закону. Для таких помех
все наблюдаемые явления зависят от интенсивности
двух произвольных взаимно ортогональных компонент
электрического вектора, перпендикулярных к направле-
нию распространения, и от существующей между ними
корреляционной связи [7].
Квазимонохроматической помехе характерны незна-
чительные изменения амплитуд и фаз ортогональных
компонент за любой интервал времени, малый по срав-
нению со временем когерентности, т. е. малый по срав-
нению с величиной, обратной эффективной ширине
спектра помехи А/. Тогда интенсивность помехи, рас-
пространяющейся вдоль оси в направлении, которое
образует угол в с положительным направлением оси
прямоугольной системы координат [ogrjg], принимает
вид
N (а; А) = cos2 а -f- sin2 а -f-
-|- 2а6а cos a'sin а | р | cos (р — А), (7.4.11)
где
<\ (0 п* (/) >
р = —........... - -1 =
/<А (0 п\ (/)> <nv (0 п\ (/)>
= |р|ехр(/р);
А — фазовое запаздывание ^-компоненты электрического
вектора относительно ^-компоненты;
2
%
р — элементы корреляционной матрицы
Яп(0) =
’tw
2
0,1
(7.4.11а)
Для неполяризованной помехи, у которой N(a; А) =
= const, из (7.4.11) находим, что N (а; А) не зависит
от а и А тогда и только тогда, когда
Р>0 и (7.4.12)
Следовательно, корреляционная матрица для неполяри-
зованной помехи гауссового шума равна
Rn(t-Q = ^- ’ ° |s(G-и. (7.4.13)
U 1 |
190
где jV0 = 3^4- 3^ — полная интенсивность непрляризован-
ной помехи; 8(^— Q — дельта-функция.
Полностью поляризованная помеха имеет корреляцион-
ную матрицу вида
’« , (7.4.14)
exp (— /х)
^n(0) =
где
Х = ^(0-^(0-
T. e. /?п(0) для немонохроматической волны, у которой
отношение амплитуд и разность фаз не зависят от вре-
мени, совпадает с корреляционной матрицей монохро-
матической волны с ортогональными компонентами
/Zt(0 = Vxp[/(a>0~<Pt)], ) (7415)
«ч(0 = *’6ехр [i(<rf — ?t + X)]. I
При повороте системы координат {og-qg-J на угол 0
вокруг оси о£ элементы матрицы (7.4.11а) трансформи-
руются в выражения
a^,= <4 cos2 9.+ sin2 9 + 23Еат;cos — ?,) cos 9 sin 9.
— a*) cos 9 sin 9 + a^p cos2 9 — <y6p sin2 9,
a^,= sin2 9 + cos2 9 — 2^ cos (?t — cos 9 sin 9,
a ,at,p' — a,,a ,p'*. (7.4.16)
Г E'r t' 4'r v '
Как видно из (7.4.16), след и определитель матрицы
/?„(0) инвариантен относительно поворота системы ко-
ординат. Модуль коэффициента корреляции зависит от
выбора системы координат, однако по своей величине
он не может превышать единицы, что следует из нера-
венства Буняковского — Шварца [7, 19].
Если оси системы координат повернуты на
угол 0 = 0', определяемый из соотношения
tg 29' = (a* — aj )/(о£ач + a^p), (7.4.17)
то из (7.4.16) находим, что а., = <з . В силу последнего
2 2
равенства, а также, вещественности и уравнение
191
(7.4.17) всегда имеет вещественное решение для 0'.
Следовательно, всегда существует пара взаимно ортого-
нальных осей координат (положение двухкомпонентной
антенны), для которых интенсивности ортогональных
компонент помехи равны, а |р| принимает максималь-
ное значение. Это позволяет судить о потенциальной
возможности подавления аддитивных помех, имеющих
корреляционную зависимость между компонентами, из-
вестными компенсационными или иными методами.
Известно, что любую квазимонохроматическую помеху
можно рассматривать как суперпозицию регулярно по-
ляризованной и неполяризованной помех, не зависящих
друг от друга, и что такое представление единственно.
Тогда интенсивность поляризованной помехи будет
равна
^I=|/'(^ + ^)=-4det^n(0), (7.4.18)
а полная интенсивность помехи
= + . (7.4.18а)
Следовательно, степень поляризации частично поляри-
зованной помехи можно характеризовать величиной
0<|/ 1 - 4det у.
(7.4.19)
Из анализа (7.4.19) следует, что, когда подкоренное
выражение равно единице, det/?п(0) =0, а |р| = 1, де-
поляризованная компонента отсутствует и, значит, поме-
ха полностью поляризована.
При равенстве подкоренного выражения (7.4.19) нулю
det /?п(0) = 3^> а 1р|— 0, помеха полностью
деполяризована. В остальных случаях, отличных от рас-
смотренных экстремальных, будем иметь частично поля-
ризованную помеху. Так как степень поляризации поме-
хи в отличие от |р| не зависит от выбора системы
координат, то из (7.4.19), раскрыв det Rn(0) и учиты-
вая, что среднее геометрическое двух положительных
чисел не может превышать их среднего арифметическо-
го, находим
1 - 4det Я„(О)/(3; + У'^ | р|. (7.4.20)
192
Для более полной характеристики аддитивных помех
необходимо рассматривать не только их векторные свой-
ства, но и вводить более общие корреляционные матри-
цы, определяющие корреляцию между компонентами
в различные моменты времени:
Д; Д
Рт£ Д’> М
Д’> М
Р,) (Д М
(7.4.21)
Если характер собственной и взаимной корреляции орто-
гональных компонент совпадает, то (7.4.21) можно упро-
стить:
Ы; Q = p(/,;Q
(7.4.22)
2
В этих случаях знак коэффициента взаимной корреля-
ции помеховых компонент определяет наиболее вероят-
ный угол ориентации случайного эллипса поляризации.
Так, при р(Л; ^)>0 наиболее вероятным значением
угла ориентации помехового эллипса поляризации явля-
ется 0п = О, а при p(fr, /г)<0 — значение 0п = л/2 [30].
Для характеристики наиболее вероятного направления
вращения вектора электрического поля помехи, пред-
ставленного в ортогонально-круговом базисе, вводится
[30] параметр
Кп — (oi—Ста)/(oi + oa)-
(7.4.23)
При 0<Лп<1 наиболее вероятным направлением враще-
ния вектора n(t) будет правое, а при —1<Лп<0—
левое. Суммарное электромагнитное поле ПМ сигнала
и аддитивной помехи на входе приемной системы можно
представить в виде
и (/; Л) = S (/; Г) + п (0- (7.4.24)
Применительно к круговому базису разложения (7.4.24)
можно записать как
u(t\ Г) = 7, [S, (t-, Г)+ я, (0] + 72 [S2(t-, 1) + «2 (01. (7.4.25)
где rit гг — единичные орты ортогонально-кругового базиса
разложения,
13—667 193
Подставляя в (7.4.25) выражения St(t; Л) и «г (0, по
лучаем
«1 я) = [SCx (t; Л) + nCi (0] COS <ot —
~ Я) - nSi (ЭД sin mt, (7 4 26)
«2 (^; я) = [SCs (t-3.) + nCi (0] cos ы 4-
+ [sSj(^; l) + «Sa(OJsin®t
где
(t; 2)’= So cos [? (О — it/4] cos 9 (t);
SC2 (I', ty = So cos [? (/)'+ ’'/4] cos в (t);
SS1 Я) — So cos [? (t) — it/4] sin в (t);
SSi (t; 2) = So cos [? (t) + it/4] sin в (t) — квадрату-
сигнала.
ры ПМ
Следовательно, квадратуры входной смеси можно пред-
ставить в виде
wCt (О ty — sCt (t; 2) -J- пс*
5 = \ (Z;f):+«S((O
(7.4.27)
Параметры поляризации электромагнитного колебания
(7.4.25) определяются из соотношений
<p(O = arctg ----1 — .
V U2ci(t-,^ + u2Si{t-, X) +
-V + u2S2 (t; Г)
+ V aca (z; M + 4 G; M
6 (0 = 0,5 [arctg«s (O Z)/«Ci'(0 2) —
— arctg«Sj(O 2)/uCi(0 2)].
(7.4.28)
Из анализа (7.4.28) с учетом (7.4.27) находим, что
аддитивные помехи изменяют по случайному закону
угол эллиптичности <р(0 и угол пространственной ориен-
тации 0(0 эллипса поляризации ПМ сигналя,
194
Входная смесь (7.4.24) будет представлять собой
нормальный случайный процесс со средним значением
<и (f; 2)> = S (t-, Г) (7.4.29)
и корреляционной матрицей
Ru (*,; Q = RnQ + S(/.; Г) ST (t2- 2), (7.4.30)
где учтена независимость ПМ сигнала и аддитивной
помехи. Проведенный анализ физических условий рабо-
ты радиолинии с ПМ сигналами, как следует из выво-
дов § 7.1, нельзя считать полным без рассмотрения воз-
действия на ПМ сигнал мультипликативных помех,
возникающих в различных звеньях радиолинии связи.
7.5. ВОЗДЕЙСТВИЕ МУЛЬТИПЛИКАТИВНЫХ ПОМЕХ
НА ПМ СИГНАЛ
Нестабильности окружающей среды, антенно-волно-
водных систем, поляризационных модуляторов и демо-
дуляторов, а также прохождение ПМ сигналов по мно-
гим заранее неизвестным путям оказывают воздействие
на параметры поляризации, которые несут информацию
о переданном сообщении. Это суммарное воздействие на
ПМ сигналы можно учесть как. воздействие некоторого
поля мультипликативной помехи
* Z,v II Н-01 + Р-? (0 ._ Г ..
- (7.5.1)
|| Рог + Р-2 (0 .
где щи и рог — средние значения ортогональных компо-
нент поля мультипликативной помехи; pi°(0 и p20(0 —
центрированные части этих случайных функций. Тогда
вектор колебаний, действующих на входе приемной
системы с учетом воздействия только мультипликатив-
ных помех, будет иметь вид
u(t; 2) = Re {S (t-, 2) н(0}- (7-5.2)
В ортогонально-круговом базисе разложения этот вход-
ной сигнал запишется как
и (t; 2) = г, Re {[р,01 + р° (0 ехр /<р, (015, (*; *)} +
+ G Re {[ног + И-" (0 ехР Мг (01 ^2 ^)}> (7-5.3)
13* 195
где <pi(O и <рг(О —фазы ортогональных компонент поля
мультипликативной помехи.
Подставляя в последнее выражение значения орто-
гональных компонент ПМ сигнала в круговом базисе
разложения
Sj (f; Я) = So cos pf> (t) — it/4] exp j [<++ 9 (0]>
S2 (t; Я) = So cos [<? (0 + x/4) exp j]wt — 9 (0],
получим
(t; 2) — |xOiS, (/) cos [urf -j- 9 (/)] (/) Sj (t) cos [orf -j-
+ 9 (0 + (01>
u2 (t-, 2) = jj.OaS2 (0 cos [<и/ — 9 (/)] 4- p-2 (0 S2 (/) cos [W —
(7.5.5)
-9(0 + ?, (0].
Отсюда находим, что квадратурные составляющие ПМ
сигнала при воздействии на него поля мультипликатив-
ной помехи имеют вид
uci *) = Si (0 {iw cos 9 (0 + (0 cos [9 (0 + <?i (0]},
«„• (t; Я) = Si (0 Ы sin 9 (0 + (0 sin [9 (0 + <pf (0]},
(7.5.6)
где введены обозначения
S, (0 = So cos [<f> (0 — It/4], S2 (t) = So cos [<? (t) + It/4].
Случайные функции
|ici(0 = ^(0cos?i(0> Hs,(0 = sin <?i(t), (7.5.7)
отражающие воздействие центрированной части поля
мультипликативной помехи, статистически независимы,
имеют нулевые средние и одинаковые корреляционные
матрицы:
h) =
(^i) l^ci i (Л) 1^62 (^2)
<Рч.'2 (^1) 1^*81 (О (^2)
I *Cp*si (^i) ^P’si (^1) Р’аг (^г)^-
I ^P*s2 (Л) Р*81 (^2)^ <^P'S2 (G) HS2 (^г)^
(Л) 1^6 2 2) >
196
= (7'5‘7а)
Поле мультипликативных помех в большинстве случаев
является нормальным, поэтом}' ортогональные компо-
ненты при представлении его в различных базисах так-
же являются нормальными. Однако обратное утвержде-
ние, вообще говоря, не всегда будет верным. В [36, 38]
показано, что в радиотехнических системах связи прини-
маемые по ортогональным каналам колебания X)
с учетом воздействия мультипликативных помех обычно
являются нормальными случайными процессами. Для
полного описания таких процессов достаточно задать их
Математические ожидания
<цг (/; Я)> = рог£г-(/; £) (7.5.76)
и корреляционные функции
Ru (Д, М = <[«г (^; я) — РоД-(^; я")] [«г- (/2; я) —
- РоА Я)]> = Re [5г- Я) £*г- (/2; Г)] R^ (/.; t2), (7.5.8}
где
Ui (/; Я)= р0 A G; Я) + р° (/) Si (t) с os [arf zL 0 (t) <рг- (/)];
Si (t\ Я) = Si (/) cos [o>Z 0 (/)];
В рамках корреляционной теории не всегда возникает
необходимость знать двумерный закон распределения
ПМ сигналов. Часто достаточно бывает ограничиться
их математическим ожиданием и корреляционной мат-
рицей, которые для рассматриваемого случая запишутся
.как
<«(/; X)> = Re {S (/; Я)} р0, (7.5.9)
ад; Q =
М •
(7.5.10)
Если положить, что процесс «(/; X) стационарный и ста-
ционарно связанный, а характер собственной и взаим-
197
( -» 1 °|Л1Р1 (^11 М
= Re 5(/,;Я);
( I стр.2ар.1Ра 1 (^11
a|X;a|j.sPi2 (Д> ^а)
°И2Р2 (^>>
S*T
ной корреляции ортогональных компонент мультиплика-
тивной помехи совпадает, то (7.5.10) можно представить
в виде
Ru (+0)=< 2)
1
(7.5.11)
Математический аппарат теории синтеза и анализа си
стем связи, использующий статистические характеристи-
ки (7.5.7—7.5.11), получается сложным и громоздким,
поэтому в инженерной практике используется сравни-
тельно редко.
Для реально существующих условий работы радио-
технических систем связи, использующих ПМ сигналы,
можно принять идеализацию — случай медленных флюк-
туаций амплитуд и фаз ортогональных компонент ПМ
сигнала. Тогда время корреляции функций цог + щДО.
(Xsi (/) или
Hz (0 — |/^[р-oz + Пег (О]2 + (0>
<?i (t) = arc tg [Isl- (0/(Hoz + Hci (0)- (7-5-12)
отражающих воздействие поля мультипликативной по-
мехи, будет значительно больше интервала наблюдения
или длительности ПМ сигнала, и (7.5.3) можно записать
как
и (t, 2) = г. Re {рч exp /«PjS, (£; 2)} -f-
—r2 Re {jx2exp/<р2 S2 (Z; Л)}, (7.5.13)
где щехр/фг имеют, хотя и случайное, но постоянное
значение на интервале наблюдения или длительности
ПМ сигнала. Полезный ПМ сигнал при этом представ-
ляет собой детерменированную векторную функцию
времени и четырех совокупностей случайных параметров
ортогональных компонент.
Квадратуры ПМ сигнала (7.5.13) запишутся в виде
«е/ (0 Я; а) — р.г50 cos Г<р (/) ^-^- cos [0 (/) -ф- ?г]>
L J (7.5.14)
usi (t-, к a) —- p-iSo cos (0 j Sin [0(0 + ?d,
где X—параметры, отражающие передаваемые сообще-
ния и подлежащие оценке (существенные параметры);
198
а —параметры, отражающие воздействие мультиплика-
тивных помех, обычно не подлежащие оценке (несуще-
ственные параметры).
Подставляя (7.5.14) в (7.4.28), находим, что- мульти-
пликативные помехи, изменяя по случайному закону
амплитуды и фазы ортогональных компонент St(t\ 7),
тем самым изменяют по случайному закону параметры
Рис. 7.2.
поляризации: угол эллиптичности <p(Z) и угол простран-
ственной ориентации 0(/) ПМ сигнала. На основании
замечаний, сделанных в этом и предыдущем параграфах,
ПМ сигнал, принимаемый на фоне мультипликативных
и аддитивных помех, можно представить в виде адди-
тивной смеси
И(t- 2) = Re {S{t- ^|7}4-/7(/)=:S(/;2;a) + <(0. (7.5.15)
199
Для описания такого сигнала в рамках корреляционной
теории достаточно задать его математическое ожидание
<и(/; Z)> — S(Z; Z; а) (7.5.16)
и корреляционную матрицу ^), которая совпадает
с корреляционной матрицей аддитивной помехи, в отли-
чие от (7.5.10), не зависит от 2, и определяется из вы-
ражения
^„(/1Д2) = <[ц(/1; я) — S(/,;X; а)] [ы(/2; Г) —
-5(/2;Г;а)]> = /?п(Л;/2). (7.5.17)
В соответствии с изложенными рассуждениями на
рис. 7.2 приведена классификация помех, которой мы
будем придерживаться в дальнейшем изложении.
ГЛАВА 8
НЕКОТОРЫЕ ВОПРОСЫ ОПТИМИЗАЦИИ ПРИЕМА ПМ
СИГНАЛОВ НА ФОНЕ ПОМЕХ
В радиолинии с ПМ сигналами происходит процесс преобразова-
ния временных процессов (напряжений, токов) в пространственно-
временные (поляризационно-модулированные электромагнитные по-
ля) и обратный процесс преобразования пространственно-временных
процессов во временные. Эти преобразования осуществляются поля-
ризационными модулирующими устройствами и передающими антен-
нами на одном конце радиолинии и приемными антеннами с поля-
ризационными селектирующими устройствами на другом. Теория,
основанная на рассмотрении только временных процессов на входе
селектирующего устройства, не охватывает синтеза антенных систем
и может считаться вполне удовлетворительной, как показано
в [36, 38], для радиолиний связи, в которых основным источником
помех являются внутренние шумы аппаратуры.
В тех случаях, когда в радиолиниях используются ПМ сигналы
и существенное значение нреобретают внешние помехи, теория, осно-
ванная на изучении только временных процессов, не позволяет опре-
делить оптимальные схемы, полностью реализующие потенциальные
возможности приемопередающих систем, ибо не используются в про-
цессе синтеза все априорно известные различия между помехами и
ПМ сигналами, т. е. различия в функциональной зависимости ПМ
сигналов и помех от пространственных координат [£г)</|. Этот недо-
статок восполнился в известных работах [13, 25, 37, 38] предложе-
ниями по пространственной и поляризационной селекции сигналов,
которые непосредственно не следуют из временной теории статисти-
ческого синтеза оптимальных систем. Рассмотрение ПМ сигналов и
помех на входах приемных антенн позволит определить потенциаль-
ные возможности радиолинии с ПМ сигналами и оптимальные си-
стемы пространственно-временной обработки таких сигналов, которые
200
реализуют как частотно-временную, Так и поляризационную се-
лекцию.
Целью настоящей главы является определение структуры опти-
мальных приемных систем, осуществляющих обнаружение ПМ сигна-
ла S(t; л) или оценку его поляризационных параметров на основа-
нии принятой смеси (7.5.15), в течение времени (0; Г].
8.1. ОТНОШЕНИЕ ПРАВДОПОДОБИЯ ДЛЯ ПМ СИГНАЛОВ
На основании выводов, сделанных в гл. 7, оптималь-
ной будем считать систему, формирующую на своем
выходе при обнаружении ПМ сигналов функционал от-
ношения правдоподобия, при оценке поляризационных
параметров — функцию правдоподобия оцениваемого па-
раметра.
Из выражения, отображающего взаимосвязь услов-
ных вероятностей
Р (и) Р (s/u) —Р (S) Р (u/S), (8.1.1)
находим апостериорную вероятность наличия ПМ сиг-
нала
Р (S/u) = P(S)P (u/S)/P (и)
и апостериорную вероятность отсутствия
Р (0/и) = Р (0) Р (и/0)/Р (и).
Принимая во внимание, что
рГ5)Н-Р(0) = ^ + <7=1,
P(S/u) + P(0/u)= 1,
и разделив (8.1.2) на (8.1.3) с учетом (8.1.4), получим
абсолютное отношение правдоподобия
=-Р. JL№) = дог[« (/; я)]. (8.1.5)
1 — Р (S/u) 4 р (и/о)
Полагая априорные вероятности P(S) и Р(0) известны-
ми, часто множитель p/q считают постоянной величиной,
и тогда выражение
P(w/S)/P(u/O) = A[u(/;T)J (8.1.6)
определяет отношение правдоподобия.
201
(8.1.2)
ПМ сигнала
(8.1.3)
(8.1.4)
Апостериорная вероятность P(S/u) из (8.1.5) связана
с Л [u (it; Z)] соотношением
(8.1.7)
q + рЛ. [и (t; А.)]
Таким образом, отношение правдоподобия определя-
ет вероятность наличия или отсутствия сигнала в реа-
лизации. Поскольку реализация позволяет определить
только указанные вероятности, то отношение правдопо-
добия содержит в себе всю доступную информацию о на-
личии ПМ сигнала, которую можно извлечь из опыта ио
его обнаружению.
При неизвестных априорных вероятностях наличия и
отсутствия ПМ сигнала, что является типичным случа-
ем в практике обнаружения, отношение правдоподобия
дает все, что можно получить из наблюдения. Иногда
в таких случаях полагают, что
р'~= <7 = 0,5 и Ло [и (/; Z)] = Л [u (/; Z)j,
т. е. отношение правдоподобия полностью характеризу-
ет вероятность наличия сигнала в реализации.
Если об априорной вероятности наличия сигнала из-
вестно только то, что она мала р<<1, получим и
P(S/u)= pA[u(t; Я)], т. е. апостериорная вероятность бу-
дет пропорциональна отношению правдоподобия. Исполь-
зуя известное в теории вероятности соотношение между
вероятностью Р и плотностью вероятности f(x) случай-
ной величины х, находим
Р (и/0) = f^(u) du, (g j gj
P (u[S) = f (и/S') du.
Подставляя выражения (8.1.8) в (8.1.6), получаем
A[u(t;Z)]=f(^S)/^(u). (8.1.9)
п
Если на входе приемной системы действует аддитив-
ная смесь (7.4.24), то вероятность получения в реализа-
ции величины Uj(t; X) совпадает с вероятностью получе-
ния шума
7ц (/) = ut (t; Z) — St (/; 1). (8- 1.10a)
202
Это, в свою очередь, означает, что вероятность полу-
чения вектора u,(Z; X) в реализации, содержащей сиг-
нал, совпадает с вероятностью получения вектора Ui(t\
2.) —Si(t; X) в реализации, содержащей только шум.
Следовательно, при аддитивности ПМ сигнала и шу-
ма имеем
f(«/S) = L(u-S). (8.1.11)
п
С учетом (8.1.11) выражение отношения правдоподо-
бия в окончательном виде запишется так
(и — $)
Л \и (t; Л)| -- f(“/5) , (8.1.12)
f (и/0) (а)
п
где f(u[O)— условный функционал плотности вероятности
реализации u(t; Z), t [0; 7], при условии, что выборка
взята из совокупности (8.1.10а) при S(/;^) = 0.
В заключение отметим, что все входящие в (7.4.24)
компоненты будем считать узкополосными со средней
частотой соо- Длина интервала наблюдения удовлетворя-
ет неравенству
7’^>2л/соо,
соотношение между степенью узкополости u(t\ Z) и ин-
тервалом наблюдения Т может быть произвольным. Ко-
нец выборки будем считать совпадающим с текущим
моментом времени • t. Обработка выборки совершается
практически мгновенно, что позволяет в момент време-
ни /1 определитьЛ [u(t; Л)], а значит, и вероятность нали-
чия или отсутствия ПМ сигнала внутри выборки в неко-
торый, вполне определенный момент времени. Этот мо-
мент определяется настройкой анализирующего устрой-
ства, заключающейся в том, что на его выходе образу-
ется отношение правдоподобия наличия ожидаемого ПМ
сигнала, совпадающее своим максимумом с моментом
времени, отстоящим на промежуток времени to от конца
выборки. Таким образом,Л[м(^; Z)] означает правдоподо-
бие того, что ПМ сигнал поступил в момент времени
t — to.
203
Известно, что запаздывание 4-момента принятия ре-
шения от момента прихода сигнала должно быть не
меньше длительности сигнала плюс время корреляции
помехи.
8.2. ФУНКЦИОНАЛ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
ПРИ ДЕТЕРМИНИРОВАННОМ ПМ СИГНАЛЕ
Для установления вида функционала А [и (f; Я.)] восполь-
зуемся разложением процесса u(t; Я) в ряд по ортогональ
ным функциям. При модуляции параметров поляризации
электромагнитной волны передаваемым сообщением бу-
дет сформирован ПМ сигнал S(t; %) с изменяющимися
амплитудами и фазам ортогональных составляющих
%) и S2(Z; X). Таким образом, обеспечивается пере-
дача и прием информации как бы по двум каналам (пер-
вому и второму).
Известно, что если элементы корреляционной матри-
цы непрерывны в интервале [0; Г], то для аддитивной
помехи справедливо выражение
= *е[0;Л, (8.2.1)
fe=l
где {УДО! — некоторая действительная ортонормиро-
ванная на данном интервале [0; Г] совокупность вектор-
ных функций, удовлетворяющих уравнению
( V Тк (0 Vi (0 dt = 8kl, 5rz = Р При * =l’ (8.2.2)
( 0 при k^l,
а случайные коэффициенты Nh определяются как
т
Nk=\nT(t)Vk[t)dt. (8.2.3)
Предполагается, что интеграл (8.2.3) сходится в сред-
нем квадратическом, а также, что ряд (8.2.1) сходится
в среднем квадратическом к процессу п(1), Статистиче-
ские характеристики процесса n(J), таким образом, во-
площаются в совокупности случайных коэффициентов
разложения {Ah}. Например, из (8.2.3) и (8.2.1) получа-
204
ем первый и второй моменты этих случайных векторов:
г
M{Nk} = \MT{n(t)} Vk(t)dt,
О
(8.2.4)
M{NkNt} = J
О
T->
V(t2)dt„
(8.2.5)
n
где Z2) — второй момент процесса n(f). Выражение
n
(8.2.5) в общем случае не обращается в нуль; следова-
тельно, Nk не являются статистически независимыми.
Если выбор действительной ортонормированной со-
вокупности векторных функций {Еь(0} является произ-
вольным, то можно выбрать эту совокупность так, чтобы
вторые моменты коэффициентов разложения были тоже
ортогональны, т. е. чтобы выполнялось равенство
(8.2.6)
где ак — некоторая положительная случайная величина,
не равная нулю.
Следовательно, некоррелированные коэффициенты
разложения поля помехи можно представить в виде
т
= [пт (t)Vk(t)dt
К J
о
(8.2.7)
при M{nft} = 0, где {Хй} — совокупность действительных
неотрицательных чисел, если процесс n(t) действитель-
ный.
Обозначив Nk^= V лкпк, можно формально представить
ряд (8.2.1), а также условия нормированности и ортого-
нальности соответственно:
^[0;Л, (8.2.8)
т у
J V>(0 Vt(t)dt=bkl, (8.2.8а)
О
М {nkni} = But, Af{/Zft}=0. (8.2.86)
Как и прежде, равенство (8.2.8) следует понимать как
сходимость ряда в среднем квадратическом к процессу
205
n(t). Таким образом, случайный векторный процесс
представляется в виде суммы квазидетермииированных
векторных процессов вида
Vh nkVk (О,
где пк -- случайные коэффициенты, определяемые взве-
шенным интегрированием этого процесса согласно
(8.2.7).
При выполнении вышеизложенных условий разложе-
ние (8.2.8) является ортогональным разложением про-
цесса n(t) па интервале [0; Т], a {14(01 и {^z<}— соответ-
ственно совокупности собственных векторных функций
и собственных значений, соответствующие этому разло-
жению. Эти собственные функции и собственные значе-
ния имеют нулевые средние, попарно не коррелированы
и имеют одинаковые, равные единице дисперсии. Они за-
висят от корреляционной матрицы /?п(4; t2) процесса
n(t) и определяются из решения однородного линейного
интегрального уравнения
f /G[0; Т]. (8.2.9)
Если среднее значение случайного процесса n(t) отлич-
но от пуля и равно п0, то разложение (8.2.8) следует
использовать для отклонения случайного процесса от
его среднего
/г(0 = «о 4- £ (Z), (8.2.10)
причем ядром интегрального уравнения (8.2.9) теперь
будет не Rn(ti, tz), a Rn(tt; t2) — ПоПот.
Считая мощность ПМ сигнала конечной величиной
т
j ST (t\ Я) S (t- Я) = S] + s[ = S2
oo (8.2.11)
и исходя из векторной формы теоремы Мерсера для дву-
мерных действительных функций, можно получить пред-
206
ставленйе
VlkSkVk(t),
k=i
(8.2.12)
где
Далее, вводя
г
Sfe = -J= fsr(Z; X)Vb(t)dt.
V f^h J
0
Г
= -L=[uT(t- Я) Vb(i)dt,
V Ah J
o
(8.2.13)
(8.2.14)
мы можем представить поступающую на вход двухком-
понентной приемной антенны аддитивную смесь электро-
магнитных полей ПМ сигнала и помехи в виде
= t К4и/Л(0^2КМ^ + ^т(0- (8.2.15)
6=1 А=1
Причем, учитывая (8.2.12) и (8.2.8), имеем
т г т 1T
Af {unut) = -J= f C Ru (t,; t2) Vh (/,) dt. Vi (t2) dtt=
V AfcAj J J I
0 Lo J
= M1— \)> (8.2.16)
где
Ruttd, Q + 5(/i; Я) ST(t2- Ty, (8.2.17)
vs характеризует мощность й-й реализации ПМ сигнала.
Пусть теперь нормальный случайный векторный про-
цесс n(f) задается Своими координатами, т. е. конечной
совокупностью п выборок п.\, п2,. . пп, взятых через ин-
тервалы времени \ = Т1п на интервале наблюдения
[0; Г]- Тогда ортогональные компоненты векторов п,,
t=l, 2, ..., п, можно рассматривать как две совокупно-
сти п нормальных случайных величин
«12........ /гт}, ’ (8.2.18)
^2 (^г) " {^21> ^22, "•> /^2п} • (8.2.19)
207
Корреляционная матрица этих случайных величин будет
блочной размером 2пХ2п:
Rn (tt\ tj) =
ft. (tf, tj)
R„Vi-, tj)
R^; 6)
RzAti; tj)
(8.2.20)
где
Rn (ti\ tj) = п. (tf) n\ (tj)— n, (t{) n\ (tj)-,
Rm ft; tj) = n2 (ti) n\ (tj) — n2 (tf) nT2 ft);
R12 (fi, tj) z= ft) ft ft) ft ft) ft ft)>
ft. ft; tj) = ft ft) n\(tj) — n2 (ti) n\ (tj)-,
i, j = 1, 2...n.
Совместное распределение 2n наблюдаемых случайных
величин представляет собой 2/г-мерную нормальную
функцию распределения
Кп (П) =------ : .... X
(2П)"Г det/?n(/i: tj)
X exp {-----\-n\ti) R~l (tf, tj) n(tj) J, (8.2.21)
где
«Г ft) = 11 «Г ft) «2 ft) II.
Аналогично, для аддитивной смеси и (t; Я.) имеем
t2n (и) =-----. X
(2")n V det/?n(^;M
X exp -----L [ит (ti- Я) - ST Г)] R~l (tf, tj) \
X[u(tj-,T)-S(tj-J)\}. (8.2.22)
Если в качестве координат выбраны случайные векторы,
определенные согласно выражениям (8.2.8) и (8.2.15),
то плотность совместного распределения 2п случайных
ортогональных компонент этих векторов существенно
упрощается. Действительно, если n(t)—нормальный
процесс с нулевым средним, то его координаты (0
208
представляют нормальные некоррелированные, а следо-
вательно, и независимые векторы. Поэтому их 2п-мерное
распределение представляет собой произведение п дву-
мерных нормальных функций распределения независи-
мых случайных величин У hknkV ik(t) и У ЛцП/гУи (/),
имеющих нулевые средние и единичную корреляционную
матрицу,
{2п
—
Ь=1
(8.2.23)
Аналогично, для аддитивной смеси ПМ сигнала и поме-
хи имеем
{2л >
—г (8-2-24)
Подставляя (8.2.23) и (8.2.24) в (8.1.12), получаем
Л [и (t; Я)] = .......цд>
fin («1. «2.......Пп)
12п 2п
А=1 А=1
(8.2.25)
12»
—2~ 54 есть опре-
S I
деленная постоянная величина, которую можно рассчитать,
зная уравнение ПМ сигнала S (/; Я) и статистические свойст-
,ва помехи n(t). Величина множителя ехр
2л
2 ukSk слу-
л=1
чайна, так как в него входят неизвестные наперед реали-
зации щ, i = l, 2, ..., п. Поэтому в случае полностью де-
терминированного ПМ сигнала оптимальным можно счи-
тать приемное устройство, формирующее на своем вы-
ходе
Л [и (/; Я)] = exp j lim
I ZWOO
2n 2n 1 ]
A=1
(8.2.26)
14—667
209
Заменяя в (8.2.26) uh и в соответствии с (8.2.13),
(8.2.14), получаем выражение
Л [и (t; 2)] = exp
(8.2.27)
из которого, меняя порядок суммирования и интегриро-
вания, получим
Л[п (/; 2)] = ехр
О й=1
где
&(/;2) =
(/; Г)
(t\ X)
= 25ftVft(0//2ft. (8,2.29)
k=i
Умножим (8.2.29) слева и справа на матрицу Rn(ti, Л,) и
проинтегрируем по t2:
Т Т 00 _>
J Rn(tc, t2) &(f2; 2)d/2 = j£n (Л; Qj] ^p~dt2. (8.2.30)
О О k=l к
Тогда, подставляя в правую часть последнего выражения
разложение /?п(/,; Q в соответствии с векторной формой
теоремы Марсера
хг- 00
Rn^, Q = 2 2ftVft(Q V[(t2), Z.^0; T^t2, (8.2.31)
A=1
и используя условие ортогональности, а также разложе-
ние (8.2.29), получаем
210
Т оо оо _>
j 2 (Q 2 dt> = S а.; Г)’ (8.2.32)
0 fe=l fe=l
или
J Rn^-, Q»(/s;Z)^2 = S*(f1;A)'. (8.2.33)
о
Исходя из (8.2.28), можем отметать, что в случае
полностью детерминированного ПМ сигнала функцио-
нал отношения правдоподобия включает в себя операции
скалярного перемножения вектора (матрицы-строки)
принимаемой смеси электромагнитных полей ПМ сигна-
ла и помехи u\t- Я) на некоторый вектор (матрицу-стол-
бец) & (t\ Я), удовлетворяющий интегральному уравнению
(8.2.33), и усреднение результата перемножения на интер-
вале времени [0; Г]. С учетом изложенных рассуждений
функционал отношения правдоподобия запишется в виде
Л [и (t; Я)] = ехр
-*Т -* -*
и (ф) & (t-, Я) dt —
т
О
(8.2.34)
где В-(/; Л.) определяется из интегрального уравнения
(8.2.33).
Выражение (8.2.34) для функционала отношения
правдоподобия можно представить в другом виде, опре-
делив &(^; А,) как
т
&(f; £)= [e(f; fos^a)^,,
о
(8.2.35)
где матрица 0(f; Q определяется из интегрально-матрич-
ного уравнения
J RnfaW;
14*
(8.2.36)
211
I—единичная матрица. Подставляя (8.2.35) в (8.2.34),
получаем
Л [и (t; Г)] = ехр К J ur (t; 1) 0 (^; t2) S (t2-, Л) dtxdt2—
I о
—г
о
t2) s(t2- X)dt2dt2
(8.2.37)
Из полученных выражений (8.2.34), (8.2.37) находим,
что функционал отношения правдоподобия зависит от
вида аддитивных помех, на фоне которых принимается
ПМ сигнал, и самого полезного сигнала. В работах [23,
25] показано, что в регулярном случае, когда функцио-
нал отношения правдоподобия существует Л [и (t; 1)]> О,
при любом конечном интервале наблюдения [0; Г] прави-
ло, использующее Л [u(^; 1)], неизбежно приводит к веро-
ятностям ошибочных решений, отличным от нуля. В син-
гулярном случае, когда функционал отношения правдо-
подобия Л[и(^; X)] обращается в нуль или неограничен-
но возрастает, существует возможность достоверных ре-
шений при любом конечном интервале наблюдения [0; 7].
Так как функционал отношения правдоподобия Л [и (/; X)]
является монотонной функцией, то на практике можно
пользоваться не самим функционалом, а произвольной
взаимно-однозначной функцией <p{A[u(t-, X)]}, в частности
его логарифмом InЛ[и(t-, X)].
8.3. СТРУКТУРА ОПТИМАЛЬНЫХ СИСТЕМ ОБНАРУЖЕНИЯ
ДЕТЕРМИНИРОВАННОГО ПМ СИГНАЛА
Положим, что приемная система должна решать про-
стейшую задачу оптимального обнаружения ПМ сигна-
ла, состоящую в проверке простой гипотезы Но, что на-
блюдаемый векторный процесс — стационарный, нор-
мальный, с нулевым средним значением, против простой
альтернативы Hit что этот процесс также нормальный,
но со средним значением S(t-, X).
Такая постановка задачи и связанный с пей расчет
функционала отношения правдоподобия имеет особую
практическую важность для проектирования приемных
212
систем ПМ сигналов, так как на этапе проектирования
часто приходится задаваться сигналом, который необхо-
димо обнаружить. Выбирая расчетный ПМ сигнал, заве-
домо неблагоприятный для обнаружения, мы в какой-то
мере следуем минимаксному критерию обнаружения и
освобождения на этапе проектирования от неопределен-
ности, связанной с незнанием априорной информации.
На основании выводов, сделанных выше, запишем
функционал отношения правдоподобия в виде
Л [u (t; Г)] == ехр [я (Г) — р. (1)], (8.3.1)
где
т
gU) = J(V(fi;l)0(fi;Q S(f2; 1)ЛХЛ2;
o'
т
(8.3.2)
(8.3.3)
В принятых обозначениях ц(Х) определяет энергетиче-
ское отношение сигнал/помеха на выходе приемной си-
стемы, а корреляционный интеграл g{X) представляет
собой выходной эффект, который должна формировать
приемная система для целей обнаружения ПМ сигнала.
В теории синтеза оптимальных приемных систем ПМ
сигналов можно считать, что определяет необходи-
мую и достаточную статистику или выходной эффект
оптимальной приемной системы ПМ сигналов, если эти
сигналы детерминированы.
Пусть ПМ сигнал принимается на фоне пеполяризо-
ванного поля аддитивной помехи с обратной корреляци-
онной матрицей
0(f1;Q=2M;178(^-Q, (8.3.4)
где Мо = 2о2 — спектральная плотность помехи. Тогда
подставляя (8.3.4) в (8.3.2) и (8.3.3), получаем, что
т
g (1) = ^- рГ (8.3.5)
О
т
= K [£,(!) + E2(1)1 = —,
(8.3.6)
213
г
где £/(!)— S? (t; V) dt представляет собой энергию i-й
б
компоненты ПМ сигнала при разложении его в ортого-
“► —►
нальном базисе; Е = Е\ (1) -ф- Ег (1) — полная энергия ПМ
сигнала.
В общем случае некоторые параметры ПМ сигнала
могут влиять на его энергию, поэтому они называются
энергетическими, в отличие от неэнергетических пара-
метров, от которых энергия сигнала не зависит.
Оптимальный выходной эффект приемной системы
(8.3.5) относится к аппроксимации аддитивной помехи
Рис. 8.1.
полем белого шума. Из его выражения находим, что
оптимальная структурная схема приемной системы об-
наружения детерминированного ПМ сигнала строится
по двухканальной схеме, как это показано па рис. 8.1.
Над принимаемым сигналом в структурной схе-
ме осуществляется линейная операция, заключающаяся
в формировании корреляционного интеграла (8.3.5)
при известных значениях параметров поляризации обна-
руживаемого ПМ сигнала. Это значит, что оптимальная
приемная система обнаружения детерминированного
ПМ сигнала должна осуществлять операцию скалярного
перемножения вектора-строки uT(t; X) на вектор-стол-
бец, описывающий ПМ сигнал Ё(/; %), и полученный
результат подвергать усреднению на интервале време-
ни [0; Г].
Выходные эффекты g’i(^) после суммирования подают-
ся на решающее устройство, которое при сравнении
ё U) = Si W 4" Sz W3C порогом, определенным в соответ-
214
ствии с выбранным критерием, выдает решение «ПМ сиг-
нал есть» или «ПМ сигнала нет». Корреляционный метод
формирования (8.3.5) можно заменить эквивалентным
методом оптимальной фильтрации. В этом случае основ-
ными элементами оптимальной приемной системы явля-
ются два линейных фильтра с импульсными характери-
стиками
/г/(0Х2М,;1 S( (/0 —//_!), (8.3.7)
включенными в ортогональные каналы приемника
(рис. 8.2). h{(t) представляют собой зеркальное отобра-
жение ортогональных компонент Si(t; 7.) относительно
Рис. 8.2.
оси / = 0, сдвинутых па t0. Ограничением, налагаемым
на временной сдвиг to, является условие физической
реализуемости этих фильтров
hi(t)— 0 при /<0. (8.3.8)
Пусть теперь аддитивная помеха имеет корреляционную
матрицу
+ о
(8.3.9)
т. е. ее взаимно независимые ортогональные компоненты
представляют собой сумму белого и коррелированного
шума. Если подставить корреляционную матрицу
(8.3.9) в (8.2.33), то получим
т
+ Z)^ = S4f2; Z),
(8.3.10)
215
где
Vi = sjз2, i = 1, 2.
r
Положив, что Sf(/; Я) и необходимое число 'их произ-
водных на концах интервала наблюдения [0; Г] обраща-
ются в нуль, а также справедливость представления
преобразования Фурье от корреляционной функции
00
F [/?,• (т)]=-^- j^(T)exp(—i^)dz =
—00
(0>2)
Pi (®2)
(8.3.11)
где Л^г-(®2) и РД®2)—полиномы с действительными
коэффициентами, мы можем интегральные уравнения
(8.3.10) свести к дифференциальным уравнениям вида
(-р2) Si (t- Я) = з2Рг- (-р2) &г- (t- Я) + Ni (-р2) &г- (t; Я),
(8.3.12)
где Л(—Р2), ^(—р2) — операторы (p = d]dt).
Изображения решений уравнений (8.3.12) запишутся
как
ft ________Л (—Р2) Si (Р) _
^ЛР)~ (_р2) + Nt (_рг)
~ Nt (-/>’) S* (р)
-^Si(p)-±-------------j--------. (8.3.13)
Pt (—Р2) + 7Г N< (—Р2)
Определив по изображениям функций 'Oi(p) их ориги-
налы, можно представить функции &,(/; X) двумя спо-
собами:
->. г -+
а) М; Я)= рг-(т; Я)/гг ^ —(8.3.14)
О
где
/00
— _L [ Л(—р)ехр(р/) d
2л J ’?Л(-Рг) + ^( -Р2)
—/00
Т
б) (f-, Я) = -i- Sj (t; Я)-f Sj (т; Я) ht (t — -t) dx,
J
о
(8.3.15)
216
где
/00
M0=i J
—/00
(—p2) exp (pt)
<s-
________________________dp.
P (-P2) + ~T Nt (-P2)
Если основной вклад в неполяризованпую помеху вносит
поле белого шума, то &;(/; Z) лучше определять в соот-
ветствии с (8.3.15). При взаимно независимых компо-
нентах, у которых pj/t—/г)=#0 при ti=^t2, значительно
превышающих по своей интенсивности в полосе спектра
ПМ сигнала компоненты поля белого шума, лучше поль-
зоваться X), определяемыми из (8.3.14). Таким
образом, структурную схему оптимальной приемной си-
стемы, осуществляющей обнаружение детерминирован-
ного ПМ сигнала па фойе поля пеполяризованной адди-
тивной помехи, ортогональные компоненты которой в об-
щем случае имеют pi(/i—/2)¥=0 при ti=£t2, можно пред-
ставить в двух вариантах, зависящих от способа получе-
ния функций &;(/; X), представляющих собой опорные
сигналы местного гетеродина корреляционного приемни-
ка или импульсные характеристики соответствующих
оптимальных линейных фильтров в ортогональных кана-
лах приемника.
На рис. 8.3 представлена структурная схема опти-
мальной приемной системы для получения выходного
эффекта g’(X), когда используются опорные сигналы,
определенные согласно (8.3.15). В этом случае каждый
ортогональный капал состоит из двух каналов, причем
один из них полностью согласован для приема 5г(/; X)
на фоне ортогональных компонент поля белого шума,
другой — па фоне ортогональных коррелированных ком-
понент поля пеполяризованной помехи.
Опорные сигналы &;(/; X) для первых каналов опти-
мального приемника определяются в соответствии
с (8.2.33) как
Л)= 1), (8.3.16)
а для вторых каналов, если положить, что в (8.3.9)
Gr—12) = о1;2 ехр (—Р; | ti—t21),
. F[o,2 exp (-p,| h-/2| )] = 2ffi2Pi/(Pi2+®2), (8.3.17)
217
как
W-, й=-К sdt-, *)-4-
2°i Pi
d2S( (t; X)
dt2
(8.3.18)
Если вместо корреляционного метода формирования
оптимального выходного эффекта используется метод
оптимальной фильтрации, то вид частотных характери-
Рис. 8.3.
стик оптимальных линейных фильтров в ортогональных
каналах с точностью до постоянных множителей опре-
деляется выражениями:
— для обнаружения детерминированного ПМ сигна-
ла на фоне поля белого шума
Ki (/<») = Ci J Si (т — i; A) exp (—jmt) dt =
—00
= CiKsi (/<») exp (—/а>от=); (8.3.19)
— для обнаружения детерминированного ПМ сигна-
ла на фоне неполяризованного поля помехи, взаимно
независимые компоненты которого имеют p^/j—/2) у=0
21?
При
Ki (/«>) = CiKsi (>) exp (-/M (1 + or/f?). (8.3.20)
Из выражений (8.3.19), (8.3.20) видно, что частотные
характеристики оптимальных линейных фильтров в орто-
гональных каналах приемника определяются для пер-
вого случая спектрами ортогональных компонент ПМ
сигнала,, а для второго случая — еще и соотношениями
частотных характеристик ортогональных компонент по-
мехи и ПМ сигнала.
В общем случае детерминированный ПМ сигнал при-
нимается на фоне частично поляризованной помехи, кор-
реляционная матрица которой отлична от диагональной.
Для этого случая функционал отношения правдоподобия
Л [и (/; Я)] =
«г(^; ’k)dtxdt2—
2 T
i, 7=1 0
i, /=1,2. (8.3.21)
Это выражение указывает на необходимость иметь
в оптимальном приемнике дополнительно два канала,
как это показано на рис. 8.4, что значительно усложняет
структурную схему оптимального обнаружения детер-
минированного ПМ сигнала на фоне частично поляри-
зованной помехи. Однако этих усложнений можно избе-
жать путем диагонализации корреляционной матрицы
tz) частично поляризованной помехи n(t).
В работах [7, 18] показано, что хотя в общем случае
элементы корреляционной матрицы Rij, не лежащие на
главной диагонали, т. е. при i=£j, комплексны, однако
они являются комплексно-сопряженными. Матрица,
у которой = при всех i и /, называется эрмитовой,
и ее можно диагонализировать с помощью униторного
преобразования. Тогда в соответствии с (8.2.36) диаго-
нализируется и обратная ей корреляционная матрица
е = я;‘.
219
Для ортогонализации компонент частично поляризо-
ванной помехи fit(t) введем линейное унитарное пре-
образование
пт (f) — Un(t), (8.3.22)
Где (0 = |]«1(0«г(0||'
Тогда корреляционная матрица частично поляризо-
ванной помехи примет вид
Rn, = й*т RnU. (8.3.23)
Известно [22], что всегда можно выбрать унитарную
матрицу U при произвольной эрмитовой матрице Rn,
такой, что матрица Rn' окажется диагональной:
Хх О
А ъ
(8.3.24)
где элементы, стоящие в диагонали хь равны собствен-
ным значениям эрмитовой матрицы Rn. Они являются
220
корнями уравнения
det (Rn— х/) = 0,
(8.3Ли)
где х — скалярный параметр.
Унитарная матрица U, выполняющая данное преоб-
разование, состоит из собственных векторов Ut, Иг матри-
цы Rn- Совершив такого рода преобразование, перейдем
от структурной схемы оптимальной приемной системы,
изображенной на рис. 8.4, к эквивалентной ей двух-
канальной структурной схеме, изображенной на рис. 8.3,
в которой необходимо заменить опорные сигналы
в соответствии с проведенным преобразованием.
Техническая реализация приведенных структурных
схем требует конкретизации применяемых ПМ сигналов.
Принципиально не исключается возможность осущест-
вления всех преобразований до выходных сумматоров
непосредственно на несущей частоте. В этом случае не-
обходимая обработка принятой смеси полей ПМ сигнала
и аддитивной помехи может осуществляться в антенно-
волноводном тракте, а последующие элементы мбгут
выполнять лишь операции усиления и нелинейного пре-
образования. Развитие техники волноводных фильтров
позволяет надеяться на возможность технической реали-
зации таких систем, которые обладают по сравнению
с обычной обработкой на промежуточной частоте тем
преимуществом, что значительно снижают уровень соб-
ственных шумов, которые велики в последних системах
из-за смесителей и усилителей промежуточной частоты.
На практике в СВЧ диапазонах мы имеем дело не
с детерминированными ПМ сигналами, а с сигналами,
имеющими случайную начальную фазу, случайную
амплитуду либо случайные фазу и амплитуды. Поэтому
необходимо рассмотреть задачу обнаружения квазиде-
терминированиого ПМ сигнала на фоне аддитивных
помех.
8.4. СТРУКТУРА ОПТИМАЛЬНЫХ СИСТЕМ
ОБНАРУЖЕНИЯ КВАЗИДЕТЕРМИНИРОВАННОГО
ПМ СИГНАЛА
Задача, которую должна решать в этом случае при-
емная система, состоит в проверке простой гипотезы Но,
что наблюдаемый векторный входной процесс стацио-
221
парный, нормальный, с пулевым средним значение^,
против сложной альтернативы Н%, что этот процесс
также нормальный, но со средним значением S(t\ X; ф),
представляющим одну из возможных реализаций, соот-
ветствующих изменению начальной фазы ф в интервале
[0; 2л].
В этом случае квазидетермпнировапный ПМ сигнал
целесообразно представить в ортогонально-круговом
базисе
3 (/; Г; ф) = Re {3 (/; 1)ехр(/ф)} =
= [Sc (/; Л; «>)-ф-35(/; Z; <ю)| соэфЦ-
+ /[Ssl(^; Я; «>)— Scl(/; Z; «фтф,
(8.4.1)
где SC±(Z; Z; «>), S^±(Z; Z; o>) — узкополосные векторные
процессы, сопряженные по Гильберту с соответствующе
ми процессами
S(. (/; Z; о>) = Sc (t; Z)cosW,
Ss(/; Z; o>) = Ss(Z; Z)sin< (8.4.2)
ф— случайная начальная фаза S(/; X; co). Подставляя
(8.4.1) в выражение функционала отношения правдо-
подобия (8.2.37), получаем
Л [и (t; Z; ф)] = exp {[gc (Z) + (Г)] cos ф -ф-
+ (*) — £с± U)l sin <? — Р- Л}' (8-4.3)
где
gc(Z)= и (ts, Z) 0(^; /2)3С(^2; Z;
О
г
gsW— «Г(Л; z) 0(^; t2) Ss (Z2; Z;
gclU)= jp7QSC±(Z2;l; ш)^;
0
gs±U)= ^«Г(Л-Л)0(Л; QSs±(/2;1; <*)dt.dt2,
‘o
222
нй-4- [joP°(/i; ш)^1;
Z; <n)dtxdt2-[-
т
(/,; Ш)0(Л; 4)Ss(/2; Z; w)dtxdt2
о
(8.4.4)
r -> *
[рсГ(^; Z; «)0(Л; ^2)Sc(/2; Z; *>)dtxdt2^
о
=^р1±(Л; MSC±(4;1; ®)d/,d/2;
0
г
Jj Z; u))0(^; ^2)Ss(t>; Z; &)dtxdt2—
oJ
= Jf ^±(Л; ^)\j_P2; Z; &)dtxdt2\
о
T
JJSr(^; Z; «)0(Л; ^)Sc±(/2; Z; <*>)dtxdt2^
о
= fpsr(^; Z; «>)0(Л; QSs±&; I; <»)= 0.
0
Принимая во внимание, что
[gc (1) + gs W1 COS Ф + [gs± (Г) — gc± (Z)l sin (p =
= Q (Z) cos (Ф —']>), (8.4.5)
где
Q Й = ]/[gc (Z) + gs (Z)]2 + [gs± (1) - gc± (Z)]2, (8.4.6)
. x ssi (M — Sc I Й /o .
Ф = arctg-----------------------, (8.4.7)
Sc (ty + Ss (M
а также полагая фазу ПМ сигнала равномерно распре-
деленной в интервале [0; 2л], находим
Л [и (t; Z)] = ехр [—р. (Z)] J ехр [Q (Z) cos (Ф + <]>)] сЩ> =
о
= ехр {-fi(Z)] Л fQ(Z)], (8.4.8)
223
где Jo [ • ] — модифицированная функция Бесселя нуле-
вого порядка.
Так как функция Бесселя Jo [Q (Z)] является монотон-
ной функцией своего аргумента, то решение о наличиии
или отсутствии квазидетерминированного ПМ сигнала
приемная система может принимать па основании срав-
нения с выбранным порогом любой взаимно-однозначной
функции от огибающей Q(X). Функция Q(X) согласно
выражению (8.4.5) представляет собой модульное зна-
чение комплексного корреляционного интеграла
(8.4.9)
где u(t\ Z) и S(/; Z) — комплексное представление век-
торных процессов (соответственно принимаемой смеси
электромагнитных полей ПМ сигнала с помехой п одно-
го ПМ сигнала).
Следовательно, при обнаружении квазидетерминиро-
ванного ПМ сигнала она играет ту же роль, что н g(X)
при обнаружении детерминированного ПМ сигнала. Если
p(X)=const, то Q(X) дает нам достаточную статистику
и может быть принята в качестве оптимального выход-
ного эффекта приемной системы ПМ сигналов. Опти-
мальная система обнаружения в рассматриваемом слу-
чае должна вычислять величину Q(X) согласно (8.4.6)
и сравнивать ее с порогом, определенным согласно
выбранному критерию, т. е. мы пришли к необходимости
выполнения существенно нелинейной обработки. В из-
вестных работах [23, 25, 36, 42] показано, что при оди-
наковых значениях ц(Х) характеристики приемной си-
стемы обнаружения квазидетерминированного сигнала
значительно ухудшаются по сравнению с приемной си-
стемой обнаружения детерминированного сигнала. В по-
следующей главе мы это покажем применительно к при-
емным системам ПМ сигналов.
Если ПМ сигнал принимается на фоне пеполяризо-
ванпого поля белого шума, то
г
ge & “ А^“ j*и dt’
б
224
т
б
т
-> 9 Р ->Т -> -> -*•
gsU)= sr и v>z) Ss(z; z; w)dt,
/v 0 J
0
T
-> 9 p -i. -» ->
^±W = mtJ u Z)\1^ b ^dt-
0
(8.4.10)
Структурная схема корреляционного метода формиро-
вания оптимального выходного эффекта (8.4.6) для слу-
чая обнаружения ПМ сигнала со случайной начальной
Рис. 8.5.
15—667
225
фазой, когда справедливы выражения (8.4.10), приве-
дена на рис. 8.5.
Схема состоит, как и прежде, из двух ортогональных
каналов, каждый из которых состоит из двух групп ак-
тивных фильтров, согласованных соответственно с Scz(Z;
Z; «)), Z; о>) и Ssi(t; Л; о>), (/; л; «>), формирующих
корреляционные интегралы
т
(4 = 777 ^«*4 4S„(/;1; <»)<#.
6
т
-> о р -> ->
P(Z; 4Sc±;(C 4 “Ж
(8.4.11)
т
ga U) = ЛГ- f ui <Л *) Ssl- (/; л; <») dt,
J'o J
о
т
о
суммирующих и вычитающего устройств, квадратичных
детекторов (КД) и устройства, осуществляющего опе-
рацию извлечения квадратного корня.
Активный фильтр, выполняющий операции согласно
(8.4.6), может быть реализован по схеме, изображенной
на рис. 8.6. Действительно, пренебрегая интегралами
с удвоенной частотой в выражениях (8.4.11), находим
т
gcW^--^-^u[(t-,l)Sc(t; l)dt,
i)
т
2)SC(Z; X)dt,
(8.4.12)
T
£s(4 = /- 1)Ss(t‘, %dt,
‘ * 0 I 8
6
T
= ^)dt,
226
Рис. 8.6.
где
a(M) = S cos [?(/) —тг/4] cos 0 (/) 4~/?,(/) cos <h(/)
° cos [<? (Z)—cos0(/) -j- «2 (0 cos % (/)
(8.4.13)
(/. Ъ = 5 ~cosI?(O~*/4lsin0(/) —M0sin?,(0
s ’ ° cos[?(0 — it/4] sin 0(/) — n2 (t) sin ?2 (t)
— квадратуры огибающей входной смеси и (t, Z).
В соответствии с выражениями (8.4.12) в оптималь-
ной структурной схеме обнаружения квазидетерминиро-
ванного ПМ сигнала (рис. 8.6) входной сигнал «(/; X)
сначала переносится на видеочастоты, а затем осущест-
вляется корреляционная обработка. В этом случае необ-
15* 227
Ходимо поддерживать хорошую идентичность ортого-
нальных каналов приемника по частоте настройки, коэф-
фициентам усиления, времени групповой задержки
и т. д.
На рис. 8.7 показан фильтровой метод формирования
модульного значения корреляционного интеграла, за-
Рис. 8.7.
ключающийся в пропускании квадратур ортогональных
составляющих входной смеси через две группы опти-
мальных фильтров с импульсными реакциями
— t- 1),
(8.4.14)
н«(О = ^5и(/о-^; я),
образовании суммы и разности соответствующих выход-
ных эффектов этих фильтров, двухполупериодном квад-
228
ратичпом детектировании суммы и разности, суммирова-
нии продетектированпых величин и извлечении квадрат-
ного корня из полученной суммы. На практике можно
использовать более простую схему (рис. 8.8), состоящую
из согласованных с ортогональными компонентами ПМ
сигнала фильтров н линейных детекторов (ЛД), выде-
ляющих огибающие этих компонент. Такая схема будет
•эквивалентна [23, 41] вышерассмотренным.
Начальные фазы импульсных характеристик, так же
как и опорных сигналов, в рассматриваемом случае
Рис. 8.8.
обнаружения ПМ сигнала могут быть произвольными.
Методы синтеза оптимальных фильтров для различных
сигналов, в том числе для сложных, в настоящее время
разработаны достаточно фундаментально в работах [23,
25, 36]. При приеме квазидетерминированного ПМ сиг-
нала на фоне пеполяризованной аддитивной помехи, у ко-
торой pi(Zi—t2) =т^0 при t^t2, paiti—ti) =0 при i^=j,
опорные сигналы для ортогональных каналов активного
фильтра определяются из решения интегральных урав-
нений
г
М; Z)= J0((; QS0((,; Z; <B)dtx,
о
т
М; Z) = QM.- Z; <»)(«,;
(8.4.15)
(t; 1) = j 0^; Z; v)dti,
и
т -
(^ Z) = J 0 it- Ssj_ Z; 0>) dtlt
и
а импульсные характеристики оптимальных пассивных
фильтров — из соотношений
229
hci (Z) = C^ci (t - Zo; Z), hc l; (0 --- C^c Lj (t - t0; Z),
(8.4.16)
(0 = hs±i(t) =Сг^±((/ — z0; z).
Если нет модуляции угла пространственной ориентации
эллипса поляризации 0, а приемная антенна согласова-
на с принимаемым ПМ сигналом так, что 0 = 0пр, то
Ssi(t; А; со) = к; со) =0 и структурные схемы опти-
мальных приемных систем, изображенные на рис. 8.5—
8.7, существенно упрощаются, так как из упомянутых
групп активных и пассивных фильтров остается одна
группа, согласованная с SC,-(Z; А,; со) и Scjj (Z; к; со).
В тех случаях, когда фоном служит частично поляризо-
ванная помеха, во избежание усложнения приемной
аппаратуры необходимо провести ортогонализацию ком-
понент помехи с помощью линейного унитарного пре-
образования, т. е. определить опорные сигналы или
импульсные характеристики фильтров из выражений
(8.4.15), (8.4.16), полагая, что
j* t7*rZ) /2)^ =/8 (/1 — 4). (8.4.17)
о
Пусть детерминированный ПМ сигнал принимается на
фоне аддитивных и мультипликативных помех, при этом
последние на основании ранее сделанных замечаний на
интервале наблюдения {0; 7] имеют случайное, но по-
стоянное значение. Тогда ПМ сигнал можно в соответ-
ствии с (8.4.1) представить в виде
S(t; Z) = Re{S(Z; Z) jx exp (/ср)} — jx, {[Sc (Z; Z; <o) +
+ Ss(Z; Z; <i>)] cos<|>-j- [Ss± (Z; Z; <») — Sc±(Z; o>)| simp},
где
Sc (Z; Z; <») = (ijSo
Ss(Z; Z; <«) — (ijSo
cos [<f> (Z) — it/4] cos 0 (Z)
cos [<f> (Z) — J—*n/4] cosG(Z)
—cos [<f> (Z) — it/4] sin 0 (Z)
=-^cos [<f> (Z)H-ic/4] sin 6 (Z)
(8.4.18)
COSeoZ;
sin <»Z;
(8.4.19)
230
"г = (Р-i — P-2)/(p-i Ч- М»
щ, [i2 — компоненты вектора-столбца р..
Подставляя (8.4.18) в (8.2.37) и учитывая (8.4.19),
получаем выражение функционала отношения правдо-
подобия для всей совокупности случайных парамет-
ров ц1( ф:
Л [и (t; Z; [i; ф)] = exp {—М (Г) -ф |1Д (Z) cos (Ф, — ф)},
(8.4.20)
где K(Z) определяется аналогично Q(Z); Л4 (/)—аналогич-
но p-(Z); Ф,— аналогично Ф, если вместо ПМ сигналов
(8.4.2) в выражения (8.4.4), (8.4.6) и (8.4.7) подставить
ПМ сигналы (8.4.19). Усреднение (8.4.26) по равномерно
распределенной на интервале [0; 2л] случайной фазе ф
дает
Л[п(ф Z; fi)] ~ 2^" У Л [«(/; л; р.; ф)](/ф —
= exp [—[ij М (Z)] Jo [нЛ U)]> (8.4.21)
а по случайной величине щ, если опа имеет релеевский
закон распределения и т = const,—
- - 1 ( ’и к (X) ]
Л[и(ф Я)]=-------!---— ехрф------1X1 I (8.4.22)
1-<М(Х) ( 2 [1 + 02м (X)] J
Вследствие монотонной зависимости Л[и(Л, А,)] от ЛфА.)
последнюю можно взять в качестве оптимального вы-
ходного эффекта приемной системы ПМ сигнала со
случайными фазой и амплитудой. Заметим, что струк-
турная схема в этом случае не отличается от структур-
ных схем, изображенных на рис. 8.5—8.7, за исключе-
нием дополнительно введенного в один из ортогональ-
ных каналов коэффициента (1—m)/(l + m). На основа-
нии выводов, сделанных в работах [23, 37], можно по-
казать, что оптимальность приведенных структурных
схем для обнаружения квазидетерминированного ПМ
сигнала сохраняется и при других законах распределе-
ния
Используя полученные соотношения, найдем струк-
турные схемы оптимальных приемных систем различе-
231
ния двух ПМ сигналов, что особенно важно для бинар-
ных систем передачи информации с помощью мани-
пуляции параметрами поляризации электромагнитной
волны.
8.5. СТРУКТУРА ОПТИМАЛЬНЫХ СИСТЕМ
РАЗЛИЧЕНИЯ ДВУХ ПМ СИГНАЛОВ
Так же как и рассмотренные выше задачи обнаруже-
ния, задача различения ПМ сигналов эквивалентна
проверке гипотез. Однако в этом случае имеется п+1
гипотеза Но, Ни ..., Нп, что наблюдаемый векторный
процесс u(t; X) является суммой одного из заданной
совокупности ПМ сигналов S(t-, Хо), S(t; Xi), ..., S(/;Xn)
и помехи и(/). При получении некоторых данных
о X) наблюдатель должен решить, какая из пере-
численных гипотез имела место. Возможны случаи, ког-
да наблюдаемый процесс обязательно содержит в себе
какой-либо из ПМ сигналов, т. е. одной помехи на входе
приемной системы быть не может. Тогда имеют место
только гипотезы Н\, Н2, ..., Нп, а гипотезу Но необхо-
димо исключить, приписав ей априорную вероятность
<7 = 0. Таким образом, здесь мы сталкиваемся с много-
альтернативными задачами обнаружения, отличающи-
мися от одноальтериативпых задач, которые являются
частными случаями задачи различения, когда число
гипотез сокращается до двух: Но и Различение двух
ПМ сигналов характерно для различных бинарных си-
стем передачи информации, работающих в условиях
наличия помех.
В начале рассмотрим простейшую задачу различения
двух детерминированных ПМ сигналов, принимаемых па
фоне аддитивных помех. Введя неизвестный параметр
Хо, принимающий значения Хо=1 (присутствует ПМ сиг-
нал S(t; Xi)) и Хо=0 (присутствует ПМ сигнал S(/; Х2)),
мы можем представить поступающую на вход приемной
системы смесь электромагнитных волн сигнала и помехи
в виде
м(/; l) = 20S(f; £) + (1 — Z0)S(f; Я2) + »(0- (8.5.1)
где S(/; X;), i=l, 2 — детерминированные ПМ сигналы
бинарной системы передачи информации.
232
Если различение двух ПМ сигналов проводится по
реализации, наблюдаемой па интервале [0; Г], то функ-
ционал отношения правдоподобия с учетом результатов
предыдущих параграфов, а также [37] будет иметь вид
, т
Л[«(/; л)]----ехр/ иг (/,; Z)0(/,; t2)S(t2; k1)dtldla—
I о
т
— j'j uT (t.; Z) 0 (Д /2) S (t2, X) dt.dK —
0
T
—W; t^S'd^dt^t,-]-
’o’
1 s
+4 fp7 (Z’; ^(/3; W^dtA. (8.5.2)
tu /
Делая замены в соответствии с введенными обозначе-
ниями (8.3.2) и (8.3.3), получаем
Л [и а; X)] = ехр {[g (X) - g (X)] — [Н (X) — Н (X)]} -
(8.5.3)
где
g(X)-g(X) = JJ и (t,-, zw,; М1$а2; *.)-
О
-sa2;X)l^A-
(8.5.4)
Выражение (8.5.4) определяет структуру оптимальной
приемной системы для различения двух детерминирован-
ных ПМ сигналов, принимаемых па фоне помех.
Если помеха представляет собой поле белого шума,
то (8.5.4) упрощается и принимает вид
т
ё (X) - ё (X) = j- f Ur а; X [S а; i)~s а; Х)| dt. (8.5.5)
2V о J
О
Интегралы, входящие в (8.5.3), могут быть интерпретиро-
ваны как расстояния реализации u(t‘, >-) До ПМ сигналов
S(f; X) и S(Z; X).
233
Поэтому правило выбора решений предписывает
оптимальной приемной системе вычислять разность этих
расстояний и сравнивать ее с порогом, зависящим от
выбранного критерия и спектральной плотности помехи.
При критерии максимального правдоподобия принима-
ется решение о присутствии того ПМ сигнала, который
находится ближе к наблюдаемой реализации и(Р, А,).
Следовательно, структурную схему оптимальной при-
емной системы, предназначенной для различения двух
детерминированных ПМ сигналов, можно представить
в виде двух вышеприведенных структурных схем обнару-
жения детерминированного ПМ сигнала, согласованных
соответственно с S(t; Ai) и S(/; Аа), выходы которых
подключены к решающему устройству.
На практике в диапазонах СВЧ, где особенно пер-
спективно использование ПМ сигналов, их начальные
фазы являются случайными величинами, равномерно
распределенными в интервале [0; 2л]. Тогда, используя
представление ПМ сигналов согласно (8.4.1)
S (/; Af) = [Sc (/; Аг-; со) + Ss (/; Аг-; <о)| со/ ф -|“
+ [Ss± (/; Аг-; (о) — Sc± (/; <о)| sin 6 (8.5.6)
и подставляя эти выражения в (8.5.2), получаем
Л[п(/; Л; ф)| --exp {[С (А,) — С (А2)] созф +.
+ [Р (А,) - Р (A2)J sin ф - [р. (А,) - р. (А2)]}, (8.5.7)
где
С(Аг-)-^с(Аг)+^(Аг);
P&) = gsl Й;
£сЙ = J J ит (/,; А)0(/,; /„) Sc (/,; Аг-; <о)Л,Л2;
о
Я)0(/1; /2)Scl5(/2; Аг-; «>W/2;
(Г
£s(X) ~- »Г(Л; Я)0(Л, t)Ss(/2; Az; ^dtxdt2-
o’-
234
gs± (X) = J J Х'(Л; Хе (Л; X; «ИД;
(8.5.8)
н(М = 4- СрГ^; X; °W‘; ^)Х(^;Х; ^dt.dt2 +
-V
Г -I
-|-JJs*(^; Z,-; <о)0(4; t2) Ss (l„\ Z,-; w)dtxdt2 .
о
Если ввести обозначение
[С (I,) - С (1)] cos ф + [Р (X) - Р (X)] sin ф =
— Q(X; X)cos(Ф + Ф)- (8.5.9)
где
Q (Xi 1)=К[С(Х)- С(Х)]= + [Р(Х)- Р(Х)]2; (8.5.10)
Ф —arctg^ , (8.5.11)
с (М) + С (л2)
и усреднить выражение (8.5.7) на всем априорном интер-
вале ф G [0; 2и], то найдем, что
Л \и (Р, X)] = j Л [и (Р, л; ф)] с?ф = ехр {— (X) —
О
— и-(X)]} j Q (X; л2) cos (Ф 4- ф) йф =
= ехр{— [р.(Х)~^(Х)]}Л[<2(Х; X)]- (8.5.12)
Учитывая, что функция Бесселя Л[С(^й iQ] являет-
ся монотонной функцией своего аргумента Q(/L,; Z2), ре-
шение о наличии того или другого ПМ сигнала со слу-
чайной начальной фазой можно принимать на основа-
нии сравнения с некоторым порогом Q(M; X). Функция
Q(M; Xz) согласно выражению (8.5.9) представляет
собой модульное,.зпачение комплексного корреляцион-
235
ного интеграла
IQ Un Ml=-r
ur (/,;!) 9 (^,; t2) [S* U; !>) —
— S*(f2; Л2)] dttdt2
(8.5.13^
Следовательно, при различении двух квазидетерминиро-
ванных ПМ сигналов S (^; Лг) со случайной начальной фа-
зой функция Q(Z,; Л2) играет ту же роль, что и функция
g (Л1)—g(22)| при различении двух детерминированных
ПМ сигналов, и ее можно принять в качестве оптималь-
ного выходного эффекта приемной системы, предназна-
ченной для решения обсуждаемой задачи.
При воздействии на различаемые ПМ сигналы по-
стоянной, но случайной на интервале наблюдения [0; Т]
мультипликативной помехи выражение (8.5.6) перепи-
шется как
S (/; — p,Z1 {|SC(/; Г/; <о) -ф- Ss (?; Гг-; со)] cos ф -ф-
•ф- [Ssj U “)— SC1 (t-, ^i\ <»)]sin'J>}, (8.5.14)
S, (/; zz; a»)-= p.Z1S0
cos О (f) — COS 0 (?)
cos <nf;
(8.5.15)
1 — Г re
TT^cos |?(0+ —
sin0 (0
Sitl co/;
— Hz2)/ Un + Pz2),
uZ1, — компоненты вектора-столбца p.z, i=l, 2.
Произведя соответствующие подстановки в выражение
для функционала отношения правдоподобия (8.5.2),
получим
Л. [и (^; ц; и)] — ехр {[рщСо (Z,) [х21С0 (22)| cos ф-|-
+ Un^oUi)-- Р-21^0(X)] ЭШф—- [р^мХ)— Н^Р-оХ)]},
(8.5.16)
236
где выражения для Со(^). Potyi) и ц0 (Л/) получаются из
(8,5.8) подстановкой Sc (t; It и>), Ss (/; a>) и им сопря-
женных по Гильберту в соответствии с (8.5.15) без
Преобразуем выражение (8.5.16) к виду
М“(4 Л; ц; ф)] = ехр {р.и [Со (1,) - [трГ С° (Лг)1 cos Ф +
+ Им 1 |>о Ui) —
Иц Г 1*° (^1)"
1 — k
1 — k
(8.5.17)
где
п = (и» — н2.)/(Ни + М; k = (1*1! — }*|2)/ (нц + Ни)-
Тогда в соответствии с (8.4.20) можем записать
A[u(Z; 1; ц; ф)] — ехр {— (X; Т2)4“
+ Н1Л(X; Xi cos (Фо — ф)}, (8.5.18)
где
М (X; X) = Но (X) — и» tX);
А(Х;Х) =
|/ [с» с» (Х)]2 + [ро (X) - г+тр» <Х)]2;
(8.5.19)
Гр» (X) - Xi]
Фо = arctg —------Г^ТГ—Г- •
|_С0 (XJ j । п Со (Х2)
Если положить, что плотность вероятности случайной
величины цц является релеевской, коэффициенты п,
k = const, а случайная фаза ф распределена равномерно
па интервале (0; 2л], то, усредняя по всей совокупности
случайных параметров (8.5.18), получим
Л [«(/; Г)|---------------- 1 х
х2)
237
X exp |--°И1,Л )• (8.5.20)
( 2Ii +<Wr. MI J
Вследствие монотонной зависимости Л [и (t; Л)] от
2,) структура оптимальной приемной системы при
выполнении оговоренных допущений будет определяться
выражением (8.5.19).
Таким образом, при различении двух квазидетерми-
нированиых ПМ сигналов приемная система должна
формировать оптимальные выходные эффекты в соот-
ветствии с выражениями (8.5.10) или (8.5.19) в зависи-
мости от того, какой ожидается сигнал: с неизвестной
фазой или неизвестными фазой и амплитудой. Эту
операцию можно осуществить включением на парал-
лельную работу двух оптимальных приемных систем
обнаружения квазпдетерминированных ПМ сигналов,
согласованных соответственно с S(/; М) и S(t; А,2),
выходы которых .подключены к решающему устройству.
Дальнейшим обобщением рассмотренных систем яв-
ляются системы различения т+1 ПМ сигналов. В из-
вестных работах [18, 23] показано, что оптимальные
приемные системы, предназначенные для различения
т+1 детерминированных или квазпдетерминированных
узкополосных сигналов на фоне аддитивных помех,
должны состоять из /71+1 согласованных фильтров,
выходные сигналы которых поступают после стробиро-
вания или детектирования на схему сравнения, опреде-
ляющую наибольшее из т+1 значений выходных эффек-
тов или их огибающих. На основании ранее сделанных
выводов эти утверждения можно распространить и на
различение т+1 детерминированных и квазидетермини-
рованпых узкополосных ПМ сигналов.
8.6. СТРУКТУРА ОПТИМАЛЬНЫХ СИСТЕМ
ОЦЕНКИ ПАРАМЕТРОВ ПОЛЯРИЗАЦИИ ПМ СИГНАЛОВ
В соответствии с выводами, сделанными в § 7.3,
оптимальная приемная система, предназначенная для
оценки параметров поляризации ПМ сигнала, должна
формировать на своем выходе функцию правдоподобия,
которая представляет собой условную плотность вероят-
ности векторного процесса «((; Л), т. е. Л(А,) =ф(м/Л).
238
Часто в качестве критерия оптимальности используется
требование получения эффективной оценки [18, 36],
характеризуемой нулевым смещением и минимальным
рассеянием. Однако эффективная оценка параметров
сигнала существует только тогда, когда удовлетворяют-
ся условия
Л (Я) = ?[«(/; Я)]Ш*Д),
(8.6.1)
где ?[«(/; Я)] — произвольная функция от и(1; Я);
/(Я*/Я)— условная плотность вероятности; k — постоян-
ный коэффициент, не зависящий от Я*.
Эти ограничения приводят к тому, что невозможно
аналитически представить апостериорное распределение
/фЛ/ц) на всем априорном интервале Л и произвести
необходимые усреднения, чтобы вычислить дисперсию
оценки
f (М --=]< J - Я*г-)2 [ Йи) dl>. (8.6.2)
л
Сложными оказываются и решающие устройства при их
практической реализации. Поэтому в настоящее время
наиболее широко используются оценки по методу мак-
симума апостериорного распределения или функции
правдоподобия. Оценка по максимуму функции правдо-
подобия, если Л (Л) в среднем обладает свойством сим-
метрии, совпадает с оценкой по минимуму среднеквад-
ратической ошибки, а в теории оценок доказывается
[22, 37] возможность определения эффективной оценки,
если она существует, методом максимума правдоподо-
бия. К тому же инвариантность функции правдоподобия
по отношению к произвольному взаимно-однозначному
преобразованию позволяет значительно упростить реа-
лизацию структурных схем для получения оценки по
методу максимума функции правдоподобия.
Для определения функции правдоподобия оценивае-
мых параметров поляризации найдем выражение функ-
ционала плотности вероятности нормального случайного
239
векторного процесса «(/; л). Пусть отсчеты при дискрет-
ном наблюдении «(/; X) берутся через равноотстоящие
моменты времени Д = /;+1—t, (z=l, 2, «).*При этом
число выборок X) равно целому числу дроби
(Г+1)/Д, где Т — длительность реализации случайного
процесса «(/; л). В общем случае математическое ожи-
дание M[u(t; Х)]=^0, поэтому совокупность значений
математического ожидания М[м(/; X)] = «o(Z; X) в выбо-
рочные моменты времени можно обозначить и0г = и0(/г; X).
Совокупности значений корреляционных функций в вы-
борочные моменты времени 7?ц(^; tj) =Rnij = Riiji,
Rz2.(ti', tj) =R22ij = RlZji', Rl2(ti, tj)—R2i(tj', h) ~Ri2ij —
— Ri2ji образуют корреляционную блочную матрицу
R(ti; tj) выборки порядка 2пХ2п. Многомерная плот-
ность вероятности 2п-го порядка стационарного нормаль-
ного случайного процесса u(t; X) определяется выра-
жением
f Ол; ^2; > ^п) — у—--------------X
(2п)пУ det«(i4; tj)
Хехр| —tj) (и — «»)*>, (8.6.3)
где
ит = 1| ит и ||; ита = \\и ит ||;
И ц 2г 11 к 0 11 oit 02г 11
“1( {^п’ tti2> ••• > ^in}> == {ч21, и22, • , Ч2П) ,
“в11 {“он> ^012, ... , Ujin}» ^02( ’ {^o2i> 4<j22, ... , Ua2n).
Для нахождения функционала плотности вероятности
необходимо вычислить предел показателя экспоненты
(8.6.3) при
\ = Т1(п—l)=/i+i—tj—>-0, п—>оо.
Определив элементы С11г-3-, C22X-j, C12l-3-, С21г-3- блоков ма-
трицы Д-1(^-; tj) из уравнений вида
п п
S ^22zj^22jfc -=
/=1 у=1
(8.6.4)
240
п п
C^ijRisjk == о, О,
/=1 /=1
мы можем показатель экспоненты (8.6.3) записать как
~ [ S(Wi/ - и°1г) д2 (u‘> ~и°^+
п
Ч- (u>t — uon)
п
IZij Д2
д2
+ Щгг — «огг)
&=1
%^A2(UJ-Hod) +
п
Н" (^2 г Ц)2г)
4,/=1
%^А2 (uj —u02j)
п п
+ S + Я “=.М“>
I, /=1 ;./=1
(8.6.5)
где
W’OIZ > ^21 ' ^2l* ~~ ^021 >
п п
У-£щ2.Д==^9,,йЛ„„Д = ^;
/^1 /^1
п п
У]^Д2= ^WW^ = 0;
/=1
п п
5]^-Д2= 5]^21лД = О;
/=1 ,=1
п п
S^22iJ Д2 _ VI О ..п * .. ,
—Д2- А — / , ^22НК223^-д—»
/=1 /=1
&»« =-£Г- — элементы матрицы 0„ == || Сиц ||;
16—667
241
^1213 Д2 — элементы матрицы
^21Z j 2 11 3 — элементы матрицы
&22ZJ ^22i3 A2 — элементы матрицы
®12-------лТ II II;
®22 Д2 II ^-'222 j || '
Осуществляя в выражениях (8.6.5) предельный пере-
ход при А—>-0, п—>-оо, получаем
{п п
—rS <*х>,+Е “"ахд!+
i, /=1 I, /=1
Таким образом, искомый функционал плотности вероят-
ности нормального случайного процесса u(t; X) с точ-
ностью до некоторого постоянного множителя k, не
зависящего от реализации процесса «(/; %) или от вида
векторной функции м0(£; Л.)> можно представить в виде
F [и (t; 2)] =
2) dttdt2 I = k exp
т
о
X«°(4;
(8.6.7)
где u°(/,; 2)— u(t; Л)— u0(t; £).
Если процессы uz(Z; 2) и Uj(t; 2.) при i^J некор-
релированны, то 0гД^; t2) = 0 при i =/; j и (8.6.7)
242
преобразуется в
, т
F \и (t; 1)] = k exp j — u° Z) 0„; t2) \
т 1
°(/2; + 1)022 (^ 4) <9^; W, •
о J
(8.6.8)
Функция правдоподобия оцениваемых параметров
поляризации при приеме детерминированного ПМ сигна-
ла на фоне в общем случае частично поляризованного
поля помехи получается путем подстановки в выраже-
ние функционала плотности вероятности (8.6.7) нормаль-
ного случайного векторного процесса
n(t)=u (t-, Z) — S (^; Z).
(8.6.9)
Полагая, что 0(^; = t2), будем иметь
A (Z) = k exp
t„) и (t2, Z) dtidt2'-j-
uT(ti- Z)0(^; 4)S(fa; 1)Л,Л2 —
т
Z)0(^;
0
t2)S(t2S)dttdt2
(8.6.10)
Первый интеграл под знаком exp не зависит от оце-
нок поляризационных параметров, поэтому значение
Г г — 1
exp 1----JJ «г(^; Z)0(^; t2)u(t2, tydtidtA
о '
может быть отнесено в постоянный множитель k. Тогда
выражение для функции правдоподобия оцениваемых
параметров % будет определяться выражением
16*
Л (Z) —- k exp
Q S(/2; 1)Л^2 —
243
QS(t2\ tydt'dtz
о
= йехр [g(l) — (*(!)].
(8.6.11)
Для неэнергетических параметров второй интеграл
(8.6.11) под знакОхМ ехр:
р,(1) =
т
i- JJ Sr(ti; 7)0(f,
о
; t2)S(t2-, tydt'dt,,
не зависит от оцениваемых параметров, поэтому по при-
нятой реализации «(/; Л.) при оценке неэнергетических
параметров достаточно сформировать корреляционный
интеграл
g(4 = jJ
о
u(ti, Л)0(^; t2)S(t2-, tydt'dt.,.
(8.6.12)
Из анализа выражений для функции правдоподобия
(8.6.11) находим, что она с точностью до некоторого
постоянного множителя k, не влияющего на структуру
оптимальных приемных систем, повторяет выражения
для функционала отношения правдоподобия, получен-
ные в § 8.2. Естественно ожидать, что для случая оценки
параметров поляризации у ПМ сигналов с неизвестной
начальной фазой, с неизвестной фазой и интенсивностью
функция правдоподобия также будет отличаться от
функционала отношения правдоподобия на постоянный
множитель k. Поэтому структурные схемы оптимальной
оценки параметров поляризации ПМ сигналов будут
строиться из п структурных схем оптимального обнару-
жения ПМ сигналов, каждая из которых настроена на
фиксированные значения параметров поляризации Л.,-.
Выходные эффекты всех этих схем подаются на решаю-
щее устройство, принимающее решение по мак-
симуму правдоподобия. Число п дискретных значений
параметров поляризации, а следовательно, и число не-
зависимых каналов в оптимальной структурной схеме
оценки определяется длиной априорных интервалов
угла эллиптичности фтак—фт/п и угла пространственной
ориентации эллипса поляризации @тах—Qmin, а также
конкретным видом ПМ сигналов. Очевидно, что число
244
каналов п должно быть таким, чтобы при любых истин-
ных значениях измеряемых параметров поляризации фи,
©и хотя бы на выходах двух схем имели место резкие
выбросы сигнальных составляющих выходных эффек-
тов (8.6.12):
gs (X) = J J (/.; X) 0 (Л; t2) S (f2; X) dt.dt,. (8.6.13)
Иначе говоря, расстройка между соседними структурны-
ми схемами обнаружения Xi+i—X должна быть ие мень-
ше ширины области высокой корреляции, которая опре-
деляется по нормированной сигнальной функции (функ-
ции неопределенности). Если нормированное напряжение
на выходе оптимальной системы при полностью детер-
минированном ПМ сигнале описывается корреляционной
функцией
Sr(/1;71)e(/1; /2) S(G; X +Х) dtxdt2
г (X = -----------г - ------------• (8.6.14)
У 2 [ц (X) + ц (X + X]
то при квазидетерминированном ПМ сигнале, когда
используется линейное детектирование для выделения
огибающей, — модулем комплексной огибающей корре-
ляционной функции
|/?(Г)1-
г .
J [ X (/,; X) е (6; h) S* (Z2; X +Х dt'dti
О__________________________________________
]/"2 [ц (X) + Р- (X +Х]
(8.6.15)
а при использовании квадратичного детектирования —
квадратом модуля | R (1) |2 комплексной огибающей. По
этой причине модулю комплексной огибающей корреля-
ционной функции уделяется в теории связи и радио-
локации большое внимание. Именно он позволяет судить
о точности измерения полезных параметров сигнала
(в нашем случае ср и 0).
Ширину области высокой корреляции ХКОрг отсчиты-
вают, как правило, по линии уровня, разделяющей тело
неопределенности на 17? (X) | >0,5 ... 0,7 и |7?(Х)|<
245
<0,5... 0,7, или определяют соотношением
00 у
Якорг= f | R U) гdXi при Zj = O, i^j. (8.6.16)
— оо
Число каналов по каждому из поляризационных па-
раметров ДОЛЖНО быть равно (Xi max—Xi min) /Хкор i, Э об-
щее искомое число
и и и .___ *?тах ^min ®тах ^min /О z? |
¥кор 9кор •
Таким образом, важнейшие качественные показатели
системы связи, использующей ПМ сигналы, — число раз-
решимых элементов пространства сообщений но каж-
дому из параметров поляризации, точность и однознач-
ность оценки этих параметров — определяются видом
функции неопределенности | R (<р; 0) |. ПМ сигнал дол-
жен быть выбран так, чтобы его функция неопределен-
ности обеспечивала заданные качественные показатели
системы.
ГЛАВА 9
НЕКОТОРЫЕ ВОПРОСЫ ПОТЕНЦИАЛЬНОЙ
ПОМЕХОУСТОЙЧИВОСТИ ПРИЕМНЫХ СИСТЕМ ПМ
СИГНАЛОВ
Определение помехоустойчивости радиолинии связи, использую-
щей ПМ сигналы, является сложной и многогранной проблемой. По-
этому в данной работе мы рассмотрим помехоустойчивость отдельно-
го звена радиолинии — приемной системы ПМ сигналов. Предельно
достижимая помехоустойчивость в соответствии с [11, 23, 36] назы-
вается потенциальной. Сравнивая потенциальную и реальную поме-
хоустойчивости приемной системы ПМ сигналов, можно дать оценку
ее качества и указать на наличие еще не использованных резервов,
т. е. в конечном итоге ответить на вопрос, близка или далека при-
емная система от совершенства. Кроме того, знание потенциальной
помехоустойчивости приемной системы при различных способах ко-
дирования и поляризационной модуляции позволяет сравнить эти
способы между собой и указать, какие из них являются наиболее
совершенными относительно помехоустойчивости.
При обнаружении и различении ПМ сигналов критерием досто-
верности, который характеризует помехоустойчивость степенью соот-
ветствия принятого сообщения переданному при заданном поле по-
мехи, обычно является средняя вероятность ошибочных решений
(при использовании критерия идеального наблюдателя или простой
функции потерь).
При оценке параметров поляризации ПМ сигнала на фоне по-
мех необходимо различать два вида ошибок. Первый вид вызван
246
Смещением максимума сигнальной составляющей выходного эффекта
под действием помех вблизи истинного значения измеряемого пара-
метра поляризации. Второй вид ошибок обусловлен возможностью
принятия помеховой составляющей выходного эффекта за сигналь-
ную составляющую.
Так как метод максимума функции правдоподобия при оценке
параметров поляризации ПМ сигналов применим в основном, когда
максимум сигнальной составляющей с вероятностью, близкой к еди-
нице, лежит в окрестности истинного значения оцениваемого пара-
метра, то для характеристики помехоустойчивости приемных систем
оценки параметров поляризации воспользуемся вероятностью падеж-
ной оценки.
Необходимо отметить, что достоверность передачи сообщений
существенно зависит от отношения сигпал/помеха, от рационального
построения всей радиолинии связи в целом и, в частности, от выбора
системы формирования и способа приема сигнала. Помехоустойчи-
вость приемной системы ПМ сигналов при заданном способе коди-
рования и поляризационной модуляции определяется в конечном
счете относительным увеличением сигнала над помехой на выходе
по сравнению со значением этого отношения па входе.
9.1. АНАЛИЗ ПРИЕМНЫХ СИСТЕМ ОБНАРУЖЕНИЯ
ПМ СИГНАЛОВ
При обнаружении ПМ сигналов на фоне аддитивных
помех использование заранее установленного правила
выбора решения связано с возможностью принятия оши-
бочных решений двух родов: ошибки первого рода,
характеризуемой вероятностью ложной тревоги
[Т=1],
s = o
и ошибки второго рода, характеризуемой вероятностью
пропуска сигнала
₽ = [Т = 0].
5^0
Эти две важнейшие величины, характеризующие каче-
ство приемной системы обнаружения ПМ сигналов, яв-
ляются условными вероятностями. Безусловные вероят-
ности ложной тревоги и пропуска сигнала равны услов-
ным аир, умноженным соответственно па априорные
вероятности отсутствия q и наличия р ПМ сигнала,
Рлт = 7«. Aip = pP- (9.1.1)
Согласно критерию идеального наблюдателя прием-
ная система обнаружения ПМ сигнала должна миними-
зировать полную вероятность неправильного решения
Arenu = 7a+P₽ = min, (9.1.2)
247
тогда полная вероятность правильного решения, опре-
деляемая как Рпрп = 1—да—рР, будет максимизирована.
Обычно в задачах обнаружения величина р неизвестна,
однако условная вероятность пропуска сигнала, равная
среднему отношению числа пропущенных ПМ сигналов
к их полному числу, находящемуся в зоне обнаружения,
важнее безусловной, поэтому именно ее целесообразно
использовать для характеристики приемной системы или
обратную ей условную вероятность правильного обна-
ружения
[Y=l] = l—р.
(9.1.3)
Для обнаружения детерминированного ПМ сигнала
оптимальная приемная система должна формировать
выходной эффект
g (% = J J [s’ (Л; 1) + (/.)] 0 (Л; Q S Д2; X) Л,Л2 -
Q
-- gs(ty U)-
Найдем плотности вероятностей f [gn (Л/ S) == 0] и
/[gGQ/S)#^]. Когда векторный процесс u(t\ Л) —S (/; Л)-|-
4~п(0 является нормальным, его ортогональные компо-
ненты также нормальны. Следовательно, g(h), получен-
ная в результате линейной комбинации случайных ве-
личин gi(%), которые, в свою очередь, определены пос-
ле линейных преобразований нормальных ортогональ-
ных компонент Ui(t\ X), нормальна, и нам достаточно
определить средине значения и дисперсии выходных
эффектов при S(t; X) —О, S(/; Л) =/=0.
Если ПМ сигнал отсутствует на входе приемной си-
стемы, то ^(Л) = ^п(2) и среднее значение
-> г —
< gn (Л) > = J J < пТ (Q > 0 (/,; S (/2; 1) dttdt2 = 0.
При наличии на входе приемной системы ПМ сигна-
ла g(K) определяется согласно (8.3.2), а
248
< g (Я) > = J J ST (^; 1) 0 ft; t2) S (t2- 1) dt.dt, =
0
= &(!) = 2h(1).
Дисперсия в обеих случаях будет одинаковой и равной
<^)>=<ffjprft)0ft; 4)Sft;l)?ftW3; QX
XS(^;1) П^> =
i=i
= fjfj^ft; A)0rft; Q<nft)nrft)>Oft; QX
o'
x s ft; Ъ П dti = [ J Sr ft; 2) QT ft; Q S ft; 2) dt.dt, =
i = l 0
= fjsrft; l)0ft; Q S ft; I)d^2 = 2p.(2), (9.1.4)
где учтено, что
J < П it.) пт (/2) > 0 (Z3; dt3 = П> (t, - Q.
о
Для проверки гипотезы о среднем значении нормаль-
ного случайного векторного процесса u(t; %) восполь-
зуемся правилом, изложенным в [23], которое для рас-
сматриваемого случая запишется в виде
g (Л) > In х 4- р. (Л),
где величина х определяется критерием качества.
Согласно этому правилу выбора решения ПМ сигнал
присутствует на входе приемной системы, если выпол-
няется неравенство
JJ иг(^; 1)0(^,; ^dt.dt^M^, (9.1.5)
где
Л10 = In X -J- }л (2),
249
и ПМ отсутствует, если выполняется неравенство, обрат-
ное (9.1.5). Следовательно, условные вероятности лож-
ной тревоги п пропуска ПМ сигнала будут определяться
из выражений
У 4Л(Л (К) 4*, I (М J
Так как для критерия идеального наблюдателя х= 1, то
из выражений (9.1.6) и (9.1.7) находим, что
<% = ?= 1 - Ф (Л)/2], (9.1.8)
где Ф(«) —интеграл вероятности.
В этом случае вероятность правильного обнаружения
в соответствии с (9.1.3) будет равна
[Т=1] = ф[/11(1)/2] . (9.1.9)
s^o
Из полученных выражений (9.1.8) и (9.1.9) находим,
что при р.(Л)~►О, т. е. при очень малом отношении сиг-
нал/помеха, хиВ—1, [1=1]—*0. а безусловные
5^!)
вероятности ложной тревоги и пропуска ПМ сигнала,
если р = <7 = 0,5, стремятся к 0,5.
Если p.(Z)~*‘Oo, что может наблюдаться при очень
больших отношениях сигнал/помеха или при det Q—*0,
аир, так же как Рар и Ра т, стремятся к нулю, а
[1=11—1-
s^o
При обнаружении ПМ сигнала со случайной начальной
фазой, равномерно распределенной на интервале [0; 2и],
250
необходимо найти распределения [|Qn(z)/S) = 0] и
j [Q(z)/S)7^0]. На основании вышеизложенных допущений
можно положить, что компоненты gc (А) + gs (А) и gsl(A)—
— gcl (А) представляют собой нормально распределенные
случайные величины, средние значения которых при от-
сутствии ПМ сигнала и «(/)>-—О равны
<gc(A)+gs(A)>|^ =0, <g,.(A)-g (А)>=0
5-0 ' х -L
при наличии i IM сигнала
<gc(A) + gs(A)>^ = 2|л(А), <gs,(a5-g (А)>=0.
5v:> х ц-
Дисперсии этих случайных величин в соответствии
с (9.1.4) и (8.4.12) определятся из выражений
< {[ge (А) + gs (А)] — 2|Л (I)}2 >
• J j S7' (/,; 1) 0 (/,; t2) So (t2- 1)dt,dt2 |xc (1), •
о
<l£sl(A)— gcl (< > =
= j f S; (/,; A) 0 (/,; /,) Ss (t2- A) dt,dt2 = |xs (A),
()'
< {[gc (A) + gs (A)l — 2p (A)} [gsl (A) — gcl (A)] > =
=- fJSr(^; А)0(Л; QSs(^; A)^,^2=0.
vo
Следовательно, при отсутствии ПМ сигнала случай-
ная величина Q(A) [23, 36] распределена по закону Релея
f[Q (A)/S) = 0] = -5# exp (—21В-1,
2(л(А) [ 4р. (A) J
а при наличии ПМ сигнала [18, 36] распределение слу-
чайной величины Q (А) имеет вид
f[Q(A)/S)^=O]=
251
= exp J — ^-(X) +_2|Х (X) 170 [C; Q (T)]. (9.1.10)
2р. (X) [ 4р. (X) J
Таким образом, случайная величина Q(X). имеет
релеевское распределение, когда верна гипотеза Но, и
распределение вида (9.1.10), когда верна гипотеза Hi.
Поэтому вероятность ложной тревоги определяется по
формуле
00
f Q (X) Q2 (X) /?. ( Л42 1
а — I Д' exp — - V- > dQ (1) = exp г------------— I
J 2р. (X) 4р. (X) ( 4р. (X) J ’
а вероятность пропуска ПМ сигнала—по формуле
С <Э(Х)
J 2р. (X)
Q2 (X) + 2р. (X)
4р. (X)
dQ(I).
ехр.
(9.1.11)
Определение интеграла (9.1.11) вызывает необходи-
мость пользоваться табулированными функциями Рай-
са [22].
Для отыскания порога ограничения, минимизирую-
щего суммарную вероятность ошибки, продифференци-
руем выражение
Q2 О)
4р. (X)
dQ(l) +
Q2 (X) + 2р. (X) | г
z; Но
4р. (X) J
<?/)
/2р. (X)
по переменному порогу ограничения, результат прирав-
няем к нулю, а затем прологарифмируем полученное
равенство. После выполнения указанных операций на-
ходим
лг _ лр + 2р. (X) j 1п ; Г М
4р. (X) 4р. (X) / 2р. (X)
(9.1.12)
Рассмотрим предельные случаи, которые позволяют
найти экстремальные значения порога М.
252
1. При малых отношениях сигнал/помеха, когда
М/ jAti (Г) > 1, In /0 [М//2|л (А)] = М//2|л (А). С учетом
последнего выражения из (9.1.12) следует, что М —
= Kti(A)/2.
2. При больших отношениях сигнал/помеха, а также
при det/?n(^; Q—”0. когда
M/V 2р. (A) < 1, info WV2р. (А)] ж М2/2р(А).
В этом случае порог ограничения определится из (9.1.12)
как М=]/" р.(А).
В остальных случаях, отличных от рассмотренных экст-
ремальных, порог ограничения будет иметь величину
}/~p.(A)/2<7H < ^Р'(А), и для ее определения следует
рекомендовать расчет с помощью табулированных функ-
ций Райса.
Проведенный анализ оптимальных приемных систем
обнаружения ПМ сигналов позволяет сделать вывод,
что вероятности ложной тревоги и пропуска ПМ сигна-
лов зависят не только от щ(А), г= 1, 2, которую по ана-
логии с одномерным случаем [36] можно принять как
отношение сигнал/помеха на выходе приемной системы,
но и от статистических свойств поля аддитивной помехи.
В частности, совершенно очевидно, что при det Rn (ti; fe)—*-
—>0, т. e. когда основной вклад в поле помехи вносит
полностью поляризованное поле, можно достичь увели-
чения вероятности правильного обнаружения ПМ сиг-
нала за счет перераспределения его мощности между
ортогональными компонентами, оставляя неизменной
.суммарную мощность ПМ сигнала.
9.2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ
ПРИЕМНЫХ СИСТЕМ БИНАРНЫХ ПМ СИГНАЛОВ
Пусть сообщение передается с помощью бинарных ПМ
сигналов S (/; А() = || S, (Ц Аг)||, i— 1, 2. При
этом положим, что сигнал S (t; А)) соответствует единице,
а сигнал S (/; А2)—нулю. На каждый из этих сигналов при
передаче воздействует аддитивная, в общем случае ча-
253
Стично поляризованная помеха, так что принимаемые
колебания представляются в виде
u(/; X) = S(/; X)+ //(/)• (9.2.1)
Определим среднюю вероятность ошибки при разли-
чении указанных ПМ сигналов, которая будет характе-
ризовать потенциальную помехоустойчивость приемной
системы при данном способе передачи сообщений. При
приеме таких сигналов реальной приемной системой
помехоустойчивость может сколь угодно приближаться
к потенциальной, но не может ее превысить. Поскольку
при бинарной передаче сообщений посылки ПМ сигна-
лов S(t; к,), соответствующие 1 и 0, являются собы-
тиями взаимно исключающими друг друга, то средняя
вероятность ошибки будет равна
Рош.ср.=Р(1)Р(0/1) +Р(0)Р(1/0), (9.2.2)
где Р(1), Р (0) — априорные вероятности передачи соот-
ветственно S(t; kj) и S(/; 22); Р(0/1), /’(I/O) — вероят-
ности того, что при передаче ПМ сигнала с индексом /
будет принят сигнал с индексом I, i^j, j=l, 2. Часто
эта задача бывает симметричной в том смысле, что
Р(1)=Р(0) и Р(0/1) =Р(1/0). Тогда для вычисления
средней вероятности ошибки РОш.ср, достаточно вычис-
лить Р(0/1) или /’(1/0).
Условная вероятность ошибочных решений /’(0/1)
будет равна вероятности удовлетворения неравенства
между выходными эффектами оптимальной приемной
системы бинарных ПМ сигналов
У.ЙЖ^Х), (9.2.3)
где в качестве выходных эффектов взяты величины
(М — 1п{Л[ц(/; 2)]}—— р- (2/) -f- g (2/; 2j) —|—In /%,
/,) S(/2; 2г)Л,Л2,
(9.2.4)
о
g&; %) = J J ur(t,- t2)S(t2-li)dt4t2,
о
Рг=Р(1) при i = 1, Pi — P(0) при i=2.
254
Подставляя в выражение для g (Рг-; М значение и (t; 2г)
в соответствии с (9.2.1), получаем
g(^t', aj) = gs(J-i', Лз) -|- gn (М> (9.2.5)
где
gs (X; M = fpr('.; МО a.; QS&;
— сигнальная составляющая выходного эффекта;
-> т -> ->->
gn(M = JJ'*7’Р,)9(Л; М5(Л; lj)dtldt2
о
— помеховая составляющая выходного эффекта.
Раскрывая выражение для сигнальной составляю-
щей выходного эффекта, будем иметь
2р. (М —• 2 [(Ац (1/) -|- р,, (Лг) -f-
+ 2pi2]/ Р„(Мр22(М] при <=/;
gs (М М —
' 2 _____________
S P;\V Pftn (X) Рчгп (М
_k, п=1
при i j, k, n—\, 2,
где введены обозначения
P*fcn (^z) '
Рчг (M
P1!! Pi)
Pi > ^г)
(9.2.6)
X)dtidt2",
У/ P*hn Pl) P*hn P2)
(9.2.7)
T
rfp* (^;
0
p
rfcn
а также принято, что
Риг (М =: Р21 (М’
С учетом полученных выражений (9.2.5) и (9.2.6)
выходные эффекты оптимальной приемной системы би-
нарных ПМ сигналов, принимаемых на фоне аддитив-
255
ной помехи, можно представить в виде
(Ф) = Р-11 (Ф) + Р-22 (Ф) + Р-11 (ф) Р-22 (Ф) +
-ф£„(ф) + 1пР(1),
(9.2.8)
(^г) — Р*11 (Ф) Р*22 (^г) %?п Ри (^г) Раг (Ф) "ф
+ 2
k, rt=l
+ 2n(X) + lnP(0). (9.2.9)
Подставляя выражения выходных эффектов (9.2.8)
и (9.2.9) в неравенство (9.2.3), получаем
ёп (Ф) ёп (^i) Ф* Ри (Ф) ~ф Р22 (Ф) "ф
~Ф 2pj2 Ри (Ф^ Р22 (Ф) ~Ф Pi 1 (Ф) ~Ф Р22 (Ф) -ф
+ 2р12 V Р-ц (ф) Р-22 (ф) —
' 2
-2 и Рйп(Ф)рйп(Ф) +ln-P(l)/-P(0).
(9.2.10)
hn
_ k, гс = 1
Случайная величина, стоящая в левой части нера-
венства (9.2.10), представляет собой нормальную слу-
чайную величину со средним значением, равным нулю,
так как <«(/)> =0. Для определения дисперсии этой
случайной величины найдем корреляционную функцию
<£ф(ФЛ£п(Ф) > =
= ЩрГ(/2; ф)0(ф Q (t3)>Q(t3; QX
X $ (Ф; ф) П dti (/,; ф) 0 (ф; ф) S (ф; ф) ЛДф=
= £ДФ;Ф). (9.2.11)
С учето*м (9.2.11) искомая дисперсия случайной ве-
личины, стоящей в левой части неравенства (9.2.10),
будет определена как
[йп (Ф) ёп (Ф)]
2 J Pi 1 (ф) -ф Р22 (Ф) -ф
256
4“ 2р12 VPi1 (40 Р-22 (4) Ч" Р-п (4) +
+ Р-22 (4) Ч" 2p}J Р-И (4) Р-22 (4) —
— 2
_k, п = \
2
S12
(4) P-ftn (4)
(9.2.12)
Вероятность выполнения неравенства (9.2.10) в соот-
ветствии со сделанными замечаниями определится по
формуле
р(о/1) = ----- JX
V^<\Sn (4)-gn(4)]2>
оо
X [ ехР
Мо
fgU4- g” (^)|2-----1 d Jg„ (X) - gn (1,)],
2<[g„ (4)-£n (4)]2> J
(9.2.13)
где
Mo — p (Я,) p(4) — 2
V*1”P-ftn (4)Pftn(4)
Подставляя в (9.2.13) соответствующие значения, по-
лучим условную вероятность ошибочного решения
Р(0/1)= 1-Ф fa +(9.2.14)
(9.2.15)
Аналогичные рассуждения, проведенные для услов-
ной вероятности ошибочного решения Р(1/0), приводят
к результату, что
Р (1/0) = 1 - Ф [а + In (9.2.16)
Подставляя полученные выражения для условных
вероятностей ошибочных решений (9.2.14) и (9.2.16)
в (9.2.2), найдем общую формулу средней вероятности
17—667 -257
ошибочных решений оптимальной приемной системы
бинарных ПМ сигналов:
Р<.шЯ.=Р(1){1-*[а + ^1Пр^]}+
+ Р(0){1-ф[о+^1п£®-]}. (9.2.17)
Из полученной формулы (9.2.17) с учетом (9.2.15)
следует, что средняя вероятность ошибочных решений
при различении двух детерминированных ПМ сигналов
зависит от величины а и априорных вероятностей Р(0)
И Р(1).
Априорные вероятности Р(0) и Р(1) определяются
статистическими свойствами передаваемых сообщений.
Величина а зависит не только от энергии эквивалент-
ного сигнала
$экв(*; *) = $(*; X)-S(/; 1)
при данном уровне помех, как это мы находим у опти-
мальных приемных систем бинарных одномерных сигна-
лов [36], но и от взаимной корреляции ортогональных
компонент ПМ сигналов и аддитивной помехи.
При равенстве априорных вероятностей появления
ПМ сигналов Р(1) = Р(0) =0,5:
1п(Р(1)/Р(0)) =1п(Р(0)/Р(1)) =0, />(1/0) =/>(0/1),
(9.2.18)
формула средней вероятности ошибочных решений упро-
щается и принимает вид
/>ошср= 1—Ф(а). (9.2.19)
Далее можно рассмотреть определение Липер для
случая различения квазидетерминировапных ПМ сигна-
лов и получить результаты, аналогичные результатам
хорошо известных работ [18, 36] с учетом двумерного
характера ПМ сигналов и аддитивных помех. Поэтому
мы остановимся здесь только на определении оптималь-
ного порога ограничения при различении ПМ сигналов
со случайной начальной фазой.
Используя свойство узкополосности принимаемых
колебаний, на основании (8.5.8), (8.5.10) и (8.5.12) для
среднего значения случайной величины Q(M; М полу-
258
чаем
<Q(X,; 0)> = 2[|i (Я,)-|a(1,; Я,)] (9.2.20)
при наличии ПМ сигнала S(t; Я,),
<Q(0,la)> = 2[p(ls; Я,)-|х(Я2)1 (9.2.21)
при наличии ПМ сигнала S(t- Я2).
Дисперсия в обеих случаях будет одна и та же:
<[<?(Я,; 0)- <Q (Я,; 0)>]2> =
= < [Q (0; Я2) - < Q (0; Я2) >]2 > =
= 2 [р (Я,) + р (Я2) - 2р. (Я,; Я2)], (9.2.22)
где т
(X; М=4 ®$(^ X)ад, ij.
о
Так как квадратурные составляющие [С (Я,) — С (Я2)|
и (Р(Я,)— Р (Я2)| распределены по нормальному закону, то
случайные величины Q (Я,; 0) и Q(0; Я2) будут иметь рас-
пределения вероятностей, описываемые законом Райса,
/ [Q (X; 0)] =---_ Q(^0)------X
2 [Р- (Я,) + р (Х2) 2,ч. (X,; Х2)]
X CXp J_____“2 0) + [Р-2 (М) Т Р2 (X,; Хг) 2,и. (Х,)р(Х,; Хг)]
| 4 [р (А.,) -|- р (Х2) 2р. (А.,; Х2)]
х J ГQ(X.; Q)[p(X)-p(X,; Х2)] 1 [,
Р (X,) + р (Х2)— 2р. (X,; Х2) |
(9.2.23)
f [Q(0; Я2)1 =---------X
2 [Р- ( Я,) 4~ р. (Х2) — 2р. ( X,; Хг)]
X еХр |_________Q2 (0; ^-г) —[р-2 (^-г) 4~ р-2 (Я2; х,) —_____*
( 4 [р. (X,) р. (Х2) —
___k 2р. (Хг) р. (Х2; X,)j j Г Q (0; Х2) [р. ( Х2; X,) — р. (Х2)] |
2р. (X,; Х2) ] । р. (X,) -|- р. (Х2) — 2р. (X,; Х2) |
(9.2.24)
71* 259
Полагая априорные вероятности наличия ПМ сигна-
лов со случайными начальными фазами равными, для
средней вероятности ошибочных решений рассматривае-
мой оптимальной приемной системы различения полу-
чаем выражение
0° у у у
Рош. ер = 1 - 0,5 J {/ [Q (Я,; 0)] - f [Q (0; Я2)]} dQ (Я,; Я2).
м
(9.2.25)
При оптимальном пороге ограничения М=М0Пт сред-
няя вероятность ошибочных решений должна быть мини-
мальной. Подставив в выражение (9.2.25) соответствую-
щие плотности вероятностей (9.2.23) и (9.3.24), продиф-
ференцируем интеграл по нижнему пределу и результат
приравняем нулю. Тогда, полагая ц(Я1; кг) =H(ta; М,
после соответствующих преобразований получим
_ Гр- <\|) + Р- <^г) — (Х1; X2)J [р. (~Х,) — р. (Х2)| _
Р (М) Н- 1х (Х2) 2р. (X,; Х2)
__Id / | TIqut [и- (X, > Яг) р ( Х2)] |
[ р. (X,) + р. (Хг) — 2р. (X,; Хг) j
__In у I 44опт [|х (Л,) р. (Л,; Xg)J j (д 2 2g)
|р (Я1) + Р (Х2) — 2р (X,; Х2) j
Рассмотрим экстремальные случаи, которые позво-
лят определить интервал изменения оптимального поро-
га ограничения.
1. При
Мош [р (X,; Х2) Р ( Х2)] ।
Р (Xi) + Р (Х2) — 2р (X,; Х2)
натуральные логарифмы от бесселевых функций нуле-
вого порядка, стоящие в правой части равенства
(9.2.26), приблизительно равны аргументам этих функ-
ций. Тогда равенство (9.2.26) можно переписать в виде
fp (Я>) Р (Х2) 2р. (X,; Х2)J [р (X,) р. (Хй)] _
Р (М) + Р (Х2) — 2р. (X,; Х2)
__ 2р (^-1« Х2) Р (X,) р. (Х2)
Р (М +Р (Х2) — 2р (Х>; Х2)
260
Откуда находим, что
(9.2.27)
2. Если х<^1, то 1п/0(х)~х'2. Тогда положив, что
Мрпт [Р* (A,', А2) Р* (^-а)i ।
р (М) + Р' (А2) 2р. (А.,; А.а)
находим
Af0I1T-—F р + р(3.2) — 2p(2j; Z2).
(9.2.28)
Следовательно, при различении двух квазидетерминиро-
ванпых ПМ сигналов оптимальный порог заключен
в интервале
Р (X) — Р (X) < Af01IT < Кр (X) + Р (X) — 2р (X; К)
и для его определения в общем случае, отличном от
рассмотренных экстремальных, необходимо пользовать-
ся табулированными функциями Райса. Величины ц(Х;),
входящие в выражения (9.2.27) и (9.2.28), определяют
качество приема для конкретного вида ПМ сигналов и
помех.
9.3. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ПОЛЯРИЗАЦИИ
ПРИ ОБНАРУЖЕНИИ ПМ СИГНАЛОВ
Из выводов, сделанных в § 9.1, следует, что полная
вероятность неправильного решения, а также вероятно-
сти ложной тревоги и пропуска при обнаружении
ПМ сигналов тем меньше, чем больше величина ц(Х),
характеризующая отношение спгпал/помеха на выходе
приемной системы. Следовательно, эта величина явля-
ется удобной мерой определения качества работы при-
емной системы, и нам необходимо определить условия,
при которых опа принимает максимальные значения.
Это позволит выяснить возможности поляризационной
селекции ПМ сигналов, основанной на различии в поля-
ризационной структуре полей сигналов и помех. Пусть
сообщение передается при помощи модуляции угла
эллиптичности <р(/) эллипса поляризации электромаг-
нитной волны сигнала. Тогда ПМф сигнал в ортогональ-
но круговом базисе разложения можно представить
261
в виде
S(<; 2) =
[5c.^c(0-5sl^(Z)] cos(«V + 0o)
[5С2ГфС(/)-5в2^(/)] cos(^-0o)
(9.3.1)
где
SC1 — So COS (<p0 — Tt/4); Ssi — So sin (<p0 — it/4);
SC2 = So cos (<p0 + it/4); SS2 = So sin (<?0 4- z/4);
/ло = cos <?(/); F«l==sm<?(t).
Полагая, что ПМ сигнал является узкополосным.
а энергетические спектры его ортогональных компонент
симметричны относительно соо, и пренебрегая слагае-
мыми, содержащими интегралы с удвоенной частотой,
получаем
т
Иф(1) =.-1- f jsr(Z,; 1)0(/,; 4)S(t; 1)«2 =
о
5о
= ~Т~ К-п + sin 2<?'>!Х-11 + 2 cos 2<Ро C0S 26оР‘112 +
+ <22- sin 2<рорЛ,2], (9.3.2)
где введены обозначения
т
<,-г = 4-+ QX
О
X cos ш — Л) dt^dt^
т
t =--- 4 £f vx F*c (^) - (^) мх х
о‘
X cos w — t2)dtidt2\
т
= 4- П F.c - F4S (X F,s О 0,= (Л; Q х
о'
X cos ш (ti —12) dt^dt^
а также принято, что 0,2 (4Х2) — 021 (^;/2). Определив
0(^; t2) из интегрального уравнения
т
J /?п(/.; О0^; 4)^-=78(Л —4) (9.3.3)
б
262
для заданного поля аддитивной помехи, можно вычис-
лить отношение ПМ^ спгиал/помеха на выходе прием-
ной системы. Если поле аддитивной помехи стационарно
и стационарно связано, а интервал наблюдения (0; 7]
много больше времени корреляции полезного сигнала,
то пределы интегрирования в (9.3.3) можно распростра-
нить от —оо до +оо и с помощью преобразования
Фурье получить:
ОО
; i=\ к +as d(°'
--ОО
00
i=4г J(ш) К ~иdu>’
— 00
00
^12= 4г J ^>2 (Ш) 1ае (ш)~ аз
— 00
а* ш l^.(<o + <O0)P + IV(<o- <O0)L,
с (<о) R22 (<о) —/?f2 (<о)
। p*s (м + I2 +1 (<° — мо)!2 ,
Ян («) Я22 (“) — ^2 (“)
i, у =1,2, 17^ j.
Положим, что частично поляризованная помеха имеет
одинаковый характер собственной н взаимной корреля-
ции ортогональных компонент, а ее корреляционная
матрица записывается как
Rn W = Р СО
2
3; 3P2V
2
3„32V з2
cos<«(^ —t2), (9.3.5)
где v — параметр, характеризующий степень взаимной
корреляции ортогональных компонент помехи; р(т) =
= Ро(т) =^ч(т)/(ТЩ.1 — коэффициент корреляции; о? —
дисперсии ортогональных компонент помехи. Введем
также в рассмотрение o2 = oi2 + o22 — суммарную мощ-
ность помехи —н Kn=(oi—o2)/(oi + o2) — параметр, ха-
рактеризующий поляризационную структуру помехи.
Тогда выражения (9.3.4) после соответствующих пре-
263
образований примут вид:
Ф 2(1+/<2) ?
Р'+П 02(1 — >2) (1 +Л„)2 Р'+’
Ф ___ 2 (1 + Кп ) ф
н_ц— о2 (1 _ ,2) (1 + Лп)2 (9.3.6)
аФ — 2(1 + FJ2 ф
^422- 02 (1 v2) (1 _ /(J2 **+
О 2(1—Л-2) „
^-22 02(|_уг)(1_Лп)г
Ф 2(1+^)
-I-’ 02 (| _ (1 _ ) -
где обозначено
[^фс (® + “о) ;2 + if (<о — <о0) 11г +
ф_ 1 С +[|Flfs(w + <o0)|2 + |Flp, (<о —<о0)|2]
8л ) р (со)
—00
li^ (W + «о»)12 + |F9C. (со — Wo)i2]—
Ф _ 1 Г — [|/\5 (со + С0,)|2 + (со — <О0)|2J
8л ) р (со)
—00
Подставляя полученные
окончательно получаем
выражения (9.3.6) в (9.3.2),
So 1 + ^
а2 2(1 — V2)
ц? /__!___I----!__4-
и+ )(1 + /<п)2^(1-^)2^
+ sin2?0 [(1 +к„)2
1 ] 2ч cos 2»0 cos 29О
(1 ~ KJ2] Y
(9.3.8)
где 0<у = pl/p’ 1, есл11 |<Р(О I ^л/4.
Очевидно, что оптимальное значение
эллипса поляризации ПМ9 сигнала
угла ориентации
определяется из
уравнения
(И
с/8о
v cos 2<р0
(l-v2)(l-^J
sin20op* —0. (9.3.9)
1\0)=--
Считая, что фо=#'л/4, а аддитивную помеху — частично
поляризованной с | Кп | < I, v=40, из уравнения (9.3.9)
264
с учетом (9.3.7) находим
6 = /0
\т./2
при
при
v < О,
0.
(9.3.10)
Таким образом, при частично поляризованной аддитив-
ной помехе наблюдается связь между оптимальным
значением угла ориентации эллипса поляризации ПМ,,
сигнала 0ОПт и параметром v, характеризующим степень
взаимной корреляции ортогональных компонент помехи.
Из (9.3.5) следует, что знак параметра v определяется
знаком р1г(т), который определяет наиболее вероятный
угол ориентации случайного эллипса поляризации поме-
хи. Причем при р1г(т)>0 наиболее вероятным значением
угла ориентации случайного эллипса поляризации поме-
хи будет 0п = О, а при р12(т) <0 — значение 0п = л/2. На
основании (9.3.10) оптимальный угол ориентации эллип-
са поляризации ПМф сигнала необходимо выбирать
таким, чтобы его большая ось была перпендикулярна
наиболее вероятному положению большой оси эллипса
поляризации помехи.
Если v = 0, то величина р.ф(Х) не зависит от угла
ориентации эллипса поляризации ПМф сигнала и его
выбор может быть произвольным. Это понятно с физи-
ческой точки зрения, так как при пеполяризоваппой
аддитивной помехе ее мощности на выходах двухкомпо-
нентпой антенны будут одинаковыми Oi2=o22 = M)/2, не
зависящими от угла ориентации эллипса поляризации
приемной антенны. При ^п|=1 и v=^0 аддитивная
помеха имеет преимущественно круговую поляризацию
левого или правого направления вращения вектора
напряженности электрического поля, определяемого
знаком Кп, поэтому 0()Пт также может быть произ-
вольным.
Очевидно, что эффективность перестройки по углу
ориентации ПМ^ сигнала будет уменьшаться по коси-
нусоидальному закону с увеличением угла эллиптично-
сти фо от пуля до л/4. Если ПМ сигнал имеет большие
значения угла эллиптичности фо~л/4, то перестройка
по углу 0о теряет свою эффективность и необходимо
переходить к перестройке по фо. Так как знак опре-
деляет наиболее вероятное направление вращения век-
тора аддитивной помехи «(/), то при —1<^7 7<?г<0 необ-
265
значения угла эл.
п<0,
(9.3.15)
Холимо добиваться максимального отношенпя’ПМ сиг-
нал/помеха иа выходе приемной системы за счет первой
компоненты
- 55 1 + Ki р.’
обеспечивая выполнение условия
sin2cp0=l- (9.3.12)
При 0<Л^п^1 максимальное значение отношения ПМ9
сигпал/помеха должна обеспечивать вторая компонента
2(1^ (Т=^р (1 — Y sin 2?0), (9.3.13)
sin2fp0 = — 1. (9.3.14)
Таким образом, из выражений (9.3.12) и (9.3.14) сле-
дует, что оптимальные
ПМф сигнала
? -J
TOUT--\ .
I— т./4
т. е. направление вращения вектора напряженности элект-
рического поля ПМф сигнала S(/;Z) должно быть проти-
воположно наиболее вероятному направлению вращения
вектора п (/).
Оптимальные значения параметров поляризации 0Опт
и фопт получены в предположении, что мощность ПМ^,
сигнала остается постоянной. Увеличение отношения
ПМ сигнал/помеха достигается за счет перераспределе-
ния мощности полезного сигнала между его ортогональ-
ными компонентами при изменении 0ОПт и фопт в зави-
симости от наиболее вероятных значений параметров
поляризации аддитивной помехи.
Подставляя в выражение (9.3.8) оптимальные значе-
ния параметров поляризации ПМф сигнала (9.3.10)
и (9.3.15), получаем
/7 S0 ’+*« ^+
%1ИоПТ;— 02 [_V2 (1+Кп)2<
(9.3.16)
266
1 + *1 IX*
1-V2 (1-Кп)2’
^<р2 Uoiit) —'
а2
Из этих выражений следует, что величина p^iUout) +
+ Н92 (^оит) имеет абсолютный минимум при Кп = 0 и v=0,
т. е. условия приема ПМф сигналов наиболее неблаго-
приятные, когда аддитивная помеха будет полностью
пеполяризованной, а ее ортогональные компоненты
имеют одинаковую мощность.
При |Kn| —1 (^опт) + !\2 UonT) °0 независимо от
значений v. В этом случае должна существовать одна
компонента ПМ^ сигнала Sz(0 Z), ортогональная вектору
i =£j, и приниматься она будет в отсутствии помех.
При | Кп [ 1, v ► 1 (^опт)—|~ Р'фЗ (^оцт) *” Следова-
тельно, при полностью поляризованной аддитивной по-
мехе всегда можно эффективно взаимно скомпенсиро-
вать воздействие ее ортогональных компонент.
В заключение рассмотрим случай, когда сообщение
передается модуляцией угла ориентации 0(0 эллипса
поляризации электромагнитной волны сигнала. Тогда
ПМ0 сигнал в ортогонально круговом базисе разложе-
ния можно представить в виде
S(/;Z) =
S! cos [ш/ -ф- 0о + О (01
S2 cos [iot — 0o — 0 (0]
(9.3.17)
гд
S, So cos Л?о — ; S2 = S0cos(<?0 + -J-
Оставляя в силе предположения относительно узкополос-
ности сигнала и симметричности спектра, а также пре-
небрегая интегралами с удвоенной частотой, для адди-
тивной помехи с матрицей вида (9.3.5) получаем
> с2 1 I
(*) = цт^) < Г0 +sin +
\ / 1 “Г *\п
4- (1 — sin 2<f>0)
2v cos 2<p„ cos 2S0
(9.3.18)
где обозначения совпадают с обозначениями для ПМф
сигнала, если заменить индексы ср на 0 и взять моду-
267
лирующие функции FBc(t) =cos 0(/), FBs (/) =sin 0(/).
Сопоставляя выражения (9.3.8) и (9.3.18), находим, что
все выводы, сделанные относительно оптимальных пара-
метров поляризации 0ОпТ и <рОпт для ПМф сигналов,
остаются в силе и для ПМ0 сигналов. Однако исполь-
зование ПМ0 сигналов позволяет получить лучшее от-
ношение сигнал/помеха на выходе приемной системы,
если 0<у<1. Это легко объяснить различием в поля-
ризационных спектрах ПМ и ПМ0 сигналов. У ПМд.
сигнала углы эллиптичности всех гармоник равны углу
эллиптичности несущей ф/, = фп = фо; угол ориентации
эллипса поляризации четных гармоник совпадает с углом
ориентации эллипса поляризации несущей 02й = 0ц,
а у нечетных гармоник 02Л+1=,ОН—л/2; направление вра-
щения вектора напряженности электрического поля чет-
ных гармоник совпадает с направлением вращения век-
тора несущего колебания K.2h=Ku, а направление вра-
щения вектора поля нечетных гармоник противоположно:
Kzk+i = — Ки. У ПМ0 сигнала фл = фн = фо; 02й = 0н; 02fe+i =
=0н—л/2; однако, в отличие от ПМф сигнала, направ-
ление вращения вектора напряженности электрического
поля всех гармоник совпадает с направлением враще-
ния вектора поля несущей.
9.4. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ПОЛЯРИЗАЦИИ
ПРИ РАЗЛИЧЕНИИ ПМ СИГНАЛОВ
При детерминированных бинарных ПМ сигналах
средняя вероятность ошибочных решений (9.2.17) пол-
ностью определяется величиной а (9.1.15) и априорными
вероятностями Р(0) и Р(1). Если эти сигналы имеют
одинаковые априорные вероятности, то Рошер зависит
только от величины а. Однако при а^>1 в (9.2.17)
вторыми членами аргументов интегралов вероятности
можно пренебречь, так как условные вероятности оши-
бок в этом случае практически не зависят от априорных
вероятностей ПМ сигналов S(/; X;), и с достаточной
для инженерной практики точностью производить рас-
четы потенциальной помехоустойчивости по формуле
(9.2.19). При малых значениях а зависимость условных
вероятностей ошибок от соотношения априорных вероят-
ностей сигналов S{t; Х<) становится существенной и ее
надо учитывать в расчетах.
268
Получим аналитические выражения для а при раз-
личных равновероятных бинарных ПМ сигналах, когда
их средняя энергия фиксирована, т. е.
p-ср (Х;Х) = и (М р (1) + р (1) р (0) - 4-+
4-|i(Z2)] = const. (9.4.1)
Бинарное сообщение может быть передано при помощи:
— манипуляции угла ориентации плоскости поляри-
зации линейно-поляризованной волны;
— манипуляции направления вращения вектора на-
пряженности электрического поля с круговой поляри-
зацией;
— манипуляцией направления вращения вектора по-
ля и угла ориентации эллипса поляризации.
При манипуляции угла ориентации плоскости поля-
ризации линейно-поляризованной волны ПМ сигнал
COS (<о/ 4“ ®0)
V 2 cos (wt — Go)
представленный в ортогонально-круговом базисе,
передаваться с одним из ПМ сигналов
cos (<о/ + М
cos (<о/ — 0о — it)
COS (оз/ -I- Go 4” *10
COS (w,t — Go — It)
COS (fot 4- Go 4- It) I ,
cos (u>t— Go — 2it)[
S(/; 2,)= °
SAt;
г А
32(/;Х) = -^
S. (f;l2) = -^
3\> 2/
(9.4.2)
может
(9.4.3)
также представленными в ортогонально-круговом ба-
зисе. Тогда в соответствии с выражениями (9.2.4),
(9.2.15) получим:
— для бинарных ПМ сигналов S (t; Л,), S! (/; Z,)
а, = /2р.22 (I) ; (9.4.4)
— для бинарных ПМ сигналов S(t; ЛД S2 (t; Л2) =
= —S(f; 1.)
аг = ]/Г211А) ; (9.4.5)
269
— для бинарных ПМ сигналов S (/; Л,), 3, (t; Л2)
as = V 2щ, (Л) .
(9.4.6)
Из полученных соотношений (9.4.4), (9.4.5) и (9.4.6) на-
ходим, что при манипуляции угла ориентации плоскости
поляризации линейно-поляризованной волны противо-
положные ПМ сигналы S(t; Xi), —S(/; Xi) позволяют
получить минимально возможное значение средней ве-
роятности ошибочных решений, т. е. aa>ai, аз- Эта пара
ПМ сигналов по сравнению с двумя другими позволяет
осуществить и более эффективную поляризационную
селекцию путем подбора 0Опт (9.3.10), в зависимости от
того, какое наиболее вероятное значение имеет угол
ориентации эллипса поляризации помехи.
При манипуляции направлением вращения вектора
напряженности электрического поля волны с круговой
поляризацией в ортогонально линейном базисе разло-
жения ПМ сигналы можно представить в виде двух
линейно-поляризованных колебаний одинаковой частоты
и амплитуды, ортогональных в пространстве и сдвину-
тых по фазе на л/2:
S(t;
cos (<ot <р,)
sin (wt 4~ Ф,)
(9.4.7)
S(t- A2) = S0
COS (<ot 4- <[>2)
— sin (u>t <p„)
где ф| и фи — начальные фазы ПМ сигналов S(t; к,).
Из выражений (9.2.4), (9.2.15), пренебрегая инте-
гралами с удвоенной частотой, находим
= V4ц22 (X) при ф, = ф2 4- kv.
(9.4.8)
Совпадение составляющих (t; Л,) = S{ (t; Z2) в выраже-
ниях (9.4.2), (9.4.3) и (9.4.7), соответствующих двум
значениям ПМ сигналов, означает, что их энергия при
различении теряется бесполезно, так как количество ин-
формации, которое они несут, равно нулю. Следователь-
но, передача бинарных сообщений манипуляцией угла
ориентации плоскости поляризации линейно-поляризо-
270
ванной волны на л и направлением вращения вектора
напряженности поля волны с круговой поляризацией
обеспечивает принципиально одинаковую помехоустой-
чивость.
Сущность метода передачи бинарных сообщений ма-
нипуляцией направления вращения вектора поля и угла
ориентации эллипса поляризации заключается в том,
что двум состояниям передаваемой информации соответ-
ствуют две ортогональные эллиптически-поляризованные
волны. В ортогонально-круговом базисе такие ПМ сиг-
налы можно представить в виде
cos (<?,-----j cos (ml -ф- ф> -ф- 601)
S
° cos ftp, +-J- ) cos(o>z + ф, — 601)
COS 0>2 — -J-) COS (mt + 4>2 + 602)
COS (<p2 + ) COS (mt -4- ф, — 0O2)
где ср, может принимать значения в дискретных точках
или интервалах, а Оси — в дискретных точках:
[ф1 = (0...и/4), 0О1 = 0О],
[ф,^^...^), 0O1==0o + JL],
0О1 = 0О-ф-z],
^ = (5/^...-^^, 0О1 = 0О + 4* ]. (9.4.10)
[фа = б*/2 — 415 У 8“2 ~ во+'гс/2 ];
Положим, что для передачи бинарных сообщений
используются два ортогональных эллиптически-поляри-
зованных сигнала с параметрами [<pi= (0,... л/4), 0Oi =
271
= 0о] п (фа - (л/2 ... Зл/4), 0о2 = 0о+л/2], тогда
-Si (У,) cos (ш/Н-<р, + 0о)
S2 (<pt) cos (<»t + <р, — 0о)
С//.-П— s, (?2)sin(<»/ + ^ + 60) |
S2 (<p,) sin (ш/ + ф2 — O0)
(9.4.11)
где |S,(ф)) | |S2((pi) |, |51(ф2) | |S2(<p2) | в зависимо-
сти от выбранных значений из (9.4.10).
Подставляя (9.4.11) в выражение (9.2.15) и пренебре-
гая интегралами с удвоенной частотой, находим
а5 = 0,5 hUi)+hU2) -н-2
^*) (^2)
kt /2—1
1/2
при k=/=n, k,n=\, 2, 4>1 = 4'2+&л. (9.4.12)
Следовательно, бинарные ПМ сигналы, представляю-
щие собой две ортогональные эллиптически-поляризо-
ванные волны, обладают лучшей потенциальной помехо-
устойчивостью по сравнению с бинарными ПМ сигналами
ортогонально-линейной поляризации. При реализации та-
кого способа передачи сообщений каждая из ортогональ-
ных составляющих является информативной и может
быть использована для различения S(t; к,), что позво-
ляет получить й5>аь аз.
Рассмотрим влияние корреляционной зависимости
ортогональных компонент аддитивной помехи n(t) на
потенциальную помехоустойчивость приемных систем би-
нарных ПМ сигналов. Для этого положим, что корре-
ляционная матрица n(t) имеет вид
2
31 3132Р
2
313гР 32
(9.4.13)
Stf.-Ч).
Тогда из выражения (9.2.15) с учетом (8.2.36) найдем
1 -> -> 1
&2 Р'аг (Л.,J X2)-|-2v а p.I2 (X,; Х2)
2 (1 — Ра)
(9.4.14)
272
где введены обозначения
Р'гД^'й^г)— 3, [Р'гг (X) Н- Нг7 (^2) ^Р4” X
X (Л-|) Ргг (Д)| >
Н12 (l;X) = I- ?;У Ри (I) Р22 (X) -
Pia^Pn (^2) Р22 ( ^-2) + (Р12-F Р.-1) Р12 U1)P12 G2) ]•
Для бинарных ПМ сигналов S(/;2j), SJ/jZJ из (9.4.2) и
(9.4.3) имеем:
12 12 1 I пД 12 12 ,
Pil=p21=1’ Р12= VCOS20.P Р22=:?12 = — 1.
р.гг(Г,) = р.гг(Г2), р12(Г1) = р12(С) = р21(лг). (9.4.15)
Подставляя полученные значения (9.4.15) в выражение
(9.4.14), находим
at =
So 1
2°г /(1 — р2) '
(9.4.16)
Аналогичные вычисления, проведенные для ПМ сигна-
лов Sj(t; 22); / = 2, 3, из (9.4.2), (9.4.3), а также
для ПМ сигналов (9.4.7) и (9.4.11), приводят соответст-
венно к выражениям:
а2
S«
2
°l 2 + 32 2 — 2v cos 20o (а^з) * 1
a =-^_____L— •
3 2all/pT^p
(9.4.17)
(9.4.18)
Л5 — 2
а4 = , при ф, = <[» Д- /гл;
=г К(1 — р2)
°1 2 [•S2 (?1) + X (¥г)1 + 2 [Sj (fl) + Sj (®2)1 —
— 2v (ata2) -1 {[S, (?i)S2(yi) {-S,(y2) S2 (?2)] cos 20о:Р
+ 0,5 [S, (y2) S2 (?,) — S, (y,) S2 (y2)] sin 29ц}
(9.4.19)
2(1-P2)
(9.4.20)
где знак плюс берется при фг=41 + 2kn, а знак минус —
при 'фг=4’1—(2& + 1)л, k=Q, 1, .п.
18—667 273
Из полученных выражений (9.4.16) — (9.4.20) нахо-
дим, что при |р|->1, at ... п5->оо, а средняя вероятность
ошибочных решений в соответствии с (9.2.19) стремится
к нулю. Это указывает на потенциальную возможность
достоверного различения рассмотренных бинарных ПМ
сигналов па фоне полностью поляризованных помех.
Однако на практике всегда присутствует неполярпзован-
иое поле помехи, за счет действия которого |р|<1,
а Липер отлично от пуля.
Легко видеть, что выражение (9.4.20) является обоб-
щенным, из которого как частные случаи можно полу-
чить выражения (9.4.16) — (9.4.19). Поэтому для нахож-
дения оптимальных, параметров поляризации ПМ сиг-
налов и их взаимосвязи с наиболее вероятными пара-
метрами поляризации помехи представим подкоренное
выражение (9.4.20) в виде
f 1 । 1/2
4fl5 — а2(1 — рг) |(1 + Kn)2 (^1 +
+ (14/^ lS2 ('?) + si (?2)1 - 2p ^5^H[S. (?1) S2 (?J) +
+ s. (?2) S2 (<P2)] cos 20o 4" [S, (?2) s2 (<?,) —
- S, (?,) S2 (?2)J sin 26j|. (9.4.21)
Так как величина Кп по модулю не превосходит единицы,
то из (9.4.21) для оптимальных значений углов ориента-
ции эллипсов поляризации бинарных ПМ сигналов на-
ходим
А ( 0 при v<0, V01 \ л 0°2 ’ (rt-rc/2 при v>0, когда ф1 = ф2-|-1г; й _ f + 1t/4 ПРИ V>°- fl °01 { .. ' °0® (— it/4 при v< 0, когда ф, = ф2 + (2k -j-1) it; а _ 1t/4 при v<0, Ч»1 { , n 0»2 14-11/4 при v>0, когда ф, =• ф2 4- 2£it. 274 _f=tit/2 при v<0, ( 0 при v>0, (9.4.22) (—u/4 при v>0, (4-i'/4 при v<0, |4~it/4 при v<0, (it/4 при v>0, (9.4.23)
Подставляя в выражение (9.4.21) значения 0ui в со-
ответствии с (9.4.22) и повторяя рассуждения, проведен-
ные в предыдущем параграфе для каждого из сигналов
S(t; Хг), находим, что углы эллиптичности должны
иметь равные по величине, но противоположные по знаку
значения.
Знак оптимального угла эллиптичности одного из сиг-
налов S(t; Xi) необходимо брать таким, чтобы направле-
ние вращения его вектора было противоположно наибо-
лее вероятному направлению вращения вектора аддитив-
ной помехи n(t), что позволяет получить максимальное
отношение сигнал/помеха в одном из поляризационно-
ортогональных каналов приемной системы. Тогда для
второго ПМ сигнала будет иметь место обратная ситуа-
ция.
Использование оптимальных значений 0оь определен-
ных в соответствии с (9.4.23), также приводит к необхо-
димости применения в качестве бинарных ПМ сигналов
двух ортогональных эллиптически-поляризованных волн.
9.5. НАДЕЖНОСТЬ ОЦЕНКИ ПАРАМЕТРОВ
ПОЛЯРИЗАЦИИ ПМ СИГНАЛОВ
Метод максимума функции правдоподобия А(Х) дает
приемлемые результаты, когда максимальный выброс
выходного эффекта одного из каналов с вероятностью,
близкой к единице, лежит вблизи истинного значения
оцениваемого параметра поляризации. С увеличением
уровня помех и априорного интервала значений пара-
метров поляризации ПМ сигнала вероятность того, что
максимум А(Х) обусловлен не действием ПМ сигнала,
а помехой и будет находиться на значительном удале-
нии от истинного значения оцениваемого параметра по-
ляризации, существенно возрастает. В этих случаях ме-
тод максимума максиморума А(Х) становится неэффек-
тивным, а оценка параметра поляризации ПМ сигнала
будет ненадежной.
Для определения вероятности надежной оценки Рн.о
воспользуемся основанной па (8.6.17) приближенной за-
мене реальной системы с непрерывными параметрами
поляризации дискретной системой с взаимно ортогональ-
ными ПМ сигналами, обеспечивающей практическую не-
18* 275
зависимость помех n(t) в интервалах дискретизации.
В этом случае определение вероятности надежной оценки
представляет собой задачу определения вероятности того,
что максимальное значение выходного эффекта, обуслов-
ленное действием ПМ сигнала и помехи на выходе одно-
го из каналов, будет больше любого из п—1 выбросов,
обусловленных помехой во всех остальных каналах.
Следовательно, эта задача совпадает с задачей обна-
ружения одного из п ортогональных ПМ сигналов. Итак,
положим, что полученные в результате дискретизации
ПМ сигналы равновероятны, имеют одинаковую энергию
и взаимно ортогональны, т. е.
Р [S (t- Я,)] = Р [S (t-Я2)] =... = Р [S (/;!„)] = 1 jn\
-i I 0 при
J S (/;MS(U-)<fl = £rf + E2l-=£.. (9.5.1)
—00
Тогда выходные эффекты каждого из п каналов при-
емной системы таких ПМ сигналов будут взаимно не-
зависимыми случайными величинами, представляющими
собой любые монотонно возрастающие функции от функ-
ции правдоподобия оцениваемого параметра поляриза-
ции,
Л (Яг-) = /с.ехр Й J u\t- Я) 0(С; t2) S (t2; Я/) dt^dt^—
(о
т
4 J]*5Г(^; ^)0(fi;QS(4; tf)dttdt2
о
/=1,2...n.
(9.5.2)
При оценке параметров поляризации детерминированно-
го ПМ сигнала в качестве оптимальных выходных эф-
фектов можно принять
Y (li) = J J У (/,; Я) 0 (/,; t2) S (/2; Яг) Л,Л2. (9.5.3)
Пусть один из п выходных эффектов (9.5.3) соответству-
ет полезному сигналу плюс помеха, а остальные п—1 —
276
только помехе. Вероятность того, что максимальное зна-
чение выходного эффекта от воздействия смеси S(i; fa) +
+ n(t) больше максимального значения любого из п—1
выходных эффектов, обусловленных воздействием только
помехи n(i), определяется хорошо известным соотноше-
нием
ОО
•’ S'4-w п
—00
(9.5.4)
где
у
F_*(Y) — f Ц (У) dY — интегральный закон распределения
п J п
—00
помеховой составляющей
^n(X)= j f п(<.)^-, t2)S (£,; l^dt.dt^, (9.5.5)
o'"
_ДУ),/_ДУ)— одномерные плотности вероятности мгно-
S + n п
венных значений выходных эффектов от воздействия
S (/; fa) + я (0 и п (t).
Ранее было показано, что выходные эффекты (9.5.3)
при выполнении оговоренных допущений представляют со-
бой нормальные случайные величины со средними значе-
ниями при u(t; Я) = S(Z; fa) -\-n(t), u(t-, Я) = n (t), соответ-
ственно равными 2р(Яг) и нулю, и дисперсиями, в
обоих случаях равными 2р (Яг-). Следовательно, законы
распределения этих случайных величин можно записать
в виде
^(у)=-Г7=^ехР
п V 4лр- (X)
при u(t\ fa = n(t);
L -> (Y) = 1 ехр .
5 + л 1 Г -*
|/ 4пр (X)
при и (/; Я) = S (/; Я) Д- п (t).
п 4 '
4р. (1) .
(9.5.6)
_>(Х)-2р (Х)]2 ]
S+n_______________I
4р. (X) j
(9.5.7)
277
Подставляя (9.5.6), (9.5.7) в соотношение (9.5.4), на-
ходим
00
[y-V 2;л(Х) П
---------2------Р’
(9.5.8)
где учтено, что
и2
4[х (1)
du —
Непосредственное вычисление по формуле (9.5.8)
в общем случае возможно только путем численного ин-
тегрирования. Приближенный метод, хорошо изложенный
в известных работах [22, 36], основан па аппроксимации
{0,5[1+Ф(У)]}И-1 ступенчатой функцией
1 + Ф (ПГ
О при Y < Уо,
~ при Y = Y0,
1 при Y > Уо>
(9.5.9)
где Уо определяется из уравнения
Ф(У0) = 2('I-2>/(”“I) — 1. (9.5.10)
При таком приближении вероятность надежной оценки
параметров поляризации ПМ сигнала определится из вы-
ражения
р
* но
1 f [У-у 2;х(Х) ]2
=vdexp-----------------2-----
Го ______
= 2_[1 __ф(уо_ j/"2р.(2)].
dY =
(9.5.11)
Из полученного выражения находим, что при и(7.)^-
—>оо вероятность надежной оценки PIK>->1. Следователь-
но, на основании выводов, сделанных в предыдущих па-
раграфах, при оценке параметров поляризации мы мо-
жем увеличить Лю за счет поляризационной селекции
при действии полностью или частично поляризованных
278
помех. При ц(л)->0 Р1Ю-> 1 /п, так как все дискретные
значения поляризационных параметров из интервала воз-
можного их изменения равновероятны. Если ПМ сигнал,
параметры поляризации которого мы оцениваем, имеет
случайную начальную фазу, равномерно распределенную
па интервале [0; 2л], то за оптимальный выходной эффект
можно принять величину
u\t- Z)0(E; t2)S* (/,; X)dtxdt2.
(9.5.12)
Тогда распределение амплитуд помеховых выходных эф-
фектов п—1 каналов подчиняется [23] при линейном
детектировании релеевскому закону
^(У) = 2к^_ехр
« 2р. (X)
при и (/; Z) = п (I),
(9.5.13)
а распределение амплитуды выходного эффекта суммар-
ного колебания ПМ сигнала и помехи — квазирелеев-
скому
к -> (П = л . (Я)] ехр - ------
S + n 2р. (X) S+n L 4р. (X) J
при u(t; Z) = S(t, Я)Ч-я(^). (9.5.14)
Подставляя (9.5.13), (9.5.14) в соотношение (9.5.4),
в соответствии с результатами работы [36] находим
И—1 т
Pao=Yi Сп-1(— OVG’+Oexpf—«>Й/«Ч-1], (9.5.15)
где С‘_, = (п~ 1)!/г! (/? — 1 — i).
При большом числе дискретных значений п вычисления
по формуле (9.5.15) становятся трудоемкими. Поэтому
при больших значениях п и и (2.) можно пользоваться
приближенным соотношением
Рно=г 1 —0,5(«—1)ехр[—ц(1)/2]. (9.5.16)
Из выражения (9.5.16) находим, что и в случае оцен-
ки параметров поляризации у квазидетерминировапного
279
ПМ сигнала эффективность поляризационной селекции
может оказаться значительной, если помеха будет пол-
ностью пли частично поляризованной.
В заключение отметим, что при анализе потенциаль-
ной помехоустойчивости приемных спсте.м ПМ сигналов
нигде не накладывалось существенного ограничения на
величину базы этих сигналов. Поэтому многие получен-
ные выше результаты могут быть использованы не толь-
ко для оценки узкополосных систем передачи информа-
ции путем поляризационной модуляции, но и для оценки
потенциальной помехоустойчивости приемных систем,
использующих широкополосные ПМ сигналы.
ПРИЛОЖЕНИЕ
Для чисел с двумя мнимыми единицами справедливы следующие
три тождества. Первое:
cos -f- i sin ас-•— cos ?cia + j sin ~. (П.1.1)
Для доказательства этого тождества достаточно преобразовать
в первой части выражения (П.1.1) тригонометрические функции в по-
казательные ио формулам Эйлера с мнимой единицей /, а показа-
тельные функции с мнимой единицей i — в тригонометрические.
Второе:
cos ае^ -ф ij sin ае—& -= cos ^е‘уа + / sin Зе—1/11 . (П. 1.2)
Справедливость этого соотношения доказывается так же, как и пер-
вого, по только необходимо оперировать с совмещенной мнимой
единицей (ij), как с обычной мнимой единицей. Очевидно, равенство
не изменится, если заменить везде в (П.1.2) i па / и наоборот. По-
этому
cos ае1^ -{- ij sin ае~'₽ - cos ?e1J I + i sin pe -,Ja . (П. 1.3)
Третье:
е±<7к/4 е/а с± i/*/4 ет_ (П j 4)
е±ш-/4е;«._е±^/4ет/« _ (П.1.5)
Докажем справедливость соотношения (П.1.4). Для этого разложим
по тригонометрическим функциям и умножим sin а на единицу, ко-
торую представим как произведение —(•/=!. Получим
gi'/11/4 ._ cos ag--1/*/4 — j, sjn ае±'/я/4 .
Объединяем в правой части этого выражения произведение ij
в совмещенную мнимую единицу (ij) (с одновременным изменением
знака в показателе степени последующего сомножителя) и представ-
ляем се в виде ±с±';,1/2. Таким образом:
e±W4e/«_cosae±<>/4 у. i Sin яс±<7*/2 е^бЖ4 = е±'7*/4 .
Соотношение (П.1.5) доказывается аналогичным образом.
280
Приведем еще ряд соотношений, которые также можно доказать
путем преобразований тригонометрических функций в показательные
и наоборот с соблюдением правил перемножения мнимых единиц и
правил объединения произведения ij в совмещенную мнимую едини-
цу (//):
е/я + z/e—/a ije^ia , (II.1.6)
1
Vi
(е^М с-/<х _|_ е—'^/4 с/«)
/2
[е— + | е~Ч (=•—~/1)j _
= sin (а л/4) е ч':'14 -ф cos j f (П.1.7)
(е±/я 'с*'7) ет‘,:'14 —
V £
•-^(e^/e^e’W4, (П.1.8)
ei«e±/"/4.r=_J_ (е±<-щ + /c+i70!), (П'1.9)
e/«e±^/4i=_J_ (е±»7а±(-ет</«). (П.1.10)
г £
СПИСОК ЛИТЕРАТУРЫ
1. Андерсон Т. Введение в многомерный статистический анализ.
Пер. с англ. Под ред. Б. В. Гнеденко. М., Физматгиз, 1963.
2. Антенны эллиптической поляризации. Пер. с англ. Под ред.
А. И. Шпунтова. М., ИЛ, 1961.
3. Ахманов С. А., Хохлов Р. И. Проблемы нелинейной
оптики (электромагнитные волны в нелинейных диспергирующих
средах). М., Изд. АН СССР, 1961.
4. Б а к у т П. А. Оценка максимума правдоподобия нормальных
сигналов. — «Известия вузов СССР. Радиотехника», 1962, № 3.
5. Бунимович В. И. Приближенное выражение вероятности
правильного обнаружения при оптимальном приеме с неизвест-
ной начальной фазой. — «Радиотехника и электроника», 1958,
№ 4.
6. Борн М., Вольф Э. Основы оптики. Пер. с англ. Под ред.
Г. П. Мотулевич. М., «Наука», 1970.
7. Б о л ь ш а к о в И. А. Выделение потока сигналов из шума. М.,
«Сов. радио», 1969.
8. В а р а к и н Л. Е. Теория сложных сигналов. М., «Сов. ра-
дио», 1970.
9. Вопросы статистической теории радиолокации. Т. 1 и 2. Под
ред. Г. П. Тартаковского. М., «Сов. радио», 1963, 1964. Авт.:
Б акут П. А., Большаков И. А., Герасимов Б. М.
и др.
10. Г и н з б у р г В. Л. Распространение электромагнитных волн
в плазме. М., «Наука», 1967.
II. Гуткин Л. С. Теория оптимальных методов радиоприема при
флюктуационных помехах. М., «Сов. радио», 1972.
12. Гусев К. Г. Возможности поляризационной селекции при
различии поляризационных параметров помех и сигналов.
ХВКИУ, 1962.
13. Гусев К. Г. Поляризационная модуляция. ХВКИУ, 1968.
14. Камнев Е. Ф., П е т р о в и ч Н. Т. Вопросы космической ра-
диосвязи. М., «Сов. радио», 1965.
15. К а н а р е й к и и Д. Б., Павлов Н. Ф., Потехин В. А.
Поляризация радиолокационных сигналов. М., «Сов. радио»,
1966.
16. К а н а р ей к н н Д. Б., Потехин В. А., Шишкин Н. Ф.
Морская поляризация. Л., «Судостроение», 1968.
17. Киселев А. 3. Оптимальный прием эллептически-поляризо-
ванного сигнала при наличии случайно поляризованного шума.—
«Радиотехника и электроника», 1969, № 2.
18. Кириллов Н. Е. Помехоустойчивая передача сообщений по
линейным каналам со случайно изменяющимися параметрами.
М., «Связь», 1971.
2§2
19. Ку рикш а Л. А. Об оптимальном использовании простран-
ственно-временных сигналов. — «Радиотехника и электроника»,
1963, № 4.
20. Кобзев В. В., Чернышев В. Н., Шереметьев А. Г.
Лазеры в системах связи. М., «Связь», 1966.
21. Королев Ф. А. Теоретическая оптика. М., «Высшая школа»,
1966.
22. Корн Г., Корн Т. Справочник по математике для научных
работников и инженеров. Пер. с англ. Под ред. И. Г. Арамано-
вича, М„ «Наука», 1968.
23. Левин Б. Р. Теоретические основы статистической радиотех-
ники. Кн. 1 и 2. М., «Сов. радио», 1969, 1968.
24. Лекции по теории связи. Под рсд. Е. Дж. Багдан. Пер. с англ.
Под ред. Б. Р. Левина. М„ :<Мир», 1964.
25. Миддлтон Д. Введение в статистическую теорию связи. Т. 1
и 2. Пер. с англ. Под ред. Б. Р. Левина. М., «Сов. радио»,
1961, 1962.
26. Микаэлян Н. Л. Теория и применение ферритов на сверхвы-
соких частотах. М., Госэнергоиздат, 1963.
27. М у с т е л ь Е. Р., П а р ы г и н В. Н. Методы модуляции и ска-
нирования света. М., «Наука», 1970.
28. Петрович Н. Т., Размахпип М. К. Системы связи сшу-
моподобными сигналами. М., «Сов. радио», 1969.
29. Петрович II. Т. Передача дискретной информации в кана-
лах с фазовой манипуляцией. М., «Сов. радио», 1965.
30. Поздняк С. И., Радзевскин В. Г., Казаков В. И.
Исследование по помехоустойчивости системы приема и обра-
ботки информации по двум поляризационно-ортогональным ка-
налам.— «Вопросы радиоэлектроники, Сер. ТРС», 1969, вып. 8.
31. Проворов К. Л. Радиогеодезия. М., «Недра», 1965.
32. Родимец А. П., Потехин В. А. О распределении вероят-
ностей положения точки поляризации частично поляризованной
волны на сфере Пуанкаре. — «Радиотехника и электроника», 1967,
т. XII, вып. 12.
33. Родпмов А. П., Глухов А. Н., Потехин В. А. Стати-
стические характеристики произвольной частично поляризованной
волны. — «Радиотехника и электроника», 1968, т. XIII, вып. 8.
34. Родим ов А. П., Глухов А. Н., Потехин В. А. К вопро-
су о поляризационной селекции радиолокационных сигналов.—
«Радиотехника и электроника», 1969, т. XIV, вып. 3.
35. Ст риги п В. С. О методах приема поляризацнонно-модули-
рованных колебаний. — «Труды ЛВИКА им. А. Ф. Можайского»,
1960, вып. 343.
36. Тихонов В. И. Статистическая радиотехника. «Сов. ра-
дио», 1966.
37. Фальков и ч С. Е. Оценка параметров сигнала. М., «Сов. ра-
дио», 1970.
38. Фалькович С. Е. О задаче определения оптимальной про-
странственно-временной системы обработки сигналов. — «Радио-
техника и электроника», 1966, № 5.
39. Фалькович С. Е., Хомяков Э. Н. Пространственно-вре-
менная обработка при наличии мультипликативных и аддитив-
ных флюктуаций. — «Радиотехника и электроника», 1967, № 3.
40. Ч а п д р а с е к а р С. Перепое лучистой энергии. Пер. с англ.
Под ред. Е. С. Кузнецова, М., ИЛ, 1953.
283
41. Шерклифф У. Поляризованный свет. Пер. с англ. Под ред.
Н. Д. Жевандрова, М., «Мир», 1965.
42. Ш е с т о в Н. С. Выделение оптических сигналов на фоне слу-
чайных помех. М., «Сов. радио», 1967.
43. N i b 1 о с k W., Wolf Е. Polarization modulation and demo-
dulation of light.— «Wescon Mechn. Conv.», 1963, Papers (3).
44. Roman P., Wolf E.— «Nuovo Cimento», 1960, pp. 17, 462,
477.
45. II uams H., Wolf E. Notes of the application of lasers for
space communications. — «Proc. Nat. Winter Conv. Mil. Electron»,
1963, v. 2.
46. Wolf E. Proc. Synp. Astr. Optics, ed. Z. Kopal, North Holland
Publ. Co. Amsterdam, 1956, p. 177.
47. M a r a t h a у A. S. Operator formalism in the theory of partial
polarization. — «J. Optical Soc. Amer.», 1965, v. 55, Aug., p. 965.
4S. Mar at hay A. S. Extension of the commutation relations in
the theory of partial polarisation. — «J. Optical Soc. America», 1966,
v. 56, may, p. 619.
ПРЕДМЕТНЫЙ
Алгоритм обработки ПМ сиг-
налов 149
Антенна двухкомпонентная 50,
58, 137, 142
Базис 15, 24
Вектор аддитивной помехи 188
— базисный 32
— качающийся 95, 96
— транспонированный 29
Волна квазимонохроматиче-
ская 45, 49, 52
— линейно-поляризованная 9,
13, 14
— монохроматическая 48
— плоская 9, 10
— эллиптически - поляризован-
ная 14, 18, 21—27
Волновод, скрутка 140
Гиротропное устройство 66, 71
Демодулятор ПМ сигнала
150-153, 158
Диаграмма поляризационная
10, 18
Единица мнимая совмещенная
16, 18, 19
Канал связи 7
Коэффициент нелинейных иска-
жений НМ сигнала 153
— эллиптичности 8
Критерий Неймана — Пирсона
175, 176
— оптимальности 174
Линотропное устройство 66,
67, 69, 70
Манипуляция поляризации
113—121
Матрица когерентности 44
— потерь 174, 175
Модулятор поляризационный
65—67, 76, 79, 80, 81, 88
Модуляция поляризационная
дискретная 82, 109
--- непрерывная 82
— — радиоимпульсов (ПМИ)
104, 105
— фазовая ПИМ 122
Направление вращения векто-
ра поля 8, 10
Неполяризованная составляю-
щая излучения 43
УКАЗАТЕЛЬ
Однозначность определения па-
раметров поляризации 10
Ориентация поляризационной
диаграммы 10
Отношение правдоподобия 178,
201
Оценка 181, 186
Параметр мгновенный 57
-- существенный 198, 199
Передатчик с импульсной мо-
дуляцией поляризации 111
Пластинка фазовая 65
Плоскость комплексная двой-
ная 7, 8
— поляризации 9
Поляризационный селектор 139
Помехоустойчивость потенци-
альная 246
Порог ограничения 252, 260
Правило выбора решения 170
Преобразование унитарное 33.
36
Преобразователь поляризации
37, 38, 64, 65, 137
Приемник ПМ сигналов 147,
148, 157, 162 163, 212, 217,
225, 234
Полуось эллипса поляризации
главная 10, 11, 13
Расщепитель волны 65
Риск 171, 172, 183
Сигнал двумерный 51, 58, 137
— поляризационно-импульсной
модуляции (ПИМ) 109
— узкополосный 49, 62
— фазомодулпрованпый 49, 87,
89
Система связи с ПМ сигнала-
ми 109, 168, 169, 172
— — смешанная 109
Степень поляризации волны 44
Спектр сигнала полный 110
— — с поляризационной мо-
дуляцией 87—90
Угол ориентации 8, 11
— эллиптичности 8, 11, 12, Н
Фаза эллиптически поляризо-
ванной волны 8, 11, 12
Фазосдвигатель 66, 67, 68, 71,
Фильтр активный 226, 228
Функция потерь 171, 180
Эллипс поляризации 8, 10
Эллипсоид рассеяния 185
285
ОГЛАВЛЕНИЕ
Предисловие................................................ 3
Введение.................................................... 5
Глава 1. Параметры поляризации монохроматической волны
в комплексном представлении ............................ 8
1.1. Поляризационная диаграмма.......................... 8
1.2. Графическое представление эллиптически-поляризо-
ванной волны............................................. 13
1.3. Представление эллиптически-поляризованной волны
на двойной комплексной плоскости.........................15
1.4. Некоторые формы представления эллиптичсски-поля-
рчзовапной волны.........................................21
1.5. Комплексные числа двойной комплексной плоскости
и комплексные векторы.................................. 28
1.6. Параметры поляризации электромагнитной волны
в произвольном базисе . 36
1.7. Параметры Стокса и матрица когерентности ... 43
Глава 2. Мгновенные параметры поляризации двумерных
сигналов................................................48
2.1. Предварительные замечания..........................48
2.2. Поляризационная диаграмма суммы двух монохрома-
тических волн.......................................... 52
2.3. Поляризационные параметры двумерных сигналов . 57
Глава 3. Принципы построения поляризационных преобра-
зователей и модуляторов ............................... 63
3.1. Основные понятия и определения.....................64
3.2. Операторы элементарных преобразователей поляриза-
ции ................................................... 69
3.3. Преобразование поляризации линейно-поляризовапнон
волны . 73
3.4. Схемы поляризационных модуляторов ..... 75
3.5. Классификация способов поляризационной модуляции 81
Глава 4. Сигналы с непрерывной поляризационной модуля-
цией ...................................................83
4.1. Модуляция угла эллиптичности.................83
-4.2. Спектр ПМ^ сигналов..........................86
4.3. ПМ8 сигналы и их спектры.....................90
4.4. Одновременная модуляция угла эллиптичности угла
ориентации поляризационной диаграммы ... 95
4.5. Поляризационно-спектральная структура ПМ^д сиг-
нала при модуляции параметров гр и 0 различными
сообщениями.........................................100
4.6. Поляризационная модуляция периодической последо-
вательности радиоимпульсов ............................ 103
286
Глава 5. Сигналы с дискретной поляризационной модуля-
цией ................................................109
5.1. Модуляция параметров поляризации периодической
последовательностью прямоугольных импульсов . . 109
5.2. Поляризационно-фазовая манипуляция (ПФМ) . . 121
5.3. Сопряжение поляризационной манипуляции и мани-
пуляции по фазе.................................... 124
Глава 6. Некоторые способы приема ПМ сигналов . 136
6.1. Поляризационные параметры антенны эллиптической
поляризации........................................ 136
6.2. Прием ПМ сигнала па двухкомпоиеитпую антенну . 142
6.3. Обработка сигналов с непрерывной ПМф .... 149
6.4. Обработка сигналов с непрерывной ПМ0 . . . 155
6.5. Обработка сигналов с непрерывной ПМ^е .... 161
Глава 7. Основные понятия и соотношения теории оптималь-
ного приема ПМ сигналов..............................164
7.1. Статистическая модель системы связи с ПМ сигна-
лами ................................................165
7.2. Задача обнаружения ПМ сигналов, являющихся за-
данными функциями поляризационных параметров . 172
7.3. Задача оценки параметров поляризации ПМ сигналов 180
7.4. Воздействие аддитивных помех на ПМ сигнал . . 186
7.5. Воздействие мультипликативных помех на ПМ сигнал 195
Глава 8. Некоторые вопросы оптимизации приема ПМ сиг-
налов на фоне помех..................................200
8.1. Отношение правдоподобия для ПМ сигналов . . . 201
8.2. Функционал отношения правдоподобия при детерми-
нированном ПМ сигнале . ............................204
8.3. Структура оптимальных систем обнаружения детерми-
нированного ПМ сигнала...............................212
8.4. Структура оптимальных систем обнаружения, квази-
детермниированного ПМ сигнала........................221
8.5. Структура оптимальных систем различения двух
ПМ сигналов .........................................232
8.6. Структура оптимальных систем оценки параметров
поляризации ПМ сигналов............................ 238
Глава 9. Некоторые вопросы потенциальной помехоустойчи-
вости приемных систем ПМ сигналов....................246
9.1. Анализ приемных систем обнаружения ПМ сигналов 247
9.2. Потенциальная помехоустойчивость приемных систем
бинарных ПМ сигналов ...............................253
9.3. Оптимизация параметров поляризации при обнаруже-
нии ПМ сигналов......................................261
9.4. Оптимизация параметров поляризации при различении
ПМ сигналов..........................................268
9.5. Надежность оценки параметров поляризации ПМ
сигналов.............................................275
Приложение...............................................280
Список литературы........................................282
Предметный указатель.....................................285
Клавдий Григорьевич Гусев
Алексей Дмитриевич Филатов
Анатолий Петрович Сополев
ПОЛЯРИЗАЦИОННАЯ МОДУЛЯЦИЯ
Редактор Ю. И. Суханов
Художественный редактор 3. Е. Вендрова
Художник Б. JJ. Николаев
Технический редактор А. А. Белоус
Корректор И. Г. Багрова
Сдан; в набор 21/11 1974 г. Подписано в печать 3/VI 1974 г. Т-09646
Формат 84x108/32 Бумага типографская № 2
Объем 15,12 усл. п. л.» 14,581 уч.-изд. л.
Тираж 5 000 экз. Зак. 637 Цена 1 р. 02 к.
Издательстзо «Советское радио", Москва, Главпочтамт, а/я 693
Московская типография № 10 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
Москва, М-114, Шлюзовая наб., 10.