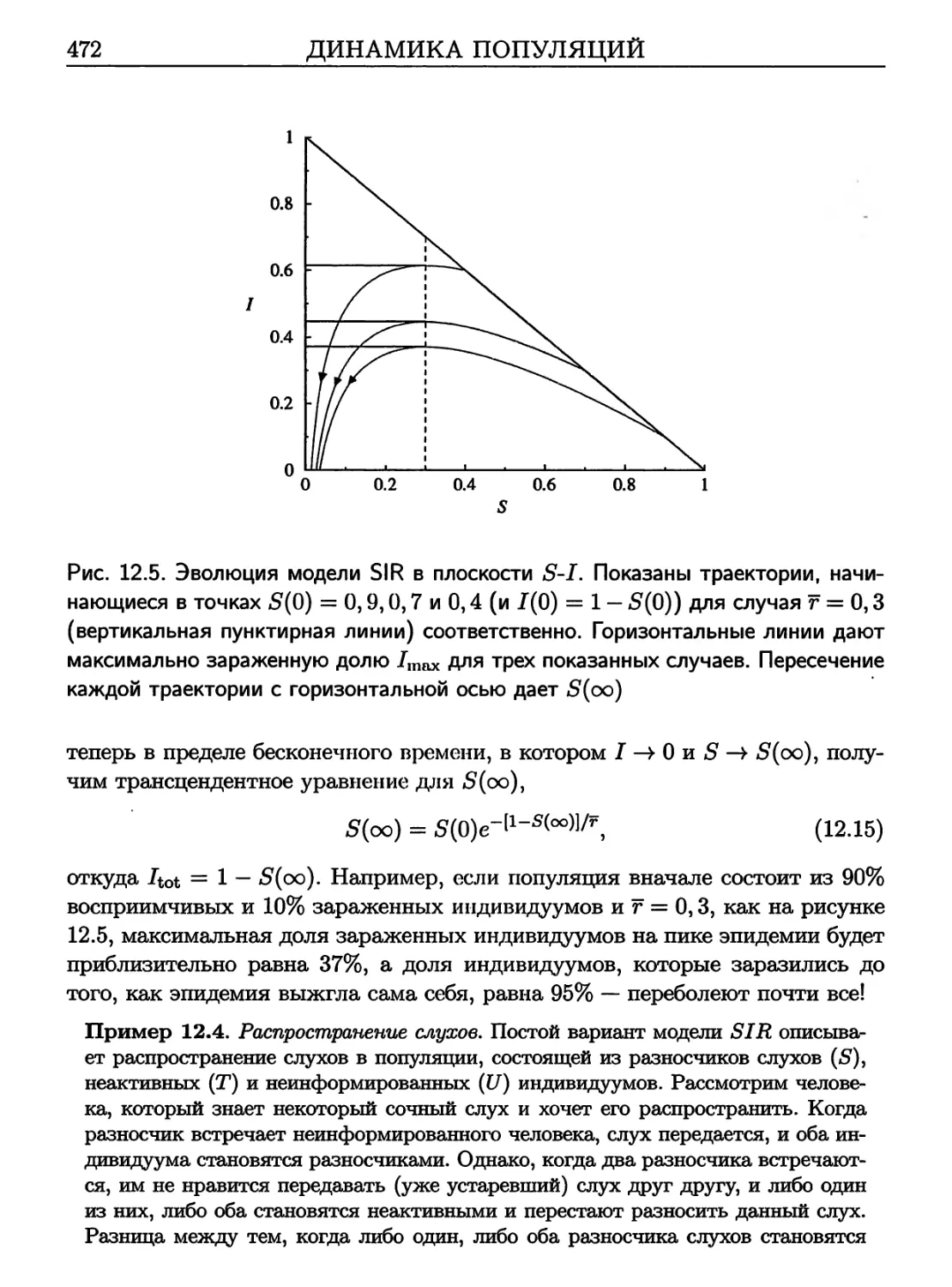
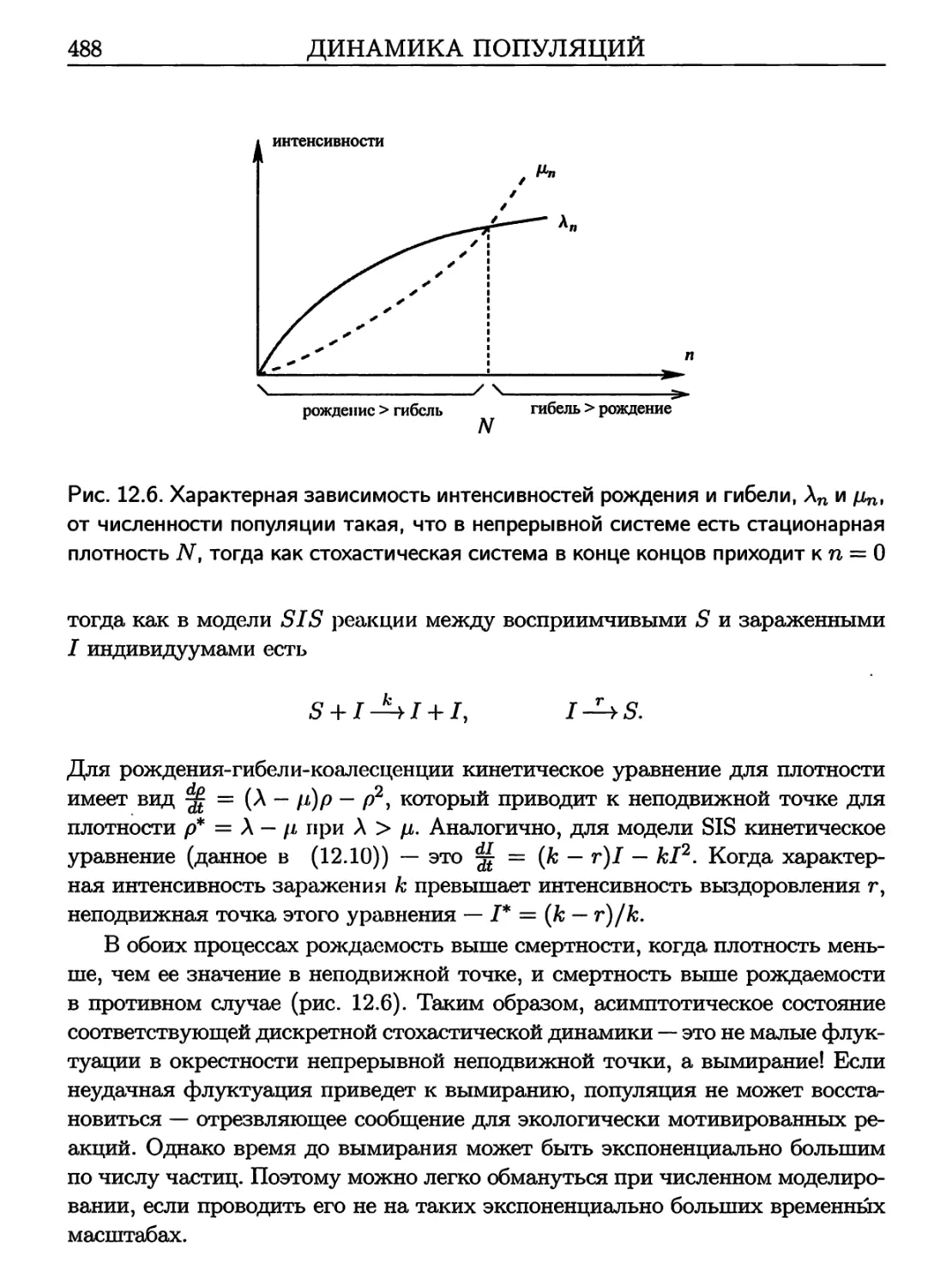
Author: Крапивский П. Реднер С. Бен-Наим Э.
Tags: сборники произведений разных авторов на разные темы серии сборники физика статистическая физика
ISBN: 978-5-91522-296-9
Year: 2012
Text
ФУНДАМЕНТАЛЬНЫЕ ОСНОВЫ НАНОТЕХНОЛОГИЙ
Павел Л. Крапивский
Сидней Реднер, Эли Е
ЛУЧШИЕ ЗАРУБЕЖНЫЕ УЧЕБНИКИ
научнообразовательный центр
по нанотехнологиям
МГУ имени М.В. Ломоносова
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ М.В. ЛОМОНОСОВА
НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ ЦЕНТР ПО НАНОТЕХНОЛОГИЯМ
ФУНДАМЕНТАЛЬНЫЕ ОСНОВЫ НАНОТЕХНОЛОГИЙ
лучшие зарубежные учебники
РОСНАНО
«РОНД ИНФРАСТРУКТУРНЫХ
И ОбРАЗОВАТЕЛЬНЫХ ПРОГРАММ
Издание осуществлено при поддержке
Фонда инфраструктурных и образовательных программ
A Kinetic View of
STATISTICAL PHYSICS
Pavel L. Krapivsky
(Boston University)
Sidney Redner
(Boston University)
Eli Ben-Naim
(Los Alamos National Laboratory)
Cambridge
UNIVERSITY PRESS
Кинетический взгляд на
СТАТИСТИЧЕСКУЮ ФИЗИКУ
Павел Л. Крапивский
(Бостонский университет)
Сидней Реднер
(Бостонский университет)
Эли Бен-Наим
(Лос-Аламосская национальная лаборатория)
перевод с английского
кандидат физ.-мат. наук
А.М. Поволоцкий
научный редактор русского издания
доктор физ.-мат. наук
В.Б. Приезжев
НАУЧНЫЙ МИР
2012
УДК 082.1; 531.3
ББК 94.3; 22.317
К 78
Серия: Фундаментальные основы нанотехнологий: лучшие зарубежные учебники
Главный редактор серии: академик А.Р. Хохлов
Ответственный редактор: канд. физ.-мат. наук А.В. Чертович
Редакционная коллегия:
Антипов Евгений Викторович, профессор химического факультета МГУ;
Гудилин Евгений Алексеевич, профессор факультета наук о материалах МГУ;
Клячко Наталья Львовна, профессор химического факультета МГУ;
Образцов Александр Николаевич, профессор физического факультета МГУ
Крапивский П., Реднер С., Бен-Наим Э.
К 78 Кинетический взгляд на статистическую физику / Пер. с англ. А.М. Поволоцкий;
науч. ред. В.Б. Приезжев. — М.: Научный мир, 2012. — 616 с.: ил. — (Фундамен¬
тальные основы нанотехнологий: лучшие зарубежные учебники). ISBN 978-5-91522-
296-9
В книге в доступной для студентов форме рассмотрены основные явления неравно¬
весной статистической физики. Она посвящена развитию и применению теоретических
методов, которые помогут студентам совершенствовать навыки решения задач.
Книга начинается с микроскопических процессов переноса: диффузии, явлений, опре¬
деляемых столкновениями, и процессов с запретами. Далее представлена кинетика агрега¬
ции, фрагментации и адсорбции, где основное внимание уделено феноменологии и методам
решений. Следующие главы посвящены кинетике спиновых систем в дискретной и непре¬
рывной формулировках, роли беспорядка в неравновесных процессах и явлению гистерези¬
са, рассматриваемому с неравновесной точки зрения. В заключительных главах обсужда¬
ются динамика популяций, химические реакции и кинетический взгляд на сложные сети.
Книга содержит более 200 упражнений для проверки понимания предмета читателем.
Книга предназначена для широкого круга читателей: студентов, аспирантов и научных
работников как физико-математических, так и смежных специальностей.
© Р. L. Krapivsky, S. Redner and Е. Ben-Naim
First published by Cambridge University Press 2010.
ISBN-13 978-0-521-85103-9 (Hardback)
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или передана
в какой бы то ни было форме и какими бы то пи было средствами, будь то электронные или
механические, включая фотокопирование и запись на магнитный носитель, а также размещение в
Интернете, если на то нет письменного разрешения правообладателя.
ISBN 978-5-91522-296-9
© Поволоцкий А.М., перевод на русский язык, 2012
© Научный мир, издание на русском языке, оформление, 2012
Оглавление
Предисловие xi
Обозначения xv
1 ВВОДНЫЕ ПРИМЕРЫ 1
1.1 Диффузия 2
1.2 Одновидовая аннигиляция/коалесценция 6
1.3 Двухвидовая аннигиляция 11
1.4 Ссылки 13
2 ДИФФУЗИЯ 15
2.1 Распределение вероятностей 15
2.2 Центральная предельная теорема 19
2.3 Блуждания с широкими распределениями 21
2.4 Применение к гравитации: распределение Хольцмарка 27
2.5 Свойства первого достижения 32
2.6 Вероятность выхода и время выхода 36
2.7 Теория скорости реакций 45
2.8 Подход Ланжевена 49
2.9 Применение к росту поверхностей 53
2.10 Ссылки 62
2.11 Задачи 62
3 СТОЛКНОВЕНИЯ 71
3.1 Кинетическая теория 71
3.2 Газ Лоренца 76
3.3 Газ Лоренца во внешнем поле 85
3.4 Волна столкновений 91
3.5 Молекулы Максвелла и очень твердые частицы 94
3.6 Неупругие газы 98
3.7 Баллистическая агломерация 109
v
vi
ОГЛАВЛЕНИЕ
3.8 Однополосное дорожное движение 112
3.9 Ссылки 117
3.10 Задачи 118
4 ЗАПРЕТЫ 125
4.1 Симметричный процесс с запретами 126
4.2 Асимметричный процесс с запретами 132
4.3 Гидродинамический подход 136
4.4 Микроскопический подход 143
4.5 Открытые системы 150
4.6 Ссылки 158
4.7 Задачи 159
5 АГРЕГАЦИЯ 163
5.1 Основное кинетическое уравнение 163
5.2 Методы точного решения 167
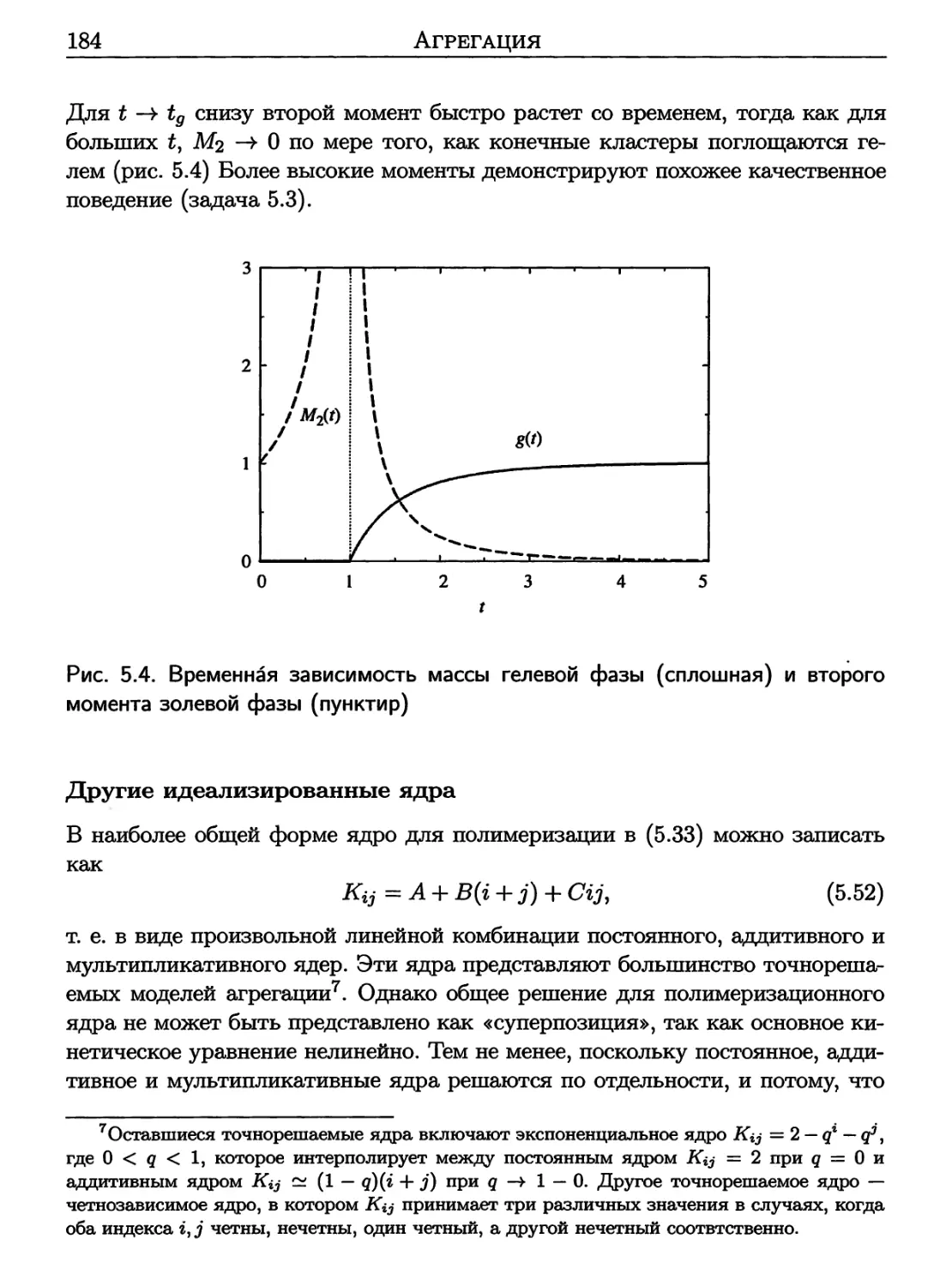
5.3 Гелеобразование 176
5.4 Скейлинг 186
5.5 Агрегация с источником 190
5.6 Рост с обменом 199
5.7 Ссылки 204
5.8 Задачи 205
6 ФРАГМЕНТАЦИЯ 210
6.1 Бинарная фрагментация 210
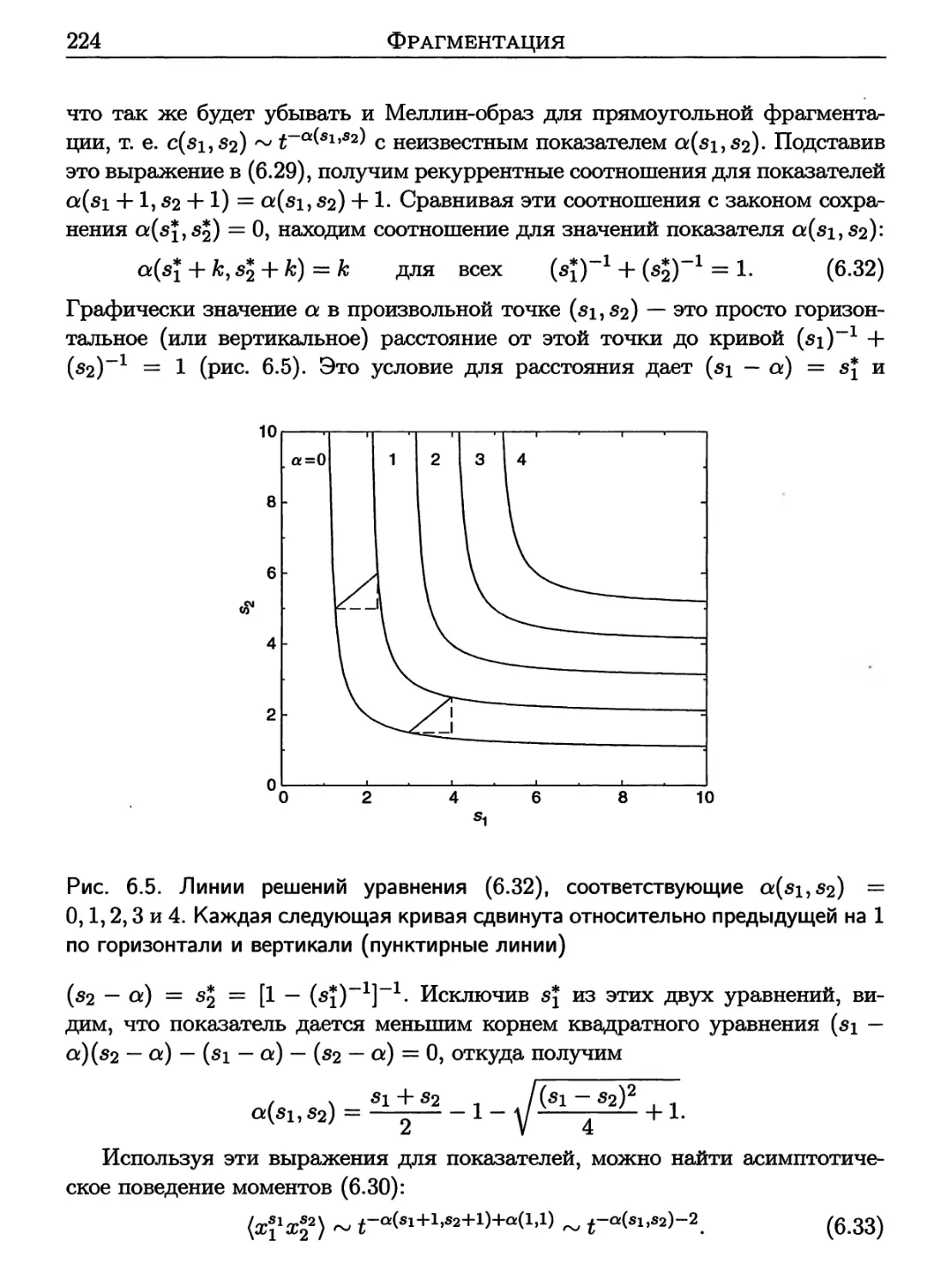
6.2 Планарная фрагментация 220
6.3 Обратимая полимеризация 226
6.4 Столкновительная фрагментация 233
6.5 Ссылки 237
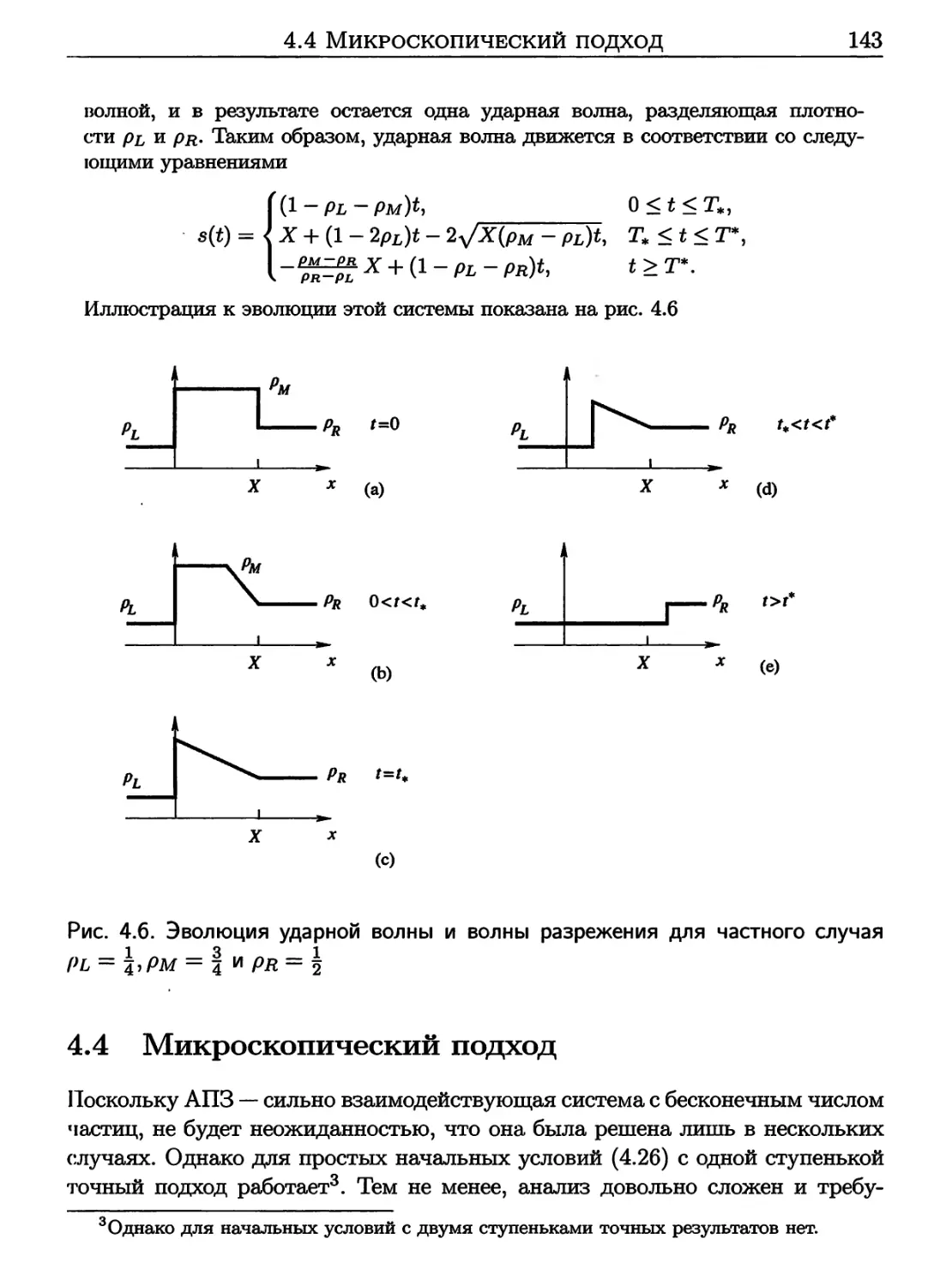
6.6 Задачи 238
7 АДСОРБЦИЯ 243
7.1 Случайная последовательная адсорбция в одномерии 243
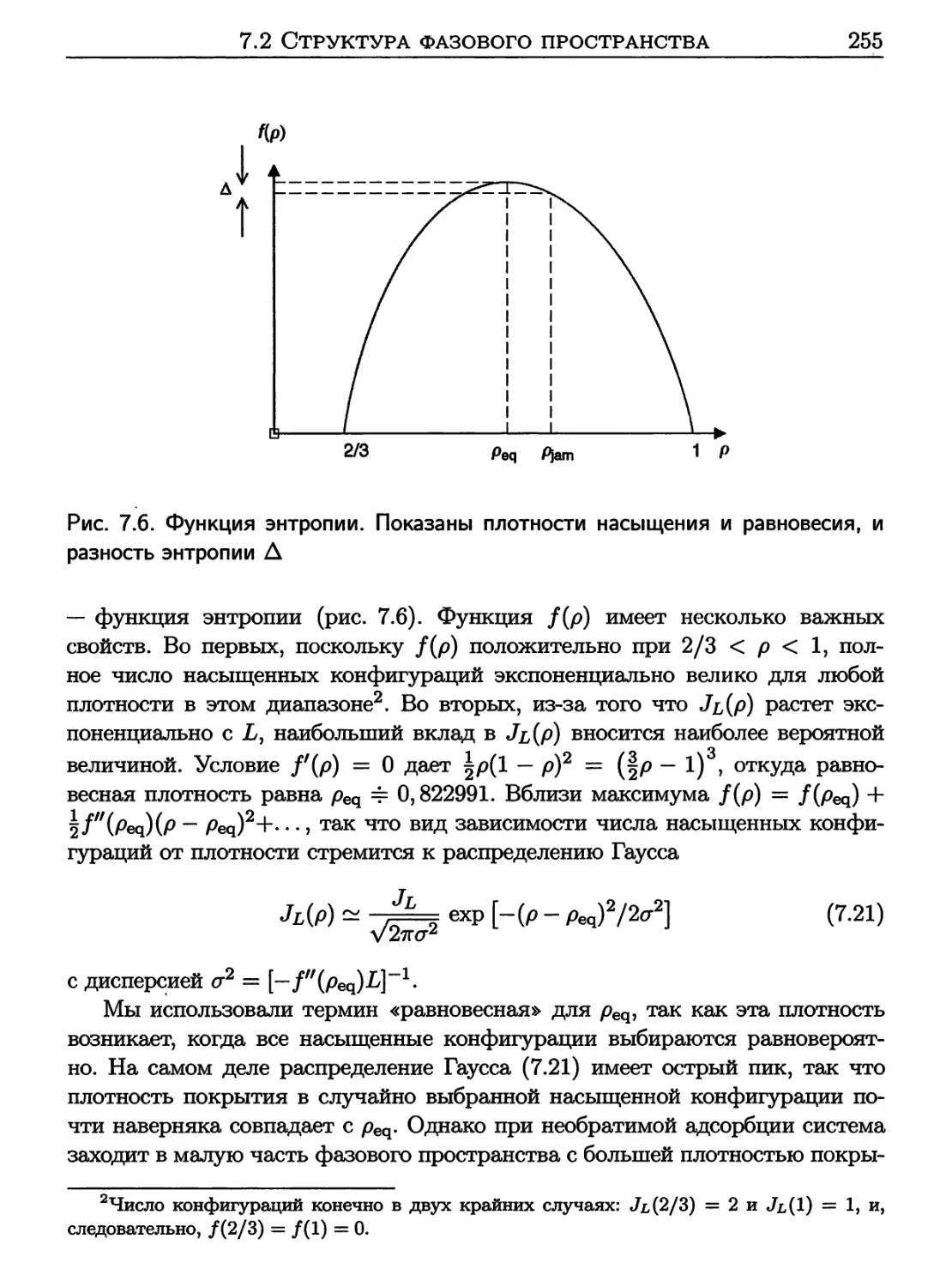
7.2 Структура фазового пространства 253
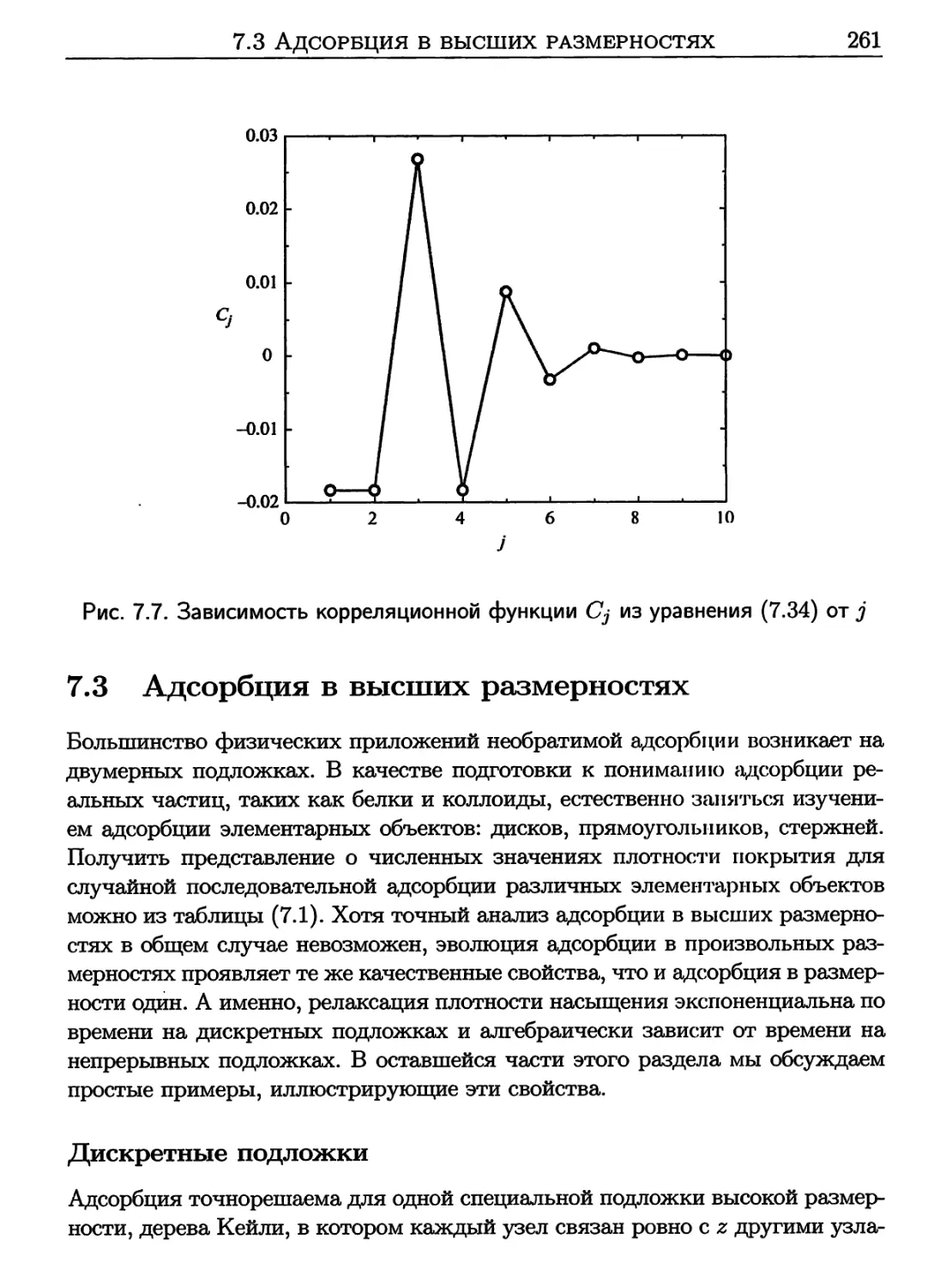
7.3 Адсорбция в высших размерностях 261
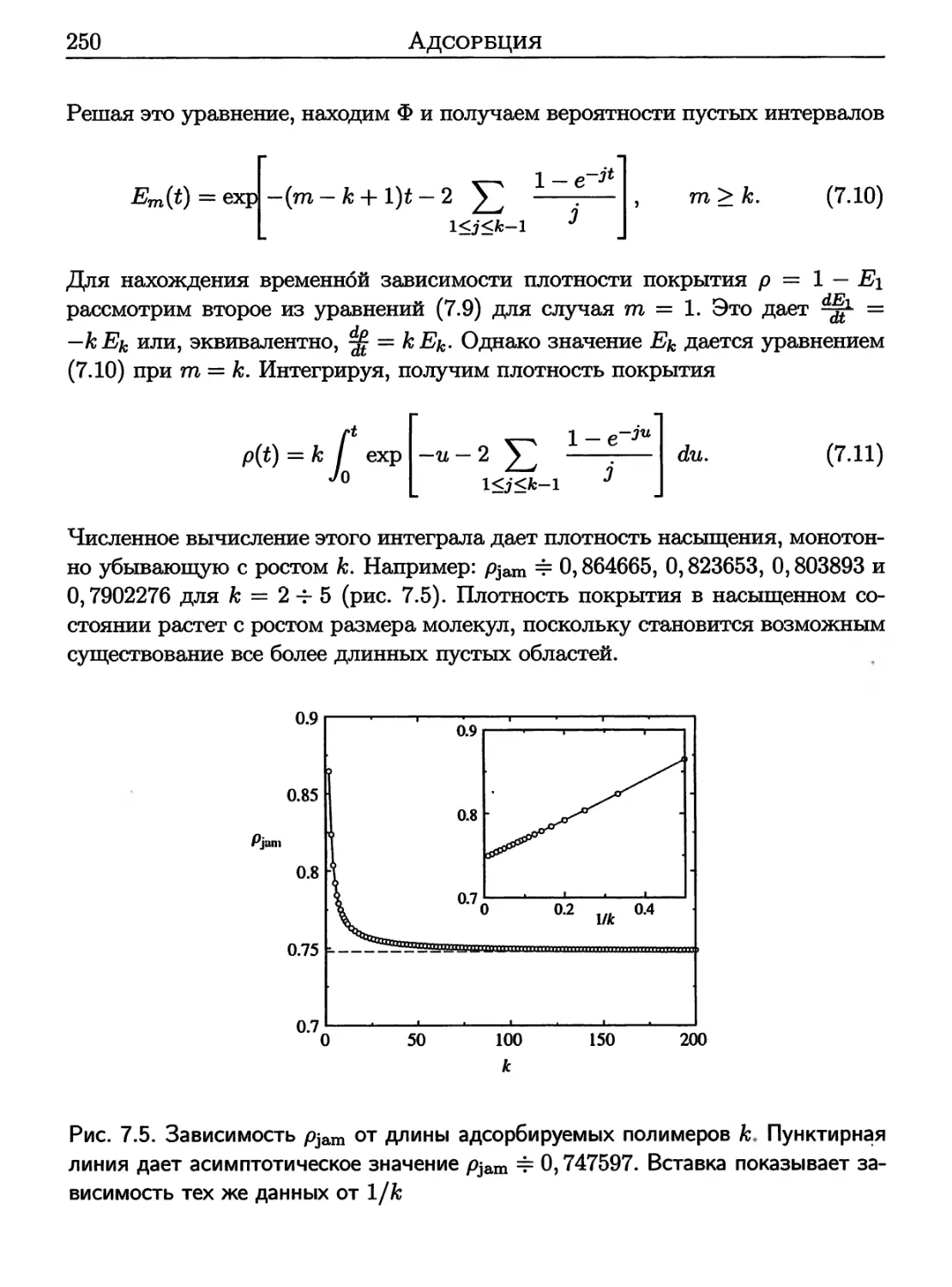
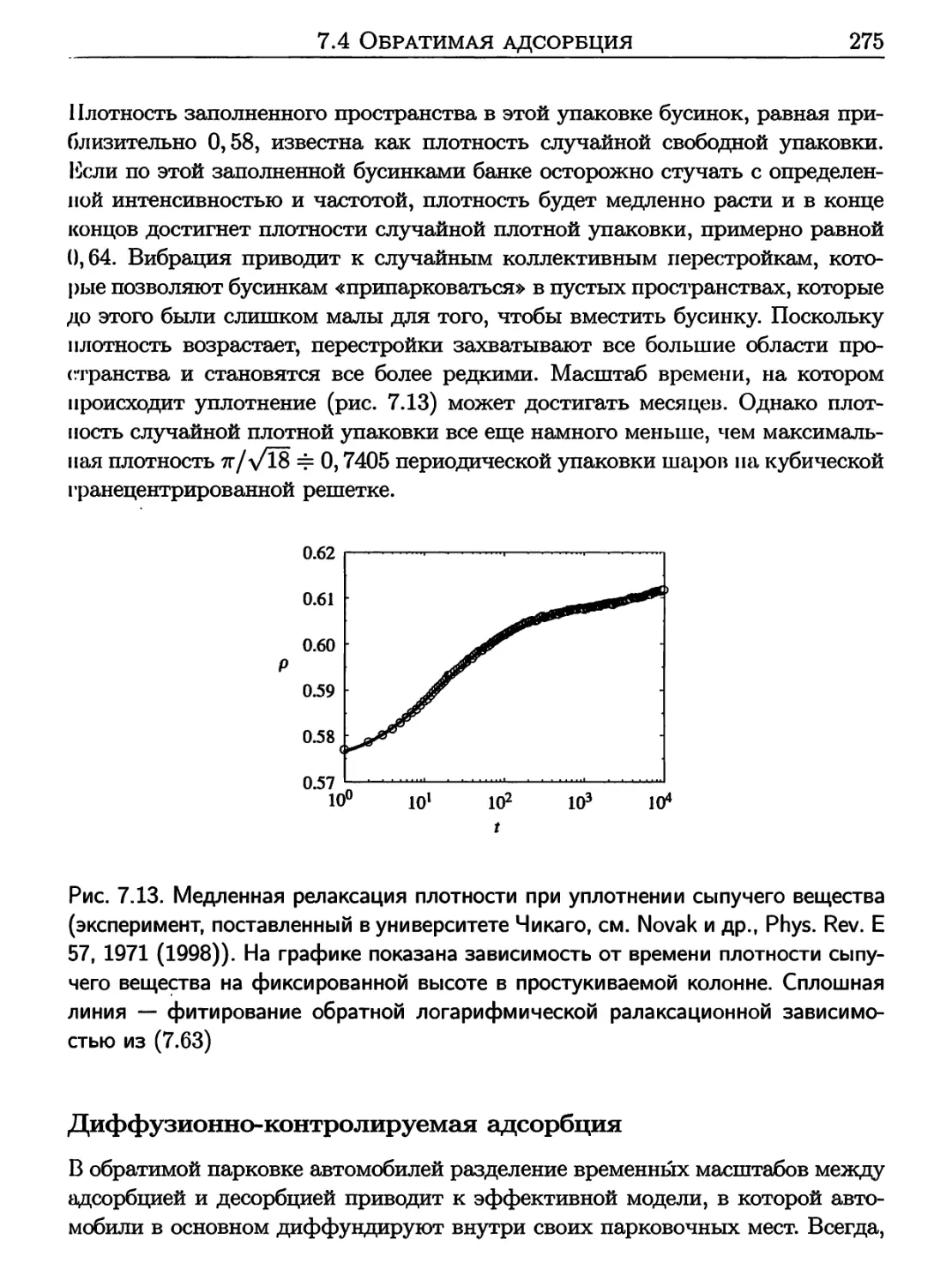
7.4 Обратимая адсорбция 270
7.5 Транслокация полимеров 277
7.6 Ссылки 282
7.7 Задачи 282
ОГЛАВЛЕНИЕ vii
8 ДИНАМИКА СПИНОВ 285
8.1 Феноменология укрупнения 285
8.2 Модель голосования 288
8.3 Модель Изинга-Глаубера 300
8.4 Приближение среднего поля 303
8.5 Глауберова динамика в одномерии 306
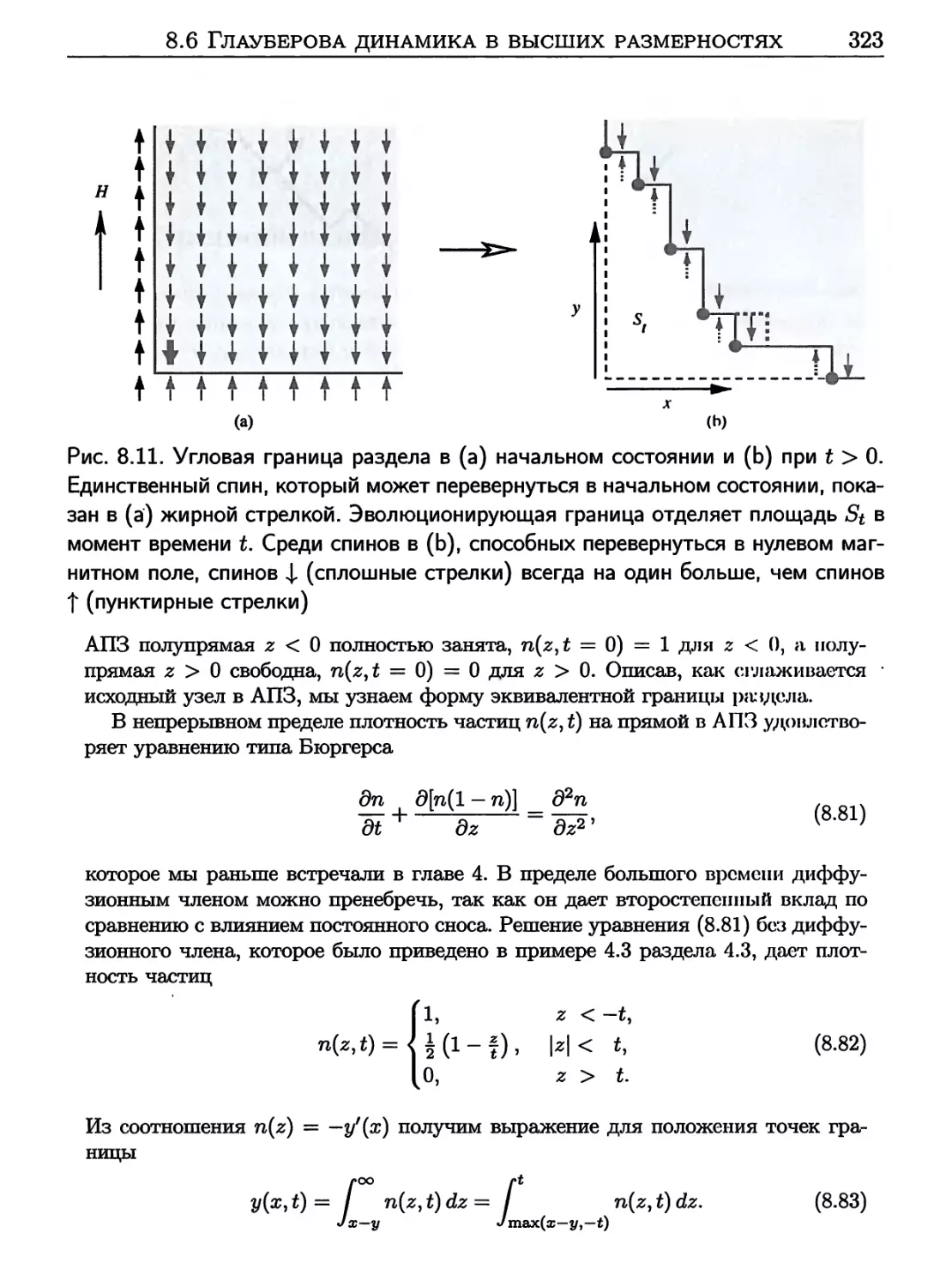
8.6 Глауберова динамика в высших размерностях 317
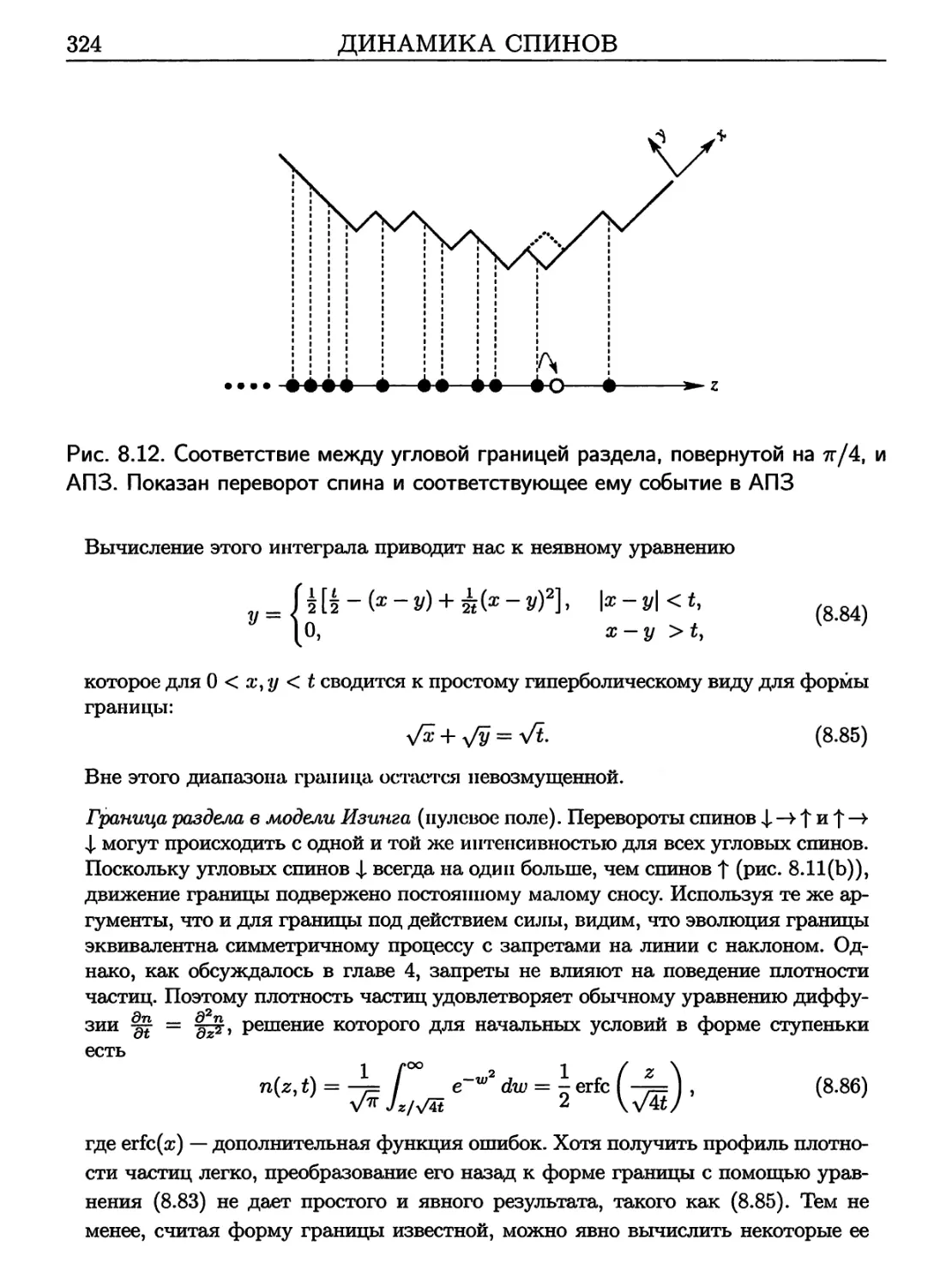
8.7 Спин-обменная динамика 325
8.8 Динамика кластеров 332
8.9 Ссылки 336
8.10 Задачи 337
9 УКРУПНЕНИЕ 341
9.1 Модели 341
9.2 Свободная эволюция 345
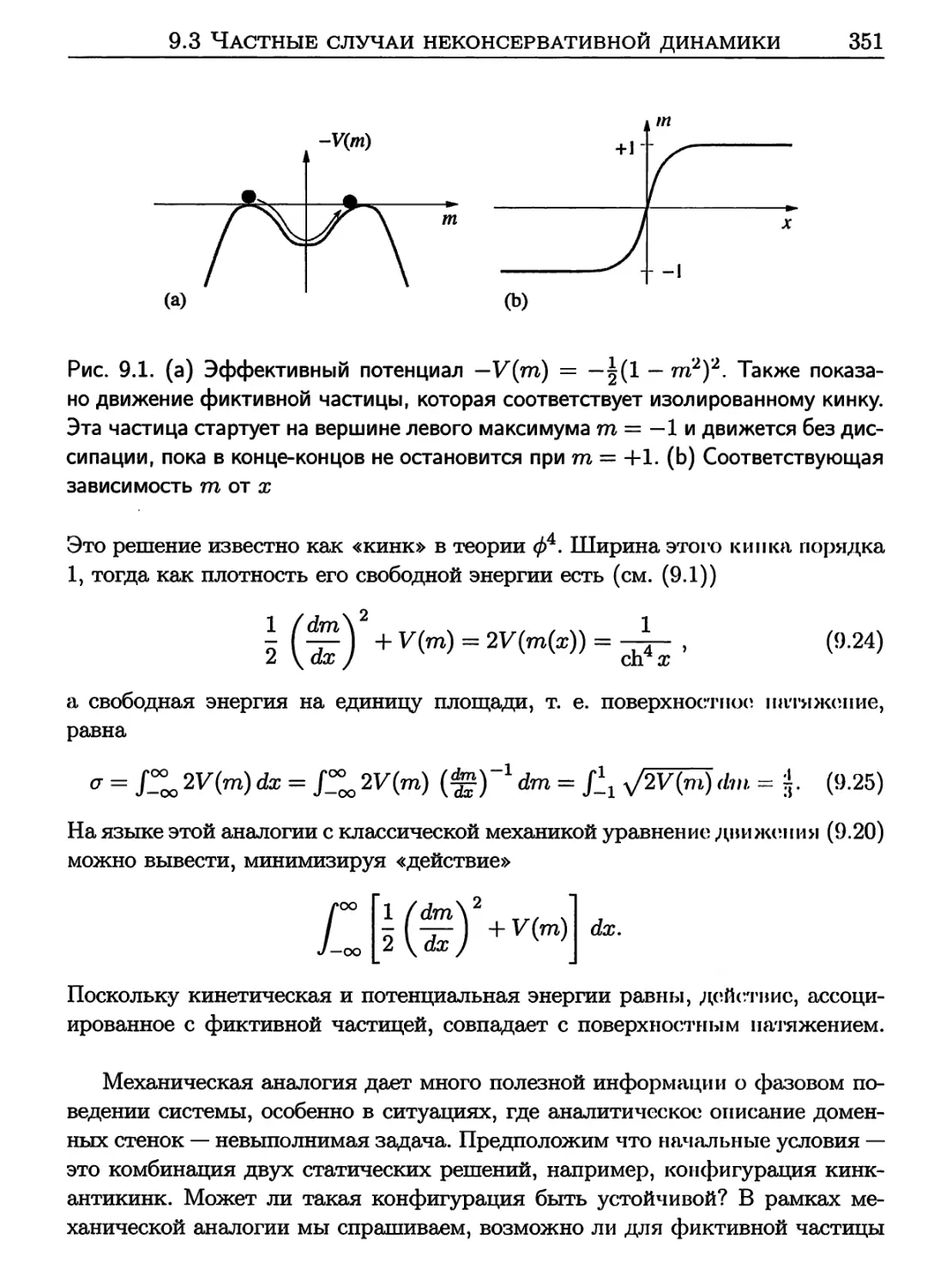
9.3 Частные случаи неконсервативной динамики 349
9.4 Финальные состояния 360
9.5 Дефекты 362
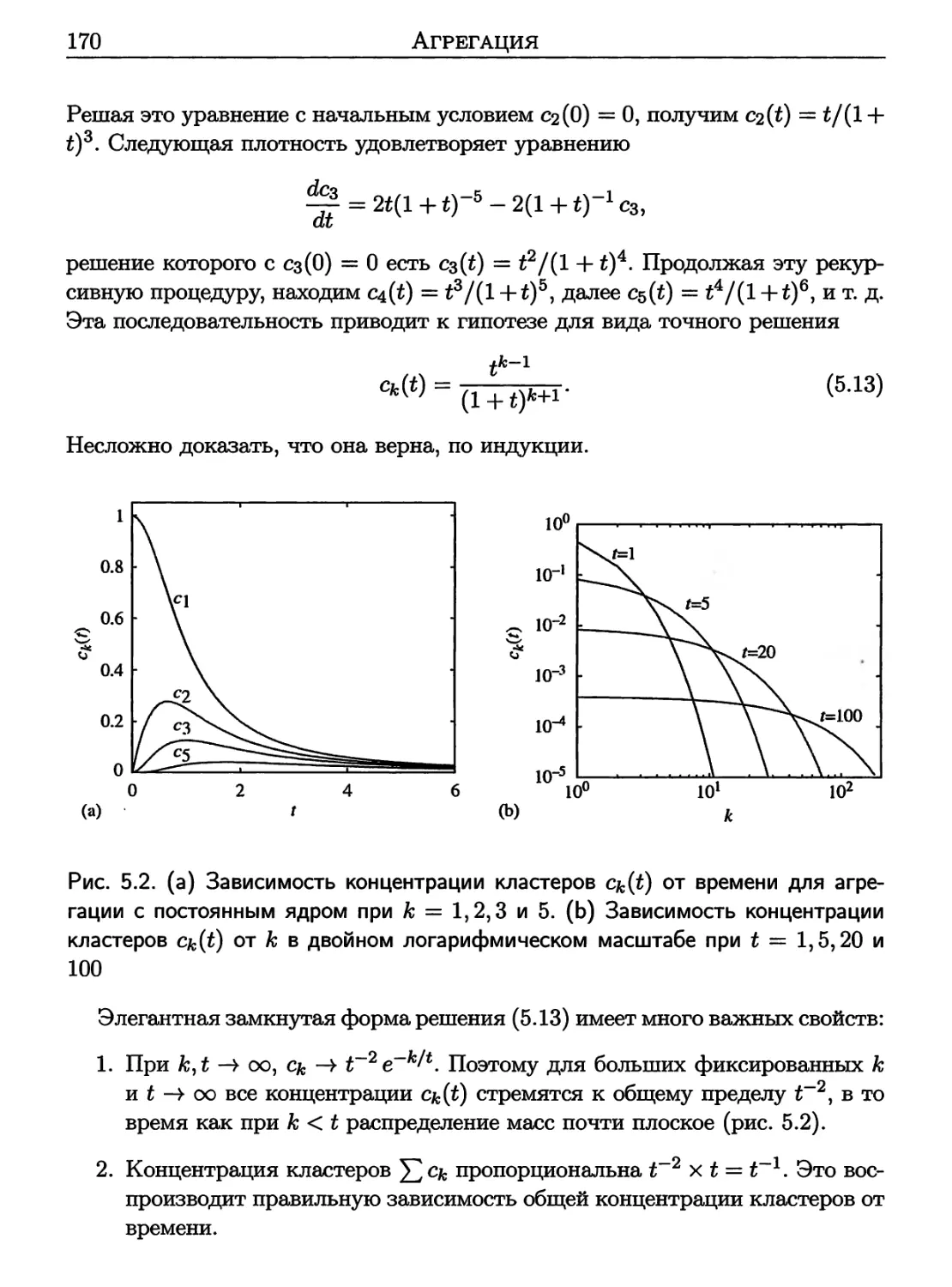
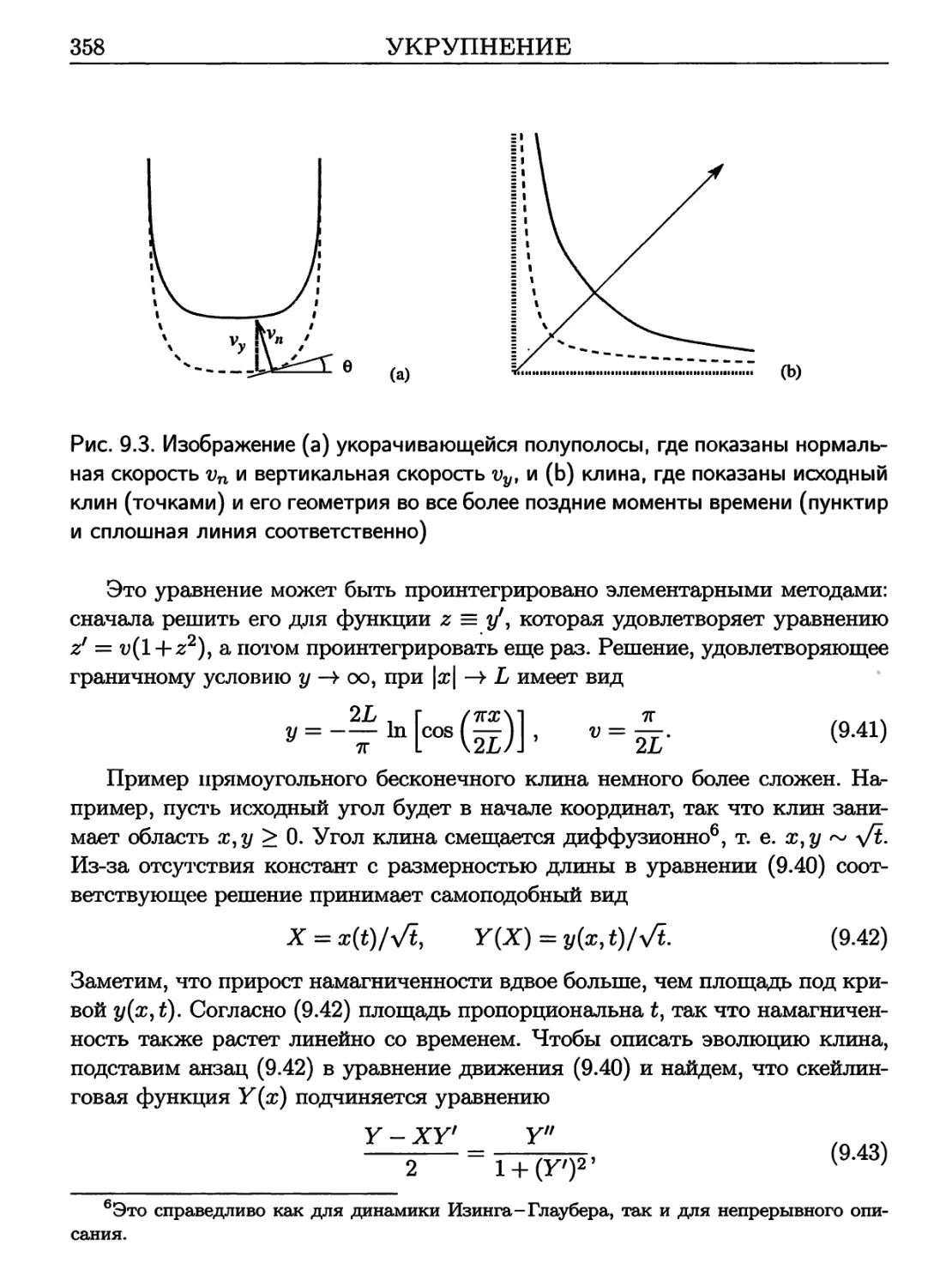
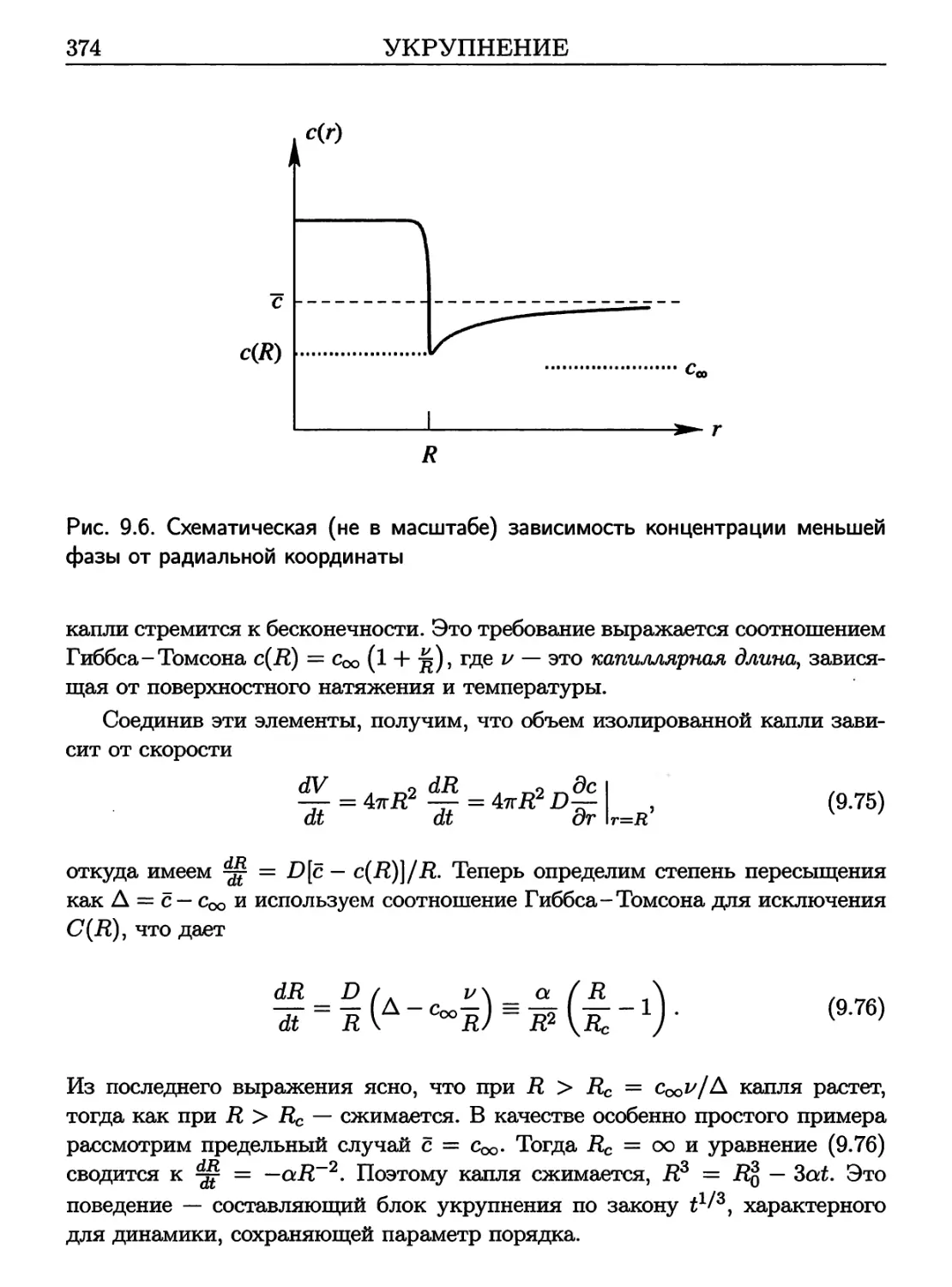
9.6 Консервативная динамика 372
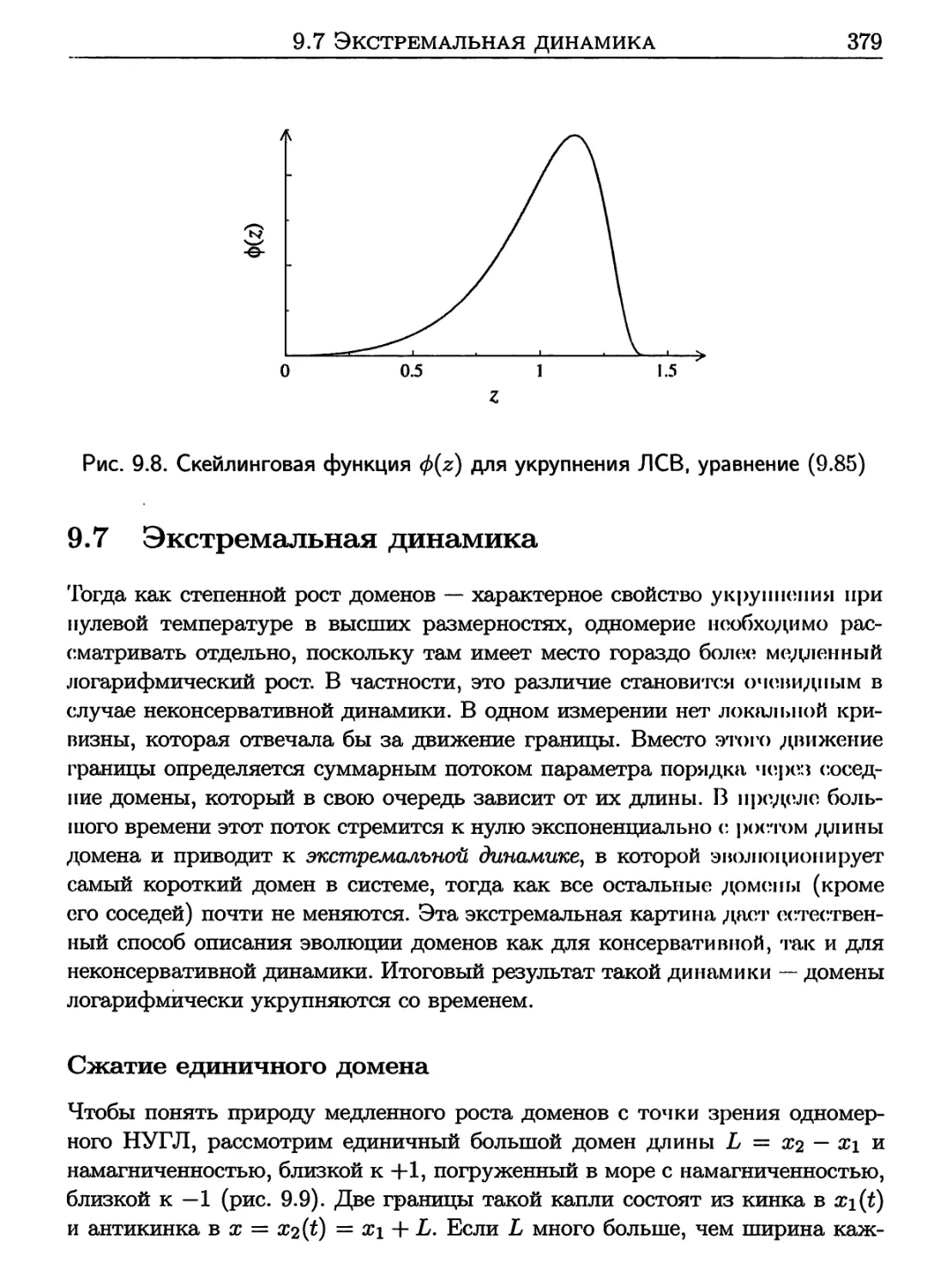
9.7 Экстремальная динамика 379
9.8 Зародышеобразование и рост 384
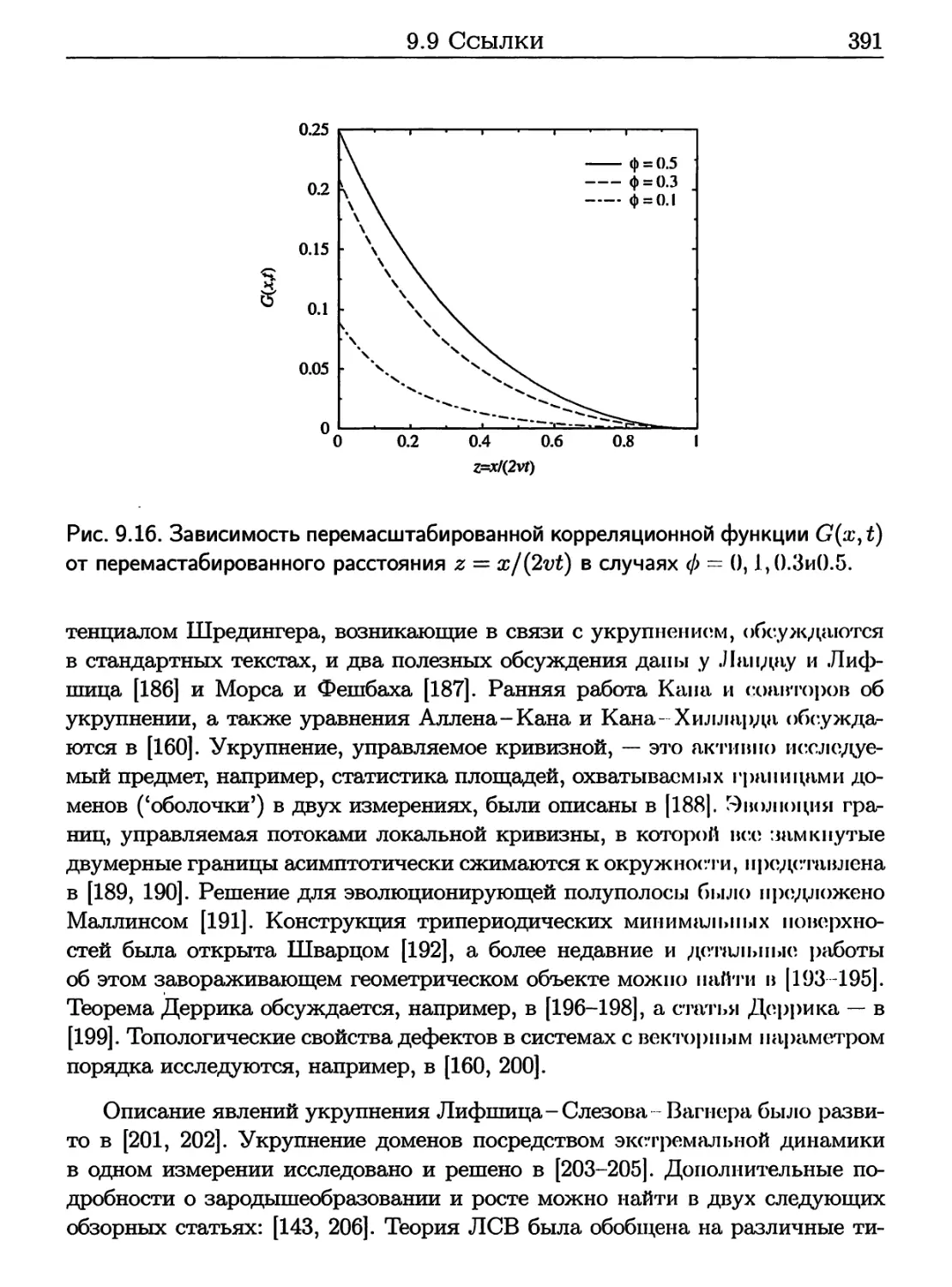
9.9 Ссылки 390
9.10 Задачи 392
10 БЕСПОРЯДОК 397
10.1 Неупорядоченная спиновая цепочка 398
10.2 Случайные блуждания в случайном потенциале 409
10.3 Случайные блуждания в поле случайных скоростей 418
10.4 Ссылки 423
10.5 Задачи 424
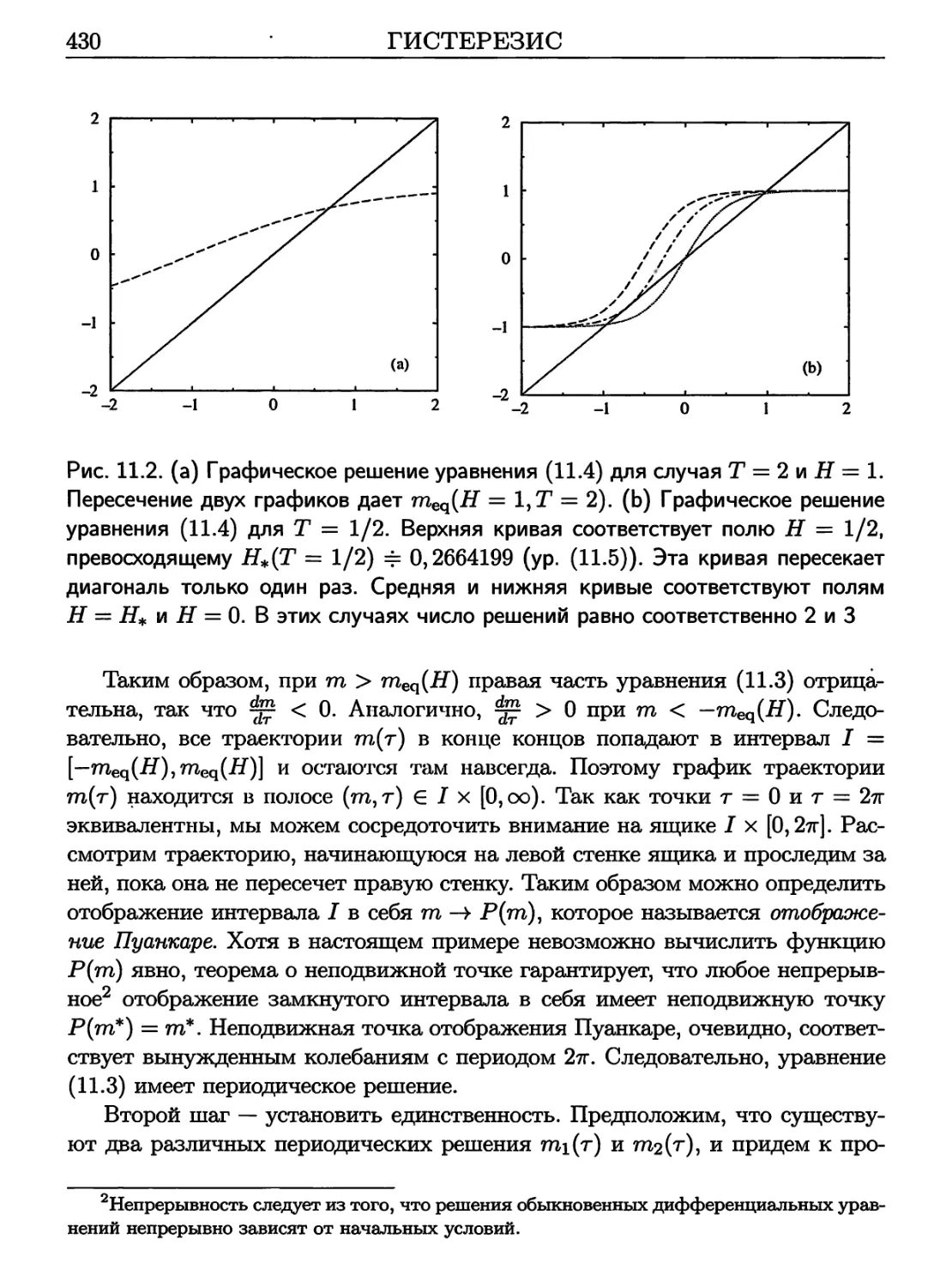
11 ГИСТЕРЕЗИС 427
11.1 Однородные ферромагнетики 427
11.2 Теория возмущений 432
11.3 Неупорядоченные ферромагнетики 441
11.4 Модель среднего поля 446
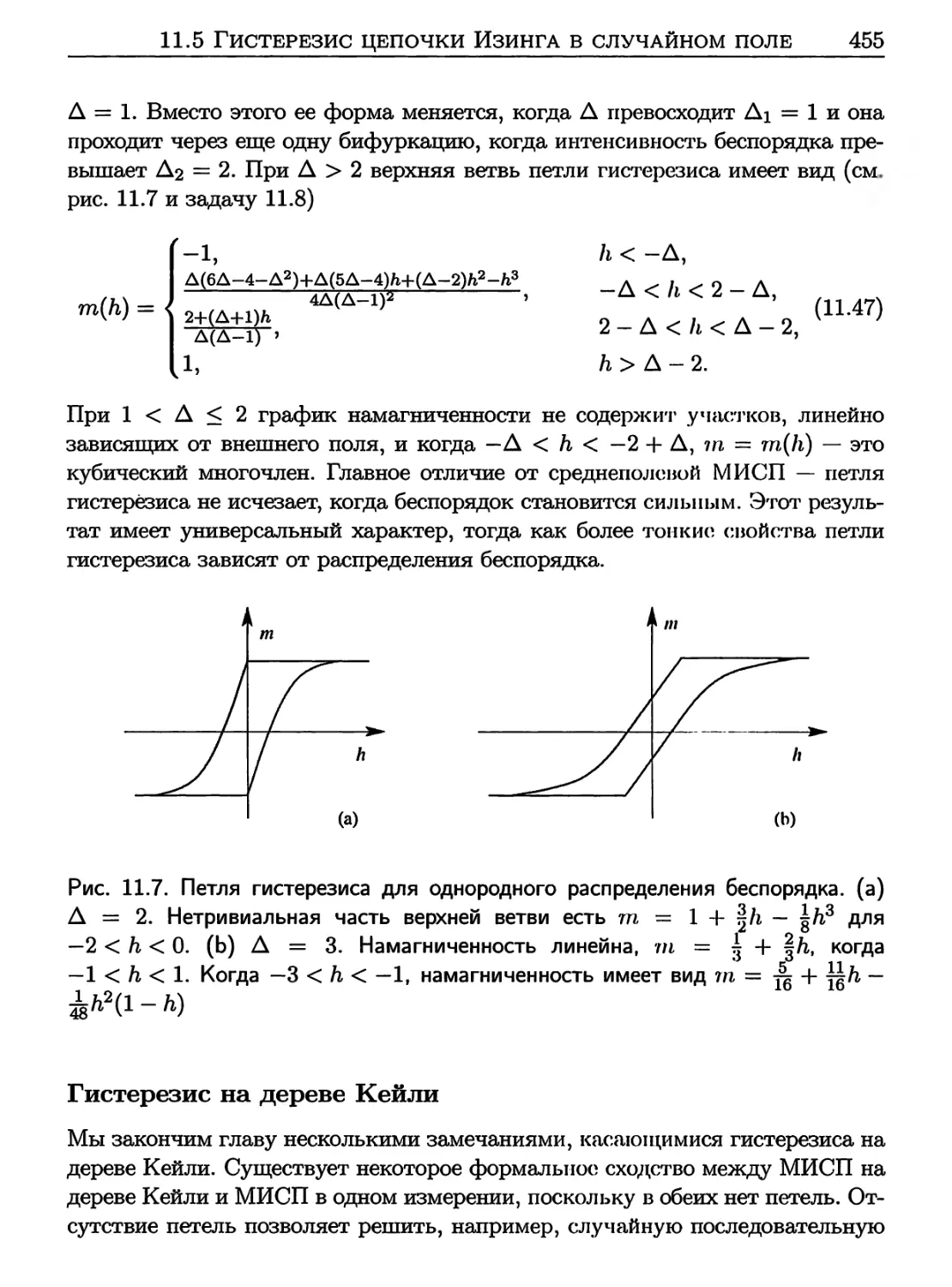
11.5 Гистерезис цепочки Изинга в случайном поле 452
11.6 Ссылки 457
11.7 Задачи 457
viii
ОГЛАВЛЕНИЕ
12 ДИНАМИКА ПОПУЛЯЦИЙ 461
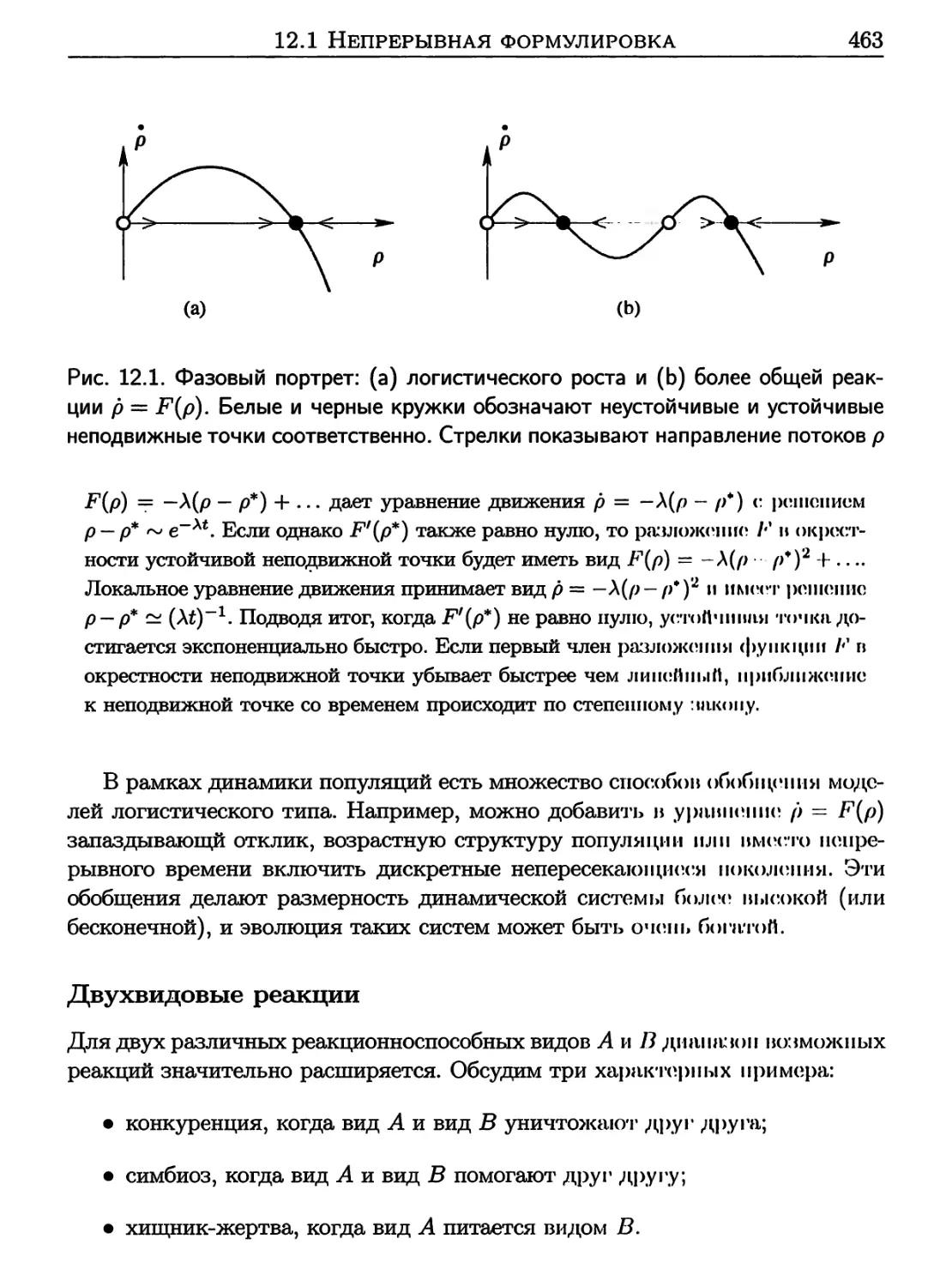
12.1 Непрерывная формулировка 461
12.2 Дискретные реакции 473
12.3 Разложение по малым флуктуациям 483
12.4 Большие флуктуации 487
12.5 Ссылки 493
12.6 Задачи 494
13 ДИФФУЗИОННЫЕ РЕАКЦИИ 498
13.1 Роль пространственной размерности 498
13.2 Реакция с захватом 504
13.3 Двухвидовая аннигиляция 510
13.4 Одновидовые реакции в одном измерении 515
13.5 Реакции с пространственным градиентом 528
13.6 Ссылки 539
13.7 Задачи 540
14 СЛОЖНЫЕ СЕТИ 543
14.1 Нерешеточные сети 543
14.2 Эволюция случайных графов 546
14.3 Случайные рекурсивные деревья 556
14.4 Преференционное присоединение 562
14.5 Флуктуации в сетях 566
14.6 Ссылки 572
14.7 Задачи 573
Литература 579
Предметный указатель 592
ПЛК благодарен Жене, Любе, Дане и другим чле¬
нам своей семьи за вещи, не имеющие ничего об¬
щего со статистической физикой. СР благодарен
своим детям Ребекке и Габриэлю и своей жене
Аните за терпение, поддержку и любовь во вре¬
мя подготовки книги. ЭБ благодарит любимую
семью: Эллен, Миху, Даниэля и Талью за все.
Авторы
Павел Львович Крапивский — доцент физики Бостонского университета.
Его научные интересы лежат в области сильно взаимодействующих многоча¬
стичных систем и их приложений к кинетическим спиновым системам, сетям
и биологическим явлениям.
Сидней Реднер — профессор физики Бостонского университета. Его науч¬
ные интересы лежат в области неравновесной статистической физики и ее
приложений к реакциям, сетям, социальным системам, биологическим явле¬
ниям и процессам первого посещения.
Эли Бен-Наим — член теоретического отделения и сотрудник центра наци¬
ональных исследований Лос-Аламосской национальной лаборатории. Он про¬
водит исследования по статистической, нелинейной физике и физике мягкого
конденсированного вещества, в том числе по коллективной динамике систем
взаимодействующих частиц и сыпучих веществ.
Предисловие
Статистическая физика — это необычный раздел науки. Он определяется не
объектом изучения как таковым, а идеями и методами, применимыми к очень
большому кругу проблем. Статистическая физика имеет дело с взаимодей¬
ствующими системами, состоящими из огромного числа составных частей:
частиц, спинов, агентов и т. д. Локальное взаимодействие этих элементов
приводит к поведению, которое часто бывает простым и ясным, хотя пове¬
дение таких же систем, но с малым числом частиц настолько запутано, что
не поддается никакой классификации. С точки зрения статистики большой
размер системы оказывается не недостатком, а преимуществом, приводящим
к проявлению простых коллективных свойств.
Если инструментарий равновесной статистической физики хорошо разра¬
ботан, статистическое описание систем вне равновесия менее развито. Нес¬
мотря на более чем вековые попытки построить формализм для неравновес¬
ных явлений, до сих пор не придумано аналога больцмановского веса или
статистической суммы в равновесной статистической физике. Кроме того,
неравновесная статистическая физика традиционно имела дело с малыми от¬
клонениями от равновесия. Мы сосредоточимся на системах, находящихся
вдали от равновесия, для которых концептуально простые и явные результа¬
ты могут быть выведены из их динамической эволюции.
Вероятно, наилучший способ вхождения в неравновесную статистическую
физику — это изучение примеров разнообразных систем и развитие техник
их описания. Мы попытались сделать наше изложение самодостаточным, так
чтобы интересующийся читатель мог перемещаться по тексту с минималь¬
ным количеством методологических подводных камней или скрытых вычис¬
лительных ловушек. Хотя основной акцент сделан на точные аналитические
инструменты, мы также, по мере необходимости, используем эвристические и
скейлинговые аргументы. Наша целевая аудитория — студенты университета
после первого года обучения, прослушавшие курс равновесной статистиче¬
ской физики и владеющие некоторым арсеналом математических методов.
Кроме того, мы надеемся, что эта книга будет полезна студентам и исследо¬
xii
Предисловие
вателям, работающим в области компьютерных наук, теории вероятности и
прикладной математики, вычислительной биологии и технических специаль¬
ностей, так как многие явления в этих областях тоже включают временную
эволюцию систем с множеством степеней свободы.
Мы начинаем с «вводных примеров», сокращенного перечисления основ¬
ных задач вместе с «намекам» на методы их решения. Основная тема следую¬
щих трех глав — процессы переноса. Глава 2 вводит случайные блуждания и
явление диффузии, механизмы, которые лежат в основе многих неравновес¬
ных явлений. Дальше в главе 3 мы обсуждаем явления, связанные со столк¬
новениями. Мы отходим от традиции концентрироваться исключительно на
уравнении Больцмана и его приложениях к гидродинамике. Вместо этого мы
приводим простые и наглядные примеры, такие как газ Лоренца и модели
Максвелла. В главе 4 мы даем краткий обзор процессов с запретами и обсуж¬
даем глубокие последствия для переноса и пространственного распределения
частиц, к которым приводит такое взаимодействие.
В следующих трех главах обсуждается кинетика фрагментации, агрега¬
ции и адсорбции. Классический процесс агрегации, в котором два кластера
необратимо сливаются, формируя больший кластер, дает возможность про¬
иллюстрировать методы точного решения и возникновение самоподобия в
распределении размеров кластеров. Многие из усвоенных при этом техниче¬
ских уроков применяются в книге в дальнейшем. Описание обратного про¬
цесса, фрагментации, следует похожей логической схеме. Далее мы рассмат¬
риваем необратимую адсорбцию протяженных объектов на поверхности. В
этом случае кинетический подход дает простой способ решения на первый
взгляд сложной геометрической проблемы: определения итогового покрытия
поверхности.
Главы 8 и 9 посвящены неравновесным спиновым системам. Сначала мы
займемся кинетическими моделями Изинга, так как они просты и широко
применяются для описания динамических систем, ассоциированных с фазо¬
выми переходами. Следующая глава об укрупнении рисует мезоскопическую
картину, в которой элементарные степени свободы — капли и фронты, а не от¬
дельные спины кинетической модели Изинга. Эти два разных подхода допол¬
няют друг друга, и каждый дает свой взгляд на предмет. Глава 10 проясняет
роль беспорядка на трех специфических примерах неравновесных процессов.
Следующая глава эксплуатирует подходы, развитые при изучении спиновых
систем и беспорядка для объяснения явления гистерезиса.
Главы 12 и 13 посвящены динамике популяций и кинетике химических
реакций. Первая из этих двух глав рассматривает также роль дискретно¬
сти. Это свойство может привести к эволюции во времени, значительно отли¬
Предисловие
xiii
чающейся от эволюции, предсказанной детерминистическими кинетически¬
ми уравнениями. В следующей главе обсуждается существенная роль про¬
странственных флуктуаций и влияние размерности на кинетику реакций. Мы
завершаем изложение подходом, вытекающим из основного кинетического
уравнения, которое используется для понимания фундаментальных свойств
сложных сетей.
В заключении к каждой главе мы поместили короткий раздел «Ссылки»,
который дает рекомендации по дополнительному чтению. В основном мы от¬
сылаем читателя к книгам и обзорным статьям. Хотя мы не ставим задачу
игнорировать оригинальную литературу, полезную информацию можно най¬
ти в этих более подробных источниках. Мы цитируем оригинальные источ¬
ники, когда это педагогически оправдано или когда обзоров по конкретному
предмету еще не написано.
Наш выбор тем был продиктован желанием осветить ключевые идеи и
основные техники, которые помогли бы превратить студентов, изучающих
неравновесную статистическую физику, в практиков. Из-за ограниченного
размера книги, нехватки знаний и из-за наших личных предпочтений многие
важные темы остались вне поля зрения. Тем не менее, мы надеемся, что
успешно изучивший книгу студент будет готов воспринять многие другие
гемы неравновесной статистической физики самостоятельно.
Хотя список тем не полон, содержащийся в книге материал слишком об¬
ширен для семестрового курса. Для такого курса мы рекомендуем бблылую
часть главы 2 (случайные блуждания/диффузия), первые три части главы 3
(столкновения), первые четыре части главы 5 (агрегация), части 7.1 и 7.4 в
главе 7, бблылую часть глав 8 и 9 (спиновые системы и укрупнение), первые
две части главы 12 (динамика популяций), первые три части главы 13 (диф¬
фузионные реакции) и главу 14 (сложные сети). Студентам рекомендуется
решать задачи — вероятно наиболее эффективный способ усвоения материа¬
ла.
Мы должны поблагодарить наших многочисленных соавторов, коллег и
студентов, которые помогли нам оформить наши мысли, а также тех, кто по¬
могал советами при подготовке книги. Каждый из нас пользовался идеями,
почерпнутыми от коллег, сотрудничавших с нами, и некоторые из этих идей
нашли место в этой книге. Мы не упоминаем всех имен, так как они слиш¬
ком многочисленны и мы наверняка упустим кого-нибудь. Тем не менее, мы
горячо благодарны им всем, и нам повезло, что многие из них — наши друзья.
Также мы благодарны студентам Бостонского университета, посещавшим
курс неравновесной статистической физики, основанный на материалах из
этой книги, который преподавали двое из нас (ПЛК и СР). Их вопросы и ре¬
xiv
Предисловие
акция на предварительные версии глав книги были очень полезны. Особенно
мы благодарны студентам Бостонского университета: Луке Д’Алессио, Кипу
Барросу и Дэвиду Шайчу, за тщательное чтение частей книги и полезные
комментарии. Кроме того, мы многое почерпнули из откликов студентов, по¬
сещавших мини-курсы, основанные на этой книге, на летней школе в Боулде¬
ре, поддержанной Национальным научным фондом, и в институте «Perimeter
Scholars» при поддержке Института Теоретической Физики «Perimeter». Мы
благодарим наших коллег за чтение ранних вариантов книги и за множество
полезных предложений и исправлений. Среди них Дани бен-Авраам, Хар¬
ви Гульд, Джон Мачта и Мауро Мобилиа. Мы особенно благодарны Кирону
Маллику, который прочитал всю книгу и внес бесчисленные предложения и
улучшения. Двое из авторов (ПЛК и СР), хотели бы поблагодарить Нацио¬
нальный научный фонд за финансовую поддержку исследований в течение
долгого периода, которая помогла написанию книги. ЭБН благодарен Лос-
Аламосской национальной лаборатории за продолжающуюся поддержку его
работы. Мы будем благодарны за сообщения о найденных ошибках и будем
выкладывать постоянно обновляемый список ошибок на наших веб-сайтах.
С любым из авторов можно связаться по адресам: paulk@bu.edu (ПЛК),
redner@bu.edu (СР), или ebn@lanl.gov (ЭБН).
Обозначения
()дин из приятных моментов в статистической физике — почти полное отсут¬
ствие необходимости задавать единицы измерения. Достаточно запомнить,
ч'го (в классической нерелятивистской физике) есть всего три независимых
единицы измерения: массы, длины и времени. Это желательное восстанов¬
ление нормального положения вещей, особенно после прохождения электро¬
динамики и магнетизма — этих удивительных областей, запутанных систе¬
мой единиц СИ. В статистической физике только один «пришелец» из систе¬
мы СИ, константа Больцмана fc, и многие физики и даже математики гор¬
до демонстрируют этот бесполезный множитель, переводящий одни единицы
в другие. Константа Больцмана — это меньшее зло, чем такие искусствен¬
ные величины, как магнитная и диэлектрическая проницаемости вакуума, а
сохранение к подобно удержанию фактора перевода между милями и кило¬
метрами. В этой книге константа Больцмана всегда единица, к = 1, то есть
температура измеряется в единицах энергии.
Неравновесная статистическая физика во многом пересекается с приклад¬
ной математикой, и мы следуем ценным урокам последней: например, мы
предпочитаем работать с уравнениями в безразмерной форме. Когда мы ис¬
пользуем размерные уравнения, мы стараемся применять анализ размерно¬
стей, который часто позволяет продвинуться неожиданно далеко с минималь¬
ными усилиями. Размерный анализ происходит из гидродинамики - дисци¬
плины, также граничащей со статистической физикой и прикладной матема¬
тикой.
Для краткости обозначений мы допускаем некоторые неоднозначности.
Например, мы используем одну и ту же букву для функции и ее Фурье обра¬
за, скажем f(x) и f(k), соответственно. В контексте риск запутаться почти
отсутствует, а принятое соглашение позволяет избежать громоздких обозна¬
чений. Таким же образом мы пишем /($) как для преобразования Лапласа,
'так и для преобразования Меллина функции /(ж). Так как преобразования
Лапласа и Меллина никогда не возникают вместе, дублирование обозначений
не вызовет затруднений.
xvi
Обозначения
Некоторые технические соглашения: везде в книге точка сверху обозна¬
чает дифференцирование по времени. Значение символов отношения: =, =,
ос, « и т. д. — расплывчато представляется большинством исследовате¬
лей, и мы должны признать, что оно было нашей постоянной головной болью
при подготовке книги. Чтобы сохранить математические отношения просты¬
ми и минимальными, мы старались избегать символов =, ос и «, так как они
близки к символам =, ~ и А именно,
= имеет промежуточное значение между = и —, так что мы используем
одну из крайностей;
ос имеет значение сходное с так что мы используем
« часто обозначает приближенное численное значение константы; так как
в наше время легко получить столько значащих цифр сколько нужно,
необходимость этого символа минимальна.
Таким образом, мы в основном пользуемся следующими символами:
= обозначает «равно по определению»;
~ обозначает «асимптотически равно»; например sin 2т ~ 2х при т —> 0; •
~ обозначает «пропорционально»; например sin2т ~ т; в более общем
смысле ~ обозначает «одного порядка с»; конечно, когда мы пишем
точное решение, мы предпочитаем стандартный знак равенства.
== обозначает равенство с точностью до необходимого количества знаков,
когда мы приводим только несколько первых; например: л/2 = 1,414213.
Глава 1
ВВОДНЫЕ ПРИМЕРЫ
Неравновесная статистическая физика описывает временную эволюцию мно¬
гочастичных систем. Индивидуальные частицы — это базовые взаимодейству¬
ющие элементы, которые в некоторых ситуациях могут изменяться в про¬
цессе взаимодействия. В самых интересных случаях взаимодействие между
частицами настолько сильное, что детерминистическое описание системы да¬
же малого числа частиц лежит за пределами любого точного теоретического
подхода. С другой стороны, когда число частиц достаточно велико, многоча¬
стичные системы часто допускают аналитическое статистическое описание. В
этом смысле они проще, чем системы с небольшим числом частиц. Это свой¬
ство имеет несколько разных названий: закон больших чисел, эргодичность
н т. д. — и это одна из причин столь впечатляющих успехов статистической
физики и теории вероятности.
Кроме того, неравновесная статистическая физика довольно сильно от¬
личается от других разделов физики, таких как «фундаментальные» разде¬
лы электродинамики, гравитации и физики высоких энергий, включающие
редукционистское описание систем нескольких частиц, и прикладных облаг
стей, таких как гидродинамика, теория упругости и т. д., которые в основ¬
ном имеют дело со следствиями фундаментальных уравнений движения. Вот
некоторые из ключевых и отличительных черт неравновесной статистической
физики:
• отсутствуют основные уравнения (как уравнения Максвелла в электро¬
динамике или Навье-Стокса в гидродинамике), из которых следовало
бы все остальное;
• она занимает промежуточное положение между прикладной и фунда¬
ментальной физикой;
2
Вводные примеры
• несмотря на разнородность области, существуют общие техники и кон¬
цепции;
• она естественно приводит к созданию методов, которые полезны для
приложений за пределами физики (например, метод Монте-Карло и ал¬
горитм имитации отжига).
Наша путеводная мысль состоит в том, что в отсутствие основополагающих
принципов и управляющих уравнений неравновесная статистическая физика
должна быть ориентирована на изучение конкретных систем взаимодейству¬
ющих частиц, а не на развитие теоретического формализма.
1.1 Диффузия
Чтобы проиллюстрировать несколько ключевых идей и ввести несколько ин¬
струментов для анализа, применимых к более общим проблемам, мы начнем
с краткого рассмотрения случайных блужданий.
Плотность вероятности для симметричной диффузии на прямой
Prob [частица Е (т, х + dx)] = Р(х, t) dx (1.1)
удовлетворяет уравнению диффузии
5Р _ д2Р
dt ~D дх2'
(1-2)
Как вскоре станет ясно, это уравнение описывает непрерывный предел несме¬
щенного случайного блуждания. Уравнение диффузии необходимо снабдить
начальными условиями, для которых положим: Р(ж,0) = 5(т), что соответ¬
ствует блужданию из начала координат.
Анализ размерностей
Притворимся, что мы не умеем решать (1.2), и попробуем понять поведение
блуждания без явного решения. Чему равно среднее смещение (ж)? Посколь¬
ку сноса нет, очевидно что
роо
х} = xP(x,t)dx = 0.
J—оо
Следующий момент, среднеквадратичное отклонение
/оо
X2
■оо
Р(х, £) dx,
1.1 Диффузия
3
уже нетривиален. Очевидно, он должен зависеть от коэффициента диффузии
D и от времени t. Применим анализ размерностей, чтобы найти эту зависи¬
мость. Если L обозначает единицы длины, а Т — единицы времени, то из
(1.2) размерности (ж2),Р и t будут
[<>=)] =/Л И=ь2/г, м=т.
Единственные величины, измеряемые в единицах квадрата длины, которые
можно получить, комбинируя эти параметры, — это само среднеквадратич¬
ное отклонение и произведение Dt. Следовательно,
(ж2) =С х Dt. (1.3)
Уравнение (1.3) — это один из центральных результатов неравновесной стати¬
стической физики, который мы получили, используя лишь анализ размерно¬
стей! Чтобы определить численную константу С = 2 в (1.3), нужно затратить
немного больше усилий, например решить (1.2) или домножить (1.2) на х2 и
проинтегрировать по пространственной координате, что дает (ж2) = 2D.
Эта, казалось бы, тривиальная аргументация работает и для гораздо бо¬
лее сложных проблем, таких как оценка возраста вселенной по ее плотности
или энергии атомного взрыва по зависимости радиуса взрывной волны от
времени. Из-за простоты и эффективности анализ размерностей должен ис¬
пользоваться как первое средство исследования реальных проблем.
Скейлинг
Применим теперь анализ размерностей к плотности вероятности P(x,t\D),
где зависимость от D указана явно, чтобы напоминать нам, что плотность су¬
щественно зависит от коэффициента диффузии. Так как [Р] = L-1, величина
y/DtP(x, t|Р) — безразмерна и, следовательно, может зависеть только от без¬
размерных величин. Из переменных х, t, D мы можем собрать единственную
безразмерную величину x/y/Dt- Поэтому самая общая зависимость плотно¬
сти от основных переменных, которая допускается анализом размерностей,
это
= « = az)
Плотность зависит от единственной скейлипговой переменной, а не от двух
основных переменных х и £. Это замечательное свойство значительно упрощаг
ет анализ типичных уравнений в частных производных, которые описывают
неравновесные системы. Уравнение (1.4) часто называют скейлинговъьм анза-
цем. Нахождение правильного скейлингового анзаца часто является большим
4
Вводные примеры
шагом на пути к решению. Подстановка анзаца (1.4) в уравнение диффузии
(1.2) сводит уравнение в частных производных к обычному дифференциаль¬
ному уравнению
2т"+ет7+Т=0.
Интегрируя дважды и используя симметрию (Т'(0) = 0) и нормировку, мы по¬
лучаем Т = (47г)-1/2 е-^ /4 и, в конце концов, приходим к распределению Гаус¬
са
P(x,t) =
y/kxDt
exp
4Dt
(1.5)
В этом примере скейлинговая форма была строго выведена только из
размерных соображений. В более сложных ситуациях аргументы в пользу
скейлинга менее строги, и скейлинг обычно достигается только в асимпто¬
тическом пределе. Рассмотренный пример, где скейлинг применим для всех
t, — исключение. Для уравнения диффузии с начальными условиями на ко¬
нечной области, а не на точечном носителе, скейлинг имеет место только в
пределе x,t —> оо, когда переменная £ остается конечной. Тем не менее мы
увидим, что там где скейлинг работает, он позволяет добиться существенного
прогресса в понимании проблемы.
Ренормализация
Стратегия метода ренормгруппы - понять поведение на большом масштабе,
в нашем случае на больших временах, итерируя свойства случайных блуж¬
даний на меньшем масштабе. Для уравнения диффузии начнем с равенства
/оо
P(y,t)P(x-y,t)dy, (1.6)
-оо
которое выражает вероятность достижения позиции х в момент времени 2t,
в терминах распространения блуждания с момента 0 до момента t и с момен¬
та t до 2t. Математически вероятность в момент времени 2t дается сверткой
вероятности пройти из (0,0) в (y,f) и вероятности пройти из (y,t) в (х, 2i).
Уравнение (1.6) называется уравнением Чепмена-Колмогорова и выражает
марковское отсутствие памяти у случайного блуждания. Более точно, мар¬
ковское свойство подразумевает, что переход из (у, £) в (ж, 2t) точно такой же,
как из (0,0) в (х — y,i). (Уравнение (1.6) также служит основой для описа¬
ния диффузионных процессов через интегралы по путям. Мы не затрагиваем
здесь эту тему.)
1.1 Диффузия
5
Свертка в уравнении (1.6) наводит на мысль применить к уравнению пре¬
образование Фурье
P(k,t) = Г eikxP(x,t)dx, (1.7)
J—оо
которое превращает (1.6) в алгебраическое соотношение Р(к, 2t) = [Р(&, i)]2.
Скейлинговая форма (1.4) показывает, что P(k,t) = Т(к), где к = ky/Dt, таи
что уравнение ренормгруппы принимает следующий вид:
?(у/2к) = [Т(к)]2.
.Логарифмируя и вводя новые обозначения z = k2,Q(z) = In У (к), мы полу¬
чим уравнение Q(2z) = 2Q(z), решение которого Q(z) = —Cz или P(k,i) =
(-2k2Dt (Константу С = 2 можно получить, например, разложив (1.7) при
малых к, P(k,t) = 1 — к2{х2} и вспомнив, что (ж2) = 2Dt). Применяя обратное
преобразование Фурье, мы снова приходим к (1.5). Таким образом, распре¬
деление Гаусса дает точное решение уравнения ренормгруппы. Этот вывод
показывает, что ренормгруппа тесно связана со скейлингом.
Основное кинетическое уравнение
Основное кинетическое уравнение дает способ детального описания эволюции
многих неравновесных систем. Такие системы могут быть охарактеризованы
статистически с помощью вероятностей того, что переменные, определяю¬
щие состояние системы, имеют заданные значения. Скорости, с которыми
эти переменные состояния изменяются со временем, входят в основное ки¬
нетическое уравнение. Проиллюстрируем это уравнение простым примером
симметричного случайного блуждания на одномерной решетке. Блуждание
описывается вероятностью Pn(t) находиться в узле п в момент времени t. Эта
вероятность меняется в соответствии с уравнением
^ = Рп_1 + Рп+1-2Рп. (1.8)
Первые два члена в правой части отвечают за рост Рп из-за прыжков из п — 1
впиизп+1вп, соответственно. Таким же образом последний член отвечает
за убывание Рп из-за прыжков из п в п ± 1.
Тот факт, что случайные блуждания лежат в основе многих аспектов
неравновесной статистической физики, обсуждается далее на протяжении
книги. Глава 2 посвящена объяснению случайных блужданий и связанных
с ними диффузионных процессов. В главах 2 и 10 мы также представим
физически мотивированные обобщения, в том числе: (i) глобальный снос в
6
Вводные примеры
интенсивностях прыжков, (ii) длинные прыжки и (iii) интенсивности прыж¬
ков, являющиеся случайными функциями координат. Понимание, полученное
при изучении случайных блужданий, обеспечит нам основной багаж, необхо¬
димый для изучения эволюционных уравнений, описывающих неравновесные
процессы в системах многих взаимодействующих тел.
1.2 Одновидовая аннигиляция/коалесценция
Неравновесная статистическая физика изучает системы, которые содержат
макроскопическое число взаимодействующих частиц. Чтобы понять их кол¬
лективное поведение, полезно игнорировать усложнения, появляющиеся из-за
ограниченности системы, т. е. сосредоточиться на ситуациях, когда количе¬
ство частиц бесконечно. Вероятно, простейшие системы бесконечного числа
частиц — это одновидовая аннигиляция, в которой частицы свободно диф¬
фундируют и мгновенно аннигилируют при контакте, и одновидовая коалес-
ценция, в которой реагенты сливаются при контакте. Эти процессы сыграли
важную роль в развитии неравновесной статистической физики и предостав¬
ляют великолепную иллюстрацию техник, применимых к другим системам,
состоящим из бесконечного числа частиц.
Оба процесса символически представимы в виде соответствующих схем
реакций:
А + А —0, (1.9а)
Л + Л —> А. (1.9Ь)
Плотность p(t) частиц А в обеих реакциях очевидно уменьшается со време¬
нем. Вопрос: «Как?»
Гидродинамическое описание
В гидродинамическом подходе предполагается, что реагенты все время иде¬
ально перемешаны. Это значит, что плотность в любом месте одна и та же и
каждая частица может вступить в реакцию в следующий момент с одной и
той же вероятностью. В пределе сильного перемешивания, взятом совместно
с непрерывным пределом, плотность частиц р в реакции коалесценции убы¬
вает со временем в соответствии с кинетическим уравнением для скорости
реакции
Tt = (1Л0)
Действительно, так как для того чтобы реакция произошла, две частицы
должны находиться в одном месте, левая часть пропорциональна квадрату
1.2 Одновидовая аннигиляция/коалесценция
7
плотности. Здесь К — скорость реакции, которая описывает склонность двух
диффундирующих частиц к взаимодействию. Вычисление скорости реакции
требует детального микроскопического анализа (см. раздел 2.7). Для реакции
аннигиляции мы можем использовать почти такое же уравнение, а именно
dp/dt = —2Кр2, теперь с коэффициентом 2, который учитывает пару частиц,
исчезающих при каждом столкновении.
Уравнения вида (1.10) типичны для гидродинамического описания. Реше¬
ние этого уравнения имеет вид
п<(’ = " W-1’ <1П’
где ро — начальная плотность. Однако истинное асимптотическое поведение
более интересно и зависит от размерности пространства d:
p(t) ~ <
fr1/2,
i_1 Ini,
i"1,
d = l;
d = 2;
d> 2.
(1-12)
Изменение асимптотики при dc = 2 иллюстрирует важное понятие критиче¬
ской размерности: выше dc кинетическое уравнение реакции воспроизводит
асимптотически верное поведение; ниже dc этот подход не верен; в dc этот
подход почти правилен — типичная ошибка на логарифмический поправоч¬
ный член.
Чтобы построить полную теорию, можно попытаться написать формаль¬
но точные уравнения для корреляционных функций. А именно, если p(r, t) —
микроскопическая плотность, правильные динамические уравнения для
p(t) = (р(г, £)) включают корреляционные функции (или просто корреля¬
торы) второго порядка (p(r, t)p(r',i)), так как две частицы должны нахо¬
диться близко друг к другу, чтобы реакция произошла. Аналогично, урав¬
нения для корреляторов второго порядка включают корреляторы третьего
порядка и т. д. Эти уравнения имеют иерархическую структуру, и единствен¬
ный способ продвинуться — применить некоторую процедуру замыкания,
в которой высокие корреляторы распадаются на корреляторы более низко¬
го порядка. В частности, гидродинамическое уравнение (1.10) воспроизво¬
дится при предположении, что коррелятор второго порядка факторизуется:
(p(r,i)p(rz,f)) = (p(r,f))(p(rz,t)) = p(t)2- Таким образом, уравнение (1.10) —
это факторизованная версия уравнения Больцмана для процесса аннигиля¬
ции (1.9а). Попытки описать эту схему реакции более честно, используя кор¬
реляторы высоких порядков, не достигли успеха. То есть, широко признан¬
ный подход, основанный на кинетической теории, оказывается практически
8
Вводные примеры
бесполезным для столь невинно выглядящего процесса А + А —> 0! Из-за того
что подходы, основанные на традиционных вычислениях, потерпели фиаско,
требуется развитие альтернативных методов.
Анализ размерностей
Определим зависимость скорости К от фундаментальных параметров реак¬
ции, т. е. от коэффициента диффузии реагентов D и радиуса частиц R. Из
уравнения (1.10) размерность скорости реакции равна [К] = Ld/Т, и, следо¬
вательно, единственная возможная зависимость имеет вид
К = DRd~2. (1.13)
Мы опустили численный множитель порядка единицы, определение которо¬
го выходит за пределы анализа размерностей. В дальнейшем мы часто иг¬
норируем такие коэффициенты без явного предупреждения. Заметьте, что
скорость реакции пропорциональна J?d“2, а не площади сечения Это
свойство происходит из особенностей диффузионного движения (см. также
раздел 2.7).
Подставляя (1.13) в (1.10) и решая это уравнение, получим
~ Rd~2Dt'
Мы ожидаем, что плотность убывает быстрее, когда радиус частиц возраста¬
ет. В соответствии с (1.14) эти ожидания оправдываются только при d > 2.
Поэтому кинетическое уравнение реакции, вероятно, верно в этом режиме.
При d = 2 убывание не зависит от размера частицы, что уже неожиданность.
Для d < 2 мы получим очевидно неверный результат, что плотность убывает
тем медленнее, чем частицы больше.
На самом деле плотность не зависит от R при d < 2. Это свойство са¬
моочевидно в d = 1, так как все, что имеет значение, — это расстояния
между частицами. Если теперь мы будем искать плотность в независящем
от R виде, р = р(7?,£), мы обнаружим, что единственная возможность — это
р ~ в соответствии с предсказанием (1.12) для одного измерения.
В контексте скорости реакции этот медленный спад эквивалентен скорости
реакции, которая убывает со временем. Мы вернемся к этому утверждению
в следующей главе.
Эвристические аргументы
Анализ размерностей часто воспроизводит правильные зависимости, но не
объясняет почему они возникают. Физический смысл одномерной асимпто¬
1.2 Одновидовая аннигиляция/коалесценция
9
тики р ~ (Dt)1/2 процесса аннигиляции (1.9а) можно понять, рассматривая
основное свойство случайного блуждания: за время t каждая частица по¬
сещает область размером i ~ y/Dt. Поэтому типичное расстояние между
выжившими частицами порядка откуда р ~ €-1 ~ (Dt)-1/2.
Руководствуясь этим объяснением, попробуем понять (1.12) во всех про¬
странственных размерностях. Полезно рассмотреть слегка модифицирован¬
ную ситуацию, в которой частицы совершают случайные блуждания по ре¬
шетке в размерности d (параметр решетки играет роль радиуса частицы).
Чему равно среднее число N различных узлов, посещенных частицей за N
шагов? Этот вопрос хорошо известен, и замечательный ответ на него:
{N1/2, d = 1;
N/lnN, d = 2; (1.15)
N, d> 2.
Немного подумав, можно убедиться, что плотность частиц в одновидовой
аннигиляции пропорциональна обратному среднему числу узлов, посещенных
частицей. Если в посещенной области больше одной частицы, они должны
были аннигилировать. Поэтому (1.15) эквивалентно (1.12).
Точное решение в одномерии
Диффузионно-контролируемая аннигиляция допускает точное решение в од¬
номерии. Это исключение — большинство взаимодействующих бесконечноча¬
стичных систем не могут быть решены даже в размерности d = 1. Более того,
даже в решаемых случаях чаще всего можно вычислить лишь ограниченное
количество физических величин. Например, если плотность частиц для од¬
номерной аннигиляции определена точно, распределение расстояний между
соседними частицами P(f, t) неизвестно даже в простейшем скейлинговом
пределе £,t —> оо при конечном £ = l/y/Dt, тр$ P(t,t) имеет вид (Dt)-1 У(£)
с до сих пор неизвестной функцией У.1
Точные результаты для диффузионно-контролируемой аннигиляции бу¬
дут представлены в главах 8 и 13, где будут развиты необходимые техниче¬
ские приемы. В данный момент ограничимся рассмотрением диффузионно¬
контролируемой коалесценции А + А —> А, которая решается в одномерии,
благодаря тому что может быть сведена к двухчастичной проблеме. Чтобы
вычислить плотность, удобно пометить частицы таким образом, чтобы при
коэффициент (Dt)-1 нужен для того, чтобы «закон сохранения» f£°£P(£,t)d£ = 1
записывался в не зависящем от времени явно виде £ У(£) df = 1
10
Вводные примеры
каждом столкновении левая частица исчезала, а правая выживала (рис. 1.1).
Тогда, чтобы вычислить вероятность выживания заданной частицы, можно
Рис. 1.1. Пространственно-временные траектории диффундирующих частиц
в размерности один, показывающие распространение помеченных частиц в
диффузионно-контролируемой коалесценции А -1- А —> А
забыть обо всех частицах слева от нее. Такой переход от изначальной двусто¬
ронней задачи к односторонней значительно упрощает анализ, так как важна
только ближайшая частица справа от заданной. Хотя ближайшая правая ча¬
стица может слиться с другой частицей справа от нее, эти реакции не влияют
на судьбу заданной частицы. Таким образом, задача свелась к решаемой про¬
блеме двух частиц.
Расстояние между заданной частицей и ее правым соседом подчиняется
диффузионному закону с коэффициентом диффузии 2D, так как расстоя¬
ние диффундирует с удвоенной скоростью каждой из частиц. Следовательно,
плотность вероятности р(£, t) расстояния i от заданной частицы до ее правого
соседа удовлетворяет уравнению диффузии с адсорбирующими граничными
условиями:
| = p(O,t) = O. (1.16)
Решение (1.16) для произвольных начальных условий р(у, £ = 0) есть
р(Л*) = p(y^ = 0) _ e-(Z+j/)2/8Di] dy
“ vhi вХР (’8^) ехр (-8^) sh (j5i)
В первой строчке решение выражается через суперпозицию распределения
Гаусса и его зеркального изображения, которая автоматически удовлетворяет
* Здесь и далее мы придерживаемся принятой в англоязычной литературе традиции
переноса формул, которая использовалась в оригинальном тексте (Прим, переводчика).
1.3 Двухвидовая аннигиляция
11
адсорбирующим граничным условиям. В пределе большого времени интеграл
во второй строчке стремится к
^iryp(v’t=o)dy=^
где ро — начальная плотность. Таким образом,
что приводит нас к решению
p(t) = ро f p(£,t)d£ ~ (2nDt) 1/2, (1-18)
Jo
независимому от начальной плотности.
Так как распределение длины интервала Р(£, t) равно рор(£, t), мы видим
что для диффузионно-контролируемой коалесценции перемасштабированное
распределение имеет вид
?(€) =
ехр
И),
£
VDt'
е
4^
е =
1.3 Двухвидовая аннигиляция
Рассмотрим диффундирующие частицы двух видов, А и В, которые вначале
случайно распределены с равными концентрациями: рл(0) = рв(О) = Ро- Ко¬
гда две частицы разных сортов сближаются до радиуса реакции, они немед¬
ленно аннигилируют в соответствии с
0.
А + В
(1-19)
В этой реакции плотности убывают по закону
p(t) ~
d < 4,
d > 4,
(1-20)
при t -> со, так что критическая размерность равна dc = 4. Этот пример пока¬
зывает, что гидродинамическое описание неверно даже в физически важном
случае трех измерений. Специфическая черта уравнения (1.20) — отсутствие
логарифмических поправок в d = dc. Обычно логарифмические поправки
12
Вводные примеры
Рис. 1.2. Снимок положений частиц в двухвидовой аннигиляции в размерности
два. Размеры частиц увеличены для наглядности
возникают в критической размерности, и их отсутствие в двухвидовой ан¬
нигиляции еще не объяснено. В данном примере ни гидродинамическое опи¬
сание (дающее р ~ £-1), ни анализ размерностей не объясняют убывания
плотности. Для того чтобы понять, почему простые подходы терпят неудачу,
рассмотрим снимок двумерной системы в некоторый момент t » 1 (рис. 1.2),
на котором система спонтанно организуется в мозаику перемежающихся об¬
ластей (доменов) А и В. Из-за такой организации аннигиляция возникает
только на границах доменов, а не во всей системе. Это эффект экранирова¬
ния, который объясняет, почему плотность больше, чем в гидродинамической
картине, где предполагается, что частицы хорошо перемешаны.
Эвристические аргументы, основанные на такой доменной структуре, поз¬
воляют определить убывание плотности в уравнении (1.20). В пространствен¬
ной области линейного размера £ начальное число частиц А равно
na = pQed ± (1.21)
и частиц В — аналогично. Здесь член со знаком ± подчеркивает, что число
частиц в конечном объеме — случайная величина с типичными флуктуаци-
1.4 Ссылки
13
ими порядка в окрестности среднего значения ро$. Следовательно,
характерная разница Na — NB в области размера € имеет вид
Na-Nb =
На эту разность не влияют события аннигиляции. Поэтому после того как
вид находящийсяв_меньшинстве исчезнет, локальная плотность принимает
значение р ~ у/p$t,d/(!,d. Из-за диффузионного размазывания (1.3) средний
размер области растет как £ r\j VDt, поэтому имеем
p(t)~V^(Pt)-d/4. (1.22)
В отличие от одновидовой аннигиляции, где начальная плотность асимпто¬
тически не важна, в двухвидовой анигиляции начальная плотность влияет
на асимптотическое поведение.
В заключение заметим, что убывание плотности не может быть получено
только с помощью анализа размерностей, так как теперь мы имеем по мень¬
шей мере два независимых характерных пространственных масштаба: размер
домена y/Dt и расстояние между частицами. Чтобы получить временную за¬
висимость плотности, необходима дополнительная физическая информация
о виде доменной картины.
1.4 Ссылки
Существует значительное количество литературы по темам обсуждавшимся
ко вводной главе. Случайные блуждания и диффузия — классические пред¬
меты, базовый материал и основные ссылки по которым можно найти в [1-6].
Анализ размерностей и концепции скейлинга восходят к Галилею [7]. Совре¬
менная перспектива и исторические корни скейлинга представлены в [8]. Об¬
ласть, в которой анализ размерностей и скейлинг особенно популярны, — это
гидродинамика. Они информативно представлены в книге Баренблатта [9],
к которой обсуждается связь между скейлингом, промежуточными асимп¬
тотиками и ренормгруппой. Позже найденные взаимосвязи выделены в кни¬
ге Голденфельда [10]. Еще одна очень полезная книга, которая обсуждает
применение скейлингового подхода к физике полимеров, — книга де Жен-
иа. Кинетика реакций обсуждается в главах 12 и 13, где мы и предложим
соответствующую литературу. Зависимость от времени числа различных уз¬
лов, посещенных случайным блужданмем, (1.15), — классический результат,
выведенный например в [1] и в [3]. Диффузионно-контролируемый процесс
14
Вводные примеры
коалесценции в размерности d, = 1 — это один из примеров немногих нерав¬
новесных реакций, которые можно обоснованно назвать «полностью решае¬
мыми». Ссылки на различные точные решения этой модели и ее обобщения
будут также даны в главах 12, 13.
Глава 2
ДИФФУЗИЯ
Случайные блуждания и их непрерывный предел, диффузия или броунов¬
ское движение находятся в самом сердце неравновесной статистической фи¬
зики. Механизм броуновского движения1 — это повторяющиеся столкнове¬
ния микроскопической частицы с молекулами среды, в которой она нахо¬
дится. Историческая важность броуновского движения в том, что оно дало
веское (косвенное) подтверждение существования атомов и молекул. Из-за их
распространенности и полезности случайные блуждания (рис. 1.2) и диффу¬
зия, вероятно, самые успешные модели теоретической физики с гораздо более
разнообразными приложениями, чем простое описание движения микроско¬
пических частиц. Здесь мы приводим основные результаты и приложения,
которые будут использоваться в книге.
2.1 Распределение вероятностей
Начнем с рассмотрения случайного блуждания в дискретном времени на од¬
номерной решетке. На каждом шаге частица смещается на единичную длину
вправо с вероятностью р или влево с вероятностью q = 1 — р. Вероятность
нахождения частицы в узле х через N шагов подчиняется рекурсии
Pn№ = pPn-i(x - 1) + qPn-i(x + 1)- (2.1)
Вместо того чтобы решать (2.1), заметим, что вероятность П^(г) того, что
броуновское движение было открыто в 1785 году Яном Игенхаузом, который наблю¬
дал беспорядочное движение частиц угольной пыли на поверхности спирта. Роберт Броун
произвел свои наблюдения в 1827 году, изучая движение взвешенных зерен пыльцы в воде.
16
Диффузия
(а)
Рис. 2.1. (а) Случайное блуждание из 5000 шагов, в котором каждый шаг фик¬
сированной длины делается в случайном направлении в двух измерениях. (Ь)
Случайное блуждание из 5000 шагов, в котором длина шага распределена по
степенному закону г-3/4
блуждание сделает г шагов вправо и N —г шагов влево, имеет биномиальный
вид
П„М = (2.2)
Биномиальный коэффициент (^f) учитывает число различных сочетаний ша¬
гов вправо и влево, включающих г шагов вправо, тогда как множитель
prqN~r — это вероятность одного такого блуждания. Если случайное блуж¬
дание начинается в начале координат, общее смещение будет х = 2г — N.
Используя приближение Стирлинга для больших 7V, чтобы упростить бино¬
миальное распределение, получим, что Pn(x) = П^[г = (ж + N)/2]\dr/dx\
превращается в2 *Рлг(ж) e-lx-Nb-gtf/SNpq (2.3)
4 ' y/8irNpq v 7
Этот гауссов вид универсален и возникает, когда среднее и среднеквадратич¬
ное смещение за один шаг конечны. Мы еще вернемся к этому утверждению
при рассмотрении центральной предельной теоремы в разделе 2.2.
Случайные блуждания в дискретном времени играют важную роль как в
математике, так и в компьютерных вычислениях, тогда как в естественных
2Точнее, Pn(x) вдвое больше, чем предсказание (2.3), когда х и N имеют одинаковую
четность, и Pn (ж) = 0, если четность х и N разная.
2.1 Распределение вероятностей
17
пауках обычно возникают случайные блуждания в непрерывном времени.
Рассмотрим симметричный случай, где прыжки вправо и влево происходят
с одинаковыми интенсивностями, которые мы без ограничения общности по¬
лагаем равными единице (рис. 2.2). Обозначим Pn(t) вероятность того, что
1 1
Рис. 2.2. Случайные блуждания в непрерывном времени с прыжками вправо и
влево с интенсивностью 1
блуждание находится в узле п в момент t. Основное кинетическое уравнение
для такой вероятности заполнения имеет вид
^=Рп+1-2Р„ + Р„_1. (2.4)
Здесь Рп растет за счет прыжков из п ± 1 в п, и, наоборот, Рп убывает из-за
прыжков изпвп — 1 и вп+1. Решение уравнения (2.4) дает
PnW = In(2t)e-2t, (2.5)
где 1п модифицированная функция Бесселя порядка п (см. уравнение (2.14)
на врезке). В пределе большого времени асимптотика функции Бесселя ведет
себя как распределение Гаусса
P„W-t^==e-"2/«. (2.6)
V47rt
В непрерывном пространстве уравнение эволюции (2.4) превращается в
уравнение диффузии — классическое уравнение из раздела физики, которо¬
му посвящена значительная часть этой книги. Чтобы сделать пространство
непрерывным, мы заменяем т —$■ х n Pn(t) на P(x,t) — плотностью веро¬
ятности координаты х в момент времени t. Далее, мы разлагаем (2.4) в ряд
Тейлора до второго порядка. Это приводит к уравнению диффузии
9P(?,t) _ d2P(x,t) (9 7,
dt дх2 {’
е коэффициентом диффузии D = 1. Решаем это уравнение при общих значе¬
ниях £>, используя прямое и обратное преобразования Фурье:
P(fc, t) = Г° Р(х, t) eikx dx, Р(х, t) = ^~ Г° P(k, t) e~ikx dk. (2.8)
J-oo 27Г /_m
18
Диффузия
2.1. Уравнение дискретных прыжков и модифицированная
функция Бесселя
Изучим несколько более общую версию уравнения (2.4)
ЯР
= 7(P»-i + Pn+i) - 2Рп. (2.9)
Это обобщение описывает эволюцию спиновой корреляционной функции в кине¬
тической модели Изинга, которая будет обсуждаться в главе 8. Для простоты
предположим, что начальное условие имеет вид: Pn(t = 0) = 5п,о- Для решения
(2.9) введем дискретное преобразование Фурье
P(k,t)= £ Pn(t)eikn, (2.10)
п= —ОО
с помощью которого уравнение перепишется в виде
= (7(е<* + е-“) _ 2] Р(к, г). (2.11)
Так как преобразование Фурье начальных условий Р(&,£ = 0) = 1, то решение
уравнения (2.11) запишется как
Р(/с, i) = e2(7COsfc_1)t. (2.12)
Производящая функция модифицированной функции Бесселя 1п имеет компакт¬
ное представление
e*cosfc = £ eikn In(z). (2.13)
п=—ОО
Сравнивая эту производящую функцию с решением (2.12) для Р(/г, t) и используя
определение (2.10) преобразования Фурье, мы сразу получаем решение
Pn(t) = /n(270e"2t. (2.14)
Как будет видно в продолжении этой главы, использование преобразования
Фурье упрощает уравнения, возникающие в случайных блужданиях. В дан¬
ном примере преобразование Фурье превращает (2.7) в
с решением P(k, £) = Р(к, 0) e~Dk2t. Используя начальные условия Р(х, t=0) =
5(ж), получим Р(к, t) = e~Dk2t. После этого обратим преобразование Фурье и
2.2 Центральная предельная теорема
19
получим распределение вероятностей Гаусса3:
Р(х,*) = -!- /°° e~Dk2te~ikxdk = * e~x2/4Dt, (2.15)
27Г J_oo у/4%Dt
которое идентично результату (2.6), полученному в дискретном времени, с
коэффициентом диффузии взятым равным 1.
2.2 Центральная предельная теорема
После множества шагов распределение вероятностей для смещения случай¬
ного блуждания сходится к распределению Гаусса независимо от вида рас¬
пределения одного шага (при легких ограничениях, обсуждаемых ниже). Эта
универсальность составляет содержание центральной предельной теоремы.
Предположим, блуждание происходит в одномерии4 и перемещается дискрет¬
ными шагами со смещением хп на n-ом шаге, выбранными независимо из
непрерывного распределения р(х). Пусть Xjy = Yli<n<Nxn будет смещение
блуждания после N шагов5. Центральная предельная теорема утвержда¬
ет, что в пределе N —> оо распределение вероятностей полного смещения
— это универсальная гауссова функция
~ (2.16)
где сг2 = (ж2) — (ж)2. Необходимые условия центральной предельной теоремы
таковы: (i)nepBbie два момента одношагового распределения
/»оо /*оо
(ж) = / xp(x)dx и (ж2) = I x2p(x)dx
J—ОО J—оо
конечны6, (ii) начальное пространственное распределение также должно
иметь конечные первый и второй моменты, и (ш)шаги независимы. Согласно
3Интеграл е-ак2-гкх dk вычисляется с помощью «приведения к полному квадрату»
и экспоненте. Мы пишем ак2 + ikx = а(к + гх/2а)2 — х21^.аь делаем замену у = к + гх/2а и
вспоминаем, что е~ау &У = у/п/а.
4 Наши аргументы можно шаг за шагом распространить на любое количество измере¬
ний.
5 Для простоты мы будем часто писать X вместо Xn.
0 Центральная предельная теорема справедлива и когда моменты выше второго расхо¬
дится.
20
Диффузия
центральной предельной теореме (2.16) среднее смещение и дисперсия имеют
вид
{XN) = N(x), var(-Xjv) = (X2N) - (XN)2 = Na2.
Чтобы вывести центральную предельную теорему, заметим, что так как
шаги случайного блуждания независимы, распределение вероятностей после
N шагов связано с вероятностью после N — 1 шагов через рекурсию (также
известную как уравнение Чепмена-Колмогорова)
PN(X) = Г Pn-^Х') р(Х - Г) dX'. (2.17)
J—оо
Действительно, чтобы дойти в X за N шагов, блуждание сначала добирает¬
ся до X' за N — 1 шаг и затем делает один шаг из X1 в X с вероятностью
р(Х' -» X) = р(Х — X'). Уравнение (2.17) — свертка, и это значит, можно
использовать преобразование Фурье, чтобы свести интегральное уравнение
(2.17) к рекуррентному соотношению Pyy(fc) = Pyv_i(fc)p(fc). Итерируя, полу¬
чим Рм(к) = Рв(к) [p(^’)]yV- Для канонических начальных условий, при кото¬
рых блуждание стартует с начала координат, Ро(ж) = &г,(Ъ имеем Po(fc) = 1.
Таким образом, Pi\i(k) = [р(^)]^, и
1 7°°
Р*Р0 = 2^/ \p(k)]N e~ikX dk. (2.18)
Так как два первых момента конечны, мы можем записать преобразование
Фурье как
p(fe) = /* р(х) егкх dx
J—оо
= J р(ж) [l + ikx — 1&2ж2 + ... J dx
= 1 + ik(x) - ^k2(x2) +
Тогда асимптотическое распределение вероятностей имеет вид
1 Г°° 1
PN(X) ~ j [1 + ik(x) - ±k2(x2)}N e~ikX dk
= у- J exp pVln (l + ik(x) — lfe2(a;2))J е~гкх dk
/ exP pv(ifc(:r) - у ((ж2) - (ж)2) )] е~гкХ dk. (2.19)
2.3 Блуждания с широкими распределениями
21
Приводя к полному квадрату выражение под экспонентой и вычисляя полу¬
чившийся гауссов интеграл, приходим к результату центральной предельной
теоремы (2.16).
2.3 Блуждания с широкими распределениями
Что происходит, когда распределение смещения за один шаг случайного
блуждания настолько широкое, что его первый момент и/или его второй мо¬
мент расходятся? Также, что происходит, когда время каждого шага не фик¬
сировано, а выбрано из распределения, первый и/или второй момент кото¬
рого расходятся? Если распределения одиночных событий достаточно широ¬
ки, распределение Р(Хм) больше не гауссово и масштаб моментов смещения
аномально растет с N. Судьба целого блуждания может тогда определяться
доминирующим вкладом единственного исключительно длинного шага, или
единственного длинного времени прыжка, которые составляют конечную до¬
лю от общего количества. Существование таких исключительных событий
приводит к нарушению центральной предельной теоремы.
(2.20)
Широкое распределение длины шага
Предположим, что одношаговое распределение имеет вид
. (дж_(1+^, X > 1,
■) = <
О, 0 < х < 1,
где р > 0. Мы ввели параметр обрезания снизу, чтобы избежать услож¬
нений из-за бесконечно малых шагов, тогда как условие р > 0 обеспечива¬
ет нормируемость распределения. Используем основные факты о статистике
жстремальных величин (см. врезку ниже по тексту), чтобы определить два
первых момента смещения за N шагов. Основная идея — заменить настоя¬
щее одношаговое распределение (2.20) эффективным распределением peff(x)>
которое описывает лишь блуждания с конечным числом шагов. Эффектив¬
ное распределение имеет ограниченный носитель, верхний предел которого
определяется самым длинным шагом, ожидаемым за конечное число шагов.
Применяя экстремальный критерий (2.22) находим жтах ~ По по¬
строению эта длина дает верхнее обрезание распределения одного шага для
блуждания из N шагов. Следовательно, мы должны заменить одношаговое
22
Диффузия
распределение р(х) для бесконечной выборки эффективным одношаговым
распределением для блуждания из N шагов:
~ 1'< X < Жщах,
Жтах (2.21)
О в противном случае.
То есть, одношаговое распределение обрезано на хтах, так как возникновение
большего шага за N шагов маловероятно.
2.2. Статистика экстремальных величин
Рассмотрим выборку N случайных величин, полученных независимо из одного
и того же непрерывного распределения р(ж), которое не ноль в области (0, оо).
Максимальная величина .т111ах из этой выборки обязательно конечна, и мы бы
хотели выяснить сс статистические характеристики. Оценка для жтах дается экс¬
тремальным критерием того, что значение одной из N переменных больше или
равно rcmax (см. рис. 2.3)
Г°° 1
/ p(x)dx~—. (2.22)
* Я-max
Более точно, мы определяем вероятностное распределение того, что макси¬
мальная из N переменных имеет значение #, откуда следует среднее значе¬
ние ж,пах. Для того чтобы максимальная переменная была равна ж, остав¬
шиеся N — 1 переменные должны быть меньше х, тогда как одна переменная
равна х. Вероятность этого события равна
MN(x) = ЛГ[1 - P(i)]w_1p(a:), (2.23)
где Р(х) = р(у) dy — вероятность того, что одна переменная лежит в
области (#,оо). В (2.23) множитель [1 — P(x)]N_1 дает вероятность того,
что N — 1 переменная меньше чем ж, а множитель ^возникает, так как лю¬
бая из N переменных может быть максимальной. Поскольку Р'(х) = —р(я),
имеем Jo°° Mn(x) dx = 1, т. е. Мм имеет правильную нормировку. Для боль¬
ших N распределение М/Дж) приблизительно равно Np(x)e~NP(x\ так что
типичное значение жтах можно найти, потребовав, чтобы выражение в экс¬
поненте было порядка единицы: NP(xmax) ~ 1. Это совпадает с полученной
«на пальцах» оценкой (2.22).
2.3 Блуждания с широкими распределениями
23
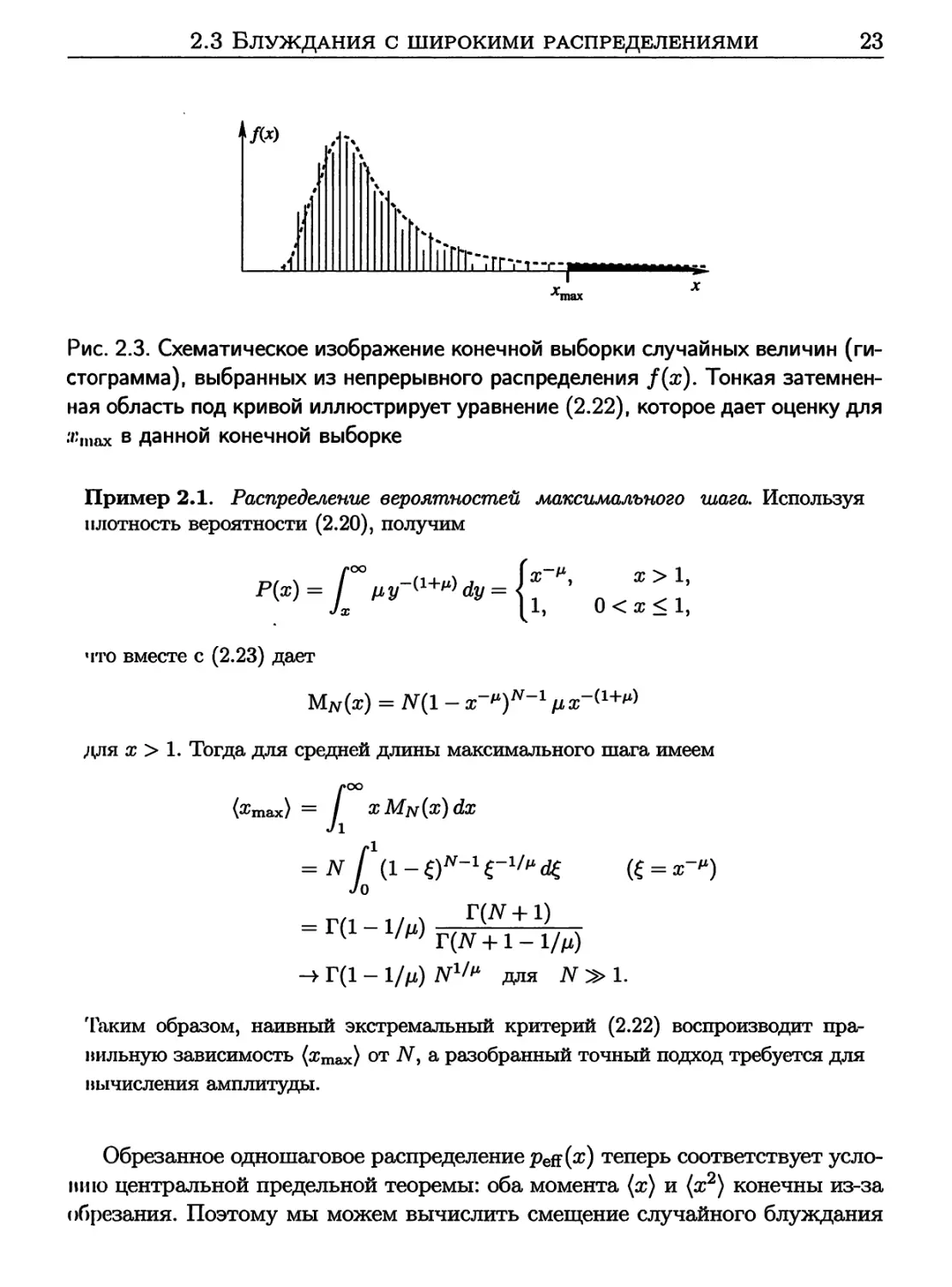
Рис. 2.3. Схематическое изображение конечной выборки случайных величин (ги¬
стограмма), выбранных из непрерывного распределения /(ж). Тонкая затемнен¬
ная область под кривой иллюстрирует уравнение (2.22), которое дает оценку для
Жшох в данной конечной выборке
Пример 2.1. Распределение вероятностей максимального шага. Используя
плотность вероятности (2.20), получим
Р(т)= Г
Jx
РУ
-(1+я)
dy
(;?
X > 1,
0 < х < 1,
что вместе с (2.23) дает
Mn(x) = 7V(1 — ^-(i+д)
для х > 1. Тогда для средней длины максимального шага имеем
(З'тах) = xMN(x)dx
= N f\l- С)*-1 r1/#1 (£ = Х-»)
Jo
-»• Г(1 - l/д) N1/ft для N » 1.
Таким образом, наивный экстремальный критерий (2.22) воспроизводит пра¬
вильную зависимость (жтах) от 7V, а разобранный точный подход требуется для
вычисления амплитуды.
Обрезанное одношаговое распределение peff (#) теперь соответствует усло¬
вию центральной предельной теоремы: оба момента (х) и (х2} конечны из-за
обрезания. Поэтому мы можем вычислить смещение случайного блуждания
24
Диффузия
из N шагов с широким распределением длин индивидуальных шагов, исполь¬
зуя Pes(x) вместо р(ж) в формулировке центральной предельной теоремы.
Таким образом, средняя длина единичного шага становится
хт£, Д < 1,
1пя;тах, /х = 1, (2.24а)
конечно, /х > 1.
(ж)ей ~ р
f^max
J1
х х dx ■
Поскольку £тах ~ величина (rr)eff имеет следующую зависимость от N:
(z)eff ~ "
In TV,
(конечно,
Д < 1,
д = 1,
р > 1.
(2.24Ь)
Аналогично, для (ж2)ея
р<2,
(z2)eff ~
jin TV,
р = 2,
(2.25)
(конечно,
р> 2.
Так как первые два момента одношагового распределения конечны, централь¬
ная предельная теорема дает среднее значение и дисперсию случайного блуж¬
дания из N шагов:
Г^/М, Д<1,
(X} ~ N(x)eg ~ < N In N, р = 1, (2.26а)
[tv, Д > 1,
И
{N2^, р < 2,
TV In TV, р = 2, (2.26Ь)
N, р > 2.
Полученные результаты говорят, что самые большие отклонения от гауссова
поведения возникают когда 0 < /х < 1; этот режим соответствует так называе¬
мым полетам Леви. Траектория типичного полета Леви показана на рисунке
2.1(b). Это блуждание состоит из множества коротких участков и несколь¬
ких длинных скачков, которые вносят основной вклад в суммарное смеще¬
ние. Такое поведение коренным образом отличается от траектории простого
случайного блуждания, изображенного на рис. 2.1(a), в котором длина шага
2.3 Блуждания с широкими распределениями
25
фиксирована. Когда хвост одношагового распределения спадает быстрее чем
х~2 при больших х, распределение вероятностей скейлинговой переменной
z = (Xjv — N(x})/\fN сходится к гауссовому виду при N —> оо. В режиме
О < д < 2 распределение вероятностей стремится к распределению Леви7, ча¬
сто обозначаемое через Важное свойство этого распределения — наличие
степенного хвоста LM(z) ~ Для 0 < д < 1 скейлинговая переменная
z = Xn/N1^ описывается распределением Леви, тогда как для 1 < М < 2
соответствующая скейлинговая переменная — это z = (Хм —
Замена смещения Хм скейлинговой переменной z обеспечивает правиль¬
ное взятие предела N —> оо. В то же время эта замена затемняет важное
различие между гауссовым режимом (// > 2) и полетами Леви (0 < /л, < 1).
Действительно, в гауссовом режиме сумма большого числа независимых оди¬
наково распределенных случайных величин становится все более и более де¬
терминированной при N —> оо. А именно, сумма сконцентрирована около
/V (х), и хотя отклонения растут (в среднем) с ростом N, относительные
флуктуации убывают как 7V-1/2 при N —> оо. Таким образом, эффектив¬
но случайность исчезает из суммы. Это объясняет, почему можно доверять
большим социологическим опросам. Это явление называется «самоусредне-
пие». Однако для полетов Леви сумма остается случайной. Эта случайность
станет очевидной, если заметить, что зависимость (X) от N такая же, как и
у (жтах)- Полеты Леви несамоусредняемы, что проявляется в больших флук¬
туациях, возникающих от выборки к выборке, которые никогда не исчезают
даже в термодинамическом пределе. В дискуссии выше мы рассматривали
распределения Леви, которые возникают в специальном случае (2.20), когда
нее шаги положительны. В более общем случае распределения Леви зави¬
сит от индекса /х и от параметра асимметрии /3, где —1 < /3 < 1, который
характеризует относительную частоту положительных шагов (/3 = 0 соот-
иггствует равным частотам положительных и отрицательных шагов, а при
/7 - 1 все шаги положительны). Распределение Леви (2.20), возникающее из
сумм случайных величин, соответствует полностью асимметричному случаю
/7 = 1. Поэтому Симметричные распределения Леви также часто
встречаются в различных приложениях. Их Фурье-образ дается элегантной
формулой
1 Г°°
L„,o(z) = ^~ e~c^~ikzdk. (2.27)
J—oo
7 Однако распространенность распределения Гаусса многократно превосходит распро¬
страненность распределений Леви. Полезное свойство, которое объединяет распределения
Лини с распределением Гаусса, — их устойчивость. По определению случайная переменная
устойчива, если взвешенная сумма двух ее копий имеет то же самое распределение, что и
исходная переменная, возможно с точностью до сдвига и растяжения.
26
Диффузия
В некоторых случаях интеграл в (2.27) можно выразить через элементарные
функции. Распределение Гаусса воспроизводится при /х = 2, а при р = 1
результатом является распределение Коши%
<2'28>
Различные аспекты блужданий с широкими распределениями длин шагов
составляют содержание задач 2.8—2.10.
Широкое распределение времени ожидания
Рассмотрим теперь другую ситуацию, когда время каждого шага — случай¬
ная величина с широким распределением. Пространственная природа блуж¬
дания не важна для дальнейшего обсуждения, и мы можем ограничиться
примером случайного блуждания, где прыжки на расстояния ±1 происхо¬
дят с одинаковой вероятностью. Когда среднее время ожидания одного шага
конечно, мы ожидаем обычное поведение, т. е. среднеквадратичное смеще¬
ние блуждания без сноса должно асимптотически расти как (X2) ~ t. Чтобы
увидеть, что происходит когда среднее время между шагами бесконечно, рас¬
смотрим распределение времени ожидания
(рт~(1+»\ т>1,
•) = <
0, 0 < т < 1.
Если 0 < д < 1, среднее время ожидания расходится, (т) = оо, и мы ожи¬
даем аномальное поведение. Действуя точно так же, как в случае с широким
распределением длин шагов, установим соответствие со случайными блуж¬
даниями с подходящим образом обрезанным распределением времени ожи¬
дания. Для 0 < /1 < 1 максимальное время ожидания за N шагов дается
экстремальным условием
роо
’^'Гтах
jut dr
-1
N
из которого максимальное время ожидания в блуждании из N шагов ттах ~
N1^. Используем обрезанное распределение, в котором ('Т") = <0(т) для т 8 *8Распределение в уравнении (2.28) также известно как распределение Лоренца, а в
ядерной физике и физике частиц его часто называют распределением Брейта-Вигнера.
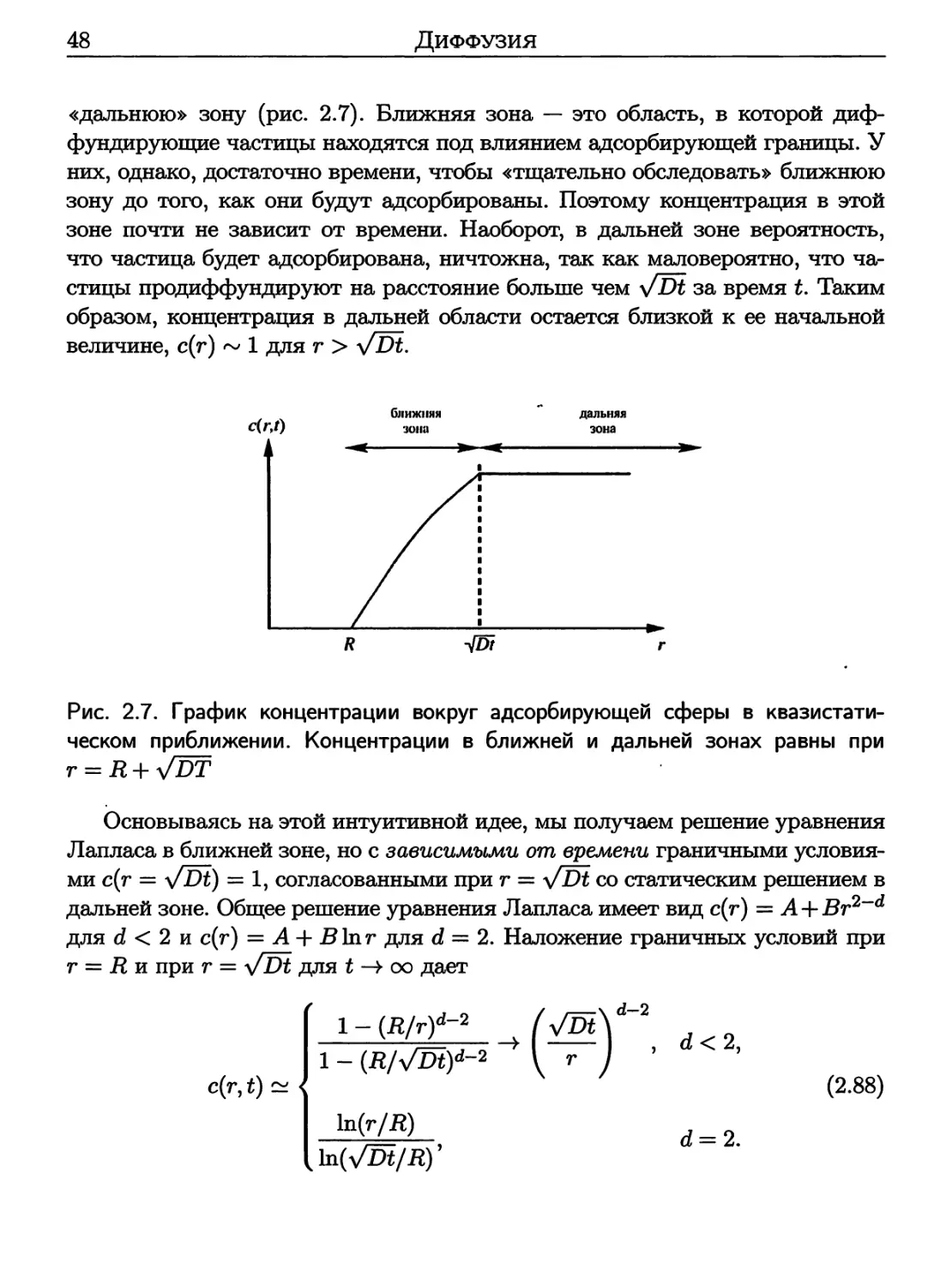
2.4 Применение к гравитации: распределение Хольцмарка 27
в диапазоне [1, ттах] и ^eff(T) = 0 вне его, для определения среднего, прихо¬
дящегося на один шаг:
Р^тах
/ рт
JQ
-*<1т
* InJV,
конечно,
д < 1,
д = 1,
д > 1.
Снова нижний индекс означает, что это среднее время относится к обрезан¬
ному распределению V’efr (■’")• Суммарное время Гдг, нужное для того, чтобы
сделать 7V шагов
м<1,
TN = N(t}eS~ < NhN, д = 1,
(TV, р > 1.
(2.29)
Среднеквадратичное смещение за N шагов растет линейно с N. Используя
(2.29), получим временнбй скейлинг:
(X2) ~ ~ <
Т»,
Т/]пТ,
[Т,
ц<1,
М = 1>
р > 1.
(2.30)
Два первых случая соответствуют субдиффузии, в которой среднеквадра¬
тичное смещение растет со временем медленнее, чем линейно.
2.4 Применение к гравитации: распределение
Хольцмарка
Физическая реализация случайного блуждания с широким распределением
смещения возникает в распределении гравитационных полей, распределении
Хольцмарка, которое возникает при случайном распределении материи. Рас¬
смотрим бесконечную систему звезд, которые случайно распределены с по¬
стоянной плотностью и без корреляций между их пространственными поло¬
жениями. Мы хотели бы рассчитать распределение гравитационных сил, дей¬
ствующих на одну «пробную» звезду, которую без потери общности можно
поместить в начало координат. Предположим для простоты, что звезды име¬
ют одинаковые массы (можно также рассмотреть общий случай случайных
28
Диффузия
масс звезд, что, однако, приводит к значительному усложнению формул). Мы
хотим найти распределение случайной величины
GM2n
(2.31)
fi =
(г,)3
Здесь Yj — координата J-той звезды, fj — сила, действующая на пробную звез¬
ду, G — гравитационная постоянная Ньютона, а М — масса каждой звезды.
Далее мы опускаем множитель GM2: он легко восстанавливается в конечном
результате из размерных соображений.
Можно интерпретировать (2.31) как случайное блуждание с широким
распределением (векторных) шагов fj. Удобно начать с конечной системы
и потом взять термодинамический предел. Рассмотрим сферу радиуса R с
центром в начале координат. Число звезд в сфере близко к N = nV, где
п — плотность звезд, и V = | тгЯ3. Сначала определим конечную сумму
F = ^2i<j<N $ 9- Так как положение rj случайно и однородно распределено
в сфере объемом V, распределение вероятностей P(F) имеет вид TV-мерного
интеграла
P(F) = J
dri
V
(2.32)
l<j<N
х
X^l
Применяя преобразование Фурье, получим
dri
V
P(k) = У dFeikPP(F) = х ... х
dr^
V
JdF^S^ fJ'_F
-I
-{L
= №x...x*" efkEf,
у у
— eikf
v e
f = 4
Теперь перепишем интеграл как
Lv <ikf-L£ I1 - f1 -e“)] -1 - v,Ldr 0-e‘k')- <2-33>
что упрощает вычисление TV-ой степени. После этого в термодинамическом
пределе TV, V оо, где отношение N/V = п остается постоянным, имеем
N г Г / \1
(2.34)
1 - у у dr (l - eikf) -> exp|-n У dr (l - eikf)
9Строго говоря, конечная сумма обозначается Fjv, но мы опускаем нижний индекс,
который можно восстановить из контекста.
2.4 Применение к гравитации: распределение Хольцмарка 29
Последний интеграл в (2.34) сходится и поэтому с шара радиуса R может
быть расширен на все пространство. Из обратного преобразования Фурье
следует распределение силы
P(F) = (2тг)“3 J dk ехр[—гк • F - пФ(к)], (2.35)
где мы используем сокращенное обозначение
Ф(к) = У dr (l - eik f) , f = (2.36)
Для получения явного результата нужно вычислить интеграл (2.36) и об¬
ратить преобразование Фурье (2.35). Однако можно определить зависимость
Ф(к) от к и без вычислений. Во первых, так как экспонента от к-г интегриру¬
ется по всем направлениям г, результат не может зависеть от направления к.
Поэтому Ф(к) = Ф(&). Во вторых, можно обезразмерить зависимость от к в
экспоненте, введя новую переменную интегрирования г —> fc_1/2r. Получаем,
что вся зависимость интеграла от к это
Ф(к) = ор/2.
(2.37)
Амплитуду а нельзя найти только из соображений симметрии. Полное вы¬
числение дает а = (27т)3/2 (задача 2.11).
Таким образом, распределение силы дается распределением Хольцмарка:
P(F) = (2тг)_3 У dk exp ik • F — arafc3/2j , a = (27r)3/2. (2.38)
Переходя в сферические координаты в k-пространстве с осью вдоль направ¬
ления F, запишем к • F = kF cos в и dk = 2л sin 9 dO k2dk. Интегрирование
уравнения (2.38) по угловой координате дает
P(F) = (2%) 2 У dk к2 У d9 sin 9 exp ikF cos 9 — ank3/2]
°°dkk2e-^2S^
kF
= (2ТГ)-2 f
Jo
= 2^рз/ dz z sin z e~^S/2, < = F/(an)2/3.
(2.39)
Чтобы осознать поведение распределения, посмотрим на предельные слу¬
чаи больших и малых сил. Интеграл в уравнении (2.39) зависит от комбина¬
30
Диффузия
ции С = F/(on)3/2, так что пределу малых сил соответствует режим £ <С 1,
больших — £ » I10.
Пример 2.2. Предел малых сил. Так как область z ~ С, вносит основной вклад
в интеграл в (2.39), асимптотическое поведение просто извлекается для £ <^С 1.
Используя sin z ~ z, сведем (2.39) к
z2 e-(z/C)3^
С3 2 /"
ЗУо
2ir2F3
1 1
dvve~
[г = <v2/3]
37Г2 (an)2’
(2.40)
Пример 2.3. Предел больших сил. При С 1 запишем sinz как мнимую часть
егг, так что имеем
Лр) = 2^F3 J(<) = /0 dzzeiZ е {z/C)3'2-
Пользуясь соотношением z = iu, получим
J«) = - / duue~u exp Q)
(2.41)
3/2'
что приводит к
Im[J(C)] = j
du и exp
1 Л
»V/21
1
»v/2l
:) J
sin
У2 v
J
Так как основной вклад дает область и ~ 1, можно заменить функцию синуса
на ее аргумент. Сохраняя первое слагаемое в экспоненте, получим
If00 1 /п\3/2
P(F^^JO duu
1 Г(7/2) 15 1 on = 1 п
2тг2ГЗ ^^з/г 8 (2тг)3/2 F9/2 2Я2’
где в последней строке мы использовали значение гамма-функции, Г(7/2) =
15^/8, и амплитуды а из уравнения (2.38).
10Нужно отметить, что типичное расстояние между звездами £ ~ п~1//3, так что ти
личная сила Ftyp ~ £~2 ~ п2^3. Следовательно, £ ~ F/Ftyp, что объясняет почему £ ~
разграничивает режимы больших и малых сил.
2.4 Применение к гравитации: распределение Хольцмарка 31
Пример 2.4. Средняя сила и ее моменты. Из асимптотического поведения рас¬
пределения сил (2.40) и (2.42) ясно, что zz-тый момент силы
(Fy) = j Fy P(F) dF = 4л j F2+v P(F) dF
существует только для — 3 < и < 3/2. Используя (2.39) и заменяя переменную
интегрирования F на С получим
(Fy) = Су (an)2у!\ С„ = — f dzz sin z f e~(z/O3/\
71 Jo Jo s
Можно вычислить интегралы в пользуясь свойствами гамма-функций:
С„ = ± Г dzz sin z Г Г2"/3 е-"3/2 4 (t = С3/2)
Зтг Jo Jq t
= ^-Г(—2i//3) f dzz1+y sin 2
Jo
= r(i-2,/3)r(2 + ,)!i^i®.
Интеграл во второй строке вычисляется заменой z = iy, т. е. z рассматривается
как комплексная переменная, контур интегрирования по которой поворачивает¬
ся с вещественной оси (0, оо) на мнимую ось (0,гоо).
В частности, средняя сила имеет вид
(F) = Ci (on)2/3, Ci = ИМ! = 3) 4Ю93.
Познавательно вывести предел больших сил (2.42) непосредственно, без ис¬
пользования распределения Хольцмарка (2.38). Пользуясь тем, что сильные
гравитационные силы вызваны ближайшими звездами, сначала вычислим
распределение вероятностей расстояния R от данной звезды до ее ближайше¬
го соседа. Так как звезды распределены случайно с однородной плотностью п,
вероятность что ближайшая звезда находится в сферическом слое (Л, R+dR)
имеет вид
ехр^—^-Л3п^ kitR?ndR.
Здесь экспонента обеспечивает условие, чтобы в сфере радиусом R с цен¬
тром в данной звезде не было других звезд. Предел большой силы соот¬
ветствует случаю, когда расстояние мало, т. е. Л3п С 1. В такой ситуации
вероятностное распределение упрощается до 47гЛ2п. Так как притяжение к
ближайшей звезде доминирует, сила асимптотически равна F — R~2. По¬
лагая 47гД2п^Д = n(F)dF и F = Л“2, в пределе большой силы получим
32
Диффузия
n(F) = Этот результат согласуется с (2.42), если вспомнить, что
распределение силы имеет вращательную симметрию 11(F) = 47tF2P(F).
2.5 Свойства первого достижения
До сих пор мы интересовались тем, где находится случайное блуждание. Сей¬
час мы рассмотрим другой вопрос: «Когда случайное блуждание достигает
данную точку впервые?» В более общем случае, чему равна вероятность
первого достижения F(r,t) точки г в момент времени t случайным блуж¬
данием? Понятие первого достижения объединяет большой круг явлений, в
которых стохастическая переменная впервые принимает заданное значение.
Примеры: эволюция химических реакций, нервные импульсы в нейронах моз¬
га и переключение биржевых опционов. Данный раздел кратко излагает идеи
процессов первого достижения.
Возвратность и невозвратность
Предположим, случайное блуждание начинается в начале координат беско¬
нечной решетки в момент t = 0. Вернется ли частица в конце концов в на¬
чальную точку? Примечательно, что ответ зависит только от размерности
пространства.
• Для d < 2 случайное частица обязательно возвращается в начало —
случайное блуждание возвратно.
• Для d> 2 существует ненулевая вероятность того, что частица никогда
не вернется — блуждание невозвратно.*
Более того, если случайное блуждание возвратно, оно возвращается беско¬
нечное число раз, но среднее время возвращения бесконечно!
Чтобы понять критерий возвратности и невозвратности, рассмотрим ти¬
пичную траекторию случайного блуждания. За время t блуждание заметает
сферическую область радиуса L VDt, тогда как число посещенных узлов
(необязательно разных) растет линейно с t. Поэтому плотность посещенных
узлов равна р ~ t/Ld ~ Для d > 2 р убывает, когда t растет, так что
некоторые точки в «охваченной» области могут никогда не быть посещены —
блуждания невозвратны. При d < 2 плотность — возрастающая функция
• Наряду с терминами возвратность и невозвратность в русскоязычной литературе часто
используются соответственно термины рекуррентность и транзиентность, которые являют¬
ся точным воспроизведением английских «recurrence» и «transience» (Прим, переводчика).
2.5 Свойства первого достижения
33
о
• +
о
Рис. 2.4. Диаграммное представление соотношения между вероятностью запол¬
нения случайного блуждания (распространение которой представлено волнистой
линией) и вероятностью первого достижения (прямая линия)
/., так что каждый узел в области обязательно будет посещен — блуждания
возвратны. Как будет показано ниже, пограничный случай d — 2 также воз¬
вратный.
Теперь вычислим вероятность первого достижения, из которого можно
извлечь критерий возвратности и невозвратности. Вероятность первого до¬
стижения связана с уже знакомой вероятностью заполнения P(r,f):
•t
P(r,t)= / F(rJ)P(O^-t')dt' + Srfie-2dt, (2.44)
о
где 5г>о — дельта-функция Кронекера. Это уравнение учитывает вероятность
того, что блуждание достигнет (г, t), посетив г в первый раз в момент времени
I1 < t, и пройдет по замкнутому пути (г, t') —> (r,t) за оставшееся время
I — t1. , Множитель е-2<й — это вероятность того, что до времени t прыжка
нс произойдет (здесь d — пространственная размерность). Из-за того что
частица может возвращаться в г в промежутке между и t, возвратный
множитель включает Р, а не F.
Интеграл в правой части (2.44) — свертка. Наличие свертки предполагает
применение преобразования Лапласа к вероятности заполнения11. В терми¬
нах преобразований Лапласа вероятностей заполнения и первого достижения
РОО роо
P(r, s) = / Р(г, t) e-st dt и Р(г, s)= P(r, t) e~st dt
Jo Jo
уравнение (2.44) становится алгебраическим: P(r, s) = F(r, s)P(O, s) + 5Г)о,
откуда имеем
11 Если свертка — это интеграл с бесконечными пределами • •), используется преоб¬
разование Фурье, как мы делали в случае уравнения Чепмена-Колмогорова (2.17). Когда
пределы интегрирования конечны, как в (2.44), предпочтительно использовать преобразо¬
вание Лапласа.
34
Диффузия
f х _ P(r,s)-5r,0/(s + 2d)
b J P(<M)
(2-45)
Возвратность или невозвратность случайного блуждания определяется пол¬
ной вероятностью возвращения в начало:
= F(0, s =
F(O,f)dt.
Блуждание возвратно, когда Я = 1, и невозвратно при SR < 1. Поскольку мы
интересуемся только возвращением в начало, в дальнейших рассуждениях
мы будем опускать пространственный аргумент.
2.3. Связь между алгебраическими хвостами функции и ее
преобразованием Лапласа
Предположим, что у f(t) есть алгебраический хвост f(t) ~ при t 1, где
р, < 1, так что интеграл /0°° f(t) dt расходится. Каково преобразование Лапласа
функции Ответ очевидно зависит от полной функции /(f), однако асимпто¬
тика преобразования Лапласа для малых 5 определяется асимптотикой f(t) для
больших t. По определению преобразования Лапласа
/(s) = f°° e~st dt
Jo
для /(f) = t fl. Подставляя x = sf, перепишем преобразование Лапласа как
f(s) = s'*-1 Г° Х-» e~x dx = Г(1 - ц) s'*"1, (2.46)
/о
где мы использовали определение гамма-функции,
r(z) = [O°xz-Ie-Xdx.
Jo
Таким образом, получим удобное соотношение между хвостами функции и ее пре¬
образованием Лапласа
f“M при /х < 1 <$=> Г(1 — (2.47)
которое широко используется, как в этой главе, так и на протяжении всей книги.
Чтобы вычислить вероятность первого достижения для случайных блуж¬
даний в непрерывном времени, мы стартуем с обобщения уравнения (2.5) для
вероятности заполнения в начале координат на d-мерной гиперкубической ре¬
шетке:
когда t —> оо.
(2.48)
2.5 Свойства первого достижения
35
Мы используем этот результат для расчета вероятности первого достижения
и вероятности возврата для d = 1,2 и 3.
Случай d = 1. Согласно уравнениям (2.48) и (2.47) преобразование Лапласа ве¬
роятности заполнения начала координат в пределе s —> 0 будет P(s) ~ l/>/4s.
Тогда уравнение (2.45) дает преобразование Лапласа вероятности первого до¬
стижения начала координат
P(s) ~ 1 - y/s. (2.49)
Таким образом, случайное блуждание в одномерии возвратно, потому что веро¬
ятность возвращения fR = F(s = 0) = 1. Однако из-за того что P(s) не расходит¬
ся при малых 5, неудобно обращать преобразование Лапласа напрямую. Вместо
этого рассмотрим производную уравнения (2.49)
dF(s)
ds
\/4s
1
Смысл этого приема в том, что при малых s преобразование Лапласа tF(t) бо¬
лее сингулярно, чем преобразование Лапласа F(t). Непосредственно применяя
(2.47), находим tF(i) ~ (47г£)-1/2, то есть
1 1
л/4^^2
F(t)~
при
оо.
(2.50)
Случай d = 2. В этом случае нужна некоторая осторожность, так как интеграл в
P(t) слабо расходится при t —> оо. Кроме того, чтобы избавиться от неприятной
сингулярности, которая появляется из-за использования вида Р(£), полученного
для больших времен, при малых временах нужно обрезать интеграл при t < 1.
Учтя эти особенности, получим
~ —— Ins.
47Г
(2-51)
Экспонента под интегралам дает малую поправку к поведению при малых s, и
можно пренебречь ей, вычисляя ведущий вклад в интеграл. Используя (2.51) и
(2.45) находим
F(s) ~ 1 + при s —> 0. (2.52)
Ins
Случайное блуждание также возвратно в двумерии, потому что F(s = 0) =
Я = 1. Чтобы найти F(£), применим —d/ds к обеим частям уравнения (2.52), что
дает
[ t F(t) e~st dt ~ -7- % ? при s -> 0. (2.53)
Jo s(lns)2
Так как Лаплас-образ константы равен 1/s, функция tF(t) должна медленно
меняться со временем, чтобы заработать дополнительный множитель (Ins)"2. В
36
Диффузия
самом деле (см. задачу 2.14)
F(t) ~ фКТр при (2-54)
Случай d = 3. Этот случай отличается от d < 2, так как
<2-55>
сходится при s 0. Заметим, что интеграл опять обрезан при t < 1, чтобы
избежать плохой сингулярности, происходящей из использования на малых вре¬
менах формы Р(£), полученной для больших времен. Чтобы найти P(s), снова
применим — к обеим сторонам уравнения (2.55) и получим
ds
dP(s)
е stdt
(4тг)3/2 tl/2 е
1
8lTy/s’
где мы использовали уравнение (2.47) для подсчета интеграла. Вследствие этого
P(s) имеет вид
P(s)~P(0)-^. (2.56)
Тогда из уравнения (2.45) получим преобразование Лапласа вероятности первого
достижения
. |1 - (бР(О))-1] -
= я-
3(1 - ft)2^
2тг
Поскольку P(s = 0) < оо, мы делаем вывод, что Л = [1 — (6Р(0))-1] < 1 и
случайное блуждание невозвратно. В заключение по аналогии с (2.47) получим
асимптотический вид F(t)
3(1 -Я)2 1
4тг3/2 t3/2'
(2.57)
2.6 Вероятность выхода и время выхода
Две самых важных характеристики первого достижения — это вероятность
выхода и время выхода. А именно, какова вероятность того, что блуждаю¬
щая частица, стартовавшая с точки г в области В, когда-нибудь дойдет до
заданной точки на границе области, и сколько времени это займет? В этом
разделе представлены основные свойства этих величин.
2.6 Вероятность выхода и время выхода
37
Вероятность выхода
Для вероятности выхода естественно разделить границу дВ на два непере-
сскающихся подмножества, дВ+ и дВ-, где дВ+ U дВ- = дВ, и спросить,
какова вероятность £(г) того, что частица выходит из области через дВ+
прежде, чем коснется дВ-. Например, в конечном одномерном интервале
[О, 2V] можно считать, что дВ- — это точка х = 0, а — точка х = N, и
интересоваться вероятностью того, что блуждание, начавшееся в любой точ¬
ке внутри интервала, в конце концов достигнет х = N, не побывав в х = 0.
Рассмотрим дискретное случайное блуждание, которое начинается в точ¬
ке п интервала [0,2V], и пусть £т — вероятность того, что блуждание до¬
стигнет точку N, не посетив 0. Эта величина удовлетворяет рекуррентному
соотношению
£п = |(£п-1 + £n+i), (2.58)
которое отражает тот факт, что для того чтобы уйти из точки N, начав дви¬
жение в точке п, частица или делает шаг влево с вероятностью после чего
следует выход с началом в точке п — 1, или шаг вправо с вероятностью с
последующим выходом с началом в точке п +1. Граничные условия £о = 0 и
£/v = 1, т. е. частица не может выйти из точки 7V, начав с точки 0, и сразу же
уходит, когда стартует с точки N. Рекурсию (2.58) часто называют обрат¬
ным уравнением, потому что оно написано как функция начальной точки
частицы; наоборот, основное кинетическое уравнение для распределения ве¬
роятностей, такое как (2.4), содержит текущее положение.
Общее решение дискретного уравнения Лапласа (2.58) линейно по про¬
странственной переменной, т. е. имеет вид А + Вп, а учет граничных условий
дает
£п = (2.59)
Аргументы, приведшие к уравнению (2.58), обобщаются на произвольную
область, и вероятность выхода в непрерывном пределе удовлетворяет непре¬
рывному уравнению Лапласа
V2£(r) = 0 (2.60)
с граничными условиями £(г € дВ+) = 1 и £(г 6 дВ_) = 0 12.
Вероятность выхода удовлетворяет такому же уравнению Лапласа, как
электростатический потенциал с аналогичными граничными условиями. Эта
12Если граничные множества дВ+ и дВ- не составляют всей границы области, то гра¬
ничные условия на оставшейся части границы будут Vn£=0, где п — производная в на¬
правлении нормали к границе.
38
Диффузия
связь позволяет легко вывести вероятность в множестве геометрий. В ка¬
честве простого примера рассмотрим диффундирующую частицу, которая
стартует с точки на расстоянии г от центра сферы радиусом R < г. Какова
вероятность того, что частица когда-нибудь коснется сферы? Чтобы ответить
на этот вопрос, мы должны решить уравнение V2£(r) = 0 с граничными усло¬
виями £(r = R) = 1. Ответ коренным образом зависит от размерности:
d = 1. Общее решение уравнения Лапласа: £(г) = А + Вг. Так как 0 < £(r) < 1,
В должно быть нулем, чтобы решение не расходилось при г -> оо. Используя
граничные условия £(г = Д) = 1, получим £(r) = 1.
d = 2. Теперь общее решение уравнения Лапласа имеет вид £(r) = А+В 1п(г/Д).
Требование 0 < £(r) < 1 снова приводит к В = 0, так что вероятность выхода
опять тривиальна: £(r) = 1.
d > 2. Общее решение £ (г) = А + Br2~d больше не расходится при г —> оо.
Решением, удовлетворяющим граничным условиям £(r) = 1, будет £ (г) = 1 +
B(r2~d — R2~d). До сих пор мы явно не использовали то, что неограниченные
решения нефизичиы: а именно, мы должны рассматривать проблему с внешней
абсорбирующей границей, находящейся далеко от внутренней сферы. Предполо¬
жим, что внешняя граница — также сфера радиуса Доо R, концентрическая
с внутренней сферой. Следовательно, мы решаем уравнение Лапласа с гранич¬
ными условиями £(г = Д) = 1 и £(г = Доо) = 0. Решение имеет вид
Взяв предел Д/Доо -> 0, получим похожую на закон Кулона формулу для веро¬
ятности выхода: £(r) = (R/r)d~2. Правдоподобно, хотя и трудно доказуемо, что
конечный результат не зависит от формы внешней поверхности, когда она очень
далеко от внутренней сферы, и мы ищем вероятность £(г) для начальной точки
г, взятой далеко от внешней поверхности.
В заключение, при d < 2 диффундирующая частица определенно касается
внутренней сферы. Для d > 2, вероятность, что частица, стартовавшая с г,
коснется внутренней сферы, дается формулой Кулона: £(г) = (Д/г)6*-2.
Время выхода
Теперь обратимся к занимательному свойству одномерного случайного блуж¬
дания: частица определенно достигает начала координат, хотя среднее время
2.6 Вероятность выхода и время выхода
39
до первого достижения бесконечно. Проще всего рассмотреть это свойство на
примере сходной проблемы непрерывной диффузии с коэффициентом диф¬
фузии D. Предположим, что частица стартует в точке х = I > 0. В некоторый
момент времени Т частица достигнет начала координат в первый раз; назо¬
вем Т временем выхода. Как мы покажем, время выхода — это случайная
величина с бесконечным средним: (Г) = оо. Тем не менее, типичное время
выхода конечно, — оно может зависеть только от D и — и анализ размер¬
ностей дает Ttyp ~ I2/D.
Чтобы понять эту двойственность, вычислим вероятностное распределе¬
ние времени выхода П(Т,^). Прямой путь — сначала вычислить плотность
вероятности P(x,t\£) того, что частица, стартовавшая в х = £, имеет коор¬
динату х в момент времени t и не достигала начала координат на интервале
времени (0, t). Для этого мы решаем уравнение диффузии (2.7) с начальными
условиями Р(ж, t = 0|^) = 8(х — £) и граничными условиями Р(х = 0, t\£) = 0,
которые гарантируют, что частица не достигает начала координат. Решение
можно получить, пользуясь методом изображений: поместим фиктивную ан¬
тичастицу в х = —£, так что начальные условия примут вид
P(x,t = 01 £) = 5(х - £) - 5(х + £).
(2.62)
О такими начальными условиями граничные условия Р(х = 0, t\£) = 0 авто¬
матически выполняются. Из-за линейности уравнения диффузии решение —
это линейная комбинация двух распределений Гаусса
Р(Ж, 11 £) = . 1 _ e-(®+€)2/4Dtl , (2.63)
y/A^Dt L -I
соответствующих источнику в x = £ и стоку в х = — I. Поток через начало
координат за интервал времени (t, t + dt) дает плотность вероятности того,
что время выхода равно t (см. задачу 2.15). Таким образом,
€ (2б4)
дР\
T[(T,£) = D—\ =
дх lx=o у/4-jtDT3
В качестве формального определения типичного времени мы используем
величину (тау/а, где (Та) это момент времени выхода порядка а
Г
(Та} = /
JQ
Г“П(Г|€) dT.
Используя (2.64), получим
, /2
/T“\V“ _
' ' 4Р
Г(|-а)
Г(|)
- 1/а
(2.65)
40
Диффузия
Типичные времена, определенные в соответствии с (2.65), конечны, когда
а < 1/2 и бесконечны в остальных случаях. В частности, среднее время (Т)
бесконечно! Однако когда а < 1/2, все моменты (Г")1/" действительно про¬
порциональны i2/D.
Теперь рассмотрим диффундирующую частицу в ограниченной области.
В этом случае среднее время выхода конечно13, и мы, в принципе, можем
вычислить точное распределение времени выхода, применив тот же метод
что и для случая полуоси. А именно, решим уравнение диффузии
яр
— = V2P (2.66)
внутри области ® со следующими начальными и адсорбирующими гранич¬
ными условиями:
fP(x,t = 0|r)=i(x-r),
Р(хе#в,г|г) = о.
Распределение времени выхода будет интегралом по поверхности
П(Г, г) = —D [ VP(x, Т | г) • da, (2.68)
JO'S
и, следовательно, среднее время выхода (которое конечно, когда область огра¬
ничена) — это
f(r) = (Г(г)) = [ Т H(T,r)dT. (2.69)
Jo
Применение процедуры, изложенной выше трудоемко14, тогда как оконча¬
тельные ответы зачастую замечательно просты. Если нас интересует только
среднее время выхода, изложенный метод для расчета этой интегральной ве¬
личины слишком громоздок, потому что он требует (i) решить задачу (2.66)-
(2.67), зависящую от времени, (ii) проинтегрировать (2.68), чтобы получить
время выхода, и (iii) произвести усреднение (2.69).
Сейчас мы опишем более элегантную процедуру, которая не требует ана¬
лиза уравнений, зависящих от времени и использования вспомогательных
величин. Проиллюстрируем этот подход с помощью блуждания в непрерыв¬
ном времени на одномерной решетке. По построению за инфенитиземальный
13Все остальные моменты, например (Г2), (Т3), тоже конечны.
14Например, когда область — конечный интервал (0, L), этот подход дает плотность
вероятности времени выхода в форме бесконечного ряда. Однако среднее время выхода
для частицы, стартующей с х Е (0, L), можно выразить в простом виде: t(x) = x(L — x)/2D,
2.6 Вероятность выхода и время выхода
41
временной интервал dt время выхода изменяется следующим образом
Т(ж) = dt + <
Т(Ж)
Т(х +1)
Г(х-1)
с вероятностью 1 — 2dt;
с вероятностью dt;
с вероятностью dt,
(2.70)
что основано на делении случайного блуждания на процесс, происходящий
за время dt, и на весь остальной путь. Например, если частица прыгает из х
в х + 1 за время dt, то она выйдет из системы через время dt (т. е. только
что сделанный шаг) плюс Т(х + 1) (время выхода из нового положения).
Два других случая имеют имеют аналогичный смысл. Усреднение уравнения
(2.70) дает
t(x) = dt + (1 — 2dtyt(x) + dt [t(x + 1) + t(x — 1)],
что сводится к
t(x + 1) — 2t(x) + t(x — 1) = —1. (2.71)
Теперь возьмем непрерывный предел уравнения (2.71), заменив вторую
разностную производную обычной производной: t(x + 1) — 2t(x) + t(x — 1) —>
Z?d2t/dx2, где D = 1 соответствует случайному блужданию в непрерывном
времени с прыжками в соседние узлы, показанному на рис. 2.2. В результате,
среднее время выхода в одномерии удовлетворяет уравнению
(2.72)
В общем случае среднее время выхода подчиняется уравнению Пуассона
PV2t(r) = -1 (2.73)
drt
dx2
D
= -1.
с граничными условиями t(r € &В) = 0, которые означают, что время выхо¬
да — ноль, есль диффундирующая частица стартует с границы области. Для
примера, рассмотрим время выхода на поверхность адсорбирующей сферы
радиуса R. Так как все зависит только от радиального расстояния, нам нуж¬
на только радиальная часть уравнения Пуассона
d2t d — 1 dt _ 1
dr2 r dr D'
решение которой имеет вид
t(r) =
Л2-г2
2dD ‘
(2.74)
42
Диффузия
Вычисление распределения времени выхода в принципе сложно, так как
включает в себя решение уравнений (2.66)—(2.67) для плотности вероятности
Р(х, t |г), и вычисление пространственного интеграла (2.68). Использование
преобразования Лапласа помогает обойти вычисления с плотностью вероят¬
ности Р(х, i|r), а вместо этого позволяет работать непосредственно с рас¬
пределением времени выхода. Не давая формального вывода, мы находим
такое распределение для случайных блужданий в непрерывном времени и
прыжками в соседние узлы и после этого переходим к непрерывному преде¬
лу. Лаплас-образ распределения времени выхода имеет вид
Tl(s,x) = e~sTH(T, х) dT = (e~sT^ } . (2.75)
Для процесса, определенного в (2.70), запишем уравнение эволюции для
(e-ST(x)^:
(e~sT^ = e~sdt {(1 - 2dt) (е~аТ^ + dt (e-aT(x+1^ + dt j. . (2.76)
Раскладывая по степеням dt и устремляя dt —> 0, получим
sll(s, x) = П($, x + 1) — 2П(5, x) + П(5, x — 1),
что в непрерывном пределе дает
»П(*,х) = /у (2.77)
или в общем случае более высоких размерностей приводит к
sn(s, х) = PV2II(s, х). (2.78)
Время выхода равно нулю, если частица стартует с границы: П(Г, х Е дВ) =
5(Г). Следовательно, к уравнению (2.78) нужно добавить граничные условия
для преобразования Лапласа: П($,х Е дВ) = 1.
Уравнения (2.60) и (2.78) вместе дают удобный и эффективный подход
к определению вероятностей выхода и времен выхода диффундирующих ча¬
стиц в произвольных областях.
Применение к недружественным случайным блужданиям
Естественное применение процессов первого достижения — это динамика вза¬
имно аннигилирующих или «недружественных» случайных блужданий. Ка¬
кова их вероятность выживания? Мы ограничимся размерностью один, так
2.6 Вероятность выхода и время выхода
43
как в этом случае возникает наиболее интересное поведение. Начнем с задачи
о двух диффундирующих частицах в точках xi и Х2 > ti с одним и тем же
коэффициентом диффузии D, которые погибают при встрече. Чтобы най¬
ти вероятность выживания, сначала отобразим эту двухчастичную задачу
на одночастичную, рассматривая координаты xi и Х2 на прямой как пози¬
цию (ж1,Т2) одной эффективной диффундирующей частицы в двух измере¬
ниях, при условии Х2 < xi (рис. 2.5). Если эффективная частица касается
Рис. 2.5. Схематическая иллюстрация эквивалентности двух диффундирующих
частиц на прямой (а) и одной диффундирующей частицы в области Х2 > х± (Ь).
Первая показывает пространственно-временное изображение траекторий частиц,
а вторая — траекторию эквивалентной частицы в плоскости (не в масштабе)
линии Х2 = xi, она погибает. Так как играет роль только расстояние до ли¬
нии xi = Х2 вдоль перпендикуляра, мы, таким образом, отобразили задачу о
двух частицах на задачу об одной диффундирующей частице в у = Х2 —
с коэффициентом диффузии D = 2 и с адсорбирующей границей в начале
координат.
Эту одночастичную задачу можно решить методом изображений. Нам
нужна плотность вероятности для частицы, диффундирующей на линии,
стартовавшей в уо > 0, так что с(у, t = 0) = 5 (у — уо), и гибнущей при дости¬
жении начала координат. Здесь уо — это начальное расстояние между двумя
частицами на прямой. Плотность вероятности имеет вид (см. также (2.63))
с(у, t) = -j== [e_(3/_3/o)2/8Pt - e-(J/+3/o)2/8Pt]. (2.79)
'Гак как начальные условия нормированы, вероятность первого достижения
начала координат в момент времени t это ничто иное как поток к этой точке
F(0,i) = 2PaC^’^
оу
У° e-y^/SDt ~ £-3/2
(2.80)
44
Диффузия
при t —> оо, что согласуется с временнбй зависимостью в (2.50). Вероятность
выживания S(t) двух частиц можно найти из S(t) = 1 — Jq F(0,V) dt'. Вводя
переменную и2 = y^/SDi', получим
2 f°° 2
<S(t) = 1 -= I е~и du = erf
V Jyo/y/iDt
У0
y/^irDt
(2.81)
при t -> оо. Как и ожидалось из возвратности диффузии, вероятность выжи¬
вания с течением времени стремится к нулю. Однако среднее время анниги¬
ляции (t) = t F(0, i) dt бесконечно.
Что происходит с тремя частицами в xi, Х2 > xi и хз > Х2 на прямой?
Если они взаимно недружественны, вероятность того, что все они доживут
до времени t, равна вероятности, что порядок тз > > xi будет сохранять¬
ся для всех t' < t. Эту задачу удобно решать опять с помощью отображения
на одну частицу, диффундирующую в трех измерениях, координаты кото¬
рой всегда удовлетворяют хз > Х2 > xi- Ограничение Х2 > xi соответствует
диффундирующей частице, всегда остающейся с одной стороны от плоскости
жх = Х2- Аналогично, ограничение хз > Х2 соответствует диффундирующей
частице, всегда остающейся с одной стороны от плоскости Х2 = хз. Чтобы
удовлетворить обоим ограничениям, частица должна оставаться в бесконеч¬
ном двумерном клине с углом раствора л/З, заданном этими ограничениями.
Известно, что вероятность выживания диффундирующей частицы внутри
бесконечного двумерного клина с углом раствора ф убывает как (см. зада¬
чу 2.25)
S(t) ~ Г*/2ф. (2.82)
Следовательно, вероятность выживания трех взаимно недружественных ча¬
стиц асимптотически убывает как t~3^.
В трехчастичной системе есть и другие тонкости. Объявим одну из частиц
«жертвой», а две другие «хищниками», которые не взаимодействуют друг с
другом, но каждый убивает жертву при встрече. Предположим, что оба вида
диффундируют с одним и тем же коэффициентом диффузии. Какова вероят¬
ность выживания жертвы? Есть два различных случая: (i) жертва в началь¬
ный момент в середине, и (ii) жертва с краю. Обе эти трехчастичные зада¬
чи могут быть решены отображением на одну диффундирующую частицу в
трех измерениях с наложением соответствующих ограничений. Для жертвы
в середине, ограничения Х2 > xi и хз > Х2 такие же, как для трех взаим¬
но недружественных блужданий, и вероятность выживания жертвы спадает
как f-3/2. Для жертвы в xi, с краю, ограничения для выживания: х± < Х2
и xi < хз. Угол раствора клина, полученного при отображении на эквива¬
2.7 Теория скорости реакций
45
лентную трехмерную задачу, теперь 27г/3, так что вероятность выживания
жертвы асимптотически убывает как £-3/4.
Нужно отметить уменьшающийся эффект добавления второго хищника
с краю: для одного хищника вероятность выживания убывает как £-1/2, то¬
гда как для двух хищников вероятность выживания убывает медленнее, чем
(Л-1/2)2. Естественно задать следующий вопрос: «Какова вероятность выжи¬
вания жертвы /Stv(£) для N > 2 хищников с одной стороны от жертвы?» Ответ
неизвестен! Численно оказывается, что асимптотическое убывание степенное:
5yv(£) ~ с 7з « 0,91342 и 74 « 1,032. Показатели ум растут медлен¬
но с 7V, например 710 « 1,4- Для N —> оо качественные аргументы дают:
7/v — |ln4JV.
2.7 Теория скорости реакций
Какова интенсивность, с которой диффундирующие молекулы попадают на
адсорбирующий объект? Ответ на этот вопрос проливает свет на диффу¬
зионно-контролируемые реакции — предмет, который будет обсуждаться в
главе 13. В таком процессе реакция происходит, когда два реагента сближа¬
ются на расстояние равное радиусу взаимодействия, т. е. реагенты эффек¬
тивно «встречаются». Эволюция реакций, таким образом, ограничена интен¬
сивностью, с которой диффузия сближает реагенты. Цель теории скорости
реакций — вычислить эту интенсивность.
Чтобы поместить теорию скорости реакций в контекст данной главы, рас¬
смотрим гораздо более простой пример скорости реакции, в которой внешние
частицы движутся баллистически, а не диффузионно. Для однородного пуч¬
ка частиц, падающего на адсорбирующий объект, скорость реакции очевидно
пропорциональна площади сечения. Совершенно по другому обстоит дело с
«пучком» диффундирующих частиц: скорость реакции растет медленнее, чем
площадь сечения, а также нетривиально зависит от формы. Используя мате¬
матическое сходство между диффузией и электростатикой, мы покажем, как
определить скорость реакции объекта на языке электростатической емкости.
Сначала изучим скорость реакций адсорбирующего объекта произвольной
формы в трех измерениях (d = 3). Объект окружен газом невзаимодейству¬
ющих молекул, каждая из которых адсорбируется, как только попадает на
поверхность объекта (рис. 2.6). Скорость реакции определяется как величи¬
на диффузионного потока к объекту в стационарном состоянии. Чтобы найти
этот поток, нужно решить уравнение диффузии для концентрации с(г, f) сна¬
ружи объекта 23 с адсорбирующей границей <923. Удобно в качестве начальных
условий выбрать пространственно однородную единичную плотность. Тогда
46
Диффузия
Рис. 2.6. Схематическое распределение диффундирующих частиц вокруг адсор¬
бирующего объекта
нужно решить уравнение диффузии с граничными и начальными условиями:
^- = £>V2c, c(red®,t) = 0, c(r,t = 0) = l. (2.83)
Оь
В d = 3 есть важное упрощение: концентрация приближается к стационар¬
ному состоянию. Интуитивно стационарное состояние возникает из-за невоз¬
вратности диффузии: убыль молекул из-за адсорбции компенсируется попол¬
нением на бесконечности. С другой стороны, диффузия возвратна в d = 2 и
в d = 1. Из-за того что диффундирующая частица в конце концов попадает
на адсорбер, стационарного решения уравнений (2.83) быть не может.
Так как в d = 3 концентрация c(r,t) приближается к стационарному со¬
стоянию Соо(г), мы исследуем дополнительную функцию </>(r) = 1 — Соо(г).
Уравнения эволюции </>(г) имеет вид
£>V20 = 0, 0(r G д'В) = 1, ф(т -> оо) = 0. (2.84)
Поскольку ф = 1 на границе и </>(г) удовлетворяет уравнению Лапласа, ф есть
просто электростатический потенциал, создаваемый идеально проводящим
объектом В, на котором поддерживается единичный потенциал.
По определению скорость реакции К — это
К = D f Vc-da = -D [ Чф- dcr. (2.85)
J&z Jd%
С другой стороны, согласно электростатике полный заряд на поверхности
эквивалентного проводника в трех измерениях равен
Q = ~ [ Чф-da.
Ьл J&2,
(2.86)
2.7 Теория скорости реакций
47
Волее того, полный заряд проводника связан с его емкостью С уравнением
Q = Сф%. Следовательно, когда на проводнике поддерживается единичный
потенциал, скорость реакции равна
К = 4nDQ = №С.
(2.87)
Ота фундаментальная эквивалентность позволяет найти скорость реакции
различных простых объектов по известным значениям их емкостей.
• Сфера радиуса R в трех измерениях15:
С = R, К = ^DR.
Вытянутый эллипсоид вращения с осями а > b = с:
К = 4nD
С =
Arch(a/b) ’ Arch(a/6)
• Сплюснутый эллипсоид вращения с осями а = Ь> с:
С =
Диск радиуса R:
\/о?
зхссав(с/а)’
К = 4nD
\Jа2, — </•
arccos(c/а)
С = 2R/n, К = 8DR.
Что можно сказать о реакциях в низкоразмерных системах с d < 2? Из-за
того что диффузия возвратна, вокруг адсорбера возникает постоянно расту¬
щая «обедненная зона». В результате адсорбируемый поток монотонно стре¬
мится к нулю при t —> оо. В этой ситуации полезно оперировать скоростью
реакции, зависящей от времени. Получим эту скорость, которая не что иное,
как зависящий от времени поток на адсорбер. Хотя вычисление зависящего
от времени потока — выполнимая задача (см. задачу 2.23), можно обойти
большинство технических трудностей, произведя приближенный квазиста-
тический расчет, который мы проиллюстрируем на примере адсорбирующей
сферы. Это мощный, хотя и простой метод для решения уравнения диффузии
п медленно меняющихся условиях.
Основа квазистатического приближения — это естественное для d < 2 раз¬
деление внешней по отношению к адсорбирующей сфере области на «ближ¬
нюю» зону протяженностью y/Dt от поверхности и дополнительную к ней
15Для сферы в d > 2 измерениях С = (d—2}Rd~2 и, следовательно, К = D (d—2) fid J?11-2,
где = 27rd/2/r(d/2) — площадь поверхности единичной d-мерной сферы.
48
Диффузия
«дальнюю» зону (рис. 2.7). Ближняя зона — это область, в которой диф¬
фундирующие частицы находятся под влиянием адсорбирующей границы. У
них, однако, достаточно времени, чтобы «тщательно обследовать» ближнюю
зону до того, как они будут адсорбированы. Поэтому концентрация в этой
зоне почти не зависит от времени. Наоборот, в дальней зоне вероятность,
что частица будет адсорбирована, ничтожна, так как маловероятно, что ча¬
стицы продиффундируют на расстояние больше чем y/Dt за время t. Таким
образом, концентрация в дальней области остается близкой к ее начальной
величине, c(r) ~ 1 для г > y/Dt.
г = R +
Рис. 2.7. График концентрации вокруг адсорбирующей сферы в квазистати-
ческом приближении. Концентрации в ближней и дальней зонах равны при
Основываясь на этой интуитивной идее, мы получаем решение уравнения
Лапласа в ближней зоне, но с зависимыми от времени граничными условия¬
ми с(г = y/Dt) = 1, согласованными при г = y/Dt со статическим решением в
дальней зоне. Общее решение уравнения Лапласа имеет вид c(r) = А + Br2~d
для d < 2 и с(г) = А + В In г для d = 2. Наложение граничных условий при
г = R и при г = y/Dt для t —» оо дает
с(г, t) ~ <
1 - (R/y/Dt)d~2
y/Dt
d-2
d<2,
(2.88)
l-(B/r)d~2
г
ln(r/R)
d = 2.
2.8 Подход Ланжевена
49
После этого, мы вычисляем поток D Vc • do к поверхности, из которого
получаем размерную зависимость скорости реакции для сферы радиуса R:
'D х (Р4)(<*-2)/2, d < 2,
47г£>
In (Dt/R2) ’
d = 2,
(2.89)
DRd~2, d> 2.
Скорость независима от времени и растет с радиусом как Rd~2 при d > 2;
при d < 2 скорость независима от радиуса сферы, что отражает возвратность
диффузии, и убывает со временем по степенному закону.
2.8 Подход Ланжевена
Как упоминалось во вступлении к этой главе, ярко выраженная случайность
движения броуновской частицы обусловлена огромным числом столкнове¬
ний с молекулами жидкости. Безнадежная и бесполезная задача — учесть
все столкновения и решить уравнения движения точно. Подход Ланжевена
основан на замене эффекта от этих очень частых столкновений эффектив¬
ной стохастической силой. Таким способом многочастичная задача сводится
к гораздо более доступной для анализа эффективной проблеме одного тела.
Чтобы проиллюстрировать подход Ланжевена, начнем с диффузионно¬
го движения в одном измерении16. Мы имитируем процессы столкновений
случайным шумом £(£). Уравнение движения для координаты x(t) частицы
5 =- (2'90)
)то стохастическое дифференциальное уравнение, потому что £(£) — стоха¬
стическая переменная, зависящая от конкретной реализации шума. Этот шум
имеет следующие основные свойства:
• не зависит от х.
• £(£) флуктуирует на микроскопически малом временном масштабе, что¬
бы имитировать эффект столкновений17.
10Такое же рассмотрение работает и в более высоких размерностях. Мы ограничиваемся
одномерием для простоты.
17Для частиц пыльцы, служивших объектом экспериментов Роберта Броуна, их линей¬
ный размер порядка 10“5м и число столкновений порядка 1О20 столкновений в секунду.
50
Диффузия
• (f(0) = т- е- нет координации столкновений, приводящей к ненуле¬
вой общей скорости. (Скобки (• • •) обозначают усреднение по разным
реализациям шума.)
• Нет корреляций между шумами на разных временах, (£(£)£(£х)) =
2D8(t — tf>). Наличие амплитуды 2D будет позже обосновано.
Интегрирование уравнения (2.90) дает формальное решение
x(t) = Г (2.91)
Jo
Когда мы усредняем (2.91) но шуму, мы получаем (x(t)} = 0, так как
= 0. Возведение в квадрат уравнения (2.91) дает
<**> = [‘ (2.92)
Jo Jo
Используя (£(£/)С(^//)) = 2D5(tf — tn\ находим (т2) = 2Dt, что воспроизво¬
дит результат, полученный из уравнения диффузии. Эта связь с диффузи¬
ей обосновывает значение амплитуды 2D в корреляционной функции шума.
Заметим, что временная зависимость следует из уравнения (2.90) и анали¬
за размерностей. Так как 5(t) имеет размерность 1/t (потому что интеграл
f 5(t) = 1), утверждение (£(i)£(iz)) = %D8(t — tf) значит, что £ имеет размер¬
ность y/D/t. Поэтому из (2.91) видно, что должно иметь размерность
y/Dt.
Не только дисперсия идентична предсказанию уравнения диффузии, но
и полное распределение вероятностей гауссово. Это можно увидеть, если по¬
делить интервал (0, £) на большое число t/fct подинтервалов продолжитель¬
ностью Д£, заменить интеграл в уравнении (2.91) суммой
ж(о = 52
>=i
(2.93)
и заметить, что смещения — независимые одинаково распределенные слу¬
чайные величины, удовлетвряющие (£у) = 0, (£2) = 2Dkt. Поэтому примене¬
ние центральной предельной теоремы дает
Очевидно невозможно (и бесполезно!) следить за изменениями, вызванными столкновени¬
ями, происходящими на чрезвычайно коротком, 10“2Ос, временном масштабе.
2.8 Подход Ланжевена
51
Р(х, t) = , 1 е-®2/4^. (2.94)
Появление распределения вероятностей Гаусса особенно поразительно, ес¬
ли учесть, что уравнение Ланжевена (2.90) приводит к нефизической бес¬
конечной скорости. Действительно, за малый временной промежуток Af
среднеквадратичное смещение броуновской частицы равно (Дж2) = 2DAt.
11оэтому типичная скорость vtyP ~ Дж/At ~ y/D/fct расходится при At —» 0.
Математически функция ж^) непрерывна, но нигде не дифференцируема. В
качестве альтернативы Ланжевен предложил уравнение
dv >./ \ dx
^ = -TV + «t), *=v (2-95)
для скорости v, которая, будучи основной переменной, остается конечной18.
Подход Ланжевена, основанный на уравнении (2.95), постулирует что влия¬
ние жидкости можно разделить на систематическую силу трения, представ¬
ленную членом —7V, и на флуктуирующую часть, обозначенную £(t). Сила
I рения как обычно подчиняется закону Стокса19 * * *, в котором 7 = Ъ'ка'ц/т, где
а радиус частицы, которая по предположению имеет сферическую фор¬
му» 77 — коэффициент вязкости жидкости, и т — масса броуновской части¬
цы. Шум имеет нулевое среднее и корреляционную функцию (&0О£?СИ) =
I 'Я у 8(t — tf). Так как оба этих вклада вносятся окружающей жидкостью, они
не независимы. Мы увидим, что 7 и Г взаимосвязаны через флуктуационно-
Ниссипационное соотношение.
Формальное решение уравнения (2.95) имеет вид
v(t) = v0 + е-^ Г<(t') е*' dt'. (2.96)
Jo
Поэтому средняя скорость убывает экспоненциально со временем: (v) =
Voc“7t. Средний квадрат скорости имеет более интересное поведение
(V2) = vg е~2^ + е~2^ Р Л^') dt"
Jo Jo
= v§ e"27* + (1 - e“27*) . (2.97)
27
,HСогласно уравнению (2.95) скорость непрерывна, но нигде не дифференцируема, так
что ускорение бесконечно. Также нужно отметить, что в пределе 7 —> оо можно пренебречь
инерционным членом v, что снова приводит нас к (2.90).
19Сила сопротивления линейна по скорости, когда скорость мала или жидкость очень
тикая. Более точно, безразмерное число Рейнольдса (которой дается отношением инер-
цш ильного члена к вязкому) должно быть мало. Для сферы число Рейнольдса равно
Не - pva/y.
52
Диффузия
Теорема о равнораспределении говорит, что в равновесии все степени свободы
имеют среднюю энергию Т/2. (Мы всегда измеряем температуру в единицах
энергии, полагая константу Больцмана к = 1.) Следовательно (v2) = 3T/m
в трех измерениях. Сравнивая с уравнением (2.97) в пределе т -> оо, мы
видим, что коэффициент трения и амплитуда шума связаны флуктуационно-
диссипационным соотношением Г = 2Т^/т.
Чтобы определить распределение вероятностей P(v,t|vo) из (2.96), мы
можем пойти по тому же пути, как при выводе (2.94) из (2.93), а именно
запишем
v(t)-voe_7t = Cj = e~yt £(t') e*'dt'. (2.98)
В правой части имеем сумму независимых (хотя и не одинаково распределен¬
ных) случайных величин. Однако центральная предельная теорема все еще
справедлива в этом случае20, и в пределе Д£ —> 0 получим распределение
(задача 2.26)
^0Mlvo)
т
3/2
m(v —voe 7t)2"
_2тгГ(1 - е-27‘)
ехр
2Т(1-е-2^) .
(2.99)
которое стремится к распределению Максвелла в пределе t —> оо.
Нашей первоначальной целью было описать распределение вероятностей
смещения. Исследуем эту величину. Интегрируя х = v, получим
x(t) = хо + 7_1vo(l - е-7*) + 7_1 £ £(*') [l - e"7^"*')] dt', (2.100)
так что среднее смещение будет (х) = xo+7_1vo(l — е-7*). Возводя в квадрат
(2.100), находим среднеквадратичное смещение
(х2) = X2 + 7’2v^ e-27t + 27-х(1 - е-7*)х0 • v0 + g(t),
g(t) = 27t - 3 + 4е“7< - e“27*. (2.101)
Поработав еще немного, приходим к полному распределению
Р(х, V, 11 Хо, Vo)
Ш72
3/2
Ш72[х - х0 - v0(l - е 7<)/7]2
27rT0(t)
ехр
2T5(t) J
20Полная дисперсия — это сумма индивидуальных дисперсий (£2).
(2.102)
2.9 Применение к росту поверхностей
53
Асимптотически это распределение вероятностей согласуется с решением
уравнения диффузии с константой диффузии, определенной как
D
Т_ - Т
ту бтсца'
(2.103)
где г/ — вязкость. Эта связь между параметрами известна как соотношение
Стокса - Эпштейна.
Существует стандартный рецепт перехода от уравнения Ланжевена для
стохастической переменной х к уравнению Фоккера-Планка для распределе¬
ния вероятностей P(x,t). Так как эта связь подробно обсуждается во многих
учебниках, мы не будем на ней останавливаться. Просто заметим, что для
общего уравнения Ланжевена
и котором шум £(t) имеет нулевое среднее, а корреляции отсутствуют, (£) = 0
и (£(£) С(^)) = 2Г5(£—t'), соответствующим уравнением Фоккера-Планка для
/’(:/;,<) будет
9Р д д2Р
й=-&№>р1+г^-
Например, для уравнения Ланжевена А = £(t) уравнение Фоккера-Планка
сводится к стандартному уравнению диффузии (2.7). Характерное свойство
уравнения Фоккера-Планка — то, что его решение имеет гауссов вид. Ниже
мы используем этот факт при обсуждении разложения по малым флуктуа¬
циям основного кинетического уравнения для систем с реакциями в разделе
12.3.
2.9 Применение к росту поверхностей
Мы видели, что комбинация простейшего шума и самого тривиального диф¬
ференциального уравнения А = 0 приводит к уравнению Ланжевена (2.90) —
тмечательному стохастическому дифференциальному уравнению, которое
содержит все свойства одномерного броуновского движения. Уравнения Лан¬
жевена, соответствующие более сложным дифференциальным уравнениям
(например для гармонического осциллятора) и более сложному шуму, также
были исследованы. Идея остается такой же: мы хотим понять, как меняет¬
ся поведение детерминистической системы из-за взаимодействия со средой.
Мы не можем описать среду точно и вместо этого имитируем ее влияние на
систему посредством стохастической силы.
54
Диффузия
В общем случае уравнение Ланжевена строится с помощью следующей
стандартной процедуры:
• Начинаем с детерминистического уравнения движения. Чаще всего это
обыкновенное дифференциальное уравнение, но возможны и другие ва¬
рианты (например разностные уравнения).
• Добавляем член с шумом. В простейшем случае шум предполагается
независимым от самой переменной, нескоррелированным во времени и
гауссовым.
Множество природных явлений описываются дифференциальными урав¬
нениями в частных производных. Амбициозное обобщение программы Лан¬
жевена — начать с детерминистического уравнения в частных производных.
Наиболее важное линейное уравнение в частных производных, возникающее в
этой книге, — это уравнение диффузии. Наиболее известное нелинейное обоб¬
щение уравнения диффузии — уравнение Бюргерса. Рассмотрим уравнения
Ланжевена, соответствующее этим двум уравнениям в частных производных.
У равнение Эдвардса - У и л кинсона
Уравнение Эдвардса-Уилкинсона (ЭУ) — это уравнение диффузии с шумом:
^ = £>V2/i + t?. (2.105)
Это уравнение Ланжевена было предложено как модель роста поверхности,
в которой атомы из внешнего источника адсорбируются поверхностью, то¬
гда как адсорбированные атомы могут испаряться. В зависимости от при¬
роды падающего потока, мобильности адатомов и механизмов релаксации
может возникать большое разнообразие морфологий поверхностей. Поверх¬
ность характеризуется высотой H(r, f) — функцией координаты г и времени
t. Удобнее рассматривать отклонение поверхности от ее средней величины:
/i(r, t) = 7Z(r,t) — (Н). Основная цель — понять свойства функции h и ее
корреляционных функций (Д(г, f)/i(r/,t/)).
Рассматриваемый в контексте модели эволюции поверхности лапласиан в
(2.105) положителен около локальных минимумов поверхности (положитель¬
ная кривизна) и отрицателен около локальных максимумов (отрицательная
кривизна). Таким образом лапласиан стремится сгладить поверхность и ими¬
тирует влияние силы упругости. Член уравнения (2.105), соответствующий
2.9 Применение к росту поверхностей
55
шуму, предполагается гауссовым с нулевым средним, независимым от h, а
также нескоррелированным в пространстве и времени. То есть:
(г)} = 0, (ri(x, f')) = 2Г<5(х — х') 5(t — tf). (2.106)
Конкуренция между влиянием этого шума и сглаживающим лапласианом
приводит к возникновению нетривиальных поверхностных морфологий.
Вычислим ширину фронта w(t) = y/(h2(x, t)) в одномерной ситуации, в
которой фронт предполагается плоским в начальный момент: h(x, t = 0) = 0.
Как всегда начнем с анализа размерностей. Из-за трансляционной инвари¬
антности ширина w не зависит от х. Поэтому w = w(t,.D,r). Из (2.105) на¬
ходим [77] = L/fT, тогда как (2.106) дает [Г] = [»7]27УГ = L?/T (в одномерном
случае). Таким образом, один лишь анализ размерностей уже приводит нас
к нетривиальному скейлинговому предсказанию для ширины:
w2 = DtF{n\ где K = Dh/Y2. (2.107)
Используя линейность уравнения уравнения ЭУ (2.105), можно продвинуться
и дальше. Высота (и ширина) должны быть пропорциональны rj или, учиты¬
вая (2.106), л/Г. Эта зависимость точно будет наблюдаться в пределе боль¬
шого времени, а для плоской в начальный момент поверхности справедлива
всегда. Из того, что w пропорционально \/Г, следует, что F(k) = СкГ1/2.
'Таким образом анализ размерностей и линейность определяют ширину
w2 = CLy/t/D (2.108)
с 'гочностью до амплитуды С.
Чтобы вывести (2.108) аналитически и, как следствие, вычислить ампли¬
туду, напишем общее решение уравнения (2.105) в одном измерении
h(x, t) = f dti Г° dXl /fe1’-1) e-^-xi)2/^^-*!). (2.109)
V ' Уо У-оо y/Mit-tx) k ’
Возведя в квадрат и усреднив, чтобы найти ш2 = (h2(x,t)}, получим (2.108)
с С = 1/2/7Г (задача 2.29).
В двух измерениях анализ размерностей дает
w2 = £>tF(K), где K = D2t/T. (2.110)
()тсюда, а также пользуясь зависимостью w ~ vT, получим интересный ре¬
зультат: ширина принимает стационарный вид w2 = СТ/D. Эта стационар¬
ность, в принципе, правдоподобна как асимптотическое поведение. Однако
56
Диффузия
в отсутствие характерного временного масштаба предсказание w2 = CT/D
должно быть (если оно правильно) справедливо для любых времен. Такое
постоянство очевидно невозможно, так как мы положили начальную шири¬
ну равной нулю. (На практике мы увидим, что ширина плохо определена, а
именно: расчет w2 = (/i2(x,t)) с Д(х,<) из (2.112) приводит нас к w = оо.)
Чтобы разрешить дилемму, рассмотрим двухточечную корреляционную
функцию
С(х, t) = (й(х, t) /i(0, t)). (2.111)
Эта функция хорошо определена и конечна для х / О. Чтобы вычислить
С(х, i), мы снова используем общее решение
/i(x,t) = J dti J dx.i
4:TTD(t — ti)
exp
(x-xi)2'
42?(i — ti)_
(2.112)
вместе c (2.106) и находим (см. задачу 2.30)
С(х, t)
Г
47гР
(2.113)
Si(£),
где Ei(z) — экспоненциальный интеграл21. Используя асимптотическое пове¬
дение
z3
Ei(z) = -hkz-'yE + z- — + — + ...,
(ryE = 0,577215 — константа Эйлера) мы видим, что в пределе большого
времени
С(Х’*) = 4^Р • (2Л14)
Расходимость ширины объясняется просто тем, что в любой физической
ситуации есть характерная микроскопическая длина, ниже которой предпо¬
ложение о том, что шум пространственно нескоррелирован, уже неверно. Это
обрезание — естественная наименьшая длина, за пределами которой непре¬
рывное описание бессмысленно. В решеточных задачах а — постоянная ре¬
шетки, в задачах об осаждении на поверхности а — размер атома. Математи¬
чески член 6(х — х') в корреляционной функции шума должен быть заменен
на функцию /(х — Xх), имеющую следующие свойства:
• /(0) конечно.
• /(у) быстро убывает при |у| » а.
21 Экспоненциальные интегралы En(z) определяются как En(z) = du и п е uz
2.9 Применение к росту поверхностей
57
• / dy f (у) = 1> так что амплитуда шума «зашита» в параметре Г.
Конечное обрезание снизу избавляет от расходимости и приводит к ширине
w = y/(T/4:TrD) ln(ZU/a2), которая расходится логарифмически по параметру
обрезания.
Хотя случай двумерия наиболее естественный с точки зрения эволюции
поверхностей, общий подход статистической физики (а также и многих дру¬
гих разделов физики) предполагает изучение поведения в произвольной про¬
странственной размерности. Такая общность помогает обнаружить законо¬
мерности, которые проливают свет на поведение в размерностях, представ¬
ляющих физический интерес. Уравнение ЭУ решаемо в любой размерности,
а привычка рассматривать произвольную размерность часто оказывается по¬
лезной. В данном случае поведение двухточечной корреляционной функции
наглядно демонстрирует важность размерности пространства:
г ( d=l,
х 1 d = 2’ (2-115)
I d = 3.
В трех измерениях двухточечная корреляционная функция становится неза¬
висимой от времени в пределе большого времени. Из (2.115) получаем следу¬
ющее асимптотическое поведение:
ш2 = С(0,£) = Г х <
y/2t/nD,
(4TTD)-1 ln(£>t/a2),
(47гРа)-1,
d = 1,
d = 2,
d = 3.
(2.116)
Таким образом, шум может увеличить шероховатость фронта описываемого
уравнением ЭУ, только когда d < 2.
Хотя ширина, а в более общем случае С(т, t), остается нестационарной в
одномерии, разность высот стремится к стационарному пределу. Это свойство
может быть извлечено из усреднения среднеквадратичной высоты. Используя
(2.115), получим
([/г(т, £) — Д(0, i)]2) = 2[(7(0,t) — С(х, t)]
= 1/2[^3/2(0) - Е3/2(С)]. (2.117)
Записывая
roo л/7/ г т
(2.118)
58
Диффузия
и дифференцируя по £, получим, что производная стремится к когда
£ —> 0. Поэтому разность (2.118) ведет себя как 2Утг£, когда £ —> 0. Подста¬
новка этого результата в (2.117) дает
([/&(#, t) — /i(0,t)]2) = |х| при t —> оо. (2.119)
Эта изящная формула говорит нам, что высота /i(#,t) — (асимптотически)
случайное блуждание по отношению к пространственной координате х.
Уравнение ЭУ дает общее представление об обширной области уравнений
Ланжевена, сконструированных на основе уравнений в частных производ¬
ных. Такие уравнения редко оказываются решаемыми. Одно из решаемых
уравнений — уравнение Маллинса (см. задачу 2.32)
Ц = _pV4/1 + t?. (2.120)
Похожие (но часто нелинейные) задачи описывают кинетику упорядочивания
фаз при положительных температурах22.
Уравнение Кардара-Паризи-Жанга
Уравнение, похожее на уравнение ЭУ, — уравнение Кардара - Паризи - Жанга
(КПЖ) было предложено для описания роста поверхностей. Это нелинейное
уравнение Ланжевена гораздо более сложно и интересно чем уравнение ЭУ.
В обоих уравнениях, как КПЖ так и ЭУ, предполагается, что поверхность
характеризуется ее высотой /i(x, f), причем /i(x,£) — однозначная функция
координат. Физически это значит, что профиль поверхности не имеет нави¬
сающих выступов. Кроме того, оба уравнения — это примеры макроскопиче¬
ского описания, в котором мы интересуемся масштабами, во много раз пре¬
восходящими атомные. Основное различие между уравнениями ЭУ и КПЖ
то, что уравнение КПЖ нелинейно. Это уравение имеет простой вид23
^ = DV2h + X(yh)2 + rj, (2.121)
хотя простота эта иллюзорна: свойства этого уравнения были полностью по¬
няты только в одномерии.
22Более подробно об этом см. главу 9.
23Уравнение (2.121) — это ланжевеновское обобщение уравнения Бюргерса (с несколько
необычным шумом). Действительно, применяя оператор градиента V к (2.121), находим,
что и = — 2Л57Д удовлетворяет уравнению и* + (и • V)u = PV2u + £, которое есть не что
иное, как уравнение Бюргерса с шумом £ = — 2XVrj.
2.9 Применение к росту поверхностей
59
Нужно подчеркнуть, что уравнение (2.121) — не случайный пример из
множества нелинейных уравнений Ланжевена, а единственный уникальный
экземпляр. Действительно, простейшее уравнение, согласующееся с с симмет¬
риями задачи, обычно оказывается самым подходящим. С этой точки зрения
заметим, что уравнение (2.121) согласуется со следующими симметриями:
1. Трансляционная инвариантность в направлении роста. Она запрещает
появление членов, содержащих h явно. Могут возникать только произ¬
водные h.
2. Инвариантность по отношению к трансляциям, вращениям и инвер¬
сии в координатной плоскости х. Эти симметрии допускают только
члены типа V2/i, V4/i, четные степени градиента (Vft)2, (V/i)4, и т. д.,
но исключают нечетные степени градиента (такие как V/i).
В принципе, уравнение вида
= PiV2/i + £>2V4/i + Ai (V/i)2 + A2(Vh)4 + /z(V2/i)(V/i)2 + 77
совместно с симметриями, перечисленными выше, и может давать даже более
хорошее описание некоторых процессов на малых временах, чем уравнение
(2.121). Асимптотически, однако, производные более высокого порядка и бо¬
лее высокие степени пренебрежимо малы, т. е. V2/i » V4h, (V/г)2 » (W,
(V/1)2 » (V2Zi)(V/i)2, и поэтому мы возвращаемся к (2.121). Если процесс
вдобавок инвариантен по отношению к замене верх-низ, h —> — h, нелиней¬
ные члены должны исчезать (Ai = А2 = 0), и мы получим (2.105). Если,
кроме того, из симметрий следует Di = 0, получим (2.120). Эти аргумен¬
ты показывают, почему такие уравнения, как ЭУ, Маллинса и КПЖ играют
выделенную роль.
Обратите внимание, что в уравнении ЭУ есть симметрия верх-низ, т. е.
симметрия по отношению к преобразованию h —> —h, которой нет в уравне¬
нии КПЖ. Это различие предполагает, что, если рост поверхности осуществ¬
ляется осаждением и испарением, причем эти процессы уравновешивают друг
друга, то уравнение ЭУ должно давать правильное описание. Если же один
из процессов доминирует, т. е. симметрия верх-низ нарушена24, то уравнение
ЭУ (а в более общем случае любое линейное уравнение Ланжевена) неприме¬
нимо.
Попробуем извлечь как можно больше из уравнения КПЖ наименее тру¬
дозатратным способом: анализом размерностей. Для простоты сосредоточим¬
ся на одномерной системе. Ширина фронта — функция времени и параметров
24 Даже в системе отсчета, связанной со средней высотой.
60
Диффузия
2?, Л, Г уравнения КПЖ: w = w(t,D, Л, Г). Записав размерности этих пере¬
менных [£] = Т, [£>] = L2/T, [Л] = L/Т, [Г] = L3/T, мы видим, что из четырех
переменных можно составить две безразмерные комбинации. Таким образом,
анализ размерностей дает
w = y/Dt F(D3t/T2, ГХ/D2). (2.122)
Вспомним, что в случае уравнения ЭУ мы выразили ширину через одну без¬
размерную переменную к = D3t/Y2 и затем использовали линейность урав¬
нения ЭУ, чтобы найти ширину. Для нелинейного уравнения КПЖ ширина
выражается в виде неизвестной функции двух переменных, и никакие даль¬
нейшие упрощения не кажутся возможными.
Сейчас мы опишем полезный трюк, который оказывается неожиданно эф¬
фективным в данном контексте. Его идея — искусственно увеличить число
размерностей. В задачах поверхностного роста есть очевидная разница меж¬
ду вертикальным и боковыми направлениями, которая предполагает, что для
них могут использоваться разные единицы измерения. Запишем L = [ж] для
поперечной и Н = [h] для вертикальной размерностей. Используя (2.106),
получим [Г] = [?7]2Z/r, тогда как (2.121) дает [77] = Н/Т и [Л] = L2/HT. Тогда
размерности интересующих нас переменных:
г 2 г 2 гт2 г
М = Г, [D} = ^, [А] = -^, [Г] = ^. (2.123)
Мы хотим выяснить, как ширина w и корреляционная длина € (типичное
поперечное расстояние между точками, на котором их высоты становятся
нескоррелированными) зависит от этих четырех переменных. Мы можем
сформировать из них только одну безразмерную комбинацию r2A4f/£>5. Учи¬
тывая, что [w] = Я, [€] = Z, и пользуясь анализом размерностей получим:
г) Г2 А4/
w = -F(t), t=/DtG(r), r = ^~. (2.124)
Совершенно неожиданно, что простой формальный трюк приводит к тако¬
му значительному упрощению. Можно спросить, действует ли этот трюк для
уравнения ЭУ. В этом случае у нас есть три переменные: t, D и Г, — с неза¬
висимыми размерностями, так что анализ размерностей выдает полную заг
висимость от параметров:
w ~ Г1/2 (t/2?)1/4, I ~ y/Dt.
Таким образом, для уравнения ЭУ применение этого трюка позволяет выве¬
сти основную зависимость ширины от физических параметров без привлече¬
ния линейности.
2.9 Применение к росту поверхностей
61
К сожалению, один анализ размерностей для уравнения КПЖ не может
дать больше, чем скейлинговые предсказания (2.124), которые все еще содер¬
жат неизвестные функции одной переменной. Также неизвестно, как действо¬
вать в случае двух и более измерений. Одномерный случай, однако, уника¬
лен, так как известно стационарное решение уравнения Фоккера-Планка для
распределения вероятностей h. Уравнение — Фоккера-Планка это основное
кинетическое уравнение для вероятности распределения П(/г). Для уравне¬
ния КПЖ (и вообще для фоккер-планковского описания любого уравнения в
частных производных) нужно учитывать, что вероятность распределения —
это функционал П(Д(х)). Поэтому частные производные по h, которые воз¬
никают в уравнении Фоккера-Планка, должны быть заменены на вариаци¬
онные производные. В случае уравнения КПЖ стандартный рецепт вывода
уравнения Фоккера-Планка из уравнения Ланжевена дает (см. обсуждение,
приводящее к уравнению (2.104))
дП
dt
= -Jd*-^ [(DV2h + A(V/i)2) П] + Г J dx ^5. (2.125)
В одномерии это уравнение допускает стационарное решение:
21
П = ехр[-/&^(^)
(2.126)
Эта формула, однако, не дает решения в высших размерностях d > 2.
Простейший способ определения закона роста в одномерном уравнении
КПЖ — заметить, что в пределе большого времени параметры D и Г воз¬
никают только в комбинации Т/D. Пользуясь этим важным свойством, мы
можем применить анализ размерностей25, чтобы найти ширину и корреля¬
ционную длину как функции переменных t, А и Г/Р. Эти параметры имеют
независимые размерности, и, таким образом, мы находим полную асимпто¬
тику зависимости от параметров модели:
w ~ (Af)x/3(r/D)2/3, I ~ (А4)2/3(Г/Р)г/3. (2.127)
Такое скейлинговое поведение согласуется с (2.124), когда F ~ -г1/3 и G ~
т1/6. Степенной рост ширины по закону i1/3 часто называют ростом КПЖ,
и критический индекс 1/3 называется индексом КПЖ26.
25Здесь требуется обобщенный анализ размерностей с двумя единицами длины, [w] = Н
и [^] = L.
26Индекс, равный 1/3, впервые возник в работе Бюргерса, посвященной детерминисти¬
ческому уравнению Бюргерса со случайными начальными условиями, задолго до работы
Кардара, Паризи и Жанга, к которой его обычно относят. Потребовалось долгое время,
чтобы осознать универсальность такого поведения.
62
Диффузия
2.10 Ссылки
Случайные блуждания, диффузия и процессы первого достижения — цен¬
тральные разделы теории вероятности, и, соответственно, по ним существует
обширная литература. Кроме ссылок, упомянутых в предыдущей главе, мы
рекомендуем [12, 13] для более вероятностных аспектов случайных блужда¬
ний и теории вероятности в целом. Полезные и подробные обзорные статьи
о диффузии в случайной среде: [14, 15]. Отсутствие самоусреднения обсуж¬
дается в [15, 16]. Распределение Хольцмарка и его применение к астрономии
даны в обзорной статье Чандрасекара [12]. Более подробное описание свойств
первого достижения есть в [13, 17]. Разнообразным аспектам недружествен¬
ных случайных блужданий и, в частности, задачам о захвате в одномерии
посвящены [18-20].
Стимулирующее обсуждение связи между электрической емкостью про¬
водящих объектов и скоростью реакций для этих объектов можно найти в
[21, 22]. Использование квазистатических методов для решения уравнения
диффузии в присутствии движущихся границ обсуждается например в [23—
27]. Решение уравнения диффузии в геометрии клина рассматривается в [17]
и в [23]. Уравнение Ланжевена подробно обсуждается в обзоре Чандрасекара
[12] и книге Ван Кампена [13]. Последняя уделяет много внимания связи меж¬
ду уравнением Ланжевена и соответствующим уравнением Фоккера-Планка.
О применении уравнений ланжевеновского типа к явлениям роста поверхно¬
стей смотри [28-30].
2.11 Задачи
2.1 На каждом шаге дискретного случайного блуждания частица прыгает вправо
с вероятностью р или влево с вероятностью q = 1—р. Пусть Pn(#) — вероят¬
ность того, что частица находится в узле х на шаге N.
(a) Напишите основное кинетическое уравнение для этой вероятности запол¬
нения.
(b) Для начальных условий Pq(x) = 5Ж)о покажите, что комбинация преоб¬
разования Фурье и производящей функции
P(k,z) = 52 zN 52 eikxpN(x)
N>0 х=—оо
имеет вид P(/c,z) = [1 — zn(fe)]"1, где и(к) = регк + qe~tk — это Фурье-
образ вероятности прыжков за один шаг.
2.11 Задачи
63
(с) Обратите преобразование Фурье и производящую функцию и получите
распределение вероятностей дискретного случайного блуждания.
2.2 Рассмотрите одномерное дискретное случайное блуждание, в котором с ве¬
роятностью 1/3 происходит шаг вправо длиной 2, а с вероятностью 2/3 —
шаг влево длиной 1. Исследуйте поправки конечного времени к асимптотиче¬
скому изотропному распределению Гаусса. Подсказка: Используйте поведение
моментов выше второго (хк} с к > 2.
2.3 Решите уравнение (2.4) для случайного блуждания в непрерывном времени,
начинающегося в начале координат, применив сначала преобразование Лапла¬
са, чтобы получить разностное уравнение
sP(n, s) - P(n, t = 0) = P(n + 1, s) + P(n - 1, s) - 2P(n, s)
для Лаплас-образа P(n, s) = /0°° Pn(t) e~st dt. Покажите, что
P(n, s) = a!T'/(s + 2 - 2A_),
где A± = (1± vl — 4a2)/2а, и a = (s + 2)-1. Покажите, что в пределе большого
времени, соответствующем s —> 0 для Лаплас-образа, обращение преобразова¬
ния Лапласа воспроизводит распределение Гаусса (2.6) для Pn(t).
2.4 Обобщите уравнение (2.4) на случайное блуждание на гиперкубической решет¬
ке в d измерениях и найдите вероятность заполнения данного узла. Проверьте,
что вероятность заполнения начального узла дается формулой (2.48).
2.5 Непрерывный предел основного кинетического уравнения (2.1).
(a) Выведите уравнение диффузии (2.7) с D = 1 для случая симметричных
прыжков, р = q = j, раскладывая основное уравнение в ряд Тейлора до
первого неисчезающего порядка.
(b) Обобщите вывод на случай несимметричных прыжков (р / q) и покажи¬
те, что непрерывный предел дает уравнение конвекции-диффузии
dP(x,t) dP(x,t) d2P(x,t)
dt + V дх дх2
Выразите коэффициент диффузии D и скорость сноса v через микроско¬
пические параметры случайного блуждания (р и q).
(c) Для начальных условий P(x,t = 0) = 5(х) покажите, что решение урав¬
нения конвекции-диффузии имеет вид
P(x,t) = —1 ■ e-^-vt)2/4Dt
V 7 y/^Dt
64
Диффузия
2.6 Решите уравнение конвекции диффузии с помощью метода преобразования
Лапласа и покажите, что Лаплас-образ распределения Р(х, s) имеет вид
«) =
y/v2 + 4Ds
где нижний индекс ± обозначает распределение в областях х > 0 и х < 0, соот¬
ветственно, и = (у ± \Л>2 + 4Ps) /2D. Обратите преобразование Лапласа
и получите распределение Гаусса.
2.7 Решите уравнение конвекции-диффузии на полуоси х > 0 с адсорбирующими
граничными условиями Р(х = 0, t) = 0 и начальными условиями Р(т, t = 0) =
5(х — I).
2.8 Предположим, что N независимых одинаково распределенных случайных ве¬
личин выбраны из распределения вероятностей р(ж). Оцените максимальную
из этих величин для случаев: (а) р(х) = е~х, где х > 0; (Ь) р(т) =
при х > 1 и р(х) = 0 при 0 < х < 1; (с) р(т) = 1 при 0 < х < 1 и р(х) = 0 в про¬
тивном случае. Пользуясь этим, оцените скорость самой быстрой молекулы в
типичной классной комнате.
2.9 Исследуйте случайное блуждание в дискретном времени с широким симмет¬
ричным распределением длины шага, имеющим алгебраический хвост р(х) ~
Л|гс|“1_м при |т| —> оо. Предположите, что 0 < р < 1.
(а) Напишите Фурье-образ распределения длины шага в виде
p(fc) = l+ /
7-с
-l)p(x)dx
и покажите, что второе слагаемое ведет себя как — С|&|** при к -> 0, где
. С = -Л0ПГ(-д/2)/[2*Т((1 + ц)/2).
(Ь) Подставьте p(fc) = 1+АГ(—p)|fc|^ в (2.18) и покажите, что распределение
смещения имеет следующую скейлинговую форму
PN(X) -> z = X/N1^,
где Ьм,о(^) взято из (2.27) с С = —2АГ(—р).
2.10 Предположим, что случайное блуждание с дискретным временем имеет рас¬
пределение длины шага р(х) = 7г""1(1-|-т2)”1 (распределение Коши).
(a) Покажите, что его преобразование Фурье равно p(fc) =
(b) Вычислите интеграл в (2.18), взяв р(к) = е~W, и покажите, что
PN(X) = 1 N
тг N2 + X2
для любого целого N > 1. Таким образом, распределение Коши — это
не просто устойчивое распределение в пределе N —> оо: оно устойчиво
для всех 7V, т. е. обладает свойством, характеризующим распределение
Гаусса.
2.11 Задачи
65
2.11 Эта задача посвящена выводу амплитуды (2.37).
(a) Используйте f вместо г как переменную интегрирования (2.36). Покажи¬
те, что dr = — | /“9/2df, так что (2.36) становится
= I / (1 - ■') ■
(b) Покажите, что интеграл выше не меняется при замене f на —f. Взяв
среднее арифметическое этих двух интегралов, покажите, что
ф(к) = |/ ^2 [1 - cos(k - f)J.
Альтернативный вывод можно проделать, заметив, что интеграл в (а)
должен иметь действительное значение.
(c) Введем сферические координаты в f-пространстве с осью z, направлен¬
ной вдоль к, так что dt = 27rsin0 dQ f2df. Покажите, что интеграл из
пункта (Ь) принимает вид
Ф(к) = 7Г У j [1 - cos(&/m)] , Д = COS0.
(d) Выполните интегрирование по д и покажите, что интеграл из пункта (с)
сводится к
Ф(к) = 27rfc3/2 У dz Z > z = kf.
(e) Вычислите интеграл из пункта (d) и воспроизведите (2.37) с амплитудой
а=£(2тг)3/2.
2.12 Предположим, звезды распределены случайно (без корреляций) и однородно с
плотностью п. Каково среднее расстояние от звезды до ее ближайшего соседа?
(a) Пользуясь анализом размерностей, покажите, что среднее расстояние
убывает как п-1/3 или в общем случае как в d измерениях.
(b) Покажите, что в d среднее расстояние равно r(l/d) (V^n)"1^, где Vd —
объем d-мерного единичного шара.
(c) Покажите, что Vd = 7rd/2/r(l + d/2).
(Подсказка: Нужно вычислить интеграл Jd = f e~r2 dr по всему про¬
странству Вычислите этот интеграл двумя методами. Первый — за¬
писать г2 = х2 + ... + х2^ dr = dxi... dxdi что превращает Jd в произ¬
ведение, Jd = (Ji)d, где Ji = е~х dx = у/п. Второй — используя
вращательную инвариантность и сферические координаты, свести ин¬
теграл к Jd = /0°° e"r Qdrd_1dr и выразить его через Гамма-функцию.
Сравнение двух ответов даст «площадь» поверхности единичной сферы
объем единичного шара часто определяется из = dVd-)
66
Диффузия
2.13 Для г / 0 и t > О проверьте явно уравнение(2.44) в одном измерении.
2.14 Выведите (2.54) из (2.53).
2.15 Объясните связь между потоком и вероятностью времени выхода и закончите
вывод (2.64).
2.16 Покажите, что решение уравнения (2.72) на интервале (0,L) имеет вид t(x) =
x(L—x}
2D ’
2.17 Выведите дифференциальные уравнения для высших моментов (Т2(ж)) и
(Т3(ж)), обобщив уравнение (2.72). Решите эти уравнения на интервале (0,L).
2.18 Рассмотрите уравнение (2.77) на интервале (—L, L).
(а) Покажите, что преобразование Лапласа времени выхода имеет вид
n(s, х)
сЬ^д/а/Р]
ch[LVsTP]’
Предположим, что случайное блуждание стартует с начала координат
х = 0. Разложите П(я,я = 0) по степеням s и выведите из разложения,
что (Тп) = Лптп, где т = L2/D и коэффициенты:
л 1 л 5 л 61 л
Ai = й, А.2 = —, Л3 = —, А4
Ап =
2’ " 24’
50521
3628800’ 6
540553
95800320’
277
8064’
.(b) Покажите, что общее выражение для моментов времени выхода порядка
п имеет вид:
где Еп — числа Эйлера, которые определены через разложение
— = V — zn
chz
п>0
2.19 Предположим, что частица, находившаяся в начале в х = Л совершает несме¬
щенное случайное блуждание с коэффициентом диффузии D. Частица на¬
ходится на полуоси (ж*,оо), где граница я*(£) движется. Предположим, что
х* = Vt, т. е. в начальный момент граница находится в нуле и она догоня¬
ет частицу со скоростью V > 0. Время выхода — это время, когда частица
впервые пересекает движущуюся границу.
(а) Покажите, что среднее время выхода не зависит от коэффициента диф¬
фузии: (Т) = i/V.
2.11 Задачи
67
(b) Покажите, что среднеквадратичное время выхода — это (Т2) = (€/У)2 +
2W/V3.
(c) Покажите, что Лаплас-образ времени выхода (e~sT) имеет вид
exp[-£(vV2 + 4s£> - V)/(2P)].
Решите эту же задачу, когда граница движется назад: ж* = — Vt.
(d) Покажите, что время выхода бесконечно с вероятностью РгоЬ(Г = оо) =
1 _
(e) Покажите, что Лаплас-образ времени выхода имеет вид
exp[-^(VV2+4sD + У)/(2Р)].
2.20 Диффундирующая частица заключена в интервале [0, Ь]. Частица имеет ко¬
эффициент диффузии D и, также, подвержена постоянному сносу v. Конечная
точка х = L отражающая, а когда частица приходит в х = 0, она адсорбиру¬
ется.
(a) Вычислите среднее и среднеквадратичное время, нужное для захвата
частицы в х = 0, когда она стартовала с х = L. Подробно исследуйте три
случая: v > 0, v < 0 и и = 0.
(b) Вычислите Лаплас-образ распределения времен захвата для случаев
v > 0, v<0hv = 0h обсудите асимптотическое поведение этих распре¬
делений в пределах t —» 0 и t оо.
2.21 Броуновская частица стартует с центра трехмерного шара радиуса R.
(a) Покажите, что Лаплас-образ распределения времени выхода имеет вид
T=R2/D-
(b) Выведите общее выражение для целых моментов времени выхода
(Тп) = (22п_2)_^_|В2п,тп
выраженное через числа Бернулли Вт , которые определены через раз¬
ложение
2.22 Рассмотрим задачу о разорении игрока. Два игрока АиВ многократно разыг¬
рывают партии, в каждой из которых оба делают ставки по одному доллару.
Вероятность того, что игрок А выиграет одну партию равна р. Пусть игрок А
начинает с п долларами, а игрок В с N — п долларами, и игра заканчивается,
когда у одного из игроков не остается денег.
68
Диффузия
(a) Чему равна вероятность £п, что игрок А в конце концов победит?
(b) Как долго будет продолжаться игра?
(c) Как долго продолжается игра при условии, что игрок А победил? Эта
формулировка определяет условное время выхода.
2.23 Решите уравнение диффузии вне адсорбирующей сферы радиуса а в одно- и
двумерии и таким образом рассчитайте точный поток к этой сфере27. То есть
решите
дс
— = PV2c; c(r = a, t) = 0, с(г > а, t = 0) = 1
и после этого вычислите зависимый от времени поток к сфере
K(t) = D f Vc(r,t)-da.
2.24 Газ сферических невзаимодействующих частиц радиуса а находится в шаре
радиуса R с центром в начале координат. При каждом событии захвата объем
этого шара увеличивается на объем захваченной частицы 47га3/328. Вдали от
адсорбирующего шара концентрация равна Соо-
(a) Используя стационарную величину скорости реакции К = ^kDRcoq, по¬
кажите, что такой процесс захвата приводит к «диффузионному росту»
радиуса R(t) адсорбирующего шара:
R = у/ADt, А = Соо а3.
о
(b) Приведите аргументы, доказывающие, что использование стационарной
скорости реакции было бы правильным, если бы полученный рост был
медленнее диффузии. Обоснуйте справедливость скейлингового анзаца
c(r,t) = Соо/(7?), где и R = y/ADt
с неизвестной амплитудой А.
(c) Подставьте вышеупомянутый скейлинговый анзац в (2.83) и покажите,
что перемасштабированная концентрация имеет вид
^ = 1_f(l)’ ГДе д^ = / С2е~Ае/4<%.
273десь а должно быть больше нуля в d = 2, но может быть нулем в d = 1.
28Это упражнение — пример задачи Стефана, в которых граница движется, а ее поло¬
жение R = y/ADt определяется в процессе решения.
2.11 Задачи
69
(d) Используйте сохранение объема для проверки того, что амплитуда дает¬
ся неявным решением уравнения
У Сооа3 = А еА'* ^°° <
(е) В приложениях доля объема, занимаемого внешними частицами, обычно
очень мала: с^а3 <С 1, откуда следует Л < 1. Покажите, что в этой
ситуации соотношение для А приближенно записывается как,
где уе =f 0,577215 — константа Эйлера.
2.25 Найдите вероятность выживания частицы, диффундирующей внутри беско¬
нечного двумерного клина, образованного лучами 0=Оив=фс адсорби¬
рующими граничными условиями на обоих лучах. Вместо вычисления пол¬
ной функции Грина воспользуйтесь начальными условиями c(r,0,t = 0) =
%sin(7T0/ф)5(г — го)/(2</>), которые задают угловую зависимость на больших
временах. Для такой усеченной проблемы требуется найти только радиаль¬
ную часть решения.
2.26 Завершите вывод уравнений (2.99) и (2.102).
2.27 Гармонически связанная броуновская частица с ненулевой массой подчиняется
уравнению движения
x(t) + 4x(i) + UQx(t) = 77(f),
где 7](t) — белый шум с нулевым средним и с (т?(£)?7(£/)) = Г$(£ — tf). Для
произвольных начальных условий т(0) и ±(0) найдите (x(t)} и В пре¬
деле большого времени t 7-1 покажите, что при правильном выборе Г ваш
результат согласуется с равновесной статистической механикой.
2.28 Проверьте уравнение (2.113) для двухточечной корреляционной функции в
двух измерениях.
2.29 Заполните пробелы в выводе точной формулы для среднеквадратичной ши¬
рины w2, уравнение (2.108), для модели Эдвардса-Уилкинсона.
2.30 Проверьте результат (2.115) для двухточечной корреляционной функции
С(ж, t) в одномерии.
2.31
Проанализируйте уравнение Эдвардса-Уилкинсона в трех измерениях. Под¬
твердите предсказание (2.115) для двухточечной корреляционной функции.
Покажите, что когда х VDt, двухточечная корреляционная функция сво¬
дится к
ч Г 1
C(x,f) = -—— -.
v ’ 7 4тг£> х
70
Диффузия
2.32 Рассмотрите уравнение Маллинса (2.120).
(a) Используйте анализ размерностей и линейность, чтобы показать, что ши¬
рина ведет себя как w ~ г1/2^-^/8^4-^)/8. Поэтому шум увеличивает
шероховатость фронта в физически значимом случае d = 2 и даже в
d = 3.
(b) Вычислите ширину и двухточечную корреляционную функцию в раз¬
мерностях d = 1,2,3.
2.33 Покажите, что распределение вероятностей (2.126) есть решение уравнения
Фоккера-Планка (2.125) в одномерии.
2.34 Покажите, что при d > 1 распределение вероятностей (2.126) не дает реше¬
ния (2.125). (Выражение под интегралом в (2.126) должно содержать (Vft)2 в
высших измерениях.)
Глава 3
СТОЛКНОВЕНИЯ
Обычно курсы неравновесной статистической физики начинаются уравнени¬
ем Больцмана и некоторыми его наиболее известными следствиями, в частно¬
сти выводом гидродинамического уравнения Навье-Стокса и определением
коэффициентов переноса. Такие вычисления обычно пугающе сложны, часто
основаны на неконтролируемых приближениях и, кроме того, обсуждаются
во множестве стандартных учебных пособий. С другой стороны, базовое по¬
нимание можно получить, рассматривая идеализированные процессы столк¬
новений, для которых уравнение Больцмана имеет настолько простой вид,
что может быть решено явно. Примеры таких процессов: газ Лоренца, где
пробная частица взаимодействует с фиксированной рассеивающей средой,
молекулы Максвелла, интенсивность столкновений которых не зависит от
относительной скорости. Мы также применяем подход, основанный на урав¬
нении Больцмана, к гранулярным и транспортным потокам.
3.1 Кинетическая теория
Неравновесная статистическая физика уходит корнями в кинетическую тео¬
рию, которая объяснила динамику разреженных газов и стала начальной точ¬
кой для рассмотрения более сложных систем. Сама кинетическая теория на¬
чалась с распределения скоростей Максвелла-Больцмана, которое было по¬
лучено даже до того, как само уравнение Больцмана, равновесным решением
которого является распределение Максвелла-Больцмана, было сформулиро¬
вано1.
1 Джеймс Кларк Максвелл вывел это распределение в 1867 году, тогда как уравнение
Больцмана было впервые написано в 1872 году.
72
Столкновения
Распределение Максвелла—Больцмана
Начнем с вывода распределения скоростей Максвелла-Больцмана для клас¬
сического газа одинаковых молекул, который находится в термодинамиче¬
ском равновесии при температуре Т. Подходя на достаточно близкие рассто¬
яния, молекулы упруго рассеиваются благодаря короткодействующему от¬
талкивающему межмолекулярному потенциалу. Пусть P(v)dv — вероятность
найти молекулу в объеме dv в окрестности v. Распределение Максвелла -
Больцмана можно вывести, исходя из двух фундаментальных предположе¬
ний:
• Вращательная симметрия в пространстве скоростей. Это значит, что
распределение скоростей изотропно (т. е. зависит только от величины
скорости v = |v|, но не от направления v):
P(v) = P(v2). (3.1)
• Отсутствие корреляций между разными компонентами скоростей.
Вместе с симметрией это предположение приводит к факторизации рас¬
пределения скоростей
Р(и2) =p(v2)p(v2)p(v2), (3.2)
где p(v2) dvi — это вероятность того, что г-тая компонента скорости на¬
ходится в объеме dvi в окрестности Vi.
Использование этих предположений позволяет вывести распределение Макс¬
велла-Больцмана, взяв логарифм
lnP(v2) = lnp(w2) + lnp(v2) + lnp(u2)
и дифференцируя его по компонентам скоростей. Это дает
dlnP(v2) __ dlnPdv2 __ dinР _ dlnp(v2)
dv2 dv2 dv2 dv2 dv2
и, так как уравнение выполняется для любой компоненты, заключаем, что
правая часть должна быть константой. Поэтому dlnP/dv2 = —6, откуда
Р = Ае~Ьу2. Константы в этом распределении фиксируются нормировкой,
f P(v) dv = п, где n — это плотность частиц. Используя стандартное опре¬
деление температуры ^m(v2) = получим
pM = "Sfe””v2/2T
(3.3)
3.1 Кинетическая теория
73
Заметим, аргументы Максвелла никак на зависят от межчастичного потенци¬
ала! Нам нужен только механизм рассеяния, который в каждом столкновении
сохраняет массу, импульс и энергию, что гарантирует само наличие равновес¬
ного состояния. При выполнении этих скромных требований распределение
скоростей имеет вид распределения Максвелла-Больцмана независимо от
межмолекулярного потенциала и плотности частиц2.
Уравнение Больцмана
Фундаментальная величина классической кинетической теории — зависящее
от пространственных координат и скорости распределение P(r,v,t)drdv,
определяемое как число частиц в объеме drdv в окрестности r,v в момент
времени t. Это распределение изменяется во времени в соответствии с урав¬
нением
4+а
a [P2(r, v'; г, w') - P2(r, v; г, w)]
х 5(v+w-v'-w')5(v2+ w2-v,2-w12') dwdv1 dw'. (3.4)
Члены в левой части уравнения (3.4) описывают изменение Р(г, v; i) из-за
движения частиц в отсутствие столкновений; последний член возникает из-за
внешней силы, вызывающей ускорение а. Правая часть показывает измене¬
ние P(r,v;t) из-за столкновений (рис. 3.1). Член ухода учитывает частицы
сА
Рис. 3.1. Парное столкновение со скоростями до столкновения (v,w) и после
(<w')
с координатами (r,v), сталкивающиеся с частицами с координатами (r,w).
Общая интенсивность столкновений включает сечение рассеяния а, умно¬
женное на вероятность того, что две частицы находятся близко друг к другу,
2Можно задать вопрос: «Не проще ли „вывести" распределение Максвелла-Больцмана
из больцмановского веса е~Е^т, появляющегося в равновесной статистической механике?»
Хотя не составит труда записать больцмановский вес, значительные усилия требуются,
чтобы развить аппарат статистической механики, из которого этот вес следует. Аргументы
Максвелла вообще не требуют никакого аппарата!
74
Столкновения
которая представлена двухчастичной корреляционной функцией Рг3* Другой
член, член прихода, дает интенсивность, с которой частицы с координатами
(г, vz) и (г, wx) сталкиваются, и одна из выходящих частиц приобретает коор¬
динаты (г, v), а другая (г, w). Дельта-функция под интегралом в уравнении
(3.4) гарантирует сохранение энергии и импульса4.
Уравнение (3.4) незамкнуто, таккак одночастичноераспределениеР(г, v; t)
выражено через двухчастичное распределение P2(r,v;r,w). Поэтому нужно
написать уравнение для двухчастичного распределения, которое, в свою оче¬
редь, будет содержать трехчастичное распределение и т. д. Продолжение это¬
го построения дает бесконечную иерархию уравнений, известную как цепочка
ББГКИ (Боголюбова-Борна-Грина-Кирквуда-Ивона). Больцман предло¬
жил обрезать эту цепочку в самом начале, заменив двухчастичное распреде¬
ление произведением двух одиочастичиых:
P2(r,v;r,w) = P(r,v)P(r,w). (3.5)
Эта замена базируется на предположении, что скорости частиц до столк¬
новения нескоррелированы, — гипотеза молекулярного хаоса (в оригинале
названная Больцманом Stosszahlansatz). На такое отсутствие корреляций в
многочастичных системах часто ссылаются как на среднеполевое поведение.
Оно позволяет представить многочастичные функции распределения в ви¬
де произведения одночастичных. С помощью гипотезы молекулярного хаоса
можно написать замкнутое уравнение Больцмана (УБ) для эволюции функ¬
ции распределения частиц
д д д\ ч
8i + V'S + a'^)F(r'v)
= j” [^(г, v') Р(г, w') - P(r, v) Р(г, w)]
х 5(v+w—vx —wx) <$(г>2+ w2 —vt2—w/2) dwdv' dw'.
(3.6)
Хотя возникновение гипотезы молекулярного хаоса самоочевидно, она не так
проста как кажется и ее использование во многих случаях приводило к пута¬
нице и непониманию. Самая трудная загадка: «Как согласовать микроскопи¬
ческую обратимость молекулярного движения с макроскопической необрати¬
мостью?» В самом деле, микроскопическая ньютоновская динамика обрати¬
ма, т. е. при обращении времени t -+ —t уравнения движения не меняются.
С другой стороны, мир вокруг нас необратим на макроскопическом уровне.
3 Здесь под близостью мы подразумеваем совпадение пространственных координат.
4Мы предполагаем, что молекулы одинаковы. В частности у них одинаковые массы.
3.1 Кинетическая теория
75
Гипотеза молекулярного хаоса нарушает симметрию по отношению к обра¬
щению времени, и получившееся уравнение Больцмана (3.6) описывает на¬
блюдаемое необратимое поведение. Чтобы рассмотреть классический пример
этого очевидного парадокса, представим, что все молекулы в начальный мо¬
мент находятся в одной половине комнаты. Впоследствии они быстро распре¬
делятся по всей комнате, и плотность станет существенно однородной. Если,
однако, мы перевернем скорости всех молекул, они должны (в определен¬
ный момент) собраться в половине комнаты. Говорят, что на это возражение
Людвиг Больцман ответил: «Давайте, попробуйте их перевернуть!» Более
адекватное объяснение, также предложенное Больцманом, основывается на
вероятностной картине: говоря простым языком — необратимое поведение
более вероятно.
Кроме гипотезы молекулярного хаоса важно помнить о других предполо¬
жениях, лежащих в основании УБ и некоторых его приложений:
• Газ разрежен, так что одноточечное распределение P(r,v;t) коррект¬
но описывает состояние газа. Более того, газ разрежен настолько, что
важны только парные столкновения.
• Частицы движутся с постоянными скоростями между столкновениями,
и их траектории изгибаются только тогда, когда частицы сближаются.
Удобно представлять себе молекулы в виде твердых сфер.
Тогда как концептуальные проблемы, связанные с УБ, решены и необходи¬
мость использования статистического описания'уже не подвергается сомне¬
нию, понимание У Б сильно затруднено отсутствием аналитических решений.
Чтобы понять теорию, необходимо применять ее к конкретным задачам: на¬
хождение энергетических уровней гармонического осциллятора и атома во¬
дорода играет огромную роль в улучшении понимания квантовой механи¬
ки. Из-за математической сложности теории эта логика не работает в ки¬
нетике. Формально уравнение Больцмана (3.6) — это нелинейное интегро-
дифференциальное уравнение с несколькими переменными5. Более того, для
реалистичных систем, таких как воздух, который состоит в основном из двух¬
атомных молекул, учет вращательных и колебательных степеней свободы
приводит к множеству дополнительных усложнений.
Даже если мы попытаемся упростить УБ насколько это возможно, мы
столкнемся с неразрешимыми проблемами. Например, один из больших успе¬
хов подхода, основанного на УБ, — это то, что он привел к выводу урав¬
нений гидродинамики, в частности через разложение Чепмена-Эсконга —
5В d измерениях одночастичное распределение Р(г, v; t) зависит от d + d + 1 = 2d + 1
переменных.
76
Столкновения
уравнения Навье-Стокса. Эта процедура очень сложна и была полностью
осуществлена только для одноатомных газов. Более того, коэффициенты пе¬
реноса не были вычислены даже в простейшем случае газа твердых сфер.
Другой путь к упрощению — рассматривать системы, где изменение в про¬
странстве возникает вдоль одной координаты, как в случае ударных волн.
Однако микроскопические скорости частиц по-прежнему трехмерные, и при
решении такой задачи нужно учитывать все компоненты скорости — услож¬
нение, компенсирующее значительное упрощение, к которому приводит зави¬
симость гидродинамических переменных от одной координаты.
Еще более радикальный подход — рассмотреть истинно одномерную си¬
стему. Однако УБ в одномерии тривиально — при соударениях частицы оди¬
наковой массы просто обмениваются скоростями. Переобозначая частицы, мы
можем рассматривать этот обмен как прохождение частиц друг через друга
без взаимодействия. Следовательно, распределение скоростей не меняется,
и равновесного состояния нет. Чтобы исправит отсутствие взаимодействия,
можно рассмотреть газ с распределением масс частиц. Однако УБ для такой
смеси снова слишком сложно. Более того, применимость УБ под вопросом,
так как частицы могут непосредственно взаимодействовать только со своими
соседями слева и справа, так что справедливость гипотезы молекулярного
хаоса становится сомнительной.
В УБ есть еще масса дополнительных усложняющих моментов, которые
не до конца прояснены. Например, нужно снабдить У Б граничными услови¬
ям, и это не просто даже для такой простой ситуации, как газ в контейнере. Не
существует «канонических» граничных условий, и, чтобы задать граничные
условия из первых принципов, мы должны формально рассматривать также
молекулы стенок и их взаимодействия с ударяющими их молекулами газа.
Парадоксально, но не удивительно, что УБ не имеет точных решений. Из-за
множества усложнений мы прибегаем к помощи идеализированных описаний
кинетической теории, в которых удается избежать технических трудностей
при работе с УБ. Несмотря на то что такие идеализации включают чрезмер¬
ные упрощения, которые делают задачу решаемой, они основаны на соответ¬
ствующей феноменологии и ухватывают суть физической кинетики.
3.2 Газ Лоренца
На заре двадцатого века Пауль Друде развил качественную теорию элек¬
трической проводимости металлов. Чтобы дать более твердое основание для
теории Друде, Хендрик Лоренц предложил идеализированную модель для
электронного транспорта, в которой (i) взаимодействия между электронами
3.2 Газ Лоренца
77
игнорируются, (ii) атомы металла рассматриваются как неподвижные сфе¬
рические рассеиватели, и (iii) электронно-атомные взаимодействия описывав
ип'ся упругим рассеянием. Предположение (ii) принципиально, так как оно
превращает проблему многих частиц в эффективную одночастичную систе¬
му, которая состоит из «пробной» частицы и неподвижного фона. Сейчас
мы понимаем, что квантовые эффекты должны учитываться при описании
ыектрической проводимости. Однако во многих случаях, например в зада¬
чах переноса, включающих медленные нейтроны, или в газовых смесях, в
которых отношение масс велико, классическая модель Лоренца дает хоро¬
шее приближение. Модель Лоренца представляет редкий источник точных
результатов в кинетической теории. Она дает конкретный пример, в кото¬
ром микроскопическую обратимость можно согласовать с макроскопической
необратимостью, и обнаруживает множество неожиданных свойств.
Модель
Рассмотрим трехмерную модель Лоренца, в которой невзаимодействующие
классические частицы (электроны) движутся среди случайно распределен¬
ных неподвижных твердых сфер (атомов) радиуса а. Электроны не взаимо¬
действуют друг с другом и упруго рассеиваются твердыми сферами. Соот¬
ветственно, только направление скорости электрона v, но не ее величина, из¬
меняется при столкновении. Плотность вероятности /(г, v, £) найти электрон
н позиции г со скоростью v в момент времени t изменяется в соответствие с
уравнением Больцмана
(
д
dt+yf
(3.7)
Здесь 1/т = v/£ — частота столкновений, € = (rwra2)-1 — средняя длина сво-
бодного пробега, и v = v/v. Левая часть состоит из стандартных потоковых
членов уравнения Больцмана. В отсутствие столкновений решение уравнения
(3.7) /(r,v,t) = /(г — vt,v,0) описывает частицу, движущуюся с постоян¬
ной скоростью. Правая часть уравнения (3.7) производит учет столкновений.
Член ухода равен распределению, умноженному на частоту столкновений,
а член прихода отражает хорошо известное свойство: рассеяние на твердой
сфере в трех измерениях изотропно (задача 3.3). Для простоты обозначений
мы запишем член прихода как
[Р/] (г, V, t) = У /(г, V, f),
(3-8)
78
Столкновения
где Р — проекционный оператор усреднения по всем направлениям скорости.
Уравнение (3.7) имеет несколько важных свойств, заслуживающих упо¬
минания:
• Линейность. Это свойство представляет огромное упрощение по срав¬
нению с нелинейным уравнением Больцмана. Чтобы подчеркнуть раз¬
ницу, уравнение (3.7) часто называют уравнением Больцмана-Лоренца
(БЛ). Физически, линейность — это следствие того, что столкновения
не влияют на рассеиватели. Благодаря линейности уравнение (3.7) ре¬
шаемо, чего не скажешь об уравнении Больцмана.
• Изотропия столкновительного члена прихода. Это свойство возникает
только в трех измерениях. В двумерии упругое рассеяние на твердой
сфере анизотропно (см. задачу 3.3).
• Разреженный предел. Средняя длина свободного пробега i а или
эквивалентно доля объема, занимаемая рассеивателями мала па3 1.
• Случайно распределенные рассеиватели6. Это условие вместе с разре¬
женностью подразумевает, что не возникает скоррелированных траек¬
торий, которые содержат множественные столкновения с парами сосед¬
них рассеивателей.
Главный вывод из уравнения (3.7) — электроны диффундируют в пределе
большого времени. Как видно из анализа размерностей, результирующий ко¬
эффициент диффузии пропорционален v£. Решение уравнения (3.7), которое
мы приводим ниже, дает точный ответ
D = ^vt. (3.9)
<5
Коэффициент диффузии
Сначала найдем распределение скоростей
= У dr/(r,v,t). (3.10)
6В физических приложениях, таких как электроны, движущиеся в кристаллах, рассеи¬
ватели выстроены в периодическую решетку. У Б неприменимо для такой геометрии, пото¬
му что могут существовать неограниченные траектории свободных частиц — бесконечный
«горизонт». Эти траектории ведут к среднеквадратичному отклонению, растущему немно¬
го быстрее, чем линейно: (г2) ~ tint Этот результат был доказан в двух измерениях и
считается также верным в трехмерии.
3.2 Газ Лоренца
79
Интегрируя (3.7), получим, что F(v,t) удовлетворяет уравнению
^F(v,t) = i{[PF](V,t)-F(v,t)}. (3.11)
11рименим проекционный оператор Р к (3.11) и используем фундаментальное
свойство Р2 = Р (которое часто приводится как определение проекционного
оператора). Это дает
^[PF](V,t) = 0. (3.12)
Таким образом, изотропная часть распределения скоростей [PF](v, t), кото¬
рую мы обозначаем как Ф(у), не меняется. Поэтому решение уравнения (3.11)
имеет вид
F(v, t) = Ф(г>) + [F0(v) - Ф(и)]е-*/т, (3.13)
т. е. распределение скоростей становится изотропным экспоненциально быст¬
ро, через время релаксации т. Для начальных условий Fo(v) = <S(v — и) общее
решение (3.13) принимает вид
F(v,t|u, 0)
5(у — и)
47Г«2
<5(v — и) —
5{у — и)
47Ttt2
-t/т
(3-14)
+
Последние два аргумента в F относятся к начальным условиям. Используя
(3.14), можно вычислить коэффициент диффузии с помощью замечательной
формулы Грина-Кубо7, которая выражает коэффициент диффузии через ав¬
токорреляционную функцию скорости8:
1 Г°°
D = j dt (v(t) • v(0))equil,
где равновесная автокорреляционная функция скорости имеет вид
(v-u)equil = У dv У du (v • u) F(v, t |u, 0) Фечш1(«).
(3.15)
(3.16)
7B общем случае формула Грина-Кубо, выведенная в 1950-х, связывает коэффициенты
переноса, такие как тепловая и электрическая проводимости и сдвиговая и объемная вяз¬
кости, с соответствующими корреляционными функциями. «Формула Грина-Кубо» для
коэффициента диффузии появилась в одной из статей Энштейна, опубликованных в тече¬
ние его annus mirabilis — чудесного 1905-го года.
8Численный множитель перед интегралом в уравнении (3.15) специфичен для трех
измерений. В d измерениях этот коэффициент равен d-1. Вывод формулы Энштейна -
Грина-Кубо (3.15) составляет содержание задачи 3.4.
80
Столкновения
Автокорреляционная функция скорости включает среднее по изотропному
равновесному $equii(^) = S(u — vq)/(4ttvq). Так как скорость остается посто¬
янной, имеем |v| = |u| = vo, интегрирования в (3.16) — это проекционные
операторы. Изотропные члены в F(v,i|u, 0) в уравнении (3.14) пропорцио¬
нальны [Pv] • [Pu] и, поскольку Pv = 0, зануляются. Только анизотропный
член, который содержит член <S(v — и), вносит неисчезающий вклад. Удер¬
живая только этот член, получим
(v • u)equil = J = V2Q е~^. (3.17)
Подставив результат в (3.16) и вычислив интеграл, получим D = §VqT, что
эквивалентно (3.9).
Точная плотность вероятности
После того как мы нашли распределение скорости, попытаемся решить пол¬
ное уравнение Б Л (3.7) для плотности вероятности /(r,v, £). Линейность
уравнения БЛ предполагает использование преобразования Лапласа по вре¬
мени, так как нас интересует t > 0, и преобразования Фурье в пространстве,
так как мы рассматриваем полное трехмерное пространство R3. Вводя Фурье-
Лаплас-образ
/(k,v,s) = У dte st jdre гкг /(r,v,f), (3.18)
сведем уравнение (3.7) к
[s + гк • v] /(к, v, s) = ^(Р - 1)/(к, v, s) + /0 (к, v), (3.19)
где /о(к, v) = /(к, v, t = 0) — Фурье-образ начальной плотности вероятности.
Переписывая, получим
/(к, V, s) = + у [Р/](к, v, s) + </>0(к, v, s), (3.20)
где мы использовали сокращающее обозначение
<^o(k,v,s)
/о (К v)
т-1 + s + гк • v '
(3-21)
Для завершения решения нам нужно вычислить Р/. Для этого применим
проекционный оператор к уравнению (3.20). Так как Р/ уже изотропно, то
3.2 Газ Лоренца
81
чтобы подействовать оператором Р на первое слагаемое в правой части (3.20),
нужно вычислить
r-i
•1 л27Г /*1
г-1
т-1 + s + гк • v
+ s + ikv cos О
1 kvr
— arctg —.
kvr st +1
Действие P на уравнение (3.20) дает
Р/ =
kvr
sr +1
Р/ + Р</>о,
откуда мы можем найти Р/. Подставляя Р/ в уравнение (3.20), придем к
полному решению для Фурье-Лаплас-образа, которое справедливо для про¬
извольных начальных условий:
г-1
/(k, v, s) = —=
' ' т-1 + s + гк • v
1 kvr
-1
Р фо + Фо- (3.22)
Обратить это точное решение, чтобы найти /(r,v,t), нелегко даже для изо¬
тропных начальных условий, таких как
/(г, v,t = 0) = 5(г)
$(v- Vq)
4tTVq
Тем не менее, как мы сейчас покажем, Фурье-Лаплас-образ позволяет извлечь
коэффициент диффузии.
Альтернативный вывод коэффициента диффузии
Займемся получением коэффициента диффузии из точного решения (3.22).
В гидродинамическом режиме на большом временнбм и пространственном
масштабе, плотность
p(r,t) = У dv/(r,v,t)
Р/
(3.23)
должна эволюционировать в соответствии с уравнением диффузии
др(М)
dt
DV2p(r,t).
(3.24)
82
Столкновения
Поэтому Фурье-образ плотности удовлетворяет соотношению
^^- = -Dk2p(k,t), (3.25)
откуда p(k,t) = e-Dfc2t, так как р(к = 0, i) = / drp(r,t) = 1. Перейдя к
Лаплас-образу p(k,i), получим
p(k, s) = (Dk2 + s)_1. (3.26)
Чтобы получить (3.26) из (3.22), заметим, что в гидродинамическом режиме
t т. Так как S t -Чк ~ t х/2, имеем т 1 » s, kv. Следовательно, (3.22)
принимает вид
/ =
1-
kvr
arctg
kvr
sr + 1
-l
P</>o + </>o-
Пользуясь формулой arctg x = x — ж3/3 + ..., разложим выражение в квад¬
ратных скобках
1-
-— arctg
kvr
kvr
st + 1
1 1 (кут)2
1 + st + 3 (1 + sr)3 + ’
= ts + -k2v2T2 +
о
откуда заключаем что D = v2t/3. Более того, в гидродинамическом режиме
уравнение (3.21) сводится к фо = т/о. С таким упрощением уравнение (3.22)
асимптотически стремится к
f =
1
Dk2 + s
P/о,
откуда действительно получим (3.26). Это вычисление также дает коэффи¬
циент диффузии D = v2t/%, который уже получен с помощью формулы Эн¬
штейна - Грина - Кубо.
Газ Лоренца в одном измерении
Уравнение БЛ решаемо в трех измерениях отчасти из-за того, что изотропия
упругого рассеяния на сфере приводит к простому виду приходного столк-
новительного члена в уравнении БЛ (3.7). Напротив, рассеяние на твердой
сфере анизотропно, когда d /= 3: обратное рассеяние усилено в двух измере¬
ниях, а в одном измерении есть только обратное рассеяние. Таким образом,
нельзя просто перенести определение газа Лоренца в одно измерение, так как
3.2 Газ Лоренца
83
частица будет заперта между двумя соседними рассеивателями. Однако мож¬
но определить газ Лоренца в одномерии, постулировав, что частица проходит
через рассеиватель с вероятностью 1 — р та. упруго рассеивается назад с ве¬
роятностью р. Упрощенно этот процесс выглядит как одномерное случайное
блуждание, и мы увидим до какой степени такое сравнение корректно.
Уравнение Б Л для такого одномерного газа Лоренца имеет вид
/(a?,-v,t)-/(a;,v,t)
т
(3.27)
где pvII = 1/т. Так как во время столкновения скорость может только поме¬
нять знак, распределение вероятности — это комбинация двух распределений:
/(ж, v, t) = р+(я, t) - vq) + р-(х, t)S(y + v0).
Тогда уравнение БЛ (3.27) распадается на два уравнения, описывающие эво¬
люцию частиц, движущихся вправо и влево:
д д\ р- - р+
Р+-Р-
(3.28а)
(3.28b)
11ерепишем эти уравнения в гидродинамической форме, заменяя плотности
/>-ь(а:, i) общей плотностью и током соответственно
р(ж, f) = р+(ж, i) + р_(ж, t)
= v0 [p+(x,t) - p-(x,t)}.
Складывая и вычитая уравнения (3.28a)-(3.28b), получим
^ + ^ = 0
dt + дх ’
dJ 2 dp 2J
~dt+V° дх ~ ~—
(3.29а)
(3.29Ь)
Первое уравнение выражает сохранение массы и могло быть написано и без
и ы вода. Отсутствие интегрального оператора во втором уравнении — след¬
ствие простоты газа Лоренца в одном измерении.
Чтобы исключить J, продифференцируем уравнение (3.29а) по t и урав¬
нение (3.29Ь) по х и, вычитая, получим уравнение
т д2р др _ VqT д2р
2^ + ~dt=~2d^'
(3.30)
84
Столкновения
известное как телеграфное уравнение. Из уравнения (3.30) могут быть извле¬
чены несколько важных уроков.
1. Значение коэффициента диффузии
£> = jv02T. (3.31)
2. Телеграфное уравнение — гиперболическое, так что возмущения рас¬
пространяются с конечной скоростью. Напротив, все стандартные гид¬
родинамические уравнения (диффузии, Навье-Стокса и т. д.) — пара¬
болические. Нежелательное последствие параболической природы гид¬
родинамических уравнений — то, что возмущения распространяются
мгновенно9.
3. Присутствие второй производной по времени подразумевает, что к стан¬
дартным начальным условиям р(ж,4 = 0) = ро(х) нужно добавить на¬
чальные условия для производной ^|t=0.
Решим телеграфное уравнение (3.30). Пусть p(fc,s) будет комбинирован¬
ный Лаплас-Фурье-образ плотности р(#,£), и рассмотрим симметричные на¬
чальные условия
№,*,< = 0) = ^) + (3.32)
Таким образом, p+(x,t = 0) = ^p-(x,t = 0) = 5(х) и J(x,t = 0) = 0, так
что начальное условие для полной плотности имеют вид р(х, t = 0) = S(x),
тогда как уравнение (3.29Ь) дает pt(x,t = 0) = 0, где нижний индекс обозна¬
чает частную производную. Для Фурье-образа эти начальные условия дают
p(k,t = 0) = 1, pt(k,t = 0) = 0. С учетом этих результатов Лаплас-Фурье-
образ полной плотности запишется как
p(fc, s)
1 + js
Dk2 + 5 + 5 52
(3.33)
9Эта нефизическая черта уравнений гидродинамики обычно игнорируется. Это малая
цена, которая платится за успех уравнения Навье-Стокса. Уравнения гидродинамики бо¬
лее высокого порядка (как например уравнение Бурнетта), которые должны быть более
точными, приводят к неустойчивостям, появляющимся из-за асимметрии временных и про¬
странственных координат: первая производная по времени против более высоких производ¬
ных по пространственным координатам.
3.3 Газ Лоренца во внешнем поле
85
Обращая это преобразование, получим (задача 3.6)
t) = - |аг|) + е-Ч-
0(yQt - И),(3.34)
где £ = r^y/t2 — (ж/^о)2 и 1п — модифицированная функция Бесселя по¬
рядка п. Первое слагаемое в правой части уравнения (3.34) учитывает части¬
цы, которые еще не принимали участия в столкновениях, а второй описыва-
<гг все остальные частицы. Последний должен оставаться внутри интервала
[-vo£,vot], что обеспечивается ступенчатой функцией Хевисайда в. В пре¬
деле большого времени асимптотическое разложение функции Бесселя дает
(задача 3.6)
р(х, () = -^== -1*1), (3.35)
где D = Vqt/2. Таким образом, мы воспроизвели классическую диффузию в
одномерии.
3.3 Газ Лоренца во внешнем поле
Хотя модели Лоренца были введены для описания электрической проводимо¬
сти в металлах, по иронии судьбы их применение к движению электронов в
однородном магнитном поле не приводит к закону Ома J = сгЕ, связывающе¬
му плотность тока J с электрическим полем Е. Причина этого несоответствия
проста: модели Лоренца не содержат диссипации, так что заряженные части¬
цы в основном движутся вдоль поля, и их энергия неограниченно возрастает.
Влияние магнитного поля может быть даже более значительным из-за суще¬
ствования циклотронных орбит.
Газ Лоренца в электричеком поле
11опробуем понять необычное поведение газа Лоренца под действием поля.
11тобы вычислить электрическую проводимость, Лоренц использовал линей¬
ное уравнение Больцмана
(3.36)
и предложил приближенное стационарное решение уравнения (3.36) в ви¬
де пертурбативного разложения относительно распределения Максвелла-
Вольцмана, которое работает, когда электрическое поле достаточно мало.
86
Столкновения
Однако отправная точка анализа Лоренца содержит ошибку10. Если рассея¬
ние упругое (без диссипации, как предполагал Лоренц), то электроны будут
неизбежно накапливать энергию и стационарное состояние будет невозмож¬
но. Однако рассеяние все еще играет значительную роль: мы увидим, что
типичная скорость растет со временем как f1/3, а не линейно, как было бы в
случае свободно ускоряемого электрона.
Перед тем как исследовать уравнение БЛ (3.36) в трех измерениях, рас¬
смотрим его одномерную версию11
й+’ +£ й]ж 4)= ? г ,х'f)' (3'37)
Здесь £ = —еЕ/т — ускорение электрона с зарядом —ей массой т в элек¬
трическом поле Е, и
Г(ж, V, t) =h/(x, V, t) + /(ж, -v, t)],
J (3.38)
fa(x,v,t) =-[f(x,v,t) - f(x, -v,t)] —
соответственно, симметричная и антисимметричная компоненты плотности
вероятности.
Хотя скорость больше не сохраняется, сохраняется энергия. Для электро¬
на, стартовавшего в точке х = со скоростью v = vo, закон сохранения
энергии дает
ж - ж0 = 2gV°. (3.39)
Следовательно, плотность вероятности сводится к распределению скоростей:
f(x,v,t\x0,v0)
F(y, 11v0) 5 (x - x0 - V 2g—) •
С учетом такой факторизации для распределения скоростей выполняется со¬
отношение
р _i_ М ра = о,
(3.40)
10 Статья Лоренца привела к созданию моделей Лоренца, которые сыграли существен¬
ную роль в развитии кинетической теории, а также инициировала математические иссле¬
дования по развитию эргодической теории. Это пример того, как новаторская статья с
ошибочным результатом может быть ценнее, чем сотни правильных статей.
11 Мы записываем частоту столкновений как |v|/€, а не 1/т, так как скорость больше не
является константой.
3.3 Газ Лоренца во внешнем поле
87
или, если разделить это уравнение на симметричную и антисимметричную
части, получим
F“ + £^-Fs = 0,
dv
(3.41)
Для канонических начальных условий, где частица покоится в начальный
момент, т. е. F(y, 0) = fi(y) (или эквивалентно Fs(y,0) = 5(у) и Fa(y, 0) = 0),
точное решение уравнения (3.41) можно записать через функцию Эйри. Од¬
нако это решение не дает интуитивно ясного объяснения двух ключевых ха¬
рактеристик газа Лоренца, находящегося под действием поля: роста скорости
но закону t1/3 и асимптотического распределения скоростей. Вместо точного
решения мы приводим качественное объяснение этих характеристик.
Аргумент для скорости роста, основанный на случайных блужда¬
ниях
Для удобства предположим, что рассеиватели расположены на расстоянии
постоянной решетки € и что электрон проходит через рассеиватель с вероят¬
ностью 1/2 или отражается назад с вероятностью 1/2. Пусть хп и vn — это
положение и скорость электрона после n-ого события рассеяния. Используя
(3.40), получим
vn+i ~vn = 2£(хп+1 - хп) = ±2£Л (3.42)
Поэтому величина v2 совершает случайное блуждание, так что среднее ее
квадрата растет линейно с числом шагов: ~ (£€)2п. Таким образом,
средняя скорость растет как v ~ (£^)х/2 п1/4. Чтобы найти рост v со временем,
выразим приращение времени между соседними столкновениями как
Vn
1
П1/4’
11оэтому время до n-ого столкновения равно
п— 1
tn = ^[fyc+1
fe=0
tk\
S>-1/4
к<п
что дает п ~ (£i2/€)2/3. Исключая п и выражая все через f, получим
(£2£f)1/3.
(3.43)
^n+l tn
88
Столкновения
Отметим, что средняя скорость (3.43) отличается от скорости сноса. Чтобы
оценить последнюю, можно представить газ Лоренца под действием поля как
несмещенное случайное блуждание (так как рассеяние изотропно) на полуоси
х > 0 с отражающей границей в х = 0. Типичное положение электрона,
деленное на время, дает скорость сноса. Для электорна, который стартует
с начала координат, находясь в покое, положение и скорость связаны как
х = v2/2£. Так как v ~ (£2^£)х/3, положение электрона равно х ~ (££2t2)1/3,
откуда получаем скорость сноса Adrift ~ (fi-^/t)1/3.
Таким образом скорость сноса убывает со временем, даже несмотря на
то, что средняя скорость неограниченно растет. Так как ток пропорционален
скорости сноса, имеем J ~ 7?1/3 f”1/3. Этот результат противоречит закону
Ома, в соответствии с которым ток должен быть стационарным и пропорци¬
ональным Е.
Асимптотическое распределение скорости
Скейлинг вместе с аргументами, основанными на симметрии, дает привлека¬
тельный способ вывода асимптотического распределения скорости. В пределе
большого времени мы ожидаем, что симметричная часть распределения ско¬
рости стремится к скейлинговой форме
Fs(v, t) = t_1/3$(u), и = vt~1/3. (3.44)
Эта форма согласуется с законом роста v ~ i1/3 из уравнения (3.43), а ко¬
эффициент обеспечивает нормировку f dv Fs(y,t) = 1. (В терминах перемас¬
штабированного распределения нормировка принимает вид f du$(u) = 1.)
Изотропия симметричной части распределения скоростей возникает из-за то¬
го, что средняя скорость сноса убывает, тогда как средняя скорость растет.
Из второго уравнения (3.41) видно, что асимметричная часть распреде¬
ления Fa ведет себя как vFsft. Поскольку v ~ t1/3, скейлинговая форма для
Fa имеет вид
Fa(v,t) = t-1u^(u), (3.45)
где Ф(и) — четная функция, так что скейлинговая форма явно антисиммет¬
рична. Подставив (3.44)-(3.45) в уравнение (3.41), получим
ф + £ф' = о,
- | [Ф + иФ'] + £ [Ф + иФ'] = 0,
О
(3.46а)
(3.46Ь)
3.3 Газ Лоренца во внешнем поле
89
где штрихи обозначают дифференцирование по и. Интегрированиё (3.46Ь) да¬
ет ф = ф/(3£). Поэтому (3.46а) превращается в Ф'/Ф = —u|u|/(3^£2), откуда
можно найти Ф(«). Собирая все вместе, получим
f‘(’’‘’ = 2t(T73) (3'47а)
= (3.47b)
/’’(v,0) = $(v). Эти результаты находятся в согласии с предельным асимпто¬
тическим распределением скорости, возникшем из полного решения уравне¬
ний (3.41) с начальными условиями F(v,0) = 6(у).
Газ Лоренца в магнитном поле
Известно, что в постоянном однородном магнитном поле В на электрон дей¬
ствует сила Лоренца, так что его ускорение равно F/m = шВ х v, где В —
единичный вектор, направленный вдоль магнитного поля. В результате полу¬
чаем движение по спирали, проекция которой на плоскость, перпендикуляр¬
ную магнитному полю, имеет форму окружности. Компонента уц скорости
электрона, параллельная полю, остается постоянной, тогда как компонента
v.l вращается с циклотронной частотой ш = где с — скорость света. Плот¬
ность вероятности /(г, v,t) удовлетворяет уравнению БЛ
+ v' £ + “ (® х v)' /(г’¥’() = 7IW,r’v7ii -№,v,()]-
(3.48)
Скорость электрона не меняется во время циклотронного движения, и она
также остается неизменной после упругого столкновения с рассеивателем
(рис. 3.2). Поэтому частота столкновений 1/т = v/X постоянна. В этом отно¬
шении уравнение Б Л в магнитном поле сходно с уравнение Б Л без внешних
сил. Из этого факта можно предположить, что при анализе уравнения (3.48)
можно применить подход, использованный для исследования уравнения (3.7).
Интегрируя (3.48) по пространственным координатам, мы получим, что
распределение скорости F(v,t), определенное в (3.10), удовлетворяет уравне¬
нию
i'| - JB х vj A j F(v,t) = i ([№](», t) - F(v, t)). (3.49)
Применяя проекционный оператор IP к (3.49), мы придем к (3.12), тому же
самому уравнению, что и в случае без сил. Таким образом, сферическая часть
90
Столкновения
Рис. 3.2. Газ Лоренца с круглыми рассеивателями. На рисунке показаны замкну¬
тая циклотронная орбита без рассеяния и часть траектории с множественным
рассеянием
распределения скоростей не меняется. Для анизотропной части F°(v,t) =
F(y,t) — [PF](v, t) имеем
(J-t + u> (В х v) ~) F°(v,t) = -r-^Cv,t), (3.50)
и она стремится к нулю экспоненциально быстро (с временем релаксации
порядка т). К этому утверждению можно прийти без вычислений. Достаточно
переписать (3.50) как
(2 + и, (в х v) • A) $(v, *) = 0, $(v, t) = (3.51)
чтобы увидеть появление экспоненциального убывания со временем релакса¬
ции т = X/v.
Анализ влияния магнитного поля на релаксацию начальной неоднород¬
ности плотности — более сложная задача, чем в ситуации без поля. Дей¬
ствительно, в последнем случае имеется естественная изотропия: даже если
начальные условия анизотропны, состояние при большом времени изотроп¬
но. Одно из следствий этой изотропии — это то, что диффузионное движе¬
ние характеризуется скалярным коэффициентом диффузии. В то же время,
в присутствии магнитного поля результирующее анизотропное движение на
больших временах характеризуется тензором диффузии. Если магнитное по¬
ле направлено вдоль оси z, симметрия между х и у и отсутствие взаимо¬
действия между движением в плоскости х-у и движением в направлении z
3.4 Волна столкновений
91
приводят к тому, что диффузионный тензор имеет вид
Dxx
DXy
DXZ\
(DL
DXy
0 \
Dyx
Dyy
Dyz
— I Dyx
Dr
° Г
(3.52)
Dzx
Dzy
Dzz)
V 0
0
D\\)
Физически очевидное, хотя и удивительное свойство модели Лоренца в од¬
нородном магнитном поле — это то, что уравнение БЛ иногда неприменимо.
В трех измерениях у электрона с вероятностью единица есть ненулевая ком¬
понента скорости, параллельная магнитному полю. Следовательно электрон,
движущийся по спирали, наверняка столкнется с одним из рассеивателей, ес¬
ли они распределены случайно. Поэтому уравнение БЛ дает верное описание
в трех измерениях12. Для электронов, находящихся на плоскости с магнит¬
ным полем, перпендикулярным этой плоскости, ситуация отличается в корне.
Теперь могут существовать замкнутые циклотронные орбиты, не проходящие
ни через один рассеиватель (рис. 3.2)13. Существование свободно вращаю¬
щихся электронов означает, что стандартная больцмановская картина, где
с толкновения происходят с постоянной скоростью, неверна.
Двумерный газ Лоренца в однородном поперечном магнитном поле может
показаться экзотикой. Однако двумерные электронные пленки повседневно
производятся с большой точностью в галлиево-арсениевых гетероструктурах.
Исследования таких систем в сильных полях — активно развивающееся на¬
правление исследований. Кроме того что они есть почти в каждом полупро¬
водниковом приборе, двумерные электронные системы породили новую ин¬
тересную физику, такую как квантовый эффект Холла. Квантовая природа
электронов имеет решающее значение в большинстве таких систем. Тем не
менее, даже на классическом уровне двумерный газ Лоренца в поперечном
магнитном поле — это источник сложных задач и интересных результатов.
3.4 Волна столкновений
Желание понять поведение газа твердых сфер послужило мотивом для иссле¬
дования гораздо более простых моделей Лоренца, описанных в двух предыду¬
щих разделах. В том же духе рассмотрим отклик неподвижного газа твердых
сфер на одну движущуюся частицу. После первого столкновения движутся
две частицы, и они, в свою очередь, сталкиваются с другими частицами, что в
12Мы предполагаем, что стандартные требования: разреженный предел, случайно рас¬
положенные рассеиватели и т. д. — выполнены.
13Более точно, свободная циклотронная орбита возникает с вероятностью е-27гД/А =
f -2тг/(ц>т), где _ радИуС ЭТОЙ орбиты.
92
Столкновения
конце концов приводит к замечательно симметричному каскаду движущихся
частиц (рис. 3.3). Хотелось бы понять основные свойства этого каскада.
Рис. 3.3. (а) Каскад столкновений размерности два, когда одна частица вдруг
начинает двигаться внутри газа, находящегося при нулевой температуре. Движу¬
щиеся сферы нарисованы с двойным радиусом, а покоящиеся с половинным. (Ь)
То же самое для ситуации, когда газ занимает полуплоскость х > 0, а движуща¬
яся частица приходит слева. (Перепечатано с любезного разрешения Т. Антала)
Мгновенный впрыск энергии в газ, находящийся при нулевой темпера¬
туре, может рассматриваться как взрыв, а каскад столкновений аналогичен
ударной волне, которая распространяется вовне от точки начальной детона¬
ции. Основные свойства ударной волны, такие как скорость распростране¬
ния, зависимость плотности от радиуса и распределение температуры поза¬
ди волны, хорошо описываются гидродинамической теорией. Как мы сейчас
увидим, каскад столкновений твердых сфер повторяет многие качественные
свойства такой ударной волны.
Две естественных характеристики каскада — это число N(t) движущихся
частиц в момент времени t и общее число столкновений C(t) до момента t. Как
и во взрывной волне, используем анализ размерностей, чтобы определить эти
характеристики, затратив минимум усилий. Число движущихся частиц мо¬
жет зависеть от времени 4, плотности п, размерности пространства d, началь¬
ной скорости vq входящей частицы и радиуса частиц a: N(t) = N[t, vo, a, n, d].
Из анализа размерностей следует, что N(t) может зависеть от безразмерно¬
го времени Т = п1^ vot и двух других безразмерных параметров, например
3.4 Волна столкновений
93
доли объема занятой частицами14 р = nVdad и d. Таким образом, имеем
N = N{T,p,d). (3.53)
Самоподобная природа каскадов столкновений предполагает, что временная
зависимость N(t) должна быть степеннбй:
N~T* (3.54)
е показателем £, который потенциально может зависеть от р и d.
Что говорит элементарная кинетическая теория о росте числа столкно¬
вений со временем? Из рис. 3.3 видно, что только частицы в оболочке тол¬
щиной порядка одной длины свободного пробега (. ~ vt ~ l/(nad_1) от края
каскада могут создать новые движущиеся частицы за время столкновения т.
Если энергия каскада распределяется приблизительно одинаково среди дви¬
жущихся частиц, каждая частица в каскаде имеет энергию порядка JV-1 от
начальной энергии, и, следовательно, v ~ /V-1/2. Так как каскад столкнове¬
ний (рис. 3.3) приближенно имеет форму шара (растущего) радиуса R, число
движущихся частиц растет со временем как
dN rxl-i f N\{d~1)/d ,occ.
~ nvRd 1 ~ nv [ — ) . (3.55)
dt ть J
Учитывая, что v ~ 7V-1/2 и решая полученное дифференциальное уравнение,
подтверждаем степенной закон роста (3.54), где £ = 2d/(d + 2). Интересно,
что показатель £ не зависит от доли объема р. Похожие аргументы можно
применить, чтобы найти число столкновений, произошедших до момента t
(задача 3.9).
Свойства каскада столкновений можно описать и с помощью анализа раз¬
мерностей, основанного на гидродинамике15. Возмущение, вызванное одной
движущейся частицей, может рассматриваться как мгновенное высвобожде¬
ние энергии Е = %mvQ. Этот точечный источник энергии напоминает детона¬
цию взрыва, задача о котором имеет элегантное скейлинговое решение, когда
давление позади ударной волны во много раз превосходит давление перед ней.
Это условие всегда выполняется в нашем случае, так как у внешнего газа ну¬
левое давление. В таком пределе бесконечного числа Маха радиус ударной
14yd = тга/2/Г(1 + d/2) — это объем единичного шара в d измерениях.
15 Это был легендарный аргумент Г. И. Тейлора, который оценил мощность первого ядер-
ного взрыва по зависимости радиуса взрывной волны от времени, найденной из фотогра¬
фий.
94
Столкновения
волны R(t) может зависеть только от высвобождающейся энергии, массовой
плотности пт, где т — масса частицы и времени t. Поэтому радиус должен
вести себя как
R(t)^(Et2/nm^d+2\ (3.56)
так как это единственная переменная размерности длины16. Этот результат
для R(t) вместе с Е = и N = nVdRd воспроизводит закон (3.54), кото-
рый был получен из кинетической теории.
Ситуация, в которой частица падает на газ, находящийся в полуплоскости
х > 0 при нулевой температуре, нормально, — особенно загадочна (рис. 3.3).
Каскад столкновений опять распространяется в газе подобно тому, как это
происходит в однородном случае, но некоторые частицы отлетают назад. Хо¬
тя визуально получившийся всплеск состоит из малого количества частиц,
в конце концов вся энергия передастся этому всплеску. Парадоксально, что
энергия переходит во всплеск очень медленно. Эвристические аргументы по¬
казывают, что энергия в первоначально занятой части пространства убывает
со временем по степенному закону с показателем, который пока неизвестен
(задача 3.10).
3.5 Молекулы Максвелла и очень твердые частицы
Уравнение Б Л правильно воспроизводит многие свойства УБ, но есть одна
существенная разница: УБ нелинейно, тогда как уравнение БЛ линейно. Как
уже упоминалось ранее в этой главе, попытки модифицировать УБ, чтобы
упростить его и построить теорию, поддающуюся анализу, имеют долгую
историю. Здесь мы обсуждаем два широко используемых примера таких по¬
пыток.
• Молекулы Максвелла взаимодействуют через потенциал U (г) = Ajr^.
УБ для этой модели сильно упрощается, так как относительная ско¬
рость в интеграле столкновений в уравнении (3.6) заменяется на кон¬
станту. Чтобы понять, почему интенсивность столкновений становится
независимой от относительной скорости гг, предположим, что межмо¬
лекулярный потенциал имеет вид U(г) = А/гу. Можно оценить наи¬
меньшее расстояние между молекулами, приравнивая кинетическую
и потенциальную энергии Ar~~y ~ mu2, что дает г ~ и~21у. Тогда
16Коэффициент в уравнении (3.56) нельзя определить с помощью анализа размерностей.
Для этого требуется решать полные гидродинамические уравнения движения.
3.5 Молекулы Максвелла и очень твердые частицы
95
сечение рассеяния а ~ rd 1 зависит от скорости как и 2(d а общая
интенсивность столкновений ведет себя как
и а urd~^ ~ и^~i)/p_
Эта интенсивность независима от относительной скорости, когда и =
2(d — 1). В трех измерениях возникает межмолекулярный потенциал
Максвелла г-4. Хотя такой потенциал не был обнаружен в природе (наг
пример потенциал Ван-дер-Ваальса между нейтральными молекулами
г-6), достоинство его в том, что он допускает аналитическое решение.
• Очень твердые частицы имеют общую интенсивность столкновений,
пропорциональную квадрату относительной скорости двух молекул. Из-
за этой квадратичной зависимости взаимодействие более «твердое», чем
взаимодействие твердых сфер в классической кинетической теории, то¬
гда как модели Максвелла «мягче» благодаря независимому от скоро¬
сти взаимодействию. Поэтому модели Максвелла и очень твердые ча¬
стицы могут рассматриваться как верхняя и нижняя границы класси¬
ческой кинетической теории.
Уравнения Больцмана для молекул Максвелла и для очень твердых ча¬
стиц все еще слишком сложны, и априори не очевидно, почему они проще, чем
УБ для твердых сфер. Можно привести некоторые подсказки, проясняющие
почему в этих моделях проще оценить температурную зависимость коэффи¬
циентов переноса. Для коэффициента диффузии мы начнем с соотношения
из кинетической теории D ~ v£ ~ и/(па), куда входит тепловая скорость
V ~ у/Т. Для молекул Максвелла интенсивность столкновений nva постули¬
руется независимой от относительной скорости, и следовательно должна быть
пропорциональна и-1. Для очень твердых частиц интенсивность столкнове¬
ний постулируется квадратичной по скорости, так что а ~ v. Таким образом
получим температурную зависимость
' v2 ~ Т,
< v ~ у/Т,
л
v
а
D
молекулы Максвелла,
твердые сферы,
очень твердые частицы.
(3.57)
Другие коэффициенты переноса (такие как кинетическая вязкость) демон¬
стрируют такую же температурную зависимость. Неаналитическая зависи¬
мость D от температуры для твердых сфер наводит на мысль о том, что
расчет коэффициентов переноса для этой базовой модели может оказаться
9G
Столкновения
трудной задачей. Действительно, точные коэффициенты переноса для газа
твердых сфер неизвестны несмотря на усилия Больцмана, Гильберта, Чеп¬
мена, Эсконга и других. Напротив, сам Максвелл посчитал коэффициенты
переноса для молекул Максвелла17.
Применение к баллистической аннигиляции
Полезность молекул Максвелла и очень твердых частиц особенно ярко про¬
является на примере необратимой баллистической аннигиляции, где части¬
цы движутся с постоянной скоростью и аннигилируют при столкновениях.
Несмотря на простоту процесса, он не решаем для газа твердых сфер, но ре¬
шаем для молекул Максвелла и очень твердых частиц. В формализме Больц¬
мана распределение скоростей P(v, t) в пространственно однородном газе из¬
меняется в соответствии с уравнением
=-P(v,t) J gaP(yv,t)dw. (3.58)
В духе больцмановского подхода вероятность того, что две частицы со ско¬
ростями v и w столкнутся, факторизуются на произведение одночастичных
плотностей. Оставшийся кинематический коэффициент состоит из относи¬
тельной скорости д = |v — w|, умноженной на сечение а, которое мы можем
включить в перемасштабированное время. Так как присутствует только ан¬
нигиляция, правая часть состоит из одного члена, соответствующего уходу.
В одномерии уравнение (3.58) принимает вид
*) [ dw\v — w\P(w,t). (3.59)
J—oo
Это невинно выглядящее уравнение не было решено, и единственные резуль¬
таты, полученные из численного анализа, свидетельствуют о том, что средняя
скорость убывает со временем алгебраически
/•оо г г°° 1 V2
n(t) = / dwP(w,t) ~ t~a, Vrms/f) = -т-r / dww2P(w,t)
J-00 Lnw J-00
t-p
(3.60)
Показатели а и /3 зависят от поведения начального распределения скоростей
Ро(у) при малых v. (Только один из двух показателей независим, так как
а + /3 = 1, см. задачу 3.15.) Например, для изотропных распределений, плос¬
ких в окрестности начала координат, показатель, характеризующий убывание
17ОтМетим еще раз: Максвелл предложил свою модель в 1867 г. — до того как было
написано уравнение Больцмана и задолго до появления метода Чепмена-Эсконга.
3.5 Молекулы Максвелла и очень твердые частицы
97
равен /3flat = 0,230472, а для начального распределения, линейно убываю¬
щего в начале координат, Po(v) ~ |v|, показатель равен Ainear Ф 0,16664918.
С другой стороны, для молекул Максвелла и очень твердых частиц уравнение
(3.58) может быть полностью решено.
Пример 3.1. Молекулы Максвелла. Так как молекулы взаимодействуют с интен¬
сивностью, не зависящей от скорости, средняя молекулярная скорость не меня¬
ется. Поэтому мы заменяем множитель д = |v—w| в уравнении (3.58) константой
и, которая, чтобы обеспечить правильную размерность, измеряется в единицах
скорости, и переписываем уравнение (3.58) в виде
= -Р(у, t) n(t) иа. (3.61)
Интегрирование по скоростям приводит к уравнению п = —п2исг, решение кото¬
рого тривиально. Используя это решение в (3.61), получим
n(t) =
п(0)
1 + n(0) иа t 9
P(v,t)
-Po(v)
1 + n(0) иа t ’
(3.62)
Получившиеся показатели убывания а = 1 и /3 = 0 универсальны и тривиальны
в модели Максвелла.
Пример 3.2. Очень твердые частицы. В этом случае, чтобы сохранить пра¬
вильную размерность, заменим д в уравнении (3.58) на #2/vrms(£). Включая мно¬
житель l/vrms(£) во временную переменную
г
=/'
Jo
^rms(^/)
(3.63)
■Z\ ’
перепишем УБ как
=-Р(у,т) УI(v -w)2|P(w, т) dw=-Р(у,т)п(т) [и2 + vr2ms(т)], (3.64)
где мы использовали |(v — w)2| = v2 + w2 — 2v • w и f dwwP^wj) = 0 (си¬
стема отсчета, в которой общий импульс равен нулю) при написании второго
равенства. Решение уравнения (3.64) имеет вид
P(v,r) = P0(v)e”v2A(T)-B(r), (3.65)
ГДе
А(т)= Лт'п(т'), В(т) = dr'п(т')и^т'). (3.66)
Jo Jo
18 Прямое моделирование баллистической аннигиляции дает показатели с точностью ме¬
нее двух знаков. Более точные значения, приведенные выше, получены с использованием
скейлинговой гипотезы P(v,t) ~ t^_O£/(vt^), подставляемой в уравнение (3.59), и последу¬
ющим численным решением полученного нелинейного уравнения на собственные значения.
98
Столкновения
Для получения явного ответа рассмотрим однопараметрическое семейство
распределений начальных скоростей общего положения
Po(v) =
fidr[(/z + d)/2]
v^e
(3.67)
где Qd = 27rd/2/r(d/2) — площадь поверхности единичной сферы в d измерени¬
ях, а коэффициент Po(v) выбран так, чтобы начальная плотность была равна
единице. Интегрируя (3.65), получим
„w _/dvP(v,T) =
= [l + A(r)]-('1+rf>/2e-B(r).
Использование этого результата вместе с (3.66) дает
= п(т) = [1 + ^4]-<M+d)/2 e-B
Таким же образом умножая (3.65) на v2, интегрируя и сравнивая с производной
от второго уравнения (3.66), получим
dB = ц + d + A,_(fl+d+2)/2 е_в
dr 2
Решая эти уравнения для Л и В с начальными условиями Л(0) = В(0) = 0.,
находим Л и В, откуда можем вычислить плотность и среднюю скорость:
П = [1 + (/Z + d + 1)т]“ (м+<*)/(м+<*+1),
Urms = у/** [1 + (/X + d + l)T]-l/[2(M+d+l)]. (3.68)
Далее, с помощью уравнения (3.63) исключим т, оставив зависимость от вре¬
мени, и выразим плотность и среднюю скорость как функции времени. Таким
образом мы получим показатели убывания плотности и средней скорости
а = 2(д + Л) = 1
1 + 2(/х -Ь d) ’ 1 + 2()la + d)
3.6 Неупругие газы
Кинетическая теория традиционно имеет дело с газами, молекулы которых
взаимодействуют посредством упругих столкновений. Напротив, столкнове¬
ния между макроскопическими частицами всегда неупругие. Из-за этого воз¬
никает множество новых неожиданных явлений - вероятно наиболее захва¬
тывающие: крупномасштабная кластеризация и неупругий коллапс свободно
3.6 Неупругие газы
99
Рис. 3.4. Неупругая кластеризация в газе из 40000 частиц с коэффициентом
восстановления 0,6. Доля площади равна 0,05 при 500 столкновениях в среднем
на одну частицу. (Взято из I.Goldhirsch and G.Zanetti, Phys.Rev.Lett. 73,1619,
(1993), с разрешения)
• нюлюционирующего неупругого газа (рис. 3.4). Основной параметр, харак¬
теризующий неупругие столкновения, — коэффициент восстановления г.
В одном измерении эта величина определяется как
г — ^12
^12 ’
где izi2 = и± — U2 и V12 = v± — V2 — относительные скорости двух частиц
до и после столкновения. Коэффициент восстановления лежит в диапазоне
0 < г < 1, где нижняя граница соответствует полностью неупругому рассе¬
янию, верхняя — упругому рассеянию. Если массы сталкивающихся частиц
одинаковы, сохранение импульса, vi+^2 = щ+иъ и определение (3.70) задают
скорости после столкновения (vi, V2) через скорости до столкновения (ui,^)’
Vi = ^(1 - r)ux + ^(1 + r)u2 = е«1 + (1 - б)«2,
V2 = |(1 + r)Ui + |(1 + r)«2 = (1 - е)и1 + eu2-
(3.71)
100
Столкновения
Для дальнейшего удобства мы параметризуем кинематику параметром дис¬
сипации б = 3(1 — г). Если положить массу частиц равной единице, потеря
энергии при столкновении будет равна
ДЕ = |(tt2 + «з) - ^(Уг + v$) = -б(1 - б)(«1 - и2)2. (3.72)
Потеря энергии максимальна для полностью неупругих соударений (г = 0,
б = 1/2) и минимальна для упругих соударений (г = 1, б = О)19.
Средняя кинетическая энергия неупруго сталкивающихся частиц, называ¬
ется гранулярной температурой, или просто температурой. Из-за неупругих
соударений температура уменьшается со временем. Какова зависимость от
времени такого остывания? Пользуясь элементарной кинетической теорией,
можно найти эту зависимость в предположении, что газ остается простран¬
ственно однородным. Однородность дает хорошее приближение на ранних
временах. Однако это простое предположение оказывается ошибочным в пре¬
деле большого времени из-за крупномасштабной кластеризации.
Проанализируем сначала исход типичного столкновения. Как видно из
уравнения (3.72), потеря кинетической энергии в неупругом столкновении
равна ДГ = —б(1 — б)(Дг»)2 ~ —е(Дг)2, где Ди — относительная скорость
сталкивающихся частиц. Обратимся к квазиупругому пределу б —> 0, для
которого предположение о пространственной однородности хорошо работает
в существенном диапазоне времен. Грубая оценка типичного времени меж¬
ду соударениями Д£ дает €/Ди, где I — средняя длина свободного пробега.
Предположим, что единственный масштаб характеризует все скорости, так
что Av ~ v ~ л/Г. Собирая эти элементы, получим, что температура умень¬
шается со временем в соответствии с
dT АТ б(Дг>)2 бТ3/2
.
dt At (,/Av (.
Зная скорость убывания, получим температуру
= + (3'73)
19В трех измерениях у относительной скорости U12 = ui — 112 есть нормальная и тан¬
генциальная составляющие
U12 = gn + gt, gn = (U12 • n) П И gt=Ui2-gn,
где n — это единичный вектор, который соединяет центры двух частиц в момент их столк¬
новения. В общем случае коэффициенты восстановления для тангенциальной и нормаль¬
ной составляющей разные. При этом необходимо учитывать вращение, даже если вначале
частицы не вращались. В дальнейшем мы пренебрегаем этим вращательным движением.
3.6 Неупругие газы
101
Газ остается эффективно упругим, T(t) ~ То, для t <С to- Этот временной
диапазон оказывается существенным, если диссипация при столкновениях
мала. За пределами этого диапазона температура алгебраически убывает со
временем: T(t) ~ (et/£)~2. Такое убывание известно как закон Хаффа.
Аргументы, лежащие в основе закона Хаффа, применимы, когда неупру-
гость достаточно мала или когда система содержит достаточно мало частиц.
В противном случае развиваются крупномасштабные неоднородности плот¬
ности, которые приводят к отклонениям от закона Хаффа и в конечном итоге
к неупругому коллапсу.
Неупругий коллапс в одном измерении
Чтобы лучше понять неупругий коллапс, рассмотрим тривиальный пример
одной неупругой частицы, ударяющейся о горизонтальную пластину. Если
частица стартует с пластины с начальной скоростью v, направленной вверх,
она снова упадет на пластину через время 2v/g (g — ускорение свободного
падения). После столкновения частица полетит вверх со скоростью rv и цикл
повторится. Время, требуемое для бесконечного числа столкновений, дается
суммой
2v ч 2г>
tc = — (1 + г + г2 + г3 + ...) = —
9 9
1
1 — г’
Таким образом, с частицей происходит неупругий коллапс, т. е. она оказы¬
вается в состоянии покоя после бесконечного числа столкновений, которые
происходят за конечное время.
Две свободные частицы участвуют, максимум, в одном столкновении, так
что коллапс в этом случае невозможен. Однако для трех одинаковых частиц
неупругий коллапс происходит, если коэффициент восстановления удовлетво¬
ряет неравенству
Г < ГС = 7 - 4\/3 = 0,071796769. (3.74)
Чтобы вывести это ограничение, перенумеруем частицы числами 1,2,3 слева
направо и предположим (без ограничения общности), что первое столкнове¬
ние — 12. Последующие столкновения — чередующиеся 23 и 12. После пары
столкновений 12 и 23 скорости частиц V» связаны со скоростями до столкно¬
вений щ соотношением (полученным из (3.71))
VI
v2
Л>3.
= .М23А/12
ttl\
U2 I,
«З/
где
/ б 1-б 0
М12 =11 — 6 6 0
\ 0 0 1
М23 =
1 о о
0 6 1-6
0 1-6
б
(3.75)
102
Столкновения
После 2п столкновений скорости частиц даются формулой v = Mnuo,
где М = М23М12 и ио — вектор начальной скорости, тогда как после 2п + 1
столкновений скорости принимают значение v = Mi2Mnuo- Эволюция после¬
довательности столкновений определяется собственными значениями матри¬
цы М:
Ai,2 = I [(е2 + 2е - 1) ± ^/(1 - 2е - - 4(2е - 1)2] , А3 = 1.
Когда б > бс = 2а/3 — 3, что соответствует коэффициенту восстановле¬
ния г < гс = 7 — 4д/3, оба собственных значения Ai^ действительны и
по модулю меньше единицы. Следовательно, в системе отсчета, движущей¬
ся со скоростью центра масс, скорости частиц асимптотически убывают как
[max(|Ai|, |А2|)]п, что приводит к полному коллапсу. В то же время для г > гс
одно из собственных значений больше 1, так что последовательность столк¬
новений в конце концов обрывается, после чего три частицы разлетаются
друг от друга. Когда N > 3, последовательность столкновений необязательно
периодична, и матричная формулировка, использованная выше, уже не да¬
ет точного критического значения коэффициента восстановления гс. Вместо
этого можно привести эвристические аргументы для объяснения зависимо¬
сти г с от N при больших N. Рассмотрим частицу со скоростью 1, которая
падает на ряд неподвижных частиц, находящихся на одинаковом расстоянии
друг от друга, с коэффициентом восстановления, близким к 1. После первого
столкновения налетающая частица становится почти покоящейся, тогда как
частица-мишень будет двигаться немного медленнее первой частицы. Удоб¬
но поменять номера этих двух частиц, так что мировая линия частицы 1
только немного изменяется, когда она «проходит через» частицу 2. То же
самое повторяется при следующих столкновениях, так что мировая линия
исходной частицы постепенно изгибается, когда проходит через ряд частиц
(рис. 3.5). Пусть v(N) — скорость исходной траектории после N столкно¬
вений. Используя правила изменения скоростей при столкновениях (3.71) и
учитывая переобозначение номеров частиц, получим v(l) = 1 — 6. Аналогич¬
но, в первом порядке по е имеем v(N) = (1 — e)N — 1 — Ne. Для достаточно
большого N начальный импульс частицы в конце концов растрачивается и
происходит неупругий коллапс. Полагая v(N) = 0, получим критическое зна¬
чение параметра диссипации 6C(7V) ~ АТ-1 или критический коэффициент
восстановления
l-rc(JV)~l (3.76)
Неупругий коллапс для почти упругих частиц неизбежен в термодинамиче¬
ском пределе.
3.6 Неупругие газы
103
Рис. 3.5. Пространственно-временное представление пробной частицы, которая
неупруго сталкивается с рядом неподвижных частиц. Справа показано экви¬
валентное представление, в котором номера частиц переставляются во время
столкновения так, что частица 1 проходит через ряд частиц, но замедляется при
столкновениях
Кроме этого простого результата асимптотическое поведение неупругого
газа в более чем одном измерении до сих пор не полностью изучено. Су¬
ществование загадочно-прекрасной крупномасштабной кластеризации, пока¬
чанной на рис. 3.5, делает неприменимым любое больцмановское описание
газа. Есть основания ожидать, что асимптотическое поведение подобно бал¬
листической агломерации (см. раздел 3.7), когда в газе происходят полностью
неупругие столкновения. Это соответствие проще всего проверить в одном
измерении. В результате такой эквивалентности закон Хаффа Т ~ 1Г2 для
остывания применим только в промежуточном временном интервале, тогда
как истинное асимптотическое убывание есть Т ~ t-2/3 (см. (3.93)) в соот¬
ветствии с предсказаниями для баллистической агломерации.
Неупругая модель Максвелла в одном измерении
Поскольку невозможно получить аналитическое решение для динамики ре¬
ального газа с неупругими столкновениями, обратимся к модели Максвелла,
в которой интенсивность столкновений не зависит от скоростей и положе¬
ний частиц. При численном моделировании мы просто случайно выбираем
две частицы, определяем их скорости после столкновения, руководствуясь
соотношениями (3.71) для одномерия (или их обобщениями для d > 1), и
увеличиваем время на случайную величину, среднее которой равно обратно¬
му полному числу частиц. Благодаря простоте такой динамики мы можем
получить решение У Б в одном измерении в явном виде как для свободного
остывания, так и для газа под действием внешних сил.
104
Столкновения
Свободное остывание
Уравнение Больцмана для для неупругой пространственно однородной моде¬
ли Максвелла имеет вид
= J{5 [v — ещ — (1 — e)u2] — 5(у — -м2)} du± du2-
(3.77)
Дельта-функции определяют два способа изменения плотности частиц со ско¬
ростью v: создание частиц, когда сталкиваются частицы с такими скоростя¬
ми, что v = еи± + (1 — e)U2 (см уравнение (3.71)), или исчезновение, когда
частицы со скоростью v взаимодействуют с любыми другими частицами. Об¬
щий множитель у/Т возникает из интенсивности, с которой встречаются две
частицы. В модели Максвелла эта интенсивность не зависит от их относи¬
тельной скорости, но чтобы сохранить правильную размерность уравнений,
должна измеряться в единицах скорости. Единственный такой масштаб в си¬
стеме — это тепловая скорость у/Т. Так как плотность фиксирована, мы ис¬
пользуем шкалу, в которой плотность равна единице, f P(v, t) dv = 1, а также
полагаем полный импульс равным нулю, / v P(v, i) dv = 0.
Исследуем моменты распределения скорости. Включая общий множитель
у/Т в перемасштабированное время т = Jq y/T(t') dt', умножая (3.77) на vn
и интегрируя по v, получим уравнения эволюции для моментов Мп(т) ’=
f vn Р(у, т) dv
+ Опмп = (”) - er~mMmMn.m, (3.78)
т=2 ' '
где а„(б) = 1 — еп — (1 — е)п. Эти уравнения можно решать рекурсивно, начи¬
ная с Mq = 1 и Mi = 0. Несколько первых нетривиальных моментов имеют
следующий вид:
М2(т) = М2(0) е-О2Т,
М3(т) = М3(0)е-ОзТ,
М4(т) = [М4(0) + ЗМ2 (0)] е-“4Т - ЗМ2(т).
Для получения явной временнбй зависимости заметим, что второй момент
совпадает с гранулярной температурой Т. Поэтому проинтегрировав с dr =
y/Tdt, где Т = Т(0) е “2Г, получим выражения для моментов:
M3(t) = М3(0) (Т/Г(0))аз/а2, (3.79)
M4(t) = [М4(0) + ЗМ22(0)] (Т/Г(0))а4/а2 - зт2.
3.6 Неупругие газы
105
В отличие от равновесной статистической механики температура не пол¬
ностью характеризует распределение скоростей. Для классического распре¬
деления Максвелла-Больцмана имеем М4 ~ Т2,М§ ~Т3ив общем случае
A/2fc ~ Тк, т. е. в системе есть всего один характерный масштаб энергии. Одна¬
ко это не так для неупругого газа Максвелла. Из on(e) = 1—en —(1—е)” имеем
«а = За2/2, так что асимптотическое поведение М3 имеет вид Мз r\J М%/2. Та¬
ким образом, второй момент все еще определяет поведение третьего. Однако
и.4 < 2о2, т. е. отношение Mi/Mf расходится при t —> 00. В общем случае
моменты ведут себя следующим образом:
М„ ~
{
грп/2
rJJQ>nl
п < гс* = 3,
п > п*,
(3.80)
где ап — независимые коэффициенты для п > п*. Так как Т —> 0 при t —> 00,
частицы постепенно замедляются и в конце концов останавливаются.
Такое изменение поведения моментов указывает на то, что у распределе¬
ния скоростей степенной, а не гауссовый хвост. Чтобы найти распределение
скоростей, заметим что член уравнения Больцмана (3.77), ответственный за
с толкновения, имеет форму свертки, которая предполагает применение пре¬
образования Фурье. Определяя Р(к, t) = f eikv Р(у, t) dv и вычисляя Фурье-
образ правой части уравнения (3.77), получим произведение
ж
etkv p(Ul) т)р(и2, т) — eui — (1 — e)u2] dui du2 dv
= У eikeui P(Ul,T)dUlJeik^UiP(u2,T)du2
= Р(ек,т) P((l — е)к,т).
To есть Фурье-преобразованное уравнение (3.77) будет иметь вид
дР^.’Т) + Р(к, т) = Р((1 - е)к, г) Р(ек, г). (3.81)
Хотя это нелинейное и нелокальное уравнение оказывается нерешаемым,
мы, тем не менее, можем продвинуться в пределе большого времени, ко¬
гда распределение скоростей должно иметь скейлинговый вид Р(у,т) =
Т-1/2У(ш) со скейлинговой переменной w = иТ-1/2. Соответствующий скей¬
линг для Фурье-образов дает Р(к,т) = 7г(г), где z = |fc| Т1/2, две скейлин-
совые функции связаны между собой: 7r(z) = / T(w) ег2Ш dw. Подставив этот
скейлинговый анзац в уравнение (3.81) и пользуясь скоростью убывания
106
Столкновения
температуры dT/dr = — 2е(1 — е)Т из уравнения (3.78), получим уравнение
для скейлинговой функции 7г(г)
—е(1 — e)z — = тг^ — ez) тг(ег), (3.82)
dz
решение которого имеет вид250
7г(г) = (1 + z) е z. (3.83)
После обращения преобразования Фурье находим, что перемасштабированное
распределение скоростей имеет вид степенного закона20 21
2 1 __2 1
' _ 7Г (1 + w2)2 "*■ тг^Т (l + w2/T)2
Это распределение неожиданно не зависит от параметра диссипации б. Более
того, подставив формулу (3.84) в уравнение Больцмана (3.77), обнаружива¬
ем, что решение (3.84) точное для любого времени. Таким образом, начальное
распределение (3.84) всегда дает точное решение, тогда как другие началь¬
ные условия эволюционируют к этому скейлинговому виду только в пределе
большого времени.
Для более реалистичного случая газа твердых сфер хвост распределения
убывает экспоненциально по скорости
3>(w) ~ e“Cw, w = -^=, (3.85)
когда w 1. Можно получить такое поведение эвристически, рассматри¬
вая только хвост распределения, соответствующий большим скоростям. При
больших скоростях член ухода дает доминирующий вклад в УБ. В этом пре¬
деле можно также заменить |v — vz| в интеграле столкновений на |v|. Решение
получившегося дифференциального уравнения ~ — | v| Р немедленно при¬
водит нас к экспоненциальному хвосту. Эти аргументы сложно сделать стро¬
гими, хотя предсказание (3.85) оказывается правильным. Однако решение
20 Не существует систематического метода решения нелинейных разностно¬
дифференциальных уравнений. Разумная попытка — начать с исследования поведения
при больших z. Предположив, что 7r(z) убывает быстрее чем экспоненциально с ростом
z, придем к противоречию, так как порядок левой части окажется меньше чем порядок
правой. Аналогично, если убывание медленнее чем экспоненциальное, левая часть будет
доминировать и решение окажется степенным, что неприемлемо. Поэтому ищем решение
в виде 7г(г) = где f изменяется медленнее чем экспоненциально с ростом z.
Предположение, что f — полином, оказывается непротиворечивым, только если это
линейный полином. Этот подход приводит к (3.83).
21 Обратное преобразование Фурье для e~KZ — это ; обратное преобразование для
zne~KZ может быть получено последовательным дифференцированием по к.
3.6 Неупругие газы
107
У Б для неупругих твердых сфер до сих пор остается одной из выдающихся
нерешенных проблем.
Газ под действием внешней силы
Когда энергия непрерывно накачивается в систему, неупругий газ достигает
стационарного состояния, в котором поступление энергии уравновешивается
ее потерей в неупругих столкновениях. Чтобы организовать такую накачку,
можно поместить неупругий газ в закрытый контейнер, который мы будем
грясти. Эксперименты такого типа показывают, что распределение скоростей
обычно имеет немаксвелловский хвост для многих геометрий и способов на¬
качки энергии. Естественный способ смоделировать накачку — придать слу¬
чайное ускорение каждой частице, так что ее движение будет описываться
уравнением Ланжевена22
^=Са, (3.86)
в котором (£а) = 0 и (£a(£)£/3(£z)) = 2D$ap $ (t — tf). Из-за того что случай¬
ное ускорение придается однородно во всей системе, связь такого способа
накачки с экспериментами, в которых во вводе энергии задействована толь¬
ко малая часть частиц у стенок контейнера, не известна. Тем не менее, мы
надеемся, что хвост распределения будет универсальной характеристикой, не
зависящей от точного вида энергетической накачки.
Так как введение силы в уравнение (3.86) приводит к диффузии в про¬
странстве скоростей, соответствующее УБ (3.77) должно быть модифициро¬
вано:
dt dt dv2
Перед тем как приступить к анализу этого уравнения, приведем сначала об¬
щие, хотя и эвристические, аргументы для вида хвоста распределения скоро¬
стей, соответствующего большим значениям скоростей. Для достаточно боль¬
ших скоростей член прихода и производная по времени, удлиненная как в
уравнений (3.87), оказываются пренебрежимо малы23. Получившееся урав¬
нение имеет вид
(3.88)
22 Здесь греческие буквы используются для обозначения различных частиц.
23 Похожее разбиение на члены прихода и ухода также присутствует в кинетике агрега¬
ции (см. главу 5), что дает простой способ нахождения асимптотических свойств распре¬
деления масс кластеров.
108
Столкновения
который приводит к экспоненциальному высокоэнергетическому хвосту
P(v) е Этот аргумент можно просто обобщить для произвольных
интенсивностей столкновений. Для интенсивности, которая пропорциональ¬
на |ui — 1X2^ при |tzi — иъ\ —> оо, правая часть уравнения (3.88) запишет¬
ся как — Н5Роо, что приводит к Роо(^) ~ ехр(—|v|7), где 7 = 1 + 5/2. Для
классического случая твердых сфер (интенсивность столкновений линейна
по относительной скорости), получим 7 = 3/2. (См. также задачу 3.18.)
Повторяя шаги, приводящие в случае свободно остывающего газа к урав¬
нению (3.81), придем к уравнению для Фурье-образа распределения скоро¬
стей в стационарном состоянии:
р{к} = T+W р((1 ■е}к} р(ек}- (3-89)
Здесь множитель, содержащий Dк2, появился из члена уравнения (3.87), со¬
ответствующего диффузии в пространстве скоростей. Один из способов реше¬
ния уравнения (3.89) — последовательно подставлять правую часть в левую
часть. Первый шаг такого подхода дает
Р(^ = \ + Dk? Х 1 + £>((1 - е)&)2 Х 1 + £>(efc)2
х Р ((1 - e)2fc) х [Р((1 - e)efc)]2 х P(e2fc).
Продолжая этот процесс и используя граничные условия Р(0) = 1 и Р'(0) = 0,
полученные из сохранения общего числа частиц и импульса, получим реше¬
ние
P(fc) = П П [х + е2то(1 - е)2(г_тп)Х»А:2] . (3.90)
/>0 тп=0
У этой функции в комплексной плоскости к имеется бесконечный набор
простых полюсов ±г [е2тп(1 — б)2^_ш) £>] 1/Z2. Хвост P(v), соответствующий
большим скоростям, определяется двумя полюсами к = ±i/y/~D} находящи¬
мися ближе всего к началу координат. Так как эти полюса простые и нахо¬
дятся на конечном расстоянии от нуля, распределение скоростей имеет чисто
экспоненциальный хвост
P(v) ~ v*1 при |v| —> оо, (3.91)
где = VD, так же как в свободно остывающем газе. Неожиданное свойство
проявляется в том, что зависимость от параметра диссипации содержится
только в предэкспоненциальном множителе.
3.7 Баллистическая агломерация
109
3.7 Баллистическая агломерация
При баллистической агломерации частицы необратимо слипаются всегда, ко¬
гда два агрегата сталкиваются. Такая модель дает идеализированное описа¬
ние крупномасштабной аккреции материи при формировании астрономиче¬
ских объектов и слияния тепловых струй или вихрей. В результате посто¬
янно происходящих столкновений агрегаты непрерывно растут, но при этом
масса и импульс сохраняются в каждом столкновении. Баллистическая аг¬
ломерация представляет простое применение идей, развитых в этой главе, к
пониманию макроскопических следствий кинетики столкновений.
Можно схематически записать процесс агломерации в виде
(mi,pi) + (m2,p2) -»• (mi +m2,pi +р2),
где mi — масса i-той группы, a Vi — ее скорость. Мы предполагаем, что
агрегаты имеют форму шара, радиус которого в трех измерениях пропорци¬
онален га1/3, и принимают такую форму сразу после столкновения (рис. 3.6).
Начальная система достаточно разрежена, так что взаимодействиями трех
о<9
. Ь
а
Рис. З.б. Схематическое изображение эволюции при баллистической агломера¬
ции
н более тел можно пренебречь. Система стартует со случайного распределе¬
ния частиц с начальными скоростями и массами, выбранными из некоторого
фиксированного распределения. Какова эволюция процесса агломерации?
Характер временнбй эволюции массы, скорости и плотности типичных
кластеров можно вывести на пальцах. Чтобы упростить наши аргументы,
предположим, что сначала все кластеры имеют единичную массу и единич¬
ную скорость со случайным направлением. Поэтому агрегат массы т будет
состоять из т частиц. Если начальные импульсы частиц нескоррелированы,
импульс агрегата массы т — это сумма т некоррелированных импульсов,
равных по модулю единице, которая имеет порядок га1/2. Следовательно,
по
Столкновения
типичная скорость такого агрегата порядка v р/т га""1/2. Чтобы опре¬
делить, как средняя масса растет со временем, заметим, что масса агрегата
за одно столкновение возрастает на массу прядка его текущей массы, а ти¬
пичное время между столкновениями т связано с длиной свободного пробега
I соотношением € ~ vt. Поэтому масса изменяется со временем следующим
образом
dm т
dt т
Столкновение происходит, когда плотность, умноженная на объем трубки,
заметенной агрегатом при движении, равна 1, т. е. n(vr)72d“1 — 1. Здесь
п — плотность агрегатов, a R — типичный радиус агрегата. Переписав эти
величины через типичную массу агрегата (n ~ га-1,г> ~ га”1/2,/? ~ га1/^),
получим
т —Rd-i ~ mx т™1/2 х га-^-1^ ~ m^d+2^2d. (3.93)
Подставляя эту зависимость т от массы в уравнение (3.92), находим
ТП ~ t2d/(d+2), v ~ t-d/(d+2) > п ~ t-2d/(d+2). (3.94)
Хотя приведенный аргумент кажется красивым, он ошибочен, когда раз¬
мерность пространства больше единицы (и конечна)24. Ошибка происходит
из неправильного предположения: импульс агрегата массы m дается суммой
m нескоррелированных импульсов. На самом же деле частицы, которые дви¬
жутся навстречу друг другу, стремятся сталкиваться чаще, а те, что разлета¬
ются, — реже. Поэтому агрегаты с массой меньше средней состоят из частиц,
импульсы которых с большей вероятностью положительно скоррелированы,
а агрегаты с массой больше средней — наоборот. В одномерии эти корреляции
не играют большой роли, потому что растущие агломераты обязательно
заметают целый отрезок прямой с нескоррелированными начальными ско¬
ростями. Однако корреляции между импульсами мономеров, составляющих
один агломерат, играют неожиданно важную роль в размерностях выше еди¬
ницы.
Чтобы увидеть влияние корреляций, полезно рассмотреть агломерацию
в реакционно-контролируемом пределе25, в котором столкновения приводят
к слиянию кластеров с вероятностью 5, где 6 — исчезающе малая величина,
или к упругому столкновению с вероятностью 1 — 5. Поскольку почти все
24Первое свидетельство того, что уравнение (3.94) неверно, было получено из численного
моделирования, которое показало, что m где а « 0.86 в двух измерениях, а не а = 1,
как следовало из (3.94).
25В глава 13 о кинетике реакций разница между пределами, управляемыми переносом
и реакциями, обсуждается более подробно.
3.7 Баллистическая агломерация
111
3.1. Численное моделирование молекулярной динамики
Совершенно незаменимый инструмент при исследовании эволюции таких систем,
как баллистически агломерирующие частицы, — численное моделирование моле¬
кулярной динамики. В простейшем варианте молекулярная динамика интегриру¬
ет уравнения движения для каждой частицы на подходящим образом определен¬
ном временном интервале. Для баллистической агломерации такое интегрирова¬
ние двигает все частицы по прямым траекториям, пока не произойдет столкнове¬
ние. После каждого столкновения нужно снова рассчитать время до следующего
столкновения каждой пары частиц, и минимальное из этих времен определяет,
когда произойдет следующее столкновение. Хотя это наиболее прямой подход,
он совершенно неэффективен. Действительно, чтобы найти минимальное время
столкновения, необходимо вычислять времена столкновений между всеми пара¬
ми, и расчет времени следующего столкновения в системе из N частиц требует
порядка N2 операций (N операций в одном измерении).
Эту неэффективность можно во многом обойти. Рассмотрим для простоты случай
d = 1; однако обсуждаемый подход можно в большей части обобщить на высшие
размерности. В одномерии полезно сначала рассортировать времена столкнове¬
ний всех пар ближайших соседей в порядке возрастания с помощью стандартного
алгоритма сортировки из O(2Vln7V) операций. Предположим, что в соответствии
с полученным списком частицы п и п +1 агломерируют. Чтобы сохранить список
времен столкновений действительным, нужно заново рассчитать и сохранить но¬
вые времена столкновений, которые включают частицу п — 1 и новый агломерат
п, а также п и п+2. Важное отличие более эффективного алгоритма — это то, что
он продолжает использовать «виртуальные» события агломерации, в которых ча¬
стицы не двигаются, чтобы пересчитывать скорости частиц после столкновений,
проходя созданный вначале список времен столкновений в порядке возрастания.
Как только одно из вновь полученных времен столкновений станет меньше чем
следующее время из списка, мы передвигаем все частицы в течение времени, по¬
лученного суммированием упорядоченных времен всех столкновений вплоть до
настоящего момента. Кроме того, мы пересчитываем и пересортируем все време¬
на столкновений. Грубо говоря, мы можем заглянуть за пределы наименьшего
времени столкновения, потому что, когда происходит ближайшее столкновение,
движение основной части частиц остается детерминистическим.
Мораль здесь — неэффективность прямого численного моделирования молеку¬
лярной динамики может быть существенно снижена благодаря тому факту, что
движение большинства частиц остается детерминистическим на временах много
больших, чем время одного столкновения.
столкновения упругие, распределение скоростей будет близко к распределе¬
нию Максвелла-Больцмана для каждого кластера независимо от его мас¬
сы. Получившуюся реакционно-контролируемую агломерацию можно опи¬
сать аналитически, и результат детального (и длинного) анализа уравнения
Вольцмана для этой модели имеет следующий вид
т ~ t2d/(-d+3\ v ~ t_(d+1)/(d+3), n~t~2d/(d+3\ (3.95)
112
Столкновения
что находится в прекрасном согласии с данными численного моделировав
ния реакционно-контролируемых моделей. Так как эвристические аргументы,
приведшие к уравнению (3.94), одинаково хорошо применимы как в реакцион¬
но-контролируемом, так и в баллистически-контролируемом пределе, их несо¬
стоятельность в последнем случае наводит на мысль, что и в баллистически-
контролируемом пределе эвристические аргументы могут быть неверны.
В задаче о баллистической агломерации в одном измерении можно точно
вычислить совместную функцию распределения масс и скоростей P(m,v,t).
Это решение громоздко, и мы ограничимся перечислением основных резуль¬
татов:
• Типичный размер кластера растет как f2/3, тогда как типичная ско¬
рость кластера убывает как i-1/3, что согласуется с эвристическими
предсказаниями уравнения (3.94). Полное распределение масс и скоро¬
стей имеет вид
P(m,v,t) = Г1/3 Т(М,У), M = mt~2^, V = vt1/3. (3.96)
• Можно вычислить перемасштабированное распределение Т(М, У), от¬
куда можно получить отдельные распределения скоростей и масс,
Ф(У) = fdM7(M,У) и Ф(М) = fdV(P(M, У). Оба распределения
стремятся к скейлинговому виду Ф(У) и Ф(М), соответственно.
• Факторизации не происходит: Т(М, У) / Ф(У) Ф(М).
• Распределение массы имеет простое асимптотическое поведение
'l/\/M, М->0,
е-СМ3^ М —> оо.
Существует также интересная связь между баллистической агломерацией и
уравнением Бюргерса в размерности один (как кратко упоминается в разделе
2.9 и более подробно обсуждается в главе 4.3). В этом отображении среднее
расстояние между частицами Z ~ £2/3 соответствует среднему расстоянию
между соседними ударными волнами, а слияние агломератов соответствует
слиянию локализованных волновых пакетов.
3.8 Однополосное дорожное движение
Как многие из нас могли убедиться на собственном опыте, езда по дороге в
сельской местности, где имеется только одна полоса для движения в каждом
направлении и обгон запрещен, неэффективна. Более быстрые машины со¬
бираются позади медленно едущих, которые догоняют еще более медленные
3.8 Однополосное дорожное движение
113
транспортные средства, так что почти никто не едет с желаемой скоростью.
Запрет обгонов приводит к тому, что однородное вначале движение эволюци¬
онирует к кластеризованному состоянию. Мы можем описать это удручающее
явление с точки зрения кинетической теории.
Смоделируем кластеризацию дорожного движения с помощью следующей
идеализированной модели. Каждая машина обладает ее собственной скоро¬
стью, с которой она двигалась бы по пустой дороге. Когда более быстрая
машина догоняет более медленную, обе машины начинают двигаться со ско¬
ростью медленной (рис. 3.7). В общем случае, если кластер из m2 машин,
Рис. 3.7. Схематическое изображение дорожного движения без обгонов. На ри¬
сунке изображены мировые линии машин для некластеризованного начального
состояния (точки)
движущихся со скоростью г?2, догоняет кластер из mi машин, движущихся
со скоростью vi < V2, произошедшее «столкновение» даст кластер из т±+т2
машин, движущийся со скоростью v±:
(m^vi) + (m2,v2) -> (mi + m2,min(vi, V2)). (3.98)
Для простоты предположим (i) мгновенные столкновения, (ii) точечные ма¬
шины, (iii) независимые случайные начальные скорости, выбранные из одного
и того же заданного распределения P(v,0), и (iv) некоррелированные на¬
чальные положения машин со средним расстоянием между ними, равным 1.
I (осле того как заданы начальные условия движение происходит детермини¬
стически в соответствии с правилами «столкновений» (3.98), запрещающими
обгон. Единственный источник случайности — это начальные условия. Опи¬
шем эволюцию такого потока машин.
Скейлинг
Как первый шаг в понимании кластеризации транспорта применим скейлинг,
позволяющий определить основные характеристики, такие как эволюция ти¬
пичного размера кластера т, расстояние между кластерами £ и их скорость v.
114
Столкновения
Эти величины зависят от начального распределения скоростей самых медлен¬
ных машин, потому что асимптотически почти все машины соберутся позади
таких медленных машин. В качестве примера общего вида предположим, что
начальное распределение скоростей имеет вид26
P(v, 0) ~ при v —> 0. (3.99)
Из размерных соображений расстояние между кластерами € и скорость v
связаны соотношением I ~ vt. Так как расстояние между кластерами должно
быть величиной, обратной концентрации кластеров, которая в свою очередь
обратно пропорциональна среднему числу машин в кластере, имеем t ~ т.
Теперь попробуем связать число машин в кластере с его скоростью. Рассмот¬
рим машину со скоростью v. Вероятность того, что кластер размера к собе¬
рется позади этой машины, может быть вычислена точно для «односторонне¬
го» случая, в котором машины существуют только позади данной машины.
Пусть P(v) = Jq P(yf,0)dvf будет вероятность того, что скорость машины
меньше v. Тогда кластер размера к в конце концов образуется, если есть
к — 1 следующих одна за другой «быстрых» машин (со скоростью больше
v), за которыми следует одна медленная машина. Вероятность такой конфи¬
гурации равна Р(г>)[1 “* P(v)]fc_1. Поэтому средний размер кластера (m(v)}
позади машины со скоростью v имеет вид
(m(v)) = 5>P(v)[l - P(v)]‘-> = Ay.
Это соотношение — точное для односторонней проблемы; оно асимптоти¬
чески точно также и для двусторонней проблемы в пределе малой скорости,
потому что столкновение медленной машины с еще более медленной мало¬
вероятно. Используя распределение скоростей (3.99) как Р(у), получим, что
средний размер кластера ведет себя как (т(у)} ~ у-1-м. Комбинируя это
соотношение cm ~ vt, получим
m~ta, t~p, где а = (3.100)
/2 “г Z /2 ~г Z
Как можно было ожидать, кластеры машин постоянно растут со временем,
а их скорости соответственно уменьшаются.
Точное распределение скоростей
Можно пойти дальше и определить распределение скоростей свободных ма¬
шин — машин, которые еще не застряли позади медленных машин. Начнем со
26 Без потери общности мы вычитаем скорость самой медленной машины из всех скоро¬
стей, так что минимальная скорость равна 0.
3.8 Однополосное дорожное движение
115
специального случая, в котором у машин есть два возможных значения соб¬
ственной скорости, vi и V2 > vi, соответственно с вероятностями Pi(0) и Р2(0).
Медленные машины никогда не догонят никакие другие так что их плотность
сохраняется, Pi(t) = Pi(0). Быстрые движутся с собственной скоростью V2,
пока не догонят медленную. Чтобы быстрая машина не догнала медленную
m время £, перед ней должен быть отрезок длины (v2 —vi)£, свободный от мед¬
ленных машин. Поскольку начальные пространственные положения машин
случайны, вероятность пустого отрезка убывает экспоненциально с его дли¬
ной exp[—Pi(0)(v2 — vi)£)]. Поэтому плотность более быстрых машин убывает
следующим образом
Р2(<) = р2(0) (3.101)
Теперь рассмотрим поток машин, движущихся с тремя различными соб¬
ственными скоростями vi < V2 < V3. На кластеры со скоростями vi и V2 не
влияет присутствие более быстрых машин, так что предыдущие результаты
для Pi(t) и Рг(£) остаются верными. С другой стороны, чтобы быстрые ма¬
шины со скоростью V3 сохраняли эту скорость, они должны избежать столк¬
новений с кластерами и с vi, и с V2- Вероятность для таких двух независимых
случайных событий равна произведению двух вероятностей пустых отрезков
P3(t) = р3(0) X e-p2(0)(v3-v2)t. (3.102)
В общем случае, когда машина имеет начальную скорость vn с вероятностью
/’„(0), для (дискретного) набора скоростей {vn}, где vi < V2 < V3 < ...,
получим распределение скоростей кластеров в виде
P„(t) = pn(0) J] е~р^п~^у
l<i<n—l
P(v, 0) exp t У dvf (v — v/)P(v/, 0) ,
(3.103)
где во второй строчке мы заменили произведение суммой в экспоненте и пе¬
релили к непрерывному пределу. Таким образом плотность машин любой ско¬
рости убывает экспоненциально с интенсивностью, которая является возрас¬
тающей функцией v.
С использованием начального распределения скоростей P(v,0) — avM
уравнение (3.103) в пределе больших времен дает
P(y,t') = avfl exp [—, где b = ^ + 1^ + 2у (3.104)
что может быть записано в скейлинговой форме
P(v, t) = i?-a Ф(У), Ф(У) = aW4 exp [-бУ^2], (3.105)
116
Столкновения
где V = vtP, а показатели а = (/x+l)/(/z+2) и /3 = 1/(/х+2) уже были эвристи¬
чески найдены в (3.100). В соответствии с житейской интуицией вероятность
того, что машина с собственной скоростью v может свободно ехать, не дого¬
няя более медленный поток, быстро убывает со временем, а также является
быстро убывающей функцией v: чем быстрее собственная скорость машины,
тем быстрее она застрянет позади автобуса.
Идеализированная модель транспортного потока замечательно иллюстри¬
рует недостатки больцмановского подхода к одномерным системам. Мы мо¬
жем записать уравнение (3.103) в больцмановской форме, дифференцируя
логарифм этого уравнения по времени, что дает линейное эволюционное урав¬
нение
дР^ = -P(v, *) f” dv'(v - 0). (3.106)
Это уравнение напоминает классическое уравнение Больцмана (3.6), кроме
того что член прихода отсутствует, потому что кластер не может быть создан,
если он не существовал до этого. Однако есть существенные отличия, которые
полезно привести:
• Уравнение (3.106) — линейное по распределению скоростей P(v,f).
• Есть бесконечная память, так как начальные условия P(v,0) продол¬
жают влиять на образование кластеров до бесконечности.
• Уравнение Больцмана для однополосного дорожного движения имеет
вид.
= -P(v,t)£dv'(v- (3.107)
В отличие от линейного (и точного!) уравнения (3.106), которое реша¬
ется для любых начальных условий, нелинейное уравнение Больцмана
(3.107) не было решено для любых начальных условий.
• Поскольку в уравнении Больцмана (3.107) используется неконтролируе¬
мое среднеполевое описание межчастичных взаимодействий, естествен¬
но ожидать, что оно неприменимо в одном измерении, где есть только
взаимодействие ближайших соседей.
• Классическое уравнение Больцмана основано на факторизации много¬
частичных корреляционных функций в произведение одночастичных
корреляционных функций. Например, в подходе Больцмана вероят¬
ность 7^2(^) w; t) того, что две машины имеют скорости v и w, где w > v,
записывалась бы в виде P(w, t)P(v, t). Однако правильный результат —
3.9 Ссылки
117
это P2(y,w;t} = P(w,t)P(v,0), так как ведущая быстрая машина «за¬
слоняет» более медленную машину позади, и поэтому достаточно га¬
рантировать, что ведущая машина не замедляется. Это самоочевид¬
ное отсутствие фактоизации иллюстрирует еще одно упущение подхода
Больцмана.
Много других корреляционных функций в модели транспортного потока
также не факторизуются. Пожалуй самые главные — совместные распределе¬
нии размеров и скоростей, а именно плотность кластеров Рт(у, £), состоящих
ил т машин, движущихся со скоростью v. Скейлинг предсказывает что
Pm(v,t) = tp-aT(M,V), M = mt~Q, V = vtP. (3.108)
Отсутствие факторизуемости означает, что скейлинговую функцию СР(М, V)
нельзя записать в виде произведения Ф(У)Ф(Л1). Строго говоря, нефакто-
ризуемость еще не означает неприменимости больцмановского подхода; по¬
следний работает с множеством взаимодействующих компонентов, тогда как
;P(M, У) описывает один кластер. Однако отсутствие факторизуемости ока¬
зывается неотъемлемым свойством основных наблюдаемых характеристик
транспортного потока, таких как Т(7И, V)27.
3.9 Ссылки
Теория столкновений — это фундамент, на котором была выстроена нерав¬
новесная статистическая физика. Симметрийный аргумент, использованный
для вывода распределения скоростей в газе, был предложен самим Максвел¬
лом [31]. Основания кинетической теории и уравнение Больцмана изложены
в лекциях Больцмана [32], а также в различных книгах [33-35] и обзорных
статьях [36, 37]. Вывод гидродинамики из уравнения Больциана — стандарт¬
ный предмет, обсуждаемый почти в каждом тексте, посвященном уравнению
Вольцмана, см. например [35, 38].
Статью Друде можно найти в [39], а модель Лоренца предложена в [40].
Для популярного изложения моделей Лоренца см. [41], тогда как подробное
обсуждение свойств этих моделей есть в [42, 43]. Одна из патологий плотно¬
го газа Лоренца — неаналитическая зависимость коэффициента диффузии от
плотности; это свойство обсуждается в [44]. Нестационарность модели Лорен¬
ца во внешнем поле и ее физические следствия обсуждаются в [45, 46]. Текст
27Как мы упоминали ранее, перемасштабированное распределение 1Р(М, V), описываю¬
щее процесс агломерации в размерности один, также не факторизуется.
118
Столкновения
Кубо и соавторов [47] представляет формализм Грина -Кубо, который мы
использовали, чтобы найти коэффициент диффузии газа Лоренца. Этот же
формализм Грина-Кубо может быть использован для нахождения множе¬
ства флуктуационно-диссипационных соотношений. Проблема ударного рас¬
пространения и близкая задача о непрерывной взрывной волне разобраны в
[9,48-50]. Модели Максвелла были введены самим Максвеллом [31], переот-
крыты Уламом [51] и обсуждаются в [35, 36]. Основные результаты о моделях
очень твердых частиц можно найти в [36]. Газ твердых сфер играет централь¬
ную роль как в равновесной, так и в неравновесной статистической физике.
Мы только кратко перечислили главные свойства этой замечательно простой
и богатой модели. Описание неравновесного поведения газов твердых сфер
можно найти в [52, 53]. Кроме того продолжают появляться и неожиданные
новые результаты [54]. Больше о баллистической аннигиляции можно найти
в [55-57].
Необычные свойства неупругих газов, а именно, крупномасштабная кла¬
стеризация и неупругий коллапс, стали популярны в 1990-х. Одна из ранних
работ на эту тему — работа Хаффа [58], в которой была объяснена скорость
охлаждения неэластичных газов. Рисунок 3.4, который показывает неупругий
коллапс, взят из статьи Голдхирш и Занетти [59]. Удивительно простое точное
решение для свободного охлаждения неупругой модели Максвелла в размер¬
ности один было открыто Балдасарри [60]. Кинетическая теория неупругих
газов подробно обсуждается в монографии Бриллиантова и Пешель [61]. Тех¬
ника преобразования Фурье в приложении к молекулам Максвелла сильно
упрощает эволюционные уравнения. Это наблюдение появилось в неопубли¬
кованной диссертации Круппа [62]. Больше подробностей об этом подходе
в контексте упругих молекул Максвелла можно найти в [36, 63]; неупругие
молекулы освещены в [64].
Баллистическая агломерация [65-68] — тема, которая продолжает раз¬
виваться [69], а детальное понимание было достигнуто только в одномерии
[65, 68, 70]. Богатый материал о техниках молекулярной динамики и об¬
щих алгоритмах сортировки и поиске по спискам можно найти, например,
в [71, 72].Применение теории столкновений к одномерному дорожному дви¬
жению основано на [73].
3.10 Задачи
3.1 Уравнение Больцмана можно применять, когда газ разрежен, а именно когда
nd3 < 1, где п — плотность, ad — радиус межмолекулярного взаимодействия.
В стандартных условиях (комнатная температура и атмосферное давление)
3.10 Задачи
119
оцените плотность атмосферы и радиус межмолекулярного взаимодействия.
Покажите при этих условиях, что атмосфера действительно разрежена.
3.2 Докажите, что квантовые эффекты принебрежимо малы для атмосферы в
стандартных условиях. В частности покажите, что длина волны де Бройля
много меньше, чем среднее расстояние между соседними молекулами:
<С п_1/3.
Для газа при атмосферном давлении оцените температуру, при которой ста¬
новятся важны квантовые эффекты. Для газа при комнатной температуре
оцените плотность, при которой квантовые эффекты становятся важны.
3.3 Рассмотрите рассеяние однородного параллельного пучка точечных частиц,
которые налетают параллельно оси z на неподвижное сферическое препят¬
ствие в d измерениях. Покажите, что отношение потока Фь, рассеянного назад,
к потоку Ф^ рассеянному вперед, имеет вид
Здесь под потоком, рассеянным вперед, понимаются частицы, имеющие поло¬
жительную г-компоненту скорости (наоборот для рассеянного назад). В част¬
ности Ai = оо (только рассеяние назад в одномерии), А2 = (у/2 — I)”1 > 1
(преимущественно рассеяние назад в двух измерениях), A3 = 1 (проявление
изотропного рассеяния в тр1х измерениях).
3.4 Эта задача посвящена выводу формулы Энштейна-Грина-Кубо.
(a) Покажите, что из уравнения диффузии следует, что среднеквадратичное
смещение Д(£) = ([г(£) — г(0)]2) растет как Д ~ 2dDt.
(b) Выведите из предыдущего результата
= 2(v(t) • [r(t) - r(0)]> = 2 dt' (v(t) • v(f)>.
(c) Обоснуйте, что равновесное среднее зависит только от разности времен¬
ных аргументов £" = £ — £', и поэтому
^ = 2/>'{v(0).v(t")).
(d) Используя соотношение Д ~ 2dDt и рассматривая предел £ —> оо, пока¬
жите, что предыдущее уравнение дает
D = По°dt <v(°) ‘ VW>-
120
Столкновения
3.5 Любое изотропное распределение скоростей — равновесное распределение мо¬
дели Лоренца. Если, однако, есть слабое взаимодействие между движущимися
частицами, они в конце концов придут к равновесию при некоторой темпера¬
туре Т, так что их распределение скоростей будет распределением Максвелла.
Покажите, что в этой ситуации средний коэффициент диффузии (3.9) стано¬
вится равен
D-— I Т - 16а / Т 1
3 V 27гт 9 V 27гтп г/’
где у = п(47га3/3) <С 1 — доля объема, занятая рассеивателями.
3.6 Проверьте, что уравнение (3.35) даст решение телеграфного уравнения.
3.7 Используя (3.47а), вычислите корень из среднеквадратичной скорости частиц
газа Лоренца в электрическом поле. Покажите, что эта скорость совпадает с
оценкой (S2^)1/3 с точностью до численного коэффициента 32/3[Г(1/3)]-1/2.
3.8 Используя формулу Грина- Кубо так же, как для случая нулевого магнитного
поля, рассчитайте нетривиальные компоненты тензора диффузии в уравнении
(3.52) и покажите, что они имеют вид
п 1 2
Я|| = з иог,
3V°T1 + (wt)2’
1 2 CJT
Dxy - -Dyx - --vot 1 + (wr)2-
3.9 Используйте кинетические аргументы, сходные с использованными для рас¬
чета числа движущихся частиц, уравнение (3.55), чтобы определить число
столкновений C(t) за время t в каскаде столкновений, обсуждавшемся в раз¬
деле 3.4.
3.10 Рассмотрите газ при нулевой температуре, который занимает полупростран¬
ство х > 0. Когда частица, движущаяся вдоль оси ж, попадает в эту систему,
она генерирует каскад столкновений, который распространяется в среду. Ча¬
стицы также отбрасываются назад, создавая структуру, похожую на всплеск.
Цель данной задачи — обосновать, что энергия частиц E(t) в изначально за¬
нятом полупространстве в конце концов стремится к нулю алгебраически со
временем.
(a) Используя анализ размерностей, покажите, что размер каскада R дается
уравнением (3.56), хотя в данном случае мы имеем дело с энергией E(t),
убывающей со временем.
(b) Покажите, что общее число частиц в каскаде ведет себя как
N~nRd~ {E/m)d/(d+2} {ntd)2/(d+2}.
(c) Покажите, что типичная скорость выброшенных частиц v связана с N и
Е соотношением Nmv2 ~ Е, откуда
\ l/(d+2)
nmtd J
3.10 Задачи
121
(d) Обоснуйте, что энергия E(t) убывает в соответствии с уравнением
dE
dt
mv
х nvR
d-l
(е) Используя результаты (а)-(с), покажите, что (d) сводится к dE/dt ~
—E/t, что приводит к алгебраическому убыванию Е со временем.
3.11 В этой задаче рассматривается теплопроводность в среде, где коэффициент
теплопроводности алгебраически зависит от температуры: к = к(Т) = АТп.
(Для молекул Максвелла, твердых сфер и очень твердых частиц показате¬
ли п = 1,1/2,0 соответственно, что следует из аргумента, который привел к
уравнению (3.57) для коэффициента диффузии.) Математически уравнение
теплопроводности
= AV • (TnVT)
— параболическое уравнение в частных производных. Когда п = 0, есть част¬
ное решение для произвольных начальных условий. Когда п / 0, получаю¬
щееся параболическое нелинейное уравнение в общем случае нерешаемо, но
точные решения известны для достаточно простых начальных условий. Рас¬
смотрим одну такую ситуацию, где тепло постоянно высвобождается на (ги¬
перплоскости х = 0, тогда как снаружи начальная температура — ноль. Тогда
нам нужно решить задачу Коши:
1=4 (ИЮ-
Наша цель — решить эту задачу Коши для п > 0.
(a) Из общих соображений имеем Т = T(x,t\A,Q). Используя анализ раз¬
мерностей, покажите, что любые три из четырех величин ж, £, Л, Q имеют
независимые размерности.
(b) Выбрав t,A,Q в качестве основных, покажите, что решение должно
иметь вид
= \ At) = (Q*Aty/V+n)'
Таким образом, один анализ размерностей показывает, что решение (ко¬
торое в принципе зависит от двух переменных х и t) с точностью до мас¬
штабного множителя есть функция одной скейлинговой переменной £.
Главная причина такого упрощения — отсутствие величины с размерно¬
стью длины в формулировке задачи Коши.
122
Столкновения
(c) Подставьте приведенный выше анзац для Т(#, t) в нелинейное уравнение
теплопроводности и покажите, что скейлинговая функция удовлетворяет
обыкновенному дифференциальному уравнению.
СТ/')'+ 777 (£/)' = о,
2 + п
где штрих означает дифференцирование по £.
(d) Покажите, что решение этого дифференциального уравнение имеет вид
ле) =
2(2 + «)
(£о2-£2)
1/п
п
в области |£| < и /(£) = 0 для |£| > £о- Обоснуйте, что £о определяется
законом сохранения теплоты
и вычислите £о-
(е) Нагревающаяся область — это область [—жо(*),яо(£)], границы которой
растут как £о№ = ^o(Qn^)1^2+n\ вне нагреваемой области среда оста¬
ется при нулевой температуре. Попробуйте объяснить противоречие с
общеизвестным фактом, что для параболического уравнения в частных
производных возмущения распространяются мгновенно.
3.12 Рассмотрите предыдущую задачу в трех измерениях и предположите, что ко¬
нечное количество тепла было мгновенно высвобождено в начале координат:
T(r,0) = QJ(r).
(а) Используя те же самые аргументы, что и в предыдущей задаче, покажи¬
те, что решение должно иметь вид
/ q2 \ l/(2+3n) г
= \А№) = (QMi)1/^3") ’
(Ь) Выведите обыкновенное дифференциальное уравнение для /(£) и решите
его
п
- 1/п
Л£) =
(й-г)
.2(2+ 3п)
(с) Нагреваемая область — шар радиуса ro(t) = fo(Qn^)1^2+3w^- Таким об¬
разом, объем нагреваемой области растет как £3/5 и £6/7 в случае молекул
Максвелла и твердых сфер соответственно; для очень твердых сфер все
пространство К3 становится нагретым при любом t > 0.
3.10 Задачи
123
3.13 Рассмотрите теплопроводность в трехмерной области R < г < оо. Предполо¬
жите, что внутренняя сферическая поверхность поддерживается при постоян¬
ной температуре, Т(Д,£) = То, и что температура зануляется на бесконечно¬
сти, Т(оо,£) = 0. Покажите, что, если к(Г) = ЛТП, стационарная температура
удовлетворяет уравнению V2(Tn+1) = 0, и что соответствующее распределе¬
ние температуры имеет вид Т(г) = То .
3.14 Рассмотрите баллистическую аннигиляцию в одном измерении. Преобразуйте
эволюционное интегро-дифференциальное уравнение Больцмана (3.59) к виду
«^1ПРМ=_2РМ.
Это (очевидно очень сложное) нелинейное уравнение в частных производных
до сих пор не было решено.
3.15 Объясните соотношение а + = 1 между показателями убывания, возникаю¬
щими в (3.60).
3.16 Рассмотрите баллистическую аннигиляцию для очень твердых частиц. Про¬
верьте выражения (3.68) для плотности и средней скорости и покажите, что
показатель убывания /3 действительно дается уравнением (3.69).
3.17 Проверьте общее поведение импульса [приведенное в уравнении (3.80)] для
одномерного неупругого максвелловского газа, используя неравиество ап <
ат + о>п-т для всех 1 < т < п — 1.
3.18 Предположите, что зависимость интенсивности столкновений от относитель¬
ной скорости имеет вид |ui — W2I5 при |ui — U2I 00. Используйте этот факт
для получения аналога уравнения (3.88) и асимптотической формы P(v, t) для
больших V.
3.19 Рассмотрите упрощенную модель баллистически-контролируемой агрегации,
в которой массы всех частиц всегда остаются одинаковыми, т. е. когда две
частицы со скоростями Vi и V2 сталкиваются, они составляют агрегат со ско¬
ростью v = Vi + V2-
(a) Покажите, что для этой упрощенной модели доля объема, занятая ча¬
стицами, неограниченно убывает.
(b) Дает ли формализм Больцмана асимптотически точное описание? Из (а)
мы видим, что система становится разреженной, так что множественные
столкновения становятся асимптотически несущественны28.
(c) Используя (упрощенный) вариант среднеполевого аргумента (3.92)-
(3.93), примененного в качестве гипотезы о поведении баллистической
28Для модели баллистической агломерации доля объема остается постоянной, так что
подход, основанный на уравнении Больцмана, работает, только если система разрежена с
самого начала.
124
Столкновения
агломерации, покажите, что для упрощенной модели аналог уравнения
(3.94) имеет вид
v п~ t~2
независимо от размерности пространства d.
(d) Покажите, что уравнение Больцмана, описывающее упрощенную модель,
записывается как
~ = / ^udwP(u,£) P(w,t)|u — w|5(u + w — v)
-2P(v,t) J dw P(w,t)|v — w|.
(Численное решение УБ показывает, что плотность убывает алгебра¬
ически п ~ t~a с показателем, возрастающим с размерностью: а «
1,33,1,55,1,65 для d = 1,2,3.)
(e) Смоделируйте численно УБ в одномерии и покажите, что показатель на
самом деле а ~ 4/3, что сильно отличается от а = 2, получающегося в
среднополевом подходе.
(f) Рассмотрите упрощенную модель в реакционно-контролируемом преде¬
ле. Покажите, что п ~ ^-^/(d+i). Для среднеполевого аргумента нет раз¬
ницы между баллистически-контролируемым пределом и реакционно¬
контролируемым пределом, так что его предсказание п ~ t~2 неверно
в любой размерности.
3.20 Предположите, что кластер состоит из т машин со скоростями, независимо
выбранными из распределения Ро(у). Используя асимптотический вид Pq(v) ~
Vм при v —> 0, покажите, что т ~
3.21 Вычислите распределение размера кластеров P(v, t) для специального случая
Ро(у) = Покажите, что результат согласуется с общим скейлинговым
поведением.
3.22 Рассмотрите простейшие неоднородные начальные условия: полупрямая х < 0
занята машинами, положения и скорости которых нескоррелированы, тогда
как другая половина прямой х > 0 вначале пуста. Покажите, что общее число
кластеров, которое проникает на изначально пустую половину прямой, растет
как alnt Здесь а = (/z +1)/(^ + 2) — показатель степени, которая характери¬
зует число машин в типичном кластере (во внутренней части потока) т ~ta.
Глава 4
ЗАПРЕТЫ
I (ель статистической физики — изучать коллективное поведение взаимодей¬
ствующих многочастичных систем. В равновесной статистической физике
простейшее взаимодействие — запрет: например твердые сферы не могут пе¬
ресекаться. Эта модель зависит от одного безразмерного параметра: доли
объема. Температура не играет роли, так как энергия взаимодействия рав¬
но нулю, когда сферы не пересекаются, и бесконечна в противном случае.
11еемотря на кажущуюся простоту, газ твердых сфер за исключением одно¬
мерного случая не до конца изучен. Похоже обстоят дела и с решеточной
версией твердых сфер; понимание необычного перехода жидкость-газ отсут¬
ствует для пространств размерности d > 2.
В этой главе мы исследуем роль запретов в простейших неравновесных
моделях под названием «процессы с запретами». В них частицы занимают
< отдельные узлы решетки, и каждая частица может прыгать в соседний узел,
если он свободен (см. рис. 4.1). Можно задать множество фундаментальных
Рис. 4.1. Симметричный процесс с запретами на квадратной решетке. Частица
может перескочить в соседний узел, если он свободен
126
Запреты
вопросов. Каково смещение единичной частицы? Как плотность влияет на
свойства переноса? Как градиенты плотности меняются со временем? В бо¬
лее чем одном измерении запреты не меняют качественно свойства переноса
по сравнению с системами независимых частиц. Интересно, что запреты при¬
водят к фундаментально новым транспортным явлениям в размерности один.
4.1 Симметричный процесс с запретами
В симметричном процессе с запретами (СПЗ) среднее движение каждой ча¬
стицы пространственно симметрично. Для одной частицы СПЗ эквивалентен
случайному блужданию. В обратном пределе, где занята вся решетка кро¬
ме одного пустого узла, эта вакансия также совершает простое случайное
блуждание. На первый взгляд неожиданннно, что для любой концентрации
частиц, 0 < с < 1, общая плотность частиц в СПЗ эволюционирует, как будто
взаимодействия нет.
Эволюция плотности
Пусть Pn(t) будет одночастичная плотность, а именно вероятность того, что
частица занимает узел решетки п в момент времени f. Нам также нужны
различные парные плотности: Pn,m(£) — совместная вероятность того, что
узлы пит заняты, и Рп,гп(£) — совместная вероятность того, что узел п
занят, а узел т свободен. В СПЗ одночастичная плотность эволюционирует
в соответствии с уравнением
(4-1)
где индекс суммирования т пробегает по всем ближайшим соседям узла п.
А именно, частица может прыгнуть в п, если этот узел свободен, а один из
его ближайших соседей т занят, тогда как частица может уйти из п, если
один из ближайших соседей свободен.
Мы можем исключить парные вероятности, заменив их одночастичными
вероятностями, если заметим, что парные вероятности удовлетворяют про¬
стым равенствам
4.1 Симметричный процесс с запретами
127
а также условиям симметрии Pn,m(£) = Рт,п(£)- Воспользовавшись этими
фактами, можно исключить Рп,т и Рп,т из уравнения (4.1), что немедленно
дает
(4-2)
Это просто основное кинетическое уравнение для случайного блуждания
единственной частицы! Эта эквивалентность выполняется на любой решетке.
Таким образом, запреты не влияют на пространственно-временную эволюцию
плотности. Таким образом, в пределе больших расстояний и времен плотность
подчиняется классическому уравнению диффузии.
Эволюция отдельной помеченной частицы
I (есмотря на сходство с классической диффузией запреты играют большую
роль в одномерии, когда мы рассматриваем движение одной выбранной «по-
меченной» частицы. Очевидно помеченная частица не может пройти так да¬
леко, как в случае свободной диффузии. Когда размерность пространства —
два или больше, эта разница проявляется просто в перенормировке коэффи¬
циента диффузии (г2) = 2dD(c)t, где коэффициент £>(с), зависящий от кон¬
центрации, уменьшается с ростом с. Однако, в одномерии запреты приводят
к тому, что корень из среднеквадратичного смещения растет как
Несмотря на такую аномальную зависимость от времени, распределение ве¬
роятности положения помеченной частицы все еще гауссово, но теперь по
переменной rr/f1/4.
Интуитивно можно, понять временную зависимость смещения помеченной
частицы, рассматривая почти заполненную решетку с —> оо. В этом преде¬
ле любая частица почти всегда окружена занятыми узлами и поэтому редко
движется. Наоборот, так как плотность вакансий 1 — с мала, вакансии редко
видят друг друга и поэтому свободно диффундируют. Ключевой момент —
что то, что свойства движения помеченной частицы можно извлечь из свойств
движения таких свободно блуждающих вакансий. Помеченная частица пры¬
гает вправо, когда в ее правом соседнем узле есть вакансия, и аналогично
для прыжка влево. Таким образом, смещение свободной частицы дается раз¬
ностью
(4-4)
128
Запреты
где N+(i) — число вакансий, которые вначале были справа от помеченной
частицы, а теперь слева, и наоборот для Так как вакансии свободно
диффундируют и их плотности слева и справа от помеченной частицы равны,
числа пересечений траекторий N+ и N- будут иметь вид
(JV+(i)) = (JV_(t))~(^. (4.5)
Среднее смещение помеченной частицы (х) равно нулю. Однако разность чи¬
сел шагов вправо и влево для случайного блуждания ведет себя как Vt1/2,
и поэтому среднеквадратичное смещение растет как t1/2, что согласуется с
(4.3).
Чтобы вывести распределение вероятности Р(х, t) смещения помеченной
частицы, гораздо проще рассмотреть непрерывный вариант СПЗ, в котором
частицы среды диффундируют независимо и свободно проходят через друг
друга при встрече (рис. 4.2). В отличие от этого процесса в исходном СПЗ
Рис. 4.2. Эквивалентность свободной диффузии и процесса с запретами. На ри¬
сунке показаны мировые линии частиц в размерности один, (а) С запретами:
частицы сталкиваются при встрече так, что порядок их номеров остается неиз¬
менным. (Ь) При свободной диффузии номер частицы остается прикрепленным
к конкретной траектории (сплошной, точечной, пунктирной)
встретившиеся частицы сталкиваются и отражаются друг от друга, так что
их порядок сохраняется. Важно, что оба взаимодействия приводят к одному
и тому же результату. Поэтому, чтобы вычислить распределение смещения
помеченной частицы, мы обратимся к более простой системе независимых
свободно диффундирующих частиц среды.
Предположим, что помеченная частица стартует с начала координат и
достигает х к моменту времени t. Тогда среднее число свободно диффунди-
4.1 Симметричный процесс с запретами
129
рующих частиц среды, которые сначала были справа от помеченной частицы,
в в момент t оказались слева от нее, дается следующим выражением (рис. 4.3)
О $
Рис. 4.3. Иллюстрация к уравнению (4.6а). Частица среды, вначале находивша¬
яся в £ — справа от помеченной частицы, прошла через помеченную частицу до
момента t и пришла в у < х
/»ОО рх
v+{x,t) = (N+(x,t)} = Уо d£J ддй е~(у~€) /4Dtdy. (4.6а)
' 1десь £ — это начальное положение частицы среды, у — ее конечное положе¬
ние, а р — плотность частиц среды. Аналогично, формула
= У d£ f dy ^£—e~^y~^2/4Dt (4.6b)
дает среднее число частиц среды, которые вначале были слева от помеченной
частицы и оказались справа в момент t. Очевидно, что = v-fai).
Какова вероятность Р+(п, ж, £) того, что п частиц среды, которые сначала
были справа от помеченной частицы, оказались слева от нее к моменту £? Так
как частицы движутся независимо, эта вероятность дается законом Пуассона
со средним значением i/+(x, i), и аналогично для Р_(п, #,£). Поэтому имеем
P±(n,x,t) = ^e-^. (4.7)
Вероятность Щ(х, £), того что есть еще к > 0 проходов справа налево (случай
к < 0 аналогичен) будет даваться выражением
Щ(ж,<) = Р+ (n + fc, ж, f )Р_ (п, ж, t).
га>0
(4-8)
130
Запреты
Подставляя выражения для P±(n,x,i) из (4.7) в эту сумму и используя при¬
веденное ниже разложение функции Бесселя в ряд, получим
щ(м) =
(4-9)
Ik(2^u+v-).
4.1. Еще один взгляд на модифицированную функцию Бес¬
селя
Стандартное определение модифицированной функции Бесселя, которое приме¬
нимо для произвольного действительного индекса /х > 0, дается через дифферен¬
циальное уравнение
(iio>
У уравнения второго порядка есть два линейно независимых решения, JM(z) и
— модифицированные функции Бесселя первого и второго рода, соответ¬
ственно. Модифицированная функция Бесселя первого рода допускает представ¬
ление в виде ряда при z —> 0:
ТП>0
1
т\ (т + /х)!
(4.П)
тогда как модифицированная функция Бесселя второго рода K^z) расходится
при z 0.
Важная новость — то что P(x,t) непосредственно связана с По(#, t). Как
показано на рис. 4.2, если мы примем частицу 2 за помеченную, ее положение
в момент t в процессе с запретами (рис. 4.2(a)) будет совпадать с положением
свободно диффундирующей частицы, через которую справа и слева прошло
одинаковое число частиц среды (рис. 4.2(b)). Поэтому Р(ж,£) и По(х,4) экви¬
валентны.
Теперь определим точное соотношение между По (ж, i) и вероятностью рас¬
пределения P(x,t) помеченной частицы в пределе большого времени. Пред¬
положим, что характерный масштаб длины меньше чем диффузионный,
|ж| <С f1/2, и мы увидим из конечного результата, что это предположение
самосогласовано. Начнем с переписывания второго интеграла в уравнении
(4.6а)
г р
J-oQ yffarDt
о-(у-$2
f
Vn J-
(x-£)/y/4Dt
~z2 dz
4.1 Симметричный процесс с запретами
131
и после этого изменим порядок интегрирования в (4.6а), что приводит I/+ к
пиду
poo
e~z dz
п px/y/^Dt px—z\/4Di
= -у= I e~z dz / d£
J—oo J 0
= f (rj — z) e~z2 dz,
J—oo
где г/ =
X
Аналогично
у- = ру/kDtpx / (z — rf) e z2 dz.
Jrj
Наше предположение |т| C i1/2 эквивалентно неравенству \rj\ <С 1. В этом
пределе имеем
i/±(??, *) = py/Dt/n (l ± rjy/n + rj2 + ...). (4.12)
Используем асимптотику функции Бесселя, /o(2t) — е2*/л/47г<, чтобы перепи¬
сать (4.9) для к = 0 как
П0(М ~ (4тг)”1/2(г/+1/_)-1/4
Подставляя (4.12) в выражение выше и оставляя только ведущие члены, по¬
лучим вероятность равного числа левых и правых проходов через помечен¬
ную частицу
Интегрирование этого выражения по всем х дает 1/р. Следовательно, веро¬
ятность распределения помеченной частицы — действительно распределение
Гаусса
P(x,t) = рПоСМ) = Л— е х2/2(х2\ где (ж2) = |а/^- (4.13)
у2(ж2) Р V 7г
Этот результат можно вывести, хотя и более громоздко, для решеточной вер¬
сии СПЗ. Общее правило — почти всегда легче решать процессы типа слу¬
чайного блуждания в непрерывном пределе, чем в дискретном варианте.
132
Запреты
4.2 Асимметричный процесс с запретами
В асимметричном процессе с запретами (АПЗ) движение частиц подвержено
общему сносу. Мы сосредоточимся на одномерном случае, так как он снова
наиболее интересен. В общем случае в АПЗ частица прыгает направо с ин¬
тенсивностью р и налево с интенсивностью </; прыжок разрешен, только если
узел назначения свободен. Традиционно общая интенсивность прыжков по¬
лагается равной единице, т. е. q+p = 1, и рассматривается снос вправо: р> q.
Если явно не указано обратное, мы будем подразумевать, что интенсивности
прыжков полностью асимметричны, (p,q) = (1,0). Причина такого выбора
в том, что, когда снос есть, все качественные характеристики АПЗ в основ¬
ном не зависят от величины сноса. Таким образом, рассматривая полностью
асимметричную модель, мы не теряем в понимании, но обычно выигрываем
в компактности формул.
Стационарные состояния
Состояние АПЗ в любой момент задается расположением всех частиц. Ве¬
роятность Р(С, <) того, что система находится в конфигурации б в момент
времени t, эволюционирует в соответствии с основным кинетическим уравне¬
нием
dP^'^ = 22 р(е'’ Q R(e> е) - р@> *) 52 л(е ->•е')- (4-14)
ez е'
Здесь Д(е' —> С) dt — вероятность перехода из С' в 6 за интервал времени dt.
Система в конце концов достигает стационарного состояния, где выполняется
равенство
J2 ^ss(e') я(е' -> е) = pss(e) 22 R@ е'). (4.15)
е' ez
Уравнение движения, приведенное выше, универсально и описывает про¬
цессы с запретами любого типа на любой решетке. Однако существуют неко¬
торые тонкие моменты, которые могут привести к путанице. Например, нель¬
зя ли использовать основной постулат равновесной статистической механики,
чтобы выразить вес конфигурации С через ее энергию 2?(6), т. е. применить
равновесное распределение Гиббса
Peq(e) = Z-1 е~Е^т, (4.16)
где Т — температура, a Z = ~ статистическая сумма? В силу
очевидных причин ответ в общем случае — нет: в неравновесных системах
4.2 Асимметричный процесс с запретами
133
обычно нет функции энергии £(С). Вместо этого такие системы определя¬
ются через динамические правила. Эти правила задают матрицу интенсив¬
ностей Р(6 —> 6'), и, чтобы найти стационарное состояние, нужно решить
соотношения стационарности (4.15). Таким образом, существует концепту¬
альная разница между стационарными и равновесными состояниями; чтобы
помнить об этом, мы будем обозначать соответствующие вероятности Pss(£)
И Peq(C).
Отсутствие функции энергии — общее свойство необратимых процессов.
Например в агрегации, фрагментации и адсорбции, которые будут изучаться
ii следующих главах, основная динамическая переменная — это число ча¬
стиц, которое не сохраняется. Это свойство — неоспоримый знак того, что
функции энергии не существует. Напротив, для процессов с законами сохра¬
нения (таких как процесс с запретами, где число частиц сохраняется) иногда
возможно построить функцию энергии. Для процесса с запретами подходит
тривиальная функция энергии: £(С) = 0, если С — разрешенная конфигу¬
рация, и £(С) = оо в противном случае. Соответствующее распределение
Гиббса на кольце простое: как будет показано ниже, все разрешенные конфи¬
гурации имеют одинаковый вес. Если так, зачем нам выводить стационарное
состояние на кольце из (4.14), вместо того чтобы просто сказать, что это про¬
стое следствие формулы Гиббса? Причина в том, что применимость формулы
Гиббса случайна; почти любое изменение микроскопических правил процес¬
са с запретами приводит к стационарным состояниям, которые не даются
формулой Гиббса.
Пример 4.1. Ослабленный запрет: Рассмотрим АПЗ на кольце и потребуем,
чтобы в одном узле было не больше двух частиц. Каждая частица прыгает с
интенсивностью один в соседний узел справа при условии, что этот узел не пе¬
ренаселен (т. е. содержит не больше одной частицы): прыжки в узлы, которые
содержат две частицы, запрещены. Например на кольце с N = 3 узлами и М = 3
частицами конфигурация {2,1,0} разрешена, и она превращается в {1,2,0} (с
интенсивностью 2, так как любая из двух частиц может прыгнуть) или в {2,0,1}
(с интенсивностью 1). Уравнения эволюции для вероятности конфигураций бу¬
дет
Р(2,1,0) = Р(1,1,1) — ЗР(2,1,0),
Р(1,2,0) = Р(0,2,1) + 2Р(2,1,0) - 2Р(1,2,0),
Р(1,1,1) = 2Р(2,0,1) + 2Р(0,1,2) 4- 2Р(1,2,0) - ЗР(1,1,1).
В стационарном состоянии левая часть исчезает, а инвариантность по отно¬
шению к вращениям дает Pss(2,1,0) = Pss(0,2,1) = Pss(l,0,2) и Pss(l,2,0) =
134
Запреты
Pss(0,1,2) = Pss(2,0,1). Решение этих уравнений дает
Pss(2,1,0) = Pss(0,2,l) = PSS(1,0,2) =
Ри(1,2,0) = Pss(0,1,2) = Pss(2,0,1) = |,
Pss(l) 1,1) — у •
В то же время есть б способов расставить частицы так, чтобы числа заполне¬
ния узлов были (2,1,0) и один единственный способ получить числа заполнения
(1,1,1). Поэтому
Peq(2,1,0) = ^ плюс все перестановки, Peq(l? 1,1) = у.
Хотя значения весов вычислены для данного конкретного примера, важное свой¬
ство состоит в том, что стационарные веса отличаются от равновесных. Поэтому
в общем случае нельзя использовать распределение Гиббса для описания стаци¬
онарных состояний в АПЗ.
Другой важный момент — это то, что вместо того чтобы иметь дело со
сложными соотношениями стационарности (4.15), хотелось бы потребовать
выполнения более сильных условий детального баланса
Pss(e2) я(е2 ej = pss(e1) я(ех -> е2). (4.17)
Решение, которое подчиняется детальному балансу, автоматически удовле¬
творяет (4.15) и поэтому дает стационарное состояние. Однако в общем слу¬
чае детальный баланс — слишком сильное ограничение. В частности, урав¬
нение (4.17) может не иметь решения, даже когда стационарное состояние
существует (и удовлетворяет (4.15)). В качестве тривиального примера рас¬
смотрим АПЗ с одной частицей (т. е. асимметричное случайное блуждание)
на кольце из N узлов. В стационарном состоянии все конфигурации (за¬
данные положением частицы в узле п) имеют равные веса. Следовательно
Pss(n) = 1/АГ для всех п - Однако условие детального баланса
(4.15) дает
Pss(n) R(n -> п + 1) = Pss(n + 1) R(n + 1 —> n),
что неправильно, так как R(n —> п + 1) = 1 и R(n + 1 —» п) = 0. Поэтому
детальный баланс не работает для полностью асимметричного случайного
блуждания. Этот же аргумент показывает, что детальный баланс нарушает¬
ся для любой величины сноса р / q и выполняется только для симметричного
4.2 Асимметричный процесс с запретами
135
случайного блуждания. Более конкретное обсуждение разницы между усло-
миями стационарности и детального баланса дано во врезке на странице 228
раздела 6.3.
Далее в этой книге мы будем изучать неравновесные системы, которые
имеют хорошо определенные равновесные аналоги. В таких примерах стаци¬
онарные состояния совпадают с равновесными состояниями, определяемы¬
ми формулой (4.16), а условие детального баланса обычно выполняется. Мы
также встретимся с неравновесными системами без функции энергии, для
которых оказывается, что детальный баланс выполнен. Как мы увидим, де¬
тальный баланс — это гораздо более сильное условие, чем требуется для су¬
ществования стационарного состояния. Хотя равновесные решения и условие
детального баланса необязательно выполняются для неравновесных систем,
когда они применяются, это мощный инструмент, который очень помогает в
понимании неравновесных систем.
Стационарные состояния на кольце
Теперь используем основное условие стационарности (4.15), чтобы вывести
неса разрешенных конфигураций на кольце. Рассмотрим разрешенную кон¬
фигурацию 6 и обозначим через /(6) общее число островов в этой конфигу¬
рации. Например, конфигурация
оеееоо •• ооо • oteetooeeto
остров остров остров остров остров
состоит из М = 13 частиц и содержит 1 = 5 островов на кольце разме¬
ра N = 23. За временной интервал dt вероятность покинуть конфигурацию
С равна 1(6) PSS(C) dt. Аналогично, вероятность создания конфигурации С
дается суммой dt Pss(ez) по всем конфигурациям С', отличающимся от
С положением одной частицы. А именно, каждая конфигурация Q' может
быть получена из 6 передвижением самой левой частицы одного из островов
на один шаг влево. Поэтому полное число таких конфигураций равно об¬
щему числу островов 1(6). Если все конфигурации имеют одинаковые веса,
^(С7) = l(e)Pss(e), условие стационарности действительно выполняет¬
ся. Полное число разрешенных конфигураций равно (^), что есть не более
чем число способов разместить М частиц в N узлах. Следовательно каждая
разрешенная конфигурация имеет вес
(4-18)
136
Запреты
Теперь вычислим ток в стационарном состоянии. Конфигурация б вносит
вклад в ток через произвольное ребро между двумя узлами (которые мы
обозначим 1 и 2), если узел 1 занят, а узел 2 свободен. Следовательно осталь¬
ные N — 2 узла 3,4,..., N должны содержать М — 1 частиц. Полное число
таких конфигураций равно (^i) • Каждая из них добавляет 1 к току (так как
интенсивность прыжков равна единице), а вес каждой конфигурации дается
формулой (4.18). Таким образом, стационарный ток дается выражением
О
©
М N — М
N N — 1
J =
(4-19)
Взяв термодинамический предел TV, М —> оо и M/N = р, видим, что ток в
стационарном состоянии J и плотность р связаны соотношением
J = p{l-p). (4.20)
Максимальный ток равен Jmax = 1/4 при р* = 1/2. При более высоких плот¬
ностях ток меньше чем Jmax из-за малого числа свободных узлов (перегру¬
женный поток); при низких плотностях ток также меньше чем Jmax из-за
малого количества частиц (разреженный поток).
Замечательное свойство макроскопического стационарного тока (4.20) —
его соответствие самым наивным ожиданиям: ток равен произведению веро¬
ятностей найти занятый узел (р) и свободный узел справа от него (1 — р).
Вероятность такой конфигурации на самом деле равняется (ni(l — n^+i)), где
Пг — число заполнения узла г (п< = 0, если узел г пуст, и щ = 1, если узел i
занят). Это выражение дает ток ji через ребро (г,г + 1). Свойство фактори¬
зации
ji = (пД1 - ni+i)) = (пг)(1 - щ+1) = р(1 - р),
которое выполняется в АПЗ — маленькое чудо. По большей части любое
изменение микроскопических правил прыжков и запретов приводит к его
нарушению.
4.3 Гидродинамический подход
Чтобы понять свойства процесса с запретами на больших масштабах и време¬
нах, необязательно следить за каждой отдельной частицей. Это же свойство
лежит в основе гидродинамики, где нам не нужно отслеживать индивиду¬
альные траектории и столкновения молекул, чтобы описать движение жид¬
кости. Поэтому вместо микроскопического описания в терминах положений
4.3 Гидродинамический подход
137
и скоростей всех молекул, мы используем макроскопическое описание, ос¬
нованное на усредненных «гидродинамических» переменных. Пример такой
переменной — плотность р(х, i), определяемая как общее число молекул в ме¬
зоскопической области, содержащей точку х, деленное на объем этой области.
Термин «мезоскопическая» означает следующее:
• область должна быть достаточно большой, чтобы содержать такое боль¬
шое число молекул, при котором относительные флуктуации этого чис¬
ла были бы пренебрежимо малы;
• область должна быть достаточно малой, чтобы плотность (или любые
другие гидродинамические переменные) были почти постоянными внут¬
ри нее.
Поэтому гидродинамическое описание имеет смысл, если, например, размер
тела, погруженного в поток газа, много больше, чем микроскопическая длина
свободного пробега молекул жидкости.
Кроме плотности гидродинамическое описание включает также ток J (х, i)
или гидродинамическую скорость v(x, t) и часто небольшое число термоди¬
намических величин, таких как давление р(х, i) и температура Т(х, i). Все
эти величины связаны между собой гидродинамическими уравнениями, са¬
мое главное из которых — закон сохранения массы, имеющий форму уравне¬
ния непрерывности
^ + V-J = 0, J = pv. (4.21)
Для АПЗ в одномерии есть всего две гидродинамических величины: плот¬
ность р(ж,£) и ток J(x,t). Они связаны соотношением (4.20) и одномерной
версией уравнения непрерывности (4.21). Эти уравнения дают полное гидро¬
динамическое описание, и представляет собой аналог эйлеровской формули¬
ровки классической гидродинамики.
Однако гидродинамика АПЗ намного проще, чем динамика газа, так как
она включает одну величину р(х,£), которая зависит от двух переменных
х и t. Эйлеровское описание — это система зависимых нелинейных диффе¬
ренциальных уравнений в частных производных для пяти1 величин: р(х, t) и
р(х, £) плюс три компоненты скорости v(x, £), которые зависят от четырех пе¬
ременных х, t. Напротив, как мы увидим, гидродинамика АПЗ компактна и
решаема. Однако самый важный аспект макроскопического подхода состоит
в том, что он показывает нам общие свойства гидродинамики. Действительно,
1 Для газов можно выразить температуру через плотность и давление, и поэтому только
две из трех термодинамических величин независимы.
138
Запреты
множество отдельных примеров АПЗ было решено точно на микроскопиче¬
ском уровне. Эти точные решения можно сравнить с предсказаниями гид¬
родинамического подхода и сделать заключение о применимости последнего.
В классических газах и жидкостях, где точных решений не было получено,
такая возможность отсутствует.
Чтобы увидеть, что гидродинамика АПЗ решаема, скомбинируем соот¬
ношение (4.20) и одномерную версию (4.21), что дает уравнение в частных
производных (УЧП) первого порядка
g + (1_2,)g=0. (4.22)
Замена и = 1 — 2р превращает (4.22) в самое известное нелинейное УЧП
первого порядка, уравнение Бюргерса в отсутствие вязкости щ+иих = 0. В
дальнейшем мы будем неявно предполагать, что плотность лежит в пределах
0 < р < 1, что обусловлено связью с АПЗ.
Все УЧП первого порядка гиперболические (т. е. волнового типа) и опи¬
сывают передачу сигнала с конечной скоростью вдоль характеристик. Для
уравнения (4.22) характеристика — это кривая в плоскости x-t с наклоном
dx
di = 1~2p- (423)
Дифференцируя р вдоль характеристики, находим
dp _др dxdp_
dt dt + dt дх ’
т. е. р не меняется вдоль характеристик. (Это и есть причина, по которой
(4.23) используется как определение характеристики.) Поскольку вдоль ха¬
рактеристики р — постоянная, наклон (4.23) тоже не меняется, т. е. харак¬
теристики — это прямые линии2. Нахождение характеристик — это ключ к
решению всей задачи. Предположим, мы хотим решить задачу Коши, т. е.
уравнение (4.22) с начальными условиями p(x,t = 0) = /(ж). Пусть (пока
неизвестная) характеристика начинается в х = £ в момент t = 0. Вдоль этой
характеристики плотность остается постоянной р = /(£), и поэтому соотно¬
шение (4.23) запишется как уравнение
^ = 1-2/(£), x(t = O) = e, (4.24)
2В более общем случае однородных квазилинейных УЧП первого порядка, т. е. уравне¬
ний вида pt + с(р)рх = 0 с произвольной функцией с = с(р), характеристика имеет наклон
= с(р) и является прямой линией.
4.3 Гидродинамический подход
139
решение которого имеет вид
z = £ +[1-2/0. (4-25)
Эта формула в принципе завершает решение: на каждой характеристи¬
ческой линии (4.25) плотность принимает значение р = /(£). Пока характе¬
ристики не пересекаются, это решение ведет себя хорошо. Однако самое ин¬
тересное поведение возникает, когда характеристики пересекаются. На пере¬
сечении гладкие или классические решения перестают существовать, и рож¬
даются ударные волны. Как будет видно ниже, построение таких разрывных
решений с ударными волнами очень показательно. Решения гиперболических
УЧП с ударными волнами отнюдь не исключительный случай. На самом де¬
ле обычно справедливо обратное, а именно решения без ударных волн — это
исключения. Например, если в решении уравнения (4.22), есть пара точек
£i < £2, таких что соответствующие начальные плотности удовлетворяют
неравенству /(£1) < /(£2), соответствующие характеристики (4.25) пересека¬
ются в момент
. _ 1 6 - £i
2/(€2)-/(€1)*
Задать начальный профиль плотности, являющийся монотонно убывающей
функцией пространственной координаты, — это единственный способ избе¬
жать появления ударных волн.
Поскольку разрывные решения — скорее правило, чем исключение, есте¬
ственно изучать эволюцию, начинающуюся с разрывных начальных условий.
Классический пример — это ступенчатая функция
рь, х < О,
рд, х > 0.
Попробуем определить, как система эволюционирует, стартовав со ступень¬
ки. Одна из причин, по которой мы рассматриваем этот простой пример —
множество важных приложений. Одно из них — эволюция углового фронта
в модели Изинга, которая обсуждается в разделе 8.3 и может быть представ¬
лена как эволюция ступеньки плотности.
Пример 4.2. Волна разрежения: рь > Pr- Поскольку начальная плотность —
невозрастающая функция координаты ж, ударных волн не должно быть. Все
характеристики начавшиеся в х < 0 имеют один и тот же наклон 1—2рь; поэтому
Р = Pl в области х < (1 — 2рь)£. Аналогично, р = pr, когда х > (1 — 2рд)£.
Нам нужно определить плотность в незаполненной (бесконечной) треугольной
области (1—2pL)t < х < (1—2рд)£ (рис. 4.4). Решение должно быть непрерывным
140
Запреты
Рис. 4.4. Пространственно-временная диаграмма, иллюстрирующая пробел в ха¬
рактеристиках. В показанном примере начальные данные р = рь = 1/2 распро¬
страняются вдоль вертикальных характеристик, а начальные данные р = pr —
вдоль характеристик с положительным наклоном
и должно связывать между собой р = рь и р = pR. Взяв р = с, где рь > с > рд,
мы видим, что соответствующие характеристики (которые должны исходить из
начала координат) определяются из уравнения (4.23), при х = (1 — 2с)£. Таким
образом, имеем
р(х, t)
PL, X < (1 - 2pL)t,
4 (1 - x/t), (1 - 2pL)t < x < (1 - 2pR)t,
pR, ж > (1 — 2рд)4.
(4-27)
Решение такого типа называется волна или веер разрежения (рис. 4.5).
г=0
t>0
Рис. 4.5. Превращение ступеньки плотности в волну разрежения, описываемое
уравнением (4.27)
То же самое решение можно также получить с помощью скейлингового под¬
хода. В уравнении движения (4.22) возникает одна и та же степень переменных
х и t. Этот факт предполагает, что решение должно иметь вид p(rr,t) = f(z),
где z — x/t. Подставив этот вид в уравнение (4.22), получим обыкновенное диф¬
ференциальное уравнение /'[(1 — 2/) — z] = 0, решение которого или f = 0,
4.3 Гидродинамический подход
141
или f = (1 — z)/2. Потребовав непрерывности этих решений, мы воспроизве¬
дем (4.27).
Пример 4.3. Ударная волна: рь < Pr- В этом случае характеристики сразу
пересекаются, так что начальная ударная волна сохраняется. Если с — скорость
ударной волны, решение будет сохранять начальную форму ступеньки
p(x,t)
Pl, х <ct,
pR, x > ct.
Чтобы определить скорость с, мы используем сохранение массы. Рассмотрим
большую область, содержащую ударную волну. Ток в эту область слева — рь(1 —
рь), а ток из этой области вправо — рд(1—Pr)- Приравнивая полный поток массы
в эту область за время At полному приращению массы, получим
[рь(1 - Pl) - Pr(1 - Ря)] At = (pL - PR)c&t,
откуда скорость ударной волны равна
с = 1 - рь - Pr-
(4.28)
Интригующий аспект решения с ударной волной возникает, при 0 < рь < PR
и PR + рь = 1> когда с=1 — рь — ря = 0. В этом случае гидродинамика не пол¬
ностью предсказывает поведение около ударной волны. Поскольку исходный
АПЗ — стохастический процесс, положение ударной волны тоже стохастиче¬
ское. В общем случае она находится в точке ct + 0(\/f) с флуктуациями по¬
рядка л/i, которые изменяются от реализации к реализации. Поэтому обычно
в пределе t —> оо ударная волна далека от х = 0. Если она оказывается далеко
справа, плотность в х = 0 будет равна рь? и это случается в 50% реализаций.
С такой же вероятностью ударная волна может быть далеко слева и плот¬
ность будет равна pr. Таким образом, в этом специальном случае плотность
в начале координат — случайная переменная, тогда как она является детер¬
министической для любых других начальных условий с ударной волной.
Теперь обсудим судьбу кусочно-постоянного начального профиля плотно¬
сти с двумя разрывами
{PL, X < 0,
РМ, о < х < X, (4.29)
Ря, х > X.
Теперь в задаче есть масштаб X. Гидродинамический подход применим, толь¬
ко когда величина X макроскопическая, т. е. много больше микроскопической
142
Запреты
постоянной решетки. Вначале разрывы в х = 0 и X далеки друг от друга,
так что не чувствуют друг друга. В рамках гиперболических УЧП это утвер¬
ждение вполне корректно, так как сигналы распространяются с конечными
скоростями. Поэтому предсказание для эволюции ступеньки (4.26) дает точ¬
ное поведение на малых временах для эволюции двух ступенек: результат —
комбинация двух решений, описанных в примерах 4.2 и 4.3. Теперь рассмот¬
рим поведение, когда два возбуждения взаимодейтсвуют.
Пример 4.4. Слияние ударных волн: Для рь < рм < Pr скорость ударной
волны слева 1 — Pl — Рм, что больше чем скорость 1 — рм — Pr ударной волны
справа. Поэтому левая волна догонит правую в момент Т = X/(pr — рь)- Потом
волны сольются и образуют одну ударную волну со скоростью 1 — рь — рд. Таким
образом, для t > Т решение принимает вид
р(х t\ = f?L’ х < (1 - pL - рм)Т + (1 - Pl- PrN - Т),
1 Pr, х > (1 - pl - рм)Т + (1 - рь - Рд)(£ - T).
Другие возможности включают в себя взаимодействие двух волн разрежения,
и взаимодействие ударной волны и волны разрежения. Приведем пример по¬
следнего.
Пример 4.5. Взаимодействие ударной волны и волны разрежения. Предполо¬
жим, что ударная волна сначала слева, так что рь < Рм, и что второй раз¬
рыв создает волну разрежения, для которой требуется рм > Pr- Для опреде¬
ленности положим рь < Pr- Сначала ударная волна движется со скоростью
с=1 — рь — PMjStee положение s = ct. Волна разрежения нетривиальна в об¬
ласти CMt < х — X < CRt, где см = 1 — 2рм и сд = 1 — 2рд. Нужно отметить,
что с > см, так что ударная волна сталкивается с волной разрежения в момент
Г* = Х/(с — см) = Х/(рм — Рь)- Потом начинается взаимодействие, и оно про¬
должается, пока ударная волна не пройдет через всю волну разрежения. На этой
стадии положение ударной волны s(t) удовлетворяет уравнению
PL-
М-
Решая это уравнение при условии s(T*) = сТ*, получим s = X + (1 — 2pb)t —
%(рм — Pb)y/tT*. В момент Т* ударная волна достигнет правого конца волны
разрежения. Из s(T*) = X + CrT* находим
Рм - Рь\2т = Рм - Рь у
Pr-Pl) * (Pr ~ Pl)2
Наконец, когда t > Т*, волна разрежения уже полностью поглощена ударной
4.4 Микроскопический подход
143
волной, и в результате остается одна ударная волна, разделяющая плотно¬
сти pl и pr. Таким образом, ударная волна движется в соответствии со следу¬
ющими уравнениями
s(t) = <
(1 — Pl — Рм )Л
X + (1 — 2рь)£ — 2у/Х{рм — pL)t,
0<t<T„,
T*<t< T*,
t > T*.
{-^X + (l-pL-PR)t,
Иллюстрация к эволюции этой системы показана на рис. 4.6
X х
"х
(с)
Рис. 4.6. Эволюция ударной волны и
PL = Ъ’РМ = 1 и PR = 5
волны разрежения для частного случая
4.4 Микроскопический подход
Поскольку АПЗ — сильно взаимодействующая система с бесконечным числом
частиц, не будет неожиданностью, что она была решена лишь в нескольких
случаях. Однако для простых начальных условий (4.26) с одной ступенькой
точный подход работает3. Тем не менее, анализ довольно сложен и требу-
3 Однако для начальных условий с двумя ступеньками точных результатов нет.
144
Запреты
ет развития серьезных аналитических инструментов, так что мы представим
здесь лишь несколько ключевых фактов и качественных результатов. Из гид¬
родинамического описания ясно, что из двух характерных примеров: ударной
волны и волны разрежения — ударную волну легче описать, так как она су¬
щественно стационарна, тогда как волна разрежения меняется со временем.
Такая же качественная разница проявляется и в микроскопическом описании:
меняющуюся волну разрежения труднее анализировать.
Ударная волна
В гидродинамическом приближении ударная волна приходит в (неравновес¬
ное) стационарное состояние в системе отсчета, которая движется вместе с
ней — свойство, которое упрощает ее анализ. В АПЗ, однако, расположение
волны флуктуирует от реализации к реализации. Нам нужно найти способ
избавиться от этих флуктуаций и поместить систему отсчета точно в место
ее расположения. Эту задачу можно выполнить, применив хитрый трюк: за¬
менив одну вакансию частицей второго сорта и задав правила прыжков, при¬
водящие эту частицу к месту расположения ударной волны. Динамические
правила
10 —> 01, 20 —> 02, 12 21, (4.30)
подходят для этой цели. Здесь частицы обозначены 1, вакансии 0 и частица
второго сорта 2. Все процессы в (4.30) происходят с интенсивностью 1, тогда
как такие процессы как 21 —> 12, которые не показаны, запрещены. Каждая
частица рассматривает частицу второго сорта как вакансию, и следовательно
АПЗ (движение частиц) не меняется. Наоборот, по отношению к вакансиям
частица 2 ведет себя как обычная частица.
Теперь рассмотрим движение частицы второго сорта со ступенчатыми на¬
чальными условиями (4.26), где pl < что обеспечивает распространение
ударной волны. Частицы второго сорта прыгает вправо с интенсивностью 1,
если ее правый сосед — вакансия, и влево с интенсивностью 1, если ее левый
сосед — частица. Поэтому, если частица второго сорта находится в однород¬
ном окружении с плотностью частиц р, ее скорость равна плотности вакансий
впереди, 1 — р, минус плотность частиц сзади, р, т. е. v = 1 — 2р. Для сту¬
пенчатых начальных условий скорость частицы второго сорта равна 1 — 2р^,
если она находится слева от ударной волны, и 1 — 2рд — справа. В первом
случае скорость больше, чем скорость ударной волны с=1 — Pl — pr, тогда
как в последнем — меньше. Поэтому частица второго сорта притягивается
к ударной волне, и мы можем определить положение волны как положение
частицы второго сорта.
4.4 Микроскопический подход
145
Это рассуждение приводит нас к пониманию того, что профиль плотно¬
сти в системе отсчета частицы второго сорта описывает микроскопическую
структуру ударной волны. Доказано, что это действительно так, а ответ для
плотности был получен через матричный анзац4 с помощью технически слож¬
ных вычислений. Однако некоторые свойства локализованных возбуждений
можно объяснить, исходя из более простых рассуждений. В следующем раз¬
деле мы рассматриваем одно такое неравновесное стационарное состояние,
обратное ударной волне: волну разрежения.
Волна разрежения
Для определенности рассмотрим начальные условия ро(#) = 1 при х < 0 и
Ро(х) = 0 при х > 0, для которых гидродинамическое решение имеет вид
р(М)
1, X < —t,
< j (1 — x/t), |ж| < t,
О, х > t.
(4-31)
Гидродинамическое решение (4.31) имеет разрыв первой производной в х =
±t. Эти сингулярности — следствие гидродинамического приближения, а
именно гиперболической природы невязкого уравнения Бюргерса. Однако
распределение вероятности того, что правая частица находится в уз¬
ле М в момент времени £, — гладкая функция. Можно найти заме¬
тив, что все остальные частицы не оказывают никакого влияния на самую
правую частицу, так что ее положение сводится к положению асимметрично¬
го случайного блуждания5. Распределение вероятности удовлетворяет
уравнению
dt
= #M-1 - ^м,
решение которого, когда самая правая частица стартует с нуля, 3^м(0) = 5м,о>
имеет вид
/М
^(<) = М!е’*- (4'32)
Из этого распределения Пуассона имеем
(М) = 52 MKM(t) = t, (М2) - (М)2 = t. (4.33)
М>0
4Мы опишем матричный анзац и его применение к открытым системам в разделе 4.5.
5Этот аргумент основан на предположении, что АПЗ — полностью асимметричный
процесс. В частично асимметричном случае положение левого соседа самой правой частицы
становится важным, а на него в свою очередь влияет положение его левого соседа и т. д.,
так что редукции к одночастичной задаче больше не происходит.
146
Запреты
Центр распределения самой правой частицы находится в М = t, что согласу¬
ется с гидродинамическими предсказаниями, а ширина этого распределения
растет диффузионно со временем.
Гидродинамическое описание можно улучшить, избавившись от разры¬
вов первой производной в х = ±t. То, что такое решение существует, кажет¬
ся естественным, если вспомнить классическую гидродинамику. Уравнение
Бюргерса в отсутствие вязкости (4.22) относится к эйлеровскому описанию
в классической гидродинамике, которое допускает ударные волны и другие
разрывные решения. Уравнение Навье - Стокса дает следующий уровень при¬
ближения, где такие разрывы сглаживаются. Для АПЗ аналог уравнения На¬
вье-Стокса — это уравнение Бюргерса
др , /-■ дР 1 д2Р
dt дх 2 дх2 ’
(4-34)
решение которого для волны разрежения действительно гладкое. В преде¬
ле большого времени это гладкое решение почти неотличимо от (4.31) для
x/t внутри (—1,1), но отклоняется от приближенного гидродинамического
решения на расстоянии порядка ±\/i от х = ± t. Качественная картина этого
отклонения согласуется с точным результатом (4.33) для ширины.
Как мы отмечали раньше при обсуждении ударных волн, классические
методы определения плотности профиля очень сложны. К счастью, неко¬
торые качественные свойства решения, соответствующего волне разрежения,
можно извлечь из эвристических аргументов. К примеру, рассмотрим полный
ток. Мы определяем ток как полное число частиц, прошедших через ребро
(0,1) к моменту времени t, или, эквивалентно, полное число частиц N(t) на
первоначально пустой полуоси х > 0. Из гидродинамического решения (4.31)
находим
Г°° 1
N(t) = / р(ж, t)dx = - f. (4.35)
Jo 4
Вместо того чтобы интегрировать профиль плотности (4.31), можно получить
(4.35), пользуясь двумя основными свойствами гидродинамического решения:
(i) плотность в х = 0 равна 1/2, a (ii) соответствующий локальный ток (см.
(4.20)) равен J = р(1 — р). Следовательно, интегрированный по времени (или
полный) ток действительно равен t/4.
Поскольку N(t) — случайная величина, уравнение (4.35) описывает толь¬
ко средний полный ток. Основная задача — рассчитать флуктуации тока.
Первое свойство — ток флуктуирует на масштабе f1/3, так что
ЛГ(0 = ^ + ?/зе
(4.36)
4.4 Микроскопический подход
147
Рис. 4.7. Отображение АПЗ на модель роста поверхности осадка: (а) ступенчатые
начальные условия, (Ь) состояние через некоторое время. Элементарное событие
осаждения (закрашенный квадрат) соответствует прыжку в АПЗ (стрелка)
для больших i, где £ — стационарная случайная переменная. Чтобы понять,
откуда берется скейлинг i1/3, отобразим АПЗ на эволюцию поверхности, опре¬
деляемую следующим образом (рис. 4.7): разрешены только элементарные
события осаждения в локальные минимумы, и все эти события происходят с
одинаковой интенсивностью 1. Интегрированный по времени ток может быть
определен как высота фронта в начале координат. Уравнение (4.36) теперь
допускает простую интерпретацию: фронт растет со скоростью 1/4 и флук¬
туирует на масштабе t1/3. Модель осаждения должна принадлежать к классу
универсальности КПЖ (раздел 2.9), и поэтому флуктуирующая часть урав¬
нения (4.36) — просто еще одна запись скейлинга КПЖ. Как уже упоми¬
налось, соответствие между АПЗ и ростом поверхности может быть исполь¬
зования для решения задачи о границе в модели Изинга-Глаубера (раздел
8.6).
Найти распределение СР(£) случайной переменной £ — нелегкая задача, так
как У(£) оказывается решением уравнения Пенлеве И6. В качестве гораздо
более простой альтернативы мы используем эвристические аргументы, что¬
бы показать, что экстремальное поведение У(£) негауссово. Сначала найдем
асимптотическое поведение У(£) в пределе £ —> —оо. Формально мы хотим
вычислить
P(JV,t) = Prob[AT(t) = AT],
когда i/4 — N » t1/3. Рассмотрим экстремальный случай, отсутствие тока,
соответствующий N = 0. В этом случае мы должны убедиться, что самая
правая частица не сдвинулась; этот критерий дает Р(0, t) = e_t. Величина £,
соответствующая величине N = 0, равна £ = — £2/3/4. Переписывая е~* как
81£|3/2, заключаем, что 1п СР(^) ~ — с_|£|3/2. Как объясняется во врезке ниже,
6Уравнение Пенлеве II имеет вид у"(х) = 2у3 + ху + а, где а — комплексная константа.
148
Запреты
4.2. Вероятность распределения из поведения хвостов
Оценки, приведенные в (4.42), дают иллюстрацию удобного общего метода нахож-
дения распределений вероятности стохастических величин из их экстремального
поведения. Такие экстремальные свойства обычно легко определить, откуда с ми¬
нимальными усилиями извлекаются ведущие асимптотики вероятностных распре¬
делений.
Как первый тривиальный пример рассмотрим распределение вероятности случай¬
ного блуждания в одномерии. Предположим, что мы не знаем, что это распреде¬
ление гауссово, но зато мы знаем, что типичное смещение растет со временем как
t1/2. Благодаря этому факту, в предположении скейлинга, распределение вероят¬
ности Р(т, £) должно иметь вид
P(x,t)~±$(x/y/t), (4.37)
Vt
где коэффициент обеспечивает нормировку fP(x,t) dx = 1. Какова скейлинговая
функция Ф(г)? Эта функция убывает для больших г, но как быстро? Очевидно,
что при больших z функция Ф(г) должна убывать быстрее, чем любая степень.
Если бы это было не так, то достаточно высокие моменты распределения расхо¬
дились бы. Естественная гипотеза тогда — это
Ф(з) ~ ехр(—zs). (4.38)
Пользуясь этим выражением, мы можем определить «хвостовой» показатель 6
следующим образом: рассмотрим «растянутое» блуждание, где каждый шаг —
шаг направо. Вероятность сделать t таких шагов подряд равна 2_t. С другой
стороны, такое растянутое блуждание соответствует скейлинговой переменной
z = жд1/2 = г1/2, а уравнение (4.38) дает Ф(г = t1/2) ~ ехр[—(t1/2)6]. Чтобы
воспроизвести точное поведение 2_t, мы должны иметь 6 = 2. Поэтому мы за¬
ключаем, что Ф(г) ~ ехр(—const, х z2). Из-за грубости оценки вероятности хвоста
мы не знаем константу внутри гауссовой функции.
В качестве немного менее тривиального примера рассмотрим сомоизбегающее
блуждание в d измерениях. Это решеточное случайное блуждание с дополнитель¬
ным ограничением: любой узел может быть посещен не более чем один раз. Типич¬
ное смещение самоизбегающего блуждания растет как tu. Известно, что и = 1/2
для d < 4. По аналогии с уравнением (4.37) мы ожидаем, что распределение кон¬
цов блужданий в момент t дается выражением
P(r, t) -> t~du exp a(r/i"/]. (4.39)
показатель степени в асимптотическом выражении У(£), полученном с помо¬
щью эвристических аргументов, вообще говоря, — правильный, хотя ампли¬
туда, входящая как множитель перед |£|3/2, ненадежна. Поэтому мы записы¬
ваем асимптотику в виде 1пТ(£) ~ —с_|£|3/2 с неизвестной амплитудой с_,
а не множителем 8, получающимся из эвристического подхода.
4.4 Микроскопический подход
149
4.2. Продолжение
Рассмотрим снова растянутое случайное блуждание, в котором t шагов сделаны в
одном направлении. Растянутое блуждание соответствует скейлинговой перемен¬
ной z = x/t'' = t1_", так что распределение конечной точки принимает вид
P(r ~ t, t) -> t-dv ехр [-а(?-*У]. (4.40)
С другой стороны, растянутое блуждание возникает с вероятностью (2d)-t, по¬
скольку все шаги должны быть в одном направлении. Сравнив (2d)-1 и (4.40),
получим общее соотношение для показателей
5 = (1-Z/)-1. (4.41)
Мы используем эту же аргументацию, чтобы получить оценки, показанные в
(4.42). Этот метод работает в различных контекстах и зарекомендовал себя как
мощный и общий подход, который, однако, прост в применении.
Для изучения поведения при больших £ нужно оценить P(7V, t) в области
N — t/4 » i1/3. С этой целью мы модифицируем АПЗ без последствий для ре¬
зультата, но так, чтобы у N был конечный верхний предел. Вместо процесса
в непрерывном времени мы определим эволюцию в дискретном времени, так
что все подходящие частицы (с вакансией справа) прыгают с вероятностью
1/2. Для этого синхронного АПЗ полное число частиц, которые перемеща¬
ются в полупространство х > 0, удовлетворяет ограничению N < t. Теперь
вычислим вероятность достижения этой верхней границы. На первом шаге
единственная подходящая частица должна прыгнуть (с вероятностью 1/2);
иа втором шаге две подходящие частицы должны прыгнуть (с вероятностью
1/4) и т. д. Поэтому имеем
Значение £ соответствующее N = t — это £ = 3t2/3/4. Переписывая 2-t(t-1)/2
через £, мы находим асимптотику In У ~ —£3. Опять мелким деталям этой
асимптотики не стоит доверять — и потому что £ расходится одновремен¬
но с t, и потому что мы модифицировали правила АПЗ — но качественная
зависимость от £ должна быть правильной.
Собрав наши результаты, получим хвосты распределения вероятности
е-с-1$|3/2) £ -4. —оо,
е~с+^3, £ -> оо.
Таким образом распределение асимметрично, и поведение хвостов негауссово.
150
Запреты
4.5 Открытые системы
Наконец, мы представляем точное решение для неравновесного стационарно¬
го состояния открытой системы (рис. 4.8), которая соединяет два бесконеч¬
ных резервуара с различными плотностями частиц. Частицы подчиняются
Рис. 4.8. АПЗ в открытой системе. Одна из двух внутренних частиц (временно)
неподвижна из-за запрета
динамическим правилам АПЗ во внутренних узлах, в самый левый узел ча¬
стица приходит с интенсивностью а, а из самого правого выходит с интен¬
сивностью /3. Символически можно записать
0 1 в узле г = 1,
в узле г = N.
Наша задача — определить свойства стационарного состояния.
Пусть щ будет число заполнения: щ = 1 ,если узел г занят, и чц = 0, если
пуст. Мы также будем использовать переменные потока ji = пД1 — n^+i).
Состояние узла i меняется в одном из следующих случаев: (i) узел свободен, а
его левый сосед занят, тогда переход 0 —> 1 происходит с интенсивностью ji-Г,
(ii) узел занят, а его правый сосед свободен, тогда переход 1 -» 0 происходит
с интенсивностью ji. С учетом того что ji = 0, если щ = 0, a ji-± = 0, если
щ = 1, мы видим
щ —> 1 — щ с интенсивностью Wi = ji—± + ji. (4.43)
Эквивалентно, за инфинитезимальный интервал времени dt число заполне¬
ния эволюционирует следующим образом
ni(t) с вероятностью 1 —Widt,
1 — rii(i) с вероятностью Wi dt,
(4.44)
Усреднение (4.44) дает эволюцию локальной плотности
= Ml - 2n»)).
(4.45)
4.5 Открытые системы
151
Используя соотношение Wj = + ji и выражение для локального тока,
перепишем (4.45) в виде
= (ni-x(l - П»)) - (ni(l - ni+i)). (4.46)
Интуитивно эти уравнения выражают изменение локальной плотности в дан¬
ном узле как ток в этот узел минус ток из этого узла. Однако одноузельные
средние перемешаны с двухузельными средними. Если мы напишем уравне¬
ния для локальных токов (двухузельные средние), мы получим трехузельные
средние. Продолжая, мы получим бесконечную иерархию уравнений, в кото¬
рой fc-узельные средние будут выражаться через (fc + 1)-узельные средние.
Эта иерархическая структура — главное препятствие, стоявшее на пути по¬
лучения зависимого от времени аналитического решения.
Динамические правила (4.43) также выполняются на границе, если поло¬
жить jo = а(1 — ni) и jtv = Используя эти результаты и уравнения
(4.46), получим уравнения движения
d(nj)
dt
- (ni(l -n2)),
< (nj_i(l - Hi)) - (n»(l - rii+i)},
-/3(пн) + (nw_i(l - tin)},
i = l,
1 < i < N,
i = N.
(4-47)
Матричный метод
Задача о стационарном состоянии АПЗ в открытой системе может быть ре¬
шена точно с помощью матричного анзаца7. Главная идея — записать рас¬
пределение вероятности для стационарного состояния в абстрактном виде
произведения матриц
Р(п) = -А- <ТУ| + (1 - ni)E] IV). (4.48)
г=1
Здесь п = (.. .Пг_1,Пг,Пг+1,...) — набор чисел заполнения узлов решетки,
D,E — матрицы, свойства которых определены ниже, и (РИ|, |V) — векто¬
ра состояния. Под знаком произведения матрица D сопоставляется занятому
узлу (ni = 1), а матрица Е — свободному. Например, можно записать веро¬
ятность для конфигурации чисел заполнения {1,0,1,0} как Р({1,0,1,0}) =
7Матричный метод напоминает анзац Бете, который был использован для получения
множества точных решений статистических моделей в физике конденсированного состоя¬
ния.
152
Запреты
Д^"1(И/’|Р£?Р£’|У). Множитель Zn в (4.48) обеспечивает нормировку распре¬
деления вероятности, т. е. P(n) = 1 при суммировании по всем 2N воз¬
можным конфигурациям N узлов решетки. Таким образом, нормировочный
множитель имеет вид
ZN = 0У|(Р + E)N\V) = (Ж|С^| V), (4.49)
где С — D + Е. Используя матричный анзац (4.48), можно записать локаль¬
ные плотность и ток в компактном виде
(ni) = <tv|c*-‘rcw-i|v>/zK.
O'i) = <Wr|Ci_1-D-ECK-i-1|V)/Zw.
Например, для (щ) состояние первых г — 1 и последних N — г — 1 узлов не
задано, что выражено множителями Сг_1 и С^-г-1, Т0Гда как у3ел занят,
что соответствует множителю D. Для применения матричного метода мы
должны найти матрицы D,E и векторы (1У|, |У), такие, чтобы матричный
анзац (4.48) давал стационарное состояние. На самом деле, как мы увидим,
нам не нужно явного представления этих матриц — важна алгебра, которой
они удовлетворяют.
В стационарном состоянии уравнение (4.47) подразумевает, что все сред¬
ние локальные токи однородны: (jo) = (Д) = ... = (j^ = ... = (jjv-i) = (jiv)-
Эти условия дают
a(W|EC'7V_1| V) = (W\DECn~2\V), (4.51а)
(WIC^DEC^-^IV) = (W\CiDECN~i~2\V), (4.51b)
(iy|CN"2PE|y) = ^(W|C'JV"1P|V). (4.51c)
Внутренние условия (4.51b) можно выполнить, положив (DE)C = C(DE),
т. e. матрица DE коммутирует с С = D + Е. Эта коммутативность будет
выполняться, если матрицы DE и D + Е пропорциональны друг другу. Ока¬
зывается, что решение будет иметь вид произведения матриц (4.48), если
мы потребуем выполнения простейшего соотношения между DE и D + E,
а именно, DE = D + Е. Подставив этот результат в (4.51а) и (4.51с), ви¬
дим, что эти соотношения действительно выполняются, если a(W|£? = (РИ|
и /3D\V) = |V), соответственно. Поэтому, если для матриц D,E и векторов
(ТУ| и |У) справедливы равенства
DE = D + Е, (W\E = а_1(М D\V) = p-^V), (4.52)
то локальные плотности действительно стационарны.
4.5 Открытые системы
153
Стационарность локальных плотностей еще не доказывает, что матрич¬
ный анзац дает стационарное состояние: мы не показали что локальные токи
(или двухточечные корреляционные функции (щгцУ) стационарны или что
трехточечные корреляционные функции стационарны, и т. д. Таким образом,
матричный анзац (4.48) вместе с соотношениями (4.52) представляет собой
обоснованное предположение, которое оказывается правильным для АПЗ в
случае открытой системы. В частности, когда одноточечные средние стаци¬
онарны, все более высокие средние и целое распределение Р(п) также обла¬
дают этим свойством.
Доказательство того, что матричный анзац дает стационарное распреде¬
ление, несложно, но громоздко. Мы иллюстрируем справедливость матрич¬
ного анзаца двумя примерами.
Пример 4.6. Маленькие системы. Рассмотрим простейший случай N = 1.
Воспользовавшись соотношениями (4.52), получаем (РИ|Р|У) = a_1(VK|V) и
(ТУ|7?|V) = /3~1 (РИ|У). Поэтому система пуста с вероятностью, равной Р(0) =
о-1/(о-1 + /З-1) = Р/(а + /?), и занята с вероятностью Р(1) = а/(а + Р}. Эти
вероятности стационарны. Поскольку пустое состояние разрушается с интенсив¬
ностью аР(0) и создается с интенсивностью /ЗР(1), равенство аР(0) = РР(1)
выполняется.
Для N = 2, пользуясь уравнением (4.52), находим
(W\EE\V) =а"2(1У|У),
(ту|рр|у) = or'p-^ww),
(W\DE\V) = (а”1 + /3-1)(ТУ|У),
(W\DD\V) = P~2(W\V).
Чтобы убедиться, например, что пустое состояние {0,0} разрушается и создается
с одинаковыми интенсивностями, нужно проверить, что
a(W\EE\V) = P(W\ED\V).
Это равенство действительно выполняется. Таким же образом показываем, что
остальные три состояния также стационарны.
Пример 4.7. Специальные конфигурации в системе произвольной длины. Рас¬
смотрим систему длины N. Попробуем доказать, что специальная конфигурация
0 — 001£—_1, (4.53)
М N—M
вероятность которой согласно матричному анзацу равна (W\EM DN~M \ V) / Zn ,
создается и исчезает с одинаковыми интенсивностями. (N и М произвольны в
пределах 1 < М < N — 1.)
154
Запреты
Конфигурация (4.53) создается с интенсивностью (ТУ|£7М XDEDN м ^У)/^,
поскольку она получается из конфигурации
0 — 010 l^J. .
М-1 N—M—1
Выход из состояния (4.53) происходит, когда частица поступает из резервуа¬
ра слева или когда самая правая частицы уходит из системы. Поэтому полная
интенсивность выхода равна (а + /3)(W\EM Dn~m\V)/Zn. Таким образом, вес
конфигурации (4.53) остается постоянным, если
(W\EM~1DEDN~M~1\V) = (а + f3)(W\EMDN-M\V). (4.54)
С помощью (4.52) легко проверить (4.54).
Обобщая анализ из предыдущего примера, можно доказать, что решение,
в виде матричного анзаца, стационарно. Этого еще недостаточно, так как мы
не доказали существования матриц D,E и векторов (ТУ|, |У), удовлетворяю¬
щих (4.52). Наилучший способ справиться с этой проблемой — игнорировать
ее: мы просто постулируем соотношения (4.52), и тогда все веса можно со¬
считать с помощью чисто алгебраических манипуляций. Этот подход очень
сильно напоминает введение повышающих и понижающих операторов для
гармонического осциллятора в квантовой механике, где нам почти никогда
не нужно явного представления этих операторов. Все что нужно — это опе¬
раторная алгебра.
Непосредственно в вычислениях мы встречаем операторы вида
(W\ ■ ■ ■ DaEbDcEd ■ ■ ■ \V).
Применяя соотношение DE = £*+£>, можно передвинуть операторы Е налево
и переписать матричное произведение как сумму канонических матричных
произведений iy\f\EADB|V). Мы можем вычислить канонические произведе¬
ния, пользуясь остальными соотношениями (4.52), что дает
(WlEpD^V) = a~p/8-g(WlV). (4.55)
Пример 4.8. Коммутирующие матрицы. Давайте выясним, возможно ли, что¬
бы матрицы D и Е коммутировали, т. е. ED — DE = 0. Используя (4.52), найдем
общее выражение для матричных элементов коммутатора
(№|(DE - ВС)|И = (I + i - (W|V> = (1У|У).
4.5 Открытые системы
155
Следовательно, матрицы D и Е могут коммутировать, только когда а + /3 = 1.
Вдоль этой линии мы можем выбрать матрицы в виде констант: Е = а-1 и
D = /З-1, а вектора будут (W| = |У) = 1. Таким образом, вдоль линии a + fi = 1
нет корреляций. В частности, все конфигурации с М занятыми узлами имеют
вероятность ам pN~M независимо от расположения частиц. Для таких величин
а и /3 ведут себя также как кольцо.
Вне линии а + /3 = 1, вдоль которой достаточно одномерного представ¬
ления, представление должно быть бесконечномерным! Это редкий случай,
когда для решения конечной проблемы (с 2N состояний) требуются беско¬
нечномерные матрицы. Мы не доказываем этого утверждения и не даем яв¬
ных представлений, поскольку, как уже было замечено, явного представления
матриц и векторов не требуется — вычисления проще проводить, формально
пользуясь соотношениями (4.52) как набором аксиом.
Стационарное состояние
Вычислим ток J = (ji}. Используя выражение (4.50) для (ji} в сочетании с
DE = D + Е = С, получим компактную общую формулу
т= (уис^-Чу)
(ТУ|С^|У) ’
из которой следует, что нам нужно вычислить только = (WIC^IV) для
всех N. Для этого мы придерживаемся стратегии представлять (D + E}N как
сумму операторов в канонической форме (с Е слева от D}. Для N — 2
(D + Е}2 = E2 + ED + DE + D2
= E2 + ED + (D + E} + D2,
поскольку в единственном члене DE нужно менять порядок. Аналогично для
N = 3 выражение
(D + Е}3 = Е3 + E2D + EDE + DE2 + ED2 + DED + D2E + D3
= E3 + E2D + E(D + E} + (D + E}E + ED2
+ (D + E}D + D(D + E} + D3
= E3 + E2D + ED + E2+ (D + E} + E2 + ED2
+ D2 + ED + D2 + (D + E) + D3
= E3 + E2D + ED2 + 2(E2 + ED + D2} + 2(E + D}
156
Запреты
дает требуемую сумму. Отметим, что канонические члены с одинаковой пол¬
ной степенью имеют одинаковые амплитуды. Из этого факта следует общая
структура
N р
(d+e)n = а(р> ю 22 E9DP~9-
р=1 д=0
Амплитуды А(р, N) для р < N и маленьких N легко вычисляются, так же
как и для произвольных N вдоль диагонали р = N, где A(N,N) = 1. Что¬
бы продвинуться дальше и найти общее поведение, нужны и усидчивость и
остроумие. Однако результат известен:
(в+Е)»=£> <4-57)
Хотя вывод этого результата совсем не прост, его проверка тривиальна. На¬
пример, можно доказать (4.57) по индукции.
Канонический член дается уравнением (4.55), которое вместе с (4.57) при¬
водит к
(WV) = А (2^-!-р)! (,
(Ж|Г) Nl(N — p)l /З-'-ог1 ' 1 ‘ ’
Уравнения (4.56) и (4.58) содержат ток для систем произвольной длины N и
с произвольными интенсивностями входа и выхода а и /3. Хотя задача фор¬
мально решена, общее решение не особенно проясняет дело: ответ — сумма
дробей. Обычно в статистической физике в термопределе возникает простое
и характерное поведение, гораздо более показательное, чем поведение систем
с малым числом частиц. Поэтому мы изучаем термопредел N оо. В данном
случае получающееся поведение действительно простое и красивое: из урав¬
нения (4.56) следует элегантная формула для тока, которая обнаруживает
существование скрытых фаз и фазовых переходов между ними
1/4, а > 1/2, /3 > 1/2 (фаза МТ),
J = { а(1 — се), а < 1/2, /3 > а (фаза НП),
/3(1 — /3), /3 < 1/2, а> /3 (фаза ВП).
(4.59)
Здесь аббревиатуры МТ, ВП и НП обозначают фазы максимального тока,
высокой плотности и низкой плотности соответственно. Вспоминая соотноше¬
ние (4.20) между током и плотностью, мы видим, что плотность в фазе МТ
равна р = 1/2. Аналогичный аргумент для фазы НП дает два решения, р — а
4.5 Открытые системы
157
и р — 1 — а; точное решение показывает, что р = а, так что плотность дей¬
ствительно низкая в фазе НП (поскольку а < 1/2). В фазе ВП р = 1 — (3.
Линии а = 1/2, /3 > 1/2 и /3 = 1/2, а > 1/2 отмечают переходы второго
рода между соседними фазами (рис. 4.9). Наконец, линия а = /3 < 1/2 пред-
Рис. 4.9. Фазовая диаграмма АПЗ. Также показаны схематические графики за¬
висимости плотности от пространственной координаты для фаз максимального
тока (МТ), высокой плотности (ВП) и низкой плотности (НП)
ставляет переход первого рода между фазами НП и ВП. В отличие от фаз
МТ, НП и ВП, которые характеризуются однородной объемной плотностью,
плотность — линейная функция х = i/JV, когда а = (3 < 1/2. Подытоживая,
получим
1/2,
а,
1-0,
а + (1 — 2а)ж,
а > 1/2, /3 > 1/2
а < 1/2, {3 > а
/3 < 1/2, а >/3
а = Р< 1/2.
(фаза МТ),
(фаза НП),
(фаза ВП),
(4.60)
Около входа и выхода локальная плотность отличается от полученных
объемных значений. Рассмотрим сначала фазу максимального тока. Самое
большое отклонение от объемного значения наблюдается при а = оо. В этом
случае самый левый узел всегда занят, = 1, и, следовательно, плотность
убывает от 1 до 1/2, когда мы движемся от левой границы. Приближение
к объемной плотности имеет алгебраический характер: (nj) — 1/2 ~ J-1/2
при j 1. Аналогично, около выхода локальная плотность также убывает
158
Запреты
алгебраически, и асимптотическое поведение имеет вид
5 -“ Ж? + °СГ“) (4'б1)
при 1 j С N. Таким образом, ведущая асимптотика не зависит8 от интен¬
сивностей а и /3. Вывод (4.61) несложен: у нас есть точное решение, и нам
нужно только применить асимптотический анализ для оценки сумм, таких
как в (4.58). (Некоторые подсказки для таких вычислений даны в задачах.)
В фазе максимального тока теория среднего поля правильно предсказывает
объемные величины, но дает хвост у-1 вместо правильного J”1,2 из уравнения
(4.61). Та же самая ситуация возникает для двух других фаз: теория средне¬
го поля дает правильное объемное поведение, но приводит к неправильному
изменению плотности вблизи границ.
Наконец, попробуем понять природу перехода первого рода между фаза¬
ми НП и ВП. Рассмотрим предельный случай aN < 1 и /3N <С 1, и пусть
а > В пределе большого времени система в основном будет находиться в
конфигурациях типа ООН ... 11 с несколькими пустыми узлами у левой гра¬
ницы. Чтобы увидеть почему такие конфигурации доминируют, представим,
что самая правая частица только что покинула систему. Тогда вся занятая,
область сдвинется влево, что потребует времени порядка 7V, много меньшего,
чем времена 1/а и 1//3, необходимые для того, чтобы частица могла войти
в систему или выйти из нее. Аналогично, если новая частица входит в си¬
стему, занятая область сдвигается на шаг влево. Следовательно, доменная
стенка между пустой и занятой стенкой совершает асимметричное случайное
блуждание с отрицательной скоростью сноса — а. Поэтому доменная стенка
смещается к левой границе, и система действительно находится в фазе вы¬
сокой плотности. Точно так же, когда а < /3, типичная конфигурация имеет
вид 00...0011 с несколькими занятыми узлами справа. Когда а = /3, сно¬
са нет. Следовательно, доменная стенка совершает симметричное случайное
блуждание на конечном интервале (с отражающими границами). Усредняя,
приходим к заключению, что профиль плотности линейный: (щ) = i/N.
4.6 Ссылки
Процесс с запретами был впервые предложен для описания диффузии боль¬
ших молекул через узкие поры [74]. После этого модель была переоткрыта
в теории вероятности, в том числе Харрисом [75] и Спицером [76]. Метод,
8Такая же универсальность наблюдается и у левой границы.
4.7 Задачи
159
использованный в разделе 4.1 для нахождения распределения вероятности
помеченной частицы в симметричном процессе с запретами, принадлежит
Левитту [77].
В книгах Бюргерса [65] и Уиттама [78] можно почерпнуть информацию о
гидродинамическом подходе к процессам с запретами. Необходимые элемен¬
ты теории нелинейных гиперболических уравнений в частных производных
(например, нелинейных волновых уравнений) содержатся в [65, 78] и в мно¬
гих других источниках; полезная ссылка общего характера — текст Логана
179].
Процессы с запретами были довольно популярны последние 20 лет. Мате¬
матические аспекты обсуждаются, например, в книгах Шпона [80] и Лиггета
[81]. Ранние работы физиков по одномерному АПЗ с открытыми границами —
[82-84]. Матричный метод для этой же системы был развит в [85]. Обзорные
статьи Шмиттман и Зиа [86], Дерриды и Эванса [87], Шютца [88], Голинелли
и Маллика [89], Блите и Эванса [90] и Дерриды [91, 92] дают множество ин¬
формации о физических и транспортных свойствах процессов с запретами.
За подробностями о применении экстремальных аргументов к оценке хвостов
распределения вероятности из врезки на странице 148 можно обратиться к
книге де Женна по физике полимеров [11]. Этот подход также имеет извест¬
ность как «хвосты Лившица»; см. [93] о вкладе Лившица в эту область.
4.7 Задачи
4.1 Рассмотрите СПЗ в экстремальном пределе, когда решетка полностью занята,
кроме одной вакансии, которая сначала находится в начале координат. Зада¬
ча — исследовать движение помеченной частицы.
(a) Покажите, что в одном измерении, если помеченная частица сначала на¬
ходится справа от вакансии, например в п > 0, то в любой последующий
момент она будет либо в начальной позиции п, либо в узле п— 1. Оцените
типичное число прыжков помеченной частицы за интервал времени (0, t).
Покажите, что вероятность того, что помеченная частица не движется,
убывает как £-1/2 в пределе большого времени.
(b) Попробуйте ответить на такой же вопрос как в (а) в двумерном случае.
Обоснуйте, что типичное число шагов ведет себя как Inf и что типичное
смещение растет9 как \/lnt
9Распределение вероятности смещения помеченной частицы негауссово; однако аргу¬
менты типа центральной предельной теоремы дают правильный скейлинг \/1п£ типичного
смещения.
160
Запреты
(с) Рассмотрите ту же самую проблему в трех измерениях. Покажите, что
помеченная частица с положительной вероятностью может никогда не
сдвинуться с места. Обоснуйте, что число прыжков за все время — ко¬
нечно.
4.2 Рассмотрите уравнение Бюргерса в отсутствие вязкости (4.22) с начальными
условиями р(ж,0) = (1 + ж2)-1. Покажите, что гладкое решение существует
до момента £* = Щу/ЧН и что ударная волна рождается в ж* = —5/\/27 в
момент £*.
4.3 Рассмотрите взаимодействие ударной волны и волны разрежения которые об¬
разуются, если начать с начальных условий (4.29). Предположите, что pi < ръ
к Р2 > Рз- Рассмотрите случай, когда, в отличие от примера 4.5, pi > рз-
4.4 Опишите эволюцию, которая начинается с начальных условий (4.29), когда
Pi > Р2 > Рз, в которой две волны взаимодействуют.
4.5 Предложите эвристический вывод уравнения Бюргерса (4.34), состоящий из
следующих шагов:
(a) Начните с кинетического уравнения
дР^д^ = Р(Х ~ МЛ1 “ Р(М)] - Р(Х, t)[l - Р(Ж + 1,*)]-
Попробуйте обосновать его правильность, пользуясь точным уравнением
эволюции (4.46). В чем сложность написания локальных токов в виде
произведения?
(b) Разложите плотности в ряд Тейлора
р(х ± 1,£) = p(x^t} ±
др(з,*) 1 d2p(s,t)
дх 2 дх2
Подставьте эти разложения в кинетическое уравнение из части (а) и вы¬
ведите уравнение Бюргерса (4.34).
4.6 Рассмотрите уравнения Бюргерса в канонической форме ut + иих — Duxx.
Цель этой задачи — решить уравнение Бюргерса для произвольных начальных
условий.
(а) Используйте преобразование Коула-Хопфа
и = -2D (1пф)х = —2Офх/ф
и покажите, что вспомогательная функция ф(х, t) удовлетворяет уравне¬
нию диффузии, 0* = Бфхх. Таким образом преобразование Коула-Хопфа
превращает нелинейное уравнение Бюргерса в линейное уравнение диф¬
фузии.
4.7 Задачи
161
(Ь) Рассмотрите произвольные начальные условия и(х, 0) = F(x). Покажите,
что функция
0(ж,О) = Ф(я) = exp -(2D) 1 [ F(y)dy
Jo
может быть выбрана как начальное условие уравнения диффузии.
(с) Начав с решения уравнения диффузии с начальными условиями ф(х, 0),
<№,t) = J Ф(у)е~^~^ /4Dtdy,
покажите, что решение уравнения Бюргерса с начальными условиями
и(х, 0) = F(x) имеет вид
G(x,y;t) = j° F(y1') dy' +
4.7 Примените общее решение, описанное в предыдущей задаче, для уравнения
Бюргерса. (4.34) с начальными условиями ро(х) = 1 для х < 0 и ро(х) = 0
для х > 0. Покажите, что во внутренней области |ж| < t решение стремится
к выражению р = j (1 — x/t). Опишите поведение внутренних слоев вокруг
х = ±£.
4.8 Рассмотрите открытую систему размера N = 3. Проверьте, что матричный
анзац дает стационарное решение.
4.9 Убедитесь в правильности соотношения (4.54).
4.10 Рассмотрите конфигурацию 1д^32д^д2 и покажите, что ее стационарность
М N—M
эквивалентна выполнению соотношения
(W\DmEn~m IV) = a{W\EDM~1EN~M\V} + p(W\DM EN~M~1D\V).
Проверьте справедливость этого соотношения, используя (4.52).
4.11 Убедитесь в правильности равенства (4.57) на линии а + р = 1, где можно
заменить операторы скалярами: Е = а_1,£> = /З-1. После этого докажите
равенство (4.57) в общем случае, используя математическую индукцию.
4.12 Вывод соотношений (4.59)-(4.60) для тока и плотности в разных фазах дли¬
нен, так как он требует асимптотического анализа различных сумм, подобных
возникающим в (4.58). Обычно бывает полезно ухватить основную идею о том,
что происходит, рассматривая линию а + ft = 1, где решение сильно упроща¬
ется (так как операторы Е и D — скаляры), и основные результаты не зависят
от N. Покажите, что на линии а + /3 = 1, среднее (щ) = а не зависит и от г,
и от N. Проверьте, согласуется ли этот результат с общими предсказаниями
(4.60).
162
Запреты
4.13 Рассмотрите АПЗ в открытой системе с одинаковыми интенсивностями входа
и выхода, а = /3.
(a) Пользуясь правилом Лопиталя, упростите сумму (4.58) и получите
<wqcw|v> (2лг-1-р)! р + 1
<W|V) ~~'1Р N'.(N-p)\ аР '
(b) Покажите что, когда а > 1/2, члены с р = 0(1) доминируют. Используй¬
те этот факт для расчета ведущей асимптотики
0У|С*|У) _ а2 4^+1
(ТУ|У) ” 7^(2а-1)3 2V3/2’
(c) Покажите, что для а < 1/2, доминируют члены с р, близким к 7V(1 —
2а)/(1 — а). Используйте этот факт для расчета ведущей асимптотики
(iy|CN|V) (1 — 2а)2 N
(1У|У) ~ (1 — а)2 а^(1 —a)N*
(d) Покажите, что когда a = 1/2,
(Ж|С^|У) лЫ
{W\V)
(e) Воспользуйтесь результатами (b)-(d), чтобы подтвердить предсказания
(4.59) на диагонали a = /3.
. (f) Подтвердите предсказания (4.60) на диагонали a = /3.
Глава 5
АГРЕГАЦИЯ
При агрегации реакционноспособные кластеры необратимо сливаются, где
бы ни встретились два из них. Агрегация повсеместна в природе: она лежит
в основе скисания молока, коагуляции крови и образования звезд посред¬
ством гравитационной аккреции. Агрегация также великолепно иллюстриру¬
ет некоторые базовые понятия неравновесной статистической физики, такие
как скейлинг, фазовые переходы и нетривиальное стационарное состояние.
Далее мы описываем эти универсальные понятия и приводим точные реше¬
ния нескольких моделей агрегации, поддающихся аналитическому исследо¬
ванию.
5.1 Основное кинетическое уравнение
В кинетической теории, которая была начальной точкой неравновесной ста¬
тистической физики, динамика включает в себя непрерывную последователь¬
ность событий рассеяния Р+Р —> Р+Р. В теории агрегации главный процесс
можно представить как
А + Aj —4 A+j, (5.1)
где два кластера массы г и j необратимо объединяются с интенсивностью
Kij и образуют кластер массы i + j (рис. 5.1). Агрегация явно необратима,
поскольку число кластеров уменьшается со временем, и в конце концов все
кластеры сливаются в один кластер. В процессе рассеяния наоборот участ¬
вующие частицы сохраняют свою идентичность. Чтобы подчеркнуть это раз¬
личие, принято называть участников процесса агрегации кластерами. Наша
цель — описать временную эволюцию концентрации кластеров с массой fc,
Cfc(i), и понять, какие из свойств интенсивностей реакции, т. е. ядра А7?, вли¬
яют на ее распределение.
164
Агрегация
Рис. 5.1. Кластеры с массами г и j необратимо сливаются, образуя кластер с
массой i + j
Везде в этой главе мы неявно подразумеваем, что масса к принимает по¬
ложительные целые значения, что означает, что мы измеряем массу в еди¬
ницах, равных наименьшей массе, а кластер массы к содержит к первичных
кластеров с наименьшей массой. Такие элементарные кластеры называются
мономерами, а кластеры массы к — fc-мерами. При таких предположениях о
массе интенсивности реакций образуют бесконечную симметричную матрицу
Kij =
Начальная точка изучения агрегации — бесконечный набор основных ки¬
нетических уравнений, описывающих эволюцию распределения масс класте¬
ров Ck(t). Эти уравнения выглядят следующим образом:
= | Е KijdCj-Ck^KikCi. (5.2)
г>1
Первое слагаемое в правой части описывает образование fc-меров в процессе
коалесценции двух кластеров с массами i и суммирование происходит по
всем парам, таким что i+j = к. Коэффициент перед членом прихода нужен,
чтобы избежать дублирования при пересчете. Например, когда к = 5, мы
должны просуммировать по (i,j) = (1,4), (2,3), (3,2), (4,1), и поэтому член
прихода равен С1С4 + 7<2,з с2Сз, что согласуется с определением матрицы
интенсивности реакций (с учетом симметрии Kij = Kj^. Для кластеров
четной массы коэффициент остается в одном из слагаемых; например, для
кластеров с массой к = 6 член прихода имеет вид
АГхд С1С5 + 7<2,4 С2С4 + - АГзд (сз)2.
Чтобы понять эту тонкость учета реакций между кластерами одинако¬
вой массы, рассмотрим конечную систему. Пусть Nk будет полное число
5.1 Основное кинетическое уравнение
165
кластеров массы к. Для г / j есть NiNj пар типа ij, тогда как число пар кла¬
стеров одинаковой массы |JVfc(7Vfc — 1) -> в термодинамическом пределе.
Поэтому коэффициент правильно учитывает относительную долю пар с
одинаковой массой.
Член ухода в правой части уравнения (5.2) производит учет реакций к-
меров с другими кластерами. Член ухода для пар кластеров с равной массой
равен KjjCjCj а не ^KjjCjCj, так как два кластера массы j исчезают при таком
столкновении. Надежный способ учесть все коэффициенты — записать
(5.2) в виде
1
2
dck
dt
, Kij CiCj [ <5i-hj,k 8i>k 8jjs ] ,
M>1
где 8ij — дельта-символ Кронекера, так что все способы, которыми fc-мер
может быть создан или уничтожен, правильно пересчитываются явным об¬
разом.
Основное кинетическое уравнение — начальная точка почти всех исследо¬
вания агрегации, и важно помнить какие предположения лежат в его основе:
• Пространственная однородность. Важнее всего, что расположение кла¬
стеров не учитывается. А именно, предполагается, что система хорошо
перемешана, так что вероятность того, что реагенты в непосредственной
близости друг к другу, факторизуется в произведение одночастичных
плотностей, — это приближение среднего поля.
• Бимолекулярные реакции. Система достаточно разрежена, так что вза¬
имодействием большего числа тел можно пренебречь.
• Независимость от формы. Масса агрегата — единственная динамиче¬
ская переменная. Форма кластера не играет роли в эволюции (как при
агрегации сферических капель жидкости.)
• Термодинамический предел. Система достаточно большая, чтобы пре¬
небречь влиянием дискретности.
Приближение среднего поля часто асимптотически точно в физическом
случае трех измерений. В главе 13 мы обсудим, что делать с низкоразмерны¬
ми системами, для которых приближение среднего поля неприменимо. Рас¬
смотрение только бимолекулярных реакций не является серьезным ограни¬
чением, поскольку плотность кластеров уменьшается при необратимой аг¬
регации. Поэтому система, которая вначале не была разреженной, в кон¬
це концов становится разреженной, и вклад множественных столкновений
166
Агрегация
асимптотически становится пренебрежимо малым1. Предположение о неза¬
висимости от формы трудно проверить. Однако в некоторых случаях до¬
полнительные физические механизмы, такие как поверхностное натяжение,
заставляют растущие кластеры принимать сферическую форму.
Нужно подчеркнуть, что в подходе, базирующемся на основном кинети¬
ческом уравнении, интенсивности предполагаются заданными, тогда как в
реальности их определение может быть частью анализа. Главная характе¬
ристика реакции, оказывающая влияние на интенсивности, — это механизм
переноса. Большинство приложений агрегации относятся к физической хи¬
мии, где перенос осуществляется посредством диффузии. Другие механиз¬
мы переноса также возможны; например, баллистический транспорт отве¬
чает за астрофизические приложения2. Такие уравнения, как (5.2), также
использовались в баллистически контролируемой агрегации. В этом случае
справедливость (5.2) трудно проверить, так как каждый кластер характери¬
зуется своими массой и скоростью, и последняя должна входить в основное
кинетическое уравнение. В таких системах правильная среднеполевая схема
включает бесконечный набор уравнений больцмановского типа3.
Уравнение (5.2) характеризуется базовым интегралом движения: плот¬
ность массы
M(t) = ^kckft) (5-3)
к>1
сохраняется. Чтобы проверить этот закон сохранения, запишем
= 53fc^ = 2 53 |-fcv(i+j)cicJ-5353-FC’ifcfcciCfc = 0- (5-4)
к к i+j=k к i
Из-за внешней суммы по к суммы по г и j становятся независимыми и неогра¬
ниченными. Поэтому члены прихода и ухода сокращаются и плотность массы
сохраняется в явном виде. Как мы увидим, закон сохранения массы играет
центральную роль в описании распределения массы кластеров.
1 Однако из этого правила есть исключения; во многих природных процессах, напри¬
мер таких, как каталитические реакции, взаимодействия большего числа тел играют суще¬
ственную роль. Более того, некоторые реакции изоморфны агрегации со многокластерным
слиянием. Далее в этой книге мы исследуем реакции, эволюционирующие посредством
слияния трех тел Ai + Aj + Ак —> УЦ+j+fc. См. разделы 8.8, 9.7 и 10.2.
2Иногда могут возникать более экзотические механизмы переноса. Например, в турбу¬
лентности среднее расстояние между частицами растет как t3/2, так что транспорт супер¬
баллистический.
3 Смотри обсуждение баллистической агломерации и автомобильного потока в разделах
3.7 и 3.8.
5.2 Методы точного решения
167
5.2 Методы точного решения
Основное кинетическое уравнение — это чудовищно сложный бесконечный
набор взаимозависимых нелинейных дифференциальных уравнений, которые
решаются только для нескольких специальных видов ядра К^. Множество
остроумных техник решения было предложено для ядер, которые мы обсуж¬
даем здесь. Мы ограничиваем наше рассуждение ядром с постоянными интен¬
сивностями, предложенного и изученного Смолуховским в 1917 году, которое
благодаря своей простоте является идеальным примером для иллюстрации
многих точных подходов.
Чтобы обосновать применение ядра с постоянными интенсивностями, нач¬
нем с ядра реакций, описывающего агрегацию кластеров, совершающих бро¬
уновское движение. Интенсивность, с которой частицы с коэффициентом
диффузии D налетают на сферу с радиуса R, пропорциональна DRd~2 или
DR в трех измерениях (см. раздел 2.7). Обобщение для набора сфериче¬
ских агрегатов с радиусами Ri и коэффициентами диффузии Di дает ~
(Di + Dj)(Ri + Rj). В этой формуле радиус кластера растет как кубический
корень из его массы, тогда как коэффициент диффузии пропорционален
обратному радиусу. Поведение последнего — следствие соотношения Сток¬
са-Энштейна между коэффициентом диффузии сферического объекта D и
коэффициентом сопротивления 67ttjR, а именно: D = T/(67tt}R) (см. также
(2.103) в разделе 2.8). В результате интенсивность реакции принимает вид
/•\1/з /.\1/з
^~(Г1/3+Г1/3)(г1/з + ?/3) = 2+ (j) + (j) . (5.5)
Основное кинетическое уравнение с броуновским ядром до сих пор не решено.
Однако броуновское ядро имеет одну общую черту с постоянным ядром: оба
инвариантны по отношению к преобразованию (г, j) —> (аг, су), т. е. Ka^aj =
A'ij. Это свойство означает, что постоянное ядро — это разумное (хотя и
неконтролируемое) приближение для физически важного броуновского ядра.
Для постоянного ядра мы для удобства положим Кц = 2, после чего
получим следующее основное кинетическое уравнение:
52 CiCj-2Ck^Ci= 52 CiCj-2ckN,
i+j=k г>1 i+j=k
(5-6)
168
Агрегация
где 2V(t) = ^к>1 Cfc(i) — концентрация кластеров любой массы. Приведем
несколько первых из полученных уравнений
ci = — 2ci TV,
С2 = Cl — 2С2 TV,
с3 = 2ci с2 - 2с3 TV,
С4 = 2ci С3 + с| — 2с4 TV,
С5 = 2ci С4 + 2с2 сз - 2с5 TV,
cq = 2ci С5 + 2с2 С4 + cl - 2сб TV,
(5.7)
где точка сверху обозначает производную по времени.
Один из главных уроков, извлеченных из исследований агрегации и дру¬
гих необратимых процессов, — это то, что поведение на больших временах
(которое является наиболее интересной характеристикой системы) зависит
от начальных условий тривиальным образом: через полную плотность мас¬
сы, тогда как детали начальных условий неважны. Поэтому естественный
выбор — начальные условия с одними мономерами
cfc(0) = дк>1. (5.8-)
В дальнейшем мы будем всегда предполагать такие начальные условия, если
обратное не указано явно.
Далее, чтобы дать почувствовать диапазон техник решения основного ки¬
нетического уравнения вида (5.6), мы кратко изложим несколько методов
решения для случая агрегации с постоянным ядром.
Моменты
Перед тем как решать задачу Коши (5.6)-(5.8), полезно изучить моменты
распределения массы
Mn(t) = ^knck(t), (5.9)
к>1
из которых с небольшими усилиями можно получить значительную инфор¬
мацию даже в тех случаях, когда полные основные кинетические уравнения
нерешаемы. Моменты также дают некоторую информацию о самом распре¬
делении масс. Например, отношение M±/Mq = М/N дает среднюю массу
кластера.
5.2 Методы точного решения
169
Для постоянной интенсивности реакций уравнения для моментов особен¬
но просты. Используя уравнения (5.6), получим
dMn
dt
к>1
— У kn [ У CiCj 2ск У Cjj
к>1 i+j=k i>l
= У {i + j)n Ci Cj - 2Mn Mo, (5.10)
i,j
где суммы no i и j во второй строчке имеют бесконечные пределы. Явный
вид уравнений для нескольких первых моментов — это
M0 = yciCj-2M02 = -M02,
. Ml = У (г + j) Ci Cj - 2MiM0 = 0,
Ji (5-п)
М2 = У (г2 + + j2) Ci Cj - 2M2M0 = 2M2,
М3 = У (г3 + 3i2j + 3ij2 + /) Ci Cj - 2M3M0 = 6M1M2.
Для начальных условий с одними мономерами имеем Mn(0) = 1 для п > 0.
Тогда решением для нулевого момента Mq = N будет
JV(t) = (5.12)
Решая уравнения (5.11) для высших моментов шаг за шагом, получим М± =
1, М2 = 1 + 2£, М3 = 1 + 6t + 6f2, и т. д. В общем случае Мп ~ n! tn_1 при
t —> оо. Заметьте, что полная масса сохраняется, М± = 1 — как и должно
быть. Естественную меру типичной массы кластера дает второй момент М2,
который растет линейно со временем.
Рекурсивный подход
Уравнения (5.6) — это рекурсия и поэтому могут решаться шаг за шагом.
Для начальных условий с одними мономерами подставим N(t) из (5.12) в
первое уравнение из (5.7) и проинтегрируем, что дает ci(f) = (l + f)“2. Найдя
ci, можно получить уравнение для С2
= (1 + £)“4 _ 2(1 + £)-1 с2.
170
Агрегация
Решая это уравнение с начальным условием сг(0) = 0, получим 02(f) = f/(l +
f)3. Следующая плотность удовлетворяет уравнению
= 2f(l + f)-5 — 2(1 + f)-1 с3,
решение которого с сз(0) = 0 есть 03(f) = t2/(1 + f)4. Продолжая эту рекур¬
сивную процедуру, находим 04(f) = f3/(l + f)5, далее 05(f) = f4/(l + f)6, и т. д.
Эта последовательность приводит к гипотезе для вида точного решения
= (1 + t)W ■ <5-13)
Несложно доказать, что она верна, по индукции.
Рис. 5.2. (а) Зависимость концентрации кластеров Cfc(i) от времени для агре¬
гации с постоянным ядром при к = 1,2,3 и 5. (Ь) Зависимость концентрации
кластеров Cfc(f) от к в двойном логарифмическом масштабе при t = 1,5,20 и
100
Элегантная замкнутая форма решения (5.13) имеет много важных свойств:
1. При fc, t —> оо, Ck —> t~2 е~к^. Поэтому для больших фиксированных к
и t —> оо все концентрации с&(£) стремятся к общему пределу t-2, в то
время как при к <t распределение масс почти плоское (рис. 5.2).
2. Концентрация кластеров пропорциональна t~2 xt = t~r. Это вос¬
производит правильную зависимость общей концентрации кластеров от
времени.
5.2 Методы точного решения
171
3. Для произвольного начального распределения масс с конечным носи¬
телем4 пределы малых и больших времен можно изучать, не решая ос¬
новное кинетическое уравнение. В пределе малого времени можно пре¬
небречь членами ухода, что дает уравнения (5.14) ниже по тексту, из
которых следует что Cfc(i) ~ при t <£ 1. Наоборот, при t —> оо отсут¬
ствует образование /с-меров для некоторого фиксированного к. Поэтому
мы пренебрегаем членом прихода в основном кинетическом уравнении,
что дает уравнение с* ~ — 2ckN, решение которого имеет вид Ск ~ t-2.
Избавление от членов ухода
11олезный трюк, который часто позволяет упростить основные кинетические
уравнения, — избавиться от членов ухода, рассматривая отношения концен¬
траций вместо самих концентраций. Например, рассмотрим отношение фк =
*'а7г:1) эволюция которого описывается уравнением
d-Фк
dt
= ci
i+j=k
(5-14)
Видно, что член ухода действительно исчез. Можно также избавиться от
множителя в правой части, введя новое время
т= f dt'ci(iz), (5.15)
Jo
так что уравнение (5.14) сведется к
= £ <м>,- (5.16)
i+j=k
Чтобы связать т и t, подставим полученную раньше плотность мономеров
П = (1 +1)~2 в (5.15) и найдем т = t/(l + i). Решая (5.16) для нескольких
первых фк, получим ф± = 1,02 = т.>фъ = т2. Легко поверить, что общее
решение есть фк = Tfc_1. Подставив его в Ск = фк ci и используя т = t/(l + t),
мы перевыведем (5.13).
Экспоненциальный анзац
Решения основного кинетического уравнения часто имеют экспоненциальный
вид: уравнение (5.13) — один из таких примеров. Используя это предполо¬
жение в качестве начального, можно значительно упростить управляющие
4Распределение с*;(0) имеет конечный носитель, если Cfc(O) = 0 для всех к > кт9Х с
КОНеЧНЫМ ктах-
172
Агрегация
уравнения. Для случая агрегации с постоянным ядром подходящий экспо¬
ненциальный анзац — это
cfe(f)=Aafe-1 (5.17)
с неизвестными функциями A(t) и a(t). Начальное условие (5.8) дает А(0) = 1
и а(0) = 0; этот факт объясняет, почему мы выбрали степень к — 1, а не к.
Подстановка анзаца (5.17) в (5.6) и деление обеих частей на Ск дает
А /. Z.
- + (A:-l)- = (fc-l)--
А а а
2А
1 — а
Если экспоненциальный анзац верен, зависимые и не зависимые от к части
этого уравнения должны зануляться по отдельности. Следовательно, задача
сводится к решению пары взаимозависимых дифференциальных уравнений
2Л2
А = -- , а = А. (5.18)
1 — а
Поскольку ^2к>1 = А^2к>1 как 1 = ^(1 “ а) 2> сохранение массы пред¬
полагает А = (1 — а)2. Подставляя А = (1 — а)2 в (5.18), получим
А =
1
(W
а =
(5.19)
1 + е
что опять воспроизводит решение (5.13) для Ck(t). Экспоненциальный анзац
имеет преимущество перед двумя предыдущими подходами в том, что он
в меньшей степени основан на догадках и требует работать всего с двумя
(а не с бесконечным набором) дифференциальными уравнениями. Этот анзац
также работает для любых экспоненциально убывающих с массой начальных
условий.
Пример 5.1. Экспоненциально убывающие начальные условия. Пусть Cfc(0) =
(1 —g)2gfc_1, где 0 < q < 1; начальные условия с одними мономерами воспроизво¬
дятся в пределе q —> 0. Используем экспоненциальный анзац (5.17) с А = (1—а)2.
Теперь мы должны решить а = (1 — а)2 при условии а(0) = q. Получим
a(t) = 1 —
1-g
i+ (!-<?)*’
A(t) =
Г 1 I2
1-g
1 + (1 — g)t
Параметр q не влияет на качественное асимптотическое поведение. Например,
для фиксированной массы концентрация /с-меров стремится к общему пределу,
который ведет себя как t~2 при t —> оо. Когда и масса и время расходятся так,
что отношение t/k остается конечным, распределение массы снова принимает
скейлинговый вид Ск — t~2 ехр(—k/t).
5.2 Методы точного решения
173
Метод производящей функции
Мощный подход к нахождению распределения масс кластеров — метод про¬
изводящей функции. Эта техника идеально подходит для агрегации, потому
•Iто основные кинетические уравнения имеют вид дискретной свертки. С по¬
мощью метода производящей функции эта свертка превращается в простое
произведение. Производящая функция определяется как
е(г> О = ^2 Ск^ zk, (5-2°)
к>1
и эта единственная функция содержит информацию о полном распределе¬
нии масс. Заметим, что производящая функция — просто дискретный аналог
преобразования Лапласа. Поэтому идею о связи функции и ее Лаплас-образа
можно обобщить и на производящую функцию.
Чтобы применить метод производящей функции к агрегации с постоян¬
ным ядром, умножим уравнение (5.6) на zk и просуммируем по всем к. Это
дает
-тг = S ZCkzk 5> = e2-2ew. (5.21)
к>1 i+j=k к>1 ъ>1
Здесь сумма по к делает две суммы по i и j независимыми, так что пер¬
вое слагаемое превращается в произведение. Такая редукция — это суще¬
ственное упрощение, которое дает метод производящей функции. Можно до¬
биться дополнительного упрощения, заметив, что уравнение движения для
/V имеет вид N = — 7V2, так что функция 6 — N удовлетворяет уравнению
— N) = (е — 7V)2. Таким образом, мы свели полный набор основных ки¬
нетических уравнений к одному дифференциальному уравнению! Это урав¬
нение нужно снабдить начальными условиями. Если вначале существовали
одни мономеры, то С(г, t = 0) = z. Решение дает 6 — N = (z — 1)/ [1 — (z — l)t],
откуда
е = — z- .
1 +1 1 — (z — l)t
После небольшой перегруппировки (5.22) и разложения в ряд по z получим
^,t) = ^zk
к>1
tk-l
(1 + t)k+1'
Из этой формулы можно непосредственно увидеть распределение массы и
таким образом воспроизвести (5.13).
174
Агрегация
5.1. Обращение производящей функции
Часто мы можем найти производящую функцию C(z) = J3fc>1 Ск zk, и нам нужно
извлечь асимптотическое поведение соответствующего распределения масс Ск при
больших к. Сейчас мы покажем, как связать хвост Ск при больших к и поведение
С(г) при z —> 1. В качестве примера общего вида предположим, что
Ск — Ск~а при к'Э» 1. (5.23)
Мы ограничимся режимом а > 1, так что Ск сходится; положим также
Sfc>i с* = 1. Сначала предположим, что а не равняется 2. Тогда в пределе z f 1
производящая функция G(z) и Ск асимптотически связаны:
e(z) = 1 + СТ(1 - а) (1 - z)“_1 + ..., (5.24)
где Г — гамма-функция Эйлера.
Чтобы получить это соотношение, заметим, что в соответствии с нашей гипотезой
G(z = 1) = 1. Далее, продифференцируем 6(z) по z, используем (5.23) для Ск и
возьмем предел z f 1, который дает
dG к_1
Tz=^kCkZ
~С /°°dfcfc1"eefclnz
Уо
~С /'TOdfcfe1_“e_fc(1_z)
Уо
= <7Г(2 — а) (1 — z)“-2.
(5.25)
Интегрирование этого уравнения дает (5.24). Мы уже применяли такой же трюк,
основанный на использовании более сингулярной функции dG/dz вместо самой G
(см. раздел 2.5), который позволяет выявить реальное асимптотическое поведение.
В пограничном случае а = 2 те же самые шаги в уравнении (5.25), которые при¬
водят к (5.24), дают
Со(2) = 1 + С (1 — z) ln(l — z) + (5.26)
Для произвольных начальных условий производящая функция принима¬
ет вид
e(z,t) = (l + t)-2—(5.27)
где = 0), и мы предполагаем, что N(t = 0) = Qq(z = 1) = 1.
Пример 5.2. Начальное распределение массы с конечным носителем. Рассмот¬
рим начальное состояние, состоящее из смеси мономеров и димеров, т. е.
ci(0), сг(0) > 0, где сДО) + сг(0) = 1, тогда как сДО) = 0 при j > 3. Тогда
5.2 Методы точного решения
175
to(z) = ci(0)2 + С2(0)г2, и формула (5.27) дает
6(z, £) = (! + £) 2
ei(0)z + C2(0)z2
1 “ I+t [ci(°)z + c2(°>2] ’
11тобы разложить эту производящую функцию по степеням г, перепишем квад¬
ратичный полином в знаменателе как (1—z/zi)(l—zjzi}, где ^1,2 — его корни. Те¬
перь представим [(1—z/zi)(l—z/z2)]~1 как произведение двух членов (1—z/zi)”1
п (1 — г/гг)-1 и разложим каждый из них как геометрическую прогрессию.
Этот же подход позволяет получить результаты в явном виде в случае с^(0) =
О при к > 5, когда полином четвертого порядка в знаменателе (5.27) можно яв¬
но факторизовать. В более общем случае решение для производящей функции
позволяет исследовать асимптотическое поведение концентрации кластеров Cfc(£)
при произвольном начальном распределении масс с конечным носителем. Про¬
цедура обращения (см. задачу 5.1) дает
°к~ М(0)£2
e-fc/[M(0)t]
(5.28)
Пример 5.3. Алгебраически убывающие начальные условия. Если начальное
распределение масс неограничено и убывает достаточно медленно, можно на¬
блюдать аномальное поведение распределения масс кластеров. Один такой при¬
мер — начальное распределение, которое ведет себя как
Cfc(0)->Cfc-a (5.29)
при к 1. Показатель а должен быть больше единицы, так как нулевой момент
распределения масс должен сходиться. В противном случае уравнения (5.6) пло¬
хо определены. За исключением этого ограничения показатель а произволен. В
частности, если а < 2, первый момент расходится, М(0) = оо и асимптотический
вид (5.26) становится неверен.
Предположим, что 1 < а < 2. Тогда в соответствии с уравнением (5.23) произ¬
водящая функция Со (2), в которой закодированы начальные условия, в пределе
z f 1 имеет следующее асимптотическое поведение:
e0(z) = 1 + СТ(1 - а) (1 - z)a~x + .... (5.30)
Пользуясь уравнением (5.30), переходя к пределам t -> 00 и z f 1 и сохраняя
только ведущий порядок, получим производящую функцию (5.27)
e(z’i)=l + o;(7-z)°-i’ где ®—СГ(1-а).
Комбинация переменных в знаменателе определяет скейлинговую переменную
w = и скейлинговый вид распределения масс
Ск — ^(Dt)""1^*”1) /a(w), w =
(5.31)
176
Агрегация
Действительно, имеем
/*оо ,-1
e(2,f) = 52 / dw fa(w) e~WS = i ■ gO_i ■
1 + 3
где s = — z). Следовательно, скейлинговая функция fa(w) дает
обратное преобразование Лапласа функции (1 + s6*-1)-1.
Асимптотики Лаплас-образа для больших и малых s определяют соответству¬
ющее поведение скейлинговой функции при больших и малых w:
fa(w) - <
Г(а-1)
1
w_>0,
(5.32)
Г(1-а)
W
W
W —> оо.
Для некоторых значений а возможно получить явный вид скейлинговой функ¬
ции. Например, когда а = 3/2, обратный Лаплас-образ функции (1 + x/s)-1
может быть представлен через функцию ошибок
/з/2(^)
/7TW
ewerfc (x/w).
В пограничном случае а = 2 скейлинговое поведение просто. Пользуясь урав¬
нением (5.26), находим, что скейлинговое решение — это по-прежнему экспонен¬
циальная функция
к
Ctint '
Cfc(£) = t 2(Clnt) 1 ехр
но с логарифмом, возникающем в скейлинговой переменной и в коэффициенте.
Эти логарифмические множители — единственное отличие пограничного случая
от стандартного скейлингового поведения при а < 2. Для а > 2 скейлинговая
функция универсальна и чисто экспоненциальна, тогда как при 1 < а < 2 скей¬
линговая функция fa(w) — это обратный Лаплас-образ функции (1 + sa-1)-1.
Эта скейлинговая функция все еще универсальна в том, что она не зависит от
деталей начальных условий (их поведения при малых массах, амплитуды С и
т. д.); единственная значимая величина — это значение показателя убывания а.
5.3 Гелеобразование
Когда интенсивность агрегации — достаточно быстро растущая функция мас¬
сы кластеров, за конечное время происходит гелеобразование, в котором
5.3 Гелеобразование
177
ненулевая доля общей массы собирается в один кластер (представим себе же¬
латиновый десерт «фруктовое желе»). Как мы сейчас увидим, мультиплика¬
тивное ядро дает точнорешаемый пример этого впечатляющего явления. По
истечении времени гелеобразования система делится на две фазы: гель, или
бесконечный кластер, и оставшийся золь конечных кластеров, общая масса
которых убывает со временем из-за того, что конечные кластеры продолжают
сливаться с гелем.
Мультипликативное ядро = ij
Мультипликативное ядро возникает, когда мономеры состоят из f реакци¬
онноспособных концевых функциональных групп (рис. 5.3). Если два таких
(а)
(Ь)
Рис. 5.3. Небольшие fc-меры 3-функциональных единиц: (а) мономер, (Ь) димер,
(с) тример
мономера соединятся, у получившегося димера будет 2/ — 2 реакционноспо¬
собных концевых группы, у тримера 3/—4, а у /г-мера kf—2(k—1) = (/—2)fc+2
реакционноспособных концевых группы. Если реакционная способность всех
концевых групп одинакова, то интенсивность реакций между двумя класте¬
рами дается произведением числа концевых групп
Kij = [(/ - 2)i + 2] [(/ - 2)j + 2] = (/ - 2)2y + 2(/ - 2)(i + j) + 4. (5.33)
Случай f = 2 соответствует линейному полимеру, для которого Kij — по¬
стоянная, тогда как мультипликативное ядро возникает при / —> оо. Для
конечных f > 2 ядро является линейной комбинацией постоянного, мульти¬
пликативного и аддитивного ядер.
178
Агрегация
Теперь обратимся к чисто мультипликативному ядру = ij, основные
кинетические уравнения для которого имеют вид5:
= 52 = i v’CiCj-AiCfc. (5.34)
i+j=k г>1 i+j=k
Удивительное свойство этой бесконечной системы уравнений — конечная до¬
ля всей массы конденсируется в один гигантский кластер, гелевый кластер,
который в конце концов поглощает всю систему.
Моменты
Математически возникновение геля проявляется как сингулярность. Попро¬
буем обнаружить эту сингулярность простейшим способом — изучая моменты
распределения массы. Рассмотрим конечную систему с начальной массой М.
Для таких систем образование «бесконечной» молекулы геля означает нали¬
чие кластера, масса которого д№ составляет конечную часть общей массы
М, а концентрация равна 1/М. Разделим моменты распределения массы
Мп = 52 кП СЬ = 52 кП Ск + (fcncfc)gel
к>1 sol
на сумму по конечным кластерам ^2sol — золю и вклад от одного «бесконечно¬
го» гелевого кластера. В соответствии с этим разделением первые несколько
моментов будут иметь следующий вид6:
Mq = »,
sol
Mi = 52 кск+9>
м2 = J2fc2cfc + p2M,
sol
Мз = 52А:Ч + 53М2.
sol
5 Агрегация с мультипликативным ядром эквивалентна случайному графу Эрдеша -
Реньи, который будет обсуждаться в разделе 14.2. Поэтому из решения для агрегации с
мультипликативным ядром бесплатно извлекается монжество фундаментальных свойств
случайного графа.
6Для нулевого момента разница между плотностью всех кластеров и конечных класте¬
ров не важна, так как есть только один бесконечный кластер.
5.3 Гелеобразование
179
11озтому в термодинамическом пределе М —> оо второй и более высокие мо¬
менты расходятся, хотя до момента гелеобразования t < tg, g(t) = 0 и все
Моменты конечны. Из этого аргумента видно, что сингулярность можно об¬
наружить, изучая второй момент.
Согласно уравнению (5.34) второй момент М2 эволюционирует следую¬
щим образом:
=Е*2 | Е Е<«+- Е
к>1 г>1 j>l к>1
= EE<iMA>=M!2. (5.35)
г>1 j>l
Решая это уравнение с начальным условием Л12(0) = 1, получим M2(t) =
(I - t)"1. Эта сингулярность — признак гелеобразования, и она приводит
к гипотезе, что гелеобразование наступает при tg = 1. Возможно ли чтобы
третий момент расходился раньше, т. е. чтобы гелеобразование наступало
раньше? Ответ — нет. Действительно, записывая уравнение эволюции для
третьего момента
dM3
dt
= + =ЗМ3М2 = -|--Мз,
i>l J>1 к>1
(5.36)
и решая с условием М3(0) = 1, получим M3(i) = (1 — i) 3. Аналогично,
решение уравнения
= IЕ + ^iCi ici ~ L fe5<* = + ЗМз (5-37)
г>1 j>l к>1
даст M^t) = (1 + 2t)(1 — £)~5- Используя индукцию, можно проверить, что
вес моменты расходятся в tg = 1. Отметим, что расположение сингулярности
lg = 1 не универсально, а зависит от нчальных условий, точнее от Л/2(0).
Для произвольных начальных условий решение уравнения (5.35) становится
сингулярным в tg = 1/М2(0), хотя характер сингулярности остается таким
же, как для монодисперсных начальных условий.
Теперь будет полезно изучить нулевой момент. Просуммировав уравнения
(5.34), находим, что Mq = N удовлетворяет уравнению
dN
dt
= 1- ^2kck = j
(5.38)
i>l j>l
k>l
1
2
180
Агрегация
Решение N(t) = 1 — зануляется при t = 2 и становится отрицательным,
когда t > 2. Такое аномальное поведение — следствие использования соотно¬
шения 53&>1 ^ск = 1 выше точки гелеобразования. На самом деле эта сумма —
сумма по конечным кластерам, так что мы должны писать ^ск = 1 — 5-
Следовательно, имеем
= = (5.39)
при t > tg, т. е. число кластеров перестает убывать только при бесконечном
времени, когда доля геля достигает единицы.
Чтобы получить поведение моментов (и распределения масс) нам нужен
более полный анализ, который можно провести с помощью производящей
функции.
Метод производящей функции
Для решения уравнений (5.34) удобно использовать экспоненциальную про¬
изводящую функцию £(у, t) = к Ck(t) еук. В этой производящей функ¬
ции закодирована последовательность ксь вместо последовательности с&, что
упрощает последующий анализ. Чтобы получить уравнение эволюции для £,
умножим основное кинетическое уравнение для каждого сь на кеук и, про¬
суммировав по А:, получим
152 52(®+№ * сзеУк ~ 52 к2°к еУк
г>1 j>l к>1
= | £ i2Ci eyi jCj е™ + | £ га е* £ Л,’ е" - J>2cfe e*fc
2 г>1 J>1 2 i>l J>1 к>1
= (£-1)|. (5.40)
Таким образом мы получили невязкое уравнение Бюргерса — простейшее ги¬
перболическое нелинейное уравнение, которое было предметом раздела 4.3,
посвященного гидродинамическому описанию процессов с запретом. Харак¬
терное свойство уравнения Бюргерса — возникновение ударных волн; оно
же соответствует возникновению геля при агрегации с мультипликативным
ядром.
Чтобы решить уравнение Бюргерса (5.40), мы используем метод харак¬
теристик, который обсуждался в разделе 4.3. Характеристики уравнения
(5.40) — это кривые в плоскости y-t с наклоном yt = 1 — £. Вдоль характе¬
ристик производящая функция £ постоянна, и поэтому у = (! — £)£ + /(£),
5.3 Гелеобразование
181
5.2. Обращение Лагранжа
Пусть дана функция X = /(У), такая, что X ~ Y при малых Y. Каково пред¬
ставление в виде степенного ряда обратной функция Y(X) = £3П>1 АпХп? Коэф¬
фициенты Ап даются формулой обращения Лагранжа. Формально коэффициенты
Лп можно получить с помощью контурного интегрирования по маленькой окруж¬
ности вокруг начала координат:
/dY- <5">
Наиболее важный шаг — перейти от интегрирования по X к интегрированию
по Y. Преобразованный контур — также маленькая окружность вокруг начала
координат, поскольку X и Y пропорциональны друг другу в окрестности ноля.
Применим формулу обращения к уравнению (5.43). Записав Y = £t и X =
мы превратим уравнение (5.43) в /(У) = У e~Y = X. Из уравнения (5.41), под¬
ставляя = (1 — У) е“у, имеем
лп = -^ / (1 - Y) e~Y dY =-^ <£ епУ dY,
2т J (У e-y)n+1 v 7 2т J Yn
Чтобы вычислить вычет, нужно разложить экспоненту в степенной ряд и взять
коэффициент при 1/У в подинтегральном выражении. Таким образом получаем
Л - — / V — (Yk~n - Yk+1~n} dY - П" 1 - 2 - —
Ап ~ 2iri f 2-< k\ \ ) (п-1)! (п-2)! n! ’
fc>0
так что представление обратной функции в виде ряда имеет вид
г""1
п!
п—1
у = _ хп
(5-42)
п>1
где /(£) определяется начальными условиями. Для начальных условий с од¬
ними мономерами начальная производящая функция имеет вид: £(t = 0) =
£ кек e3/fc|t=0 — еУ или y(t = 0) = /(£) = In £. Таким образом, получаем явное
решение
£е-£‘ = ег/-*. (5.43)
Саму производящую функцию можно получить по формуле обращения
Лагранжа (см. текст во врезке выше). Подставив Y = ££ и X = в
уравнение (5.42), получим
ък-1
к>1
к\
182
Агрегация
Пользуясь тем, что плотность с*, равна fc-тому коэффициенту ряда £, де¬
ленному на /г, придем к замечательно простому результату
= (5.44)
Применив формулу Стирлинга, найдем асимптотическое выражение этого
распределения
Cfe(t)
кк~2
e~k(l—t)2/2
•\/27rfc5/2 ’
(5.45)
где мы аппроксимировали выражением е~к^~^2^2 при t -+ 1. При
t / 1 распределение массы Ск экспоненциально убывает с к. В момент геле¬
образования t = tg = 1 распределение массы имеет степенной хвост, сигнали¬
зирующий о сингулярности там, где впервые возникает гель. Для t, близких
к tg, выражение (5.45) приводит к скейлинговому виду распределения массы
Cfc(f) ~ s 5/2Ф(А:/5),
где
е~^2
£5/2 ’
(5.46)
ад =
1
у/2тг
. в котором характерная масса s = (1 — t)~2.
Производящая функция позволяет определить долю общей массы, при¬
надлежащей гелю. Пользуясь неявным выражением для производящей функ¬
ции (5.43), найдем, что д — 1 — Mi = 1 — £(у = 0, t) удовлетворяет уравнению
д = 1 — е 9t
(5-47)
Это уравнение всегда имеет тривиальное решение д = 0. Однако при t > 1
есть дополнительное нетривиальное решение, в котором гель имеет ненуле¬
вую массу. Это решение дает правильное выражение для д при t > tg = 1.
Хотя уравнение (5.47) не может быть решено явно, его предельное поведение
можно изучать пертурбативно. Сразу после момента гелеобразования мы за¬
пишем t = 1+5 и разложим (5.47) при малых 5, а при t —> оо положим д = 1—е
и разложим при малых е. Это дает следующие предельные выражения
{0, при t < 1,
2(t — 1) - 8(t - 1)2/3 + ..., при 14 1,
1 — e-t — te-2* + ..., при t -ь оо.
(5.48)
5.3 Гелеобразование
183
Комбинируя (5.38)-(5.39) с результатами (5.48)
плотности кластеров
M0 = N =
< 1 — i/2 + 2(i — 1)3/3 + ..
ke-* + (V2)e-2t + ...,
для з, получим убывание
при t < 1,
, при 14 1, (5.49)
при t —> оо.
fl-t/2,
Плотность кластеров, как и две ее первые производные непрерывны в точке
гелеобразования, тогда как третья производная испытывает скачок.
Наконец можно найти все моменты распределения размера конечных кла¬
стеров, которые будут конечными всегда, кроме момента гелеобразования.
1Ьшример, чтобы вычислить М2, можно воспользоваться кинетическим урав¬
нением
г>1 j>l к>1
= ^2^2i2cij2 ч+52 *3 <*52-^ - 52fc3 ск
г>1 j>l i>l j>l к>1
= М%- дМ3.
До точки гелеобразования воспроизводится уже известное решение M2(t) =
(I - t)_1. Для t > tg уравнения содержат неизвестные д и М3. Соответственно,
чтот подход не дает явных выражений для М2 или для Мп при п > 2. Тем не
менее, можно выразить моменты числа конечных кластеров непосредственно
через д как производные производящей функции £:
9П 1£
дуп~^
y=Q
Для второго момента мы берем логарифм уравнения (5.43), дифференцируем
но у и полагаем у = 0, что дает
М2(<) =
£(y=O,t)
(5.50)
где £(у = Q,t) = 1 в золевой фазе и £(у = 0,f) = 1 — д = е 9t (см. (5.47)) в
гелевой фазе. Таким оёразом,
M2(t) = <
(1 — t) 1 при t < 1;
(е9* — £)-1 при t > 1.
(5.51)
184
Агрегация
Для t —> tg снизу второй момент быстро растет со временем, тогда как для
больших i, М2 —> 0 по мере того, как конечные кластеры поглощаются ге¬
лем (рис. 5.4) Более высокие моменты демонстрируют похожее качественное
поведение (задача 5.3).
t
Рис. 5.4. Временная зависимость массы гелевой фазы (сплошная) и второго
момента золевой фазы (пунктир)
Другие идеализированные ядра
В наиболее общей форме ядро для полимеризации в (5.33) можно записать
как
Kij = А + В (i + J) + Cij, (5.52)
т. е. в виде произвольной линейной комбинации постоянного, аддитивного и
мультипликативного ядер. Эти ядра представляют большинство точнореша¬
емых моделей агрегации7. Однако общее решение для полимеризационного
ядра не может быть представлено как «суперпозиция», так как основное ки¬
нетическое уравнение нелинейно. Тем не менее, поскольку постоянное, адди¬
тивное и мультипликативные ядра решаются по отдельности, и потому, что
7 Оставшиеся точнорешаемые ядра включают экспоненциальное ядро Kij = 2 — q1 — qi,
где 0 < q < 1, которое интерполирует между постоянным ядром Kij = 2 при q = 0 и
аддитивным ядром Kij ~ (1 — q)(i + J) при q —> 1 — 0. Другое точнорешаемое ядро —
четнозависимое ядро, в котором Kij принимает три различных значения в случаях, когда
оба индекса г, j четны, нечетны, один четный, а другой нечетный соотвтственно.
5.3 Гелеобразование
185
нддитивное и мультипликативное ядра тесно связаны (см. задачу 5.4), есте-
гтиеиио было бы ожидать, что общее ядро (5.52) тоже решается. Решение
(Г».52) оправдывает естественные ожидания: при С > 0 мультипликативная
чисть доминирует, и в системе происходит гелеобразование; при С = 0 и В > О
вддитивная часть доминирует, и типичная масса растет экспоненциально со
Временем как в решении для аддитивного ядра.
Ядра с более быстрой агрегацией, такие как
Ку = (i + j)2 или = (ij)2, (5.53)
гораздо более сложны. Формально к этим ядрам применим метод производя¬
щей функции, с помощью которого основное кинетическое уравнение можно
Переписать в виде одного уравнения в частных производных для производя¬
щей функции. Однако это уравнение нелинейно и выше первого порядка (в
отличие от уравнения (5.40) для мультипликативного ядра). Можно попробо-
ппть добиться прогресса, используя метод моментов для получения основной
информации, такой, например, как типичная масса, или для обнаружения
гелсобразования. К сожалению, метод моментов не работает для таких ядер,
как (5.53). Чтобы увидеть источник проблем, рассмотрим ядро Kij = (i +j)2,
для которого уравнения, описывающие несколько первых моментов имеют
вид:
М2 = 2MiM3 + 2М%,
Мз = ЗУИ1М4 + 9М2М3,
М4 = ШхМь + 14М2М4 + 10УИ32,
УИ5 = 5 М± М§ + 2ОМ2М5 + З5А/3Л44.
Уравнения (5.54) имеют иерархическую структуру: уравнение для каждого
Мп содержит более высокий момент Mn+i и в общем случае не решается.
В предыдущем примере уравнения моментов были рекуррентными и потому
решались шаг за шагом. Более того, эта иерархическая структура приводит
к большой неожиданности: для специального примера Ку = (i + j)2 гель
возникает мгновенно — tg = 0+ ! Это странное поведение обычно возникает в
моделях с асимптотически однородным ядром вида
Kltj = Kjtl ~ j” при j -> 00, (5.55)
где у > I8. Доказательство того, что tg = 0+ в агрегации с ядром (5.55)
при у > 1, технически сложно. В разделе 5.6 мы покажем, что мгновенное
8 Применимость таких моделей к реальным процессам агрегации находится под вопро¬
сом, потому что число активных узлов в кластере не должно расти быстрее, чем его размер.
186
Агрегация
гелеобразование происходит в процессе массового обмена, анализ которого
оказывается проще, чем анализ простой агрегации.
5.4 Скейлинг
Скейлинг основан на наблюдении, что типичная масса кластера систематиче¬
ски растет со временем. Поэтому изменение временнбй шкалы соответствует
изменению масштаба массы, так что распределение масс остается инвари¬
антным при подходящем совместном перемасштабировании массы и времени.
Эту инвариантность можно записать в виде скейлингового анзаца
c(M) = ^/(j)- (5.56)
Здесь s = s(t) — типичная масса кластера в момент t, x/t — перемасштаби¬
рованная масса, и f(x/t) — скейлинговая функция. Таким образом, фунда¬
ментальные переменные не масса и время по отдельности, а перемасштаби¬
рованная масса x/s и время. Множитель s~2 перед скейлинговой функцией
обеспечивает сохранение массы f xc(x,i)dx = 1. В перемасштабированных
единицах этот закон сохранения сводится к не зависящему от времени явно
соотношению J* и f(u) du = 1.
Скейлинг помогает понять многие неравновесные явления. Есть несколько
причин полезности скейлингового подхода:
• Скейлинг упрощает и концентрирует описание неравновесных систем.
• Когда точные решения сложно или невозможно получить, скейлинг
предоставляет кратчайший путь к асимптотическим решениям благо¬
даря тому, что он разделяет основные кинетические уравнения с двумя
переменными на уравнения с одной переменной, которые можно про¬
анализировать по отдельности.
• Скейлинговое решение не зависит от начальных условий* * * * * 9 и потому со¬
средоточено только на самом существенном асимптотическом поведе¬
нии.
Это означает, что отношение K(l,j)/j ограничено при j —> оо, откуда следует ограничение
I/ < 1. Однако ядра с у > 1 были предложены, например, для описания гравитационно
притягивающихся частиц. Такие ядра в принципе могут быть использованы для конеч¬
ных систем. В термодинамическом пределе агрегация с такими ядрами плохо определена
и эволюция останавливается мгновенно.
9Кроме тривиальной зависимости от полной массы (см. уравнение (5.28)). Если, однако,
начальное распределение масс имеет достаточно медленно убывающий хвост, то асимптоти¬
ческое решение существенно зависит от начальных условий (см. пример 5.3 в разделе 5.2).
5.4 Скейлинг
187
• Наконец, скейлинг дает надежный способ классификации решений в
зависимости от общих свойств ядра реакций. В следующих главах мы
также увидим этот подход в действии.
Чтобы применить скейлинг, нужно «правильно» определить типичную
массу. В соответствии со скейлинговым анзацем n-ый момент распределения
масс имеет вид
Мп = / dx^sn~1-
Следовательно, 1/Мо, М2 или даже отношения Мп+\/Мп для произвольного
п — подходящие кандидаты для типичной массы s. Когда скейлинг приме¬
ним, можно выбрать определение типичной массы наиболее удобное в данной
ситуации. Для изучения следствий скейлинга нам также нужна основная ин¬
формация о матрице интенсивностей реакций Кц. Оказывается, что только
два свойства матрицы определяют асимптотическое поведение распределе¬
ния масс. Первое — это индекс однородности, определяемый соотношением
K(ai,aj') ~ axK(i,j),
которое показывает общую зависимость интенсивности реакций от массы, где
мы записали аргументы вместо матричных индексов матрицы К, поскольку
/ и j рассматриваются как непрерывные. Второе — индекс I/, определенный в
(5.55), который характеризует относительную важность реакций между кла¬
стерами с несоизмеримой массой. Как пример, постоянное ядро имеет индек¬
сы (Л, и) = (0,0), мультипликативное ядро — (Л, v) = (2,1), а «броуновское»
ядро (5.5), которое дает интенсивности реакций для сферических диффун¬
дирующих агрегатов, — (А, р) = (0,1/3).
Влияние индексов Л и v на кинетику реакций можно оценить, рассматри¬
вая следующее наглядное представление матрицы реакций:
188
Агрегация
Матричные блоки SS, SL{~ LS\ и LL содержат соответственно интенсив¬
ности реакций маленьких кластеров с другими маленькими кластерами, ма¬
леньких с большими и больших с большими. Точнорешаемые примеры, об¬
суждавшиеся в разделе 5.2, представляют «архетипы» трех разных классов
универсальности:
• Tun I: LL » LS, SS, что соответствует случаю Л > у. В этом слу¬
чае высокая реакционная способность больших кластеров приводит к
их быстрому исчезновению, в то время как маленькие кластеры имеют
тенденцию сохраняться. Соответственно, распределения массы класте¬
ров убывает монотонно с ростом массы. Мультипликативное ядро —
типичный представитель этого класса.
• Тип II: Все три реакции одного порядка. Пограничный класс содержит
постоянное ядро Kij = 1. Асимптотическое поведение в этом классе
чувствительно к деталям интенсивностей реакций.
• Тип III: LS » LL, SS или X < и. В процессе реакции число маленьких
кластеров быстро уменьшается из-за доминирования взаимодействий
типа «большой — маленький». Поэтому в системе наблюдается дефицит
маленьких кластеров, что приводит к пику в распределении масс.
Теперь применим скейлинг для нахождения основных свойств распреде¬
ления масс кластеров. В непрерывном пределе основное кинетическое урав¬
нение для агрегации принимает вид 10
дс 1 Iх Г°°
dt = 2J0 dyK(y,x-y)c(y,t)c(x-y,t)-J dyК(х,у) c(x,t)c(y,t). (5.57)
Подставив скейлинговую форму с(х, t) = s~2 f(x/s) в уравнение (5.57) и поль¬
зуясь однородностью К (ах, ау) = ахК(х,у), получим для левой части
^ = ~^з W(u) + uf'(u)],
где и = x/s. Аналогично, правая часть равна sA-33C(tt), где
1 PU гоо
5C(iz) = — / dvK(v,u-v)f(y)f(u-v)- / dv K(u,v) f(u) f(v) (5.58)
* Jo Jo
10Нижний предел интегралов в (5.57) должен быть равен наименьшей начальной массе.
Когда распределение масс не слишком сингулярно около ноля, можно заменить нижний
предел на 0.
5.4 Скейлинг
189
и и = у/х. Приравнивание этих двух частей после несложного преобразоваг
мня дает
s(t) _ Х(и) _
s(t)x 2f(u) + uf'(u) ~
(5.59)
Таким образом, как и было заявлено ранее, зависимости от времени и пере¬
масштабированной массы и разделяются, и две части уравнения (5.59) долж¬
ны равняться константе по отдельности: константе разделения Л.
Зависимость типичной массы от времени определяется из уравнения s =
Л«Л и дает
р/(1-А) =
s(t) ~ <
-1
л< 1,
А = 1,
1 < А < 2.
(5.60)
Для негелеобразующих систем зависимость типичной массы от времени опре¬
деляется только индексом однородности А. Другие черты интенсивности ре¬
акций, такие как второй индекс и, влияют только на детали, как, например,
общая амплитуда в асимптотическом законе убывания. Степенною зависи¬
мость от времени (5.60) также можно извлечь из простых аргументов. Ес¬
ли s(t) представляет типичную массу кластера в момент t, соответствующая
плотность кластеров имеет порядок 1/s. Рассмотрим интервал времени Af, за
который все кластеры прореагировали. При этом типичная масса возрастает
на As ~ s, тогда как время, необходимое, чтобы все эти события произошли,
ведет себя как величина, обратная полной интенсивности реакций. Последняя
в свою очередь пропорциональна ядру реакций K(s, s) ~ sA, умноженному
на концентрацию 1/s. Следовательно, &.s/&.t ~ s х (sA/s), что воспроизводит
(5.60).
Зависимость скейлинговой функции f от перемасштабированной массы и
подчиняется зависящей от и части уравнения (5.59)
2f{u) + uf’(u) + Л^ад = 0, (5.61)
где Х(и) дано в (5.58). Нелинейное интегрально-дифференциальное уравне¬
ние (5.61) — сложно, и полное понимание поведения скейлинговой функции
/(«) до сих пор отсутствует. Хотя найти решение (5.61) для произвольно¬
го ядра не представляется возможным, можно разобраться во многих его
качественных свойствах, используя простые средства. Например, было пока¬
зано, что, когда перемасштабированная масса велика, и 1, скейлинговая
функция демонстрирует экспоненциальную зависимость f(u) ~ е_аи; деталь¬
ные свойства ядра влияют только на предэкспоненциальный множитель это¬
го экспоненциального хвоста. Поведение скейлинговой функции при малых
190
Агрегация
значениях перемасштабированной массы менее устойчиво. Различные чис¬
ленные результаты показывают, что f(u) ~ и~т при и 1. Вследствие этого
зависимость плотности кластеров малой массы от времени имеет вид
Ск ~
~fc~Tr(2_r)z.
(5.62)
Эвристический подход к определению т предполагает, что временная зави¬
симость, полученная для мономеров, дает представление о поведении скей¬
линговой функции в пределе и —> 0. Эволюционное уравнение для плотности
мономеров имеет вид
^ = -Cl^KljCj. (5.63)
Так как K±j ~ ju и Cj ~ j~~T, сумма в правой части уравнения (5.63) схо¬
дится, если у — т + 1<0. В этом случае первый член дает хорошую оценку
всей суммы. Поэтому мы пишем ci ~ — Кц Ср что дает с± ~ 1/t. Сравнивая
эту временную зависимость с уравнением (5.62), находим соотношение для
индексов т = 1 + Л. Этот степенной хвост возникает при у — т + 1 = и — Л < 0,
т. е. для ядер типа I. Такая временная зависимость для кластеров малой
массы — это одно из хорошо установленных свойств хвоста распределения
размера кластеров.
5.5 Агрегация с источником
Многие физические реализации агрегации происходят не в замкнутой систе¬
ме, напротив, реакция поддерживается из постоянного источника. Примеры
агрегации с источником разнообразны: от химического процесса в реакцион¬
ном аппарате с мешалкой до распределения звезд в галактиках. Здесь мы
изучим взаимодействие между источником и агрегацией в простом случае
постоянного источника мономеров, который начинает действовать в момент
t = 0. Поскольку асимптотическое поведение независимо от начальных усло¬
вий, мы рассматриваем изначально пустую систему: с&(0) = 0.
Постоянное ядро
В этом случае распределение массы изменяется в соответствии с уравнением
dck
i+j=k
CiCj - 2ckN + 6к<1.
(5.64)
5.5 Агрегация с источником
191
11олная плотность удовлетворяет уравнению N = —N2 +1, решение которого
для изначально пустой системы имеет вид
N(t) = th t. (5.65)
Следовательно, плотность кластеров сначала растет линейно со временем, но
в конце концов стремится к единице.
Плотность кластеров данной массы можно в принципе вычислить, решая
основные кинетические уравнения одно за другим. Однако метод производя¬
щей функции снова оказывается более эффективным инструментом. Введя
производящую функцию Q(z,t) = ^2k>ick(^zkj мы превращаем уравнения
(5.64) в дифференциальное уравнение (сравните с уравнением (5.21))
ё(г, t) = C(z, t)2 - 2е(г, i)JV(t) + z. (5.66)
'Гак же как в необратимой агрегации, удобно работать с величиной С — 7V,
удовлетворяющей замкнутому дифференциальному уравнению ж(е - ло =
(6 — TV)2 + (z — 1). Решив это уравнение, получим
C(z, £) = th £ — y/l — z th (t л/l — z) , (5.67)
и таким образом в пределе t —> оо имеем
C(jz, t = оо) = 1 — л/1 — z.
Производящую функцию на бесконечном времени можно обратить, разлагая
>/1 — z в степенной ряд по 2, что приводит к следующему хвосту стационар¬
ного распределения масс11:
ct 7S *375’ к *L (5'в8)
При конечных временах закон сохранения массы требует выполнения равен¬
ства ^3 kck(t) = t, так что стационарный степенной хвост распределения мас¬
сы должен быть обрезан в конце. Можно определить точку перехода между
стационарным режимом при к < и режимом к > &*, где кластеры еще не
были созданы, потребовав, чтобы полная масса в системе была пропорцио¬
нальна прошедшему времени:
t = kck(t) ~ ^2 ^ск ~ ~ (&*)1/2 > (5.69)
к>1 к=1 к=1
11В этом разделе мы пользуемся обозначением Ск вместо Ck(t = оо). Когда мы работаем
с нестационарным распределением масс, мы пишем сь(£).
192
Агрегация
5.3. Игры с гамма-функциями
Гамма-функция Эйлера предоставляет удобный и мощный метод обращения про¬
изводящей функции для агрегации с источником. Рассмотрим функцию у/1 — z,
которая возникает в производящей при конечном времени. Разложение Тейлора
этой функции имеет вид
-1 + К--) + i К) + i (-1) (-1)
+1 (-1) (-1) (-!) + •■■■
Такая форма записи неудобна для выявления поведения произвольного члена это¬
го ряда. Однако можно избавиться от длинных произведений, используя основное
тождества для гамма-функций
а(а + 1)... (а + fc — 1) = (5.70)
чтобы получить компактное выражение для ряда
1 _ — I)
2Г(|) Г(Л+1)’
После этого, воспользовавшись равенством Г(|) = 5/7F, получим
1 r(fe-j)
^/4% r(fc +1)
(5.71)
Для асимптотического поведения можно воспользоваться удобным асимптотиче¬
ским соотношением, справедливым при к 1,
Г(Ас + а)
Г(Ь + 5)
(5.72)
Из уравнений (5.71) и (5.72) получаем стационарное распределение масс (5.68).
Еще одно применение гамма-функций будет дано во врезке на стр. 482.
и поэтому к* ~ t2. Соответственно, стационарное степенное распределение
(5.68) распространяется только до этой точки обрезания.
Эту качественную картину можно улучшить с помощью точного анали¬
за. Чтобы получить плотность кластеров из производящей функции (5.67),
подставим в (5.67) представление в виде ряда
7Г
th(7nr) =
00
£
X
х2 + (п+±/
5.5 Агрегация с источником
193
м ризложим по степеням z, что дает
(5.73)
И пределе большого времени заменим сумму в правой части (5.73) на инте¬
грал по переменной х = (| + n) j. При к С t2 получим
1 [°° х2 dx
Ск~ тг J-ж (1 + ж2)*4-1 ‘
Вычисление интеграла дает (5.71).
С другой стороны, когда и к, и t стремятся к бесконечности, так что
к ~ k/t2 остается конечным, (5.73) упрощается:
2
Cfc(t) =
? L ("+!)
п=—оо х 7
7Г2 К,
(5.74)
Для масс к » к* можно сохранить только первый член (5.74), чтобы получить
ведущее асимптотическое поведение плотности массы
Cfc(t) =
е"7^4.
(5.75)
Обобщенное аддитивное ядро
Кстественная реализация агрегации с источником возникает при эпитакси¬
альном росте поверхностей. При этом атомы ударяются о чистую поверх¬
ность с постоянной интенсивностью, необратимо адсорбируются и в некото¬
ром температурном диапазоне могут диффундировать по поверхности. Такие
мобильные адатомы могут соединяться, образуя димеры, тримеры и т. д.,
так что острова всех размеров могут диффундировать по поверхности, про¬
должая агрегировать. Таким образом, рост острова подвержен комбиниро¬
ванному влиянию необратимой агрегации, диффузии островов и постоянного
источника мономеров.
Механизм, лежащий в основе диффузии островов, включает адатомы на
границе острова, которые могут прыгать в соседние узлы рядом с границей
острова (рис. 5.5). Рассмотрим большой остров с линейным размером R. За
время Д£ ~ R2 граничный адатом может обойти всю границу острова12. За
12Мы неявно предполагаем, что граничная диффузия сглаживает границу так, что пе¬
риметр острова пропорционален R и адатом остается близко к границе острова.
194
Агрегация
Рис. 5.5. Схематическое изображение эффективной диффузии острова посред¬
ством движения адатомов вдоль границы острова
время Д£ каждый граничный адатом перемещается на расстояние R от его
первоначального положения. Смещение центра масс острова из-за смещениея
одного адатома равно Sx ~ R/В? ~ R-1. Если каждый граничный адатом
диффундирует независимо от других, то общее смещение Дж будет суммой R
независимых одинаково распределенных случайных величин, так что Дж ~
•УД(5ж)2 ~ Д-1/2. Поэтому эффективный коэффициент диффузии острова
линейного размера R ведет себя как Dr ~ (Дж)2/Д< ~ R~3. Так как масса к
острова линейного размера R пропорциональна его площади, эффективный
коэффициент диффузии острова имеет массовую зависимость
Dk ~ к~3'2. (5.76)
Формула Смолуховского = (Di + Dj)(Ri + Rj)d~2 для интенсивно-
сти агрегации г-мера и J-мера на поверхности в двух измерениях сводится к
Di + Dj13. Запишем Dj = j а, где а — показатель подвижности, рав¬
ный 3/2 для граничной диффузии, который может принимать и другие зна¬
чения при других механизмах релаксации поверхности. В физическом случае
двумерной поверхности мы получаем обобщенное аддитивное ядро
Кц = Га + Га. (5.77)
Найдем стационарное состояние для обобщенного аддитивного ядра с ис¬
точником мономеров. Основные кинетические уравнения имеют вид
(5.78)
J>1
13Для диффузии по двумерной поверхности член (Ri+Rj)d 2 нужно заменить медленно
меняющейся зависимостью 1/1п(#г + Rj), которой мы пренебрегаем.
5.5 Агрегация с источником
195
Определив производящие функции
•A(z)=52 к~°ск zk> =^2Ск*к (5-79)
к>1 к>1
и введя сокращенное обозначение А = A(z = 1), можно свести уравнение
(5.78) к
Л(г)б(г) - Л(г)ЛГ - e(z)A + z = 0. (5.80)
11оскольку при а = 0 распределение массы убывает алгебраически, естествен¬
но предположить, что это убывание имеет место и при а / 0, т. е. Ск —> С к~т
при А: » 1. Эта гипотеза предполагает, что при z f 1 производящие функ¬
ции демонстрируют следующее сингулярное поведение (см. (5.24) во врезке
ни стр. 174):
ЛМ = Л + СГ(1 - т - и) (1 - г)'-1-”"1 + ...
e(z) = N + СГ(1 - т) (1 - z)r-‘ + ....
Чтобы найти показатель убывания т и амплитуду С, подставим эти разло¬
жения Л и 6 в (5.80) и потребуем, чтобы они были согласованы в пределе
z -> 1. Уравнение для константных членов дает AN = 1. Уравнение для чле¬
нов первого порядка по (1 — z) и формула отражения для гамма-функции
Г(г)Г(1 — z) = 7г/sin(jrz) приводят нас к выражениям
3 — а „ Il — а2 (пах
r=— ^ = v^tcos(t)- (5-82)
После нахождения показателя убывания стационарной плотности fc-меров т
с помощью аргументов, использованных при выводе (5.69), можно оценить
время перехода:
. t=52 fcCfc(t) ~ 5>с* ~ 52 к1^ ~ к^-т = $+а)/2.
к>1 к=1 к=1
Таким образом, мы получаем характерную массу
fc*~t2/(1+a). (5.83)
Наш анализ основывался на том, что система достигает стационарного
состояния. Практически, мы неявно предполагали, что суммы N = ^Ск и
А = ^2^аск сходятся. Для этого требуется, чтобы показатель убывания
одновременно удовлетворял ограничениям т > 1 и т > 1 — а. Эти неравенства
196
Агрегация
вместе с равенством т = (3 — о)/2 накладывают ограничения на показатель
подвижности
-1 < а < 1, (5.84)
следующие из требования существования стационарного состояния. Парадок¬
сально, что механизм граничной диффузии, который привел нас к обобщен¬
ному аддитивному ядру, не достигает стационарного состояния а непрерывно
меняется.
Модель роста островов
Экстремальный предел а —> оо, в котором только мономеры движутся, а
бблыние агрегаты (острова) неподвижны (рис. 5.6), особенно интересен. В
Рис. 5'6. Изображение элементарных процессов в модели роста острова: адсорб¬
ции с интенсивностью F (вертикальные стрелки); столкновение двух подвижных
мономеров, образующих неподвижный димер (справа вверху); присоединение
подвижного мономера к неподвижному кластеру (слева снизу).
модели роста островов кластеры массы 2 или больше могут расти только
за счет присоединения подвижных адатомов к их границам. Элементарные
шаги роста островов — это
О—>Ai, Ai + Ai —> А2, Ai + Ад, —> А&+1.
Первый процесс учитывает осаждение мономеров на поверхность с интенсив¬
ностью F, тогда как два последних отвечают за рост кластеров при присо¬
единении мономеров. Когда только мономеры подвижны, ядро реакций имеет
вид Kij ~ Di + Dj = D(Siti + <5j,i), так что эволюция системы описывается
уравнениями
5.5 Агрегация с источником
197
-с e«+f,
к=1
= ci(cfc_i - Cfc), к >2.
' {дссь мы включили коэффициент диффузии D в переменную времени, так
что параметр F стал отношением интенсивности осаждения (измеряемой в
единицах числа адатомов на один узел за единичное время) к коэффициенту
диффузии D. В экспериментальных приложениях F обычно мало и может
изменяться в широком диапазоне.
Следующие предположения стоят за применением основного кинетиче¬
ского уравнения к модели роста островов:
• Острова разрежены, так что они не могут сливаться непосредственно
друг с другом. Этот предел соответствует субмонослойному режиму,
определяемому как Ft 1.
• Острова рассматриваются как точки. Это слабое ограничение, так как
интенсивность реакций в двух измерениях зависит от радиуса логариф¬
мически.
• Выполняется приближение среднего поля. В реальности это предполо¬
жение нельзя обосновать, так как неподвижные острова могут рассмат¬
риваться как случайно распределенные ловушки, для которых средне¬
полевое описание неприменимо (см. раздел 13.2).
• Имеются свободно диффундирующие адатомы и неподвижные остро¬
ва. Это предположение определенно находится под вопросом, поскольку
острова обычно диффундируют посредством отсоединения и повторно¬
го присоединения мономеров на границе острова.
Несмотря на такую идеализацию, модель роста островов хорошо иллюстриру¬
ет использование асимптотического анализа для решения основных кинети¬
ческих уравнений, а также достоинства и недостатки скейлингового анализа.
Для решения уравнений (5.85) сначала сложим их, что даст кинетическое
уравнение для полной плотности N
(5.86)
Также полезно явно разделить все кластеры на мономеры и неподвижные
острова массы 2 и более. Пусть I будет плотность неподвижных островов, I =
- = F-c1N.
at
198
Агрегация
5Dfc>2 ск- Тогда мономеры и острова удовлетворяют системе взаимозависимых
уравнений
=-2cl - c,I + F,
di 2
Tt=c"
для которых асимптотика решения имеет вид (см задачу 5.11)
i(t) ~ f2/3 (зг)1/3, ci(t) ~ F1/3(3t)_1/3,
(5.87)
(5.88)
Однако эти законы роста не могут выполняться до бесконечности, потому что
в конце концов покрытие окажется за пределами субмонослоя. Окончание
субмонослойного режима определяется как fmax ~ F-1, что соответствует
оценке Imax ~ F1/3.
Чтобы найти плотности островов в субмонолслойном режиме, введем
вспомогательную переменную времени т = J^ci (t') dt' и запишем уравнение
(5.85) для неподвижных островов (к > 2) в виде пуассоновского процесса
= Cfc_i - ск. (5.89)
Теперь, рассматривая к как непрерывную переменную и аппроксимируя раз¬
ность производной, получим линейное волновое уравнение
(£+^)-*м=0- (8'90)
Его общее решение имеет вид с&(т) = f(r — fc), где f — произвольная функ¬
ция, определяемая сравнением решения с решением для ci, которое играет
роль граничных условий. Поскольку ci(t) = /(т — 1), искомое решение — это
просто Cfc+i(r) = ci(t —к). Используя определение т и формулу (5.88) для ci,
получим
т ~ | F1/3 (Зг)2/3, ci(t) ~ F1/2(2t)"1/2 (5.91)
что приводит нас к
= (М2)
Таким образом, распределение размеров островов описывается решением в
виде распространяющейся волны.
5.6 Рост С ОБМЕНОМ
199
Решение (5.92) не дает точного описания, когда к мало, так как замена ед,—
q.1 становится неприемлемой. Волновое решение (5.92) также неприменимо,
когда к > т. Последняя проблема решается более сложным непрерывным
приближением, сохраняющим два члена тейлоровского разложения,
Cfc-l - cfc ~
дс 1 д2с
дк + 2 дк?'
'Тогда вместо волнового уравнения (5.90) получается уравнение конвекции-
диффузии
дс дс _ 1 д2с
дт + дк 2 дк? ’
(5.93)
которое имеет хорошо определенные решения для всех к. Это решение очень
близко к волновому решению, когда к < т. Сингулярность волнового решения
(5.92) заменяется пиком конечной ширины в точке к = т (см. задачу 5.12).
5.6 Рост с обменом
Паша последняя тема — процесс обмена массы, в котором взаимодействие
между двумя кластерами имеет вид
Ai + AjK^nAm + An. (5.94)
Мы рассматриваем только события, сохраняющие массу, в которых i + j =
m + п. Примерами реализации обменных процессов являются рост капли с
испарением и повторной конденсацией и изменение благосостояния с обменом
капиталом между экономически взаимодействующими индивидуумами. Как
показано на рис. 5.7, массовый обмен — это гибрид рассеяния и агрегации:
два входящих кластера превращаются в два выходящих кластера, хотя если
одна из масс m или п мала, процесс напоминает агрегацию, потому что масса
одного из выходящих кластеров почти равна сумме масс входящих кластеров.
В качестве простого примера предположим, что в каждом событии обмена
переносится единичная масса. Тогда взаимодействие сводится к
Ai + Aj —4 Aj±i + Aj^i. (5.95)
Далее предположим, что кластер с одинаковой вероятностью приобретает
или теряет массу во время взаимодействия, т. е. матрица реакции симмет¬
рична: K^j = Kjti. Таким образом, когда один из реагирующих кластеров —
200
Агрегация
Рис. 5.7. Изображение массового обмена, в котором взаимодействие кластеров
с массами г и j приводит к рождению кластеров с массами т и п
мономер, число кластеров возрастает на 1 с вероятностью 1/2; если оба входя¬
щих кластера — мономеры, число кластеров с необходимостью уменьшается
на 1.
Одна из приятных сторон обменных процессов — простота их решения.
Эта простота на первый взгляд неожиданна, так как моменты распределения
масс (которые так помогли в случае обычной агрегации) не удовлетворяют
замкнутым уравнениям14. Однако основное кинетическое уравнение для об¬
менного ядра часто можно линеаризовать и таким образом решить. Рассмот¬
рим, например, мультипликативное ядро 7f(i,J) = (ij)A. Эволюция с& для
такого обменного процесса описывается уравнением
~ = МХ [(А: + l)ACfc+i + {к - l)ACfc_i - 2fcACfc] , (5.96)
где М\ = 53. jxCj — это момент степени Л распределения масс. Эти уравнения
будут справедливы для всех к > 1, если мы потребуем выполнения условия
со = 0. Первый эффективный шаг к решению уравнения (5.96) — включить
член М\ в определение переменной времени
т= Г dtf (5.97)
Jo
таким образом лианеризовав основные уравнения:
= (к + l)Acfc+i + (k- l)Acfc_1 - 2кхск. (5.98)
Теперь решим уравнения (5.98) для показательных случаев Л = 0,1,2, и
покажем мгновенное гелеобразование в случае Л > 2.
14Единственной исключение — первый момент, который снова с необходимостью сохра¬
няется, Mi = 1.
5.6 Рост С ОБМЕНОМ
201
Пример 5.4. Постоянное ядро (А = 0). Когда K(i,j) = 1, уравнения (5.98)
принимают вид
= Cfc+i + Ck—i 2с&, (5.99)
который есть ни что иное, как уравнение диффузии в непрерывном времени и
дискретном пространстве. Удобно смотреть на к как на пространственное по¬
ложение «частицы», так что Ck(t) — вероятность того, что частица находится в
точке к в момент времени t. Для мономерных начальных условий Cfc(0) = 5^1
частица стартует с fc = 1 и начинает диффундировать. Требование со = 0 можно
интерпретировать как адсорбирующие граничные условия.
В отсутствие адсорбирующих граничных условий решение для концентрации
имеет вид Ск = е~2тIk-i(2r) (см. обсуждение диффузии в дискретном простран¬
стве в разделе 2.1). Сдвиг индекса в модифицированной функции Бесселя по
сравнению с решением в разделе 2.1, отражает тот факт, что частица стартует
в fc = 1, а не в fc = 0. Можно включить адсорбирующие граничные условия, по¬
местив изображение частицы в fc = — 1, и рассматривая уравнение (5.99) на всей
прямой15, с начальными условиями сЦО) = 5кд — Комбинация исходного
и отраженного решений дает
Cfc(r) = е~2т [Д_х(2т) - Д+1 (2т)], (5.100)
где Iv — модифицированная функция Бесселя порядка у. Из этого решения
можно найти полную плотность кластеров, N(t) = J2fc>iCfc(r), для которой
получим
7V(t) = е~2г [Л)(2т) + Л(2т)] ~ (7гт)-1/2, т —> оо.
Этот результат совпадает с вероятностью выживания для диффузии иа полу¬
прямой. Чтобы выразить это решение через физическое время £, проинтегрируем
£(т) = £ dr'/N^r'), что в пределе большого времени дает N ~ [2/(37г£)]1/<3, тогда
как для плотности массы имеем
с(т) ~ ехр
1/3
fc2 ‘
£2/3
Заметьте, что типичный размер кластера растет как £2/3.
Пример 5.5. Мультипликативное ядро (А = 1). Мультипликативное ядро
= ij оказывается простейшей решаемой моделью обмена, поскольку пер¬
вый момент Mi равен 1, так что t и г в уравнении (5.97) совпадают. В этом
случае уравнения (5.98) имеют вид
= (к + l)cfe+i + (к - l)cfc_! - 2kck. (5.101)
15Этот стандартный прием часто используется в электростатике, а также применим к
уравнению диффузии.
202
Агрегация
Уравнения (5.101) решаются с помощью экспоненциального анзаца Ск = Аак~г,
который обсуждался на странице 171. После подстановки этого анзаца в (5.101)
бесконечный набор уравнений сведется к двум взаимозависимым уравнениям
а = (1 — а)2, А = —2А(1 — а),
откуда имеем: а = t/(l +t) и А = (1 + £)“2. Отсюда получим Ск = £fc_1/(l +
£)fc+1. Мы могли бы прийти к тому же самому результату с меньшими усилиями,
заметив, что условие ^кск = 1 приводит нас к равенству А = (1—а)2, и поэтому
нам нужно решить только одно дифференциальное уравнение для а.
Распределение массы точно такое же, как в случае агрегации с посто¬
янным ядром (см. уравнение (5.13)). Это неожиданное совпадение также
имеет место для экспоненциально спадающих начальных условий. Это
совпадение уникально: в общем случае не существует точного соответ¬
ствия между линейным основным кинетическим уравнением для агрега¬
ции и нелинейным для обмена.
Пример 5.6. Квадратичное мультипликативное ядро (Л = 2). Квадратичное
мультипликативное ядро К (г, J) = (<?)2 приводит к «полному» гелеобразованию,
при котором плотности всех кластеров конечного размера равны нулю за точкой
гелеобразования. Эту сингулярность можно обнаружить, анализируя кинетиче¬
ские уравнения для моментов. В терминах вспомогательной временнбй перемен¬
ной, определенной в уравнении (5.97), первые несколько уравнений имеют вид16
dM2
dr
= 2М2,
dM3
dr
= 6М3,
dM4
dr
— 12Л/4 + 2M2,
а их решения даются комбинациями экспонент: М2 = e2r, М3 = e6r, М4 =
|е12т - |е2т. Переходя к физическому времени t = fj dr' М^1 (т'), получим
t = j[l — е“2т]. Выражая моменты через £, находим
M2 = (l-2i)~\ М3 = (1 — 2f)-3, Mi = ^(1 - 2t)-6 - |(1 - 2t)-1. (5.102)
5 5
В общем случае Мп ~ (1 — 2t) n(jl 1^/2. Поэтому гелеобразование происходит в
момент tg = 1/2.
Пример 5.7. Мгновенное гелеобразование (А > 2). Чтобы продемонстрировать
необычное (или на чей-то вкус ненормальное) явление мгновенного гелеобра¬
зования, мы предположим, что гелеобразования не происходит и затем придем
16Полная плотность подчиняется уравнению dM^/dr = —ci для всех ядер, и следова¬
тельно, чтобы определить нулевой момент, нужно знать плотность мономеров.
5.6 РОСТ С ОБМЕНОМ
203
к противоречию. Согласно гипотезе догелевый режим хорошо определен когда
моменты существуют и удовлетворяют уравнению17
dMn
dr
L«/2J X ч
\2l)Mn~2l+X'
(5.103)
5.4. Неравенство Йенсена
Предположим, что Pj для j = 1,2,... — неотрицательные числа, pj >0, которые
удовлетворяют неравенству SjPj = 1- Пусть Ф(т) — произвольная выпуклая
функция. Тогда неравенство
> Ф((5.104)
j>i S>i '
называется неравенством Йенсена. Это неравенство эквивалентно утверждению
о выпуклости, т. е. функция выпукла, если неравенство (5.104) выполняется. Под¬
ставим в неравенство Йенсена pj = jcj (условие = 1 тогДа следует из за¬
кона сохранения массы .jcj = 1) и выпуклую функцию Ф(ж) = ж1+д (р > 0
для Л > 2). Выбирая Xj = Jn_1, используя равенства ^PjXj = 53Jncj = Мп и
2р^Ф(^’) = -Wn-2+А, видим, что неравенство Йенсена сводится к (5.106).
Нижнюю границу скорости роста можно получить, удерживая несколько первых
членов в этой сумме:
> п(п - 1)МП_2+Л. (5.105)
Это все еще иерархический набор уравнений, поскольку для Л > 2 индекс мо¬
мента в правой части п — 2 + А превосходит индекс момента в левой. К счастью,
можно воспользоваться неравенством Йенсена (см. врезку выше), которое дает
Мп_2+А > (Мп)1+^, д = (5.106)
72—1
Сравнивая (5.105) и (5.106), получим dMn/dr > n(n — 1)(МП)1+М. Из этого урав¬
нения видно, что удобно использовать вспомогательные функции Мп, эволюция
которых задается уравнением
= п(п - 1)(МП)14Л (5.107)
ат
Решая (5.107) с начальными условиями Mn(0) = 1, получим Mn = [1 — п(А —
2)т]“(п_1)/(л_2\ Следовательно, Мп —> оо, когда т —> тп = [n(A — 2)]-1. По¬
скольку Мп > Мп, момент Мп расходится максимум в тп. Последовательность
17Функция |_xj в (5.103) дает наибольшее целое число, которое не превосходит действи-
гельное число х.
204
Агрегация
времен тп дает верхнюю оценку для времени гелеобразования тд, так как все
моменты должны быть конечны при т < тд. Поскольку тп —> 0 при п —> оо,
можно заключить, что тд = 0. Поэтому для А > 2 гелеобразование мгновенное:
tg = 0-
5.7 Ссылки
Некоторые из ранних работ по агрегации представлены в обзоре Чандрас¬
екара [12], а более поздние рассмотрены в [94, 95] в контексте физической
химии. Дополнительные приложения агрегации, опять в основном с точки
зрения физической химии, обсуждаются в [96, 97]. Одно из предположений,
лежащих в основе метода кинетических уравнений, о том, что интенсивность
агрегации не зависит от формы кластера, было численно подтверждено в [98].
Общее обсуждение соотношения Стокса-Энштейна и других аспектов физи¬
ческой гидродинамики можно найти в [99]. Производящие функции, которые
кратко упоминались в главе 2, существенно используются в этой главе для
решения основных кинетических уравнений, при обращении Лагранжа и при
анализе сингулярностей. Три полезные книги по производящим функциям —
[100-102]. Другая более специализированная ссылка [103] особенно хороша
для асимптотического анализа. Обзоры по агрегации с упором на скейлинг
недавно представили Алдоус [104] и Лейвраз [105].
Вероятно, первый вывод гелеобразования для мультипликативного ядра,
базирующийся целиком на решении основного кинетического уравнения, дан
в [106]. Подробное исследование гелеобразования при агрегации есть в [107].
Исследования агрегации в конечных системах, которые показывают возник¬
новение геля и обсуждают флуктуации проводились в [108, 109].
Ранние ссылки по агрегации в присутствии стационарного источника —
[110, 111]. Первая рассматривает астрофизическую задачу о распределении
размера звезд с учетом гравитационной аккреции материи и постоянного при¬
тока нового материала в результате взрывов сверхновых. Вторая имеет дело
с теми же явлениями, но в контексте аэрозолей. Модели эпитаксии и их связь
с агрегацией обсуждаются, например, в [112-115]. Идея, стоящая за массовым
обменом, была сформулирована Мельзаком в [116]. О применениях этой идеи
к статфизическому моделированию обмена богатствами см. [117]. Дополни¬
тельную информацию о тонкостях, связанных с мгновенным гелеобразова-
нием, можно почерпнуть в [118-121]. Онлайн-энциклопедия целочисленных
последовательностей, упоминаемая в задачах, находится по адресу [122].
5.8 Задачи
205
5.8 Задачи
5.1 Рассмотрите агрегацию с постоянным ядром с начальным распределением
масс cj(O) = 0 для )>т + 1ит>4. Опишите асимптотическое поведе¬
ние распределения масс кластеров, обобщив метод из примера 5.2 (стр. 175)
следующим образом:
(a) Хотя невозможно явно вычислить корни производящей функции, пока¬
жите, что начальную производящую функцию Q(z,t = 0) можно запи¬
сать как
C(zi, 0) = Ci(0)zi + С2(0)г2 + ... + Cm(0)z™ = 1 + M (0)б + О(б2),
где ci(0) + сг(О) + ... + cm(0) = 1 — начальная плотность кластеров,
ci(0) + 2с2(0) + ... + тСтп(О) = Л1(0) — начальная плотность массы, а
zi = 1 + е — наименьший корень e(^i, 0).
(b) Воспользуйтесь результатом для C(z,t = 0) и покажите, что производя¬
щую функцию можно записать как
“ г2ти(о) 1 - z/zr ’
где zi = 1 + 1/[М(0)£] — наименьший корень производящей функции.
Разложите это выражение в степенной ряд по z и покажите, что скей¬
линговый вид распределения массы дается уравнением (5.2).
5.2 Найдите концентрацию кластеров сь(£) для агрегации с постоянным ядром с
начальными условиями Cfc(0) = 2~к.
5.3 Покажите, что третий и четвертый моменты распределения масс кластеров
для агрегации с мультипликативным ядром с мономерными начальными усло¬
виями имеют вид
f(l-t)-3
_ f)-3
M3(t) =
при t < 1;
при t > 1;
и
M4(t) =
f (1 + 2t)(l -1)-5
(e4flt + 2fe3fft)(eat -t)"5
при t < 1;
при t > 1.
В более общем случае покажите, что около точки гелеобразования моменты
Мп расходятся как
_ 2—2 Г(п — 3/2) . ,2п_з,
Г(1/2) 11 4
что следует из уравнения (5.46).
206
Агрегация
5.4 Рассмотрите агрегацию с аддитивным ядром, в котором Ку = г + j.
(а) Покажите, что основные кинетические уравнения имеют вид
dck
dt
52 CiCj - cfc(fcM0 + 1),
k
2
где плотность массы равна единице: Mi = ^2k>1 kck = 1.
(b) Напишите кинетические уравнения для моментов. Покажите, что для мо¬
номерных начальных условий несколько первых моментов даются выра¬
жениями: Mq = е~\ М2 = е2*, М3 = 3 e4t — 2 e3t, М4 = 15 e6t — 20 e5t+6 e4t.
(c) Решите основные кинетические уравнения, выписанные выше, для моно¬
мерных начальных условий и получите точное решение
Cfc(t) = (1 - е-‘ е-*1-*-*).
5.5 Рассмотрите модель роста островов в отсутствие источника с реакциями Ai +
Ak —> Afc+i, где интенсивность каждой реакции равна 1, кроме реакции между
мономерами А± + А^ —> Аг, интенсивность которой равна 2 (почему?). Пред¬
положите, что система изначально содержит одни мономеры.
(a) Введите вспомогательную переменную времени, которая линеаризует ос¬
новное кинетическое уравнение.
(b) Определите распределение размера островов при бесконечном времени.
(c) Покажите, что конечное состояние достигается экспоненциально быстро.
5.6 Рассмотрите процесс сложения из предыдущей задачи, но с ядром = iSjyi +
jSi^. Покажите, что
Cfe(t) = [(1 - e-t)fe_1 - - e-‘)fc] (2 - e-‘)-fc
5.7 Используйте скейлинговый подход для определения распределения массы в
агрегации с постоянным ядром, т. е. решите уравнение (5.59) и найдите скей-
линговую функцию.
5.8 Рассмотрите агрегацию с постоянным ядром18.
(а) Покажите, что плотность мономеров имеет вид
С1 = 2
ch2 t
+ tht
18В этой и других задачах с источником мы предполагаем, что система сначала пуста,
а интенсивность источника полагается равной единице, так что М = t.
5.8 Задачи
207
(Ь) Решите уравнение (5.64) с помощью рекурсии и выведите формальное
решение (для к > 1)
CfcG) =-Д- / dt' ch2t' ^2
5.9 Рассмотрите агрегацию с аддитивным ядром с источником.
(a) Проверьте, что плотность кластеров дается выражением
N(t} = fdt'e^-^2.
Jq
Покажите, что N(t) сначала растет, достигает максимума, а потом стре¬
мится к нулю как N ~ 1Г1 при t 1.
(b) Покажите, что плотность мономеров также сначала растет, потом умень¬
шается и асимптотически убывает как ci — £-1.
(c) Покажите, что плотность димеров убывает как сг — t~3.
(d) Проверьте, что в общем случае в пределе большого времени имеет место
зависимость Ck — Akt~^2k~^.
(e) Найдите рекурсию для амплитуд и покажите, что эти амплитуды
образуют последовательность А088716 из онлайн-энциклопедии целочис¬
ленных последовательностей.
5.10 Исследуйте мультипликативное ядро с источником.
(a) Покажите, что в догелевом режиме второй момент имеет вид М2 = tgt
Используйте это решение, чтобы доказать, что гелеобразование проис¬
ходит при tg = 7Г/2.
(b) Покажите, что в догелевом режиме N = t — t3/§.
(c) Покажите, что в догелевом режиме М3 = tgt + | tg31.
(d) Покажите, что плотность мономеров равна Ci(t) = dtf e^'2~t2^2 при
любом времени.
5.11 Стартуя с эволюционного уравнения (5.87) для модели роста островов, найди¬
те временную зависимость 1(f) и плотность мономеров ci(t) с помощью сле¬
дующих шагов.
(a) Покажите, что плотность островов монотонно возрастает со временем,
и что ci —> 0 при t 00. Подсказка: Предположите противоположное,
а именно — ci —> const, при t 00, и покажите, что такое поведение
приводит к противоречию.
(b) Воспользовавшись тем, что ci -4 0 при t 00, найдите асимптотическое
решение основного кинетического уравнения для ср Используйте этот
результат при выводе уравнения (5.88).
208
Агрегация
5.12 Проанализируйте улучшенное непрерывное описание модели роста островов
(5.93).
(a) Покажите, что этот подход избавляет от сингулярностей решения вол¬
нового уравнения (5.92), а именно, сингулярное поведение заменяется
пиком конечной ширины.
(b) Найдите высоту пика, т. е. плотность с^(т), когда к = т.
(c) Оцените ширину пика.
5.13 Исследуйте модель роста островов с нестабильными димерами, в которой ди¬
мер может распасться на два подвижных адатома с интенсивностью А, тогда
как все бблыпие острова стабильны.
(a) Запишите и решите основное кинетическое уравнение для этого про¬
цесса и покажите, что I = JF’3/4(4t/A)1/4, ci = F1/4(4t/A)”1/4, и С2 =
F1/2(4tA)_1/2.
(b) Покажите, что максимальная плотность островов, достигаемая в конце
субмонослойиого режима, растет с F как /тах ~ F1/2.
5.14 Предположите, что острова массы > п стабильны, тогда как более легкие
острова нестабильны.
(a) Покажите, что ci г>и £ 1/С71-!-!) ф
(b) Покажите, что сп £-(n-l)/(n+l)
(c) Покажите, что /тах r\J p(n-l)/(n+l).
5.15 Рассмотрите «жадный» обмен, при котором больший из двух взаимодейству¬
ющих кластеров всегда получает мономер, а меньший теряет мономер. В сим¬
волической записи реакция может быть представлена как (J, к) —> (j +1, к — 1)
для j > к.
(a) Покажите, что эволюция системы описывается уравнениями
к-1
Cfc = Ck—1 Cj + Cfc+i Cj CfcTV — с^.
J=1 j>k+l
(b) Проверьте, что полная плотность кластеров удовлетворяет уравнению
% = -ciN.
(c) Покажите, что основное кинетическое уравнение сводится к
дс(к, t)
dt
-ск(ск + cfc+i) + N(ck-i - ск) + (Cfc+i - cfc-i)
5.8 Задачи
209
(d) Используйте скейлинговый анзац с* ~ N2Q(kN), чтобы в непрерывном
пределе разделить основное кинетическое уравнение на две части
dN
dt
= -e(o)jv3,
e(o)[2e-i- же'] = 2е2 -ь е'
/»ОО
- 2 / dye(y) .
J X
Решите эти уравнения. Подсказка: Используйте уравнения на Ф(т) =
fgdyG(y), чтобы показать, что перемасштабированное распределение
е(я) = ®'(т) совпадает с распределением Ферми при нулевой температу¬
ре
< 6(0), х < ж*;
0, х > х*.
Используя закон сохранения массы, найдите х*.
Глава 6
ФРАГМЕНТАЦИЯ
Непрерывное разрушение кластеров либо под действием внешней силы, либо
из-за взаимных столкновений известно как фрагментация. На геологических
масштабах фрагментация отвечает за песчинки и за поля гальки. Фрагмен¬
тация из-за столкновений ответственна за космический мусор, представляю¬
щий потенциальную долгосрочную угрозу искусственным спутникам земли.
На молекулярном уровне разрушение химических связей лежит в основе де¬
градации полимеров и тления. Одновременные агрегация и фрагментация от¬
вечают за облака межзвездной пыли, планетарные кольца и другие небесные
структуры. Многочисленные биохимические реакции в клетках дают более
приземленные примеры. Фрагментация выглядит как агрегация, обращенная
во времени, и совсем неудивительно, что для этих двух процессов использу¬
ются схожие теоретические подходы. В этой главе мы представляем основную
феноменологию фрагментации, а также исследуем связь между фрагмента¬
цией и агрегацией.
6.1 Бинарная фрагментация
Бинарную фрагментацию можно представить как реакцию
F(x,y)
fc + y] > [ж] + [у],
в которой фрагмент массы х+у распадается на два меньших фрагмента масс
х и у с интенсивностью F(x, у), которая обязательно симметрична по х и
у1. В отличие от комплементарного явления агрегации, естественно рассмат¬
ривать массы кластеров как непрерывные. Точно так же, как в агрегации,
1 Определение интенсивности распада F(rc,y) — это отдельная задача, зависящая от
микроскопических деталей процесса распада. Здесь мы предполагаем, что интенсивность
6.1 Бинарная фрагментация
211
нужно найти возникающее распределение размеров фрагментов. Поскольку
число фрагментов растет до бесконечности, а начальное число фрагментов
и большинстве физических приложений велико, простейшее статистическое
описание, основанное на средних плотностях и пренебрегающее флуктуаци¬
ями, должно давать приближение, постоянно улучшающееся со временем.
Поэтому главная переменная — c(x,t)dx, плотность фрагментов с массой в
интервале (ж, х + dx) в момент времени t. Эта величина изменяется в соот¬
ветствии с уравнением
= ~с{х, t) j F(y, х - у) dy + 2 / c(y,t)F(x,y - x)dy. (6.1a)
Первый член в правой части отвечает за убывание фрагментов массы х из-
за их распада, а второй — за образование таких фрагментов при распаде
кластера массы у > х. Множитель 2 учитывает возможность того, что любой
из двух фрагментов, полученных при распаде у-фрагмента, имеет массу х.
Полезно проверить правильность основного кинетического уравнения (6.1а),
проверив, что полная масса /xc(x,i)dx постоянна.
Когда интенсивность распада зависит только от начальной массы и не
зависит от масс дочерних кластеров, то F{x^ у) — функция одной переменной
х + у. Удобно записывать F в виде (х + у)-1 R(x + у), где R(x + у) — полная
интенсивность распада фрагмента размера х + у. В этом случае основное
кинетическое уравнение приводится к виду
■■ = -R(x) с(х, t) + 2 j y~1R{y) с(у, t) dy. (6.1b)
Кинетические уравнения для фрагментации (6.1а) и (6.lb) основаны на
нескольких предположениях, которые стоит описать отдельно:
• Линейность. Внешние силы, а не взаимодействия между фрагментами
приводят к фрагментации. Поэтому интенсивность распада фрагмента
не зависит от состояния других фрагментов.
• Пространственная однородность. Плотность фрагментов не зависит от
точки в пространстве.
• Термодинамический предел. Система настолько большая, что эффекта¬
ми дискретности можно пренебречь.
распада известна. С помощью основного кинетического уравнения возможно также изучать
распад объекта на произвольное число фрагментов.
212
Фрагментация
• Независимость от формы. Форма фрагмента не играет роли для эво¬
люции.
• Бинарная фрагментация. При каждом распаде образуются два фраг¬
мента.
Последнее предположение вторично, и большую часть нашего обсуждения
можно обобщить на ситуации, в которых число фрагментов, образующихся
при каждом распаде, произвольно. Далее в этой главе (раздел 6.2) мы будем
упрощенно учитывать зависимость от формы в модели планарной фрагмен¬
тации. Мы также рассмотрим простую модель нелинейной фрагментации,
в которой столкновения между фрагментами приводят к событиям распада
(раздел 6.4).
Случайное разрезание
Вероятно, простейший пример фрагментации — это случайное разрезание
(рис. 6.1), в котором объект распадается с интенсивностью, пропорциональ¬
ной его размеру. Эта интерпретация хорошо подходит для описания дегра-
у х-у
время
V
Рис. 6.1. Случайное разрезание. Начальный отрезок длины х разрезается в слу¬
чайной точке на два отрезка длин у и х — у. Последняя линяя показывает ре¬
зультат многих событий распада; эквивалентно, это может рассматриваться как
случайное размещение точек разрезов
дации полимеров, где фрагменты — это полимерные цепочки, и каждая по¬
лимерная связь может разорваться с одной и той же фиксированной интен¬
сивностью. В этом случае можно определить полную интенсивность распада
как R(x) = х. Тогда уравнение (6. lb) сводится к
=-xc(x,t) + 2 J c(y,t)dy. (6.2)
И снова, первый член справа отвечает за убывание фрагментов размера х с
интенсивностью R(x) = х, а второй — за образование таких фрагментов при
6.1 Бинарная фрагментация
213
распаде большего фрагмента размера у. Интегрируя (6.2) по всем размерам,
видим, что полное число фрагментов N = f с(ж) dx растет линейно со време¬
нем, dN/dt = 1 (при массе равной /xc(x,t) dx — 1). Поэтому N(t) = N(0)+t,
и средний размер фрагмента (х) = 1/N асимптотически убывает как
(ж)~4-1. (6.3)
Начнем с вероятностного объяснения распределения размера фрагмен¬
тов. В этой формулировке отрезок разрезается в случайно выбранных ме¬
стах с единичной интенсивностью. Таким образом, среднее число разрезов
на отрезке длины L равняется Lt в момент времени t. При начальном отрез¬
ке длины L через некоторое время будут существовать три типа сегментов
(рис. 6.2):
• Сегменты без разрезов. Отрезок длины L не содержит разрезов с веро¬
ятностью e~Lt.
• Сегменты с одним разрезом. Сегмент, длина которого находится в диа¬
пазоне (ж, x+dx), получается, когда на расстоянии меньшем х от одного
конца разрезов нет (с вероятностью e~xt), а интервал (ж, х + dx) содер¬
жит разрез (с вероятностью t dx). Нам не нужно заботиться о состоянии
оставшейся части длиной L—х. Полный вклад от сегментов с одним раз¬
резом равен 2te~xt, так как такой сегмент может возникнуть с любого
конца.
• Сегменты с двумя разрезами. Такие сегменты возникают, когда есть
два разреза в интервалах dy и dz с двух концов сегмента длины ж, внут¬
ренняя часть которого не содержит разрезов. Вероятность этого собы¬
тия равна t^dydze-3^. Можно опять игнорировать состояние внешней
по отношению к сегменту части. Интегрирование по всем возможным
положениям сегмента дает i2(L — x)e~xt.
(а)
(Ь)
►
L
У У
х
(с)
Рис. 6.2. Три типа сегментов на отрезке: (а) сегмент без разрезов, (Ь) сегмент с
одним разрезом, (с) сегмент с двумя разрезами
214
Фрагментация
Комбинируя эти три вклада, найдем вероятность Рь(ж, t) сегмента длины
х в момент времени t
PL(x,f) = e~xt {<5(L - x) + [2t + f2(L - ж)] 0(L - ж)} . (6.4)
Теперь проинтегрируем (6.4) по начальному распределению длины с(ж, t) =
CQ(L)Pi,(x,t) dL и получим распределение размера
c(x,t) = e_xt |со(ж) + / со(у) [2< + 1?(у - ж)] dy} . (6.5)
В пределе большого времени распределение длины (6.5) стремится к скей¬
линговому виду. Поскольку типичная длина сегмента стремится к нулю, име¬
ем оо ж
У со(у)(у - х) dy -> у Со(у) у dy = 1,
и поэтому асимптотическое распределение массы имеет очень простой скей¬
линговый вид
c(#,t) ~ t2e~xt. (6.6)
Однородная интенсивность распада
Во многих физических ситуациях скорость распада — однородная функция
размера фрагмента. Например, при случайном разрезании линейного объ¬
екта интенсивность распада пропорциональна его длине. В случаях, когда
фрагментация определяется площадью поверхности объекта, интенсивность
распада — как масса в степени 2/3. Как и в агрегации, основной параметр —
индекс однородности А, который определяется равенством R(ax) = axR(x)2.
Теперь исследуем кинетику фрагментации как функцию индекса однородно¬
сти. Для чистого степенного закона R(x) = основное кинетическое урав¬
нение (6.lb) принимает вид
дс^ = -Xх с(ж, *) + 2 / уЛ_1с(у, t) dy. (6.7)
Структура уравнения (6.7) предполагает, что его решение можно искать
в форме
с(х,£) = Ф(£) e~txX.
2Благодаря тому, что фрагменты постоянно уменьшаются, достаточно, чтобы однород¬
ность выполнялась асимптотически в пределе маленького размера.
6.1 Бинарная фрагментация
215
11одставив этот анзац в основное кинетическое уравнение (6.1), получим урав¬
нение
Ф _
Ф ~ At’
которое дает Ф = Поскольку уравнение (6.7) инвариантно по отношению
к преобразованию t —> t + а, существует семейство точных решений этого
уравнения вида
с(ж, t) = (t + а)2/Л ехр[—(t + а) жл]. (6.8)
Теперь используем линейность уравнения (6.7) и построим общее точное
решение для c(x,t) в виде линейной комбинации элементарных решений:
с(я, t) = f С (a) (t + а)2/Л ехр[—(t + а) хл] da, (6.9)
Jo
где амплитуда С (а) определяется из начальных условий. В пределе большого
времени решение (6.9) демонстрирует универсальное поведение
c(x,t)^t2^e~tx\ (6.10)
Это распределение массы фрагментов снова можно записать в скейлинговом
виде c(#,t) ~ £_2/(я/£) с типичной массой £ = t_1/A и скейлинговой функци¬
ей /(г) = e~z ; выражение (6.6) — частный случай этой общей скейлинговой
формы.
Распыление
Предыдущий анализ неявно предполагает, что А > 0. Когда А < 0, фраг¬
ментация становится взрывоподобной, приводящей к удивительному явлению
распыления, в котором масса исчезает, переходя в «пылевую» фазу, состоя¬
щую из частиц нулевой массы. Переход распыления при фрагментации — это
аналог перехода гелеобразования в агрегации.
Как и в случае гелеобразования, изучение поведения моментов — это са¬
мый быстрый путь к обнаружению сингулярности. Интегрируя (6.lb) по х,
мы находим, что моменты
N(t) = Mo(t) = [ c(x,t)dx, M\(t) = f xxc(x,t)dx
JQ Jq
связаны между собой соотношением
dN м
(6.11)
216
Фрагментация
Уравнение (6.11) — точное и справедливо для всех Л. Чтобы найти асимпто¬
тическое поведение, мы следуем нашему обсуждению скейлинга в агрегации3,
используя то свойство, что распределение масс фрагментов имеет скейлиго-
вый вид c(x,t) = £~2f{x/£). В результате нулевой момент принимает вид
N = f c(x,t) dx = f €~2f(x/£) dx ~ £-1.
Jo Jo
Аналогично, для момента M\ имеем
Мд — [ хх с(х, t) dx ~ £a_1 .
Jo
Сравнение этих двух соотношений дает М\ ~ А1_л. Подставив эту зависи¬
мость для М\ в (6.11), получим замкнутое уравнение для плотности фраг¬
ментов
(6-12)
Как следствие, асимптотическая зависимость плотности фрагментов от вре¬
мени имеет вид
при
еш1,
при
(*с-*)-1/|Л|,
при
А > О,
А = О,
А < 0 и t —> tc.
(6.13)
Когда А < 0, фрагментация самых мелких фрагментов происходит так быст¬
ро, что плотность фрагментов расходится при конечном времени tc. При t > tc
часть массы превращается в пыль, состоящую из бесконечного числа частиц
нулевой массы, которая тем не менее содержит конечную долю полной массы.
Фрагментация с источником
Фрагментация со стационарным источником материи возникает во многих
физических процессах, таких как дробление стационарного потока сырой ми¬
неральной руды. В таких ситуациях распределение размера фрагментов до¬
стигает стационарного состояния. Фактически, кроме не зависящего от вре¬
мени решения (6.8), основное кинетическое уравнение (6.7) в общем случае
допускает целый класс стационарных решений вида с(ж) = Сх~2~х (задача
6.4). Проанализируем влияние источника для однородных интенсивностей
3См. раздел 5.4 и уравнение (5.56).
6.1 Бинарная фрагментация
217
6.1. Преобразование Меллина
Преобразование Меллина f(s) функции f(x) и соответствующее обратное преоб¬
разование даются формулами
/•оо -I /*с+гоо
f(s) = J^ xa~1f{x)dx, f(x) = — J x~8f(s)ds. (6.14)
Обозначения подразумевают, что s должна рассматриваться как комплексная пе¬
ременная, а интеграл в обратном преобразовании вычисляется по вертикальной
прямой в комплексной плоскости. Преобразование Меллина есть не что иное, как
момент степени s — 1 функции f(x), а также замаскированное преобразование Ла¬
пласа: преобразование Меллина становится преобразованием Лапласа после за¬
мены переменных х = е~у. Поэтому, чтобы вычислять обратные преобразования
Меллина, можно адаптировать известные правила обращения преобразования Ла¬
пласа.
Приведем таблицу преобразований Меллина для нескольких распространенных
функций:
/(*)
е ®
2е-®2
1п(1 + ж)
(1+х)-1
Г(а)/(1+х)а
(1 + я2)-1
х/тг crfc(x)
/(«)
Г(э)
Г(з/2)
7Г
7Г
Г(а - s) Г(«)
7Г
«“'гки-^/г]
S sin(7rs)
sin(7rs)
2 sin(7r.s/2)
В этой главе мы будем часто пользоваться двумя свойствами преобразования
Меллина.
1. Если /(s) — Меллин-образ функции /(т), то f(s—n) — Мел л ин-образ функ¬
ции х~п f(x).
2. Меллин-образ функции д(х) = утп~1 f(y) dy — это .s"1 Это соот¬
ношение становится очевидным после изменения порядка интегрирования:
/* жв_1р(т)с/ж= /* Xs-1 dx Z* 2/т_1 f(y)dy
J О «/О J х
- Г ym~x f {у) d.y Гх-'dx
Jo Jo
= ~ [ ys+m_1 f(y) dy = a”1 f(s + m).
s Jo
распада. Если I(x) — интенсивность добавления источником объектов массы
.т, распределение массы меняется в соответствии с уравнением
= -Ххс{х, t) + 2 J уХ_1с(у, t)dy + 1(х).
(6.15)
218
Фрагментация
Можно решить это уравнение, применяя преобразование Меллина c(s,t) =
f£° xs~l c(x,t) dx. В терминах этого преобразования уравнение (6.15) запи¬
шется как
dc(s, t) = 2_s + Л + (6.16)
где /(s) = xs_11(ж) dx — преобразование Меллина интенсивности источ¬
ника.
В стационарном состоянии преобразование Меллина уравнения (6.16) дает
(после замены индекса s на s — А)
Ф) = ~2^Л ~ Л)' (6-17)
Перепишем теперь Меллин-образ как c(s) = (l + J(s — Л) и, восполь¬
зовавшись основными свойствами преобразованиея Меллина, приведенными
выше в рамке, получим стационарное распределение масс фрагменов
с(х) =х~х1(х) + 2х~2~х f 1(у) у dy. (6.18)
Jx
В пределе маленьких масс фрагментов второе слагаемое доминирует, так что
распределение масс имеет универсальный алгебраический хвост
2J
с(х) ^2+л ПРИ х 0» (6.19)
который упоминался в начале этого раздела; здесь J = х I(x) dx — пол¬
ная интесивность источника. Таким образом, кроме общей амплитуды J в
стационарное распределение масс не входят никакие параметры распределе¬
ния интенсивности источника.
Асимптотическое распределение также можно получить из следующих
эвристических аргументов. В качестве примера рассмотрим линейную ин¬
тенсивность фрагментации R(x) = х. Из-за стационарного источника полная
масса в системе M(t) = c(s = 2,t) растет линейно со временем, M(t) = Jt.
Аналогично, из уравнения (6.15) видно, что полное число фрагментов N(t) =
c(s = l,t) удовлетворяет уравнению N(t) = Jt + ц, где ц = / I(x)dx — чис¬
ло фрагментов, добавляемых за единичное время. Следовательно, N(t) =
5 Jt2 + y,t. Из двух первых моментов видно, что типичная масса фрагмен¬
та ведет себя как M/N ~ t-1. Таким образом, распределение массы должно
стремиться к скейлинговому виду
с(ж, t) ~ tzF(xt) при t —> оо.
(6.20)
6.1 Бинарная фрагментация
219
Множитель t3 обеспечивает линейный рост полной массы в системе, а аргу¬
мент скейлинговой функции отвечает за то, чтобы характерная масса убыва¬
ла как 1/t С таким скейлинговым видом стационарное состояние возможно,
только если F(z) ~ z~3 ддя. больших z. Этот факт означает, что с(ж) х~3.
Пример 6.1. Метод Чарльсби для фрагментации с источником. Чтобы полу¬
чить полное зависящее от времени решение для фрагментации с источником в
случае случайного разрезания (А = 1), начнем с разложения преобразования
Меллина в бесконечный степенной ряд по времени4 *с(М) = I2ziCfc(s) (6-21)
fc>l
и найдем коэффициенты разложения с помощью итераций.
Подставим разложение (6.21) в уравнение (6.16) и приравняем коэффициенты
при одинаковых степенях времени. Это дает Ci(s) = I(s) и Cfc+i(s) = — (1 —
2/s)cfc(s + 1) для k > 2. Рекурсивно решая полученную систему уравнений,
получим
-(-■>* (3+(:L 2)
Чтобы обратить преобразование Меллина, перепишем Cfc+i(s) как сумму элемен¬
тарных дробей
“ f-1’411 - гтй + ттй] I6-22’
Используя (6.21) и применяя обратное преобразование Меллина почленно, по¬
лучим распределение массы в виде степенного ряда
с(х, t) = 52 \fcini с*(ж)’ (6-23)
fc>0 +
где обратное преобразование от Cfc+i записано в удобном виде (-x)kCk(x). Три
слагаемых в (6.22) можно обратить, пользуясь правилами, приведенными во
врезке на стр. 217, посвященной преобразованию Меллина. Это дает
cfc(a;) = А (ж) - 2г(аг) + к^2 13(х), (6.24)
4Этот метод редко используется, потому что выглядит как магия. Действительно, метод
основан на разложении в ряд Тейлора, обычно используемом для малых времен, хотя на
самом деле нас интересует поведение при большом времени. Этот прием работает, когда
только конечное число членов ряда Тейлора не равны нулю. Метод восходит к Эйлеру; в
контексте фрагментации эта техника была использована Чарльсби.
220
Фрагментация
где
Ii(x) = I(x), I2(x) = f I(y)dy, I3(x)= f yl(y)dy. (6.25)
Jx Jx
Уравнение (6.24) позволяет разбить бесконечный ряд (6.23) на три суммируемых
ряда. Это дает распределение масс в виде суммы всего трех слагаемых
з
с(х, f) = tk Fk{xt), (6.26)
к=1
со скейлинговыми функциями5
Fi(z) = 2-1(1 — е-2),
F2(z) = е-2, (6.27)
F3(z) = z~3 [2 - (2 + 2z + z2)e~z].
Уравнения (6.26) и (6.27) дают полное зависимое от времени решение для
произвольного стационарного источника /(ж). В пределе х -> 0 и t -> оо, когда
скейлиговая переменная z = xt остается конечной, третье слагаемое в сумме
в (6.26) доминирует, и воспроизводится ожидаемое скейлинговое поведение со
скейлинговой функцией F(z) = Fs(z).
6.2 Планарная фрагментация
До сих пор, рассуждая о кинетике фрагментации, мы рассматривали влия¬
ние на фрагментацию единственного фактора: размера фрагмента. Однако из
нашего повседневного опыта разбивания хрупких объектов ясно, что геомет¬
рические аспекты также важны. Сейчас мы обсудим модель фрагментации,
учитывающую влияние формы минималистским образом, а именно планар¬
ную модель фрагментации, в которой один прямоугольник фрагментируется
на много маленьких прямоугольников с помощью последовательности пря¬
мых разрезов. Индивидуальное событие обновления в прямоугольной фраг¬
ментации состоит из следующих шагов (рис. 6.3):
1) случайно выбирается прямоугольник с вероятностью пропорциональ¬
ной его площади;
5Функция Рз(г) получена из степенного ряда Рз(г) = 53fc>o •
6.2 Планарная фрагментация
221
Рис. 6.3. Несколько шагов планарной прямоугольной фрагментации
2) из случайной точки внутри выбранного прямоугольника проводится
разрез (либо горизонтальный, либо вертикальный с одинаковой веро¬
ятностью), который делит прямоугольник на два меньших прямоуголь¬
ника, сохраняя при этом площадь6.
Похожие модели предлагались для описания образования мартенситов
в двух измерениях, где измельчение микрообластей визуально напомина¬
ет результат большого количества событий прямоугольной фрагментации
(рис. 6.4(a) показывает фрагментацию единичного квадрата после 500 разре¬
заний.). Важнейшее свойство прямоугольной фрагментации — наличие беско¬
нечного числа «скрытых» законов сохранения. Как следствие, распределение
масс описывается «мультифрактальным» скейлингом, а не чистым, обычно
возникающим в кинетических моделях агрегации и фрагментации.
Без потери общности предположим, что система стартует с одного квадра¬
та 1 х 1 и положим полную интенсивность фрагментации, равной 1. Посколь¬
ку в каждом событии распада разрушается один прямоугольник и образу¬
ются два дочерних прямоугольника, среднее число прямоугольников растет
со временем линейно: N = 1 + t. Набор прямоугольников характеризует-
6 Очевидно обобщение на произвольную размерность пространства d, в котором (d — За¬
мерная гиперплоскость вырастает из данного зародыша в одном из d — 1 возможных орто¬
гональных направлений.
222
Фрагментация
Рис. 6.4. Результат планарной фрагментации единичного квадрата по истечении
большого времени: (а) прямоугольная фрагментация после 500 событий распада,
(Ь) изотропная фрагментация после 1000 событий распада
ся распределением вероятности c(xi,X2,t), так что c(xi,X2,t) dx^dx2 — это
плотность прямоугольников с длиной и шириной соответственно в диапазо¬
нах (ац, xi + dxi) и (х2,Х2 + dxi) в момент времени t. Это распределение
эволюционирует в соответствии с уравнением
=-xiX2c(x1,X2,t) + X2 У c(yi,X2,t)dyi+xi f c(xx,y2,i) dy2-
(6.28)
Первое слагаемое в правой части отвечает за убывание прямоугольников с
площадью А = Х1Х2 из-за фрагментации. Так как начальная точка разреза
выбирается случайно, полная интенсивность деления любого прямоугольни¬
ка пропорциональна его площади. Второе слагаемое отвечает за возникно¬
вение фрагмента длиной xi и высотой х% пъолъ вертикального разреза пря¬
моугольника длиной yi > xi и высотой Х2- Коэффициент Х2 отвечает за то,
что начальная точка может быть расположена в любом месте вертикально¬
го разреза. Последнее слагаемое также учитывает вклад от горизонтальных
разрезов.
Для упрощения уравнения (6.28) применим к нему преобразование Мел¬
лина
c(5i,S2?i)= / / #i1_1 ^22-1 c(xi^X2^t)dxidx2-
Jo Jo
6.2 Планарная фрагментация
223
Умножая обе части уравнения на гср-1^2-1 и интегрируя по х± и Х2, мы на¬
ходим, что Меллин-образ удовлетворяет линейному функциональному урав¬
нению.
dc(s^,t) _ (А + _ Л с(51 + 1, s2 + 1,г). (6.29)
ОТ \Si S2 )
Вместо того чтобы пытаться решить это уравнение, исследуем моменты рас¬
пределения масс фрагментов. Согласно определению преобразования Мелли-
иа эти моменты даются выражением
«“4а> - с(п1фд)2 + 1)- (6'3°)
Мы знаем, что сохранение общей площади фрагментов дает с(2,2,£) = 1.
Также нам известно, что среднее число фрагментов дается выражением
с(1,1, t) = 1 + t. Следовательно, средняя площадь фрагмента равна (А) =
(®1®2) = 1/(1 + t).
Важнейшее свойство уравнения движения (6.29) — это то, что оно имеет
бесконечно много законов сохранения, определяемых следующей кривой в
ПЛОСКОСТИ 51 — 52 7
М)-1 + К)-1 = 1. (6-31)
вдоль которой Меллин-образ c(5j,52) постоянен во времени. Эти скрытые
законы сохранения выполняются только для средних значений. Это значит,
что хотя значение с(5р 5^) не остается постоянным в каждом индивидуальном
событии распада, усредненное по всем реализациям прямоугольной фрагмен¬
тации c(5j, 52) сохраняется. Единственный строгий закон сохранения — общая
площадь не меняется в любых событиях прямоугольной фрагментации. Кри¬
вую (6.31) можно представить в параметрическом виде 5J = я+1, = /€“1+1,
из которого следует, что сохранение с(5^, t) гарантирует сохранение момен¬
тов вида
c(#i,tf25i)dxiGte2
для всех к > —1. Случай к = 1 соответствует сохранению площади; дру¬
гие значения я, даже простейшие из них, как например к, = 2, приводят к
сохраняющимся моментам, не имеющим ясного физического смысла.
Так как в линейной фрагментации с однородным ядром распада сред¬
няя масса убывает алгебраически со временем, естественно предположить,
7Переписав (6.31) как (si — l)(s2 — 1) = 1, мы видим, что геометрически кривая (6.31) —
это гипербола.
224
Фрагментация
что так же будет убывать и Меллин-образ для прямоугольной фрагмента¬
ции, т. е. c(si,$2) ~ i-a(Sl,S2) с неизвестным показателем a(si,S2)- Подставив
это выражение в (6.29), получим рекуррентные соотношения для показателей
a(si + 1, S2 + 1) = a($i, S2) + 1. Сравнивая эти соотношения с законом сохра¬
нения q(s*, $2) ~ 0, находим соотношение для значений показателя a(si, S2):
а($1 + к, ^2 + к) = к для всех (^)“1 + С^)-1 = 1. (6.32)
Графически значение а в произвольной точке ($1,52) ~ это просто горизон¬
тальное (или вертикальное) расстояние от этой точки до кривой (si)-1 +
(S2)”1 = 1 (рис. 6.5). Это условие для расстояния дает (si — а) = sj и
Рис. 6.5. Линии решений уравнения (6.32), соответствующие ce(si,S2) =
0,1,2,3 и 4. Каждая следующая кривая сдвинута относительно предыдущей на 1
по горизонтали и вертикали (пунктирные линии)
($2 — а) = S2 = [1 — (^i)-1]-1. Исключив sj из этих двух уравнений, ви¬
дим, что показатель дается меньшим корнем квадратного уравнения (si —
а) (52 — а) — (si — а) — (s2 — а) = 0, откуда получим
/ ч si + S2 /(si - S2)2
a(si,s2) = 1 - у y~l- + 1.
Используя эти выражения для показателей, можно найти асимптотиче¬
ское поведение моментов (6.30):
(жрЖз2) ~ £-a(«l+l,«2+l)+a(l,l) ^-a(si,s2)-2
(6.33)
6.2 Планарная фрагментация
225
IS качестве примера приведем выражение для моментов длины фрагментов
(Г) = (х?) ~ г(п+2-ТТО)/2? (б.34)
ИЗ которого следует, ЧТО (£) ~ £~(3”^)/2 ~ £-0,382 и (^1/2 ~ £-(2-\/2)/2
I -0,293 Этн моменты убывают медленнее, чем можно было ожидать из по¬
ведения средней площади. Так как (А) = (1 + f)""1, естественный масштаб
длины должен по идее быть порядка t-1/2, что убывает намного быстрее чем
((). Другое интересное свойство прямоугольной фрагментации — это то, что
типичный фрагмент становится все более вытянутым с течением времени (см.
рис. 6.3 и рис. 6.4(a)). Эту асимметрию можно количественно охарактеризо¬
вать моментами отношения сторон ((xi/#2)n)> которые согласно уравнению
(6.33) расходятся как ((Ж1/Ж2)71) ~ £^'п2+1~1 в пределе большого времени.
Нелинейный спектр скейлинговых показателей a(si,S2) дает пример
мультискейлинга, в котором нет прямой связи между моментами высоких и
низких порядков. Для прямоугольной фрагментации следствия мультискей¬
линга хорошо иллюстрируется аномальными свойствами моментов длины и
отношения сторон. Нужно отметить, что использование только ориентиро¬
ванных разрезов - это важная составляющая мультискейлинга. Как можно
визуально убедиться на примере планарной изотропной фрагментации, по¬
казанной на рис. 6.4(b), изотропия разрезов восстанавливает чистый скей¬
линг. В такой изотропной фрагментации фрагмент выбирается с вероятно¬
стью, пропорциональной его площади, и потом разрезается вдоль случайно
расположенной и ориентированной линии. В этой модели характерный ли¬
нейный размер I и площадь А фрагментов подчиняются обычному скейлингу
(С2 ~
Пример 6.2. Распределение площади. Обозначим через F(A, t) плотность пря¬
моугольников площади А. Это распределение площади может быть выражено
через c(rri,rc2,t) как
c(xi,X2,t)S(xiX2 — A) dxidx2- (6.35)
Уравнение (6.35) не очень полезно для конкретных вычислений, так как у нас
нет явного выражения для c(rci,X2,t). Однако мы можем найти распределе¬
ние площади, используя его Меллин-образ F(s,t). Из уравнения (6.35) имеем
F(s,£) = c(s,s,£). Следовательно, уравнение движения для F(s,t) — это просто
диагональный вид уравнения (6.29), т. е.
тч = //
(6.36)
226
Фрагментация
Так же как в случае моментов длины предположим, что c(s, 5) = и
подставим это в уравнение (6.36), что дает a(s) = s—2. Из этого уравнения также
получим соотношение для амплитуд p(s 4- 1) = s/z(s). Пользуясь граничными
значениями /z(l) = 1 (нормировка) и ц(2) = 1 (общая площадь равна 1), получим,
что /z(s + 1) = s/x(s), и, наконец, находим
F(s, t) — T(s) t2~s при t » 1. (6.37)
Обращение преобразования Меллина дает
F(A,t)-t2e-At. (6.38)
Перемасштабированное распределение площади имеет тот же самый вид, что и
распределение длины в модели случайного разрезания.
6.3 Обратимая полимеризация
В науке о полимерах агрегация и фрагментация часто происходят одновре¬
менно, приводя к обратимой полимеризации. Рассмотрим набор полимерных
цепочек, состоящих из идентичных мономеров, каждый из которых содержит
две реакционноспособные концевые группы. Символически каждая группа
может быть представлена как -А-А А-А-. При связывании два полиме¬
ра длин i и j агрегируют с интенсивностью Ку с образованием более длин¬
ного полимера, тогда как распад на два более коротких полимера длин г и j
происходит с интенсивностью Fy:
К’ ’ F’ •
M + L?] —+ и [i + j] —> [i] + [j].
Интенсивности агрегации и фрагментации даются полубесконечными сим¬
метричными матрицами Ку = Kji и РУ/ — Fji.
Плотность Cfc(f) полимеров, состоящих из к мономеров, эволюционирует
в соответствии с основным кинетическим уравнением
"37" = 9 У^ &У Ci Cj — Ск Kkj Cj + У2 FkjCj+k — ъск У Fy. (6.39)
i+3=k j>l j>l i+j=k
Распределение масс обычно становится стационарным благодаря соревнова¬
нию между агрегацией и фрагментацией. В простейшей ситуации стацио¬
нарное распределение можно найти, приравняв интенсивность процесса аг¬
регации [г] + [J] —> [г + j] интенсивности обратного процесса фрагментации
[г + j] [г] + [j]. Это условие детального равновесия (см. врезку ниже)
Ку Ci Cj = Fy Ci+j (6.40)
определяет равновесное распределение.
6.3 Обратимая полимеризация
227
Так как релаксация к равновесию обычно происходит экспоненциально
быстро и часто ей можно пренебречь, нам нужно только исследовать рав¬
новесную систему алгебраических уравнений (6.40), а не дифференциальных
уравнений (6.39). Это упрощение возвращает нас к пройденному уроку из
кинетической теории (глава 3): эволюционное уравнение Больцмана, пугаю¬
ще сложное и чаще всего не имеющее аналитического решения, тогда как
соответствующий аналог уравнений (6.40) имеет решение — распределение
Максвелла - Больцмана.
Однако есть одно важное различие между обратимой полимеризацией и
кинетической теорией: уравнения (6.40) могут не иметь решения вовсе.
Чтобы осознать это утверждение, выпишем первые несколько уравнений
системы (6.40).
Kll С? = #11 С2,
к 12 С1С2 = #12 Сз,
#13 С1С3 = #13 С4,
#22 = #22 С4.
(6.41)
Мы видим, что С2 и сз, выраженные через ci, допускают единственное реше¬
ние:
#11 2 #11 #12 з
С2 — rp с1> Сз — Ср
Л1 *11 *12
Подставив эти выражения в уравнения (6.41), получим два независимых
уравнения для С4:
#11 #12 #13 4
^4 тр ry ry ^1,
2*11 2*12 2*13
(6.42)
Если условие
*12 *13 = ^2 (6.43)
*12 *13 *11 *22
удовлетворяется, уравнения (6.42) совместны; в обратном случае решения
нет. Таким образом, в общем случае уравнения (6.40) образуют переопреде¬
ленную систему: существует бесконечно много условий типа (6.43), а мно¬
жество решений как правило пусто. Когда многие интенсивности реакций
равны нулю, система уравнений (6.40) может быть нерешаема, либо система
может стать недоопределенной, т. е. она может иметь много решений. Даже
если уравнения (6.40) имеют единственное решение, нужно убедиться, что
это решение является притягивающей неподвижной точкой и что начальные
228
Фрагментация
условия находятся в области ее притяжения. В общем случае комбинации аг¬
регации и фрагментации существует два типа стационарных распределений:
(i) равновесное стационарное состояние, удовлетворяющее условию детально¬
го равновесия (6.45) и (ii) неравновесные стационарные состояния, которые
6.2. Детальное равновесие
Условие детального равновесия отличает два типа стационарных состояний. В об¬
щем случае поток Ji^j из состояния i в состояние j дается произведением вероят¬
ности pi того, что система находится в состоянии г, умноженной на интенсивность
Wi-tj перехода из г в J, т. е. Ji->j = piWi-+j. В стационарном состоянии общий
поток в состояние г должен быть равен потоку из этого состояния
^рш^ = ^p-jWj-n (6.44)
для всех г. С другой стороны, детальное равновесие требует, чтобы потоки между
любыми двумя состояниями уравновешивались, т. е. Ji—— Jj—yi, ИЛИ
PiWi^j = pjWj-ц для всех i,j. (6.45)
Очевидно, что детальное равновесие (6.45) гарантирует выполнение условия
стационарности (6.44), но стационарное состояние еще не означает выполне¬
ния детального равновесия. Простой пример неравновесного стационарного со¬
стояния приведен на рис. 6.6(a), где разрешены только переходы по циклу
wi_>2, W2->3, wa->i 0, тогда как все остальные переходы не происходят. Стацио¬
нарный поток J = piwi_>2 = P2W2->3 = рзгиз-п удовлетворяет (6.44), но нарушает
детальное равновесие (6.45) (задача 6.7). Для системы с N состояниями существу¬
ет N условий стационарности и гораздо большее число, (^) = jJV(2V — 1), условий
детального равновесия.
2 3
(а)
Рис. б.б. (а) Неравновесное стационарное состояние с циклическим потоком; (Ь)
равновесное состояние с детальным равновесием
6.3 Обратимая полимеризация
229
удовлетворяют основному кинетическому уравнению (6.44), но нарушают де¬
тальное равновесие. В последнем случае существует ненулевой суммарный
поток между состояниями. Рассмотрим более подробно две показательных
модели, которые иллюстрируют предыдущее обсуждение.
Модель струны
Классическое описание эволюции линейной полимеризации при конечных
температурах дает модель струны, в которой интенсивности агрегации и
фрагментации предполагаются постоянными. Модель основана на разумном
предположении, что реакционная способность всех химических связей оди¬
накова. Для этой модели уравнения (6.40) принимают вид
CiCj = Xci+j, (6.46)
где Л = Fij/Kjj — отношение интенсивностей фрагментации и агрегации.
Уравнения (6.46) имеют однопараметрическое семейство решений
cfe = A/3fe, (6.47)
в котором значение параметра f3 фиксируется условием, что полная масса
^ск равна 1. Это условие приводит к квадратному уравнению А/?/(1 —
/З)2 = 1, из которого нужно выбрать один корень
/3 = 1 + -- ^А + —, (6.48)
потребовав, чтобы распределение было убывающей функцией к.
Пример 6.3. Равновесная полимеризация. Выберем = 2 и = 2А, так что
зависимое от времени основное кинетическое уравнение (6.39) принимает вид
Ск = c^j - 2cfeM0+ 2A^2cj - A(fc-l)cfe, (6.49)
i+j=k j>k
где Mq = 52fe>i ck ~ нулевой момент распределения массы является плотностью
кластеров. Уравнение (6.49) решается с помощью экспоненциального анзаца
ск = (1 -a)2afe_1,
который явным образом обеспечивает сохранение массы кек = 1. Для мо¬
номерного начального состояния имеем a(t = 0) = 0. Экспоненциальный анзац
230
Фрагментация
превращает бесконечный набор дифференциальных уравнений (6.49)в одно диф¬
ференциальное уравнение о = (1 — а)2 — Ха. Его решение:
1 _ е—(<*—£)*
а -/3 ’
А+т-
a{t) =
где
“=1+2+
(6.50)
Поскольку a(t = оо) = а 1 = /3, результатом для стационарного распределения
массы является Cfc(f=oo) = (1—/З)2/З^-1 = A что согласуетсяс (6.47)-(6.48).
Модель откалывания краев
Как пример неравновесного стационарного состояния рассмотрим ситуацию,
в которой рост полимера конкурирует с деградацией или отрывом концов
полимера. Поскольку мономеры на концах прикреплены к полимеру един¬
ственной связью, тогда как внутренние полимеры прикреплены двумя свя¬
зями, концевые мономеры отрываются скорее. Модель откалывания краев
представляет экстремальный случай, когда могут отсоединиться только кон¬
цевые мономеры (рис. 6.7):
Г2, Л i = 1 или j = 1,
.Г29 “—
[о, г / 1 и j / 1.
Мы рассматриваем простейший процесс агрегации с постоянным ядром
2
(a) СНХ) 0-0-0 ► о-О-О-О-О-О
2
(b) 0-0-000 О ► 000-0-0-0
2Х
Рис. 6.7. Процессы составляющие модель откалывания краев: (а) необратимая
агрегация и (Ь) обратимое отсоединение мономеров. На рисунке показаны ин¬
тенсивности каждого процесса.
= 2), который естественным образом применим к полимеризации. Ин¬
тенсивности отсоединения концов [к + 1] —> [/с] + [1] также предполагаются
независимыми от массы и мы обозначаем их 2Л. В модели откалывания краев
6.3 Обратимая полимеризация
231
детальное равновесие явным образом нарушено, потому что не все микроско¬
пические шаги обратимы. Как мы увидим, модель откалывания краев приво¬
дит к необычному распределению длины полимеров, в котором критическая
золевая фаза сосуществует с гелевой фазой.
Плотности cjfe(t) полимеров длины к эволюционируют в соответствии с
уравнениями
= -2ск N + ^2 <*сз + 2A(cfc+i “ cfc), к >2, (6.52а)
= -2а TV + 2А (с2 + с,), (6.52b)
3>2
где N(t) = Cj(t) — полная плотность полимеров. Как мы уже виде¬
ли, для решения таких уравнений можно ввести производящую функцию.
В данной ситуации удобно использовать производящую функцию C(z,i) =
— l)cj(f), которая превращает уравнения (6.52а)-(б.52Ь) в уравне¬
ние Риккати
= е2 + 2А—-е + 2А^~^2 N. (6.53)
dt z z
В стационарном состоянии (i —ь оо) уравнение (6.53) сводится к квадратному
уравнению
e(z) = А (1 - г-1) (l - у/1 - 2Nz/\j. (6.54)
Плотность массы можно вычислить, продифференцировав (6.54) по z и по¬
ложив z = 1. Так как начальная плотность массы равна единице, получим
1 = ci = Э2=1 = А (* - л/1 -27V/A), (6.55)
J>1 z
что дает N = 1 — (2А)-1.
Это решение не может быть правильным при А < 1/2, потому что плот¬
ность полимеров будет отрицательной. На самом деле уравнение (6.55) несов¬
местно уже при А < 1 из-за того, что выражение под корнем становится
отрицательным. Физически эта несовместность вызвана возникновением бес¬
конечного полимера («геля»). Математически сумма j Cj, учитывающая
конечные полимеры («золь»), становится меньше единицы при А < 1; осталь¬
ная часть начальной массы содержится в геле д = 1 — j cj. Из уравне¬
ния (6.54) следует, что в гелевой фазе N = А/2 (задача 6.10). В итоге полная
232
Фрагментация
плотность полимеров равна
N=<
'l-(2A)-x,
[А/2,
А > 1
А< 1
(фаза золя),
(фаза геля).
(6.56)
Это изменение поведения указывает на то, что при А = 1 в системе про¬
исходит неравновесный фазовый переход. Так как плотность N непрерывна
в критической точке Ас = 1, фазовый переход является переходом второго
рода.
В гелевой фазе производящая функция (6.54) принимает вид
e(z) = А (1 - г-1) (1 - y/l^z) . (6.57)
Дифференцируя (6.57) по г и полагая z = 1, находим массу золя ^2j>i 3 сз —
А. Таким образом, масса геля:
9 =
О,
1-А,
А > 1,
А< 1.
(6.58)
Такое поведение — еще одно проявление фазового перехода второго рода, в
котором масса геля играет роль, аналогичную параметру порядка в обычном
(равновесном) фазовом переходе второго рода.
Хотя эти свойства предполагают, что в системе происходит обычный фа¬
зовый переход второго рода, более естественно представлять гель как неко¬
торую критическую фазу для всех А < 1. Чтобы проиллюстрировать это
утверждение, исследуем распределение длины полимера, разложив (6.54) по
степеням z. В золевой фазе (А > 1) получим
Ск = е
-Afc
г(*-Ю
r(i) Г(* + 1)
'(A-l)2 3 1 — (2А)~Х
2А 2 к +1
(6.59)
где Л = 2 In А—1п(2А—1). Асимптотически плотность полимеров длины к 1
убывает экспоненциально с к, но с алгебраическим экспоненциальным мно¬
жителем fc-3/2
Ck — С к~3/2 е~^к, С = 22. . (6.60)
A V47T
Этот результат не является неожиданностью: вне критической точки пове¬
дение должно быть некритическим. Однако для гелевой фазы разложение
(6.57) дает
ЗА Г(к —|) ЗА
°к~ 4^ r(fc + 2) “4^
к~5/2
при к^> 1.
(6.61)
6.4 Столкновительная фрагментация
233
Примечательно, что распределение массы полимера является алгебраиче¬
ским не только в критической точке Ас = 1, но и во всем диапазоне А < Ас = 1!
Эта критичность находится в противоречии с традиционными представления¬
ми о фазовых переходах второго рода, согласно которым критическое поведе¬
ние возникает только в критической точке. В режиме А < 1 избыточная масса
(а именно доля 1 — А от всей массы системы) конденсируется в гигантский
полимер (гель), тогда как остальная часть системы остается в критическом
состоянии.
6.4 Столкновительная фрагментация
В астрофизике и материаловедении столкновения между различными класте¬
рами могут приводить к фрагментации (рис. 6.8). В таком процессе, который
Рис. 6.8. Вид на окрестности звезды HD 23514 из скопления Плеяд в представ¬
лении художника, иллюстрирующий столкновительную фрагментацию. (Изобра¬
жение создано Линеттом Р. Куком и воспроизведено с разрешения обсерватории
Gemini/AURA)
можно представить в виде схемы
[ж] + [у + z] —> [ж] + [у] + [г]
234
Фрагментация
столкновение двух фрагментов приводит к распаду одного из фрагментов,
так что на выходе получается три фрагмента. Часто фрагментация, вызван¬
ная столкновениями, может включать и более интенсивные процессы, где в
событиях распада образуется много фрагментов. Тем не менее, характерная
интенсивность столкновительной фрагментации проявляется даже в слабей¬
шем случае бинарных распадов.
Начнем с определения самых общих свойств столкновительной фрагмен¬
тации. Так как распады вызваны столкновениями, они возникают с интенсив¬
ностью, пропорциональной квадрату плотности фрагментов8. В правильно
выбранных единицах плотность N изменяется в соответствии с уравнением
ллг
(6.62)
решение которого с начальной плотностью, равной 1, имеет вид
(6.63)
Поэтому число фрагментов расходится при конечном времени распыления
tc = 1, когда средняя масса фрагмента зануляется. Хотя распыление мо¬
жет также возникнуть и при линейной фрагментации, оно происходит только
для неестественных распадных ядер, когда маленькие частицы распадаются
легче, чем большие; в реальности обычно происходит обратное. Однако при
столкновительной фрагментации распыление имеет место в общем случае для
любых типов ядер.
Чтобы найти распределение массы при столкновительной фрагментации,
мы построим идеализированные модели, в которых заданы два основных ин-
гридиента:
1. Что распадается. Естественные правила включают в себя: (i) деление
случайной частицы при столкновении или (ii) деление большей части¬
цы.
2. Как распадаются фрагменты. Мы предполагаем детерминистический
распад, при котором распадающийся фрагмент всегда делится на две
части одинаковой массы. Если вначале все частицы были единичной
массы, после п распадов масса фрагмента будет т = 2~п.
8Это утверждение игнорирует уменьшение размера фрагментов. Более физическая си¬
туация рассмотрена ниже.
6.4 СТОЛКНОВИТЕЛЬНАЯ ФРАГМЕНТАЦИЯ
235
Для фрагментов, которые делятся на две равные части9, cn(t) будет обозна¬
чать плотность фрагментов, участвовавших в п распадах за время t и потому
имеющих массу 2-"71.
Пример 6.4. Деление случайной частицы. Предположим, что случайно выбран¬
ная частица распадается при столкновении (эквивалентно тому, что обе частицы
делятся с половинной интенсивностью). Плотность cn(t) эволюционирует соглас¬
но уравнению
= N [ 2c„_i - с„], (6.64)
с полной плотностью N(t) = Множитель 2 в члене прихода воз¬
никает потому, что при делении частицы массой создаются две части¬
цы массой 2“п. Для проверки самосогласованное™ просуммируем уравнения
(6.64) по всем п и воспроизведем кинетическое уравнение (6.62) для плотности
кластеров любого размера. Аналогично можно проверить, что плотность массы
Af(t) = также сохраняется, M(t) = М(0) = 1.
Уравнения (6.64) становятся линейными, если вместо t мы используем г =
dt' N(t') = — ln(l — t) как переменную времени10. Решая уравнение dcn/dr =
2cn-i — сп с монодисперсными начальными условиями сп(0) = <5П)о, получаем
пуассоновское распределение плотности: сп(т) = е~т (2т)п/п!. Выразив ее через
обычное время, получим
cn(f) = (1 - t)
[—21n(l — t)]ra
n!
(6.65)
В момент распыления tc = 1 все плотности зануляются и в системе происхо¬
дит фазовый переход первого рода, вся масса превращена в пыль, и частицы с
положительной массой отсутствуют.
Пример 6.5. Деление большей частицы. Теперь пусть бблыпая частица делится
на две равные части. Масса фрагментов удовлетворяет основному кинетическо¬
му уравнению
— 4cn—iAn 2cnAn+i + 2сп_т сп,
(6.66)
где Ап = J2j>nCj — кумулятивная плотность фрагментов массы 2~п и мень¬
ше. Снова полезно проверить, что плотность массы сохраняется, а плотность
фрагментов удовлетворяет уравнению (6.62).
Плотность co(t) частиц единичной массы удовлетворяет уравнению dc^/dt =
Cq — 2cqN, которое легко решить, так как Cq 1 удовлетворяет линейному уравне¬
нию. Пользуясь уравнением (6.63) и начальным условием со(0) = 1, получим
3(1 —t)2
2 + (1 —t)3’
9Более физическое правило, при котором деление стохастическое, приводит к поведе¬
нию, похожему на детерминистическое деление; см. задачу 6.14.
10Физический смысл модифицированного времени т — это среднее число столкновений,
в которых фрагмент успевает поучаствовать за время t.
236
Фрагментация
Плотности фрагментов сп с п > 1 удовлетворяют уравнениям Риккати, и
их общее решение неизвестно. Тем не менее, асимптотическое поведение можно
исследовать, используя технику бегущих волн (задача 6.13). Здесь мы исследуем
только поведение около перехода распыления.
Так как Ап —> N при t —> 1, и последними двумя членами в уравнении
(6.66) можно асимптотически пренебречь, уравнения (6.66) приводятся к ви¬
ду dcn/dr = 2АГ(2сп_1 — сп), идентичному (с точностью до коэффициента 2)
уравнению (6.64). Следовательно, имеем сп(т)~е 2т (4т)п/п! или
Cn^(l-t)2
[—41n(l —t)]n
п\
С точностью до логарифмических поправок плотность убывает квадратично
сп ~ (1 — t)2. Поэтому переход распыления — снова первого рода.
В нашем упрощенном описании столкновительной фрагментации с помо¬
щью бимолекулярных взаимодействий мы пренебрегли импульсами фрагмен¬
тов, а также уменьшением размера фрагментов со временем. Можно испра¬
вить этот недостаток, воспользовавшись подходом кинетической теории, па¬
раллельным подходу, примененному в разделе 3.7 для учета роста кластеров
при баллистической агломерации. Начнем с переписывания кинетического
уравнения (6.62) в виде
dN N
dt т ’
где т — это среднее время между двумя столкновениями, следующими одно
за другим. Если бы у всех фрагментов был один и тот же размер, который
не зависит от их массы, то время между столкновениями вело бы себя как
7V-1, таким образом воспроизводя результат решения уравнения (6.62).
Чтобы найти т при убывающем размере фрагментов, воспользуемся стан¬
дартным аргументом кинетической теории: число фрагментов в трубке столк¬
новений, заметаемой данным фрагментом за время т, должно быть поряд¬
ка единицы, а именно N^Vr^R^1 ~ 1. Поскольку средняя масса фрагмен¬
та имеет порядок m ~ 7V-1, типичный радиус фрагмента ведет себя как
R ~ ~ 7V_1/d, что также дает и радиус трубки столкновений. Более то¬
го, типичная скорость фрагмента не меняется со временем вследствие закона
сохранения энергии. Поэтому имеем
т ~ ~ TV-1 AT(d_1)/d = N~1/d.
Подставив эту оценку для т в уравнение (6.67), получим кинетическое урав¬
нение для плотности
— ~ N1+1/d.
dt
(6.68)
6.5 Ссылки
237
Это модифицированное кинетическое уравнение приводит к переходу распы¬
ления, в котором
N~N0(l-t/tc)-d, где (6.69)
Заметим, что показатель степени равен пространственной размерности, и,
следовательно, наивный результат (6.63) справедлив только в одномерии.
Можно использовать этот более точный метод для вычисления распреде¬
ления массы. В случае, когда делится случайная частица (как в примере 6.4),
вместо уравнения (6.64) имеем
= 2Сп-! ]Г(Дп-1 + - Сп + Rtf-'cj, (6.70)
j>0 j>Q
еде Rn = Хотя эти уравнения не допускают линеаризации, можно ис¬
следовать асимптотическое поведение в окрестности перехода распыления.
Например, плотность самых больших фрагментов можно найти из уравне¬
ния
dco
dt
Cq ^2(1 + Rj)d ~ — CqN,
j>Q
что дает
In Cq ~
1
(l-t/te)^-1
при t —> tc.
Плотности меньших фрагментов демонстрируют похожее чрезвычайно быст¬
рое обращение в ноль со временем при t tc, когда d > 1, так что переход
распыления остается первого рода.
6.5 Ссылки
Обзор ранних работы по фрагментации дан в [123]. Было найдено множество
точных решений моделей фрагментации со специальными интенсивностями
распадов; репрезентативная выборка таких публикаций — [124-128]. Скей¬
линговая теория фрагментации, которая является зеркальным отражением
комплементарного процесса агрегации, была развита в [129]. Переход распы¬
ления был впервые исследован Филипповым [130], и многие свойства этого
явления были выяснены в [127, 129].
Решение для фрагментации со стационарным источником материи дано в
1131]. Оно основано на разложении в ряд, которое было разработано Чарльсби
|132]. Модель прямоугольной фрагментации введена в [133], и эта же мето¬
дология решения будет использована в следующей главе для рассмотрения
238
Фрагментация
адсорбции игл. Стандартная ссылка по обратимой полимеризации — Блац и
Тобольски [134]. Применения детального равновесия к обратимой фрагмента¬
ции исследуются в [135]. Необычные кинетические свойства модели откалы¬
вания краев впервые обсуждались в [136], тогда как неравновесный фазовый
переход в этой модели был открыт в [137]. Модель столкновительной фраг¬
ментации введена в [129], и многие ее свойства исследованы в [138].
6.6 Задачи
6.1 Получите ведущее асимптотическое поведение моментов для модели случай¬
ного разрезания.
6.2 Решите модель случайного разрезания с экспоненциальным начальным рас¬
пределением длины и покажите, что это распределение остается экспоненци¬
альным.
6.3 Рассмотрите однородное ядро распадов R(x) = 1 с показателем однородности
Л = 0, которое таким образом лежит на границе между скейлингом и распы¬
лением.
(а) Покажите, что для монодисперсных начальных условий с(я,£ = 0) =
5(х — €), распределение массы фрагментов имеет вид
с(ж,£) = е *й(х — €) +
2te-*
£
п>0
[2Пп(е/х)]п
п! (п + 1)!
i
(b) Выразите ряд, дающий решение в пункте (а), через модифицированную
функцию Бесселя Д ^2y/2t ln(€/rr)J.
(c) Покажите, что моменты распределения массы даются выражением Мп =
Р1 ехр[(1 — ri)t/(l + п)].
6.4 Получите стационарное решение основного кинетического уравнения (6. lb)
для произвольных интенсивностей распада R(x) / 0.
6.5 Рассмотрите трехмерное обобщение прямоугольной фрагментации из разде¬
ла 6.2. Предположите, что начальный фрагмент — это куб 1 х 1 х 1 и что
каждая трещина приводит к разрезу в одном из трех взаимно ортогональных
направлений.
(а) Покажите, что Меллин-образ удовлетворяет уравнению
dc(si,s2,s3,t) _ [2 /£ 1 1 \ _
dt [з S2 S3/
c(si + 1,s2 + 1, S3 + 1, £).
6.6 Задачи
239
(b) Получите асимптотическое поведение Меллин-образа в виде
c(si,S2,s3,t) ~ t-a(5i’s2,s3)
и вычислите показатель a(si, s2, $з)-
(c) Убедитесь, что распределение объема принимает скейлинговый вид
F(V,t) ~ t2 e~vt, такой же как в модели случайного разрезания.
6.6 Рассмотрите геометрический процесс фрагментации, в котором прямоуголь¬
ник делится на четыре меньших фрагмента, как показано ниже.
(a) Убедитесь, что Меллин-образ c($i,s2,£) удовлетворяет уравнению
(b) Проверьте, что это уравнение согласуется с законом сохранения плотно¬
сти, и покажите, что среднее число фрагментов равно 1 + 3£.
(c) Пользуясь уравнением для c($i,s2,t) из пункта (а) и асимптотическим
поведением c(si,s2,f) ~ £-<*(«1^2), покажите, что
a(si,s2) = [(si + s2) - У(в1 - s2)2 + 16]/2.
(d) Покажите, что распределение площади имеет скейлинговый вид
F(A, t) ~ t~2f(At), f(z) = 6 [' d£ (f-1 - 1)е-г/«.
Jo
(e) Пользуясь результатами пункта (с), покажите, что распределение пло¬
щади слабо расходится в пределе малой площади, f(z) ~ 61п|. Убеди¬
тесь, что в противоположном пределе перемасштабированное распреде¬
ление площади демонстрирует экспоненциальное убывание, напоминаю¬
щее распределение в одномерной модели случайного разрезания, но с
алгебраической поправкой: f(z) ~ 6z~2 ехр(—z) as z Э> 1.
6.7 Рассмотрите систему с тремя состояниями с ненулевыми интенсивностями пе¬
реходов / 0 для всех i / j. Какому условию или условиям должны
удовлетворять эти интенсивности для того, чтобы в стационарном состоянии
выполнялся принцип детального равновесия (6.45)?
6.8 Рассмотрите комбинированную полимеризацию / фрагментацию в непрерыв¬
ном пределе, где длина полимеров — непрерывная величина.
(а) Покажите, что основное кинетическое уравнение для этой непрерывной
модели имеет вид
I
с(ж) с(£ — x)dx — 2с(£)
п;
г
Jo
с(х) cte + А
с(ж) dx — i с(£)
240
Фрагментация
(Ь) Убедитесь, что стационарное решение этого уравнения дается выраже¬
нием с(^) = е_€/£° и найдите €о-
6.9 Обобщите предыдущую задачу для определения стационарного распределе¬
ния длины замкнутых струн при комбинированной агрегации / фрагментации.
При фрагментации замкнутой струны она разрезается в двух случайно вы¬
бранных точках, и получившиеся отрезки немедленно образуют замкнутые
петли. При агрегации две петли объединяются, образуя большую петлю, дли¬
на которой равна сумме длин исходных петель.
(а) Обоснуйте, что основное кинетическое уравнение имеет вид
ас(€)
dt
ft Z»OO
= / х(£ — х) с(ж) с(£ — x)dx — / х c(rr) dx
Jq Jq
+А 2 У х с(т) dx — £2 с(£)
Первые два члена с правой стороны отвечают за события агрегации, то¬
гда как последние два — за события фрагментации.
(b) Покажите, что уравнение имеет стационарное решение с = (А/£)е_€/€°.
(c) Покажите, что то же самое распределение длины следует из принципа
детального равновесия.
6.10 Покажите, что в модели откалывания краев плотность фрагментов в гелевой
фазе, (А < 1), равна N = А/2, и таким образом получите вторую строчку в
(6.56).
6.11 Убедитесь в правильности выражений (6.59) и (6.61) для плотности массы в
. модели откалывания краев в золевой и гелевой фазах.
6.12 Рассмотрите модель столкновительной фрагментации из примера 6.4, где одна
из двух сталкивающихся частиц делится на две.
(a) Покажите, что в окрестности перехода распыления пуассоновский вид
(6.65) плотности массы стремится к распределению Гаусса.
(b) Покажите, что типичная масса га* (соответствующая пику распределе¬
ния массы) стремится к нулю как
га* ~ (1 — £)а, где а = 2In2 = 1,386294.
6.13 Рассмотрите модель столкновительной фрагментации из примера 6.5, где
бблыпая из двух сталкивающихся частиц делится на две.
(а) Покажите, что в терминах кумулятивной плотности уравнение (6.66)
приводится к виду
dAn
dt
— од2 _ Л2
— ^п-1 лгг
6.6 Задачи
241
(Ь) Отнормировав кумулятивное распределение Fn(r) = N ХАП(£), перепи¬
шите уравнение в пункте (а) в виде
(с) Покажите, что уравнение для F имеет решение в виде бегущей волны
Fn(r) —> f(n — vt). Подставьте этот волновой вид в уравнение для F и
получите уравнение
v4:f(x) = /(я) + /2(ж) - 2/2(ж -1).
(d) Покажите, что граничные условия для этого уравнения — это /(—оо) = 1
и /(оо) = 0. Попытайтесь угадать характер приближения к конечной
асимптотике в пределах х —> ±оо.
(e) Чтобы определить скорость v, нужно искать асимптотическое поведение
функции f{x) дрлеко позади фронта в виде 1 — /(ж) ~ еХх при х —> —оо.
Подставив этот вид в уравнение из пункта (с), получите «дисперсионное»
соотношение v = (3 — 4е”Л)/А между скоростью v и показателем убыва¬
ния А. Постройте график v = v(A) для А > 0 и покажите, что спектр
возможных скоростей ограничен сверху: v Е (—oo,vmax].
(f) Максимальная величина выбирается из спектра v Е (—оо,?;П1ах]. Пока¬
жите, ЧТО V = Vmax =F 1, 52961.
(h) Покажите, что типичная масса стремится к нулю в соответствии с урав¬
нением из пункта (Ь) задачи 6.12, где cr = vln2 = 1,06024.
6.14 Рассмотрите модель столкновительной фрагментации, в которой случайно вы¬
бранный участник столкновения стохастически распадается: а именно, части¬
ца массы т делится на два фрагмента с массами га' и га — га', где величина
га' выбрана однородно из [0,га].
(а) Покажите, что плотность массы с(га, т) удовлетворяет уравнению
(Ь) Решите основное кинетическое уравнение из пункта (а), пользуясь преоб¬
разованием Меллина. Покажите, что для начального условия с(га, 0) =
8 (т — 1) распределение массы имеет вид
с(га, т) = е Т8(т—1) + е Т
8т In А
га
где Ii — модифицированная функция Бесселя.
242
Фрагментация
(с) Покажите, что в окрестности перехода распыления с(ш, t) ~ 1—t с точно¬
стью до логарифмического множителя. (В основном такое же поведение
было обнаружено для столкновительной фрагментации с детерминисти¬
ческим правилом деления.)
Глава 7
АДСОРБЦИЯ
Предположим, что молекулы газа сталкиваются с поверхностью или подлож¬
кой и адсорбируются ей. Если падающие молекулы — мономеры, которые
непрерывно присоединяются к изолированным адсорбирующим узлам на по¬
верхности, и взаимодействие между адсорбированными мономерами отсут¬
ствует, то плотность занятых узлов растет со временем с интенсивностью,
пропорциональной плотности вакансий, а именно, dp/dt = 1 — р. Поэтому
p(t) = 1 — е“*, а вакансии убывают со временем экспоненциально, Однако,
если каждая молекула занимает больше одного узла на подложке, то пустая
область, меньше размера молекулы, не может быть заполнена. Подложка до¬
стигает насыщенного, но не до конца заполненного состояния, которое больше
не может поддерживать адсорбцию. Какова доля заполненных узлов в этом
состоянии? С какой скоростью достигается это заполнение? Это основные
вопросы кинетики адсорбции.
7.1 Случайная последовательная адсорбция в одно¬
мерии
Адсорбция димеров
Простой пример с нетривиальным коллективным поведением — это случай¬
ная последовательная адсорбция димеров — молекул, занимающих два со¬
седних узла одномерной решетки (рис. 7.1). Мы моделируем стационарный
приток молекул как попытки адсорбции, предпринимаемые по одной за раз в
случайно выбранных узлах подложки. Попытка становится успешной, толь¬
ко если димер попадает в два соседних пустых узла. Если димер попадает в
два занятых узла или в один занятый и один пустой узел, попытка считается
244
Адсорбция
Рис. 7.1. Изображение необратимого осаждения димеров. Димер слева успешно
адсорбируется двумя соседними вакантными узлами, тогда как димер справа не
адсорбируется
неудачной. После каждой успешной попытки доля покрытия возрастает. В
конце концов остаются только изолированные вакансии. Когда это состояние
достигается, подложка насыщена, поскольку дальнейшая адсорбция невоз¬
можна.
Как показано на рис. 7.2, при адсорбции димеров насыщенное состояние
состоит из цепочек с четным числом занятых узлов (•), разделенных изо¬
лированными вакантными узлами (о). В принципе, доля занятых узлов в
Рис. 7.2. Насыщенная конфигурация случайной последовательной адсорбции ди¬
меров
насыщенном состоянии pjam = p(t = оо) может принимать любое значение от
2/3 до 1. Предельные случаи достигаются соответственно на конфигурациях
с одним пустым узлом между адсорбированными димерами (• • ••"•оф-фоф-ф- ••)
и без пустых узлов (• • • •—• • • •). Замечательный результат, впервые
выведенный Флори с использованием комбинаторного подхода, — то, что из¬
начально пустая подложка стремится к плотности насыщения pjam, которая
имеет значение
Pjam = 1 - е 2 = 0,864664.
(7.1)
Мы найдем плотность насыщения, используя кинетический подход.
7.1 Случайная последовательная адсорбция в одномерии 245
Метод пустых интервалов
Мы будем придерживаться кинетической точки зрения и опишем полную
временную эволюцию плотности покрытия. Тогда окончательная плотность
покрытия получится как простое следствие. Для полного описания эволю¬
ции требуется знание вероятностей всех возможных конфигураций молекул,
адсорбированных подложкой. Однако эти вероятности содержат больше ин¬
формации, чем это необходимо для описания эволюции плотности покрытия.
Что нам действительно понадобится в одномерии, так это вероятности пу¬
стых интервалов, т. е. вероятности того, что цепочка из т последовательных
узлов пуста:
Ет = Т[о - • -о].
(7-2)
т
Здесь У обозначает вероятность конфигурации. Заметим, что состояние внеш¬
них по отношению к цепочке узлов не задано. Таким образом, Ет — это ве¬
роятность найти пустой интервал длины т или больше. В частности, Ei —
»*го плотность пустых, а р = 1 — Е± — плотность занятых узлов.
Для необратимой адсорбции димеров уравнения, которые описывают эво¬
люцию вероятностей пустых интервалов Ет, имеют вид
— 2.Еш+1, 772 > 1.
(7-3)
Обычно мы полагаем внутреннюю интенсивность адсорбции равной 1, что со¬
ответствует измерению времени в единицах, обратных величине интенсивно¬
сти адсорбции. Первое слагаемое в правой части уравнения (7.3) отвечает за
исчезновение 772-интервала из-за адсорбции димеров внутри интервала. Мно¬
житель 772—1 перечисляет 772—1 различных положений, где может быть адсор¬
бирован димер, так что он находится полностью внутри интервала (рис. 7.3).
Второе слагаемое отвечает за два различных события адсорбции, в которых
один конец адсорбированного димера находится вне 772-интервала. Для таких
событий пустой интервал должен содержать по меньшей мере 772 + 1 пустых
узлов, чтобы димер адсорбировался на конце 772-интервала, откуда следует
множитель Яш+1. Заметим, что уравнение (7.3) содержит только члены ухо¬
да. Это свойство — следствие использования вероятностей пустых интервалов
Ет в качестве основных динамических переменных. Можно считать, что мы
смотрим на подложку через линзу, через которую каждый раз видно только
т последовательных узлов, и Ет — это просто доля тех интервалов, которые
пусты. При таком рассмотрении не существует способа создать пустой интер¬
вал длиной > 772 посредством адсорбции димера на на еще больший пустой
интервал.
246
Адсорбция
(а) (Ь) СГ^
Рис. 7.3. Изменения вероятностей пустых интервалов Ет для т = 5с событиями
адсорбции (а) внутри интервала и (Ь) на конце интервала (пунктирная часть)
Для решения уравнения (7.3) заметим, что однородная часть этого урав¬
нения имеет решение в виде Этот факт подсказывает нам, что ис¬
кать решение полного уравнения нужно в виде
ЕГп(*) = е-^-1)‘Ф(4), (7.4)
где Ф(£) совпадает с Ei(t). Для естественных начальных условий, т. е. пустой
системы, имеем Ет(0) = 1, что дает Ф(0) = 1. После подстановки анзаца для
Em(t) бесконечный набор эволюционных уравнений (7.3) чудесным образом
сводится к единственному уравнению = —2е“* Ф, решение которого имеет
вид Ф(£) = ехр [—2(1 — е“4)]. Отсюда получаем вероятности пустых интерва¬
лов
Em(t) = ехр [-(т - l)t - 2 (l - е *)] . (7.5)
Пустые промежутки длины, больше, чем 1, исчезают экспоненциально со вре¬
менем, и только промежутки длины 1 остаются в конечном насыщенном со¬
стоянии. Согласно уравнению (7.5) асимптотическая плотность таких проме¬
жутков равна Е±оо = е“2, так что плотность насыщенного покрытия будет
Pjam = 1 — е“2. Таким образом, проделав небольшую работу, мы воспроизве¬
ли результат Флори, а также получили намного больше — долю покрытия в
течение всей эволюции:
p(t) = 1 - ехр [-2 (1 - е *)] • (7-6)
Плотность покрытия приближается к насыщению экспоненциально по време¬
ни, Pjam—p(t) — С где С = 2 е~2. Такое быстрое приближение к конечному
состоянию типично для моделей необратимой адсорбции (задачи 7.3 и 7.4).
7.1 Случайная последовательная адсорбция в одномерии 247
Пустые интервалы и лакуны
Альтернативой использованию вероятностей пустых интервалов Ет в каче¬
стве основных переменных для описания необратимой адсорбции могут слу¬
жить вероятности лакун. Лакуна длины т определяется как группа из т
последовательных пустых узлов, ограниченная с двух сторон занятыми уз¬
лами. Графически вероятность тп-лакуны определяется как
Vm = — о»].
т
Чтобы связать вероятности лакун Vm с вероятностями пустых интервалов
Ет, начнем с простейших конфигураций. Очевидно, выполняется равенство
?[•] + СР[о] = р + Е± = 1. Для двух узлов существуют следующие законы
сохранения:
Т[оо] + Т[ое] = Т[о] и Т[оо ] + Т[о*] + Т[*о] + ?*[••] = 1,
а для интервалов произвольной длины имеем
- о о] = 1Р[о_^до]. (7.7а)
ТП Ш+1 771
Мы также определяем вспомогательную вероятность сегмента S7H, в кото¬
ром состояние узла на одном конце сегмента задано как
т
(7.7Ь)
Пользуясь соотношением (7.7а), вероятность сегмента можно выразить через
вероятности пустого интервала, Sm = Ет — Em+i. Аналогично, вероятности
лакун — это разность вероятностей сегментов,
Кп — Sm+1 — Ет 2Em+i + Ет+2. (7.8)
Не существует твердого правила, говорящего какой из наборов величин, Ет
или Vm, полезнее для описания адсорбции и других кинетических задач. Хотя
вероятности лакун проще понять, эволюционные уравнения для Vm содержат
как члены ухода, так и прихода (задача 7.5), и анализ этих уравнений сложнее
анализа уравнений для Ет.
248
Адсорбция
Численное моделирование адсорбции
Существует два основных метода моделировать адсорбцию димеров в одно¬
мерии численно.
1. Бесполезный алгоритм. На каждом шаге алгоритма: (i) случайно вы¬
бираем узел ; (ii) принимаем попытку адсорбции в узле тогда и только
тогда, когда этот узел и его сосед справа не заняты; и (iii) увеличива¬
ем время на величину, обратную полному числу узлов L: t —> t + Ь~г.
Повторяем эти шаги, пока не достигнем заданной плотности покрытия.
Такой алгоритм легко реализовать, но он требует больших затрат вы¬
числительного времени, так как большинство попыток адсорбции на
больших временах оказываются неудачными.
2. Более эффективный алгоритм. На каждом шаге алгоритма: (i) случай¬
но выбираем один разрешенный узел; (ii) помещаем димер в разрешен¬
ный узел и в соседний справа; и (iii) увеличиваем время на величину,
обратно пропорциональную полному числу La узлов, разрешенных для
адсорбции: t —> t + L”1. Повторяем эти шаги, пока не достигнем насы¬
щения (La = 0). Для этого алгоритма требуется постоянно следить за
всеми узлами, где разрешена адсорбция. Дополнительные расходы на
ведение такого учета (рис. 7.4) окупятся с лихвой потому, что каждая
попытка адсорбции всегда удачна, а вычислительная стоимость каждой
попытки фиксирована. Рисунок 7.4 иллюстрирует ведение этого учета.
В общем случае более эффективный алгоритм может быть реализован для
численного моделирования адсорбции произвольных форм как на дискрет¬
ной, так и на непрерывной подложке с помощью постоянного учета областей,
где адсорбция разрешена.
Адсорбция длинных молекул
Что если налетающие молекулы занимают к последовательных узлов? (Такие
линейные полимеры называются /с-мерами.) Плотность покрытия для такого
обобщенного процесса адсорбции может быть получена с помощью прямого
развития подхода, примененного к димерам. Уравнения для вероятностей
7.1 Случайная последовательная адсорбция в одномерии 249
-1—2 ■ 3—4 5 6 7 8
<ТХ2) 3 4 5 6 7 8
<ТХ2ХЗХ4) 5 6 7 8
физическая подложка
1 2 3 4 5 6 7 8
I Т'“ " J 1
6 7 3 4 5
{ '
6 7 5
события
список разрешенных узлов
Рис. 7.4. Эффективный алгоритм, моделирующий адсорбцию димеров на кольце
размером L = 8. Левая часть показывает физическую подложку после каждого
индивидуального события адсорбции, а правая часть показывает соответству¬
ющий список узлов, где разрешена адсорбция (предполагаются переодические
граничные условия). Этот список чисел сжимается на каждом шаге при замене
положений узлов, где адсорбция больше не разрешена, положениями разрешен¬
ных узлов. Например, после первого события адсорбции узлы 1,2 и 8 становятся
запрещенными. Мы меняем нумерацию, так что первый разрешенный узел те¬
перь — 6, второй — 7, а узел 8 просто удаляется
пустых интервалов Ет при адсорбции fc-меров имеют вид
dE„
dt
-(m- k + l)Em(t) -2 ^2 m>k,
<
-(fc - m + l)-Efc(t) - 2 У2 Ek+j(t), m < k.
(7-9)
Слагаемые в этих уравнениях аналогичны слагаемым в уравнении (7.3), опи¬
сывающем адсорбцию димеров. Для т > к первое слагаемое отвечает за
т — к + 1 различных способов адсорбции fc-мера внутри пустого интервала
длины т. Второе слагаемое отвечает за 2(fc — 1) способов адсорбции fc-мера
частично внутри и частично снаружи исходного m-интервала. Для т < к
первое слагаемое отвечает за к — т + 1 способов, которыми га-интервал мо¬
жет быть полностью покрыт fc-мером, а второе слагаемое учитывает способы
покрыть интервал частично. Заметим, что уравнение для т < к может быть
получено простой перестановкой к и т в уравнении для т> к.
По аналогии с (7.4) воспользуемся анзацем Em(t) = е~^т"к+1^ Ф(£), под¬
становка которого в уравнение (7.9) для т > к дает = — 2Ф
250
Адсорбция
Решая это уравнение, находим Ф и получаем вероятности пустых интервалов
Em(t) = exp — (т — к + l)t — 2 52
1 - e~jt
j
т> к. (7.10)
Для нахождения временнбй зависимости плотности покрытия р = 1 — Ei
рассмотрим второе из уравнений (7.9) для случая т = 1. Это дает =
—кЕк или, эквивалентно, = кЕк- Однако значение Ек дается уравнением
(7.10) при т = к. Интегрируя, получим плотность покрытия
1 - е"^
-«_2 52
du.
(7-11)
Численное вычисление этого интеграла дает плотность насыщения, монотон¬
но убывающую с ростом к. Например: pjam Ф 0,864665, 0,823653, 0,803893 и
0,7902276 для к = 2 4- 5 (рис. 7.5). Плотность покрытия в насыщенном со¬
стоянии растет с ростом размера молекул, поскольку становится возможным
существование все более длинных пустых областей.
Рис. 7.5. Зависимость от длины адсорбируемых полимеров к. Пунктирная
линия дает асимптотическое значение pjam = 0,747597. Вставка показывает за¬
висимость тех же данных от 1/к
7.1 Случайная последовательная адсорбция в одномерии 251
Необратимая парковка автомобилей
Предел адсорбции fc-меров при к —> оо приводит нас к задаче о парковке ав¬
томобилей. В этом пределе положение адсорбируемых fc-меров становится
непрерывным, и можно думать об «автомобилях» единичной длины, необра¬
тимо паркующихся в любом месте у одномероного бордюра (при отсутствии
разметки парковочных мест). Единственное ограничение — автомобили не
могут пересекаться. Однако автомобиль может въехать на парковочное ме¬
сто, которое длиннее, чем сам автомобиль, на бесконечно малую величину.
Плотность покрытия в этой задаче о парковке была найдена Реньи и состав¬
ляет Pjam Ф 0, 74597.
Для решения задачи о парковке автомобилей мы снова применим метод
основного кинетического уравнения. Длина автомобиля не важна, если мы
ищем долю прямой, покрытую автомобилями, и поэтому мы полагаем ее рав¬
ной единице. Подходящая динамическая переменная теперь Е(х, t) — веро¬
ятность того, что случайно выбранный интервал длины х пуст. Как и в дис¬
кретном случае, эта область может быть частью большего пустого интерва¬
ла. Если интенсивность, с которой паркуются автомобили, равна 1, эволюция
E(x,t) описывается уравнениями (сравните с уравнениями (7.9))
гх 4-1
-(х - 1)Е(жД) - 2 / E(y,t)dy, х>1,
Jx
(7-12)
/•аН-1
-(1 -x)£(l,t) - 2 J E(y,t)dy, х<1.
Слагаемые в этих уравнениях находятся в точном соответствии со слагае¬
мыми из уравнений (7.9), описывающих адсорбцию fc-меров. Для х > 1 пер¬
вое слагаемое в правой части (7.12) отвечает за адсорбцию, происходящую
полностью внутри интервала, а второе слагаемое — за адсорбцию, частично
выходящую за его пределы. Такое же соответствие применимо и ко второй
строке (7.12), где снова заметим, как х и 1 меняются ролями.
Также для иллюстрации связи между вероятностями пустых интервалов
и вероятностями лакун полезно выписать основное кинетическое уравнение
для плотности лакун V(х, t)
-(ж - 1)У(жД) + 2 [ V(y,t)dy, х>1,
Jx+l
(7-13)
2 [ V(y,t)dy,
Jx+l
dE(x, t)
dt
dV (x, t)
dt
x <1.
252
Адсорбция
В случае х > 1 первое слагаемое, так же как в уравнении (7.12), отвечает за
адсорбцию внутри интервала длины х. Второе слагаемое отвечает за образо¬
вание х-лакуны при «фрагментации» лакуны длиной у > (х + 1), происходя¬
щей в результате адсорбции внутри последней (отметим близкую аналогию с
основным кинетическим уравнением фрагментации (6.2)). Существует только
два возможных положения для таких событий адсорбции, которые приводят
к образованию х-лакуны. В случае х < 1 член ухода отсутствует, так как
адсорбция не может произойти в такой короткой лакуне, а член прихода со¬
ответствует фрагментации лакуны длины х + 1 или больше. (Использование
вероятностей лакун для описания адсорбции димеров — предмет задачи 7.5.)
Чтобы найти £?(x,t), рассмотрим первый режим х > 1. Так же как в
дискретном случае, будем искать решение в виде E(x,i) = J5(l,f).
После подстановки этого выражения в первое из уравнений (7.12) члены,
зависимые от х, сокращаются, а интегрирование полученного уравнения для
£7(1, £) дает
£?(!,£) = exp
du ,
(7-14)
откуда немедленно получаем Е(х, t) для х > 1. Для второго из уравнений
(7.12) имеем = —F(l,i), так что плотность покрытия p(t) = 1 — E(0,t)
дается следующим выражением
1 - e_wl
и
dv.
(7-15)
Численный расчет этого интеграла при t оо дает плотность насыщения
Pjam = 0,747597х.
Качественно новое свойство непрерывной парковки автомобилей — это то,
что приближение к насыщению происходит существенно медленнее, чем при
адсорбции на решетке. Посмотрим, как отклонение от предельной плотности
покрытия pjam — p(t) убывает при t —> оо. Для этого выпишем асимптотиче¬
ское поведение интеграла из уравнения (7.15)
d« = lnf + 7£ + t хе * + ...,
и
где = 0,577215 — константа Эйлера. Используя этот результат, получим,
что приближение к плотности насыщения происходит следующим образом
1Этот же результат можно также получить рассматривая предел к оо и t —> оо в
уравнении (7.11).
7.2 Структура фазового пространства
253
Pjam - p(t) = J ехр [-2 J^ (1 - е “) dv
ехр [—2(1пг> + 7#)] dv
= е~^Е Г1. (7.16)
Медленное приближение к насыщению происходит из-за того, что могут воз¬
никать парковочные места, которые инфинитезимально длиннее автомобиля,
и такие места заполняются очень медленно. В пространственной размерно¬
сти d происходит аналогичная степенная релаксация, при которой плотность
стремится к плотности насыщения как (см. раздел 7.3).
7.2 Структура фазового пространства
Нарушение эргодичности
Основополагающий принцип равновесной статистической физики — это по¬
стулат равной априорной вероятности: микроскопические состояния с од¬
ной и той же энергией реализуется с одинаковой вероятностью. Это свой¬
ство идентично понятию эргодичности, лежащему в основе эквивалентности
между формальным усреднением по ансамблю в статистической механике
и усреднением по времени в реальных равновесных системах. Неравновес¬
ные системы в общем случае и системы с насыщенными конфигурациями в
частности не подходят под такое описание, так как они не дают однородной
выборки из пространства состояний, состоящего из всех конфигураций.
Это явление известно как нарушение эргодичности. Поскольку в необ¬
ратимой адсорбции вероятности всех конфигураций можно непосредственно
вычислить, это идеальная модель понимания нарушения эргодичности.
Мы начнем с подсчета полного числа насыщенных состояний в конечной
системе для необратимой адсорбции димеров. Пусть Jl — полное число насы¬
щенных конфигураций на конечной цепочке из L узлов. Мы можем легко рас¬
считать число насыщенных конфигураций на малых цепочках: J2 = 1 (•-•),
J3 = 2 (•-• о и о •-*), J4 = 2 (•+ и о о) и J5 = 3 (•-• о, о *-•
и о •-•). В общем случае есть два типа насыщенных конфигураций: в
которых (i) первый узел цепочки занят или (ii) свободен. Типичные конфи¬
гурации из этих этих двух категорий — это
х • • • х и о х • • • X,
L—2
L-3
254
Адсорбция
соответственно. Поэтому первая категория состоит из Jl-2, а вторая — из
Jl-з конфигураций. Таким образом, при L > 2 числа Jl удовлетворяют ре¬
куррентному соотношению, подобному соотношению для чисел Фибоначчи,
Jl = Jl-2 + Jl-з (7-17)
с граничными условиями Jo = Ji = Jz = 1- Для асимптотического решения
подставляем экспоненту Jl = zL в рекурсию для Jl и находим, что пара¬
метр z должен удовлетворять кубическому уравнению z3 — z — 1 = 0. Только
один из его корней (z = 1,32472) действительный и имеет величину больше,
чем 1. В результате асимптотическое поведение числа насыщенных конфигу¬
раций действительно растет экспоненциально с размером системы (см. задачу
7.8)
Jl ~ zL, (7.18)
так что конфигурационная энтропия равна S = — L\az,
Также интересно найти число конфигураций с заданной плотностью по¬
крытия. Пусть Jyv,L ~ число насыщенных конфигураций, которые содер¬
жат N димеров в системе размера L. Для того чтобы конфигурация бы¬
ла насыщена, число димеров должно находиться в диапазоне [(L + 1/3)J <
7V|_L/2J, где |xj — целая часть х. В насыщенной конфигурации за диме¬
ром должен следовать другой димер или одиночный свободный узел. По¬
этому различные насыщенные конфигурации можно символически записать
как ... DDDODDOD..., т. е. между каждой парой димеров (представленной
как DD) может быть или единичная вакансия (О) или ничего. Поскольку
вакансия может возникать между любой парой димеров, а также между ди¬
мером и концом цепочки, существует N +1 способов возможного размещения
L — 2N вакантных узлов. Таким образом, число различных конфигураций с
N димерами дается биномиальным коэффициентом
а полное число разрешенных конфигураций равно Jl = Jn,l-
В термодинамическом пределе мы фиксируем плотность покрытия рав¬
ной р = 2N/L и вычисляем общее число конфигураций с данной плотностью,
Jl(p) = JpL/2,L^ удерживая только два ведущих члена в формуле Стирлинга
In х\ ~ х In х — х. В этом приближении полное число конфигураций с фикси¬
рованной плотностью растет как Jl(p) ~ где
f(p) = ^ - (1 - р) 1п(1 - р) - (^ - l) In (^ - l) (7.20)
7.2 Структура фазового пространства
255
Рис. 7.6. Функция энтропии. Показаны плотности насыщения и равновесия, и
разность энтропии Л
— функция энтропии (рис. 7.6). Функция f(p) имеет несколько важных
свойств. Во первых, поскольку /(р) положительно при 2/3 < р < 1, пол¬
ное число насыщенных конфигураций экспоненциально велико для любой
плотности в этом диапазоне2. Во вторых, из-за того что Jl(p} растет экс¬
поненциально с L, наибольший вклад в Jl(p) вносится наиболее вероятной
величиной. Условие f'(p) = 0 дает |р(1 — р)2 = (|р — I)3, откуда равно¬
весная плотность равна peq = 0,822991. Вблизи максимума /(р) = /(peq) +
|/,,(peq)(p — Peq)2+- • •, так что вид зависимости числа насыщенных конфи¬
гураций от плотности стремится к распределению Гаусса
Jl(p) - ехР [~(Р - Peq)2/2<x2] (7.21)
У27Г<72
С дисперсией <72 = [-/"(peq)^]-1.
Мы использовали термин «равновесная» для peq, так как эта плотность
возникает, когда все насыщенные конфигурации выбираются равновероят¬
но. На самом деле распределение Гаусса (7.21) имеет острый пик, так что
плотность покрытия в случайно выбранной насыщенной конфигурации по¬
чти наверняка совпадает с peq- Однако при необратимой адсорбции система
заходит в малую часть фазового пространства с большей плотностью покры¬
2Число конфигураций конечно в двух крайних случаях: Jl (2/3) = 2 и Jl(1) = 1, и,
следовательно, /(2/3) = /(1) = 0.
256
Адсорбция
тия, pjam = 0,864644 > peq Ф 0,822991. Относительный вес этой области фа¬
зового пространства убывает экспоненциально с размером системы е”ЛЬ, где
Д = /(peq)~/(Pjam) (рис. 7.6). Для неравновесных систем, таких как показан¬
ная на примере необратимой адсорбции, динамика диктует, как посещается
фазовое пространство, и нет никаких причин, по которым все макроскопиче¬
ские конфигурации возникали бы с равной вероятностью.
Поправки конечного объема
Анализ кинетики адсорбции методом основного кинетического уравнения
описывает только бесконечно большие системы, тогда как реальные системы
конечны. Чтобы оценить влияние конечного размера, адаптируем комбина¬
торный подход Флори для рассмотрения необратимой адсорбции димеров на
конечном интервале длины L. Обозначим через Al среднее число занятых
узлов во всех насыщенных конфигурациях при адсорбции димеров на интер¬
вале длины L. Можно непосредственно вычислить эту величину для малых
систем.
Пример 7.1. Насыщение в малых системах. Для систем, которые состоят из
одного узла, очевидно, что А± равно нулю. В двух- и трехузловых интервалах
может адсорбироваться только один димер, так что Аъ = A3 = 2. Первый нетри¬
виальный случай — это интервал с четырьмя узлами. С вероятностью | первый
димер располагается на двух средних узлах, и никакая дальнейшая адсорбция
невозможна. С вероятностью | первый димер занимает узел на конце интерва¬
ла и его соседний, так что остается место для второго димера. Таким образом,
среднее число занятых узлов равно: | + | х 4 = Следовательно Ai = 0,
А2 = Л3 = 2, А4 = ~ и т. д.
Непрактично производить такое перечисление шаг за шагом вручную. Тем
не менее, можно найти Al для произвольных L, записав рекурсию для плот¬
ности насыщения на конечном интервале L, выраженной через плотности
насыщения на меньших интервалах. Если первый димер находится в узлах
(j, J+1), где 1 < j < L—1, то возникают два интервала длин J—1 и L—j— 1, ко¬
торые впоследствии заполняются независимо. Поэтому для L >2 плотность
покрытия удовлетворяет соотношению
1 L_1 2 L"2
Al = У2 (2 + Aj-i + A-l-j-i) = 2 + Aj (7.22)
J=1 j=o
с граничными условиями Aq = A± = 0.
7.2 Структура фазового пространства
257
Для того, чтобы найти Al, мы используем производящую функцию
*^(z) = Sl>2 Al zl х. Умножая уравнение (7.22) на (L — 1) zL 2 и суммируя
по всем L > 2, мы превращаем левую часть в а первое слагаемое в правой
части в — 2/(1 — z)2. Во втором слагаемом в правой части мы меняем порядок
суммирования, что дает
L—2
2z
1-Z
A(z).
Ь>2 j=0 j>0 L>j+2 j>0
В результате рекуррентные соотношения (7.22) превращаются в дифферен¬
циальное уравнение
dA _ 2 2z п
d^~ (l-z)2 + l^
(7.23)
с граничными условиями Л (г = 0) = А± = 0 и A'(z = 0) = Л2 = 2. Чтобы
решить уравнение (7.23), заметим, что множитель I = (1 — z)2 e2z qkqrwy
уравнение (7.23) к виду = 2e2z. Решение уравнения (7.23) имеет вид
Из поведения при малых г, Л = 2z + 2z2 + ^z3 + ..., мы снова выводим
средние числа занятых узлов в насыщенном состоянии для малых систем.
Когда L —> оо, можно найти коэффициенты ряда производящей функции
из поведения A(z) при z f 1. Если плотность покрытия линейна по размеру
системы, т. е. Al —> Lp + С при L -> оо, где р и С — константы, то в этом
пределе функция A(z) должна стремиться к виду
A(z) ~^(pL+C)zL 1 = p4z^2zL + C^2zb 1
L>2 L>2 L>2
(1 - z)2 1 - z
(7-25)
в пределе 3 f 1. Сравнивая с уравнениями (7.24), находим, что p = pjam =
1 — e"2, таким образом воспроизводя результат Флори (7.1). Также находим
ведущую асимптотическую поправку С = —2е”2. Таким образом, плотность
покрытия в системе длины L, p(L) = Al/L содержит поправки конечного
объема
p(L) ~ pjam + CL Х.
(7.26)
258
Адсорбция
Такие поправки к асимптотическому поведению из-за конечного размера си¬
стемы часто имеют степенной вид, как в (7.26). Поправки конечного объема
полезны при численных расчетах, так как они позволяют экстраполировать
свойства бесконечных систем из расчетов для конечных систем (задача 7.9).
Величина поправочного члена (пропорциональная L”1) возникает из-из того,
что плотность близка к значению Флори везде, кроме нескольких узлов на
краях интервала.
Корреляции и флуктуации
Отклонение пространственного расположения молекул в насыщенном состо¬
янии от случайного можно охарактеризовать парной корреляционной функ¬
цией Cj:
Cj = (nonj) - (no)(nj). (7.27a)
Здесь nj — индикаторная функция заполнения узла j: nj = 0, когда узел j ва¬
кантный, и nj = 1, когда он занят. Эквивалентно, корреляционную функцию
можно записать как3
С,- = (е0 еу) - (е0) (еу) = Pj - Е%, (7.27b)
где еу = 1 — nj — индикаторная функция пустых узлов, a Pj = (еоеу). Пред¬
почтительно работать с еу и Pj, поскольку они непосредственно связаны с
вероятностями пустых интервалов. Величина Pj может быть представлена
как вероятность конфигурации
Pj = 3>[ох-хо], (7.28)
J-1
где х обозначает узел, состояние которого не задано.
Чтобы найти корреляционную функцию, нам нужны вероятности для бо¬
лее общего класса конфигураций, которые состоят из пустых интервалов дли-
ны > г и > к, окружающих j — 1 неопределенных узлов:
Ei,j,k = ? [ •
г j—1 k
3В выражении Cj = ((1 — ео)(1 — е5)) — (1 — ео)(1 — ej) константы и линейные слагаемые
сокращаются.
7.2 Структура фазового пространства
259
Тогда Pj из (7.28) — это просто Pj = Вероятности удовлетворяют
иерархии кинетических уравнений, структурно схожих с (7.3):
= ” (^ ” к “
— (fc — — Eij'k+1 ~ ■£'i,<7-l,fc+l (7.29)
для г, к > 1 и j > 2: Слагаемые в первой строке отвечают за изменения в
пустом интервале из г узлов. Они описывают события адсорбции с участи¬
ем внутренних узлов, внутреннего граничного узла и внешнего граничного
узла г-интервала. Слагаемые во второй строке отвечают за соответствующие
события в fc-интервале.
Уравнения (7.29) решаются, и, как следствие, мы можем получить корре¬
ляционные функции. Начнем с обобщения анзаца (7.4), записывая
EijjM = e-(i+fc-2)t где г,к>1 (7.30)
с начальными условиями Eijj^t = 0) = Р/(£ = 0) = 1. Для j > 2 этот анзац
приводит уравнения (7.29) к виду
HP
= —2e-t [Pj + BhJ . (7.31)
Для j = 1 имеем Pi — Е%- Для решения этого уравнения мы вводим мно¬
житель I = ехр ( f 2e-t di) = ехр [2(1 — e-t)], совпадающий с 1 из (7.5),
который упрощает вид уравнения (7.31):
= —2е t Qj—i) где Pj = Ei Qj.
Наконец, мы заменяем явную зависимость от времени зависимостью от пе¬
ремасштабированной временнбй переменной dr = —2e-t dt, что дает
^- = Qj-i, где T = ln£i. (7.32)
Это уравнение снабжено начальными условиями Qj(O) = 1 и граничными
условиями Qi = Pi/Ei = Е2/Е1 = е"г, где последнее равенство следует из
4 Заметим, что Ei^k = Ег+k, где справа стоит введенная раньше вероятность пустого
интервала, а также что для адсорбции димеров Eit2,k = tP(° • • • о х о • • • о) = £?i+i+fc, по¬
скольку одиночный узел, зажатый между кластерами пустых узлов, также должен быть
пустым.
260
Адсорбция
(7.5). Интегрируя уравнения (7.32) пошагово, начиная с Qi = l + ^r, получим
Q2 = 1 + т + 5^, Q3 = 1 + т + + 5^, и т. д., и для общего случая
3^тк
^' = 2тг +
к=0
1 TJ
2?!*
В заключение запишем конечную сумму в виде разности бесконечной сум¬
мы и конечной суммы, начинающейся с J, перепишем Qj через Pj и т = In Е±
и получим парную корреляционную функцию (рис. 7.7)
Cj = Pj - El = -Ei
(lnEi)J'
2 j!
(In El)*
k>j+l
В насыщенном состоянии Ei(oo) = e-2, так что
ki
j > 1. (7.33)
Cj -> —e"
при ] —> оо,
(7.34)
и мы получили более быстрое убывание, чем обычное экспоненциальное, ко¬
торое типично для корреляций в равновесных системах с близкодействием,
таких как газ твердых сфер. Отметим также положительные (отрицатель¬
ные) корреляции между узлами на нечетном (четном) расстоянии.
7.1. Флуктуации плотности
Дисперсия <т2 = (р2) — (р)2 — это стандартная характеристика флуктуаций плот¬
ности покрытия. Пользуясь определением р = L-1 Пг, где L — размер системы,
дисперсию можно записать через парную корреляционную функцию (niUj):
6Т2 = L~2 [(ninj) - . (7.35)
Теперь запишем корреляционную функцию как Ск = (ni7ii+fc) — (ni)(ni+fc) с ин¬
дексом к, принимающим любые положительные или отрицательные целые значе¬
ния. Пользуясь трансляционной инвариантностью и суммируя по одному из двух
индексов, находим
оо
сг2 = £-1 Cfc- (7.36)
к=—оо
Следовательно, существует прямая связь между флуктуациями и корреляциями
плотности. Для систем с быстро убывающими корреляциями, как при адсорб¬
ции, флуктуации исчезают в термодинамическом пределе, и плотность становит¬
ся детерминистической величиной. Например, при адсорбции димеров, подставив
(7.33) в (7.36), получим дисперсию а2 = 2Е2 ln(l/£q)/L, равную 4e“4L“1 в насы¬
щенном состоянии.
7.3 Адсорбция в высших размерностях
261
Рис. 7.7. Зависимость корреляционной функции Cj из уравнения (7.34) от j
7.3 Адсорбция в высших размерностях
Большинство физических приложений необратимой адсорбции возникает на
двумерных подложках. В качестве подготовки к пониманию адсорбции ре¬
альных частиц, таких как белки и коллоиды, естественно заняться изучени¬
ем адсорбции элементарных объектов: дисков, прямоугольников, стержней.
Получить представление о численных значениях плотности покрытия для
случайной последовательной адсорбции различных элементарных объектов
можно из таблицы (7.1). Хотя точный анализ адсорбции в высших размерно¬
стях в общем случае невозможен, эволюция адсорбции в произвольных раз¬
мерностях проявляет те же качественные свойства, что и адсорбция в размер¬
ности один. А именно, релаксация плотности насыщения экспоненциальна по
времени на дискретных подложках и алгебраически зависит от времени на
непрерывных подложках. В оставшейся части этого раздела мы обсуждаем
простые примеры, иллюстрирующие эти свойства.
Дискретные подложки
Адсорбция точнорешаема для одной специальной подложки высокой размер¬
ности, дерева Кейли, в котором каждый узел связан ровно с z другими узлаг
262
Адсорбция
объект
подложка
Pjam
неориентированные димеры
квадраты 2x2
квадратная решетка
квадратная решетка
0,9068
0,74788
параллельные квадраты
диски
континуум
континуум
0,562009
0,5472
Таблица 7.1. Плотность насыщения для различных объектов в двух измерениях,
полученная из численного эксперимента
ми дерева. При адсорбции димеров на дереве Кейли димер может с равной
вероятностью расположиться на любой паре соседних узлов дерева. В этом
случае фундаментальными объектами являются не пустые интервалы дли¬
ны > т, а пустые связные кластеры из > т узлов, вероятность которых
мы снова обозначаем через Ет. Поскольку эти кластеры имеют структуру
дерева, нужно следить только за «граничными» конфигурациями, которые
входят в эволюционные уравнения для Ет (рис. 7.8). Это свойство позволяет
решить задачу об адсорбции на дереве Кейли.
Рис. 7.8. Кластер из т = 3 узлов (черные круги) и 8 узлов периметра (белые
круги) на дереве Кейли с координационным числом z = 4
Вероятность Ет того, что все узлы в пустом m-кластере остаются пусты¬
ми при адсорбции димеров, удовлетворяет уравнению (сравните с уравнением
(7-3))
= -(тп - 1)Ят - [(г - 2)тп + 2]Ет+1 (7.37)
для т > 1 с начальными условиями £^(0) = 1. Первое слагаемое в пра¬
вой части отвечает за события, в которых димер адсорбируется где-нибудь
внутри кластера. Число доступных расположений для такой «внутренней»
7.3 Адсорбция в высших размерностях
263
адсорбции — это просто число ребер внутри кластера. Так как каждый кла¬
стер имеет топологию дерева, число ребер в кластере равно т — 1. Второе
слагаемое отвечает за события адсорбции, в которых один конец димера нахо¬
дится внутри кластера, а другой — снаружи. Число способов возникновения
таких событий равно числу узлов периметра — узлов, которые связаны с кла¬
стером, но не являются его частью (рис. 7.8). Для m-кластера число узлов
периметра равно (z — 2)m+2 независимо от его топологии. У начального узла
есть z узлов периметра, а добавление каждого нового узла приводит к обще¬
му росту периметра на z — 2. Таким образом, полное число узлов периметра
равно z + (т — l)(z — 2) = (z — 2)т + 2.
Для решения уравнения (7.37) мы используем экспоненциальный анзац
Em(t) = Ф(0 [<^(^)]ГП_1, где начальные условия удовлетворяются равенством
у>(0) = Ф(0) = 1 (см. врезку на стр. 264). Тогда иерархия уравнений (7.37)
сводится к паре взаимозависимых уравнений
dip
dt
-<p-(z- 2)ip2,
d<&
Уравнение (Бернулли) для у? можно превратить в решаемое линейное урав¬
нение = и + (г — 2), сделав замену и = 1/<р, откуда имеем —
1) — (г — 2)е“*] . Использовав этот результат в уравнении для Ф, получим
Ф(£) = [(z — 1) — (z — 2)e_t] Следовательно, вероятности пустых кла¬
стеров имеют вид
ETO(t) = e-(’n-i)* [(z _ 1) _ (z _ 2) е"‘] ~m~2/(z~2). (7.38)
В итоге, из выражения для плотности p(t) = 1 — Е± заключаем, что при¬
ближение к плотности насыщения происходит экспоненциально по времени,
а значение плотности насыщения равно
Ржп = 1-(2-1)"г/(г-2). (7.39)
В пределе z 2 воспроизводится одномерный результат pjam = 1 — е~2
(задача 7.14), тогда как для больших z непокрытая часть обратно пропорци¬
ональна координационному числу 1 — pjam ~ г-1. Дерево Кейли дает хорошее
приближение для pjam на регулярной решетке с таким же координационным
числом, как у дерева. Например, когда z = 4, адсорбция димеров на дереве
Кейли дает pjam = 8/9, тогда как на квадратной решетке р^т = 0,9068.
264
Адсорбция
7.2. Второй взгляд на экспоненциальное решение (в про¬
должение раздела 5.2, стр. 171)
Рассмотрим основное кинетическое уравнение общего вида
= \(т + а)Ет+ р.(т + P)Em+i, (7.40)
которое содержит уравнение (7.37) как частный случай. И снова экспоненциаль¬
ный анзац дает простой путь к решению. Предположим, что Ет имеет вид
Em = $(t)[v(t)]m. (7.41)
Подставляя в уравнение (7.40) и деля его на Ет, получаем
¥ + т^р = + + +
Так же как при использовании экспоненциального анзаца в разделе 5.2, это урав¬
нение естественным образом распадается на части линейные по т и не зависящие
от т. Из линейной части имеем
= А + (7.42)
откуда получаем Независимая от т часть дает
5 = Аа + р&р, (7.43)
откуда находим Ф(£).
Важное свойство — член в анзаце (7.41) разделяет исходный набор уравнений
(7.40) на два уравнения: одно линейное по т и одно независимое от т.
Кроме решения для дерева Кейли, не существует точных результатов об
эволюции плотности покрытия для адсорбции в более чем одном измерении.
В ситуации общего вида и, как показано в примере 7.2 (ниже), для адсорбции
димеров на квадратной решетке релаксация к плотности насыщения экспо¬
ненциальна по времени:
Pjam - p(t) ~ e~xt. (7.44)
Такое же поведение возникает при адсорбции объектов произвольной формы
на дискретных подложках в любой размерности. Чтобы почувствовать при¬
роду зависимости (7.44), рассмотрим простейший пример адсорбции димеров
на квадратной решетке.
Пример 7.2. Адсорбция димеров на квадратной решетке. Рассмотрим состоя¬
ние решетки при большом времени, когда места, доступные для адсорбции до¬
полнительных димеров, достаточно редки, а расстояния между ними велики.
7.3 Адсорбция в высших размерностях
265
Эти разрешенные области представляют из себя последовательность малень¬
ких кластеров из незанятых узлов: димеры, тримеры (линейные и изогнутые),
квадраты 2 х 2 и т. д. Чтобы определить интенсивность заполнения этих так
называемых «решеточных зверей», нам нужны вероятности того, что эти кон¬
фигурации пусты. Свойство, упрощающее жизнь на больших временах, — это
то, что остаются только самые маленькие звери, и доминирующую роль в их
асимптотическом убывании играет адсорбция димеров внутри них. Таким обра¬
зом, для адсорбции димеров на квадратной решетке вероятности конфигураций
наименьших порядков (димеров, тримеров, и квадратов 2x2) изменяются в
соответствии с уравнениями
1у[оо]~-Т[оо], 1 J>[ooo] ~ -2Т[ооо], АУ [£] ~ -4У [£].
Здесь У [ • ] обозначает вероятность конфигурации, а численный множитель пере¬
числяет число способов адсорбции димера в кластере. Таким образом, плотность
этих конфигураций убывает со временем как
У[оо] ~ У[ооо] ~ e“2t, У [оо] ~ e~4t. (7.45)
В общем случае вероятность, что данный решеточный зверь пуст, убывает как
У(£) ~ e~At, где А — число способов адсорбции димера внутри данного зверя.
Плотность покрытия определяется уравнением самого малого порядка, ~
-2У[оо], так что pjam - ~ е_<.
Непрерывные подложки
Характер кинетики адсорбции на непрерывных подложках довольно сильно
отличается от дискретных подложек. Главное новое свойство — то, что про¬
межутки между соседними адсорбированными объектами могут быть сколь
угодно малы (смотри рис. 7.9), что в итоге приводит к алгебраической релак¬
сации плотности
Pjam — р($ ~ t ° ч (7-^6)
где сг — индекс насыщения. Такое же медленное по сравнению с дискретны¬
ми подложками приближение к плотности насыщения возникает в задаче о
парковке автомобилей в одномерии (уравнение (7.16)), где расстояния между
автомобилями тоже могут быть сколь угодно малыми.
Обратимся к кинетике необратимой адсорбции дисков в двух измерениях.
Вокруг каждого адсорбированного диска есть «запрещенная зона», радиус
которой равен двум радиусам диска (рис. 7.9(b)). Если центр налетающего
диска лежит в запрещенной зоне любого адсорбированного диска, попытка
266
Адсорбция
Рис. 7.9. (а) Насыщенное состояние случайной последовательной адсорбции дис¬
ков единичного радиуса на квадрате 50. (Ь) Изображение разрешенной зоны (бе¬
лая), запрещенных зон (серые) и адсорбированных дисков (черные) в небольшом
кластере. В пределе большого времени существуют только разрешенные зоны в
виде треугольников из дуг, такие как маленький треугольник линейного размера
€, показанный на рисунке
адсорбции считается неудачной. Поэтому диск может адсорбироваться, толь¬
ко если его центр попадает в дополнение к объединению всех запрещенных
зон. Мы называем такие разрешенные части подложки «разрешенными зо¬
нами». Когда подложка близка к насыщению, на ней есть только небольшое
число маленьких независимых разрешенных зон. В насыщенной конфигу¬
рации разрешенных зон нет, несмотря на то что адсорбированные частицы
не покрывают подложку полностью. Эволюцию плотности покрытия можно
описать, рассматривая эволюцию разрешенных зон.
Когда, например, диски 1 и 2 уже адсорбированы и диск 3 адсорбирует¬
ся следующим, (рис. 7.9(b)), то между этими тремя дисками образуется ма¬
ленькая разрешенная зона. Пусть I — линейный размер разрешенной зоны.
По построению размер I однородно распределен между некоторым верхним
пределом и нулем. Пусть с(^, t) — плотность разрешенных зон линейного раз¬
мера I. Поскольку площадь разрешенных зон квадратична по <£, их плотность
эволюционирует как dc/dt ~ —12с, что приводит нас к оценке
(7.47)
7.3 Адсорбция в высших размерностях
267
Интенсивность адсорбции пропорциональна доле площади разрешенных зон:
~ [°° e2c(£,t)d£ ~ ~ Г3/2. (7.48)
dt Jq Jq
Поэтому отклонение плотности покрытия подложки от значения насыщения
ведет себя как Pjam“P(£) ~ е"1/2, т. е. индекс насыщения равен а = Важный
факт — разрешенные зоны могут быть сколь угодно малы, и суперпозиция
экспоненциально убывающих зависимостей приводит к убывающему степен¬
ному закону (задача 7.15). Этот эвристический подход легко можно обобщить
на произвольную пространственную размерность d. Теперь площадь разре¬
шенной зоны линейного размера I пропорциональна £d, а соответствующая
плотность разрешенных зон линейного размера £ убывает как с(£, £) ~ e~^dt.
Аналог уравнения (7.48) тогда дает индекс насыщения а = 1/d в d измере¬
ниях. Релаксация замедляется с ростом размерности.
Иглы
Интригующий пример необратимой адсорбции — осаждение идентичных слу¬
чайно ориентированных игл единичной длины. Плотность игл на единицу
площади неограниченно возрастает, и главная задача — определить скорость
этого возрастания. Ранние попытки осаждения почти всегда успешны, пото¬
му что подложка почти пуста. Следовательно, число адсорбированных игл
вначале растет линейно со временем, и эти начальные иглы имеют слабую
упорядоченность положений и ориентаций. Однако, когда плотность игл ста¬
новится порядка 1, адсорбированные иглы сильно ограничивают возможно¬
сти выбора положения и ориентации для последующих событий адсорбции.
В пределе большого времени образуются области, в которых соседние иглы
почти параллельны, а их местоположения упорядочены (рис. 7.10). Ориента¬
ция каждой области фиксирована после нескольких первых попыток адсорб¬
ции, и результат — это порядок в расположении игл на малых масштабах
и его отсутствие на больших. Когда области хорошо определены, большин¬
ство попыток адсорбции оказывается неудачными, и число адсорбированных
игл растет со временем медленнее, чем линейно. Образование почти строго
упорядоченных по направлению игл областей существенно упрощает анализ
поведения на больших временах. Для адсорбции новой иглы между двумя
близкими иглами, она должна почти совпадать с ними и по положению, и
по направлению. На больших временах типичная разрешенная область — это
трапеция с единичной высотой и основаниями х± и Х2 « xi (рис. 7.10(b)).
При адсорбции новой иглы положение ее нижнего конца меняется в диапа¬
зоне 0 < yi < xi, а верхнего конца — в диапазоне 0 < у2 < #2- Такое событие
268
Адсорбция
адсорбции делит трапецию на две меньших трапеции с основаниями у\, У2 п
xi — yi,X2 — У2, таким образом определяя процесс планарной фрагментации
(раздел 6.2).
Рис. 7.10. (а) Конфигурация, полученная в результате случайной последова¬
тельной адсорбции игл в двух измерениях в течение большого времени. (Ь) Ло¬
кальная геометрия одиночного события адсорбции иглы и его эквивалентность
фрагментации трапеций
Используя метод основного кинетического уравнения и эквивалентность
планарной фрагментации, получим, что плотность с(ж1,Ж2) трапеций с осно¬
ваниями (жх,Ж2) эволюционирует согласно уравнению
= _XlX2 С(Х1, я2) + 2 у у c(yi, у2) dy! dy2. (7.49)
Член ухода пропорционален полному числу способов, которыми каждый ко¬
нец иглы может быть расположен на основании трапеции. Член прихода учи¬
тывает два способы, которыми можно образовать трапецию с основаниями
Ж1,Ж2 при делении большей трапеции. Преобразование Меллина c(si,S2) =
ff Ж|1-1Ж22-1с(ж1,а;2) dx! dx2 подчиняется уравнению
3c(si,s2) _ ( 2 Л , , , , 1Ч
(7.50)
7.3 Адсорбция в высших размерностях
269
'Гак же как и в планарной фрагментации, снова появляется бесконечное се¬
мейство скрытых законов сохранения, определяемых равенством в^в^ = 2.
Пели мы предположим, что Меллин-образ алгебраически зависит от времени
c(ei,e2) ~
то уравнение (7.50) приведет нас к рекурсии o:(si + 1, *2 + 1) = a(ei, вг) + 1-
I [ользуясь этой рекурсией и условием «(ej, s^) = 0 вдоль параболы в*в2 = 2,
показатель o:(si, вг) можно определить с помощью аргументов из раздела 6.2,
и результат имеет вид
, ч «1 + S2 — д/(51 — s2)2 + 8 <
a(ei, 52) = . (7.51)
Одно из важнейших следствий этой формулы — что плотность числа игл
меняется сублинейно со временем с иррациональным показателем
N ~ tv, где v = а(1,1) = \/2 — 1. (7.52)
Чем больше игл адсорбировано, тем ближе их направления друг к другу. Эту
близость можно количественно охарактеризовать величиной (n-n') — (cos0),
где пип'- единичные векторы вдоль каждой иглы, а 0 — это угол между
ними. Этот угол связан с длинами оснований трапеции, построенной из двух
игл, как в = |a:i — ж2| при х± < ж2 С 1. Таким образом, ориентационная кор¬
реляционная функция (cos0) связана с моментами размеров трапеций через
равенства
1 - (cos 0) ~ ((жх - ж2)2) = 2((ж2) - (ацжг)),
где (ж2) = (х%) = (ж2). Пользуясь зависимостью (ж2) ~ t~“(ЗД-МЧ), нахо¬
дим, что ориентационная корреляционная функция убывает алгебраически с
еще одним иррациональным показателем
1- (cos 0) ~t-», где ц = а(3,1) - а(1,1) = 1 + Л - \/3. (7.53)
Таким образом, соседние иглы асимптотически становятся идеально парал¬
лельными.
Связь с планарной фрагментацией замечательным образом приводит нас
к мультискейлинговым свойствам и иррациональным показателям степеней,
которые характеризуют адсорбцию игл. Важный урок — это то, что на пер¬
вый взгляд трудную проблему, в данном случае адсорбции игл, можно сильно
упростить, посмотрев на нее в правильной геометрической перспективе. Ко¬
гда удалось охарактеризовать доминантное поведение на больших временах,
точный асимптотический анализ стал доступным.
270
Адсорбция
7.4 Обратимая адсорбция
Физические ситуации, в которых энергия связи адсорбированных молекул
с подложкой конечна, заставляют нас обратиться к изучению обратимой
адсорбции-десорбции, в которой молекулы адсорбируются с интенсивностью
г+ и десорбируются с интенсивностью г_. В качестве жизненного макроско¬
пического примера представим автомобили, которые пытаются парковать¬
ся вдоль одномерного бордюра (рис. 7.11). В соответствии с повседневным
опытом, если интенсивность с которой автомобили покидают парковку (де¬
сорбируются) мала, вероятность найти парковочное место также будет ма¬
ленькой. Поскольку единственный существенный параметр — это отношение
г = г+/г_, мы переопределяем время t —> r-t и записываем все формулы в
терминах г.
Рис. 7.11. Адсорбция-десорбция автомобилей. Попытки десорбции всегда успеш¬
ные (сплошная стрелка), тогда как изображенная попытка адсорбции (пунктир¬
ная стрелка) неудачна из-за того, что парковочное место слишком мало
Пример 7.3. Обратимая адсорбция мономеров. В качестве предварительного
примера рассмотрим ситуацию, когда мономеры адсорбируются на изолирован¬
ные узлы подложки. Тогда задача элементарна, поскольку нет запретов, возни¬
кающих при автомобильной парковке. Плотность адсорбированных частиц удо¬
влетворяет уравнению Ленгмюра
^ = -р + г(1-р), (7.54)
откуда находим, что релаксация к стационарному состоянию происходит экспо¬
ненциально быстро:
p(t) = Poo + (ро - Poo) e~t/T. (7.55)
Здесь время релаксации г = (1 + г)”1, и окончательная плотность покрытия
Роо = г/(1 + г). Заметьте, что при г -> оо, асимптотическая плотность покрытия
1 — poo ~ 1 — г”1, и этот предел достигается за время порядка г”1.
В обратимой парковке автомобилей мы будем интересоваться эволюцией
плотности покрытия единичной длины автомобилями, которые паркуются
7.4 Обратимая адсорбция
271
с интенсивностью г и уезжают с интенсивностью 1. В этом случае удобнее
пользоваться плотностью V(x,t) лакун длины х в момент времени t, чем
плотностью пустых интервалов Е(х, f). Физически нулевой и первый момен¬
ты плотности лакун равны, соответственно, удельным долям занятого и сво¬
бодного места
=f
V (х) dx л 1
х V (ж) dx.
(7.56)
11ервое условие происходит из взаимно однозначного соответствия между ла¬
кунами и паркующимися автомобилями, в соответствии с которым плотность
лакун любого размера равна плотности автомобилей.
При х < 1 основное кинетическое уравнение для плотности лакун имеет
вид
= -2У(ж, t) + 2г Г V(y, t)dy, х < 1. (7.57а)
Jx+l
Первое слагаемое справа отвечает за убыль ж-лакун из-за десорбции авто¬
мобилей на любом конце лакуны. Второе слагаемое учитывает образование
лакун длины х из больших лакун в результате адсорбции (задача 7.1G). Для
лакун длины х > 1 эволюционное уравнение содержит два дополнительных
слагаемых
= —2У(ж, t) + 2г f™V(y, t) dy - r(x -1) У(ж, t)
+ - Pv(y,t)V(x-y-l,t)dy, x > 1. (7.57b)
pJo
Третье слагаемое в правой части отвечает за исчезновение лакун из-за ад¬
сорбции внутри лакуны. Интенсивность исчезновения пропорциональна ко¬
личеству доступного для адсорбции места х—1. Член со сверткой представля¬
ет образование х-лакун, происходящее, когда автомобиль единичной длины
покидает парковочное место, в котором есть свободные пространства дли¬
ны у с одной стороны от автомобиля и длины х — у — 1 с другой стороны.
Правильный способ выражения вероятности такого составного события —
использовать двухлакунную плотность. Однако такое описание не замкну¬
то: эволюция одной лакуны зависит от двухлакунной плотности, двух лакун
от трехлакунной и т. д. до бесконечности. Простейший способ обрезать эту
иерархию — предположить, что соседние лакуны нескоррелированы и запи¬
сать двухлакунную плотность (для двух лакун длин х и х—у—1 с двух сторон
272
Адсорбция
от автомобиля) в виде произведения плотностей одиночных лакун. Множи¬
тель р в знаменателе дает правильную нормировку. Можно проверить, что
основное кинетическое уравнение сохраняет интеграл f(x + l)V(x)dx, что
согласуется с (7.56).
Равновесные стационарные состояния
Хотя эволюционные уравнения, такие как (7.57а) и особенно (7.57Ь), кажутся
пугающе сложными, они допускают простое и точное решение для стационар¬
ного состояния. Заметим, что уравнение (7.57а) связывает вероятности лакун
с их пространственными интегралами. Это означает, что решение имеет экс¬
поненциальный вид V(x) = Ае~ах. Два нормировочных условия (7.55) опре¬
деляют коэффициент А = р2/(1 — р) и индекс убывания а = р/(1 — р). Далее
мы обнаруживаем, что уравнение (7.57а) имеет стационарное решение, когда
индекс убывания удовлетворяет соотношению аеа = г. Наконец, подставим
V(x) = Ае~ах с А и а, полученными выше, в член со сверткой и потребуем,
чтобы два дополнительных члена сокращались. Это требование опять при¬
водит нас к соотношению а = р/(1 — р). Таким образом, вероятность лакун
имеет экспоненциальный вид
У(ж) = (7.58)
1 — р
для всех х. Нужно отметить, что, несмотря на то, что в уравнениях (7.57а)-
(7.57Ь) делается различие между лакунами больше и меньше, чем размер
автомобиля, плотность лакун остается неизменной. Более того, в отличие от
необратимой адсорбции, где большие лакуны не существуют, здесь возможны
промежутки любых размеров. Обратимость позволяет системе посещать все
фазовое пространство. В этом смысле мы можем рассматривать плотность
лакун (7.58) как равновесное распределение. Кроме того, это равновесное
распределение дает нам апостериорное подтверждение нашего предположе¬
ния об отсутствии корреляций между соседними лакунами (задачи 7.16 и
7.17).
Равновесная плотность находится из трансцедентного уравнения, где
а = р/(1 —р). В интересном пределе большой интенсивности адсорбции имеем
p(r) ~ 1 — (Inг)-1. (7.59)
Таким образом, для достижения высокой плотности значение г должно быть
астрономически большим. Например, чтобы получить р = 0,99, нужно иметь
г = е100. В заключение заметим, что поведение в пределе г —> оо отличается
7.4 Обратимая адсорбция
273
от ситуации, когда десорбция запрещена. Действительно, в последнем случае
не существует механизма использования очень маленьких парковочных мест,
и плотность насыщения принимает значение pjam Ф 0,747597.
Медленная релаксация
Зависимость плотности от времени описывается уравнением
(7.60)
Это обобщенное уравнение Ленгмюра (сравните с (7.54)) имеет простую ин¬
терпретацию: первое слагаемое в правой части отвечает за припаркованные
автомобили, которые десорбируются с интенсивностью р и, таким образом,
понижают плотность. Второе слагаемое соответствует приросту плотности
из-за автомобилей, паркующихся на свободных местах длины х > 1. Нужно
отметить, что уравнение (7.60) может быть также получено интегрированием
по всем длинам в уравнениях (7.57а)-(7.57Ь).
Интересная ситуация, соответствующая десорбционно-контролируемому
режиму, возникает в пределе г —> оо, в котором любое освобождаемое пар¬
ковочное место немедленно заполняется. В этом пределе можно заменить
точное уравнение (7.60) приближенным, вид которого можно обосновать сле¬
дующим образом. На масштабе времени, который велик по сравнению с ха¬
рактерным временем десорбции, автомобили просто диффундируют в их пар¬
ковочных местах в результате десорбции и немедленного последующего за¬
полнения, хотя сами автомобили при этом меняются. Таким образом, чле¬
ном ухода в уравнении (7.60) можно пренебречь. Более того, из-за быстрой
диффузии автомобилей по их парковочным местам вероятность лакун имеет
экспоненциальный вид (7.58). Поэтому в уравнении (7.60) мы опускаем член
ухода, а также подставляем равновесное распределение лакун (7.58) в член
прихода, в результате получая
at
(7.61)
Сравнивая уравнения (7.54) и (7.61), мы видим, что коэффициент
S(p) = e-p^-^
(7.62)
может рассматриваться как вероятность того, что адсорбция успешна — собы¬
тие, которое становится очень маловероятным в пределе р —> 1. Вид зависимо¬
сти плотности от такой эффективной вероятности прилипания имеет простое
274
Адсорбция
объяснение. Для почти заполненной системы можно записать плотность как
р = (I + (х)У~х, где (х) 1 — это маленькое расстояние между бамперами
автомобилей, припаркованных по соседству. На масштабе времени порядка
единицы автомобиль покидает свое парковочное место, которое в свою оче¬
редь немедленно заполняется. Однако на гораздо большем временном мас¬
штабе в результате коллективной перестройки N = (х)~г = р/(1 — р) при¬
паркованных автомобилей десорбция может привести к освобождению двух
парковочных мест. Такое удачное стечение обстоятельств будет иметь место,
если десорбция и немедленная реадсорбция (на масштабе времени порядка
единицы) приводят к тому, что первый автомобиль сдвигается на (ж), второй
на 2 (я), третий на 3(ж) и т. д., пока в конце концов не освобождается новое
парковочное место (рис. 7.12). Вероятность такой коллективной перестройки
экспоненциально убывает с числом автомобилей 7\7, так что эффективная ве¬
роятность прилипания имеет порядок S ~ e~N, что согласуется с (7.62). Так
как система приближается к полному покрытию, коллективная перестройка
включает расходящееся число автомобилей, так что вероятность прилипа¬
ния становится пренебрежимо малой. Чтобы найти зависимость от времени
плотности автомобилей из уравнения (7.61), сначала запишем д = (1 — р)”1.
В низшем порядке эта замена приводит к уравнению dg/d(rt} ~ е~9, решение
которого имеет вид
(7'СЗ)
Поэтому, когда плотность возрастает, адсорбция автомобилей становится
очень медленной из-за того, что вероятность прилипания экспоненциально
убывает с плотностью.
1 2 3 4 5 -у-
-•LL'l'YCl.7-
Рис. 7.12. Изображение шести шагов коллективного события, в котором пять
припаркованных друг за другом автомобилей двигаются налево в результате де¬
сорбции и немедленной последующей адсорбции. В конце концов, освобождается
дополнительное парковочное место, которое немедленно заполняется
Модель обратимой парковки автомобилей дает полезную информацию о
кинетике уплотнения сыпучих веществ. Предположим, что одинаковые сфе¬
рические стеклянные бусинки случайно помещаются в банку одна за другой.
7.4 Обратимая адсорбция
275
11лотность заполненного пространства в этой упаковке бусинок, равная при¬
близительно 0,58, известна как плотность случайной свободной упаковки.
Если по этой заполненной бусинками банке осторожно стучать с определен¬
ной интенсивностью и частотой, плотность будет медленно расти и в конце
концов достигнет плотности случайной плотной упаковки, примерно равной
0,64. Вибрация приводит к случайным коллективным перестройкам, кото¬
рые позволяют бусинкам «припарковаться» в пустых пространствах, которые
до этого были слишком малы для того, чтобы вместить бусинку. Поскольку
плотность возрастает, перестройки захватывают все большие области про¬
странства и становятся все более редкими. Масштаб времени, на котором
происходит уплотнение (рис. 7.13) может достигать месяцев. Однако плот¬
ность случайной плотной упаковки все еще намного меньше, чем максималь¬
ная плотность 7г/\/18 = 0,7405 периодической упаковки шаров на кубической
гранецентрированной решетке.
Рис. 7.13. Медленная релаксация плотности при уплотнении сыпучего вещества
(эксперимент, поставленный в университете Чикаго, см. Novak и др., Phys. Rev. Е
57, 1971 (1998)). На графике показана зависимость от времени плотности сыпу¬
чего вещества на фиксированной высоте в простукиваемой колонне. Сплошная
линия — фитирование обратной логарифмической ралаксационной зависимо¬
стью из (7.63)
Диффузионно-контролируемая адсорбция
В обратимой парковке автомобилей разделение временных масштабов между
адсорбцией и десорбцией приводит к эффективной модели, в которой авто¬
мобили в основном диффундируют внутри своих парковочных мест. Всегда,
276
Адсорбция
когда достаточное пустое место образуется в результате коллективной пе¬
рестройки припаркованных автомобилей, немедленно адсорбируется новый
автомобиль. Здесь мы изучаем ситуацию, когда адсорбированные молекулы
явным образом диффундируют по подложке и дополнительная адсорбция
происходит всегда, когда открывается достаточно свободного места. Без по¬
тери общности мы полагаем интенсивность диффузии равной единице, а ин¬
тенсивность адсорбции — бесконечности. Таким образом, как только конфи¬
гурация адсорбированных молекул допускает еще одно событие адсорбции,
оно немедленно происходит, как показано на рис. 7.14.
Рис. 7.14. Подвижные адсорбированные димеры в одномерии. Каждый следую¬
щий ряд показывает систему после одного события. Когда две дырки становятся
соседними, они немедленно заполняются димером
Когда димеры адсорбируются с бесконечной интенсивностью на одномер¬
ной решетке, немедленно достигается насыщенное состояние, в котором все
пустые узлы — изолированные. Мы назовем такие узлы «дырками». Это на¬
сыщенное состояние неустойчиво, потому что, если рядом с димером есть
дырка, димер может перепрыгнуть в соседний узел. Как показано на рис. 7.14,
прыжок димера соответствует эффективному прыжку дырки на два шага в
обратном направлении. В результате таких прыжков две дырки могут слу¬
чайно оказаться ближайшими соседями. Эта пара дырок немедленно и необ¬
ратимо заполняется димером. Такая комбинация диффузии и заполнения пар
соседних дырок эквивалентна диффузионно-контролируемой бинарной анни¬
гиляции
Н + Н 0, (7.64)
динамика которой хорошо изучена (см. подробности в главе 13). Здесь термин
«Диффузионно-контролируемая» подчеркивает, что диффузия ограничивает
общую реакцию, поскольку аннигиляция происходит немедленно, как толь¬
ко два реагента оказываются в непосредственной близости. Из результатов,
7.5 Транслокация полимеров
277
которые будут представлены в главе 13, плотность дырок ф убывает как
р-1/2, d = l;
t-1 In t, d = 2; (7.65)
(t-1, d > 2,
где d — это пространственная размерность подложки5. Изменение поведения
в двумерии означает, что d = dc = 2 — критическая размерность диффузи-
оиио-контролируемой аннигиляции.
Можно похожим образом проанализировать осаждение подвижных fc-ме¬
ров. Теперь, когда fc-мер смещается на одну постоянную решетки, дырка пры¬
гает на к постоянных решетки. Эта диффузия и последующая адсорбция эк¬
вивалентны fc-частичной диффузионно-контролируемой аннигиляции
Н + - . + Н ->0.
4 V '
к
Для этой реакции кинетическое уравнение имеет вид ~ —фк^ и оно приме¬
нимо при к > 4. Решением будет6
ф~Г1/{к~1\ к >4, (7.66)
для всех d > 1. Убывание плотности дырок становится все более медленным
для длинных молекул. В пределе к -+ оо, соответствующем задаче о парковке
автомобилей, степенная релаксация (7.66) превращается в логарифмическую
(7.63). Действительно медленная поверхностная диффузия оказывает такое
же влияние как десорбция и последующая реадсорбция с маленьким смеще¬
нием.
7.5 Транслокация полимеров
Поучительное применение кинетики адсорбции — облегченная транслокация
полимера через маленькую пору в мембране. Любой биологически значимый
полимер, движимый одними только тепловыми флуктуациями, проходил бы
5 Адсорбция имеет физический смысл в пространственных размерностях d = 1 и d =
2, где все узлы подложки находятся на границе фаз, но остается математически хорошо
определенной для всех d.
6Для тримеров (к = 3) критическая размерность dc = 1 и в одномерии имеются лога¬
рифмические поправки ф ~ £-1/2\/1п£. В остальных случаях уравнение (7.66) справедливо
для d > 1.
278
Адсорбция
через пору слишком медленно, чтобы быть вовлеченным в клеточные процес¬
сы. Один из способов ускорить транслокацию — «выпрямить» флуктуации
таким образом, чтобы обратное движение было подавлено. Как мы сейчас по¬
кажем, транслокация, ускоренная шаперонами, предоставляет как раз такой
механизм выпрямления. Предположим, что среда справа от мембраны содер¬
жит фиксированную плотность «шаперонов», которые необратимо адсорби¬
руются на узлах полимера с интенсивностью Л. Если шапероны достаточно
велики для того, чтобы они могли пройти через пору, диффузия оказывает¬
ся направленной, так что полимер будет проходить через пору с ненулевой
скоростью V.
Характер зависимости скорости v от существенных параметров D и Л
можно объяснить с помощью простого физического рассуждения. Рассмот¬
рим предел малой интенсивности адсорбции, и пусть т = 1/(А€) — типичное
время между событиями адсорбции в самом левом сегменте полимера длины
в котором отсутствуют шапероны (рис. 7.15(c)). В течение этого времени
полимер продиффундирует на расстояние ~ y/DX. Собирая эти два соотно¬
шения, получим т (ОА2)-'/з
и Л ~ (Р/Л)1/3. Из размерных соображений
скорость транслокации ведет себя как
v ~ ~ (Р2 Л)1/3. (7.67)
т
Рис. 7.15. Изображение облегченной шаперонной транслокации, (а) Полимер мо¬
жет прыгнуть в любом направлении. (Ь) Полимер может прыгать только направо
из-за того, что адсорбированный шаперон (черный кружок) находится рядом с
порой (промежутком в барьере) и слишком велик, чтобы войти в нее. (с) Ад¬
сорбция нового шаперона (серый круг) в самом левом сегменте, свободном от
шаперонов
Теперь применим метод пустых интервалов, развитый в разделе 7.1 для
необратимой адсорбции, к расчету скорости транслокации v. Для. этой цели
нам нужно разобраться в динамике самого левого сегмента полимера [1, тп], не
содержащего шаперонов. Нужно рассмотреть две ситуации, (i) Длина m этого
7.5 Транслокация полимеров
279
сегмента может измениться на ±1 в результате изотропных скачков полимера
(г отражением в т = 1, см. рис. 7.15(b)); здесь мы полагаем интенсивность
скачков равной 1, что соответствует «голому» коэффициенту диффузии D =
I. (ii) Кроме того, из-за адсорбции число т может ровновероятно замениться
на любое число из [1,т — 1] (рис. 7.15(c)).
Полимер продвигается, только если шаперон находится рядом с порой.
В противном случае он диффундирует изотропно. Следовательно, скорость
равна вероятности, что длина самого левого безшаперонного сегмента равна
I. Чтобы вычислить эту величину, нам нужны вероятности Ет того, что
интервал длины т справа от поры не содержит шаперонов
Ет = ?(| °_^_°);
т
здесь | обозначает пору, а о — пустой узел. Это аналоги вероятностей пустых
интервалов, определенных в (7.2). Скорость просто равна v = 1 — £1; т. е.,
когда узел рядом с порой содержит шаперон, полимер сдвигается с единичной
скоростью. Нам также нужна вероятность сегмента (см. (7.7Ь))
Sm — *Р( | Р В *) — Е!т+\, (7.68)
т
а именно вероятность того, что самый левый шаперон находится на расстоя¬
нии т + 1 от поры. Здесь • обозначает шаперон.
Для вычисления Е± нужен полный набор вероятностей Ет, поскольку
нахождение Е± требует знания £2, в свою очередь связанного с £3, и т. д. Ве¬
роятности Ет при т>1 эволюционируют со временем согласно уравнению
НЕ
= Sm-1 -Sm- ХтЕт. (7.69)
Определенный как в (7.68) член Sm-i отвечает за создание пустого интервала
длины т из пустого сегмента длины т—1 в результате скачка полимера впра¬
во. Аналогично, для пустого интервала длины т, когда самый левый шаперон
длины т находится на расстоянии т + 1 от поры, и полимер прыгает влево,
возникает член —Sm. Член —ХтЕт описывает исчезновение m-интервала из-
за адсорбции внутри этого интервала, которая происходит в любом из т его
узлов. Подставляя определение (7.68) в уравнение (7.69), находим, что для
т > 1 эволюция вероятности пустых интервалов описывается уравнением
= Ет—1 + Em+i 2Ет ХчпЕт.
(7.70)
dt
280
Адсорбция
Граничное условие Eq = 1 для уравнения (7.70) следует из условия норми¬
ровки Eq = £ш>0 Sm = 1. Как мы увидим в главе 13, вероятности сегментов
описываются такой же дискретной диффузией, которая возникает в реакции
А + А -> 0 с одночастичным источником (уравнение (13.35)).
В пределе большого времени достигается стационарное состояние, и левая
часть уравнения (7.70) обращается в ноль
Em—1 + -Sra+l (2 + ТпХ^Ет = 0. (7.71)
Нам нужно решить это уравнение при условии Eq = 1 и потом найти скорость
из соотношения v = 1 — Е±. Уравнение (7.71) — дискретный аналог уравне¬
ния Эйри Е" = ХхЕ, и оно имеет компактное решение, выраженное через
функции Бесселя. Пользуясь хорошо известным соотношением для функций
Бесселя
2г/
+ Л+Дг) Л(г) = 0
Z
и сравнивая его с уравнением (7.71), получаем
2р
z
— 2 + т\ = 2
772 + 2/А
2/Л
Таким образом, полагаем у = т + 2/Л и z = 2/А. Хотя есть только одно
условие, фиксирующее значение обоих параметров у и г, сделанный выбор
единственный, потому что разность между ними должна быть целым числом.
В итоге, требование Eq = 1 дает
Ет —
_ Лп+2/л(2/А)
J2/a(2/A) ’
откуда находим скорость транслокации
Л+2/а(2/А)
Л/а(2/Л) •
(7.72)
Интересны предельные случаи поведения этой скорости. В пределе малых Л
индекс v = ш + 2/А функции Бесселя становится большим, и мы пользуемся
асимптотической формулой
Jv(y + ал/1/3) ~ (2/р)1/3Ai(-21/3a:), (7.73)
которая связывает функцию Бесселя с функцией Эйри. Для больших Л фор¬
мула (7.73) дает представление в виде степенного ряда
Jv{v + х) = (2/iz)1/3 Ai(0) - (2/i/)2/3 Ai'(0) x + ..., i/ —> oo, (7.74)
7.5 Транслокация полимеров
281
где Ai(0) = [32/3Г(2/3)] 1 и Aiz(0) = —[3Х/3Г(1/3)] х. Подставив этот резуль¬
тат в (7.72), получим ведущую асимптотику скорости (задача 7.18)
fCA1/3, А->0,
1 — j + ^2 + 0(А-3), А —>• оо,
где С = —Ai'(0)/Ai(0) = 3Х/3Г(2/3)/Г(1/3).
(7-75)
7.3. Метод ВКБ
Метод Вентцеля-Крамерса-Бриллюэна (ВКБ) — это эффективный способ по¬
лучения асимптотик решений дифференциальных уравнений около существен¬
но особых сингулярностей. Известный пример — непрерывный предел уравне¬
ния (7.71), а именно Е"(х) = АхЕ, или в общем случае у" = ху. Уравнение
такого вида возникает из стационарного уравнения Шредингера около класси¬
ческой точки поворота. В подходе ВКБ мы записываем у в виде разложения
у = exp[0i(:c) + $2(ж) Ч ] и потом ищем решение для функций фп с помощью
рекурсии. В ведущем порядке получим ($)2 -Ь ф" ~ х. При больших х одним
слагаемым в этом уравнении можно пренебречь. Рассмотрев все возможности,
находим, что самосогласованный выбор — это (ф'\)2 — .т, где ф" (0i)2. У этого
уравнения есть два решения, и правильным будет фг = — |ж3/2, которое убывает
при х оо. На следующем шаге приближение дает ф2 = — |ж-1, откуда получаем
ведущую асимптотику
у^х-'/лс~2^/2/3. (7.76)
Делая следующие шаги приближения, можно получить все члены высших поряд¬
ков, дающие исчезающие поправки к ведущей асимптотике при х —> оо.
Как побочный результат находим вероятность Рт = Sm-i = Em-i — Ет,
что самый левый шаперон находится в т
«Ап—1+2/а(2/А) <Лп+2/а(2/А)
J2/a(2/A)
(7.77)
В пределе большого расстояния проще исследовать непрерывную версию
уравнения на стационарное состояние (7.71), Еуу = уЕ> где у = А1/3?™. Для
этого мы применяем приближение ВКБ (см. врезку выше) и получаем
£(у) ~ У-1/4ехр (—j у3/2). В заключение, используя равенство Р = —
находим
рт ~ А-1/12 тх/4 ехр [-(2/3) А1/2 т3/2] . (7.78)
Таким образом, маловероятно, что самый левый шаперон находится на рас¬
стоянии много большем чем среднее расстояние от поры до шаперона, равное
А-1/3.
282
Адсорбция
7.6 Ссылки
Формула (7.1), дающая плотность покрытия при необратимой адсорбции ди¬
меров, была первым точным результатом в этой области. Она была выведена
Флори [139] в контексте реакции циклизации в полимерных цепочках. Со¬
ответствующая плотность покрытия для модели парковки автомобилей бы¬
ла найдена Реньи [140]. Впоследствии выяснилось, что кинетический подход
предоставляет более короткий путь к пониманию основных свойств необрати¬
мой адсорбции. Обзор первых результатов дан в [141]. Более свежие обзоры
включают [142-144]. Они содержат множество полезных тем, которые не об¬
суждались в этой главе. Суперэкспоненциальное убывание корреляционных
функций при адсорбции димеров обнаружили Монтус и Хилхорст [145].
Хотя в ранних работах были найдены точные решения для необратимой
адсорбции в одном измерении, подходы к нахождению точных решений в
высших измерениях отсутствуют до сих пор. Для развития таких подходов
потребовалось бы точно перечислить все связные кластеры любого размера
на двумерной решетке (так называемые «решеточные звери») и потом ре¬
шить связанные уравнения, описывающие вероятности пустых конфигураций
для каждого решеточного зверя. Дополнительный материал по асимптотиче¬
скому подходу к адсорбции дисков, эллипсов и ориентированных квадратов
можно найти в [146-149]. Аномальный скейлинг плотности покрытия для оса¬
ждения игл изучали Тарджюс и Виот [150].
Модель обратимой парковки [151] стала популярной благодаря ее успеху
в объяснении ультрамедленного уплотнения сыпучих материалов на масшта¬
бах времени порядка месяцев. Эксперименты по уплотнению представлены
в [152]. Связь между диффузионно-контролируемой адсорбцией и диффу¬
зионно-контролируемой аннигиляцией обсуждается в [153]. Облегченная ша¬
перонная транслокация полимеров обсуждается в [154]. Недавние статьи, с
подходом близким к нашему изложению, см. в [155, 156]. Книга Ватсона [157]
содержит (почти) все, что известно про функции Бесселя. Метод ВКБ опи¬
сан в любой книге по квантовой механике и многих книгах по прикладной
математике; прекрасное изложение дается в [158].
7.7 Задачи
7.1 Для необратимой адсорбции димеров выразите полную плотность лакун и
плотность островов через вероятности пустых интервалов.
7.2 Найдите плотность покрытия для ограниченной адсорбции мономеров, в ко¬
торой мономеры могут адсорбироваться только на занятые узлы, окруженные
7.7 Задачи
283
двумя незанятыми узлами. (Подсказка: отобразите эту задачу на подходящим
образом определенный процесс адсорбции димеров.)
7.3 Предположите, что димеры необратимо адсорбируются на одномерной решет¬
ке, каждый узел которой независимо занят с вероятностью ро в начальном
состоянии. Вычислите плотность покрытия.
7.4 Используя (7.11), определите поведение на больших временах величины Pjam —
p(t) для необратимой адсорбции fe-меров. Найдите предельное поведение плот¬
ности покрытия для к —> оо.
7.5 Запишите и решите уравнение для необратимой адсорбции димеров в терми¬
нах вероятностей лакун. Сравните ваше уравнение с уравнением (6.2), описы¬
вающем случайное разрезание интервала.
7.6 Выведите уравнение (7.15) из (7.11), взяв непрерывный предел (к —> оо) в
последнем уравнении.
7.7 Решите модель необратимой парковки автомобилей, если вначале задана плот¬
ность А случайно распределенных дефектов пулевого размера.
7.8 Обобщите рекурсивное уравнение (7.17) для полного числа Jl насыщенных
конфигураций на адсорбцию fc-меров и выведите уравнение для г, для случая
Jl ~ zL. Вычислите z для к = 3,4,5 и ведущую асимптотику z для к —> оо.
7.9 Используйте поправки конечного объема, приведенные в уравнении (7.26),
чтобы получить термодинамическую плотность покрытия в случайной после¬
довательной адсорбции, экстраполируя результаты численного моделирова¬
ния на конечных решетках.
(a) Воспользуйтесь эффективным алгоритмом, описанным в разделе 7.1, для
численного моделирования необратимой адсорбции димеров на одномер¬
ной решетке длины L . Найдите численно плотность покрытия pjam с
максимальной точностью, доступной при оптимальной настройке числа
реализаций и размера системы. (Подсказка: произведите отдельные экс¬
траполяции для четных и нечетных L.)
(b) Найдите плотность покрытия для двумерной необратимой адсорбции ди¬
меров, в которой попытки адсорбции вертикальных и горизонтальных
димеров происходят с равными вероятностями.
7.10 Вычислите дисперсию (7.36) с помощью суммирования корреляционной функ¬
ции (7.33).
7.11 Выведите структурный фактор S(q) = ^е^Ст из уравнения (7.33) для
насыщенного состояния необратимой адсорбции мономеров.
7.12 Вероятности Fm заполненной струны длины т й вероятности 1т острова дли¬
ны т определяются как
тп
ТП
284
Адсорбция
Покажите, что вероятность острова дается второй разностной производной
вероятности заполненной струны
Лп = Fm — 2Fm+1 4“ Fm+2*
7.13 Рассмотрите адсорбцию димеров в одномерии. Используйте законы сохране¬
ния, чтобы найти следующие соотношения между Fm и вероятностями пустых
интервалов Ет для т < 3:
2^1 = 1 - J57i,
F2 = 1 — 2jE?i -Ь -Ё/2,
2*з = 1 — 37?1 4- 22?2.
Заметьте, что общий вид последнего равенства:
2*з = 1 — ЗСР[о] + 2У[оо] 4- У [о х о] — У [о о о],
но для адсорбции димеров имеем У [о х о] = У [о о о], так что трехчастичный
член в этом равенстве сокращается.
Для 3 < т < 7 выразите Fm через Ej и через вероятность двух разделенных
пустых интервалов Ei^k. Например, для F& должно быть
2*5 = 1 — 52?i + 4Я2 — 2jE?4 + Е§ 4- 2(1 — е *)Фз 4- Ф4.
7.14 Проверьте, что выражение (7.38) для дерева Кейли сводится к выражению
(7.5) для адсорбции димеров в одномерии в пределе z 4 2 и воспроизведите
плотность покрытия для адсорбции димеров в одномерии.
7.15 Исследуйте необратимую адсорбцию ориентированных квадратов на непре¬
рывной плоской подложке. Обобщите результаты (7.47) и (7.48) и опишите
приближение плотности покрытия к плотности насыщения.
7.16 Запишите основное кинетическое уравнение для плотности лакун при адсорб¬
ции-десорбции Л-меров в одномерии аналогичное уравнениям (7.57а)-(7.57Ь).
Покажите, что плотность лакун всегда экспоненциальна и найдите уравне¬
ния, описывающее эволюцию этой плотности. Получите плотность в пределе
г —> оо.
7.17 Рассмотрите задачу облегченной шаперонной транслокации, где шапероны —
это димеры, которые занимают два соседних узла полимера. Вычислите ско¬
рость транслокации для этого случая. Чтобы продвинуться еще дальше, обоб¬
щите результат на случай, когда шапероны — это fc-меры, занимающие к узлов
полимера, следующих один за другим.
Глава 8
ДИНАМИКА СПИНОВ
Два классических раздела статистической физики — это кинетическая теория
и фазовые переходы. Последний традиционно изучается в контексте равно¬
весного формализма, цель которого охарактеризовать упорядоченные фазы,
возникающие при температуре ниже критической в системах с локальным
взаимодействием. Недавние достижения связаны с вопросом, как порядок
формируется динамически. В настоящей и следующих главах мы сосредото¬
чимся на такой динамике.
8.1 Феноменология укрупнения
Изначально теория фазовых переходов ставила своей целью объяснение фер¬
ромагнетизма. Модель Изинга сыграла центральную роль в этих попытках,
а также предоставила полезное средство для изучения динамики. Основная
величина в модели Изинга — это спиновая переменная, которая может при¬
нимать два значения s = ±1. Локальное ферромагнитное взаимодействие
способствует координации направлений спинов, тогда как тепловой шум стре¬
мится сделать их ориентации случайными. Результат такой конкуренции —
неупорядоченное состояние при достаточно высоких температурах, тогда как
ниже критической температуры превалирует тенденция выстраивать спины
в одном направлении и возникает упорядоченное состояние, в котором пара¬
метр порядка, т. е. средняя намагниченность, не равен нулю.
Предположим, что мы стартуем с модели Изинга в равновесной неупоря¬
доченной фазе и начинаем понижать температуру. Чтобы понять, как систе¬
ма эволюционирует к конечному состоянию, мы должны снабдить эту модель
динамикой, а также определить процедуру закалки. Закалка обычно произ¬
водится следующим образом:
286
ДИНАМИКА СПИНОВ
• Начинаем с высокой начальной температуры > Тс, при которой спи¬
ны неупорядочены, где Тс — критическая температура.
• Мгновенно охлаждаем систему до более низкой температуры Tf.
В различных приложениях (от образования стекол до охлаждения Вселен¬
ной) больше подходит медленное охлаждение, но и быстрое охлаждение есте¬
ственным образом возникает во многих других случаях. Отсутствие вре¬
менного масштаба при мгновенном охлаждении очень полезно, так как поз¬
воляет сосредоточиться на временном масштабе, связанном с укрупнением,
а не на масштабе, связанном с процедурой закалки.
Саму по себе динамику можно определить достаточно произвольным об¬
разом. Поскольку элементарные спины являются базовыми объектами, мы
должны, в принципе, пользоваться квантовыми уравнениями движения Гей¬
зенберга или Шредингера. Такое полностью микроскопическое теоретическое
описание сильно взаимодействующих квантовых многочастичных систем в
большинстве случаев не может быть завершено. Уже для нескольких десят¬
ков таких частиц численный расчет становится чрезвычайно трудоемким. Бо¬
лее того, даже в случае разреженных классических газов не многое возмож¬
но понять в рамках уравнений движения Ньютона, и требуется огрубленный
(и вероятностный) подход Больцмана. Таким же образом для кинетических
спиновых систем требуется развитие менее фундаментальных и более эффек¬
тивных методов.
Главное упрощение, используемое для изучении эволюции спиновых си¬
стем, состоит в том, что мы можем игнорировать квантовые эффекты. При¬
менимость этого приближения обосновывается тем, что фазовые переходы
в ферромагнетиках происходят при температурах много больших, чем тем¬
пература, при которой квантовые эффекты оказываются важны1. В рамках
классического описания инструментом, который мы в первую очередь ис¬
пользуем для вероятностного описания многочастичных систем, является ос¬
новное кинетическое уравнение. Здесь мы применяем это подход к моделям с
простыми микроскопическими правилами эволюции, которые ведут систему
к равновесию. В следующей главе мы исследуем системы такого типа с более
макроскопической (феноменологической) точки зрения.
Для эволюционных уравнений, которые возникают в этих двух главах,
установлено мало строгих результатов. Несмотря на обилие теорий и нехват¬
1 Влияние квантовых флуктуаций существенно при нулевой температуре, когда исче¬
зают тепловые флуктуации. В этой книге мы не обсуждаем эту молодую бурно разви¬
вающуюся область квантовых фазовых переходов при нулевой температуре. Даже когда
мы исследуем динамику при нулевой температуре, мы делаем это в рамках классической
физики.
8.1 Феноменология укрупнения
287
ку твердо установленных фактов, то, что известно из численного моделиро¬
вания, приблизительных и эвристических аргументов и исследования точ¬
норешаемых (обычно одномерных) моделей, указывает на справедливость
простой центральной догмы. Это догма предполагает, что есть три больших
класса динамического поведения спиновых систем, в зависти от того, выше
или ниже критической точки находится значение конечной температуры.
• Надкритическая динамика, Tf > Тс. Равновесное неупорядоченное со¬
стояние, соответствующее конечной температуре Tf, достигается экспо¬
ненциально быстро.
• Критическая динамика, Tf = Тс. Критическая динамика применима
только при одном значении температуры Тс. Существует столько же
критических динамик, сколько типов равновесного критического пове¬
дения.
• Подкритическая динамика, Tf < Тс. Динамическое поведение универ¬
сально и в большой степени такое же, как динамика при нулевой тем¬
пературе.
Большинство исследований были сосредоточены на динамике при нулевой
температуре из-за ее универсального характера и потому, что она приводит
к лаконичным результатам, а также потому, что она гораздо проще, чем ди¬
намика при конечной температуре. Самое удивительное свойство динамики
при нулевой температуре (и в более общем случае подкритической динами¬
ки) — это возникновение замысловатой укрупняющейся доменной мозаики
(рис. 8.1 и рис. 8.6). Свойства таких доменных мозаик демонстрируют заме¬
чательную универсальность. Эту универсальность можно сформулировать в
виде так называемой динамической гипотезы подобия.
• Единственный масштаб. На поздних стадиях укрупнения система ха¬
рактеризуется единственным масштабом длины L(i), т. е., если мы пе¬
ремасштабируем пространственные координаты х —> x/L(£), доменная
мозаика на разных временах будет выглядеть одинаково.
• Алгебраический скейлинг. Характерный масштаб длины L(i) растет со
временем как tz в пределе большого времени, где z — универсальный
динамический индекс.
• Универсальность динамического индекса. Индекс z не зависит от про¬
странственной размерности и от большинства деталей системы, но чув¬
ствителен к наличию законов сохранения.
288
ДИНАМИКА СПИНОВ
Центральная догма и динамическая гипотеза подобия предоставляют де¬
тальную схему для понимания процессов укрупнения. Существование такой
схемы — выдающийся факт, поскольку большинство неравновесных процес¬
сов находятся за пределами применимости математической аналитики. Перед
тем как приступить к анализу, заметим, что одномерные системы со ска¬
лярным параметром порядка предоставляют наилучшую возможность каче¬
ственно протестировать динамическое поведение. Как мы увидим, это дей¬
ствительно так, хотя одномерная система это исключительный случай по той
причине, что фазовый переход происходит при Тс = О2. Поэтому априори
не ясно, соответствуют ли решения одномерных задач критической или под¬
критической динамике. Мы увидим, однако, что предсказания, основанные
на решении кинетических уравнений для одномерных моделей дают такие
же качественные результаты, как динамика при нулевой температуре в выс¬
ших размерностях. Однако существуют и исключения из общей картины.
В частности, динамика Ланжевена предсказывает медленное логарифмиче¬
ское укрупнение, противоречащее динамической гипотезе подобия. Однако
существование единственного масштаба длины остается справедливым. Есть
и другие усложнения, которые будут обсуждаться в этой главе, например:
закаленная система, охлажденная до нулевой температуры, может навсегда
застрять в метастабильном состоянии. Фундаментальное утверждение — цен¬
тральная догма и динамическая гипотеза подобия правильны по сути, хотя
фактически могут не соблюдаться в некоторых специальных случаях.
8.2 Модель голосования
Мы начнем изучение спиновой динамики с модели голосования — упрощен¬
ной модели, преимуществом которой является ее решаемость в любой про¬
странственной размерности. Эта модель описывает возникновение консенсуса
в популяции безспиновых индивидуумов. Каждый индивидуум находится в
вершине графа3 и может находиться в одном из q эквивалентных состояний,
соответствующих определенному мнению. Индивидуум не имеет собственных
убеждений и во время обновления просто соглашается с мнением одного из
своих ближайших соседей. При такой динамике конечная популяция в конце
2Другой такой пример — система с векторным параметром порядка в двух измерениях,
где опять Тс = 0.
3Граф — конечный или бесконечный — это набор вершин, некоторые из которых соеди¬
нены ребрами. Для пространственно регулярных бесконечных решеток и вообще в физике
вершины называются узлами, а ребра — связями. В данной главе мы придерживаемся этой
терминологии, а также в основном рассматриваем регулярные решетки.
8.2 Модель голосования
289
Рис. 8.1. Эволюция модели голосования на квадратной решетке размером
256 х 256. Верхний ряд показывает фотографии, сделанные на временах t =
4,16,64и256 в системе, которая стартует с круглого пятна радиуса 180, изобра¬
жающего участников голосования с одним мнением в море голосующих с проти¬
воположным мнением. Нижний ряд показывает такую же эволюцию, начинаю¬
щуюся со случайных начальных условий с одинаковыми плотностями участников
голосования с двумя мнениями. (Рисунок взят из статьи Dornic и др., Phys. Rev.
Lett. 87, 045701 (2001) с любезного согласия И. Дорника)
концов приходит к консенсусу за время, которое зависит от размера системы,
пространственной размерности и числа мнений q. Консенсус по одному из q
эквивалентных мнений обязательно достигается, поскольку это единственное
абсорбирующее состояние стохастической динамики. Для простоты в даль¬
нейшем мы будем иметь дело с моделью голосования с двумя состояниями.
На рис. 8.1, где изображена эволюция модели голосования, видно, как в си¬
стеме с течением времени организуются домены с единым мнением.
Таким образом, в каждом узле решетки х находится участник голосова¬
ния с мнением s(x), которое может находиться в одном из двух состояний
±1. Можно рассматривать эти мнения как изинговские переменные. Каж¬
дый спин переворачивается с интенсивностью равной доле его соседей, име¬
ющих противоположное мнение (рис. 8.2). Такое правило переворотов можно
определить, задав интенсивность w(s), с которой изменяется мнение s(x)
участника голосования в узле х:
Wx(s) = | [1 - 22 >
уе(х>
(8-1)
290
ДИНАМИКА СПИНОВ
t
t t t —
t
t
t 4 t
I
t
t t I —
t
I
t 4 I
I
t
t ♦ 4 —
I
t
I 4 I
I
интенсивность r=0
r=l/4
r=l/2
I
t t 4 —*
I
I
t 4 1
I
I
4 t 4 -*
I
I
I 4 I
1
r=3/4
Рис. 8.2. Интенсивность переворота центрального участника голосования из
уравнения (8.1) как функция состояния его ближайшего окружения на квад¬
ратной решетке
где суммирование проводится по всем ближайшим соседям (х) узла х, a z —
координационное число решетки. Нижний индекс х в интенсивности wx(s)
указывает на то, что только участник голосования в узле х меняет свое мне¬
ние во время обновления. Отметим, что интенсивность перехода для голосу¬
ющего в узле х равна доле несогласных с ним соседей. Как мы увидим, эта
пропорциональность в правиле обновления и есть главная причина того, что
модель решаема.
Полное описание модели голосования дается вероятностью P(s,£) того,
что множество всех участников голосования находится в состоянии s в мо¬
мент времени t. Распределение этой вероятности эволюционирует в соответ¬
ствии с уравнением4
= - 53 Wx(s)P(s) + 53 ^x(sX)P(sX).
(8-2)
X
X
Здесь sx обозначает состояние, которое отличается от состояния s только
тем, что участник голосования в узле х поменял свое мнение, т. е. sx(y) = s(y)
для у ^х и sx(x) = — s(x). В уравнении (8.2)'член ухода отвечает за перехо¬
ды из состояния s, а член прихода соответствует переходам в состояние s из
состояний, отличающихся от состояния s одним спином. Вместо нахождения
4В уравнении (8.2) мы опускаем временной аргумент, чтобы сделать формулы менее
громоздкими. Кроме того, обозначение P(s, t) не вполне правильное, так как распределе¬
ние вероятности не зависит от времени явно. На самом деле, распределение — это функция
состояния s, которое в свою очередь зависит от времени, так что P(s[Z]) — функционал,
зависящий от s. Мы стараемся избегать излишней педантичности и часто опускаем пере¬
менную времени даже для величин, явно зависящих от времени. Например, в уравнении
(8.5) мы пишем S(x) вместо S(x,t).
8.2 Модель голосования
291
полного распределения вероятности мы обратимся к вычислению корреля¬
ционных функций, из которых можно извлечь важнейшие свойства модели
голосования.
8.1. Численное моделирование модели голосования
Алгоритм обновления модели голосования определяется следующим образом:
1. Случайно и равновероятно выбираем участника голосования, например в
узле х.
2. Выбранный участник принимает состояние случайно выбранного соседа,
например в узле у. (Таким образом, голосующий меняет свое мнение, только
когда взаимодействующий с ним партнер имеет противоположное мнение.)
3. Увеличиваем время на подходящим образом выбранное приращение време¬
ни t —> t + At.
Эти шаги повторяются до наступления заданного момента времени или до до¬
стижения консенсуса. Естественный выбор приращения времени Ai = 1/7V, так
что за единицу времени каждый участник голосования делает в среднем по одной
попытке сменить мнение.
При реальном численном моделировании не следует пользоваться этой простей¬
шей процедурой обновления, поскольку она безнадежно неэффективна. Когда
популяция приближается к консенсусу, все более и более вероятным становит¬
ся выбор двух участников голосования в одном и том же состоянии, в результате
которого ничего не происходит. Вместо того чтобы тратить время па модели¬
рование пустых событий, можно применить событийно-зависимый алгоритм, в
котором выбираются только «гарантирующие успех» противоположно ориенти¬
рованные участники голосования. Среднее приращение времени для успешного
события (2N^ )-1, где — число противоположно ориентированных, соеди¬
ненных между собой участников голосования.
Корреляционные функции
В принципе, основное кинетическое уравнение (8.2) можно использовать
для вывода замкнутых уравнений для всех моментов распределения веро¬
ятностей, а именно всех многочастичных корреляционных функций вида
5Хг..)У = (s(x) • • • s(y)), где угловые скобки обозначают усреднение (/(s)) =
£s/(s)P(s). Начнем с рассмотрения простейшей из таких корреляционных
функций 5(х) = (s(x)). Возможно получить описание эволюции этой функ¬
ции, так же как и всех многочастичных функций, прямо из уравнения (8.2).
Однако этот подход достаточно громоздок, и при его использовании легко
ошибиться. Более простой путь — заметить, что за инфинитезимальный ин¬
тервал времени At, состояние данного участника голосования меняется еле-
292
ДИНАМИКА СПИНОВ
дующим образом 5:
s(x, t + At)
< s(x,t)
-s(x,t)
с вероятностью 1 — wxA£,
с вероятностью wxAf.
(8-3)
Поскольку мнение в х меняется на — 2s(x) с интенсивностью wx, среднее
мнение меняется в соответствии с уравнением
= -2(.(х)ч,>. (8.4)
Подставив интенсивность перехода из (8.1) и воспользовавшись тождеством
[s(x)]2 = 1, получим уравнение для среднего мнения в модели голосования
= -S(x) + i «М-
уе(х)
где z — координационное число решетки.
Математически уравнение (8.5) совпадает с основным кинетическим урав¬
нением для случайных блужданий в непрерывном времени. В результате
средняя намагниченность т = ^Зх5(х)/ЛГ играет роль полной вероятности
и, следовательно, сохраняется. Такой же результат следует из суммирования
уравнения (8.5) по всем узлам. Заметим, что, хотя намагниченность конкрет¬
ной системы меняется при единичном событии обновления, среднее по всем
узлам и по всем траекториям системы сохраняется.
Факт сохранения намагниченности имеет далеко идущие последствия
(рис. 8.3). Рассмотрим конечную систему с начальной долей участников го¬
лосования в состоянии +1 и долей 1 — р в состоянии —1, так что начальная
намагниченность равна mo = 2р — 1. В конце концов эта система приходит к
консенсусу, в котором состояние т = +1 достигается с вероятностью 2?(р), а
состояние т = — 1 — с вероятностью 1 — Е(р). Финальная намагниченность
дается величиной
Шоо = Е(р) х 1 + [1 - Е(р)] х (-1) = 2Е(р) - 1,
которая равна начальной намагниченности mo = 2р— 1. Следовательно, веро¬
ятность достижения консенсуса с мнением +1 равна Е(р) = р, а, вероятность
достижения консенсуса с мнением —1 равна 1 — р. Эти вероятности зависят
только от р; зависимость от размера системы и от структуры графа отсут¬
ствует6.
5Мы часто используем запись wx вместо wx(s). Как указывалось в предыдущей сноске,
правильное обозначение было бы wx(s[f]).
6Эти утверждения неприменимы, если граф состоит из несвязных частей или у разных
узлов разное число соседей.
8.2 Модель голосования
293
А | (1+ОТо)/2
(1-«оУ2|| |v
(а) -1 т0 1 (b) -1 1
Рис. 8.3. Иллюстрация к сохранению намагниченности.(а) Начальное состояние
с намагниченностью то- (Ь) Финальное состояние — это либо положительный
(ш = +1), либо отрицательный (т = —1) консенсус, и сохранение намагничен¬
ности фиксирует вероятности достижения этих двух состояний
Решим уравнение (8.5) с начальными условиями S(x, t = 0) = <V;e,o> т. е.
один участник голосования находится в состоянии +1 на фоне популяции
голосующих, находящихся в состояниях либо +1, либо —1с равной вероят¬
ностью. В размерности один имеем
= -SW +1 № - 1) + S(x + 1)]. (8.6)
Используя результаты из врезки, посвященной решениям разностных урав¬
нений такого типа в функциях Бесселя (стр. 18 в разделе 2.1), получаем
S(x,t) = e~4x(t). (8.7)
Этот же подход работает на решетках более высокой размерности. Для
начальных условий с одним участником голосования в состоянии +1, нахо¬
дящемся в начале координат в море иеопределившихся участников, средним
мнением в узле х = (a?i,..., Xd) будет
d
Sfct) = e~tIx(t/d>), где Ix(t/d) = JJ^Xt/d)- (8-8)
i=l
Поэтому среднее мнение участника голосования в начале координат монотон¬
но стремится к нулю, тогда как среднее мнение всех остальных сначала воз¬
растает, достигает максимальной величины (зависящей от координаты х) и
потом асимптотически убывает до нуля. Асимптотически S(x, i) ~ (d/27rt)d/2
для любого х. Таким образом, единственный участник голосования постепен¬
но принимает среднее неопределенное мнение остальной популяции.
Хотя эти результаты точны, они не дают нам информации о том, как
именно достигается консенсус. Нам нужно количественно охарактеризовать,
до какой степени находятся в согласии два отдаленных друг от друга участни¬
ка голосования. Такая характеристика дается двухточечной корреляционной
294
ДИНАМИКА СПИНОВ
функцией <S(x,y) = (s(x)s(y)). По аналогии с (8.5) эволюция двухточечной
функции имеет вид
s(x, t + Ai)s(y, t + Д£) = <
s(x, £)s(y, f) с вероятностью 1 — (wx + wy) Д£,
—s(x, £)s(y, t) с вероятностью (wx + wy)Д£,
(8-9)
т. e. s(x)s(y) изменяется на —2s(x)s(y), если любой из двух участников голо¬
сования либо в х, либо в у изменяет состояние с интенсивностями wx и шу,
соответственно, так что уравнение эволюции 5(х,у) имеет вид
= -2(s(x)s(y)(wx + wy)>.
dt
На гиперкубической решетке явный вид этого уравнения:
^(х,у)
dt
= -2S(x,y) + i £ S(x',y) + i
x'E(x) y'G(y>
(8.10)
Далее мы обсудим пространственно однородные системы, в которых кор¬
реляционные функции зависят только от расстояния между участниками го¬
лосования S(x, у) = G(x — у). Для таких систем два последних слагаемых в
правой части уравнения (8.10) идентичны, и с точностью до общего множи¬
теля 2 уравнение сводится к уравнению (8.5) для среднего спина. Однако мы
не можем просто использовать решение для среднего спина, так как двухто¬
чечная корреляционная функция должна также удовлетворять граничному
условию С?(0,£) = 1.
Непрерывный подход
Решение уравнения (8.10) с граничным условием G(O,t) = 1 технически до¬
вольно сложное, так что сначала попробуем получить самые интересные ре¬
зультаты более простым способом, как обычно понимая под «самыми инте¬
ресными» асимптотические результаты. Когда масштаб времени становится
большим, ожидается, что характерный пространственный масштаб также бу¬
дет большим7. Поэтому сначала мы исследуем модель голосования в непре¬
рывном пределе, в котором уравнение (8.10) становится уравнением диффу¬
зии
«С „.,2,
(8.П)
7Мы увидим, характерный масштаб в модели голосования действительно неограничен¬
но растет, когда d = 1,2. В более высоких размерностях (d > 2) такого роста больше не
наблюдается. Тем не менее, даже в этой ситуации непрерывный подход оказывается поле¬
зен для понимания сути.
8.2 Модель голосования
295
а коэффициент диффузии, возникающий в непрерывном пределе, равен D =
1/d. Для неопределенного начального состояния, в котором состояние каж¬
дого участника голосования независимо с равными вероятностями принима¬
ет значения ±1, начальные условия имеют вид G(r,f = 0) = О для г > 0.
С другой стороны, каждый участник голосования полностью скоррелирован
с самим собой, т. е. S(x,x) = 1. В непрерывном пределе в аргументе кор¬
реляционной функции необходимо ввести нижнее обрезание а > 0, так что
утверждение о полной скоррелированности будет иметь вид G(a, £) = 1. Хотя
решеточная система и не изотропна, корреляционная функция G(r) должна
становиться изотропной, когда расстояние много больше параметра решетки
г » а. Поскольку начальное условие (?(а, i) = 1 изотропно, соответствующее
решение G(r, t) непрерывного уравнения диффузии (характеризуемое враща¬
тельной инвариантностью) также изотропно. Таким образом, мы ожидаем,
что корреляционная функция 5(х,у) решеточной системы будет стремиться
к G(r, t) при г = |х — у | » а.
Чтобы понять, как эволюционирует корреляционная функция, целесооб¬
разно работать с функцией с = 1 — G, которая также удовлетворяет уравне¬
нию диффузии, но с начальным условием c(r > a, t = 0) = 1 и граничным
условием c(r = a, f) = 0, т. е. адсорбирующая точка в начале координат заме¬
няется на маленькую адсорбирующую сферу радиуса а. Величина а играет
роль параметра решетки: ненулевой радиус требуется, чтобы диффундиру¬
ющие частицы могли попасть на сферу. Таким образом мы исследуем, как
начальный профиль постоянной плотности эволюционирует в присутствии
маленькой адсорбирующей сферы в начале координат. Эта задача уже ана¬
лизировалась в квазистатическом приближении (см. раздел 2.7). Тогда мы
выяснили, что в трех измерениях профиль концентрации становится стацио¬
нарным c(r) = 1—а/r. В более общем случае при d > 2 профиль концентрации
стремится к электростатическому решению c(r) = 1 — {a/r)d~2. В размерно¬
стях один и два профиль концентрации стремится к тривиальному решению
с = 0. Из уравнения (2.88) из раздела 2.7 получим асимптотическое поведение
двухспиновой корреляционной функции
1-
г
d = 1 и 0 < г < y/Dt,
G(r, t) ~ <
ln(r/a)
ln(\/Di/a)’
5
d-2
d = 2 и a <r < y/Dt,
d> 2 и a < r.
(8-12)
296
ДИНАМИКА СПИНОВ
Таким образом, для d < 2 корреляционная функция стремится к 1 при фик¬
сированном расстоянии г , т. е. удаленные спины постепенно становятся все
более скоррелированными. Это свойство — проявление укрупнения, при ко¬
тором участники голосования организуются в анклавы с единым мнением,
характерный размер которых растет с течением времени. С другой сторо¬
ны, при d > 2 модель голосования стремится к стационарному состоянию,
и укрупнения в пространственном распределении участников голосования в
бесконечной популяции не происходит.
Есть два важных следствия для модели голосования, которые могут быть
выведены из корреляционной функции. Первое — временная зависимость
плотности границы раздела, а именно плотности р соседних участников го¬
лосования, имеющих противоположные мнения. Как мы будем делать еще
не раз в этой главе, представим границу раздела как эффективную квази¬
частицу, которая находится на связи между двумя соседними участниками
голосования, придерживающимися противоположных мнений. Плотность до¬
менных стенок характеризует удаленность системы от консенсуса. Корреля¬
ционные функции для соседних узлов х и у можно связать с плотностью
доменных стенок
G(x,y) = (s(x)s(y)) = [Prob(++) + Prob(—)] - [Prob(d—) + Prob(—h)]
= [1-P]-M = l~2p. (8.13)
Таким образом, плотность границ и корреляционная функция для ближай¬
ших соседей связаны соотношением р = [1—G(x, у)]/2. Пользуясь уравнением
(8.12) для корреляционных функций, можно получить зависимость плотно¬
сти границ от времени:
г
p(t) ~ <
t-v2,
(lnt)-1,
0(1).
d= 1,
d = 2,
d>2.
(8-14)
При d <2 вероятность того, что два участника голосования на данном рассто¬
янии друг от друга имеют противоположные мнения, асимптотически стре¬
мится к нулю, и возникает укрупненная мозаика доменов с единым мнением.
В пограничной размерности d = 2 процесс укрупнения медленный, и плот¬
ность границы раздела асимптотически убывает только как 1/ In t (рис. 8.1).
В высших размерностях бесконечная система достигает динамически фруст-
рированного состояния, в котором участники голосования с противополож¬
ными мнениями сосуществуют и эволюционируют таким образом, что сред¬
няя плотность участников каждого типа остается постоянной.
8.2 Модель голосования
297
Второе главное следствие из корреляционной функции — это значение
времени Tjy достижения консенсуса в конечной системе из N участников го¬
лосования. Чтобы оценить время достижения консенсуса, мы воспользуем¬
ся диффузионным характером распространения влияния любого участника
голосования, ввиду которого размер области влияния имеет порядок y/Dt.
Постулируем, что консенсус наступает, когда суммарная корреляция на рас¬
стояниях до y/Dt от любого участника голосования равна полному числу
участников голосования. Тогда критерий консенсуса имеет вид
y/Dt
G(r)rd_1 dr = N. (8.15)
Нижний предел интегрирования может быть положен равным 0 в d = 1 и дол¬
жен быть взят равным обрезанию а для d > 2. После подстановки выражения
(8.12) для корреляционной функции в этот интеграл, извлечем из скейлинга
временную зависимость, в результате чего получим следующее асимптотиче¬
ское поведение (задача 8.2):
Tn ~ <
N2,
NkN,
N,
d — 1,
d = 2,
d> 2.
(8.16)
При уменьшении размерности меньше 2 для достижения консенсуса требует¬
ся все больше времени. Это свойство отражает возрастание трудностей пере¬
дачи информации при понижении размерности.
Точный анализ
На гиперкубической d-мерной решетке эволюция парной корреляционной
функции, описывается дискретным уравнением диффузии (сравните с урав¬
нением (8.16))
У€(х)
с некоррелированным начальным условием G(x,0) = <5(х) и граничным усло¬
вием G(O,t) = 1. Без граничных условий решение имеет вид Ix(2t/d)e~2t (см.
уравнение (8.8)). Это решение согласуется с граничным условием, только ко¬
гда t = 0. Для выполнения G(0, t) = 1 в течение всей эволюции рассмотрим
298
ДИНАМИКА СПИНОВ
задачу Коши с источником, локализованным в начале координат, и выбе¬
рем интенсивность источника так, чтобы удовлетворить граничным услови¬
ям. Поскольку уравнение эволюции линейно, общее решение — это линейная
комбинация
G(x, t) = Ix(2t/d)e~2t +f dr J(t — т) Ix{2r/d} е~2т. (8.18)
Jq
Интеграл содержит вклад от эффективного зависимого от времени источника
J(t) dr за время (т,т + dr). В начале координат уравнение (8.18) принимает
вид
1= [7o(2£/d)e 2t/d^ + J dr J(t - т) ро(2т/б/)е 2r/d^ . (8.19)
Теперь решим это интегральное уравнение, чтобы найти интенсивность ис¬
точника J(t). Присутствие свертки под интегралом (8.19) предполагает при¬
менение преобразования Лапласа. В терминах Лаплас-образов
J(cr) = jf °° dt e~at J(t) и Jd(a) = jf °° dt e~at [z0(2t/d) ‘
получим простое соотношение
J(tr) = [aJd(cr)]_1 - 1.
Пользуясь интегральным представлением функции Бесселя
р27Г
/о(т) = (27г)-1 / ет
Jo
cosq
dq,
перепишем последний Лаплас-образ в (8.20) в виде интеграла
(•27Г /»27Г
U/Щ j.
cos qi)
(8.20)
(8.21)
(8.22)
Уравнения (8.21) и (8.22) дают точное выражение для Лаплас-образа интен¬
сивности источника.
Поведение на больших временах тесно связано с поведением соответству¬
ющего Лаплас-образа при малых а. Используя (8.22), получаем ведущую
асимптотику Jd(<r) (задача 8.3)
р-'а-1/2, d=l,
Jd(<r) - \ (2тг)-х 1п(1/сг), d = 2,
Щ0), d > 2.
(8.23)
8.2 Модель голосования
299
Таким образом, когда сг —> О, интеграл (8.22)расходится при d < 2, и остается
конечным при d > 2. В частности, в трех измерениях явное выражение для
константы имеет вид
а3(о) = Г Л Л dgldg2dg3 *
3 Уо Уо Уо (2л)3 2 — | (cos + COS <J2 + COS 9з)
=^гШгШгШг(Ю-
Интегралы такого типа называются интегралами Ватсона, и они повсе¬
местно возникают в задачах с решеточными функциями Грина. Комбини¬
руя (8.21) и (8.23), получим ведущую асимптотику Лаплас-образа интенсив¬
ности источника при а —> О
2 а-1/2,
2 л <7—1 [1п(1/<г)]
-1
5
d= 1,
d = 2,
d>2.
(8.24)
Переходя к переменной времени, получим асимптотику интенсивности источ¬
ника на больших временах
(2тг~1/2Г1/2,
J(t) — <
2л (In Z) 1,
Pd(O))-1,
d=l,
d = 2,
d>2.
(8.25)
Наконец, чтобы извлечь асимптотическое поведение плотности реакционно-
способных границ раздела, воспользуемся уравнениями (8.18) и (8.19), что
дает8
р(0 = Ie_2t Uo^/d)]*-1 [iQ{2t/d) - h(2t/d)\
+ I Г drJ(t - т) [I0(2T/d')]d-1 [J0(2r/d) - Ji(2r/d)] е~2т. (8.26)
* Jo
Используя этот результат вместе с (8.25), находим поведение плотности ре¬
акционноспособных границ
Г(4тгё) V2, d = l,
p(t) ~ < л/(21п£), d = 2,
(const, d> 2,
(8.27)
8Для простоты мы рассматриваем границы раздела, перпендикулярные одной из осей.
Полная плотность границ в d раз больше. Поэтому в данном случае мы определяем p(t) =
j[l — <7(1®, £)], где lx соответствует узлу решетки (1,0,0,...).
J(a) ~ <
300
ДИНАМИКА СПИНОВ
в пределе большого времени. Эти асимптотически точные результаты под¬
тверждают предсказания непрерывного подхода, см. уравнение (8.14).
8.3 Модель Изинга-Глаубера
Модель Изинга является наиболее широко исследуемой моделью статисти¬
ческой механики из-за ее простоты, ее полезности для объяснения фазовых
переходов и необычайно широкого диапазона ее приложений. В классической
модели Изинга спины с двумя состояниями живут в узлах регулярной решет¬
ки. Спины могут принимать одно из двух значений s(x) = ±1. Гамильтониан
этой системы имеет вид
JsiSj, (8.28)
где суммирование производится по всем парам соседних спинов (i,j). Та¬
ким образом, каждая параллельная пара соседних спинов дает вклад — J в
энергию, а каждая антипараллельная пара — вклад + J. Все термодинамиче¬
ские свойства модели Изинга могут быть получены из статистической суммы
Z = 53ехр(—где суммирование производится по всем конфигурациям
спинов в системе, а /3 = 1/Т — обратная температура9. Для J > 0 ферро¬
магнетизм возникает спонтанно, т. е. в нулевом внешнем магнитном поле,
когда температура Т ниже критической Тс, а пространственная размерность
d > 2. В этом упорядоченном состоянии намагниченность ненулевая и уда¬
ленные друг от друга спины сильно скоррелированы. Выше Тс спины про¬
странственно неупорядочены при равных количествах спинов со значениями
+1 и —1, так что намагниченность равна нулю. Более того, пространственные
корреляции между спинами экспоненциально убывают с расстоянием.
Хотя равновесные свойства модели Изинга следуют из статистической
суммы, неравновесные свойства зависят от природы спиновой динамики. Су¬
ществует большая свобода формулировок для динамики, которая ограничена
только условием детального равновесия (см. ниже, а также врезку на стр.
228). Например, спины могут меняться один за раз или скоррелированными
блоками, а динамика может сохранять или не сохранять намагниченность.
Динамика, сохраняющая намагниченность, будет рассмотрена в разделе 8.7.
Такое отсутствие единственности динамических правил часто встречается в
неравновесной статистической физике и отражает отсутствие универсальных
9Как уже упоминалось, мы всегда измеряем температуру в единицах энергии или, эк¬
вивалентно, полагаем константу Больцмана къ равной 1.
8.3 Модель Изинга-Глаубера
301
принципов эволюции неравновесных систем, таких как минимизация свобод¬
ной энергии в равновесной статистической механике.
Интенсивности переходов
В модели Глаубера спины выбираются по одному в случайном порядке, и
состояние каждого спина изменяется sj —> — Sj с интенсивностью, которая
зависит от изменения энергии в процессе обновления. По построению наг
магниченность не сохраняется в каждом событии обновления. Есть три ти¬
па переходов, в которых переворачиваются спины: с увеличением энергии,
с уменьшением энергии, энергетически нейтральные (рис. 8.4). События с
I II II I
I ♦ I I 4 I lll^ltl t ♦ I -* III
I t I II t
(a) (b) (c)
Рис. 8.4. Перевороты спинов (а) с понижением энергии, (b) с увеличением энер¬
гии и (с) с сохранением энергии в модели Изинга-Глаубера на квадратной ре¬
шетке
увеличением энергии происходят, когда спин направлен так же, как боль¬
шинство его соседей, а события с понижением энергии — когда он направлен
против большинства спинов в его локальном окружении. Энергетически ней¬
тральные или сохраняющие энергию события происходят, когда локальная
намагниченность равна нулю. Основной принцип, помогающий фиксировать
интенсивности переходов, — это условие детального равновесия (см. уравне¬
ние (6.44))
Peq(s) Wj(s) = Peq(sJ) (8.29)
Здесь s обозначает любое из 2N состояний всех N спинов системы, sJ — это
состояние, полученное из s переворотом спина в j, wy(s) — интенсивность
перехода из s в sJ , и -Peq(s) — равновесный больцмановский вес
D л,\ _ ехр[-^ JC(s)]
-teqVS; — —
Детальное равновесие — это утверждение о балансе токов, протекающих че¬
рез каждую связь в пространстве состояния: токи вероятности из s в sJ и из
302
ДИНАМИКА СПИНОВ
sJ в s — левая и правая части уравнения (8.29) — равны. По определению
равновесные веса удовлетворяют условию детального равновесия. С весами,
определенными в (8.29), любое начальное спиновое состояние будет релак-
сировать к равновесному состоянию при всех положительных температурах.
Детальное равновесие — ключевой принцип, который обосновывает способ
введения динамики. Однако необходимо сделать несколько пояснений.
• Интенсивности определяются условием детального равновесия, а не вы¬
водятся из какой-либо микроскопической модели. Равновесная стати¬
стическая физика утверждает, что равновесные больцмановские веса
(8.30) должны давать решение для неравновесной динамики. Это дела¬
ет выбор интенсивностей (8.29) естественным для систем стартующих с
равновесия. Однако, если начальная конфигурация находится далеко от
равновесия, другие интенсивности могут вести систему к равновесию.
• Интенсивности (8.29) обеспечивают достижение равновесия при любой
положительной температуре, потому что через любую связь в простран¬
стве состояний существует ненулевой ток вероятности. Однако при Т =
0 перевороты, повышающие энергию, запрещены, и соответствующие
интенсивности переходов равны нулю. Следовательно, изинговская си¬
стема может попасть в локальный минимум — состояние энергия кото¬
рого ниже, чем энергия любого состояния, отличающегося переворотом
одного спина. Из такого метастабильного состояния нет выхода, и си¬
стема не может достигнуть основного состояния.
Примечательно, что условие детального равновесия можно удовлетворить
простым выбором интенсивностей переходов. Рассмотрим общую неоднород¬
ную модель Изинга с гамильтонианом
СК = — JijSiSj. (8.31)
М
Константы взаимодействия могут быть произвольными (ферромагнитными
или антиферромагнитными), а их величина может меняться от связи к связи,
и число соседей может быть разным для разных спинов. Уравнение (8.29)
дает
Wi(s) _ Peq(s*) _ е _ 1 - Si th(/3 JijSj)
W;(s2) Peq(s) e^Si £ 1 + Si tll(/3 ^VSj) ’
(8.32)
8.4 Приближение среднего поля
303
Wi(s) = - [
где суммирование производится по ближайшим соседям (г) узла г. При выво¬
де последнего равенства мы использовали полезное тождество (которое вы¬
полняется для s = ±1)
eAs = chA + sshA = chA (1 + sth Л). (8.33)
Простейший набор интенсивностей, удовлетворяющих соотношению (8.32),
je<*>
где мы положили равными 1/2 интенсивности переходов для сохраняющих
энергию переворотов10. Перед тем как обратиться к ситуации с конечной раз¬
мерностью, рассмотрим более простую версию глауберовой динамики, иллю¬
стрирующую ее работу, — предел среднего поля.
8.4 Приближение среднего поля
Термин приближение среднего поля относится к эффективному полю, кото¬
рым заменяется локальное взаимодействие между спинами. На начальной
стадии приближение среднего поля не содержит никакого приближения: мы
просто переписываем гамильтониан (8.31) в виде
IK = - 52 his^ = Js3 (8.35)
*
и рассматриваем его, как гамильтониан набора спинов на каждый из
которых действует локальное неоднородное магнитное поле hi, происходящее
от соседних спинов j Е (г)11. Приближение появляется, когда мы заменяем
спины Sj в каждом узле j Е (г) их средним значением, средней намагни¬
ченностью т, так что локальное поле hi сводится к однородному «среднему
полю» h = Jzm/2, где z — координационное число решетки. Это приближе¬
ние заменяет исходную взаимодействующую систему системой эффективно
независимых спинов, которые взаимодействуют только с внешним полем h,
а не напрямую со своими соседями.
Отсутствие прямого взаимодействия между соседями приводит к важ¬
нейшему свойству — соседние спины нескоррелированы. Математически это
значит, что
{SiSj} = (Si)(sj) для i/j, (8.36)
10В одномерном случае интенсивность (8.34) была предложена Глаубером.
11 Множитель 1/2 в hi исправляет двойной переучет, возникающий из-за того, что каж¬
дая связь входит в гамильтониан (8.35) дважды.
304
ДИНАМИКА СПИНОВ
и аналогично для корреляционных функций более высоких порядков. Во
многих ситуациях, в частности, в неравновесных процессах, которые не до¬
пускают гамильтонова описания, невозможно ввести «среднее поле», которое
действует на все отдельные спины (или частицы) в системе. Такие систе¬
мы естественным образом могут быть описаны с помощью корреляционных
функций. Однако уравнения эволюции для корреляционных функций обычно
имеют иерархическую структуру, т. е. n-частичная корреляционная функция
связана с (п + 1)-частичной корреляционной функцией. В этом случае фак-
торизуемость корреляционных функций, как в (8.36), определяет приближе¬
ние среднего поля. Это приближение заменяет точную иерархию уравнений
для корреляционных функций среднеполевыми уравнениями, которые име¬
ют вид рекурсии, замкнуты и, таким образом, решаемы. В общем случае
факторизация корреляционных функций представляет собой неконтролиру¬
емое приближение, но оно часто схватывает основные качественные свойства
взаимодействующих систем.
По построению среднеполевое описание не может быть количественно точ¬
ным для систем с локальными взаимодействиями, но оно точно в специальном
случае, когда все пары элементов взаимодействуют. Особенно простой пример
дается ферромагнитной моделью Изинга на полном графе из N узлов12, где
точное решение совпадает со среднеполевым. Гамильтониан системы имеет
вид
= (8.37)
i<j
Здесь величина взаимодействия выбрана обратно пропорциональной разме¬
ру системы, чтобы энергия была экстенсивной, т. е. пропорциональной N.
Поскольку каждый спин взаимодействует со всеми остальными спинами, ло¬
кальное поле совпадает с намагниченностью13. Исследуем глауберову дина¬
мику на полном графе, для которого интенсивности переходов из уравне¬
ния (8.34) равны
1
2
Wi =
i-s’th(4s,sj)
4 з 7
(8.38)
12В полном графе из N узлов есть N(N — 1)/2 связей, так как все узлы связаны.
13Есть еще одна сеть, дерево Кейли, где возможен точный анализ, который приводит
к такому же критическому поведению, как для полного графа. Эти примеры представля¬
ют собой две противоположные топологические крайности: полный граф содержит макси¬
мально возможное число петель, тогда как дерево Кейли — регулярный граф вообще без
петель.
8.4 Приближение среднего поля
305
Штрих при сумме означает, что суммирование производится по всем спи¬
нам кроме Si. Когда TV 3> 1, спин S; может быть включен в сумму, что дает
пренебрежимо малую ошибку. Можно также заменить точную намагничен¬
ность N-1 Sj ее средним значением т = N-1 Sj, где Sj = (sj). Тогда
уравнение движения среднего спина dSi/dt = —2(siWi) принимает вид
+ (8.39)
at
Просуммировав уравнение (8.39) по всем узлам, получим уравнение для сред¬
ней намагниченности
= — т + th /Зт. (8.40)
dt
В отличие от одномерия намагниченность в общем случае не сохраняется. В
равновесии уравнение (8.40) предсказывает, что фазовый переход возникает
при /Зс = 1. Когда /3 < Д = 1, единственное решение уравнения т = th/3m —
это т = 0. Для /3 > /Зс, кроме решения с нулевой намагниченностью, суще¬
ствует два нетривиальных равновесных решения: т = ±meq, где mcq — по¬
ложительный корень трансцедентного уравнения т = th(/3Jm). С помощью
линейного анализа устойчивости можно показать, что состояния с т = ±meq
устойчивы при /3 > 1, а состояния с нулевой намагниченностью неустойчивы.
Вблизи критической температуры имеем meq ~ ^/3(/3 — 1) = \/'А(Тс — Т)/Т
при Т Тс = 1. Появление двух эквивалентных, но нарушающих симметрию
основных состояний, в то время как сам гамильтониан симметричен, известно
как спонтанное нарушение симметрии.
Теперь вернемся к динамике. Выше критической температуры разложим
th /Зт из уравнения (8.40) по степеням /Зт, что дает
= -<J3C - (3)т - ±(/Зт)3 + 0(т5). (8.41)
В высокотемпературной фазе кубический член и члены более высоких по¬
рядков пренебрежимо малы, и намагниченность убывает экспоненциально
со временем т ~ е“*/т, где г = (/Зс — /З)-1. В критической точке =
—т3/3 + О(тп5), так что намагниченность демонстрирует степенную релак¬
сацию
т ~ t-1/2. (8.42)
Ниже критической температуры решение т = 0 неустойчиво, и намагни¬
ченность стремится к ±meq. Разлагая уравнение (8.41) вблизи равновесной
намагниченности, находим, что намагниченность убывает к ее равновесно¬
му значению экспоненциально со временем |m — meq| ~ е~^Т, где т-1 =
306
ДИНАМИКА СПИНОВ
1 — /3/ ch2(/3raeq). Таким образом, при приближении к критической точке сни¬
зу или сверху время релаксации расходится как
т^\Тс-Т\-\ (8.43)
Расходимость времени релаксации при Т -> Тс — это сигнал критического
замедления приближения к равновесию.
Такие различные типы поведения для надкритической, критической и
подкритической динамики есть отражение центральной догмы, изложенной
в начале этой главы. Выше критической температуры система быстро релак-
сирует к равновесному неупорядоченному состоянию с m = 0. Корреляции
спинов локальны для всех конечных Т > Тс и отсутствуют при Т = оо.
При критической температуре система релаксирует гораздо медленнее. Для
всех температур ниже критической точки система релаксирует к одному из
равновесных состояний с дальним порядком. Из-за такого универсального по¬
ведения мы сосредоточимся на динамике при нулевой температуре, которая
представляет подкритическую динамику в ее чистейшем виде.
8.5 Глауберова динамика в одномерии
В размерности один интенсивность переворота (8.34) имеет вид
w<(s) = -
1 4.к (п/э т 1 + $г+1
1 - Si th ( 2/3 J
-7$г
(8.44)
Sj-1 + Sj+1
2
где 7 = th(2/3J). На последнем шаге мы использовали тождество thex =
еth#, справедливое при е = 0,±1, так же как в глауберовой интенсивности
переворота. Хотя такая интенсивность согласуется с детальным равновесием,
это лишь одна из возможных интенсивностей. Чтобы лучше почувствовать
специфику глауберовой динамики, найдем самую общую интенсивность пе¬
реворота спинов, которая удовлетворяем следующим естественным требова¬
ниям:
• Локальность. Поскольку гамильтониан СК = —J^SjSj+i содержит
только взаимодействия между ближайшими соседями, интенсивности
переворотов должны также зависеть только от ближайших соседей каж¬
дого спина: Wi(s) = Si+i).
• Симметрия правое /левое. Инвариантность по отношению к замене
i + 1 о г — 1.
8.5 Глауберова динамика в одномерии
307
• Симметрия верх/низ. Инвариантность по отношению к обращению
всех спинов, которая отражает инвариантность гамильтониана по от¬
ношению к этому же преобразованию. В ненулевом магнитном поле
симметрия верх/низ не выполняется, и интенсивности переворотов не
инвариантны относительно обращения спинов.
Самая общая интенсивность переворота, удовлетворяющая этим условиям,
имеет вид
Si, Si+i) = А + Bsi(si-\ + Si+i) + Csi-iSi+i. (8.45)
Поучительный способ получения этого результата — разложить интенсив¬
ность в ряд Тейлора
Wifa-1, Si, Si+l) = A-abc &i—
a,b,c>0
Поскольку s2 = 1, бесконечный ряд сводится к конечной сумме, в которой
а,Ь,с равны 0 или 1. Привлекая симметрии правое/левое и верх/низ, сведем
сумму к интенсивности в (8.45).
С помощью переопределения времени t —> 2At можно положить А = 1/2.
Результирующая интенсивность переворота зависит только от двух парамет¬
ров и традиционно записывается в виде
Wi = | [l - ^Si (Si-! + Sj+i) + <5si_iSj+ij . (8.46)
Наглядно эту интенсивность можно изобразить как
Wi = -X
'1-7 + 5
< 1 — 5
к1 + 7 + 5
ДЛЯ СПИНОВЫХ СОСТОЯНИЙ ТГТ> 4-4-4-»
для спиновых состояний tf4) 444> 444) 444)(8-47)
ДЛЯ СПИНОВЫХ СОСТОЯНИЙ "444) 444)
где константы 7 и 5 удовлетворяют условию детального равновесия
1 - |7gj(gj-i + Sj+i) + 5sj-igi+i = 1 - th(2^J)sj(sj-i + sJ+i) 4g)
1 + + Sj+i) + foi-iSi+i 1 + j th(2^J)sj(sj-i + sJ+i)
Проверяя выполнение этого условия для всех конфигураций спиновых троек
Si+i), находим, что детальное равновесие выполняется, когда
7 = (1 + 5) th(20J),
(8.49)
308
ДИНАМИКА СПИНОВ
а физическое требование, чтобы все интенсивности переворотов были неот¬
рицательными, дает ограничения на параметр 5, а именно — 1 < S < 1. Хо¬
тя интенсивности переворотов (8.46) самые общие, интенсивности Глаубера
(8.44) наиболее естественны. Например, глауберовы интенсивности предска¬
зывают, что в пределе Т —> оо все перевороты равновероятны, тогда как для
общих интенсивностей это не так. Более того, кинетическая модель Изинга
в одном измерении решаема только для глауберовых интенсивностей (и еще
для одного исключительного случая, который мы не обсуждаем). Далее, если
не оговорено обратное, мы всегда пользуемся глауберовыми интенсивностями
переворотов.
Намагниченность и корреляционные функции
Следуя той же линии анализа, что и для модели голосования (уравнения
(8.3) и (8.5)), запишем уравнения движения для корреляционных функций
низших порядков
(8.50а)
= -2(siSj[wi + wj]), (8.50b)
где Si = (si) и Sitj = (siSj).
Используя интенсивность перехода (8.44) и тождество = 1, получим
уравнение эволюции для среднего спина Sj
= -Sj + I (Sj-г + SJ+i). (8.51)
Решение с начальным условием Sj(O) = 5jto имеет вид (см. врезку на стр. 18
про функции Бесселя)
SjV^IjMe-1, (8.52)
где Ij — модифицированная функция Бесселя порядка j. Заметим, что при
Т = 0 (что соответствует 7 = 1) уравнение движения (8.51) идентично тако¬
му же уравнению для одномерной модели голосования. Действительно, при
Т = 0 эти две модели оказываются идентичны. При Т > 0 новая черта моде¬
ли Изинга-Глаубера по сравнению с моделью голосования — это присутствие
зависимого от температуры множителя 7. В этой ситуации средний спин в
любом узле асимптотически убывает как Sj(t) (27гт£) х/2е т. е. на¬
блюдается экспоненциальное убывание с временем релаксации г = (1 — -у)-1
8.5 Глауберова динамика в одномерии
309
и алгебраическое убывание при Г = 0. Намагниченность т = N 1 Sj удо¬
влетворяет уравнению = — (1 — 7)ш, так что т убывает экспоненциально
со временем при любой положительной температуре
m(t) = m(0) (8.53)
и сохраняется только при нулевой температуре, так же как и в модели го¬
лосования. Одномерная модель Изинга-Глаубера претерпевает критическое
замедление — более медленная релаксация в критической точке (Т = 0 в
одномерии), чем при Т > 0. Для общих начальных условий общее решение
уравнения (8.51) дается линейной комбинацией частных решений (8.52), ко¬
торая имеет вид
ОО
<%(*) = 52 a»n^-m(7^)e_t, (8.54)
m=—оо
где ат — это начальное значение спина в узле т. Исследуем парную кор¬
реляционную функцию, Sij. Функция для ближайших соседей особенно по¬
лезна, так как имеет простую интерпретацию в терминах доменных стенок
(рис. 8.5). Два соседних антипараллельных спина соответствую!’ находящей-
t t t t t t t t t t t t°J°t ) t t t t to* | | |
A V \
t t t tol'ot t t t t t t t t t t t t t t t°l I I
(a) (b) (c)
Рис. 8.5. Соответствие между состояниями моделей Изинга или голосования в
размерности один и соответствующих квазичастиц- доменных стенок: (а) по¬
вышающий энергию шаг и образование пары доменных стенок; (Ь) понижающий
энергию шаг и аннигиляция доменных стенок;(с) сохраняющий энергию шаг и
диффузия доменных стенок
ся между ними доменной стенке-квазичастице, а два соседних параллель¬
ных спина соответствуют отсутствию доменной стенки. Таким образом, связь
(к, fe + l) несет доменную стенку, если ^(1 —s^s^+i) = 1. Плотность доменных
стенок дается выражением
Р = (it1 “ skSk+ii) = |(1 - Gi)>
310
ДИНАМИКА СПИНОВ
Для трансляционно инвариантных систем корреляционная функция зави¬
сит только от расстояния между двумя спинами, Gk = Sij+к, так что основное
кинетическое уравнение (8.50Ь) принимает вид
dGk
dt
— ~^Gk + 7 (Gk-i + Gfc+i)
(8.55)
для к > 0 с граничным условием <7o(i) = (s2) = 1. Чтобы получить равновес¬
ное решение уравнения (8.55), подставим Gfc(oo) ~ т]к и найдем, что правая
часть равна нулю, когда 2 = 7(77 + т?-1). Из этого соотношения выводим
— 72]/7 = th/3J. Таким образом, равновесное решение запишется
как
Gfc(oo) = где £ = [ln(coth/3J)]_1, (8.56)
что находится в согласии с равновесной статистической физикой. Как и ожи¬
далось, корреляционная длина расходится при Т —> 0, что указывает на нали¬
чие фазового перехода, и £ обращается в ноль при бесконечной температуре.
Чтобы найти временную зависимость корреляционной функции, заметим, что
эволюционное уравнение (8.55) имеет такой же вид, как уравнение на средний
спин, с точностью до общего множителя 2 и фиксированного граничного усло¬
вия в начале координат. Поэтому общее решение должно строиться из ком¬
понентов такого же вида, как в (8.54), с заменой t —> 2t. Теперь нужно найти
подходящую линейную комбинацию этих компонент, которая одновременно
удовлетворяет специальному начальному условию Gk(t = 0) и граничному
условию Gq = 1. Одна часть полного решения дается просто равновесной
корреляционной функцией С&(оо) = т)к. К ней мы должны прибавить общее
однородное решение, которое удовлетворяет наложенным ограничениям. По
форме подходящее начальное условие для однородного решения состоит из
произвольной нечетной функции плюс антисимметричная часть, которая со¬
кращается с равновесной частью для к > 0. Антисимметричность этих частей
обеспечивает выполнение условия Gq = 1 и выполнение начального условия
для к > 0. Общее решение для к > 0 имеет вид
<3fc(*) = rf + е 2t ^2
€=—оо
= Г? + e~2t £[<?Х0) - rf]Ik-№t) + e-2t 2 (G,(0) +
€>1 €<-1
= rf + e_2t £[Gz(0) - rie][Ik-e(2yt) - Д+г(2т*)],
e>i
(8.57)
8.5 Глауберова динамика в одномерии
311
где Ае. — набор констант, определяемый из произвольно заданных начальных
условий G^(0).
Самое интересное поведение возникает, когда температура равна нулю и
поэтому, если не оговорено обратное, мы предполагаем Т = 0. Для случайных
начальных условий с начальной намагниченностью то = 0 имеем СДО) = 0,
н временная зависимость корреляционной функции дается выражением
к-1
Gk(t) = 1 - e~2t [j0(2t) + Ik(2t) + 2^2 Z,(2f)] . (8.58)
J=1
Отсюда плотность доменных стенок равна
PM = ^(l-Gi) = ^~2‘M2t) + W)] '“(“М |/2. (8.59)
Другой иллюстративный пример — антиферромагнитные начальные условия,
для которых Gt(0) = (—1/. В этом случае плотность доменных стенок есть
p(t) = e~2t Io(2t) ~ (47г^)-1/2, (8.60)
и она характеризуется таким же асимптотическим убыванием, что и для
случайных начальных условий. В общем случае плотность доменных сте¬
нок зависит только от начальной намагниченности, другие детали начальных
условий не важны. Наконец заметим, что при нулевой темперач'уре динами¬
ка доменных стенок совпадает с необратимой диффузионно-контролируемой
аннигиляцией, в которой популяция идентичных частиц свободно диффунди¬
рует и две частицы всегда аннигилируют при встрече. Аналогично, при Т > 0
динамика Изинга-Глаубера эквивалентна диффузионно-контролируемой ан¬
нигиляции с образованием пар. Мы вернемся к этому предмету в главе 13.
Пример 8.1. Мулътиплеты доменных стенок. Можно обобщить анализ домен¬
ных стенок и найти вероятность того, что две соседние связи содержат доменные
стенки. Связи (fc — 1, fc) и (fc, k + 1) несут доменные стенки, если |(1 — Sk-iSk) х
(1 — SfeS/j+i) = 1. Поэтому плотность дублетов доменных стенок равна
Р2 — (|(1 — Sk-iSk) х (1 — SfcSfc+i)) — |(1 — 2Gi + G2).
Подставляя Gi и G2 из (8.58), находим, что для некоррелированных начальных
условий то = 0 плотность дублетов равна
Р2(*) = | e-2t [J0(2t) - h(2f)} = 1 e-2t A(2t) c
при t —> 00. (8.61)
312
ДИНАМИКА СПИНОВ
Таким же образом плотность триплетов
РЗ = ( g(l - Sk-lSk) х (1 “ SfcSfc+l) X (1 - Sfc+lSfc+2)\
можно выразить как
Рз = |(1 — 3<?1 + 2G2 — G3 + (sk-iSkSk+iSk+2Y)- (8.62)
Для нахождения плотности триплетов нам нужно вычислить четырехспиновую
корреляционную функцию (sk-iSkSk+iSk+2)- Это непросто, но для самых есте¬
ственных начальных условий шо = 0 ответ относительно прост (задача 8.6):
(sfe-iSfcSfc+iSfc+2) = Gj 4- G1G3 — G|. (8.63)
Комбинируя этот результат с (8.62) и используя Gi,G2,G3 из (8.58), приходим
к выражению
Рз = [/02(2i) + /o(2t)A(2t) + Z0(2t)J3(2t) - A2(2t)
- 2A(2t)/2(2t) + A(2t)/3(2t) - (2t)] • (8.64)
Асимптотически имеем рз — 1/(87г£3).
В присутствии ненулевого магнитного поля Н гамильтониан ферромагнитной
модели Изинга имеет вид
X = -J£ W+i - Н 52 Sj, (8.65)
3 3
и мы ожидаем, что спины будут выстроены по полю. Введение поля приводит
к нерешаемому эволюционному уравнению для кинетической модели Изинга
при положительной температуре. Однако при нулевой температуре модель
проста и решаема и красиво иллюстрирует асимптотическое выстраивание
спинов вдоль поля.
Пример 8.2. Цепочка Изинга в магнитном поле. Условия детального равнове¬
сия дают
Wj(s) = _ 1 _ (s._1 + g.+1) 1 _ fag.
W^S*) “ e^Jsi(si_i+si+i)+pHsi 1 + (s._1 + s.+1) 1 _|_ hs. ’ * '
где 7 = th 2/3 J и ft = th f3H, и без потери общности мы предполагаем, что поле
положительно. Естественным выбором интенсивностей переходов будет
Wi(s) = i [l - (Si-! + si+i) - hSi + (Si-! + si+i)] . (8.67)
8.5 Глауберова динамика в одномерии
313
Магнитное поле приводит к появлению линейных по спиновым переменным
членов, которые имеют более низкий порядок, чем квадратичный не зависимый
от поля член. Эта линейность позволяет надеяться, что уравнения для спино¬
вой динамики в ненулевом поле могут быть решены. К сожалению, это не так.
Например, средний спин удовлетворяет уравнению
в которое входит парная корреляционная функция для соседних спинов
Таким же образом уравнения для парной корреляционной функции содержат
трехспиновые корреляторы, и такая иерархическая структура продолжается до
бесконечности.
Хотя поведение при положительных температурах не поддастся аналитиче¬
скому рассмотрению, случай Т = 0 оказывается проще и все еще является ин¬
тересным. Для определения интенсивностей переходов при Т = 0 целесообразно
воспользоваться правилом арок, гласящим, что перевороты спинов, понижаю¬
щие энергию разрешены, а все остальные события запрещены. Это правило при¬
водит нас к заключению, что есть две различных динамики, в зависимости от
того Н > 2J или Н < 2J.
Сильное поле (Н > 2J). В этом тривиальном случае спины, направленные вверх,
не изменяются, а спины, направленные вниз, переворачиваются с интенсивно¬
стью 1 независимо от состояния соседних спинов. Поэтому распределение длины
доменов равно Wi = (1 — Si)/2, а средний спин эволюционирует в соответствии
с уравнением Si = 1 — Si. Стартовав с некоррелированных начальных условий с
нулевой намагниченностью, получим решение Si = 1 — e-t, из которого видим,
что полностью упорядоченное состояние достигается экспоненциально быстро.
Поскольку все спины независимы, все корреляционные функции факторизуют-
ся: Silt...>in = (1 - е *)".
Слабое поле (0 < Н < 2J). В этом случае из восьми возможных конфигура¬
ций трех последовательных спинов центральный спин может перевернуться с
единичной интенсивностью только в следующих трех случаях:
ш=^ш, •
В доменной картине домены со спинами, направленными вниз, систематически
сжимаются. Плотность Рп таких доменов длины п эволюционирует в соответ¬
ствии с уравнением
^=2(Рп+1-Рп)
(8.69)
при п > 2. Немного другое уравнение описывает эволюцию доменов длины один
с направленными вниз спинами: dP-y/dt = 2Р% — Р±. Эти уравнения легко реша¬
ются (задача 8.10).
314
ДИНАМИКА СПИНОВ
Распределение длины доменов
При нулевой температуре доменные стенки, которые диффундируют и анни¬
гилируют при встрече, — это фундаментальные возбуждения цепочки Изинга
с глауберовой динамикой. Основной характеристикой таких возбуждений яв¬
ляется среднее расстояние между ними (эквивалентное обратной плотности
доменных стенок), которое при нулевой температуре растет как i1/2. Более
фундаментальная величина — распределение расстояний, т. е. вероятность Рк
найти домен размером к. Чтобы получить интенсивную величину, мы опреде¬
ляем эту вероятность на единицу длины. Домен состоит из к последователь¬
ных сонаправленных спинов, ограниченных с двух концов противоположно
направленными спинами. Частичная информация об этом распределении мо¬
жет быть получена из наблюдения, что плотность доменных стенок — это
просто Рк, что должно быть пропорционально i-1/2. Аналогично, усло¬
вие нормировки дает Y^k>i ^Pk = 1- Эти факты приводят нас к скейлинговой
форме для распределения длины доменов
Pfc(t) ~ СГ1 Ф(А:Г1/2). (8.70)
Тогда требование нормировки дает f^°x&(x)dx = 1, а приравнивание
Рк К Р и использование асимптотического убывания в (8.59) дает
/0°° Ф(т) dx = (47г)-1/2 = С.
Из убывания плотности доменов на больших временах мы также можем
извлечь хвост скейлинговой функции Ф(гг) для малых расстояний. Рассмот¬
рим роль кратчайшего возможного домена длины 1 в уравнении для плот¬
ности доменов р. Как показано на иллюстрации, когда односпиновый домен
переворачивается, три домена сливаются в один больший домен:
• ■ ■ 4- J- • ■ • • ■ • 4 г4 • • •.
Э г+J+l
Поскольку такие события возникают с единичной интенсивностью, плот¬
ность доменов убывает как
= ~2P1- (8-71)
Пользуясь уравнением (8.59), получим Pj. ~ jCt-3/2. С другой стороны,
разложение перемасштабированного распределения Ф в ряд Тейлора дает
8.5 Глауберова динамика в одномерии
315
Pi = Ф(0)£-1 + Ф'(0) t~3/2 + • • •. Сравнивая эти два результата, мы заклю¬
чаем, что Ф(0) = 0 и Ф'(0) = Поэтому в пределе малого аргумента х
скейлинговая функция убывает линейно:
Ф(ж) = Сж + ... при х -> 0. (8.72)
Линейность функции на малых расстояниях — это черта, присущая мно¬
гим одномерным многочастичным взаимодействующим системам. Эта линей¬
ность возникает из-за того, что диффузионная аннигиляция доменных стенок
связана с динамикой расстояния между случайным блужданием и адсорби¬
рующим началом координат. Обычно эта последняя система демонстрирует
линейную зависимость распределения вероятности вблизи начала координат.
Хотя скейлинг позволяет получить общую идею о природе распределе¬
ния длины, полное решение для этого распределения неизвестно. Здесь мы
представляем приблизительное решение, основанное на приближении неза¬
висимых интервалов, в котором длины соседних доменов предполагаются
нескоррелированными. Это приближение успешно применялось для нахожде¬
ния приближенных, но довольно точных решений для множества одномерных
эволюционных процессов и процессов с реакциями. В рамках приближения
независимых интервалов распределение длины эволюционирует как
^ = -2ft + A+1+ft., + « (8.73)
' Р Р i+j=k—l Р
11ервый член отвечает за изменение длины из-за прыжков доменных стенок.
Коэффициент (1 — Pi/p) при Р^-i обеспечивает, чтобы сосед домена длины
(к — 1) имел длину больше 1, так чтобы процесс роста домена к — 1 —> к
приводил к (к — 1, j) —> (k,j — 1), а не к (к — 1,1, j) —> (fc + j). Послед¬
ние два слагаемых отвечают за изменение длины из-за слияния доменов. Так
как любое слияние требует домена длины 1, оба эти члена пропорциональ¬
ны Pi. Член прихода соответствует слиянию трех доменов длин i,j и 1, где
i + j + 1 = к. Член ухода отвечает за слияние домена длины к с доменом лю¬
бой длины. Приближение независимых интервалов было использовано, чтобы
записать вероятность найти три (либо два) соседних домена заданных длин
как произведение плотностей отдельных доменов. Уравнение (8.73) останется
справедливым, когда к = 1, если мы положим Ро = 0.
Поскольку типичная длина доменов непрерывно растет со временем, за¬
меним суммы интегралами, а целое к непрерывной переменной х = к/y/i и
превратим (8.73) в непрерывное уравнение. Теперь подставим скейлинговый
316
ДИНАМИКА СПИНОВ
вид (8.70), а также р a Ct-1/2 и Pi ~ | CvW1 в эту непрерывную версию
основного кинетического уравнения и найдем уравнение для скейлинговой
функции
1 d(a#)
dx2 + 2 dx
i ix
4С Jo ^^Х~У^У = О.
(8-74)
+
Поскольку последний член — это свертка, чтобы выразить ее в виде произве¬
дения, введем Лаплас-образ Ф(в) = /0°° Ф(х) e~sx dx (хотя и с дополнитель¬
ным коэффициентом) и перепишем уравнение (8.74) в виде обыкновенного
дифференциального уравнения
d|
ds
Ф2 « * 1
— + 2вФ - —
2s 2s
(8.75)
с граничным условием Ф(в = 0) = 1, которое обеспечивает нормировку.
Уравнение (8.75) — это уравнение Риккати. По случайности такое урав¬
нение возможно решить, превратив его в линейное дифференциальное урав¬
нение второго порядка, которое оказывается решаемым. В данном случае
замена Ф = — 2s^g^ превращает уравнение (8.75) в
d2V> dV>
ds2 ds
Теперь можно переписать его в виде уравнения Шредингера, применив стан¬
дартный трюк избавления от линейного члена
§ + (2 - «2)У = 0. (8.76)
Для избавления нужно искать решение в виде 'ф = yv та потом потребо¬
вать, чтобы линейный член в у' обратился в ноль. Это условие фиксирует
константу интегрирования v = ехр [—| / (| — 2s) ds]. Связь между исход¬
ной переменной и переменной у дается соотношением Ф = 1 — 2s2 — 2s
Уравнение (8.76) — это уравнение параболического цилиндра, которое воз¬
никает, например, в квантовом гармоническом осцилляторе. Общее реше¬
ние этого уравнения дается линейной комбинацией двух независимых членов
у = C+Di/2(y/2s) + C-D^/2^ — a/2s), где £>„(х) — функция параболического
цилиндра порядка v. Из поведения Ф ~ (2s)-2 при больших s и асимптотики
D„(s) следует, что С- = 0. Поэтому Лаплас-образ имеет вид
Ф = 1 — 2s2 — 2s-y- In Di/2(\/2 s).
CLS
(8.77)
8.6 Глауберова динамика в высших размерностях
317
Для нахождения хвоста распределения длины доменов на больших рас¬
стояниях исследуем предел малых s Лаплас-образа (8.77). В этом преде¬
ле функция параболического цилиндра имеет простой полюс вида Ф с±
2A(s +А)-1, где А = 0,5409 — первый ноль функции параболического ци¬
линдра, = 0. Обратив преобразование Лапласа, получим наш
главный результат — хвост Ф(ж) на больших расстояниях спадает экспонен¬
циально с х, Ф(ж) с± Ае~Хх.
Хотя приближение независимых интервалов не точное, оно приводит к
решаемым уравнениям для распределения длины доменов, решение которых
воспроизводит главные качественные свойства распределения, в том числе:
(i) линейный предел малых длин, (ii) экспоненциальный хвост на больших
длинах и (iii) правильные интегральные свойства, такие как убывание числа
доменов как t-1/2.
8.6 Глауберова динамика в высших размерностях
Спиновая эволюция обычно приводит к причудливой картине роста или к
укрупнению доменов (рис. 8.6). Хотя общее понимание модели Изинга-Гла-
Рис. 8.6. Эволюция модели Изинга-Глаубера при Т = 0 на квадратной решетке
размером 256 х 256 для случайных начальных условий с равными плотностями
спинов, направленных вверх и вниз, на временах t — 4,16,64 и 256. Рисунок
воспроизводится с любезного разрешения В. Спирина
убера в d > 1 чаще всего основано на непрерывных теориях (глава 9), можно
почерпнуть многие факты, изучая кинетические дискретные спиновые систе¬
мы.
318
ДИНАМИКА СПИНОВ
Интенсивности переходов
Для глауберовой динамики в d > 1 интенсивности переходов имеют вид
w*(s) = [l - Si th (/? J «j)], (8-78)
je(i>
где суммирование производится по всем 2d ближайшим соседям спина г на
d-мерной гиперкубической решетке. Сначала попробуем разобраться, почему
модель Изинга-Глаубера не решается при нулевой температуре, хотя близ¬
ко связанная с ней модель голосования решается для всех d. При нулевой
температуре разрешенные перевороты спинов и соответствующие интенсив¬
ности определяются правилом большинства: спин переворачивается, чтобы
совпасть с большинством его соседей (рис. 8.7). Иначе устроена динамика мо-
' t I
t t t
I t
t I
t I t
I t
модель Изинга-Глаубсра
t I 2/3 f |
t ♦ t — t ♦ t
It It
А модель голосования
Рис. 8.7. Сравнение интенсивностей событий обновления в (а) модели Изинга-
Глаубера и (Ь) модели голосования на треугольной решетке
дели голосования, которая подчиняется правилу пропорциональности: участ¬
ник голосования принимает состояние большей части своего локального окру¬
жения с вероятностью, равной доле соседей в этом состоянии. Эта пропор¬
циональность приводит к факторизации основного кинетического уравнения
для модели голосования в d измерениях в произведение решаемых одномер¬
ных уравнений. Напротив, как мы проиллюстрируем сейчас для d = 2, в
размерности d > 1 корреляционные функции модели Изинга-Глаубера удо¬
влетворяют бесконечной иерархии уравнений, а не замкнутым рекуррентным
соотношениям.
Пример 8.3. Интенсивности переворотов в модели Изинга-Глаубера при ну¬
левой температуре. Если так же как и в одном измерении, потребовать ло¬
кальности и симметрий верх/низ и правое / левое, (раздел 8.5), самая общая
интенсивность переворота спина Si должна иметь вид
U)j, = a “h b Sj, “Н С Si S(^SfiSy •
ае(г) а,/3,7б(г)
8.6 Глауберова динамика в высших размерностях
319
Первая сумма пробегает по всем четырем соседям узла i = (х, у), т. е. (#± 1, у) и
(х,у ± 1); второе суммирование производится по четырем возможным способам
выбрать три попарно различных соседа узла г, т. е. а / /3, /3 / 7,7 / а. Теперь
потребуем выполнения следующих условий на интенсивности переворотов для
динамики при нулевой температуре (рис. 8.8):
а — 46 — 4с = 1, рис. 8.8(a),
а — 26 + 2с = 1, рис. 8.8(6),
а = 1/2, рис. 8.8(c).
(Есть три других вырожденных уравнения, которые возникают из конфигу-
t
t t
t
t 1
tit —
t
(а)
t 1 t
t I I —* t t I
I 1 1
t I I —* I t I
Рис. 8.8. Различные спиновые конфигурации на квадратной решетке, использу¬
емые для определения интенсивностей переворотов
раций, подобных изображенным на рис. 8.8, ио с переверну ты м центральным
спином.) Из этих условий следуют следующие интенсивности переворотов
wi = 2 [l ~ g Si 53 Sa + g Si 53 . (8.79)
aE(i) a,Psy£(i)
С этими интенсивностями переворотов можно определить эволюцию корреля¬
ционных функций. Например, комбинируя уравнения (8.50а) и (8.79), получим
уравнение
а€(г> а,/3,7С(г>
которое связывает односпиновую корреляционную функцию Si = (s^) с трехспи¬
новой корреляционной функцией Sapy = (saspSy). Поэтому нам нужны урав¬
нения для трехспиновой корреляционной функции Sapy. Эти уравнения содер¬
жат пятиспиновую корреляционую функцию, приводя к никогда не заканчиваю¬
щейся спирали. В общем случае эволюционные уравнения для корреляционных
функций имеют иерархическую, а не рекурсивную природу. Такие иерархиче¬
ские уравнения в общем случае не поддаются точному анализу, и поэтому глау¬
берова динамика спиновых переворотов в двух измерениях не решаема.
Ключевой чертой глауберовой динамики при нулевой температуре в раз¬
мерностях больше единицы является несохранение средней намагниченно¬
320
ДИНАМИКА СПИНОВ
сти. Математически, несохранение возникает из-за того, что сумма уравне¬
ний (8.80) по всем узлам (и ее обобщение на более высокие размерности)
не равна нулю. Интуитивно понять такое несохранение можно, рассматри¬
вая рост изолированной капли радиуса Л, состоящей из одной фазы, в море
противоположной фазы (рис. 8.9). Действие правила большинства в глау-
Рис. 8.9. Эволюция изначально квадратной капли в модели Изинга. Рисунок взят
из R. Cerf и S.Louhichi, Prob.Theory Rel.Fields 137, 379 (2007). Воспроизводится
с разрешения Р. Серфа.
беровой динамике приводит к возникновению эффективного поверхностного
натяжения, такого что радиус R(t) изолированной капли уменьшается как
R?(t) = Rq — at (непрерывное описание этого сжатия будет дано в разделе
9.3). В модели голосования сохранение намагниченности, наоборот, приводит
к тому, что изолированная капля становится более диффузионно размазан¬
ной и систематического сжатия не происходит (рис. 8.1).
Свойства модели Изинга-Глаубера на больших временах особенно инте¬
ресны. Когда изначально случайная конечная система линейного размера L
внезапно замораживается, будучи охлажденной до нулевой температуры, фи¬
нальное состояние фундаментальным образом зависит от пространственной
размерности. В одном измерении конечная система в конце концов достигает
полного упорядочения — основного состояния. В двух измерениях основное
состояние достигается с вероятностью р, строго меньшей 1, а с вероятно¬
стью 1 — р система приходит к конфигурациям, состоящим из четного числа
8.6 Глауберова динамика в высших размерностях
321
идеально ровных полос шириной > 2 (рис. 8.10)14. Эти полосатые состоя-
Рис. 8.10. (а) Метастабильная конфигурация на периодической прямоугольной
решетке, состоящая из шести горизонтальных полос; (Ь) метастабильная кон¬
фигурация на кубической решетке из 203 узлов с периодическими граничными
условиями. Самые светлые блоки показывают «мерцающие» спины, перевороты
которых оставляют систему в изоэнергетическом множестве. Воспроизводится
благодаря любезности Дж. Оледжарца
ния статичны и являются возможными финальными состояниями эволюции.
Полное число М этих метастабильных состояний очень велико, М y/N
(задача 8.15). В более чем двух измерениях основное состояние никогда не
достигается15, а полное описание структуры метастабильных состояний не из¬
вестно. Типичные метастабильные состояния могут рассматриваться как ана¬
лог минимальных поверхностей (рис. 8.10, а также см. непрерывный аналог
на рис. 9.4), для которых граница раздела между двумя фазами состоит из
14Мы всегда неявно подразумеваем, что начальная намагниченность то = 0. Если
то 0, то система в термодинамическом пределе всегда достигает основного состояния
со спинами, направленными по полю, при любом d > 2. Это утверждение не очевидно, но
существуют эвристические аргументы, а также численные свидетельства в его пользу.
15Под «никогда» мы подразумеваем, что вероятность достижения основного состояния
убывает крайне быстро с ростом L.
322
ДИНАМИКА СПИНОВ
участков как с положительной, так и с отрицательной кривизной, так что вся
граница статична. Неожиданно то, что финальное состояние — это не изоли¬
рованное метастабильное состояние, а связное изоэнергетическое множество,
в котором система бесконечно долго блуждает под действием глауберовой
динамики спиновых переворотов при нулевой температуре.
Пример 8.4. Угловая граница раздела. Угловая граница раздела на квадратной
решетке (рис. 8.11) — это, вероятно, простейший пример двумерной границы,
для которой эволюция, управляемая глауберовой динамикой, допускает точное
решение. Сначала угол находится в начале координат, так что спины в первом
квадранте направлены вниз, а все остальные — вверх. В первый момент только
угловой спин в узле (0,0) может перевернуться, потому что это единственный
спин с окружением с нулевой энергией. После того как он перевернулся, могут
перевернуться спины в узлах (1,0) и (0,1), а угловой спин в (0,0) может вер¬
нуться назад к исходной ориентации. Далее процесс продолжается по тому же
принципу: в любой момент некоторое число N спинов могут перевернуться, пе¬
рейдя в фазу большинства, и ровно N — 1 спинов может вернуться назад в фазу
меньшинства. Все эти перевороты сохраняют энергию, так что длина границы
остается постоянной. Более того, такая граница сохраняет свою целостность: об¬
разование капель или отделение капель от начальной границы невозможно. Эти
свойства делают задачу об угловой границе раздела решаемой.
Есть два типа динамики, которые зависят от магнитного поля:
Граница под действием внешней силы (слабое положительное поле 0 < Н <
2 J). В этом случае события ф —> ф происходят только в углах, а события ф —> ф
никогда не происходят. Например, на рис. 8.11 есть шесть мест, где может про¬
изойти переворот спина типа ф —> ф. Чтобы найти форму интерфейса, отобразим
спиновую динамику на асимметричный процесс с запретом (АПЗ), обсуждав¬
шийся в главе 4. Соответствие устанавливается за два шага: сначала мы разво¬
рачиваем угол вокруг начала координат на 7г/4 против часовой стрелки. Далее
проектируем единичные отрезки, направленные с северо-запада на юго-восток
на занятые узлы на горизонтальной оси, а направленные с северо-востока на
юго-запад на незанятые узлы (8.12). Один переворот спина соответствует за¬
мене участка границы раздела вида I на участок вида I. В эквивалентном
АПЗ это соответствует прыжку частицы вправо • о —» о •, который может про¬
изойти, только если соседний узел не занят. Поскольку все частицы, которым
разрешены прыжки, прыгают с одинаковыми интенсивностями, эволюция сов¬
падает с АПЗ.
В силу того, что угол между границей раздела и эквивалентным АПЗ равен
7г/4, событие переворота спина, происходящее в точке (х,у) на границе, отоб¬
ражается в точку z = х — у на наклонной линии. Наличие частицы в узле z
на линии соответствует тому, что высота границы в (х,у) уменьшается на 1.
Поэтому в непрерывном пределе наклон линии границы и плотность частиц в
соответствующем АПЗ связаны соотношением у'(х) = —n(z). Исходная угловая
граница раздела в спиновой системе соответствует тому, что в эквивалентном
8.6 Глауберова динамика в высших размерностях
323
Рис. 8.11. Угловая граница раздела в (а) начальном состоянии и (Ь) при t > 0.
Единственный спин, который может перевернуться в начальном состоянии, пока¬
зан в (а) жирной стрелкой. Эволюционирующая граница отделяет площадь St в
момент времени t. Среди спинов в (Ь), способных перевернуться в нулевом маг¬
нитном поле, спинов | (сплошные стрелки) всегда на один больше, чем спинов
f (пунктирные стрелки)
АПЗ полупрямая z < 0 полностью занята, n(z,t = 0) = 1 для г < 0, а полу¬
прямая z > 0 свободна, n(z,t = 0) = 0 для z > 0. Описав, как сглаживается
исходный узел в АПЗ, мы узнаем форму эквивалентной границы раздела.
В непрерывном пределе плотность частиц n(z, t) на прямой в АПЗ удовлетво¬
ряет уравнению типа Бюргерса
дп 9[п(1 — п)] _ д2п
dt + “ dz2'
(8.81)
которое мы раньше встречали в главе 4. В пределе большого времени диффу¬
зионным членом можно пренебречь, так как он дает второстепенный вклад по
сравнению с влиянием постоянного сноса. Решение уравнения (8.81) без диффу¬
зионного члена, которое было приведено в примере 4.3 раздела 4.3, дает плот¬
ность частиц
{1, z < -t,
|(l-f), \z\< t, (8.82)
0, z > t.
Из соотношения n(z) = —у'(х) получим выражение для положения точек гра¬
ницы
2/(ж, £) = f n(z, t)dz = /* n(z, t) dz. (8.83)
Jx—y Jmax(x-y-t)
324
ДИНАМИКА СПИНОВ
Рис. 8.12. Соответствие между угловой границей раздела, повернутой на 7г/4, и
АПЗ. Показан переворот спина и соответствующее ему событие в АПЗ
Вычисление этого интеграла приводит нас к неявному уравнению
(| [| — (х — 2/) + 5t(x ~ У)2]> к - 2/| < zg g^x
[О, х-у >t, V '
которое для 0 < х, у < t сводится к простому гиперболическому виду для формы
границы:
Vх + у/у = Vt. (8.85)
Вне этого диапазона граница остается иевозмущенной.
Граница раздела в модели Изинга (нулевое поле). Перевороты спинов 4 —> f и f —>
4 могут происходить с одной и той же интенсивностью для всех угловых спинов.
Поскольку угловых спинов 4 всегда на один больше, чем спинов | (рис. 8.11(b)),
движение границы подвержено постоянному малому сносу. Используя те же ар¬
гументы, что и для границы под действием силы, видим, что эволюция границы
эквивалентна симметричному процессу с запретами на линии с наклоном. Од¬
нако, как обсуждалось в главе 4, запреты не влияют на поведение плотности
частиц. Поэтому плотность частиц удовлетворяет обычному уравнению диффу¬
зии решение которого для начальных условий в форме ступеньки
есть
n(z, t) = -^= [ e~w2 dw = ^ erfc (-^=) , (8.86)
V^ Jz/VTi 2 \v4t/
где erfc(rr) — дополнительная функция ошибок. Хотя получить профиль плотно¬
сти частиц легко, преобразование его назад к форме границы с помощью урав¬
нения (8.83) не дает простого и явного результата, такого как (8.85). Тем не
менее, считая форму границы известной, можно явно вычислить некоторые ее
8.7 СПИН-ОБМЕННАЯ ДИНАМИКА
325
свойства: например, пересечение границы с диагональю у = х происходит при
8.7 Спин-обменная динамика
Как уже упоминалось в разделе 8.3, существует два фундаментальных класса
спиновых динамик: сохраняющие и несохраняющие намагниченность. Пер¬
вый класс подходит для описания сплавов, где два различных спиновых со¬
стояния соответствуют атомам двух компонент, из которых состоит сплав. В
области разделения на фазы, когда в сплаве образуются домены чистого ме¬
талла, естественна динамика, при которой атомы различных сортов меняют¬
ся местами. На спиновом языке эта эволюция соответствует обмену соседних
аитипараллельных спинов:
Эта эволюция, известная как спин-обменная динамика Кавасаки, точно со¬
храняет намагниченность при каждом событии обновления. Это точное со¬
хранение имеет далеко идущие последствия, которые станут понятнее далее
при обсуждении непрерывных теорий спиновой динамики в следующей главе.
Интенсивности переходов
Существует три типа событий обновления: увеличивающие энергию, умень¬
шающие энергию и энергетически нейтральные. Как показано на рис. 8.13,
энергетически нейтральные обновления происходят при одновременном пе¬
рескоке двух соседних доменных стенок. Эквивалентно, это происходит, ко¬
гда один спин, направленный вниз, находящийся в море спинов, направлен¬
ных вверх, меняется местами с соседним спином. Пока такая пара доменных
стенок остается изолирована от всех остальных доменных стенок, она сво¬
бодно перескакивает между соседними узлами решетки. Такие пары могут
рассматриваться как элементарные возбуждения в спиновой системе. Интен¬
сивность прыжков пары доменных стенок просто задает шкалу времени, так
что без потери общности можно положить ее равной 1/2, как в глауберо¬
вой динамике. Так как такие диффузионные перескоки не изменяют энергии,
они автоматически удовлетворяют условию детального равновесия. Тогда ин¬
тенсивности двух оставшихся событий обновления определяются из условия
детального равновесия. Поскольку спиновый обмен включает в себя взаимо¬
действия между четырьмя спинами — двумя, которые переворачиваются, и
326
ДИНАМИКА СПИНОВ
1/2
♦44 ♦
1/2
(1+У)/2
♦444
(1-у)/2
1 14 1
\\
//
V
А
♦ 144
144 *
♦ 14 *
1444
(а)
(Ь)
(С)
(d)
Рис. 8.13. Энергетически нейтральные события обновления (а) и (Ь), понижа¬
ющее энергию событие (с) и повышающее энергию событие (d) в динамике
Кавасаки в одном измерении. Переворачивающиеся спины показаны жирными
стрелками. Также показаны частицы, соответствующие доменным стенкам (•) и
интенсивности переходов для этих событий
двумя их соседями — интенсивности зависят от полной энергии трех связей,
соединяющих эти четыре спина. Условие детального равновесия имеет вид
— = — = exp(4/3J), (8.87)
W-1 Рз
где wq — интенсивность перехода из состояния с энергией q J, а рд — равно¬
весная вероятность этого состояния. Используя обозначения Глаубера W3 =
(1 + 7)/2 и w_i = (1 — 7)/2 для повышающих и понижающих энергию пере¬
ходов соответственно, получим такой же вид условия детального равновесия,
как а глауберовой динамике: = exp(4/3J) или 7 = th2/3J.
Чтобы определить интенсивности переходов, мы сначала должны обеспе¬
чить, чтобы спины г и г+1 были антипараллельны . Это условие выполняется
с помощью множителя (1 — SiSi+i)/2, равного +1, если два спина антипарал¬
лельны, и нулю в противном случае. Тогда вид интенсивности переворота
зависит от энергии взаимодействия между парами и и s^+i и 5^+2.
Интенсивность переворота должна быть симметричной функцией этих двух
энергий связи и должна быть пропорциональна соответственно (1+7)/2, 1/2,
и (1 — 7)/2, когда эти энергии имеют знаки —, -I—, ++. Эти условия при¬
водят к следующей интенсивности переходов
Wi(si,si+i) = I [l - (si-iSi + Si+isi+2)] X I(1 - SiSi+i). (8.88)
С такой интенсивностью переходов эволюция спиновых корреляционных
функций незамкнута. Односпиновые средние связаны с трехспиновыми,
8.7 Спин-овменная ДИНАМИКА
327
двухспиновые с четырехспиновыми и т. д. Поэтому мы снова наталкиваемся
на техническое препятствие, заключающееся в том, что уравнение движения
для определенной корреляционной функции генерирует бесконечную иерар¬
хию уравнений для корреляторов более высоких порядков. Требуются значи¬
тельные технические усилия и изобретательность, чтобы найти правильную и
разрешимую схему обрывания таких бесконечных иерархий, превращающую
их в конечный набор решаемых уравнений.
Фрустрация при нулевой температуре
Из-за сохранения намагниченности в динамике Кавасаки система, охлажден¬
ная до нулевой температуры, должна всегда застревать в метастабильном со¬
стоянии. Метастабильные состояния характеризуются тем, что каждая части¬
ца, соответствующая доменной стенке, отделена от других доменных стенок
более чем одним расстоянием между ближайшими соседями. Эквивалентно,
длина всех спиновых доменов — два или более параметра решетки. Число
таких конфигураций в системе длины L асимптотически растет как gL, где
д = (1 + л/б)/2 — золотое сечение. При нулевой температуре эти метаста¬
бильные состояния не дают системе достигнуть основного состояния. При
ненулевой температуре они просто замедляют приближение к равновесию.
Изучим теперь фрустрацию при нулевой температуре (разрешены толь¬
ко понижающие энергию переходы) для простейшего случая антиферромаг-
нитного начального состояния (рис. 8.14). Разница со случаем, когда также
t ы t.M.t H H.J.H
I t.{ I {.t | M H.J.M '
Рис. 8.14. Эволюция антиферромагнитного начального состояния под действием
понижающей энергию динамики Кавасаки. Спины, которые могут перевернуться,
выделены. Также показаны доменные стенки между соседними антипараллель-
ными спинами
328
ДИНАМИКА СПИНОВ
могут происходить сохраняющие энергию переходы (диффузия пар сосед¬
них стенок), невелика, однако первый случай легче рассматривать анали¬
тически. Полезно визуализировать эволюцию в терминах доменных стенок,
находящихся в узлах дуальной решетки. При нулевой температуре шаг спин-
обменного обновления динамики Кавасаки эквивалентен случайному выбору
трех находящихся друг за другом частиц-доменных стенок и удалению двух
внешних частиц. Такой шаг превращает любой триплет • • • в о • о. Теперь
для решения этой задачи используем инструментарий случайной последова¬
тельной адсорбции (см. раздел 7.1).
Пусть Ек вероятность того, что интервал из к узлов, расположенных один
за другим (на дуальной решетке), весь занят доменными стенками. При к > 3
эта вероятность эволюционирует согласно уравнению
= ~{к - 2)Ек - 2Ек+1 - 2Ек+2. (8.89)
Это уравнение отражает различные способы, которыми могут происходить
переходы • ••—>офои меняться число занятых интервалов длины к. Су¬
ществует к — 2 способов такого перехода внутри fc-интервала. Также есть
два способа такого перехода, который происходит с двумя узлами на границе
fc-интервала и одним узлом снаружи. В этом случае событие должно проис¬
ходить в занятом интервале длины к + 1. Наконец, существуют два способа
с одним узлом на границе и двумя узлами снаружи fc-интервала.
Сформулировав задачу в терминах эволюции занятых интервалов, при¬
меним методы, развитые в разделе 7.1, к решению уравнений (8.89). Сделаем
экспоненциальный анзац Ек = Ф(£) чтобы свести бесконечный на¬
бор уравнений (8.89) к одному уравнению (см. обсуждение, сопутствующее
уравнению (7.4))
= —2</>(е_* + е-2*). (8.90)
Для антиферромагнитных начальных условий дуальная решетка полностью
занята. Поэтому вначале Ек = 1, так что Ф(0) = 1. Интегрируя ((8.90)) с
такими начальными условиями, получаем вероятности интервалов для к > 2
Ek(t) = exp [—(/г — 2)t + e~2t + 2e-t — 3] . (8.91)
Поскольку две частицы-доменные стенки — исчезают при каждом собы¬
тии обновления, а такие события происходят с интенсивностью Е$, плотность
доменных стенок р = Ei удовлетворяет уравнению = — 2Ез. Используя
уравнение (8.91) для Е$ и интегрируя, получим плотность доменных стенок
p(t) = 1 — 2 f du exp Г—it + e~2u + 2e~u — 3] ,
Jo
(8.92)
8.7 Спин-обменная динамика
329
откуда финальная плотность покрытия равна pjam = р(оо) = 0,450898. От¬
метим также, что релаксация к плотности насыщения экспоненциальна по
времени
p(t) - pjam - е“3 е~*. (8.93)
Именно такую релаксацию и следовало ожидать из-за связи со случайной
последовательной адсорбцией на решетке.
Укрупнение при бесконечно малой температуре
Хотя при нулевой температуре одномерная цепочка с динамикой Кавасаки
быстро достигает насыщенного состояния, при любой ненулевой темпера¬
туре система приходит к равновесному состоянию независимо от того, на¬
сколько мала температура. Поскольку равновесная корреляционная длина
£ = [ln(coth/3J)]_1 ~ e2$J (см. уравнение (8.56)) расходится, когда темпера¬
тура приближается к нулю, можно положить температуру достаточно малой,
для того чтобы корреляционная длина была много больше размера системы.
Тогда равновесное состояние будет состоять из единственного домена с фер¬
ромагнитным упорядочением, так что эволюция напоминает укрупнение при
нулевой температуре.
Сильное разделение временных масштабов между увеличивающими энер¬
гию и всеми остальными событиями обновлений делает возможным элегант¬
ное описание эволюции доменов в терминах экстремальной динамики. По¬
скольку интенсивность увеличивающих энергию событий равняется e“4^J,
типичное время на одно событие есть т = е4^*7. Примем т за элементар¬
ную единицу времени. В таких единицах времени события, увеличивающие
и сохраняющие энергию, происходят мгновенно. Начиная с начального со¬
стояния, система мгновенно достигает фрустрированного состояния, в кото¬
ром дальнейшие обновления как с понижением, так и сохраняющие энергию,
невозможны. По прошествии времени т (в среднем) происходит повышаю¬
щее энергию событие, за которым следует взрывоподобный каскад энергети¬
чески нейтральных и понижающих энергию событий, в результате которого
система достигает нового фрустрированного метастабильного состояния. Эта
последовательность из повышающих энергию обновлений, за которыми сле¬
дуют взрывные каскады комплементарных им событий, продолжается, пока
конечная система не достигнет состояния с одним доменом. Как мы сейчас
покажем, эта динамика приводит к росту типичного домена со временем по
закону Z1/3. Одна из приятных черт динамики Кавасаки в одном измерении —
то, что укрупнение по закону i1/3 возникает очень простым образом. В еле-
330
ДИНАМИКА СПИНОВ
дующей главе мы увидим, что вывод закона укрупнения t1/3 из непрерывной
картины, напротив, требует значительных усилий.
При некотором промежуточном, но достаточно большом времени система
достигает состояния с низкой энергией, которое состоит из перемежающихся
доменов с характерным размером t. Последующая эволюция при низкой тем¬
пературе управляется редкими увеличивающими энергию событиями, требу¬
ющими времени т = e^J\ при которых пара доменных стенок возникает
рядом с существующей изолированной доменной стенкой. Когда образуется
такой триплет, две соседние стенки в нем могут свободно диффундировать,
как связанная пара доменных стенок, пока им снова не встретится изолиро¬
ванная доменная стенка. Это может быть как первая доменная стенка, остав¬
ленная позади, когда дублет начал диффундировать, так и стенка на следу¬
ющей границе раздела. В последнем случае можно рассматривать спин как
движущийся от одной границе к другой, так что размер одного домена уве¬
личивается на единицу, а другого становится на единицу меньше (рис. 8.15).
Определение вероятности того, что спин дойдет до соседней границы разде-
111f(им *i* 1111
i t t t..i i i i Tffi 11 t..i
Рис. 8.15. Эффективная доменная диффузия в динамике Кавасаки при беско¬
нечно малой температуре. Спин (в пунктирном овале) отделяется от домена
размера j и с вероятностью 1/к в конце концов достигает правого края соседне¬
го домена размера к. Конечный результат диффузии спина через домен размера
к — движение этого домена как целого на один шаг решетки влево
л а, — это задача о первом посещении, разобранная в разделе 2.5. После того
как спин отделился, он находится на расстоянии 1 от исходной границы и
расстоянии к — 1 от другой границы. Поскольку спин диффундирует почти
свободно16, он с вероятностью l/(2fe — 2) в конце концов достигает другого
края, а с вероятностью 1 — l/(2fc — 2) возвращается к начальному положе¬
нию. Следовательно, вероятность того, что домен размера к прыгает на один
16Когда спин находится рядом с его начальным положением или другим краем домена,
его прыжки не симметричны (см. задачу 8.17).
8.7 Спин-обменная динамика
331
шаг решетки, равна к *, что соответствует коэффициенту диффузии домена
1){к) - АГ1.
Таким образом, в пределе низких температур спиновая динамика отоб¬
ражается на эффективные изотропные перескоки целых доменов на один
шаг вправо и влево17 (рис. 8.15). Однако домены длины 1 исчезают все¬
гда в тот момент, когда один из их соседних доменов прыгает по направ¬
лению к ним, так что четыре соседних домена сливаются, превращаясь в два
(рис. ??). Конечный результат последнего процесса — укрупнение доменов.
,11111 l„t„l * I I l„t t t t,
alb c
,1111111111 l,,t 1111,
a+b <+l
Рис. 8.16. Процесс слияния доменов
Оценим скорость такого укрупнения с помощью скейлииговых аргументов.
Поскольку каждый домен совершает случайное блуждание, всегда, когда до¬
мен продиффундировал на расстояние порядка его длины, возникает коалес-
ценция. При этом домен характерной длины £ растет на величину Д/?, которая
также порядка тогда как время между событиями коалесценции порядка
At ~ т€2/Р(^). Поэтому имеем
Д€ £ 1
At ~ r£2/D(£) ~ rf2'
так что домены растут как
€ ~ (8.94)
Традиционно определяют динамический индекс г, задающий рост харак¬
терного масштаба длины при укрупнении через £ ~tz. Для иеконсервативной
глауберовой динамики и консервативной динамики Кавасаки динамический
17Для домена длины 2 наблюдается аномалия, которая не важна для целей данного
обсуждения.
332
ДИНАМИКА СПИНОВ
индекс равен
1/2, неконсервативная динамика.
1/3, консервативная динамика.
(8.95)
Хотя мы вывели эти результаты в одном измерении, они справедливы для
всех пространственных размерностей. Законы сохранения накладывают силь¬
ные ограничения на неравновесную динамику.
8.8 Динамика кластеров
До сих пор мы обсуждали локальную глауберову динамику переворотов от¬
дельных спинов и спин-обменную динамику Кавасаки. Несмотря на их идеа¬
лизированный характер и благадаря их связи с эволюцией реальных систем,
эти правила дали основу для множества численных исследований укрупнения
и динамики критических явлений. Однако динамика, которая основана на пе¬
реворотах отдельных спинов или двух соседних спинов, неэффективна для
численных расчетов. Из-за этой неэффективности динамика значительно за¬
медляется вблизи критической точки. Для смягчения этих трудностей были
предложены динамические правила, в которых целый подходящим образом
определенный кластер спинов переворачивается одновременно, в то же время
сохраняя правильные равновесные свойства. Благодаря их эффективности,
такие кластерные алгоритмы интенсивно используются для численного мо¬
делирования равновесного поведения моделей статистической механики мно¬
гих тел и теорий поля на решетке. Алгоритмы Сведсена-Ванга и Вольфа —
одни из первых и самых известных примеров кластерной динамики.
Как мы увидим, кинетические уравнения, описывающие эти алгоритмы,
решаются точно в одном измерении. Эти два примера служат прекрасной
иллюстрацией эффективности подхода основных кинетических уравнений.
Алгоритм Сведсена—Ванга
В алгоритме Сведсена-Ванга случайно выбирается целый домен однонаправ¬
ленных спинов, и все его спины переворачиваются одновременно, как пока¬
зано на рисунке:
• • • tt-UIUtt —> • • • tttttwt • • • •
8.8 Динамика кластеров
333
При каждом обновлении энергия всегда убывает, и это событие сопровож¬
дается исчезновением двух доменов, так что их плотность р убывает в соот-
нстствии с уравнением = — 2р. Здесь без потери общности мы принимаем
вероятность переворота равной 1. Для антиферромагнитиых начальных усло¬
вий имеем р(0) = 1, так что плотность доменов равна p(t) = e~2t. Поскольку
средняя длина домена (€) обратна плотности доменов, получим (£.} = e2t.
Когда эта средняя длина становится порядка размера системы L, динами¬
ка завершается. Из этого критерия время достижения основного состояния
~lnL.
Теперь рассмотрим распределение длины доменов. Определим плотность
ее доменов длины £. Когда домен переворачивается, он сливае гея с двумя со¬
седними доменами, так что его длина равна длине трех исходных доменов. В
результате такой трехчастичной агрегации се эволюционирует в соответствие
с уравнением
= -$се + 52 сз Ск' (8-96)
? i+j+k=Z
Слагаемое —Зс^ отвечает за исчезновение домена длины t при перевороте это¬
го домена или одного из двух соседних доменов. Второе слагаемое описывает
увеличение щ из-за переворота домена длины J, который при этом сливается с
двумя соседними доменами с длинами г и к, где £ = i+j+k. Вероятность тако¬
го слияния равна вероятности с^с^/р2 того, что домен длины j лежит между
доменами длин гик. Заметим, что ни вновь созданные домены не влияют на
своих соседей, ни соседи не оказывают влияния на них. Поэтому если сначала
домены не скоррелированы, они и останутся нескоррелированным и. 'Гак как
не возникает пространственных корреляций, уравнение (8.96) точное.
Введя вероятность Pg = c#Jр существования домена длины Z7, можно по¬
лучить уравнение в более ясном виде. По построению имеем ’ = 1- Вы¬
ражая уравнение (8.96) через и используя уравнение движения для плот¬
ности р = — 2р, находим уравнение эволюции для Р^
dPt
dt
-Ре+ £ PiPjPk.
i+j+k=£
(8.97)
Как и во многих рассмотренных примерах, удобно ввести производящую
функцию Т(г) = 52^7^-И, которая упрощает свертку в члене прихода и
приводит уравнение (8.97) к виду = —У + У3. Разложив 1/(У3 — У) на
простейшие дроби, получим уравнение для которое может быть проинте¬
334
ДИНАМИКА СПИНОВ
грировано элементарными методами, и интегрирование дает решение
У0(г)е~*
^l-T0(z)2(i_e-2t)’
(8.98)
где Уо(^) — это начальная производящая функция.
Для простого случая антиферромагнитных начальных условий все на¬
чальные домены имеют длину 1, а соответствующее начальное условие для
производящей функции — это То(^) = 2. Теперь разложим производящую
функцию в (8.98) по степеням z и получим распределение числа доменов:
(“) е_‘- (8'99)
Заметим, что такая производящая функция приводит к доменам, которые
имеют только нечетные длины. Из этого распределения видно, что сред¬
няя длина домена растет экспоненциально со временем, (/?) = е2*, как и
было найдено раньше. Наконец, используя формулу Стирлинга, получим,
что асимптотическое распределение длины стремится к скейлинговому ви¬
ду Ре e~2t Ф(^е“2<) со скейлинговой функцией
Ф(т) =
(8.100)
В перемасштабированных единицах в распределении доминирует сингуляр¬
ность в числе малых доменов.
Алгоритм Вольфа
В кластерном алгоритме Вольфа случайно выбирается спин, и домен, кото¬
рому он принадлежит, переворачивается. Эта процедура ускоряет динамику
сильнее, чем алгоритм Сведсена-Ванга, так как обновление больших кла¬
стеров более вероятно. Схематически алгоритм Вольфа представляется как
тш • • • Htt
так что переворачивающийся домен опять сливается со своими соседями.
Так как каждый спин выбирается случайно, приращения времени, ассоции¬
рованные с любыми обновлениями, одинаковы. Поэтому плотность доменов
убывает с постоянной скоростью р = —2. Следовательно, p(t) = 1 — 2t, так
8.8 Динамика кластеров
335
что полная система превращается в единственный домен за конечное время
1/2. Соответственно, средняя длина домена (€) = (1 — 2t)_1 расходится
При t —> tc.
’Эволюция распределения длины домена описывается прямым обобщенн¬
ом уравнения (8.97)
^ = -€Р€+ 52 jPiPjPk. (8.101)
Производящая функция У(з,£) = теперь удовлетворяет уравнению
<8'102’
Чтобы его решить, мы сначала запишем линейные члены в виде одной про¬
изводной, перейдя от переменных (£, z) к переменным (т,у) = (£,£ — In г)
дт ду
(8.103)
Теперь применим такую же процедуру, как при решении агрегации с мульти¬
пликативным ядром (см. обсуждение, ведущее к уравнению (5.43) в главе 5).
Вдоль характеристической линии, определяемой уравнением = СР2, СР —
константа. Поэтому у = СР2т + (7(СР) или, эквивалентно,
t-lnz = CP2f + G(CP),
(8.104)
где <7(СР) определяется начальными условиями. Для антиферромагпитного
начального состояния имеем ‘Pq(z') = z, так что (7(СР) = — In У. Подставляя
6'(СР) = — 1пСР в (8.104) и экспоненцируя, получим следующее неявное урав¬
нения для производящей функции
г = (8.105)
Распределение длины Pg — это не что иное, как коэффициент разложения
функции CP(z) степени Формально этот коэффициент можно записать в
виде контурного интеграла
=-f
2m J
Pi
dz
и, заменив переменную интегрирования z на СР, воспользоваться формулой
инверсии Лагранжа (см. врезку на стр. 181 в главе 5). Это дает
ад, . 1
^+i az - 2m
e~et
2m
CP dz
г(СР)^1 dCP
,£P2t
CP*
2t
7e~2
dV,
(8.106)
336
ДИНАМИКА СПИНОВ
где мы использовали формулу = е* *р2< (1 — 2‘J>2t) под интегралом. Теперь
находим вычеты, разлагая е^2* в степенной ряд и оставляя в подинтеграль¬
ном выражении только коэффициенты при j. Поскольку степенной ряд четен
по У, только Pg нечетных значений (, не равны нулю, и мы находим
Ре = e~tl
“(W 2‘
После несложных вычислений получим формулу распределения длины до¬
менов
P2W (!) = (2€+€,1)£ " te (8.107)
8.9 Ссылки
Несмотря на центральную роль, которую кинетические спиновые системы
сыграли в неравновесной статистической физике, нет книг для физиков, по¬
священных глауберовой динамике или связанным с ней микроскопическим
моделям. Два полезных обзора об основной феноменологии неравновесных
спиновых систем, преимущественно с точки зрения непрерывного описания,
даны в [159, 160]. Исследования модели голосования были начаты в теоре¬
тико-вероятностном сообществе и главная ссылка — это монография Лиггета
[161]. Численные исследования, показавшие отсутствие поверхностного на¬
тяжения в модели голосования, как показано на рис. 8.1, появились в [162].
Точное решение модели голосования с помощью техник из неравновесной ста¬
тистической физики представлено в [163, 164]. Хорошая начальная точка для
изучения глауберовой динамики — это великолепная статья самого Глаубера
[165]. Ссылки [166, 167] делают следующий за Глаубером шаг и анализируют
корреляционные функции более высоких порядков — предмет, которого мы
коснулись в примере 8.1. Временная эволюция распределения длины доменов
в цепочке Изинга-Глаубера при нулевой температуре до сих пор не известна
во всех подробностях, но эта интригующая проблема кажется, в конце кон¬
цов, решаемой. Однако несколько главных свойств этого распределения было
установлено с помощью приближения независимых интервалов [168] и точ¬
ных методов [169]. Приближение независимых интервалов полезно, когда мы
имеем дело с задачами многих тел в одном измерении и иногда даже является
асимптотически точным [170].
Эволюция модели Изинга-Глаубера при нулевой температуре и явление
замораживания в метастабильное состояние изучались в [171, 172]. Точная
8.10 Задачи
337
эволюция одной границы раздела по правилам глауберовой кинетики, такая
как задача с углом, была описана Ростом [173] с помощью техники, похо¬
жей на используемую здесь. Дополнительный материал о сжатии квадратной
капли можно найти в [174-176]. Спин-обменная динамика, явно сохраняющая
намагниченность, была введена Кавасаки [177]. В ссылке [178] построена кар¬
тина укрупнения доменов по закону ti/3
при низкотемпературной динамике
Кавасаки. Идея радикального ускорения численного моделирования кинети¬
ческой модели Изинга с помощью переворотов коррелированных групп спи¬
нов была сформулирована Сведсеном и Вангом [179], а соответствующая ди¬
намика Вольфа предложена в [180]. Обзор общей темы ускорения алгоритмов
численного моделирования кинетической модели Изинга дан в [181]. Динами¬
ки Сведсена-Ванга и Вольфа для цепочки Изинга обсуждались в [182, 183].
8.10 Задачи
8.1 Рассмотрте модель голосования в одном измерении.
(a) Предположите, что начальное состояние состоит из двух участников го¬
лосования с мнением +1 в море «иеопределившихся» участников голосо¬
вания, а именно тех, которые могут иметь одно из двух мнений с равной
вероятностью: S(x,t = 0) = £ж,-1 + £®д.
i. Найдите S(x,t) для всех целых х.
й. Покажите, что 5(0,t) = 2e_t/i(t). Пользуясь определением функ¬
ции Бесселя Ii(t), докажите справедливость (физически очевидно¬
го) неравенства 5(0, t) < 1.
(b) Теперь рассмотрите «дипольные» начальные условия, 5(ж, t, = 0) = <5х.д —
5Xi-1, а именно, один участник голосования с мнением +1 и один с мне¬
нием —1 в море иеопределившихся участников голосования. Для таких
начальных условий покажите, что
5(я,г) = ^е-4Ш.
С
8.2 Используйте корреляционную функцию (8.12)для модели голосования в кри¬
терии консенсуса (8.15), чтобы вывести асимптотические результаты из (8.16).
8.3 В этой задаче рассматривается точное решение для парной корреляционной
функции модели голосования в произвольной пространственной размерно¬
сти d.
(a) Выведите ведущую асимптотику (8.23).
(b) Покажите, что в пределе большого времени интенсивность источника
изменяется в соответствии с уравнением (8.25).
338
ДИНАМИКА СПИНОВ
(с) Завершите вывод уравнения (8.27). Вам может понадобиться вычислить
интегралы вида
[ е~х1о(х^х, f e~xIi{x)dx, f е“2я70(я) 1\{х) dx.
Jq Jq Jq
Для этих вычислений могут быть полезны следующие интегральные
представления:
1 /»27Г -| /»27Г
Ш = —]о excosgdq, I1(x) = —J cosqeXCOS4 dq.
8.4 Исследуйте динамику Изига-Глаубера в приближении среднего поля. Пусть
число спинов будет конечным но очень большим.
(a) Для динамики при нулевой температуре найдите вероятность Р/и(^)
иметь М спинов вверх и N — М спинов вниз.
(b) Найдите Рм(^) для критической динамики.
(c) В низкотемпературном режиме (/Зс < /3 < оо) распределение Рм(£) имеет
два пика ширины порядка y/N вокруг М± = | А(1 ± Шоо). Система
проводит почти все время около одного из пиков, но случайно переходит
из одного пика в другой. Оцените время перехода.
8.5 Рассмотрите динамику Изинга-Глаубера при нулевой температуре в одном
измерении с антиферромагнитным начальным состоянием.
(a) Вычислите парную корреляционную функцию Gk(t).
(b) Проверьте, что плотность доменных стенок дается формулой (8.60).
(c) Покажите, что плотность дублетов доменных стенок равна
Р2 = e“2t[/o(2t) — Л (2t)].
Проверьте, что ее асимптотическое поведение то же самое, что и для
нескоррелированных начальных условий (8.61).
8.6 Рассмотрите одномерную модель Изинга-Глаубера (с то).
(a) Напишите уравнения эволюции для трехспиновой корреляционной функ¬
ции (siSjSk), где г < j < fc, а в остальном произвольны.
(b) Проверьте (здесь важны начальные условия), что решение этих уравне¬
ний тривиально: (SiSjSk) = 0.
(c) Напишите уравнения эволюции для четырехспиновой корреляционной
функции (siSjSkSe), Tp$i<j<k<i.
(d) Проверьте, что четырехстпиновую корреляционную функцию можно вы¬
разить через парную корреляционную функцию:
{siSjSkSz} = (siSj)(skSt) + (siSt^SjSk) - (siSk)(sjSe).
8.10 Задачи
339
(е) Покажите, что предыдущая формула сводится к (8.63)для четырех со¬
седних спинов.
8.7 Покажите, что плотность доменных стенок р и плотность дублетов доменных
стенок р2 связаны соотношением р = —2р2- Проверьте, что плотности (8.59) и
(8.61) согласуются с р = —2р2-
8.8 Опишите асимптотическое поведение плотности триплетов доменных стенок,
определенной в уравнении (8.62). С помощью эвристических аргументов объ¬
ясните, почему и рз, и (рг)2 убывают как £”3.
8.9 Предположите, что модель Изинга снабжена динамикой, определенной в урав-
нении(8.46) с параметрами = 2,5 = 1.
(a) Покажите, что эта динамика соответствует нулевой температуре.
(b) Проверьте, что и повышающие энергию, и понижающие энергию перево¬
роты в такой динамике запрещены.
(c) Покажите, что система попадает в насыщенное состояние, где расстояния
между соседними доменными стенками больше, чем шаг решетки.
(d) Отобразите спиновую эволюцию на процесс случайной последователь¬
ной адсорбции. Покажите, что аитиферромагнитное начальное состояние
соответствует пустой системе, так что финальную плотность доменных
стенок можно извлечь из результатов главы 7.
(e) Вычислите финальную плотность доменных стенок в случае, когда на¬
чальное состояние нескоррелировано.
8.10 Рассмотрите цепочку Изинга в ненулевом магнитном иоле с глауберовой ди¬
намикой при нулевой температуре. Найдите плотность п доменов со спинами
вниз для начального состояния с перемежающимися доменами спинов вверх
и вниз одной и той же длины L.
8.11 Стартуя с основного кинетического уравнения (8.73), проверьте, что полная
плотность доменов р = Рь удовлетворяет уравнению (8.71) и полная длина
доменов сохраняется к = 0.
8.12 Найдите распределение числа доменов в модели Поттса с глауберовой дина¬
микой при нулевой температуре. Подсказка: Р\ заменяется на Pi/(g — 1) в
уравнении (8.73).
8.13 Для модели Изинга на квадратной решетке при положительной температуре
покажите, что интенсивность переворотов спинов может быть записана в виде,
похожем на (8.79), с коэффициентами
th(2/3J) + | th(40J) и th(2j8J) - | th(40J)
4 8 4 8
вместо 3/8 и 1/8.
340
ДИНАМИКА СПИНОВ
8.14 Обобщите вывод уравнения (8.79) и выведите интенсивность переворотов спи¬
на в модели Изинга на кубической решетке (d = 3) с глауберовой динамикой
при нулевой температуре.
8.15 Рассмотрите модель Изинга на квадратной решетке L х L. Для свободных
граничных условий вычислите полное число «полосатых» состояний, которых
система может достичь в результате глауберовой динамики при нулевой тем¬
пературе. (Учтите: Ответ связан с числами Фибоначчи.) Также оцените со¬
ответствующее число «полосатых» состояний для периодических граничных
условий.
8.16 Исследуйте модель Изинга с динамикой Кавасаки при нулевой температуре.
(a) Напишите уравнение эволюции для среднего спина Si в узле г.
(b) Покажите, что корреляционные функции подчиняются бесконечной ие¬
рархии уравнений.
(c) Найдите плотность доменных стенок для случайных начальных усло¬
вий. Сравните ваши результаты с результатами из уравнения (8.92) для
антиферромагнитиых начальных условий.
(d) Найдите число замороженных конфигураций.
8.17 Рассмотрите цепочку Кавасаки - Изинга при нулевой температуре. Рассмотри¬
те домен спинов вверх длины L, который содержит единственный спин вниз
в положении х. Проделав следующие шаги, вычислите вероятность выхода
Е(х), т. е. того, что этот диффундирующий спин вниз достигнет правой гра¬
ницы, не касаясь левой границы:
(a) Найдите уравнения, которым удовлетворяют вероятности выхода, уделяя
особое внимание случаям я = 1 и ж = L - 1.
(b) Решите эти уравнения и покажите, что Е(х) = (2х — 1)/(2L — 2) для всех
0 < х < L.
8.18 Рассмотрите динамику Сведсена-Ванга при нулевой температуре для модели
Поттса с q = оо, в которой могут возникать только события, понижающие
энергию. В этом случае переворот домена приводит к его слиянию с соседними
доменами. Найдите плотность доменов и распределение их длины.
Глава 9
УКРУПНЕНИЕ
В предыдущей главе мы обсуждали кинетику разделения фаз или укрупне¬
нии доменов в кинетической модели Изинга после закалки с переходом из од¬
нородной высокотемпературной фазы к двухфазному низкотемпературному
режиму. Ввиду сложности результирующего процесса укрупнения значитель¬
ные усилия были направлены на построение непрерывных и более доступных
дли аналитического описания теорий укрупнения. Хотя в такой непрерывной
формулировке потеряна прямая связь с индивидуальными спинами, непре¬
рывный подход дает много новых сведений, которые трудно получить из
описания на уровне индивидуальных спинов.
9.1 Модели
Мы неявно предполагаем параметр порядка скалярным, если обратное не
указано явно. В общем случае мы будем иметь ввиду магнитные система¬
ми и будем пользоваться терминологией таких систем. Это дань традиции, а
но указание на основную область применения укрупнения. Есть существен¬
ная разница между неконсервативной и консервативной динамиками, и мы
начинаем с описания характерных моделей для этих двух динамик.
Нсконсервативная динамика
Основные составляющие неконсервативной динамики:
• Основная переменная — это непрерывный огрубленный параметр по¬
рядка ra(x,t) = средняя намагниченность в блоке линейного
размера I с центром в х, заменяющая бинарную переменную модели
342
УКРУПНЕНИЕ
Изинга а = ±1. Здесь, для того чтобы иметь плавно меняющуюся огруб¬
ленную намагниченность на масштабе большем €, размер (. ррлжея быть
много больше шага решетки а и много меньше размера системы. Это
огрубление применимо во временном диапазоне, в котором типичный
размер домена велик по сравнению с параметром решетки.
• Термодинамика системы описывается огрубленным функционалом сво¬
бодной энергии Ландау
F[m(x)] = У |Vm(x)|2 + У(тп(х)) dx, (9.1)
где потенциал V(m) имеет два минимума, соответствующих равновес¬
ным состояниям. Стандартный пример — это V(т) = % (1—т2)2 с двумя
вырожденными минимумами.
• Последний шаг построения огрубленного описания также феноменоло¬
гический: мы предполагаем, что параметр порядка меняется со ско¬
ростью, пропорциональной локальной термодинамической силе х ,
функциональной производной F по отношению к т в точке х. Мы рас¬
сматриваем сильно демпфированную динамику: математически в урав¬
нении движения нет второй производной по времени. Это предполо¬
жение эквивалентно пренебрежению инерцией. Включив коэффициент
пропорциональности в масштаб времени, мы получаем нестационарное
уравнение Гинзбурга-Ландау (НУГЛ)
<9-2’
которое является одним из главных уравнений, описывающих укрупне¬
ние.
Важно помнить о некоторых аспектах НУГЛ:
1. Хотя вид (9.1) огрубленной свободной энергии интуитивно ожидаем (он
сочетает теорию среднего поля Ландау с вкладом низшего порядка от
пространственного изменения параметра порядка), невозможно выве¬
сти уравнение (9.1) и НУГЛ из первых принципов, стартуя с микроско¬
пических спиновых моделей
2. НУГЛ — чисто диссипативное уравнение, т. е. для изменения свободной
энергии как функции времени имеем
dF_ [№дт, __ Г (SF\2
dt J Sm dt X J
dx < 0.
9.1 Модели
343
Поэтому система, описываемая НУ ГЛ, спускается по градиенту свобод¬
ной энергии, пока не достигнет потенциального минимума.
3. НУГЛ в виде (9.2) применимо при нулевой температуре. При положи¬
тельных температурах к уравнению (9.2) должен быть добавлен член
с шумом, интенсивность которого растет с температурой. Поэтому в
более общем случае НУГЛ — это нелинейное стохастическое уравнение
в частных производных. Ниже критической температуры динамическое
поведение в основном универсально (это часть центральной догмы, упо¬
мянутой в главе 8), и поэтому мы можем сосредоточиться иа динамике
при нулевой температуре.
d. При нулевой температуре НУГЛ — это детерминистическое уравнение.
В отличие от него описание Изинга-Глаубера остается стохастическим
при нулевой температуре.
5. НУГЛ можно интерпретировать как реакционно-диффузионный про¬
цесс. Например, для потенциала V(m) = j (1 — га2)2 НУГЛ имеет вид
= V2ra + 2га(1 — га2). (9.3)
Если мы рассматриваем га как плотность, то это уравнение описыва¬
ет эволюцию диффундирующей популяции частиц, которые порожда¬
ют новые частицы А —> 2 А и подвержены трехчастичной коалесцен¬
ции, ЗА —> А (альтернативно процесс ухода может быть аннигиляцией
ЗА —> 0). В этой реакции плотность эволюционирует в соответствии с
уравнением = 2га(1 — га2), у которого есть неустойчивая неподвиж¬
ная точка га = 0 и устойчивая неподвижная точка в т = 1. Когда
диффузия включена, результирующее уравнение движения (9.3) опи¬
сывает инфильтрацию стабильной фазы высокой плотности (га = 1) в
область низкой плотности (га = 0). Фактически, уравнение (9.3) — это
один из примеров1 из множества саморегулируемых реакций вида
^ = V2m + /(m), (9.4)
где /(0) = /(1) = 0 и /(га) имеет один максимум на отрезке [0,1].
Эта интерпретация, однако, требует оговорки. Для реакционно-диффу¬
зионных процессов га представляет плотность, которая должна быть
1 Самый известный из таких примеров, уравнение Фишера-Колмогорова-
Петровского-Пискунова (ФКПП), возникает для /(то) = то(1 — то). Этот пример
будет обсуждаться в главе 13.
344
УКРУПНЕНИЕ
положительна. В то же время в НУГЛ скалярный параметр порядка т
может быть отрицательным. Тем не менее, математическая эквивалент¬
ность реакционно-диффузионным процессам полезна в качестве интуи¬
тивного ориентира для вывода результирующей феноменологии.
Консервативная динамика
В системах двухкомпонентных сплавов естественный параметр порядка -
разность концентраций составляющих элементов. По построению параметр
порядка сохраняется в изолированном куске материала. Поэтому, чтобы
учесть это сохранение, необходима динамика, отличающаяся от НУГЛ. На
уровне феноменологии мы ищем эволюционное уравнение, которое гаранти¬
рует выполнение уравнения непрерывности для потока атомов каждого эле¬
мента сплава
дт „ ,
8r + V'J = °’
(9.5)
которое явным образом обеспечивает сохранение параметра порядка. Заме¬
тим, что мы снова рассматриваем сильно демпфированную динамику. В урав¬
нении (9.5) вектор потока J должен зависеть от параметра порядка через
свободную энергию (9.1). Простейший выбор, одновременно и консерватив¬
ный, и включающий градиентный ток — это J ~ — V^. Мы снова включаем
коэффициент пропорциональности в масштаб времени и получаем уравнение
Кана-Хилларда (КХ)
дт
~dt
v2Sr = -v2[V2m-V»],
Sm
(9-6)
которое играет ту же роль для консервативной динамики при нулевой тем¬
пературе, что и НУГЛ для неконсервативной динамики.
В виде, данном в (9.6), эволюционное уравнение КХ — детерминистиче¬
ское. Это означает, что мы имеем дело с системой при нулевой температу¬
ре. Чтобы феноменологически смоделировать поведение при положительной
температуре, так же как в НУГЛ, в правую часть уравнения нужно доба¬
вить (ланжевеновский) член с шумом. Как отмечено в центральной догме
в начале предыдущей главы, этот добавочный член не должен качественно
менять динамическое поведение, пока температура находится ниже критиче¬
ской температуры Тс.
Обычно начинают с начальной температуры Ti = оо, при которой система
полностью разупорядочена, и замораживают систему до Tf = 0. Огрубленно
9.2 Свободная эволюция
345
*тн неупорядоченные начальные условия имеют вид
(га(х, 0)) = 0, (га(х, 0) т(х', 0)) = 5(х — х'). (9.7)
Пиша цель — определить поведение решений детеминистических уравнений
НУГЛ и КХ с такими случайными начальными условиями. В настоящее вре¬
мя достоверно установлено, что на больших временах из решений таких урав¬
нений получается масштабно-инвариантная укрупненная доменная мозаика.
Данная морфология (статистически) не зависит от времени, если перемас¬
штабировать все длины на характерный размер кластера £(£), который ал-
И’браически растет со временем. Для систем со скалярным параметром по¬
рядка этот характерный масштаб длины обычно записывается как L(t) ~ tz,
где z — динамический индекс, величина которого (как и в (8.95)) равна
'l/2 (НУГЛ);
Ч/З (КХ).
(9.8)
Существование такого универсального динамического индекса, для которого
единственная важная черта — сохранение или несохраиепие параметра по¬
рядка, — это один из краеугольных камней центральной догмы.
0.2 Свободная эволюция
Теперь используем скейлинг, чтобы упростить описание динамики. Хотя не¬
оспоримые факты свидетельствуют в пользу скейлинга, его выполнение дока-
1ШЮ только для НУГЛ в одном измерении и для специальных микроскопиче¬
ских моделей, таких как одномерная модель Изинга-Глаубера и п-векториая
модель с п = оо. Поэтому возникновение скейлинга в НУГЛ и уравнении
КХ служит еще одним подтверждением этого факта, несмотря на то, что
рассматриваемые примеры сильно идеализированы. Двигаясь в этом направ¬
лении, рассмотрим простейший пример, в котором потенциал равен нулю,
V(m) = 0. Тогда динамическое уравнение сводится к уравнению диффузии
= V2ra для неконсервативной динамики параметра порядка и к уравне¬
нию бидиффузии = —V4m для динамики, в которой параметр порядка
сохраняется. В этих двух примерах анализ размерностей предполагает суще¬
ствование единственного растущего масштаба длины: L(t) t1/2 (НУГЛ) и
b(t) ~ t1'4 (КХ)2.
Если спиновая система вначале находится в случайном состоянии, задава¬
емом уравнением (9.7), то глобальная намагниченность остается нулевой на
2 См. дополнительное обсуждение анализа размерностей и скейлинга в разделе 1.1.
346
УКРУПНЕНИЕ
протяжении всей эволюции. Поэтому для изучения природы укрупнения нам
нужна двухточечная корреляционная функция; мы уже встречались с той
же проблемой при изучении модели голосования и модели Изинга-Глаубера
в предыдущей главе. Чтобы охарактеризовать доменную структуру в двух
различных точках пространства-времени, определим двухточечную корреля¬
ционную функцию
(ш(г1,Ь)тп(г2,^2))
(9-9)
Мы нормировали корреляционную функцию, чтобы сделать ее безразмер¬
ной. Для краткости мы используем сокращенные обозначения 1 = (гх, ti) и
2 = (г2,*2)- Трансляционная инвариантность подразумевает, что С(1,2) =
C(r,tx,i2)> где г = гх - г2. Также полезно явным образом изучить автокор¬
реляционную функцию Л(^х,<2) = которая является мерой веро¬
ятности того, что знак намагниченности совпадает в моменты t± к t%.
Начнем с изучения укрупнения в НУГЛ (уравнении диффузии) без по¬
тенциала
дт „о
5i- = V”
(9.10)
для случайных начальных условий (9.7). Оно имеет решение
m(ri,t)= (4тгг)<*/2/m(zi’0)e (ri Zl)2/4t<fei.
Среднее значение произведения намагниченностей в двух различных точках
пространства-времени равно
(ro(ri,fi)m(r2,t2))
$(zi-Z2)
e dzidz2
e-(ri-z)2/4ii g—(r2—z)2/4t2
- (ri- zi)2/4ti - (r2— z2)2/4i2
х е
[(47r)2^2]d/2 /
= - [ e~ri/4tl e~r
-r|/4t2 g-z2(l/4ti+l/4t2) ez-(n/2ti+r2/2t2)
Интеграл в последней строчке вычисляется с помощью приведения выраже¬
ния в экспоненте к полному квадрату, что дает
1
(m(ri,«i)m(r2,t2)) =
[47г(< 1 + t2)]d/2
a-(ri-r2)2/4(ti+t2)
(9.П)
9.2 Свободная эволюция
347
В результате получаем нормированную двухточечную корреляционную
функцию, определенную в (9.9)
С(1,2)
qd/4
e_(n-r2)2/4(M+t2)
(9.12)
2^гЗг'
<1 + <2
Таким образом, корреляционная функция быстро убывает (как распределе¬
ние Гаусса) как функция расстояния, но медленно (ио степенному закону)
как функция разницы во времени.
Уравнение КХ без потенциала (бидиффузия)
дт
~dt
= -V4m
(9.13)
также дает законченное аналитическое описание укрупнения. Простейший
способ решить бидиффузионное уравнение (и диффузионное) - - преобразова¬
ние Фурье. Используя Фурье-образ m(r, t) = (27r)_d f m(k, t) е~гк г б/k, мы сво¬
дим (9.13) к обыкновенному дифференциальному уравнению dm/dt = —к^т,
решение которого имеет вид ra(k, t) = гао(к) e”fe4*, где гао(к) = m(k, t = 0).
Обращая преобразование Фурье, находим
m(r,£) = (2%) d J m0(k)
e-ikr-fe44k.
(9-14)
Более полезная характеристика — это среднеквадратичная намагниченность,
поскольку в ней проведено усреднение по стохастическим начальным услови¬
ям, точно так же, как в случае классического уравнения Ланжевена (раздел
2.8). Для начальных условий с белым шумом (9.7) среднее Фурье-образа и
корреляции между компонентами имеют вид
(гао(к)) = 0, (ш0(к) га0(к')) = (27r)d5(k + к'). (9.15)
Используя эти результаты вместе с уравнениями (9.7) и (9.14), получаем сред¬
неквадратичную намагниченность
(m2(r,t)) = (2тг)~л / e~2k4tdk = Bd(2i)~d/\ (9.16)
где Bd = (2тг)-^Г(сг/4)/4. Здесь Qd = 2тг^/2/Г(<//2) — площадь единичной
сферы в размерности d, а Г — гамма-функция Эйлера.
Аналогично находим корреляционную функцию
(m(l)m(2)) = (2ir)~d J e~ik-r~k4^+t^ dk.
(9.17)
348
УКРУПНЕНИЕ
Когда пространственные точки совпадают, г = 0, получаем автокорреляци¬
онную функцию
x(fl'i2)= [ir+l]*4’ (9Л8)
которая имеет одинаковый вид для диффузии и бидиффузии. Когда про¬
странственные точки различны, ri / г2, можно вычислить интеграл в (9.17),
вводя сферические координаты в k-пространстве для d > 2. Тогда к • г =
кг cos в п dk = kd~1 Q^-i sin4-2 в dd dk, и мы получаем
(ш(1) m(2)) = jT kd~' е-*4(‘1+*’) Fd(kr) dk,
где
Fd(u) = f (sin 0)d"2 e~iucose dO.
Jo
Вычисляя этот интеграл, получаем двухточечную корреляционную функцию
C(r,ti,i2):
С(г, ti,t2)
' 2(4<!*2)1/8
Г(1/4)г
4(4t1t2)1/4
2(4txt2)3/8
. Г(3/4)г3
cos q e q T
qlo(q) e q4r dq,
q sin q e q T
dq,
dq,
d= 1,
d = 2, (9.19)
d = 3.
Здесь мы использовали сокращенные обозначения q — кг, т = (ii + f2)/r4, и
Iq — модифицированная функция Бесселя порядка 0.
Наконец, корреляционная функция с временнбй нормировкой G(r, ii, i2) =
C'(r,ti,t2)/A(ti,<2) — это функция единственной скейлинговой переменной т
(здесь «временная нормировка» отражает свойство, что G(0, ii,i2) = 1). Та¬
кой однопараметрический скейлинг есть особенность упрощенной модели, а
не универсальное правило. В общем случае вращательная симметрия и дина¬
мический скейлинг подразумевали бы, что G(r, ti, t2) — функция двух пере¬
менных. Когда ti — t2 = t, обе корреляционные функции С (г, t, t) и G(r,t,t)
сводятся к одновременнбй корреляционной функции G(t), которая зависит
от единственной скейлинговой переменной т = 2i/r4. Для уравнения КХ без
9.3 Частные случаи неконсервативной динамики
349
потенциала точный вид одновременнбй корреляционной функции G(r) сле¬
дующий:
G(r) =
( 2т1/4 f°° .
• Г дЫд) e-^dg,
у/п Jo
2т3/4 [°° .
1г(3/4)Уо 9ЯП’е
d= 1,
cl = 2,
d = 3.
В отсутствие потенциала динамика параметра порядка и его корреляци¬
онные функции могут быть полностью вычислены. К тому же для описа¬
ния роста типичного масштаба длины есть более детальные характеристики,
например, скорость убывания автокорреляционной функции. Возможность
точного решения дает сильную мотивацию для исследования таких моделей
свободных полей. Кроме того, хорошо понятен механизм, приводящий к раз¬
личным динамическим индексам для диффузии и бидиффузии. Тем не менее,
необходимо помнить об ограниченности моделей свободных нолей. Например,
зависимость от времени, полученная из анализа бидиффузиоиного уравнения
L(i) t1/2, отличается от хорошо установленного закона роста Л1/3, который
характеризует процесс укрупнения с сохраняющимся параметром порядка3.
9.3 Частные случаи неконсервативной динамики
Теперь обратимся к явным решениям уравнений движения. Поскольку гра¬
ницы доменов при укрупнении геометрически сложны, мы сначала изучим
идеализированные системы, которые допускают точный анализ, ио все еще
динамически нетривиальны. Есть несколько классических примеров такого
рода, например, единичная доменная стенка и единичная сферическая кап¬
ля. Мы также обсуждаем геометрии полуполосы и клина, которые проливают
дополнительный свет на динамику одиночных границ.
Перед тем как рассматривать пространственно нетривиальные конфигу¬
рации, убедимся, что однородные конфигурации эволюционируют к основно¬
му состоянию. Для пространственно однородных состояний НУГЛ (9.2) упро¬
щается к виду и поэтому в пределе большого времени система
3Однако рост по закону t1//4 действительно возникает для консервативных систем с
векторным параметром порядка (с некоторыми исключениями в случае ХУ-модели).
350
УКРУПНЕНИЕ
действительно достигает одного из минимумов V(m). Далее, если обратное не
указано явно, мы рассматриваем двухъямный потенциал V(m) = ^(1 — га2)2.
Для такого потенциала пространственно однородное и стационарное реше¬
ние или га = 1, или га = — 1. Теперь обратимся к эволюции пространственно
неоднородных систем.
Прямая доменная стенка
Простейший пример пространственной неоднородности — единичная граница
в виде прямой доменной стенки. Для дискретной модели Изинга-Глаубера
намагниченность — это просто ступенчатая функция. Для непрерывного
НУГЛ плоская линия раздела более интересна, поскольку огрубленная на¬
магниченность нетривиально меняется в пространстве при пересечении ли¬
нии. Для плоской стационарной границы НУГЛ сводится к обыкновенному
дифференциальному уравнению
(fim ,
=v (m)'
(9.20)
где х — координата вдоль оси, перпендикулярной границе. Вдали от гра¬
ницы параметр порядка неоднородный и стационарный. Для двухъямного
потенциала общего вида граничные условия для уравнения (9.20) имеют вид
га(±оо) = ±1.
Перед тем как решать уравнение (9.20), дадим красивую интерпретацию
доменных стенок на языке классической механики. Рассматривая х как пе¬
ременную времени, а га — как координату, мы видим, что прямая доменная
стенка эквивалентна движению фиктивной частицы единичной массы в по¬
тенциале —V (рис. 9.1). Энергия этой фиктивной частицы имеет вид
Е =
(9.21)
и не меняется со «временем» х. Граничные условия подразумевают, что Е =
0. Поэтому = y/2V(m) или
ГтЮ dfi
ш(о)
(9.22)
Обычно «начальные условия» полагают равными т(х = 0) = 0. Для потен¬
циала У(т) = (1 — т2)2 решение уравнения (9.22) дает профиль доменной
стенки
т(х) = thx.
(9.23)
9.3 Частные случаи неконсервативной динамики
351
(а)
-У(т)
т
(Ь)
т
х
Рис. 9.1. (а) Эффективный потенциал —V(m) = — ^(1 — га2)2. Также показа¬
но движение фиктивной частицы, которая соответствует изолированному кинку.
Эта частица стартует на вершине левого максимума т = — 1 и движется без дис¬
сипации, пока в конце-концов не остановится при т — +1. (Ь) Соответствующая
зависимость т от х
Это решение известно как «кинк» в теории </>4. Ширина этого кинка порядка
1, тогда как плотность его свободной энергии есть (см. (9.1))
(9.24)
а свободная энергия на единицу площади, т. е. поверхностное натяжение,
равна
° = f-oo 2V (m) ^ = 1-00^ (m) (1йг) 1 dm = f-1 V2V(m) dm = П • (9-25)
На языке этой аналогии с классической механикой уравнение движении (9.20)
можно вывести, минимизируя «действие»
Поскольку кинетическая и потенциальная энергии равны, действие, ассоци¬
ированное с фиктивной частицей, совпадает с поверхностным натяжением.
Механическая аналогия дает много полезной информации о фазовом по¬
ведении системы, особенно в ситуациях, где аналитическое описание домен¬
ных стенок — невыполнимая задача. Предположим что начальные условия —
это комбинация двух статических решений, например, конфигурация кинк-
антикинк. Может ли такая конфигурация быть устойчивой? В рамках ме¬
ханической аналогии мы спрашиваем, возможно ли для фиктивной частицы
352
УКРУПНЕНИЕ
стартовать в максимуме т = — 1, дойти до максимума т = +1 и потом
вернуться назад в максимум т = — 1 (см. рис. 9.1). Очевидно, это движе¬
ние невозможно, так что без вычислений можно заключить, что пара кинк-
антикинк не может быть устойчивой. Численное моделирование показывает,
что кинк и антикинк медленно двигаются по направлению друг к другу и в
конце концов аннигилируют.
Еще один полезный аспект механической аналогии — мы можем исполь¬
зовать ее, чтобы охарактеризовать все возможные одномерные стационарные
решения, соответствующие конечной свободной энергии на единицу площади.
Для любой функции потенциала (i) фиктивная частица должна стартовать с
одного максимума потенциала [—V] в момент «времени» х = —оо и достигать
другого максимума потенциала [—V] при х = оо, и (ii) максимумы должны
быть соседними. Поэтому для потенциалов с двумя вырожденными мини¬
мумами (в т = ±1) есть два типа статических решений, кинк и атикинк,
которые мы символически обозначаем соответственно как [—1,1] и [1,-1].
Аналогично для потенциалов с тремя вырожденными минимумами, напри¬
мер, для системы спинов с тремя состояниями с минимумами в т = ±1 и
т = 0 (например, потенциал V(га) = га2 (1 — га2)2) есть четыре типа стати¬
ческих решений: [—1,0], [0, —1], [1,0]и[0,1]. Точное статическое решение урав¬
нения (9.22), которое разделяет фазы га = 0 и га = ±1 для этого потенциала,
дается выражением (см. задачу 9.3)
(9.26)
Более того, из механической аналогии очевидно, что фиктивная частица не
может стартовать в максимуме га = —1 и двигаться к максимуму га = +1.
Поэтому доменная стенка [—1,1] не может возникнуть.
Устойчивость доменных стенок и основных состояний
В одном измерении НУГЛ допускает меняющиеся в пространстве стационар¬
ные решения (доменные стенки), если система имеет по меньшей мере два
основных состояния. Физически устойчивость основных состояний и домен¬
ных стенок очевидна. НУГЛ описывает градиентную динамику, так что сво¬
бодная энергия убывает и в конце концов достигает минимума. Поскольку
доменные стенки и основные состояния — это единственные возможные ми¬
нимумы, система должна попасть в одно из этих состояний. Потенциальный
подводный камень в этих аргументах — неявное предположение существова¬
ния конечного числа доменных стенок, таких как кинк и антикинк, в случае,
когда потенциал имеет два вырожденных минимума. Число типов доменных
9.3 Частные случаи неконсервативной динамики
353
стенок действительно конечно. Однако из-за трансляционной инвариантно¬
сти существует бесконечно много доменных стенок данного типа. Поэтому,
если начать с доменной стенки и произвести над ней небольшое возмущение,
мы ожидаем, что намагниченность в конечном итоге релаксирует к доменной
стенке такого же типа, но сдвинутой на некоторое расстояние.
Чтобы охарактеризовать применимость этой картины и сделать ее более
количественной, изучим малые возмущения около стационарной доменной
стенки. Для этого запишем намагниченность как сумму стационарного реше¬
ния mo = thrr плюс произвольное малое возмущение </>(&•, />):
т(я, t) = то(я) + ф(х, t). (9.27)
Подставляя этот анзац в НУГЛ (9.2) и разлагая, получим (в ведущем поряд¬
ке)
| = (в-28)
Это нестационарное одномерное уравнение Шредингера с потенциалом
V"(mo), решение которого имеет вид4
ф(х, f) = ^2 Ane~Entijjn(<x'), (9.29)
n>0
где Ап определяется из начальных условий, а Еп и фп — это, соответствен¬
но, собственные значения и собственные функции, которые удовлетворяют
уравнению
Здп = +(9.30)
Решение то устойчиво по отношению к малым возмущениям, если все
собственные значения уравнения Шредингера (9.30) неотрицательны. Убе¬
димся в этом для потенциала V = ^(1 — т2)2. Для кинка с центром в начале
координат mo = thx уравнение (9.30) принимает вид
ЕПфП —
-^ + (6«А:-2)
Фг,
(9.31)
Такое уравнение Шредингера встречается во многих учебниках по кванто¬
вой механике5. Энергетический спектр состоит из малого числа дискретных
4На самом деле уравнение (9.28) — это уравнение Шредингера в мнимом времени. За¬
метим также, что сумма в (9.29) - символическая, поскольку включает как дискретный
спектр, который содержит несколько элементов (иногда только один), так и интегрирова¬
ние по сплошной части спектра.
5Потенциал обычно записывается как —Уо(chare)-2. Выбирая Уо = 6 и а = 1, мы
воспроизводим (с точностью до сдвига энергии) потенциал из уравнения (9.31).
354
УКРУПНЕНИЕ
уровней, за которыми следует непрерывный спектр. Адаптируя эти резуль¬
таты к нашему конкретному примеру, мы приходим к следующему выводу:
существует два дискретных уровня
Eq = 0, чро = 1/ ch2x, (9.32а)
Ei = 3, V’l = shx/ ch2T (9.32b)
и непрерывный спектр для Е > 4. (Последний результат ожидаем, так как
потенциал б th2 х — 2 в уравнении Шредингера (9.30) стремится к 4 при х —>
±оо, так что непрерывный спектр должен быть при более высокой энергии.)
Некоторые детали предсказаний (9.32а)-(9.32Ь), в частности, относящие¬
ся к первому возбужденному состоянию V’l, чувствительны к выбору V(m),
тогда как другие универсальны и могут быть получены без вычислений. На¬
пример, уравнение (9.30) всегда имеет собственную функцию
V’o =
dmo
~fa'
(9.33)
соответствующую собственному значению Ео = 0. В самом деле, продиффе¬
ренцировав НУГЛ
d2mo
dx2
V'(mo),
мы видим, что V’o, определенное в (9.33), удовлетворяет уравнению (9.30) с
Eq = 0. Более концептуальный способ вывода этого результата — заметить,
что функция то(х + а) является стационарным решением, и если мы разло¬
жим его по степеням а, то в ведущем порядке получим
то(х + а) = шо(т) + aipo(x).
Поэтому функция афо(а) удовлетворяет уравнению (9.28), и, поскольку эта
функция не зависит от времени, мы снова находим, что ipo — собственная
функция с Eq = 0.
Сжатие капли
Решаемый пример динамики границы раздела в высших измерениях дает
эволюция капли одной фазы, например т = — 1, в море противоположной
фазы с т = +1. В картине с индивидуальными спинами мы ожидаем, что
конечный кластер спинового меньшинства будет подавляться большинством
спинов, направленных в противоположную сторону. Такое же поведение воз¬
никает и при непрерывном описании.
9.3 Частные случаи неконсервативной динамики
355
Поскольку капля сжимается, для описания ее эволюции нужно использо¬
вать зависимое от времени НУГЛ. Благодаря сферической симметрии, НУГЛ
(9.2) сводится к виду
дт _ д2т
dt дг2
d-lдт ,
(9.34)
При условии, что радиус капли R значительно превосходит ширину границы,
мы ожидаем, что намагниченность имеет вид m(r,t) = /(г — /?.(£)). Подстав¬
ляя этот анзац в (9.34), получаем
(
/" +
d-l
/'-И/) = 0.
(9.35)
Умножим это уравнение на f и проинтегрируем по переменной х поперек
границы. Граница большой капли локализована в узкой области вокруг R(t).
Поэтому мы можем положить нижний предел интегрирования —R равным
-оо. Получаем
(/')2
°° Г° Р-1 1?'
-оо + У_то [г + dt.
(f'^dx “Г(а:)|_оо = 0.
(9.36)
Первое и третье слагаемое в этом уравнении очевидно равны нулю. Поскольку
(/')2 отлично от нуля только вблизи х = 0, зануление второго слагаемого
приводит к следующему уравнению для движения границы:
d-l dR
R + dt
= 0.
(9.37)
Решая это уравнение, мы находим, что радиус капли уменьшается как R2 =
Rq — 2(d —1)£. Следовательно, время исчезновения капли равно 7?q/[2(cZ — 1)].
Благодаря тому, что мы сосредоточились на приграничной области, мы
получили решаемое уравнение для ее динамики вместо нерешаемого НУГЛ
вида (9.34). Такое эффективное описание динамики границы раздела приме¬
нимо для для произвольной сложной геометрии домена при условии, что ха¬
рактерный масштаб длины ассоциированный с морфологией границы быстро
растет со временем. Эта конструкция особенно полезна в двух измерениях.
Локально кривизна границы есть 1/Л, и поэтому границу можно аппрок¬
симировать окружностью радиуса R. В результате, скорость, нормальная к
границе, равна v = — 1/R. В общем случае d измерений граница это (d — 1)-
мерное многообразие. Если обозначить ее главные радиусы кривизны через
7?1,..., Rd-i (они зависят от положения точки на границе), то нормальная
356
УКРУПНЕНИЕ
скорость границы — это сумма главных кривизн 1/Rj- Это приводит к урав¬
нению Аллена-Кана
v = -(d-l)K, (9.38)
где К — средняя кривизна, К = (d — I)-1 ^-/Rj- Необходимо сделать нес¬
колько замечаний об уравнении Аллена-Кана:
1. Динамика чисто локальная, а именно, скорость определяется локаль¬
ной кривизной и не зависит от остальной границы, присутствия других
границ и т. д. Эта локальность характеризует НУГЛ в асимптотическом
режиме и не выполняется для консервативной динамики.
2. Динамика не зависит от точной формы потенциала V(m).
3. Уравнение Аллена - Кана не применимо в одном измерении, где граница
между двумя доменами — это одна точка. В этом случае скорость гра¬
ницы — это экспоненциально малая функция длины домена по любую
сторону от границы. Это свойство приводит к ультрамедленному лога¬
рифмическому росту доменов, который описывается с помощью экстре¬
мальной динамики (см. раздел 9.7).
Рис. 9.2. При сжатии замкнутая двумерная граница, эволюционирующая как
управляемый кривизной поток, с необходимостью принимает все более круглую
форму
Динамика границы раздела, выведенная из НУГЛ, — это пример потока,
управляемого кривизной, в котором эволюция произвольной формы зависит
от локальной кривизны. Многое известно об эволюции изолированной за¬
мкнутой границы, эволюционирующей как управляемый кривизной поток. В
двух измерениях каждая такая граница независимо от ее начальной формы
9.3 Частные случаи неконсервативной динамики
357
асимптотически стремится (сжимаясь) к круглой форме. На первый взгляд,
является неожиданностью то, что кривая, нарисованная на рис. 9.2, асимп¬
тотически сжимается в окружность под действием управляемого кривизной
потока без отрыва самых заметных выступов. В трех измерениях, если ис¬
ходная граница раздела везде выпуклая, результат управляемого кривизной
потока на больших временах — сфера. Однако граница, содержащая и вы¬
пуклые и вогнутые участки, может подвергнуться делению, если вогнутые
участки достаточно тонкие, как, например, удлиненная капля жидкости с
тонкой талией посередине. Полная классификация всех возможных измене¬
ний топологии в высших размерностях под действием потока, управляемого
кривизной, все еще неполна.
Двумерные неограниченные домены
В двух измерениях эволюция одиночной замкнутой границы раздела, харак¬
терный размер которой значительно превосходит ее ширину, проста в пределе
большого времени — граница становится круглой и сжимается в соответствии
с уравнением (9.37). Что можно сказать о неограниченном домене? Это снова
случай, в котором достаточно простая исходная геометрия эволюционирует
к стационарному состоянию, свойства которого могут быть найдены. Здесь
мы рассматриваем решаемые примеры бесконечной полуполосы и бесконеч¬
ного клина (рис. 9.3). Последний есть непрерывный аналог системы с углом,
исследованной в разделе 8.6.
Для полуполосы меньшая фаза вначале занимает полубесконечную об¬
ласть у > 0 и |я| < L. Интересен предел t » L2, когда прошло достаточно
времени, чтобы два угла исходной полуполосы начали взаимодействовать.
В таком пределе большого времени полуполоса релаксирует к предельной
форме, которая укорачивается с постоянной скоростью, и граница у(.т) ста¬
ционарна в движущейся с той же скоростью системе отсчета. Для такой гео¬
метрии уравнение Аллена-Кана имеет вид
- у”
Vn [1 + (у')2]3/2’
где vn — скорость, нормальная к границе. Правая часть — это просто кри¬
визна кривой у (я), которая задает границу полуполосы, а штрих обозначает
производную по х. Вертикальная компонента скорости равна vy = vnfcos# =
^n\/l + (у')2 (рис. 9.3). В стационарном состоянии вертикальная скорость по¬
стоянна, vy = v и, следовательно, у(х) удовлетворяет уравнению
у”
1 + (у')2 ’
(9.40)
V =
358
УКРУПНЕНИЕ
Рис. 9.3. Изображение (а) укорачивающейся полуполосы, где показаны нормаль¬
ная скорость vn и вертикальная скорость vy, и (Ь) клина, где показаны исходный
клин (точками) и его геометрия во все более поздние моменты времени (пунктир
и сплошная линия соответственно)
Это уравнение может быть проинтегрировано элементарными методами:
сначала решить его для функции z = у', которая удовлетворяет уравнению
z' = v(l + z2), а потом проинтегрировать еще раз. Решение, удовлетворяющее
граничному условию у —> оо, при |ж| —> L имеет вид
Пример прямоугольного бесконечного клина немного более сложен. На¬
пример, пусть исходный угол будет в начале координат, так что клин зани¬
мает область ж, у > 0. Угол клина смещается диффузионно6, т. е. ж, у ~ y/t.
Из-за отсутствия констант с размерностью длины в уравнении (9.40) соот¬
ветствующее решение принимает самоподобный вид
X = Y (X) = у(х, (9.42)
Заметим, что прирост намагниченности вдвое больше, чем площадь под кри¬
вой y(x,t). Согласно (9.42) площадь пропорциональна t, так что намагничен¬
ность также растет линейно со временем. Чтобы описать эволюцию клина,
подставим анзац (9.42) в уравнение движения (9.40) и найдем, что скейлин¬
говая функция Y(ж) подчиняется уравнению
у - XY' _ У"
2 _1 + (У')2’
(9.43)
6 Это справедливо как для динамики Изинга-Глаубера, так и для непрерывного опи¬
сания.
9.3 Частные случаи неконсервативной динамики
359
где штрих теперь обозначает дифференцирование по X. Уравнение (9.43)
должно решаться при условиях limx->oo Y(X) = 0 и Нтх->+оУрО = °°>
которые соответствуют геометрии клина.
Полезно ввести полярные координаты (X, У) = (г cos в, г sin в), с помощью
которых уравнение (9.43) упрощается к следующему уравнению для г = г (в):
2r$-(4+r^)2=r2(2+r2)' (9'44)
Записывая = Л (г), мы сводим уравнения (9.44) к уравнению первого по¬
рядка с решением R2 = г4 er F(r, го), где
F(r, го) = У (^5 + е-р2/2 dp (9.45)
и го — перемасштабированное расстояние от начала координат до ближайшей
точки на границе. Линия границы теперь определяется уравнением
= ± г2 ег2/4 y/Ffaro) (9.46)
со знаком плюс для в > 7г/4 и минус для в < 7г/4, что делает решение симмет¬
ричным относительно диагонали в < 7г/4. Интегрирование уравнения (9.46)
дает явное решение для в = 0(г)
роо р-р2!^
Jr P^y/F^)
при в < 7г/4. Для 7г/4 < в < 7г/2 мы используем соотношение г(0) = г(^ — 0),
обеспечивающее симметрию границы по отношению к диагонали. Значение
неизвестной константы г о получается из условия О = 7г/4 при г = Гц. Отсюда
получаем критерий
/•оо g—г2/4 п
k r^VFM)dr~e
численное решение которого дает го = 1,0445. Уравнение (9.47) с F, опреде¬
ленной в (9.45), дает явное представление для 0(г)на границе, выраженное че¬
рез (перемасштабированное) расстояние г G [го, оо) от начала координат. При
г —> оо уравнение границы значительно упрощается. В этом пределе уравне¬
ния (9.45) и (9.47) дают в -> А г-3 е~г /4, где А = 2/i/F(oo,ro). В декартовых
координатах соотношение между виг приводит к У —» АХ~2 е~х2/4.
360
УКРУПНЕНИЕ
9.4 Финальные состояния
Так же как в нашем обсуждении эволюции модели Изинга-Глаубера при ну¬
левой температуре в разделах 8.5 и 8.6, есть некоторые фундаментальные
вопросы об укрупнении в пределе большого времени, (i) Каково финальное
состояние системы? Какие имеются низкоэнергетические возбуждения? Име¬
ется как сходство, так и некоторые важные различия между НУ ГД и дина¬
микой модели Изинга-Глаубера, которые мы сейчас обсудим.
Мы видели (стр.352), что элементарные возбуждения в НУГЛ в одном из¬
мерении — это кинки и антикинки. Они являются аналогами доменнах стенок
в модели Изинга-Глаубера. В системе Изинга-Глаубера доменные стенки
свободно диффундируют и аннигилируют при встрече. Следовательно, вре¬
мя достижения финального основного состояния растет как квадрат длины
системы. С другой стороны, взаимодействие между кинками и антикинками
в НУГЛ экспоненциально мало, когда расстояние между ними превышает их
ширину (это свойство будет обсуждаться в разделе 9.7). Поэтому основной
вклад в динамику вносит пара возбуждений с наименьшем расстоянием меж¬
ду ними. Такая картина экстремальной динамики, которая будет разобрана в
разделе 9.7, приводит к медленной эволюции, для которой время достижения
основного состояния посредством динамики НУГЛ растет экспоненциально
(а не по степенному закону) с размером системы.
При d > 2 результаты динамик НУГЛ и Изинга-Глаубера при нулевой
температуре на первый взгляд похожи. Обе динамики порождают при укруп¬
нении сходные структуры, которые эволюционируют по одним степенным
законам. Более того, когда эти системы приготовлены в одном и том же на¬
чальном состоянии, они достигают одного и того же финального состояния
(или основного, или полосатого) с одинаковыми вероятностями для каждо¬
го из этих двух возможных исходов. Поскольку НУГЛ было построено как
естественный макроскопический аналог микроскопической глауберовой ди¬
намики, это соответствие ожидаемо. Однако НУГЛ при нулевой температу¬
ре — детерминистическое уравнение, тогда как глауберова динамика остает¬
ся стохастической. Поэтому природа связи между этими двумя динамиками
требует более пристального рассмотрения.
Здесь есть две тонкости. Во первых, поскольку эволюция НУГЛ детер¬
министическая, финальное состояние однозначно определяется начальными
условиями. С другой стороны, если начать с данного начального состояния и
позволить системе эволюционировать под действием глауберовой динамики
при нулевой температуре, различные реализации динамики могут привести
к различным финальным состояниям. Поэтому, чтобы найти вероятность до-
9.4 Финальные состояния
361
етижения полосатого состояния, нужно усреднять по многим разным началь¬
ным условием, имеющим нулевую намагниченность. Однако, если мы старту¬
ем с «достаточно случайных» начальных условий, можно просто усреднить
но многим реализациям динамики7.
Вторая тонкость — это огромное разделение временных шкал в динамике
НУГЛ между режимами укрупнения и финальным состоянием. Когда дости¬
гается полосатое состояние в НУГЛ, это происходит за время порядка Ь2, где
L — это линейный размер системы. В этом полосатом состоянии экспоненци¬
альное взаимодействие между соседними стенками в конце концов приводит
систему к основному состоянию, истинному финальному состоянию динами¬
ки. Однако это финальное состояние достигается за время, растущее как eL,
а не как степень L. Для типичного макроскопического образца, например
с L = 108, это время жизни во много раз превосходит любые временные
масштабы во вселенной, так что этот экстрамедленный процесс можно ис¬
ключить из рассмотрения.
В трех измерениях финальные8 состояния похожи на состояния, возни¬
кающие в динамике Изинга-Глаубера (см.рис. 8.10), хотя сходство немного
менее точное, чем в двух измерениях. Из уравнения Аллена-Кана видно,
что финальные состояния состоят из статичной границы раздела с нулевой
средней кривизной. Такие состояния называются минимальными поверхно¬
стями потому, что они имеют минимальную возможную площадь поверхно¬
сти, покрывающей границу. Мыльные пленки дают практический пример
минимальных поверхностей. Для динамики НУГЛ на периодическом домене
минимальная поверхность распространяется на все пространство R3, приводя
к так называемым трипериодическим минимальным поверхностям9. Некото¬
рые простые примеры минимальных поверхностей даны на рис. 9.4. Даже
несмотря на то, что граница имеет нулевую среднюю кривизну, снова су¬
ществует остаточное экспоненциально малое взаимодействие между грани¬
цами, которое в конце концов должно привести систему к основному состоя¬
нию. Еще одно отличие от модели Изинга-Глаубера — система, описываемая
7Термин «достаточно случайные» сложно определить. Пример «плохого» начального
состояния — это конфигурация, состоящая из двух прямых полос. Такое состояние статично
для глауберовой динамики. С другой стороны, антиферромагнитное начальное состояние,
полностью детерминистическое состояние, имеющее максимальную энергию, вероятно, мо¬
жет служить хорошей стартовой точкой глауберовой динамики.
8Снова в пренебрежении процессами, возникающими на масштабах порядка eL.
9Первые пять примеров трипериодических минимальных поверхностей были найдены
Шварцом и его учениками во второй половине девятнадцатого столетия. Многие примеры
были обнаружены уже после 1970.
362
УКРУПНЕНИЕ
Рис. 9.4. Примеры три периодических минимальных поверхностей в трех измере¬
ниях. Рисунки любезно предоставлены К. Бракке
НУГЛ, не блуждает вечно по изоэнергетическому множеству метастабильных
состояний, как это происходит в дискретной спиновой модели.
9.5 Дефекты
Доменная стенка, которая обсуждалась в разделе 9.3, — это простейший то¬
пологический дефект. Чтобы почувствовать его важность, рассмотрим все
возможные решения НУГЛ с конечной свободной энергией
F[m] = j dx + V{m) . (9.49)
В любое время намагниченность на пространственной бесконечности долж¬
на стремиться к нулям потенциала. В противном случае была бы бесконеч¬
на свободная энергия (9.49). Для одномерной системы с двумя вырожден¬
ными минимумами потенциала, например, находящимися в т = ±1, про¬
странство всех решений подразделяется на четыре сектора, характеризуе¬
мые величинами т(х = ±оо). Например, сектора с кинками соответствуют
т(х = —оо, t) = =Fl и т(х = оо, t) = ±1. Эти сектора топологически не связа¬
ны, поскольку путь от решения в одном секторе к решению в другом секторе
обязательно прошел бы через бесконечную свободную энергию10, что невоз¬
можно: в эволюции, описываемой НУГЛ, свободная энергия может только
10Например, если т{х = оо,£) непрерывно изменяется от +1 до —1, свободная энергия
будет бесконечной всегда, когда т{х = oo,t) ±1.
9.5 Дефекты
363
убывать. В каждом секторе намагниченность эволюционирует, так что сво¬
бодная энергия убывает и, в конце концов, достигает минимума. Есть только
четыре таких минимума: стационарный кинк в секторе [—1,1], стационарный
шггикинк в секторе [Г, —1] и одно из двух основных состояний в каждом из
двух оставшихся секторов. Поэтому доменные стенки (и основные состояния)
играют выделенную роль как финальные состояния динамики НУГЛ.
Теорема вириала
В высших размерностях доменные стенки больше не имеют конечной свобод¬
ной энергии, но это не приводит к новой физике, так как они существенно
одномерные. Есть ли стационарные решения с конечной свободной энергией в
высших измерениях? Как это ни удивительно, но ответ отрицательный: когда
параметр порядка скалярный, основные состояния — это единственные ста¬
ционарные состояния. Это утверждение известно как теорема вириала (или
теорема Деррика).
Чтобы доказать теорему вириала, предположим, что т = 7/2* (х) нетри¬
виальное стационарное решение НУГЛ
V2ra = Ух(ш), (9.50)
которое получается из минимизации свободной энергии, 6F = 0. Здесь V2 —
это d—мерный лапласиан. Полезно разбить свободную энергию на «кинети¬
ческую» и «потенциальную» компоненты, Р[772] = А[т72] + Р[т], где
А[77г] = У (V772)2 > 0, Р[т] = f dxV(m) > 0.
Сделаем масштабное преобразование стационарного решения
772* (х) -> 772а(х) = 772* (ах).
Из этого преобразования получим
А[772а] = a2_dA[m*], Р[772а] = a“dP[m*], (9.51)
и поэтому
Р[т72а] = a2”dA[772*] + a_dP[772*]. (9.52)
Поскольку 772i = 772* — это экстремум функционала Р[т], это также экстре¬
мум на однопараметрическом семействе намагниченностей /ня(х). Поэтому
dF[ma] I
dCL la=l
(9.53)
364
УКРУПНЕНИЕ
откуда, используя (9.52), находим
(2 - d)K[m*] = dP[m*]. (9.54)
Уравнение (9.54) вместе с неравенствами К[га*] > 0 и Р[ш*] > 0 накла¬
дывает строгие ограничения на существование стационарных решений:
1. d > 2. Равенство (9.54) выполняется, только когда /С [га*] = Р[т*] =
0. Это условие показывает, что тп* должно быть константой и равно
одному из нулей V[ra], т. е. решением является тривиальное основное
состояние.
2. d = 2. Уравнение (9.54) дает Р[га*] = 0. Этого условия все еще доста¬
точно (когда минимумы V[ra] дискретны), чтобы исключить нетриви¬
альные стационарные решения.
3. d = 1. Равенство (9.54) выполняется, когда K[m*] = Р[га*]. Похожее
соотношение возникает в классической механике, где оно называется
теоремой вириала. Эта связь объясняет, почему мы пользуемся «вири-
альной» терминологией.
Отсутствие нетривиальных стационарных решений при d > 2 также очевидно
из формулы (9.52). В самом деле, это соотношение показывает, что при а > 1
состояние с гаа(х) имеет меньшую энергию, чем состояние с ш* = rai(x).
Поэтому характерный размер, характеризующий гаа(х), в а раз меньше, чем
размер в ш* (х). Поэтому энергетически выгодно, чтобы конфигурация га*(х)
сжалась в точку, например, обратившись в основное состояние.
Теорема вириала говорит нам, что система со скалярным параметром по¬
рядка может иметь нетривиальные стационарные решения только в размер¬
ности один. Она ничего не говорит о зависимых от времени решениях. По¬
следние действительно существуют в некоторых моделях. Здесь мы интересу¬
емся только независимыми от времени решениями, и поэтому единственный
способ обойти теорему вириала — рассмотреть модели с более экзотическими
параметрами порядка.
Векторный параметр порядка
Следующий уровень сложности - это векторный параметр порядка. Это обоб¬
щение очевидно, и все предыдущие результаты остаются справедливыми,
кроме того, что скалярный параметр порядка заменяется на вектор m =
(ttii, ... ,77in). Например, уравнение (9.54) принимает вид
(2 - d)7f[m*] = dP[m*].
(9.55)
9.5 Дефекты
365
На первый взгляд, ничего не изменилось по сравнению со скалярным парат
метром порядка: например, при d > 2 не существует нетривиального стаци¬
онарного решения. Однако в двух пространственных измерениях ситуация
более интересна. Стационарные решения для системы с нулевым потенци¬
алом V[m] = 0 удовлетворяют уравнению Лапласа V2m = 0. Поскольку
(несингулярные) решения в бесконечном пространстве постоянны, модель без
потенциала не имеет нетривиальных стационарных решений.
Однако, если мы снабдим модель без потенциала физическим условием
п
ш(х) • ш(х) = £[го,(х)]2 = 1, (9.56)
j=i
может возникнуть нетривиальное состояние. В отличие от моделей с ненуле¬
вым потенциалом это условие дает более адекватное макроскопическое опи¬
сание (классического) ферромагнетика Гейзенберга, который состоит из спи¬
нов фиксированной длины11. Наивно было бы ожидать, что определяющим
уравнением снова будет V2m = 0. Однако это уравнение ошибочно: пра¬
вильная величина, которую нужно минимизировать в случае системы со свя¬
зями, — это исходная функция плюс связь, умноженная иа правильно вы¬
бранный множитель Лагранжа. В данном случае эта процедура приводит к
функционалу
F[m] = | J dx {(Vm)2 + A[m2 - 1]} ,
с пока неизвестным множителем Лагранжа А(х). Применяя рецепт Эйлера-
Лагранжа = 0 к этому функционалу, получаем
V2m = Am. (9.57)
Умножив уравнение на m и используя условие (9.56), выразим множитель
Лагранжа А через намагниченность: А(х) = m • V2m. Таким образом, урав¬
нение (9.57) принимает вид
V2m = (m • V2m) m. (9.58)
В отличие от линейного уравнения Лапласа V2m = 0, которое получается
в отсутствие связи, уравнение (9.58) — элегантное, но не простое нелинейное
уравнение в частных производных. Попробуем выяснить, когда у (9.58) есть
11 Модель с нулевым потенциалом и намагниченностью, определенной на единичной сфе¬
ре в d измерениях, называется (нелинейной) (Э(п)-моделью. 0(2)-модель также известна как
ХУ-модель, а 0(3)-модель — как модель Гейзенберга.
366
УКРУПНЕНИЕ
решения, не решая его. В силу условия (9.56) мы можем представить т(х)
как отображение двумерного физического пространства, в котором опреде¬
лена модель, на единичную сферу §п-1 в n-мерном внутреннем спиновом
пространстве:
m : К1 2 -> §n_1. (9.59)
Отметим, что в пространственной бесконечности намагниченность должна
стремиться к некоторому постоянному единичному вектору Шоо во внутрен¬
нем спиновом пространстве
lim m(x) = moo- (9.60)
|х|->оо
Если бы не такие граничные условия, намагниченность зависела бы от поляр¬
ного угла 0, даже в пределе г —> оо. Этот факт подразумевал бы для угловой
компоненты градиента г~1дт/дв ~ г-1. А следовательно свободная энергия
г dr d0(Vm)2
расходилась бы (логарифмически).
Поскольку намагниченность т(х) должна стремиться к одной и той же
величине Шоо для всех точек пространственной бесконечности, можно до¬
полнить двумерную плоскость R2 до сферы S2. Следовательно, (9.59) можно
рассматривать как отображение
m : §2 §п_1 (9.61)
двумерной сферы на (п — 1)-мерную сферу.
Примечательно, что такие отображения образуют сектора. Отображения
из одних и тех же секторов могут быть деформированы друг в друга, то¬
гда как отображения из разных секторов не могут. Эти сектора называются
гомотопическими группами и обозначаются ^(S71”1). Известны следующие
группы:
1. Если п> 4, есть только один сектор, который содержит тождественное
отображение. В этом случае группа гомотопии тривиальна: ^(S*5) =
0, когда к > 3. Этот факт не дает формального доказательства того,
что существуют только тривиальные стационарные состояния, но, как
минимум, делает это свойство ожидаемым.
2. Когда п = 3, т. е. в случае модели Гейзенберга, есть бесконечно много
секторов. Это свойство может быть компактно записано как 7Г2(§2) = Z,
9.5 Дефекты
367
что означает, что сектора могут быть помечены целыми числами (а так¬
же наводит на мысль, что гомотопические классы можно складывать
и они образуют группу, изоморфную группе целых чисел Z). Целый
«топологический» заряд отображения (9.61) дается интегралом12
[б^т • (c^m х djm)]. (9.62)
Здесь индексы нумеруют пространственные координаты, dx = drridx2,
c^m = dm/dxi, и т. д.; по повторяющимся индексам подразумевает¬
ся суммирование, и б^ обозначает антисимметричный тензор: 612 =
—^21 = 1) €ц = 622 = 0.
3. Наконец, ^(S1) = 0 означает, что для ХУ-модели не существует нетри¬
виальных стационарных решений для параметра порядка., которые име¬
ли бы конечную свободную энергию.
Стационарные решения модели Гейзенберга
Приведенные аргументы предполагают, что нетривиальные решения с конеч¬
ной свободной энергией и, в частности, стационарные решения существуют
для модели Гейзенберга в двух измерениях. Вспомним, что свободная энергия
модели Гейзенберга есть
F[m] = | J dx(djm) • (<%т), (9.63)
с параметром порядка, равным трехмерному единичному вектору m =
(ш1,Ш2,тз), т. е. с m • m = 1. Каждое решение с конечной свободной энер¬
гией принадлежит одному из секторов. Полное число секторов бесконечно,
и эволюционирующее решение ограничено одним единственным сектором. В
любом секторе трудно найти решение, потому что даже простейшие стацио¬
нарные решения должны удовлетворять сложному уравнению (9.58). Един¬
ственное исключение — это тривиальное решение ш(х) = Шоо13, соответству¬
ющее основному состоянию с нулевой свободной энергией F = 0.
Однако с помощью пары умных трюков были построены и некоторые
нетривиальные решения.
12Совсем неочевидно, что правая часть — это целое число. Свойство, что для любого
отображения m : §2 —> S2 интеграл (9.62), поделенный на 87Г, дает целое число — это
типичный сжимающий результат алгебраической топологии.
13Есть бесконечно много основных состояний, каждое из которых описывается единич¬
ным вектором т<эо • Эта неопределенность — проявление «спонтанного нарушения симмет¬
рии» на классическом уровне.
368
УКРУПНЕНИЕ
Первый трюк
Начнем с очевидного неравенства
У dx [(dim ± х djm) • (dim ± x d^m)] > 0.
Расписывая это неравенство, получим
У dx [(dim) • (dim) + б^б^(т х djm) • (т х d^m)]
> ±2 У dx [б^-т • (dim х djm)].
Слагаемые в левой части равны между собой
(9.64)
х д7т) • (т х d^m) = Sjk[{m • m)(djm • d^m) + (m • djm)(m • d^m)]
= (d^m-dim).
(Здесь мы использовали тождество e^ik = $jk, условие m • m = 1 и его
производную m • djm = 0.) Таким образом, (9.64) превращается в
У dx (dim) • (dim) >± J dx [e^m • (dim x djm)]. (9.65)
Вспомнив выражение (9.62) для топологического заряда и уравнение (9.64),
можно переписать (9.65) в компактном виде
^>4тг|д|. (9.66)
Следовательно, в каждом ^-секторе свободная энергия не может быть ни¬
же 47г|д|. Напомним, что стационарные решения находятся из минимизации
F[m], а минимизацию можно производить внутри каждого сектора по отдель¬
ности. Таким образом, минимальное возможное значение F[m] в g-секторе —
это 47г|д|. Вывод уравнения (9.65) показывает, что минимальное значение воз¬
никает тогда и только тогда, когда выполняется равенство
dim = ±6ijm х djm. (9.67)
Это уравнение в частных производных первого порядка, и поэтому оно пред¬
ставляет собой огромное упрощение по сравнению с уравнением второго по¬
рядка (9.58). В принципе возможно, что у (9.58) есть стационарное решение,
соответствующее локальному минимуму F[m], превосходящему глобальный
минимум 47г|д|. Тем не менее мы сосредоточимся на решениях более простого
уравнения первого порядка (9.67).
9.5 Дефекты
369
Второй трюк
Теперь цель — свести нелинейное уравнение (9.67) к линейному. Идея - ис¬
пользовать стереографическую проекцию сферы m • m = 1 на плоскость.
Выберем плоскость, параллельную (mi,m2) и содержащую южный полюс.
Координаты (у 1,1/2) в этой плоскости связаны с m посредством
У1
2mi 2ш2
з , У2 = з
1 — Шз 1 — Шз
(9.68)
Теперь, используя (9.67), вычислим d±yi и д2У2 и убедимся, что они совпадают
(или противоположны), и аналогично для двух других производных. Тогда
имеем о о
<9yi = ду2
дх± дх2* дх2 ^dxi'
Это не просто линейные уравнения, а уравнения Коши-Римана! Они сооб¬
щают нам о том, что комплексная переменная £ = yi + 4/2 является ана¬
литической функцией переменной z* = xi — ix2 для верхних знаков в фор¬
мулах (9.69). Для нижних знаков £ — аналитическая функция переменной
z = xi + гх2- Подведем итог:
1. Цель была — найти решение нелинейного уравнения второго порядка в
частных производных (9.58), описывающего стационарное решение мо¬
дели Гейзенберга с конечной свободной энергией.
2. Используя первый трюк, мы пришли к гораздо более простой задаче
нахождения решений уравнения первого порядка (9.67). Эти решения
удовлетворяют начальному уравнению (9.58), хотя не все решения (9.58)
являются решениями (9.67).
3. Используя второй трюк, мы установили, что после отображения (9.68)
уравнение (9.67) сводится к уравнениям Коши-Римана. Следовательно,
любая аналитическая функция дает решение.
Вихри
Теперь дадим примеры стационарных решений. Из-за их локализованной
формы имеет смысл называть их вихрями для любой величины q. Такие ре¬
шения представляются аналитическими функциями £ = £(z), где £ = 2/1 +^У2
и (уьУг) задаются уравнениями (9.68). Выраженные через эти функции сво¬
бодная энергия (9.63) и топологический заряд q будут иметь вид
-/
К/^12
F
dx
(1 + ICIW’
где
(9.70)
370
УКРУПНЕНИЕ
Например, рассмотрим
где п — положительное целое число. Подставив это в (9.70), мы найдем
F = 47гп и \q\ = п. Если выбрать более общую функцию Q = [(г — zo)/R]n,
мы получим тот же результат для F. Здесь zq задает положение вихря. Неза¬
висимость F от zq отражает трансляционную инвариантность. Аналогично,
параметр R — это размер вихря, а независимость F от R есть отражение
инвариантности свободной энергии по отношению к масштабному преобразо¬
ванию х —> Дх.
Простейший вихрь, соответствующий £ = 2z, имеет элегантное явное
представление в исходных переменных
mi =
2xi
|х|2 + 1’
Ш2 =
2X2
|х|2 + 1’
ТПз =
|*12 -1
|х|2 + 1'
(9-71)
Далеко от центра вихря (центр задан в начале координат) намагниченность
стремится к Шоо = (0,0, —1). Топологический заряд вихря (9.71) равен q = — 1
Вихрь с зарядом q = 1 получается обращением знака у шз в (9.71). Это дает
2xiR
Ш1~ |х|2 + Д2’
2x2R
Ш2~ |Х|2 + Д2 ’
тз =
R2 - |х|2
|х|2 + Д2’
(9.72)
где дополнительно восстановили размер вихря R, который может быть про¬
извольным. Самое общее решение для вихря с зарядом q = 1 совпадает с
(9.72) с точностью до сдвигов и вращений.
Визуализировать т(х) — непростая задача. Вместо того чтобы строить
эту векторную функцию, построим график скалярной плотности энергии Д,
определенной как F = / с1хЭ^ (рис. 9.5). Согласно формулам (9.70) имеем
Рис. 9.5. Плотности энергии (a) Ti, (Ь)Дг и (с) Дц (при а = 1) в двух измерениях
как функция (ж, у). Эти плотности ассоциированы с вихрями топологических
зарядов q = —1, —2 и —2 соответственно. С любезного согласия Д. Воловика
9.5 Дефекты
371
(1 + KIW
Для С, = 2z плотность энергии принимает вид
4 4
7Х =
(1 + И2)2 (1 + ж2 + ж2)2'
(9.73а)
(9.73Ь)
7 =
Нижний индекс означает, что данная плотность энергии соответствует вихрю
с топологическим зарядом q = — 1. Аналогично, взяв £ = 2z2, получим вихрь
(! зарядом q = —2, плотность энергии которого равна
16|г|2 _ 16(х1 + х%)
2 (1 + N4)2 [l + (®i+^)2]2'
Наконец, взяв £ = 2(z —а)(г + а), получим нелинейную суперпозицию вихрей
с q = — 1, которая дает возбуждение с топологическим зарядом q = — 2 и
плотностью энергии
16(ж’| + xi)
(1 + [(xi - а)2 + х%] [(Ж1 + о)2 + ж|])2 ■
(9.73d)
Когда а » 1, составляющие вихри приблизительно расположены в (£1,22) =
(±а,0).
Роль вихрей
Чтобы понять роль вихрей, вспомним некоторые главные свойства домен¬
ных стенок в одном измерении. Поскольку доменные стенки имеют конеч¬
ную свободную энергию, при любой положительной температуре плотность
доменных стенок будет конечной14. Существование конечной плотности до¬
менных стенок разрушает дальний порядок в одном измерении при любой
ненулевой температуре. Локализованные вихри с конечной свободной энерги¬
ей, которые возникают в классической модели Гейзенберга, играют похожую
роль: само их существование указывает на то, что для любой положительной
температуры их плотность имеет порядок e~FtT. Поэтому вихри позволяют
установить важнейшее свойство равновесного поведения модели Гейзенберга
в двух измерениях: при любой положительной температуре дальний порядок
невозможен.
Вихри гораздо более разнообразны по характеру, чем доменные стенки. В
самом деле, есть бесконечное число типов вихрей (каждый с топологическим
14Она имеет порядок е-1/т, если положить энергию доменной стенки равной единице.
372
УКРУПНЕНИЕ
зарядом, равным произвольному целому числу). Более того, вихри с одним и
тем же зарядом могут отличаться по размеру. Доменных стенок, напротив,
всего два типа15, и все их размеры одинаковы. Наличие множества типов
вихрей отличает модель Гейзенберга от модели Изинга. Однако при низких
температурах почти все вихри будут иметь заряд q = ±1. В этом отношении
ситуация похожа на одномерную модель Изинга, которая также имеет два
типа доменных стенок: кинки и антикинки.
Доменные стенки и вихри различаются еще в нескольких важных аспек¬
тах. Например, одномерные кинки перемежаются с антикинками. В двух
измерениях такие топологические ограничения отсутствуют. Также гораз¬
до труднее описать взаимодействие между вихрями, чем между доменными
стенками. Поскольку определяющие уравнения нелинейны, мы можем гово¬
рить о хорошо определенных вихрях только тогда, когда расстояние между
ними достаточно велико, т. е. когда L значительно превосходит их размеры,
L » Ri + R2. Такие сильно разделенные вихри приблизительно сохраняют
свою индивидуальность с точностью до малых возмущений. Два таких вихря
будут отталкиваться или притягиваться. Вихри с противоположным тополо¬
гическим зарядом вероятно могут аннигилировать. Детали этого типа взаи¬
модействий неизвестны. С другой стороны, кинки и антикинки притягивают
друг друга со взаимодействием, спадающим экспоненциально с расстоянием
(см. раздел 9.7).
9.6 Консервативная динамика
Влияние закона сохранения сильно ограничивает число способов, которы¬
ми может передвигаться граница между двумя доменами. Хотя отдельная
граница может двигаться так, чтобы снизить свою локальную кривизну и
энергию, такая эволюция должна сопровождаться глобальными перестрой¬
ками границ, которые обеспечат сохранение параметра порядка. Поэтому да¬
же эволюция изолированной капли нетривиальна в консервативном случае.
Поэтому мы начнем наше обсуждение с единичной капли, а потом перейдем
к эволюции разреженной популяции капель, погруженных в фазу большин¬
ства. В разреженном пределе капли сильно отдалены друг от друга и поэтому
почти сферичны. Рассматривая капли как сферические на протяжении всей
эволюции, можно избежать трудностей, связанных со случайными граница¬
ми. Тем не менее, этот предел все еще имеет свои тонкости: капли размером
15Это утверждение относится к потенциалам с двумя вырожденными минимумами. Для
потенциалов с т вырожденными минимумами есть 2(т-1) типов доменных стенок.
9.6 Консервативная динамика
373
меньше среднего сжимаются, тогда как ббльшие капли растут, и средний
размер нужно определять самосогласованно, требуя выполнения закона со¬
хранения.
Эволюция единичной капли
Рассмотрим эволюцию изолированной капли одной фазы, погруженной в сре¬
ду, находящуюся в противоположной фазе. Несогласованность возникает уже
па уровне формулировки задачи: если бы две фазы были идеально разделе¬
ны, капля не могла бы эволюционировать, так как любое изменение разме¬
ра капли нарушало бы сохранение параметра порядка. Альтернативно, мож¬
но представлять единичную каплю жидкости вместе с паром в замкнутом
резервуаре. На поверхности капли могут происходить как испарение, так и
конденсация молекул пара. Капля может эволюционировать с сохранением
параметра порядка через комбинацию этих двух процессов.
Скорость конденсации определяется потоком молекул пара к капле, ко¬
торый в свою очередь зависит от концентрации пара в газе. В принципе кон¬
центрация пара вне капли подчиняется уравнению диффузии. Однако, по¬
скольку радиус капли медленно меняется со временем, мы применим квази-
статическое приближение (см. раздел 2.7), в котором мы пренебрегаем явной
зависимостью от времени и, чтобы определить внешнюю концентрацию пара,
работаем с более простым уравнением Лапласа. Концентрация меньшей фа¬
зы как функция расстояния от центра капли радиусом R должна вести себя
как показано на рисунке рис. 9.6. Средняя концентрация с мсныпсй фазы во
всей системе должна быть больше, чем концентрация пересыщения c^O, т. е.
сначала, чтобы капля могла образоваться, нужно достигнуть пересыщения.
(При с < Соо меньшая фаза остается в виде пара в газе.) Внутри капли концен¬
трация много больше, чем с, по самому определению капли. Снаружи капли
концентрация пара подчиняется уравнению Лапласа с граничными условия¬
ми с(г —> оо) —> с, а с(7?) определяется из. соотношения Гиббса - Томсона (см.
ниже). В трех измерениях с(г) меняется по закону
с(г) = с-[с-с(Д)]^. (9.74)
Соотношение Гиббса-Томсона связывает с(Д) с Cqo, исходя из следующей
физической картины. В объемной части жидкости в равновесии с насыщен¬
ным паром концентрация пара равна Cqo по определению. Для маленькой
капли концентрация пара на границе больше, чем в объеме с(Д), потому что
большая часть молекул находится на границе. Поэтому значение с(R) должно
быть больше, чем Cqq, на величину, которая стремится к нулю, когда размер
374
УКРУПНЕНИЕ
R
Рис. 9.6. Схематическая (не в масштабе) зависимость концентрации меньшей
фазы от радиальной координаты
капли стремится к бесконечности. Это требование выражается соотношением
Гиббса-Томсона с(Л) = Coo (1 + ^), где v — это капиллярная длина, завися¬
щая от поверхностного натяжения и температуры.
Соединив эти элементы, получим, что объем изолированной капли зави¬
сит от скорости
dV_
dt
——— = 47гЛ2 = 47г/22 D^-
dt
дс I
dr 1г=я’
(9.75)
откуда имеем = Р[с — с(Д)]/Д. Теперь определим степень пересыщения
как Д = с — Cqo и используем соотношение Гиббса-Томсона для исключения
C(R), что дает
dJ? _ D / v\ _ а / R \
~dt ~ ~R\~ C°°r) = R?\Rc~ J'
(9.76)
Из последнего выражения ясно, что при R > Rc = Cqo^/Д капля растет,
тогда как при R > Rc — сжимается. В качестве особенно простого примера
рассмотрим предельный случай с = Соо- Тогда Rc = оо и уравнение (9.76)
сводится к = —aR~2. Поэтому капля сжимается, R3 = Rq — 3at. Это
поведение — составляющий блок укрупнения по закону f1/3, характерного
для динамики, сохраняющей параметр порядка.
9.6 КОНСЕРВАТИВНАЯ ДИНАМИКА
375
Укрупнение Лифшица—Слезова—Вагнера
Дальнейшее обсуждение дает основу для понимания укрупнения в разрежен¬
ной популяции капель в пересыщенной среде. Это явление (проанализирован¬
ное Лифшицом, Слезовым и Вагнером) известно как укрупнение ЛСВ. Раз¬
реженный режим позволяет использовать приближение, в котором частицы
не взаимодействуют, так что поле концентрации вокруг каждой капли такое
же, как вокруг изолированной капли. Главное свойство такого укрупнения
уже содержится в уравнении (9.76): капли, радиус которых превышает Rc,
растут, а те, что меньше, сжимаются. В популяции однородных капель вели¬
чина Rc должна определяться самосогласованно и, как мы покажем, равна
II,.. ~ t1/3.
Пусть f(R,t) будет концентрация капель радиуса R в момент времени t.
Эта концентрация эволюционрует согласно уравнению непрерывности
dJ п
dt + dR~ °’
(9.77)
где поток J = t) — это просто разность между возрастанием и убыва¬
нием количества капель радиуса R из-за их эволюции. Хотелось бы решить
это уравнение движения с из формулы (9.76) при условии, что полная
масса меньшей фазы сохраняется. Это условие можно записать как
с — Соо + ^7 /* R3 f(R, i) dR = const. (9.78)
3 Jo
В разреженном пределе объемная доля фазы меньшинства, существующей в
виде свободно диффундирующих мономеров, исчезающе мала. I 1оэ'гому закон
сохранения сводится к условию, что полный объем капель фиксирован. С
этой оговоркой уравнения (9.76)-(9.78) дают эволюционные уравнения для
укрупнения, сохраняющего параметр порядка в разреженном пределе.
Чтобы решить эти уравнения движения для укрупнения, мы снова при¬
меним скейлинг. Естественный скелинговый анзац для такой системы имеет
вид
/(Д,0 = -fit <№, z=^~- (9-79)
Здесь коэффициент задается исходя из сохранения полной массы меньшей
фазы, а именно f R3 f(R,t)dR = const., что вместе с (9.79) дает соотно¬
шение f z3<t>(z}dz = const, которое явным образом не зависит от времени.
Подставляя скейлинговый анзац (9.79) в (9.77), получаем первый член этого
376
УКРУПНЕНИЕ
уравнения
4Дс _х 1 jj RRc Rc!л л , jj\
М=-Щф-КФ^^~№^Ф + гф)'
где штрих обозначает дифференцирование по скейлинговой переменной z =
R/Rc. Аналогично, второй член в (9.77) принимает вид
д \а (R Д 1 /I а Г/1 1 \ ±, /2 1\ /
dR [я2 V-Rc / R4C U “ R7C LV 2;27^ + V3 z1 )
После этого уравнение в частных производных (9.77) можно превратить в
обыкновенное дифференциальное уравнение
RcRc = ct
KhiWfci)’].
4:ф +
= Q7,
(9.80)
где мы перегруппировали члены так, чтобы перенести всю зависимость от
времени влево, а всю зависимость от z — вправо. Поскольку две части явля¬
ются функциями разных переменных, каждая из них должна быть констан¬
той. В элементарных приложениях скейлинга, таких как скейлинговое реше¬
ние уравнения диффузии в разделе 1.1, величина постоянной разделения’7
играет определяющую роль: в зависимости от величины 7 есть три разных
режима поведения, только один из которых имеет физический смысл.
Теперь рассмотрим разделенные уравнения и найдем условия, определя¬
ющие физически оправданную величину параметра 7. Для временной зави¬
симости имеем
Д*Дс = а7, => Rc(t) = (Зсгу*)1/3. (9.81)
Таким образом укрупнение при условии сохранения параметра порядка при¬
водит нас к росту типичного радиуса капли по закону t1/3. Этот более медлен¬
ный, чем в случае диффузии, рост также обосновывает квазистатическое при¬
ближение, которое было использовано для определения концентрации снару¬
жи капли. После перегруппировки членов получим уравнения для зависимо¬
сти скейлинговой функции от переменной z
дф1 -Кф = Ъ, где g(z) = - - - zy, h(z) = + 47. (9.82)
Z % Z Z
Тогда формальное выражение для скейлинговой функции принимает вид
-ф-Г^-Г
2-у- kyy3 dy
1 - У + ГУ3 у'
(9.83)
9.6 Консервативная динамика
377
Пока мы использовали наш стандартный прием: применили скейлинг для
разделения уравнения в частных производных (9.77) на два обыкновенных
дифференциальных уравнения. Как это часто бывает, найти зависимость от
времени достаточно просто. Анализ зависимости от z требует аккуратности,
поскольку существенную роль играет постоянная разделения 7. Неожиданное
следствие уравнения (9.83) — функция </>(г) должна иметь резкое обрезание
на величине zmax, после которой = 0. Чтобы обосновать это утверждение,
предположим, что это не так. Тогда при z —> 00 из уравнения (9.83) следовало
бы, что </>(г) асимптотически ведет себя как
In ~ 4 — = —4 In z —> ф ~ .
J У
Однако степенной хвост невозможен, поскольку при таком асимптотическом
убывании расходится полная масса меньшей фазы
R3 ф (R, t)dR~ У z3 z~4 dz —> 00.
Поэтому мы заключаем, что </>(г) имеет резкое обрезание при некоторой ве¬
личине гтах-
Рис. 9.7. Схематическое изображение зависимости решения z = g(z)/(3yt) от z
в трех случаях: (а)7 < 7*, (6)7 > 7*, (с)7 = 7*. Стрелки на оси z показывают
потоки z из уравнения (9.84)
Второе и более важное свойство состоит в том, что только одно значе¬
ние постоянной разделения физически приемлемо. Чтобы увидеть, почему
это так, рассмотрим поведение Д, выраженной в скейлииговых переменных.
Используя уравнения (9.83) и (9.81), после простых вычислений получим
(9.84)
378
УКРУПНЕНИЕ
где функция g(z) определена в (9.82). Теперь посмотрим на поведение g(z)
при различных значениях параметра 7. Существует три различных случая
(см. рис. 9.7):
(а) 7 < 7* = ЩТ!. В этом случае при z(0) > 21 значение z(t) экспоненци¬
ально быстро приближается к устойчивой неподвижной точке 22, т. е.
радиусы капель достигают общего значения RCZ2, которое расходится
при t —> 00. Такое распределение не может удовлетворять закону сохра¬
нения массы.
(Ь) 7 > 7*. В этом случае z(t) —> 0 экспоненциально быстро по времени при
любом начальном значении z. Поэтому все капли сжимаются в ноль, и
закон сохранения массы снова нарушается.
(с) 7 = 7*. В этом случае z = 3/2 — неподвижная точка, но такая, при¬
ближение к которой описывается степенным законом по времени. Такое
специфичное поведение позволяет выполнить закон сохранения массы.
Если бы неподвижная точка в z = 3/2 достигалась экспоненциально
быстро, то опять радиусы капель достигли бы общего значения ЗЛс/20,
и сохранение массы нарушилось бы. Медленное убывание z обеспечива¬
ет деликатное равновесие между ростом и уменьшением кластеров так,
что масса сохраняется.
В физическом случае 7 = 7* уравнение (9.83) для скейлинговой функции
можно факторизовать
2 - » - 57»3 dy
(т?-1)2(з + Ч У'
Вычисление этого интеграла с помощью разложения на простейшие дроби
дает интересный вид скейлинговой функции в трех измерениях (рис. 9.8)
0(z)
Cz2 (z + З)-7/3 (3 — 2г)-11/3 е~3/(3_2г) z < 3/2,
< 0 г >3/2,
(9.85)
в котором амплитуда С фиксируется с помощью закона сохранения (9.78).
Эта же величина феноменологически возникает для укрупнения ЛСВ в про¬
извольной пространственной размерности (задачи 9.15 и 9.16).
9.7 Экстремальная динамика
379
Рис. 9.8. Скейлинговая функция </>(z) для укрупнения ЛСВ, уравнение (9.85)
9.7 Экстремальная динамика
Тогда как степенной рост доменов — характерное свойство укрупнения при
нулевой температуре в высших размерностях, одномерие необходимо рас¬
сматривать отдельно, поскольку там имеет место гораздо более медленный
логарифмический рост. В частности, это различие становится очевидным в
случае неконсервативной динамики. В одном измерении нет локальной кри¬
визны, которая отвечала бы за движение границы. Вместо этого движение
границы определяется суммарным потоком параметра порядка через сосед¬
ние домены, который в свою очередь зависит от их длины. В пределе боль¬
шого времени этот поток стремится к нулю экспоненциально с ростом длины
домена и приводит к экстремальной динамике, в которой эволюционирует
самый короткий домен в системе, тогда как все остальные домены (кроме
его соседей) почти не меняются. Эта экстремальная картина даст естествен¬
ный способ описания эволюции доменов как для консервативной, 'гак и для
неконсервативной динамики. Итоговый результат такой динамики — домены
логарифмически укрупняются со временем.
Сжатие единичного домена
Чтобы понять природу медленного роста доменов с точки зрения одномер¬
ного НУГЛ, рассмотрим единичный большой домен длины L = Х2 — a?i и
намагниченностью, близкой к +1, погруженный в море с намагниченностью,
близкой к —1 (рис. 9.9). Две границы такой капли состоят из кинка в
и антикинка в х = жг(4) = х± + L. Если L много больше, чем ширина каж-
380
УКРУПНЕНИЕ
Рис. 9.9. Единичный домен с намагниченностью близкой к +1 в среде с намаг¬
ниченностью близкой к —1
дой границы, что является хорошим приближением на больших временах,
то кинк и антикинк почти независимы. При этих предположениях простран¬
ственную зависимость намагниченности можно записать как
ш(ж, t) ~ th[x — a?i(t)] — th[a; — жг(<)] — 1, (9.86)
где мы использовали профиль (9.23) для кинка и антикинка.
Теперь оценим, как движутся границы в паре кинк-антикинк. Подставив
профиль (9.86) в НУГЛ (9.2), получим
[d,(x-\))2 = 6[th(l - ~th(l -12)1
х[1 — th(x — xi)][l + th(x — Ж2)]. (9.87)
Удерживая только члены низших порядков по х — х± и х — Х2^ асимптотически
находим
X! ~ -ж2 = 12e“2(l2_:El). (9.88)
Следовательно, длина домена L = Х2 — xi уменьшается согдасно уравне¬
нию ~ —24e_2L, решение которого имеет вид L(t) = jin [e2L® — 48£].
Поэтому время исчезновения домена аномально длинное: т = ^e2L(Q\ Та¬
кая экспоненциальная зависимость от длины имеет далеко идущие следствия
для эволюции гетерогенного массива доменов в одном измерении. В преде¬
ле большого времени продолжительность сжатия самого маленького домена
на порядки меньше, чем для следующего по величине домена. В результате
домены сливаются с ближайшими соседями в порядке возрастания разме¬
ра, т. е. детерминистическим образом. Такая упорядоченность приводит к
экстремальной динамике и предполагает следующий эффективный алгоритм
для эволюции доменов в НУГЛ: (i) выбираем наименьший домен и соединя¬
ем его с двумя его соседями, тогда как все остальные домены сохраняются
неизменными; (ii) повторяем так до бесконечности (рис. 9.10).
9.7 Экстремальная динамика
381
Рис. 9.10. Эволюция с экстремальной динамикой. Кратчайший домен на любой
стадии (в круге) сливается с двумя соседними доменами, тогда как все остальные
остаются статичными. Домены, вновь созданные на каждом шаге, выделены
Распределение длины доменов
Теперь исследуем как в экстремальной динамике эволюционирует распреде¬
ление длины доменов16. Более конкретно, мы определим с(.т,€), плотность
доменов длины ж, когда длина кратчайшего домепа равна Э'га минималь¬
ная длина играет роль времени для экстремелы-юй динамики. Выберем на¬
чальные длины доменов из непрерывного распределения, так что все длины
различны. Также предположим, что полная начальная намагниченность рав¬
но нулю, так что средние длины доменов с положительной и отрицательной
намагниченностью равны между собой. По определению полная плотность
доменов есть р = f£°c(x,£)dx, а условие, что домены покрывают прямую
целиком, приводит к соотношению х с(х, f)dx = 1.
Сначала покажем, каким образом длина кратчайшего домена может иг¬
рать роль переменной времени. Предположим, что при длине кратчайшего
домена I происходит столько слияний соседних доменов, чтобы уничтожить
все домены с длинами в диапазоне (^,^+Д€). Следовательно, длина кратчай¬
шего домена увеличивается с t до Д£. Плотность доменов в этом диапазоне
равна с(^,^)Д^. Поскольку при каждом слиянии всего исчезают два домена,
p(t + Д£) = р(£) — 2с((,.>£)М, плотность доменов описывается уравнением
^ = -2с(€Л). (9.89)
Поэтому в данном кинетическом уравнении для полной плотности доменов
минимальная длина I играет роль времени.
16Получающееся в результате укрупнение похоже на кластерные динамики Сведсена -
Ванга и Вольфа, которые обсуждались в разделе 8.8.
382
УКРУПНЕНИЕ
Теперь уравнение движения для распределения длины доменов можно на¬
писать в терминах временнбй переменной А Когда длина кратчайшего домена
увеличивается с £ до £ + Д€, распределение длины с(ж,^) меняется согласно
уравнению
с(т, I + А€) — с(т, €)
с(М)
—2
рх—2€
+ 0(ж-3€) J
с(у,£) с(х-£- у,£)
dy
(9.90)
Первое слагаемое в правой части отвечает за исчезновение домена длины х
из-за его слияния. Коэффициент 2 возникает потому, что домен длины х или
слева, или справа от кратчайшего домена. Второе слагаемое отвечает за по¬
явление домена длины х в результате слияния трех доменов длины £, у и
х — £ — у. Ступенчатая функция Хевисайда ©(ж — 3^) накладывает условие,
что когда длина минимального домена равна £, кратчайший домен, кото¬
рый может возникнуть при слиянии, должен иметь длину > ЗЛ Последний
множитель учитывает число событий слияния, которые происходят,
когда минимальный размер возрастает с £ до I + ДЛ Как уже было выяс¬
нено при обсуждении кластерной динамики в разделе 8.8, важное свойство
экстремальной динамики — если домены не скоррелированы сначала, то они
остаются нескоррелированными все время. Слияние доменов не влияет на
соседние домены, так же как на сами домены не влияют их соседи.
Сейчас нам удобно работать с нормированным распределением Р(х, £) =
с{х^£)/р. Пользуясь уравнениями (9.89) и (9.90) (после деления на Д£), нахо¬
дим уравнение для Р(т, £)
= jT *p(y,e)P(x-e-y,e)dy, (9.91)
которое содержит только член прихода. Воспользуемся уравнением (9.91) для
нахождения асимптотического поведения распределения длины доменов. По¬
стоянно растущая минимальная длина доменов £ задает масштаб, который
мы постулируем как характерный для системы в пределе большого времени.
Предположим, что Р(ж, £) стремится к скейлинговому виду
Р(ж,€)^|ф(ж/€) (9.92)
при I -> оо. Коэффициент в уравнении (9.92) обеспечивает нормировку
Р(х,£) dx = 1. Как следствие, скейлинговая функция Ф(-г) должна удо¬
влетворять условию Ф(г) dz = 1. Подставляя скейлинговый анзац Р(т,€)
9.7 Экстремальная динамика
383
it (9.91), находим, что Ф(г) удовлетворяет уравнению
+ Ф(г) + ©(г — 3) Ф(1) [ Ф(у) $(z - 1 - у) dy = 0. (9.93)
аг Ji
Поскольку уравнение содержит свертку, удобно работать в области приме¬
нения преобразовани Лапласа. Для этого конкретного примера удобно опре¬
делить Лаплас-образ как 0(s) = /х°° Ф(г)е_в2^, т. е. с нижним пределом,
равным 1. Теперь умножим (9.93) на e~sz и, проинтегрировав ио частям, по¬
лучим, что Лаплас-образ удовлетворяет уравнению
5^ = -ф(1)(1-</>2)е-в (9.94)
as
с граничным условием 0(0) = 1. Чтобы найти константу Ф(1) (нормиро¬
ванную плотность кратчайших доменов), подставим разложен же 0(.ч) = 1 +
s0'(O) + ... и, взяв предел s = 0, получим Ф(1) = ^17. Используя Ф(1) = j,
можно переписать уравнение (9.94) в виде
где
s
и решение для Лаплас-образа принимает вид
</>(s) =th[Ei(s)/2], (9.95)
где Ei(s) — экспоненциальный интеграл Ei(s) = /s°° ± е~и du.
Есть несколько основных свойств экстремальной динамики, которые сто¬
ит выделить:
1. Уравнения движения решаемы. Для одномерной модели Изинга Глау¬
бера распределение длины доменов, напротив, неизвестно.
2. Экстремальная динамика детерминистическая. Случайность происхо¬
дит только из начальных условий.
3. В отличие от стохастических эволюционных процессов корреляции не
генерируются динамикой.
4. Скейлинговый анализ эффективно переопределяет длину кратчайшего
домена после каждого слияния, полагая ее равной единице. Эту проце¬
дуру можно рассматривать как неподвижную точку пространственной
ренормгруппы18.
17Следовательно, асимптотическая плотность кратчайших доменов равна Р(€, £) =
(2Q-1.
18Похожая ренормализация сильного беспорядка будет использована в разделе 10.2.
384
УКРУПНЕНИЕ
Теперь используем предшествующие результаты, чтобы найти среднюю
длину домена (х) = (z}£. Из поведения Лаплас-образа при малом аргументе
= 1—s(z)+O(s2) и асимптотических свойств экспоненциального интегра¬
ла19 мы заключаем, что (х) = 2 ехр(7в) €. Заметим, что отношение средней и
минимальной длин стремится к 2 ехр(7#) = 3,562144, так что, действительно,
в распределении есть единственный характерный масштаб длины. Из закона
сохранения р(х) = 1 полная плотность доменов равна
ехр(—2тб)
Р 2€
Наконец хвост распределения на малых длинах можно вычислить непосред¬
ственно из уравнения (9.93). В диапазоне длин 1 < z < 3 интеграл выпадает,
так что скейлинговая функция удовлетворяет уравнению гФ'(г) = — Ф(г) с
граничным условием Ф(1) = 1/2. Это дает Ф(г) = (2г)-1 для 1 < z < 3.
Неожиданно в диапазоне € < х < 3€ нормированная плотность длины доме¬
нов Р(ж,^) -4- (2я)-1 не зависит от I.
9.8 Зародышеобразование и рост
Фазовые переходы могут быть непрерывными (второго порядка) и разрыв¬
ными (первого порядка). До сих пор наш анализ был сконцентрирован на
непрерывных фазовых переходах, в которых мы изучали кинетику закалки
при охлаждении от температуры выше критической до температуры ниже
критической. Такую же закалку можно использовать для изучения кинетики
систем, в которых происходит разрывный фазовый переход. В этом разделе
мы описываем простую модель зародышеобразования и роста Колмогорова -
Аврами-Джонсона-Мейла (КАДМ) (рис. 9.11). При зародышеобразовании
и росте вещество в одной термодинамической фазе превращается в другую
фазу с помощью следующих двух шагов:
• Зародышеобразование. Инфинитезимальные острова или «зародыши»
стабильной фазы образуются в «море» нестабильной фазы.
• Рост. Из этих зародышей за счет нестабильных областей вырастают
стабильные острова, которые превращают вещество в стабильную фазу.
Граница между стабильной и нестабильной фазами распространяется в
нестабильную фазу с постоянной скоростью в направлении, перпенди¬
кулярном границе (рис. 9.11).
19Для малых ж, Ei (х) — — — In ж, где ув Ф 0,577215 — постоянная Эйлера.
9.8 Зародышеобразование и рост
385
(а)
(Ь)
(с)
Рис. 9.11. Иллюстрация к зародышеобразованию и росту в двух измерениях с
начальным посевом: (а) одного зародыша, (Ь) двух зародышей и (с) четырех
зародышей. Последний случай показан в четыре разных момента времени, раз¬
деленных равными промежутками
Чтобы завершить описание модели, нужно определить как именно обра¬
зуются зародыши стабильной фазы. Есть две естественные возможности:
• Начальный посев. Система стартует с заданной конфигурации зароды¬
шей.
• Непрерывное зародышеобразование. Зародыши образуются в системе
непрерывно и однородно с фиксированной интенсивностью.
В реальности у зародышей есть ненулевой размер, которым мы пренебрегаем
в настоящей модели. Таким образом, область стабильной фазы состоит из
объединения растущих сферических доменов. Геометрическая природа эво¬
люции позволяет извлечь из простых вероятностных аргументов долю пре¬
вращенного вещества.
Начальный посев
Когда все зародыши образованы в момент t = 0 на неограниченной двумер¬
ной подложке, есть два основных параметра: с — концентрация зародышей и
v — скорость распространения из стабильной фазы в нестабильную. Посколь¬
ку направление распространения всегда перпендикулярно границе раздела,
растущий остров, появившийся из единственного круглого зародыша, неогра¬
ниченно долго сохраняет форму круга радиуса vt (рис. 9.11(a)). Множествен¬
ные изолированные зародыши в конце концов сливаются в расширяющуюся
386
УКРУПНЕНИЕ
область, которая является объединением кругов радиусов vt, растущих из
каждого зародыша (рис. 9.11(b) и (с)). Поэтому все точки, находившиеся
вначале на расстоянии vt от любого зародыша, превращаются в стабильную
фазу за время t.
Для произвольного числа зародышей точка на плоскости остается в неста¬
бильной фазе тогда и только тогда, когда окружность радиуса vt и площа¬
ди 7r(ut)2 в начальной конфигурации свободны от зародышей (рис. 9.12).
Поскольку зародышеобразование случайно в пространстве, эта круглая за-
Рис. 9.12. В начальной конфигурации точка (показанная маленькой окружно¬
стью), находящаяся на расстоянии более vt от любого зародыша (точки) оста¬
нется в нестабильной фазе до времени t
прещенная зона не содержит зародышей с вероятностью ехр[—C7r(vt)2], убыва¬
ющей экспоненциально с ожидаемым в этой зоне числом зародышей C7r(vi)2.
Следовательно, доля площади ф нестабильной фазы есть просто
ф(/) = ехр[—C7r(vi)2], d = 2. (9.97а)
Этот результат похож по духу на уравнение (7.47), которое дает распреде¬
ление площади разрешенных зон при необратимой адсорбции дисков. Доля
площади стабильной фазы р — это просто р = 1 — ф, и. в конце концов все
пространство оказывается занятым стабильной фазой.
В d измерениях форма запрещенной зоны есть шар радиуса vt и объема
Vd(yt)d, где Vd — это объем единичного шара в d измерениях20. Таким обра¬
зом, доля площади нестабильной фазы дается прямым обобщением формулы
20Единичный шар определяется как множество {я | ||я|| < 1}, тогда как единичная
сфера - это множество {я | ||я|| = 1}. Объем единичного шара в d измерениях равен Vd =
тга/2/[Г(1 + d/2)], где Vi = 2, V2 = тг и V3 = 4тг/3.
9.8 Зародышеобразование и рост
387
(9.97а)
</>(£) = ехр[ —cVd(yt)d ].
(9.97b)
Система опять достигает финального состояния, полностью занятого ста¬
бильной фазой, экспоненциально по времени.
Непрерывное зародышеобразование
При непрерывном зародышеобразовании зародыши, начиная с пустой исход¬
ной системы, постоянно образуются с интенсивностью 7 на единицу объе¬
ма. Теперь размер острова зависит от его возраста, различного для разных
островов (рис. 9.13). Поэтому нам нужно следить за всей историей процесса
Рис. 9.13. Снимки непрерывного зародышеобразования и роста в двумерной си¬
стеме через равные промежутки времени
зародышеобразования. Рассмотрим сначала случай одного измерения, в кото¬
ром стабильную область, растушую из изолированного зародыша, можно рас¬
сматривать как расширяющийся треугольник в пространственно-временном
представлении (рис. 9.14(a)) Аналогично, стабильные области, растущие из
множественных зародышей, — это объединения треугольников в простран¬
ственно-временном представлении. Для того чтобы точка осталась в неста¬
бильной фазе, события зародышеобразования не должны происходить в пе¬
ревернутом треугольнике с шириной основания 2vt, высотой t и площадью
vt2 в плоскости x-t (рис. 9.14(b)). Ожидаемое число событий зародышеобраг
зования в этой запрещенной зоне есть yvt2. Таким образом, доля системы,
которая остается в нестабильной фазе, равна
</>(£) = exp [—7vi2] , d = 1.
(9.98a)
Поэтому непрерывное зародышеобразование и рост приводят к гораздо бо¬
лее быстрому приближению к асимптотическому поведению, чем в случае
начального посева и последующего роста.
388
УКРУПНЕНИЕ
X
(а)
t
Рис. 9.14. Зародышеобразование и рост в одном измерении с непрерывным за¬
родышеобразованием. (а) Пространственно-временная эволюция островов из за¬
родышей, возникающих в разные моменты (точки); получившаяся стабильная
область показана серой. (Ь) Чтобы кружок остался в нестабильной фазе, долж¬
на существовать перевернутая треугольная запрещенная область с основанием
2vt и высотой t
Обобщение на d измерений снова очевидно. Теперь запрещенная зона —
это (d + 1)-мерный гиперконус с радиусом vt, высотой t и объемом
Следовательно, результат из уравнения (9.98а) принимает вид
<£(<) = ехр [-gjy 7 Vd vd td+1 ]
(9.98b)
для всех d. Эти результаты также можно легко обобщить для учета зави¬
симости интенсивностей зародышеобразования от времени и пространства, а
также для зависящих от времени скоростей роста.
Пространственные корреляции
Более полную характеристику пространственного распределения стабильной
и нестабильной фаз дает двухточечная корреляционная функция
G(a;,f) = (v?(O,t)v?(a5,f)) - t)><v?(O, t)>, где х = |аг|, (9.99)
которая дает количественную характеристику вероятности, что две точки,
разнесенные на расстояние х, находятся в нестабильной фазе в момент t.
Здесь <p(x,t) — функция индикатора фазы такая, что у?(ж) = 1, когда х
находится в нестабильной фазе, и <^(ж) = 0 в противном случае. Поэтому
(</?(ж)) = ф — доля площади нестабильной фазы. Мы неявно предполагаем,
9.8 Зародышеобразование и рост
389
что корреляционная функция изотропна, потому что система пространствен¬
но однородна. По определению у?2 = <р, так что корреляционная функция G
удовлетворяет граничному условию G(x = 0) = ф — ф2. Поскольку величина
ф = (v(®)) Уже была вычислена, нам нужно найти
д{х, t) = (<р(0, t)), (9.100)
откуда получим G = д — ф2.
Рассмотрим сначала непрерывное зародышеобразование в одном измере¬
нии. Мы уже видели, что пространственно-временная запрещеная зона — это
перевернутый треугольник и что в ней не должно быть зародышей, чтобы
точка осталась в нестабильной фазе. Аналогично, вероятность, что две точ¬
ки на расстоянии х останутся в нестабильной фазе, определяется объедине¬
нием двух запрещенных треугольников (рис. 9.15). Если — это площадь
такого объединения, то, поскольку события зародышеобразования не могут
происходить внутри этой составной запрещенной зоны, д(х) = exp(-~7Aj).
Когда х > 2vt, мы имеем Au = 2А, где А = vt2 — площадь одного треуголь¬
ника (рис. 9.15(a)). Пользуясь формулой (9.98а), получим, д = ф2, и, таким
х
Рис. 9.15. Иллюстрация к корреляционной функции в одном измерении с непре¬
рывным зародышеобразованием для: (а) двух нескоррелированных точек, и (Ь)
двух скоррелированных точек. Наложение двух запрещенных зон (штрихованный
треугольник) определяет корреляции между двумя точками
образом, две точки нескоррелированы.
Однако точки, разнесенные на расстояние, меньшее чем 2vt, скоррели¬
рованы, потому что их запрещенные зоны пересекаются. Площадь пересече¬
ния — это треугольник с основанием 2vt—x, высотой (2vt — x)/2v и площадью
(рис. 9.15(b))
4т —
(2vt — хУ
4v
= ^2(1 - г)2
где
х
2vt
(9.101)
390
УКРУПНЕНИЕ
Наконец, площадь объединения двух запрещенных зон — это просто Ли =
2А — Лп. Подставляя эту площадь в д(х) = ехр(—7Ли), получаем д(х) =
ф2-р(г) с нормированной функцией пересечения F(z) = Лп/Л = (1 — г)2.
Используя (9.99), получаем корреляционную функцию
G(x, t)
'ф2 pH1-*)2 - l] z < 1;
ч0 z>l.
где
X
2vt
(9.102а)
Положительные корреляции имеют место между точками на расстоянии,
меньшем 2и£, и отсутствуют в противоположном случае. Корреляционная
функция — универсальная функция доли покрытия ф: две разные системы
на разных стадиях эволюции, но с одинаковым общим покрытием, имеют
идентичные двухчастичные корреляторы.
Корреляционная функция (9.102а) непосредственно обобщается на произ¬
вольную размерность
G(x) = ф2 (ф~р<№ - l) (9.102b)
для z < 1, где ф дается выражением (9.98Ь). Здесь F^(^) — функция пере¬
сечения в d измерениях, которая равна нормированному объему пересечения
между двумя (d + 1)-мерными гиперконусами единичной высоты и единич¬
ного радиуса 2^, разделенными расстоянием 2z
f (1 - г)2, d = 1,
Fd(z) = Н [arccosz — 2zVl — z2 + z3 In , d = 2, (9.103)
I (1 - z)3(l + z), d = 3.
Функция пересечения удовлетворяет условиям F(0) = 1 и F(l) = 0, так что
G(x = 0) = ф — ф2 и G(x = 2vt) = 0. Так как функция пересечения моно¬
тонно убывает с перемасштабированной длиной г, корреляционная функция
(9.102Ь) также монотонно убывает с расстоянием и становится равной ну¬
лю на перемасштабированных расстояниях z > 1 (рис. 9.16). Приведенные
выводы естественным образом обобщаются для расчета следующих корреля¬
ционных функций. Например, чтобы получить n-точечную корреляционную
функцию, нужно вычислить объем объединения п запрещенных зон. Это вы¬
числение является предметом задач 9.22 и 9.23.
9.9 Ссылки
Общую информацию по явлениям укрупнения можно найти в ссылках, упо¬
мянутых в предыдущей главе [159, 160], а также в [184, 185]. Задачи с по-
9.9 Ссылки
391
Рис. 9.16. Зависимость перемасштабированной корреляционной функции G(x,<)
от перемастабированного расстояния z = x/(2t;i) в случаях ф = 0,1,0.3и0.5.
тенциалом Шредингера, возникающие в связи с укрупнением, обсуждаются
в стандартных текстах, и два полезных обсуждения даны у Ландау и Лиф¬
шица [186] и Морса и Фешбаха [187]. Ранняя работа Кана и соавторов об
укрупнении, а также уравнения Аллена-Кана и Кана- Хилларда обсужда¬
ются в [160]. Укрупнение, управляемое кривизной, — это активно исследуе¬
мый предмет, например, статистика площадей, охватываемых границами до¬
менов (‘оболочки’) в двух измерениях, были описаны в [188|. Эволюция гра¬
ниц, управляемая потоками локальной кривизны, в которой все замкнутые
двумерные границы асимптотически сжимаются к окружности, представлена
в [189, 190]. Решение для эволюционирующей полуполосы было предложено
Маллинсом [191]. Конструкция трипериодических минимальных поверхно¬
стей была открыта Шварцом [192], а более недавние и детальные работы
об этом завораживающем геометрическом объекте можно найти в [193 -195].
Теорема Деррика обсуждается, например, в [196-198], а статьи Деррика — в
[199]. Топологические свойства дефектов в системах с векторным параметром
порядка исследуются, например, в [160, 200].
Описание явлений укрупнения Лифшица-Слезова Вагнера было разви¬
то в [201, 202]. Укрупнение доменов посредством экстремальной динамики
в одном измерении исследовано и решено в [203-205]. Дополнительные по¬
дробности о зародышеобразовании и росте можно найти в двух следующих
обзорных статьях: [143, 206]. Теория ЛСВ была обобщена на различные ти¬
392
УКРУПНЕНИЕ
пы динамики. Хорошая стартовая точка для работы над этой темой — это
ссылки [207, 208].
9.10 Задачи
9.1 Исследуйте уравнение mt = V4m с «неправильным» знаком плюс в правой
части. Проанализируйте решения вида m(x,t = 0) = sin fere. Покажите, что
коротковолновые возмущения быстро растут со временем.
9.2 Завершите вывод автокорреляционной функции (9.18) и двухчастичной кор¬
реляционной функции (9.19).
9.3 Проверьте, что кинки в модели с потенциалом V = jm2(l — га2)2 даются
формулой (9.26).
9.4 С помощью следующих аргументов покажите, что V’o из (9.33) соответствует
самому низкому уровню энергии:
(a) Проверьте, что то (ж) — монотонная функция х.
(b) Убедитесь, что из пункта (а) следует, что фо не имеет узлов, т. е. нулей.
(c) Примените теорему о том, что для одномерного уравнения Шредингера
с произвольным потенциалом собственная функция без узлов соответ¬
ствует самой низкой энергии.
9.5 Исследуйте устойчивость основного состояния mo = 1 для модели с потенци¬
алом V = |(1 — т2)2. Покажите, что убывание малых возмущений намагни¬
ченности на больших временах происходит по закону ф ~ e~4t.
9.6 Исследуйте устойчивость кинка mo = (1 Ч-е-®)-1/2 для модели с потенциалом
V = |т2(1 — т2)2 с помощью следующих шагов:
(a) Запишите соответствующее уравнение Шредингера.
(b) Опишите потенциал соответствующего уравнения Шредингера и пока¬
жите, что он монотонно возрастает от 1 при х = —оо до 4 при х = оо.
(c) Используя пункт (Ь) и основные результаты об одномерном уравнении
Шредингера, покажите что у него есть: (i) только один дискретный уро¬
вень Ео = 0, (ii) непрерывный спектр в интервале 1 < Е < 4 с невырож¬
денными собственными значениями (все собственные функции осцилли¬
руют при х —> —оо и убывают как е~Ху^4~Е при х —> оо) и (iii), наконец,
непрерывный спектр при Е > 4, не содержащий дважды вырожденных
собственных значений.
9.7 Подтвердите вид зависимости от параметра а слагаемых в свободной энергии
(9.51).
9.10 Задачи
393
9.8 Группа гомотопии я-* (^классифицирует отображения г-мерной сферы §г в J-
мерную сферу Эта классификация не отличает отображения, которые мож¬
но непрерывно деформировать друг в друга. Когда i = каждое отображение
сферы в себя имеет целый топологический заряд, измеряющий сколько раз
сфера обернута в саму себя. Поэтому ^(S7) = Z для всех j > 1. Проанали¬
зируйте простейший случай отображения окружности в окружность. Отобра¬
жение S1 —> S1 можно записать как в —» /(0). Угол 0 определен по модулю
27Г.
(а) Покажите, что /(27т) — /(0) = 27гп, где п — целое число, называющееся
числом намоток, w(/) = п. Число намоток играет роль топологического
заряда в случае окружности. Число намоток можно переписать в инте¬
гральном виде
п =
_1_ /27Г
2тг Уо
Это выражение — аналог формулы (9.62), которая дает топологический
заряд отображения обычной сферы S2 в себя
(Ь) Покажите, что отображение
при 0 < в < 7Г,
при 7Г < в < 27Г
можно деформировать в тривиальное отображение /о(0) = 0.
(c) Покажите, что отображение /о($) = 0 нельзя деформировать в отобра¬
жение /i(0) = в-
(d) Покажите, что отображение fn(&) = п0 нельзя деформировать в отобра¬
жение fm(6) = тв, когда п / т.
(e) Рассмотрите два отображения /(0) и д(в) и определив их произведение
f * д как отображение идентичное f при 0 < в < 7г, применяемое с удво¬
енной скоростью, а далее равное д, применяемое с удвоенной скоростью.
На языке формул это значит
/ * 0(0) = <
7(20)
/(2%) + д(26 - 27г)
при 0 < 0 < 7Г,
при 7Г < 0 < 27Г.
Покажите, что fn*fm = fn+m и что в общем случае числа намоток
складываются, w(f *д) = w(/) + w(p). Это объясняет, что ^(S1) = Z
обладает структурой аддитивной группы целых чисел.
9.9 Покажите, что намагниченность удовлетворяет уравнению (9.67) и, конечно,
условию (9.56), а также является решением уравнения (9.58).
9.10 Рассмотрите вихрь (9.72).
394
УКРУПНЕНИЕ
(a) Убедитесь, что он дает решение уравнения (9.67).
(b) Проверьте, что топологический заряд вихря (9.72) равен q = 1.
(c) Вычислите свободную энергию вихря (9.72) и покажите, что она равна
47Г.
(d) Постройте явное выражение (похожее на (9.72)) для распределения на¬
магниченности q = 2.
9.11 Рассмотрите ХУ-модель в двух измерениях.
(a) Покажите, что от условия (9.56) можно избавиться, используя представ¬
ление m = (cos </>, sin 0).
(b) Выразите свободную энергию через ф и покажите, что ее минимизация
дает V20 = 0.
(c) Найдите решение уравнения V2</> = 0 в полярных координатах. Пока¬
жите, что решения зависят только от угловой координаты, ф = ф(6), и
имеют вид ф = пв + const., где п — целое число (число намоток).
(d) Вычислите свободную энергию вихря фп = пв и покажите, что она равна
F = |/dx(VK>2 = ™2/°°^.
Эта свободная энергия логарифмически расходится (в соответствии с на¬
шим общим результатом, что ХУ-модель не имеет стационарного реше¬
ния с конечной свободной энергей)21. Самые важные вихри — это снова
вихри с п = ±1. В исходных переменных они могут быть представлены
как m = ±х/|х|. На гидродинамическом языке первый вихрь — это ис¬
точник, а второй — сток. Эти вихри сингулярны не только потому, что
они имеют расходящуюся свободную энергию, но у них также есть син¬
гулярность в начале координат, где намагниченность плохо определена.
9.12 Рассмотрите потенциал «Мексиканская шляпа» (или «винная бутылка»), V =
(1 — т2)2, который является обобщением двухямного потенциала V = (1 —
га2)2. Покажите, что в любой пространственной размерности d > 2 существует
стационарное решение, независимое от размерности внутреннего пространства
параметра порядка.
9.13 Квазистатическое приближение дает ведущую асимптотику поведения закона
роста в (9.81). Оцените поправку к закону t1/3 роста в трех измерениях.
9.14 Убедитесь, для функции <j(z), определенной в (9.82), уравнение g(z) = 0 имеет
двойной корень (z = 3/2), когда 7 = 7*= 4/27.
21 Расходимость на малых расстояниях — это артефакт непрерывного описания. В мик¬
роскопической модели параметр решетки дает нижнее обрезание. Расходимость на боль¬
ших расстояниях действительно имеет место. Следовательно, в конечной системе свободная
энергия вихря пропорциональна логарифму размера системы.
9.10 Задачи
395
9.15 Обобщите теорию ЛСВ на произвольную размерность d > 2. Убедитесь, что
скейлинг t1/3 соблюдается независимо от d. Покажите, что скейлинговая
функция принимает вид
ф = Cdz2 (z + З)-1"4^9 (3 - 2z)“2_5d/9 e-d^3-2^
при z < 3/2 и </>(z) = 0 при z > 3/2.
9.16 Рассмотрите укрупнение ЛСВ в d = 2. Отсутствие изотропного стационарного
решения уравнения Лапласа, которое исчезает на бесконечности, приводит к
тому, что стандартная теория оказывается неэффективна. Используйте под¬
ход, развитый в разделе 2.7 для скорости реакции, и покажите, что в резуль¬
тате получается слегка более медленный рост R(. ~ (/./1»01/3.
9.17 Завершите вывод уравнения (9.88).
9.18 Эта задача посвящена скейлинговой функции Ф(г) дли экстремальной дина¬
мики, которая возникает в формуле (9.92).
(a) Вычислите Ф(г) в диапазоне 3 < z < 5.
(b) Вычислите Ф(г) в диапазоне 5 < z < 7.
(c) Покажите, что у Ф(г) есть разрывы в нечетных целых значениях z =
1,3,5,7,..., которые становятся слабее и слабее: разрыв функции Ф при
z = 1, разрыв первой производной Ф' при z = 3, разрыв второй произ¬
водной Ф" в z = 5, и т. д.
(d) Покажите, что Ф(г) экспоненциально убывает в пределе z —> оо, Ф(г) ~
Ae_az. Найдите А и а.
9.19 Рассмотрите процесс одномерного зародышеобразования и роста.
(а) Пусть Д(ж, t) будет плотностью дырок длины х в момент времени t. Пока¬
жите, что это распределение длины дырок эволюционирует следующим
образом
(^ - 2w J“) h(x> Q = 27(*) / Мг/, 0 dy - 7(<) j: li(x, t).
(b) Покажите, что плотность дырок (или островов) n(t) и доля 1 — p(t) неза¬
нятого пространства дается выражением
/*ОО /*ОО
n(t) = / h(x,t)dx, 1 — p(t) = / xh(x,t)dx.
Jq Jq
(c) Покажите, что для мгновенного зародышеобразования, y(t) = cr5(t), эво¬
люционное уравнение превращается в волновое уравнение ht — 2vhx = 0,
общее решение которого имеет вид h(rc,t) = ho (я + 2vt). Покажите, что
подходящее начальное условие есть ho (ж) = а2 е~ах и, поэтому, Ь(ж, £) =
a2 е~ах e~2avt.
396
УКРУПНЕНИЕ
(d) Покажите, что при однородном зародышеобразование, 7(f) = 7 при t > О,
распределение длины дырок имеет вид
h(x,t) = (7t)2 e~yxt e-4vt\
(e) Пусть д(х, t) — плотность дырок длины х в момент времени t. Покажите,
что это распределение подчиняется уравнению
(й + 9(”’= 7(t)[1 - + 2’ Sr
Х \/о 9^y,t^x~y,t^dy _2n(tMa:>f) •
9.20 Рассмотрите зародышеобразование и рост в одном измерении с начальным
посевом.
(a) Выведите двухточечную корреляционную функцию (9.99).
(b) Выразите корреляционную функцию через z — rc/(2vt) и покажите, что
корреляционная функция зависит от плотности покрытия и простран¬
ственной размерности только как (9.102Ь).
(c) Получите функцию пересечения Fi(z).
9.21 Вычислите нормированную функцию пересечения для случая началь¬
ного посева зародышей.
9.22 Найдите формальное выражение для n-точечной корреляционной функции
0п(®1,®2,...,®») = (<^(®l)v>(®2) • • •
в d измерениях для зародышеобразования и роста с непрерывным зародыше¬
образованием с постоянной интенсивностью 7.
9.23 Трехточечная корреляционная функция зависит от объединения трех запре¬
щенных зон. Выразите это объединение запрещенных зон как линейную ком¬
бинацию одноточечных запрещенных объемов и объемов пересечений между
двумя и тремя запрещенными зонами.
Глава 10
БЕСПОРЯДОК
Порядок ассоциируется с симметрией, красотой и простотой. Некоторые из
самых значительных прорывов в физике использовали эти понятии для по¬
нимания фундаментальных свойств пространства и времени, а также струк-
туры материи на элементарном масштабе. С другой стороны, понятие бесио-
рядка созвучно с хаосом, запутанностью и сложностью. Это предубеждение
сдерживало научный прогресс в неупорядоченных системах до тех пор, пока
в середине 1970-х не обнаружилось, что многие неупорядоченные системы
демонстрируют замечательно красивые свойства, не уступающие свойствам
самых симметричных систем. Также было понято, что в неупорядоченных
системах динамические свойства намного более важны, чем в однородных
системах. В частности, некоторые неупорядоченные системы не могут быть
адекватно рассмотрены в рамках равновесного подхода, и им необходимо ди¬
намическое описание.
Одно из предубеждений о неупорядоченных системах действительно от¬
ражает реальность: они могут быть сколь угодно сложны. Тем не менее су¬
ществует достаточно возможностей для построения «хороших» моделей, ко¬
торые в основном улавливают то, как беспорядок влияет на физические яв¬
ления, и, кроме того, или поддаются аналитической трактовке, или на разум¬
ном временном масштабе могут быть смоделированы численно. Харак'герный
пример — это модель Изинга с неоднородным взаимодействием, гамильтони¬
ан которой имеет вид
JijSiSj. (10.1)
(v>
Параметры Jij взаимодействия между соседними спинами Si и Sj — случай¬
ные (а также независимые и одинаково распределенные) величины. В неупо¬
рядоченных ферромагнетиках все взаимодействия имеют одинаковые знаки,
398
БЕСПОРЯДОК
и главный вопрос — как беспорядок влияет на переход к ферромагнетизму,
который происходит при понижении температуры. Когда есть ферромагнит¬
ные (Ту > 0) и антиферромагнитные (Ту < 0) взаимодействия с близкими
суммарными величинами взаимодействий, низкотемпературная фаза оказы¬
вается более сложной. В ней есть не ферромагнитный дальний порядок, а
спин-стекольный порядок, в котором каждый спин направлен вдоль своего
собственного локального, случайно ориентированного поля (рис. 10.1). Мно¬
гие аспекты этого перехода и самой спин-стекольной фазы до сих пор оста¬
ются загадкой.
удовлетворенные
связи
Рис. 10.1. Ячейка неупорядоченной модели Изинга (10.1) на треугольной решет¬
ке, показывающая ферромагнитные (сплошные) и антиферромагнитную (пунк¬
тирную) связи. Их толщина пропорциональна величине взаимодействия вдоль
связи. Показано состояние с минимальной энергией, в котором каждый спин на¬
правлен вдоль локального поля, создаваемого соседними спинами. Самая тонкая
связь фрустрирована, потому что ориентации спинов на концах противоположны
знаку взаимодействия
Эта глава описывает несколько основных систем, в которых динамика
управляется беспорядком. Эти примеры дают пять кратких экскурсов в уди¬
вительный мир неупорядоченных систем.
10.1 Неупорядоченная спиновая цепочка
Начнем с цепочки Изинга с неупорядоченным взаимодействием ближайших
соседей и глауберовой динамикой с единичными переворотами. Параметры
взаимодействия между соседними спинами выбраны из распределения
p(J). Для конкретности сделаем три упрощающих предположения о распре¬
делении взаимодействия:
10.1НЕУПОРЯДОЧЕННАЯ СПИНОВАЯ ЦЕПОЧКА
399
• Л,г+1 — независимые одинаково распределенные случайные величины;
• распределение р( J) непрерывно;
• распределение p(J) симметрично, p(J) = р(—J).
Самое важное свойство — это непрерывность р( J), так что невозможно иметь
два параметра взаимодействия с одинаковым значением. Это ограничение
обеспечивает увеличение или уменьшение энергии при каждом перевороте
спина. Переворотов с сохранением энергии не происходит. Когда система эво¬
люционирует по правилам глауберовой динамики при нулевой температуре,
перевороты спинов, повышающие энергию, запрещены, и остаются только
понижающие энергию перевороты.
Так же как в однородной цепочке Изинга, фазовый переход возникает при
нулевой температуре, и поэтому мы сосредоточимся на эволюции при нуле¬
вой температуре. В отличие от однородной цепочки Изинга, которая имеет
два тривиальных основных состояния, у неупорядоченной спиновой цепочки
огромное число метастабильных состояний, которое растет экспоненциально
с размером системы. Мы увидим, что система застревает в одном из таких
метастабильных состояний, а не достигает основного состояния. Хотя в ре¬
зультате можно было бы ожидать сложной временнбй эволюции, некоторые
динамические свойства оказываются замечательно простыми. В частности,
система, вначале выстроенная вдоль одного направления, в конце концов ре-
лаксирует к состоянию, где намагниченность равна |, независимо от осталь¬
ных деталей системы.
Существование огромного числа метастабильных состояний не гаранти¬
рует, что система придет в такое состояние: область притяжения основного
состояния может в принципе доминировать и подавлять влияние метаста¬
бильных состояний. Например в главе 8 мы видели, что однородная модель
Изинга-Глаубера в двух измерениях не обязательно достигает полосатого
состояния, несмотря на то что число таких состояний макроскопическое (оно
растет как [(л/5 + 1)/2]для квадратной системы из N спинов). Тем не
менее, когда число таких состояний растет экспоненциально с размером си¬
стемы, часто в самом деле оказывается так, что система приходит в метаста¬
бильное состояние.
Метастабильные состояния
В метастабильном состоянии каждый спин направлен вдоль своего локаль¬
ного поля. Если такое состояние достигается глауберовой динамикой при ну-
400
БЕСПОРЯДОК
левой температуре, покинуть его невозможно. Значение г-того спина в мета¬
стабильном состоянии определяется равенством
Si = sgn(Jj_iSi_i + JiSi+i), (10.2)
где Ji = Jiti+i. Из-за непрерывности распределения параметров взаимодей¬
ствия, условие | Ji_i| / |Л| выполняется с вероятностью 1, и только сильней¬
шее из двух взаимодействий определяет s». Например, если |Л| > |«A-i|, то
(10.2) дает Si = sgn(JiS,+i), так что спин Si жестко связан со спином Sj+i.
Метастабильные состояния удобно характеризовать относительной вели¬
чиной взаимодействия на соседних связях. Будем называть связь г «сильной»,
когда |Л| > max(|Ji_i|, |Ji+i|), и «слабой», когда |JJ < min(|Jj_i|, |Ji+i|). В
остальных случаях связь будет «средней». Конкретные величины параметров
взаимодействия на связях не важны для эволюции. Важно лишь, является
ли связь сильной, слабой или средней. Поэтому конфигурацию связей можно
представить как последовательность букв W, М, S (см. рис. 10.2).
UI
I i
WS WMS MWS MWSM W
Рис. 10.2. Рельеф параметров взаимодействия |«7<| и соответствующий трехбук¬
венный алфавит — W, М, S — для слабых (weak), средних (medium) и сильных
(strong) связей. Пары стрелок отделяют кластеры в метастабильных состояни¬
ях, внутри которых спины упорядочены, тогда как в разных кластерах они не
скоррелированы
Назовем кластером часть цепи между двумя слабыми связями. По опре¬
делению слабые связи не могут быть соседними, поэтому каждый кластер
содержит по меньшей мере одну связь. В кластере есть ровно одна сильная
связь, а соседние кластеры отделены друг от друга изолированными сла¬
быми связями. При нулевой температуре состояние, в котором каждая не
слабая связь «удовлетворена», т. е. Si = Sj+i, если связь i ферромагнитна,
и Si = — Sj+i, если связь антиферромагнитна, минимизирует энергию. Одна¬
ко спины на концах слабой связи, не связаны между собой, и связь может
10.1 Неупорядоченная спиновая цепочка
401
быть как удовлетворенной, так и фрустрированной, когда ориентация сосед¬
них спинов противоположна знаку взаимодействия между ними. Поскольку
состояние каждой слабой связи может быть задано независимо, полное число
метастабильных состояний равно
М = 2^, £2 = число слабых связей. (10.3)
10.1. Случайный мультипликативный процесс и экспонен¬
циальные средние
Рассмотрим произведение N случайных величин, в котором с вероятностью 1/2
каждый множитель может принимать значение либо 2, либо 1/2. Каково среднее
этого произведения (П)? Поскольку к сомножителей 2 и N — к сомножителей 1/2
возникают с вероятностью 2"N (^), среднее значение произведения равно
= 2~n (2 + l/2)w = (5/4)w = (е1пП). (10.4)
Экспоненциально большое среднее значение (П) находится в противоречии с ин¬
туитивным ожиданием, что произведение должно состоять из равного количества
множителей 2 и 1/2 и, поэтому, быть равным 1. На самом деле единица дает наи¬
более вероятное значение произведения Птр. Можно записать ПШ|> как
Птр=2^2(1/2)^2
_ e[ln2+ln(l/2)]N/2 _ е(1пП> _ J (10 5)
Логарифм произведения — это сумма N слагаемых, равных либо In 2, либо ln( 1 /2),
и каждое из этих значений возникает с вероятностью 1/2. Тогда среднее значение
величины 1пП равно N, умноженному на среднее этих двух величин. Мы пришли
к основному результату
(е1пП) »е(1пП>. (10.6)
Какова же интуитивная причина того, что среднее и наиболее вероятное значения
так сильно отличаются? Типичное произведение состоит не из одинакового коли¬
чества чисел 2 и 1/2, а эти числа возникают N/2 ± y/N раз. Поэтому типичное
слагаемое будет порядка
2JV/2±v^V (1/2)N/2=FV^ — 2±2л/^
что уже довольно далеко от наиболее вероятного значения. На самом деле макси¬
мальное слагаемое в сумме (10.4) асимптотически растет как (5/л/87гЛГ) х (5/4)N,
что свидетельствует о том, что редкие события вносят существенный вклад в (П)
и приводят к тому, что (П) отличается от Птр.
402
БЕСПОРЯДОК
Чтобы найти среднее число слабых связей, рассмотрим три соседних связи.
Очевидно, что средняя связь будет самой слабой с вероятностью |, так что
среднее число слабых связей равно (fi) = N/3. Что же можно узнать отсюда
о числе метастабильных состояний? Наивная гипотеза, что оно равно 2^, не
верна. Различие возникает из-за того, что М экспоненциально растет с Q. Хо¬
тя статистические свойства Q могут быть хорошими, статистические свойства
экспоненциальной функции от П могут не быть таковыми, так что значение
2^ может сильно отличаться от (2П) (см. врезку выше). Таким образом,
нужно с аккуратностью подходить к различию между наиболее вероятным
числом метастабильных состояний (которое дается упомянутой гипотезой)
Mmp = 2<n> = 2n/3 (10.7а)
и средним числом метастабильных состояний
(М) = (2П), (10.76)
которое, как мы покажем, растет как (4/л)'ЛГ.
Чтобы вполне понять природу числа метастабильных состояний, нужно
найти вероятность П;у(9) того, что цепочка из N спинов содержит Q слабых
связей. Это можно сделать с помощью рекурсивного метода, эквивалентного
трансфер-матричной технике из равновесной статистической механики.
Распределение Плг(П)
Идея метода трансфер-матрицы — записать и решить рекуррентные соотно¬
шения для зависимой от N статистической величины1. В нашем случае мы
хотим выразить IIyv-ы через Пуу. Однако просто Щг не подходит для построе¬
ния рекурсии. Нам нужно знать величину взаимодействия на последней свя¬
зи, а также сильнее или слабее предпоследняя связь последней. Чтобы хра¬
нить информацию о величинах соседних связей, введем Pyv(Q, ж), вероятность
иметь Q слабых связей в системе с N связями при условии, что | J/y-i| = х и
| Jjv—21 > Аналогично определим Q;v(Q, х) как вероятность иметь Q слабых
связей при условии, что = х и |Jjy_2I < х. Эти вероятности подчиня¬
1 Например числа Фибоначчи определены скалярными рекуррентными соотношениями
Fw+i = F/v+Fw_i. Когда Fn — векторная величина, рекуррентные соотношения включают
трасфер-матрицу.
10.1 Неупорядоченная спиновая цепочка
403
ются рекуррентным соотношениям
Ptv+i(Q, х) = ^(x) f [Pn№, у) + Qn(&, у)] dy,
Jxrx (Ю.8)
Qw+i(Q,x) = / [P7v(fi-i,y) + Qyv(^,y)]dy,
Jq
где *ф(х) = p(x) + p(—x) — это плотность вероятности того2, что параметр
взаимодействия по модулю равен х. Члены этих рекуррентных соотношений
показаны на рис. 10.3. Например, вероятность P;v+i(fi,a;) можно построить
N-l N N+1
N-l N N+1
1 .г
' у
• У
• У
х
.г
У
Рис. 10.3. Схематическое изображение четырех слагаемых в уравнениях (10.8).
Рисунок слева соответствует вкладу в Pn+i(£1,x) (последняя связь слабее
предыдущей), а справа — вкладу в Q^+i(Q,a;) (последняя связь сильнее преды-
дущей)
либо из P/v(fi,y), либо из Qjv(Q,y), в которых величина взаимодействия у
предпоследней связи больше х. Таким же образом Q7v+i(^).'',)mo>k,i° постро¬
ить из PN(tt — 1, у) или из О/у(О,у), где у меньше х. Число слабых связей
возрастает только при добавлении связи с величиной взаимодействия х > у к
множеству конфигураций в Р#(П —1,у) (в верхнем правом углу на рис. 10.3).
Хотя следующий далее вывод технически сложен, каждый его шаг кон¬
цептуально очевиден, а конечный результат, приведенный в формуле (10.14),
очень постой. Для решения рекуррентных соотношений (10.8) введем произ¬
водящие функции
^(w, ж) = 52 х), Qn(w, х) = 52 Qn(^, х),
Q>0 П>0
2Для симметричного распределения параметров взаимодействия р(х) = р(—х), и поэто¬
му ifi(x) = 2р{х). Эта симметрия не влияет на концепцию «слабой связи», и поэтому вывод
остается справедливым и для несимметричных распределений р(х). Однако выражение
М = 2П для числа метастабильных состояний предполагает наличие симметрии.
404
БЕСПОРЯДОК
и перепишем (10.8) в виде
?jv+i(w, ж) = ^(х) f [Tjv(w, у) + Q/v(w, у)] dy,
JxfX (Ю.9)
Qjv+i(cd,ж) = ^(ж) / [еш Tn(u,у) + Qjv(w, у)] dy.
Jo
Таким образом, (T/v+i, Q/v+i) связано с (Tjv,Qjv) через действие линейного
оператора. Обозначим его максимальное собственное значение через е\ Ве¬
личина Л = A(w) известна как показатель Ляпунова. В пределе N —> оо ре¬
шения уравнения (10.9) растут экспоненциально с N: 7^(ш,х') ~ p(aj,x)eXN
и Qpf(u},x~) ~ q(u,x)eXN. Подставив эти асимптотики в (10.9), получим
еЛ р(ш, х) = -ф(х) f [p(w, у) + g(w, у)] dy,
Jx
РХ
ех q(w, ж) = ^(ж) / [еш р(ш, у)+ q(w, у)] dy.
Jq
Разделив эти уравнения на *ф(х) и продифференцировав по найдем
еА(^) = _р“9’ еЛ(^) = ешр+<1- (101°)
Теперь введем вспомогательную переменную dz = dx и перенормируем
функции амплитуд p(cj,z) = р(ш,х)/'ф(х) и q(u,z} = q{bo^x}/^{x)y так что
уравнения (10.10) примут вид
\ dp
г1 = е"г+’-
Исключая q(w, z) из этой пары уравнений, получаем
„2А d2P
(10.11)
По определению Qn(x} имеем Qn(x = 0) = 0. Это дает <?(w,0) = 0 и
g(w,0) = 0. Аналогично, равенство р(ш,оо) = 0 приводит нас к р(ш, 1) = О3.
Решение уравнения (10.11), которое удовлетворяет условию р(ш, 1) = 0, имеет
вид
р(ш, z) = С{ш) sin [(1 — z) е~х у/еш — 1 j ,
3В соответствии с определениями функций р, q и ip значению х = оо соответствует
2 = /о°° ^(у) аУ = f-ao dv = !•
10.1 Неупорядоченная спиновая цепочка
405
откуда получим
q(u>, z) = С(ш) у/еР — 1 cos [(1 — z) е Л \/еш — 1 ]
-C(w) sin [(1 - 2)е-Л \/еш- l] .
Граничное условие g(w, 0) = 0 определяет показатель Ляпунова
(10.12)
После того как мы вычислили Рм(£1,х) и Qtv(Q, ж), мы можем найти
Щг(П). Поскольку Р#(П,ж) + Qn(£1,x) — это вероятность иметь Q слабых
с величиной взаимодействия на последней связи |J/v_i| = величина
Pn(SI,x) + Qn(Q,x), будучи проинтегрирована по х, дает вероятность числа
Q в цепочке с всего N связями
Щг(П) = / -ф(х) [Р/ДП, х) + Qn№, ж)] dx.
Тогда соответствующая производящая функция Gjv(w) = П^(П) =
(ewft) имеет вид
/»ОО
Gjv(tv) ~ e^N I “ф(х) [p(w, ж) + g(u>, ж)] dx
= С(о>) sin [е Уе" — 1 ] . (10.13)
Среднее число метастабильных состояний
Используя функцию Gn(oj) = Плг(П) = (ешГг) и ее явное выражение
(10.13), можно найти среднее число метастабильных состояний. Действитель¬
но, поскольку (М) = (2П) = (еП1п2), среднее число метастабильных состояний
равно (?лг(1п2). Поэтому из (10.12) имеем
(М) ~ (4/tt)n.
(10.14)
В общем случае
lim 1п(Мп) = А(п1п2) = In
х/2п - 1
W-»-oo N
arctg у/2п — 1
406
БЕСПОРЯДОК
для произвольного п. Поведение при малых п позволяет найти наиболее ве¬
роятное число метастабильных состояний. В самом деле,
2пПЩг(£2) —» (Mmp)n при п —> 0,
п>о
тогда как (Mmp)n растет как e^(nln2)N Следовательно,
lim ilnMap=lim^^ = Jln2,
TV—>оо N Р п->0 п 3
что служит подтверждением результата (10.7). Когда N большое, среднее
число метастабильных состояний сильно превосходит его наиболее вероятное
значение
п5/Э
С= = 1,01057.
7Г
Поэтому число метастабильных состояний демонстрирует огромные флукту¬
ации от реализации к реализации, и иногда число метастабильных состояний
может быть много больше наиболее вероятного значения.
Остаточная намагниченность
Важная характеристика спиновых стекол — остаточная намагниченность,
возникающая, когда лабораторное спиновое стекло подготавливают в сильно
намагниченном состоянии при температуре Т, обычно с помощью наложения
сильного внешнего магнитного поля, а потом при фиксированной темпера¬
туре выключают поле и ждут, пока не будет достигнуто конечное состоя¬
ние. Остаточная намагниченность конечного состояния гаоо(Т) = га(Т, t = oo)
характеризует структуру фазового пространства и содержит информацию о
метастабильных состояниях системы. Хотя в реальных спиновых стеклах эти
метастабильные состояния чрезвычайно сложны, в неупорядоченной изингов-
ской цепочке их легче описывать, поскольку цепочка разбивается на невзаи¬
модействующие кластеры, отделенные друг от друга слабыми связями.
Начнем с определения остаточной намагниченности при нулевой темпе¬
ратуре для симметричного распределения р( J) параметров взаимодействия.
Рассмотрим любой спин, не соединенный с сильной связью. Каждый такой
спин жестко скоррелирован со своим соседом на другом конце более сильной
из двух присоединенных к нему связей. При симметричном распределении
параметров на связях каждый такой спин может быть направлен вверх или
вниз с одинаковыми вероятностями и не дает вклада в остаточную намаг¬
ниченность. Только спины на концах сильных связей вносят в нее вклад.
10.1 Неупорядоченная спиновая цепочка
407
Если сильная связь ферромагнитная, два ее концевых спина направлены
вверх4, а если связь антиферромагнитная, эти спины антипараллельны. При
симметричном распределении параметров взаимодействия ферромагнитные
и антиферромагнитные параметры имеют равные вероятности, гак что вклад
в остаточную намагниченность равен доле сильных связей, умноженной на
(2+0)/2. Это дает
1
тоо = -.
Следовательно, остаточная намагниченность не зависит от распределения па¬
раметров взаимодействия, пока оно симметрично и непрерывно.
Исследуем спиновую эволюцию по правилам глауберовой динамики при
нулевой температуре. Рассмотрим кластер из И спинов .sj,... , .57 с сильной
связью (J, j + 1). За инфинитезимальный временной интервал At спин .ч; слева
от сильной связи (1 < г < j) эволюционирует как
Si(t + dt)
Si(t) с вероятностью 1 - dt,
с вероятностью dt,
где ei = sgn(Л). Вторая строчка в (10.15) отвечает за событие, когда, спин Si
становится равным Si+i при обновлении, когда взаимодействие между двумя
спинами ферромагнитное, или противоположным, Si = —при аптифер-
ромагнитном взаимодействии. Поэтому среднее значение спина ,5Д/.) (.ч/(£))
удовлетворяет уравнению
j с.
-57 = -Si + 6iSi+i, l<i<j (10.16а)
at
Аналогично, спины справа от сильной связи (J +1 < i < () эволюционируют
согласно уравнению
= -^ + 6i_iSi_i, j +1 < i < e.. (Ю.166)
at
Чтобы описать эволюцию макроскопической системы, нужно усреднить
ее по распределению параметров взаимодействия. Поскольку параметры вза¬
имодействия — независимые одинаково распределенные случайные величи¬
ны, параметры ei также являются независимыми одинаково распределенны¬
ми случайными величинами, принимающими только значения ±1. Для сим¬
метричного распределения параметров взаимодействия p(Ji), они принимают
значения ei = ±1 независимо и с равной вероятностью.
4 Напомним, что в начальном состоянии все спины направлены вверх.
408
БЕСПОРЯДОК
Пусть (...) обозначает среднее величины (...) по распределению пара¬
метров взаимодействия. Тогда Т = 0 по определению. Вместо того чтобы
решать уравнения (10.16) и потом усреднять решение по беспорядку, мы сна¬
чала усредним уравнения, а потом решим. Усреднение линейных членов дает
Si —> Si. Усреднить квадратичные также просто, поскольку множители в
произведениях нескоррелированы. Например tiSi+i = eiSi+i = 0 для i < j.
Поэтому Si зависит от и <Si+i, a S'i+i в свою очередь зависит от е^-ы и
Si+2, и т. д. Таким образом, Si зависит от с индексами i' > г. Посколь¬
ку разные е независимы, мы заключаем, что €» и 5j+i в уравнении (10.16а)
нескоррелированы. Поэтому усреднив (10.16) и (10.16), мы получим
^Si = -Si для всех i / j, j + 1,
и решением будет Si(t) = <%(0) е-*.
Для двух спинов на концах сильной связи (j, j+1) эта процедура не вполне
работает, так как в этом случае sj+i не определяется левым соседом Sj. Тем
не менее можно непосредственно решить исходные уравнения
= ^tl = -S'+1+eJ5/, (10.17)
а потом усреднить. Прибавляя и вычитая два уравнения (10.17), мы в конце
концов получаем, что Sj = Sj+i = ехр[(б^ — 1)£] для ферромагнитного на¬
чального состояния со всеми спинами вверх: $Д0) = 1 для всех г. Усредняя по
беспорядку, мы находим, что средние значения спина в кластере имеют вид
Si = е~* для i / j,j + 1, тогда как для спинов, соединенных сильной связью
Sj = Sj+i = j(l + e“2t). В кластере из i спинов два спина на концах сильной
связи эволюционируют согласно этой формуле, а остальные & — 2 спина экс¬
поненциально релаксируют. Пусть будет доля кластеров, состоящих из i
спинов. Тогда средняя намагниченность имеет вид
m(t) = (1 + e-2t) 52 xi + е~* 52(£ “ 2)x*- (10.18)
€>2 €>2
Заметим, что ]>^>2 “ это плотность кластеров, равная плотности слабых
связей |, так как имеется взаимнооднозначное соответствие между класте¬
рами и слабыми связями. К тому же сумма дает долю системы,
покрытую кластерами любого размера, и поэтому равна 1. С учетом этих
результатов выражение для намагниченности сводится к
”*(*) = j (1 + e_t + e-2t) .
10.2 Случайные блуждания в случайном потенциале 409
Поэтому не только остаточная намагниченность равна j, независимо от рас¬
пределения параметров взаимодействия, но и эволюция к конечному состоя¬
нию имеет универсальный характер.
Теперь вычислим финальную энергию на один спин £. Каждая слабая
связь либо удовлетворена, либо фрустрирована с одинаковыми вероятностя¬
ми, так что их вклад в энергию нулевой. Все не слабые связи — удовлетво¬
ренные, и доля таких связей составляет |, что дает £ = -||J|nw Поскольку
||J|nw + 5\J\w = |«/|, где нижние индексы nw и w указывают соответствен¬
но на не слабые (non-weak) и слабые (weak) связи, энергия метас/габильного
состояния равна
= -Й + (10.19)
что больше, чем энергия основного состояния £qs = —|«/|. Чтобы вычис¬
лить £м, рассмотрим введенную ранее плотность вероятности ^(ж) того, что
параметр взаимодействия имеет абсолютное значение х = |J|. Тогда плот¬
ность вероятности для слабой связи с параметром х дается выражением
ip(x) (f£° 1р(у) dy)2. В результате имеем
£M-£GS = gJo (J ^(y)dy] xtfi(x)dx, (10.20)
т. е. энергию можно вычислить явно, если задано распределение параметров
взаимодействия (задача 10.2).
10.2 Случайные блуждания в случайном потенциа¬
ле
Существует два типа беспорядка, естественно возникающих в задачах о слу¬
чайном блуждании. Первый — случайность индивидуальных шагов блужда¬
ния, вызвана столкновениями с другими частицами в системе. Эти столкно¬
вения обычно моделируются случайным выбором направления каждого шага
блуждания. Как обсуждалось в главе 2, существуют хорошо развитые техни¬
ки для работы с такой случайностью и нахождения распределения вероятно¬
сти случайного блуждания. Второй источник случайности — среда, в которой
происходит случайное блуждание, редко бывает однородной. Во многих ситу¬
ациях временные изменения в среде возникают на гораздо бблыних масшта¬
бах, чем временной масштаб, ассоциированный со случайным блужданием.
Следовательно, можно предположить, что характеристики среды случайно
410
БЕСПОРЯДОК
изменяются в пространстве, но не во времени. Такой вмороженный беспоря¬
док используется для моделирования материалов, содержащих примеси или,
в более общем случае, имеющих внутреннюю случайность.
Феноменология
Подход Ланжевена дает простое непрерывное описание случайного блужда¬
ния в случайной среде. Начнем с уравнения Ланжевена х = £, которое соот¬
ветствует броуновскому движению и, добавив случайную силу, моделирую¬
щую среду, получим
^ = F(X)+£(i). (10.21)
Здесь £(t) — гауссов белый шум (во времени), который моделирует тепловой
шум и имеет следующие свойства:
(О = 0, &(t) ej(t')) = 5(t - t'Y (10.22)
Случайная сила F(x) обычно также принимается гауссовой5, а именно:
(F} = 0, (ЕДх) ЕДх')) = 2Г<^ 5(х - х'). (10.23)
Анализ уравнений (10.21)—(10.23) и связанных с ними моделей случайных
блужданий в случайной среде привели к следующим замечательно простым
наблюдениям:
• Одно измерение. Вмороженный беспорядок существенно замедляет слу¬
чайное блуждание. Характерное смещение в случае нулевого сноса рас¬
тет как (Inf)2.
• Два и более измерений. Вмороженный беспорядок не влияет на времен¬
ной скейлинг смещения, но влияет на коэффициент диффузии6.
Хотя сложно доказать справедливость этой классификации, можно понять
ее, пользуясь эвристическими аргументами. Для случайных блужданий, ко¬
торые дискретны в пространстве и времени, число различных узлов, посе¬
щенных случайным блужданием, растет как y/i, t/lnt, t, когда d = 1,2,3,
5Уравнение (10.23) иногда может оказаться неприменимым. Например, случайная сила
может быть бездивергентной (V • F = 0) или потенциальной (F = — W).
6Для некоторых специальных случайных сил в двух измерениях появляются логариф¬
мические поправки.
10.2 Случайные блуждания в случайном потенциале 411
соответственно. Если беспорядок слабый, простейшая гипотеза — он не влия¬
ет на блуждание. Оценим типичное добавочное смещение <5х, вызванное слу¬
чайной силой. Мы имеем: 5х = ^i<r<t F[x(r)]. Когда d > 2, любой узел посе¬
щается максимум несколько раз, и поэтому корреляции в последовательности
сил под этой суммой практически отсутствуют. Следовательно, центральная
предельная теорема говорит нам, что 5х ~ еу/i, где е — характерная сила.
Это такой же рост, как и в обыкновенном случайном блуждании, а коэф¬
фициент б показывает, что слабый беспорядок влияет только па амплитуду
смещения. Этот аргумент заставляет нас ожидать, что выше двух измерений
имеет место обычное диффузионное поведение (с перенормированным коэф¬
фициентом диффузии). Также ясно, что логарифмические поправки могут
возникнуть максимум в двух измерениях.
Самое интересное явление возникает в одном измерении. Сначала заме¬
тим, что в одном измерении силу всегда можно записать как градиент потен¬
циала, F = В частности, можно положить У(0) = 0 и затем определить
V(x) = — F(y)dy, как показано на рис. 10.4. Поскольку сама сила имеет
(а)
Чк
к
Рис. 10.4. (а)Локальный снос для прыжка из узла к с вероятностями pk и qk
прыжков вправо и влево. (Ь) Локальный снос в цепочке узлов, (с) Локальный
потенциал, индуцированный локальным сносом
нулевое среднее, случайный потенциал также имеет нулевое среднее и диф¬
фузионные флуктуации
(У2(ж)) ~ ж.
Таким образом, частица движется в случайном потенциале. Чтобы пройти
расстояние L от начального положения, частица должна преодолеть потенци¬
альный барьер, типичная высота которого растет как vTZ. Как мы покажем
в следующем разделе, для больших L случайный потенциал можно заменить
412
БЕСПОРЯДОК
на линейно растущий потенциал с таким же средним градиентом. Из резуль¬
тата задачи 2.23 время, требуемое для того, чтобы диффундирующая частица
преодолела барьер высоты vTT растет как 7
t ~ t* е^/о, (10.24)
где i* = Г2/Р3. Поэтому мы делаем вывод, что типичный масштаб длины
случайного блуждания растет как
7)2
— [ln(i/i*)f. (10.25)
Сколь угодно малый вмороженный беспорядок коренным образом меняет
движение диффундирующих частиц: вместо диффузионного роста L Vt,
частица подчиняется ультрамедленному логарифмическому закону L (Ini)2.
Это поведение известно как закон Синая,
Другое замечательное проявление влияния случайного потенциала на
диффузионное движение возникает, когда две невзаимодействующие частицы
находятся под действием одного и того же случайного потенциала. Если бы
не было беспорядка, положения двух блужданий давались выражениями
(x2) = (T2)=f, ((Т!-Т2)2)=2<,
т. е. расстояние между двумя частицами также диффундирует, но со вдвое
большим коэффициентом диффузии, чем при движении одной частицы. Бес¬
порядок полностью меняет ситуацию. Теперь среднее расстояние между ча¬
стицами стремится к конечному пределу на бесконечном времени! Причина
такого неожиданного поведения — при возрастании времени каждая частица
стремится находится ближе ко дну ее локального потенциала. В некоторый
момент обе частицы попадают в одну и ту же впадину, и после этого их по¬
ложения сильно скоррелированы, так как обе частицы стремятся находиться
в одной и той же локальной впадине. Это явление называется феноменом
Голосова,
Процедура децимации
Теперь рассмотрим одномерную модель (10.21)—(10.23), также известную как
модель Синая, более подробно. Для простоты, вместо того чтобы рассматри¬
вать случайную силу (10.23) или, что тоже самое, случайный потенциал в ви¬
де броуновского движения, мы изучим кусочно-линейный случайный потен¬
циал. Наклоны каждого линейного сегмента имеют одинаковую абсолютную
7 Это один из вариантов закона Аррениуса, который утверждает, что при температуре
Т частица может преодолеть потенциальный барьер V за время порядка еу^т.
10.2 Случайные блуждания в случайном потенциале 413
величину, а их знаки — случайные переменные с одинаковой долей положи¬
тельных и отрицательных наклонов. Асимптотическое поведение случайного
блуждания в таком случайном потенциале — такое же, как в модели Синая.
Пусть £п будет длина n-ого сегмента, вдоль которого потенциал растет
линейно от Vn до Vn+i. Концевые точки разделены барьером высоты Вп =
|1п—Нг+i |- Когда частица движется в таком потенциале, опа обычно остается
около дна впадины. Если барьер мал, частица вскоре преодолеет его и попа¬
дет в более глубокую впадину. Ключевой момент состоит в том, что малень¬
кие барьеры не играют роли на большом временнбм масштабе. Это наблю¬
дение предполагает следующую рекурсивную процедуру, которая упрощает
случайный потенциал, но не влияет на асимптотическое движение частиц. На
каждом шаге мы убираем участок (I, Bmin) с наименьшим барьером, соединяя
вместе соседние участки (€х, Вх) и (€г, Вг). Эта процедура децимации являет¬
ся вариантом пространственной ренормализации и схематически изображена
на рис. 10.5.
Li L- к
Рис. 10.5. В децимации участок с наименьшим барьером В,,,,,, убирается со
слиянием соседних участков
Формально децимация определяется как
(€х,Вх)ф(€ ) -®min ) © (^2) В2) > (^1 + I + ^2? Bl + B2) (10.26)
и сохраняет зигзагообразную форму кусочно-линейного потенциала. Свой¬
ство, которое делает возможным анализ, — это отсутствие спонтанного раз¬
вития корреляций при такой ренормализации: если вначале барьеры не скор¬
релированы, они остаются нескоррелированными. Уравнение (10.26) — это
пример экстремальной динамики, а подробности ренормализационного преоб¬
414
БЕСПОРЯДОК
разования напоминают детали укрупнения с экстремальной динамикой, при¬
веденные в разделе 9.7. Процедура децимации (10.26) — это специфический
двухкомпонентный процесс агрегации. Его анализ технически длинный, но
простой по сути, а конечный результат (10.38) для распределения вероятно¬
сти положения частицы имеет компактный вид и очень простую интерпрета¬
цию.
Для начала забудем о длине барьеров и сосредоточимся на распределении
их высоты с(В, £>), определенном как концентрация барьеров высоты В при
минимальной высоте барьера, равной Ь. Основное кинетическое уравнение
для этого распределения имеет вид
дс(В,Ъ)
дЬ
= с(Ъ,Ъ)
<АВ,Ь)
р(Ь)
с(В',Ъ) с(В-В' + Ь,ЪУ
р(Ь) Р(Ь)
(10.27)
Здесь минимальная высота барьера может рассматриваться как временипо-
добная переменная, более удобная для вычислений, чем само время. Первое
слагаемое в правой части отвечает за исчезновение барьера высоты В из-за
того, что он оказался по соседству (с любой стороны) с минимальным ба¬
рьером. Второе слагаемое соответствует образованию барьера высоты В при
слиянии барьеров с высотами В', В — В' + Ь и отрицательного барьера глу¬
бины Ь. Здесь р(Ь) = /ь°° dB с(В, Ь) — это плотность барьеров любой высоты,
которая эволюционирует согласно уравнению
= —2с(£>, Ь), (10.28)
поскольку при каждом слиянии исчезают три барьера и появляется один.
Используя асимптотически точную оценку Аррениуса t ~ еь, запишем мини¬
мальную высоту барьера b как In t, так что мы можем перевыразить конечный
результат через исходную переменную времени.
В пределе Ъ —> оо мы ожидаем, что высота барьера стремится к скейлин¬
говому виду
(10.29)
Подставляя этот скейлинговый анзац в (10.27), мы видим, что уравнение для
распределения высоты барьеров приводится к виду
(1 + Z) + Ф(г) + Ф(0) Г Ф(ж) Ф(г - ж) dx = 0. (10.30)
dz Jq
Можно решить уравнение (10.30) с помощью преобразования Лапласа, ко¬
торое позволяет выразить свертку в виде произведения. С другой стороны,
10.2 Случайные блуждания в случайном потенциале 415
заметим, что это уравнение напоминает уравнение (5.61) для скейлинговой
функции для агрегации с постоянным ядром, решением которого является
экспоненциальная функция. Поэтому мы также ищем8 экспоненциальное ре¬
шение Ф = ae~az. Подставляя этот вид в уравнение (10.30), находим, что
согласованное решение получается, когда а = 1. Поэтому имеем
ф(г) = e”z. (10.31)
Теперь, используя равенство = Ь_1Ф(0) = Ь""1 в сочетании с (10.28),
находим, что полная плотность барьеров равна р(Ь) = Ь"~2, а плотность ми¬
нимальных барьеров равна с(Ь, Ь) = 6_3.
Чтобы найти полное распределение барьеров, нам нужно узнать с(£, В, Ь),
концентрацию участков длины I с барьером высотой В. Это совместное рас¬
пределение эволюционирует в соответствии с уравнением
(^ + 2 ) с(А В,Ь) = I dtx dt>2 М3 8(£i
х J dBi dB2 8(Bi + B2 — b — B) c(£3, b, £>)
c(A,Bi,6) c(€2,B2,6)
p(6) p(b) ’
где дельта-функции обеспечивают, чтобы перемасштабированный барьер
имел длину и высоту, определенные правилом композиции (10.26). В пре¬
деле Ъ -> оо совместное распределение стремится к скейлинговому виду
с(^, В, Ь) = Ь“5 V>(w, ^), где w = и z = & b. (10.32)
1г о
Этот вид можно обосновать, заметив, что минимальная высота барьера Ъ
устанавливает масштаб для отклонений от минимальной длины В — Ь, а об¬
ратная плотность барьеров р-1 = Ъ2 задает масштаб Подставляя скей¬
линговый вид (10.32) в уравнение для с(-^, В,Ь), приходим к уравнению на
скейлиноговую функцию
3, + (1 + 2)g + 2wg
+ /dWldK,2dW3«(w1+W2 + WS-l)
х Jd2idz25(zi+z2-2)V’(wi,2i)-0(w2,22)V’(w3,O) = 0.
8Экспоненциальная функция содержит два параметра, Ф = Ае~аг, но мы должны
выбрать А = а, чтобы обеспечить выполнение равенства р(Ь) = /6°°c(B,b)dB.
416
БЕСПОРЯДОК
Теперь введем Лаплас-образ ^(р, z) = е v™ tp(w, z) dw, чтобы перепи¬
сать уравнение как
1+(1+г)й-2р^
+'0(Р?О) [ 'tp{p1x)'i/}(p^z — x>)dx = O, (10.33)
Jo
Это уравнение является обобщением уравнения (10.30), решение которого
имеет экспоненциальный вид (10.31). Этот факт позволяет предположить,
что нужно искать экспоненциальное решение
^(р, ^) = <Хр) e~z^. (10.34)
Подставляя (10.34) в (10.33), находим, что экспоненциальный анзац самосо¬
гласован, если
2р - а = —aft, = -а2. (10.35)
По определению if)(p = 0, г) = /0°° dwip(w,z) = $(z) = e~z, см. (10.31). По¬
этому а(0) = /5(0) = 1. Уравнения (10.35) имеют элементарный вид и могут
быть упрощены с помощью замены
а(р) = qA(q), 0(р) = qB(q), q = y/p,
которая превращает (10.35) в следующие уравнения:
dA
dq
-АВ,
dB
dq
-А2.
Эти уравнения удовлетворяют закону сохранения В2 — Л2 = const, и их ре¬
шения имеют качественно разный характер в зависимости от того, положи¬
тельна константа, равна нулю или отрицательна9.
Решением, имеющим физический смысл, являются А = (shq)-1 и В =
coth q. В исходных переменных q = у/p мы имеем
а(р) =
shy/p’
Р(р) = у/Р
chy/p
shy/p'
(10.36)
Поэтому функция -ф(р, z) дается выражениями (10.34) и (10.36), а ее обратное
преобразование Лапласа дает ip(w,z). Результат громоздок, так что ограни¬
чимся распределениями одной переменной. Мы уже знаем распределение вы¬
соты барьеров Ф(г), но нам также нужен скейлинговый вид распределения
9Например, если бы константа была равна нулю, мы бы имели А = В =
Л(0)/[1 + 9-4(0)], и поэтому а(р) = /3(р) = Л(0)-^/р/[1 + 4(0)y/pj, что не согласуется с гра¬
ничным условием а(0) = /3(0) = 1.
10.2 Случайные блуждания в случайном потенциале 417
длины барьеров Ф(ги) = f 'if)(w,z)dz (аналогично, Лаплас-образы связаны
соотношением Ф(р) = /if>(p,z)dz). Из (10.34) мы находим
ад = = _J_
5(р)
Интересно, что этот результат совпадает с Лаплас-образом вероятности пер¬
вого посещения для диффундирующей частицы на конечном адсорбирую¬
щем интервале. Эта связь с вероятностью первого посещения — совершенно
неожиданное свойство, которое упоминалось в начале этого подраздела.
Обратное преобразование Лапласа функции (сЬ^ф)-1 можно получить,
взяв интеграл через вычеты, что для перемасштабированного распределения
длины дает
Ф(ш) = 7Г (—1)” (п + 3) exp |— tt2w (п + ^)2j (10.37)
п=—оо
= ^Т/2^3/2 Z (-1Г(П+5)ехр[-^(«+1)2 ’
n=—оо J
Мы привели ответ в двух эквивалентных видах, которые удобны для полу¬
чения поведения при больших и малых w соответственно.
Предшествующее обсуждение было посвящено ренормализации случай¬
ного потенциала. Чтобы определить положение блуждающей частицы, мы
используем фундаментальное наблюдение (кратко изложенное в начале это¬
го раздела): частица находится на дне перенормированной потенциальной
ямы, которая содержит начальную точку. Пусть Prob(x, t) будет плотность
вероятности того, что эта частица находится в положении х в момент вре¬
мени t при условии, что она была в х = 0 в t = 0. Нам понадобится эта
вероятность, усредненная по реализациям среды. Обозначим среднее через
РгоЬ(ж,£). Если Р(^, Ь) — это вероятность того, что длина перенормирован¬
ного сегмента равна i, тогда частица будет в этом сегменте с вероятностью
lP(i,b)/ f iP(t,b) di. Дно впадины однородно распределено на отрезке [0,1},
так что все сегменты длины i > |я| вносят вклад в Prob(rc,f):
Prob(rc, t) = 2 jf °° е. Р(£, Ь)
-1
/•оо
/ Р(£,Ь)М.
Jill
Мы знаем, что Р(€, Ь) ~ Ь 2Ф(€/62), где функция Ф(гг) дана в (10.37). Ис¬
пользуя этот факт и вспомнив, что b = In t, получим
РгоЬ(х, 1) = (Inf)"2 F(X), X = pip,
418
БЕСПОРЯДОК
где
*U) = 11?"1)" (n + i)"1 exP H2I*I (” + i)2] • (10.38)
n>0
Это распределение Голосова- Кестена, которое является аналогом распре¬
деления Гаусса в обыкновенном случайном блуждании. Хотя распределение
Голосова-Кестена (10.38) имеет вид бесконечного ряда, моменты смещения
(усредненные по шуму и реализациям среды) достаточно просты. Например,
М-^(М4,
(ж4) Ci
50521
75600
(In t)8,
(ж6) Ci
199360981 ,12
(lnt) .
60540480 7
(10.39)
10.3 Случайные блуждания в поле случайных ско¬
ростей
Как обсуждалось в предыдущем разделе, пространственный беспорядок в ин¬
тенсивностях прыжков случайного блуждания приводит к более медленному
росту среднеквадратичного смещения со временем, чем линейный рост. На¬
оборот, есть ситуации, когда может реализоваться супердиффузионное дви¬
жение, в котором среднеквадратичное отклонение растет со временем быст¬
рее, чем линейно. Один такой пример — модель Матерона-де Марсили
(МдМ), которая была предложена для описания переноса почвенных вод че¬
рез осадочные породы.
В модели МдМ осадочная среда моделируется как набор параллельных
слоев, каждый с немного разными свойствами материала (рис. 10.6). В каж-
(а)
Рис. 10.6. (а) Поле потоков в двумерной слоистой среде. (Ь) Тот же поток в си¬
стеме центра масс, откуда извлекается абстрактная формулировка модели МдМ,
показанная в (с)
10.3 Случайные блуждания в поле случайных скоростей 419
дом слое жидкость движется с постоянной скоростью, характерной для этого
слоя. В системе отсчета, которая движется со средней по всем слоям ско¬
ростью, относительная скорость в каждом слое превращается в случайную
функцию поперечной координаты с нулевым средним. Рассмотрим движение
частицы, которая диффундирует, а также подвержена пассивной конвекции
в поле потока. Пока частица находится в данном слое, па нес действует поле
скорости этого слоя. Однако из-за наложенной диффузии частица совершает
переходы между слоями. Вследствие этого продольная скорость частицы сто¬
хастически меняется. Такая комбинация поперечной диффузии и случайной
конвекции в продольном направлении приводит к супердиффузии.
Простой подход к пониманию движения частиц — рассмотреть уравнения
движения Ланжевена. В двух измерениях эти уравнения для броуновской
частицы, подверженной добавочной горизонтальной случайной конвекции,
имеют вид
(10.40)
Здесь n[y(t)] — поле скоростей в направлении ж, зависящее только от попе¬
речной координаты. Чтобы еще упростить эту систему, заменим непрерыв¬
ную картину на рисунке 10.6(b) дискретной картиной на рисунке 10.6(c), на
котором скорости в каждом слое принимают случайные значения ±но. По
построению средняя по всем слоям продольная скорость равна нулю, и нет
корреляций между скоростями в разных слоях. Как мы увидим, влияние кон¬
векции доминирует над диффузией, так что мы можем пренебречь второсте¬
пенным влиянием шума rjx в направлении х.
Мы можем найти зависимость среднеквадратичного смещении в продоль¬
ном направлении от времени, оценивая величину эффективного зависимого
от времени сноса, который действует на броуновскую частицу до времени t.
Если бы каждый слой дискретной системы на рисунке 10.6(c) посещался с
одинаковой частотой, то средний снос был бы равен нулю. Однако диффун¬
дирующая частица обычно отходит на перпендикулярное расстояние y/Dt и
поэтому посещает N ~ y/~Dt/a слоев за время i, где а - шаг решетки. Сред¬
няя скорость сноса в таком конечном числе слоев равна
Поэтому типичное продольное смещение растет супердиффузионно
х ~ ut ~ а1//2 D-1/4 no t3/4.
(10.42)
420
БЕСПОРЯДОК
Более полная характеристика движения частицы — распределение вероятно¬
сти смещения. Мы ожидаем, что усредненное по всем траекториям частиц и
по всем реализациям скоростей распределение смещения на больших време¬
нах будет иметь скейлинговый вид
Р(ж, t) ~ t-3/4 /(жГ3/4). (10.43)
В терминах скейлинговой переменной £ = xt-3/4 естественно ожидать, что
скейлинговая функция будет убывать быстрее любого степенного закона при
£ » 1. Такое поведение было обнаружено практически для всех процессов
типа случайного блуждания. Таким образом, запишем
/(£) ~ ехр(—const х £г). (10.44)
Теперь для определения индекса формы 5 мы привлечем аргумент, основан¬
ный на экстремальной статистике, который в первый раз был использован
для определения индекса формы 5 во врезке на странице 149.
В случае модели МдМ в применении этого аргумента есть свои тонко¬
сти, поскольку существует два типа беспорядка: беспорядок в траекториях и
беспорядок в среде. Взаимодействие этих двух факторов приводит к блуж¬
данию с максимальным возможным смещением. Очевидно, что блуждание
уходит дальше в продольном направлении, если оно содержится в подмноже¬
стве слоев с одинаковыми скоростями. Какова вероятность такого события?
В дискретной модели МдМ, где скорость для данного значения х может быть
±«о с равной вероятностью, вероятность, что область ширины w состоит из
слоев с одной и той же скоростью, равна 2-то. В пределе большого времени
вероятность, что поперечная координата блуждания останется в этой обла¬
сти10, убывает как ехр(—Dt/w2). Тогда вероятность нахождения в области,
усредненная по всем ширинам, будет иметь вид
2-w dw = J eF(w) dw> (10.45)
где F(w) = Dt/w2 — win2 — функция, имеющая единственный максимум в
области интегрирования. Интегралы такого типа, как в (10.45), известны как
интегралы Лапласа и их можно легко оценить пользуясь методом Лапласа.
10Эта вероятность, что случайное блуждание останется заключенным в интервале фик¬
сированной длины, также стоит за вероятностью выживания одномерного случайного
блуждания в присутствии случайно распределенных ловушек — система которая будет
обсуждаться в разделе 13.2.
10.3 Случайные блуждания в поле случайных скоростей 421
10.2. Интегралы Лапласа
Интеграл Лапласа имеет общий вид
J(AT)= [°° eNF(x) dx,
Jo
где у F(x) есть один максимум в 0 < хо < оо. Нас интересует значение этого инте¬
грала в пределе N -> оо. Метод Лапласа вычисления этого интеграла основан на
разложении функции F(x) около ее максимума F(x) = F(xo) — ± (ж-жо)2 |F"(то)| +
— Пользуясь разложением до второго порядка, мы оцениваем этот интеграл как
/(AT) = ^°° exp pV(F(®0) - - zo)2 |F"(a:o)| + •..) dx
~ exp[ATF(a;o)] f exp [-j(s - zo)2 |F"(xo)|] dx
J — oo
= e*PpWo)].
Более точно, экспоненциально большой множитель — это главный член, а приве¬
денное выражение дает ведущий вклад в интеграл. Полное выражение в общем
случае содержит ведущий вклад, умноженный на бесконечный асимптотический
ряд по обратным степеням N.
Применяя метод Далласа из врезки, мы находим, что оптимальное значе¬
ние w растет как (Di)1/3. Следовательно, главный член в (10.45) имеет вид
ехр[—const, х (Di)1/3].
Теперь, используя (10.44) для распределения вероятности в модели МдМ и
применяя такое же сравнение с вероятностью растянутого блуждания (как
во врезке на странице 149) получаем
Р(х ~ i,i) ~ i-3/4 exp const, х i5/4].
Сравнивая эти два выражения, находим, что S = 4/3. Неожиданное свойство
модели МдМ — это то, что индексы формы и расстояния не подчиняются
общему соотношению 5 = (1 —i/)-1 (см. уравнение (4.41)), которое характерно
для многих типов случайных блужданий.
Что происходит с моделью МдМ в физическом случае трех измерений?
Есть две ситуации, которые естественным образом приходят на ум: парал¬
лельные осадочные пласты или осадочные волокна (рис. 10.7). Первый слу¬
чай более вероятен с точки зрения геологии, и он проявляет то же самое
422
БЕСПОРЯДОК
L 1
1 J
1 1
1 1
1 1
1
Г '
(b)
Рис. 10.7. (а) Поле потоков в модели МдМ в трех измерениях. (Ь) Изотропная
версия модели МдМ — решетка случайный Манхэттен — в двух измерениях
поведение, что и двумерная система. Второй случай может рассматривать¬
ся как истинная трехмерная модель МдМ. Теперь уравнения движения для
броуновской частицы имеют вид
=
где мы рассматриваем х как продольную координату, а у\ и у? как попереч¬
ные. Нам снова удобно думать о решеточной модели, в которой есть случай¬
ные скорости в направлении х, которые с равными вероятностями принимают
значения ±«о для фиксированных поперечных координат (yi, уг)- Чтобы най¬
ти продольное смещение, снова полезно разделить движение на продольную
и поперечные компоненты. Движение частицы в поперечном направлении —
это просто обыкновенное случайное блуждание в двух измерениях. Мы зна¬
ем, что частица обычно посещает порядка t/hit разных узлов (мы опуска¬
ем множители, содержащие D и параметр решетки). Поэтому средний снос,
которому подвержено блуждание за время t, дается обобщением формулы
(10.41) для трех измерений. Поскольку число разных узлов, посещенных за
время t, растет как t/lnt, мы имеем
Тогда оценка характерного смещения дает
х ~ ut ~ (tint)1/2.
10.4 Ссылки
423
Модель МдМ можно также естественным образом обобщить на изотроп¬
ное поле случайных скоростей. Особенно интересная реализация — решетка
«случайный Манхэттен», в которой скорость вдоль всей длины любой авеню,
идущей с севера на юг, или улицы с востока на запад фиксирована, а доли
путей каждого типа равны. Можно найти среднеквадратичное смещение слу¬
чайного блуждания, движущегося по манхэттенской решетке, обобщив аргу¬
менты, приведшие нас к (10.42). Сначала мы произвольно делим изотропное
движение блуждания на различные поперечные и продольные компоненты,
даже несмотря на то, что движение изотропно. Теперь найдем остаточный
продольный снос в типичной области, заметаемой поперечным случайным
блужданием. Для (неизвестного) смещения в поперечном направлении запи¬
шем у ~ ty. Тогда, согласно уравнению (10.41), средняя продольная скорость
в направлении х в момент времени i, усредненная по ty слоям, которые по¬
сещаются типичным случайным блужданием за время его уходов в направ¬
лении у, убывает как t~y/2. Из аналога уравнения (10.42) мы заключаем,
что х ~ £1-1//2. Однако из-за изотропии мы должны иметь // = I — у/2 или
у = 2/3. Поэтому блуждание на решетке случайный Маихэ'гген также супер¬
диффузионное со смещением, растущим как t2/3 (в сравнении с х ~ Л3/4 для
модели МдМ). Обобщение этих аргументов для решетки случайный Манх¬
эттен в произвольной пространственной размерности d дает у — 2/(d + 1).
Поскольку движение не может быть медленнее чистой диффузии, мы дела¬
ем вывод, что для d > 3, х ~ t1/2. Поэтому критическая размерность для
случайного блуждания на решетке случайный Манхэттен равна. dc = 3. Для
d > dc у = 1/2, тогда как для d < dc у = 2/(d + 1), и естественно ожидать
возникновения логарифмических поправок при d = dc, точно так же как в
модели МдМ при d = 3.
10.4 Ссылки
Наше изложение сосредоточено вокруг нескольких специфичных систем, в
кинетическом поведении которых беспорядок играет центральную роль, и
для которых возможно аналитическое решение. Свойства релаксации и оста¬
точная намагниченность неупорядоченной кинетической модели Изинга опи¬
саны в [209, 210]. Элементарное педагогическое введение в случайные муль¬
типликативные процессы, дающее основные сведения, нужные для подсчета
числа слабых связей, и дополняющее врезку на странице 401, даны в [211].
Более обширную информация о слабых связях и случайных рельефах (см.
также задачи 10.3-10.5) можно найти в [209,Ё212 -214].
424
БЕСПОРЯДОК
В настоящее время неизвестно, как считать остаточную намагниченность
в двух- и трехмерных спиновых стеклах при нулевой температуре (аналог
результата Шоо в одном измерении). Больше узнать об этой интригующей
загадке можно в [215].
Обзор ранних работ по модели Синая и другим моделям в случайном по¬
тенциале сделан в [216]. Метод пространственной ренормализации для иссле¬
дования этих моделей был развит в [217]. Элементарное введение в этот метод
есть в [17], глава 4. Общая экспозиция случайных блужданий в неупорядочен¬
ных средах и обзоры модели Матерона и де Марсили даны в [14,15, 218, 219].
Дополнительная информация по случайным блужданиям в случайных сре¬
дах есть в [220, 221]. Основные результаты о числе случайных узлов, посе¬
щенных случайным блужданием, приведены в [1, 3]. Наконец, в [158] Бендер
и Орсзаг дали блестящую экспозицию интегралов Лапласа.
10.5 Задачи
10.1 Эта задача посвящена моментам числа слабых связей.
(a) Начните с явной формулы (10.13) для поизводящей функции Gn(w) =
52п>о П^(£2) = (ешП) и разложите ее по степеням си.
(b) Используя разложение из пункта (а), найдите дисперсию
(Q2) — (fi)2 = N при N —> оо.
45
(с) Выведите дисперсию прямым способом, не использующим (10.13), с по¬
мощью обобщения вероятностных аргументов, приведших к (£i) = 7V/3.
10.2 Используя (10.19) и (10.20), покажите, что для однородного рапределения па¬
раметров взаимодействия = 1 для 0 < х < 1 и ^{х) = 0 в остальных
случаях, энергия основного состояния равна £qs = а энергия метаста¬
бильного состояния равна £м = —Таким же образом покажите, что для
экспоненциального распределения ^{х) = е~х эти энергии равны £qs = — 1 и
£м = -Ц.
10.3
Рассмотрите распределение размеров кластеров, которое возникает в (10.18).
Найдите это распределение, используя трансфер-матричный подход. У вас
должно получиться
(1-1)(1 + 2)
(£ + 3)!
Хе = 2е
Заметьте, что это распределение также не зависит от распределения парамет¬
ров взаимодействия. Убедитесь в справедливости правила сумм =
1/3 и У^£>? = 1*
10.5 Задачи
425
10.4 Подумайте о рисунке (10.2) как об одномерном рельефе: каждый узел име¬
ет определенную высоту; высоты — независимые одинаково распределенные
случайные величины; распределение высот не важно, если оно не содержит
дельта-функций. (Для вычислений удобно выбирать высоты из однородного
распределения на единичном интервале (0,1).) На языке рельефа слабая связь
соответствует впадине, а сильная — пику.
(a) Покажите, что вероятность убывающей последовательности из £ высот
подряд равна 1/£!
(b) Покажите, что вероятность Р^- того, что последовательность из i + j + 1
высот содержит впадину, которая находится на расстоянии i от пика
слева и на расстоянии j от пика справа, равна
Pij (i + l)!(j + l)!
+
£ + 1 £ + з
(с) Пусть Хе будет распределением длины между соседними пиками или,
что то же самое, между соседними впадинами. Покажите, что
хе= £
Подставьте выражение для Pij , найденное выше, и, вычислив сумму,
найдите выражение для Хе из предыдущей задачи.
10.5 Рассмотрите двумерный рельеф, в котором каждый узел квадратной решетки
имеет определенную величину, а распределение этих высот подчиняется таким
же предположениям, как в предыдущей задаче.
(a) Покажите, что плотность впадин равна 1/5. (Плотность пиков такая же.)
(b) Покажите, что плотность Мз с тремя направлениями спуска равна
Мз = 1/5. (Плотность точек с одним направлением спуска такая же,
Mi = 1/5.)
(c) Покажите, что плотность М2 с двумя направлениями спуска равна
М2 = 1/5.
(d) Покажите, что плотность седел равна 1/15.
(e) Покажите, что дисперсия полного числа впадин равна
(V2) - (V)2 = N при 7V -> оо.
Полное число впадин пропорциаиально плотности, т. е. (V) = 7V/5.
426
БЕСПОРЯДОК
10.6 Рассмотрите одномерное случайное блуждание в случайной среде, подчиняю¬
щееся уравнениям (10.21)-(10.23). Повторите аргументы, приведшие к (10.25),
в правильном размерном виде и покажите, что
L ~ L*
L*
Г ’
рз
Г2'
Пользуясь анализом размерностей, выведите £* = Р3/Г2 и L* = D2/Г.
10.7 Рассмотрите одномерное случайное блуждание в случайной среде с общим
сносом, а именно: вместо уравнения (10.23) будет
(Р) = Ро, №) F(x')) - F$ = 2Г 6(х - х').
Покажите, что есть одна безразмерная комбинация трех параметров D, Fq и
Г, а именно р = или любая ее функция. В качестве заметки на полях
отметим, что случайное блуждание движется баллистически при р > 1,
lim = У, У = Ро (1 - М-1) •
(Заметьте, что скорость V меньше «голой» скорости Vo = Ль которая бы¬
ла бы у блуждания в отсутствие беспорядка.) Когда 0 < р < 1, движение
суббалистическос: (.т) ~ V1.
10.8 Выведите амплитуды моментов, приведенные в (10.39).
Глава 11
ГИСТЕРЕЗИС
Толковые словари (как, например, словарь Вебстера) определяют гистерезис
как «запаздывание влияния изменения сил, действующих па 'гело, особенно
отставание значения результирующей величины намагниченности в магнит¬
ных материалах (таких как железо) при изменении намагничивающей силы.»
Понятие гистерезиса возникло при изучении магнетизма, ио он присутствует
в разнообразных системах (механических, химических, биологических, опти¬
ческих, электронных и т. д.). В этой главе мы рассматриваем магнетизм и
изучаем отклик спиновой системы на осциллирующее магнитное поле. Мы
исследуем как площадь и форма петли гистерезиса зависят от амплитуды и
частоты осциллирующего магнитного поля. Мы используем идеи и методы,
описанные в предыдущих главах, посвященных кинетическим спиновым мо¬
делям и неупорядоченным системам, а также инструменты из динамических
систем и асимптотические техники.
11.1 Однородные ферромагнетики
Качественное понимание гистерезиса можно получить уже при изучении по¬
ведения однородного изинговского ферромагнетика в осциллирующем внеш¬
нем магнитном поле h(t) = if sin fit. Мы хотим узнать, как намагниченность
m(t) зависит от температуры Т, амплитуды Н и частоты fi внешнего поля.
Мы увидим, что намагниченность m(t) отстает от поля и после некоторого
переходного периода га(£) описывает динамическую петлю в плоскости га(£)-
h(t) площади
(11-1)
428
ГИСТЕРЕЗИС
Если эта площадь остается ненулевой даже в квазистатическом пределе П —>
О, система демонстрирует статический гистерезис. Этот традиционный вид
гистерезиса возникает ниже точки ферромагнитного перехода, Т < Тс, а вы¬
ше точки фазового перехода статический гистерезис отсутствует (рис. 11.1).
Когда магнитное поле меняется неадиабатически (О > 0), характер петли
гистерезиса качественно другой.
Рис. 11.1. (а) Петля статического гистерезиса (сплошная линия) ниже точки фа¬
зового перехода. Пунктирная кривая показывает равновесное решение. Система
может застрять в метастабильном состоянии с т < 0, хотя h > 0, и наоборот. Ко¬
гда поле превышает коэрцитивное поле 7/*, система возвращается в равновесие,
в котором т и h имеют одинаковые знаки. (Ь) Петля динамического гистерезиса
(сплошная линия) выше точки фазового перехода. В квазистатическом пределе
намагниченность описывает пунктирное равновесное решение raeq(/i) и площадь
петли становится равной нулю
Площадь Л(Г, Н, Q) или избыточная площадь Л(Г, Я, Q) — Л(Г, Н, 0) в
случае, когда в системе есть статический гистерезис, называется площадью
динамического гистерезиса. Площадь динамического гистерезиса важна для
многих технологических приложений. Например, гистерезис характеризует
добавочную мощность, теряемую при многократно повторяющихся циклах
работы оптических и магнитных переключателей. Площадь динамического
гистерезиса демонстрирует интересную зависимость от Н и Q. При Н <С 1
предельное поведение имеет вид
A(T,ff,fi) -
напь
' НаО,-0
при П <С 1,
при Q >• 1.
(П-2)
Попробуем понять эти феноменологические законы в рамках простей¬
шей системы, а именно, среднеполевого ферромагнетика в осциллирующем
11.1 Однородные ферромагнетики
429
магнитном поле. Взаимодействие между любой парой спинов Si и sj есть
Jij = 1/2V, а эволюционируют спины по правилам глауберовой динамики. Га¬
мильтониан и интенсивность переворотов спинов имеют вид (см раздел 8.4)
i<j
N
- h(t) 22
i=l
Wi =
1 — Si th
m + h(t) \
1
2
Из общего соотношения Si — —2(siWi) (см. уравнение (8.50a)) получим, что
локальная намагниченность Si = (s^ эволюционирует как
dSi
dt
—Si + th
m + h(t)
T
)'
Суммируя эти уравнения и используя равенство h(t) = Н sin -г, позволяю¬
щее выразить т через натуральную временною переменную т = ilt, найдем
зависимость намагниченности т = N-1 ^2 Si от времени1
Л dm
S2 -г- = —т + th
dr
(т + Н sinr^
т /‘
(п-з)
Поскольку сила периодическая, мы интуитивно ожидаем, что после переход¬
ного периода система будет совершать вынужденные колебания с периодом
27г. Наша цель — найти характеристики этих вынужденных колебаний.
Общие свойства
Выше точки фазового перехода, Т > Тс = 1, система независимо от на¬
чальных условий приходит к чистым вынужденным колебаниям периода 27г.
Математически, уравнение (11.3) допускает единственный устойчивый пре¬
дельный цикл. Доказательство этого утверждения основано на нескольких
базовых фактах об обыкновенных дифференциальных уравнениях. Первый
шаг — показать, что периодическое решение в самом деле существует. Заме¬
тим, что уравнение
m — th
имеет единственное решение meq(fir,T’) — равновесную намагниченность.
Единственность стационарного решения очевидна, поскольку наклон кривой
F(m) = th[(m+H)/T] меньше чем 1 при Т > Тс = 1. Поэтому кривая должна
пересечь диагональ ровно в одной точке (рис. 11.2(a)).
1 Практически самая важная ситуация соответствует пределу Q 1. Поэтому перемен¬
ную т = Q,t часто называют «медленным» временем.
т-
(П-4)
430
ГИСТЕРЕЗИС
Рис. 11.2. (а) Графическое решение уравнения (11.4) для случая Т = 2 и Н = 1.
Пересечение двух графиков дает meq(H = 1,Т = 2). (Ь) Графическое решение
уравнения (11.4) для Т = 1/2. Верхняя кривая соответствует полю Н = 1/2,
превосходящему Н*(Т = 1/2) = 0,2664199 (ур. (11.5)). Эта кривая пересекает
диагональ только один раз. Средняя и нижняя кривые соответствуют полям
Н = Я* и Н = 0. В этих случаях число решений равно соответственно 2 и 3
Таким образом, при m > meq(H) правая часть уравнения (11.3) отрица¬
тельна, так что < 0. Аналогично, > 0 при m < —meq(H). Следо¬
вательно, все траектории га(т) в конце концов попадают в интервал I =
[—,n^eq(H\meq(H>)] и остаются там навсегда. Поэтому график траектории
га(т) находится в полосе (т,т) Е I х [0, оо). Так как точки т = 0 и т = 27т
эквивалентны, мы можем сосредоточить внимание на ящике I х [0,27г]. Рас¬
смотрим траекторию, начинающуюся на левой стенке ящика и проследим за
ней, пока она не пересечет правую стенку. Таким образом можно определить
отображение интервала I в себя m —> -Р(га), которое называется отображе¬
ние Пуанкаре. Хотя в настоящем примере невозможно вычислить функцию
Р(т) явно, теорема о неподвижной точке гарантирует, что любое непрерыв¬
ное2 отображение замкнутого интервала в себя имеет неподвижную точку
Р(га*) = т*. Неподвижная точка отображения Пуанкаре, очевидно, соответ¬
ствует вынужденным колебаниям с периодом 27г. Следовательно, уравнение
(11.3) имеет периодическое решение.
Второй шаг — установить единственность. Предположим, что существу¬
ют два различных периодических решения mi(r) и гп2(т), и придем к про¬
2Непрерывность следует из того, что решения обыкновенных дифференциальных урав¬
нений непрерывно зависят от начальных условий.
11.1 Однородные ферромагнетики
431
тиворечию. Заметим, что поскольку траектории не могут пересекаться, одно
решение строго больше другого, тг(т) > mi(r)3. Из уравнения (11.3) полу¬
чим
П -у- (m2 - mi) = -(m2 - mJ + FT(m2) - FT(mi),
ат
Fr(mj) = в
rrij + H sin т
T
Неравенство |FT(m2) — FT(mi)| < |тг — mi|, которое справедливо при Т >
Тс = 1, означает, что m2 — mi строго убывает. Следовательно, неравенство
Р(тг) — F(mi) < m2 — mi находится в противоречии с F(mj) = mj.
Ниже точки фазового перехода, Т < Тс = 1, есть единственное поло¬
жительное стационарное решение уравнения (11.4), которое мы обозначим
через meq(F). В самом деле, кривая th[(m + Н)/Т\ проходит выше начала
координат4 в m = 0, а наклон этой кривой монотонно убывает сти быст¬
ро стремится к нулю. Поэтому кривая пересекает диагональ ровно в одной
точке, где намагниченность m = meq(H) положительна. Пересечение кри¬
вой th[(m + Н)/Т] и диагонали при отрицательных m может иметь место,
только если Н достаточно мало. Пороговое поле Н*, выше которого решение
с отрицательным m исчезает, называется коэрцитивным полем. Амплитуда
коэрцитивного поля имеет вид (см. задачу 11.1)
Я* = - FArcth\/T^T. (11.5)
При Н = Н* есть еще одно стационарное решение —т*, где то» = \/1 — Т.
При Н < Н* кроме тед(Я) есть два отрицательных стационарных решения.
Отображение Пуанкаре показывает существование периодического реше¬
ния, находящегося в интервале I = [—meq(H\meq(H)]. Однако может суще¬
ствовать больше одного решения. Это легче понять в пределе малой часто¬
ты. При Н < Н* петля намагниченности не достигает точек бифуркации
(±Я*,я=га*), а просто колеблется вокруг квазиравновесной кривой meq(h)
или —meq(h). Эти периодические решения называются ферромагнитными,
так как у них есть ненулевая средняя намагниченность. При Н > Н* петля
намагниченности имеет нулевую среднюю намагниченность. Соответствую¬
щее периодическое решение называется парамагнитным. В общем случае при
9 > 0 фазовая диаграмма в плоскости (Т, Я) содержит: (i) парамагнитную
Пересечение запрещено из-за единственности решений обыкновенных дифференци¬
альных уравнений.
4Мы предполагаем, что Н > 0. Если бы Н было отрицательным, мы могли бы обратить
его знак, сдвинув временную переменную т —> т -Ь 7г.
432
ГИСТЕРЕЗИС
область Р, где парамагнитное решение устойчиво, (ii) ферромагнитную об¬
ласть F, где устойчивы два ферромагнитных решения и (iii) область P+F,
где устойчивы и парамагнитное, и ферромагнитные решения. Вопрос о пол¬
ном аналитическом исследовании фазовой диаграммы до сих пор остается
открытым.
11.2 Теория возмущений
Теперь проанализируем петлю гистерезиса среднеполевого ферромагнетика
с глауберовой динамикой спиновых переворотов, сосредоточившись при этом
на зависимости площади петли от амплитуды Н и частоты Q осциллирую¬
щего магнитного поля. В конце этого раздела мы изучим гистерезис в фер¬
ромагнитной спиновой цепочке.
Высокотемпературный режим (Т > Тс)
Когда Н = 0, решение уравнения (11.3) даст равновесную намагниченность,
которая стремится к нулю в высокотемпературном режиме: meq(H = 0) = 0.
Хотя для Н > 0 невозможно представить meq(H) явной формулой, можно
решить задачу пертурбативно в пределе Н —> 0. Раскладывая гиперболиче¬
ский тангенс в правой части уравнения (11.3) и оставляя только линейный
член, получаем
П—= -^l--Jm+ —эшт. (11.6)
Это линейное уравнение с периодической силой имеет единственное периоди¬
ческое решение т = Msin(r — ф). Это выражение удовлетворяет уравнению
(11.6), когда параметры Миф имеют вид
м —/= — - ., Ф = агсап I , ) (11.7)
Т Ф* + (1 - т) \# + (1-Ш
Общее решение уравнения (11.6) — это сумма периодического решения и об¬
щего решения однородного уравнения. Поэтому имеем
т = Msin(r -ф) + Се-(1"г'1)т/п, (11.8)
где амплитуду С нужно определить из начальных условий. Равенство (11.8)
показывает, что любое решение притягивается к периодическому решению
экспоненциально быстро независимо от величины внешнего поля Н.
11.2 Теория возмущений
433
Теперь перепишем т = М sin(r — </>) в виде = sin т cos ф — cos т sin ф и,
воспользовавшись равенством jy = sinr, найдем параметрическое представ¬
ление петли гистерезиса в координатах m-h. Исключив параметр т, получим
h \2 /т\2 га Л
н) +\м) ~2мн
cos ф = sin2 ф.
Повернув перемасштабированные координаты h/H и т/М па 7г/4,
h_ х — у т __ х + у
н = "7Г’ м = Р/Р
можно переписать петлю гистерезиса в стандартной форме уравнения ЭЛЛИП-
Са о о
х% у^
2cos2(0/2) + 2sin2(</>/2) 1
с полуосями л/2 cos(</>/2) и л/2 sin(</>/2). Поэтому когда внешнее поле мало,
петля динамического гистерезиса — эллипс.
Угол •& = arctg(M/flr) между главной (горизонтальной) оеыо эллипса и
осью h — возрастающая функция частоты
•& = arctg
1 1
Рисунок 11.1(b) схематически изображает петлю динамического гистерезиса
только в пределе низкой частоты. В противоположном пределе высокой ча¬
стоты г? ~ (TQ)-1 —> 0, и петля динамического гистерезиса лежит вдоль оси
Л.
Площадь эллипса в плоскости (ж, у) равна 7г х у/2 cos(</>/2) х \/2 sin(</>/2) =
7rsin^>, так что площадь петли динамического гистерезиса в плоскости m-h
есть тгМНвгаф. Из (11.7) получим
тг Я2П
ГП2 + (1_ 1)2
(П-9)
Это выражение справедливо, когда Я 1, и согласуется с общим предска¬
занием (11.2) для значения показателей a = a = 2ub = (3 = l.
Эти асимптотические результаты выполняются, когда магнитное поле
слабое. Теперь мы покажем, что они справедливы в общем случае. Например,
в среднеполевой модели Изинга теория возмущений показывает, что площадь
434
ГИСТЕРЕЗИС
петли динамического гистерезиса продолжает демонстрировать предельное
поведение А ~ £2 при Q < 1 и Л £2-1 при £2 » 1 независимо от величины
внешнего поля.
Пример 11.1. Предел низкой частоты. Будем искать решение уравнения (11.3)
в виде степенного ряда
тп(т) = гао(т) + Qmi(r) + £22тп2(т) + (11.10)
Подставив (11.10) в (11.3), мы находим рекурсивное уравнение для ш^(т). В
нулевом порядке по £2 получим
= + "sinT),
(11-П)
тогда как поправка первого порядка имеет вид
тп^т)
= _dmo Л _ 1 -тп§(т)\
dr k Т ) •
(11.12)
Аналогично можно определить и поправки более высоких порядков (см. зада¬
чу 11.2). Однако эти члены имеют ограниченное значение, потому что площадь
петли гистерезиса в общем случае пропорциональна £2 (см (11.14) ниже). Поэто¬
му член первого порядка дает ведущий вклад.
Формальное решение уравнений (11.11) и (11.12) имеет вид
ш0(т) = racq(ft),
mi(r) = -
dh dmcq
dr dh
1-
1 - Weq(^)
-1
(11.13)
T
т. e. вклад нулевого порядка Шо(т) совпадает с равновесным решением. Пло¬
щадь петли динамического гистерезиса А = <fmdh в нулевом порядке равна
нулю, так как отсутствует задержка во времени между гао(т) = meq(h) и h. По¬
скольку rai(r) ~ временная задержка между шх(т) и й(т) равна 7г/2, т. е.
четверти периода. Следовательно, ведущий вклад в площадь петли динамиче¬
ского гистерезиса равен
/»27Г JL
А = П/ mi(r)^dr. (11.14)
Jo dT
Пример 11.2. Предел высокой частоты. Когда £2 1, используя £1 1 как па¬
раметр разложения5, запишем
га(т) = гао(т) + ^_1 пгх(т) + £2"2 Ш2(т) + — (11.15)
5Мы используем те же обозначения т7 (т), что и в (11.10), хотя функции разные.
11.2 Теория возмущений
435
Подставив (11.15) в (11.3), получим
dm0
dr
^ = -n,o(r) + th(’"°(T) + HsinT),
и т. д. Первое уравнение показывает, что гао(т) — константа. Следующее урав¬
нение имеет периодическое решение, только когда шо(т) = 0. Поэтому ведущее
поведение намагниченности следующее:
га(т) = П 1mi(r), гах(т) = f th sin£^ cff + Cj, (11.16)
где постоянная С± фиксируется требованием, что следующий член Ш2(т) раз¬
ложения (11.15) — периодическая функция переменной т. Из соотношений m ~
П”1 и h ~ 1 мы снова делаем вывод, что петля динамического гистерезиса в
пределе высокой частоты лежит вдоль оси h. Ведущий вклад в площадь петли
динамического гистерезиса есть
А = П-1 [ (11.17)
Jo wr
Подставляя rai(r) из (11.16) в (11.17) и интегрируя по частям, получим
А=1Т / U.[y7l-iJ] ix.
(11.18)
Предыдущий результат (11.9), А = пН2/О.Т восстанавливается, когда II Т.
Критический режим (Т = Тс)
В критическом режиме система все еще приходит к единственным вынуж¬
денным колебаниям, качественное поведение которых такое же, как в высо¬
котемпературном режиме, но возникает количественная разница. Например,
когда внешнее поле мало, член линейный по m в правой части уравнения
(11.6) становится равным нулю. Поэтому уравнение (11.6) не дает правиль¬
ного приближения для уравнения (11.3). Взамен этого, чтобы получить со¬
гласованное приближение, нужно удерживать следующий (кубический) член
разложения.
Теперь рассмотрим пределы высокой и низкой частоты подробнее. В пер¬
вом случае природа гистерезиса такая же, как в высокотемпературном режи¬
ме. Результаты (11.15)—(11.18) продолжают выполняться, и площадь петли
динамического гистерезиса дается уравнением (11.18), где Т равняется 1:
‘ь[я'/ГТЯЛх-
(11.19)
436
ГИСТЕРЕЗИС
В пределе низкой частоты ситуация более богатая. Будем искать решение в
виде ряда (11.10). Это приводит к решениям (11.11) и (11.12), где Т = 1, а
именно
mo = теп = th(m0 + h), mi(r) = (— ). (11.20)
от \то )
Теперь дополнительно предположим, что внешнее поле мало, так что то
также мало. Разложив первое из уравнений (11.20) в ряд, получим
mo = mo + h-^ (то + h)3 + ...,
откуда то ~ (З/i)1/3 при h —> 0. Поэтому то — (ЗНт)1/3 в окрестности
т = 0. Тогда второе из уравнений(11.20) дает т± ~ — Н~1^3(Зт')~4^3. Эта
сингулярность показывает, что разложение (11.10), сделанное в предполо¬
жении mo » Qmi, становится неприменимым при то ~ Qmi, т. е. при
т ~ Н~2/3 Q3/5. Такая несовместность часто возникает при применении про¬
стого пертурбативного разложения. Хороший способ преодоления этих труд¬
ностей — применение метода граничного слоя. Содержание этого метода мож¬
но вкратце представить следующим образом:
1. Ряд (11.10) рассматривается как внешнее разложение, применимое во
внешней области, которая в данном случае определяется неравенством
т » П3/5.
2. Область, комплементарную внутренней области, обычно называют гра¬
ничным слоем. Внутри граничного слоя мы используем подходящим
образом перемасштабированные переменные и ищем решение в виде
внутреннего разложения по такой переменной.
3. Внутреннее и внешнее решения сшиваются в области перекрытия.
Поскольку ширина граничного слоя пропорциональна Л-2/5П3/5, мы на¬
чинаем применение метода граничного слоя с замены переменной т на 0 с
помощью преобразования
T = Q3/5tf“2/50. (11.21)
Когда в » 1, мы все еще находимся во внешней области, так что m ~
(ЗЯт)1/3 = (ПД’)1/5(30)1/3. Из этого следует, что правильный скейлинг ве¬
дущего члена внутреннего разложения имеет вид
тп(т) = (ПЯ)1/5М0(^) + ....
(11.22)
11.2 Теория возмущений
437
Подставляя (11.21)—(11.22) в (11.3), получаем
!! +th [(W'M + (Mf)V5«] .
Раскладывая гиперболический тангенс и приравнивая члены ведущего по¬
рядка, находим
<п-23>
Следующий за доминирующим член имеет вид QH х Чтобы скомпен¬
сировать его, введем поправку Сравнивая порядок поправки
с порядком ведущего члена (11.22), мы делаем вывод, что правильным пара¬
метром теории возмущений будет (ШТ-)2/5. Таким образом, получаем внут¬
реннее разложение в виде
ш(т) = (fitf)1/5 [Мо(0) + (ПЯ)2/5ЛЛ(0) + (Qff)4/5M2(0) + ...]. (11.24)
Подставляя (11.24) в (11.3), мы воспроизводим (11.23) в ведущем порядке и
в следующем порядке получаем
Внешнее и внутреннее разложения применимы, когда |т| J и М »1,
соответственно, и теперь мы сшиваем результаты в области перекрытия
П3/5Я’ ■2/5 т <С I6. Эта сшивка очевидна в ведущем порядке: потребовав
Mq ~ (30)1/3 при |0| —> оо, мы воспроизводим асимптотику т ~ (ЗЯт)1/3,
которая применима при |т| <С 1. Сшивка более высоких порядков не так
очевидна. К счастью, нам не нужны эти высшие поправки, поскольку ве¬
дущий член / modh не равен нулю. Наконец, мы используем соотношение
то dh = (ПНу/5М0(в) х (ПЯ)3/5 <1в = (ПЯ)4/5Мо(0) <№ и видим, что основной
вклад в площадь петли динамического гистерезиса вносит граничный слой.
Поскольку граничный слой в окрестности г = 7г вносит такой же вклад, как
и окрестность т = 0, то для площади петли динамического гистерезиса в
пределе низкой частоты получим7
а = ся№ н4'5,
Мо(0) М.
(11.25)
6Когда внешнее магнитное поле мало, правильное определение предела низкой частоты
есть Q Я2/3, а не Q 1.
7Константа С в самом деле положительна (задача 11.4).
438
ГИСТЕРЕЗИС
Таким образом, площадь петли динамического гистерезиса дается выра¬
жениями (11.19) и (11.25), соответственно, в пределах большой и малой ча¬
стот. Это результат справедлив, когда вдобавок Н <С 1. Переходя к такому
же приближению малого Н в уравнении (11.19), получаем асимптотический
результат
А(ГС,Я,П)~
7гЯ2Г2—х,
СЯ4/5П4/5,
Я2/3 «fi.; Я« 1,
Q < Я2/3 < 1.
(11.26)
Это предельное поведение предполагает, что площадь петли удовлетворяет
динамическому скейлинговому анзацу вида
Л(ТС,Я,П) = Я4/5П4/5 A(z), z =
который должен выполняться в скейлинговом пределе Н —> 0 и Q —> 0, где
значение z фиксировано. Тогда уравнение (11.26) дает Л(0) = С и A(z) —>
7Г2-9/5 при z » 1.
Низкотемпературный режим (Т < Тс)
Рассмотрим сначала наиболее интересный предел малой частоты. При Н <
Н* периодические решения ферромагнитны. Если мы будем искать т(т) в
виде ряда вида (11.10), то найдем (11.11) и (11.12) для то и т±. Площадь
петли динамического гистерезиса линейна по ft и дается выражением (11.14).
Ведущий вклад в среднюю намагниченность дается выражением
М =
- Г"
TTJ-H VH2 - h2
Если мы к тому же предположим, что магнитное поле мало, h <С 1, средняя
намагниченность будет близка к /х = теч(Н = О)8. Чтобы упростить выраг
жение (11.14) для площади петли, разложим равновесную намагниченность
в ряд Тейлора
me4(4 = m«,(O) + ^!|)i=o/,+ ... = M+(T^?-l) h + ...
и подставим это разложение в (11.12), что в низшем порядке дает
mi
Т
1-м2
1 1 \~х dh
Tl-fj?) dr'
ч
8 Величина ц — положительное решение уравнения /х = th(/Lx/T).
11.2 Теория возмущений
439
При малых Н и Q площадь петли динамического гистерезиса равна
А = тгН2О,
(1-Л2)2
1 + (1 - м2)2 - (1 - Л2)(Г-1 4- Г)'
(11.27)
Согласно уравнению (11.27), зависимость площади от поля Н и частоты П
похожа на зависимость из уравнения (11.9), применимого выше критической
температуры, а зависимость от температуры оказывается сложнее:
А(Т,Н,О) -> тгЯ2П х
16 • е-4/т,
i(i -тг2,
(11.28)
т -> о,
Т -> I.
При Н > Н* периодическое решение парамагнитное. В пределе низкой ча¬
стоты площадь петли динамического гистерезиса стремится к площади <"га-
тической петли
А(Т\ Я, Q) —> Ло = 2 / raeq(/i) dh.
J-н*
Избыток площади, находящийся за пределами Aq, растет как Q2/3. Элемен¬
тарный вывод этого скейлинга отсутствует, и здесь мы просто опишем идею.
Вывод станет технически проще, если предположить, что температуря близ¬
ка к Тс. Далее разложим гиперболический тангенс в правой части уравнения
(11.3) и получим зависимое от времени уравнение Гинзбурга. Ландау с пе¬
риодической вешней силой
dm . m\ 1 ч тт •
Q -г- = (1 — Т)т — - га3 + Н sm т.
dr 3
Петля статического гистерезиса находится на неустойчивой ветви до ’точки
(га, h) = (га*, —Я*), где тп* = у/1 — Т и Я* = | (1 — Г)3/2, откуда перескаки¬
вает в (га, h) = (—Зл/l ~ Г, —Я*), и далее следует по устойчивой в(гтви. Если
мы будем искать решение в виде регулярного разложения (11.10), то около
/i = Я* возникнет сингулярность. От нее можно избавиться, вводя граничный
слой. Анализ похож на то, что мы делали раньше для критического режи¬
ма и дает масштаб отклонения петли динамического гистерезиса от петли
статического гистерезиса. Если и частота мала, и амплитуда II лишь слегка
превосходит коэрцитивное поле Я*, то избыточная площадь растет как
Л(Г,Я,Г2) - Ло ~ Г22/3(Я - Я*)*/3.
440
ГИСТЕРЕЗИС
Гистерезис в ферромагнитной спиновой цепочке
Хотя одномерная ферромагнитная спиновая цепочка — это в некотором смыс¬
ле исключительный случай, поскольку Тс = 0 и статический гистерезис от¬
сутствует, эта система особенно проста и поэтому хороша для понимания
динамического гистерезиса при Т > 0. Воспользовавшись стандартной глау¬
беровой интенсивностью переворотов спинов
Wi =
gj+i) + M*)1A
Т \) ’
получим уравнение для локальной намагниченности Si = (s^
Как мы узнали из главы 8, среднее можно легко вычислить при h = 0:
(
Si-i + Sj+i \ 7
7
— 2 (^*-1 + ^»+i) >
2
где 7 = th(2J/T). Этот трюк не работает при h / 0, и в этом случае нель¬
зя получить замкнутых уравнений для локальной намагниченности. Однако
в слабых полях Н min(J, Г) возможно продвинуться аналитически. Вос¬
пользуемся разложением
th
и, усреднив, получим
2 1 + (Sj-iSj+l)
2
— ~Si + (Si-i + Si+i) + — 1 — 7‘
Просуммировав эти уравнения, мы придем к замкнутому уравнению для на¬
магниченности m = N-152 Si,
(11.29)
где Gk = (siSi+к) ~ спиновая корреляционная функция. После окончания
переходных процессов, намагниченность будет совершать вынужденные ко¬
лебания с амплитудой m ~ h. Спиновая корреляционная функция также
11.3 Неупорядоченные ферромагнетики
441
совершает периодическую нутацию порядка h вокруг своего равновесного
значения G*^ = r)k, где rj = th(J/T). Поскольку умножена на h 1, мы
пренебрегаем вкладом нутации9. Заменяя G2 на г/2 и сохраняя только члены
порядка до 0(h), мы преобразуем (11.29) к виду
Л dm . Н
nd7 = _(1“7)m + T
1-
72 (1 + 772)‘|
SUIT.
С точностью до коэффициентов это уравнение идентично (11.6). Поэтому
выполняется аналог результатов (11.7)-(11.9). В частности, петля динамиче¬
ского гистерезиса — это эллипс площади10
•тг 1 - т/2 Н2 Q
“ Т 1 + rf П2 + (1-7)2’
а амплитуда намагниченности равна
Я 1 - т/2 1
Т 1 + 7?2 -^/П2+ (1 — 7)2
(11.30)
В пределе низкой частоты это выражение сводится к равновесной статиче¬
ской восприимчивости ферромагнитной цепочки Изинга (зпдача 11.5).
11.3 Неупорядоченные ферромагнетики
В большинстве приложений материалы, которые демонстрируют миленке ги¬
стерезиса, находятся при температурах существенно ниже критической, так
что полезно рассмотреть случай нулевой температуры. В адиабатическом
пределе (Г2 0) петля гистерезиса однородных ферромагнетиков при II > Н*
имеет форму прямоугольника11. Однако реальные петли гистерезиса могут
быть разными, а медленное изменение поля может сопровождаться прыжком
намагниченности. Можно было бы ожидать, что эти скачки исчезнут при пре-
цезионных измерениях, но тем не менее они остаются. Вероятно, самое впе¬
чатляющее проявление такого скачкообразного отклика шум Баркгаузепа,
происходящий от внезапных изменений ориентации локальной намагничен¬
ности при изменении поля.
9Если бы мы хотели сохранить этот вклад, нам пришлось бы разложить гиперболиче¬
ский тангенс до порядка О(Д2).
10Мы упростили формулы с помощью равенства 7 = 2у/ (1 4- 7/2).
11 Этот результат справедлив в произвольной пространственной размерности. От раз¬
мерности зависит только амплитуда Н* коэрцитивного поля.
442
ГИСТЕРЕЗИС
Простейшая теоретическая картина, которая дает хотя бы качественное
объяснение некоторых из экспериментально наблюдаемых фактов, — модель
Изинга в случайном поле (МИСП), где на все спины действует различное
магнитное поле. Преимущество МИСП состоит в том, что она решаема в
отличие от большинства более экзотических спиновых моделей, таких как
спиновые стекла. Некоторые качественные свойства МИСП универсальны, и
поэтому ее анализ проливает свет на гистерезис в других неупорядоченных
магнетиках.
Гамильтониан имеет вид
где локальные магнитные поля в узлах hi — вмороженные, независимые и
одинаково распределенные случайные переменные с плотностью вероятно¬
сти p(hi). Мы предполагаем, что p(hi) непрерывна и что вначале hi = О12. К
тому же, если распределение беспорядка четное, т. е. p(hi) = p(—hi), то петля
гистерезиса симметрична, т. е. инвариантна по отношению к преобразованию
т —> — т и Л —> —h. Важное для дальнейшего анализа предположение —
взаимодействие между спинами ферромагнитное, (J > 0). Мы сосредоточим¬
ся на статическом гистерезисе, предполагая, что магнитное поле меняется
адиабатически, если обратное не оговорено явно. Эквивалентно, все перево¬
рачиваемые спины переворачиваются мгновенно. При нулевой температуре
разрешены только понижающие энергию перевороты, и каждый спин Si на¬
правлен вдоль локального поля Li в узле i
которое является суммой внешнего однородного поля, случайных полей и вза¬
имодействий с ближайшими спинами Sj спина При нулевой температуре
имеем Si = sgn(Li).
Прежде чем обсуждать динамику МИСП, покажем, как сильно случайное
поле может влиять на ферромагнитное упорядочение при нулевой температу¬
ре. Начиная с ферромагнитного состояния, в котором все спины направлены
вверх, рассмотрим изменение энергии компактной капли радиуса Д, которая
переворачивается вниз. Есть два вклада в изменение энергии этой капли: (i)
123десь (...) обозначает усреднение величины (...) по беспорядку. Если среднее случай¬
ного поля не ноль, можно сделать его нулем, вычтя среднее из случайного поля в каждом
узле и добавив это среднее к случайному внешнему полю.
11.3 Неупорядоченные ферромагнетики
443
увеличение на J Rd 1 за счет образования границы капли, (ii) уменьшение на
5ДД4*/2, где 8h — типичное значение случайного поля, если спины в области
объемом Rd разворачиваются вдоль среднего магнитного поля. Энергетиче¬
ские затраты на такую каплю положительны, если J Rd~r > 5hRd/2 или
при d > 2. Поэтому изинговский ферромагнетизм при нулевой температуре
устойчив к возмущениям случайного магнитного поля в пространственной
размерности больше двух.
Теперь опишем общие свойства МИСП, которые не зависят от простран¬
ственной размерности и структуры решетки. Начнем с h = оо, когда все
спины принимают значение +1. При уменьшении h локальное поле Li в неко¬
тором узле i в конце концов перейдет через ноль. В этот момент спин в узле г
перевернется, Si = —1. Это событие уменьшает локальные поля соседних спи¬
нов, возможно, заставляя перевернуться некоторые из них. Это, в свою оче¬
редь, приводит к уменьшению локальных полей следующих спинов, которые
также могут перевернуться и т. д. Следовательно, переворот одного спина
может сопровождаться лавиной спиновых переворотов. Когда лавина закан¬
чивается, мы снова понижаем внешнее магнитное поле h до тех пор, пока не
перевернется новый спин, возможно, вызвав новую лавину. Этот процесс про¬
должается до тех пор, пока не перевернутся все спины, и как результат мы
получим верхнюю половину петли гистерезиса га+(Д). Между лавинами на¬
магниченность остается постоянной, таким образом приводя к скачкам петли
гистерезиса и соответственно шуму Баркгаузена (рис. 11.3).
Рис. 11.3. (а) Статический гистерезис в МИСП. (Ь) Увеличение кривой гистере¬
зиса, показывающее скачки намагниченности, приводящие к шуму Баркгаузена.
Также показаны малые петли возврата, лежащие внутри главной петли. Они
получены при циклическом изменении поля h в уменьшенном диапазоне
444
ГИСТЕРЕЗИС
Другое интересное свойство МИСП — существование малых петель воз¬
врата. Такая петля получается, например, если начать в точке А на нижней
половине главной петли и уменьшать поле до достижения точки С. Если
затем увеличивать поле, система вернется точно в начальную точку А, за¬
мкнув малую петлю. Если увеличение поля остановить раньше (например,
в точке В), а потом уменьшать его, то образуется другая малая петля, ко¬
торая снова вернется в точку А. Хотя эти свойства характеризуют любую
неупорядоченную систему с переворачивающей спины динамикой при нуле¬
вой температуре, некоторые черты специфичны для ферромагнитной МИСП.
Мы перечислим их ввиду их полезности для для анализа петель гистерезиса:
1. Абелево свойство. Порядок, в котором назначенные (направленные про¬
тив локального поля) спины переворачиваются в течение лавины, не
имеет значения.
2. Один переворот. Когда h меняется от +оо до — оо, каждый спин пере¬
ворачивается ровно один раз.
3. Симметрия. Нижняя часть петли гистерезиса га_(/г), полученная уве¬
личением магнитного поля от h = —оо до h = +оо, является зеркальным
отражением верхней половины13: т_(Л) = —га+(—Д).
4. Непрохождение. Обозначим всю спиновую конфигурацию через s =
{si,... ,syv}« Предположим, что две конфигурации и s(2)(t) эво¬
люционируют под действием полей h№(t) и h(2)(t), удовлетворяющих
неравенству h№(t) > Если одна конфигурации изначально «вы¬
ше» другой, т. е. s(l)(0) > s(2)(0) (сокращенная запись множества нера¬
венств s^(0) > б’Р\о) для всех i = 1,... ,7V), то s^t) > s^(f) при
всех t.
5. Память о точке возврата. Предположим, что s(0) эволюционирует
под действием поля /г(£), удовлетворяющего неравенству Д(0) < h(t) <
h(tf). Финальное состояние s(tf) зависит только от Zi(t/) и не зависит
от продолжительности tf и истории h(t).
Чтобы понять абелево свойство, предположим, что переворот спина i при¬
вел к тому, что два соседних спина j и к могут перевернуться (т. е. Lj и Lk
стали отрицательными). Если сначала перевернется Sj, то когда узел к —
сосед узла J, это еще более уменьшит локальное поле в узле к (если все
константы взаимодействий ферромагнитные). В противном случае магнит¬
ное поле в узле к не изменится. В любом случае возможность переворота
13Это условие выполняется только в термодинамическом пределе, когда распределение
случайного поля четное: p(hi) = p(—hi).
11.3 Неупорядоченные ферромагнетики
445
спина в узле к сохранится. Аналогично, при перевороте сначала спина Sk со¬
храняется возможность переворота спина Sj. Для любого другого узла I / j,k
любой порядок переворотов спинов Sj и Sk приводит к одинаковому локаль¬
ному полю в узла £. Повторяя эти рассуждения для следующих переворотов,
мы заключаем, что порядок переворотов действительно не важен для конеч¬
ного результата, и полная лавина будет состоять из одних и тех же спинов.
Второе и третье свойства очевидны. Чтобы обосновать правило непрохожде-
ния, предположим, что прохождение возможно и впервые происходит в узле
г, т. е. s^(0) > 5р\о), но s^\t) < Тогда локальные поля удовле¬
творяют неравенству L^\t) < 0 < Но это невозможно, поскольку
и > h№(t). Наконец, память о точке возврата оче¬
видна, если поле монотонно возрастает (или убывает) со временем. Чтобы
рассмотреть общий случай, когда h(t) не обязательно монотонная функция,
построим два вспомогательных поля /imin и /imax, определенных как
^min(^) = t<t'<tf h(t ), ^тах(^) = таХ//;о<//</. /&(/' )•
Эти вспомогательные поля монотонны по построению, и исходное поле зажа¬
то между ними: /imin(i) < h(t) < Zimax(t)- Пусть smin(t), s(Z) и HIIiax(Z) все
вначале равны s(0) и эволюционируют под действием //.(/) и йтах(0-
Правило непрохождения говорит, что smin(i) < s(£) < s,llax(/J. Мы знаем, что
Smin(fy) = smax(fy) из-за уже установленного свойства памяти о ч’очке воз¬
врата для монотонных путей14. Поэтому конфигурация s(/j) должна также
зависеть только от tf для произвольного (не обязательно монотонного)
Свойства, перечисленные выше, лежат в основе статического гис/герезиса
в ферромагнитной МИСП. Более тонкие характеристики, чакне как распреде¬
ление размера лавин, зависят от конкретного вида распределения случайных
полей. Более серьезное препятствие на пути теоретического прогресса про¬
странственная размерность. В общем случае отсутствуют методы, позволя¬
ющие теоретически описать гистерезис в ферромагнитной МИСП на решет¬
ках с петлями. Поэтому гистерезис в двух- и трехмермерной МИСП изучался
главным образом численно. Однако гистерезис изучен иа одномерных (безпе-
телевых) решетках, а также на полном графе, который содержи г максималь¬
ное число петель. Сейчас в качестве примера, дающего полезное понимание,
мы обсудим последнюю систему (часто называемую моделью среднего поля).
^Предполагается, что поле остается в границах /ь(0) < h(J.) < h(t.f). Поэтому опреде¬
ление вспомогательных полей hmin и hmax подразумевает выполнение равенств /i,njn(0) =
Л-(О) = ^шах(О) И = h(tf) =
446
ГИСТЕРЕЗИС
11.4 Модель среднего поля
В модели среднего поля или на полном графе все пары узлов соединены меж¬
ду собой. Если положить константу взаимодействия равной 1/7V, локальное
поле в узле г будет равно т + hi + h. Случайное магнитное поле в узлах со
спинами, направленными вниз, удовлетворяет неравенству hi < —т — h. До¬
ля таких спинов дается интегралом р(х) dx, так что намагниченность
равна
/—m(h)—h
р{х) dx. (11.31)
-оо
В общем случае уравнение (11.31) не поддается аналитическому исследова¬
нию, но для некоторых простых распределений беспорядка решение суще¬
ствует (рис. 11.4).
Пример 11.3. Однородное распределение беспорядка. Для однородного распре¬
деления случайных магнитных полей
/>(М = (2Д) 1 х
✓
1,
(О,
Iftil < д,
|/ч| > Д,
(11.32)
из (11.31) находим, что m(/i) = 1, если — m(ti) — h < —Д, или, эквивалентно,
h > Д — 1. Этот результат показывает, что критической величиной беспорядка,
ниже которой возникает прямоугольная петля гистерезиса, является Дс = 1
(рис. 11.4(a)). Продолжая этот анализ (задача 11.6) при Д > Дс = 1, найдем
намагниченность
m(Ji) = <
-1,
МД-1),
+1?
Л<-(д-1),
|Л| < д -1,
h > +(Д — !)•
(11.33)
Исчезновение петли гистерезиса при достаточно слабом беспорядке ти¬
пично, хотя ее форма зависит от распределения беспорядка. Прямоугольная
петля характерна для однородного распределения.
Пример 11.4. Экспоненциальное распределение беспорядка. При распределении
беспорядка
p(hi) = (2Д)-1 e-|hi|/A, (11.34)
петля гистерезиса тоже исчезает, когда беспорядок превосходит критическую
величину Дс = 1 (рис. 11.4(b)). Чтобы понять, откуда берется это критическое
11.4 Модель среднегополя
447
Рис. 11.4. Петли гистерезиса и графики намагниченности, (а) Однородное рас¬
пределение случайных полей. При слабом беспорядке (Д < I,слева) коэрцитив¬
ное поле равно Я* = 1 — Д, тогда как при сильном беспорядке (Д > I , справа)
петля гистерезиса исчезает. (Ь)Экспоненциальное распределение случайного по¬
ля. При слабом беспорядке (Д < 1, слева) в точках бифуркации (///.*,-Я*) и
(—т*, Я*), где 771* = 1 — Ди Я* = 1 — Д + Д1пД, возникают бесконечные
лавины, а при сильном беспорядке (Д > 1, справа) петля гистерезиса исчезает
значение, продифференцируем уравнение (11.31), чтобы избавиться от интегра¬
ла. Тогда находим
dm _ 2р(—га - h) _ б-1^+й|/Д
dh 1 — 2р(—771 — h) Д — е~ 1т+,11/А ’
где последнее равенство справедливо для экспоненциального распределе¬
ния (11.34).
Когда Д > 1, знаменатель в (11.35) остается положительным и т гладко
возрастает от 77i(—оо) = —1 до тп(оо) = 1, так что петли гистерезиса п<гг. Ко¬
гда Д < Дс = 1, знаменатель зануляется и намагниченность перескакивает па
другую ветвь.
Подставим экспоненциальное распределение (11.34) в (11.31) и получим на¬
магниченность
771
e(m+h)/A _
1 _ е-(тп+/1)/Д,
771 + h < О,
771 + h > 0.
(11.36)
При Д > 1 разложим (11.36) в окрестности начала координат, что дасгг (задача
11.6)
_ Гy/2h — + ^(2/i)3^2 + ..., Д — I,
( д=Т ~ j (д-1)з h2 + ..., Д > 1.
Теперь предположим, что Д < Дс = 1. Если мы будем уменьшать магнитное
поле, то когда достигается точка (т, h) = (га*,—Я*), намагниченность претер¬
певает скачок с верхней ветви на нижнюю. Если потом увеличивать магнитное
поле, скачок назад на верхнюю ветвь произойдет при (/л , //.) = (-га*, Я*). Первая
771 =
(11.37)
448
ГИСТЕРЕЗИС
строка в (11.36) представляет эту верхнюю ветвь. Поэтому в точке бифуркации
(га*, —Д*) мы будем иметь га* = 1 — в этой точке знаменатель в
(11.35) должен быть равен нулю. Это дает Д = Из двух получен¬
ных соотношений мы находим га* = 1 — Д и Я* = 1 - Д + Д1пД.
В общем случае произвольного симметричного распределения магнитных
полей, которое имеет единственный максимум в нуле, т. е. когда р(—х) = р(х)
и р(х) < р(0) для всех х, мы используем уравнение (11.35) и находим, что
равенство р(0) = 1/2 определяет случай критического беспорядка. Когда ве¬
личина беспорядка превосходит критическое значение, зависимость намагни¬
ченности от h в пределе малого поля линейна (задача 11.6)
т = + 0(/г2). (11.38)
Чтобы описать предел малых h для критической величины беспорядка, нуж¬
но знать поведение распределения случайных полей около нуля. Если p(hi) =
| - A\hi|м + ... при \hi\ С 1, то для 0 < h <С 1 имеем
т —
1 + р
2А
д1/(1+/х)
(11.39)
Такое неаналитическое поведение неуниверсально, поскольку оно зависит от
деталей (и, в частности, от показателя степени р) распределения случайных
полей.
Распределение размеров лавин
Лавины — это выраженное свойство гистерезиса в неупорядоченных ферро¬
магнетиках, проявляющееся при адиабатическом изменении магнитного по¬
ля. Здесь мы изучим распределение их размеров. Предположим, что лавина
начинается при (Л, t), т. е. самый «податливый» спин со случайным полем
х = — т — h переворачивается вниз. Это событие уменьшает намагничен¬
ность с т до т — 2/N (см. рис. 11.5). Лавина закончится, если не осталось
других спинов, случайное поле которых находится в диапазоне [ж,х + 2/N}.
Среднее число таких спинов есть Л = 2р(—т — Zi), а вероятность того, что
ни один спин не перевернется, равна е“Л. Следовательно, размер лавины ра¬
вен 1 с вероятностью Ai(A) = е“Л. Аналогично, первый переворот приводит
только к одному последующему перевороту, когда существует ровно один
спин со случайным полем в диапазоне [х,х + 2/N] и не существует спинов
11.4 Модель среднего поля
449
I <, 11 , ,
I •
t ,
л,-
2/N 4/N (JN UN
Рис. 11.5. Изображение лавины в среднеполевой МИСП. Спины выстроены в по¬
рядке возрастания случайных магнитных полей. После переворота самого «по¬
датливого» спина спин, случайное поле которого hi лежит внутри пунктирного
отрезка (длиной 2/N от значения случайного поля самого «податливого» спи¬
на), переворачивается. Как видно из рисунка, лавина (длины 4) заканчивается
после переворота четырех спинов, когда случайные поля /ц. всех спинов вверх
оказываются вне пунктирного отрезка
с полем в интервале [ж + 2/N,x + 4/2V]. Вероятность такого события рав¬
на Аг(А) = Ае-Л х е_А = Ае-2А. Продолжая рассуждать таким же образом
(задача 11.7), приходим к распределению размера лавин
АДА) = 1 e~s\ (11.40)
S!
Мы уже встречали эту изящную формулу при изучении агрегации с муль¬
типликативным ядром (см. уравнение (5.44)). В этой агрегирующей системе
распределение размеров кластеров cs(t) было равно Таким образом,
утверждение о сохранении массы ^2s>iScs(i) = 1 эквивалентно нормировке
53s>i АДА) = 1-
Эти результаты имеют общий характер, но зависимость от распределе¬
ния случайных полей спрятана в параметре А = 2р(—т — //.). Теперь, чтобы
выяснить, как ведет себя распределение размеров лавин в плоскости (m, Zi),
рассмотрим два конкретных примера.
Пример 11.5. Однородное распределение беспорядка. В этом случае имеем
—т — h < — 1 + Н* = —Д на верхней ветви. Поскольку р(.т) = 0 при х < — Д для
450
ГИСТЕРЕЗИС
однородного распределения беспорядка (11.32), получим А = 2р(—т — ft) = 0.
Таким образом, как показано на рисунке 11.4(b), лавины отсутствуют, за исклю¬
чением бесконечных лавин, которые проводят систему из (га,ti) = (1,—Я*) по
всему пути вниз до (га, h) = (—1, —Я*).
Пример 11.6. Экспоненциальное распределение беспорядка. Теперь А > 0, и
распределение размеров лавин везде нетривиально. Точка (га, Л) проходит из
точки (1, оо) в точку (1 — Д, —1 + Д — Д In Д) вдоль верхней ветви, определенной
уравнением га = 1 — е-(»»+л)/Дв Следовательно, —(га + ft) возрастает от —оо до
Д1пД, а А = 2р(—га — ft) = Д~1е”(т+Л)/Л возрастает от 0 до 1. При А < 1
распределение размеров лавин имеет на больших размерах экспоненциальный
хвост
л-(а)Ч7ЯГ'<1'л+,"а’
который следует из (11.40) после применения формулы Стирлинга. При дости¬
жении точки бифуркации, в которой начинаются бесконечные лавины, мы имеем
(га, ft) = (га*, —Я*), где га* = 1—Д и Я* = 1—Д+Д In Д. Эта точка соответствует
пределу А -> 1, где хвост распределения, соответствующий большим размерам,
имеет вид
Л (А)
е-5(1-Л)2/2
1
Полезно переписать эту формулу в терминах переменной ft + Я*, либо га — га*
вместо 1 — А. Подставив га = га* + е и ft = —Я* + S в га = 1 — е-(™+ь)/Д и
разложив, получим, что в ведущем порядке е = \/2Д5. Поскольку А = 2р(—га—ft)
равно Д“1е“(ш+,1)/д = Д_1(1 — га), то для экспоненциального распределения
беспорядка (11.34) получим
1-А =
га — га*
(11.41)
е
Д
Д
Тогда соответствующий большим размерам хвост распределения размеров лавин
примет вид
Д 1 г-д(тп-77гФ)2/2А2 _ 1
S~y/2^
Средний размер лавин равен (s) = J2S>1 sAs —> (1 — А)""1, т. е. он расходится как
(в) ~ А = .
' ' т - m* V h + Я*
11.4 Модель среднего поля
451
Бесконечные лавины
Точно в точке бифуркации (т, fi) = (т*, —Н*) распределение размеров лавин
имеет алгебраический хвост
Ps—1
As
s!
v27TS^
(11.42)
Это распределение не содержит бесконечных лавии, остается загадкой почему
результат (рис. 11.4(b)) выглядит так, как будто есть бесконечная лавина, пе¬
реводящая систему из точки (тп, К) = (тп*, —Н*) в точку (тп, /».) = (—тп*, — Н*),
где т* дается решением уравнения m* = 1—е-(т*+#*)/д, трго()и увидеть, как
возникает бесконечная лавина, заметим, что при уменьшении поля до —Н*
и далее, так что точка бифуркации оказывается пройденной, намагничен¬
ность проходит через множество лавин. После М таких лавин с размерами
Sj намагниченность уменьшается на
Каждое слагаемое этой суммы — случайная величина с распределением As,
заданным формулой (11.42). Оценим самое большое слагаемое с по¬
мощью экстремального критерия (см. врезку на стр. 22)
ОО
Е
а—Smax(M)
который означает, что величина > 5тах(Л/) возникает максимум один раз в
М испытаниях. В сочетании с соотношением As ~ s-3/2 этот критерий дает
SmaY(M) ~ М2. Поэтому > smax(M) ~ М2. Оказывается, эта оценка
снизу максимального слагаемого воспроизводит правильное асимптотическое
поведение всей суммы. Чтобы показать, что это так, запишем яз =
где (s)m — среднее значение распределения As, обрезанного в s,nax(Al)- Это
дает15
М 5тах(Л/)
^Sj~M(s)M = M sAs~M[smax(M)]'/2~M2,
J=1 S=1
откуда 8m ~ M2/JV. Пользуясь математической аналогией между лавина¬
ми и компонентами эволюционирующего случайного графа, оценим, как М
15Поэтому максимальное слагаемое дает правильный скейлинг полной суммы.
452
ГИСТЕРЕЗИС
зависит от N. Сначала заметим, что бесконечная лавина возникает с поло¬
жительной вероятностью (А) = 1 — AS(A), которая ведет себя как
2(А — 1) при А —> 1. С другой стороны, используя (11.41), мы заключаем,
что А — 1 ~ M2/N. Бесконечная лавина будет в конце концов выбрана, когда
число лавин М будет одного порядка с обратной вероятностью Это да¬
ет М ~ N/М2 или М ~ 2V1/3. Поэтому бесконечная лавина возникает после
2V1/3 конечных лавин.
11.5 Гистерезис цепочки Изинга в случайном поле
Рассмотрим гамильтониан МИСП в одном измерении с (ферромагнитной)
константой взаимодействия ,7=1
Л = — SjSi+i h^Si h У Si,
iii
в котором внешнее ноле растет адиабатически. Отсутствие петель в одномер¬
ной решетке сильно упрощает анализ гистерезиса16. Сначала h = оо, и все
спины направлены вверх. Спин в узле г переворачивается, когда его локаль¬
ное поле Si_i + s7:+i + hi + h проходит через ноль. Поэтому состояние спина
зависит не только от hi и Л, но и от числа соседей /, которые уже перевер¬
нулись. В одном измерении число соседей направленных вниз есть f = 0,1
или 2.
Пусть Пу (Л) будет условная вероятность того, что спин с f направлен¬
ными вниз соседями сам направлен вниз. Тогда в терминах распределения
случайных полей р(Д) мы будем иметь
f-2(l-/)-h
Пу(/г) = / p(x)dx. (11.43)
J—оо
Когда убывает внешнее поле, полная история спиновых переворотов может
быть чрезвычайно сложна. К счастью, свойства МИСП — абелево свойство и
свойство памяти о точке возврата — значительно упрощают анализ. Память
о точке возврата позволяет нам уменьшать внешнее поле с оо до h по своему
усмотрению, например, мгновенно, а не медленно с тщательной фиксацией
истории лавин. Абелево свойство позволяет переворачивать спины, направ¬
ленные против их локальных полей, в любом порядке, который нам удобен.
Таким образом, начнем со всех спинов вверх (Д = сю) и мгновенно умень¬
шим поле до h. Теперь спросим: какова вероятность p(Ji) того, что произ¬
вольный спин, который мы назовем зародышем, перевернется? Пользуясь
16Похожее упрощение возникало в неупорядоченных спиновых цепочках в разделе 10.1.
11.5 Гистерезис цепочки Изинга в случайном поле
453
абелевым свойством, мы вычисляем эту вероятность в предположении, что
спин-зародыш перевернется в лавине последним. Вероятность того, что спин-
зародыш перевернется, зависит от состояния его соседей. Обозначим через
П(Д) вероятность того, что правый сосед зародыша (который мы будем на¬
зывать спином R) перевернется. Тогда
р(Д) = [ВД]2П2(/г) + 2П(Л) [1 - П(/0]П1(Л) + [1 - П(Л)]2По(Д). (11.44)
Например, множитель II2(Zi) в первом слагаемом отвечает за то, что и пра¬
вый, и левый соседи зародыша направлены вниз. Поскольку спин-зародыш
фиксирован и направлен вверх, полубесконечные цепочки справа и слева от
зародыша нескоррелированы, и поэтому возникает фактор П2(Д). Умножение
П2(Ь) на соответствующую условную вероятность П<2(/ь) дает первое слагае¬
мое. Другие слагаемые объясняются аналогично.
-I
зародыш r VZ VZ
I I I I {
зародыш Я лавина
Рис. 11.6. Лавина, приводящая к перевороту спина-зародыша. В этом примере
после уменьшения поля до заданного значения h появляются два готовых пе¬
ревернуться спина (в овалах). Ближайший к зародышу готовый перевернуться
спин (жирная стрелка) инициирует лавину размера 4, которая распространяется
влево и достигает R. Пунктирные спины можно игнорировать в этой лавине
Определение П(Л,) концептуально проще, чем нахождение потому
что задача становится односторонней. В самом деле, спин /?. может перевер¬
нуться только в результате лавины, распространяющейся справа налево или
начинающейся на самом спине R. Когда внешнее поле мгновенно уменьшает¬
ся с оо до Л, создается доля По(/г) спинов, готовых перевернуться (рис. 11.6).
Мы можем игнорировать все спины справа от ближайшего готового к пере¬
вороту спина (пунктирные стрелки на рисунке), поскольку они не влияют на
судьбу спина R. Когда ближайший готовый к перевороту спин перевернется,
он инициирует лавину, которая будет распространяться влево и достигнет R.
454
ГИСТЕРЕЗИС
Согласно абелевому свойству можно проходить эту лавину последовательно
справа налево.
Поскольку достаточно учитывать только это конечное число спиновых пе¬
реворотов, можно быстро вычислить их вероятности. Например, для конфи¬
гурации на рис. 11.6 вероятность такой лавины размера 4 равна По(/ь)[П1(Д) —
По(/г)]3. Множитель По(Д) — это вероятность существования ближайшего го¬
тового перевернуться спина, который инициирует лавину, a pli(/i)—По(/ь)]3 —
вероятность того, что каждый из следующих трех спинов перевернется, то¬
гда как ни один из них не мог перевернуться вначале. Суммируя по всем
размерам лавин I > 1, получаем
П(„) = g IW)[nlW - По(Ч]« = (11.45)
Как это часто бывает с комбинаторными аргументами, результат уравнения
(11.45) прост, хотя его вывод далеко не очевиден. Поэтому мы даем еще
один короткий, но абстрактный вероятностный вывод. Из-за трансляцион¬
ной инвариантности правый сосед спина R также переворачивается с веро¬
ятностью П(/г). Тогда есть два вклада в вероятность П(/&) переворота спина
R: n(/i)ni(/i), когда его правый сосед переворачивается, и [1 — П(/&)]По(Д),
когда нет. Поэтому имеем
П(/г) = П(Л) Щ(Л) + [1 - П(Д)] По(Д), (11.46)
что эквивалентно (11.45).
Уравнения (11.44)-(11.45) дают общее решение для произвольного рас¬
пределения беспорядка. Прямым вычислением найдем ПЦ/ь) = р(х) dx.
Тогда две другие условные вероятности можно найти из По(/ь) = Щ(Д + 2)
и П2(/ь) = П1 (Д — 2). Подставив их в (11.44)—(11.45), мы найдем p(h). Для
случая однородного распределения беспорядка (11.32) получаем
1,
h < —Д,
IN < А,
h > Д.
ПДД) =
< (Д —Д)/(2Д),
.0,
Когда беспорядок слабый (Д < 1), петля гистерезиса прямоугольная, как
в случае среднеполевой МИСП с однородным распределением беспорядка
(рис. 11.4(a)). Единственная разница — это амплитуда коэрцитивного поля
Н* = 2 — Д, вместо H^F = 1 — Д. В отличие от случая среднего поля петля
статического гистерезиса не исчезает при критическом значении беспорядка
11.5 Гистерезис цепочки Изинга в случайном поле
455
Д = 1. Вместо этого ее форма меняется, когда Д превосходит Д1 = 1 и она
проходит через еще одну бифуркацию, когда интенсивность беспорядка пре¬
вышает Дг = 2. При Д > 2 верхняя ветвь петли гистерезиса имеет вид (см.
рис. 11.7 и задачу 11.8)
m(h) = <
-1,
Д(6Д-4-Д2)+Д(5Д-4)/1+(Д-2)/12-Л3
4Д(Д—I)2 ’
2+(Д+1)/1
Д(Д-1) ’
11,
h < —Д,
-Д < 1к 2 - Д,
2 — Д<Д<Д — 2,
h > Д - 2.
(11.47)
При 1 < Д < 2 график намагниченности не содержит участков, линейно
зависящих от внешнего поля, и когда —Д < h < — 2 + Д, т = m(h) — это
кубический многочлен. Главное отличие от среднеполевой МИСП — петля
гистерезиса не исчезает, когда беспорядок становится сильным. Этот резуль¬
тат имеет универсальный характер, тогда как более топкие свойства петли
гистерезиса зависят от распределения беспорядка.
Рис. 11.7. Петля гистерезиса для однородного распределения беспорядка, (а)
Д = 2. Нетривиальная часть верхней ветви есть т = 1 + |/i — j/i3 для
—2 < h < 0. (Ь) Д = 3. Намагниченность линейна, т = 3 + %h, когда
—1 < h < 1. Когда — 3 < h < —1, намагниченность имеет вид т = —
^2(!-Ь)
Гистерезис на дереве Кейли
Мы закончим главу несколькими замечаниями, касающимися гистерезиса на
дереве Кейли. Существует некоторое формальное сходство между МИСП на
дереве Кейли и МИСП в одном измерении, поскольку в обеих нет петель. От¬
сутствие петель позволяет решить, например, случайную последовательную
456
ГИСТЕРЕЗИС
адсорбцию димеров на дереве Кейли используя ту же технику, что и в од¬
ном измерении (см. главу 7). Однако равновесные свойства ферромагнитной
МИСП на дереве Кейли, такие как средняя свободная энергия или намаг¬
ниченность, не известны даже при нулевой температуре и нулевом внешнем
однородном поле17. Несмотря на эти трудности, петлю гистерезиса в МИСП
на дереве Кейли можно найти аналитически для произвольного непрерывно¬
го распределения случайных полей.
Линия атаки включает прямое обобщение уравнения (11.44), которое при¬
меняется в одномерном случае. Для спина-зародыша вероятность того, что он
перевернется, связана с вероятностью П(/&) переворота одного из его соседей
соотношением
Р = (у)П/ - П)2_/Па, (11.48)
где Tlf(h) = р(х) dx — условные вероятности, и z > 2 — коор¬
динационное число дерева Кейли. Аналогично, обобщение уравнения (11.46)
имеет вид
П=£ О11'(1 _ п)г_1_/п/- (п.49)
При расчете вероятности П(Д) того, что соседний спин j спина-зародыша
перевернется, нужно задать состояние остальных z — 1 соседей спина j. Би¬
номиальный коэффициент (^у1) соответствует числу конфигураций с / спи¬
нами вниз и z — 1 — f спинами вверх, П^ (1 — П)г_1”^ дает вероятность этой
конфигурации, а Пу — условная вероятность переворота спина j.
Уравнения (11.48)—(11.49) дают общее решение для петли гистерезиса в
МИСП на дереве Кейли, которое справедливо для произвольного распреде¬
ления беспорядка и произвольного координационного числа. Полный ана¬
лиз петли намагниченности га(/г), который можно проделать, решив (11.48)-
(11.49), громоздок даже для однородного распределения беспорядка. Однако
конечный результат — простой и неожиданный. Для z = 3 петли намагни¬
ченности качественно похожи на найденные в случае z = 2, т. е. в одномерии.
Напротив, для z > 4 петли намагниченности качественно похожи на петли,
найденные в модели среднего поля. Этот результат не является неожидан¬
ным, поскольку дерево Кейли эффективно бесконечномерное. Что странно —
характеристики гистерезиса на дереве Кейли для случая z = 3 квазиодно-
мерны.
17 Свойства основного состояния МИСП на дереве Кейли были описаны только для слу¬
чая бимодального распределения случайных полей р(х) = — l) + jd(rc + l).
11.6 Ссылки
457
11.6 Ссылки
Гистерезис играл большую роль в записи на пленку и других технологиях
хранения данных, основанных на магнетизме. Например, главное свойство,
отставание намагниченности от поля записывающей головки, использовалось
для хранения музыки. Тем не менее, гистерезис часто рассматривается как
помеха, от которой нужно избавиться, чтобы «исправить» равновесные дан¬
ные. С теоретической точки зрения гистерезис содержит множество сложных
задач. Хорошее описание гистерезиса требует использования неравновесных
методов, учета беспорядка (распространенный термин «грязные материалы»
вероятно лучше отражает существо дела, в отличие от научного названия
«неупорядоченные системы» ) и, возможно, учета эффектов далыюдейству-
ющих магнитных и даже упругих взаимодействий.
Наше изложение гистерезиса сосредоточено вокруг двух специальных мо¬
делей. Первая, даже будучи сформулированной на магнитном языке (одно¬
родный ферромагнетик в осциллирующем магнитном поле), довольно об¬
щая и может быть применена к другим динамическим системам под дей¬
ствием осциллирующего магнитного поля. Больше информации об этом типе
моделей можно найти в [222, 223]. Скейлинговые законы в динамическом ги¬
стерезисе обсуждаются в [224, 225], где также использую'гся асимп'готические
разложения. Книга Бендера и Орсзага [158] — отличная ссылка по асимпто¬
тическим методам такого типа. Для экспозиции отображении Пуанкаре и
элементарным топологическим методам, используемым при анализе обык¬
новенных дифференциальных уравнений, можно обратиться к монографии
Строгача [226].
Аргумент об устойчивости ферромагнитного состояния в присутствии
магнитных полей предложен Имри и Ма [227]. Фейнман [228] в главе 37 то¬
ма II дает хорошее описание скачкообразного графика намагниченности как
функции магнитного поля. МИСП, описывающая это явление, была пред¬
ложена и проанализирована Сетной и соавторами: см. обзор в |229| и книгу
[230]. Эта модель допускает аналитическое решение в одном измерении, а
также на дереве Кейли. Наше изложение было основано на |231 233]. Обзо¬
ры гистерезиса в магнитных материалах см. в [229, 234].
11.7 Задачи
11.1 Покажите, что для среднеполевого ферромагнетика, амплитуда коэрцитивно¬
го поля имеет вид (11.5).
458
ГИСТЕРЕЗИС
Подсказка'. Чтобы найти Я* и га* = у/1 — Т, воспользуйтесь применимостью
(11.4) в точке (—га*, Я*) плоскости (га, Я) и фактом, что, когда график функ¬
ции F(ra) = th[(ra + Н)/Т] касается диагонали в точке (—га*, Я*), он имеет
наклон равный 1.
11.2 Покажите, что второй член разложения (11.10) имеет вид
cfrai _2шо(1 —^о)
■d7 + rni т*
1-
2"|
l-mg
-1
где гао и rai находятся из (11.13).
11.3 Покажите, что второй член разложения (11.15) удовлетворяет уравнению
!^ = _„11 + М1_и?рЦ2Л1
dr Т L \ т J\
и что это уравнение имеет периодическое решение, если
11.4 Цель этой задачи — показать, что константа С, возникающая в (11.25), хорошо
определена и положительна, т. е. интеграл Iq = Mq(O)<10 существует и
отрицателен.
(a) Установите расходимость Mq(0) при больших |0|, а именно, используя
(11.23) выведите асимптотику
Mq —> (30)1/3 — (30)-4/3 при |0| —> оо.
(b) Покажите справедливость соотношения /^(З#)1/3 d0 = 0. (Интегралы
• •) d0 определяются как lim©-^ /&е(. . •) d0.)
(c) Воспользовавшись этими соотношениями, перепишите Iq в виде интегра¬
ла Iq = w(0) d0, где w(0) = Mq(0) — (30)1/3. Покажите, что асимпто¬
тическое поведение функции w(0) подразумевает, что она интегрируема
и, следовательно, интеграл Iq существует.
(d) Чтобы доказать, что интеграл Iq отрицателен, достаточно показать, что
w(0) отрицательно. К этому факту можно прийти следующим образом:
i. Вспомните, что w(0) отрицательно при 0 —> —оо.
ii. Воспользовавшись предыдущим утверждением, покажите, что, ес¬
ли ю(0)где нибудь положительно, должна быть первая точка #, где
w(0) = 0. Объясните, что производная w'($) в этой точке должна
быть неотрицательна, поскольку график w(0) пересекает w = 0 сни¬
зу вверх в точке -0.
11.7 Задачи
459
iii. Покажите прямым вычислением, что
Используя этот результат вместе с предположенным соотношением
Л/о(т?) = (Зт?)1/3, выведите, что производная и точке А равна w'($) =
—(Зт?)-2/3, т. е. отрицательна. Это противоречие доказывает, что w
в самом деле отрицательно.
11.5 Эта задача связана с гистерезисом в ферромагнитной цепочке Изинга в пре¬
деле слабого поля: Н <С min( J,T).
(a) Покажите, что в пределе низкой частоты П <£ 1 - 7 уравнение (11.30)
упрощается к виду
_М 11- г/2 1 11-Z/1 /2./\
Х~ Н - Т 1 + J72 1-7 _ Т 1 + 77 “ Т ех|>\7’7 ■
(b) Убедитесь, что это выражение совпадает со стандартным выражением
для статической восприимчивости % = М/Н ферромагнитной цепочки
Изинга.
11.6 Рассмотрим среднеполевую МИСП с константой взаимодействии I /N между
всеми парами спинов при нулевой температуре.
(a) Покажите, что для однородного распределения беспорядка (11.32) на¬
магниченность имеет вид (11.33).
(b) Получите асимптотическое поведение (11.37) для экспоненциального рас¬
пределения беспорядка.
(c) Рассмотрите распределение Гаусса p(hi) = (27гД2)-1/2 ехр('“ 23^) СЛУ"
чайных полей. Убедитесь, что критическая величина беспорядка есть
Дс = д/2/7г. Покажите, что когда петля гистерезиса отсутствует, Д > Дс,
намагниченность демонстрирует следующее асимптотическое поведение:
/(А-1)’114-ву.2),
{(Зтг/4) W/3 + o(ft2/3), Д Д,..
(d) Получите асимптотическое поведение (11.38) и (11.39).
11.7 Продолжите рассуждение, используемое на странице 448 для нахождения
распределения размеров лавин АДА), записанное в виде уравнения (11.40) для
среднеполевой МИСП. Нам нужна вероятность того, что ровно .ч спинов могут
перевернутся в одной лавине. Для того чтобы это событие могло произойти,
значения случайных полей для этих s спинов должны лежать в диапазоне
[#, a;-l-2s/7V], а расстояния между соседними значениями случайных полей не
могут быть больше чем 2/N.
460
ГИСТЕРЕЗИС
11.8 Выведите верхнюю ветвь петли гистерезиса для однородного распределения
беспорядка при Д > 2, (11.47).
Глава 12
ДИНАМИКА ПОПУЛЯЦИЙ
Динамика взаимодействующих популяций обычно моделируется с помощью
систем нелинейных дифференциальных уравнений. В этой главе мы обсу¬
дим базовую феноменологию нескольких классических моделей динамики
популяций. Как мы увидим, даже в простейших ситуациях стохастичиость
вопреки ожиданиям может играть ключевую роль. Далее мы представим
статфизический подход к явлениям, лежащим за пределами применимости
непрерывного динамического описания, таким как большие уклонения и су¬
ществование различных асимптотических состояний в непрерывной и стоха¬
стической динамике.
12.1 Непрерывная формулировка
Рассмотрим популяцию, содержащую N различных видов. Мы предполагаем,
что все виды идеально перемешаны в течение эволюции, так ччч> основные
переменные — это их глобальные плотности pi. Эволюция этих плотностей в
непрерывном пределе описывается набором уравнений
Pi = Щр).
Здесь точка сверху обозначает производную по времени, а р = (pi, Р2>Рз? • • •)
обозначает набор плотностей различных видов. В функциях Fi зашифрова¬
ны реакции, и обычно это нелинейные функции р*. Для более чем двух видов
результирующая динамика может быть сколь угодно сложной, содержащей
странные аттракторы, топологически сложные орбиты и хаос. Мы сосредо¬
точимся на простых системах, в которых не возникает таких усложнений и
при этом стохастические эффекты могут быть важны.
462
ДИНАМИКА ПОПУЛЯЦИЙ
Логистический рост
Начнем с одновидового логистического роста, описывающего эволюцию по¬
пуляции самовоспроизводящихся конкурирующих между собой организмов.
Индивидуумы воспроизводятся с помощью бесполого размножения (с интен¬
сивностью г) и умирают из-за конкуренции с другими членами популяции.
Плотность подчиняется уравнению р = гр — /ср2. Это уравнение можно за¬
писать в безразмерном виде, перемасштабировав время t —> rt и плотность
р kp/r, что дает логистическое уравнение
р = р{1- р), (12.1)
решение которого есть
р(0) е*
1 + р(0)(е* - 1)*
Таким образом, начальная плотность экспоненциально быстро приближается
к своему стационарному значению р = 1.
Рассмотрим более общий случай реакций, которые описываются уравне¬
нием р = F(p\ где у F(p) есть множество нулей и экстремумов. Можно по¬
нять динамическое поведение почти без вычислений, изучая фазовый порт¬
рет системы, а именно, график р как функции р. Точки, где F = 0, — это
неподвижные точки динамики. В пределе большого времени одновидовая
система должна в конце концов прийти в одну из этих неподвижных то¬
чек. Существует два типа неподвижных точек: устойчивые и неустойчивые.
Если система начинает эволюцию в неустойчивой неподвижной точке, она
останется там навсегда. Если система стартует инфинитезимально близко к
неустойчивой неподвижной точке, она в конце концов придет в устойчивую
неподвижную точку. Множество начальных состояний, стартуя с которых
система достигает данной неподвижной точки, называется ее областью при¬
тяжения. Если мы не можем решить уравнение р = F(p) в явном виде (а
обычно мы не можем), мы тем не менее можем понять его динамическое пове¬
дение из его фазового портрета. Нужно просто найти все неподвижные точки
р*, в которых F(p*) = 0, и определить их устойчивость по знаку производ¬
ной Ff в каждой неподвижной точке. Тогда поведение на больших временах
можно извлечь из направления «потока», как показано на рис. 12.1. Таким
образом можно описать поведение любой одномерной динамической системы.
Пример 12.1. Приближение к неподвижной точке. Рассмотрим уравнение р =
F(p) в окрестности устойчивой неподвижной точки, где F(p*) = 0. Разложение
12.1 Непрерывная формулировка
463
Рис. 12.1. Фазовый портрет: (а) логистического роста и (Ь) более общей реак¬
ции р = F(p). Белые и черные кружки обозначают неустойчивые и устойчивые
неподвижные точки соответственно. Стрелки показывают направление потоков р
F(p) = — А(р — р*) -h ... дает уравнение движения р = -А(р - р*) с решением
р — р* ~ e~xt. Если однако F'(p*) также равно нулю, то разложение /*’ и окрест¬
ности устойчивой неподвижной точки будет иметь вид F(p) = -А(р р*)2 -Ь —
Локальное уравнение движения принимает вид р = —А(р-р*)2 и пмее г решение
р — р* ~ (At)-1. Подводя итог, когда F'(p*) не равно нулю, устойчннаи точка до¬
стигается экспоненциально быстро. Если первый член разложения функции F п
окрестности неподвижной точки убывает быстрее чем линейный, приближение
к неподвижной точке со временем происходит по степенному закону.
В рамках динамики популяций есть множество способов обобщения моде¬
лей логистического типа. Например, можно добавить в уравнение р — F(p)
запаздывающй отклик, возрастную структуру популяции пли вместо непре¬
рывного времени включить дискретные непересекающиесн поколении. Эти
обобщения делают размерность динамической системы более высокой (или
бесконечной), и эволюция таких систем может быть очень богатой.
Двухвидовые реакции
Для двух различных реакционноспособных видов А и В диапазон возможных
реакций значительно расширяется. Обсудим три характерных примера:
• конкуренция, когда вид А и вид В уничтожают друг др.уеа;
• симбиоз, когда вид А и вид В помогают друг другу;
• хищник-жертва, когда вид А питается видом В.
464
ДИНАМИКА ПОПУЛЯЦИЙ
Для внутривидовых реакций естественно рассматривать логистический
рост. Однако для реакций хищник-жертва мы будем рассматривать более
простое внутривидовое взаимодействие, чтобы подчеркнуть уникальные
свойства этой системы.
Конкуренция и симбиоз
В двухвидовой конкуренции каждый вид демонстрирует логистический рост,
к которому добавляется конкурирующее взаимодействие. Эволюция плотно¬
стей, которые теперь обозначаются также А и В, описывается уравнениями
А = А(1 — А —еВ) = Fa(A,B),
В = В(1 — В — еА) = Fb(A,B),
где величина конкуренции задается параметром е. Для простоты предполо¬
жим, что каждый вид имеет такую же динамику в отсутствие взаимодей¬
ствия, а влияние конкуренции также симметрично (несимметричные внут¬
ривидовые взаимодействия рассматриваются в задачах 12.1 и 12.2). Чтобы
понять поведение системы на больших временах, сначала найдем неподвиж¬
ные точки, где А = В = 0. Они имеют координаты
(А*,В*) = (0,0), (1,0), (0,1) и (1/(1 + е), 1/(1 + б)).
Последняя неподвижная точка — самая интересная, поскольку она описывает
влияние конкуренции на сосуществование видов. Чтобы узнать, действитель¬
но ли она описывает влияние конкуренции, нужно изучить ее устойчивость.
Для двумерной динамической системы (12.3) аналогами производной в непо¬
движной точке являются собственные значения и собственные векторы ли¬
неаризованных кинетических уравнений в неподвижной точке
fdFA
dFA\
дА
дВ
9FB
dFB
0А
дВ /
(12-4)
Собственные значения матрицы (12.4) в каждой из четырех неподвижных
точек равны
в (0,0)
в (1,0)
в (0,1)
В (1/(1 + с), 1/(1 + €)),
Ai = l,
Ai = -1,
Ai = 1 - б,
A1 = l
Аг = 1,
Аг = 1 — б,
Аг = —1,
Аг = (б — 1)/(б +1).
12.1 Непрерывная формулировка
465
В (0,0) оба собственных значения положительны. Поэтому потоки расходят¬
ся и (0,0) — неустойчивая неподвижная точка. В трех других неподвижных
точках может быть либо два отрицательных собственных значения, что озна¬
чает, что неподвижная точка устойчива, либо одно положительное и одно
отрицательное собственное значение. В последнем случае потоки сходятся к
неподвижной точке в одном направлении и расходятся от нее в ортогональном
направлении. Такие неподвижные точки называются седловыми точками.
В общем случае проще и физически нагляднее описывать глобальный по¬
ток, рассматривая нулевые изоклины, а именно геометрические места точек,
в которых выполняются равенства А = 0 и В = 0. Полагая А = 0 и В = 0,
получаем уравнения для нулевых изоклин
А = 1 — еВ, В = 1 — еА,
которые показаны на рисунке 12.2 для е < 1 и е > 1, что соответствует слабой
и сильной конкуренци соответственно1. Пересечение нулевых изоклин оиреде-
Рис. 12.2. Плоскость A-В плотностей двух конкурирующих видов (уравнение
(12.3)) с нулевыми изоклинами А = 0 и В = 0 (показаны пунктиром) для (а)
е<1и(Ь) б > 1. Маленькие стрелки рядом с данной нулевой изоклиной показы¬
вают направление потока соответствующей плотности. Также белыми, серыми и
черными кружками показаны неподвижные точки — неустойчивые, седловые и
устойчивые соответственно. Толстые стрелки показывают потоки А и В
ляет неподвижную точку. Поскольку мы знаем направление! потока одной из
плотностей с двух сторон от нулевой изоклины, мы можем построить изобра¬
жение глобального потока в плоскости A-В, пользуясь ин<|х>рмацисй с обеих
1Есгь еще две нулевые изоклины А = 0 и В = 0, но они по играют роли, когда обе
плотности не равны нулю.
466
ДИНАМИКАПОПУЛЯЦИЙ
нулевых изоклин. Таким образом мы узнаем, что при слабой конкуренции
неподвижная точка, в которой сосуществуют две плотности, устойчива, хо¬
тя и с меньшими значениями по сравнению со случаем, когда конкуренции
нет. Однако при сильной конкуренции любая разница между двумя видами
увеличивается, и только сильнейший выживает в пределе большого времени.
Позволив параметру е в уравнении (12.3) быть отрицательным, можно
также рассматривать симбиоз, при котором присутствие одного вида усили¬
вает другой. Если определить S = — е, то неподвижная точка сосуществования
видов будет расположена в
(л*, В’) = (1/(1 -J), 1/(1 -г)).
Из уравнений, линеаризованных в окрестности каждой неподвижной точки,
следует два типа возможного поведения. При 6 < 1 наблюдается умеренный
симбиоз, такой что стационарные плотности просто возрастают по сравне¬
нию со случаем отсутствия симбиоза. Однако при 5 > 1 неподвижная точка
сосуществования видов неустойчива, и плотности неограниченно растут для
большинства начальных условий.
Взаимодействие хищник-жертва
Особенно привлекательная модель динамики популяций была предложена
Вольтерра в 1926 году для объяснения наблюдаемых колебаний улова ры¬
бы в Адриатическом море. Основная идея модели была в том, что популя¬
ция состоит из вида-жертвы, который свободно воспроизводится в отсутствие
хищников, и вида-хищника, который должен поедать жертв, чтобы выжить.
Напишем простейшее динамическое уравнение для этих двух процессов:
А = А-АВ,
В =-В + АВ.
(12.5)
Здесь АиВ соответствуют жертве и хищнику. Эта система известна как мо¬
дель Лотки-Вольтерра. Чтобы избежать нагромождения обозначений, мы
полагаем четыре потенциально разные константы интенсивностей равными
единице. Без потери общности можно исключить три из них, соответствен¬
но перемасштабировав время и две плотности, так что в общей модели есть
лишь одна константа интенсивности. Для простоты мы также обходимся без
квадратичных слагаемых, обеспечивающих саморегуляцию для каждого ви¬
да (этому обобщению посвящена задача 12.2). Из уравнений (12.5) следует,
что если бы мир был свободен от хищников В, плотность жертв А росла
12.1 Непрерывная формулировка
467
бы со временем экспоненциально. Однако жертв поедают с интенсивностью,
пропорциональной частоте встреч хищников с жертвами. Аналогично, хищ¬
ники вымерли бы от голода экспоненциально быстро в отсутствие жертв, но
выживают, поедая их.
Две неподвижные точки этой системы — это (А*, 7?*) = (0,0) и (1,1). Про¬
изводя линейный анализ устойчивости в окрестности каждой неподвижной
точки, мы находим, что неподвижная точка в начале координат — седловая,
устойчивая в вертикальном направлении и неусточивая в горизонтальном на¬
правлении, тогда как неподвижная точка (1,1) — нейтральный центр. Слово
«центр» означает, что оба собственных значения комплексные, так что поток
около центра имеет вращательную компоненту. От неустойчивого центра по¬
ток расходится, поскольку у собственных значений есть положительная дей¬
ствительная часть, а для неустойчивого центра — наоборот. Для нейтраль¬
ного центра действительные части собственных значений равны нулю, а по¬
ток — чисто круговой. Опять несложно сшить глобальное поведение, изучая
нулевые изоклины. Полагая А = 0 и В = 0, получаем нулевые изоклины в
виде
А(1 - В) = 0, В(А - 1) = 0,
откуда видим, что глобальный поток вращается вокруг неподвижной точ¬
ки сосуществования видов (рис. 12.3). Фактически все орбиты замкнуты —
свойство, которое следует из скрытого закона сохранения модели Лотки -
Вольтерра. Любая модификация уравнений движения (12.5), делающая мо-
Рис. 12.3. Модель Лотки-Вольтерра в плоскости А-В. Пунктирные линии по¬
казывают нулевые изоклины, а замкнутые кривые представляют периодические
орбиты для данного значения сохраняющейся величины G из уравнения (12.6)
468
ДИНАМИКА ПОПУЛЯЦИЙ
дель более реалистичной, такая как включение саморегуляции для каждого
вида, нарушает закон сохранения и меняет глобальную структуру потока.
Для нахождения закона сохранения разделим первое из уравнений (12.5)
на А, а второе — на В и получим уравнения для In А и In В:
din А , _ din В .
—;— = 1 - В, —;— = А - 1.
dt ’ dt
После сложения этих двух уравнений правая часть будет равна А — В, что
согласно уравнению (12.5) то же самое, что А + В. Таким образом, имеем
закон сохранения
1п(АВ) — (А + В) = б = const. (12.6)
Если начальные условия не (0,0) и не (1,1), последующее движение происхо¬
дит вдоль замкнутой орбиты, характеризуемой данным значением б. Каждая
из этих орбит маргинально устойчива; это означает, что мгновенное инфини¬
тезимальное возмущение переводит систему с одной орбиты на другую близ¬
кую орбиту, где система остается навечно в отсутствии новых возмущений.
Пример 12.2. Циклическая конкуренция. Прекрасный пример взаимодействия
хищник-жертва с более чем двумя видами дает модель названная Г.Ф. Гаузе
«борьба за существование» (рис. 12.4). В ней три вида борются за превосходство
Рис. 12.4. Динамика модели «борьба за существование» (уравнения (12.7)) в
пространстве АВС. Показаны две периодические орбиты, которые даются пере¬
сечением плоскости А + В + С = 1 и гиперболоида АВС = const
12.1 Непрерывная формулировка
469
через циклический набор взаимодействий
А + В 2Л, В + С 2В, С + А-+2С.
Плотности этих трех видов Л, В и С эволюционируют согласно уравнениям
А = Л(В-С),
В = В(С-Л), (12.7)
С = С(Л-В).
Этот симметричный набор уравнений имеет два закона сохранении. Сначала,
складывая уравнения (12.7), мы видим, что сохраняется общая плотность А +
В + С = 1. Далее, записывая уравнения для Л/Л, В/В и С/С и складывая
их, находим, что произведение плотностей АВС также сохраняется. Поэтому
для данного значения константы 6 = АВС эволюция ограничена замкнутыми
орбитами в плоскости, определенной уравнением Л + В -Ь С = 1.
Пример 12.3. Трехвидовая конкуренция. В качестве примера сложностей, ко¬
торые могут возникнуть в трехвидовой системе, рассмотрим модель, и которой с
каждым видом происходит логистический рост и все виды попарно циклически
конкурируют. Эволюция такой системы описывается уравнениями
Л = Л(1- А-аВ-рС),
В = В(1 — В — аС — рА), (12.8)
С = С(1-С-аА-рВ),
а и Р характеризуют интенсивность истребления видов друг другом. Есть
три различных асимптотических исхода этой динамики в зависимости от значе¬
ний параметров конкуренции а и Р:
• Слабая конкуренция: а + Р <2. Неподвижная точка, в которой плотности
всех трех видов не равны нулю, устойчива.
• Сильная конкуренция: а > 1 и Р > 1. Неподвижные 'точки, в которых
плотность только одного вида не равна нулю, устойчивы. Какая из непо¬
движных точек (1,0,0), (0,1,0) или (0,0,1) станет аттрактором динамики
зависит от начальных условий.
• Асимметричная конкуренция. Для всех остальных значений а и Р непо¬
движные точки отсутствуют и эволюция становится динамически сложной.
Последний случай особенно интересен. Можно показать, что плотность каждо¬
го вида колеблется непериодическим образом, с периодом, пропорциональным
общему прошедшему времени.
470
ДИНАМИКА ПОПУЛЯЦИЙ
Эпидемии
Распространение эпидемий можно смоделировать как набор реакций, в кото-
рых здоровые, восприимчивые и зараженные индивидуумы взаимодейству¬
ют и распространяют болезнь. Два классических описания распространения
эпидемий — это модель SIS (susceptible-infected-susceptible, т. e. восприим¬
чивый-зараженный-восприимчивый) и модель SIR (susceptible-infected -
recovered, т. e. восприимчивый-зараженный-выздоровевший). Первая явля¬
ется карикатурным изображением распространения простуды, при котором
с индивидуумом могут происходить бесконечные циклы заражений и выздо¬
ровлений. Вторая описывает болезнь, которой индивидуум может заболеть
только один раз в жизни, после чего он либо приобретает полный иммуни¬
тет, либо умирает. Оба результата могут быть отнесены к категории «удален».
В модели SIS мы принимаем обозначения S и I для плотностей восприим¬
чивых и зараженных индивидуумов соответственно. Когда восприимчивый и
зараженный индивидуумы встречаются, восприимчивый заражается с интен¬
сивностью fc, которая характеризует вирулентность инфекции. Зараженный
индивидуум выздоравливает с интенсивностью г. Их плотности подчиняются
уравнениям
S= rl — kSI,
I = -г/ + kSI.
(12.9)
Модель SIS — это не что иное, как замаскированный логистический рост.
Из уравнений (12.9) видно, что полная плотность S +1 сохраняется (можно
положить ее равной 1). Поэтому, используя равенство S = 1 — I, получаем
уравнение эволюции для I
i=(k-r)I- kl2,
(12.10)
которое есть просто логистическое уравнение (12.1), но с заданными интен¬
сивностями. Если интенсивность заражения к превосходит интенсивность вы¬
здоровления г, плотность инфицированных индивидуумов приближается к
стационарному значению 1 — £ с такой же экспоненциальной зависимостью
от времени, как в (12.2). Соответственно, плотность восприимчивых индиви¬
дуумов достигает стационарного значения £. В противном случае, если к < г,
то I —>0, & S —> 1. В обоих случаях плотность зараженных индивидуумов S
задается плотностью I, т. е., как только найдена плотность I, сразу опреде¬
ляется и плотность S.
12.1 Непрерывная формулировка
471
Более интересна динамика модели SIR. Хотя шаг заражения такой же, как
в модели SIS, выздоровевшие индивидуумы эффективно удаляются из попу¬
ляции, и их плотность R никогда не убывает. Плотности восприимчивых, за¬
раженных и выздоровевших индивидуумов эволюционируют в соответствии
с системой уравнений
S = —kSI,
i=-rI + kSI, (12.11)
R= ri.
Главный вопрос о модели SIR следующий: может ли малая доля заражен¬
ных индивидуумов, находящаяся среди восприимчивых индивидуумов, запу¬
стить макроскопическую эпидемию? Чтобы определить кри терий эпидемии,
заметим, что в соответствии с первым из уравнений (12.11) плотность вос¬
приимчивых индивидуумов со временем может только убывать. 'Горда для
S < г/к = г второе уравнение I = I(kS — г) показывает, что плотность за¬
раженных индивидуумов убывает со временем — вспышки заболевания не
происходит. Поскольку S убывает со временем, если вспышки пот вначале,
ее не может быть никогда.
Наоборот, для S >г величина I будет изначально положи тельной, и нач¬
нется эпидемия. Чтобы узнать масштаб эпидемии, разделим второе из урав¬
нений (12.11) на первое, и получим
di
dS
„ г
_1+5’
(12.12)
Интегрирование этого уравнения показывает, что иа данной траектории в
плоскости S-I величины S и I связаны соотношением
I + S-r In S = /(0) + 5(0) - г In 5(0). (12.13)
Из уравнения (12.12) следует, что эпидемия может начаться 'только при
5(0) > г,, когда плотность зараженных индивидуумов вначиле возрастает
(рис. 12.5).
Максимальная плотность зараженных индивидуумов /,,тх возникает, ко¬
гда 5(f) = г. Используя этот факт в уравнении (12.13), получим
1 — г + г In
г
(12.14)
Другая важная характеристика — это доля индивидуумов /tot, которые за¬
ражались в течение всей эпидемии. Снова используя уравнение (12.13), но
472
ДИНАМИКА ПОПУЛЯЦИЙ
Рис. 12.5. Эволюция модели SIR в плоскости S-I. Показаны траектории, начи¬
нающиеся в точках 5(0) = 0,9,0,7 и 0,4 (и /(0) = 1 — 5(0)) для случая г = 0,3
(вертикальная пунктирная линии) соответственно. Горизонтальные линии дают
максимально зараженную долю /,пах для трех показанных случаев. Пересечение
каждой траектории с горизонтальной осью дает 5(оо)
теперь в пределе бесконечного времени, в котором I —> 0 и 5 —> 5(оо), полу¬
чим трансцендентное уравнение для 5(оо),
5(оо) = 5(0)e"t1_s(oo)'/F, (12.15)
откуда Aot = 1 — S(oo). Например, если популяция вначале состоит из 90%
восприимчивых и 10% зараженных индивидуумов и г = 0,3, как на рисунке
12.5, максимальная доля зараженных индивидуумов на пике эпидемии будет
приблизительно равна 37%, а доля индивидуумов, которые заразились до
того, как эпидемия выжгла сама себя, равна 95% — переболеют почти все!
Пример 12.4. Распространение слухов. Постой вариант модели SIR описыва¬
ет распространение слухов в популяции, состоящей из разносчиков слухов (5),
неактивных (Т) и неинформированных (U) индивидуумов. Рассмотрим челове¬
ка, который знает некоторый сочный слух и хочет его распространить. Когда
разносчик встречает неинформированного человека, слух передается, и оба ин¬
дивидуума становятся разносчиками. Однако, когда два разносчика встречают¬
ся, им не нравится передавать (уже устаревший) слух друг другу, и либо один
из них, либо оба становятся неактивными и перестают разносить данный слух.
Разница между тем, когда либо один, либо оба разносчика слухов становятся
12.2 Дискретные реакции
473
неактивными, лишь количественная. Когда разносчик и неактивный индивиду¬
ум встречаются, разносчик становится неактивным. Все остальные взаимодей¬
ствия двух индивидуумов ни к чему не приводят.
Плотности трех типов индивидуумов эволюционирую'!’ согласно системе
S =—aS2 - ST + SU,
Т= aS2 + ST, (12.16)
U = -US.
Когда а = 1, один разносчик слухов становится неактивным, когда встречают¬
ся два разносчика (модель Маки-Томсона), тогда как при а = 2 неактивными
становятся оба (модель Далея-Кендалла). Какова доля населении, осгавшаяся
в благагополучном неведении относительно данного слуха, после того как тот
начал распространяться от одного разносчика слухов и исчез, когда все раз¬
носчики слухов стали неактивными? В модели Маки-Томсона эта доля дастся
решением трансцедентного уравнения = 1; х = 0,203188 (задача 2.14).
Для модели Далея-Кендалла соответствующая доля несведущих индивидуумов
равна 0,283.
12.2 Дискретные реакции
В непрерывном описании динамики популяций и химической кинетики ос¬
новные переменные — это глобальные плотности каждого вида. Иол ее полное
описание конечной системы дается вероятностью того, что система содержит
пд реагентов типа А, пв реагентов типа В и т. д. Можно ожидать, что с ро¬
стом размера системы это распределение становится более острым, так что
средние плотности начинают полностью характеризовать эволюцию реаген¬
тов. Тем не менее, иногда эти естественные ожидания могуч' не оправдаться:
дискретность может играть существенную роль даже в термодинамическом
пределе. Сейчас мы обсудим влияние дискретности в двух общих ситуациях:
процессы рождения-гибели и бимолекулярные реакции, в которых элемен¬
тарные реакции включают две частицы.
Процессы рождения-гибели
В процессе рождения система содержит идентичные частицы, каждая из ко¬
торых может породить точно такого же потомка с постоянной интенсивно¬
стью, которую мы без потери общности полагаем равной 1. Как число ча¬
стиц растет со временем? В непрерывном пределе средний размер популяции
474
ДИНАМИКА ПОПУЛЯЦИЙ
N = (п) удовлетворяет уравнению N = N и, следовательно, растет со време¬
нем экспоненциально, N = Nq е1.
Учтем теперь, что число частиц в данной реализации реакции в момент
времени t не детерминировано, а зависит от времен индивидуальных событий
рождения. Поэтому стохастическое описание дается набором вероятностей
Pn(i), где п — это размер популяции. Распределение численности популяции
меняется в соответствии с уравнением
Рп = (n - l)Pn_i - пРп. (12.17)
Первый член справа отвечает за увеличение вероятности того, что существует
п частиц за счет изменения числа частиц с п — 1 до п. Поскольку любая
из п — 1 частиц может породить частицу, интенсивность процесса рождения
равна (n — l)Pn_i. Член ухода имеет похожую природу.
Предположим, что процесс начинается с одной частицы, Рп(0) = 5пд. Для
решения уравнения (12.17) с таким начальным условием мы снова применим
экспоненциальный анзац (см. стр. 173 и 264) вида Pn = Aan_1. Можно упро¬
стить задачу еще больше, заметив, что из J2n>i Рп = 1 следует А = 1 — а.
Таким образом, используя анзац Рп = (1 — a)an_1, мы переписываем беско¬
нечный набор уравнений (12.17) в виде одного уравнения а = 1 — а, откуда
получаем а = 1 — с~1 и
Рп(0 = е-‘ (1-е-у1"1
(12.18)
Заметим, что средний размер популяции
(«) = 53пРп = т~ ~е*
1-а
воспроизводит детерминистический прогноз. Однако такое согласие не рас¬
пространяется на высшие моменты распределения численности популяции.
В частности, сг2 = (n2) — (n)2 = e2t — е*, и поэтому а ~ (п). Таким образом,
флуктуации огромны, и они выживают всегда. Эти большие флуктуации воз¬
никают из-за того, что распределение численности популяции (12.18) не имеет
острого пика в (п), а вместо этого имеет пик п = 1. Более того, в пределе
большого времени распределение (12.18) в основном плоское, когда п С (п).
Теперь предположим, что в дополнение к тому, что каждый индивидуум
может с интенсивностью Л породить такого же потомка, он может еще уме¬
реть с интенсивностью /х. В непрерывном пределе эволюция среднего размера
популяции описывается уравнением dN/dt = (Л — Решение имеет вид
12.2 Дискретные реакции
475
N = No е(л“д^, так что популяция растет со временем экспоненциально, если
А / /2, и стационарна, когда А = /2. В стохастическом описании распределе¬
ние численности популяции этого процесса рождения-гибели удовлетворяет
основному кинетическому уравнению
Рп = Л(п - l)Pn-i - (А + р)пРп + ^(n + 1)Рп+1- (12.19)
Для п > 1 мы снова ищем решение в экспоненциальном виде Рп = Аа71”1.
Этот анзац немедленно дает2
*0 = №) (ж^л)2 ’ “<f> = ЁО? ад "
(12.20)
Эти формулы имеют много интересных следствий. Рассмотрим сначала
вероятность Pq того, что в системе нет частиц, т. е. популяция оказывается
вымершей. Это абсорбирующее состояние дискретной динамики. Если си¬
стема попала в такое абсорбирующее состояние, она остается там навсегда.
Существование абсорбирующих состояний — одна из главных причин того,
что судьба конечной системы обычно сильно отличается от предсказаний,
следующих из непрерывного описания. Из уравнений (12.20) получим
м £(£) -1
0 А£(0 —/х/А'
В пределе большого времени имеем
Po(t = оо)
Л’
1,
А > /2,
А < /2.
Поэтому, если интенсивность гибели превышает интенсивность рождения,
вымирание обязательно происходит. Наоборот, если интенсивность рождения
больше, чем интенсивность гибели, существует ненулевая вероятность, что
популяция никогда не вымрет, хотя даже в этой ситуации вероятность вы¬
мирания не равна нулю. Из (12.21) мы находим, что вероятность выживания
S(t) = 1 — PQ(t) убывает, асимптотически приближаясь к своему предельному
значению при А/^и5 = (1 + А^)""1 при А = /г. Расчет среднего размера
популяции и его дисперсии дает (см. задачу 12.10)
(п) = £(*), а2 = {п2} - (п)2 = £(i)[£(t) - 1]. (12.22)
А — /2
2Снова в предположении, что вначале система содержит одну частицу, Рп(0) = 5пд.
476
ДИНАМИКА ПОПУЛЯЦИЙ
Средний размер популяции опять точно ухвачен детерминистическим непре¬
рывным подходом. Однако детерминистический подход остается «морально»
неправильным: в интересном случае, когда интенсивность рождения превы¬
шает интенсивность гибели, снова существуют огромные флуктуации от од¬
ной реализации процесса к другой.
Заметим также, что пограничный «стационарный» случай совсем не явля¬
ется стационарным: в самом деле, средний размер (п) остается постоянным;
однако вымирание происходит с вероятностью единица, а дисперсия растет
как сг2 = 2At. Этот рост дисперсии возникает из-за того, что в конце концов
должно произойти вымирание при том, что (п) остается постоянным. Сле¬
довательно, в реализациях процесса, которые выживают в течение долгого
времени, численность популяции имеет тенденцию увеличиваться.
Если оглянуться назад, легко понять неприменимость непрерывного под¬
хода. Если мы начинаем с одной частицы, случайная природа индивидуаль¬
ных событий рождения и гибели очевидно имеет значение. Поэтому флукту¬
ации, возникающие в самом начале, играют огромную роль. Эти флуктуации
закрепляются при росте популяции, и рост становится все более и более детер¬
минированным. Чтобы проверить эту идею, рассмотрим процесс рождения и
предположим, что процесс начинается с no > 1 частиц, т. е. -Pyv(O) = 5П}По.
Для no > 1 экспоненциальный анзац неприменим, но задачу можно решить
с помощью более систематических методов (см. задачу 12.6). В этом случае
распределение вероятности снова имеет компактный вид (задача 12.8)
P„(f) = (^“^ е-п°* (1 - e-t)n_n° . (12.23)
Используя это распределение, можно найти средний размер популяции и дис¬
персию:
(n) = no е1, а2 = по (e2t — е() . (12.24)
Относительные флуктуации сг/(п) = [(1 — е-*)/^]1/2 остаются конечными в
течение всей эволюции. Поскольку их величина ведет себя как (по)-1/2, мы
заключаем, что относительные флуктуации действительно малы при no S> 1.
Бимолекулярная реакция: аннигиляция
Два предыдущих примера описывали системы невзаимодействующих частиц.
Взаимодействия обычно делают многочастичную задачу нерешаемой. Среди
немногих исключений — одновидовая аннигиляция и коалесценция, и сей¬
час мы обсудим первую из них. Плотность в одновидовой аннигиляции эво¬
люционирует согласно кинетическому уравнению реакции = — р2, откуда
12.2 Дискретные реакции
477
р — (1 + t} Ч Полное описание снова дается набором вероятностей Pn(t).
Эволюционные уравнения имеют вид
Рп = | [(п + 1)(га + 2)Рп+2 - га(п - 1)Р„]
= | (Е2 - 1) п{п - 1)РП. (12.25)
Для простоты обозначений мы используем повышающий оператор Е , опре¬
деленный как E/(n) = /(n + 1), где / — произвольная функция п. Соответ¬
ственно, обратный или понижающий оператор определяется как Е"1/(п) =
f(n — 1). Первое слагаемое в правой части уравнения (12.25) отвечает за уве¬
личение Pn(t) из-за событий аннигиляции, в котором изменение числа частиц
есть п + 2 —> п. Интенсивность таких событий равна числу различных пар
частиц в системе из п + 2 частиц, а именно |(n + 1)(?г + 2). Второе слагаемое
описывает исчезновение частиц из-за аннигиляции при переходе п —> п — 2.
Чтобы воспроизвести кинетическое уравнение реакции = —/У2, нужно раз¬
делить правую часть на квадрат объема системы (см. задачу 12.12 и следу¬
ющий раздел). Здесь мы опускаем этот коэффициент для прос/готы.
Прежде чем анализировать уравнения (12.25), сделаем паузу и подумаем,
как это возможно, что линейные уравнения (12.25) описывают взаимодей¬
ствующую систему. В непрерывном приближении взаимодействую! цан систе¬
ма обычно описывается несколькими связанными нелинейными дифферен¬
циальными уравнениями. Хотя точное описание взаимодействующей систе¬
мы может включать в себя линейные уравнения, сложность в том, что этих
уравнений бесконечно много. (Пример того как, превратить нелинейное урав¬
нение в бесконечный набор линейных, дан в задаче 12.11.)
Возвращаясь назад к уравнениям (12.25), заметим, что они похожи на
уравнения (12.19). Например, уравнения в обоих наборах линейны, что поз¬
воляет надеяться на решаемость уравнений (12.19). К сожалению, у нас не
получится воспользоваться простотой и эффективностью экспоненциально¬
го анзаца (стр. 264), так как этот подход работает, 'голько когда коэффи¬
циенты — линейные функции п, тогда как коэффициенты в (12.19) квад¬
ратичны по п3. Поэтому нам придется использовать тяжелую артиллерию,
а именно метод производящих функций. Введем производящую функцию
?(М) = 53п>о Рп(£)гп и перепишем (12.19) в виде уравнения в частных про-
3Можно попытаться обобщить экспоненциальный анзац следующим образом: Рп =
A(t) exp(a(£)n + 6(£)n2), но поскольку аннигиляция ведет к уменьшению числа частиц, нам
нужно решение в диапазоне 0 < п < No. Из-за дополнительного «граничного» условия в
Nq кажется невозможным, чтобы решение имело такой простой вид.
478
ДИНАМИКА ПОПУЛЯЦИЙ
изводных
dt 2( } dz2'
(12.26)
Двухчастичная природа реакции приводит нас к уравнению в частных про¬
изводных второго, а не первого порядка. Это свойство делает решения для
бимолекулярных реакций более сложными, чем для одночастичных. Реше¬
ние уравнения (12.26) можно найти стандартными методами, но подробности
громоздки и не добавляют ясности. Поэтому мы лишь кратко остановимся на
важнейших чертах метода и решения. Мы начинаем искать решение с разде¬
ления переменных V(z, t) = Z(z)T(t). Подставляя это выражение в уравнение
(12.26), находим, что Т ~ e~xt, a Z удовлетворяет дифференциальному урав¬
нению Лежандра
2А
Z" + ~ Z = 0. (12.27)
1 — z£
Если начальное число частиц по четное, то число частиц п всегда остается
четным. Для дальнейшего удобства запишем TVo — 2fco и п = 2к. Более того,
решение уравнения (12.27) — четная функция z. Нормированные собственные
функции уравнения (12.27) имеют вид
<Ы*) = - ^-2(^)1 ,
где Р2к — стандартный полином Лежандра порядка 2к и соответствующие
собственные значения равны А = 2k(k — 1). Требуя выполнения граничного
условия CP(z,t = 0) = z2k° и пользуясь соотношением ортогональности для
полиномов Лежандра, получим производящую функцию
Ж t) = 1 + £ AkQ2k(z) (12.28)
к=1
где
Ак =
4fc — 1 Г(&о + l)r(fco + 5)
к(2к - 1) r(fc0 + fc + i)r(fc0-fc + l)’
Из производящей функции можно извлечь моменты числа частиц
= (гй)’’’(г)|-‘-
Для вычисления производных мы воспользуемся формулой Стирлинга, с по¬
мощью которой запишем Ак при больших к в виде
Ак
~ 1 —fc(2fc—X)/2fc0
fc(2fe — 1)
12.2 Дискретные реакции
479
Кроме того, выражения для производных полиномов Лежандра в точке z = 1
даются выражениями4
= 1) =
+1)
2
p,,f~ i 'i ~ i)k(k + i)(k + 2)
Pn\Z = 1) = Q
и т. д.
Собирая все вместе и работая в промежуточном скейлинговом пределе 1 <С
к <С ко, получаем
(п) ~ 524Jfce-2fe2/JV (n2) ~^8k3e~2f^N, (12.29)
к=1 к=1
где N = 7V(O)/(l + p(O)t) — это зависимое от времени число частиц из средне¬
полевого решения. Асимптотическое поведение этих сумм можно получить,
устремляя верхний предел к бесконечности и заменяя сумму интегралом. Это
приближение дает
N (п2) ~ 27V2,
так что среднее число частиц совпадает со среднеполевым прогнозом.
Время завершения при коалесценции
До сих пор мы занимались временнбй эволюцией числа реагентов. Компле¬
ментарный вопрос — время, нужное, чтобы число реагентов достигло опреде¬
ленного предела. Например, за какое время популяция вырастот до заданно¬
го размера (задача 12.7)? Наоборот, как долго популяция будет выживать до
того, как вымрет? В аннигиляции и коалесценции вымирание означает, что
в конце концов система либо становится пустой (аннигиляция), либо в ней
остается одна частица (коалесценция). Как время Т достижения финально¬
го состояния — время завершения — зависит от исходного числа реагентов?
Каково распределение времени завершения?
Наивную оценку времени завершения можно получить из непрерывного
описания, которое дает плотность p(t) = 1/(1 + t). Реакция считается закон¬
ченной, когда остается одна частица, чгго соответствует р(Г) = 1/N. Этот
4Эти выражения выведены с помощью представления полиномов Лежандра через про¬
изводящую функцию
(1 - 2hz + z2)~1/2 = 52
к>и
Для этого нужно продифференцировать обе части этого равенства требуемое число раз,
положить z = 1 и разложить получившуюся в левой части формулу в степенной ряд.
480
ДИНАМИКА ПОПУЛЯЦИЙ
критерий немедленно дает Т ^ N. Это только оценка. Непрерывный подход
справедлив, когда число частиц велико, и неприменим на поздних стадиях,
когда остается лишь несколько частиц.
Теперь попробуем найти время завершения, пользуясь точным подходом.
Идея состоит в том, чтобы построить основное кинетическое уравнение для
этого времени как функции текущего состояния системы. Эта же идея была
использована в разделе 2.6 для расчета времени выхода случайных блуж¬
даний. Применим этот метод для нахождения среднего времени завершения
для коалесценции.
Число реагентов в любой момент — это стохастическая переменная, кото¬
рая меняется с п на п — 1 с интенсивностью гп = п(п — 1)/АГ5. Тогда каждое
индивидуальное время перехода распределено по экспоненциальному закону
n(tn) = rn exp(-rntn),
где среднее время перехода и его дисперсия равны (tn) = r~r и —
(in)2 = г“2. Поскольку среднее время возникновения события п-^ п—1 равно
in = г”1, время проходящее до того, как останутся к частиц, есть
fc+i
Тк = 2 tn = N
n=N
= N
N(N - 1) + (TV - 1)(TV - 2) + "
(tV-1 ~n) + (a-2 “
fc(fc + l)
i)+- +
(~ - —'ll
k + lj
1
к
= N
N
(12.30)
Поэтому среднее время завершения, которое проходит до того, как остается
одна частица, — это (Т) = Ту = N — 1. Похожий результат возникает для
аннигиляции (задача 12.14). Заметим, что непрерывный подход дает каче¬
ственно правильный результат.
Можно обобщить этот прямой подход для расчета второго момента вре¬
мени завершения. При TV —> оо результат имеет вид (задача 12.15):
(Т2) _ тг2
(Г)2 “ 3
(12.31)
который указывает на то, что распределение времени завершения нетриви¬
ально.
5Как было отмечено ранее, коэффициент нужен, чтобы воспроизвести среднеполевое
кинетическое уравнение для плотности = _р2 (см. также задачу 12.12).
12.2 Дискретные реакции
481
Чтобы вычислить моменты времени завершения систематическим путем,
нам нужно распределение Pn(t) вероятности того, что система содержит п
частиц в момент времени t. Аналогично уравнению (12.25), уравнение для
этой вероятности есть
= ^n+1-Pn+l “ ГпРц (12.32)
с начальным условием Pn(0) = 5n,w- Мы также накладываем граничные усло¬
вия Pn+i = 0, так что это уравнение справедливо для всех I < п < N. Чтобы
решить (12.32), применим преобразование Лапласа, которое даст
(s + Ty^Pn^s) —"И ^n+l-^n+l (*^)’ (12.33)
При п = N получим Pn(s) = (r^ + s)”1. после чего остальные уравнения
(12.33) могут быть решены рекурсивно. Самая важная величина для времени
завершения — это Pi(s), Лаплас-образ вероятности того, что система состоит
из одной частицы. Он равен
N
п
п=2
Гп
S + rn
=п
п=2
sN
л -I
п(п — 1)
(12.34)
Эти результаты справедливы для любого N, но нам нужно поведение при
больших N. В этом пределе произведение в (12.34) становится бесконечным.
Чтобы понять, как работать с произведением sN, заметим, что время завер¬
шения растет как Т ~ N, и поэтому лапласовская переменная .ч должна быть
порядка 2V-1. Следовательно, чтобы взять предел N —> оо, нужно рассмат¬
ривать переменную S = sN, остающуюся конечной. Таким обраюм (12.34)
принимает вид
Л(5) = П
п>2
п(п — 1)
(12.35)
N
1 +
1 +
т -1
Теперь используем результаты из врезки (ниже), чтобы выразить P\(S) в
компактном виде
Pi(S) =
irS
cos — 45)
(12.36)
Моменты времени завершения (Г”) можно найти, раскладывая Лаплас-
образ (12.36) в степенной ряд вида Pi(cr) = ^,n>o(-’4N)n(Tfl)/п\. Главная
482
ДИНАМИКА ПОПУЛЯЦИЙ
12.1. Еще об играх с гамма-функциями
Основываясь на врезке «Игры с гамма-функциями» на странице 192, мы вычис¬
лим
Pl(S) = 5 I1 + ^4^1)] = Д (п-п+)(п-п-)’ (12-37)
где п± = |(l ± Vl — 45). Как это часто бывает, проще оказывается проанализи¬
ровать более общий случай. Рассмотрим конечное произведение
_ ут1 (п4-а)(п + а*)
ДА (п+ь)(п+и
(12.38)
Нас интересует П = limyv-*oo П/v с параметрами а, а*, 6, 6*, которые удовлетворяют
равенству а + а* = b + b*. Начиная с равенства (5.70)
(2 + а)(3 + а)... (N - 1 + а) = ’
перепишем (12.38) в виде
= Г(АГ 4- а) Г(АГ + а*) Г(2 + 6) Г(2 + 5*)
N Г(АГ 4-6) Г(АГ 4-6*) Г(2 + а) Г(2 + а*)
(12.39)
Теперь, используя асимптотическое соотношение (5.72),
Г(АГ + а)
V(N -I- b)
~N*
при АГ —> оо,
находим, что зависимая от АГ часть выражения в (12.39) сводится к Na+a* b ь
что равно 1, если а + о* = 64-6*. Таким образом, имеем
П = Нт Плг
N - >оо
Г(2 + 6) Г(2 + 6*)
Г(2 4- сь) Г(2 4~ а*)
(12.40)
Для Pi (5) в (12.37) а = 0, а* = -1, 6 = -j(l-/l -45), и 6* = - j (l-Ь дД - 45),
так что а 4- а* = 6 4- 6*. Специализируя (12.40) на этих значениях параметров
а,а*,6,6*, находим
Pl(5) = Г(3 4S) Г(3 + ^ 45) . (12.41)
Наконец, используя равенства
Г(1 + *) = *ГМ, r(|-I)r(i + I) = 53i_,
приводим уравнение (12.41) к виду, данному в (12.36).
асимптотика этих моментов имеет вид (Тп) ~ CnNn со следующими зна¬
чениями трех первых коэффициентов: Ci = 1, С% = — 2 и Сз = 12 — 7г2.
12.3 Разложение по малым флуктуациям
483
Так как Лаплас-образ (12.36) демонстрирует скейлинг в пределе большого N,
т. е. Pi(s) —> Pi (S'), где S = sN, распределение времени завершения является
функцией перемасштабированной переменной T/N
Pi(T) = N-1 Ф (T/N).
Чтобы найти поведение Pi(T) на больших временах, заметим, что Лаплас-
образ Pi(<S) имеет бесконечно много полюсов на отрицательной части дей¬
ствительной оси в точках Sk = — fc(fc + l), где fc — положиичшьиое целое. Бли¬
жайший к началу координат полюс S = —2, где Pi(S) = 6(5 -|- 2) 1 -I- Это
соответствует поведению вида Pi(T) — 6е-2Г на больших временах. Анало¬
гично, поведение Р(5) при больших S определяет асимптотику 1\(Т) на ма¬
лых временах. Из (12.36) получим асимптотику Р(5) 27г5г "’г^, которую
можно обратить методом Лапласа. Отсюда получаем предельное поведение
распределения времени завершения
Ф(ж) ~
■ 1^7/2^/^
(12.42)
бе"
X —г ОО.
Мы видим, что распределение времени завершения очень быстро стремится к
нулю при удалении от пика, так что время завершения, сильно отличающееся
от своего среднего значения, очень маловероятно.
12.3 Разложение по малым флуктуациям
Динамика популяций и химических реакций обычно сложнее, чем динамика
идеализированных примеров, приведенных выше. Поэтому обычно не пред¬
ставляется возможным провести их точный анализ. Если, однако, флуктуа¬
ции плотностей реагентов около их средних значений достаточно малы, есте¬
ственный способ получения информации — разложение основного кинети¬
ческого уравнения по малым флуктуациям Ван-Камиспа. В этом подходе
ведущий член воспроизводит кинетическое уравнение для средних плотно¬
стей, а первая поправка отвечает за флуктуации около этих средних. До¬
стоинства этого разложения — его общность и систематический характер.
Недостаток — то, что оно применимо, только когда флуктуации малы. Как
показало обсуждение в предыдущих разделах, область применимости малых
флуктуаций уже, чем можно было бы ожидать.
484
ДИНАМИКА ПОПУЛЯЦИЙ
Чтобы проиллюстрировать разложение по малым флуктуациям, рассмот¬
рим одновидовые реакции общего вида, в которых фундаментальная пере¬
менная — это число частиц п. Предположив, что флуктуации малы, запишем
число частиц в виде
п = Vp(t) + У1/2£, (12.43)
где V — это объем системы, p(i) — плотность, а £ — случайная переменная.
Таким образом, мы разделяем число частиц на экстенсивную детерминисти¬
ческую компоненту Vp(t) и стохастическую компоненту V£. При этом мы
явно учли предположение о том, что величина стохастической части имеет
порядок квадратного корня из экстенсивной компоненты. Запишем также
Pn(t) = n(6t), . (12.44)
чтобы разделить гладкую явную зависимость от времени и зависимость от
случайной переменной Нас интересуют реакции, в которых число частиц
меняется на маленькую величину при каждом микроскопическом взаимодей¬
ствии. Такие изменения кратко записываются с помощью повышающего и
понижающего операторов Е и Е-1 соответственно (см. уравнение (12.25) и
последующее обсуждение). Поскольку оператор Е меняет число частиц на 1,
переменная £ меняется на V-1/2. В результате имеем
, 1 д , 1 а2
~ + yi/2 д£ + 2Vdt2+""
Наконец, чтобы привести производную по времени Рп в основном кинети¬
ческом уравнении (£,t), заметим, что при взятии производной число п со¬
храняется постоянным, dn = Vdp + У1/2^ = 0 или d£ = —У1/2 dp. Тогда
производная по времени от Рп принимает вид
dPn = dR(£,t) = Ж _ 1/2 . ЭЛ
dt dt dt Р
После проделанной подготовки для написания разложения основного ки¬
нетического уравнения остается собрать все вместе. Как мы увидим из следу¬
ющих примеров, это разложение естественным образом разделяется на экс¬
тенсивные члены, описывающие эволюцию средней плотности, и субэкстен¬
сивные члены, которые описывают флуктуации около средней плотности.
Пример 12.5. Распад А -> 0. Уравнение Рп для реакции распада имеет вид
Рп = -пРп + (п + 1)Р„+1 = (Е - 1)тгРп.
(12.47)
12.3 Разложение по малым флуктуациям
485
Подставив выражения из уравнений (12.43)-(12.46) в это основное кинетическое
уравнение, получим
ЦП
dt
_ у1/2
1 а2
) (vP + V,/2<;) П.
(12.48)
. ап
д
+
yi/2^ 2V d£2
Собирая слагаемые разных порядков, находим
т/1/2 • 5П 9П
порядка V1'2 : р — = _р —,
(12.49а)
(12.49Ь)
порядка V0 :
ап _ а(еп) р а2п
dt ~ d£ + 2 d? '
Первое уравнение воспроизводит кинетическое уравнение р = -р с решением
р = е“*. Второе — это уравнение Фоккера-Планка с зависимыми сп* времени
коэффициентами. Общее решение последнего — это обычно функции Гаусса. В
нашем случае, однако, все, что нам нужно, это моменты стохастически флуктуи¬
рующей переменной Mk = (£к) = f £кП d£. Их можно найти, умножив уравнение
(12.49Ь) на £к и проинтегрировав по всем Правую часть можно проинтегри¬
ровать по частям. Например, два слагаемых в уравнении дли первого момента
имеют вид
Аналогично из уравнения для второго момента находим
/= -/2С(^п)^ = -2м2, I= =
где во второй строчке интегрирование по частям выполнено дважды. Во всех
этих интегрированиях по частям граничные члены равны нулю, так как И убы¬
вает быстрее, чем любая степень при £ ±оо. Таким образом, первые два
момента эволюционируют со временем согласно уравнениям
Mi = -Mi, М2 = -2М2 •+• Р-
Поскольку система стартует с детерминированного начального состояния, на¬
чальные условия суть Mfc(O) = 0. Тогда Mi(t) = 0, и мы также находим, что
M2(t) = е“* — e"2t, что согласуется с точным решением (зпдача 12.9). Используя
эти результаты вместе с (12.43), получим (n) = Vp (поскольку (£) = 0) и
(n2) = V2p2 + V(£2) = V2p2 + V (е-< - с. 2'),
откуда находим а2 = (n2) — (n)2 = V (e_t — e-2t). Поэтому относительная флук¬
туация числа частиц равна
сг _ /е‘ - 1
W~V V ’
486
ДИНАМИКА ПОПУЛЯЦИЙ
Она растет со временем и становится порядка единицы, когда остается одна
частица.
Пример 12.6. Аннигиляция. Начнем с уравнения Рп = (Е2 — 1) п{п—1)РП/(2У),
которое совпадает с (12.25) с точностью до множителя У”1, который мы вклю¬
чили, чтобы правильно воспроизвести кинетическое уравнение для плотности.
Разлагая плотность, находим
_ Vl/2P— - — +
(у2р2+2y3/Mп+• • • • (12-5°)
Собирая члены соответственно их порядку, находим
порядка У1/2 :
порядка У° :
.ап 2 ап
р ае ~ р вс
дп п д(£П) 2а2п
(12.51а)
(12.51Ь)
Снова из первого уравнения воспроизводим уравнение р = — р2, из которого
следует, что р = 1/(1 + £). Производя те же вычислительные шаги, что и в
предыдущем примере, находим уравнение эволюции для первых двух моментов
Mi = -2pMi, М2 = -4рМ2 + 2р2,
откуда Mi = 0 и М2 = j [(1 + £) 1 — (1 +t) 4], так что относительная флукту¬
ация равна
<т _ / М2 _ /2 1 + t — (1 4-1)~2
(n) уур2 V3 У ’
Снова относительная флуктуация растет со временем и становится порядка еди¬
ницы, когда остается единственная частица.
Пример 12.7. Комбинорованные процессы рождения-аннигиляции А —> А + А
и А + А —> 0. Уравнение для Рп теперь имеет вид
Рп = (Е2 - 1) п(п - l)Pn + (Е-1 - 1) пРп.
(12.52)
Производя разложение плотности и собирая члены разных порядков, находим
(12.53а)
т.1/2 . ЗП . 2. ап
порядка V1/2 : р = (р - р2) ,
порядка V0 :
ап а(£п) р а2п
_ = (2р-1)—+ -(1+2р)-^..
(12.53Ь)
12.4 Большие флуктуации
487
Как обычно, первое уравнение воспроизводит уравнение р = р(1 — р), тогда как
второе уравнение описывает моменты. Из второго уравнения получаем
JW2 = 2(1 — 2p)A^2 + р(1 И- 2р).
(12.54)
Если система начинает со стационарного состояния р = 1, чо М<2 = -(1 - е 2t).
Сухой остаток, который можно извлечь из использования разложения по
малым флуктуациям, — оно предоставляет собой систематический метод для
работы с малыми отклонениями от среднего поведения в стохастически вза¬
имодействующих системах частиц. Пока нас интересует поведение в преде¬
лах нескольких стандартных отклонений от среднего, статистики флуктуаций
гауссова
(12.55)
Поэтому среднее и дисперсия полностью задают все остальные моменты. В
рамках разложений по малым флуктуациям эволюция систем сводится к де¬
терминистическим уравнениям для первого и второго моментов.
12.4 Большие флуктуации
Разложение по малым флуктуациям, обсуждавшееся выше, предоставляет
систематический подход для понимания сложных реакций. Однако в ситуа¬
ции, когда в системе есть абсорбирующее состояние, в этом разложении при¬
сутствует серьезный подводный камень. В этом случае разложение кинети¬
ческого уравнения по малым флуктуациям в окрестности аттрактора может
работать для некоторого конечного времени, но в конце концов оно становит¬
ся неприменимо, и система приходит в абсорбирующее состояние. Процесс
рождения, обсуждавшийся выше, дает один из примеров такой двойственно¬
сти. В общем случае разложение по малым флуктуациям неприменимо для
зависящих от состояния процессов рождения-гибели, где интенсивность рож¬
дения превосходит интенсивность гибели в маленьких популяциях, а в боль¬
ших интенсивность гибели больше, чем интенсивность рождения (рис. 12.6).
Две специфических ситуации, в которых разложение по малым флук¬
туациям оказывается неприменимо, — это рождениогибель-коалесценция и
модель эпидемий SIS. В первой элементарные реакции имеют вид
х
л + л,
Л + А
488
ДИНАМИКА ПОПУЛЯЦИЙ
Рис. 12.6. Характерная зависимость интенсивностей рождения и гибели, Лп и дп,
от численности популяции такая, что в непрерывной системе есть стационарная
плотность N, тогда как стохастическая система в конце концов приходит к п = О
тогда как в модели SIS реакции между восприимчивыми S и зараженными
I индивидуумами есть
S + I-^I + I, I-^S.
Для рождения-гибели-коалесценции кинетическое уравнение для плотности
имеет вид = (А — р)р — р2, который приводит к неподвижной точке для
плотности р* = А — /z при А > //. Аналогично, для модели SIS кинетическое
уравнение (данное в (12.10)) — это = (к — г)/ — kl2. Когда характер¬
ная интенсивность заражения к превышает интенсивность выздоровления г,
неподвижная точка этого уравнения — /* = (& — г)/к.
В обоих процессах рождаемость выше смертности, когда плотность мень¬
ше, чем ее значение в неподвижной точке, и смертность выше рождаемости
в противном случае (рис. 12.6). Таким образом, асимптотическое состояние
соответствующей дискретной стохастической динамики — это не малые флук¬
туации в окрестности непрерывной неподвижной точки, а вымирание! Если
неудачная флуктуация приведет к вымиранию, популяция не может восста¬
новиться — отрезвляющее сообщение для экологически мотивированных ре¬
акций. Однако время до вымирания может быть экспоненциально большим
по числу частиц. Поэтому можно легко обмануться при численном моделиро¬
вании, если проводить его не на таких экспоненциально больших временных
масштабах.
12.4 Большие флуктуации
489
В качестве разминки перед изучением времени вымирания в классе моде¬
лей, изображенных на рисунке 12.6, рассмотрим сначала идеализированный
пример броуновской частицы с коэффициентом диффузии D на конечном
интервале [О, L] с отражающей границей х = L и адсорбирующей границей
х = 0. Предположим, что у частицы есть постоянная скорость сноса вправо v.
Бблыпую часть времени частица остается около х — L, на дне эффектив¬
ной потенциальной ямы образовавшейся из-за сноса. Однако в конце концов
возникнет достаточно большая флуктуация, которая позволит частице до¬
стигнуть х = 0, где она останется захваченной навсегда. Среднее время Т,
которое должно пройти до захвата, ведет себя как (задача 2.20):
{exp(uL/P), v > 0,
L2/D, v = 0,
L/v, v < 0.
Огромное время захвата при v > 0 представляет собой аналог большого вре¬
мени вымирания в стохастических реакциях, упомянутых выше.
Теперь изучим динамику вымирания в общем случае реакций рождения-
гибели, в которых популяция изменяется следующими шагами:
п—>п+1 с интенсивностью А,,.,
п —> п — 1 с интенсивностью //„.
Как и на рисунке 12.6, интенсивности рождения и гибели, А„ и /t„, удовле¬
творяют неравенствам Хп > Рп для п < N и Ап < рп для п > N. Чтобы
охарактеризовать вымирание в системе, сначала сосредоточимся па вероят¬
ности Еп вымирания, когда в системе изначально было п частиц, и времени
Тп, проходящего до вымирания при том же начальном состоянии. Вероят¬
ность вымирания удовлетворяет обратному уравнению (ем. уравнение (2.58))
Еп = Рп.Еп+1 + Яп-Еп—1, (12.56)
гдерп = Ап/(Ап + рп) и qn = Рп/(Ап+Рп) —вероятности переходов п -> п±1,
соответственно. Граничные условия для системы уравнений (12.56) есть Eq =
1.
Чтобы решить уравнения (12.56), сначала перепишем их в видерп(-Еп+1 —
Еп) = Яп(Еп - En-i). Определяя Fn = En+i - Еп и рп = Яп/Рп = Рп/Хп,
получаем Fn = рп Fn-i с решением
п
Rn = JJ Pj •
j=i
(12.57)
Fn = F0Rn,
490
ДИНАМИКА ПОПУЛЯЦИЙ
Теперь, чтобы найти вероятность вымирания для любых начальных условий,
сложим Fn:
п
Еп+1 = Ег + (Ei - 1) Ri- (12-58)
г=1
Если сумма Az расходится, то мы обязательно должны иметь Е\ = 1, так
что ни одна из вероятностей вымирания Еп не может превосходить 1 или быть
отрицательной. Соответственно, мы получили бы Еп = 1 для всех п > 1.
Заметим, что Ri — возрастающая функция г для всех i > N, поскольку в
этом диапазоне pi > А^, и таким образом pi = pi/Xi > 1. Поэтому бесконечная
сумма Ri расходится. Следовательно, мы делаем вывод, что вероятность
вымирания равна 1 с любым (конечным) исходным числом частиц.
Теперь исследуем время вымирания. Пусть Тп обозначает время вымира¬
ния в системе, в которой вначале было п частиц. Эта величина удовлетворяет
обратному уравнению (см. уравнения (2.70)-(2.71))
Тп =
An rp I rp I 1
Т— J-n+1 + у— J-n-1 + -у—
Лп ~г рп Лп -г Рп Лп “г Рп
(12.59)
с начальным условием То = 0. Действуя таким же образом, как с вероятно¬
стью вымирания, определим Un = Tn — Tn+i, чтобы переписать (12.59) в виде
рекурсии Un = (An)_1 + PnUn-i- Му уже знаем решение однородной части
этого уравнения, см. (12.57), так что мы используем его как коэффициент
интегрирования, т. е. мы ищем решение для Un в виде Un = VnRn- Эта под¬
становка приводит к рекурсии Vn = Vn-i + (An-Rn)”1- Мы находим Vn, откуда
следует С/п, и затем определяем Тп (задача 12.18). Результат для общего п
имеет вид
п оо
J=1 i=j
1
XiRi
(12.60)
при условии, ЧТО Rq = 1.
Рассмотрим время вымирания , когда начальная точка находится в од¬
ном шаге от вымирания, исходя из того, что эта ситуация проста и естествен¬
на для многих приложений. Математически Ti содержит важную составля¬
ющую выражения Тп для общего п, но выглядит немного проще:
г^Егй? (12-м>
ё?лл
В качестве разминочного упражнения рассмотрим интенсивности
-2
п
tin=N-
Ап —
(12.62)
12.4 Большие флуктуации
491
В этом случае рп = n/N и Rn = n\/Nn, так что
П>1
Nn
П'п\'
(12.63)
Сумма в уравнении (12.63) похожа на разложение экспоненты
' г? !
Л
(12.64)
п>0
Когда N » 1, распределение Nn/n\ имеет острый ник в п = N. То же самое
справедливо для распределения Nn/(n • п!). Поэтому члены, вносящие ос¬
новной вклад в сумму (12.63), в N раз меньше, чем соответствующие члены
в сумме (12.64). Соответственно, когда интенсивности даны в (12.62), веду¬
щее асимптотическое поведение времени вымирания есть Т\ ~ N"leN. Что¬
бы вычислить субдоминантные члены, используем следующею интегральное
представление суммы в (12.63),
N ех-1
т1='Е—, = [ 4^dx’
и воспользуемся его асимптотическим разложением вблизи верхнего предела
Ti
е^_ ( 1! _2!_ _3!_
N V1 + N + N2 + 7V3 +
(12.65)
Возвращаясь к общей ситуации, заметим, что N обычно очень велико,
так что интенсивности Хп и цп могут рассматриваться как гладкие (функции
непрерывной переменной х = n/N. Более точно, мы рассматриваем семейство
интенсивностей, которые в пределе большого N демонстрируют следующий
скейлинг:
An = TV/(a:), = Ng(x), x = ~fi' (12.66)
Интенсивности из (12.62) принадлежат к этому семейству, а именно /(т) = х
и д(х) = х2. Другой пример дается интенсивностями
п2
Ап = (1 + б)п-е — и = (12.67)
которые соответствуют процессу рождение-гибель-коал сс цел щи я, обсуждав¬
шемуся в начале этого раздела. В этом случае /(т) = х + сш(1 — х) и д(х) = х.
492
ДИНАМИКА ПОПУЛЯЦИЙ
Мы увидим, что функция (Л»Лг)-1 имеет острый пик в i = N, что со¬
ответствует х = 1. Пользуясь определением (12.57) для мультипликативных
переменных, беря логарифм и заменяя суммирование интегрированием, по¬
лучаем
1пДг= 52 In Pj = 52 ln(Mj/Aj)
l<j<i l<j<i
~ —N f In 44 dy (x = i/N, у = j/N).
Jo 9{У)
Используя этот результат и заменяя суммирование в (12.61) интегрировани¬
ем, находим
/-00 eNH(x)
т'~1 (12'68)
где мы использовали сокращенное обозначение
Н(-ХЧУ^- (12'69)
Наше предположение об интенсивностях рождения и гибели подразумева¬
ет, что /(ж) > 5(х), когда х < 1, и f(x) < д(х), когда х > 1, что означает, что
Н(х) монотонно возрастает в интервале 0 < х < 1, а потом убывает, когда
х > 1. Пик под интегралом (12.68) очень острый (из-за члена N » 1), и он
вносит основной вклад в интеграл. Удерживая только ведущее экспоненци¬
альное поведение, мы находим
1\ ~ eNH*, Я* ее Я(1) = In Д4 dy- (12-7°)
Jq 9\У)
Для интенсивностей (12.62) мы воспроизвели Т\ ~ eN. Для интенсивностей
(12.67) мы получили Я* = (1 + б”1) 1п(1 + б) — 1.
Подводя итог, мы видим, что когда у детерминистической динамики в ко¬
нечной системе есть притягивающая неподвижная точка, это состояние яв¬
ляется метастаби л ьным, а не настоящим равновесным, если система также
имеет другое абсорбирующее для стохастической динамики состояние. Вре¬
мя достижения абсорбирующего состояния обычно растет как eNH*, где N —
размер популяции в метастабильном состоянии, а амплитуда Я* может быть
вычислена во многих ситуациях. Конечно во многих ситуациях детермини¬
стическое поведение может быть гораздо более сложным — например, си¬
стема может иметь притягивающий предельный цикл или демонстрировать
детерминистический хаос. Нет необходимости объяснять, что в таких ситуа¬
циях время вымирания вычисляется в очень редких случаях.
12.5 Ссылки
493
12.5 Ссылки
Полезная ссылка, которая дает общее введение в математические методы
анализа нелинейных уравнений динамики популяций содержится в моногра¬
фиях Бендера и Орсзага [158] и Сторгача [226]. Многие модели популяци¬
онной биологии и распространения эпидемий, рассмотренные в разделе 12.1,
представлены в [235]. Модель «Борьба за существоваиеи» была впервые опуб¬
ликована в 1934 году Г.Ф. Гаузе [236]. Подробное обсуждение модели трех¬
видовой конкуренции (пример 12.3 в этой главе) дано Мэем и Леонардом
[237]. Прекрасное изложение моделей распространения слухов дано в [238], а
дополнительную информацию об этих моделях можно найти в [239].
Процессы коалесценции, описанные в разделе 12.2, довольно популярны в
популяционной биологии. Фактически коалесценция представляет собой мо¬
дель Райта-Фишера [240, 241] без отбора. Если пустить процесс коалесценции
назад во времени, время коалесценции, которое вычислялось в разделе 12.4 —
это то же самое, что возраст последнего общего предка. Читатель может об¬
ратиться к книгам [242, 243] за дополнительной информацией об этой связи
между моделями. Статьи [244, 245] иллюстрируют применение физических
методов к модели Райта-Фишера.
На появление больших флуктуаций в при одновидовом рождении было
давно указано Дельбрюком [246]. Полезное обсуждение комбинированной ре¬
акции рождения-гибели дано Кендаллом [247], кроме toix), в этой статье со¬
держится подробный список предшествующей литературы по этой *геме. Точ¬
ный вывод вероятности распределения для двухчастичной аннигиляции дан
Маккуори [248, 249]. Наш подход следует методу, развитому в [250|. Разложе¬
ние по малым флуктуациям подробно обсуждается в книге Бан-Кампена [13].
Использование стохастических методов для явлений вымирания — классиче¬
ская область, которая остаются актуальной по сей день. Две полезные книги
по этому предмету — [251, 252]. Подход, использованный для определения
вероятности вымирания для общих процессов рождения-гибели, представлен
в книге Карлина и Тейлора [2]. Более поздние достижения в этой области
можно найти в [253-256].
494
ДИНАМИКА ПОПУЛЯЦИЙ
12.6 Задачи
12.1 Обобщите двухвидовую модель соревнования, чтобы учесть асимметричную
конкуренцию. Эволюция этой реакции описывается уравнениями
Л = Л(1-А-елВ)=Гл(Л,В),
В = В(1 - В - ев А) = FB(A, В).
Исследуйте динамическое поведение этих уравнений как функцию ел и ев и
перечислите все возможные типы поведения.
12.2 Проделайте линеаризованный анализ уравнений Лотки-Вольтерра (12.5) и
опишите структуру локальных потоков в окрестности двух неподвижных то¬
чек (0,0) и (1,1). Далее исследуйте два следующих обобщения модели Лот¬
ки-Вольтерра:
(a) Константы в правой части уравнений модели Лотки-Вольтерра — раз¬
ные:
А = гаА — клвАВ,
В = —гвВ + кВлАВ.
(b) Для вида жертвы реализована соморегуляция:
А = А(1-А)-А£,
В = -В + АВ.
Найдите неподвижные точки этих двух моделей и опишите глобальнае потоки
в плоскости А-В
12.3 Рассмотрите модель трехвидовой конкуренции из примера 12.3 (стр. 469).
(a) Проверьте устойчивость неподвижной точки сосуществования видов в
области пространства параметров, определяемой неравнеством а+/3 < 2,
и устойчивость однобитовой неподвижной точки в области (а > 1) П
(£>!)•
(b) Исследуйте динамическое поведение для случая, когда а и fi находятся
в комплементарной области [а + /3 < 2] U [(а > 1) П (/3 > 1)]. Начните
с написания уравнений эволюции для суммы S = Л + В + С и приве¬
дения П = АВС. Покажите, что, пренебрегая квадратичными членами
в уравнении для £, мы придем к асимптотическому решению £ —> 1.
В этом приближении покажите, что П асимптотически убывает экспо¬
ненциально со временем. Поэтому траектория находится в треугольнике
Л + В + С = 1, но, так как П —> 0, смещается ближе и ближе к грани¬
цам треугольника. Наконец, исследуйте траекторию в окрестности точки
12.6 Задачи
495
(1,0,0), предположив, что члены квадратичные по В и С исчезающе ма¬
лы, а А близко 1. Используйте эту информацию, чтобы показать, что
время т, которое траектория проводит в окрестности точки (1,0,0), при¬
близительно равно
(а +/3 — 2)(/3 — a)t
Т 2(/3 — 1)(1 — а) •
Таким образом, время, которое траектория проводит в окрестности лю¬
бой одновидовой неподвижной точки, пропорциаиалыю всему прошед¬
шему времени.
12.4 Воспользуйтесь методом, развитым для модели SIR, дли определения доли
большой популяции, которая никогда не узнает слуха, начавшего распростра¬
няться с единственного разносчика.
12.5 Стартуя с уравнения эволюции для процесса рождении (12.17), запишите урав¬
нения для эволюции первых трех моментов распределении численности, Му =
(nj). Решите эти уравнения и покажите, что зависимость моментов от времени
имеет вид М± = е1, М2 = 2e2t - е* и М3 = 6e3t - 6е2/ + с1.
12.6 Вместо того чтобы использовать экспоненциальный анзац, найдите распреде¬
ление вероятности для процесса рождения методом производящей функции.
Потом попробуйте найти решение по индукции: решите (12.17) дли п = 1,2,3
(это можно сделать благодаря рекуррентной структуре уравнений), йогом уга¬
дайте Рп ддя. общего случая и проверьте вашу догадку.
12.7 Для процесса рождения вычислите среднее время (T/v), за которое* число ча¬
стиц достигает N, если исходная система содержала одну частицу. Также вы¬
числите распределение времен Tn- Каково наиболее вероятное время, па ко¬
тором это распределение достигает максимума?
12.8 Рассмотрите процесс рождения, стартующий с n0 > 1 частиц. Выведите ре¬
зультаты, объявленные в уравнениях (12.23)-(12.24).
12.9 Рассмотрите процесс распада А—> 0.
(a) Используйте метод производящей функции дли решения основного ки¬
нетического уравнения и таким образом найдите дли случаи, когда
исходная система содержала N > 1 частиц.
(b) Найдите (п) и (п2) и покажите, что флуктуации числа частиц малы.
(c) Начиная с N частиц, найдите среднее время, за которое исчезнут все
частицы.
Замечание: Можно найти Pn(t), не вычисляя. Если вы можете сделать это,
пропустите шаг (а).
12.10 Для процесса рождения-гибели вычислите (п) и (п2), которые возникают в
(12.22).
496
ДИНАМИКА ПОПУЛЯЦИЙ
12.11 Линеаризация. Возьмем нелинейное обыкновенное дифференциальное урав¬
нение и превратим его в бесконечную систему линейных дифференциальных
уравнений. Например, рассмотрим дифференциальное уравнение первогопо-
рядка х = х2 с начальным условием ж(0) = 1.
(a) Пусть xi = х, Х2 = ж2, и в общем случае Xj = х^. Покажите, что это пре¬
образование позволяет переписать исходное нелинейное дифференциаль¬
ное уравнение в виде системы линейных дифференциальных уравнений
=J^+i, j = 1,2,3,...
Начальные условия суть ж ДО) = 1 для всех j.
(b) Попробуйте решить уравнения из (а), пользуясь линейными методами.
Если удастся, вы найдете Xj = (1 — что конечно гораздо легче по¬
лучить, если просто решать уравнение х = х2.
(c) Вспомните теорему о том, что система линейных дифференциальных
уравнений с постоянными коэффициентами имеет решение во временном
интервале 0 < t < оо. Можете ли вы согласовать эту теорему с результа¬
том нашей задачи, а именно с существованием решения только в интер¬
вале 0 < t < 1?
12.12 Начиная с уравнения (12.25) для Рп для аннигиляции, получите уравнения
эволюции первых трех моментов распределения числа частиц Mj = (nJ)..B
частности, покажите, что правильное среднеполевое кинетическое уравнение
воспроизводится, если время перемасштабировано на 1/У, где V — объем си¬
стемы.
12.13 Напишите основное кинетическое уравнение для процесса коалесценции А +
А —> А. Используйте метод производящей функции и подходящую замену
переменных, чтобы показать, что производящая функция для коалесценции
такая же, как производящая функция (12.26) для аннигиляции. Выведите про¬
изводящую функцию для начальных условий с N частиц. Прокомментируйте
разницу, существующую между производящими функциями аннигиляции и
коалесценции, хотя уравнения для производящих функций одинаковые.
12.14 Пользуясь тем же методом, который привел нас к уравнению (12.30), вычис¬
лите среднее время достижения состояния, в котором не осталось частиц для
аннигиляции А + А 0, если система стартовала с N частиц.
12.15 Покажите, что среднеквадратичное время завершения для коалесценции да¬
ется выражением (12.31). Подсказка: Нужно учесть, что для экспоненциально
распределенной случайной переменной х справедливо равенство (ж2) = 2(ж)2.
Следовательно, для индивидуального времени перехода имеем (t2) = 2(tn)2 =
2r-2.
12.16 Найдите массу максимального кластера в конечной системе при агрегации с
постоянным ядром.
12.6 Задачи
497
12.17 Это расширенная задача, иллюстрирующая, что время гелеобразования стре-
мится к нулю для агрегации в конечной системе с индексом однородности
А > 1. Рассмотрите обобщенное мультипликативное ядро = (ij)\ с
А > 1, для которого основные кинетические уравнения имеют вид
£ 52 * ci ~ кХ Ск И 'Хе‘-
i+j=k i
Предположите, что полное число частиц N велико, 'гак что основные кинети¬
ческие уравнения (с Ск = Nk/N, где Nk — среднее число кластеров массы к)
дают хорошее приближение.
(а) На малых временах пренебрегите членом ухода и покажите', что с-к —
где коэффициенты удовлетворяют рекуррентным соотношениям
(к- 1)Ак = |
i+j=k
для к > 2 и с Ai = 1.
(b) Найдите главный вклад в эти рекуррентные соотношения и таким обра¬
зом получите среднее число кластеров массы А:, ранное
Nk = Nck ~ N[(k - 1)!]a_1 tk~l.
(c) Найдите время первого возникновения fc-мера, наложив условие Nk = 1.
(d) Воспользуйтесь этим результатом для времени первого возникновения,
чтобы оценить время гелеобразования и показать, что оно является убы¬
вающей функцией N при А > 1. Таким образом, при N —> сю происходит
мгновенное гелеоборазование.
12.18 Завершите вывод среднего времени вымирания (12.61), начиная с уравнения
(12.60).
Глава 13
ДИФФУЗИОННЫЕ
РЕАКЦИИ
В предыдущей главе обсуждались модели динамики популяций, в которых
реагенты рассматривались как идеально перемешанные, а кинетика харак¬
теризовалась только глобальными плотностями. В этой главе мы изучим
диффузионно-контролируемые реакции, в которых молекулярная диффузия
накладывает ограничения на интенсивности, с которыми встречаются реа¬
генты. В этой ситуации пространственные градиенты и пространственные
флуктуации играют существенную роль в управлении кинетикой. Как мы
увидим в этой главе, пространственная размерность играет ключевую роль
в определении важности этих неоднородностей.
13.1 Роль пространственной размерности
Когда размерность пространства d превосходит критическую размерность,
диффундирующие молекулы имеют тенденцию оставаться хорошо переме¬
шанными. Хорошее перемешивание есть следствие невозвратного характера
диффузии в высших пространственных размерностях, что означает, что мо¬
лекула с одинаковой вероятностью может прореагировать как с удаленным,
так и с ближайшим соседом. Из-за такого хорошего перемешивания простран¬
ственная размерность играет пренебрежимо малую роль, в конце концов при¬
водя к среднеполевой кинетике. Наоборот, когда d < dc, ближайшие частицы
вступают в реакцию с большой вероятностью. Такая локальность приводит
к развитию крупномасштабных неоднородностей, даже когда начальное со¬
стояние однородно, и это делает среднеполевое описание кинетики неприме¬
нимым.
13.1 Роль ПРОСТРАНСТВЕННОЙ РАЗМЕРНОСТИ
499
Чтобы проиллюстрировать роль пространственной размерности на про¬
стом языке, рассмотрим эволюцию газа одинаковых диффундирующих ча¬
стиц, с которыми происходит либо необратимая аннигиляции, либо коалес¬
ценция (см. также раздел 1.2). Предположим, что каждая частица имеет ра¬
диус R и коэффициент диффузии D. Изменение концентрации с за типичное
время реакции пропорционально вероятности того, ч'го две частицы войдут в
контакт, тогда как время реакции — это обратная интенсивность реакции. В
предположении о пространственной однородности вероятность встречи фак¬
торизуется в произведение одночастичных плотностей, а интенсивность ре¬
акции двух диффундирующих частиц пропорциональна к ~ I)Rd 2, что сле¬
дует из анализа размерностей (раздел 1.2), а также выведено в разделе 2.7.
Следовательно, плотность эволюционирует согласно уравнению 1
Tt = 'k<?' (131)
асимптотическое решение которого дает с — (fct) 1 (DRa 2Z.) ’.
При d > 2 интенсивность реакции — возрастающая функция радиуса ча¬
стиц, так что концентрация — убывающая функция R. Эти результаты согла¬
суются с интуицией: чем больше частицы, тем они более реакционноспособны.
Однако для d = 1 этот прогноз очевидно не верен. Интуитивно ясно, что в
одномерии радиусы частиц не влияют на асимптотическое поведение роль
играют только расстояния между соседними частицами. Следовательно, кон¬
центрация зависит только от D и t, и анализ размерностей даст с ~ (Л/.)-1/2
при d = 1. Другой способ получить тот же результат, а также понять, как
убывает плотность в критической размерности, — вспомнить, что при d <2
у интенсивности реакции появляется зависимость от времени (см. (2.89) в
разделе 2.7):
d<2
' Dd/2t(d-2)/2^
D/]n(Dt/R2), d = 2
DR?~2, d> 2.
k(t)
(13.2)
Зависимость интенсивности реакции от времени в d < 2 измерениях происте¬
кает из возвратности диффузии, которая систематически обедняет плотность
реагентов около адсорбера. Используя эти выражения для k(t) в кинетиче¬
ском уравнении (13.1), получим асимптотическое поведение плотности:
{(pf)-d/2? d < 2)
(Р^-Зп^/Л2), d = 2, (13.3)
(DRd-2t)-x, d> 2.
ХВ кинетических уравнениях для аннигиляции и коалесценции есть разница на коэф¬
фициент 2, которая не меняет динамику качественно.
500
ДИФФУЗИОННЫЕ РЕАКЦИИ
Следовательно, плотность убывает медленнее, чем в среднеполевом прогнозе
с ~ t”1, всегда, когда d < dc = 2. Поэтому для диффузионно-контролируемой
одновидовой аннигиляции критическая размерность равна dc = 2. Этот ре¬
зультат может показаться немного академическим, поскольку реальный мир
трехмерен. Однако для многих диффузионно-контролируемых реакций сред¬
неполевое описание неприменимо уже в трех измерениях. Вероятно, самый
известный пример — диффузионно-контролируемая двухвидовая аннигиля¬
ция, для которой, как будет показано в разделе 13.3, dc = 4.
Предсказание (13.3) специфично для одновидовой аннигиляции, но его
качественные свойства имеют общий характер. А именно, для большинства
неравновесных реакций существует критическая размерность б?с, для которой
справедливы следующие утверждения:
• Для d < dc среднегюлевой подход неверен. Настоящее убывание более
медленное.
• В пограничном случае d = dc среднеполевой подход почти верный. Ча¬
сто он дает правильный, обычно степенной ведущий член, но при этом
упускает логарифмический коэффициент.
• Когда d> dc, среднеполевое приближение дает асимптотически верный
результат.
Поэтому для диффузионно-контролируемой необратимой реакции плотность
обычно демонстрирует следующее поведение:
с~ < r^(lnip,
d < dc,
d — dc,
d > dc,
(13.4)
где (3(d) < (Зс, котдр, d < dc, и (3C = (3(dc). Показатель (3(d) не просто мень¬
ше, чем /Зс, это обычно строго возрастающая функция d в интервале d < dc.
Пример такой зависимости дает поведение показателя (3(d) в одновидовой и
двухвидовой аннигиляции, где (3(d) = d/2 и (3(d) = d/4, соответственно. В
критической размерности показатель 7 неотрицателен, так как среднеполе¬
вой результат либо медленнее на логарифмический множитель (как в одно¬
видовой аннигиляции в dc = 2, где 7=1), либо верен (как в двухвидовой
аннигиляции в dc = 4, где 7 = 0).
Значения dc = 2 и dc = 4 критических размерностей для одно- и двухви¬
довой аннигиляции встречаются часто. Например, возвратность случайных
13.1 Роль ПРОСТРАНСТВЕННОЙ РАЗМЕРНОСТИ
501
блужданий в d < 2 и их невозвратность в d > 2 (раздел 2.5) в основном опре¬
деляют критическую размерность dc = 2 для одиовидовой аннигиляции. Кри¬
тическая размерность dc = 4 характеризует множество взаимодействующих
диффузионных систем, таких как самоизбегающие блуждания, (раздел 2.5)
Пример 13.1. Самоизбегающие блуждания. В самоизбегаю1цпх решеточных
блужданиях в дискретном времени частица прыгает в случайно выбранный со¬
седний узел, если этот узел не был посещен ранее. Чтобы правильно описывать
самоизбегающее блуждание, приходится следить за всей его траекторией. Эта
бесконечная память делает самоизбегающие блуждания гораздо более сложны¬
ми, чем обыкновенные случайные блуждания. Тем не менее, асимп'готическое
поведение самоизбегающих блужданий хорошо изучено, за исключением трех¬
мерного случая, где индексы известны только численно2. После I 1 временных
шагов смещение самоизбегающих блужданий, усредненное по всем возможным
траекториям, растет как
t3/4,
R ~ t\ где у ~ 0,59,
t1/2,
d= 1,
d = 2,
d = 3,
d = 4,
d > 4.
Поэтому критическая размерность равна dc = 4.
Есть ли ситуации, в которых критическая размерность отличается от двух
и четырех? Вот два примера, где критическая размерность принимает экс¬
тремальные значения dc = 1 и dc = оо, соответственно.
Пример 13.2. Трехчастичные реакции. Рассмотрим одповидовый диффузион¬
но-контролируемый процесс, в котором реакция происходи'!’ только тогда, когда
три частицы оказываются в контакте, например, трехчастичпан аннигиляция
А + А + А -> 0 или трехчастичная коалесценция А + А + Л —> Л. Хотя трехча¬
стичный процесс может показаться искусственным, мы видели, что он возника¬
ет в адсорбции (раздел 7.4), кластерной динамике (раздел 8.8) и экстремальной
динамике (раздел 9.7). Кроме того, большинство биологических реакций меж¬
ду двумя молекулами требуют присутствия катализатора. Это не одновидовые
процессы, но они также включают по меньшей мере три молекулы.
Теперь используем кинетические уравнения и анализ размерностей, чтобы
показать, что dc = 1. Так же как в бинарных реакциях, запишем (среднеполевое)
2Прекрасное приближение дается формулой Флори и = 3/(d+2), которая точна в одном
измерении, оказывается точной в двух измерениях и становится точной в критической
размерности.
502
ДИФФУЗИОННЫЕ РЕАКЦИИ
кинетическое уравнение
асимптотическое решение которого имеет вид с ~ (2/ct)-1/2. Далее мы использу¬
ем анализ размерностей, чтобы выразить интенсивность реакции через радиус3
и коэффициент диффузии: к ~ DR2d~2. Поэтому
с ~ (2fct) 1у<2 ~
1 1
Ж-1 y/Dt
Зависимость от R кажется разумной, когда d > 1, тогда как для d < 1 она
очевидно не верна. Таким образом мы заключаем, что dc = 1. В критической
размерности появляется логарифмическая поправка
1п(£>*/Д2)
Dt
когда d = 1.
Этот пример показывает, что полезно думать о размерности d как о веще¬
ственном числе, хотя физически она должна принимать одно из трех целых
значений d = 1,2 или 3. В самом деле мы можем предсказать, что dc = 1,
обобщая пространственную размерность на нефизическую область d < 1.
Чтобы получить реакционно-диффузионный процесс с dc = оо (т. е. средне¬
полевые результаты неверны во всех размерностях), мы должны обеспечить
отсутствие перемешивания. Приведем простой пример.
Пример 13.3. Реакция захвата. Рассмотрим среду, содержащую неподвижные
ловушки и диффундирующие частицы, которые не взаимодействуют между со¬
бой. Когда частица попадает в ловушку, она адсорбируется. Естественно пред¬
полагать, что в системе имеются точечные частицы и сферические ловушки оди¬
накового радиуса Д, которые случайно распределены в системе с концентраци¬
ей р. Отсутствие взаимодействия между частицами позволяет нам работать с
одночастичной задачей. На первый взгляд, задача кажется простой: если мы
знаем расположения всех ловушек и начальное положение частицы, мы долж¬
ны решить уравнение диффузии с адсорбирующими граничными условиями на
поверхности всех ловушек, а потом усреднить по всем начальным положениям,
чтобы найти вероятность выживания S(f). Однако граница очень сложна, и с
помощью такого прямого подхода невозможно извлечь никаких осмысленных
результатов.
3Мы определяем трехчастичную реакцию очевидным образом: когда центры трех ча¬
стиц сближаются на расстояние < Д, они вступают в реакцию. В решеточной формулиров¬
ке реакция возникает, когда три частицы занимают один и тот же узел решетки. В этом
случае параметр решетки играет роль Д.
13.1 Роль ПРОСТРАНСТВЕННОЙ РАЗМЕРНОСТИ
503
Среднеполевое описание основано на кинетическом уравнении
^ = -кр§, (13.5)
которое приводит к экспоненциальному убыванию плотности
§ = e~kpt. (13.6)
В следующем разделе мы увидим, что это предсказание неверно во всех измере¬
ниях. Правильная асимптотика имеет вид
S ~ ехр[—const, х p2/(d+2) (Pf)d/(rf+2)j . (13.7)
Среднеполевой прогноз асимптотически неверен, потому что ловушки неподвиж¬
ны, неупорядоченность их начальных положений заморожена, и перемешивания
никогда не происходит.
Пример 13.4. Рост островов. Здесь каждый кластер занимает один решеточ¬
ный узел. Мономеры (М) подвижны, тогда как острова (I), т. е. кластеры массы
> 2, статичны. Символическая запись процесса имеет вид
M + M-+I, М + 1^1.
На среднеполевом уровне кинетические уравнения
dM
dt
= —2М2 - MI,
di
dt
предсказывают экспоненциальное убывание плотности мономеров. (Этому рас¬
чету посвящена задача 5.5.) Модель роста островов похожа на реакцию с за¬
хватом за исключением того, что острова (играющие роль ловушек) образуются
динамически. Если вначале островов нет, они возникают во время эволюции.
Пространственное распределение островов задается этим процессом, а не на¬
чальными условиями (как в реакции с захватом), а точная скорость убывания
плотности мономеров до сих пор не вычислена. Это убывание! определенно зави¬
сит от пространственной размерности и должно напоминать зависимоеть (13.7),
которая характеризует реакцию с захватом. Эти факты позволяют предполо¬
жить, что критическая размерность должна быть бесконечной, dc = оо.
Наконец, ниже мы покажем, как искусственно менять пространственную
размерность в диффузионно-контролируемых реакциях.
504
ДИФФУЗИОННЫЕ РЕАКЦИИ
Пример 13.5. Нецелые размерности. Рассмотрим систему невзаимодействую¬
щих пассивных частиц, которые диффундируют и находятся под действием по¬
ля скоростей V = V(r,£). Плотность частиц с = c(r,f) описывается уравнением
конвекции-диффузии
^ + (V-V)c = PV2c.
Для радиального поля скоростей V = V (г) г/г и радиально симметричных на¬
чальных условий уравнение конвекции-диффузии для плотности с = c(r, £) сво¬
дится к
дс дс __ f д2с d — 1 дс\
dt + дг \5г2 + г дг) '
Теперь представим, что радиальное поле скоростей обратно пропорционально
расстоянию от начала координат V = В этом случае конвекционное слага¬
емое можно включить в диффузионное, изменив размерность. Поэтому можно
интерпретировать конвекционно-диффузионный процесс как диффузию в про¬
странстве нецелой размерности. Радиальное поле скоростей V = естественно
в двух измерениях, где оно подчиняется уравнению непрерывности V-V = 0 и со¬
ответствует потоку, индуцированному точечным источником интенсивности Q.
Поэтому рассмотрим двумерный случай dphys = 2 с полем скоростей V =
Этот конвекционно-диффузионный процесс в двух пространственных измерени¬
ях математически описывается уравнением диффузии в фиктивной размерности
dfict> которая не обязательно целое число:
дс = (№с_ dfict - 1 9с\
dt \ дг2 г дг /
dfict — 2
Q
2nD'
Для источника (Q > 0) фиктивная размерность меньше физической, dfict < 2, а
для стока (Q < 0) наоборот.
13.2 Реакция с захватом
В реакции с захватом частицы диффундируют и адсорбируются тогда, когда
они вступают в контакт с ловушками, случайно распределенными в системе.
Какова вероятность, что частица выживет до времени t? Наивный способ ис¬
следования этого вопроса — заменить конфигурацию ловушек эффективной
усредненной средой. Такая замена (см. пример 13.2 в предыдущем разделе)
приводит к вероятности выживания, экспоненциально убывающей со време¬
нем, (13.6). Это предсказание не верно. Можно попытаться улучшить это
усредненное описание, вспомнив, что интенсивность реакции, которая рас¬
сматривалась как постоянная при решении уравнения (13.5), на самом деле
13.2 Реакция с захватом
505
приобретает временную зависимость при d < 2. Решив (13.5) с k(t) из (13.3),
найдем асимптотику
InS ~ — р х
'(Dt)d/2,
< Dt/]n(Dt/R2),
DRd~2t,
d<2,
d = 2,
d>2,
(13.8)
очевидно подразумевающую, что dc = 2. Приближение эффективной среды
(13.8) ближе к истинной асимптотике, но все еще неправильно. Результаты
(13.6) и (13.8) ошибочны по интересным причинам. Как мы увидим, экстре¬
мальные флуктуации пространственного распределения ловушек приводят
к более медленному, чем экспоненциальное, убыванию вероятности выжива¬
ния. Это аномально медленное убывание устанавливается только на очень
больших временах, на которых плотность исчезающе мала. Следовательно,
хотя экстремальные флуктуации играют решающую роль с точки зрения тео¬
рии, их практические следствия весьма ограничены.
Точное решение в одном измерении
Суть реакции с захватом можно лучше всего понять в одном измерении. Что¬
бы найти среднюю вероятность выживания, сначала нужно получить веро¬
ятность выживания диффундирующей частицы при заданной конфигурации
ловушек, потом усреднить по всем начальным точкам блуждания и, нако¬
нец, по всем конфигурациям ловушек. В одном измерении это вычисление
не представляет труда, поскольку диффундирующая частица «видит» толь¬
ко единственный содержащий ее интервал, определяемый положениями бли¬
жайших ловушек. Предположим, что частица находится в хо, а ближайшие
ловушки вя = 0ия = £. Точная концентрация в момент времени t > 0 для
такой конфигурации дается рядом Фурье (задача 13.1)
«0М|Ы = |ZS1" О ™ (Т) (13.9)
П>1
Теперь вычислим вероятность выживания на интервале [0, L], усредняя по
всем начальным положениям частицы и интегрируя по всем финальным по¬
ложениям в интервале, что дает
Sb(t) = ^r [ [ cL(x,t\xo)dxdxQ
ь Jo Jo
= —V
•я-2
7Г^о(2ш + 1)2
,-(2m+l)2n2Dt/L2
(13.10)
506
ДИФФУЗИОННЫЕ РЕАКЦИИ
где черта сверху обозначает усреднение по начальным положениям. Нако-
нец, найдем среднюю по конфигурациям вероятность выживания, усреднив
Sb(i) по распределению длин интервалов, не содержащих ловушек. Если ло¬
вушки случайно распределены с плотностью р, плотность вероятности того,
что интервал длины L не содержит ловушек, равна e~pLp. Таким образом,
формальное решение для средней вероятности выживания дается двойным
усреднением по всем начальным положениям блуждания и по всем областям
без ловушек
о /*оо
s(t) = №(t)) = i / dt £
J° m>0
(2m +1)2
exp
(2m +1)2
2^2
-£
, (13.11)
где угловые скобки обозначают усреднение по длинам интервала, а вместо t
и L мы использовали безразмерные переменные
т = 2ir2p2Dt, & = pL.
Зависимость S от времени достаточно хитрая, с различным поведением
в пределе малого и большого времени. Сначала рассмотрим поведение S на
больших временах, когда первый член найденного ряда доминирует. Оставив
только этот член, получим
о /»оо
§(т) - ^2 Уо М efW' где L
У функции /(^) есть пик в (,* = т1/3, который становится все более и более
острым при т —> оо. Поэтому мы можем найти поведение S при большом
времени, воспользовавшись методом Лапласа, который дает (задача 13.2)
§(т) ~
ехр(-|г1/3),
т —> ОО.
(13.12)
Неожиданный растянуто-экспоненциальный характер асимптотического убы¬
вания происходит из-за конкуренции между экспоненциально малой вероят¬
ностью найти область без ловушек и длинным временем жизни частицы в
такой области. Оптимизация по отношению к этим двум свойствам эквива¬
лентна максимизации /(€). Эта максимизация предсказывает, что длина €*
оптимального интервала без ловушек растет как т1/3.
Чтобы найти поведение вероятности выживания на малых временах, про¬
ще сначала рассмотреть производную выражения (13.11) по т
13.2 Реакция с захватом
507
dS
dr
м 53 ехр
га>0
(2т + 1)2т
(13.13)
При т —> 0 можно заменить суммирование интегрированием
53ехР
т > 0
(2п.+ 1)2т1 ~ Г
2Р ] “ Уо
dm ехр
2т
--^т
1 /я-/?2
2 V "2т"
(13.14)
Таким образом, уравнение (13.13) принимает вид
(13.15)
Нижний предел интегрирования теперь равен I = у/г, а не (. = 0, потому что
замена суммы интегралом корректна только при т С €2. Ведущая асимптоти¬
ка интеграла в (13.15) есть 1п(т-1/2), и поэтому dS/dr ~ -(27г3т)_|/21и(1/т),
откуда
ад,1-Д1п(1/Т) при т -> 0. (13.16)
Изменение поведения от малых времен к большим происходит постепен¬
но. Поэтому обнаружить длинновременную асимптотику в экенеремситаль-
ных данных или численно трудно. Асимптотическую вероятность выживания
вида ехр(—f1/3) можно наблюдать, используя тонкие численные методы, ко¬
торые созданы специально для выявления режимов, в которых вероятность
выживания становится действительно мизерной.
Произвольная пространственная размерность
Можно обобщить рассуждение об оптимальных флуктуациях с размерно¬
сти один на произвольную пространственную размерность, чтобы получить
нижнюю оценку для асимптотики вероятности выживания. Мы приведем
аргументы в пользу того, что эта оценка асимптотически точна в пределе
маленькой концентрации ловушек. Без потери общности рассмотрим части¬
цу, стартующую из начала координат. Для заданной конфигурации ловушек
вероятность выживания очевидным образом ограничена снизу конфигура¬
цией, в которой ловушки заменены на адсорбирующую сферу с центром в
начале координат и радиусом, равным расстоянию до ближайшей ловуш¬
ки (рис. 13.1(a)). Не составит труда вычислить вероятность выживания для
такой сферы. Нужно решить уравнение диффузии с граничным условием
c(|r|,t) = 0 и начальным условием с(г, t = 0) = 5(г). С помощью метода
508
ДИФФУЗИОННЫЕ РЕАКЦИИ
• • • •••*.• •
• • • • . ••
• ж
Ж \ А • ж
* '^5\ '■ .* *
•Л"‘
• ••
(а)
•••*••%• • • ••
(Ь)
• • •
• •
• •
• •
Рис. 13.1. (а)Конфигурация ловушек (круги) и диффузионная траектория, ко¬
торая остается внутри свободной от ловушек сферической области радиуса а с
центром в точке начального положения частицы. (Ь) При увеличении радиуса а
область без ловушек становится все более сферической
разделения переменных можно записать решение в виде разложения по соб¬
ственным функциям (задача 13.3)
c(r,£) = Апху J„(\nx) e-xnDt/a\ х = -. (13.17)
У1>1 а
Здесь Jy — функция Бесселя порядка у = (2 — rf)/2, Ап — это n-ый ноль этой
функции Бесселя, а амплитуды Ап определяются из начальных условий.
Теперь мы усредним по всем конфигурациям ловушек. Эта процедура
эквивалентна усреднению по радиусу сферической области без ловушек. Ве¬
роятность существования шара радиуса г без ловушек равна e~pv, где V =
Vdrd — объем rf-мерного шара радиуса г. Так же как в одномерии, первый
член этого ряда доминирует в пределе большого времени, и нижняя оценка
для вероятности выживания имеет вид
S(t) > У ехр (—A2 Dt/a2 — pVdad^ p^d^1 da, (13.18)
где Qd — площадь поверхности rf-мерного шара.
Теперь определим асимптотическое поведение этого интеграла с помощью
метода Лапласа. Подробности вывода повторяют то, что было проделано в
одномерном случае, а конечный результат следующий:
lnS^-Cdp2/^2)^)^2), Cd=^[^\ . (13.19)
13.2 Реакция с захватом
509
Таким образом, асимптотическое поведение зависит только от наименьшего
собственного значения Ах. В двух измерениях Ai — это наименьший положи¬
тельный корень функции Бесселя Jo- Численно Ах = 2,4048. В трех измере¬
ниях Ах = 7г/2, и асимптотика (13.19) принимает вид
с /^2\4/5
P2/5(W/5-
Так же как в случае одного измерения, это убывание по растянутой экспо¬
ненте не получается с помощью традиционных подходов, таких как теория
возмущений в пределе малой плотности ловушек, а асимптотическая вероят¬
ность выживания не может быть обнаружена, пока плотность не уменьшится
до исчезающе малого значения4.
Наконец, определим качество нижней оценки (13.19). Замечательно то,
что она асимптотически точна5. Это свойство далеко не очевидно: сохране¬
ние только доминирующего члена в разложении по собственным функциям
не уменьшает асимптотики, тогда как искусственно вставленная сферическая
адсорбирующая граница с радиусом, равным расстоянию до ближайшей ло¬
вушки, понижает вероятность выживания. Сравним реальную полость с мак¬
симальной вставленной сферой. В пределе большого времени, когда полости,
вносящие основной вклад, также велики, они становятся все более и более
сферическими, как показано на рис. 13.1(b). Это свойство интуитивно понят¬
но, но трудно доказуемо. Поэтому мы приведем другой аргумент в пользу
оптимальности сферы.
Лучшая возможность для частицы выжить — быть в большой полости.
Однако плотность таких полостей мала. Конкуренция между двумя этими
тенденциями выбирает оптимальную полость. В высших размерностях поло¬
сти отличаются не только по объему, но также и по форме. Внутри произволь¬
ной полости V большого объема V = vol(V) (т. е. pV 1) решение уравнения
диффузии с адсорбирующей границей можно записать в виде разложения по
собственным функциям
с(г>*) = 52 Агфп(г)е A"Dt, (13.20)
П>1
4Даже в одномерии плотность должна уменьшиться более чем на 13 порядков, чтобы
асимптотическое поведение стало видно. В трех измерениях асимптотическое поведение
еще не наблюдалось численно.
5В пределе, когда доля объема, занятого ловушками, пренебрежимо мала, pRd —> 0.
510
ДИФФУЗИОННЫЕ РЕАКЦИИ
где собственные значения и собственные функции определяются для опера¬
тора Лапласа с граничными условиями Дирихле (адсорбирующими)
\72Ф„ = -Л2 Ф„ Ф J =0
Размерный анализ дает Лп = V-1/dAn с безразмерным собственным зна¬
чением Ап, не зависящим от объема полости. Теперь, повторяя стандартные
аргументы, записываем асимптотику на больших временах
S ~ f ехр (—A2Dt/V2/d - pv) pdV
и находим
/ л \ 2/(d+2) / 9 \ d/ (d+2)
InS ~ -Bdp2/^ (\lDt)d^d+2\ Bd = n) + n) . (13.21)
Самое медленное убывание (вносящее основной вклад в асимптотику) соот¬
ветствует полости с минимальным первым собственным значением. Известно,
что такие полости сферические6.
13.3 Двухвидовая аннигиляция
В двухвидовой аннигиляции диффундирующие комплементарные виды А и
В аннигилируют, а частицы одинаковых видов не взаимодействуют. Физи¬
ческие примеры этой реакции включают электронно-дырочную рекомбина¬
цию в полупроводниках или в космологической формулировке аннигиляцию
материи-антиматерии. Вероятно, самый интересный аспект диффузионно -
контролируемой двухвидовой аннигиляции — это то, что плотность медленно
убывает со временем как для пространственной размерности d < 4, ко¬
гда начальные плотности частиц равны. Это убывание медленнее, чем пред¬
сказание кинетического уравнения t”1, а также медленнее, чем убывание в
одновидовых реакциях при d <2. Аномально медленная кинетика возникает
из-за того, что реагенты противоположных видов организуются в укрупнен¬
ную доменную мозаику (рис. 13.2). В результате, реакции могут возникать
только вдоль границ доменов, а не однородно по всей системе. Ограничение
реакций на малое подмножество всей системы лежит в основе медленного
6 Это свойство обеспечивается теоремой Фабера-Крана. Эта теорема утверждает, что
квантовая частица в ящике данного объема с непроницаемыми стенками имеет минималь¬
ную энергию основного состояния, если ящик — сферический.
13.3 Двухвидовая аннигиляция
511
Рис. 13.2. Снимок положений частиц в двухвидовой аннигиляции в двух изме¬
рениях. Радиусы частиц увеличены для наглядности. При рассмотрении этой
картинки можно увидеть три независимых масштаба длины: маленькие рассто¬
яния между соседними частицами одного вида, характерный размер домена и
ширину границы раздела между доменами противоположных видов
убывания плотности. Убывание плотности как f~d/A дока «ано с помощью пре¬
вращения эвристических аргументов из раздела 1.3 в строгие утверждения.
Несмотря на то, что мы узнали из эвристического и строгого подходов, ампли¬
туды асимптотического поведения и полный функциональный вид плотности
неизвестны и остаются предметом для исследования даже в одном измерении.
Главное следствие убывания как t~dl^ — то, что ниже критической раз¬
мерности среднее расстояние между соседними частицами растет по универ¬
сальному (т. е. не зависящему от размерности) закону f ~ c{/d ~ Можно
предположить, что масштаб длины I — единственная характеристика укруп¬
ненной доменной мозаики в двухвидовой аннигиляции. Однако, как видно из
рис. 13.2, это предположение ошибочно. В оставшейся части этого раздела мы
512
ДИФФУЗИОННЫЕ РЕАКЦИИ
используем эвристический метод, чтобы показать, что укрупненную мозаику
в двухвидовой аннигиляции характеризуют по меньшей мере три масштаба
длины.
Существование трех масштабов легче всего понять в одномерии, где си¬
стема в пределе большого времени организуется в перемежающиеся домены
видов Аи В (рис. 13.3). Типичная длина домена равна
L ~ y/Dt. (13.22)
Этот масштаб возникает потому, что диффузионный транспорт обеспечива¬
ет хорошее перемешивание иа масштабе L ~ y/Dt во время t, так что вид,
который был в локальном меньшинстве, в таком домене будет уничтожен.
Поскольку среднее начальное число частиц каждого вида на этом простран¬
ственном масштабе равно c(0)L, а флуктуации имеют порядок д/с(0)Ь, плот¬
ность в домене во время t равна
с ~ ~ Уфу (Dt)-1/4, (13.23)
ХУ
как уже было показано в разделе 1.3. Используя (13.22) и соотношение I ~
с-1, получим типичное расстояние между соседними частицами одного вида
t-лл = ?вв ~ [с(О)]-1/2 (Dt)1!4. (13.24)
Таким образом, существует по крайней мере два масштаба: межчастичное
расстояние (,аа = ?вв и размер домена L. Неожиданностью становится то,
что есть еще третий независимый масштаб #ав, характеризующий расстояние
между соседними частицами противоположных видов, или, что то же самое,
расстояние между соседними доменами (рис. 13.3). Чтобы найти £ав, заме-
^лл 1ав
••••ААААА ВВВ АААА В ВВВ В ААА —
н И
L
Рис. 13.3. Схематическое изображение трех главных масштабов длины в двухви¬
довой аннигиляции: размер домена L ~ t1/2, межчастичное расстояние, которое
ведет себя как £аа = £вв ~ t1/4, и обедненная зона между доменами, которая
растет как £ав t3/8
в одном измерении
тим, что типичная пара АВ вступает в реакцию за время At ~ £2AB/D. Число
13.3 Двухвидовая аннигиляция
513
реакций на единицу длины порядка одной реакции на домен, т. е. (Dt) х/2.
Следовательно, скорость изменения концентрации равна
dc Дс (Dt)-1/2
dt~ Д* ~ £2ab/D '
(13.25)
Однако, dc/dt независимо известно из (13.23). Используя этот результат для
dc/dt вместе с соотношением (13.25), находим
Zab ~ [с(О)]-1/4 (2?t)3/8. (13.26)
Асимптотически имеем £ав » ^АА = ^ВВ, и £дв <£ Ь. Свойство ^дя ?АА
можно рассматривать как проявление эффективного отталкивании между
частицами противоположных видов, как следует из хорошо видных пустых
промежутков между доменами противоположных видов на рис. 13.2.
Можно обобщить это объяснение на два измерении. Снова, па врсмсинбм
масштабе порядка Д£ ~ все частицы на окраине доменов будут вза¬
имодействовать между собой. Число таких частиц имеет порядок периметра
доменов, деленного на расстояние между частицами на окраине доменов. Тон¬
кость в том, что расстояние между этими частицами — это /'дя, а не /?дд. По¬
этому концентрация периферических частиц имеет порядок [(/?/.)1 /2/( AB\/Dt.
С этими компонентами аналогом соотношения (13.25) будет
dc ~ Дс ~ [(Pt^/tABl/Pt
dt ~ At~ #ab/d k '
Опять, используя известный результат для c(t) из уравнения (13.23), получим
£ав ~ [с(О)]"1/6 (Dt)1/3. (13.28)
В размерности больше двух случайные блуждания невозвратны, и мы боль¬
ше не можем быть уверены, что все периферические частицы прореагируют
за время порядка ^ab/D. И обобщение эвристических аргументов, представ¬
ленных здесь, и численные наблюдения свидетельствуют в пользу того, что
аномальный скейлинг расстояний АВ пропадает в трех измерениях, так что
Раб ~ #АА ~ t1/4-
514
ДИФФУЗИОННЫЕ РЕАКЦИИ
13.1. Численное моделирование диффузионных реакций
Наивный способ моделирования диффузионных реакций — выбрать реагент на¬
угад, позволить ему продиффундировать на короткое расстояние (или прыгнуть
в случайный ближайший узел) и произвести реакцию, если передвинутая частица
попала в радиус реакции другого реагента. В необратимой реакции, где плотность
непрерывно убывает, такой подход становится безнадежно неэффективным. Когда
реагенты становятся сильно отдаленными друг от друга, большинство прыжков
не приводят к изменению плотности реагентов. Поэтому наивное моделирование
тратит большую часть времени на диффузионные шаги и почти не производит
наиболее важные шаги с реакциями.
Событийно ориентированное численное моделирование исправляет этот недоста¬
ток, обеспечивая, чтобы каждый шаг обновления соответствовал событию реак¬
ции. Рассмотрим конкретно случай аннигиляции (Л + А —> 0) для простоты на
одномерном кольце. Однако с небольшой доработкой подход, о котором мы здесь
рассказываем, может быть обобщен на любую пространственную размерность.
Для данного пространственного распределения частиц из раздела 2.6 мы знаем
распределение времени первого посещения, необходимого для столкновения лю¬
бой пары ближайших соседей. Поэтому мы можем мгновенно продвинуть время
вперед до времени первого столкновения и удалить соответствующую прореаги¬
ровавшую пару. Все остальные частицы перемещаются в новые положения, в со¬
ответствии с распределением Гаусса свободной диффузии за это время столкно¬
вения. Таким способом единичный шаг обновления соответствует все более воз¬
растающему приращению времени, по мере того как система становится все более
разреженной.
Важная мораль: никогда и ни в каких приложениях не нужно моделировать дви¬
жение индивидуального случайного блуждания. Так как свойства времени перво¬
го посещения известны, всегда имеется способ избежать построения путей диф¬
фундирующих частиц с помощью бессмысленных пошаговых прыжков. Вместо
этого нужно определить обновление времени через важные физические события
в системе.
Пространственная организация реагентов в домены одного вида разруша¬
ется при d > 4, потому что домены становятся прозрачными для проникнове¬
ния частиц противоположного вида. Рассмотрим, например, судьбу частицы
А, помещенной в центр домена В линейного размера L. Для такого домена,
локальная концентрация частиц В, согласно уравнению (13.23), имеет поря¬
док L~d/2. Чтобы покинуть домен, гостю из А нужно L2 временных шагов, во
время которых он посетит L2 различных узлов (снова предполагается d> 4).
В каждом узле частица А вступает в реакцию с вероятностью порядка кон¬
центрации В, равной L~d/2. Поэтому вероятность того, что частица вида А
прореагирует с любой частицей вида В, до того как выйдет из домена, имеет
порядок Z,(4_d)/2. Поскольку эта вероятность стремится к нулю при L оо
13.4 Одновидовые реакции в одном измерении
515
в d > 4, домен прозрачен для частиц противоположного вида, и поэтому
система остается пространственно однородной.
13.4 Одновидовые реакции в одном измерении
Диффузионно-лимитированные реакции в одном измерении специфичны тем,
что они часто имеют точное решение. В этом разделе мы представляем точ¬
ное решение двух классических одновидовых реакций: (i) необратимая ко¬
алесценция А + А —>■ А и (ii) аннигиляция Л + А —> 0, как необратимых, так
и соответствующих стационарному состоянию.
Необратимая коалесценция А + А —> А
В коалесценции частицы прыгают между соседними узлами с интенсивно¬
стью, которую мы полагаем равной 1/2. Когда частица прыгает в занятый
узел, две частицы мгновенно сливаются и образуют одну частицу (рис. 13.4).
I
I
(а)
(Ь)
Рис. 13.4. Коалесценция в одном измерении: (а) прыжок в соседний узел и (Ь)
коалесценция
Удобно анализировать эту реакцию методом пустых интервалов, (см.
главу 7), который работает с лакунами между соседними частицами. Длина
лакуны может или расти, или уменьшаться на 1 только из-за прыжка части¬
цы на конце лакуны. Этот факт позволяет нам записать решаемое уравнение
для распределения длины лакуны. Пусть Vn будет плотность лакун длины п.
Как показано на рис. (13.5) длина лакуны совершает одномерное случайное
блуждание, и плотность вероятности ее длины эволюционирует следующим
образом (для п > 0):
= Vn+1 - 2Vn + V„_x.
(13.29)
516
ДИФФУЗИОННЫЕ РЕАКЦИИ
ш L
(а)
(Ь)
(с)
Рис. 13.5. Изменения лакуны длиной п = 3 из-за прыжков. Показаны прыжки,
приводящие к уходу (а) и к двум типам процессов прихода (Ь) и (с)
Это уравнение можно обобщить иа случай п = 0, заметив, что уравнение для
плотности лакун нулевой длины = —214) + И приводится к тому же виду,
что и (13.29), с помощью наложения граничного условия V_i = 0.
Как было показано в разделе 2.1, элементарное решение уравнения (13.29)
имеет вид In(2£)e_2t, где 1п — модифицированная функция Бесселя перво¬
го рода (см. (2.14)). Теперь нам нужна правильная комбинация элементар¬
ных решений, удовлетворяющая начальным условиям. Для канонического
начального состояния, в котором каждый узел занят, начальные условия для
пустот 14(0) = 5пд. Чтобы удовлетворить граничному условию = 0,
используем метод изображений, поместив в начальный момент отрицатель¬
ное изображение с коэффициентом — 1 в п = —2. Тогда граничное условие
= 0 автоматически удовлетворяются по построению. Суммируя вкла¬
ды исходного и отраженного решений, находим плотность лакун
Vn(t) = [ln(2t) - Jn+2(2£)] e-2t = 1^(2t) e~2t, (13.30)
где для получения конечного результата мы использовали тождество
277,
7n-l(®) ~ Лг+1(ж) = 1п(х).
X
Поскольку частицы и лакуны находятся во взаимнооднозначном соот¬
ветствии, плотность частиц равна плотности лакун любой длины, с(£) =
Zdfc>0 W)- ПОЭТОМУ
с = [Z0(2t) + /i(2t)le"2t ~ -4=, t -> оо. (13.31)
У/ТГЬ
Замечательное свойство этого решения — при правильном взгляде взаимо¬
действующая многочастичная система сводится к одномерному случайному
блужданию. В данном случае ключевой факт — это то, что длина лакуны
соответствует положению случайного блуждания. В основном все точные ре¬
шения для одномерных реакций — это вариации на ту же тему.
13.4 Одновидовые реакции в одном измерении
517
Из этой аналогии можно немедленно извлечь несколько главных свойств
распределения длины лакун: (i) средняя длина лакуны растет как t1/2, (ii)
вероятность иметь длинную лакуну длины х » t1/2 убывает как е~ах , (iii)
вероятность короткой лакуны длины х t1/2 убывает линейно с х. Последнее
свойство — это появление эффективного отталкивания между частицами,
индуцированного реакцией. Если бы взаимодействия не было, вероятность
найти короткую лакуну длины х убывала бы как
Необратимая аннигиляция в одном измерении
При необратимой аннигиляции обе частицы исчезают, когда частица прыга¬
ет в занятый узел. Если каждая частица прыгает с интенсивностью 1/2, то
аннигиляция возникает с интенсивностью 1, поскольку любая из двух частиц
может прыгнуть и вызвать реакцию. Необратимая аннигиляция решаема, по¬
скольку она эквивалентна динамике Изинга-Глаубера, при нулевой темпера¬
туре (раздел 8.5). Конкретно, прыжок частицы эквивалептеи сохраняющему
энергию перевороту спина, тогда как аннигиляция эквивалентна перевороту,
понижающему энергию (рис. 13.6). Формально, число наполнении в узле i
I
I
(a)
(H)
Рис. 13.6. Одновидовая аннигиляция в одном измерении: (а) прыжки в сосед¬
ние узлы с интенсивностью 1/2 и (Ь) аннигиляция с интенсивностью I. Также
показано эквивалентное представление в терминах изинговских спинов, где пара
противоположно ориентированных спинов эквивалентна частице на месте домен¬
ной стенки
(rii = 1, если узел занят, и п* = 0 в противном случае) получается из соот¬
ветствующей спиновой конфигурации на дуальной ренкггке, если положить
ni = (1 — SiSi+i)/2. Таким образом, мы можем просто использовать результа¬
ты решения Глаубера для решения реакции аннигиляции.
518
ДИФФУЗИОННЫЕ РЕАКЦИИ
Для изначально заполненной решетки, с(0) = 1, соответствующей анти-
ферромагнитному начальному состоянию в эквивалентной спиновой системе,
зависимость концентрации от времени имеет вид (см. (8.59))
c(t) = Io(2i) e~2t —> - при t —> оо. (13.32)
V47rt
Асимптотическая плотность равна половине плотности при коалесценции
(13.31), поскольку при каждом событии аннигиляции исчезают две частицы, а
при коалесценции только одна. Можно найти поведение на больших временах
из следующего физического аргумента. Случайное блуждание посещает об¬
ласть размером y/Dt за время t. Из-за аннигиляции число частиц, оставшихся
в этой области, должно быть порядка 1 — если бы было больше частиц, они
бы аннигилировали. Поэтому типичное расстояние между частицами имеет
порядок y/Dt, а концентрация обратна этому расстоянию. Заметим, что и в
приближенных аргументах, и в точных результатах асимптотическая плот¬
ность не зависит от начальной плотности.
Главные качественные свойства распределения длин лакун известны бла¬
годаря их связи с распределением длин доменов в модели Изинга-Глаубера
(раздел 8.5, стр. 314). Эти свойства включают: типичная длина лакуны рас¬
тет как f1/2; (ii) плотность малых лакун длины х t1/2 линейно зависит от
х и (iii) плотность больших лакун длины х » t1/2 экспоненциально убывает
с х.
Стационарная аннигиляция
Когда частицы поступают в систему с постоянной интенсивностью, возни¬
кает стационарное состояние, для которого снова можно получить точное
решение. Тонкость заключается в том, что от деталей свойств источника за¬
висит, устанавливается ли в системе в пределе большого времени термодина¬
мическое равновесие или же неравновесное стационарное состояние. Сначала
рассмотрим рождение пар соседних частиц с интенсивностью h, в то время
как с интенсивностью единица происходит реакция А + А -> 0. Из рисунка
13.7(a) видно, что рождение пар соответствует повышающим энергию перево¬
ротам одного спина в эквивалентной модели Изинга-Глаубера. Следователь¬
но, аннигиляция с рождением пар соответствует модели Изинга-Глаубера
при ненулевой температуре, и мы можем использовать известные результаты
для последней, чтобы изучить свойства реакции с источником.
Благодаря соответствию между рождением пар и равновесной спиновой
системой выполняется условие детального равновесия, и мы можем приме¬
нить это условие, чтобы вывести равновесную плотность. Поскольку реакция
13.4 Одновидовые реакции в одном измерении
519
o+ofofo-fo+o ofofofofofo
| | л
ofo f • J • f p-fo
(a) (b)
Рис. 13.7. Эквивалентность (а) между добавлением с интенсивностью h пары со¬
седних частиц и повышающими энергию событиями в модели Изинга-Глаубера
и (Ь) между добавлением с интенсивностью h одной частицы и нелокальными
повышающими энергию событиями в модели Изинга-Глаубера, в которой все
спины справа от частицы переворачиваются
А + А —> 0 происходит с интенсивностью 1, а 0 А + А с интенсивностью
Л, условие детального равновесия принимает вид
1 х Р(..., 1,1,...) = Л, х Р(... ,0,0,...),
где Р(... П£_1, ni+i...) обозначает вероятность конфигурации чисел запол¬
нения {п^}. В тепловом равновесии каждая пара спинов в модели Изинга
независима, и распределение доменных стенок факторизуется в произведение
всех вероятностей отдельных доменных стенок. Поэтому условие детального
равновесия запишется в виде с2 = h(l — с)2, где с плотность доменных
стенок, совпадающая с плотностью частиц. Тогда стационарная плотность
имеет вид
Этот результат очевиден апостериори, потому что соседиие узлы нсскоррели-
рованы. Для таких пар интенсивность притока частиц равна вероятности най¬
ти два свободных узла, умноженной на интенсивность рождения. Аналогич¬
но, интенсивность исчезновения частиц равна вероятности найти два занятых
узла, умноженной на интенсивность аннигиляции. Эти два процесса приво¬
дят к эволюционному уравнению ленгмюровского типа = -2с2 + 2Д(1 — с)2,
равновесное решение которого имеет вид (13.33).
Стационарное состояние имеет совершенно другую структуру, когда с ин¬
тенсивностью h добавляется только одна частица (рис. 13.7(b)). Для одно¬
частичного источника нельзя удовлетворить условие детального равновесия,
520
ДИФФУЗИОННЫЕ РЕАКЦИИ
поскольку отсутствуют процессы, обращающие аннигиляцию и рождение7.
Таким образом, система достигает существенно неравновесного стационарно¬
го состояния. Тем не менее, с помощью формализма Глаубера можно опреде¬
лить свойства этого состояния. Когда единичная частица создается в узле г,
число заполнения щ изменяется с 0 на 1. В эквивалентной модели Изинга-
Глаубера это одночастичное рождение соответствует перевороту всех спинов
справа от i-ого ребра (рис. 13.7(b)), т. е.
. . .Si_i,Si,Si+i,Si+2 • • • —I . . . Si-i, Si, — Si+1, — Si+2 (13.34)
Когда частица рождается в узеле i, где 1 < г < к, произведение gk = SQSk
меняет знак. Поэтому </&(£ +Ai) = —gk(t) с вероятностью hkAt, a gk(t + At) =
gk(t) с вероятностью 1 — (hk)At. Таким образом, скорость изменения корре¬
ляционной функции Gk = (gk) вследствие процесса (13.34) равна — 2hkGk-
Теперь добавим это слагаемое к основному кинетическому уравнению (8.55)
для корреляционной функции модели Изинга-Глаубера, что дает
dGk
dt
—2(1 + kh)Gk + Gk-i + Gfc+i
(13.35)
для к > 1. Граничное условие для этого уравнения есть Gq = 1. В стационар¬
ном состоянии уравнение (13.35) очень похоже на рекуррентные соотношения
для функции Бесселя первого рода8
—Jy{x) = + Jy+i{x). (13.36)
Эту рекурсию можно привести в соответствие с уравнением (13.35), положив
2и/х = 2(1 + kh). Это задает однопараметрическое семейство соотношений,
связывающих (fc, h) с (z/,:/;). Простейший выбор х = l/hnv = k + 1/h дает
парную корреляционную функцию для к > 0:
G‘(ft)=(1з-з7)
В пределе слабого источника, используя асимптотику функции Бесселя, вы¬
раженную через функцию Эйри, Л^ + ал/1/3) ~ (2/z/)1/3Ai(—2Х/Зх) (формула
7Если частица добавляется в уже занятый узел, то по определению аннигиляция про¬
исходит мгновенно, так что результатом будет пустой узел. Однако в интересующем нас
пределе h —> 0 влиянием этого процесса, А —> 0, можно пренебречь.
8Многие из нижеследующих вычислительных шагов почти идентичны шагам, проде¬
ланным в разделе 7.5 для полимерной транслокации, облегченной шаперонами.
13.4 Одновидовые реакции в одном измерении
521
(7.73)), мы записываем плотность частиц в виде
с= id= А
Ai((2/i)V3)
Ai(0)
(13.38)
а раскладывая функцию Эйри при малом h до первого порядка, находим
с-С^/з, с =-2-2/3 = Q)1/3 ^| = 0,459248. (13.39)
Стационарные плотности из (13.39) и (13.33) на первый взгляд противоре¬
чат интуиции. Для маленькой интенсивности h добавление пар дает плот¬
ность, пропорциональную h,1'2, тогда как добавление единичных частиц с
вдвое меньшим количеством добавляемых в единицу времени частиц дает
большую плотность, пропорциональную /11/3. Однако при добавлении пар
эффективная интенсивность перенормируется до нуля, потому что пары со¬
седних частиц с определенностью в конце концов аннигилируют.
Пример 13.6. Убывание корреляций на большом расстоянии. Рассмотрим пре¬
дел к —> оо точного решения (13.37) для парной корреляционной функции.
Вместо того чтобы вычислять асимптотический предел точного решении, про¬
ще иметь дело с уравнением эволюции в асимптотическом режиме. В пределе
к -> оо мы заменяем Gk+i — 2Gk + Gk-i на d2G/dfc2, так что уравнение на
стационарное состояние (13.35) приводится к виду
j^ = 2hkG. (13.40)
Асимптотическое поведение решений этого дифференциального уравнения9 лег¬
ко найти, используя метод ВКБ (см. врезку в разделе 7.5, стр. 281). Решение
имеет вид
Gk ~ ехр[-д/8Л/9 fc3/2] .
Убывание неожиданно быстрое: оно быстрее, чем экспоненциальное убывание в
(8.56), характеризующее равновесную модель Изинга.
В дополнение к точному анализу попробуем понять свойства стационарного
состояния и приближения к нему, пользуясь скейлинговыми аргументами. В
пределе слабого источника реакция с самого начала является доминирую¬
щим механизмом. В конце концов плотность убывает до уровня, когда ин¬
тенсивности реакций и источника соизмеримы. Определим время t* ~ h~P,
9Уравнение (13.40) называется уравнением Эйри.
522
ДИФФУЗИОННЫЕ РЕАКЦИИ
при котором плотность, вначале убывавшая как t-1/2, выходит на постоян¬
ное значение. Эти два предельных поведения объединяются скейлинговым
анзацем
c(h,t)~ha$(hPt),
где
fl/3,
[1/2,
рожд. пар частиц,
рожд. одиночных частиц.
(13.41)
а = <
Чтобы обеспечить убывание со временем по закону с ~ Г-1/2 при t t*, скей¬
линговая функция должна иметь степенной хвост Ф(г) ~ z-1/2 при z —> 0.
Эта зависимость приводит к соотношению между индексами fi = 2а, ко¬
торое уничтожает зависимость от интенсивности источника для достаточно
маленьких времен. Таким образом, мы заключаем, что
fl,
[2/3,
рожд. пар частиц,
рожд. одиночных частиц.
(13.42)
Когда частицы рождаются парами, переход к стационарному состоянию про¬
исходит при t* ~ /i-1, что существенно позже, чем t* ~ /г-2/3 для одноча¬
стичного источника.
Одномерная агрегация
Задачу об агрегации в одном измерении можно решить аналитически, обоб¬
щив метод пустых интервалов. Этот подход применим только к идеализиро¬
ванной ситуации, когда кластеры прыгают с независимыми от массы интен¬
сивностями. Мы также предполагаем, что каждый кластер занимает только
один узел. Когда кластер прыгает в узел, занятый другим кластером, они
немедленно объединяются в больший кластер: А г I *
Необратимая агрегация
Пусть Cfc(t) — это плотность кластеров массы к в момент времени t. Мы бу¬
дем рассматривать начальное условие с&(0) = б^д, в котором каждый узел
вначале занят мономером, так что свойства системы трансляционно инва¬
риантны. Чтобы найти ед,, удобно ввести вероятность того, что полная
масса содержащаяся в п узлах, расположенных друг за другом, равна к. По
построению 22д.>о Qn = 1, а Qn ~ эт0 вероятность того, что в интервале дли¬
ны п не содержится массы. Поэтому совпадает с вероятностью пустого
интервала, введенной в главе 7 для описания явлений адсорбции, Еп = Q3.
13.4 Одновидовые реакции в одном измерении
523
Распределение массы кластеров просто равно вероятности того, что масса к
содержится в интервале длины 1, т. е. Ск = Qi-
Свойство, которое делает агрегацию решаемой, — это то, что вероятности
занятия интервала эволюционируют в соответствии с тем же дискретным
уравнением диффузии, которое описывает плотность лакун при одновидовой
коалесценции . Чтобы записать уравнение для Q*, нам также нужна условная
вероятность того, что п стоящих подряд узлов содержат полную массу
к, а следующий узел не занят. Пользуясь этими условными вероятностями,
можно перечислить процессы, в которых Q* изменяется из-за прыжков на
правой границе (рис. 13.8). Подобный набор вкладов приходит и от левой
>• > » !
I
+ •
• • •
• • •
I I
(а)
(Ь)
Рис. 13.8. Конфигурации, которые вносят вклад в изменения множества состоя¬
ний, в которых интервал длиной п содержит полную массу А:: (а) четыре процесса
прихода в и (Ь) четыре процесса ухода
границы. Интервалы размера п и массы к появляются (-(-) и исчезают (—) со
следующими интенсивностями:
+ Масса в n-интервале меньше к, и кластер прыгает в этот интервал, со¬
здавая в результате кластер массы к. Поэтому масса, содержащаяся в
интервале длины п + 1, должна быть равна к. Интенсивность этого со¬
бытия равна — Qn+il/2- Разность Q отвечает за вероятность того,
что масса к содержится в интервале длины п+1, в котором занят самый
правый узел. Коэффициент 1/2 соответствует прыжку этого последнего
кластера влево с образованием интервала длины п, содержащего мас¬
су к.
524
ДИФФУЗИОННЫЕ РЕАКЦИИ
+ Масса интервала больше к, и кластер в конце интервала выпрыгива¬
ет, так что итоговая масса становится ранной к. Интенсивность этого
события равна [<5^_х - Qn-d/2-
— Масса в интервале равна к, и кластер запрыгивает в него с интенсив¬
ностью -[Q* - Q*+1]/2.
— Масса в интервале равна к, и кластер выпрыгивает из него с интенсив¬
ностью -[Q* - Qn-il/2-
При сложении этих интенсивностей переходов условные вероятности чу¬
десным образом сокращаются! Включая идентичный набор вкладов от левой
границы, находим, что эволюция плотности интервалов с массой к снова опи¬
сывается дискретным уравнением диффузии
^ = Qn+i-^Qn + Qn-i (13.43)
для всех к > 0. Граничное условие имеет вид Qg(£) = 0 для к > 0 (в самом
деле, Eq = Qq = 1), а начальное условие — каждый узел решетки сначала
занят мономером — суть £?^(0) = 8п^. Приятное свойство уравнения (13.43) —
это то, что различные массы не связаны, так что решение для всех к можно
снова получить методом изображений (см. (13.30)), который дает Q^(i) =
[/n_fc(2£) + Jn+fc(2i)]e“2t, где Im — снова модифицированная функция Бесселя
порядка т. Из этого результата находим плотность массы кластеров Ck = Qi,
Cfe(t) = [Ik-i(2t) - IM(2Q]e~2t ~ -^= e-fe2/4t t -> oo. (13.44)
v47Tf3
Забавный постскриптум: плотность массы кластеров содержит решения для
одновидовой коалесценции и одновидовой аннигиляции. Плотность кластеров
любой массы в агрегации идентична плотности кластеров ссоа в коалесценции,
т. е, ссоа = С1+С2+С3 + — Аналогично, если система сначала содержит только
мономеры, плотность кластеров в одновидовой аннигиляции саПп совпадает
с плотностью кластеров нечетной массы при агрегации, и, следовательно,
Сапп = Cl + С3 + С5 +
Требование, чтобы коэффициенты диффузии кластеров не зависели от
массы, Dk = D, принципиально важно для применимости математическо¬
го формализма, представленного выше. Лучшее, что мы можем сделать, —
использовать скейлинговые аргументы, чтобы оценить временную эволюцию
плотности кластеров.
13.4 Одновидовые реакции в одном измерении
525
Пример 13.7. Агрегация с коэффициентом диффузии, зависящим от массы.
В простейшем случае диффузии, не зависящей от массы, диффундирующие ча¬
стицы покрывают интервал длины порядка y/Dt за временной интервал (0,f).
Следовательно, каждый такой интервал содержит в среднем один кластер. По¬
этому средняя масса кластера равна
т ~ y/Dt. (13.45)
Рассмотрим ситуацию, когда коэффициенты диффузии алгебраически зависят
от массы, Dk ~ к~у. Скейлинговая гипотеза характеризует популяцию класте¬
ров типичной массой. Поэтому мы подставляем D = Dm ~ т~у в (13.45), что
дает т ~ t1^2^. Соответственно, плотность кластеров убывает как
с ~ га-1 ~ f“1/(2+IZ). (13.46)
Теперь мы ожидаем, что распределение массы стремится к скейлинговому виду
Ck(t) = с2 F(ck). Однако наши эвристические аргументы, которые приводят к
убыванию плотности (13.46), недостаточны для того, чтобы сделать какие-либо
выводы о перемасштабированной функции распределения масс F.
Агрегация с источником
Что происходит, когда мы добавляем мономеры в систему равномерно в про¬
странстве и с постоянной интенсивностью? Раньше мы нашли, что для посто¬
янного ядра реакции в среднеполевом пределе стационарное распределение
масс есть Ck(t —> оо) ~ /с-3/2 в диапазоне масс 1 к <$С t2 (раздел 5.5).
Опишем соответствующее поведение в одном измерении.
Когда мономеры добавляются в каждый узел с постоянной интенсивно¬
стью h, основные кинетические уравнения для вероятностей пустых интерва¬
лов все еще решаются. Влияние источника на вероятности пустых интервалов
простое: если n-интервал содержит массу к—1 и случается добавление, то про¬
исходит увеличение вероятности заполнения интервала Интенсивность,
с которой масса добавляется в n-интервал равна h п, поскольку добавление
может произойти в любой узел интервала. Аналогично, если интервал со¬
держит массу к, добавление приводит к убыванию с интенсивностью hn.
Поэтому уравнение (13.43) для обобщается следующим образом:
= -2Qk + Qk_, + Qk+1 + hn [q£-x - <?£] . (13.47)
Это уравнение выполняется для всех к > 0 с граничным условием = 0.
Эти уравнения зависят от вероятностей интервалов с различными масса¬
ми и различными длинами. Поэтому их сложнее решать, чем независящие
526
ДИФФУЗИОННЫЕ РЕАКЦИИ
13.2. Случайные речные сети
Агрегация с источником эквивалентна классической случайной речной се¬
ти Шейдеггера (рис. 13.9). В этой модели координата, нисходящая вдоль
реки, эквивалентна времени, а поперечные извилины реки эквивалент¬
ны одномерному случайному блужданию. Слияние двух рек соответству¬
ет агрегации. Площадь речного бассейна (пунктирная линия на рисун¬
ке 13.9) равна потоку через устье реки. Этот поток эквивалентен мас¬
се агрегата на пространственно-временной диаграмме, когда в каждом
узле одномерной решетки осуществляется постоянное добавление массы.
время
пространство
Рис. 13.9. Пространственно-временное представление варианта агрегации с
источником в дискретном времени. Отрезки с наклоном 45° представляют
траектории агрегатов, которые совершают синхронное случайное блуждание
в одном измерении. В речном представлении более широкая река образует¬
ся, когда встречаются два притока. Приток частиц задается массой агрегата,
определенной как площадь соответствующего речного бассейна
Можно использовать эту картинку, чтобы привести эвристические аргументы,
характеризующие распределение массы агрегата. Площадь данного бассейна про¬
порциональна его высоте h, умноженной на ширину. Поскольку траектории гра¬
ниц совершают обыкновенные случайные блуждания, его ширина растет как h1/2,
а площадь — как h3^2. Эта площадь соответствует массе агрегата к. С другой сто¬
роны, h может рассматриваться как время первой встречи двух случайных блуж¬
даний, вероятность которого асимптотически убывает как p(/i) ~ h~3^2. Переходя
от h к fc, получаем распределение массы
ск = P(h) % ~ h~3'2 % ~ к-1 к-1'3 ~ к-*'3, (13.48)
ак ак
которое согласуется с асимптотическим результатом (13.52).
13.4 Одновидовые реакции в одном измерении
527
от массы уравнения в отсутствие источника. Однако ситуация упрощается в
стационарном состоянии. В этом случае мы используем производящую функ¬
цию Qn(z) = ^k>0Qkzk, чтобы превратить уравнение (13.47) в
Qn-i(z) + Qn+i(z) = [2 + hn(l - z)] Qn(z). (13.49)
Если правильно подобрать индекс, эта рекуррентная формула совпадет с
формулой для функций Бесселя (см. (13.36)). Таким образом, следуя тем
же аргументам, которые привели к результату (13.37), получим выражение
для Qn
Jn+l/gQ/я)
Qn(z} —
(13.50)
где д = g(z,h) = h(l — z)^. Нас интересует поведение распределения масс
при больших fc, которое соответствует пределу z -> 1 производящей функ¬
ции. В этой ситуации д <С 1, и мы можем воспользоваться асимптотической
формулой (7.73) для функции Бесселя, которая дает
Qi(z)
Ai{(2g)V3)
Ai(0)
Ai'(0)
Ai(0)
/г1/3 (1 - z)
1/3
(13.51)
~ 1 +
Сингулярное поведение производящей функции, (1 - z)1/3, подразумевает,
что (см. формулу (5.24) во врезке на стр. 174) хвост распределения масс имеет
характер fc“4/3. Точнее, для к 1, получим
Ai'fOl I
Г(—l/3)Ai(0) = 32/3Г(1/3) Ф 179455‘
(13.52)
Полное распределение масс дается формулой (13.50) при п = I, или эквива¬
лентно
Ji+i/gd/d) „ _ /1(1 - г)
Cfc-Ch1/3^4/3,
! + У^ск(гк-1) =
к>1
Jl/дШ ’
(13.53)
Явные результаты легко извлечь в пределе слабого источника. В самом деле,
при h —> 0 правые части в (13.53) и (13.51) совпадают. Поэтому, когда h «С 1,
имеем
fc>l ' '
(13.54)
В отличие от формулы (13.51), которая справедлива в пределе z 1, равен¬
ство (13.54) справедливо для всех z. Используя (13.54) вместе с биномиаль¬
ным тождеством
fc>0
Г(А: - а)
Г(—а)Г(/г + 1)
С =
Я
2
J
528
ДИФФУЗИОННЫЕ РЕАКЦИИ
получим распределение масс
с‘=с'‘1/зЕ^тц2’ (13-м)
с такой же амплитудой С, как в (13.52).
13.5 Реакции с пространственным градиентом
Логистический рост и уравнение ФКПП
Диффузия играет определяющую роль в выборе пути, по которому устойчи¬
вое состояние распространяется в область неустойчивого. Простейший при¬
мер этого типа — уравнение Фишера-Колмогорова-Покровского-Пискуно¬
ва (ФКПП), которое содержит логистический рост (раздел 12.1) и диффузию
яд
— = DV2А + М(1 - А). (13.56)
В этой системе устойчивое состояние соответствует однородной плотности
А = 1, тогда как неустойчивое состояние соответствует пустой системе.
Рис. 13.10. Захват неустойчивой области с плотностью А = 0 устойчивой попу¬
ляцией с А = 1
В более общем случае, когда пространственно однородная система име¬
ет одно устойчивое и одно неустойчивое состояние, поведение реакционно¬
диффузионного уравнения
яд
— = £>V2A + F(A) (13.57)
похоже на поведение уравнения ФКПП. Как мы узнали из предыдущей гла¬
вы, это состояние соответствует неподвижным точкам динамики, где реакци¬
онный член зануляется, F(A) = 0. Неподвижная точка F(A*) = 0 устойчива,
13.5 Реакции с пространственным градиентом
529
если F'(A*) < 0, и неустойчива, если F'(A*) > 0. Для простоты мы берем
неустойчивую неподвижную точку в А = 0 (этого всегда можно добиться
сдвигом переменной Л).
Предположим теперь, что пространственно протяженная система нахо¬
дится в неустойчивом состоянии (Л = 0) везде, за исключением простран¬
ственно локализованной области, где Л > 0. Мы ожидаем, чгго в этой обла¬
сти плотность быстро достигнет устойчивого стационарного состояния. Из-за
диффузии устойчивое состояние будет также вторгаться в пустую область.
Вопрос: как? Типичный ответ на этот вопрос прост: поело короткого переход¬
ного периода образуется бегущая волна, которая распространяется в область
пустоты. Такое распространение удивительно, поскольку диффузия и волны
не имеют ничего общего. Еще более поразительна универсальность 'какого
распространения. Форма области, в которой начальная плотность положи¬
тельна, детали начального условия Ло(гг), точная форма реакционного члена
F(A) не важны. Единственное, что имеет значение для скорости распростра¬
нения, — это коэффициент диффузии и наклон F'(0):
V = 2y/DF'(G}. (13.58)
Хотя результат (13.58) для скорости и связанные с ним свойства были
доказаны только для уравнения ФКПП и небольшого числа, уравнений та¬
кого же типа, нет сомнений в применимости10 этого результата, к общему
реакционно-диффузионному уравнению (13.57). Здесь мы представим эври¬
стический аргумент, обосновывающий (13.58). Начнем с уравнения ФКПП и
перемасштабируем время, t —> kt, и пространство, х —> х \/к/1), чтобы обез-
размерить уравнение (13.57), приведя его к виду
ял
^ = V2A + A(l-A). (13.59)
Рассмотрим режим большого времени, когда бегущая волна уже приняла
стационарную форму, а кривизна фронта стала пренебрежимо мала. Обозна¬
чая координату, нормальную по отношению к фронту, через х и выбирая +ж
вдоль направления распространения фронта, видим, что плотность исчезаю¬
ще мала далеко справа от фронта. В этой области уравнение (13.59) сводится
к линейному уравнению
дА_&А
dt ~ дх2+ ’
10Результат о скорости распространения верен для класса реакционно-диффузионных
уравнений с выпуклым реакционным членом F,z(A)<0 и, вероятно, применим к большему
классу реакционно-диффузионных уравнений.
530
ДИФФУЗИОННЫЕРЕАКЦИИ
для которого естественно искать экспоненциальное решение для бегущей вол¬
ны
A(x,t) ~ (13.61)
Подставляя (13.61) в (13.60), получаем дисперсионное соотношение
v(A)=A + A-1. (13.62)
Таким образом, самое грубое предположение о природе распространения
дает нетривиальное соотношение между скоростью распространения и фор¬
мой волны. Однако уравнение (13.62) неполное, так как мы нашли только,
что скорость зависит от А и удовлетворяет неравенству v > vm[n = 2, где
tynin — это минимальная скорость из дисперсионного соотношения (13.62).
Какая скорость выбирается осталось неопределенным. Однако природа муд¬
ра; для разумных начальных условий выбирается именно v = Здесь
термин «разумные начальные условия» означает начальный профиль, кото¬
рый зануляется за пределами некоторой области.
Можно привести слегка более сильный, хотя все еще эвристический аргу¬
мент в пользу того, какая скорость выбирается. Рассмотрим начальное усло¬
вие
А(х, t = 0) = / Х_Л X<Q' (13.63)
е Ах х > 0,
или любые другие начальные условия, убывающие как е_Лаг, когда х » 1
(имеет значение только поведение хвоста). Естественно, хвост (13.61) бегу¬
щей волны должен удовлетворять начальным условиям. Это действительно
так, если параметр А в обоих уравнениях один и тот же. Следовательно,
для начального условия (13.63) скорость может имеет вид (13.62). Теперь по¬
смотрим на зависимость v = v(A). Когда А возрастает от 0 до 1, скорость
уменьшается. Такое поведение естественно: при росте А хвост становится все
круче, так что система движется дальше от устойчивого состояния. Следова¬
тельно, скорость распространения должна уменьшаться. С другой стороны,
соотношение предсказывает, что когда А возрастает от 1 до оо, скорость так¬
же возрастает. Как мы только что заметили, такая зависимость невозможна.
Поэтому мы заключаем, что для начального условия (13.63) скорость рас¬
пространения равна
v(A) =
А < 1,
А > 1.
(13.64)
13.5 Реакции с пространственным градиентом
531
Обобщение реакционно-диффузионного уравнения (13.57) очевидно, и аналог
формулы (13.64) имеет вид
1 ’ рувг'(о), л > 7Г'(о)/с.
Таким образом, в уравнении ФКПП быстро образуется бегущая волна,
которая распространяется со скоростью vm;n = 2 (для самых естественных
начальных условий). Мы знаем, что далеко впереди фронта профиль плот¬
ности убывает экспоненциально. Чтобы найти весь профиль, подставим анзац
бегущей волны
A(x,t) = А(£), где £ = х — 2t (13.65)
в уравнение ФКПП (13.59) и перепишем его в виде обыкновенного диффе¬
ренциального уравнения
d?A ndA ..
^+2 —+ Л(1-Л)-0.
(13.66)
Явное аналитическое решение этого нелинейного обыкновенного дифферен¬
циального уравнения не было найдено. Однако его легко решить численно, и
в основном мы хорошо понимаем решение для бегущей волны.
Пример 13.8. Обобщенное уравнение Фишера-Колмогорова (ОУФК). Чтобы
продемонстрировать эффективность метода бегущей волны, рассмотрим кажу¬
щееся сложным уравнение в частных производных
дА д2А д*А Л л3
dt ~ дх2 7 dxi+A А
(13.67)
Слагаемое с четвертой производной может быть проинтерпретировано как ги¬
пердиффузия. Заметим также, что (13.67) — это гибрид нестационарного урав¬
нения Гинзбурга-Ландау (9.2) и уравнения Кана-Хилларда (9.6). Численное
интегрирование ОУФК приводит к решению в виде бегущей волны, если коэф¬
фициент гипердиффузии 7 достаточно мал. Попробуем понять эти предсказания
и найти скорость бегущей волны. Мы будем действовать так же, как раньше, и
подставим экспоненциальный хвост (13.61) в (13.67). Это дает дисперсионное
соотношение
v(A) = А — 7А3 + А-1. (13.68)
Скорость v(A) имеет локальный минимум в
А*
1 - 7~1 - 127
67
1/2
(13.69)
532
ДИФФУЗИОННЫЕ РЕАКЦИИ
и, следовательно, для наиболее естественных (т. е. быстро убывающих) началь¬
ных условий начальная скорость распространения равна v* = г>(А*). При написа¬
нии (13.69) мы неявно предполагали, что 7 < 1/12. Для 7 > 1/12 дисперсионные
соотношения (13.68) не имеют минимума. Таким образом, пользуясь простыми
средствами, мы обнаружили радикальное изменение поведения, когда коэффи¬
циент гипердиффузии 7 переходит порог 1/12. Этот прогноз подтверждается
численным моделированием11.
Агрегация с пространственно локализованным источником
Другая формулировка, в которой пространственные градиенты влияют на
кинетику реакций, это агрегация в присутствии пространственно локализо¬
ванного источника, например, постоянного притока мономеров в одной точке.
Уравнения эволюции для распределения кластеров в этой системе имеют вид
= D^2ck + К 52 d Cj - 2KckN + J<5M5(r). (13.70)
i+j=k
Здесь сЦг, f) — это плотность кластеров массы к в точке (г, i). Первое слага¬
емое в правой части уравнения (13.70) описывает перемешивание из-за диф¬
фузии, следующие два слагаемых отвечают за агрегацию с постоянным яд¬
ром, и последнее слагаемое — это приток мономеров в начале координат с
интенсивностью J.
Начнем с изучения эволюции пространственно зависимой плотности мас¬
сы M(r,i) = &Cfc(r, £). Поскольку агрегация сохраняет массу, реакция не
влияет на распределение массы. Плотность массы подчиняется уравнению
диффузии с дополнительным слагаемым, соответствующим источнику
= PV2M + J5(r). (13.71)
Предположим, что источник включается в момент t = 0 в изначально пустой
системе. Тогда распределение массы будет задаваться суперпозицией гауссо-
вого пропагатора от всех источников с t = 0 до настоящего времени:
Jo
dt'
(4TrDt')d/2
,-r2/4Dt'
(13.72)
11Метод бегущей волны ничего не говорит о поведении при 7 > 1/2. Численно фронт
движется неоднородно и создает периодические структуры.
13.5 Реакции с пространственным градиентом
533
Решение уравнения (13.72) в пределе t —> оо и г y/Dt дает плотность массы
(задача 13.5)
{4y/irDt, d = 1,
ln(4P£/r* 2) - 7Е + O(r2/4P£), d = 2, (13.73)
l/г, d = 3,
где = 0,577215 — константа Эйлера. Заметим, что плотность массы дости¬
гает стационарного предела только в пространственной размерности d > 2.
В этой ситуации плотность массы дается просто решением (стационарного)
уравнения Лапласа12.
Далее рассмотрим плотность кластеров N(r, t) = 23fc>i с/-(г, £). Поскольку
мы используем кинетическое уравнение (13.70), справедливое выше критиче¬
ской размерности (dc = 2 в случае агрегации с постоянным ядром), мы неяв¬
но предполагаем, что наше пространство трехмерное. Однако эффективная
размерность может быть больше, если рассматривать следующие геометрии:
• Однородный приток на плоскости х = 0 в d = 3: эффективно
одномерная система;
• Однородный приток вдоль прямой х = у = 0в</ = 3: эффективно
двумерная система;
• Приток в начале координат х = у = z = 0 для d = 3.
Мы также проанализируем что происходит, когда d > 3. Как мы узнали
раньше, такое обобщение помогает взглянуть на результаты под правильным
углом и улучшить понимание физически важной трехмерной системы.
Уравнение эволюции для плотности кластеров получается суммировани¬
ем уравнений (13.70). В пределе t —> оо мы получим реакционно-диффузион¬
ное уравнение
DV2N - KN2 + J5(r) = 0. (13.74)
Здесь мы неявно предположили, что плотность кластеров достигает стаци¬
онарного предела. Эта стационарность не является самоочевидной. Мы ви¬
дели, что плотность массы не стационарна, когда d < 2. В принципе, мы
должны рассмотреть нестационарную версию уравнения (13.74), решить это
уравнение и показать, что его решение стремится к стационарному пределу.
12Эта стационарность отражает важнейшее свойство диффузии: она невозвратна в d>
2, и поэтому частицы не скапливаются в начале координат. Напротив, при d < 2 диффузия
возвратна и плотность около начала координат неограниченно растет, так как частицы,
родившиеся ранее, возвращаются бесконечно часто.
534
ДИФФУЗИОННЫЕ РЕАКЦИИ
Эту процедуру невозможно осуществить для нестационарной версии (13.74)
потому, что это — нелинейное уравнение в частных производных. Поэтому мы
не можем описать 7V(r, t) аналитически, но можем понять его асимптотиче¬
ское поведение, предполагая стационарность и проверяя самосогласованность
апостериори.
Стационарное решение уравнения (13.74) демонстрирует интересную за¬
висимость от размерности пространства. Когда d превосходит верхнюю кри¬
тическую размерность dc (которую мы позже найдем из требования само¬
согласованное™), реакционным членом можно пренебречь, когда он далеко
от источника. Следовательно, когда г —> оо, уравнение (13.74) сводится к
уравнению Лапласа с асимптотическим решением
N -JZ2 при > dC- (13.75а)
Наоборот, когда мы не можем пренебречь реакционным членом в (13.74), мы
используем простой подсчет степеней для определения зависимости плотно¬
сти от г. Записывая V2TV ~ N/r2 ~ 7V2, мы видим, что N ~ г-2. Поэтому
подставляем анзац N = А/г2 в (13.74). Простое вычисление дает асимптоти¬
ческое решение
2D 1
N ~ (4 — d) ——5- при d < dc. (13.75b)
К
Так как зависимости от г для d> dc и для d < dc совпадают в четырех изме¬
рениях, мы заключаем, что верхняя критическая размерность равна dc = 4.
В d = dc = 4 естественно ожидать логарифмических поправок. Поэтому
мы ищем решение (13.74) в виде N = iz/r2, где и = и(р) и р = lnr. Мы ожи¬
даем, что и зануляется, когда р —> оо, поскольку согласно (13.75Ь) амплитуда
стремится к нулю, когда d f dc = 4. В четырех измерениях имеем
V2W
d2N 3 dN
dr2 r dr ’
Теперь подставим N = u(p)/r2 и воспользуемся равенствами
du _ uf d2u _ 2uf u,f
dr r ’ dr2 r2 + r2 ’
где штрих означает дифференцирование по р, чтобы переписать уравнение
(13.74) в виде
-2и' + и"=^и2.
13.5 Реакции с пространственным градиентом
535
Поскольку и —> 0 при р —»• оо, мы предполагаем, что и" г/ и сохраняем
только член и'13. Это дает и' = —Ки2/2D, и поэтому в четырех измерениях
далеко от источника плотность кластеров убывает как
~ 2D 1
— К г2 In г
(13.75с)
Пример 13.9. Плотность кластеров в одном измерении. Умножая уравнение
(13.74) на 2N' и интегрируя от ненулевого значения х до х = оо, получим
D(N')2 - I KN3 = 0, (13.76)
<5
где константа в правой части — это ноль, поскольку N 0 при |ж| —> оо. Инте¬
грируя (13.76), находим
6D
N =-—
К (|ж| + ж0)2’
(13.77)
Чтобы найти константу интегрирования жо, проинтегрируем (13.74) по инфи¬
нитезимальному отрезку (~б, е) вокруг начала координат и рассмотрим предел
б 0. Это дает D [7V'(+0) - N'(—0)] + J = 0, и, используя (13.77), получим
(13.78)
Амплитуда 6D/K в (13.77) согласуется с асимптотическим решением (13.75Ь).
Точное решение (13.77) выходит на асимптотический режим, когда
|ж| ~ жо- В двух и трех измерениях мы ожидаем похожий переход при г ~ го-
Как го зависит от параметров задачи 7?, К, J? К сожалению, чтобы ответить
на этот вопрос, анализа размерностей недостаточно. Например, в трех из¬
мерениях мы могли бы использовать (79/J)1/2 и {K/J}1/3 как независимые
единицы измерения с размерностью длины. Этот трюк оказывается полез¬
ным в данном случае. Руководствуясь видом решения в одном измерении,
будем искать 7V(r) в виде
W) = |/W- (13.79)
Подставляя этот анзац в уравнение (13.74), получим
ту- Т
V2f-f2 + -^6(r) = 0. (13.80)
13Это предположение верно для функций, спадающих медленнее, чем экспоненциально
(например алгебраически). Чтобы добиться самосогласованности, мы должны проверить
неравенство и" <£. и апостериори. В данном случае мы имеем и ~ р~\ и поэтому членом
и” ~ р~3 действительно можно пренебречь в сравнении с и' ~ р~2.
536
ДИФФУЗИОННЫЕ РЕАКЦИИ
Это уравнение показывает, что вместо трех переменных D,K и J решение
зависит от единственной комбинации KJ/D2. Эта комбинация имеет размер¬
ность длины в степени d — 4 и приводит к оценке
/ Г)2 \ 1/(4-<г)
Г0~ Н77 > d<4- (13.81)
Наконец, определим полное число кластеров. В принципе,
N(f) = f N(r,i) £ldrd-1 dr.
Jo
(13.82)
В одном измерении мы используем (в пределе t —> оо) точное стационарное
решение (13.77) и получаем
’И-Ш'
Поэтому в одном измерении полное число кластеров стремится к конечной
величине.
В двух и трех измерениях мы не можем просто подставить стационар¬
ную плотность кластеров в правую часть равенства (13.82), поскольку ин¬
теграл расходится при г —> оо. Однако так как кластеры совершают слу¬
чайные блуждания с (зависимым от массы) коэффициентом диффузии 7?,
плотность кластеров быстро убывает при г » y/Dt. Поэтому, чтобы оценит
полное число кластеров, можно использовать стационарные результаты, но
нужно обрезать интегрирование в y/Dt.
Вдобавок, нужно обрезать нижний предел в гц. Проделав эти шаги, мы
переписываем (13.82) в виде
L)t
N(r) dr.
(13.84)
Используя это выражение вместе с (13.75Ь), находим
X(t) ~ |
'1п(КЛ/Р),
* VDt,
d = 2,
d = 3.
(13.85)
Примечательно, как слабо влияет интенсивность источника на плотность кла¬
стеров и на полное число кластеров в этом процессе агрегации с источником.
13.5 Реакции с пространственным градиентом
537
Неоднородная двухвидовая аннигиляция
Давайте вернемся к базовой двухвидовой реакции аннигиляции из раздела
13.3, но вместо однородной начальной плотности рассмотрим пространствен¬
но разделенные реагенты. В силу их противоположности два вида не могут
сосуществовать, и более физично изучать эту реакцию, когда реагенты вна¬
чале пространственно разделены, а потом сближаются. Здесь мы обсужда¬
ем эту реакцию, в которой две исходно разделенные компоненты реагируют
вдоль плоской границы. Комплементарная ситуация стационарного отклика,
которая возникает, когда два вида непрерывно вводятся в систему из лока¬
лизованных источников, рассматривается в задачах 13.9 и 13.10.
Рассмотрим d-мерную систему, разделенную (d — 1)-мерной гиперплоско¬
стью в х = 0, где частицы вида А сначала случайно распределены в области
х > 0, и аналогично для В в области х < 0. Последующая реакция описыва¬
ется реакционно-диффузионными уравнениями
дсА д2сА
-§r = D~s^- Ксясв’
дсв п д2св „
~at=D~S^~ Кслсе’
где с а = и св = св(х,£) обозначают концентрации каждого вида в
точке х в момент времени t, а К — постоянная реакции. Начальные плотности
равны
/ , п\ f СО, # > 0,
cA(x,t = 0) = t
[0, х < 0
и св(х,Ъ = 0) = cA(—x,t = 0). Основные свойства этой реакции — шири¬
на зоны реакции w и интенсивность производства реагентов. Как мы сейчас
увидим, эти величины могут быть найдены с помощью только анализа раз¬
мерностей.
Для геометрии на рисунке 13.11, когда постоянная реакции К велика,
область с одним видом работает почти как адсорбирующая граница для про¬
тивоположного вида. Поэтому, например, профиль плотности А близок к
профилю плотности независимых диффундирующих частиц в присутствии
адсорбирующей границы в х = 0, а именно, cA(x,t) = cq erf (х / у/4Dt). Из
асимптотики функции ошибок, плотность меняется как c(x,t) ~ CQx/y/4Dt
для 0 < х < y/^Dt. Поэтому размер обедненной зоны равен I y/Dt.
Теперь мы можем оценить ширину зоны реакции w, уравновесив диф¬
фузионный поток в эту зону, J = 2|Р(/| = 2coy/D/t, с интенсивностью ан¬
нигиляции частиц. Из реакционно-диффузионного уравнения (13.86) следу-
538
ДИФФУЗИОННЫЕ РЕАКЦИИ
Рис. 13.11. Схематические профили концентраций (сплошные кривые) и интен¬
сивность реакции Ксдсв (пунктирная линия, показана в сильном увеличении)
в двухвидовой аннигиляции с исходно разделенными компонентами. Ширина
обедненной зоны равна € ~ VDt, тогда как ширина зоны реакции есть w ~ £1/6
ет, что число в единицу времени равно интегралу от К са св по зоне ре¬
акции. Мы оцениваем этот интеграл как квадрат типичной концентрации
в зоне, а именно, сД.т = w,£), умноженный на ширину зоны w. Используя
вид са ~ с$х/у/4£)t для малых ж, получаем полную интенсивность реакции
JCc(w,i)2w ~ KcQW3/(Dt). Приравнивая эту интенсивность и поток съу/Dft,
находим ширину зоны реакции
w ~ (Г^/К2^)1/6
(13.87)
Соответственно, локальная интенсивность производства в зоне реакции
/Cc(w,^)2, стремится к нулю как i-2/3.
Существует множество интересных вариаций этой системы. Например,
когда интенсивность реакции достаточно мала, изначально разделенные ре¬
агенты будут сначала проникать друг в друга на расстояние, которое растет
как y/Dt. В следствие этого реакция будет происходить однородно в этой сме¬
шанной области, что дает начальную интенсивность реакции, которая также
растет как y/Dt до тех пор, пока не установится асимптотическое убыва¬
ние i“2/3. Движение границы может быть также немонотонным во времени,
когда Da > Db, но с ДО) < св(0). На ранних временах доминирует более
быстрая диффузия вида А, и граница движется налево. Однако на больших
временах граница движется вправо, и вид В, находясь в большинстве, подав¬
ляет вид А.
13.6 Ссылки
539
13.6 Ссылки
Одна из выдающихся черт диффузионно-контролируемых реакций — это то,
что пространственная размерность играет ключевую роль в их кинетике. Это
понимание было достигнуто с помощью исследований разнообразных приме¬
ров. Самоизбегающие блуждания описаны в [11, 257]. Свойство, что dc = 1
для реакции трех тел обсуждается в [258, 259]. Аргумент об оптимальных
флуктуациях для определения асимптотики убывания плотности в реакции
с захватом предложен Балагуровым и Баксом [260]; см. также [261]. Эти ра¬
боты показали, что отклонения от теории среднего поля имеют место во всех
пространственных размерностях, хотя время, необходимое, чтобы наблюдать
истинное асимптотическое поведение астрономически велико. Точные асимп¬
тотики для плотности были найдены Донскером и Вараданом [262]. Свой¬
ство, что из всех односвязных множеств фиксированного объема шар дает
наименьшее собственное значение оператора Лапласа-Дирихле известно как
теорема Фабера - Крана, которая была доказана в 1920-х для двух измерений.
Эта теорема описана в [263]. Далее она была обобщена на произвольные раз¬
мерности, и доказательство можно найти в [264].
Аномально медленная кинетика двухвидовой аннигиляции была открыта
Зельдовичем в 1949 году [265]. Тема диффузионно-контролируемых реакций
стала довольно популярной в конце 1970-х вплоть до 1980-х. Примеры важ¬
ных ранних работ — [266, 267]. Некоторые пионерские работы вышли в мало¬
известных советских журналах. К счастью, часть этих работ освещена в [268].
Обзоры эффектов пространственной организации в двухвидовой аннигиля¬
ции представлены в [269, 270]. Строгие результаты по убыванию плотности
в двухвидовой аннигиляции были получены Брамсоном и Лебовицем [271].
Попытки разработать эффективные алгоритмы численного моделирования
реакций имеют долгую историю. Ранняя работа по построению метода пер¬
вого посещения, упомянутого во врезке в разделе 13.3 на странице 514, есть
в [272]. Этот подход был поднят до уровня высокого искусства в [273].
Точные решения процессов с одномерными одновидовыми реакциями об¬
суждаются в обзорной статье в [270]. Точное решение одномерной аннигиля¬
ции в стационарном состоянии и ее связь с кинетической моделью Изинга
представлены Рацем в [274]. Точное решение для распределения массы кла¬
стеров в необратимой агрегации в одном измерении было предложено Спод-
жем [275]. Далее этот подход был развит Томсоном [276] и Такаясу и др. [277]
для описания агрегации со стационарным источником мономеров.
Явления вторжения устойчивой популяции в неустойчивую область были
описаны Колмогоровым и др. [278] и Фишером [279]. Педагогическое введе-
540
ДИФФУЗИОННЫЕ РЕАКЦИИ
ние в этот важный пример дано в книге Мюррея по математической биологии
[235] и в обзоре Саарлоса [280]. Математические аспекты уравнения ФКПП
рассмотрены в [281]. Явление агрегации с локализованным источником мо¬
номеров обсуждается в [282, 283]. Динамика фронта реакции А + В -> 0
обсуждалась в ранней публикации Зельдовича [265] и независимо переоткры-
та Гальфи и Рацем [284]. Стационарная версия этой задачи рассмотрена в
[285].
13.7 Задачи
13.1 Дополните подробностями нахождение вероятности выживания диффундиру¬
ющей частицы на адсорбирующем интервале [0, £]:
(a) Сначала решите уравнение диффузии в одном измерении с граничными
условиями с(0, £) = c(L, f) = 0 и начальным условием с(ж,£ = 0) = S(x —
#o) и таким образом получите концентрацию частиц, данную в (13.9).
(b) Далее, проинтегрировав по всем финальным положениям частиц и усред¬
нив по всем начальным положениям, получите интегральное выражение
для вероятности выживания, данное в (13.11).
13.2 Примените метод Лапласа к интегралу в (13.11) и покажите, что его асимп¬
тотика на большом времени действительно имеет вид (13.12).
13.3 Рассмотрите диффундирующую частицу, которая стартует в центре адсорби¬
рующей сферы а. Используя сферическую симметрию и разделение перемен¬
ных, покажите, что решение радиального уравнения имеет вид (13.17). Вы¬
числите амплитуду Ап. Покажите, что в трех измерениях функцию Бесселя
можно выразить через тригонометрические функции.
13.4 Смоделируйте агрегацию в одном измерении в предположении, что коэффи¬
циент диффузии равен обратной массе кластера, Dk = 1/к, Покажите, что
плотность кластеров убывает как £-1/3, что согласуется с эвристическими ар¬
гументами (13.46) с и = 1.
13.5 Вычислите интеграл в (13.72) и проверьте результаты (13.73).
13.6 Используйте производящую функцию 6(ж, z) = ^2k>i %к Для описания
стационарного предела уравнения (13.70).
(а) Покажите, что
где xq задан в (13.78).
13.7 Задачи
541
(Ь) В положении источника (х = 0) производящая функция принимает вид
6П_
-2
к>1 "■С°
Разложите правую часть и получите
4D Г(Л-2/3)
Cfc(°) =
Кх% Г(1/3)Г(Л + 1)
(с) Покажите, что далеко от источника, |ж| xq,
аЫ = 12D r<fc + i/3) ~ (21\1/3 ,,,^-2/3
к[ ) Krrg |£|3 Г(1/3)Г(Л + 1) \DKJ
13.7 Рассмотрите агрегацию с пространственно локализованным источником. За¬
вершите обсуждение в тексте для произвольной пространственной размерно¬
сти и покажите, что полное число кластеров асимптотически растет следую¬
щим образом:
£, d > 4,
t/ lnt,
^-2)/2?
In £,
N ~ <
d = dc = 4,
2 < d < 4,
cf = cfc = 2,
const, d < 2.
13.8 Исследуйте агрегацию в полупространстве х > 0 с адсорбцией на плоскости
х = 0. (Истинная размерность пространства равна d = 3, так что выполняются
среднеполевые кинетические уравнения.)
(a) Покажите, что плотность кластеров 7V(rr, £) удовлетворяет реакционно¬
диффузионному уравнению из
= DV2N - KN2,
ot
с граничным условием N(x = 0, t) = 0 и начальным условием ЛГ(ж, t =
0) = 1 для х > 0.
(b) Объясните, почему решение должно иметь скейлинговый вид, и что пра¬
вильным скелинговым анзацем будет N(x,t) = (Kt)-1 /(£), где £ =
x/y/Dt.
(c) Покажите, что анзац из (Ь) сводит эволюционные уравнения в частных
производных, а именно реакционно-диффузионные уравнения из пункта
(а), к обыкновенному дифференциальному уравнению
r+|er+/(i-/)=o.
542
ДИФФУЗИОННЫЕ РЕАКЦИИ
(d) Найдите скейлиноговую функцию f численно.
13.9 Рассмотрите двухвидовую аннигиляцию А+В -+ 0 в области [—L, L\ со стаци¬
онарными источниками частиц вида Авх=ЬиВвх= —L. Интенсивности
источников равны. Граничные условия имеют вид:
DcA\x=L = — Dcb\x__l = —J, ^ca\x=-l = D°b\x=l = О’
соответствующий постоянным потокам частиц А в точке х = L и В в точке
х = — L и отражению на противоположных сторонах. Стартуя с реакционно¬
диффузионного уравнения (13.86) в стационарном состоянии с такими гра¬
ничными условиями, примените аргумент, аналогичный аргументу для пере¬
ходного случая, чтобы показать, что ширина зоны реакции равна
/Г2\1/з
w ~ I
\JKJ
13.10 Снова рассмотрите стационарное поведение реакционно-диффузионного урав¬
нения для двухвидовой аннигиляции А + В -+ 0 со стационарным источником
частиц Авх = ЬиВвх = —L.
(a) Рассмотрите комбинации с± = сл ± сд. Покажите, что решение для с_,
удовлетворяющее граничным условиям, есть с-(х) = jx/D.
(b) Используйте результат для с_, чтобы переписать уравнение для с+ в
виде
где штрихи обозначают дифференцирование по ж, и граничные условия
есть: £>с'+ = j вх = L и Dc'+ = —j вх = —L. Покажите, что для большого
потока, определяемого как j > jo = D2/(KL3}, у c+ есть разложение в
ряд Тейлора
= <4У/3 , *2
Со \5) (10)2/3 40 ’
где z = x/xq « 1, = (P2/jK)1/3 и сб = (f/KD}1/3.
(с) Покажите, что концентрация вида, находящегося в меньшинстве вне зо¬
ны реакции, асимптотически выглядит как
ср(ж)/со ~ г-1/4 ехр ( - 2г3/2/3).
Чтобы получить этот результат, подставьте приближение с а — св +
(jx/D} для малых х в стационарное уравнение для Св, получите урав¬
нение Dcfp = ксв(св + jx/D} и найдите приближенное решение этого
уравнения при больших х.
Глава 14
СЛОЖНЫЕ СЕТИ
Равновесное и неравновесное поведение решеточных систем составляет боль¬
шую часть физики твердого тела, статистической физики и пр. Хотя свой¬
ства решетки могут влиять на поведение многочастичных систем, в первую
очередь решетка предоставляет остов, на котором строится физическая си¬
стема. Если, однако, мы хотим изучать динамическую систему на сложной
сети, (рис. 14.1) ее структура становится существенным ингредиентом зада¬
чи. Хотя может показаться, что структура таких сетей имеет статическую
природу, мы покажем, что кинетический подход предоставляет простой путь
к описанию многих свойств сложных сетей.
14.1 Нерешеточные сети
Нерешеточные сети были впервые введены для иллюстрации равновесного
и неравновесного поведения, которое оказывается проще, чем в решеточных
системах. Два особенно полезных примера — это полный граф и дерево Кей¬
ли. Важная черта этих примеров — это то, что коллективное поведение на
этих графах дает среднеполевое приближение коллективного поведения на
решетках., Однако полный граф и деревья Кейли однородны, а чтобы опи¬
сать взаимодействие нейронов в мозге или интернет-трафик между сообщаю¬
щимися интернет-страницами, требуются сети высокой сложности. Если мы
хотим изучать динамику на таких сетях, мы должны полностью задать сеть,
т. е. составить список всех связей между узлами1. Эта задача сложна сама
по себе: структура разнообразных биологических сетей в лучшем случае из¬
вестна лишь приблизительно, а их огромный размер требует значительных
вычислительных ресурсов. В добавок к трудностям при описании структуры
ХВ этой главе мы используем термин «связи» для обозначения ребер.
544
СЛОЖНЫЕ СЕТИ
(а) (Ь)
Рис. 14.1. Примеры сложных сетей: (а) сеть взаимодействия белков, перепеча¬
тано из «Lethality and centrality in protein network», H. Jeong et al., Nature 411,
41 (2011); (b) представление социальной сети старшей школы, перепечатано из
«Race, school integration and friendship segregation in America», J. Moody, Am.J.
Sociol. 107, 679 (2001)
сети, мы обычно хотим рассматривать сложную динамическую систему на
этой сети. Для решения некоторых из этих проблем мы принимаем статфи-
зическое представление о том, что в большой сети мелкие детали вторичны:
если сеть достаточно велика и случайна, ее статистические свойства будут
близки к характеристикам «типичной» сети.
Пример 14.1. Планарный регулярный случайный граф. Рассмотрим сеть, в ко¬
торой каждый узел соединен ровно с z другими узлами и предположим, что сеть
можно положить на плоскость так, чтобы связи не пересекались. В остальном
сеть произвольна. Такие сети называются планарными регулярными случайны¬
ми графами. Существует много таких графов, например, деревья Кейли с ко¬
ординационным числом z и двумерные решетки (которые существуют только
для z = 3,4,6). Эти примеры, однако, очень специфичны и производят ложное
впечатление: типичный планарный регулярный случайный граф имеет размер¬
ность, равную 4, несмотря на то, что граф планарный.
Конечно нужно объяснить, что мы подразумеваем под размерностью. Про¬
стейшее определение множества размерности D основано на том свойстве, что
объем шара радиуса R растет как RD. Поэтому сосчитаем число узлов N(R)
на расстоянии < R от данного узла2. Интересное поведение возникает, когда
2Расстояние между узлами определяется как число связей вдоль кратчайшего пути,
соединяющего эти узлы.
14.1 Нерешеточные сети
545
R 1. Для решеток N ~ R2, так что планарные решетки действительно дву¬
мерны. Для дерева Кейли N ~ (z — 1)я; экспоненциальный рост N с R отражает
(скрытую) бесконечномерную природу дерева Кейли. Для типичного планарного
регулярного случайного графа асимптотическое поведение отличается коренным
образом: N ~ R4, так что его размерность D = 4. Подавляющее большинство
планарных регулярных случайных графов имеют размерность D = 4. Только
некоторые исключительные сети, вероятность которых исчезающе мала, име¬
ют другие размерности. Взаимосвязь между планарностью и присущей ей
размерностью D = 4 приводит к необычному поведению различных взаи¬
модействующих систем, определенных на планарных регулярных случай¬
ных графах. Например, модель Изинга на таких графах демонстрирует
критическое поведение, совершенно не похожее на критическое поведение
модели Изинга на двумерных решетках.
Кроме предположения, что типичная сеть, выбранная случайно из неко¬
торого ансамбля, дает хорошее представление реальной сети, мы принимаем
динамическую точку зрения и пользуемся средствами неравновесной стати¬
стической физики для описания разных геометрических свойств сложных
сетей. На первый взгляд кажется неожиданностью тот факт, что такая точ¬
ка зрения жизнеспособна и пригодна для описания геометрических свойств
сетей, особенно когда сеть статична. Однако при рассмотрении статической
сети как единичной фотографии подходящего эволюционного процесса ди¬
намический подход оказывается применимым и эффективным. Здесь можно
провести полезную параллель с главой 7 об адсробции, где трудновычисли¬
мая финальная плотность покрытия — существенно статическая величина —
была получена гораздо более простым способом как побочный продукт ре¬
шения для зависящей от времени плотности покрытия.
Тем не менее, такая динамическая перспектива не всегда реалистична или
полезна. Например, глобальное ограничение планарности, по-видимому, ис¬
ключает возможность динамического описания регулярных планарных слу¬
чайных графов3. Если мы ослабим требование планарности и регулярности
(например, вместо требования строгой регулярности предположим, что каж¬
дый узел в среднем соединен с z соседями), ситуация коренным образом упро¬
стится. Получившийся случайный граф допускает динамическое описание,
несмотря на его статическое определение.
3 Планарность накладывает ограничения на структуру регулярных случайных графов
в случае когда z больше или равно трем. Для z = 1 и z = 2 планарность автоматически
выполняется, и динамический рассмотрение оказывается возможным (задача 14.1).
546
СЛОЖНЫЕ СЕТИ
14.2 Эволюция случайных графов
Хотя мы в первую очередь будем изучать эволюцию случайных графов,
удобно начать со статического определения. Эволюционирующие случай¬
ные графы в этой картине часто называются графами Эрдеша-Реньи (ЭР)
(рис. 14.2). Существует две общие формулировки этой модели, тесно связан¬
ные между собой. В вероятностной версии вероятность того, что каждая па¬
ра узлов графа, состоящего из N узлов, соединена связью, равна p/N, тд$
О < р < N. Множитель 1/N включен для удобства, поскольку он приводит
к перколяционному переходу при р = 1 (см. ниже). Так как у каждого узла
N — 1 соседей, среднее число связей, присоединенных к узлу, также известное
как степень узла, равно p(N — 1)/7V (и стремится к р при N —> оо). В отли¬
чие от регулярных решеток степень (или координационное число) каждого
узла на графе ЭР не одинакова (как и для всех сложных сетей). Поэтому
распределение степени — это новая характеристика сложных сетей.
Рис. 14.2. Реализация графа ЭР из 13 узлов и 14 связей. Сеть разбита на 4
кластера: один размера 8, один размера 3 и два размера 1. В этом графе есть
один узел степени 5, четыре узла степени 3, четыре узла степени 2, один степени
1 и два узла степени ноль. В кластере размера 3 степень каждого узла равна 2
Альтернативная модель получается, если случайно соединить N(N —1)/2
пар узлов с помощью фиксированного числа связей L. Соответственно, доля
соединенных пар равна 2L/(N(N — 1)). Приравнивая это отношение к p/N,
получим, что в пределе TV, L —> оо граф с фиксированным числом связей —
это почти то же самое, что и вероятностный граф ЭР с р = 2L/N.
Хотя построение графа ЭР элементарно, его геометрические свойства уди¬
вительно богаты. Вероятно, самая интересная его особенность — существо¬
вание перколяционного перехода, когда значение р проходит через критиче¬
ское значение рс = 1, при котором вид распределения кластеров кардинально
меняется. Кластер определяется как максимальное множество узлов, соеди¬
14.2 Эволюция СЛУЧАЙНЫХ ГРАФОВ
547
ненных связями, так что граф состоит из объединения непересекающихся
кластеров (рис. 14.2). При р < рс кластеры малы и древовидны. При р > рс
существует «гигантский» кластер, содержащий ненулевую долю всех узлов.
При р = рс распределение размера кластеров алгебраически убывает с ростом
размера. Многие из этих свойств были выявлены с помощью вероятностного
подхода. В данном разделе мы представляем альтернативный кинетический
подход к прояснению структуры графа ЭР.
Кинетическая формулировка
Чтобы представить граф ЭР как кинетическую задачу, мы начнем с N изо¬
лированных узлов и будем вводить связи одну за другой между случайно
выбранными парами узлов. Эти два узла могут быть одним и тем же узлом,
а также более одной связи может быть создано между одной парой узлов.
Однако при N —> оо эти два процесса имеют исчезающе малую вероятность,
и ими можно пренебречь4. Для удобства положим интенсивность, с которой
вводятся связи, равной N/2. Следовательно, общее число связей ко времени t
будет 7VY/2, так что средняя степень NL/2 равна t. Поэтому средняя степень
растет со скоростью 1.
Сначала найдем распределение степени узлов в графе ЭР. Удобно рабо¬
тать с нормированным распределением степени пь, определяемым как доля
узлов степени к. Узлы степени к создаются с интенсивностью 1 при добавле¬
нии связи, которая присоединяется к узлу степени к — 1. Аналогично, узлы
степени к исчезают (они становятся узлами степени А;+1) с интенсивностью 1,
связываясь с другими узлами. Поэтому распределение степени удовлетворяет
уравнению
(14-1)
Это уравнение будет применимо для всех к > 0 при наложении дополнитель¬
ного условия п-i = 0. Для начального условия п&(0) = 5^о, соответствующе¬
го N изначально изолированным узлам, решение уравнения (14.1) является
распределение Пуассона (см. задачу 14.2)
tk -t
Пк=йе
(14-2)
Из этого решения мы находим, что средняя степень действительно равна
4Ниже дадим описание образования циклов, в котором возможность возникновения
множественных связей и петель будет учитываться.
548
СЛОЖНЫЕ СЕТИ
Теперь исследуем временную эволюцию распределения размеров класте¬
ров, в котором можно будет увидеть перколяционный переход на графе ЭР.
Вначале сеть состоит из N изолированных одноузельных кластеров. По мере
того как в систему вводятся связи, кластеры могут только сливаться, так
что число кластеров систематически убывает, а их средний размер растет.
Вероятность того, что два несвязанных кластера размеров i и j объединятся,
образовав новый кластер размера к = i + j, равна (iCi/N) х (J Cj/N}\ здесь
Cj — полное число кластеров размера j. Следуя тому же самому рецепту,
который привел нас к уравнению (5.34) в разделе 5.2, получим основное ки¬
нетическое уравнение для плотности Ck(t) = Ck(t)/N кластеров с к узлов в
момент времени t
1
dt 2
22 icijcj-kck-
i+j=k
(14.3)
Это уравнение совпадает с уравнением для распределения масс кластеров в
агрегации с мультипликативным ядром. Поскольку сеть стартует с изолиро¬
ванных узлов, начальные условия имеют вид Cfc(O) = 5*.д. Из уравнения (5.44)
получим распределение размера кластеров
Cfc(t) =
кк~2
к\
tk-i e-kt
(14.4)
Теперь мы используем этот основной результат, а также несколько других
важных результатов из раздела 5.2, чтобы описать множество геометриче¬
ских свойств графа ЭР.
Перколяционный переход
Первое главное следствие уравнения (14.4) — это переход, происходящий,
когда значение t проходит через 1. Применяя формулу Стирлинга к этому
уравнению, получаем асимптотическое поведение сд, (см. также уравнение
(5-45))
Cfc(f) ~
1 — k(t—lnt—1)
fc5/2
1 e-fc(l-t)2/2
л/27г А:5/2
(14.5)
при t f 1. При t < 1 распределение размера кластеров убывает экспонен¬
циально с к, так что средний размер кластера конечен. Естественно было
бы записать средний размер кластера как к°к- Однако по построению эта
сумма равна полной плотности массы, которая равна единице. Более инфор¬
мативная мера среднего размера кластеров — второй момент М2 = к2Ск-
14.2 Эволюция СЛУЧАЙНЫХ ГРАФОВ
549
При t = 1 распределение размера кластеров имеет степенной хвост с показа¬
телем —5/2, и это означает, что в бесконечной сети средний размер кластера
расходится. Поэтому при t = 1 происходит перколяционный переход.
Сингулярное поведение бесконечного графа ЭР вблизи перколяционного
перехода лучше всего описывать, изучая несколько первых моментов распре¬
деления размера кластеров Мп = knCk- Важно понимать (см. раздел 5.3 и
особенно обсуждение на стр. 178), что эта сумма не содержит вклада гигант¬
ской компоненты, или, на более неформальном языке, бесконечного кластера
тогда, когда он существует. Для нулевого момента имеем
[ 1 - */2, t < 1,
Мо = < 1 - t/2 + 2(< - 1)3/3 + ..., t ф 1, (14.6)
(е е , t —оо.
Отличительный признак перколяционного перехода определяется долей геля
g = 1—Mi, а именно, долей узлов, входящих в гигантский кластер. Эволюция
доли геля неявно задается соотношением g = 1 — e~9t (уравнение (5.47)), а
предельное поведение доли геля имеет следующий характер
9= <
О,
2(£ - 1) - 8(£ - 1)2/3 +
—2t
t < 1,
Ц1,
t, —> OO.
(14-7)
Наконец, для начальных условий М2(0) = 1 второй момент задается выра¬
жением
f(l-t)-1,
1(est —t)-1,
M2(t) =
t< 1,
t > 1.
(14.8)
Таким образом, при t = 1 в бесконечном графе ЭР образуется бесконечный
кластер. Когда значение t растет, уходя далеко за перколяционную точку,
средний размер остальных конечных кластеров стремится к единице.
Поскольку обычно изучается большой но конечный граф ЭР, конечно¬
размерный скейлинг является неотъемлемой частью описания перколяцион¬
ного перехода. Чтобы ощутить роль эффектов конечного объема, сначала
определим размер М* максимального кластера в конечном эволюционирую¬
щем случайном графе. Этот размер можно оценить, воспользовавшись экс¬
тремальным критерием (см. врезку на стр. 22)
N 22 ск = 1, (14.9)
k>M*
550
СЛОЖНЫЕ СЕТИ
который утверждает, что будет существовать единственный кластер разме¬
ра > М*. Используя асимптотическое выражение для Cfc(t) из уравнения
(14.5) и аппроксимируя сумму интегралом, получаем из асимптотического
критерия, что
{kiN/(l — t)2, t<l,
N2/3, t = 1, (14.10)
gN, t > 1.
Для конечной сети сумма для среднего размера кластера должна быть обре¬
зана на размере наибольшего кластера М*, так что вблизи точки перколяци-
онного перехода имеем
/>М*
М2 ~ к2ск ~ / к2 к~5/2 dk ~ ~ я1/3-
к<М* d
Для конечного графа ЭР выражение М2 = (1 — t)-1 для среднего размера
кластера в бесконечной сети обрезается, когда он становится порядка IV1/3.
Соответственно, точка острого перехода размазывается, что приводит к су¬
ществованию критического режима, также известного как скейлинговое окно,
которое определяется соотношением
|1 -t| ~ IV-1/3. (14.11)
Кроме перколяционного перехода, в котором рождается гигантский кластер,
существует второй переход при более позднем времени t\, отделяющий ре¬
жим, когда граф состоит из многих кластеров, от режима, в котором вся
сеть становится связной, объединяясь в единый кластер. Таким образом, в
момент ti гигантский кластер поглощает всю сеть, и конечных кластеров
больше не остается. С помощью критерия NMo(ti) ~ 1 и уравнения (14.6)
находим, что ti а In N.
Геометрические свойства
Геометрические свойства большого графа ЭР можно понять, исходя из ло¬
гических следствий кинетической формулировки и пользуясь вероятностны¬
ми аргументами. Сначала рассмотрим режим ниже перколяционного порога.
Поскольку при t < 1 существует порядка N маленьких кластеров (уравне¬
ние (14.6)), типична ситуация, когда новая связь добавляется между двумя
несвязанными кластерами, а не между двумя узлами одного и того же кла¬
стера. Следовательно, подавляющее большинство кластеров — деревья.
14.2 Эволюция СЛУЧАЙНЫХ ГРАФОВ
551
Выше перколяционного порога размер самого большого кластера равен
gN, а размер второго по величине кластера убывает по такому же экспонен¬
циальному закону, как размер самого большого кластера ниже точки перко-
ляции (см. уравнение (14.10)). Поэтому размер второго по величине кластера
ведет себя как (t — l)“2lnTV. Сразу выше порога перколяции, когда средняя
степень узлов р больше (но порядка) единицы, структура графа ЭР — это,
грубо говоря, структура ветвящегося дерева. Можно воспользоваться этой
картиной, чтобы получить простую оценку диаметра сети. Для р > 1 произ¬
вольный узел связан в среднем с р узлами первого поколения. Каждый узел
первого поколения связан с р— 1 узлами второго поколения, и т. д., а каждый
узел поколения (к — 1) связан с р — 1 узлами поколения к. Из-за того, что
p/N 1, вероятность образования замкнутых петель имеет порядок 1/N в
первых поколениях этого ветвящегося дерева. Поэтому диаметр сети возрас¬
тает на единицу при каждом добавлении нового поколения. Однако, когда
общее число узлов р(р — 1)к в дереве из к поколений становится порядка TV,
новые поколения должны приводить к образованию петель и рост диаметра
в этот момент останавливается. Поэтому диаметр графа ЭР имеет порядок
In TV/In р. Такая логарифмическая зависимость диаметра от N — свойство,
присущее многим сложным сетям.
Благодаря длинным связям, которые не могут появиться при перколя¬
ции на регулярных решетках, граф ЭР демонстрирует некоторые необычные
свойства. Вероятно, самое выдающееся из них — существование последова¬
тельности порогов, на которых исчезают все кластеры данного конечного
размера. Начнем с нахождения точки, где больше не могут существовать мо¬
номеры. Из выражения для q в уравнении (14.4) следует, что полное число
мономеров Ci имеет вид С± = Ne~f‘. Поэтому типичный единичный мономер
живет до момента t± = In TV, такого же, как найденное ранее время, когда сеть
становится полностью связной. Таким же образом число fc-меров Ск = Nek
сначала возрастает, а позже убывает обратно до 1, когда In TV. Поэтому
существует ряд пороговых времен, равных tk — % In TV, при которых исчезает
последний fc-мер. Во временном интервале (t'2,ii) сеть содержит гигантскую
компоненту и изолированные узлы (мономеры). Таким образом, мономеры —
последний тип маленьких компонент, который исчезает в сети.
Циклы
В общем случае различают три типа кластеров: деревья, унициклические и
сложные кластеры. По определению дерево не содержит замкнутых путей
(циклов), унициклические кластеры содержат единственный цикл, а слож¬
552
СЛОЖНЫЕ СЕТИ
ный кластер содержит минимум два цикла. Альтернативно, можно описать
эти типы кластеров, пользуясь понятием эйлеровой характеристики. Для гра¬
фа эйлерова характеристика определяется как полное число связей минус
полное число узлов. Эйлерова характеристика любого дерева равна —1. Для
унициклического кластера эйлерова характеристика равна 0. Сложный кла¬
стер имеет положительную эйлерову характеристику. Например, граф на ри¬
сунке 14.2 содержит два дерева (изолированных узла), один унициклический
кластер размера 3 и сложный кластер размера 8 (эйлерова характеристика
которого равна 11 — 8 = 3).
Граф ЭР стартует с N изолированных узлов, т. е. с N деревьев размера
1. Добавление связи между двумя деревьями порождает большее дерево. На
начальной стадии эволюции случайный граф представляет собой лес, т. е. все
кластеры — деревья. В конце концов, связь добавляется внутри дерева, и это
дерево становится унициклической компонентой. Добавление связи между
деревом и унициклическим кластером дает унициклический кластер, тогда
как связь между унициклическими кластерами порождает сложный кластер.
Может показаться, что классификация, основанная на выделении деревьев,
унициклических и сложных кластеров, недостаточна, поскольку возникнет
целый спектр кластеров разной сложности. Вместо этого мы должны были
бы рассматривать сложные кластеры более детально и классифицировать их
соответственно их эйлеровой характеристике. Замечательно, что для боль¬
ших сетей (N —> оо) в такой детальности нет необходимости, так как суще¬
ствует максимум один сложный кластер. Более точно:
• ниже перколяционного порога есть макроскопическое число (~ N) де¬
ревьев и конечное число (флуктуирующее от реализации к реализации)
ацикличных кластеров;
• выше перколяционного порога ситуация такая же, как ниже порога, за
исключением того, что существует единственный сложный кластер —
гигантская компонента.
Найдем интенсивность, с которой возникают кластеры данного типа. Для
деревьев эта интенсивность пропорциональна N-1 х АГ2, где АГ-1 — интенсив¬
ность добавления связи к узлу, а АГ2 учитывает число пар деревьев. Уницик-
лические кластеры образуются с интенсивностью, пропорциональной АГ-1 х
АГ, поскольку они возникают при добавлении связи внутри дерева. Кластеры
сложности 1 образуются с интенсивностью АГ-1, и поэтому число сложных
кластеров стремится к нулю в пределе АГ —> оо. Единственное исключение из
этого правила — гигантская компонента, которая сложна из-за постоянного
14.2 Эволюция СЛУЧАЙНЫХ ГРАФОВ
553
добавления новых связей внутри нее. Отсюда мы заключаем, что не суще¬
ствует сложных кластеров, кроме гигантской компоненты. Мы также видим,
что среди Ск кластеров размера к все являются деревьями, кроме конечного
числа Uk унициклических кластеров.
В принципе и Ск, и Uk — случайные величины, которые флуктуируют от
реализации к реализации. Однако мы знаем, что С к ~ N, тогда как Uk ~ 1.
Из такого скейлинга следует, что флуктуации первой величины относительно
малы
Ск = Nck + у/N£*., (14.12)
где Ск — это детерминистическая плотность, удовлетворяющая кинетическо¬
му уравнению (14.3). Эволюцию случайных величин £& можно в принципе
проанализировать, воспользовавшись техникой, описанной в главе 12. Однако
это технически сложно, и, если флуктуации малы по сравнению со средним,
такие вычисления мало что добавят.
Поскольку число унициклических кластеров конечно, эта величина силь¬
но отличается для разных реализаций сети, так что ее среднее Uk = (Uk) несет
в себе мало информации. К сожалению, найти распределение Pk(Uk) — труд¬
ная задача. Более того, распределения одной переменной Pk(Uk) не особенно
полезны, так как величины Uk сильно скоррелированы ((UiUj) (Ui)(Uj)).
Следовательно, подходящей характеристикой является вероятность чисел
унициклических кластеров всех размеров, т. е., P(U,t), где U = {C/fc}-
Несмотря на обсуждаемые выше трудности, определим средние числа Uk
унициклических кластеров всех размеров. Их уравнения эволюции имеют вид
(сравните с уравнением (14.3))
1
2
duk
dt
k2Ck + iuijcj - кик-
i+j=k
(14.13)
Первый член справа описывает образование унициклического кластера при
добавлении связи внутри дерева5. Следующие два члена отвечают за слияние
двух разных кластеров, один из которых ацикличен. Перед тем как решать
уравнение (14.13), сначала определим среднее число унициклических компо¬
нент U = ^ик в золевой фазе (t < tg = 1). Суммируя уравнения (14.13) и
используя (14.8), получим
dU
dt
1
2(1 ~tV
(14.14)
5Напомним, что в соответствии с нашим определением узел может быть связан с самим
собой, а два узла могут быть связаны более чем одной связью (таким образом образуя
мультиграф).
554
СЛОЖНЫЕ СЕТИ
откуда имеем
ад==11пг^- (14-15)
Полное число унициклических компонент остается конечным в золевой фазе
и расходится на пороге перколяции. В конечной системе перколяционная точ¬
ка уширяется, образуя скейлинговое окно (14.11), где l — t~ TV-1/3. Поэтому
в критическом режиме полное число унициклических кластеров расходится
логарифмически
Ug = j InJV. (14.16)
Естественный путь решения уравнений для Uk — переписать бесконечный
набор уравнений (14.13) в виде дифференциального уравнения в частных
производных — стратегия, которая оказалась особенно эффективной при ре¬
шении уравнений для агрегации в главе 5. Здесь мы используем немного ви¬
доизмененный метод, который позволяет найти решение с меньшими трудо¬
затратами. Чтобы извлечь общую зависимость от времени, решим уравнение
(14.13) для нескольких первых fe, при условии 7/^(0) = 0. Находим
Ul = -te\ u2 = -t2e2t, u3 = —t6e6t и т. д.,
откуда видим, что Uk ~ tk e~kt. Следовательно, мы можем искать решение в
виде6 * *kuk(t) = ^Aktke~kt. (14.17)
Подставляя (14.14) и (14.17) в (14.13), получим
kk „-J-1
Л‘ = Г + £ <14 *-18>
i+j=k
Это рекуррентное соотношение можно решить, записав его в виде обык¬
новенного дифференциального уравнения7 * * * для производящей функции
6Так как величина кик входит в правую часть уравнения (14.13), естественно записать
анзац (14.17) для кик-
7Это обыкновенное дифференциальное уравнение проще решать, чем дифференциаль¬
ное уравнение в частных производных для производящей функции ^,Uk(t) ekz. Трюк, со¬
стоящий в выделении временной зависимости, применим к многим другим примерам, рас¬
смотренным в этой книге. Например, для распределения размера кластеров cjt(t) в эво¬
люционирующем случайном графе легко догадаться, что Ск ~ £fc_1 e~kl. Тогда зависимый
от к коэффициент, а, следовательно, и полное решение (14.4) находится с несколько мень¬
шими усилиями, чем с помощью оригинального решения, основанного на производящей
функции. Недостаток этого метода в том, что он применим только в случае специальных
начальных условий.
14.2 Эволюция СЛУЧАЙНЫХ ГРАФОВ
555
Л (г) = ^A^ekz. С помощью этого метода получим коэффициенты А^ =
52o<n<fc-i (задача 14.4), так что
(14.19)
0<п</с—1
В пределе больших к эта сумма стремится к ^у/тг/{2к) (задача 14.5). Таким
образом, имеем
Uk(t) ~ ^к е~^ к L (14-20)
Точно в точке перколяции среднее число унициклических кластеров размера
к меняется как
= S (14.21)
0<n<fc—1
Благодаря большим флуктуациям Uk их средние дают мало информации о
циклах. Однако методы, которыми мы воспользовались, несут важную веро¬
ятностную информацию. Посмотрим на одно такое свойство вероятность
того, что существует определенное число циклов.
Пример 14.2. Отсутствие циклов. Какова вероятность яо(£), что система не
содержит циклов вплоть до времени t? Достаточно ответить на этот вопрос в
предгелевом режиме, так как в гигантской компоненте они определенно есть.
Согласно уравнению (14.14) скорость образования циклов равна ./ = . Так
как образование циклов — это случайный процесс, вероятность их отсутствия
подчиняется уравнению
dsp
dt
= —Jsq
(14.22)
с начальным условием $о(О) = 1. Решение имеет вид .ч()(А) = \/1 - £ при t < 1.
В точке перколяции мы оцениваем вероятность отсутствии циклов, используя
ширину критической области TV-1/3 для |1 — £| (уравнепие(14.11)). Поэтому ве¬
роятность отсутствия циклов равна so ~ л/TV-1/3 = TV-1/6.
Аналогично можно вычислить вероятность sn(t) наличия ровно п ацикли¬
ческих кластеров. Учитывая, что образование циклов — случайный процесс,
запишем для вероятностей sn(t)
dsn т/ \
— J\$п—1 Sn)-
556
СЛОЖНЫЕ СЕТИ
Решая это уравнение с начальным условием sn(0) = <5п,о> находим, что реше¬
ние дается распределением Пуассона
Sn. —
(1 — f)1/2
ni
1, 1
21пГТ7
(14.23)
14.3 Случайные рекурсивные деревья
Характерным показательным примером растущих сетей являются случай¬
ные рекурсивные деревья (СРД). В этой сети узлы добавляются по одному и
каждый новый узел присоединяется к единственному «целевому» узлу, вы¬
бранному случайно из уже существующих узлов. Из-за условия, что каждый
новый узел присоединяется к единственному узлу, получающаяся сеть имеет
структуру дерева8. Это свойство сильно упрощает анализ системы. Таким
образом, рост СРД подчиняется следующим правилам (см. также рис. 14.3):
1. Выбираем один узел из СРД — целевой узел — с однородной вероятно¬
стью.
2. Добавляем один узел, который связывается с целевым узлом.
Стартуя с начального состояния, которое состоит из единственного узла, по¬
вторяем эти два шага, пока сеть не достигнет заданного количества узлов N.
СРД — это особенно полезная модель, так как можно без особых усилий
найти многие ее геометрические свойства. Более того, существует множество
физически обоснованных путей обобщения СРД, ведущих к более богатой
структуре сети.
Распределение степени
Основная локальная характеристика СРД, как и любой сложной сети, это
ее распределение степени. Сначала мы кратко изложим шаги, необходимые
для вывода точного распределения степени (см. также задачу 14.7), а по¬
том обратимся к асимптотическому анализу распределения степени в пре¬
деле больших N. Состояние степеней любой сети характеризуется вектором
N = {Ni,N2, ■..}, где Nk обозначает число узлов степени к. В случае СРД
8Если новый узел соединяется с более чем одним узлом из существовавших ранее, то
могут образовываться замкнутые петли. По сравнению с растущим деревом распределение
степени в такой сети меняется слабо, тогда как на другие свойства, такие как диаметр,
присутствие петель оказывает существенное влияние.
14.3 Случайные рекурсивные деревья
557
(МЛ2)->(^,Л2 + 1),
(14.24)
Рис. 14.3. Несколько первых шагов эволюции случайного рекурсивного дерева
вектор состояния сети N эволюционирует при добавлении узла следующим
образом:
присоединение
к узлу степени 1:
присоединение
к узлу степени к > 1
Хотя можно в принципе написать уравнение эволюции для полного рас¬
пределения вероятности P(N), это уравнение дает «слишком много» инфор¬
мации. Чаще всего нас интересует среднее число узлов заданной степени (Nk)
(распределение степени) или иногда двухточечная корреляционная функция
(NiNj). Здесь угловые скобки обозначают усреднение по всем возможным
историям сети. Как мы сейчас увидим, метод основного кинетического урав¬
нения идеально подходит для нахождения этих величин.
Как видно из уравнения (14.24), узлы степени 1 и узлы степени боль¬
ше чем 1 нужно рассматривать отдельно. Число Ni(N) узлов степени 1 есть
случайная переменная, которая после добавления каждого узла меняется со¬
гласно следующим правилам:
N±(N) с вероятностью Ni/N,
Ni(N) + l с вероятностью 1 — N±/N,
а именно, с вероятностью N±/N новый узел присоединяется к узлу степени
1, и число таких узлов не меняется. В противном случае с вероятностью
1 — Ni/N новый узел присоединяется к узлу степени больше чем 1 и YVi
возрастает на 1. Таким образом, уравнение эволюции для среднего числа
4
М(АГ + 1)
558
СЛОЖНЫЕ СЕТИ
узлов степени 1 будет иметь вид
<M(7V + 1)> = (М(АГ) х + ((ВД +1) х (l -
= l+(l-l)<M(AT)>. (14.26)
Это уравнение можно решить и найти среднее число узлов степени 1. Для
N > 2 ответом будет
<М(АГ)> = у + ]7^1. (14.27)
Этот результат можно получить с помощью метода производящих функций
(задача 14.7) и непосредственно проверить прямой подстановкой в уравнение
(14.26).
Похожее рассуждение показывает, что при добавлении нового узла число
узлов Nk = Nk(N) степени к > 2 эволюционирует как
1^-1
7Vfc(W + l) = Ы + 1
(Ль
с вероятностью Nk /N,
с вероятностью Nk-i/N, (14.28)
с вероятностью 1 — (Nk-i + Nk)/N.
Проследовав по тому же пути, который привел нас к уравнению (14.26), по¬
лучаем уравнение для эволюции (Nk}
(Nk(N + l}} = (Nk(N}} +
Nk-i(N) - Nk(N}
N
(14.29)
Уравнение (14.29) также можно решить, что дает точное распределение сте¬
пени для конечных сетей (задача 14.7).
Далее мы ограничимся более простым рассмотрением ведущего порядка
распределения в пределе N —> оо. Чтобы минимизировать нагромождение
обозначений, мы опускаем угловые скобки и используем обозначение Nk для
среднего числа узлов степени к в сети, состоящей из N узлов. Далее в уравне¬
ниях (14.29) и (14.29) заменим дискретные разности производными, так что
асимптотическое распределение степени будет эволюционировать следующим
образом:
dNk Nk-i-Nk , г
In = —N— + {н
Это уравнение похоже на уравнение (14.1) для графа ЭР с точностью до
дополнительного члена с дельта-функцией, который отвечает за добавление
14.3 Случайные рекурсивные деревья
559
нового узла степени 1. Чтобы получить представление о виде решения, по¬
пробуем решать уравнения (14.30) одно за другим. Уравнение для TVi имеет
вид dNi/dN = — Ni/N + 1, и решение М = N/2. Тогда уравнение для N2
есть dN2/dN = (TVi — N2)/N с решением N2 = 7V/4. Продолжая таким же
образом, видим что все Nk пропорциональны N. Поэтому удобно работать
с плотностью узлов пк = Nk/N степени fc, в терминах которой уравнение
(14.30) сведется к
пк = пк-\ -пк + 5к1. (14.31)
Стартуя с по = 0, получим щ = j, П2 = | и т. д., а общее решение есть
пк = 2~к. Из этого распределения видим, что средняя степень равна (fc) = 2,
тогда как максимальная степень fcmax, которая следует из экстремального
критерия = 1 (см. врезку на стр 22), равна fcmax — In TV/In 2.
Поскольку распределение степеней в СРД быстро убывает с ростом fc, даже
максимальная степень в некотором смысле мала.
Переброс
Теперь мы обобщим СРД, включив механизм переброса. Главный мотив для
такого построения — то, что переброс неожиданно приводит к линейному пре¬
ференционному присоединению, фундаментальному механизму роста слож¬
ных сетей, который будет подробно обсуждаться в следующем разделе9. С
перебросом сеть строится с помощью многократного последовательного вы¬
полнения следующих шагов (рис. 14.4):
1. Случайно выбираем узел х с равной вероятностью из всех ранее суще¬
ствовавших узлов сети.
2. С вероятностью 1 — г новый узел п присоединяется к х.
3. С вероятностью г узел п присоединяется к узлу у, предшественнику
узла х10.
9 Поскольку добавление каждого узла требует выполнения только двух элементарных
инструкций, переброс предоставляет эффективный способ моделирования очень большой
сети, растущей посредством преференционного присоединения.
10Здесь есть техническая тонкость, так как переброс требует, чтобы у каждого узла
был предшественник. Чтобы обеспечить выполнение этого условия, начальное состояние
должно состоять по меньшей мере из двух узлов и одной связи. При этом каждый узел
считается предшественником другого.
560
СЛОЖНЫЕ СЕТИ
Рис. 14.4. Изображение переброса. Интенсивность, с которой происходит при¬
соединение к предшественнику у узла х при перебросе, пропорциональна числу
узлов предшествующих у (темных)
Из-за переброса распределение степени теперь ведет себя в соответствии с
уравнением
dNk
dN
1—г
“ N
= я
JVfc_x - 7Vfc] + Skl + £ [(fe - 2)7Vfc_x -(к- l)7Vfc]
к - 1 + (| - 2)] Nk-i - [fc + (A - 2)] Nk} + §kl,
(14.32)
где вторая строчка получается в результате простой перегруппировки слага¬
емых. Первые три слагаемых в первой строке соответствуют СРД, эволюци¬
онное уравнение которого воспроизводится для вероятности переброса г = 0.
Два последних слагаемых отвечают за изменение из-за переброса. Чтобы
понять, откуда они берутся, рассмотрим член прихода. Поскольку начальный
узел выбирается из всех узлов равновероятно, если переброс осуществляется,
вероятность того, что узел степени к — 1 получит переброшенную связь, про¬
порциональна числу предшествующих ей соседей (темные узлы на рис. 14.4),
которое равно к — 2. Такой же аргумент применяется к соответствующим
перебросу членам ухода. Такое однородное присоединение в сочетании с пе¬
ребросом приводит к линейному преференционному присоединению, так как
интенсивность, с которой новый узел присоединяется к существующему узлу
степени fc, есть линейная функция к, Ак = к + (| — 2). В следующем разде¬
ле мы исследуем сеть с преференционным присоединением систематическим
методом, из которого немедленно следует распределение степени.
14.3 Случайные рекурсивные деревья
561
Генеалогическое дерево и диаметр
Показательное свойство СРД — его генеалогия. Чтобы задать генеалогию,
поместим начальный узел в поколение д = 0. Узлы, соединенные с узлами
поколения 5, образуют поколение д + 1 независимо от того, когда именно
произошло присоединение во время роста сети. Например, в финальной сети
на рис. 14.3 (воспроизведенной на рис. 14.5) узел 1 — предшественник узла
2, а узлы 3 и 7 — потомки узла 2. В поколении д = 1 пять узлов, а в д = 2 —
три, что приводит к генеалогии, показанной рисунке 14.5 справа.
Рис. 14.5. Случайное рекурсивное дерево из девяти узлов (с рис. 14.3) и соот¬
ветствующее генеалогическое дерево
Сколько поколений содержится в дереве с N узлами? Каков размер Lg(N)
поколения д? Чтобы ответить на эти вопросы, заметим, что Lg(N) возраста¬
ет на 1, когда новый узел соединяется с узлом из поколения д — 1. Когда
новый узел соединяется с любым из существовавших ранее узлов равноверо¬
ятно, присоединение к поколению д — 1 происходит с вероятностью Lg-i/N.
Следовательно, Lg эволюционирует согласно уравнению
dLg ^д—1
~dN = “лГ’
решение которого имеет вид Ьд(т) = т9/д\, где т = In N. Применив формулу
Стирлинга, получим, что Lg(N) сначала растет с д при д < т, а потом убывает
и становится порядка 1 при д = ет. Поэтому генеалогическое дерево, соот¬
ветствующее дереву из N узлов, содержит е т поколений. Поскольку диаметр
равен двум расстояниям от корня генеалогического дерева до последнего по¬
коления (а также максимальному расстоянию между любой парой узлов), он
ведет себя как 2ет ~2е InN.
562
СЛОЖНЫЕ СЕТИ
14.4 Преференционное присоединение
При преференционном присоединении интенсивность с которой узлы при¬
соединяются к существовавшим ранее узлам степени fc, — возрастающая
функция fc. Смысл этого правила может быть выражен фразой: «Богатые
становятся богаче». Например, в контексте научного цитирования преферен¬
ционное присоединение соответствует тому, что публикации с высокой цити-
руемостью будут хорошо цитироваться и в будущем только потому, что они
хорошо цитируются сейчас. Характерная черта преференционного присоеди¬
нения — распределения степеней узлов в сетях, построенных таким образом,
имеют широкий хвост. Это свойство идет вразрез с традиционными моделями
сетей, таких как граф ЭР, обсуждавшийся в разделе 14.2, который характе¬
ризуется гораздо более крутым пуассоновским распределением степеней.
Основное кинетическое уравнение
Эволюция распределения степеней для сети, рост которой определяется ин¬
тенсивностью присоединения описывается уравнением (сравните с урав¬
нением (14.30) для СРД)
dNk _ Ak-jNk-i - AkNk
dN — A
+ 5ki-
(14.34)
Первое слагаемое справа отвечает за новый узел, соединяющийся с узлом,
у которого уже есть fc — 1 связь, таким образом увеличивая Nk на еди¬
ницу. Поскольку существует Nk-i узлов степени fc — 1, полная интенсив¬
ность, с которой происходят такие процессы пропорциональна Ak-iNk-i-
Член A(N) = AjNj в числителе обеспечивает правильную нормиров¬
ку. Второй член играет соответствующую роль. Полная амплитуда Ak не
важна, поскольку в кинетическое уравнение входит только отношение Ak/A.
Последнее слагаемое отвечает за добавление нового узла, который имеет одну
исходящую связь и не имеет входящих связей. Чтобы найти распределение
степени в таких сетях, нужно задать интенсивность присоединения Мы
рассмотрим общий случай Ak = fc7, где 7 > 0. Совершенно разное поведе¬
ние возникает для сублинейной (7 < 1), суперлинейной (7 > 1) и линейной
(7 = 1) интенсивности присоединения.
Моменты и распределение степеней
В качестве первого шага к распределению степени изучим моменты Ma(N} =
Как обсуждалось в разделе 5.2 (см. стр. 168), тот же самый предва¬
14.4 Преференционное присоединение
563
рительный шаг оказывается исключительно полезным при изучении кинети¬
ки агрегации. Зависимость нулевого и первого моментов этого распределения
от N имеет простой вид:
<£Л4о dNj dMi . dNj
~dN=^~dN= ’ ~dN = ~dN =
3 3
(14.35)
Уравнение для Mq говорит нам, что полное число узлов всех степеней возрас¬
тает на 1 каждый раз, когда добавляется новый узел. Аналогично, уравнение
для М± показывает, что полная степень сети увеличивается на 2 при
добавлении одной связи. Поэтому и первый и второй моменты распределения
степени растут линейно с N. Для интенсивности присоединения Ak = &7, где
О < 7 < 1, полная интенсивность А = 22jj7Nj также рас/гет линейно с АГ,
14.1. Линейные, логарифмические и оптимальные алгорит¬
мы
Как на практике конструируется сеть с преференционным присоединением? Для
линейного преференционного присоединения вероятность присоединении нового
узла к узлу а степени ка имеет вид ка/^р кр. Поэтому нам нужен метод выбора
узла а с такой вероятностью. Существует три естественных возможности:
Линейный алгоритм: Сначала задаем последовательность кумулятивных ве¬
роятностей {Pm}, где Pm = Zl<Q<m^> ГДв Ш = 1,2, . . . ,/V (ilO OI1 рСДСЛО!IИЮ
Pn = 1). Далее выбираем случайное число г, равномерно распределенное на от¬
резке [0,1]. Наконец, линейно просканировав последовательность Рт, присоеди¬
няемся к узлу, удовлетворяющему условиям г > Р1П и г < / ш , i ■
Логарифмический алгоритм: Посвященные алгоритмам курсы, преподаваемые
при обучении компьютерным специальностям, учат нас, что линейный поиск по
списку достаточно неэффективен. Было разработано множество методов, позво¬
ляющих производить поиск по списку за время, растущее? как логарифм его дли¬
ны. Например, когда мы ищем номер в телефонной книге, мы неявно производим
логарифмический поиск. При поиске аивиакомпании «Юнайтед Эйрлайнс» мы
сначала ищем страницу с буквой «Ю», далее страницу содержащую «Юн», по¬
том «Юна» и т. д., пока не окажемся на нужной странице?. Этот метод позволяет
найти целевой узел за время, растущее линейно с размером се?ти.
Оптимальный алгоритм: При использовании алгоритма переброса из предыду¬
щего раздела, число операций, требуемых для нахождения целевого узла порядка
единицы, независимо от размера сети. Такой 0(1)-поиск эквивалентен тому, как
если бы в любой телефонной книге мы немедленно находили бы запись «Юнайтед
Эйрлайнс», неважно в маленькой деревне или в Нью-Йорке.
поскольку А находится между первым и вторым моментом. Таким образом,
асимптотически А ~ /j,N с пока не определенной амплитудой ц, гладко меня¬
ющейся от 1 до 2, когда 7 растет от 0 до 1 (задача 14.6).
564
СЛОЖНЫЕ СЕТИ
После нахождения нескольких первых Nk из уравнения (14.34) становится
ясно, что Nk также пропорционально N (задача 14.10). Поэтому после под¬
становки Nk(N) = nkN и А ~ fiN в основное уравнение, общая зависимость
от N исчезает, и мы приходим к рекуррентным соотношениям
Пк =
Ак-гПк-i - АкПк
Д
П1 — h 1,
м
формальное решение которых имеет вид
-1
(14.36)
к > 1
и
Чтобы это решение было явным, нам нужно найти амплитуду р в A(N) = pN.
Пользуясь определением р = Ylj>i Ajnj и (14.36), получаем
(14.37)
Таким образом, амплитуда р в общем случае зависит от функциональной
формы интенсивности присоединения. Уравнения (14.36) и (14.37) дают фор¬
мальное решение для распределения вероятности степени в сетях с преферен¬
ционным присоединением. Чтобы понять физический смысл этого решения,
исследуем его асимптотическое поведение при различных значениях 7 в ин¬
тенсивности присоединения.
Пример 14.3. Сублинейная интенсивность присоединения. Аля. Ак = fc7, где
7 < 1, перепишем произведение в уравнении (14.36) в виде экспоненты суммы,
заменим сумму интегралом, а потом разложим логарифм под интегралом в ряд
Тейлора. Эти очевидные шаги приводят нас к выражениям
'к 7 ехр [-д . j < Т' <
/j(m2-1)/2 еХр |_2цу/к] ,
(14.38)
7=1
fc-^exD fcl—1 I<-7<1
eXP [ Д 1_7 2 1-27 J ’ 3 2’
и т. д. Каждый раз, когда при уменьшении значения 7 оно проходит через 1/т,
где т — целое число, в экспоненте появляется дополнительное слагаемое, кото¬
рое является возрастающей функцией к. Тем не менее, ведущая асимптотика —
это универсальное убывание по растянутой экспоненте, ехр(—const. х fc1”7), то¬
гда как все остальные члены дают малые поправки.
14.4 Преференционное присоединение
565
Рис. 14.6. Создание «Библии», при котором каждый новый узел соединяется
только с «Библией» (темным узлом)
Пример 14.4. Суперлинейная интенсивность присоединения. Для 7 > 1 про¬
исходит аналог гелеобразования, когда почти все связи конденсируются на од¬
ной вершине. Для 7 > 2 наблюдается ультрасингулярное поведение, в котором
с ненулевой вероятностью существует «Библия» — один узел, который связан
со всеми остальными узлами бесконечной сети, тогда как между другими уз¬
лами есть лишь конечное число связей. Для нахождения вероятности возник¬
новения «Библии» предположим, что «Библия» существует в сети из N + 1
узлов (рис. 14.6). Действуя по индукции, видим, что вероятность присоедине¬
ния к «Библии» следующего узла равна Ny/(N + TV7), а вероятность того,
что такая структура связей будет продолжаться до бесконечности имеет вид
Т = Пдг>1 (1 + 2V1-7)-1. Применение такого же асимптотического анализа как
тот, что использовался для сублинейной интенсивности присоединения, приво¬
дит нас к следующему асимптотическому поведению этого произведения
? = О при 7 < 2;
Т > 0 при 7 > 2.
Таким образом, при 7 > 2 есть ненулевая вероятность возникновения «Библии»
в бесконечной сети.
Когда 1 < 7 < 2, картина связей для узлов маленькой степени менее триви¬
альна, чем на рис. 14.6, но единственный узел, связанный с почти всеми узлами,
продолжает существовать. Когда 7 проходит через т/(т — 1), где т — целое
больше двух, также наблюдается бесконечная серия точек переходов, в которых
число узлов со степенями к < т растет как TV*-^”1)7, тогда как число узлов
большей степени остается конечным, когда N стремится к бесконечности.
Пример 14.5. Линейная интенсивность присоединения. Мы различаем строго
линейное присоединение Ак = к и асимптотически линейное присоединение. В
566
СЛОЖНЫЕ СЕТИ
первом случае полная интенсивность событий равна А = AkNk = kNk —
2N. Подставляя это значение д = 2 в уравнение (14.36), немедленно приходим к
дискретному степенному закону
4 4Г(Л)
Пк~ к(к + 1)(к + 2) ~ Г(Л + 3)’ >
где Г — гамма-функция Эйлера. Поскольку это распределение не содержит ха¬
рактерного масштаба степени, такие сети были названы безмасштабными. Такие
распределения обычно противопоставляются дельта-функциональному распре¬
делению степеней регулярных решеток и пуассоновскому распределению графа
ЭР.
При асимптотически линейном присоединении неожиданностью является то,
что распределение степени неуниверсально. Эта неуниверсальность находится в
противоречии с общепринятым в статистической физике убеждением о том, что
отсутствие характерного масштаба при фазовых переходах приводит к универ¬
сальному степенному скейлинговому поведению. Легко показать неуниверсаль¬
ность распределения степеней для асимптотически линейных интенсивностей
присоединения Ак ~ к. В этом случае уравнение (14.36) принимает вид
Пк
м
~ -г ехр
к
-ЛИ)18
(14.40)
Поэтому показатель распределения степеней может принимать любое значение
большее 2 в результате простой подстройки амплитуды в полной интенсивности
А ~ pN. Некоторые специальные примеры асимптотически линейных интенсив¬
ностей присоединения приводятся в задачах 14.11-14.15.
14.5 Флуктуации в сетях
При исследовании сетей, которые образуются в результате процесса роста, мы
неявно подразумеваем, что экстенсивные11 характеристики таких сетей при¬
мерно одинаковы. Это предположение не может в точности выполняться, но
оно верно по сути. Например, в эволюционирующем случайном графе число
11 Экстенсивные величины растут линейно с размером системы. Стандартный пример —
энергия системы с близкодействием. (Рост быстрее линейного возникает когда есть дально¬
действие. Например, гравитационная энергия системы массы М растет как М2/R ~ М5^3.)
14.5 Флуктуации в сетях
567
кластеров данного размера — самоусредняемая величина, т. е. ее относитель¬
ные флуктуации исчезают, когда размер системы стремится к бесконечно¬
сти (см. уравнение (14.12)). Проверка сомоусредняемости данной величины
может оказаться сложной задачей. Еще более сложно исследовать природу
флуктуаций даже в тех случаях, когда величина действительно самоусред-
няется. Проиллюстрируем возможное поведение экстенсивных характеристик
на примере двух различных процессов роста сетей.
Случайные рекурсивные деревья
Исследуем поведение общего числа Ni(N) узлов степени один (такие узлы
часто называют листьями или висящими концами). Среднее число листьев —
это экстенсивная величина. Согласно уравнению 14.31 каждый второй узел
в СРД — лист, т. е. (TVi) ~ N/2. Подробное описание случайной величины
Ni(N) дает распределение вероятности P(Ni,N). Если TVi самоусредняется,
распределение вероятности P(TVi,TV) будет иметь острый пик в окрестности
TVi = N/2 и быстро убывать, когда TVi удаляется от N/2. Хотя найти P(Ni,N)
сложно, поведение на хвостах для крайних случаев Ni = N — 1 (звезда) и
N± = 2 (линейная цепочка) можно легко просчитать.
Какова вероятность §jv = P(N — 1, TV) образовать звезду? Для начальных
условий с одним узлом СРД точно является звездой до TV = 3. Для больших
СРД эта вероятность находится из рекуррентного соотношения
Stv+i =
которое обеспечивает присоединение всех узлов к центру звезды. Таким об¬
разом, Syy = 2/(TV — 1)! при TV > 3. Аналогично, при TV > 2 вероятность
£>n = P(2,TV) того, что процесс роста СРД приводит к линейной цепочке,
удовлетворяет рекуррентному соотношению
&N+1 =
Следовательно, £>n = 2n~2/(N — 1)! при TV > 3. Таким образом, для TV > 3
предельные значения распределения вероятностей P(TVi, TV) даются выраже¬
ниями
P(TVi,TV)
1/(TV-1)!,
2^-2/(TV-l)!,
звезда (TVi = TV — 1),
линейная цепочка (TVi = 2).
(14.41)
Вероятности образования этих двух экстремальных деревьев быстро убывают
с ростом размера сети.
568
СЛОЖНЫЕ СЕТИ
Хотя мы ничего не доказали, две вещи, которые мы узнали: число ли¬
стьев Ni — экстенсивная величина, и вероятности того, что Ni принимает
экстремальные значения, очень быстро убывают с увеличением размера си¬
стемы — говорят, что флуктуации Ni малы. Более смелое предположение —
что флуктуации гауссовы. А именно, их амплитуда растет как y/N, так что
дисперсия растет линейно с N
a2(JV) = - (М(АГ))2 ~ N
и асимптотическая форма также гауссова
21
(14.42а)
Р(М,АГ)~
а/27ГСГ2
ехр
(М ~ W)
2<т2
(14.42Ъ)
Этот тип поведения необыкновенно устойчив и возникает далеко за предела¬
ми применимости центральной предельной теоремы.
Чтобы проверить справедливость предположения о гауссовости, сначала
попробуем аналитически подтвердить уравнение (14.42а). Извлекая квадрат¬
ный корень из уравнения (14.25) и усредняя, получаем
W(N + 1)> = (l _ A) <JVf (^)) + (2 - A) <7Vi{JV)> + 1. (14.43)
Проще работать с дисперсией <г2(АГ) = (АГ2(АГ)) — (АГх(АГ))2. Воспользовав¬
шись уравнением (14.26), получим
a\N + 1) = (l - -^) a\N) + 1 (N^N)) - ± (М(АГ))2. (14.44)
Далее подставим результат для в (14.44), что превратит это урав¬
нение в разрешимое рекуррентное соотношение. Однако точное решение
этого соотношения громоздко, и поскольку мы главным образом интере¬
суемся асимптотическим поведением, рассмотрим предел N -> оо. Тогда
-> 1/2, и мы можем применить непрерывное приближение,
чтобы свести разностное уравнение (14.44) к дифференциальному
da2 2 сг2 1
dN = ~“FT + 4’
решение которого имеет вид сг2 = 7V/12.
Чтобы показать, что распределение флуктуаций гауссово, применим раз¬
ложение по малым флуктуациям, которое уже применялось в разделе 12.3.
14.5 Флуктуации в сетях
569
Этот анализ довольно громоздок, но идея проста: мы просто переписываем
правила роста (14.25) через распределение вероятности P(Ni,N),
P(Nlt N + 1) = P(Nlt N) + (l - P(M - 1 ,N), (14.46)
и затем применяем непрерывный подход, который позволяет использовать
ряд Тейлора
Р(М,АГ + 1) = Р(М,Я) + ^Р(М,АГ) + 1^Р(М,ЛГ) + ...,
Р(М - 1,7V) = Р(МЛ) ~Р(МЛ) +1 Р(МЛ) + • • •
Теперь заменим переменные (JVi,7V) на (г/, 7V), где
V = Nx - (14.47)
В важной области вокруг пика распределения имеем // y/N, и поэтому
мы удерживаем вторую производную д2/dv2» которая имеет порядок d/dN,
но опускаем d2/dvdN ~ TV-3/2, d2/dN2 ~ TV-2 и остальные более высокие
производные . В результате этих шагов уравнение (14.46) запишется в виде
дифференциального уравнения в частных производных
ЭП _ 1 — — 1 д2д
dN ~ N П + N ди + 8 ди2
(14.48)
для П(р, N) = Р(р + 2V/2, N). Опыт работы с уравнением диффузии предпо¬
лагает, что решение можно искать как функцию единственной скейлинговой
переменной г/ = и/y/N, т. е.
П(1/,ЛГ) = -^=Ф(т7),
(14.49)
где коэффициент 7V-1/2 обеспечивает нормировку f dvH(v,N) = 1. Подста¬
вив (14.49) в (14.48), получим обыкновенное дифференциальное уравнение с
решением Ф(т/) = д/б/л е~&т> (задача 14.17). Таким образом, мы проверили
распределение Гаусса (14.42Ь) с дисперсией а2 = N/12.
Сеть друзей
Здесь мы рассмотрим обобщение СРД, в котором каждый новый узел со¬
единяется с целевым узлом, а также пытается соединиться с его соседями
570
СЛОЖНЫЕ СЕТИ
(«друзьями»)12. На каждом временном шаге добавляется новый узел, кото¬
рый соединяется с целевым узлом, выбранным случайно среди уже суще¬
ствующих узлов. Далее, с вероятностью р новый узел также соединяется с
со всеми соседями целевого узла13. Поэтому эта модель дружбы или копи¬
рования зависит от единственного параметра, вероятности копирования р.
Простейшая глобальная характеристика — число связей Ln. В отличие от
СРД, где Lpi детерминировано (Ln = N —1),в модели копирования величина
Ln — случайная переменная. Попробуем вычислить ее среднее L(N) = (Ln)
и дисперсию cr2(JV) = (L^-) — [L(7V)]2. Добавление нового узла увеличивает
полное число связей в среднем на 1 +р(к), где (к} = 2L(N)/N — это средняя
степень узлов в сети. Поэтому среднее полное число связей эволюционирует
следующим образом:
L(N + l) = L(N) + l + 2p^p-. (14.50)
В рамках непрерывного подхода (N » 1) разностное уравнение (14.50)
становится дифференциальным
^=1+24 <14-51>
Для СРД (р = 0) имеем L = N — 1, и мы ожидаем, что для достаточно
малых р будет наблюдаться экстенсивное поведение L ~ N. Подставляя эту
линейную зависимость в уравнение (14.51), находим L = (1 — 2p)_17V. Таким
образом, экстенсивное поведение сохраняется для р < 1/2. В пограничном
случае р = 1/2 решение уравнения (14.51) приобретает логарифмический
множитель, тогда как для р > 1/2 число связей растет быстрее чем линейно14:
f(l-2p)-17V, р < 1/2,
Ь(ЛГ) ~ < N InJV, р = 1/2, (14.52)
[л(р)ЛГ2Р, 1/2<р<1.
12Копирование — ключевой механизм роста всемирной паутины (World-Wide Web), сети
цитирования и других социальных, технологических и информационных сетей. Копирова¬
ние также наблюдается в природе: например, дупликация генов, которая играет важней¬
шую роль в эволюции, в большой степени основана на копировании.
13Вариант, демонстрирующий качественно похожее поведение, — соединяться с каждым
соседом независимо с одной и той же вероятностью р.
14Непрерывный подход дает правильную зависимость от N и правильную амплитуду
для р < 1/2. Для р > 1/2 непрерывный подход дает только показатель степени L ~ N2p,
а для определения амплитуды А(р) нужно решать точные рекуррентные соотношения
(14.50).
14.5 Флуктуации в сетях
571
Важный результат, следующий отсюда, состоит в том, что при р < |, средняя
степень узлов в сети остается конечной при N —> оо, или, эквивалентно, число
связей — экстенсивная переменная. Такие сети называются разреженными.
Наоборот, для р> 1/2 мы получаем плотную сеть, в которой средняя степень
узла расходится при N —> оо.
Теперь вычислим дисперсию числа связей. По построению новый узел
присоединяется к случайно выбранному целевому узлу и либо ко всем его
соседям, либо ни к кому из них. Это значит, что
м,
1°>
Ln+i = Ln + 1 +
probability р,
probability 1 — р,
(14.53)
где к — степень целевого узла. Возведя в квадрат и усреднив, получим
— p((Ln + 1 + fc)2) + (1 — p)((Ln + l)2)
= ((Lw + l)2) + 2p(Ljvfc) + 2p(fe) + p(fc2). (14.54)
Нам известно, что (fc) = <2.L(N)/N, тогда как (L^k) = (Lp/^k) /N. Однако
(53 fc) = так что получаем (L^k) = 2(L^)/JV. Таким образом, уравнение
(14.54) принимает вид
(ln+i) - (l + -jf) (ln) + 2 (l + L(N) + l+p(fc2).
Вычтя из этого уравнения квадрат уравнения (14.50), получим
a\N + 1) = (l + ^) a2(N) + p(fc2) - p2(fc)2. (14.55)
В непрерывном приближении уравнение (14.50) превращается в диффе¬
ренциальное уравнение
da2 4р 2 2
решение которого дает
а2 ~ P(fc2)-P2(fc)2
1 — 4р
р < 1/4.
(14.56)
При 1/4 < р < 1 находим, что рост быстрее линейного15
а2 ~ TV4p.
(14.57)
15 Плюс логарифмические поправки при р=1/4ир=1/2.
572
СЛОЖНЫЕ СЕТИ
При р > 1/2 среднее число связей и его стандартное отклонение растет так
же, L ~ а ~ N2p. Таким образом, плотные сети, которые строятся с помощью
копирования, сильно флуктуируют от реализации к реализации.
Пример 14.6. Урновая схема. Рассмотрим модель копирования с р = 1, т. е.
новый узел выбирает целевой узел и соединяется с ним и всеми его соседями.
Предположим, что сначала сеть содержит два несвязанных узла16. Получивша¬
яся сеть будет всегда состоять из двух несвязанных между собой полных графов,
например, размеров А и В, где А+В = N. Какова доля узлов А/(А+В) в одном
из этих графов? Примечательно, что в каждой реализации эта доля достигает
предельной случайной величины, которая однородно распределена между еди¬
ницей и нулем17.
Чтобы понять, откуда берется этот результат, обозначим через On долю узлов
в одном из подграфов и исследуем ее эволюцию как функцию размера сети
N. Сначала 02 = 1/2. На следующем шаге $з = 1/3 или 0з = 2/3 с равной
вероятностью. Далее имеем РгоЬ(04 = 1/4) = Prob(04 = 2/4) = Prob(04 = 3/4) =
1/3. В общем случае Prob(0/v = j/N) = (N — I)-1 для всех j = 1,... ,7V — 1.
В данной реализации доля On флуктуирует все меньше и меньше, по мере того
как N возрастает, и в конце концов останавливается на некоторой предельной
величине. Однако предельная величина совершенно непредсказуема, а именно
она однородно распределена в интервале (0,1). Самые первые шаги — самые
важные, так как они фиксируют начальные флуктуации. Это яркий пример
отсутствия самоусреднения.
14.6 Ссылки
Сети, воспроизведенные на рис. 14.1, появились в [286, 287]. Теория графов и
сложных сетей различных типов долго изучалась математиками. Литерату¬
ра, посвященная планарным регулярным случайным графам, необъятна, так
как они связаны с многими разделами математики и физики, такими как ком¬
бинаторика, случайные матрицы, упрощенные модели из теории струн. Хоро¬
шей стартовой точкой послужит обзорная статья [288] и книга [289]. Статья
Эрдеша и Реньи [290] по случайным графам предоставляет математическую
мотивировку для исследований этого неожиданно богатого предмета. Самая
16Если начальная сеть содержит только один узел, то получившаяся сеть будет полным
графом.
17 Эта модель известна как урновая схема Эггенбергера-Пойа: начинаем с двух шаров
разного цвета в урне; достаем один шар наугад и кладем его назад вместе с еще одним
шаром такого же цвета.
14.7 Задачи
573
захватывающая черта случайного графа — это рождение гигантской ком¬
поненты, происходящее, когда плотность превышает критическое значение.
Хороший анализ этого явления дан в обзорной статье [291]. Два полезных
текста по случайным графам содержатся в [292, 293]. Построение со скейлин¬
говым окном было развито в [294]. Разнообразные геометрические свойства
случайных графов обсуждаются в [295] с кинетической точки зрения.
Ранняя работа об основных геометрических свойствах случайных рекур¬
сивных деревьев — [296], а обзор этого предмета дан в [297]. «Зачатки» префе¬
ренционного присоединения можно обнаружить в работе Йуле о распределе¬
нии видового разнообразия [298]. Вероятно, саман первая работа собственно
по сетям с преференционным присоединением — работа Саймона [299]. Этот
класс сетей приобрел значительную популярность после того, как было об¬
наружено, что такие сети воспроизводят многие свойства технологических
и реальных биологических сетей. Обзор этой работы дан в [300], тогда как
недавние монографии по этому предмету включают в себя [301-304]. Подход
к нахождению распределения степеней и связанных с ним геометрических
свойств, основанный на кинетических уравнениях, был развит в [305]. Более
подробно о влиянии конечного размера на структуру сети можно узнать из
[306, 307].
14.7 Задачи
14.1 Покажите, что регулярный случайный граф с z = 1 и г = 2 можно определить
динамически, и условие планарности автоматически соблюдается. Для z = 1
граф — это набор димеров, а для z = 2 граф — это набор петель. Покажи¬
те, что для z = 1 финальное число компонент равно 7V/2, а для z = 2 оно
логарифмически растет с размером системы.
14.2 Решите уравнение эволюции (14.1) для распределения степени узлов графа
ЭР с начальным условием rik(t = 0) = 5к,о и покажите, что решение дает¬
ся формулой (14.2). Попробуйте использовать разные методы (прямое — шаг
за шагом — решение уравнений по одному, метод преобразования Лапласа,
техника производящих функций).
14.3 Выведите уравнения эволюции моментов U± = и ^2 = 53fc>i к2 Uk и
решите их. Покажите, что в золевой фазе
t п _ t(l+t)
2(1—t)2’ 2 2(1 —t)4*
14.4 Найдите решение рекуррентных соотношений (14.18). Один из методов — ис¬
пользовать производящие функции:
574
СЛОЖНЫЕ СЕТИ
(a) Пользуясь экспоненциальными производящими функциями
к>1 к>1
перепишите рекуррентные соотношения (14.18) в виде дифференциаль¬
ного уравнения
(b) Производящая функция 3C(z) заключает в себе распределение размера
кластеров в точке перколяции. Пользуясь результатами из главы 5, по¬
кажите, что ЗС e_IK = ez. Используя это выражение вместе с полученным
дифференциальным уравнением, покажите, что А = (1 — 3€)“2ЗС.
(c) Примените метод инверсии Лагранжа для вычисления
14.5 Найдите асимптотическое поведение суммы 23o<n<fc-i^n 1/п- ПРИ больших
fc. Вот один из возможных способов:
(а) Заметим, что последний член суммы самый большой. Это позволяет
предположить, что нужно поменять порядок суммирования, записав сум¬
му в виде
кк~2 S, 5 11 fc~1 I (fc-W-2) | (fc-l)(fc-2)(fc-3) |
(fc-1)!
k2
k3
(b) Для вычисления S покажите, что в пределе больших к можно восполь¬
зоваться непрерывным приближением, которое дает
+ 1)
Jo
dj ехр
21
2fc
= у/як/2.
(с) Сочетая (а) и (Ь) и пользуясь формулой Стирлинга fc! ~ (к/е)ку/2тгк,
покажите, что
ул &71-1 _ кк-' кк ПГ _ ек
п'- ~ fc! 5 ~ fc! V 2к ~ 2к
Q<n<k-1 ’
и выведите из этого результата формулу (14.21).
14.6 Покажите, что для большого, но конечного эволюционирующего случайного
графа вероятность sn(N) иметь п унициклических кластеров в точке перко¬
ляции равна
14.7 ЗАДАЧИ
575
14.7 Вычислите точное среднее распределение степеней (Nk{N)} в случайном ре¬
курсивном дереве для нескольких первых N = 1,2,3,... с помощью решения
рекуррентного соотношения
№<« + Ц) - <ВД>
При этом нужно воспользоваться производящей функцией
Gfc(w)=
N>1
чтобы превратить это рекуррентное соотношение в решаемое уравнение. Да¬
лее, разложите решения Gfc(w) степенной ряд по N и получите распределения
степеней. В частности, покажите, что среднее число узлов степени один дает¬
ся формулой (14.27). Наконец , сравните ваши результаты с асимптотическим
средним распределения степени Nk(N) ~ N/2k.
14.8 Обобщите построение генеалогического дерева на СРД с перебросом.
(а) Сначала покажите, что кинетическое уравнение для числа 1/рузлов в
поколении д имеет вид:
dLg = (1 - г)£д_1 + rLg
dN N
(Ь) Покажите, что решение для Lg дается формулой
W) = [
Jo
9-
где т = In N.
14.9 Покажите, что р в формуле A(N) = pN демонстрирует следующее предельное
поведение:
ц = 1 + Воу + О (72), 7 4-0,
Д = 2 - Вх(1 - 7) + О ((1 - 7)2), 7|1,
где
Во = V = 0,5078, Bi = 4 V ———— = 2,407.
’ ’ ^0 + 1)0 + 2)
Здесь 7 — это показатель степени в интенсивности присоединения опре¬
деляемой как Ak = ку.
14.10 Для линейного преференционного присоединения А^ = к вычислите Nk явно,
пользуясь основным кинетическим уравнением (14.34) при к = 1,2,3 и 4.
576
СЛОЖНЫЕ СЕТИ
14.11 Найдите распределение степени узлов для преференционного присоединения
со сдвинутой линейной интенсивностью Ak = к + А. Сначала упростите нор¬
мировочный коэффициент А = AjNj до A(N) = Мх + АМо = (2 + A)7V,
подразумевающий, что /х = 2 + А. Используя этот результат, покажите, что
распределение степени имеет вид
nj; = (2 + А)
Г(3 + 2А) Г(к + А)
Г(1 + А) Г(& + 3 + 2А)’
Покажите, что асимптотически это распределение убывает как fc“3“A. Заметь¬
те, что уравнение (14.34) со сдвинутой линейной интенсивностью присоедине¬
ния Ak = к + А идентично уравнению для модели с перебросом (14.32), когда
установлено соответствие А = ± — 2.
14.12 Найдите распределение степени для процесса роста, в котором с вероятностью
р новый узел соединяется с существовавшим узлом по правилам преферен¬
ционного присоединения, а с вероятностью 1 — р — по правилам случайного
однородного присоединения.
14.13 Рассмотрите интенсивность присоединения Ах = 1 и Ak = ак для к > 2. По¬
кажите, что получающееся распределение степени асимптотически стремится
к степенному закону nk ~ к~у, где показатель у = (3 + у/1 + 8/а)/2 может
быть равен любому числу больше 2.
14.14 Обобщите сети с линейным преференционным присоединением на случай, ко¬
гда каждый новый узел соединяется с т существовавших ранее узлов. Напи¬
шите основное кинетическое уравнение для этого процесса и, применив тот же
подход, что и при решении уравнения (14.34), найдите распределение степени.
14.15 Предположите, что каждому узлу присвоена начальная «привлекательность»
77 > 0, выбранная из распределения /?о(^)« Интенсивность присоединения к
узлу со степенью к и привлекательностью rj определяется как Ak(rf). Пусть
Nk(rj) будет число узлов со степенью к и привлекательностью 77. Покажите, что
это совместное распределение степени и привлекательности эволюционирует
в соответствии с уравнением
dNk(r,) Ak.1(r,)Nk.1(rj) - Ak(rj)Nk(ij) , „
~dN~ = A +PoO?)fci,
где A = f drj^2k Ak(rf)Nk(rf) — полная интенсивность присоединения. Ис¬
пользуя подстановки А = pN и Nk(rf) = Nnk(ri), сведите это уравнение к
рекуррентному соотношению с решением
Пк(л) =ро(??)
4/fa)
-1
14.7 Задачи
577
Для специального примера, в котором интенсивность присоединения линейна
по степени и привлекательности Ak(rf) = rjk, покажите, что распределение
степени имеет вид
(.P.W rwr(i+;)
ч г(/г + 1 + *)‘
14.16 Рассмотрите растущую сеть, в которой узлы добавляются по одному, и каж¬
дый может присоединиться к одному существовавшему ранее узлу степени к
с интенсивностью Ak = к\ где 7 > 1.
(a) Начните с основного кинетического уравнения для TVi и покажите, что
в общем случае М пропорционально N для любых значений 7.
(b) Далее исследуйте основное кинетическое уравнение для N2. Покажите,
что асимптотически dNz/dN ~ TV1”7 и таким образом продемонстрируй¬
те, что для 1 < 7 < 2 N2 растет как 7V2-7.
(c) Продолжая рассуждать в том же направлении, покажите, что при Ду <
7 < справедливы соотношения Nk ~ для к < J, тогда как
Nk ~ 0(1) для к > j.
14.17 Заполните пробелы в выводе распределения Гаусса, который был кратко обо¬
значен в уравнениях (14.46)-(14.49). В частности, выведите дифференциаль¬
ное уравнение для скейлинговой функции $(77) и решите его.
14.18 Цель этой задачи — решить уравнение(14.50).
(а) Покажите, что однородная версия уравнения (14.50) имеет следующее
решение
r(2p + 2V)
Г(2р +1) Г(ЛГ) ’
П С117) -
1<?<W
(b) Обоснуйте идею использовать решение однородной версии (14.50) как
интегрирующий множитель, т. е. искать решение в виде
L(N) = U(N)
Г(2р + ЛГ)
Г(2р + 1) Г(ЛГ) ’
Покажите, что этот анзац превращает уравнение (14.50) в соотношение
U(N + 1) = U(N) +
Г(2р + 1)Г(ЛГ + 1)
r(2p + lV + l)
(с) Найдите решение этого рекуррентного соотношения в виде
b(lV) =
Г(2р + ЛГ)
Г(ЛГ)
V гв)
578
СЛОЖНЫЕ СЕТИ
(d) Используя хорошо известное асимптотическое соотношение
Г(2р + ж)
Г(гг)
когда ж » 1,
г2р
подтвердите асимптотику (14.52) для р < 1/2.
(e) Покажите, что когда р = 1/2, точный результат имеет вид L(N) =
N(Hn — 1), где Hn = J-1 — это гармоническое число. Исполь¬
зуя асимптотики гармонических чисел, подтвердите предсказание (14.52)
для р = 1/2.
(f) Покажите, что сумма в правой части уравнения из пункта (с) сходится.
Вычислите эту сумму, пользуясь соотношением
vr(6 + fc) _ Г(&)
£Г(с + к) (с — 6 — 1)Г(с — 1)
Подтвердите результат (14.52) для р > 1/2 с А(р) = 1/[(2р — 1) Г(1 + 2р)].
*
Литература
Глава 1. Вводные примеры
[1
[2
[3
[4
[5
[6
[7
[8
[9
[Ю
[П
W. Feller, An Introduction to Probability Theory and its Applications, Vol. I
(Wiley, New York, 1968).
S. Karlin, H.M. Taylor, Л First Course in Stochastic Processes, 2nd edn.
(Academic Press, New York, 1975).
G.H. Weiss, Aspects and Applications of the Random Walk (North-Holland,
Amsterdam, 1994).
J. Rudnick, G. Gaspari, Elements of the Random Walk (Cambridge University
Press, New York, 2004).
P. Morders, Y. Peres, Brownian Motion,
http://www.stat.berkelcy.edu/users/peres/ bmbook.pdf.
B. Duplantier, “Einstein, 1905-2005”, eds Th. Damour, O. Darrigol, B. Duplantier
and V. Rivasscau (Birkhauser, Basel, 2006); arXiv:0705.1951.
Galileo Galilei, Discourses and Mathematical Demonstrations Relating to Two
New Sciences (Dover, New York, 1954; originally published by Elzevir, Leiden,
1638).
Yu.I. Manin, Mathematics and Physics (Birkhauser, Basel, 1981).
G.I. Barenblatt, Scaling, Self-Similarity, and Intermediate Asymptotics
(Cambridge University Press, Cambridge, 1996).
N. Goldenfcld, Lectures on Phase Transitions and the Renormalization Group
(Addison-Wesley, Reading, MA, 1992).
P.G. de Gennes, Scaling Concepts in Polymer Physics (Cornell University Press,
Ithaca, NY, 1979).
Глава 2. Диффузия
[12] S. Chandrasekhar, Rev. Mod. Phys. 15, 1 (1943).
[13] N.G. van Kampen, Stochastic Processes in Physics and Chemistry (North-
Holland, Amsterdam, 2001).
[14] S. Alexander, J. Bernasconi, W.R. Schneider, R. Orbach, Rev. Mod. Phys. 53,
175 (1981).
*Bce библиографические ссылки приведены без изменения по оригинальному тексту
(Прим, переводчика).
580
ЛИТЕРАТУРА
[15] J.-P. Bouchaud, A. Georges, Phys. Rep. 195, 127 (1990).
[16] B. Derrida, Physica D 107, 186 (1997).
[17] S. Redner, A Guide to First-Passage Processes (Cambridge University Press,
Cambridge, 2001).
[18] M. E. Fisher, M. P. Gelfand, J. Stat. Phys. 53, 175 (1988).
[19] M. Bramson, D. Griffeath, in: RandomWalks, Brownian Motion, and Interacting
Particle Systems: A Festshrift in Honor of Frank Spitzer, eds R. Durrett,
H. Kesten (Birkhauser, Boston, 1991).
[20] D. ben-Avraham, В. M. Johnson, C. A. Monaco, P. L. Krapivsky, S. Redner,
J. Phys. A 36, 1789 (2003); arXiv:cond-mat/0210501.
[21] H. C. Bergand E. M. Purcell, Biophys. J. 20, 193 (1977).
[22] H. C. Berg, Random Walks in Biology (Princeton University Press, Princeton,
NJ, 1993).
[23] H. S. Carslaw, J. C. Jaeger, Conduction of Heat in Solids (Clarendon Press,
Oxford, 1959).
[24] J. Crank, Free and Moving Boundary Problems (Oxford University Press, Oxford,
1984).
[25] J. S. Langer, in: Chance and Matter, eds J. Souletie, J. Vannimenus, R. Stora
(North-Holland, Amsterdam, 1986).
[26] S. Redner, D. ben-Avraham, J. Phys. A 23, L1169 (1990).
[27] P. L. Krapivsky, Phys. Rev. E 47, 1199 (1993).
[28] T. Halpin-Healey, Y.-C. Zhang, Phys. Rep. 254, 215 (1995).
[29] A.-L. Barabasi, H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge
University Press, Cambridge, 1995).
[30] M. Kardar, in: Les Houches session LXII on Fluctuating Geometries in Statistical
Mechanics and Field Theory eds F. David, P. Ginzparg, J. Zinn-Justin (Elsevier,
Amsterdam, 1996); arXiv:cond-mat/9411022.
Глава 3. Столкновения
[31] J. C. Maxwell, Phil. Trans. Roy. Soc. 157, 49 (1867).
[32] L. Boltzmann, Lectures on Gas Theory (Dover, New York, 1964).
[33] M. Kac, Probability and Related Topics in Physical Sciences (Interscience,
London, 1959).
[34] P. Resibois, M. De Leener, Classical Kinetic Theory of Fluids (Wiley, NewYork,
1977).
[35] C. Truesdell, R. G. Muncaster, Fundamentals of Maxwell’s Kinetic Theory of a
Simple Monatomic Gas (Academic Press, New York, 1980).
[36] M. H. Ernst, Phys. Rep. 78, 1 (1981).
[37] C.Villani, A review of mathematical topics in collisional kinetic theory in:
“Handbook of Mathematical Fluid Dynamics”, eds S. Friedlander, D. Serre
(Elsevier Science, Amsterdam, 2007).
ЛИТЕРАТУРА
581
[38] К. Huang, Statistical Mechanics (Wiley, New York, 1987).
[39] P. Drude, Annalen Phys. 1, 566 (1900); 3, 369 (1900).
[40] H. A. Lorentz, Arch. Neerl. 10, 336 (1905); reprinted in: Collected Papers Vol.
Ill, p. 180 (Martinus Nijhoff, The Hague, 1936).
[41] Иногда газ Лоренца называют Доска Гальтона, см. например М. Кас,
Scientific American 211, 2, 92 (1964).
[42] Е. Н. Hauge, in “Transport Phenomena”, eds G. Kirczenow, J. Marro, Lecture
Notes in Physics, Vol. 31, p. 337 (Springer, Berlin, 1974).
[43] L. A. Bunimovich, Ya. G. Sinai, Comm. Math. Phys. 78, 247 (1980);
L. A. Bunimovich and Ya. G. Sinai, Comm. Math. Phys. 78, 479 (1981).
[44] J. M. J. van Leeuwen, A. Weijland, Physica 36, 457 (1967); A. Weijland,
J. M. J. van Leeuwen, Physica 38, 35 (1968).
[45] J. Piasecki, E.Wajnryb, J. Stat. Phys. 21, 549 (1979).
[46] P. L. Krapivsky, S. Redner, Phys. Rev. E 56, 3822 (1997); arXiv:condmat/
9612037.
[47] R. Kubo, M. Toda, N. Hashitsumi, Nonequilibrium Statistical Mechanics
(Springer, Berlin, 1985).
[48] T. Antal, P. L. Krapivsky, S. Redner, Phys. Rev. E 78, 030301 (2008);
(arXiv:0805.3783).
[49] L. I. Sedov, Similarity and Dimensional Methods in Mechanics (Academic Press,
New York, 1959).
[50] L. D. Landau, E. M. Lifshitz, Fluid Mechanics (Pergamon Press, New York, 1987).
[51] S. Ulam, Adv. Appl. Math. 1, 7 (1980).
[52] J. P. Hansen, I. R. McDonald, Theory of Simple Liquids (Academic Press,
London, 1986).
[53] J. R. Dorfman, An Introduction to Chaos in Nonequilibrium Statistical Mechanics
(Cambridge University Press, Cambridge, UK, 1999).
[54] P. Visco, F. van Wijland, E. Trizac, Phys. Rev. E 77, 041117 (2008);
arXiv:0803.1291.
[55] E. Ben-Naim, S. Redner, F. Leyvraz, Phys. Rev. Lett. 70, 1890 (1993).
[56] P. L. Krapivsky, C. Sire, Phys. Rev. Lett. 86, 2494 (2001); arXiv:condmat/
0005539.
[57] E. Trizac, Phys. Rev. Lett. 88, 160601 (2002); M. I. Garcia de Soria, P. Maynar,
G. Schehr, A. Barrat, E. Trizac, Phys. Rev. E 77, 051127 (2008).
[58] P. K. Haff, J. Fluid Meeh. 134, 401 (1983).
[59] I. Goldhirsch, G. Zanetti, Phys. Rev. Lett. 73, 1619 (1993).
[60] A. Baldassari, U. M. B. Marconi, A. Puglisi, Europhys. Lett. 58, 14 (2002).
[61] N. V. Brilliantov, T. Poschel, Kinetic Theory of Granular Gases (Oxford
University Press, Oxford, 2004).
582
ЛИТЕРАТУРА
[62] R. S. Krupp, A nonequilibrium solution of the Fourier transformed Boltzmann
equation, M.S. Thesis, MIT (1967); Investigation of solutions to the Fourier
transformed Boltzmann equation, Ph.D. Thesis, MIT (1970).
[63] A. V. Bobylev, Sov. Sci. Rev. C. Math. Phys. 7, 111 (1988).
[64] E. Ben-Naim, P. L. Krapivsky, The inelastic Maxwell model, in: Granular Gases,
Lecture Notes in Physics, Vol. 624, p. 63 (Springer, Berlin, 2004); arXiv:cond-
mat/0301238.
[65] J. M. Burgers, The Nonlinear Diffusion Equation (Reidel, Dordrecht, 1974).
[66] S. Kida, J. Fluid Meeh. 93, 337 (1979).
[67] S. F. Shandarin, Ya. B. Zeldovich Rev. Mod. Phys. 61, 185 (1989).
[68] G. F. Carnevale, Y. Pomeau, W. R. Young, Phys. Rev. Lett. 64, 2913 (1990).
[69] E. Trizac, P. L. Krapivsky, Phys. Rev. Lett. 91, 218302 (2003); arXiv:condmat/
0310133.
[70] L. Frachebourg, Phys. Rev. Lett. 82, 1502 (1999); arXiv:cond-mat/9808077.
[71] D. C. Rapaport, The Art of Molecular Dynamics Simulation, 2nd edn.
(Cambridge University Press, Cambridge, 2004).
[72] W. H. Press, S.A. Teukolsky,W. T.Vetterling, В. P. Flannery, Numerical Recipes,
2nd edn. (Cambridge University Press, Cambridge, 1992).
[73] E. Ben-Naim, P. L. Krapivsky, S. Redner, Phys. Rev. E 50, 822 (1994);
arXiv:cond-mat/9402054.
Глава 4. Запреты
[74] A. L. Hodgkin, R. D. Keynes, J. Phys. 128, 61 (1955).
[75] T. E. Harris, J. Appl. Prob. 2, 323 (1965).
[76] F. Spitzer, Adv. Math. 5, 246 (1970).
[77] D. G. Levitt, Phys. Rev. A 8, 3050 (1973).
[78] G. B. Whitham, Linear and Nonlinear Waves (Wiley, New York, 1974).
[791 J. D. Logan, An Introduction to Nonlinear Partial Differential Equations (Wiley,
New York, 1994).
[80] H. Spohn, Large Scale Dynamics of Interacting Particles (Springer-Verlag, Berlin,
1991).
[81] T. M. Liggett, Stochastic Interacting Systems: Contact, Voter, and Exclusion
Processes (Springer, New York, 1999).
[82] J. Krug, Phys. Rev. Lett. 67, 1882 (1991).
[83] B. Derrida, E. Domany, D. Mukamel, J. Stat. Phys. 69, 667 (1992).
[84] G. Schutz, E. Domany, J. Stat. Phys. 72, 277 (1993).
[85] B. Derrida, M. R. Evans, V. Hakim, V. Pasquier, J. Phys. A 26, 1493 (1993).
[86] B. Schmittmann, R. К. P. Zia, Statistical mechanics of driven diffusive systems,
in: “Phase Transitions and Critical Phenomena”, Vol. 17, eds C. Domb,
J. L. Lebowitz (Academic Press, London, 1995).
ЛИТЕРАТУРА
583
[87] Nonequilibrium Statistical Mechanics in One Dimension, eds V. Privman
(Cambridge University Press, New York, 1997). Эта книга содержит много по¬
лезных обзоров. О запретах см. В. Derrida, М. R. Evans, The asymmetric
exclusion model: exact results through a matrix approach, chapter 14.
[88] G. Schutz, Exactly solvable models for many-body systems far from equilibrium,
in: “Phase Transitions and Critical Phenomena”, Vol. 19, eds C. Domb,
J. L. Lebowitz (Academic Press, London, 2000).
[89] O. Golinelli, K. Mallick, J. Phys. A 39, 12679 (2006); arXiv:cond-mat/ 0611701.
[90] R. A. Blythe, M. R. Evans, J. Phys. A 40, R333 (2007); arXiv:0706.1678.
[91] B. Derrida, Phys. Rep. 301, 65 (1998).
[92] B. Derrida, J. Stat. Meeh. P07023 (2007); arXiv:cond-mat/0703762.
[93] M. Lifshits, S. A. Gredeskul, L. A. Pastur, Introduction to the Theory of
Disordered Systems (Wiley, New York, 1988).
Глава 5. Агрегация
[94] P. J. Flory, Principles of Polymer Chemistry (Cornell University Press, Ithaca,
NY, 1953).
[95] R. L. Drake, in: Topics in Current Aerosol Researches, eds G. M. Hidy,
J. R. Brock, p. 201 (Pergamon Press, New York, 1972).
[96] S. K. Frielander, Smoke, Dust and Haze: Fundamentals of Aerosol Behavior
(Wiley, New York, 1977).
[97] H. Pruppacher, J. Klett, Microphysics of Clouds and Precipitations (Kluwer,
Dordrecht, 1998).
[98] R. M. Ziff, E. D. McGrady, P. Meakin, J. Chem. Phys. 82, 5269 (1985).
[99] R. Probstein, Physicochemical Hydrodynamics:An Introduction(Wiley-
Interscience, New York, 2003).
[100] S. K. Lando, Lectures on Generating Functions, Student Mathematical Library,
Vol. 23 (American Mathematical Society, Providence, RI, 2003).
[101] R. L. Graham, D. E. Knuth, O. Patashnik, Concrete Mathematics: A Foundation
for Computer Science (Addison-Wesley, Reading, MA, 1989).
[102] H.S. Wilf, Generating functionology (Academic Press, Boston, 1990).
[103] P. Flajolet, R. Sedgewick, Analytic Combinatorics (Cambridge University Press,
New York, 2009).
[104] D. J. Aldous, Bernoulli 5, 3 (1999).
[105] F. Leyvraz, Phys. Rep. 383, 95 (2003); arXiv:cond-mat/0305670.
[106] J. B. McLeod, Quart. J. Math. Oxford 13, 119 (1962); ibid 13, 193 (1962); ibid
13, 283 (1962).
[107] E. M. Hendriks, M. H. Ernst, R. M. Ziff, J. Stat. Phys. 31, 519 (1983).
[108] A. A. Lushnikov, J. Colloid. Inter. Sci. 65, 276 (1977).
[109] P. G. J. van Dongen, M. H. Ernst, J. Stat. Phys. 49, 879 (1987).
584
ЛИТЕРАТУРА
[110] G. В. Field, W. C. Saslaw, Astrophys. J. 142, 568 (1965).
[111] W. H. White, J. Colloid Interface Sci. 87, 204 (1982).
[112] N. V. Brilliantov, P. L. Krapivsky, J. Phys. A 24, 4787 (1991).
[113] L.-H. Tang, J. Phys. I (France) 3, 935 (1993).
[114] P. L. Krapivsky, J. F. F. Mendes, S. Redner, Phys. Rev. В 59, 15950 (1999);
arXiv:cond-mat/9808054.
[115] M. N. Popescu, J. G. Amar, F. Family, Phys. Rev. В 64, 205404 (2001).
[116] Z. A. Melzak, Mathematical Ideas, Modeling and Applications (Wiley, New York,
1976).
[117] S. Ispolatov, P. L. Krapivsky, S. Redner, Eur. Phys. J.B 2, 267 (1998);
arXiv:condmat/ 9708018.
[118] E. R. Domilovskii, A. A. Lushnikov, V. N. Piskunov, Dokl. Phys. Chem. 240, 108
(1978).
[119] P. G. J. van Dongen, J. Phys. A 20, 1889 (1987).
[120] L. Malyshkin, J. Goodman, Icarus 150, 314 (2001).
[121] E. Ben-Naim, P. L. Krapivsky, Phys. Rev. E 68, 031104 (2003); arXiv:condmat/
0305154.
[122] http://www.research.att.com/ njas/sequences/
Глава 6. Фрагментация
[123] См. статьи из “Statistical Models for the Fracture of Disordered Media” eds
H. J. Herrmann, S. Roux (North-Holland, New York, 1990).
[124] T. Harris, The Theory of Branching Processes (Springer, Berlin, 1963).
[125] R. M. Ziff, J. Stat. Phys. 23, 241 (1980).
[126] E. D. McGrady, R. M. Ziff, Phys. Rev. Lett. 58, 892 (1987).
[127] R. M. Ziff, E. D. McGrady, J. Phys. A 18, 3027 (1985).
[128] M. H. Ernst, G. Szamel, J. Phys. A 26, 6085 (1993).
[129] Z. Chengand S. Redner, J. Phys. A 23, 1233 (1990).
[130] A. F. Filippov, Theory Prob. Appl. 6, 275 (1961).
[131] E. Ben-Naim, P. L. Krapivsky, Phys. Lett. A 293, 48 (2000); arXiv:condmat/
0006456.
[132] A. Charlesby, Proc. Roy. Soc. London Ser. A 224, 120 (1954).
[133] P. L. Krapivsky, E. Ben-Naim, Phys. Rev. E 50, 3502 (1994); arXiv:condmat/
9407084.
[134] P. J. Blatz, A. V. Tobolsky, J. Phys. Chem. 49, 77 (1945).
[135] E. Ben-Naim, P. L. Krapivsky, Phys. Rev. E 77, 061132 (2008); arXiv:0803. 2875.
[136] P. L. Krapivsky, S. Redner, Phys. Rev. E 54, 3553 (1996); arXiv:condmat/
9509129.
[137] S. N. Majumdar, S. Krishnamurthy, M. Barma, Phys. Rev. Lett. 81, 3691 (1998);
arXiv:cond-mat/9806353.
ЛИТЕРАТУРА
585
[138] Р. L. Krapivsky, Е. Ben-Naim, Phys. Rev. E 68, 021102 (2003); arXiv:condmat/
0302525.
Глава 7. Адсорбция
[139] P. J. Flory, J. Amer. Chem. Soc. 61, 1518 (1939).
[140] A. Renyi, Publ. Math. Inst. Hung. Acad. Sci. 3, 109 (1958).
[141] J. J. Gonzalez, P. C. Hemmer, J. S. Hoye, Chem. Phys. 3, 228 (1974).
[142] M. C. Bartelt, V. Privman, lnt. J. Mod. Phys. 5, 2883 (1991).
[143] J. W. Evans, Rev. Mod. Phys. 65, 1281 (1993); см. также Random and
cooperative sequential adsorption: exactly solvable models on ID lattices,
continuum limits, and 2D extensions, chapter 10 from [87].
[144] J.Talbot, G.Tarjus, P. R.VanTassel, P.Viot, Colloids SurfacesA165, 287 (2000).
[145] C. Monthus, H. J. Hilhorst, Physica A 175 263 (1991).
[146] Y. Pomeau, J. Phys. A 13 L193 (1980).
[147] R. H. Swendsen, Phys. Rev. A 24, 504 (1981).
[148] J. Talbot, G. Tarjus, P. Schaaf, Phys. Rev. A 40, 4808 (1989).
[149] V. Privman, J.-S.Wang, P. Nielaba, Phys. Rev. В 43, 3366 (1991).
[150] G. Tarjus, P. Viot, Phys. Rev. Lett. 67, 1875 (1991).
[151] P. L. Krapivsky, E. Ben-Naim, J. Chem. Phys. 100, 6778 (1994); arXiv:condmat/
9310065; X. Jin, G. Tarjus, J. Talbot, J. Phys. A 27, L195 (1994).
[152] E. R. Nowak, J. B. Knight, E. Ben-Naim, H. Jaeger, S. Nagel, Phys. Rev. E 57,
1971 (1998).
[153] P. Nielaba, Lattice models of irreversible adsorption and diffusion, chapter 11
from [87].
[154] S. M. Simon, C. S. Peskin, G. F. Oster, Proc. Natl. Acad. Sci. (USA) 89, 3770
(1992).
[155] M. R. D’Orsogna, T. Chou, T. Antal, J. Phys. A 40, 5575 (2007); arXiv:condmat/
0703742.
[156] P. L. Krapivsky, K. Mallick, J. Stat. Meeh. P07007 (2010); arXiv: 1005.3626.
[157] G. N.Watson, A Treatise on the Theory of Bessel Functions (Cambridge
University Press, Cambridge, 1922).
[158] С. M. Bender, S. A. Orszag, Advanced Mathematical Methods for Scientists and
Engineers (McGraw-Hill, New York, 1978).
Глава 8. Динамика спинов
[159] J. D. Gunton, M. San Miguel, P. S. Sahni, in: Phase Transitions and Critical
Phenomena, Vol. 8, eds. C. Domb, J. L. Lebowitz (Academic Press, New York,
1983).
[160] A. J. Bray, Adv. Phys. 43, 357 (1994).
[161] T. M. Liggett, Interacting Particle Systems (Springer, New York, 1985).
586
ЛИТЕРАТУРА
[162] I. Dornic, H. Chate, J. Chave, H. Hinrichsen, Phys. Rev. Lett. 87, 045701 (2001);
arXiv:cond-mat/0101202.
[163] P. L. Krapivsky, Phys. Rev. A 45, 1067 (1992).
[164] L. Frachebourgand P. L. Krapivsky, Phys. Rev. E 53, R3009 (1996);
arXiv:condmat/ 9508123.
[165] R. J. Glauber, J. Math. Phys. 4, 294 (1963).
[166] B. U. Felderhof, Rep. Math. Phys. 2, 215 (1970).
[167] D. Bedeaux, К. E. Shuler, I. Oppenheim, J. Stat. Phys. 2, 1 (1970).
[168] P. L. Krapivsky, E. Ben-Naim, Phys. Rev. E 56, 3788 (1997); arXiv:condmat/
9705155.
[169] B. Derrida, R. Zeitak, Phys. Rev. E 54, 2513 (1996); arXiv:cond-mat/9606042.
[170] S. N. Majumdar, D. S. Dean, P. Grassberger, Phys. Rev. Lett. 86, 2301 (2001);
arXiv:cond-mat /0004486.
[171] V. Spirin, P. L. Krapivsky, S. Redner, Phys. Rev. E 63, 036118 (2001); Phys.
Rev. E 65, 016119 (2001).
[172] K. Barros, P. L. Krapivsky, S. Redner, Phys. Rev. E 80, 040101 (R) (2009);
arXiv:0905.3521.
[173] H. Rost, Theor. Prob. Rel. Fields 58, 41 (1981).
[174] L. Chayes, R. H. Schonmann, G. Swindle, J. Stat. Phys. 79, 821 (1995).
[175] A. Karma, A. E. Lobkovsky, Phys. Rev. E 71, 036114 (2005); arXiv:condmat/
0502219.
[176] R. Cerf, S. Louhichi, Prob. Theory Rel. Fields 137, 379 (2007);
arXi v: math/0411545.
[177] K. Kawasaki, Phys. Rev. 145, 224 (1966).
[178] S. J. Cornell, K. Kaski, R. B. Stinchcombe, Phys. Rev. В 44, 12263 (1991).
[179] R. H. Swendsen, J. S.Wang, Phys. Rev. Lett. 58, 86 (1987).
[180] U.Wolff, Phys. Rev. Lett. 62, 361 (1989).
[181] D. P. Landau, K. Binder, A Guide to Monte Carlo Simulations in Statistical
Physics (Cambridge University Press, Cambridge, 2000).
[182] B. Derrida, V. Hakim, J. Phys. A 29, L589 (1996).
[183] P. L. Krapivsky, J. Phys. A 37, 6917 (2004); arXiv:cond-mat/0405469.
Глава 9. Укрупнение
[184] J. S. Langer,An introduction to the kinetics of first-order phase transitions, in:
“Solids Far From Equilibrium” eds C. Godreche (Cambridge University Press,
Cambridge, 1992).
[185] P. C. Hohenbergand В. I. Halperin, Rev. Mod. Phys. 49, 435 (1977).
[186] L. D. Landau, E. M. Lifshitz, Quantum Mechanics (Pergamon Press, Oxford,
1987).
ЛИТЕРАТУРА
587
[187] Р. М. Morse, Н. Feshbach, Methods of Theoretical Physics (McGraw-Hill, New
York, 1953).
[188] A. Sicilia, J. J. Arenzon, A. J. Bray, L. F. Cugliandolo, Phys. Rev. E 76, 061116
(2007).
[189] M. E. Gage, R. S. Hamilton, J. Differential Geom. 23, 69 (1986).
[190] M. A. Grayson, J. Differential Geom. 26, 285 (1987).
[191] W.W. Mullins, J. Appl. Phys. 27, 900 (1956).
[192] H. A. Schwarz, Gesammelte Mathcmatische Abhandlungen, Vol. 1 (Julius
Springer, Berlin, 1890).
[193] A. H. Schoen, Infinite Periodic Minimal Surfaces without Self-Intersection, NASA
Technical Note TN D-5541 (1970).
[194] H. Karcher, Manuscripta Math. 64, 291 (1989).
[195] S. Fujimori, M.Weber, Manuscripta Math. 129, 29 (2009).
[196] S. Coleman, Aspects of Symmetry (Cambridge University Press, Cambridge,
1988).
[197] R. Rajaraman, Solitons and Instantons (North-Holland, Amsterdam, 1989).
[198] N. Manton, P. Sutcliffe, Topological Solitons (Cambridge University Press,
Cambridge, 2004).
[199] G. H. Derrick, J. Math. Phys. 5, 1252 (1964).
[200] M. Zapotocky, W. Zakrzewski, Phys. Rev. E 51, R5189 (1995); arXiv:condmat/
9502005.
[201] I. M. Lifshitz, V. V. Slyozov, Zh. Eksp. Tcor. Fiz. 35, 479 (1959).
[202] C.Wagner, Z. Elektrochem. 65, 581 (1961).
[203] T. Nagai, K. Kawasaki, Physica A 120, 587 (1983); K. Kawasaki, T. Nagai,
Physica A 121, 175 (1983).
[204] A. J. Bray, B. Derrida, Phys. Rev. E 51, 1633 (1995); arXiv:cond-mat/9411037.
[205] A. J. Bray, B. Derrida, C. Godreche, Europhys. Lett. 27 175 (1994).
[206] K. Sekimoto, Int. J. Mod. Phys. В 5, 1843 (1991).
[207] C. Sire, S. N. Majumdar, Phys. Rev. E 52, 244 (1995); arXiv:cond-mat/9503163.
[208] B. Meerson, P. V. Sasorov, Phys. Rev. E 53, 3491 (1996); B. Giron, B. Meerson,
P. V. Sasorov, Phys. Rev. E 58, 4213 (1998).
Глава 10. Беспорядок
[209] В. Derrida, E. Gardner, J. Physique 47, 959 (1986).
[210] P. L. Krapivsky, J. Physique I 1, 1013 (1991).
[211] S. Redner, Am. J. Phys. 58, 267 (1990).
[212] S. N. Majumdar, О. C. Martin, Phys. Rev. E 74, 061112 (2006); arXiv:condmat/
0609735.
[213] F. Hivert, S. Nechaev, G. Oshanin, O. Vasilyev, J. Stat. Phys. 126, 243 (2007);
arXiv:cond-mat/0509584.
588
ЛИТЕРАТУРА
[214] S. Carmi, P. L. Krapivsky, D. ben-Avraham, Phys. Rev. E 78, 066111 (2008);
arXiv:0808.0388.
[215] С. M. Newman, D. L. Stein, Phys. Rev. E 60, 5244 (1999); arXivxondmat/
9908455.
[216] J.-P. Bouchaud, A. Comtet, A. Georges, P. Le Doussal, Ann. Phys. 201, 285
(1990).
[217] P. Le Doussal, C. Monthus, D. S. Fisher, Phys. Rev. E 59, 4795 (1999);
arXiv:cond-mat/9811300.
[218] D. ben-Avraham, S. Havlin, Diffusion and Reactions in Fractals and Disordered
Systems (Cambridge University Press, Cambridge, 2000).
[219] S. Redner, Physica D 38, 287 (1989).
[220] B. D. Hughes, Random Walks and Random Environments, Vol. 1, Random Walks,
Vol. 2, Random Environments (Oxford University Press, Oxford, 1995, 1995).
[221] M. Kardar, Statistical Physics of Fields (Cambridge University Press, Cambridge,
2007).
Глава 11. Гистерезис
[222] T. Tome, M. J. de Oliveira, Phys. Rev. A 41, 4251 (1990).
[223] M. Rao, H. R. Krishnamurthy, R. Pandit, Phys. Rev. В 42, 856 (1990).
[224] G. H. Goldsztein, F. Broner, S. H. Strogatz, SIAM J. Appl. Math. 57,1163 (1997).
[225] N. Berglund, H. Kunz, J. Phys. A 32, 15 (1999); arXiv:chao-dyn/9807025.
[226] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics,
Biology, Chemistry, and Engineering (Perseus, Cambridge, MA, 2000).
[227] Y. Imry, S.-K. Ma, Phys. Rev. Lett. 39, 1399 (1975).
[228] R. P. Feynman, R. B. Leighton, M. L. Sands, The Feynman Lectures on Physics,
Vol. II (Addison-Wesley, Reading, MA, 1964).
[229] Science of Hysteresis, eds G. Bertotti, I. D. Mayergoyz (Academic Press,
New York, 2006). Эта книга содержит много полезных обзоров, в частно¬
сти J. Р. Sethna, К. A. Dahmen, О. Perkovic, Random-field Ising models of
hysteresis (arXiv:cond-mat/0406320); G. Durin, S. Zapperi, The Barkhausen
effect (arXiv:cond-mat/0404512).
[230] J. P. Sethna, Statistical Mechanics: Entropy, Order Parameters, and Complexity
(Oxford University Press, New York, 2006).
[231] D. Dhar, P. Shukla, J. P. Sethna, J. Phys. A 30, 5259 (1997); arXivxondmat/
9611028.
[232] P. Shukla, Phys. Rev. E 62, 4725 (2000); arXiv:cond-mat/0004125; Phys. Rev. E
63, 027102 (2001); arXiv:cond-mat/0007370.
[233] F. Colaiori,A. Gabrielli, S. Zapperi, Phys. Rev. В 65, 224404 (2002);
arXivxondmat/ 0112190.
ЛИТЕРАТУРА
589
[234] В. К. Chakrabarti, М. Acharyya, Rev. Mod. Phys. 71, 847 (1999).
Глава 12. Динамика популяций
[235] J. D. Murray, Mathematical Biology (Springer, Berlin, 1989).
[236] G. F. Gause, The Struggle for Existence (Dover, New York, 2003).
[237] R. M. May, W. J. Leonard, SIAM J. Appl. Math. 29, 243 (1975).
[238] B. Hayes, American Scientist 93, 207 (2005).
[239] D. P. Maki, M.Thompson, Mathematical Models and Applications (Prentice-Hall,
Englewood Cliffs, NJ, 1973).
[240] R. A. Fisher, The Genetical Theory of Natural Selection (Clarendon Press,
Oxford, 1930).
[241] S.Wright, Genetics 16, 97 (1931).
[242] J. Hein, M. H. Schierup, C. Wiuf, Gene Genealogies, Variation and Evolution:
a Primer in Coalescent Theory (Oxford University Press, Oxford, 2005).
[243] J.Wakeley, Coalescent Theory: An Introduction (Roberts & Co.,
GreenwoodVillage, CO, 2008).
[244] M. Serva, J. Stat. Meeh. P07011 (2005); arXiv:q-bio/0503036.
[245] D. Simon, B. Derrida, J. Stat. Meeh. P05002 (2006); arXiv:cond-mat/0601167.
[246] M. Delbruck, J. Chem. Phys. 8, 120 (1940).
[247] D. G. Kendall, J. Roy. Statist. Soc. Ser. В 11, 230 (1949).
[248] D. A. McQuarrie, J. Chem. Phys. 38, 433 (1963).
[249] D. A. McQuarrie, C. J. Jachimowski, M. E. Russell, J. Chem. Phys. 40, 2914
(1964).
[250] M.Assaf, B. Meerson, Phys. Rev. E 74, 041115 (2006); arXiv:cond-mat/0606210.
[251] M. I. Freidlin, A. D. Wentzell, Random Perturbations of Dynamical Systems
(Springer, New York, 1984).
[252] N. T. J. Bailey, The Mathematical Theory of Infectious Diseases (Oxford
University Press, Oxford, 1987).
[253] V. Elgart, A. Kamenev, Phys. Rev.E 70, 041106 (2004); arXiv:cond-mat/0404241.
[254] C. R. Doering, К. V. Sargsyan, L. M. Sander, Multiscale Model. Simul. 3, 283
(2005); arXiv:q-bio/0401016.
[255] M.Assaf, B. Meerson, Phys. Rev. E 75, 031122 (2007); arXiv:cond-mat/0612157.
[256] M. Khasin, M. I. Dykman, Phys. Rev. Lett. 103, 068101 (2009); arXiv:0904.1737.
Глава 13. Диффузионные реакции
[257] В. Duplantier, Proc. Symp. Pure Math. 72, Part 2, p. 365-482 (AMS, Providence,
RI, 2004); arXiv:math-ph/0303034.
[258] В. P. Lee, J. Phys. A 27, 2633 (1994); arXiv:cond-mat/9311064.
[259] P. L. Krapivsky, Phys. Rev. E 49, 3233 (1994); arXiv:cond-mat/9403041.
[260] B. Ya. Balagurov, V. G. Vaks, Sov. Phys. JETP 38, 968 (1974).
590
ЛИТЕРАТУРА
[261] Р. Grassberger, I. Procaccia, J. Chem. Phys. 77, 6281 (1982).
[262] M. D. Donsker, S. R. S. Varadhan, Comm. Pure Appl. Math. 32, 721 (1979).
[263] G. Polya, G. Szego, Isoperimetric Inequalities in Mathematical Physics (Princeton
University Press, Princeton, NJ, 1951).
[264] I. Chavel, Eigenvalues in Riemannian Geometry (Academic Press, Orlando, FL,
1984).
[265] Ya. B. Zeldovich, Zh. Tekh. Fiz. 19, 1199 (1949); Ya. B. Zeldovich,
A. S. Mikhailov, Sov. Phys. Usp. 30, 23 (1988).
[266] A. A. Ovchinnikov, Ya. B. Zeldovich, Chem. Phys. 28, 215 (1978).
[267] D. Toussaint, F.Wilczek, J. Chem. Phys. 78, 2642 (1983).
[268] A. A. Ovchinnikov, S. F. Timashev, A. A. Belyi, Kinetics of Diffusion Controlled
Chemical Processes (Nova Science, Hauppage, NY, 1989).
[269] S. Redner, F. Leyvraz, in: Fractals and Disordered Systems, Vol. II, eds A. Bunde
and S. Havlin (Springer, Berlin, 1993).
[270] S. Redner, Scalingtheories of diffusion-controlled and ballistically controlled
bimolecular reactions, chapter 1 from [87].
[271] M. Bramson, J. L. Lebowitz, J. Stat. Phys. 65, 941 (1991).
[272] D. ben-Avraham, J. Chem. Phys. 88, 941 (1988).
[273] T. Oppelstrup, V. V. Bulatov, A. Donev, M. H. Kalos, G. H. Gilmer, B. Sadigh,
Phys. Rev. E 80, 066701 (2009); arXiv:0905.3575.
[274] Z. Racz, Phys. Rev. Lett. 55, 1707 (1985).
[275] J. L. Spouge, Phys. Rev. Lett. 60, 871 (1988).
[276] B. R. Thomson, J. Phys. A 22, 879 (1989).
[277] H. Takayasu, I. Nishikawa, H. Tasaki, Phys. Rev. A 37, 3110 (1988).
[278] A. Kolmogorov, I. Petrovsky, N. Piscounov, Moscow Univ. Bull. Math. 1,1 (1937);
translated and reprinted in P. Pelce, Dynamics of Curved Fronts (Academic Press,
San Diego, 1988).
[279] R. A. Fisher, Ann. Eugenics 7, 353 (1937).
[280] W. van Saarloos, Phys. Rep. 386, 29 (2003); arXiv:cond-mat/0308540.
[281] M. Bramson, Memoirs of the AMS, No. 285 (AMS, Providence, 1983).
[282] Z. Cheng, S. Redner, F. Leyvraz, Phys. Rev. Lett. 62, 2321 (1989).
[283] H. Hinrichsen, V. Rittenberg, H. Simon, J. Stat. Phys. 86, 1203 (1997);
arXiv:cond-mat /9606088.
[284] L. Galfi, Z. Racz, Phys. Rev. A 38, 3151 (1988).
[285] E. Ben-Naim, S. Redner, J. Phys. A 25, L575 (1992).
Глава 14. Сложные сети
[286] H. Jeong, S. P. Mason, A.-L. Barabasi, Z. N. Oltvai, Nature 411, 41 (2001).
[287] J. Moody, Am. J. Sociol. 107, 679 (2001).
ЛИТЕРАТУРА
591
[288] Р. Di Francesco, Р. Ginsparg, J. Zinn-Justin, Phys. Rep. 254, 1 (1995);
arXiv:hepth/ 9306153.
[289] J. Ambjprn, B. Durhuus, T. Jonsson, Quantum Geometry: A Statistical Field
Theory Approach (Cambridge University Press, Cambridge, 2005).
[290] P. Erdos, A. Renyi, Publ. Math. Inst. Hung. Acad. Sci. 5, 17 (1960).
[291] S. Janson, D. E. Knuth, T. Luczak, B. Pittcl, The birth of the giant component,
Random Struct. Algorithms 4, 233 (1993).
[292] B. Bollobas, Random Graphs (Academic Press, London, 1985).
[293] S. Janson, T. Luczak, A. Rucinski, Random Graphs (Wiley, New York, 2000).
[294] B. Bollobas, C. Borgs, J. T. Chayes, J. H. Kim, D. B. Wilson, Random Struct.
Algorithms 18, 201 (2001); arXiv:math/9909031.
[295] E. Ben-Naim, P. L. Krapivsky, Phys. Rev. E 71, 026129 (2005); arXivxondmat/
0408620.
[296] R. Otter, Ann. Math. 49, 583 (1948).
[297] R. T. Smythe, H. Mahmoud, Theory Prob. Math. Statist. 51, 1 (1995).
[298] G. U. Yule, Phil. Trans. Roy. Soc. В 213, 21 (1925).
[299] H. A. Simon, Biometrica 42, 425 (1955).
[300] R. Albert, A.-L. Barabasi, Rev. Mod. Phys. 74, 47 (2002); arXivxondmat/
0106096.
[301] S. N. Dorogovtsev, J. F. F. Mendes, Evolution of Networks: FVoin Biological Nets
to the Internet and WWW (Oxford University Press, Oxford, 2003).
[302] M. E. J. Newman, A.-L. Barabasi, D. J. Watts, The Structure and Dynamics of
Networks (Princeton University Press, Princeton, NJ, 2006).
[303] A. Barrat, M. Barthelemy, A. Vespignani, Dynamical Processes on Complex
Networks (Cambridge University Press, Cambridge, 2008).
[304] M. E. J. Newman, Networks: An Introduction (Oxford University Press, Oxford,
2010).
[305] P. L. Krapivsky, S. Redner, Phys. Rev. E 63, 066123 (2001); arXivxondmat/
0011094.
[306] S. N. Dorogovtsev, J. F. F. Mendes, A. N. Samukhin, Phys. Rev. E 63, 062101
(2001); arXiv:cond-mat/0011115.
[307] P. L. Krapivsky, S. Redner, J. Phys. A 35, 9517 (2002); arXiv:cond-mat/0207107
Предметный указатель
абсорбирующее состояние 475
автокорреляционная функция 346
агрегация 163
—, броуновское ядро 167
—, гелеобразование 176
—, диффузия, зависящая от массы 525
—, локализованный источник 532
—, моменты для постоянного ядра 168
—, мультипликативное ядро 176
—, обобщенное аддитивное ядро 193
—, постоянное ядро 167
—, приближение среднего поля 165
—, рост островов 196
—, скейлинг 186
— одномерная 522
с источником 525
— с источником 190
адсорбция 243
—, запрещенная зона 266
—, коллективная перестройка 274
—, насыщенное состояние 244
—, обратная логарифмическая релакса¬
ция 274
—, парковка автомобилей 251
—, поправки конечного объема 256
—, транслокация полимеров 277
—, , скорость 281
—, флуктуации плотности 260
—, число насыщенных конфигураций
254
— fc-меров 248
— в двух измерениях 261
— димеров 243
— димеров на квадратной решетке 265
— диффузионно-контролируемая 275
— игл 267
— на дереве Кейли 261
— на непрерывной подложке 265
— обратимая 270
анализ размерностей 2, 8
, взрывная волна 94
, волна столкновений 120
, время выхода 39
, кинетика реакций 499
, коэффициент диффузии 78
, модель ЭУ 55
, реакции с захватом 510
, случайное блуждание в неупоря¬
доченной среде 426
, теплопроводность 121
, транслокация полимеров 278
, трехчастичная реакция 502
, укрупнение 345
, уравнение КПЖ 59
, уравнение ланжевена 50
аннигиляция 517
Аррениуса закон 412
асимметричный процесс с запретами (АПЗ)
132
, взаимодействие волн ударных/
разрежения 142
, волна разрежения 141
, гидродинамический подход 136
, матричный метод 151
, микроскопический подход 143
, ослабленный запрет 134
, открытая система 150
, связь с осаждением 147
, стационарное состояние 155
, стационарные состояния 132
, ударная волна 139
, фаза высокой плотности (ВП)
157
, фаза максимального тока (МТ)
157
, фаза низкой плотности (НП) 157
, флуктуации тока 146
асимметричный процесс с запретом (АПЗ)
, связь с границей раздела в мо¬
дели Изинга 322
Баркгаузена шум 441
, лавины 443
бегущая волна 530
бегущих волн техника 236, 241
бидиффузии уравнение 345, 347
592
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
593
Больцмана уравнение 73
, газ Лоренца в поле 86
для газа Лоренца 77
большие флуктуации 487
Бюргерса уравнение 54, 112, 138, 146, 323
Ватсона интегралы 299
вероятности лакун 247
вероятности сегментов 247
взрывная волна 94
ВКБ метод 281
возвратность/невозвратность 32
волна разрежения 141, 145
волна столкновений 91
волновое уравнение 198
время завершения 479
выбор скорости 530
выживания вероятность 44
вымирания вероятность 489
вымирания время 492
, коалесценция 480
выхода вероятность 36
, формула кулона 38
и электростатика 38
выхода время 38
Гаусса распределение 4
Гейзенберга модель 367
гелеобразование 176
—, агрегация 176
—, модель откалывания краев 232
— мгновенное в агрегации 204
гелеобразования время 182
Гиббса-Томсона соотношение 373
гидродинамическое описание 6
гипотеза молекулярного хаоса 74
гистерезис 427
—, глауберова динамика 429
—, дерево Кейли 455
—, коэрцитивное поле 431
—, лавины
—, —, абелевы 444
—, —, распределение размеров 448
—, —, связь с агрегацией 449
—, малые петли возврата 444
—, модель среднего поля 446
—, неупорядоченные ферромагнетики
441
—, память о точке возврата 444
—, петля в плоскости 427
—, спиновая цепочка 440
—, теория возмущений 432
—, цепочка Изинга в случайном поле
452
—, эллиптическая петля гистерезиса 433
Голосова-Кестена распределение 418
голосования модель 288
, время консенсуса 297
, корреляционные функции 291, 296
, непрерывный подход 294
, сохранение намагниченности 292
Голосова феномен 412
гомотопические группы 366
граница раздела выпуклая 357
граничного слоя теория 436, 439
гранулярная температура 100
Грина-Кубо формула 79
детальное равновесие 132, 226, 228, 302, 326
дефект топологический 362
дефекты 362
—, вихри 369
—, теорема вириала 363
динамика критическая 287
динамика популяций 461
динамика при нуле температуры 287
динамика спинов 285
, глауберова динамика 300
, , доменные стенки 308, 314
, , корреляционные функции
308
, , распределение длины до¬
менов 314
, , связь с аннигиляцией 311
, , среднее поле 304
, в высших размерностях 317
, в магнитном поле 312
, в од помори и 306
, динамика кластеров 332
, диффузия домена 331
, кластерная динамика
, , алгоритм Вольфа 334
, , алгоритм Сведсена-Ванга
332
, метастабильные состояния 321
, сжатие капли 320
, угловая граница раздела 322
, центральная догма 287
обменная 325
, укрупнение 329
при нулевой температуре 328
динамическая гипотеза подобия 287
динамический индекс 288, 345
диффузии тензор 91
диффузии уравнение 2, 17
диффузия 15-27
—, распределение вероятностей 15
—, субдиффузия 27
—, широкое распределение времени
ожидания 26
—, широкое распределение длины шага
21
594
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
диффузия острова 194
доменная мозаика 287
доменные стенки 350
, кинки 351
, клин 357
, механическая аналогия 350
—, модель Изинга-Глаубера 296
, модель Изинга-Глаубера 308
, полуполоса 357
, сжатие капли 354
, устойчивость 352
дорожное движение 112
, распределение скоростей 114
единичный шар 65
, объем Vd 66, 93, 387, 508
, площадь поверхности Qj 66, 93,
387, 508
закалка температурная 285
Зародышеобразования и роста модель 384
Изенга модель
в случайном поле 441
Изига модель
в случайном поле
, лавины 443
Изинга модель 300
, приближение среднего поля 303
изображений метод 39, 43, 201, 524
интенсивность реакции
, ядро 164
Йенсена неравенство 203
Кана-Хилларда (КХ) уравнение 344
капиллярная длина 374
Кардара-Паризи-Жанга (КПЖ) уравне¬
ние 58
, индекс КПЖ 61
квазилинейное волновое уравнение 138
квазистатическое приближение 47, 295
кинетическое уравнение 6
, к-частичная аннигиляция 277
, аннигиляция и коалесценция 499
, двухвидовая аннигиляция:
А + В —> 0 511
, логистический рост 529
, столкновительная фрагментация
234
, трехчастичная аннигиляция:
ЗА -> 0 502
для моментов, с мультипликатив¬
ным ядром 183
— для плотности доменов 381
кластерные алгоритмы 332
конкуренция и симбиоз 464
корреляционные функции 258, 346, 521
, автокорреляции 346
, адсорбция 258
, аналогия с электростатикой 295
, зародышеобразование и рост 388
, модель голосования 291
, непрерывная модель голосования
294
двухспиновые 308
кривизна средняя 356
критическая размерность 500
лавины 448
Лагранжа обращение 181, 335
Ланжевена уравнение 49-53
, поле случайных скоростей 419
, применение к росту поверхностей
53
, случайный потенциал 410
для броуновской частицы 51
нелинейное 58
Лапласа метод 420, 508
Лапласа уравнение 37, 48, 365, 373
— дискретное 37
Лаплас-образ степенного закона 34
Леви
— полеты 25
— распределение 25
линейный анализ устойчивости 467
логарифмические поправки 500, 534
логистический рост 462, 528
локальная динамика 356
Лоренца газ 76
, аргумент, основанный на случай¬
ных блужданиях 87
, коэффициент диффузии 78, 81
, плотность вероятности 80
в магнитном поле 89
в одном измерении 82
в электрическом поле 85
Лотки - Вольтерра модель 466
Ляпунова показатель 404
Максвелла-Больцмана распределение 72
Максвелла молекулы 94, 97
Маллинса уравнение 58, 70
Матерона-де Марсили де Марсили модель
418
медленное время 429
мезоскопический 137
Меллина преобразование 217, 219, 222
метастабильные состояния 402, 492
молекулярная динамика 111
моменты
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
595
—, агрегация с мультпликативным яд¬
ром 178
—, , постгелевая фаза 183
—, агрегация с постоянным ядром 168
—, мультискейлинг 105
—, планарная фрагментация 223
—, распыление при фрагментации 216
— времени выхода 40
— одношагового распределения 19
— распределения размеров кластеров
549
— распределения сил 31
— распределения скоростей в неупругих
газах 104
— распределения степеней узлов 563
мультискейлинг 105
—, адсорбция игл 269
—, модель Максвелла 105
—, планарная фрагментация 225
мультифрактальный скейлинг 221
Навье - Стокса уравнение 76
недоопределенные системы 228
независимых интервалов приближение
, модель Изинга-Глаубера 315
—, точность 382
, точность 333
неподвижные точки 462
непрерывности уравнение 137
неупорядоченная спиновая цепочка 398
, метастабильные состояния 399
, сильные, средние и слабые связи
400
неупорядоченный ферромагнетик 398
неупругие газы 98
, закон Хаффа 101
, коллапс 101
, коэффициент восстановления 99
, модель Максвелла 103
, , с внешней силой 107
, модель Максвелла, , , сво¬
бодное остывание 104
, неупругий коллапс 98
, параметр диссипации 100
нецелые размерности 504
НУГЛ 341
—, реакционно-диффузионное уравне
- ние 344
нулевая изоклина 465
обеднённая зона 47
обратимая полимеризация 226
, линейные полимеры 229
, модель откалывания краев 230
, равновесие 230
обратное уравнение 37
для вероятности выхода 37
огрубление 342
однородности индекс 187
, агрегация 187
, фрагментация 214
основное кинетическое уравнение 5, 17
, агрегация 164
, агрегация, мультипликативное
ядро 178
, агрегация с источником 190
, адсорбция fc-меров 249
, адсорбция димеров 245
, адсорбция игл 268
—, алгоритм Вольфа 334
, алгоритм Сведсена-Ванга 333
, граф ЭР 548
, двухспиновые корреляции 310
, диффузия 17
, модель голосования 290
, модель откалывания краев 231
, обратимая парковка автомоби¬
лей 271
, обратимая поимеризация 226
, парковка автомобилей 251
, планарная фрагментация 222
, разложение по малым флукту¬
ациям 484
, распределение барьеров 414
, распределение длины доменов
315
, распределение степеней узлов
557
, сети 562
, транслокация полимеров 279
, фрагментация 211
, фрагментация стол к новител ь-
ная 235
, фраментацпя однородная 214
, экстремальная динамика 382
остаточная намагниченность 406
откалывания краев модель 230
очень твердые частицы 98
очень твёрдые частицы 94
парабол и ческ нс/ ги i юрбол и ческ ие уравнения
84
параметр порядка векторный 364
первого посещения вероятность 33-36, 417
первого посещения свойства 32-42, 514
переопределенные системы 227
пересыщение 373
периодические минимальные поверхности
361
плотность насыщения 244
помеченная частица 127
поправки конечного объема 256
596
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
поток, управляемый кривизной 356
предельный цикл 468
приближение независимых интервалов 272
, обратимая адсорбция 272
приближение среднего поля 500
проекционный оператор 78
производящая функция 18, 173
, А + А -> 0 478
, агрегация, мультипликативное яд¬
ро 180
, агрегация, постоянное ядро 173
, агрегация с источником 191, 195,
527
, адсорбция димеров 257
, алгоритм Вольфа 335
, алгоритм Сведсена-Ванга 334
, граф ЭР 554
, модель откалывания краев 231
, неупорядоченная цепочка Изинга
403
, обращение 174
, случайные рекурсивные деревья
558
функций Бесселя 18
Пуанкаре отображение 430
Пуассона распределение 145
Пуассона уравнение 41
пустых интервалов метод
, агрегация 523
, адсорбция 245
, дерево Кейли 262
, динамика Кавасаки 328
, коалесценция 515
, связь с лакунами 247
—, транслокация полимеров 279
равной априорной вероятности постулат 253
разложение по малым флуктуациям 483-487
размерность критическая 7
распределение сил 28
распыление 215
реакции 6, 498
—, агрегация 163
—, —, локализованный источник 532
—, — одномерная 522, 525
—, аннигиляция 517
—, —, глауберова динамика 517
—, —, стационарное состояние 518
—, баллистическая агломерация 109
—, , реакционно-контролируемый
предел 111
—, баллистическая аннигиляция 96
—, большие флуктуации 474, 476
—, двухвидовая аннигиляция 11, 510-
515
—, , зона реакции 537
—, двухвидовая аннииляция
—, , пространственная организа¬
ция 513
—, диффузионно-контролируемые 498
—, захват 503, 504
—, —, одно измерение 505
—, —, оптимальные флуктуации 509
—, —, произвольная размерность 507
, критическая размерность 503
—, коалесценция 6, 479, 515
—, одновидовая аннигиляция 6, 476
—, пространственная размерность 498
—, трехвидовая аннигиляция 502
— дискретные 473-483
, аннигиляция: А + А —> 0 486
, большие флуктуации 487
, распад: А —> 0 484
, рождение: А —> А + А 474
рождения-гибели 476, 487
реакционно-диффузионное уравнение
528, 533
ренормализация 4
—, децимация 412
—, экстремальная динамика 383
речные сети 526
Риккати уравнение 236, 316
рождения-гибели реакции 476
рост поверхностей 53
рост с обменом 199
самоизбегающие случайные блуждания 501
самоусреднение 25
—, отсутствие 572
седловая точка 465
сети 543
—, генеалогия 561
—, деревья 544, 552
—, диаметр 551
—, звезды 567
—, линейное присоединение 565
—, листья 567
—, переброс 559
—, перколяционный переход 548
—, планарные случайные графы 545
—, пороговое время fc-меров 551
—, преференционное присоединение 562
—, распределение размеров кластеров
550
—, распределение степеней узлов 546,
556, 562
—, скейлинговое окно 554
—, сложные кластеры 552
—, случайные графы 546
—, случайные рекурсивные деревья 556
—, случайный граф Эрдеша-Реньи 546
—, сублинейное присоединение 564
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
597
—, суперлинейное присоединение 565
—, унициклические кластеры 552, 553
—, флуктуации 566
—, циклы 551
— друзей 569
сильно демпфированная динамика 342
симметричный процесс с запретами (СПЗ)
126
, гауссова субдиффузия 131
, помеченная частица 127
, частица второго сорта 144
, эволюция плотности 127
Синая закон 412
Синая модель 409
скейлиг
—, агрегация 186
скейлинг 3
—, баллистическая агломерация 110
—, одновидовая аннигиляция 522
—, скейлинговый анзац 3
—, фрагментация 214
— Лифшица-Слезова-Вагнера 375
скорость реакции 45, 499
, электростатическая аналогия 47
случайная манхэттенская решетка 423
случайное ускорение 107
случайные блуждания 2, 5, 15, 19
, возвратность/невозвратность 32
, самоизбегающие 501
недружественные 42
случайные блуждания в поле случайных ско¬
ростей 418
случайные блуждания в случайном потенци¬
але 409
, ультрамедленная диффузия
412
случайный мультипликативный процесс 401
событийно-ориентированное численное моде¬
лирование 514
специальные функции
, гамма-функция 192, 482, 527
, полиномы лежандра 478
, функции параболического цилин¬
дра 316
1 функция Бесселя 17, 521, 527
, модифицированная 18, 85,
130, 201, 293, 298, 308, 516, 524
, функция Эйри 521, 527
, экспоненциальный интеграл 56,
383
функция Бесселя 280
— функция Эйри 280
среднее и наибролее вероятное значения 401
Стирлинга приближение 182, 254, 478
Стокса-Энштейна соотношение 53, 167
стохастический шум 49
твердые сферы 75, 95
телеграфное уравнение 84
, диффузионный предел 85
топологический заряд 367
трансферматрицы метод 402
ударная волна 139, 144
укрупнение 285, 341
—, консервативная динамика 344, 372
—, , капля 373
—, неконсервативная динамика 341
—, свободная эволюция 345
—, скейлинг 375
—, уравнение бидиффузии 345
—, уравнение Кала-Хилларда (КХ) 344
—, финальные состояния 360
—, экстремальная динамика 379
— Лифшица-Слезова-Вагнера 375
урновая схема 572
фазовый портрет 462
ФКПП уравнение 528
флуктуационно-диссипацианное соотноше¬
ние 51
Фоккера-Планка уравнение 53, 61, 485
фрагментация 210
—, метод Чарльсби 219
—, однородный распад 214
—, распыление 215, 234
—, —, кинетический аргумент 237
—, случайное разрезание 212
—, стационарный источник 216
— бинарная 210
— планарная 220
— столкновительная 233
фрустрация 401
характеристик метод 138
хищник-жертва, 3 вида 469
хищник-жертва, модель 466
—, —, закон сохранения 468
Хольцмарка распределение 27
центральная догма 287, 345
центральная предельная теорема 19, 50
Чепмена-Колмогорова уравнение 4, 20
Шредингера уравнение 316, 353
Эдвардса-Уилкинсона (ЭУ) уравнение 54
, ширина фронта 57
эйлерова характеристика 552
экспоненциальный анзац 171
, агрегация 171
, адсорбция 264
598
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
экстремальная статистика 22
, АПЗ 148
, граф ЭР 549
, максимальная степень узла в сети
559
, максимальное время ожидания 27
, максимальный шаг 23
, поле случайных скоростей 420, 421
, распределение вероятности 149
, распределение лавин 451
, флуктуации в сетях 568
экстремальная стстистика
, беспорядок 414
эктремальная статистика
, укрупнение 379
эпидемий модели 470
, модель SIR 471
, модель SIS 470
, порог эпидемии 472
, распространение слухов 473
эргодичности нарушение 253
эргодичность 253
ядро реакции 163
ячейка 398
Фонд инфраструктурных и образовшельных
программ создан в 2010 году в соответс i вин с <1>с
деральным законом № 211-ФЗ «О peoprniiirutuiiu
Российской корпорации нанотехнологий», I (елью
деятельности Фонда является развитие 11111 ionn ни
онной инфраструктуры в сфере naiini exinwioi ий,
включая реализацию уже начатых Р()(’I IАIК) об
разовательных и инфраструктурных программ,
РОСНАНО
Основными направлениями деятельности Фонда инфраструктурных и
образовательных программ являются:
• Формирование технологической инфраструктуры.
• Разит не кадрового потенциала отрасли.
• (‘тимулировапие спроса на нанотехнологическую продукцию.
• ('Овертоне Iкование законодательства.
• ( Гайдар! изакии, сертификация и оценка безопасности ианопродукции,
• Метроло1ил.
• 11онулнрпзацня нанотехнологий.
Председателем высшего коллегиального органа управления Фонда
наблюдательного совета - является вице-президент Сколковского циститу ! в
науки и технологий (С’колтех) Алексей Пономарев. Согласно уставу Фонда,
к комне leintiiii совет, в частности, относятся вопросы определения приор!!
тетных направлений деятельности Фонда, его стратегии и бюджет. Предсе¬
дателем 11равлсния Фонда, являющегося коллегиальным органом управлении,
яилистсн 11рсдссдагель Правления ОАО «РОСНАНО» Анатолий Чубайс,
генеральным директором Фонда-Андрей Свинаренко.
Научное издание
Павел Л. Крапивский
Сидней Реднер
Эли Бен-Наим
Кинетический взгляд
на статистическую физику
Перевод с английского языка
А.М. Поволоцкий
Научный редактор русского издания
В. Б. Приезжее
Художественное оформление
Ю.В. Зайцевская
ООО «Издательство «Научный мир»
Тел./факс: +7 (499) 973-2513;
E-mail: sale@naumir.ru. E-mail: naumir@naumir.ru
Internet: http://www.naumir.ru
Подписано к печати 2.07.2012
Формат 70x100/16
Гарнитура Таймс. Печать офсетная. Печ. л. 38,5
Тираж 1 000 экз. Заказ №6583
При участии ООО Агентство печати «Столица»
Отпечатано с готовых файлов заказчика
в ОАО «Первая Образцовая типография»,
филиал «УЛЬЯНОВСКИЙ ДОМ ПЕЧАТИ»
432980, г. Ульяновск, ул. Гончарова, 14
ФУНДАМЕНТАЛЬНЫЕ ОСНОВЫ НАНОТЕХНОЛОГИЙ
Издательство «Научный мир» и Научно-образовательный центр по нанотехнологиям
МГУ имени М.В. Ломоносова представляют книгу из серии «Фундаментальные основы
нанотехнологий»: Павел Л. Крапивский, Сидней Реднер, Эли Бен-Наим «Кинетический
взгляд на статистическую физику» (перевод с английского языка).
В книге в доступной для читателя форме рассмотрены основные явления неравновес¬
ной статистической физики. Она посвящена развитию и применению теоретических
методов, которые помогут студентам совершенствовать навыки решения задач.
1
Список тем:
-Диффузия -Адсорбция -Гистерезис
-Столкновения - Динамика спинов - Динамика популяций
-Запреты -Укрупнение - Диффузионные реакции
- Агрегация - Беспорядок - Сложные сети
- Фрагментация
Книга содержит более 200 упражнений для проверки понимания предмета студен¬
тами. Ссылку на веб-страницу, поддерживаемую авторами, содержащую текущий спи¬
сок ошибок и решений упражнений для преподавателей, можно найти по адресу
www.cambridge.org/9780521851039.
У неравновесной статистической механики так много приложений, и она наполнена
таким количеством искусных трюков, что единственный способ ее преподавания - через
примеры. Крапивский, Реднер и Бен-Наим написали прекрасную книгу, которая в легкой
и непринужденной манере представляет многие из таких примеров: одни - классические,
а другие - на переднем крае современного научного знания.
Ж.Ф. Буше, председатель компании Capital Fund Management (Париж),
профессор статистической механики Парижской политехнической школы
В последнем десятилетии наше понимание неравновесной статистической физики и
сложных систем развивалось большими шагами, но до сих пор отсутствовали подробные
учебные пособия, которые могли бы служить для студентов введением в эту область. На¬
писанная в простом и доступном стиле, который также характерен для оригинальных
научных работ авторов, книга осторожно проводит читателя от самых элементарных по¬
нятий до передового рубежа современных исследований.
Иохйм, Круг, Кельнский университет
Это великолепное педагогическое введение в широкий круг современных разделов не¬
равновесной статистической физики... Текст полон примеров и упражнений и является обя¬
зательным чтением для студентов, которые хотят работать в этой области.
Сатья Мажумдар, НЦНИ, Университет Париж-юг
ЛУЧШИЕ ЗАРУБЕЖНЫЕ УЧЕБНИКИ
785915 222969
WTOCThinmiifliffinn