Author: Баканина Л.П. Белонучкин В.Е. Козел С.М. Колачевский Н.Н. Косоуров Г.И.
Tags: физика задачи по физике общая механика кинематика общая физика сборник задач
Year: 1967
Л.П.Баканина, В.Е.Белонучкин, С.М.Козел, Н.Н.Колачевский, Г.И.Косоуров,
И.П.Мазанъко
СБОРНИК ЗАДАЧ ПО ФИЗИКЕ
Книга представляет собой сборник задач (повышенной трудности) по физике в объеме программы средней школы. Предназначается для лиц, самостоятельно готовящихся к поступлению в вузы с повышенными требованиями по физике. Может быть использована в работе школьных физических кружков и юношеских физико-математических школ. Может также служить дополнительным пособием для студентов педагогических вузов и для преподавателей физики в средних школах.
Содержание
Предисловие ко второму изданию 5
Из предисловия к первому изданию 6
I. МЕХАНИКА Задачи Решения
Кинематика 7 132
Статика 9 138
Динамика 13 144
Работа, мощность, энергия 20 156
Динамика вращательного движения 25 165
Закон сохранения количества движения 31 177
Разные задачи 33 189
II. ТЕПЛОТА И МОЛЕКУЛЯРНАЯ ФИЗИКА Поверхностное натяжение 44 209
Закон сохранения энергии для тепловых явлений 45 213
Тепловое расширение тел 48 218
Уравнение газового состояния 49 222
Насыщающие и ненасыщающие пары 61 243
Разные задачи 66 250
III. ЭЛЕКТРИЧЕСТВО Электрический заряд. Закон Кулона 73 261
Электроемкость. Потенциал 74 265
Заряженная частица в электрическом поле 89 279
Электрические цепи. Закон Ома 84 289
Работа и мощность электрического тока. Закон Джоуля — 92 307
Ленца Электромагнитная индукция 96 320
Разные задачи 99 323
IV. ОПТИКА Преломление и отражение света на границе двух сред 105 311
Тонкие линзы 108 350
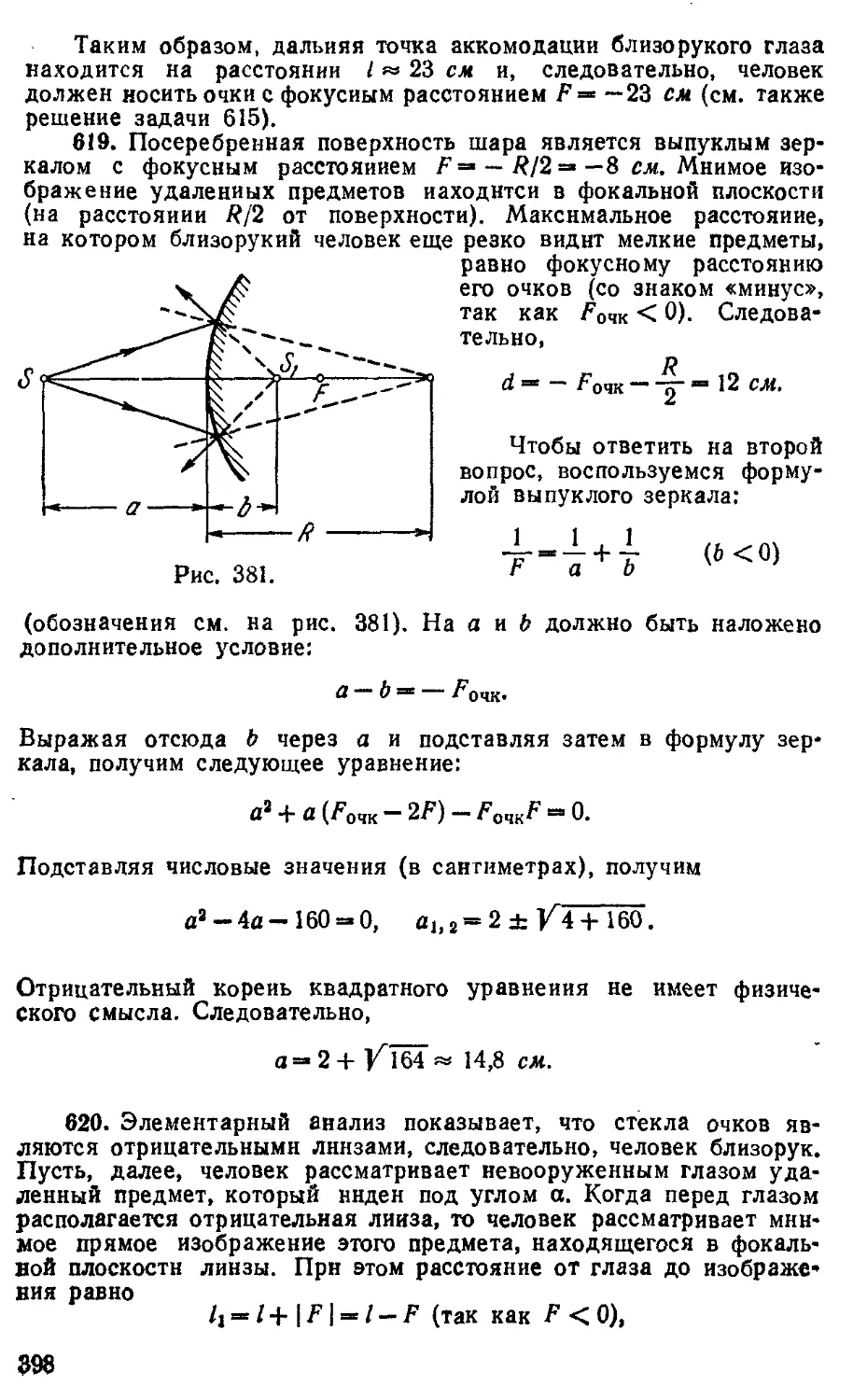
Сферические зеркала 115 369
Элементы фотометрии 118 377
Оптические приборы 125 397
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
В настоящем втором, дополненном и исправленном издании сборник включает большинство физически интересных задач из числа предлагавшихся на приемных экзаменах в Московском физико-техническом институте за период с 1947 по 1967 гг.
Авторы сборника, принимавшие в разное время участие в составлении и подборе экзаменационных задач, заново отредактировали и привели в систему этот обширный материал.
В сборник дополнительно включено более двухсот новых задач. Заново проверены условия и решения задач и внесены необходимые исправления. В ряде случаев было сочтено целесообразным дать более подробные пояснения к задачам. Некоторая часть задач, не представляющих физического интереса, из сборника исключена.
Все авторы в той или иной мере принимали участие в работе над каждым разделом сборника. При подготовке к печати рукописи второго издания разделы были распределены между авторами следующим образом:
механика — Л. П. Баканина и И. П. Мазанько, теплота и молекулярная физика — Г. И. Косоуров и С. М. Козел,
электричество — В. Е. Белонучкин и И. П. Мазанько, оптика — Н. Н. Колачевский и С. М. Козел.
Авторы приносят благодарность всем преподавателям кафедры физики МФТИ, принимавшим участие в составлении задач, собранных в настоящей книге. Авторы также считают своим долгом выразить признательность рецензенту книги Б. Б. Буховцеву за ценные замечания.
Авторы Март 1969 г.
5
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Настоящий сборник в основном предназначается для лиц со средним образованием, самостоятельно готовящихся к поступлению в такие высшие учебные заведения, где предъявляются повышенные требования по физике.
Кроме того, он может быть использован в работе школьных физических кружков и юношеских физико-математических школ. Сборник может явиться полезным дополнительным пособием для студентов педагогических вузов и для преподавателей физики в средних школах.
Авторы сборника пытались подобрать задачи, решение которых требует не просто механической подстановки исходных данных в готовые уравнения, а прежде всего осмысливания самого явления, описанного в условии задачи, и свободного владения физическими законами, изучаемыми в средней школе. Это, по мнению авторов, должно способствовать не только развитию у поступающих навыков решения физических задач, но и более глубокому усвоению теории.
Для решения задач, содержащихся в данном сборнике, требуются знания в объеме программы средней школы. Следует, однако, подчеркнуть, что большинство предлагаемых задач является задачами повышенной трудности. Учитывая это, авторы снабдили значительное число задач указаниями или подробными решениями.
Сборник состоит из четырех разделов: «Механика», «Теплота и молекулярная физика», «Электричество» и «Оптика», каждый из которых разбит на ряд подразделов. Как правило, внутри подразделов задачи располагаются в порядке возрастающей трудности.
При составлении указаний и решений особое внимание уделено принципиальным вопросам, связанным с применением физических законов к решению конкретных задач. Второстепенные моменты рассуждений, как правило, опущены.
Апрель 1965 г,
Авторы
ЗАДАЧИ
I. МЕХАНИКА
Кинематика
1. Небольшой шарик движется без трения один раз по желобу АВС (рис. 1), а другой раз по желобу ADC. Части желоба AD и ВС вертикальны, а углы АВС и ADC закруглены. Изобразить графически для обоих случаев зависимость скорости и шарика от времени *, если AB = BC=AD = DC = h. Скорость шарика в точке .4 равна нулю. По какому пути (АВС или ADC) шарик скорее попадет из точки А в точку С?
2. Из точки А, лежащей на верхнем конце вертикального диаметра некоторой окружности, по желобам, установленным вдоль различных хорд этой окружности (рис. 2), одновременно начинают скользить грузы. Определить, через какое время грузы достигнут окружности? Как это время зависит от угла а наклона хорды к вертикали? Трением пренебречь,
7
3. На тонкой невесомой нити длины I подвешен небольшой груз. Определить приближенно период Т колебаний груза, предполагая, что его истинное движение по дуге окружности АВС (рис. 3) можно заменить дип-
лом а к горизонту. Если на высоте Н и попасть тс
жением по соответствующим хордам АВ и ВС.
4. Горизонтально направленный пучок атомов серебра при вылете из источника обладает кинетической энергией W = 9,8 • 10-!0 эрг. Определить снижение атомов под действием силы тяжести на расстоянии L = 5m от источника. Атомный вес серебра А — 108.
5. Бомбардировщик пикирует по прямой под уг-пилот хочет сбросить бомбу шо в цель, то на каком рас
стоянии по горизонтали от цели он должен это сделать? Скорость бомбардировщика v. Сопротивление воздуха
не учитывать.
6. Из трех труб, расположенных на земле, с одинаковой скоростью 'бьют струи воды под углами 60, 45 и 30° к горизонту. Найти отношение наибольших высот подъема струй воды, вытекающих из труб, и отношение дальностей падения воды на землю.
7. Камень бросают горизонтально с горы, уклон которой равен а. Определить, с какой скоростью v был брошен камень, если он упал на склон на расстоянии L от точки бросания.
8. Шарик с высоты й=2 м вертикально падает на наклонную плоскость и упруго отражается. На каком расстоянии S от места падения он снова ударится о ту же плоскость? Угол наклона плоскости к горизонту а = 30°.
9. Два тяжелых шарика брошены с одинаковыми начальными скоростями из одной точки вертикально вверх, один через t секунд после другого. Они встретились в воздухе через Т секунд после вылета первого шарика. Определить начальную скорость шариков. Сопротивлением воздуха пренебречь.
8
10. На учебных стрельбах поставлена задача: в минимальное время поразить снаряд, выпущенный вертикально вверх со скоростью щ = 1000 м/сек, вторым снарядом, скорость v-2 которого на 10% меньше. Через сколько секунд после первого выстрела следует произвести второй, если стрелять с того же места?
11. На реке на расстоянии Л = 60 м от берега стоит на якоре плот. Скорость и течения реки у самого берега
равна нулю и растет пропорционально расстоянию от берега, так что у плота она равна uL = 2 м/сек. Моторная лодка отправляется с берега к плоту. Относительно воды лодка развивает скорость и = 7,2 км/час. Как дол-
жен моторист ориентировать лодку перед отплытием, чтобы без дальнейшей корректировки скорости лодки пристать к плоту точно напротив места отплытия? Какое время Т лодка будет при этом находиться в пути?
12. Самолет летит горизонтально на высоте Н — Ь км над поверхностью земли со сверхзвуковой скоростью. Звук дошел до наблюдателя через t — 10 сек после того, как над ним пролетел самолет.
Определить скорость v самолета, если скорость звука с = 330 м/сек.
13. Самолет летит горизонтально со скоростью v — 470 м/сек. Человек услышал звук от самолета через t = 21 сек после того, как ним. На какой Скорость звука <
: самолет пролетел над высоте летит самолет? с — 330 м/сек.
Статика
С
14. Нижний конец В стержня АВ В укреплен шарнирно (рис. 4). К верхнему концу А привязана веревка АС, удержи- 1!С' 4’ вающая стержень в равновесии. Найти натяжение вёревки, если вес стержня Р, Z.ABC = Z ВСА — а. Точки В и С находятся на одной вер-
тикали.
15. Если к нижнему концу вертикально висящей пружины прикрепить груз, то ее длина станет равной L\. Если другой такой же груз прикрепить к середине
9
пружины, то ее длина возрастет до величины L2. Найти длину пружины в недеформированном состоянии, пред-
полагая, что ее удлинение прямо пропорционально на-
грузке. Весом пружины при расчете пренебречь.
16. Два одинаковых цилиндра (рис. 5) подвешены на нерастяжимых нитях одинаковой длины. Между ними положен цилиндр того же диаметра, но вдвое большего веса. Система находится в равновесии. Определить угол р, если угол между нитями равен 2а. Трение отсутствует.
17. На земле вплотную друг к другу лежат два одинаковых цилиндрических бревна. Сверху на них кладут такое же бревно (рис. 6). При каком максимальном коэффициенте трения k между бревнами
они еще будут раскатываться? Скольжения бревен по
поверхности не происходит.
18. Грузовик общим весом р = 8 Т преодолевает крутой подъем (рис. 7). К грузовику присоединен прицеп
общим весом р = 4 Т. Буксирный трос расположен на высоте h=\ м. Центр тяжести С грузовика находится на высоте Н = 2 м; расстояние между осями передних и задних колес грузовика L = 4 м. При езде по горизонтальной дороге на задние колеса приходится 3/4 веса грузовика. При каком угле подъема грузовик опрокинется назад? Существует ли такая опасность реально,
10
если мощность двигателя достаточна лишь для преодоления подъемов, не превышающих 10°? (tglO? = = 0,18.)
19. Однородная тонкая пластинка имеет форму круга радиуса R, в котором вырезано отверстие вдвое мень-
касающееся (рис. 8). Где тяжести пла-
шего радиуса, края пластинки находится центр стинки?
Рис. 8.
Рис. 9.
20. На круглом столе, крышка которого имеет радиус R и массу М, лежит, касаясь края крышки, диск радиуса г и массы т. Как должны быть расположены три равноотстоящие друг от друга ножки стола, чтобы их давление на пол было одинаково?
21. Катушку тянут за нитку по полу, как указано стрелкой на рис. 9, причем ускорение катушки постоянно и равно а. При каком значении коэффициента трения между ободами катушки и полом катушка будет скользить не вращаясь? Радиус вала катушки г, а ободьев — R.
22. В цилиндре на расстоянии 2AJ/3 от центра параллельно оси просверлено отверстие радиуса /?/4 (рис. 10)*
Рис. 10.
Отверстие залито веществом, плотность которого в 11 раз больше плотности вещества цилиндра. Цилиндр
И
лежит на дощечке, которую медленно поднимают за один конец. Каков максимальный угол наклона дощечки, при котором цилиндр еще может находиться на ней в равновесии? Коэффициент трения 6 = 0,3.
23. Вдоль оси цилиндра на расстоянии /?/2 от его центра просверлено отверстие (рис. 11). Радиус отверстия /?/2. Цилиндр лежит на дощечке, которую медленно
Рис. 11.
поднимают за один конец. Найти предельный угол наклона дощечки, при котором цилиндр еще может на
ней удержаться. Коэффициент трения k — 0,2.
24. Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду, как указано на рис. 12. Равновесие достигается, когда палочка расположена наклонно и погружена в воду на половину своей длины. Какова плотность материала, пз которого сделана палочка?
25. Поверх жидкости плотности pi налита жидкость плотности р2 < Pi, причем жидкости не смешиваются. Очевидно, что тело плот-
Рис. 12.
ности р (pi > р > рг) будет плавать у границы раздела этих жидкостей. Определить, какая часть объема тела будет погружена в более плотную жидкость.
26. В цилиндрический банке с площадью дна S высота воды //=15 см. Когда в эту банку опустили порожнюю латунную чашку (плотность латуни рл=8,8 г/слр) так, чтобы она плавала, то вода в банке поднялась на /г=2,2 см. Какова будет высота //х уровня воды в банке, если чашку утопить в ней?
12
27. В бак с водой опущена длинная трубка диаметром d, к которой снизу плотно прилегает цилиндрический диск толщины h и диамет
ром D (рис. 13). Плотность р материала диска больше плотности воды рв. Трубку медленно поднимают вверх. Определить, на какбй глубине Н диск оторвется от трубки?
28. Автомобиль массы Л1 = 1 т равномерно поднимается по наклонному участку шоссе с углом наклона а = 12° (sin 12° = 0,2). Определить, насколько отличаются давления передних и задних колес автомобиля на шоссе, если известно, что расстояние между
осями L == 2,5 лг, а центр тяже-
сти расположен па равных расстояниях от осей на высоте Н = 0,75 м.
Динамика
29. На горизонтально расположенную штангу надета муфта, которая может скользить вдоль штанги (рис. 14). Штанга перемещается поступательно в горизонтальной плоскости с ускорением а в направлении,
составляющим угол а со штангой. При каком мини-мальном коэффициенте k трения муфта не будет двигаться относительно штанги?
30. Горизонтальная доска А имеет ступеньку высотой Н, в которую упирается свободно лежащий на доске однородный цилиндр В радиуса R>H (рис. 15). Доску двигают в горизонтальном направлении с ускорением я. Определить максимальное значение этого ускорения,
13
при котором цилиндр еще не будет подниматься на ступеньку, Трением пренебречь.
Рис. 15,
31. Однородный цилиндр массы т лежит на подставке в форме желоба, расстояние между боковыми стенками которого равно радиусу цилиндра R (рис. 16). Подставку двигают в горизонтальном направлении с ускорением а. Найти силы давления на стенки желоба. Трением пренебречь.
32. Тонкая U-образная трубка, размеры которой указаны на рис. 17, заполнена ртутью до половины вертикальных колен. Трубка движется горизонтально с ускорением а. Найти разность высот h ртути в вертикальных частях трубки и давление в точке А. При каком ускорении ртуть начнет выливаться из трубки? Атмосферное давление равно Ро, плотность ртути р.
Рис. 17.
Рис. 16.
33. На каком минимальном расстоянии I от перекрестка должен начинать тормозить шофер при красном свете светофора, если автомобиль движется со скоростью v = 100 км/час,, а коэффициент трения k между шинами и дорогой равен 0,4?
34. Два груза с массами и т2 (рис. 18) лежат на гладкой горизонтальной плоскости и связаны между собой тонкой нитью, способной выдерживать наиболь-
14
шую нагрузку Р. Определить максимальную силу F, с которой можно тянуть за груз т\, чтобы нить не оборвалась. Изменится ли величина этой силы, если тянуть за груз /т?2? Трением грузов о плоскость пренебречь.
Рис. 18.
35. К грузу А массы тА = 1 кг подвешен на веревке груз В массы тв = 5 кг. Масса веревки т = 4 кг. К грузу А приложена направленная вверх сила F = 188,8 н. Найти натяжение в верхнем конце и в середине веревки.
36. От поезда, идущего по горизонтальному участку пути с постоянной скоростью v0, отцепляется 1/3 состава. Через некоторое время скорость отцепившихся вагонов уменьшилась в два раза. Считая, что сила тяги при разрыве состава не изменилась, определить скорость головной части поезда в этот момент. Сила трения пропорциональна весу и не зависит от скорости.
37. Два грузика с массами mi = 300 г и т2 = 200 г соединены нитью, перекинутой через блок, подвешенный на пружинных весах. Определить ускорение грузов, показание пружинных весов и натяжение нити. Трением в оси блока и его массой пренебречь.
38. Две гири неравного веса висят на концах нити, перекинутой через невесомый блок, причем более легкая гиря расположена на h = 2 м ниже более тяжелой. Если предоставить гирям двигаться под действием силы тяжести, то через 1 = 2сек они будут на одной высоте. Определить отношение весов гирь.
39. На штанге укреплен неподвижный невесомый блок, через ко
торый перекинута нить с двумя грузами массы nii = 500 г и т2 — 100 г. В грузе т2 имеется отверстие, через которое проходит штанга (рис. 19). Сила FTP трения груза т2 о штангу постоянна и равна 300 Г. Найти ускорение а грузов и силу Т натяжения нити.
ЖЖ»
Рис. 19.
15
ходится все время
Рис. 20.
40. Предполагая массы грузов Afi и М2 известными, найти их ускорения ai и а2 в системе, состоящей из неподвижного блока А и подвижного В (рис. 20). Массой блоков п трением в их осях пренебречь.
41. Через неподвижный блок, масса которого пренебрежимо мала, перекинута веревка. На одном конце веревки висит груз с массой М = 25 кг, а за другой конец ухватилась обезьяна и карабкается вверх. С каким ускорением а поднимается обезьяна, если груз на-на одной высоте? Масса обезьяны т = 20 кг. Через какое время t обезьяна достигнет блока, если первоначально она находилась от него на расстоянии I = 20 л?
42. Внутри колеса, всю массу т которого можно считать сосредоточенной в ободе, бежит белка, причем отношение массы колеса к массе М белки равно ф 2. Колесо без трения вращается вокруг неподвижной горизонтальной оси. Коэффициент трения между ободом колеса и белкой k—\. Какое макси
мальное постоянное линейное ускорение а белка может сообщить колесу?
43. На горизонтальной доске лежит груз. Коэффициент трения между доской и грузом ,4=0,1. Какое ускорение а в горизонтальном направлении следует сообщить доске, чтобы груз мог с нее соскользнуть?
44. Груз весом /’=100 н привязан к свободно свисающему концу веревки, намотанной на лебедку. И груз и лебедка находятся на некоторой высоте. Груз начинает падать, причем веревка натянулась, когда груз пролетел h — 12 м. После этого при помощи лебедки начали тормозить движение груза. Какую минимальную длину I веревки пришлось вытравить до полной остановки груза, если прочность веревки Т—180 н?
45. Маховик, состоящий из тяжелого обода с массой М и радиусом R и легкой ступицы, соединенной с ободом с помощью тонких спиц, вращается вокруг горизонтальной оси с угловой скоростью со. К ободу маховика прижимается с силой F тормозная колодка. Коэффициент трения между колодкой и ободом равен k.
16
Рис. 21.
Чему равно время торможения t и сколько оборотов п сделает маховик до полной остановки? Массой ступицы и спиц можно пренебречь.
46. Тяжелое колесо с массой М и радиусом R вращается на оси с угловой скоростью to. С колесом жестко связан легкий тормозной барабан радиусом г, к которому прижимается тормозная колодка (рис. 21). Определить, сколько оборотов сделает колесо до полной остановки, если колодка прижимается силой F, а коэффициент трения между колодкой и барабаном равен k. Всю массу колеса считать сосредоточенной в ободе.
47. За какое время тело с массой т сосколь
знет с наклонной плоскости высотой h и с углом наклона р, если по наклонной плоскости с углом наклона а оно движется вниз равномерно?
48. Чему должен быть равен минимальный коэффициент трения k между шинами и поверхностью наклонной дороги с уклоном сс = 30°, чтобы автомобиль мог двигаться по ней вверх с ускорением а=0,6 М/сек2?
49. С наклонной плоскости соскальзывает небольшая шайба и в конце спуска ударяется о стенку ВО (рис. 22). Считая удар абсолютно упругим, определить, на какую высоту поднимется шайба. Известно, что Z.AOC=a, BOFOA, AC = h. Коэффициент трения шайбы о плоскость k.
50. На наклонной плоскости лежит брусок. К бруску приложена сила F, равная удвоенному весу бруска и направленная вверх вдоль наклонной плоскости (рис. 23). Коэффициент k трения между бруском и
2 Л. П. Баканина и
17
нутой через невесомый блок
наклонной плоскостью равен 1. При каком угле а наклона ускорение а бруска будет минимальным и каково это минимальное ускорение?
51. На гладком горизонтальном столе лежит брусок массы М = 2 кг, на котором находится брусок массы т = 1 кг. Оба бруска соединены легкой нитью, переки-(рис. 24). Какую силу К нужно приложить к нижнему бруску, чтобы он начал двигаться от блока с постоянным ускорением а = g/2? Коэффициент трения между брусками k = 0,5. Трением между нижним бруском и столом пренебречь.
52. По легкому клину с углом а, лежащему на горизонтальном полу, скользит тело. Коэффициент трения между клином и полом k. Каков должен быть минимальный коэффициент трения k\ между телом и клином, чтобы последний оставался неподвижным? Массу клина
I м ----7
ШВЖЖВЖЖЖ
Рис. 24.
при расчетах не учитывать.
53. Через блок, укрепленный плоскости, перекинута веревка наковой массы М (рис. 25). Найти силу давления на ось, если коэффициент тре
в вершине наклонной двумя грузами оди-
Рис. 25.
ния между наклонной плоскостью и лежащим на ней грузом равен k, а угол наклонной плоскости равен а. Трением в оси блока и его массой пренебречь.
54. Через блок/ укрепленный на краю гладкого горизонтального стола, перекинута веревка, соединяющая два груза т и М, как указано на рис. 26. Стол движется вверх с ускорением Ь. Найти ускорение груза т. Трением и массой блока пренебречь.
18
b
Рис. 27.
55. Определить ускорение груза т в предыдущей задаче, если стол движется вертикально нием b < g.
56. Через невесомый блок перекинута зами т и 2т. Блок движется вверх с Пренебрегая трением, найти давление (рис. 27).
57. Решить предыдущую задачу в предположении, что блок движется вниз с ускорением b < g.
58. На наклонной плоскости с углом наклона а неподвижно лежит кубик, причем коэффициент трения между кубиком и плоскостью равен k. Наклонная плоскость движется с ускорением а в направлении, указанном стрелкой (рис. 28). При каком минимальном значении этого ускорения кубик начнет соскальзывать?
59. Наклонная плоскость с углом
жется с ускорением а в сторону, указанную стрелкой (рис. 29). Начиная с какого значения а тело, лежащее
вниз с ускоре-
веревка с гру-ускорением Ь. блока на ось
наклона а дви-
Рис. 28.
Рис. 29,
на наклонной плоскости, начнет подниматься? Коэффициент трения между телом и наклонной плоскостью равен k.
60. В автомобиле укреплена герметически закупоренная банка с бензином, имеющая вид прямоугольного параллелепипеда, две грани которого перпендикулярны к оси автомобиля и находятся на расстоянии 30 см друг от друга. Какова разность давлений бензина на стенки банки во время разгона автомобиля, если он набирает скорость 65 км/час за 1 мин (плотность бензина 0,7 а/сл*3)? Ускорение автомобиля при разгоне считать постоянным.
2*
19
61. С какой средней силой F давит на плечо ручной пулемет при стрельбе, если масса пули т=10 г, ее ско-рость при вылете о=800 м/сек и скорострельность пулемета 600 выстрелов в минуту?
62. Космический корабль, имеющий лобовое сечение S = 50 лг2 и скорость о=10 км/сек, попадает в облако микрометеоров. В одном кубометре пространства находится один микрометеор. Масса каждого микрометеора Л1 = 0,02 г. Насколько должна возрасти сила F тяги двигателя, чтобы скорость корабля не изменилась? Удар микрометеоров об обшивку корабля считать неупругим.
63. Какова должна быть минимальная сила трения между колесами автомобиля и дорогой, чтобы он мог двигаться со скоростью о = 30 м/сек под вертикальным дождем? Масса дождевой капли т = 0,1 г. Ежесекундно на 1 с.и2 горизонтальной поверхности попадает дне капли дождя (а = 2). Площадь поверхности автомобиля, смачиваемой дождем, S = 5 .и2. Считать, что вся поверхность смачивается дождем равномерно.
64. Огнетушитель выбрасывает ежесекундно т — 0,2 кг пены со скоростью v = 20 м/сек. Вес полного огнетушителя Р=20 н. Какую силу должен развить человек, чтобы удержать огнетушитель неподвижно в вертикальном положении в начальный момент его работы?
Работа, мощность, энергия
65. Какой путь S пройдут санки по горизонтальной поверхности после спуска с горы высотой /г=15 м, имеющей уклон а = 30°? Коэффициент трения /г = 0,2.
66. Какой путь пройдут до полной остановки санки, имеющие начальную скорость v0, при подъеме на гору с углом наклона а? Известно, что на горизонтальном участке пути с тем же коэффициентом трения санки, имеющие такую же начальную скорость, проходят путь /0.
67. Легковой автомобиль с массой М = 1000 кг равномерно движется* по наклонному участку шоссе, поднимаясь на /г = 10 м на каждый километр пути. Насколько в этом случае расход бензина больше, чем при движении с той же скоростью по горизонтальному участку шоссе? Теплотворная способность бензина равна
20
<7=11 000 ккал/кг. Коэффициент полезного действия двигателя равен т] = 10%.
Примечание. Расход бензина принято относить к пути /=100 км.
68. Вверх по наклонной плоскости равномерно со скоростью v поднимают тело массы т, причем сила направлена вдоль наклонной плоскости. При каком угле наклона затрачиваемая мощность Р будет максимальной и каково значение максимальной мощности? Коэффициент трения k между телом и наклонной плоскостью равен 1.
69. От удара копра весом Р = 5000 н, свободно падающего с некоторой высоты, свая погружается в грунт на s=l см. Определить силу F сопротивления грунта, считая ее постоянной, если скорость копра перед ударом о=10 м/сек. Весом сваи при расчете пренебречь.
70. Чему была равна средняя сила сопротивления воды движению парохода, если он в течение трех суток при средней скорости 10 км/час потребил <2 = 6,5 т угля? Коэффициент полезного действия судового двигателя 11=0,1. Теплотворная способность угля 103 ккал/кг (—33,5 • 106 дж/кг).
71. Шарик для игры в настольный теннис радиусом /? = 15 мм и массой т — 5 г погружен в воду на глубину h = 30 см. Когда шарик отпустили, он выпрыгнул из воды на высоту hi = 10 см. Какая энергия перешла при этом в тепло вследствие трения шарика о воду?
72. Веревка длиной /=20 м переброшена через блок. В начальный момент веревка висит симметрично и покоится, а затем, в результате незначительного толчка, начинает двигаться по блоку. Будет ли движение веревки равномерно ускоренным? Какова будет скорость веревки, когда она сойдет с блока? Массой блока пренебречь, радиус блока считать малым.
73. Небольшой по размерам груз массой Л4] прикреплен к веревке длиной / и массой М2, лежащей на гладком горизонтальном столе. Под тяжестью груза веревка начинает соскальзывать без начальной скорости через отверстие в столе. Какова будет скорость v веревки в тот момент, когда ее конец соскользнет со стола?
74. В водоеме укреплена вертикальная труба с поршнем таким образом, что нижний ее конец погружен в воду. Поршень, лежавший вначале на поверхности
21
воды, медленно поднимают на высоту Н~15 м (рис.30), Какую работу пришлось на это затратить, если пло-
Рис. 30.
щадь поршня S = 1 дм2, атмосферное давление Р = 1 атм? Весом поршня пренебречь.
75. Санки, движущиеся по горизонтальному льду со скоростью v == = 6 м!сек, выезжают на асфальт. Длина полозьев санок А = 2 м, коэффициент трения об асфальт /?=1. Какой путь S пройдут санки до полной остановки?
76. Какую работу необходимо за* тратить, чтобы вытащить пробку из горлышка бутылки (рис. 31)? Длина пробки а. Пробка находится от края горлышка тоже на расстоянии а. Сила трения между пробкой и бутылкой F. Весом пробки пренебречь.
77. Легкая цилиндрическая палочка
длиной L и плотностью р погружена вертикально в жидкость с плотностью ро (р0> р). Нижний конец палочки находится на глубине Но под уровнем жидкости (Н0>Ь). На какую высоту Н выпрыгнет палочка из жидкости, если ей дать возможность двигаться? Вяз-
костью жидкости пренебречь.
Рис. 31.
Рис. 32.
78. Какую работу нужно совершить, чтобы длинную доску, лежащую на земле, повернуть в горизонтальной плоскости вокруг одного из концов на угол а? Длина доски L, масса М, коэффициент трения между доской и землей k.
79. В цилиндрическом стакане с водой плавает бру*, сок высоты L и сечения Si (рис. 32). При помощи тон*
22
кой спицы брусок медленно опускают на дно стакана. Какая работа при этом была совершена? Сечение стакана 32=251, начальная высота воды в стакане тоже L, плотность материала бруска р = 0,5рв, где рв — плот-
ность воды.
80. На поверхности земли шарнирно закреплена легкая штанга длины расположенная вначале верти-
кально. На верхнем конце штанги укреплен груз массы /пь а на
Рис. 34.
расстоянии 12 от нижнего конца — груз т2 (рис. 33). С какой скоростью масса т, коснется земли, если штанга начнет падать без начальной скорости? Массой
штанги можно пренебречь по сравнению с массой грузов.
81. Вокруг горизонтальной оси О может свободно вращаться легкий рычаг, плечи которого равны /] и 12 (рис. 34). На концах рычага укреплены грузы с массами соответственно пц и т2. Какую скорость будет иметь в нижней точке один из грузов, если первоначально рычаг находился в горизонтальном положении?
82. На легкий барабан радиуса г с горизонтальной осью намотана нить, на конце которой подвешен груз массой т\. На ба
рабане укреплены радиально четыре спицы длиной /о с тяжелыми шариками массы т на концах (рис. 35).
Первоначально груз висит на высоте ho над полом. Груз
23
предоставляют самому себе, и система приходит в ускоренное движение. Когда груз достигает пола, нить продолжает свободно сматываться с барабана, после чего барабан начинает снова наматывать на себя нить. Нг< какую максимальную высоту от пола поднимется груз? Массой барабана, нити и спиц, а также трением в оси блока можно пренебречь и удар груза об пол считать неупругим.
83. Два груза с массами mt и т2 (пц > пг2) связаны нитью, перекинутой через легкий блок радиуса г, ось
Рис. 37.
которого горизонтальна. На одной оси с блоком укреплены по радиусам четыре тонкие спицы длиной I, на концах которых укреплены небольшие тяжелые шарики массы т (рис. 36). Система приходит в ускоренное движение без начальной скорости. Найти ускорение грузов /П1 и т2, считая, что трение в оси блока отсутствует, нить не проскальзывает по блоку и массами нити, блока и спиц можно пренебречь.
84. Какова должна быть минимальная мощность насоса, поднимающего воду по трубе на высоту й? Сечение трубы S; насос за 1 сек, перекачивает Q литров воды (рис. 37).
85. Вентилятор гонит струю воздуха через отверстие в стене. Во сколько раз надо увеличить мощность Wt вентилятора, чтобы ежесекундно перегоняемое вентилятором количество воздуха увеличилось в два раза?
24
Закон сохранения количества движения
86. Два небольших тела одновременно начинают соскальзывать без трения внутрь полусферы радиуса /? (рис. 38). Происходит абсолютно неупругий удар, после которого тела продолжают двигаться вместе. Найти угловую амплитуду колебаний тел, если отношение их —a —•
масс равно 2. ’ Р \Р Н
87. Пуля с массой т = \\ Л \ у
= 10 г подлетает к доске со \ /
скоростью Vo = 600 м/сек и, _____
пробив ее в центре, вылетает со скоростью v = Рис. 33.
= 400 м/сек. Определить,
какая часть потерянной кинетической энергии пули пошла на кинетическую энергию доски и какая выделилась в виде тепла. Масса доски М = 1 кг.
88. На железнодорожной платформе, движущейся по инерции со скоростью V, укреплено орудие. Ствол орудия направлен в сторону движения платформы и приподнят над горизонтом. Орудие произвело выстрел, после чего скорость платформы уменьшилась в три раза. Найти скорость v снаряда (относительно земли), если он вылетает из ствола под углом а к горизонту. Масса снаряда т, масса платформы с орудием М.
89. На гладкой горизонтальной поверхности лежит длинный брусок массой ЛЬ. На бруске стоит пушка массой М2. Из пушки производится выстрел в горизонтальном направлении снарядом массы т, вылетающим со скоростью v относительно земли. Пушка, испытав отдачу, проходит некоторое расстояние по бруску, затем под влиянием сил трения она перестает двигаться относительно бруска. Определить количество механической энергии Q, превратившейся в тепло за счет сил трения между пушкой и бруском.
90. Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние h сдвинется лодка, если масса человека т = 60 кг, масса лодки Л1=120 кг, длина лодки L = 3 ju? Сопротивлением воды пренебречь.
91. Плот массой mi свободно скользит по поверхности воды со скоростью vj. На плот с берега прыгает
25
человек массы т2. Скорость человека перпендикулярна к скорости плота и равна ц2- Определить скорость и плота с человеком. Силами трения плота о воду пренебречь.
92. Открытая "цистерна с водой стоит на рельсах, по которым может двигаться без трения. Alacca цистерны М, масса воды т. Сверху в цистерну на расстоянии I от ее центра падает вертикально груз массой ц. В какую сторону и насколько сдвинется цистерна к тому времени, когда движение воды успокоится и груз будет плавать? Объясните механизм явления.
93. Пуля с массой т попадает в деревянный брусок массы М., подвешенный на нити длиной I (баллистический маятник), и застревает в нем. Определить, на какой угол а отклонится маятник, если скорость пули равна V.
94. Атом распадается на две части, массы которых Mi и М2, а общая кинетическая энергия частей Е. Определить их скорости.
95. При p-распаде одного атома радиоактивного элемента RaB (атомный вес А = 214) из атома вылетает электрон с энергией IR = 5-10~15 дж. В результате атом RaB превращается в атом нового элемента RaC с тем же атомным весом. Определить кинетическую энергию атома RaC.
96. Нейтрон с энергией М7=10~15 дж поглощается первоначально неподвижным ядром кадмия. Определить скорость и вновь образовавшегося ядра.
97. Нейтрон испытывает упругое соударение с ядром гелия и затем, отразившись, упруго соударяется с другим ядром гелия (при упругих соударениях суммарная кинетическая энергия сохраняется). Ядра гелия до соударения были неподвижны. Считая оба соударения центральными (т. е. скорости до и после соударения направлены вдоль линии центров соударяющихся частиц), определить, во сколько раз изменится энергия нейтрона после двух соударений.
98. Реакцию синтеза тяжелого и сверхтяжелого изотопов водорода (Н2 + Н3 = п + Не4) изучают, направляя ускоренные до энергии Е^ — 2 Мэв ионы дейтерия на тритиевую мишень. Детектор регистрирует нейтроны, вылетающие перпендикулярно к направлению пучка
26
На расстоянии Z/2 под
ЬшШШШ
Рис. 39.
дейтронов. Определить энергию регистрируемых нейтронов, если в реакции выделяется энергия Q = 14 Мэе.
99. Математический >маятник, т. е. небольшой шарик на тонкой нити, массой которой можно пренебречь, первоначально находится в горизонтальном положении. Длина нити маятника равна I. точкой подвеса маятника расположена горизонтальная стальная плита. На какую высоту поднимется шарик после удара о плиту, если удар считать абсолютно упругим (рис. 39)?
100. Вертикально вверх произведен выстрел из пуш
ки. Начальная скорость снаряда равна п0- В точке максимального подъема снаряд разорвался на две одинаковые части. Первая из них упала на землю вблизи точки выстрела, имея скорость 2оо. Через какое время после выстрела упадет на землю вторая половина? Какую скорость она будет иметь в момент падения? Сопротивлением воздуха пренебречь.
101. При разрыве снаряда, летящего со скоростью v — 800 м/сек, образовалось три осколка с равными массами т=20 кг. Суммарная кинетическая энергия всех осколков 7=2,9 • 107 дж. Какую наибольшую скорость может приобрести один из осколков? Вращением осколков пренебречь.
102. Два упругих шарика подвешены на тонких нитях рядом так, что они находятся на одной высоте и соприкасаются. Нити подвеса разной длины: /1=10 см, 12 = & см. Массы шариков mi =8 г и тг = 20 г соответственно. Шарик с массой mi отклоняют на угол а = 60э и отпускают. Определить максимальное отклонение шариков от вертикали после удара. Удар считать абсолютно упругим.
103. Два шара — стальной массой М и свинцовой массой М/4 — подвешены в одной точке на нитях. Свинцовый шар отклоняют, так что нить образует угол а с вертикалью» и отпускают. После соударения он отклоняется на угол р. Удар центральный. Определить количество энергии, перешедшее в тепло.
27
104. На гладкой горизонтальной поверхности на некотором расстоянии от вертикальной стенки находится шар массой М. Другой шар, массой т, скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный упругий удар (при упругом ударе суммарная кинетическая энергия сохраняется). При каком соотношении масс М и т второй шар после удара достигнет стенки и, упруго отразившись от нее, догонит первый шар?
105. На гладкой горизонтальной поверхности, на расстоянии L=3 м от вертикальной стенки, находится шар массой М = 800 а; другой шар массой т = 200 г скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный упругий удар. Второй шар после удара достигает стенки и, упруго отразившись от нее, догоняет и вторично ударяет первый шар. Определить, на каком расстоянии от стенки произойдет второе соударение.
106. Три абсолютно упругих шара одинаковых радиусов, массы которых равны mi, т2 и т3, лежат на гладкой горизонтальной поверхности так, что их центры расположены на одной прямой. Крайнему шару mt сообщается скорость Цо вдоль линии центров шаров, и он сталкивается с шаром т2. Шар т2 сталкивается с третьим шаром т3. При каком соотношении масс все три шара будут иметь после этих столкновений одинаковые количества движения? Возможны ли в этом случае дальнейшие столкновения шаров?
107. Горизонтально летящая пуля с массой т попадает в деревянный шар, лежащий на полу, и пробивает его. Определить, какая часть энергии пули перешла в тепло, если ее начальная скорость была скорость после вылета из шара V2, масса шара М. Трение между шаром п полом отсутствует, траектория пули проходит через центр шара.
108. Деревянный шар массой М лежит на тонкой подставке. Снизу в шар попадает вертикально летящая пуля с массой rrf и пробивает его. При этом шар подскакивает на высоту h. На какую высоту х поднимется пуля над подставкой с шаром, если ее скорость перед ударом о шар была v? Считать, что скорость пули при прохождении через подставку не изменяется.
28
109. В покоящийся клин с массой М попадает горизонтально летящая пуля с массой т и после абсолютно упругого удара о поверхность клина отскакивает вертикально вверх (рис. 40). На какую высоту поднимется пуля, если горизонтальная скорость клина после удара оказалась равной V? Трением пренебречь.
ЖЯЙШтЖШЖ ‘777777^7777^^
Рис. 40.
Рис. 41.
ПО. На стоящий на горизонтальном полу клин массы М с высоты /г падает шар массы т и отскакивает в горизонтальном направлении (рис. 41). Найти горизонтальную скорость V клина после удара. Трением пренебречь; удар шара о клин считать абсолютно упругим.
111. Призма с массой Л4 с углом наклона а стоит на гладкой горизонтальной поверхности льда. На призме стоит собака, масса которой т. С какой скоростью будет двигаться призма, если собака побежит вверх со скоростью v относительно призмы? Трением между призмой и льдом пренебречь.
112. С клина, стоящего на гладкой горизонтальной поверхности, соскальзывает тело массы т. Угол наклона клина плавно ме-
в нижней (рис. 42). При . переходе на горизонталь-ную плоскость скорость этого тела равна v. Опре- Рис. 42.
делить высоту, с которой
соскальзывало тело, если известно, что масса клина равна М. Трением при движении обоих тел пренебречь. Считать, что тело начинает движение по клину из состояния покоя.
29
113. Ыа пути тела А, скользящего по гладкому горизонтальному столу, находится незакрепленная «горка» высотой Н = 2 м. Профиль горки изображен на рис. 43. При какой минимальной скорости тело сможет
Рис. 43.
преодолеть горку? Масса горки в пять раз больше массы тела. Считать, что тело движется, не отрываясь от горки. Тело по горке, а также «горка» по столу скользят без трения.
114. Профиль железнодорожной горки, используемой на сортировочной станции показан на рис. 44. На
4
Н i
Рис. 44.
горизонтальном участке на расстоянии L от конца уклона стоит вагон 1. С горки скатывается без начальной скорости вагон 2, а через t сек — вагон 3. На каком рас-
стоянии от конца уклона все три вагона окажутся сцепленными? Вагоны одинаковы и снабжены автосцепкой. Трением пренебречь. Высота горки Н.
115. В цилиндре, наполненном газом (рис. 45),
Рис. 45.
поршень перемещается со скоростью и. Определить часть энергии, теряемую молекулой, скорость которой перпендикулярна к поверхности поршня, при столкновении с поршнем. Скорость молекулы равна v (oJ5>xz). Столкновение молекулы с поршнем считать абсолютно упругим,
30
Динамика вращательного движения
116. Вокруг планеты по круговой орбите обращается спутник. Определить радиус орбиты, если период обращения спутника равен Т, масса планеты М.
117. Внутри камеры автомобильного колеса находится небольшое тело (рис. 46) Радиус колеса равен
Р — 0,4 м. При какой минимальной скорости автомобиля v тело будет вращаться вместе с колесом? Толщиной шины пренебречь.
118. На вертикальной осн укреплена горизонтальная штанга, по которой могут свободно перемещаться два груза с массами 1Щ п т2, связанные нитью длиной I. Система вращается с угловой скоростью io. На каких расстояниях от оси будут находиться грузы в равновесии? Чему равны при этом натяжение нити п кинетическая энергия грузов? Вернутся ли грузы в положение равновесия, если их сме
стить на малое расстояние из положения равновесия?
119. Груз, подвешенный на нити длиной L, равномерно вращается по кругу в горизонтальной плоскости. Найти период оборота груза, если при его вращении
нить отклонена от вертикали на угол а.
120. На вращающемся горизонтальном диске укреплен отвес, который устанавливается под углом а = 45°
।
Рис. 47,
к вертикали. Расстояние от точки подвеса до оси вращения d = 10 см, длина нити L = 6 см. Определить угловую скорость вращения со (рис. 47).
121. К концу вертикального вала с помощью горизонтальной оси подвешена невесомая штанга с грузом массой т=10 к,г так, что точка подвеса штанги нахо
31
дится на оси вала (рис. 48). Найти натяжение штанги, если вал вращается с угловой скоростью wi = 2 рад/сек. ‘Длина штанги L=1 м. Как изменится натяжение штан-
Рис. 48.
ги, если угловая скорость возрастает до со2 = 4 рад/сек?
122. Определить, какую скорость нужно сообщить снаряду, чтобы он облетел Землю параллельно ее поверхности при отсутствии трения о воздух. Радиус Земли R = 6370 км.
123. Две звезды под действием силы их взаимного гравитационного притяжения описывают круговые орбиты вокруг их общего центра масс с периодом Т, равным двум годам. Сумма масс звезд равна двум солнечным массам. Найти расстояние между звездами, зная, что среднее расстояние от Земли до Солнца равно 150•10s км (масса Земли по сравнению с массой Солнца пренебрежимо мала).
124. Определить радиус R горбатого
мостика, имеющего вид дуги окружности, при условии, что давление автомобиля, движущегося со скоростью v = 90 км/час, в верхней точке мостика
уменьшилось вдвое.
125. Автомобиль движется по горбатому мосту, имеющему форму дуги окружности радиусом R — 40 м. Какое максимальное горизонтальное ускорение может развить автомобиль в высшей точке моста, если скорость его в этой точке v = 50,4 км/час, а коэффициент трения колес автомобиля о мост & = 0,6?
126. С какой минимальной угловой скоростью ы нужно вращать ведро в вертикальной плоскости, чтобы из него не выливалась вода? Расстояние от поверхности воды до центра вращения I.
127. На тонкой нити подвешен шарик с массой т = 100 г. Прочность нити (максимальный груз, который она может выдерживать) f0=l>96 н. Определить, на какой минимальный угол нужно отклонить нить от вертикали, чтобы после того как шарик будет отпущен, нить оборвалась при прохождении шарика через положение равновесия. При какой прочности нити шарик не оборвется даже при начальном отклонении на 90°?
128. Груз с массой т = 100 г подвешен на нити и совершает колебания, отклоняясь на угол а=60° в ту и другую сторону. Определить натяжение нити в момент, когда нить составляет угол 0 = 30° с вертикалью.
129. Определить плотность планеты, продолжительность суток которой составляет Г = 24 часа, если на ее
экваторе тела невесомы.
130. Для создания искусственной тяжести на пассивном участке полета две части космического корабля (отношение масс 1:2) разводятся на расстояние L и
приводятся во вращение вспомогательными двигателями относительно их общего центра масс. Определить период вращения, если маятниковые часы в кабине космонавта, расположенной в более массивной части корабля, идут вдвое медленнее, чем на Земле.
131. Определить расстояние х от центра Земли до
искусственного спутника и скорость последнего v, если спутник запущен таким образом, что он вращается в
плоскости земного экватора и притом так, что с Земли он все время кажется неподвижным. Радиус Земли R = 6400 км.
132. Тележка массой т совершает «мертвую петлю» (рис. 49), скатываясь с наименьшей необходимой для
этого высоты. Определить,
с какой силой F тележка давит на рельсы в той точке петли, радиус которой составляет угол а с вертикалью. Трением пренебречь.
133. Тележка, скатившаяся по наклонному желобу с высоты Н = 10 м, описывает в вертикальной плоскости «мертвую петлю» радиусом г—Н13. Что показывают в верхней точке петли стоящие на тележке пружинные весы, на которых подвешен груз массы т = 1,2 кг?
134. Небольшая тележка описывает в вертикальной плоскости «мертвую петлю» радиусом R, скатываясь с минимальной высоты, обеспечивающей прохождение всей петли. Чему равно полное ускорение тележки в тот момент, когда ее скорость вертикальна? На какой высоте h сила давления на рельсы равна 3/2 веса тележки? Трением можно пренебречь.
3 Л. П. Баканияа и др.
33
135. С высшей точки сферического купола вниз скользит небольшое тело. На какой высоте h тело оторвется от купола? Радиус купола R. Трением пренебречь.
136. На внутренней поверхности полого шара радиуса /?, вращающегося вокруг вертикальной оси с постоянной угловой скоростью со, находится маленькая шайба А (рис. 50).
Считая угол а известным, найти минимальное значение коэффициента трения, при котором шайба не сорвется вниз.
137. Небольшое тело соскальзывает без начальной скорости в яму, имеющую форму полу* сферы с радиусом R. До глубины R/2 стенки ямы полированные, трение при этом пренебрежимо мало. Далее тело движется с постоянной скоростью. Определить коэффициент трения.
138. Какую минимальную скорость должен иметь математический маятник, проходя через положение устойчивого равновесия, чтобы он мог вращаться но кругу в вертикальной плоскости? Задачу решить для
двух случаев:
а) Маятник подвешен на невесомой недеформируе-мой штанге.
б) Маятник подвешен на нерастяжимой нити.
139. В кабине подъемника висит маятник. Когда кабина неподвижна, его период 7' = 1 сек. В движущейся с постоянным ускорением кабине период Ту = 1,2 сек. Определить величину и направление ускорения кабины.
140. Определить, какого радиуса R круг может описать велосипедист, если он едет со скоростью v = = 25 км/час, а предельный угол а наклона велосипедиста к земле равен 60°.
141. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу с радиусом 7? = 90 м, если коэффициент трения k резины о почву равен 0,42? На какой угол от вертикали он должен при этом отклониться?
142. Во сколько раз увеличится максимально допустимая скорость движения велосипедиста по наклонному греку с углом наклона а по сравнению с допустимой
34
скоростью по горизонтальному треку при одинаковом радиусе закругления и коэффициенте трения Л?
143. В известном аттракционе «автомобиль на вер* тикальной стене» автомобиль движется на внутренней поверхности вертикального цилиндра по горизонталь* ному замкнутому кругу. Каков должен быть минимальный коэффициент трения k скольжения между шинами и поверхностью цилиндра, чтобы автомобиль не падал при скорости а? Радиус цилиндра R.
144. Какова должна быть скорость ' мотоциклиста, чтобы он мог ездить на внутренней поверхности вертикального кругового цилиндра по горизонтальному кругу, если известно, что при езде по горизонтальной поверхности с тем же коэффициентом трения скольжения минимальный радиус поворота на скорости v равен R? Радиус цилиндра Ri. Под каким углом а к поверхности цилиндра наклонится мотоциклист?
Разные задачи
145. Спутник вращается вокруг Земли по круговой орбите с радиусом R. В результате кратковременного действия тормозного устройства скорость спутника уменьшилась так, что он начинает двигаться по эллиптической орбите, касающейся поверхности Земли (рис. 51). 1 \
Через какое время после это- I f J\
го спутник приземлится? Ра- I—Z------
диус Земли /?;!. Трением в ат- I 1
мосфере пренебречь. „„ J I ;
146. Известно, что вследст- т—V------
вие вращения планеты сила | \
веса на экваторе меньше, чем j_________
на полюсе. На какой высоте h
над поверхностью планеты на Рис- 51.
полюсе сила веса сравняется-
с силой веса на поверхности на экваторе? Считать планету шаром радиуса R. Время обращения планеты вокруг оси Т, средняя плотность вещества р.
147. Радиус одного из астероидов г = 5 км. Допустив, что плотность астероида равна ра = 5,5 г/см3, .
1) найти ускорение силы тяжести ga на его поверхности;
3* 35
2) определить, на какую высоту поднялся бы человек, находящийся на астероиде и подпрыгнувший с усилием, достаточным для прыжка на высоту 5 см на Земле (астероид имеет форму шара).
148. Каково ускорение силы тяжести на поверхности Солнца, если радиус его в 108 раз больше радиуса Земли, а плотность относится к плотности Земли, как 1 к 4?
149. Подсчитать ускорение свободно падающих тел на поверхности Солнца, если известны: радиус земной орбиты R —1,5-108 км, радиус Солнца r = 7- 103 км и время обращения Земли вокруг Солнца Т=\ год.
150. Считая орбиты Земли и Луны приблизительно круговыми, вычислить отношение масс Земли и Солнца. Известно, что Луна совершает 13 обращений в течение года и что расстояние от Солнца до Земли в 390 раз больше расстояния от Луны до Земли.
151. Какую длину будет иметь подвес маятника Фуко, если представить себе, что маятник установлен на планете, плотность которой равна плотности Земли, а радиус в два раза меньше? Маятник совершает 3 колебания в минуту.
152. В свинцовом шаре с радиусом R сделана сферическая полость, поверхность которой касается шара и проходит через его центр (рис.
52) . Масса сплошного шара равнялась М. С какой силой свинцовый шар будет притягивать маленький шарик массы т, находящийся на расстоянии d от
Рис. 53.
центра свинцового шара, на продолжении прямой, соединяющей центр свинцового шара с центром полости?
153. На неподвижной оси без трения может вращаться тяжелое колесо, вся масса которого сосредсто-
36
A
2
Рис. 54.
г = 6 см, v = 72 км/час,
чена в ободе (рис. 53). Радиус колеса равен R, его масса М. С колесом связан легкий шкив радиуса г, на который намотана нить. На конце нити висит груз массы т. Какую скорость будет иметь груз т после того, как он опустился на расстояние Н? В верхней точке скорость груза была равна нулю.
154. На рис. 54 изображена шестеренчатая передача. На вал двигателя насажена шестерня 1, сцепленная с шестерней 2, сидящей на рабочем валу. Известно, что полезная мощность двигателя равна U7 = 63 кет, а рабочий вал вращается со скоростью п — 3000 об/мин.
Определить моменты Л11 и М2 сил, действующие на вал двигателя и рабочий вал, если отношение чисел зубьев шестерен 1 и 2 равно т = 5.
155. Ведущее колесо мотоцикла приводится во вращение с помощью цепной передачи. Радиус колеса равен R, радиус ведущей шестерни равен г. Определить полезную мощность двигателя, если известно, что мотоцикл идет со скоростью v, а натяжение верхнего и нижнего участков цепи равны Fi и F2. Произвести числовой расчет для R = 30 см, F2 — Fy = 500 н.
156. С наклонной плоскости одновременно начинают соскальзывать‘брусок и скатываться без проскальзывания обруч. Определить, при каком коэффициенте трения k между бруском и плоскостью оба тела будут двигаться, не обгоняя друг друга. Угол наклона плоскости вен а.
157. На полый
линдр намотана нить, конец которой закреплен на стойке в верхней точке наклонной плоскости так, что при соскальзывании цилиндра нить все время параллельна наклонной плоскости (рис. 55). Определить скорость va цилиндра в конце плоскости, наклоненной к
pa-
пи-
37
а
Рис. 56.
т?
ение
а
горизонту под углом а = 60®, если при наклоне р = 30® она равна up. Длина наклонной плоскости в обоих случаях равна L.
158. Наклонная плоскость имеет угол наклона а, который можно изменять. Тяжелая пластинка, соскальзывая по ней, проходит при cti=45° и «2 = 60° за одинаковое время пути с одинаковыми горизонтальными проекциями. Начиная с какого угла наклона а3 пластинка не будет соскальзывать?
159. На гладком горизонтальном столе лежит груз с массой т. Коэффициент трения между грузом и столом k. К грузу привязана нить, перекинутая через блок на краю стола. На другом конце нити подвешен максимально возможный груз, еще не вызывающий скольжения первого груза. Стол начинает двигаться в горизонтальном направлении, как показано на рис. 56. Чему будет равно при этом ускорение гру-стола мало по сравнению с g, так
что отклонением второго груза от вертикали можно пренебречь.
160. Математический маятник, вращающийся в вертикальной плоскости, находится в лифте, движущемся вниз с ускорением 2g. Когда маятник находится в нижней точке своей траектории, натяжение нити равно нулю. Определить натяжение нити в момент, когда маятник находится в верхней точке траектории. Масса маятника т.
161. В высотной ракете помещены часы с маятником, который можно считать математическим, и часы с пружинным маятником. Ракета движется вертикально вверх с ускорением а=10 g. На высоте й = 50 км двигатель выключается, и ракета продолжает подниматься по инерции. Каковы будут показания тех и других часов в наивысшей точке подъема ракеты? Сопротивлением воздуха и уменьшением силы земного тяготения с высотой пренебречь.
162. Какова высота h столбика ртути в ртутном барометре, помещенном в лифте, который опускается с ускорением а, если атмосферное давление равно Н мм рт. ст.?
38
163. Какая сила необходима для вытаскивания из доски гвоздя длиной 80 мм, если он забит с шести ударов молотка весом 5 н при скорости молотка непосредственно перед ударом 2 м!сек? Массой гвоздя можно пренебречь.
164. Один конец пружины прикреплен к гвоздю О, вбитому в стол, а другой —к грузу В (рис. 57). Груз, скользя по столу без трения, совершает круговые движения с линейной скоростью и вокруг гвоздя. Найти радиус окружности, по которой движется груз,
О В
П—\,\./У\АЛ/УЛАА/У\7'^^'
Рис. 57.
если известно, что длина
недеформированной пружины /0 и возрастает вдвое, если к пружине подвесить груз В. Массой пружины пренебречь и считать, что ее удлинение прямо пропорционально нагрузке.
165. Стержень ОА вращается относительно вертикальной оси ОВ с угловой скоростью со (рис. 58). Угол
между осью и стержнем равен а. По стержню без трения скользит муфта массой М, связанная с точкой О пружиной. Определить положение муфты при вращении, если известно, что длина пружины в недеформированном состоянии равна 10, жесткость пружины k.
\т
Рис. 58. Рис. 59.
Примечание. Сила F натяжения пружины пропорциональна ее удлинению: F = kx, где х = /— lo-
166. Шайба массой т двумя одинаковыми пружинами прикреплена к концам стержня, вращающегося вокруг вертикальной оси, проходящей через его середину (рис. 59). Пренебрегая трением между шайбой и
39
стержнем, найти угловую скорость со последнего, при которой возможны круговые движения шайбы. На каком расстоянии от середины стержня должна при этом находиться шайба. Отношение силы, деформирующей пружину, к изменению ее длины постоянно и равно k.
167. К концу вертикально висящей пружины длиной I прикрепили груз Л, в результате чего ее длина возросла до 21. Предполагая, что удлинение пружины пропорционально нагрузке, найти угловую скорость груза А, вращающегося на этой пружине по кругу в горизонтальной плоскости (рис. 60), если длина пружины в этом случае L. Массой пружины пренебречь.
Рис. 60.
168. Две штанги, ОА и ОВ (рис. 61), расположены под углом а к вертикальной оси 00'. Ось и штанги расположены в одной плоскости. На каждую штангу надета муфта массой М. Муфты соединены пружиной и находятся на одной высоте. Система вращается с постоянной угловой скоростью о вокруг оси 00'. Определить положение равновесия муфт (величину И). Трение не учитывать. Длина пружины в недеформиро* ванном состоянии равна /о- Отношение силы F, деформирующей пружину, к изменению / — /о ее длины /, постоянно и равно k.
169. Имеется два тонкостенных цилиндра. Один из них, радиус которого равен /?, вращается с угловой скоростью о вокруг своей оси, а второй покоится. Цилиндры приводятся в соприкосновение так, что их оси
40
количество энергии
вращения параллельны (рис. 62). Через некоторое время (за счет трения) цилиндры начинают вращаться без проскальзывания. Найти, какое перешло в тепло. Массы цилиндров равны Л4[ и М2.
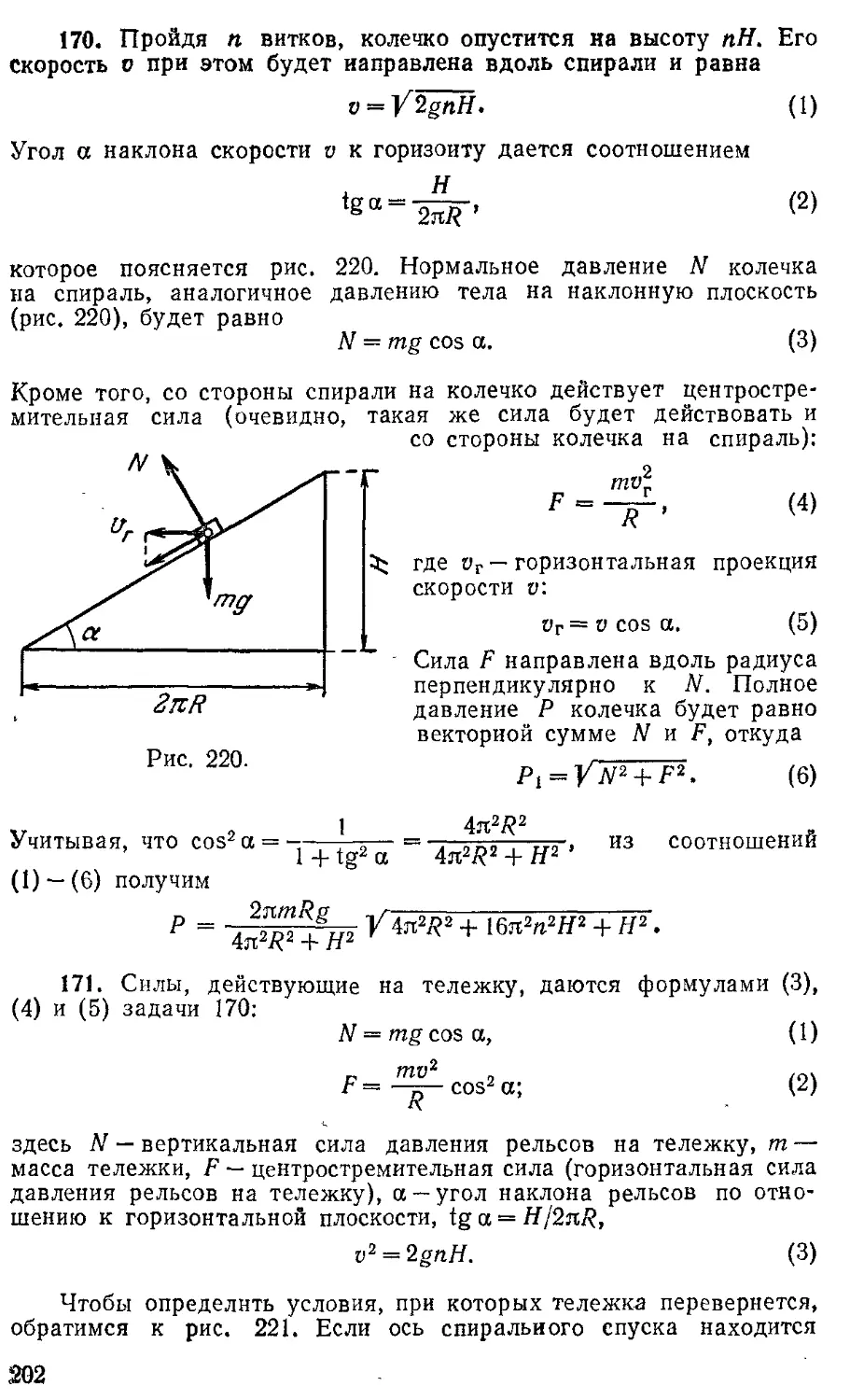
170. Радиус витка цилиндрической спирали, ось которой вертикальна, 7? и расстояние между соседними витками («шаг винта») Н. На спираль надевают маленькое колечко массы т, ко* торое без трения начинает скользить вдоль спирали. С какой
силой колечко будет давить на спираль после того, как оно пройдет п полных витков?
171. По дорожке, выполненной в виде спирального спуска с радиусом витка спирали R и расстоянием между соседними витками («шаг винта») Н, положены рельсы. По рельсам скатывается небольшая тележка, причем расстояние между рельсами h и центр тяжести тележки находится от рельсов тоже на высоте h. Какое максимальное количество п витков должно быть в спиральном спуске, чтобы тележка в конце спуска не перевернулась? Ширину тележки считать много меньше радиуса спирали.
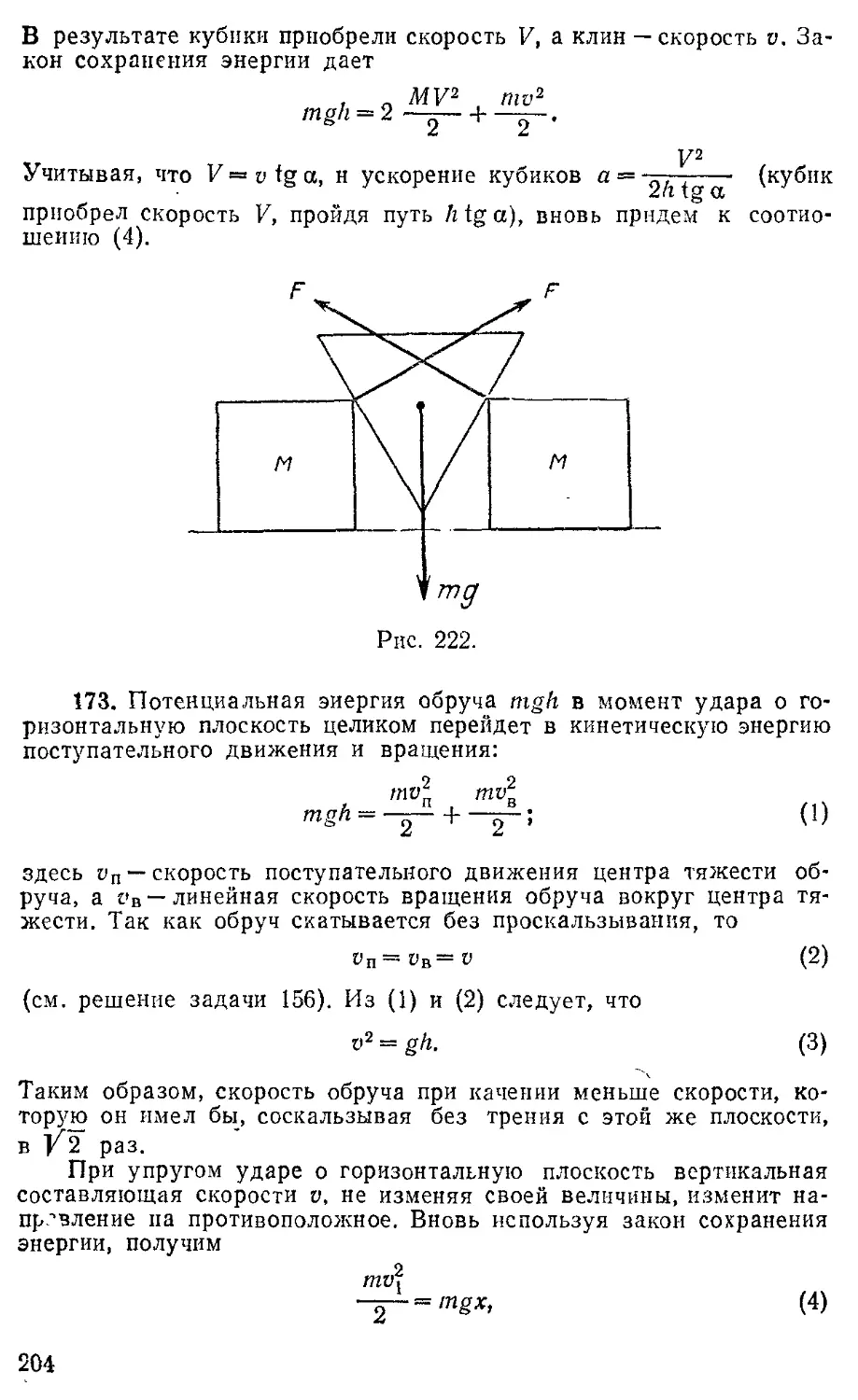
172. На горизонтальной поверхности (рис. 63) стоят два одинаковых кубика массой М. Между кубиками вводится тяжелый клин массой т с углом при вершине 2а. Чему равны ускорения кубиков? Трением пренебречь.
Рис. 63.
173. Тонкий обруч скатывается без проскальзывания с наклонной плоскости на горизонтальную плоскость. На какую высоту х подпрыгнет обруч, если он скатится с высоты h (рис. 64)? Обруч и плоскость считать
41
абсолютно упругими. Угол наклона плоскости к горизонту равен ос.
174. Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине давление обруча на стенку ямы станет равно его весу? Радиус ямы 7? значительно больше радиуса обруча г.
175. Как изменится сила давления передних колес автомобиля массы т=1500 кг, движущегося по горизонтальной дороге (с коэффициентом трения k = 0,4), при максимально возможном без возникновения скольжения торможении задних колес? Центр тяжести автомобиля находится посередине между колесами и приподнят над землей на г = 60 см, расстояние между передними и задними колесами d = 3,5 м.
176. Две пластинки с массами т\ и т2 соединены спиральной пружиной и расположены таким образом, что пластинка т\ находится над пластинкой т2, лежащей на столе (рис. 65).
С какой силой нужно надавить на верхнюю пластинку, чтобы после прекращения действия силы верхняя пластинка, подпрыгнув, приподняла и нижнюю? Массой пружины пренебречь.
Рис. 65.
Рис. 66.
177. Два одинаковых шарика связаны невесомой нитью, перекинутой через невесомый блок, причем один из шариков погружен в сосуд с жидкостью (рис. 66). С какой установившейся скоростью v будут двигаться шарики, если известно, что установившаяся скорость падения одиночного шарика в той же жидкости равна Pg?
42
Силу сопротивления считать пропорциональной скорости. Плотность жидкости равна рж, плотность материала шариков равна р.
178. Лестница вместе с находящимся на ней человеком уравновешена противовесом на веревке, перекинутой через блок. Масса т человека равна массе лестницы, а массой и трением блока можно пренебречь. На какой высоте Н над землей будет находиться человек, если он поднимется по лестнице на п перекладин вверх (п = 6)? Расстояние между перекладинами I — 40 см. Первоначально человек находился на нижней перекладине на высоте h = 2 м над землей. Можно считать, что при подъеме на каждую перекладину человек движется равноускоренно.
II. ТЕПЛОТА И МОЛЕКУЛЯРНАЯ ФИЗИКА
Поверхностное натяжение
179. Чему равен коэффициент поверхностного натяжения воды, если с помощью пипетки, имеющей кончик диаметром 0,4 мм, можно дозировать воду с точностью до 0,01 г?
180. Мыльный пузырь имеет радиус г. Коэффициент поверхностного натяжения мыльной воды о. Чему равно дополнительное давление внутри мыльного пузыря?
181. В вертикальную цилиндрическую трубку, закрытую снизу пористым фильтром, налит слой ртути толщиной 0,1 м. Чему равны диаметры каналов фильтра, если ртуть начинает продавливаться через фильтр при дополнительном давлении на поверхность ртути 0,8 атм? Коэффициент поверхностного натяжения ртути от=0,465 н/м.
182. Грамм ртути помещен между двумя параллельными стеклянными пластинками. Какую силу надо приложить к верхней пластинке, чтобы ртуть имела форму круглой лепешки радиусом г=5 см. Поверхностное натяжение ртути <т=0,465 н/см. Считать, что ртуть совершенно не смачивает стекло, так что угол между краем свободной поверхности ртути и стеклянной пластинкой равен нулю.
183. Капля воды с массой т = 0,01 г введена между двумя плоскопараллельными стеклянными пластинками, полностью смачиваемыми водой. Как велика сила притяжения между пластинками, если они находятся на расстоянии t/=10“4 см друг от друга? Коэффициент поверхностного натяжения воды о = 0,073 н/см.
184. Капиллярная трубка погружена в воду таким образом, что длина непогруженной ее части составляет
44
1 = 0,2 м. Вода поднялась в трубке на высоту //2=0,1 м. В этом положении верхний конец трубки зажимают
пальцем и трубка погружается пока уровень воды в трубке не сравняется с уровнем воды в сосуде. Найти длину h выступающей из воды части трубки в этом положении. Внешнее давление равно 105 н/м2.
185. В вакууме в чашку с маслом, имеющим весьма низкую упругость пара и хорошо
в воду до тех пор,
смачивающим стекло, погружена Рис. 67.
стеклянная трубка радиусом
1 мм. Найти давление в масле на высоте Л/3 над уров-
нем масла в чашке (/г — высота, на которую поднимается масло в капиллярной трубке) (рис. 67). Коэффициент поверхностного натяжения масла о = 0,03 н/я.
Закон сохранения энергии для тепловых явлений
186. В кастрюлю налили холодной воды (7=10° С) и поставили на электроплитку. Через 10 минут вода закипела. Через какое время она полностью испарится?
187. На электрической плитке мощностью IF=1 кет кипит чайник с водой. Найти скорость истечения пара из носика чайника. Площадь сечения носика 5=1 см2, пар можно считать идеальным газом; давление на конце носика равно атмосферному. Считать, что вся энергия, выделяемая плиткой, передается воде.
Рис. 68.
188. В устройстве для измерения мощности электромагнитного излучения энергия излучения полностью поглощается в цилиндре АВ (рис. 68), через который
45
прогоняется с определенной скоростью жидкость. Определить энергию, поглощаемую в цилиндре в единицу времени, если известно, что температуры жидкости в трубках на входе и выходе цилиндра равны соответственно 7\ и Т2. Процесс поглощения считать установившимся. Изменением плотности жидкости и ее удельной теплоемкости с температурой пренебречь. Плотность жидкости равна р, удельная теплоемкость с, скорость течения жидкости v, площадь поперечного сечения трубок 5.
189. Свинцовая пуля пробивает деревянную стену, причем скорость в момент удара о стену была 400м/сек, а после прохождения стены 300 м/сек. Температура пули в момент удара 7'0 = 323°К. Какая часть пули расплавилась, если теплота плавления свинца Х= = 2,5 • 104 дж/кг, температура плавления 7’ = 600°К, удельная теплоемкость с=125 дж/кг • град. Считать, что все выделяющееся тепло получает пуля.
190. Железный шарик радиусом 1 см, нагретый до 393° К, положен на лед. На какую глубину погрузится шарик в лед, если удельная теплоемкость железа с = 475 дж/кг • град? Плотность льда ро = 900 кг/мА. Плотность железа р = 7,9-103 кг/м3. Температура льда 273°К; удельная теплота плавления /1 = 3,34-105 дж/кг. Теплопроводностью льда и нагревом воды пренебречь,.
191. При изготовлении льда в комнатном холодильнике потребовалось 5 мин, чтобы охладить воду от 277 до 273° К и еще 1 час 40 минут, чтобы превратить ее в лед. Определить из этих данных удельную теплоту плавления льда.
192. Сколько тепла выделится в комнате за четыре часа работы холодильника, потребляющего мощность №7 = 90 вт, если его производительность — 2 кг льда при температуре 7'1 = 271° К в сутки, а охлаждение начинается с температуры Т'=293°К. Теплота плавления льда К = 3,34- 10s дж/кг, теплоемкость воды
св = 4,2 • 103 дж/кг • град-,
теплоемкость льда
сл = 2,1 • 103 дж/кг • град.
193. В теплоизолированный откачанный сосуд объема 17=11 л положили рядом кусок льда с массой Afj= 1 кг и кусок меди с массой 7142=3 кг. Температура
льда То = 273° К- Определить первоначальную темпе* ратуру меди, если в конце процесса в сосуде установилась температура Л = 373° К. Теплоемкость меди см = 376 дж)кг-град. Теплота плавления льда % = 3,34-10s дж/кг-, теплота парообразования воды q = 2,26 • 106 дж[кг. Изменением объема воды можно пренебречь.
194. Какое количество тепла необходимо для того, чтобы нагреть от 283 до 298° К 7 г азота, находящегося в цилиндре под поршнем, на котором лежит постоянный груз, если теплоемкость одной грамм-молекулы азота при нагревании при постоянном объеме равна cr=20,9 дж]моль • град?
195. 50 г льда при температуре 0°С заключено в теплонепроницаемую оболочку и подвергнуто давлению 600 атм. Сколько льда расплавилось, если при повышении давления на 138 атм температура плавления льда понижается на 1°К? Считать понижение температуры плавления пропорциональным повышению давления,. Теплоемкость и теплоту плавления считать такими же, как и при нормальном давлении: Х=3,34-105 дж)кг, сл=2,1 • 103 дж[кг • град.
196. Вода при соблюдении необходимых предосторожностей может быть переохлаждена до 7 = 263° К. Какая масса льда образуется, если в такую воду в количестве М = 1 кг бросить кусочек льда и вызвать этим замерзание? Теплоемкость переохлажденной воды с = 4180 дж/кг-град.
197. Генератор излучает импульсы сверхвысокой частоты с энергией в каждом импульсе w = Q дж. Частота повторения импульсов f = 500 гц. Коэффициент полезного действия генератора ц = 60%• Сколько литров воды в час надо прогонять через охлаждающую систему генератора, чтобы вода нагревалась не выше, чем на Ю°?
198. В дьюаровском сосуде хранится жидкий азот при температуре Т\ = 78° К в количестве 2 л. За сутки испарилась половина этого количества. Определить удельную теплоту испарения азота, если известно, что 40 г льда в том же дьюаре растает в течение 22 часов 30 минут. Скорость подвода тепла внутрь дьюара может считаться пропорциональной разности температур внутри и снаружи дьюара. Температура окружающего
47
воздуха Т — 293° К- Плотность жидкого азота при 78° К равна 800 кг/м3.
199. На сколько градусов нагреется медная пластинка площадью S = 12 см2 при нарезании в ней резьбы с шагом 0,75 мм, если при нарезке к воротку нужно приложить момент сил 4,9 н-м? Удельная теплоемкость меди 376 дж/кг- град. Плотность меди 8,8 г)см3. Считать, что все выделяющееся тепло получает пластинка.
Тепловое расширение тел
200. Стальная и бронзовая пластинки толщиной 0,2 мм каждая склепаны на концах так, что при температуре 293° К образуют плоскую биметаллическую пластинку. Каков будет радиус изгиба этой биметаллической пластинки при температуре 393° К? Коэффициент линейного расширения стали <zi = l-10"5 \/град, а бронзы «2=2-10-5 \/град.
201. Бронзовый стержень был охлажден в жидком азоте до температуры 72° К. Охлажденный стержень плотно вставили в прямоугольное отверстие жесткой обоймы, имеющей температуру 293° К так, что зазор между торцами стержня и соответствующими плоскостями отверстия обоймы можно считать равным нулю. Каким стало давление стержня на обойму после того, как он нагрелся до температуры 293°К? Коэффициент линейного расширения бронзы сс. = 1,75 • 10-5 \/град. Модуль Юнга E = l,04-1011 н/м2.
202. Латунное кольцо сечением 2X5 мм и диаметром в несколько сантиметров было нагрето до температуры 573° К и плотно надето на стальной цилиндр, имеющий температуру 291° К. Какое усилие на разрыв испытывает кольцо после охлаждения до 291° К? Коэффициент линейного расширения латуни а=1,84-10~5 \/град. Модуль Юнга £=6,47-1010 н/.и2.
203. В центре стального диска имеется отверстие диаметром 4,99 мм (при 0°С). До какой температуры следует нагреть диск, чтобы в отверстие начал проходить шарик диаметром 5,00 мм? Линейный коэффициент теплового расширения стали а=1,1 • 10~5 град~}.
204. Между двумя стенками помещен стержень постоянного сечения 5, состоящий из двух частей одинаковой длины 1/2, имеющих коэффициент теплового рас
48
Ширения cci и аг и модули Юнга Е} и Е2 соответственно. При температуре 1\ торцы стержня лишь касаются стенок. С какой силой стержень будет давить на стенки, и насколько сместится место стыка частей стержня, если стержень нагреть до температуры Т2? Деформацией стенок пренебречь.
205. В одном из двух сообщающихся сосудов, наполненных жидкостью при 10°С до уровня Но~ 10 см, температура жидкости поднялась на Д7'=6°. Какая возникнет при этом разность уровней, если объемный коэффициент расширения жидкости [3 = 0,0026 град-1? Расширением сосуда можно пренебречь.
206. В цилиндрический калориметр с площадью дна 30 см2 налито 200 см3 воды при температуре 303° К и опущен кусок льда массой 10 г, имеющий температуру 273° К. Определить изменение уровня воды к моменту, когда лед растает, по сравнению с начальным, когда лед уже был в калориметре. Объемный коэффициент теплового расширения воды [3 = 2,6. 10'3 \/град. Теплота плавления льда Х = 3,34-105 дж!кг.
207. Брусок меди, имеющий температуру 273° К, и одинаковый с ним по объему брусок алюминия с температурой 373° К, сложены вместе, и их температуры выравниваются. Каково будет относительное изменение общего объема? Плотности, удельные теплоемкости и коэффициенты линейного расширения меди и алюминия равны соответственно:
pi=8,5 г)см3, ci = 376 дж[кг-град, а| = 1,7-10*5 1/град; р2 = 2,6 г!см3, <?2 = 920 дж!кг- град, а2 = 2,3-10'5 \/град.
208. Стеклянный шарик с коэффициентом объемного расширения [3 взвешивается в жидкости при температурах t\ и t2. Вес вытесненной жидкости равен соответственно Р\ и Р2. Определить коэффициент объемного расширения жидкости рь
Уравнение газового состояния
209. Какое давление имеет 1 кг азота в объеме 1 .и3 при температуре 27° С? Атомный вес азота 14.
210. Определить массу аммиака NH3, содержащегося в баллоне емкостью 20 л при температуре 27° С и под давлением 190 ж.ирт. ст.
211. Температура комнаты была 10° С, а после того, как комнату натопили, температура поднялась до 20° С. Объем комнаты 50 м3, давление в ней постоянно и равно 730 мм рт. ст. Насколько изменилась масса воздуха, находящегося в комнате? Считать, что РвОЗД = 29.
212. В легкой герметичной оболочке воздушного шара находится водород. Определить подъемную силу шара. Считать, что оболочка сделана из неупругого материала и может свободно растягиваться. Масса водорода т. Молекулярный вес воздуха принять равным 29.
213. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу р=1 кг!м2. Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимет сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0°С. Молекулярный вес воздуха принять равным 29.
214. Объем воздушного шара равен К=224 м3, масса оболочки М~ 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура воздуха вне оболочки равна 0°С. Молекулярный вес воздуха принять равным 29.
215. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр Юли весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм рт. ст., температура 27° С, молекулярный вес воздуха принять равным 29.
216. Определить подъемную силу воздушного шара, наполненного гелием. Радиус шара 6 м; шар сообщается с наружным воздухом. Давление воздуха 640 мм рт. ст., температура 17° С. Молекулярный вес гелия 4, воздуха 29.
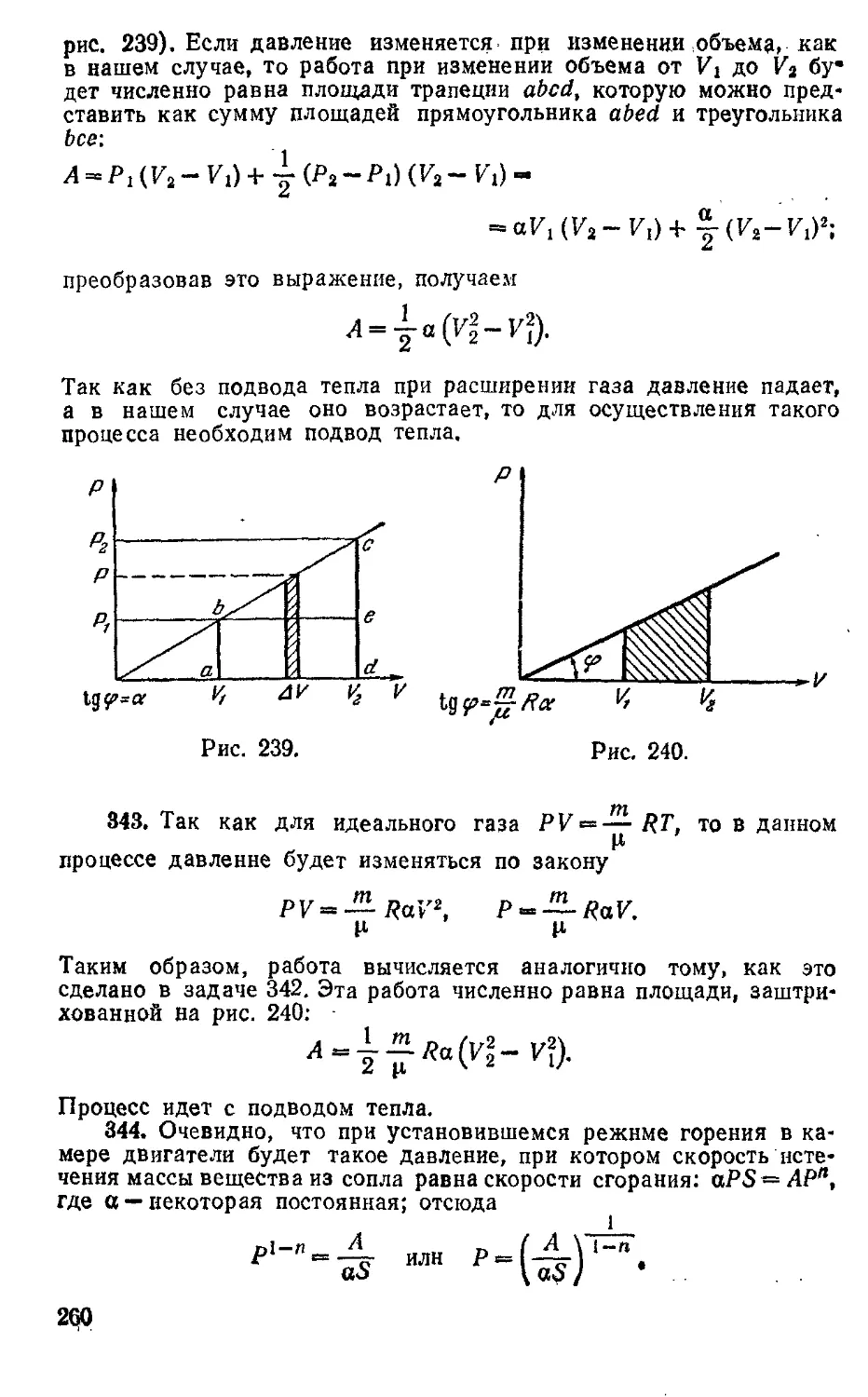
217. 716 мг органического соединения с формулой (С3Н6О)П дают при 200° С и давлении 750 мм рт. ст. 242,6 см3 пара. Найти число п.
218. Определить молекулярную формулу некоторого соединения углерода с водородом, если известно, что При температуре t=2T С и давлении Р = 760 мм рт. ст,
50
объем V=1 л этого вещества в газообразном состоянии имеет массу т = 0,65 г. Атомный вес углерода pi=12, водорода [Л2= 1-
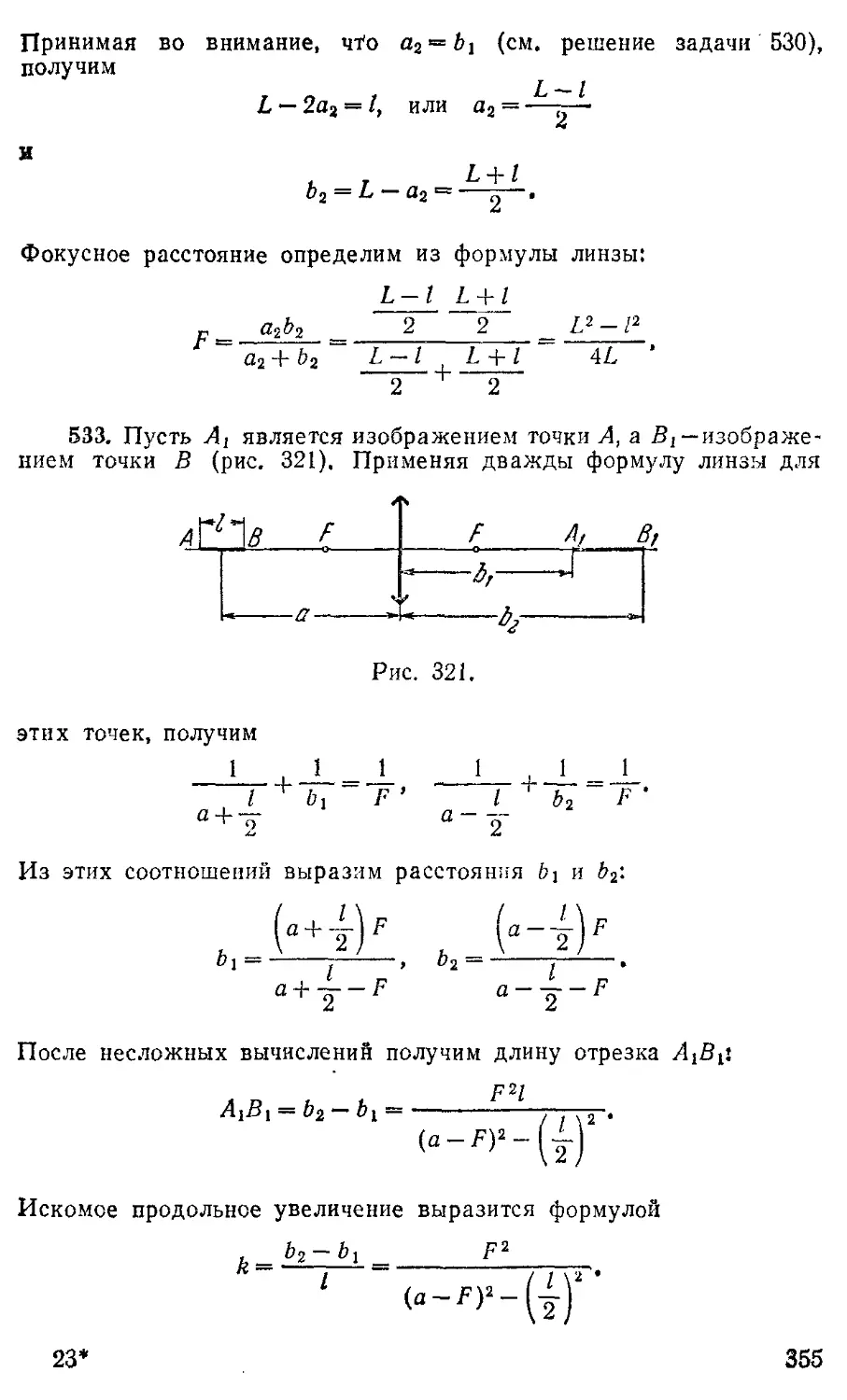
219. Найти молекулярную формулу некоторого соединения углерода с кислородом, если известно, что т=\ а этого вещества в газообразном состоянии создает в сосуде с объемом У=1 л при температуре t — 27° С давление /’ = 0,56 атм. Атомные веса углерода и кислорода равны соответственно p,i = 12 и Ц2= 16.
220. Сколько электронов заключается в одном литре кислорода при давлении 10 атм и температуре 200°С?
221. При бомбардировке лития 3Li7 протонами он превращается в гелий 2Не4. Определить объем гелия, образовавшегося из 1 г лития, если гелий после опыта имеет температуру 30°С и давление 700 мм рт. ст.
222. Барометр дает неверные показания вследствие присутствия небольшого количества воздуха над столбиком ртути. При давлении 755 мм рт. ст. барометр показывает 748 мм рт. ст., а при 740 мм рт. ст. — показывает 736 мм рт. ст. Какое давление будет показывать барометр, если действительное давление будет равно 760 мм рт. ст.?
223. Баллон емкостью V, наполненный газом при давлении Р и температуре Т, взвешивают. Его вес оказывается равным N. Из баллона откачивают газ, пока его давление не упадет до Pi при той же температуре Т. Вес баллона в этом случае оказывается Nr. Определить из этих данных плотность газа при нормальных условиях: давлении Ро и температуре То.
224. Сколько качаний надо сделать, чтобы при помощи насоса, захватывающего при каждом качании 40 c.w3 воздуха, наполнить пустую камеру шины велосипеда настолько, чтобы площадь его соприкосновения с дорогой была равна 60 см2? Нагрузка на колесо равна 35 кГ. Объем камеры равен 2000 см3. Атмосферное давление 1 атм. Считать, что объем шины при накачивании не изменяется. При нагреве во время езды давление в камере возрастает. Определить уменьшение площади соприкосновения с дорогой, если шина нагрелась от 20 до 60° С. Объем по-прежнему считать постоянным.
225. Известно, что 1 г радия в 1 сек дает 3,7 • 1010 а-частиц. Каково будет давление гелия, образующегося в герметичной ампуле объемом 1 см3, в которой
•Г
51
в течение года находилось 100 мг радия? Температура ампулы 15° С.
226. Из баллона со сжатым водородом емкостью 10 л вследствие неисправности вентиля утекает газ. При температуре 7° С манометр показывает 50 атм. Через некоторое время при температуре 17° С манометр показал такое же давление. Ка^ая масса газа утекла из баллона?
227. По газопроводной трубе идет углекислый газ при давлении Р = 4 атм и температуре Т = 7°С. Какова средняя скорость движения газа в трубе, если за время /=10 мин протекает т=2 кг углекислого газа и если площадь сечения канала трубы S = 5 см2?
228. Определить плотность смеси тщ = 4 г водорода и /?i2 = 32 г кислорода при температуре / = 7°С и давлении Р = 700 мм рт. ст. (pj = 2 г!моль, ц2 — 32 г!моль).
223. Цилиндрическая трубка длиной I наполовину погружена в ртуть. Ее закрывают пальцем и вынимают. Часть ртути при этом вытекает. Какой длины столбик ртути остается в трубке? Атмосферное давление равно Н мм рт. ст.
230. Аэростат наполнен водородом при температуре /1 = 15° С и давлении 1 атм. При неизменном давлении атмосферы под влиянием солнечной радиации его температура поднялась до /2 = 37°С, а излишек газа М вышел через клапан, благодаря чему вес аэростата с газом уменьшился. Известно, что Л4 = 6 кг. Определить объем аэростата V.
231. На дне цилиндра, заполненного воздухом, лежит полый стальной шарик радиусом 2 см, весящий 5 г. До какого давления надо сжать газ, чтобы шарик поднялся наверх? Считать, что воздух при больших давлениях подчиняется уравнению газового состояния. Температура воздуха 20° С.
232. В сосуд, на дне которого лежит твердый шар, нагнетают воздух при температуре / = 27° С. Когда давление в сосуде стало равно Р = 20 атм, шар поднялся вверх. Чему равна масса шара т, если его радиус /•=5 см? Молекулярный вес воздуха равен 29.
233. Электрическая лампа накаливания наполнена азотом при давлении 600 мм рт. ст. Объем колбы лампы равен 500 см3. Какое количество воды войдет в лампу, если у нее отломить кончик под водой на глубине 1 .«
52
от поверхности? Атмосферное давление считать равным 760 мм рт. ст.
234. Объем некоторой массы идеального газа при нагревании на 1°С при постоянном давлении увеличился на 1/335 своего первоначального значения. При какой температуре находился газ вначале?
235. Определить плотность паров ртути при ^=420° С и давлении Р = 2,3 мм рт. ст. Атомный вес ртути ц=200.
236. Узкая цилиндрическая трубка, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути. Когда трубка обращена закрытым концом кверху, воздух внутри нее занимает длину /ь когда же трубка обращена кверху открытым концом, воздух внутри нее занимает длину /2, меньшую Ц. Длина ртутного столба h. Плотность ртути р. Определить атмосферное давление.
237. В двух стеклянных шарах, емкостью в 1 л каждый, находится воздух при 0°С. Шары соединены трубкой длиной в 1 .и и диаметром 4 мм. На сколько переместится капелька ртути длиной в 1 см, помещенная посередине трубки, если один шар нагреть до +1°С, а другой охладить до —ГС?
238. До какой температуры нужно нагреть запаянный шар, содержащий 17,5 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление не более 100 атм, а объем его 1 д?
239. Сжиженные газы хранят в сосудах, сообщающихся с атмосферой. В одном из таких сосудов объемом в 10 л находилось 0,5 л жидкого азота, плотность которого 0,81 г!см3. По ошибке сосуд был плотно закупорен. Разорвет ли сосуд, когда азот испарится и нагреется до комнатной температуры? Сосуд может выдерживать давление 20 атм.
240. Горизонтальный цилиндрический сосуд делится на две части подвижным теплопроводящим поршнем. Каково будет равновесное положение поршня, когда в одну часть сосуда помещено некоторое весовое количество кислорода, а в другую — такое же количество водорода, если общая длина сосуда 85 с.и?
241. В бомбе объемом 10 л содержится смесь водорода и кислорода в равных количествах (масса каждого газа т = 2 г). Весь кислород, соединяясь с частью
53
водорода, образует воду. Каково давление оставшегося водорода при 17° С?
242. Внутри закрытого с обоих концов горизонтального цилиндра имеется поршень, который скользит в цилиндре без трения. С одной стороны поршня находится 3 г водорода, а с другой—17 г азота. Какую часть объема цилиндра занимает водород?
243. При нагревании газа при постоянном объеме на 1°С давление увеличилось на 0,2%. При какой начальной температуре находился газ?
244. Вертикальный цилиндрический сосуд, закрытый с обеих сторон, разделен тяжелым теплонепроницаемым поршнем на две части; обе части сосуда содержат одинаковое количество воздуха. При одинаковой температуре Т\ =400° К воздуха в обеих частях, давление Р2 в нижней части сосуда вдвое больше давления Pi в верхней части. До какой температуры Т2 надо нагреть воздух в нижней части сосуда, чтобы объемы верхней и нижней частей стали одинаковыми?
245. Вертикальный цилиндр с объемом V и площадью основания S разделен на две части тонким тепло-
________________________ _______________________ непроницаемым поршнем, у} z____________________" н В нижней части цилинд-
]________________________ра находится m грамм
ДуууДД-— Д-ДД; водорода при темпера------- - туре Т2, в верхней — 2m
' ‘. / /. грамм гелия при темпера-
туре 7]. Найти массу пор-1 ~ ~ | | шня, если при равнове-
Ь-------.- -- сии объемы газов равны.
рис. 69. 246. Два закрытых
сосуда, частично заполненных ртутью, соединены трубкой (рис. 69). В сосудах находится воздух при температуре То и давлении Ро. Уровни ртути в сосудах расположены на расстоянии Н от крышек. Затем воздух в сосуде 2 нагревают до некоторой температуры, а давление воздуха в сосуде 1 увеличивается в два раза. Определить, до какой температуры был нагрет воздух в сосуде 2. Отношение площадей поперечного сечения сосудов Si/S2 = 2. Плотность ртути равна р. Давлением паров ртути пренебречь.
247. Шахта глубиной /г = 224 м пробурена в склоне горы и имеет горизонтальный выход (рис. 70). Темпе-.
54
ратура наружного воздуха равна /о = О°С, средняя температура воздуха внутри шахты равна 1=14° С. Вертикальный ствол шахты имеет сечение S = 3,5 м2. Какую силу нужно приложить к заслонке, чтобы закрыть сверху вертикальный ствол? Давление воздуха на уровне горизонтального ствола шахты равно 760 мм рт. ст. Молекулярный вес воздуха ц принять равным 29.
Рас. 70.
Рис. 71.
248. Фабричная труба имеет высоту h = 22,4 м. Входное отверстие трубы наглухо закрыто заслонкой .4 (рис. 71), имеющей сечение S = l м2. Температура наружного воздуха равна /о = О°С, давление равно Ро = 76О мм рт. ст. Определить среднюю температуру воздуха в трубе, если известно, что из-за разности температур на заслонку действует сила / = 8,7 кг. Молекулярный вес воздуха принять равным 29.
249. Закрытый сосуд разделен на две равные части твердой неподвижной полупроницаемой перегородкой. В первую половину сосуда введена смесь аргона и водорода при давлении /’ = 1,5 атм, во второй половине — вакуум. Через перегородку может диффундировать только водород. После окончания процесса диффузии давление в первой половине оказалось Р' = 1 атм. Во время процесса температура поддерживалась постоянной. Определить отношение масс аргона и водорода в смеси, которая была первоначально введена в первую половину сосуда. Атомный вес аргона ца = 40, молекулярный вес водорода цв = 2.
250. Закрытый сосуд объемом V=2 л разделен на две равные части твердой полупроницаемой неподвижной перегородкой. В одной половине сосуда первоначально находится mi =20 г аргона и т2 — 2 г водорода.
55
В другой половине — вакуум. Через перегородку может диффундировать только водород. Какое давление установится в первой половине сосуда после окончания процесса диффузии? Во время процесса температура поддерживается постоянной и равной / = 20° С. Атомный вес аргона ца = 40, молекулярный вес водорода цв = 2.
251. Сколько балласта должен выбросить аэростат объемом 300 ж3, чтобы подняться с высоты, на которой барометр показывал давление 730 мм рт. ст. при температуре —15° С, до высоты, на которой барометр показывает давление 710 мм рт. ст., а температура равна —20° С?
252. Баллон, содержащий 1 кг азота, при испытании взорвался при температуре 350° С. Какое количество водорода (в граммах) можно хранить в этом баллоне при 20° С, имея пятикратный запас прочности? Считать прочность баллона не зависящей от температуры.
253. В баллоне находилось некоторое количество газа при атмосферном давлении Pi = l атм. При открытом вентиле баллон был нагрет, после чего вентиль закрыли и газ остыл до температуры Т2= 10°С. При этом давление в баллоне упало до Р2=0,7 атм. На сколько градусов баллон нагревали?
254. Стеклянный баллон при постоянной температуре был взвешен трижды: 1) откачанный, 2) заполненный воздухом при атмосферном давлении, 3) заполненный неизвестным газом при давлении 1,5 атм. Оказалось, что pi = 200 Г, р2 = 204 Г, р3 = 210 Г. Определить молекулярный вес неизвестного газа. Молекулярный вес воздуха принять равным 29.
255. В цилиндре под поршнем площадью 5=100 см2 находится т = 28 г азота при температуре Т •, = 273*’ К. Цилиндр нагревается до температуры 7’2=373°К. На какую высоту h поднимется поршень массой Л4=100 кг? Атмосферное давление Ро=1 атм.
256. В цилиндрическом сосуде с площадью основания 5 = 250 см2 находятся 10 г азота, сжатого поршнем, на котором лежит гиря массой М = 12,5 кг. Какую работу совершит газ при нагревании его от температуры 25° С до 625° С? Насколько увеличится при этом объем газа? Атмосферное давление Ро= 1 атм.
257. Сколько водорода находится под поршнем в цилиндрическом сосуде, если при нагревании его от
56
Ti =250° К до 7'2 = 680° К при постоянном давлении на поршень газ произвел работу, равную 400 дж?
258. Какое количество тепла необходимо для нагревания т = 7 г азота от 10 до 25°С? Газ находится в цилиндре под поршнем, на котором лежит постоянный груз. Теплоемкость одной граум-молекулы азота при нагревании его при постоянном объеме равна с„ = = 21 дж/моль • град.
259. Поршни двух одинаковых цилиндров жестко связаны таким образом, что объемы под поршнями равны между собой. В цилиндры при температуре Т введен воздух таким образом, что давление в одном из цилиндров равно Р. Затем этот цилиндр нагревается до температуры Ti. Какое установится в нем давление? Во втором цилиндре поддерживается температура 7'. Атмосферное давление равно Ро- Весом поршней пренебречь.
260. Поршни двух одинаковых цилиндров связаны жестко таким образом, что объемы под поршнями равны между собой. В оба цилиндра введена одинаковая масса воздуха при температуре Т. Затем один из цилиндров нагревается до температуры 1\, а другой поддерживается при начальной температуре Т. Каково будет давление в цилиндрах? Весом поршней пренебречь. Атмосферное давление Ро.
261. Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом и находится при температуре Т. Во сколько раз изменится давление в такой системе, если один из сосудов нагреть до температуры 7\, а другой оставить при температуре 7?
262. Три одинаковых сосуда, соединенные тонкими непроводящими тепло трубками, заполнены при температуре 4° К некоторым количеством газообразного ге-лия. Затем один из сосудов нагрели до 20° К, а второй — до 80° К- Температура третьего сосуда осталась неизменной. Во сколько раз изменилось давление в системе?
263. К цилиндру с площадью поперечного сечения S со свободно скользящим невесомым поршнем, наполненному газом, подключен через тонкую трубку с краном откачанный баллон объема V. На какую высоту опустится поршекь, если открыть кран? Цилиндр
57
поддерживается при температуре Tt, а баллон— при температуре Т.
264. Теплоизолированный сосуд емкостью К=22,4 л разделен тонкой непроницаемой, проводящей тепло перегородкой на две равные части. В одну половину сосуда вводят «11 = 11,2 г азота при Zi = 20°C, во вторую «12=16,8 г азота при /2=15ОС, Какие давления установятся в каждой части сосуда после выравнивания температуры? Молекулярный вес азота р = 28.
265. В сосуде, разделенном пополам перегородкой, находятся 2 г водорода и 32 а кислорода при температуре То. После того как перегородку убрали и газы прореагировали, установилась температура Т и давление Р. Определить первоначальное давление в обеих частях сосуда.
266. Цилиндрический сосуд с газом разделен двумя невесомыми поршнями А и В на три секции, в каждой из которых находится газ (объем и давление газа для
А в
Шинмаппн
?2 ^2
щщщщщ
Рис. 72.
Рис. 73.
каждой секции указаны на рис. 72), Поршни освобождаются и получают возможность свободно скользить вдоль цилиндра. Найти объем и давление газа в каждой секции после того как поршни перестанут перемещаться. Температура газа во всем цилиндре одна и та же и поддерживается неизменной.
267. Запаянная с одного конца цилиндрическая трубка длиной L погружается в воду до тех пор, пока ее запаянный конец не окажется на одном уровне с поверхностью воды (рис. 73). Когда температура воздуха в трубке и воды уравнялась, оказалось, что вода в трубке поднялась на высоту -g- L. Найти начальную
68
температуру воздуха в трубке, если температура воды Т, а атмосферное давление Ро.
268. Цилиндрическая пробирка длины L, содержа* щая некоторое количество газа при температуре Т, пол* ностью погружена в жидкость с плотностью р, так что дно пробирки касается поверхности жидкости. При этом жидкость заполняет половину про- бирки. Пробирку поднимают вверх так, т f: что она едва касается поверхности жид- [7
КОСТИ СВОИМ ОТКрЫТЫМ КОНЦОМ. Как 7?' | £7
надо изменить температуру газа в про- £__| н
бирке, чтобы жидкость снова заполняла у- с-
половину пробирки? Атмосферное дав-ление равно Ро. '-2
269. В запаянную у одного конца Ц ?.
U-образную трубку налита вода, причем v\ М3
за счет присутствия в трубке воздуха разность уровней воды оказалась равной h (рис. 74). Как нужно изменить Рис. 74. температуру воздуха в трубке, чтобы
разность уровней воды у ее концов уменьшилась вдвое? Атмосферное давление Ро. Давлением паров воды пренебречь.
270. Сосуд емкостью 2К=200 см3 разделен пополам полупроницаемой перегородкой. В одну половину введено nii = 2 мг водорода и т2 == — 4 мг гелия. Через перегородку может диффундировать только гелий. Во время процесса поддерживается температура Т = 27° К. Какие давления Pi и Р2 установятся в обеих частях сосуда?
271. В цилиндре под поршнем находится некоторая масса водорода при температуре 30° С,
занимающая при давлении в 2 атм объем 8 л. Как изменилась температура водорода, если при неизменном давлении объем его уменьшился настолько, что при этом была совершена работа 50 дж?
272. В цилиндре под поршнем площадью S = 100 см2 находится т = 28 г азота при температуре 100° С, К поршню через систему блоков привешен груз Л1 = 50 кг (рис. 75). Цилиндр охлаждается до 0°С. На
59
какую высоту поднимется груз? Атмосферное давление Ро= 1 о-тм. Весом поршня пренебречь.
273. В цилиндре под поршнем находится некоторая масса воздуха. На его нагревание при постоянном давлении затрачено Q — 5 кдж. Найти работу, произведенную при этом газом. Теплоемкость воздуха при постоянном давлении ср=103 дж/кг^рад, молекулярный вес воздуха принять равным 29.
274. В комнате объемом V=50 м3 затопили печь, и температура воздуха поднялась с /1 = 11 до /2 = 23°С. Давление воздуха в комнате не изменилось и осталось равным 1 атм. Какая часть воздуха ушла при этом из комнаты? Какую работу совершил при расширении воздух, оставшийся в комнате?
275. В баллоне объемом 10 л содержался при температуре 20°С водород под давлением 100 атм. Какое количество водорода израсходовано, если при сжигании оставшегося водорода образовалось 0,5 л воды?
276. В баллоне с метаном емкостью 60 л при 0°С было давление Р = 80 атм. Баллон подключили к газовой горелке с к. п.д. 80% и, сжигая метан, нагревали воду. Если после этого нагреть баллон до 80° С, в нем снова установится давление Р. Сколько воды можно было нагреть от 0°С до кипения? Теплотворная способность метана <7 = 41,8 кдж!г, молекулярный вес 16.
277. В баллоне с метаном емкостью 50 л при температуре /0 =—23°С было давление Ро= 150 атм. Баллон подключили к газовой горелке и, сжигая метан, расплавили 10 кг льда с той же начальной температурой, превратив его в воду с температурой 0°С; к. п. д. горелки 80%. Да какой температуры надо нагреть баллон, чтобы в нем снова установилось давление Ро? Теплотворная способность метана <7=41,8 кдж/г. Удельная теплоемкость льда 2,1 дж/г • град.
278. В цилиндре сечением S, закрытом поршнем с массой М, находится иг г азота при температуре Т и давлении Р. Какова сила трения между поршнем и стенками цилиндра, если для того, чтобы сдвинуть поршень, газу сообщили количество тепла Q. Атмосферное давление равно Ро, а удельная теплоемкость азота при постоянном объеме cv.
279. Некоторая масса молекулярного водорода занимает объем Vi = 1 м3 при температуре Л = 250° К и дав
60
лении Pj=2 атм. Какое давление Р2 будет иметь та же масса водорода при температуре 72 = 5000°К в объеме 1'2=10 Л13, если при столь высокой температуре молекулы водорода полностью диссоциируют на атомы?
280. В сосуде объемом V = 0,5 л находится т = 1 г парообразного иода (J2). При температуре /=1000°С давление в сосуде оказалось равным 7=700 мм рт. ст. Найти степень диссоциации молекул иода J2 на атомы иода J при этих условиях. Молекулярный вес иода J2 (х = 254.
Примечание. Степенью диссоциации называют отношение числа диссоциированных молекул к общему числу молекул до диссоциации.
281. В сосуде объемом К=1 л находится т —0,2 г углекислого газа СО2. При температуре 7 = 2600° К некоторая часть молекул СО2 диссоциировала на молекулы окиси углерода СО и молекулы кислорода О2. При этом давление в сосуде оказалось равным 7 = 810 мм рт. ст. Найти степень диссоциации молекул СО2 на молекулы СО и О2 при этих условиях.
Насыщающие и ненасыщающие пары
282. Относительная влажность воздуха, заполняющего сосуд объемом 0,7 At3, при 24°С равна 60%. Сколько нужно испарить в этот объем воды до полного насыщения пара? Давление насыщающих паров при этой температуре рн = 22,4 лш„рт. ст.
283. В запаянной трубке объемом 0,4 л находится водяной пар под давлением 60 мм рт. ст. при температуре 150° С. Какое количество росы выпадает на стенках трубки при охлаждении ее до 22° С? Давление насыщающих паров воды при 22° С равно 19 мм рт. ст.
284. Давление насыщающего водяного пара при температуре 36° С равно 44,6 мм рт. ст. Сколько весит при этой температуре 1 м3 влажного воздуха при относительной влажности 80% и давлении 1 атм?
285. Определить отношение веса 1 .я3 сухого воздуха к весу 1 Л13 воздуха с влажностью 50%. Обе порции взяты при атмосферном давлении и температуре 20° С. Отношение молекулярного веса воды к молекулярному весу воздуха принять равным 0,6. Упругость водяных паров при температуре 20° С равна 17,5 мм рт. ст.
61
286. На сколько изменится подъемная сила воздушного шара объема V, если относительная влажность воздуха увеличится на 20%? Давление и температура влажного воздуха осталисъ неизменными. Известно, что плотность насыщающих паров при данной температуре равна р. Молекулярные веса воздуха и паров воды соответственно равны 29 и 18.
287. Какое количество ртути содержится в 1 м3 воздуха зараженного ртутью помещения при температуре 20° С, если давление насыщающего пара ртути при этой температуре равно 0,0011 мм рт. ст.? Атомный вес ртути ц = 200,6.
288. Сколько молекул ртути содержится в 1 см3 воздуха в помещении, зараженном ртутью, при температуре 30° С, если давление насыщающего пара ртути при этой температуре равно 0,0056 мм рт. ст.? Число Аво-гадро Ао = 6,023- 1023.
289. Найти среднее расстояние между молекулами насыщающего водяного пара при Т =100° С. Отношение универсальной газовой постоянной R к числу Авогадро No, называемое постоянной Больцмана, k = = 1,4 • 10~16 эрг)град.
290. В теплоизолированном цилиндре под невесомым подвижным поршнем находится 30 г воды при температуре 0°С, причем поршень лежит на поверхности воды. Воду нагревают электрическим кипятильником, сопротивление спирали которого г=100 ом. На какую высоту поднимется поршень, ’если внешнее давление 1 атм, а через кипятильник в течение 1 мин протекал ток 2 а? Площадь поршня 512 см2. Удельная теплота парообразования воды 2,25 кдж[г.
291. Смешали 1 м3 воздуха с влажностью 20% и 2 м3 воздуха с влажностью 30%. При этом обе порции были взяты при одинаковых температурах. Смесь занимает объем 3 м3. Определить ее относительную влажность.
292. В цилиндре под поршнем находится воздух при 100°С и с относительной влажностью 40%. Объем воздуха при этом 100 см3. Цилиндр охлаждается до 20° С. Как надо изменить его объем для того, чтобы роса на стенках не выпадала? Давление насыщающих паров воды при 20° С равно 17,5 мм рт. ст.
62
293. Чему равнялась относительная влажность воздуха под поршнем при 20° С и давлении 1 атм, если конденсация воды из этого воздуха при 100° С началась при давлении 60 атм? Давление насыщающих паров воды при 20° С равно 17,5 мм рт. ст.
294. В сосуд объемом V= 10 л, наполненный сухим воздухом при давлении P — i атм и температуре 0°С, вводят 3 г воды и нагревают сосуд до 100° С. Определить давление влажного воздуха в сосуде при этой температуре.
295. Некоторый объем воздуха, температура которого 25° С, давление 745 мм рт. ст. и относительная влажность а = 40%, имеет массу 1 г. Найти этот объем. Давление ра насыщающих паров при 25° С равно 23,5 мм рт. ст.
296. Сосуд с небольшим отверстием находится при температуре, равной 76° С. Атмосферное давление Ро = 750 мм рт. ст. В сосуд налито немного воды, давление насыщающих паров которой при этой температуре равно pi = 300 мм рт. ст. Затем сосуд закупоривают и погружают в жидкий воздух, кипящий при 80° К. Каково будет давление в сосуде? Давлением насыщающего водяного пара при 80° К можно пренебречь.
297. Под поршнем, закрывающим цилиндрический сосуд, имеющий объем Ко=Ю л и помещенный в термостат при %=—57°С, находится т = 1,9 г газообразного аммиака (молекулярный вес 17). Сколько аммиака сконденсируется при сжатии газа поршнем до объема V = Ко/2? Давление насыщенного пара аммиака при .—57° С равно 200 мм рт. ст.
298. В камеру объемом 1 л, сообщающуюся с воздухом при 20° С и нормальном атмосферном давлении, бросают кусочек сухого льда массой 0,5 г. Камеру сразу же герметически закрывают. Какое давление установится в камере после установления равновесия при неизменной температуре? Давление насыщающего пара углекислоты при 20° С ра = 56,5 атм.
299. В сосуде К=100 л при 30° С находится воздух с относительной влажностью а ==30%. Какова будет относительная влажность аь если в сосуд ввести т=1 г воды? Давление насыщающих паров воды при 30° С рн=31,8 мм рт. ст.
63
300. В сосуде V=1 л при 30°С находится воздух с относительной влажностью а = 30%- Какова будет относительная влажность ait если в сосуд ввести ш = 1 г воды? Давление насыщающих водяных паров при 30°С ра = 31,8 мм рт.ст.
301. В закрытом с обоих концов цилиндре объема К=1 л свободно ходит невесомый тонкий поршень. В пространство под поршнем вводится m^l г воды, в пространство над поршнем — т.2—2 г азота. Какую часть объема цилиндра займет азот при 100° С?
302. В закрытом с обоих концов цилиндре объемом 1 л свободно ходит невесомый тонкий поршень. В пространство под поршнем вводится mi = 0,1 г воды, в пространство над поршем — /«2 = 0,5 г азота. На какой высоте установится поршень при 100° С (в долях от общей высоты цилиндра)?
303. В закрытом с обоих концов цилиндре объемом 1 л свободно ходит невесомый тонкий поршень. В пространство под поршнем вводится mi = 0,5 г воды, в пространство над поршнем — т2 = 0,5 г азота. На какой высоте установится поршень при 100° С (в долях от общей высоты цилиндра)?
304. В цилиндре объемом 10 л под поршнем находится влажный воздух при температуре 20° С. Относительная влажность его 70%. Каково будет давление в цилиндре, если его объем при той же температуре уменьшить в 10 раз? Начальное давление равно 100 мм рт. ст. Давление насыщающего пара при температуре / = 20° С равно 18 мм рт.ст.
305. Температура воздуха в комнате Zi = 14°C, а относительная влажность «1=60%. В комнате затопили печь, и температура воздуха повысилась до /2 = 22°С. При этом некоторая часть воздуха вместе с содержащимся в нем водяным паром ушла наружу и давление в комнате не изменилось. Определить относительную влажность воздуха при температуре t2. Давления насыщающих паров при температурах £i = 14°C и /2 = 22° С равны р11( = 12 мм рт.ст. и рП2 = 20 мм рт.ст.
306. В герметически закрытом ящике при ^ = 50° С находится воздух с влажностью а=40%. В ящик введен змеевик, который можно охлаждать потоком воды. Сколько воды сконденсируется на змеевике, если через него пропускать воду температуры /2 = 20°С, а ящик
64
поддерживать при 50° С? Давления насыщающих паров воды при температурах ti и /2 равны Д1 = 92,5 мм рт. ст. и р2—17,5 мм рт. ст. Объем ящика 1 м3.
307. В стеклянном баллоне, присоединенном к вакуумному насосу, содержались капельки ртути общей массой 0,87 г. Баллон помещен в печь, имеющую температуру 120° С. Производительность насоса 7 л!мин. Чему равно давление насыщающих паров ртути при 120° С, если давление в баллоне резко упало после 20 мин работы насоса? Молекулярный вес ртути 200.
308. Под колоколом насоса находится стакан, содержащий 20 г воды. Скорость откачки насоса 50 a)muh. Через сколько времени вся вода испарится, если установившаяся температура воды 5° С? Давление насыщающих паров воды при 5° С равно 6,54 мм рт. ст.
309. В откачанный сосуд объемом 500 см3 ввели водород до давления 200 мм рт.ст. при температуре 20° С. В другой такой же сосуд ввели кислород до давления 100 мм рт. ст. Оба сосуда соединили и после того, как газы перемешались, пропустили электрическую искру; гремучая смесь сгорела. Сколько воды сконденсировалось на степках сосуда после того, как установка приняла первоначальную температуру? Давление насыщающих паров воды при 20°С равно 17,5 мм рт.ст.
310. Кубический метр влажного воздуха при относительной влажности 60%, температуре 20° С и давлении 1 атм весит 10,76 н. Определить давление насыщающего водяного пара при температуре 20° С.
311. Герметически закрытый сосуд, содержащий некоторое количество воздуха, наполовину заполнен водой. При температуре Л =27° С давление в сосуде оказалось равным />1 = 626,7 мм рт.ст., а при температуре /2 = 60°С
равным /,2=815 мм рт.ст. Определить давление насыщающих паров при температуре /2, если известно, что при температуре оно равно 26,7 мм рт.ст.
312. Два цилиндрических сосуда одинаковой высоты //=150 см соединены снизу тонкой трубкой (рис. 76).
5 Л. П. Баканина и др.
65
Сосуд А плотно закрыт крышкой, сосуд В открыт. Сначала в сосудах находился сухой воздух При давлении Ро = 76О мм рт. ст. Затем сосуд В при неизменной температуре до краев наполнили водой; уровень воды в сосуде А оказался равным й = 14 см. Определить давление насыщающих паров воды при температуре опыта.
Разные задачи
313. Кристаллическая решетка железа кубическая. Считая, что на каждый элементарный куб приходится один атом железа, определить постоянную решетки, т. е. расстояние между ближайшими атомами железа. Плотность железа 7,9 г)см\ атомный вес 56. Число Авогадро 6,02- 1023.
314. С какой скоростью растет толщина покрытия стенки серебром при распылении, если атомы серебра, обладая энергией 10~17 дж, производят давление на стенку, равное 0,1 н/м2? Плотность серебра 10,5 г/см3. Молекулярный вес серебра 108.
315. В цилиндрическом сосуде под поршнем находятся пары воды при температуре 100° С и внешнем давлении 1 атм. Начальный объем сосуда 20 л. При постоянном внешнем давлении поршень опускается, так что объем Пара уменьшается вдвое. Какое количество тепла надо отвести от сосуда, чтобы температура пара осталась постоянной? Объемом сконденсировавшейся воды пренебречь. Теплота парообразования воды при 100° С равна 2246 дж!г.
316. В цилиндре под невесомым поршнем площадью S —100 см2 находится Л4=1 кг воды при температуре 0°С. В цидиндре включают нагреватель мощностью W = 500 вт. Через какое время поршень поднимется относительно своего первоначального положения на высоту Л=1 Л1? Атмосферное давление Ро=1 атм. Теплота парообразования воды <7 = 2,25-106 дж!кг. Теплоотдачей и теплоемкостью цилиндра пренебречь. Теплоемкость воды 1 кал/г • грп5 = 4,18 дж/г • град.
317. В цилиндре под невесомым подвижным поршнем находится V=1 Л13 насыщающего водяного пара. Какую массу воды температуры 0°С надо впрыснуть в сосуд, чтобы весь пар сконденсировался? Атмосферное давление Р=1 атм. Теплоемкостью и теплоотдачей
66
цилиндра пренебречь* Теплота конденсации воды <7=2,25- 106 дж/кг.
318. Под невесомым поршнем в цилиндре находится 1 кг воды при температуре 0°С. В воду опускают кусок железа массы 1 кг, нагретый до температуры 1100° С. На какую высоту поднимется поршень? Атмосферное
давление 1 атм, удельная теплоемкость железа с = 0,5 дж/г • град. Площадь поршня 5=1000 см2. Тепло-
отдачей и теплоемкостью цилиндра пренебречь.
319. В цилиндре под невесомым поршнем площадью 100 см2 находится 18 г насыщающего водяного пара.
В сосуд впрыскивают 18 г воды при температуре 0°С. На какую высоту опустится поршень? Атмосферное давление 1 атм. Теплоемкостью и теплопроводностью цилиндра пренебречь.
320. В цилиндре под поршнем площадью 5 = 100 см2 находится 18 г воды
при 0°С (рис. 77). Цилиндр нагревается до 200° С. На какую высоту поднимется
поршень с лежащим на нем грузом
М = 100 г? Атмосферное давление 1 атм; давление на* сыщающих водяных паров при 200° С равно 16 атм.
321. В цилиндре под поршнем площадью 5=100 см2 находится 18 г водяного пара при температуре 100° С, К поршню через систему блоков подвешен груз М = 50кг (см. рис. 75). Цилиндр охлаждается до 0°С. На какую высоту поднимется груз? Атмосферное давление 1 атм. Весом поршня пренебречь. Давление насыщающего водяного пара при 0°С равно 4 мм рт.ст.
322. В теплоизолированный откачанный сосуд объемом 15 л налито 2 кг воды при 300° К. На дне в сосуд впаяна проволока с сопротивлением 100 см, по которой течет ток 2 а. Определить время, в течение которого в сосуде установится температура 100° С. Изменением объема воды пренебречь.
323. Балластный резервуар подводной лодки объемом И=5000 л целиком заполнен водой. Какое давление воздуха должно быть в баллоне емкостью v = 200 л, чтобы при подсоединении баллона к балластному резервуару подводная лодка полностью освободилась от балласта на глубине 77=100 м? Температуру воздуха считать неизменной.
5*
67
324. Балластный резервуар подводной лодки объемом V=5000 л заполнен водой. Для сброса балласта в верхнюю часть резервуара подается воздух из компрессора и вода через трубу сечением 5=100 см2, расположенную в нижней части резервуара, вытекает наружу. Какова должна быть мощность компрессора, чтобы лодка на глубине Я=100 м могла полностью освободиться от балласта за время / = 50 сек?
325. В вертикально расположенном цилиндрическом сосуде находится газ массы М с молекулярным весом ц. Газ отделен от атмосферы поршнем, соединенным с дном сосуда пружиной жесткости k (рис. 78). При температуре Т{ поршень расположен на расстоянии/г от дна сосуда. До какой температуры надо нагреть газ, чтобы поршень поднялся до высоты Н?
326. В цилиндре под невесомым поршнем находится газ под давлением Р, равным внешнему давлению, и с температурой Т. Поршень удерживается упругой пружиной (см. рис. 78). Во сколько раз нужно увеличить температуру газа, чтобы его объем увеличился в полтора раза? Если газ из-под поршня полностью откачать, поршень находится в равновесии у дна цилиндра.
327. Цилиндрический тонкостенный сосуд высотой Н плавает, погрузившись в воду на глубину h. Сосуд переворачивают вверх дном и опускают на воду в таком положении. На какую глубину погрузится при этом нижний край сосуда, если сосуд плавает? Атмосферное давление Ро. Плотность воды р. Давлением насыщающего пара воды внутри сосуда пренебречь.
328. Тонкостенный стакан массы М = 50 г ставят вверх дном на поверхность воды и медленно отпускают его в глубь таким образом, что он все время остается вертикальным. На какую минимальную глубину надо опустить стакан, чтобы он утонул? Высота стакана Я = 10 см, площадь дна 5=20 см2. Давлением паров воды в стакане пренебречь. Атмосферное давление Ро=1 атм.
329. В U-образную запаянную с одного конца трубку длины 2L налита жидкость таким образом, что в пра-
68
вом запаянном колене остался воздух.-Уровень жидкости в открытом колене совпадает с краем трубки. Разность между уровнями равна Z./3 (рис. 79). Какую часть жидкости нужно выпустить через кран в нижней части сосуда, чтобы уровни жидкости в открытом и закрытом коленах сравнялись? Давлением паров жидкости пренебречь. 1 КП Л Д Плотность жидкости р, атмосферное давление Ро. Y-
330. В вертикальной узкой трубке L --
длины 2L нижний конец запаян, а f- L-
верхний открыт. В нижней половине Д па-
трубки находится газ при темпера-туре Т, а верхняя до конца заполнена ртутью. До какой минимальной тем- гТ0
пературы надо нагреть газ в трубке, Ц
чтобы он вытеснил всю ртуть? Внеш- _
нее давление L мм рт. ст. Поверхност- рнс> /9' ное натяжение не учитывать.
331. Опрокинутый гидравлический пресс (рис. 80) находится в равновесии. При каком соотношении между массами поршней m и М это возможно? Размеры даны на рисунке 80. Плотность жидкости р; трением пренебречь.
Рис. 81.
332. В закрытом с обоих концов откачанном цилиндре подвешен на пружине скользящий без трения поршень, положение равновесия которого находится у дна цилиндра. В пространство под поршнем вводится такое количество газа, что поршень поднимается на высоту h (рис. 81). На какой высоте hi установится поршень, если этот газ нагреть от начальной температуры Т
69
до 7\? Сила, действующая co стороны пружины на пор-
шень, пропорциональна смещению поршня.
333. Герметически закрытый откачанный цилиндр соединен тонкой трубкой с краном с откачанным сосудом объема V. В цилиндре подвешен на пружине скользящий без трения поршень, положение равновесия ко-
торого находится у дна цилиндра. В пространство под поршнем при закрытом кране вводится такое количество газа, что поршень поднимается на высоту h (рис. 82). На какой высоте h\ установится поршень, если открыть кран? Площадь сечения цилиндра S, температура постоянна. Сила, действующая со стороны пружины на поршень, пропорциональна смещению поршня.
334. В мензурке высотой Н и сечением S, закрытой невесомым поршнем,
Рис. 82. находится газ с молекулярным весом ц.
Поршень опускают и освободившуюся .часть мензурки до краев заливают ртутью. При каких значениях температуры газа можно найти такое положение поршня, при котором поршень будет находиться в равновесии (т. е. ртуть, налитая в мензурку, не будет выбрасываться давлением газа)? Масса газа в мензурке т, внешнее давление принять равным нулю.
335. Пробирка погружена в воду своим открытым концом на глубину, равную половине ее длины. Уровень воды в пробирке совпадает с уровнем воды в резервуаре. Начальная температура всей системы 71 = 273° К. При какой максимальной длине пробирки воздух из нее начнет выходить, если температуру си
стемы довести до Т? — 373° К? Наружное давление Ро = 1 атм. Давлением паров воды при 0° С пренебречь.
336. Пробирку длиной L заполнили водородом под давлением Ро, закрыли легким подвижным поршнем и погрузили в сосуд со ртутью на глубину Н (рис. 83). Какая часть длины пробирки будет при этом заполнена
Рис. 83.
70
водородом? При каких значениях Н задача имеет решение? Плотность ртути р, внешнее давление Ра, температура водорода поддерживается неизменной.
337. В контейнере высотной ракеты сначала было давление Ро=1 атм. Во сколько раз увеличилась тем-
пература внутри ракеты при ее взлете, если установленный в контейнере ртутнйй барометр стал показывать 0,6 Ро? Ракета взлетает вертикально с постоянным ускорением g.
338. Одна грамм-молекула идеального газа находится в цилиндре под поршнем при температуре Tt. Газ при постоянном давлении нагревают до температуры Т2, затем при постоянном объеме нагревают до температуры Т3. Далее газ охлаждают при постоянном давлении так, что его объем падает до первоначального значения. Наконец при постоянном объеме газ возвращают
в первоначальное состояние. Таким образом, над газом совершен замкнутый процесс (цикл). Какую работу совершил газ в этом процессе?
339. Над одной грамм-молекулой идеального газа совершают цикл (замкнутый процесс), состоящий из двух изохор и двух изобар (рис.84). Температуры в точках 1 и 3 равны Ti и Тз- Определить
Рис. 84.
работу, совершенную газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме.
340. Некоторая масса газа имеет давление Р\, объем Vi и температуру Т\. Затем газ при постоянном объеме нагревают до температуры 7'2 = 27’1, после этого
происходит расширение газа при постоянном давлении до объема V2 = 4Vi. Из получившегося состояния газ возвращают к начальному (Pi, Vt, Ti), причем так, что во время этого процесса PVn — const. Опреде-
лить п.
341. Нагревается или ох-лаждается идеальный газ, если он расширяется по закону P = bjVn, где b и п— некоторые постоянные, причем 0<п<1?
342. Идеальный газ расширяется по закону P = aV. Найти графически работу, произведенную газом при
71
увеличении объема от V/ до V2. Поглощается или выделяется тепло при таком процессе?
343. Температура некоторой массы т идеального газа с молекулярным весом р меняется по закону Т = аР2. Найти графически работу, совершенную газом при увеличении объема от V] до V2. Поглощается или выделяется тепло при таком процессе?
344. Масса М пороха, сгорающего в одну секунду в камере ракетного двигателя, зависит от давления Р по закону М—АРп (А и п — некоторые постоянные). Скорость расхода массы газа за счет истечения из сопла пропорциональна давлению в камере. Во сколько раз отличаются давления в камерах ракетных двигателей, если сечение их сопел равны Si и So? Рассмотреть частный случай, когда п — 2/3, Si/S2 = 2.
345. Масса М пороха, сгорающего в одну секунду в камере реактивного двигателя, зависит от давления Р по закону М=АРп. Найти показатель степени п, если при уменьшении сечения сопла двигателя в два раза давление в камере возрастает в четыре раза. Скорость расхода массы газа за счет истечения из сопла пропорциональна давлению в камере Р,
III. ЭЛЕКТРИЧЕСТВО
Электрический заряд. Закон Кулона
346. Какой заряд Q приобрел бы медный шар с радиусом /?=10 см, если бы удалось удалить все электроны проводимости? Плотность меди р = 8,9 г)см3, атомный вес Л = 64. Заряд электрона е=1,6-10'1э к, число Авогадро М> = 6 - 1023. Считать, что на каждый атом меди приходится один электрон проводимости.
347. С какой силой f будут притягиваться два одинаковых свинцовых шарика радиусом г = 1 см, расположенные на расстоянии R = 1 м друг от друга, если у каждого атома первого шарика отнять по одному электрону и все эти электроны перенести на второй шарик? Атомный вес свинца А =207, плотность р = 11,3 г!см3.
348. На двух одинаковых капельках воды находится по одному лишнему электрону, причем сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек?
349. Три точечных заряда, попарно помещенные на расстоянии г = 10 см друг от друга, взаимодействуют с силами: 5 Г, 8 Г, 12 Г. Найти величины зарядов.
350. По кольцу могут свободно перемещаться три шарика, несущие заряды: + <71 на одном шарике и +g-i на каждом из двух других. Чему равно отношение зарядов <71 и «/г, если при равновесии дуга между зарядами </г составляет 60°?
351. Два одинаковых заряженных шарика, подвешенные на нитях равной длины, опускаются в керосин. Какова должна быть плотность р материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Плотность керосина рк = 0,8 г/см3, относительная диэлектрическая проницаемость е = 2. (И в дальнейшем е означает относительную диэлектрическую проницаемость диэлектрика. Абсолютная прэ-
73
ницаемость равна 88о, где ео=(1/36л) 10-9 ф/м — диэлектрическая проницаемость вакуума.)
352. Вокруг неподвижного точечного заряда qo — = + Ю"9 к равномерно вращается под действием сил притяжения маленький шарик, заряженный отрицательно. Чему равно отношение заряда q шарика к его массе т, если радиус орбиты R = 2 см, а угловая скорость вращения ы = 3 padfceKi
Электроемкость. Потенциал
353. Три последовательно соединенных конденсатора Ci, С2 и С3 подключаются к батарее с электродвижущей силой <о. Какова разность потенциалов на каждом из конденсаторов?
А
Рис. 85.
Рис. 89.
354. Найти заряд на каждом из конденсаторов Ci, С2 и С3, схема соединения которых дана на рис. 85. Э. д. с. батареи равна <S.
335. Двенадцать одинаковых конденсаторов с емкостью С каждый собраны в батарею в виде восми-гранника ACDEFB (рис.86). Какова емкость этой батареи конденсаторов между точками А и В?
356. В схеме, изображен
ной на рис. 87, емкость батареи конденсаторов не изменяется при замыкании ключа К. Определить Сх, -
74
357. Батарея конденсаторов, изображенная на рис. 88, составлена из конденсаторов одинаковой емкости. Во сколько раз изменится общая емкость батареи, если замкнуть ключи /<1 и К2?
Рис. 89.
Рис. 88.
358. У трех конденсаторов емкости равны С, 2С и ЗС, а пробойные напряжения соответственно V, V/4 и V/2. При каком из всех возможных способов соеди* нения батарея из этих трех конденсаторов выдержит наибольшее напряжение?
359. Конденсаторы Ci и С2 (рис. 89) при помощи переключателя К присоединяются сначала к батарее с э. д. с., равной сТ, а потом к незаряженному конденсатору Сз. Найти заряд q3, который появится на конденсаторе С3.
360. Два конденсатора с емкостями Ci и С2, обладающие зарядами qi и q2, включаются в замкнутую цепочку так, что положительная оболочка одного конденсатора соединяется с отрицательной обкладкой другого. Определить заряд каждого конденсатора в этом случае.
361. Конденсатор емкости С первоначально заряжен от батареи с э. д. с. & и отключен от батареи. К нему подключается другой (незаряженный) конденсатор емкости 6?! (рис. 90,а). Затем конденсатор С] от
соединяют от С и вновь подсоединяют, но так, что теперь верхняя пластина конденсатора С оказывается соединенной с нижней пластиной конденсатора С\
75
(рис. 90,6). Определить разность потенциалов на конденсаторе С. .
362. Конденсатор емкостью 20 мкф заряжен до напряжения 400 в. К нему подключается конденсатор с емкостью 1 мкф, в результате чего последний заряжается. Затем, отключив этот конденсатор, заряжают таким же образом второй конденсатор с той же емкостью (1 мкф), третий и т. д. Затем конденсаторы соединяют последовательно. Какое максимальное напряжение можно получить таким способом?
363. Плоский конденсатор с размерами пластин 25 X 25 см и расстоянием между ними d\ =0,5 мм заряжен до разности потенциалов Vi = 10 в и отключен от источника. Какова будет разность потенциалов V2, если пластины раздвинуть до расстояния d2 = 5 мм?
364. Два изолированных плоских конденсатора емкостью Со каждый заряжены до разности потенциалов Ио и соединены параллельно. В одном из конденсаторов расстояние между пластинами увеличено в три раза. Найти заряды конденсаторов и напряжение на них.
365. Воздушный конденсатор емкостью С заполняют диэлектриком с диэлектрической постоянной е. Конденсатор какой емкости надо включить последовательно с данным, чтобы такая батарея вновь имела емкость С?
366. Плоский конденсатор имеет площадь пластин S = 2000 см2, расстояние между ними 0,5 мм. В конденсаторе находится пластинка слюды (е = 7) толщиной dj = 0,3 мм, в остальной части — воздух. Определить емкость С конденсатора.
367. Плоский конденсатор, пластины которого расположены горизонтально, наполовину залит жидким диэлектриком. Какую часть k аналогичного конденсатора надо залить жидкостью при вертикальном расположении пластин, чтобы емкости в обоих случаях были одинаковы? Диэлектрическая постоянная жидкости е.
368. N одинаковых шарообразных капелек ртути заряжены до одного и того же потенциала V. Каков будет потенциал Vj большой капли, получившейся в результате слияния этих капелек?
369. Металлический шар радиуса Ri, имеющий потенциал V, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара, если заземлить внешнюю оболочку?
76
370. Металлический шар радиуса /?ь заряженный до потенциала V, окружают сферической проводящей оболочкой радиуса /?2. Как изменится потенциал шара после того как он будет на некоторое время соединен проводником с оболочкой?
371. Два одинаковых металлических шарика радиуса г расположены в вакууме на расстоянии а друг от друга, причем а?$>г. Шарики заряжены разноименными и равными по абсолютной величине зарядами. Какова емкость конденсатора, образованного шариками?
372. Найти разность
С С потенциалов между точ-
_____а______11 ками а, b в схеме, изо-s '' ~1 браженной на рис. 91.
Рис. 92.
Рис. 91.
373. Найти разность потенциалов между точками а, b в схеме, изображенной ла рис. 92.
Рис. 93.
Рис. 94.
374. Какой заряд протечет ме, изображенной на рис. 93,
375. Какой заряд протечет ме, показанной на рис. 94,
через гальванометр в схе-при замыкании ключа Л'? через гальванометр в схе-если замкнуть ключ К?
77
Здесь Ci, С2, С3 и С4 — емкость конденсаторов, S-*» э. д. с. батареи. До замыкания ключа конденсаторы были незаряжеиы.
376. Два металлических шара, радиусы которых и и г2, соединены тонкой проволокой. Второй шар окру-О—жен концентрической оболочкой радиуса /?, соединенной с зем-=d Я п лей (рис. 95). Шарам сообщает-ся заряд Q. Как распределится Т этот заряд между шарами? Счи’ ~ тать, что R — г2</?, а длина
Рис. 95. проволоки велика по сравнению
с радиусами шаров.
377. Найти напряженность электрического поля Е вблизи металлической пластины площадью S с равномерно распределенным зарядом q. Поле вблизи плоскости можно считать однородным.
378. Две параллельные металлические пластины площадью S каждая заряжены одинаковыми по величине и знаку зарядами Q. Найти напряженность электрического поля между пластинами и вне их. Поля считать однородными. .✓ +
379. Четыре одинаковые метал- £ £
лические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравнению с размером пластин). Площадь каждой из пластин равна S. Пла- 12 3 4
стина 1 соединена проводником с £__________J
пластинкой 3, а от пластин 2 и 4 сделаны выводы (рис. 96). Опре- р б делить емкость такого сложного 1С’
конденсатора.
380. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях d друг от друга (рис. 97). Площадь каждой из пластин равна S. Крайние пластины соединены между собой, средние пластины подсоединены к батарее, э. д. с. которой равна S. Найти заряды средних пластин. Считать, что расстояние d между соседними пластинами мало по сравнению с их размерами.
381. У расположенного горизонтально незаряженного плоского конденсатора нижняя пластина закре* 78
плена, а верхняя подвешена к коромыслу весов (рис. 98). Весы находятся в равновесии, когда расстояние между пластинами d = 1 мм. Как нужно изменить нагрузку второй чашки весов, чтобы сохранить равновесие при том же расстоянии между пластинами, если конденсатор зарядить до напряжения V = 1000 в? Площадь пластин конденсатора S = 50 см2,
Рис. 98.
Рис. 97.
382. Одна пластина конденсатора закреплена неподвижно, вторая подвешена на пружине с коэффициентом жесткости k. Площадь пластин S. Насколько удлинится пружина, если пластинам сообщить равные, но противоположные по знаку, заряды Q? Поле между пластинами считать однородным. (Коэффициентом жесткости называется отношение силы, растягивающей пружину, к удлинению последней.)
383. Одна пластина конденсатора закреплена неподвижно на дне широкого сосуда с жидким диэлектриком (диэлектрическая проницаемость его е, плотность р). Вторая, имеющая вид бруска высотой Н, плавает над ней, погрузившись на 1/4 своего объема, если пластины не заряжены. Какую разность потенциалов надо приложить к пластинам, чтобы верхняя пластина погрузилась наполовину? Первоначальное расстояние между пластинами конденсатора Н. Поле между пластинами считать однородным.
384. Пластины изолированного плоского конденсатора раздвигают так, что емкость его меняется от Ci до С2 (Ci>C2). Какую работу на это затратили, если
79
заряд конденсатора q? Поле между пластинами в время остается однородным.
385. Плоский воздушный конденсатор с расстоянием между пластинами d—5 см и площадью 5 = 500 см2 подсоединен к источнику с э. д. с. <F = 2000 в. Параллельно пластинам в конденсатор вводится металлическая плита толщиной di = 1 см. Какую работу А совершает при этом батарея?
Заряженная частица в электрическом поле
386. Капелька масла радиусом г = 1 мк, несущая на себе заряд двух электронов, находится в равновесии в поле расположенного горизонтально плоского конденсатора, когда к нему приложено напряжение V = 820 в. Расстояние между пластинами d = 8 мм. Плотность масла р = 0,8 г!см3. Чему равен заряд электрона?
387. Заряженная капелька масла уравновешена электростатическим полем горизонтально расположенного плоского конденсатора. Какое напряжение V подано па пластины конденсатора, если капелька при радиусе г = 2 мк несет на себе три электрона? Расстояние между пластинами d = 8 мм. Что произойдет при раздвижении пластин в случае, когда:
а) пластины соединены с источником напряжения?
б) пластины отключены?
Плотность масла р = 0,8 г]см3.
388. Энергию движущейся заряженной частицы принято выражать в электронвольтах (эв). Один электронвольт — это энергия, которую приобретает первоначально покоящийся электрон после прохождения в вакууме разности потенциалов в 1 в. Вычислить, какая энергия соответствует 1 эв в системе СГСЭ и в системе СИ.
389. Ядро атома неона ускоряется разностью потенциалов V — 2000 в. Найти скорость v ядра, если атомный вес А неона 20 и его номер в периодической системе Z = 10.
390. Электрон движется по направлению силовых линий однородного поля, напряженность Е которого равна 1,2 в/см. Какое расстояние он пролетит в вакууме до полной потери скорости, если его начальная скорость
80
t’o = 1OOO км/сек? Сколько времени будет длиться этот полет?
391. С поверхности металлического шара радиусом /?, несущего на себе заряд —Q, вылетает электрон. Скорость этого электрона на бесконечно большом расстоянии от шара оказалась равной v. С какой скоростью 1>0 электрон покинул поверхность шара? Отношение заряда электрона к _ —
его массе elm предпола- х yq2
гается известным. / 4
392. Сфера радиуса ZXJ' \
несущая на себе заряд / / / \ \
+ ^1, окружена металли- / [’ \+е \
ческой сеткой радиуса r2 I }-•--;----*
(рис. 99), на которую ' Зи- / /
нанесен заряд + q2. Ша- 2 у
рик с массой т, несу- \ щий заряд + е, начинает \ -z
движение вблизи сферы х z
без начальной скорости. ----"
Пролетев через сетку, Рис 99
шарик удаляется на бесконечность. Какова будет его скорость на большом (бесконечном) расстоянии от сферы?
393. Маленький металлический шарик с массой m = 1 г, которому сообщен заряд q= +10*7 к, брошен издалека со скоростью v — 1 м/сек в металлическую сферу, с зарядом Q =+3- !0’7 к. При каком минимальном значении радиуса сферы шарик достигнет ее поверхности?
394. Какая энергия выделится при ударе электрона о положительно заряженный шар радиуса R, если на бесконечном расстоянии от шара скорость электрона была направлена к центру шара и равна у? Заряд шара +q, заряд электрона —е, масса его т. Удар считать неупругим.
395. Одна из пластин плоского конденсатора с расстоянием между пластинами 10 мм освещается рентгеновскими лучами, вырывающими из нее фотоэлектроны со скоростью v = 106 м!сек. Электроны собираются на второй пластине. Через какое время фототок между пластинами прекратится, если с каждого квадратного сантиметра площади вырывается в 1 сек п = 1013 электронов?
6 Л. П. Баканииа и др.
81
396. Под действием светового облучения с поверхности изолированного металлического шара радусом г вылетают электроны с начальными скоростями v, в результате чего шарик заряжается. До какого максимального заряда Q можно зарядить шарик таким образом? Отношение заряда электрона к его массе е/т предполагается известным.
397. Электроны, вылетающие без начальной скорости с одной из пластин заряженного плоского конденсатора, достигают другой пластины, имея скорость щ. Как изменится конечная скорость электронов, если па-
раллельно к этому конденсатору подсоединить незаряженный конденсатор вдвое большей
I } емкости?
1 । 398. Пластины А и D (рис. 100)
। I заземлены, сетки В и С имеют по
I 1 отношению к земле потенциалы 200
I 1 и 100 в соответственно. Из пла-
| j стины А без начальной скорости вы-
। । летает электрон. С какими скоро-
I । стями он пересекает сетки В, С и
I I достигает пластины D? Отношение
1 1 заряда электрона к его массе равно
А В £ Л 1,76-1011 к/кг.
399. Электрон со скоростью у0
Рис. 100. вылетает с катода лампы, выпол-
ненной в виде плоского конденса-
тора. Потенциал анода через равные промежутки времени Т меняет знак на противоположный, оставаясь внутри промежутка постоянным и равным ± V, Если заряд е, массу т электрона и расстояние L между
электродами считать известными, то за какое время т электрон долетит до анода? Известно, что Т <С х и на первом из промежутков времени потенциал анода по-
ложителен.
400. Электрон испускается с малой начальной скоростью катодом лампы, выполненной в виде плоского конденсатора. Если потенциал анода поддерживается равным V, то электрон достигнет анода через время Т. За какое время электрон достигнет анода, если потенциал последнего попеременно принимает значения V и нуль? Длительность промежутков времени, в течение которых потенциал анода равен V, Ti = T/10, длитель
ность промежутков с нулевым значением потенциала Т2=*Т/2(к
401. Катод и анод двухэлектродной лампы (диода), выполненной в виде плоского конденсатора, расположены вертикально в поле тяжести. Катод испускает электроны, скорость которых можно считать равной нулю. Определить вертикальное смещение S электрона при полете между электродами. Отношение заряда электрона к его массе равно Л; анодное напряжение V, межэлектродное расстояние d.
402. Электрон со скоростью v0 = 4» 109 см]сек влетает в плоский конденсатор, причем вектор его скорости лежит в плоскости, параллельной пластинам. Насколько сместится точка вылета электрона из конденсатора, если к конденсатору приложена разность потенциалов V = 300 в? Расстояние между пластинами конденсатора d = 1 см, длина конденсатора I = 5 см. Пластины горизонтальны.
403. Поток электронов, получивших свою скорость в результате прохождения разности потенциалов V = 5000 в, влетает в середину между пластинами плоского конденсатора. Какое наименьшее напряжение нужно наложить на конденсатор, чтобы электроны не вылетали из него, если размеры конденсатора таковы:-длина I = 5 см, расстояние между пластинами d = 1 см? I*- I -*+*-L -----”
404. Электрон с кине- ।---------
тической энергией W = 1
= 10 000 эв влетает в пло- j
ский конденсатор, между J
обкладками которого под-
держивается постоянная Рис- 101-
разность потенциалов
V = 40 в (рис. 101). Расстояние между обкладками d = 1 см, длина пластин конденсатора I = 10 см. На расстоянии L = 20 см от конденсатора находится экран. Первоначальная скорость электрона направлена параллельно пластинам. Найти смещение х электрона на экране. Как изменится ответ, если вместо электрона взять протон той же энергии?
405. Пучок ионов хлора С135 и С137, несущих каждый По одному элементарному положительному заряду,
6*
83
разгоняется так, что скорости ионов к моменту попадания пучка в пространство между пластинами плоского конденсатора одинаковы и равны t'o=lO7 см!сек. Пучок влетает в середину конденсатора параллельно его пластинам. Длина пластин / = 5 см, расстояние между ними d = 5 мм. Какое напряжение V нужно приложить между пластинами конденсатора, чтобы точки попадания ионов С135 и С137 отстояли на приемном экране на 0,6 мм друг от друга? Приемный экран расположен на расстоянии L = 10 см от заднего края пластин конденсатора.
406. Электроны влетают в плоский конденсатор длиной L под углом а к плоскости пластин, а вылетают под углом р. Определить первоначальную кинетическую энергию 117 электронов, если напряженность поля внутри конденсатора равна Е.
407. Определить, насколько сместится относительно ядра плоскость круговой орбиты электрона в атоме водорода, если его поместить в электрическое поле с напряженностью Е. Заряд электрона равен в. Считать, что расстояние от ядра до электрона равно R и не меняется при наложении поля.
Электрические цепи. Закон Ома
408. Определить общее сопротивление цепи, изображенной на рис. 102. Сделать численный расчет при
Рис. 102.
следующих значениях сопротивления: 13 2
/?!=2- ом, R2^-2OM> = = ом, R5 = -^-om.
409. Из проволоки с сопротивлением R = 10 ом сделано кольцо. Где следует присоединить провода, подводящие ток, чтобы сопротивление равнялось 1 ом?
84
410. В приемнике применены три радиолампы, Л2 и Лз, с напряжением накала V = 6 в и током накала соответственно 0,1, 0,2, 0,3 а. Нарисовать схемы бес-трансформаторного питания цепи накала от сети с напряжением Vo = 120 в в случае последовательного и параллельного соединения ламп. Определить величину дополнительных сопротивлений, при которых лампы в обоих случаях будут работать в заданных режимах.
411. Все нити накала пятилампового приемника и добавочное гасящее сопротивление включены последовательно. Для нормального накала всех нитей требуется ток I = 0,3 а. Напряжение накала одной из ламп V’i = 30 в, остальных V = 6 в. Какое добавочное сопротивление нужно включить, если напряжение питающего источника Ко = 120 в? Указать схему включения и подобрать величину дополнительных сопротивлений, при которых лампы работают в заданных режимах, для случая, когда все лампы с напряжением накала 6 в включены параллельно. При каком включении мощность, рассеиваемая на дополнительных сопротивлениях, будет больше?
412. Чтобы определить место повреждения изоляции двухпроводной телефонной линии длиной L = 4 км, к одному ее концу присоединили батарею с э. д. с., — 15 в. При этом оказалось, что если провода у другого конца линии разомкнуты, ток через батарею /1 = 1 а, если замкнуты накоротко, то ток через батарею /2 = 1,8 а. Найти место повреждения и сопротивление /? изоляции в месте повреждения. Сопротивление каждого провода линии 5 ом. Сопротивлением батареи пренебречь.
413. К одному концу двухпроводной линии передачи электроэнергии подсоединен источник постоянной э. д. с., а к другому — потребитель с сопротивлением /?о- В линии произошло повреждение изоляции, в результате чего ток через источник возрос в два раза, а ток через нагрузку Rq упал в восемь раз. Найти сопротивление изоляции в месте повреждения, если длина каждого провода линии равна L, а сопротивление единицы длины провода равно р.
414. Гальванометр с чувствительностью 3,0-10'5 а на деление шкалы, с внутренним сопротивлением
85
fi =* 20 ом, включенный в цепь термопары, дал отклонение в 11 делений шкалы. Другой гальванометр, чувствительностью 5,0-10'5 а на деление шкалы, с внутренним сопротивлением г2 ~ 30 ом, включенный вместо первого, дал отклонение в пять делений шкалы. Определить сопротивление термопары R и ее э. д. с. &.
415. К гальванометру, сопротивление которого г = 290 ом, присоединили шунт, понижающий чувствительность гальванометра в 10 раз. Какое сопротивление, надо включить последовательно с шунтированным гальванометром, чтобы общее сопротивление осталось неизменным?
416. Имеется прибор с ценой деления г'о = 10 мка. Шкала прибора имеет п = 100 делений, внутреннее сопротивление прибора г = 50 ом. Как из этого прибора сделать вольтметр для измерения напряжения до V = 200 в или миллиамперметр для измерения токов до /о = 800 ма?
417. В цепь гальванометра включена термопара, состоящая из медной и константановой проволочек длиной по 1 ж и диаметра 0,2 мм. Чувствительность гальванометра 10~6 а на одно деление шкалы; его внутреннее сопротивление равно 50 ом. На сколько делений отклонится стрелка гальванометра, если спай термопары перегреть на 50° С по отношению к температуре окружающей среды? Э. д. с. термопары 40 мкв/град, удельное сопротивление константана 0,50 • 10~4 ом-см и меди 0.17-10”5 ом-см.
418. К батарее через переменное сопротивление R подключен вольтметр. Если сопротивление R уменьшить втрое, то показания вольтметра возрастут вдвое. Во сколько раз изменятся показания вольтметра, если сопротивление R уменьшить до нуля?
419. В цепь, состоящую из аккумулятора и сопротивления R = 10 ом, включают вольтметр, сначала последовательно, затем параллельно сопротивлению R. Оба показания вольтметра одинаковы. Сопротивление вольтметра г = 1000 ом. Каково внутреннее сопротивление аккумулятора?
420. Аккумулятор (э. д. с. равна 6 в) замкнут на некоторое сопротивление. В цепь включаются параллельно друг другу два амперметра и показывают соответственно 2 а и 3 а. Затем эти амперметры включаются 86
в цепь последовательно и показывают 4 а. Какой ток течет в цепи в отсутствие амперметров?
421. При включении шунта сопротивлением 100 ом параллельно измерительному прибору стрелка отклоняется на всю шкалу при токе во внешней цепи 3 а. При включении добавочного сопротивления 300 ом к не-зашунтированному гальванометру шкала прибора становится в четыре раза грубее, чем без добавочного сопротивления и шунта. Какой шунт надо взять для того, чтобы стрелка отклонялась на всю шкалу при токе во внешней цепи 7,5 а?
422. В схему, указанную на рис. 103, включены два микроамперметра и два одинаковых вольтметра. Показания микроамперметров h — 100 мка, 1% = 99 мка\ показание вольтметра Ki = 10 в. Найти показание вольт* метра Кг- Сопротивлением проводов пренебречь.
Рис. 103.
423. В схеме, изображенной на рис. 104, значения сопротивлений и э. д. с. батареи неизвестны. Вольтметр с неизвестным внутренним сопротивлением подключают сначала к сопротивлению 7?i, затем к и, наконец, к R. При этом вольтметр дает показания Ki = 4 о, Кг = 6 в, К = 12 в. Пренебрегая внутренним сопротивлением батареи, определить падение напряжения Ui и (7г на сопротивлениях Rt и Ri при отключенном вольтметре.
424. Какое количество аккумуляторов нужно соединить последовательно, чтобы получить в цепи ток 4 а при разности потенциалов на полюсах батареи 220 в? Э. д. с. каждого аккумулятора 2 в, внутреннее сопротивление 0,25 ом.
425. По медному проводу сечением S = 1 мм2 Tenet ток / = 10 м.а. Найти среднюю скорость и упорядочен* ного движения электронов вдоль проводника, есл?1
87
считать, что на каждый атом меди приходится один электрон проводимости. Атомный вес меди А = 63,6, плотность р = 8,9 г/си3.
426. Плоский конденсатор с расстоянием между пластинами d, заполненный средой с диэлектрической проницаемостью е и удельным сопротивлением р, включен в цепь батареи э. д.с. равной %>, с внутренним сопротивлением г. Чему равна напряженность Е электрического поля конденсатора, если его емкость равна С?
427. Два плоских воздушных конденсатора с емкостями С\ и С2 соединены последовательно и подключены к батарее, э. д. с. которой равна <8. Определить, какие разности потенциалов будут на конденсаторах, если их заполнить веществами с удельными сопротивлениями р! и р2 и диэлектрическими проницаемостями ei и е2 соответственно.
428. Воздух в пространстве между пластинами плоского конденсатора, размеры которого 10X10X2,5 см,
ионизуется рентгеновскими лучами так, что в 1 см3 образуется 109 пар ионов в секунду. Пластины конденсатора соединены с источником напряжения 1300 в через сопротивление 1010 ом. Такое же сопротивление 1010 ом включено параллельно конденсатору (рис. 105). Какой ток протекает через источник? (Можно считать, что ионы достигают пластин конденсатора, не успев рекомбинировать, и что заряд каждого иона равен заряду одного электрона.)
429. Три одинаковых медных кольца радиусом а соединены между собой так, как показано на рис. 106,
88
Определить сопротивление полученной таким образом фигуры, если внешняя разность потенциалов подведена к точкам А и В. Диаметр проволоки d. Удельное сопротивление меди р,
CD = о DE = о EF = о FC.
430. Пять одинаковых соединены между ками соединения
собой в каждый
никелевых прутьев длины I виде звезды (рис. 107). Точ-прут делится на три равные
a
части (АВ = BD = DE и ние этой фигуры между перечного сечения прута ние никеля р.
431. Сопротивление одного ребра проволочного куба г — 1 ом. Каково будет сопротивление R между вершинами, лежащими на пространственной диагонали куба?
432. Найти ток через перемычку ab в схеме, представленной на рис. 108. Считать, что сопротивление перемычки, сопротивление подводящих проводов и внутреннее сопротивление батареи пренебрежимо малы.
433. Два аккумулятора, э. д. с. которых <^1 = 57 в и <^2 = 32 в, соединены, как указано на рис. 109. Чему равна разность потенциалов между точками а и Ь, если
т. д.). Определить сопротивле-точками А и F. Площадь пора вна S, удельное сопротивле-
6,
b
Рис. 109.
89
отношение внутренних сопротивлений аккумуляторов Гг/п = 1,5? Сопротивлением соединительных проводов пренебречь.
434. Две батареи с э. д. с. <8\ и <F2 включены, как указано на рис. НО. При каком соотношении между внутренними сопротивлениями батареи ток через гальванометр не пойдет?
Сопротивлением подво- ------------------------
дящих проводов пренебречь.
Рис. ПО.
Рис. 111.
435. Две батареи с э. д. с. <5^ и <82 и внутренними сопротивлениями Г\ и г2 включены, как указано на рис. 111. Пренебрегая сопротивлением подводящих проводов, найти ток через перемычку ab. Сопротивление перемычки считать равным нулю.
Рис. 112.
Рис. 113.
436. В цепи, указанной на рис. 112, /?2 > Ri. При каком R3 можно подобрать такое R4, чтобы ток через гальванометр был равен нулю? Электродвижущие силы батарей одинаковы. Внутренним сопротивлением батарей пренебречь.
437. В схеме, изображенной на рис. 113, величины э. д. с. батарей, их внутренние сопротивления
90
rlt r2, сопротивление R и емкость С заданы. Определить заряд конденсатора.
438. Определить разность потенциалов на конденсаторе С в схеме, изображенной на рис. 114. Величины сопротивлений, э. д. с. батарей и их полярность указаны
на рисунке. Внутренними сопротивлениями батарей пренебречь. Какой знак будет иметь заряд на верхней пластине конденсатора?
439. Какой заряд протечет в схеме, показанной на рис. 115, Здесь С{ и С2 — емкости конденсаторов, Ri и — сопротивления, to и г — э. д. с. и внутреннее сопротивление батареи. При каком соотношении между параметрами схемы заряд через гальванометр при замыкании ключа не будет протекать?
440. Определить разность потенциалов на конденсаторе С в схеме, изображенной на рис. 116. Величины сопротивлений, э. д. с. батарей и их
через гальванометр Q если замкнуть ключ К?
полярность указаны на ри-
сунке. Внутренними сопротивлениями батарей пренебречь. Какой знак будет иметь заряд на верхней пластине конденсатора С при = ^2?
91
Работа и мощность электрического тока.
Закон Джоуля — Ленца
441. Электрический чайник имеет две обмотки. При включении одной из них чайник вскипает через 10 мин, при включении другой — через 15 мин. Через сколько времени чайник вскипит, если эти обмотки включить вместе: а) параллельно, б) последовательно?
442. Нагреватель кипятильника состоит из четырех секций, каждая из которых имеет сопротивление 1 ом. Нагреватель питают от аккумуляторной батареи с э. д. с., равной 8 в, и внутренним сопротивлением 1 ом. Как нужно включить элементы нагревателя, чтобы вода в кипятильнике нагревалась быстрее? Какова при этом мощность, расходуемая аккумулятором?
443. Проволочное кольцо включено в цепь, в которой течет ток 9 а. Контакты делят длину кольца в отношении 1 :2. При этом в кольце выделяется мощность 108 вт. Какая мощность выделялась бы (при том же токе во внешней цепи), если бы контакты были расположены по диаметру кольца?
444. Аккумулятор с внутренним сопротивлением 0,08 ом при токе 4 а отдает во внешнюю цепь 8 вг. Какую мощность отдаст он во внешнюю цепь при токе 6 а?
445. Мощность, рассеиваемая на сопротивлении Ri, подсоединенном к батарее, равна W. Чему равна э. д. с. батареи, если эта мощность не изменилась при замене Ri на /?2?
446. Параллельно сопротивлению R, подключенному к батарее, включили неизвестное сопротивление. Оказалось, что мощность, выделяемая на внешнем участке цепи, не изменилась. Определить величину неизвестного сопротивления. Внутреннее сопротивление батареи равно г.
447. Напряжение в сети, измеренное до включения нагрузки, равно 120 в. При включении лампочки с номинальной мощностью 100 вт напряжение упало до ПО в. Какой номинальной мощности электроплитку включили параллельно лампочке, если напряжение ча лампочке упало до 90 в? Лампочка и плитка рассчитаны на одинаковое напряжение. Изменением сопро-
92
тивления лампочки и плитки при изменении накала пренебречь.
448. При включении в сеть электроплитки с номинальной (т. е. при нормальном напряжении в сети) мощностью 300 вт фактически выделяющаяся мощность равна 250 вт. Какая мощность будет выделяться в двух таких плитках, одновременно включенных параллельно в эту сеть? Изменением сопротивления плиток пренебречь.
449. Какой ток пойдет по подводящим проводам при
Р-г
Рг
должны сопротив-в схеме, рис. 117, напряже-
g _=L_
Я,
коротком замыкании, если на двух плитках с сопротивлением в 200 и 500 ом выделяется при поочередном включении одинаковая мощность 200 вт?
450. Какими быть выбраны ления Rx и /?2 показанной на для того, чтобы ние на нагрузке /?0 было
Рис. 117.
в а раз меньше напря-
жения на той же нагрузке при непосредственном подключении ее к зажимам батареи, а мощность, расходуемая батареей, равнялась мощности, расходуемой при непосредственном подключении?
451. Газоразрядная трубка загорается при напряжении 2 кв. При этом ее сопротивление резко падает, и для поддержания номинального тока, равного 40 ма, необходимо включить последовательно с трубкой балластное сопротивление. В наличии имеются сопротивления R по 100 ком, рассчитанные на мощность 10 вт. Сколько потребуется таких сопротивлений и как их надо соединить, чтобы обеспечить необходимую величину рабочего тока? Сопротивлением трубки в зажженном состоянии и внутренним сопротивлением источника тока можно пренебречь.
452. Чему равно внутреннее сопротивление аккумулятора, если при включении восьми аккумуляторов в две параллельные группы по четыре на сопротивление в три ома в нем выделяется такая же мощность, как и в случае последовательного соединения всех аккумуляторов?
93
453. Электроэнергия генератора мощностью Н?о передается потребителю по проводам, общее сопротивление которых г. Э. д. с, генератора <5. Определить к. п. д. линии передачи, т, е. отношение мощности, выделяемой на полезной нагрузке R, к мощности генератора. Внутренним сопротивлением генератора пренебречь.
454. Электроэнергия передается от генератора потребителю по проводам, общее сопротивление которых г, К. п. д. линии передачи, т. е. отношение мощности, выделяемой на полезной нагрузке, к мощности генератора, равен р. Определить сопротивление нагрузки. Внутренним сопротивлением генератора пренебречь.
455. Во сколько раз следует повысить напряжение источника, чтобы потери мощности (в подводящих проводах от источника к потребителю) снизить в 100 раз при условии постоянства отдаваемой генератором мощности?
456. При передаче электроэнергии на большое расстояние используется трансформатор, повышающий напряжение до 6 кв и загруженный до номинальной мощности 1000 кет. При этом разность показаний счетчиков электроэнергии, установленных на трансформаторной подстанции и в приемном пункте, увеличивается ежесуточно на 216 квТ'Час. Во сколько раз необходимо повысить напряжение, чтобы при передаче потери электроэнергии не превышали 0,1 %?
457. Линия имеет сопротивление 300 ом. Какое напряжение должен иметь генератор, чтобы при передаче по этой линии к потребителю мощности 25 кет потери в линии не превышали 4% передаваемой мощности?
458. Определить количество меди, нужное для устройства двухпроводной линии длиной 5 км. Напряжение на шинах станции 2400 в. Передаваемая потребителю мощность 60 кет. Допускаемая потеря напряжения в проводке 8%, удельный вес меди 8,9 Г)см\ удельное сопротивление 0,017 • 10~4 ом • см.
459. Сопротивление 100-ваттной электролампы, работающей при напряжении 120 в, в накаленном состоянии в 10 раз больше, чем в холодном. Найти ее сопротивление в холодном состоянии (при 20° С) и средний температурный коэффициент сопротивления, если температура накала нити 2000° С. ----- --
94
460. К концам свинцовой проволоки длиной 1 м приложена разность потенциалов 10 в. Сколько времени пройдет с начала пропускания тока до момента, когда свинец начнет плавиться? Температура плавления свинца 327° С, начальная температура 20° С, среднее удельное сопротивление 1,7 • 10~4 ом-см, средняя удельная теплоемкость 0,125 дж/г-град, плотность 11,3 г!см3. Потерей тепла в окружающее пространство пренебречь.
461. Два параллельно включенных в электрическую цепь нагревателя представляют собой отрезки проволоки из одинакового материала с диаметрами и £)2 соответственно. Длина первой проволоки I. Определить длину второй проволоки, если известно, что при длительной работе их температуры оказались одинаковыми. Теплоотдача пропорциональна площади поверхности проволоки.
462. При длительном пропускании тока Л = 1,4 а через проволоку последняя нагрелась до Т\ = 55° С, а при силе тока 12 = 2,8 а — до Т2 = 160° С. До какой температуры Тх нагревается проволока при токе 7з — 5,6 п? Сопротивление проволоки не зависит от температуры. Температура окружающего воздуха постоянна. Теплоотдача пропорциональна разности температур прово
локи и воздуха.
463. Конденсатор емкостью С = 10 мкф, заряженный до напряжения Ко = 1000 в и отключенный от источника
напряжения, замыкается на электрическую лампочку. Какая энергия выделится в лампочке?
464. Конденсатор, присоединенный к батарее с напряжением 2000 в проводами с сопротивлением 100 ом, имеет первоначальную емкость 2 мкф. Затем его ем
кость равномерно увеличивают в течение 10 сек до 10 мкф. Какая энергия выделяется при этом в виде тепла в подводящих проводах?
465. Батарея с э. д с. <S = 4 в
и внутренним сопротивлением
г — 1 ом, изображенная на Рис. 118.
рис. 118, входит в состав не-
известной цепи. К полюсам батареи подключен
вольт-
метр так, что положительная клемма вольтметра подсое-
95
динена к положительному полюсу батареи. Вольтметр показывает напряжение V = 6 в. Определить количе-
ство тепла, выделяющееся за единицу времени на внутреннем сопротивлении батареи.
466. Батарея с э. д. с. 3 = 4 в и внутренним сопротивлением г — 1 ом, изображенная на рис. 119, входит
в состав неизвестной цепи. К полюсам батареи подсоединен вольтметр так, что положительная клемма вольтметра подключена к отрицательному полюсу батареи. Вольтметр при этом показывает напряжение V — 2 в. Какое коли-
Рис. 119.
чество тепла выделяется за
единицу времени на внутреннем сопротивлении батареи?
Электромагнитная индукция
467. В однородном магнитном поле с напряженностью Н расположен плоский проволочный виток таким образом, что его плоскость перпендикулярна к силовым линиям. Виток замкнут на гальванометр. Полный заряд, протекший через гальванометр при повороте витка, равен Q. На какой угол повернули виток? Произвести численный расчет для случая Q = 9,5 • 10 3 к, Н — = 105 а/м, площадь витка S = 103 см2, сопротивление витка R = 2 ом.
468. При включении магнитного поля, перпендикулярного к плоскости витка радиуса R, по витку протек заряд Q.
Какой заряд протечет по витку, если его, при неизменном поле, сложить «восьмеркой», состоящей из двух окружностей, причем радиус меньшей окружности равен R/4? Плоскость «восьмерки» также перпендикулярна к магнитному полю.
469. Проволочный виток, имеющий площадь S = — 102 см2, разрезан в некоторой точке, и в разрез включен конденсатор емкости С = 10 мкф. Виток помещен в однородное магнитное поле, силовые линии которого перпендикулярны к плоскости витка. Индукция магнитного поля равномерно изменяется во времени со
96
скоростью 5 • 10~3 тл]сек. Определить заряд конденсатора.
470. Коротко замкнутая катушка, состоящая из N = 1000 витков проволоки, помещена в магнитное поле, направленное вдоль оси катушки. Площадь поперечного сечения катушки 5=40 см2, ее полное сопротивление R = 160 ом. Найти мощность W джоулевых потерь, если индукция магнитного поля равномерно изменяется со скоростью 10~3 тл!сек.
471. Прямоугольная проволочная рамка со стороной L находится в магнитном поле с напряженностью Н, перпендикулярном к плоскости рамки. По рамке параллельно одной из ее сторон без нарушения контакта скользит с постоянной скоростью v перемычка ab (рис. 120), сопротивление которой R. Определить ток
Рис. 121.
Рис. 120.
472. На железный сердечник, форма которого показана па рис. 121, намотаны две катушки. Магнитный поток, создаваемый каждой катушкой, не выходит из
железного сердечника и делится поровну между разветвлениями. При включении катушки 1 в цепь переменного тока с напряжением 40 в напряжение на катушке 2 равно V. Какое напряжение будет на зажимах ка-
Рис. 122.
тушки /, если катушку 2 включить в цепь переменного тока с напряжением V?
473. На симметричный железный сердечник, показанный на рис. 122, намотаны две катушки. При включении катушки 1 в сеть переменного тока напряжение на
7 Л. П. Бакалина и др.
97
зажимах катушки 2 Vz = 13,2 в. При включении катушки 2 в ту же сеть напряжение на зажимах катушки 1 Vi = 120 в. Чему равно отношение чисел витков катушек?
Считать, что магнитный поток, создаваемый каждой катушкой, не выходит из сердечника.
474. Электромотор питается от батареи с э. д. с. <S = 12 в. Какую механическую работу W совершает мотор за 1 сек при протекании по его обмотке тока I = 2 а, если при полном затормаживании якоря по цепи течет ток /0 = 3 а?
475. Чему равен коэффициент полезного действия электромотора, если при включении его в сеть постоянного тока пусковой ток Л> = 15 а, а в установившемся режиме ток снижается до I = 9 а?
476. Электровоз движется со скоростью и = 36 км!час и развивает в среднем силу тяги F = 5 Т. Найти ток, проходящий через мотор электровоза (без учета потерь), если напряжение на нем V = 500 в.
477. На горизонтальный вал мотора равномерно наматывается нитка, на которой подвешен груз весом ,Р = 800 Г. Мотор питается от батареи аккумуляторов с э. д. с. <§’=12 в и внутренним сопротивлением Г[ = 0,4 ом. Сопротивление цепи мотора равно Гг = 3 ом. Сколько оборотов в секунду делает якорь, если по обмоткам мотора течет ток I = 3,3 а? Радиус вала а = 0,5 см.
478. Какую э. д. с. развивает динамо-машина постоянного тока, если при сопротивлении цепи 300 ом на вращение машины затрачивается мощность 50 вт, а потери на трение составляют 4% от затраченной мощности. Какую мощность для поддержания того же числа оборотов необходимо затрачивать при сопротивлении цепи 60 ом?
479. Электромотор постоянного тока, включенный в цепь батареи с э. д. с., равной 24 в, при полном сопротивлении цепи 20 ом делает 600 оборотов в минуту при токе в цепи 0,2 а. Какую э. д. с. разовьет тот же мотор, работая в качестве динамо-машины при 1400 оборотах в минуту?
480. Электромотор, включенный в сеть постоянного тока напряжением 120 в, при полном сопротивлении цепи 20 ом передает при некоторой нагрузке приводу
98
мощность 160 вт. Какую э. д. с. разовьет тот же мотор, если его использовать как динамо-машину, вращая якорь с той же угловой скоростью, которую он имел, работая как двигатель? Какой смысл имеет неодно-значность полученного результата?
481. Груз с массой tn подвешен на нити, намотанной на ось якоря динамо-машины с постоянным магнитом. Нить сматывается с оси так, что груз опускается с постоянной скоростью V. Динамо-машина замкнута на сопротивление R. С какой скоростью будет подниматься вверх тот же груз, если динамо-машину включить как электромотор в цепь постоянного тока с э. д. с., равной S, и с тем же сопротивлением цепи R?
Разные задачи
482. Определить, какое количество алюминия отложится на катоде за 10 часов при электролизе A12(SO4)3, если ток через электролит равен 1 а. Атомный вес алюминия 27.
483. Какое количество электричества Q проходит через электролитическую ванну за время t = 10 сек, если ток за это время равномерно возрастает от 0 до 3 а? Какое количество меди выделяется при этом на катоде ванны, если электролитом является медный купорос? Атомный вес меди 63,6?
484. Определить, сколько меди выделилось из раствора CuSO4 за 100 сек, если ток, протекавший через электролит, менялся при этом по закону I = (5 — 0,02/) a (t— время в сек). Постоянная Фарадея F = 96 500 к/г -.же; атомный вес меди А — 63,6.
485. Никелирование металлического изделия с поверхностью 120 см2 продолжалось 5 часов при силе тока 0,3 а. Валентность никеля 2, атомный вес 58,7, плотность 9 г/см3. Определить толщину слоя никеля.
486. Какое количество электричества нужно пропустить через электролитическую ванну с подкисленной водой, чтобы получить 1 л гремучего газа при 27° С и 760 мм рт.ст.?
487. Сколько времени нужно производить электролиз подкисленной воды, чтобы полученным водородом наполнить при нормальных условиях воздушный шар с подъемной силой 200 кГ? Ток при электролизе равен
7*
99
100 а. Средний молекулярный вес воздуха принять равным 29.
488. Два одинаковых плоских конденсатора с площадью пластин S соединены параллельно, заряжены до разности потенциалов Vo от батареи и затем отключены от нее. Пластины одного из конденсаторов начинают сближать так, что расстояние между ними изменяется во времени по закону
где do — первоначальное расстояние между пластинами, t — время, to — некоторая постоянная величина. Определить ток I в проводах, соединяющих конденсаторы.
489. Между пластинами накоротко замкнутого плоского конденсатора, суммарный заряд пластин которого равен —q, с постоянной скоростью v движется тонкая
Рис. 123.
I | I
! i i
1 1 I
I I J
/I 2*1 oi
Рис. 124.
пластина с зарядом +q (рис. 123). Определить величину тока I, текущего при этом во внешней цепи конденсатора. Расстояние между пластинами конденсатора d.
490. Из вертикально расположенного плоского конденсатора равномерно вытекает заполняющий его керосин (е = 2). При этом в цепи, соединяющей конденсатор с батареей, имеющей э. д. с. <$ = 100 в, течет ток / = 2-10*и а. С какой скоростью понижается уровень керосина? Пластины конденсатора — квадраты со стороной I = 10 см, зазор между ними d = 1 мм.
491. Вблизи сетки 1 (справа от нее, рис. 124) в результате ионизации атома азота образовался свобод-100
ный электрон, начальную скорость которого можно принять равной нулю. Определить максимальную длину Л электромагнитных волн, излучаемых электроном, движущимся между сетками 1 и 3, если его заряд е = 1,6 • 10~19 к, а масса т = 9,1 • 10-28 г. Остальные данные приведены на рис. 124.
Как следует изменить потенциал сетки 2, чтобы оставшийся ион азота начал двигаться между сетками 1 и 3, излучая электромагнитные волны той же максимальной длины X?
492. Металлический круг радиуса R вращается вокруг своей оси с угловой скоростью ю. Определить напряженность Е электрического поля внутри металла и показание вольтметра, клеммы которого соединены с контактами, один из которых касается круга в центре, а другой — у края. Отношение заряда электрона к его массе равно X.
493. Через двухэлектродную лампу (диод) с плоскими электродами идет ток I. Напряжение на лампе равно V. С какой силой F действуют на анод лампы попадающие на него электроны, если скорость их вблизи 0 | п
катода равна нулю? Отноше- _
ние заряда электрона к его 'у'
массе равно X. в г~------*— —'
494. К точкам А, В
(рис. 125) прикладывают по- I I
стоянное напряжение от источ- ~
ника, который заряжает кон- Рис- 125.
денсатор С. К обмотке элек-
тромагнита М прикладывают переменное напряжение. Электромагнит приводит в колебание язычок D. Язычок поочередно замыкает цепь питания конденсатора и цепь гальванометра G. Какова средняя величина тока через гальванометр, если частота переменного тока v = 500 гц, емкость конденсатора С — 1 мкф, постоянное напряжение V ~ 100 в? Стержень электромагнита и язычок изготовлены из мягкого магнитного материала, т. е. остаточным намагничиванием можно пренебречь. Считать, что конденсатор успевает полностью зарядиться за время, пока замкнута цепь зарядки, и полностью разрядиться, пока он замыкается на гальванометр.
101
495. Найти разности потенциалов на конденсаторах С| и С2 в цепи, указанной на рис. 126, если изве-
стно, что при замыкании сопротивления накоротко ток
через батарею возрастает равна S.
496. Для стабилизации няют газоразрядную лампу
в три раза. Э. д. с. батареи напряжения иногда приме-(стабиловольт), схема включения которой показана на рис. 127. При изменении
Рис. 127.
тока, протекающего через стабиловольт от 5 до 15 ма, напряжение на нем практически не меняется и остается равным 150 в. Сопротивление нагрузки RB = 10 ком. Определить величину сопротивления R и напряжение <F, при которых напряжение на нагрузке остается постоянным при изменениях входного напряжения S на ±10%.
497. Через аккумулятор в конце зарядки течет ток / = 4 а. При этом напряжение на его клеммах Vi — 12,8 в. При разрядке того же аккумулятора током /2 ~ 6 а напряжение составляет У2 = 11,1 в. Найти ток короткого замыкания.
498. Два аккумулятора с одинаковым внутренним сопротивлением г = 0,05 ом и э. д. с. <Fi = 1,8 в и Si = 2,0 в включены параллельно в качестве источников в цепь, сопротивление которой R = 2 ом. Найти токи во внешней цепи и в каждом аккумуляторе.
499. Динамо-машина имеет э. д. с. <^1=12 в. Ее внутреннее сопротивление Г] = 0,2 ом. Она заряжает батарею аккумуляторов с э.д. с. <^2 = 10 в и внутренним сопротивлением г2 = 0,6 ом. Параллельно батарее включена лампочка с сопротивлением R = 3 ом. Определить токи в батарее и в лампочке.
102
500. Цепь состоит из двух батарей с э. д. с. <$\ = 4 в и«?2 — 12 в, реостата со скользящим контактом, полное сопротивление которого R — 1500 ом, проводника, сопротивление которого г = 200 ом, и амперметра, включенных как указано на рнс. 128. С каким полюсом батареи $2 надо соединить скользящий контакт и какое
положение он должен занимать на реостате, чтобы ток через амперметр был равен нулю? Какая мощность при этом будет рассеиваться на сопротивлениях R и г? Внутренним сопротивлением батарей пренебречь.
501. Между каждыми двумя
из N точек включено сопротив-
ление R. Какая мощность будет выделяться в этой
сети, если к каким-либо двум точкам подсоедини гь источник э.д. с. <S, внутреннее сопротивление которого тоже R?
502. В однородном магнитном поле с индукцией В расположены вертикально на расстоянии L два метал-
Рис. 129.
лических прута, замкнутых наверху. Плоскость, в которой
Рис. 130.
расположены прутья, перпендикулярна к направлению индукции магнитного поля. По прутьям без трения и без нарушения контакта скользит вниз с постоянной скоростью v пермычка ab массы т (рис. 129). Определить электрическое сопротивление R перемычки ab, если сопротивлением остальной части системы можно пренебречь. В = 10~2 тл, v = 1 м)сек, пг = 1 г, L = 50 см.
503. Плоскость прямоугольной проволочной рамки abed перпендикулярна к однородному магнитному полю с индукцией В (рис. 130). Одна сторона рамки be = L
103
подвижна и скользит без нарушения контакта с постоянной скоростью v по сторонам ab и de. Между точками а и d включена лампочка с сопротивлением R. Сопротивлением остальной части рамки можно пренебречь. Какую силу необходимо приложить к стороне Ьс для осуществления такого движения?
В=10~3тл, L = 1 см, v = 10 см/сек, R — 5 ом.
504. Квадратный замкнутый виток проволоки, длина стороны которого L, а сопротивление единицы длины р,
Рис. 131.
проходит с постоянной скоростью V между башмаками электромагнита, создающего однородное магнитное поле с напряженностью Н (рис. 131). Продольный размер башмаков значительно превышает L. Считая поле вне башмаков равным нулю, определить энергию, превратившуюся в тепло, для случаев, когда поперечный размер башмаков Lo > L и когда Ao < L.
505. Какое число п оборотов в секунду разовьет электромотор постоянного тока с постоянным магнитом, включенный в цепь с э. д. с., равной <S, при полном сопротивлении цепи R,
если, работая в качестве динамо-машины, он развивает э. д. с., равную при числе обо-
ротов в секунду, равном nb а момент сил трения на оси мотора равен Л4? Какой ток будет течь по цепи и чему будет равно число оборотов при М — 0?
506. Один конец провода трамвайной линии находится под постоянным напряжением V относительно земли. На каком расстоянии от этого конца линии находится трамвай, снабженный двумя одинаковыми двигателями, и с какой скоростью он движется, если при последовательном включении двигателей ток в линии равен /1, при параллельном — равен /г и скорость трамвая при таком переключении не меняется? Сила трения, приложенная к колесам трамвая, равна F, сопротивление единицы длины провода р, омическое сопротивление обмотки каждого из двигателей R.
IV. ОПТИКА
Переломление и отражение света на границе двух сред
507. Два плоских зеркала, образующие между собой постоянный двугранный угол <р, вращаются относительно оси, параллельной ребру двугранного угла. Свет от удаленного источника после отражения от обоих зеркал попадает в зрительную трубу. Как будет двигаться изображение источника света в поле зрения трубы при вращении зеркал?
508. Параллельный пучок света проходит через плоскопараллельную стеклянную пластинку (п = 1,5), толщина которой d — 1 см. Угол падения i = 30°. Определить величину смещения пучка, т. е. расстояние между осями пучка до и после преломления.
509. Стеклянная пластинка толщины d = 3 мм имеет на верхней и нижней сторонах царапины. Чему равен показатель преломления стекла, если при наведении микроскопа с верхней царапины на нижнюю его тубус пришлось опустить на 2 мм? Углы отклонения лучей, попадающих в объектив от оси микроскопа, считать малыми.
510. Палка длины 2Z с изломом посередине погружена в пруд так, что наблюдателю, находящемуся на берегу и смотрящему приблизительно вдоль надводной части палки, она кажется прямой, составляющей угол с горизонтом. Какой угол излома имеет палка? Пока-4
затель преломления воды п = -^-.
511. Луч света падает на границу раздела двух сред под углом 30°. Показатель преломления первой
105
среды rtj = 2,4- Определить показатель преломления второй среды, если известно, что отраженный и преломленный лучи перпендикулярны друг к другу.
512. Равнобедренная стеклянная призма с малыми преломляющими углами а помещена в параллельный пучок лучей, падающих нормально на ее основание (рис. 132). Коэффициент преломления стекла н=1,57, размер основания 2а = 5 см. Найти * ” Г Г величину преломляющего угла а,
._____„ А если в середине экрана, располо-
“А женного на расстоянии L — 100 см ------*--- ) 2а от призмы, образуется темная по-cj лоса шириной 2d = 1 см.
' ” у 513. Свет от удаленного источ-
______д У ника, состоящий из красных и зеленых волн, параллельным пучком
Рис. 132. падает перпендикулярно на одну из преломляющих граней призмы с малым углом преломления а. За призмой установлена линза с фокусным расстоянием F так, что ее оптическая ось совпадает по направлению с падающим на призму пучком света. Оказалось, что расстояние между изображениями источника в фокальной плоскости линзы в красном и зеленом свете равно I. Определить разность значений показателя преломления материала призмы для красного и зеленого света. Для простоты расчетов углы отклонения лучей от оптической оси лин-
зы считать малыми, так что синусы и тангенсы этих углов можно приближенно заменять самими углами.
514. Между двумя стеклянными пластинками с показателями преломления щ и П'2 находится тонкий слой жидкости. Луч света, распространяющийся в первой пластинке под
углом i, пройдя через слой жидкости, входит во вторую пластину под углом г (рис. 133). Показать, что
угол падения i и угол преломления г подчиняются обычному закону преломления sin i: sin г = н2: «1 независимо от наличия слоя жидкости между первой и вто* рой пластинами. -
106
515. На тонкую сферическую колбу, наполненную жидкостью, падает узкий параллельный пучок света так, что ось пучка проходит через центр колбы. На противоположной стороне колбы пучок света имеет диаметр в два раза меньше диаметра пучка, падающего на колбу. Каков показатель преломления жидкости в колбе?
516. Где видит наблюдатель рыбку, находящуюся в диаметрально противоположной от него точке шарообразного аквариума? Радиус аквариума /?, показатель преломления воды п = 4/3.
517. Стеклянная пластинка, коэффициент преломления которой «1, касается поверхности жидкости с коэффициентом преломления п2 < пг. Показать, что ни один из лучей, падающих на верхнюю поверхность стеклянной пластинки, не испытывает полного внутреннего отражения на границе между стеклом и жидкостью.
518. В широкий плоский сосуд с водой, показатель преломления которой равен п, помещена линза. Фокусное расстояние этой линзы в воде равно F. Линза расположена горизонтально на расстоянии F от дна сосуда и окружена непрозрачным плоским экраном. Поверхность воды освещается рассеянным светом. Найти диаметр светлого пятна на дне сосуда.
519. На дне сосуда, наполненного водой до высоты h, находится точечный источник света. На поверхности воды плавает круглый диск так, что центр диска находится над источником света. При каком минимальном радиусе диска ни один луч не выйдет через поверхность воды? Коэффициент преломления воды равен п.
520. Прямоугольный стеклянный сосуд наполнен жидкостью и освещается снизу лампочкой, расположенной под сосудом вблизи его дна. Каково минимальное значение показателя преломления жидкости п, при котором лампочку нельзя увидеть сквозь боковые стенки сосуда?
521. На основании равносторонней стеклянной призмы находится пылинка. При каких значениях показателя преломления п пылинку еще можно увидеть через боковые грани призмы с помощью лучей, на претерпевших ни одного отражения на границе стекло — воздух?
522. Для измерения показателя преломления п стеклянной призмы с углом а = 30° была использована
107
Рис. 134.
схема, показанная на рис. 134. Призма помещалась перед положительной линзой Л так, что грань АВ была перпендикулярна к оптической оси линзы. В фокальной плоскости линзы помещался экран, на котором при освещении грани АС рассеянньш светом можно было наблюдать две области: освещенную и неосвещенную. Отрезок, соединяющий границу между областями (точку D) с центром линзы, оказался расположен
ным под углом 30° к оптической оси линзы. Определить
показатель преломления п призмы.
Тонкие линзы
523. На рис. 135 дан ход одного луча АВС через тонкую отрицательную линзу. Определить построением фокусное расстояние линзы.
Рис. 135.
Рис. 136.
524. Положительная линза Л \ дает в точке Sj действительное изображение точечного источника S, расположенного на оптической Оси линзы. Между Лх и Si поставлена отрицательная линза Л^, положения фокусов которой заданы (рис. 136). Найти построением новое положение изображения источника. Рассмотреть случай, когда расстояние между Si и Л2 больше фокусного расстояния линзы Л2.
108
525. На рис. 137 дан ход одного луча АВС через тонкую положительную линзу. Построить ход произвольного луча DE. Рассмотреть случаи, когда точка пересечения лучей АВ и DE лежит слева и справа ог линзы.
52G. Положительная линза Л\ дает в точке S] действительное изображение точечного источника S, расположенного на оптической оси линзы. Между источником S и линзой Л\ поставлена еще одна положительная линза, Л2, положения фокусов которой заданы (рис. 138). Найти построением новое положение изображения источника. Рассмотреть случай, когда расстояние между S и Л2 меньше фокусного расстояния линзы Л2.
527. С помощью собирающей линзы получают изображения двух точечных источников А и В. Один из них расположен на оптической оси на двойном фокусном
расстоянии от линзы; другой смещен от оси на небольшое расстояние так, что линия, соединяющая оба источника, образует с оптической осью угол <р = 30° (рис. 139). Под каким углом к оптической оси следует расположить плоский экран, чтобы одновременно получить на нем четкие изображения обоих источников?
528. Каков диаметр действительного изображения Солнца, если это изображение получается с помощью линзы с фокусным расстоянием 3 м? Диаметр Солнца 1,4 • 106 км, расстояние от Солнца до Земли 150- 10б км.
529. Положительная линза дает действительное изображение с увеличением в два раза. Определить фокусное расстояние линзы, если расстояние между линзой и изображением равно 24 см.
530. С помощью собирающей линзы получено уменьшенное действительное изображение предмета на экране. Размер предмета х = 6 см, размер изображения r/i = 3 см. Оставляя предмет и экран неподвижными, перемещают линзу в сторону предмета и получают на экране второе четкое изображение предмета. Определить его величину.
531. С помощью линзы с фокусным расстоянием F на экране получают уменьшенное и увеличенное изображения предмета, находящегося на расстоянии L от экрана. Найти отношение размеров изображений в обоих случаях.
532. Расстояние между источником света и экраном равно L. Линза, помещенная между ними, дает четкое изображение при двух положениях, расстояние между которыми I. Определить фокусное расстояние линзы.
533. Предмет в виде отрезка длиной / расположен вдоль оптической оси тонкой положительной линзы с фокусным расстоянием F. Середина отрезка расположена на расстоянии а от линзы и линза дает действительное изображение всех точек предмета. Определить продольное увеличение предмета.
534. Источник света находится на расстоянии 1,5 м от экрана, на котором с помощью собирающей линзы получают увеличенное изображение источника. Затем экран отодвигают еще на 3 м и снова получают увеличенное изображение источника. Чему равны фокусное расстояние линзы и размер источника, если размер изображения в первом случае 18 мм, а во втором 96 мм?
535. На некотором расстоянии от тонкой собирающей линзы помещен предмет и на экране получено его изображение. При этом линейное увеличение оказалось равным Vi. Затем предмет был приближен к линзе на расстояние L от своего предыдущего положения. Передвижением экрана снова получено четкое изображение
110
и измерено линейное увеличение. Оно оказалось равным Vi. Определить фокусное расстояние линзы.
536. Предмет помещен на расстоянии 25 с.м перед передним фокусом собирающей линзы. Изображение предмета получается на расстоянии 36 см за задним фокусом. Определить фокусное расстояние.
537. Точечный источник света расположен на расстоянии а = 30 см от тонкой положительной линзы, оптическая сила которой 5 диоптрий. На какое расстояние сместится изображение источника, если между линзой и источником поместить толстую стеклянную пластинку толщины L — 15 см с показателем преломления п = 1'57?
538. Небольшой источник света расположен на оптической оси отрицательной линзы. Изображение источника рассматривается глазом. Из каких точек пространства можно одновременно видеть как источник, так и его изображение? Заштриховать эту область на чертеже. Существует ли такое положение источника, при котором такой области не будет?
539. Источник света расположен на двойном фокусном расстоянии от собирающей линзы на ее оси. За линзой перпендикулярно к оптической оси помещено плоское зеркало. На каком расстоянии от линзы нужно поместить зеркало, чтобы лучи, отраженные от зеркала, пройдя вторично через линзу, стали параллельными?
540. На тонкую отрицательную линзу падает параллельный пучок лучей от удаленного источника, расположенного на оптической оси. На расстоянии а за линзой перпендикулярно к ее оптической оси расположено плоское зеркало. После прохождения лучей через линзу отражения от зеркала и вторичного прохождения через линзу образуется мнимое изображение, расположенное между линзой и зеркалом на расстоянии За/4 от линзы. Определить фокусное расстояние линзы.
541. Человек держит в руке короткофокусную линзу на расстоянии ах = 55 см от глаза и смотрит на удаленное здание. Через линзу он видит уменьшенное обратное изображение здания на фоне самого здания, видимого вторым (невооруженным) глазом — это дает ему возможность судить о размерах изображения, видимого через линзу. Приблизив линзу к глазу на расстояние «2 = 30 см, человек находит, что видимая величина
111
изображения увеличивается в два раза. Найти фокусное расстояние линзы.
542. Плоская поверхность плоско-выпуклой линзы с фокусным расстоянием F покрыта хорошо отражающим слоем. На расстоянии а от линзы со стороны выпуклой поверхности расположен точечный источник света. Определить положение изображения. При каких значениях а изображение будет действительным и при каких мнимым?
543. Плоская поверхность плоско-вогнутой линзы с фокусным расстоянием F покрыта хорошо отражающим слоем. На расстоянии а от линзы со стороны вогнутой поверхности расположен точечный источник света. Определить положение изображения. Можно ли в такой системе получить действительное изображение?
544. Расположить две линзы так, чтобы параллельные лучи, пройдя сквозь обе линзы, оставались параллельными. Сделать это: а) в случае двух собирающих линз; б) в случае одной рассеивающей и одной собирающей линзы.
545. Две одинаковые тонкие положительные линзы с фокусным расстоянием +F расположены на расстоянии F друг от друга, так что их оптические оси совпадают. На расстоянии а от одной из них находится источник света. Найти положение изображения.
546. Две тонкие линзы: положительная с фокусным расстоянием +F и отрицательная с фокусным расстоянием —F расположены на расстоянии а друг от друга так, что их оптические оси совпадают. На некотором расстоянии а перед положительной линзой находится источник света; изображение этого источника, даваемое системой линз, располагается на таком же расстоянии а за отрицательной линзой. Определить это расстояние.
547. Изображение удаленного источника света S проектируется на экран с помощью линзы с фокусным расстоянием Fj = 20 см. На расстоянии I = 10 см от этой линзы со стороны источника ставится вторая линза с фокусным расстоянием F% = 30 см. В какую сторону и на какое расстояние надо передвинуть экран, чтобы получить на нем снова резкое изображение источника?
548. Точечный источник света помещен на оптической оси собирающей линзы с фокусным расстоянием Fi == 30 см на расстоянии = 120 см от нее. По дру-
112
гую сторону линзы в ее фокальной плоскости помещена рассеивающая линза. Чему равно фокусное расстояние F2 рассеивающей линзы, если лучи после прохождения второй линзы кажутся исходящими из самого источника?
549. Источник света помещен на расстоянии 20 см от собирающей линзы с фокусным расстоянием 12 см. На каком расстоянии за собирающей линзой может быть помещена рассеивающая линза с фокусным расстоянием 16 см с тем, чтобы изображение источника света оставалось действительным?
550. Две положительные линзы с фокусными расстояниями F] и F2 = 3Fi расположены на расстоянии 2F] друг от друга. Предмет находится на оптической оси со стороны короткофокусной линзы. При каких положениях предмета эта оптическая система дает прямое изображение?
551. Оптическая система состоит из двух одинаковых линз с фокусными расстояниями /д = F2 = F, расположенных на расстоянии F/2 друг от друга. При каких положениях предмета его изображение будет мнимым? Предмет находится на оптической оси системы.
552. Две положительные линзы Л\ и Л2 с фокусными расстояниями F} и F2 расположены на расстоянии L друг от друга. На каком расстоянии от первой линзы следует расположить предмет, чтобы получить прямое изображение с увеличением, равным 1? При каких значениях L это возможно?
553. Две одинаковые отрицательные линзы с фокусным расстоянием Fi = F2 = —F расположены на расстоянии 2F друг от друга. Предмет находится на оптической оси системы перед одной из линз. Какую линзу следует поместить посередине между отрицательными линзами, чтобы при любых положениях предмета его изображение, даваемое системой из трех линз, было действительным?
554. Показать, что оптическая сила системы, состоящей из двух тонких линз, приложенных вплотную друг к другу, равна сумме оптических сил этих линз.
555. Из тонкой плоскопараллельной стеклянной пластинки изготовлены три линзы (рис. 140). Оказалось, что фокусное расстояние линз 1 и 2, составленных вместе, равно F < 0; фокусное расстояние линз 2 и 3, также приложенных вплотную друг к другу, равно / < 0.
8 Л. П. Баканина и др. 113
Предполагая, что линзы тонкие, найти фокусные расстояния каждой из трех линз.
556. Тонкая двояковыпуклая линза получена из двух
Рис. 140.
одинаковых часовых стекол, пространство между которыми заполнено водой. Фокусное расстояние линзы равно F — 20 см. Определить фокусное расстояние f тонкой плосковогнутой линзы, состоящей из одного такого часового стекла и плоскопараллельной пластинки, пространство между которыми также заполнено водой.
557. Две одинаковые тонкие плоско-выпуклые линзы, фокусные расстояния которых равны F, помещены в оправу так, что их выпуклые поверхности соприкасаются. Определить фокусное расстояние такой системы в воде, коэффициент преломления кото
рой равен п. Считать, что внутрь оправы вода не попадет. Рассматривать только такие лучи, которые пере-
секаются с оптической осью под достаточно малыми
углами, чтобы тангенсы этих углов можно было приближенно заменить синусами.
558. Границей раздела двух сред является сфера некоторого радиуса (рис. 141). Первой средой является воздух, второй — стекло, коэффициент преломления ко- * // 4
торого равен п. На поверх- £п '
ность раздела со стороны ? *
первой среды падает узкий —*----------// ,/
пучок лучей, параллельный-------------у— ---------
одному из диаметров сферы. ___________т'л/ к
Найти точку схождения лу- V f .
чей во второй среде, зная, у к г
что тонкая плоско-выпук- Л,/ ,{t
лая линза, изготовленная
из того же стекла и имею
Рис. 141.
щая радиус кривизны вы-
пуклой поверхности такой же, как и граница раздела, имеет фокусное расстояние F. Углы между падающими и преломленными лучами считать малыми.
559. В очень толстой пластине из стекла с показателем преломления п сделано сферическое углубление.
114
На это углубление направляется узкий пучок параллельных лучей. Найти положение фокуса f такой системы в стекле, если тонкая плоско-вогнутая линза из того же стекла и с тем же радиусом кривизны, что и углубление, имеет фокусное расстояние F. Углы между падающими и преломленными лучами считать малыми.
560. Воздушная полость в стекле имеет форму плоско-вогнутой линзы. Найти фокусное расстояние f этой линзы в стекле. Известно, что линза, изготовленная из этого же стекла и совпадающая по форме с полостью, имеет в воздухе фокусное расстояние F. Показатель преломления стекла равен п. Углы между падающими и преломленными лучами считать малыми.
561. Воздушная полость в стекле имеет форму тонкой плоско-выпуклой линзы. Найти фокусное расстояние f этой линзы в стекле. Известно, что фокусное расстояние линзы из этого же стекла, совпадающей по форме с Полостью, равно F в воздухе. Показатель преломления стекла равен п. Углы между падающими и преломленными лучами считать малыми.
Сферические зеркала
562. Чему равна величина изображения Солнца в
подшипниковом шарике диаметром 4 мм? Диаметр Солнца 1,4-106 км, а расстояние до него 150- 106 км?
563. Чему равны продольный (относительно оси цилиндра) и поперечный угловые размеры изображения Солнца в полированном металлическом прутке диаметра 4 мм? Диаметр Солнца 1,4-106 км, а расстояние до него 150- 106 км.
564. С помощью вогну
Рис. 142.
того зеркала получают изо-
бражения двух точечных источников А и В. Один из них расположен на оптической оси на расстоянии 4/zF от зеркала, другой смещен от оси на небольшое расстояние так, что линия, соединяющая оба источника, образует с оптической осью угол <р = 60° (рис. 142), Под каким углом ф к оптической оси следует
8*
115
расположить плоский экран, чтобы одновременно полу-чить на нем четкие изображения обоих источников?
565. В фокусе сферического зеркала прожектора помещен источник света в виде светящегося диска радиусом г = 1 см. Найти диаметр освещенного пятна на стене на расстоянии 50 м от прожектора, если фокусное расстояние сферического зеркала F — 40 см, а диаметр зеркала 1 м.
566. Предмет высотой h = 5 см находится на расстоянии а = 12 'см от вогнутого зеркала с фокусным расстоянием F = 10 см. Где и какого размера получится изображение?
567. Вогнутое сферическое зеркало дает действительное изображение, которое в три раза больше предмета. Определить фокусное расстояние зеркала, если расстояние между предметом и его изображением I = 20 см.
568. Два одинаковых вогнутых сферических зеркала поставлены одно против другого на расстоянии, равном учетверенному фокусному расстоянию. В фокусе одного зеркала помещен источник света. Найти изображения источника.
569. Два одинаковых вогнутых зеркала поставлены друг против друга так, что их главные фокусы совпадают. Светящаяся точка S помещена на общей оси зеркал на расстоянии а от первого зеркала. Где получится изображение после отражения лучей от обоих зеркал?
570. Радиус вогнутого сферического зеркала R = 40 см. На главной оптической оси этого зеркала помещен точечный источник света S на расстоянии «,= 30 см от зеркала. На каком расстоянии от вогнутого зеркала надо поставить плоское зеркало, чтобы лучи, отраженные вогнутым, а затем плоским зеркалом, вернулись в точку S?
571. Сходящиеся лучи падают на вогнутое зеркало с радиусом кривизны R = 60 см так, что их продолжения пересекаются на оси зеркала в точке S на расстоянии а — 15 см за зеркалом. На каком расстоянии от зеркала сойдутся эти лучи после отражения от зеркала? Будет ли точка их пересечения действительной?
572. Сходящиеся лучи падают на выпуклое зеркало с радиусом кривизны R = 60 см так, что их продолжения пересекаются на оси зеркала на расстоянии а = 15 см за зеркалом. На каком расстоянии от зеркала сойдутся эти лучи после отражения? Будет ли
116
точка их пересечения действительной? Решить ту же задачу для R = 60 см и а = 40 см.
573. На расстоянии 102 см от вогнутого зеркала, оптическая сила которого равна +2 диоптрии, находится точечный источник света. Между зеркалом и источником расположена плоскопараллельная стеклянная пластинка, показатель преломления которой равен 1,5. При какой толщине пластинки изображение будет совпадать с источником? Считать, что размер зеркала достаточно мал, так что отношение тангенсов углов падения и преломления лучей в пластинке можно заменить отношением их синусов.
574. Свет от точечного источника, расположенного на оптической оси линзы за ее фокусом, после прохождения линзы отражается обратно от вогнутого сферического зеркала с радиусом сферы R и, вторично пройдя через линзу, дает изображение. В каких точках оптической оси может быть помещено зеркало для того, чтобы изображение совпало с самим предметом? Как будет перемещаться изображение, если зеркало перемещать между этими точками?
575. К вогнутому зеркалу приложена вплотную небольшая собирающая линза, закрывающая центральную часть отражающей поверхности зеркала. Такая оптическая система дает два действительных изображения при одном и том же положении предмета перед зеркалом; одно изображение получается на расстоянии bi = 50 см, а другое на расстоянии &2 = 10 см от зеркала. Найти фокусное расстояние линзы.
576. К вогнутому сферическому зеркалу, радиус кривизны которого равен R = 1 м, приложена вплотную тонкая положительная линза. На расстоянии а = 20 см перед этой системой, перпендикулярно к ее оптической оси, расположен плоский предмет. Оказалось, что плоскость предмета совпадает с плоскостью изображения, образованного после прохождения света через линзу, отражения от зеркала и вторичного прохождения через линзу. Определить фокусное расстояние линзы.
577. Плоский предмет помещен на расстоянии а = 60 см перед выпуклым сферическим зеркалом, к которому вплотную приложена тонкая положительная линза с фокусным расстоянием F — 20 см. Плоскость предмета перпендикулярна к оптической оси системы.
117
Оказалось, что плоскость предмета совпадает с плоскостью изображения, образовавшегося после прохождения света через линзу, отражения от зеркала и вторичного прохождения через линзу. Определить радиус кривизны выпуклого зеркала.
578. Наблюдатель стоит в комнате спиной к удаленному окну и держит перед глазом на вытянутой руке тонкую двояковыпуклую линзу с фокусным расстоянием Р = 28 см. Радиус кривизны каждой поверхности линзы R = 28 см. Какие изображения окна видит наблюдатель и каковы их положения относительно линзы?
579. Наблюдатель стоит спиной к удаленному яркому источнику света и держит на вытянутой руке плоско-выпуклую тонкую линзу, обращенную плоской стороной к глазу. Он видит два изображения источника, одно из которых обратное и уменьшенное. Повернув линзу выпуклой стороной к глазу, не меняя расстояния до нее, наблюдатель замечает, что обратное изображение смещается. Объяснить происхождение изображений. Найти величину смещения обратного изображения. Фокусное расстояние линзы F = 30 см, радиус кривизны ее выпуклой поверхности R = 16 см.
Элементы фотометрии
580. Точечный источник монохроматического света излучает мощность 1Г0 = 10 вт на длине волны X = 0,5 мк. На каком максимальном расстоянии этот источник будет замечен человеком, если глаз реагирует на световой поток в 60 фотонов в секунду? Диаметр зрачка d — 0,5 см, постоянная Планка h = — 6,6 • 10~34 дж-сек.
581. При перпендикулярном падении света на плоскопараллельную стеклянную пластинку отношение световых энергий в отраженном и падающем лучах (коэффициент отражения) равно R. Выразить R через коэффициенты отражения света от границ воздух — стекло и стекло — воздух, предполагая их одинаковыми и равными г. При решении учесть многократные отражения света в плоскопараллельной пластинке. Поглощением света в пластинке пренебречь.
582. Коэффициент отражения света от плоских границ воздух — стекло и стекло — воздух одинаков и ра
118
вен г. Какая часть световой энергии пройдет через плоскопараллельную стеклянную пластинку при нор« мальном падении света? При решении учесть многократные отражения света от границ. Поглощением света пренебречь.
583. Точечный источник света помещен на некото^ ром расстоянии d от экрана и дает в центре освещенность, равную 1 лк. Как изменится освещенность, если по другую сторону от источника на том же расстоянии поместить плоское, идеально отражающее зеркало? Плоскости экрана и зеркала параллельны.
584. На некотором расстоянии d от идеального плоского зеркала находится точечный источник света S. Перпендикулярно к плоскости зеркала поставлен экран. Во сколько раз изменится освещенность в точке экрана, расстояние которой от зеркала равно d/2, если убрать зеркало? Расстояние между экраном и источником d.
585. Два точечных источника света 3j и S2 расположены на расстоянии 2d = 2 м друг от друга. На перпендикуляре, восстановленном в середине линии, соединяющей источники, расположена под углом а
Рис. 143.
/ ।
Рис. 144.
к перпендикуляру небольшая площадка на расстоянии d = 1 .йот этой линии (рис. 143). При а = 15° освещенности обеих сторон площадки одинаковы и равны 20 лк. Определить силы света /1 и /2 источников.
586. Две одинаковые матовые пластинки ГЦ и П2 образуют прямой двугранный угол. Ребро этого угла помещается на одинаковых расстояниях от источников света Si и S2 на прямой, соединяющей источники .(рис. 144). Оказалось, что освещенность обеих пластинок одинакова, когда биссектриса двугранного угла образует с перпендикуляром к линии SiS2 угол а. Найти отношение Л//2 сил света источников. Считать, что
119
линейные размеры пластинок много меньше расстоя-ния SiS2.
587. На расстоянии d под поверхностью воды (с показателем преломления п) помещен точечный источник света S, сила света которого равна I (рис. 145). Небольшая площадка перемещается вдоль линии 5Л, оставаясь все время перпендикулярной к этой линии (линия 5Л параллельна поверхности воды). Каково минимальное расстояние между площадкой и источником, при котором, подсчитывая освещенность площадки, можно считать поверхность воды идеально отражающим зеркалом? Какова освещенность площадки на таком расстоянии? Потерями света в толще воды пренебречь.
588. Определить силу света лампы уличного освещения, необходимую для того, чтобы освещенность на земле на середине расстояния между фонарями была равна 0,2 лк. Лампы подвешены на высоте 10 м, расстояние между столбами 40 м. При расчете учитывать освещенность, даваемую двумя соседними фонарями.
589. В воде на глубине Я расположен точечный источник света силой I, а на одной с ним вертикали на высоте Н над поверхностью воды находится круглый экран с радиусом а, значительно меньшим Н. Найти полный световой поток, попадающий на экран, принимая во внимание, что энергетический коэффициент отражения для лучей, нормально падающих на границу раздела, равен R. Показатель преломления воды равен п.
Указание. Воспользоваться тем, что при малых углах sin а ~ tga.
590. Параллельный пучок света, проходящий через плоскопараллельную пластинку толщиной Н с показателем преломления п, направляется линзой на катод фотоэлемента. Фокусное расстояние линзы F значительно больше ее диаметра D. Взаимное расположение Линзы и фотоэлемента таково, что круглый фотокатод в точности перекрывает световой поток. При этом гальванометр в цепи фотоэлемента показывает ток I. Какой 120
ток покажет гальванометр, если поставить пластинку между линзой и фотоэлементом, не меняя положения последних?
591. Точечный источник света расположен на главной оптической оси собирающей линзы на расстоянии 30 см от нее. Освещенность светлого пятна на белом экране, помещенном за линзой на расстоянии 60 см от нее, в четыре раза меньше освещенности того же экрана, расположенного вплотную к линзе. Определить фокусное расстояние линзы.
592. В фокусе собирающей линзы с фокусным расстоянием F = 10 см находится точечный источник света. На расстоянии L = 1 м от линзы помещен экран, перпендикулярный к оптической оси линзы. Во сколько раз освещенность в центре светового пятна, получающегося на экране, больше, чем освещенность в том же месте экрана, создаваемая источником при отсутствии линзы? Потерями света в воздухе и в линзе пренебречь.
593. На оси собирающей линзы на расстоянии а = 25 см от нее находится весьма малый источник света. По другую сторону' линзы один раз на расстоянии /1 = 27 см, а другой раз на расстоянии /г = 48 см ставится экран. Освещенность светового пятна на экране в обоих случаях оказывается одинаковой. Определить фокусное расстояние линзы.
594. Точечный источник света расположен на главной оптической оси рассеивающей линзы на расстоянии а = 30 см от нее. На экране, расположенном по д |
другую сторону линзы на____________S_______Д____
расстоянии /1 = 10 см от И ТГ~
линзы, получается све- V |
товое пятно, освещен- __Ц-__г? »[./•»!
ность которого Е. Когда экран отодвигают на рас- Рис. 146.
стояние /2 = 40 см от линзы, освещенность светового пятна становится равной F/4. Найти фокусное расстояние линзы.
595. На оптической скамье последовательно расположены экран, точечный источник света S, положительная линза и плоское зеркало. Расстояния указаны на рис. 146. Во сколько раз изменится освещенность в центре экрана, если плоское зеркало передвинуть
121
вправо на расстояние F, равное фокусному расстоянию линзы?
596. Точечный источник света, равномерно излучающий во все стороны, расположен на расстоянии 3 At от идеального отражающего плоского зеркала. На расстоянии 1 м с другой стороны от источника расположен экран. На сколько процентов изменится освещенность в центре экрана, если на расстоянии 1 м от зеркала поместить тонкую положительную линзу с оптической силой в 1 диоптрию?
597. Источник света помещен на расстоянии L>SF от экрана. Между источником и экраном вводятся две одинаковые собирающие линзы с фокусными расстояниями, равными F. При каких положениях линз источник будет изображаться в натуральную величину? Чему равно при этом отношение освещенностей изображений? При расчете освещенностей источники считать малыми но сравнению с диаметром линзы, а ее диаметр — малым по сравнению с ее фокусным расстоянием.
598. В главном фокусе вогнутого зеркала с радиусом кривизны R = 2 м находится точечный источник света. На расстоянии L = 10 м от источника помещен экран, перпендикулярный к главной оптической оси зеркала. Во сколько раз освещенность в центре светового пятна, получающегося на экране, больше, чем освещенность в том же месте экрана, создаваемая источником при отсутствии зеркала? Потерями света в воздухе и при отражении пренебречь.
599. На оси выпуклого сферического зеркала радиуса R находится точечный источник света. Расстояние между зеркалом и источником равно R/2. Определить освещенность Е площадки, находящейся на расстоянии R от зеркала, если освещенность площадки на расстоянии 2R равна Ед. Зеркало считать идеально отражающим. ।
600. Точечный источник света находится на расстоянии а — 20 см от вогнутого сферического зеркала радиусом R = 50 см. Найти освещенность экрана на расстоянии d = 60 см от поверхности зеркала, если на расстоянии = 100 см освещенность равна £i = 290 лк.
601. Чем легче поджечь кусок дерева: вогнутым зеркалом с диаметром оправы D = 1 м и радиусом 122
кривизны R = 10 м или линзой с диаметром d = 2 см и фокусным расстоянием F2 = 4 см? Источником света служит Солнце.
602. Изображение Солнца получено на экране при -помощи тонкой положительной линзы. Определить светосилу линзы, если известно, что освещенность изображения Солнца лучами, прошедшими через линзу, равна освещенности экрана прямыми солнечными лучами. Угловой размер Солнца а = 30 мин. Светосилой линзы называют отношение квадрата диаметра к квадрату фокусного расстояния^
603. Изображение Солнца получено на экране при помощи системы из двух одинаковых линз с фокусным расстоянием F, расположенных на расстоянии F/2 друг от друга. Во сколько раз освещенность изображения Солнца лучами, прошедшими систему линз, больше освещенности экрана прямыми лучами? Угловой размер Солнца равен а, диаметры линз равны D.
604. Небольшой черный шарик, поглощающий все световые лучи, при освещении Солнцем нагревается до температуры t\. До какой температуры t2 нагреется шарик, если сфокусировать на нем изображение Солнца с помощью линзы с фокусным расстоянием F и диаметром D? Считать, что энергия, теряемая шариком в единицу времени за счет теплообмена, пропорциональна площади его поверхности и разности температур шарика и окружающего воздуха. Температуру воздуха принять равной to. Рассмотреть случай, когда диаметр шарика меньше диаметра изображения Солнца. Угловой диаметр Солнца равен а.
605. Наблюдатель, находящийся между двумя почти параллельными плоскими зеркалами, видит в одном из них несколько изображений своего лица. Как относятся между собой освещенности второго и третьего изображений на сетчатке глаза, если коэффициент отражения от каждого зеркала равен k = 0,8?
606. Солнечные лучи проходят через круглое отверстие в непрозрачном экране и освещают расположенный за ним белый экран. Диаметр отверстия d = 20 лш. На каком расстоянии L следует расположить белый экран, чтобы освещенность в его центре была в три раза меньше освещенности, создаваемой лучами в плоскости отверстия? Известно, что линза с фокусным
123
расстоянием F = 2 м дает изображение Солнца диаметром D = 17,4 мм.
607. Экран освещается прямыми солнечными лучами. Как изменится освещенность экрана, если между ним и Солнцем в метре от экрана поместить матовый стеклянный шарик диаметром 5 см, равномерно рассеивающий во все стороны падающий на него свет?
608. Источник света с площадью S = 0,5 см2 проектируется линзой с фокусным расстоянием F = 30 см на экран. Расстояние между источником и линзой а = 120 см. Диаметр линзы 0 = 5 см. Определить освещенность изображения источника света на экране, если сила света источника / = 40 св.
609. Источник света в виде шарика диаметром 10 мм, помещенный на расстоянии 1 м от белого экрана, дает в точке экрана, ближайшей к источнику, освещенность Е. С помощью линзы с фокусным расстоянием 21 см и диаметром 3 см на экране получают увеличенное изображение источника. Найти освещенность изображения. _
610. Действительное изображение протяженного источника получено при помощи линзы, находящейся на расстоянии а от источника. Определить фокусное расстояние F линзы, если при увеличении расстояния между линзой и источником в два раза освещенность резкого изображения меняется в четыре раза.
611. Протяженный источник находится на расстоянии а от линзы с фокусным расстоянием F. Во сколько раз изменится освещенность изображения, если расстояние между источником и линзой увеличить в два раза? Рассмотреть случай а = = 2F.
612. На некотором расстоянии а от равномерно светящейся плоскости А рас
положен непрозрачный экран В с круглым отверстием диаметром d (рис. 147). На таком же расстоянии а за экраном В расположено матовое стекло С. Найти освещенность центрального участка матового стекла (точка D), если известно, что светящаяся плоскость излучает за 1 сек с 1 см2 поверхности в единицу телесного
124
Рис. 147.
угла световую энергию Ф. Считать, что диаметр отвер* стия d значительно меньше расстояния а.
613. На расстоянии 2F от равномерно светящейся плоскости большого размера находится собирающая линза с фокусным расстоянием F и диаметром D. Чему равна освещенность в центре светового пятна на экране, находящемся на расстоянии а < 2F от линзы, если светящаяся плоскость излучает за 1 сек с 1 см2 поверхности в единицу телесного угла энергию Ф? Считать, что диаметр линзы D значительно меньше расстояния а. Свет, падающий на экран мимо линзы, не учитывать.
Оптические приборы
614. Определить главное фокусное расстояние и оптическую силу очков, восполняющих недостатки дальнозоркого глаза, для которого расстояние наилучшего зрения равно 50 см.
615. Человек с близорукими глазами может читать мелкий шрифт на расстоянии не более 20 см от глаз. Чему равны оптическая сила и фокусное расстояние очков, восполняющих недостаток таких близоруких глаз?
616. На каком максимальном расстоянии близорукий человек может читать без очков мелкий шрифт, если обычно он пользуется очками с оптической силой —4 диоптрии?
617. Пределы аккомодации у близорукого человека лежат между 10 и 25 см. Определить, как изменятся эти пределы, если человек наденет очки с оптической силой —4 диоптрии.
618. Близорукий человек без очков рассматривает предмет, находящийся на некотором расстоянии под поверхностью воды. Оказалось, что если глаз расположен вблизи поверхности воды, то максимальное погружение предмета, при котором человек еще различает его мелкие детали, равно 30 см. Принимая показатель преломления воды равным 1,3, определить, какие очки следует носить этому человеку.
619. В парке установлен посеребренный шар диаметром 32 см. С какого максимального расстояния близорукий человек без очков будет резко видеть
125
отраженные в шаре далекие предметы, если обычно он пользуется очками с оптической силой —5 диоптрий? С какого максимального расстояния он увидит резко свое отражение в шаре?
620. Человек носит очки. Из нормального положения он постепенно удаляет их, все время смотря сквозь стекла очков. При удалении видимые предметы представляются ему уменьшающимися. Какие он носит очки: для близоруких или для дальнозорких? Одним глазом человек смотрит сквозь очковое стекло, а другим помимо очков на удаленный предмет, совмещая оба изображения. Второе изображение, получаемое невооруженным глазом, ему кажется в 1,5 раза больше первого. При этом расстояние очкового стекла от глаза равно 20 см. Определить оптическую силу этих очков.
621. Телеобъектив фотоаппарата состоит из двух линз: положительной линзы с фокусным расстоянием F= +6 см, обращенной к объекту, и отрицательной линзы с фокусным расстоянием F2 — —2,5 см. Расстояние между линзами d — 4 см. На каком расстоянии о г отрицательной линзы должна располагаться фотопленка при фотографировании удаленных предметов?
622. Изображение предмета на матовом стекле фотоаппарата с расстояния 15 м получилось высотой 30 мм, а с расстояния 9 м — высотой 51 мм. Найти фокусное расстояние объектива.
623. Ближайшая точка, на которую может быть сфокусирован фотоаппарат, находится на расстоянии а = 2 м от объектива. Куда переместится эта точка, если к объективу вплотную приставить тонкую положительную линзу с оптической силой D = +5 диоптрий?
624. При фотографировании предмета объективом с фокусным расстоянием Fi размер изображения оказался равным h[. Каков будет размер изображения, если на объектив надеть насадочную рассеивающую линзу с фокусным расстоянием F2 (|F21 > Fi). Расстояние от предмета до объектива в обоих случаях одинаково и равно а.
625. Проекционный аппарат, объектив которого имеет фокусное расстояние Fi, установлен на расстоянии L от экрана. Во сколько раз изменится размер изобра-126
жения, если на объектив надеть насадочную положительную линзу с фокусным расстоянием F2.
626. Фотоаппаратом, объектив которого имеет фокусное расстояние F = 50 мм, а размер кадра 24 X 35 мм, фотографируют чертеж размером 480 X X 600 мм. С какого расстояния нужно производить фотосъемку, чтобы получить максимальный размер изображения? Какая часть кадра (по площади) будет при этом занята изображением?
627. Какое время может быть открыт затвор фотографического аппарата при съемке прыжка в воду с вышки? Фотографируется момент погружения в воду. Высота вышки 5 м. Фотограф стоит в лодке на расстоянии 10 м от места погружения прыгуна. Объектив фотоаппарата имеет фокусное расстояние 10 см. На негативе допустимо размытие изображения 0,5 мм.
628. Какая экспозиция нужна при фотографировании чертежа с линейным увеличением Уь если при фотографировании с увеличением V2 экспозиция равняется /г?
629. В фокальной плоскости положительной линзы установлено матовое стекло. Оказалось, что размытость деталей изображения предметов, находящихся на расстоянии а = 5 м от линзы, составила d = 0,2 мм. Определить светосилу линзы, если ее фокусное расстояние F = 10 см.
Примечание. Светосилой линзы называют квадрат отношения диаметра линзы к ее фокусному расстоянию.
630. Фотоаппарат, объектив которого имеет фокусное расстояние F = 20 см, наведен на предмет, находящийся на расстоянии щ = 4 м. До какого диаметра нужно задиафрагмировать объектив, чтобы размытость изображения предметов, находящихся на расстоянии а2 = 5 м от фотоаппарата, не превышала 0,2 мм"?
631. При фотографировании удаленного точечного источника на фотографии из-за невысокого качества объектива и применяемого фотоматериала получается светлый кружок диаметром d = 0,1 мм. С какого максимального расстояния можно сфотографировать в тех же условиях два точечных источника, расположенных на расстоянии I = 1 см друг от друга, чтобы на
127
фотографии их изображения еще не перекрывались? Фокусное расстояние объектива F = 5 см.
632. В микроскопе главное фокусное расстояние объектива F, = 5,4 мм, а окуляра F2 = 2 см. Предмет находится от объектива на расстоянии а1= 5,6 мм. Определить линейное увеличение микроскопа для нормального глаза и длину микроскопа (расстояние между объективом и окуляром), предполагая, что глаз аккомодирован на расстояние наилучшего зрения d = 25 см.
633. Объектив зрительной трубы имеет фокусное расстояние Fi = 30 см, а окуляр — фокусное расстояние Г2 = 4 см. Труба установлена на бесконечность*). В каком месте нужно поставить диафрагму, чтобы поле зрения было резко ограничено? Какова величина угла поля зрения, если диаметр диафрагмы 12 мм? Каково угловое увеличение трубы?
Примечание. Угловым увеличением называют отношение тангенсов углов, образованных выходящими и входящими пучками с оптической осью.
634. Между источником света и зрительной трубой помещена рассеивающая линза с фокусным расстоянием Fi = —15 см на расстоянии 1\ = 85 см от источника. Где в промежутке между источником и рассеивающей линзой нужно поместить собирающую линзу с фокусным расстоянием Г2 = 16 см, чтобы источник света был виден резко в трубу, установленную на бесконечность? При каком из возможных положений линзы изображение в трубе будет иметь наибольшие угловые размеры?
635. Объектив зрительной трубы имеет фокусное расстояние Fi =25 см и диаметр 5 см, а окуляр — фокусное расстояние Г2 = 5 см. Труба установлена на бесконечность. Если за окуляром поместить матовое стекло, то при некотором его положении освещенный кружок на матовом стекле имеет наименьшие размеры и резко ограниченные края. Чему равно при этом расстояние от матового стекла до окуляра и чему равен диаметр кружка?
*) В тексте данной и ряда последующих задач не содержится указаний относительно аккомодации глаза наблюдателя, В подобных случаях рекомендуется решать задачи в предположении, что глаз аккомодирован на бесконечность (см. примечание к решению данной задачи).
128
636. Зрительная труба с фокусным расстоянием объектива F = 50 см установлена на бесконечность. На какое расстояние надо передвинуть окуляр трубы, чтобы ясно видеть предметы на расстоянии а — 50 xi?
637. Зрительная труба перемещением окуляра может фокусироваться на предметы, находящиеся на расстоянии от й1 = 2 м до а2 — Ю м. Какую линзу нужно приложить к объективу, чтобы труба могла настраиваться на бесконечность? Где при этом будет находиться ближняя точка фокусировки?
•638. Перед объективом зрительной трубы Кеплера (с собирающей линзой в качестве окуляра) помещен предмет на расстоянии а < F{. Отношение фокусных расстояний объектива и окуляра F\fF2 = 10. Труба установлена на бесконечность. Найти линейное увеличение V = у/х (х—размер предмета, у — размер изображения). Определить характер изображения.
639. Перед объективом зрительной трубы Галилея (с рассеивающей линзой в качестве окуляра) помещен предмет на расстоянии а > Гь Отношение фокусных расстояний объектива и окуляра FJF2 = —10. Труба наведена на бесконечность. Найти линейное увеличение V = у/х, где х — размер предмета, у — размер изображения. Определить характер изображения.
640. Зрительная труба имеет фокусное расстояние объектива Fi = 50 см и фокусное расстояние окуляра F2 = 10 см. Чему равен угол, под которым видны через трубу два удаленных предмета, если при наблюдении невооруженным глазом этот угол равен 30'? Труба установлена на бесконечность.
641. Объектив и окуляр зрительной трубы Галилея имеют фокусные расстояния, равные Г1 = 57 см и 1'2 = —4 см соответственно. Труба наведена на Солнце. На расстоянии b — 12 см от окуляра расположен белый экран. При каком расстоянии L между объективом и окуляром на экране получится четкое изображение Солнца. Каков будет диаметр D этого изображения, если угловой размер Солнца а = 30'?
Решить ту же задачу, когда использована трубг< Кеплера с фокусными расстояниями объектива и окуляра Fi = 40 см, F2 = 3 см, а экран расположен на расстоянии b = 15 см от окуляра.
9 Л. П. Баканина и др.
129
642. Объективом театрального бинокля служит собирающая линза с фокусным расстоянием F[ = 8 см, а окуляром — рассеивающая линза с фокусным расстоянием F2 = —4 см. Чему равно расстояние между объективом и окуляром, если изображение рассматривается глазом с расстояния наилучшего зрения? На сколько нужно переместить окуляр для того, чтобы изображение можно было рассматривать глазом, аккомодированным на бесконечность?
643. Наблюдатель с нормальным зрением рассматривает Луну в телескоп, объектив которого имеет фокусное расстояние F] = 2 м, а окуляр F2 = 5 см. Глаз наблюдателя аккомодирован на расстояние наилучшего зрения d = 25 см. На сколько нужно переместить окуляр для того, чтобы получить изображение Луны на экране на расстоянии d = 25 см от окуляра? Чему равны при этом размеры изображения Луны на экране, если ее угловые размеры а = 30'?
644. Два зрителя — близорукий и дальнозоркий—» смотрят по очереди на сцену в один и тот же театральный бинокль. Которому из них приходится сильнее раздвигать трубку бинокля, если в обоих случаях изображение рассматривается с расстояния наилучшего зрения? Подсчитать изменение длины трубки бинокля при передаче его одним зрителем другому, если фокусное расстояние окуляра (рассеивающей линзы) F — —4 см, а расстояния наилучшего зрения близорукого и дальнозоркого зрителей равны di = 20 см и d2 = 50 см.
645. Зритель с нормальным зрением смотрит на сцену, находящуюся на расстоянии а = 15 м, в бинокль. Фокусное расстояние объектива бинокля /д = 20 см, окуляра F2=—5 см. На каком расстоянии должны быть расположены объектив и окуляр бинокля, чтобы зритель наиболее четко видел сцену, если изображение рассматривается с расстояния наилучшего зрения d = 25 см?
646. Объективом зрительной трубы Кеплера служит линза с фокусным расстоянием Fi = 500 мм, имеющая диаметр D = 75 мм. Каково фокусное расстояние окуляра, если при наблюдении с помощью этой трубы Луна кажется в четыре раза менее яркой по сравнению с наблюдением невооруженным глазом? Диаметр зрачка принять равным 3 мм.
130
647. Во сколько раз изменится освещенность изображения Луны на сетчатке глаза при наблюдении с помощью телескопа (труба Кеплера), если уменьшить диаметр объектива в три раза (диафрагмирование)? Первоначальный диаметр объектива равен 150 мм, увеличение трубы равно 25. Диаметр зрачка глаза считать равным 3 мм.
648. С помощью зрительной трубы Кеплера наблюдают изображение лунной поверхности. Перед объективом трубы расположена круглая диафрагма переменного диаметра. При увеличении диаметра диафрагмы освещенность изображения Луны на сетчатке глаза постепенно увеличивается до тех пор, пока диаметр диафрагмы не превосходит 30 мм. При D > 30 мм яркость изображения не зависит от величины диафрагмы. Принимая диаметр зрачка глаза равным 3 мм, определить увеличение трубы.
649. Во сколько раз изменится освещенность изображения Луны на сетчатке глаза при переходе от наблюдения невооруженным глазом к наблюдению с помощью телескопа (труба Кеплера)? Объектив телескопа имеет диаметр 100 мм; увеличение трубы равно 50. Диаметр зрачка глаза считать равным 3 мм.
650. С помощью зрительной трубы, состоящей из объектива с фокусным расстоянием Fi = 50 см и диаметром di — 10 см. и окуляра с фокусным расстоянием К2 = 2,5 см и диаметром d2 = 0,5 см, получено изображение Солнца на экране, расположенном на расстоянии Ь = 20 см за окуляром. Определить, во сколько раз освещенность изображения больше освещенности экрана прямыми солнечными лучами. Угловой диаметр Солнца а = 0,01 рад. Потерями света в оптической системе пренебречь.
651. Изображение Солнца получено с помощью объектива, состоящего из собирающей и рассеивающей линз (Fi = +10 см, F2 — —10 см), расположенных на расстоянии I = 5 см. Посередине между линзами помещена круглая диафрагма диаметром D — 0,75 см. Предполагая, что линзы имеют достаточно большие размеры и не ограничивают световых пучков, определить, во сколько раз освещенность изображения больше освещенности экрана прямыми солнечными лучами. Угловой диаметр Солнца а принять равным 0,01 рад. Потерями света в линзах пренебречь.
9*
131
РЕШЕНИЯ ЗАДАЧ
1. МЕХАНИКА Кинематика
1. Так как трения нет, то независимо от пути скорость шарика в точке С будет одинакова. Зависимость скорости от времени изобразится линиями, наклон которых на участках желоба АВ и DC, ВС н AD Одинаков. На рис. 148 путь равен площади под кривыми
ode н ой</. Так как путь одинаков, площади эти должны быть равны, и уже поэтому ясно, что tABC > t ADC-
Проведем расчет времени соскальзывания по обоим путям:
и так как
gt2nr sin а DC = ft = oD/DC + -^------------,
то
/DC=-—^-+1/ +
gsma у g2sin2a 1 gsina
132
Следовательно, ____
+ V -у (И + sin а + sin а-1).
Аналогично для iABC‘.
'«'/уЖТ' -j-ra^slna,
,ас._^+1/ 4+“,
вс g V g2 g
откуда __
/2h / 1 - sin a , ,/——:— \ — —— + V 1 + sin a . g \ /sin a 1
Теперь легко найти разность
/вс ~ /вс = l/4" ~(К sin a + 1 - /1 -I- sina) > О, две adc y g sin a
поскольку l^sina+l >’Ksina+l, и знаки перед корнями всюду, разумеется, положительны.
2. Время t движения груза вдоль хорды определится из соотношения
а
где а — ускорение груза, L — длина хорды. Если хорда составляет с вертикалью угол а, то а — g cos a, L = D cos а, где D — диаметр окружности. Таким образом,
g
Время движения груза вдоль любой из хорд одинаково.
3. Если h — длина хорды АВ, то ускорение при движении вдоль , h . Г 2h Г I .
нее будет a = g — , а время движения гАВ = у — = 2 у >
нетрудно видеть, что tAB = tвс, поэтому
Полученное приближенное выражение для периода несколько больше точного Т — 2л Почему?
4.
2 2ti2 ’
здесь t — время полета, v — горизонтальная скорость атомов:
, 21Г 2WN m А
133
где т — масса атома, N — 6,02 • 1023 \]моль — число Авогадро. Окончательно получим
h=J^T ~ 11>2*10~5 см.
4WN
5. Время I падения бомбы можно найти из уравнения
Н =• + vt sin а;
s»*' здесь v sin а — вертикальная составляющая скорости бомбардировщика (рис. 149). За это время бомба пройдет в горизонтальном направлении путь L;
L = vt cos а.
Исключая отсюда время t, получим
у2 cos asin а /~, 2gH Д g \ V v2 sin2 а )'
6. Пусть струя воды вылетает со скоростью v из”трубы, направленной под углом а к горизонту (рис. 150). Тогда максимальная
высота й, на которую поднимается вода, будет равна , v2 sin2 g Ь--------------------------------
где v sin a — вертикальная составляющая скорости v. Обозначая через й], Л2, йз максимальные высоты подъема, соответствующие углам g = 60, 45 и 30°, получим
ht : h2 : h3 = (sin 6O0)2: (sin 45°)2: (sin 3O0)2 = 3:2: 1.
Время t полета воды равно удвоенному времени подъема на высоту h:
^=2 пзша
S
За это время вода пройдет в горизонтальном направлении путь L".
V2
L = vt cos а — — sin 2а, g
откуда
1/ 7Г VT
Lt: L2: L3 = sin 120°: sin 90°; sin 60° = : 1;
Z 4b
134
7. За время полета t камень прошел в горизонтальном направлении путь (рис. 151)
vt — L cos а.
Снижение камня за то же время равно
= L sin а.
Исключая из этих двух уравнений время, получим . 2t>2 sin g
~ geos2а ’ отсюда находим о.
8. Скорость v шарика перед ударом о плоскость v-V^gh. (1)
При упругом ударе о неподвижную поверхность потерь энергии шарика не происходит, поэтому величина скорости при отражении
будет такой же. Составляющая скорости, направленная вдоль наклонной плоскости, останется неизменной, а составляющая скорости, перпендикулярная к наклонной плоскости, не меняя своей величины, после удара изменяет направление на противоположное. Иными словами, при упругом ударе угол падения шарика равен углу отражения (рис. 152).
Перейдем теперь к решению задачи. Для этого введем систему координат, начало которой поместим в точку удара шарика о наклонную плоскость, ось х направим горизонтально, а ось у—вертикально (см. рис. 152). Координаты точки наклонной плоскости, в которую попадает шарик после отскока, обозначим через и у0. Очевидно, что
(2)
За время t шарнк пройдет в вертикальном направлении путь у, причем
у = vi cos 2a — , (3)
135
а в горизонтальном направлении — путь х:
х = pt sin 2а. (4)
Исключая из (3) и (4) времи t, найдем траекторию движения шарика:
у = х cig 2а - f п . (5)
у ь 2с2 sin2 2а
Заметим теперь, что в момент повторного удара шарика о наклонную плоскость значения х и у в уравнении (5) станут соответственно х0 и уй. Если затем из (2) и (5) исключить х0, то легко получим следующее выражение для уа:
... ~ ctg2a\
уа — — 4л tg2 a sin- 2a 1 -I—~J.
Учитывая, что sin 2a = 2 sin a cos a и cos 2a = cos2 a — sin2 a, окончательно найдем
у о “ — 8ft sin2 a.
Теперь нетрудно найти искомое расстояние S, которое, очевидно, равно
5 = 1д!_ = 8ft sin а = 4Л = 8 м. sin a
Заметим, что выражение для S не зависит от ускорения свободного падения и будет тем же самым при любых g ф 0. Читателю предоставляется возможность самому истолковать этот результат.
9. Через время Т первый шарик окажется над землей на высоте fti, причем
gT2
=
где v — начальная скорость шарика. Второй шарик к моменту времени Т находился в воздухе (Т — I) сек, поэтому его высота h над землей будет
ft2 — о (Г — t)-----g-----.
При встрече шариков hi = h2, откуда
р=Н7'“4)-
10. Первый снаряд будет поражен в минимальное время» если встреча снарядов произойдет на максимально возможной высоте, т. е. на максимальной высоте, на которую сможет подняться второй снаряд.
Максимальные высоты, на которые поднялись соответственно первый и второй снаряды,
of vl
Н 1 и Я2 = -jr2-;
2g 2g
13S
отсюда время t( полета первого снаряда до встречи будет
- 4.1/2(//Х-//2)
‘~Т + У g—
а время /2 второго снаряда будет t2 = v2/g. Значит, время между
выстрелами
/1 — /2 =
54 сек.
g
11. Скорость течения реки на расстоянии х от берега (рис. 153)
Составляющие скорости лодки относительно берега вдоль осей х и у соответственно будут
vx = v cos <р, vy — v sin <р — и
(о—скорость лодки относительно o^ = osin<p—jb-ti/costp. Таким образом, движение лодки вдоль сси х — равномерное, а вдоль у —равнозамедленное.
Через t сек после отплытия лодка будет иметь координаты х и у, причем
х = vt cos <p, 1
. ur vt2 COS ф f у =1,/81пф _______
воды) и так как х ~ vt cos ф, то
Рис. 153.
Момент встречи лодки с плотом определяется равенствами t — Т, У = 0, х~ L, следовательно,
L = vT cos ф,
u.vT2 cos ф
О = vT cos ф----L -------;
отсюда 5Шф = ид/2о и Т = L/a cos гр. Подставляя заданные значения, получим ф = 30°, 7' « 35 сек. Очевидно, что если 2v, то встреча лодки с плотом невозможна.
12. Из каждой точки, которую пролетает самолет, распространяется сферическая звуковая волна (несколько таких волн в момент нахождения самолета в точке А, изображены на рис. 154). Границей зоны, в которую дошел звук, служит коиус, являющийся огибающей для этих волн; АВ и АС — линии пересечения этого конуса с плоскостью чертежа (плоскость чертежа перпендикулярна
137
к земле). Сначала до точки В, как видно из рисунка, дойдет звук из точки O[(BOi ± АВ). ОД —путь, пройденный самолетом с того момента, как он пролетел над наблюдателем, до того, когда наблюдатель услышал звук. OD— путь, пройденный за то же время звуковой волной из точки О (OD ± АВ). Углы ВАО и BOD равны, как углы со взаимно перпендикулярными сторонами (обозначим эти углы через . Как видно из рисунка,
OD ci cos a - QB “ н >
OD ct c
sin a == “7ГТ — OA vt v
a).
(1)
(2)
Решая совместно уравнения (1) и (2), получаем гН
v — ....... 583 м/сек.
КН2 - с212
13, Ответ;
Я =
ct tn
— = 10 км
(решение аналогично решению задачи 12).
Статика
14, Условием равновесия стержня является равенство момен-относительно
тов сил тяжести Р и натяжения веревки Т (рис. 155) шарнира В;
Р -~sina=TL cos р, где £—длина стержня, или
Р
-g- sin a — Т cos р,
J_(„_2a) = 2a--^,
cos 2a —
Таким образом, _ Р sin a Р I в — ---- । за । #
2 sin 2a 4 cos a
15. Пусть P —груз, растягивающий
как удлинение пружины пропорционально нагрузке, то
£t —£0 = аР,
Рис, 155.
Пружину ДО ДЛИНЫ L1.
Так
(О
138
где Lo —длина недеформированной пружины, а — коэффициент пропорциональности. Очевидно, что под действием той же нагрузки половина пружины растянется до длины Lj/2. Обозначив cq аналогичный коэффициент для половины пружины, получим
b^o=^ = aip, откуда
<4 = у. (2)
Таким образом, коэффициент а упругости зависит от длины пружины. Теперь можно записать выражение для L2:
= + «!?) + (^- + a,2p).
(3)
Здесь первая скобка дает длину нижней половины растянутой пру-псключая из (1) и (3)
жины, а вторая — верхней. Учитывая величину аР, получим
L0 = 3Li-2L2.
16. Силы, действующие на цилиндры, изображены на рис. 156: Т — натяжение нитей, W — сила давления между цилиндрами. Для среднего цилиндра условие равновесия запишется так:
2mg = 2:V cos р. (1)
Для любого из крайних цилиндров
(2)
(3)
(3) на
(2)
mg + N cos р = Т cos a, N sin P = T sin a.
Подставляя (1) в (2) и деля (2), получаем
tg Р = 2 fg a.'
и
?т3
Рис. 156.
Заметим, что при наличии трения продолжение нитей может не проходить через центры боковых цилиндров и решение задачи усложнится. Читателю полезно попытаться записать условия равновесия для этого случая.
17. На рис. 157 изображены силы, действующие на нижнее левое бревно: Г —сила давления со стороны верхнего бревна, FTp — сила трения между бревнами, /тр — сила трения между бревнами и землей, Р — сила тяжести. Кроме того, в точке В действует сила N реакции опоры, направленная вертикально вверх. Бревна не будут раскатываться, если сумма моментов сил FTp и ftp относительно точки О равна нулю. Так как АО — ОВ, то это условие приводит к соотношению
F тр — /тр.
(1)
139
Кроме того, в случае равновесия бревна будет
ftp + F-rp cos 30° = F cos 60° (2)
(сумма горизонтальных проекций всех сил равна нулю). Но FTp = kF. Подставляя это соотношение в (1) и (2) и исключая из (1) и (2) fTp, получим
. cos 60° 1
k =-----------=,------ .
1 + cos 30° 2 + V 3
При меньшем коэффициенте трения бревна раскатятся.
18. Центр тяжести грузовика находится на расстоянии x — L)4 от его задних колес. Вычисляя моменты относительно точки
соприкосновения заднего колеса грузовика с землей, получим вие опрокидывания грузовика:
Fh + MgH sin а Mgx cos а,
где F — натяжение троса,
F = mg sin a, Mg = Р, mg = р.
Условие (1) можно переписать в следующем виде: g (mh + МН) sin а cos а>
усло-
(1)
(2)
откуда
. ML/4
tg а > —, ,-т. « 0,4,
ь mL + MH
т. е. реальной опасности опрокидывания для а =10° нет.
19. Предположим, что в пластине симметрично первому отверстию вырезано второе (пунктир на рис. 158), тогда центр тяжести оставшейся части пластины будет расположен в ее геометрическом центре, т. е. в точке О. Центр тяжести части пластины, заключенной внутри пунктирной линии, находится на расстоянии R/2 от точки О. Если М — масса целой пластины, а т — масса вырезанной
140
ее части, то положение центра тяжести пластины с отверстием
определится из соотношения
(М — 2т) х=т — х
Здесь х — расстояние искомого центра тяжести от точки О, Отсюда, т 1 , учитывая, что (массы относятся как площади соответ-
ствующих частей диска), сразу получим
20. Решение аналогично предыдущему. Положение центра тяжести крышки стола с диском найдем из соотношения (рис. 159)
Мх = т (R—r — х).
где х— расстояние искомого центра тяжести от точки О (центр крышки). Ножки стола должны быть расположены симметрично относительно этого центра тяжести, т. е. в вершинах равносторон
него треугольника, центр которого совпадает с центром тяжести стола с диском.
21. Катушка не будет вращаться, если момент сил трения
Рис. 160.
(2)
относительно центра тяжести будет равен моменту силы f, приводящей катушку в движение (рис. 160), т. е. если
RFTp = rf. (1)
Очевидно, что Ftp = mgk, a f=mgk + ma, где т — масса катушки. Подставив эти выражения в (1), получим k =_____________________________™___
(R~r)g
Примечание. В тех случаях, когда тело не имеет фиксированной оси вращения и может под действием внешних сил перемещаться, моменты сил рекомендуется вычислять относительно осн, проходящей через центр тяжести этого тела. Если же такая фиксированная ось вращения существует (как, например, в задаче 14), то моменты сил удобнее вычислять относительно этой оси, так как это избавляет от необходимости учитывать моменты сил реакции.
141
22. При увеличении угла а (рис. 161) цилиндр может либо соскользнуть, либо скатиться. Скольжение наступит, когда составляющая веса цилиндра вдоль дощечки станет больше максимального значения силы трения. Обозначая cti — угол, при котором начинается
скольжение, Pi — избыточный вес вещества, заполняющего отверстие, а Р — вес однородного цилиндра, получим
(P+Pj) sin (Х| =
= k (Р + Pj) cosab (1)
откуда
fgai = A. (2)
Определим теперь угол a = a2, начиная с которого возникнет чистое (без проскальзывания) качение цилиндра. Для этого заметим, что поскольку
Рис. 161.
скольжения нет, сила трения меньше своего максимального значения, и равна составляющей силы веса вдоль дощечки, т. е. величине (Р 4- Р;) sin a2. Очевидно, цилиндр сможет удерживаться на дощечке, пока момент силы трения относительно его оси не превысит максимально возможного значения момента силы Р1( который
соответствует горизонтальному расположению линии центров отверстия и цилиндра. Таким образом, для a = a2 будем иметь
9
R (Р + Р,) sin а2 =-х-ДР). (3) <5
Поскольку, как нетрудно видеть Р{ = = 5Р/8, то равенство (3) дает
10 sin a2 - 39 .
При этом
tg a2 « 0,26 < fg ab
Следовательно, равенство моментов нарушится раньше и цилиндр начнет скатываться без скольжения.
Заметим, что ось, относительно которой вычисляются моменты, можно выбирать произвольно, однако в данном случае вычисления получаются наиболее простыми, если эта ось совпадает с осью цилиндра. (См. примечание к задаче 21.)
23. sin a =1/6 (решение аналогично решению задачи 22).
24. Силы, действующие на палочку, указаны на рис. 162. Палочка будет находиться в равновесии, если сумма моментов архимедовой силы FА и силы тяжести mg относительно точки О равна
нулю.
142
Если длина палочки L, то (см. примечание к решению задачи 21)
FA-lL = mS^ L
(FА приложена в центре тяжести жидкости, вытесненной палочкой). Обозначим плотность воды рв, плотность материала палочки р, сечение палочки S. Тогда
mg^SLpg,
и условие равновесия примет вид
3
Р - J Рв-
25. Условие равновесия тела можно записать так!
Р V = р 1 Т’1 + р2Г2,
где Vt и V2 — части объема тела, находящиеся в более плотной и менее плотной жидкости соответственно; учитывая, что V = + V2,
получим
у. = у Р ~
Р1-Р2
26. Обозначим через V объем латуни, из которой сделана чашка, а через п — часть объема чашки, погруженную в воду. Чашка будет плавать, если
Урл = ПРв. . (I)
Здесь рл и рв —плотности латуни и воды соответственно, объем погруженной части чашки v связан с высотой изменения Л уровня жидкости соотношением
v = Sh. (2)
Это соотношение можно пояснить, например, следующим образом. При погружении чашки давление р воды на дно возросло и стало равным
где Рв н Рч — вес воды и чашки соответственно. С другой стороны, Р = Peg (Я + /<)• (4)
Соотношения (3) н (4) дают
-у- + рлИ = рв£ (Я + А).
143
Отсюда, учитывая, что Рв= pBgSH, сразу получим (2). Высота воды в банке при утопленной чашке:
Я1 = Я+-^=>Я+-^Л= 15,25 см.
О рд
27. Диск оторвется от трубки, когда сила Ft давления воды на его нижнее основание уравновесится весом Р диска и силой F? давления воды на выступающую д, д,. за пределы трубки верхнюю часть
к 7 ^s?s!a4_f— основания,
p + f2 = f{,
/\ (м\ или
yrt£>2Apg + yrt(£)2-rf2) Ярв§ =
--------------------------------- л£)2 (Н + h) pBg.
‘^9 Отсюда
Г, ( D V t Р-Рв рис. 163. h~^r-
Атмосферное давление на верхнюю н нижнюю части диска предполагается одинаковым.
28. Допустим, для определенности, что у автомобиля только задние колеса — ведущие. Условие равномерного движения позволяет утверждать, что, во-первых, суммы действующих на автомобиль сил и моментов снд равны нулю и, во-вторых, что сила трения в точности равна Afgsina (рис. 163):
JV| + JV2 = Afgeos a, Nt-^-=N2-^ + FTpH, Ftp = Mg sin a. Отсюда
Nt = Mg + -y sin aj « 0,56 T,
A'2 = Mg — -£ sin « 0,44 T.
Динамика
29. На муфту в горизонтальной плоскости действуют сила тре. нпя FTp и реакция опоры У, причем FTp <1 kN. Муфта не будет двигаться относительно штанги, если сумма этих сил будет равна та и направлена вдоль направления ускорения. Поэтому в предельном случае
* N N ,
tga = -7;— = -ттг» отсюда fe = ctga.
Атр kN
144
i/У
wwwww
Рис. 164.
30. Поскольку трение отсутствует, то. на цилиндр не будут действовать никакие силы, касательные к его поверхности. Поэтому при увеличении ускорения доски цилиндр будет подниматься на ступеньку, не поворачиваясь. Используя рис. 164, представляющий действующие на цилиндр силы, можно записать второй закон Ньютона для горизонтального и вертикального направлений:
та = N\ cos а,
0 = mg — Ni sin а — N.
Учитывая, что sin а = (R — Н)/R и что при максимально возможном ускорении агаах будет N — 0, получим
На цилиндр действуют реакции 165)
2 = m
VH (2R — H)
«max — S R — Н '
31. Так как цилиндр движется с ускорением а, то сумма действующих на него сил равна та. опоры и и вес его mg (рис.
та = N1 cos а — N2 cos а,
mg = Azj sin а + N2 sin а,
где cos а = RI2R, а = 60°. Решая эти уравнения, получаем
N\ = т (-4=- + а), \/з /
Что произойдет при а > gl\,r3 ?
32. Ртуть движется с ускорением а, следовательно, на нее действует горизонтальная сила, равная та. На ртутные столбики DB
и ЕС (рис. 166) действует сила со стороны трубки. На горизонтальном
участке ВС на ртуть будет действовать сила за счет разности давления Рв — Рс в точках В и С: Р в~ Рс = pgh,
p2LSa = pghS, отсюда h = ~±-.
10 Л. П. Баканина н др.
145
_ , 2La „ gH „
Ртуть начнет выливаться, если h —-----> Н, т. е. а> Дав*
ление в точке А
Рд + Рг 1
РЛ=-------g---=2‘ lP° + PS (h + Л1) + ро + pgfti],
но h + 2hi = Н; поэтому
Рл = ро + уРЙ7Л
33. На основании второго закона Ньютона запишем та = kmg,
где т — масса автомобиля, а а — его ускорение: о2
а~ 2Г
Таким образом,
1)2
1 = ~Г « 100 м.
34. (mi + 'п2) а = F. Здесь а — максимально допустимое ускорение грузов. Так как наибольшая нагрузка, которую выдерживает нить, равна Р, то максимальное ускорение груза т2, а значит, и всей системы, будет а = Р1т2, откуда
Р = р т{ + т2
т2
Если сила действует на груз т2, то
Р = р mi + m2 -mt
35. По второму закону Ньютона ускорение а равно
F — (т . + т„ + т\ g 188,8 н — 16 кг 9,8 м/сек2
а =-----L_A----£-----Lt. =----------- --------------= 2 м/сек?.
т . + т _ + т 16 кг
A D
Натяжение у верхнего конца веревки
/в = (тв + ш) (а + g) = 106,2 н,
а в середине веревки
4 = ("гв + -у) “ 82’6 «
Зв. Пусть коэффициент трения k. Тогда на отцепившуюся часть состава действует сила k Mg; ускорение этой части опреде-V лится из уравнения
о о
146
следовательно, скорость ее меняется по закону v — v0 — kgt. Время, по прошествии которого скорость уменьшится в два раза,
= v°
1 2kg ‘
На остальную часть состава действуют две силы — сила тяги и сила трения. До разрыва состава сила тяги уравновешивала силу трения: F\ = kMg. После разрыва — ускорение а2
оставшейся части легко найти:
4 Ма2 = FT- Дтр = kMg - ~ kMg = 4 kMg, О Ou
1 .
= k8’ скорость этой части
, 1 г.
1’2 = + у
и в момент времени ti равна . 1 , t'o 5 и2 = сй+^к3-~-с0.
37. Так как трение в оси блока и его масса пренебрежимо малы, то натяжение Т вдоль веревки, связывающей грузы, будет постоянным. Поэтому уравнения движения для грузов mi и т2 соответственно будут (рис. 167):
Рис. 167.
т-.а — mig — Т, m2a =Т — m2g,
где Из
а —ускорение грузов. Пружинные весы растягиваются силой 2Г. уравнений движения легко найдем
2Т = = 4 7 т = 2 35
m 1 + m2
mi — m2 , п„ , >
а —----:---Я=1,96 м сек2.
mi + m2
38. По аналогии с решением задачи 37 найдем
а = m । ~ П'2 р mi + т2
где а — ускорение каждой гири, a и т2— массы гирь (mi > т2). За время t каждая гиря пройдет путь й/2. Значит,
h
а ~ ~[Г
10*
147
Подставляя это выражение в исходное равенство, нолучим g + ^г
—г-1-11-
mi
т2
39. Уравнения движения грузов: Ш\а = ni\g — Т, т2а — Т — m2g - Етр, (т, — m2)g — FTp 1
а — ---------------— as-- О
тх + т2 6
2/n2g + FTp 7 = m1------------«
rni + m2
40. Натяжение вдоль всей веревки задачи 37). Поэтому уравнения движения грузов М\ и М2 соответственно будут
Mtai = Mtg-T, М2а2 = 2Т — M2g.
Нетрудно видеть, что а\ = 2а2 (почему?). Учтя это, получим
2Mi -М2 !"
откуда
1,6 м1сек2,
417 Г.
постоянно (см. решение
--------g_
2М + ~М2
Если 2Mt > М2, 41. Так как время постоянно
то груз М\ будет опускаться.
груз М неподвижен, то натяжение веревки все равно весу груза М. На обезьяну действуют сила тяжести (вниз) и сила натяжения веревки (вверх). Отсюда ускорение обезьяны
М — т а =-------g.
т
Время /, очевидно, равно t=V21/а = 4 сек.
42. Пусть белка находится в точке 4 (рис. 168). Сила, действующая на колесо со стороны белки, равна весу белки Р и направлена вертикально вниз. Ускорение колесу будет сообщать касательная составляющая F силы Р
F = та,
а— ускорение колеса. Так как F есть не что
где т — масса, иное, как сила трения, то
Fmax = kP cos а.
С другой стороны
F ~ Р sin а.
н
а
148
Исключая нз двух последних равенств угол а, получим (ЛТ—масса белки)
с _ п k kgM
max гт+f= ’
откуда &£ М g
amax“7TTP т ~ 2'
Читателю рекомендуется подумать, где в приведенных выше рассуждениях было использовано условие постоянства ускорения колеса.
43. Максимальное ускорение доски, при котором груз еще не будет соскальзывать, атах> очевидно, будет
Потл.ч = — kg — 0,98 м/сек2.
Если ускорение доски больше атах, то груз начнет скользить по доске.
44. После того как веревка натянулась, груз некоторое время продолжает двигаться вниз, но ускорение а груза направлено вверх и равно
Т-Р
где т — масса груза. Чтобы, двигаясь с таким ускорением, погасить скорость v = У2gh, груз должен пройти путь I, причем
v2 _ 2ghm Ph
2а “ 2 (Т-Р) “ Т-Р ~ 15 м'
45, Решение задачи поясняет рис. 169. Сила FTp, тормозящая маховик, равна
FTp — kF. (1)
С другой стороны,
FTp ~ Ма, (2)
где а —линейное ускорение точек обода. Так как конечная скорость обода равна нулю, то а — v/t. Учтя, кроме того, что v — а/?, получим
<о/? а~ t
из равенств (1), (2) и (3) следует, что
, г, ,. а« kF = М---------------------
(3)
(4)
Отсюда
Ма/?
kF '
(5)
149
Для того чтобы найти п, можно воспользоваться соотношением S = at2/2, где 5 = 2nRn — путь, пройденный до остановки точками обода
(6)
Подставляя сюда выражения для t и а, получим = а/2 = = Afto2/?
П 4aR 4nRt 4nkF
46. Задачу можно решать аналогично предыдущей (читателю предлагается проделать это сахмостоятельно), но более простым в этом случае оказывается энергетическое решение. Кинетическая энергия, запасенная вначале в колесе, равна М (aR)2/2. Она вся переходит в работу против сил трения
--------•» kF2nrn,
где п — число обо-ротов, которое сделает новки. Таким образом,
колесо до полной оста-
MaFR2
П 4nkFr
47, На тело действуют силы: тяжести стороны наклонной плоскости и
па рис. 170. По наклонной плоскости с углом на-
клона а тело движется равномерно, поэтому
mg sin а = mgk cos а,
mg, нормального давле-трения FTp, как указано
вил N со
где k — коэффициент трения. Отсюда k = tg а.
По наклонной плоскости с углом наклона р > а тело будет двигаться вниз с ускорением а под действием силы /:
f = F - FTp = mg sin p - FTp,
где FTp= kmgcos [3. Так как f = та, то из этих уравнений
, • „ х „ч sin (Р~а)
а = 8 (sin Р - tg a cos ₽) = g-.
Зная длину наклонной плоскости 1 = Л/sin р, можно время скатывания t определить из равенства
. — а^2
1~ 2 ’
откуда
2Л cos а
g sin р sin (р - а) ’
150
48. Обратившись к рис. 171, легко понять, что FTp = kmg cos а, F = mg sin а,
где nt — масса автомобиля, FTp — сила трения, F — равнодействую-
щая (сумма) сил тяжести mg и реакция Л'. Отсюда
та = Ftp — F, или
а = g (k cos а — sin а)
и, окончательно,
й = А±£^А«о,66.
g cos а
49, Путь, пройденный шайбой,
Рис. 171.
5 = -Д-sm а
Для вычисления сил, действующих па шайбу, можно воспользоваться рис. 170. Очевидно, что сила трения Ртр шайбы о плоскость
FTp = kmg cos а,
где т — масса шайбы. Ускорение шайбы а определяется из второго закона Ньютона
та — mg sin а — kmg cos а,
или а = g (sin а — k cos а). Скорость шайбы в момент удара
Рис. 172.
По =• K2as = к2gh (1 - k ctg а).
При упругом ударе величина скорости не изменится. Ускорение а, при подъеме шайбы будет (рис. 172)
Л-р + mg sin а at =--------------= g (sin а + k cos а).
Если Sj — путь, который прошла
то высота ее подъема
шайба после удара о стенку,
°б
hi = Si sin а = -ц— sin а = h 2д j
sin а — k cos а
sin а + k cos а ’
50. Силы, действующие на брусок, изображены на рис. 173. Так как движение возможно лишь вдоль наклонной плоскости,
151
та N = mg cos а, а сила трення FJp = kN — kmg cos а. Второй закон Ньютона дает
ma — 2mg — mg sin a — mg cos a, откуда
a = g [2 — (sin a + cos a)].
Ускорение будет минимальным, если сумма sin a + cos a примет максимально возможное значение. Как известно,
_ . ЭТ / \
sin a + cos a = 2 sm — cos la-— .
4 \ 4 )
Отсюда видно, что максимальное значение этой суммы будет при а = л/4. Следовательно,
51. Уравнения движения для нижнего и верхнего брусков соответственно будут (рис. 174)
Ma = F-T-FTp,
ma = Т — F тр,
где Г —сила натяжения веревки. Учитывая, что FTp = mgk, из (1) получим
F = а (Л4 + m) + 2mgk = 24,5 н.
52. Сила F, сообщающая телу ускорение, равна
F = mg sin a — mgkt cos a = mg (sin a — k\ cos a)
(см. задачу 47). Горизонтальная составляющая Fr этой силы будет
Fr = mg cos a (sin a — ki cos a).
Очевидно, такая же сила Fr будет в горизонтальном направлении действовать со стороны тела на клин, стремясь сдвинуть его с места. Препятствовать этому будет сила трения клина о пол, максимальная величина которой
FtP = kN,
где N — сила давления клина на пол. Нетрудно видеть, что
N = mg — F sin a,
152
где F sin a — вертикальная составляющая сила F. Подставляя значение F, получим
У = nig-(l — sin2 a + fei sin a cos a) = mg cos a (cos a + kt sin a).
Для того чтобы клии оставался неподвижным, необходимо выполнение неравенства Frp Fc или, подставляя сюда значения Гтр и Fr, найдем
, '' tg a - fe 1 k tg a + I
53. Обозначим силу натяжения веревки Г, Уравнения движения грузов будут
Ma — Mg — Т,
Ма = Т — (Етр + F);
здесь а — ускорение грузов, Етр — сила трения, а сила F = Mg cos a. Нетрудно видеть, что FTp = kMg cos а. Подставляя эти значения в исходную систему уравнений и исключая из них а, найдем
2 Г = Afg + Fjp + F = Mg (1 + k cos a + sin a).
На блок действуют две одинаковые силы Т, угол между которыми я/2 — а. Сила F давления блока на ось будет равна векторной сумме этих сил:
£? П'Г' / SX Ct \
Г —2Т COS —;---,
\ 4 2 ]
54. На груз М в горизонтальном направлении действует только сила Т натяжения веревки, поэтому
Ма=Т, (I)
где а — ускорение груза М относительно стола. На груз m действуют силы: тяжести mg и натяжения веревки Т, направленные в разные стороны. Поскольку ускорение груза m относительно стола тоже будет а, а ускорение стола относительно Земли Ь, то ускорение груза относительно Земли равно а — Ь. Следовательно,
mg — T — m (a — b). (2)
Из равенств (1) и (2) получим
m(g + b) а М + т •
Ускорение относительно Земли
_ , mg- Mb а — b — —г7~,--.
М + т
Из последнего выражения, в частности, следует, что если Mb —mg, то а — b = 0. В этом случае груз т находится в покое относительно Земли. Если Mb > mg, то а — b < 0 и груз относительно Земли будет двигаться вверх.
153
Примечание. Заметим, что (2) можно переписать так: m(g + Ь) — Т = та.
Следовательно, для того чтобы найти ускорение а груза т относи-тельно стола, можно считать, что стол неподвижен, а укорение силы тяжести g возросло на величину Ь.
55. Решение этой задачи можно получить из решения предыдущей, если везде знаки перед b заменить на обратные. В итоге получим
т (g - b) М + т '
, , mg + Mb a + b = .. ,
М + т
Из последнего выражения видно, что ускорение груза т относительно Земли не может быть больше g.
56. Задача решается так же, как и задачи 54 н 55. Пусть а —ускорение груза 2т относительно блока. Тогда ускорение этого груза относительно Земли а — Ь. Второй закон Ньютона дает
2mg — Т — 2т (а — &);
(1)
Рис. 175.
веревки. Для груза т аналогично имеем Т — mg — т(а + Ь).
Из (1) и (2) находим давление блока на
2T=|m(g + &), О
(2) ось:
т. е. здесь, как и в задаче 54, сразу можно считать блок неподвижным, а ускорение силы тяжести возросшим на величину Ь.
57. Задача аналогична задаче 56. Ответ: 2Т ~^m(g-b).
58. Силы, действующие на тело, находящееся на наклонной плоскости, указаны на рис. 175. М —реакция опоры, F — сила тре-
ния. Тело будет двигаться вместе с наклонной плоскостью (т. е. с ускорением а), если суммарная сила, действующая на него, направлена горизонтально и равна та, vjifi т — масса тела. Отсюда:
М cos а + F sin а — mg = О, F cos а — N sin а = та.
Максимальная сила трения F = kN. Учтя это, получим
_ k cos а — sin а _ fe — tg а cos а + k sin a 1 + k tg а ’
Если fe = tga, то тело начнет соскальзывать при любом сколь угодно малом ускорении.
154
59. Задача аналогична задаче 58, с той только разницей, что теперь сила трения будет направлена вниз по наклонной плоскости (рис. 176). И в этом случае для того, чтобы тело двигалось вместе с наклонной плоскостью, сумма горизонтальных проекций всех снл должна равняться та (т — масса тела), а вертикальных — нулю:
та = У sin а + F cos а, О = Д' cos а — F sin а — mg. Максимальная сила трения F = kN. Отсюда k + tg а а = ------------------гт— •
1 — k tg а
Если k tga= 1, то ни прп каких сколь угодно и
больших а тело не будет подниматься.
60. Положим, что автомобиль во время "
разгона движется с некоторым ускорением а. _ . -
Тогда разность давлений Р бензина на пе- ”ис' реднюю и заднюю стенки банки должна быть равна силе, вызывающей ускорение всего бензина, деленной на площадь боковой стенки
По второму закону Ньютона сила F, вызывающая ускорение бензина, равна та. Кроме того, т = S/p, где т — масса бензина, S — площадь стенки банки,/—длина банки н р — плотность бензина. Окончательно искомая разность давлений равна
„ Slpa .
Р = —f — = p/a.
О
Ускорение а находится по формуле
а = v/t.
Подставляя численные данные, получим
г, п-7 m3 1(2 по 18 м/сек с„ н
Р « 0,7 • 103 —г • 0,3 м ----= 63 —г.
л3 60 сек м2
61. Средняя сила давления F равна изменению количества движения пуль за 1 сек: F = mvn, где /г =10 \/сек — число выстрелов в секунду. Подставляя данные задачи, получим
F = 10-2 кг • 8 • 102 м/сек • 10 \/сек = 80 н.
62. Изменение силы тяги двигателя можно найти, воспользовавшись вторым законом Ньютона, записанным в следующей форме:
Д(то) = F Д/, (1)
где Д/ —некоторый промежуток времени, а Д (то) — изменение количества движения микрометеоров, столкнувшихся с кораблем за время Д/. Так как, по условию, скорость корабля постоянна, тонз (1)
(2)
155
Здесь Am — масса микрометеоров, столкнувшихся с кораблем за время Л/. Если р — плотность микрометеоров (т. е. масса в единице объема), то, очевидно, что
Am = oSp \t. (3)
Из (2) и (3) окончательно получаем
E = n2Sp = 98- 108 дин~ ЮГ.
63. Задача аналогична двум предыдущим. Сила, тормозящая движение автомобиля, равна изменению количества движения до-
ждевых капель за 1 сек в горизонтальном направлении. Эта сила преодолевается силой трения. Отсюда
Утр = tnvSa — 300 н.
64. При вытекании струн пены на огнетушитель действует сила реакции струн. Ее величину можно определить из соотношения
Ер t = tnv, где т — масса пены, выброшенной за время t,
Fp — v = 0,2 кг!сек • 20 м!сек = 4 н.
Сила N, с которой человек должен держать огнетушитель, как видно из рис. 177, должна быть равной по величине силе F и противоположной ей по направлению:
N=F = VF2p + P2~2O,4 н.
Работа, мощность, энергия
65. Начальная потенциальная энергия mgfi саней целиком расходуется на преодоление сил треиия
mgh = Ftl + Fs S,
где т — масса саией, Fx — сила трения при движении по горе. Е2 — сила трения на горизонтальной поверхности, I — длина горы. Нетрудно видеть, что
h
E, = mgfecosa, , F2= mgk.
1 sma 6
Используя эти соотношения и (1) получим
S = /; — cig aj ~ 49,05 л.
156
66. При подъеме на гору первоначальная кинетическая энергия саиок расходуется на преодоление трения н переходит в потенциальную энергию:
mvQ
—2— = kmgl cos а + tngl sin а.
Коэффициент трения k находится из условия
2 2
«г0 к , . "о
-X— = ktngls, откуда k = -Х-—,
* 4gl{)
и, окончательно, __________________________________v0*0_______
Vq cos a + 2g/0 sin a
67. На горизонтальном участке пути энергия двигателя расходуется только на работу против сил сопротивления движению автомобиля (сопротивление воздуха, треине о дорогу и в осях колес). Обозначив результирующую силу сопротивления F, а расход бензина на горизонтальном участке пути ац можем поэтому написать
aiqr\ = Fl.
Так как при подъеме автомобиля сила сопротивления не изменится. Но гателя будет возрастать еще и потенциальная энергия автомобиля. Закон сохранения энергии запишется теперь так:
a2<74 — Fl-F Mghi,
где я2 — расход бензина при подъеме. Таким образом,
Mg/г/
а2 — я. = —5— = 2,2 кг.
скорость остается прежней, теперь за счет энергии дви-
68. На рис. 178 изображены силы, действующие на тело. Та:с как тело поднимается равномерно, то
F = Ftp + mg sin a, Ftp = kmg cos a = mg cos a
(здесь учтено, что fe=l). Затрачинаемая мощность
p = Fv = mgv (sin a + cos a) = 2mgv sin • cos — a
Мощность максимальна при a =
fmax = mgv V2.
157
69. Энергия копра целиком расходуется на преодоление сопротивлении грунта. Поэтому
/по2 , D Р -у- + Ps = Fs.
Так как m = P/g, то окончательно
F = Л « 2,5 • 10s н«250Т.
\ 2gs 1
Отсюда видно, что Р <С F, поэтому поправка Ps в исходном уравнении существенной роли не играет. Заметим, что приведенное решение справедливо только при пренебрежении массой сваи. Если массы сваи н копра сравнимы, то величина F будет зависеть как от массы сваи, так и от характера удара («упругого» или «неупругого») копра о сваю. Мы рекомендуем читателю в качестве полезного упражнения самостоятельно получить точные выражения для F в случае «упругого» и «неупругого» ударов.
70. Среднюю силу F можно найти из закона сохранения энергии. Пусть IT — работа, совершенная двигателем в течение трех суток. Тогда W = FS, где S — путь парохода за трое суток. Очевидно, что
F — Qqr\.
Вычисляя S и подставляя эти данные в исходное уравнение, получим
кЗ О
71. Всплывающий шарик вблизи поверхности воды будет обладать кинетической энергией
где IP'— потери энергии на тепло, а Ед —сила Архимеда. Так как шарик выпрыгнул из воды на высоту Ль то закон сохранения энергии дает
(fA - mS) h - F = mgh lt
или
W^F^h-rng (Л-F/zJ.
Учтя, что
4
f A = у
где p — плотность воды, и подставляя численные значения, получим Г = 219 520 эрг 2,2 • 10“2 дж.
Рекомендуем читателю самостоятельно разобраться в том, какие допущения были сделаны при решении задачи.
72. Когда веревка весит симметрично относительно блока, ее центр тяжести находится на расстоянии 1/4 от ее концов и на та
158
ком же расстоянии от блока. В момент соскальзывания с блока центр тяжести опустился на //4 и, следовательно, потенциальная энергия уменьшилась на mgl[4. За счет убыли потенциальной энергии веревка приобретает кинетическую энергию znv2/2. По закону сохранения энергии
nw1 mgl Г gl ,
—у =—у, v=y ~ Ю3 см/сек.
Движение веревки не будет равноускоренным. Объяснение этому может быть легко получено с помощью второго закона Ньютона и явится полезным упражнением для читателя.
73. Задача аналогична предыдущей. Закон сохранения энергии, записанный для того момента, когда конец веревки соскользнет со стола, дает
7! 2 т
(Ml + М2) -у = М<gl + M2g-^-, откуда
= 1/ M2gL + 2MlgL v V Mt + M2
74. Эту и ряд следующих задач проще всего решать графически. Отложим по оси абсцисс высоту h, на которую поднимается поршень, а по осн ординат — действующую на него силу F (рис. 179),
Так как атмосферное давление Р = 1 кГ/см2 = 9,8 • 104 н/м2, то поршень поднимет воду до высоты 10 м (почему?); при этом сила, действующая на поршень и равная весу поднятой воды, меняется пропорционально высоте h. На высоте 10 м вода оторвется от поршня, и поршень пройдет последние 5 м, совершая работу против снл атмосферного давления. Очевидно, работа А по поднятию поршня равна площади, ограниченной графиком. Так как сила атмосферного давления Fo = PS = 9,8 • 102 н, то
А = у10 м • 980 н + 5 м • 980 н = 9,8 • 103 дж.
75. Используем тот же прием, что и в задаче 74, т. е. представим силу трения Ртр в зависимости от пути й, пройденного санками по асфальту, в виде графика (рнс, 180). Тогда площадь под
159
графиком равна работе сил трения. На основании закона сохранения энергии
mv2 1 ,, .
-у- = у mgkL + mgkx,
отсюда х = 0,84.и, а весь путь, пройденный санями до полной остановки, составит
S — L + х — 2 м + 0,84 м = 2,84 м.
76. Из рис. 181 следует, что искомая работа Л будет (см. решения задач 74 и 75)
А = Fа + у Fa = Fa.
77. Общая работа, совершенная против силы тяжести,
U7-= SZ.pg (Яо +/7), (1)
где S —сечение палочки. Эта работа равна работе W+ архимедовой силы, вычисление которой, как и в задачах 74—76, удобно провести графически.
Введя обозначения: х — смещение палочки из начального положения, fA — архимедова сила, a FQ = SLgf>0 — ее максимальное значение, легко заметить, что W+ будет равна площади под кривой на рис. 182
W+ = (>0SLg(H0-L} + ^^8_i (2)
Приравнивая (1) и (2), найдем Н:
"-vt""-'?)-''-
Примечание. Приведенное решение предполагает, что палочка целиком выскакивает из жидкости, т. е. L < 2Н0 (1 — р/р0). Однако подобным методом можно решить задачу и в том случае, когда палочка выскакивает не полностью.
160
78. Так как доска однородна, то сила трения, действующая на кусочек длиной Дх, есть AF = kMg hx/L. Пути, проходимые различными точками доски при повороте, s — ax, где х — расстояние данной точки от неподвижного конца. На рис. 183 приведен график зависимости пути s (х). Работа против сил трения для кусочка доски длиной Дх, удалеииого от неподвижного конца на расстояние х, очевидно, равна
, ,, Дх
ДЛ = kMg —j- ах,
т. е. с точностью до постоянного множителя kMgjL равна площади, заштрихованной на рис. 183.
Вся работа по повороту доски равна площади под графиком, умноженной на kMgjL'
kMgaL.
79. Так как S2 = 2Sb то при погружении бруска па глубину L/4 уровень воды в стакане поднимется на высоту L/4. Таким образом, для того чтобы брусок оказался полностью под водой, его достаточно погрузить на 1/4, а для того, чтобы он достиг дна, его нужно опустить на L/2. График зависимости разности между выталкивающей силой и силой тяжести от глубины погружения h дан на рис. 184. Из этого графика, по аналогии с задачами 74—77, находим работу:
J О / Q
8Э. На основании закона сохранения энергии 5 2
• v, m<yV7>
(milt + m2l2) g = + -g—,
где О] и о2 —скорости грузов и т2. Легко видеть, что
£1_ = Ц2_
/j i2
И Л. П. Баканина и др.
161
Из этих уравнений находим
V
?=
2g(mil{ +т21^ I* 2 т1 + т2~д ‘1
81. Положим, для определеииости, что mjj > zn2/2. Это значит, что груз mt пойдет вниз (рис. 185). Закон сохранения дает
Рис. 185.
2 ‘
IУ? m9V<
(т it 1 ~ т2^г) ~ —2---1"
где о1 и и2 — скорости грузов ms и т2. Так как сч ' lt = с2 : 1г, то
..2 2g (т^ - т212)
°i--------------р •
12
ПЦ + /и2 —
82. В начальный момент энергия системы равняется потенциальной энергии груза массы
Ea = migh0. (i)
Предоставленный самому себе груз mt начинает опускаться с некоторым ускорением, приводя во вращение спицы с грузами т. Когда груз mi достигнет Нола, его потенциальная энергия Еп перейдет в кинетическую энергию самого груза т{, равную EKi, и грузов т, расположенных на концах спиц, равную EKit
9 9
niyVi 4mv?
might = —2~ +—g—
(2)
где Vi — скорость груза непосредственно перед соприкосновением с полом, а о2 —скорость грузов т в тот же момент. Когда груз достигнет пола, произойдет неупругий удар, при котором кинетическая энергия груза /п1 целиком перейдет в энергию неупругой деформации. После этого механическая энергия системы становится равной кинетической энергии вращающихся грузов т:
4mv« Р —______£.
KS 2 ‘
Пока груз тг находится на полу (нить свободно сматывается и затем свободно наматывается на барабан), механическая энергия системы не меняется. Когда вить снова натягивается и начинает поднимать груз гпр то ЕКг переходит в потенциальную энергию груза /Пр Так как Ек? меньше, чем начальный запас энергии Еа (ЕКг= Еп —EKt), то груз т[ поднимется на некоторую высоту йр меньшую ha. Очевидно, чтобы найтн hi, надо знать скорость о2
162
вращения грузов т. Угловая скорость точек обода барабана, на который намотана нить, и угловая скорость грузов на спицах одинаковы. Линейная скорость »i обода (и груза гщ) и линейная скорость с>2 грузов т на спицах выражаются через угловую скорость <в следующим образом:
v! = <вг, v2 = Следовательно,
= (3)
Для нахождения скорости v2 подставим (3) в (2). В результате
получим
-? niigha
°2- 1 г2
—/П] -J- + 2OT
Теперь находим высоту hi поднятия груза Ир
4mv2 mighi=—g—.
Вгспользовавшись (4), сразу найдем
9 9 * (5)
mlr2 + 4mlQ
Приведенное решение поясняется рис. 186.
Примечание. При решении пред- У/////////////////. полагалось, что груз тъ отрываясь от пола, мгновенно приобретает конечную скорость, Рис- 1°°'
т. е. испытывает бесконечно большое ускорение. Поэтому в момент рывка в нити возникнут бесконечные силы натяжения, которые растянут нить, продеформируют ось блока и т. д„ как бы прочны эти детали ни были. Энергия, затраченная на деформацию системы, нами не учитывалась н поэтому результат (5) несколько завышен. Однако отметим, что рывок будет тем слабее (и неучтенные потери энергии — тем меньше), чем лучше при сравнимых по величине массах т и nit выполняется неравенство
г < 10.
Поскольку в задаче требуется иайти максимальную высоту подъема груза mit то решение (5) является правильным, но оно может быть реализовано, как теперь видно, только при г = 0.
83. Наиболее простое решение задачи может быть получено при помощи закона сохранения энергии. Допустим, что в начальный момент система находилась в покое. Так как тх > nl2 то, предоставленная самой себе, система придет в движение, и груз начнет опускаться с некоторым ускорением а. Пусть груз mt опустился на h см, груз т2, очевидно, при этом поднимется на ту же высоту h. Изменение потенциальной энергии системы будет
(«! - т2) gh.
11
163
На основании закона сохранения энергии
. О 9 9
4mv m,v, m9v,
(mi - m2) gh = —— + -у1 + -у,
(1)
где v, Vi и t>2 ~ скорости грузов т, mt и т2 соответственно. Нетрудно заметить, что
= 4 » = Viy. (2)
Подставляя (2) в (1), получим
-.2 2 (и1 — m2)gh
”i---------------JT-
mi + m2 + 4m —
Воспользовавшись известным кинематическим равенством г»1 = 2аЛ, найдем а:
° I2 '
m1 + m2 + 4m —
Задачу можно решить и при помощи второго закона Ньютона. Для этого обратимся к рис. 187. Груз т 2 движется с ускорением а под действием силы Тt натяжения веревки и силы тяжести, поэтому
пца = mi g — Т2. (3)
Аналогично для груза т2
m2a = T2-m2g. (4)
Ясно, что силы натяжения Tt и Т2 неодинаковы и разность этих сил приводит в движение грузы т. Ускорение at грузов т связано с а очевидным соотношением:
ai=ay. (5)
Разность сил Тх — Т2 создает относительно оси блока момент (Ti — T2)r. Этот сти компенсироваться моментом сил F дав
ления грузов m на спицы, т. е.
(Tt-Tt)r-Fl, (6)
где
F — 4mai. (7)
Действительно, так как барабан н спицы невесомы, то они начали бы вращаться с бесконечно большим ускорением, если бы равенство (6)
164
не выполнялось точно. Совместное решение (3)-(7) приводит к полученному ранее выражению для а.
84. За 1 сек насос на высоту h поднимает р(?кгводы (р—плотность воды). Мощность Ni, расходуемая на это,
Nt = pQgh.
Кроме того, насос сообщает воде скорость v = Q/S. Мощность расходуемая на ускорение воды,
mv2 ~1Г
= р
полная мощность
/ О2 \
N = Ni + Л'2 = pQ \gh + j.
85. Первоначальная мощность вентилятора IF| = mo2/2, где т — масса воздуха, перегоняемого за 1 сек, а о — его скорость. Для того чтобы через то же отверстие перегонять в единицу времени массу воздуха в два раза большую, его скорость нужно увеличить в два раза. Поэтому мощность вентилятора
Закон сохранения количества движения
86. Скорости тел непосредственно перед соударением: o1 = o2«=o0 = lz2g/?.
Так как удар неупругий, скорость тел после соударения одинакова (тела «слипаются»). Эту скорость о можно найти из закона сохранения количества движения:
2mo0— mv0 = 3/но,
1
0 = _0о = __.
Максимальная высота Н подъема тел после удара
2g
Я.
9
Угловую амплитуду можно найти из геометрических соображений (рис. 188)
О А = R - ~ ~ R, cosa = -S-,
V У V
8 а •= arccos
165
87. Скорость о । доски после того, как ее пробила пуля, находится из закона сохранения количества движения:
тоо = то + Л1Р|, vt = (с0 — v).
Кинетическая энергия доски, таким образом, равна
1 .. Г т . ,12 «2 (оо - о)2
Г = Т м [лГ (t,° “ • =— —~
2Л1
m2(fQ-^2
В тепло перешла энергия 2 °
mvQ mv~
Q = 2 2 2М ’
Q =i™ £o^L=o,998>
И7! М Vq+v
т (tig - с2)
где F| = ——----------потерянная пулей энергия;
= 0,002.
U71 М v0 + v
88. Так как в горизонтальном направлении на платформу внешние силы не действуют, то полное количество движения в этом направлении должно остаться неизменным, т. е.
у
(т + М) V = mv cos а + М -г-, О
откуда
V m + -5-, \ о и =---------------
т cos а
(1)
89. Сразу после выстрела пушка приобретает скорость t-'i — mv/M2. При этом ее кинетическая энергия
г = т2°2
После того как пушка перестанет двигаться относительно бруска, их общую скорость снова можно определить из закона сохранения количества движения
т
V*~ М, + М2 °’
их общая кинетическая энергия прн этом
г тЧг
2(Mt + M3)'
Из (1) и (2) легко найти энергию Q, перешедшую в тепло:
Afi
(2)
90. На основании закона сохранения количества движения
mv — MV,
где V — скорость лодки, а о — скорость человека относительно берега. Но о = (L — h)/t, V = h/t, где / — время, за которое человек перешел с носа на корму. Подставляя эти значения v и V в исходное уравнение, получим
Из последней формулы следует, что центр тяжести всей системы остается неподвижным.
Примечание. Выражение для h было получено в предположении, что скорость v постоянна. Однако исходное выражение mv=MV сохраняет свою силу для любых сколь угодно малых перемещений человека относительно лодки. Центр тяжести всей системы при таких перемещениях, очевидно, остается на месте. Поэтому положение центра тяжести сохранится и при конечном перемещении человека по лодке. Таким образом, сохранение положения центра тяжести можно принять за исходное условие при решении задачи.
91. Так как внешних сил в момент прыжка нет, выполняется закон сохранения количества движения, причем в данной задаче существенно, что он имеет векторную форму (рис. 189):
[(/«! + т2) v ]2 = (тtvt)2 + (m2v2)2;
v=тггЪг
Эта скорость образует с первоначальным направлением движения плота угол а, причем tg а = m2o2/m1oi.
/77/
Рнс. 189.
"(М+т)д
Рис. 190.
92. Центр масс системы цистерна — вода — груз по горизонтали сдвинуться не может, так как силы в этом направлении не действуют. Вначале, пока груз ие погрузился в воду, положение центра масс относительно центра цистерны у2 (рис. 190) определим из условия
(M + m)yo = p(/-yo),
167
Когда груз плавает в воде, вытесненная им вода, вес которой как раз равен весу груза, равномерно распределится по всей поверхности и центр масс всей системы будет совпадать с центром цистерны. Следовательно, цистерна должна сдвинуться на расстояние Уй в сторону груза.
Теперь о механизме явления. Когда груз входит в воду, он «расталкивает» ее, посылая через иее импульсы давления во все стороны. Но до правой (иа рис. 190) стенки импульс дойдет быстрее и даст цистерне толчок вправо. Когда до левой стенки импульс тоже дойдет, тележка получит толчок влево и остановится. Так как импульсы могут частично отражаться, то окончательное положение цистерны установится ие сразу, а после нескольких колебаний.
93. Начальную скорость V маятника можно определить при помощи закона сохранения количества движения:
mv = (Л1 + т) V, откуда V — mv/(M + т).
Высоту h, на которую поднимется маятник после удара пулн (рис. 191), найдем из закона сохранения энергии:
-----— = (М + т) gh,
откуда
Рис. 191.
Теперь легко определить угол а:
, h , m2v2
cos а — I---г- = 1 —ТТТ-.—•;.
Z (M + m)22gl
94. Движение частей атома после распада может быть описано уравнениями
М ! = Л12и2,
первое из которых является законом сохранения количества движения, а второе — законом сохранения энергии. н о2 — скорости масс Afi и Afj. Отсюда
М, У2Ё Mt У2Ё
V! = —__-___ , V2 =» — - - 11 .
У MtM% + м2м? У м tM% + м^
95. Кинетическая энергия Е атома RaC равна
MV2
Е----2“’
где V — скорость атома, М = Ат0 = 214т0, т0 — масса протона, равная 1,67-10“ 24 г. Для нахождения V воспользуемся законом сохранения количества движения:
М V = mev,
168
где о —скорость, me— масса электрона: me = 9,l • 10-2s г. (В левой части последнего соотношения мы пренебрегли массой электрона по сравнению с М.) Величину о найдем из очевидного соотношения т^3 .
2 '
Из полученных уравнений
£ = яз 1,3 . IO"13 эрг= 1,3- Ю"20 дж.
Л/7?о
96. Если v — скорость нейтрона, тп — его масса, a mCd — масса ядра кадмия, то
тп<> = («П + «Cd) V-
Учтя, что тп = 1,67 • 10~24 г, mcd= 112,4 тд,
22^ = 17
2
получим
.. y^rrinW
И =----------- « 104 м/сек.
mn + mcd
97. Обозначим массу нейтрона т, его начальную скорость о0. После первого соударения
mv0 — 4mv{ — mop
2 , г3 2
mv/. 4mvt mv\
~2~‘ 2 + -2-’
где 4т — масса ядра гелия, — его скорость после соударения, t>i —скорость нейтрона после соударения. Решая эти уравнения, определяем
3
01 = ¥оо.
После второго соударения аналогично имеем mv{ — 4mv2 — mv2, 9 z2
mv{ 4mv2
__ _
О tnvi + ~Г’
и
3
9 °2==“С1=25
Следовательно, энергия нейтрона уменьшится в 625/81 « 7,7 раза.
169
98. Запишем закон сохранения количества движения для направления полета ядра дейтерия и перпендикулярного к нему направления полета нейтрона (рис. 192);
mDVD = тНе • У„6 • cos ф, mnVn~mHe' rHesin Ф-
По закону сохранения энергии
mnvn , "'Не^Не „
—2~ +-----2---------2~ + Q-
Решая уравнения, получим
99. При ударе маятника о плиту горизонтальная составляю-
велнчину, изменит направление на противоположное. Так как
v = 2g и cosa = ~-,
ТО
/ад
пв = v cos а —-~—•
(рис. 193). Высота ft, на которую поднимется маятник, равна
2g = 8g 8 h
100. В момент взрыва полное количество движения снаряда равно нулю. Если т— масса каждого осколка, a и t>2 — их скорости, то
tnvt + moa = 0, или vi = — о2-
170
Высота, на которой взорвался снаряд,
2g ‘
Из закона сохранения энергии для первого осколка получим т01 „ т (2с,о)2 /—
2— + mS" =—~2 ’ отсюда 01 = о» УЗ. Следовательно, v2— = —v0V3, на землю второй осколок упадет с такой же скоростью, что и первый осколок. Время его падения t складывается из времени ti подъема на максимальную высоту и времени /2 падения вниз:
= Z==£0(2 + /3-).
g g g g
101. Скорость одного из осколков, например, olt будет максимальной, если он будет лететь в ту же сторону, куда прежде летел снаряд, а два других осколка — в противоположную. Тогда из закона сохранения количества движения
tnvi = 3mv + mv2 + tnv3,
а нз закона сохранения энергии
2 2 9
mv\ mv?*
~~2~~T ~~2 2~•
причем сумма o2+»3 Д°лжна быть как можно больше, а »2 + t>| — как можно меньше. Оптимальные условия достигаются при и2 = о3 (можно представить + о|= (о2 + о3)2 —2о2о3; но о2 • и3 при заданном о2 + °з максимально, когда п2=о3). Окончательно имеем
»! = Зо + 2о2/
о2=Ат-2о|.
1 т 2
Решая эту систему, находим
Oj ~ 1500 м!сгк.
102. Скорость V шарика nit перед ударом можно найти из соотношения
V2 = 2gh = 2g(It-It cos a) = glt (1)
(здесь a = 60°). Так как в момент удара маятников на них никакие внешние силы в горизонтальном направлении не действуют, то справедлив закон сохранения количества движения:
tniV — niiVt + m2o2. (2)
171
Удар упругий, поэтому в момент удара можно воспользоваться законом сохранения энергии
mtV2 mrf т^>1
-2-=-2“ + “^“- (3)
Из (2) и (3) получим
т1 — т2 ту 2«17
V1 =------ V, О2 = ---у---.
mi + т2 mt + т2
Так как mt < т2, то направление t>i противоположно направлению V. Иными словами, после удара шарик mt отскочит назад и поднимется на высоту h^v^ig. Высота подъема второго шарика будет h^v^lZg. Углы «ц и а2 (рис. 194), на которые отклоняется
первый и второй шарики после удара, легко определяются:
cosai=l— cos <х2 = 1 —-т^-. (4)
/1 <2
Воспользовавшись соотношениями (1) и (4), окончательно получим
COS <X| =-g- +
(m, + m2)2 ’
mf тг f 2m2/|
Рис. 194. cosa2—1 — /2 (OT1 4-•
103. Из закона сохранения энергии можно определить скорости Ci и v2 свинцового шара непосредственно до и после соударения:
О) = 2 sin у KgL,
о2 = 2 sin ~ V~gL
Закон сохранения стального шара непосредственно после удара:
М М , ,,
-т-О1“ -т-Ог + ЛГо.
4 4
количества движения позволит найти скорость
Отсюда
1 / 0=,_.(С|_С2).
В тепло, таким образом, перешла энергия:
М of М о| Afo2
MgL (> 1 а P.«₽,o.a.
= —|—|3sin2^- - 5 sin2 + 2 sin — sin ту),
О \ Z Z Z Z /
172
Заметим, что если шары разлетелись после удара в противоположные стороны, то знаки углов а и fJ будут различными, если же после удара шары продолжали двигаться в одном направлении, то а и р будут иметь одинаковые знаки.
104. Если начальная скорость второго шара о0, а скорости первого и второго шаров после удара равны соответственно и с2, то по законам сохранения количества движения и энергии можно написать:
mva = Mvi — mv2, mvl Mv2t mv2 ~2~==~2~ + 2 1
Решая эту систему уравнений, находим связь между о, и v2:
Очевидно, что второй шар догонит первый, если о2 > °1, т. е.
105. Воспользуемся решением и обозначениями задачи 104. Связь между скоростями первого и второго шаров найдем из соотношения
1 /М 3
и2 = -ТГ-----1 =ТГ »!•
2 \ т I 2 1
Если шары вторично столкнутся
на расстоянии Z от стенки, первый
шар пройдет между столкновениями путь (Z — L), а второй — (Z + L) (рис. 195). Так как время, за которое они проходят этот путь*
одинаково, получаем
1-L »1
1+L 3
Т Vi
1= 5L— 15 м.
106. При соударении первого шара законов сохранения количества движения
со вторым на основании и энергии имеем
Ш]О0= mtvt + ш2а2>
2 2'
m{VQ mtOj m2v2 ~~2~' 2~ + 2 •
Аналогично, при соударении второго и третьего шаров m2v2 + m3u3’ /2 9 2
/Л2°2 m2V2 m3V3
2 =~2 + 2 *
(1)
(2)
(3)
(4)
173
По условию задачи
mitij =» т2о2 = m3v3.
(5)
Найдем связь оь v2 и о3. Из уравнений (1) н (2), (3) н (4) находим
Z , «3
О2=°2 + 7^°3-
(6)
(7)
а уравнения (5) и (7) в свою очередь дают
Рис. 196.
(8)
(9)
Теперь из уравнений (5), (8) и (9) найдем m| = 2m2 = 6m3. Таким образом c3>»2>yi и дальнейшие столкновения
шаров невозможны.
107. Скорость v шара после удара пули сохранения количества движения (рис. 196):
mVi — Mv -г mV2, откуда
Энергия IF, перешедшая в тепло, равна mVf mV2 Mv2
т
~2
[tn 1
найдется из закона
108. Решение задачи поясняет рис. 197. В момент удара пули о шар справедлив закон сохранения количества движения:
mv — MV+tnvi, (1)
где V — начальная скорость шара, oi —скорость пули после вылета из шара. Так как V2 = 2gh, а
of = 2gx,
ТО ___
{mv -MV2gh У
Х 2gm2
Примечание. Применение закона сохранения количества движения (1) в данном случае может вызвать сомнения, так как,
174
кроме «внутренних» сил взаимодействия (трения), на шар и пулю действует «внешняя» сила тяжести. Чтобы обосновать (1), запишем для шара второй закон Ньютона:
V
= Л1
(2)
Здесь Frp — сила треиия между пулей н шаром, t — время пролета пули через шар. Аналогичное уравнение для пулн будет
г v — v1 ,п.
Ftp - mg = т —pi j (3)
т (о — Oi) — изменение количества движения пули при пролете через шар. Теперь видно, что (2) и (3) дают (1), если можно пренебречь действием сил Mg и mg по сравнению с силой трения F\p.
109. Будем считать, что сначала происходит соударение пули с клином, а потом — клииа со столом. Так как количество движения—вектор, применим закон сохранения количества движения отдельно для вертикальной и горизонтальной составляющих. Если vt — начальная скорость пули, а о2 — конечная, и V — вертикальная скорость клина после удара, то
mvi = MV,
mv2 = MV, mv2 mv\ MV2 MV’
(1)
(2)
(3)
так как удар упругий.
Выражая vt и V из (1) и (2) и подставив их в (3), полу чае ш
M2V2 mv22 AfV2
‘ 2m ' = ~~2~ + ~2~ + 2M ’
откуда находим
2 M2 (M — m) ,2
2 m2 (M + m) 1
высота подъема пули
v2 M2 (М - т)
2g~ 2gm2 (М + т) ’
Примечание. В решении не рассмотрено второе соударение клина со столом, так как в условии задачи оговорено, что трением можно пренебречь, и, следовательно, горизонтальная составляющая скорости клииа при этом не изменится. Однако в реальных случаях, поскольку нормальное давление при таком соударении очень велико, даже при малых коэффициентах трения сила трения достигает большой величины и может изменить горизонтальную скорость,
175
НО. Задача решается аналогично предыдущей:
moi=MV', (1)
mv2 = MV, (2)
mv2 MV2 MV'2
mgh “ ~~2~ + ~2--1--2—’
откуда ______________
V~l/
111. В нашей задаче сохраняется составляющая количества движения по горизонтали, так как в этом направлении внешние силы не действуют. Пусть <?] — скорость призмы. Горизонтальная составляющая скорости собаки относительно льда будет v cos a — тогда Moi = т (v cos a — t>i),
mv cos а
Vi = M + m
112. Так как горизонтальная составляющая количества движения системы, «тело» + «клин» равно нулю и не меняется, то при соскальзывании тела клин приобретает скорость, направленную в противоположную сторону и равную
Следовательно, потенциальная энергия тела т перешла в кинетическую энергию тела и клина (трения нет):
Итак,
113. Минимальная скорость тела определится нз условия, что в верхней точке горки скорость его относительно горки равна нулю; при этом по закону сохранения количества движения
mva = (М + т) t»i, (1)
где т н М — массы тела и «горки», р0 — начальная скорость тела, V] — скорость горки в тот момент, когда тело достигнет ее вершины. Из закона сохранения энергии имеем:
mv% (М + т) v2
-jj— = mgH +-----------»
7~2gH(M + m)
t>o = Т/ —2—~ 6,9 м1сек,
114. Скатившись с горки, вагон 2 приобретает скорость оа «= V2gH , когда он сцепится с вагоном 1, то, по закону сохранения
т
количества движения, скорость их будет в два раза меньше. Вагой 3 достигнет этой точки через время t со скоростью о0. Расстояние х, которое они пройдут до столкновения, найдется из условия
^ + /=Т^2’ _____
Расстояние этой точки от конпа уклона будет L + tVigH.
115. Рассмотрим столкновение молекулы с поршнем в системе координат, связанной с поршнем. В этой системе скорость молекулы равна о — и. После упругого удара молекула отскочит от поршня с той же по величине скоростью, но направленной в противоположную сторону (так как масса поршня бесконечно велика по сравнению с массой молекулы). В неподвижной системе координат скорость отскочившей молекулы будет равна г>| — — (о — и) + и = = — v + 2и. Следовательно, кинетическая анергия ее изменилась на величину
„ _ т ,п .„ mv2 т , miuv mv2 mv2 „
Д5 = у (2u - о)2 - -у = у 4и2------у + ---------у * - 2muv.
Так как то u2 С по, и первым членом можно пренебречь.
Относительная часть теряемой энергии равна, таким образом,
| | _ 2тиу и_
Е то2 v ‘
2
Динамика вращательного движения
116. Центростремительной силой в данном случае является сила притяжения между планетой и спутником. Поэтому
тМ
V R2
= mw2/?,
(О
где т — масса спутника, у — гравитационная постоянная, ш — угло-„ 2 л ...
вая скорость. Поскольку <о = —, то нз (1)
получим
R
Т2.
117. Проще всего телу оторваться отшниы и упасть в самой верхней точке (рис. 198), так как там все силы (вес mg и реакции N опоры) направлены вертикально вниз. В предельном случае W = 0 н роль центростремительной силы будет играть вес:
откуда v — VRg = 2 м/сек.
К
118. На грузы mi и т2, движущиеся по окружности, действует только сила FH натяжения нити. Так как грузы движутся с ускорениями (центростремительными) a>2fj н <в2г2, то, воспользовавшись
12 Л. П. Бакалина и др.
177
вторым законом Ньютона, можно написать mi<o2ri — FH, т2<а2г2 = F^,
откуда miri = т2г2. Воспользовавшись этим уравнением и условием fi + r2 = I, найдем 1т2 1т,
г,=----------, г 2 =---=--,
тх + т2 mt + т2
Найденные значения п и г2 соответствуют положению неустойчивого равновесия. В положении равновесия натяжение нити равно
„ т}т2
* Я ““ . —
тх -г
Кинетическая энергия грузов
СО2/.
т,а>2г^
т1т2
m2<i>2r22 1 „ч„.2
2 2 mt + m2 ° 1 '
119. Так как груз вращается то его ускорение, а следовательно,
в горизонтальной плоскости, н действующая на пего сила
(р а'недействующая сил тяжести и натяжения нити /V) направлены по горизонтальной линии АВ (рис. 199). Очевидно, что
f — ma>2R,
где <о — угловая скорость, R = АВ, т — масса груза. Подставляя следующие соотношения:
t х 2л _ , .
f=mgtga, —, /? = Isina
в исходное уравнение, получим
4л2/. sin а 4л2£ cos a I ‘ —---т----------------.
gtga Я
120. В данном случае = АС (рис. 200)
= L sin a + d.
178
Используя соотношения, выведенные прн решении предыдущей задачи, будем иметь
Г L sin а + d сек.
121. Если при вращении вала груз остается висеть вертикально, то натяжение штанги не изменится и будет равно весу груза.
Если же груз отклонится из положения равновесия на угол а, как показано на рис. 201, то при этом тоже возможно равновесие, при условии muPL sin a=mg tg а, или cos a = g/a>2£; любое другое положение штаиги будет неустойчивым. Так как cos a 1, груз может отклоняться лишь при а > Yg/L = 3 рад/сек. Следовательно, в первом случае, при а>] — 2 рад; сек, груз отлониться не может, н 7" =7’1 = 100 н. Во втором случае груз отклонится, так как вертикальное положение штанги соответствует неустойчивому положению равновесия, а отклоненное — устойчивому (почему?). При этом Т = Т2 =* mg/cos а = muRL = 160 н.
122. Единственной силой, действующей на снаряд и сообщающей ему центростремительное ускорение, является сила тяжести. Поэтому mg— mt^lR (о —скорость снаряда, 7? — радиус Земли). Отсюда
v = V Rg « 8 км!сек.
"У
Рис. 201.
123. Если mi н т2 — массы звезд, а Г\ и г2 —их расстояния от общего центра масс, то т^. т2 = г2'.Г\. Принимая во внимание, что mt + т2 — 2М, где М — масса Солнца, и обозначая расстояние между звездами через R, получим
2Мг,
т2-—^~.
(О
Так как сила их гравитационного притяжения является для каждой звезды центростремительной силой, звезды вращаются вокруг их общего центра масс. При этом
Из (1) и (2) получаем
4л2 2уМ .
J-2 рЗ • W
Для системы Солнце — Земля можно написать аналогичное соотношение:
(4) (7’/2)2 R30
где Ro — расстояние от Земли до Солнца, а М & т3 + М. Из (3) и (4) получаем R — 2R0 — 300 • 10е км.
12* 179
124. На автомобиль действуют сила тяжести mg н сила реакции W моста (равная, по третьему закону Ньютона, силе давления автомобиля на мост). Поэтому второй закон Ньютона сразу дает то2 „ о* „
mg — N =—5— . Здесь — центростремительное ускорение. Так
к К
mg
как, по условию, N = —, то окончательно:
Рис. 202.
вается силой
откуда
/? = №. ~ 127 м. g
125. На движущийся автомобиль действуют сила тяжести Р, реакция опоры (моста) N и сила трения Ftp (рис. 202). Горизонтальное ускорение автомобиля вызы-
трения, максимальное значение которой равно
(Т'тр)тах — — тОтах>
kN вшах= _, •
Разность сил Р и У сообщает автомобилю центростремительное ускорение
/\
Отсюда
N = P-F
Окончательно получаем
вшах —
k
= 2,94 м/сек2.
126. Наиболее «опасным» при таком эксперименте является момент прохождения ведром высшей точки траектории. В этой точке на некоторый элемент воды с массой т будут действовать сила тяжести mg и давление У слоев воды, расположенных ближе к дну, причем обе силы направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение
mg + N = та>21. (1)
Угловая скорость <о будет минимальной, если N — 0. При дальнейшем уменьшении <о правая часть (1) станет меньше левой и вода потечет вниз, Таким образом, из (1) (полагая У = 0) получим
<в2 = -|
180
127. В положении равновесия на шарик действуют сила тяжести Р и реакция нити /V, направленные по одной прямой в разные стороны (рис. 203). Так как шарик движется по окружности, он обладает центростремительным ускорением. По втопому закону Ньютона имеем
Поскольку v2 — 2gh, a h = L (1 — cos а), то N — mg (1 +2 — 2 cos а) = mg (3 — 2 cos а).
Подставляя вместо предельное значение fQ, найдем
cos а = 77 — тг5— = 4-, т. е. а = 60°. 2 2
Если а = 90°, то cos а — 0. Величина /0 для этого случая будет
,fo = З/ng = 2,94 н.
128. При колебаниях маятника натяжение нити N уравновешивает составляющую силы тяжести Р, направленную вдоль нити, и сообщает маятнику центростремительное ускорение. Следовательно, при отклонении маятника на угол 0
.. о tn°i
N — mg cos 0 = ——.
Для скорости v из закона сохранения энергии имеем соотношение v2 = 2gh, где h есть разность высот маятника при отклонении от вертикали на углы а и р, т. е.
h = L (1 — cos а) — L (1 — cos р) = L (cos 0 — cos а).
Из этих уравнений получим
,V = mg cos 0 + 2mg (cos 0 — cos а) = mg (3 cos 0—2 cos a).
Подставив численные значения, найдем N — 1,6 н.
129. Поскольку, по условию, на экваторе тела невесомы,
где со — угловая т — масса тела. mg = ma>2R, (1) скорость вращения планеты, R — ее радиус, Величину g найдем из известного соотношения = (2)
здесь М ~~ масса как плотность р планеты, а у — гравитационная постоянная. Так по определению равна Af Р- 4 . (3) о
181
то из (1) и (3), учитывая, что <в = 2я/Г, получим
Зя
0,02
см1
133. Период колебаний маятника обратно пропорционален ускорению силы тяжести, следовательно, последнее в кабине корабля в четыре раза меньше, чем на Земле:
1
(1)
Но gi является центростремительным ускорением, поэтому _ 4л2 g 1 2’2 ^2*
Г 1 (2)
г2 + п = £, =
Г ] 2
Следовательно, г2=4-Д. (3)
о
Из (1) —(3) получаем
131. Так как спутник кажется неподвижным, значит, его угловая скорость <в равна угловой скорости Земли. Единственная сила, которая действует на спутник и сообщает ему центростремительное ускорение, есть сила земного притяжения. Следовательно,
здесь Л1 — масса Земли. На поверхности Земли тМ , ,
= (2)
2jt
Учитывая, что ш = — , Т = 24 часа, из (1) и (2) получим
x = 42400 КМ.
Скорость спутника v — ах ® 3 км! сек..
132. Пусть Я —минимальная высота, скатываясь с которой тележка сможет пройти мертвую петлю. Тогда давление тележки на рельсы в точке О (рис. 204) будет равно нулю. (Если давление на рельсы обратится в нуль в любой другой точке, то тележка в этой точке сорвется и не сможет пройти всей петли.) Значит,
182
в точке О на тележку действует сила тяжести, сообщая ей центростремительное ускорение:
здесь R — радиус петлн, т — масса тележки, о0 — ее скорость в точке О. Воспользуемся зако-
ном сохранения энергии;
В точке А на тележку действует сила тяжести й дав- Рис. 204.
леиие рельсов ?/. Центростремительное ускорение тележки будет определяться полной силой, действующей в направлении радиуса петли, т. е.
mg cos а + N = —5—. (4)
л
Скорость v тележки в точке А можно найти нз закона сохранения энергии:
mgH~ + mgR (1 + cos а). (5)
Из (3), (4) н (5) получим
N = 3mg (1 — cos а). (6)
Если а = 0, то N = 0 в соответствии с условием задачи.
133. В верхней точке петли на груз, подвешенный к пружинным весам, будут действовать силы тяжести mg и натяжения пружины f. Если пренебречь длиной пружины, то можно считать, что груз движется по окружности радиуса г. Сумма сил f и mg сообщает грузу центростремительное ускорение;
. , mv2 ...
f + mg---— ; (1)
здесь о —скорость тележки в верхней точке петли. Ее величина может быть легко определена нз закона сохранения энергии;
2
v2 = 2g(H-2r) — -^-gH. (2)
О
Из (1) и (2) получим
/ + mg = 2mg. (3)
183
Таким образом, f <= +mg и, следовательно, сила, действующая на пружину в верхней точке петли, направлена вверх и равна
/=11,76 н.
134. В точке А на
Для определения h
тележку действует сила давления со стотяжести mg (рис. 205). Воспользовавшись формулой (6) задачи 132 и положив в ней а = 90°, найдем
N = 3mg.
Полная сила F, действующая на тележку, определится как векторная сумма сил V и mg-.
F = /№ + (mg)2 = mgV 10.
Следовательно, полное ускорение а на-правлено вдоль F н равно а = — — gV 10.
вновь обратимся к формуле (6) задачи 132:
Отсюда
3
— mg = 3mg (1 — cos а).
1 3
cosa = -g, h — R (1 + cos a) = — R.
135. В момент отрыва давление купола на тело равно нулю; следовательно, единственной действующей на тело силой будет сила тяжести mg. Пусть тело отрывается в точке А (рис. 206).
Тогда то2 ,п
/ngcosa = —(1)
где о — скорость тела в точке А. Нетрудно видеть, что
v2 = 2gR (1 — cos a). (2)
Из (1) и (2) следует, что 2 2
cos a = -5-, h = R cos a = -= R. о О
136. На шайбу действуют следующие силы (рис. 207); IV —сила нормального давления (направлена по радиусу), F — сила трения, касательная к поверхности шара, Р — mg — сила тяжести (здесь т — масса шайбы). Максимальная сила трения равна
F^kN, (1)
где k — коэффициент трения. Шайба вращается вокруг вертикальной оси. На основании второго закона Ньютона сумма проекций
184
всех сил на горизонтальную плоскость (АО' на рис. 207) будет создавать центростремительное ускорение &2R cos а, -т. е.
N cos а — F sin а = maFR cos а. (2)
Так как шайба относительно поверхности шара покоится, то сумма проекций всех сил на вертикаль должна равняться нулю: mg — F cos a — N sin а — 0. (3)
Отметим, что ошибкой было бы писать условие равновесия шайбы относительно шара в виде mg cos a — F = 0. Действительно, центро-
стремительное ускорение направлено по линии АО и его проекция на направление АВ равна <о2/? cos a sin а. Поэтому разность mg cos а — F равна не нулю, а массе шайбы, умноженной на эту проекцию: mg cos а — F — — mciFR cos а sin а.
Последнее соотношение вполне эквивалентно (3). Исключая из (1), (2) н (3) силы F и N, найдем
h — cos а (g ~ s*n а) g sin а + <о2Д cos2 а
Рис. 207.
137. В нижней части ямы тело движется с той скоростью, которой оно достигло на глубине R/2. хранения энергии
Определим ее из закона со-
v = VgR.
(О
Так как в нижней части ямы скорость постоянна, сумма сил, действующих на тело по касательной, равна нулю и (рис. 208)
Рис. 208.
FTp = mg sin а. (2) Сумма сил, действующих на тело по радиусу, сообщает ему центростремительное ускорение
mv2
N — mg cos а = К
где N — сила давления стенки. Из (1) и (2) следует
т°2 . о , а
N = —R— + mg cos а = mg 2 cos2— .
(3)
Коэффициент трения k, по определению, равен F^/N. Используя (2) и (3), получим
185
138. а) На первый вопрос задачи ответить просто. Закон со» хранения энергии сразу дает
то2 о .
-у- - 2mgL,
(1)
где L — длина штаиги, о — искомая скорость, т — масса маятника. Отсюда v2 = 4gL.
б) Этот случай отличается от предыдущего тем, что при прохождении маятником высшей точки своей траектории нить должна быть натянута. В этот момент иа маятник будут действовать силы тяжести mg н натяжения нити Т, направленные вертикально вниз (рис. 209). Сумма этих сил сообщает маятнику центростремительное ускорение of/t, где Vi — скорость маятника в точке В. В предельном случае Т = 0
2
(2)
При меньших значениях Vi маятник не достигает точки В и пройдет под ней, как указано на рис. 209 пунктиром. Поскольку скорость маятника в точке В не равна нулю, то в данном случае вместо (1) надо записать
2 2
mv mv.
Из (2) и (3) получаем
v ==l'5gT.
(3)
139. Период маятника в неподвижной кабине
здесь I — длина нити маятника. Ускоренное движение кабины вниз эквивалентно уменьшению силы тяжести на а (см. по этому поводу примечание к решению задачи 54). Поэтому
Г, = 2л Т/ —— = 1, 2 сек.
V g-a
Из этих двух уравнений находим
а « 0,3g = 3,23 м{сек2.
140. При движении по тяжести mg, нормального видно, что
кругу иа велосипедиста действуют силы давления N и трения F (рис. 210). Оче-
Л?«“ mg (1)
186
(m — масса велосипедиста). Силой, сообщающей велосипедисту центростремительное ускорение, является сила трения; поэтому
В
mff
Рис. 210. одинаковы, а их расстояния
Момент силы треиия относительно центра тяжести велосипедиста равен Fd sin а, а момент силы N — соответственно Nd cos а (где d расстояние от точки касания до центра тяжести). Велосипедист не перевернется, если эти моменты равны
Fd sin а = Nd cos а. (3) Подставляя (1) и (2) в (3), получим
/? = 2^«8,5л<.
g
Примечание. Полученное решение не является точным, так как в нем не учтено, что различные точки велосипедиста имеют различные центростремительные ускорения. Это легко понять, если учесть, что угловые скорости точек А и В (см. рис. 210)
от оси вращения различны. Однако в дальнейшем при решении аналогичных задач мы будем пользоваться той же методикой, потому что, во-первых, строгое решение требует специальных знаний, выходящих за пределы программы средней школы, во-вторых, в большинстве практически интересных случаев такие приближенные решения дают вполне удовлетворительную точность.
141. На мотоциклиста действуют те же силы, что и на велосипедиста в предыдущей задаче (см. рис. 210). Принимая обозначения предыдущей задачи, запишем ряд очевидных соотношений:
M = (1)
F=kN, (2)
Равенство моментов сил N и F относительно точки О (центра тяжести) дает:
F sin а = N cos а. (4)
Из (1) —(4) получаем
cig а = k = 0,4, v = VRgk « 18,8 м/сек.
Мотоциклист отклонится от вертикали на угол 90° —а« 22° (см. примечание к решению задачи 140).
142. Максимальную скорость v движения велосипедиста по горизонтальному треку найдем, используя решения задач 140 и 141:
v=V Rgk,
(1)
187
где R — радиус трека, клониом треке, даиы
Силы, действующие иа велосипедиста иаиа-иа рис. 211. Здесь V — сила нормального давления, mg — сила тяжести, F сила
треиия
F = kN. (2)
В создании центростремительного ускорения участвуют проекции сил F и N на горизонтальное направление О
F cos а + N sin а — —5—, (3)
где 01 —скорость велосипедиста при
Рие' "I*- движении по наклонному треку. Так
как в вертикальном направлении перемещения велосипедиста не происходит, то сумма проекций всех сил иа это направление должна равняться нулю:
<V cos а — F sin а — mg = 0.
Из (2) —(4) получим
2 п й + tg а
н, используя (1), окончательно найдем
Qi = д/" fe + tg а о V k(l — ktga)‘
Подчеркнем, что найденное значение действительно является
максимальным, так как (2) дает максимальное центростремительное
ускорение (см. примечание к решению задачи 140).
143. Силы, действующие на автомобиль, указаны на рис. 212. Условие равновесия автомобиля выглядит так: FTp = mg. С другой стороны,
FTp - kN
(N — сила давления стенки на автомобиль). Центростремительная сила в данном случае совпадает с N:
Приведенные соотношения сразу дают
Рис. 212.
(см. примечание к решению задачи 140).
144. Чтобы найти коэффициент трения k, воспользуемся реше^ пием задачи 141;
188
Силы, действующие на мотоциклиста при движении по стенке цилиндра, указаны иа рис. 213. По определению,
FTp = kN.
Мотоциклист не будет соскальзывать вниз по стенке, если
FTp = mg.
(2)
(3)
Так как в данном случае реакция стенки М есть центростремитель-
ная сила, то
щог
N =----
Ri
Соотношения (1) —(4) дают
2 Riz _ RiRz2 = k
Чтобы мотоцикл не опрокидывался, не -обходимо равенство моментов сил N и FTp относительно центра тяжести О:
Рис. 213.
FT?d sin а = Nd cos а (5)
(где d — расстояние от точки касания до центра тяжести). Из (2) и (5) имеем
ctga = fe = ~H—
Kg
(см. примечание к решению задачи 140).
Разные задачи
145. После торможения спутник движется по эллиптической орбите, большая полуось которой а — ~^,^3 . Если применить за-
коны Кеплера к движению спутника по круговой и эллиптической орбитам, получим: (7'/7'0)2= (а//?)3. Период обращения спутника по круговой орбите __
т 2л/? .2л _//?3
т°~~ ягУ т
(см. задачу 131). Таким образом, период обращения его по эллиптической орбите
т = 2л /~W ( R+Rn УД
Лз У g \ 2R ) •
189
С момента торможения до посадки спутник пройдет как раз половину орбиты (см. рис. 51). Поэтому
t = Т_ = л (R + R3 \312
2 2 /
146. Под силой веса здесь подразумевается сила давления тела на поверхность планеты, равная, очевидно, силе N, с которой планета давит на тело (эту силу можно измерять с помощью пружинного динамометра). На полюсе эта сила в точности равна силе всемирного тяготения yMm/R2 (у — гравитационная постоянная, М — масса планеты, ш — масса тела). На экваторе разность сил yMm/R2 и N сообщает ему центростремительное ускорение a2R = = -р- R. С другой стороны, как следует из условия задачи, в этом последнем
.. Мт
~Y (R + h)2 ’
Поэтому
Мт Мт Мт 4л2 „
¥~Я2" tf-y \ {R + h]2 ~т—R.
(О
4
М = -5-эт/?3р, то из (1) получим:
Поскольку
/г = r(± —У.рГг-----1
V И урТ2 —Зя /
Величина h по смыслу задачи положительна, поэтому перед корнем следует брать знак « + ».
147. Пусть Ма — масса астероида. Как следует из закона всемирного тяготения,
(1)
Здесь ga — ускорение свободного падения на астероиде, у —гравитационная постоянная. Учитывая, что
4
Ma = -s- яК’ра, (2)
<5
получим
4
ga = — лра/?у ~ 0,008 м/сек2. (3)
и
По условию задачи человек в момент прыжка на Земле и на астероиде обладает одной и той же кинетической энергией. Поэтому потенциальная энергия в высшей точке подъема как на Земле, так и на астероиде тоже будет одинакова:
mgaha = mgh, (4)
190
где т — масса человека, йа — высота прыжка на астероиде, a h — на Земле. Из (3) и (4)
ha = S— h 64 м.
ga
Заметим, что на самом деле прыжок будет выше, так как значение ga убывает с высотой по закону, даваемому формулой (1).
148. Ускорение силы тяжести gc на поверхности Солнца
уМс V 4 , 4
gc = -75- = • Т л/?сРс = - я«сРсУ>
*'С 2'С
(1)
где Rc — радиус Солнца, рс — плотность Солнца. Для Земли по аналогии с (1) имеем
4
й3 = 3-^зРзУ, (2)
где /?3 —радиус Земли, р3 — плотность Земли. Из (1) и (2)
_ #з^сРс Sc ~ R3P3
Дс Рс
Поскольку 55—= 108, — =0,25, из (3) окончательно получим R3 Рз
(3)
gc « 265 м/сек2.
149. Допустим, что земная орбита имеет форму круга. Центростремительное ускорение, с которым Земля движется по орбите, определяется силой всемирного тяготения:
Мст 4л2
=т ~R- (D
(2)
Здесь Л4С — масса Солнца, т— масса Земли, у — гравитационная постоянная. Ускорение свободного падения gc на поверхности Солнца тоже дается законом всемирного тяготения:
Мсу Sc-----
Из (1) и (2) легко получим
4л2/?3 ,
gc = -727-2" 2о5 м!секг.
150. Как для Земли, так и для Луны центростремительное ускорение определяется силой всемирного тяготения. Следовательно,
М3&3%3 = V 72“ >
К3
«л
191
Здесь введены обозначения: М3, Мл, Мс — массы ЗеМли, Луны и Солнца, R3 и Ял —радиусы орбит Земли и Луны, и>3и'<ол —угловые скорости по орбите. Земли, и Луны.
Исходная система уравнений легко приводит к выражению
Мс , юз^з
^3 ®л^л
« 351 • 10’.
При подстановке числовых данных л последнее выражение было учтено, что
«з _ 1
®л 13
«з
ТГ390-
151. Ускорение силы тяжести на поверхности планеты найдем так же, как в задачах 147 и 148:
Sn =у я2?чРпУ-
Аналогично для Земли:
4
2 = уЛ/?зР3у.
Здесь Z?3 и Rn — радиусы, а р3 и рп — плотности Земли и планеты. Так как р3 — ри, a R3 — 2Rn, то
„ _ „ Rn R
Sa g R3 = 2 ’
Длина маятника связана с периодом известным соотношением:
Z =
Т2 g3
-г-5- —= 49,6
4л2 2
м.
152. Сила F, действующая на шарик с массой т, равна
„ Мт Мпт
F ~ ~ Y (d-Rfi)2'
Здесь Л!п — масса свинца в объеме полости. Очевидно, что Мп — М/8 (объем полости составляет 1/8 объема шара). Написанные соотно-
шения дают
F = у Мт
1 d2
1
( R \2
153. По мере опускания груза колесо будет раскручиваться и потенциальная энергия груза будет переходить в кинетическую энергию груза и колеса:
mu? Л4и?
192
где и 1 —скорость груза, а ~ линейная скорость обода колеса. Из равенства угловых скоростей шкива и колеса следует
t>i ^2
г R ’
поэтому
mv\ MR2v2
mgff = -r-+-^r- н и,=
154. Определим сначала момент, действующий на вал двигателя. По определению II7 = Fvt = где F — сила, действующая в точке зацепления, О] — линейная, а <0] угловая скорость шестерни 1. Число зубьев у шестеренок пропорционально их радиусам, а линейные скорости в точке зацепления равны, тельно,
следова-
г2 1 1
«>1 = со,— = со,— = 2m —, fi m m
Wm
~ 1000 н-м.
2m
Так как силы, действующие в зацеплении на каждую из нок, согласно третьему закону Ньютона равны между собой, то
44 2 _ г2 г 1 Л4] r\ m ’
поэтому
М,
Мг = = 200 н м.
пг
шестере-
Рис. 214.
155. Угловая скорость колеса <о=и//?. Силы, действующие на ведущую шестерню, изображены на рис. гателя
214. Полезная мощность
дви-
У=(Р2-Р,)г<о=(Р1-Г2)~.
Подставляя числовые значения, получаем
N — 2000 н м'сек = 2 к.вт.
156. Ускорение ci] бруска, соскальзывающего с наклонной скости, определяется с помощью второго закона Ньютона:
ma\ = mg sin а — kmg cos а, ai = g (sin а — k cos а).
Движение обруча сложнее. Во-первых, каждая его точка движется вниз по наклонной плоскости с ускорением а2 и, кроме того,
193
пло-
(1)
13 Л, П, Баканнна и др.
вращается вокруг оси обруча. Так как обруч скатывается без проскальзывания, скорость его поступательного движения оп и линейная скорость вращения вокруг оси ив в каждый момент равны между собой. Действительно, представим себе, что обруч совершил один полный Оборот. Тогда его центр тяжести пройдет вдоль наклонной плоскости путь 2л/?, а любая точка обруча повернется вокруг центра на угол 2л, т. е. пройдет вдоль обруча путь 2л/?. Эти пути равны и проходятся за одинаковое время, поэтому va = va= v.
Согласно закону сохранения энергии
2 2
mv mgh = —g— + —— = mv2.
(2)
(работа против сил трения не совершается, так как скорость нижней точки равна нулю).
Из кинематики следует, что
А = sin а, (3)
о = a^t. (4)
Из (2) — (4) получаем
“2 = -% g sin а. (5)
Тела не будут обгонять друг друга, если <Z] = a2; отсюда
А = у tga.
157. Потенциальная энергия Еп цилиндра в конце пути частично израсходуется на работу Лтр против сил трения о плоскость, а частично перейдет в кинетическую энергию поступательного движения и вращения:
где цп-поступательная скорость центра цилиндра, а ив— линейная скорость поверхности цилиндра при вращении вокруг центра тяжести. Как и в предыдущей задаче, в данном случае
On=oB=f, (2)
так как цилиндр скатывается без проскальзывания по нити. При этом скорость нижней точки цилиндра, касающейся плоскости, будет 2v, и работа против сил трения
Лтр = 2kNL, (3)
где N — сила нормального давления на плоскость, a k — коэффициент трения. Используя (2) и (3), запишем (1) для углов наклона а н (5:
mgL sin a = mv2a + 2Lkmg cos a,
mgL sin (} = + 2Lkmg cos fJ.
194
Отсюда, исключая k, получим выражение для va:
corp"aP + gL(sin“~cos“fg^’ (5)
которое после подстановки значений а и £ примет следующий вид:
2 Vl + SL
V?, = ----•
а Кз
158. Если k — коэффициент трения, то угол а3, при котором пластинка еще будет удерживаться на наклонной плоскости, определится нз соотношения
& = tga3 (1)
(см. решение задачи 47). Время t движения тела дается известной кинематической формулой
О’?
/2 = —. (<2\
где S — путь, пройденный телом, а — его ускорение. В данном случае
(3)
at а2
где Sj и в] — путь и ускорение, соответствующие углу ab а $2 и а2 — те же величины для а2. Если Л — горизонтальная проекция пути, то
Из решения задачи 47 следует, что
= g (sin a( — k cos aO, (5)
a2 = g (sin a2 — fc’cos a2).'
Подставляя (4) и (5) в (3), получим
, _ sin ai cos a( — sin a2 cos a2 cos2 a2 — cos2 a2
Подставляя в (6) числовые значения и учитывая (1), окончательно найдем:
й = 2 —К 3 = tga3.
159. Сначала найдем массу М груза, подвешенного к веревке. Так как величина М максимально возможная, при которой еще не начинается скольжение груза т, то, очевидно, что Mg=mgk, или
М = km.
13*
(О
195
Рассмотрим силы, действующие иа каждый из грузов в случае движущегося стола. Если b — ускорение груза М относительно стола, а Т — сила натяжения веревки, то
Mg-Mb = T. (2)
Это уравнение вытекает из второго закона Ньютона для тела с массой М. Ускорение груза m относительно Земли будет b — а, поэтому
Т — mgk — m(b — а). (3)
Из (1) —(3) получим
Знак « —» в правой части (4) говорит о том, что а > Ь, т. е. груз m будет увлекаться столом.
160. Если бы лифт двигался вниз с ускорением g, то это соответствовало бы состоянию невесомости внутри лифта. Действительно, в этом случае сам лифт и все тела в нем находились бы в состоянии свободного падения и силы давления тел друг на друга отсутствовали.
Если же ускорение лифта направлено вниз и равно 2g, то это эквивалентно изменению знака силы тяжести. Иначе говоря, все процессы будут происходить точно так же, как и в неподвижном лифте, только «верх» и «низ» поменяются местами. Воспользовавшись результатами решения задачи 139, получим о2 = §Lg, где L — длина нити маятника, а о — его скорость в верхней точке траектории. Очевидно, в этом случае разность сил натяжения Т и «веса» mg сообщает маятнику центростремительное ускорение:
7. , mV2 а
Т = mg -1—= bmg.
161. Часы с математическим маятником («ходики») в ракете, движущейся вверх с ускорением, будут идти быстрее, чем в неподвижной. Если Го —период колебаний математического маятника в неподвижной ракете, а Т — в движущейся, то, как следует из решения задачи 139,
Отсюда
Истинное время ta, за которое ракета прошла первые 50 км, найдем по известной формуле:
/ 2/г
t0 = 1/ — « 32 сек. (2)
«Ходики», помещенные в ракете, за то же время t0 совершат в "/11 раз больше колебаний, чем «неподвижные» часы. Поэтому время /, показанное ими к моменту выключения двигателя, будет
1 = /о/1Т « Ю6 сек. (3)
196
После выключения двигателя ракета начнет двигаться только под действием, силы тяжести с ускорением g. Все процессы в ракете будут протекать так же, как и при свободном падении (наступит «состояние невесомости»). Поэтому часы с математическим маятником остановятся, и их показания в дальнейшем для любой точки траектории будут даваться формулой (3). Что же касается пружинных часов, то их ход не зависит от характера движения ракеты; поэтому в верхней части траектории они покажут истинное время, равное /0 + Ч, где /0 определяется (2), а Ч — время, прошедшее с момента выключения двигателя до достижения ракетой высшей точки траектории. Так как скорость ракеты в момент выключения двигателя была
с.' = ]/Г2а/г « 3130 м[сек,
то, как нетрудно видеть,
/; = - « 320 сек, g
откуда окончательно
/0 + Ч « 352 сек.
162. Рассмотрим силы, действующие на столбик ртути (рис. 215). Вниз действует вес pSgh, вверх сила pSgH атмосферного давления. По второму закону Ньютона pSha = = pShg—pSHg, откуда h = Hgl(g-a).
163. Решение задачи аналогично решению задачи 75. Поскольку сопроти-
Рис. 215.
влсние движению гвоздя обусловлено в основном трением его боковой поверхности о доску, а это трение в свою очередь пропорционально длине гвоздя, то график зависимости силы трения F от длины h забитой части гвоздя будет иметь вид, изображенный иа рис. 216. При этом, если й = //о = 8О мм = 0,08 м, то, очевидно, что Fo — искомая сила.
Чтобы найти Ро, определим полную энергию, ушедшую на забивание гвоздя. Поскольку предполагалось, что масса последнего равна нулю, то вся энергия молотка при каждом ударе затрачивалась на преодоление сил трения. Значит, полная энергия W, пошедшая на преодоление трения, W = 6mv2/2. Здесь т — масса,
197
а о — скорость молотка. Как видно из рис. 216, W*=F0/i0/2; следо
вательно,
эй/
150 н. Ло
В заключение заметим, что решение задачи верно, если гвоздь входит в доску горизонтально. Если же он стоит вертикально, то ситуация несколько осложняется тем, что при ударе молоток некоторое время движется вместе с гвоздем, а при этом меняется не только кинетическая, но и потенциальная энергия молотка (см. по этому поводу решение задачи 72), Однако поправка к решению в этом случае получается не очень существенной (около 3%). Мы предлагаем читателю самостоятельно получить точное решение при вертикальном расположении гвоздя.
164. Тот факт, что удлинение пружины пропорционально нагрузке, можно записать так (см. задачу 15):
/~/о = бР,
(О
где Р — нагрузка, 1а — длина недеформированной пружины, /—длина, которую приобрела пружина под действием груза Р, д —коэффициент пропорциональности. По условию задачи, если Р = mg, где т — масса груза В, то / = 2/0, поэтому из (1) получим
mg
Пусть R — радиус окружности, описываемой грузом В. Тогда сила F натяжения пружины, в соответствии с (1), будет
Рис. 217,
С другой стороны, при движении по кругу
Е = -^. (4)
Из равенств (2) — (4) получим
Так как величина R положительна, то перед корнем следует брать знак « + ».
165. Силы, действующие на муфту, указаны на рис. 217: F = k (/ — /0) — сила
упругости пружины, Mg — вес муфты и N — сила реакции со стороны стержня. Поскольку в установившемся режиме муфта вращается в горизонтальной плоскости с постоянной угловой скоростью, сумма всех действующих на нее сил должна быть центростремительной силой, направленной по радиусу окружности, описываемой муфтой. Следовательно, сумма проекций всех сил иа
198
вертикаль должна быть равна нулю:
откуда
N sin а - Mg - k(l — /0) cos а = О,
Mg sin а
+ k {I — Zq)
cos а sin а ‘
Рассмотрим теперь сумму проекций всех сил да радиус вращения муфты:
г , /• > \ . . , cos a k (I —— In)
ft = k (Z — Zo) sin a + N cos а = Mg —:--1---\
sin a sin а
Как уже было сказано, эта сила в установившемся режиме должна являться центростремительной силой /2 = AZco2Z sin а. Равновесной
значение Z найдется из равенства fi-fi-
_ klq — Mg cos a k — Afco2 sin2 a
Исследуем, является ли найденное положение муфты устойчивым. Для этого построим графики ft (О и fz U) (рис. 218). Это прямые линии, одна из которых (f2) всегда проходит через начало координат, ее наклон задается условием tgy=Afco2 sin а. Расположение и наклон второй прямой (f;) зависит от параметров системы tg Р = -3-^ > а ft (0) = (Mg cos a - kl,
Рис. 218.
i)—г-—. Равновесное значе-sin a
ние определяется точкой пересечения. Возможны два типа пересечения этих прямых, изображенные на рис. 218 (случаи а и б). Случай а соответствует положению устойчивого равновесия, так как если Z немного увеличится, ft возрастет больше, чем необходимо для устойчивого вращения, и система вернется к исходному положению. Точно так же, если Z уменьшится, ft окажется меньше, чем f2, и радиус окружности будет возрастать, т. е. система и в этом случае вернется в положение равновесия. Из тех же соображений видно, что случай б соответствует положению неустойчивого равновесия.
Как видно из рис. 218, случай а реализуется при выполнении следующих двух условий:
sin a sin a
ИЛИ kla> Mg cos a, (1)
и fa —: > Afco2 sin a, sin a
или 1 . г k ... о < — 1/ • (2) sin a V M
199
Таким образом, муфта имеет устойчивое положение равновесия на штанге лишь при выполнении условий (1) и (2). Заметим в заключение, что в данной задаче не учитываются силы трения и, следовательно, любые возмущения равновесного режима не должны затухать. Различие между положениями устойчивого и неустойчивого равновесия проявится в следующем: при малом смешении муфты из устойчивого положения равновесия оиа будет в дальнейшем совершать малые колебания около этого положения; при малом смещении из неустойчивого положения муфта уйдет далеко и никогда не вернется в положение, близкое к равновесному.
166. Если Г —сила, деформирующая пружину, /0 —ее начальная длина, а / — длина при действии силы F, то из условия задачи следует, что
При вращении штаигн сила натяжения пружин является центростремительной силой. Поэтому тсо2/? = 267?; здесь /? — радиус окружности, описываемой шайбой. Двойка учитывает влияние обеих пружин. Отсюда найдем:
Угловая скорость не зависит от R. Это значит, что шайба на вращающейся штанге будет находиться в положении безразличного равновесия.
167. Воспользовавшись результатами решения задач 164, 166, сразу запишем:
2l — l = l = 6mg. (1)
Здесь /—начальная длина пружины, т — масса груза А, б —коэффициент пропорциональности. Из (1)
6 = —
Mg
(2)
Пусть при вращении пружина отклонилась от вертикали на угол а. Тогда радиус окружности, описываемой грузом А в горизонтальной плоскости, будет L sin а и центростремительное ускорение груза £<в2 sin а. Это ускорение будет вызываться горизонтальной составляющей силы F натяжения пружины, откуда
F sin а = mco2L sin а, .
F = m<a2T;
на основании (1)
о
Из (2) — (4) окончательно имеем:
200
.168. Задача аналогична предыдущим (задачи 165— 167). Силы, действующие на каждую из муфт, изображены на рис. 219, а их горизонтальная и вертикальная проекции соответственно:
k (/—/о) ~ cos а =Л4со2
Afg — N sin а — 0.
Исключая отсюда силу N нормального давления и учитывая, что I — 2fl tg а, получим
Mg+klotga {2k — Л1и2) tg2 а
Рекомендуем читателю исследовать это решение на устойчивость, подобно тому как это сделано в задаче 165.
169. Цилиндры начнут двигаться друг относительно друга без проскальзывания, если их линейные скорости г»! и v2 станут одинаковыми, т. е. если
о1 = и2=ц. (1)
Обозначим начальную линейную скорость первого цилиндра По. Тогда
v0 = со/?.
Сила трения F, одинаковая для обоих цилиндров, будет первый из них тормозить, а второй ускорять. Второй закон Ньютона для этого случая сразу дает
f = (2)
ч
f = m2~. (3)
Если учесть, что время t действия силы F для обоих цилиндров одно и то же, то из (2) и (3) получим
Л12о = Мj (t>o — v), откуда
Чтобы найти тепловые потери, заметим, что начальная энергия си-сгемы была М^2, а конечная стала равна —% 1 —. Разность этих величин дает потери на тепло. Учитывая (4), после несложных преобразований получим
AIjOq (Mtv2 M2v2 M^M^R2
~~2 \ 2 *" 2 J 2(Mi + M2) ’
201
170. Пройдя п витков, колечко опустится на высоту пН. Его скорость v при этом будет направлена вдоль спирали и равна
о = /2^. (1)
Угол а наклона скорости v к горизонту дается соотношением
которое поясняется рис. 220. Нормальное давление N колечка на спираль, аналогичное давлению тела на наклонную плоскость (рис. 220), будет равно
N = mg cos а. (3)
Кроме того, со стороны спирали на колечко действует центростремительная сила (очевидно, такая же сила будет действовать и со стороны колечка на спираль):
Рис. 220.
Учитывая, что cos2 а = --——— 1 + tg2 а
где ог — горизонтальная проекция скорости V.
ог = v cos а. (5)
Сила F направлена вдоль радиуса перпендикулярно к N. Полное давление Р колечка будет равно векторной сумме N и F, откуда
p1==J/№ + F2. (6)
- л 9П9 . tw'i из соотношений 4л2/?2 + Нг
(1) —(6) получим
Р = + 16rtV//2 + Н2'
171. Силы, действующие на тележку, даются формулами (3), (4) и (5) задачи 170:
N = mg cos а, (1)
с mv2 2 <<>\
F=—g— cos2 а; (2)
здесь N — вертикальная сила давления рельсов на тележку, т — масса тележки, F — центростремительная сила (горизонтальная сила давления рельсов на тележку), а —угол наклона рельсов по отношению к горизонтальной плоскости, tg а = H/'2ztR,
v2 = 2gnH. (3)
Чтобы определить условия, при которых тележка перевернется, обратимся к рис. 221. Если ось спирального спуска находится
202
справа от тележки, т. е. рельс А наружный, a D — внутренний, то в момент переворота давление на рельс D исчезнет (тележка переворачивается вокруг наружного рельса); поэтому сила N, определяемая формулой (1), окажется приложенной к точке А. К этой же точке будет приложена и центростремительная сила F. Для равновесия тележки необходимо, чтобы сумма моментов всех сил отно-
сительно центра тяжести тележки (точ--h
ка О) равнялась нулю. Отсюда N у= = Fh и, следовательно,
^- = F. (4)
Принимая во внимание (1) —(3), а также очевидное соотношение
, 1 4л2/?2
cos а = j + tg2 а = 4л2/?2 + Н2 ,
из (4) получим
7? /4л2/?2 + Я2 1
SX ...— ' — =ss I — г=
4Н cos а 8лН 8л sin а
В г ИС. ZZ1.
заключение отметим, что момент исчезновения давления на рельс D действительно является критическим. При повороте тележки вокруг рельса А центр тяжести О будет подниматься и приближаться к линии действия силы N. Так как величины сил F и N при этом практически меняться не будут, то в результате поворота тележки момент силы N будет уменьшаться, а момент силы F — увеличиваться. Таким образом, тележке достаточно лишь немного оторваться от рельса D, чтобы она перевернулась.
172. Единственной силой, сообщающей кубикам ускорение а, будет горизонтальная составляющая силы давления клина, поэтому
Ma = F cos а
(О
(силы, действующие на клин, указаны на рис. 222). Если Ь — ускорение клина, то
mb — mg — 2F sin а. (2)
Так как смещение клина вниз на некоторую величину h вызывает горизонтальное смещение кубика на h tg а, то ускорения а и b связаны очевидным соотношением:
а = & tg а. (3)
Совместное решение (1) —(3) приводит к окончательному результату:
«gig а т + 2/И tg2 а
(4)
Эту же задачу можно просто решить энергетически. Пусть h— путь, пройденный клином по вертикали после начала движения.
203
В результате кубики приобрели скорость V, а клин — скорость v. Закон сохранения энергии дает
, MV2 mv2
V2
Учитывая, что V = v tg а, н ускорение кубиков а = (кубик
приобрел скорость V, пройдя путь h tg а), вновь придем к соотношению (4).
173. Потенциальная энергия обруча nigh в момент удара о горизонтальную плоскость целиком перейдет в кинетическую энергию поступательного движения и вращения:
2 2
mv^ mvQ
(1)
здесь t>n — скорость поступательного движения центра тяжести обруча, а с'в —линейная скорость вращения обруча вокруг центра тяжести. Так как обруч скатывается без проскальзывания, то
ап=ав=а (2)
(см. решение задачи 156). Из (1) и (2) следует, что
(3)
Таким образом, скорость обруча при качении меньше скорости, которую он имел бы, соскальзывая без трения с этой же плоскости, в V2 раз.
При упругом ударе о горизонтальную плоскость вертикальная составляющая скорости v, не изменяя своей величины, изменит направление па противоположное. Вновь используя закон сохранения энергии, получим
О mv\ —^~=mgx, (4)
204
где Vi — вертикальная составляющая скорости v. Очевидно, что
t>i = v sin а; (5)
(4) и (5) дают
А . „
x = -g-sin2 а.
174. Как в задачах 156 и можно записать следующим образом:
оп=ов=о, (1)
где оп— скорость центра тяжести обруча, направленная вдоль стенок ямы, а ов — линейная скорость вращения точек обода вокруг центра тяжести. Скорость центра тяжести о легко найти, используя формулу (3) задачи 173,
v2 = gh, (2) где
h = (/? — г) cos a~R cos а. (3)
Здесь мы пренебрегли г по сравнению с R. Силы, действующие на обруч, указаны на рис. 223. На основании второго закона Нью-
тона имеем
N — mg cos а = т
V2
~R’
(4)
где N — сила нормального
А^ А^
давления. (В правой части (4) мы вновь учли, что г С R.) Так как в интересующей нас точке по условию задачи
Рис. 224.
TV = mg, (5)
то из (2) — (5) получим:
175. Действие различных сил на автомобиль поясняется рис. 224, где N! и Л'2 — силы нормального давления,
Ктр — сила трения. Для равновесия автомобиля необходимо, чтобы
сумма моментов всех сил относительно центра тяжести равнялась
нулю, т. е.
(О
Поскольку сила трения действует только в заднем колесе, то
Ктр — kN р
(2)
205
Кроме того, очевидно, что W1 + — mg = 0.
Исключая из (1) —(3) величины и FTD, получим д. mg(d + 2kr)
3 2(d + kr) ’
Подстановка числовых данных дает
Л'2 « 7820 н.
(3)
(4)
Если £ = 0, то из (4), как и следовало ожидать, №2=> mg{2. Если k очень велико, то в (4) можно пренебречь d по сравнению с kr. Тогда получим N2 = mg. Изменение силы давления передних колес при торможении, очевидно, будет
ДДО = N2-17° = -^ -£-г- « 500 н. г z 2 d + kr
176, Представим себе, что мы надавили на пластинку с некоторой силой f. В результате этого сила F, сжимающая пружину, оказалась равной
F = mig + f. (1)
Обратимся теперь к рис. 225. На нем АО соответствует длине пружины в недеформированном состоянии (при /^ = 0), а АО — х2 равно длине пружины после того, как на нее подействовала сила F, Если мы перестанем давить на пластинку, то последняя устремится
и
вверх, растягивая пружину, сможет оторваться от стола,
достигнет точки В. Пластинка т2 если максимальная сила натяжения пружины будет по крайней мере равна m2g (или больше). Как известно (см., например, задачу 164), сила натяжения (или сжатия) пружины пропорциональна удлинению. Поэтому сила F, определяемая (1), будет
F = kx2, (2)
где k — коэффициент пропорциональности. Эта зависимость графически изображена на рис. 226. Как следует из этого графика
206
энергия пружины, сжатой силой F, будет
Fx2 kx2
(3)
Эта энергия пойдет на изменение потенциальной энергии пластинки /И], которое, очевидно, равно mtg (х2 + h), где h = OB, и на растяжение пружины на длину Л. Таким образом,
kx2 kh2
—g- ~ mi8 (хз + h) -1—g—. (4)
Условие задачи требует, чтобы по крайней мере
kh = m2g. (5)
Исключая из (4) и (5) величину h, найдем
2 2mxg / mgi2 2m.-lm2g2\ х2 х2 ~ I ^2 । ^2 / О’
откуда
v - ч- («1 + ОТ2)Я
*2-—*-----------~k---. (6)
Из (1) и (2) следует, что
f = F - mtg = kXi-mig.
Подставляя в последнее соотношение х2 из (6), окончательно получим
+ т2) g.
177. На левый шарик действует вес mg и сила Т натяжения нити. На правый шарик, кроме того, архимедова сила ржУ£, и сила kv сопротивления жидкости (здесь V — объем шарика, k — постоянная величина, v — скорость шарика). При свободном падении в жидкости шарик имеет установившуюся скорость с0> следовательно,
kv0 +pxVg = pVg, (1)
И
Л = ^Я(Р-Рж)
о0
При установившемся движении суммы сил, действующих на левый и правый шарики, будут равны нулю:
pVg = T,
т + РжГя = pVg + 7g(p~ Р^ v,
v0
откуда
207
178. Введем обозначения: Г —натяжение веревки, Af —сила давления человека на лестницу, ач, ал и аП“ ускорения, а /пч, тл и
znn — массы
соответственно человека, лестницы и противовеса (рис. 227). Тогда уравнения движения системы будет иметь следующий вид:
тчач ~ N —
тлал = N — Т + tnng,
тпап = Т - m„g.
(1)
Отсюда, учитывая, что
тл + тч = т„, (2)
получим: тлал + тпап — тчач = 0 или (вспомните вывод закона сохранения количества движения!)
тлил + >ПпУп — m4v4 = const, (3)
где v — соответствующие скорости. Заметим, что хотя (3) п очень внешне похоже, но не является законом сохранения количества движения. Действительно, закон сохранения количества движения
имеет векторный смысл. В данном случае до начала движения человека количество движения системы равнялось нулю, а после того как человек стал подниматься, количество движения его и противовеса оказались направлены к блоку, и только лестницы —от блока. Учитывая, что скорости лестницы и противовеса численно равны, а масса противовеса вдвое больше, нетрудно видеть, что противовес и человек имеют значительно большее количество движения, чем лестница, и их векторная сумма отлична от нуля.
Поскольку начальное количество движения системы, как уже t говорилось, равно нулю, соотношение (3) примет вид
тлъл + mnvn — m4v4 = 0.
(4)
Если теперь вспомнить, что пути S, проходимые различными частями системы, пропорциональны скоростям (времена движения одинаковы), та — 2тч = 2тл и е>п=Ул, то вместо (4) получим
Sq = Ззц — Ззд, (5)
Перемещения s4, «л и Дп, так же как и ускорения в системе (1), должны, разумеется, измеряться относительно блока. Относительно лестницы (веревки) путь человека, очевидно, будет ач + «л> и в данном случае
s4 + «л = nl. (6)
Равенства (5) и (6) сразу дают
s4 = nl, (7)
а общая высота Н, на которой окажется человек,
3
Н - h + s4 = h + — nl = 3,8 м.
4
208
ТЕПЛОТА И МОЛЕКУЛЯРНАЯ ФИЗИКА
Поверхностное натяжение
179. Жидкость с помощью пипетки можно дозировать с точностью до веса одной капли. В нашем случае вес одной капли воды равен 0,01 г. Пока капля не оторвалась, она принимает такую форму, при которой вертикальная составляющая силы поверхностного натяжения уравновешивает вес капли (рис. 228). Вертикальная составляющая силы поверхностного натяжения примет свое максимальнее значение 2лг<т (г — радиус отверстия пипетки, а — коэффициент поверхностного натяжения) в момент, предшествующий отрыву, когда под действием веса капля вытянется так, что _________
ее верхняя часть примет цилиндрическую форму. 7
Таким образом, вес капли mg в момент отрыва под- U .1/ чиняется условию ЦТ
mg = 2лгсг, Л К
откуда /J \х
Подставляя числовые значения, находим
10~5 кг 9,8 м/сег? . , 1 р„„ ооо
а ----------—j-------- 0,078 нм. нис-
6,28-2-10-4 м
180. Вырежем на поверхности мыльного пузыря маленький квадратик со стороной а и рассмотрим его равновесие под действием сил поверхностного натяжения и сил давления (рис. 229).
На каждую сторону квадратика по касательной к поверхности действует сила Р = аа.
Равнодействующая двух таких сил, приложенных к противоположным сторонам квадратика, как видно из рис. 229, равна 2сга sin а. Так как мыльная пленка имеет две поверхности, таких пар всего будет 4. Сила, обусловленная дополнительным давлением Р внутри пузыря, равна Ра2.
14 Л. П, Баканина и др.
209
Условие равновесия рассматриваемого элемента поверхности пузыря запишется в виде:
Ра2 = 4 • 2<та sin а, откуда
р 8g sin а а
Так как для малых углов sin a « а, выражение для Р может быть записано в виде
р _ 8ga _ 4g 2га г
При написании этого выражения принято во внимание, что а = 2га.
Примечание. Заметим, что при решении данной задачи были учтены силы поверхностного натяжения, действующие на обеих поверхностях мыльной пленки. Дополнительное давление внутри капли жидкости (когда имеется только одна поверхность) оказалась бы поэтому равным 2a/r.
181. Так как ртуть не смачивает фильтр, то у входа в канал образуется мениск с такой кривизной, что действие сил поверхностного натяжения уравновешивает давление на поверхность мениска, создаваемое весом столбика ртути и дополнительным давлением Ро-.
Р = Ро + pgh.
Условие равновесия мениска может быть записано в виде (см. задачу 180)
где г —радиус поверхности ртути в канале. Минимальное значение этого радиуса равно радиусу канала гк. Поэтому ртуть начнет продавливаться через фильтр при условии
Ро + РЗ^ = ~-> " к откуда
=____2a___
Гк Ро + pah •
Во всех формулах под Ро нужно, очевидно, понимать избыточное (над атмосферным) давление на поверхность ртути. Подставляя числовые значения, найдем: гк=8ж
182. Приближенно объем V ртутной капли равен объему цилиндра радиуса Р и высоты d, которая найдется из условия nP2d — т/р, откуда
d = — -4т = 9,36 • 10~4 см - 9,36 • 1СП6 м.
‘ р лР?
210
Ввиду малости отношения d/R, при вычислении d можно пренебречь дополнительным объемом V’ выпуклой части капли (легко подсчитать, что V: V — nd: 47?) и считать d равным полученному выше значению. Поверхностное натяжение создает внутри капли дополнительное давление
что можно получить, рассмотрев, как и в задаче 181, равновесие вырезанного из боковой поверхности капли квадратика. Разница только в том, что в данном случае силы поверхностного натяжения, даюшие составляющую внутри капли, приложены только к двум сторонам. Силы, приложенные к двум другим сторонам, действуют практически по касательной к поверхности капли. (Свободную поверхность ртути с очень хорошим приближением можно рассматривать как цилиндрическую.)
Сила, которую надо приложить к пластинке, равна дополнительному давлению Р, умноженному иа площадь соприкосновения капли с пластинкой:
г 2сг 2-0,465-3,14-25 • 10~4
F = — nR2-------------------------
d
= 780 н.
9,36 -10-6
183. Так как боковая поверхность капли воды между стеклами будет вогнутой (рис. 230), то поверхностное натяжение вызовет уменьшение Дввления внутри капли на величину, равную (см. задачу 182) |
d г:" " т~ т
В этой формуле учтено, что (как и в случае полного иесмачивания) радиус кривизны бо- р
ковой поверхности — можно считать равным рис'
d/2. Сила притяжения между пластинками будет равна разности давлений снаружи и изнутри капли, умноженной на плошадь соприкосновения капли с пластинкой:
2<т т 2ffrn 2 • 0,073 • 10~5 п,
F = PS = — • — =--------=------5----75— = 1,46 • 10- я.
d pd pd2 103.10"12
184. Вода поднимается под действием сил поверхностного натяжения. Высота поднятия в первом случае определяется условием
о 2 1
2nra = nr2pg g-,
где а —коэффициент поверхностного натяжения, а г —радиус трубки.
Во втором случае сила поверхностного натяжения уравновешивает силу, возникающую за счет разности давления Р внутри трубки и атмосферного давления Р<>:
2nru = nr2 (Р — Ро).
14:
211
Из этих двух уравнений находим
Р-Ро = Pg Z/2.
Давление Р можно найти из закона Бойля — Мариотта PV =P0V0:
Pnr2h = Р0Лг2 откуда р —
Таким образом,
Р°(2й ~1) = Р^’2 ’
Из этого соотношения получим:
I h = —---------j-г- = 9,9 см.
2(' + р" аАг)
185. Легко видеть, что давление внутри столба масла, втянутого силами поверхностного натяжения в трубку, будет отрицательным (т. е. столб растянут, а не сжат). Действительно, в условиях данной задачи внешнее давление на поверхность масла равно нулю. Поэтому давление внутри столба на уровне масла в чашке тоже равно нулю, так как давления в жидкости в точках, расположенных на одном уровне, всегда одинаковы. Во всех точках внутри столба Давление будет меньше нуля на величину гидростатического давления, В частности, для точки, находящейся на уровне й/3, будем иметь
3 •
Высоту h можно определить, записав условие равновесия столба под действием силы тяжести и сил поверхностного натяжения
лг2/гр g = 2лг(Г, откуда
, 2<т
h =-----.
Pgr
Подставляя это выражение в формулу для Р, найдем
Примечание. Интересно отметить, что давление в точке, находящейся непосредственно под мениском, будет минимальным и равным
„ , 2<х
Р= - pgh= - —.
Поскольку внешнее давление равно нулю, эта формула, по существу, определяет скачок давления при переходе через сферическую поверхность жидкости, которая в данном случае является вогнутой (см. задачу 180 и 181).
212
Закон сохранения энергии для тепловых явлений
186. Если за время t масса m воды нагрелась от температуры Т( до температуры Т2, то при теплоемкости с это требовало подвода мощности:
t
При той же подводимой мощности для испарения воды необходимо время
. mq q 2,26.10®
Zl W “ciTt-Ti)* 4,2 • 103 • 90 ' 10 G0 MUH
(q = 2,26- 106 дж/кг — удельная теплота испарения воды, с — = 4,2 • 103 дж/кг • град — удельная теплоемкость воды).
187. Масса испарившейся в секунду воды равна
W пг — —, q
где q = 2,26 • 10е дж/кг — удельная теплота испарения воды. Объем образовавшегося за секунду пара находится по уравнению газового состояния (см. решение задач 209)
у = _т RT _ W RT 11 Р W
Р ’
где Р= 1 атм—давление паров воды при 100° С, R = 0,082 —- аТМ моль • град
Т = 373° — абсолютная температура кипящей воды.
С другой стороны, этот объем равен произведению скорости истечения v пара на площадь сечения носика S. Тогда
W RT 103- 103 • 0,082 • 373 ,
— — -------- = 75 дм/сек = 7,5 м/сек.
v —-----------
qp. PS
2,26- 106- 18-1 - 10 2
188. Так как процесс установившийся, то энергия в цилиндре не накапливается. Поэтому энергия излучения, поглощенная за единицу времени, равна дополнительной энергии, выносимой из цилиндра нагревшейся жидкостью. Эта дополнительная энергия равна
W = тс (Тг - Т,),
где m = pvS. Таким образом,
Г = (Гг-Л).
189. Тепло Q, выделившееся при ударе, равно уменьшению кинетической энергии пули. Это тепло пошло на нагревание пули до температуры плавления и на расплавление части пули:
Q = _А_!_—У = тс {т _ То} +
213
где т — масса пуди, mi — масса расплавившегося свинца. Отсюда
т
0,015.
190. Шарик, охладившись до температуры 273° К, отдает тепло Q, которое пойдет на плавление льда:
Q = тс (Т — То) = тД.
о 4 , , 2 \
Здесь т = -г лг3р, mi = «г2 ( h + — г р0.
О \ О ]
Подставив выражения Для т и т{ в первое уравнение и разрешая его относительно Л, находим
Нижняя точка шарика будет находиться от поверхности льда на расстоянии
191. Из данных по охлаждению воды легко определить производительность холодильника (т. е. количества тепла Q, которое холодильник отнимает у воды в единицу времени):
тс \Т
где т — масса воды, с — ее удельная теплоемкость, t — время, в течение которого вода охладилась на АГ.
При замерзании воды в течение времени tt холодильник отнимает у нее тепло, равное Qtt. С другой стороны, это количество тепла равно, очевидно, Am, где Л —удельная теплота плавления льда.
Таким образом,
. _ Q/i тс АГ/1 _ с АГ/; ~ т = mt t
Подставляя в эту формулу числовые значения, найдем Л = 3,34 • 105 дж/кг.
192,. Тепло, отнятое рабочим веществом холодильника у воды н льда, переносится им и отдается комнатному воздуху. За время t работы холодильника это тепло равно
Qi= [mcB (Г-Г0) + Лт + тсл(Г0-Г1)]-^,
<о
где То — температура замерзания воды, а т — масса льда, образующегося за время f0. Кроме того, комнатному воздуху передается энергия, потребляемая холодильником из электросети. Эта энергия
Qn = Wt
214
идет на то, чтобы сжать рабочее вещество после его теплообмена со льдом в холодильной камере холодильника и тем повысить температуру рабочего вещества выше комнатной. Это необходимо для того, чтобы стала возможна передача тепла от рабочего вещества холодильника комнатному воздуху. После теплообмена с воздухом рабочее вещество вновь расширяется и охлаждается до температуры холодильной камеры. При этом оно совершает работу, которая также в конечном счете идет на нагревание воздуха. Таким образом, воздух комнаты получает больше тепла, чем отнимается у охлаждаемого тела на величину энергии, необходимой для проведения рабочего цикла. Подставляя числовые значения, имеем
1,41 • 10s дж, Q2 = 1,29 • 106 дж, Q = Qi + Q2 = 1,43 • 106 дж.
Примечание. В идеальном холодильнике, свободном от непроизводительных потерь энергии, тепло, отданное комнате, и тепло, отнятое от охлаждаемого тела, связаны соотношением
Q = Qiy-; * 1
в нашем случае это дало бы Q = 1,53 • 105 дж.
193. В процессе установления теплового равновесия лед расплавился, вода нагрелась до 100° С и часть воды испарилась, так что в сосуде установилось давление насыщенных паров воды при 100° С, т. е. 1 атм. Массу испарившейся воды найдем по известным температуре (373° К), давлению (1 атм) н объему (Юл) из уравнения газового состояния (см. решение задачи 209)
PV
Запишем теперь уравнение теплового баланса:
М2См (Т — Тi) = (Тi — Го) + ш<7,
где То = 273° К, св —удельная теплоемкость воды, равная 4,2 • 103 дж/кг • град. Из этих двух уравнений может быть найдена начальная температура меди:
Л4] [Л + св (Г] — Та) + ц q т — т. j 44' 1
Подстановка числовых значений в эту формулу дает
Г = 1053° К.
194. В цилиндре под поршнем находится m/ц грамм-молекул азота, где от —масса азота, ц — его молекулярный вес. Для нагревания этой массы азота при постоянном объеме потребовалось бы количество тепла
<2>=-^сг,(Га-Г1).
J*
215
В нашем случае газ при нагревании расширяется в условиях по’-стоянного давления. Следовательно, как это вытекает нз закона сохранения энергии, полное количество тепла Q, необходимое для нагрева газа от Ti до Тг, превышает Q] на величину работы А, совершенной газом при расширении. Обозначая давление газа через Р, а изменение объема при расширении через ЛИ, получим
m
A = PAV = -R(T2-T1).
Р-
В последнем соотношении изменение объема ДИ газа при расширении в условиях постоянного давления Р выражено с помощью уравнения газового состояния через изменение температур Га —Г]. Таким образом, m
Q=Q1+4 = — (cv + R)(T2-Ti).
и
Подстановка числовых значений дает Q = ПО дж.
Примечание. Следует обратить внимание на то, что величину Cy + R можно рассматривать как теплоемкость одного моля газа в процессах, протекающих при постоянном давлении (ср).
195. Температура плавления льда понизится на
ду = = 4 4°
138 ’
После повышения давления лед окажется при температуре выше температуры плавления и начнет плавиться. Его температура при этом будет понижаться. Плавление будет продолжаться до тех пор, гока температура льда не упадет до точки плавления при новом давлении. Массу расплавившегося льда nij можно найти из уравнения теплового баланса:
т Д = тс АТ,
откуда
тс АТ , , тх = —5— = 1,4 г,
Л
196. При образовании льда в переохлажденной воде выделяется теплота плавления в количестве Л на каждую единицу массы образовавшегося льда. Это тепло идет на нагревание льда и воды. Процесс прекратится, когда выделится количество тепла, достаточное для нагревания системы до температуры плавления, В силу закона сохранения энергии, так как все тепло в конечном счете идет только на нагревание, при расчете можно считать, что сначала вся вода нагрелась до температуры плавления То, а потом образовалось необходимое количество льда при температуре То.
На основании уравнения теплового баланса можно написать:
1 IT -г \ МС (Т — То)
т/. = Me (Т — То), откуда от =--Ц:---—.
Л
В этих соотношениях X есть удельная теплота плавления льда при температуре То =273’ К (и нормальном давлении), равная 3,34-Ю3 дж/кг. Подстановка числовых значений дает
m 0,125 кг.
216
197. Полная энергия излучения генератора за время t равна
За это же время в виде тепла в генераторе выделится энергия Ю0-г)Гв 1р0-г)
11 11
Объем воды, который нагревается таким количеством тепла на ДГ = 10°, будет
,,___Q______100 — т) wft
ср ДГ г) ср АГ'
За час это составит
100-60 6 • 500 3600 • 103 “° 60 4180 • 103-10 ~т л-
198. Количества тепла Q] и Q2, необходимые для испарения азота и плавления льда, могут быть записаны в таком виде:
Q] = а (Т — Тi) ti = miKi, Q2 = а(Т — Т2) t2<= m2X2>
где а — некоторый коэффициент пропорциональности.
Поделив эти выражения почленно и исключив таким образом а, найдем
Подставив числовые значения, получим
Л, j = 1,8 • 105 дж/кг.
199. При повороте воротка на угол Л<р его концы описывают путь Д/ = гДф, где г —плечо воротка. При этом приложенные к концам воротка силы F совершают работу
ДЛ — 2Fr Д<р — М Д<р,
где М — момент сил, приложенный к воротку.
Если толщина пластинки //, а шаг резьбы h, то для нарезания резьбы нужно совершить n = H/h оборотов воротка. При этом будет произведена работа
А = М • 2л/г = М • 2л Д-.
п
Нагрев пластинки можно наити из условия, что вся работа переходит в тепло, выделяющееся в пластинке. Тогда
А = тс ДГ,
. М-2я4- _
_ А _ _______h = 2.п.М
тс pSHc hSpc
Нагрев пластинки не зависит от ее толщины, так как и объем и работа пропорциональны Н,
217
Тепловое расширение тел
200. Будем считать, что средняя линия каждой пластинки (рис. 231) сохраняет длину, которая была бы в неизогнутом состоянии. Радиус г определяется нз условий:
Рис. 231.
Ф (г — -у J = / + Л/ь А/1 = /а1Д7’, Ф + -g-j = /+ Л/2, Д/2 = /«2 АЛ (1+а1АГ)(г + у) = (1+а2АГ)(г--|-).
Следовательно,
— [2 + (ct] + ct2) АГ]
---------------—----------= 25 см.
(а2 — а|) ДГ
201. При охлаждении стержень сжимается. Его длина становится равной
/ = /0[1-а(Т’2-Л)], откуда - = а (Т2 - Г,). <о
После отогрева стержня, зажатого в обойму, его длина остается равной I, а сжатие 1^ — 1 будет теперь вызвано упругими силами. Запишем закон Гука
1»~1 » п
/о Е '
где Р —давление со стороны обоймы на стержень в направлении оси стержня. Сравнивая два выражения для (/0“ОАо> найдем искомое давление:
Р = Еа (Т2 - Г1) = 4,02 108 н/ж2 = 40,2 атм.
Обратим внимание на то, что давление не зависит от длины стержня.
202. Прн нагревании длина внутренней окружности кольца увеличилась:
/ = 10[1+а(Т1-Г2)], -^^- = a(Tj-r2),
<о
где I и /0 —длины внутренней окружности при температурах 1\ = 573° К и Г2 —29ГК соответственно, а а — коэффициент линейного расширения. Пренебрегая уменьшением диаметра стального цилиндра под действием сжимающих усилий со стороны кольца, можно считать, что после охлаждения кольца длина его внутренней окружности остается равной I и кольцо окажется растянутым упругими силами. Так как в нашем случае толщина кольца мала по сравнению с его диаметром, можно считать, что относительные удлинения всех слоев кольца одинаковы и равны (/ — 1о)/1о- Тогда
218
растяжение кольца можно связать с растягивающим усилием при помощи закона Гука:
/-/о 1 F
10 = Е S'
где F — растягивающая сила, S —сечение кольца, а Е — модуль Юнга. Окончательно для F получаем
F = Еа (Т1 — Т2) == 3360 н.
Это решение не вполне точно не только потому, что мы заменили неоднородную деформацию кольца однородным растяжением, но и потому, что радиальные напряжения в кольце вызывают изменение длины его окружности. Чем меньше толщина кольца по сравнению с его диаметром, тем меньше поправки, вносимые этими обстоятельствами.
203. Результат может быть получен из общих соображений о том, что при равномерном нагреве однородного материала в нем не должно возникать механических напряжений, если его внешние границы не закреплены. Следовательно, изменение любого линейного размера образца может быть определено по формуле линейного расширения
/,-1(1 4-аДГ). (1)
(2)
Для доказательства этого утверждения рассмотрим, например, однородное кольцо с внешним диаметром D и внутренним диаметром d. После нагрева на ДГ его внешний и внутренний диаметры станут равными
= D (1 + аАТ), dj = d (1 + аДТ).
Толщина кольца при этом будет равна
Di—di D — d ... .
---2 = —g— (1 + а ДТ).
(3)
Таким образом, толщина кольца также преобразуется по формуле линейного расширения. В нашем случае формулу (1) следует применить непосредственно к диаметру отверстия в диске. Это дает
ДГ — 1^ = 182°,
а \ D )
т. е. диск нужно нагреть до 182° С.
204. При нагревании стержня от температуры до температуры Т2 без ограничивающих стенок он удлинится на величину
М = Mi + Д/2 = (a, + а2) (Г2 - Г,).
(1)
При ограничивающих стенках нагретый стержень окажется сжатым на такую же величину. По закону Гука (сжимающая сила F в обеих половинах стержня одинакова)
д>_. F 12
Г II 1 1 \ F
S м 2 \ Ei Е2 ) S *
(2)
219
Это соотношение, вообще говоря, является приближенным, так как мы заменили длины /] и /2 обеих частей стержня при температуре Г2 нх длинами 1/2 при температуре Тъ Легко, одиако, понять, что относительная ошибка при определении Д/ по этой формуле будет порядка А/// и, следовательно, наше приближение является очень хорошим (так как А/ /).
Из соотношений (1) и (2) найдем
h2
Смещение ДА места стыка можно определить, приняв во внимание, что оно складывается из перемещения за счет температурного расширения (например, первой половины стержня) и обратного перемещения за счет сжатия:
=4 [а> и2 - го - -/$]=4 ^444— -Г1)-
L -С jO J £
205. Условие равновесия жидкости в двух сообщающихся сосудах запишется в виде
Р18^1 = Р2§Я2.
где Н\ и Н2 — высоты столбов жидкости в сосудах, Р1 и р2 —их плотности. В нашем случае
р2 = Р1 (1 — Р ДГ), поэтому
Р1я, = Р1(1-рдг)//2, откуда
//2 - Н1 = р \ТН2 « р \ТН{.
Подстановка числовых значений в эту формулу дает
Я2 — = 1,56 мм.
206. Изменение уровня воды произойдет из-за того, что объем воды зависит от температуры. Если не учитывать теплового расширения, то изменения уровня воды вообще не будет, так как лед вытеснит точно такой же объем воды, какой он займет, когда растает.
Чтобы найти изменение объема воды, составим уравнение теплового баланса:
Л/и + me (Т — То) = Me — Т),
где tn и М — массы льда н воды, Л — теплота плавления льда, с — теплоемкость воды, Т<, — температура плавления льда и Tf — начальная температура воды в калориметре. Из этого уравнения найдем установившуюся температуру Т:
X
МТ j + mT0 — m —
Г =щ
m + М
220
Обозначая через Уо объем воды с массой (т + М) при температуре Ti, найдем изменение объема и соответствующее изменение уровня воды нз уравнений
АЛ =
АУ У„р
S S
АУ = ПР (Г-ГО, л
МТ] 4- тТ0 — т —
т + М
= — 0,95 мм.
Таким образом, уровень воды в калориметре понизится на 0,95 мм.
207. Из уравнения теплового баланса находим конечную температуру:
У — ОТ1С1^ 1 + ,n2C2^2 _ Р 1С1Г] + Р2С2Г2
1Н\С\ + ZZ12C2 Р1С1 Ч- Ргс2
Как известно, объемный коэффициент теплового расширения твердого тела равен утроенному линейному коэффициенту теплового расширения. Поэтому изменение-объема меди будет равно
ДУ| = ИЗаЛГ-Г,).
изменение объема алюминия
АУ2 = Уо3а2 (Г - Г2).
Общее относительное изменение объема
—^оА-2' = у [а. (Г- Г.) + а2 (Г - Г2)] =
= 4 [(«1 + а2) " а1?1 "аЛ1 = ~ 8-9 • 1О’Л
Z L Р1С1 + р2с2 J
Общий объем уменьшится.
208. Пусть при t = 0° С объем шарика равен Уо, а плотность жидкости р0. Вес вытесненной шариком жидкости в обоих случаях равен произведению удельного веса жидкости на объем шарика, взятых при соответствующих температурах. Поэтому
Pi PigH
Р2 P2gH
Отношение объемов шарика при температурах и /2 равно
У. П(1+РЛ)
У2 Уо(1+₽/2)’
а отношение плотностей жидкости
Pi Ро(1 + (Мг)
Р2 Ро(1+₽Л)’
Отсюда
Pi _ (1 + РЛ) (1 + PH) 1 + РЛ + Рi^2
Рг (1+РШ1+РЛ) 1+Р^ + РЛ'
221
Мы пренебрегли слагаемыми p[Mif2 потому, что они малы по сравнению с членами, содержащими первые степени р и Рр
Разрешая последнее уравнение относительно рь имеем
Р2(1 +р/2)- Р, (1 +рЛ)
Р^-Р2/2
Примечание. Заметим, что проведенное решение справедливо в том случае, если в рассматриваемом интервале температур коэффициент объемного расширения жидкости не зависит от температуры. Это следует иметь в виду, так как некоторые жидкости в определенном интервале температур обладают аномальным объемным расширением. Например, коэффициент объемного расширения воды при температуре около 4° С равен нулю.
Уравнение газового состояния
209. При решении данной и большинства последующих задач на газовые законы объединенный газовый закон (называемый в дальнейшем уравнением газового состояния) удобно записывать в универсальной форме
PV = — RT,
Н
где т — масса газа, р. — его молекулярный вес, a R — универсальная (т. е. одинаковая для всех газов) газовая постоянная. Значение R легко получить из закона Авогадро, согласно которому одна грамм-молекула любого газа при нормальных условиях занимает объем 22,4 л. Таким образом, если т/р, = 1 (одна грамм-молекула), Р = Р0=1 атм, То = То = 273° К, то V ~ = 22,4 л. Отсюда
R -= 0,082 = 8,31--д*..
То 273 моль • град моль • град
Поскольку m/V = р — плотность газа, уравнение газового состояния может быть также переписано в виде
т цР
P=V= RT ’
Это последнюю запись уравнения газового состояния также удобно использовать при решении ряда задач.
Решение данной задачи сводится к подстановке числовых значений в уравнение газового состояния. Нужно только учесть, что молекула азота состоит из двух атомов и, следовательно, ц = 28 г)моль = 28 • 10~3 кг/моль
т РТ 1 0,082 - 300
ц V = 28 • 10-3 103
атм.
222
210. Разрешив уравнение газового состояния относительно массы, получим
pPV т= RT
Принимая теперь во внимание, что молекулярный вес аммиака равен 18, и выражая давление в атмосферах (190 мм рт. ст. = «= 0,25 атм), получим
17 -0,25 -20
т 0,082 • 300 34,6
г.
211. Применяя к воздуху, занимающему объем комнаты при температурах 10° С и 20° С, уравнение газового состояния, разрешенное относительно массы, н выражая давление в атмосферах, а температуры в °К, имеем
. РУр ( 1 1 \
Am R Т J - 2,2 кг.
212. Очевидно, что давление внутри шара равно давлению окружающего воздуха. Тогда масса вытесненного шаром воздуха щРУ .. .. mRT р,] _
т} =• Но У =—=—, следовательно, = Подъем-RT ]lP р
ная сила
F = m^g — mg = I —— 1) mg = 13,5mg.
213. Из уравнения газового состояния найдем
тНе _
RT0
1-ЩР рУ
та~~РТГ'
где отНе и тв — массы гелия н воздуха в объеме шара V, gHe и Цв — молекулярные веса гелия и воздуха, R — универсальная газовая постоянная. На основании закона Архимеда условие, при котором шар будет поднимать сам себя, запишется в виде
Р V
Mg<g (mB - mHe) = g (|*B - PHe)>
где M — масса оболочки. Обозначая через Ио величину RTq/Pc, равную 22,4 л, н выражая М и V через радиус шара г, получим следующее условие:
1 4
4лг2р<-^(1Хв-Нне) y^3-
Отсюда
ЗУ0р
Г mln —7 “ •
Ив “ ИНе
223
Подставляя числовые значения, получим
Tlllln —
3 -22,4- 10~3- 1 (29-4)- 10-3
« 2,71 м.
214. Пусть Го и Г —абсолютные температуры воздуха вне и внутри оболочки. Тогда массы т0 и т воздуха при температурах Та и Г в объеме оболочки равны
т0 =
цР0У рУ
RT0 ~ Vo ’
_ p,P0V _ jxV Го
RT Vo T
где [Л — молекулярный вес воздуха, 7? — универсальная газовая постоянная, Vo = RTo/Po = 22,4 л —объем одной грамм-молекулы при нормальных условиях.
Условие, при выполнении которого шар будет подниматься, запишется в виде
Mg С g («о - m) = f 1 - .
vo \ I /
Из этого соотношения можно найтн минимальное значение Tmia температуры воздуха внутри оболочки:
j____То = _Ко = 145-22,4- 10~3 = _1_
Гт1п р V 29- 10~3- 224 2 *
Гппп = 2Г0 = 546° К = 273° С.
215. Условие подъема шара запишется в виде
где р0 — вес оболочки, pt = V Pig — вес вытесненного воздуха в объеме шара, р2— Vp2g —вес теплого воздуха в шаре. Плотность воздуха может быть найдена из уравнения газового состояния
m _ рР
Р =
Таким образом,
VvPg п , VuPg Vp.TxPg
-W>Po + “W’ Г2>1¥р?-роРГ-305 к‘
Следовательно, воздух нужно нагреть не менее, чем на 5° С.
216. F=Kg(pB-Pr), Р = ЪУ-АI
F = (Ив - Иг) = 7870 я = 803 кГ.
224
217. Молекулярный вес соединения ц = пц0, где Цо = 12 3 +• + 6+ 16 = 58. Из уравнения газового состояния находим, выражая т в граммах, Р в атм и V в литрах,
т RT 0,716-0,082-473 _
П~ цо PV = 58-0,987-0,2426 ~2,
218. Предполагаемая формула вещества С.уНу, а его молекулярный вес ц=12х + у. Молекулярный вес ц может быть определен с помощью уравнения газового состояния из данных задачи:
mRT 0,65-0,082-300
= =------ГП------= 16-
Подбором находим х=1, у = 4. Таким образом, формула соединения будет СН4.
219. Предполагаемая формула вещества СЛОУ. Его молекулярный вес ц=12х4-16у. Из данных задачи с помощью уравнения газового состояния найдем:
_ mRT _ Ц ру 44.
Подбором находим х=1, у = 2. Формула вещества СО2.
220. Число грамм-молекул кислорода согласно уравнению газового состояния равно
т РУ П ц RT •
Число молекул в одной грамм-молекуле дается числом Авогадро No = 6,023 • Ю23. Число электронов в атоме равно его порядковому номеру. Принимая во внимание, что молекула кислорода состоит из двух атомов, найдем
W = 2 — JV0Z = 2 JV0Z = 4,3 • 102«. ц Nl
221. Напишем реакцию образования гелия
Li7 + p> =2Не4.
Таким образом, масса образовавшегося гелия равна
8
mH= = 7 mLi = 1^ г-
Объем гелия найдем по уравнению газового состояния
Т7 т RT 1,14 - 0,082 - 303 „„
у = = —Го£2— = 7’7 л-
222. Будем считать, что площадь поверхности ртути в чашке много больше площади сечения трубки, и пренебрежем изменением уровня ртути в чашке. Обозначим внешние давления через Plt Р2
15 Л. П. Баканииа и др. 225
223. Плотность
и Р3, давления воздуха в трубке через р', Р2 и Р3 и высоты столбов ртути —через Н}, Н2 и Н3 соответственно (рис. 232). Тогда, обозначая давления (в мм рт. ст.) теми же буквами, что и высоты столбов ртути (в мм), получим
pi = p'i+Hi, р2=р'2 + н2, р3 = р'з + н3.
Все величины, входящие в эти формулы, выражены в мм рт. ст.
Если обозначить в первом случае расстояние от уровня ртутн до верха трубки через /г, то во втором случае это расстояние будет Л + Hi — Н2, а в третьем h + Я] — Я3. Считая сеченне трубки постоянным, можно записать закон Бойля — Мариотта для воздуха в трубке так:
p{hS = P'2(h + Hi ~H2)S = P'3 (h + Hi - Я3) S.
Определив отсюда
= (Pi-Hj)(Hi~H2) _ (Pi-Ps)-(ffi-ffs) 1 M’
подставим это значение в уравнение для определения неизвестного давления Я3:
H23-(Hi + h + P3) н3 +
+ (P3-Pi+Hi')h + P3Hl^Q, и получим Я3 = 751,2 мм рт. ст.
газа при давлении Ро и температуре То равна ш _ р Ро
V ~~R то
Пусть вес пустого баллона равен Яо. Тогда его масса равна Na/g, а масса газа в первом и во втором случаях (Я — Na)/g и (Hi — Na)/g соответственно. Следовательно,
PV = - р V = RT
fig Pg
Ро =
откуда
(P-Pi)V=N -'RT, 4 ng
Отсюда следует, что p Я-Я, Т R ~ (P~Pi)g V‘
Подставляя это значение в выражение для р0, получим
Я-Я, РаТ Ро (P~Pi)g VT0‘
224. Давление в камере определяется из условия
Р — Ро = -тг = 0,58 атм.
Таким образом, /*=1,58 атм.
226
Так как при накачивании температура не меняется, объем воздуха, который насос должен захватить из атмосферы, равен
v° р0 '
Число качаний
„ = _Kl = ^.=79.
При езде за счет изменения температуры изменяется и давление в камере. Новое давление Р] при температуре Г] будет равно
Pi = р 2-L
1 1 * J* •
Площадь S] соприкосновения с дорогой при этом будет si = F = —-----------------------= 50 см2.
Pi-Рь PJl_po
225. Число атомов гелия, образующихся за год, равно А = 3,7 • 1010 • 0,1 • 60 • 60 • 24 • 365 « 1,17 • 1017.
Эта формула написана в предположении, что можно пренебречь изменением массы радия в течение года. Действительно, первоначальное число атомов радия Ni = 2,2 • 1020, н таким образом, это число изменилось меньше, чем на 0,1%. Число грамм-молекул гелия A = .M7J.0”=194,10-7 Na 6,02-1023 ’ ш ’
п =
где .Wj —число Авогадро. Поэтому
4,6 • 10-3 атм.
226. PV^^-RTt, PV=^-RT2, = - = 1,6 a.
И К U i “ 2)
227. Определим объемную скорость газа, протекающего по трубе,
= V 1 m RT q t ~ t p P ’
Объемная скорость связана с линейной скоростью <7 = vS,
соотношением
откуда
q 1 m RT no~ , °= s-=sFT~ = 0’87 MlceK-
общее давление, которое этот газ
228. Каждый сорт газа в смеси дает вклад в равный парциальному давлению, т. е. давлению, оказывал бы на стенки сосуда, если бы других газов в сосуде ие
227
15*
было (закон Дальтона). Для парциальных давлений можем написать так:
P1V=^±RT, p2v = ~^rt.
Отсюда
(Р, + Р2) F = |i + ^-) RT.
\ Mi На /
Следовательно,
= = (m, + m2)(P. + P2) =
V ^ + ^\RT \ Hi Нз /
229. Столбик ртути находится в равновесии, когда pghS = = P0S — PS, P=pg(H — h). Так как температура не менялась,
PV~PBV0, P(l-h)S = P0-t S,
пли
Р-Т(&р +
откуда
Л,.! = ^±|От’.
Во всех формулах для давлений (в мм. рт. ст.) и для соответствующих высот столбов ртутн (в мм) использованы одинаковые обозначения. Но 0 < h < I по смыслу задачи, a + у V Н2 + l2>l
и, следовательно, не может быть решением задачи. Остается
h = ^~- -уЬ/Л+Т.
Заметим, что при решении данной задачи силы поверхностного натяжения во внимание не принимались.
230. Применяя уравнение газового состояния к водороду, находящемуся в аэростате до и после нагрева, имеем
PV^—RT,
И
PV = ^RTit
Р откуда
тТ ~ miTl.
Таким образом,
/ Т \ m — m [ = m i —— = M \ 11 /
или
228
Тогда для объема аэростата имеем
mRT
MRT
I T \
= 985 .и3.
231. Шарик поднимается, когда rnmg < pVmg, где р - плотность воздуха. Отсюда
Р RT
muiRT или Р > -т-.---124 атм.
4 }ЛГ3Ц
232. Шар всплыл, когда масса воздуха в объеме шара стала равна массе шара. Воспользовавшись уравнением газового состояния, найдем ,
р.РК цР 4 3 _ „
RT RT 3 ПГ 12,3 г'
233. При постоянной температуре
PV=PiVit где Р=Ро + О,1Ро = 1,1Р0.
Отсюда
Р 17
У=-Б7р- = 360 см3.
В лампу войдет V; — V = 500 — 360 = 140 см3 веды.
Рис. 233.
234. При постоянном давлении -г7- = тр-.
' 1 ‘ 1
Записав Г] = Т + АГ и Р, = У(1+рЛГ), где р — коэффициент объемного расширения, равный по условию задачи 1/335, получим
1 Г
1 + р АГ Г + АГ ’ откуда
Г = 4- = 335° К.
Р
235. р = 0,0107 г/сл3.
236. Из рис. 233 видно, что условие равновесия ртути в первом и втором случаях будет
PiS = P0S - mg,
Рг$ = P0S + mg.
Кроме того, по закону Бойля — Мариотта Pi/]S] = P2I2S2.
Таким образом,
(Ро - pgh) lt = (Ро + pgh) 1г,
Po-Pgh^.
Ч “ *2
229
237. Так как массы воздуха в обоих шарах одинаковы, можно записать
Р I У1 _ Р 2^2
Ti Т2 *
Из условий равновесия капельки Pi = Р2, следовательно,
Учитывая, что У, = Уо + ДУ, У2 = Уо - ДУ, Т\ = Та + АГ, Т2 = Тв - АГ,
У0+АУ Уо-АУ ... Уо ._ д, АУ
получаем = —---—или ДУ = -=-ДГ, откуда AZ ==-„-=
1 Q~T 1Л1 1 Q — LX1 1 о О
= « 29 см. Из условия задачи видно, что объем шара (1 л)
о/ О
значительно больше объема трубки (12 см3); поэтому при вычислении Уо объемом трубки можно пренебречь.
238. Т = 1250° К. Расчет был проведен в предположении, что вся вода превратилась в пар. В нашем случае это заведомо справедливо, так как при температуре, превышающей ZK = 374,1°C (критическая температура воды), водяной пар не может быть превращен в жидкость ни при каком давлении.
239. Давление в сосуде, которое установилось бы После испарения азота (при условии, что сосуд не разорвался), находим нз уравнения газового состояния
_ tn RT 0,5 • 103 • 0,81 • 0,082 • 293
Р=т—------------------------------34.7 атм.
Так как Р > 20 атм, сосуд разорвется.
240. Условия равновесия системы запишутся в виде
Pi = P2 = P и Tt~T2 = T.
Кроме того, по условию задачи, mi = т2 = пг. Применяя уравнение газового состояния к
Принимая теперь во
У1 =
обеим частям сосуда, получим
VI _ 1*2
У2 1*1
внимание, что У] 4- У2=У, найдем
—У и У2 = —У, 1*1 + 1*2 1*1 + 1*2
откуда следует /] = 5 см (кислород), /2 — 80 см (водород).
241. 2 г кислорода составляют 1/8 грамм-атома кислорода. Они прореагируют с 1/8 моля Н2 (0,25 г). Таким образом, останется непрореагировавшнм 1,75 г водорода. Он создает давление
D ni RT
Р =-----= 2 атм.
1* У
242. При равновесии поршня
Р1^Р2=-Р, Г1 = Г2 = Г.
Для каждого из газов
PV^-^-RT, PV2 = ~RT. 1*1 1*2
230
Следовательно,
Fi . W1H2
V2 m2g!
Учитывая, что 1Л + V2 — V, находим
£ =----=
V m1p2 + ^2l4'i
P T
243. При постоянном объеме = Pi 11
Положив Р2 = Р1 + ДГ, имеем
£1_1 = Л£
?1 Г, ’
откуда
Т^. ..- = 500° К
1 Рг-Р\ 1,002?!- Pi °UU *••
244. По условию задачи, до нагрева Р2 = 2?!, V2=Fi/2; после нагрева
Так как температура в верхней части сосуда неизменна, можно записать:
Р^^Р^, откуда Р[ = 4-Рр О
Принимая во внимание, что вес тяжелого поршня создает в нижнем сосуде неизменное дополнительное давление (равное Р\, как это вытекает из соотношения Р2 = 2Р1), будем иметь
P2=Pi+p;=yp,.
Для ннжнен части сосуда нз уравнения газового состояния получим
Р'У' _ P2V2
Ti Pl
Выражая давления н объемы в этом равенстве через Рг и Vi, найдем 7 7
?2 = т Г1 = V 400 = 700° К-
245. Давления гелия Pi и водорода Р2 определяется из уравнения газового состояния:
р _ 2m RTi _ tn RT2
' 4 V ’ 2 2 V ’
но Р2 — Pi ~ Mg,!S, откуда
(P2-P,)S mR(T2-Ti) g 2gV/S '
231
246. Так как при неизменной температуре давление в сосуде / увеличилось вдвое, то его объем уменьшился в два раза. Так как Si/S2 — 2, объем газа в сосуде 2 увеличился вдвое, а новое давление Р в сосуде 2 стало равным
О
Из уравнения газового состояния имеем
2HSt (2Р0+8/2р^Я) HS2P0 “ То откуда
247. Поскольку горизонтальный ствол шахты сообщается с атмосферой, давление воздуха здесь равно атмосферному: РО“760 мм рт. ст. В верхней части шахты (под заслонкой) давление воздуха будет равно
Pi = Po~pigh,
где р!~ плотность воздуха внутри шахты. Аналогичным образом давление воздуха над заслонкой будет равно
Pi = Ро ~ p2gh,
где р2 — плотность наружного воздуха.
Прн написании этих соотношений, очевидно, предполагалось, что плотности воздуха р] и р2 не меняются заметным образом при изменении высоты па величину /г. Это предположение справедливо, если изменения давления с высотой (т. е. pigfi и р2§Л) были малы по сравнению с Ро. Плртности воздуха р! и р2 могут быть определены нз уравнения газового состояния
о = Р° о - УР°
P1 RT ’ р2 RT0 '
где Т н То — абсолютные температуры воздуха внутри и вне шахты соответственно, R — универсальная газовая постоянная (см. решение задачи 209). Разность давлений
Pi - Р2 = gh (у— у) = ghp (1 - .
f д \ / о •*/ А-/ о \ 1 !
Поскольку Го = 273° К (нормальная температура), величина RT0/Pa имеет смысл объема, который занимает одна грамм-молекула газа при нормальных условиях. Обозначим эту величину через 1/0=22,4 л. Запишем теперь выражение для силы, действующей на заслонку нз-за разности давлений:
F=S(P1-P2) = Sg/i-jH-(l-^-'j.
VQ \ 1 I
Эта сила направлена вверх, так как Р\ > Р2. Для удержания заслонки в равновесии к ней нужно приложить внешнюю силу, на
232
правленную вниз и равную по величине F. Подстановка числовых значений в выражение для F дает
3,5-9,8-224-29- 10~3(1 --|gy)
F --------------------=-*--------- «500 н ~ 50 кГ.
22,4- 10~3
В справедливости сделанного выше предположения о постоянстве pj и р2 можно убедиться с помощью несложного числового расчета, который здесь не приводится.
248. Решение данной задачи аналогично решению задачи 247. Обозначая абсолютные температуры воздуха вне н внутри трубы через Га и Т соответственно, получим
Отсюда
= ! _ FV0 = j _ 8,7-9,8-22,4 • 10~3
Т Sg/щ 1.9,8 •22,4.29 10~3
Таким образом, Т 974
т = W = ’oT = 39O°K = 117°с
Следует отметить, что система находится в неустойчивом состоянии, так как теплый воздух может свободно выходить вверх, и значит, полученный результат относится только к первому моменту после закрытия заслонки.
249. Первоначальное давление Р в первой половине сосуда равно сумме парциальных давлений аргона и водорода;
p = p1 + p2 = AL
После окончания диффузии
так как водород теперь занимает объем 2Р. Принимая теперь во внимание, что Р=1,5 атм, а Р'=1 атм, найдем после несложных преобразований
= 1 ра _ 40 = ,
тв 2 цв 2 2
250. Давление в первой половине сосуда будет равно сумме парциальных давлений аргона и водорода
/’=Р1+Р2
V \ Ра 2цв )
0,082-293 /20 , 2 \
----i---(ТО + 272) = 24
(см. решение задачи 249).
атм
233
251. Условия равновесия аэростата на первой и второй высотах запишутся в виде
Mg = piVg, (М- Am)g = p2Vg,
где pi и р2 — соответствующие плотности воздуха, Ат —масса выброшенного балласта. Из этих соотношений следует
Дт = (р,-р2) V.
Выражая теперь плотности р] и р2 с помощью уравнения газового состояния через температуры Г] н Т2 и давления Pi и Р2 (см. задачу 209), получим
Am = ~ (у1— 44 V = 4,2 кГ. К \ 1 \ lit
252. Баллон с азотом взорвался при давлении р mi RTi
Давление водорода, по условию, равно Р2 = Т’1/5. Массу водорода найдем из уравнения газового состояния:
р2Р2У т, ц2 Т, _ 103 -2-623 а
2 RT2 5 |i| Т2 5-28-293 ’
253. Для той части газа, которая осталась в баллоне, справедливо соотношение
Рг _ Pi
Т2 Ti'
Следовательно,
Ti~T2 = T2 = 121,Г.
254. При первом взвешивании вес был равен весу баллона минус вес воздуха в объеме баллона (выталкивающая сила):
Pi = Р - Рв-
Во втором случае вес равен весу самого баллона: р2 = р. В третьем случае р3 = р — рв + рг.
Таким образом, р2 = р3 — р{. Массы газа, заполнявшего баллон, и воздуха в объеме баллона, находятся из уравнения газового состояния:
цгРгУ _ рвРвУ mr , тв
Следовательно, Иг = = 118 = ИВ (P2- Pi)Pr
тсРв
РгР в
(Рз-Р1) Рв
234
255. Давление в цилиндре определяется условием равновесия поршня и остается постоянным:
р = р0 + “. о
Изменение объема ЛИ можно выразить с помощью уравнения газового состояния через изменение температуры Т2 — Т
ду=у2_у1=^-А(7’2_Г1))
откуда
.. ЛИ m 7? . m R .
ЛЛ S |л PS (?2 р. P0S + Mg (’2 ?1' 4
266. Давление газа под поршнем постоянно и равно
P=P!l + ^-. О
Работа газа по поднятию поршня
A = F(h2-h1) = PS (й2-Л1) = Р(И2-И1).
Выражая изменение объема ЛИ = И2 — V\ через изменение температуры газа (при постоянном давлении), найдем с помощью уравнения газового состояния:
A=^R (T2-Ti) =1715 дж, д
др = у2 - у, = -Д- = 0,0167 л3.
257. Используя результаты решения задачи 256, найдем
„ РА
И(Тг-Т,)'
Подставляя числовые значения, получим
т = 0,23 г.
258. При нагревании газа при постоянном давлении тепла требуется больше, чем при нагревании при постоянном объеме, так как в этом случае, кроме нагревания самого газа (повышения его температуры), производится еще работа по расширению газа A — P(V2—Vi) (см- задачу 256). Поэтому требуемое количество тепла
Q = v cv (Т2 - Л) + v * ~ = 7Г (^ + V ~ = 109 дж'
н м> в>
235
259. Так как поршни находятся в равновесии (рис. 234), то Ро ~ Р = Р2 — Ро, где Р2 — давление во втором цилиндре. Таким образом, Р2 = 2РС, — Р. После
нагревания первого цилиндра получим аналогичное соотношение Р'2 = 2Р() — — Р . Из уравнения газового состояния для первого найдем
Р'У' РУ Tt ~ Т
и второго цилиндров
Подставляя сюда выражения которого определится Р':
и, следовательно, V V7
Р' = ~
Ti Р2
Т Р2
для Р2 и Р'2, получим уравнение, из
2P0PTt
Р •2Р.,Т--Р<Г1 -Т) •
260. Условие равновесия системы (см. решение задачи 259)
Р2 = 2Р0-Р1.
(О
Так как массы воздуха в обоих цилиндрах и их объемы одинаковы, можно написать
Из (1) и (2) найдем
261. Первоначальное давление в сосуде определится из уравнения газового состояния:
И 2V ’
При нагревании давление в обоих сосудах остается одинаковым, но плотности, а следовательно, и массы газа будут различны;
РХУ = — РТЪ
Н
py = -^-RT-,
н
отсюда
m1T l = т2Т.
236
Принимая во внимание, что
т ] + т2 = т, получим
Т1
т2-т T+Ti-
Окончательно,
m,TJR 2\xVPTiTR Т,' Р, = 27,
р. (Jt + T) V цУ (?’+ 7',) РГ T+Tt’ Р T + Tt'
262. Пусть Иц, т2 11 «г3 —массы гелия в первом, втором и третьем сосудах при температурах Тi = 4° К, Т2 = 20° К и Т3 = 80° К. Поскольку сосуды соединены трубками, давления в них одинаковы и, следовательно, на основании уравнения газового состояния будем иметь
rn, PTi m2 RT2 m3 RT3
и V p. V p V ’
где P — установившееся давление в сосудах в конце опыта, ц — молекулярный вес гелия, V — объем каждого сосуда.
Первоначальное давление Ро, когда все три сосуда находились при одинаковой температуре Т,, было равно
d m PTl
° р ЗУ ’
где ш — т,+ т2 + тз- Найдем теперь отношение давлений
Р 3/п, 3
ро ~ т ~ 1 + '"2 + т-- '
, + «1 mi
Как следует из первой формулы, отношение масс газов в двух сообщающихся сосудах одинакового объема, находящихся при разных температурах, равно обратному отношению абсолютных температур. Поэтому
263. Давление в цилиндре всегда равно атмосферному давлению Ро. После открытия крана в баллон перейдет некоторая масса газа, которая при температуре Г, занимала объем Sh, поэтому
Sh V , V Ti
~тГ- = -тГ, отсюда Л =
1 | 1 о 1
264. Установившаяся температура определяется из уравнения теплового баланса
t = J у» с = 290° К.
nii + т2
237
Теперь можно определить давление в каждой части сосуда:
mt 2RT пй - тг 2RT
Pi -------п— в 0,85 атм, Ра -------= 1,27 атм.
у. V * у V
26?.. Так как каждого газа взято по 1 молю и объемы их и температуры одинаковы, то давление тоже должно быть одинаково и равно Ро = RT0/V. После реакции образуется 1 грамм-молекула паров воды Н2О и останется 0,5 грамм-молекулы кислорода. Давление в сосуде равно сумме давлений этих газов (предполагается, что вода не конденсируется). Если Р{ — давление паров воды, a Pi — давление кислорода, то 2yPj = Pr, 2УР2 = 0,5РГ. Сложив эти равенства, получаем >
2VP = 1,5RT, у = -1,5-Г- Р = АГ°2^.. = Р.
’ Л ’ 2Р ’ ° 1.5РГ ЭД) •
266. Для каждой секции справедлив закон Бойля — Мариотта. Кроме того, при равновесии давление во всех секциях одинаково: Р, = Р2 = P'i = Р- Следовательно, У[: V'2: V'z= P^j: Р2У2 : Р'<У'л' Кроме того, Kj + + Из = Fj + К, + У3. Поэтому
P (V! + У2 + У3) = P1K1 + РгУ2 + P3K3.
Из этих соотношений найдем
Р,К1 + Р2К24-РзКэ , Р,У, Р1У,(У,+ У2+У,)
У,+ У2+Уз ’ 1 Р Р1У!+Р2У2+РзУз ’
Р2У2(У1 +V2+Уз) v, РзУзСУ. + Уз + Уз)
2= PiV^PiVi + P^Vi ’ V'^ Р1У1 + Р2У2 + РзУз •
267. Из уравнения газового состояния для воздуха, заключенного внутри трубки, имеем
p,ls PiiLS
Го Г •
Принимая во внимание, что
Pl =Po + j-pgL’ получим
та~т------ф-------.
Ро + у PgL
238
268. Так как в обоих случаях объем газа в пробирке одинаков можно написать
р р, р
Т=У7 и™
во
Pi = Po-yPg£, P = P0+^-pgi,
откуда
_ _ 2Р0 - pgL
1 2Po + pgL’
При решении предполагалось, что в верхнем положении пробирка не сообщалась с наружным воздухом.
269. Сначала давление и объем газа равны
Pi = Ро + pgh, V1 = Sh.
Потом
Р2 = Р0 + -^, V2 = S-~h
(вода опустилась в правом колене на й/4 и поднялась в левом на /г/4). Теперь можно написать
(Po + pgh)Sh +
Ti Т2
откуда
т = 3. т 2Ро + pgh
2 8 1 Po + pg/г ‘
270. В результате процесса водород останется в первой половине сосуда, тогда как гелий распределится по всему сосуду. По закону Дальтона давление в смеси газа равно сумме давлений, оказываемых каждым газом в отдельности; поэтому давление в первой половине Р1 = Рн + РНе, во второй Р2 = РНе.
Из уравнения газового состояния
_ mt РТ _ m2 РТ_
Н gH v > Рн. Цне 2V *
Отсюда
Pi
т2 2Нне
„ RT т2 „ „ атм, P2=—tt-q----= 0,12 атм.
v
271. Работа, совершаемая газом, равна A = P(V1 — V2) (см. решение задачи 256). Таким образом,
но
Ti Vi'
239
следовательно,
т — г — т
Таким образом,
лт,
А7- = Г2-Л=--^.
Подставляя числа, находим ЛГ = — 9,5°.
272. В обоих случаях груз будет в равновесии, если давление внутри сосуда будет удовлетворять условию
PS = P0S - Mg, или Р = Ро - = 0,5 атм.
0
Так как в сосуде находится 1 моль азота, то
PVi = RTlt
PV2 = RT2-
\Т —2 Ч
следовательно, ДУ = ———=1,64-10 м. Груз поднимется на вы-
соту 164 см.
273. Работа газа Д = Р(Р2- 7,). Но Р (V2 - Pi) = — R (Т2 - Л), н
Затраченное тепло
Q = mcp(T2-Ti)t откуда
ш(Г2-Л) = ^-. ср Итак,
д = -^_= 1 37 - 103 дж.
МСр
274. Из уравнения газового состояния
PV= — RT u
следует, что при постоянных Р и V отношение масс газа равно обратному отношению абсолютных температур:
— = = 41! = 0,96, т. е. m2 = 96%mi:
mj Т2 296
из комнаты ушло 4% воздуха.
Работа газа при расширении (при Р = const) равна произведению давления на изменение объема (см. решение задачи 256);
I V, \
A’=P(V2-Vl) = PV2[l-~L\.
\ У 2/
240
В этой формуле по смыслу V2 — есть объем комнаты V, a Vi — объем, который до расширения занимал газ, оставшийся в комнате. Легко видеть из уравнения газового состояния, что
Vi т2‘
Таким образом,
А = PV (1 - = 1,033 • 10’ • 50 • 0,04 « 2,07 • 10’ кГм = 2 • 10s дж.
\ 1 2 )
275. Первоначально в баллоне содержалось — = -^у = — 41,7 грамм-молекул водорода. Дли образования 0,5 л воды (0,5 кг) требуется 500/18 = 27,7 грамм-молекулы. Следовательно, потерялось 14 молей, или 28 г Н2.
количество метана в баллоне сжигания в баллоне осталось
276. Первоначальное PV
= р. = 3430 г; после КI
Ш1 =
тг —
= р. -jpp- = 2650 г; сожжено, следовательно, 780 г и получено тепла Л < 2
Q = 26,l-10е дж. Так как теплоемкость воды с = 4,18 дж/г • град, этим теплом можно нагреть на 100°
М = •—— = 62 кг воды. с ДГ
277. Первоначальная масса метана в баллоне была
М = = 5,8 кг.
РI
На нагревание льда и его расплавление израсходовано тепла
Q = ст AZ + тК = 3,84 • 106 дж.
Для этого потребовалось сжечь метан в количестве
Масса оставшегося метана
М2 = 5800-92 = 5708 г.
При постоянных объеме и давлении
МТ = М2Т1;
откуда
М
7’1 = 7-77-=254° К.
278. Поршень сдвинется, когда сила давления азота на поршень уравновесит вес поршня, силу внешнего давления и силу треиия F:
PlS = Mg + P0S + F.
16 л. п. Баканина и др.
241
Повышение температуры газа в нашем случае будет равно
ДР---
mcv
имеем
Из уравнения газового состояния (при постоянном объеме)
Р1 = Р^- = р(1+-у-) = р(1 +
mcvT )
Следовательно, P=(P1_p0)S-JMg=[p(l+-J— )-Р01 S-Mg.
L \ ГПС / J
279. Число молей водорода после полной диссоциации увеличится в два раза. Следовательно, как это вытекает из уравнения газового состояния, давление Р2 в сосуде будет в два раза больше того давления Р, которое установилось бы в сосуде в отсутствии диссоциации. Из уравнения газового состояния имеем
PV2 PiVi
Т2 Т, ’
откуда
Р2 = 2Р = 2Р1-р-4Х = 8 атм.
И2 1 j
289. Если бы молекулы J2 не были диссоциированы, давление в сосуде было бы равно
„ m РТ 1 0,082 • 1273 .
Ро =——у~= 254---------------= 0>82 «’’•« = 625 мм рт. ст.
Если степень диссоциации молекул J2 на атомы J равна а, то n пг т ., . m
в сосуде находится 2а— молен атомарного иода J и (1—а) —
М- т „ И
молей молекулярного иода J2. При этом полное давление в сосуде на основании закона Дальтона будет равно сумме парциоиальных давлений J и J2, т. е.
пг РТ . m РТ .т РТ р 2а р V +(1 ) Ц У 1 + а)р V ( +а)р°-
Отсюда следует, что 1 + а —
Таким образом,
Р 700
Ро ~ 625
= 1,12.
т. е. 12%.
281. Решение данной задачи аналогично решению задачи 280. Если бы диссоциации молекул СО2 не было, давление Ро в сосуде оказалось бы равным
n m РТ 0,2 0,082 - 2800
Рс =-----77- = -77—’--;-----= 0,97 атм = 735 мм рт. ст.
ц У 44 1
Здесь ц — молекулярный вес СО2, равный 44.
242
а = 0,12,
Пусхь_теперь степень диссоциации молекул СО2 равна а. Поскольку формула диссоциации в данном случае записывается в виде
2 СО2 2 СО + О2,
на каждую пару диссоциированных молекул СО2 приходится две молекулы СО и одна молекула О2. Таким образом, в сосуде будет ,, х т . т . ат .
(I — а) — молей СО2, а— молей СО и -------молей О,,
ц р 2 (х 2
Применяя закон Дальтона для смеси газов, найдем полное давление Р в сосуде:
л к т от х т RT а т РТ
р = (1_а)_^ + а_ —+ ___.
Таким образом,
т RT ( Н V =V
+ ^)Р°
а
¥
Ро 735 ’
а = 0,2, т. е. 20%.
Насыщающие и ненасыщающие пары
282. Давление паров воды в сосуде р = 22,4 • 0,6 = 13,4 мм рт. ст. Дополнительно нужно создать давление 9 мм рт. ст. Масса воды, создающая такое давление, найдется из уравнения газового состояния
PV=^RT, /п = -^ = 6,2 а.
283. Масса пара в трубке при 150° С т, — 0,0164 г.
Rl I
Масса насыщающего пара при 22° С тг = — 0,0075 г. Значит,
К!2
выпадет 0,0089 г росы.
284. Полное давление влажного воздуха равно сумме давлений воздуха и водяного пара: Р0 = Р + р, р = 44,6 0,8 = 35,7 мм рт. ст., Р = 724,3 мм рт. ст.
тп = -^^Д-=33,4 г, тв = -^~=Ю90 г.
Таким образом, искомый вес равен
(та + тв) g = 11 « = 112Э Г.
285. Давление паров воды при 50% влажности и температуре 20° С равно 8,75 мм рт. ст. Масса сухого воздуха по уравнейшо газового состояния равна
PV
mBt = ^в f •
16*
243
Масса воздуха во втором случае равна . Рв(Р-Рн) V 7?V P»v а‘ RT !в>7’ !n RT ’
а масса пара
т _ гп~^т^-
Искомое отношение после преобразований имеет вид
тя Р 760
и 1
760 - 0,4 • 8,75 1 ’°05'
"Ч + тп
Рп
286, Подъемная сила во влажном воздухе равна F = [V (рв + ар) — М] g,
где М — масса шара, « — относительная влажность. Увеличившаяся влажность а' = а + 0,2. Следовательно,
F' = [ V (Рв + Дрв + ар + 0,2р) — Л7] g,
где Дрв — изменение плотности воздуха. Таким образом,
&F = F' — F = V (Дрв + 0,2р) g.
При неизменном общем давлении изменение давления воздуха будет, очевидно, равно — 0,2рн, где ра — давление насыщающих паров при заданной температуре, равное
pRT Рч = ~Т—-Нп
Следовательно, изменение плотности воздуха Дрв будет равно
Дрв=_Д^н^_0,2^р.
К1 Цп
этой формуле означает, что при увеличении влаж-парциальное давление воздуха уменьшается. Иско-: подъемной силы будет, таким образом, равно kF=- 0,27 (-Н2--б pg= - 0,l22Vpg.
\ Рп /
Подъемная сила уменьшается, так как уменьшается плотность влажного воздуха.
287. Из уравнения газового состояния, разрешая его относительно массы, находим
ррн7 200,6 - 0,0011 Ю3
т = -РТ" = “б,082.7С0”293“ “ °’0'2 3 " 12 Мг'
288. Число молекул равно N = Л'ош/р, где Л’о —число Лвогадро. Из уравнения газового состояния
т _ раУ р RT •
Знак минус в нести воздуха мое изменение
244
Следовательно,
N=.-^N0 = —jT Na = 760.0 082.303 6,023-1023 = 1,78- 10H молекул.
289. Одна грамм-молекула газа занимает объем
V --р-.
На одну молекулу приходится объем ,, _ RT kT
Ь N0P Р ’
где No — 6,023 • 1023 — число Авогадро, a k~ постоянная Больцмана; среднее расстояние между молекулами будет, таким образом, равно
При Т — 100° С давление насыщающих паров воды равно 1 атм = = 1,033-—С- = 10® -^г, поэтому см- слР
, Л Г 1,4- 10-16-373 „„ ,„_7
I — у ------урё---- =3,7-10 см.
290. Количество тепла, выделенное кипятильником, Q=Prt. Это тепло идет на нагревание воды до 100° С и на испарение ее части:
Q = ст Д7' + qnii.
Объем паров может быть определен из уравнения газового состояния у uh RT
Н Рн
где ра — давление насыщающих паров воды при Т — 373° К, равное 1 атм. Следовательно,
h = — = RT (-J2rt~cm Л7~> S Sppuq
Подстановка числовых значений в эту формулу дает h =17 см.
Следует обратить внимание, что н уравнении энергетического баланса не нужно писать члена рнК, соответствующего работе, совершаемой насыщающим паром. Дело в том, что теплота испарения определяется всегда при постоянном внешнем давлении, равном давлению насыщающего пара при этой температуре, и работа расширения пара уже учтена н величине q.
291. При неизменной температуре давление пара пропорционально плотности. Поэтому относительная влажность
а = —= —
Ра Ри
245
Плотность пара будет равна сумме плотностей, которые создает пар нз первого и второго объемов
p=p! + p2 = (-v + Рн = 4 <°>2 + 2 ’ °’3) Рн = °>27Р«-\ о о / о
Относительная влажность будет равна а = 27 %.
292. Давление паров при 1003С pi = 760 • 0,4 = 304 мм рт. ст. Так как масса паров не меняется,
р i V1 p2V2 PiViT2 .. „
Чр— = -^—, отсюда К2 = - „ = 1ч00 см3.
' 1 J 2 J 1Р2
Следовательно, объем надо увеличить на 1300 см3.
293. Давление водяного пара, пока не началась его конденсация, будет изменяться пропорционально общему давлению. Поэтому в конечном состоянии, когда началась конденсация, его давление, равное 760 мм рт. ст., было в 60 раз больше начального давления, т & 760 „
Таким образом, начальное давление пара р = = 12,7 мм рт. ст.,
а относительная влажность 72%.
294. Давление влажного воздуха н сосуде складывается из давления воздуха и пара:
Т
P — Pi + p, Pi — Р = 1,37 атм. i о
Считая пар идеальным газом н предполагая, что вся вода испарилась, найдем: р = mPT/pV — 0,51 атм. Так как давление насыщающего пара при 100° С равно 1 атм, пар не насыщен н, следовательно, наше предположение было правильным. Таким образом, Ро= 1,88 атм.
295. Массу воздуха и массу паров воды н искомом, объеме находим из уравнения состояния для воздуха и пара:
_ (Ро-арн)Г __ арпУ
тв------РВ» ГГ1П — РП»
где Pq — суммарное давление. Учитывая, что тв + тп~ т, находим
V = ------= 0,86 л.
(Ро «Рн) U-B 4" йРнЦп
296. Давление воздуха н сосуде при 76° С Pi — Po — Pi — = 450 мм рт. ст. При 80° К давление будет ранно Р2 = PiT^/T^ = = 103 мм рт. ст.
297. При объеме Т0/2 и известном давлении насыщающего пара масса газообразного аммиака найдется из уравнения
т = п„ = 1,26 г.
Следовательно, сконденсировалось 0,64 г аммвака.
298. Предположим, что весь сухой лед испарится. Тогда р = тРТ/р V = 0,27 атм. Это давление меньше давления насыщаю
246
щего пара; значит, наше предположение верно. Давление н камере равно 1,27 атм.
299. Найдем первоначальную массу паров воды в сосуде:
/7»1= ^г~ = 0,909 г, где pi = apa.
При внеденни еще 1 г воды масса станет равной 1,900 г и давление
m2RT
р2 ~ = "О мм рт. ст.
r р7
Относительная влажность cti = — = G3°6.
рн
300. Первоначальная масса воды в сосуде ж^О.ООЭг (см. задачу 299). После введения добавочной воды т2 = 1,009 г. Давление такой массы паров, если бы нся вода испарилась, было бы Рг = m2RT/p.V = 1,37 атм— 1041 мм рт. ст. Это значительно больше, чем давление насыщающих паров. Следовательно, вода, введенная дополнительно, испарится не вся и в сосуде будут насыщающие пары воды. Относительная влажность а^ЮОй.
301. Максимальное давление, которое могут иметь пары воды при 100° С, равно 1 атм. При равновесии азот должен иметь то же давление. Определим его объем Va = m2RT/naP = 2,18 л. Это превышает полный объем сосуда. Следовательно, вода сконденсируется и азот займет весь объем (за вычетом части, занятой жидкостью).
302. Будем решать задачу в предположении, что испарится вся вода. Поскольку при равнонесии данлеиия и температуры водяных парой и азота одинаковы, из уравнения газового состояния найдем
^. = ^£l = 0,31.
Са Рв m2
Таким образом, искомая доля высоты будет равна
__« 0 24 Гв+7а ’
Для того чтобы убедиться в спранедливости нашего предположения, нужно найти давление в сосуде:
maRT 0,1-0,082-373
Р = 1ГД24— ~°" а™~
Поскольку р<рн=1 атм (при /=100° С), пар не насыщен и, следовательно, наше предположение было верным.
303. Легко убедиться в том, что н условиях данной задачи предположение об испарении нсей ноды несправедливо (см. решение задачи 302), и при раннонеснн под поршнем будет находиться вода и насыщающий пар при давлении 1 атм. Давление азота над поршнем также должно равняться 1 атм. Поэтому объем азота будет равен
m2RT _ Va =—i---= 0,55 л.
PaP
247
Таким образом, поршень установится на уровне 0,45 от полней высоты цилиндра. Определим теперь массу т испарившейся воды из уравнения газоного состояния
= г.
Ki
304. Давление паров ноды при 70% влажности составляло
р = рна=12,6 мм рт. ст.
Следовательно, давление воздуха составляло 87,4 мм рт. ст. При изотермическом сжатии давление воздуха возрастет в 10 раз и будет раввым 874 мм рт. ст. Пары воды при уменьшении объема станут насыщающими и часть воды сконденсируется.
Полное давление в цилиндре после сжатия будет
Pi — 874 + 18 = 892 мм рт. ст.
Уменьшение объема за счет сконденсировавшейся воды можно не учитывать, так как общий объем равен 1 л, а объем сконденсировавшейся воды даже при полной конденсации составит
И = — = -£-т??- = 0,11 см3. р pRT
305. Полное давление в комнате при изменении температуры не изменилось, следовательно,
(Рв + Рп) 1 = (Рв + Рп) 2-
Поскольку из комнаты ушли одинаковые части воздуха и пара, можно записать так:
(— 'l = f j
\ Рп /1 \ Рп /2
Отсюда следует, что при изменении температуры каждое нз давлений рв и рп осталось неизменным. Таким образом,
(pu)l = а1РН1 = (Рп)2 = а2Риг
а2 = cti =36%.
Рпг
306. Вначале давление паров воды в ящике pa — api — 37 мм рт. ст. Это давление выше, чем р2, и на змеенике будет конденсироваться вода до тех пор, пока давление паров воды н ящике не станет равным р2. При этом масса паров н воздухе будет равна
Начальная масса паров была равна
m =
0 ЦТ
243
Следовательно, на змеевике сконденсируется
н у
Ат = та - т = (р0 - Рг! = 17,5 г.
307. Пока вся ртуть не испарится, в баллоне будет сохраняться давление насыщающих паров ртути при 120° С. За 20 мин насос откачал 140 л этих паров. Применяя к парам ртути уравнение газового состояния, можно найти их давление:
т/?Т
р =——— = 0.001 атм.
ц У
308. При температуре 5° С 20 г воды в виде насыщающеге пара займут объем, равный
т RT 20 • 0,82 278 • 760 „
V -------=-------~ 3 • 103 Л.
р. р 18-6,54
Насос откачает такой объем за время t—\ час.
309. Найдем число грамм-молекул (молей) водорода и кислорода:
/ т \ РН У
I — I = ——— = 0,00550 грамм-молекулы,
V И /ц2 RT
/ т\ POV
I—I =—=0,00275 грамм-молекулы.
' И 'сь
Таким образом, весь водород и кислород прореагирует, и образуется 0,00550 грамм-молекул воды. Так как давление паров воды не может превышать 17,5 мм рт. ст., найдем, какому числу молей это давление соответствует:
/ т \ рн П2У
(—I =—— = 0,00096 грамм-молекулы.
\ н /нгО RT
Итак, сконденсируется 0,0045 моля, или 82 мг воды.
310. Масса т влажного воздуха, равная сумме масс сухого воздуха и пара, определится из уравнения газового состояния: цв(Ро-арн) V , ИпарнУ
m-------+ RT .
Разрешая это уравнение относительно ра, найдем
_ 1 ( D т%Т\
Рн а(цв-рп)Гв0 V Г
Подстановка числовых значений в это выражение дает рц = 18 мм рт. ст.
311. По условию задачи сосуд содержит достаточно большое количество воды (половину объема); следовательно, при повышении температуры до Т2 испарится не нся вода, и в сосуде установится
249
новое данлеине Р2, складывающееся из давления возДуха, равного Р.Т21Т1 (Рп — давление воздуха при температуре Т^, и давления насыщающего водяного пара рн?
= + Рнр
~~ т
Р2==РВ-^- + Ра,-& в у * ид
Отсюда
Т Т
Р^Р2-РВ^-Р2-{РХ~Р^Т; =
= 815,5 - (626,7 - 26,7)-^. = 149,5 мм рт. ст,
OvU
При решении задачи предполагалось, что испарение некоторой дополнительной части воды при повышении температуры до Т2 практически не меняет объема, занимаемого воздухом и паром.
312. В сосуде А после установления равновесия будет находиться воздух и насыщающий пар. Давление Рв в сосуде найдется из закона Бойля — Мариотта (7 = const):
Рв = Р° H^—h = 760 "1360 ~ 838 мм рт‘ Ст’
Полное давление Р в сосуде А из условия равновесия столба веды равно
р = pQ + -£2- (Я - h) = 760 + -5L 1360 = 860 мм рт. ст. Ррт 10,0
Здесь Рз и ррт — плотности воды и ртути соответственно.
Следует отметить, что второе слагаемое в этой формуле записано н виде, выражающем давление сразу н мм рт. ст.; при этом (Я —й) следует, конечно, выражать в мм водяного столба. Таким образом, для обозначения давлений (в мм водяного столба) и соответствующих высот столбов воды (в мм) здесь используются одинаковые буквы.
Давление насыщающих парой воды найдется из соотношения
рн = Р — Рв = 22 мм рт. ст.
Разные задачи
313. Число атомон в 1 см3 железа п = Nop/p = 8,5 • 1022. Объем одного элементарного куба о = 1/и= 1,18 • 10“23 см3. Длина ребра куба I = j^v = 2,3 • 10“8 см.
314. На 1 см2 площади стейки за 1 сек попадает масса серебра М = mN = pd, d — где АГ —число частиц, попадающих на 1 см2 стенки за 1 сек. Давление на стенку P = mNv, a v = ^2W/m.
250
Итак,
Ц 2rwo ’
где И — молекулярный нес, a No — число Авогадро,
^ = — уЛ 2100' = 9'10 3 сМ!сек-
315. Давление насыщающих парой ноды при 100° С равно 1 атм. Следовательно, пар в сосуде насыщающий и при уменьшении объема конденсируется в воду. При этом выделяется тепло Q = qm. где q— удельная теплота испарения воды, а т — масса сконденсировавшейся ноды (пар, содержащийся н половине объема):
т = = 5,9 г, Q = 13251 дж.
Работу, которую совершают внешние силы при опускании поршня (Р ЛИ), отдельно учитывать не надо. Она включена в теплоту конденсации (см. решение задачи 290).
316. Если поршень поднимается не слишком быстро, давление паров воды в сосуде практически равно Рй = 1 атм. Такое давление пары ноды имеют при 100° С. Так как поршень поднялся на высоту h, объем паров равен hS, а масса
li.PohS т = = 5,9 г.
Тепло идет на нагревание всей ноды до 100° С и испарение массы т ноды. Работа по поднятию поршня включена в q (см. решение задачи 290). Итак,
Q — Me &.Т + qm.
Время, необходимое для выделения такого количества тепла,
Q _ Мс ЬТ + qm 41,6 • 104 + 1,3 • 104
W W 500
= 858 сек = 14 мин 18 сек.
Из сравнения тепла, затраченного на нагренание и испарение, видно, что испарение продолжалось примерно 1/40 всего времени, т. е. около 20 сек. Это дает скорость поднятия поршня 5 см/сек, что действительно можно считать малой скоростью.
317. Так как поршень свободен, очевидно, начальное давление пара 1 атм. и, следовательно, температура 100° С. Масса пара
PV
При конденсации этого пара выделится тепло Q = qm. Это тепло пойдет на нагренание впрыснутой ноды, причем вода должна нагреться не выше 100° С. Поэтому
M~TW=TwSr=3’17 кг-
251
318- Вода нагреется до температуры, при которой давление ее насыщающих паров будет равно атмосферному давлению (100° С), после чего часть воды, в соответствии с запасом тепла, испарится. Массу испарившейся воды т найдем из уравнения теплового баланса:
Al1 (Т — Т+ срп — М2С2 (Т2 — Т),
m=~ [М2с2 (Т2 — Т) — MiCl (Т - Г()] = 38 г.
- v mRT _л
Это количество пара займет объем V — —~ = 64 л. Следовательно, поршень поднимется на высот5^
V
Д/г = -g- = 64 см.
319. Очевидно, что температура пара в сосуде 100° С. Введенная вода должна нагреться до 100° С за счет конденсации некоторого количества пара:
me (Т — То) = kniq.
Отсюда
тс (Г-Го) о,.
Ат =------------= 3,34 г.
Ч
MnRT
Объем этой массы пара Л/ = ——— = 5,3 л. Итак,
AV ..
ап — = 53 см.
329. Поршень будет в равновесии, когда сумма действующих на него сил равна пулю: PS = P0S + Mg. Следовательно,
Р = Ро + -щт- = 2 атм.
При 0°С данлеиие насыщающих паров меньше 2 атм, и поэтому вся вода скоиденсиронана. При 200° С данлеиие насыщающих паров больше 2 атм, поэтому нся вода испарится, и пар будет расширяться до тех пор, пока его давление не станет равным 2 атм. Найдем ' ”
нимется
его объем при этом: У=трГ/цР; высота, на которую подпоршень,
, V _ mRT _ , „
h S y,PS 1,9 М'
Условие равновесия груза и поршня:
PS = P0S -Mg, Р-Ро- = 0,5 атм.
321.
Это давление меньше давления насыщающих парой при 100° С (1 атм), следовательно, вся вода испарится н займет объем, при котором давление равно 0,5 атм:
. mRT к
У = —7~- = 61 л.
цР
252
При 0° С давление насыщающих паров меньше 0,5 атм, следовательно, нся вода сконденсируется и ее объем практически будет равен нулю. Поршень опустится до диа сосуда, а груз поднимется на такую же высоту:
h = -£- = 6,1 м.
Мс <Т2 - Г,) +
322. t = ----------— — 26 мин.
323. Давление на глубине 100 м Р{— Ро + pgH = 11 атм. Из закона Бойля — Мариотта находим необходимое давление в баллоне:
Р = 1К±£1£1_ = 286 атм. v
324. Энергии компрессора расходуется на работу А против сил давления на глубине 100 м и сообщение кинетической энергии вытекающей струе воды 1Г:
Д = РУ=(Ро + рйЯ) у,
= Mv2_,
2 ’
скорость струи v — V/St-, M — pV. Итак, еК3_ » A+W РУ , рУ*
IT 2S2,2 , Л t t + 2S2t3 113 мт.
325. Запишем условия равновесия поршня в начальном и конечном состояниях:
Л4 jgf -j- P0S kx2 ~ R2S,
где Mi — масса поршня, S — сечение цилиндра, X] и х2 — изменения длины пружины, Pi и Р2 — начальное и конечное давления газа, Ра —внешнее давление. Из этих двух соотношений имеем
fe(x2-x1) = S(P2-P1).
Но х2 — xi = H — /г; Р2 — Р] ныразим из уравнения газового состояния
Pi Pl~ pS\H h )
Из этих соотношений найдем
_ _ Н pkH (Н - Л)
Г2==71Т+ MR----------•
326. Так как в начальном положении давление газа равно внеш*, нему давлению, то в этом положении пружина не сжата. Пусть первоначально поршень находится на высоте h. Если газ полностью откачать из-под поршня, то внешнее давление сожмет пружину как раз на величину h. Это дает возможность прокалибровать
253
пружину. По закону Гука F = kx, k — жесткость пружины, х — изменение ее длины.
При х=/г, F = PS и, следовательно, k^PS/h.. Давление, которое пружина оказывает через поршень на газ, будет
D, F Р Р-^-^х.
Когда объем газа увеличится в 1,5 раза, пружина удлинится на h/2 и будет оказывать давление:
Р 1 . Р
Применяя теперь уравнение газового состояния, получим
PV^—RT и + V~ ~ ц \ 2 ) 2 |Х
отсюда
о
Л = т = 2,25 Т.
того чтобы сосуд плавал во втором случае, объем им воды должен по-прежнему равняться hS, где
327. Для вытесненной 8 — сечение сосуда, и давление воздуха в ием должно поэтому равняться P0 + pgft. Обозначив через высоту столба воздуха в стакане во втором случае, получим из закона Бойля — Мариотта:
Р0Я8 = (Р0 + Р^)Я18,
откуда
H P*H
1 Po + pgA’
Найдем теперь глубину погружения Л] нижнего края стакана
hx - H-Hi + h—H (1 - ) +• h = h (1 + k
\ T’o + PgA/ \ T’o + pg/г/
328. Стакан утонет, если масса воды в объеме, занимаемом воздухом на глубине Л, будет равна (или меньше) массе стакана. Объем воздуха на глубине h определяется законом Бойля — Мариотта
Po + pgA’
где V0 = SH.
На критической глубине
fo + pgft
откуда
Л = —
— 1 ] = 30 м.
254
329. Состояние воздуха в правом колене трубки подчиняется закону Бойля — Мариотта. В первом случае
= +^Lpg, Vi — ~LS. О о
L [ 1 Лр?\
J V з
Если обозначить через х высоту столба воздуха во втором случае (после слива части жидкости), то
Pz — Po> Vi = xS.
Следовательно,
Po + v Z-pJ 4 О J О откуда
х =
Полная длина столба жидкости до слива равнялась 2L— L 5 т
----— после слива части жидкости длина столба уменьши-о б
лась на
L L {. , 2 £ра \
2х~"з'"з' v + 'з ТГ/'
Таким образом, относительное изменение массы равно
2х~~
3 1/2 Lpg \
2L-А 5 ' 3 f->'
О
жидкости будет
330. Применим уравнение газового состоянию и состоянию при температуре
состояния к начальному 7\ -----
(Ро + L) LS (Ро + L — х) (L + х) S Г Ту
где Ро = L — атмосферное давление, S — сечение трубки, х — увеличение длины столба газа в трубке *)• После преобразований получаем
Т + 2 L V Р)' т
Отношение достигает максимума при
х 1
Т“ 2 ’
*) Заметим, что в этой формуле х обозначает и длину, и давление. Это возможно потому, что в условии задачи давление дано в мм рт. ст.
255
что н определяет необходимую степень нагрева. Дальнейшего повышения температуры не потребуется — газ, изотермически расширяясь, вытесинт всю ртуть. Таким образом,
Г,-4 г.
331. Давление внутри жидкости будет меньше атмосферного (жидкость растянута). Если система находится в равновесии, то вес поршней уравновешивается разностью сил внешнего давления и давления жидкости на поршень. Кроме того, внутри жидкости устанавливается гидростатическая разность давлений, уравновешивающая вес столба жидкости. Пусть давление в верхней части жидкости будет Р. Тогда давления жидкости у поверхности поршней будут
Pi = P + pgh и P2 = P + pg/7.
Условие равновесия поршней
mg = (Ро -Pi)s = (Po-P~ pgh) s,
Mg = (Po -P2)S = (P0-P- pgH) S.
Исключая Pq — P, находим условие равновесия в виде т , М т + р/г = -т+рЯ.
Легко видеть, что равновесие системы будет неустойчивым.
332. Поршень всегда будет устанавливаться в таком положении, при котором сила давления газа равна силе сжатой пружины F=kh.
kh
При температуре Т Р — V—
при температуре Р^-—-, V1 = /z1S.
Из уравнения газового состояния получим
khhS khihiS
ST Sl\ ’
еткуда ___
даче 332.
Задача решается аналогично за-
256
334. Давление газа P = pg(H — х) (рнс. 235). Его объем V = хЗ. Следовательно,
г.-гЯ + ^..о,
Н Л Г Н* mRT
Х 2 “ V 4 pSpg *
Для того чтобы задача имела решение, необходимо, чтобы
mRT . Н1 „ . №p,Spg
—ё С—г> следовательно, Т <—т—
piSpg 4 4mR
Рис, 235.
Рис. 236.
335. При 100° С в пробирке будут воздух и водяные пары. Они могут выходить из пробирки, если их общее давление будет больше или по крайней мере равно внешнему давлению иа глубине L/2; давление насыщающих паров воды при 100° С равно 1 атм, т. е. равно Ро,
Eo + Pi>pg-|- + Po. Pi>Pg-^-
В начале опыта давление воздуха в пробирке, очевидно, равнялось атмосферному. Из рис. 236 видно, что
0 2 PJ.S _ _ Т2 L . _ Т2
т Т2 9 Р* Р°2Т или pg 2 *
Итак,
J < 2k— }Q R и
pg
336. Поршень будет в равновесии, если давление в пробирке будет равно Ра + pg(ff — х). Тогда по закону Бойля — Мариотта получаем
[Pa + pg(W-x)]xS-=P0Z,S,
х2 - х (н + -2лЛ + -£«£ = 0,
\ Pg / РЙ
17 Л. П, Баканина н др.
257
Определим, какое из полученных решений годится. Для этого изобразим на графике закон Бойля — Мариотта для газа внутри пробирки. В данном случае закон Бойля — Мариотта можно записать так: Рх = const (кривая 1 на рис. 237). Кроме того, на том же графике построим зависимость давления в жидкости на глубине
Н — х как функцию х: Р = = Ра + pg (Н — х) (прямая II).
Для равновесия поршня нужно, чтобы оба давления были равны; этому соответствуют точки пересечения кривой I и прямой II — точки a и Ь. Но нетрудно видеть, что положение поршня в точке b является положением неустойчивого равновесия. Действительно, если объем газа случайно немного увеличится, гидростатическое давление умень-
рис „ЗУ шится сильнее, чем давление
газа в сосуде, и газ вытолкнет пробку. Если же объем немного уменьшится, то гидростатическое давление возрастет сильнее, чем давление газа, а пробка будет проваливаться внутрь пробирки до положения ха. Из тех же соображений видно, что ха — положение устойчивого равновесия. Итак,
Задача имеет решение, если подкоренное выражение больше нуля, т. е.
4 \ pg) pg
или
1 / РуР _Ра_ V Pg Pg'
На рис. 237 это соответствует условию, что прямая II проходит правее прямой III.
337. В покоящейся ракете высота столбика ртути в барометре определяется условием pgH0 = Ра. В ракете, взлетающей вверх с ускорением а, столбик ртути тоже должен двигаться с ускорением а, т. е. сумма действующих на него сил должна равняться та: та = PS — mg, где Р — давление в контейнере т — р -ОД/ДЗ, a—g в нашем случае.
Итак, PS = т(а + g) = l,2pg//0S или Р — 1,2Р0- Но Ро : Т0=Р : Т, следовательно, Т/То= 1,2.
338. Работа совершается на пути 1 — 2 н на пути 3 — 4 (рис. 238). Так как давление на этих участках постоянно, то
2^12 = Pi(V2—V^, Л34 = Рг (Kj — И2).
Из уравнения газового состояния
Р1У2 = РТг, PiV^RTi, Р2У2 = Р1\.
258
Комбинируя эти равенства, находим
P^-R^.
1 2
Полная работа за цикл
Л=Л12 + Л34-
Знак минус означает, что на участке 3 — 4 иа большая работа, чем работа газа на участке 1 — 2. Р
339. Газ совершает работу, расширяясь по изобаре 2 — 3. Эта работа равна
Л23 — Рц (Уз ~ Vz) — R — Т2).
При этом для сохранения постоянства давления при расширении к газу подводят тепло. На второй изобаре совершается от-
рицательная работа у
Л1 = Р4(’/2-1лз) = «(Г1-Г2). Рис. 238. '
Чтобы давление не поднималось, несмотря иа сжатие, от газа отводят тепло. Полная работа газа
Л — ^23 + ^41 = Р (Гз + Г1 — 2Т2):
Т2 может быть определено из условия, что на изохоре 3 — 4: Р2:Т2 — Р^: Т2, а иа изохоре 1 — 2: Рг:Т2 = Pt: Th откуда
Т3 = Vrfc.
газом совершена
4 , 3
/ 2
Окончательно работа, совершенная газом, есть
A~R{Px + T2-2.VT(FzY
340. В результате нагревания и расширения газ из состояния Р1, V\ перешел в состояние 2Pt, 4Vi. Эти состояния связаны уравнением PV>1= const, т. е.
Р1У" = 2Р1(471)П,
лп 1 1
откуда 4П = — п = — -^.
341. Так как кривые PVn — const при 0<n< 1 идут на графике зависимости Р от V более полого, чем проведенные через те же точки изотермы PV = const, то при расширении газа по этому закону давление падает медленнее, чем при изотермическом расширении. Следовательно, газ нагревается.
342. Если объем газа при некотором давлении увеличивается на величину ДР за счет смещения поршня площадью S на величину А/г, то при этом газ совершает работу против силы, действующей на поршень и уравновешивающей силы давления газа. Эта работа равна АЛ = F&h = РДV. Графически работа изобразится прямоугольником с высотой Р и шириной ДГ (заштрихован иа
17* 259
рис. 239). Если давление изменяется при изменении объема, как в нашем случае, то работа при изменении объема от 7! до Vj бу дет численно равна площади трапеции abed, которую можно представить как сумму площадей прямоугольника abed и треугольника Ьсе:
преобразовав это выражение, получаем
A = ±a(y22-V*).
Так как без подвода тепла при расширении газа давление падает, а в нашем случае оно возрастает, то для осуществления такого процесса необходим подвод тепла.
= — RT, то в данном Й
закону
P~~RaV. И
343. Так как для идеального газа процессе давление будет изменяться по
PV= — RaV2, И
Таким образом, работа вычисляется аналогично тому, как это сделано в задаче 342. Эта работа численно равна площади, заштрихованной на рис. 240:
Процесс идет с подводом тепла.
344. Очевидно, что при установившемся режиме горения в камере двигатели будет такое давление, при котором скорость истечения массы вещества из сопла равна скорости сгорания: aPS — AP", где a — некоторая постоянная; отсюда
1
илн P = (-±V-n.
aS \ aS /
260
Отношение давленый в камерах 2 и 1 будет
1 Pg ( «$1 \l— п Pl \sj •
2 S P
В частном случае п — -тг- = 2 получим -=^- = 23 = 8.
О о2 г\
345. Задача решается аналогично задаче 344. В нашем случае
Р
-—- = 2, —2-= 4. Таким образом
г>2 Pi
4==2ь^ т е —=2 » = 1
1 — п 2
III. ЭЛЕКТРИЧЕСТВО
Электрический заряд. Закон Кулона
346. Заряд шара, очевидно, равен заряду электрона, умноженному на число п атомов в.шаре:
Q — ne. (1)
Подсчитаем число атомов. Ойо равно произведению числа грамм-атомов меди па число Авогадро:
п = у Na. (2)
Масса же меди
/п = ул/?3р. (3)
Таким образом,
Q = .ey°..-^P-=5)6.1Q7
347. После того как электроны у одного шарика отняты и перенесены на другой, шарики приобретают равные и противоположные по знаку заряды, поэтому (если шарики находятся в Вакууме) сила притяжения
' 4ле0/?2
8о= otL-10"9 ООД
(1)
где R — расстояние между центрами шариков. Заряд q определится следующим соотношением (см. решение задачи 346):
еМ0 еМ0 4
q = т = у л/?3р. (2)
Здесь Мо—число Авогадро.
261
Подставляя (2) в (1), получим
№е2 4лЛ^6₽2е2
f - -л-ВТ = - » ляЬГ = 4,38 • 10"» н.
4ле0Р2 QeaA2R2
348. Применив законы Кулона и всемирного тяготения, получим два уравнения для силы электрического отталкивания f3si и силы тяготения fiar:
е2 ^“Ine^2
Здесь е= 1,6-10~19 /с — заряд электрона,
е°= ЗблГ ‘10 9 ^м'
, tn2
/тяг = Y
т — масса капельки, R — расстояние между у=6,7-10-11 кг-1 м3 сек~2 — гравитационная иивая }ЭЛ и /тяг и выразив массу капельки плотность р, получим
4ле0/?2 R2 9 Р ’
центрами капелек, постоянная. Прирав-через ее радиус г и
откуда
Окончательно получим:
гв. 9е2
64л38оур2 г = 7,6 • 10~5 м.
349. На основании закона Кулона силы fit f2 и f3 взаимодействия между зарядами будут иметь следующий вид:
f =, г _. г _ УгУз
'* 4яе0г2’ 2 4ле0г2 ’ '3 4ле0г2’
где е0 — диэлектрическая проницаемость вакуума. (Предполагается, что заряды расположены либо в вакууме либо в среде с проницаемостью, близкой к е0.) Из этих уравнений нетрудно получить
(7)=r-j/taWJ1 = li9.10-7 к>
= 2,9 10~7 к,
350. Для равновесия зарядов необходимо, чтобы сумма проекций всех электрических сил, приложенных к каждому заряду, на направление касательной к кольцу равнялась нулю (рис. 241). Результирующая электрическая сила в этом случае перпендикулярна к окружности и уравновешивается силой реакции кольца.
262
Так как заряды в точках В1 и В2 равны между собой, то заряд <71 может быть расположен только в точке, находящейся на равных расстояниях от точек В, и Вг. В соответствии со сказанным, проекции сил /л и }2г, действующих на заряд q2 в точке Bt со стороны двух других зарядов, на направление касательной к ок
ружности TTi в точке В] должны быть равны друг друг^, т. е.
f21cosY1 = f22COSY2. (1)
Но f2i = —?1%~, где (из треу-4ne0rf2
п
гольника ABfi) rI2 = 2R cos — :
kl =--------. (2)
16ne0/?2cos2-^-
<?2
Далее, f22 =-----
4ле04,
„Г> • О
где r22 = 2R sin , т. е.
<?2
=--------------О)
16ле0/?2 sin2 -%
Рассматривая углы при вершине Blt мы можем написать
4+Yi = 90°, (4)
90°-y + Y1 + Y2 + -|“ 180°. (5)
Рис. 241.
Из уравнений (1) —(5), учитывая, что Р = а/2, получим а , Р а
cos -к- cos2 -т- cos
— в------?-------1_ --------2 = 12 5>
^2 sin2 — sin 4sin3-^ 2 2 4
351. Ha каждый из шариков в воздухе действует сила тяжести mg, сила натяжения нити Т и сила электрического отталки-л2
вания f=-z-------т£-—.—ту (рис. 242, а). При равновесии выпол-
(«ь/ SIH Ct/
пяются условия:
Т cos а = mg,
Т sin а = f,
263
откуда
tga =
f
mg ’
(2)
При погружении шариков в керосин добавится выталкивающая сила F, а сила электрического отталкивания уменьшится в е раз, где е — относительная диэлектрическая проницаемость
керосина (рис. 242, б). Сила натяжения нити, естественно, тоже изменится и станет равной Гр Условия равновесия пишутся теперь следующим образом:
Т] cos а + F = mg, |
Г1 sin а =
(3)
откуда
tg а — —;------777 .
e(mg —Г)
(4)
Приравнивая правые части (2) и (4), получим
1 1 mg n(mg-F)'
(5)
Определим теперь m и F: m = i/3ar3{>, где р —плотность материала шариков, г —радиус шарика; r = 4/3w3pKg, где рк —плотность керосина. Подставим полученные выражения в (5):
р = е(р-рк).
f
264
Отсюда
р = -5Ц--=1,б-^.
г е — 1 см3
352. Поскольку шарик вращается равномерно, сила электрического притяжения создает необходимое центростремительное ускорение;
4л80/с
Искомое отношение
<7 4леою2Я3 о ,п-б к — = ---------- KQ ‘ 1U ----
гп до кг
Электроемкость. Потенциал
353. Последовательно соединенные конденсаторы имеют одинаковые заряды (почему?):
<71“<72 = <7з = <7, (1)
поэтому разность потенциалов на каждом из них соответственно будет
V^/-, У2=^-, V3 = 4-. (2)
С 1 ^2 Ьз
Учитывая, кроме того, что
Vj + ^+Vs-S, (3)
из уравнений (1) —(3) находим
У ___________________
1 CjC2 + С2С3 + С3С1 ’
У „_______gC,C3______
2 С1С2 + С2С3 + СзС1’
у ________jC}________
3 CjC 2 + СгС3 + С3С1
Заметим, между прочим, что из (1) —(3) легко получается и формула для обшей емкости С трех последовательных конденсаторов:
1
С
7г-+ -р~ + -J4—> где С’в—. UI U 2 <-» 3 ©
354. Решение задачи аналогично предыдущей. Результирующая емкость системы Со удовлетворяет равенству:
_L=_L+__L_, Cq Ci С2 + С3 откуда
С —
° С, + С2 + С3 ’
265
Заряд этого результирующего конденсатора равен
<7 гс0 „ „ „ .
Этой же величине q равен заряд q} конденсатора Ct и суммарный заряд группы конденсаторов Сг и С3:
<72 + <7з = q.
Кроме того, разности потенциалов на С2 и С3 равны друг другу (параллельное соединение); следовательно,
<-2 Оз
Решая совместно полученную систему уравнений, определим q2 и qz. Окончательно имеем
годСз + Сз) ______ гс,с2 _ ?С|Сз
<7,~ С1 + С2 + СГ’ 92 - С1 + С2 + С3’ q3~ С, + С2 + Сз •
355. Потенциалы точек С, D, Е и F равны, что ясно из симметрии батареи. Следовательно, конденсаторы, включенные между этими точками, не заряжены, и их при расчете емкости батареи можно не учитывать. Но тогда батарея состоит из четырех параллельных ветвей по два последовательно включенных конденсатора в каждой. Емкость каждой ветви равна С/2, общая емкость, следовательно, равна 2С.
356. Емкость батареи конденсаторов при разомкнутом ключе
а при замкнутом ключе
ЗС (С 4- Сх) ЗС + С -Е Сх
Рис. 243.
Приравняв эти выражения, получим Сх —
357. Емкость батареи до замыкания ключей составляет 2/3С. Разберем схему, получившуюся после замыкания ключей. Из соображений симметрии ясно, что потенциалы точек А и В равны; то же можно сказать о точках F и D. Но, с другой стороны, равны потенциалы точек А и D, а также В и F, так как они соединены проводниками. Следовательно, средние конденсаторы ие заряжены. Теперь нетрудно понять, что емкость батареи равна С, т. е. она возросла в полтора раза.
358. Наибольшее напряжение выдержит такая батарея, в которой конденсатор с наибольшим пробойным напряжением присоединен последовательно к параллельно соединенным двум другим (рис. 243). Непосредственной проверкой можно убедиться, что такая
2€6
батарея способна выдержать напряжение e/tV; это больше, чем при любой другой схеме соединения.
359. Обозначим через Сх результирующую емкость конденсаторов Ct и С2; тогда
С — CiC2
х Cl + C2"
Заряд, приобретенный конденсатором Сх при подключении его к батарее, равен
После замыкания конденсатора Сх на конденсатор С3 заряд q0 распределится между Сх и С3 так, что
дх + дз — 9о-
Разность потенциалов и та же. Это дает
на Сх и С3 после их замыкания будет одна
V = у. = _?2_ = _£3_
-v 3 Сх С3‘
Решая совместно полученные уравнения, можно найти д$: C3Q0 (С[ + С2) ______уС1С2С3_______
3 CjC2 + С2С3 + С{С3 <?jC2 + С2С3 + С3С3
360. Согласно закону сохранения электрического заряда полный заряд Q системы из двух конденсаторов должен оставаться постоянным до и после соединения их в замкнутую цепочку:
91 + 92 = </{ + 92 = Q> (О
где gt и д2 — искомые заряды. О чевидно, что после соединения конденсаторов разности потенциалов на обкладках одного и другого конденсатора будут равны между собой:
Z г
Ci с2
Из равенств (1) и (2) получим
z _ С, (g] 4- д2У г __ С2 (ffi + дг) 91 С, + С2 ’ С; + С2 '
Из условия задачи следует, что qi и q2 имеют разные знаки, следовательно, q{ и q2 могут равняться нулю. Заметим также, что знаки qt и q2 всегда одинаковы.
361. Заряд Cg, полученный вначале первым конденсатором, после подключения второго распределится между ними пропорцио
267
нально их емкости (так как разность потенциалов на конденсаторах должна быть одна и та же). Вычислим эти заряды:
С2? CC,g
qc С + С,’ С+С,*
После переключения заряды частично скомпенсируются, и суммарный заряд будет
Разность потенциалов V на конденсаторе С будет равна , .. Q C(C-Ct)
С, + С2 (С + С,)2
362. Начальный заряд конденсатора q = CV0, где Уо — начальное напряжение. После подключения конденсатора емкости С, заряд q распределится между конденсаторами С и С1 так, что на конденсаторе С останется заряд <?,. Найдем qt. При параллельном соединении С и С, разности потенциалов V, на пластинах С и С, будут одинаковы. Поэтому
q=V, (С + С,).
После отсоединения С, от С иа обоих конденсаторах будет разность потенциалов
V q CVq
1 С 4- С] С 4- С]
Оставшийся на С заряд равен
Я1 Ск, ю , л*
После подсоединения нового незаряженного конденсатора С, заряд q\ распределится снова между С и С, и на конденсаторе С останется заряд q2. Мы можем определить q2 тем же способом:
Я2 = Н2 (С + С,).
Напряжение на конденсаторах С и С, после их разъединения будет
V q' CiV°
2 С + С, (С + С,)2’ оставшийся заряд равен
„ Z-V <^0
<72-СИ2- (С + С1)2.
Повторяя эту операцию, мы будем иметь набор конденсаторов, заряженных до напряжения V,, V2, V3, V< и т. д., где V, и V2 нами определены, a V3, И4 и т. д. легко определить, пользуясь методом математической индукции:
Уо(сТсг) ‘
268
Общее напряжение
у^у 4-V2 + V3+ ... - —ft + —S—,+—с* —. + ...) V vi-r 2f 3+ C + Ci I C + Ci (C + Ci)2 + )
Просуммировав получившуюся геометрическую прогрессию, определим максимальное напряжение:
У = £Е°_ = 8ООО в.
L1
363. Заряд конденсатора q после раздвигания пластин не изменяется, следовательно,
q — где
_ e0S „ _ 6qS
С| rfi ’ 2~ d2 ’
Отсюда получаем
г2 = А к1== юо в.
“ 1
Замечание. На первый взгляд может показаться, что увеличивая расстояние rf2 между пластинами заряженного плоского конденсатора, можно получить сколь угодно высокие потенциалы. Заметим, однако, что приведенные выше формулы для С| и С2 справедливы только для плоских конденсаторов, у которых расстояние между пластинами значительно меньше линейных размеров пластины (в данном случае для rf2<}^S = 25 см). Чтобы лучше понять это обстоятельство, рекомендуем обратиться к решению задачи 371, где показано, что прн увеличении расстояния между электродами (правда,— сферическими) емкость —а следовательно, И разность потенциалов — стремятся к постоянному значению.
364. Обозначим через qi и q2 заряды на конденсаторах после раздвижения пластин одного из них, а через V напряжение на них. Тогда
<71 + <?2 = <7о, t/о “ ЭСоИо, V = ‘
Из этих соотношений найдем
<7. = yCoVo, <72 = 4C°V” V = JV°-
365. После заполнения диэлектрической жидкостью емкость конденсатора увеличивается в е раз:
С,=еС.
Результирующая емкость С2 системы, образовавшейся при последовательном соединении конденсатора С! н конденсатора с искомой емкостью Сх определяется из соотношении
_L=_L + _L с2 с, + сх •
269
Рис. 244.
Так как по условию задачи С2 = С, то нз этих уравнений получаем
Х 8—1
366. Рассмотрим рис. 244. Нижияя плоская граница диэлектрика 00' будет являться эквипотенциальной поверхностью, поскольку вектор напряженности электрического поля всюду перпендикулярен к ней. Можно представить себе, что эта плоскость покрыта тонким слоем идеально проводящего металла. Этот слой не нарушит эквипотенциальности данной плоскости и не изменит ее потенциала. Таким образом, разность потенциалов между основными пластинами, а следовательно, и емкость останутся такими же,
как и до металлизации. Но теперь уже конденсатор С можно рассматривать как два последовательно соединенных конденсатора Ci и С2, т. е.
J___L . 1 п
с с, + с2’ или с~ cl + c2-
Вычислим Cj и С2:
С - eeo,S 1 di ’
— e°S 2~^г-
Результирующая емкость С равна
=7-3' 10-9 Ф-dt + edi
367. Пусть S н d — площадь пластин конденсатора и расстояние между ними. Тогда в первом случае мы имеем (см. решение задачи 365) последовательно соединенные конденсаторы с параметрами S и rf/2, а во втором — параллельно соединенные — один с параметрами kS н d, другой (1— k) S и d. В обоих случаях один из конденсаторов заполнен диэлектриком. Емкость первой системы
р _________1__________2ee0S
* d d — d(l+e)’
2ee0S 2e0S
Для второй системы
80efeS 80(l-fe)S e0S ь.ь<л
Из равенства Ct и C2 получаем fe = 1/(1 -j-e).
368. Потенциал большой капли
V, = —, 4ле0/?
(I)
270
где Q — заряд капли, а /? — ее радиус, е0 — диэлектрическая проницаемость вакуума (воздуха). Заряд Q равен сумме зарядов всех капелек, т. е.
Q - Nq = 4ae0NVr, (2)
где г —радиус малых капелек. Подставляя (2) в (1), найдем
1 R .
Так как объем ртути при слиянии капелек сохраняется, то
N лг3 = ~ xR3, О О
откуда
г3 _ 1
R3 N'
Окончательно получаем
7) =. у№/3.
369. После заземления внешней оболочки она приобретает электрический заряд из-за явления электростатической индукции. Этот заряд будет противоположен по знаку заряду внутренней сферы и равен ему по абсолютной величине. Это равенство следует из условия равенства нулю потенциала внешней сферы. Действительно, потенциал внешней сферы слагается из потенциала, обусловленного ее зарядом Q' и потенциала в поле внутренней сферы, т. е.
Q' О
—-— 4------— — О
4ле0Я2 4ле0#2
откуда Q' = — Q.
Потенциал внутренней сферы будет складываться из потенциала Vlt обусловленного ее собственным зарядом Q и потенциала V2, обусловленного наведенным зарядом Q' = — Q на внешней сфере.
Для определения V2 представим себе уединенную металлическую сферу, заряженную зарядом — Q. Напряженность поля внутри такой сферы равна нулю, следовательно, перемещение пробного заряда внутри сферы не требует совершения работы. Это значит, что потенциал внутри сферы постоянен и равен потенциалу самой сферы. Итак,
2 4ле0/?2 ’
Но Q = 4леоП1/?1, откуда
Результирующий потенциал внутренней сферы
‘<z
271
370. После замыкания шара с оболочкой весь заряд шара перейдет иа оболочку. (Одноименные заряды стремятся разойтись как можно дальше друг от друга.) Потенциал шара после этого будет равен потенциалу оболочки (см. задачу 369). Потенциал оболочки в свою очередь равен
„ Q
|/л SS 1 -
4ле0/?2 где
Q = 4ле0У1/?1.
Потенциал оболочки (и шара) равен окончательно
371. Емкость конденсатора, по определению, равна
где q — заряд конденсатора, И —разность потенциалов между обкладками.
Определим V. Потенциал первого шарика несущего заряд + q, слагается из его собственного потенциала <?/4ле0г и потенциала в поле второго шарика, равного — q/4neaa. Итак,
4ne()7I = — - — г а аналогично
4ле0У2’=- — — + ~ г а
Разность потенциалов
2 а
Поскольку нам дано, что а 2> г, то с хорошей точностью имеем
у =
4ле0г Следовательно,
С = 2ле0г.
Замечание. При решении неявно предполагалось, что заряды по поверхности шариков распределены равномерно. На самом же деле взаимное влияние шариков нарушит равномерность распределения зарядов таким образом, что их поверхности окажутся эквипотенциальными. Однако неравенство а г позволяет пренебречь этим эффектом (почему?) и пользоваться приведенными в решении выражениями для потенциалов.
372. Пусть разность потенциалов между точками а, b равна Известно, что работа, совершаемая при переносе заряда вдоль любого замкнутого контура в электрическом поле, равна нулю (если в контуре отсутствуют электродвижущие силы); следова
272
тельно, равно нулю и полное изменение потенциала. Будем мысленно переносить пробный заряд вдоль контура dabd по часовой стрелке; тогда, учитывая направление электрического поля в конденсаторах, в Ci совпадающее с направлением обхода, а в С2 противоположное ему, получим
Vda + Vab — Vdb “0. (1)
Отсюда
Vab ~ Veil) — Vrfa, (2)
НО
Результирующая емкость цепочки Cb С равна
г> CCi
с*“с + с?
(4)
Заряд конденсатора Cj равен заряду конденсатора С] (последовательное соединение):
С С qC-<= С + ci’ аналогично,
Используя (3), (5) и (6), получаем на основании (2)
V = v 1 ~
аЬ (С + С,)(С + С2)-
Знак разности потенциалов 7aj зависит от соотношения величин емкостей конденсаторов Ct и С2.
Задачу можно решить и так:
^ = г-РС1> Vb~Z-VCi, va-vb = vab~vc-vc.
Нетрудно убедиться, что результаты в обоих случаях получаются тождественными.
373. Электродвижущая сила измеряетси работой, совершаемой при перемещении единичного положительного заряда по некоторому замкнутому контуру. Будем мысленно переносить пробный заряд вдоль контура dabd (по часовой стрелке); тогда на основании указанного выше имеем
*С, + Vab =
ПО
где
('С1 = (гГ?2) Ci'+C2
18 Л. П. Баканина и др.
273
(см. задачу 372). Отсюда
Vab~
Cj + c2
374. До замыкания ключа конденсаторы С, н С2 были соединены последовательно и подключены к батарее. Их заряды были равны. На правой пластине конденсатора и на верхней пластине конденсатора С2 заряды имели разные знаки, суммарный заряд этих пластин был равен нулю. После замыкания ключа разность потенциалов между пластинами конденсатора С, и заряды на них стали равны нулю, а пластины конденсатора С2 приобрели заряды ± С2Ч (на верхней пластине заряд +С2%). Таким образом, суммарный заряд правой пластины конденсатора С1 и верхней пластины конденсатора С2 теперь стал С2%. Этот заряд н протек через гальванометр при замыкании ключа К.
375. Суммарные заряды левой и правой пар конденсаторов должны быть равны между собой, так как эти пары соединены последовательно. Тогда разность потенциалов на них обратно пропорциональна емкостям. Получаем для левых конденсаторов
V C^ + Ct
1 Сj + С2 + С3 + С4 ’
и для правых
V - у С‘ + Сз
2 С1 + С2 + Сз + С4
Заряды конденсаторов С3 и С4:
= (С2 4- С4) _ С4 (С] + С3)
3 СI + с2 + С3 т С4 ’ 4 С{ + С2 + С'з + С4
Правая пластина конденсатора С3 заряжена отрицательно, левая пластина конденсатора С4 — положительно. Суммарный заряд этих
двух пластин
? = 94~<7з =
<f(C)C4 — С2С3)
С1 + С2~ЬСз + С4
Так как до замыкания ключа все конденсаторы были незаряжены, то и заряды этих двух пластин, очевидно, были равны нулю. Следовательно, q и есть искомый заряд, протекший через гальванометр.
376. Потенциалы сфер должны быть равны между собой, следовательно,
<71 <?2
Ci = С2 ’
где q2, Сь С2—заряды и емкости соответственно первой и второй сфер. Первую сферу ввиду большой длины соединительной проволочки можно считать уединенным проводником, а емкость ее равной 'Iw,.
По условию задачи расстояние между второй сферой и оболочкой мало по сравнению с их радиусами. Следовательно, шар с оболочкой можно рассматривать как плоский конденсатор с пло-
274
шадью 4лг$, расстоянием между пластинами Л — г2 и соответственно емкостью
R — r2 '
Учитывая, что q! + q2 — Q, получаем ответ:
п = Л Г1 (£~Гг) „ = о______1__
Г1(^-Г2) + Г2 ’ 2 г1(^-г2) + г2
(так как г2 « /?2, то площадь «конденсатора» можно принять равной 4лЛ?2; тогда ответ несколько видоизменится). Отметим, что при решении существенным образом использовано то обстоятельство, что длина проволоки (т. е. расстояние между шарами) значительно превосходит радиусы шаров. Понять это поможет замечание к решению задачи 371.
377. Так как заряды пластин плоского конденсатора равны по абсолютной величине и противоположны по знаку, то они создают внутри конденсатора равные по напряженности и одинаково направленные электрические поля. Эти поля, складываясь, образуют полное поле Е внутри конденсатора. Поле равномерно заряженной плоскости Е1 можно рассматривать как поле, создаваемое одной из пластин плоского конденсатора. Тогда, очевидно,
Полное поле Е внутри конденсатора связано с разностью потенциалов на его пластинах V и расстоянием между пластинами d следующей формулой:
Разность потенциалов V в свою очередь равна
Е_ <7
С e0S •
Отсюда
р =__!L_
e0S '
Итак, для напряженности поля одной пластины (равномерно заряженной плоскости) получаем
р Ч 1 2e0S '
378. Напряженности полей, создаваемых каждой нз пластин 1 и 2, равны (см. задачу 377)
= £* = 2г,-S '
Направление векторов напряженности между пластинами (область /), а также вне их (области И и Ш) ясно из рис. 245. Между
18*
275
пластинами напряженности вычитаются, а вне пластин — склады* ваются, следовательно,
£, = 0.
г, _ г. _ q а Еп Еш e0S = еа
q
где = поверхностная плотность заряда па пластине.
п Е, Ег
1 Е, Ег Ед-
ш Е, Ег
Рис. 245.
379. Образовавшийся сложный конденсатор можно рассматри-
вать как батарею, образованную тремя одинаковыми конденсаторами с емкостью Со = e,0S/d: конденсатор / с пластинами 1 и 2, конденсатора // — с пластинами 2 и 3 и конденсатора /И —с пластинами 3 и 4. Тогда конденсаторы / и II соединены параллельно — пластины 1 н 3 имеют равные потенциалы, так как они соединены |,<5
Рис. 246.
Рис. 247.
проводником, а пластина 2 у них общая. Конденсатор III присоединен к этой паре последовательно: его «плюсовая» пластина 3 является в то же время «минусовой» пластиной конденсатора II. Получаем схему соединения (рис. 246), по которой легко подсчитать емкость:
1 2(?о 2воК
~ 1 1 " 3 ~~М~'
2Са + Са
380. Будем рассуждать, как в предыдущей задаче. При включении по рис. 97 конденсаторы I (пластины 1—2) и III (пластины 3—4) соединены последовательно — равны потенциалы пластин I и 4, а конденсатор II (пластины 2—3) включен параллельно этой паре (рис. 247).
276
' Заряд конденсатора И
„ <, e0S‘<f 9// = <V = —
а заряды конденсаторов / н III
^~^7/~COY = ~2d'-
На пластине 2 находятся положительные заряды конденсаторов / и 11, следовательно, общий ее заряд
3e.0S£
-^1 + <>11 ~ 2d ‘
Заряд пластины 3, очевидно, имеет ту же величину, но отрицателен.
381. Вычислим сначала силу притяжения F между пластинами конденсатора. В плоском конденсаторе одна из пластин находится в однородном поле создаваемом другой пластиной. Рассмотрим силу, действующую на одну нз пластин, например, положительно заряженную. Эта пластина находится в поле, создаваемом отрицательно заряженной пластиной. Напряженность этого поля равна половине полной напряженности поля внутри конденсатора (см. задачу 377):
Р =
1 2e0S ’
(1)
(2)
Сила, действующая иа положительно заряженную пластину,
Такая же по величине и противоположная по направлению сила будет действовать и на отрицательно заряженную пластину. Как видно из (2), сила притяжения между пластинами не зависит от расстояния между пластинами. Это утверждение справедливо только в том случае, когда пластины находятся так близко друг от друга, что искривлением силовых линий на краях пластин («поле рассеяния») можно, пренебречь и рассматривать поле между пластинами как однородное. Применяя эти рассуждения к данной задаче и учитывая, что
9 = УС = у а
получаем
2,2- 10~2 н.
Очевидно, что для сохранения равновесия нужно добавить на вторую чашку весов перегрузок весом Р = F.
382. Сила, действующая на пружину, изменилась на Q2/2e0S (см. задачу 381). По определению, k — &F/M, откуда удлинение пружины
О2
Л/ = 2ee/fS '
277
383. Напряженность поля в конденсаторе, заполненном диэлектриком, при равных зарядах, в е раз меньше, чем в воздушном Следовательно, сила, действующая на пластину (см. задачу 381),
<?2 У2С2
2ee0S 2se0S ’
где С —емкость конденсатора, V— разность потенциалов на нем, S —площадь пластин. Эта сила равна при равновесии изменению выталкивающей силы, действующей на верхнюю пластину,
F'~±HSpg.
(1)
(2)
Из равенства сил F и F' получаем 1'2С2 1 ое
2ee0S 4 HSpS'
Но C = ee0S/d, следовательно, (с/= 3/7/4) и2 /ee°sV
*1 я
1
откуда
V
f
384. Для того чтобы пластины не притянулись друг к другу, мы должны нх
Рис. 248.
2 батареей, равна
цепи при вдвига-
удерживать с силой, равной по величине F — q2)2eaS (см. задачу 381). Подсчитаем работу этой внешней силы, если расстояние между пластинами изменяется от dj до d.2-
А= F(d2-dj ~ (d2-dt)=
£bQ*J £ * ’ *
385. Работа, совершаемая Д = Q'£, где Q — заряд протекшей по нии металлической пластинки, а напряжение на клеммах батареи аккумуляторов. Заряд Q определяется изменением емкости конденсатора;
Q = g(C1-C0), где Со — начальное значение емкости, a Cj —емкость конденсатора с металлической пластинкой.
После вдвигания пластинки образуются два конденсатора С' и С", соединенные последовательно (рис. 248). Их общая емкость определяется из соотношения
1 = 1 1 d-dt
Cj ~ С' + С" ~ e0S ’
278
В этом равенстве d — зазор между пластинами конденсатора, a d\ — толщина металлической пластинки. Таким образом,
_ _ e0S
Учитывая, что Са = ecS/d, получаем
л 8o<l2Sd| о_ ,л —6 а
А = -Г7~,—т т = 8,8а • 10 дж.
d (d — dt)
Заряженная частица в электрическом поле
386. Условие равновесия капельки имеет вид
mg = 2eE, (1)
где т — масса капельки, е — заряд электрона, Е — напряженность электрического поля внутри конденсатора. Учитывая, кроме того, что
у
т — 4 лг3р, (3)
О
и решая совместно полученные равенства(1) — (3), найдем
е=4^£=]6.10_19к_
и • Z V
387. Напряжение, при котором капелька находится в равновесии, равно (см. решение задачи 386)
v= ±eW = 4350 в,
9е
а) Если раздвигать пластины, когда они соединены с источником напряжения, т. е, при V — const, то напряженность поля внутри конденсатора уменьшится, так как
V=Eyll = E2d2, E2=^-Elt
U2
где d2 > <Л- Электрическая сила, действующая на капельку, F= ЗеЕ, определяется величиной напряженности; следовательно, эта сила уменьшится и капелька начнет падать.
б) Если раздвигать пластины, когда они отключены от источника напряжения, то заряд конденсатора сохраняется: q — const. В этом случае сохраняется и величина напряженности электрического поля, поскольку она определяется зарядом конденсатора и не зависит от расстояния между пластинами (см. задачу 377), Равновесие капельки не нарушится.
279
388. Кинетическая энергия, которую приобретает первоначально покоящийся электрон, проходя разность потенциалов V, определяется выражением
Подставляя заряд электрона в СГСЭ и учитывая, что 1 в =777; СГСЭ, UVV
получим
1 эв = 4,8 • 1О~10 -А- [г • см2/сек2] = 1,6 • 10-12 эрг. uUv
В системе СИ
1 эв = 1,6 • 10~19 дж.
389. На основании закона сохранения энергии ядро приобретает кинетическую энергию за счет работы, совершаемой над ним электрическим полем:
те2 т,
где q = Ze (е —заряд электрона), т = Ата
(та— масса протона, равная 1,67 10~27 кг). Отсюда
М/сек.
390. Запишем для электрона уравнение движения. Пусть пг — масса электрона, е — заряд, а — ускорение, Е — напряженность электрического поля. Тогда
та = еЕ.
Для равномерно-замедленного новки имеем соотношения:
О = по — at,
движения электрона до его оста-
c. , at2
S — not------
где с0 — начальная скорость, S — путь, пройденный электроном до полной потерн скорости, t — время движения. Решая систему равенств, получим
2 9
е V0 V0'n о л
$ — —— — ——— *= 2,4 см, t —
2а 2еЬ
г’о лтг in-8
— = —=- = 4,75 • 10 ° сек.
а еЕ
391. Из закона сохранения энергии имеем
2 2
тс «Со
—--------__ = — ev,
где о0 — начальная скорость электрона, а V = — Q/4ne0R — потенциал шара относительно бесконечности (заряд электрона равен — е).
280
' -Отсюда
2g Q
4ле0„1У?
392. На основании закона сохранения энергии имеем
т°2 TZ
где /пс^ — кинетическая энергия шарика, а I7 — пройденная им разность потенциалов. Если потенциал бесконечно удаленной точки принят равным нулю, то V есть потенциал внутренней сферы. Он равен (см. задачу 369)
Следовательно,
1 ? <7i , <7; \
4ле0 \ Г[ г2 )
(<71г2 ~Е <7;г 1) 4ne0mrir2
393. Шарик, обладающий запасом кинетической энергии /ncf^2, будет совершать работу qV против сил электрического поля, где V — разность потенциалов, пройденная шариком, a q — его заряд:
2 2
mu, tiivZ
Шарик достигнет сферы, если на ее поверхности о2 О- В пре-дельном случае о2=0. Итак,
то?
где V — потенциал сферы (потенциал бесконечно удаленной точки принят равным нулю). Но
4ле0/? ’
где’ Q — заряд сферы, a R — ее радиус. Отсюда
о 2qQ ял
R =----——у = 54 см.
4ne0mof
Если сфера будет меньшего радиуса, то шарик пе долетит до нее, а остановится на расстоянии 54 см от центра сферы и полетит обратно.
394. Энергия электрона у поверхности шара будет равна (см. задачу 400)
1Г = +
2 4ле0« '
281
Поскольку удар неупругий, вся эта энергия выделится в виде тепла.
395. По мере оседания электронов на второй пластине конденсатор заряжается. Нетрудно видеть, что поле в промежутке между пластинами препятствует движению последующих электронов. Для того чтобы попасть на вторую пластину, вылетевший электрон должен совершить некоторую работу. Фототок прекратится, когда весь запас кинетической энергии, которым обладает электрон, израсходуется на совершение работы против сил электрического поля, так что скорость электрона у второй пластины равна нулю:
= (I)
здесь V — разность потенциалов между пластинами, при которой прекратится фототок. Но
V=£d, (2)
где (см. задачу 377)
В формуле (3) Q — заряд конденсатора в момент прекращения фототока. Заряд конденсатора Q связан с числом электронов, поступающих на пластину в единицу времени:
Q = entS. (4)
Решая совместно уравнения (1) —(4), получим
е0то2 . _ . -7
» = ~х~5—г = 1,56 • 10 сек.
2e2nd
396. Чтобы покинуть шарик (удалиться в бесконечность), электрон должен совершить работу eQ/4ne0r. Значит, запас кинетической энергии электрона не должен быть меньше этой величины, иначе, отлетев на какое-то расстояние от шарика, электрон остановится и под действием притяжения со стороны шарика возвратится на него. Отсюда получаем условие для величины заряда:
eQ _ mv2
4леог 2
Следовательно,
_ т 4neQr2r
У 7 2 •
397. Движение электрона под действием постоянного электрического поля будет равномерно-ускоренным. Скорость i>b с которой электрон достигает противоположной пластины, очевидно, равна
v^Vza^d, (1)
где at — ускорение электрона, a d — расстояние между пластинами. Ускорение определится из уравнения движения
таг — eEi. (2)
282
Тогда
fi
2eEid m
(3)
Если подключить к заряженному конденсатору С, еще один незаряженный, то часть заряда перейдет на пластины незаряженного конденсатора, в результате чего напряженность поля внутри исходного конденсатора уменьшится. Общая емкость возросла в три раза, следовательно, разность потенциалов в три раза уменьшилась, поэтому
^=4-. (4)
о
Конечная скорость электронов при подсоединении нового конденсатора определится соотношением, аналогичным (3):
/ 2eE2d ,Г1
Из (3) н (5) на основании (4) следует v2 —
t'i
/3 ’
398. Так как разность потенциалов между пластинами А и D VAD = ®, то результирующая кинетическая энергия, с которой электрон достигает пластины D, также равна нулю. Следовательно,
скорость
го = °.
Далее, на основании закона сохранения энергии имеем
"гов nwl
2 eVAB' 2 eVA&
откуда
./2^ т
~ 8,4 • 10е м/сек, t>c
2eE,r
----= 6 • 106 м/сек. т
VB
399. Электрон в течение времени Т движется с ускорением a = eVjmL и к концу этого промежутка времени приобретает скорость Оо + аТ, а через время 2/’ после вылета скорость электрона снова падает до t>0. Средняя скорость элек трона за такой цикл очевидно, равна
, аТ
г’ = Оо + -2-.
Время пролета от катода до анода равно
L 2mL2 д; __ —
v 2mr0L + епТ ‘
Так как, по условию, т Т, равенство справедливо всегда, по крайней мере приближенно. Если т кратно 27", равенство переходит в точное. Получить точное решение для случая т — (2л + а) Т, где а < 2, предоставляется читателю.
283
400. Так как в первом случае электрон проходит расстояние L от катода до анода с некоторым постоянным ускорением а, справедлива формула для равноускоренного движения
__ аТ2
L~ 2
(начальной скоростью, малой по условию задачи, пренебрегаем)-
Во втором случае электрон, очевидно, движется с ускорением а в течение времени Т i, затем равномерно в течение времени Т2, затем снова с ускорением а и т. д. Подсчитав путь Ln, пройденный электроном за п таких циклов, получаем (Т2= Т]/2)
аТ2,
Тп = ~~(Зп+1).
Время достижения анода определится из условия Ln = L. Отсюда получаем п = 8, и искомое время t — 1,7Т.
401. Будем рассматривать независимо друг от друга вертикальное и горизонтальное движения электрона:
е gt2
по вертикали S=-^r-,
at2
по горизонтали d = ——,
где вызываемое электростатическими силами ускорение —
а
Рис. 249.
у
а = 4-Л, d
/ — время пролета. Отсюда с_ gd2
УЛ'
402. Рассмотрим рис. 249. Движение электрона внутри конденсатора можно рассматривать как результат движения по оси х, которое является равномерным, так как в этом
направлении на электрон не действуют никакие силы, н равномерно-ускоренного движения по оси у в постоянном электрическом поле и поле силы тяжести (ось у мы направили в сторону действия на электрон электрической силы). Итак,
«х = Со,
Vy = at,
(1)
(2)
где а определяется из второго закона Ньютона:
ma — еЕ ± mg.
Знаки «±» означают, что направление силы тяжести может совпадать с направлением электрической силы, а может быть ей про-
284
тивоположно. Нетрудно видеть, что еЕ > mg (для электрона й»= 1,6* 10~19 к, т*»9,1 • IO"28 г). Следовательно, силой тяжести можно пренебречь по сравнению с электрической силой, и мы ее в дальнейшем учитывать не будем. Тогда
Но
<Ч
где V— напряжение на конденсаторе. Следовательно,
Время пролета
электрона через конденсатор
Со
Из уравнений (2), (6) н (7) можно определить составляющую vy, которую имеет электрон при вылете из конденсатора:
eVl vy-—1—• я т dva
Искомое расстояние, на которое отклонится электрон при вылете
из конденсатора, v2 eVl2 h •» — “=-------------------------5- “= 0,41 см.
2а 2т dv$
403. Очевидно, что условие того, что электроны не вылетят из конденсатора, таково (см. рис. 249):
h>~. (1)
Величина h определена в решении задачи 402:
. eVl2 h°=------г.
2т dvQ
На основании (1) н (2) определяем минимальное напряжение: md2$ v—ъг-
(2)
(3)
Скорость »о находится из закона сохранения энергии:
9
—2“=еИ0, (4)
где 7о — ускоряющее наприженне.
285
Подставляя о0> определенное нз (4), в (3), получаем окончательно:
^2^=400 .
404. Рассчитаем смещение h электрона внутри конденсатора и вертикальную скорость vy при вылете нз него, как в задаче 402.
т”о
Учтя, что И7 = —, получаем
eW2
4dW '
eVl vv = —j—• * т av0
По вылете нз конденсатора электрон летит по инерции, значит, прямолинейно. Угол 0 между горизонталью и направлением полета электрона (см. рис. 101) определяется следующим соотношением:
vu eVl tg0==7T= 2rfT •
Добавочное смещение
Отсюда
о г 4 a eV!L s-Ltge~ 2dW.
eVl ! I \
x=ft+s=SHi +L)=o-5 см-
Так как в ответ масса частицы не входит, а заряд протона равен заряду электрона (по абсолютной величине), то численный ответ для протона будет тот же; направление смещения, естественно, должно измениться на противоположное.
405. Рассмотрим рис. 250. Расстояние между точками попадания ионов С135 и С137 равно — h®7* (более легкие ионы С135 отклоняются электрическим полем сильнее). Расстояния и Л(37> зависят от приложенного к конденсатору напряжения V, Определим
286
эту зависимость. Прежде всего (см. решение задачи 402):
Далее,
• /,(35) eVl2
1 Zm^dv*' h<37) eVl2
2m(37> dug '
h^ = LiSa^\ h^ = Ltg a<37>.
(0
(2)
Но согласно той же задаче 402
Л35’ eVl (3)
(35) j 2 * f и /п' > dv^
Из рис. 250 видно, что
Л<35> = Л<35) 4-й^б). (4)
На основании (i) —(4) имеем
/,(35) и eVl rn^dv*
и аналогично,
Отсюда
, (37) = eVl m^dv*
dvl \2
Искомое напряжение
ГЛ(35) _ A(37)j dv2
TL 31 ,
U Дт(ад m<37>/
Отметим, что описанное в задаче устройство может быть использовано для разделения изотопов.
406. Рассмотрим рис. 251. Напряженность электрического поля направлена вдоль оси у, следовательно, силы, действующие вдоль оси х, отсутствуют и составляющая скорости vx постоянна. Составляющая скорости Vy определяется из соотношения
vy = voy + at>
где ускорение а находится из уравнения движения та = еЕ.
287
Далее,
, "w 4о v'y
tga = ——, tg0=——
fox ’'lx
здесь t>Ox H
t>ot, - составляющие скорости при влете электрона
в конденсатор, a vtx и viy — при вылете (о0Л- = ои). Легко видеть, что
„2 eEL
Рис. 252. Ox т р _ fg a) •
Учитывая, что = t>2x tg2 а, найдем первоначальную кинетическую энергию электронов:
mv% + eB£(l + tg2a)
2 2 = 2(tgp-tga) *
Читателю предлагается самостоятельно рассмотреть случай, когда аир имеют разные знаки.
407. После наложения электростатического поля электрон будет двигаться по новой круговой орбите (иа рис. 252 пунктиром показана старая орбита, а сплошной линией — новая). Равнодействующая силы притяжения к ядру e2/4ne<>R2 и силы, действующей со
288
<;тороиы поля еЕ, должна быть направлена к центру окружности, по которой движется электрон.
Из подобия треугольников eOOt н eBA следует;
d еЕ
R “ е2/4ле0/?2 '
Отсюда
4ae0ER3 d ' •
е
Электрические цепи. Закон Ома
408. Если схему рис. 102 нарисовать несколько иначе (рис. 253), то становится очевидным, что сопротивления и R3 соединены параллельно, затем к ним последовательно подсоединено сопротивление /?2, параллельно к этим трем сопротивлениям присоединено R$,
вновь последовательно R-, и, наконец, параллельно всей цепочке Rf. Расчет произведем последовательно.
Сопротивление параллельно соединенных сопротивлений R3 и R6 будет
R3 + Rs 2 ’
Подсоединили /?2:
Rim ~ R3e + Rz — 2 ом.
Далее,
г, ____ Rsm * R5 _ 1 ,
A3S25 “ ~п--Г"п ЯГ 0М’ ''3625) = 1 ОМ.
*'362 + *'5 i
Окончательно имеем п 1
“общ = ОМ.
409. Рассмотрим рис. 254. Обозначим длину участка 1 через х, тогда длина оставшейся части кольца будет 2яа — х. Сопротивление единицы длины проволоки р определится очевидным соотношением:
n_ *
₽“ 2ла"’
где R — сопротивление всей проволоки, из которой сделано кольцо.
19 Л. П. Еаканина и др. 289
Сопротивление участка 1 есть Rx •» рх; аналогично сопротивление участка 2:
J?2 = p (2ла — х).
Сопротивление параллельно соединенных участков 1 и 2:
п _ _ р2х(2яп —х) _ Rx(2ita — x)
**’2 Ri + R2 рх + р(2лп-х) = (2ла)2
Отсюда получаем квадратное уравнение для х:
Рис. 254.
Rx2 — 2itaRx + (2яа)2 Ri2 — 0.
Для упрощения уравнения поделим все уравнение на (2пп)2 и введем новую величину у = х/2яп; тогда
Ry2 - Ry + Rt2 = 0, откуда
Р± //?2-4/?Р,2
У1,2=
Итак, расстояние между точками подсоединения должно составлять либо z/i = 0,89, либо 1/2 = 0,11 от всей длины
провода.
410. Так как все три лампы рассчитаны на одно и то же напряжение, то они могут быть включены параллельно друг другу.
Рис. 255.
Для питания этих ламп от сети 120 в придется включить добавочное сопротивление, на котором должно упасть напряжение; 120 в — 6 в = 114 в. Величину этого сопротивления Ra легко определить (рис. 255) нз уравнений /
V=Va — IaR0, /
/о = Л + Л + Л> \ откуда \
У/ — 190 ом. \
220
Для последовательного включения ламп придется первые две лампы зашунтировать сопротивлениями, так как они рассчитаны на меиыпий ток, чем третья, и включить в цепь добавочное сопротивление, на котором бы падало напряжение; 120 —3-6= 102 в
(рис. 256). Величины добавочного сопротивления и шунтов легко определить из следующих соотношений:
D _ Ио —3V --------У —-340 ом,
V V Ri = —г —--------— 30 ом,
Л) "Л
V V
R2 — — —----------- 60 ом.
h Л) ~
411. Последовательное включение ламп легко осуществляется, поскольку ток накала всех ламп одинаков. Для того чтобы обеспечить нормальную работу ламп, необходимо, чтобы напряжения на
них соответствовали номинальным. Избыточное напряжение гасится добавочным сопротивлением Ro (рис. 257). Его величину легко определить;
1
ом.
19*
291
Мощность, выделяющаяся на этом сопротивлении, равна
19,8 ег.
При включении ламп с накалом 6 в (JIit Лг, Л3 и Л4) в параллельную группу в цепи источника должен течь ток, равный 4/, следовательно, лампа Л5, включенной последовательно с этой группой, должна быть зашунтирована. Кроме того, в цепь должно быть
Рассчитаем величины сопротивлений:
ом, /?2=-р_ = _К^ = зз ом, 11 4/ — I
Мощность, выделяющаяся на этих сопротивлениях,
Рис. 259.
Г2 = (4/)21?1+/^2=127 вт.
Очевидно, что 1Г2 > Я7).
412. Рассмотрим рис. 259. Нарушение изоляции в каком-либо месте линии эквивалентно включению в этом месте некоторого сопротивлении R. Если конец линии разомкнут, то согласно закону Ома
g = (2xp+ /?)/,, (1)
где р — сопротивление единицы длины провода, х — расстояние до поврежденного участка, а Ц — ток в цепи источника.
При замыкании конца линии параллельно сопротивлению R подключается еще короткозамкнутый участок линии
g = 2хр +
R-2(L-x)p ]
R + 2(L — x)p J'2!
(2)
где /2 — ток в цепи источника при замкнутом конце линии.
292
Из уравнения (1) получаем выражение для х:
Ч R
Х 2р/, 2р •
(3)
Подставив х в уравнение (2), получим квадратное уравнение
I2R2 - 2g - 1 ^R + - 1) (jJ- - 2Lpg) = 0,
откуда
_ а(т7-1)±/
Подставим числа, учитывая, что р = 1,25 ом/км:
_ 24 ± /Пб"
------ ом>
откуда
/?1 « 10 ом, /?2«=3,3 ом.
Соответствующие значения х получим, подставив Rt и R2 в уравнение (3):
xt = 2 км, х2 = 4,7 км.
Очевидно, что значение х2 не соответствует условию задачи (вся длина линии равна 4 км), следовательно, не годится также и R2. Итак, ответ: R =10 ом.
х = 2 км.
413. Рассмотрим рис. 260. Вначале, когда линия была исправна, можно было записать следующее уравнение для цепи, содержащей источник, линию н нагрузку:
g = 2LpIa + R0I0, (1)
Повреждение изоляции можно рассматривать как
включение в месте поврежде-
ния (на расстоянии х от источника) некоторого сопротивления Rt, в результате чего ток через батарею станет равным I, через нагрузку 12 и через сопротивление Rt станет равным Для контура, содержащего источник, участок линии длиной х и сопротивление Rt можно записать:
g = 2хр/ 4- RJt.
(2)
Условие равенства напряжений на сопротивлении Rt и на участке, содержащем отрезок линии L — х и сопротивление Rt>, есть
Наконец, имеем
/j/?i — 12 [^?о + 2 (L — х) р].
(4)
293
I = 11 +12>
где, по условию,
/ = 2/о, 4 = -^. (5)
Из уравнения (4). учитывая (5), получим
2/о = Л+4> (6)
откуда
л=4/о- <7>
Далее, на основании (2), (3), (5) н (7) имеем
<f = 4%р/о + -g- Pi<o> (8)
y-/o^=4[/?i+2(z'~x)pL (о)
Решая совместно уравнения (1), (8) н (9), получим
*1=9^ («о + 2£р).
414. При выключении первого гальванометра в цепи термопары протекает ток
Л ri + Я ’
Аналогично, при включении второго гальванометра
415. Условие равенства напряжений на сопротивлении шунта ??ш и гальванометре (рис. 261) есть
ir = (/ - <) Рш,
где / — ток во внешней цепи, / — ток через гальванометр, г — сопротивление гальванометра. Следовательно,
Рш =
ir
T^i
г
п — 1 '
294
где п — число, показывающее, во сколько раз понизилась чувствительность гальванометра. Далее, согласно условию
, п . .
"Б—— + Ко —г, К'Л + Г
откуда
Ro = ~-------- = 260 ом-
Rui + г п
416. Очевидно, что вся шкала прибора соответствует току через прибор
7 = /оп = 10~3 а,
где io — цена деления, а п — число делений шкалы.
Рис. 262.
Рис. 263.
Чтобы сделать из этого прибора вольтметр, необходимо включить последовательно с ним добавочное сопротивление (рис. 262), величина которого Ro находится из уравнения
откуда
P = Zr + ZZ?0,
V — ]г
Z?o = —j-----~ 2 105 ом = 200 ком.
Для измерения токов, превышающих Z = 10 3 а, необходимо зашунтнровать прибор (рис. 263). Имеем:
Zr = (Z0-Z) Z?m,
откуда
Z?m = -------г 0,0625 ом.
'о ~ 1
417. Стрелка отклонится на п делений, причем
Z п = —. г0
где Z — ток в цепи термопары, a ia — чувствительность гальванометра.
295
Согласно закону Ома
, g 8V R ° R ’
здесь g0 — э. д. с. термопары на один градус, / — температура перегретого спая, R — полное сопротивление цепи. Далее,
Я=г + Р1-£- + Р2= г + "^2 (Pi + Рг),
где г —сопротивление гальванометра, Pj и р2 —удельные сопротивления меди и константана, I — длина проволочек, а — радиус проволочек. Следовательно,
С? /
л — —--------j-----------у == 3 деления.
,0|_Г + + P2d
418. Для схемы, изображенной на рис. 264, имеем, согласно условию задачи трн уравнения (показания вольтметра пропорциональны току в цепи):
g = Ir + IR + Ira,
g = 2/r + 2/ 4 + 2/r0,
g = nlr + ft/r0;
здесь / — начальная сила тока, г —внутреннее сопротивление источ
Рис. 264.
ника, г0 — сопротивление вольтметра.
Преобразуем эти уравнения:
/ (г + гр) IR
g g
2/(r + r0) 2IR
g + 3g ’
nl + r0)
g
Заметим, что неизвестные г, го, g, /, R входят в уравнения одинаковыми группами. Обозначим поэтому
/(г + го) IR
х =-----, У~~^г>
о О
и приведем уравнения к такому виду:
х + у = 1,
2
2х + -у у = 1, О
пх = 1.
296
Решая полученные три уравнения с тремя неизвестными (х, у, п), найдем
п = 4.
Итак, показания вольтметра увеличатся в четыре раза.
419. Так как показания вольтметра одинаковы, значит, падение напряжения на вольметре в первом случае (последовательное включение) равно падению напряжения на вольтметре и параллельно включенном сопротивлении во втором случае.
Подсчитаем ток и падение напряжения на вольтметре в обоих случаях. Пусть Ч — э. д. с. аккумулятора, — его внутреннее сопротивление. Тогда:
а) ток в цепи при последовательном включении вольтметра
R + r + r{ ’
падение напряжения на вольтметре
б) ток в цепи при параллельном включении вольтметра
Rr х ’
RT7 + ri
падение напряжения на вольтметре
V * + Пг
2 (/?r + 7?ri+rrI)(/? + r)*
Условие Vi= У2 дает г _________________________________Rr______
R + г + /') Rr + Rry + ’
откуда
R2 О 1 Г1 —----= 0,1 ом.
1 г
420. В первом случае, применяя закон Ома для всей цепи, можно записать
где R — неизвестное внешнее сопротивление, R{ — внутреннее сопротивление батареи, гх и г2 — сопротивление амперметров, а Ц и /г — протекающие через них токи. Кроме того, падения напряжения на амперметрах At и А2 равны друг другу:
г,/1 = г2/г.
297
Во втором случае имеем
7? + Г1 + Г2 + 7?!
Решая совместно эти уравнения, находим
R + R^
Искомый же ток Л протекающий в отсутствие амперметров, равен
7=-^_.
/?+/?,'
Окончательно получаем
///(/? + /1/2+/2) 7"(/1 + 72)-7172
а.
421. Сопротивление шунта, при котором стрелка отклонится на всю шкалу при силе тока во внешней цепи 7 = 7,5 а, определится нз соотношения (рис. 265)
С г — (7 — г'о) 7?ш, или 7?ш = — —,
1 — it>
где ('о — сила тока через прибор, при которой стрелка прибора отклоняется на всю шкалу, г — сопротивление прибора. Необходимо
/ >. I I
4
-----О-
Рис. 265.
теперь определить 1й и г. Нам задано, что при включении шунта с сопротивлением Rm — 100 ом стрелка прибора отклоняется на всю шкалу при токе во внешней цепи 1' = За. Следовательно,
V (z< “ г'о) С'
Далее, при включении добавочного сопротивления Ro = 300 ом (рис. 266) прибор отклоняется на всю шкалу, когда напряжение V
в четыре раза больше 170 = гсг:
ioi' + ioRo — 17 — 4/oG
откуда
г = 4-=Ю0ОЛ.
298
Решая систему уравнений, найдем
а,
а также
/?щ — 25 ом.
422. Обозначим через г2 сопротивление второго амперметра, а через R} и R2 — сопротивления вольтметров. Очевидно, что показания вольтметров будут
Р1 = /17?1, У2 — ^2г2-
С другой стороны,
V2 = (Z,-Z2)Z?2.
Используя условие Z?1 = Z?2, получим
V2 = -^-^VI = 0,I в.
423. Так как внутреннее сопротивление батареи пренебрежимо мало, V равно э. д. с. батареи. Тогда напряжение на сопротивлении Ri при подключении к нему вольтметра составит
у -К.1-— у =-----/?| + г._
R + R'r
Ri+WTr
(1)
где г — сопротивление вольтметра. Аналогично для V2 получим
Из (1) и (2) получаем
у - Z?2 + r
Rl+ R2 +Г
(2)
V2 _ Ri
Vt R2 ‘
= 4,8 а.
И 2
Теперь нетрудно подсчитать искомые напряжения Ut и U2 на сопротивлениях Rt и R2 при отключенном вольтметре. Так как Ut + и2 = V, то
и VR> - v ^1 + ^2 1J.A + R1
Аналогично получаем U2 = 7,2 в.
424. Для всей цепи можно написать уравнение ZVgo = V + AZtq,
где g0 —э. д. с. каждого аккумулятора, AZ — число аккумуляторов, соединенных в батарею, V — напряжение на внешней нагрузке
299
(напряжение на полюсах батареи), 1 — сила тока в цепи, ^'внутреннее сопротивление одного аккумулятора. Отсюда
---Н— = 220.
О'”
425. Электрический ток в металле создается благодаря тому, что под действием внешнего электрического поля электроны начинают двигаться в некотором определенном направлении (упорядоченное движение). По определению, величина тока
где Д<? — количество электричества, протекшее через поперечное сечение проводника за интервал времени At. Очевидно, что
А? = Ne At, (2)
где N — число электронов, прошедших через поперечное сечение проводника за 1 сек, а е — заряд электрона.
Рассмотрим теперь отрезок нашего провода (рис. 267). Путь А/, проходимый электронами при упорядоченном движении за время ДА равен
А/ = v At. (3)
Очевидно, что за время А/ через поперечное сечение успеют пройти только электроны, находящиеся в столбике, длина которого равна v At. Учитывая, что по
Рис. 267.
условию задачи на каждый атом меди приходится только один электрон проводимости, подсчитаем число атомов, содержащихся в столбике с сечением S и длиной, равной v Ы. Объем этого столбика
AV - Sv At. (4)
Пусть Am —масса меди, содержащаяся в объеме АР, тогда число атомов ДМ в этом объеме
= (5)
/1
где А'о — число Авогадро, А — атомный вес меди. Но
Azn = pAV, (6)
где р — плотность меди.
Из уравнений (1), (2), (4) — (6) получаем
V NtfSe 7
10-5 _£^L сек
300
426. Напряженность электрического поля внутри плоского конденсатора равна
где V — напряжение на конденсаторе.
Эта же формула остается справедливой при заполнении конденсатора средой, обладающей некоторой электропроводностью, так как поле внутри конденсатора остается однородным. Итак, задача сводится к нахождению V. Используя закон Ома для цепи, состоящей из конденсатора, подключенного к батарее, получаем формулу для тока в этой цепи:
здесь через R обозначено полное сопротивление конденсатора. Напряжение на конденсаторе будет равно
(3)
Сопротивление конденсатора выражается формулой
Я = р4’ Н)
где S —площадь пластин конденсатора.
С другой стороны, емкость конденсатора (в системе СИ)
Исключая S нз (4) п (5), получаем
R = (6)
Решая совместно уравнения (1), (3) и (6), получаем
s eepg’p
(ееэр + Cr) d "
427. Сопротивления конденсаторов будут равны (см. задачу 426) г> _ е1еоР1 „ п е28оР2
Л1------с\ ” /''2 С~2 •
Несложный расчет показывает, что падения напряжения на них соответственно составят
у = = ^^aPigi у _ 1СiP2gz
+ 6iC2p 1 4" i^CjPi 2 ВгСip2 + 6jC2pj
428. Ионы, возникающие под действием рентгеновских лучей внутри конденсатора, начинают двигаться к обкладкам конденсатора
301
под действием приложенного к нему напряжения. Ток через конденсатор равен
Zc = «eo, (1)
где /г —число пар ионов, образующихся в 1 сек в 1 см3 объема конденсатора, е — заряд одного иона (равный заряду электрона), о —объем конденсатора. Имеем
v = vab + vbo = (2)
Кроме того, сумма токов в разветвлении АВ должна быть равна току в неразветвленной цепи
= ‘С + ^2- (3)
Из уравнений (2), (3), следует, что
, У + 1Л
R‘ Ri + R2 •
Так как Ri = R2 = R = 1010 ом, то искомый ток I равен , , V + nevR ‘-‘Ъ- 2R
Подставляя данные задачи, получим 7 = 8,5- 10~8 а.
. 429. Из соображений симметрии ясно, что точки С, D, Е и F имеют один и тот же потенциал. Следовательно, в кольце CDEF тока нет, н фактически схема состоит из четырех параллельно соединенных полуколец (АСВ, ADB, АЕВ и AFB). Сопротивление одного полукольца
_ ла _ 4ра г° ~р
Общее сопротивление, очевидно, равно
г0 ра
Г 4 d2 '
430. Потенциалы точек В и В' равны, то же можно сказать о точках D и D'. Очевидно, сопротивление участка ВВ' можно не рассматривать вообще (по нему ток не идет), а остальная часть фигуры распадается на двр одинаковые параллельные цепочки. Рассмотрим одну нз них. Между точками А н В сопротивление равно сопротивлению трети прута — Сопротивление между точками В и D — это параллельно соединенные г0 (участок BD) н 2г0 (участок BCD). Всего 2г0/3; такое же сопротивление между D и F. Таким образом, сопротивление цепочки ABDF равно 7г0!3. Таким же сопротивлением обладает и цепочка AB'D'F. Общее сопротивление
_ 1 7 _ 7 I
ri 2 3 г° 18 р S *
302
431. Пусть напряжение подведено к вершинам А и С' (рнс. 268). Тогда потенциалы точек В, D и А' равны между собой, так же как и потенциалы точек В', С и £>'. Если мы мысленно соединим
каждую нз этих троек точек в одну, то наша цепь распадется на три последовательно соединенные части. От точки А до «точки* BDA' сопротивление */з ом, такое же сопротивление
у участка, прилегающего к вершине С'. Сопротивление среднего участка !/е ом. Общее сопротивление равно 5/6 ом.
Рис. 269.
Рис. 268.
432. Пусть токи через сопротивления 1, 2, 3, 4 равны /2, /3, Ц, через перемычку — Z н через батарею — 1а (рис. 269). Пренебрегая внутренним сопротивлением батареи, определим ток в цепи источника:
= (1)
где R — сопротивление между точками с и d. Очевидно, что
^ = "2 + V = б"Г‘
В узле а имеем
Л = Л + л (3)
Равенство напряжений па сопротивлениях 1 и 2 дает
гЛ = г/2, но в узле с
1о — Ii + ^2> откуда
Л = /2=4- (4)
Равенство напряжений на сопротивлениях 3 и 4 дает
/73 = 2/74, но в узле d
1з + Ц = /ог
303
откуда
(Б) о о
Из уравнения (3), используя (4) и (5), получим
/ = Л-/з = -|/о.
Учитывая равенства (1) и (2), получим окончательно:
433. Обозначим напряжение между точками а и b через V, причем потенциал точки а относительно точки b будем считать положительным (рис. 270). Coi-.асно определению электродвижущая сила измеряется работой, совершае-
мой при перемещении единичного положительного заряда по замкнутому контуру. (В отсутствие э. д. с. эта работа равна нулю.) Выберем в качестве контура, по которому мы мысленно будем переносить единичный положительный заряд, контур defed. Обходить контур будем по часовой стрелке. При выбранном направлении обхода аккумулятор совершает положительную работу (разряжается), а ?2 - отрицательную (заряжается). Разность этих работ,
Рпс. 270.
равная разности электродвижущих сил аккумуляторов, равна в свою очередь сумме падений напряжений на внутренних сопротивлениях батарей:
(1)
Аналогично, если пронести единичный положительный заряд вдоль контура abeda по часовой стрелке, то аккумулятор соверщит-положительную работу, которая равняется сумме падений напряжения на внешнем (V) и внутреннем (/гх) участках цепи:
«1=/Г1+Р.
На основании уравнений (1) и (2) получаем
Г1 + r2
g’l-g’z .-
_!----i. к 47 01
434. Применяя метод, использованный в решении задачи 433, составляем уравнения:
V=g1-/rJ = 0,
+ (fj + r2);
304
здесь / — ток в цепи батарей (ток через гальванометр по условию равен нулю), V — падение напряжения на гальванометре, rt и г2 — внутренние сопротивления батарей и g2 соответственно. Исключая ток / из этих уравнений, получаем условие
гг h
'!= и'
435. Пусть ток в цепи первой батареи равен 1\, а ток в цепи второй батареи равен /2 (рис. 271). Очевидно, ток /, идущий через перемычку, равен
Z = Z] — /2,
где —ток короткого замыкания батареи gj!
12 — ток короткого замыкания батареи g2:
Следовательно, I = ~ ।
Г,Г2
Напомним, что решение получено в предположении, что сопротивление перемычки пренебрежимо мало! Если такого предположения не делать, то выражение для / будет, разумеется, зависеть от
сопротивления перемычки, однако условие отсутствия тока, i a b
?1Г2 = ?2''|, сохранится. Почему? + ЯВ
436. Учитывая, что ток 7 через гальванометр равен ну- “ лю, напишем выражение для тока в цепи батарей: ! . Ri + Ri + Rs + Rt - <f, '7 <S2 » T
b Рис. 271.
Напряжение V на гальванометре также равно нулю (см. решение задач 433 и 434):
V = -1 + Rf) — 0.
Следовательно, „ (Ri + Ri) 0
Ri + Ri + Rs + Rt ’ откуда
/?i + R2 + R3 + Ri = 2Ri + 2/?4, или
Rt = R3 Ri + Ri.
20 Л. П, Баканина и др.
305
Поскольку Л?2 > Ri, то необходимо (/?40) выполнение условия R3 /?2 ~ /?ь
437. После того как конденсатор зарядится, ток через него прекратится. Рассматривая цепь 4i42R по способу, изложенному в задаче 433, определим разность потенциалов V на батарее
gl ~ С2
Г] + 7*2 + R
4j(r2+ R) + %2Г [ г 1 + 7*2 + R
Такая же разность потенциалов будет н на конденсаторе, еле довательно, заряд на нем
_ r ?1 0*2 + Ю +
Я ri+r2 + R "
438. Разность потенциалов между точками а и b подсчитаем, как падение напряжения на левой ветви схемы, изображенной на рис. 114:
4
Vai> = g - IR = v Ч.
Очевидно, что
Val>=vc-^
где Vc — искомая разность потенциалов на конденсаторе. Следовательно,
7
VC-Vat> + ^3 g>0-
Потенциал верхней пластины выше, чем нижней, т. е. верхняя пластина заряжена положительно.
439. До замыкания ключа конденсаторы были незаряжепы, очевидно, сумма зарядов правой пластины конденсатора С] и левой пластины С2 была равна нулю. После включения батареи на первом конденсаторе напряжение стало tz RV4
V2 = -б—г-н—:—, соответственно
/?1+/?2 + Г
CtRi4
сатора Cj стал =----------------
C2R24
q2~+ Ri + Ri + r"
Сумма этих зарядов
через гальванометр. Если CiRi = C2R2, то заряды конденсаторов равны, т. е. заряд с левой пластины С2 перетекает на правую пластину С[, а через гальванометр заряд не протекает.
440. Падение напряжения на участке АВ равно 41. Потенциал точки а относительно А составит
17 R&
Vi Ri + Ri + r' на заряд правой
пластины
втором
кондеи-
~ ri + r2+7' заряд левой
У+ъУ* * н есть
А 1 + А 2 + Г
пластины
С2 стал
заряд, протекший
v -у _?__А
Va зц ~ з •
306
Потенциал точки Ь:
Vb ЗУ? 3
Разность потенциалов точек а н Ь:
Vab^~ О
Далее,
и окончательно
Vc = Vab + ?2= ?2— з"
2
При ?2 = ?| = ^ получаем Vc = -g-g>0, т. е. верхняя пластина конденсатора заряжена положительно.
Работа и мощность электрического тока. Закон Джоуля — Ленца
441. Для того чтобы вскипятить чайник, требуется энергия W. Эта энергия выделяется при нагревании обмоток электрическим током (пренебрегаем рассеиванием тепла в окружающее пространство).
Если включить первую обмотку, то
1/2
(1) откуда
. V2/.
^1=-^-; (2)
здесь V — напряжение сети, У?] —сопротивление первой обмотки, У, — время, за которое чайник вскипает при включении одной первой обмотки.
Аналогично, если включить вторую обмотку,
V2
(3)
откуда
*2=~2-. (4)
Соединим обмотки параллельно. Энергия IF теперь выделяется при нагревании обеих обмоток. Поскольку напряжение на обеих обмотках одинаково и равно V, то
V2 1/2
У?! + У?2
(5)
здесь /3 — время, за которое чайник вскипает при параллельном соединении обмоток.
20*
307
На основании уравнений (2), (4) и (5) получим
<3 = “ 6 мин- (6)
I1 т • >
Пусть теперь обмотки соединены последовательно. В этом случае
Снова используя равенства (2) и (4), получим
= f! + /2 = 25 мин.
442. Мощность, выделяющаяся на нагрузке с сопротивлением R, равна
где г —внутреннее сопротивление батареи аккумуляторов. Нужно определить, прн каком R мощность W максимальна. С этой целью преобразуем выражение (1), использовав соотношение
?-/(Ш (2)
Имеем
W=4I-Pr. (3)
Для нахождения максимума W представим выражение (3) в виде
Так как выражение (/ \,г7 — 4/2 Vг )2 всегда положительно, то максимум W наступает, когда выражение в скобке равно нулю, т. е. когда
Из уравнения (2) следует, что при этом сопротивление нагрузки R должно равняться внутреннему сопротивлению источника, т. е. R = r=\ ом. Для получения такого сопротивления нагрузки обмотки нагревателя кипятильника можно включить следующим образом: во-первых, можно включить только одну секцию, во-вторых, возможна комбинация, изображенная на рнс. 272 (перемычка между сопротивлениями не обязательна).
Итак, полная мощность, расходуехмая аккумулятором при R — r,
Fo = -^ = 32 вт.
На нагрузке выделяется мощность
1Т = 47Г»16вг.
308
Отметим, что, в отличие от предыдущей задачи, при уменьшении сопротивления нагрузки мощность на ней не будет неограниченно нарастать, а проходит через максимум. С чем это связано?
443. Рассмотрим рис. 273. Пусть сопротивление участка / равно Ri, а участка 2 равно R?, тех что полное сопротивление кольца
R--=R,+R?_,
причем
1 2
Ri = ~R, Ri=^R.
О О
Мощность, выделяющаяся в кольце,
W = Rrf+R2ll
Далее,
/ = Л+Л-
Кроме того,
hRi ~ IzRz,
откуда
I = 1R' = А / / 1
’ Rt + R2 3 ’ 2 Ri+R2 3
Сопротивление всего кольца
о 27IF „
P = -gp-=6 ом.
Если бы контакты были расположе выделившаяся в кольце, была бы
В7=4-/2 = 121,5 вт.
4
444. В первом случае (/] = 4<я) мощность, отдаваемая аккумулятором во внешнюю цепь,
W^l]Rlt где
г—внутреннее сопротивление
здесь /?] —сопротивление нагрузки, аккумулятора.
Ток в цепи изменился из-за изменения сопротивления нагрузки, которое стало равным Д2. В этом случае
^2 ~ ^2R2’
где
I = _А_
2 Rz + г '
Решая совместно полученные уравнения, найдем выражение для W2t
' J
309
445. Обозначим искомую э. д. с. батареи ?, а ее внутреннее сопротивление г. Тогда мощность, рассеиваемая на Rlt будет
Ц7 = —-----
(tf.W
Та же мощность рассеивается и на сопротивлении R2:
№ =___12-2_
№ + г)2’
Приравняв правые части уравнений (1) и (2), получаем г = Vr^.
Теперь находим э. д. с.:
г = (/лГ+VrT)
Замечание. Обсудим полученные результаты более
дробно. Для этого еще раз перепишем выражение для мощности IF, рассеиваемой на нагрузке R:
т %2R 72
(*+г)2 Р + +
Л + 2.1 +
(1)
(2)
(3)
(4)
ПО"
(5)
из которого следует, что как при уменьшении, так и при неограниченном возрастании R мощность ' ' ’
Рис. 274.
будет падать до нуля (рис. 274). Значит, прн некотором промежуточном значении R = Ra мощность W должна достигать своего максимального значения I7max. Для всех остальных каждому V7=y=V7max будет соответствовать два значения сопротивления нагрузки, Ri и /?2, связанные между собой соотношением (3). Если, однако, допустить, что в (3) будет Rt = r, то должно быть и R? = г, т. е. в этом случае = Ri — г. Очевидно, что это возможно только в точке IF = lFraax. Отсюда следует важный вывод: от источника с внутренним сопротивлением г максимальная мощность будет отбираться только в том случае, если сопротивление нагрузки тоже будет равно г. Эта мощность —
<f2 )Fraax = —.
(6)
446. По аналогии с решением задачи 445 можно записать
r = VRiR2,
RR
где Ri—R, a R2 = -р , д. (Rx~ искомое сопротивление),
л -г Rx
310
Отсюда
tf.v-
r2R
R2-r2’
Если R = г, to Rx -> то. Это значит, что любое конечное Rr изменит (точнее, уменьшит) мощность, отдаваемую внешней цепи (см. по этому поводу замечание к решению задачи 445). Очевидно, при R < г задача не имеет решения.
447. Уменьшение напряжения сети связано с тем, что при протекании по цепи тока I создается падение напряжения на сопротивлении подводящих проводов г и внутреннем сопротивлении генератора (которое, впрочем, обычно весьма мало). Рассматривая рис. 275, где под. R подразумевается сопротивление нагрузки, а под г — сопротивление подводящих проводов, можем сделать следующие выводы:
1. Включена одна лампочка:
р — /
? = 7oWo + r), (1)
причем
«2
/?0 = 'К’ (2)
где 1У0 — номинальная мощность лампочки (мощность, потребляемая лампочкой в накальном состоянии) при нормальном для нее напряжении сети (в нашем случае g,). С другой стороны,
Vo = Zo/?o, (3)
где Vo — напряжение на лампочке (сетевое напряжение). Из уравнений (1) —(3) определим г:
g2 / g \
r~ ~w~ (дт 1 )•
"с \ о /
2. Включены параллельно лампочка н плитка:
Ч = Л(г + R), (5)
где
<6>
(/?] — сопротивление плитки). С другой стороны,
V^IiRi, (7)
где Vi — напряжение сети при параллельно включенных лампочке и плитке.
Из уравнений (2), (4) — (7) определим сопротивление плитки:
RorVl
Ro (% — Vi) — V\r “ йГо(Уо-VJ-
311
Номинальная мощность плитки находится из уравнения
_ S(V0-7;)
1 Я, ~ V^-Vo)
Го « 270 вт.
448. Решение задачи аналогично решению задачи 447.
1. Включена одна плитка (рис. 275):
= /i (7? + г)
(/? = ё2/Гн — сопротивление одной плитки, Ги — номинальная мощность плитки, г — сопротивление подводящих проводов и источника, питающего сеть). Фактически выделяющаяся мощность
Из этих уравнений определяем сопротивление подводящих проводов г = [ 1 _ 1 1
/ЖГ L К г? /ЖГ J ’
2. Включены две плитки:
« = / Г*
‘ '2 2
Фактически выделяющаяся мощность в двух плитках
2 ‘2 2 (7?+2r)2'
Подставив в это уравнение найденные значения г и R, получим
Г2 =
2Г,Г„
---.----7=72 — 423 вт. (2/Гн - /Г, )2
449. Ток при коротком замыкании (в точках а н b на рис. 275) равен
Но (см. решение задачи 445):
Г=К/?1.,?2 и
Окончательно будем иметь
« = (Г/?1 +К«2)Кг.
4 = ]/ +]/ 1,63
459. Из условия постоянства расходуемой батареей мощности следует, что сопротивления нагрузки в обоих случаях должны быть одинаковы:
7?о = Т?2 4-j------j----> (1)
ТЖГ + Rz + Ro
откуда
(2)
312
По другому условию напряжение Ki на Ra в случае, указанном на рис. 117, в а раз меньше, чем при непосредственном подключении 7?о к батарее:
/Ro = <х7о7?о, (3)
где /о-ток через Ro в случае, указанном на рис. 117. Но сопротивление нагрузки, а следовательно, и ток I через батарею в обоих случаях одинаковы. Имеем
I = 71 + /а, (1)
7iPi = 70 (Т?2 + 7?0), (:>)
где 7j —ток через
Из уравнений (4) и (5) найдем
° Ro + Ri + Rt' (б)
Подставляя найденное значение 70 в (3), получим уравнение
нли (8)
Из уравнений (2) и (8) получаем
_ 2а/?0 о = «~ I п
Рис. 276.
451. Ход рассуждений может быть, например, таким. При напряжении 2 кв и токе 40 ма необходимо сопротивление 50 ком, рассеивающее мощность 80 вт. Минимальное количество сопротивлений, на которых может рассеиваться эта мощность, равно восьми. Как их соединить, чтобы обеспёчнть номинальный ток? Расчетная величина добавочного сопротивления (50 ком) должна быть вдвое меньше R, следовательно, при симметричном соединении число параллельных ветвей должно вдвое превышать число последовательно стоящих сопротивлений. Отсюда ответ: 8 сопротивлений должны быть собраны в цепь нз четырех параллельных ветвей по два последовательно соединенных сопротивления в каждой ветви.
452. При последовательном соединении аккумуляторов на сопротивлении 7? выделяется мощность
117,=
(8g0)2 R
(7? + 8г0)г ’
где g0 — э. д. с. одного аккумулятора, а г0 — его внутреннее сопротивление.
Прн параллельном соединении двух групп аккумуляторов (рис. 276) через нагрузку R протекает ток
, 8g0
4г0 + 2/?’
313
и выделяется мощность
16?£₽
Но IF, = Uy2, откуда
64'гц/? 16^/?
(R + 8г0)2 = (2г0 + /?)2 '
Решая это уравнение относительно г0, получим г0 = 0,25/? = 0,75 ом.
453. Мощность, развиваемая генератором, равна
где /? —сопротивление нагрузки. Отсюда у 2
R—w~-r-
Рассчитаем полезную мощность
Й7П = Z2/?
Таким образом, коэффициент полезного действия т] равен ^7п . , Wor
1 Го й2 •
454. Мощность генератора IF0 равна
ч2
г + R
где —э. д. с. генератора, R — сопротивление нагрузки. Полезная мощность составляет
Таким образом, Гп R
П Fo r+R'
Отсюда
455. Полная мощность, выделяющаяся в цепи (см. рис. 275):
Гв =
%2
R+r
(1)
314
где R — сопротивление нагрузки, а г — сопротивление линии передачи и источника. При R = Ri мощность потерь
(2)
где %i — начальное напряжение источника. Повысив напряжение до ^2. необходимо изменить и сопротивление нагрузки, так как отдаваемая генератором мощность должна оставаться постоянной (см. формулу (1)). Имеем
М/Йг) г- (3)
По условию,
Полная мощность в первом случае (g = yb R = Ri) равна
<5>
Во втором случае (г = %2> R = R2)
Используя условие U7i = W'2, получим
R2 + r = 7 J^\2 fli+r UJ ’
Подставим равенство (7) в уравнение (4):
Таким образом, напряжение следует повысить в п = -|у- = 1О раз.
456. Разность показаний счетчиков увеличивается из-за потерь электроэнергии на нагревание подводящих проводов, обладающих сопротивлением г (рис. 277), Пусть начальное напряжение источника равно V и соответственно ток в цепи равен Ц, В этом случае мощность потерь
причем
где W — полная мощность, отдаваемая трансформатором (1000 квт)^
Wy можно выразить через разность показаний счетчиков N и N2:
t
где t — времи, за которое разность показаний увеличивается на &N.
Рис. 277.
При повышении напряжения до У2 и токе в цепи /2 имеем мощность потерь
Г2 = 4г,
причем
/ = 2
Система уравнений приводит к соотношению
1Р2 Р,
"»7=
Учитывая условие
r2= io-3rb получаем ,
V2 = 1/ - .. Vy = 18 кв.
V ю 3wt
457. Рассмотрим рис. 275. Полезная мощность, отдаваемая нагрузке, равна
W =
соответственно мощность потерь
1 r + R
R,
По условию,
1Р0 = 4- 10~2Г.
Отсюда определяем сопротивление нагрузки R и напряжение генератора
/? = 25г, jf«=(r + J?)-|/rX. = ^.r j/'i = i4 кв.
458. Рассчитаем сначала сопротнвленне линии 7?0, которое удовлетворяет условиям задачи (потери напряжения — 8%). Падение
316
напряжения на сопротивлении Ro
R + Ro Ro’
где V — напряжение на шинах станции, R — сопротивление нагрузки. По условию, 70 = 0,087, откуда
V
Ro = 0,087, или R=ll,5Ro.
А "Г АО
Мощность, отдаваемая потребителю (сопротивлению /?), определяется выражением
I 7 «7 = ------
\R + Ro
Следовательно,
„ 11,5 V2
^""156^" ~7’1 ом-
Выразим Ро через геометрические размеры провода:
Ro = »
О
где Z — длина линии, S — сечение провода, р — удельное сопротивление меди.
Вес меди, требующейся для проводки такой линии, равен Р - 2 dlS,
где d — удельный вес медн. Исключив S из последних равенств, получим
р = 2140 кГ.
Ко
459. Пусть сопротивление лампочки при 0° С равно Ro, при комнатной температуре Rj и в накаленном состоянии R2; тогда
Ri = Ro 0 4-cc/j), R2 = Ro (1 4- <х/2),
где а —средний температурный коэффициент сопротивления, Н— комнатная температура, /2 — температура накаленной нитн. Но
Ro 1 +а/2 10
Ri 1+аН ’
откуда
а = 5-10 3\/град.
Мощность, рассеиваемая лампой в накаленном состоянии:
У2
W= R?
= “14’4 ом-
откуда
317
460. Составим уравнение теплового баланса!
V2 cm
В этом уравнении справа стоит количество теплоты (в джоулях), выделившееся в проволоке при пропускании через нее тока за время х. Вся эта теплота идет на нагревание проволоки (с —удельная теплоемкость свинца, т — масса проволоки, 10 — комнатная температура, / — температура плавления). Отсюда находим
cm (t — toj R
т= уз •
где р —удельное сопротивление свинцовой проволоки, /—ее длина, S — сеченне. Кроме того,
т = dlS,
где d — плотность свинца. Окончательно имеем:
cdl2p(t—t0)
х = --------— = 7,5 сек.
461. Обозначим через /? j и R2 величины сопротивлений соответственно первого и второго отрезков проволоки, а через V — разность потенциалов на их концах. На основании условий теплового равновесия имеем
1/2 172
-w- = kDll, = kD2L,
«1 Кг
где k — некоторый коэффициент пропорциональности, L — длина второй проволоки. Отсюда
Ri __D2L
R2
С другой стороны,
п . / n L
*\ 1 ’ Р О I > 2 Р Г) / J
ntf/i л/>|/4
где р—удельное сопротивление материала проволок. Из этих соотношений находим
Ri 11%
~R^~1%l'
Сравнивая два полученных выражения для Ri/R2, имеем окончательно
318
462. Количество тепла, выделяемое в единицу времени при пропускании тока через проволоку пропорционально квадрату силы тока
Q~I2R. (1)
Количество же тепла, отдаваемое в окружающее пространство, пропорционально разности температуры проволоки и воздуха
Q, = fe(r-r0), (2)
где k— множитель, постоянный во всех трех рассматриваемых случаях, Г — температура проволоки, Го —температура воздуха. При длительном пропускании тока устанавливается тепловое равновесие:
Q = Qi. (3)
Значит, во всех трех режимах выделяемое и отводимое тепло равно:
(Г, - Го),
/^ = fe(T2-T0),
4я = цгх-г0).
Решая эту систему, получаем Гу = 580° С.
463. Построим график зависимости напряжения на конденсаторе V от его заряда q во время разрядки в соответствии с формулой
(рис. 278). Прн изменении заряда конденсатора на малую величину bq совершается работа
ДЛ = V kq,
которая приближенно равна заштрихованной площади. Очевидно, это последнее утверж-
дение выполняется тем точнее, рпс 278
чем меньше Д<? (мы считаем, что когда заряд изменяется от
q до <? + Д<?, напряжение V постоянно). Полная работа электрических сил, являющаяся, очевидно, энергией, выделившейся в лампочке, равна площади треугольника О АВ, т. е.
A = W =
2
СГо к ~ = 5
дж.
464. Количество электричества, которое протекло по проводам за время изменения емкости конденсатора, равно
Q^HCs-C,);
319
здесь V—напряжение на конденсаторе, равнее напряжению батареи (падением напряжения на проводах пренебрегаем), Ct — начальное, С2 —конечное значение емкости. Ток, протекающий по цепи при равномерном изменении емкости,
1 Л У^г-С,) t t '
Тепловая энергия, выделяющаяся в проводах,
Окончательно
W - V..2 (£? ж о,ОО25 дж.
465. Если воспользоваться законом Ома
g=y + /r, (1)
то легко получить величину тока I — — 2а. Отрицательное значение говорит о том, что во внешней цепи ток течет против того направления, куда бы он тек, если бы
наша батарея была единственным источником э. д. с. в цепи (рис. 279). Теперь подсчитываем выделяющееся тепло:
Q = 12г = 4 дж.
466. Так как положительный полюс батареи для нормальной работы вольтметра должен быть
подсоединен к отрицательной клемме последнего, потенциал точки Ь (рнс. 119) выше потенциала точки а. Следовательно, напряжение V в формуле (1) (см. решение задачи 465) мы должны считать отрицательной величиной. Тогда
I ------------ 6д
г
Q = /2r = 36 дж.
Электромагнитная индукция
467. При повороте витка в нем возникает э. д. с. индукции На основании закона Фарадея
(1)
где ЛФ — изменение магнитного потока через плоскость витка, происшедшее за время Ы. С другой стороны, по закону Ома
(2)
320
где ДО — заряд, протекший через поперечное сечение провода, из которого сделан виток (через гальванометр), за время ДД
Сравнивая равенства (1) и (2), получаем ДФ
(3)
Подсчитаем теперь изменение магнитного потока ДФ (рис. 280) В начальный момент, когда плоскость витка была перпендикулярна к силовым линиям магнитного поля, магнитный поток, пронизывающий плоскость витка, был равен
Ф, = ]i0HS, (4)
где ро— магнитная проницаемость вакуума. После поворота витка на угол а магнитный поток изменился до величины
Ф2 = ЦоНЗ cos а. (5) Следовательно, дф = ф2 _ ф1 = _ ^HS (1 - cos а). (6) Подставив значение ДФ из равенства вая, что в данном случае 3Q = Q, получим . RQ cos а = 1---------------------------77-=-.
ИоНЗ Подставим числовые значения, учитывая, что надо выражать в вольтах, Ф в веберах, Н — в амперах/метр, S — в м2; получим cos а — — 0,5, откуда а = 120°.
Напомним, что |х0=4л- 10~7 гн/м.
468. Заряд, протекающий по витку, пропорционален изменению магнитного потока, пронизывающего виток. По условию задачи
Первоначальное положение
Рис. 281.
вначале магнитное поле отсутствовало, следовательно, изменение магнитного потока при включении поля равно просто потоку Ф, пронизывающему виток при включенном поле.
Изменение потока при складывании витка восьмеркой зависит ют того, каким из трех возможных способов получили восьмерку (рис. 281). Учитывая, что в перевернутых петлях потоку необходимо
21 Л. П. Баканина и др.
321
приписать противоположные знак, получаем для трех случаев (стрелки на рис. 281 поставлены для того, чтобы пояснить изменение ориентировки различных частей витка и к направлению протекания заряда не имеют отношения):
1) виток «пережат»:
Ф1=-|-Ф, ДФ.--1-Ф, ООО
2) перевернута меньшая петля:
Ф2 = 1ф, ДФ2=-1ф, Q2=-1q;
3) перевернута большая петля:
Ф3 = - -у Ф, АФз - - -|- Ф, <2з “ - -|~ Q-
Знак минус во всех трех ответах показывает, что в неперевер-иутых частях витка направление протекания заряда противоположно
тому, в котором он протекал при включении магнитного поля.
469. Рассмотрим рис. 282. На основании закона электромагнитной индукции Фарадея
ДФ
Д/
дв
Д/ •
Заряд конденсатора равен q = Cg.
Окончательно получаем абсолютную величину заряда: |9|-CS-^--5- Ю"10 к.
470. По закону индукции
ю'4 в, Д/ Д/ ’
где S — площадь витка катушкн, N — число витков, ДВ/Д^ — скорость изменения индукции магнитного поля.
Мощность джоулевых потерь равна
где Л —сопротивление катушки. Следовательно, JF -10“9 вт,
322
471. Перемычка ab делит рамку на два контура, причем при движении перемычки изменяется магнитный поток через оба контура и в обоих контурах наводится э. д. с. индукции.
Так как магнитный поток через правый контур уменьшается, а через левый увеличивается с одинаковой по абсолютной величине скоростью, то э. д. с. индукции равны по абсолютной величине и имеют разные знаки по отношению к заданному направлению обхода контуров (рис. 283):
Подсчитаем теперь изменение магнитного потока.
Поскольку напряженность магнитного поля постоянна, то
ДФ = ЦоЯ AS = n0HLx
(AS равно плошадн заштрихованного прямоугольника на рис. 283). Итак,
Av
I I = I г2 | = = ii^HLv,
где v — скорость движения перемычки.
Применяя метод, изложенный в решения задачи 433 к правому и левому контурам, получаем два совпадающих уравнения:
I = । I _ I ^2 I Lv
Ri R2 = R
472. При синусоидальной зависимости тока от времени магнитный поток и скорость его изменения (если иметь в виду средние значения их абсолютных величин за период) связаны прямой пропорциональной зависимостью. Поэтому э. д. с. индукции в этом случае пропорциональна величине магнитного потока, а следовательно, пропорциональна току в возбуждающей катушке или напряжению на ней.
Рассмотрим первый случай. Катушка I создает магнитный поток
<b=kVx,
где = 40 в, a k — некоторый множитель пропорциональности. Половина этого потока проходит через катушку 2 и возбуждает там напряжение V. Следовательно, если мы подведем к катушке 2 то же напряжение V, она создаст поток ®:2 = felzi:2. Из этого потока в силу симметричности сердечника половина, т. е. feKi/4, пойдет через катушку 1. Следовательно, в первой катушке возбудится напряжение, в четыре раза меньше, чем Vi, т. е. 10 в.
21*
323
473. Если весь поток, создаваемый одной из катушек (обмоток) трансформатора, проходит через вторую катушку, то выполняется соотношение
V, Ni
где Nt н — числа витков катушек 1 н 2.
Так как в нашем сердечнике лишь некоторая часть потока проходит через вторую катушку, то эта пропорция несколько видоизменяется, а именно, напряжение, возбуждаемое в катушке, пе подключенной к сети, будет меньше во столько раз, во сколько раз часть потока, пронизывающая ее, меньше всего потока, создаваемого другой катушкой. В первом случае (к сети подключена катушка /) имеем
V, _ Л’2
У -/!1 7V,
(1)
Во втором случае
Ле
V П2 Nt
(2)
симметричен, следовательно,
пх — п2. Учитывая это условие,
Но по условию задачи находим из уравнений (1) и (2)
А/ЛН2
R
и окончательно
N2 V v2
Рис. 284.
474. В рассматриваемой электрической цепи (рис. 284) действуют э. д. с. батареи, равная £ и э. д. с. индукции ^инд, возникающая при вращении якоря
и направленная навстречу $Г; следовательно, для этой цепи закон Ома будет выглядеть следующим образом:
+<?иид, (1)
где R — омическое сопротивление цепи, слагаемое из сопротивления соединительных проводов, обмоток якоря мотора, батареи и т. д. При заторможенном якоре, очевидно, = 0 и
2 = (2)
Подстановка (2) в (1) дает
? = -т-+ ^инд. (3)
Умножая обе части равенства (3) на ток /, получим
/2
8/“^-у Ь/^иид- (4)
'о
324
Левая часть (4) является не чем иным, как полной мощностью, расходуемой батареей. Первый член справа дает мощность джоулевых (тепловых) потерь, а /сНнл = W — это полезная (механическая) мощность мотора. Следовательно,
I2
W = = 8 вт.
475. Закон Ома для цепи, состоящей из источника с э. д. с. У и электромотора постоянного тока, выглядит следующим образом (см. решение задачи 474):
г = 77? + йш,д, (1)
где R — омическое сопротивление цепи, ?инг~“э- Д- с. индукции якоря мотора. В момент пуска якорь еще неподвижен, поэтому
?иид= 0 и ’t — laR. (2)
Мощность, расходуемая источником, питающим мотор в установившемся режиме, будет %1, а полезная мощность 21шд/, следовательно,
476. Поскольку джоулевыми (тепловыми) потерями можно пренебречь, то (см. решение задачи 474) механическая мощность электровоза будет
1Г=Г0 = ?Ш1Д/ = Vf, откуда
F V 1=^ = 980а.
477. Уравнение цепи, содержащей электромотор (см. решение задачи 474):
t ~ (Г1 + г2) I + ¥ипд, (1)
где 7ипд — э. Д- с. индукции якоря.
Полезная мощность /?ИНд, расходуемая мотором, равна механической работе IV, совершаемой мотором за одну секунду,
^инд/ = I*7 = P2nav. (2)
Соотношения (1) и (2) дают
v =
7 [% — / Од + г2)] 2лаР
— 10 }/сек.
478. Закон сохранения энергии для динамо-машины запишется в виде
Г = -^- + а)Г,
А
325
где W — затрачиваемая на вращение мощность, а — коэффициент потерь на трение, g — э. д. с. индукции, развиваемая машиной, Д — сопротивление цепи. Из этого уравнения находим
g = — а) = 120 в.
Согласно условию при изменении нагрузки динамо-машины число оборотов поддерживается прежним. Поскольку э. д. с. динамо-машины зависит только от скорости изменения магнитного потока, пронизывающего обмотку якоря, то при постоянном числе оборотов э. д. с. индукции постоянна.
На основании закона сохранения энергии имеем
%2 R
= 4- + aW^ = IF = 250 вт.
Al Ki
479. Для цепи, содержащей батарею и якорь электромотора (рис. 285), закон Ома имеет вид
«-?! = //?, (1)
где ?! —э. д. с. индукции, возникающая в обмотке якоря, который вращается с числом оборотов в постоянном магнитном поле, создаваемом статором.
Если мотор будет работать в качестве динамо-машины, то при той же скорости вращения якоря э. д. с. динамо-машины будет равна которая определяется равенством (1). Так как э. д. с. индукции пропорциональна скорости вращения якоря (т. е. скорости изменения магнитного потока), то при числе оборотов в минуту п2 э. д. с. динамо-машины будет равна
= (2)
Используя уравнения (1) и (2), получим
= — (S - IR) = 46',7 в. п\
480. Для цепи, изображенной на рис. 285, запишем уравнение, выражающее закон Ома,
$ — ?ИНД ~ IRl
где 2Иид— Э. д. с. индукции, возникающая в обмотке якоря при его вращении.
Полная мощность, затрачиваемая батареей, расходуется на совершение механической работы и иа нагревание сопротивления R. Поэтому
41 = W + PR.
326
Написанные равенства дают квадратное уравнение для £ицд:
«внд-^ннд+^’О. (О
откуда
(1, 2) = g±/g2-4/?tl7
®инд 2 *
Подставив числовые значения, получим
4нд = 40 в, 42нд = 80*
Неоднозначность полученного результата можно понять, если по* строить график зависимости механической мощности IP7, отдаваемой
мотором, от скорости вращения
его ротора <а. Для этого необходимо принять во внимание, что э. д. с. индукции пропорциональна скорости вращения, т. е. Ун11л = k&, где k — некоторый коэффициент пропорциональности. Тогда из уравнения (1) получим
%k®~k2e>2
R
Зависимость IT (<а) изображена на
рис. 286. Из графика видно, что
при 1Го > 0 одному н тому же значению IP7 о соответствуют две скорости вращения (со, и <а2)- Поскольку механическая мощность
равна произведению момента внешних сил, приложенных к валу
мотора, на скорость его вращения, следовательно, два значения скорости вращения реализуются при разных условиях (прн различных значениях момента внешних сил). При использовании мотора в качестве динамо-машины двум скоростям вращения (coi и со2), совместимым с условиями задачи, соответствуют различные э. д. с. «, = 40 в и « = 80 в).
Физический смысл отрицательных значений W (рис. 286) читателям предлагается выяснить самостоятельно.
481. Груз, опускаясь со скоростью и Рис. 287. (рис. 287), заставляет вращаться якорь ди-
намо-машины. Витки обмотки якоря при
своем вращении пересекают силовые линии магнитного поля, создаваемого статором, и в обмотке якоря возникает э. д. с. индукции ?инл- Цепь якоря замкнута на сопротивление R, следовательно, ток в цепи равен
?иид
327
По закону сохранения энергии мощность, развиваемая динамо-машиной, равняется ежесекундной убыли энергии опускающегося груза:
^2 синд —nigv,
откуда ____
Еинд = VmgvR.
Если динамо-машина будет работать'как мотор, то при той же скорости вращения якоря э. д. с. индукции в обмотке мотора будет равна э. д. с. индукции динамо-машины $инд. Так как э. д. с. индукции пропорциональна скорости вращения якоря, то э. д. с. индукции, возникающая в моторе, в том случае, когда груз поднимается со скоростью vb будет равна —
L ИНД ьиид 0 •
Для мотора имеем (см. решение задачи 480)
^~^инд = /1^ и = I2R + mgvh
где <f — э. д. с. внешнего источника, /[ —ток в цепи якоря электромотора.
Решая совместно найденную систему уравнений, получим
_ VmgvR (<? - mgvR)
01 mgR
Разные задачи
482. На основании законов Фарадея имеем
где А — атомный вес алюминия, z — валентность, Q — количество протекшего электричества, F — число Фарадея (F = 96500 к/г-экв).
Количество электричества
Q = Д,
следовательно,
483. Так как ток возрастает равномерно, заряд определяется средней величиной тока:
Q = yf = 15 к.
Масса меди тогда равна
т = — 4 = 5 • 10~3 г,
z F
328
484. Как нетрудно убедиться, ток меняется от 5 а в канале опыта до 3 а в конце. Заряд
Q = t = 400 к.
Теперь подсчитаем количество выделившейся меди:
иг = — —. = 0,13 г. Z Г
485. Масса никеля, выделившегося на поверхности изделия,
т = = 1>65 г- (1)
z F
с другой стороны,
т — S dp,
где S — площадь изделия, d — толщина покрытия, р — плотность никеля. Следовательно,
= -Z2- = 1,53.10-3 см.
pS
486. Давление гремучего газа складывается из парциальных давлений кислорода ро, и водорода рн,:
Ро = Рог + PH/ (1)
Парциальные давления легко найти из уравнений газового состояния:
т,, «гп
(2) РНа Но,
где V— объем газа, ц — молекулярный вес, 7? — универсальная газовая постоянная, Т — абсолютная температура.
Массы водорода /иНь и кислорода то определим на основании законов электролиза:
где атомный вес водорода, — валентность водорода, Aq2 — атомный вес кислорода, го, — его валентность.
На основании уравнений (1) —(3) получим
Q =------——-------------- = 5200 к.
4 / Ан Ап \
RT (—+ —2г-
\ гн211н2 го!М'О2 /
487. Подъемная сила F равна разности между архимедовой силой ГА н весом водорода в шаре Р (весом оболочки шара пренебрегаем)
Fh = mBg,
329
где тв — масса воздуха в объеме шара V. Массу воздуха найдем из уравнения газового состояния:
PqV = ^.RT,
Рв
откуда
₽ poVfW
Аналогично,
Po^Hig
RT ’
где рв и цн? — соответственно молекулярные веса воздуха и водорода. Далее,
р-р п PoWb-M
откуда
F=_____™______
Ро£(Рв-Рн2) ’
Водород, заполнивший шар объема V, получен электролизом подкисленной воды; следовательно, масса водорода
где Рф — число Фарадея.
Применив уравнение газового состояния, получим
т,т pBV=-Th.RT, ^Н2
откуда
г AHHRT
М'НгРо ZhZ®Hh2P0
Сравнивая выражения для объемов, получим
AnJg (Нв-Нн,)
= 4000 часов.
488. Пусть Со и С — емкости конденсаторов в некоторый момент времени, q0 — полный заряд на конденсаторах. Поскольку полный заряд не меняется со временем, а потенциалы на конденсаторах одинаковы, можно записать
- °zT"- -7г или (?0- <7) da=* qd; (1)
330
здесь q nd — заряд и расстояние между пластинами переменного конденсатора в некоторый момент времени t. Тогда
Чо<1 = d° + d я .и d0 + do
qBd _ др (t0 + 0 to — t 2tB to +1
(2)
Таким образом, заряд q линейно меняется со временем, а значит, искомый ток I будет постоянным.
В начальный момент времени С = Св и, следовательно, q qBft-Поэтому заряд на переменном конденсаторе изменился за время t от значения q0/2 до qo(to + t)/2ta. Изменение заряда за время t, очевидно, равно qat/2t0. Это изменение заряда обусловлено протеканием тока I по соединительным проводам:
(fot т tfo
Н ~ 2tB ’ “ЛИ 1 ~ 2tB '
Теперь можно определить начальный заряд конденсаторов:
_ . т/ eoSVo qa — -iC о V о---—.
«о
Подставляя значение qB в выражение для тока, получим окончательно
dBt0
(3)
(4)
(5)
Примечание. При решении данной задачи предполагалось, что в каждый момент времени заряды распределяются пропорционально. значениям емкостей (как это бывает в электростатике). Это условие будет выполнено, если емкости конденсаторов (или одного нз них, как в данном случае) меняются достаточно медленно. Количественное рассмотрение, выходящее, однако, за рамки школьного курса, приводит в данной задаче к условию RCa to, где /? —сопротивление соединительных проводов.
489. Если части конденсатора, расположенные левее и правее пластины, рассматривать как самостоятельные емкости, то можно представить всю систему как два параллельно соединенных конденсатора. Заряды между ними распределены пропорционально емкостям, т. е. обратно пропорционально расстояниям между пластинами. Пусть в некоторый момент времени (t = 0) расстояние от пластины до левой обкладки конденсатора db а до правой d — d^. Через время At они станут равны соответственно d, — о At и d — di + v td. Проследим за зарядом какого-нибудь из конденсаторов, г» « d — d j
для определенности левого. В первый момент он равен q —-—
d — di + v&t
а затем q------—-----. Так как ток равен отношению изменения
заряда ко времени, то
d — dj + vAt__ d — di
. _ AQ d_________d_______d d________qv_
J~ M M d
(см. примечание к решению задачи 488).
331
490. Искомая скорость понижения уровня керосина
» = 7, (1)
где I — длина пластины, / — время вытекания керосина. Время вытекания в свою очередь определяется из соотношения
£
1 ’
(2)
где / — ток в цепи, Q — изменение заряда конденсатора за время t, т. е. разность зарядов конденсатора до и после вытекания керосина:
Q - Qi - Qs, (3)
где Q2 — (4)
Но г ee0S d ’ r e0S (5)
Решая совместно (3) — (5), получим - 1)23 d (6)
Учитывая, что S = Z2, и использовав уравнения (1), (2) и (6), найдем окончательно
V — —7~~ТГ^7 = 2,26 10~2 лг, сек е0(е - 1) 41
(см. примечание к решению задачи 488).
491. Потенциал сетки 3 по условию (см. рис. 124) равен потенциалу сетки 1, следовательно электрон, разогнанный полем между сетками 1 и 2, при подлете к сетке 3 затормозится, повернет обратно и будет колебаться между сетками 1 и 3 (положительный ион азота, разумеется, будет вытолкнут нз пространства между сетками I и 3), Так как движение электрона не синусоидально, то он будет излучать целый спектр электромагнитных воли, однако минимальная длина волны в этом спектре (несущая, кстати, основную энергию излучения) будет соответствовать полному периоду колебаний электрона. Если с —скорость электромагнитных волн (скорость света), то
Л = сГ.
Очевидно, период Т в четыре раза больше времени пролета электронов от сетки 1 до сетки 2. Поскольку ускорение а н время t движения на этом участке соответственно будут
а =
eV
niL ’
1
У eV '
то для X получаем окончательно
А = 4с L 1/~ - 3,6 м.
Г eV
332
Чтобы ион азота начал двигаться между сетками 1 и 3 и излучать волны с длиной X, необходимо знак потенциала V2 изменить на обратный и добиться того, чтобы отношение m/eV осталось таким же, как для электрона.
492. Так как электроны проводимости в проводнике практически не связаны с ионной решеткой металла, они при вращении диска будут отбрасываться к его краю; во внешней части диска концентрация электронов повысится, во внутренней понизится, в результате чего возникнет некоторая разность потенциалов. Равновесие наступит тогда, когда образовавшееся поле будет таким, что в каждой точке действующая на электрон сила заставит его двигаться по окружности с угловой скоростью и, т. е. двигаться вместе с диском:
ma2r = еЕ,
где г —расстояние от центра диска. Таким образом, напряженность поля
растет пропорционально г, изменяясь от нуля в центре диска до значения
„ о?/?
на внешней окружности. Разность потенциалов можно получить умножив среднее значение напряженности поля
Е 2/. на расстояние /?:
2А,
Заметим, что это справедливо только при линейной зависимости Е от г, т. е. при зависимости вида Е = а + Ьг, где а и b — постоянные множители (в этой задаче а = 0, Ь = <в2/Л). В общем случае величина V будет равна площади под кривой зависимости Е от г.
493. За некоторый промежуток времени т на анод попадет п электронов, причем
Каждый из этих электронов передает аноду импульс
п — mv = т ~\/ =yr2emV .
V т
Можно записать, что
пр *= Fx,
333
где F— средняя сила давления электронов на анод. Отсюда
Небезынтересно провести и численную оценку этой величины. Для типичных значений / = 10 ма, V •= 100 в, величина силы F = = 3,4 • 10~6 н.
494. Так как стержень электромагнита и язычок изготовлены нз материала, не обладающего остаточным намагничиванием, то язычок дважды за период переменного тока будет притягиваться электромагнитом н замыкать цепь заряда конденсатора. При каждом замыкании цепи разряда через гальванометр проходит количество электричества
Q = CV.
По определению, ток измеряется количеством электричества, протекшим за 1 сек. Таким образом,
I = Q • п,
где п — число замыканий цепи разряда за 1 сек; поскольку п = 2v, то l = CVn = 0,\ а.
495. Прежде всего определим напряжение на сопротивлении R; для этого запишем уравнение, выражающее собой закон Ома, для двух случаев — разомкнутого и замкнутого накоротко сопротивления /?:
Ч = (R + г} !,
? = г • 3/,
где г —внутреннее сопротивление батареи.
Теперь легко определить напряжение на разомкнутом сопротивлении R-.
V„ — IR = 4 — 1г = 4 -^- = ^-4.
К 3 3
Обозначим напряжение на конденсаторе С( через Уц а на С2 — через У2. Имеем
У1 + У2=УЛ.
Равенство зарядов конденсаторов дает = V2C2.
Решая систему уравнений, получим
V = %ЧС2 2% С]
1 3(С1 + С2) ’ к2= З^ + С,) ‘
496. Ток через нагрузку /н, очевидно, постоянен и равен , 150 в
In = Тл----= 15 ма.
10 ком
334
Так как ток через стабиловольт /с изменяется от 5 ма до 15 ма, то общий ток, протекающий через сопротивление R, меняется в пределах от /min = 20 ма до /max = 30 ма.
Запишем закон Ома для предельных режимов работы стабилизатора (К=150 а —напряжение на нагрузке):
1,1<J — И = 7?/тах,
0,9g V = /?/ш1п-
Решая эти уравнения, получаем
jLymax-/mln)„300 д<
и,У/тах — b’min
/< = —------= § ком.
'max
497. При зарядке аккумулятора внешнее напряжение Vj идет на совершение работы против э. д. с. аккумулятора g и на компенсацию падения напряжения на внутреннем сопротивлении г аккумулятора:
Vt = g + /ir.
При разрядке иа основании закона Ома будем иметь
g = V 2 + Izr.
Решая этн уравнения, получаем
г = 0,17 ом, g = 12 в.
Отсюда ток короткого замыкания (т. е. ток при нулевом сопротивлении внешней цепи)
= ——80а.
г
498. Рассмотрим рис. 288. Внутренние сопротивления батерей ri и г2 показаны включенными последовательно с каждой батареей. Перенесем мысленно единичный положительный заряд вдоль кои-тура acdfa (см. решение задачи 433). Тогда (Г] = гг = г)
^-Цг + Ш.
Аналогично для контура bcdeb
Кроме того, Отсюда
$2 — /а^ 4" //?• /1 + Л = /.
, g2(r + /?)~gl/?
а = г (г + 27?)
~ 2,47 а.
335
Знак минус для тока Ц означает, что направление для !\ (см. рнс. 288) выбрано неправильно и ток через батарею течет в противоположную сторону по сравнению с указанным на рисунке направлением.
499. Вернемся намо-машину, под
к рис. 288. Здесь под нужно понимать ди-?2 —батарею аккумуляторов, а сопротивление Р обозначает лампочку. Составляя уравнения таким же образом, как и в предыдущем решении, учитывая, что ri =И= Г2, найдем ток в лампочке:
, _ ?1Т2 + <?2Г 1 о д- _
— ~i гГ i п ' в о,оо й,
rtr2 + Rrt + Rr2
ток в батарее аккумуляторов:
, 22-lR
= -1,58 а.
Г2
Знак минус для тока /2 означает, что ток через аккумулятор (зарядный ток) течет в противоположную сторону по сравнению с указанным на рисунке направлением.
500. Напишем уравнение, выражающее закон Ома для контура, содержащего источник 'гь амперметр и реостат:
Si = 'iWc;
здесь /( — ток через амперметр, АД — полное сопротивление, в которое входят: внутреннее сопротивление батареи, сопротивление амперметра и участка ab реостата; VЬс — напряженке между точками 6нс реостата. По условию /( = 0, значит,
<£ I = VЬс-
Отсюда видно, что батарея 'А2 должна быть присоединена положительным полюсом к точке 6. Далее,
Vbc = Rbch — $2 — “= <?i,
где /2 — ток через батарею g2. Отсюда находим
Rbc^~~r^ ЮО ом-, г2 — с 1
на сопротивлениях R и г будет рассеиваться мощность
V2 -т2
= ~ = 0,16 вт, К Rbc Rbc
ур = (%2 Vbc)2 _ (с 2
— = 0,32 er.
501. Разберем для определенности сеть с N == 5 (рис. 289). Пусть батарея подсоединяется к точкам 1 и 2. Непосредственно между точками 1 н 2 включено сопротивление
336
Параллельно через точку 3 подсоединено сопротивление 2R, то же через точку 4 и т. д. Тот факт, что точки 3 и 4, 3 и 5, 4 и J соединены между собой, не играет роли, так как при подключении батареи к точкам 1 и 2 потенциалы точек 3, 4, 5 будут одинаковы и, следовательно, включенные между ними сопротивления не оказывают влияния иа суммарное сопротивление сети. Таким образом, сеть состоит из сопротивления R и параллельно с ним соединенных N — 2 сопротивлений 2R. Общее сопротивление
R 1 .
К 2 1 N - 2 .V •
R + 2R
Теперь нетрудно подсчитать искомую мощность:
WN
2 (N + 2У R *
2 /
502. Так как перемычка движется Рис. 289.
вниз с постоянной скоростью, то сила
тяжести уравновешена силон, действующей на перемычку со стороны магнитного поля (рнс. 290):
mg = F.
Определим теперь силу F.
При движении перемычки в контуре abcda наводится э. д. с. индукции g:
__ АФ
* ~ ~ьГ'
Мощность джоулевых потерь равна «2
№ = — R '
Согласно закону сохранения энергии
W — Fv, или F = Rv
Но
Решая систему уравнений, получаем
/? = = 2,55 10“3 ом.
mg
503. Для осуществления равномерного движения перемычки к ней необходимо приложить силу
г «2 В2А2о
/’ S3S -- » -----
Rv R
22 Л. П, Баканнна и др.
337
(см. решение задачи 502). Подставляя числовые значения, получим Е = 2-10“'2 н.
604. Мощность джоулевых потерь равна (см. решение задачи 502)
И7 =__п .
R 4Lp •
Энергия, превратившаяся в тепло, равна А = Wt,
где t — время, в течение которого происходит изменение потока, пронизывающего рамку, т. е. время существования э. д. с. индукции.
В том случае, когда размеры башмаков Ло > L, изменение потока происходит при входе рамкн в поле и при выходе нз него.
Внутри башмаков, когда вся рамка находится в поле, поток через нее постоянен и 2 = 0 (рис. 291). Так как рамка движется равно-
мерно, то
I »
Отсюда
2L v
H20ff2L2v 2р
Если La < L, то изменение магнитного потока происходит за время, пока башмаки «входят» внутрь рамкн и «выходят» из нее. Пока рамка движется так, что башмаки находятся внутри рамкн (вертикальные края рамкн находятся за пределами магнитного поля), изменения магнитного потока, пронизывающего рамку, не происходит, и g = 0 (рис. 292). Итак, при La < L
, 2Лр
и
338
откуда
nlH2LvLQ
А~ 2р •
505. Э. д. с. индукции ?1Шд> возникшая в обмотке якоря электромотора, пропорциональна скорости вращения якоря (см. решение задачи 481):
?инд = ?! ~~~ • (1)
На основании закон сохранения энергии, примененного к электромотору, имеем
<gI = PR + Fv,
(2)
где / — сила тока в цепи якоря, г—сила трения, приложенная к валу мотора н направленная по касательной к валу (рис. 293), о—линейная скорость точек на окруж-
ности вала, R, —сопротивление цепи ™ । i S
якоря. Можно записать
Fv = F • 2лап = 2лМп,
где а —радиус вала, М — момент трения.
На основании закона Ома
? — ?ИНД —
Сравнивая уравнения (2) н (4). лучаем
й’инд/ = Fv — 2лМп.
Учитывая равенство (I), на основании уравнения (5) получаем 1-^. (6)
с 1
Подставив выражение (6) в уравнение (2), имеем окончательно ? 2пМм^/?
п=пх---------------.
г,
При Л4 — О
П ?! П'’
Ток находится нз уравнения (2): ?/ = /2Л
Отсюда получаются два значения тока: /1 = 0 — ток холостого хода, = —ток прн полностью остановленном якоре.
22*
339
506. Пусть х — расстояние от конца линии до места, где находится трамвай. Тогда прн последовательном соединении двигате-
лей (рис. 294) имеем на основании закона Ома уравнение
= Л (27? 4- рх);
здесь р—сопротивление еди-вицы длины провода трамвайной линии, синд — э. д. с. индукции, возникающая в двух соединенных последовательно обмотках двига-
телей.
Прн параллельном соединении (рис. 295) получаем аналогичное уравнение:
К-?инд = /2(4+ РХ)'
где %"ал — э. д. с. индукции, возникающая в параллельно соедииеп-
Механическая мощность, затрачиваемая трамваем, равна (см. решение задачи 505)
“ ^иидЛ = ^инДг-
Из полученных уравнений определяем х:
Затем находим скорость трамвая:
v =,hs^L „ Ik [v _ ц {2R - рХ)1.
340
IV. ОПТИКА
Преломление и отражение света на границе двух сред
507. Чтобы определить, как будет двигаться изображение источника в поле зрения трубы, найдем, как меняется угол у между падающим и отраженным лучами (рис. 296). Легко видеть, что у = 2а+ 2(5 (как внешний угол А ЛВС). С другой стороны, Ф = а + (J, так как в Л АВО
Z АВО = — ZBAO = у- a, a Z ЛОВ = ф
и, следовательно.
л п , л
— - Р + J - а + <р = л .
Таким образом, у = 2ф при любых а и р. Это означает, что параллельный пучок лучей от удаленного предмета после отражения от обоих зеркал отклоняется на постоянный угол у и изображение в поле зрения трубы не будет перемещаться при повороте зеркал. Однако зеркала могут повернуться
таким образом, что луч вообще ;:е попадет на отражающие поверхности зеркал и изображение в поле зрения трубы исчезнет. Прн вращении зеркал с постоянной скоростью изображение источника будет, таким образом, периодически появляться и исчезать.
508. Рассмотрим прямоугольный Д ЛВС (рис. 297). Интересующее нас смещение луча х равно длине катета СВ. Из построений видно, что Z САВ — i~r, поэтому
х = СВ = АВ sin (/' — г).
Замечая далее, что АВ = rf/cos г, получим
d sin (i — г) ,, . . . . .
X =-------->----— Д (sin j — COS / fg A,
cos r '
341
Из закона преломления света на границе двух сред имеем slnr = sin i
—------и, следовательно,
sin I Уп2 — sin21
Таким образом,
х — d sin 111 —
cos I
У n2 — sin2 i
Подставляя значения d—1 см, n= 1,5 и ( = 30°,
получим оконча-
тельио
2/2-/3 п9
х =---—---«s 0,2 см.
4/2
539. Лучи от нижней царапины А после преломления на верхней границе стеклянной пластинки будут казаться исходящими из некоторой точки At, которую можно рассматривать как изображение нижней царапины в плоскопараллельной пластинке (рис. 298).
При наведении микроскопа с верхней царапины на нижнюю его тубус, очевидно, следует передвинуть на расстояние I = BAt. Из Д АВС и Д А[ВС получим
tgi _ d tgr I ’
По условию в объектив микроскопа попадают лишь лучи, наклоненные к осн микроскопа под достаточно малыми углами. Для таких лучей можно приближенно принять
tg / _ sin i tgr ~ sine
(синусы и тангенсы малых углов приблизительно равны). Таким образом,
Примечание. Из решения вытекает, что положение точки 4| не зависит от углов i и г только при достаточно малых значениях этих углов. Таким образом, изображение нижней царапины в микроскопе будет резким лишь в том случае, когда условие малости углов отклонения будет выполнено для всех лучей, попадающих в объектив.
510. Палка будет казаться прямой наблюдателю, смотрящему вдоль ее надводной части, если направление подводной части сов
342
падает с направлением преломленного луча (рис. 299). Угол излома |) равен I — г, причем
sin i
sin г ♦
Отсюда легко получаем
о л . cos а
р = — — а — arcsin--------
2 п
511. По условию задачи отраженный н преломленный лучи перпендикулярны друг к другу. Это означает, что i + г = 90° (рнс. 300).
Рис. 299.
Учитывая это и применяя закон преломления света иа границе двух сред, получим
sin I______sin i . _
sin г sin (90° — г) &1 nt *
Таким образом, _
V з
n2 = ni tg i = 2,4 —z— « 1,39.
512. Появление темной полосы на экране следует из построения, приведенного на рис. 301. Пучок параллельных лучен, падающий на призму, разделяется на два пучка, каждый из которых
отклоняется на некоторый угол <р по отношению к направлению падающего пучка (каждый пучок изображен на рис. 301 своей
343
штриховкой). Найдем сначала связь между преломляющим углом призмы а и углом отклонения лучей ф. Для этого, очевидно, достаточно рассмотреть преломление лучей на второй поверхности призмы. Угол падения лучей иа эту поверхность равен а, угол преломления а + ф, следовательно,
sin а _ 1 sinfa + ф) п'
Как видно из рис. 301,
, а + d 30 .>
tg4>=~£—=Лог = 3' ° рад'
Угол ф оказался весьма малым,
будет малым. Мы заменим синусы
углами:
а 1 ф
—— = _ а = X—
а + ф п п — I
Можно ожидать, что и угол а и тангенсы малых углов самими
рад — 3°.
Решение показывает, что наше предположение о малости преломляющего угла а было правильным.
513. Рассмотрим сначала ход лучей с длиной волны Л| (рис. 302). На передней грани лучи не преломляются. Для преломления на задней грани можно записать (см. задачу 512):
П|а = ф| + а.
Отсюда определяем угол отклонения лучей от первоначального направления
ф! = а(п— 1).
Очевидно, что ф( есть угол между направлением преломленных лучен и оптической осью лиизы. На экране лучн соберутся в точке, отстоящей от оптической оси иа расстояние
/] « ф]? = а («1 — 1) F.
Повторим те же рассуждения для лучей с длиной волны А2;
/2 « ф2Д = a (н2 - 1) F.
344
Вычитая полученные уравнения, получаем
514, Обозначим угол преломления светового луча в жидкости через ф (рис. 303). Тогда для первой границы имеем
sin'z _ и sin ф ’
где и —показатель преломления жидкости. Для второй границы sin ф п2
si п г п '
Перемножая почленно оба равенства, получим sin i _ п2 sin r nt
Отсюда следует, что прозрачный плоскопараллельный слой вещества с любым коэффициентом преломления, расположенный на границе между двумя средами, не изменяет условий преломления.
Рис. 303. Рис. 304.
Исключение представляет случай, когда луч света испытывает на первой границе полное внутреннее отражение. jB этом случае угол преломления луча в слое не имеет физического смысла и приводимое решение неверно.
515. Из построения (рис. 304) видно, что
Л, = R sin i, A2 = 7?sina,
где а = 2r — i. Учитывая узость пучка и, следовательно, малую величину углов падения, имеем приближенно:
hi _ sin I _ i_______________n ~ .
й2 sin (2r — i) 2r — i 2 — n ~ ’
откуда n — 4/3.
Случай, когда лучи пересекаются внутри колбы, предоставляем рассмотреть читателю.
345
Примечание. При решении задачи мы не учитывали влияния тонких стенок сферической колбы. Легко видеть, что для такой колбы угол преломления на границе воздух — стекло ? приблизи
тельно равен углу падения иа границе стекло — вода I' (рис. 305), откуда
sin i sin I’ n
-у = Пет и —------= ----,
sin Г sin Г Пет
где Ист — показатель преломления стекла колбы, и — показатель преломления воды. Учитывая, что sin г' ~ sin i', получаем
sin I
—;--= И.
sin г
516. Рассматривая рыбку как источ-
ник, находящийся в точке А, построим изображение рыбки (точка В на рис. 306). Искомое расстояние х = АВ. Принимая во внимание, что в глаз попадает узкий пучок
Рис. 307,
и, следовательно, углы Z, г и <р малы, запишем: h = xqp= х (2т — i).
С другой стороны, h = Ra = 2R (i — г), откуда 2P(i-r) n-t
2г-i 2~п"
х =
Подставляя значение и =4/3, получим x — R.
517. Из закона преломления света на границе воздух — стекло следует (рис. 307)
sin ггС ~ и,
(знак равенства соответствует скользящему падению 1 = 90°), С другой стороны, условие полного внутреннего отражения на границе стекло — жидкость имеет вид
346
При п2 > 1 неравенства несовместны. Это означает, что утлы преломления лучей г после прохождения светом первой границы недостаточно велики, чтобы свет испытал полное отражение на второй границе.
518. Допустим, что на поверхность воды падает под углом I параллельный пучок света (рис. 308). Угол преломления такого пучка получим из условия sin г = sin i/n. Параллельный пучок преломленных лучей, пройдя через линзу, соберется в некоторой точке фокальной плоскости, которая по
условию задачи совпадает с дном сосуда. Расстояние х от точки схождения лучей до оптической оси линзы равно Fig г, или
F sin i х — —7==, у п2 — sin2I
Для скользящего луча (Z = 90°) это расстояние принимает максимальное значение, равное
Рис. 308.
При освещении поверхности воды рассеянным светом, т. е. светом, состоящим из лучей всевозможных направлений, на дне сосуда образуется светлое пятно, диаметр d которого равен 2хтзх:
d — 2хтах — z •
У и2 — 1
519. Ни одни луч не выйдет через поверхность воды, если луч SA (рнс. 309) испытывает полное внутреннее отражение на
границе вода — воздух. Запишем условие полного внутреннего отражения для луча SA:
г----.
Уй2 + Р2 «
Отсюда после несложных преобразований найдем
520. Лампочку нельзя увидеть сквозь боковые стенки сосуда в том случае, когда все лучи, падающие на эти стенки, испытывают полное внутреннее отражение. Условие полного внутреннего отражения иа боковой стейке имеет вид
sin г
_£ п ’
347
где п — показатель преломления жидкости, а / — угол падения луча на боковую стенку (рис. 310). Рассмотрим теперь лучи от источника S, проникающие в жидкость через дно сосуда. Поскольку жидкость по сравнению с воздухом является средой оптически более плотной, угол преломления лучей г не может быть больше некоторого предельного угла г0, соответствующего скользящему падению луча от источника на дно сосуда. Предельный угол г0 определится из условия sinr0=l/ra.
Из A SOA следует, что г' = 90° — г.
Предельному углу г0 соответствует минимальное значение угла падения лучен г0 на боковую грань, равное 90 — г0 Если условие полного отражения на боковой грани будет выполнено для г = г,. = = 90° — го (предельный луч), то оно, конечно, будет выполнено и для всех других лучей. Таким образом, решение задачи запишется в виде
sin rn — и п
, Г. i . i
ИЛИ COS ГЛ — I/ 1-5- —
Оу п2 п
Отсюда следует: 1,41 и nratn ~ 1,41.
Примечал и е. При решении задачи стеклянные стенки сосуда между жидкостью и воздухом не принимались во внимание, так как условия преломления света на границе двух сред не зависят от наличия прослойки (см. задачу 514).
521. Лучи от пылинки S, которую можно рассматривать как точечный источник, находящийся вблизи основания призмы, падают па нижнюю грань под всевозможными углами. Максимальный угол преломления г ~ го соответствует, очевидно, скользящему падению. Этот угол определяется соотношением
1
sin г0 = —.
п
Из A SOA (рис. 311) следует: г + г' = 60° (так как Z SOA = 120°), Таким образом,
г == 60° — г > 60° — г0 = Гц,
348
(Здесь предполагается, что г0 < 60°, в противном случае всегда найдется такой луч, который падает на боковую грань призмы перпендикулярно и не испытывает поэтому полного отражения.) Если для наименьшего угла падения света на боковую грань призмы г » rQ будет выполнено условие полного внутреннего отражения, то ни один луч не выйдет наружу и, следовательно, пылинка будет не видна. Таким образом, условие, при котором ее еще можно увидеть, запишется в виде
' I
sin г0 < -
или
sin (60° — го) — sin 60° cos r0 — cos 60° sin г0 •»
Ч-i/1 -Л--/“/[>/з(«2-1)-1] <-• 2 Г ti! 2ti 2п ' п
Отсюда следует, что и < 2.
522. Рассмотрим преломление света в некоторой точке а. расположенной на грани АС (рис. 312). Эта грань по условию задачи
освещается лучами всевозможных направлений (рассеянный свет). Так как стеклянная призма представляет собой оптически более плотную среду по сравнению с воздухом, угол преломления не может быть больше некоторого предельного угла г0, определяемого соотношением
1
S1I1 Гп = —.
п
Крайние лучи светового конуса, исходящего из точки а, будут падать на грань АВ под углами г0 = г0 — а и Гд = г0 + а в точках b и е соответственно. Заметим, что г0 < г0, а го > го> это означает, что луч ab не
испытает полного отражения на гра-
нице стекло — воздух, в то время как луч ае полностью отразится. Угол преломления г0 луча, выходящего из призмы в точке Ь, найдется из соотношения
sin г0 1
sin i0 п ’
или
sin(r0 —a) sin а cos г0 — cos а sin го
sin «о sin i0
-i 1 1
sin а I/ 1------5— cos а— .
Г и2 n 1
sin i0 n
349
Отсюда получим
п
sin Zo . \2 , ,
—-—cig а) + 1.
sin а )
Все лучи, выходящие из призмы под углом i0> соберутся в некоторой точке фокальной плоскости линзы (точка D на рис. 134), направление на которую из центра линзы составляет угол i0 с оптической осью. Выше точки D свет попасть не может (неосвещенная область), так как лучн, выходящие из призмы, не могут быть отклонены вверх от оптической оси на угол, больший чем ia. Ниже точки D располагается освещенная область; угол отклонения лучей от оптической оси вниз может быть любым в интервале от 0 до 90° (например, в точке d на рис. 312 выходящий из призмы луч отклонен на 90° вниз от оптической оси). В нашем случае а = 30°, io = 30° и, следовательно,
п = = ^5-21'3 ~ 1,24.
Тонкие линзы
523. Проведем вспомогательный луч аа’, проходящий через оптический центр линзы параллельно лучу АВ (рис. 313). Продолжение луча ВС пересекается с лучом аа! в фокальной плоскости линзы //'.
524. Проведем вспомогательный луч аа параллельно
лучу ВС через оптический центр линзы Л2 (рис. 314). Луч аа! должен пересечь продолжение преломленного луча CD в фокальной плоскости ff' линзы Л2. Таким образом, мнимое изображение источника S будет в точке S2. Как видно из построения, на линзу Л2 падает сходящийся в St пу
чок лучей. В подобных случаях принято говорить, что Si играет ДЛЯ ЛИНЗЫ Л2 роль «мнимого» источника.
525. Сначала построением вспомогательного луча аа!, параллельного АВ, определим положение фокальной плоскости ff' (рис. 315). Затем при помощи вспомогательного луча bb', параллельного DE, определим направление преломленного луча EF. Случай, когда точка пересечения лучей АВ и DE лежит справа от линзы, предо-
ставляем рассмотреть читателю.
526. Обычным построением вспомогательного луча аа', параллельного лучу АВ, найдем направление преломленного луча ВС (рис. 316). Далее построением, аналогичным рассмотренному в задаче 525, определим положение фокальной плоскости лиизы Лц направление преломленного луча CD и тем самым положение изображения S2.
350
Рис. 316.
527. Построим изображение источников А и В. Изображение источника А будет на главной оптической оси в точке А' на расстоянии 2F от линзы. Построение изображения источника В ясно из чертежа (рис. 317). Искомый угол определяется из соотношения
tg = b _ 2F , (1)
где у — расстояние от изображения В' до главной оптической оси, а b — расстояние от В' до линзы. С другой стороны,
где х и а —расстояния от источника В до главной оптической оси и линзы соответственно. Из подобия треугольников ВСО и В'С'О имеем
гт к 1,11
По формуле линзы — = —, откуда
а b г
t Р-а b a — F"
(4)
Вычислим отношение tg ip/tgq>, используя уравнения (1) —(3): tg ф У (2F — a) b (2F-a)
tg qp х (b-2F) a (b — 2F) ’ ' }
Учитывая выражение (4), получим tgi|)/tg<p = 1, следовательно, •ф = 30°.
Очевидно, что если расположить экран под углом 30° к главной оптической оси так, чтобы он пересекал главную оптическую ось в точке, отстоящей на расстоянии 2F от линзы, то изображения обоих источников будут четкими.
528. Проведем лучи от противоположных краев солнечного диска через оптический центр линзы (лучи АО и ВО на рис. 318). Изображения краев будут находиться в точках пересечения этих лучей с фокальной плоскостью линзы (точки As и Bj). Из рис. 318 имеем
D =d_
R F ’
352
где О —диаметр Солнца, R— расстояние от Солнца до Земли, d — диаметр изображения. Подставляя числовые значения, получим d х 2,8 см.
Рис. 319.
529. Из формулы линзы имеем (рис. 319)
ab а + b '
Принимая теперь во внимание, что линейное увеличение
получим
х а
530. Пусть at и bt, а2 н b источником и линзой и линзой линзы (рис. 320) так, что
at + bi = а2 + b2 = const. (1)
Из построения видно, что искомое увеличенное изображение предмета определится из соотношения
У2=*~. (2)
142
Кроме того,
(3) “1
обозначают расстояния между и экраном прн двух положениях
Используем далее формулу лннзы для обоих случаев:
ai + bl ” F ’ а2 + Ь2 “ К •
(4)
Учитывая соотношение (1), легко видеть, что
а2 = b2, a2=bi. (5)
23 Л. П. Баканива и др.
353
Решая совместно (2), (3) и (5), получим
(6) откуда уг=\2см.
531. Для первого положения линзы имеем (см. рис. 320)
для второго положения:
здесь ijt и у2~ размеры изображений, х — размер предмета. Найдем теперь расстояния at и Z>i, а2 и Ь2. Из формулы лиизы имеем
at + bi "= F ' а2 + Ь2 F '
Следовательно,
a^i = F (ai + bi) = FL*= a2b2.
Кроме того, at + bi •= a2 + b2 = L.
Из этих соотношений следует, что все величины at, bi, а2, b2 удовлетворяют квадратному уравнению
гг — zL + LF = 0
(где z = at, bt, а2 или Ь2).
Решая это уравнение^ принимая во внимание, что ai > а2, bt < b2 (см. рис. 320), получим
. L-fl2 . L ..fl2
+ y — -LF, bi>=a2^-^— у -^-LF,
Заметим, что действительные решения квадратного уравнения суше-ствуют только при ! ^4Л Физически это означает, что при L < 4F нельзя получить ни одного действительного изображения. Отношение размеров изображений у2/у1 в обоих случаях есть
~ L Г L2 2 п ь । 1 / Д / р , .__________,
У2 <4 2 + И 4 (L + VL2~4LF )4
уГ bia^ ьС “ 16Д2/г2
_ 2 К 4
532. Пусть «1 и bi, а2 и Ь2 обозначают расстояния между источником н линзой и линзой и экраном при двух положениях линзы (см. рис. 320). Тогда
Принимая во внимание, что a2 = fc] (см. решение задачи 530), получим
L — 2а3 = I, или аг =
Ь2 — ~~ П2
L + 1
2
Фокусное расстояние определим из формулы линзы:
L — l L+1
г а2Ь2 2 2 £2-/2
Г =-----— = —:-------; — —
0-2 + b2 В — I L А-1
~2- + “Т“
533. Пусть At является изображением точки A, a Bj—изображением точки В (рис. 321). Применяя дважды формулу линзы для
4 в.
аГ^В F
Рис. 321.
этих точек, получим
Из этих соотношений выразим расстояния bi и Ь2:
a~i~F
После несложных вычислений получим длину отрезка
F2l Л1В] = b2 — bi --------г-. .2 .
(a-FY- (I)
Искомое продольное увеличение выразится формулой к b2-bi F2
o-n--(j)"
23*
355
534. Из рис. 322 следует:
£L = 1l Уг t>2 х «] ’ х а2
Здесь ух и уг~ размеры изображений, х — размер источника, £ В первом случае
=
Рис. 322. 1 х+У1’
Записывая теперь формулу линзы, получим
1 = Я1 + &1 Ц = (х + У1)2
F “ aib! *° xLi ijiLi Lixiji ’
x + yi x+iji
ИЛИ
Llxy1 = F (x + yi)2.
Аналогичным образом во втором случае
F (X + у2)2'9
здесь через ь2 обозначена сумма а2 4- Ь2. Разделим почленно два
последних равенства:
LiVi (x+yi)2 L2IJ2 = (х + у2)2 •
Отсюда
х У2КД1У1 -У1КЦуГ = ^2У2 ~ L{yi
= 8 мм
Найдем теперь фокусное расстояние линзы:
F = = Vlj72 [-V2+£i _ L^+Ly\ = 32 см^
(х + У1)2 (Уа~У1)2 \ VУ2У1 VF2Lx I
535. Как следует из рис. 323, линейные увеличения в первом
И втором случаях суть
356
Согласно формуле Линзы
----1—
«1 bi
±^JL + ±, F а2 b2
F
или
4?- = 1 + -ТГ- “ 1 + Т7-F bi V,
Беря разности левых и правых частей этих соотношений, получим ai~a2 1 1
~~F Vi ~ W
Отсюда „ di — L
°'ZZ'T'
У1 v2 V! v2
536. Используя заданные формулу линзы (рис. 324):
в условии задачи расстояния, запишем
1.1 1 ..— -4- 1 SS ——. F + li F + l2 F
Решая это уравнение относительно F, получим для фокусного расстояния формулу:
F^lil2.
Подставляя численные значения, найдем F = 30 см. 537. В отсутствие стеклянной до изображения равно
Рис. 324. пластинки расстояние от линзы
b — ——г- = 60 см, aD— 1 ’
где D= 1/F — оптическая сила линзы.
Рассмотрим теперь преломление лучей н пластинке. Как видно из рис. 325, вертикальное смещение d луча, прошедшего через пластинку, равно
(tgj-tgr),
357
где I и г —углы падения и преломления. Отсюда
= £ (1 -
, d а — а — -т—г tg'
tgr\ tg'/
Дли малых углов шениеги синусов:
Таким образом,
и г отношение тангенсов можно заменить отно-
tgr sin г 1
---— = -1
tg Z sin г n
, L(n-l) a ~ a------------ 2o cm
n
и
У -Г = 100 CM.
a D — 1
Искомое расстояние l между изображениями равно b'— b:
. ,, , L(n-l)
I = b' — b = 77-7=-rr-=7=7--7- ------77 = 40 CM.
[(aD — 1) n — LD (n — 1)] (aD — 1)
538. Мнимое изображение источника света, даваемое отрицательной линзой, всегда располагается ближе к линзе, чем сам источник. Поэтому всегда будет существовать область, заштрихованная на рис. 326, из которой можно одновременно увидеть и источник света и его изображение. Исключение составляет случай, когда расстояние между источником и линзой равно нулю.
539. В отсутствие плоского зеркала изображение Si источника располагается на двойном фокусном расстоянии от линзы. Для того чтобы лучи, отраженные от зеркала, пройдя вторично через линзу, стали параллельными, необходимо, чтобы они пересекались в заднем фокусе линзы. Это, очевидно, произойдет в том случае,
3
когда расстояние между линзой и зеркалом будет равно F. Ход лучей показан на рис. 327.
540. Параллельный пучок лучей от удаленного источника прн прохождении через отрицательную лннзу дает мнимое изображе-
858
иие Si источника в фокусе линзы (рис. 328). В плоском зеркале получается второе изображение S2. Это изображение находится иа расстоянии 2а — F от линзы, где F < 0 — искомое фокусное расстояние линзы. При вторичном прохождении лучей через линзу получается изображение S3. Можно записать
1 1 1
F 2а — F 3 " ~г а
3
Решая это уравнение, находим F= — а. Второе решение Г = + — а
Рис. 328.
для нашей задачи смысла не имеет.
541. Рассмотрим лучи, исходящие из краев удаленного здания. Пересечение этих лучей с фокальной плоскостью ffi определяет размер у
Рис. 329.
изображения здания (рис. 329). Это изображение рассматривается глазом под углом ф1#
Ограничиваясь случаем малых углов, нетрудно видеть, что
Ф1 =
У
at-F'
Приблизив линзу к глазу на расстояние а2, человек будет рассматривать изображение глазом уже под углом
*₽2----Z р~’
^2 “
Изменением размеров изображения при малом перемещении линзы мы пренебрегаем. Поскольку видимая величина изображения определяется величиной углов <р] и <р2, то изменение этих размеров при приближении линзы к глазу будет
откуда
<р2 _ fli - F
Ф1 а.2 — F
L, ka2
359
Подставляя значения Я] и я2 и учитывая, что в нашем случае й = 2, получаем F — 5 см.
542. Плоско-выпуклую линзу, плоская поверхность которой покрыта хорошо отражающим слоем, можно рассматривать как систему, состоящую из линзы и плоского зеркала. Ход одного из лучей в такой системе показан на рис. 330. Расстояние Ь до первого изображения, S], даваемого линзой, найдется из формулы линзы:
ь= aF
a — F '
После отражения лучей от плоского зеркала образуется второе изображение, S2, лежащее па расстоянии bx — — b от линзы. Наконец, после повторного прохождения лучей через линзу лучи сойдутся в точке S3; расстояние от этой точки до линзы найдется из формулы линзы:
btF aF
а' bx-F 2а-F"
При Я] > 0 изображение S3 является действительным, при at <0 — мнимым. Таким образом, условие получения действительного изображения запишется в виде 2я > F.
Примечание. Во всех задачах настоящего «Сборника» формулы положительной н отрицательной линз, а также формулы вогнутого и выпуклого зеркал, записываются всегда в единообразной форме
При этом должно соблюдаться следующее правило знаков: действительным предметам или изображениям соответствуют положительные значения а и Ь; мнимым предметам (сходящиеся луч.и; см. решение задачи 524) или изображениям соответствуют отрицательные я н Ь. Наконец, для положительной линзы и вогнутого зеркала F > 0, для отрицательной линзы и выпуклого зеркала F < 0.
В данной задаче источник S действительный, промежуточное изображение S] также действительно (для однократного прохождения лучей через линзу). Второе промежуточное изображение S2 играет роль мнимого источника для повторного прохождения лучей через линзу. Наконец, окончательное изображение оказалрсь действительным. В соответствии с изложенным выше правилом знаков было принято: а > 0, b > 0, bi < 0, ai > 0 и F > 0.
543. Будем рассматривать плоско-вогнутую линзу с посеребренной плоской поверхностью как систему, состоящую из линзы и прижатого к ней вплотную плоского зеркала. Ход лучей в такой 360
системе показан на рис. 331. Положение первого изображения определится по формуле линзы:
6 =
aF
а — F
(F < 0).
Второе изображение, S2, образующееся после отражения лучей
рт зеркала, но без учета повторного прохождения через линзу,
расположится на расстоянии — Ь. Наконец, после повторного прохождения через линзу лучи сойдутся в точке S3, положение которой найдется по формуле линзы:
bxF aF
а'~ bx — F ~ 2a — F'
Поскольку F < 0, при любых значениях а изображение S3 оказывается мнимым
(т. е. Hi < 0).
544. Требуемые расположения линз показаны на рис. 332. Первое расположение (а) реализуется в зрительной трубе Кеплера, второе (б) — в зрительной трубе Галилея.
Рис. 332.
545. Решение задачи поясняется рис. 333. Источник света расположен в точке S на расстоянии а перед линзой. Его изображение, даваемое первой линзой, находится в точке Sb Из формулы для линзы следует, что
361
Для второй линзы это изображение служит мнимым источником, находящимся на расстоянии ai= — (b — F) от этой линзы. Искомое изображение S2 находится на расстоянии bt от второй линзы. Это
расстояние можно определить из формулы
Подставляя сюда выражение для а1( получаем
Здесь возможны два случая а^> F п а < F
лучей в первом случае показан на рис. 333. Ход лучей во втором случае предлагается рассмотреть читателю.
546. Решение этой задачи аналогично решению предыдущей задачи. Необходимо только принять во внимание, что теперь вторая линза — рассеивающая с фокусным расстоянием Ft= — F, поэтому формулу для второй линзы следует записать в виде
b-F + а ~~ F '
В этом случае приходим к уравнению а2 - 2Fa -F2 = 0, откуда следует, что _
а=(1+К2)Л
Второй корень — отрицательный — здесь не имеет смысла.
547. В первом случае экран следует поместить в фокальной плоскости линзы Л], Во втором случае расстояние между линзами
Рис. 334.
Л} и Л2 подобрано так, что их задние фокусы совпадают. Изображение, даваемое линзой Л2, играет для линзы Л\ роль мнимого источника, расположенного в фокусе (рис. 334). Отсюда следует
1,11 Ft
Fi a Fi ' 2
362
Таким образом, экран следует приблизить к линзе Л{ на расстояние, равное Fj —а = р!/2.
548. Если бы не было лиизы Л2, то изображение источника располагалось бы в точке S] (рис. 335), причем расстояние b можно найти из формулы линзы:
Изображение Sj можно рассматривать, как мнимый источник для линзы Л2. Для того чтобы лучи после прохождения линзы Л2
Л,
Рис. 335.
казались исходящими из источника S, необходимо, чтобы мнимое изображение источника Si совпало с S. Учитывая правило знаков, запишем:
Подставляя в последнюю формулу значение Ь, получим
549. Изображение, даваемое положительной линзой, играет роль источника для отрицательной линзы. Положение этого изображения определим по формуле лннзы:
Ьх= а|ГЕ-^зО см. ai-Fi
Запишем теперь формулу для отрицательной линзы:
-------V 885
#2 o’2 *2
здесь F2—— 16 см — фокусное расстояние отрицательной линзы. В этой формуле знаки расставлены так, что действительному предмету или изображению соответствуют положительные а2 и Ь2, мнимому — отрицательные. Анализ формулы отрицательной линзм
363
показывает, что величина Ь2 > 0 (действительное изображение) будет при F2 < а2 < 0. Таким образом, расстояние между линзами может изменяться в пределах от bt - | F21 = 14 см до Ьх = 30 см. Ход лучен показан иа рис. 336.
трудно увидеть, что
Рис. 337.
550. Если последовательно строить изображения в системе из двух линз, считая первое изображение, даваемое линзой Лi (рис. 337), источником (действительным или мнимым) для линзы Л2, то не-I система может давать прямое изображение предмета в двух случаях. Во-первых, когда каждое последовательное преобразование оставляет изображение прямым, во-вторых, когда после каждого преобразования изображение получается обратным. Расположение линз исключает второй случай. Таким образом, необходимо, чтобы мнимое прямое изображение, даваемое линзой Л;, находилось на участке O|Fi слева от линзы Л]. Это изображение будет играть роль действительного источника для
линзы Л2, расположенного на расстоянии а2 < F2, следовательно, его изображение (которое и будет окончательным) будет прямым и мнимым.
Применим для Л1 формулу линзы
_L + _L = _L ai + 6, F]
Расстояния 01 и bi отсчитываются от линзы Ль причем bt может изменяться от нуля до — /л (61 < 0, изображение мнимое).
Учитывая интервал изменения bt, получаем интервал возможных положений предмета:
о<01<4.
551. Результирующее изображение предмета будет мнимым, если промежуточное мнимое изображение, даваемое линзой будет находиться на участке OtF2 слева от ЛИЯЗЙ 338).
364
Это промежуточное изображение играет для линзы Л2 роль действительного источника, находящегося ближе ее фокуса. Применим для JIt формулу линзы
— + 01
F ’
Расстояния О] и &i отсчитываются от линзы Ль причем bi может изменяться от нуля до — F/2 (&[<0, изображение мнимое).
Учитывая интервал изменения blt получаем интервал возможных положений предмета:
„ . F
о< Д1С-5-.
о
Рис. 338.
552. Увеличение, даваемое первой линзой Ль будет (рис. 339)
ki =
61
а, ‘
(1)
Соответственно увеличение, даваемое Л2,
Результирующее
Расстояния &i, 62
Если учесть, что
(2)
k2 = -± а2
увеличение k=ktk2 по условию равно единице:
0^2
по формуле лиизы г. a2F2 62 =------ГТ".
02 — F2
решая совместно уравнения (3),
(3)
и а2 определим
г. a\F\ и I — --Ё—t
at-Fi
a2 — L — bi, то,
Л,
(4)
Рис. 339.
(4) получим
п
1 L-(Fi + F2)’
(5)
Равенство (5) имеет смысл при L > Ft + F2. Легко видеть, что это решение единственно возможное.
365
линз Л\Л3 (рис. 340), должно
Применяя к Л3 формулу линзы
а = 2Е a = F
b>F, b^2F.
1
получить, что
553. Изображение, даваемое отрицательной линзой Л2, будет действительным только в том случае, когда на линзу падает сходящийся пучок лучей, продолжение которых пересекает главную оптическую ось на расстоянии от линзы Л2, не превышающем фокусного расстояния лиизы Р2 (мнимый источник). Таким образом, при любых положениях предмета изображение, даваемое системой
”. ”. ' > находиться в интервале [О2Е2]. От-
сюда следует, что линза Л3 обязательно должна быть положительной.
Далее, при перемещении предмета из бесконечности к линзе Л; мнимое изображение, даваемое этой линзой, перемещается от точки Fi к Oi, Таким образом, линза Л3 должна удовлетворять следующим условиям:
при
при
---= легко а Ь F3
первое условие выполняется при F3 2F[3, а второе —при F3 ^.2F/3. Таким образом, оба условия оказываются непротиворечивыми при F3 — 2F/3. Следует подчеркнуть, что однозначный результат для F3 получается вследствие симметрии хода лучей в двух крайних случаях (рис. 340).
554. Пусть малый источник света находится в фокусе первой линзы Л{ (рис. 341). Световые лучи после преломления в первой линзе будут параллельны оптической оси, а после преломления во второй линзе соберутся в ,ее фокусе. Если расстояние между линзами значительно из линз, то систему из двух линз можно рассматривать как тонкую линзу. Применяя теперь формулу тонкой линзы к системе из двух линз, получим
—I—или Д|4-Д2 = Д, г I г2 г
где F — фокусное расстояние системы из двух линз, а D — ее оптическая сила.
555. Принимая во внимание, что оптические силы тонких линз, приложенных вплотную задачи 554), получим
JL + J_=±
Ft + F2 F’
меньше фокусного расстояния каждой
друг к другу, складываются (см. решение
jL+J_ = _L JL + J_ + JL = 0 + f3 f' F.‘ f2 + f3 •
366
Последнее соотношение вытекает из того, что при сложении всех трех линз получается система с нулевой оптической силой — плоскопараллельная пластинка. Решая этн уравнения, найдем
f3=_f>0, £|=_f>o, Fs = -Jf_<o.
г + l
556. Тонкие часовые стекла имеют одинаковую кривизну передней и задней поверхности. Поэтому они не влияют на условия преломления в «водяной» линзе и можно рассматривать преломление света на границе воздух —вода (см. задачу 515). Если теперь рассмотреть систему, изображенную на рис. 342, то ее оптическая сила равна нулю и можно написать:
-у- + -у + у = 0, откуда / = - 2F = - 40 см.
557. Фокусное расстояние системы нз двух приложенных друг к другу одинаковых тонких линз в воздухе равно F/2 (см. решение
Рис. 342,
задачи 554). Пусть теперь система помещена в воду и на нее падает параллельный пучок лучей, распространяющийся вдоль оптической оси. Рассмотрим один из лучей этого пучка (рис. 343).
Условия преломления луча на всех границах, кроме последней, не зависят от того, помещена система в воду или нет. Обозначим угол падения луча на вторую плоскую границу через I, а углы преломления для случаев, когда система находится в воздухе н в воде, через и г2 соответственно. Тогда на основании закона преломления получим
sin I____1 sin i п
sin гi sin Г2 /1ст
здесь «—коэффициент преломления воды, «ст — коэффициент преломления стекла; коэффициент преломления воздуха принят равным единице. Таким образом,
sin ri
—:----= Л.
sm гц
367
Принимая теперь во внимание малость углов rt н г2, заменим отношение синусов этих углов отношением нх тангенсов:
откуда следует
Рис. 344.
tgri F’
tgr2 F/2’
„ nF
• «-g-.
558. Проведем мысленно плоскость АВ так, чтобы образовалась тонкая плоско-выпуклая линза АВС (рис. 344). Вторую среду можно
рассматривать теперь как плоско-выпуклую линзу, приложенную вплотную к плоской поверхности толстой стеклянной пластинки.
Лучи, параллельные оптической осн, пересекутся в некоторой точке О. Заметим, что если бы справа от линзы был воздух (а не стекло), то эти лучи сходились бы в фокусе линзы (в точке О', ЕО' = F). Таким образом, лучи DO и DO'отличаются только тем, что первый не испытывает преломления на границе АВ, в то
время как второй испытывает такое преломление, переходя из стекла в воздух. Закон преломления дает
sin < _ 1 sin г п "
Принимая во внимание малость углов I и г, получим
2. п
sin i ~ tg I ЕО' F sin г ~ tgr = ЕО = f ’
или f ~ nF.
559. Решение данной задачи аналогично решению задачи 558
f ~ nF < 0 (так как F < 0).
560. Рассмотрим луч света, падающий на воздушную линзу (рис. 345) параллельно оптической оси со стороны плоской поверхности. Этот луч, пройдя без отклонения плоскую границу DE, упадет на выпуклую поверхность стекла АВС. Задача сводится теперь к определению положения точки пересечения луча с оптической осью после преломления
на выпуклой границе воздух —
стекло. Для решения достаточно Рис. 345.
знать фокусное расстояние сте-
клянной плоско-выпуклой линзы АВС, плоская поверхность которой изображена на рис. 345 пунктиром (см. задачу 558). Это фокусное
расстояние легко определить, замечая, что две стеклянные линзы — плоско-выпуклая АВС и плоско-вогнутая ABCDE — прн сложении
368
образуют плоскопараллельную пластинку н что, следовательно, их оптические силы отличаются только знаком:
1 _ 1
F' “ F"
Принимая теперь во внимание решение задачи 558 получим j ~ nF' = — nF > 0 (так как F < 0).
561. Решение этой задачи аналогично решению задачи 560: f « - nF < 0.
Сферические зеркала
5S2. Подшипниковый шарнк диаметром а можно рассматривать как выпуклое зеркало с фокусным расстоянием равным а/4. Про-
ведем лучи от противоположных краев солнечного диска через центр зеркала (лучи АО и ВО на рис. 346). Изображение краев будет находиться в точках пересечения продолжения этих лучей с фокальной плоскостью ff' (точки и В,). Из рис. 346
Рис. 346.
Имеем
Д d_ F’
где Д —диаметр Солнца, В — расстояние от Земли до Солнца, d — диаметр изображения, равный XjBp Подставляя числовые значения, получим d ~ 10~2 ММ.
563. Рассмотрим случай, когда лучи АО и ВО, проведенные от краев солнечного диска, лежат в плоскости, перпендикулярной к осн цилиндра (рис. 347, а). В этом случае поперечный размер прямого мнимого изображения Солнца AiBt = d определяется отражением солнечных лучей от выпуклого зеркала (см. задачу 562)
. Дг .„-2
d = « 10 мм;
К
здесь использованы те же обозначения, что и в задаче 562.
Если это изображение рассматривать глазом, то угловой размер этого изображения <р зависит от положения глаза:
где / — расстояние от глаза до изображения AtBt. Когда это изображение рассматривается нормальным глазом с расстояния иаи-лучшего зрения, имеем
Ф = Г -8".
*0
24 Л. П. Бакалина и др.
369
Рассмотрим теперь случай, когда лучи СО и DO, проведенные от краев солнечного диска, лежат в плоскости, проходящей через ось цилиндра. Здесь ход лучей совпадает с отражением в плоском
зеркале (рис. 347, б). Мнимое прямое изображение Солнца нахо-~ v 1 размер, который равен угло-
вому размеру Солнца, не зависит от положения глаза наблюдателя:
q>--£-«0,5»,
564. Рассмотрим рис. 348. Изображение точки А, лежащей на оптической оси, будет в точке причем
a — F'
дится в бесконечности и его угловой
Рис. 348.
(О
Изображение Bi источника В, смещенного относительно оптической оси, будет находиться иа расстоянии bt от линзы:
1 — г
(2)
Далее замечаем, что tgq> =
х . . и a —at bi— b
где х и у соответственно расстояния источника В и изображения Bj от оптической осн. Далее замечаем, что
У bi _ х ai ’
Используя уравнения (3) и (4), имеем tgip bi(a-ai) tg<₽ ailb-bi)
(3)
(4)
(5)
870
Подставляя в (5) значения b и bt из формул (1) и (2), после несложных преобразований получаем
tgip a — F _ 1
tg<₽ F ~3‘ W
Поскольку tg <p = 1^3 , to tg ф = 1/V3 , следовательно, ф = 30°. Вычислим теперь расстояние Ь нз формулы (1):
& = 4F.
Итак, если расположить экран под углом 30° к оптической оси так, чтобы он пересекал ее в точке b — 4F, то изображение обоих источников будут резкими.
565. После отражения от зеркала лучи от каждой точки источника будут распространяться параллельным пучком, наклоненным к оптической оси. Рассмотрим одну нз крайних точек ис- ]_
точника (например, нижнюю |
точку S на рис. 349). Угол ।
наклона а отраженных лучей легко найти, рассмотрев луч, |
проходящий через точку О. Из I
рис. 349 следует, что --------------------
1£а==7Г- ----------- 7. -----—*
Рис. 349.
Теперь найдем радиус £)/2 освещенного пятна на стене, отстоящей от зеркала на расстояние L:
~ = L tg v + R.,
где R — радиус зеркала. Таким образом, 2£г
D = 2L tg а+ 27?-=-^4-2/? = 3,5 м. Г
566. Построения показаны на рис. 350. Применяя формулу зеркала, получим
, aF о =-----=- = 60 см.
a — F
Из рис. 350 следует, что
Н_= h_ b а ’
где Я —размер изображения. Таким образом,
И = — h ~ 25 см. а
24*
371
567. Используя обозначения, принятые на рис. 350, найдем
a b F
II Ъ „ , .
“ — = 3, 6- а«I.
h а
двух последних соотношений получим
Учитывая данные задачи, из а — 10 см, 6 = 30 см и, следовательно, аЬ 7 Г F = —-г- = 7,5 см. а + b
568. Изображения располагаются на расстояниях —-— F от каждого из зеркал; п — любое целое положительное число.
569. Найдем положение изображения, которое образуется при отражении лучей сначала от первого, затем от второго зеркала
(при этом учтем, что изображение, получаемое в первом зеркале, играет роль источника для второго зеркала):
1,11 aF
или о =-----=г:
а Ь F a—F
здесь Ь — расстояние от изображения до первого зеркала. При b > 0 изображение в первом зеркале действительное, при b < 0 — мнимое. Расстояние от изображения до второго зеркала равно, очевидно, 2F — b (рис. 351). Следовательно,
-J—+ 1 = ±;
2F — b с F
здесь с — расстояние от второго изображения S2 до второго зеркала. После несложных преобразований получим
F(2F—b) С!в f , 63 О»
г —Ь
Таким образом, изображение, получающееся после отражения лучей от обоих зеркал, совпадает с самим источником.
570. Чтобы после отражения от вогнутого, д. затем от .плоского зеркала световые лучи вернулись в точку S, плоское зеркало
872
нёобходимо расположить от вогнутого на расстоянии
а + b 2
d =
(ход лучен показан на рис. 352).
Применяя формулу сферического зеркала и учитывая, что фокусное расстояние зеркала равно /?/2, получим
aF aR
Ь~ a — F ~ 2a-R “
a + b a2 d=~2-=2^ = 45 CM-
571. Точка схождения лучей 5 играет роль мнимого источника, расположенного на расстоянии at = — а (рис, 353). Применяя фор-
мулу зеркала, получим
Следовательно,
aR
2а+ R
= 10 см.
В данном случае & > 0; это озна-
чает, что точка пересечения лучей дей-
ствительная.
572. Точка схождения лучей S играет |1с'
роль мнимого источника, расположен-
ного на расстоянии at = — а (рис. 354). Для нахождения расстояния Ь от зеркала до изображения Sj запишем формулу зеркала;
Отсюда
2 }'
aF aR
b~ a+F ~ R-2<i
. . aF а + F
F
При a= 15 см и R — 60 см получим b = 30 см. В данном случае Ь > 0, изображение действительное.
При а = 40 см и R — 60 см получим b — — 120 см. Здесь b < О, изображение мнимое.
373
573. Световые лучи, проходящие через плоскопараллельную пластинку, испытывают смещение. Точку 5[ (рис. 355), в которой пересекаются продолжения лучей, прошедших пластинку, можно рассматривать как мнимое изображение источника S, даваемое плоскопараллельной пластинкой. Это изображение играет роль источника по отношению к вогнутому зеркалу. Если точка 5[ ока-
жется расположенной в геометрическом центре зеркала (т. е. на расстоянии 2F), отраженные лучи пойдут точно навстречу падающим и, следовательно, после вторичного прохождения через пластинку соберутся в точке S. Таким образом,
о
I = а — 2F = а — = 2 см.
С другой стороны, если углы падения и преломления лучей в пластинке достаточно малы, так что отношение тангенсов этих углсв
можно с хорошей точностью заменить отношением их синусов, расстояние I между S и 5] определяется соотношением (см. задачу 537)
Таким образом,
L(n — 1) п
I о
L =-----— = 6 СМ.
п- 1
574. Зеркало можно располагать либо на расстоянии /? за изображением источника, либо в месте изображения. В первом случае отраженные лучи идут в об-
ратном направлении по тому же пути, во втором случае лучи при отражении меняются местами, но выходят нз той же точки (рис. 356). При перемещении зеркала вправо от S[ изображение начинает перемещаться вправо от 5 и уходит в + оо; затем изображение появляется при х= — оо и стремится к S (при смещении зеркала на R).
575. Изображение S, обрдзуется при отражении лучей от той части зеркала, которая не перекрыта линзой. Изображение S2 образуется при отражении лучей от зеркала и двукратном прохождении через линзу (рис, 357). Обозначим через F фокусное расстояние
874
зеркала, а через Ft фокусное расстояние системы из сложенных вплотную линзы и зеркала. Тогда
1 + JL=± ±+_L = _L
a bi F ' a b2 Ft ’
Вычитая почленно первое уравнение из второго, получим
j_____1_ = J____L
bi Fi F '
Легко показать, что
-L = ±+2,
Fi F l
Рис. 357.
^7 —
где f — фокусное расстояние линзы. Для доказательства этого соотношения допустим, что точечный источник света помещен на рас-' стоянии f (в фокусе линзы) от системы линза — зеркало. Световые лучи, пройдя через линзу, будут падать па зеркало параллельно оптической оси. После отражения от зеркала эти лучи сошлись бы, если не учитывать вторичного прохождения через линзу, в фокусе зеркала, т. е. на расстоянии F от системы. Фактически же после вторичного прохождения через линзу лучи сойдутся на некотором расстоянии d от системы, которое легко определить по формуле линзы; при этом фокус зеркала следует рассматривать по отношению к линзе как мнимый источник;
_± + ± = ±. F d f
Это соотношение можно переписать в виде
_L + l=±+2 f + d F + f
и рассматривать как формулу для системы линза — зеркало. Как видно из последней формулы, оптическая сила системы l/Fi— i/F+2ff, что и требовалось доказать. Таким образом,
_1____1_ = _1__1_ = _2
bi Fi F f’ откуда . 2bib2 n-f=-r—~— = 25 щи. bi-b2
576. Так как положительная линза приложена вплотную к вогнутому зеркалу, то для оптической силы D полученной системы имеем (см. задачу 575) .
375
где R — радиус кривизны зеркала, F — фокусное расстояние линзы-С другой стороны, можно напирать такое уравнение:
1+1 = D,
а b
где а — расстояние от предмета до системы, b — расстояние от системы до изображения. Учитывая, что по условию задачи а = Ь, из приведенных уравнений получаем
= 25 см.
R — a
577. Эта задача аналогична предыдущей. Необходимо только учесть, что теперь зеркало выпуклое. Поэтому в тех же обозначениях имеем
и £> = - + 4-а b
F R
Учитывая, что по условию а = Ь, получаем
R =------р- = 30 см.
а — г
578. На границе стекло — воздух часть лучей отражается, поэтому наблюдатель видит два изображения. Первое изображение образовано отраженными лучами от передней (считая от глаза), выпуклой поверхности линзы. Это изображение, мнимое и прямое, расположено в фокальной плоскости выпуклого зеркала, т. е. на расстоянии Fi = R/2 = 14 см за линзой. Второе изображение образовано лучами, отраженными от задней, вогнутой поверхности линзы. Изображение удаленного окна находится в фокальной плоскости системы линза — вогнутое зеркало. Необходимо учесть, что лучн дважды проходят через линзу. Следовательно, можно записать (см. задачу 575)
4-2-f F + R'
Итак, второе действительное перевернутое изображение находится перед линзой на расстоянии
t RF
1 2 (F + R) 7 СМ-
579. В первом случае изображения образованы лучами, отраженными от передней (считая от глаза) плоской поверхности линзы (мнимое прямое) н от задней, вогнутой поверхности (действительное перевернутое). Это второе изображение находится перед линзой на расстоянии
t го
2(R + F) ~ °'2 СМ
376
(см. задачу 578). Когда линза обращена выпуклой стороной к наблюдателю, изображения образованы лучами, отраженными от передней выпуклой поверхности линзы (мнимое прямое) и от задней, плоской поверхности (действительное перевернутое). Это изображение находится в фокальной плоскости системы линза — плоское зеркало /2. Для этого случая можно записать
1 2
h F’
откуда f2 = —= 15сл.
Смещение перевернутого изображения, таким образом, равно f2 — fi 9,8 см. Изображение перемещается ближе к глазу.
Элементы фотометрии
580. Вся световая мощность точечного источника 1Г0 излучается в телесный угол 4л стерад, следовательно, в глаз, находящийся на расстоянии R от источника
(рис. 358), попадает мощность
Рис. 358.
Подсчитаем, какое число квантов энергии (фотонов) ежесекундно попадает в глаз, находящийся па этом расстоянии. Энергия одного фотона Е — 1п, где /г — постоянная Планка, v — частота электромагнитного излучения. Поскольку v = с/%, где с — скорость света, Л —длина волны излучения, имеем
Итак, ежесекундно в глаз попадает N=W/E фотонов:
IFo d2%
16 R2hc '
По условию, глаз реагирует на свет, если N — No — fjO l/сек. Такое число фотонов попадает в глаз на расстоянии
« 108 сл(=103 км.
4 К Nahc
581. Рассмотрим рнс. 359, где схематически изображены последовательные многократные отражения и преломления света в плоскопараллельной пластинке, причем угол падения i по условию задачи близок к нулю. Пусть энергия падающего света равна £а. Полная энергия отраженного света равна £1 + £2 + Е3+ ... Коэффициентом отражения называется отношение отраженной Энергии к падающей, т. е. отношение
Е1 + Е2 + Е% +
377
Поскольку при каждом отражении луча на границе раздела стекло — воздух отражается г-я часть энергии падающего луча, следовательно, проходить через границу по закону сохранения энергии будет (1 — г)-я часть. Поэтому энергия Et первого отраженного луча, испытавшего однократное отражение, будет равна гЕ0. Второй отраженный луч дважды проходит через границу раздела и один раз отражается (на нижней границе). Его энергия Е2 будет равна г(1—г)аЕ0. Третий луч снова дважды проходит через границу и три раза отражается, следовательно, Е3 = г3 (1 — г)2 Еа и т. д. Таким образом,
R = r + r(l-r)2 + r3(l-г)2 +
+ г5(1 -г)2+ ... =
Нетрудно заметить, что выражение, стоящее в квадратных скобках, представляет собой бесконечно убывающую геометрическую прогрессию (г2<1). Сумма ее членов равна 1/(1—г2). Поэтому окончательно получим для R следующее выражение:
R = -t——7.
582. Назовем коэффициентом пропускания D отношение световой энергии, прошедшей сквозь пластинку, к энергии, падающей на пластинку (см. рис. 359)
Вместо последовательного вычисления Е{, Е'2 и т. д. можно воспользоваться законом сохранения энергии. Если пренебречь поглощением света в пластинке, то DEa= Eq— REo, где R — коэффициент отражения, следовательно,
1 -R.
Но (см. задачу 581)
О»* 1 — г
R = > откуда D = ——-.
1+г 1 + г
583. В отсутствие зеркала освещенность £] в центре экрана равна
здесь / — сила света источника, т. е. поток световой энергии, отнесенный к единице телесного угла. При наличии зеркала освещенность Е определится соотношением
£=2_ + _Л_.
л сЕ (3rf)2 ’
378
здесь I — по-прежнему сила света источника, /t — сила света изображения St источника в плоском зеркале. Легко показать, что для идеально отражающего зеркала Ц — I. Действительно, световой поток в некотором телесном угле £2 (рис. 360) после отражения
от зеркала будет распространяться в том же телесном угле £2; при этом поток не изменяется н по величине (идеальное отражение). Это как раз и означает, что /;=/. Таким образом,
£ = jL + _L_ = JO
rf2 (3d)2 9
584. Обозначим расстояние SA через г и расстояние через Г\ (рис. 361). Принимая во внимание, что сила света изображения Si источника в идеальном плоском зеркале равна силе света I самого источника (см. решение задачи 583), найдем
„ / cos а
Е~Л~
„ / cos а I cos ai
где Е и Ei —освещенности экрана в точке А в отсутствие и при наличии зеркала соответственно. Поделив почленно второе урав-
Рис. 361.
нение на первое, получим
9 . . Ч
r^cos а, ( г \
-—L=1+ — ту cos а \Г1 /
При написании последнего выражения принято во внимание, что г cos а = ri cos аь Найдем теперь г и по теореме Пифагора:
Г V d + \ 2 ) = 2 d’
-1 /лз Л3/J V УТз й
Таким образом,
Ei _ , , (_5_\з/2
Е +113)
1,24.
585. Обозначим углы, образованные лучами S^ н S2O с перпендикуляром к площадке, через а; и а2 соответственно (рис. 362). Легко показать, что
а, = 45° — а = 30°, а2 = 45° + а = 60°.
Применяя теперь формулу для освещенности, создаваемой точечным источником, будем иметь
р _ dicoscti Кз/; р /2 cos а2 _ /2
Ь1 - г2 ~ 2г2 ' 2 ~ г2 2г2 ’
Е
379
Здесь Е, и Ё2 — освещенности обеих сторон площадки, Ц и 73 — силы света источников Sj и S2; г —расстояние от площадки до источников,
Рис. 363.
равное rf 7Z2. Принимая во внимание, что £t = £2 = 20 лк, получим
4d2
Ц = —7^ £1 = 46 св, 12 = 4 d2£2 = 80 св.
уТ
586. Восставим перпендикуляры к освещаемым поверхностям пластинок и обозначим углы между этими перпендикулярами и лучами от и S2 через и а2 (рис, 363). Легко показать, что
а> = 45° + а, а2 = 45° — а.
Применяя формулу для освещенности, создаваемой точечным источником, получим
с 71 coso! „ /2 cos а2
= г2 ’ С2 ~ г2 ;
здесь 71 и 12 — силы света источников Si и S2, г —расстояние от пластинок до источников. В нашем случае £'i = £2 и, следовательно, /1 _ cos ct2 _ cos (45° — а) _ 72 cos a; cos (45° + a) ~~
1 + tg a
1 - tg a '
587. Поверхность воды можно рассматривать как идеальное зеркало при полном внутреннем отражении (рис. 364), т. е. при условии
. _ 1
Sin I .
п
Принимая во внимание, что sin i = у ' --——, перепишем усло-
вие полного отражения в виде Х
4d2
п2-1 *
х2>
380
Отсюда следует, что
*mln = г—^ ~~
F п2 — 1
Найдем теперь освещенность площадки, находящейся на расстоянии xmin от источника:
„ / I cos а
£=-2—+------— .
*min Г
Здесь первое слагаемое дает освещенность, создаваемую прямыми лучами от источника, второе — освещенность, создаваемую лучами от его изображения г —расстояние между изображением источника и площадкой, а —угол между перпендикуляром к площадке и лучом от изображения.
В соответствии с решением задачи 583 сила света изображения принята равной силе света 1 источника. Учитывая, что xmin = г cos а,
получим
4» и '
При написании последнего соотношения было принято во внимание, , . . 1
что (при х = Xmln) cos а = sin t = —.
588. £ = 22£2^L = 2_^=;
l2 + cP /(P + cP)3
здесь £ —освещенность, / — сила света лампы; обозначения I, d и а см. на рнс. 365;
2d
589. Решим сначала задачу, пренебрегая отражением лучей от
Рис. 365.
поверхности воды. Из рис. 366 ясно, что на площадку падает световой поток
Ф = Л2, (1)
где £2 —телесный угол, образованный лучами, попадающими иа края площадки после преломления на границе вода —воздух. Заметим,
381
далее, что
й=^, н2 * (2)
Из подобия треугольников AtBC и AjBfii имеем b h а Н + Л ’ (3)
где Л = Л1В1. С другой стороны, из треугольников ЛВ1С1 и
находим
h tg г = Н tg i, (4)
НО
tg i sin i 1
tgr ~ sinr n’ (5)
откуда
h = —♦ n (6)
Теперь легко найти величину 6: , _ h а ° H+ha п+1‘ (7)
Объединив выражения (1), (2) н (7), получаем окончательно
ф= /---_---
Н2(п + I)2'
Учтем теперь отражение от поверхности воды. На основании закона сохранения энергии имеем
D = 1 - R,
где D — доля световой энергии, проходящая через границы раздела (см. задачу 582), таким образом,
ТГ
'•’•-“’-(‘-«'W+iF-
590. Когда стеклянная пластинка находилась в параллельном пучке света, падающем на линзу, опа не оказывала влияния иа ход лучей и лучи фокусировались в точке S (рис. 367). Фотоэлемент в этом случае располагался таким образом, что его круглый катод диаметром d в точности перекрывал световой поток. Если теперь стеклянная пластинка помещена между линзой и фотоэлементом, то вследствие преломления в пластинке лучи сфокусируются в точке Следовательно, катод фотоэлемента уже не перекрывает весь световой пучок, диаметр которого в плоскости расположения катода равен теперь Если обозначить через А вертикальное смещение луча после введения пластинки, то
dj = d + 2A.
(1)
382
При первом расположении весь световой поток Фо падал на площадку диаметром d, при втором —этот же поток в плоскости катода проходит через площадку диаметром db следовательно, освещенность катода фотоэлемента во втором случае г- с г- d2 d2 (d + 2A)2’
(2)
где Ео — освещенность в первом случае.
Ток, протекающий через фотоэлемент, пропорционален освещенности его катода, следовательно, во втором случае гальванометр покажет ток
Нетрудно увидеть, что
(4)
Учитывая малую величину угла падения, а также замечая, что i = а, имеем
Д « Н tg а ^1 — (5)
Но
tga = '^r’ (6)
откуда получаем
591. Возможны два случая, когда расстояние от источника S до линзы больше и меньше фокусного растояния линзы. Решение для первого случая поясняется рис. 368, а. Для того чтобы освещенность экрана была в четыре раза меньше освещенности того же экрана, расположенного вплотную к линзе, необходимо, чтобы площадь светового пятна на экране была в четыре раза больше площади линзы, т. е.
D2 ( с-Ь\2 .
~d^[~b) ~4’
откуда с = 36.
Теперь, принимая во внимание, что
, aF
b =----F ,
а — F ’
получим с (а — F) = ZaF, откуда
са
Ъа + с
— 12 см.
383
Во втором случае линза дает мнимое изображение Si источника S (рис. 368, б), и после линзы идет расходящийся пучок лучей. Рассмотрение этого второго случая, которое представляется читателю, дает F = 60 см.
Я
Рис. 368.
592. Освещенность экрана в отсутствие линзы
Е -- 1
1 (Г + Д)2’
где 7 —сила света источника.
При наличии линзы освещенность Ez в цейтре светового пятна такая же, как н освещенность в плоскости линзы, поскольку за линзой лучи идут параллельным пучком;
УТ-
Таким образом,
Е2 (F + L)2
Et F2
593. Освещенность светового пятна на экране одинакова, если в обоих положениях экран удален на одинаковые расстояния от изображения S; (рис. 369). В этом случае один и тот же световой
384
поток распределяется по одинаковым площадям и, следовательно, Ех*= Е2. Таким образом,
, Л Т- /2 от С Г" if
b = —5— = 37,5 см и F = —— = 15 см.
* о т о
594. Освещенность экрана в обоих положениях обратно пропорциональна квадрату расстояния до мнимого изображения, даваемого линзой:
. (1Н + -'г)2 .
Е2 (|И + Мг
Здесь через |6| обозначено расстояние от линзы до изображения. Решая это уравнение относительно | b |, найдем
| 6 / = /2 — 2/j = 20 см.
Применяя теперь формулу линзы, найдем фокусное расстояние:
F = Г|Н - = - GO см.
|£>| —а
В последней формуле мы учли, что b = — | b | (изображение мнимое).
Рис. 369.
Рис. 370.
595. На рис. 370 показан ход лучей, прошедших через линзу и отразившихся от зеркала при первом положении зеркала. Освещенность экрана создается источником S и изображением Sb причем силы света источника и изображения в данном случае одинаковы (если пренебречь потерями энергии при прохождении света через линзу и при отражении от зеркала). Это следует из того, что телесные углы Q и Й1 равны между собой и в этих телесных углах распространяются одинаковые световые потоки. Таким образом, прн нервом положении зеркала освещенность равна
£, = 5+4
4 4
здесь Е — освещенность в центре экрана, создаваемая прямыми лучами от источника. При втором положении зеркала изображение Sj совпадает с источником S и, следовательно,
Е2 = 2Е.
25 71. П. Баканина в др.
385
Отсюда следует, что
Ег 2Е 8
£> “ 5 “ 5
~4Ь
1,6.
596. Когда линза отсутствовала, освещенность в центре экрана Et создавалась самим источником и его изображением в плоском
зеркале: I I 50
1 “ а3 + (7а)3 “ 49 а3
здесь I — сила света источника, а — расстояние от источника до экрана. Сила света источника и изображения равны друг другу (см. задачу 583). Во втором случае изображение источника совпадает с центром лннзы (см. задачу 595). Освещенность экрана в этом случае равна
р 1 7 222_
2 " а3 + (За)2 “ 9 а2 '
Таким образом, освещенность увеличилась на
100% -9%.
С1
597. Изображение источника на экране в натуральную величину может быть получено при трех различных расположениях линз, обеспечивающих симметричный ход лучен.
а;
Первый случай. Первая линза расположена иа расстоянии F от источника, а вторая —на расстоянии F от экрана (рис. 371, а).
Второй случай. Первая линза расположена так, что она дает изображение источника на расстоянии Z./2. Расстояние между первой линзой и источником равно а. Вторая линза расположена на расстоянии а от экрана (рис. 371, б). Применяя формулу линзы
385
и учитывая, что в данном случае а + 6 = L/2, найдем
L - Vl3-8LF t L + Vl2-8LF
Третий случай. Этот случай аналогичен второму; только на этот раз первая линза расположена на расстоянии 6 от источника, а вторая —иа расстоянии b от экрана.
Отношение освещенностей изображений во всех трех случаях будет зависеть от телесных углов, под которыми видна первая линза из нсточннка S:
Ei: Е2: Е$ ~ : Q2: Q3 = -^7: -^7: -^7 •
598. В отсутствие зеркала освещенность экрана равна
где / — сила света источника.
При наличии зеркала освещенность экрана создается не только прямыми лучами от источника, но и лучами, отраженными от зеркала. Поскольку от зеркала отражается параллельный пучок лучей, эта дополнительная освещенность такая же, как и освещенность самого зеркала. Таким образом,
г F,
Е^Е+~пгу и е “1 + 7^v=I01'
) \2J
599. Определим по формуле зеркала положение изображения Sp
R ( R\
. aF 2 \ 2 ) R
rJJTrS—
2 \ 2 }
(обозначения см. на рис. 372). Освещенность Е площадки, находя-
щейся на расстоянии R от зеркала, найдется по следующей формуле:
/ , /.
£ “ (R — a)2 + (Я + |И)2 “
41 + 16/' . "° R2 + 25/?2 1
здесь / и Ц — силы света источника S и изображения Si соответственно. Освещенность Ео пло-
щадки, находящейся на расстоянии 2R от зеркала, запишется в виде
Е 1 Л 4/ . 16Л
0 “ (2R — a)2 + (2R + | b I)2 = ВД2 + 81/?2 ’
25*
387
Найдем теперь связь между I и Заметим, что поток световой энергии от источника S в некотором телесном угле Q после отражения от зеркала распространяется в телесном угле Qi (см. рис. 372). При идеальном отражении имеем
70 = 7,0,.
С другой стороны, при достаточно малых й и Й, можно записать и, следовательно,
Выражения для Е и £0 теперь можно записать в виде
р = АСЛ = р
ЯЧ +25/ /?2 25 ’ 0 °+ 81 / /?2 8Г
Отсюда следует
е-1М£,.8.4£„
600. Задача аналогична задаче 599:
41
Е = ~ Ei ~ 60° лк.
601. Очевидно, что кусок дерева легче поджечь при помощи той оптической системы, которая создает на поверхности дерева большую освещенность, т. е. концентрирует большую мощность излучения на единицу поверхности. Подсчитаем освещенность, создаваемую линзой Ei и вогнутым зеркалом Е2:
Ф, — Ф2
£,= S? E2°~s^-
Здесь Ф, и Ф2 — световые потоки, падающие на изображения Солнца, S, и S2 — площади этих изображений.
Если не учитывать потерь в линзе и зеркале, то световые потоки Ф1 и Ф2 пропорциональны площадям линзы и зеркала:
Ф, Ф2 “ D2 •
Диаметры изображений равны
R
li = aFi, l2 = aF2 = a-~,
где а —угловой размер Солнца (см. задачу 528), Ft и F2 — фокусные расстояния линзы н зеркала. Поскольку S, прямо пропорцио
388
нально /2 и Sy прямо пропорционально /|, имеем
Е2 Ф2 S] D2 4Ef
Таким образом, кусок дерева легче поджечь при помощи линзы.
602. Освещенность изображения Солнца Et определяется величиной светового потока Фь падающего на изображение площади S:
Диаметр изображения определяется формулой
d = aF,
где а — угловой размер Солнца, Г —фокусное расстояние линзы (см. задачу 528), следовательно, его площадь
о nd2 ла2/22
d “~4~ “ 4 *
Таким образом,
Р = 4Ф-
1 ла2/22
Нетрудно видеть, что освещенность экрана прямыми лучами равна освещенности линзы:
„ 4Ф2
здесь D — диаметр линзы, Ф2 — поток, падающяй на поверхность линзы. Если пренебречь потерями в линзе, то Ф1 = Ф2. Учитывая, что, по условию, Е^ — Ег, имеем
£ = Т>2 = .
Ег d2F2 *’
откуда светосила линзы
-21 = а2 = 7,6- ю~5.
603. Если не учитывать потерь света в линзах, то можно за
писать:
£, _ Г)2 d2 ’
где Ei — освещенность изображения Солнца образованной системой линз, Ег — освещенность экрана прямыми лучами, D — диаметр линзы, d — диаметр изображения (см. задачу 602). Найдем теперь диаметр изображения. Первая лииза создает изображение Солнца в своей фокальной плоскости, причем диаметр этого изображения rfj равен
d , = aF.
389
Это изображение, расположенное иа расстоянии F/2 от второй линзы, служит для иее мнимым источником. Учитывая правило знаков в формуле линзы, запишем
2,11 t Р
+ откуда 6”Т;
здесь b — расстояние от второй лиизы до окончательного изображения. Далее нетрудно видеть, что
d 26 2
dj ” F ~ 3 •
Таким образом, диаметр изображения Солица, создаваемого системой лииз, равен
2 „
d-yoF.
Подставляя это значение в исходную формулу, получаем ответ:
Е, W2
Е2 “ 4с№ *
604. При установившейся температуре шарика энергия, получаемая в единицу времени за счет поглощения световых лучей, равна энергии, рассеиваемой за то же время вследствие теплообмена с окружающим воздухом. Когда шарик освещается прямыми солнечными лучами, уравнение теплового баланса запишется в виде
Ф, = kinr2 (d( — d0);
здесь Ф, —световой поток, падающий на поверхность шарика, — температура шарика, t0 — температура окружающей среды, k — коэффициент пропорцнональиости, г —радиус шарика. Если на шарик спроектировано изображение Солнца, имеем
Ф2 — 64№ (d2 — f0).
Обозначим световой поток, падающий на линзу, через Ф3. Очевидно, что
Ф1 _ -Si
Ф3 S3
где Si — площадь поперечного сечеиия шарика и S3 — площадь лиизы. С другой стороны,
Ф3
Ф2 5 J 9
где Sj — площадь изображения Солнца -------------------------------—
(см. задачу 602). Таким образом,
Ф1 S2 a2F2
Ф2 “ S3 ” D2 ’
390
Следовательно,
откуда
t2-ta D2
№’
D2
^2 “ ^0 "Ь q2pi (?! A))*
605. Рассмотрим сначала случай, когда зеркала идеально отражают падающий на них свет. Построим ряд последовательных изображений небольшого источника А площади а (или участка поверхности протяженного источника), равномерно излучающего во все
Рис. 373.
стороны (рис. 373). Если рассматривать эти изображения как источники света, то нетрудно заметить, что силы света I всех этих источников одинаковы, поскольку онн испускают одинаковые световые потоки в одинаковых телесных углах Q. Освещенность, создаваемую на сетчатке глаза некоторым источником, можно определить из формулы
где S —площадь изображения на сетчатке глаза, а
0 = 4- (2)
а1
В последней формуле So —площадь зрачка глаза, at — расстояние от глаза до некоторого (например, первого) изображения лица наблюдателя в зеркале.
С другой стороны, рассматривая хрусталик глаза как тонкую положительную линзу, можно записать так:
где b — неизменяемое расстояние от хрусталика до сетчатки глаза1 Объединяя формулы (1) —(3), получим
391
таким образом, освещенность на сетчатке глаза не зависит от расстояния до последовательных изображений лица наблюдателя в идеально отражающем зеркале.
Если теперь учесть, что прн отражении от зеркала величина светового потока уменьшается в k раз, то это эквивалентно уменьшению в k раз силы света изображения по сравнению с силой света источника I. Следовательно, первое изображение имеет силу света Ц — kI, второе /2 = ^3Л третье /3 — k5l и т. д. Отношение освещенностей на сетчатке глаза, создаваемое вторым и третьим изображениями лица наблюдателя, равно l/fe2= 1,56.
606. Решение поясняется рис. 374. На этом рисунке ф представляет собой угловой размер Солнца (угол, под которым виден
Рис. 374.
с Земли диаметр солнечного диска), а <р — угол, под которым видно отверстие из центральной точки белого экрана (точка А). Если <р < ф, то освещенность в точке А будет меньше освещенности прямыми солнечными лучами, так как световые лучи к точке А доходят не от всех участков солнечного диска. В нашем случае до точки А доходят лучи только от */з части солнечного диска и, следовательно,
В силу малости углов ф и <р можно тангенсы этих углов заменить самими углами, поэтому
t D
и Ф = у
d_ L
Последнее выражение вытекает из того, что линза с известным фокусным расстоянием F дает изображение Солнца в виде кружка диаметра D. Из этих соотношений легко найти
607. Обозначим освещенность экрана прямыми солнечными лучами через Ео. Нетрудно видеть, что на матовый шарик падает световой поток
А Г* п^2 Фо — Ео ,
392
По закону сохранения энергии тот же световой поток рассеивается шариком равномерно во все стороны. Следовательно, шарик излу. чает в единицу телесного угла све-
товой поток
4л 16
Выберем в области тени малую площадку о, видимую с поверхности шарика под телесным углом Q = olH'1 (рис. 375). Освещенность площадки равна
В светлой области освещенность площадки Е' складывается из освещенности, создаваемой прямыми лу-
чами Еа и рассеянным светом Е\.
Учитывая, что рассеянный свет падает на площадку под углом а, а расстояние от шарика до площадки Н H/cosa, имеем „ о cos a a cos’ а „ Er,d2 ,
Ci •= --х—=-------5— и> следовательно, Es = -.-тт/г cos3 а.
Я? Н2 л is//2
Освещенность в этой области
равна
р — г (f > rf2cos3 а
Ь h°V + 1б№
т. е. практически не зависит от наличия шарика.
608. Освещенность изображения равна
где Ф — световой поток, падающий на изображение площадью Sj. Имеем (рис. 376)
ф=./о = /^,
4а2
Если х — линейный размер источника, а у — изображения, то х2 S а2 у2 “ S, “ ft2 ’
где расстояние от линзы до изображения находится из формулы линзы
. aF b~T=F-
Таким образом, nIDHa-FY ~ £ 4а2№ ***
398
609. Освещенность экрана в отсутствие линзы
здесь / — сила света источника, L—расстояние от источника до экрана. При наличии линзы
Е______
* ЯП?/4 ’
где Ф —световой поток, проникающий через линзу, Dt— диаметр изображения. Обозначим через а расстояние от шарика до линзы, через 6 —расстояние от лиизы до экрана и через d — диаметр шарика. Тогда
D, = - d. а
Принимая теперь во внимание, что
4 а2 4
где Е'— освещенность линзы, a D — ее диаметр, получим
I яйг
а2 4 ID2 L2D2
я I b ,\2 “ b2d2 “ b2d2 E'
Величину b найдем по формуле линзы:
Отсюда
причем плюс соответствует увеличенному изображению, а минус — уменьшенному. Подставляя числовые значения, получим
ft =70 см, Ei ~ 18,4/?.
610. Освещенность изображения прямо пропорциональна телесному углу Q, под которым видна линза из некоторой точки источника. С другой стороны, освещенность обратно пропорциональна площади а изображения. Таким образом, Е прямо пропорционально 0,/а.
Принимая во внимание, что а <т~(6/а)2, получим
здесь а и ft — расстояния между источником и линзой н между линзой и изображением соответственно, а с —некоторый коэффициент
394
пропорциональности. Из этой формулы следует, что с увеличением расстояния между источником и линзой освещенность изображения растет (уменьшается Ь). Выражая теперь b через а и F, из формулы линзы найдем для первого случая
для второго случая
/2а-К\2 k 2aF ) ’
4Е •- с
Разделив почленно второе соотношение на первое, получим
, Г 2а —F у 4 = L 2 (а — К) J ’
Л „2
Отсюда следует F = -5- а.
Г 2а —F I2
611. Освещенность возрастет в [ 2 (д — F)"J раз‘ ^ри а = освещенность возрастет в 9/4 раза (см. решение задачи 610).
612. Рассмотрим достаточно малый элемент а поверхности протяженного источника. Световые лучи от этого элемента, пройдя
через отверстие, дадут на экране С пятио, диаметр R которого равен, очевидно," 2d (рис. 377). Освещенность этого пятна, создаваемая лучами от элемента а,
р ФОо Фйо
= л/?2/4 “ nd2 *
Здесь Q —телесный угол, под которым видно отверстие из рассматриваемого элемента источника. При выполнении условия d <С а можно записать
и, следовательно,
Отношение Etf<J имеет смысл освещенности, создаваемой на матовом стекле световыми лучами с единичной площадки источника. Для определения полной освещенности Е достаточно умножить отношение Et/a на площадь S той части поверхности протяженного источника, которая посылает световые лучи в точку D. Проведем прямые линии из точки D через края отверстия (пунктир на рис. 377). Конус этих прямых выделяет на поверхности протяженного источника круг с диаметром R — 2d. Таким образом,
е я^2 л в с яФ<^2
4 a 4a2
395
613. Рассмотрим малый элемент о поверхности протяженного источника А (рис. 378). Светввая энергия от этого элемента, проходящая через линзу, распределяется по площадке S экрана В. Поскольку по формуле линзы b = 2F (& —расстояние от лиизы до изображения оД имеем согласно рис. 378
_ лР2 ( Ь-а\2 лР2 р_ 2
4 \ b ) 16F2 { '
где Р~ диаметр лиизы. Принимая во внимание, что при Р <С 2F телесный угол Q, под которым видна линза из элемента о, равен siZ>74 (2F)2, можно записать так:
S = Q(2F — a)2.
Освещенность Et площадки S, обусловленная лучами от малого элемента о, равна
Фйа Фа
= (2F — a)2‘
Рассмотрим теперь другой малый элемент поверхности источника А, смещенный от оптической оси. Свет от этого элемента распределится в плоскости экрана В по площадке, площадь которой по-прежнему равна 5, а центр смещен от оптической оси на некоторое расстояние х (пунктир на рис. 378).
Легко видеть, что вклад в освещенность центра экрана В будут давать световые лучи только от тех площадок источника А, для которых х не превышает радиуса площадки S.
Полная площадь S, поверхности протяженного источника А, световые лучи с которой достигают центра площадки S, найдется, если провести лучи от крайних точек площадки S через оптический центр линзы:
„ „ / 2F \2 лР2{2Е-а\2
о j «= о I- = —-— I------
\ а ) 4 \ а /
Полную освещенность Е центра экрана найдем по формуле
Ф$! пФ/)2
а (2F — а}2 “ 4а2 '
Заметим, что £ оказалась не зависящей от фокусного расстояния линзы.
396
Оптические приборы
d,
Рис. 379.
614. Рассмотрим ход лучей в очковой линзе (рис. 379). Глаз, вооруженный очковой линзой, рассматривает мнимое изображение Sj предмета S. Оптическая сила линзы должна быть подобрана так, чтобы это изображение находилось на расстоянии b = dt наилучшего зрения дальнозоркого глаза, если предмет помещен на расстоянии иаилучшего зрения нормального глаза (rf = 25 см). В этом случае дальнозоркий глаз, вооруженный очковой линзой, будет эквивалентен нормальному глазу. Таким образом, n t 1 1
D = = —----— = 2 диоптрии.
615. Дальняя точка аккомодации нормального глаза находится на бесконечности; дальняя точка аккомодации близорукого глаза —
на расстоянии 20 см. Очки, восполняющие недостаток такого глаза, должны быть таковы, чтобы бесконечно удаленный предмет казался находящимся на расстоянии 20 см. Следовательно, F = — 20 см и D = — 5 диоптрий.
Примечание. В данном случае речь идет об очках для дальнего зрения. Такие очки, вообще говоря, могут оказаться неподходящими для ближнего зрения (например, для чтения).
616. На расстоянии 25 см (см. решение задачи 615).
617. Для ближней точки аккомодации имеем
Рис. 380.
dt F ’
а.
где 01 и rf] — расстояния до ближних точек аккомодации глаза, вооруженного очками и без очков соответственно, F—фокусное расстояние очковой линзы. Таким образом,
й|= rfT+T^16’7^
Аналогично для дальней точки аккомодации получим rfjF
618. В данном случае глаз рассматривает мнимое изображение S] предмета S, образовавшееся при преломлении световых лучей иа границе вода — воздух (рис. 380). Расстояние / от изображения до поверхности воды связано с глубиной погружения предмета d соотношением Z= djn (см. решение задачи 509).
397
Таким образом, дальняя точка аккомодации близорукого глаза находится на расстоянии I«23 см и, следовательно, человек должен носить очки с фокусным расстоянием К = — 23 см (см. также решение задачи 615).
619. Посеребренная поверхность шара является выпуклым зеркалом с фокусным расстоянием Р= — R/2 = —8 см. Мнимое изображение удаленных предметов иаходнтси в фокальной плоскости (на расстоянии R/2 от поверхности). Максимальное расстояние, на котором близорукий человек еще резко виднт мелкие предметы,
равно фокусному расстоянию его очков (со знаком «минус», так как РОчк < 0). Следовательно,
R «— «12 см.
Чтобы ответить на второй вопрос, воспользуемся формулой выпуклого зеркала:
4---+1 <б<°)
Fab ' 7
(обозначения см. на рис. 381). На а и Ъ должно быть наложено дополнительное условие:
а Ь “ F очк*
Выражая отсюда Ъ через а и подставляя затем в формулу зеркала, получим следующее уравнение:
в® + в (Fочк ” 2F) — Fочк^7 м 0*
Подставляя числовые значения (в сантиметрах), получим а8 —4а—160 = 0, а1>2=2 ±/4+160.
Отрицательный корень квадратного уравнения не имеет физического смысла. Следовательно,
а = 2 + р4 164 ~ 14,8 см.
620. Элементарный анализ показывает, что стекла очков являются отрицательными линзами, следовательно, человек близорук. Пусть, далее, человек рассматривает невооруженным глазом удаленный предмет, который ннден под углом а. Когда перед глазом располагается отрицательная линза, то человек рассматривает мнимое прямое изображение этого предмета, находящегося в фокальной плоскости линзы. Прн этом расстояние от глаза до изображения равно
/, = Z + | К | = / — F (так как F < 0),
398
где I— расстояние от глаза до очкового стекла. Линейный размер этого изображения d определяется нз формулы d = а | FI. Глаз видит это изображение под углом р:
я d «1^1
P=/i / + IFI *
По условию, а/₽ = 1,5, следовательно,
1Я
-1,5,
откуда IF| = 40 см, следовательно, £> = 1/F= —2,5 диоптрии.
621. Ход лучей показан на рис. 382. Предполагается, что фотографируемый предмет находится в бесконечности. Расстояние а от изображения St, даваемого линзой объектива до второй (отрицательной) линзы, равно а = Ft — d = 2 см. Это изображение слу-
жит для линзы мнимым источником, расположенным на расстоянии at = — а, следовательно,
Отсюда следует, что фотопленка должна располагаться иа расстоянии
aF2 a + F2
10
см.
622. Обозначим в первом случае через at расстояние от предмета до объектива, через Ь\ — расстояние от объектива до матового стекла и через у\ — размер изображения. Соответствующие величины для второго случая обозначим через а2, Ь2 и у2. Тогда по формуле линзы имеем
_L+_L ' JL + J_=±.
at bt F a2 b2 F
Применяя теперь формулу для увеличения, получим
fri""V'ai- Ь2^^-а2, Л л
где х — размер предмета. Подставляя выражения для &i и Ь2 в формулу линзы и исключая затем х, найдем
Отсюда
^-Ipi = ^-у-1р,.
^42,9
У2-У1
899
623. При наличии дополнительной линзы фотоаппарат фокусируется иа мнимое изображение, даваемое линзой. Это мнимое изображение должно быть расположено на расстоянии а= —2 м от объектива, следовательно, сам предмет находиться на расстоянии Ь, которое согласно формуле линзы равно
' h aF а 1
а — г aD — ]
624. В первом случае, когда на объектив еще не надета насадочная линза, размер предмета у и размер изображения Л] связаны соотношением
hi bi У а ’
где а —расстояние от предмета до объектива, a bt — расстояние от объектива до фотопленки (изображения). По формуле линзы имеем
Если иа объектив надета насадочная линза, то оптическая сила этой системы Г/F равна сумме оптических сил отдельных линз (см. задачу 554), откуда
>° <F>>0’ ^<°>-+ Ьг
Теперь снова можно записать:
^2 = Ь2 У = а ’
где h2 — новый размер изображения, а Ь2 — новое расстояние от объектива до фотопленки
а — F ]
Используя отношение h2: hi*= b2: bt и подставив в него значения bt и 62, получим
Лг = Л1Т(77
625. Задача аналогична предыдущей. Необходимо только учесть, что линза F2 — положительна, и что в данном случае остается постоянным расстояние L от объектива до изображения:
626. Очевидно, для того чтобы весь чертеж поместился в кадре при максимальной площади изображения, необходимо получить
400
изображение чертежа размером 24 X 30 мм; уменьшение дается в 20 раз, поэтому мы можем написать
где а —расстояние от чертежа до объектива, Ь— расстояние от объектива до фотопленки. Применим формулу линзы;
Из этих двух уравнений получаем
а = 217' = 105 см.
Нетрудно видеть, далее, что
•Зкадр 7
627. Рассчитаем допустимое смещение L человека за время экспозиции, чтобы размытие изображения не превышало заданного значения d, Поскольку по условию задачи расстояние а от объекта до фотоаппарата существенно больше F, с хорошим приближением можно считать, что изображение располагается в фокальной плоскости и, следовательно, линейное увеличение равно F/а. Отсюда следует, что при смещении изображения на расстояние d объект должен сместиться па расстояние L = ad/F.
Скорость человека при погружении в воду равна v = V Таким образом, время экспозиции не должно превышать значения
t = — <= « 0,005 сек.
v V2gH
628. Произведение освещенности на время экспозиции в обоих случаях должно быть одинаковым:
Fdl ~ £*2^2*
Освещенность изображения обратно пропорциональна квадрату расстояния от объектива до фотопластинки (см. задачу 610);
здесь 6] и bt — расстояния между объективом и фотопластинкой в первом и втором случаях. Следовательно,
26 Л. П. Баканипа в др.
401
Выразим теперь 6| и Ьг через линейные увеличения 71 и V, н через фокусное расстояние объектива F-.
Отсюда
_L+_L.±, V
ai bi F
bi
*.-£(7, + !).
Аналогично, для второго случая получим
fr2-F(72+l).
Таким образом,
629. Для получения четкого изображения предметов, находящихся на расстоянии а от объектива, матовое стекло следовало бы расположить не в фокальной плоскости, а на расстоянии
Если матовое стекло расположено в фокальной плоскости, каждая
точка предмета даст на ием пятио диаметра d (рис. 383), причем
b-F “ b ’
здесь О —диаметр объектива. Подставляя в эту формулу выражение для Ь, получим
d D
F “ а’
Отсюда найдем светосилу объектива С, равную отношению О*/Рг;
nl Г ad 12 с“7Г“[тг] =0'01'
402
630. Каждая точка предмета, находящегося на расстоянии а2, даст на фотопластинке пятио диаметра d (рнс. 384), причем
d ш D .
~~ Ь?*
здесь D — диаметр диафрагмы, bt —расстояние от объектива до фотопластинки, &2 — расстояние от объектива до плоскости, в
которой располагается резкое изображение предметов, удаленных на расстояние а2. Применяя формулу линзы, получим
н, следовательно,
d D d(al-F) D
a\F_____a2F a2F aa
ai — F a2—F a2 — F
Отсюда
a2(ai-F)d F(a2-ax}
= 1,9 cm.
631. Для того чтобы изображения двух точечных источников Sa и S2 не перекрывались, необходимо, чтобы расстояние между центрами светлых кружков х равнялось илн превышало диаметр кружка d (рис. 385).
Если а значительно больше F, изображения источников S2 и Sa будут располагаться практически в фокальной плоскости линзы, т. е. b & F. Поэтому
26*
403
Для того чтобы изображения источников не перекрывались, должно выполняться условие:
£ а
l^d.
Отсюда Отах = -у- “5 м.
632. Расстояние bt от объектива найдем по формуле линзы
до первого изображения
t O|F| bi ------р~ •
at- rt
Величина первого изображения
b. Fi y^x-—
-----F X-
a, - Fj
где х— размер предмета.
Расстояние а2 от первого по формуле линзы, принимая изображение должно располагаться на расстоянии Ь2 = d — расстояние иаилучшего зрения для нормального глаза:
изображения до окуляра определим во внимание, что второе (мнимое) d, где
dF2
“2 = d + F2 •
Величина второго изображения
„ = А „ ZlAAL
Ji а2У' Ft(ai~Fl)
x.
Отсюда найдем линейное увеличение:
V = А •= ?' + F*\- « 370. X т? о \
F2(al-F1)
Определим теперь длину микроскопа:
l“bt + а2=~~-+ dF* « 16,8 см. — г\ a-v
633. В трубе, установленной на бесконечность, расстояние между объективом н окуляром равно сумме F] + F2. Первое изображение удаленных предметов располагается в общей фокальной плоскости объектива и окуляра; в этой плоскости и следует расположить диафрагму поля зрения. Размер диафрагмы определяет угол поля зрения. Он равен, очевидно, 2а (рис. 386). Принимая во внимание малость угла а, можно записать:
2а « 2 tg а = — = 0,04 рад « 2° 15'. Г1
404
Параллельный пучок света, входящий в объектив под углом а, выйдет из окуляра под углом р. Угловое увеличение у равно
D
V tga D F2 ' 2F,
Примечание. Глаз обладает значительной областью аккомодации. У нормального человеческого глаза эта область простирается с расстояния около Ю см до бесконечности. В тех случаях, когда глаз вооружен зрительным прибором (очки, лупа, микроскоп, зрительная труба), мнимое изображение предмета, рассматриваемое глазом, должно, конечно, располагаться в области аккомодации. Однако его положение даже для одного и того же наблюдателя может в широких пределах изменяться от опыта
Рис. 386.
к опыту, что практически не отражается на качестве наблюдаемого изображения. При изменении аккомодации оптический прибор, вооружающий глаз, должен быть перефокусирован (в случае микроскопа, например, это достигается перемещением тубуса относительно предмета, а в случае зрительной трубы — перемещением окуляра относительно объектива; см., например, задачу 642). Таким образом, ход лучен в приборе зависит от того, как в данном случае аккомодирован глаз.
При рассмотрении хода лучей в оптических приборах обычно полагают, что глаз аккомодирован либо на бесконечность (в этом случае ход лучей оказывается наиболее простым), либо на расстояние нанлучшего зрения (равное для нормального глаза 25 см). Если в тексте задачи нет соответствующего указания, рекомендуется решать задачу в предположении, что глаз аккомодирован на бесконечность. В данной задаче это приводит к заключению о том, что длина зрительной трубы должна быть равной сумме фокусных расстояний объектива и окуляра.
634. Предмет будет резко виден в трубу, если в объектив будет попадать параллельный пучок лучей. Для этого необходимо, чтобы изображение предмета S, даваемое собирающей линзой, располагалось в фокусе рассеивающей линзы, лежащем со стороны
405
зрительной трубы (рис. 387). В этом Случае расстояние /2 между S и Sj будет равно
Z2 “ Zi +1 Ft |e li — Ft “ ZOO см.
Расстояние x между предметом и собирающей линзой определитси
из уравнения — + , или х2 — l2x + Z2f2 — 0, откуда
X X Г 2
х-т±
X; =» 20 см, х2 = 80 см.
Таким образом, в промежутке между источником 5 и рассеивающей линзой существуют два положения собирающей линзы, при которых источник будет резко виден в трубу; при этом первое положение (х, — 20 см) соответствует увеличенному изображению,
а второе (х2 = 80 см) — уменьшенному. Отсюда следует, что в первом положении собирающей линзы угловые размеры изображения видимого в трубу, будут больше, чем во втором.
635. На матовом стекле, помещенном за окуляром, получается изображение оправы объективной лиизы. Расстояние b от окуляра до матового стекла определится из формулы линзы:
Здесь а —расстояние между объективом и окуляром, равное сумме их фокусных расстояний Ft + F2 (так как труба, по условию, наведена на бесконечность; см. примечание к решению задачи 633); Ft и F2 — фокусные расстояния объектива и окуляра соответственно (рис. 388). Таким образом,
aF2 F2(Fi + F2)
b = ——=— —-----=------“б см.
a — F2 Ft
Диаметр D' изображения оправы объектива определится из фор' мулы уаеличения:
D °° а “° Ft*
406
здесь D = 5 см — диаметр объектива. При Ft = 25 см, Ft получим D' — 1 см.
5 см,
636. Изображение удаленных предметов, даваемое объективом, располагается в его фокальной плоскости. Изображение предметов, находящихся на расстоянии а, будет расположено на некотором растоянни b от объектива, равном, согласно формуле лиизы, aF/(a — F). Окуляр зрительной трубы играет роль лупы, при помощи которой рассматривают изображение предметов, даваемое объективом. Если это изображение переместится, то на такое же расстояние следует переместить и окуляр. В нашем случае окуляр следует отодвинуть от объектива на расстояние
При а = 50 м, F = 50 см смещение окуляра равно 0,5 см.
637. Длн того чтобы дальння точка фокусировки переместилась в бесконечность, необходимо поместить перед объективом такую лиизу, которая дает изображение (мнимое) удаленных предметов на расстоянии а2=10 м от объектива. Фокусное расстояние F такой линзы должно быть равно — а2 =—10 м. Положение ближней точки фокусировки найдем по формуле линзы
1 1 1
—--------= —, или
a, a, F
j a\F а, at =--------=----------
ai + F a2 — at
Подставляя числовые значения, получим = 2,5 м.
638. Поскольку а < Fit объектив даст мнимое изображение предмета, положение которого определим по формуле линзы (обозначения см. на рис. 389)
- + -г = тг> или ь------(&<0).
a b Fi a — Ft v '
Размер мнимого изображения
a Fi—a
х,
«П
где х — размер предмета. Так как труба настроена иа бесконечность, расстояние между объективом и окуляром равно сумме фокуеных расстояний Ft + F2 (см. примечание к решению задачи 633)
н, следовательно, расстояние а' от мнимого изображения до оку-
ляра равно
о7 = —ь । 4- F2 —
Fl+ FiF2~ ар2
F2-a
Расстояние d > F2, поэтому изображение, даваемое окуляром, будет действительным. Расстояние Ь' от окуляра до изображения найдем по формуле линзы:
Найдем теперь размер изображения:
b' , Ь' Fi а' a' Ft—а
F2 х~ X.
Fi
Таким образом, линейное увеличение равно
У F2 1
“ х “ Fi = 10 •
Следует отметить, что У не зависит от положения источника.
639. Мнимое изображение расположено на расстоянии — F2(Fi + F{F2 — от окуляра. Линейно увеличение равно — F2: Fi<= 1 : 10 (см. аналогичную задачу 638).
640. Расстояние между объективом и окуляром трубы равно сумме их фокусных расстояний Fi + F2, так как труба наведена на бесконечность (см. примечание к решению задачи 633). Изображения Sj и S2 удаленных предметов Sj и S2, находящихся иа угловом расстоянии а, расположены в общей фокальной плоскости объектива и окуляра и при наблюдении через окуляр будут казаться
408
расположенными иа угловом расстоянии 0. Из рис. 390 видно, что
MLa
Fi'.
В нашем случае углы а/2 и р/2 малы, поэтому отношения тангенсов
этих углов можно с хорошим приближением заменить отношением самих углов. Это дает
₽«4La=2-5°-
Г 2
641. Объектив зрительной трубы дает в своей фокальной плоскости изображение Солнца диаметром d — аД]. Это изображение
служит мнимым источником для окуляра (рис. 391). Имеем
4 + 4 = 4 («<0. F2<0),
а о г 2
но
a — L — Fu откуда
L = F} + =54 см.
Ь — Г 2
n D Ъ
Далее из соотношения = р _ находим диаметр изображения Солнца
„ „ Ь „
D = аг 1 ~р _ = 2 см.
Для трубы Кеплера читателю предлагается решить задачу самостоятельно. Ответ: £«=43,7 см, £>= 1,4 см.
409
642. С помощью бинокля рассматриваются удаленные предметы, находящиеся на расстоянии, много большем Ft, поэтому можно считать, что первое изображение S], даваемое объективом, находится в его фокальной плоскости (рис. 392). Это изображение
играет по отношению к окуляру роль мнимого источника, находящегося на расстоянии at •=> — а от окуляра. Изображение S2, даваемое окуляром, находится на расстоянии bi =—d, где d — расстояние наилучшего зрения нормального глаза (d = 25 см).
ГТ ж 1 , 1 1
Применив формулу линзы— + -г— = -=—, получим
01 °1 ^2
а = — ° 4,76 см.
d + F2
Расстояние между объективом и окуляром
L = Fi — а = 3,24 см.
В том случае, когда глаз аккомодирован на бесконечность, фокусы объектива и окуляра совмещены и, следовательно,
с Ft + F2 >= 4 см и Li — L = 0,76 см.
643. Изображение S Луны, даваемое объективом, располагается в его фокальной плоскости. Расстояние at от этого изображения до окуляра при наблюдении
глазом найдем по формуле линзы (рис. 393):
1 , 1 1
<h + bi F2 ’
где 6] = — d (изображение, даваемое окуляром, мнимое), или
а‘ = 7Тг2 ~4’17 см’
Найдем теперь расстояние а2 от изображения S до окуляра при наблюдении на экране (рис. 394):
1 , 1 1 dF2
— + —= -£г~, или а2 — ——= 6,25 см.
а2 d Ft , d — F,2
410
Смешение окуляра a2 — at равно, таким образом, 2,08 см. Линейный размер К изображения Луны легко найти, рассматривая подобные треугольники иа рнс. 394:
Здесь Л —линейный размер изображения S, даваемого объективом/ При написании последней формулы принята во внимание малость
f
Л'-
d ----и
Рис. 394.
угла а; это позволяет с хорошим приближением записать Л « aFt. Подставляя числовые значения, получим Л' —7 см.
644. Изображение удаленного предмета, даваемое объективом, располагается в его фокальной плоскости. Это изображение играет по отношению к рассеивающей окулярной линзе роль мнимого предмета. Мнимое изображение, рассматриваемое глазом, должно располагаться на расстоянии 61“ — d, где d — расстояние наилучшего зрения. Обозначим через а расстояние между окуляром и фокальной плоскостью объектива. По формуле линзы
Учитывая, что а2 = —а, найдем
Fd
При d«=af1 = 20 см получим
При af“af2«=>50 см будем иметь
а" -----“4,35 см-
F + d2
Расстояние между объективом и окуляром равно, очевидно, Fi — а, где Ft — фокусное расстояние объектива. Таким образом, дальнозоркому зрителю приходитси сильнее раздвигать трубку бинокля. При передаче бинокля от близорукого зрителя дальнозоркому длина трубки должна быть увеличена на а — а" “0,65 см.
411
645. Найдем по формуле лиизы расстояние Ь между объективом и промежуточным изображением предмета (изображение предмета, которое дает объектив):
здесь а — расстояние до предмета. Для того чтобы изображение, даваемое окуляром, находилось на расстоянии наилучшего зрения d от глаза, окуляр следует расположить на некотором расстоянии а, перед промежуточным изображением. Это расстояние равно (см. решение задачи 644)
dF2 ai~~ d + F2‘
Расстояние I между объективом и окуляром равно, очевидно. b — аг
, , aFt dF2
l= b — дц •=-=~ + 14 см.
a-Fi d+ F2
Примечание. Поскольку a 3» Fb без большой ошибки можно было бы считать, что промежуточное изображение находится в фокальной плоскости объектива (b^Fi), как это делалось, например, в задаче 644.
646. Рассмотрим параллельный пучок лучей от некоторого малого элемента лунного диска, лежащего на оптической оси трубы. Диаметр d пучка, выходящего из трубы, равен, очевидно, (Р2/Л) D,
Рис. 395.
где Ft и F2 — фокусное расстояние объектива и окуляра соответственно, a D — диаметр объектива. Освещенность изображения на сетчатке глаза зависит от соотношения между диаметром пучка и диаметром зрачка d3p.
Рассмотрим случай d d3p. В этом случае вся световая энергия, поступающая в объектив, доходит до сетчатки. Освещенность изображения пропорциональна энергии световых лучей, проникающих в зрачок (т. е. пропорциональна D2), и обратно пропорциональна площади изображения на сетчатке (т. е. обратно пропорциональна квадрату увеличения трубы (Pi/Pz)2; см. задачу 633). Таким образом, при d^d3p имеем
I F. \2
E~D2 -У-) .
412
В случав d > d3? в зрачок будет проиикать’только часть световой энергии, поступающей в объектна, так как лучи, идущие через периферические части объектива, в зрачок не попадут. Из рис. §95 видно, что в этом случае диаметр О' входного пучка лучей, проникающих в зрачок, равен (Fi/F2) d3p и, следовательно,
Освещенность Еа изображения на сетчатке в случае невооруженного глаза пропорциональна, очевидно, d^p. Таким образом, при выполнении условия d^d3p освещенность изображения на сетчатке глаза, вооруженного трубой, такая же, как и в случае невооруженного глаза. При d < d3p освещенность изображения на сетчатке глаза, вооруженного трубой, меньше Еа.
По условию задачи,
£о
Е
d3D
, р < 2 = отсюда F2 = —— = 10 мм. I * 2 I
647. При уменьшении диаметра объектива трубы от 150 до 75 мм освещенность изображения лунной поверхности иа сетчатке глаза не будет изменяться. При дальнейшем уменьшении диаметра объектива освещенность начнет уменьшаться. Прн D = 50 мм она окажется равной 4Еа/9, где Еа — освещенность в случае недиафраг-мированиого объектива (см. задачу 646).
648. Увеличение трубы, равное отношению фокусных расстояний объектива и окуляра, равно 10 (см. задачу 646).
649. Освещенность изображения лунной поверхности иа сетчатке уменьшится в 2,25 раза (см. задачу 646).
Рис. 396.
650. Для определения освещенности изображения Солнца на экране необходимо найтн площадь изображения и поток световой энергии, достигающий экрана. Рассмотрим рис. 396. Промежуточное изображение Солнца Si будет располагаться в фокальной плоскости объектива. Диаметр этого изображения з1 равен аГь Диаметр st
413
изображения.S2 на экране найдем по формуле
Z> „ b
s2 “Si— =аг. — г 1 а а
где через а обозначено расстояние между изображением S, и окуляром.
При расчете светового потока следует принять во внимание ограничения световых пучков. В условии данной задачи расположение линз и их размеры таковы, что часть светового потока диафрагмируется оправой окуляра. Как видно нз рис. 396, через окуляр проходят только те лучи, которые прошли через центральную часть объектива. Диаметр d работающей части объектива может быть найден по формуле
Теперь запишем выражение для освещенности изображения Солнца на экране:
d2
£=» Ео-^- = Ео s.
где через Ео обозначена освещенность, создаваемая солнечными лучами в плоскости объектива (а следовательно, освещенность любого экрана, расположенного перпендикулярно к солнечным лучам). Подставляя в последнюю формулу числовые значения, получим
Примечание. Как видно из решения, некоторые данные из условия задачи непосредственно в ответ не вошли (диаметр объектива d], фокусные расстояния Ft н F2). Это, однако, не означает, что оии не нужны для решения задачи. Числовые значения d], Fi и F2 необходимы для анализа хода лучен в системе (см. рис. 396).
651. Ход лучей в системе изображен на рис. 397. Промежуточное изображение Солнца Si будет располагаться в фокальной плоскости собирающей линзы. Диаметр s2 изображения S2 на экране будет равен
6 „ b
S2 = S1-=aF1-
Здесь через 3| обозначен диаметр изображения S], равный aFi-По условию задачи световые пучки ограничиваются диафрагмой D. Пучок лучей, достигающий экрана, имеет на входе системы диаметр d, который может быть определен из подобия треугольников
414
на рнс. 397:
D Ft-1/2'
Обозначая теперь освещенность, создаваемую прямыми солнечными
лучами, через Ео, найдем поток световой энергии Ф, проходящей
через систему
Б°~ ’
Этот поток энергии распределяется по изображению S2, создавая осэещенность Е:
/ а
пг I 1 4- —-
р Ф d2 ₽ р ' F*)
nsl si a2F2b2
4 \ 2/
В последнем выражении отношение а?/Ьг в соответствии с формулой тонкой линзы заменено на (l+a/F2)2, Подставляя числовые значения .О— 0,75 см, а —5 см, 1^5 см, Ft*= 10 см, Ft~ — 10 см на— 10~2 рад,
Е=25£о.