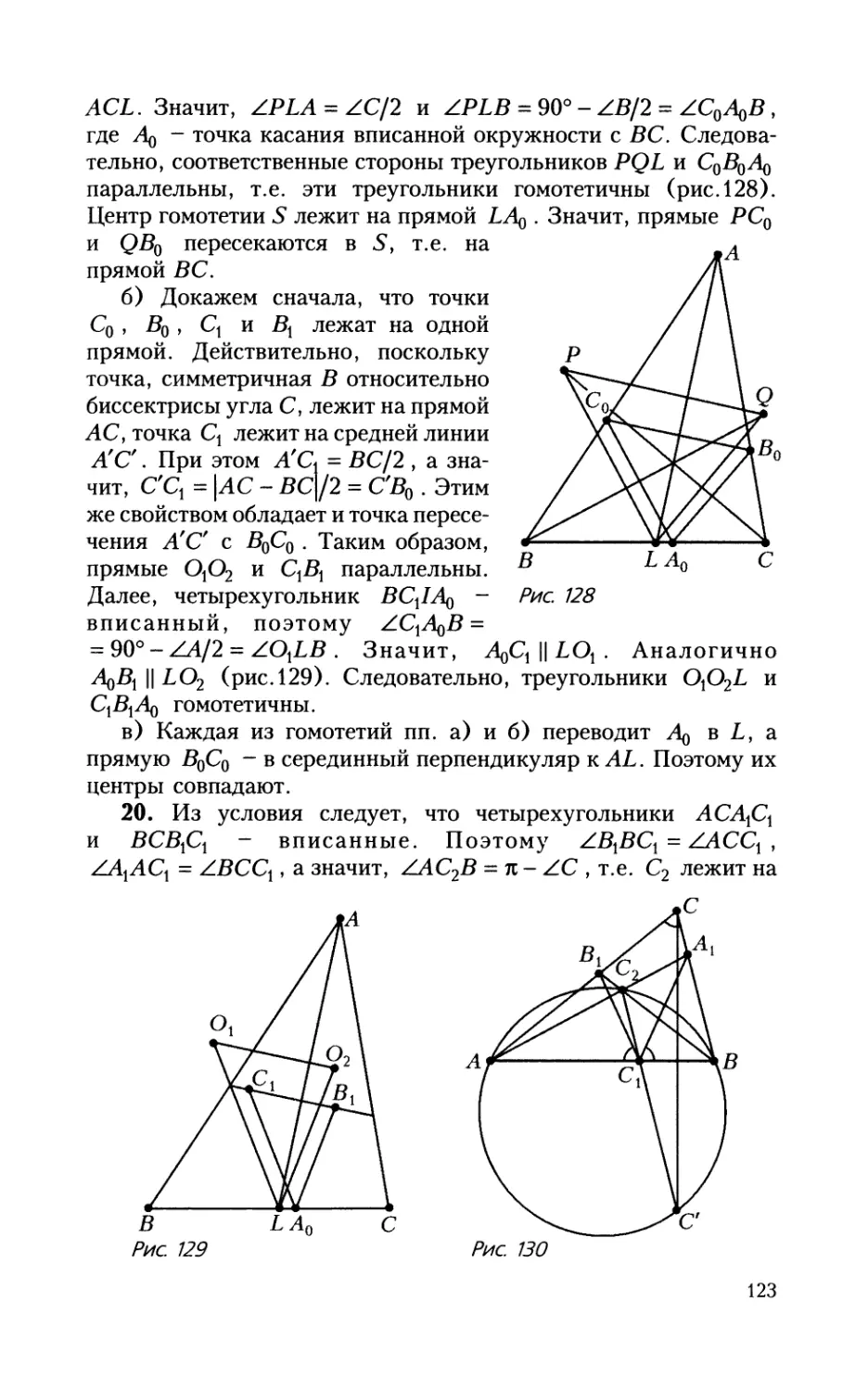
Author: Заславский А.А.
Tags: геометрия топология математика квант
ISBN: 978-5-4439-0626-3
Year: 2015
Text
134
ВЫПУСК d'B'*
Библиотечка КВАНТ
Библиотечка КВ/
АА Заславский
Олимпиады имени
И.Ф. Шарыгина
Приложение к журналу
«Квант»№2 / 2015
БИБЛИОТЕЧКА
КВАНТ
ВЫПУСК
АА Заславский
Олимпиады имени
И.Ф. Шарыгина
(2010-2014)
Москва
Издательство МЦНМО
2015
УДК 514.112
ББК 22.151.0
3-36
Серия «Библиотечка «Квант»
основана в 1980 году
Редакционная коллегия:
Б.М.Болотовский, А.А.Варламов, Г.С.Голицын, Ю.В.Гуля-
ев, М.И.Каганов, С.С.Кротов, С.П.Новиков, В.В.Произволов,
Н.Х.Розов, А.Л.Стасенко, В.Г.Сурдин, В.М.Тихомиров,
А.Р.Хохлов, А.И.Черноуцан
Заславский А.А.
3-36 Олимпиады имени И.Ф.Шарыгина (2010—2014). - М.:
Издательство МЦНМО, 2015. - 168 с. (Библиотечка «Квант».
Вып. 134. Приложение к журналу «Квант» №2/2015.)
ISBN 978-5-4439-0626-3
В книге приведены задачи геометрических олимпиад имени И.Ф.
Шарыгина, прошедших в 2010 - 2014 годах. Ко всем задачам даны
подробные решения.
Сборник предназначен школьникам, учителям математики и
руководителям математических кружков, а также всем любителям
геометрии.
ББК 22.151.0
СОДЕРЖАНИЕ
Вступление 4
Условия Ответы
VI ОЛИМПИАДА 5 43
VII ОЛИМПИАДА 12 70
VIII ОЛИМПИАДА 20 90
IX ОЛИМПИАДА 27 116
X ОЛИМПИАДА 35 143
ВСТУПЛЕНИЕ
Олимпиады по геометрии имени И.Ф.Шарыгина
проходят, начиная с 2005 года, в память об известном математике и
педагоге Игоре Федоровиче Шарыгине (1937-2004). В жюри олим-
пиады входят профессиональные математики, школьные учителя,
студенты - победители и призеры олимпиад прошлых лет. К
участию в олимпиаде приглашаются ученики 8-11 классов из
России, ближнего и дальнего зарубежья. Олимпиада проходит в два
тура. Первый тур - заочный. Вариант из 20-25 задач (для каждой
задачи указываются классы, которым она предназначена) в начале
года публикуется в газете «Математика» и на интернет-порталах
www.mccme.ru и www.geometry.ru. Варианты публикуются на
русском и английском языках. Решения можно присылать как по
электронной, так и по обычной почте, крайний срок, как правило,
- начало апреля. Иностранные участники могут присылать решения
на английском языке. По результатам заочного тура жюри опреде-
ляет победителей, которые приглашаются на финальный тур, про-
ходящий в Дубне (Московская область) в конце июля. Кроме того,
к участию в финальном туре допускаются победители региональных
геометрических олимпиад, проходящих в ряде городов России,
Украины и Казахстана. Финальный тур проводится в два дня.
Каждый день участники решают по 4 задачи. Решение каждой
задачи школьник должен защитить сам, объясняя его (устно)
членам жюри. Для каждого класса варианты финального тура
составляются отдельно. Как правило, в каждом классе находятся
1-2 человека, решившие все задачи. Во время финального тура для
ребят и их родителей и учителей организуются популярные лекции
по геометрии, которые читают профессора МГУ, а также культур-
ная и спортивная программа.
В этой книге содержатся условия и решения задач VI-X олим-
пиад, проведенных в 2010-2014 гг. Условия и решения задач первых
пяти олимпиад можно найти в книге «Олимпиады им. И.Ф.Шары-
гина» («Библиотечка «Квант», вып.ИЗ, 2009 г.). Автор благодарит
И.И.Богданова, Н.Белухова, А.Д.Блинкова, Ю.А.Блинкова,
Е.С.Горскую, П.А.Кожевникова, Д.В.Прокопенко, В.Ю.Протасо-
ва, Б.Р.Френкина, Д.В.Швецова и А.Якубова, написавших и про-
иллюстрировавших часть решений, а также регулярно проверявших
и исправлявших материалы олимпиад.
УСЛОВИЯ ЗАДАЧ
VI ОЛИМПИАДА
Заочный тур
1. (8)1 Существует ли треугольник, в котором
одна сторона равна какой-то из его высот, другая - какой-то из
биссектрис, а третья - какой-то из медиан?
Б. Френкин
2. (8) В прямоугольном треугольнике АВС (ZC = 90°)
биссектрисы AAt и ВВХ пересекаются в точке I. Пусть О - центр
описанной окружности треугольника СА{В}. Докажите, что
OI1 АВ.
Д. Швецов
3. (8) Точки А', В' , С' лежат на сторонах ВС, СА, АВ
треугольника АВС. ТочкаХ такова, что ZAXB = ZA'C'B' + ZACB
и ХВХС = ХВ'А'С' + ZBAC . Докажите, что четырехугольник
ХА'ВС' - вписанный.
Ф. Нилов
4. (8) Диагонали вписанного четырехугольника АВ CD пере-
секаются в точке N. Окружности, описанные вокруг треугольни-
ков AN В и CND, повторно пересекают стороны ВС и AD в
точках At, В1 , Ct , Dx. Докажите, что четырехугольник A\B£\DX
вписан в окружность с центром N.
Д. Швецов
5. (8-9) На высоте BD треугольника АВС взята точка Е
такая, что ХАЕ С = 90°. Точки Ot и О2 - центры описанных
окружностей треугольников АЕВ и СЕВ; F, L - середины
отрезков АС и ОХО2 . Докажите, что точки L, Е, F лежат на одной
прямой.
Д. Швецов
6. (8-9) На стороне ВС равностороннего треугольника АВС
взяты точки М и N (М лежит между В и N) такие, что 1
1 В скобках после номера задачи указан класс, для которого она
предназначена.
5
Z.MAN = 30° . Описанные окружности треугольников АМС и
AN В пересекаются в точке К. Докажите, что прямая АК содер-
жит центр описанной окружности треугольника AMN.
Д. Швецов
7. (8-9) Через вершину В треугольника АВС проведена
прямая, перпендикулярная медиане ВМ. Эта прямая пересека-
ет высоты, выходящие из А и С (или их продолжения), в
точках К и ЛГ. Точки Ot и О2 - центры описанных окружнос-
тей треугольников АВ К и CBN соответственно. Докажите, что
OtM = О2М .
Д. Швецов
8. (8-10) В треугольнике АВС проведена высота ЛЯ. Точки
1Ь и 1С - центры вписанных окружностей треугольников АВН
и САН; L - точка касания вписанной окружности треугольника
АВС со стороной ВС. Найдите угол LIbIc.
Д. Швецов
9. (8 -10) Назовем точку внутри треугольника хорошей, если
три чевианы, проходящие через нее, равны. В треугольнике АВС
стороны АВ и ВС равны, а количество хороших точек нечетно.
Чему оно может быть равно?
Б. Френкин
10. (8-11) Дан треугольник АВС. С помощью двусторонней
линейки, проведя не более восьми линий, постройте на стороне
АВ такую точку D, что AD/BD = ВС/АС.
И. Богданов
11. (8-11) Выпуклый гг-угольник разрезан на 3 выпуклых
многоугольника. У одного из них п сторон, у другого - боль-
ше, чем п, у третьего - меньше, чем п. Каковы возможные
значения п?
Б. Френкин
12. (9) В прямоугольном треугольнике АВС АС - больший
катет, СН - высота, проведенная к гипотенузе. Окружность с
центром Н и радиусом СН пересекает катет АС в точке М. Точка
В' симметрична точке В относительно Н. В точке В' восставлен
перпендикуляр к гипотенузе, который пересекает окружность в
точке К. Докажите, что:
а) В'М || ВС ;
б) АК - касательная к окружности.
А. Блинков, Ю.Блинков, М.Сандрикова
6
13. (9) В выпуклом четырехугольнике ABCD АВ = ВС. На
диагонали BD выбрана точка К такая, что ЛА К В + ZBKC =
= /А + ZC . Докажите, что АК • CD = КС • AD .
С. Берлов
14. (9-10) На стороне AD выпуклого четырехугольника
ABCD нашлась такая точка М, что СМ и ВМ параллельны АВ
и CD соответственно. Докажите, что SABCD > 3SBCM .
С. Берлов
15. (9-11) В остроугольном треугольнике АВС ЛА1, ВВХ и
CCt - высоты. Прямые АА} и В}С} пересекаются в точке К.
Окружности, описанные вокруг треугольников АХКСХ и А{КВХ ,
вторично пересекают прямые АВ и АС в точках N и L соответ-
ственно. Докажите, что
а) сумма диаметров этих окружностей равна стороне ВС;
6) AXN/BBX + A^/CQ = 1.
Д. Прокопенко, А. Блинков
16. (9-11) В угол с вершиной А вписана окружность,
касающаяся сторон угла в точках В и С. Прямая, проходящая
через А, пересекает окружность в точках D и Е. Хорда ВХ
параллельна прямой DE. Докажите, что отрезок ХС проходит
через середину отрезка DE.
Ф. Нилов
17. (9-11) Постройте треугольник по высоте и биссектрисе,
проведенным из одной вершины, и медиане, проведенной из
другой вершины.
Предложил С. Токарев
18. (9-11) На хорде АС окружности со выбрали точку В. На
отрезках АВ и ВС как на диаметрах построили окружности
и <02 с центрами Ох и О2, которые пересекают со второй раз в
точках D и Е соответственно. Лучи ОД) и О2Е пересекаются в
точке F. Лучи AD и СЕ пересекаются в точке G. Докажите, что
прямая FG проходит через середину АС.
Д. Прокопенко
19. (9-11) Четырехугольник ABCD вписан в окружность с
центром О. Точки Р и Q диаметрально противоположны С и D
соответственно. Касательные к окружности в этих точках пере-
секают прямую АВ в точках Е и F (А лежит между Е и В, В -
между А и F). Прямая ЕО пересекает АС и ВС в точках X и У,
а прямая FO пересекает AD и BD в точках U и V. Докажите, что
XV = YU.
В. Ясинский, Украина
7
20. (10) Вписанная окружность остроугольного треугольни-
ка АВС касается его сторон АВ, ВС, СА в точках Ct , At, Bt
соответственно. Пусть А2, В2 ~ середины отрезков В}С{,
А£\ соответственно, О - центр описанной окружности треу-
гольника, Р - одна из точек пересечения прямой СО с вписан-
ной окружностью. Прямые РА2 и РВ2 вторично пересекают
вписанную окружность в точках А' и S'. Докажите, что
прямые АА' и В S' пересекаются на высоте треугольника,
опущенной на АВ.
Ф. Иелее
21. (10-11) Дан выпуклый четырехугольник АВ СО. Извес-
тно, что AABD + AACD > ABAC + Z.BDC . Докажите, что
$ABD + $ACD > $ВАС + $BDC •
А.Акопян
22. (10-11) Окружность с центром F и парабола с фокусом
F пересекаются в двух точках. Докажите, что на окружности
найдутся такие четыре точки А, В, С, D, что прямые АВ, ВС, CD
и DA касаются параболы.
А. Заславский
23. (10-11) Шестиугольник ABCDEF вписан в окружность.
Известно, что АВ • CF = 2ВС • FA , CD • ЕВ = 2DE • ВС ,
EF AD = 2FA DE. Докажите, что прямые AD, BE и CF
пересекаются в одной точке.
Н.Белухов, Болгария
24. (10-11) Дана прямая I в пространстве и точка А, не
лежащая на ней. Для каждой прямой /', проходящей через А,
построим общий перпендикуляр XY (У лежит на Г ) к прямым
I и Г. Найдите ГМТ точек У.
А.Акопян
25. (И) Среди вершин двух неравных икосаэдров можно
выбрать шесть, являющихся вершинами правильного октаэдра.
Найдите отношение ребер икосаэдров.
Н.Белухов
Финальный тур
8 класс
1. В неравнобедренном треугольнике АВС прове-
дены высота из вершины А и биссектрисы из двух других
вершин. Докажите, что описанная окружность треугольника,
8
образованного этими тремя прямыми, касается биссектрисы,
проведенной из вершины А.
М.Рожкова, Украина
2. Даны две точки А и В. Найдите геометрическое место точек
С таких, что точки А, В и С можно накрыть кругом единичного
радиуса.
А.Акопян
3. В выпуклом четырехугольнике АВ CD лучи АВ и DC
пересекаются в точке К. На биссектрисе угла AKD нашлась
точка Р такая, что прямые ВР и СР делят пополам отрезки АС
и BD соответственно. Докажите, что АВ = CD.
С. Берлов, Д. Прокопенко
4. В равные углы XxOY и YOX2 вписаны окружности и
о>2 , касающиеся сторон ОХх и ОХ2 в точках At и Л2
соответственно, а стороны ОУ - в точках Вх и В2 . Точка Ct -
вторая точка пересечения АХВ2 и , а точка С2 - вторая точка
пересечения А2ВХ и о>2 . Докажите, что CtC2 - общая касатель-
ная к окружностям.
И. Богданов
5. В треугольнике АВС проведены высота АН, биссектриса
BL и медиана СМ. Известно, что в треугольнике HLM прямая
АН является высотой, a BL - биссектрисой. Докажите, что СМ
является в этом треугольнике медианой.
Б. Френкин
6. Точки Е, F - середины сторон ВС, CD квадрата ABCD.
Прямые АЕ и BF пересекаются в точке Р. Докажите, что
ZPDA = ZAED .
Д. Прокопенко
7. Каждый из двух правильных многоугольников Р и Q
разрезали прямой на две части. Одну из частей Р и одну из
частей Q сложили друг с другом по линии разреза. Может ли
получиться правильный многоугольник, не равный ни одному из
исходных, и если да, то сколько у него может быть сторон?
Б. Френкин
8. Биссектрисы ААХ и ВВХ треугольника АВС пересекаются
в точке I. На отрезках АД и ВД построены как на основаниях
равнобедренные треугольники с вершинами Л2 и В2 , лежащими
на прямой АВ. Известно, что прямая CI делит отрезок А2В2
пополам. Верно ли, что треугольник АВС - равнобедренный?
А. Заславский
9
9 класс
1. Для каждой вершины треугольника ЛВС нашли
угол между высотой и биссектрисой, проведенными из этой
вершины. Оказалось, что эти углы в вершинах Л и В равны друг
другу и меньше, чем угол в вершине С. Чему равен угол С
треугольника?
В. Френкин
2. Два треугольника пересекаются. Докажите, что внутри
описанной окружности одного из них лежит хотя бы одна
вершина другого. (Здесь треугольником считается часть плоско-
сти, ограниченная замкнутой трехзвенной ломаной; точка, лежа-
щая на окружности, считается лежащей внутри нее.)
А.Акопян
3. На прямой лежат точки X, У, Z (именно в таком порядке).
Треугольники ХАВ, YBC, ZCD - правильные, причем вершины
первого и третьего ориентированы против часовой стрелки, а
второго по часовой стрелке. Докажите, что прямые ЛС, BD и XY
пересекаются в одной точке.
В. Ясинский
В треугольнике ЛВС отметили точки Л', В7 касания
сторон ВС, ЛС с вписанной окружностью и точку G пересечения
отрезков ЛЛ' и В В7. После этого сам треугольник стерли.
Восстановите его с помощью циркуля и линейки.
А. Заславский
5. Окружность, вписанная в прямоугольный треугольник
ЛВС ( ZABC = 90° ), касается сторон ЛВ, ВС, ЛС в точках Сх ,
Л1, В1 соответственно. Вневписанная окружность касается
стороны ВС в точке Л2. Точка А$ - центр окружности,
описанной около треугольника АХА2ВХ; аналогично определяется
точка Со . Найдите угол А$ВС$.
Д. Швецов
6. Произвольная прямая, проходящая через вершину В
треугольника ЛВС, пересекает сторону ЛС в точке К, а описан-
ную окружность в точке М. Найдите геометрическое место
центров описанных окружностей треугольников AM К.
Ю. Блинков
7. В треугольнике ЛВС ALa и АМа - внутренняя и внешняя
биссектрисы угла Л. Пусть - окружность, симметричная
описанной окружности треугольника ALaMa относительно сере-
10
дины ВС. Окружность соь определена аналогично. Докажите,
что (Од и соь касаются тогда и только тогда, когда треугольник
АВС прямоугольный.
Н.Белухов
8. На доске нарисован правильный многоугольник. Володя
хочет отметить k точек на его периметре так, чтобы не существо-
вало другого правильного многоугольника (не обязательно с тем
же числом сторон), также содержащего отмеченные точки на
своем периметре. Найдите наименьшее k, достаточное для любо-
го исходного многоугольника.
В.Гуровиц
10 класс
1. Пусть О, I - центры описанной и вписанной
окружностей прямоугольного треугольника; R, г- радиусы этих
окружностей; J - точка, симметричная вершине прямого угла
относительно I. Найдите OJ.
А. Заславский
2. Каждая из двух равных окружностей cot и СО2 проходит
через центр другой. Треугольник АВС вписан в , а прямые
АС, ВС касаются СО2 • Докажите, что cosZA + cos ZB = 1.
П. Кожевников
3. Два выпуклых многоугольника А^А^.А^ и В}В2...ВП
(п> 4 ) таковы, что любая сторона первого больше соответству-
ющей стороны второго. Может ли оказаться, что любая диаго-
наль второго больше соответствующей диагонали первого?
А.Акопян
4. Проекции двух точек на стороны четырехугольника лежат
на двух различных концентрических окружностях (проекции
каждой точки образуют вписанный четырехугольник, а радиусы
соответствующих окружностей различны). Докажите, что четы-
рехугольник - параллелограмм.
Ф. Нилов
5. В прямоугольном треугольнике АВС ( ZB = 90° ) проведе-
на высота ВН. Окружность, вписанная в треугольник АВН,
касается сторон АВ, АН в точках соответственно;
окружность, вписанная в треугольник СВН, касается сторон СВ,
СН в точках Н2 , В2 соответственно. Пусть О - центр описанной
окружности треугольника Н\ВН2 . Докажите, что ОВ{ - ОВ2.
Д. Швецов
И
6. Вписанная окружность треугольника АВС касается его
сторон в точках А', В7 и С'. Известно, что ортоцентры
треугольников АВС и A'S'С' совпадают. Верно ли, что АВС -
правильный?
Ф. Нилов
7. Каждый из двух правильных многогранников Р и Q
разрезали плоскостью на две части. Одну из частей Р и одну из
частей Q приложили друг к другу по плоскости разреза. Может
ли получиться правильный многогранник, не равный ни одному
из исходных, и если да, то сколько у него может быть граней?
Б.Френкин
8. Вокруг треугольника АВС описали окружность k. На
сторонах треугольника отметили три точки А1, В1 и Q , после
чего сам треугольник стерли. Докажите, что его можно однознач-
но восстановить тогда и только тогда, когда прямые АЛ1, ВВ{ и
CQ пересекаются в одной точке.
Н.Белухов
VII ОЛИМПИАДА
Заочный тур
1. (8) Существует ли выпуклый семиугольник,
который можно разрезать на 2011 равных треугольников?
А. Заславский
2. (8) В треугольнике АВС со сторонами АВ = 4, АС = 6
проведена биссектриса угла А. Из вершины В опущен на эту
биссектрису перпендикуляр ВН. Найдите МН, где М - середина
ВС.
Из сингапурских олимпиад
3. (8) В треугольнике ABC ZA = 60° . Серединный перпенди-
куляр к отрезку АВ пересекает прямую АС в точке Q . Середин-
ный перпендикуляр к отрезку АС пересекает прямую АВ в точке
В1 . Докажите, что прямая В1С] касается окружности, вписан-
ной в треугольник АВС.
Д. Швецов
4. (8) В треугольнике АВС проведены биссектрисы АА',
ВВ', СС'. Известно, что в треугольнике А'В'С' эти прямые
также являются биссектрисами. Верно ли, что треугольник АВС
равносторонний ?
В. Френкин
12
5. (8) В треугольнике АВС проведен серединный перпенди-
куляр к стороне АВ до пересечения с другой стороной в некото-
рой точке С'. Аналогично построены точки А' и В'. Для каких
исходных треугольников треугольник А'В'С' будет равносто-
ронним?
В. Френкин
6. (8) Даны две единичные окружности coj и > пересека-
ющиеся в точках А и В. На окружности (ty взяли произвольную
точку М, а на окружности - точку N. Через точки М и N
провели еще две единичные окружности СО3 и со4 . Обозначим
повторное пересечение со1 и (О3 через С, повторное пересечение
окружностей 0)2 и 0)4 - через D. Докажите, что ACBD -
паралле лограмм.
А.Акопян
7. (8-9) На сторонах АВ и АС треугольника АВС выбрали
точки Р и Q так, что РВ = QC. Докажите, что PQ < ВС.
А.Акопян
8. (8-9) Окружность, вписанная в прямоугольный треуголь-
ник АВС ( ZB = 90° ), касается сторон АВ, ВС, СА в точках Ct ,
At, Вх соответственно; А2, С2 - точки, симметричные точке В{
относительно прямых ВС, АВ соответственно. Докажите, что
прямые AtA2, CtC2 пересекаются на медиане треугольника
АВС.
Д. Швецов
9. (8-9) Точка Н - ортоцентр треугольника АВС. Касатель-
ные, проведенные к описанным окружностям треугольников
СНВ и АН В в точке Н, пересекают прямую АС в точках At и Ct
соответственно. Докажите, что AtH = СЛН .
Д. Швецов
10. (8~9) В трапеции ABCD диагонали пересекаются в точке
О. На боковой стороне CD выбрана точка М, а на основаниях
ВС и AD - точки Р и Q так, что отрезки МР и MQ параллельны
диагоналям трапеции. Докажите, что прямая PQ проходит через
точку О.
М.Волчкевич
11. (8-10) Вневписанная окружность прямоугольного треу-
гольника АВС ( АВ = 90° ) касается стороны ВС в точке At, а
прямой АС в точке А2. Прямая AtA2 пересекает (первый раз)
окружность, вписанную в треугольник АВС, в точке А'; анало-
гично определяется точка С'. Докажите, что АС || А'С'.
Д. Швецов
13
12. (8—10) Пусть АР и BQ - высоты данного остроугольного
треугольника АВС. Постройте циркулем и линейкой на стороне
АВ такую точку М, чтобы AAQM = ZBPM .
В. Ясинский
13. а) (8-10) Найдите геометрическое место центров тяжести
треугольников, вершины которых лежат на сторонах данного
треугольника (по одной вершине внутри каждой стороны).
6) (11) Найдите геометрическое место центров тяжести тетра-
эдров, вершины которых лежат на гранях данного тетраэдра (по
одной вершине внутри каждой грани).
Б. Френкин
14. (9) В треугольнике АВС высота и медиана из вершины А
образуют (вместе с прямой ВС) треугольник, в котором биссек-
триса угла А является медианой, а высота и медиана из вершины
В образуют (вместе с прямой АС) треугольник, в котором
биссектриса угла В является биссектрисой. Найдите отношение
сторон треугольника АВС.
Б. Френкин
15. (9-10) Дана окружность с центром О и радиусом 1. Из
точки А к ней проведены касательные АВ и АС. Точка М,
лежащая на окружности, такова, что четырехугольники ОВМС
и АВМС имеют равные площади. Найдите МА.
В. Протасов
16. (9-10) Дан треугольник АВС и прямая /. Прямые,
симметричные I относительно АВ и АС, пересекаются в точке
At. Точки Вх, С} определяются аналогично. Докажите, что
а) прямые AAt, ВВХ, ССХ пересекаются в одной точке;
6) эта точка лежит на описанной около треугольника АВС
окружности;
в) точки, построенные указанным способом для двух перпен-
дикулярных прямых, диаметрально противоположны.
П.Долгирев
17. (9-11) а) Существует ли треугольник, в котором наи-
меньшая медиана длиннее, чем наибольшая биссектриса?
б) Существует ли треугольник, в котором наименьшая бис-
сектриса длиннее, чем наибольшая высота?
Б. Френкин
18. (9-11) На плоскости проведены п прямых общего поло-
жения, т.е. никакие две прямые не параллельны и никакие три
14
не пересекаются в одной точке. Эти прямые разрезали плоскость
на несколько частей. Какое
а) наименьшее;
б) наибольшее
количество углов может быть среди этих частей?
А. Заславский
19. (9-11) Существует ли неравнобедренный треугольник, у
которого медиана, проведенная из одной вершины, биссектриса,
проведенная из другой, и высота, проведенная из третьей,
равны?
А. Заславский
20. (9-11) Четырехугольник АВ CD описан около окружно-
сти с центром I. Точки М и N - середины диагоналей АС и BD.
Докажите, что АВ CD вписанный тогда и только тогда, когда
IM : АС = IN : BD.
Н.Белухов, А. Заславский
21. (10-11) На окружности с диаметром АС выбрана произ-
вольная точка В, отличная от А и С. Пусть M,N - середины хорд
АВ, ВС, а Р, Q - середины меньших дуг, стягиваемых этими
хордами. Прямые AQ и ВС пересекаются в точке К, а прямые СР
и АВ - в точке L. Докажите, что прямые MQ, NP и KL
пересекаются в одной точке.
В. Ясинский
22. (10-11) Из вершины С треугольника АВС проведены
касательные СХ, СУ к окружности, проходящей через середины
сторон треугольника. Докажите, что прямые XY, АВ и касатель-
ная в точке С к окружности, описанной около треугольника
АВС, пересекаются в одной точке.
Г. Фельдман
23. (10-11) Дан треугольник АВС и прямая I, пересекающая
ВС, СА и АВ в точках At, Вх и Ct соответственно. Точка А' -
середина отрезка, соединяющего проекции At на АВ и АС.
Аналогично определяются точки В7 и С .
а) Докажите, что А', В» и С лежат на некоторой прямой /'.
б) Докажите, что, если I проходит через центр описанной
окружности ДАВС , то Г проходит через центр его окружности
девяти точек.
Н.Белухов, М.Маринов, Болгария
24. (10-11) Дан остроугольный треугольник АВС. Най-
дите на сторонах ВС, СА, АВ такие точки А7, В7, С7, что-
15
бы наибольшая сторона треугольника А'В'С' была мини-
мальна.
А. Заславский
25. (10-11) Три равных правильных тетраэдра имеют общий
центр. Могут ли все грани многогранника, являющегося их
пересечением, быть равны?
Н. Б слухов
Финальный тур
8 класс
1. В трапеции с перпендикулярными диагоналями
высота равна средней линии. Докажите, что трапеция равно-
бокая.
А. Блинков
2. Петя вырезал из бумаги прямоугольник, положил на него
такой же прямоугольник и склеил их по периметру. В верхнем
прямоугольнике он провел диагональ, опустил на нее перпенди-
куляры из двух оставшихся вершин, разрезал верхний прямоу-
гольник по этим линиям и отогнул полученные треугольники во
внешнюю сторону, так что вместе с нижним прямоугольником
они образовали прямоугольник.
Как по полученному прямоугольнику восстановить исходный
с помощью циркуля и линейки?
Т. Голенищева-Кутузова
3. Около треугольника АВС описали окружность. Пусть At
- точка пересечения с нею прямой, параллельной ВС и проходя-
щей через А. Точки Bt и Ct определяются аналогично. Из точек
At, , Ct опустили перпендикуляры на ВС, СА, АВ соответ-
ственно. Докажите, что эти три перпендикуляра пересекаются в
одной точке.
А.Мякишев, Д.Мавло
4. В окружности радиуса 1 проведено несколько хорд,
суммарная длина которых тоже равна 1. Докажите, что в
окружность можно вписать правильный шестиугольник, сторо-
ны которого не пересекают этих хорд.
А. Шаповалов
5. Через вершину А равностороннего треугольника АВС
проведена прямая, не пересекающая отрезок ВС. По разные
стороны от точки А на этой прямой взяты точки М и N так,
что AM = AN = АВ (точка В внутри угла МАС). Докажите,
16
что прямые АВ, AC, BN, СМ образуют вписанный четырех-
угольник.
С. Маркелов
6. В остроугольном треугольнике АВС проведены высоты
ВВХ и CCt ; Д - середина стороны ВС. Прямые А$ВХ и A0Ci
пересекают прямую, проходящую через вершину Л параллельно
прямой ВС, в точках Р и Q. Докажите, что центр вписанной
окружности треугольника PA$Q лежит на высоте треугольника
АВС.
Д. Прокопенко
7. На плоскости отмечена точка М, не лежащая на осях
координат. По оси ординат движется точка Q, а по оси абсцисс
точка Р так, что угол PMQ всегда остается прямым. Найдите
геометрическое место точек, симметричных М относительно PQ.
А.Акопян
8. Пользуясь только линейкой, разделите сторону квадратно-
го стола на п равных частей. Линии можно проводить только на
поверхности стола.
А. Заславский
9 класс
1. Высоты AAj и BBt треугольника АВС пересе-
каются в точке Н. Прямая СН пересекает полуокружность с
диаметром АВ, проходящую через Ах, Вх в точке D. Отрезки
AD и ВВ} пересекаются в точке М, BD и ЛЛ1 - в точке N.
Докажите, что описанные окружности треугольников BXDM и
AXDN касаются.
М.Кунгожин, Казахстан
2. В треугольнике ABC ЛВ -2ЛС. Точки Р и Q на середин-
ном перпендикуляре к СВ таковы, что АС АР = APAQ = AQAB =
ЛА
- . Докажите, что Q - центр описанной окружности тре-
угольника СРВ.
Д.Кеян, Молдова
3. Восстановите равнобедренный треугольник АВС (АВ =
= АС) по точкам I, М, Н пересечения биссектрис, медиан и высот
соответственно.
А.Карлюченко, Украина
4. Четырехугольник ABCD вписан в окружность с центром
О. Биссектрисы его углов образуют четырехугольник, вписан-
17
ный в окружность с центром Z, а биссектрисы внешних углов -
четырехугольник, вписанный в окружность с центром J. Дока-
жите, что О - середина IJ.
А. Заславский
5. Из высот треугольника можно составить треугольник.
Верно ли, что из его биссектрис также можно составить треуголь-
ник?
Б. Френкин
6. В треугольнике АВС AAq и ВВ0 - медианы, AAt и BBt
- высоты. Описанные окружности треугольников CAqBq и
CAtBt вторично пересекаются в точке Мс, Аналогично опреде-
ляются точки Ма, Мь. Докажите, что точки Ма, Мь,
Мс лежат на одной прямой, а прямые АМа , ВМЬ , СМс
параллельны.
П.Долгирев
7. В угол вписаны две окружности со и Q. Прямая /
пересекает стороны угла в точках А и F, окружность со - в
точках В и С, окружность Q - в точках D и Е (порядок точек
на прямой - А, В, С, D, Е, F). Пусть ВС = DE. Докажите, что
АВ = EF.
И. Богданов
8. Выпуклый n-угольник Р, где п > 3, разрезан на равные
треугольники диагоналями, не пересекающимися внутри него.
Каковы возможные значения п, если n-угольник описанный?
Б. Френкин
10 класс
1. В треугольнике АВС середины сторон АС, ВС,
вершина С и точка пересечения медиан лежат на одной окруж-
ности. Докажите, что она касается окружности, проходящей
через вершины А, В и ортоцентр треугольника АВС.
М. Рожкова
2. Четырехугольник АВ CD описан вокруг окружности, каса-
ющейся сторон АВ, ВС, CD, DA в точках К, L, М, N соответ-
ственно. Точки А', В', С , D' - середины отрезков LM, MN,
NK, KL. Докажите, что четырехугольник, образованный пря-
мыми АА', В В', СС', DD' - вписанный.
Л. Емельянов
3. Дано два тетраэдра А1А2А3А4 и ВХВ2В3ВА . Рассмотрим
шесть пар ребер ДАу и BkBi , где (i, /, k, I) - перестановка
18
чисел (1, 2, 3, 4) (например, АХА2 и В3В4 ). Известно, что во
всех парах, кроме одной, ребра перпендикулярны. Докажите,
что в оставшейся паре ребра тоже перпендикулярны.
А.Акопян
4. На стороне АВ треугольника АВС взята точка D. В угол
ADC вписана окружность, касающаяся изнутри описанной ок-
ружности треугольника ACD, а в угол BDC - окружность,
касающаяся изнутри описанной окружности треугольника BCD.
Оказалось, что эти окружности касаются отрезка CD в одной и
той же точке X. Докажите, что перпендикуляр, опущенный из X
па АВ, проходит через центр вписанной окружности треугольни-
ка АВС.
В.Мокин
5. Точка касания вневписанной окружности со стороной
треугольника и основание высоты, проведенной к этой стороне,
симметричны относительно основания биссектрисы, проведен-
ной к этой же стороне. Докажите, что эта сторона составляет
треть периметра треугольника.
А. Блинков
6. Докажите, что для любого неравнобедренного треугольни-
ка /2 > V35 > 12 , где /1, 12 - наибольшая и наименьшая биссек-
трисы треугольника, 5 - его площадь.
М.Рожкова
7. В остроугольном треугольнике АВС О - центр описанной
окружности, At, Bt, - основания высот. На прямых OAt,
OBt, OCt нашли такие точки А', В', С' соответственно, что
четырехугольники АОВС', ВОСА', СОАВ7 вписанные. Дока-
жите, что окружности, описанные около треугольников AAtA',
BBjB', CQC', имеют общую точку.
Г. Фельдман
8. Есть лист жести размером 6x6. Разрешается надрезать
его, но так, чтобы он не распадался на части, и сгибать. Как
сделать куб с ребром 2, разделенный перегородками на единич-
ные кубики?
С.Токарев
19
VIII ОЛИМПИАДА
Заочный тур
1. (8) В треугольнике АВС точка М - середина
АВ, а точка D - основание высоты CD. Докажите, что ZA - 2ZB
тогда и только тогда, когда АС = 2MD.
М. Рожкова
2. (8) Вписанный w-угольник разбит непересекающимися (во
внутренних точках) диагоналями на треугольники. Каждый из
получившихся треугольников подобен хотя бы одному из осталь-
ных.
При каких п возможна описанная ситуация?
Б.Френкин
3. (8) Окружность с центром I касается сторон АВ, ВС, СА
треугольника АВС в точках Q , А1 , Д . Прямые Al, CI, ВД
пересекают А1С1 в точках X, Y, Z соответственно. Докажите, что
ZYB^Z = ZXBxZ .
Д. Швецов
4. (8) Дан треугольник АВС. Пусть М - середина стороны
ВС, а Р - проекция вершины В на серединный перпендикуляр
к АС. Прямая РМ пересекает сторону АВ в точке Q. Докажите,
что треугольник QPB равнобедренный.
А.Акопян
5. (8) На стороне АС треугольника АВС произвольно выбра-
на точка D. Касательная, проведенная в точке D к описанной
окружности треугольника BDC, пересекает сторону АВ в точке
Ct; аналогично определяется точка At. Докажите, что А1С1 || АС .
Д. Швецов
6. (8-9) На гипотенузе АС прямоугольного треугольника
АВС отметили точку Ct такую, что ВС = CCt .Затем на катете
АВ отметили точку С2 такую, что АС2 = ACt; аналогично
определяется точка А2. Найдите угол AM С, где М - середина
отрезка А2С2.
Д. Швецов
7. (8-9) В неравнобедренном треугольнике АВС биссектрисы
углов А и В обратно пропорциональны противолежащим сторо-
нам. Найдите угол С.
Б.Френкин
8. (8-9) Пусть ВМ - медиана прямоугольного треугольника
АВС ( ZB = 90° ). Окружность, вписанная в треугольник АВМ,
20
касается сторон АВ, AM в точках Ах, А2 ; аналогично опреде-
ляются точки Сх , С2. Докажите, что прямые АХА2 и СХС2
пересекаются на биссектрисе угла АВС.
Д. Швецов
9. (8-9) Восстановите треугольник АВС по прямым 1Ь и 1С,
содержащим биссектрисы углов В и С, и основанию биссектрисы
угла А - точке Ц .
А.Карлюченко
10. В выпуклом четырехугольнике все стороны и все углы
попарно различны.
а) (8-9) Может ли наибольший угол примыкать к наиболь-
шей стороне, и при этом наименьший - к наименьшей?
6) (9-11) Может ли наибольший угол не примыкать к
наименьшей стороне, и при этом наименьший - к наибольшей?
Б. Френкин, А.Заславский
11. Дан треугольник АВС и точка Р. Точки А', В', С' -
проекции Р на ВС, СА, АВ. Прямая, проходящая через Р и
параллельная АВ, вторично пересекает описанную окружность
треугольника РА'S' в точке Сх . Точки Ах, Вх определены
аналогично. Докажите, что
а) (8-10) прямые ААХ, ВВХ, ССХ пересекаются в одной
точке;
6) (9-11) треугольники АВС и АХВХСХ подобны.
Чан Куанг Хюнг, Вьетнам
12. (9-10) Пусть О - центр описанной окружности остро-
угольного треугольника АВС. Прямая, проходящая через О и
параллельная ВС, пересекает АВ и АС в точках Р и Q соответ-
ственно. Известно, что сумма расстояний от точки О до сторон
АВ и АС равна ОА. Докажите, что сумма отрезков РВ и QC
равна PQ.
М.Жанбулатулы, Казахстан
13. (9-10) Даны точки А, В. Найдите геометрическое место
таких точек С, что С, середины отрезков АС, ВС и точка пере-
сечения медиан треугольника АВС лежат на одной окружности.
А. Заславский
14. (9-10) В выпуклом четырехугольнике ABCD
АС П BD = О и М - середина ВС. Пусть МО П AD - Е .
АЕ S^abq
Докажите, что - —-------
Ш) ^acdo
М.Волчкевич
21
15. (9-11) Дан треугольник ЛВС. Рассматриваются прямые
/, обладающие следующим свойством: три прямые, симметрич-
ные / относительно сторон треугольника, пересекаются в одной
точке. Докажите, что все такие прямые проходят через одну
точку.
А. Заславский
16. (9-11) Дан прямоугольный треугольник ЛВС, гдеЛВ -
гипотенуза. Пусть М - середина ЛВ, О - центр описанной
окружности со треугольника СМ В. Прямая АС вторично пере-
секает окружность со в точке К. Отрезок КО пересекает описан-
ную окружность треугольника ЛВС в точке L. Докажите, что
отрезки AL и КМ пересекаются на описанной окружности
треугольника АСМ.
Ф. Ивлев
17. (9-11) Квадрат ABCD вписан в окружность. Точка М
лежит на дуге ВС, прямая AM пересекает BD в точке Р, прямая
DM пересекает ЛС в точке Q. Докажите, что площадь четырех-
угольника APQD равна половине площади квадрата.
М. Рожков а
18. (9-11) На плоскости начерчен треугольник и в нем
отмечены две точки. Известно, что какой-то из углов равен 58° ,
какой-то из остальных 59°, какая-то из отмеченных точек
является центром вписанной окружности, а другая - центром
описанной. Используя только линейку без делений, определите,
где какой угол и где какая точка.
Б. Френкин
19. (10-11) Две окружности радиуса 1 пересекаются в точках
X, У, расстояние между которыми тоже равно 1. Из точки С
одной окружности проведены к другой касательные СЛ, СВ,
вторично пересекающие первую окружность в точках В', Л'.
Прямые ЛЛ' и ВВ7 пересекаются в точке Z. Найдите угол XZУ.
А. Заславский
20. (10-11) В треугольнике ЛВС на стороне ЛВ отметили
точку D. Пусть о)| и Qj, (1)2 и Q2 > соответственно, вписанные
и вневписанные (касающиесяЛВ во внутренней точке) окружно-
сти треугольников ACD и BCD. Докажите, что общие внешние
касательные к и о>2 , Ц и О2 пересекаются на прямой ЛВ.
Г. Фельдман
21. (10-11) Через ортоцентр остроугольного треугольника
проведены две перпендикулярные прямые. Стороны треуголь-
22
ника высекают на каждой из этих прямых два отрезка: один -
лежащий внутри треугольника, второй - вне его. Докажите, что
произведение двух внутренних отрезков равно произведению
двух внешних.
Н.Белухов, Э.Колев, Болгария
22. (10-11) В сегмент, ограниченный хордой и дугой АВ
окружности, вписана окружность со с центром I. Обозначим
середину указанной дуги АВ через М, а середину дополнитель-
ной дуги через N. Из точки N проведены две прямые, касающи-
еся сов точках С и О. Противоположные стороны АС и BD
четырехугольника ABCD пересекаются в точке X, диагонали
ABCD пересекаются в точке У. Докажите, что точки X, У, I и М
лежат на одной прямой.
Ф. Нилов
23. (10-11) На каждой из двенадцати диагоналей граней куба
выбирается произвольная точка. Определяется центр тяжести
этих двенадцати точек. Найдите геометрическое место всех таких
центров тяжести.
А.Канель
24. (10-11) На плоскости даны п (п > 2) точек, никакие три
из которых не лежат на одной прямой. Сколькими различными
способами это множество точек можно разбить на два непустых
подмножества так, чтобы выпуклые оболочки этих подмножеств
не пересекались?
В. Ясинский
Финальный тур
8 класс
1. Точка М - середина основания АС остроуголь-
ного равнобедренного треугольника АВС. Точка N симметрична
М относительно ВС. Прямая, параллельная АС и проходящая
через точку N, пересекает сторону АВ в точке К. Найдите угол
АКС.
А. Блинков
2. В треугольнике АВС провели биссектрисы В В' и СС', а
затем стерли весь рисунок, кроме точек А, В' и С'. Восстановите
треугольник АВС при помощи циркуля и линейки.
А.Карлюченко
3. Квадратный лист бумаги согнули по прямой так, что
одна из вершин квадрата оказалась на несмежной стороне
23
(рис.1). При этом образовалось три
треугольника. В эти треугольники
вписали окружности. Докажите, что
радиус одной из этих окружностей
равен сумме радиусов двух других.
Л.Штейнгарц, Израиль
4. Дан равнобедренный треуголь-
ник АВС, в котором /-В = 120°. На
продолжениях сторон АВ и СВ за
точку В взяли точки Р и Q соответ-
ственно так, что лучи AQ и СР пересе-
каются под прямым углом. Докажите, что ZPQB = 2Z.PCQ .
А.Акопян, Д. Швецов
5. Существует ли выпуклый четырехугольник и точка Р
внутри него такие, что сумма расстояний от Р до вершин больше
периметра четырехугольника?
А.Акопян
6. Окружность со описана около треугольника АВС. На
продолжении стороны АВ за точку В взяли точку В} такую,
что АВ} = АС. Биссектриса угла А пересекает со вторично в
точке W. Докажите, что ортоцентр треугольника AWBX лежит
на со.
А.Туманян, Украина
7. Высоты AAt, CCt остроугольного треугольника АВС
пересекаются в точке Н. Точка Q симметрична середине стороны
АС относительно AAt. Точка Р - середина отрезка Л1С1.
Докажите, что ZQPH = 90°.
Д. Швецов
8. Квадрат разрезан на несколько (больше одного) выпуклых
многоугольников с попарно различным числом сторон. Докажи-
те, что среди них есть треугольник.
А.Заславский
9 класс
1. В остроугольном треугольнике АВС провели
высоты ААХ и ВВХ, которые пересекаются в точке О. Затем
провели высоту AtA2 в треугольнике OBAt и высоту BtB2 в
треугольнике AOBt. Докажите, что отрезок А2В2 параллелен
стороне АВ.
Л.Штейнгарц
24
2. Через вершины А, В, С треугольника АВС проведены три
параллельные прямые, пересекающие вторично описанную око-
ло него окружность в точках Д , Вх , Q соответственно. Точки
Л2, В2 , С2 симметричны точкам , Вх , Q относительно
сторон ВС, СА, АВ соответственно. Докажите, что прямые АА2 ,
ВВ2, СС2 пересекаются в одной точке.
Д. Швецов, А. Заславский
3. В треугольнике АВС провели биссектрису CL. В треу-
гольники CAL и CBL вписали окружности, которые касаются
прямой АВ в точках М и П соответственно. Затем все, кроме
точек A, L, М и П, стерли. С помощью циркуля и линейки
восстановите треугольник.
В. Протасов
4. При каких п > 3 правильный n-угольник можно разрезать
диагоналями (возможно, пересекающимися внутри него) на
равные треугольники?
Б. Френкин
5. Пусть АВС - равнобедренный прямоугольный треуголь-
ник. На продолжении гипотенузы АВ за точку А взята точка D
такая, что АВ = 2AD. Точки М и П на стороне АС таковы, что
AM = ПС. На продолжении стороны СВ за точку В взята точка
К такая, что СП = ВК. Найдите угол между прямыми ПК и DM.
М.Кунгожин
6. Дан равнобедренный треугольник АВС, в котором ВС =
= а, АВ = АС = Ь. На стороне АС во внешнюю сторону
построен треугольник ADC, в котором AD = DC = а. Пусть
СМ и СП - биссектрисы в треугольниках АВС и ADC соответ-
ственно. Найдите радиус окружности, описанной около треу-
гольника СМП.
М. Рожкова
7. В выпуклом пятиугольнике Р провели все диагонали, в
результате чего он оказался разбитым на десять треугольников
и один пятиугольник Р'. Из суммы площадей треугольников,
прилегающих к сторонам Р, вычли площадь Р'; получилось
число П. Совершив те же операции с пятиугольником Р',
получили число П'. Докажите, что П > П'.
А. Белов
8. Пусть АН - высота остроугольного треугольника АВС.
Точки К и L - проекции Н на стороны АВ и АС. Окружность,
описанная около треугольника АВС, пересекает прямую KL в
25
точках Р и Q, а прямую АН - в точках А и Т. Докажите, что
точка Н является центром окружности, вписанной в треуголь-
ник PQT.
М. Плотников, Украина
10 класс
1. При каких п можно оклеить в один слой
поверхность клетчатого куба п х п х п бумажными прямоуголь-
никами 1x2 так, чтобы каждый прямоугольник граничил по
отрезкам сторон ровно с пятью другими?
А. Шаповалов
2. Точку внутри треугольника назовем хорошей, если длины
проходящих через нее чевиан обратно пропорциональны длинам
соответствующих сторон. Найдите все треугольники, для кото-
рых число хороших точек - максимальное возможное.
А.Заславский, Б. Френкин
3. Пусть М и I - точки пересечения медиан и биссектрис
неравнобедренного треугольника АВС, а г - радиус вписанной в
него окружности. Докажите, что MI = r/З тогда и только тогда,
когда прямая MI перпендикулярна одной из сторон треугольни-
ка.
А.Карлюченко
к. Дан квадрат. Найдите геометрическое место середин гипо-
тенуз прямоугольных треугольников, вершины которых лежат
на попарно различных сторонах квадрата и не совпадают с его
вершинами.
Б. Френкин
5. В окружность со вписан четырехугольник ABCD, диагона-
ли АС и BD которого перпендикулярны. На сторонах АВ и CD
во внешнюю сторону как на диаметрах построены дуги аир.
Рассмотрим две луночки, образованные окружностью со и
дугами аир (рис.2). Дока-
жите, что максимальные ради-
усы окружностей, вписанных в
эти луночки, равны.
Ф. Нилов
6. Дан тетраэдр ABCD. Точ-
ка X выбрана вне тетраэдра
так, что отрезок XD пересекает
грань АВС во внутренней точ-
ке. Обозначим через А', В',
26
С' проекции точки D на плоскости ХВС, ХСА, ХАВ соответ-
ственно. Докажите, что А'В' + В'С' + С'А' < DA + DB + DC .
В. Ясинский
7. Дан треугольник АВС. Касательная в точке С к его
описанной окружности пересекает прямую АВ в точке D. Каса-
тельные к описанной окружности треугольника ACD в точках А
и С пересекаются в точке К. Докажите, что прямая DK делит
отрезок ВС пополам.
Ф. Ивлев
8. На стороне ВС квадрата ABCD выбрали точку М. Пусть
X, У, Z - центры окружностей, вписанных в треугольники АВМ,
CMD, AMD соответственно. Пусть Нх , Ну , Hz - ортоцентры
треугольников АХВ, CYD, AZD соответственно. Докажите, что
точки Нх , Ну t Hz лежат на одной прямой.
Д. Швецов
IX ОЛИМПИАДА
Заочный тур
1. (8) В треугольнике АВС АВ = ВС. Из точки Е
на стороне АВ опущен перпендикуляр ED на ВС. Оказалось, что
АЕ = DE. Найдите угол DAC.
Н.Москвитин
2. (8) В равнобедренном треугольнике АВС (АС = ВС)
угол при вершине С равен 20°. Биссектрисы углов А и В
пересекают боковые стороны треугольника соответственно в
точках At и Bt. Докажите, что треугольник AiOBi (где О -
центр окружности, описанной около треугольника АВС) явля-
ется равносторонним.
Л.Штейнгарц
3. (8) Вневписанная окружность, соответствующая вершине
А прямоугольного треугольника АВС (ХВ = 9О°), касается
продолжений сторон АВ, АС в точках At, А2 соответственно;
аналогично определим точки Ct , С2. Докажите, что перпенди-
куляры, опущенные из точек А, В, С на прямые CtC2, А1С1 ,
AtA2, пересекаются в одной точке.
Д. Швецов
4. (8) Дан неравнобедренный треугольник АВС. Точка О -
центр описанной около него окружности, а точка К - центр
окружности w, описанной около треугольника ВСО. Высота
27
треугольника, проведенная из точки А, пересекает окружность w
в точке Р. Прямая РК пересекает описанную окружность треу-
гольника в точках Е и F. Докажите, что один из отрезков ЕР и
FP равен отрезку РА.
Ф. Ивлев
5. (8) Точка внутри выпуклого четырехугольника соединена
с вершинами. Получились четыре равных треугольника. Верно
ли, что четырехугольник - ромб?
Б. Френкин
6. (8-9) Диагонали AC, BD трапеции ABCD пересекаются в
точке Р. Описанные окружности треугольников АВР, CDP
пересекают прямую AD в точках X, Y. Точка М - середина XY.
Докажите, что ВМ = СМ.
Д. Швецов
7. (8-9) Пусть BD - биссектриса треугольника АВС. Точки
1а , 1С - центры вписанных окружностей треугольников ABD,
CBD. Прямая 1а1с пересекает прямую АС в точке Q. Докажите,
что XDBQ - 90° .
Д. Швецов
8. (8-9) Вокруг треугольника АВС описана окружность.
Пусть X - точка внутри окружности, К и L - точки пересечения
окружности и прямых ВХ и СХ соответственно. Прямая LK
пересекает ВА в точке Е, а прямую АС в точке F. Найдите
геометрическое место таких точек X, что окружности, описанные
около треугольников AFK и AEL, касаются.
М. Плотников
9. (8-9) Пусть , Т2 ~ точки касания вневписанных
окружностей треугольника АВС со сторонами ВС и АС соответ-
ственно. Оказалось, что точка, симметричная центру вписанной
окружности треугольника относительно середины АВ, лежит на
окружности, описанной около треугольника С1\Т2 • Найдите
угол ВС А.
М. Плотников
10. (8-9) Окружность, вписанная в треугольник АВС, каса-
ется стороны АВ в точке С'. Окружность, вписанная в треуголь-
ник АСС', касается сторон АВ и АС в точках Сх , Вх ; окруж-
ность, вписанная в треугольник ВСС', касается сторон АВ и ВС
в точках С2, А2 . Докажите, что прямые В}СГ, А2С2 и СС'
пересекаются в одной точке.
Д. Швецов
28
11. (8-9) а) Дан выпуклый четырехугольник ABCD. Пусть
<т2 <г3 <г£ - взятые в порядке возрастания радиусы окруж-
ностей, вписанных в треугольники ABC, BCD, CDA, DAB.
Может ли оказаться, что г4 > 2г3 ?
б) В выпуклом четырехугольнике ABCD диагонали пере-
секаются в точке Е. Пусть < г2 < г3 < г4 - взятые в порядке
возрастания радиусы окружностей, вписанных в треугольники
АВЕ, ВСЕ, CDE, DAE. Может ли оказаться, что г2 > 2г{ ?
П. Кожевников
12. (8-11) На каждой стороне треугольника АВС отмечены
две различные точки. Известно, что это основания высот и
биссектрис.
а) Пользуясь только линейкой без делений, определите, где
высоты, а где биссектрисы.
б) Решите пункт а), проведя только три прямых.
Б. Френкин
13. (9-10) Пусть At и Ct - точки касания вписанной
окружности со сторонами ВС и АВ соответственно, а А' и С'
- точки касания вневписанной окружности треугольника, впи-
санной в угол В, с продолжениями сторон ВС и АВ соответ-
ственно. Докажите, что ортоцентр Н треугольника АВС лежит
на А£\ тогда и только тогда, когда прямые A'Q и В А
перпендикулярны.
Ф. Ивлев
14. (9-11) Точки М, N - середины диагоналей AC, BD
прямоугольной трапеции ABCD ( ZA - ZD = 90° ). Описанные
окружности треугольников ABN, CDM пересекают прямую ВС
в точках Q, R. Докажите, что точки Q, R равноудалены от
середины отрезка MN.
Д. Швецов
15. (9-11) а) В треугольник АВС вписаны треугольники
А\ВХСХ и А2В2С2 так, что CtAt ± ВС , AtBt ± С А , ВХСХ ± АВ ,
В2А2 1 ВС , С2В2 1 СА , А2С2 1 АВ . Докажите, что эти тре-
угольники равны.
В.Расторгуев
б) Внутри треугольника АВС взяли точки At, Вх, Ct , А2 ,
В2, С2 так, что At - на отрезке АВ{, - на отрезке ВС}, Сх
- на отрезке CAt, А2 - на отрезке АС2, В2 - на отрезке ВА2,
С2 - на отрезке СВ2 и углы ВААХ, СВВХ, ACCt, САА2, АВВ2 ,
29
ВСС2 равны. Докажите, что треугольники AiBiCi и А2В2С2
равны.
П. Кожевников
16. (9-11) Вписанная в треугольник АВС окружность каса-
ется сторон ВС, СА, АВ в точках А', ff, С' соответственно.
Перпендикуляр из центра I этой окружности на медиану из
вершины С пересекает прямую А'В' в точке К. Докажите, что
СК || АВ.
Ф. Ивлев
17. (9-11) Дан вписанный четырехугольник, острый угол
между диагоналями которого равен <р. Докажите, что острый
угол между диагоналями любого другого четырехугольника с
теми же длинами сторон меньше <р.
А. Заславский
18. (9-11) В треугольнике АВС проведена биссектриса AD.
Точки М и N являются проекциями В и С на AD. Окружность
с диаметром MN пересекает ВС в точках X и У. Докажите, что
ZBAX = ZCAY.
А. Иванов
19. (10-11) а) Вписанная окружность треугольника АВС
касается сторон АС и АВ в точках Во и Со соответственно.
Биссектрисы углов В и С треугольника АВС пересекают сере-
динный перпендикуляр к биссектрисе AL в точках Q и Р
соответственно. Докажите, что прямые РС0 и QB0 пересекают-
ся на прямой ВС.
6) В треугольнике АВС провели биссектрису AL. Точки С\ и
О2 - центры описанных окружностей треугольников ABL мАСЬ
соответственно. Точки Д и С, - проекции вершин С и В на
биссектрисы углов В иС соответственно. Докажите, что прямые
О1С1 и О1В1 пересекаются на прямой ВС.
в) Докажите, что точки, полученные в пунктах а) и б),
совпадают.
Д. Прокопенко
20. (10-11) На стороне АВ треугольника АВС взята произ-
вольная точка С\ . Точки А1, Вх на лучах ВС и АС таковы, что
ZACjBf = ZBCfAj = ZACB . Прямые AAt и BBi пересекаются в
точке С2. Докажите, что все прямые CtC2 проходят через одну
точку.
В. Ясинский
21. (10-11) Дана окружность со и точка А вне ее. Через А
проведены две прямые, одна из которых пересекает со в точках
30
В и С, а другая - в точках DnE (D лежит между А и Е). Прямая,
проходящая через D и параллельная ВС, вторично пересекает со
в точке F, а прямая AF - в точке Т. Пусть М - точка пересечения
прямых ЕТ и ВС, а X - точка, симметричная А относительно М.
Докажите, что описанная около треугольника DEN окружность
проходит через середину отрезка ВС.
В. Ясинский
22. (10-11) Общие перпендикуляры к противоположным
сторонам пространственного четырехугольника взаимно перпен-
дикулярны. Докажите, что они пересекаются.
А.Заславский
23. (10-11) Выпуклые многогранники А и В не имеют общих
точек. Многогранник А имеет ровно 2012 плоскостей симметрии.
Каково наибольшее возможное количество плоскостей симмет-
рии у фигуры, состоящей из А и В, если В имеет а) 2012; б) 2013
плоскостей симметрии?
в) Каков будет ответ в пункте б), если плоскости симметрии
заменить на оси симметрии?
В. Френкин
Финальный тур
8 класс
1. Дан равносторонний пятиугольник ABCDE с
прямыми углами АВС и AED. Диагонали BD и СЕ пересекаются
в точке F. Докажите, что отрезок FA равен стороне пятиуголь-
ника.
Н.Москвитин
2. Две окружности с центрами Ot и О2 пересекаются в точках
А и В. Биссектриса угла OtAO2 повторно пересекает окружности
в точках С и D.
Докажите, что центр описанной окружности треугольника
CBD равноудален от точек Ot и О2.
Д. Швецов
3. В выпуклом многоугольнике из каждой вершины опущены
перпендикуляры на все не смежные с ней стороны. Может ли
оказаться так, что основание каждого перпендикуляра попало на
продолжение стороны, а не на саму сторону?
Б. Френкин
4. Диагонали выпуклого четырехугольника ABCD пересека-
ются в точке В. В треугольнике ABL отметили точку пересечения
31
высот Н, а в треугольниках BCL, CDL и DAL - центры , О2
и О3 описанных окружностей. Затем весь рисунок, кроме точек
Н, , О2, О3, стерли. Восстановите его.
А. Заславский
5. Высота АА', медиана ВВ> и биссектриса СС' треугольни-
ка АВС пересекаются в точке К. Известно, что А'К = В?К .
Докажите, что и отрезок С'К имеет ту же длину.
Б. Френкин
6. На отрезке АВ построена дуга а . Окружность со касается
АВ в точке Т и пересекает а в точках С и D. Лучи АС и TD
пересекаются в точке Е, лучи BD и ТС - в точке F. Докажите,
что прямые EF и АВ параллельны.
Ф. Нилов
7. Три окружности касаются друг друга извне и касаются
четвертой окружности изнутри. Их центры были отмечены, а
сами окружности стерты. Оказалось, что невозможно устано-
вить, какая из отмеченных точек - центр объемлющей окружно-
сти. Докажите, что отмеченные точки образуют прямоугольник.
Б. Френкин
8. Пусть Р - произвольная точка на дуге АС описанной
окружности треугольника АВС, не содержащей точки В. Биссек-
триса угла АР В пересекает биссектрису угла ВАС в точке Ра ;
биссектриса угла СРВ пересекает биссектрису угла ВСА в точке
Рс. Докажите, что для всех точек Р центры описанных окруж-
ностей треугольников РРаРс лежат на одной прямой.
И. Дмитриев
9 класс
1. Пятиугольник ABCDE, все углы которого ту-
пые, вписан в окружность со. Продолжения сторон АВ и CD
пересекаются в точке Ех; продолжения сторон ВС и DE - в точке
Ai. Касательная, проведенная в точке В к описанной окружно-
сти треугольника ВЕХС , пересекает со в точке В{ ; аналогично
определяется точка Dx. Докажите, что BXDX || АЕ .
Д. Швецов
2. Две окружности со1 и СО2 с центрами Ох и О2 пересекаются
в точках А и В. Точки Си/), лежащие соответственно на и
о>2 по разные стороны от прямой АВ, равноудалены от этой
прямой. Докажите, что точки С и D равноудалены от середины
отрезка ОХО2 .
Ф. Нилов
32
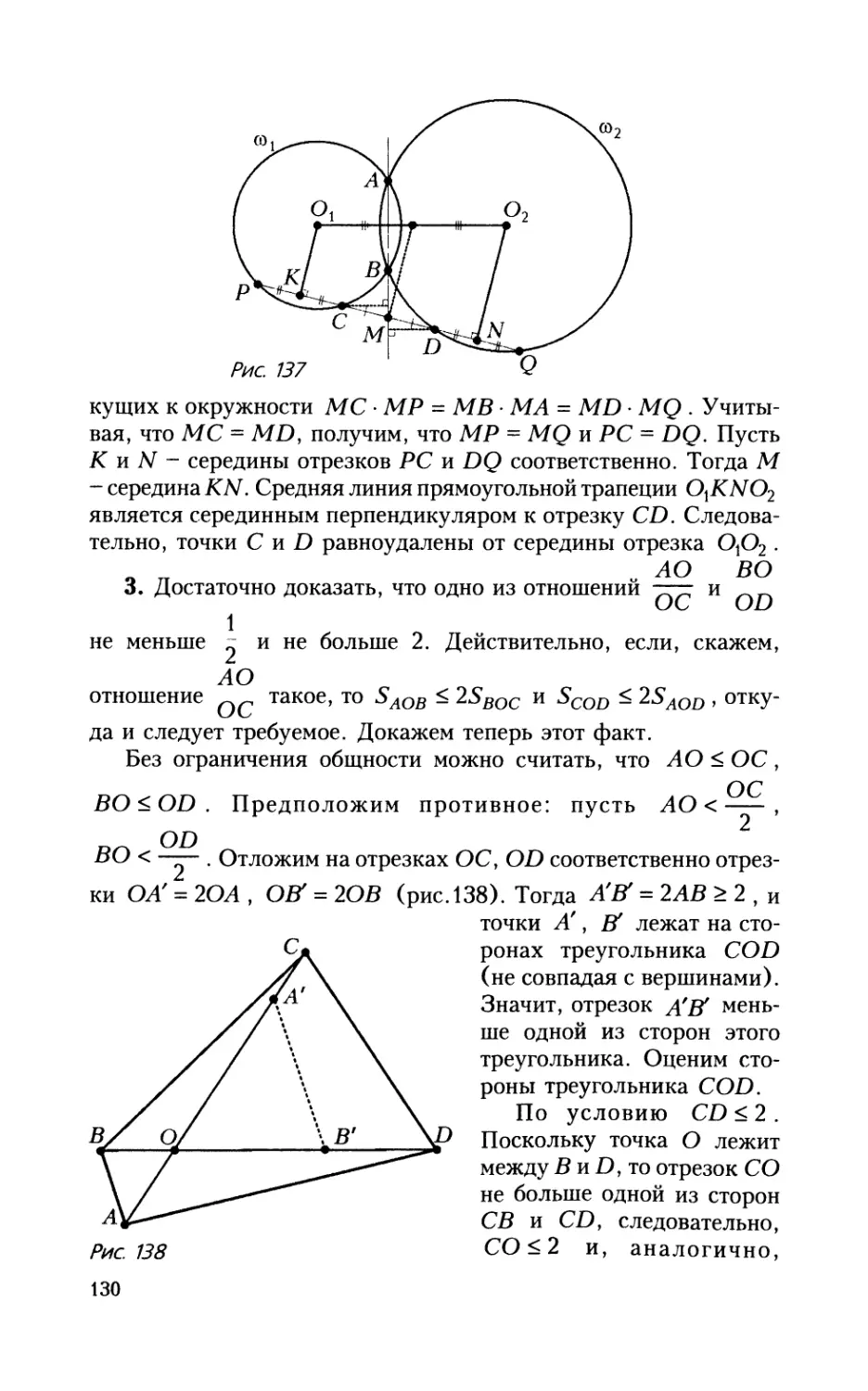
3. Длина каждой стороны выпуклого четырехугольника
ABCD не меньше 1 и не больше 2. Его диагонали пересекаются
в точке О. Докажите, что SAOB + SCOD < 2(SAOD + SBOC).
И. Богданов
Дан треугольник АВС и точка F, такая что XAFB =
= XBFC = XCFA . Прямая, проходящая через F и перпендику-
лярная ВС, пересекает медиану, проведенную из вершины А, в
точке At, Точки Bt и Q определяются аналогично. Докажите,
что At, Bt и Ct являются тремя вершинами правильного
шестиугольника, три другие вершины которого лежат на сторо-
нах треугольника АВС.
Н.Белухов
5. На сторонах АВ и АС треугольника АВС взяты точки Е и
F. Прямые EF и ВС пересекаются в точке S. Точки М и -
середины отрезков ВС и EF соответственно. Прямая, проходя-
щая через вершину А и параллельная ЛГЛГ, пересекает ВС в точке
К. Докажите, что ВК/СК = FS/ES.
В. Ясинский
6. Через вершину В правильного треугольника АВС проведе-
на прямая I. Окружность сой с центром 1а касается стороны ВС
в точке Ах и прямых /, АС. Окружность сос с центром 1С
касается стороны В А в точке Q и прямых I, АС. Докажите, что
ортоцентр треугольника АХВС} лежит на прямой 1а1с.
Д. Швецов, Ю.Зайцева, А. Соколов
7. Две окружности со1 и пересекаются в точке О.
Окружность с центром О и произвольным радиусом R пересека-
ет со1 в точках А и В, а ©2 _ в точках С и D. Пусть X - точка
пересечения прямых АС и BD. Докажите, что при изменении
радиуса R все точки X лежат на одной прямой.
А.Карлюченко
8. Три велосипедиста ездят по кольцевой дороге радиуса 1 км
против часовой стрелки с постоянными различными скоростями.
Верно ли, что, если они будут кататься достаточно долго, то
найдется момент, когда расстояние между любыми двумя из них
будет больше 1 км?
В. Протасов
Ю класс
1. Окружность k проходит через вершины В и С
треугольника АВС (АВ > АС) и пересекает продолжения сторон
АВ и АС за точки В и С в точках Р и Q соответственно. Пусть
33
AAt - высота треугольника АВС. Известно, что АХР = AXQ.
Докажите, что угол PAXQ в два раза больше угла А треугольни-
ка АВС.
В. Ясинский
2. В описанном четырехугольнике ABCD АВ = CD Ф ВС .
Диагонали четырехугольника пересекаются в точке L. Докажи-
те, что угол ALB острый.
А. Полянский
3. Пусть X - такая точка внутри треугольника АВС, что
ХА • ВС = ХВ • АС = ХС • АВ; Ц , 12, /3 - центры вписанных
окружностей треугольников ХВС, ХСА и ХАВ соответственно.
Докажите, что прямые АЦ , В12 и С13 пересекаются в одной
точке.
А.Карлюченко
4. Дан бумажный треугольник, площадь которого равна
1 /2, а квадраты всех сторон - целые числа. Докажите, что в него
можно завернуть квадрат с площадью 1/4 (треугольник можно
сгибать, но нельзя резать).
Н. Б слухов
5. Четырехугольник ABCD вписан в окружность с центром в
точке О. Точки Е nF - середины не содержащих других вершин
дуг АВ и CD соответственно. Прямые, проходящие через точки
Е и F параллельно диагоналям четырехугольника ABCD, пере-
секаются в точках К и L. Докажите, что прямая KL содержит
точку О.
Д. Швецов
6. В остроугольном треугольнике АВС высоты АА}, ВВ{ и
CQ пересекаются в точке Н. Из точки Н провели перпендику-
ляры к прямым В{СХ и AiQ , которые пересекли лучи СА и СВ
в точках Р и Q соответственно. Докажите, что перпендикуляр из
точки С к прямой A}B} проходит через середину отрезка PQ.
Д. Прокопенко
7. В пространстве отмечены 5 точек. Известно, что это центры
сфер, четыре из которых попарно касаются извне и касаются
изнутри пятой сферы. При этом невозможно определить, какая
точка является центром объемлющей сферы. Найдите отношение
радиусов наибольшей и наименьшей сферы.
Б. Френкин
8. Даны две окружности, одна из которых лежит внутри
другой. Из произвольной точки С внешней окружности проведе-
34
ны касательные к внутренней, вторично пересекающие внешнюю
в точках А и В. Найдите геометрическое место центров вписан-
ных окружностей треугольников АВС.
А. Заславский
X ОЛИМПИАДА
Заочный тур
1. (8) Дан прямоугольный треугольник АВС. На
катете АВ во внешнюю сторону построен равносторонний треу-
гольник ADB, а на гипотенузе АС во внутреннюю сторону -
равносторонний треугольник АЕС. Прямые DE и АВ пересека-
ются в точке М. Весь чертеж стерли, оставив только точки А и
В. Восстановите точку М.
Н.Москвитин, В. Протасов
2. (8) Есть бумажный квадрат со стороной 2. Можно ли
вырезать из него 12-угольник, у которого длины всех сторон
равны 1, а все углы кратны 45° ?
К.Кноп
3. (8) Вокруг равнобедренного треугольника АВС с основа-
нием АВ описана окружность и в точке В проведена касательная
к ней. Из С проведен перпендикуляр CD к касательной, также
проведены высоты АЕ и BF. Докажите, что D, Е, F лежат на
одной прямой.
Н.Москвитин
4. (8) В треугольник вписан квадрат (две вершины на одной
стороне и по одной на остальных). Докажите, что центр вписан-
ной окружности треугольника лежит внутри квадрата.
Б. Френкин
5. (8) В остроугольном треугольнике АВС проведены меди-
ана AM, биссектриса AL и высота АН (Н лежит между L и В).
При этом ML = LH = НВ. Найдите отношение сторон треуголь-
ника АВС.
Б. Френкин
6. (8-9) Дана окружность с центром О и не лежащая на ней
точка Р. Пусть X - произвольная точка окружности, У - точка
пересечения биссектрисы угла РОХ и серединного перпендику-
ляра к отрезку РХ. Найдите геометрическое место точек У.
А. Заславский
7. (8~9) Перпендикуляр, восставленный в вершине С парал-
лелограмма ABCD к прямой CD, пересекает в точке F перпенди-
35
куляр, опущенный из вершины А на диагональ BD, а перпенди-
куляр, восставленный из точки В к прямой АВ, пересекает в
точке Е серединный перпендикуляр к отрезку АС. В каком
отношении отрезок EF делится стороной ВС?
В. Румянцев
8. (8-9) Дан прямоугольник ABCD. Через точку В провели
две перпендикулярные прямые. Первая прямая пересекает сто-
рону AD в точке К, вторая прямая пересекает продолжение
стороны CD в точке L. Пусть F - точка пересечения KL и АС.
Докажите, что BF перпендикулярно KL.
Р. Садыков
9. (8-9) Окружности cot и СО2 , касающиеся внешним образом
в точке L, вписаны в угол ВАС. Окружность cot касается луча
АВ в точке Е, а окружность СО2 ~ луча АС в точке М. Прямая EL
пересекает повторно окружность СО2 в точке Q. Докажите, что
MQ || AL .
Д. Швецов
10. (8-9) В угол вписаны непересекающиеся окружности cot
и о>2 • Рассмотрим все пары параллельных прямых Zt и 12 таких,
что 1Х касается , 12 касается СО2 (> ^2 между Zt и 12 ).
Докажите, что средние линии всех трапеций, образованных
прямыми Zt , Z2 и сторонами данного угла, касаются фиксиро-
ванной окружности.
М. Кунгожин
И. (8-9) Точки К, L, М и N на сторонах АВ, ВС, CD и DA
квадрата ABCD образуют еще один квадрат. DK пересекает NM
в точке Е, а КС пересекает LM в точке F. Докажите, что
AF || АВ.
М. Плотников
12. (9-10) Окружности и СО2 пересекаются в точках А и
В. Пусть Кх и К2 - точки на и (О2 такие, что К{А касается
(О2, а К2А касается соответственно. Описанная окружность
треугольника К}ВК2 пересекает вторично прямые АКХ и АК2
в точках £4 и £2 соответственно. Докажите, что точки 1^ и Ь2
равноудалены от прямой АВ.
И. Макаров
13. (9-10) В окружности со с центром О фиксирована хорда
АС. Точка В движется по дуге АС. Точка Р - фиксированная
точка хорды АС. Прямая, проходящая через Р параллельно АО,
пересекает прямую В А в точке At; прямая, проходящая через Р
36
параллельно СО, пересекает прямую ВС в точке . Докажите,
что центр описанной окружности треугольника А1ВС1 движется
по прямой.
Д. Прокопенко, Д. Швецов
14. (9-11) Постройте подмножество круга, площадью в
половину площади круга, такое что его образ при симметрии
относительно любого диаметра пересекается с ним по площади,
равной четверти круга.
Фольклор
15. (9-11) В неравнобедренном треугольнике АВС высота из
вершины А, биссектриса из вершины В и медиана из вершины С
пересекаются в одной точке К.
а) Какая из сторон треугольника - средняя по величине?
Б. Френкин
б) Какой из отрезков АК, ВК, СК средний по величине?
А.Заславский
16. (9-11) Из некоторой точки D в плоскости треугольника
АВС провели прямые, перпендикулярные к отрезкам DA, DB,
DC, которые пересекают прямые ВС, АС, АВ в точках At, В{ ,
Q соответственно. Докажите, что середины отрезков ААХ, ВВХ,
СС} лежат на одной прямой.
Д. Прокопенко
17. (10-11) Дан прямоугольный треугольник с гипотенузой
АС, проведена биссектриса треугольника BD; отмечены середи-
ны Е и F дуг BD окружностей, описанных около треугольников
ADB и CD В соответственно (сами окружности не проведены).
Постройте одной линейкой центры окружностей.
П.Москвитин
18. (10-11) Пусть четырехугольник ABCD описан около
окружности с центром I. Касательные к окружности AIC в
точках А, С пересекаются в точке X. Касательные к окружности
BID в точках В, D пересекаются в точке У. Докажите, что точки
X, I, Y лежат на одной прямой.
А.Заславский
19. (10-11) Окружности и о>2 касаются друг друга
внешним образом в точке Р. Из точки А окружности , не
лежащей на линии центров окружностей, проведены касатель-
ные АВ, АС к (ty . Прямые ВР, СР вторично пересекают СО2 в
точках Е и F. Докажите, что прямая EF, касательная к СО2 в
37
точке А и общая касательная к окружностям в точке Р пересека-
ются в одной точке.
В. Ясинский
20. (10-11) Дан четырехугольник KLMN. Окружность с
центром О пересекает его сторону KL в точках А и А{, сторону
LM в точках Ви Bt, и т.д. Докажите, что
а) если описанные окружности треугольников KDA, LAB,
МВС и NCD пересекаются в одной точке Р, то описанные
окружности треугольников KD{A{, LA{B{, МВ{С{ и NCXD{
также пересекаются в одной точке Q;
6) точка О лежит на серединном перпендикуляре к PQ.
Н. Б слухов
21. (10-11) В четырехугольнике ABCD вписанная окруж-
ность со касается сторон ВС и DA в точках Е и F соответственно.
Оказалось, что прямые ЛВ, FE и CD пересекаются в одной
точке. Окружности, описанные около треугольников AED и
BFC, вторично пересекают окружность со в точках Е^ и Ft.
Докажите, что прямые EF и ЕД\ параллельны.
Н. Полянский, Д.Скробот
22. (10-11) Существует ли выпуклый многогранник, у
которого есть диагонали и любая диагональ меньше любого
ребра?
А. Блинков
23. (И) Дана тригармоническая четверка точек Л, В, С и D,
т.е. такая, что
АВ • CD = АС • BD = AD • ВС .
Пусть А^ - отличная от Л точка такая, что четверка точек At, В,
С и D тригармоническая. Точки Bt, Ct и Dx определяются
аналогично. Докажите, что
а) Л, В, Ct, £>t лежат на одной окружности;
б) точки At, Bt, Ct, Dt образуют тригармоническую
четверку.
А.Акопян
24. (11) Дана описанная четырехугольная пирамида АВ CDS.
Противоположные стороны основания пересекаются в точках Р
и Q, причем точки Л и В лежат на отрезках PD и PC. Вписанная
сфера касается боковых граней ABS и BCS в точках К и L.
Докажите, что если прямые РК и QL пересекаются, то точка
касания сферы и основания лежит на BD.
Ф. Нилов
38
Финальный тур
8 класс
1. Окружность, вписанная в прямоугольный тре-
угольник АВС, касается катетов АС и ВС в точках Bt и Д, а
гипотенузы - в точке Q . Прямые СХАХ и СХВХ пересекают С А
и СВ в точках Во и Aq соответственно. Докажите, что
АВ0 = BAq .
Ю. Зайцева, Д. Швецов
2. Пусть АНа и ВНЬ - высоты, a ALa и BLb - биссектрисы
треугольника АВС. Известно, что HaHb || LaLb . Верно ли, что
АС = ВС?
Б.Френкин
3. В треугольнике АВС отмечены середины сторон АС и ВС
- точки М nN соответственно. Угол MAN равен 15° , а угол BAN
равен 45° • Найдите угол АВМ.
А. Блинков
4. Таня вырезала из клетчатой бумаги треугольник, изобра-
женный на рисунке 3. Через некоторое время линии сетки
выцвели. Сможет ли Таня их вос-
становить, не пользуясь никаки-
ми инструментами, а только пере-
гибая треугольник (длины сто-
рон треугольника Таня помнит)?
Т. Казицына
5. Дан треугольник с углами
30, 70 и 80 градусов. Разрежьте
его отрезком на два треугольника
так, чтобы биссектриса одного из
этих треугольников и медиана
второго, проведенные из концов
разрезающего отрезка, были параллельны друг другу (достаточ-
но найти одно решение).
А. Шаповалов
6. Две окружности и k2 с центрами Ot и Q касаются
внешним образом в точке О. Точки X и У лежат на и k2
соответственно так, что лучи ОхХ и О2У одинаково направле-
ны. Из точки X проведены касательные к k2, а из точки У - к
. Докажите, что эти четыре прямые касаются одной окружно-
сти, проходящей через точку О.
В. Ясинский
39
7. Две точки окружности соединили ломаной, длина которой
меньше диаметра окружности. Докажите, что существует диа-
метр, не пересекающий эту ломаную.
Фольклор
8. Пусть М - середина хорды АВ окружности с центром О.
Точка К симметрична М относительно О, Р - произвольная
точка окружности. Перпендикуляр к АВ в точке А и перпенди-
куляр к РК в точке Р пересекаются в точке Q. Точка Н -
проекция Р на АВ. Докажите, что прямая QB делит отрезок PH
пополам.
Чан Куанг Хюнг
9 класс
1. Пусть ABCD - вписанный четырехугольник.
Докажите, что АС > BD тогда и только тогда, когда
(AD-BC)(AB-CD)>0 .
В. Ясинский
2. В четырехугольнике ABCD углы Л и С - прямые. На
сторонах АВ и CD как на диаметрах построены окружности,
пересекающиеся в точках X и У. Докажите, что прямая XY
проходит через середину диагонали АС.
Ф. Нилов
3. Дан острый угол А и точка Е внутри него. Постройте на
сторонах угла точки В, С так, чтобы Е была центром окружности
Эйлера треугольника АВС.
Е. Диомидов
4. Ортоцентр Н треугольника АВС лежит на вписанной в
треугольник окружности. Докажите, что три окружности с цен-
трами А, Bt С, проходящие через Н, имеют общую касательную.
Махди Этесами Фард, Иран
5. В треугольнике ABC Z.B = 60° , О - центр описанной
окружности, BL - биссектриса. Описанная окружность треу-
гольника BOL пересекает описанную окружность треугольника
АВС в точке D. Докажите, что BD ± АС .
Д. Швецов
6. Пусть I - центр вписанной окружности треугольника АВС,
М, N - середины дуг АВС и ВАС описанной окружности.
Докажите, что точки М, 7, N лежат на одной прямой тогда и
только тогда, когда АС + ВС = ЗАВ.
А. Полянский
40
7. Девять окружностей рас-
положены вокруг произвольно-
го треугольника, как показано
на рисунке 4. Окружности, каса-
ющиеся одной и той же стороны
треугольника, равны между со-
бой. Докажите, что три прямые
на рисунке пересекаются в од-
ной точке.
Н.Белухов
8. Выпуклый фанерный мно-
гоугольник Р лежит на деревян-
ном столе. В стол можно вбивать
гвозди, которые не должны проходить через Р, но могут касаться
его границы. Фиксирующим назовем набор гвоздей, не позволя-
ющий двигать Р по столу. Найдите минимальное количество
гвоздей, позволяющее зафиксировать любой выпуклый много-
угольник.
Н.Белухов, С.Герджиков, Болгария
10 класс
1. Вершины равнобедренного треугольника и центр
его описанной окружности лежат на четырех различных сторо-
нах квадрата. Найдите углы треугольника.
И.Богданов, Б. Френкин
2. Дана окружность, ее хорда АВ и W - середина меньшей
дуги АВ. На большей дуге АВ выбирается произвольная точка С.
Касательная к окружности из точки С пересекает касательные из
точек А и В в точках X и Y соответственно. Прямые WX и WY
пересекают прямую АВ в точках N и М соответственно. Докажи-
те, что длина отрезка НМ не зависит от выбора точки С.
А.Зерцалов, Д.Скробот
3. Верно ли, что существуют выпуклые многогранники с
любым количеством диагоналей (диагональю называется отре-
зок, соединяющий две вершины многогранника и не лежащий на
его поверхности)?
А. Блинков
4. Дан треугольник АВС и точка D, не совпадающая с
вершинами треугольника. Окружность с центром в D, проходя-
щая через А, пересекает прямые АВ и АС в точках А^ и Ас
соответственно. Аналогично определяются точки Ва , Вс, Са и
41
Cb . Сколько может существовать таких точек D, что точки ,
Ас , Ва , Вс, Са и Сь лежат на одной окружности?
А.Гаркавый, А. Соколов
5. В треугольнике провели высоту из одной вершины, биссек-
трису из другой и медиану из третьей, отметили точки их
пересечения, а затем все, кроме этих отмеченных точек, стерли.
Восстановите треугольник.
А.Заславский
6. Вписанная окружность треугольника АВС касается АВ в
точке с' • Окружность с диаметром ВС' пересекает вписанную
окружность в точке Д , а биссектрису угла В в точке А2 .
Окружность с диаметром АС' пересекает вписанную окруж-
ность в точке , а биссектрису угла А в точке В2 . Докажите,
что прямые АВ, АХВХ, А2В2 пересекаются в одной точке.
Э.Х. Гарсиа, Испания
7. Докажите, что для любого тетраэдра его самый маленький
(из шести) двугранный угол не больше, чем двугранный угол
правильного тетраэдра.
С.Шлосман, О.Огиевецкий
8. Дан вписанный четырехугольник ABCD. Внутри треуголь-
ника BCD взяли точку La, расстояния от которой до сторон
треугольника пропорциональны этим сторонам. Аналогично внут-
ри треугольников ACD, ABD, АВС взяли точки Lb , Lc , и Ld
соответственно. Оказалось, что четырехугольник LaLbLcLd впи-
санный. Докажите, что ABCD - трапеция.
Н.Белухов
РЕШЕНИЯ ЗАДАЧ
VI ОЛИМПИАДА
Заочный тур
1. Нет, так как наибольшая сторона треугольника
длиннее любой из его высот, медиан или биссектрис. Действи-
тельно, любой отрезок, соединяющий вершину треугольника с
точкой на противоположной стороне, короче, по крайней мере,
одной из двух других сторон. Поэтому любая медиана или
биссектриса короче хотя бы одной из сторон и, тем самым,
короче наибольшей стороны. Тем более это верно для высот.
2. Первое решение. Пусть А2, В2 Q ” проекции точек Ах,
Вх, I на АВ (рис.5). Так как AAt - биссектриса, то АА2 = АС .
С другой стороны, АС2 -
касательная из А к вписан-
ной окружности треугольни-
ка, и, значит, отрезок
А2С2 = АА2 - АС2 равен ка-
сательной к этой окружности
из точки С. Аналогично по-
лучаем, что отрезок В2С2
равен той же касательной,
т.е. С2 - середина А2В2. По теореме Фалеса С21 пересекает
отрезок AtBt в его середине, а так как треугольник САХВХ
прямоугольный, эта середина совпадает с центром его описанной
окружности.
Второе решение. (Райко Арсений, школа 179, Москва)
Обозначим через А2, В2 основания перпендикуляров, опущен-
ных из точек At, Bt на гипотенузу АВ соответственно. Из
равенства прямоугольных треугольников ВСВХ и ВВ2ВХ следу-
ет, что ХВВхС = ЛВВХВ2. Получаем, что для треугольника
АВхВ2 точка I является центром вневписанной окружности.
Следовательно, В21 - биссектриса прямого угла ВХВ2А2 . Таки-
ми же рассуждениями показываем, что А21 является биссектри-
сой прямого угла АХА2В2. Таким образом, треугольник В21А2 -
равнобедренный прямоугольный, т.е. точка I лежит на середин-
ном перпендикуляре к А2В2. Точка О, будучи серединой боко-
43
вой стороны В1А1 прямоугольной трапеции В2ВХАХА2 , также
обладает этим свойством. Поэтому OI ± В2А2 .
3. Пусть Y - отличная от С' точка пересечения окружностей
АВ'С' и ВС'А'. Тогда, так как XB'YC' = я - ХВАС и
ZC'KA' = я - ХСВА , то XA'YB' = я - ZACB , т.е. У лежит так-
же на окружности С A'S'. Заметим теперь, что
XAYB = XAYC' + ZC'KB = ZAB'C' + ZC'A'B =
= 2я - ZC'B'C - ZCA'C' = ZACB + ZA'C'B' = XAXB
(рис.6). Аналогично, ZBYC = ZBXC , т.е. точки X и У совпа-
дают.
4. Рассматривая вписанный пятиугольник AXNBXCD , полу-
чаем, что AXN = BXN , так как равны опирающиеся на эти дуги
углы BDA и ВС А. Аналогично, NCX = NDX. Кроме того,
ZNAXA = ZACD = ZABD = ZDDXN (рис.7). Следовательно,
NDX = NAX, что и требовалось доказать.
5. Прежде всего заметим, что серединные перпендикуляры к
отрезкам АЕ и ЕС являются средними линиями треугольника
АЕС и, значит, проходят через F. Таким образом, надо доказать,
44
совпадает с точкой, симмет-
что FE ~ медиана треугольника FO1O2 . При этом ОХО2 || АС,
так как оба эти отрезка перпендикулярны BD. Пусть прямая,
проходящая через Е и параллельная АС, пересекает FOX и FO2
в точках X и Y (рис.8). Так как FCEX и FAEY - параллелограм-
мы, то ХЕ = FC = FA = EY. Следовательно, FE - медиана
треугольника FXY, а значит, и треугольника FOXO2 .
6. Так как ХВАМ + XNAC = XMAN и АВ = АС, точка,
симметричная В относительно AM,
ричной С относительно AN. Обо-
значим эту точку через L. Тогда
XALM = ХАВМ = ХАСМ , т.е. L
лежит на окружности АСМ. Анало-
гично, L лежит на окружности ABN
и, значит, совпадает с К (рис.9).
Поэтому XKAN = XNAC = 30° -
- ХВАМ = 90° - XNMA . Но по те-
ореме о вписанном угле прямая,
соединяющая А с центром описан-
ной около треугольника AMN ок-
ружности, образует с прямой AN
такой же угол.
7. Достроим данный треугольник до параллелограмма ABCD
(рис. 10). Так как ХВКА = XDKC = XBDA , точки А, В, К, D
лежат на одной окружности и ОХМ ± BD. Аналогично,
О2М ± BD . Кроме того, так как треугольники ABD и BCD
равны, то равны и расстояния от центров описанных около них
окружностей до точки М.
8. Докажем, что треугольник LIbIc - равнобедренный и
прямоугольный. Пусть Lb , Lc - проекции точек 1Ь, 1С на ВС,
45
Так как эти треугольники прямоугольные, то
гь = (АН + ВН- АВ)/2 , гс = (АН + СН- АС)/2 и
rb - rc = (ВН - СН)/2 - (АВ - АС)/2 =
= (ВН - СН)/2 - (BL - CL)/2 = LH .
Следовательно, IbLb = LIC = rb , ICLC = LIb = rc, т.е. треугольни-
ки LIbLb и ICLCL равны, LIb - LIC и ZIbLIc = 90° . Соответ-
ственно, ^LIbIc = 45°.
Замечание. Пусть Ц, /2 ~ центры вписанных окружностей
треугольников ABD и CBD соответственно (D - произвольная
точка на AC); L - точка касания вписанной окружности треу-
гольника АВС со стороной АС. Тогда точки , £, D и /2 лежат
на одной окружности.
9. Так как хорошие точки симметричны относительно высоты
треугольника из вершины В, а число их нечетно, то найдется
хорошая точка, лежащая на этой высоте. Так как чевиана через
эту точку из вершины А не короче высоты из той же вершины,
высота треугольника из А не длиннее, чем из В, т.е. АС < АВ .
Более того, АС не может быть длиннее высоты из В, так как
иначе на этой высоте было бы две хороших точки. Предположим
теперь, что некоторая хорошая точка не лежит на высоте. Пусть
АА', ВВ', С С' ~ проходящие через нее чевианы, a AAt, CCt -
высоты треугольника. Тогда AtA' = CtC', причем одна из точек
А', С' лежит между основанием соответствующей высоты и
точкой В, а другая - нет. Но отсюда следует, что соответствую-
щие чевианы короче АС и тем более короче BBt - противоречие.
Значит, хорошая точка только одна.
10. Проведем прямые а, Ь, с, параллельные ВС, СА, АВ и
лежащие от них на расстоянии ширины линейки с внешней
стороны треугольника. Прямые а,
Ь, ВС, АС образуют ромб, диаго-
/ I \ наль которого является биссект-
/ 1С \ рисой угла С. Пусть Е - точка
/ / \ \ пересечения этой биссектрисы с
Ь/ / I \ \ прямой с, &F- точка пересечения
/ / I \ \« диагоналей трапеции, образован-
/ / I \ \ ной прямыми с, АВ, АС и ВС
/ / I \ \ (рис. 12). Тогда прямая EF пере-
/д/ jj I \о \ секает АВ в искомой точке D.
Л— \ И- п = 4 или и = 5.
Очевидно, п > 3. Предполо-
жив 12 жим, что п > 5. Тогда одна из
46
частей n-угольника имеет не менее п + 1 стороны, вторая - и,
третья - не менее 3. При соединении этих частей либо три пары
сторон соединяются внутри многоугольника и не более трех пар
образуют его стороны, либо две пары соединяются внутри и не
более четырех образуют стороны. В любом случае суммарное
количество сторон частей превосходит п не более чем на 9, что
при п > 5 невозможно. Примеры для п = 4, 5 показаны на
рисунке 13.
12. а) Первое решение. Проведем высоту HN к основанию
равнобедренного треугольника СНМ, тогда CLV = NM. Так как
ВН = В'Н и NH || ВС , то прямая, проходящая через точку В'
параллельно HN, пересечет АС в точке М (по теореме Фалеса).
Второе решение. Имеем АСМН = АМСН = АСВВ' =
= ЛСВ^В = а , поэтому точки С, Н, & и М лежат на одной
окружности. Следовательно, ZCB'M = АС НМ = 180° - 2а , тог-
да ААВ'М = а , что и требовалось.
б) Из прямоугольного треугольника АВС: СН2 = АН • ВН .
Так как В'Н = ВН и КН = СН, то КН2 = АН • В'Н , т.е.
треугольники АКН и АН К подобны, откуда и вытекает утвер-
ждение задачи.
13. Возьмем на BD такую точку L, что AALB = АЛ . Так как
треугольники ABL и DBA подобны, BL • BD = АВ2 = ВС2 .
Значит, треугольники CBL и DBC тоже подобны, т.е.
ABLC = ZC и L совпадает с К. Требуемое равенство, очевидно,
следует из указанных подобий.
14. Так как ААВМ = АВМС = AM CD, то SABM/SBMC-
= АВ МС и SBMC SCMD = ВМ CD . Но треугольники АВМ и
MCD подобны, так что эти отношения равны и SBMC =
= $авм ’ $мсо • По неравенству о среднем арифметическом и
среднем геометрическом SBMC <(SABM + $mcd)m , что равно-
сильно утверждению задачи.
15. а) Треугольники ЛВ^СА , А}ВСХ и АХВХС подобны треу-
гольнику АВС с коэффициентами cos АЛ , cos ZB , cos ZC
47
соответственно. Поэтому ХКАхСх = ХКАхВх = 90° - ZA , и по те-
ореме синусов диаметры описанных окружностей треугольников
АКВХ и АХКСХ равны соответственно BxKlcosXA и QX/cosZA .
Следовательно, их сумма равна B^CjcosXA = ВС .
б) Доказанное в предыдущем пункте равенство можно пере-
писать в виде
AXN t AXL
sin ZB sin ZC
= BC .
Разделив его на ВС, получим искомое соотношение.
16. Первое решение. Прежде всего заметим, что
XBCD = ХЕСХ, так как соответствующие дуги заключены
между параллельными хордами. Кроме того, из равенства углов
ABD и АЕВ следует подобие треугольников ABD и АЕВ и,
значит, равенство BD/BE =
= AD/AB. Аналогично, по-
лучаем, что CD/CE =
= AD/AB, т.е. BD CE =
= CDBE = BC- DE/2 (пос-
леднее равенство следует из
теоремы Птолемея).
Пусть теперь СХ пересе-
кает DE в точке М (рис. 14).
Тогда треугольники CBD и
СМЕ подобны, следователь-
и из предыдущего равенства
но, BD СЕ = CB EM .
получаем, что EM = ED/2.
Второе решение. (Руденко Александр, лицей 171 «Лидер»,
Киев) Заметим, что XDMC = ^(u£)C + иХЕ). По условию
DE || ВХ => uBD = uEX . С другой стороны,
Отсюда
ZCOB = uCB = uCD + uDB = uCD + uEX = 2XCMD .
Откуда следует, что ZCOA = ХСОВ = XCMD , поэтому точки
А, С, М, О лежат на одной окружности. Следовательно,
ХАМО = ХАСО = 90° , т.е. МО 1 DE =» DM = ME .
17. Первое решение. Пусть I = CL, h = СН - биссектриса и
высота из вершины С, т = ВМ - медиана из вершины В, (р - угол,
который в прямоугольном треугольнике с гипотенузой длины /
противолежит катету длины h. Через р обозначим прямую,
содержащую точку С и параллельную прямой АВ, а через В' -
точку, симметричную точке В относительно прямой р.
48
Предположим, что треугольник АВС построен. Тогда выпол-
нено хотя бы одно из равенств ZCLB = ф или ZCLB = 180°-
- Ф , и в любом случае имеем Z.B>СМ = 2ф. В самом деле, если,
например, ZCLB = ф, то Х&СМ = 360° - 2ХСВА - ХВСА =
= 2(180° - ХСВА - /.ВСЕ) = 2ф (рис. 15). Второй случай разби-
рается аналогично.
Итак, отрезок В'М виден из
точки С под углом 2ф. Отсюда
получаем следующее построение.
Проведем две параллельные
прямые на расстоянии h друг от
друга и отметим на одной из них
точку В; другая прямая будет
прямой р. Далее отмечаем точку
Ё , а затем - точку М, удален-
ную на расстояние т от В и
равноудаленную от параллельных прямых. Построив угол ф,
строим две дуги окружностей с концами в точках В> и М и
угловой величиной 360° - 4ф.
Если Q и С2 - точки пересечения дуг с прямой р, а Д- (г =
= 1,2)- точка, симметричная Ci относительно М, то каждый из
треугольников АХВСХ и А2ВС2 является искомым.
Действительно, высоты этих треугольников, проведенные из
вершин Q , С2, равны Л, а отрезок ВМ = т является в каждом
из них медианой. Кроме того, если Ц , Е - основания соответ-
ствующих биссектрис, то из построения следует, что один из
углов СХЦВ и С2ЕВ равен ф, а другой 180° - ф, откуда, в силу
определения угла ф, получаем С/^ = С2Е = /.
Примечание 1. Ясно, что если / < h или т < h/2, то решений
нет. Если I = h и т > h/2 , решением является единственный
равнобедренный треугольник (при т = h/2 вырождающийся в
отрезок). В случае, когда / > h и т = h/2, получаем два равных
треугольника, симметричных относительно прямой В В'.
При I > h п т — 1/2 один из построенных треугольников
оказывается вырожденным, так что решение единственно. Во
всех остальных случаях задача имеет два решения.
Второе решение. Зная высоту и биссектрису из вершины С,
можно построить эту вершину и прямую АВ. Рассмотрим теперь
следующее отображение этой прямой в себя. Для произвольной
точки X найдем точку У, удаленную от X и АВ на расстояния,
равные данной медиане из вершины В и половине данной высоты
(рис. 16). Затем отразим прямую СУ относительно биссектрисы
и найдем точку X' пересечения полученной прямой с АВ.
49
в=х
Рис 16
Очевидно, что это отображе-
ние сохраняет двойные отно-
шения точек и переводит точку
В в себя. Таким образом, зада-
ча сводится к известной задаче
построения неподвижной точ-
ки проективного преобразова-
ния прямой.
Примечание 2. В 1938 г. в
журнале «Математика в шко-
ле» была напечатана статья В.Фурсенко, в которой разбирались
все задачи на построение треугольника по трем элементам. Эта
задача там была ошибочно названа неразрешимой.
18. Так как углы ADB и ВЕС прямые, точки D и Е лежат на
окружности с диаметром BG. При этом XFDG = XADOx =
= XDAC = XGED . Следовательно,
FD (и аналогично FE) - касательная
к этой окружности (рис. 17). Значит,
эта прямая симметрична медиане тре-
угольника GED из вершины G отно-
сительно биссектрисы из этой же вер-
шины. Поскольку треугольник GDE
подобен треугольнику GCA, в этом
последнем треугольнике данная пря-
мая будет медианой.
19. Достаточно доказать, что ХО =
= OY. Действительно, тогда анало-
гично получим, что UO = OV и,
значит, XUYV - параллелограмм.
Пусть прямая ЕО пересекает ок-
ружность в точках Р и Q (рис. 18). Искомое равенство равно-
сильно равенству двойных отношений (РХ; OY) = (0У; ОХ).
Спроецировав прямую ЕО на
окружность из точки С, полу-
чим эквивалентное равенство
(РЛ; С'В) = (QB; С'Л), кото-
рое верно, так как прямые
PQ, АВ и касательная к ок-
ружности в точке С' пересе-
каются в одной точке.
20. Достаточно доказать,
что ХСАР = ХА'АР . Дей-
ствительно, это означает, что
Рис. 18
50
прямая АЛ' симметрична АР относительно биссектрисы угла А.
Тогда аналогично В S' симметрична ВР относительно биссектри-
сы угла В, а значит, точка пересечения этих прямых лежит на
прямой, симметричной СР относительно
биссектрисы угла С, т.е. на высоте треу-
гольника.
Пусть Q - точка пересечения прямой
АР с окружностью, 5 - середина дуги
В]С] (рис. 19). Композиция проекций ок-
ружности на себя из точек А и А2 меняет
местами точки и Ct , переводит Q в А'
и оставляет 5 на месте. Значит,
(B1Q;5C1) = (C1A';5B1), т.е. точки А' и
Q симметричны относительно прямой
АА2, что равносильно искомому равен-
ству.
21. Если бы стороны АВ и CD были
параллельны, то выполнялись бы равен-
ства ZABD = АВ DC и AACD = ABAC . Поэтому условие зада-
чи равносильно тому, что лучи АВ и DC пересекаются, т.е.
расстояние от С до прямой АВ меньше, чем от D, а расстояние
от В до прямой CD меньше, чем от А. Поэтому SABD > SABC и
$ACD > $BCD •
22. Возьмем произвольную точку окружности А, лежащую
вне параболы. Так как прямая AF и прямая, проходящая через
А и параллельная оси параболы, вторично пересекают окруж-
ность в точках, симметричных относительно оси, касательные из
А к параболе также пересекают окружность в точках В и D,
симметричных относительно оси. Аналогично получаем, что
вторые касательные из В и D вторично пересекают окружность
в точке С, симметричной А. Следовательно, А, В, С, D - искомые
точки.
23. Пусть Р - точка пересечения FC и AD; G - вторая точка
пересечения описанной окружности шестиугольника с прямой
ВР. Тогда 2 = (AC; BF) = (DF; GB) = (DF; ЕВ), и, следова-
тельно, точки G и F совпадают.
24. Пусть плоскость, проходящая через А и перпендикуляр-
ная I, пересекает I в точке В, а С - проекция У на эту плоскость.
Так как ВС || XY , то ВС ± А У и по теореме о трех перпенди-
кулярах ВС ± АС. Следовательно, С лежит на окружности с
диаметром АВ, а У - на цилиндре, образующие которого
проходят через точки этой окружности. Очевидно, что любая
точка цилиндра принадлежит искомому ГМТ.
51
25. Заметим, что ни один из икосаэдров не может содержать
четырех вершин октаэдра. Действительно, среди четырех вер-
шин октаэдра обязательно найдутся две противоположные, а
любая из остальных вершин образует с ними равнобедренный
прямоугольный треугольник. Но среди вершин икосаэдра нельзя
выбрать три вершины такого треугольника.
Таким образом, одному из данных икосаэдров принадлежат
три вершины одной грани октаэдра, а другому - три вершины
противоположной грани. Заметим теперь, что между вершинами
икосаэдра существуют только три различных расстояния: одно
равно ребру икосаэдра, другое - диагонали правильного пяти-
угольника со стороной, равной ребру, третье - расстоянию
между противоположными вершинами. При этом правильный
треугольник могут образовывать только вершины с расстояния-
ми первых двух видов. Так как икосаэдры неравны, то для
одного из них грань октаэдра совпадает с гранью, а для другого
с треугольником, образованным диагоналями. Следовательно,
отношение ребер равно отношению диагонали правильного пяти-
л/5 + 1
угольника к его стороне, т.е. —-— .
Финальный тур
8 класс
1. Обозначим через I точку пересечения биссект-
рис, а через X и Y - точки пересечения высоты с биссектрисами
углов В и С соответственно (рис.20). Пусть для определенности
АВ > АС; тогда точки I и У лежат
на отрезках BY и АХ соответствен-
но. Значит, ZA/y = ZA/2 +
+ ZB/2 = 90° - ZC/2 = Z.IXY , от-
куда (по теореме об угле между
касательной и хордой) сразу сле-
дует утверждение задачи.
2. Обозначим искомое ГМТ че-
рез Ф . Очевидно, что Ф пусто при
АВ > 2, а при АВ = 2 является
кругом с диаметром АВ. Пусть
АВ < 2, а окружности сол, сов с
центрами А, Ви радиусами, равными 1, пересекаются в точках
Р и Q. Рассмотрим круги единичного радиуса, покрывающие
точки А и В; ГМТ их центров есть «линза», образованная дугами
PQ окружностей сол и сов. Значит, Ф есть объединение кругов
52
единичного радиуса с центрами в
этой линзе.
Построим точки Pt, Р2, Qi, Q2
такие, что Р - середина отрезков
АР[, ВР2, a Q - середина отрез-
ков AQX, BQ2, и проведем четы-
ре дуги окружностей: PXQ} с цен-
тром А и радиусом 2, P2Q2 с
центром В и радиусом 2, PtP2 с
центром Р и радиусом 1, QXQ2 с
Рис. 21
центром Q и радиусом 1 (рис.21). Докажем, что Ф есть фигура,
ограниченная этими дугами. Ясно, что любая точка X этой
фигуры принадлежит Ф . В самом деле, если X лежит в секторе
PtPP2, то она лежит в круге с центром Р; если же она лежит в
секторе PXAQX, то она лежит в круге с центром У, где У - точка
пересечения луча АХ и дуги PQ
окружности cot. Остальные слу-
чаи аналогичны.
Осталось показать, что любая
точка X вне нашей фигуры не при-
надлежат Ф . Если X лежит в угле
P1AQ1, то АХ > 2, и точки А и X не
накрываются единичным кругом.
Пусть теперь X лежит в угле PtPP2 ;
нам надо доказать, что расстояние
от X до любой точки У, лежащей в линзе, больше 1. Для этого
покажем, что XXPY > 90° (и, следовательно, XY > ХР > 1 ).
Пусть для определенности в угле XPY лежит точка Pt (рис.22);
тогда Z.XPY > XPxPY . С другой стороны, AY < 1 , а АРХ = 2 ,
откуда PtY > 1 > AY . Это и означает, что точки А и У лежат по
одну сторону от серединного пер-
пендикуляра к АРХ , т.е.
90° < ДРУ < Z.XPY .
3. Поскольку прямые ВР и
СР являются медианами тре-
угольников АВС и BCD, то точ-
ки А и С равноудалены от ВР, а
В и D - от СР (рис.23). Это
значит, что SPAB = SPBC =
= SPCD . С другой стороны, вы-
соты треугольников РАВ и PCD
из точки Р равны, так как Р
53
лежит на биссектрисе; значит, равны и их основания, что и
требовалось доказать.
4. Можно считать, что ОА2 > ОАХ (рис.24). Треугольники
ОАХВ2 и ОВхА2 равны по двум сторонам и углу между ними,
значит, ЛОВ2АХ = ЛОА2Вх и АОАхВ2 = ЛОВХА2. Далее, из ра-
венства ААХОВ{ = ЛВ2ОА2 = ф следует, что ЛАХСХВХ = 90° -
- ф/2 = 180° - (90° + ф/2) = 180° - ЛА2С2В2. Следовательно, че-
тырехугольник В2С2ВХСХ вписан, поэтому ZB1C2C1 = ZB1B2C1 =
= Z.OA2BX . Наконец, поскольку прямые CtC2 и ОА2 образуют
равные углы с хордой А2С2 окружности g>2 , а ОА2 - касатель-
ная, то и CtC2 - также касательная. Касание CtC2 и cty
доказывается аналогично.
Замечание. Другое решение можно получить, заметив, что из
равенства треугольников ОАХВ2 и ОА2ВХ следует АХВ2 = А2ВХ,
а затем, применив теорему о секущей и касательной:
ВХС2 • ВХА2 = ВХВ2 = В2СХ • В2Ах , откуда В2СХ = ВХС2. Теперь,
поскольку четырехугольник ВХС2В2СХ вписан, он является рав-
нобокой трапецией и, следовательно, симметричен относительно
линии центров наших окружностей.
5. Так как АН ± LM , то LM || ВС , т.е. LM - средняя линия
треугольника. Значит, BL - биссектриса и медиана треугольни-
ка ЛВС, т.е. АВ = ВС. Поскольку BL является биссектрисой
углов АВС и HLM, точки Н и М симметричны относительно нее;
1 1
значит, - АВ = ВМ = ВН = ~ВС , и высота АН является меди-
аной треугольника АВС. Таким образом, АС = АВ = ВС,
треугольник АВС - равносторонний, и из симметрии СМ делит
HL пополам, что и требовалось доказать.
6. Первое решение. Заметим, что прямые АЕ и BF перпенди-
кулярны, поскольку получаются друг из друга поворотом на 90°
54
G
Рис. 25
вокруг центра квадрата. Пусть пря-
мая, проходящая через А и парал-
лельная BF, пересекает прямую CD в
точке G. Так как ABFG - параллело-
грамм, то FG = АВ и, значит, FD =
= DG. По теореме Фалеса прямая,
проходящая через D и параллельная
BF, является медианой треугольника
ADP. Поскольку АЕ ± BF , эта пря-
мая является и высотой (рис.25). Сле-
довательно, треугольник ADP - рав-
нобедренный, как и треугольник AED.
Угол EAD в обоих треугольниках
является углом при основании, поэто-
му углы при вершинах также равны.
Второе решение. Опять же заметим, что AAPF = 90° =
= ZADF. Значит, четырехугольник APFD вписан, откуда
2ADP = AAFP = ZAFB . С другой стороны, AAFB = AAED ,
поскольку треугольники ABF и ADE равны.
Третье решение. Пусть АВ = 1. Поскольку ВР - высота
1
прямоугольного треугольника с катетами 1 и - , получаем АР :
РЕ = 4 : 1. Тогда по теореме Фалеса проекция отрезка DP на CD
4
равна —. Аналогично получаем, что его проекция на AD равна
3
5 . Значит, по теореме Пифагора DP = 1 = AD. Дальнейшие
рассуждения такие же, как в первом решении.
7. Да, может; 3 или 4 стороны.
Примеры, как может получиться правильный треугольник
или квадрат, приведены на рисунке 26. Предположим, что у
полученного многоугольника М хотя
бы 5 сторон. Разрез пересекает его
по двум точкам, каждая из которых
принадлежит максимум двум сторо-
нам. Значит, у М есть сторона АВ,
не имеющая общих точек (даже вер-
шин) с разрезом. Пусть она лежит в
куске, полученном из Р; тогда сто-
рона Р равна АВ, и углы при ней
равны углам многоугольника М.
Поскольку правильный многоугольник однозначно задается сто-
роной и углом при ней, то Р = М, что невозможно.
Ik-
Рис 26
55
8. Нет, не обязательно.
Покажем, что условию задачи удовлетворяет любой треу-
гольник с ZC = 120°. Пусть CQ - биссектриса угла С. Тогда
САХ - внешняя биссектриса угла АССХ, т.е. точка Ах равноуда-
лена от прямых АС и CQ . Но она также равноудалена от
прямых АС и АВ, поэтому CtAt - биссектриса угла CCtB .
Значит, точка J, симметричная I относительно С^А} , лежит
на прямой АВ (рис.27). Заметим, что
ZAAfii = ЛА^В - ЛА^АВ = - (ZCCjB - АС АВ} = 1АССХ = 30°,
откуда
ZIAXJ = 2ZAAtC = 60°.
Итого, в равнобедренном треугольнике IAXJ ( ZAt = AXJ ) угол
равен 60°; значит, он равносторонний, IJ = /А1, и потому
А2 = J . Таким образом, мы получили, что A2Q = JCX = ICX.
Аналогично получаем A2Ct = JC{ = ICX, что и требовалось дока-
зать.
Замечание. Можно показать, что в треугольнике, удовлетво-
ряющем условию задачи, обязательно либо АС = ВС, либо
ZC = 120° .
9 класс
1. 60°.
Нетрудно посчитать, что угол между биссектрисой
и высотой в вершине X треугольника XYZ равен - ZZ|.
Следовательно, если эти углы в вершинах А и В треугольника
АВС равны, то ZA - ZC = ZB - ZC или ZA - ZC = ZC - ZB .
В первом случае треугольник равнобедренный, т.е. высота и
биссектриса из вершины С совпадают, что противоречит усло-
вию. Во втором случае
ZC = | (ZA + ZB) = | (180° - ZC) = 60° .
56
Замечание. Условие задачи выполняется в любом неравнос-
тороннем треугольнике с ZC = 60° .
2. Очевидно, что, если одна из описанных окружностей
лежит внутри другой, то утверждение задачи выполнено, а если
каждая из окружностей лежит вне другой, то треугольники не
могут пересекаться. Поэтому будем считать, что описанные
окружности треугольников пересекаются в точках Р и Q (воз-
можно, совпадающих), и предположим, что утверждение задачи
не выполняется. Тогда вершины каждого из треугольников
лежат на дуге PQ соответствующей окружности, расположенной
вне другой окружности. Но эти дуги лежат по разные стороны от
прямой PQ. Значит, сами треугольники тоже лежат по разные
стороны от этой прямой и не могут пересекаться. (В случае, если
Р = Q, в качестве прямой PQ
рассматривается общая каса-
тельная к окружностям.)
3. Через Z(fe, /) будем обо-
значать направленный угол
между прямыми k и / (счита-
ющийся против часовой стрел-
ки).
При повороте на 60° по
часовой стрелке вокруг В точ-
ки А и С переходят соответ-
ственно в X и Y (рис.28). Сле-
довательно, Z(XY, АС) = 60°.
Пусть Р - точка пересечения прямых XY и АС. Тогда
Х(ХР, АР) = 60° = Х(ХВ, АВ),
т.е. точки А, X, Р, В лежат на одной окружности. Отсюда
Z(CP, РВ) = Z(AX, ХВ) = 60° = Z(CY, YB),
т.е. точки В, С, Р, У также лежат на одной окружности. Таким
образом, точка Р является второй точкой пересечения прямой XZ
и описанной окружности треугольника BCY. Аналогично пока-
зывается, что прямая BD также проходит через эту точку. (В
случае, если эти окружность и прямая касаются, получаем Р = У,
и все три прямые проходят через У.)
4. Первое решение. Обозначим через с' точку касания
вписанной окружности со стороной АВ. Сделаем инверсию с
центром в точке ff • Будем обозначать образы точек индексами
«1», т.е. образом точки А' будет А( и т.п. Тогда образами
прямых АВ и ВС будут окружности АХВХВ> и СХВХВ>, а образом
57
вписанной окружности - прямая
АХСХ, касающаяся обеих окруж-
ностей (рис.29). Далее, радикаль-
ная ось В'ВХ этих окружностей,
содержащая точку , делит от-
резок пополам.
Отсюда вытекает построение.
Построим 1Х - образ прямой B'G
(на которой лежит Вх ) при гомо-
тетии с центром Ах и коэффици-
ентом 2; эта прямая содержит С{. Значит, ее инверсный образ
содержит точку С'. Проведя аналогичное построение, начиная с
инверсии в точке А', получим вто-
рую окружность, содержащую С' и,
значит, сможем восстановить точку
С' (вообще говоря, двумя способа-
ми). После этого восстанавливается
описанная окружность треугольника
А'В'С' и стороны исходного тре-
угольника, являющиеся касательны-
ми к ней.
Второе решение. Пусть С' - точ-
ка касания вписанной окружности со
стороной АВ, At, Вх , Q - проекции
G на стороны треугольника А'В'С'
(рис.30). Заметим, что
GBX = р(С, А'С') = СА'sin ZCA'C' = sin ZA'B'C'
GAX ~ р(С, B'G') ~ OB' sin ZCB'C' “ sin ZB'A'C' ’
т.е.
GBt sin ZB'A'C' = GAX sin ZA'B'C'.
Это означает, что проекции отрезков GAX и GBX напрямую А'В'
равны, и Cfi является медианой в треугольнике АХВХСХ. Анало-
гично, AXG также является медианой в этом треугольнике, т.е.
G - его центр тяжести.
Отсюда получаем искомое построение. Построим точку Сх и
ее образ С2 при гомотетии с центром G и коэффициентом -~
(таким образом, С2 - середина АХВХ ). Далее построим окруж-
ности сол, сов с диаметрами GA', GB' и найдем точку пересе-
чения окружности сол с окружностью, симметричной сов отно-
сительно С2 ; мы получили точку Вх (опять же, вообще говоря,
58
двумя способами). Точка At симметрична ей относительно С2.
Теперь можно восстановить прямые А'С' и ВС' как перпенди-
куляры к GAi и GBt в точках Д и Д; дальнейшее ясно.
Замечание. В первом абзаце по сути доказывается, что точка
Лемуана G (треугольника А'В'С') является центром тяжести
своего педального треуголь-
ника АХВХСХ.
5. Поскольку точки At и
А2 симметричны относи-
тельно середины отрезка
ВС, то А$В = А$С (рис.31).
С другой стороны, А$ ле-
жит на серединном перпен-
дикуляре к отрезку ,
который совпадает с бис-
сектрисой угла С. Следовательно,
ZCBHo = ZAqCB = 2 ZC •
Аналогично,
АВС0 =-ЛА
0 2
и, значит,
Z^BQ = ZC - |(ZA + ZB) = 45° .
6. Пусть угол С - острый. Пусть О - центр описанной
окружности треу гол ьникаАМК. Так как ЛАМ К = ЛАМ В = ЛС ,
то ЛАОК = 2ЛС и ЛОКА = ЛОАС = 90° - ЛС , т.е. этот угол не
зависит от положения точек К, М (рис.32). Следовательно, все
центры лежат на одной прямой. Бо-
лее того, поскольку все прямые КО
при различных положениях точки
К параллельны друг другу, то, ког-
да точка К пробегает отрезок АС,
точка О пробегает боковую сторону
равнобедренного треугольника с ос-
нованием АС и углом при основании
90° - ЛС (этот треугольник и точка
В лежат в разных полуплоскостях
относительно АС).
Если угол С тупой, то рассужде-
ния аналогичны; получается боковая сторона равнобедренного
треугольника с углом при основании ЛС - 90° , лежащего по ту
же сторону от АС, что и В.
59
7. Первое решение. Известно, что описанная окружность
треугольника ALaMa перпендикулярна описанной окружности
Q треугольника АВС и является геометрическим местом точек
X, для которых ВХ : СХ = В А : СА. Окружность сой симметрич-
на ее относительно серединного перпендикуляра к ВС; поэтому
сой также перпендикулярна Q и является геометрическим мес-
том точек X, для которых ВХ : СХ = СА : ВА. Аналогичный факт
верен и для соь . Значит, множество общих точек сой и cofc
переходит в себя при инверсии относительно Q; поэтому они
касаются тогда и только тогда, когда некоторая их общая точка
X лежит на Q ; при этом АХ : ВХ : СХ = ВС : С А : АВ.
Итак, если окружности касаются, то по теореме Птолемея
одно из произведений АХ • ВС , ВХ • СА , СХ • АВ равно сумме
двух других. Так как эти произведения пропорциональны квад-
ратам сторон треугольника АВС, он должен быть прямоуголь-
ным.
Наоборот, пусть треугольник АВС прямоугольный, и точки
А, В, С, X (в некотором порядке) образуют прямоугольник.
Тогда эти точки лежат на одной окружности, и нетрудно убедить-
ся, что АХ : ВХ : СХ - ВС : С А : АВ; это значит, что X - общая
точка сой и соь , а это равносильно тому, что они касаются.
Второе решение. Опять же напомним, что описанная окруж-
ность треугольника ALaMa является геометрическим местом
точек X, для которых ВХ : СХ = В А : СА, а ее центр Оа лежит
на касательной к Q в точке А. Кроме того, известно, что точки
Оа , Оь, Ос лежат на одной прямой. Получаем, что центр О'
окружности сод симметричен Оа относительно середины ВС, а
ее радиус равен длине касательной О'аА', проведенной из О'а к
Q (точка А' симметрична к А относительно серединного перпен-
дикуляра к ВС).
Далее, точка X пересечения двух из окружностей сод , со6 , сос
удовлетворяет соотношениям АХ : ВХ : СХ = ВС : СА : АВ, т.е.
лежит и на третьей окружности. Значит, если две из окружнос-
тей сой , со6 , сос касаются в точке X, то третья также проходит
через эту точку и касается их обеих (ибо больше не имеет с ними
общих точек).
Это замечание позволяет ограничиться случаем, когда С -
наибольший угол треугольника АВС. Если ZC = 90° , то каса-
тельные из точек О'а и О'ь к Q касаются ее в одной и той же
точке А' = В', диаметрально противоположной С (рис.33). Зна-
чит, точки О'а , О'ь , А' лежат на одной прямой и, следовательно,
окружности с центрами О'а , О'ь , проходящие через А', касаются
в ней.
60
Пусть угол С острый; проведем вторые касательные из точек
О' и О'ь к Q ; тогда точки касания будут расположены так, как
на рисунке 34, и, следовательно, дуги В'В" и С'СЖ окружностей
соа и с% пересекутся. Наконец, если угол С тупой (рис.35), то
отрезок О'аО'ь пересекает Q в двух точках К и L; тогда
ОаА' + ОЬК = у]ОаК OaL + ylobK ObL <
OaK + OaL ObK + ObL .
2 2 а b’
значит, сумма радиусов меньше расстояния между центрами, и
окружности не имеют общих точек.
8. k = 5.
Докажем сначала, что пяти точек достаточно. Пусть А, В, С,
D - четыре последовательные вершины многоугольника (воз-
можно, А = D). Отметим точки А, В, произвольную точку X на
61
стороне АВ, точку У на стороне ВС, достаточно близкую к В, и
точку Z на стороне CD, достаточно близкую к С.
Пусть Р - исходный многоугольник, Q - некоторый правиль-
ный многоугольник, содержащий на периметре наши пять точек,
аир- углы этих многоугольников. Прямая АВ должна
содержать сторону многоугольника Q, так как на ней лежат три
отмеченных точки. Пусть эта сто-
рона- А'В' (рис.36). Далее, пусть
сторона Q, содержащая У, лежит
на прямой I; тогда точки В и Z
должны лежать по одну сторону от
нее. Поскольку Z близка к С, это
означает, что угол между прямыми
I и ВС мал. С другой стороны,
a = ZABY >ZAB'Y >р, т.е. ко-
личество сторон у Q не больше, чем
у Р. Значит, угол между I и ВС
может быть достаточно мал лишь
тогда, когда эти прямые совпадают. Итак, прямая ВС также
содержит сторону Q, а точка В тогда является его вершиной.
Отсюда следует, что Р и Q гомотетичны с центром в точке В, и
контур Q может содержать Z только тогда, когда Р = Q. Итак,
многоугольник восстановился однозначно.
Докажем теперь, что при достаточно большом числе сторон п
правильного многоугольника Р четырех точек не хватит для его
задания. Предположим, что три из этих точек лежат на одной
стороне АВ многоугольника Р. Правильный треугольник, пост-
роенный на АВ, лежит целиком внутри Р, т.е. четвертая из
отмеченных точек лежит вне его. Поэтому, применив к нашему
треугольнику гомотетию с центром в середине АВ и подходящим
коэффициентом, большим 1, можно добиться того, что и четвер-
тая отмеченная точка окажется на
его контуре. Значит, в этом случае
многоугольник однозначно не вос-
станавливается .
Если же наше предположение
неверно, то отмеченные точки об-
разуют выпуклый четырехуголь-
ник АВ CD, «достаточно близкий»
ко вписанному. Именно, покажем,
что ZX + ZC > 180° - 360°/п .
Пусть точки В и С лежат на сто-
ронах KL и MN многоугольника
62
Р, причем точки А, К и N лежат по одну сторону от BD
(рис.37). Опишем вокруг Р окружность со с центром О.
ZA + ZC > ZLAM + XKCN =
Аналогично,
= | (иЛ YM + uKXN) = 180° - 360°/п .
ZB + ZD > 180° - 360°/и , т.е. ZA + ZC < 180° + 360°/п.
Мы покажем, что ABCD можно вписать либо в квадрат,
либо в правильный треугольник. Пусть ZA - наибольший
угол 4-угольника ABCD, a ZB > ZD. Возможны несколько
случаев.
Случай /. Пусть ZB < 90°. Тогда ясно, что ABCD можно
вписать в квадрат так, чтобы точки А, В попали на одну из сторон
(одним из способов, показанных на рисунке 38, в зависимости от
того, что больше: проекция CD на АВ или проекция ABCD на
прямую, перпендикулярную АВ).
Случай 2. Пусть теперь Z£> < ZB < 90° , но при этом обе
суммы ZA + ZD и ZB + ZC не превосходят 240° . Проведем
через С и D прямые, составляющие с АВ углы 60° (рис.39).
Тогда из наших неравенств следует, что все точки А, В, С, D
лежат на сторонах этого треугольника.
Случай 3. Нам остался случай, когда Z£> < ZB < 90° (а
значит, оба этих угла близки к 90° ), но одна
из сумм ZA + ZD и ZB + ZC больше 240°
(поскольку ZA - наибольший, это может
быть лишь сумма ZA + ZD ). Покажем, что в
этом случае можно вписать ABCD в квадрат
так, как показано на рисунке 40. Пусть X и Y
~ проекции точек С и D на АВ; тогда нам
достаточно проверить, что YB < СХ . Но
ZDCX = 270° - (ZA + ZD) < 30° ,
63
поэтому
XY <CXtg30°<CX/V3 ;
с другой стороны,
ZB > | (ZB + ZD) > 90° -180°/и ,
т.е. при большом п имеем tgZB > 10 ; значит,
ХВ = CXctgZB < CX/10 , и YB < CX/Ji, + CX/10 < СХ ,
что и требовалось.
Замечание. Пять точек требуются не для любого правильного
многоугольника. Так, например, правильный треугольник мож-
но восстановить и по четырем точкам: трем вершинам и внутрен-
ней точке одной из сторон.
10 класс
1. R - 2г.
Пусть АВС - данный прямоугольный треуголь-
ник, ZC = 90°. Очевидно, что окружность с центром J и
радиусом 2г касается АС и ВС. Докажем, что она касается также
описанной около треугольника АВС окружности Q ; отсюда как
раз будет следовать, что OJ = R - 2г.
Рассмотрим окружность со, касающуюся АС, ВС в точках Р,
Q соответственно, и касающуюся Q изнутри в точке Т; нам надо
доказать, что J - центр со. Так как Т - центр гомотетии со и Q ,
прямые TP, TQ вторично пересекают описанную окружность в
точках, касательные в которых параллельны АС и ВС, т.е. в
серединах В', А' дуг АС, ВС. Поэтому прямые АА' и ВВ'
пересекаются в точке I. Применяя теорему Паскаля к ломаной
САА'ТВ'В , получаем, что точки Р, I, Q лежат на одной прямой.
Рис 41
Наконец, поскольку прямая PQ
перпендикулярна биссектрисе
угла С, получаем, что Р, Q
- проекции J на АС и ВС
(рис.41), что и означает, что J -
центр со.
Второе решение. По форму-
ле Эйлера, OI = y]R(R - 2г).
Поскольку OI - медиана в тре-
угольнике OCJ, получаем
4OI2 = 2 (ос2 + OJ2)- СJ2 ,
64
или
47? (7? - 2r) = 27?2 + 20J2 - 8r2,
откуда и следует
OJ2 = (R- 2r)2.
2. Пусть R - радиус окружностей, О - центр , Р - точка
на (Oj , диаметрально противоположная к О, а А' - точка
касания ЛС и СО2 • Так как СО - биссектриса угла А СВ, точки А
и В симметричны относительно прямой ОР.
Заменим сумму косинусов произведением:
/D _ . ZC ZA-ZB
cos ZA + cos ZB = 2 sin-cos-------
2 2
Из отмеченной выше симметрии следует, что
~ = ZCOP , т.е. OP cos264 ~Zg = СО.
2 2
Наконец, поскольку
/С /С ОР
— = Z.OCA = Z.OCA' , то COsin—— = ОА' = R = —
2 2 2
(рис.42). Итого,
п СО ОР 4
cos ZA + cos ZB = 2-------= 1,
OP 2CO
что и требовалось.
3. Нет.
Докажем сначала следующую лемму.
Лемма. Пусть АВС, АВС' - два таких треугольника, что
АС > АС', ВС > ВС'. Тогда для любой точки К отрезка АВ
имеем СК > С'К .
Доказательство. Из условия следует, что точки А, В, С'
лежат по одну сторону от серединного перпендикуляра к отрезку
65
С С' • Значит, и точка К лежит по ту же сторону, что равносильно
искомому неравенству.
Докажем сначала утверждение задачи при п = 4. Предполо-
л. Ач/Т> А2А4 „
жим противное. Можно считать, что > — . Применив
в,в:) ВА
гомотетию (с коэффициентом )
ко второму четырехугольнику, мож-
но считать, что В}В3 = AtA3 ,
В2В4 > А2А4 . Теперь, передвинув
второй четырехугольник, можно
также считать, что Вх = At , В3 = А3 ;
при этом А^А2 > АХВ2 , А2 А3 > Д2Л3 >
А3А4 > А3В4 , А4 Д > В4 Ах. Пусть Е
- точка пересечения диагоналей
АХА3 и А2А4; тогда по лемме имеем
А2Е > В2Е , АЛЕ > ВХЕ и, следовательно, А2А4 = А2Е + АХЕ >
> В2Е + В^Е > В2В4 (рис. 43). Противоречие.
Теперь докажем утверждение задачи индукцией по п. База
при п = 4 уже доказана. Пусть п > 5. Немного подвигав
вершины второго многоугольника, можно добиться того, что все
неравенства из задачи сохранятся, но при этом все отношения
длин соответствующих диагоналей станут различными. Пусть
ДА
В В - максимальное такое отношение. Тогда, применив соот-
ветствующую гомотетию (с коэффициентом, меньшим 1) ко
второму многоугольнику, МЫ получим, ЧТО ДД > BtBj , но
любая другая диагональ первого многоугольника меньше соот-
ветствующей диагонали второго. Теперь осталось применить
предположение индукции к многоугольникам АХА2... Д и
BtB2...Bz (если i > 3) или AiAn+x...An и В^В„+1...В„ (если i <
< п - 1).
4. Пусть проекции точки Р на стороны лежат на окружности
с центром О, а Р' - точка, симметричная Р относительно О. Тогда
проекции Р' на стороны лежат на той же окружности. При этом Р
и Р' являются фокусами некоторой коники, касающейся прямых,
содержащих стороны четырехугольника. Поэтому, если выпол-
нены условия задачи, то стороны четырехугольника являются
общими касательными к двум коникам с общим центром. Таких
касательных может быть не больше четырех, и они разбиваются
на две пары симметричных (а значит, параллельных). Значит,
стороны четырехугольника и являются этими четырьмя касатель-
ными, а следовательно, образуют параллелограмм.
66
5. Обозначим а = ZAC В . Пусть Ц , 12 ~ центры вписанных
окружностей треугольников ABH, СВН. Из подобия этих тре-
угольников следует, что
отрезки ЦНХ, 12Н2 пер-
пендикулярны АВ и ВС
соответственно, то про-
екции этих отрезков на
АС равны /j/^cosa и
/2H2sina, т.е. равны
друг другу. Тогда, по-
скольку О - середина
НХН2, то проекция О на
ЦНХ : 12Н2 = АВ : ВС = tga . Так как
АС совпадает с серединой ВХВ2 , что равносильно утверждению
задачи (рис.44).
6. Да.
Первое решение. Предположим противное. Пусть О, I -
центры описанной и вписанной окружностей треугольника ЛВС,
Н - совпадающий ортоцентр треугольников АВС и А'В'С', Л*,
В*, С* - вторые точки пересечения прямых А'Н', В'Н', С'Н'
со вписанной окружностью со. Тогда
ZA'C'C' = ZA'A'C' = 90° - ZA'C'B' = ZB'B'C' = ZB'C'C';
это значит, что А'В" парал-
лельна касательной к со в
точке С', т.е. А*В* || АВ. Зна-
чит, стороны треугольников
АВС и А*В*С* параллельны
друг другу, а Н - центр впи-
санной окружности треуголь-
ника А'/ГС*. Следователь-
но, существует гомотетия, пе-
реводящая треугольник АВС
в A*B*C* . При этой гомоте-
тии центр описанной окруж-
ности О переходит в I, а точка
Рис 45
пересечения биссектрис I - в Н. Таким образом, точка Н лежит
на прямой OI, причем OI : IH = R : г (рис.45).
Какие-то две вершины треугольника ЛВС (например, А и В)
не лежат на прямой OI. Так как Al, BI - биссектрисы углов
ОАН, ОВН соответственно, то OI : IH = АО : АН = ВО : ВН.
Следовательно, АН = ВН = г, что невозможно, ибо
АН + ВН > АВ > 2г . Полученное противоречие показывает, что
треугольник АВС - правильный.
67
Второе решение. Опять же предположим противное и обо-
значим через Н совпадающий ортоцентр. Имеем IC' || НС ± АВ .
Значит, либо точки С, I, С' ,Н лежат на одной прямой (и тогда
АС = ВС), либо четырехугольник CIC'H - параллелограмм;
аналогичное утверждение верно про остальные вершины. У
треугольника АВС найдется сторона (скажем, АВ), не равная ни
одной другой его стороне. Тогда четырехугольники AIA'H и
BIB'H - параллелограммы, и АН = А7 = г = Hl = ВН = г ,
что опять же невозможно, ибо АН + ВН > АВ > 2г .
7. Да, может; 4 или 8 граней.
Пусть R - полученный многогранник. Ясно, что часть много-
гранника Р содержит хотя бы одну его вершину А, не лежащую
в плоскости разреза. Многогранный угол многогранника Р при
ней будет также многогранным углом при вершине многогранни-
ка В; это означает, что все многогранники Р и Q подобны.
Аналогично, Q также подобен им. Более того, если хотя бы одно
ребро многогранника Р, выходящее из А, не имеет общих точек
(даже другой вершины!) с плоскостью разреза, то оно также
будет являться ребром в R. Тогда в подобных многогранниках Р
и R ребра равны, а следовательно, равны и многогранники, что
невозможно.
Итак, часть Р, вошедшая в R - это пирамида с вершиной А.
Аналогично, часть Q, вошедшая в R - это пирамида с вершиной
В. Следовательно, не менее половины граней в R примыкает к
одной и той же вершине.
Это исключает додекаэдр
и икосаэдр. Если наши мно-
гогранники - кубы, то от Р
и Q отрезаются треуголь-
ные пирамиды, и в итого-
вом многограннике не боль-
ше 5 вершин, что неверно.
Оставшиеся случаи ок-
таэдра и тетраэдра возмож-
ны, как показано на ри-
сунке 46.
Рис 46
8. Докажем сначала следующую лемму.
Лемма. Рассмотрим треугольники АВС и А'НС', вписан-
ные в окружность k; пусть их соответствующие стороны
пересекаются в точках At, Bt, Ct (рис. 47). Тогда
АС, СВ^ (А'С, В'А, СВ, t
С,В ’ А,С В,A j [ С,В' А,С В,A' ) ~
68
Доказательство. Из подоб-
ных треугольников АСХА' и
лд _ АА'
&СХВ имеем ~ && и
Л'д _ АА' 1
~ . Перемножая эти
равенства с четырьмя аналогич-
ными, получаем требуемое.
Перейдем к решению задачи.
Докажем сначала, что для лю-
бых точек А{, Вх на сторонах
ВС и АС найдется не более одной
точки g на стороне АВ такой,
что треугольник АВС восстанав-
ливается однозначно. Зафиксируем треугольник АВС и точки
Л t. Пусть А2, В2 - вторые точки пересечения прямых АА{,
ВВ} с окружностью k; С' - произвольная точка дуги А2СВ2;
А', В* - вторые точки пересечения прямых С'А1, C'Bt с k ; Ct
- точка пересечения АВ и А'В7. Когда точка с' близка к А2 или
к В2 , точка g близка к А или В соответственно. Далее, при
движении точки С' от А2 до В2 точка g непрерывно движется
от Л до В (в случае, когда С = С', рассмотрим предельное
положение точки С2; то, что оно существует, гарантируется
леммой). Значит, для любой точки g , кроме, возможно, выше-
упомянутого предельного положения, треугольник АВС одно-
значно не восстанавливается, ибо существует второй треуголь-
ник А'В'С'.
Осталось доказать, что если ААа, ВВ}, CCt пересекаются в
одной точке Г, то треугольник восстанавливается однозначно
(тогда из выше доказанного следует, что других случаев нет).
Пусть это не так; тогда из леммы мы получаем
Лд BAt CBt = A'Q B'Ai C'BX
CXB А£ ВХА “ дв7 ДС' ВХА'
т.е. отрезки A'At, B'Bt, C'g так-
же пересекаются в одной точке Г'.
Но это невозможно. Действитель-
но, пусть, например, точка Л' ле-
жит на дуге Л С (рис. 48); тогда Т'
не может лежать в угле АТ В, так
как его не пересекает отрезок A'At.
Остальные случаи разбираются
аналогично.
Рис 48
69
VII ОЛИМПИАДА
Заочный тур
1. Да.
Первое решение. Пусть Т - прямоугольный треугольник,
гипотенуза которого равна 1003, а один из катетов - 1. Из
двух таких треугольников составим пря-
моугольник, а из 1003 таких прямоу-
гольников - прямоугольник со сторо-
ной 1003. Теперь приложим к одной из
сторон этого прямоугольника равнобед-
ренный треугольник, составленный из
двух треугольников, равных Г, а к про-
тивоположной стороне четырехугольник
из трех таких треугольников (рис.49).
Второе решение. Возьмем квадрат
со стороной 34 и отрежем от трех его
углов равнобедренные прямоугольные
треугольники с катетами 3, 6 и 16. По-
лучится семиугольник, который можно
разрезать на равнобедренные прямоугольные треугольники
с катетом 1, причем число этих треугольников равно
2 - 342 - 9 - 36 - 256 = 2011.
Вместо квадрата можно взять прямоугольник т х п и отре-
зать от него равнобедренные прямоугольные треугольники с
катетами х, у, z такими, что 2тп - х2 - у2 - z2 =2011. Участни-
ки олимпиады нашли несколько решений такого вида.
Третье решение. (М.Аманжолов, Казахстан) Пусть Т -
равнобедренный треугольник с основанием 1 и углом при верши-
не 120° . Тогда правильный треугольник со стороной 1 можно
разрезать на три треугольника, рав-
ных Т. С другой стороны, из 335
правильных треугольников можно
сложить равнобедренную трапецию
с основаниями 168 и 167 и боковыми
сторонами 1. Две таких трапеции,
соединенные большими основания-
ми, образуют выпуклый шестиуголь-
ник, который можно разрезать на
2010 треугольников, равных Т. При-
ложив к его меньшей стороне еще
один такой треугольник, получим
искомый семиугольник.
70
2. Пусть D - точка пересечения прямых ВН и АС (рис.50).
Тогда в треугольнике ABD АН - биссектриса и высота. Следо-
вательно, этот треугольник равнобедренный, т.е. AD = BD и
ВН = HD. Значит, МН - средняя линия в треугольнике BCD и
МН = CD/2 = (АС - АВ)/2 = 1.
3. Пусть BQ , Со - середины сторон АС, АВ соответственно.
Так как треугольники AB0Bt , AC0Ct прямоугольные с ZA = 60° ,
то ABt = 2ABq = АС и АС} = 2ACq = АВ . Следовательно, пря-
мая В}С} симметрична ВС относительно биссектрисы угла А.
Поскольку эта биссектриса проходит через центр вписанной
окружности, а ВС касается этой окружности, то и В}С} тоже
касается вписанной окружности.
4. Да.
Из условия следует, что в четырехугольнике А'С'В'С диаго-
наль с С' является биссектрисой углов Си С', а значит, осью
симметрии. Поэтому А'С = В'С , А'С' = В'С', ХСВ'А' = ХСА'В'
и ХАВ'С' = ХВА'С'. Аналогично получаем, что
ХВС'А' = ХВА'С' = ХАВ'С' = ХАС'Н .
Следовательно, треугольники АВ>С' и BA'С' равны, т.е.
АВ> = В At и АС = ВС. Равенство АВ = ВС доказывается
аналогично.
5. Для равносторонних и треугольников с углами 30, 30 и 120
градусов.
Пусть треугольник АВС - не равносторонний и АВ - его
наибольшая сторона. Тогда точки А', S' лежат на отрезке АВ.
Из условия следует, что С'С0 , где Со - середина АВ, -
серединный перпендикуляр к A'S', значит,
СА' = А'В = АВ'= СВ',
т.е. С' совпадает с С и треугольник АВС равнобедренный. Кроме
того,
2ZA = ХА + ZCAB' = ХСВ'В = 60° ,
следовательно,
ХА = ХВ = 30° .
6. Пусть Ог - центр окружности сог. Из условия следует, что
ОХАО2В , О^СО3М , O3MO4N , O4NO2D - ромбы со сторонами
1. Значит, QC = МО3 = O4N = DO2 и QA = ВО2 . Следова-
тельно, АС = DB , что равносильно утверждению задачи.
7. Пусть Т - четвертая вершина параллелограмма СВРТ.
71
Тогда PT = ВС и СТ = = ВР = CQ (рис.51). Следовательно,
ZPQT > ZTQC = ZQTC > ZQTP , т.е. PT > > PQ.
8. Пусть I - центр вписан-
пересечения прямой AtA2 с медианой ВВ0 (рис.52). Так как
Z/ДР = Z/A1B1 = ZC/2 = ZPBAt/2 , то ZBAtP = ZBPAt , т.е.
ВР = BAt. Так как BAt = BCt, прямая CtC2 тоже проходит
через Р.
9. Из условия следует, что ZAHCt = ААВН . Значит,
ЛСХНК = ZAHB' - ZABH = ZHAB = л/2 - ZABC ( В' - осно-
вание высоты). Аналогично, ЛВ>НАХ = л/2 - ААВС , т.е. треу-
гольник АХНС - равнобедренный.
10. По теореме Фалеса AQ/QD = AM/МВ = СР/РВ.
Значит, AQ/PC = AD/ВС = АО/СО. Следовательно, треуголь-
ники AOQ и СОР подобны и AAOQ = ZCOP .
11. Проведем через центр вписанной окружности I диаметр
PQ, параллельный АС (рис.53). Так как ZPIC = ZACI = ZBCI
и CAt = (АВ + ВС - АС)/2 = r = IP , четырехугольник 1РАХС
является равнобедренной трапецией. Значит, прямая AtP па-
раллельна IC, т.е. совпадает с AtA2 . Соответственно, Р совпада-
ет с А', и, аналогично, Q совпадает с С'.
12. Так как точки Р, Q лежат
на окружности с диаметром АВ,
Рис 54
72
ZBPQ = 180° - ZA . Значит,
ZMPQ = ZBPQ - ZBPM = 180° - ZA - ZAQM = ZAMQ .
Следовательно, окружность, проходящая через точки Р, Q, М,
касается прямой АВ (рис.54).
13. а) Пусть точки А', В7, С' лежат на сторонах ВС, СА, АВ
треугольника АВС. Так как середина Со отрезка А'В" лежит
внутри треугольника АВС, расстояние от нее до стороны АВ
меньше опущенной на эту сторону высоты треугольника. По-
скольку центр тяжести М треугольника А'В'С' делит отрезок
С'С0 в отношении 2 : 1, то расстояние от М до АВ меньше, чем
2/3 этой высоты. Аналогично получаем, что расстояния от М до
двух других сторон меньше, чем 2/3 соответствующих высот,
т.е. М лежит внутри шестиугольника, образованного сторонами
данного треугольника и прямыми, симметричными им относи-
тельно точки пересечения его медиан. При этом, если две
вершины треугольника А'В'С' приближаются к одной вершине
треугольника АВС, то центр тяжести приближается к границе
указанного шестиугольника, так что все его внутренние точки
принадлежат искомому ГМТ.
6) Рассуждая аналогично п.а), получаем, что искомое ГМТ
является телом, ограниченным гранями данного тетраэдра и
параллельными им плоскостями, каждая из которых делит
соответствующую высоту в отношении 1:3, считая от вершины.
Четыре из восьми граней этого тела являются треугольниками,
а остальные - шестиугольниками.
14. 1: 2>/3 : 3 .
Так как биссектриса угла В делит пополам угол между
высотой и медианой, то угол В прямой. Значит, высота из
вершины А совпадает со стороной АВ, т.е. биссектриса угла А
делит сторону ВС в отношении 1:3. Следовательно, отношение
АВ : АС тоже равно 1 : 3 и по теореме Пифагора ВС : АВ = 2у[2 .
15. Так как SOBMC - SABMC = SABC - SOBC + 2SMBC , геомет-
рическим местом точек, для которых SOMBC = SAMBC , является
серединный перпендикуляр к отрезку ОА. Поэтому AM =
= ОМ=1.
16. Прежде всего заметим, что когда прямая / движется
параллельно себе с постоянной скоростью, прямые, симметрич-
ные / относительно АС и ВС, также перемещаются параллельно
себе с постоянной скоростью. Поэтому точка Сг движется по
прямой, проходящей через С, т.е. точка пересечения CQ с
описанной окружностью зависит только от направления прямой
I. Пусть теперь А', В7 - точки пересечения / с ВС и АС (рис. 55).
73
с Тогда ZQB'C = ZCB'A',
иЛ ZC'AC = ZBA'Q . Значит, С -
// \ центр вписанной или вневписан-
// \ ной окружности треугольника
/ / \ X'B'Q , т.е. CtC - биссектриса
/ / \ угла АСХВ! или смежного с ним.
------/ -^Лв7 Н° угол между прямыми А'С} и
/ /-В'С^ не зависит от /, значит, не
/ / зависит от / и угол между CCt и
/ / CtA'. Поэтому при вращении / с
постоянной скоростью прямые
AAt, ВВХ, CQ вращаются с той
Рис. 55 же скоростью, откуда следуют
все три утверждения задачи.
17. а) Нет.
Пусть в треугольнике АВС длины сторон ВС, АС, АВ равны
а, Ь, с соответственно, причем а < b < с. Далее, пусть СМ -
медиана, AL - биссектриса. Если угол С тупой или прямой, то
AL > АС. Так как ВС < АС , то ZCMA - тупой или прямой,
поэтому СМ < АС и, значит, AM < AL.
Пусть теперь ZC острый. Так как сторона АВ наибольшая,
то ZC > 60° и углы А, В острые. Тогда основание Н высоты АН
лежит на стороне ВС, а не на ее продолжении. Поэтому длина
АН (а тогда и длина AL) не меньше, чем AC cos 60° = . В
то же время квадрат длины медианы СМ равен
2д2 + 2Ь2 - с2 < 2д2 + Ь2 <
4 4 ‘ 4 '
Поэтому длина СМ не превосходит Ьл/з/2 и, значит, не превос-
ходит длины биссектрисы угла А.
б) Нет.
Пусть опять а <Ь < с и I - длина биссектрисы угла С. Тогда
, n . ZC . 2ez6cos(ZC/2)
(al + b/)sin-= 2SABC = ezb sin ZC , т.е. I =-------— .
2 a + b
С другой стороны, высота из вершины А равна h = 6sinZC. Так
, _ , (я+ b)sin(ZC 2) л
как а + b > 2а , a ZC > 60 , h I - ' v ' >1 .
а
Примечание. Нетрудно построить треугольник, в котором
наименьшая медиана длиннее наибольшей высоты.
18. а) 3.
Первое решение. Рассмотрим выпуклую оболочку всех точек
пересечения данных прямых. Две прямые, проходящие через
74
вершину этой оболочки, делят плоскость на четыре угла, в одном
из которых лежат все остальные точки пересечения. Соответ-
ственно, угол, вертикальный этому, не пересекается остальными
прямыми, так что количество углов не может быть меньше трех.
Пример с тремя углами легко строится по индукции: очередную
прямую надо проводить так, чтобы она пересекала все предыду-
щие внутри треугольника, являющегося выпуклой оболочкой
точек пересечения.
Второе решение. (А.Гончарук, Харьков) Рассмотрим много-
угольник Т, являющийся объединением всех ограниченных
частей. Ясно, что все углы являются вертикальными к углам Т,
меньшим 180° • Из формулы для суммы углов сразу следует, что
таких углов не меньше трех. Многоугольник с тремя углами
можно построить следующим образом. Возьмем точку D внутри
треугольника АВС, впишем в угол ADB окружность достаточно
малого радиуса, возьмем на меньшей из ее дуг, образованных
точками касания, п - 4 точки и проведем касательные в этих
точках. Эти касательные вместе с прямыми АС, ВС, AD, BD
образуют искомый многоугольник.
б) п при нечетном п, п - 1 при четном, большем 2.
Построим окружность, внутри которой лежат все точки
пересечения. Данные прямые разбивают ее на 2п дуг. Пусть АВ,
ВС - две соседние дуги, X, Y - точки пересечения прямой,
проходящей через В, с прямыми, проходящими через А и С.
Тогда, если X лежит на отрезке BY, то часть плоскости,
содержащая дугу ВС, не является углом, т.е. из двух частей,
содержащих соседние дуги, углом может быть только одна.
Следовательно, количество углов не превосходит п, причем
равенство возможно только тогда, когда углом является часть,
содержащая каждую вторую дугу. Но при четном п это означает,
что есть два угла, содержащие противоположные дуги, т.е.
образованные одной и той же парой прямых. При п > 2 это,
очевидно, невозможно. При нечетном п прямые, содержащие
стороны правильного и-угольника, разбивают плоскость на час-
ти, из которых п являются углами. Очевидно, что можно
добавить к ним еще одну прямую так, чтобы количество углов не
уменьшилось.
19. Да.
Зафиксируем вершины А, В, построим точку D, симметрич-
ную А относительно В, и возьмем произвольную точку С такую,
что XBCD = 150° . Тогда высота треугольника АВС из вершины
А равна расстоянию DH от D до прямой ВС, т.е. половине CD.
С другой стороны, медиана ВМ из вершины В является средней
75
линией в треугольнике ACD, т.е. тоже равна половине CD
(рис.56). Будем теперь двигать точку С по дуге BD, вмещающей
Рис 56
угол 150° . Когда С стремится к В, биссектриса угла С стремится
к нулю, а медиана из В - к АВ/2. Когда С стремится к D,
медиана из В стремится к нулю, а биссектриса не меньше, чем
ВС. Значит, существует положение точки С, при котором
биссектриса равна двум другим отрезкам.
Примечание. Нетрудно видеть, что при движении С от В к D
биссектриса возрастает, а высота и медиана убывают. Следова-
тельно, углы искомого треугольника определяются однозначно.
20. Будем считать, что ABCD не является трапецией. Против-
ный случай требует лишь незначительных изменений решения.
По теореме Ньютона I лежит на MN. Пусть X = MI : IN.
Возьмем на сторонах четырехугольника точки Р, Q, R и 5 такие,
что АР : РВ = CQ : QB = CR : RD - DS : SA= А. Покажем, что
I - середина отрезков PR и QS.
Это можно сделать, например, методом масс: поместим еди-
ничные массы в точки А и С, а массы X в В и D. Две первые
массы можно заменить массой 2 в точке М, две вторые - массой
2 А в точке N, следовательно, I - центр всех четырех масс. С
другой стороны, можно заменить массы в Л и В на массу 1 + А
в точке Р, а две оставшихся на такую же массу в точке R.
Теперь, так как I - середина PR, а прямые АВ и CD - не
параллельные касательные к окружности с центром /, то они
образуют равные углы с PR, т.е. PR параллельна биссектрисе
одного из образованных этими прямыми углов. Аналогично, QS
параллельна биссектрисе одного из углов между AD и ВС.
Следовательно, ABCD вписанный тогда и только тогда, когда
PRLQS. Так как PQRS - параллелограмм (со сторонами,
параллельными АС и BD), это равносильно тому, что PQRS -
ромб. Но
1 А
PQ = QR & ——АС = ——BD А = АС : BD ,
1 + А 1 + А
что и требовалось доказать.
21. Прямые РМ и QN пересекаются в центре окружности О.
Поэтому утверждение задачи следует из теоремы Дезарга, при-
мененной к треугольникам PML и NQK.
76
22. При гомотетии с центром С и коэффициентом 1/2 прямая
XY перейдет в радикальную ось точки С и окружности, прохо-
дящей через середины А', В', С' сторон ВС, СА, АВ. С другой
стороны, касательная в точке С к описанной окружности касает-
ся также окружности А'В'С', т.е. является радикальной осью
этой окружности и точки С. Следовательно, точка пересечения
этих радикальных осей лежит на прямой A'S'. Сделав обратную
гомотетию, получим утверждение задачи.
23. Пусть Ра , Рь , Рс - середины высот АНа , ВНЬ, СНс.
Очевидно, что точки А', В', С' лежат на сторонах треугольни-
ка РаРъРс и делят их в тех же отношениях, в каких точки At, В1 ,
Q делят стороны треугольника АВС. Поэтому п.а) сразу
следует из теоремы Менелая. Кроме того, если I проходит через
некоторую фиксированную
точку, то Г также проходит
через некоторую фиксирован-
ную точку, так что для доказа-
тельства п.б) достаточно про-
верить его для каких-то двух
прямых, проходящих через
центр О описанной окружнос-
ти. Например, для прямых,
проходящих через какую-ни-
будь вершину треугольника.
Пусть Ct - точка пересече-
ния СО и АВ ; X, Y - проекции
С{ на АС и ВС; Aq , Во , Со -
середины ВС, СА, АВ, U, V - середины XY и A$BQ , Q - точка
пересечения серединного перпендикуляра к A^Bq 0 с UPC (рис.57).
Так как XY || АВ , точки С, V, U лежат на одной прямой.
Значит, VQ СРс =UV UC = CtO CCt , т.е. VQ = OCJ2 и Q -
центр окружности AqBqCq .
24. Докажем сначала, что искомый треугольник - педаль-
ный, т.е. перпендикуляры, восставленные из его вершин к
соответствующим сторонам АВС, пересекаются в одной точке.
Действительно, для произвольного треугольника А'В'С' окруж-
ности АВ'С', В С'А' и С A'S' пересекаются в некоторой точке Р.
Пусть А*, В*, С* - проекции Р на ВС, СА, АВ. Так как
ХА'РВ'= ХА"РВ^ = п-ХС и т.д., то ХА'РА'= ХВ'РВ'=
= ХС'РС', и, значит, треугольник А'В'С* получается из А'В'С'
поворотной гомотетией с коэффициентом, меньшим 1.
Рассмотрим теперь точку Т, педальный треугольник которой
правильный, и докажем, что педальный треугольник любой
77
другой точки Р имеет хотя бы одну сторону большей длины.
Пусть Л', & - проекции Р на ВС и АС. Тогда А'В' = PC sin ZC ,
т.е. A'tf не превосходит стороны педального треугольника Т
тогда и только тогда, когда PC < ТС. Аналогично должны
выполняться неравенства РВ < ТВ , РА < ТА . Очевидно, что
три эти неравенства выполнены только для точки Т.
Осталось описать построение точки Т. Из ее определения
следует, что ТА • ВС ~ТВ • АС = ТС • АВ . Геометрическим мес-
том точек, удовлетворяющих первому равенству, является ок-
ружность Аполлония, проходящая через С и основания внешней
и внутренней биссектрис угла С. Аналогично строится окруж-
ность - геометрическое место точек, удовлетворяющих второму
равенству. Точка Т будет общей точкой этих окружностей,
лежащей внутри треугольника АВС.
25. Да.
Пусть Л, В, С, D - точки касания правильного тетраэдра с
вписанной сферой. Повернув их на 120° относительно общего
перпендикуляра к отрезкам АВ и CD, получим точки Л', # ,
С', D', а повернув на 240°, - точки Л*, В*, С*, D*.
Плоскости, касающиеся сферы в этих двенадцати точках, обра-
зуют три искомых тетраэдра.
Действительно, для любых двух из этих точек существует
движение, переводящее все множество из двенадцати точек в
себя, а одну из выбранных точек в другую. Такими движениями
можно перевести любую грань полученного многогранника в
любую другую.
Финальный тур
8 класс
1. Первое решение. Пусть AD, ВС - основания
трапеции. Проведем через вершину С прямую, параллельную
диагонали BD. Пусть Е - точка пересечения этой прямой с
продолжением основания AD. Тогда треугольник АСЕ - прямо-
угольный и, значит, его медиана из вершины С равна половине
гипотенузы, т.е. средней линии трапеции. Из условия задачи
следует, что высота этого треугольника совпадает с медианой,
поэтому диагонали трапеции равны.
Второе решение. Пусть AD, ВС - основания трапеции, О -
точка пересечения ее диагоналей. Тогда медианы прямоуголь-
ных треугольников OAD, ОВС равны половинам их гипотенуз,
т.е. сумма этих медиан равна средней линии трапеции. С другой
стороны, высота трапеции равна сумме высот этих же треуголь-
78
ников. Поэтому из условия задачи следует, что медианы совпа-
дают с высотами, т.е треугольники OAD, ОВС - равнобедрен-
ные, откуда, очевидно, вытекает, что АВ = CD.
2. Пусть ABCD - полученный прямоугольник; О - его центр;
К, М - середины его коротких сторон АВ, CD; L, N - точки
пересечения окружности с ди-
аметром КМ с отрезками ВС и
AD соответственно (рис.58).
Тогда прямоугольник KLMN
- искомый. Действительно,
пусть Р - проекция М на LN.
Так как ACLM = AOML =
= ZMLO , то треугольники
MCL и MPL равны и при
перегибании по ML они совме-
стятся. Аналогично, при пере-
Рис. 58
гибании по MN совместятся треугольники MDN и MPN. Нако-
нец, поскольку конструкция симметрична относительно точки О,
то при перегибании по KL и KN треугольники BKL и AKN
наложатся на треугольник NKL.
3. Первое решение. Так как точка Ах симметрична А относи-
тельно серединного перпендикуляра к ВС, то перпендикуляр из
А1 симметричен высоте из А. По теореме Фалеса, он пересекает
прямую ОН, где О и Н - центр описанной окружности и точка
М
Рис 59
пересечения высот треуголь-
ника, в точке, симметричной
Н относительно О. Через эту
же точку проходят два других
перпендикуляра.
Второе решение. Пусть К,
LnM- точки попарного пере-
сечения прямых AAt, ВВХ и
CQ (рис.59). Докажем, что
КСХ - высота треугольника
KLM. Поскольку КВСА - па-
раллелограмм, а AQCB - рав-
нобокая трапеция, то КА = ВС = AQ , АКАВ = ААВС = ZBAQ .
Таким образом, в равнобедренном треугольнике КАСХ АВ
является биссектрисой, а следовательно, и высотой. Таким
образом, АВ ± КСХ, откуда ССХ ± КСХ. Аналогично доказыва-
ется, что LAX и МВХ также являются высотами треугольника
KLM. Поскольку высоты пересекаются в одной точке, то утвер-
ждение задачи доказано.
79
Закрасим меньшие из дуг, стягиваемых проведенными
хордами. Если сдвинуть закрашенные дуги так, чтобы соответ-
ствующие хорды образовали ломаную, то расстояние между
концами этой ломаной будет меньше 1, а поскольку хорда длины
1 стягивает дугу, равную 1/6 круга, то сумма закрашенных дуг
будет меньше, чем 1/6 круга.
Теперь впишем в окружность правильный шестиугольник и
отметим одну из его вершин. Будем вращать этот шестиугольник
и каждый раз, когда отмеченная вершина попадает в закрашен-
ную точку, закрашивать точки, в которые попадут остальные
вершины. Тогда общая длина закрашенных дуг увеличится не
более чем в 6 раз, следовательно, найдется положение шести-
угольника, при котором все его вершины попадут в незакрашен-
ные точки. Очевидно, что в этом положении стороны шести-
угольника не будут пересекать проведенных хорд.
5. Так как треугольник BAN - равнобедренный, то
ХМАВ
2
(рис. 60). Аналогично ХАМ С =
XNAC
2
Зна-
XANB =
чит, сумма этих углов равна 60° , а
угол между прямыми BN и СМ
равен 120° , что равносильно ут-
верждению задачи.
6. Первое решение. Так как
треугольники ВСВ} и ВСС} пря-
моугольные, то их медианы ВхАц ,
QAq равны половине гипотенузы,
т.е. В}А$ = А$С = А$В = С}Ац . Да-
лее, ХРВ^А = ХСВхА$ = ХВ^САц = ХРАС , и, значит, РА - РВХ
(рис.61). Аналогично, AQ = QCt. Следовательно, вписанная
окружность треугольника A$PQ касается его сторон в точках А,
В) , С1 , откуда и следует утверждение задачи.
Второе решение. Пусть Н - точка пересечения высот тре-
угольника АВС, О ~ середина АН. Тогда точки А$ , В{ , Ct , О
80
лежат на окружности девяти точек треугольника АВС, причем
Д)О ~ диаметр этой окружности. С другой стороны, точки Вх ,
Q лежат на окружности с диаметром АН, которая, следователь-
но, и является вписанной окружностью треугольника APQ
(рис.62).
7. Из условия задачи следует,
что точки Р, Q, М и начало коорди-
нат О лежат на окружности с диа-
метром PQ. Значит, точка N, сим-
метричная М относительно PQ,
тоже лежит на этой окружности
и XPON = APMN = XPNM =
= ХРОМ (рис.63). Таким обра-
зом, N лежит на прямой, симмет-
ричной ОМ относительно осей ко-
ординат. С другой стороны, если N
- произвольная точка этой прямой, а Р, Q - точки пересечения
осей координат с окружностью OMN, то
XPMN = XPON = ХРОМ = XPNM
и
XPMQ = XPOQ = XPNQ = 90° ,
поэтому точки М и N симметричны относительно PQ.
8. Сначала разделим сторону пополам. Проведя диагонали,
найдем центр О квадрата ABCD. Теперь пусть X - точка на
стороне ВС, Y - точка пересече-
ния ХО и AD, U - точка пересе-
чения АХ и BY, V - точка пере-
сечения прямых UC и XY
(рис.64). Тогда прямая BV делит
основания трапеции CYUX попо-
лам. Соединив О с серединой CY,
разделим пополам стороны АВ и
CD.
Покажем теперь, что если две
противоположные стороны разде-
лены на k равных частей, то их
можно разделить на k + 1 равных
частей. Пусть АХ{ = Х}Х2 = ...
Рис 64
... = Xk_xB , DYX = YyY2 = ... = Yk_xC . Тогда по теореме Фалеса
прямые AY{, Xty2,..., Xk_xC делят диагональ BD на k + 1 равных
81
частей (рис.65). Аналогично разде-
лив вторую диагональ и проведя
через соответствующие точки пря-
мые, параллельные ВС, разделим
на k + 1 равных частей сторону АВ.
9 класс
1. Угол между каса-
тельной к окружности B/DM в точ-
ке D и прямой AD равен углу MB^D ,
который, в свою очередь, равен углу BAD (рис.66). Аналогично,
угол между касательной к окружности A/DN и BD равен углу
ABD. Поскольку ZBAD + ZABD = 90° = AADB , касательные к
обеим окружностям совпадают.
2. Пусть точка D симметрична А относительно серединного
перпендикуляра к ВС. Тогда ABCD - равнобокая трапеция, а
диагональ BD - биссектриса угла В. Следовательно, CD = DA =
= АВ. Далее, = ZC + ZA/3 = (ZA + ZB + ZC)/3 = 60°.
Поэтому треугольник ADP равносторонний и АР = АВ. Посколь-
ку AQ - биссектриса угла РАВ, то QP = QB = QC (рис.67).
3. Центр О описанной окружности треугольника лежит на
продолжении НМ за точку М, и МО = НМ/2. Кроме того,
прямые BI, CI являются биссектрисами углов ОВН, ОСН
( ЛСВН = ZABO = п/!-Z.C ). Следовательно, ВО/ВН =
= СО/СН = Ю/IH, т.е. точки В, С лежат на окружности
Аполлония точек О и Н, проходящей через I. Но центр окруж-
ности BIC лежит на описанной окружности треугольника АВС.
Таким образом, получаем следующее построение.
Построим точку О и окружность Аполлония. Затем построим
окружность с центром О, проходящую через центр этой окруж-
82
ности. Две окружности пересе-
кутся в точках В, С, а прямая
ОН вторично пересечет описан-
ную окружность в точке А.
4. Пусть биссектрисы углов
А и В пересекаются в точке К, В
и С - в точке L, С и D - в точке
М, D и А - в точке N (рис.68).
Тогда прямая КМ - биссектриса
угла между AD и ВС. Обозначив
этот угол через <р, по теореме о
внешнем угле получаем, что
ЛЬКМ = ЛВ/2 - ф/2 =
= (я - ZA)/2 = ZC/2
и, значит, ZLIM = ZC. С другой стороны, перпендикуляры
из L на ВС и из М на CD образуют с ML углы, равные
(я- ZC)/2, т.е. треугольник, образованный этими перпенди-
кулярами и ML, равнобедренный с углом при вершине, рав-
ным углу С. Поэтому вершина этого треугольника совпадает с
I. Таким образом, перпендикуляры, опущенные из вершин
четырехугольника KLMN на соответствующие стороны ABCD,
проходят через I. Аналогично получаем, что перпендикуляры
из вершин четырехугольника, образованного внешними бис-
сектрисами, проходят через J.
Пусть теперь К' - точка пересечения биссектрис внешних
углов А и В. Так как четырехугольник АКВК' вписан в
окружность с диаметром КК', то проекции ТС и ТС' на АВ
симметричны относительно середины АВ. Отсюда и из утверж-
дения, доказанного выше, следует, что проекции I и J на каждую
из сторон ABCD симметричны относительно середины этой
стороны, что равносильно утверждению задачи.
Примечание. Известно аналогичное утверждение для треу-
гольника: центр описанной окружности является серединой
отрезка между центром вписанной окружности и центром опи-
санной окружности треугольника, образованного биссектрисами
внешних углов.
5. Нет. Возьмем треугольник, две стороны которого равны 2
и 3, и будем увеличивать угол между этими сторонами. При
стремлении угла к 180° отношение высот треугольника будет
стремиться к 1/2 : 1/3 : 1/5, так что из них при любом
значении угла можно будет составить треугольник. С другой
стороны, наименьшая из биссектрис стремится к нулю, а две
83
другие - к неравным величинам. Значит, при больших значени-
ях угла треугольник из биссектрис составить нельзя.
Приведем точные оценки. Прежде всего отметим, что, если
две стороны треугольника равны а и 6, угол между ними - С, а
биссектриса этого угла - 1С, то площадь треугольника равна
о . ZC (й + 6)/с sin(ZC/2)
2 2
откуда
2ab cos(ZC/2)
{а + 6)
Аналогично находятся длины биссектрис la , 1Ь .
Пусть теперь а = 2, b = 3. Тогда
ZB
cos---.
2
Поэтому
cos---->
2
п 2
2с cos-----
2
ZAf b
L -lb > 2c cos- ---- , - z
2^6 + c a + c) (c + 2)(c + 3)
а
Возьмем угол С достаточно большим, чтобы выполнялись нера-
ZA пл ZC Л .
венства с > 4, cos-^- > , cos-^- < 0,1. Тогда la-lb > 1С и
треугольник из биссектрис составить нельзя. С другой стороны,
для отношений высот имеем hb/ha = 2/3 , 2/5 < hc/ha < 1/2 . Сле-
довательно, + hc > ha > hb > hcH из высот можно составить
треугольник.
6. Пусть О - центр описанной окружности треугольника
АВС, а Н - точка пересечения его высот. Так как
ZCAqO = ZCB0O = ZCAtH = ZCRH = 90° , то CO и CH - диа-
Рис 69
метры окружностей СА$В$
и САХВ\ соответственно.
Поэтому проекция С на
прямую ОН лежит на обе-
их окружностях, т.е. со-
впадает с Мс (рис.69).
Отсюда, очевидно, следует
утверждение задачи.
7. Первое решение.
Пусть одна сторона угла
касается со и Q в точках
Хх, Yx, а другая - в точ-
ках Х2 , Y2 ; U, V - точки
84
пересечения ХхХ2 и YXY2 с AF. Середина отрезка CD лежит
на радикальной оси окружностей, т.е. средней линии трапеции
Х^У^Х-г у поэтому BU = EV и CU = DV (рис. 70). Следо-
вательно, X{U X2U = YXV Y2V . Отсюда получаем, что
FY2/FX2=Y2V/X2U = хр/уу = АХх/АУх , т.е. АХ{ = FY2 .
Теперь утверждение задачи вытекает из равенств
АВ • АС = AXf = ГУ22 = FEFD
Второе решение. Зафиксируем точку А на стороне угла и
покажем, что через нее проходит ровно одна прямая, удовлет-
воряющая условиям задачи. Действительно, середина К отрез-
ка CD равноудалена от проекций центров окружностей на
искомую прямую и, значит, совпадает с проекцией середины L
отрезка между центрами. Следовательно, К - точка пересече-
ния окружности с диаметром AL и радикальной оси окружнос-
тей, отличная от середины отрезка Х^Ух. С другой стороны,
если взять точку F так, что AXt = Y2F , то АВ • АС = FE • FD и
AD • АЕ = FC • FB , откуда следует, что прямая AF - искомая.
8. Докажем, что п = 4.
Лемма. Пусть выпуклый п-угольник разрезан на равные
треугольники диагоналями, не пересекающимися внутри него.
Тогда у каждого из треугольников разбиения хотя бы одна
сторона является стороной (а не диагональю) п-угольника.
Доказательство леммы. Пусть треугольник разбиения имеет
углы а < р < у с вершинами А, В, С соответственно, причем АС
и ВС - диагонали n-угольника. К вершине С примыкают еще
хотя бы два угла треугольников разбиения. Если хотя бы один
из них больше а , то сумма углов при С не меньше у + р + а = я,
но она не больше угла выпуклого многоугольника - противоре-
чие. Значит, все углы при С, кроме ХА С В, равны а , причем а
строго меньше р .
Рассмотрим второй треугольник разбиения, примыкающий к
ВС. Так как он равен ААВС , то против стороны ВС в нем лежит
85
угол, равный а . Но угол при С в этом треугольнике также равен
а, тогда как он должен равняться р или у - противоречие.
Лемма доказана.
Перейдем к решению задачи.
Так как сумма углов многоугольника Р равна л (и - 2) и они
складываются из всех углов треугольников разбиения, то коли-
чество этих треугольников равно п - 2. По лемме, в каждом из
этих треугольников хотя бы одна сторона является стороной Р.
Отсюда вытекает, что у двух треугольников разбиения по две
стороны являются сторонами Р.
Пусть KLM - один из этих треугольников, причем KL и LM
- стороны Р. К стороне КМ примыкает другой треугольник
разбиения KMN. Одна из его сторон (для определенности KN)
является стороной Р. Так как треугольники разбиения равны, то
ZNKM равен либо ZLKM , либо ZKML . В первом случае
КМ - биссектриса угла описанного многоугольника Р и потому
содержит центр I вписанной окружности. Во втором случае
KN || LM. Тогда I лежит на общем перпендикуляре к этим
отрезкам и потому содержится (по выпуклости) в параллелог-
рамме KLMN, а значит - хотя бы в одном из треугольников
KLM, KMN.
Пусть K'L'M' - другой треугольник разбиения, две стороны
которого являются сторонами Р. Аналогично предыдущему, I
содержится либо в этом, либо в смежном с ним треугольнике
разбиения. Если I содержится хотя бы одном из треугольников
KLM, K'L'M', то они имеют общую сторону, и тогда п = 4. В
противном случае треугольник KMN - смежный с обоими этими
треугольниками и содержит /.При этом сторона MN - общая с
AK'L'M'; можно положить М = М', N = К'. Рассуждая как
выше, получаем, что LM || KN || L'M . Но тогда LM и L'M
лежат на одной прямой, тогда как это две стороны выпуклого п-
угольника - противоречие.
Из приведенного рассуждения видно, что выпуклый четы-
рехугольник удовлетворяет условию задачи тогда и только
тогда, когда он симметричен относительно одной из своих
диагоналей.
Ю класс
1. Пусть С' ~ точка, симметричная С относитель-
но середины АВ. Тогда точки А, В, С' и ортоцентр треугольника
АВС лежат на одной окружности. С другой стороны, если Д,
Bq - середины сторон ВС, АС, то треугольник AqBqC гомотети-
чен треугольнику АВС' относительно центра тяжести М тре-
86
угольника АВС с коэффициентом -1/2 .
Следовательно, описанные окружности этих
треугольников касаются в точке М (рис.71).
2. Прежде всего сформулируем следую-
щее утверждение, вытекающее из непос-
редственного вычисления углов.
Лемма. Точки А, В, С, D лежат на
одной окружности тогда и только тогда,
когда биссектрисы углов, образованных
прямыми АВ и CD, параллельны биссект-
рисам углов, образованных прямыми AD
и ВС.
Доказательство леммы. Действитель-
но, рассмотрим для определенности слу-
чай, когда ABCD - выпуклый четырехугольник, лучи В А и DC
пересекаются в точке Е, DA и ВС - в точке F. Тогда углы между
биссектрисами углов BED и BFD равны полусуммам противопо-
ложных углов четырехугольника, откуда, очевидно, следует
утверждение леммы. Другие случаи рассматриваются аналогич-
но.
Перейдем к решению задачи. Пусть I центр вписанной
окружности, г - ее радиус. Тогда /С' • IA = г2 = IA' • IC , т.е.
точки А, С, А', С' лежат на одной окружности. Применяя
лемму, получаем, что биссектрисы углов между АА' и СС'
параллельны биссектрисам углов между IA и IC, а значит, и
углов между перпендикулярными им прямыми KN и LM.
Аналогично, биссектрисы углов между В В' и DD' параллельны
биссектрисам углов между KL и MN. Еще раз применив лемму,
получим утверждение задачи.
3. Сначала докажем следующую лемму.
Лемма. Ребра AtA2 и В3В4 перпендикулярны тогда и
только тогда, когда перпендикуляры из точек Aif А2 на
плоскости В2В3В4 и В}В3В4 соответственно пересекаются.
Доказательство леммы. Пусть АХА2 ± В3В4 . Тогда суще-
ствует плоскость, проходящая через AtA2 и перпендикулярная
В3В4 . Перпендикуляры из условия леммы лежат в этой плоско-
сти и, значит, пересекаются. Обратно, если перпендикуляры
пересекаются, то проходящая через них плоскость перпендику-
лярна В3В4 и содержит AtA2 .
Пусть теперь AtA2 ± В3В4 , AtA3 ± В2В4 , А2А3 ± ВХВ4 . Тогда
любые два из трех перпендикуляров, опущенных из Д , А2 , А3
на соответствующие грани ВХВ2В3В4 , пересекаются. Так как эти
перпендикуляры не лежат в одной плоскости, отсюда следует,
87
что они проходят через одну точку. Следовательно, если выпол-
нены условия задачи, то все четыре перпендикуляра из вершин
одного тетраэдра на соответствующие грани другого проходят
через одну точку, что влечет перпендикулярность шестой пары
ребер.
4. Сначала докажем следующую лемму.
Лемма. Пусть окружность касается сторон АС, ВС треу-
гольника АВС в точках U, V, а описанной около него окружно-
сти - изнутри в точке Т. Тогда прямая UV проходит через
центр I окружности, вписанной в треугольник АВС.
Доказательство леммы. Пусть прямые TU, TV вторично
пересекают описанную окружность в точках X, Y. Так как
окружности АВС и TUV гомотетичны с центром Т, то X, Y -
середины дуг АС, ВС, т.е. прямые А У и ВХ пересекаются в точке
I (рис.72). Поэтому утверждение леммы следует из теоремы
Паскаля, примененной к шести-
угольнику AYTXBC.
Рис 72
Из леммы следует, что в условиях задачи DIxXI2 , где Ц, 12
- центры вписанных окружностей треугольников A CD, BCD, -
прямоугольник (рис.73). Пусть У, Ct , С2 - проекции точек X,
Ц , 12 на АВ. Тогда
BY - АУ = ВС2 + С2У - ACt - Cty = (ВС2 - DC2) - (ACt - DQ) =
= (ВС - CD) - (AC - CD) = BC - AC .
Следовательно, У - точка касания стороны АВ с вписанной
окружностью.
5. Из условия следует, что радиус гс вневписанной окружно-
сти, касающейся стороны АВ треугольника АВС, равен высоте
hc, проведенной к этой стороне. Поскольку площадь треуголь-
ника S = (р - c)rc = chc/2 , то
с = 2(р - с) = 2р/3 .
88
6. Пусть а > b > с - стороны треугольника. Тогда /2 “
биссектриса угла А и
_ , . ZA (b + c)Z2sin(ZA/2)
S - be sin-= -----—-------—.
2 2
Поэтому правое неравенство можно переписать в виде
л/3 (b + с) sin (ZA/2) 2bc cos (ZA/2)
2 b + с
или
л,»/-’J'"_
2 (Ь + с)2'
Но л/6 < А/2 < л/2 , следовательно, левая часть больше 1, а
правая меньше 1 по неравенству о средних.
Так как С < л/3 , то л/35 < ЪаЬ/^. С другой стороны,
Z?
4й2Ь2 cos2 (ZC/2) _ 2a2b2 (1 + cosZC)
(а + Ь)2 (а + Ь)2
Поскольку b > с, cosZC > а/2Ъ , т.е. I2 > а2Ь(а + 2Ь)/(я + Ь)2.
Поэтому левое неравенство следует из того, что
а (а + 2b)/(а + b)2 = 1 - Ь2/{а + Ь)2 > 3/4 .
7. Пусть Н - ортоцентр треугольника АВС. Тогда
АН • НА\ = ВН • НВХ = СН • НСХ, т.е степени Н относительно
окружностей АА{А', ВВХН , CCtC' равны, причем Н лежит
внутри этих окружностей. С другой стороны,
ZBC'O = Z.BAO = ZOBCt, т.е. треугольники ОС'В и ОВС{
подобны и OCt • ОС' = OBq (рис.74). Следовательно, степени О
89
относительно всех трех окружностей
также равны и, значит, эти окружности
пересекаются в двух точках, лежащих
на прямой ОН.
8. Искомая развертка изображена
на рисунке 75. Жирные линии обозна-
чают разрезы, тонкие и пунктирные -
сгибы вверх и вниз. Центральный квад-
рат 2x2 соответствует горизонталь-
ной перегородке куба.
VIII ОЛИМПИАДА
Заочный тур
1. Пусть К - середина АС (рис.76). Так как DK - медиана
прямоугольного треугольника AD С, то АК = KD и ZADK = ZA.
С другой стороны, МК - средняя линия треугольника АВС,
следовательно, ADMК = Z.B.
Применяя к треугольнику
/ DM К теорему о внешнем угле,
получаем, что равенства KD =
/ = Ж и AKDA = 2ZKMD
И/ уР ХМ_______________равносильны.
рис 76 2. При п = 4 и при п > 5.
Очевидно, что п > 3. Ясно
также, что при четном п можно разрезать правильный п-
угольник на два равных многоугольника диагональю, проходя-
щей через его центр, а потом разрезать эти два многоугольника
одинаковым образом. Кроме того, можно на трех сторонах
правильного 2/г-угольника построить равные треугольники с
вершинами на описанной окружности. Поэтому при нечетном
п > 5 искомая ситуация тоже возможна. Осталось доказать, что
она невозможна при п = 5.
Если центр описанной около пятиугольника окружности не
лежит ни на одной из проведенных диагоналей, то треугольник,
содержащий его, - остроугольный, а остальные - тупоугольные,
т.е. описанная ситуация не может иметь места. Если же центр
лежит на диагонали, то два треугольника, примыкающие к этой
диагонали, - прямоугольные, а третий - тупоугольный. Следо-
вательно, указанная ситуация также невозможна.
3. Так как В}11 АС , достаточно доказать, что
ZYB1Z = ZXB1C. Так как CI - серединный перпендикуляр к
90
, то ZYBXA} = ZC^A^ , а по-
скольку ZAJ^C = ZBXAXC , то
ZYBXA = zqAtB (рис.77). Анало-
гично ZXBxC = ZA{CXB = ZqAtB.
4. Пусть точка D симметрична В
относительно серединного перпенди-
куляра к АС, а Г - точка пересечения
АВ и CD. Тогда ACBD - равнобокая
трапеция, и, значит, треугольник BDT
- равнобедренный (рис.78). Так как
прямая РМ содержит среднюю ли-
нию этого треугольника, треугольник QPB тоже равнобедрен-
ный.
Рис. 78
Рис 79
5. Из условия задачи следует, что ZCXDA = ZDBC и
ZAXDC = ZD В А (рис. 79). Следовательно, четырехугольник
AXBCXD - вписанный, т.е. ZqAtD = ZC{BD = ZCDAX.
6. 135°.
Пусть I - центр вписан-
ной окружности треуголь-
ника АВС. Так как точка
q симметрична В относи-
тельно CI, а С2 симметрич-
на q относительно А/, то
BI = 1С2 и ZBIC2 = 90° .
Аналогично BI = 1А2 и ZBIA2 = 90° (рис.80). Следовательно,
I - середина А2С2 , a ZA/C = 135° .
7. 60°.
Пусть AAt, BBt - биссектрисы треугольника, АА2, ВВ2 -
его высоты. Из условия задачи следует, что ААХ/АА2 = ВВХ/ВВ2
и, значит, ZAXAA2 = ZBXBB2 . Но ZA1AA2 = |ZB - ZCj ,
ZBXBB2 = |ZA - ZC|. Так как треугольник неравнобедренный,
91
равенство ZA - ZC = ZB - ZC невозможно. Следовательно,
ZC = (ZA + ZB)/2 = 60° .
8. Так как треугольники ABM, CBM - равнобедренные,
точки Aj, Cj - середины соответствующих катетов. Кроме того,
прямая AjA2 перпендикулярна бис-
сектрисе угла А и, значит, является
биссектрисой угла AAiQ (рис.81).
/ / /\ 1 Аналогично, CtC2 - биссектриса угла
А^—------CCjAj. Следовательно, точка их пе-
\ // 2 ресечения - центр вневписанной ок-
\ / ружности треугольника АХВСХ - ле-
v жит на биссектрисе угла В.
Рис. 81 9. Пусть I - точка пересечения 1Ь
и 1С. Тогда 1Ц - биссектриса угла А.
Поэтому нам известны углы между биссектрисами треугольника,
а значит, и углы треугольника. Построим произвольный треу-
гольник А'В'С' с такими углами, найдем центр Г вписанной в
него окружности, отложим на прямых 1Ь , 1С отрезки /В* = Г В' ,
/С* = /'С' и проведем через Ц прямую, параллельную В"С' .
Эта прямая пересечет 1Ь , 1С в вершинах В, С искомого треуголь-
ника. После этого вершина А строится очевидным образом.
10. а) Да; б) нет.
а) Рассмотрим треугольник АВС, в котором АС > ВС > > АВ.
Возьмем на отрезке АС такую точку Р, что АР = ВС, восставим
о из нее перпендикуляр к АС и
возьмем на этом перпендикуляре
точку D, лежащую вне треуголь-
ника и достаточно близкую к Р.
Тогда в четырехугольнике АВ CD
AD ~ наибольшая сторона, CD -
наименьшая, D - наибольший
угол, С - наименьший (рис.82).
6) Предположим, что ABCD
- четырехугольник, удовлетворяющий условию. Без ограниче-
ния общности можно считать, что угол В наибольший, а сторона
CD наименьшая. Тогда из равенства
АС2 = АВ2 + ВС2 - 2АВ ВС cos ZB =
= AD2 + CD2 - 2 AD CD cos ZD
следует, что AD - наибольшая сторона и, значит, С - наимень-
ший угол. Так как ZC + ZZ) < я, лучи СВ и DA пересекаются в
некоторой точке Р. Так как угол С острый и ZC + ZA < я , то
92
sin ZA > sin ZC . Поскольку
РВ/sin ZA = AB/sin ZP > CD/sin ZP = PD/sin ZC ,
из этого следует, что РВ > PD. Но РВ = PC - ВС < PC -
- CD < PD - противоречие.
11. Так как PC - диаметр описанной около треугольника
РА'S' окружности, угол PQC прямой, т.е. точка С{ лежит на
высоте треугольника АВС. Аналогично точки At, Bt лежат на
двух других высотах. Поэтому прямые AAt, ВВ{, СС{ пересе-
каются в ортоцентре Н и утверждение а) доказано. Кроме того,
точки А1, В{, С{ лежат на окружности с диаметром PH,
поскольку углы РАХН , PBtH , РСХН прямые. Следовательно,
угол между прямыми AtCt и ВГС{ равен углу между прямыми
HAt и НВ{, который как угол между высотами треугольника
АВС равен углу между его сторонами АС и ВС. Таким образом,
углы треугольников АВС и АХВХС{ равны, т.е. эти треугольники
подобны.
12. Из равенства cos ZA + cos ZB + cos Z.C = 1 + г/R следует,
что в остроугольном треугольнике сумма расстояний от О до
сторон равна сумме радиусов описанной и вписанной окружно-
стей. Поэтому из условия задачи следует, что прямая PQ
проходит через центр I вписанной окружности. Тогда
ZPZB = ZZBA = ZZBP и РВ = IP. Аналогично QC = IQ.
13. Окружность с центром в середине АВ и радиусом, равным
АВл/з/2 без точек пересечения с прямой АВ.
Пусть медианы AAq и ВВо треугольника пересекаются в
точке М. Из условия задачи следует, что AM • AAq = АВ0 • АС ,
т.е. АА^ = АС2 . Аналогично, BBq = ~&С2 . Поскольку в лю-
бом треугольнике отношение суммы квадратов медиан к сумме
квадратов сторон равно 3/4, из этих равенств следует, что
медиана из вершины С равна АВл/з/2 . Нетрудно видеть, что
любая точка окружности, кроме точек пересечения с прямой АВ,
входит в искомое ГМТ.
14. Пусть Р - точка пересечения АВ и МО. Применяя теорему
Менелая к треугольникам АВС и ABD, получаем
АР ВО РЕ АР ВМ СО
РВ OD АЕ ~ РВ МС ОА
Следовательно,
ЛЕ _ ОА • OB _ S^abo
ED ОС • OD S^cdo
93
15. Пусть прямые, симметричные Z, пересекаются в точке Р.
Тогда точки, симметричные Р, лежат на Z, а значит, проекции Р
на стороны треугольника лежат на одной прямой. Следователь-
но, по теореме Симеона Р лежит на описанной окружности
треугольника АВС. Кроме того, так как прямая Симеона точки
Р делит пополам отрезок между Р и ортоцентром Н треугольника
АВС, то / проходит через Н.
16. Первое решение. Так как четырехугольник ВМКС впи-
санный, то АВМК = 90° и О лежит на ВК. Поэтому
AABL = АМВК = Z.MCK = ZA . Значит, Z.MAL = ZB , а угол
между прямыми АТ и КМ равен углу А, т.е. углу АСМ (рис.83).
Второе решение. Так как угол КС В прямой, то О лежит на
КВ. Так как АВ - диаметр описанной около треугольника АВС
окружности, то угол ALB также прямой. Угол КМ В прямой,
поскольку КС В прямой. А тогда К - точка пересечения высот
треугольника из точек А, В и
точки пересечения AL с МК. Значит, два прямых угла с
вершинами С и М опираются на один и тот же диаметр и все
доказано.
17. Так как ZAMD = 45° = ZOAD = AODA , то ZAQD =
= ZAMD + Z.MAQ = Z.PAD . Аналогично, ZAPJD = ZADQ
(рис.84). Следовательно, треугольники APD и QDA подобны,
т.е. AQ • PD = AD2 , что равносильно утверждению задачи.
18. Проведем прямую через отмеченные точки. Она пересечет
две стороны треугольника (скажем, АВ и АС) и продолжение
третьей (скажем, за вершиной С). Тогда АВ - наибольшая сто-
рона треугольника, ВС - наименьшая и центром вписанной ок-
ружности является та из отмеченных точек, которая ближе к ВС.
Докажем сделанные утверждения. Пусть I - центр вписанной
окружности треугольника, О - центр описанной. Соединим их с
94
вершинами треугольника и вычислим углы. Получим, что О
лежит в треугольнике, образованном наибольшей стороной и /,
а I лежит в треугольнике, образованном наименьшей стороной и
О. Значит, прямая OI пересекает наибольшую и наименьшую
стороны треугольника и, следовательно, пересекает продолже-
ние средней стороны. При этом О лежит ближе к наибольшей
стороне, а I - к наименьшей.
Остается узнать, с какой стороны OI пересекает продолже-
ние средней стороны АС. Для этого надо сравнить длину
перпендикуляров из О и I на прямую АС. Если г и R - радиусы
вписанной и описанной окружности, то перпендикуляр из I
равен г, а перпендикуляр из О равен R cos 59° > R/2 > г , откуда
следует ответ.
19. 150°.
Из условия следует, что расстояние между центрами ок-
ружностей равно >/3 , значит, по формуле Эйлера эти окружно-
сти для треугольника А'В'С являются описанной и вневписан-
ной, т.е. А'В' касается второй окружности в точке С', лежащей
на прямой CZ (рис.85).
Пусть 0,0' — центры окружностей. Тогда
1
ZA'O'A = ZAO'C' + - ZC'O'B = 2ZABC' + ZC'AB =
2
1
= ZCB'A'+ — ZC'A'B',
2
го’а’о = го'a'# + гв'л'о = -- гс'о'А'+-- гвсл =
2 2
1 1
= п - ZBCA - - ZCA'B' = zee А' + - ZCA'B'
2 2
и, так как О'А = ОА', то АО'А'О ~ равнобедренная трапеция.
Поэтому ZO'AA' = ZA'OO' и, аналогично, ZO'BB' = ZB'OO'.
95
Следовательно, ZA'ZB7 = 2л - ZAO'B - ХА'OB' = п-ХС , т.е.
точка Z лежит на описанной окружности треугольника и
XXZY = 150°.
Примечание. Доказать, что Z лежит на окружности, можно и
по-другому. При изогональном сопряжении относительно треу-
гольника А'В'С Z перейдет в центр гомотетии окружностей,
который в силу равенства их радиусов является бесконечно
удаленным.
20. Первое решение. Пусть Ix, Jx, I2, J2 ~ центры CDj , Ц ,
СО2 , Q2 , a , ^2 “ точки пересечения прямых IXJX, /2/2 с АВ
(рис.86). Тогда ЦКхЩС = ]хКхихС , 12К2/12С = J2K2/J2C и,
дважды применив к треуголь-
нику СКХК2 теорему Мене-
лая, получим, что прямые
1Х12 и JXJ2 пересекают АВ в
одной и той же точке. Через
эту точку проходят и общие
внешние касательные.
Второе решение. Возьмем
пересечение общих внешних
касательных к окружностям
CDi и Q2 - точку Р. Тогда,
применяя теорему о трех кол-
паках для троек окружнос-
тей cot, , Q2 и cot , о>2 ,
Q2 , получаем, что точки пе-
ресечения общих внешних
касательных сначала к ок-
ружностям и Q2 , а потом
К Ц И являются точкой
пересечения прямой PC с
прямой АВ, т.е. совпадают и
лежат на АВ.
21. Пусть одна из прямых
пересекает ВС, СА, АВ в точ-
ках Ха , Хь , Хс , а другая -
в точках Уа , Yb , Yc (рис.87).
Тогда ZHYaB = ZXbHA и
ZHXbA = ZYaHB , так как
стороны этих углов перпен-
дикулярны. Поэтому треу-
гольники HBYa и ХЬАН
подобны. Аналогично, подоб-
96
ны треугольники НХаВ и YbAH . Значит, АХЬ • BYa =
= АН • ВН = AYb- ВХа . С другой стороны, применив теорему
Менелая к треугольникам CXaXb , CYaYb и прямой АВ, получим
СА XbXc ХаВ _ СЛ YbYc YaB_^
АХЬ ХсХа ВС AYb YcYa ВС '
Из этих трех равенств следует утверждение задачи.
22. Пусть К, L - точки касания со с АВ и большой
окружностью. Так как L - центр гомотетии окружности, а
касательные к ним в точках К и N параллельны, точки L, К, N
лежат на одной прямой. При этом ZKAN = ZNLA , так как эти
углы опираются на равные дуги. Значит, треугольники К AN и
ALN подобны и AN2 = NK • NL = NC2 , т.е. четырехугольник
ABCD вписан в окружность с центром N (рис.88). Относительно
этой окружности прямая
XY является полярой точ-
ки пересечения АВ и CD.
При этом, поскольку
ZNAM = ZNBM = ZNCI =
= ZNDI = 90° , точки М и
I являются полюсами пря-
мых АВ и CD и, следова-
тельно, лежат на ХУ.
23. Прежде всего, заме-
тим, что множеством сере-
дин отрезков, концы кото-
рых лежат на двух диаго-
налях квадрата, будет квад-
рат с вершинами в середи-
нах сторон исходного. По-
Рис 88
этому множеством центров тяжести четырех точек, лежащих на
диагоналях двух противоположных граней куба, будет квадрат
с вершинами в центрах четырех остальных граней. Таким
образом, задача равносильна определению ГМТ - центров тяже-
сти трех точек, каждая из которых выбирается в одном из трех
таких квадратов. Очевидно, что все такие центры тяжести лежат
в октаэдре, образованном центрами граней куба. Кроме того,
если одна из точек лежит в центральной плоскости этого октаэд-
ра, а две другие удалены от этой плоскости на расстояние, не
превышающее половины ребра куба, то расстояние от центра
тяжести до плоскости не может быть больше трети ребра.
Значит, все центры тяжести лежат в многограннике, полученном
в результате отсечения от октаэдра шести четырехугольных
97
пирамидок с ребрами, равными одной трети ребра октаэдра. С
другой стороны, все вершины этого многогранника, а значит, и
все его внутренние точки принадлежат искомому ГМТ.
24. п(п - 1) 2 .
Так как выпуклые оболочки двух подмножеств не пересека-
ются, они лежат по разные стороны от некоторой прямой. Таким
образом, требуется узнать, сколькими способами данное множе-
ство точек можно разделить прямой на два подмножества.
Возьмем в плоскости точку О, не лежащую ни на одной из
прямых, соединяющих данные точки, и рассмотрим полярное
соответствие с центром О. Данным точкам будут соответствовать
п прямых, никакие две из которых не параллельны и никакие
три не пересекаются в одной точке. По индукции легко доказать,
что эти прямые делят плоскость на гг(гг + 1)/2 + 1 частей, из
которых 2п неограниченных.
Лемма. Пусть поляры а, Ъ точек А, В делят плоскость на
4 угла. Тогда полюса прямых, пересекающих отрезок АВ,
лежат в двух вертикальных углах, а полюса прямых, не
пересекающих отрезок АВ, - в двух других углах.
Действительно, пусть прямая I пересекает прямую АВ в точке
X. Тогда поляра X проходит через точку пересечения а и Ь. Если
вращать I вокруг X, то ее полюс будет двигаться по этой прямой,
т.е. внутри пары вертикальных углов, образованных а и Ь. При
движении точки X по АВ ее поляра вращается вокруг точки
пересечения а и Ь, переходя из одной пары вертикальных углов
в другую в моменты прохождения X точки А или В. Лемма
доказана.
Вернемся к задаче. Из леммы следует, что две прямые
разбивают данное множество точек одинаковым образом тогда и
только тогда, когда их полюсы либо лежат в одной из частей, на
которые плоскость разбивается полярами данных точек, либо
лежат по разные стороны от всех п прямых. Но второй случай
возможен тогда и только тогда, когда обе точки лежат в неогра-
ниченных областях. Действительно, если точки Р, Q лежат по
разные стороны от всех прямых, то каждая из этих прямых
пересекает отрезок PQ. Значит, каждый из продолжающих этот
отрезок лучей целиком лежит в одной части. Обратно, если точка
Р лежит в неограниченной части, то возьмем луч с началом в ней,
целиком лежащий в этой части и не параллельный ни одной из
п прямых. Точки противоположного луча, лежащие дальше от Р,
чем все точки пересечения с прямыми, лежат по разные стороны
с Р от этих прямых.
Таким образом, 2п неограниченных областей разбиваются на
98
пары, каждой из которых соответствует один способ разбиения
данного множества точек, а каждой из остальных областей
соответствует свой способ разбиения. Всего получаем
и(я-1)/2 + 1 способов, при одном из которых все п точек
попадают в одно подмножество.
Финальный тур
8 класс
1. 90°.
Пусть L - точка пересечения NK и ВС (рис. 89).
Из симметрии относительно ВС видим, что AM = МС = CN и
ZMCB = ZNCB . Далее, из
LN || АС получаем ZCNL =
= ZLCM , а значит, треуголь-
ник CNL равнобедренный, и
LN = CN = AM. Итак, отрезки
AM и LN параллельны и равны,
поэтому ALNM - параллелог-
рамм, и AL || MN ± LC . Нако-
нец, из симметрии относитель-
но ВМ получаем ZAKC =
= ZALC = 90°.
2. Первое решение. Пусть I -
центр окружности, вписанной в треугольник АВС. Тогда
1
ZB'IC' = 180° - (ZIBC + ZICB) = 90° + | ZB'AC'.
Значит, если О ~ центр окружности со, описанной около ABCI,
то ZB'OC' = 180° - ZB'АС'. Таким образом, можно построить
точку О, а затем - точку I (как точку пересечения меньшей дуги
В'С' окружности со с биссектрисой угла S'АС', рис.90). Теперь
точки В и С строятся как .... .
пересечение прямых В'С,
АС' и С'1, АВ' соответ-
ственно.
Второе решение. Так как
ВВ> ~ биссектриса угла В,
точка В' равноудалена от
прямых ВС и АВ. Поэтому
окружность с центром В',
касающаяся АС', касается
также ВС. Аналогично, пря-
мая ВС касается окружности
Рис 90
99
с центром с'> касающейся АВ' (см. рис.90). Следовательно,
для восстановления точек В и С достаточно провести общую
внешнюю касательную к этим двум окружностям (лежащую по
другую сторону от В'С', чем А) и найти точки ее пересечения с
АВ' и АС'.
3. Пусть квадрат АВ CD перегнули по прямой XY; обозначим
получившиеся точки, как показано на рисунке 91. Заметим, что
в прямоугольном треугольнике
центр вписанной окружности,
точки ее касания с катетами и
вершина прямого угла образуют
квадрат, поэтому ее радиус ра-
вен отрезку касательной из этой
вершины. Значит, диаметры
окружностей, вписанных в
треугольники UDX, UAP и
PVУ, равны соответственно dx =
= UD + DX - XU, d2 = UA +
+ АР - UP и J3 = PV + VY -
- PY. Обозначив сторону квад-
рата через а и заметив, что UX =
= ХС и VY = YB, получаем
d{ + d3 - d2 = DU + (a - CX) - CX + PV + BY - PY -
-(a - DU) -(a-PY- BY) + (a - PV) = 2(DC + ВУ - CX).
Опустим перпендикуляр YK на CD. Точки С и U симметричны
относительно XY, поэтому XY ± CU , и Z.DCU = Z.KYX. Кро-
ме того, KY = CD = а. Следовательно, прямоугольные треуголь-
ники CDU и YKX равны, поэтому DU = КХ = СХ -
- СК = CX - BY. Это и значит, что dx+ d3-d2 = 0 .
Замечание. В первой части решения можно рассуждать по-
другому. Прямоугольные треугольники DXY, VYP и AUP
подобны; значит, радиусы вписанных в них окружностей отно-
сятся так же, как соответствующие катеты. Поэтому достаточно
доказать равенство DX + VY = AU, или DX + СК = a- DU. Но
из второй части решения следует, что DU = КХ, откуда и следует
требуемое.
4. Выберем на луче ВС точки X и Q' такие, что ВХ = ВР,
BQ' = ВР + BQ. Тогда треугольник ВРХ - равнобедренный с
углом 60° , значит, он равносторонний, и РХ = ВР, Z.PXQ' - 120° .
Тогда треугольники PBQ и PXQ' равны по двум сторонам и
углу между ними, поэтому PQ' = PQ и XPQ'B = Z.PQB . Ана-
100
логично, выбрав на луче В А точку Р' такую, что ВР' = ВР +
+ BQ, получаем, что PQ' = QP и AQP'B - AQPB (рис.92).
Рис. 92
Отложим теперь на продолжениях отрезков ВР' и BQ' за
точки Р' и Q' отрезки Q'A' = Р'С' = PQ . Тогда
ВА' = ВР' + Р'А' = ВР + BQ + PQ = BQ' + Q'C' = ВС'.
Далее, треугольники QP'A' и PQ'C' равнобедренные, поэтому
AP'Q'Q + AQ'C'P =
1 1
= |(ZQP'B + ZPQ'B) = |(ZBPQ + ZBQP) = 30° .
Значит, угол между прямыми QA' и PC' равен
180° - (ZP'A'Q + ZQ'C'P + ABA'С' + ABC'А') = 90° .
Но если ВА' = ВС' < ВА , то этот угол должен быть меньше 90° ,
а если ВА' > ВА , то больше. Значит, А' = А , С' = С , и
APQB = APQ'B = 2APCQ', что и требова-
лось доказать.
5. Да. —4 q
Пусть в четырехугольнике ABCD AD = \ /
= BD = CD = х, АВ = ВС = у < х/4, а Р - 1 /
такая точка на диагонали BD, что PD = у vy !
(рис.93). Тогда РВ + PD = BD = х, РА = V /
= PC > AD - PD = х у, следовательно, \\ //
РА + РВ + PC + PD > Зх - 2у > 2х + 2у = \\р//
= АВ + ВС + CD + DA. WZ
6. Пусть Н - вторая точка пересечения со \ Т /
с прямой CBt. Поскольку АТУ - биссектриса \м
равнобедренного треугольника ABtC , имеем Di
B^HIAW. Рис 93
101
Далее, если точки С и W лежат по одну сторону от АН, то
ZAWH = ZACH = 90° - ZCAW = 90° - ZWAB ,
т.е.
WH 1 АВг
(рис.94). Если они лежат по разные стороны, то
ZAWH = 180° - ZCH = 90° + ZWAB ,
откуда опять же следует
WH ± ABt. Наконец, если эти
точки совпадают, то треуголь-
ник AWBi прямоугольный, и
Н = W - его ортоцентр.
Итак, в любом случае точка
Н лежит на двух высотах треу-
гольника AWBt, т.е. является
его ортоцентром.
7. Первое решение. Пусть К
- середина АС. Так как
KQ || ВС , то KQ делит высоту
AAi пополам. Значит, в четы-
рехугольнике AKA^Q диагонали перпендикулярны и делятся
точкой пересечения пополам, т.е. он - ромб. Кроме того, из
симметрии HQ = НК.
Аналогично, пусть R - точ
CCt ; тогда CKQR - ромб,
Рис 95
., симметричная К относительно
HQ = HR (рис. 95). Значит,
отрезки AtQ , АК, КС и CXR
параллельны и равны, откуда
QA^RC^ - параллелограмм, а
тогда Р ~ середина RQ. Зна-
чит, HP - медиана в равнобед-
ренном треугольнике HQR, а
значит, и высота, что и требо-
валось доказать.
Второе решение. Пусть L -
середина AAt. Тогда PL - сред-
няя линия треугольника
АА^С , поэтому ZPLH =
= ZBAAi и, следовательно,
ZPLQ = 90° - ZPLH = ZCXHA.
С другой стороны, точки At и Q лежат на окружности с
диаметром АС, поэтому треугольники АХСХН и САН подобны;
значит, их медианы HP и НК образуют равные углы со сторона-
102
ми НСХ и НА соответственно.
Значит, ZQHA = ZKHA =
= ZPHC} и поэтому ZPHQ =
= ZCXHA (рис.96). Итак,
ZPHQ = ZCXHA = ZPLQ , следо-
вательно, точки Р, Q, L, Н лежат
на одной окружности и
ZQPH = 180° - ZQLH = 90° .
8. Пусть квадрат разрезан на п
многоугольников. Тогда каждый
из этих многоугольников имеет не
более одной стороны на каждой
из сторон квадрата; с любым же из остальных многоугольников
разбиения он граничит не более чем по одной стороне. Следова-
тельно, всего у него может быть не более 4 + (п-1) = и + 3
сторон.
Итак, количество сторон любого многоугольника разбиения
не меньше 3 и не больше п + 3. Значит, если среди них нет
треугольника, то количества их сторон должны быть равны 4,5,
..., п + 3. Но тогда (п + 3)-угольник должен примыкать ко всем
сторонам квадрата. Поэтому каждый из остальных многоуголь-
ников может примыкать не более чем к двум сторонам квадрата
и, следовательно, иметь не более 2 +(и-• 1) = и +1 стороны.
Значит, среди многоугольников разбиения нет (п + 2) -угольни-
ка. Противоречие.
9 класс
= 90° - ZACB = ZCBBX, пря-
и ОВХА подобны (рис.97).
1. Поскольку ZCAAX
моугольные треугольники ОАХВ
Значит, их высоты АХА2 и ВХВ2
делят отрезки ОВ и ОА в одном и
том же отношении. Отсюда по
обратной теореме Фалеса получа-
ем утверждение задачи.
2. Проведем через At, и Ct
прямые д, b и с, параллельные
соответственно ВС, СА и АВ; по-
кажем, что они вторично пересе-
кают описанную окружность в
одной и той же точке. Действи-
тельно, пусть с пересекает окруж-
ность вторично в точке Р (если она касается окружности, то
P = Ci). Тогда, поскольку АВ || СХР и AAt || CQ , получаем
103
Рис 98
точке Р относительно середин
треугольника АВС. Таким об
uBP = kjC^A = uA}C (здесь че-
рез иХУ обозначается величи-
на дуги, проходимой от X к У по
часовой стрелке). Это и означа-
ет, что АХР || ВС , т.е. а прохо-
дит через Р. Аналогично, b про-
ходит через Р (рис.98).
Далее, точки Ct и Р симмет-
ричны относительно серединно-
го перпендикуляра к АВ, а точ-
ки Q и С2 симметричны отно-
сительно АВ; это значит, что Р и
С2 симметричны относительно
середины Со отрезка АВ; ана-
логично, А2 и В2 симметричны
Aq и Во соответствующих сторон
эазом, А2В2 = 2A^Bq = -АВ ; ана-
что
логично, А2С2 = — АС и
В2С2 = -ВС . Следовательно,
треугольники АВС и А2В2С2 цен-
трально симметричны, и прямые,
соединяющие их соответствую-
щие вершины, проходят через
центр симметрии.
3. Первое решение. Пусть К -
точка касания вписанной окруж-
ности треугольника АВС со сто-
роной АВ (точка К лежит на
отрезке MN; рис.99). Заметим,
МК = АК - AM =
АВ+АС-ВС AL+AC-LC BL+LC-BC г кт
2 2 2
Далее, пусть Ia , 1Ь и I - центры окружностей (£>а , Cty, и <о,
вписанных в треугольники ACL, BCL и АВС соответственно. По
AL _ AIa _ AM
свойству биссектрисы и теореме Фалеса имеем ,
тт ALMN
т е 1L —- ~ —
AM '
Итак, мы можем последовательно построить точку К, затем I
(как пересечение окружности с центром в £ и перпендикуляра к
104
MN в точке К), 1а и 1Ь (как пересечение биссектрис углов ALI
и CLI с перпендикулярами к отрезку MN в его концах),
окружности сой и , и, наконец, точки С (как пересечение
касательных к сод из А и L) и В (как пересечение MN с
касательной к cofe из точки С).
Второе решение. Докажем равенство 1 /AM + 1 /ML -
= 1 /LN + 1 /NB. Обозначим через х- АС, у = CL, z = LA длины
сторон треугольника ACL, через р, S и г - его полупериметр,
площадь и радиус вписанной окружности соответственно, а
через h - его высоту из вершины С. Тогда
1 1 = 1 1 = z
AM ML p-у р — х (р - х)(р - у)'
Далее, из формулы Герона получаем
I ч S2 rpzh/2
(Р ~ *)(Р ~У) = —----г = ----Ч- ,
p(p-z) р(р-г)
откуда
1 1 _ 2(р-г) _ 2
AM + ML~ rh ~ htg(ZACL/2)-
В треугольнике BCL угол при вершине С и высота из этой
вершины такие же, откуда и следует искомое равенство.
Таким образом, зная отрезки AM, ML, LN, мы можем найти
отрезок NB и построить точку В. Далее, из соотношений АС -
- CL = AM - LM и ВС - CL = BN - LN мы находим разность
АС - ВС = AM - LM - BN + LN = p, а из равенства АС/ВС =
= AL/BL = q~nx отношение. Из этих двух условий можно найти
длины сторон АС = - и ВС = , а значит - и построить
^“1
точку С.
4. При четных.
Первое решение. Если п = 2k, то k главных диагоналей
разрезают правильный n-угольник на п равных треугольников.
Пусть теперь п нечетно; предположим, что правильный п-
угольник Р получилось разрезать требуемым образом. Рассмот-
рим треугольники разрезания, в которых одна из сторон являет-
ся стороной Р. Против этих равных сторон в каждом таком
треугольнике лежит одинаковый угол а . Пусть остальные два
угла треугольника равны р и у. Возможны два случая.
Случай 1. Пусть эти углы не равны между собой, скажем,
р < у. Назовем сторону w-угольника р -стороной или у -сторо-
ной в соответствии с тем, какой угол примыкает к ее левому
концу (если смотреть изнутри). Выберем некоторую р -сторону
105
бив примыкающем треугольнике разреза-
ния рассмотрим сторону угла р , лежащую
внутри Р. Она лежит на диагонали, и на
другом конце эта диагональ также образу-
ет угол р с некоторой стороной с много-
угольника (рис. 100). Этот угол не может
быть разрезан на углы другими диагоналя-
ми; действительно, иначе угол разбиения,
примыкающий к с, должен быть равен р
или р > у, но он меньше, чем р - противо-
речие. Итак, наш угол р принадлежит
треугольнику, примыкающему к у-сторо-
не. Наоборот, рассматривая угол р , примыкающий к произволь-
ной у-стороне с, мы найдем р-сторону б, сопоставленную ей.
Итак, р- и у-стороны разбиваются на пары, и общее их
количество четно; противоречие.
Случай 2. Пусть теперь р = у, ив треугольнике разрезания
АВС, содержащем «нижнюю» сторону АВ многоугольника, угол
при С равен а . Вертикальный к этому угол, равный а , лежит
в некотором другом треугольнике разрезания, а против него -
сторона, равная и параллельная АВ. По
другую сторону от нее в некотором треу-
гольнике разрезания лежит угол, равный
а , и т.д. Получилась цепочка треуголь-
ников (рис. 101); рассмотрим последний
треугольник UVW этой цепочки. Если
он ориентирован не так, как АВС, то его
верхняя сторона, равная и параллельная
АВ, является стороной Р, а тогда п четно,
поскольку в правильном нечетноуголь-
нике нет параллельных сторон. В про-
тивном случае угол при верхней вершине W треугольника U VW
равен а , и W - вершина Р. Тогда обе стороны UV и VW либо
являются сторонами Р, либо лежат на диагоналях. В первом
случае получаем а = р = у = 60°, и угол w-угольника также
равен 60° , откуда п = 3 вопреки условию. Во втором же случае
угол w-угольника при вершине W содержит как минимум угол а
и два угла по р, откуда а + 2р<180°. С другой стороны,
а + 2р = 180° как сумма углов треугольника. Противоречие.
Второе решение. Приведем другое доказательство того, что
при нечетном п указанное разрезание невозможно. Так как п
нечетно, никакие две диагонали не перпендикулярны. Поэтому
через любую точку пересечения двух диагоналей должна прохо-
106
дить по крайней мере еще одна диагональ (в противном случае
образованные диагоналями смежные углы равны двум разным
углам одного треугольника, что невозможно). Докажем теперь,
что из каждой вершины многоугольника выходит не меньше
двух диагоналей.
Предположим, что из вершины Д не выходит ни одной
диагонали. Тогда треугольником, содержащим эту вершину,
будет Д_.|ДД+1, и один из углов треугольника разбиения равен
углу 72-угольника. Но тогда каждая сторона 72-угольника лежит
в треугольнике разбиения, содержащем еще одну его сторону.
Значит, стороны разбиваются на пары, что невозможно.
Предположим теперь, что из вершины Д выходит одна
диагональ. Тогда она делит угол при этой вершине на два
неравных угла [3 < у. Оба эти угла примыкают к сторонам
тг-угольника; значит, в любом треугольнике разбиения к стороне,
равной стороне тг-угольника, примыкают углы, равные £ и у.
Итак, сумма всех углов треугольников разбиения, примыкаю-
щих к сторонам тг-угольника, равна п (Р + у), что равно сумме
углов я-угольника. Значит, из каждой вершины выходит ровно
одна диагональ, что опять же невозможно в силу нечетности п.
Утверждение доказано.
Итак, пусть гг-угольник разрезан на k треугольников; сумма
всех их углов равна 180° • k. Вклад углов 72-угольника в эту
сумму равен 180° (п- 2), значит, сумма углов при точках пере-
сечения диагоналей равна 180° (/г - п + 2); каждая такая точка
добавляет 360°, поэтому количество этих вершин равно
(/? - 72 + 2)/2 . Поскольку каждая такая точка принадлежит по
крайней мере шести треугольникам, а каждая вершина много-
угольника - трем, то общее число треугольников не меньше, чем
(3(6 - 72 + 2) + 3тг)/3 = k + 2 > k - противоречие.
5. 45°.
Пусть L - проекция М
на АВ. Заметим, что
ML _ AL _ АР _ 1
CN ~ ВК~ ВС ~ у[1'’
поэтому и
LD ALiAD l
СК ~ ВК + ВС ~ V2 '
Значит, прямоугольные тре-
угольники MLP и NCK
подобны, и ZMPL =
= ZNKC (рис. 102). Поэто- Рис 102 с
107
му угол между прямыми NK и MD равен углу между прямыми
КС и LD, т.е. 45° .
ab
6. ---Г.
а + Ь
Пусть К - такая точка на отрезке АС, что МК ± ВС . Тогда
ZMCA = ZMCB = Z.CMK , поэтому МК = КС; кроме того, из
симметрии КС = МВ. Далее, по теореме Фалеса и свойству
z СК ВМ a DN „
биссектрисы имеем = = = Следовательно,
АК AM b AN
KN || CD; аналогично предыдущему, получаем KN = КС.
Таким образом, К - центр описанной окружности треугольника
CMN, а ее радиус по теореме о
биссектрисе равен КС = МВ =
= ab (a + b) (рис. 103).
7. Пусть А1А2^з^4^5 “ исходный пятиугольник, ВХВ2В3В4В5
~ пятиугольник, образованный его диагоналями, а С}С2С3С4С5
- пятиугольник, образованный диагоналями ВХВ2В3В4В5
(рис. 104). Продолжим нумерацию вершин циклически (т.е.
А^+5 = А^ и т.д.). Для удобства будем обозначать площадь
многоугольника Р через [Р].
Заметим, что
N' = ЕДвд+1вг+2] - [В&В&В,],
поскольку в сумме справа как раз пятиугольник СХС2С3С4С5
учтен с кратностью -1, треугольники вида ДД+1Ц+3 - с коэф-
фициентом 1, а треугольники вида CzCi+1Bz+3 - с нулевым
коэффициентом. Значит, требуемое неравенство равносильно
неравенству
^[дд+д+3]>£[в1вг+1д+2].
108
Докажем, что [ДД+1Вг+3] > [B/+2B/+3Bi+4 ]; тогда, сложив пять
неравенств такого вида, получим требуемое.
Ясно, что достаточно это доказать при i = 1. Присоединив к
каждому из треугольников At А2В4 и В3В4В5 треугольник ДВ3В4 ,
получим треугольники АХВ3А2 и АХВ3В5 с общим основанием
АХВ3 . При этом расстояние от точки В5 до этого основания
меньше, чем от точки А2 ; значит, [AiB3A2] > [AtB3B5], что и
требовалось доказать.
8. Пусть О - центр окружности Q, описанной около треу-
гольника АВС. Из прямоугольных треугольников АВН и АСН
имеем АК АВ = АН2 = ALAC, т.е. AK/AL = АС/АВ. Зна-
чит, треугольники ALK и АВС подобны, т.е. ZAKL = ZACB .
Поскольку ZOAB = я/2 - ZACB ,
получаем О А ± KL , значит, О А -
серединный перпендикуляр к хор-
де PQ, и поэтому АР = AQ. Отсюда
ТА - биссектриса угла PTQ
(рис. 105).
Итак, центр I окружности, впи-
санной в PQT, лежит на ТА. Кроме
того, по лемме о трезубце AI = АР.
Значит, для доказательства того,
что I = Н, достаточно показать, что
АН = АР. Пусть D - точка пересе-
чения АО и KL, аг- радиус Q . По
теореме Пифагора,
AQ2 — г2 — AQ2 - OQ2 =
= (AD2 + DQ2) - (О£>2 + DQ2) = AD2 -(AD-r)2 ,
откуда AQ2 = 2г AD . Далее, заметим, что АН - диаметр
окружности, описанной около треугольника AKL, поскольку
ЛА КН = ЛАЬН = 90° ; значит, коэффициент подобия треуголь-
ников AKL и АВС равен АН/ (2г). Отрезки AD и АН -
соответственные высоты в этих треугольниках, поэтому
AD АН = АН (2г) , или АН2 = 2г • AD = AQ2 , что и требова-
лось доказать.
Замечание. Доказательство того, что AQ = АН, можно
упростить, рассмотрев инверсию с центром А и радиусом AQ.
При этой инверсии прямая PQ и окружность Q переходят друг
в друга, поэтому точки В и К также переходят друг в друга.
Следовательно, AQ2 = АВ • АК = АН2 .
109
Ю класс
1. При четных.
Если п четно, разобьем каждую грань куба на
квадраты 2x2й заклеим каждый квадрат двумя прямоугольни-
ками так, чтобы к длинным сторонам прямоугольников, лежа-
щих в одном квадрате, примыкали короткие стороны прямоу-
гольников, лежащих в соседних квадратах. Покажем, почему
так можно оклеить все грани. Легко понять, что можно оклеить
четыре боковые грани, образующие кольцо. При этом на верхней
грани один ряд квадратов 2x2 заполнить можно (в углах
оклейка будет выглядеть так, как на
/ /----------У рисунке 106 или симметрично); этот ряд
/ / / / определяет однозначно всю оклейку вер-
____/ / /\/ . хней грани; при этом остальные четыре
/ / К \/\ крайних слоя квадратов будут заполне-
——г—( \ X \ ны аналогично, поэтому на остальных
V---------\ у \ ребрах прямоугольники также будут сты-
\ у / коваться требуемым образом. Аналогич-
\ \ \ / но оклеивается нижняя грань.
\ \ \ При нечетных п общее число прямо-
те 106 угольников равно бп1 /2 = Зя* 2 . Если у
каждого пять соседей, то общее количе-
ство пар соседних прямоугольников будет равно Зя2 • 5/2 ;
однако это число нецелое. Значит, требуемая оклейка невоз-
можна.
2. Для остроугольных.
Пусть AAt, ВВХ, ССХ - высоты треугольника АВС, Н - его
ортоцентр. Рассмотрим любую хорошую точку Р; пусть ААР ,
ВВР, ССР - проходящие через нее чевианы. Из условия
получаем, что ААР АА1 = ВВР ВВХ =ССР CCt ; значит, прямо-
угольные треугольники АА^Ар, ВВ}ВР и СС^СР подобны,
поэтому ЛА^ААр = ZB{BBP = АСХССР . При этом возможны два
различных случая ориентации этих углов. (Напомним, что
ориентированным углом А(1,т) называется угол, на который
надо повернуть против часовой стрелки прямую I, чтобы она
стала параллельна т.)
Случай 1. Пусть Z(AtA, ААР) = /_(ВХВ, ВВР) = Z(CtC, ССР)
(в частности, треугольник АВС остроугольный; действительно,
если, скажем, Z.BAC не острый, то углы ЛВХВВР и АСХССР
острые и ориентированы по-разному). Из первого равенства
следует, что точки Р, Н, А, В лежат на одной окружности;
аналогично, точка Р лежит на окружностях, описанных около
110
треугольников АСН и ВСН. Но эти три окружности имеют ровно
одну общую точку Я; значит, Р совпадает с Н.
Случай 2. Два из трех ориентированных углов равны, а
третий (для определенности, Z(CtC, ССР)) им противополо-
жен. Тогда, как и в первом случае, точка Р лежит на окружности
Qc , описанной около треугольника АВН (поскольку
Z(AH, НВ) = -Х(АС, СВ), эта окружность симметрична опи-
санной окружности Q треугольника АВС относительно прямой
АВ). Пусть прямая СН вторично пересекает Qc в точке X (тогда
точки С и X симметричны относительно АВ; на рисунках 107 и
108 показаны две таких потенциально возможных конфигура-
ции). Тогда Z(PX, ХС) = Х(РВ, ВН) = -Z(PC, СХ); если эти
углы ненулевые, то это означает, что треугольник PCX равно-
бедренный, PC = РХ. Но тогда точка Р лежит на серединном
перпендикуляре АВ к отрезку СХ, что невозможно. Значит,
Z(PB, ВН) = 0 , И Р = Н.
Таким образом, хорошей точкой может быть только орто-
центр треугольника (ив остроугольном треугольнике он ею,
очевидно, является). Следовательно, в остроугольном треуголь-
нике хорошая точка одна, а в неостроугольном - ни одной.
Замечание. В случае 2 есть более короткое, но менее элемен-
тарное решение. Геометрическим местом точек Р, удовлетворяю-
щих одному равенству Z(B1B, ВВР) = -Z(CtC, ССР), является
описанная около треугольника АВС равносторонняя гипербола.
Две таких гиперболы могут иметь максимум четыре общих
точки, и эти точки - А, В, С и Н.
3. Первое решение. Пусть Q и С2 ~ точки касания окруж-
ностей о) и (ос, соответственно, вписанной и вневписанной в
111
треугольник АВС, со стороной АВ; пусть также С' - середина
этой стороны. Тогда, как известно, CtC' = С2С'. Далее, при
гомотетии с центром С, переводящей сос в со, точка С2
переходит в точку С3 на со, диаметрально противоположную Ct
(так как касательные к со в этих точках параллельны; см. рис.
109). Значит, IC' - средняя линия треугольника СХС2С3,
поэтому С'11| СС2. Значит, при гомотетии с центром М и
коэффициентом -2 точка I переходит в точку N, лежащую на
СС2 (аналогично, она лежит на отрезках, соединяющих другие
вершины с соответствующими точками касания вневписанных
окружностей; точка N называется точкой Нагеля треугольника
АВС). Значит, N получается из М' гомотетией с центром I и
коэффициентом 3.
Перейдем к решению задачи. Пусть MI -г/3 . Тогда точка N
лежит на со. Пусть для определенности касательная к со в этой
точке пересекает стороны Л С и ВС; тогда со и С лежат по разные
стороны от этой касательной, а значит, N = С3. Так как
IC3 1 ЛВ , то и Mil. АВ (рис. 110).
Обратно, пусть АВ ± IM . Тогда точка N лежит на прямой
1С2; кроме того, она лежит на СС2 . Поскольку треугольник
АВС неравнобедренный, эти прямые различны, а значит, N = С2,
и г = IN =31М.
Второе решение. Пусть АВ ± IM . Тогда по теореме Пифа-
гора
AM2 - ВМ2 = (AQ2 + CjM2) - (sq2 + QM2) =
= (р~а)2 -(р-b)2 =с(Ь-а)
112
(здесь Ct - точка касания АВ со вписанной окружностью).
Пользуясь формулой длины медианы, получаем
AM2 = |(2Ь2 + 2с2 - а2), ВМ2 = |(2а2 + 2с2 - Ь2),
откуда
с(6 - а) = — (b - а)(а + b) t или а + b = Зс, т.е. р = 2с.
Легко показать, что верно и обратное: если р = 2с, то АВ ± IM .
Наконец, поскольку c(IM + r)/2 = SABM = SABC/3- pr/3 , по-
лучаем IM + г = 4r/3, или IM = r/3 .
Пусть, наоборот, MI = r/3 . Заметим, что
iА2 + ib2 + ic2 = (7м + мл)2 + (7м + мв)2 + (7м + мс)2 =
= МЛ2 + МВ2 + МС2 + 21М • (Ш + МВ + МС) + 3MI2 =
= МЛ2 + МВ2 + МС2 + 3MI2.
Значит, если MI = г/3 , то
/Л2 + IB2 + IC2 = МЛ2 4- МВ2 4- МС2 4--г2 = -(а2 4-Ъ2 4- с2 4-г2)
3 3' 1
Далее, по теореме Пифагора IA2 =г2 +(р- а)2; наконец, по
формуле Герона
г2 = s2/p2 = (р- а)(р - Ь)(р - с)/р .
Итак,
а +Ь +Г =(Р~ а)2 +(р~ Ь)2 + (р- с)2 + Зг2,
ИЛИ
fl2 4-Ь2 4-С2 , ч2 / »\2 / \2
-----3-----(Р~а) -(Р~с) =
_ 8г2 _ 8(в~ д)(в~ь)(/?~с)
“ ~ ~ Зр
что приводится к виду (в - 2«)(р - 2Ь)(в - 2с). Как показано
выше, одна из скобок обращается в нуль тогда и только тогда,
когда IM перпендикулярно соответствующей стороне.
4. Все точки криволинейного восьмиугольника, ограниченно-
го дугами восьми парабол с фокусами в вершинах квадрата и
директрисами, содержащими несмежную сторону, кроме сере-
дин сторон квадрата (рис.111).
Заметим сразу, что середина гипотенузы лежит внутри квад-
рата. Если концы гипотенузы лежат на противоположных сторо-
113
нах квадрата, то ее середина лежит на соответствующей средней
линии. Пусть теперь концы X и Y гипотенузы треугольника XYZ
принадлежат соответственно сторонам АВ nAD квадрата ABCD,
а вершина Z - стороне ВС (рис.112). Обозначим через О
середину XY. Точки AnZ лежат на окружности с диаметром XY;
поэтому О А = ОХ = OY = OZ, и расстояние от О до А меньше,
чем до других вершин квадрата, но не меньше, чем расстояние от
О до прямой ВС.
Геометрическим местом точек, равноудаленных от А и ВС,
является парабола с фокусом А и директрисой ВС (вершиной
этой параболы является середина АВ). Значит, точка О лежит
между ВС и этой параболой в четверти квадрата, содержащей А.
При этом точка О может попасть на параболу, но не может - на
среднюю линию (иначе точка У совпадет с В).
Рассмотрев аналогично другие случаи расположения вершин
треугольника и объединив полученные области, получим криво-
линейный восьмиугольник Р, ограниченный дугами восьми па-
рабол. Вершинами Р являются середины сторон квадрата (они
не лежат в ГМТ) и точки пересечения парабол с его диагоналями.
При этом средние линии квадрата лежат в Р; значит, и искомое
ГМТ содержится в нем. Осталось показать, что любая точка О
этого восьмиугольника, кроме середин сторон квадрата, принад-
лежит ГМТ.
Если О лежит на средней линии, параллельной АВ, и
расстояние от нее до AD не превосходит расстояния до ВС, то
можно в качестве концов гипотенузы X и У взять проекции О на
АВ и CD, а в качестве вершины прямого угла - одну из точек
пересечения окружности с диаметром XY и стороны AD. Если же
точка О лежит в четверти квадрата, содержащей А, между
параболой с фокусом А и директрисой ВС и соответствующей
114
средней линиеи, то в качестве X и Y возьмем вторые точки
пересечения окружности с центром О и радиусом ОА, а в
качестве Z - точку пересечения этой окружности со стороной ВС
(такая точка существует, так как расстояние от О до ВС не
превосходит ОА, а расстояния до точек В и С - превосходят).
5. Пусть X и Y - середи-
ны дуги а и дуги АВ окруж-
ности со соответственно, а О
- центр со. Тогда луночка с
вершинами А и В находится
между концентрическими ок-
ружностями с центром О и
радиусами ОУ и ОХ
(рисЛ13). Значит, диаметр
окружности, вписанной в лу-
ночку, не превосходит XY; с
другой стороны, окружность
с диаметром ХУ касается со и
а и лежит в луночке. Итак, максимальный диаметр окружнос-
ти, вписанной в эту луночку, равен XY.
Поскольку AC ± BD , сумма дуг АВ и CD окружности со
равна 180° . Пусть К и L - середины отрезков АВ и CD
соответственно; тогда ХОК = 90° - XCOL = Z.OCL , поэтому пря-
моугольные треугольники АО К и ОСЬ равны по гипотенузе и
острому углу. Поэтому ОХ = ОК + КХ = ОК + КА =
= (АВ + CD)/2 , поэтому XY = (АВ + CD}/! - г , где г - радиус
со. Аналогично, максимальный диаметр окружности, вписанной
в луночку с вершинами С и D, также равен (АВ + CD)/2 - г .
6. Поскольку DA' ± (ХВС), получаем XDA'C = 90° ; анало-
гично, XD&C = 90° (рис. 114). Значит, точки А' и В7 лежат на
сфере с диаметром DC, поэтому расстояние между ними не
превосходит диаметра: А7В7 < DC .
Аналогично, А'С7 < DB и В'С' <
< DA . Складывая эти три неравен-
ства, получаем требуемое.
7. Как известно, в произвольном
треугольнике XYZ симедиана XX'
(т.е. прямая, симметричная медиане
из вершины X относительно угла X)
проходит через точку пересечения
касательных к описанной окружнос-
ти в точках Y и Z. Значит, прямая
DK является симедианой треуголь-
115
с
ника Л CD. Далее, треугольники Л CD и CBD подобны. Значит,
если DL и DM - их медианы, то ZCDK = ZADL = ZCDM ,
откуда и следует, что точка М лежит на DK (рис. 115).
8. Ясно, что точки X и У лежат на диагоналях BD и АС
соответственно; поэтому прямые АС и BD содержат высоты
треугольников АХ В и CYD соответственно. Отметим на отрез-
ках AM и DM точки Р и Q
соответственно так, что АР =
= DQ = AD. Тогда АХ - биссек-
триса и, следовательно, высота в
равнобедренном треугольнике
АВР', значит, ортоцентр Нх -
это точка пересечения прямых
ВР и АС. Аналогично, Ну - это
точка пересечения CQ и BD.
Наконец, из тех же соображений
получаем AZ ± DP , BZ ± AQ ,
так что Н2 - точка пересечения
прямых AQ и ВР (рис. 116).
Применим теорему Дезарга к
Рис 116
треугольникам BPD и CAQ; поскольку прямые ВС, РА и DQ,
соединяющие их соответственные точки, пересекаются в точке
М, получаем, что точки пересечения прямых, содержащих
соответственные стороны этих треугольников, лежат на одной
прямой. Как показано выше, эти точки и есть Нх , Ну и Н2.
IX ОЛИМПИАДА
Заочный тур
1. 45°.
По теореме о внешнем угле ZAED = 90° + ZB =
= 270°-2ZA (рис. 117).
116
Следовательно,
ZEAD = (180° - ZAED)/2 = ZA - 45° .
2. Возьмем на сторонах
ВС и АС точки А' и В' так,
что АВ' = В» О = ОА' =
= А'В . Очевидно, что
А'В'\\АВ, т.е. ХСА'В'=
- ZCBA = 80° . Кроме того,
ZA'OB = ZA'BO = ZBCO =
= 10°.Значит, ZCA'O = 20° ,
a ZOA'B' = 60° , т.е. треу-
гольник ОА'В' - равносто-
ронний. Тогда А'В' = А'В и
ХА'ВВ' = ХА'К В = ХАВВ'
(рис. 118). Следовательно,
точка В7 совпадает с Bt .
Аналогично, А' совпадает с А
3
Рис. 117
Рис. 118
t, что и требовалось доказать.
Пусть I - центр вписанной окружности треугольника АВС,
D - четвертая вершина прямоугольника ABCD. Так как
Al X AtA2 , CI X CtC2 , то перпендикуляры из А на ССХ и из С
на AAt пересекаются в центре J окружности, вписанной в
треугольник A CD. Поэтому достаточно доказать, что DI X AtCt.
Пусть X, Y, Z - проекции I на АВ, ВС, CD соответственно. Тогда
BCt = ХС2 = ZD и AtB = СУ = IZ , значит, треугольники AtBCt
и IZD равны, т.е. XIDZ = ХА£\В (рис.119), откуда и следует
искомая перпендикулярность.
4. Так как точки О, К лежат на серединном перпендикуляре
к ВС, то ОК || АР . Поэтому ХОРК = ХРОК = ХОРА . Значит,
точка А', симметричная А относительно ОР, лежит на прямой
2 РК. При этом ОА' = ОА , т.е.
117
ности треугольника АВС (рис. 120) и, следовательно, совпадает
с одной из точек Е, F.
5. Да.
Пусть ABCD и О - четырехугольник и точка из условия. В
равных треугольниках против равных сторон лежат равные
углы. Так как ААВО = АСВО , то углы В АО и ВСО равны как
лежащие против ВО. Аналогично XDAO = XDCO, откуда
XBAD = XBCD . Точно так же равны и два других противопо-
ложных угла четырехугольника, поэтому сумма любых двух
соседних углов равна я, т.е. ABCD - параллелограмм.
При точке О найдутся два соседних угла, сумма которых не
меньше я, скажем ZAOB и ХСОВ. Второй из них равен
одному из углов треугольника АОВ. Это может быть только
ZAOB, так как его сумма с любым другим углом треугольника
АОВ меньше я. В равных треугольниках АОВ и СОВ против
Рис. 121
равных углов лежат равные сторо-
ны, поэтому АВ = ВС и, значит,
ABCD - ромб.
6. Из условия следует, что
ХВХА = ХВРА = XCYD ( рис.
121). Значит, трапеция ВХ У С рав-
нобокая, что равносильно утверж-
дению задачи.
7. Прямые А1а и С1с пересе-
каются в центре I вписанной ок-
ружности треугольника АВС. При этом AIa/IaI = AD/ID ,
CIc ICI = CD ID . По теореме Менелая получаем, что QA/QC =
= AD/CD = АВ/ВС. Следовательно, BQ - внешняя биссектриса
угла В, что и требовалось доказать.
8. Дуга окружности, проходящей через В, С и центр О
описанной окружности треугольника АВС.
Пусть окружности касаются. Тогда углы, образованные их
общей касательной с прямыми АС и АВ, равны соответственно
углам ALE и AKF, которые в свою очередь равны углам АВХ и
АСХ. Поскольку сумма этих углов равна углу А треугольника,
то ХВХС = 2ZA = Х.ВОС . Аналогично получаем, что любая
точка дуги удовлетворяет условию.
9. 90°.
Пусть D - четвертая вершина параллелограмма ACBD, J -
центр вписанной окружности треугольника ABD, Sx, S2 - точки
касания этой окружности с AD и BD. Тогда SJ\ || АС , S2T2 || ВС
и ZT1JT2 - ZS^JLS^ = я “ ZC . Кроме того, DSX = DS2 , а значит,
прямые SJ\, S2T2 и DJ пересекаются в одной точке. Следова-
118
тельно, J совпадает с точкой пересечения прямых SXTX и S2T2
т.е. ZC = 90° (рис.122).
10. Поскольку АС' - ВС' = АС - ВС , вписанные окружнос-
ти треугольников АС С' и В С С' касаются стороны С С' в одной
и той же точке. Поэтому СВ{ = СА2 . Кроме того, АВ} = AQ,
ВА2 = ВС2, и, вычислив углы четырехугольника А2В1С1С2,
получаем, что он вписанный. Следовательно, прямые В{С{,
А2С2 и С С' пересекаются в радикальном центре трех окружно-
стей: описанной окружности четырехугольника А2В1С1С2 и впи-
санных окружностей треугольников ACC', ВСС' (рис. 123).
11. а) Нет; б) нет.
а) Пусть для определенности г4 = г (АВС). Достаточно пока-
зать, что r(ABC)/2 < m^x\r(ABD),r(CBD')\ . Середина К диа-
гонали АС лежит в одном из треугольников ABD, CBD, скажем,
в треугольнике ABD. Тогда треугольник AKL, где L - середина
АВ, целиком содержится в треугольнике ABD, поэтому
r(ABC)/2 = r(AKL) < г (ABD).
б) Пусть г = гх - радиус окружности, вписанной в треуголь-
ник АВЕ. Так как диаметры окружностей, вписанных в треу-
гольники ВСЕ, ADE, меньше высот этих треугольников, совпа-
дающих с высотами ha, треугольника АВЕ, достаточно
доказать, что одна из этих высот не превосходит 4г. Пусть
АЕ > BE . Тогда полупериметр треугольника р < АЕ + BE <
< 2АЕ и hb= 2S/AE = 2рг/АЕ < 4г .
Примечание. Отметим, что в обоих пунктах ответ изменится
на положительный, если константу 2 заменить на меньшую
12. Предварительные замечания. Поскольку все основания
высот и биссектрис по условию различны, треугольник неравно-
бедренный. На любой стороне треугольника основание высоты
лежит ближе к меньшей из прилежащих сторон, чем основание
биссектрисы, и поэтому достаточно определить, какая сторона
119
треугольника наибольшая, наименьшая и средняя. Основания
биссектрисы и высоты, проведенных из некоторой вершины X,
будем обозначать Lx и Нх соответственно.
Лемма. Если АС > ВС, то прямые LBLA и НВНА пересека-
ют продолжение стороны АВ за вершину В.
Доказательство леммы. Пусть LBD - перпендикуляр из LB
на АВ, а СН - высота. Поскольку биссектриса делит сторону
пропорционально прилежащим, выполнено равенство
LBD : СН = АВ : (ВС + АВ). Аналогично, если LAE - перпен-
дикуляр из La tt'dAB, то LaE : СН = АВ : (АС + АВ) ). Так как
АС > ВС, то LBD > LaE , поэтому LBLA пересекает АВ за
вершиной В, что и требовалось.
Точки Нв , НА лежат на полуокружности с диаметром АВ.
Если бы углы НаАВ и НвВА были равны, то перпендикуляры
из НА и Нв на АВ также были бы равны. Но первый из углов
меньше, поэтому и соответствующий перпендикуляр меньше.
Лемма доказана.
а) Соединим отмеченные точки с противолежащими верши-
нами. Получим два семейства конкурентных прямых. На двух
сторонах треугольника возьмем точки, принадлежащие одному
и тому же семейству, и проведем через них прямую. Согласно
лемме, она пересекает продолжение третьей стороны за мень-
шей из двух выбранных сторон - независимо от того, какому
семейству соответствуют выбранные точки. Отсюда определя-
ется, какая сторона треугольника меньше какой, что и требу-
ется.
б) Для каждой вершины треугольника выберем на прилежа-
щих сторонах ближайшие отмеченные точки и соединим их
прямой. Как показано ниже, эти прямые пересекут продолже-
ние наибольшей стороны треугольника за вершину среднего
угла и продолжения остальных двух сторон за вершину наи-
большего угла. Отсюда определяется, какая сторона треугольни-
ка меньше какой, что и требуется.
Докажем утверждение, выделенное курсивом. Пусть АВ >
> АС > ВС. Отмеченные точки, ближайшие (по сторонам) к
вершине наименьшего угла, - основания биссектрис, а ближай-
шие к вершине наибольшего угла - основания высот. Согласно
лемме, соединяющие их прямые пересекают соответственно про-
должение ВС за С и продолжение АВ за В. Отмеченные точки,
ближайшие по сторонам к вершине среднего угла В, - это Нс и
La . Согласно лемме, прямая LCLA пересекает продолжение АС
за С в некоторой точке Р. Луч HCLA направлен внутрь треуголь-
ника НсСР и потому пересекает СР, что и требуется.
120
13. Пусть A'Ct ± BA . Тогда по теореме Фалеса высота,
проведенная из С, делит отрезок A^Q в отношении
AtC : С А' = (р - с): (р - а). Через ту же точку проходит и высо-
та из А. Обратное утверждение доказывается аналогично.
14. Пусть X, Y - проекции N и М на ВС. Тогда утвержде-
ние задачи равносильно равенству RY = XQ. Так как
Z.NQX = Z.NAB = Z.DBA , тре-
угольники XQN и ABD подобны
(рис. 124). Значит,
XQ = AB NX/AD .
Но
NX = CD sin Z BCD 2-
= CD • AD/2BC ,
следовательно,
XQ = АВ CD/2BC = RY .
15. а) Опишем вокруг треугольника А2В2С2 треугольник
А'В'С'. А так, что С2А2 1 В'С', А2В2 1 С'А', В2С2 1 А'В'.
Очевидно, что соответствующие стороны треугольников АВС и
В'С'А' симметричны относительно центра описанной окружности
треугольника А2В2С2 . При этой симметрии треугольник А2В2С2
переходит в треугольник В^Ср^ . Следовательно, эти треуголь-
ники равны и имеют общий центр описанной окружности.
б) В описанной окружности треугольника АВС рассмотрим
хорды АА', ВВ', СС', АА" , ВВ" , СС" , лежащие соответ-
ственно на прямых AtBt, ВХС}, СГА^ , А2С2 , В2А2 , С2В2. Из
условия задачи следует равенство дуг АС', В А', СВ', АВ" ,
СА", ВС". Пусть каждая из этих дуг равна ф. Тогда при
повороте вокруг центра описанной окружности хорды АА',
В S', С С' переходят соответственно в В В" , СС" , АА" , зна-
чит, этот поворот совмещает тре-
угольники А1В£\ и А2В2С2
(рис. 125).
Примечание. Как частный слу-
чай этой задачи получаем, что,
если треугольник АХВХСХ вырож-
дается в точку, то треугольник
А2В2С2 также вырождается в точ-
ку, причем обе точки равноудале-
ны от центра описанной окружно-
сти. Эти точки называются точ-
ками Брокара треугольника.
121
16. При полярном преобразовании относительно вписанной
окружности перпендикуляр из I на медиану перейдет в бесконеч-
но удаленную точку этой медианы, прямая А'В - в точку С, а
прямая, проходящая через С и параллельная АВ, - в точку Р
пересечения А'В с I С'. Таким образом, надо доказать, что эта
точка лежит на медиане.
Поскольку IA' = IB ,
APIB = AA, APIA'= АВ, то
ВР : А'Р = ВС : АС. А так как
СА' = СВ, то
sin ААСР : sin АВСР =
=ВС:АС,
т.е. СР делит АВ пополам
(рис. 126).
17. Пусть диагонали четы-
рехугольника ABCD пересе-
ис каются в точке Р. Обозначив
РА = а, РВ = b, PC = с, PD = d, выразим стороны четырехуголь-
ника по теореме косинусов через a, b, с, d и coscp:
|АВ2 - ВС2 + CD2 - СА2\ =
= 2cos<p(6z6 + be + cd + da) = 2AC • BDcoscp .
Но по теореме Птолемея AC • BD < AB • CD + BC AD , причем
равенство достигается только на вписанном четырехугольнике.
18. Пусть В, С', X', Y' - точки, симметричные В, С, X,
У относительно MN. Тогда ВВСС' - равнобокая трапеция,
диагонали которой пересекаются в точке L, инверсной А отно-
сительно окружности с диаметром MN. В этой же точке пере-
секаются диагонали равнобокой
трапеции XX'YY', вписанной в эту
окружность. Боковые стороны этой
трапеции пересекаются на поляре
точки L, которая проходит через А
и параллельна основаниям трапе-
ции. В силу симметрии точка пере-
сечения боковых сторон совпадает
с А, что равносильно утверждению
задачи (рис. 127).
19. а) Очевидно, что PQ || В0С0 .
Кроме того, точка Р лежит на опи-
санной окружности треугольника
122
ACL. Значит, AP LA = AC/2 и APLB = 90° - AB/2 = AC0AqB ,
где Лф - точка касания вписанной окружности с ВС. Следова-
тельно, соответственные стороны треугольников PQL и CqBqAq
параллельны, т.е. эти треугольники гомотетичны (рис. 128).
Центр гомотетии 5 лежит на прямой LAq . Значит, прямые РС0
и QBq пересекаются в 5, т.е. на
прямой ВС.
б) Докажем сначала, что точки
Со, Во, Ct и Вх лежат на одной
прямой. Действительно, поскольку
точка, симметричная В относительно
биссектрисы угла С, лежит на прямой
АС, точка Ct лежит на средней линии
Л'С'. При этом Л'С< = ВС/2 , а зна-
чит, C'Q = |ЛС - ВС\/2 = С"Bq . Этим
же свойством обладает и точка пересе-
чения Л'С' с BqCq . Таким образом,
прямые ОХО2 и СХВХ параллельны.
Далее, четырехугольник BCxIAq -
вписанный, поэтому ACxAqB =
= 90° - ZA/2 = AOXLB . Значит, AqCx || LOX . Аналогично
AqBi И LO2 (рис. 129). Следовательно, треугольники OXO2L и
CxBxAq гомотетичны.
в) Каждая из гомотетий пп. а) и б) переводит Aq в L, а
прямую BqCq - в серединный перпендикуляр к AL. Поэтому их
центры совпадают.
20. Из условия следует, что четырехугольники АСА£\
и ВСВХСХ - вписанные. Поэтому АВХВСХ = ААСС\ ,
ААХАСХ = АВССХ, а значит, ААС2В = тс - АС , т.е. С2 лежит на
123
окружности, проходящей через А, В и точку С', симметричную
С относительно АВ. При этом ZBC'Q = ZBAC2 , следовательно,
прямая C'Ct проходит через С2 (рис. 130).
21. Спроецируем сначала прямую АВ на окружность из точки
D, а затем окружность на прямую АВ из точки Т. В результате
А перейдет в М, бесконечно удаленная точка - в А, а точки В и
С останутся на месте. Приравняв двойные отношения, получим
МВ/МС = {АВ/АС)2. Из этого соотношения получаем, что
AM = АВ АС/(АВ + АС}. Пусть теперь К - середина ВС.
Тогда AN АК = 2АМ(АВ + АС} 2 = АВ АС = AD АЕ , т.е.
точки D, Е, К, N лежат на окружности.
22. Пусть К, L, М, N - точки на сторонах АВ, ВС, CD, DA
пространственного четырехугольника ABCD, являющиеся осно-
ваниями общих перпендикуляров. При проекции на плоскость,
параллельную КМ и LN, эти прямые перейдут в перпендикуляр-
ные прямые К'М' и L'N'. По теореме о трех перпендикулярах
проекции прямых АВ и CD будут перпендикулярны К'М', а
проекции прямых ВС и AD перпендикулярны L'N'. Следова-
тельно, четырехугольник ABCD проецируется в прямоугольник
A'&C'D', причем А'К' = D'M', B'L' = A'N'. Значит, АК/КВ =
= DM/MC, BL/LC = AN/ND и по теореме Менелая точки К,
L, М, N лежат в одной плоскости.
23. а) 2013; б) 2012; в) 1.
а) Оценка. Симметрия либо меняет многогранники А и В
местами, либо оставляет каждый из них на месте. В первом
случае она меняет местами их центры тяжести, поэтому плос-
кость симметрии перпендикулярна отрезку между центрами
тяжести и проходит через его середину. Во втором случае
плоскость симметрии фигуры является плоскостью симметрии
каждого из многогранников А и В. Отсюда оценка 1 + 2012 =
= 2013. Пример. Пусть А - правильная 2012-угольная пирамида.
На ее оси симметрии (очевидно, единственной) выберем точку
вне А и проведем через нее плоскость Р перпендикулярно оси.
Пусть В получается из А отражением относительно Р. Все
условия задачи выполнены, при этом Р и 2012 плоскостей
симметрии пирамиды А являются плоскостями симметрии полу-
ченной фигуры.
б) Оценка. Поскольку многогранники А и В имеют разное
количество плоскостей симметрии, они не равны и не могут
перейти друг в друга при симметрии всей фигуры. Следователь-
но, эта симметрия оставляет каждый из них на месте и, в
частности, является симметрией многогранника А, но он по
условию имеет только 2012 плоскостей симметрии. Пример.
124
Пусть А, как и в п.а), - правильная 2012-угольная пирамида.
Выберем на ее оси точку вне Л, проведем через нее плоскость
перпендикулярно оси и отразим основание пирамиды относи-
тельно этой плоскости. Над этим основанием построим прямую
призму, не имеющую общих точек с А, это и будет В. Ясно, что
В имеет 2013 плоскостей симметрии: одна из них параллельна
плоскостям оснований призмы и расположена посредине между
ними, а остальные 2012 проходят через ось призмы и две
противоположные вершины основания. Они являются плоско-
стями симметрии также для А и для всей фигуры.
в) Оценка. Поскольку многогранники А и В имеют разное
количество осей симметрии, они не равны и не могут перейти
друг в друга при симметрии всей фигуры. Значит, эта симметрия
оставляет каждый из них на месте. Поэтому она оставляет на
месте центр тяжести каждого из многогранников. Эти центры не
совпадают, поскольку многогранники выпуклые (это существен-
но!). Таким образом, у соединяющей прямой есть две неподвиж-
ные точки. Значит, она и есть ось симметрии. Пример. Пусть А
- прямая призма, основания которой - правильные 2011-уголь-
ники. Плоскости оснований считаем горизонтальными. Тогда у
призмы одна вертикальная ось симметрии, и через середину ее
отрезка между основаниями проходят 2011 горизонтальных осей
симметрии. Далее, пусть В - прямая призма, ее основания
горизонтальны и являются правильными 2012-угольниками, а
вертикальная ось та же, что у А, причем Л и В не имеют общих
точек. Тогда Л имеет 2012 осей симметрии, В - 2013, а составлен-
ная из них фигура имеет вертикальную ось симметрии.
Финальный тур
8 класс
1. Первое решение. Из
условия задачи следует, что равнобед- В
ренные прямоугольные треугольники 4
АВС и AED равны, т.е. треугольник / X. / А
ACD - также равнобедренный (рис. j- ,Х / \
131). Тогда ZBCD = 45° + ZACD = / ,/ ....-К’ \
= 45° + ZADC = ZCDE .Следовательно,
равнобедренные треугольники BCD и ............7 V^D
CDE равны. Таким образом, ZCBD = \. /
= ZCDB = ZECD = ZDEC . \ / X
Из того, что треугольник CFD -
равнобедренный, и из равенства отрез- Е
ков BD и СЕ получим, что BF = FE. Рис. 131
125
Следовательно, AABF = AAEF . Тогда
z A r?D Z.BFE 180° - 2Z.FCD
2 2
= 90° - Z.ECD = 90° - ZDBC = ZABF ,
откуда AB = AF, что и требовалось.
Второе решение. Пусть ВС пересекает DE в точке Р.
Заметим, что Z.CBD = АСОВ = ADBE , т.е. BD ~ биссектриса
АСВЕ . Значит, F - инцентр АР BE . Из симметрии и вписанно-
сти РВАЕ получаем, что А - середина дуги BE описанной
окружности АР BE , а значит по лемме о трезубце AF = АВ, что
и требовалось доказать.
Примечание. Задача верна с более слабым условием на
равенство сторон. Достаточно потребовать АВ = АЕ и ВС =
= CD = DE.
2. Первое решение. Не умаляя общности, предположим, что
С лежит на отрезке AD. Пусть Р - точка пересечения прямых
OtC и O2D (рис. 132). Треугольник АОХС - равнобедренный,
поэтому ZOtCA = ZOtAC = ZCAO2, следовательно, OtC || ЛО2.
Аналогично получаем, что ОХА || O2jD . Таким образом, О1ЛО2Р
- параллелограмм.
Докажем, что четырехугольник BCPD - вписанный, а О1О2РВ
- равнобокая трапеция, из чего и будет следовать утверждение
задачи. Действительно, тогда точка О (центр описанной окруж-
ности треугольника BCD) будет равноудалена от точек В и Р, а,
следовательно, равноудалена и от точек Ох и О2.
Заметим, что OtP =АО2 = ВО2 и С\В = ОХА = О2Р , т.е.
треугольники ВОХР и РО2В равны. Следовательно, АВОХР =
126
= ZPO2B , откуда OXO2PB - вписанный четырехугольник. Тог-
да АО£)2В = ЛОХРВ.
С другой стороны, ZBDA = ±ZAO2B = ZAO2Q = Z.OXO2B и
ЛО2ОХР = ZAO2Q . Следовательно, Z.BDA = Z.O{PB = ZO2OXP ,
т.е. BCPD - вписанный и ОХО2 || ВР . Поскольку ОХВ = О2Р , то
О1О2РВ - равнобокая трапеция.
Второе решение. Так как ОО} ± ВС , OtO2 ± АВ , то
/Л ТУГ' ААС^А AAO2D
ZOOXO2 = ААВС = —-— . Аналогично ZOC^Ot —------------.
Но, как показано в предыдущем решении, ZAO}C = ZAO2D .
3. Нет.
Пусть АВ - наибольшая сторона многоугольника. Спроеци-
руем все вершины, отличные от А и В, на АВ. Если ни одна из
проекций не попадает на отрезок АВ, то проекция некоторой
стороны 5, отличной от АВ, строго содержит АВ, следовательно,
5 > АВ - противоречие.
4. Пусть О - центр описанной окружности треугольника
LAB. Тогда прямые ОО} и О2О3 перпендикулярны BD, а
прямые О}О2 и О3О перпендикулярны АС. Следовательно, мы
можем восстановить середин-
ные перпендикуляры OOt и
ОО3 к сторонам LB, LA треу-
гольника LAB. Прямые ha , hb ,
проходящие через ортоцентр
Н этого треугольника и парал-
лельные ОО1 и ОО3, являют-
ся высотами этого треугольни-
ка, т.е. проходят через точки А
и В соответственно (рис. 133).
Поэтому прямые, симметрич-
ные ha , hb относительно соот-
ветственно ОО3 , ОО1, пересе-
каются в точке L. Дальнейшее
построение очевидно.
5. Так как точка К лежит на биссектрисе угла С, расстояние
от нее до прямой АС равно расстоянию до ВС, т.е. КА'.
Поскольку КА' = КВ', отсюда следует, что КВ' ± АС . Значит,
медиана ВВ' является также высотой и АВ = ВС. Тогда ВК и СК
- биссектрисы треугольника, следовательно, АК - тоже биссек-
триса, а поскольку АК - высота, то АВ = АС. Таким образом,
треугольник АВС - равносторонний и А'К = S'К = С'К .
6. Докажем, что четырехугольник CDEF - вписанный
127
(рис. 134), из чего будет следовать утверждение задачи. Действи-
тельно, тогда ZFEC = AFDC и ZFDC = 180° - ZBDC =
= ЛСАВ , т.е. FE || АВ .
Поскольку АВ - касательная к окружности со, то
ZTCD = ZBTD . Кроме того,
AFCE = ЛАСТ = ЛАСЕ - Z.TCD =
= (180° - ZABJD) - ЛВТЕ = Z.TDB = ZFDE .
Следовательно, CDEF - вписанный четырехугольник, что и
требовалось.
7. Пусть О0 и Rq - соответственно центр и радиус объемлю-
щей окружности, , О2,О3 и , R2, R3 - центры и радиусы
остальных. Тогда О0Ог = G = 1, 2, 3), ОгО; = Rj + Rj
(i,j =1,2,3, i Ф j ). Отсюда OQOX - O2O3 = O0O2 - O3OX = OQO3 -
- OXO2 = Rq - Rx - R2 - R3 = d . Если d >(<) 0, то расстояние от
O0 до любой из точек Ot, О2, О3 больше (меньше), чем
расстояние между остальными двумя точками. Это определяет
О0 однозначно, вопреки условию. Действительно, если в каж-
дой из пар ( OqC\ , О2О3 ), (О0О2, ОХО3 ), и (О0О3 , О<О2 )
раскрасить длинный отрезок в
красный цвет, а короткий - в
синий, то О0 - единственная
точка, в которой сходятся три
отрезка одного цвета. Если же
d = 0, то в несамопересекаю-
щемся четырехугольнике, об-
разованном данными точками,
противоположные стороны
равны и диагонали равны.
Значит, это прямоугольник.
8. Прежде всего заметим,
что прямые РРа , РРС вторич-
но пересекают описанную ок-
128
ружность треугольника в серединах С', А' дуг АВ, ВС (рис. 135).
Поэтому
ЛРаРРс = (ZA + /-С)/2 = 180° - ZA7C ,
где I - центр вписанной окружности треугольника. Значит,
окружность РРаРс всегда проходит через точку I. Зафиксируем
теперь какое-нибудь положение точки Р и найдем вторую точку
J пересечения окружностей РРаРс и АВС. Для любой другой
точки р' имеем
ZJP'P; = AJP'A' = 180° - ZJPA' = 180° - ZJPPC = ZJIPC = ZJIP;
(если P и P' расположены, как на рисунке 135, в других случаях
рассуждения аналогичны), т.е. окружность Р'РдРс также прохо-
дит через J. Следовательно, центры всех окружностей РРаРс
лежат на серединном перпендикуляре к отрезку IJ.
Примечание. Рассмотрим «полувписанную окружность» со
(касающуюся отрезков ВА, ВС и дуги АРС).
В частном случае, когда Р - точка касания окружностей со и
(АВС), видим, что J совпадает с Р. Отсюда получаем описание
точки J как точки касания с полувписанной окружностью. Как
известно (см., например, параграф «По л у вписанная окруж-
ность» книги «Математика в задачах»), J также лежит на
прямой IS, где 5 - середина дуги АВС.
9 класс
1. Отметим вне окружности на луче BtB точку М,
а на луче DXD точку N (рис. 136). По теореме об угле между
касательной и хордой равны углы МВЕХ и ВСЕ} , а также NDA1
и DCA} . Используя равенство
вертикальных углов, получим, что
ZABBt = АМВЕХ = АВСЕХ =
= ADCAX = Z^DA1 = ZEDD}.
Следовательно, дуги АД и £В1
равны, откуда и следует утверж-
дение задачи.
2. Точки С и D равноудалены
от прямой АВ. Следовательно,
прямая АВ проходит через сере-
дину М отрезка CD (рис. 137).
Пусть прямая CD вторично пере-
секает coj и ©2 в точках Р и Q
соответственно. По теореме о се- рИС
129
кущих к окружности МС • MP = МВ • МА = MD • MQ . Учиты-
вая, что МС = MD, получим, что MP = MQ и PC = DQ. Пусть
К и N - середины отрезков PC и DQ соответственно. Тогда М
- середина KN. Средняя линия прямоугольной трапеции O}KNO2
является серединным перпендикуляром к отрезку CD. Следова-
тельно, точки С и D равноудалены от середины отрезка О}О2 .
о тт АО ВО
3. Достаточно доказать, что одно из отношений ттт; и
1
не меньше ~ и не больше 2. Действительно, если, скажем,
АО
отношение QQ такое, то SAOB < 2SBOC и SCOD < 2SAOD , отку-
да и следует требуемое. Докажем теперь этот факт.
Без ограничения общности можно считать, что АО < ОС,
ОС
BO<OD. Предположим противное: пусть АО <-----------,
D_ OD 2
ВО < -у. Отложим на отрезках ОС, OD соответственно отрез-
ки ОА' = 2ОА , OB' = 2ОВ (рис. 138). Тогда А'В' = 2АВ > 2 , и
точки А', S' лежат на сто-
ронах треугольника COD
(не совпадая с вершинами).
Значит, отрезок д'& мень-
ше одной из сторон этого
треугольника. Оценим сто-
роны треугольника COD.
По условию CD < 2 .
Поскольку точка О лежит
между В и D, то отрезок СО
не больше одной из сторон
СВ и CD, следовательно,
СО < 2 и, аналогично,
130
DO <2 . Отрезок A'B' должен быть меньше одной из этих
сторон, но A'S' > 2 . Получили противоречие.
Примечание. Равенство достигается, например, на следую-
щем (вырожденном) четырехугольнике. Рассмотрим треуголь-
ник АВС, в котором 1 < АВ , ВС < 2 и АС = 3, и выберем точку
D на отрезке АС так, что CD = 1, DA = 2.
Из решения нетрудно видеть, что для невырожденных четы-
рехугольников неравенство строгое.
4. Первое решение. Будем рисовать данную конфигурацию с
конца (рис. 139). Возьмем правильный шестиугольник
АХВ?СХА'ВХС' и такую точку
М внутри треугольника
АХВХСХ , что АВХМСХ =
= 180-а, ЛСХМАХ =
= 180 - р , и т.д. (эта точка
лежит внутри ААХВХСХ , по-
тому что F лежит внутри
ААВС ). Пусть прямые, про-
ходящие через А', В7 и С'
и перпендикулярные АХМ,
ВХМ и СХМ , образуют
ААВС. Очевидно, что он
подобен данному треуголь-
нику. Значит, осталось по-
казать, что ААХ, ВВХ и ССХ являются его медианами, а М -
точкой Торричелли (т.е. М = F ).
Пусть прямая, проходящая через Сх и параллельная АВ,
пересекает СА и СВ в точках Р и Q соответственно. Построим
точку Т = АХМ П СА'В . Так как ZAtTA' = 90 , Т лежит на
описанной окружности шестиугольника Ах&СхА'ВаС' и четыре-
хугольник MCXQT вписанный. Следовательно,
ZQQM = ЛСХТМ = ЛСХТАХ = ЛСХВХАХ = 60° .
Аналогично, ZQPM = 60° , т.е. треугольник MPQ равносторон-
ний, а С1 - середина PQ. Рассмотрев гомотетию с центром С,
получаем, что ССХ - медиана, а СМ проходит через третью
вершину равностороннего треугольник с основанием АВ и,
значит, через точку Торричелли.
Второе решение. Пусть Ар - первая точка Аполлония.
Известно, что ее педальный треугольник A^BqCq правильный.
Точки Аполлония и Торричелли изогонально сопряжены. Следо-
вательно, их педальные треугольники имеют общую описанную
окружность со.
131
ZABIC + /СВ1а = 60° = /АВС ,
Определим точку Д
(рис. 140). Пусть Е - проекция
F на ВС, тогда Е лежит на со.
Прямая EF пересекает со вто-
рично в точке At . Угол
AqEAi = 90° . Следовательно,
AqAi - диаметр. Аналогично
определяются точки и Ct.
Треугольники AtBtCt и AqB0Cq
центрально симметричны отно-
сительно центра окружности со.
Следовательно, шестиугольник
AiBQCiAQBiCQ правильный. Ос-
талось доказать, что точки А{, В{ и Ct лежат на соответствую-
щих медианах. Это можно сделать как в первом решении.
(О свойствах педальных (подерных) треугольников см.,
например, в книге: В.В.Прасолов «Задачи по планиметрии»,
§10. Подерный треугольник.)
5. Проведем через F и Е прямые, параллельные АК и
пересекающие ВС в точках Р и Q (рис. 141). По теореме Фалеса
PM = MQ, значит, СР = BQ и
ВК = СР ВК CF ВА
СК~ СК BQ FA' BE'
Применив теперь теорему Ме-
нелая к треугольнику AFE и
прямой СВ, получим
CF BA ES t
FA BE FS ~ ’
что и требовалось доказать.
6. Так как /ВА1С =
= /ВС1а = 60° , точки, сим-
метричные 1С, 1а относитель-
но ВА, ВС соответственно,
лежат на прямой АС (рис.
142). С другой стороны,
следовательно, прямые, сим-
метричные В1С, В1а относительно АВ, ВС, пересекают АС в
одной и той же точке J. Значит, AtCt - средняя линия треуголь-
ника JIaIc. Тогда высоты треугольника АХВСХ из вершин Ах,
Ct , параллельные радиусам 1сСх, 1аАх соответственно, тоже
являются средними линиями этого треугольника и пересекаются
в середине отрезка 1а1с.
132
7. Первое решение.
Пусть К - вторая точка
пересечения и СО2 • Для
доказательства утвержде-
ния задачи достаточно по-
казать, что ZOKX = 90°.
По условию задачи
ОА = ОВ = ОС = OD.
Следовательно, треуголь-
ники АОВ и COD равно-
бедренные (рис. 143).
Пусть аир- углы при
их основаниях соответ-
ственно. Тогда, по свойству вписанных углов, имеем
ZBKC = ZBKO + ZCKO = ZBAO + ZCDO = а + р .
Учитывая, что четырехугольник ACBD вписанный, получим
цепочку равенств
ZBXC = 180° - ZXBC - ZXCB =
= 180° - ZCAD - ZADB = 180° - |(иАВ + иСО),
где АВ и CD - дуги окружности с центром О, о АВ = 180° - 2а,
uCD = 180° - 2р . Следовательно, ZBXC = ZBKC , т.е. четыре-
хугольник ВХКС вписанный. Значит,
ZXKB = 180° - ZXCB = 180° - ZACB = 90° + а .
Таким образом, ZOKX = ZBKX - ZBKO = 90° , что и требова-
лось доказать.
Второе решение. Пусть ОР и OQ - диаметры и СО2
(рис. 144). Докажем, что все такие точки X лежат на прямой PQ.
133
Рассмотрим инверсию
относительно окружности
со. Тогда перейдет в
АВ, а СО2 - в CD, следо-
вательно, точка К перей-
дет в точку 5 пересечения
АВ и CD. Кроме того,
PQ ± OS , т.е. PQ ~ по-
ляра точки 5 относитель-
но окружности со. С дру-
гой стороны, X (как точка
пересечения АС и BD) так-
же лежит на поляре точки
5. Следовательно, X принадлежит PQ.
Определение и свойства поляры см., например, в книге:
Я.П.Понарин, «Элементарная геометрия», том 1, §18.
8. Нет.
Очевидно, что вопрос задачи можно переформулировать
следующим образом: верно ли, что найдется момент, когда все
три отрезка между велосипедистами видны из центра под угла-
ми, большими 60° ? Ответ на этот вопрос не изменится, если
изменить скорости всех велосипедистов на одну и ту же величи-
ну. Поэтому можно считать, что первый велосипедист стоит на
месте в некоторой точке А.
Впишем в данную окружность правильный шестиугольник
ABCDEF и обозначим через М и N середины дуг ВС и EF
соответственно (рис. 145). Пусть
второй и третий велосипедисты
стартуют из точки М с равными
скоростями в противоположных
направлениях: второй - к точке
В, третий - к точке С. Пока они
не достигли этих точек, рассто-
яние между ними меньше 1 км.
Затем второй велосипедист бу-
дет удален от первого, т.е. от
точки А, меньше чем на 1 км,
пока не приедет в точку F. Од-
новременно третий приедет в
точку Е, и расстояние между
вторым и третьим станет равно 1 км. Затем оно уменьшается,
пока велосипедисты не встретятся в точке N. Получили располо-
жение, симметричное первоначальному относительно прямой
134
AD, с переменой местами второго и третьего велосипедистов.
Далее процесс повторяется.
Примечание. Можно показать, что построенный пример -
единственный с точностью до прибавления ко всем скоростям
одной и той же величины. Он соответствует случаю, когда
скорости образуют арифметическую прогрессию. Во всех осталь-
ных случаях обязательно найдется момент времени, когда рас-
стояния между велосипедистами не только больше 1 км, но даже
больше V2 км! Это следует из теоремы, доказательство которой
мы оставляем читателю:
Теорема. Если в условии задачи 8 скорости велосипедистов
не составляют арифметическую прогрессию, то найдется
момент времени, когда три радиуса, проведенные к велосипе-
дистам, образуют тупые углы.
Пользуясь этим фактом, античные астрономы могли бы
строго обосновать невозможность геоцентрической системы мира.
Причем для этого достаточно было бы рассмотреть движения
только трех небесных тел : Сол-
нца, Венеры и Меркурия.
Обозначим их точками S,
V, Мсоответственно (рис. 146).
Предположим, что они враща-
ются вокруг Земли (точки О)
по круговым орбитам. Счита-
ем, что они вращаются в одной
плоскости (в реальности плос-
кости их орбит почти совпада-
ют). Их угловые скорости раз-
личны и не составляют ариф-
метическую прогрессию (это
известно). Тогда в некоторый
момент времени все три угла
между лучами OS, ОМ и OV
тупые. Предположим, наблюдатель находится на поверхности
Земли в точке, противоположной направлению луча OS. Он
находится на неосвещенной стороне Земли, т.е. ночью, и видит
Меркурий и Венеру, поскольку углы SOM и SOV - тупые.
Угловое расстояние между двумя этими планетами, угол MOV,
больше 90° • Однако, по данным многолетних наблюдений,
которыми располагали античные астрономы, угловое расстояние
между Меркурием и Венерой никогда не превосходит 76° •
Полученное противоречие доказывает невозможность геоцент-
рической системы с круговыми орбитами.
Daysiae
JM
S
О
V
Рис. 146
135
10 класс
1. Поскольку
ЛАХАР = 90° - ZABC = 90° - XAQP ,
луч АА< проходит через центр О описанной окружности треу-
гольника APQ (рис. 147). Этот
центр также лежит на серединном
перпендикуляре I к отрезку PQ.
Поскольку АВ Ф АС , прямые АО
и / не параллельны. Но и О, и
являются их общими точками;
значит, At = О . Следовательно,
вписанный угол PAQ равен поло-
вине центрального угла PA^Q .
2. Предположим, что
ZALB > 90° . Тогда АВ2 >
> AL2 + BL2 и CD2 > CL2 + DL2 ;
отсюда же получаем AD2 <
< AL2 + DL2 и ВС2 < BL2 + CL2.
Значит, 2 АВ2 = АВ2 + CD2 > AD2 + ВС2 . С другой стороны, из
описанности имеем 2АВ - АВ + CD = ВС + AD. Значит,
AD * ВС , и
2(Л£>2 + ВС2) = (AD + ВС)2 + (AD - ВС)2 > (2 АВ)2 = 4ЛВ2 .
Противоречие.
3. Первый способ. Пусть АВСХ' - тетраэдр, в котором
АВ СХ' = ВС АХ'= СА -ВХ'. ( * )
Обозначим через Га , Гь и Гс центры вписанных окружностей
треугольников ВСХ', АСХ' и АВХ'. Из (*) следует, что
биссектрисы А1'ь и В1'а углов Х'АС и Х'ВС пересекают отрезок
Х'С в одной точке. Значит, отрезки А/' и В1'ь пересекаются.
Аналогично, каждый из них пересекается с отрезком СГс.
Поскольку эти три отрезка некомпланарны, они пересекаются в
одной общей точке.
Устремив X' к X вдоль окружности, по которой пересекают-
ся три сферы Аполлония для пар точек (А, В), (В, С), (А, С),
получим утверждение задачи.
Второй способ. Пусть I - центр вписанной окружности
треугольника ABC, a At, Вх и С1 - основания соответствующих
биссектрис в этом треугольнике. Пусть прямая С/3 пересекает
XI в точке Тс; точки Та и Ть определим аналогично. Мы
136
хв
собираемся доказать, что Та = Тъ = Тс. Поскольку -т-т -
ХА
вс
АС ’
биссектриса Х13 угла ВХА проходит через Ct. Применяя
теорему Менелая к АХ1С} и используя свойство биссектрисы
А/3 угла ХА С, имеем
ХТС _ Х/3 С,С ХА QC _ ХА С,С _ ХА sin ХА
TCI ~ I3C\ CI “ AC, CI ~ CI АС, “ CI sin(ZC/2) ’
Аналогично получаем
ХТЬ ХА sin ХА
TbI ~ BI sin(ZB/2)’
BI _sin(ZC/2) хтс XTb
Но qj “ sin(ZB/2) ’ откУда TI TI ’ что и тРе6овалось.
4. Разобьем решение для удобства на 4 этапа.
1. Будем называть элементарным треугольник с площадью
1
— и целыми квадратами сторон. Элементарный треугольник со
сторонами 1, 1, и у/2 обозначим через Д.
Назовем переклейкой операцию разрезания ДА В С по меди-
ане AM и склеивания получившихся треугольников АВМнАСМ
по равным отрезкам ВМ и СМ в новый треугольник со сторона-
ми АВ, АС и 2АМ.
2. Покажем, что из любого элементарного треугольника 8
можно переклейками получить Д .
Прежде всего заметим, что переклейка переводит элементар-
ный треугольник в элементарный: площадь не меняется, а из
формулы медианы 4m2 = 2Ь2 + 2с2 - а следует, что целочислен-
ность квадратов сторон тоже сохраняется.
Будем теперь переклеивать произвольный элементарный тре-
угольник 8 следующим образом: если у 8 есть тупой угол, то
будем разрезать его по медиане из этого угла. Тогда наибольшая
сторона треугольника будет уменьшаться, и так как квадраты
сторон целые, то когда-нибудь мы получим элементарный тре-
угольник 8', являющийся прямоугольным или остроугольным.
П А
В этом случае синус наибольшего угла не меньше » поэтому
2 2 /э
произведение сторон, прилегающих к нему, не больше ;
значит, они обе единичные, а тогда угол между ними - прямой.
Таким образом, мы получили Д .
3. Если 8' получен переклейками из 8, то и 8 можно
137
получить переклейками из 8'. Следовательно, любой элемен-
тарный треугольник 8 может быть получен переклейками
из А .
4. Будем называть треугольник 8 оберткой, если квадрат со
1
стороной можно завернуть в 8 так, чтобы любые две точки,
лежащие на одной стороне 8 и равноудаленные от середины этой
стороны, совместились.
Из треугольника А можно получить обертку, перегнув его по
средним линиям, параллельным катетам.
Предположим, что треугольник 8 = АВС является оберткой,
и пусть AM - одна из его медиан. Рассмотрим способ заворачи-
вания в нее квадрата, склеим в нем все пары точек стороны ВС,
равноудаленные от М, и разрежем ее вдоль AM. В результате
получим, что переклейка ААВС по медиане AM также является
оберткой. Отсюда, вкупе с пунктом 3, следует утверждение
задачи.
Замечание 1. Как нетрудно видеть из решения, следующие
условия эквивалентны:
а) ААВС элементарный;
б) существует треугольник, равный ААВС , с целыми коорди-
натами вершин;
в) существуют такие шесть целых чисел р, q, г, s, t, и, что р +
+ q + r = s + t + u = Onp2+s2 = АВ , q2 +t2 = ВС , г2 + и2 =СА .
Замечание 2. Равносильность условий б) и в) очевидна. То,
что условие а) также им равносильно, можно показать и по-
другому. Можно воспользоваться методами теории чисел, стар-
товав с формулы Терона: согласно ей, для элементарного треу-
гольника со сторонами 4а , 4Ь , 4с верно равенство
2 (ab + be + cd) - (а2 + b2 + с2 j = 1.
Рис 148
138
Можно показать - например, методом спуска - что все ее
решения удовлетворяют в).
Другой метод состоит в следующем. Рассмотрим наш треу-
гольник АВС и породим им решетку (т.е. отложим от точки А
всевозможные векторы вида kAB + 1АС с целыми k и /; см.
рис. 148). Используя формулу косинусов, нетрудно понять, что
расстояния между любыми точками этой решетки - корни из
целых чисел. Из условия на площадь теперь следует, что
минимальная площадь параллелограмма с вершинами в точках
решетки равна 1; теперь, рассмотрев такой параллелограмм
наименьшего диаметра, нетрудно убедиться, что он - единичный
квадрат1.
Эта же решетка помогает после этого получить другое реше-
ние задачи. Для удобства совершим гомотетию с коэффициентом
2; тогда наш треугольник имеет четные координаты вершин и
площадь 2, и надо завернуть в него единичный квадрат. Раскра-
сим теперь клетчатую плоскость шахматным образом и располо-
жим на ней решетку из наших треугольников; вершинами
треугольников будут все точки с четными координатами. Заме-
тим, что все треугольники разбиения разбиты на два класса:
получающиеся из исходного параллельным переносом, и полу-
чающиеся из него центральной симметрией.
Будем теперь оборачивать (черный) квадрат с вершиной в
одной из вершин нашего треугольника этим треугольником,
сгибая его по сторонам квадрата. На черную сторону попадут все
части треугольника из черных частей плоскости; при этом части
из строк с четными номерами претерпят параллельный перенос,
а с нечетными - центральную симметрию.
С другой стороны, все черные квадраты в строках с четными
номерами разбиты одинаково, а разбиение остальных черных
квадратов получается из предыдущего центральной симметрией.
Такая симметрия меняет местами два класса треугольников
разбиения. Теперь нетрудно понять, что наш черный квадрат
окажется замощен полностью: те его части, которые попадают в
треугольники первого класса, будут накрыты параллельными
переносами частей исходного треугольника, остальные - симмет-
риями остальных его частей. То же произойдет и с обратной
стороной нашего квадрата.
5. Пусть К - точка пересечения прямой, проходящей через Е
параллельно АС, и прямой, проходящей через F параллельно
1 См. также по этому поводу задачу 7 для 10 класса с финала V
олимпиады имени И.Ф.Шарыгина, 2009 г.
139
BD (рис. 149). Заметим, что
Z(EE, EF) = Z(AC, EF) =
= uCF + uAE = uFD + uEB = ^BD FFj = ^(KF, FFj
Это значит, что треугольник KEF равнобедренный, KE = KF.
Значит, параллелограмм EKFL - ромб, и KL - серединный
перпендикуляр к EF. Поэтому KL проходит через О.
Рис. 149
6. Первое решение. Пусть N - проекция точки С на AtBt
(рис. 150). Рассмотрим гомотетию с центром в точке С, при
которой Н перейдет в Ct , Р - в Pt , Q - в Q1. Тогда CJ\ 1 ,
QQi ± СХАХ, и достаточно доказать, что прямая CN проходит
через середину P1Q1.
Пусть К и L - проекции точек Pt и Qt на прямую А{ВХ. Как
известно, АСВ^ = ААВХС^ ; значит, АР&К = АРХВ£\, и пря-
моугольные треугольники Р\ВХК и PiBiCi равны по гипотенузе
и острому углу. Отсюда В^К = В{С{ . Аналогично, AXL = АХСХ,
т.е. длина отрезка KL равна периметру 2р треугольника АХВХСХ .
Поскольку С - центр вневписанной окружности треугольни-
ка АХВ\СХ , точка N - точка касания этой окружности с A1Bi , и
BXN = р- В{С{. Тогда KN = ВХСХ + р- В{С{ = р . Следователь-
но, К - середина отрезка KL. Наконец, поскольку прямые РХК ,
CN и QXL параллельны, по теореме Фалеса прямая CN прохо-
дит через середину PtQt, что и требовалось.
Второе решение. Обозначим ABAC = а , ААВС - р ; тогда
ААССХ =90°- a, АВССХ = 90°-р. Поскольку ДАВД ~
~ ААХВСХ ~ ААВС , имеем АН PC = 90° - ААВХСХ = 90° - Р и,
аналогично, AHQC = 90°-а. Наконец, пусть перпендикуляр
из С на AtBt пересекает PQ в точке X (рис. 151). Тогда
АРСХ = 90° - р, AQCX = 90° - а .
140
Нам нужно доказать, что СХ - медиана в &CPQ ; поскольку
ХРСХ = Z.QCH , это равносильно тому, что СН - симедиана.
Итого, мы свели задачу к следующему известному факту (см.
книгу: А.Акопян, «Геометрия в картинках», задача 4.4.6).
Лемма. Пусть в треугольнике CPQ точка Н такова, что
ХСРН = XQCH и Z.CQH = Х.РСН . Тогда СН - симедиана в
этом треугольнике.
Доказательство. Пусть L - точка пересечения СН и PQ
(рис. 152). Тогда HL - биссектриса угла PHQ. Далее можно
рассуждать по-разному.
Первый способ. Заметим, что треугольники PH С и CHQ
PH СН PC
подобны по двум углам. Следовательно, -------=-----=-----,
PC2 PH СН PH PL СН
°"УДа CQ2 = СН ' HQ ' HQ ‘ LQ ' Таким о6ра”"’ СН "
симедиана по определению.
Второй способ. Пусть описанная окружность треугольника
CPQ пересекает СН вторично в точке У (см. рис. 152). Тогда
XQPY = ZQCY = Z.CPH , аналогично, Z.PQY = Z.CQH . Сле-
довательно, биссектрисы углов HPL и CPY совпадают, равно
как и биссектрисы углов HQL и CQY. Поскольку HY -
биссектриса угла PHQ, то биссектрисы углов CPY и CQY
г РС Qc
пересекаются на СУ. Следовательно, , т.е. четырех-
угольник CPYQ - гармонический. Отсюда и следует требуемое
утверждение.
у/7 + Л 5 + V21
7. г- г- =
J1 -у/З 2
141
Пусть О и О' - два возможных положения центра большой
сферы (среди данных пяти точек), а А, В, С - три оставшиеся
отмеченные точки.
Рассмотрим точки О, О', А, В. Пусть в конфигурации, когда
О - центр большой сферы, радиусы сфер с соответствующими
центрами равны R, г' , га и гь . Тогда ОО' = R -г , О А = R-ra,
OB = R-rb, О'А = г'+ га , О'В = г + rb, АВ = ra+rb , откуда
получаем ОО' - АВ = ОА - О'В = ОВ - О'А ; обозначим эту раз-
ность через d. Аналогично, из конфигурации, в которой О' -
центр большой сферы, имеем d = ОО' - АВ = О'А - ОВ =
= О'В - ОА = -d . Значит, d = 0, т.е. ОО' = АВ , ОА = О'В ,
ОВ = О'А .
Рассматривая аналогично четверки точек (О, О', Af С) и
(О, О', В, С), мы получаем ОО' = АВ = АС = ВС и ОА = О'В =
= ОС = О'А = ОВ = О'С . Итак, треугольник АВС - правильный
(пусть его сторона равна 2>/3 ), а правильные пирамиды ОАВС
и О'АВС равны; значит, О и О' симметричны относительно
(АВС). Кроме того, ОО' = 2>/3 , т.е. высота каждой пирамиды
равна >/3 . Пусть Н - общее основание этих высот, тогда
НО = НО' = л/З и НА = НВ = НС = 2, откуда ОА = О'А = V7 .
Значит, радиусы трех сфер с центрами в А, В, С равны л/З , а
радиусы остальных двух сфер равны V? - >/3 и V7 + >/3 ,
откуда и следует ответ.
8. Обозначим через R иг радиусы внешней ( Q ) и внутренней
(со ) окружностей соответственно, а через D - центр со (рис. 153).
Пусть С' - середина дуги АВ
окружности Q , не содержащей
точку С, а I - центр вписанной
окружности треугольника АВС.
Тогда точки I и D лежат на С С',
а по лемме о трезубце имеем
C'l = С'А = 2R sin ХАСС'.
С другой стороны, если Р -
точка касания АС с со, то
, PD г
sin ХАСС —-----=------ кооме
CD CD ’ р
того, произведение d - CD • C'D
- это минус степень D относи-
тельно Q , т.е. оно постоянно.
Значит,
, 2Rr C'D • 2Rr
С 7 —--- — “
CD d
142
откуда
__. . ( 2Rr\
ID = CD -CI = CD • 1 - —
I d )
Итак, точка I лежит на окружности, полученной из Q гомотети-
2Rr .
ей с центром D и коэффициентом -1 .
Наоборот, для любой точки I этой окружности можно восста-
новить точки С и С как точки пересечения ID с Q; при этом
точка С выбирается как образ I при обратной гомотетии. Для
полученной точки С точка I является требуемым центром;
значит, каждая точка полученной окружности подходит.
Замечание. Если 2Rr = с/, то полученная окружность вырож-
дается в точку; в этом случае из приведенного решения легко
получить формулу Эйлера для расстояния между центрами
вписанной и описанной окружностей.
X ОЛИМПИАДА
Заочный тур
1. Так как A DAB = АЕАС = 60° , то
ZDAE = ABAC , следовательно, треугольники ADE и АВС
равны и /ADE = 90°. Поэтому треугольник ADM - прямо-
угольный с углом ZA = 60° . Значит, AD= АВ =АМ/2 (рис. 154),
т.е. точка М симметрична А относительно В.
2. Да, см. рисунок 155. Точки А, В, С, D лежат на средних
линиях данного квадрата и образуют квадрат со стороной
>/2-1.
3. Пусть СН - третья высота треугольника. Так как
ZCBH = АСАВ = ZCBH , треугольники CBD и СВН равны,
т.е. BD = ВН. Кроме того, в прямоугольном треугольнике АЕВ
143
с
ЕН - медиана, значит, ЕН =
= HB = BDh АВЕН = АЕВН =
/ / \ \ = AEBD. Следовательно,
/ / \ \ EDBH- параллелограмм (рис.
/ / \ \ 156) и DE \\ АВ. Поскольку
I / \ j ЕЕ также параллельна АВ,
I р /___________YE I прямые DE и EF совпадают.
\ j / Пусть в треугольнике
\ \ I/ АВС с инцентром I вершины
,4^4^ < квадрата К и L лежат на сторо-
Н s' не АВ, вершина М на стороне
Рис. 15(5 "— АС и вершина N на стороне ВС
(очевидно, углы А и В ост-
рые). Опустим из I перпендикуляр IH на АВ, и пусть отрезок DE
проходит через I, параллелен АВ и его концы D и Е лежат
соответственно на АС и ВС. Нужно доказать, что DE > IH и
II е KL . Первое следует из того, что IH = г и DE > 2г, где г -
радиус вписанной окружности. Теперь продолжим IH за точку
I до пересечения с одной из сторон треугольника АВС в
некоторой точке F. Пусть для определенности F е АС. Тогда
заведомо Н и ТС по одну сторону от L. Проведем через F прямую,
параллельную АВ, до пересечения с ВС в точке G. Достаточно
доказать, что FG < FH: тогда I и L по одну сторону от ТС и потому
I е KL , что и требуется.
Заметим, что FH - диаметр вписанной окружности, продол-
женный до пересечения с АС, поэтому F вне окружности и
FH > 2г. Перпендикулярная прямая через F не имеет общих
точек с окружностью. Поэтому точки касания окружности с АС
и ВС находятся между FG и АВ. Следовательно, соединяющая
их хорда больше, чем FG. А так как она меньше 2г, то FG <
< 2r < FH, что и требовалось.
Комментарий. Из решения видно, что вместо квадрата
можно взять любой прямоугольник, у которого большая сторона
лежит на стороне треугольника и не превосходит удвоенной
меньшей стороны.
3>/2
5. АВ : АС : ВС = 1 : 2 : -у-.
По свойству биссектрисы, АС : АВ = LA : LB = 2:1. Это
следует также из свойства медианы: именно, продолжим АВ за
точку В на отрезок BD = АВ. Тогда ВС - медиана треугольника
ADC, и так как AL : LB = 2 : 1, то AL также лежит на медиане.
Но это и биссектриса, поэтому AC = AD = 2АВ. Теперь по теореме
Пифагора получаем: АС2 - АН2 = АВ2 - ВН2, или 4АВ2 -
144
- 25ВН2 = AB2 - ВН2, откуда АВ = 2J2BH и ВС : АВ =
= QBH : АВ = — .
2
6. Прямая, перпендикулярная лучу ОР и пересекающая его
в точке, удаленной от О на расстояние (ОР + ОХ)/2 .
Пусть К, L - проекции точки У на ОР и ОХ. Из определения
точки У следует, что УР = YX и YK = YL. Значит, треугольники
YKP и YLX равны, т.е. XL = РК.
Кроме того, OL = ОК. Посколь-
ку длины отрезков ОР и ОХ не
равны, одна из них равна сумме
длин отрезков ОК и КР, а другая
- их разности. Следовательно,
ОК = (ОР + ОХ)/2 (рис. 157).
Очевидно, что любая точка пря-
мой принадлежит искомому ГМТ.
7. Пусть точка К симметрична
А относительно В. Тогда Е -
центр описанной окружности тре-
угольника АСК. С другой сторо-
ны, так как BKCD - параллелог-
рамм, то AF ± СК и F - орто-
центр треугольника АСК. Следовательно, медиана СВ делит EF
в отношении 1 : 2 (рис. 158).
8. Первое решение. Так как ХАВК = ZCBL , треугольники
АВ К и CBL подобны. Значит треугольники АВС и KBL также
подобны и XBKF - ZBAF . Следовательно, четырехугольник
ABFK - вписанный и XBFK = 90° (рис. 159).
Второе решение. Заметим, что точка В лежит на описанной
окружности треугольника KLD. Точки А и С являются основа-
ниями перпендикуляров из точки В на прямые KD и DL. А
145
значит, основание перпендикуляра из точки В на прямую KL по
теореме о прямой Симеона лежит на прямой АС, т.е. совпадает
с точкой F, что и требовалось доказать.
9. Пусть N - вторая точка пересечения coj с AL (рис. 160).
Тогда композиция симметрии относительно AL и гомотетии с
центром А переводит дугу NE в
дугу LM. Следовательно, опи-
рающиеся на эти дуги углы ALE
и MQE равны, что равносильно
утверждению задачи.
10. Пусть Ох, О2 ~ центры
данных окружностей, , г2 ~
их радиусы, О - середина от-
резка С\О2 , - прямая, па-
раллельная и проходящая через Ot, Г2 - прямая, симметрич-
ная относительно средней линии (рис. 161). Тогда расстояние
от О2 до Г2 равно |г2 - rj .
Применив гомотетию с
центром Ох и коэффици-
ентом 1/2, получаем, что
расстояние d от О до сред-
ней линии равно
|r2 - rJ/2 , т.е. все средние
линии касаются окружно-
сти с центром О и радиу-
сом d.
11. Обозначим точки пересечения прямых MN и LM с
прямой АВ как Р и Q соответственно. Треугольники AKN, BLK,
CML и DMN равны по гипотенузе и острому углу. Пусть АК =
= аиВК = Ь, тогда BL = СМ = DN = a, CL = MD = NA = Ь.
Поскольку треугольники PKN и QLK прямоугольные, РА а = Ь2
и В К • b = а2 . Из подобия треугольников РЕК и DEM получим,
что
Рис. 161
КЕ _ а + Ъ2/а _а2 + Ъ2
DE b ab
но из подобия треугольников QFK и CFM следует, что
FK b + a2/b а2 + Ь2
CF a ab
Значит, KE/DE = FK/CF и EF || АВ , что и требовалось дока-
зать.
146
12. Так как ЛК^АВ =
= ХАК2В, ХК2АВ = ХАК{В,
треугольники АКХВ и К2АВ
подобны (рис. 162). Применяя
к ним теорему синусов, полу-
чаем:
sinZKtAB _ АКХ _ AL}
sinZK2AB АК2 АЦ
что равносильно утверждению
задачи.
13. Пусть Q - вторая точка
пересечения прямой АС с ок-
ружностью AiPCi. Тогда
ZQA^ = ZQPQ = ZQCO = ZQAO = ZAOAX = ZQCAX.
Следовательно, QA< = QCt и ZA<QC< = ХАОС = 2XA1BC1, т.е.
Q - центр описанной окружно-
сти треугольника AtBCt
(рис. 163). Таким образом, этот
центр движется по прямой АС.
14. Построим круг, концен-
тричный данному, вдвое мень-
шей площади. Разделим внут-
ренний круг пополам произ-
вольным диаметром, а внеш-
нее кольцо - перпендикуляр-
ным диаметром. Объединив
половину внутреннего круга с
половиной внешнего кольца,
Рис 163
получим искомое множество.
15. а) АС; б) ВК.
а) Вспомним, что в неравнобедренном треугольнике биссек-
триса проходит между медианой и высотой, а высота - между
биссектрисой и меньшей из прилежащих сторон. Предположим,
что АВ < АС. Тогда биссектриса угла А пересекает биссектрису
угла В в точке, лежащей между К и АС. Через эту точку
проходит и биссектриса угла С. Так как она лежит между
медианой и меньшей из прилежащих сторон, то АС < ВС.
Значит, АС - средняя по величине из сторон треугольника.
Пусть теперь АВ > АС. Тогда рассуждение аналогичное:
точка пересечения биссектрис лежит между прямыми АК и АВ,
147
биссектриса угла С лежит между СК и ВС, поэтому АС > ВС.
Снова АС - средняя по величине.
6) Из условия задачи следует, что высота из А проходит
внутри треугольника, т.е. углы В и С - острые. Применив
теорему Чевы, получаем, что sin ZA = cos ZC tgZB или
, _ х z_.l- cos ZB
tgZC-tgZB--------—- . Поэтому при ZB < 60° имеем ZC <
cos ZB J
< ZB < 60° < ZA , а при ZB > 60° - ZC > ZB > 60° > ZA .
В первом случае ZKBA < 30° < АКАВ и АКСВ < АС/2 <
< АВ/2 = АКВС , следовательно, КА < КВ < КС. Аналогично,
во втором случае получаем КА > КВ > КС.
Комментарий. Из условий задачи невозможно определить,
какая сторона наибольшая и какая наименьшая, а также, какой
из отрезков КА, КС наибольший и какой наименьший.
16. Окружности с диаметрами AAt, ВВ1, ССХ проходят
через основания соответствующих высот треугольника, поэтому
степени ортоцентра Н относительно всех трех окружностей
равны. Следовательно, прямая DH является их общей радикаль-
ной осью и центры окружностей лежат на одной прямой.
Комментарий. Применяя теорему Менелая к треугольнику
АВС и треугольнику, образованному его средними линиями,
нетрудно показать, что точки Ах, Вх , Сх также лежат на одной
прямой.
17. Будем пользоваться следующими известными фактами.
1) Если даны две параллельные прямые, то, пользуясь только
линейкой, можно разделить отрезок на одной из этих прямых
пополам.
2) Если даны две параллельные прямые, то, пользуясь
только линейкой, можно провести через не лежащую на них
точку параллельную им прямую.
Заметим теперь, что прямая EF является серединным перпен-
дикуляром к BD. Поэтому точки К, L ее пересечения с АВ и ВС
являются вершинами квадрата BKDL. Используя параллельные
прямые ВС и KD, разделим отрезок ВС пополам. Используя
параллельные прямые АВ и DL, построим параллельную им
прямую, проходящую через середину ВС. Эта прямая является
серединным перпендикуляром к ВС и, значит, пересекает EF в
центре описанной окружности треугольника BCD. Аналогично
строится центр описанной окружности треугольника ABD.
18. Пусть J - вторая точка пересечения окружностей AIC и
BID. При инверсии относительно вписанной в ABCD окружно-
сти точки А, В, С, D перейдут в вершины параллелограмма, а/
- в его центр. Следовательно, AJ/СJ = AI/CI , т.е. прямая IJ
148
является симедианой треугольника AIC и, значит, проходит
через X. Аналогично получаем, что эта прямая проходит через У.
19. При гомотетии с центром Р точки В, С переходят в Е, F.
Значит, А переходит в полюс прямой EF относительно СО2 , т.е.
полюс EF лежит на прямой АР, что равносильно утверждению
задачи.
20. Пусть А'ХВ{ - переменная хорда окружности, равная
АХВХ, т.е. полученная из АХВХ поворотом вокруг центра О. Легко
видеть, что окружность (LAB) будет геометрическим местом
точек К' = ААХ П В£% при вращении хорды Ах£%. Тогда, так как
точка Р является пересечением четырех таких ГМТ, прямые АР,
ВР, СР и DP пересекают окружность в точках А', В', С', D',
образующих четырехугольник, равный AXBXCXDX . Рассмотрим
поворот вокруг О, переводящий A'B'C'D' в AXBXCXDX , а Р в
некоторую точку Q. Прямые AXQ , BXQ , CXQ и DXQ пересекают
окружность в четырех точках, образующих четырехугольник,
равный ABCD. Применив аналогичные рассуждения к описан-
ным окружностям треугольников KDXAX , LAXBX , МВХСХ и
NCXDX, получим, что все они проходят через Q. Кроме того, так
как OQ - образ ОР при повороте, то OP = OQ, что равносильно
п.б).
21. Рассмотрим точку пересечения ВС и AD. Обозначим ее
через R. Тогда R лежит на одной прямой с двумя другими
точками касания (Р и Q) окружности со сторонами четыреху-
гольника.
Пусть ЕЕХ пересекает AD в точке М. Рассмотрим три
окружности: вписанную в четырехугольник, а также окружнос-
ти AED и AID, где I - центр л
вписанной окружности. Легко ви-
деть, что радикальная ось AID и // /
вписанной окружности является // /
средней линией треугольника / / /
FPQ. Так как две другие ради- / / /
кальные оси пересекаются в точке / / I
М, получаем, что RM = MF /
( рис .164).
Аналогично, FFX пересекает \/
ВС в точке N, такой, что RN =
NE. Следовательно, прямые ЕЕХ
и FFX симметричны относительно
биссектрисы угла ERF. Значит, А
точки Ех и Fx также симметричны /
и EFFXEX - равнобокая трапеция. Рис. 164 vD
149
22. Да, возьмем правильный треугольник АВС со стороной 1
и две точки St, S2 , симметричные относительно его плоскости
и такие, что 5t52 < SiA = S^B = StC < 1. Очевидно, что един-
ственная диагональ StS2 полученного многогранника меньше
любого из его ребер.
23. а) Рассмотрим три сферы, касающиеся плоскости в
точках А, В, Си друг друга внешним образом. Легко видеть, что
если радиусы этих сфер равны х, у, z, то АВ = 2у]ху и т.д.
Поэтому две сферы, касающиеся трех данных и плоскости, будут
касаться плоскости в точках D и Z)t. Таким образом можно
построить восемь сфер a, b, с, d, ах, b}, q, dx, касающихся
плоскости в точках А, В, С, D, А}, , Q , Dx, причем сферы
а и ах касаются Ь, с, d и т.д.
Сделаем инверсию пространства с центром в точке касания
сфер с и d. Тогда эти сферы перейдут в две параллельные
плоскости, а исходная плоскость, а и b - в три равные сферы,
расположенные между этими плоскостями и попарно касающи-
еся. Сферы q и перейдут в две сферы, касающиеся этих трех,
кроме того, каждая из этих сфер касается одной из плоскостей,
следовательно, они симметричны относительно плоскости цент-
ров трех остальных сфер. Поэтому образы точек Л, В, Q , Dx
лежат в одной плоскости, а сами эти точки на одной окружности.
6) Сделаем теперь инверсию с центром в точке D. Тогда сфера
d перейдет в плоскость, параллельную плоскости АВС, а сферы
а, Ь, с - в три равные попарно касающиеся сферы. Следователь-
но, точки их касания с плоскостью будут вершинами правильно-
го треугольника, а точка Dx перейдет в центр этого треугольни-
ка. Образы точек At, Bt , Q будут образовывать правильный
треугольник с тем же центром, т.е. четверка At, В1 , Ct , D}
тригармоническая.
24. Первое решение. Поскольку точки Р, Q, К и L лежат в
одной плоскости, то отрезки PL и QP пересекаются в точке В,
принадлежащей прямой BS. Обозначим через Т точку касания
сферы и основания пирамиды. Заметим, что равны треугольники
QBK и QBT, PBL и РВТ (равны соответствующие касательные
к сфере). Аналогично равны треугольники RKB и RLB. Значит,
ZQTB = z^QKB = ZPLB = Z.PTB . Но в любой описанной пира-
миде ZCTQ = ZPTA и ZCTD = ZATB = 180° , следовательно,
ZPTB = 180° .
Второе решение. Сделаем проективное преобразование, со-
храняющее сферу и переводящее плоскость PQS в бесконечно
удаленную. Тогда пирамида перейдет в бесконечную четыреху-
гольную призму, а условие пересечения прямых РК и QL будет
150
равносильно тому, что грани этой призмы, проходящие через АВ
и ВС, образуют равные углы с плоскостью ABCD. Но тогда
призма будет симметрична относительно плоскости, проходящей
через BD и перпендикулярной ABCD. Значит, точка касания
сферы с основанием лежит в плоскости симметрии.
Финальный тур
8 класс
Рис. 165
1. Первый способ. Пусть 1А - центр вневписанной
окружности треугольника АВС, касающейся стороны АС и
продолжения стороны ВС в
точках В2 и 4 соответствен-
но (рис. 165). Тогда 1аВ2СА^ -
квадрат, а значит, 1ЛА^ = В2С .
Как известно, В2С - АВХ, зна-
чит, IaAq = АВХ. Следователь-
но, четырехугольник А^1аАВх
- параллелограмм, т.е.
AqBx || 1аА . С другой сторо-
ны, 1аА || , следователь-
но, точки А^ , Вх и Q лежат
на одной прямой и А^ совпа-
дает с Д. Тогда BAq - отре-
зок касательной к вневписанной окружности,
полу периметру треугольника АВС. Аналогично
отрезок АВ0 равен полупериметру этого же
откуда АВ0 = BAq .
Второй способ. Так как отрезки СД и СВХ равны радиусу
г вписанной окружности, а прямые CtAt , CtBt перпендикуляр-
ны биссектрисам углов В нА соответственно, из прямоугольных
треугольников СА$ВХ и СВ$АХ получаем, что
т.е. он равен
получаем, что
треугольника,
Д)С =
С другой стороны,
ZA ’ BoC “ —•
tgV tg~
АС =
ZA ’ ВС Г+ ЛВ •
tg— tg —
Следовательно,
ABq = АС + CBq = ВС + СА$ = ВА$ .
2. Да.
151
Первый способ. Так как треугольники ПаПьС и АВС подоб-
ны (рис. 166), треугольники LaLbC и АВС также подобны, т.е.
LC LbC
—— ~ • Значит, подобны треугольники ALaC и BLbC
АС ВС
(рис. 167). Следовательно, ALaBLb = ALbALa , но эти углы рав-
ны половинам углов В п А тре-
угольника. Значит, АС = ВС.
и
АВ антипараллельны относи-
Второй способ. Так НаНь
тельно прямых АС и ВС, LaLb и АВ также антипараллельны
относительно АС и ВС, значит, четырехугольник ALbLaB впи-
санный. Тогда, как и в предыдущем решении, получаем, что
ALaBLb = ALbALa и АС = ВС.
3. 75°
Первый способ. Продолжим отрезок MN на его длину в
обе стороны и получим -- -
Рис 168
152
точки К и L (рис. 168). Так как М -
общая середина АС и KN, то
AKCN - параллелограмм. Тогда
ХСКМ = 45°, АКСМ = 15°. От-
метим на отрезке СМ точку Р так,
чтобы угол СКР был равен 15° .
Тогда отрезок КР разобьет треу-
гольник КСМ на два равнобедрен-
ных треугольника. Кроме того,
АРМЫ = 60° , поэтому треуголь-
ник MPN - равносторонний. Тре-
угольники PLN и РКМ равны,
треугольник CPL - равнобедрен-
ный и прямоугольный, отсюда
ZCLM = ZCLP + AMLP = 75° =
= ААВМ , так как CLBM - па-
раллелограмм.
Можно использовать также то, что
построенная точка Р - центр описанной
окружности треугольника KCL.
Второй способ. Пусть G - точка пере-
сечения медиан треугольника ABC, F -
середина GB, треугольник GFO равно-
сторонний, причем точки О и А лежат в
одной полуплоскости относительно МВ
(рис. 169). Поскольку ZMOB = 120° , то
О - центр окружности, описанной около
треугольника МАВ, при этом
AMOG = 30° = 2ZMAG , значит, AG и
OG пересекаются на описанной окруж-
ности треугольника AM В, т.е. точки А, О
и G лежат на одной прямой. Тогда
ZABM = ZMOA = 75°
2
Рис. 169
4. Пусть АВС - данный треугольник (АС = ВС). Заметим,
что, сгибая бумагу, можно найти
отрезка. Построим медиану АА$ .
По теореме Фалеса вертикальные
линии сетки делят ее на четыре
равные части. Поэтому, построив
точку Ах , такую что ААХ =
= AAq/4 , и перегнув треугольник
по прямой САХ, получим точку
Q , такую что АСХ = ABfl
(рис. 170). Теперь, построив от-
резки СХС2 = С2С3 = ... = С5Сб =
= АСХ, мы найдем все узлы сет-
ки, лежащие на стороне АВ. Пе-
регнув треугольник по прямой, проходящей через С2, так, чтобы
точка С3 попала на прямую ССХ , мы получим линию сетки,
проходящую через С2, и т.д. Перпендикулярные линии строятся
аналогично.
5. Пусть в треугольнике АВС
ZA = 30°, Z.B = 70° , ZC = 80°
(рис. 171). Проведем высоту АН.
Тогда АСАН = ХМ НА = 10°, где
М - середина АС. При этом
Z.HAL = 10° , где L - основание
биссектрисы треугольника НАВ,
проведенной из вершины А. Зна-
середину любого заданного
153
чит, медиана треугольника АН С, проведенная из вершины Н, и
биссектриса треугольника ВАН, проведенная из вершины А,
параллельны, а высота АН является искомым разделяющим
отрезком.
6. Обозначим через 5 точку пересечения ХО2 и YC\ (рис.172).
Пусть и г2 ~ радиусы соответствующих окружностей. Тогда
Х5 = 015 = = QO
SO2 ~ SY ~ г2~ ОО2 ’
Значит, SO || O2Y и
SO = —^—O2Y =
П + г2 Г1 + Г2
Пусть XZ - одна из касатель-
ных из X ко второй окружно-
сти, a Z' - проекция S HaXZ.
Тогда
SZ' = -^—O2Z = = SO .
r( + r2 rt+ r2
Аналогично доказывается, что расстояние от 5 до остальных
касательных также равно SO, т.е. S и есть центр требуемой
окружности.
7. Пусть точки А и В - концы ломаной. Рассмотрим диаметр
XY, параллельный АВ (рис. 173). Пусть точка С симметрична В
относительно XY, тогда АС - диаметр окружности. Рассмотрим
любую точку Z хорды XY. Так как AZ + BZ = AZ + CZ > АС ,
Z не может лежать на ломаной,
а значит, диаметр XY подходит.
8. Первый способ. Пусть со
- данная окружность (с центром
154
в точке О) и QA пересекает со в точке С, отличной от А
(рис. 174). Так как ВС - диаметр со, то отрезки ВС и МК делят
друг друга пополам, т.е. СКВМ - параллелограмм. Тогда,
поскольку М - середина АВ, то СКМА - прямоугольник.
Докажем, что отрезки MQ и PC перпендикулярны. Мы имеем:
МС2 - MP2 - QC2 + QP2 =
= (ск2 + МК2) - (2РО2 + 2ОК2 - РК2) -
- (QK2 - СК2) + (QK2 - РК2) =
= 2СК2 + ЮК2 - 2PQ2 - 2ОК2 = 2СК2 + 2ОК2 - 2ОС2 = 0 .
Значит, MQ 1 PC . Пусть ВР пересекает QA в точке R. Так как
СВ - диаметр со, BR ± PC . Следовательно, MQ || BR , и
поскольку М - середина АВ, то Q - середина AR. Значит, QB
делит PH пополам.
Второй способ. Заметим, что ZPBA Ф 90° ; иначе РК || АВ ,
и точка Q не существует. Тогда
прямая ВР пересекает AQ в не-
которой точке R (рис. 175). Тре-
угольники ВРН и BRA гомоте-
тичны, так что достаточно дока-
зать, что Q - середина AR.
Пусть Р' - точка, диамет-
рально противоположная к Р.
Тогда РА 1 Р'А , PR 1 Р'В ,
AR ± АВ , т.е. в треугольниках
Р'АВ и PAR соответственные
стороны перпендикулярны. Зна-
чит, треугольники подобны, и их
медианы из вершин Р и Р' также
перпендикулярны. Но из сим-
метрии относительно О следует,
что Р'М || РК и Р'М 1 PQ . Это
и означает, что PQ - медиана в APAR .
9 класс
1. Первый способ. Без ограничения общности
можно считать, что дуги АВС и BCD не превосходят полуокруж-
ности. Тогда uAD = 2тс - иАВС - uBCD + иВС > иВС . По-
скольку дуга ABCD также больше дуги ВС, получаем, что AD >
>ВС.
155
В Теперь, если АС > BD, то
s'^'_________________° АВС > uBCD 1 иАВ > uCD и
АВ > CD. При АС < BD все
/ / у\ неравенства меняются на проти-
/ / s' \ \\ вопо ложные.
/ / s' \ \ ] Второй способ. Пусть AL -
I /s' \ \ I самый длинный из отрезков AL,
у>^__________________Ч/ BL, CL, DL (рис. 176). Тогда,
А\/D в силу равенства AL • CL =
\к / = BL • DL , CL - самый короткий
^s^ из этих отрезков. Тогда AL -
Рис. 176 - CL > \BL - DL\, отсюда
АС2 = (AL + CL)2 = (AL - CL)2 + 4AL CL >
> \BL - DL\2 + 4BL DL = {BL + £>L)2 = BD2 ,
т.е. AC > BD. Кроме того, из подобия треугольников ALB и DLC
АВ AL
получаем, что -г— = , т.е. АВ > CD. Аналогично из подобия
C^JL-Z jL/A-z
треугольников ALD и BLC получаем AD > ВС.
Третий способ. Заметим, что AC = 2BsinZB и
BD = 2В sin ZA , поэтому неравенство АС > BD эквивалентно
неравенству sin Z.B > sin ZA .
Далее,
(AD - ВС)(АВ - CD) > 0
& AD -АВ + ВС -CD > AD -CD + ВС- АВ ,
что эквивалентно (домножим на
1 1 1
sin ZA sin ZB = sin ZA sin Z£) = sin ZC sin ZB )
2 2 2 7
(AD-ABsinZA BC • CD sin ZC A .
---------------+-------------- sin ZB >
I 2 2 J
(AD-CDsinZD BC-ABsinZB}.
---------------+--------------- sin ZA,
I 2 2 J
значит,
(5 (DAB) + 5 (DCB))sin ZB > (5 (CDA) + 5 (ABC))sin ZA,
откуда
5 (ABCD) sin ZB > 5 (ABCD) sin ZA, т.е. sin ZB > sin ZA.
156
2. Первый способ. Пусть М, N, К - середины АВ, CD и АС
соответственно (рис. 177). Тогда степень точки К относительно
ЯП r^A/f2 л2 СВ2 -АВ2
окружности с диаметром АВ равна КМ - МА =------------------, а
относительно окружности с диаметром CD----------------. Так
4
как АВ2 + AD2 = BD2 = ВС2 + CD2, получаем, что степени равны.
Второй способ. Пусть прямые АВ и CD пересекаются в точке
Z. Центры данных в условии окружностей и й)2 - середины
О! и О2 отрезков АВ и CD соответственно. Пусть со -
окружность ABCD (с диаметром BD). Тогда АВ - радикальная
ось окружностей со и 0^ , CD - радикальная ось окружностей со
и о>2 , a XY - радикальная ось окружностей cty и (О2 , значит, XY
проходит через Z. Теперь для
решения задачи достаточно до-
казать, что ZK ± О}О2 (где К
- середина диагонали АС). Но
нетрудно заметить (из сред-
них линий треугольников АВС
и ADC), что ОХК V ZO2 и
О2К 1 ZOt.
3. Первый способ. Пусть
М, К и L - середины сторон
АВ, ВС и АС соответственно
(рис.178). Тогда ZLEM =
= 2Z.LKM = 2ZA . Обозначим
стороны ZA через и 12 так,
чтобы при повороте вокруг А
на ZA против часовой стрел-
ки /1 переходила в 12 . Тогда
157
при повороте по часовой стрелке вокруг Е на угол 2ZA середина
стороны треугольника, лежащей на /t , перейдет в середину
стороны, лежащей на /2. Поэтому точка, симметричная А
относительно М, будет вершиной треугольника. Вторая вершина
строится аналогично.
Второй способ. Пусть О и Н - центр описанной окружности
и ортоцентр треугольника. Тогда Е - середина отрезка ОН,
/ВАО = /.НАС и АН = 2АО cos ZA . Следовательно, компози-
ция симметрии относительно биссектрисы угла А, гомотетии с
центром А и коэффициентом 2 cos ZA и симметрии относительно
Е является подобием с центром О. Соответственно, найдя центр
этого подобия, можно построить точки В и С как вторые точки
пересечения сторон данного угла и окружности с центром О,
проходящей через А.
Примечание. При ZA = 60° рассмотренное подобие будет
симметрией относительно прямой, проходящей через Е и перпен-
дикулярной биссектрисе угла А. Соответственно, в качестве О
можно брать любую точку этой прямой. В остальных случаях
решение единственно.
4. Первый способ. Пусть На , Нь, Нс - основания высот
треугольника. Так как АН • ННа = ВН • ННЬ = СН • ННС, то
существует инверсия с центром Н, переводящая точки А, В, С в
На , Нь, Нс соответственно (в случае остроугольного треуголь-
ника надо взять композицию инверсии и центральной симметрии
относительно Н). При этой инверсии стороны треугольника
перейдут в окружности с диаметрами АН, ВН, СН, а вписанная
окружность - в прямую, касающуюся этих окружностей. Иско-
мая прямая получается из этой гомотетией с центром Н и
коэффициентом 2.
Второй способ. Пусть I - центр вписанной окружности, At,
Bt , Ct - точки ее касания со сторонами ВС, АС, АВ соответ-
ственно, а А2, В2, С2 - такие точки (на трех окружностях из
условия), что ААХ1Н ~ ДЯАА2 , ABJH ~ АНВВ2 и АСХ1Н ~
~ ДЯСС2 (подобные треугольники расположены так, что их
стороны соответственно параллельны). Касательные в этих
точках к этим окружностям параллельны касательной в Н ко
вписанной; достаточно доказать, что эти касательные совпадают,
а для этого достаточно показать, что проекции векторов НА2 ,
НВ2 и НС2 на IH равны. Нетрудно видеть, что они сонаправ-
лены. Поскольку НА2 составляет равные углы с IH и 1АХ, длина
первой проекции равна длине проекции НА2 на АН, т.е.
АН
-----НА , где А - основание высоты. Аналогично вычисляют-
г
158
ся остальные проекции; осталось
заметить, что АННА'=
= ВНН^=СН- НС'.
5. Пусть Н - ортоцентр треу-
гольника ЛВС, D' - точка, сим-
метричная Н относительно АС
(рис. 179). Тогда D' лежит на
описанной окружности, а так как
ZB = 60° , то ВО = ВН (этот факт
можно доказать, например, так:
заметим, что поскольку ZB = 60° ,
то описанные окружности треу-
гольников ЛВС и АОС равны и
совмещаются параллельным переносом на вектор ВН, поэтому
ВН = R = ВО). Значит, поскольку BL - биссектриса угла ОВН,
то LO = LH = LD'. Треугольники LBO и LBH равны (по двум
сторонам и углу между ними), отсюда Z.BOL = Z.BHL. Из
симметрии относительно ЛС: Z.BD'L = Z.LHD' = 180° - Z.BHL ,
отсюда ZBOL + Z.BD'L = 180° . Следовательно, четырехуголь-
ник BOLD' вписанный и D' совпадает с D.
6. Первый способ. Обозначим через Ах, Вх и Ct середины
дуг ВС, С А и АВ, не содержащих других вершин треугольника
ЛВС (рис. 180), кроме того, пусть и Во - точки касания
вписанной окружности со
сторонами ВС и С А соот-
ветственно.
Пусть MN проходит че-
рез /.Так как AXN и BtM
- диаметры, то АХВХ и MN
равны и параллельны. Как
известно, Л^ ± CQ и
СС2 = С2/ . Из симметрии
относительно серединного
перпендикуляра к СС] име-
ем СС2 = СХ1, кроме того,
из прямоугольного треу-
гольника CAqI получим,
что C2Aq = С2С . Тогда, по
теореме о трезубце, C2Aq = С2С = /Q = СХА = СХВ . Значит, тре-
угольники С2САц и СхАВ равны ( АВ = СА$ ). Отсюда и полу-
чаем равенство
ЛС + СВ = ЛВ0 + В0С + СЛ0 + AqB = 2АВ + А^В = ЗАВ .
159
с
Рис. 181
В обратную сторону аналогич-
но.
Второй способ. Пусть J - центр
вневписанной окружности, касаю-
щейся стороны АВ (рис. 181). По
теореме о трилистнике точки М и
N являются центрами окружнос-
тей ACJ и BCJ, следовательно,
MN - серединный перпендикуляр
к отрезку CJ, т.е. I - середина CJ.
Применив гомотетию с центром С
и коэффициентом 1/2, получим,
что вписанная окружность касает-
ся средней линии треугольника,
параллельной АВ. Условие опи-
санности трапеции, образованной этой средней линией и сторо-
нами, равносильно требуемому равенству. Обратное утвержде-
ние доказывается аналогично.
7. Первый способ. Введем обозначения, как на рисунке 182.
Пусть ra, гь и гс - радиусы окружностей с центрами Оа , Оь и
Ос соответственно, da(X} - расстояние от точки X до ВС, db и
dc определены аналогично.
Фигура, состоящая из лучей СА, СВ и трех первых, считая
от С, окружностей, касающихся СА, подобна фигуре из лучей
160
СВ, С А и окружностей, касающихся СВ. Следовательно,
da (Pb) :rb = db (Оа): га . Аналогичные равенства верны для вер-
шин А и В.
Теперь мы имеем
<(Ч) da(Ob) db(Oc) _dc(Oa) db(Oc) da(Ob)_
dbtPa) dc(Ob) da(Oc) da(Oc) dc(Ob) db(Oa)
rc rb ra
что по теореме Чевы влечет утверждение задачи.
Второй способ. Пусть АС П ВОЬ = К , СВ П АОа = М ,
В А П СОс = N . Проведем через Оь отрезок А'С' || АС , где л'
и С' ~ на прямых В А и ВС соответственно. Тогда
АК = А'ОЬ
СК ” С'ОЬ ~
= f Гь +2гь\/[ — + 4 rb ) = f —-— + 2 Vf—-— + 41
sin ZA J/ sin ZC J sin ZA J/ sin ZC J
Аналогично выразив отношения CM/ВМ и BN/AN, завер-
шаем решение, воспользовавшись теоремой Чевы.
8. Если Р - параллелограмм, то нужно не менее четырех
гвоздей. Действительно, если сторона s не касается никакого
гвоздя, то Р можно двигать в направлении двух смежных с 5
сторон.
Покажем теперь, что любой выпуклый многоугольник Р
можно зафиксировать четырьмя гвоздями.
Пусть окружность с с центром О наибольшая из окружнос-
тей, лежащих внутри Р, At, А2 , ..., Ak - точки касания с со
сторонами Р, Н - выпуклая оболочка этих точек.
Предположим, что существуют две вершины U и V много-
угольника Н такие, что UV -
диаметр с (рис. 183). Вобьем
два гвоздя в точки U и V.
Очевидно, что стороны Р, со-
держащие U и V, параллель-
ны, следовательно, Р можно
двигать только в направлении,
перпендикулярном UV. Чтобы
зафиксировать Р, достаточно
вбить еще два гвоздя, препят-
ствующих его движению влево
и вправо от UV .
161
Рис. 184
В и С, фиксируют Р.
Будем теперь считать, что сто-
роны и диагонали Н не содержат
О.
Предположим, что ОёН.
Пусть PQ - сторона Н, разделяю-
щая Н и О, а касательные к с в
точках Р и Q пересекаются в точке
Т. Тогда существует гомотетия с
центром Т и коэффициентом, боль-
шим 1, переводящая с в большую
окружность, лежащую внутри Р -
противоречие.
Таким образом, О е Н . Тогда
существует треугольник АВС, со-
держащий О (рис. 184). (А, В, С - три точки касания с со
сторонами Р). Легко видеть, что три гвоздя, вбитые в точки А,
Ю класс
1. 15, 15 и 150 градусов.
Пусть ABCD - квадрат, вершины X, У, Z равно-
бедренного треугольника лежат на сторонах ВС, CD, DA соот-
ветственно, а центр описанной окружности О треугольника XYZ
лежит на АВ (рис. 185). Так как отрезок ОУ пересекает отрезок
XZ, угол XYZ тупой, поэтому основанием равнобедренного
треугольника является именно XZ. Тогда отрезки ОУ и XZ
перпендикулярны. Поскольку их соответственные проекции на
перпендикулярные прямые ВС и АВ равны, они и сами равны,
т.е. сторона треугольника XYZ равна радиусу его описанной
окружности.
2. Первый способ. Пусть отрезки АВ и CW пересекаются в
точке Т (рис. 186). Тогда ZACW = ZABW = ZTAW , т.е. треу-
гольники CAW и ATW подобны. Тогда, поскольку прямая WX
- симедиана в треугольнике CAW, она является медианой в
треугольника ATW, т.е. точка N - середина АТ. Аналогично,
точка М - середина ВТ, откуда MN = АВ/2.
Второй способ. Поскольку W - середина дуги АВ, касатель-
ная в ней параллельна АВ. Совершим гомотетию с центром С,
переводящую эту касательную в АВ; пусть наша окружность
при этой гомотетии переходит в окружность со, а точка W - в
точку Т.
Из подобия треугольников CAW и ATW, доказанного в
предыдущем способе, следует, что AW2 = WC -WT , т.е. W
лежит на радикальной оси со и точки А. Поскольку ХА = ХС,
точка X также на ней лежит. Значит, эта радикальная ось есть
WX, откуда ХА2 - NT2 , и N - середина АТ. Аналогично, М -
середина ВТ, откуда MN = АВ/2.
3. Да.
Построим выпуклый многогранник с п диагоналями. При п =
= 0 годится любая пирамида.
Пусть п > 0. Возьмем (п 4- 2) -угольную пирамиду 5At... А^ .
Построим вовне нее на грани SA^An+z как на основании
пирамиду TSA^An+z (так, чтобы все п + 4 построенные верши-
ны находились в выпуклом положении). Объединение этих двух
пирамид - выпуклый многогранник Т5А1...Дг+2 , диагоналями
которого являются ровно отрезки ТА1,...,ТАП .
4. 2, 3 или 4.
Очевидно, что центр О описанной окружности Q треуголь-
ника АВС -хорошая точка, поскольку в этом случае Ва = Са = А ,
Аь - Сь - В к Ас - Вс - С .
Рассмотрим теперь любую хорошую точку D Ф О . Пусть А',
В? , С - проекции D на ВС, СА, АВ соответственно. Точки А и
Аь симметричны относительно С',
также как и точки В и Ва . Значит,
середины отрезков АВ и А^ так-
же симметричны относительно С';
следовательно, серединный перпен-
дикуляр к АъВа проходит через
точку О', симметричную О относи-
тельно D (рис.187). Аналогично,
серединные перпендикуляры к
АсСа и ВсСь также проходят через
О', при этом они не параллельны;
значит, О' и является центром окружности, проходящей через
шесть точек.
163
Далее, каждая из точек D и О' равноудалена от Д и Ас ;
при этом Z) / О', ибо D Ф О . Значит, прямая DO' является
серединным перпендикуляром к АЬАС. Но В'С' - средняя
линия в треугольнике ААЬАС, следовательно, DO' ± В'С'. Ана-
логично получаем, что
DO' ± А'В', т.е. точки А', В'
и С' лежат на одной прямой.
Значит, D лежит на Q, а
А'В'С' ~ ее прямая Симеона.
Кроме того, эта прямая пер-
пендикулярна прямой DO', т.е.
радиусу DO (рис. 188).
Наоборот, пусть точка D ок-
ружности Q такова, что ее пря-
мая Симеона перпендикулярна
OD. Обращая рассуждения пре-
дыдущих двух абзацев, получаем, что точка О' лежит на
серединных перпендикулярах к отрезкам АьВа, ВсСь, АсСа ,
АЬАС, ВаВс и СаСъ , т.е. все шесть точек равноудалены от О'.
Значит, точка D - хорошая.
Найдем теперь количество описанных точек. Пусть точка X
движется по Q так, что угловая скорость радиуса ОХ постоянна.
Как известно (и нетрудно показать счетом углов), прямая
Симеона точки X вращается со вдвое меньшей угловой скорос-
тью в противоположном направлении. Значит, угол между ОХ
и этой прямой меняется с полуторной скоростью, поэтому на
описанной окружности существуют три описанных точки. До-
бавляя центр О, получаем, что хороших точек не больше
четырех.
Осталось учесть, что некоторые из них могут совпасть с
вершинами. Поскольку прямая Симеона вершины А - это высота
из нее, такое происходит, если радиус О А параллелен ВС, т.е.
|ZB - ZC| = 90° . Это может произойти и с двумя вершинами -
ровно в треугольнике с углами 30° , 30° и 120° . Отсюда и
следует ответ.
5. Пусть X, У, Z - отмеченные точки. Нам требуется
построить на прямых ХУ, YZ и ZX точки А, В и С соответственно
так, чтобы в треугольнике АВС высота из А, биссектриса из В и
медиана из С лежали соответственно на этих прямых.
Выберем произвольную точку В' и проведем через нее
прямую Ц , перпендикулярную ХУ; тогда 1Х должна быть
параллельна ВС (рис. 189). Проведем через В' прямую, парал-
лельную У7, и отразим 1Х относительно этой прямой; мы
164
Рис. 189
получим прямую /2 , параллельную АВ. На /2 выберем произ-
вольную точку л' и проведем через середину отрезка А'В'
прямую, параллельную ZX, до пересечения с Ц в точке С'.
Построенный треугольник А'В'С' гомотетичен искомому (он
переводится в АВС гомотетией, переводящей А' и В' в А и В
соответственно; здесь мы считаем параллельный перенос част-
ным случаем гомотетии с бесконечно удаленным центром).
Построим в этом треугольнике точки X', Y' и Z', соответ-
ствующие X, Y и Z соответственно. Из этих данных гомотетия
однозначно восстанавливается, а после этого восстанавливается
и исходный треугольник.
Замечание. Из решения видно, что задача имеет единствен-
ное решение, если точки X, Y и Z различны.
6. Пусть I - центр вписанной окружности со, a J - ее
точка, диаметрально противоположная С' (рис. 190). Посколь-
ку ZABXC' = ZC'B^J = ZBAXC' - ZC'AXJ = 90° , точки At и Bx -
Рис 190
это точки пересечения AJ и BJ с со. Точки же А2 и В2 ~
это основания перпендикуляров из С' на BI и AI соответст-
венно.
165
Теперь из прямоугольных треугольников АС7 , BC'I , AC'J
и BC'J с высотами С'В2 , С'Л2 , С'ВХ и С'АХ имеем
ABi JAX _ AC'2 J С2 _ AC2 МС'2
BXJ A'B ~ CJ2 C'B'2 ~ iC'I2 C'B2
_ AC'2 IC'2 AB2 IA2
~ C'l2 C'B2 ~ B2I A2B
Согласно теореме Менелая, примененной к треугольникам
AIB и AJВ, это означает, что прямые АХВХ и А2В2 пересекают
АВ в одной точке (или обе параллельны ей).
7. Будем считать, что наибольшая из площадей граней
тетраэдра равна 1; обозначим эту грань через & . Пусть , S2
и 53 - площади остальных трех граней, а оц , а2 и а3 -
соответственно двугранные углы, образованные этими гранями с
. Проектируя эти три грани на , получаем, что
cos oq + S2 cos a2 + S3 cos a3 = 1.
Следовательно, одно из выражений вида Sz- cosaz не меньше
3 ’ т е'
1 > 1
35; ” 3 '
В правильном тетраэдре все три выражения равны, как и все
четыре площади, так что в нем косинус двугранного угла равен
1
— . Отсюда и следует требуемое.
8. Предположим, что четырехугольник LaLbLcLd вписанный,
но в четырехугольнике ABCD нет параллельных сторон. Обо-
значим Р = АВ П CD , Q = АППВС иВ = АСПВП (рис.191).
Далее, пусть касательные к окружности в точках А, В, С и D
образуют четырехугольник STUV, как показано на рисунке;
некоторые из точек S, Т, U и V могут быть бесконечно удален-
ными, но точки Р, Q и R таковыми не являются.
По теореме Ньютона для описанного четырехугольника STU V
имеем R = SU Г\ТУ . Далее, нетрудно понять, что точки La и
Lb являются точками Лемуана треугольников BCD и BAD
соответственно, поэтому La = BU П DT и Lc = BV П DS . При-
менив теорему Паппа к шестиугольнику BUSDTV, получаем,
что точка R лежит на прямой LaLc. Аналогично, точка R лежит
на LbLd , т.е. R = LaLc П LbLd .
Обозначим также W = ST П CV и X = SV П UT (эти точки
166
5
Рис. 191
могут быть бесконечно удаленными). Точно так же, применяя
теорему Паппа к шестиугольникам ATVBXW и аналогичным,
получаем, что Р - LaLb П LcLd и Q = LaLd П LbLc.
Так как вершины треугольника PQR являются точками
пересечения диагоналей и противоположных сторон четыреху-
гольника ABCD, вершины этого треугольника являются полюса-
ми его сторон относительно описанной окружности k четыреху-
гольника ABCD (такая окружность называется автополярной
окружностью треугольника PQR). По тем же причинам, опи-
санная окружность 5 четырехугольника LaLbLcLd также являет-
ся автополярной относительно PQR. Но для треугольника может
существовать максимум одна автополярная окружность. Следо-
вательно, k = 5 , что невозможно, так как точки La , Lb , Lc и Ld
лежит внутри k.
Замечание. Покажем, что автополярная окружность может
быть только одна. Если со автополярна для треугольника PQR,
О ~ ее центр, а г - ее радиус, то РО ± QR и QO ± PR , т.е. О
-ортоцентр треугольника PQR. Кроме того, РО • р(О, QR) = г2 ,
откуда восстанавливается ее радиус.
Алексей Александрович ЗАСЛАВСКИЙ
ОЛИМПИАДЫ ИМЕНИ И.Ф.ШАРЫГИНА
(2010-2014)
Библиотечка «Квант». Выпуск 134
Приложение к журналу «Квант» №2/2015
Редактор А. Ю.Котова
Обложка А.Е.Пацхверия
Макет и компьютерная верстка Е. В. Морозова
Компьютерная группа М.Н.Грицук, Е.А.Митченко
Формат 84x108 1/32. Бум. офсетная. Гарнитура кудряшевская
Печать офсетная. Объем 5,25 печ.л. Тираж: 1-й завод 900 экз.
Заказ №6621
119296 Москва, Ленинский пр., 64-А, «Квант»
Тел.: (495)930-56-48, e-mail: math@kvant.ras.ru, phys@kvant.ras.ru
Отпечатано «ТДДС-СТОЛИЦА-8»
Тел.: 8(495)363-48-86, http://capitalpress.ru
Индекс 90064
Библиотечка КВАНТ
ВЫПУСК