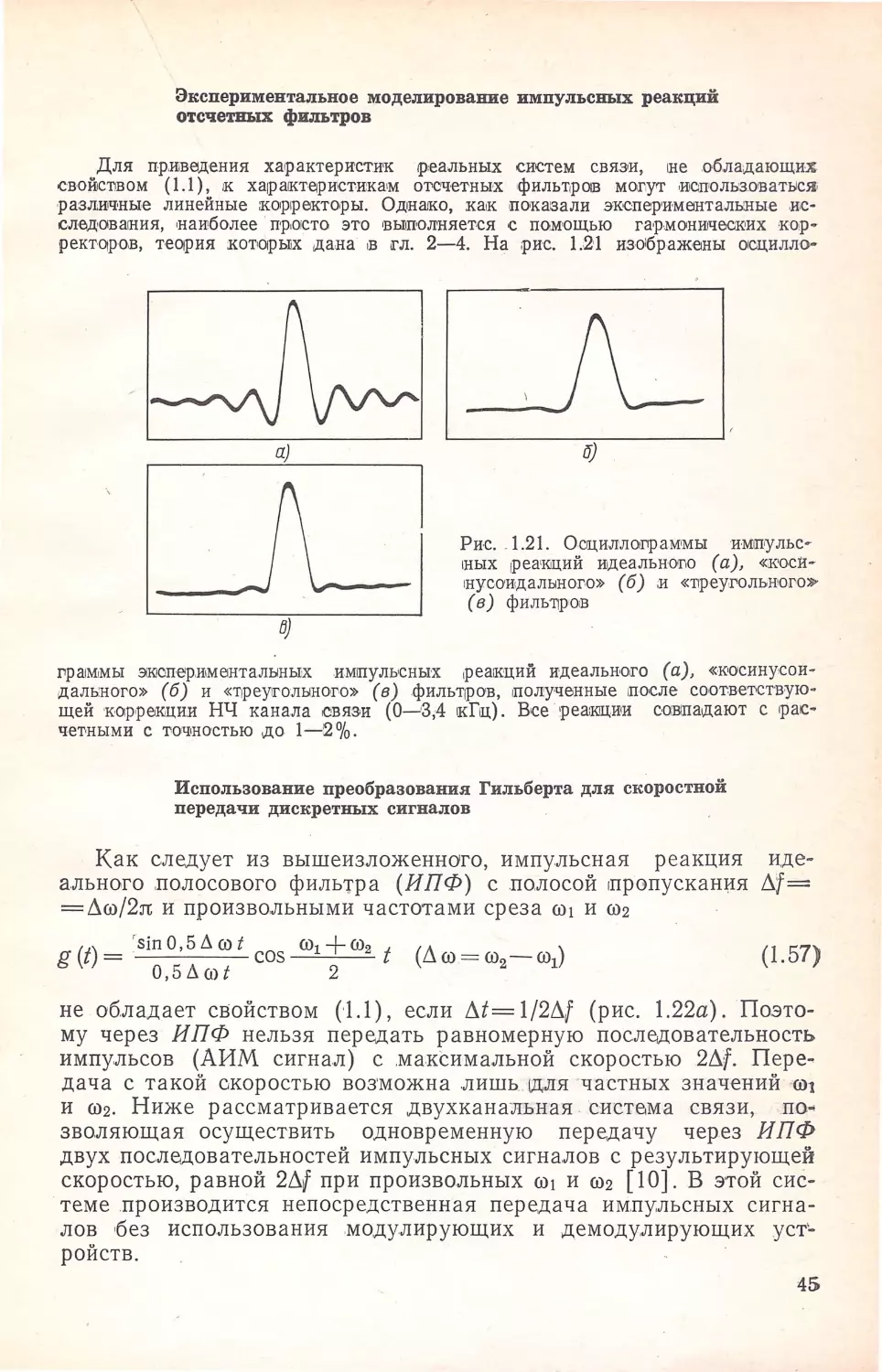
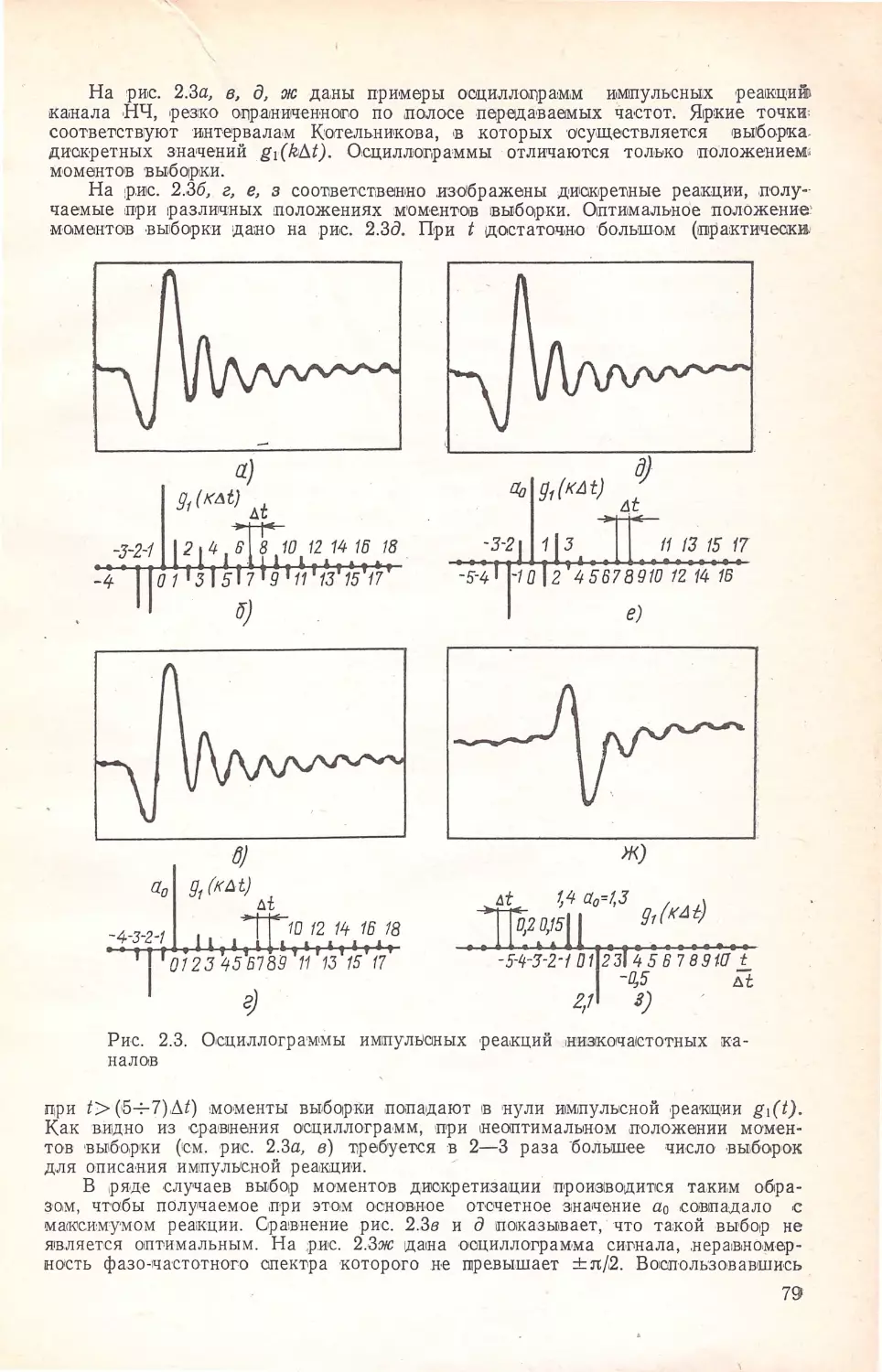
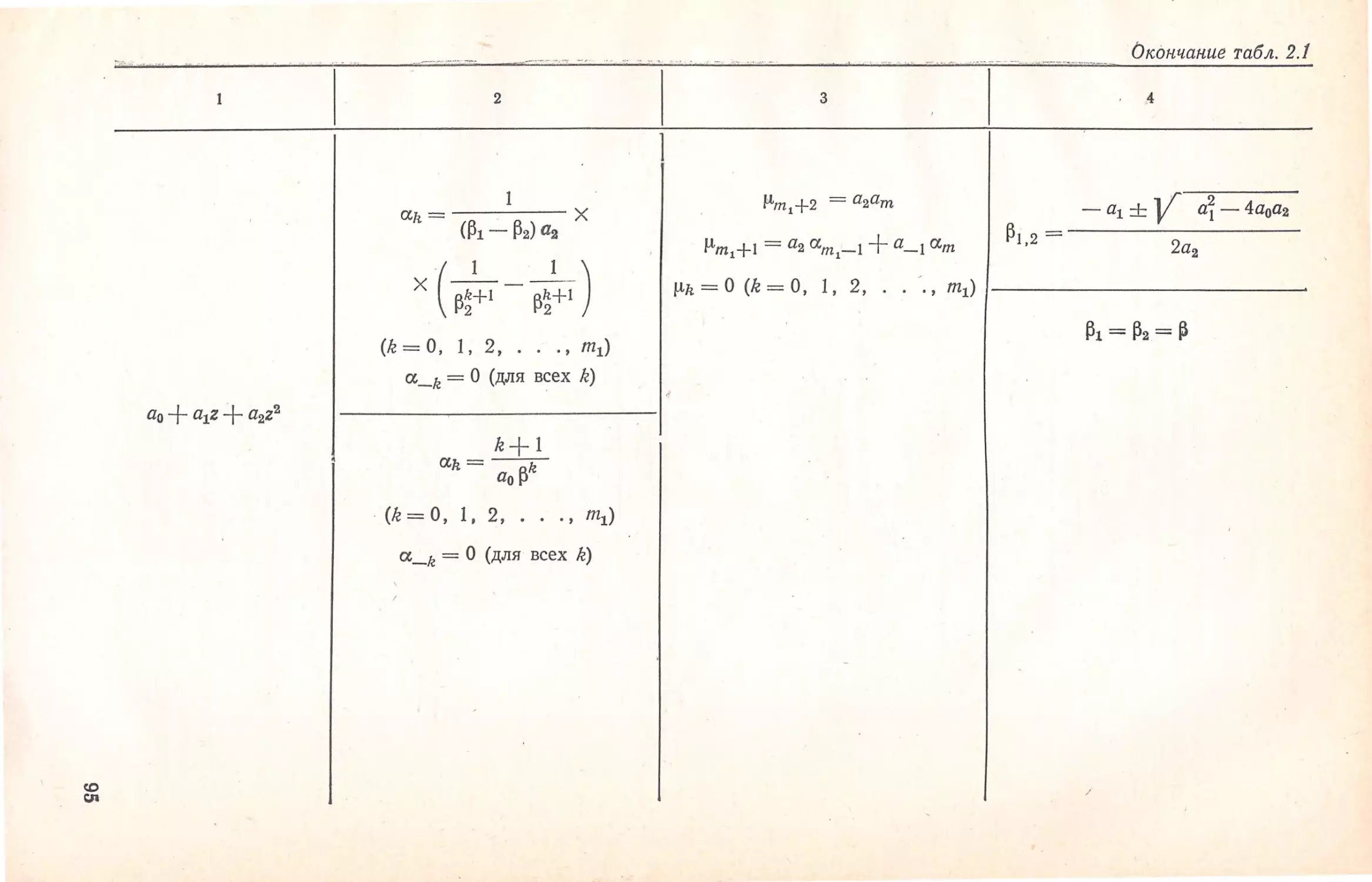
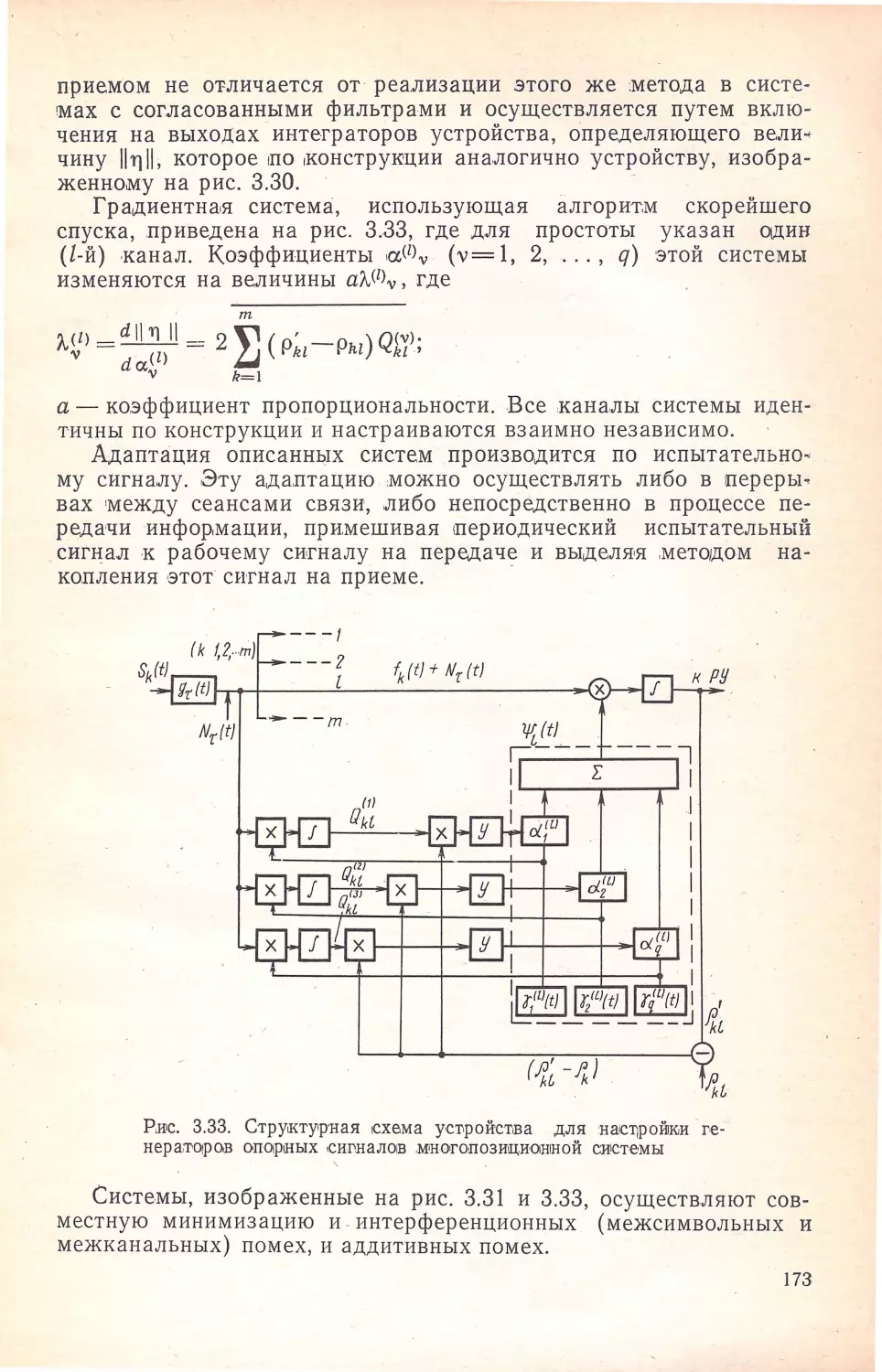
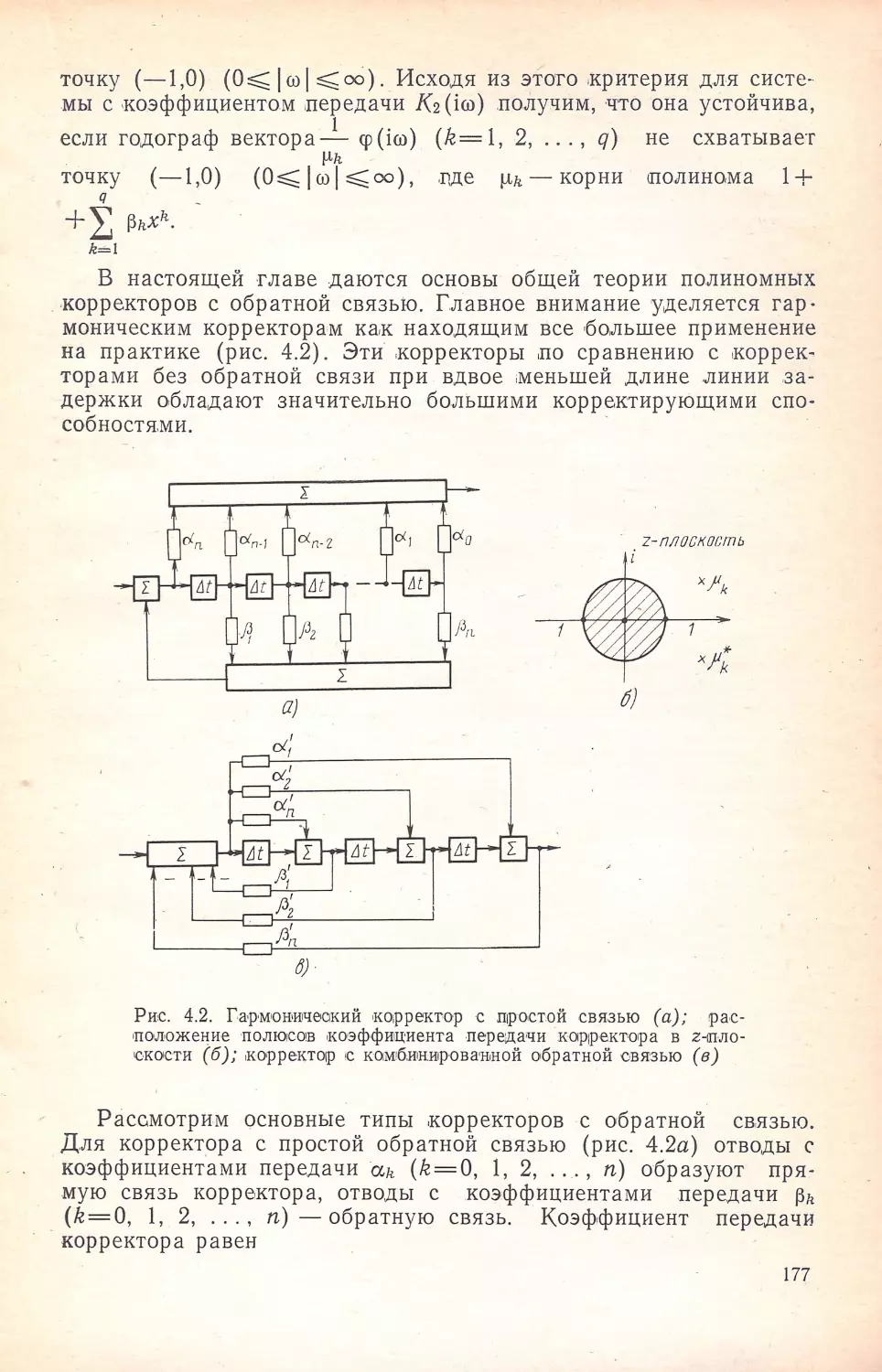
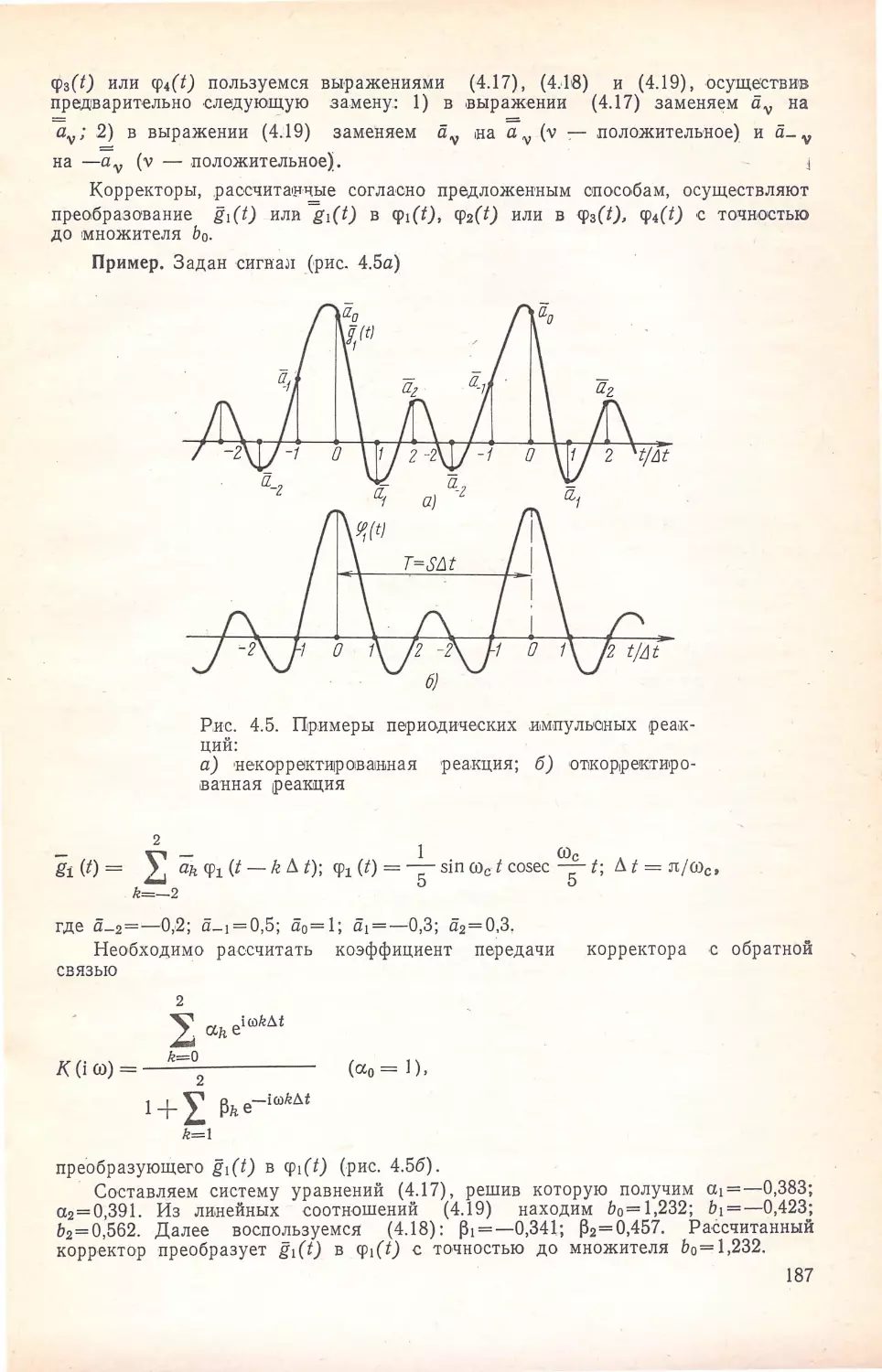
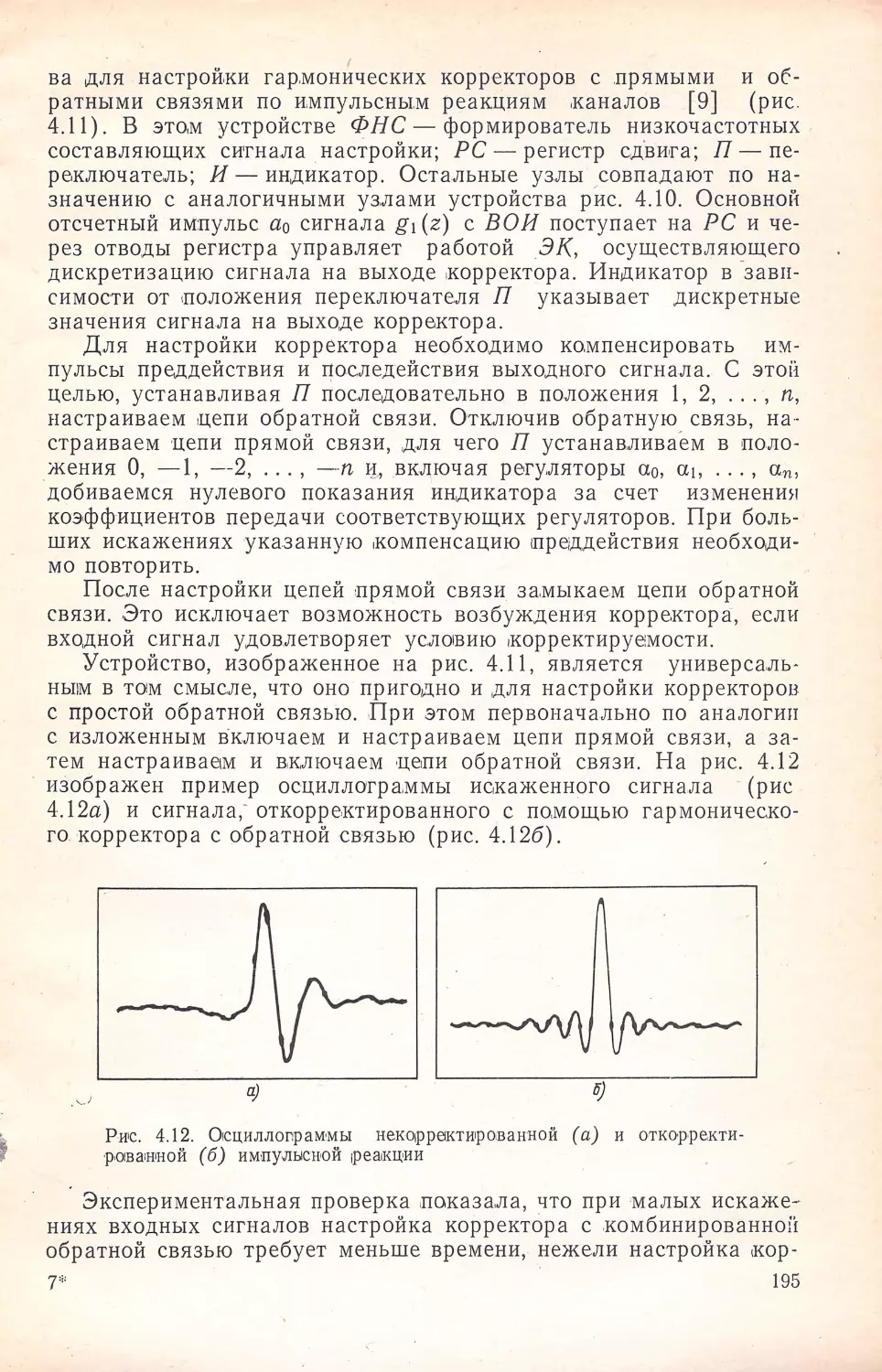
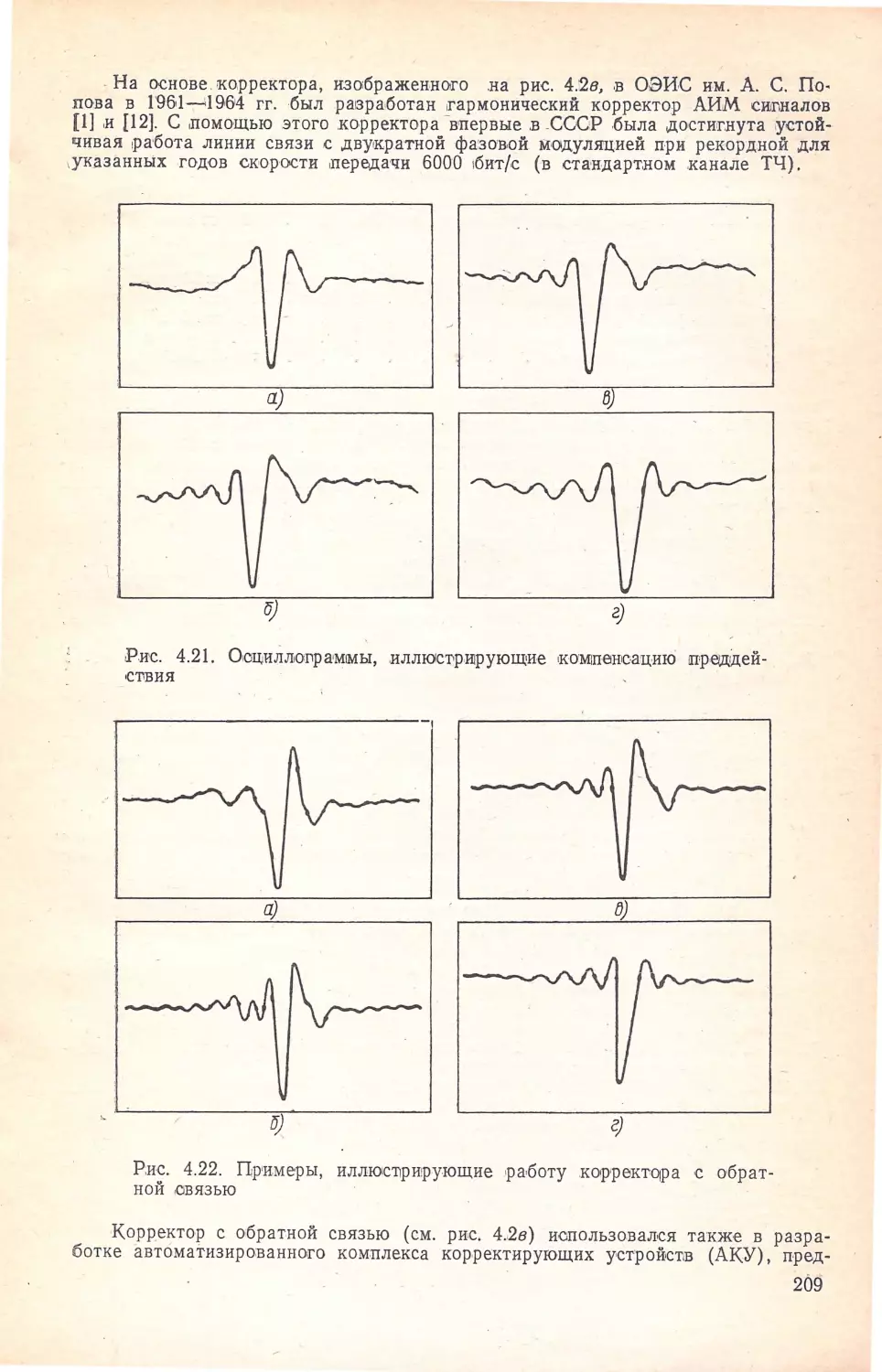
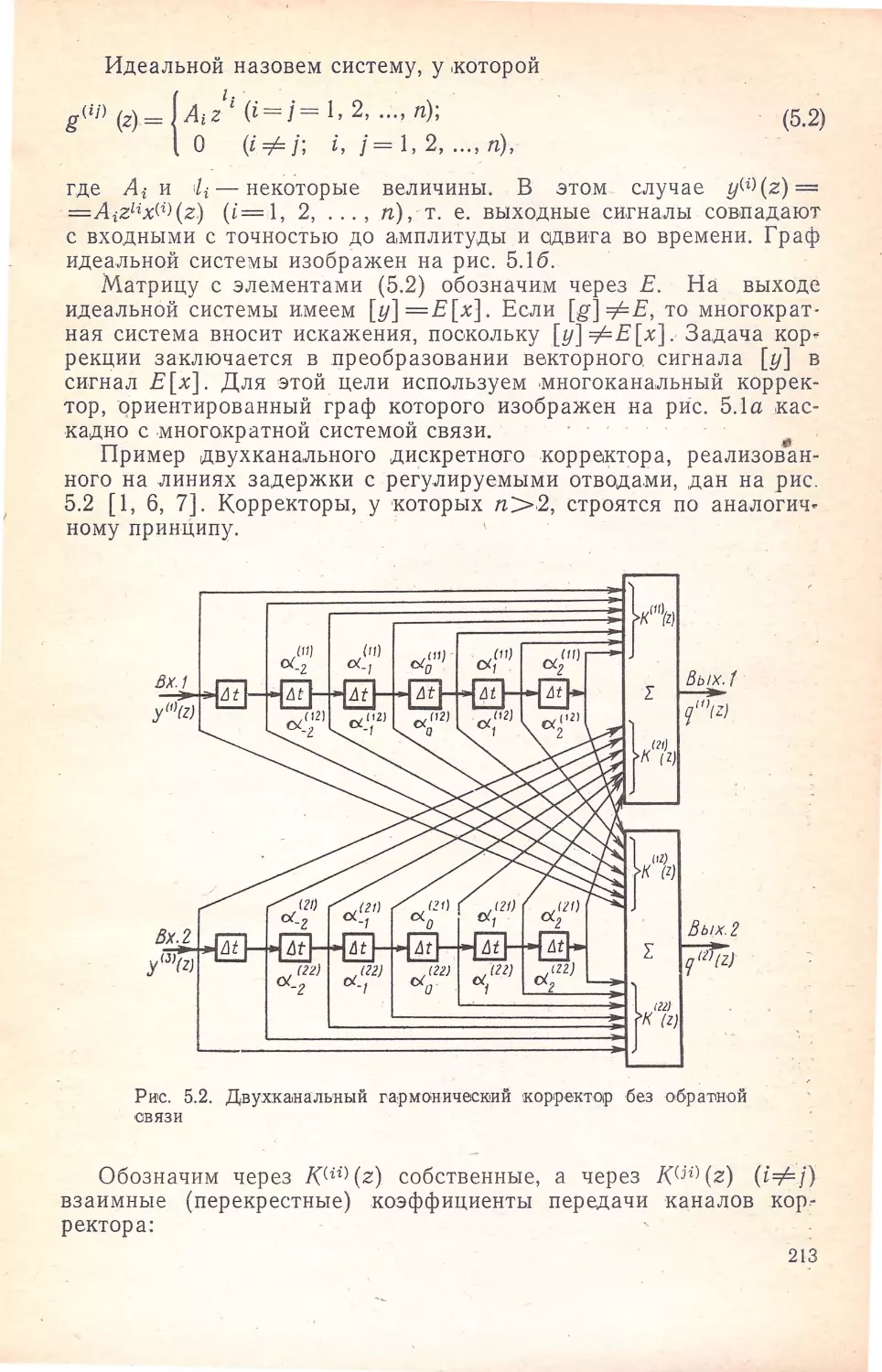
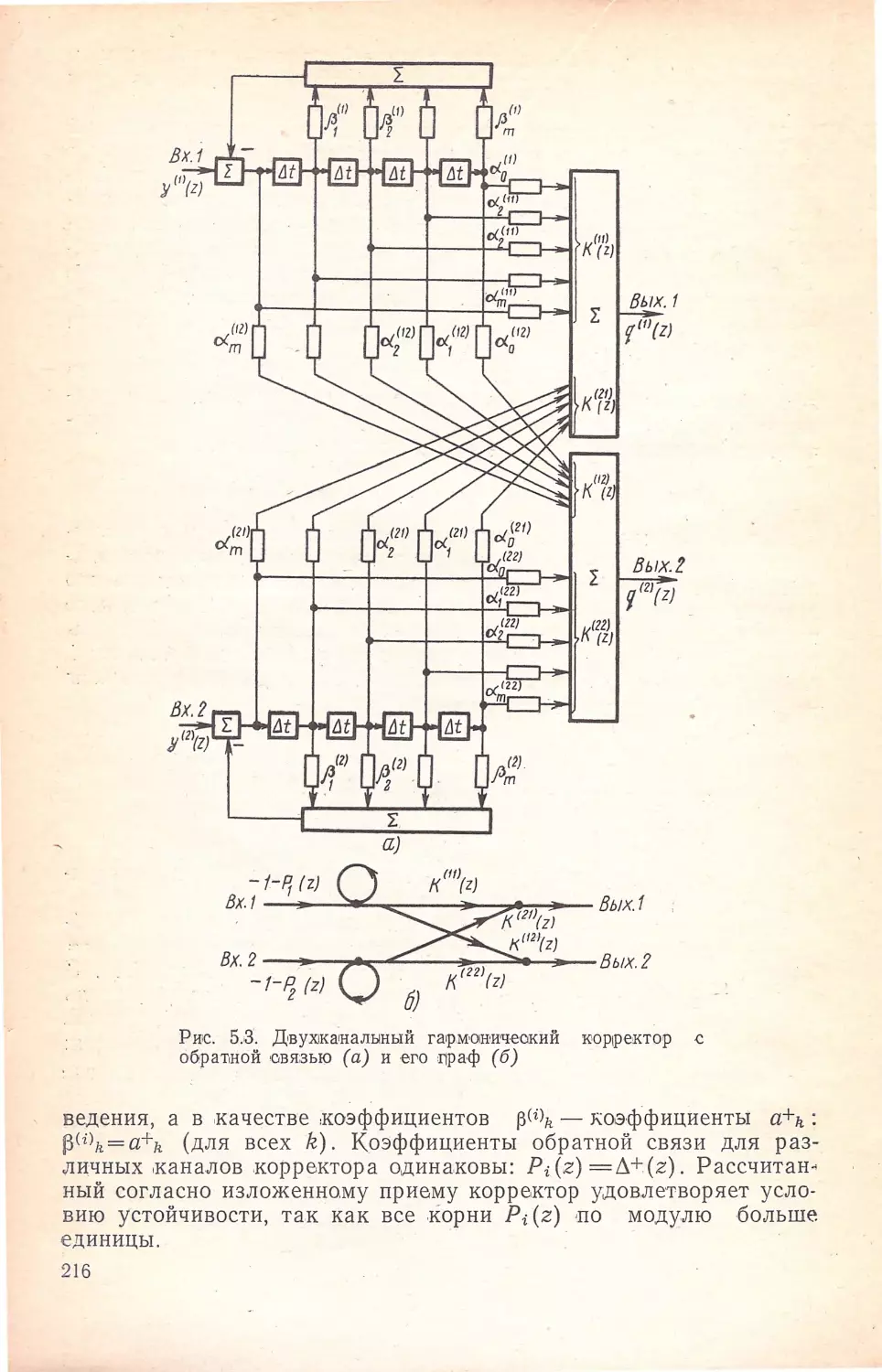
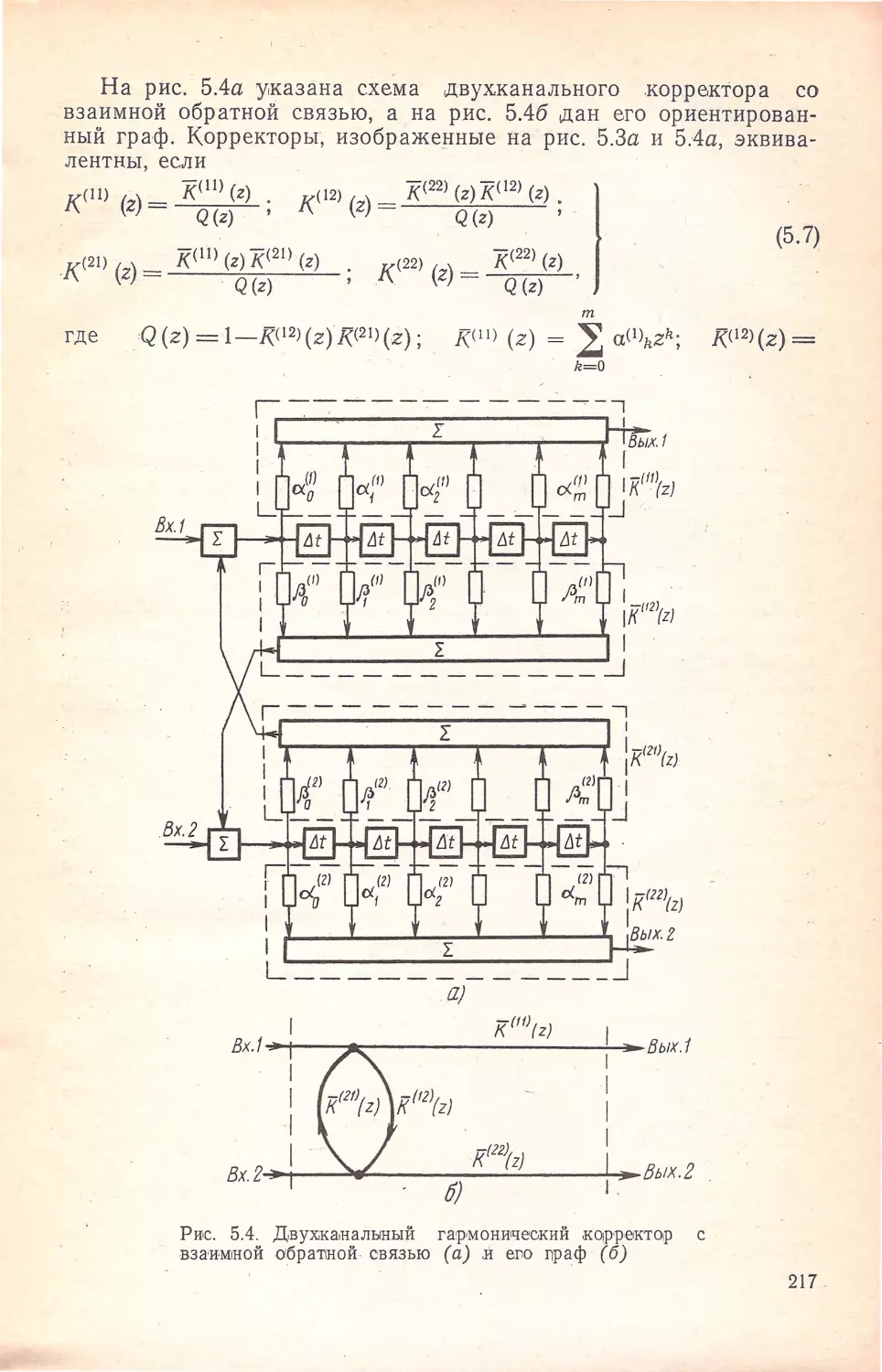
Author: Кисель В.А.
Tags: электротехника компьютерные технологии технология древесины связь цифровые устройства издательство связь
Year: 1979
Text
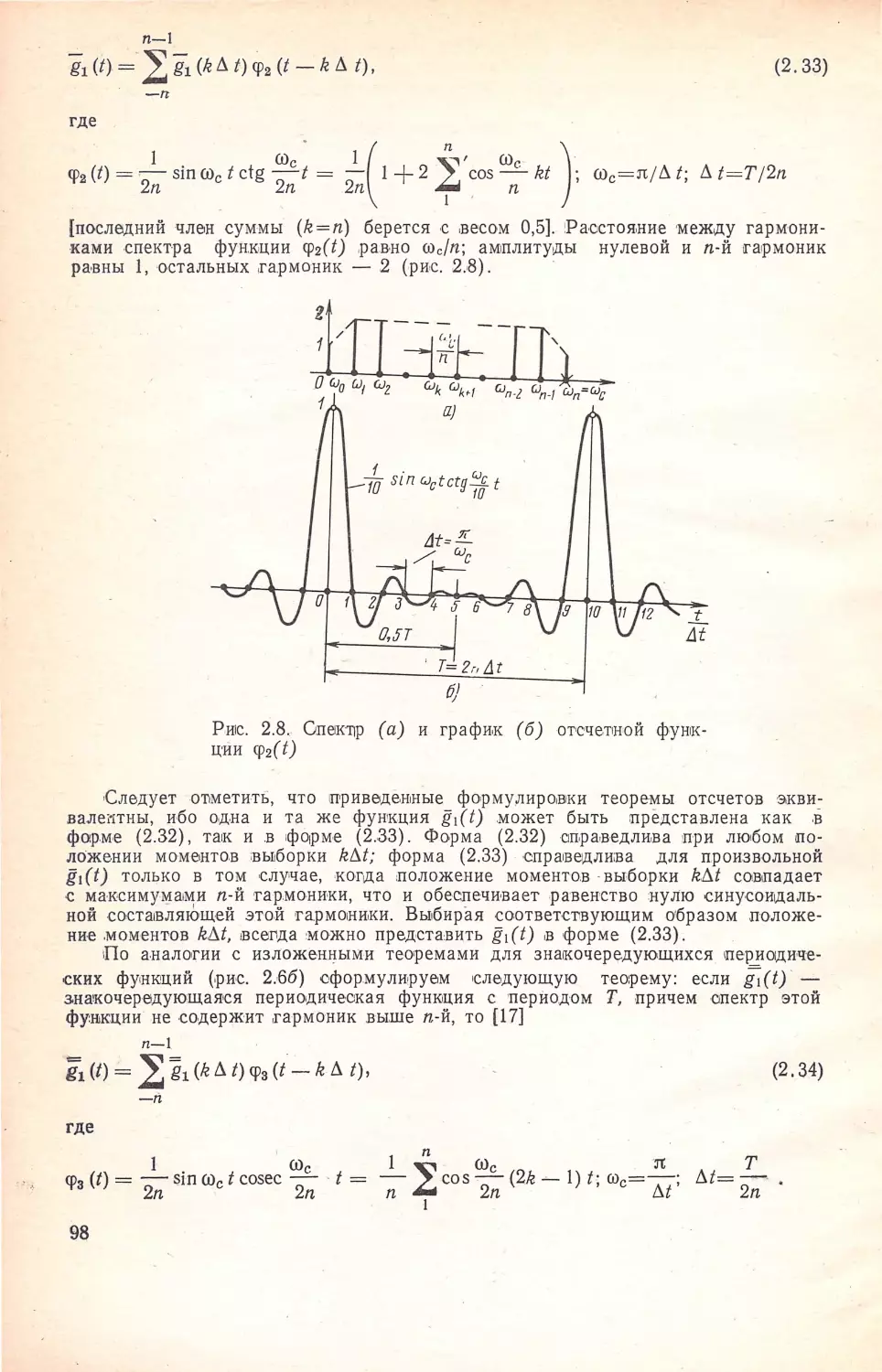
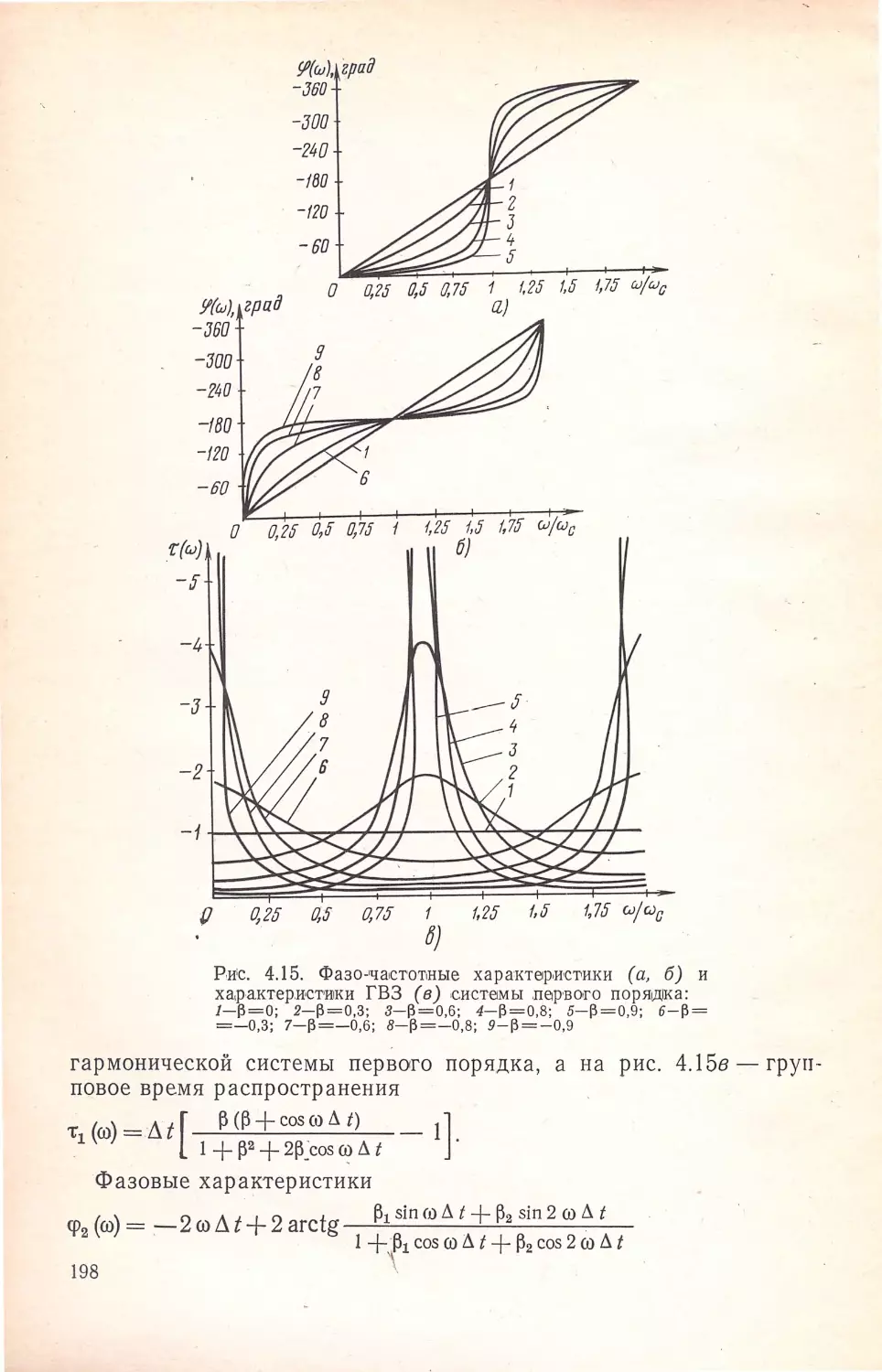
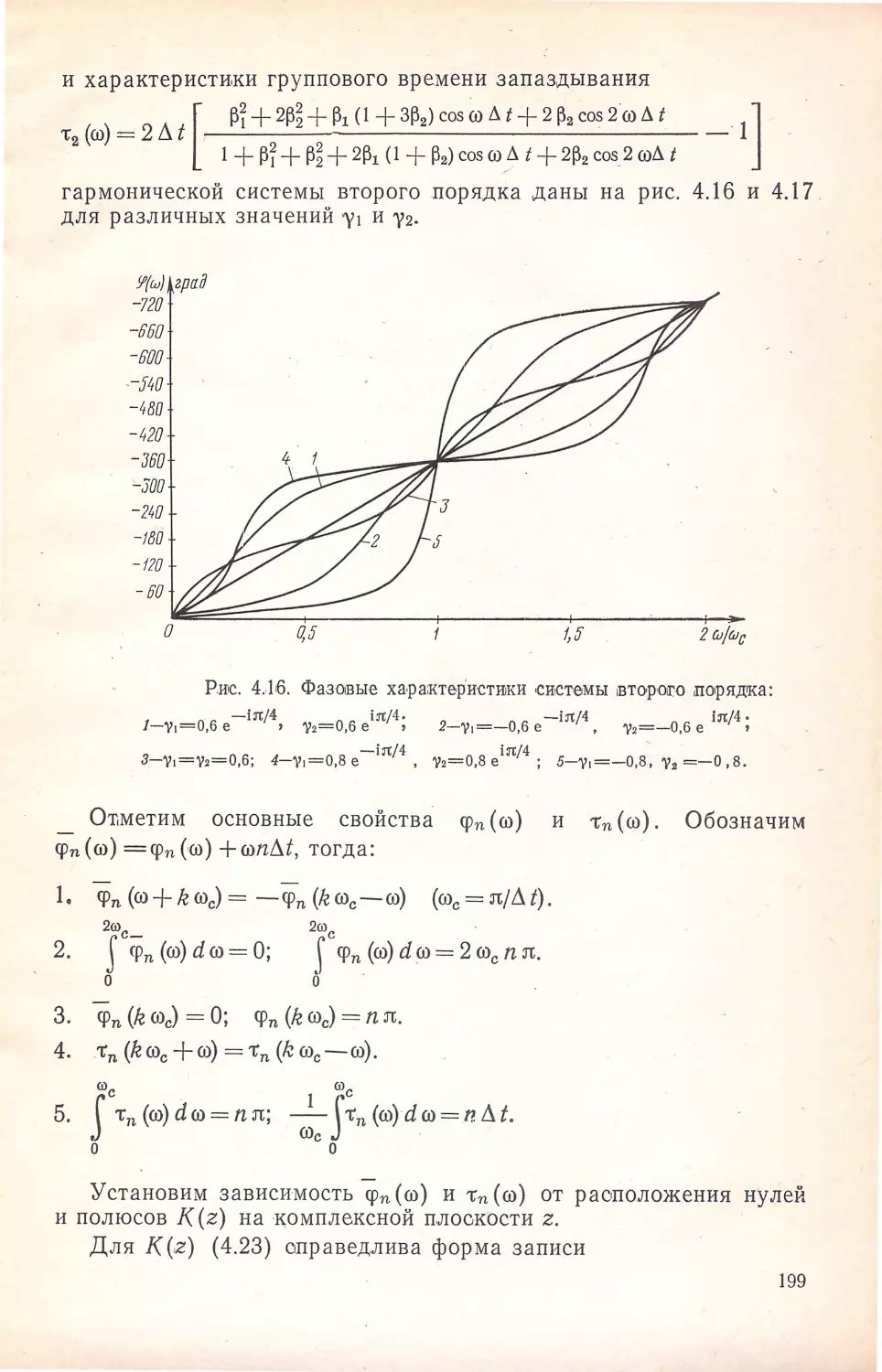
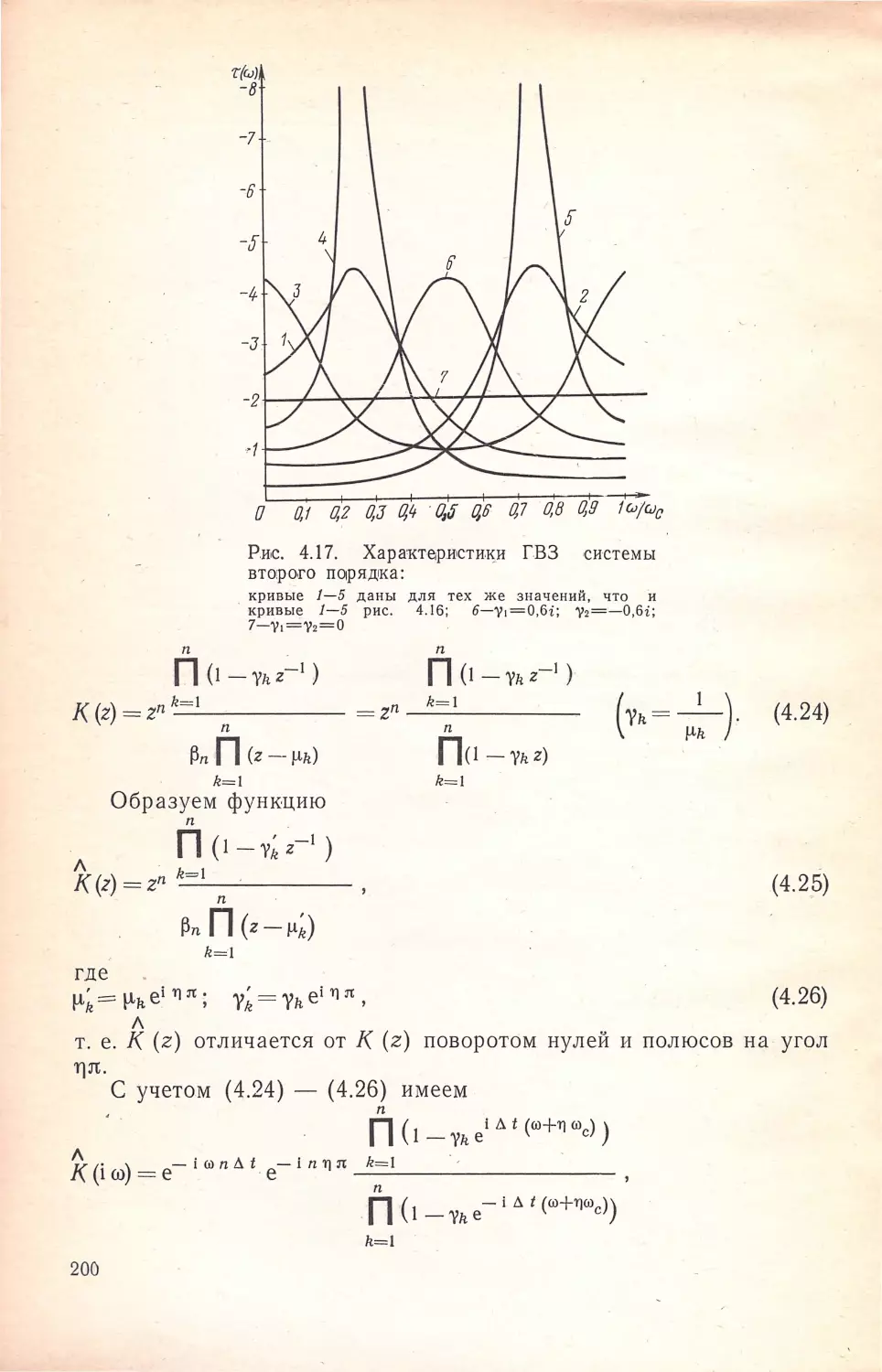
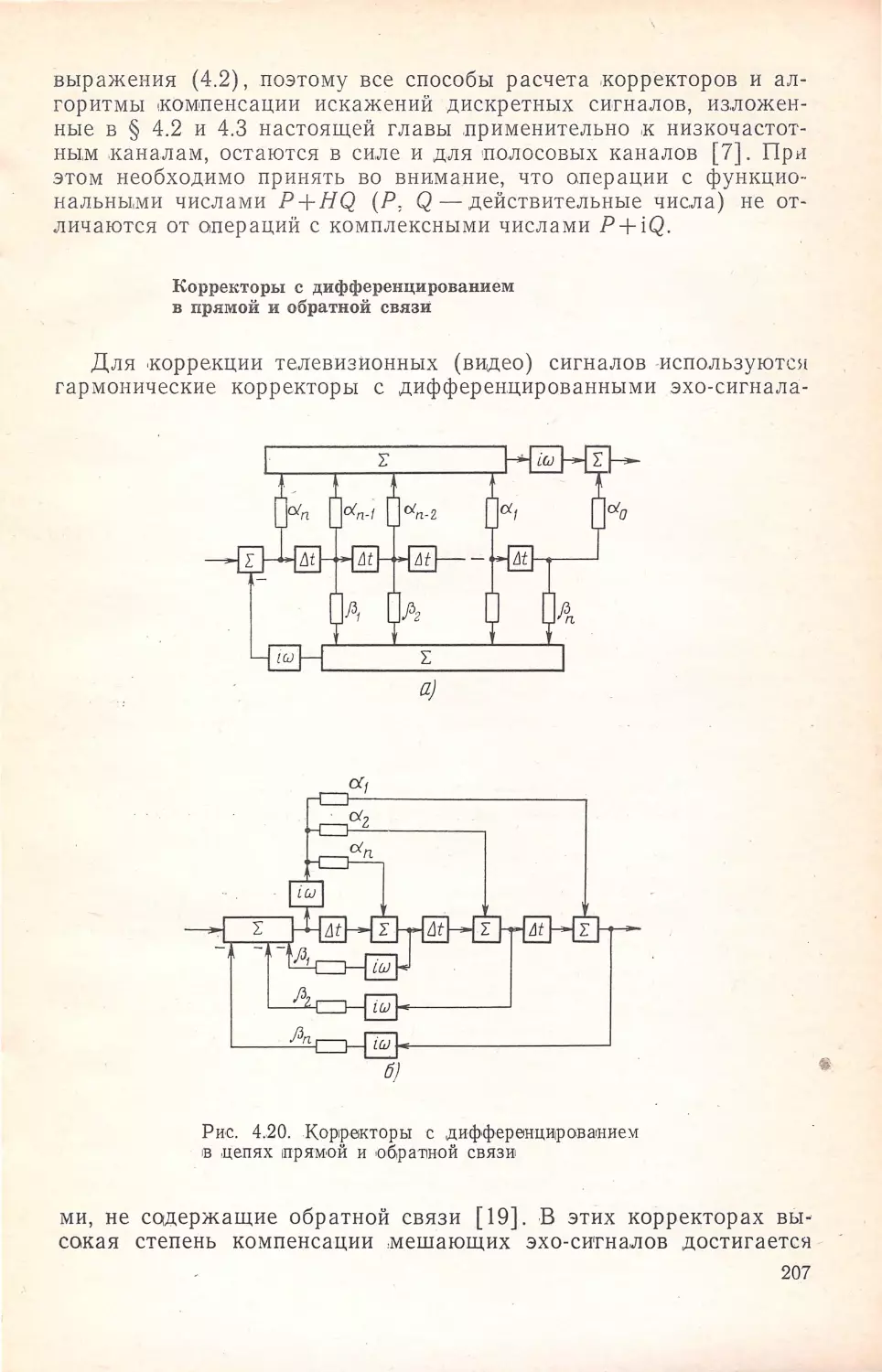
сuн,ез
rврмонuqесиuх
иорреИiоров
gnн
высоиосиорос,ных
сuстем
GBR3U
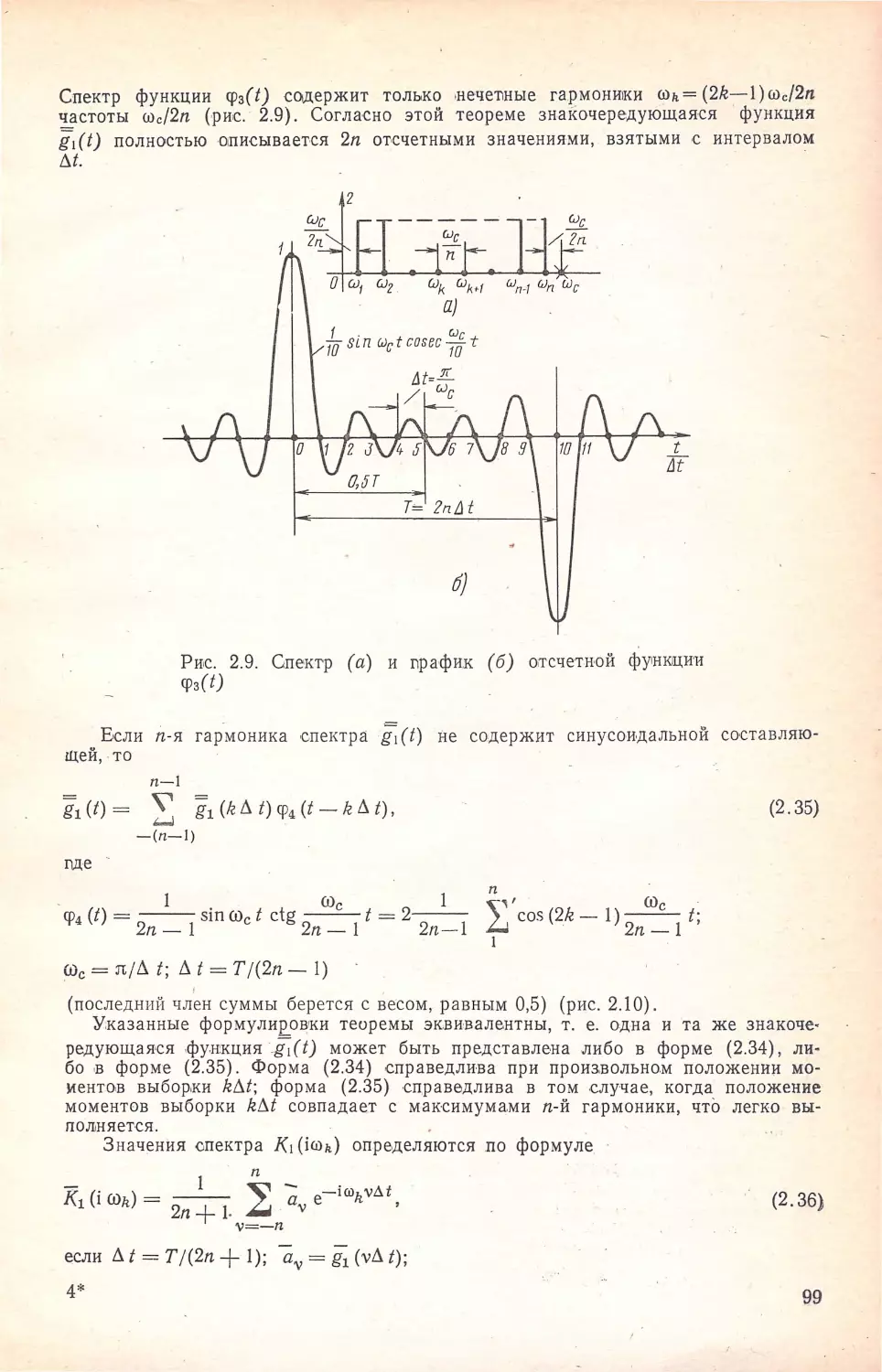
В. А. КИСЕдЬ
СИНТЕЗ
ГАРМОНИЧЕСКИХ
КОРРЕКТОРОВ _ -
·--··-·- ·· _,..,, ., -
--
. ДЛЯ
ВЫСОКОСКОРОСТНЫХ
-- .. СИСТЕМ
, связи
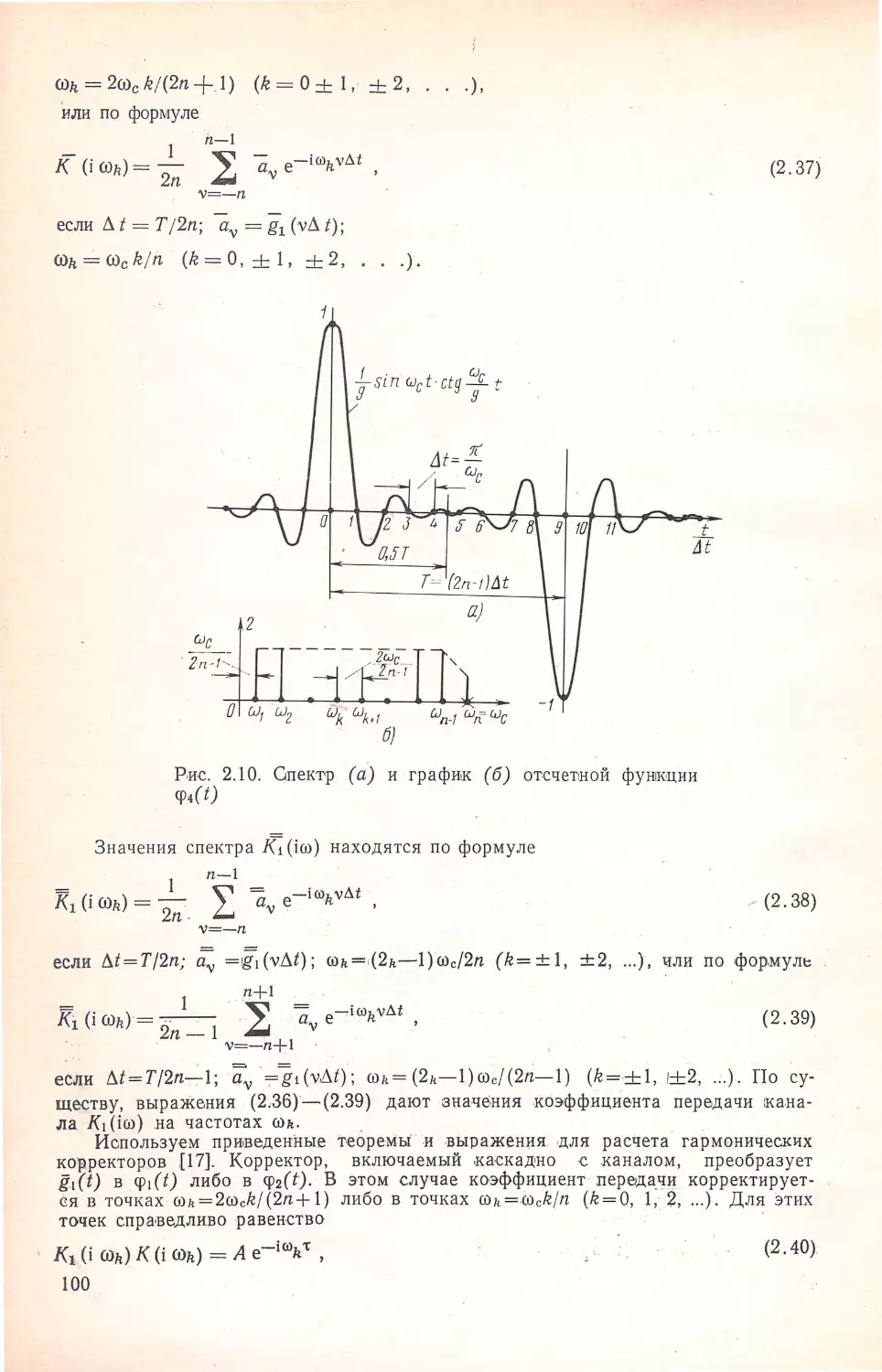
\
076129 ~=
[
. .. ~~"' а.1. ,-~
..-
......
:
,.
~
.
.
••
. ,.. _, _i:;:
".11 ~,а '!'- -
1
-
..1~&!
•
ь.
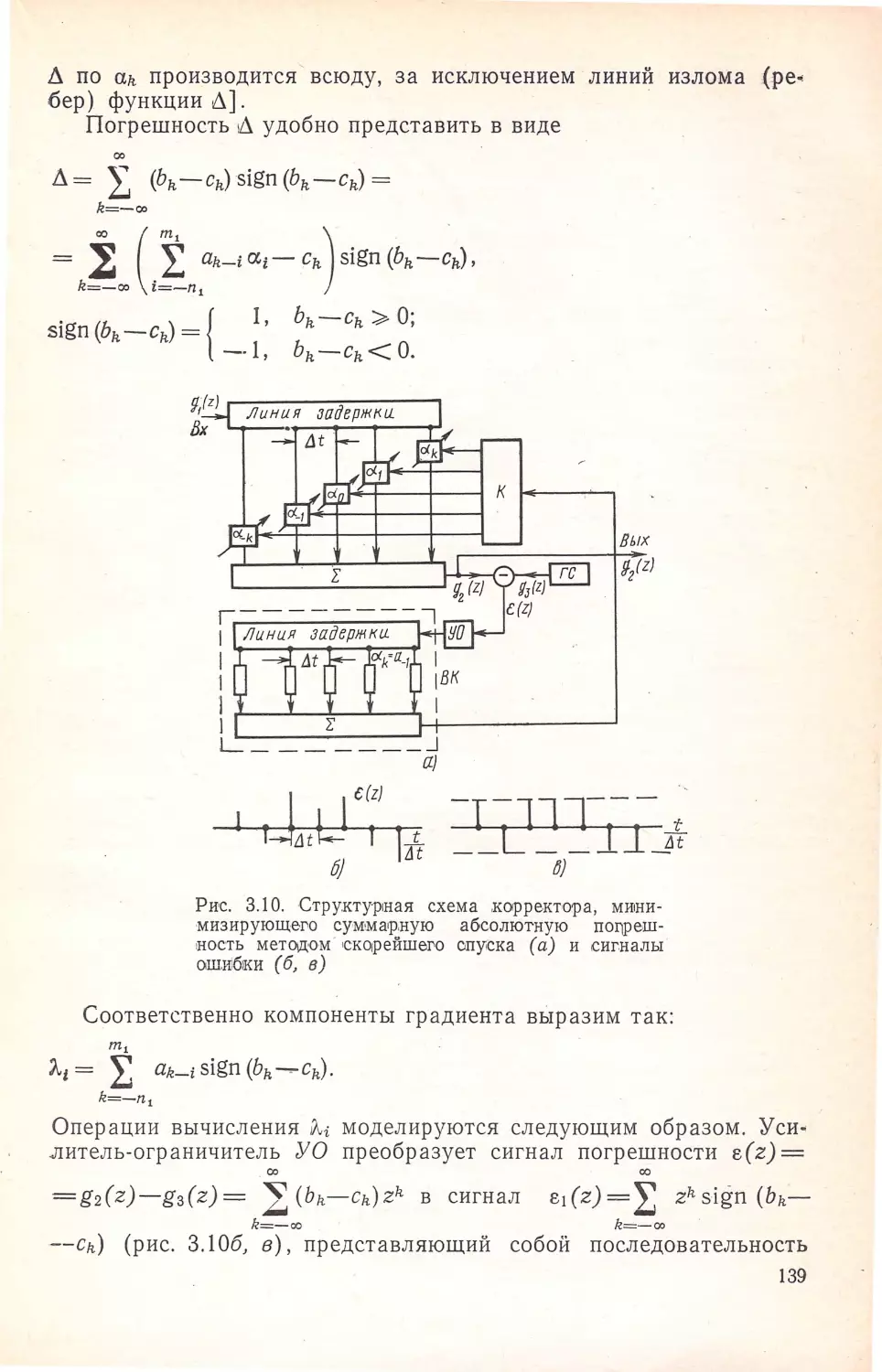
37.1
К44
УДК 621 .372.55 :681.327.8
Кисель В. А.
К44
Синт~з гармонических корректоров для высокоско-
ростных систем связи . - М.: Связь, 1979. -
252 с., ил.
1р.80к.
Рассматриваются вопросы устранения интерференционных помех в
высокоскоростных многоуровневых системах, работающих по частотно
ограниченным каналам . Излагается теория гармонических корректоров
временнЬ1х и частотных характеристик каналов . связи.
•
К н ига предназначена для научных · работников, специали з ирующихся
в об л асти высокоскоростной передачи сигналов. -
30401 - 092
ко45(О1)-79 102 - 79
3701000000
ББК 37.1
бФО.1
© Издательство «Связь», 1979 r.
..-
ПРЕДИСЛОВИЕ
Испо.ль'Зование достижений теории оптимально.го приема сиrнэ..
лов, теории помехоустойчивости и надежности, теории преобра,
зования и кодирования, новых :методов синтеза цепей и т. д. при
вело в последние годы ,к существенному росту 0ффективности сис
тем связи. Тем не менее дальнейшему увеличению скорости пере
дачи .данных в реальных частотно-ограниченных коммутируемы~ •
каналах связи с искажениями (ра_ссеянием во времени), а также
в параметрических каналах препятствует наличие интерферен
ционных (межсимво.льных) помех, ,которые не ·могут быть устра•
нены на основе существующих теорий. Это выдвигает перед раз
работчиками комплексную проблему борьбы с ,межсимвольными
помеха. ми в высокоскоростных системах связи, которая распа1дает
ся на два относительно самостоятельн.ых направления:
1. Синтез сигналов с финитным спектром для высокоскорост"
ной многоуровневой (в общем случае - многопозиционной) пере
дачи по частотно-ограниченным каналам. Эти сигналы оптималь
ны в том смысле, что их использование в ,корректированщ,rх ,ка
налах, в принципе, устраняет межсимво.льные помехи, вызывае
мые неиз-бежной интерференцией многоуровневых сигналов с рез
ко ограниченным по ширине спектром при их высокоскоростнqй
передаче (при скоростях, приближающихся к теоретическому пре-
делу - скорости Найквиста).
.
2. Синтез регулируемых корректоров, позволяющих оператив
но («вручную>> либо автоматически) скомпенсировать все виды ли~
нейных собс-~:венных и перекрестных искажений временнь1х и час
тотных характеристик (либо совокупности некоторых параметров)
,кана.лов ·многократных систем связи и произвольным характером:
селекции си.гнала на фоне шумов .
.
Первое из указанных на1_правлений рассмотрено в настоящей
монографии в гл. 1. Полученные результаты важны для построе"
ния многоуровневых высокоскоростных систем передачи дискрет
ной информации, использующих стандартные телефонные каналы .
Одна.ко в равной степени они пригодны для радиоканалов с ин
тегральными мето1дами приема, та-к 1как указьrвают общие треба"
вания, которым должны удовлетворять . ,финитные_ спектры сигна
лов на входах решающего устрой,ства .либо приведенные характе ."
рис_тики частотно 0 ограниченных каналов связи так, чтобы в мо ..
-
менты принятия решений устранялись межсимво.льные по.мехи при
неизбежной интерференции сигналов, передаваемых . с высокими
скоростя.ми.
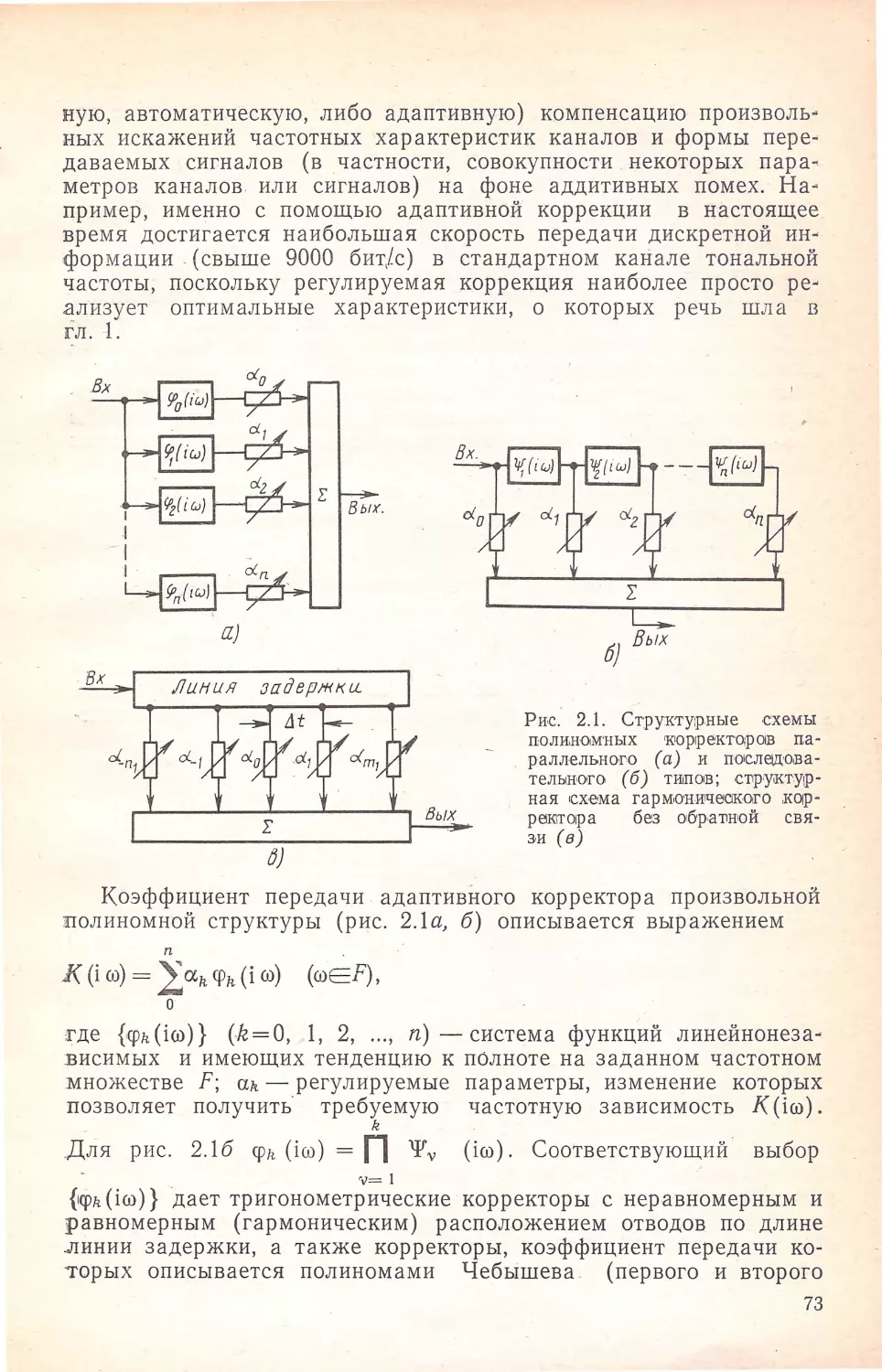
Второе направ.лени~ является комплексным и распадается на
несколько самостоятельных частей, таких, 1как общая теория по
линомных (в частности, гармонических) корректоров; алгоритмы
автоматической хоррекщии дискретных сигналов на фоне шумов;
гармонические корректоры с обратной связью; совместная мини
:мизация собственных и перекрестных иокажений •каналов много
кратных систем связи . По етой причине вопросы синтеза адаптив
ных ,корректоров освещены в гл . 2-4 .
Спецификой вопросов синтеза автоматических корректоров яв
ляется то, что, хотя эти вопросы и носят четко выраженыый «цеп
ной» хара,ктер, они, однако, не .могут быть решены на основе су
ществующих ·методов синтеза ,цепей с _сосредоточенными И:ли рас
пределенными параметрами (методов синтеза классических фазо
вых и амплитудных ·корректоров, ,корректоров БОiде и т. д.), по•
скольку указанные методы не учитывают принципиально ново["'О
требования, предъявляемого к автоматическим корректорам, -
возможности автоматической минимизации заданной целевой
функции (погрешности). Главную роль в теории таких корректо
ров играет синтез алгоритмов автоматической 1корреwции, и этому
JЗОпросу в гл. 3 и 4 уделяется основное внимание.
Актуальность и общая пра,ктическая значимость проблематики
и резу.льтатов синтеза гармонических корректоров подтверждают
ся, на1при,мер, следующими фактами. Применение автоматической
коррекции в сочетании с различными видами модуляции позво
лило осуществить в стандартном телефонном ,канале (полоса час
тот 300-3400 Гц) передачу инфор.мадии последовательными .мето
да·ми в 1964 и 1965 гг. со скоростями , с9ответственно 6800 и
9600 бит/с и после~днее время - со акоростью 'Порядка 12 ООО бит/с
[ 1-4] . В системах без корре1щии относительная скорость переда
чи многоуровневых дискретнь1х сигналов (кодовых .комбинацийJ
не превышает 0,3-0,5 Бод/Гц полосы пропускания канала, в то
время как лри использовании сигналов без межсимвольной интер
ференции совместно с коррек,цией линейных искажений · скорость
приближается ,к предельно воз.можной (скорости Найквиста1 ;1
равной 2 Бод/Гц .
Хорошо известно, что приемниками, обеспечивающими мини
мально возможную величину средней вероятности ошибки, когда
принятый сигнал искажается как случайными помехами, так и
межсимвольной интерференцией, являются не.линейные приемники,
основанные на сложном решении [5-8].
• Тем не менее линейные
оптимальные приемники, главное~
частью ,которых являются ,гар.монические корректоры, обеспечи
вают хорошее приближение ,к оптимальному решению. Кроме того,
.гармоничесжие корректоры вх~дят ка.к составная часть и в опти
'Ма.льные не.линейные приемники, например в ~приемники с ре
шающей обратной связью, в приемники максимального правдо
подобия и др. [5-8]. С другой стороны, приемники; с гармониче
скими ,корректорами (автоматическими или адаптивными) сущест:
венно проще нелинейных приемников. По указанным ~причинам
4
разработка .гармонических ,корректоров различных типов являет
ся в настоящее время qдной из центральных тем исследований спе
циалистов в области теории и техники высо·коскоростных систем
.связи [1-8].
Естественно, вопросы, рассмотренные в настоящей .книге, не
,ограничиваются только ,коррек,цией интерференционных помех в
системах передачи данных. Они в равной степени относятся и к
коррекции искажений в широкополосных системах ,связи с различ
ными видами частотного и временного уп.лотнения, к коррек,ции
линейных искажений в телевизионных системах, в видеотелефон
ных системах и др.
СПИСОК ЛИТЕРАТУРЫ
1. Lucky R. W . Automatic Equalization for Digital Communication.-«BSTJ»,
1965, v . 44, р. 54 7-588, April.
2. Rudin Н. R. А Continuously Adaptive Equalizer for General-purpose Commu-
nication Channels . -«BSТJ», 1969, v. 48, N 6, р. 1865-1884.
3. Niessen С. W., Willim D.- К. Adaptive Equalizer for Pulse Transmission .-
«IEEE , Transactions оп Сот . Techn.», 1970, v. СОМ-18, N 4, р . 377-395.
4 . Lucky R. W., Salz J., Weldom Е. F. Principles of Data Communication .-
New York ; Мс. Graw-Hill Book Со., 1968, 433 р.
5. Lucky R. W . А Survey of the Communication Theory Literature: 1963-1973. -
«IEEE Traпs . Inform. Theory», 197t3, v. 19 , N 6, р. 725-739.
6. Messerschmitt D. G. А Geometric Theory of Intersymbol Interference. Part I:
Zero -Forcing and Decision-Feedback Equalization.-«BSТJ», 1973 , v. 52, N 9,
р. 1483--1520.
7,. Messerschmitt D. G. А Geometric Theory of Intersymbol Interference. Part II :
Performance of the Maximum Likelihood Detector . -«BSТJ», 1973, v. 52, N 9,
р. 1521-1540.
8. Fa!coner D. D ., Magee Jr . . F. R. Adaptive Channel Memory Truncation for
Maximum Likelihood Sequence Estimation .-«BSTJ»,
1973, v. 52, N9, .
р . 1541-1562.
Глава 1
УСЛОВИЯ ОТСУТСТВИЯ ИНТЕРФЕРЕНЦИОННЫХ
ПОМЕХ В ВЫСОКОСКОРОСТНЫХ
МНОГОУРОВНЕВЫХ СИСТЕМАХ С ЧАСТОТНО
ОГРАНИЧЕННЫМИ КАНАЛАМИ
-+--
1.1. Задачи, решаемые в главе
В настоящее время основной объем цифровой информации пе,
редается по существующей сети стандартных каналов тональной
частоты (,СКТЧ) (телефонные каналы, среди ·которых исполь
зуются, главным образом, .каналы лроводной и радиорелейной свя •
зи с ЧМ). Эти каналы относятся, .как известно, .к помехозащищен•
ным каналам (в СКТЧ, у,довлетворяющих нормам МККТТ , уро,
вень аддитивного шума более чем на 30 дБ ниже уровня полезно •
го сигнала) . Согласно Шеннону скорость передачи дискретной ин
формации в таких .каналах может достигать 30 000~ 50 ООО -бит/с
[2}. Однако в действительности с-корости передачи на ~порядок ни
же указанных в еличин. Главным ограничи~ающим фактором по
вышения с.корости передачи в ОКТЧ -является чрез.мерно высокий
уровень интерференционных помех, который для скоростей, при •
б.лижающихся к скорости Найквиста, намного превосходит - уровень
полезного сигнала . Поэтому проб.лему синтеза высокоакоростных
систем связи, предна.значенных для работы ,по СКТЧ, принято раз
бивать на две относительно самостоятельные части : 1) получение
по возможности большой скорости передачи путем устране
ния, в первую очередь, межсимво.льной интерференции в предполо
жении, что аддитивный шум в канале пренебрежимо мал, и
2) повышение достоверности передачи за счет снижения влияния
аддитивных шумов.
.
Необходимо оговориться, что основной _ резерв повышения эф•
фективности использования пропускной способности СКТЧ дает
решение именно первой части проб.лемы. К_ак mоказали исследова•
ния отечественных и эарубежных специалистов, при поэлементном
приеме вероятность ошибки в СКТЧ без учета второй части проб •
лемы, ·т. е . без принятия специальных мер защиты от влияния -ад•
дитивных шумо~, сравнительно .мало зависит от с.корости пере
дачи и составляет величину ,порядка Рош = 10-3+10- 5 , что для ря ~
да случаев вполне приемлемо.
6
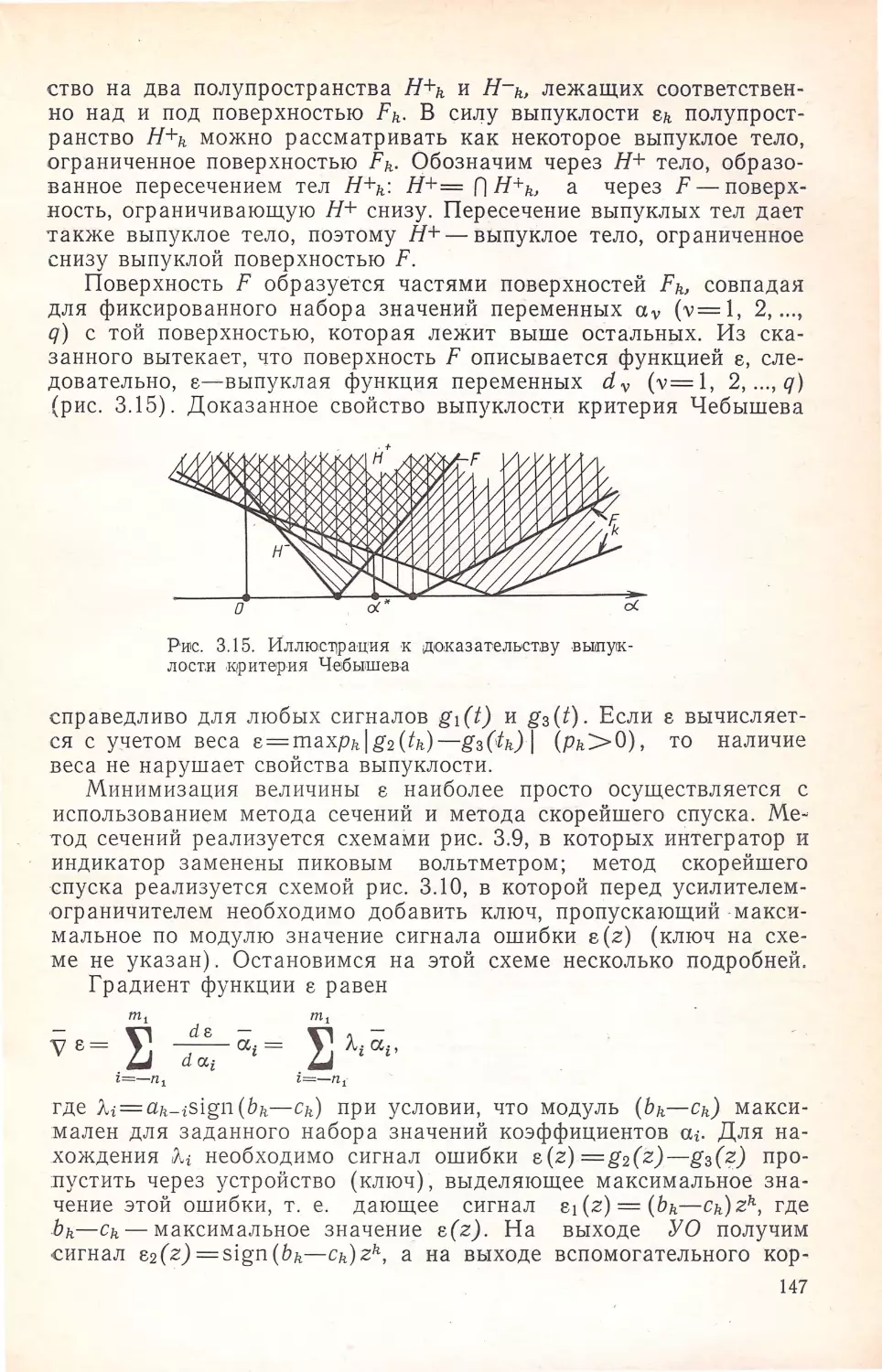
Суть _решаемых в главе вопросов свмится к следующему.
Однозначное восстановление многоуровневых импульсных сиг
налов (АФМ сигналов или кодовых комбинаций) при их переда
че через частотно-ограниченную систему (канал) возможно лишь
в случае, если реа1кция g (t) этой системы на одиночный много
уровневый сигнал (кодовый многоуровневый импульс) и (,t) об
ладает свойством отсчетности (селективности):
g(kЛt)={1,k=О;
·_
O,k= + l, +2,.,.,
(1.1)
где Лt - интервал следования им,пульсов. Выражение ( 1.1) из
вестно как ,критерий Найквиста [7, 8, 11-27, ,39 ] . Поэтому в г.ла-
ве определяются сквозные частотные характеристи,ки систем, ущов
летворяющих условию ( 1.1). Системы такого типа будем называть
отсчетными фильтрами, а соответствующие им сигналы со свойст
вом ( 1.1) - отсчетными сигналами или функциями. Условие (1. ·1)
является универсальным в том смысле, что ему д_олжны удовлет- ~ .
ворять системы с различными метмами обработки лринятоrо мно
гоуровневого сигнала, например системы, использующие метод
однократной пробы (метод укороченного ~контакта), системьr с ин- :
теrральными методами приема (метод накопления в форме интег
рального приема, взаимокорреляционный и •автокорреляционный
приемы, прием на соr.ласованный фильтр) . Во всех перечислен
цьrх системах для устранения межсимвольной интерференции при
высокоскоростной ра,боте по частотно - ограниченным ,каналам сиг- ·
нал на выходе приемника (выход приемного фильтра, выход ин
тегратора или согласованного фильтра) щолжен обладать свойс.т- .
БОМ ( 1.1).
Волрос об определении характеристик отсчетных фильтров 'иг
рает основную роль как в теоретическом, так и в пра•ктичесжом:
плане, посколь-ку позволяет оценить возможности частотно-огра
ниченных систем связи с точ,ки зрения высокоскоростной передачи
м:ноrоуровневых дискретных сигналов (независимо от вида ис
пользуемой в .канале .модуляции) . Этот же вопрос является осно
вополатающим и для высокоскоростных систем с временньrм де
лением каналов.
Исследования настоящей главы пригодны ,д.ля синтеза сигна
лов и взаимокорреляционных или автокорреляционных .функций,
обладающих свойством ( 1.1), поэтому их можно использовать для ·
построения скоростных систем передачи многоуровневых сигналов ·
с интегральной обработкой сигналов на приеме. Таким _ образом,
цсследования главы относятся не только к помехозащищенным
!{анала:м (СКТЧ), но и ,к каналам с большим уровнем шумов (ра
диоканалов), в которых исполь.зуется интегральная обработ,ка сиr
н,алов.
Под высокоскоростными в да,льнейшем подразумеваются сие-
те_мы, для ,ко_торых
fc~fm~2fc,
( 1.2)
7
где fm= 1/Лt- скорость передачи многоуровневых сигналов (ко
довых импульсов); fc - ширина 1Полосы пропуекания системы. Сле•
дует подчеркнуть, ·что применение отсчетных фильтров обеспечи
вает скорость передачи, приближающуюся -к теоретическому пре➔
делу - екорости Най,квиста, равной двум многоуровневым ,кодо
вым импульсам в секунду на l 1Гц полосы прсщускания системы,
что эквива.лентно ущельной скорости пере.дачи двоичных сигналов,
превышающей 2 ,бит/с. Например, при передаче в СКТЧ четырех
уровней е,квивалентная скорость передачи двоичных сигналов со~
ставляет свыше 9000 бит/с (с выделением одной ,боковой полосы
частот), а при передаче восьми уровней - свыше 1!2 ООО .бит/с, т. е.
удельная екорость передачи равна примерно 3-4 ,бит/с на 1 Гц.
1.2 . Передача сигналов по низкочастотным
каналам. Оптимальные отсчетные фильтры
Низкочастотные отсчетиые фильтры
Первоначально будем считать, что система связи (канал) эк
вивалентна фильтру низкой частоты (рис. 1.1). Положим, • что
~; ~t/ Pwc . 1..1 . У1п,рощенная экв!!U!а
лентная схема ~канала овязи
и (,t) = ·6 (t) - функция Дира,ка, тогда g,(t) - импу,льсная реа·кция2
""
g(t) =-
1- JK(i ro) ei ыt dro,
2:л
-оо
где K(,iro) __: комплексный коэффициент передачи отсчетного
фильтра.
В [ 13] показано, что iдЛЯ выполнения ( 1.1) в случае нулевой
(или ,линейной) фаза-частотной характеристи,ки .модуль коэффи
циента передачи низкочастотного отсчетного фильтра K(roJ
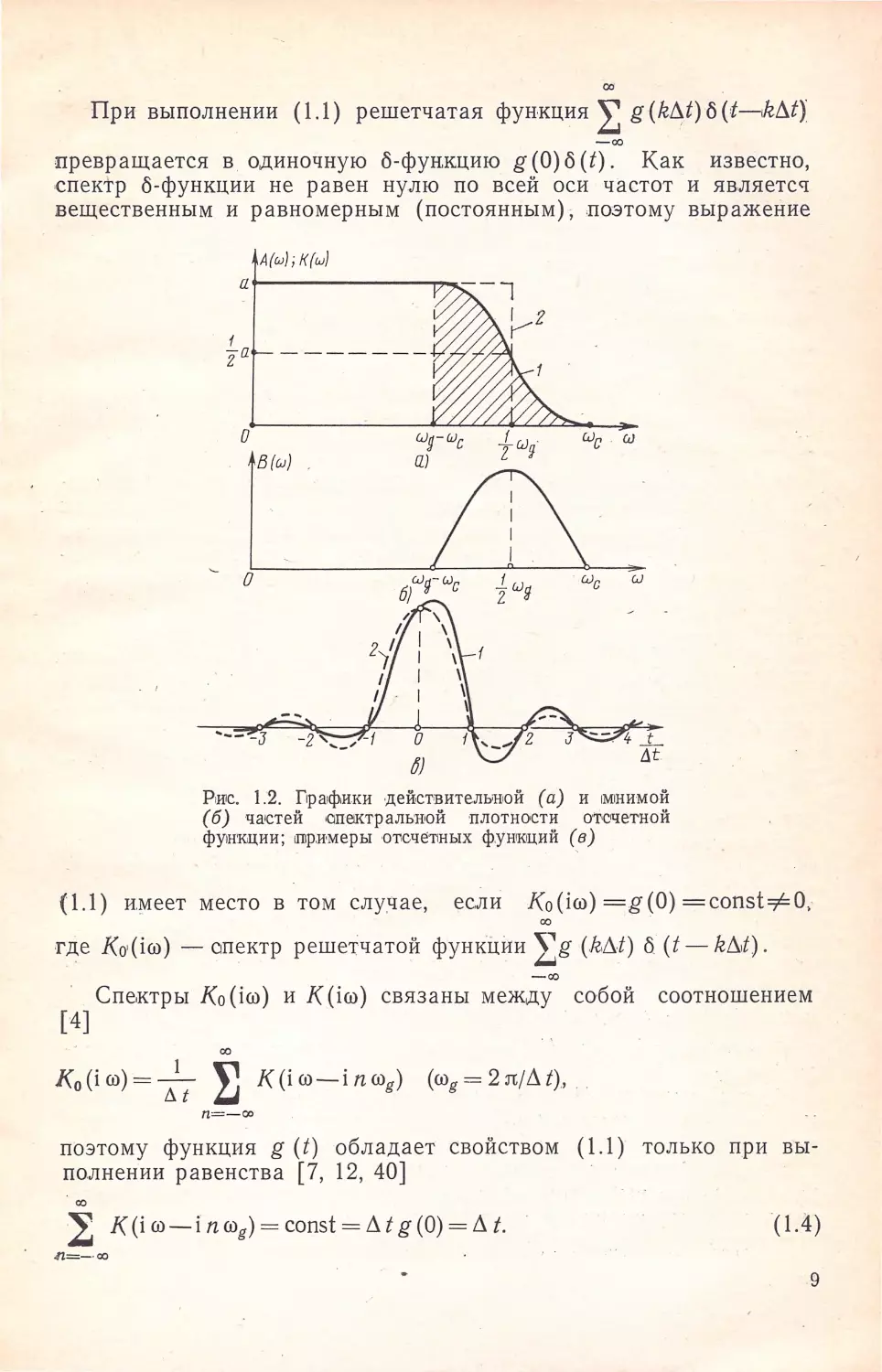
[ спектр функ;ции g (t)] должен удовлетворять условию (рис. 1. 2а ,
кривая 1):
K(ro)+K(rog-ro)=a=coпst (rog-roc < !rol < roc);)
K((J)) = О (1 ro 1 >roc);
K(ro) =а= Л t = coпst (1 ro 1< rog-(J)c),
(1.3)
где Фg=2rc/Лt -- частота стробирования (дискретизации); Фе -
граничная частота (rog/2~ (J)c). При этом g (t) - симметричная от■
носительно нуля функция (рис. 1.2в, кривая 2). Из выражения
• ( 1.3) вытекает, что в диапазоне '(J)g-•Фс--:-Фс К (ro) является не
четной функцией относительн0 точки (rog/2, а/,2) . Системы с ха~ ·
рактеристиками (11.3) принято называть фильтрами Найквиста.
Выведем общие условия отсчетности, считая, что фаза-частот•
ная хара,ктеристика фильтра является нелинейной .
•
8.
00
При выполнении (1.1) решетчатая функция L g(kЛJ)б(t-jkЛt)
-ro
превращается в . одиночную б-функцию g (О) б (t). Как известно,
спектр б-функции не равен нулю по всей оси частот и являетсq
вещественным и равномерным (постоянным), поэтому выражение
о
(,)Г(,)с
r!,).
!,)с l,J
гiа)у;J
&"'
о
1
2 (,jg
(,)с (,)
Р,ис. 1:2. Г,рафики действите.лыной (а) и 1м1 нимой
(б) ча,стей оп€1Ктральной плотности о1'очетной
фу1нкции; I111римеры от,сче11ных функций (в)
(1.1) имеет место в том случае, если Ko(iw) = g(O) =const=i=O,
"'
где 1(0,(iw) - апектр решетчатой функци:и 1) (k.Лt) б_ (t-kЛ,t) .
-ro
Спеюры Ко ( iw) и К (iw) связаны между собой соотношением
[4]
"'
/(0(iw)= -
1- ~ К(iw-iпwg) (wg= 2л/Лt),
Лt /,,J
n= -oo
поэтому функция g (t) обладает свойством (1.1) только при вы
полнении равенства [7, 12, 40]
"'
~ K(iw-inwg)= const= Лtg(O)= Лt.
( 1.4)
Л=-·оО
9
Спектральная плотность Ko(iw) получается путем сдвига (перено"
са) по шкале частот и последующего суммирования спектральной
плотности K(iw) . Нетрудно видеть, что равенство (1.4) выполняет
ся в том · случае, если комплексный ,коэффициент передачи К (iw)
обладает сво·йствами: -
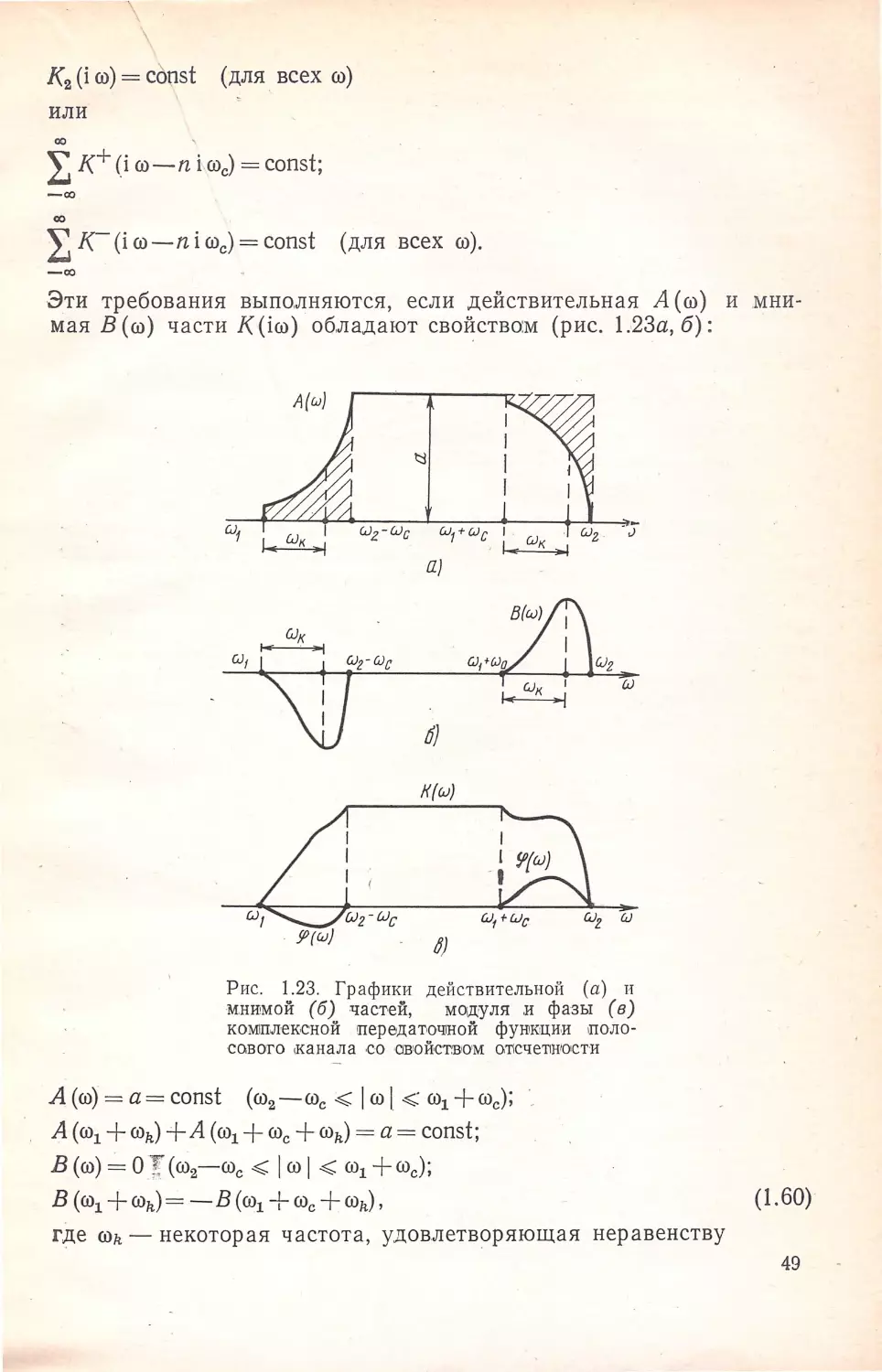
А (w) +А (wg-Ш) =а= соnst, }(
II
ffig-ffic < (J) < ffic,
В(w) =В(wg-w)
A(w)=B(w)=O
(l wl>wc),
A(w)=a=const,}(I I
)
,
(J) < ffig - ffic
B(w)= О
.
•
или
К(i w)+К*(iWg-:-i w)-= а= const (шg-:-Шс < Jw1 < wc),
K(iw)=a (JwJ<wg-wc),
(1.5)
где А (w) и В (w) - соответственно действительная и мнимая час
ти К (iw); К; (i,w} - функция, сопряженная К (iw) *). При этом
g(it) - несимметрическая функция (рис. 1.2в, кривая 2). Согласно
выражениям (1 .5) 1 в диапазоне Wg - Wc -:- Wc А (w) является нечет
ной функцией относительно точ·ки ,(wg/,2, а/2) , (рис. 1.2а, ,кривая
1), а В (w) является четной функцией относительно частоты wg/2
(рис. 1.26).
Выражения (1.3) получаются из (1.5) ,как частный случай, ес
ли В (w) = 0 , (О~ 1w 1 ~wc). •Использование низ , кочастотных систем
с характеристиками (11.3) и (1.5) позволяет пер·едавать импульсы
со скоростью fm = wg/2,л, ,которая находится в пределах
ffic f
ffic
-
< т<-,·
2n
n
(1.6)>
что совпадает с ( 1.2).
,Максимальная с,корость fт = Шс/л достигается в случае, ко гда
ffig/2 = Шс. Этот случай согласно ,( 1.5) соответствует . ш ироко из
вестному идеальному фильтру низ.ких частот (рис. 1.2а, кривая 2) 1
Коэффициент Передачи КОТОрОГО В диапазоне O - Wgf2 равен ПО -.
стоянной величине, а вне этого диапазона тождественно равен ну
лю. Импульсная реакция такого фильтра о п исывается выражени
ем
g(t)=sin0,5Шgt/0,5Шgt
и обладает с~;юйством ( 1.1 J при минимально возможном интерва
ле Лt = л/wс.
Ка!К следует из (1.5), если ffig /2 < ffic, существует бесконечное·
множество отсчетных фильтров, реакции которых g (,t) об.лада ют
свойством ( 1.1) при одн.ом и том же интервале Л.t. Поэтому Во
каждом •конкретном случае, исходя из потребностей пра,ктики,.
целесообразно выбирать из указанно го .множества те харак;герис"
тики, которые являются оп т има.льными в том или ином смысле.
*) Здесь ;1 в дальнейшем * означает комплексное сопряжение.
10
Оптимальный отсчетный фильтр для систем с натуральной
дискретизацией
При передаче импульсных сигналов через фильтр с характе
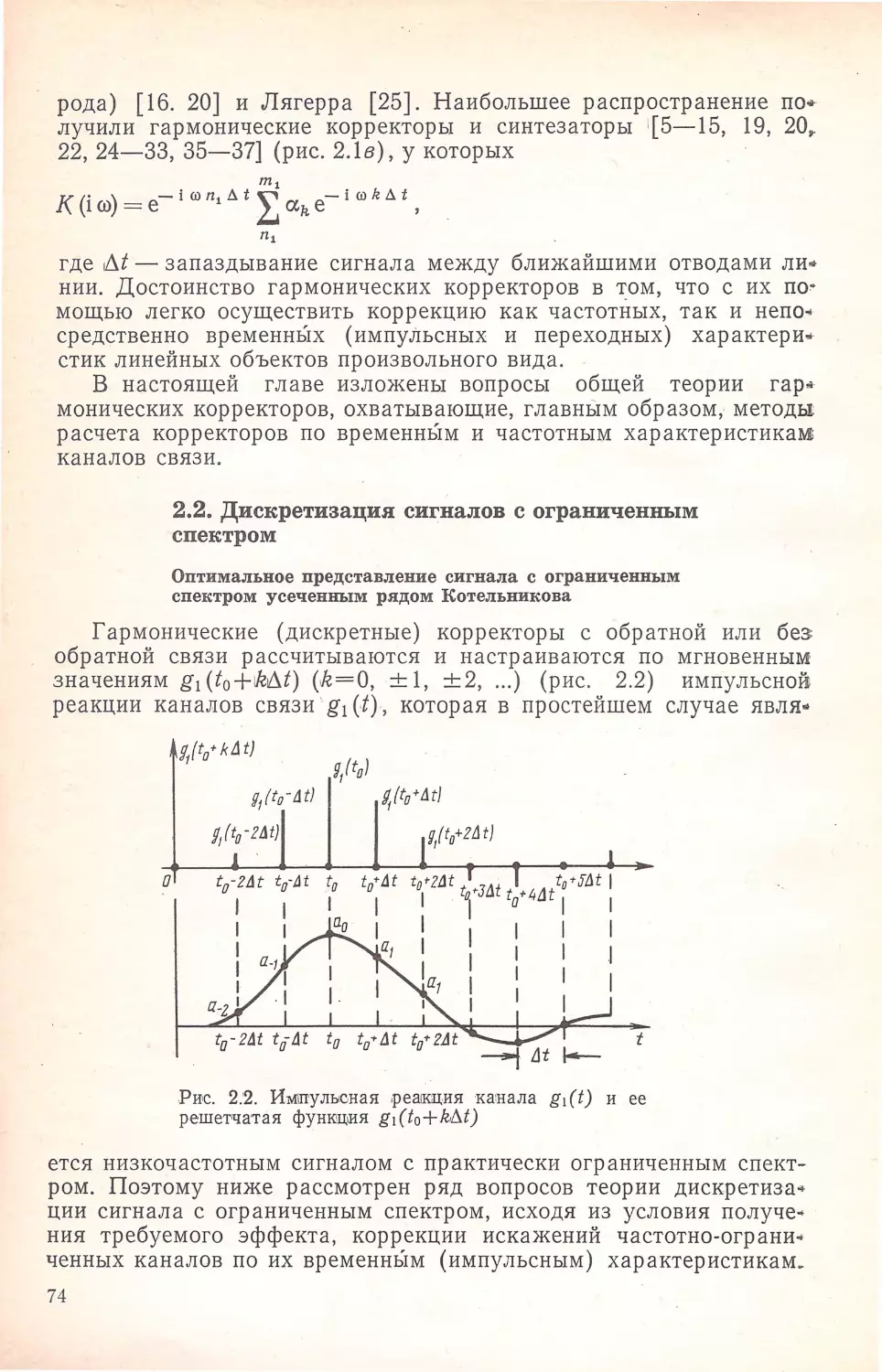
ристиками 1( 1.3) или ( 1.5) необходимо диокретизировать реа,кцию
g .(,t) строго в моменты времеJ-J:и t1<, = ,kЛt (k = O, ± 1, ±2). Такую
диакретизацию будем в дальнейшем называть идеальной. В этом
"'
случае ;цискретизирующая функция 1f (,t) имеет вид f (t) = L б (t-
-oo
- kЛt), где б U) - функция Дира·ка.
В реальных системах связи из-за неидельного фазированин
.задающих геf!ераторов передачи и приема возникает девиация
моментов дискретизации. По указанной причине дискретизация
реакции g(t) производится не в моменты времени <!1<, = kЛt, а в мо•
менты времени tk'=kЛt+т: ,(k= O, ± 1, ± ~, . : . ), где т-'случай
ная величина, изменяющаяся в пределах - Л,t/2 ~ ·т~Лt/2. При
этом дискретизирующая функция if (t) принимает вид f Щ =
00•
= ~ б (,t :_ 1k:M- т). Указанную дискретизацию будем называть
-
00
натуральной либо естественной .
Считаем, что т не зависит от k, т . е. в процессе дис-кретиза,ции
некоторой конкретной реакции g,(t) величина т не меняется, а 1-\З·
меняется при переходе от одной реализации g(t) ,к другой. Из-за
девиации · моментов дискретизации возникает «временной» дис.крет
ный шум, который воспринимается системой связи в виде последо
вательности импу,льсов с амплитудами
~(kЛt+т)=g (k Лt.+т:)-g (k Лt)={ g(т)-l, k= О;
-
.
g(kЛt+т), kc:/=O, k= ± 1, ±2, ..
Средняя мощность этой последовательности равна
Лt/2
S= Sр(т:)Е(т:)dт,
-Лt/2
где р (т:) - плотность вероятности величины т :
Л t/2
f р(т)dт = 1,
-
Лt/2
""
00
Е(т)= ~ е2 (kЛt+т) . [g(т)-1] 2 + ~ g2 (kЛt+т:).
k=-co
k=-co
k4'0
(1. 7)
( 1.8)
.
Определим коэффициент rпередачи K(iffi) отсчетного фильтра,
для ,которого средняя мощность S временного дискретного шума
nри заданной плотности вероятности р (т:) принимает минимально
:возможное значение. Такой фильтр в дальнейшем называетсн
-оптимальным, так как он максимально устойчив к девиации фазы
-
11
тактовой частоты. Использование оптимального отсчетного фильт
ра позволяет минимизировать шум, возникающий за счет неиде
а,льного фазирования дискретных систем связи.
Поставленная задача решается в частотной области [24] ,
Спектр одной реализации дискретного временного шума можно,
представить в виде
• Kш(iro)=[n~oo K(iro-nirog)ei(w- nwg)i-_a]e-iwi-
(1.9)1
(в ,правой части опущен множитель 1/Лt, не имеющий принци•
пиального значения).
На основе равенства Парсеваля с учетом ( 1.6) и (1.9) длЯ:
Е ('r:) получим
Юg/ 2
Юg/2
_
E(t)= J !Kш(iro)l 2 d@= J IK(iro)eiwi-+
о
о
+ K(iro-nirog)е1(w-wg) i-- a\2dro.
(1.10)1
Перед интегралом в этом выражении опущен множитель, пс
имеющий принципиального значения. Верхний п редел интегриро
вания rog/2 выбран на том основании, что IКш (iro j 2 - четная пе
риодическая функция с периодом rog . При записи Е (т) учтено, что
на отрезке [О, rog/2 ] все сла·гаемы е _ вида К (iro - nirog) e 1<w-пwg Jr·
равны нулю в силу (1 .5) и (1.6), если п~2, .п~ -1 1 .
Подставив выражение (1.10) в (1 ·.7) и изменив порядок интег
рирования .по независимым переменным ro и ,:, приходим ,к выра ~
жению S=S1+S2, где
•
wc
Лt/2
S1 =J dro S p(т) l ~(iro)eiwi- _al2 dт;
(1.11 )3
О
-
Л t/2
Wg/2
Л t/2
S2= Sdro ,Jр(,:)\К(iro)еIwi-+
'
-лt /2
wc
Из (1 .5) вытекает, что в диапазо н е lw l ~roc' ком плексный коэф
фициент .передачи отсчетного фильтра не зависит от частоты и
имеет единственное возможное значение, равное
K(iro)=a=const (lrol <ffiJ
(1.13};
По этой причине
wc
Л t/2
S1 =2a2 5dro J p(т)(l - cosroт)dт.
•О
-Лt/2
•
12
Таким образом, S 1 не влияет на процесс минимизации средней
мощности S «временного» шума .
Найдем условие минимума S2. Учитывая (1.5) и принимая во
внимание, что К* (i(J)g-i(J)) = К (i(J) - i(J)g), запишем S2 в следующей
форме:
•
ffig/2
S2= i J((J))d(J),
wc
где обозначено
Л t/2
J((J))= J p(-r)!K(i(J))eiro1:(1-e -irog1:)+
-Лt/2
+ а [ ei_(ro-rog),; -1] 12 d-r.
Поскольку J ( (!)) >0 (ffig/2 ~ 1(!) 1 ~(!)с'), .минимум S2 буLдет до~
стигнут в случае, если J ( (!)) принимает минимально возможное
значение для :каждой частоты (!) отрезка [ (!)/; (J)g/2]. Задача мини~
мизации ]((!)) является вариационной, и ее решение находится из
условия [3] б! ((!)) = 0, где 8/,((J)) - вариация J ((!)), вызванная бес~
конечно малой вариацией K(i(J)). ,Воспользовавшись у,казанны11
условием, после соответствующих ,преобразований, которые в си
лу их громоздкости опущены, окончательно приходим к выраже
нию
К (i (!)) = а [l +'Ф(i (J))-'Ф(i (J)g)-'Ф (i (!)- i (J)g)] ((!)~ < 1 (!) 1 < _21 wg). (1.14)
2 - 'Ф (i (J)g) -'Ф* (i (J)g)
где
Лt/2
,P(i(J))= Sp('t)e-i w-r d-r.
(1.15)
-Лt/2
Выражение ( 1.14) определяет оптимальный коэффициент пере
дачи отсчетного фильтра в диапазоне (J)c'-0,S(J)g. С целью нахож
дения оптимального 1( (i(J)) в диапазоне O,S(J)g-(J)c воспользуемся
выражением ( 1,5), которое справеtдливо во всем диашrзоне 0-шс,
включая диапазон O,Swg - (J)c, Из этого выражения вытекает
K(i ш) = а [l +'Ф(i (1))-'Ф (i Шg)-'Ф (i (1)- i Wg)] (wg/2 < lwl < Шс), (1. 16)
2- Ф(iwg)- Ф*(i(J)g)
что по форме совпадает с (1.14).
Если взять де~ ствительную часть K(iw), то получим коэффи
циент передачи фильтра Найквиста с нулевой фаз9й, у ,ко.торого
средняя мощность временного шу,ма также принимает минималь~
ное значение. Подчер,кнем, что ,полученные решения у,довлетво
ряют (1.5).
Для нахождения K(iw) согласно выражениям (1.14) и (1.JJ>)
необходимо знать функцию 'ljJ(iw), которая является комплексным
~"з
спектром плотности вероятности , временного шума р ('t). В реаль•
ных системах связи, иоrюльзуемых на практике, за·кон распределе
ния р ('t) обычно неизвестен и его необходимо измерять экспери
:ментально, что затрудняет вычисление К (iffi) . Поэтому .целесооб
разно определить .квазиоптимальный коэффициент передачи
фильтра Найквиста, ,который дает близ.кое ,к минимально воз.мож
ному .значение мощности временно.го шума при произвольных за
конах распределения р ('t).
_
В нормально функционирующих системах связи величина ,де
виаiЦии моментов выборки 't невелика по сравнению с интервалом
следования импульсов Лt (большие значения 't маловероятны) .
Для таких систем а~плитуды им.пульсов «временного» дискретно
го шума в силу малости ,; можно записать в виде в (kЛt + -i;) =
=1:g' (kЛt), ,где g' (kЛt) - значения первой производной (скорость
изменения) импульсной реакции g (,t) в ,моменты времени kЛt (k-: -
=0, ± '1, ± i2, . . . ) . Соответственно 0нергия этого шума опреще
ляется выражением
00
Е('t)= 't2~ [g'(kЛt)]2•
( 1.17)
-со
Минимум Е ('t) получится в том случае, если скорость изменения
импульсной реа,кции фильтра Найквиста в ,моменты времени k.Л,t
(k=O; ± 11; ± 12; . .. минимальная, в частности равна нулю. Фильтр
с таким свойством, по существу, является квазиоптимальным, та;{
как обеспечивает -близ,кое к минимальному значение средней мощ
ности S (1 .7) для любых р (т) при условии , что ,; - достаточно
малая величина. Исходя из с-казанного задача синтеза квазиолти- _
мального коэффициента передачи фильтра Найквиста •сводится к
определению К (iffi), минимизирующего 1энергию шума (1.17).
Воспользовавшись теоремой о ll{Вадратичном эффе,кте решетча •
той функции [4], получим
"'
ffig/2 "'
1J \g'(kЛt)l2 = ::2 J. 1J [i(ffi-nffig)A(ffi-nffig)+
k=-oo
- ffig/ 2 -оо
2
(1.18)
Поскольку выполняется неравенство ( 1.6), .правую часть выра •
жения -( 1. 18) запишем в виде
00
ffig/2
t'1 lg' (kЛt)\ 2 = ffig С J;(ffi)dffi,
l,,J
4л2•J
•
k=-oo
- ffig/2
где
J (ffi) = {ffi А (ffi)-[Л t-A (ffi)] (ffig-ffi)}2 + {ffiB {ffi)+B(ffi) (ffig-ffi) }2• •
14
Минимум этото выражения может быть найден ,путем дифферен
цирования J(@) по А(@) и В(@) и приравнивания нулю получен •
ного результата . Пр0tделав у,казанные операции, приходим к ана •
Рис. 1.3 . Каэфф111Ц11е1нты Пеjреда,чи
юва:зию,mгимального фильтра (:кри
вая 1) и филы1ров с «т:реуu:-оль
ным» и <~кас,инусиJlдалыным» сре
зами (~кривые 2 .и 3) (а); за,виси
масть энергии ,в;ременн6го шума
от частоты v:щощреrи:защии i/l;ЛЯ
.квази,опти,малыно['О фильтра (rюр.и
вая 1) и фильтров с «треуголь
ным» и «юосwнусщ.щальным» оре
зами (~кривые 2 и 3) (б)
0,2
0,1
l,J
(})
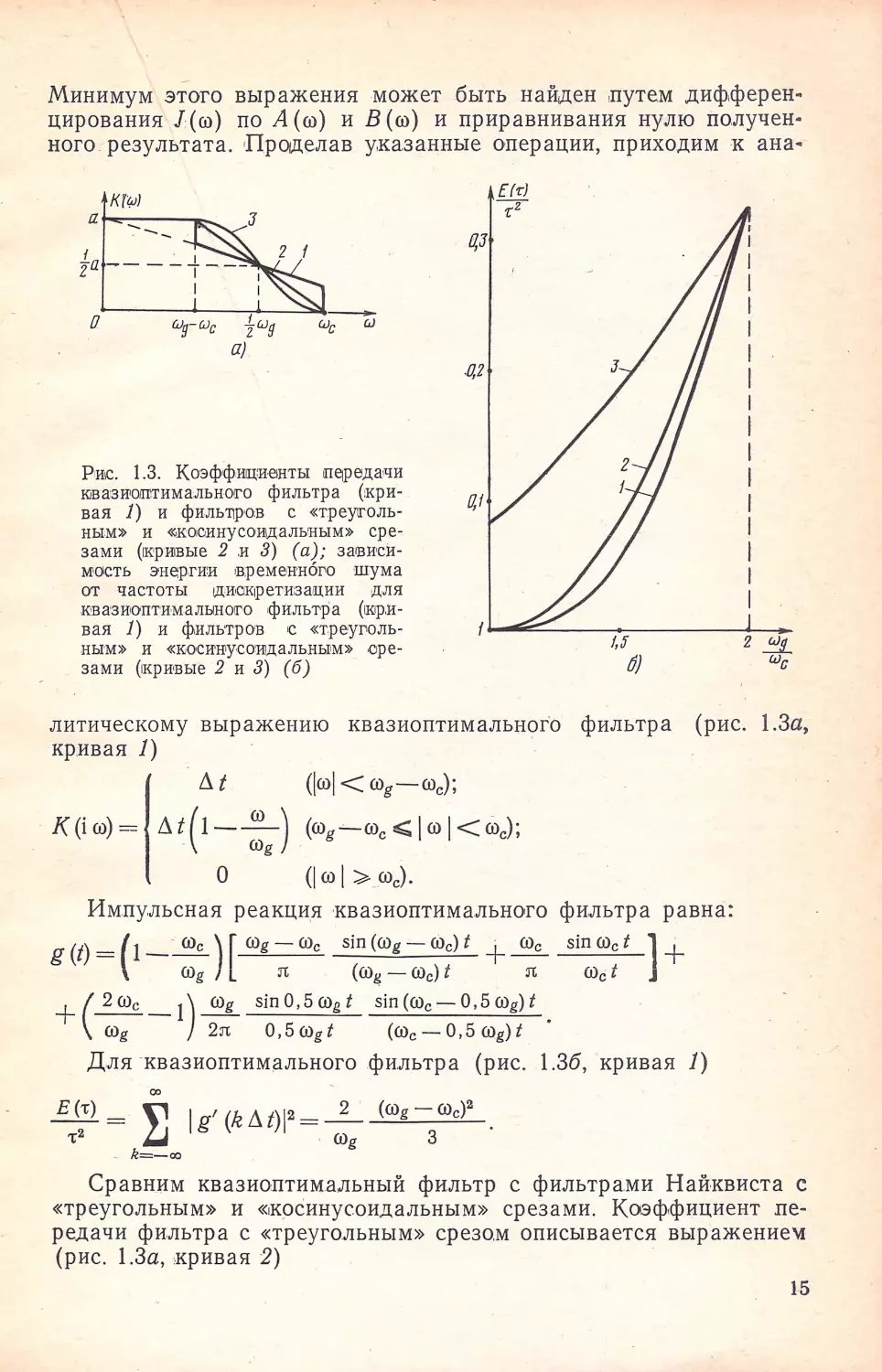
литическому выражению квазиоптимальног'о фильтра (рис. 1.За,
кр.иван 1)
1
Лt
(\@\ < ffig-@c);
K(i@)= лt(l- :J (@g"'-ffic~l@\<roc);
О
(1(J) 1>.@с),
Импульсная реакция квазиоптимального фильтра равна :
g(t)=(1-· ffic)[@g- @с sin(@g- <i:Jc)t + @с sinffict ]+
ffig
:n:
(@11 -@с) t
n
@ct
+(2u>c_ 1) @g sin0,5@gt sin(@c - 0,5@g)t
@g
2:n: O,Б@gt
(@c-0,Б@g)t
Для · квазиоптим .ального фильтра (рис. 1.36, кривая 1)
Сравщrм квазиоптимальный фильтр с фильтрами Найквиста с
«треугольным» и «,косинусоидальным» срезами. Коэффициент пе
редачи фильтра с «треугольным» срезом описывается выражение\!
(рис. 1.За, жрива я 2)
15
••
· 1Лt (O</ffi/<ffig-ffic);
К (i ffi) = Л t [ 1- (J) -(ffig - ffic) ] ((J)g-(J)c < /ffil <(!)с);
ffic - (Wg - <чс)
о (1 w 1>(!)~).
а импульсная реакция - выражением
g (t)= sin0,5(t)gf sin((t)c-0,5(t)g)t.
0,5(t)gf
(Wc-0,5(t)g)t
Для ,этого фильтра (рис. 1.36, кривая 2)
Е~. ~т)= 2
{[-21 (t)g(l-m)+m((t)g-(t)c)}з -((t)g-(t)c)3}+
•
3 (1-т) (t)g
+-2- ((t)g-(t)c)3
(t)g
3
где
т=
(t)g
(t)c- (Wg- (t)c) •
(1.19)
(1.20)
В пределе, подставив в (1.19) (t)g=2(t)c, получим идеальный ФНЧ
К(i(t))={Лt (О< 1(J)1< (t)c);
•
О (1(t) J>(t)c),
д.ля которого (рис. 1.36, .кривая 3)
Е(т) = _l _(t)2_
•т2
12g
Из рис. 1.36 следует, что .квазиоптимальный фильтр обеопечивает
определенный выигрыш в величине Е ('т) /т:2 по сравнению с иде
альным фильтром и фильтром с «треу;гольным» срезом.
В технике связи наряду с фильтром с «треугольным» срезом
используется также фильтр с «косинусоидальным» срезом
(рис. 1.За, кривая 3):
!Лt (О< Jw/< (t)g-(t)c);
K(i(t))= ~(l+cos_::_ w-(Wg-Wc)) ((t)g-(t)c</w/<(t)c); (1.21)
2
2
Лw
О (/w/ >wc),
1
где Л(t)=(t)c- - (t)g. У этого фильтра импульсная реакция
2
(t)= sin0,5(t)gf
ГcosЛ(t)t .
g
0,5-(t)gf
(2Л(t) )2
1-
--t
..
n
Допустим, что им,пульсные сигналы передаются со скоростью
fm (t)c/2n, т. е. (t)g=(t)c. Рассмотрим фильтр, ,коэффициент переда
чи которого имеет треугольную форму ( «треугольный» фильтр
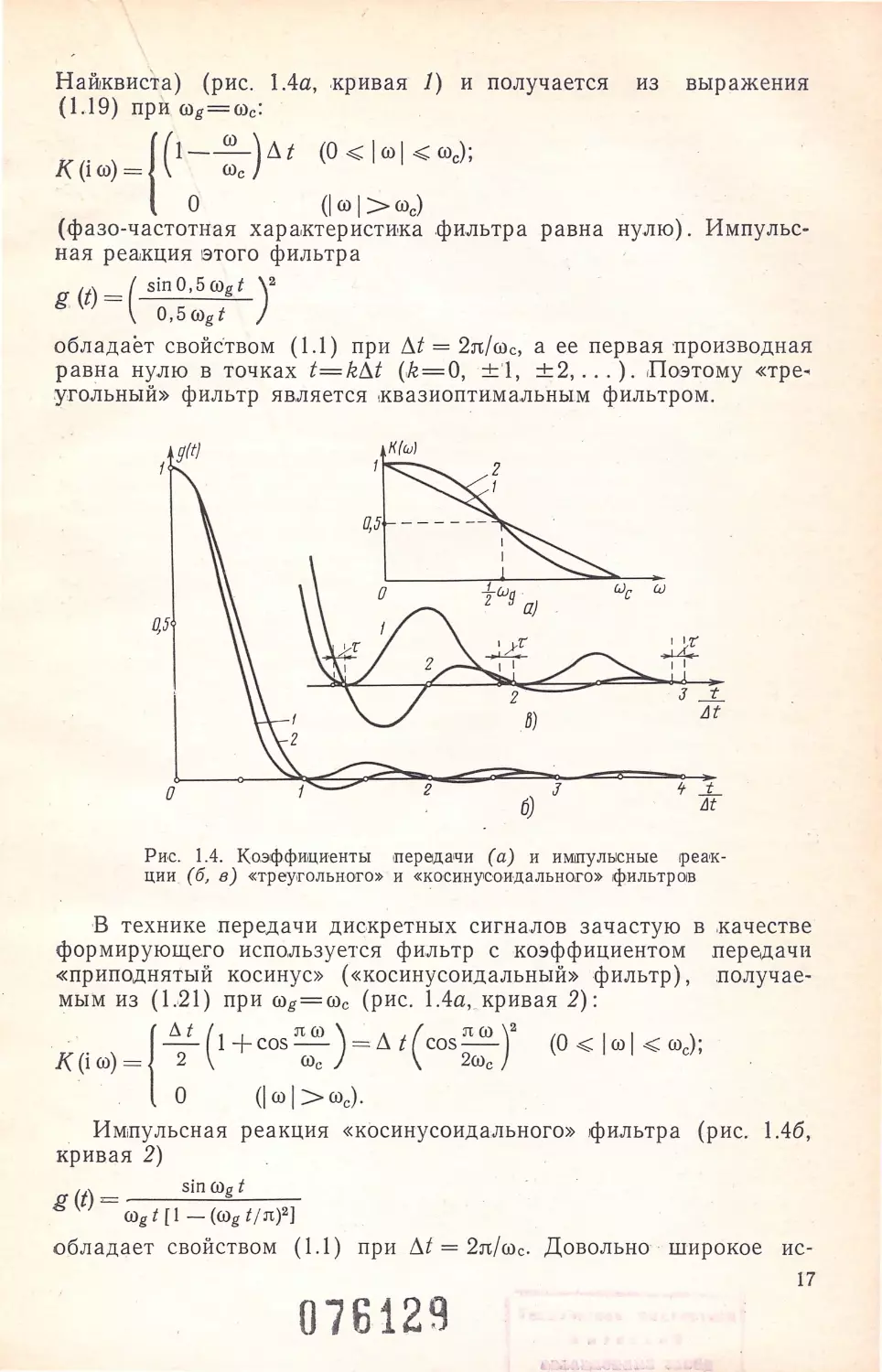
16
Найквиста) (рис . I.4a, .кривая 1) и получается из выражения
(1.19) при ffig=ffic:
.
1(1-~)Лt (О< JWj<Wc);
К(1w)=
ffic
о
(iffi l >ffic)
(фаза - частотная хара,ктеристика фильтра равна нулю) . Импульс
ная реа,кция этого фильтра
g,(t)=( sinО,5Wgt )2
0,5 Wgt
обладает свойством ( 1.1) п ри Лt = 2n/wc, а ее первая производная
равна нулю в точках f=kЛt (,k = O, ± '1, ±2, . .. ). Поэтому «тре•
.у,гольный» фильтр является ,квазиоптимальным фильтром.
g(t/
f
o,s
о
2
6)
J
/41 1
J _i_
лt
'ti._
L1t
Ри-с. 1.4 . Ко.эффи,циенты mередаrчи (а) и имmулысные ,реак
ции (6, в) «треу,гольного» и «косину,с-оидально,го» фильтрС!В
В технике передачи диекретных сигналов зачастую в ,качестве
формирующего используется фильтр с коэффициентом пере,дачн
«приподнятый косинус» ( «косинусоидальный» фильтр), получае
мым из (1..21) при ffig = Wc (рис. 1.4а, _ кривая 2):
··
1~(1+cosпw) =Лt(cosпffi)
2
(О<Jwj<wc);
К(i(i))=
2
ffic
2Wc
О
(jw j>wc).
_
Импульсная реакция «косинусоидального» фильтра (рис. 1.46,
кривая 2)
(t) _
sinWgt
g - ffigt [1-(Wg t / n)2]
обладает свойством (1 .1) при Лt = 2n/wc. Довольно широкое ис-
17
076129
..
пользование «,косинусоидального» фильтра объясняется тем, что
величина побочных выбросов импульсной реа,кции этого ' фильтра
вне интервала [ -Лt, Лt] меньше, чем у импульсных реющий дру
гих фильтров Най,квиста (например, меньше, чем у «треугольно
го» фильтра, как это видно из рис. 1.46). Однако в моменты вре ~
мени kЛt (k=0, ± 1, ±2, .. . ) первая .произвОlдная им,пульсной
реакции «косинусоид<!,ЛЬного» ,фильтра не равна нулю . Поэтому
использование косинусоидального фильтра не обспечивает .полу-·
чения минимума энергии «временного» _ шума. На рис. 1.4в д.ля
удобства сравнения импульсные реакции -«треугольного'>> и «коси
нусоидального» фильтров даны в увеличенном ,масштабе (t~~t) .
Из этого рисунка видно, что при девиации моментов выборки на
достаточно малую величину т амплитуды мешающих импульсов
«временн6:го» шума для треугольного фильтра (,кривая 1) значи.
тельно меньше, чем для «косинусоидального» фильтра (,кривая 2) ..
Таким образом, использование фильтров с ~<<,косинусоидаль~
ным» срезом с точ·ки зрения минимизации энергии .«временного»
шума является нецелесообразным, та,к .как они уступают не толь
ко квазиоптимальным фильтрам; но и фильтрам с 1«треуго.льным)>
срезом. Подчеркнем, что отсчетный фильтр, _уменьшающий энер
гию шума, вызванного девиацией ,фазы тактовой частоты, одновре
менно у,меньшает и энергию шума, вызванного девиацией величи
ны тактовой частоты.
·Максимизация отношения сигнал/шум в отсчетиом фильтре
.
Пусть в канале, э,квивалентном отсчетному фильтру, действует
аддитивная помеха (,белый шум). Отношение сигнал/шум на вы
ходе канала описывается выражением
00
00
где Q= ~.f IК(iw) J2dw = 5g2(,t) dt - энергия импульсной реак-
о
- .оо
ции отсчетного фильтра; No - спектра ,льная плотность белого шу ~
ма.
Определим отсчетный фильтр, максимизирующий величину h.
Поставленная задача _ э·квивалентна задаче [,8, 41): • ОIПределить
функщию g (t), удовлетворяющую ( 1.1), ,для которой •
g (0)/Q = шах.
(1.22)
При ограничении Q = const та ·кая функция , максимально вытянута
в ,момент · отсчета t = O. Поскольку функция g,(,t) нормирована по
мощности, искомая функция g(t), максимизирующая (1. ·2 2), бу-
18
дет функцией, принимающей при t=O .ма,ксима,льно возможное
значение из всех отсчетных функций с энергией Q.
Если нормировать функцию g(t) по значению g(O) и считать,
что g (О) = const, то в силу (1.22) искомая функция будет функ
цией с минимально воз.можной енергией. Поэтому .задача .макси
.мизации h эквивалентна задаче: минимизировать выражение
°'
, ffic
S/K(i@)/2 d@= S /A2 (@)+B2 (@}/d@=min
(1.23)
о
о
при ограничении g (О)= const и при выполнении ( 1.1). З~цесь
А(@} и В(@} - действительная и мнимая части K(i@}; @с -
граничная частота.
Поскольку В (@) не влияет на величину g (О), для получения
миниму,ма в (1.23) необходимо прежде всего положить В(@}=О
для всех @, что дает
roc
JА2 (@} d@ = min.
о
(1.24)
Так ,как g.(t) удовлетворяет ( 1.,1), в силу (l .4) должно вы
полняться равенство .
о,
(1.25)
n= -CO
Правая часть этого равенства является 1периодичеокой функцие1i'
с периодам Wg, поэтому разобьем ось частот на отрезки •
1
l
-(l-l}@g <@ < -@g (l= 1, 2, 3, ...).
(1 .26)
2
2
Допустим, что скорость передачи сигналов ,кратна скорости:
Найквиста @c=m@g, где т - целое число (скорость Найквиста
равна n/@c} .
Графики отдельных слагаемых правой ча~ти равенства (1.25)
при m=2 изображены на рис . 1.5.
и)
Рис. 1.5 . Наложе>1ие спектров при дискретизации функций
19
Выражение (1.24) с учетом (1.26) для рассматриваемого слу~
чая за:пишется в виде
(j)g/2 2m
f l:Af(ro)dro = min,
(1.27)
О 1=1
г,де А1 =АС 2 1 rog+ro) (l - нечетное); А1 = А (+@g-@) (l - чет•
ное); o:::;;;ro:::;;; +ffig.
Для получения минимума в ( 1.27) необходимо, чтобы лодын ~
тегральное выражение принимало минимальное значение на каж
дой частоте диапазона 0:::;;;ro:::;;;rog/2, поэтому выражение (1.27) эк
вивалентно выражению
2m
•
_!Ai (ro) = min.
1=1
Равенство (,1.25) с учетом ( 1.26) преобразуем в равенство
2m
~А1(ro) =Лt.
l=l
Та,ким образом , задача свелась к определению условного э,кст
ремума фун,кции .многих переменных с учетом линейных ограниче
ний . Решение ·будем искать, используя метод множителей Лагран ~
жа.
Введем неопр_еделенный -множитель л и рассмотрим функцию
2т+ 1 mеременных [3]
F(A1, А2,••• , А2т,л)=~/i(rо)_:.____л[~1 А1 (rо)-Лt]-
Эта функция принимает минимальное значение, если выполняется
система 2т+:1 уравнений
dF
dF
_
dF '=dF_:О
dA1 (@)
dA2(@)
dА 2т(@)
d'J,,,
с неизвестными А 1(ro), А2 (ro), ... , 'А. После вычислений получи_!:!.
Лt
А1(ro)=А2(ro)= ...= А2т(ro)= -
.
(1.28)
.
2m
Проведя подобное доказательство для скорости, не ,кратной ско •
рости Найквиста, запишем общие условия, которым должен удоD - .
летворять спектр А (ro), максимизирующий отношение сигнал/шум
[23]:
-
•
1) ffic=m@g+б (m=l,2,3, . . . ; 0-,,;;:б ' <+@g}
А(@)= лt j(\ro\~б);
2т+1 \(nrog-б<\@\<nrog+б); (n=1,2, ... ,т),
20
Лt
•
A(ro)=-(nrog-rog+б < \ro\ < nrog-8); (n= 1, 2, ... , т);
2m
.
А(ro) = О
(\ ffi \ > ffic),
Если б=Ф, то
Лt
А(ro) = -
(1ro1<ffic); (m= 1,2, ...);
2m
А(ro) =О (1ffi\> ffic),
0,J
m=f o=0 ,2JuJg
о
0,JuJg
а)
P,!fc. 1 .- 6 . Коэффициенты переда"Ш отсчет,ных •
фильтрQв,
•мак-С'имизи.рующих -отношение сиг
·нал/шу,м для :различшых 1ок,с~р·о.стей передачи
.
что совпадает с ,(1 .28). Примеры приведены на рис. 1.ба.
2) ffic=mrog+0,5rog+8 (m=0, 1, 2, ... ; О< 8 < 0,5mg);
А(ro) =Лt/(2m+1) (1ro1<0,5ffig- 8);
(пrog-0,5ffig+ 8< 1ro 1< пffig+ 0,5rog-8);
(п=1,2, ..., m);
А(ro) = Лt/(2m+ 2) (пrog + 0,5 rog-8< 1ro \< nrog + 0,5rog+б);
(п=О,1,2, ..., m);
A(ro)=0
(Jro J >roc)-
21
Если б=О, то
А(ffi)= Лt/(2m+1) (1(J) 1< ffig); •
(т=О, 1,2, ...);
А(ffi)=О (1(J)1>ffic).
Примеры .приведены на рис. ,1.66.
1· g(tf
-2
2
1/
.._/
Рис. '1 .7. ИМiпулыаная реакция - и,деального фильтра
(,кри1Вая J) .и филь11ра, ма,К'сим-изи,рующего отн•ошен.ие
сигнал/шум (юр-ивая 2)
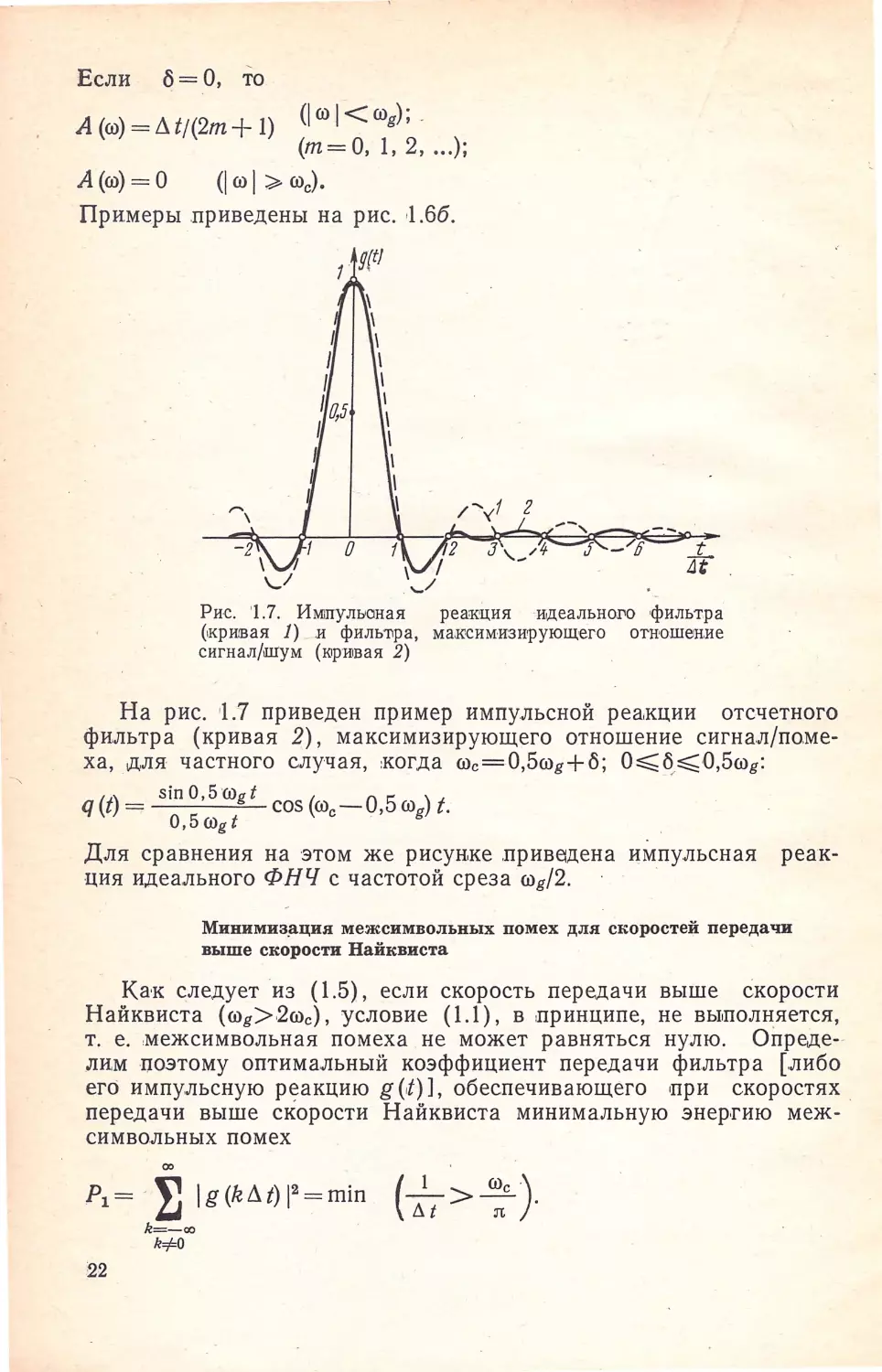
На рис. '1.7 приведен пример импульсной реа,кции отсчетного
фильтра (кривая 2), максимизирующего отношение сигнал/по.ме
ха, для частного случая, ,когда ffic=0,5ffig+б; O:::;;;б,:::;;;0 ,5ffig:
q(t)= sinO,Sffigf cos(ffic-0,5ffig)t.
0,5 ffig t
Для сравнения на этом же рисунке прив€jдена импульсная реак
ция идеального ФНЧ с частотой среза ffig/2.
Мииимиз_ация межсимволъиых помех для скоростей передачи
выше скорости Найквиста
Ка·к следует из ( 1.5), если скорость передачи выше скорости
Найквиста (ffig >2ffic), условие ( 1.1), в принципе, не выполняется,
т. е. межсимвольная помеха не может равняться нулю. Опреде
лим поэтому оптимальный коэффициент передачи фильтра [либо
его импульсную реакцию g (,t)], обеспечивающего при скоростях
передачи выше скорости Найквиста минимальную энер,гию меж
символьных помех
СХ>
Р1= Е lg(kЛt)l2 =min
22
k=-oo
kcf=O
( _1 >~)-
Лt
:п
Поставленную задачу сформулируем в таком виде : найти g (i).
дл_я ,которой ·
со
Р=Р1+А2= ~ l'g(kЛt) l2=min (_! >~)
лt
:n:
•
k=-a>
при ограничениях g(0) =A=const,
/( (i oo)-IJ g (l)e-• ы, dil = О (oo>ooJ,
где К (iffi) - ,комплексн ый ,коэффи циент передачи фильтра; ffic -
граничная частота.
.
С учетом .последнего ограничения имеем:
u>c
р-= ---'- --
2 :n:Лt
sIК(iffi) 12 dffi;
(1.29)
u>c
·,
g(О)=2
1:n: SК (i ffi) d ffi =А= const.
(1.30)
-(i)
.
с
Таким образом, необхсщимо минимизировать ,квадратичный
функционал (1.29) при ограничении (1. ,30) в виде линейного функ•
ционала. Иопользуем для етой цели методику отыскания экстре◄
мума функционала, изложенную в [25] .
-
Представим ( 1.29) в виде скалярного произведения
I(К)=(ВК,К),
где К=К(iffi).Аналогично для (1.30) J(K)=(K, G). Необходи
мое условие экстремума при наличии ограничений
v1+лvJ=о,
(1 .31)
где '\1/ ....:_: (В+В')К; Vl=G-соответственно векторы .градиента
квадратичного и _линейного функционалов; 'А - множитель Лаг•
ранжа; В, В', G - операторы.
Длярешаемойзадачи/(К)= (К,К);J(К)= (К,1),т.е.8=
=В' = 1; G = 1. Поэтому условие экстремума ( 1.3,1) принимает
вид 2K(iffi) + :л=О, 011ку1да К,(iffi) =-л/2. Множитель найдем из
условия (11.3 0):
_ I s(i)c(- ~ )dffi=A
2:n:
2
-
-u>c
или 'A=-2:rtA/ffic. С учетом этого выражения окончательно полу-.
чим
l~:n: А
•-=const
K(iffi) = ~с
-
--- --- ---
2
1
f
2
3
3
2
Полученное выражение показы
вает, что идеальный ФНЧ является
оптимальным фильтром, обеспечи
вающим минимальную
энергию
межсимвольных помех при произ
вольных скоростях передачи выше
скорости Найквиста.
Рис. 1.8. Зависимость энергии межсим
воль н ых помех от скорости передачи для
идеального, ,«косинусоидального» и «тре
угольного» фильтров (кривые 1, 2, 3)
На рис. 1.8 изображены графики зависимости энергии меж
-символьных помех от скорости передачи для идеального фильтра
НЧ (кривая 1), «треугольного» фильтра (кривая 2) и ,косинусои
дального фильтра («приподнятый ,косинус», ,кривая 3) . Указанные
кривые описываются соответственно выражениями:
Р1/А2=(0,5 rog/ffic)-1;
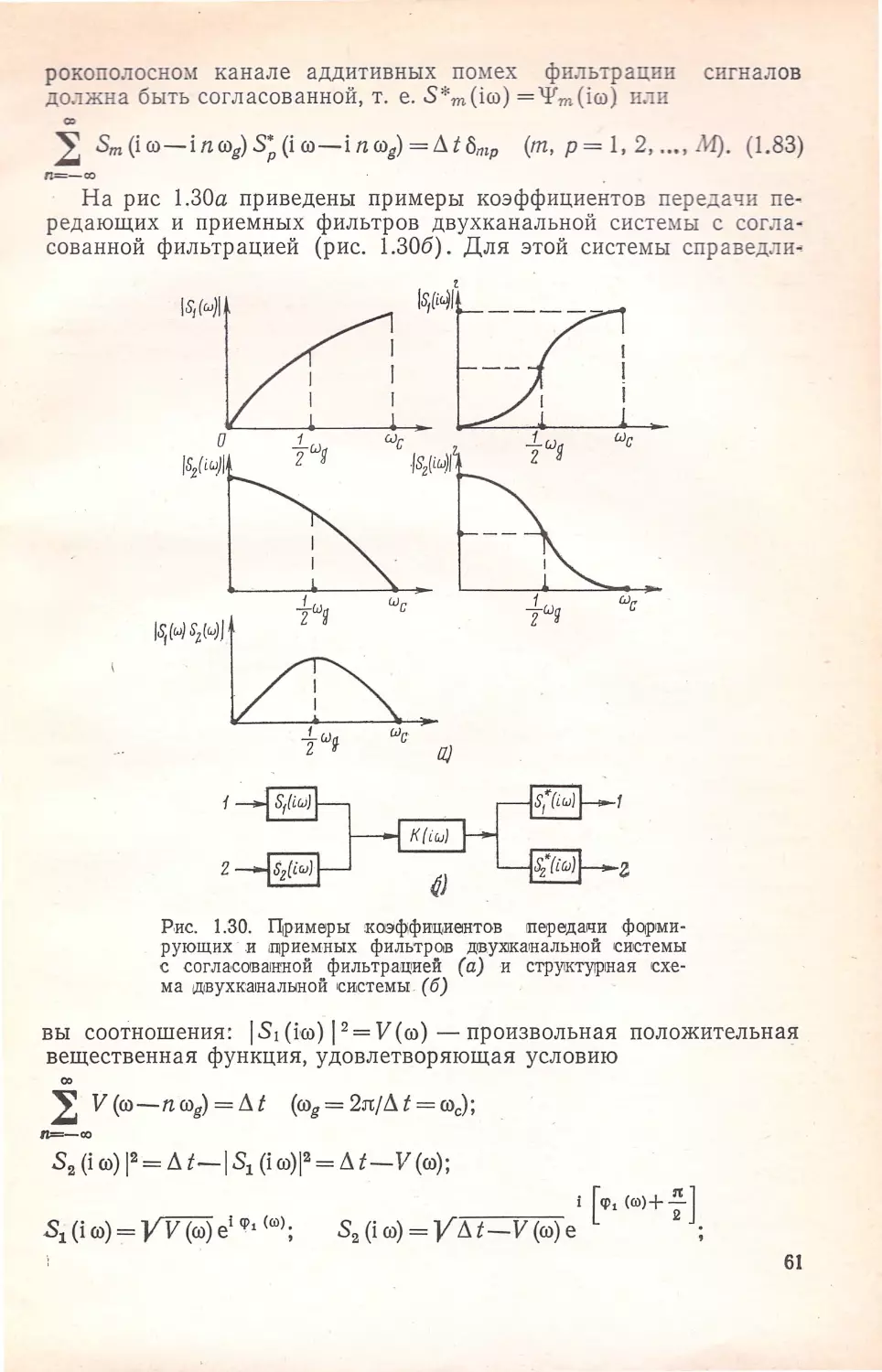
pi=~ffig-1·
___!j_=~ffig-1 (ffig>2),
No4~
'
No3~1
~
-
из которых следует, что найденный оптимальный фильтр обеспе
чивает существенный выигрыш по сравнению с фильтрами иных
типов. Обращает на себя внимание, что энергия межсимвольных
помех линейно зависит от скорости передачи.
В существующей литературе [ 19) для скоростей выше скорости
Найквиста рекомендуется использовать сигналы с пологим срезом
:Спектра, аргу,ментируя это тем, что скорость затухания бо,ковых
лепестков у таких сигналов выше, чем у сИ1гналов, спектр ,которых
имеет прямоугольный срез. Полученные в настоящем параграфе
_резу,льтаты
.показывают, что для уменьшения межсимвольных до
мех необходимо использовать именно сигналы с прямоугольным
-спектрам. Объясняется это тем, что для высоких скоростей пере
дачи основную роль в накоплении ,межсимвольных помех играет
главный .лепесток сигнала, а он наи-более узок у сигнала с пря
моугольным срезом.
1.3. Передача дискретных сигналов через
полосовые системы .
Отсчетиость •огибающей реакции полосовой системы
Определим требования к частотным хара,ктеристикам полосо
вых систем, реакции которых обладают свойством ( 1.1).
В [ 17) показано, что если сдвинуть характеристики низкочас
тотной системы с коэффициентам ( 1.3) в область высоких частот
на частоту roo (rоа - несущая частота) (рис . 1.9а), то огибающая
24
реакции п9лученной полосовой системы будет обладать свойством
(1.1). На основе результатов § 1.2 нетрудно видеть, что, проделав
аналогичный сдвиг характеристик низ.кочастотной системы с ко
эффициентом передачи ( 1.5), получим полосовую систему
о
о
(,)1 {,Jo-1(,J!I
i,Ja
{,)а- !{,J!J {,Jz (,)
а)
Р,ис. 1.9 . Частот,ные ха1рактеристи,ки по:л,осовых
каналов, огwбающие им'IТуль,оныос реакций кото
рьrх dбладают свойством 011очетности
(рис . 1.96), огибающая реакции которой та,кже будет обладать ,
свойством ( 1.1).
При использовании рассмотренных полосовых систем ( см.
рис . 1.9а, 6) скорость пере.дачи сигналов fт= rog/2n находится в
пределах
Лro/4n < fm < Лro/2n,
(1 .32)
где Лro = ro2-ro1 - ширина полосы пропускания системы. Макси ◄-
мальная скорость fm = Лro/,2n достигается в случае, когда rog=
=Лrо/2. Этот случай, как следует из рис. 1.9, соответствует ши•
роко известному . идеа,льному ,полосовому ,фильтру, коэффициент
передачи которого в диапазонах ffi1 - ro2 и -
·r o2---; ---\(J}) равен посто
янной величине, а вне этих диапазонов тождественно равен нулю .
Импульсная реакция такого фильтра описывается выражением
.
ffi2 - (J)f
SlП---"--=- t
g(t)=А~--
2--1 cos f roi:+(!)2 t
ffi2 - (J)i
•
•
2
2
t
Огибающая этой реа,кции
.
ffi2 - ffi:(
S!П
2
t
ffi2-;- (J)i t
(А = const) .
обладает свойством (1.1) при Лt=2n/(ffi2-ffi1) .
25
Из сопоставления выражений (1. ,6) и (1 .32) вытекает, что д.лн
полосовых систем, огибающая реа;к.ций ,которых об.ла~дает свойст
вом (1.1), относительная скорость передачи импульсов (т . е. ско
рость переtдачи на единицу ширины полосы пропускания) в 2 ра
за . меньше по сравнению с низкочастотными система , ми, реакции
которых обладают свойством ( 1.11). Таким образом, использование
указанных полосовых систем не ~позволяет получить высокую от
носительную скор _ость передачи, равную скорости .передачи в низ
кочастотных системах .
Оптимальный выбор несущей частоты
Выясним, возможно ,ли увеличение скорости передачи импульс
нь1х сигналов в полосовой системе ' за счет рациона,льного выбора
несущей частоты wo.
Импульсная реа,кция полосовой системы (см. рис. 1.9) может
бьпь представлена в виде
f(t)=g(t)cosw0t,
(1.33)
где огибающая g.(t) удовлетворяет (1.1) с интервалом
= -2n/wg. Для повышения окорости передачи необходимо,
реакция ,f ,(1t) обладала свойством (11.1) с интервалом Лt',
шим Лt. Это возможно лишь в случаях, ког~да
2п:-:- 1
w0= Wg
2
(n=1,2, ...)
-
26
/Jt
/
/
/
/
/
кr1.и)
\
\
\
\
\
{,)
t
м
Ри-с. l .I10. Пр и мер, иллюс11рИ:рующий - у,вели,че1н,и•е
числа эюв'И~И!стаIнтных ,нулей 'ИМ1!11улыаной реак
ции системы за ,ачет рационально,го 1выбор·а несу,
щей час-rоты
л,t =
чтобы
,мень-
(1.34)
или
2@о
(j)g _:_
---''---
2п- 1
(п= 1; 2, ... ).,
1В этих случаях
f (kЛt')={ 1, k=O;
О, k=±l,±2, ... , .
где Лt' =Лt/2=тc/rog. •Системы, в .которых несущая выбрана со
r,ласно ( 1.34), позволяют передавать импульсные сигналы со ско
ростью в 2 раза <больше, нежели системы, у которых только оги
бающая реаrкции облщдает свойством ,( 1.1). Увеличение скорости
достигается за счет того, что используIQтся не только эквидистант
ные ну,ли огибающей реакции, следующие через интервал Л:t, но
и те из нулей заполнения, .которые расположены между нуляtМи
огибающей на интервалах Лt'=М/,2.
Пример if (t) с треугольной спектральной ~плотностью дан на
рис. l.lOa, где @g = Лrо/'2:', @о = ЗЛ,rо/4. Аналитическое выражение
для<{ (rt) имеет вид (рис . 1.106)
f (t)=Лro cos0 ,75Лrot(sin0,5Лrot )2·
2л
0,5Лrot
Допустим, что несущая частота выбрана исходя из условия
@ 0 = ffig (l+т),
(1.35)
.2
где m=O, 1, 2, 3, . .. ; l принимает только нечетные значени'1!
независимо от т: ,l= 1, 3, 5, . : . При 1этом
f(kЛt±т:')=0
'
'
'
(С36)
f(kЛt)=О; }(k=+l +2 ...)·1
f (О)= 1;
•
f(±т:') = о,
где т:'=лl/2rоа. Пример реакции if(t) <для m=l, l = l дан на
рис. 1.lla.
Через систему, в которой несущая частота @о выбрана соглас
но •(1.35), можно осуществить передачу двух взаимно независи
мых импульсных последовательностей S(l>(kЛt) и S(2)(kЛt), сдви.
нутых на время т:', причем каждая последовательность пер~дается
со скоростью 1/Лt (рис. 1.11 ,б). Общая скорость передачи 2/лt.
Структурная схема та,кой системы <дана на рис. 1.111 в. Положив в
(1.35) rl=m=l, •приходим как частный случай к системе, рассмот
ренной в [18]. Согласно (1 .35), если l + т = М>2, то одна и та
же функция if (t) у<довлетворяет (1.36) с разными значениями т:',
так ,ка,к одно и то же число М можно по.лучить разными наборами
l и т. Кроме того, если М - нечетное, то вычисления по форму- .
ла.м (1.34) и (1.35) дают одинаковые зна_чения ro 0. Из вышеизло
женного вытекает, что рациональный выбор несущей частоты по-
27.
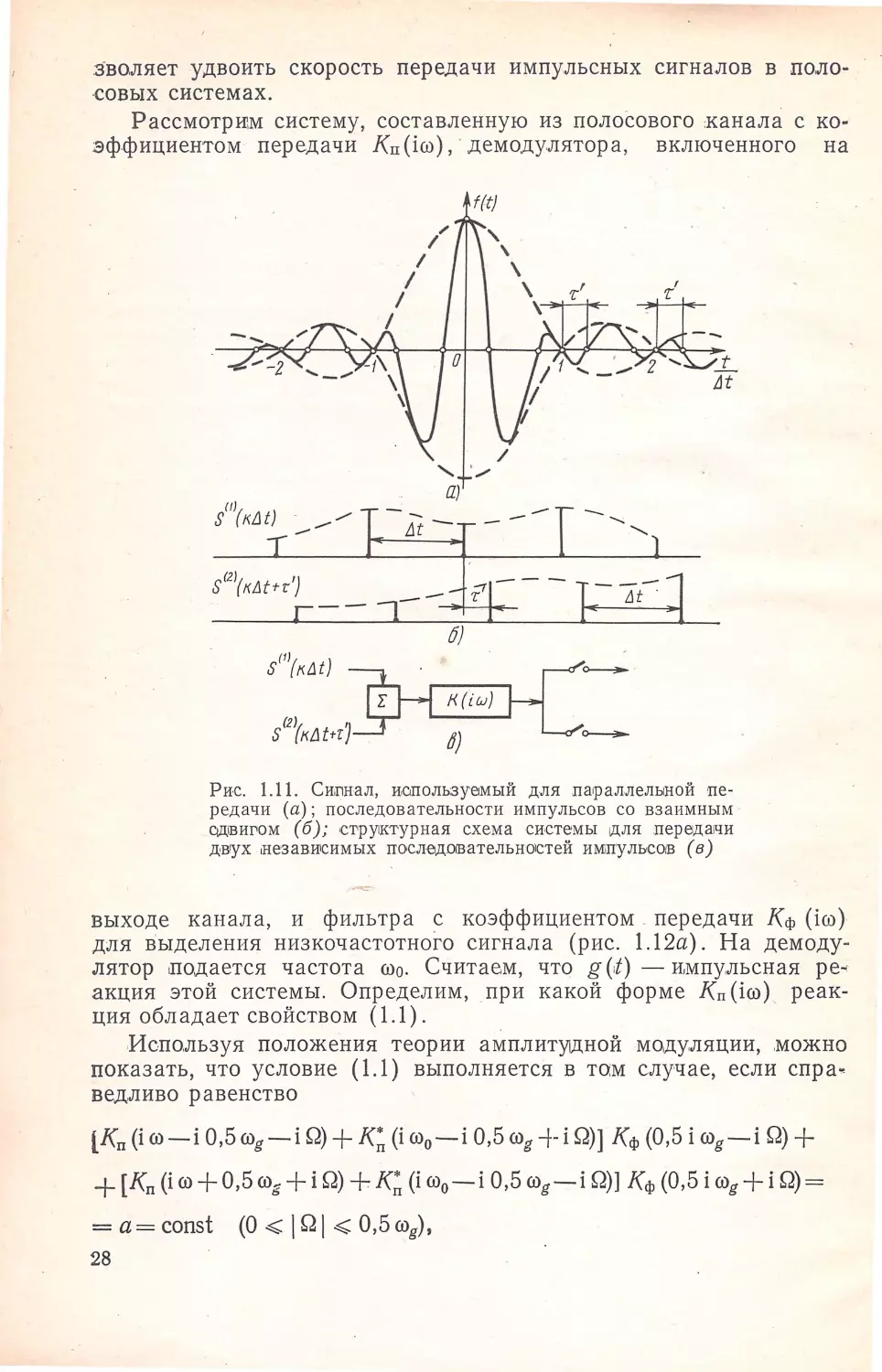
зволяет удвоить скорость передачи импульсных сигналов в поло
совых системах.
Рассмотрим систему, составленную из полосового канала с ко
эффициентом передачи Кп (iffi), •демодулятора,
включенного на
f(t}
f
't
1/)
S (к/Jt)
/Jt
oJ
/tJ(кtJt) ~0-------, -
'[
/<, (ii.J)
(2)
1
s '(клtнJ
d}
О-----,-
Рис. 1.11. Си,nнал, иапользуемый для ла,раллелыной тте
редачи (а); последовательности импульсов со взаимным ·
QД1вигом (6); стру~ктурная схема системы щля лереда1Чи
дв1ух ,неэавwсимых последооательнОlстей имrrульсо1в (в)
выходе канала, и фильтра с коэффициентом . передачи КФ (iffi)
для выделения низкочастотного сигнала (рис. 1.12а). На демоду
лятор подается частота ffio. Считаем, что g (,t) - и.мпульсная ре
акция этой системы. Определим, . при какой форме Кп (iffi) реак
ция обладает свойством ( 1.1) .
Используя положения теории амплитуtдной модуляции, можно
показать, что условие (1.1) выполняется в там случае, если спра
ведливо равенство
[Кп(iro-i0,5rog-iQ)+ К~(iffi0-i0,5 rog +iQ)] КФ(0,5irog-iQ)+
+[Кп(iro+0,5rog+ iQ)+К~(iro0-i0,5rog-iQ)JКФ(0,5irog+iQ)=
=а=const (О< 1Q 1 < 0,5ffig),
28
где частота wg должна удовлетворять неравенствам:
0,5(w2-w0) <0,5Wg < w2-w0, w2-@0> w0-w1;
0,5 (wo-W1) < 0,5 (J)g < Wo-W1, Wo-W1 > (1)2-(J)l;
Рисунок 1.126 иллюстрирует расположение частот wo ± 0,5wg±Q.
KФ(ii,J) g(t)
Яис. 1.·1,2. С1'ру,кту~рная ,схема пюлосовой системы
с демо1ПJуляцией ( а) J1 ее ыоэффиц-иент п~реда
чи (б)
Если КФ (iw) = 1, ReKп(iw) - четная и ImKп(iw)
-
нечетнан
функции относительно частоты wo, приходим к системам с харак
теристиками, указанными на рис. 1.9.
В ряде случаев при передаче дискретных сигна,лов интересу
ются только синфазной составляющей сигнала (синхрон_ный при
,ем). Поэтому определим требования, при выполнении которых
синфазная составляющая обладает свойством (·1J) . Положим н
(1.33) wo=wo' + Q, тде Q- некоторая частота; w0 - «старая» несу
щая частота; w0' -
«новая» несущая частота (демоду.лирующая
частота). Тогда
f(t)=Х(t)cosw~t+У(t)siпw~t,
где Х (t) = g (,t) cos ,Q ,t - синфазная составляющая; у (t) =
=g(,t) siп Qt - квадратурная составляющая f(t).
·Вб"-
2n-1(-+1+2+3
)
.
ыирая~~-
wg2
п-_
,
_
,
_
, ...
и считая, что
g(,t) обладает свойством (1 . 1) (Лt = 2n/wg; wg~12wc), получим
х (.t) со свойством
Х(kЛt') ={l' k=О
О, k==/=- О
(Лt' = Лt/2= n/wg);
(k= +1, +2, ... ).
Минимальное значение Лt': Лt'мин = n/Лw, -где Лw ~ ширина опект-
ра ,f (t).
.
Как следует из приведенных выражений, Х (,t) имеет эквиди
стантные нули, если g (1t) обладает свойством ( 1.1), а демодулиру
ющая частота wo' связана с несущей частотой wo соотношением
<0~=w0-wg2n- 1
(п= ± 1, ±2, ±3,... ).
2
29
Для того чтобы X(t) обладало свойствам ,(11.36), т. е .
X(kЛt)=O; } (k= ±l, ± 2,.. .); _
X(kЛt ± -r')=O
-
Х(О)=1; Х(±т')=О,
необходимо ,Q выбрать из условия ,Q = 0,5ffig (l + т) (т ~ О, 1, 2,
_
3, ... , l принимает нечетные значения независимо от т), а .- ' -
из
условия .- ' =1Тll/2Q.
Разделение перекрывающихся · реакций, спектр которых
не содержит нуле~ых частот
Определим требования -к частотным хара,ктеристика:м полосо
вых сист~м, реакции ,которых в целом (а не только огибающие)
обладают свойством .( 1.1). Эти требования позволяют указать об
щие условия _безошибочного разделения реа,кций полосовых сис-•
тем на произвольную равномерную последователъность импуль
сов, а также указать возможные скорости пере~дачи импульсов ,
при .которых выполнимо .безошибочное разделение [ 11].
Пусть g (t) - некоторая реа:к)Ция, спектральная плотность ко
торой К (iffi) существует на отрез,ке [ ffi1, ffi2], вне ·которого она тож ~
дественно равна нулю. _Найдем К (iw), для которых выполняется
( 1.1) при заданном интервале стробирования Лt. По аналогии с
§ 1.1 получим, что ( 1.1) имеет место в том случае, если
00
K0 (iw)=-
1- ~ K(iw-niwg)= l=const=#=O,
Лt~
(1.37)
где Ka(iw) - опектральная плотность решетчатой функции g(kЛt).
А,бстрагируясь первоначально от требований .к форме К (iw),
определим, при каких значенцях частоты стробирования wg=
30-
Е
..
-(J
(J
,- ..... ...
1
С,)
rJ)
Рис. 1.13. Опектр п.олосавого сиnнала (а); ,наложение
спектрав .при сд:и,окретизации ,сигнала (б)
= ,2л/М, в принципе, возможно перекрытие (взаимное наложение)
{'Двинутых спектров K(iffi _; _ niffig). Перекрытие спектров является
необходимым условием выполнения ( 1.1). Действительно, если
спектры K(iffi - niffig) для разных п (п = О, ± 1, ± :2, ...) взаимно
не ,перекрываются, то существуют области, в ,которых Ko(iffi) = 0
и равенство -(,1.37) не выполняется. Сказанное .поясняется рис. 1.13. _
_
Для наглядности на рис. 1.136 .пунктиром изобр-iз.жены те части
Ka(iffi), которые получены путем сдвига по оси ffi части спектраль
ной ,плотности К (iffi), наJ\одящейся в области отрицательных час
тот (рис. 1.13а, пунктирная кривая). Фаза-частотные характерис
тики на этих рисунках не указаны. В областях Лffi' спектрьI
К (iffi - niffig) взаимно перекрываются (накладываются), а в об
ластях Лffi" - не перекрываются, т. е. в областях Лffi" имеем
Ко (iffi) = 0. Для выполнения равенства ( 1.37) необходимо выби
рать частоту ffig так, чтобы отсутствовали области Лffi~'.
Подробный анализ рис. 1.136 показывает, что перекрытие
функций K(i(() - niffig) происходит в том случае, если ffig удовлетво
ряет неравенству
где
Ni= [ ffi1;ffi2];
(л(J) ~(i)g<2л(();).
Лffi =:= ffi2-ffi1
(1.38)
Функции N1 и N2 обозначают .целые части выражений, за,к.лючен
ных в квадратные ск_обки : Если ffig<Лffi, .перекрытие ,происходит
для любых (i)g.
.
.
Пусть, например, 1f1 = 2,2, кГц; (2 = 3,2 ,кГц (f = ffi/2л) . Выбрав
fg= 1,5 кГц, .получим N1 = 3, N2 = 1. Подставляя эти значения
.в·
( 1.38), убеждаемся, что для частоты стробирования fg= 1,5 ,кГц
выполняется требование перекрытия спектров. Одна,ко при выбо
ре ifg = 1,4 кГц< 1,.5 кГц неравенство (1 .38) не выполняется, что
свидетельствует о неперекры-'гии опектров.
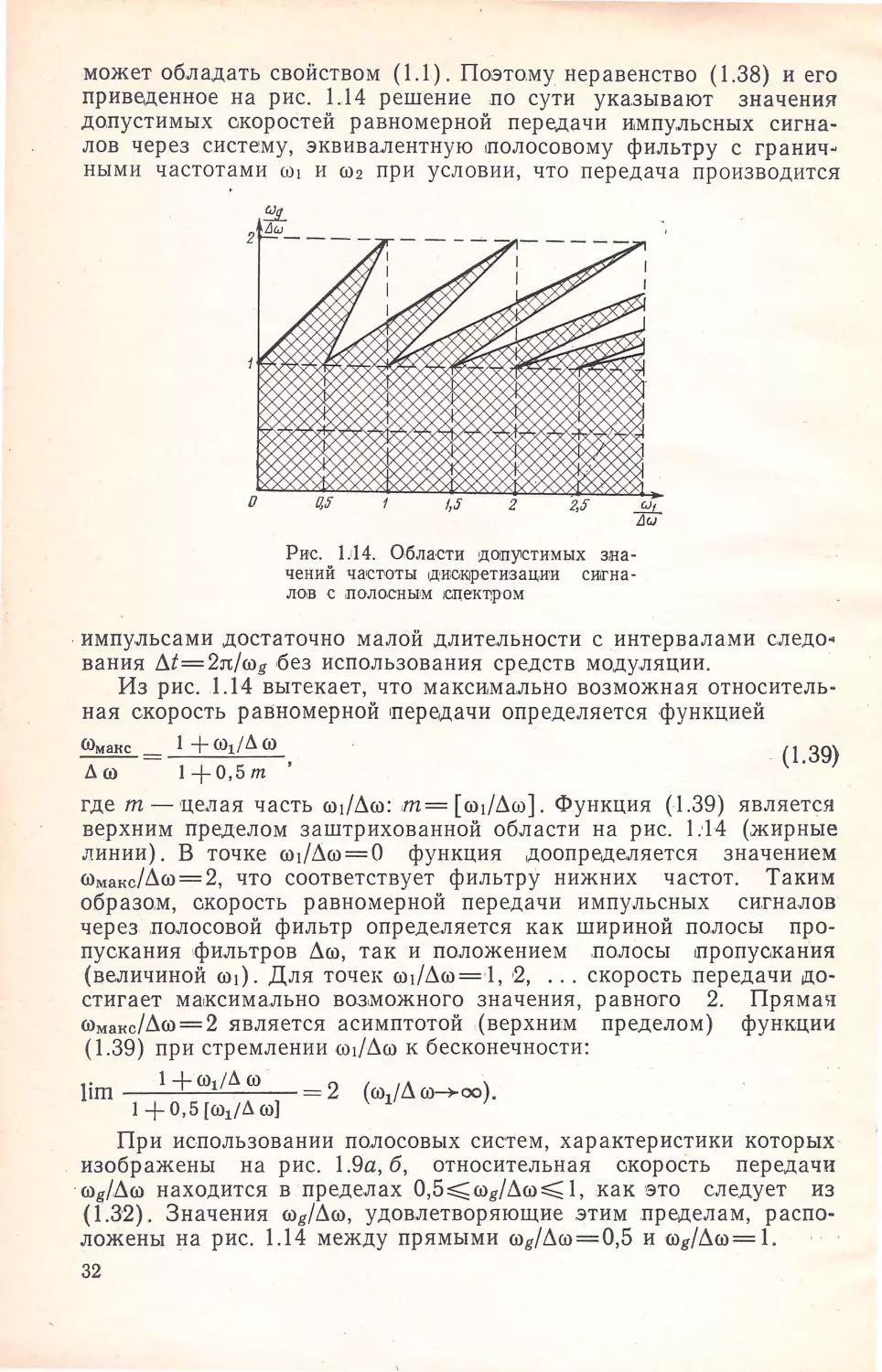
Решение неравенства ( 1.38) приведено на рис. 1J14 (заштри
хованная область) в виде функции
rog/Л ffi = 'Ф (ffi1/Л ffi),
где Л(i)=ffi2-ffi1. Функция 'Ф (ffi1/Л-ffi) представляет собой облас:ть,
ограниченную щью абсцисс и дву,мя сериями прямых, из .которых
одна проходит через точки с ,координатами Х1 = О,-5п; У1 = 1; х2 =
= п + I; У2 = 2, другая -через точки х1 =0,5п; У1 = 1; X2=n; У2=2,
где n1= 0, 1, 2, _. . ; X=ffi1/Лffi; y = ffig/Лffi. В точ,ке (i) 1 /Лffi = 0 функ
ция '\jJ (ffi1/Лffi), кроме значений, находящихся внутри заштрихо
ванной области, принимает та,кже значения на оси ординат от I_
до -2, что соответствует низкочастотным . системам, эквивалентным
фильтру нижних · частот.
Полученное решение показывает, при каких значениях частоты
стробирования (i)g осуществляется перекрытие спектров, и, следо
вательно, при этих же значениях ffig функция g(,t), в ,прин,ципе,
31
может обладать свойством ( 1.1) . По.этому неравенство (1 .38) и его
приведенное на рис . 1.14 решение по сути указывают значения
допустимых окоростей равномерной передачи импульсных сигна
лов через систему, эквивалентную ~полосовому фильтру с гранич
ными частотами w1 и w2 при условии, что передача производится
2,.}
. !::!L
L](J
Рис. l .1 14 . Обла,сти :дОIПу,стимых зна
чений ча,с·юты 1Jщ<ж1р-етизации си;гна
л-с>в с поло.сным к:.цект:р ·ом
. импульсами
достаточно малой длительности с интервалами следо•
вания Лt=2n/wg без использования средств моду,ляции.
Из рис . .1 .14 вытекает, что максимально возможная относитель
ная скорость равномерной передачи определяется •функцией
ffiмaнc 1 +@1/Лrо
.
(1.39)
Лrо
1+0,sт '
где m-целая часть ro1/Лro: m = [ro 1 /Лro]. Функция (1 .39) являетс я
верхним пределом заштрихованной области на рис. 1:14 (жирные
линии). В точке ro 1 /Лro = 0 функция доопределяется значением
ffiмaнc/Лro=2, что соответствует фильтру нижних частот. Таким
образом, скорость равномерной передачи импульсных сигналов
через полосовой фильтр определяется как шириной полосы про
пускания фильтров Лrо, так и положением полосы пропускан'ия
(величиной ro 1). Для точек ro1/Лro = · l, 12,
...
скорость передачи до
стигает ма,ксимально воз,можного значения, равного 2. Пряма я
ffiмaнc/Лro=2 является асимптотой , (верхним пределом) функции
( 1.39) при стремлении w1/ Лrо к бесконечности:
}im 1+roi/Л ro
= 2 (rо1/Л rо-ню).
1+ 0,5 [@1/Л ю]
При использовании полосовых систем, характеристики которых
изображены на рис . 1.9а, б, относительная скорость передачи
rog/Лw находится в пределах O,S~rog/Лro~ 1, как это следует из
(1 .32) . Значения wg/Лro, удовлетворяющие этим пределам, распо
ложены на рис . 1.14 между прямыми rog/Лro=0,5 и rog/Лro=l.
32
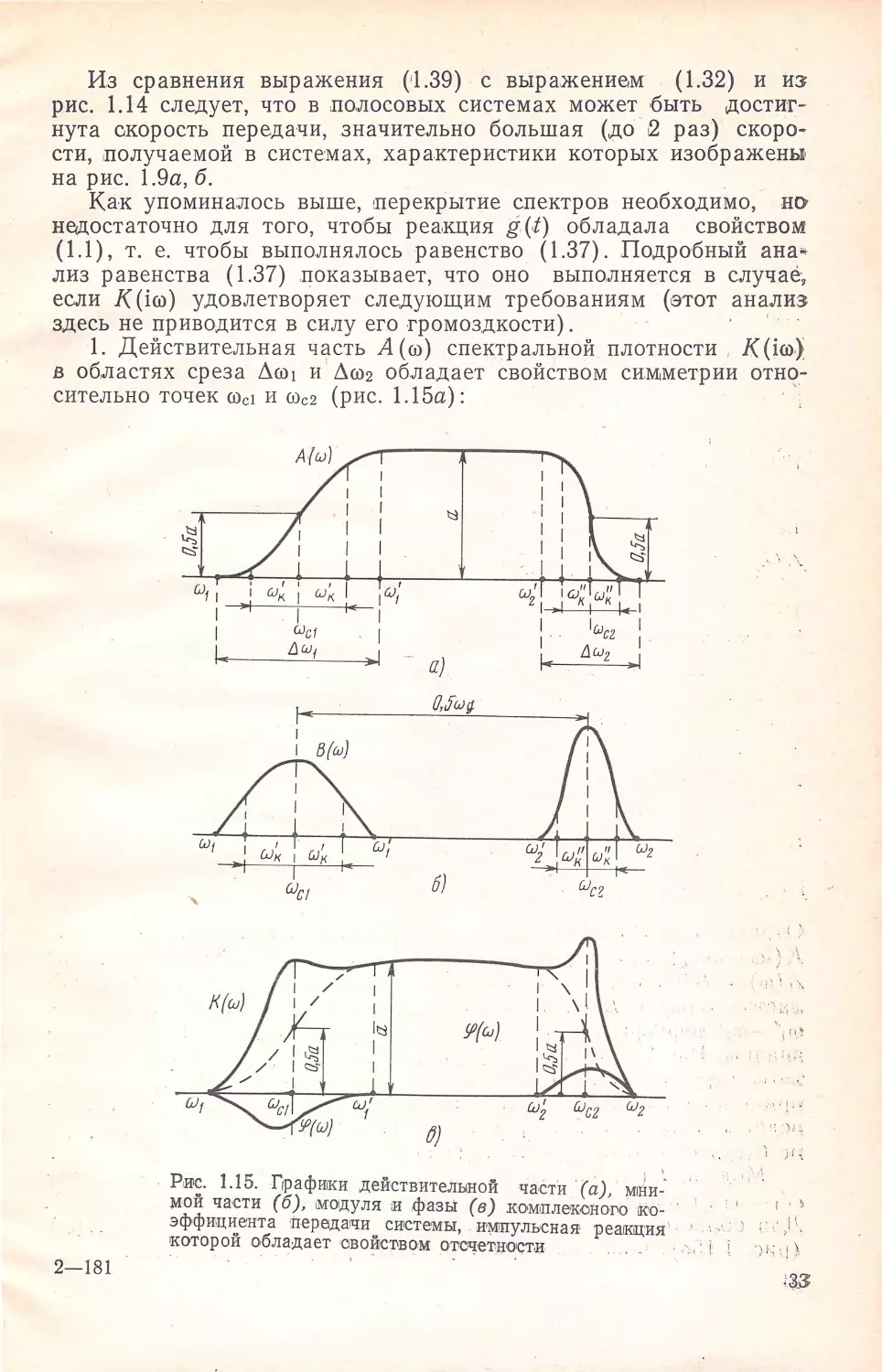
Из сравнения выражения ('1.39) с выражением (1.32) и из
рис. 1.14 следует, что в ,полосовых системах может быть достиг
нута окорость передачи, .значительно большая (до ,2 раз) скоро
сти, ,получаемой в системах, характеристики которых изображены
на рис. 1.9а, 6.
_
Как упоминалось выше, перекрытие спектров необходимо, но
н~остаточно для того, чтобы реа,КЦИя g.(,t) обладала свойством
(1 .1), т. е . чтобы выполнялось равенство (1.37). Подробный ана "
лиз равенства ( 1.37) .показывает, что оно выполняется в случае,
если К (iffi) удовлетворяет следующим требованиям (етот анализ
здесь не приводится в силу его громоздкости) .
1. Действительная часть А (ffi) спектральной плотности . K(iffi)
в областях среза Лffi1 и ' Лffi2 обладает свойством симметрии отно
сительно точек fficr и ffic2 (рис. 1.15а):
2- 181
~1
1
1~
1-t -- ---~
1- ----1-,.__ 1
1
CJct
1
1
lJ (и/
/
...
-
а)
Си'
1
1
1
1,:,
1
(J,,fщ
б)
1
1
-1
1
1
1
-
Р,и~. 1.15. Г~рафrnки действителыной части (а), м,Jи :·
мои ча,сти (6) , ,мО1дуля л фазь1 (в) комсrтлеконою ко
эффи,ц1;,ента ·передаrчи системы, wм1пулысная· реа1Кция ·
которои обла,дает •овойство:м отс,чещю·с;ти
.l
''
''
.
'i\
• >-'.
')t-~~J\
A.(fficr+ffik)+A (ffici -ffi~) = const = а;
А (Фс2 +ffi!)+A (ffic 2 -ffi;) = const = а,
г,де
N1 = [(ffi1 +ffi2~/ffig ]; ]
N2 = [2co2/cog];
Лffi <. ffig < 2Лсо;
roh.' и ю,t'' - любые частоты, удовлетворяющие требованиям:
•,
1
Jwk 1-3⁄4 2 Лю1, Л ffi1= N1cog-2 со1;
Jffi; / <. +Л(()2, Л со2=2:со2- N2 cog.
(1.40)
il3 диапазоне ю,'- со2' функция А(со) равна лостоянной величи
-не:
А(ffi)=coпst =а (ffi; <. 1Ф1<со;),
:где
(J); = N1cog-co1; со;= N2 Wg - co2•
(1.41)
Для точек ffic1 и СОс2 имее:м А (сос,) = А (сос2) = 0,5а ..
2. Мнимая часть В (со) спектральной плотности J( (ico) в облас
т ях среза Лсо1 и Асо2 четна относительно точек сос1 и СОс2 • (рис.
l .1'56): •
~(ffic1 +со;)=В(СОс1-cok) (/со;/ < + Лсо1);
_ B(f fic2 +Ф;)=B(coc2 -co;) (/roZ/ <+Лсо1) ;
в(ro) = о (~; < l(J)I <rco;).
О трезки Л со 1 и Лсо2 являются областями перекрытия спектров
i( (iffi-inщg) при стробировании g (t) . Естественно, ,поведен;ие
А (ю) и В(@) в областях Лсо1 и Лсо2 взаимонезависимо . В этих об
л астях А (со) и В (со) не являются однозначными. В щиапазоне
ro/- co2' ,перекрытия спектров нет, поэтому А (ro) и В (со) · одно•
зн:ачны. Расстояние -между точ,ками ffic1 и сос2 равно половине час•
7ОТЫ 1.С-~;робир,ования cog = 2 (сос2- сос1). Перечисленные требовани я
щринципиально необходимы . Невыполнение любо.го из них при
JВедет к не'Въпюлнению равенства (1.37), в результат е чего g(t)
!Н е .будет обладать св о йством ( 1.1) .
Модуль K (ffi) спектральной плотности K(iro) в диапазоне
l(J)11-(!)'2 'Совпадает с А (,со), т. е. К (ro) = А (ro) = а (ro'1 ~ ffi ~ ro'2).
Для областей Лffi1 и Лrо2 при В (ro) =#=О K(ro) отличается от А (ffi)
( рис. l. 15в) . Фазовая характеристика <р (ro) спектральной плотно •
:~
сти K(iro) в ,диапазоне ro1'-ro2' равна нулю (либо линей-на), а в
.
.
в~-
областях Лrо1 и Лrо2 нелинейна, если B(ffi)=jЬO: ср(ш) · aгctg-- .
•
А(Ф),
(ш1~1ш1 ~ 1ro"1, ro'2~ \ш\ ~ro2). В частном случае при В (ш) = О
(ro1~ ш ~ш2) (см. рис. 1.15в, лунктирные .линии) ср(ш) .:.....:о;
К(ш) = А(ш) (ro1~1\ro\~ro2) .
.
Типичным для рис. 1,15в является то, что в диапазоне wi'-w:/
/((ro) не зависит · от частоты и равен ~постоянной величине; при
этом ер (ш) = О; в областях ,Лrо1 и Лlro2 К (ш) и ер (ш) имеют доволь
но ·сложный хара,ктер. При изображении А (ш) и В (ш), а также ·
при записи вышеприведенных требований .линейная составляющая
фазы, вызывающая сдвиг g (t) во времени, · не учитывалась.
•
Рассмотрим несколько примеров. На рис. 1.16а, б приведены ,·
модуль К (ш) и соответствующая ему временная функция g (t), об -
ладающие свойством (1.1) при wg= 1,5Лш. Фазовая характериспr
ка ср(ш) предполагается линейной и в рассуждениях не учитывает-
К(1и}
оfч
Л1и
а)
g(t)
oJ
.-Рис. ·1.16-' . ТТ•ример к,о·;эф,фйан1t~.нта : Передачи ·: (а~
~?.~:; J,' ~·,•
.
J {'1 0 ~:с.")
. и~пульсной
1реаК'ции (б) _ rполосQвой _системь; , ~,а;'.\ >t, :{ ; , s т ,GH
своист,в,ом отсчетности; ~наложение спектра.в п~и ,.·,.-,,,•,:.·-'с··, . . .,., _ 1
.
дискретизации (в)
·..
•' ••·•'•..•("'•
зfJ~
ся, т. е. B(w) =0. Наложение спектров K(-w -nwg} при стробиро•
вани~ g (t) изображено на рис. 1J бв. На этом рисунке спектр
К(w)заштрихован,аспектрыК(w- n@g) (п= ±1, ±2, ...)изо
,бражены пунктиром.
Аналитическое выражение для g (t) имеет вид
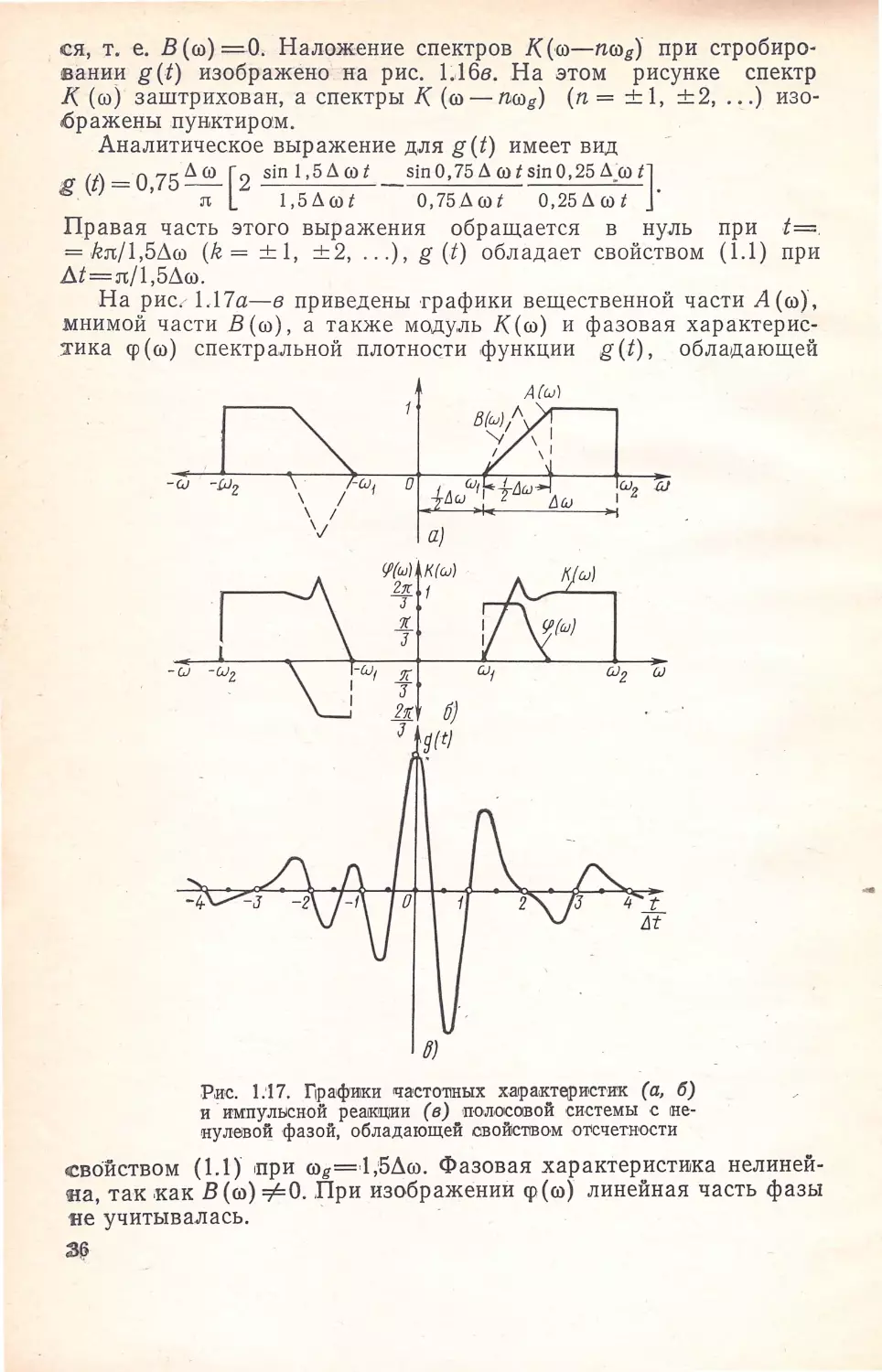
g (t)=0,?SЛffi [2 sin1,5Лwt _ sinО,75Лwtsin0,25Л_wt]·
•
п
I,5Лwt
О,75Лwt О,25Лwt
Правая часть этого выражения обращается в нуль при t = .
=
kn/1,SЛw (k = ± 1, ±2, ... ), g (t) обладает свойством (1.1) при
Лt=n/1,БЛw.
На рис , l.l 7a-в приведены трафики вещественной части А (w),
мнимой части В (w), а также моду,ль К (w) и фазовая характерис
тика ср (w) спектральной плотнщти функции g (t), обла~ающей
·ц)
-(J
-Ыz
- {,)
о
IWz {,J
\
/1
\/
\✓
а)
1/(1.и) K(w)
/( {;J)
2:Jr f
J
2f__
J
-C Jz
r,
[,}2 (;J
J
2r,
б)
т g(tJ
о
(})
Рмс. 1:17. Г1рафики чаСТО'!1ИЫХ х.а~ра~Кт~и,спn< (а, б)
и •имлулысиой peacr<!IIJИИ (в) ,полосовой системы с не
rн:у л,евой фазой, обладающей авоЙiс'!1вом о'Гсчетн,ости
свойством (1.1) ,при wg = • l,'5Лw. Фазовая характеристика нелиней
на, так ,как В (w) :#=О. При изображении cp(w) линейна я часть фазы
яе учитывалась.
~~
...
Функция g(t) равна:
g(t)=O, 25 лu> · [в sin l , 5Лu>t
n
·
l,5Лu>t
ЗsinО,75Лu>tsinО,25Лu>t_
•
0 , 75Лu>t 0 , 25Лu>t
~sin0 , 75Лu>t( sin0,125Лu>t )2]·
О,125Лu>t
Рисунки 1.16 и 1.17 на,глядно показывают, что возможно по
-строение полосовых систем с нулевой либо ненулевой фазовой х а
р актеристикой ( без учета линейной составляющей), реакции ко
торых обладают свойством ( 1.1) . При этом частотные характери с
тики систем принципиально отличаются от хара,ктеристик, изобра
женных на рис . 1.9.
Изложенные выше соображения о .многозначности формы
-спектральной плотности K(iru>) в областях Лu> 1 и Лu> 2 справедливы
для случая 1u>g<2Лu>. Если u>g=2Л·u>, что имеет ·место при u>i=
=nЛu> (п-целое число), то Лu>1=Лw2=О, поэтому форм а
К (iu>) однозначна:
К(u>)= const= а; } (u>1< \u>j< ffi2)•
<p(u>)=O
В точках u>1 и u>2, совпадающих с точ ,ками u>c1 и u>c2,
K(u>1) =K(u>2) =0,5а. Импульсная реакция g(t) в этом
определяется выражением
g(t)= Лu> cos(п+0,5)Лu>t sin0,5Лu>t (п=u>1/Лu>) ,
n
0,5Лu>t
имеем
случае
Для n=l трафики g(t) и K(ffi) даны на рис. 1 . 18а , б, и з ,которых
/{(GJ)
f ------.----,
а)
g(t/
6)
__J_
лt
Рис. 1. 18. ~оэффи,циент nередачи системы
(а), им,пулыаная р·еа:юция ка11ор·ой (б) ха
,ра:ктеризуе11ся МИiнималИ!ым 1ра•с•ст.оянием
,между эквидистантными нулями
37
следует, что g(t) обладает свойством (1.1) при минимальном ин
тервале Лlt= ,2n/шg = n/Лш.
Опреде.Jiим ·частотные характеристики полосового канала, им ~
пу.льсная реакция которого устойчива к девиации фазы та,ктовой
частоты. По аналогии с результатами § ,1.2 получим, что ,квазиопа
тимальным является фильтр, ,коэффициент передачи которого
представляет собой неравнобочную трапецию (рис. 1.19, .кривая
1), а импульсная реакция которого описывается выражением
Р,ис. 1.19. ~оэффициен-
ты [1ередачи полосового
,канала, у~стойчи,вого к
iдевиации фа:зы такто1Вой
частоты (,кри,вая 1), и
•ка1нала,
ма·wсимизирую-
щего
,QTHOШffiJИe СИГ·
,нал/шум (,к,ривая 2)
g(t) = (J)c2 sin (J)c2 t sin ((1)2 - (J)c2) t __ (J)ci sin (J)ci t
1t
(J)C2 t
((1)2 - (J)c2) f
n
(J)Cl f
sin((1)1 - (J)c1) t
((1)1 -
. (J)c1) t
где Шс1 и (J)c2 находятся по ( 1.40).
Используя тот же прием, что и в § 1.,2, можно показать, что
импульсная реакция поJ1осового канала, :максимизирующего соот•
яошение сигнал/шум, равна:
2 sin
(1)2-(1)1
t
g(t)=
2
(J)l + (1)2
t+
cos
nt
2
,
,
2 sin
W2-W1
t
w; +w;
+
2
t,
cos
nt
2
где (1)1' и (1)2' . определяются из ( 1 .Фl). Частотные характеристики
такого канала даны на рис. 1.19 (кривая 2). Для сравнения на
этом же рисунке приведен коэффИiциент передачи идеального по•
лосового .канала (пунктирная ·кривая).
Условия неискаженной передачи однополосного сигнала
Во многих системах связ_и используется ам1Плитудная модуля•
ция с передачей одной ,боковой полосы частот . .Выведем требова•
:ния, которым должен удовлетворять формирующий фильтр таких
систем для :неискаженной пере!дачи однополосного сигнала [6]. В
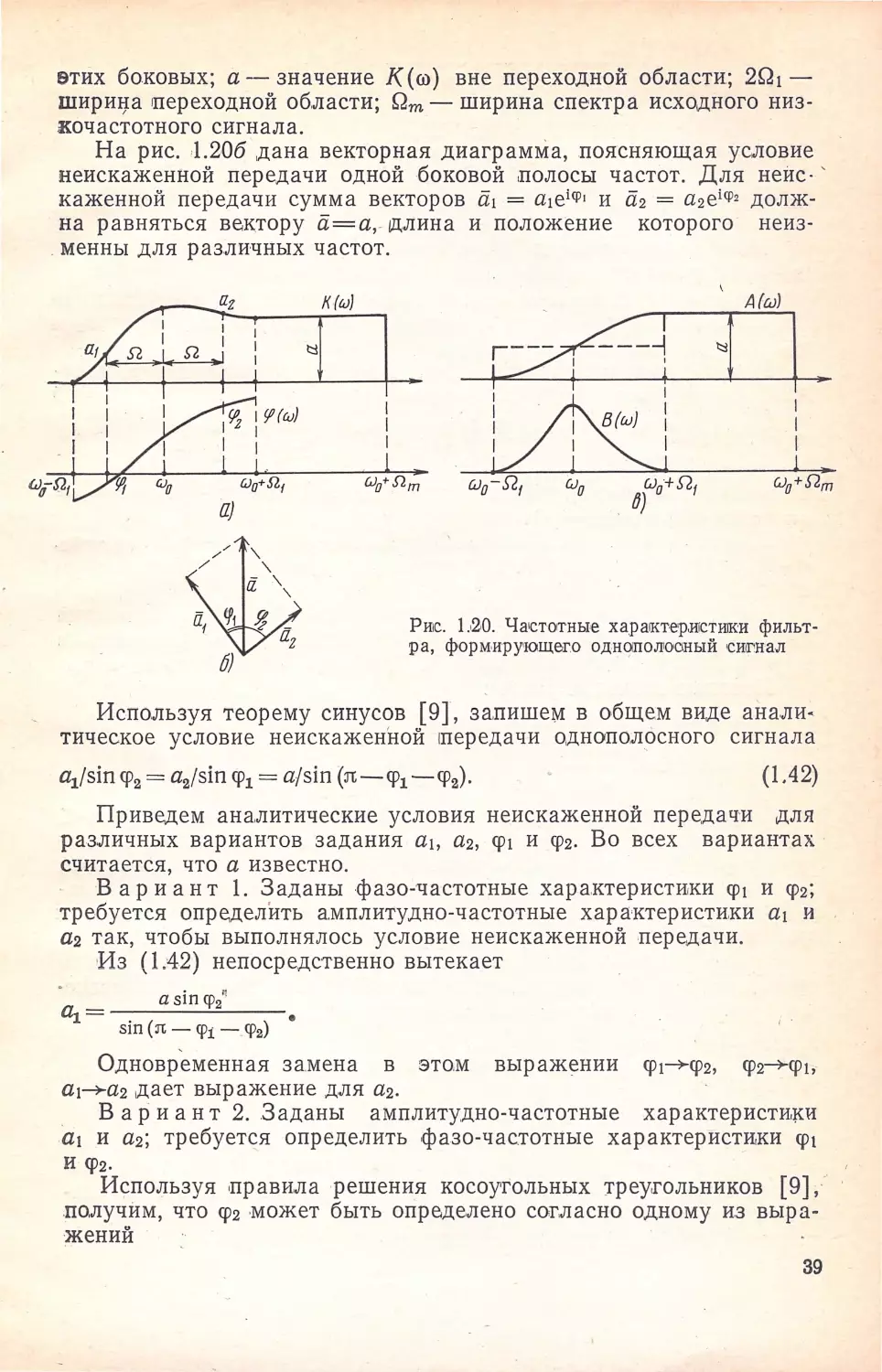
дальнейшем используются с.Jiедующие обозначения (рис. 1.20а):
К(шо-·Q)=а1; cp(wo -Q)=cp1; K(wo+Q)=a2; cp(wo+Q)=cp2;
К(W)=а ((!)о+Ql -< 1W 1-< (!)о+Qm),
где а 1 и а 2 - амплитудно-частотные характеристики соответствен•
но нижней (отрезок [ (J)o-Q, , wo]) и . верхней (отрезок [ (!)о, (!)о+'
+ Q 1]) боковых полос частот; ер, и ср2 - фазовые характеристики
38
r
етих боковых; а-- значение K(ro) вне переходной области; 2Q1 -
шири!jа переходной области; Qm - ширина спектра исходного низ
кочастотного сигнала .
На рис. ,1.206 дана векторная диаграмма, поясняющая условие
неискаженной передачи одной боковой полосы частот. Для неис- '
каженной передачи сумма векторов ii1 = a,eiq,, и ii2 = a2eiq,, долж
на равняться вектору ii= a, - ~длина и положение
которого неиз
менны для различных частот .
Ри1с. 1.,2,0. Ча•СТОО'НЫе хара1Ктер ,ИIСТИIКИ фильт
ра, форм,ирующе,го ОДНОПО JЮСJНЫЙ СIИ~нал
Используя теорему синусов [9], запишем в общем виде ана.ли
тическое условие неискаженной ~передачи однополосного сигнала
a1 /sin ср2 = a 2/sin ср1 = a/sin (л:-ср1 -ср2).
(1.42)
Приведем аналитические условия неискаженной передач-и для
различных вариантов задания а1, а2, <:р1 и <:р2 . Во всех вариантах
считается, что а известно .
Вар и ан т 1. Заданы фаза-частотные характеристики <:р1 и ср2;
требуется определить амплитудно-частотные характеристики а1 и
а2 так, чтобы выполнялось условие неискаженной передачи.
Из ( 1.42) непосредственно вытекает
•
asinqJ/
~=
.
•
S!П(Jt- (j)f-
. (J)2)
Одновременная замена в этом выражении срг+ср2 , ср2-+ср1,
а1-+а2 дает выражение для а2.
В ар и ан т 2. .Заданы амплитудно-частотные характеристщпr
а1 и а2; требует~я определить фаза-частотные характеристики ср 1
И (j)2.
Используя ,правила решения косоугольных треу,гольников [9],
.получим, что ср2 -может быть определено согласно одному из выра
жений
39
= 2arccos 1/ (а+а1+а21(а+а2-:---- а1)
r
аа2
Если в приведенных выражениях заменить (j)2-+<p1, а г~а2 ,
а2-+-а1, пол у чим выражение для определения <р1.
• Вар и ан т 3. .Заданы амплитудно-частотная и фаза-частотная
характеристики для одной боковой полосы частот, на п ример а2 и
. <р2,
треб у ется опре1делить а1 и <р1 .
Используя те же правила, что и в предыдущем варианте, полу~_
чи,м, что <р1 :может быть найдено сог,ласно одному из выражений
ср1= arctg а2sin(J)2 = ~-
_1
_
<р2+arc tg[а2.-
а ctg _1_ <р2].
а- а2cosср2 2
2
а2+а
2
Значение а1 нахмится из выражений а 1 = V a22+a2- 2a2acoscp2=,
= а sin cp2/siп(:rt-<p1-<p2).
Замена в этих выражениях а2-+-а1, <р2-+-<р1, <р1-+-<р2,
а 1 -+-а2 дает выражения для определения а2 и <р2 по известным а1
И <р1.
В ар и ан т 4. ,Заданы амплитудно-частотная хара,ктеристика
ьдной боковой полосы частот и фаза-частотная характеристика
другой боковой, на~пример а2 и <р1 . Требуется определить а 1 и <р2.
Искомые ,значения равны :
<р2 . ':rt - <p1-'Ф; а1 = а2 sin <p2/sin <р1,
где
•
asinm
'Ф= arcsш
"'
1•
а2
Если а2?::::а, то 'Ф<:rt/2 и имеет лишь одно значение; если · а2<
.<а, то: ,1) 'ljJ имеет два значения \\) 1 и 'I\J2 при а si n ср1<а 2 , причем
\\J2=:rt-<p1; 2) 'ljJ имеет одно значение (\\J = :rt/2) . • при
аsin<р1=а;
3) 'ljJ не существует при а sin ср1>а2. Ка,к и ранее, заменив в при
веденных выражениях а1-+-а2, а2-+-а1, <р1-+-<р2, 1ср2-+-<р1 , приходим к
выражениям для определения а2 и <р1 по известны, м а1 и <р1.
Кроме условия ( 1.42), которым можно ,пользоваться только
при <р1*О, <р2*О, справедливы также более общие аналитиче
с,кие условия неискаженной передачи :
а2c~sср2+а1c~s<р1=а;}(IRI< R1), j
alS!П<pl= а2S!П<р2
( 1. 43)-,
a(ffi)=a (ffi0+Q1 < [ffil <ffio+Rm).
Из этих выражений вытекает, что действительная А (ffi} =
= а cos ср и •мнимая В (ffi) = а sin ср части ·комплбксного коэффи•
циента передачи формирующего фильтра должны иметь вид, у.ка- -
занный на рис. 1.20в, т. е. формирующий фильтр, по существу,
является вышерассм9тренным полосовь1м фильтром Найквиста .
.40
Поэтому все свойства фильтра Най.квиста: справедливы и для
фильтра, формирующего однополосный сигнал. Так, на основе ре
зультатов § 1.2 можно сказать, что соотношение · сигнал/шум бу
дет максимальным для формирующего фильтра с характеристи ~
,кой, указанной на рис. 1.20в пунктиром.
:Выражения (1.42) и ( 1.43) справедливы для случая, когда фаза
несущей частоты на передаче совпадает с фазой несущей· на прие
,ме. Если разность фаз этих несущих равна ,а, то для получени,
условий неискаженной передачи во всех полученных выражениях
не(Убходимо заменить ср1 на ср1 -1а и ср2 на ср2-а,
Расширение теории передачи Найквиста
Выше получены частотные характеристики систем, импульсные
реакции .которых обладают свойством отсчетности ( 1.1). Опре,де
JIИМ теперь частотные характеристики систем, импульсные реак
ции которых облщдают. обобщенным свойством отсчетности:
g(kЛt)=CR (k=O, +1, +2, ... ),
(1.44)
где с11. - произвольные заданные величины, с которыми должны
совпадать значения g(kЛt) при заданном Лt.
'
Представим левую и правую части выражения (1.44) в виде
00
00
g(t) ~ ' б(t - kЛt)= L cJ<б(t-kЛt).
k=- oo
k=- oo
Взяв преобразование Фурье от обеих ~астей этого выражения, по
лучим
· :. [ K(iro)@,t."',B(iro-ikoo,)]- ].с,е-,.,л, (oo,~2n/ЛI),
·где ® обозначает операцию свертки . .Вычислив свертку, оконча
тельно п олучи,м
00
00
~ K(iffi-ikffig)=Лt I
(1.45)
k=-oo
k=- oo
Это выражение устанавливает требования к ,комплексному ,ко
эффициенту .передачи системы, им.пульсная реакция .которой обла
дает обобщенным свойством отсчетности ( 1.44).
Рассмотри.м частные случаи.
1. Условия отсутствия межсимвольных помех (.первый •крите•
рий Найквиста) (1.1) требуют, чтобы Co = l, С11. = О (k = ±l, ±2, ... )
или
00
I К(iffi-ikffig)= Лt= const,
,k?'- 00
·что сов1Падает с (1.4) и (1.37).
41
2. Условия отсутствия искажений длительности импульсов тре•
.
буют, чтобы
.(2k-I )1-
1
, k=O,k=1;
g --Лt= 2
2
О, k=l=O, k=I= 1, k= -1, ±2, ±3, .. .
Введем функцию g 1 (t) =g(t-Лt/2) со спектром
-lw~t
= J((iro)e
2
.
Тогда условия ('1.46) принимают вид
g1(kЛt)=1+• k=O, k--- .:. 1;
О, ,k=i=О,k=I=1;k= -1,±2,±3, ...
(1.46)
K1(iro)=
(1.47)
Подставив эти значения в (1.45) и заменив K(iro) на K1(iro), по • .
лучим
00
~ K(iro-ik~rog)(-l)k =Лtcos ro:t.
=-оо
Выражение ( 1.48) известно как второй ,критерий Найквиста [,26].
3. При одновременном отсутствии :межсимвольных помех и
искажений длительности импульсов имее,м [26]
00
k=O ;
k=±l;
k=±2, +3, ...
В этом случае на К (iro) накладывается условие
~ K(iro-i2krog)= ~t (1+cosro:t) (rog=2n/Лt),
k= -oo
.
.
.
•
.
(1.49) '
(1 .50),
которое получается из (1.45) заменой Лt на Лt/2 и подстановкой .
вместо с11, соответствующих .значений (•1.49) .
Таким образом, уС,JJовие (,1.45) позволяет с единых позиций
получить первый и второй критерии Найквиста, • а также услов ие'
одновременного отсутствия :межсимвольных по.мех и искажений ·
длительности импульсов.
''
•,,
'
'
•
-
1
•
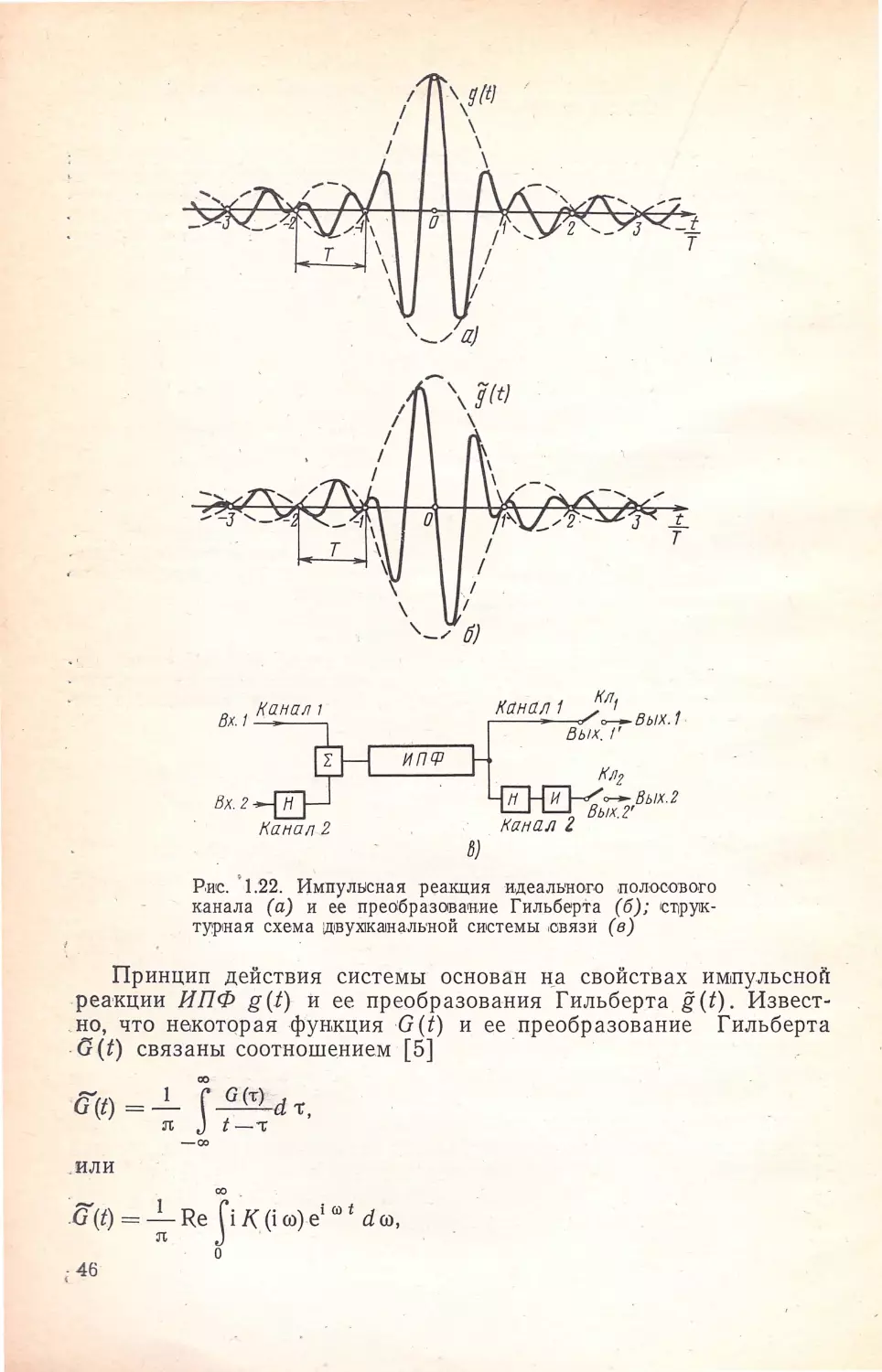
Отсчетш.1е фильтры и восстановление сигналов
по их дискретным значениям
Овяж,ем · теqрию оточе11ных фильтрЮiВ ,с BOl!lipo.caми ,вооста~новлен,ия зада,нн,о •·
го а,Н1сам1бля фу,н3⁄4ций [Ю их мг,новенным зна,чения,м. ,]3 теоР'ИИ пер~а,ч;и ,сиnна.•
л ов фу,1ща'Менталь1iу,ю ,роль 1иnрает теорема Котелы~:ИJКава (теорема выборок) ,.
согла>сно которой п1р•оизво~ьная ча,сто11но-оr~ра1ниченная фу,н,юция f(t) , опектр :ко- .
торой ,не ,оадержит ча1стот ,выше Wc, ·МО*ет бы т ь nре,д1ста 1влена · 1рящом ;r1, 2, 5]
42
00
j(t)= ~f(kЛt)sinffic(t- kЛt)_
/.J
ffic(t- kЛt)
(1.51)
-со
.
Особеюн·ость · з-гою рЯlда ,в том, ч110 его 1ко,эффициентшми являю'J\Ся 3на<rен ия
функ,ции f (t), о,осчятаIн,ные ic инте1рuзал,ом ди,ок~ретизации Лt=n/roc . В [1] л др.
паказа,но, что если интерIвал д.wощретизаци,и большiе n/roc, · то ряд (1 .- 51) •воапро
извОЩ:ит исхоiЩную фу~н'КIЦ:ИЮ f(t) ,с о1еко-горюй nагр ешнастью, которая 1в оз.ра<ста ет
с увели·чени-ем И1нтерIвала ди,ОК1ретизации.
Покажем, что Iцрои~вольная (,не обяза-гелыно частотно-ог,раtНиченная) фу,нк
·ция f(t) может быть n,рещ,сташлена ряд,ам, аналогичным ,РЯiдУ К:отелын.ИJкава
(:1.5 1) с п,роиз.нолы1ы,м Iи,нтер,вало,м tди,окретиза,ции Лт (Лт$Лt) , лри у,е,лов.ии,
sinffic,(t- kЛt)
что элемента~рIные фу~ююции ------ замене11ы •не1ю'!'орыми, О!Пределен
ffiс(t- kЛt)
ным о·бра 9 ом sыбра,н~ными фуtН,кциями v(t-kЛт).
Соста,ви,м для f (t) ,ряд:
со
f(t) = Lf(kЛт)v(t- kЛт),
(1. 52)
-со
где Лт - Пiр•оиЗ1Вольная за,да,нная величина. Определим, при каких v (t-kЛт)
это ~разложение является опра13,е,1щнвым.
Нзяrв nреобр азава,ние Ф,у,рье от ,обеих ча,стей ( 1.52), приходим к выражению
tJO
F (i ffi) = 'V (i ffi) Lf (k Л~) e-kiooл,_,
-со
г.це F(iro) и v(iro) - ошжr1ры f(t) и v(t).
Посжолыку
.
со
со
I f(kЛт)e-iookЛ,=Л~ ~ F (iw-ki ffig),
-со
-со
где ro 8 =2ri/Лт,
F (iffi)=Л~ v(iffi)iF(iuJ- kiffig)
(1. 53)
-оо
и.ли
V(iuJ)= 00
ЛтF(iffi)
(1.54)
~F(iuJ- kiШg)
-со
00
Проанализируем 'V (iro). Принимая во внимаtНие, ЧТО r F (iro-kirog) =;
-оо
00
= ~ F1[iro-(k-n)irog] (п - nроизвольное), из (1.53) или (1.54) получим
-се
со
~v(iw - kiffig)=Лт = const.
'
(1.55)
-со
Как nоказа,но ,в § 1.2, если спек'I'р некоторой функции v(t) удавлетворяет
(1.55), то она неизбежно обладает свойс'!'вом (1.1):
43
{1,
'V(t)=
'
о,
t=О;
t=kЛт,k=f,О,k=±1,±2,
.
.
-
.
(1. 56)
Из этого ,вытекает, что для ,р,азложения F(t) ·в рщц (1.51) ПiРИ п·роиз,вООiыном эа
дан,ао:м Л,: •необхсщи,мо ,в качес-лве v(t-kЛt) и,епользавать ,НJМ1Пуль,сиые Iреаrк,ции
оточетиооо филь11ра с ,коэффиrциеитом пер€1дач,н (:l .i54), кот-орый ·в общем случае
эавюсит каIк от Л-r, .та:к :и от спектра фу~нщии f(t).
В час11иом му~чае, еми
IF(iffi)i =0 (lffii >ffic)
(roc - ,11раиичиая частота), то, сrэыlбраrв Лто,;;,_,Лt=n/rос, и:з (1.54) получим, что,
v(iro) является коэффициентом переща-чи идеаль.ног-о фильтра ,низ,кюй частоты:
_
{ Лт , 1ffi 1:( ffig/2;
v(iffi) = О, 1(J) / > ffig/2 (ffig = 2:rt/Лт, ffig/2 = ffic),
имшульаиая ,реа1кrция ,которого описьювае11ся ,вьюраж,ением
sin 0,5 ffig t
v(t) =--~-
0,5rogt
~ •обла.дает свойством (•1"56). Ищеальиый филь11р низкой час11оты прещ,стасrэляет
собой ·чаrстный случай о'Гочетио.го фильт,ра. В ит,оге Iряд (,1!52) оовпщда,ет с ря
дJОМ ('1.'5"1). В этом случае фор1ма v(t) •не заIв·юоит от .ис1хЮIП!ИОЙ функции f(t).
Опрещмим опти,малыиую фу,нюцию v(t), для ,котор,ой ~ящ (1.52) в оредIием
на.илу,ч;шим обраэ•ам (•в смысле J<:вшд·рати~ЧiИО!ГО IЮJ)Ит,ерия) 1юоо,роизIвод:ит функ
~:щи из .зщzщи.ного клаоса . .Раоомотрим ,некоторую фу~и,~щию f m(t) со опектром
Fm'(iro) , пришащлежащую защанном,у ,кла•осу сrэеществещ1ых фуи,кций к-онечной
~шергии. Со1стаrвим для fm(t) ,рящ (,1.152)_ Если v(iro) ,не ущовлетвО1ряет (1 .54) ;
то э·ют 1ряд пIредJста1вляет fm(t) с ,по11решиостью, котоIрую оценим •величиной
Лт = Jx:I fm(t)- k=~
00
fm (kЛт) V (t-kдт{ dt = 2:rt 1, 1Fm (i ffi)-
-
Л~ v(iro) ki"'Fт(iro-kirog{ dro.
УюредJинм Лm по ,в•оему кла,ссу функций
•
1"'
Л= IртЛт= 2:rt S {IFm(iro) l2 -v(iro)C(iffi)-v*(iro)C*(i ro) +
т
- СХ)
+ \v(iffi)l 2 D(iffi)}dro,
где /Fm•(iro) /2
Fm·(iro); C(iro)
у~qр-е;дщеи,иьiй юва:,щр-ат -мо'дулей опектралЬ'иых ллот,иGстей'
00
.у~оредиеииая фу,и,кция ,вы,ражеиий ~F*m•(iro) ~ Fm(iro-
, k=-oo
11;
- k i@g); D(i,w) - .уоред,иеи,иая фу,Иiюция ,выражений Л,2 k~~ Fm 1(iro-kiro8)\ 2i.
Р т - некоторые весовые коэффициенты.
Найrдем _оптИJмалыиое rвыражеиие для v (i,ro), мииим,изwрующее п,огреши·ость
t:,. _ Минимум
Л достигается в том случае, е-сли бЛ = О, 11д·е l:JЛ - беок•оиечио ма
лая ваIриа;ция Iп оnрешиости Л, :вызванная бесконеЧ!ио ма\JIОЙ ,ва•р иаrцией фунюции,
v(Lro). Исходя из этого у,слювия шюнчателыио получим v(iro) =C*(iro)/D(iro).
МИJиlfмалыиое значение уюред:иенной ,по11решиости Iра,вио
1"'{
.
1с(iffi)\2} •
Лмин= 2:rt s IFm(1ffi)12С:-. D(iffi) d(J).
-ао
44
Эхспериментальиое моделирование импульсных реахций
отсчетных фильтров
Для пр,Иiвед;ения ха,рактеристwк р,еальных снстем связи, Iне .обла:Дающих
свойс11вом ( 1.1) , к хаIра~кте,ристика,м оrоqетных фильт,ров мо,луrг ,июполнз.о~атыся
-разли,q,ные линейные ,корlJ)екторы. Однако, ка,к показали эк-спеР'именталыные .и,с
следовашия, ,наwболее просто это •выполняет-ся с помощью га•рмон:и~qос.wих ко,р•
ректqро.в, теО1рия ко11О1рых ода.на ,в гл. 2-4. На рис. 1.- 21 изображены осцилло•
о)
Рис. . 1.21 . Ооци.л·ло11рам<мы иМ1пульс
Iных Iреа•Кiций Иiдеальног,о ( а), <i;K'OC!I •
,нуеои,далыног,о» (6) л «11реу,гольнюго ~
(в) фильТ1рОrВ
в)
граIммы эюопер,и,м енталыных импулысных реа1кций идеального (а), «ыосинусои
,дального» (6) и «Т1реу,голыног-о» (в) фильТ1ров, получен·ные после соот:ветствую •
щей ·к-ор,рек,ци.и НЧ канала овя~и (0-'3;4 !КГц). Все IJ)еа:юции сюВII!а,дают с ,рас•
четными с 'J1оq,ностью .цо 1-:2 %.
Использование преобразования Гильберта для схоростиой
передачи дисхретных сигналов
Как следует из вышеизложенного, импульсная реакция
ального .полосового фильтра (ИПФ) с полосой 1п ропускащrя
= Лrо/2:л и произвольными частотами среза ro 1 и ro2
(t) 'sin0,5Лffit
ffi1 +ffi2 t
g = • О,5Л(t)t cos
2
иде •
Лf=
(1.57)
не обладает свойством ('1.1), если Лf = l/2Лf (рис. 1.22а). Поэто
му через ИПФ нельзя передать равномерную после,довательность
импульсов (АИМ сигнал) с .максимальной скоростью 2Лf. Пере
дача с такой скоростью воз·можна .лишь 1д,ля · частных значений ro1
и ro2. Ниже рассматривается двухканальная . система связи, .по~
зволяющая осуществить одновременную передачу через ИПФ
двух последовательностей импульсных сигналов с результирующей
скоростью, равной 2Лf при произвольных ro1 и ro2 [ 1О]. В этой сис
теме .производится непосредственная передача импульсных сигна
лов без исп ользования модулирующих и д.емодулирующих уст'-
ройств.
45
/
/
/
/
\ g(tj
\
\
\
\
'·-../ 11)
,...\ 'j(t}
\
./
\
j
,_,, tf)
t
т
Каа1 кл,
сн л -вых.1.
вых, !'
ипq; !f и ~Вых2
2 Вых.2'
.
канал
В)
Р,и,с. ' 1:22. Импулысная реакция идеальног,о полос,овоrо
канала (а) и ее преdбразова11ше Гильберта (б); 1с11ру~к
т>7:р1ная схема tщвуХ1ка1Наль·ной системы ,с;вяз!i (в)
Принцип действия системы основан н_а свойствах импульсной
реа·кции ИПФ g(t) и ее преобразования Гильберта g(t). Извест
. но,
что некотqрая функция G (t) и ее преобразование Гильберта
G(t) связаны соотношением [5]
•
со
G(t) = _1 sG('t)d .-,
:rt
t- ,:
-оо
. ИЛИ
·~
1
s'"' .
.
t
.G(t) =
-
Re iК(iffi)e1 w dffi,
:n;
'
о
где К (.iro) -:- спектральная плотность функции G (t). Воспользовав- •
шись этими соотношения.ми, получ:и;м преобразование Гильберта,
от импульсной реакции ИПФ (рис. 11.226)
~(t)
sin0,5Лrot • ffi1 +ro2 t
g=
-
О,5Л(()t SlП
2
•
Преобразование Гильберта от е (t) дает функщию g (t)
ком минус: .
ао~
_ 1 s~d-r= -g(t).
:l't
t-т:
-оо
Функции g_(t) (1.57) и g (t) ( 1.58) обладают свойствами:
g(kТ)={1, k =О;
О, k:=i=O, k=±I, +2, ... (Т= 1/Лf),
g(kТ)=О (длявсехk).
(1 .58}
со зна-
(1.59)
Учитывая это свойс-~:во, рассмотрим работу двухканальной систе•
мы дисжретной передач и, приведенную на рис. 1.2.2в. Здесь Н -
преобразователь Гильберта, т. е. фазовращатель с фазовой харак"
теристикой, не зависящей от частоты и равной n/2 для диапазона •
ro,-ro2 . Коэффициент передачи преобразователя Гильберта равею
К(iro)=Н={ i (ro1-<:ro-<:ro2); .
н.
•
(
)
-t
- (J)z ,(: (J) ,(: -(J)l ·
Блок И - инвертор с коэффициентам передачи
-
1; блок ИПФ
идеальный полосовой фильтр, эквивалентный некоторому каналу
связи . Ключи Кл, и Кл2 работают синхронно и синфазно с часта.
той fm = 1/Т = Л{ и осуществляIQт выборку постуtПающих на них •
сигналов в моменты времени kT.
Передача импульсных сигналов через такую систему осуществ• ,
ляется слмующим образом. Пусть на вход канала 1 в некоторый
момент времени kT подано воздействие в виде прямоугольного
импульса амплитуды С и длительности -с, на1много ,меньшей интер- •
вала T(-r:«T) . При этом на выходе 11 возникает сигнал Cg('t), а
на выходе 1 - одиночный импульс амплитуды С . На выходе
.2'•
появится сигнал Cg (,t), а на выходе 2 в силу соотношения ( 1.59):
импульсный сигнал не возникнет. Аналогично ,при подаче на · вход . ·
канала 2 импульсно"го воздействия импульсный сигнал появи·тс'ii • .
толь.ко на· выходе канала 2; на выходе канала 1 сигнал не возник- ••
нет.
Из вышеизложенного следует, что ·каналы 1 и 2 взаимонеза
висимы в ·мо.менты времени .kT: воздействия, подаваемые на вход ·,
канала 1 в _ некоторые моменты времени kT, появятся только на
выходе .канала 1 также в некоторые моменты времени kT; воз·
действия, подаваемые на вход ,канала 2 в ,моменты времени kT,
появятся толь-ко на выходе канала 2. Вза:и;мный переход инфор•
.
·мации из каналов 1 и 2 в у,казанной системе отсутствует. Поэтому
47·
через такую систе,му можно передавать информацию одновремен
н о по каналам 1 и 2 ·без взаиrмной интерференции . По ,кажщому
из ,каналов информация передается в виде последовательности
э мплитудномодулированных импульсов со скоростью fm= 1/Т=Лf,
~ля которых т:«Т (Т-длительность импульсов), ,причем ско
р ость передачи не зависит от ,положения частот ffi1 и ffi2 и опре
деляется толь,ко их разностью. Скорость передачи для системы в
.целом равна ,2Лf . Данная система при замене ИПФ на ИФНЧ сов
падает с системой, приведенной в [22] .
Допустим, что в описанной системе вместо ИПФ используется
н екоторый ,полосовой фильтр с ,коэффициентом передачи К (iro).
Опрмели,м требования, которым должен удовлетворять К (iro) таn:,
чтобы импульсная реа,кция канала и ее преобразование Гильбер
та обладали свойством ( 1.59) .
Для решения поставленной задачи образуем вспомогательные
• дискретные функции:
00
01(kТ)=I [g(kT)-ig(kT)J,
-оо
00
0 2 (kT)= :I [g(kT)+ig(k Т)].
-оо
Спектры ~этих функций соответственно равны :
-00
00
K2 (iro)= ~ ~([g(kT)+ig(kТ)Je-iwkт_
-оо
Функции K,(iro) и K2(iffi) связаны с K(iro) соотношениями:
00
К1(iro) = ~к+(iro-niffic),
-оо
00
-
00
где roc=2n/T; K+(iro) и K-(iro) - правая и левая части функции
/( (,iro), расположенные соответственно в области положител~ных
и отрицательных частот~
При ВЫП(?ЛНении (1.59} имеем:
01(k,Т) =02(kТ)= 1= const (k= О);
01(kT)=G2(kT)=0 (k=l=O, k=+ 1, + 2, ...),
поэтому
К1 (i ro) = const;
48
\
\
К2 (i ro) = cdnst (для всех ro)
или
00
'
2i к+(i ro-n i roc) = const;
-оо
00
2iK-(iro-niroc)=const (для всех ro).
Эти требования выполняются, если действительная А (ro) и мни
мая В (ro) части К (iro) обладают свойство:м (рис. 1 . 23а, 6):
(,)z. -1 ,Jc
j
(,J
/J}
!((i,J)
d)
Рис. 1.23 . Графики действительной (а) и
мнимой (6) час'!'еЙ, моrд:уля л фазы (в)
коМIПлек,сной rпереда1'очшой функ,ции ,поло•
сс,вото ,канала -со -ав,ойст:1юм 011сче11н1ости
А(ffi) = а= const (ffi2- roc < 1(!) [ < ffi1 +roc);
А (ffi1 + ffik) +А (w1 + wc +wk) =а= const;
В(w) _:__ OJ (ro2- Wc< 1ffi 1< w1+wc);
В (ffi1 +wk)= - B(ro1 +roc +rok),
где rok - некоторая частота, удовлетворяющая неравенству
(1.60)
49
О< (J)h. < ffi2-ffi1-ffic ( ffic=2л/T; +Лffi < ffic < Лffi)•
При написании данных выражений не учитывалось постоянное за •
паздывание.
Моду,ль K(ffi) и фазовая характеристика cp(ffi) спектральной
плотности K(iffi) ,приведены на рис . 1.23в . Если - ffic = ffi2-ffi1, то
ffi2 - ffi1 - ffi c =O и единственно возможной формой K(iffi) является
фор;ма ,коэффициента передачи и~деального ~полосового фильтра .
В системе передачи, изображенной на рис. 1.22в, вместо ИПФ
можно использовать фильтр, коэффициент передачи которого удов,
летворяет (1,60). Для максимиза,ции соотношения сигна.л/шуrуr этог
фильтр должен обладать характеристиками
1
0,5а (ffi1< 1ffi 1< ffi2-ffic);
А(ffi)= а
- (ffi2-ffic < 1 ffi 1 < ffi1 +ffic);
0,5а (ffi1+ ffic< 1ffi 1< ffi2);
в(ffi)= о.
Из сравнения рис. 1.9 и. '1.23 вытекает, что если огибающая ре•
акции полосовой системы обладает свойством ( 1.1), то эта же
реакция обладает и свойством (1 .59) при условии, что ,Лt=Т .
Система , изображенная на рис . 1.22, осуществляет передачу
дискретных сигналов через синхронные полосовые каналы, харак•
теристики которых не меняются с течением времени. Покажем,
что использование преобразователя Гильберта позволяет переда ~
вать дискретные сигналы непосредственно и через несинхронные
кана,!JЫ. Рассмотрим систему, изображенную на рис . 1.24, в кото ,
!(анал
Pwc . 1 .24 . Стр~кту:ряая ,сх-ема пр,ием,ни
ка, ·работающего по не синхронно мrу ка
налу
рой Кд - квадратичные детекторы . Допустим, что канал являет ~
ся несинхронным, т . е . фазовая характеристика канала с течением
времени меняется на некоторую частотнонезависимую величину
(J)o . Коэффициент передачи такого канала можно представить в
виде ,Kнc(iffi) = K(i1ffi)eH(j)o, где K(iiffi) - коэффициент передачи сип .. •
хронного канала (без учета rcp 0); Н - коэффициент передачи пре ~
образователя Гильберта.
Квддрат аналитической огибающей импульсной реакции канала
описьiвается выражением g 20 (t) = g 2 (,t)+g2 (t) . Форма g 20 (t}
не зависит от ,ср0 . Если g(t) и g(.t) о(Sладают свойством
( 1.59), то g 20 (t) обладает свойством отсчетности (1.1) при
50
Лit= Т. Поэтому в системе рис. 1.24 можно передавать однополяр·
ньiе дискретные сдгналы непосредственно через несинхронный ка
нал со скоростью 1/Т, которая в 2 раза меньше скорости переда
чи в системах с синхронным каналом (см. рис. 1.22 в) и совпада
ет со скоростью передачи по синхронным каналам с характеристи
ками, изображенными на рис. 1.9.
1.4 . Минимизация межсимвольных помех
-в системах с интегральными методами приема
Системы с корреляционным приемом
Распространим результаты § 1.1 и 1.2 на системы с интеграль
ной обработкой 'принимаемого сигнала.
Структурная схема корреляционного приемника изображена на
рис. 1.25 . Используемые обозначения. : S(t) - рабочий (информа-
N(tl
Канал
S(t!
y(kЛt)
Рис. 1.125. К:орреляциюнный 1П1рием1ник
ционный) сигнал со спектром S (i{J)); ЧГ (t) - опорный (эталонный)
сигнал длительности ,Л,t со спектром ЧГ (i,(!)):
ЧГ(t)=О (t<-Лt/2; t>Лt/2).
(1.61)
Интегрирование ведется на отрезке [-М/2; ,:1t/2].
В широкополосном канале без линейных искажений S (t) =
= Ч1' (t), поэтому возможна передача сигналов со скоростью 1/,Лt
без межсимвольных (интерференционных) помех. В реальных ка
налах имеется рассеивание во времени, вызываемое многолучево
стью , ограничением рабочей полосы частот, линейными искаже•
ниями и т. д. В таких каналах S(t)=;i=ЧГ(t), в результате чего воз·
никают межсимвольные помехи, величины которых определяются
•соотношением
(2k+l) Лt / 2
.Y(kЛt)= S S(t)ЧГ(t-kЛt)dt (k=;i=O; k~- +l, +2, ... ). (1.62)
(2k- l) лt/2
Условие отсутствия межсимвол:ьных помех можно записать в
виде
g(kЛt)={ 1, k=O;
О, k=1=О, k=+1, +2, ...
(1.63)
Определим требования, которым должен удовлетворять спектр ра•
бочего сигнала S (t) при заданном спектре опорного сигнала ЧГ(t),
так, чтобы выполнялось условие ( 1.63). Эту зада чу решим в об
щем виде, не накладывая на опорный сигнал никаких ограничений,
кроме (1.61) .
51
'
С учетом (1.61) заменим в (1.62) пределы интегрирования на
бесконечные, что дает
00
00
y(kЛt)= 5s(t)ЧГ(t-kЛt)dt= 2~ 5s(iro)ЧГ*(iro)eiCJJkЛtdro.
-оо
-оо
Обозначим F(i,ro)=S(iro)Ч'*(i,ro), тогда y(kЛt) можно рассмат•
ривать как дискретные значения некоторой функции y(t) со спект~
ром F(i,ro):
с,,
у(t)= -
1- 1F(iro)ei(J)t dro.
2л J-оо
Очевидно , что для выполнения условия (1.59) функция y(t) долж~
на обладать свойством отсчетности ( 1.1), что возможно только в
том случае, если спектр этой функции удовлетворяет равенству
(1.4) ; т. е.
00
L F(iro-inrog)=Лt (rog=2л/Лt),
_
(1.64)
n=-oo
или
00
~S(iro- iпrog)ЧГ*(iro- i.пrog)=Лt.
(1.65)
n=-oo
Полученное равенство является решени(;м поставленной задачи,
т. е. указывает, каким образом должны быть связаны между с.о•
бой спектры рабочего и опорного сигналов так, чтобы выполня~
лось условие ( 1.63). Из этого равенства следует, что межсимволь "
ные помехи в корреляционном приемнике отсутствуют, если
спектр F(iro)=S(iro)Ч'*(iro) удовлетворяет первому критерию Най •
квиста . Поэтому, задаваясь P(iro), удовлетворяющим (1 .64) или
(1.4), можно по спектру опорного сигнала определить спектр pa w
бочего сигнала S(iro)=P(:iro)/Ч'*(iro) и наоборот.
Как видно из вышеизложенного, если скорость передачи -сигна ~
.тюв меньше скорости Найквиста (rog<2ffic), где ffic - граничная ча
стота спектра сигнала S (t), существует бесчисленное множество
пар рабочих и опорных сигналов, удовлетворяющих ( 1.63), так как
при этом существует бесчисленное множество F (iffi), удовлетворя
ющих ( 1.64) . Если уже ffig > 2ffic, то для ЧГ (t), имеющих конечную
энергию, не существует пар рабочих и опорных сигналов, удовле ~
творяющих (1 .63).
в частном случае, положив
(-Лt/2-< t-< Лt/2),
(t>Лt/2, t<-Лt/2)
или Ч' (iш) = 2 sin 'ffi ~, получим из (1.62), (1.63) и (1.65)
(1)
2
52
(2k+I) Лt/2
k=O;
5 S(t)dt={l,
(2k- l) Лt/2
О,.k=+1,±2, ...,
и
00
~S(i(J)- ikffig)
k=-oo
Лt
2sin(ffi- kffig)2
(ffi - k ffig)
(1.66)
(1.67)
или S(i,ffi) = 1wF(il(J))/2sin@~, где F(iffi) -пр оизвольный спектр,
2
, удовлетворяющий ( 1.64).
Выражения (1 .66) и (1.67) известны как третий критерий Най•
квиста [27]. По существу, третий критерий Найквиста позволяет
определить рабочий сигнал, использование которого устраняет
межсимвольные помехи в высокоскоростных системах с приемом
по методу накопления .
Приведем ряд примеров, иллюстрирующих изложенный мате•
риал. Пусть @c~ffig~21@c, что соответ~твует случаю высокоскоро·
стной передачи. Здесь '@с - граничная частота спектра рабочего
сигнала: /S(i,@) 1=0 (l@l>!(J)c). Допустим, что сигналы передают•
ся с максимально возможной скоростью ( скоростью Найквиста):
(!)g=2,wc. Спектр F(i@) определяется в этом случае однозначно:
F (i@)=Лt (1 (J)1< ffic); IP,(iffi)\=о (\(J) 1>@с)-
Выбрав в качестве опорного сигнала 1ЧГ(t) прямоугольный им"
пульс единичной амплитуды и длительности ,Лt, получим из (1.67)
.,
!ffiЛt/2sinffi~ (О<1ffi\<@с);
S(1ffi)=
2
О
(\ (J) 1> ffic)
(рис. 1.26, кривая 1).
Если выбрать в качестве опорного «треу гольный ~> импульс еди"
ничной амплитуды и длительности ,Лt, получим
.
!(ffiЛt/2) 2 /(1-cosffi~) (О< \ffil < ffic);
S(1@)=
2
•О
(\ ffi \> ffic)
(рис. 1.26, кривая 2) .
Для скоростей, меньших скорости Найквиста, спектр S (i@)
определяется неоднозначно. Н~шример, положив (J)g = iffic и выбрав
спектр F(i@) вида «приподнятый косинус»
F(iffi)=Лt(cos :п;ffi)2 (1@1<@с),
2@с
для прямоугольного опорного сигнала получим (рис. 1.26, кри•
вая 3)
53
1
(i)лt ctg(i)лt
S(i(i)) =
4
4
о
(О<J(i)1<(i)c);
(\ (i) \ > (i)c).
Как вытекает из приведенных рисунков, при скоростях, близ •
ких к предельной скорости, спектр рабочего сигнала резко изме •
няется в области граничной частоты wc ; если же скорость переда
чи существенно ниже предельной скорости, спектр рабочего сигна
ла имеет пологий скат в области граничной частоты .
1
Р.и,с. 1.,26. Опек11р Iрабочего сиnнала [DРИ 1П1рямоуголь
ном опорном си11нале (сr<iрл ,вая 1), «треу,голь-ном»
сшор,ном сигнале (,кривая 2) и апар,ном сигJiале
, <~!11р11Jпа,щнятый \КОСИН)IС» (юри,вая 3)
Оценим помехоустойчивость системы с корреля ционным при
_емником, в которой спектры рабочего и опорного сигналов связа•
ны соотношением (1.65) .
В реальных условиях сигнал на входе приемника X(t) пред
ставляет собой смесь п олезного сигнала S (t) и аддитивной поме·
х~ 1 N(t) (см. рис. 1.25). На выходе приемника имеем
Л t/2
SХ(t)Ч'(t)dt= а+Ь,
,-Лt/2
Лt/2
где
а= 5S(t)ЧГ(t)d(t) = у(О)
-Лt/2
,
полезный сигнал; Ь =
Л t/2
-
J N(t)'Jf(,t)dt- помеха.
-Лt/2 ,
При высокоскоростной передаче отношение сигнал/шум с уче
• том межсимвольных помех равно h = a/ V Р1 +Р2, где Р1 - энергия
со
аддитивной помехи; Р2 = I у2 (kЛt) - энергия межсимвольных
k=-o o
k=/= -0
,
1 Здесь и в далЬ'нейшем предполагается, что- соответствующий аддитив,ному
' шу,му п.роцесс N(t) является ,стаци,она,р,ным гау~ссов,ским про,цес·оом с .нулевым
средним.
54
помех; а=у(О) - значение полезного сигнала в момент регист~
рации.
Если спектры рабочего и полезного сигналов связаны между
собой соотношением (1.65), то в силу ('1.63) Р2=О, поэтому h=
=a/VP1 ,
Таким образом, отношение сигнал/шум на выходе корреляцие
онного приемника при высокоскоростной передаче определяется по
той же формуле, что и в случае низкоскоростной передачи, когда
нет в заим ного наложения передаваемых сигналов. Иными словами,
если выполняется условие ( 1.63), помехоустойчивость узкополос~
ного канала определяется только аддитивным шумом так же, как
и помехоустойчивость широкополосного канала.
Распростаним результаты § 1.3 на системы с корреляционным
приемом . Определим связь между S (iw) и 11' (i,w) исходя из ус•
ловия
(2k+l) Лt/2
y(kЛt)= S S(t)Ч!(t-kЛt)dt=C1i (k=O, ±1, ±2, ... ), (1.68)
(2k-l} Лt/2
где Ck - заданные величины .
После ряда преобразований, аналогичных вышеприведенным ,
выражение (1.68) с учетом (1.61) приобретает вид
00
y(kЛt)= 21л SP(iw)eiwkлtdw=C1i _(k=O, +1, +2, ... ),
-оо
где y(,t) - функция со спектром F(iw) =S(iw)Ч'*(iw) . Поскольку ·
это выражение не отличается по форме от выражения (1.44) , по
аналогии с ( 1.45) можно записать
00
00
:I F(iw-ihwg) = Лt I C1,,e-iwkлt
n=-oo
k=-oo
(wg= 2 л/Л t)
или
00
00
~ S(iw-inwg)Ч'*(iw___-_inwg)=Лt I C1,,e-iwkл_ t .
п,;=-оо
k=-oo
-' (1.69)
П о лученное выражение определяет связь между спектрами рабо
чего и опорного сигналов с учетом выполнения условия ( 1.64) . По- ·
ложив в (1 .68) и ('1.69) C1,,=l(k=O) , С1,,=О (,k=l=O, k =± 1,
±2, ... ), приходим к выражениям (1.63) и (1 .65).
Из сопоставления выражений (1.69) и ( 1.45) вытекает, что,
заменив в выражениях (1.48) и (1.50) K(iw) на F(i1w) = ,
= S (iw) Ч'* (iw), получим соответственно условия отсутствия иска - •
жений длительности импульсов и условия одновременного отсутст ◄
вия межсимвольных помех и искажений длительности 1rмпульсов •
в системах с корреляционным приемом .
•
"
55
-.
Нетрудно видеть, что, заменив во всех выражениях § 1.2 К (iю)
на F(iю)=S(iю)ЧF*(i<ю), получим формулы, позволяющие опреде
лить связь между спектрами рабочего и опорного сигналов, ис
пользование которых в корреляционных системах уменьшает по
меху, вызванную девиацией моментов выборок (девиаций периода
интегрирования), увеличивает отношение сигнал/шум в корреля
ционном приемнике при одновременном устранении межсимволь
ных помех и уменьшает межсимвольные помехи при скоростях пе
редачи выше скорости Найквиста.
Многоканальные корреляционные системы
.
В многоканальной системе с корреляционным приемом (рис.
1.27) рабочие сигналы Sт(t) со спектрами Sm(iю) (m = 1, 2, ... , М)
одновременно передаются в одном канале со скоростью 1/,Лt (М -
11t (t)
Канал
--
--
-
--
......
м
11-Цt}
Р,нс. 1.27. М1ногока1нальная си-стема ,с К()р
. рел яциоН1 Ным
приемом
заданный интервал). На
М - входы многоканального
корреляционного приемника
поступают рабочие сигналы
Sm (t) и подаются заданные
опорные сигналы ЧFm(,t) со
спектрами ЧFm(iю). Сигналы
чr т (,t) - конечной длитель
ности: ЧFm(t) = 0 (t< -Лt/2,
t>Лt/2), где Лt - период
интегрирования .
Найдем, какая связь
должна быть между Sm(iю) и ЧFm(iю) так, чтобы выполнялось
условие
(2k+I) Лt/2
!Jтp(kЛt)= J Sm(t)Wp(t-kЛt)dt=CmpCkO
(2k-l) Лt/2
(т,р=1,2,...,М;k=0,+ 1,+2,...),
(1. 70)
где Стр и Cko - заданные величины; YmP (kЛt) - значения сигна
лов на выходах корреляционного приемника в моменты регистра
ции k.Лt. При k = 0, т = р получаем полезное значение сигнала, ко
торое должно совпасть с СттС00 ; при k =!= 0, т=/=р получаем меш а
ющее значение сигнала (межсимвольные и межканальные поме
хи), которые должны совпасть с СmрСя.о-
После ряда преобразований выражения ( 1.70) получим
ro
ro
~с,("
•
)пr*("
•
) Лt~.,
СС--iwk_Лt
_..
,Jm 1(J)--;-1nffig I 1(J)-1nffig =
.!..J
mp kое
n= -oo
k=-oo
(юg=2л/Лt, т, р = 1, 2, ... , М).
56
(1. 71)
Это равенство указывает связь между спектрами рабочего и
о п о р но го сигналов с учетом вы п олнения (1.70).
Для отсутствия межсимвольных и межканальных помех на
М - выходах корреляционного приемника необходимо и достаточно,
чтобы
Стр = бтр;}
(1.72)
Cko=бko,
/
где бij - символ Кронекера (бij= 1 при i= j; бij=O при 1i=l=j) .,
Подстановка (1.72) в (1.71) дает
со
~ Sm(iffi - i'1ffig)ЧГ*(iffi-inffig)=Лtбmp (m, р= 1, 2, ... , М) .
(1.73)
n=-CO
П олученное равенство представляет собой, по существу, обобщен•
ный критерий Найквиста для систем с многоканальным корреля"
ционным приемником.
00
Изменим форму записи равенства (1.73) .
Обозначим
~ Sm(iffi-iпffi!)чr;(iffi-iпffig)=G0(iffi).
n=- oo
Функция Go (iffi) - периодическая с периодом ffig, имеющая чет
ный модуль и нечетный аргумент, поэтому G0 (iffi) полностью оп "
ределяется на отрезке (О, ffig/2). Разобьем положительную ось
частот на неперекрывающиеся полосы
O,S(q - l)ffig < ffi < 0,5qffig (q= 1, 2, 3, ...).
Спектры Sm(iffi) и Ч'p(iffi) в пределах каждой полосы будем
рассматривать как отдельные функции, которые обозначим соот
ветственно через Smq и ЧJ'pq . Тогда равенство (1.73) можно запи_..
сать в виде бесконечной системы уравнений
00
1 t,S ЧГ"
Лtl,J mq •;q = бmр•
(1 .74)
. q=I
В реальных каналах спектры рабочих сигналов Sm(i ffi) всегда
ограничены некоторой частотой ffic. Птному бесконечная система
уравнений (1.74) превращается в конечную; Задавшись спектра•
ми опорных сигналов, из этой системы можно определить спектры
рабочих сигналов при условии, что определитель системы уравне -.
ний не обращается в нуль. Подчеркнем, что решение системы
(1. 74) существует только пр и М л,,/Лt ~ 1ffic-
Ha рис. 1.28 приведены примеры графиков спектров рабочих и
опорных сигналов для случая М = 2, 1ffig = ffic (ffiс-rраничная частота
канала, т. е. граничная частота спектров рабочих сигналов) . В ка:..
честве опор н ых выбраны сигналы:
57
Рис. 1.128. Г:рафики ап ектров опОIJ)ных и ра<боч:и,х с и11наJ1101В
двух;кана,лыной кор~реля~циоюrой системы
1
'l' (О<t<Лt/2);
'I'1 (t) =
-1 (-Лt/2<t< О);
О (ltl>Лt/2);
'У(t)={1 (-Лt/2<t<Лt/2);
2
о (1t1>лt/2).
Спектры рабочих сигналов найдены с помощью уравнений (1.74).
Согласованная фильтрация
Пусть на вход приемника, представляющего собой линейный
фильтр с коэффициентом передачи K(iffi), поступают сигнал S(t)
со спектром S(iffi) и аддитивный шум N(t) с энергетическим
спектром N (Ф). Отклик приемника на сигнал S (,t) в некоторый
момент времени Т равен
00
V(1)= -1
-
Js(iФ)К(iФ)е1wтdФ.
2:rt
.
-оо
.
Известно [29], что максимум отношения сигнал/шум
q . V (1)/V]\,
00
где Р1 = 2: f N(Ф) IK(iФ) j2d,ffi достигается при
·о
К(iФ)=С S*(iФ) е-1wТ
N(Ф)
(C=const). В этом случае имеем:
(1.75)
(1.76)
00
ir(Т) = _.!2_ S!\S(iffi)i2 dffi=А=max.
.
2n
N (ffi)
-
00
Определим, для какого спектра S (i,ffi) эн_ергия межсимвольных по "
мех на выходе согласованного фильтра равна нулю:
00
Р2= L IV(T+ kЛt)l2=0,
r,11e
k=-ro
k=pO
00
V(T+kЛt)=-1- Jv(u?)eirokЛtdffi,
2n
-оо
i' (ffi)·= С IS (i ffi)\ 2/N (ffi).
Для выполнения ( 1:77) необх9димо и достаточно, чтобы
V(T+kЛt)={A, k=O;
·
О, k=:/=O, k=+I, + 2, ... ,
что выполняется при
,,,
~ 11· (ffi-nffig)=AЛt (ffig=2л/Лt).
n=-ro
(1. 77)
(1. 78)
(1. 79)
Как показано в 1§ 1.2 и 1.3, если lffig ~ 2ffic ,[1wc - ширина спектра
S(iffi), т. е. ширина спектра V(.ffi)J, то существует бесчисленное
м н ожество V(ffi), удовлетворяющих (1.79) . Поэтому всегда можно
выбрать V(,ffi) >О и далее с учетом (1.78) и (1.75) получим:
s(i ffi) 1 = Vv(ffi)N(ffi)/C;
к(iffi) \ = Vсv(ffi)/N(ffi) .
Фазовые характеристики ,ср 1 (ffi) и ,cp 2(,ffi) сигнала и фильтра -
произвольные, но такие, что ср 1 (1ffi)+1cp2(ffi) =-wT.
Отношение сигнал/шум (1 .76) для найденных характеристик
сигнала и фильтра принимает вид
/1~т
qмакс= t - \t (ffi) dffi .
1tс '
-00
Если ffig> 2ffic, то равенство ( 1.77), в принципе, не выполняется.
Однако, выбрав в качестве V(w) характеристику фильтра, най •
денную в § 1.2, пол учим характеристики сигнала и согласованного
фильтра, обладающие те м свойством, что энергия межсимвольных
поме х на выходе согласованного фильтра будет минимально воз"
можной. Очевидно, что , использовав в качестве V(w) характери•
стики отсчетного фильтра, синтезированные в §. 1 .2, получим ха•
рактеристики сигнала и •согласованного фильтра, минимизирую•'
щие энергию поме х и, вызванной неидеальной синхронизацией .
59
Мяогокаяальиые фильтровые системы
На рис . 1.29 изображена структурная схема многоканальной
системы , в которой прием осуществляется линейной I фильтраци
ей - сигналов. Используемые обозначения : Sm(i(J)) и ЧГm(i(J)) (т=
2
м
1
1
1
/
= 1,2, ..., М) - коэффици-
енты передачи соответствен
но перед ающих (формирую-
z щих) и приемных фильтров;
К (i(J)) - коэффициент пере
дачи гр у ппового канала свя
зи.
L-@З---м Пусть Y m P (t) - импульс
ная реакция р-го приемного
фильтра на воздействие ('б-
Р,ис: 1.29 . Мно11ака11rальная филь11ровая си- ф
)
от ема
ункцию , поданное на вход
т-го передающего фильтра.
Потребуем, чтобы выполнялось условие
Утр(kЛt)=СтрС1,, 0 (т, р= 1, 2, ... , М ; k=0, +1, +2, ... ), (1.80)
где YmP (kЛt) - значения сигналов на выходах приемных фильт •
ров в моменты регистрации ,kЛt; Стр и См - заданные величины.
При ,k=0, m=p получаем полезное значение сигнала, совпадаю
щее с СттС00 ; при k=l=-0, m=l=-p получаем межсимвольные и меж •
канальные (интерференционные) помехи.
.
Воспользовавшись результатами § 1.2 и 1.3 , получим, что вы
полнение условия ( 1.80) эквивалентно выполнению равенства
со
L Sm (i (J)-i nrog) K(i (J)-i n(J)g) Ч'р (i ro-i n(J)g) = -
n=-oo
00
=Лt }: СтрС1,,0е-1(J)kлt((J)g=2л/Лt; т, р= 1, 2, ... , М). (1.81)
k=-"'
Межсимвольные и межканальные помехи на выходах прием •
ных фильтров отсутствуют, если Стр= 1бтр, См= ,бм, где бij - сим•
вол К:ронекера. Подстановка этих значений в (1.81) дает [15]
со
V Sm(i(J)-iпrog)К(iro-iпrog)ЧГР(i(J)-
...i
n=-co
-inrog)=Лtбmp (т, р=1, 2, ..., М) .
(1.82)
Если в рассматриваемом диапазоне частот K(iw) =const= 1l, то
равенство ( 1.82) принимает вид
00
~ Sm(iro-inrog)Ч'p(iro-inrog)=Лtбmp (т, р= 1, 2, .. . , М) .
n=-oo
Для максимизации соотношения сигнал/шум при наличии в ШИ 4
60
рокопо лосн ом к анале аддити вны х помех фильтрации сигнал ов
до.1жна быть согласованной, т. е. S *m( iw) = Ч'm(iw) и.1и
О>
n=- co
На рис 1 . ЗОа приведены примеры коэффициентов передачи пе
ред ающих и приемных фильтров двухканальной с истемы с согла
с ованной фильтрацией (рис. 1.306) . Для этой систе м ы справедли.
(Jj
2
z
Рис. 1.30 . Пiримеры коэффищиентов передаl'!и фQр~ми
рующих и 1цриемных фильтро,в д<ВуХJКа,нальнюй си,стемы
с сог.ла,сава1нной фильтра,ц;ией (а) и стр}'lкту:р1ная схе
ма сl!!Бухка1налыной о~стемы (6)
вы соотношения: IS1(i,w) / 2 =V(w)-произвольная положительная
вещественная функция , удовлетворяющая условию
00
I V(w-nwg)=Лt (wg=2л/Лt =wc);
11=- 00
S2(iro) 12 = Лt-1S1(iw)l2 = Лt-V(ro);
1[q,,(oo)+: ]
S1 (iro) = YV(w)eiq,,(oo>;
S2 (iw) = VЛt-V(ro)e
;
61
, где 1ср 1 (ш) - произвольная нечетная функция; 1ffic -
граничная час·
тота полосы пропускания фильтров. По каждому из каналов си•
стемы передаются сигналы без межсимвольных и межканальных
помех со скоростью 1/1Л:t = шg/2л = ш◊/2л. Суммарная скорость пере•
дачи равна ,ш◊/л, т . е. совпадает со скоростью Найквиста.
Заслуживает внимания частный случай многоканальной систе~
мы с согласованными фильтрами [28], в которой коэффициенты
передачи фильтров вы:_браны, как указано на рис. 1.31, где жир•
ной кривой изображена амплитудно-частотная характеристика
m -ro фильтра с шириной полосы проп уска ния 2Q (шm - средняя
/K(ir. , )/
CJ
Рис. ·1.311. Раюположени-е 1коэф.фи~циентов 1Jiереда,чи мно
гока,налыrой оистемы с согJшсаван,ной фильтрацией, ин- ·
ва1риа1нтной .к линейным .и,с'Кажениям гр,у1ппового ка
на·ла
частота полосы пропускания фильтра). Все фильтры имеют оди•
наковые по ·ширине полосы пропускания и одинаковые п о форме
амплитудно - частотные характеристики. Коэффициенты передачи
двух расположенных рядом фильтров [например , • Sm(iw) и
Sm+ 1 (iш)] в диапазоне частот •ffim -
ffim+ 1 связаны между собой
теми же зависимостями, что и коэффициенты передачи фильтров
двухканальной системы, изображенной на рис. 1.30 . Особенность
рассматриваемой системы в том, что, выбрав 2Q достаточно ма
лым (т. е. выбрав число каналов достаточно большим), можно
сделать каждый из каналов системы малочувствительным к ли- _
нейным искажениям в групповом канале с коэффициентом переда
чи К (iw). Это объясняется тем, что в пределах полосы пропуска
ния · каждого из каналов (2Q) коэффициент передачи группового
канала К (iш) изменяется незначительно. Такая многоканальная
система в целом малочувствительна (инвариантна) к линейным
искажениям группового канала. Естественно, аналогичный резуль-
, тат получается и· в многоканальных корреляционных системах (см.
рис. 1.27), если расположить соответствующим образом спектры
рабочих . и опорных сигналов.
.
Отметим . важную особенность рассматриваемых систем. Квад•
раты модулей спектральных плотностей сигналов на выходах пе
редающих фильтров удовлетворяют равенству (1.83). Поэтому
62
со
2n SISm(iw)l2dw= ЛtQ= const,
-оо
т. е. энергии указанных сигналов одинаковы и не зависят от
Sm(i1ro) (т= 1, 2, ..., М) . Следовательно, с точки зрения загрузки
группового канала безразличен выбор формы частотных характе
ристик формирующих фильтров ![ естественно, в предположении,
что при выборе удовлетворяется равенство (1.83)] . Для корреля·
ционных систем (см. рис. 1.27) этот вывод несправедлив.
Выбор оптимального опорного сигнала в системах
·с
корреляционным приемом
Выражение (1 .65) позволяет, задавшись опорным сигналом
ЧГ (t), определить рабочий сигнал S (,t), исходя из условия отсутст
вия интерференционных помех на выходе интегрального приемни•
·ка (см. рис. 1.25). Однако это выражение не отвечает на вопрос,
как оптимальным образом выбрать опорный сигнал . Поэтому по•
.
дойдем к вопросу выбора опорного сигнала с позиций максимиза
ции отношения полезного сигнала к энергии аддитивной помехи
на выходе корреляционного · приемника.
При выполнении (1.65) отношение сигнал/шум равно
h=y (0)!VP1,
где у(О) - значение полезного сигнала ; Р 1 - энергия аддитивной
помехи :
Лt/2 Лt/2
Р1 =Ь2 = S S K(t, 0)ЧГ(0)ЧГ(t)d0dt>О,
-Лt / 2-Лt /2
Л t/2
Ь= SN(t)ЧГ(t)dt
-Лt/2
(1.84)
i[ черта над соответствующим выражением означает ст а тистическое
усреднение i:ro всем реализациям аддитивного шума N (it)] . Здесь
K(t, 0) =N(t)N(0) - положительно определенное симметричное
ядро, имеющее смысл функции корреляции шума N(t) .
Если выполняется (1 .65), то у(О) = 1 =const и для максимиза
ции . h необходимо минимизировать Р 1 . Поскольку Р 1 зависит от
;\1' (1t), найдем опорный сигнал из условия получения минимума
Р 1 . Чтобы эта задача имела смысл , минимум Р 1 необходимо искать
при условии, что энергия сигнала конечна:
Лt/2
JЧГ2 (t) dt = const.
(1 .85)
--Лt/2
Итак, мы пришли к- классической вариационной задаче минимиза ~
.ции квадратичного функционала (1.84) при ограничении (1 .85) .
Известно [З], что квадратичный функционал принимает стационар -
63
ные значения, если чr (t) удовлетворяет однородному интеграль~
ному уравнению •[32]
Лt/2
лЧ'(t)= SК(t, 0)Ч'(0)d0.
(1.86)
-Лt/2
где rл - множитель Лагранжа.
Для нахождения оптимального сигнала чr (t) необходимо вы ~
числить собственные функции полученного уравнения и выбрать из
них ту, которая имеет наименьшее собственное значение (Л , т. е.
дает миним у м Р 1 . При использовании данного подхода, однако,
нужно учитывать следующее. У некоторых квадратичных функцио •
налов собственные функции могут и не соответствовать минимуму
функционала , например, если ядро K(t , 0) - вырожденное , то
п
K(,t,0)=~
,am(10) ·Pm(t). В этом случае любая функция Ч'(t) ,
m=I
ортогональная на отрезке [-1М/2, М/2] ко всем функциям am(t)
либо ко всем функциям Pm(t), обращает квадратичный функцио ~
нал (1.84) в ноль и в то же время может и не являться его собст"
венной функц_ией . Вырожденные ядр·а получаются, например, если
помеха N(i) - детерминированная . Другим примером может слу"
жить помеха N(t) , имеющая случайный характер, но такая, что
можно выбрать сигнал - чr (t), ортогональный на отрезке
i [-Л,t/2, :Л-t/2] ко всем реализациям N(t) . Для этих частных ситуа .
ций ядро функционала (1.84) является положительно полуопреде•
л е нным. Подобные ситуации, в силу их тривиальности, в дальней
шем не рассматриваются .
Решим рассмотренную задачу на основе локально-оптимального
синтеза, для чего будем считать, что
т
Ч'(t) = ~ a1Jn(t),
(1.87)
k=I
где Fn(t) - ортонормальные на отрезке [-Лi,/2, tЛt/2] базисные
функции . Такое представление опорного сигнала превращает
квадратичный функционал (1.84) в положительно определенную
квадратичную форму
т
Р1= ~ Akiai a1t,
(1.88)
•
i, k=I
где
Лt/2
A1ti=AiA1t , A1t= S Fп(t)N(t)dt (k=l, 2, .. . ,т),
-Лt/2
Ограничение (1 .85) эквивалентно ограничению
т
~ а~= const .
(1.89)
k=I
64
Итак, мы пришли к задаче минимизациI:I квадратичной формьщ
(1.88) при ограничении- (1.89). Полное решение таких задач дает
спектральная теория квадратичных форм (приведение квадратич
ных форм к главным осям). Не останавливаясь на особенностях
этой теории, которая хорошо разработана и изложена в ма~ема
тической литературе , например в ,[3, 30, 31], укажем общин по
рядок нахождения оптимальных коэффициентов а"- (k=J, 2, ... , m).
минимизирующих · Р 1-
•
• 1. Определяем характеристические числа x,Jk= 1, 2, ... , m )'
(спектр) · и соответствующие им собственные векторы L"- (k =;с 1,
2, ... , m) матрицы А, составленной из элементов А;"-. Числа Xk яв
ляются корнями характеристического (векового) уравнения
l·xE - А 1~О, где Е - единичная матрица: 1 • 1 - определитель,
разности матриц. Векторы L"- удовлетворяют
уравнению AL"- =
=x"-L" (Li, -
вектор-столбец).
·2. Выбираем вектор · L1, с минимальным характеристическим
числом хмин- Компоненты этого вектора и являются оптимальны~
ми искомыми коэффициентами а"- (k= 1, 2, .. ., m), минимизирующи
ми максимум Р 1 , причем величина этого минимизированного мак ~
симума равна Хмин•
В общем случае квадратичная форма Р 1 имеет т собственнъж
взаимно ортогональных и нормированных по длине векторов ;.
сводящих максимумы Р 1 к минимально возможным значениям;,,
равным характеристическим числам. Наряду с оптимальным век-·
тором (с характеристическим числом Хмин) остальные собственны~
векторы также представляюt интерес, так как позволяют получить._
набор взаимно ортогональных оптимальных опорных сигналов
чr(t), использование которых в многопозиционных системах при
ведет к минимизации влияния аддитивных помех на передачу мно
гопозиционных си~налов.
Несмотря на то что локально-оптимальный синтез не дает тех
предельных оптимальных форм эталонных сигналов, которые полу..
чаются с использованием интегрального уравнения (1 .86), пред"
ставление сигналов в виде полиномов ( 1.87) оправдывается сооб,~.
ражениями простоты их практической реализации и простоты вы
числения этих сигналов. Указанные _представления важны в осо...,
бенности при синтезе адаптивных систем с интегральным приемом "
а именно систем, в которых формы эталонных и рабочих сигналов:
меняются при изменении характера искажений и шумов в канале::
связи. В таких системах сигналы должны описываться полиномами ;
( 1.87), а в генераторах этих сигналов необходимо предусмотреть.
возможность регулировки коэффициента а"- (k= 1, 2, ... , m). Оче.
видно, _ что алгоритмами оптимальной адаптации (алгоритмами·
подбора оптимальных ak) должны быть алгоритмы приведения P t;.
к главным осям (в частности, динамическое программирование) ..
В настоящее время разработаны различные вычислительные,
алгоритмы приведения квадратичных форм к главным осям [31]~
Однако согласно закону инерции квадратичных форм конечный:
. результат,
т. е. спектр формы, не зависит от способа его получения ..,
3-181
65,
Это подчеркивает оптимальность •и единственность указанного
выше конечного результата определения искомых коэффициен
-тов ak.
Примеры синтеза опорных сигналов
Представим аддитивный шум N (t) на отрезке ,[ -iЛt/2, tЛt/2] в
в виде канонического разложения [34]:
N(t)=I
zk s1i (t)
k=-oo
(рассматриваются стационарные шумы с нулевым средним, что,
впрочем, не нарушает общности рассуждений). При этом ядро
уравнения (1.86) (корреляционная функция шума) имеет вид
00
К(t, 0)= ~ а~ s1i (tH1i(0),
(1.90)
k=-oo
тде r:fk=Z21< - дисперсия коэффициента Z1< . Считаем, что разложе
: ние ортогональное, т. е. функции s1i (t) ортонормальны на отрезке
u -лit/2; ,Лt/2] (разложение Карунена - Лоэва) [34]
Лt/2
Zik= 5N (t) Sk (t) dt.
-Лt/2
·с учетом (1 .90) решением интегрального уравнения (1 .86) яв
~ яется любая функция 'Sk(t) с характеристическим числом, равным
1()'2 11, .
П оскол ьку в общем случае последовательность {a 2k, k= 1,
2, ... } не имеет наимен:ьшеtо числа, а только оtраничена снизу
н улем, то- в качестве оптимального сигнала 'P'(t) необходимо выб -
1() ать ту функцию sk(t) из базисных функций ортогонального кано
!Н Ического разложения, которой соответствует доп устимое значение
td2k, В итоге получим Р1 = -a21i.
Базисные функции канонического ортогонального разложения
удовлетворяют интегральному уравнению [34]
At/2
fк(t, енk(0)d0=лk s1i (t),
(.1 .91)
-,·Лt/2
кошрое идентично уравнению (1.84). Это подчеркивает, что опти
м альный эталонный сигнал чr (,t) действительно должен совпадать
tC щдной из базисных функций канонического ортогонального разло
жения шума N(t). Полученные результаты указывают на связь
i!:интез а оптимальных эталонных сигналов для систем с интеграль•
!НЫМ приемом с каноническими разложениями случайных процес•
rеов . Приведем ряд примеров синтеза оптимальных опорных сиг•
,налов .
Пример 1. Пусть N(t) - белый шум с бесконечным спектром и сред,ней
ающностью .на elдИIIЫ!JliJY ШJ11рюны 1по.1юсы Nо(О-:;;;;.ы/2п-,;;;;.оо), т. е.
tfi.6
N
K(t. 8)=-fo(t-8),
где б (t) - дельта-фу,нкция. Для та1ког-о ,процесса любая сист,ем·а OIJ)TOHD!P•Maль -:
,ных фун.к,ций 1;.(t) дает ка,но,н,и,чеок,ое ~разложение, та1к .ка,к любые функ,ции
,ущ,авле11в,о,ряют уравнению (1 .91) . Для ~,с€х этих фу,н,к,ций и2.= ,л.=Nо/2 . Та,ки м
обра:зом, 1в слу,чае белого шу,ма с беок,онечным апек11ром 1ра1В1ноценен ,выбор в- .
качест.ве ЧГ(t) лю:бой фу1нкции из nр,оиз'в,ош,ной ,ортон,ормал ь.ной ,на отре31Ке
[-;Лf/2, лt/2] еистемы фу,н,щий.
Пример 2. Шум , N (t) - б е лый с ограниченным частотой Wc спектром , таю
N0 siпu>c(t- 8)
К1(t,8)=2
-
8.
л
t-
Для ,пр остоты ,считаем, чт,о No/2= ,1.
Оптимальный си,г.нал ЧГ(t) долж ен удовлет,ворять у,ра,вшению (1 .' 86), ,кото-
рое принимает сrш,д
Лt/2sinffi (t- 8)
лчr(t)= 5 ,
с •чr(8)d0.
-Лt/2 Л(t- 8)
Решением это,~,о у,ра,в1нения я,вляю11ся, как из,вестно, ,волновые сферондаль
ные функщии, обра:з,ующи-е для любых Лt> 'О и wc>O оче11ную ,бесконеч,ную ,по
сле_щовательность ортонор,малыных ,на от.ре3ке [---4лt/,2, лt/,2] функций Ч'0 (t) •.
Ч'i(t) , ЧГ2 (t), ... с ха,ра,ктер:и:ст,ичеокими ч·ислами ло>л1>л2 .. . Пер 1вая функция- ·
Ч'о(t) - описывает сигнал с максималь
ной избирательностью по частоте, т. е .
сигнал, спектр которого максимально
сжат в заданном частотном диапазоне
'[35, 36] . Однако оптимальный опорный
с и гнал Ч' (t) описывается, в отличие от
сигнала с м аксимальной избирательно
с тью по частоте , не первой волновой сфе
роидальной ф ункцией, а ф ункцией, кото
рой соответств у ет по во зм ожности малое
значение л ,, . Величина Р 1 при этом бу
дет равна Л k- В канале без интерферен
ционных по м ех величина 1 /лk равна от- 0
ношению сигнал/шум. Важным свойст- - ,
5
во м волновых сфероидальных функций
является то, что значения л. резко умень- Рис . 1.32 . Лрафики ,волно1вых оферои
шаются с ростом k, если k>wc,лt/л. далыных фу~нкций
Этим свойством и необходимо пользо-
ваться при выборе оптимальных опорных сигналов. На рис . 1.32 приведены гра-
фики ф ункций Ч'k(t) (k=O , 1, 2, 3) для W oЛt/2=4 (ло=О,995 ; Л1=O,912; л2 = O,519 ;
лз=О,11O).
О11мети,м одну оообенность волновых ,сфероидалыных фу:нк;ций.
Из~естно, чт-о
'
(!)с
sIЧ'k(ffi)l2 d(t)
-roc
Лk = -~------
где Ч'" ('w) -спектр Ч' k (t). Э:го свойство показывает, что для больших k спект
ры функций Ч'1, (t) соср ед оточены вне диапазона [-wc, Wc] и выбирать Лk
сколь .уго;що малой величины нель.зя .
З*
\ ~..)
67f
Пример 3. Пусть N(t) - белый шум с полосным опектром.
Для ЭTOII'•O ,слу,чая полу,чи,м
Дt/2
,._
_
N0 s[siпffi2(t- 0) siпffi1(t- 0)] 0 0
чr (t)---:- 2:п
t-0
-
t_0
чr<>d •
-Ы/2
•
где No - плот;1-юсть шума; W1 и W2 - нююняя и •в1:1росняя гр_ани<Dные частоты
опек11ральн·ой ПЛОТН·ОСТИ . Из этого • ,ура-В1нения, JIОЛОЖ·и:в W1 = 0, IЩР,ИХОДИМ ка,к
ча•стный .случай :к примеру 2.
Пример 4. Шум N (t) - стационарный в широком смысле случайный _ про
-цеос ,с ДIЮКiрет ,ны,м га·рмониче С'ким апектром
п
N(t)=~(511.cosffikt+11ksinffikt).
k=I
где \;2 h = '11 2 k = ak/2, а ,оре1дн,ие ,случайных в-елwчиIн 51t -и 1']k и ,всех их ~взаимных
к о,р1реля:ций равны · ~нулю; Wk =kw 1.
-
за,дан,ные ча~стоты.
Шу,м N(t) я1Вляется ,наложением га,р,моничвс-ких колебаний ,с,о слу,чайными
V22
11k
. а,мrплитуда,ми Gk + 11k и фазами ar,ctg ~
Кор,реля,i.щонная функ,ция шума имеет ,ви,д
J<: (t, 0)= t а; COSffik(t-0) .
k=I
2:rt
1Gчитаем чrо Лt= q -
(q - любое целое число).
'
• ffi1
(1.92)
Поаколь.ку в даIнном примере K(t, 0) - вырожден,н-ое ЯдJр·о у]Jа,внения
r( I .86) , то любая функция Ч'(t)= ,cos wht, где k = n+m+ 1 - ,произв•оль,ное це
.лое .положительное число, обраща,ет функционал (1 .'84) в нуль. Однако допу
с тим, что «зшп,р-ещен» выбор в ,ка,чвс1:ве опо,рных ,сиnналав Ч' (t) отрез:к ов гаIр
м онически-х фу,нк:ций с частотам-и, 66льши1ми Wn - Решая ,интеnраш,ное уравIнение
1( 1.87), полу,чим, что его С()бственными фу,н,кциями являют,ся О'!)резки -кооиIну
.с оид Ч'1t· (t)= 1cos(.wkt+cp) с ха,рактеристи-ческими чи,слами Лk = a2 k.Лt/4 (k=l ,
:2, ..., п)
(,фаза ер - ,произ,в·ольная). Поэтому опти,малыным будет си,r,нал, п,ред
•ста1вляющий со,бой •O11рез,о,к коои,ну,сои,ды с ,наим-еньшей дисперсией a2k. При э том
lP1 =a2kЛt/4.
~Ре зультаты _раосмо11ренно•го лрим1:1ра моЖrн,о сущест.венно .обобщить. Пусть
:к ор•реляци онная функц.ия 11J1роцесса N(t) - периодическая с периодам Лt.
rРа1злож·wв эту кор,реляrЦионную фу,нкцию в ,ря,д Фурье Iна отрезке [-Лt/2,
д t/2], црих,одиIм 1к .выражению, а,на.логичному ( 1.92), в ,ко,тqро,м n= оо, а а2 п/2
!И меют смысл :коэффиrЦиенто1в Фурье. Поетому для таких nр-ацес,сюв аптималь
!НЫМ•И опарными си,гнала,м.и бу~дут O11рез:ки 'КО,сину,сои~д, ,которым ,;OO11ветсrвуют
~наи,м-еньшие значения ко,эффициенто.в Фу,рье.
Пример 5. Известно [33], ч_то коэффициенты Фурье
1 Дt/2
(
2:rt
2:п )
211. = ЛtJN(t). ,;oskЛtt+sinkЛtt dt
-Дt/2
сщ:-ацион·ар,ного гау-осов•акого n,роцес,са N(t) ста,н овят-ся статwс т ичеоки ,неза,вwси
,м ыми, ·когда Лt-+оо. Дл,я продеоса с .нулевым Qре,д,ним сл,у,чайная :велw1шна Zn
'И меет нулевое среднее, а ее дисперсия ,а 2 " удовлетворяет соотношению
GimЛt.ak=W(f),
Лf-+00
'k -+oo
lfi8
•
.
.
k
i1Де W(f) - энергетwчеок,ий апектр ,пpoцeoca;}=Iim -Л.
-
на~стота, Лц.
Лt-+оо t
k-+oo
Та,ким ·обра,зом, 1рЯ1д Фу,рье (1в обознаqениях {33])
•
·Еоо ( 2n:
•
2n: )
N(t)=
Zk cos - t+siп -· - t [-Лt/2,,;;;ti,;;;Лt/2]
Лt·
Лt.
-00
:siвляется ·ка1наничеокИ1м ~разложением лроцеоса N(t) i[.34]. Ноопользо,ва·вшись по- .
Jiучен.ными выше !результатами, -мож,но оделать ~вывод, '!ТО для -больших Лt вы
б о.р отрез1кав га•рмоничеоких фу,111юц,ий пз качестве о,rюрных сиг,налов ЧГ(t) бли-
. зок
:к оптимальному, если ча-стоты этих фу,111кций еов1па,дают с ча,стотами, на ко-
-торы х энергетический сп е ктр шума нмеет наименьшее значение.
Выбор опорного сигнала в виде части рабочего сигнала
Значение полезного сигнала на выходе корреляционного при
~мника (см. рис. 1.25) определяется выражением
Лt/2
а =у (0)= . S S(t)W(t)dt,
-Лt/2
где tЛt - время интегрирования. Известно [37], как максимум это .. _
го выражения достигается при 'V(t) =S(t). Как оговорено в § 1.4 ,
6порный сигнал чr (t) - конечной длительности Лt. Поэтому в слу•
чае высокоскоростной передачи опорный сигнал может быть ра
вен лишь части рабочего сигнала:
[-Лt/2 < t < Лt/2];
(t>Лt/2, t<-Лt/2).
чг(t) = {s(t)'
О,
(1. 93)
С другой стороны, для устранения межсимвольных помех спектры
рабочего и опорного сигналов должны быть связаны между собой
;равенством ( 1.65). Определим, каким требованиям должен удов-
.
летворять спектр рабочего сигнала, так, чтобы при выборе 'V(t)
с огласно (1 .93) выполнялось равенство (1.65). В этом случае ос
новная часть рабочего сигнала, расположенная на отрезке [--Лt/2 ,
Лt/2], ортогональна ко всем остальным частям рабочего сигнала ,
расположенным на отрезках
{(2k-l)Лt/2, (2k+l)Лt/2] (k*O, k=+1; ±2, ... ).
При выполнении (1 .93) имеем
Лt
•
00
sin(w- v)--
'P' (i w) = IS(iv)2
2 dv,
J
(J)-V
-оо
где S(iv) - спектр S(t) . Подстановка этого спектра в (1 .65) дает
Лt
00
sin(w-v) 2
F(iw)=S(iw) JS(iv) 2----dv,
(J)-V
(1. 94)
-оо
69
где F(i,ш) - произIJольная функция, удовлетворяющая (1 .64). По
лученное выражение позволяет определить спектр рабочего сигна
ла, обладающего вышеуказанным}! свойствами.
Недостаток изложенного приема в том, что, выбрав спектр ра •
бочего сигнала S(t) согласно (1 .94) и устранив тем самым интер "
ференционные помехи, мы не будем гарантированы в том, что при
этом достигнут максимум отношения сигнал/шум (для аддитивных
шумов), поскольку для достижения максимума указанного отно~
шения необходимо, чтобы рабочий сигнал минимизировал квадра~
тичный функционал (1.84) при ограничении (1.85) · [с заменой
ЧГ(,t) на S(t)]. Последнее требование с учетом (1.94) в общем
случае не всегда выполняется.
Синтез спектров сигналов, ортогональных с временнь'1м сдвигом
Под сигналами, ортогональными с временнь1м сдвигом, подразу•
мевается класс сигналов f (t - k,Лt) (k = O, ± 1, 1± 2, ...) со свойст
вом
jf(t)f(t - kЛt)dt={Co = const (~=О);
_
00
О (k=#=O, k-+1, + 2, ...),
(1.95)
где Лt - заданный интервал. Например, известно, что этим свой~
б•ф
sinШc(t-kЛt)
· [ЗS]
ством о ладают ункции вида - -----
так как 1
Шс(t-kЛt)
Soo sinШс(t- kЛt) sinШrt dt= lш:
Шс(t- kЛt) Шсt
0
-оо
(k=О);
(k=O, k=+I,+2, ...),
(Лt = л/шс).
Укажем простой способ синтеза сигналов, ортогональных с
временнь1м сдвигом, основанный на использовании сигна·лов со
свойством отсчетности, рассмотренных в настоящей главе.
Обозначим через В (>r) корреляционную функцию:
00
В(т:) = Jf(t)f(t-т)dt.
-оо
Спектр К(ш) корреляционной функции В(т:) равен: К(ш) =
= IP(iw) \2, где F(iw) -спектр f(t).
.
Для выполнения (1.95) необходимо, чтобы В(т:) удовлетворяла
первому критерию Найквиста ( 1. 1)
В(пЛt)={l (n= O);
О (п=#=О; п=±1, +2, ...).
что возможно, если K(l(J)) удовлетворяет равенству (1.4)
00
(1.96)
11=-а:,
70
Таким образом, функции вида f (t-kМ) (,k=O, ± 1, ±2, ... )
,образуют класс ортогональных функций, если квадрат модуля
спектра функции f(t) удовлетворяет (1.96).
Из изложенного вытекает, что
F(iffi)=УК(ffi)е1q, <<и> ,
где cp(ffi) - произвольная нечетная функция; K(1ffi) - произвольная
положительная четная функция, удовлетворяющая ( 1.96).
СПИСОК ЛИТЕРАТУРЫ
1. Турбович И. Т. Метод близких систем и его ,применение для создания ИН·
,женерных методов ра·счета линейных и нелинейных радиотехнич,еских си·
стем. М.: АН СССР, 1961 .
2. Каналы передачи данных. М.: Связь, 1970 .
3. Курант Р., Гильберт Д. Методы математической физики. Т. I, М.-Л.; Гос
издат технико-теорет,ичес~кой литературы, 1951.
4. Цыпкин Я:. 3. Теория линейных импульсных систем. М.: Госиздат физико
математичеокой литературы, 1963.
5. Голдман С. Тео·рия информации. М.: И.-Л., 1957.
•6. Кисель В. А. О требо.ваниях к характеристика,м • фильт,ра, фо·рмирующего
однополосный ,сигнал. - Электросвязь. 1968, No 12, с. 76-77.
7. Кисель В. А. О коррекции ча·стО1'НЫХ характеристик по импульсной реак
rrии. - В кн.: Труды конференции, по·священной 70-летию изобретения ра
дио. Киев: ТеХ'Нi-ка, 1966, с. 5-12.
:8. Кисель В. А. Выбо·р оптимальиых ха,рактеристИiк фильтров для си,стем ди
скретной связи. - В кн.: Методы математического моделирования и тео
рия электрических цепей. Киев: Инсrnтут кибернетики АН УССР, 1967,
'ВЫП. 4, С. 51-63.
.
9. Бронштейн Н. Н., Семендяев К. А. Справочник по математике. М . : Госиз
дат технико -теоретической литературы, 1957.
10. Кисель В. А. Об иополЬЗ'овании преобразоtВа,ния Гильберта при передаче
·дискретных сигнал·ов через полосовые каналы. - В кн .: Отбор и передача
информации. - Киев: Наукова думка, АН УССР, 1969, вып. 19, с. 58-62.
11 . Кисель В. А. О передаче импулыС'ных сигналов через поло,совые системы.
-
Радиотехника. 1972, т. 27, No 2, с. 36-45.
.1 2 . Кисель В. А. Дискретный синтез корректирующих цепей: Автореф. дис. на
соиск. учен . степени канд. техн . наук. Одесса, 1967.
13. Nyquist Н. Certain Topics in Telegraph Transmission Theory.-«AIEE,
Trans.», 1928, April, v. 47, р. 617-644.
14. Gibby R. А., Smith J. W . Some · Extention of Nyquist's Telegraph Transmissio11
Theory.-«BSTJ», 1965, September, v. 44, р. 1487-1510.
15. Smith J. W. А Unified View 011 Syпchronous Data Transmission System De-
sign.- «BSTJ», 1968, 1'vlarc h, v. 47, р. 273-300.
16. Croisier А., Pierret J. -M.D. The Digital Echo Madulation.- «IEEE, Trans.»,
1970, August, v. СОМ-18, N 4, р. 367-376.
17. Sunde Е. D. Theoretical Fundamentals of Pulse Transmission.,
Part I.-
<<BSTJ», 1954, Мау, v. 33, N 3, р. 721-788.
18. Bennet W. R., Feldman С. R. Н. Prevention of Interpulse Interference iп
Pulse Multiplex Transmission. U. S . Patent N 2719189.
19. Bennet W. R ., Davey J. R . Data Transmission. New York, Мс. Grow-Hill
Book Со., 1965.
•
20. Schnidman D. А. А Generalized Nyquist Criterion and an Optimum Linear
Receiver for а Pulse Modulation System. -«BSTJ»,
1967, November, v. 46,
N 9, р. 2163-2177.
21. SchiiBler W. Der Echoentzerrer als Model eines Ubertragungkanals.-«NTZ»,
1963, В. 16, Heft 3, S. 155-163.
71
22. Kettel Е. Ein automatischer Optimisator fiir den Abgleich des Impulsentzer-
rers in einer Datenubeгtragung.- «AEU», 1964, Мау, В. 18, Heft 5, S. 271-
278.
·
'
23. ХосGно Тосио, Хината Такаси. Синтез сигналов. с ограниченной поло с ой ча
стот д; ш передачи без меж,символьных искажений. Обобщение отсчетной
rфушщии. •-
Денси цуси,н 1гаккай р.ом,бун'си: 1971, No 5, с. 283-290.
24. Кисель В . А . Опти,мальный фяльтр Найквиста д л я систем с натура л ьной
дискретизацией. - Электросвязь. 1972, No 8, .с. 62-67.
25. Френкс Л. Теория .сигналов. М.: Советское радио, 1974.
26. Риккерт де Ку, Ван -дер-Вюрф . О некоторых расширениях теории передачи
телеграфных ·си11налов Най.квиста. - ТИИЭР. 1969, No 3, с. 144-145.
27. Пасупатхи. Третий крятерий Найквиста.
-
ТИИЭР. 1974, No 7, с. 204-205.
28. Chang R. W. Synthesis of Band-Limited Orthogonal Signals for Multicha:1-
nel Data Tгansmission.-«BSTJ», 1966, v. XIV, N 10, р. 1775- 1796.
29. Варакин 'Л. Е. Теория сложных сигналов. М . : СОiвет,с,кое радио, 1970:
30. Гантмахер Ф. Р . Теория матриц. М.: Наука, 1967.
31 . Березин И. С., Жидков Н. П. Методы вычислений. Т. I. М . : Наука, 1966.
32. Кисель В . А. Синтез оптимальных сигналов для систем с интегральным
1пряемом. - Радиотехника. 1976, No 3, ,с. 6-12.
33. Фано Р. Передача информации. Статистичеокая · теория связи. М.: Ми·р,
1965.
34. Мидлтон Д. Введение в статистическую теорию связи. Т . I. М.: Советское
,радио, 1961.
35. Кисель В. А. Синтез радио.сигналов с максимумом энергии на заданном от
резке времени или в заданной полосе частот. - Радиотехника и электрони- •
ка. 1971, No 12, с . 2243-2253.
••
36. Функции с двойной ор-tогональностью в радиоэлектронике и оптике . США.
1961-1968 rr. Перевод
и научная обра601'ка М. К. Размахнина и
В. П . Яковлева. М. : Советокое радио, 1971.
37. Зюко А. Г., Коробов Ю. Ф. Теория передачи сигнало1в. М.: Связь, 1972.
38. Хургин Я. И., Яковлев В. П. Фини'!'ные фующии в физике и технике. М.:
Наука, 1971.
39 . Lucky R. W., Salz J., Weldon Е. J. Principles of Data Communication . New
York, Мс. Gra,v-Hill Book Со., 1968, 433 р.
40. Тамм Ю. А., Садовский В. Б. Спектральные методы оцешrn качества пере•
дачи цифровых сИr){алов. М.: Овязь, 1974.
41 . Кисель В. А., Зюко В. А . Синтез рабочих сигналов, ма,ксимизирующих от
ношение сигнал/шум и минимизирующих мощность интерференционных по
мех при корреляционном приеме. - В кн.: Труды учебных институтов свя
зи. Л.: 1976, ВЫ!П. 78, с. 21-28.
Глава 2
ОБЩАЯ ТЕОРИЯ ГАРМОНИЧЕСКИХ
КОРРЕКТОРОВ
-+--
2.1. Основные положения .
Одним из главных путей повышения качества работы систем
связи является использование регулируемой коррекции, которая
б
Iu
(
о еспечивает с высокои степенью точности оперативную
«руч"
72
ную, автоматическую, либо адаптивную) компенсацию произволь
ных искажений частотных характеристик каналов и формы пере
даваемых сигналов (в частности, совокупности . некоторых пара
метров каналов или сигналов) на фоне аддитивных помех. На
пример, именно с помощью адаптивной коррекции в настоящее
время достигается наибольшая скорость передачи дискретной ин
формации . (свыше 9000 бит/.с) в стандартном канале тональной
частоты, поскольку регулируемая коррекция наиболее просто ре
ализует оптимальные характеристики, о которых речь шла в
гл. 1.
а)
Вх
/ltшил Jаdерм1н1..
r
t})
б} Вых
Рис. 2.1. Струкrу1р.ные схемы
поли.н-с~ю~ых wорIре-кт0;ров nа
раллельно,г.о ( а) и поIслещ•ава
телыного (6) типов; с11р,у;ктуIр•
ная ,сх-~ма гарм,онwчеюкаго KQJ)·
реютора без обра11ной свя
зи (в)
Коэффициент передачи . адаптивного корректора произвольной
nолиномной структуры (рис. 2. la, 6) описывается выражением
п
К. (i w) = ).:ан (f)1i (i ro) (roEF),
о
где {1cp1i (iw)} (k = 0, 1, 2,
... , п) - система функций линейнонеза
висимых и имеющих тенденцию к полноте на заданном частотном
множестве F; a1t - регулируемые параметры, изменение которых
позволяет получить· требуемую частотную зависимость К (iw).
k
Для рис. 2.16 (j)н (ico) = П Ч1'v (iro). Соответствующий выбор
·v= 1
{1cp1t (iro)} дает тригонометрические корректоры с неравномерным и
равномерным (гармоническим) расположением отводов по длине
.линии задержки, а также корректоры, коэффициент передачи ко
;орых описывается полиномами Чебышева . (первого и второго
73
рода) [ 16. 20] и Лягерра [25]. Наибольшее распространение по ♦
лучили гармонические корректоры и синтезаторы ·[5-15, 19, 20 ~
22, 24-33, 35-37] (рис. 2.lв), у которых
где ,Лt - запаздывание сигнала между ближайшими отводами ли"
нии. Достоинство гармонических корректоров в -~:ом, что с их по•
мощью легко осуществить коррекцию как частотных, так и непо•
средственно временнь1х (импульсных и переходных) характери~
стик линейных объектов произвольного вида.
В настоящей главе изложены вопросы общей теории гар~
монических корректоров, охватывающие, главнь1м образом,• методы
расчета корректоров по временнь1м и частотным характеристикам
каналов связи.
2.2 . Дискретизация сигналов с ограниченным
спектром
Оптимальное представление сигнала с ограниченным
спектром усеченным рядом Котельникова
Гармонические (дискретные) корректоры с обратной или бе3
обратной связи рассчитываются и настраиваются по мгновенным
значениям g 1 (t0 +~M) (,k=O, ± 1, ±2, .. . ) (рис. 2.2) импульсной
реакции каналов связи g 1 (.t), которая в простейшем случае явля•
1tft0 +kM)
u/toJ
f,ft0 -Лtl
~(t0 •Лt}
1Jt0 -2Лt)
u,f t0+2Лt}
о
t0-ZЛt t0-At .to
t0•Z!Jt t JЛt
t0+J!Jt 1
1
1
1
1,•
ta•4Лt 1 1
1
1
1
1
1
1
1
1
1
1
1
1
1а1 1
11
1
а-2 i
1
1
to t0•Лt
t
Рис. 2.2. И:м1Пульоная ,реапщ.ия ка:нала g 1(t) и
реше'!'чатая фунюц,ия gi(to+k.лt)
ее
ется низкочастотным сигналом с практически ограниченным спект
ром. Поэтому ниже рассмотрен ряд вопросов теории дискретиза;,
ции сигнала с ограниченным спектром, исходя из условия получе"
ния требуемого эффекта, коррекции искажений частотно-ограни "
ченных каналов по их временнь1м (импульсным) характеристикам .
74
Пусть g 1 (t) - функция времени со спектром G1 (i(J)), ограни•
ченным частотой
1G1(i(i))1== О (\(i)\>(i)с)-
Разложим g 1 (t) в ряд Котельникова [21]
00
(t)~\1 а (t +.kЛt) sin(J)c[t-(t0 +!,Лt)]*)
g1
~ь1 о
(J)c [t-(to +kЛ t)]
(2.1)
-оо
при выполнении условий:
1) спектральная плотность ряда (2:1) равна спектральной
плотности функции g 1 (t) всюду на отрезке ,[ - (J)c, (J)c], включая
граничные точки ± i(J)c , следовательно, знак соответствия ,_,
мож
но заменить знаком равенства;
2) разложеIJ:ие должно быть осуществлено так, чтобы коэффи •
циенты g 1(t0 + 1kЛt) убывали с максимально возможной скоростью,
т. е. ряд сходился с максимальной скоростью и при 1k конечном
(например, m?::, :k?::,n) аппроксимировал g1 (,t) на l[-1(J)c, (J)c] на-
илучшим образом .
_
Невыполнение указанных условий ведет к неоправданному ус
ложнению процесса коррекции из - за необходимости учитывать
большое число членов ряда (2.1) . и к уменьшению точности кор
рекции, в особенности на краях диапазона .
Разложим G1 (i(i)) в ряд Фурье на отрезке [-(J)c, .wc] :
00
G1(i(J))~е-iwto\--, Gнei wkлt (Лt='Л/(J)с),
--
(2.2)
-оо
где G_li = Лtg1 (t0+kл.t) (k = 0, ± 1, ±2, . .. ). Обозначим:
~(i(i))=е:iwt.01(i(i)); ]
Gi(i(i))=~Gliе+i wkлt.
-со
(2.3)
Известно, что ряд Фурье сходится всюду в промежутке 1 (i) 1 < 1(J)c,
если функция непрерывна в указанном промежутке:
(2.4)
Рассмотр им поведение ряда (2 .2) в точке скачка функции
G1 (i(i)) для следующих случаев (t0 не учитывается: t0 = 0).
1. \ G1 ( i(i)) 1 имеет разрыв в точке (()1<; arg G1 (i(J)) - непрерыв•
ная функци я ( \1(!) [ <1(J)c).
Ряд Фурье такой фун кции сходится в точке (i)1< к значениям мо
дуля и ар гумента
G1 (i (!)1<)/ = 0,5 {\G 1 (i (i)li +О)\+ \G1 (i wli - 0)[}, arg 01 (i w1<) = argG (i (i)).
*) З,на,к •соответс11вия ~ показывает, что спектралыные пло11но·сти пра,вой и
левой частей ,равны .пр.и .всех (i), за .исключением ,некоторых точек.
75
2. Аргумент сп ектральной плоскости 0 1(iro) имеет разрыв з
точке Фk_, а IG 1 (i1rо)\ - непрерывная функция ( i1ro\<roe).
Этот случай представляет наибольший интерес, ибо раскрывает
одну из особенностей сходимости ряда Фурье ком п лексной функ
ции, которая заключается в том, что ряд Фурье ком п лексной функ
ции с разрывом аргумента сходится к значениям
!Gi (i rok)\ = IG1 (i rok) cos Cfi1-; Cfi2 1• arg G~ (irok) = Cfi1 2 Cfi2 ,
где 1ср1= arg 0 1(irrok+O), ,cp2 = arg 0 1(irok- 0).
Разрыв фазы приводит к изменению амплитуды спектральной
составляющей Фk . Погрешность амплитуды зависит от величины
скачка.фазы ,ср1 - ,ср2, и при qJ1-1cp2=nл (п=1, 3, 5, .. .) 1G1(iffik) 1=0~
т . е. составляющей 'ffik нет в спектре G(jtffi). Для четных п (п = О, 2~
4,
... ) 1 G1 (Iffik) 1 = 1 G1(irok) 1 и искажения амплитуды составляю
щей ffik ОТСУТСТВУЮТ.
3. Модуль и аргумент G1(i,ffi) имеют разрывы в . точке Фk. Ряд
Фурье такой функции сходится в точке Фk к значениям
\G1 (i rok)I = +{\G1 (irok +O)I + IG 1 (irok - 0)1}· \ cos JJJi-; ср2 j,
arg G1 (i rok) = Cfi1 + Cfi2,
2
4. Пусть 0 1 (i1ffi) непрерывна на отрезке [-roe, 'ffie]. При этом
равенство (2.4) выполняется для всех значений Iffi\ <roe, за ис ~
ключением граничных точек ± lffie, в которых ряд Фурье сходитс.s~
по модулю и аргументу к значениям IG1 (iroe) 1= 11G1 (i•ffie) cos (j)e 1,
arg G1 ('iroe) =' О, где icpc = arg 0 1(i,ffie) . Таким образом, толЪко при ВЫ •
полнении граничного условия
ере=argG1(iroc) =О
(2.5}
и при отсутствии в 0 1(i1ffi) рассмотренных разрывов справедливо
равенство G1 (iffi) = G1 (iffi) ( 1 ro 1 :::;;ffie) и знак ~ заменяется в (2.2},
знаком равенства.
•
Любую функцию G1(iш), непрерывную на отрезке [-1ffie, roe],
можно преобразовать так, чтобы она удовлетворяла (2.5), умно •
жив ее на eiwt,, где .t0 =-,сре/Фе . Ряд Фурье полученной функции
со
Gз_(iro)=G1(iffi)е;wt,= LGkeiwkлt
(2,6))
-
00
сходится всюду на отрезке [-rffie, Фе]. Определив 0 1 (iffi) через-.
01 (iro) (2.3) и взяв _ обратное преобразование Фурье от обеих
·частей полученного ·выражения, приходим к ряду Котельникова,
(2.1), который точно представляет исходную функцию g 1(t).
•
Покажем теперь, что при выборе to согласно (2.6) значения ре -
шетчатой функции g 1 (t0 +kЛt) при росте k убывают с максималь -
но возможной скоростью, следовательно, ряд (2.1) сходится с
максимально возможной скоростью и при заданных значениях
76
k(-n ~k~im) частная сумма ряда наилучшим образом аппрок..-
симирует g1(t).
_
•
При разложении G1 (i(i)) в ряд Фурье ее действительная часть
A((i)) = JG 1 (i(i)) 1 cos ,ЧJ(,(i)) представляется рядом по косинусам, а
мнимая часть В ((i)) = 1G1 (i1(i)) 1 sin ЧJ((i)) - рядом по синусам:
00
00
А((i))=~AkcoskЛt(i); В((i))=~BksinkЛt(i)
-' .!
~
О
1
(Ak=Gk+G- k, Bk=Gk-G -k).
Функции А(1(!)) и B(t(i)) непрерывны на отрезке J1(i)I ~(!)с и удо "
влетворяют граничным условиям: А ((i)c) =А (-(!)с), В (1(i)c) =
= В (~wc) = О. Следовательно, коэффициенты Ak убывают не менее
чем со скоростью 1/k2 , а коэффициенты Bk - со скоростью
1/k3 [12]. Коэффициенты Gk убывают со скоростью не менее lfik 2 ,
ибо Gт,. = (Ат,.+Вт,.)/2 и Gт,.= (Ат,.-Вт,.)/2. Граничное условие для
В (1(!)) выполняе·тся только при выборе t0 согласно (2.6), в про"
тивном случае В (t(i)c) =l=B (-1(i)c) =1= О, следовательно, коэффициенты
Вт,. убывают со скоростью 1/k и скорость убывания Gт,. уменьшает.. _
ся до 1/k, т . е. в ,k раз. В силу соотношения (2.2) рассуждения о·
скорости убывания коэффициентов Gт,. справедливы и дJIЯ значений
решетчатой функции g 1 (t0 +krЛt). Изложенные соображения пока -.
зывают, что правильный выбор параметра ,t0 увеличивает скорость
убывания значений g 1 (t0 +kM) не менее чем в ,k раз, поэтому ука "
занное свойство следует учитыв_ать при осуществлении процесс а
выборки функций с ограниченным спектром.
Отметим одну особенность рассмотренного оптимального стро
бирования. Поскольку коэффициенты ряда (2.1) g 1 (t0 +,kiЛt) убы -.
вают на бесконечности со скоростью 1,/k 2 , а огибающие функци й
sin(!)c(t-t0-тЛt) (т=О, l, 2, .. .)
(i)c(t- t0- тЛt)
1
.
убывают со скоростью k (t • kЛt), то при .t достаточно большом
(t-+oo) ряд (2.1) асимптотически описывается функцией
g1(t)~D sin(i)c(t-to)
(i)cU-to)
(D - некоторая постоянная), нули которой р·асположены равно
мерно в точках t0+ ikЛt. Поэтому можно сказать, что qптимальное
стробирование подразумевает такой выбор ,t0, при котором строби
рование осуществляется в нулях функции g 1 (t) при ,t достаточ1fо
большом.
Очевидно, если g 1(t) _: _ _ четная функция относительно некоторо
го момента времени 1t'•, т о нео бходи мо выбр ать t0= ,t', что обеспечи -.
вает оптимальное стробирование .
Выбор основного отсчетного импульса
Расчет и настройка гармонических корректоров осуществляют "
ся по дискретной реакции g 1 (t0 +kЛt) без учета 1t 0 , т. е. по спект-
77
. ральной
плотности G1 (iu>) функции g1 (t+:ta) (запаздывание ,fa не
корректируется). Гармонический корректор компенсирует искаже-
ния частотной характеристики И1 (i1w) во всем диап~оне частот
10-u>c, включая точку u>c только в том случае, если G(iu>) удов
летворяет граничным условиям по фазе (2.5).
В связи с этим возникает вопрос о прав,ильной нумерации дис
'Кретной импульсной реакции g 1 (t0 +kЛt), который можно сформу
лировать в следующей форме. Пусть задана конечная последова
тельность чисел ak (,k = О, 1, 2, ... , п), о которых известно, что
они
являются мгновенными значениями функции g 1 (t). Необходимо
· пронумеровать эту последовательность, т . е. определить, какое из
значений ak равно g1(to), g 1(to+M), g 1 (to-rЛt) и т. д. так, чтобы
' nри этом выполнялось требование (2.5). В основном задача сво
дится к нахождению значения g 1(t0), которое называется основным
.отсчетным значением (или основным · отсчетным импульсом). -
•
Анализируя спектр дискретной реакции g 1 (t0 +kЛt), можно
· убедиться, что для выполнения (2 ,5) необходимо в качестве основ
н ого отсчетного . значения выбрать (п 1 + 1)-й импульс, где п 1 - чис.
п
..ло
корней алгебраического полинома Р 1 (х) ='2.akxk, по модулю
•
k=O
:меньших единицы . (т. е. расположенных в комплексной плоскости
z внутри окружности единичного радиуса) 1[7, 8, 21, 31]. Считаем,
',что полином Р 1 (х) не содержит корней, расположенных на окруж
ности единичного радиуса, что соответствует случаю J G 1 (i1u>) J =рО
i( !u> 1 ~ u>c) (см. далее).
Заметим, что основной отсчетный импульс, выбранный соглас
но сформулированному правилу, не всегда имеет максимальное
значение . Максимальный из импульсов ak является отсчетным
·rолько при сравнительно небольших неравномерностях амплитуд
но -частотных и фаза - частотных характеристик сигнала g 1 (t) . На
пример, максимальное значение дискретного сигнала а_ 1 = 1,82;
. а0 =2,7; а 1 = 1 равно 2,7, в то время как за отсчетный следует при•
нять импульс а_ 1 = 1,82, так как все корни полинома Р 1 (х) =
=1,82+2,7х+х2 расположены вне круга единичного радиуса. Сле
довательно, отклик необходимо перенумеровать, положив ао = 1,82;
а1 =2,7; a2 = 1l;
Легко показать, что если -:rc/2<arg •G1(iw)<:rc/2, то
00
1ао 1> ~ 1ak +a-kl-
•
1
(2.7)
Это неравенство может быть использовано для определения ос
новного отсчетного импульа а0 в случае небольших неравномерно
стей фазовой характеристики сигнала g 1 (t). Можно также польза-
ва ть ся неравенством Ja0 J> ~ Jak\ (k=pO), при выполнении кото-
-оо
· рого всегда выполняется (2,7).
78
На ·рис. 2.3а, в, д, ж даны примеры осщилл0t11ра.м,м и,мIпульсных ,реа1кцию
iКа1нала НЧ, ,ре3ко о,11р.а,ни,чен•НО!Г,О по ,полосе переда,ваемых ча,стот . Я~р:кие точки ,
соотве11ствуют инт•ервала,м Котельни1кова, ,в которых ·осуществляе11ся ,выIбарка.
дноК'ретных з,начений g 1 (kЛt). ОсцилJDО!Г,раммы отличаю1'Ся тол,ько ,положением ,
м,оменто,в ·выбQр,ки.
На :р,111с. 2.36 , г, е, з соо11ве'!'сТ1вен,но .из•Ображены дwС1КJрет,ные реакции, .полу-
чаемые ,при IразлИ1ч:ных !Положениях м'ом,ен'!'ов ~ыбарки. Оптимальное положени•е:
м-оментов выборки ща,но на рис. 2.3д. При t tп;остатО/JiНО большо.м (1п~ра,ктичоокп.
-4
а)
g1 (клt) дt
{})
а0 g/кt:.t)
дt
1214tб18
131517
_
4_3
_
2_1
1012141б18
1 111111#,
0123456789'111:3 15 17
г)
iJ)
11/31517
Ж)
458789Шt
0,5
лt
S)
Рис. 2.3 . Осциллогра •м1мы имrпуль>оных ,реа,кций ,низ11ючаIстотных ;ка
налов
ПiРИ t> (,5 ...;.- 7) ,Лt) ,моменты вы6Qр1ш Jюпа,дают cr1 •нули и1м111улысной ,реа'КIЦИИ g 1(t).
Как в.ИJдно из ср-а,вне,н-ия ае,циллогра,мм, ,при ,неаптималын-ом Jюложении момен
тов •выбар,ки (~см. ·ри,с. 2.3а, в) 11ре,буется в 2-3 раза ·болышее число ,выборок
для описа,ния имmулысн-ой реа,кдии.
•
В ,ря,де случаев выбо1р моментов доокретиза,ции ,п,рош~во1ди11ся та,ки,м обра
зом, что:бы пол у,чаемое .при эт-ом оонов,ное от,с-четное ·зна,че,ние а0 совmадало ,с
ма,ысимумом реаuщии . Gра1в-нение ри,с. 2.3в и д [юказывает, что та,кой выбо1р не
яrвляется оп'I'имальным. На ;р.и,с. 2..Зж IдаIна -ооциллограмма си,!'нала, .нера ,в,ном-ер
насть фазо -:частотного апек'I'ра ·которого .н-е превышает ± л/,2. Во:ополь:зо,вавшись
79
нера,венrст,в-ом ('2.7), нет,ру,щно найти ,о.оновное оточетное з н аrче-ние а 0 = ' 1,з •• (,ом .
рис. 2.Зз) , ·которое, од,нако, rНе -оав1падает с ,ма,ксималыным з1начением, rа·в
ным 2,1.
Критерий корректируемости канала по импульсной реакции
К корр е ктирующему устройств у предъявляется требование :
!О бе с печить коэффициент передачи 'K(iw), «обратный» коэффициен
ту п ер едачи канала К1 (iw) в з аданно м диапазоне ·частот (в частно
сти , в диап азоне 0-wc) с точностью до. заданных величин модул я
.и з апаздывания
(0 - wc);
(А= const,
-r = const).
Канал не корректируем Е строгом смысле, если ег о коэффици
е нт передачи обращается в нуль на какой-либо частоте диапазо
на 0-i(J)c, поскольку в этом случае корректор должен обеспечить
-бесконечно большое усиление . Поэтому требование I К 1 (Lw) 1 =1=0
явля ~тся необходимым и достаточным условием корректируемости
канала. При невыполнении данного требования речь может идти
только о приближенной коррекции.
Перейдем от частотного критерия корректируемости канала к
критерию вр.еменн6му, т. е. исходя из решетчатой функции
g 1 (k.Лt) = а11. (k = O, ± 1, ± 2) импульсной реакции канала опреде
делим, не обращается ли его коэффи циент передачи в нуль
( !,w 1~ffic, ,Л.rt = п), шс, Шс - граничная частота канала) .
С.:читаем, что решетчатая функция ,g·1 (kM) конечна, а11. =
=g1(ikЛt) =0 (k>m , ,k< - n) . Вычислив спектр этой функции,
нетр удно видеть, что он обращается в нуль , если хотя бы для
т
/
одного· из корней л11. уравнения xn У' а11.х'' = О имеет место равен
...
-п
ство l1л11.·1= 1 [7].
Таким образом, временнои критерий корректируемости ка н ала
с формулируем в следую щ ем виде [[7, 31 ]: канал, дискретный отклик
•которого конечен, является корректируемым
в том случае, если
алгебраический полином, составленный из отсчетных значений· им
пульсной реакции, не имеет корней, по модулю р авных 1, т. е. рас
положенных в комплексной плоскости на окружности единичного
радиуса.
Ряд алгебраических. п риемов по определению наличия корней
на окружности единичного радиуса дан в ,[7].
2.3 . Аналитические методы расчета гармонических
корректоров без обратной связи
Частотная область
•В ча,стотнай ,области ,раочет схем ко,р1р е~кторов n1равощ-и тся и,схощя из извес т
ного коэффициента п ередач и 1шрректируемого объекта К1 ( i ш) = IK1 ( i,ш ) l eЩ 1 ( w )
:so
, {ro1,;;; 1ro 1,;;; ro2). Гармонтеский кар,р,ектQр в ,пределе n,редставляет сабой бооко-
111еqную линию задерж,ки с коэффициентом передачи (,без у~чета в,носи.м·ого кор
ректором запазЩЫlва.ния)
со
К(iw) =t rxk e-iwkлt_
(2.8)
-со
Зада ча 1щр,~ект,о,ра состоит в комIпе,н,сации с зщданш,ой степенью точности ,не
ра1В<НО·~н~рност и iK1(iro)I и ,нелинейности cp 11(ro), что возмшюно п,р,и
K(iw)=
А e- iQJ, (w)
1 K1(iW)I
где А и ,; - ,нек оторые постоянные.
Если ro1 = -ro2, ro2 = roc I К1 (iro) 1 - четная, а ср1 (,ro) - нечетная функции,
'!'О [12)
-wc
A 'ei [-<р 1 {w) - W't'+wkЛt]
IK1(iw) 1
где Лt = л/rос; ,;' =ср1 (,roc) /roc.
dw,
(2. 9)
Такой вЫ1б0<р ,;' эювивалентен ,вьгчитанию ,из ,cp 1.(ro) линейной фазы roi:' , что
,устраняет разрыв 1р·ез,ультщрующей фазо,вой ха1раIк теристиIк и канала и кор ·рект10-
,ра ,в точках ±roc. Псююолыку у 1реалыных ка,нало,в I K1(iro) :I и Ф1(rо) непрерыв
ны на [-roc, roc], у,каза,н,ное ~вычитание увеличи·вает скор,асть у,бьuвания коэффи-
циент ов ak в k Iраз.
•
Фив,ически :реализуемые ,кQр·ректо,ры сО1держат конечное Чljсло ak, что при
водит ,к ,необходи,м•ости ,ра,ооматриIвать усеченные 'j)Яды
т,
К(i(J))n т =
~
.
rxk e-iwkЛt .
11
...
-п,
Это обусловливает погрешность 11 (iro)n,m,
= K(iro)-K(iro) n ,т, , которая в силу
экстр ем алЬ'ных своikт,в '~оэффи,циентов Фу1рье являе'I'СЯ ми,нималыной •В· с,мысле
-
.
wc
!Квщд,ратичного ,критерия 1'] 1= J!'] (iro) n ,т, 11*,(iro) n ,т, dro =min. Запаздыва,ние
't',
-wc
вносимое .каналом и ,корректором, рав:но n 1дt+i:'.
,Кач ес '!'во ,ра·боты кор,ректо,р,а о,цен,ивается ,величиной ,nогреШ1ности ,к,ор,ректи
рования 1;(i,w)=Ae-1ffi't-K1(iro)K( iro) n 1m 1 (I\Ol~(i)c), nде
Ae-1w1: и
K(iro) п ,т, К1 (iro) - IкомIплек,сные •1юэффи,циенты пер~ачи ндеалыно,го ,канала и
системы <~канал+ ,корректо,р» , либо 1величи1Ной интегральной пог,решности
wc
VJ= J p(wH(iw)s*(iw)dw,
(2.10)
-
(i) -
c'
где p(ro) - ,нео11рицателыная весо,вая функция. Поскольку 11(i(i))n,m, K1(i.ro)=
= 1;(iro), ,нет,рущ,но ·виIдеть , что раючет согла,сно (2.9) дает мини,ма льную величи-
111у 1'] только ,в .каналах, для кото~рых IK1(iro) l 2p(ro)=rconst ( l rol,;;; •roc). Кос,инус -
111ый ·кор'j)ектор, .комmе,н,сирующий не.рав;номерrн·асть I К1 (iro) 1, о:nись11ваетIся ,кос;;ф-
т,
фи;циентом ,передачи K(iro),,,, =ао+2 I: ak•coskroЛt (n1=m1), где
k=l
гIК1(iw)1-1e-iwkЛtdw.
-wc
81
ИзложеNoный· -метОIД ,ра,счета отличает,ся .nростотой, од,на1юо для каналов • с
произвольными искажениями он ,не обеспечивает полу,чения ,минимума ,величи
il!Ы 'l'J. Ко.nда этот ,м·и1нимум 1необжщим, зна1t1ения а" ооределяюrея ,из у,р-авнений
{J:lJ
-в0 Bi В2 • • .Вп,+т,
BiВ0BiВ2•
,'•
...В1Во
В1В2 .
Bi
Bi
,В1 Во Bi
_
вп,+т,· . Bi.
В1Во
ме
а;
-
1
х
а:о
ат,
wc
wc
D-1
Do
_Dm,
Bk = sР(Ш)/К1(iffi) [2e-iwkЛt ; Dk = sр(Ш)К~(iffi)К2(iffi)e-iwkЛtdш.
В 1результате ,мини,мизируется интеnральшая пm~решн·ость (2.10), в которой
s(iw) = K2(iw)-K1(i<w)K(iw)n 1 m" nде K2(iw) - заданный •коэффициент пере
да1t1и.
1Раюсмотрим теперь общий слу,чай, когда коэффициент передачи канала
К1 (i,w) ·за,дан на лроиз,воль·ном отрез,ке [w1, w2]. Ра 1счет корректо,ра путем ,разло
жения [K11(iw)J- 1 -в рЯ1д Фурье на от,рез,ке [w1, w2] ,приводит к ,комттлеконым ak,
если К1 (i,w) 1не удовлет,воряет условия-м: 1) 1К1 (iw) 1 - чет,ная функция 011носи
телыно точки Wo=I0, ,5 (w1 +w2); 2) arg Kii(iw) - нече11ная фу.н~щия отно-сительно
ffio; 3) w2+W1=n{w2-w1), .где n=O, 1, 2, ... С целью полу,чения
,вещес11венных
ak функцию K1(iw) за,мени1м новой фу,н.кцией R1 ·(iw), зада,нной ,на 011рез,ке
[w'1, w'2] (w'1 :;;;;;w1), w'2:;;,,: W2, кот.с~рая ,у1довле11воряет ,условиям : 1) w' 1+ ,ffi' 2=
=n(w'2--,w'1) (n=O, 1, 2, ...); 2) IR1(iffi) 1 - че11ная функция относительно точ
lКИ w'o=0,5(w'1+1w'2); 3) arg K11(iw) - ,нечетная фу,н•юция относител~,но точки
ffi'o; 4) R1•(iw) = K1 1(iw) (w1 :;;;;; ,w :;;;;; ,w2) .
Для уменышения О'статочной 1Величи,ны '1] 1 функция /(1 (i,w) вне отреЗtКа
[w 1w2] долж;на я,влятыся аналитичесюим продолжением функции К1 (iw), т. е.
.мсщуль и а-р,гу,мент R 1(iw), а также ее ,цроиз,вод!ные (1По крайней ,ме,ре, ,первая
•произ,водная) не ,должны претерmевать окачкюв на ча,стотах w1 и w2 . По
1(1 (iw) определяем а" из выражения (,2.9).
Ха·рактерист.ики ка ,нало,в овязи, ка ,к пра .вило, ,не за1даются .аналитиче ски, а
зщдаются в .виде та1блицы з,на,чений, которые они ~принимают в ;ра,в-ноотстоящих
точк,ах wv =wc/m (v=0, 1, 2, ... , т) . Ко.м1Пен-са,ц ия искажений
в этих точках
т
осуществ.ляе'flся 1юр,ректором с ,коэффициентом пе,редачи1 K(iw) = L ake- 1wkЛt,
-т
щ1;е
т -iq,'
1 \1'е v -iw -kЛt
CGk= -
/,J --- е
'll
,
2m
xv
-т
.
,
,
'
,т
гдеX-v =Xv;,
-v =-,
v;,v =,v-v-;:;;;хv,,v - з-начения,м0дуляи
фазы 1шрректируемого канала. Число корректирующих отводов CG1< равно 2m + 1. ·
1 1В тех •случаях, к•олда с памощью ,гар·м1оничесжого ·кор ·ректора ,во·спроизво
дят,ся ,не толыко значения функции, но и значения ее N ,произвсщных, -необ,JсОДИ·
мо ,воополь·зо,ва тЬ'ся .результата,ми .ра1б-оты ,[1 4], в которой предложен мето:д ,по
строения и,ит1;1р1Поляци он1ных триго;нометрич-еоких поли1ном -ов с ~ратными узлами.
82
Зна'К ~'- ,показывает, что два крайних чле,на суммы ,взяты с весом 0,5. В слу,чае
косину,сного кар-ректора ;выражение для ak у;nр-ощается:
1т
п
ak= -
L- coskv-
8
mv=OXV
m
Заша здывание, в1носим·ое ,си,стемой «ка;нал+['а~р-моничеакий корректQр», ра,вно
тЛt+q;т /.Шс,
Временная область
Использование бесконечных матриц Теплица. Во временной ·о'6ла,сти з а1дача
1юрректи•рующего уст,р·ойства состоит 1в ,цреО1бра"Зова1нии .имшуль·оной реа1юции
g 1(t) в •реа,~щию g 2(t), со1в[]адающую с 1'р,е6уемой точностью с сигналом заща.н-
111ой формы g 3 (t) . В :дальнейшем бу~де-м интересаватыся фор,м-ой этих -сиг-нало,в,
а 111е их .положением ,во .~р емени.
-
Пусть опектры сигнал ов gr(t) и g 3 (t) 011ра-ни-чены ло протяженности часто
той Ш с. Пре,ц,ста :вим gr(t) 1рядом (2.1), в 1котор ,ом обоз,нач.им g1(kлt+to) =ak ,
Дискретизация g 1(t) с ча,стотой Шс/п да-ет [IОСледо.вател ьно,сть им,пульtов
{ak} (k=0, ± 1, ± :2, ... ), состоящую из ,основного от,очетного им,пулыса а0 и се
рии ,мешающих, из кото,рых одну группу им1Пуль·сов, предшест,вующих оонав-но
му, принято .называть лредщейст,вием си:nнала, а другую гру,rюу, ,следующую пос
ле -ос;нов,н ого, - послещейс11вием. Сигнал g 3( t) та.кже пред1ста1щм рrодом (2.,1) с
коэффициентами gз(kЛt+t'o)=ck, Ilдe t'0 о[]lред-еляется по а -налогии с t0 . Оово
~ку1пно·сть с" дает последовательность {ck} (k=O, ± 11, ±2, ... ) . К:о,р:ректор пре
оqраэует {ak} в {ck}, При полной .кор,ре~щии нера1вн-омер.но:сти а,мплитудно-ча
ст-от,ной и нели1нейности фаэо-ча1стотной ха1ра-ктериеги~к ·канала имеем gз(t) =
=c0sinш c t/,шct, т. е. {с1<} =Со, ck = ,0 (k,i= ,0). ,В этом случае за;да,ча корр,е:к-гора
св-сщится к комшж-сации •им,пулысав пре~дJдеЙJс11вия и последействия , Поэтому
:~юр1ректо,р мож,но у~подо,бить нек1оторо,му линейному ди,сщретному или им,пул,ыс
ному фильтру, пропускающему определенный импульс из заданной последова
тельности {ak} и пада·вляющему остальные им,пульсы.
Оп,редетrм неизвестные 1ш~ффициенты ak гармонического ,ко,р1ректора по
вада,н,ным {ah} и {ck}.
Корректор последействия и корректор преддействия. Си,гналы g 1(t) и g 3 (t)
111а ,входе .и ,выходе 1кор1ректора ,свя,заны и-нтеграл,ом свертки
t
gз(t)= sf('r:)gi(t- , )d.:,
(2.11)
-ао
rде f (-r:) - им1пулыаная ,реакция ·Jюр,ректора. Считая, что g 1(t) не .сощержит
прещ,дейс11вия, ,и учитьшая, что ,коэффициент ,передачи га,рм-оничЕю1юг-о хо•рректо
ра опи,сывается рядом (2 "8) , получим .из (2.11) бесконечную т,реуrолыную си-сте
му у.равнений 1[6] l[a+ JX[a]=.[ c] или
(2. 12)
t
t
~де (а] и ,[с] - -бесконе<tные матрицы-1столб,цы; [a+J - беско,неч,ная 1шжняя тре
угольная ма11рица Теплица (,нулн 1в ,мат.рице l[a+J не ,выпи-сываются). Искомые
!Коэффициенты ak ра,в,ны [а]=И+J - 1 Х 1[с], где [A+J- 1
-
,матрица, об.ратная
Ia+J: [A+J- 1 x:[a+J={E], [Е] - еди-ничная матрица.
83
Для суще,с11Вования ~решения rнеобх,сщнмо и .цостаточно, rчтобы [A+ J- 1 сущест
вовала. ФоР'мально если a0 =i=O , то i[a+J ~имеет обрат,ную 'И+J- 1 , которая являет
ся нижней треугол ьн ой матрицей Теплица:
---
Ао
[А+ГI= А1 Ао
А2 .А1 .Ао
t•
где Ak определяются из рекуррентных соотношений
Ak-mam+ ... +· лk_Ja1 +Akao=O(k=0, 1, 2, .. . ).
(2. 13)
•У.кажем :некото,рые ,особенности обращения беск-онеrч,ных матриц, .которыми
они отличаются 01: матриц конечных размеров {2, 9, 23] .
1. Бели l[a] - беюконечная ,матри,ца:
[а]=
t
и матрица i[a]- 1 обрат.на l[a]: [a] X l[a]- 1 = 1[E], ,nде 1[Е] - единичная мат,рица, то в
общем .случае .[a]- 1 X 1[a]c;t= ;[a]Xl[aJ- 1, т . е . закон ком.мутати,вности • матрицы [а] со
своей , обратной [а]- 1 [2 ] в общем случае для бесконечных матриц несправедлив.
IМ.атрица [а] - 1, ,у1д·овле11воряющая у~равнени!Q
[а] х [аГ1 = [Е],
(2.14)
называе'I'СЯ п,р.аво1сторонней ,обра11ной.
Мат,рица - 1 [а], у~д1овле11во·ряющая у1ра,внению
-l[a] х [а] = [Е],
(2.15)
назьi,вае-гся левосто1рон,ней обрат,ной к 1ма11рИ1це (а].
Ма11рица ,[AJ-
1
,
удовлетворяющая ,как у,р -,нию (2.14), та,к и ур-1нию (2.15)
[a]X[AJ- 1 = t[AJ- 1 X l[a]=i[E], -называется двусторонней обрат,ной.
,2 . Беоконечшые ,ма-лри,цы обращаются неод,ноз,на•чно.
Сущес11вует множес11во (.конечное или беско:нечное) матриц ,[а]- 1 , - 11[а], [AJ- 1,
раз1мерность которого , (,число ли.нейнонезавнсимых о('iратных матриц) или ко-
rнечно, или ·бесж,о,нечно. Дейс11ВителЬ1но, -если [AJ-
1
-
дву,сто,рон,няя обрат,ная, то
матрица l[AJ-
1
+k1[A 0 ]
бу~дет об,рат,ной •к [а]: (,[A J-
1
+k[A0 ]) Xi[a]= ,[E], [Ще [А0] -
~д!ву,сторо.нний -нулъ -.делитель матрицы [а]: [Ao]X 1[a]=1[a]X i[Ao]=O (k - любое ве
ществ-енное или комrrле1юное чи-сло).
~роме .ПJВУ,сторон,них ,нуль -щелителей, ,матрица [а] : может иметь левос·юрон
ние 01[а] и право·стО1рон,ние [а]0 ,нуль-делители, удовлетворяющие ,равенствам .
0[a]X l[a]=O; [a]Xl[a] 0 =0, ,но [а]х 0[а] с;= ,О; (a]0 x{a] c;t=O.
Наличие ,нуль-.целителей гово,рит о нео.п,нозначно•сти обращения •матрицы
[а]. Со,воку~пность ,нуль -.целителей образует м,ножест-во ,нуль -щелителей мат1ри,цы
[а]. КаiК л.ра,вило, ,при обсуж~дении ,в,оmро,са обращения ,бесжо,н ечных матриц ,не
пооред,ственно инт-ересуют,ся ,не ,раз·мер,но.стью множества обратных матриц, а
размерностью м,ножес11ва ,нуль-делителей, ибо •размерность ·м1ножества о{~ратных
ма11риц О1д,н оз,на1чно определяе11ся размерностью ,множест,ва ,нуль-делит-елей.
Из множества обратньiх ма11ри,ц 1на·с интересуют толЬ1ко матрицы, у,довлет
воряющие условию физи,чеокой реализуемости корректора. По1д '!)ребо.ванием
«фи-зи,ческая ,реализуемость» под'разумевае'гся •следующее: 1) вещесТ1Венно,сть
коэффициенто,в ,переда,чи 1по от-во1дам КОiрректора при 1Вещест~венных ak и c_k;
00
2) ·сущест,вует ~ 1ak 1, ,следовательно, 1ak l-rO при k-r± оо . При ·выполнении
- С,,
.
84
указа,1:;ных т:ребова,ний мож,но п остроить физически 1реашrз.уем ый (а значит, ,ко
нечныи /ПО чи,слу 011В·Одав) tКOPP·elКTQP, 1ВЫ\ПОЛНЯЮЩИЙ С вадаlННОЙ TO'LHQCTЬIO по
ст авленную за1да.чу кор·р екции. С у,четом ,у,каза-н.ных ,ос обенностей ра◊СМО'!1р,и,м
обращение м&трицы [a +J. Для у1до1бст.ва lбу1дем очитат ь, что число мешающих
иМlпулысов ,КОН:ечно : ан= ·О при k<O, k>m. МаТ1рица [a+J Iпри ao'i=O име ет бес
конечное множество левосторонних обратных - 1[a+ J и одну правостороннюю·
обратную [ a+ J---.
1, которая совпадает с {A+J- 1
.
Из соотношения (2.13) следует
что .коэффициенты Ан образуют ,воз:в:ратную 1ПОследователь,ность ПОIJ)Яд'Ка т _
Обозначим через Вн .(k=·I, 2, .. .- , т) корни у.равнения
ао+а1х+а2х2+ ...+атхт =О.
Пу,сть В, *,В2# ... * Вт- Тома
Ak = А(tу+В(i-у+ .
·(1)k
.. +с
Вт'
11де А, В, ..., С нахадятся из сwс темы ура,вн ений:
А+в+ .. . +С=Ао;
1
1
1
А!\+в~+ •••+СВт=А1;
.
. .-~
.
.
.
.
.
.
.
.
.
.
.
( 1)"-'-1 (1)т-1
(1)т-1
А~. +в~
+...+сВт
)
1
}
=Am-1 • 11
(2.16)
(2. 17)
Эта ~си-стема в·с-е11да ·раз·реши,ма ,ооно,сительно ,неиз·вест,ных А, В, .. ., С , ибо ее
определитель (опре1делитель Ва:н.дермонда) не равен нулю. Очевидно, J A1t I-+О
ттри k-+oo, если
Bk>1(длявсехk),
(2. 18)
т . е. корни у,ра,в,нения (2.11 16) Iра•оположены ,в 1коМ1плексн·ой ,плоскости z ,вне ,юру га
единичного ,ра,диу,са. Из (,2.17) следует, что цри ,выполнении (2.18) ,сущест,вует
00
о:,
~ 1ан 1, если ,существует ~ 1сн I-
-оо
-оо
•Т ребования (,2. •118) являю11ся необходимым и 1достаточ:ным у,слоIвием ,с уще
ствова,ния ма1,рицы .[A +J- 1
,
удо,вле11во:ряющей условию физической реализуемо
сти . Если ,чи-сло iдискретных значений ан ,бес,конеч,но, то для сущест,вования мат
rрицы .[A+J- 1
,
у,довлет,воряющей условию физической •реализуемости, ,необхОiдИМ·О
и ~достаточно, ,чтобы
со
нули функции F(z) , -о,пределяемой ряд-ом F(z)= \" ' анz\
,l,,, ,J
-
00
раюполагались .в Iплоско·сти z ,вне .круга единичного ,ра,д,иу,са.
,Коэффициенты Ан определяются •из соотношений (2.13), (2.17) или вычи,с
ляют-ся IПО формула•м
(2. 19)
где Лн - ОIП,редели т ель k - го ,пс.р1щка . Физически ,реализуемые tКQр ,ре1Кторы со
держат конечное ,число ,от.во1дов a1tO,;;;;k,;;;;m 1 (т 1 - задаНlн·ое чи-сло). Поэтому
беско ,неtLную ,систему у:ра-внений (2.12) заменяем . конеtLной •с т,реугольной мат.ри
цей [a+] m 1 поряiд,ка т1 . Вычи,сление •обрат.ной ,ма1'рицы fa+J- 1m 1 произвс.дит-ся
аналогич но вычислениям бЕюконечн ых матриц· по ф-ла.м (2 .13, 2 .17 , 2 .19). Про
цесс ,ограничения •беоко,нечной •си,стемы у1ра,в.нений иллюстри,р уе11ся схемой
85
1
ао
\
[а+Jт, Щ ао
j
а2а1а0
1
a3a2aiao I
-- ---- --
1~-- --
х
[а+]т,
а1jао
а2 Jщ ·ао
]
•1
1
•1
Замена бесж,онвчных ма'I'риц [а+] и ,[а] .конвч,ными ,приводит к по11решно.сти, т. е.
в•место отсчетных з~на,чений ст, +1, Ст ,+ 2, Ст, +з,
...
и т . д. полу,чаются значения
81, 82, •83,
...
и т. д. Матрица значений [[8] оп,ределяе'!'ся из ,ра1вt1нства {a+Jm, х
X l[a]m, = 1[8] . Матрица [a+Jm, имеет ,в •общем случае 1раз,ме,ры 00Xm1+ 'l . При
!Конечном ,числе элементов а1<(а1< = 0, k>m) •матрицы [iI+Jm, и ,[8] ;конеч,ны и
,имеют с оотве'ГСт,венно ,раз.меры mXm1+l, mXI . При 1Полной .кор ·рЕшции С1<=0
{ k=,Ь .Q), поэтому зна,чения 8; указывают величины поnрешностей, :возникающих
в точках m1+i (i=·l, 2, ... ). В тоIDках k=l, ,2, ... , т1 имеем С1<=0. ,Кроме то·rо,
n:ри пол~ной кор1реюции ak = А1<, что упроща,ет раочет ,кор,ректора. Согласно (,2.17)
1а1< J-+O, если выполняет.ся (2 .,18) . Не11рудно :видеть, что ,в эт,о,м случае 18; J-+O,
поэтому, ,выбирая т1 соqJJве'!'ствующим образом, можно юввсти I е; 1 ·к нruперед
зruданным ,ок·оль угодно rмалым эначениям. •
Д опустим теперь, что сиг,нал g 1(t) ,не содержит 1Последейс11Вия: а1<=0
(k>0). Павторяя операции и ра,осуждения, выполнен.ные при анализе корректо
р а последействия, ,п.ри.менителыно к 1корректо,ру п,реддейс11вия, получим
-+
eto
сх- 1
сх- 2
х
(2. 20)
а_п а_ (n-1) а_ (n-2)
.ао
!
.
.
.
.
.
.
.
.
.
.
или [а-]Х{а]= 1[с], 11де {a_J
-
ниж11яя треугольная матрица, ооста•вленная .из от
счетных з,начений a-k • В ,силу ищентич,ности ,у:равнений (2 .1 2) и (2.20) анализ,
проделан·ный для -кор,ректо·ра последейст,вия, оправ-едли:в та,кже для ,корректора
пред1дейст,вия при замене ,в •соот;вет.ствующиос :выражениях ak, ан и С1< на a_k,
C-k •И C-k•
Одновременная корр екция преддействия и · последействия. КоррекТQр пре~д
действия и последейст,вия ОIПИ·СЫвае'ГСя ма11рич,ным у,ра,внением, .вытекаю щи-м -не
пооредс11венно из (2 . 11) [9 ]:
йт
,а2а1аоа-1
а-п
сх- 2
С_2
ат
.а2 а1 ао
а_1
.а- п
сх- 1
c_l
ат
.а2 а1
ао
а-1
.а -п
х eto
Со
ат
,а2
щ
ао
а-1
~ .а_п
СХ1
С1
ат
а2
а1
аоа-1·••а_п
Ct2
С2
86
или r[a]X i[aJ=r[c], т.ку,да [а]=[а]- 1 Х{с]. Матрица т бешюн~на ,во ;в-се стороны
и •содерж,ит т зна,чащих ,ншкних и п значащих •верх~них sдиагоналеи (,по rчислу
елементо·в ak, • отличных от нуля); [а] и {с]
-
ма'J\рицьн:толбцы, ,беоконечные ·в
обе ,стороны .
Иоследуем обращенные матрицы [а]. Обоз,начИ1м rчерез Н" бесконечrную мат
рИ1цу, у ,к,ото:рой •элементы k-й ,пмдиа,гонали равны единице, а все •Остальные
элементы ,ра.вны ,нулю (О). На,п,ри.мер,
~t о:!
о
оо
о
но=
Hl=
... ..
.О\ 11О о...
о11о10
➔
--------
-- --
,
о 1оо
о
оо
о 1Оо...
о 1ОО
1
Если
(2.21)
т
алгебраичеокий полином отнооительн.о х, то [а]=Iа,,.Н"-матричный полино~~
-п
011носительно Н, обладающий форм<'\ЛЬНО овойствами полинома f (х).
'Мат,рицу [AJ- 1, ,обрат,н.ую [а], бущем иокать ,в форме
00
[АГ1= I'Vkнk.
(2. 22)
-оо
Особенности о·бращения ·мат,рицы [а] следующие.
11. Матрица ,[а] имеет ,беок•онечное множес тво линейнонезаrвисим ых левосто
ронниос обратных - 1i[a] и 1бе-сконеч,ное ,м,ножество ли,нейнонеза,ви,си,мых ,пра rно
сторонних обратных l[a]- 1
.
Множест,ва :нуль-щелителей 0,[а] и ,[а]0 та1кже бесжонеч
:ны, ,причем :раз·мерность •этих ,множест,в беоконечно ,вели.ка.
12. М1-южество матриц r[AJ- 1 ,конфигу,ра,ции (,2.2,2) бе:сконечно. Множест.во
нуль,делителей ,[А] 0 та,кже , беско,нечно, ,одна rко ,размерность ,множе.ства ,коне,ч,на и
сшределяе11ся величи,нами т и п.
3. Мат,рица r[a ] имеет единственную двустороннюю о:братную, у.довлет.воряю-
щую тр ебо,ванию физи ческой реализуемости, если полином f(x) (2 ..21) ,не имеет
кор,ней, •ра,вных по мо1дулю е,дини.це . Коэффициенты '\'k такой :матри,цы ,выr<шс
ляются в ·следующем п,а;р,я~дrке. Пусть л.1 , л.2, ... ,
Л.n - ,к ор·ни полинома (2.21),
ра1оположенные в ком1пле1юной плоскости ,внутри R:pyra единичного ра,диуса;
В1, В2, ...,
Вт - ,корни, ·ра,опол,ожен:ные в,не ~руга еди,ничного ,ращиуса . Фактори
зуем •матрицу {а] относительно единич,ной аюружно·сти
[а]= Q1Q2,
п
п
гдеQl= Gm п (Но - н-Iл.;) =r dkH-k;
i=l
k=O
т
т
Q2=п(Н1-
~iН0)=Lekнk,
J=l
k=O
87
rще
QlQJI = flO; Q2Q2! = н~.
Коэффициещы D" ,и ,Е" .нахощят,ся из соотношений (2.13), (2.17), (2.19) при за
мене ал ,на dk и е1< . Перемножая Qi- 1 и Q2 - 1, получим ,ря,д Лора,на 1по степеням
матрицы Н, коэффи,циенты ,которо.го я,вщ1ются искомыми коэффициентами V1<e;=
о,
= I Eн1<D;. Описанный .прием фо.р,мально .не отличает,ся от возведения полино
i=О
ма f(x) в ,степень -1 -на ,окружности едини,чного :ра1диуса :ком,плекс.ной плоско
сти z.
1Коррект,ор, ,ра•сочита,нный •согла·сно •П!ри,веденной методике, при точном п,ре
образ овании последовательности {ал} в {ел} требует ,бесжонечн-о большо,го за
павщывания •входно,го сиг,нала. БесЖО'Нечно большое заtпаз,дывание :возни:кает
из-за требования 1rюлной к,о,ррекции ,прещ1действия. ПоС:колыку такая задержка
йJе может быть реалwзова ,на, преддейс11вие :ко;рректи:рует,ся []риближен.но, п,ричем
величи,на за1дер •жки си,гнала •ОП!ределяет,ся желаемой точ,ностью ко,рректи,ро-вания.
Rор:р е1пор, осуще'С'!шляющий приlближенную ,rщрре юцию прещдейсТ1Вия при . точ
ной •корре1щии 1последейст,вия, описывается уравнением [9]
➔
аоа а2
.а
а-2
с-l
-1
-п
а1 ао а-1 а-2
.а-п
а2а1аоа а
.а
х
а-1
с-1
-1
-2
-п
ао
Со
1 ат am-l
.а0 а_1 а_2 .. .а_п
а1
с1 -\,
:или {ii] Х [,а]= 1[с] (1- число корректируемых точек преддействия), откуда .
1a]=l[XJ- 1 Х[с], ,где [JJ- 1
-
мат,ри,ца, обрат,ная {а] .
Особенности об,ращения ма11ри~цы {ii] ,следующие .
,! . Матрица :[а] имеет ,бесконечное множест,во ~как левост,оро,нiних, так и п,ра
востор,он,них о,братных. Множества .нуль-1делителей 0,[ii] и [ii] 0 также ,бесжонеч·ны.
2. Множест.во матри,ц l[XJ- 1 lбес;ко:нечно. Раз- мер,ность ,множест ,ва конеч,на и
ра.в,на mxn.
3. Матрица [ii] имеет ЕJдинственную щвусто:роннюю обратную [д]- 1 , у,дщJлет
воряющу.ю услов-ию физической ·реализуемости, толыко в том случае, если число
корней 'полинома (,2:21), .по ,мощулю меньших -единицы, :ра1Jно п, а •число корней,
no •модулю .болыших единицы, •ра11~но т [!По ,чи,слу импульсо,в ,пред1действия и ,пос
ледействия ,в ,,rщс.юрет,ном отклике gi(kЛt)].
Из с11:а:нного свойства ,выт,екает, чт,о если полином (2.21) имеет п кар-не~,
;ра,слоложенных ,в 1Плоскости z ,в,нутри юру,га еди- ничного ра,диуса, и m ко:рнеи,
расположен,ных вне круга еди,ничного ра1диуса, то в ашчестве основного им1Пуль
са а 0 -следует ,принять •(n+ :J )-й импульс, перед ,которым ,ра-аположено п им,пуль
сов ,цреддейс'!'вия и по.еле которого следу,ет т импульсо,в ,п оследейст,вия. При
веденное п,ра 1вил.о нумерации зна,чений ал сов.падает с аналогич,ным правил.ом,
дан,ньпм ,в § ,2. 12 на,стоящей гла,вы . !Правило -спра,ведли:во ,не толь.ко п.ри расчете
КО!рректоро:в с 1Помощью бесжон,ечных матри,ц, но и п.ри раочеrах ,кор·ректоров с
и,ополюова,нием .матриц ко,неч-ных ,ра·змеро1в .
.Элементы А;п ма'!)ри1цы [XJ- 1 1находяг-ся из соотн()ше.ний:
Aj1 == EjDo; Aj2 = EjD1+Ei- IDo;
Аjз= EjD2+Ei-ID1+Ei_2 D0
и т. ,д. (} - номер ст,роки; k - .номер столбца). Элемент ао :ра•сположен всег-
88
да ,на глав,ной диагонали ,ма11рицы ,[ii]. ,Если оточетный имfflуль-с ао выrбра.н со
гласно у~казан,ному аrра,вилу, ·ма1'ри,ца ,[а] имеет оrбра11ную, ущовле11воряющую ус
ловию физической ,реализуемости. В противном слу,чае •матрица ,[iiJ ,не им-еет О'б
ра-г.ной , .даже €'ели полином (2.21) .не содержит корней, .по ,модул ю ,равны х ед-я
нище (отличие от матри,цы ra]).
,Раосмот~рим 1слу,чай, кома число 011в0~дов ,кор:ректора ak ,конеч.но, на~пример
-п 1 ,;;;;k,;;;;m 1. Бес.коне~ч,ная матрища-•стмбец коэффищиентов ak .п1ревращается s
конечную, а из беско-нечной мат,рищы (а] ,вырезае11ся к,вадрат.ная ,матрица ,раз
меромn1+т1+1:
{, ..
1
1
[а]' : a_z
1
1
1а, а.1•••
1
~- -- -----
--
--- --- --i --- ---
1йоа.,G.z•••
1
а, йо а., й-2
1
1
Gzа,йоа_,G.z
1
rr,_2
С.2
1
G3Gzа,йоа.,a.z...
1
rr, _,
с_,
1
1
[iiJ ,.
1
1а.а,а,а,йоа.,a.z
... ,.
х
Ci, о
Со
'
а, G3
'
1• ••
Gzа,(/0а.,G.z1
«,
с,
1
...а.а,а,а,йоа.,1
e;;z .
Cz
1
а0:а.,
1
...
а.а,а,а,
{r
...
а. -------!-
-
-
---
---
а, а, а,:а0
[,)" i
...
а" G3
а21а,
а" а3/а2
а,i
За -счет огра.н-ичения числа отвода.в ;возникает 1пог,решность, ~ричем nог.реш
.ности кор•ректироваtНия пре~дiдеikтвия и последейс11Вия, воdбще •ГOBOIJJЯ, различ
ны: {е]' = l[a]' Х [а]; l[e]" = l[a]" Х :[а]; {е]' и l[e]" -
матрицы погр ешностей пр еддей
с11вия и •лоследейст,вия. От-метим , что ~матрица [а]' •составлена только из эле
ментов лрещ,действия, а мат-рища [а]" - толыко из элементов после.дейс11вия. !Вы
ш есказанное ,поя,сняется ,рис. Q.4 (,ра,ссмат,рювае11Ся слу,чай полной i!Юр,рекщи,и).
-г-1О
2
Р.ис. 2.4°. Дwскре11ный сиr-нал на вых'О.де кор :ректора
В п 1 тО'Чка~х полу,чается пм,ная ,ко,ррек,ция прещ1дейст,вия, а :в т 1 точках - пол-
1ная кор:ре1щия послещейс11вия. В ,остальных точ:ках .воэникают 11югрешности
e'k и e"k*>.
Метод факторизации z-изображения импульсной реакции канала. При рас
ч ете rа1р-м0~ничеоких корректоров принимаются .во в-ни-ма ,ние ра,вномер-ные ди
скретные значения вх•одiных и выходных ситналов. Поэтому для та,коrrо ра,с,чета
*> Полная коррекция инот,да ~называется «кор.рек:цией по нулям» (zero-
- forcing).
89
!Может •быть применен метод z-m,реобра·завания 1[1, 4], являющийся м.сщифика
цией диокреТ1н-ого п:рео1бра•зава,ния Лапла,са. ,вместо •непр •ерывных сиnналав бу-
"'
-оо
циента ,передачи гармоничес1юго :к,оррект~ра без у,чета вносимого запаздывания
имеет :ви,д
т,
К.(z) =I r.ц,,zk •
(2 .23)
-п,
На е,ди~нИ'Ч,НОЙ окружности ,ком1Плеюсной плоскасти z фу,н,кции gv (z) совпа
дают со апеклральными плотностями G v (ico) дискретных сигналов g v (kiЛt)
{k-=10, ± ,!' ± ,2, .. .) с точностью ,ДО Iмнш1штеля Лt:MgV rz) =GV (icoн z= е-!rоЛ/
(v= ·l, 2, •3). Следовательно, gv ,(z) однознач,но определяют исходные непрерыв
l!!Ые ,сиr,налы gv (t) (v='l, 2, 3) только .в моменты вр,емени kЛt. В 01бщем случае
.существует беоконечное ,м,н•ожесТ1во ,непрерывных сИ1rналов с одинак·о,выми z-изо
· бражениями. Одна•ко если ,е,пе·ктры с-иrналов ограничены некоторой част.отой
•ffic, то, вьJiби -рая .Л.t =nf.coc, [юлу,чим z-изображ,ения, од:ноа.начiНО
описывающие
исходные сигналы Iво в·се моменты Iв.ремени. В этом слу,чае z-изображения [1:ри
Z= •e- 1 roлi •СОВ/Падают со спектральными, пло'!)ностями ,сиr,нало,в ·на О'!'ре·зке
[-п/,Лt, лfiлt].
Коэффицц,ент передачи корректо,ра, преобразующего g 1(z) ,в gз(z), ,ра
вен [8]
J((z)=g3 (z)/g1 (z).
(2.24)
,Определим ali Iпо за,данным gi(z) и gз(z). Предста,вим л,равую часть выражения
(12"24) ·в .ви~де ,ряда по положительным ,и отрицательным ,степеням z. С этой
целью разложим •l/.g1(z) в ряд Ло.рана на ок,руж,ности еди,нич,ного ·радиуса ~1,5]:
(2 .25)
ме
h_k= 2~i ф
г,
{k =l,2,3, .. . ).
Инте11ралы берут,ся Iв ком1Плек·сной пласкости z по окружностям (ли.бо за,м1Кну
тым конту~ра,м) Г 1 и Г2 с цент,ром ,в точ~ке О, прИ'Чем .радиусы •окруж,ностей
,1г1, I и JГ2I должны ~овлет.ворять требо.ванию l<JГ1l<l~мип • I; lл~raнc · I<
<JГ2 J<Il, 11де ~мия - ,минимальный rrю модулю нз [JОЛЮсов l/g1(z), 1р аополо
Жt}ННЫХ ,вне к,ру·га ед:и~нич,ного ращиуса; J •лмакс 1 - ,максимальный [10 •ммулю
из полюсов, расположенных внутри круга единичного радиуса.
Ряд (2 .:25) схощИ'!'Сi!, если g 1(z) Iне имеет ,нулей на окружно1ст,и еди,ни,чн,ого
радиуса, что эквивалентно выполнению условия корректируемости канала
·1G1,(iro) 1 = 1K!'(i{I)) 1=#0( 1со 1~ (uc) . В дальнейшем цредпола,гает,ся, что это усло-
11ше •ВЫIПОЛНЯ·е'I'СЯ.
Та,ки,м ,обрааом,
(2. 26)
-со
-оо
90
~
~
где hk = ~ cv h v +k, Этот ряд также сходите'!, если ~ \ Cv \< оо, поэтому, заме-
v=-оо
-оо
нив его конечным rполи,номом степени n 1+ т 1 ( -п1 ~k~ т1), получим и•скомый
коэффициент ,передачи кор:ректора (2 .23), для .которого 1ak = hk,
Сигнал ,на Iвых-оде .корректора
т,
g2(z) = g1(z)~hhzk
-п,
отличается от gз(z) ,на .вели,чину по11решно,сти ri(z)=gз(z) -g2 (z), которая в си
лу •СХОДИМОСТИ ,ряда (2. ,26) стреМИ'I'СЯ IK ,нулю ,дри n1, тг>-ОО. 'В ьJiбирая n1 и т1
соотве'J'\сТrвующим образом, rмож,но свести ri(z) к ,наперед заданной ,величине .
Для -аграюtчеаных ·по ,сп,ек11ру сигналов ·непрерьпв,ная пог.решн-ость rкор:рек-
00
sinroc(t- kЛt)
ции ,рав,на 11 (t) = ~ μh --~~
-
-~
~
Wc(t - kЛt)
-00
где μk - коэффициенты 1ряда
ri(z).
,Вычи,сление ,коэ.ффициент,ав hя су:щест.вен но :упрощает,ся, если наложить •на
т
g 1(z) ограничения: :1) g 1 (z) - полином степени п+т: ,g 1(z) = ~ akzk; 2) g\(z)
-п
смер:>Wит п .корней, .мо.цуль которых меньше единицы, и т •ко,рней, .модуль ко
торых ,больше единицы (соо'J'\Ве'I'ст,венно числу о'I'рицателыных и положителыных
сте111,еней z) . Корни на единичной окружности отсутст,вуют .
.Разложение ~функции 1/g1.(z) ,в :ря.ц Лора,на эквивалентно решению ,у.рав-
нения
К(z)g1(z)=1.
(2.27)
Здесь R.(z) - ·беоко,нечный ряд Лора.на, ,посжольку полиномиаль·ное уравнение
(2 .27) не ,может ,быть •разrрешеио .в лолинЬ,мах 1к,он-ечной степени . Заметим, что
,уравнение (,2.27) формально ,ре1Шается несщнооначно . Для полинома степени,
наrп,ример, N . существует ,сист•е.ма из N + 11 линейнонеза,висимых ря,дов, •Образую
щих бази•с,. и ,бесконечное множест,во рядов, Яlвляющи.х:ся линейной ,ком·бинацией
N+I
этого базиеа: Р = ~ АkРя, !Где Р1, Р2, ... ,
Ря - бази,сные ·ряды, ущавлетворяющие
k=I
(2.27); А1, А2, ... ,
Ak, ... •
-
любые 'Числа, поли.но.мы или rряды :no ст•епеням z та
N+1
кие, что \" Ая = 1. ,В,ведем дополнителыное огра.нич·ение, ,которое поз.валило бы
,1,,..,,
k=I
вычи,слить R(z) ,однозначно. Этим 011раничени•ем являет,ся требование физиче
ской rРеализуемости ра,ооч и т ываемой •сх-емы rкорректора ·. Факторизуем полином
g 1(z) относительно акру.жно•сти единичного ·ра.циуса g 1(z) = Q1(z)Q2(z), ме
п
п
Q 1 (z)-полином ло отриrцательным степеням z: Q,(z)= ~dяz - k=B П (1-
1
т
-ляz- 1 ); Q2 (z) - полином по положительным степеням z: Qiz)= ~ eяzk=
о
т
= П (z- ~ k); Ля - ,корни полинома g1(z), rрааположенные ·внутри круга единич-
,ною ,радиуса; ~k
-
,корни, расположенные ,вне •круга единичного радиу,са; В -
некоторый коэффициент. С учетом фак'I'оризации 1/g 1(z) = Q-) (z)Q- 12(z), где
91
00
Q- 11(z) и Q- 12(z)-ряды, обратные Q1(z) и Q2(z): Q- 11(z) = Ioяz~; Q- 12 (z)=
о
00
= ~Е1,zя. Коэффициенты Dя и Е1, находятся из рекуррентных соотношений (2.13)
о
цри замене A1t и a1t соот,ве'!'с11вен,но на D1t(d1t) и E1t(e1i). Перемножив Q- 1 11(z)
о,
н Q- 12 (z), получим ряд Лорана .с искомыми ко.с,ффициента,ми h1i°= ~ Eн1iD;. -
i=O
Описанный tП-рием формально соJ3JПа ,дает с ,процессом вычи,сления ма'I'ри.цы
IAJ- 1
,
обрат,ной [а], как зто дано ,в предыдущем разделе на-стоящей rла,вы.
Частные случаи: ·1. Кор,ни ,полинома g 1(z) •ра,сnоложены ,в,ну'I'ри единичной
ок:руж,насти. В ,результат,е h-1i=a-1i=D1t и мы приходим ,к ,кор,ректору n~ре.п.дей
с11вия. ,2. Кор ·ни n-алинома g 1(z) распаложены .в.не единичной окружности. Это
дает ,к·орректо.р ~послмейс11вия, ,у которого a1t=hя=Eft.
Укажем еще оди,н опособ определения h1t [1 ,5]. Ум.нажим ,числитель и з,на
менатель (,2.25) на zn и разложим полученный ,результат ,на сумму элементар
ных .дробей ,ви,да
Ка2КJ(ая из элемента1рных дробей sЦалее ,разлагается ,в ,ряд по формуле геомет
рической ,11ро1среосии· :
00
_ _A_1i _z - _1_ = A1i. ~ л1⁄2 z-<v+I);
• l -' A1tz-1
'11=0
В ито,rе получим
1.п
--=z
gl (z)
где
00
V=-
00
о,
'
1 \.!:,
v-1
1тB1t
h_v=~~A1t'Ak ;h' =- ~
-- (v=O, 1, 2,.
т k=l
"'
ат k=I ~k+l
•.
Коэффициенты h~ и hv связаны ,соотношением hv =h·~-п·
(2.28)
(2.29)
.).
/
,Корректор с .каэффисr.щентом ,передачи (2.23) ,вносит постояшное эалазды;ва
~ше -т:=п 1 Лt, из ,чего слмует, ,что ,в о:бщем случае 1Погрешность .хорр-екти·рова,ния
11(z), (Шре~деляемая 1велисшнами п 1 и m1, ,связана с временем -т: об.рат,ной зави
симостью. Уменьшение по11решности -корректирования цри за,данном си11нале
g 1(z) ,п:риводит ,к у~величению эапаз,дыва.ния ,выходного ·сигнала и ,наобО!рот . Ну
левая погрешность лолучается при 't' =, oo. Этот ,вывод соот,вет,с11вует случаю на
личия в полиноме g1(z) корней, по ,модулю -меньших .единицы ('A1t); если лоли
иом ,саде,ржит толы.ко 3⁄4орни, по модулю :большие единицы (~1t), ,величи,на -т:
рашна нулю и не из-меняе'ГСЯ ,при .изменении 1по11решности ·корр,ектиро1ва.ния.
92
Для а1< апра·ведли,ва также .фQ\рмула
(2. 30)
позволяющая ,при неv,бхмимости находить а1< ,приближ,енно, ..и,апользуя методы
приближенно.го ,гармонич,ескоrо анализа. Эта фо:рмула вытекает из :ра'Зложения,
я1вляющеrося обобщением .ря:да Котельникова (2:1)
ct)
g3(t)=I CGkg1(t- kЛt),
(2.31)
- ct:,
которое оп:раведли1во для 111.роизвольных -сиr-налс;в ,g1(t) и gз(t) с одина ,к·овыми
по протяженности опектрами, ,ог.ра,ниченными ча,стотой n/Лt. Подобным соотно
шением ·связаны си,nналы на входе и выходе гармонического коррект-ора при
бесконечно большом чи,сле оТfiюдов ап. IВэя,в преобра>зова,ние Фу,рье ,от о:беих ча
ст,ей (,2 ..31), ,непосред,ственно получим (2 .30).
В изложен.ных ме'!'о1дах з.на·чения п 1 и m 1 определяются ,на последнем эта1пе
ра,счета, исхо,дя и,з требуемой погрешности ,корректи:рования. Ра,с•смоТJрим опо
соб ,ра -счета, ,который поз,воляет вычислить 'Значения ко1эффициентов а1, лри _
фи,к,сИ):юва.н,ных n1 и т1, иохо:дя из условия получения . минимума суммарной
1Ювад,рати,чной ,погрешности : (энергии) уклонения выходного ·си,г.нала к~р·ректора
g 2 (z) от сигнала за1дан,ной ,фор,мы gз(z):
ф
00
1
_
1dz
.
f)= --.
11(z)11(z ) -
·=
~(bk- Ck)2 = mm,
2ni
z
~
г
-оо .
где 11(z)=K(z)g 1 (z)-gз(z); K(z) - коэффи,циент передачи кор:ректо.ра (2.23);
.Г - контур единичной с;к,руж,ности \ z \ = 1. Иокомый 111оли.ном К (z), ми.нимизи
lРУЮЩИЙ 11, ,наЙiдем из ,у,сло,вия ,ра,венс11ва -нулю 111ри.ращени_я 11, выз,ванного бе-с
конечно ,малой вариацией K(z). После соответ-ствующих преобразований л,ри-
ХОiдИМ ,к ,системе у,ра,в,нений {Jl]
•
gi
gz
• gп+т
а
-
-d
-
go
-п,
-п,
gi
go
g1
g2
gi
go
g1
gz_
х а_!
d_l
gz
g1g0 gi
ао
do
·_
gп+т
gz
.gi
,go
ат, -
dm, -
,где gi= ~ а._;ап; di = ~ an-iCn.
k
k
Пример. На осно·ве ф-л (2.28) и (2 .29) •в табл. 2.1 даны ,в общем виде вы
-ражения для ко·эффициентов ak гармо ,ническоrо корректо.ра, преаб.разующеrо
- сиnнал g 1(z) с д,вумя мешающими импульсами в сигнал -gs(z)=l. Кроме того,
_ да:ны .выражения для ,коэффициентов μ1,, позволяющие вычи-слить погрешность
tJ(t).
Ра-оочитаем •корректор . для слу,чая а-1 =0,8; ао=2,4; а1 = 1; n1 =3; m1=4. По
та,бл . 2.1 ,находим: а0 =0,625; а 1 =-0,312; а2= 10,156; аз=-0,078; а4=0,039;
, а_ 1 =-0,25; а- 2 =0,1; а- 3 =-0,04; μs=I0,039; μ,=0,016; μ_з=-0,016; μ-•=
- = 0,032 . Ма!{симум \11 (t)!\ = 0;039.
93
<.D
н>-
Исходный сигнал
1
а_1 z-1+ао+a1z
а_2 z-2 + a1z+ а0
Значение коэффициентов alt
2
1,
a1t =
а1 (а-~) ~k
(k=D ,1,2 ,
..
.,т1)
')..,k
a_k=а1(а-
~)
(k=1,2, . .., n1)
лk+I лk+I
1-2
ak=
ао (л1+л2)
(k=O, 1, 2,
• ..' n1)
a.1t = О (для всех k)
(1 +k)лk
a,_ k=
ао
(k=O,1,2, . . ., п1)
a1t=О(длявсехk)
rт.аблица 2.1
Значение коэффициен'l'ов μlt
Примечанnе
3
4
μ-(n,+I> = ai а_п,
μп, = а1 а_(п,-1) + ао ап,
т1 ,щ - число отводов корректора
μт,+1 = а1 ат,
-
ао± Vа~_:_4а_1а1
μп,= аоат,+а1ат, - 1
') ..,,
~=
2а1 ;
μlt=О(k=т1,т1+1, . . .,
1л1<1; 1~1>1
- n1,
-n1-1, .. .)
-
-
а_1 ± V а:__1- 4а0а_2
μ-(п,+2) = а_2 а_п,
л1.2=
2ао
μ-(п,+I) = а2 а,-(п,+I) +
+a-la-n,
μ_k=О(k=О,1,2
..
.'n1)
лi=л2=л
(О
1:11
ао+ a1z+ a2z2
2
1
х
a1i = (~1
_
~
2) й2
.(1
1)
Х~~+1-
~~+1
(k=О,1,2, . . ., m1)
a_k=О(длявсехk)
k+l
a11,=--
ao~k
(k=O, 1, 2, ... , m1)
a_k=О(длявсехk)
Окончание табл. 2.1
3
4
μт,+2 = а2ат
μт,+1 = а2 ат,-1 + a_l ат
V2
-
а1±
а1 - 4а0а2
~1.2=
2а2
μ1i=О(k=О,1,2, ..
-.,m1)
~1= ~2=~
Расчет корректоров по последовательности импульсных
реакций при их взаимной интерференции.
Теоремы отсчетов для периодических частотно-ограниченных
сигналов
Ранее шла речь о р_асчете 1к,орректоро;в по дисКJретным з.начения,м импульс
ной 1реак,ции ,ка,нала, т. е. ,по ди-оюретным значения-м сиrr,нала, 1Возникающего на
~выхОlде каrнала при 1пода1Че яа его ,вход о,диночног-о воэдейс11вия ,в ,вид-е функ,ци,и
Дира1ка b(t). В реальных условиях на в•хад ,ка,нала ,пощается· не миночное воз-
t 1Ет
~t1t
а}
t
t
1·
т
~t
t
it
б)
Рис. 2.5. ОднО1Поля1р.ная ( а) и д'ВУХiПОЛЯl)J,ная ( 6)
последо.ват-ель-ноС'Ги б-функций
а}
P,wc. 2.6. О11кли1К ка,нала ла ощно.полярн1ую ( а) и двух,поля·р
.ную (б) ,последоrвательности б-фу~mщий
действие, а адн0tполяр.ная или ,двуюполяр.ная последовательность б - им.пульсов
(.фующий Дирака) (рис . 12.5). Соответственно .на ,выходе канал! возни,кают пе-
риодичеокие последовательности и.м1Пульоных реакций il1(t) и g1(t) (рис. 2.6) .
Бели -кор ,ректор комrпен-сирует • .искажения одиночной •реакции, то, естественно,
он ,бу~дет ком[lен-сировать и иокажения паследо.вательности ·реаюций при любом
9б
интер .вале сле1дования Т. Однако о,брат,ное утверж,дение, - строго говоря, Не<:[]ра
ведливо , так ка,к коррекция периОiдической ,после1довательности не соот,ве11Ствует
корр1с1щии одиночной реакции {в о·собенности для Т, меньших .длительности
реа,1щии). Объясннется э то тем, что в силу фактора повторения сnектр перио
дической ,последо·вательности отличае~,ся от спект,ра о.ди,ночной ,реакции. Поэто
му рассмотрим, .какой ,получится результат ко,р.рекции характери,сти ,к ка,нала,
е-сли осущест,вляет,ся комлен•сация искажений перио.дическо_й .последовательно
сти им,пуль,сных реа·кций канала при п-роизвольно за.данном интервале Т.
Спектры од.нополярной и двух поля,рной по,следовательностей б-имmульсо,в -
. дискретные
и ра , в ,номер .ные и ,соде,ржат гармоники ,с-оотв-етст,венно с ча,стотами
1.!!_k=2nk/T (k=O, 1, 2, .. 1 и w1,=2n(2k-1)/T (k=l, 2, ... ) . Опектры R1(iw) и
1( 1 (iw) ,реакций g1(t) и j;(t) - дискретные и ограничены частотой среза кана.
ЛЗ Wc,
Для одиночной реакции g 1(t), я.вляющейся функцией с ограниченным ,опе:кт
,ром, справедли,ва теорема отсчетов (тео_рема 1Котельнико:ва) (2.1). У,кажем ана-
логичные теоремы для реЗiщий й1t) и g2(t). Согла-оно оснав,ной ·теореме отсче
тов ,[З] , если g1 (t) - периодическая функция с п ериодом Т (рис. 2.ба) и все
коэффициенты Фурье ,для ,нее, начиная с п-,го , ра.вны нулю, то
п
i1(t)=! R1(kЛt)(J)1(t- kЛt),
(2.32)
-п
1 ,_.
ffic
rp1(t) = -
-
sшffictcosec ---t =
2п+ 1
2п+ 1
1(
п~2Шс)
--
1+2" ~cos--kt ;
2п+1
,._
2п+ 1
1
ffic= л/Лt; Лt= Т/2n+1.
Сп ектр cp 1(t) - .дискретный и содержит n+l гармоник (в.ключая нулевую) . Рас·-
стояние меж ду спектральными составляющими равно 2,wc/ (2n + 1); амплит уд а ну
левой гармоники рав,на 1, амплитуJJ,ы остальных га •рмони~к ,ра ,в.ны 2 (рис. 2.7) .
Таки,м о,бразом, g1(t) однозначно определяется 2п+ 1 отсчет-ными значениями , ,
взятыми с интервалом Лt.
21/1т- --=-тц)с::
~Zд,1
О GJO GJI (,)2
GJ, 1,J; ,/ GJn -1 GJn GJc
а}
f·
(,)с
ттsт (,)ctcosec тt
T={2rz+f)Лt
tJ)
Р.ис . 2.7 . Спек11р (а) и 11рафик (б) о~,оче11н ой ф)пНК·
ции (J)1(t)
ВИiдоизменен,ная теорема отсчетов гласит: если п-я га,рмоника ооектра g1(t)
не -со.держит си.нусои~дальной соста ,вляющей, то
4-181
97
п-1
fi1(t)=~~(kЛt)ср2(t- kЛt),
(2. 33)
-п
где
1.
ffic
(р2(t)= --
sшffictctg-t =
2n
2n
[последний член суммы (k=n) берется -с ,весом 0,5]. Раостоя,ние ·между гармони
ками -спектра фующии cp2(t) ,рав-но (i)c/n; ам,плитуды нулевой и п-й rа,рмоник
равны 1, ·остальных ,rа.рмоник - 2 (рис. 2. ,8).
f.
(J
7if Stn (,Jctctg tf t
t
L1t
РИ1с. 2.8. О.пек11р (а) и графи,к (6) оrсче11ной фунrк
щ-iи cp2(t)
Следует -011метить, что rприведен,ные формулиро,вrки теоремы отсчетов •экви
вале,-пны, ибо о,.zща и та же функция g1(t) .может быть rпредставлена как ,в
фор.м,е (2.32), та ,к и в фо1рме (2.33) . Форма (2.32) оп,ра ,ведли,ва при любом по
ложении моме,нтов :выборки kЛt; форма (2.33) спра,ве,дли:ва для произвольной
g1(t) только в том ,слу,чае, -когда положение моменrов - выбо,рки k.Лt совпадает
с ма-ксиму1,_1а,ми п-й ·гар.мо-ники, что и обеспечи-вает -равен·ство нулю сину-соиtЦаль
ной соста,вляющей этой ·гармо,ни,ки. Выбирая соответс11вую щим о·бразом по-ложе
ние .моментов k.Лt, ,все11да ,можно пред,ставить й1(t) ,в форме (2.33).
rПо а.налогии с изложенными тео•ремами для зна1Кочередующихся rпе~сщи,че
ских фу,нюций (,ри-с. 2.66) оформули,руем ,следующую тео:рему: если gi(t) -
з.на•кочередующая,ся период иче-окая функция с ·периодом Т, причем спектр этой
фу,нкции не со-держит ,гармоник выше п - й, то (17]
п-1
gl(t)= .Igl(kЛt)ср3и-kЛt),
(2. 34)
-п
где
1
ffic
I In ffic
л:
Т
m 3 (t) = - sinfficfcosec -
·
·t=-
cos - (2k ~ l)t·(j)= -
·
Лt= -
"'
2n
2n
п
2n
'
с Лt'
2n
1
98
Спектр функции <р3 (t) содержит только ,нече-nные гармони1ки (i)k = (2k-1) (i)c/2n
~стоты (i)c/2n (,рнс . 2.9). Согласно этой теореме знаi(очередующанся функция
g1(t) полностью -описывается 2n от-счетными значе.ниями, взятыми •С интервалом
Лt.
2
GJz
GJk GJk,f f,Jn -1 f,Jn Wc
а)
f.
{,)с t
То sin wct casec 10
!Jt=.E . .
/
(,)с
Т= 2nL! t
d}
t
м
Ри,с. 2.9 . Спектр (а) и nрафи.к (6) отсчетной фу~нк,ции
(j)з( t)
Бели п-я гармоника спектра: gi(t) не содержит синусоидальной составляю
щей, · ТО
п-1
"i1(t)= ~ g1(kЛt)[f!4(t- kЛt),
. ...J
-(п-1)
nде
п
•
1
ffic
1~'
ffic
(f!4 (t) =
--sinffict ctg--t = 2--
cos (2k - 1)-- t;
2n- 1
2n- 1
2п-1
2n- 1
1
ffic=л/Лt;Лt=Т/(2п-1)
(последний чл1ен суммы берется с весом, равным 0,5) (рис. 2.1 О).
(2.35)
У.казанные формули2._овl]{И теоремы эквивалентны, т. е. одна и та же знакоче•
редующаяся функция .gi(t) может быть представлена либо в форме (2.34), ли
бо ,в форме (2.35). Форма (2.34) справедли-ва при произ.вольно.м положении мо
иентов выбор.кн kЛt; форма (2.35) -справедлива в том ,случае, когда положение
моментов выборки kЛt совпадает с максимумами п-й гармоники, что легко вы-
rюлняет-ся .
.
Значения опектра К1 (i(i)k) определяются .по формуле
-
1
п-
.
К(iffik)=
--
~ а e-iwkvлt
(2.36)
l
2n+1-~
V
'
V=- n
если Лt = Т/(2п+1); av = ii_(vЛt);
4*
99
ffik=2ffick / (2п+.l) (k=0±l,±2, . . . ),
или по формуле
-
1
К (i ffik)= -
2n
h-l
V= -n
еслиЛt= Т/2п; av= &_(vЛt);
ffik=ffick / n (k=0,±1, ±2, .. . ) .
Т~ (Zп - 1)Лt
-1
t
Лt
Р,и-с . 2.10. Gпектр (а) и графи,к (6) отсчет,ной фуН1к,ции
cp4(t)
Значения спектра к-;: (iw) находятся п о формуле
n-l
=
·
1L=
-iw vЛt
К1(1ffik)= -
avеk,
2n.
V=- n
(2.37)
? (2.38)
если Лt=T/2n; ~ = 1g,(vЛt); Ы1t= , (21t-l)wc/2n (k = ±1, ±2, .. .), \!ЛИ по фор.мулt:
п+l
к(.)
••-~
=
~iwkvлt
i1ffik=2n••1 •,,._
avе
'
•
V=- n+I
(2. 39)
если Лt=T/2n----,-1; 3⁄4 c=g1(vЛt); W1t=(2k-l)wc/(2n-1) (k = ±l, !±2, ... ) . По су
ществу, выражения (2 . - 36)-(2.39) дают значе,ния -коэффициента передачи кана-
ла К1 (iw) .на частотах W1t .
.
_
_
Используем ттри,ведекные т-еоремьi и ,выражения ,для расчета гармоничес.1п~х
корректоров [17J. Корректор, включаемый ,ка-ска~но с каналом, преобразует
g1(t) в cp 1(t) либо в cp 2 (t). В этом случае коэффициент лере,да_чи корректирует
GЯ в точках w.=2wck/(2n+l) либо в точках Ын=-Wсk/п (k=0, 1, 2, ... ) . Для :Этих
точек спра,ведливо равен-ство
К1(i ffik)К(i ffih) = А e-iwk't ,
(2. 40).
100
где К1 (i(i)k) и K(i(i)k) - соо:rветст,венно значения коэффициента ,передачи ка
!fала и корректора на ча,стотаос Шk; А и ,; - .некоторые постоянные. В дальней- ·
шем для удобства расчета пола г аем -т__:=0, А= 1.
Аналогичн-о при п:реобразова,нии gi(t) в cp 3(t) или в cp 4(t) 1корре1щия ха,рак
теристик .ка.нала производится 1в точках (i)k = (2k- l)(i)c/n ли1бо ,в точках (i)k =
=(2k-l)(i)c/2n-1 (k=1, 2, ... ), для которых ,выполняется (2.40) . В (2.40) не
обходимо доба 1влять вес 0,5 ,на частотах , для которых спектральные составляю
щие <pv (t) (v=l, 2, 4) уменьшены вдвое. К.ак следует из (2.40), преобраэова-
ние g1 '(t) в (J)1(t) или •в (J)2(t), а также преобразование g1(~ ,в (J)з(t) или в
<p4(t) возможно тол1>ко ,в там случае, ,когда ,епектры R1 (i(i)) и К1 (i(i)) не обра
щают,ся .в ,нуль на частотах Wk.
Расчет корректо,ра, ~преобразующего g1(t) ,в cp 1(t), выполняется ,в та.ком Jю
рядке. Воспользовавшись {Зti), оп:ределяем значе·ния коэффициента передачи
2ffic
канала К1 (i(i)) на чаетотах (i)v = - + v , затем вычисляем значения коэффи-
2п1
диенто1в переда,чи ,п о отводам линии ak п-о фо.рмуле
п
1
-
~
[-К (' )]-1
-
iuJ kЛt (
,,,k~)
a,k =
-
2--
1 1ffiv
еv
-
n""' ~n.
п+1 v=- n
Значения ak могут быть вычислены также из системы урав н е н ий [17 , 36]
-,
йо_а,Gz ..
О,п
i'l.z а.,
с;,п
о
1
а_, 7io а, ёiz
ёi., li.z
о
li.z а., 7io а, 7iz
а.,
if.3 а..2 7i: 1 lio а,
U..п ...
d:,1
о
(2.41)
~ 1$,0
7io ii1 az
о
а., iio а, ёiz
°-2 а.., 7io а,
a".z li.1 lio
о
При расчете корректора, преобразующего g1(t) в q; 2 (t) , 1пользуем,ся выра
жением
1 п-1
a1t=2n L [R;_(iffiv)Гle-iuJvkЛt ( - n,(k,(n-1),
v=-n
где R1 (i(i) v ) о,пре.деляе11ся согла,сно (2.37). Бстест,венно, ко•~ффициенты ak в
этом случае . можно найти из си,стемы у1ра.внений, аналог.ичной (2.41), в которой
отсутствует~ значение iiп-
Расчет коэффициентов ak кор ,ректо :ра, преобразующего gi(t) в -<p3(t), про
изводи1'СЯ по формуле
п-1
1~=
]
ak-= 2n .l... [К1(i(l)v) -l e-iuJvkЛt (- п ,,;;;k~п-1),
v=-n
101
где K1 (iшv) испол~,зуем из (2 .38). В случае преобразования i:(t) в cp4·(t) ко
эффи,циенты a1t ,вычисляются ,по формуле
п-1
IXk= -
1- .-
,, . [А\(iffiv)]-!e-iwvkЛt(-п+1,;;;;k~п- l),
2n-l ~
V=-n+I
где K7(iшv ) иаполызуе,м ,из (2.39).
КоэффИiцие,нты а. мо,гут быть ,найдены та~же . из ,системы уравнений типа
(2 .41), в 'Которой з,начения ii_v внутри -очерчвнной о·бла,сти за.меняются :на av,
а 1вне этой о,бла,сти - .на
-av . Подчер ,кнем, что изложенные ,опос обы ра ,ачета
позволяют О1Пределить ·коэффициент пе,ре~ачи корректора, осущес1'вляющего
·т!Уч.ное .п:рео'бразование ,сигнала.в g1(t) и g1(t) соответствен,но в cp 1(t), cp 2(t),
({)з(t) и cp4(t).
В пр~кти•ческих условиях коррекцию 1шнало,в целесообразно выпqлнять по
сигналу gi(t) .как не ,содержащему нулевой ча,сто ты, а ,качест.в·о, 'Коррвкции при
этом целесоо•бра'ЗНО оценwвать mo g1(t), по скольку ча1стоты ,гармони,к апектров
этих ,сигналов 1взаимяо не сов1па1дают.
'
1
Пример. Задан сигнал g1(t)= !g1(v,Лt) ·cp1(t-v,Лt), где g1(-<Лt)=ii-1=0,3;
-1
g 1(0)=iio=l; g1(,Лt) = ii1 = 0,5;
1.
ffic
<р1 (t) =
-
sшffictcosec - t; Лt= n/ffic.
.
3
3
Рассчитаем кор,ректор, преобразующий g1(t) в ({)1 (t). Из системы (2.41)
находи м: а- 1 =0,:07; а0 =1,21; ai =-0,59. Корректор ,с коэффициентом передачи
K(iw)=-0,07e 1 wлt+J,21-0,59e- 1 wЛt преобразует g 1 (t) в cp 1 (t) с нулевой по
грешностью.
2.4 . Особенности коррекции полосовых каналов
по импульсным реакциям
Постановка задачи. Обобщенная теорема отсчетов для сигналов
с полосным спектром
Полосовые каналы обладают рядом особенностей, отличающих
их от каналов НЧ. Поэтому не все результаты предыдущих разде
лов могут быть использованы для коррекции искажений полосовых
каналов . Сказанное подчеркивает необходимость разработки са.мо
стоятелыюй теории синтеза корректоров импульсных характерис•
тик полосовых каналов связи.
• Пусть К.1 (iffi) и g 1 (t) - комплексный коэффициент передачи и
импульсная реакция полосового канала с частотами среза uJ 1 и
(!)2. Считаем, что IК.1(iuJ)j=0 :( l1uJj>uJ2, \uJl<ffi1) . В случае
идеального полосового канала, в котором отсутствуют амплитуд
ные и фазовые искажения, имеем:
. К.1(iffi)1 = const;
<р1(ffi)= argК.1(iffi)= uJ-r+k:п:(k= О, +1, +2,...) (ffi1 -<liffil~uJ2)f
(2.42)
102
В реальных каналах содержатся как амплитудные, так и фа
зовые искажения, поэтому импульсная реакция g 1 (t) такого кана
ла существенно отличается от g 3 (t). Корректор, включаемый на
выходе канала, должен преобразовать g 1 (t) в ,g 3 (t) [ см. (2.42)] с
допустимой погрешностью, в резульwте . чего будут скомпенсиро
ваны все виды линейных искажений, имеющихся в канале.
Поставим задачу коррекции в более общей формулировке :[13] .
Пусть g 1(t) - произвольный сигнал, спектр которого К, (iffi) отли
чен от нуля только на некотором отрезке 1[/ 1ffi 11, jlffi2/], (rffi 1=F0).
Требуется преобразовать сигнал g 1 (,t) в сигнал заданной формы
g 3 (t) со спектральной плотностью Кз (iш), которая также отлична
от нуля только в диапа~оне ,ш 1 - ш2 . Подразумевая в этой форму
лировке под g· 3 (t) импульсную реакцию идеального полосо
вого канала, приходим к задаче 1):оррекции характеристик полосо
вого канала.
При выполнении ограничений: 1) /К,(iш) 1 и /К3 (i,ш) 1 - чет
ные функции, arg К, (i1ш) и arg К3 (iш) - нечетные функции относи
тельно точки 1ш0=0,5 (,ш1 +1ш2); 2) ш2+ш1= ,k (1ш2-ш1), k - любое
целое число - преобразование g 1 (i) в g 3 (t) осуществляется обыч
ным гармоническим корректором (см. рис. 2.lв). Если k - нечет
ное число, расчет корректора производится непосредственно по
дискретным значениям g1 (,kЛt) и gз (,k,Л.t) в полной аналогии с кор
рекцией низкочастотных сигналов [uЛ,t = л (,ш2-ш1) ]. В общем слу
чае, когда указанные ограничения не выполняются, для преобразо
вания g1 (t) в g з (t) используется полосовой гармонический коррек
тор (ри.с. 2.11) с коэффициентом передачи [13]
~--... ....__ ........_ ~__,__ _. . .. . 1.. _~
Вых
.____________-.J UzftJ
Р,и-с. 2.11. С'I'рукту,р.ная схема rа~рм,о-ни,че
ского ,корректора nолсюовых каналов
-п,
(2.43)
где ak = а' k+ Н~а" k; Н - коэффициент передачи преобразователя
Гильберта (фазовращателя с фазовой характеристикой, равной
л,/2, и единичной амплитудной характеристикой в диапазоне
ш1 - ,ш2'):
103
=
1s1gn ffi =
_
н. ..
• { i (ffi1 <: (J) ;'{. ffi2);
·
- i (-(J)2 <: (J) <: -ffi1);
Л<f = 2n/ (,ffi 2-ffi 1) . В дальнейшем множитель е-1wп,'лt, характер изу
ющий запаздывания выходного сигнала во времени, не учитыва~
ется.
.
Неизвестными в (2.43) являются коэффициенты ,а',,_ и а'1.ь.,
которые определим по заданным g 1 (t) и gз(f) либо по К1 (iffi) и
Кз (i(J)).
Входной g 1 (t) и выходной g 2 (t) сигналы корректора связаны
между собой соотношением
т1
m1
.
g2(t)= Lа~g1(t--:-kЛt)+}:.а~g1(t--kЛt),
(2.44)
-п,
-п,
где й1 (t) - преобразование Гильберта:
00
uJ2
g1(t)= .-
.
-
1-
dт:=Re-_
-
iК1(iffi)е'w dffi.
;....,
1 sg(,)
1j'
·t
л
t-т
л
Спектральная плоскость К1 (iffi) функции g1(t) равна R1 (iffi) =
=HK 1 (i,ffi). Потребуем, чтобы сигнал g 2 (t) совпадал с gз(t) за
данной степенью точности.
Представим g 3 (t) в виде ряда
00
00
g3(t)=}.:а~g1(t-kЛt)+La~g1(t-f?Лt),
(2 .45)
-00
-
00
где ,лt = 2л/ (ffi 2- 1ffi 1); а',,_, а",,_ - некоторые · коэффициенты. Выра
ж ение (2.44) является ч астной суммой данного ряда.
Определим, при каких ограничениях разложение (2.45) прав о
мочно. Ответ на этот вопрос является одновременно ответом и на ·
вопрос о возможности коррекции полосового канала с помощью
корректора, изображенного на р ис . 2.11.
Взяв преоб р азование Фурь е от обеих частей выражения (2.45),
п осле соответствующих упрощений получим:
а~ = ReF,,_,
а~=JmFk,
где
iwkЛtd •
е
.
ffi.
Таким образом, для вып·олнения (2.45) коэффициенты а',,_ и а",,
должны находиться как действитещ,ная. и. мнимая части .коэффи
циентов Ф урье функции F(i,ffi) =Kз(iffi) / K1, (i,ffi) .. Поэтом у в случае , .
когда F(iffi) удовлетворяет условиям ДИрJ-!ХЛе; на__ отрезке [1(J)1, ffi2] ,,
разложение (2.45) правомочно и является сходящимся.
104
'
;
При выполнении указанных ограничений ряд (2.45) сходится, в
силу чего ограничим его членами - n 1 и m 1, считая н'k=a"k=O
(k<-n 1 , ,k>m 1), что приводит к частной сумме вида (2.44), ко
торая совпадает с исходным рядом с некоторой погрешностьJО. Со
·ответствующим выбором -п1 и m1 можно свести эту погрешность
к требуемому значению.
Ряд (2.45), по существу, является обобщением широко исполь
зуемой теоремы отсчетов для сигналов с полосным ограниченным
спектром [3], так как позволяет представить один заданный сиг
· нал в виде взвешенной суммы запаздывающих значений другого
заданного сигнала и его преобразования Гильберта.
В случае сигналов с узкой относительной , шириной спектра
ЛQ= ,Лш/шо~ 1, Л·w=w2-ш 1 , 1w0 = (w 1+ш2 ) ,/2 преобразование Гиль
берта можно заменить дифференцированием, интегрированием с
изменением полярности сигнала, задержкой сигнала во времени с
изменением его полярности, а также рядом других операций. На
пример, при использовании дифференциатора или интегратора с ко
эффициентами передачи соответственно Кд = i,w/w 0 , Ки = iw 0 /w полу
· чим преобразователь Гильберта · с максимальной относительной
неравномерностью модуля коэффициента передачи ЛК = (Кмакс
-К~шн) /Ко =: 1ЛQ (,w1:::;;; 1w 1 :::;;; ,w2), где Кмакс, Кмин, Ко - максималь
ное, минимальное и среднее значе ния модуля коэффициента пере
дачи. Звено задержки с коэффициентом передачи K3 =-e -iw/wo реа
лизует преобра зователь Гильберта с максимальной абсолютной
погрешностью фазы Л1<р =l(j)макс-(j)мин = Л,Q (,w1:::;;; 1,w 1:::;;; W2); <рмакс,
(/)мин - максимальное и минимальное значе ния фазы преобразова
теля.
Метод h-преобразовання
Известно [3], что сигнал с огр _аниченным спектром однозначно
определяется своими дискретными значениями и дискретными зна
чениями его преобразования Гильберта, поэтому
Лw
sin- 2
-
(t- kдt)
g1 (t) = {1g1 (kЛt) .
cos wi+w2 (t-kЛt)+
/.J
лw
2
2- (t-kдt)
00
-оо
Лw
оо
si n-(t-kд t)
+ ~iз_(kЛt) Лw 2
siп Witw2 (t-kЛt)
-оо
2 (t- kдt}
[Лt=2:rt/ (w2 -w1)].
(2.46)
•Сигнал gз (t) записывается в аналогичной форме,
Под h-изображением непрерывных сигналов g 1 (t) и g3 (t) будем
подразумевать пределы, к которым ~ходятся ряды
105
00
00
h1(z) = ~hi1>zk, h3(z)~Lhi3)zk(z= е- Р л1),
-00
-со
где .hk< 1>= g 1 (kЛt)-:-Нg 1 (,k,Лi); hk< 2)= ,g2 (М.t)-Нй2 (k,M). Выражения
hk, в дальнейшем называемые функциональными числами, обла
дают свойствами: 1. Если А = а+НЬ
-
функциональное число (а и
Ь-вещественные числа), то JАJ=Vа2 + ,Ь 2- модуль, а ер =
= arctg Ь,/а - угол функционального числа (при изменении знака
ы угол (J) также меняет знак на противоположный) А = 1А I еН<Р=
= 1А I cosер+НIА I sin1ер. 2. Для функциональных чисел А=а+НЬ
и B=c -:-Hd справедливы операции:
н(<Р+<Р)
A+B=(a+c)+H(b+d); AB=IA//B/e А в=
=ac-bd+H(bc+ad); ерА, ер8 - углы А, В;
АJВ=~ен (<Рл+<Рв).
IBI
При выполнении операций следует учитывать, что Н2 =- 1 ;
1./Н =- Н.
На единичной окружности z::e-i(J)лt комплексной плоскости z
. Функции ,h 1 (z) и ,hз(z) совпадают на отрезках [ -1со2,-1со 1 ], [со1, со2]
соответственно со сnектра·льными плотностями К1 (iш) и К3 (iю)
'
1
'
'
сигналов g1 (t) и gз (t) с точностью до множителя- Лt=л/ (,ю2-Сu1) ,
2
т. е. Kv(i,ю)= -1-Mhv(z) (v=l, 3). Из этого вытекает, что си~налы
2
,
g 1 (t) и g 3 (t) однозначно определяются своими h - изображениями .
Замена hvk=gv (,k,Л,t)-Hgv (k,Лt) на fi,(v)k=g v (k,Лt)-ig v (k:Лt)
приводит к тому, что hv (z) на единичной окружности превращает
ся в ряд Фурье, совпадающий с Kv (iю) только на отрезке [,со 1 , w2]
(на отрезке 1 [-:со2, -со 1 ] совпадения нет). Поэтому h<v)k можно по
лучить . из коэффициентов ряда Фурье спектральной плотност и
Kv (i,co) заменой i на Н.
По аналогии, .h-изображение коэффициента nеред-ачи корректо-
т,
ра (2.43) имеет вид K(z) = ~ -akzk . Преобразование h 1 (z) в h3 (z)
возможно, если
К (z) = h3 (z)Jh1 (z).
(2.47)
Поскольку K(.z) - полином, а h3 (z) ,/h 1 (z) - рациональная
функция от z, равенство (2.47) в общем случае выполняется лишь
приближенно.
Для нахождения K(z) необходимо h3 (z)/,h1(z) разложить в ряд
Лорана на окружности Jzl =1. Получаемый при этом ряд будет
сходящимся, если h1 (.z) не содержит нулей на единичной окружно
сти; что возможно в случае, когда IK1 (i,co)l*O (co1~lcol~ffi2) ,
В качестве K(z) берем отрезок полученного ряда .
106 •
Согласно изложенному при использовании h-преобразования
расчет корректор' а полосных сигналов формально аналогичен рас
чет у корректора низкочастотных сигналов с использованием z - пре
образования .
Теоремы отсчетов для сигналов с полосным 1;1граниченным
по протяженности дискретным спектром
Те Gре м ы оточетс.в для периодических сигналов с ограниченны м низкQ!Ча~тот
ны м спектром даны в § ,2"2. ДGкажем теперь тео.ремы оточето:в для с игналов с
дискретным полосным спектром, т. е. для сиг.налов, спектр которы х состоит из
,ко.нечного на,бора ди·ск·рет,ных ,ра&ноо'!'стоящих ча,стот, не ,начи,нающих-ся с .нуля.
Теоремы mоз-воляют точно восстано,вить •си.гнал •ПО конечному числу зн а чений
сиг н ала и его ,п.реобразования Гилыберта. Эти тео1ремы могут быть лапользова.ны
при т а рм о,ническом а.нализе и ~синтезе, а также при ,ра,очетах диск,рет,ных си
сте м, ,на :пример · ,при ра ,с,чете (иiи на,стройке) гар моничес•ких корректоров.
Теорема 1 ,[1-8]. Е·сли f (t) - сигнал со спектром, •со,держащим N дискрет
ных ,равноо11стоящих частот Wk= ,wн+kQ (k = O, 1, ... , N- 1) (,рис . 2 .1 12а) :
N-l
f(t)=~ akCOS(ffikf+cpk),
k=O
гд е ,W н, Q - произвольные частоты , то
NQ
N-l
sin- (t- qдt)
f(t)= ~f(qдt)
2Q
cos
q=O
Nsiп2 (t- qдt)
NQ
siп-2-(t-qдt)
N-l
ffiнtffiв(t- qДt)+Еf(qДt)Х
q=O
х
ffiн + ffiв
Q
sin
2
(t-qЛt),
Nsin- (t- qдt)
2
-
(2. 48)
где Q - ,расстояние между ча,стотами апектра f (t) ; ak и cpk - ампл-иту,ды и
фазы этих часто.т; Wн - ·наинизшая частота; Wв ={wн+ (N-1 )Q] - .наивысшая
ча стот а ; 1!11=2л/NQ; r(qдl) - дискретные значения преобразования Гильберта
от f(t):
N-l
j(t)= - ~ aksin(ffikt+cpk)-
•=O
С огласно данной теореме сиг:нал f(t) со спектром·, ,с одержащим N ди,скрет
ных •р ав,ноотстоящих ча ·стот , полностью определяется своими N .равноотстоящи
ми дис кретными значениями и N ,ра,в.ноотстоящими дискретными значениями
прео бра з ования Гильберта.
Выражение (2.48) может быть преобразов а но к ви д у
NQ
N-1
sin -
(t- qдt)
f(t)=~Vt~+f~
2Q
cos[ffiнtCOв(t - qЛl)-Ч.'q],
q=O
Nsin2(t- qдt)
где
fq = f (qдt); fч=t(qдt) ; Ч'q= arctg 1⁄2_ .
tq
107
Докажем опра-ведливость с-форму лироваНJной теоремы . Ра ссмотрим _ с лучай ,
когда N - ,нечетное. Пронумеруем ча,стоты сп ектра f (t), как указано ,на ,рис.
2.126, и будем считать, что ооектр f(t) содержит •ча,стоты (J)k=(J)o+kQ (k=O ,
± 1, ... , 1±п) , гд е 1(1)0 = (1(J)n +(J)n) /2. С учетом сказанного:
п
п
f(t) = eiro0t LAk eikQt+e-iro0t _IAZe-ikQt ;
-п
-п
п
п
-
i t(t) = eiroot L Ak eikQt - e -iroot LAZ e-ikQt
-п
-п
(ak, <j)k - [lроиз,вольные ,числа, .не о,бладающие отно-снтельно (J)o ,ка 1кой-либо
си-мме11рией). Из этих -выражений получим
-п
где
1
~
.
t
F(t)=2 [f(t)- if(t)]e-iroo .
k
N-1
GJk=wн +kn wв
а)
1~iIi Н"НJг1 •"
-п -k
-2
-!О12kn
(,J_к = (.Ja - l<Sl {.)а r,;k = wc• kfl
б)
Рис . 2.12 . Ди-ск1ретный полос
ный опектр ,J]рИ несимме11р,ич
ной (а) и ·си,мметР'ич,ной (6)
нумерациях ча 1стот
Р,нс . 2.13. Gпектры .компози
циоНJных фу1НКЦИЙ (а, 6) , ОТ
ЛНЧаЮщие,ся ам,пл-итущой ,пе~р
вой и по•слещней частот
Согласно формулам т,ри,гон-ометри·ческой интерполяции {ЗJ
J 2;:,
-i
~kq
Ak=N L F(qЛt)e N (Лt=2л/NQ , N=2n+I),
q=O
поэтому
2n
lп
F(t)= _IF(qЛt)N' ~ eikQ(t-2лq/NQ) .
q=O
k= -n
108
•У'Читывая тригономет,рическое тождество
2п+ 1
п
п
sin- -2
-
Qх
IeikQx = 1 +2 LcoskQx= ----
Q---
-
n
I
siп2х
прихо,ди.м ,к ·выражению
NQ
2n
sin-- (t- qЛt)
f(t)- if(t)= ~[f(qЛt)- iJ(qЛt)]=
-
-
2-Q _
_
_
_
eiroo (1-qЛt) . •
q=O
Nsin2 (t- qЛt)
Выделяя действительную ча.сть этого выражения, в итоге получим (2.48), ,что и
требовалась доказать. Случай, ,когда N - четное, доказывает•ся аналогично .
На .ри,с. 2.!За изображен ам1плитуд.ный ,спектр композиционных функций:
NQ
siп-2- t
Q
Nsin2 t
NQ
sin2 t
Q
Nsin2 t
ffiн + ffiв
cos -~-- t;
2
ffiн + ffiв
sin
2
t,
а .на рис. 2.7 ,и 2.9
-
оги•бающие этих фун:к,ций, т. е. функции
,
NQ
sin-2
-
t
1
ffic
--
--- =
-
sin ffi t cosec -
t
N
с
N
Q
Nsin2 t
(
NQ.
)
ffic= -
2- ;Т=2n/Q
для N - нечетного (N= 2n+ 1l = II, ,см. рис. 2.7) и N - чет.наго (N=2n=l0,
см. •рис. 2.9) .
Т.еорема II. Если f(t) - сигнал со спектром, со1держащим N дискретных
,ра·в,ноо'Гстоящих ча,стот (l)k = ,(l)в+kQ (k = O, !, 2, ... , N - 1), ,11де (!)н и Q - произ-.
вольные частоты, п,ри'Чем ком ,плексные амплитуды наинизшей и ,наивысшей ча
стот одинаковы, то
Q(N-1)
N-2
. sin
2
(t- qЛt)
f(t)= ~f(qлt)_____Q
_____
cos
q=O
(N- 1)tg- (t- qЛt)
2
N-2
+ ~ f(qЛt)
q=O
Q(N.:__ !)
siп
2
(t- qЛt)
Q
(N- 1)tg2 (t~qЛt)
ffiн + ffiв
sin
2
(t-qЛt),
(2,49)
nде
10.9
2n
2n
(N- l)Q
Выражение · (2.49) может _ ,быть запи-са.но также ,в форме
N-2
tи)=LV,~+,~
q=O
где
Q(N- 1)
sin ---(t-qЛt)
2
Q
(N -1) tg-(t-qЛ t)
2
fq= f(qлt);т;=f(qлt);
т;
Ч'k = arctg т;; .
[Wн+Wв
•
]
cos
2
(t - qЛt)-'I'k,
До-казатель~тво теоремы II аналоги,чно доказатель,ству теоремы I и поэтому
не •приводится. При до,каэательстве теоремы II используется тождество
п
п
sinпQх
'"'eikQx = 1+2~' cos k Q х = ----
k'
!..J
Q
k=- n
k=I
tg- x
2
где знак ~, показывает, что крайние члены суммы бе р утся с весом 0,5. Сигнал,
• удовлетворяющий теореме II, полностью определяется N - 1 зна,чениями f (qЛt)
и N-1 значениями f (qЛt). На рис. 2. 136 изо~ражен амплитудный спектр ком
позиционных фун,кций:
.
Q(N-1)
SIП ---' --
-'- f
2
w~+wв
---
-
--cos
-
---t·
Q
2
•
(N-1) tgz t
.
Q(N-1)
sш---~t
2
Q
(N- -l)tg - t
2
Wн+Шв
sin
2
t,
а на ,рис. 2.8 и 2.1О - огибающие этих функций, т. е. функции
.
Q(N- 1)
sш-. --- t
2
1..
Шс
-----
-
= --sinШсtctg---t.
Q
N-1
N-1
(N-1)tg2 t
(Wc = Q(N- 1)/2; Т= 2n/Q),
для N - нечетного (N=2n+l= I I, см. рис . 2.8) и N - четного (N=2n = l0,
см. ,рис. 2. 1О).
Рассмотрим предельный случай, когда N-+-oo п ри фиксированных частотах
Шн и Wn . В этом случае R-+ -0 и мы приходим к сигналу f(t) со сплошным
спект'ро~1. существующи,м .на отрез.ке [wн, u1. ]. Принимая во внимание, что R =
= (w a-•Wн)/(N-1) и изменяя пределы суммирования в выражении (2.48), получим
'
N Wв-Wн
п,
sin- -
----
(t- qЛt)
}:
N-1
2
f(t)=
f (qЛt) ----------
Wв-Шн
Nsin ---"'--"-- (t- qЛf)
2(N- 1)
q=- n
х
110
NWn-W
sin --
н (t-qЛt)
п,
N-1
2
+
Х V t(qЛt) ----------- sinWн 2• Wв (t - qЛt),
." -i
Wв-Wн
Q=-
n
Nsin----(t- qЛt)
2(N- 1)
·
где п1 = п = (N - 1)/2 при N-нечетном;
n=N/2, n1 =N/2- l при N-четном.
1 ,Учитывая, что
N
Wв-Wн
sin -- --- (t-qЛt)
N-1
2
Wв -(i)
sin
•
н(t- qЛt)
2
lim
NsinWв-Wн(t Лt)
2(N- l) -q
(t- qЛt)
2л
2л
N-1
2л
Лt= lim-
=lim------------
NQ
W.в- Wн
N
Wв- Wн
(2. 50)
и переходя .к цределу (N-+oo) в .выражении (2.50), получим выражение, а·н·а
лоrичное выражению {2:4'6), ,с оставляющее содержа.ние тео1ремы от1счетов для
сиr,наJюв со ,сплошным полосным апек т,р,ом (1n>ри этом нео'бходимо изменить обо
значения Wн ,на W1 и Wn . ,на w2) .[33].
Нетру,дно •в идеть, что ряд, аналогичный ряду (2.46) , яsляется пределом
та·кже для ,выращения (2.49) при N-+oo.
СПИСОК ЛИТЕР АТУРЫ
1. Во~rин Л. Н. Элементы теории у,правляющих машин. М . : , Оове'!'ское ра-
дио, 1962.
2. Гантмахер Ф. Р. Теория матр•иц. М.: Наука, 1967 .
3. Голдман С. Теория информации. М.: ИЛ, · 1951.
4. Джури Э. Импуль·сные си·стемы автоматического регул ирования . М.: Госиз
дат физико->математической литературы, 1963.
5. Игнатьев Н. К. Си•нтез ам,плитудно - ча,стотной хара,ктеристи1ки по коэффи
циентам ее разложения в р'яд. - Эл ект роовязь . 1960, No 1, с. 3-10.
6. Кисель В. А. Применение бесконечных матри ц .при расчете корре~ктирующ11х
схем, использующих звенья идеального за,паздывания. - В кн.: Труды
учебных институтов связи. Л.: 1962, вып. 13, .с. 42 ---!52.
7. Кисель В. А. Критерий корре-ктируемости канала связи по имп ульоному от-
клику. - В кн.: Т·рудь! учебных ин·ституто,в сsязи. Л.: 1963, вып. 17,
с 142-150 .
8. Кисель В. А. Методика расчета корректора канал.а ювяз и по импульсному
отклику . - В кн.: Труд ы учебных инстит утов связи. Л.: 1963, вып. 18,
с. 114- 120 .
9. Кисель В. А. К расчету rармониче•оких корректоро'В с помощью бесконеч
·ных матриц . - В кн.: Труды учебных институтов связи. Л.: 1964, вып. 19,
с. 106-116 .
•
10 . Кисель в : А. К расчету гармонических корректоров двух видов.
В кн.:
Тр уды учебн ых ин·ститутов связи. Л.: 1964, ,вып. 20, с . 140-149.
11. Кисель В. А. ОптимаЛЬ'НЫЙ расчет rа·рмоническоrо корр ектора.
В кн.:
Тр уд ы учебных ин•ститутов связи. Л. : 1965, ,вып. 27, •с. 177-187.
12. Кисель В. А. Элемент ы ра,счета rа·рмоничеоких корре•кторов.
-
Электро
,связь. 1964, No 7 С. 4_6-53 .
13. Кисель В. А. Коррекция полосо ,вы х ка·налов 1по имп ул ь·сным реа1кциям.
-
В кн.: XXII В·сесоюзная научная сессия, посвященная Дню радио . Секция
общей радиотехни.ки. М.: Связь, 1966, с. 126-133 .
111
14. Кисель В. А., Кицул И. В. О тригонометрическом интер,полиро·вании с крат
ными •рав,ноотстоящими узлами . ~ В кн.: Труды учебных институтов связи .
Л.: 1965, вып. 24, с. 169-176.
15. Кисель 8. А. Об одном методе ра·счета гармоничес'КОГО си·нтезатора по вре
меннь1м характеристикам сигнала. - Электросвязь. 1967, No 7, ·с . 62-70.
16. Кисель В. А., Одесский В. Я. Построение и анализ ортогонального коррек
тора чебышевского тиrпа. - В кн . : Методы от,бора и преобразования ин
формации. Киев: Наукова думка АН УССР, 1967, вып. 6, с. 87-97.
17. Кисель В. А. Расчет гар-мон·ичес,ких корректо·ров по периодической ,последо
·вательностн взаимно1перекрьiвающихся им,пульсных реакций. - В кн.: От
бор и перtодача информащш. Киев: Нау,кова думка АН УССР, '1968, вып. 16,
с. 152-164
18. Кисель В. А. Теоремы отсчетов для функций с дискретным полосовым
опектром. ·--
В кн.: Труды учебных институтов связи. Л. : 1968, вып . 39,
с. 41-48.
19. Кисель В А., Крухмалев В. В . Синтез гребенчатых фильтров с -изоэкстре
мальными характеристиками на линиях задерж·ки без обратной связи. -
Радиотехника и электрони·ка. 1968, No 1О , ,с. 1799~1 -8107.
20. Кисель В. А., Лев А. Ю., Одесский В. Я . .Оценка
сложности гармонического
и чебышс,в,окlQ.rо корректоров фазо-ча •стотных характеристик трактов пер·вич
ных гру~!lп. - В кн.: Труды. Централь,ный научно-•исследоватет,ский инсти
тут связu. Киевский филиал. Киев: 1968, вып. 1, с. 13-20 .
21. Лев А. Ю., Кисель В. А. Об оптималь,ном пред:ставлении сигнала с ограни-
•
ченным спектро1м усеченным рядом Котельникова. - Электросвязь. 1967,
с. 25-32.
22. Ееркович Д. л:, Лев А. Ю. Система коррекции станда•ртных каналов то-
нальной чапоты с автоматиче,сиюй настройкой . М.: Связь, 1972.
.
23. Кук Р. Бесконечные матрицы и пространства последо·вательностей. М.: Гос
издат физико-математической литературы, 1960.
24 . Стрижевский Н. 3. Коррекция произвольных линейных искажений в трак
тах телевизио·нно,rо вещания. М. : Связь, 1966.
25 . Нудельман П. Я. Полиномные синтезаторы час'!'отных и временных харак
тер·истик. М.: . Связь, 1975.
26. Liпke J. W. А Va ri aЫe Time-Equa lizer for Video -Freq u ency Waveform Cor-
rection.-«Proc. IEE», 1952, v. 99, Ша, N 18, р. 427-435.
27 . Gutsche Н. Ein Echoentzerrer zur Entzerrung vоп Fernseh signalen in Vid~ -
ofrequenzbereich. -«NTZ», 1964, Н. 17, N 6, S. 280-282.
28. Amoroso F. Further History of the Tapped De l ay Line Pulse Shaper.-«IEEE,
Trans. оп Inform . Theory», 1965, v. 11-11, July, р. 450 .
•29. Kallmaп Н. Е. Traпsversa\ Fi lters.- «Proc. IRE», 1940, July, v. 28, р. 302-
310 .
30 . Scl1iissler W. Der Echoentzerrers als Model\ eines Ubertragungskanals. -
«NTZ», 1963, N 3, S. 155-163.
31. Lytle D. W . Coпvergence Criteria for Transversal Equal izers. -«BSTJ», 1968,
V. 47, N 8, р. 1775-1800.
~2 . Rupprecht , W. Verallgemeinter Verzweigungsnetzwerke zur Entzerrung vоп
Капа\еn fi.ir die digitale Dateпйbertragung.-«NTZ», 1968, N 6, S . 316-322 .
. 33 . Гоноровский И. С. Радиотехнические цепи и ~сигналы. М.: Советско~ ра
дио, 1971.
34. Di Того М. J. Communication in Time -Freq u e n cy Spread Media Using Adap -
t ive Equa\ization. - «Proc. of the IEEE», 1968, v. 56, N 16, р. 1653-1679.
35. Кисель В. А. Ди1скретный синтез ,корректирующих ц·е,nей. А1Вто·реф. дис. на
соиск . учен. степени кан,д . т·ехн. наук Одесса, 1967.
36. Bernd Meister. An Application of the Со \ еу- Turkey Algotith to Equa\izati-
011 . -«IВM. Journal of Research and Development», 1968, v. 12, N 4, р.331-
334.
-
37. Lucky R. W . Aut o m atic Equalization . for Digital Communication . - «BSTЬ,
1965, V. 44, N 4, р. 547-588.
112
Глава 3
АЛГОРИТМЫ АВТОМАТИЧЕСКОЙ ДИСКРЕТНОЙ
КОРРЕКЦИИ
........
3.1. Задачи, решаемые при разработке алгоритмов
:корре1щии
Применение полиномных корректоров на коммутируемых сетях
связи, использующих стандартные каналы тональной - частоты, и
на каналах с изменяющимися во времени параметрами выдвигает
проблему разработки алгоритмов автоматической и адаптивной
коррекции, которые позволили бы оперативно (в течение несколь-
• ких секунд или долей секунд) получить нужный коэффициент пе
редачи корректора без предварительного расчета так, чтобы кор
ректор преобразовывал произвольный искаженный сигнал g 1(t) в
заданный (эталонный) сигнал g 3 (t) с допустимой погрешностью.
Современные корректоры, используемые в технике передачи
сигналов (например, в технике телевидения), содержат до 50 ре
гулируемых отводов ak. Отсутствие определенных алгоритмов прев
ращает процесс коррекции в сложную
и утомительную о п ерацию, которая 9,(t}•Nlt}
92 (t}
уже при сравнительно небольших иска- Вх I l<орре1<mар~----=-в.;_ь,➔х-
жениях сигналов не приводит к дости
жению желаемой цели.
Автоматическую коррекцию в про
стейшей интерпретации можно пред
ставить следующим образом. Смесь
искаженного сигнала g1 (t) и аддитив
ного шума N (t) подается на вход кор-
ректора. Возникающий при этом на
выходе сигнал g2 (t) сравнивается по
!/прабление
t<OJф_ сiк
Сра ненuе
fz(tJ и !J3 (t}
Рис, ЗJ _ С;гр у~кту1р ,ная схе-
свои м параметрам с эталонным сигна- ма .на,с11рой~ки корректора
лом · gз(t) согласно тому или иному
критерию (рис. 3.1). Если отличие параметров превышает
заданную норму, меняем величины коэффициентов ak, добиваясь
совпадения g 2 (t) и g 3 (t) с требуемой степенью точности. При адап~
тивной коррекции автоматическая настройка корректора произво
дится непосредственно по рабочему сигналу. Естественно, с целью
автоматизации процесса коррекции · с применением несложных
113
технических средств алгоритмы подбора ak (алгоритмы адаптации)
должны сводиться к последовательности однотипных простейших
операций .
В настоящей главе излагаются разнообразные алгоритмы, поз- ·
валяющие синтезировать корректоры с автоматической нас,тройкой
по различным критериям. Все алгоритмы соответствуют дискрет
ной (точечной) коррекции, при которой сигналы g 2 (.t) и g3(t) сов
падают с требуемой степенью точности в дискрет н ые моменты вpe
мeниts: g2(ts)=gз(fs)(s= l,2, ...) .
В общем случае критерий совпадения не задан. Непосредствен
ный выбор той или иной погрешности (степени точности, целевой
функции) в качестве критерия со.впадения (меры близости) сиг
налов определяется специфическими требованиями решаемой тех
нической задачи и всецело зависит от особенностей функциониро ,
вания конкретных систем связи и способов приема сигналов. По
этой причине в главе рассматриваются критерии близости , такие ,
как квадратичный, суммарный абсолютный, суммарный обобщен
ный, μ-критерий, критерий Чебышева, критерии, требующие точно
го совпадения заданных параметров выходного и эталонного сиг
налов (в частности, критерии, требующие точного совпадения зна
чений сигналов в заданные моменты времени) и др. Целесообраз
ность рассмотрения алгоритмов обусловл~на потребностями прак
тики.
Исходя из разнообразия критериев близости, в основу алгорит
мов автоматической коррекции положен разнообразный математи
ческий аппарат, адэкватный сущности процесса коррекции: итера
ционные алгоритмы решения полиномиальных ур·авнений и систем
линейных уравнений, методы минимизации многомерных выпук
лых функций, ряд свойств сигналов и т . д.
В реальных каналах связи коррекция производится неизбежно
на фоне аддитивных шумов . С учетом шумов алгоритмы коррек
ции можно разделить на две группы: 1) алгоритмы, обеспечиваю.
щие, несмотря на наличие шума N (t), преобразование сигнала
g1 (t) в сигнал g 3 (t) (шум является помехой процессу коррекции),
и 2) алгоритмы,' минимизирующие совместно и искажения пере
даваемых сигналов, и влияние аддитивных шумов, например сов
местная минимизация и межсимвольных искажений и аддитивных
шумов. Алгоритмы первой группы используются при коррекции
частотных характеристик каналов связи по их временнь1м (импуль
сным, переходным) характеристикам. Алгоритмы второй группы
применяются в скоростных системах передачи дискретной инфор
мации . В главе даются алгоритмы как первой, так и второй групп.
В дальнейшем принят следующий порядок : первоначально изложе
ние алгоритмов ведется без учета шумов; далее указывается, ка
ковы будут изменения в конечных результатах при наличии шу
мов . Все алгоритмы соответствуют коррекции по зондирующим им
пульсам, в качестве которых могут использо?,аться как специаль
ные ис п ытательные, так и неп осредственно рабочие сигналы, по-
114
скольку именно такая коррекция позволяет компенсировать, в
принципе, произвольные искажения сигналов или каналов.
Следует подчеркнуть, что вопросам синтеза автоматически х кор
ректоров в настоящее время уделяется все_ возрастающее · внима
ние, что подтверждается многочисленными публикациями на эту
тему [ 19, 25-50].
3.2 . Итерационные алгоритмы коррекции на основе
z-преобразования (коррекция дискретных сигналов
на бесконечной оси времени)
Общие сведения
Считаем, что моменты времени .fs, в которые производится кор
рекция, выбраны равномерно: -ts = sЛt (s=O, ± 1, ±2, . .. )
(Лt
интервал дискретизации). Введем обозначения: g1 (z), g2 (z), gз (z),
К(z)-z - преобразования непрерывных сигналов - g1(t), g2(t), gз(t)
и коэффициента передачи корректора :
со
со
00
)
(•
~·
-,
k
g2(Z)=~ b,,_i, gз (z) = ~
k
1
g1z)=,,tЫa,,_z ,
c,,_z ,
-со
-со
-00
j (3.1)
со
I k g 2(z)=K(z)g1 (z) - (z=e-pлt).
К(z)=
akz ,
-со
где а~, ь,,_ и с,,_ - дискретные значения сигналов g 1(t), g2(t) и gз(t)
в моменты времени kЛt. Корректор с коэффициентом передачи
K(z) представляет собой линию задержки с бесконечно большим
ЧИСЛОМ ОТВОДОВ (J,k .
В терминах z-преобразования задача автоматической коррек
ции дискретных сигналов формулируется в следующем виде : не
вычисляя К (z), путем экспериментальных регулировок коэффици
ентов а"- подобрать их значения по заданным сигналам g 1 (z) и
g 3 (z) таким образом, чтобы выполнялось равенство
Указанная постановка задачи соответствует коррекции сигна
лов н· а бесконечной дискретной оси времени . Как будет показано
ниже, эта постановка задачи удобна тем, что позволяет сравни
тельно просто оценить влияние величины искажений сигналов и
воздейtтвия помех на процесс автоматической коррекции.
Полученные результаты, строго говоря, справедливы для кор
ректоров с бесконечно большим (практически с достаточно боль
шим) числом отводов а,,. Однако эти же результаты, естественно,
справедливы приближенно и для корректоров с конечным числом
коэффициентов а,,_.
115
Коррекция сигналов в случае малых фазо-частотных искажений
Общие положения. Для K(z) с учетом (3.2) формально спра
ведливо соотношение 1 1[2, 3]
сх,
К(z)= .gз(z) = g3(z)~(- 1)kв7(z),
g1 (z)
l.J
(3.3)
k=O
где в1 (z) = g1 (z)-1 . Ограничим этот ряд некоторым членом N:
N
к_(N)(z) =-= g3(z) ~(-1)kв7(z) = gз(z) [1-(-l)N+t вf+' (z)].
(3.4)
l.J
g1 (z)
k=O
При подаче на вход корректора с коэффициентом передачи
ION)(,z) сигнала g 1 (z) на его выходе возникает сигнал
g~N) (z) = g1(z) K(N) (z) = g3(z)[1-(- l)N+t вf+1 (z)],
(3.5)
абсолютная погрешность (уклонение) которого по сравнению с
требуемым сигналом g 3 (z) равна:
в~N) (z) = gJN)(z)-g3(z) = g3(z)(- l)N+i ef+1(z).
(3.6)
Относительная поrрешность находится из выражения
B(N)
л(N) (z) =
-
2-
=
(- l)N+l вf+ 1 (z)
(3. 7)
gз (z)
и не зависит от сигнала g3 (z). Очевидно, что ION+l) (z) ,
=ION)(z)-в2(N)(z) .
Из выражений (3.3)-(3.7) вытекает следующий алгоритм под
бора коэффициентов ak[2, 3]: 1. Устанавливаем начальные значе
ния ak<0J = ck или Ю0> (z) = g 3 (z). 2. Коэффициенты
«k(i) для i-го
шага настройки определяются соотношениями •ak(i) = ,ak(i-lJ_
-Bk(i-l)(i=1, 2, 3, ...}
или
(3 .8)
где Вk(i- 1 )-дискретные значения погрешности e2<i-1J(z) = gii-l)(z)-
-gз(z); gii-lJ(z) = .g 1 (z)I0i-lJ(z). Полагая в этих формулах по~
следовательно i = 1, 2, 3, ... , после N шагов получим выражения
I0N)(z), g 2(N)(z) и e2(NJ(z), совпадающие с выражениями (3.4)-
(3.6). Предлагаемый алгоритм настройки корректора заключается
в многократном изменении коэффициентов ak на величину разно
сти выходного и эталонного сигналов. Эти изменения производят•
ся шагами, что и объясняет название алгоритма.
Описанный алгоритм требовал установки начальных условий
I0°)z = g 3 (z) . Рассмотрим алгоритмы, которые отличаются от опи-
1 ,В :основе соотношения лежит п.ра,вило суммирования геометричеекой про
грессии 1/(1 +х) = l-x+x2-x3 + ...
116
санного измененными начальными условиями. Допустим, что в ка•
честве начальных условий мы приняли I0°J(z)=l, т. е. щ.(0)=0
(k=l=O), a 0(0J=l. После N шагов получим:
•
(N)
gз(z)- [gз(z)- g1 (z)] -( - l)N ef(z)
К (z)=
.
gl (z)
·
.
g~NJ (z) = g 3 (z)-[g3 (z) -g1 (z)] (- l)N ef (z);
1
(3 .9)
Предположим теперь, что начальные условия выбраны произ
вольно: I0°J(z) =g(z) или a1t=a1t, где g(z) - произвольная функ ,
ция с дискретными значениями ak, Осуществляя настройку со,
гласно (3.8), после N шагов приходим к выражениям:
K(NJ (z) = gз (z) [l-( - l)N+i'ef+1 (z)] + (- l)N [g (z)-g3 (z)] ef(z); ) ·
gl (z)
g~NJ (z) ~ g3 (z) [1-(- l)N+I ei"+1 (z)] + (- l)N [g (z)-g3 (z)] ef (z).
(3.1 О)
Пример. Применим ал.горитм (3.8) для сигналов g 1(z) =0,27z'-- 1 + 1 +0,3z;
g 3 (z)= •l. Здесь e 1(z)=0,.2z- 1 +0,3.
Исходное состояние: a1t< 0J=O (k,,60); a 0<0J=l; e2<0J(z)=0,2z- 1 +0,3z. Первый
шаг: a 1<1J=~0,2; ао< 1 )= 1; a 1<1J=-0,3; e2<1J(z)=-e2 1 (z)=-(0,04z- 2 +0,112+
+I0,09z2) . Второй ша-г: а(2)_ 2 =0,04; а<2)_ 1 =-0,,2; a 0<2J= ·J,12; а/2)=~0,3; а2< 2)=
= ·0,09;
ei2J(z) =e1< 3J(z) =0,008z-з+o ,03•6z- 1 +0,054z+0,027z 3 . Т1ретий ша,г:
а< 3 J_з=~ООО8· а<3)_ 2 =004· а< 3 ) 1=----<0 ,23·6·
· a 0(3)=1l 112· а1<3)=____,0354· ai3)=
=0,09; аз<3J=:_·0,,027; e~< 3 )(z) =-=-е41 (z) ~0,001,6z-ЧI0,,0096z-2+ О,0216+() ;021-бz2 +
+ •0,008 lz4.
Мак-сим ум e2(3J( z) при1близительно ,равен O,Q22 , поэтому погрешностью
ei4J(z) можно пренебречь, что поз,воляет п,рекратить процес•с коррекции на дан
ном ша,ге.
После осуществления предельного перехода N--roo в выражени •
ях (3.4)-(3.6), а также в выражениях (3.9) и (3.10) нетрудно
заметить, что если
Iimef(z) =О,
(3.11)
N➔oo·
то
!imK(NJ(z)= g2(z) ;
•
gl (z)
lim g~NJ (z) = g 3 (z); (N -+оо),
lime~NJ(z) =О
т. е. процесс настройки сходится (обеспечивае.т получение требу
емого результата). Стремление eN 1 (z) к нулю (N-+oo) является
необходимым и достаточным условием сходимости описанных ал•
горитмов.
Из выражений (3.4)-(3.6), (3.9) и (3.10) вытекает, что ско
рость сходимости процесса коррекции определяется только сиг·
налом g 1 (z) (величиной e 1 (z)) и не зависит от сигнала g3 (z).
117
Анализ сходимости алгоритма. Укажем ог.раничения; .на-кладываемые .на
спектральную плот.насть G1(iro) си,гнала g1 (z) , при выполне-нии которых вы.ше
опи,са:нные ал.го.ритмы обес.печиJВают сходимость юро.цеоса коррекции.
У-слови-е (3.1 ,1) ,вьmолняе'!iся, если
что может иметь место только
спектральная плотность €1 (z).
(3. 12)
Допустим, что фа:зовые иокажения в G1 (iw) отсут,ст,в уют, т. е. arg G1 (iw) =
=О (зде,сь и в дальнейшем линейный фа:зовый ,сдв111г не у,читывае'!'ся). При этом
если модуль 11G1 (i1w) 1 плотности G1 (iw) не обращается в нуль, то, выб и рая
амплитуду сигнала ,g 1(z) соответствующ и м образом, всегда можно добиться,
чтобы 1€1 (iw) 1< 1. Это свидетельствует о сходимости алгоритмов коррекции.
Проанализируем сходимость при -наличии фазовых wска.жений в спе ктре
·G1(iw). Первоначалыно ·цред'IIоложим, что нера,в.ном-ерность .модуля G1(iw) от
сутствует: G1,(iw) =ae1q,(wJ, rще а - модуль; cp(-w) - фа'За G1-(iw). У.кажем nра
_ ницы ep(w), для кото рых le1(iw)l < l. Так как
-
€1(iw)=ae 1q> (w) -::- 1, то l e1(iw) I ~=
= V1 +а2-2а cos ер (<u). Максимальное значение 1€1 (iw) 1, при котором нарушает
ся -схо.димо·сть ал,rоритмов, ,равно единице . Из этого у,словия . получим ермаис ' (w) =
а
= ar,c ,cos 2 . Таким образом, алгоритмы обеапечивают -сходимость процесса ,кор-
. рекции,.
если фаза сигнала g1 (z) удовлетворяет ограничению Iер (ro) 1<
о
Рис. 3.2 . Предельные з,на
чения фавы сиг.нала в за
висимости от модуля оп ект-
ра сигнала
IL
а
< l arccos 2 l=epмaкc(w) . При а = О достига-
ются
максимально
возможные
значении
ермакс = ±л/2 (рис. 3.2), поэтому алгоритмы,
в принципе, могут обеспечить сходимость кор
рекции только дли сигналов g1 (z), фаза кота-
• рых находитси в пределах
-л/2 <ер((!))< n/2.
(3. 13)
-Эти пределы справедливы и дли сходимости
коррекции в случае произвольных сигналов, у
которых max l G1(iw)l<a и IG1(iw)J=;t=0
(lwl~л/,Лt).
Изложенные соображении показывают, что
дли расширения пределов по фазовой характе
ристике величина а должна быть возможно
малой, поэтому сигнал g1 (z) необходимо умень
шать по амплитуде.
Итерационные алгоритмы обеспечивают
сходимость процесса коррекции, если фаза
входного сигнала находитси в пределах (3.13),
а модуль спектральной плотности этого сиг
н а л а не обращаетси в нуль. Эти алгоритмы, по существу, можно при ме нять пр11
мал ы х - фаза-частотных искаж ен ия х ..
00
Спектр 01 (iw) запишем в виде G1 (i,w) = I a.e- iw kЛt ( 1,w 1~n/1!::.t), поэтому
00
~(a_k
-
ak)-siп k (!)Л t
1
ср ((!)) = arctg ---
00---------
ао+}:(ak+a_k)coskuJЛt
1
118
-
00
(3. 14)
Очитаем, что
"'
~1ah +a_k 1<оо,
1
(3. 15)
кроме того, ,считаем, что JG1(iw)#O. Из (3.:14) ,получим, ,по е•сли
00
1ао1>~\ah+a- k1,
1
то •(j)(w) находится в пределах (3.13).
(3.16)
Неравенства · (3.15) и (3.16) . являются условиями, показывающими возмо ж
ность .применения итерационных алгоритмов для ,коррекции дисюретного сиг.на -
•
•
"'
ла g1 (z). Эти нерав-енства выполняются одновременно, если j ао j > ~ j ak 1, по
k=-оо h,ЬО
этс}Му дан.ное ,неравенство можно также рассма1'ривать как, ,критерий ,сходимо
сти ,проце сса коррекции .
Оценим ,влияние нера,вномер•ности фазового апектра
п:рощеоса корреюции. Скорость сходимости определяет1ся
рые :необходим .о выполнить для того, чтобы ма:к,С-ИМ3/М
превышал зада.иной ,величины 5:
max 18f+ 1 (i ffi) 13⁄4 1;,
на скорость сходимости
•числом шасr-о,в N, кото
мо,дуля 81N+ 1 (iw) ,не
где 8 1N+ 1,(iw) - ,спектральная ,плот,но,сть относителЬ'ной пог,решности кор.ректи-
рова·ния (3 .7).
Пусть (j)(,w) лежит в некоторых пределах 1± ,0: -103⁄4(/)(w) 3⁄4.0 (0<:п: /2). Оп
ределим, при како.м значении а модуль погрешности 1811(iw) j принимает мини
маль,но возможное зн-ачение, что обеапечивает .оптимальную по быстроте сходи
мост,ь ,процесса на,стройки . Максимум j 81 (iw) 1 достигается .на грающах у,ча,ст,ка
- 0+ +.в при (j) (,w) = 1± 10, поэтому max,I81 (i,w) 1= r 1+ а2-2а cos tJ. Анализ на
эюстремум (мини,мум) дает
minmax181(iffi)1= 1sin0j= YI __:_а2,а=cos0..
(3.17)
С увеличением Г1раниц ep(w) скорость сходимости процеоса -кор,реюции умень
ша ет,ся, поск олЬ'ку min max .\181 (i,w) 1 увеличивается. В •пределе при 0 = ± :п:/2
(т. е . а= О) имеем min max , j,81l(i,w),j = 1 и схо,димость алгоритма нарушается.
Требования. увеличения скорости схо!П;имости процес-са корреюции и преще
ло•в по - фа.за.вой характеристи .ке являются противоречи,выми, та к как с ростс,м
цредело,в rp(w) ,ск орость ,настройки уменЬ'lliается и наоборот.
Выражения (,3. ,17) поз:воляют также ответить ,на вопрос: .какой должна
быть взаимоовязь мо,дуля IG1:(iffi) ,I и фазы ер(ш) так, что1бы аJiсr-оритм о,беюпе
чил максимальную скорость сходимости проц есса настройки 1,орр е ктора? Для
ответа на этот вопрос необходимо в (3.17) заменить а на I G1 (iw) 1 и 0 на
{IJ(,w) JG1(iw)j =cos(j)(w); j81(i,w)I = jsinep(,w) I =Vl-JG1(iw)j. В этом
случае [81 (iw) [ является минимально возможной величиной для теку-
щей частоты w при заданной фаза - частотной характеристике ер (w). Н;~
при.мер, положи:м q,(w) =-1O,,25:п: sin ,w (линейный ,фа,зовый сдвиг не учитывает
ся), тогда (рис. 3.3): [G1(iw)[= cos 1[O,25:n:sinw ]; [81(iw)[=Jsin[O,25:n:sinw][. И з
nриведенного примера вытекает, что при откл·онении фаза-частотной характери
сти.ки ер (w) от линейной :в ,некоторой обла,сти ча,стот налич·ие завала амплитуд
.но - ча·стотной хара,ктеристшш [G1 (iw]) 1 в этой же. области ча,стот улучшает ,с.хо
димость процеоса коррекщии. •
Помехоустойчивость процесса коррекции. В процеосе ' 'На.стройки схема кор
ректора пощ,вер,гае-гся дейс11вию помех. Под помехами мы -будем па:дразумевать
неточную уста новк у коэффищ1ентов ak <iJ или суммирование н екоторого мешаю
щего сигнала ·С вхощным сигналом ,g 1( z ) . Поскольку в конечном итосr--е действие
119
помех выражает,ся ,в ,неточной у,становке ап<i), считаем, что все помехи пере
считаны ,к коэффи,циенту ,переда1чи l((i>(z), а сиг,нал g,(z) не []Одвержен дейст
вию помех.
Оценим влия,ние одиночной по мехи ,на процес-с на ,стройки га·рмонического
,КОр ,ректора 1 . Пусть на N 1 -м шаге на,стройки на корректор с коэффициентом пе
редачи (3.4) ,воэдейст,вует помеха, меняющая J((N, >(z) на .величину
'l'](Z): 1(1(1:i ,) (z)=ION,) '(z)+'YJ(z). Продолжая ,на·стройку согласно (3.8), после
л шагов получим 1(1<N, +л>(z) =IO N, +л>+(-· J)ле 1 л(z)'У](Z), Проа.нализи:руем да.н
,ное 1вы,ражение. Ка .к упо ми,налось выше, при правильно выбранных пределах
(J)(w) имеем lim е 1 л (z)=О (л-+оо), следовательно,
.
(N +л)
gз (z)
l1m1( 1 (z)=1((z)= -
(л ....... ·оо).
•
1
gl (z)
·таким образом, ,при воз~действии рдиночной помехи ,п огрешность .не возра-стает
с у.вели•чением числа ша,rов ·на-стройки (в системе ,нет размножения ошибок).
о
а)
д.
2
11'
(,}
6)
о
7(
т
d)
7(
с.,
Рис. 3.3 . Г,рафшки фазы ,си,гнала (а), модуля опект,ра сигнала (б)" ,и мо
дуля погрешности сп ектра си,nнала (в) , ,для кот орых доститаеТ1ся ма ,1~си
малыная ,с1юрость сх,одимости .на,сТ1р,ойки кор'рект,ора
Допустим теперь, что на ,си,стем,у воздействовал - ря,д помех 'Y]1(z), 'Y]2(z), ... ,
'Y lμ (z) соощ1етст,венно на N ,; N2, ... , Nμ ша•гах на ,стройки (N,<N2<•·· <Nμ)-
Послtс лμ шагов получи,м 1(1 <Nμ+"μ)(z)=J((Nμ+лμ)(z)+:(-J) л ,e~ 1 (z)'Y]i(z)-f
+ (-J) л, е} 2 (z)'Y]2(z)+ ... +(-J)лμ е}μ (z)'YJ μ (z), где л,=Nμ -N,+лμ ; л2 =
=N μ-N2+лμ и
т. ед. (счет лμ веде'!'ся после ша,га Nμ ) . Очевидно,
,μ
lim !, (-J)лie,лi(z)'Y]i(Z)=O (лμ -+оо), если lim s1л,μ(z)=0 (Лμ-+оо), поэтому
i=I
lim К,<Nμ+лμ) (z)=K(z) (лμ-+оо). Вывод: при ,ВОЗ1действии на систему конечно -
го чwсла ,помех 'Y]1(z), 'Y]2(z), ... , 'YJμ (z) ,на,стройка корректо,ра в пределе не на
рушается .
,Ра<с,смотрим теmерь общий случай, кс,гда помехи в·оздействуют на схему
корректора в течение всего процесса ,на,сТ1ройки. Коэффициент JJередачи ,кор ,рек
тора ,для т-го шага настройки в •этом ·случае равен
т
кfm> (z) = к<т) (z) + I (- l)m-n вr-п (z) 'У]п (z),
(3. 18)
n=O
где J((m>(z) - коэффициент передачи кор,ректора для т-го шага при отсутст
вии помех; 'У]п(z) - помеха, действующая ,на п-м шаге ,настройки. Обозначим
т
M(z) = ~ (-!) 111 - n e 1 111 -n(z)'Y]п(z). Оценим суммарную погрешность M(z) nрн
n=O
m-+oo. Оценку прове,дем в частот.ной области, т. е. при z=е- 1 ыл 1 . Допустим,
1 В дальнейшем рассмаТ1ри .вают,ся ~детерминированные помехи.
120
что -модули по11решностей ТJn(z) лежат .в некоторых пределах О~ 1ТJ n (z) 1~ 6
(z=e-1wл1, \wl~n/,Лt), тогда max!M(iw)l~6f \81(iw)ln=6
,~
1.
n=O
l- 1 1(1W)\
Аргумент M(i{I)) для да,ниой ча•стоты w _ мож-ет при.ни-мать любое значен и е, по
скольку на .а1р,rументы погрешностей Т]n (iw) ,огранwчеиия не ,на ,кла,дысrзают с я. С
учетом сказанного пределыные значения для К1 (iw) 001ределяются выражени ем
К1(i<D) = limK\mJ (iw) =КUw)+Ммаис(i<D),
(3.19)
где К(iш) - кооффиrци-ент ~передачи .кор.ректора 1При .отсутствии по м ех;
ei'I' (w)
Ммаис(i<D)=61-181(iW)/;
y(w) - произвольная фу,н•юция .
(3. 20)
С огла1сно (3 ..20) Ммакс~(i{!)) за,ви-сит как от 6 (точ.ность .на 1ст ро йки), та к и от
e 1(iw). На1пример, .е,сли l81(iw) 1 близо1к к 1, по11решность Ммакс · (iw) -сильно
в озрастает даж е при малом значвнии 6· Таким dбразом, суммар .ная погрешн о.сть
Mмaкci ( iw ) может дости,гать больших значений, хотя катдый шаг настройки
выпо лняетс я с м а лой лоnрешностью.
Из (3. 19) .получим зна,чения для амплитудно-чжтотной IK1•(iw) 1 и фазо
ча,стот.ной (j)i (,w) характери-стик ко'Эlффициента передачи К , (iw) ,при ,наличии
по мех:
1К1(iw)1~1К(iw)1±1- I8:(im)I
1
~
(JJ1 (w) = (jJ(W)± arcsiп {1-181(iW)i}1К(iw) 1 '
где IK(i,w) 1 и (j),(,w) - ам1плитудно-чжтотная и фазо -lljаrстотная
к оэффициен та пере.дачи корре•ктора при ог-су 11ствии п омех.
хара :ктеристики
Итерационный ал гори тм для произвольных фазо-частотиых
искажений
Обоснование алгорuпtа. В настояще м параграфе изла гается
итерационный алгоритм, позволяющий осу ществ ить автомат иче
скую коррекци ю в п р и н ципе при произволь ны х фазовых иска же
н и я х дискретных сигналов •[6, 28).
Запишем K(z) в виде
К(z)= g8(г) = g3(z)'g;_(z) ,
g1 (z)
gl (z)g1(z)
где g,(z) - ряд, сопряженный ряду
g·1 (z): g1(z)~g,(г1) =
00
-00
00
К(2) = ~зt)l\~/- = g3(2)g1(z) :Е (- 1/ Е1 (z).
k=O
Ограничи м этот р яд некоторым членом N : .
N
к<N)(z)=g3(z)'i1(z)~(- 1)kЕ~(z)=gв(i)ii(z)
k=O
1- ( - l)N+l Ef+I(г)
1+Е1 (z)
Если подать сигнал ,g 1(z) на вход корректора с коэффициентом
передачи (3.21), на выходе возникнет сигнал
g~NJ (z) = g1 (z) К(z) = g8 (z) [1-(-l)N+i Ef+1(z)],
(3 ,22)
абсолютная и относительная погрешности которого соответствен
но равны:
вiN> (z) = g~NJ (z)-g3(i) = (- l)NEf+1(z) g8(z);
(3 .23)
-
E(N) (z)
-
л<N) (z) =
2
=
(-l)Nвf+1(z).
(3 .24)
g3 (z)
-
Из (3.21)-(3.23) получим
к<N+I) (.z) = к<N) (z)-gl (z) E~N) (z).
(3.25)
Выражение (3 .25) лежит в основе следующего алгоритма кор
рекции : 1. Исходное состояние (начальные значения): a1,< 0 >= Ak,
где А" --; -- коэффициент при - z" произведения g1 (z) и g 3 (z):
к< 0 ) (z) = g, (z) gз (,z). 2 . Коэффициенты a,,(i) для ,i-го шага настройки
корректора определяется соотношениями
aki) = aii-I>-Dki-1)'
где Dk<i-1>- коэффициенты при zk произвед~ния g1 (z)E2<i- 1>(z):
к<i) (z) = к<i-l) (z)-g1 (z) вit-I) (z);
E~i -l) (z) =gii-l) (z)-g8 (z);
g~i-1) (z) = gl (z) K(i-1) (z) .
После N шагов получим К(N)(z), g2<N>(z) и E 2(N>(z), совпадаю-
щие соответственно с выражениями (3.21), (3.22) и (3.23) .
•
Описанный алгоритм заключается в многократном - изменении
коэффициентов a1t на величину разности выходного сигнала кор
ректора и эталонного сигнала, пропущенных через устройство с
коэффициентом передачи g1 (z).
Пример . Пусть требуется откvрректировать си.гнал g1 (z) =-' -0,3+0,9z+.0,3z2,
при,близив его к :си:гиалу gз(z)=.l.
,1. Исх<щное состоя-ние:
К(О) (z) = gi (z) g8 (z) = 0,3Г2 + 0,9z-1
-0,3.
:Вых<щной сl!iГнал g2(0J(z) и 1Погрешность E2' 0>.(z) .равны:
g~0)(z) = g1(z)к<0>(z) =
-
О,09Г2+0,99 - 0 ,09z2 ;
Е~0>(z)= g~O)(z)- g3(z)=
-
0,09z-2
-0,01-0 ,09 z2•
2. Первый шаа, ,настройки
К(!)(z) = /((О)(1)- g1(z)Е~О)(z)сO,027 z-4+0,08JZ-3 +0,276Г2+
+ 0,909,- 1
- 0,276 -0,081, -
0,027 zi.
Определяем nогрешность
Е~1) (z) = 0,0081 i-i + 0,0018 Г2 + 0,016+0,001811 + 0,0081 z' .
122
В силу малости ,этой 11юrрешности прекращаем процесс кор,рекции, считая,
что K(z)=K(l>(,z).
Сходимость и по.ме хоустойчивость алгоритма. Соrла,сно (.З .23 ) для сходи
мости алrо.ритма нео,бходи-мо и достаточ,но, чтобы \imE2<N)(z) = О или
limE 1N+ 1(z)=0 (N-+oo). Это свидетельствует о Т()М , что с.хсщимасть алrоритма
оп,ределяет,ся толыко вхо\дным си,r.нал-ом g1(z) . .
.Спектральная плотность ,по~решнасти Ei(z) ран.на E1(w)=IG11(iw) l2 - l,
rд-е I G1(iw) -12 -
квадрат мо,дуля спектраль:ной плотности сиr.нала g1(z). Счи
таем, что .модуль G1 (i{J)) нормиро.ван по максимуму: max I G1 (i,w) 1= 1. Бели
g 1(z) удовлетворяет условию 1корректи,руемости IG11(iw)!+O ( lwl~:n/ Лt), то
. max!E 1(w) 1< ,! , 111оэто'Му limE1N+l(,w) =0 (N-+oo) и алгоритм сходит•ся.
Д()пусти,м , что условие кор1ректируемости не .выполняется, т. е . модуль
1G1(iw) 1 обращается ,в нуль на некоторой частоте Wk . При этом
max!E 1(w)!<1I (,w :c# ,wk); max!E1(w)l=l (w=,wk) и limE1N+ 1(·w) =O (w:c#{J)k);
\imE 1N+ 1(w)=•l (w=Wk, N-+oo) . Из да,нных выражений вытека-ет, что алгоритм
обеап ечивает сходим ()сть .кор.реюции во в,сем диа~паэо-не ча,стот •1ш 1~ :n/,Лt, за
и,с-ключени-ем тех ,ч астот, на ко,торых не выпол.няеrся у,словие коррект,ируемости.
Функция Е 1 (ш) не зави,сит от фа.за -ча стотной хара•кте,ри,стики сигнала ,g1(z), по
этому скорость сх-одимо,сти ал,горит,ма определяется только модулем спектраль
ной :ПЛ01'НОСТИ вход.нога СИirнала.
Оценим ,влия,ние ,помех ,на ,на1стройку ~кор1ректора.
Допустим, что на корре к тор воздей ство вал ряд пом ех 1']1 (z), 1']2 (z), ... ,
~
~:: ,:~:,,::sc:,::y::. N:,:.' ~ ~ ;:)~g, : :~::,i['~f~:1::~:(:;:Н (:N] ~,:~
k=O
μ
H(z)= ~ (-li,,i E/'i (z)'l';(z); 'l';(z) .находится из .выражения
rJ;(z)=
i=I
=g 1(z)g 3 (z)'l';(z) и характеризует ·помеху rJ;(z). Очевидно, lim H(z) =0
(л-+оо), т . е. 1во3д,ейст,вие ,на ко,рректор ряда помех не нарушает процес-са ,на
строй ки .
Ра•с-смот,рим . общий случай, ког,да помехи воздействуют в течение ,всего про
цесса нае11ройки 1{орректора. 1Коэффициент ,переда,чи корректо-ра для т-,го шага
наст ройк и в э том случае равен
•
т
K\m> (z) = i<_(m) {z) + I (- l)m-n Ет-п (z) 1'Jп (z),
1 (3.26)
n=O
ме ют>(z) - .коэффицие·нт .передачи корректора для т-го шага ,при отfутствии
п омех; Y]n(z) - ,помеха , действующая ,на п-м шаге настройки.
Вы,ражение (3.2 6) по характеру .не отличает-си от аналогич ного выражения
(3.1 8), поэтому при дальнейшем а,нализе 1(1<m>(z) воапользуем,ся результатами
пр едыдущего па,раграфа. Как и ранее, ,считаем, ,что модули п огрешностей Y]n (z)
лежат ,в ,некоторых пределах 0- ,!;;.
Во·опользовавши,сь (3 .19) и (-3. '20), получим, что амriлитуд·но-частотная ха
р актери-сти,ка IК1 (iw) 1 и фазо-:частотная характеристика ср1 (ш) коэффициента
передач.и корректора при .нали,ши ,помех находятся ,в ,пределах:
1К1(i()))1 = 1К(iffi)1±
~•
1- 1Е1(ffi)\ '
<р1 (ffi) = <Р (ffi) ± arcsiп
Эти выражения позволяют сделать вывод о то м, что влияние помех на про
цесс настройки существенно зависит от величины Е1 (,w) , т. е. от величины не
.равномерности амплиту.11JН0-частотно,rо спектра сигнала g1(z). Так, если в .неко
торых областях частот а,мnлитудно-частотный спектр сигнала g 1(z) ,близок к
нулю ( 1Е1 (ш) ~ 1), влияние помех . резко воз:растает.
123
3.3 . Коррекция сигналов на конечном отрезке
-
времени
Общий итерационный алгоритм -
Используемые на практике корректоры содержат конечное
число отводов ak, Рассмотрим итерационные алгоритмы примени
тельно к настройке таких корректоров.
В настоящем разделе излагаются алгоритмы дискретной кор
рекции, при которой сигнал g2 (t) совпадает с g 3 (t) в конечном
числе произвольных (не обязательно равноотстающих) моментов
времени is(s=l, 2, ... , q) [18]. Число точек совпадения полагается
равным числу регулируемых коэффициентов 'C/,/i .
Считаем, что задан произвольный полиномный корр·ектор с ко
эффициентом передачи
q
К(i(J))=~ ah(l)h(i(J)),
.....
k=I
На входе корректора сигнал g 1 (t), на выходе сигнал
q
g2 (t) = ,I ahfh (t),
k=I
где
00
fh(t)= -
1- 5G1 (i (J)) cph (i (J)) е1 00 t d ffi, G1 (i (J))-спектр g1 (t).
2л;
-оо
(3.27)
(3.28)
Задачу коррекции сигналов на конечной дискретной оси време
ни можно сформулировать в следующем виде: указать алгоритмы
автоматического подбора коэффициентов ah (k= 1, 2, ... , q) из ус
лови~ выполнения равенства
gz(t5)=g3(ts) (s=1,2,..., q).
(3.29)
Предлагаемые в настоящем разделе алгоритмы основаны на
итерационных методах решения систем линейных уравнений.
С учетом (3.28) и (3.29) имеем
q
g 3 (t 5 )=ja11.f11.(t8 ) (s=l,2, ... ,q)
k=I
или АХ=В, где
as11.=fh(ts); bh=q2(ts) (s, k=l, 2, ... , q).
124
(3.30)
Если А- неособенная матрица, /А 1*О, где /А 1 - определи
тель А, то
Х*=А- 1 В.
(3.31)
Здесь Х* - точное решение системы (3 .30) ~
Требование неособенности матрицы А является_ необходимым и
достаточным условием выполнения равенства (3.29), т. е. необхо
димым и достаточным условием корректируемости сигнала g1 (t) (в
строгом смысле) при заданной системе функций {<pk (iw)}.
Значения a*k(k=1, 2, ... , q), при которых строго выполняется
(3 .30), неизвестны, поэтому, не производя вычисления А- 1 , подбе
рем коэффициенты ak таким образом, чтобы уравнение (3 .30) вы
полнялось с заданной степенью точности. Воспользуемся для этой
цели итерационными методами решения систем линейных уравне
ний, которые сводятся к следующему.
Строим последовательность векторов X< 0J, X(I), Х<2 ), ... , X<iJ, .. . по
рекуррентным формулам 1[22]
x<i> = x<i-1>+н<i) [B-Ax<i-1>J (i = 1, 2, ... ),
(3.32)
где Н<i> - некоторая последовательность матриц; X< 0J - начальное
· приближение,
которое в общем случае может быть произвольным.
О точности приближенного решения X(iJ системы (3.30) обычно
судят по вектору ошибки Y<i) =X* - XU> либо по вектору невязки
R<i>=A Y<iJ = B-AX<i)_ С учетом вектора невязки выражение (3.32)
записывается в форме
x<i) = x<i-l) + н<i> R(i-1>.
(З.ЗЗ)
Эквивалентное выражение для Y<i): Y<i)= (E-Н<iJA) (E-Н<i- 1 JA) .. .
. . . (Е- н< 1 >А) (Х*-Х< 0 >), где Е - единичная матрица. Из этого сле
дует, что если какая-нибудь норма матрицы T(i)= (E-Н<iJA) (Е
-н<н>А) ... (E- H(i>A) стремится к нулю:
11т<0 11-о (i-oo),
то итерационный процесс
JIR<i)/1-+0 (i-+oo).
Под нормой матрицы
T(i) = [ t_П>_ ••.• ~i?]
•
f(O f(i)
.
ql ... qq
является
подра:зумевается одно из выражений:
(3.34)
сходящимся, т. е. 11 Y<iJ/1-+0,
q
q
11т<;>l\1 = m~x I It}l>I; JIT<i>l\n = m~x I]t~i>[;
1 k=I
i=I
125
. где
(А - максимальное собственное значение матрицы T•<i)Т(i);
T•<i) - матрица, сопряженная T(i)_
[У\]
Под нормой вектора ошибки }'(i) =
:_
подразумевается
y(l)
q
какое-либо из выражений :
.
q
1 IY<i% = m;x IYi0 1; JIY<O/lн = L IYi0 1;
k=I
' Y<i)llш= Vf (Yki))2 ·
k=I
Норма вектора невяз1ш II R<iJII определяется аналогично.
Условие (3 .34) является необходимым и достаточным для с х о
димости итерационных процессов . Матрицы H(i) обычно выбирают
ся так, чтобы по возможности ускорить сходимость процесса.
г -------- - ---
Ри,с . 3.4 . С11рукту1р1ная схема а-втомаrгического
!КОij)ректо•ра •с 1на,стройкой по метО1Ду послещо
ватель:ных 1п·р·иближе,ний
На рис. 3.4 изображена структурная схема, реализующая кор
рекцию согласно (3.33). Исходное состояние этой схемы: устанав-
:::•:;.;:::::::еХ~::~е[и;f,]коэ::к•:::::::л:~:·8:т:е~:~:,,ив•:::::
а(О)
q
.
ципе, м-ожет быть выбрано произвольно. На вход кор р ектора по
дается сигнал g1 (t); на выходе возникает сигнал , g2< 0 J (t), а на вы
ходе • вычитающего устройства - сигнал r< 0)(t) = g 3(.t)-g2<0)(t).
Ключ Кл осуществляет выборку дискретных значе н ий r< 0 ) (ts) (s=
= 1, 2, .. ., q) сигнала r <0)(t). Значения r< 0)(ts) являются компонен
тами вектора невязки
R.<O) = [ ~\О)]; rio>= Го ( ts).
r (O)
-
q
126
Управляющее устройство УУ! выполняет операцию умножения мат•
рицы Н<0J на матрицу-столбец ,R<0J. На
q
выходах УУ возникают
напряжения uk(o) (ik = 1, 2, ... , q), являющиеся компонентами мат
рицы-столбца H< 0J,R<0J. Напряжения uk<0J управляют коэффициента
ми щ,<0J, изменяя их величину на uk<0J, что дает _ первое прибли
жение
а11)=ako)+uko) (k=1,2, ...' q)
или X(l)=X<0~+H<0W.< 0).
Повторяя указанный процесс i раз, получим
akiJ= а11:-о+иii-I)(k= 1,2, ..., q; i= 1,2, ...)
или X(iJ = X(i-1J+H<i-I),R(i- 1), что совпадает с (3.33). В этом выра•
жении компонентами матриц X(i), X(i-1), H(i- 1), R<i- 1) являются со
ответственно величины uk(iJ, ,щ/i- 1 ), uk<i - 1).
В процессе коррекции для каждого шага ,i производится изме •
нение матрицы H(i) согласно тому или иному заранее - выбранному
правилу. Если при заданной матрице А последовательность мат
риц H<iJ выбрана так, что выполняется (3.34), процесс коррекции
является сходящимся, т . е . .
x(t)-+X*, ak-+aZ (k = 1, 2, . . . , q; i-+oo);
gfi)
(
ts)-+:gз( ts )
(S=1,2, ..., q;
i- -+
оо),
где giiJ(ts) - дискретные значения сигнала на выходе корректора
после i шагов настройки.
Для итерационных процессов, описываемых выражением (3.33),
точное решение Х* (3.31) является неподвижной точкой 1[22]. Это
значит, что если за начальное приближение взято Х*, то все после
дующие приближения будут равны Х*. С физической точки зрения
данное свойство означает следующее . Если корректор . настроен,
т. е. установлены коэффициенты ,a*k, то, продолжая настройку со·
гласно (3 .33), мы не будем удаляться от установленных коэффи
циентов a*k • Иными словами, п родолжение настройки не приводит
к расстройке корректора.
Рассмотрим возможные итерационные алгоритмы , которые по
лучаются из общего итерационного алгоритма при различных спо
собах выбора матриц H(iJ.
Простая итерациs
,к простейшlf,м итера,ционным процеосам относятся стациощэ.р.ные процессы,
в которых мат,рицы H<i> не . зависят от номера ша .га i.
Положим в (3.32) H (i >=Е для всех i, то гда
xu)=nxu-1)+в
(З .35)
или
X(i) = x(t-l) + R(i-l),
(3 .36)
·г,де
D=Е-А=[d11•••dнl .
.
dq1 .. .dqq
127
Итерационный ,про:деос, опи,сываемый (3.35) , являет,ся 1Классически м м ет.а
дом последовательных -прwближений. Нет,ру,дно .вкдеть, что X( 1>=DiX0 + (Е +
+D+D2+ ... +D(i-!))B; Y(i)=(- J)iD i (X*- X{O)J; R (i)=(-J)iDiR (O); R(O)=B-
- - A X( O), откуда следует, что процесс последовательных приближений сходится,
если .ка,Кая-ли,бо норма .матри,цы D ,меньше единицы :
11D11<1.
(3 .37)
rПри выполнении (3.37)
11 y<i> 11 = 11D 11; 11х<0)11 + 111в!._\\~11:;
11y(i)11~11D1111yU-l)11;
11RU>11~11D1111R(i-O11.
Данные выражения поз.валяют по -известным ма11рицам D и Х( 0> оценит ь сж о•
рость схсщк,м ости пр оцесса последовательных приб л ижений.
У·каже м ,простейшие достаточные •признаки сходим ости процеоса п ослед ова•
т,ельных приближений [22].
q
!) Если max ~ jds;I =μ< ,! , то процесс сходится и
i=l
la• -
aU>,~ μmax/ ~-a\i-l)j·
V
V
..__,
Gtj
J
'
lbv-b~i)\~μmax\bj-ь?-1>/ (v, j = l ,2 , .. . , q).
q
.
• 2) Если max ·}: 11is; 1 = 11 < 1, то процесс сходится и
J S=l
q
q
q
q
(3 .38)
'\~ / а* -aU>l:;;::11 Y' /а• -a(i- l) 1
~V
V.~
,__
'V
V
'\"' 1ь - ьи> 1:;;:: ,., '\:"" 1ь - ьи-1> 1
.,
V
V °"" '1L
V
V
•
v=l
v=l
V=l
v=l
q
,....,
З) Бел и ].,,
= ip <l, то проце,с,с сх одит-ся и
s,j=l _
q
q
q
q
(3. 39)
}2(а;- а?>)2~рL(а:- a~i -1))2 ; ~(Ьs- ь;i>)2~р~(bs - b~i - 1))2 .
S=l
S=l
B=l
>=1
(3. 40)
Для га,рмо.нич есюло корректора
r
ао а-1 а_2
.:J
а1 ао а-1.
А=
а2 QI
ао
..
.
а2
а1
ао
Нормируя з,нач ения этой ,м атрицы так, -чтобы ао= 1, получим
[
оа-1а-2 •
..J
а1оа-1
.
.
-D=
-~~-
а1
о
а2а1о
128
Учитывая особен,ности ма11ри,цы D, 11ри укаванных выше достаточных усло-
q
.
вия 1мож,но заменить одним у,словием: если L Iая 1 =v< 1, то про,цеос по.слещо
k=-q, kcfaO
вателыных ,приближений схадится, ,при этом в выражениях (3 .38)-(3.40) необ
хмимо за,ме_нить μ, Т] и '() ,на 'У·
,На,стр()Й!Ка 1ПОли,номнО1Г-о корректора :по !Методу лоследо.ватель.ных 1пр_иближе
ний осуще-ствляет-ся ,охемой, приведен.ной ,на ри,с. 3.4, ,в :которой ,блок УУ 111ре.д
ставляет со'бой коммутирующее уст1ройст,во, -ра -спределяющее ди,скретные эначе
,ния .выходно,го сигнала r<i)(ts) ло q ,выходам. Напряжения r<i>(ts) меняют коэф
фипиенты as(i) на величину r(i)(ts):
a,~i+I)=aii)+r(i){t8 ) (s=1,2, . . . , q; i=l,2, ...). •
(3.41)
Бели а.,= ' 1 (s= 1l, 2, ... , . q), г,де _ а,s - диагоналыные 13лементы ма'I'ри,цы А,
то П!ро,цеос поi::ледователь,ных 1прюближений ог.носит-ся к мето,ду ,простой итера
ции , (мет-од Якоби). 1В случа-е гармонич,ес.кого кор,ректора можно считать, чт-о
а0 = 1, поэтому ,на,стройка ,гармони~ческо.го 1кор,р-ектора ,оGглаоно ,выражению (3.41)
произ:водится 1110 ,методу простой игера,ции .
Однош аrовый циклический алгоритм
За1пишем ,систему у,равнений (3 .,30) 1в ,вюде
X=DX+B,
(3.42)
где -D=E-A. В ,слу,чае О1Дношато1во,tо ~циклwчес,кого ,процесса (метоtд Зей,деля)
вычислени,е i-,ro 1приlближения k-й ком,поненты ,произвади'Гся по ,формуле
k-l
q
a,(i) = ~ dk•t,1,U)+~ dk•aU-l)+Dk
(3.43)
k
f..J
JJ
.:;..i
lk
•
i=l
j=k
Та:ким 01бразом, -i -e · ,I]ри,ближение для k-й ком.по .ненты вычисляется ,на основе
полученного ранее i -г о ,при,ближ-ен .ия ,коМ1лонент a1(iJ, aii), ... , а(i)h -I
Одноша,го·вый цикличес.кий про,цеос может ,быгь mредста,влен ка~к ·ра з,новид
ность процеоса последователь,ных 111ри,ближений, если ва,пи,сать ~выражение (3.42)
,в ,виде
(3.44)
,Матричная за11шсь ,выражения \З.43) X(i)=MX(i)+NX(i- 1)+B, 011ку,да ,следует
x(i)=(Е - мг1нхи-1)+(Е- мг1в.
(3.45)
Полный· ~цикл -одношаговоrо ,ци,кличеокого 1прсщесса сЦля ,системы (3.44) равноси
лен одному шагу ,процесса по·следо,вателыных 1Пjриближений, 111ри-менеино,го :к си
-стеме
Х=(Е-МГ 1 NХ+(Е-МГ 1 В,
(3.46)
которая эквивалентна систвме (3.44). Из ,(,3.45) следуег, что щля схми,мости
одно.ша,гово.го ,циклич-ес.ко,го 1про,цесса _ щостаточно, ~чтобы
11(Е-мг11111N11<1.•
(3 .47) .
-~В силу ·оказанно,го щля о,ценки скорости ,сх-оди;маст-и ,однашаговосо цикличе
око.го Пiроцеоса лримен.имы те же выражения, что и для процесса последователь
ных 111риближений.
5-181
129
Одной -из ,р аз<новщдщ-остей адноша,гового цкклJDЧ,еского mроцесх:а являеТ1Ся
метод Некра.сова (22], mри ,иоnолызовании которого система (3.30) 1Записывается
В !ВИIДе
k-1
q
~ akj
~ akj
bk
IXk== -
kl-CX,j-~
-
CX,j+-
i=I akk '
i=k+I akk
akk
и последовательные ,при~ближения ,ведутся по формулам
k-1
q
(i) -
\...., akj (i)
\'1 akj (i-l) + ~
a,k
-
-
,t_; а a,i
-
_,:
a,i
j=l kk
i=k+Iakk
akk
Метод Некржова ,своди11ся к •методу последовательных приближений, если
в выражения ,х (З.45)-(3.47) ~цроиз:вести замену:
М= -P-1L; N=-P- 1Q,
где
L=[а;1
о
о
JQ~ [
О а12
.aiq]
о
о
оо
. a2q
aqi Gq2
о
оо
.а
-
1
о
ан
р-1=
о
а22
,.
. (!i ,••
-~
,.
-
На.ст.ройка ~корректора ,на •основе аднош а,гового ~циклического ,процесса осу
ществляется ,схемой, 1изо:бра:жсенной на •р-и,с . 3.5, 1в ,кото1рой УС - у~стройств о
ср.авнения, на:пример двухлучевой •осциллограф. Регулируя последовательно ~ко
эффициенты ak •(k= 1, 2, ..., q), iдОlбиваем,ся совпадения .си:гнала gii>(t) ,с сигна
лом gз(t) ,последовательно ,в точках t 8 (s=k= ,1, .2, ... , q), :что соот,ветегвует ад
_ ному ,циклу на,стройки. Для каждО1Го ~цикла 1при ,регулировке ,коэффициента
fft(t}
•
1}0m•.
~Корректор 1
•~ Р,ис . 3.5 . С'1'>"'УР"" схема лас,ройю,
1юр,ректqра ,на оенаве одно1llи11овоiГо
•
fз (t) цИJклического процесса
a1t< 1 ) добиваем,ся 1вьmолнен,ия 1равенс11ва ,gi1>(t1t) =,gз(t1t) . .Затем ци,клы повторя
ются. В ,случае гармониrческого корректор .а а"" = 11 (,для ,в1сех k), поэтому можно
оказать, что на,ст,ройка ;rармониче,екого ко1рр ,ектора ~производится по методу Не
к.ра ,сова.
'
При ,на:стройк,е кар-ректора .на осно,ве юдноша,го.ваго процесса ,коэффициенты
а~ ,регулируются mослед,о'Вательно в ш~ря,дке 13озра1стания их ИНiдек,сов k (k = 1,
2, ... , q). Однако скорость сходимости п,роцесса ,на ,стройки зна:чительно увелич,и
,ва,е11ся, если индекс k ,регулируемого .коэффициента а" ,выбирать по одному irз
11ш:жсесл,едующих ~mра,вил f2 ,2]:
,1. Индеюс ,k 1вЬDбирае1'СЯ так, чтобы :число
среди вс-ех аналогичных ;q.и,сел (iпра,вило Зейделя).
130
1 ,ii-1) 12
~ ---
•было ,ма,к,еимальным
1akkJ
2. Индекс k ,выбирается так, чтобы ЧН•СЛО
,было ,ма:,ксималыным
('Правило ,Гаусса).
З. Инtдекс k ,выбнрает:ся так, чтобы числ-о \rA<i- 1>\ ,было 1ма,кси,мальным
(правило Сау,осела) .
,в этих ,выражениях r1<(i-I) - компоненты вектора невязки. С уч,етом тех
ннчеакой •реалнза,цнн 'Цра.вило ,Сауосела явля,ется ,наиlболее простым. !При ~а
стройке корректора с использованием правила Сау,осела необходимо регулиро
вать тот коэффициент ,а1<, .которому соответствует ма,к,симальное уклонение сиг
нала g2'i>(t) и g3(t) ,в ,момент ,времени tA. Для ·гармо.ннческого к,орректора
ан = 1, поэтому по сути дела правила Зейделя и Гаусса совпадают с правилом
Са у-осела.
Достоинство алгорит,мо:в коррекции, основанных .на одношаговых цикличе
ских 1про1Цесса.х, ,заключает,ся ,в •ИХ ~максимальной 11:р.остот,е (с учетом тех~ничоокой
реализации), что 1выгмно отличает их ,от ,дру,гнх итерационных процесоов.
Групповая релаксация
Выделим некоторую лру,ппу G нндек,сов k регулируемых ,коэффициентов а,,_
и ,при ~переходе от 111реtдшествующего ~приближения 1к по,слещующему будем ·на
страивать толь,ко ;коэффициенты ,а" с ин,дексамн из !выбранной ,гру,п:пы G (,kEG) .
Настройку буtдем ~производить так, чтибы для моментов времени t1<(kEG) сиг
нал gii>(t) -ст1рото ,сов1паtдал с сиrnалом g 3 (t):
gJi> Uk) = gз Uп) (kEG).
Нетр·у,дно ,видеть, что. в аснове такого алгоритма на,ст,ройки лежит ,метод
гру,пmовой ,рела·ксации ~22). ~Можно получюь 1ра'З личные ,мо,дификации 1этог.о ал
горитма, ,зада·вая,сь ,различными .правила.ми ,выбора ,г,рупп G. Простейшей .моди
фика,цией является ,цикличеокий тру.пповбй алгоритм, в ~котором 1в,се ищдек,сы
k ·разбивают,ся ·на ,несколько ,неперекрывающихся •груп,п , которые по ходу на
ст,ройки ,циклически ,повторяют,ся. ,Возможен та·кже св•о·беiд1ный 1гру~п,повой алго
рнт,м, ·в ,котором ,допJакает,ся .не толь·ко ,нециклическо,е чередо'Ва•ние вы:бра1нных
г.ру:п,п индек,сов, но и изменение ,с,остава г,ру,пп ,на каждом ша ,rу.
1Как правило, алгс;ритмы, ,о,снованные ,на 1ГJУJ1шовой ·релаксации, ·о'беспечи,ва
ют i более . , быструю ,сходимость процес,са ко,рре1щии, ·нежели ал-горитмы, осно
ванные 1на одноша,го-вом .циклическом лроцеосе.
1Лрушповые алгоритмы 1Целесообразно ~применять ,для 1кор,ректоров с ~больш и м
числом ,регулируемых ,коэф:фи,циент0~в 1а1<.
3.4. Оптимизация искажений на основе суммарных
критериев
Суммарный квадратичный критерий
Степень близости сигналов g2 (z) и g 3 (z) удобно оценивать по
величине функционала (целевой функции)
Q=Ф[g2 (z)-g3 (z)]= ~ D(bп-ck),
(3 .48)
k=- oo
где Ф ( ·), D ( ·) указывают некоторые операции под соответству4
ющими сигналами или величинами. Этот функционал в дальней•
шем называется обобщенным суммарным критерием или обобщен •
ной суммарной погрешностью . По существу, функционал (3.48)
дает обобщенное уклонение дискретных сигналов на выходе. кор~
5*
1з1:
ректора. Частными случаями обобщенного критерия являются
широко известный суммарный квадратичный критерий (суммар
ная квадратичная погрешность или уклонение)
со
YJ = ~ (Ь,. -с,.)2
k=-oo
и суммарный абсолютный критерий (суммарная абсолютная пог
решность или уклонени е)
,
00
Л= ~ \b,.- c,.J .
..,,J
,
k=-oo
Укажем алгоритмы, позволяющие настроить дискретный кор
ректор с коэффициентом передачи
(3.49)
-п,
либо полиномный корректор с коэффициентом передачи (3.27)
таким образом, чтобы величина обобщенной погрешности -Q при
няла минимально возможное значение.
Поскольку суммарный квадратичный и суммарный абсолю~
ный критерии представляют самостоятельный интерес, первона
чально коротко рассмотрим минимизацию искажений дискретных
сигналов на основе этих критериев.
Здесь и в дальнейшем предполагается, что сигналы g 2 (t,.) и
gз (t,.) удовлетворяют условию абсолютной интегрируемости:
00
00
I \Ь,.\ < оо; ~ \с,.\<оо.
k=-oo
,
k=-oo
Большой интерес, проявляемый в настоящее время к вопросу
коррекции ,искажений на основе квадратичного критерия, 9бъяс
няется, во-первых, относительной простотой его техническои реа
JIИзации и, во-вторых, относительной простотой учета влияния ад
дитивных помех на процесс настройки корректора [5, 23, 27, 30,
32].
При прохождении сигнала g 1(z) через корректор с коэффици
ентом передачи K(z) (3.49) на выходе получим сигнал g2(z) =
00
т,
=g 1 (z)K(z) = ~ bkzk, где bk= ~ щ_;а;.
k= -со
i=-n1
_
С учетом этого выражения суммарная квадратичная погреш- •
ность принимает вид [6]
'l'j=,= kfoo (Jn, ak-i ai -ckУ= Во~' а~+
т1+п,
m 1-i
т,
+2 La. Bi Li a"ak+i -2 ~ D"a,. +А,
(3.50)
i=I
k =-n,
-п,
iЗ2
«г
"'
А=I cI>O; Bi= L akak-i(i=1,2, ..., n1+m1);
k=-oo
k=-«>
"'
Dk= Lс1ai-k (-п1<k<m1).
i =-0',)
Коэффициенты А и. В 0 , равные энергии дискретных сигналов
g 3 (z) и g· 1 (z), больше нуля, так как мы рассматриваем сигналы,
не равные тожд.ественно нулю.
.
Погрешность '1']-многомерная функц·ия второго порядка от пе
ременных ak (-п1 ,-:;;; .k,-:;;; т1). Поскольку при старших членах стоит
один и тот же коэффициент Во, выражение (3.50) представляет
-собой уравнение многомерной · параболы. Известно, что многомер
ная парабола имеет только один экстремум. В нашем случае
·ri >0, поэтому парабола обращена «вверх» (положительна) и
ямеет минимум, т. е . является выпуклой вниз функцией. Это свой
-ство погрешности 'l'J справедливо для любых сигналов g 1(z) и
• gз(z).
Проведенные рассуждения показывают, что квадратичная по
грешность, вычисленная на выходе корректора, является много
мерной выпуклой функцией коэффициентов передачи регуляторов
(X,k,
Очевидно, что свойство выпуклости погрешности 'l'J не нарушит
•ся, если вычислить 11 _с у четом дискретной функции веса {Pk}:
С()
'1'] = I Pk(b1<-Ck) 2 , где Pk>O для всех 1k. В дальнейшем вес не
k=-r:,,
•
учитывается, что, однако, · не нарушает общности полученных ре
зультатов.
Для нахождения ex,k , минимизирующих величину
'l'J, необходи
мо решить систему урав нений
,d11/dex,k=О (- n1<k<m.t).
(3.51)
• Значения ex,k, удовлетвор яющие этой системе, обозначим через
,a*k• Используя свойство выпуклости погрешности 'l'J в сочетании с
известными математическими методами поиска экстремума функ
ций многих переменны х [24], ниже рассмотрим два алгоритма на
стройки дискретных корректоров с целью минимизации суммарной
квадратичной погр ешности. Первый алг.оритм, называемый алго
-ритмом последовательной оптимизации, основывается на методе
сечений (оптимизация по переменной илк по направлению); вто
рой алгорит м, называемый алгоритмом одновременной оптимиза
·ции, о сновывается на методе скорейшего спуска (метод градиен
та).
Техническая ,реализация алгоритма атоследовательной оптимизации осуще
•ствляет,ся ,с ~помощью структурной схемы, .из-обр·аженн1;>й на рис. 3.ба, где ГС -
:г енератор .эталонного сиnнала gз(z); W - ~ваттметр, указывающий величину f]'.
133
IПроцоос tПоследовательной оптн.ми'Зации ,непосредственно заключается ,в ,вы
полнении сл,едующих Q[!ераций:
,J. 'По ,всем ,регуляторам ,а1, устана ,вл.нваем Iпро!!IЗ'вольные (на,п.ример, .нуле
вые) ,начальные значе:ния коэффициентов передачи.
Rt(z) (
I< z) t---
~rкл
[~}z
6)
Pwc . 3 .16. Ст,руктурные схемы . минимиза,ции ~вад~атич
ной погрешности (а) и минимизации энергии эхо - сигна
ЛОIВ (б) ,метQIДiом сечений
2. ~Поочередным ,многократным изм-енением ,коэффициентов минимизируем
покаIзания Iваттмет,ра W. IВ кажщом случае при изменении кон,кретнаго .регулято
ра •а1, доби-ва-ем-ся 1мwнималыного пока-зания ,ватт,метра W, что Iв силу свойства
вьюпу.клости Iпрнв l)дит к абоолютн·ому (,глобальному) минимуму ~погрешности ТJ.
ПрО1Цесс на-стройки я.вляе'l'ся ,сходящимся, т. е. мы ,неиз,бежно приходим к з1на
чениям а*1,, соот,ве-гствующим -мини,муму ТJ.
Описанный алгоритм отличается простотой, поэтому настройку
корректора можно осуществлять автоматически.
В большинстве практически важ_ных случаев требуется откор
ректировать сигнал g 2 (z) так, чтобы он наименее уклонялся от
сигнала g 3 (z)=ca , где со-произвольная , не равная нулю вели
чина. Для этого случая структурная схема ·настройки корректора
упрощается и принимает вид, указанный на рис. 3.615, где Кл -
ключ, проп ускающий все значения сигнала g2(z), кроме Ьа. На
стройка производится в соответствии с изложенным алгоритмом
с той лишь разницей, что регулятор ао настройке не подвергается
(ao = const=t=O).
На рис. 3.7 изображена структурная схема автоматической
системы, реализующая алгоритм одновременной оптимизации
[6].
•
Градиент функции погрешности 'У] равен
dТJ -
--· ая.=
dah
т,
~ 'л,hah,
k=-n,
где ая. - единичный вектор переменной ан; Лн - компоненты гра~
диента:
Лн= 2( i~-n~h-i СХ; -Dh)-
В точке 'У]мин градиент равен нулю, так как его компоненты со"
гласно (3.51) обращаются в нуль. Градиент указывает направле-
134
ние и скорость быстрейшего нарастания функции для заданной
точки. Поэтому вектор, равный по величине градиенту и противо
положный ему по знаку, указывает направление и скорость быст-.
рейшего убывания функции в этой же точке. Если менять коэф
фициенты a,k одновременно таким образом, чтобы соответств у ю
щий этим · изменениям вектор был противоположен градиенту, то
мы скорейшим образом достигнем минимума функции, в к а кой бы
исходной точке мы не находились. Движение при этом осущест
вляется по геодезической линии (брахистохроме), которая явля
ется линией кратчайшего расстояния или скорейшего спуска.
Для движения по геодезической линии коэффициенты a,k необ
ходимо менять со · скоростями, пропорциональными-tсk. В резуль
тате для настройки корректор_ а понадобится минимально возмож
ное время. Таким образом, алгоритм, основанный на методике
скорейше го спуска, является оптимальным по быстродействию.
Указанные особенности лежат в основе принципа действия си
стемы, изображенной на рис. 3.7. Вспомогательный корректор
g,(zJ /!шюя
9z (z)
Ри~с. 3.7. С'!)рукту1р;ная ~схема ·к-оррекrго!ра,
мюнимизирующею квщщрат.и,чшую погреш
ность метащом окqрейшего апуока
ВК, используемый только в процессе настройки, имеет коэффици
ент передачи R(z) =g1 (z-1). В случае гармонического корректора
R(z) = L a_kzk (ak=a-k), где ak - дискретные значения входно•
k
-
го сигнала. В этом случае вспомогательный корректор реализуем
только при конечном сигнале g 1(z). На выходе ВК сигнал равен
[K(z)g 1(z)-g~(z)]g 1 (z- 1). Его дискретные значения пропорцио
нальны величинам 'л1<( - пс~;;_k~т 1) . Коммутатор распределяет
значения Лk по выходам, каждый из которых управляет работой
соответствующего регулятора, меняя его коэффициент · передачи
на величину, пропорциональную - v ,,,11..
Пример. Пусть
g1(z) =
-
О,5.Г1 + 1+ O,5z;
_g8(z) = 1
и
К(z) = ix_1 z-1+а0+щz1.
Согласно (3 :50) 1'} = 1 1,б('а2-1 +а20+ 1а2 1}-'О,15а_ 1 а1·-<а_1~2а0 +1а 1 + 1.
Искомые значения коэффИlЦиентав а*1<, удовлетворяющие (3.51), ,рав!ы:
,а*-1=O,285; а*о=О,666; ,a*i=-O,285.
135
Осущест,вим ~настройку ,методом посл,едователыной оптимизаiЦИИ.
11. Исходное ,состояние: a1t< 0>=0 (kc;6 10). Изменением а0 ,добива,емся ми,ни
мума юогрешности '1'], чт,о дает ·ао< 1 >=0,<666.
:2. Ми.ни,мизируем 'У] еа счет изменения а1 , ,в ~результате ·чего получим а1(1>=
=-0,3'33.
3. Мини,м~rзируем 'У] изменением 13еличины а- 1 , что приводит к результату
a(l)_I = '0,12718.
.
4. ,Уточня,ем значение -а1 < 1 ). 3'начение a0 <1J не уточняекя, та,к как а0<1>= ·а0*.
Повторная минимизация ·' 1 '] за ~счет ,вариации 1а1 дает a1<~J =- ,0,286 .
На этом эта,пе на,стройку можно 1ПIрек·ратить, ,поскольку а 1 <2>, ,а< 1 >_ 1 совпа
дают ,с а1"' ,и .а* -1 ,с ,хорошей степенью точности .
Опи,санная ,на,стройка ,1ю::~ффициентов ·а 1 и а_ 1 1После под1бора ,величи'!!ы а ()
иллюстрирует,ся •рис. 3.8, ,на 1котором для наглядности за положительное ,направ
ление ,пIринято ,на1пра·вление ·оси 'У] вниз .
Рис. 3.8 . Динам,ика М'И11Гимиз-ации к,ва,д!ра
тич;,Iой 'ПОI1решнасти ,методом сечений .и ме•
·юдом ок qр-ейшего апусrка
Минимальному значению Т]мин ,соответствует точка М с •координатами а 1 *
и а* -1. Последовательная ·мини,мизация ;происходит по ,крwв-ой abcd, однов.ремен
ная минимизация - rпо ,кривой lИ]мин,
Суммарный абсолютный критерий
Суммарная . абсолютная погрешность на . выходе дискретного
корректора определяется выражением [78, 33, 34]
Л= k~ " ' 1 i~n,щ_;a1-Ckl•
(3 .52)
Впервые использовать суммарный абсолютный критерий пред
ложено в [33] для коррекции малых искажений, которые удов J1ет
воряют ограничению
00
1: 1ak/<1ао1-
k= -"'· k=/ =O
136
(3.53)
Для многоуровневых систем передачи данн ы х значение величи
ны суммарной абсолютной погрешности позволяет просто оценить
• работос п особность системы. В случае, . когда величина Л меньше
половины расстояния между соседними передаваемыми уровня
ми, неискаженный прием возможен для любых комбинаций сиг•
налов . В многомерном пространстве с координатными осями а1,
выражение (3.52) описывает некоторую поверхность Л . Проанали
зируем характер этой поверхности.
Рассмотрим сечение поверхности Л плоскостями Х'п, пара.тr•
.лельными координатным плоскостям. Пересечение поверхности Л
с плоскостью Х'п дает кривую Ln, лежащую в Х' п, для нахожде
ния уравнения которой необходимо в (3.52) подставить а 1 =
=rx'i (i =;i= n) (а';-фиксированные значения ai), В результате
о,
подстановки
получим Ln = IL1ш, L1,n=lak-nl an+Ъknl, где
k=- oo
т,
Ь 1,п = ~ a1,-ia'; - c1, (.i=;i=n). Очевидно, L1,n - непрерывная кусочно-
i=-п1
.линейная выпуклая вниз функция, так как
•
(а~+а~) Lkn(а~)+Lkn(а~)
Lkn --- <
--------,
2
2
rде а'п и а"п-произвольные значения переменной •ап.
Поскольку сумма выпуклых функций и предел последователь
ности выпуклых функций также являются выпуклыми функциями,
то Ln--:: выпуклая функция. Таким образом, сечение поверхности '
Л произ.вольной плоскостью Х'п, параллельной любой координат
ной плоскости Хп, всегда дает выпуклую функцию Ln, имеющую
минимум . Следовательно, поверхность Л - выпуклая вниз.
Учет дискретной функции веса {р1,} при вычислении суммар•
-
о,
ной абсолютной погрешности Л = . "r р1, 1Ь1,-с1, 1 не нарушае~ свой~
k=-o,.
ства выпуклости.
Для нахождения значений а,*1,, минимизирующих л; в данном
случае нет возможности непосредственно применить аналитичес•
кий способ отыскания экстремума функций нескольких перемен•
ных, который заключается в составлении и решении системы урав•
нений вида dЛ/da1, = 0 ( - п 1 ~k ~ m 1), поскольку 1Л-кусочно-ли•
нейная функция с разрывными частными производными dЛ/da1,,
причем минимум Л может достигаться в точке излома, в которой
частные производные претерпевают разрыв, т. е. не существуют.
Используя свойство Л как выпуклой функции; определим а*1,
методом сечений (последовательная оптимизация) либо методом
,е корейшего спуска (одновременная оптимизация) .
Последовательная оптимизация погрешностм Л методом сече
~ ий· реализуется с помощью структурной схемы, изображенной
на рис . 3 . 9а, . в которой используется цепочка из линейно_го детек-
13.7:
тора ЛД, интегратора и индикатора И, указывающего значение
Л. Настройка корректора производится по минимуму показаний
индикатора И. В тех случаях, когда g3(z) = с0 , для минимизации
К (z}
а)
Рис. 3.9. С11ру~кту-р·ные схемы м.инимИ1Защии сум
марной а1 бсолю1шой IЮ[1решнасти ( а) и ,м-и:ни,м·и
зац,ии ,суммы .мо,дулей эх-о-,сигналов (6) методом
,сечений
д
искажений целесообразно воспользоваться системой, изображенной
на рис. 3.96, в которой ключ Кл пропускает все дискретные значе
ния сигнала g 2(z), за исключением значения . Ь 0 . В этом случае
суммарная абсолютная погрешность принимает вид
•
со
Л'=~1bk1-
(3.54)
k=- ro
k=f=O
Требования Л'мин зачастую недостаточно для практических це•
лей, поскольку для повышения помехоустойчивости дискретных
систем связи · необходимо максимизировать отношение
ЬO/Л' = max.
(3. 55)
Настройка корректора по схеме рис . 3.9а приводит к выполне
нию условия (3.55), ~ то время как при настройке по схеме
рис. 3.96 это условие может не выполняться. Максимизация отно
шения (3.55) эквивалентна минимизации Л' при ограничении :
bo=Co=const. Это ограничение учитывается введением в схему
рис. 3.96 усилителя с автоматической регулировкой уровня РУ.
который в процессе настройки корректора поддерживает неизмен
ным значение Ь 0 .
Одновременная оптимизация . методом скорейшего спуска реа
лизуется системой, изображенной на рис. 3.1 Оа, в которой вектор
изменений коэффициентов ak пропорционален дл .ине и противопо
ложен направлению градиента функции погрешности ~ -
Градиент погрешности Л находится ,из выражения "vlЛ=
= ~ Лkak, где Лk=dЛ/d,ak (-n1~k ~<m1) {дифференцирование
138
Л по a1t производится всюду, за исключением линий излома (ре•
бер) функции Л] .
Погрешность ;Л удобно представить в виде
00
Л = Li (b1t -c1t) sign (b1t -c1t) =
k=-oo
b1t-C1t > О;
b1t-C1t<0.
1
r
L:_
-- ____ _J
а;
d e(zJ
1тЛtu,ti
6)
Лt
вых
Рис. 3.1 О . Структурная схема .корректора, мини
мизирующего сум,ма,р.ную абсолютную ПОf!реш
,ность мето.п:ом · 1скQрейшего опуска ( а) и с игналы
ошюбiки (6, в)
Соответственно компоненты градиента выразим так:
т,
л1 = L ak-i sign (b1t--, ..C1t).
k=-n,
Операции вычисления J..,i моделируются следующим образом. Уси•
литель - ограничитель УО преобразует сигнал погрешности e(z) =
оо
ro
=g2(z)-g3 (z)= ~ (b1t-C1t)zk в сигнал e1(z)=L zksign (b1t-
k=-ro
k=-oo
--с") (рис . 3. 1Об, в), представляющий собой последовательность
139
импульсов' , одинаковой амплитудьr, полярность которых совпадает _
с полярностью (знаком) разностей Ь1<-С1<.
Вспомогательный . корректор с коэффициентом передачи К (z) =
=gi (z-1) преобразует е 1 (z) в сигнал g2(z) = е1 (z)K(z) =
00
= 'r л"z", дискретные значения которого совпадают с 'л1<. В ка-
-
k=- "'
честве вспомогательного корректора можно использовать два од
нополярных двоичных регистра сдвига либо один двухполярный
pffиcrp.
•
·-
Сигнал g2 (z) через коммутатор управляет работой регуляторов
а,,, меняя их коэффициенты передачи со скоростями, пропорцио- -
нальными -fл1<.
Описанная система пригодна для коррекции произвольных ис
кажений. Ее можно существенно упростить, считая, что ,искажения
00
невелики, т , е. выполняются условия: ao = l, la"I «1, ~ lakl <1 .
С учетом . этих условий
'A,h =dЛ/dah~sigп(bh-ch)
и
т,
Vл= I sigп(bh-ck)ah.
k=- n,
k=- oo
k=/ =O
Полученные выражения показывают, что модули кампонент
градиента равны между собой, а знаки компонент совпадают с;.)
знаками Ь1<-С1<. Поэтому для минимизации Л по методу скорейше
го спуска необходимо все коэффициенты а менять на одну и ту
же величину, а направления изменений должны быть противопо
ложны знакам Ь,,-сk. В этом случае необходимость во вспомога
тельном корректоре отпадает и сигнал с выхода УО (см. рис .
3.10а) непосредственно подается на коммутатор К. В итоге мы
приходим к системе, совпадающей по принципу действия с систе
мой, предложенной в [ЗЗJ.
Пример. Пусть g 1(z) = - 0,Sz+ 1 +0,6z (рис . 3.1 la); gз(z) =со+О (со - про
И3вольн6е); K(z)=a- 1z- 1 +1+arz.
Погрешность Л~(З.54) для данного ,при.мера имеет -вид (рис. 3.1 lв)
Л'=L /Ь1</ = /О,5а_ 1 / + /а_1 -О,5/ + /О,6+щl + /О,6а1 /
k= ~2
kif=O
Минимизируем Л' м-етодом ,сечений с ,нулевыми 1началь·ными условиями (точ- •
ка· с). Из ,рис. 3.11 ,следует, ·что ,для достижения ,Л' мин= 0,61 требуется два шага -
(перех-о,д из точки с в точку ,Л'мин 1прои,сходит по кр!llвой cbf). Си.г.нал g:i(z)'
изображен ,на ,рис. 3.116.
Видоизменим сигн ал ,g1(z), считая, что g1(z)=-z- 1 +l+z (рис . 3.12ai.-
B •результате ,Л'= \а-1\ + \a-1-l l + /ar+l l + /a2I-
•·
•
1Лра,фик Л' привед:ен на ,рис. 3.12, из ,которого ,видно, что Л' ,принимает ,ми
нимальное -значение, ,равное .2, ,не в -одной точке, а ,в ,целой области, ·ограничен
ной кривой О, -1, М, 1.
140
!При на~стройке 'КО,рректора ,по методу последовательной О1Птимизации либо по
методу 1о_корейшего спуска ,мы можем получить любые значения а 1 и а_ 1 , лежа
щие •В пределах -'!,;;;; а1,;;;; О, IO,;;;; ,a_ 1 ,;;;; ! , т. е . настройка может прекратит-ься в
любой точке ·прямоу,гольника abcd . Это происходит ,потому, что мы н-е ,учиты
ваем :значения Ь 0 , так 1ка.к ·Оl'ВО\д ао не ,регулируется. Одна:ко мы заинтер -есова,ны .
не только ,в том, ,чтобы получить ми-нимальное значение д', ·но также ,в том, 'IT·O ·
бы вьnполнялось соотношение (3.55) . В ·связи с этим настройку ,следует ,произ
водить та.к, чтобы для .даННО['О •эначения по.nрешности ,Л' -величина Ьо :была ма,к
симальной . ,МаК1симальному з-начению Ь 0 = 3 ,в :пределах 1прямоу,гольника М, -1,
О, 1 соответствует точка М ,с :координатами а- 1 =1, a1 = ---<l. Бели стремиться
не только уменьшить IЛ', но и увелиrчить Ьо, то на,стройка кор1ректо,ра прекра
тится в точке а, в которой Л' =
= min, bo=max, a*1=- l, а*-1=1.
Сигнал g2(z) равен (рис. 3.126):
g2(z) =-z2+3-z2.
Приведем некоторые дан-
а=1
,Q
ные, характеризующие воз-
-1
можности дискретных кор- а =·aJ
ректоров с настройкой по •1
'
aJ
·1t
iTT
-2
-f
~ =-0,?,5
о
oJ
1Zt
ь, = -О.Jб Лt
2'
минимуму суммарной квад
ратичной или суммарной аб
солютной погрешности. Как
цоказано многими авторами,
использование дискретных
корректоров позволяет пере
давать в телефонном канале
(полоса частот 300- 3400
Гц) информацию со скоро
стями 4800, 7200 и 9600 бит/с
{26-36, 40-44] и со скоро
стью порядка 12 ООО бит1/ с
[35, 45]. Сложность коррек
торов (чиЕло отводов линии
задержки) при этом варьи
руется в за!Зисимости от ка
чества канала от 13-20 до
40'--50 ОТВОДОВ (35, 42, 46].
Указанная сложность в на-
стоящее время является до
пустимой. Число передавае
мых уровней (г,радаций)
дискретных сигналов - от 2
до 16. Время автомати.ческой
настройки корректоров -
порядка нес~юльких секунд
и может быть уменьшено до
.л'
т
d.
oi_,
IJJ
Рис. 3 .' 1'!. Иллюстрация минимизации сум
мщрной а,боолют.ной погреJШност,и: -иокажен
ный и ,011кО1р1р-ектюр-ова,н,ный дисК1ретные
сигналы (а, б); фу~нк.ция суммщр,ной абсо.
.лютной mогрешности (в), до.стигающая ми
н.и1мума в од,ной точке
величины порядка 100 мс 1[47]. Вероятность ошибки в системах с
автоматической коррекцией, работающих по стандартным телефон
ным каналам, Раш= 10- 4
--:- 10-5
.
Корректоры автоматически настраи
ваются при соотношении сигнал/шум в канале порядка 20-30 дБ
(каналы удовлетворяют нормам МККТТ), однако за счет _ увеличе-
141
ния времени настройки работоспособность корректоров сохраняется
и при значительном уменьшении соотношения сигнал/шум. Обзор
опубликованных работ ' показывает, что использование гармониче
ских корректоров является важным фактором повышения скорости
передачи данных по сети стандартных телефонных каналов.
а=1
,(J
-1
а
t
Jt
-2
-
1
ь=-!
-2
ь=J
.
о
а
2
Ь2= 1
.1_
LIt
О, =-1
-1
а)
б)
л'
f
п
Рис. 3..1 ,2. Иллюс11рация минимизащш сум
марной а(kолюТ1н-ой 11011реШiност,и: ,и,скажен
,ный и ,откорректи1рова1нный ди,сюрwные
сигналы (а, 6); функция суммарной абсо
ЛЮТIНОЙ л,оnрешности (в), достигающая ми - ·
нИJму,ма ,в ,некоторой -обла ,сти
К достоинству гармонических корректоров по сравнению с
полиномными корректорами других видов (лягеровскими, чебы
шевскими др.) следует отнести возможность реализации гармо
нических !(Орректоров, используемых в системах передачи данных,
I:Ie только в аналоговом, но и в цифроаналоговом и цифровом ви
де с заменой линии эадержки корректора регистрами сдвига. Это
резко упрощает реализацию корректора, так как позволяет ис
пользовать элементы дискретной техники .
142
Условил выпуклости суммарного обобщеввоrо критерия
Автоматическая минимизация суммарной погрешности на вы •
ходе корректора реализуется с использовющем несложных техни "'
ческих средств только в том случае, если эта погрешность явля .
стся выпуклой вниз функцией относительно регулируемых пара.
метров ak. По указанной причине \з проблеме синтеза автомати "'
ческих и адаптивных корректоров \~сновополагающее значение
имеет вопрос об определении выпуклости используемого критерия
близости сигналов.
,
Определим необходимые и достаточные условия выпукл ост и
со
обобщенного критерия Q= L pkD(Ьk-Ck) для произвольных сиг~
k=-oo
налов g·1 (z), gз(z) и произвольного неотрицательного веса {pk }.
Первоначально допустим , что · D(и)-выпуклая вниз функция од•
ной переменной и, обладающая тем свойством, что каждая дуга
ее лежит не выше своей хорды (рис . 3.13):
D [И1 +л (и2-И1)] -< . -D (и1) +л [D (u2)-D (и1)],
(3.56)
где u1, И2-произвольные значения переменной
число, удовлетворяющее неравенству О~ ~ ~ 1.
Полагая D (и)= и2, D (и)= ~и 1, приходим
как частный случай соответственно к суммар
ной квадратичной и суммарной абсолютной
погрешностям. Для общности считаем, что за
дан произвольный полиномный корректор с ко
эффициентом передачи (3.27), у которого
Ьи=~Gtvfv(tи)(k=O,±1,,±2, ...) .
V=l
и; л-прош~вольное
П(и)
11
Яwс. 3.13. График
вьшгу,кл.ой
ф,у~нщи1и
вниз
Докажем, что если .D(и) - выпуклая вниз функция переменной
и, то Q - выпуклая вниз функция переменных ,ak (k=il, 2, ... , q) ,
С этой целью убедимся, что выражение D(Ьk-ck) =
= D·[~
1
av fv (tk)-ck) является выпуклой вниз функцией перемен •
ных а "(v = 1, 2, ... , q). Рассечем поверхность Pk, описываемую
функцией D (bk - ck) в декартовой системе координат, при помо"
щи· плоскостей Х'п(а'1, -а'2, ..., а'п-1, ап, а'п+1, ..., a'q), параллель
ных координатным плоскостям Х(а'1, ,а'2, ... , а'п-1, О, а'п+1, ... , a'q).
Пересечение поверхности Pk с плоскостью Х'п дает кривую Fn,
уравнение которой относительно пере_менной ап имеет вид
Fn = D(апank+Ьпk),
(3.57)
q
где ank = fп(tk); Ьпk = ~a~fv(tk)-ck. Если все кривые Fn, полу •
v=l, v=f=k
чаемые в результате указанных сечений, выпуклые вниз, то функ•
ция D ( bk - ck) также выпуклая. Для выпуклости Fn необходимо
143
и достаточно, чтобы выполнялось условие d2Fn/d,a-2n~O или с уче
том (3.57) (ank) 2 d 2D(u)/du2 ~0. Последнее условие выполняется
всегда, если d 2D(u)/du2 ~0, т. е . если D(u) выпуклая вниз функ
ция. Если D(u) недифференцируемая выпуклая функция, то Fn
также выпуклая, поскольку лин~йные преобразования координат,
имеющие место при замене и . 'СGпап+Ьпk, не изменяют свойства
выпуклости кривых.
Принимая во внимание, ч;rо предел арифметической суммы вы
пуклых функций с положительными весами дает выпуклую функ
цию, в итоге получим, что Q - выпуклая функция переменных CG
(k---: 1, 2, ... , q), если D(u) выпуклая функция переменной и. До
статочн·ость этого условия вытекает из вышеизложенного, а необ
ходимость доказывается следующими рассуждениями . Поскольку
обобщенный критерий должен обладать свойством выпуклости
~ри любом неотрицательном весе {Pk}, то, выбрав
{p1J= {l, k=m, (т-любое),
О, k=l=m
получим функцию Q = D (Ьт-Ст), для выпуклости которой необ
ходимо, чтобы D(u) была выпуклой функцией, что требовалось
.
доказать.
Учтем влияние аддитивного шума на свойства обобщенно,о
критерия Q. Пусть на входе корректора к сигналу g 1 (t) добавля
ется случайный шумовой процесс Na(tj. На выходе корректора
полный сигнал описывается выражением v(t) = g 2 (1t) + N(t), где
q
t
N(t)= ~CGvFv(t);
-
Fv(t) = Jчrv (т)Nо(t-т)dт; 1:P'v (т) - импульс-
V=l
-оо
ная реакция блока корректора с коэффициентом передачи (J)v (iw)'.
Обобщенная погрешность при наличии . шума принимает вид
.со
Q1= ~
- pkD(b1i-ck+nk) [nk=N(tk)].
k=-oo
со
Считаем, что I Ink 1< оо.
k=- oo
_
Очевидно, что свойство выпуклости погрешности Q не нару
шится в результате . добавления к g 1 (t) какой-либо конкретной
реализации шумового процесса N 0 (t), так как такое добавление
всего лишь эквивалентно изменению входного сигнала (как дока
зано выше, погрешность Q .обладает свойством выпуклости при
произвольном входном сигнале). Следовательно, Q, для каждой
конкретной реализации шума является выпуклой вниз функцией
переменных a,i (k = 1, 2, . .. , q). Поскольку операция статистическо
t'О усреднения обобщенной погрешности эквивалентна суммирова- .
.
Q
.
1
нию с определенным весом значении 1 для разных реализации
шума, то Q - выпуклая функция переменных ak (,k = 1, · 2, :.::, q)
(здесь и ниже черта означает -статистическое усреднение). •
144
Таким образом, добавление произвольного случайного - шума
на входе корректора не нарушает свойства выпуклости усреднен
ного обобщенного критерия. Это свидетельствует о том, что мини
мизация Q приведет к совместной минимизации уклонения диск
ретных сигналов g 2(tk) и g 3(t11,) при наличии шума на выходе кор
ректор а.
В частном случае, когда D(и)=и2, обобщенный критерий сов
падает с квадратичным критерием:
00
Q1= ~ Pk(bk-c1J 2 _+2 I Pk(bk-ck)nk+ ~ Pknk.
k=-o o
k=-ro
k=-o o
Из этого выражения вытекает, что при минимизации суммар
ной квадратичной погрешности минимизируется сумма дисперсий
шума и разности выходного и эталонного сигналов, а также их
взаимная корреляционная функция.
Отметим, что из свойства выпуклости критерия Q вытекает
принципиальная возможность постро·ения корректора, минимизи~
рующего величину Q.
Минимизацию величины Q (или Q) практически М-ожно выпол
нить многими способами, например методом сечений или методом
ско рейшего спуска. При использовании метода сечений в схемах
рис. 3.9 линейный детектор заменяется обобщенным детектором с
характерист икой передачи D(и) (и- входное воздействие), а при
ис пользовании метода скорейшего спуска в схеме рис. 3.10а уси
литель-ограничитель УО заменяется функциональным блоком, ко
торый преобразует входное воздействие и по закону D'.(и), гд~
D'(u) - производная D(и) по и.
Отметим основной недостаток, присущий методу сечений. Ме
тод сечений гарантирует сходимость процесса оптимальной наст
ройки параметров ak (k = ,1, 2, ... , q), т . е. отыскание абсолютного
• (глобального) минимума обобщенной погрешности Q, если выпук
лая функция не содержит оврагов. На-
;rичие оврагов, несмотря на свойство
с1-
выпуклости, затрудняет отыскание ми
нимума погрешности. В частности, воз
можно так называемое зацикливание ;
nри котором методом сечений нельзя
достичь минимума, поскольку процесс
минимизации оканчивается в некото-
-
~
u
рои точке, расположеннои в овраге
функции. Сказанное иллюстрируется
рис. 3.14, на котором сплошными кри-
/
выми изображены линии одинакового P,wc. 3
.1 4• Ли,нии у~рО1Вней
фу~ыюции с не1раэ1решимым ов
уровня, а пунктиром - овраг функции ра,лом
Q. Начав поиск минимума функции _
методом сечений из некоторой начальной точки, например из точ-
ки А. мы неизбежно попадаем в точку В или С, лежащую в овраге
функции, из которых уже поочередной регулировкой параметров
145
ak нельзя достичь минимума Q. Зацикливание существенно ограни
чивает область применения метода сечений . Для устранения зацик
ливания необходимо одновременно менять не один, а несколько па
раметров ak, Наличие оврагов зависит от характера функции Q и
в общем случае не является обязательным. Например, суммарная
квадратичная погрешность, в принципе, не содержит оврагов , в то·
время как суммарная абсолютная погрешность может содержат ь
овраги.
•
Минима:ксный :критерий близости дискретных сигналов
(:критерий Чебышева)
К предельному случаю обобщенного суммарного критерия от
носится критерий Чебышева, который оценивает меру близоста
сигналов g2(t,i,) и g3(t,,) по величине модуль-максимума их разно
сти (по максимальной абсолютной погрешности) [7, 10] в=
=maxl g·2(t1<)-gз(t1<) 1 =max Ibk-Ck 1 (k=O, ± 1, ±2, ... ) . Справед
ливость этого утверждения непосредственно вытекает из теоремы
Полиа-Джексона [21]. Действительно, рассмотрим степенно й
критерий (среднее степенное уклонение или погрешность)
N
Qт= _l_ t, 1bk-Cklm
2N /.J
k=-co
(m> 1, N-+ оо, N-произвольное),
(3.58)
который получается лз обобщенного критерия при выборе D(u) =
= 1и Im. Согласно теореме Поли а
-
Джексона имеет место асимпто-
тическое равенство 1 ~/ Qm=в(m-+oo) [21], откуда вытекает, что
критерий Чебышева можно рассматривать как предельный случай
обобщенного критерия.
Степенной критерий (3.58) обладает свойством выпуклости,
так как D(и) = lиlm-выпуклая функция переменной и, посколь
ку 0,S( l и1+и2lm)~0,S( l и1 l m+lи2lm) (m>l) (и, и и2-про
извольные, и,=l=и2). Поэтому в-выпуклая вниз функция перемен
ныхav(v= 1,2, ..., q).
Выпуклость критерия Чебышева можно доказать также иным,
более наглядным путем, не опираясь на теорему Полиа - Джексо
q
на. Обозначим B1< = lbk-ck[ = [~ avfv(lf1<) - c1<I, тогда в=mа ~_ .в,1 ,
v=I
в;;?-==вk (-oo~k ~oo). Нетрудно видеть, что Вk-кусочно-линейная
выпуклая вниз функция переменных av (v = 1, 2, ... , q), имеющая
единственный минимум. Это свойство справедливо для всех k и
при любых значениях ,f v (k) и ck, В многомерном пространстве В1<
описывает не.которую поверхность· Fk, которая делит все простран-
1 Это ;равенст,во сrюкавывает, что чем больше m, тем !ближе v' Qт к мо
дуль - ма!{{:иму,му -рааностей Ь11. -и C1t,
146
ство на два полупространства H+k и H-k, лежащих соответствен
но над и под поверхностью F k• В силу выпуклости Bk полупрост
ранство H+k можно рассматривать как некоторое выпуклое тело,
ограниченное поверхностью Fk, Обозначим через Н+ тело, образо
ванное пересечением тел H+k; Н+ = nн+k, а через F - поверх
ность, ограничивающую Н+ снизу. Пересечение выпуклых тел дает
также выпуклое тело, поэтому Н+ - вьrпуклое тело, ограниченное
снизу выпуклой поверхностью F.
Поверхность F образуется частями поверхностей Fk, совпадая
для фиксированного набора значений переменных av (v = 1, 2, . .. ,
q) с той поверхностью, которая лежит выше остальных. Из ска
занного вытекает, что поверхность F описывается функцией в, сле
довательно, в-выпуклая функция переменных d v (v = 1, 2, ... , q)
(рис. 3.15). Доказанное свойство выпуклости критерия Чебышева
d.
Ри~с. 3. 15. Иллюс'flрация -к д,оказателыству -выпу1к
лост.и щритерия Че1бышев-а
справедливо для любых сигналов g 1(t) и g 3 (t). Если в вычисляет
ся с учетом веса в=maxpklg2(tk) -gз(,tk) 1 (Pk>O), то наличие
веса не нарушает свойства выпуклости.
Минимизация величины в наиболее просто осуществляется с
использованием метода сечений и метода скорейшего спуска. Ме
тод сечений реализуется схемами рис. 3.9, в которых интегратор и
индикатор заменены пиковым вольтметром; метод скорейшего
спуска реализуется схемой рис. 3.10, в которой перед усилителем
-ограничителем необходимо добавить ключ, пропускающий - макси
мальное по модулю значение сигнала ошибки в (z) (ключ на схе
ме не указан). Остановимся на этой схеме несколько подробней .
Градиент функции в равен
тде л;=ak_ ; sigп (bk- ck) при условии, что модуль (bk-Ck) макси
мален для заданного набора значений коэффициентов а; . Для на
хождения ,л; необходимо сигнал ошибки в(z) = g 2(z) - g 3(?) про
пустить через устройство (ключ), выделяющее максимальное зна
чение этой ошибки, т. е. дающее сигнал в 1 (z) = ( bk-ck) zk, где
.Ьk-ck - максимальное значение в(z). На выходе УО получим
с игнал в2(z) = sign(bk-ck)z", а на выходе вспомогательного кор-
147
ректора-сигнал вз(z) = ,I ak-isign(bk- ck)zk, дискретные значе-
f
ния которого, совпада}l со значениями .'Лi , упра_вляют регулятора
ми ai, обеспечивая настройку корректора методом скорейшего,
спуска.
Пример. Пусть g1(z)=l+0,8z (рис . 3.!ба) ; gз(z)=l; K(z)=l+a1z+a2 z 2 •
•
•
-2
-1
Оf2J_
-1
а)
Llt
Pwc. 3 .16 . Иллюстра,rщя мюнимиза:ции ,rю:грешно
сти Чебышева: искаженный и откор1ректирава·н
ный ,сиrшалы (а, б); функция погрешности Ч~бы
шева (в)
Погрешность e(z) имеет ви,д e(z)=g1(z)K(z)-gз(z)= , (,a1+0,8)z+(a2 +
+0,8a1)z2 +0;8a2z3, т . е. Ь1 - С1=а1+О,8; b2- c2=ci2+0;8a1; Ьз-Сз=О ;8а2.
_
Необходимо IПОдобрать •а1 и 1а2 так, - чтобы погреши ')СТЬ e=maoc Ibk-,:;k 1
(k= 1, 2, 3) приняла минимально ,возможное значение.
Ха~рактер ,е указан на рис. 3.1 бв, из ·которого ,ви-дно, что •е - ,выпуклая
вниз ,функ.ция, имеющая ,минимум . Отыщем минимум -е ,методом последователь
ной ,о.п тимиза,ции. Изменение ,коэффициентов ,а 1 и а2 ,в зависимости от регули
ро.вки иллюстри,руется та, бл. 3.1.
Таблица 3.1
После 1
регулиров-
2
3
4
5
6
ки
ai
- 0,44
- 0,44
- 0,55
- 0,55
- 0,58 -0,58
СХ2
о
0,2
0,2
0,25
0,25
0,26
После шестой ,регули·ровки е=О,22. На этом подбор а 1 и а2 заканчивается,
так ~как tдальнейшие уточнения .не приво,дят •К •существенному уменьшению е .
Сиг.нал g2(z) = 1+ 0,22z-0,204z2 + 0,2082 3 изображен •на рис. 3.166 .
На ,ри,с. 3.17 даны осциллограммы, иллюстрирующие ,работу rармо.нического,
корректора . Искаженный сигнал (,рис . 3.17а) преобразовывался ,в сигнал, обла
дающий свойством -от-счетности (ти,па импуль-сной .реакции идеального низкоча
стотного фильтра: с0 =1, Ck =0, k= ± I, ±2, .. .) и в сиг.нал ,с ,косинус- к,ва1дратной:
148
сr:~ектралыной ,плотностью (с0 =1, с 1 =с- 1 =0,5, C1t=0, k=±,2, ±3, ... ) . Для этой
цели иапользовался ю::1рректор с а.нало.говой ли.нией аад,ерж,ки с •16 отводами
а" (n1=7, m1=8) . СИJrналы · ,рис. 3.176 и в •со.впадают с расчетными с точность !{)I
1·-
.3 %. il(a,к ашдно из ,срав,нения pwc. 3 .17 а и 6, ,корректор обеспечивает rrюдавле
ние мешающих импульсов в деся'!'ки раз .
tJ)
о)
Рис. 3..17 . Ооцилло11ра,м,мы, ил
л!оотрирующие ра6оту га~рмо
ничеокого к.с1р1ректора : JFС'Ка-
жеюный (а) и ОТК!~ррекщро
ва1111ные си11налы (6, в)
Минимизация модуль-максимума интерференционных помех
в многоуровневых дискретных системах связи
Обоснование критерия коррекции межсимвольных помех"
Пусть g 2 (О - реакция системы «канал+корректор» на одиноч
ный рабочий сигнал единичной амплитуды x(t) (единичный циф
ровой символ) . Дискретные значения этой реакции bk=g2 (kЛt )·
(/i*0, k= ± 1, ±2, .. .) вызывают интерференционные искажения ,.
оценка которых может быть произведена на основе суммарног о
квадратичного критерия
1') = Lь~ +(Ьо-1)2,
(3. 59}
k4=0
суммарного абсолютного критерия
Л=\-, 1bk 1+/Ьо-11
~
.
(3 .60);
k=f.O
и критерия Чебышева
8=Шах{ ... 1ь-21, ib-11, ibo-11", /b1I, 1ь21 , .. .}.
(3.61 )
В выражениях (3.59) и (3 .60) суммирование производится по
всем k, за исключением k = 0 , соответствующего основному зна
чению принятого сигнала. Основной недостаток этих критериев а
149,
том, что получение минимума 'У), Л или в в системах передачи циф
ровых сигналов с помощью корректора конечной структуры не
nриводит к уменьшению интерференционных искажений до мини
мально возможных 1[37].
Для доказательства справедливости приведенного утверждения
рассмотрим многоуровневую цифровую систему связи, в которой
информация передается при помощи дискретных сигналов, следу
ющих через интервал Лt, причем амплитуды сигналов могут при
нимать любое из значений 6мин = 61, 62, .. . , 61 = 6макс (l - число гра
даций амплитуд). Прием осуществляется выборкой дискретных
значений сигнала в моменты времени kЛt (k = O, ± 1, ±2, ... ) и
с равнением этих значений с ближайшими эталонными (опорными)
величинами 61, 62, ... , 61.
Величина межсимвольной помехи, возникающей в произволь
.ный момент времени -тЛt за счет интерференции передаваемых
случайных сигналов (влияние шума не учитывается), представля
ет собой взвешенную сумму эхо-с1цналов и определяется выра
жением
.
μ= ~ бнi Ь11, -t-бо i (Ь0 -1),
k=t -O
(3.62)
где ,611,,i принимает любое из значений 6v (v= 1, 2 , ... , l) независи
мо от ,индекса k .
Анализ выражения (3.62) показывает, что максимальная μманс
и минимальная μмин межсимвольные помехи соответственно рав
ны:
μ• .,,:быа,ш (~Ь~Н,)Н... ( fЬ:+~,) ;]
:μмин- бманс(~bk --f--В2) --f--бмин (~bk --f--В1) ,
(3.63)
где 6макс И
градации;
6мин - максимальная и минимальная передаваемые
~ Ь+11, - сумма положительных значений 611, ;}: b-11,-
k
k
сумма отрицательных значений Ь11, (суммирование ведется п'ь всем
k=l=O);
J3i={b0 ~l
(Ь0-1 > О);
(Ь0-1 < О);
(Ь0-1 -< О);
(Ь0-1 > О).
Все значения μ находятся в пределах μмин:::;;μ,:::;;; μмакс .
Максимальная по модулю межсимвольная помеха μ0 =max 1μ 1
совпадает либо с 1 μми~I, либо· с 1 μмакс\. Поэтому целесообразно
оценивать интерференционные искажения по величине
'!..to = {/μмакс 1, /μмакс 1 > /μмин 1; }
(3.64)
1μмин\, /μмин/> / μмакс 1,
В однополярных системах, в которых передаются, например,
150
только сигналы положительной полярности, 8мин=0, что, упроща .
ет выражение (3.63): μманс = 18мю,с (~Ь+а+~1); μмин=6маисХ
х(~ь-,,+~2) .
Из изложенного следует, что при передаче дискретных сигна•
лов ·с амплитудами Sh= '8h на приеме получим сигналы с ампли •
тудами S' = ,81,+~L, где lμl~;μo . Межсимвольные помехи будут
минимизированы в том случае, если переданный и принятый сиг•
налы наименее отличаются по амплитуде, т. е. модуль-максимум
разности их амплитуд достигает минимально возможного значе•
ния max JS,, --S'hi =min или maxl •μ:I = 1μ0 =min. Это требование·
• наглядно показывает, что для оптимальной коррекции
межсим
вольных искажений, под которой будем в дальнейшем подразуме
вать минимизацию амплитуд помех μ , необходимо минимизиро •
вать μо.
Рассмотрим, можно ли уменьшить значение μ 0 путем миними•
зации величины 'У), Л или 8. Сравним μ 0 с 'У), Л и 8. Сравнение про ~
ведем для общего случая, когда амплитуды ah в зависимости от
k имеют случайный характер. Именно эта особенность присуща
реальным радиоканалам, в которых ,искажения сигналов сложны
по своей структуре и не повторяются в разных каналах.
Среднеквадратичный критерий указывает энергию эхо-сигна
лов. Недостаток этого критерия, как известно, заключается в.
том, что по энергии последовательности нельзя в общем случае
однозначно определить амплитуды отдельных эхо-сигналов и, сле
довательно, величину μ0 . Пользуясь 'У), можно дать лишь макси-
мальную границу
bh <V11 (k=1=О), μ0<п181V11,
(3.65)
где l8I - максимальное по модулю значение 81, 82, .. . , 01. Знак
равенства в этих выражениях имеет место только при n = 1, г.де
п - ,число мешающих эхо - сигналов.
Среднеабсолютный критерий в общем случае также не позво
ляет однозначно определить μо. Из (3.60) и (3.63) вытекает
(3.66)'
Знак равенства в этом выражении достигается, когда: 1) n = 1;
2) 8мин= -8макс или J оl =l 8макс /=l 8минl; в этом случае μмакс=
= :8мане1Л; μмиН: =- ОмансЛ; J μманс = l 'μм1m l · = μо; μо = 18м~нс,Л; 3) все·
bh - одного знака:
b0-l>0, bh>0;·}
b0 --l <О, bh<0
(k= +1, +2, ...).
Критерий Чебышева связан с μ 0 неравенством
μ0<n8,
которое для п-:-1 переходит в равенство.
(3.67)
1st
При высокоскоростной передаче в реальных каналах обычно
m> 1, поэтому выражения (3.65)-(3.67) дают завышенное зна-
'Чение μо. Сопоставляя (3.59), (3.60) и (3.61), получим nV11~
~пе~~. · где знак равенства достигается при n = 1. Это выраже
:н ие показывает, что Л дает менее завьiшенную границу для μо, не
~ели 'YJ и е.
.
Таким образом, среднеквадратичный, среднеабсолютный и че
·бышевскиf,r критер.ии оценивают интерференционные искажения
.л ишь косвенно, так как по известным значениям 'У}, Л и е в общем
-i:лу чае можно лишь приближенно определить, в каких же грани
дах находятся мгновенные значения μ межсимвольных помех.
Косвенный характер оценок и завышенные значения границ обус
.ловлены тем, что 'У}, Л и' е не учитывают, каким образом. происхо
дит суммирование мешающих эхо-им п ульсов в реальных каналах
·связи применительно к передаче дискретных сигналов. Критерий
μо свободен от этого недостатка .
Эк.стрелшльные свойства критерия μ0 . Используем для компен
-с ации искажений полиномный · корректор с коэффициентом переда
q
ч и (3.27), для которого (3.28) bk = g 2 (kЛt) = L avfv (,tk). Данное
v=l
·выражение с учетом (3.63) показывает, что J 1μмакс J и J ,μминl
многомерные функции переменных av (-v= 1, 2, ... , q). Определим
·характер этих функций. Считаем, что
(3.68)
Запишем J ·μмакс l в виде J 1μмаксl = 1μмакс = li D1[g(k,Лt)], где
k
•
D/(u) = {бмакс U, И> О;
(3.69)
бминU, U<О, U=g(kЛf).
·Функция D1 (и) является характеристикой передачи линейного не
· симметричного детектора, у которого тангенсы углов наклона ха
;рактеристики для и>О и и<О равнqr соответственно ~макс и
~~~
'
Из (3.69) видно, что D 1 (и) - выпуклая вниз функция перемен
яой и, поэтому / ~μмакс !- выпуклая вниз функция переменных а
(v= l,2, ...,q).
С учетом (3.63) и (3,68) представим 1μмин/ в виде . / 1μмин/ =
.•
-μмин = L D2,[g (kM)], где
k
Dz(и)={-бминU, U>О;
(3_7О)
--бмакс U, U < О.
Очевидно, что D2(u) = D1 ( - и), т. е. D2 (и) - выпуклая вниз функ
ция переменной и, а D2 [g (kЛt)] и 1 μмин / - выпуклые вниз функ
ции переменных av (v = 1, 2, .. ., q). Величина максимальной · по
модулю межсимвольной помехи μо совпадает либо с 1μмакс 1, либо
152
с 1μминl, следовательно, μо - выпуклая вниз функ ц ия перемен ...
НЫХav(-v= 1,2, ...,q).
Свойство выпуклости показывает , что функция μ0 не
бочных (локальных) минимумов, а имеет один основной
ный) минимум, который достигается соответствующим
переменных av (v = 1, 2, ... , q).
имеет по.;.
(глобаль•
выбором.
Расчет оптимальных значений av, доставляющих минимум μо ,_
можно провести численно методами линейного программирования.
Действительно, задачу' выбора оптимальных av можно сформули •
ровать в следующем ви,р,е: _найти av (-v = 1, 2, ..., q), для которых.
maxlμI = μo = min, гдеμ с учетом (3.63) и (3.28) линейно зависит
от av. Эта формулиро_вка идентична задаче приближения по Че
бышеву несовместной системы линейных уравнений без учета ог ~
раничений и является одной из разновидностей задач линейног ~
программирования 1 [ 1, 20J.
~(t/
.---.......
.------,
Канал
Коррехтор
gJtj
f
oJ
l
1
1
1
1
1
1~1
L ____J
Рис. 3.18. С~рукту,р1ные -схемы 1юр1ре'Кторо ·в, мин·ими
зи,рующих мо1дуль -маыстт,му;м •ИIНТе\рферен.ционных по
мех методо,м сечений ( а) и методом окорейшего ооу
-сжа (б)
Однако практичес1ш минимизацию .μо целесообразно осуществить с помощью·
изображен.нога ,на ·рис. 3. 18а ,устройства tl'6]. Оснонные узлы •этого у,стройства :
ГС - -генератор ра;бочих сигналов единичной амплитуsды; П
-
!Приемник, ,на
1 К линейному 1Программирова1нию аналогичным образом сво,дится числен-ное
решение задач минимизации -суммарнОго аrбсолютнаго и чебышевскоrо ,критериев .
В силу своей очевидности та.кая интерпретация ~здесь .не описывается.
153.
~ыходе ,которого ,получаем имnульоную последо,вательность ... Ь_ 1 , Ь0-1, Ь 1 , ... ;
,D1 и D2 ~ детекто,ры ,соот.ветств-енно с характеристика-ми (3.69) и (3.70); ин -
тег,раторы S ; схема сравнения С .и индикатор И, .указывающий ,величину μ 0 .
Регулируя тем или иным способом ,коэффициенты av(v=l, 2, .. ., q), tдобиваем
•СЯ -минималЬ'ного значения μо, 1что свидетельствует об -оптимальной ~компенсации
интерференционных .искажений .
На IJ)ИC. 3.186 изо'бражена структурная ,схема корректора, автоматически
ми·нимизирующего !В еличину μо {37]. ,Коэффициент передачи i-го рег улятора ,ме
няется ,на -величину, пропорциональную ,i-й ,компоненте л'; гр адиента μмаис:
,
dμмаис ~ ,
Л;=
=
D 1 (и)fi(kЛt) (i=l,2, .. . , q),
da;
k
если μ,ш,с ~ 1μ,шн 1, либо на величину , пропорциональную i-й , компон е нте 'А'';
·градиента :
"-;=dlμмииl ='1D;(u)fi(kЛt) (i=l,2, .., q),
da;
i,J
k
-если /μмин / >μмаис-. Здесь
, D; (и) =<'>маис+ <'>мин + <'>маис - <'>мин sign и;
2
2
Омане + <'>мин + Омане - <'>мин
.
s1gп 11,
2
2
{ 1,и>О;
- sign и=
и=g2(kЛt).
-1, и<О,
По ,существу, D'1(и) и D'2 (и) описывают усилители-огра1Ничители, работаю
щие в .режиме ж-ест,кого ограничения (на схеме рис. 3.18 , узлы D'1 и D'2 ) . Уп
ра·вляющее у,стройство УУ подключает ко входам перемножающих устройст.в
либо выход D'1 (если μмаис>/μ,шн/), либо выход D'2 (если /μминl>μмаис) .
·Функция μо -содержит ребра (грани), на которых градиент ·не -сущес"Dвует. Одна
ко для реальных ,систем в силу их интер-ционности, а также в силу того, что ре
rуларовка ,коэффи,циентов ak производится шагами конечной длительности, и .в
·силу приближенного вычh•Сления градиента наличие ребер не ,предсставляет опас
ности. Если удалить в ра,ссматрива-емой системе узлы, обведенные пунктиром, то
-придем к ,системе, описанной ,в [32], ,которая минимизирует среднеквадратич,ную
погрешно,сть 'У].
Пример. Сра1вним критерий μ 0 ·с критериями 'У], Л и в на конкретном ,при
. мере.
Ра,с:смотрим канал, в котором от.клик g 1(t) обла,дает -свойствам~;; g 1-(0) =
=1,0; g1(Ы)=а1; g1(kЛt)=0 для всех k, не :равных О или 1. Такой ,отклик полу
чается, · нап.ример, при сд,вухлучевом распространении.
Для компенсации интерфереицион1ных искажений воспользуемся га,рмониче
,ским корректором с коэфициентом передачи K(iw) = ,1 +a 1 e- 1 wЛt. На выходе
.корр ектора Ьо = 1; Ь1 = ( L1 +а1, Ь2= а1а1, остальные значения Ь 1, равны О.
Допустим, что по каналу работает двоичная ди скретная система, в rкото
·рой передаются два уро.вня: 1 и О, т. е. <'>маис= 1; <'>мин= О. Возможные значе
ния меж,символЬ'Ных помех находятся -со-гла•сно (3.,62), г,де бli .и 152 i при·нимают
:з.начения 1 и О :
1
Ь1+Ь2= а1+щ+а1а1;
μо= Ь1 =а1+а1;
Ь2=а1а1.
154
Поскольку .в общем случае а 1 - произ·вольная положительная или отрица
тельная -велwчи.на, μ 0 ,должно совпадать с одним И'З знаrчений IЬ1 + b2 I, 1Ь 11,
l b2 j , Погрешности (,3 ,' 59), ,(3,,60) и , (3.61) имеют rвид:
ТJ = (а1 +а1)2+(а1 а1)2;
Л= 1а1+а11+ 1а1а11;
е=max{1а1+щ1, •1а1а11},
Раосчитаем ко.рректор, т. е , определим а 1 , нижеследующими четырь·мя ,опо
собами, каждый из которых ,соответствует минимизации ,какой - либо погрешно
сти rJ, Л, ,е или μо,
1. Минимум ri имеет ,место при дri/да~ = О , ,что дает
,.
2)
ai=
-
а1/\1+а1•
,2. З,начен-ия а 1 , минимизирующие Л, :наход ятся из условий
а1=
-
а1,если Iщ 1<1;
а 1 п1ринимает любое •значение меж,ду ,О и -а 1 , е-сли Iа11 = 11;
а1=О,если Iщ1>1.
-
3. Мини.мум е получается при вьnполнении условия
1а1+а11 = а1а1, откуда а1=
-
а1/(1+ 1а11). ,
4. Определяем а 1 из у,сло,вия ми.нимизации ма,ксимального из выражений
1а 1 +а 1 +а1а11; 1а1+а11; 1а,а1 j. Для всех четырех способов расчета по найден
ны м .а 1 вычисляем μ 0. Г:р·афики зави,симости μо от а, даны ,на рис. 3.19, r.де
кривые 1-4 ,соот.ветст.вуют указанным четырем способам .расчета а1, Естествен-
Р,и,с. 3.19. При-меры за,вwсимо
сти мощуль-ма1к,симума инт~р
фер енцио,нных п омех на выхо
де Iюр,ректора от а,м,плиту.ды
и пол яр,ности эхо-1сю1нала n1ри
м.инимизации искажений ,по
ювадрат.ичному • (к1ри,вая 1) ,
суммарному абсолютному (кри
вая 2), чебышевскому (кривая
3) и μ-критерию (кривая 4) •
но, наи мень шая -межсим,вольная помеха ,получа-ется :при -использова-н ии критерия
μ 0 (кривая 4). Остальные к,ритерии rJ , ,Л и е .в общем случае не ,гарантируют
достижения минимума μо. Однако при определенных з·начениях а1 критерии /'!/ ,._
и е обеспечивают минимизацию μ 0, о чем •сви.детель-ствует .совпа -дение кривы х:
3и4лриа1>Оикривых2и4приа,<О.
3.5. ИспQльзование алгоритмов дискретной
:коррекции для минимизации искажений частотных
характеристик :каналов связи
Каналы низкой частоты
Алгоритмы коррекции дискретных сигналов реализуются прак•
тически относительно несложными техническими средствами. Поэ
тому естественной является тенденция их широкого применения
не только для коррекции формы сигналов в системах передачи
155
цифровой информации, но и для компенсации искажений частот
но-ограниченных каналов связи путем дискретной коррекции их
.импульсных реакций. Ниже описывается ряд с пособов и уст
ройств, реализующих указанную возможность.
· канал
Ри,с. 3.20 . С11р"у,кту,рная схема ,ко·рректо-ра ,ча,сто11ных ха~ра,к
терwстwк 1шнала овязи с ·настройкой к·ор·ректQра по им
пульсной ,реакции каtНала
На рис. 3.20 изображена структурная схема устройства для од
Jювременной коррекции амплитудных и фазовых искажений, ра
ботающего по принципу минимизации суммарного квадратичного
уклонения импульсной реакции реального канала от реакции
sin2лf t
идеального низкочастотного канала (14] g 3(t)=C0 . с (:fc-
2лfct
граничная частота канала). Генератор ГС передает в корректируе
мый канал последовательность б-импульсов с периодом Т = m/2.f с,
где т - целое число, выбираемое так, чтобы за время Т переход
ный процесс в канале практически окончился. Узкополосный фильтр
Ф, фазовращатель Фв, генератор тактовых импульсов Г с периодом
- следования Лt = 1/2,f c, дели_тель частоты ДИ, электронный ключ Кл -
и индикатор мощности W являются вспомогательными узлами, пред
назначенными для получения суммарной квадратичной погрешно
,сти
00
00
ТJ =}: [g2 (kЛt)-g3 (kЛt)] 2 = ~ - g~(kЛt)+lg2 (0)-C0 ! 2•
k=-oo
k=a-oo
k=f=O
Амплитудные и фазовые искажения канала скомпенсированы оп
тимальным (в смысле квадратичного критерия) образом в том
случае, если 'l'J = min. Поэтому компенсация искажений сводится
к регулировке корректора (например, методом последовательной
оптимизации) по минимальному показанию индикатора W.
По аналогии с описанным устройством возможен также син
тез довольно обширного класса корректоров частотных характе
ристик с использованием д·ругих алгоритмов (например, итераци
онных), изложенных в § 3.1-3.3 настоящей главы. Эти корректо-
156
ры з десь не приводятся, поско л ьку по принцип у построения о н и
не отл ичаю т ся от корр е ктора, изображенного на рис . 3.20 .
При .использовании дискретных алгоритмов происходит преоб
р азование реакции канал а g·1 (kлt) в р еа кцию g 2 ( kЛt) , которая
_удов л етворяет условию о тсчетности (селективности) , т. е. не содер
жит эхо-сигналов
j1 k=O;
g2(kЛt) =
'
(О,k=+1,+2, ...
(3.71)
Естественно, возникает вопрос, как изменились амплитудная и
- -Фазо в ая характеристики канала в результате указанной коррек
ции. Этот вопрос имеет важное п рактическое значение для слу
чаев, когда канал нестрого ограничен по передаваемой полосе
частот или когда частота стробирования if g = 1/ Лt меньше 2,fc. •
Для случая, когда преобразова н ие g1 (kЛt) в g2 (kлt) осущест
вляется корректором, коэффициент передачи которого равен от
ношению спектров решетчатых функций g2 (kЛt) и g1 (kЛt), полу
чим результирующий коэффициент передачи системы «канал+
корректор» в виде [4]
К2(iffi)=
со
t
~ К1 (i ffi-ni COg)
(cog=2п/Лt),
(3. 72)
n=-
co
тде К1 (ico) - коэффициент передачи канала [спектр g 1(t)] (запаз
дывание, вносимое корректором, не учитывается). Данное выра
жение является коэффициентом передачи отсчетного фильтра (см.
ГЛ. 1) и · им:еет СМЫСЛ ДЛЯ случая, КО ГДа ,(t)g~2COc [случай ffig>2coc
соответствует физически нереализуемой схеме корректора, т. е.
невозможно строго выполнить условие (3.71)]. Пример построе-
Рис. 3.21 . Цр .имер ча,стотных ха
рак т ерист,ик 'Н•екар,ректиро,ваIнIноr о
и откарIректи,р·ава·ннGго
.ка,налов
д ля случая, IIOГill.a коррекция осу
ществляе'!'СЯ п0 импульсной Iреа'к
ции канала
- Jr,
-Zr,
-
7i'
ния К2 (iсо) по К1 (ico) приведен на рис. 3.21, где ffi"c=COg - 1coc.
Кривые 1 и 2 соответствуют модулю и фазе К1 (iffi), кривые 3 и
4 - модулю и фазе К2 (ico).
Выражение (3.72) показывает, что коэффициент передачи сис
темы «канал+корректор» приближается к коэффициенту переда-
157
чи идеального фильтра НЧ лишь при wg=2wc, в противном слу"
чае (wg<2wc) получим коэффициент передачи отсчетного фильт
ра с нелинейной фазовой и неравномерной амплитудной характе
ристиками в диапазоне w"c - Wc (,w"c=O, если ,wg = 2wc).
На рис. 3.22 даны осциллограммы откорректированных им
пульсных реакций, получаемых из одной и той же некорректиро
ванной ·импульсной реакции при различных соотношениях (J)g и
(J)c:wg=2wc(a); Wg= 1,8wc(6); (J)g=(J)c(в). Как следует из этих
осциллограмм, полная компенсация амплитудно-частотных и фа -
д)
Ри,с. 3.22 . Ооцилло11р-ам1мы от
карректи,р ова,нных и,м:пульс·ны,х
реакщий ка,нала ,при ,различ
,ных соотношениях меж:ду ча
стотой дис1Qретиза,ции и 11ра
•НИ<юной ,ча,стот,ой ка,нала
зо-частотных искажений достигается лишь при (J)g=2,wc (импульс
ная реакция с высокой степенью точности совпадает с реакцией
идеального низкочастотного фильтра); если же (J)g<2wc, нет сов
падения откорректированных реакций с реакцией идеального
фильтра.
В технике телевидения коррекция частотных характеристик
производится не по импульсной реакции канала, а по реакции ка
нала {1 (ikЛt) на определенный испытательный (контрольный) сиг
нал S (t). Корректор преобразует {1 (kM) в сигнал f 2 (t), совпадаю
щий в дискретные моменты времени с сигналом S (t): 1f2 (kM) =
=
S (kЛt) (,k = О, ± 1, ±2, ... ) . В результате такой коррекции коэф
фициент передачи системы «канал + корректор» принимает вид
00
·к1 (iw) ~ S(iw-ni(J)g)
К2(iw)=
_____..:.:п_
=_-_оо'-------
00
(3.73)
~ S(iw- пi(J)g)К1(i(J)_.:пiWg)
n=-oo
где S (iw) - спектральная п.потность сигнала S(t). На рис. 3.23
дан пример построения K2 (iw) (кривая 3) по ,цqвестным K1(i,w) п
158
'--- ._
S (iш) (кривые 1 -и 2) (фазовые характеристики для простоты не
учитывались). В этом примере в качестве S(t) использован сиг•
.нал с косинус-квадратной спектраль
ной плотностью. Из выражения (3.73)
:и приведенного примера следует,
что полная компенсация амплитуд
.ных и фазовых искажений (харак
теристики канала приближаются к
ха рактеристикам идеального фильт
ра НЧ) имеет место только в слу
чае, когда ffig=2шc и граничная ча- .. __
___,'":;-- _ __ ._ _
__ ::,... __
о
ц;"
f
(и
(,J
-стота спектральной плотности S (iш)
с 2(,Jg
с
равна Шс. Поэтому в качестве ис
пытательного следует выбирать сиг
нал со спектром, ограниченным часто-
ТОЙ ffic.
Полосовые каналы
Рис. 3.23. Ча,сто11ные ха·ра1кте
·рwст-ики . к-а•налов nри коrррек
ции по сигналу
с wосину,с
к;ва,д,ратной ,апек11ральной .плот
.н,о ,стью
Коррекция фазовых искажений. По своим свойствам характе
ристики полосовых каналов отличаются от характеристик низко
частотных каналов, что не позволяет механически распространять
способы коррекции искажений низкочастотных каналов на слу
чай полосовых каналов. В связи с этим • вопрос автоматической
_коррекции частотных характеристик полосовых каналов по их им
пульсным реакциям требует самостоятельного рассмотрения.
На ,рис. 3.24 изабражен ,корректор ,[17], ком1Пенсирующий фазовые искаже-
11ия полосового ,ханала •без прео·бразования !Полосового канала -в низкочастот
ный. Корректор ,на-страивается однократно за ·ми.нимально ,возможное ,время.
Рис. 3.24. Гармонич еский корректор фазовых искажений полосовых
каналов
159
Осно.вные узлы ко,рректора: ГС - .генератор испытательных сигналов , (б-им ~
пульсов); К - корректи,руемый полосовой канал; АК
-
ам,плитудный ,коррек
тор, компенсирующий а.мiПлитудно-часто,тные и-скажения канала; .ТЧ - узел
выделения тактовой ча-стоты, численно равной шири·не полосы пропускания ка
нала; СС - ,генератор ,считывающих ,сигналов; УИ
-
г-енератор управляющих
импульсов; Н - преобразователи , Гиль:берта; ЭК
·_
элект,ронные ~ключи. Регу
ляторы .а\ и а"k (k= 1, 2, ... ) , -сумматоры ~ 1 и ~ 2 , линия за,держки и преобра
зователь Н образуют гармонический ко:рректор с ·,коэффи,циентом передачи
q
K(iffi)= ~ ( а~+на~) e-iwkл_t,
(3.74)
k=O
г,де Н =i si-gn w; Лt= ·2л/1Л!.w; Л,w - ширина полосы про1nус1<ания ,канала .
rКор,реюция фазовых искажений ~производится в ,два этапа : 1. Переключатели
П 1, П2,_, П3 переводятся •в ,положе·ние II и регуляторы ,а' k на,страиваются автома
тически, исходя из условия a'k=g 1 (-kЛt) (k=O, 1, 2 , ... ), где g 1(t) ~ реа,1~ция
системы «канал+амплит уд1ный корректор» . 2. Перевадим переключатели П 1 , П2,
-П3 в положение I , и ре,гуляторы а'\ настраиваются , 1кходя из условия a"k=
=й 1· (-kЛt) (k=O, 1, 2, ... , q), где й1(t) - ,преобразование Гильберта от g 1(t) .
В ,результате .настройки имеем K(i,w)=G*(iw), ,г-де G1(i,w) - спектр g 1(t) . Об
щий .коэ.фф нциент передачи системы «канал+ амплитудный корректор + ,гармони- ·
чеокий ,корректор» ,при.ни.мает вид K2 (i,w)=G1(iw)K(iw)=1IG1(iw)l 2 , что сви,:~.е
телыствует об отсутст,вии фазовых искажений . Если амплиту,дный кор•ректо р
• компенсирует
неравномерность модуля коэффи.циента передачи ка1нала, т а
1 G1(iw) 1 =А и K2(i,w) =A 2=const (А-некоторая постоянная) .
Оптимальная коррекция несинхронных каналов . Алгоритмы ,
рассмотренные в предыдущих разделах , непригодны для компен
сации искажений в несинхронных каналах, так как форма импуль
сной реакции несинхронного канала меняется во времени. Обос
нуем воз можность оптимальной (в смысле квадратичного крите
рия) одновременной коррекции_ фазовых и амплитудньrх искаже
ний несинхронных каналов непосредственно по их импульсным
реакциям.
Рассмотрим случай, когда канал представляет собой полосовую
систему с частотами среза ffiJ, ,ffi 2 и комплексным коэффициентом
передачи I К1 (iffi) 1 =0 ( 1 ffi 1 > •ffi2, J ·юJ <ffi1) . Функция К1 (i,ffi) обла
дает следующими свойствами: 1К1 (iffi) !-частотная функция, не за-
Р,и,с. 3. ,25. Чаего11ные ха·рактеристики 1реалыното (а) и
иlдеа.лыно,г-о (6) неслнхр·онных ка•налов
висящая от времени t;. ср1 (ffi, i) = arg К1 (,iш) - частотная функция ,
форма которой не зависит от t, а положение меняется во времени
(рис. З.25а): cp 1((J)'t) = cp1(ffi) + y(t), где 1ср1(ш) -значение <:p1(ffi, t)
160
для некоторого фиксированного ,t; 'V U) - произвольная, медленно
меняющаяся функция, не зависящая от частоты ffi.
Корректор компенсирует нели н ейность фазо-частотной харак
теристики ср 1 (,ffi, t) и неравномерность амплитудно-частотной ха
рактеристики IK1(iffi) 1, в результате _ чего коrу1плексный коэффи
циент передачи системы «канал + корректор» приближается к ко
эффициенту передачи идеального несинхронного полосового кана
ла (рис. 3.256) 1[11]: I Kз(iffi) 1 = da = const, cpз(ffi, 1i) = -ffi't +(!)о+ _
+'V(t); K3 (iffi)d0ei(-wi:+q,o +Y(t)J, где i-,
ср 0 -некоторые постоянные, не
зависящие от ffi, t. •
Обозначим через g 1(t) реакцию канала с коэффициентом пе
редачи К 1 (iffi), а через g 3 (t) - реакцию идеального полосового
канала с коэффициентом передачи K3 (iffi) на воздействие в виде
функции Дирака б (t). Необходимо разработать алгоритм, кото
рый позволил бы настроить корректор непосредственно по им
пульсной реакции несинхрон.ного канала таким образом, чтобы
происходило преобразование ~той реакции в реакцию идеального
несинхронного канала.
Представим н,есинхронный канал в виде каскадного включе-•
ния синхронного канала (СК) с комплексным коэффициентом пе--
редачи R1(iffi): IJ<1(iffi)l= IK1(iffi) I, argR(iffi) = cp1(ffi)=,cp1(ffi) и
идеально._го несинхронного 19-нала (ИНСК) с к-оэффициентом пе-
редачи K1(iffi) (рис. 3.26): K1(iffi)=eiv(tJ (ffi1~lffil:::;;ffi2); K1(iffi) =
г-- -- --:--- -1
arr11I
~ I1;,rr; I
~rr;
1"' _ СХ !! инск 1 -:+1~--':а~ Корректор ~
1
1
L___ ______J
Канал
·Рие. 3.26. Изображение Iреалын,ого .несинх,р,онно!'о ,ка,нала в
•ви,де .каска,дноло ,соединения си1Юсрои,но!'о и<анала СК и
и.деалыного неси'Нхро,н,ног-о ,каIнала ИН СК
= К1 (i,(J)) К1 (iw). Коэффициент передачи системьr «канал+коррек
тор» равен K2(iffi) = К1 (i,ffi)K(iw) = R 1 (iw)K(iffi) e1V( 1J, где К(iw)
коэффициент передачи корректора, в качестве которого исполь•
зуем полосовой гармонический корректор (3.74).
Степень коррекции оценим по величине . суммарного квадра
тичного уклонения коэффициентов передачи К2 ( iw) ,и Кз (iffi)
w,
11=
L s /К1(iffi)К(iffi)- d0ei <Ро/2dffi,
ffi2 - ffi1
(3. 75)
(i)f
откуда следует, что 'У] не зависит от "?(i), т. е. не меняется с тече
нием времени t. При записи 1'J для простоты предполагалось · i - = 0,
что, в принципе, несущественно с точки зрения решаемой задачи.
Разложим R1 (iffi) в ряд
R-181
161.
00
К1(iffi)= 1:А1,е-i wkлt (ffi1 < 1ffi 1< ffi:a},
(3 .76)
где Ak отличаются от коэффициентов Фурье, получаемых при раз
ложении К1 (i<ffi) в ряд Фурье на отрезке [rw 1, w2] заменой i на Н.
С учетом (3 .75) и (3.76)
со
11= V B1,в:+(Bo-doei<Po)(в;-doe-i<P0 ),
.... .
•k=-co
k4=0
где
В1,= t Ak-i ai (ai = а; +На';).
. (3.77)
1=-n,
Вместо погрешности 11 в дальнейшем будем рассматривать пог-
решность
•
00
:ч= ~ В1,В~,
1_k= -co
1<4=0
которая совпадает с 11 при
в-d el<Ро
о-о
.
(3 .78)
Значения do и сро обычно не задаются, поэтому можно считать, что
они выбраны .так, чтобы вь~олнялось (3.78).
.
Выразим погрешность 11 через дискретные значения импульс
ной реакции несинхронного канала g 1 (t). Обозначим через g 1 (t)
и g2 (t) импульсные реакции на выходе СК и на выходе корректо
ра. Согласно теореме отсчетов
00
-
(t)=~а sinо,5Лw(t- kЛt) cos ffii+ffi2 (t-•kЛt)+
g1
/,J k 0,5Лffi(t-kЛt)
2
-со
(3.79)
-со
где Лt = 2n/Лffi; ' Лw = w2--W1; G,1J. =
g 1(kЛt)' ak=g1 (kЛt) - дискрет
ные значения преобразования Гильберта от g1(t):
-
2
-
=·
2
-
С1⁄2,.= - ReA1,; a1,=--JmA.
Лt
Лt
(Здесь под мнимой частью подразумевается часть выражения, со
держ~щая Н.) Для g 1 (<i) справедлив аналогичный ряд, в котором
ii,"- и ak заменены на ak--:- .
g 1(k,лt) и аk = Й1 (kЛt), изменяющиеся во
времен и.
162
Спектральная плотность К1 (iffi) функции g 1 (.t) равна
К1(iffi)=К~_(iffi)ei v(о =
- С,,
гд~ Ан= Aнeiv(t) = (ан - На") Лt/2 или а" = 2-ReA" = aнcosv(t) +
.
Лt
+~siny(t), а" = - :t JmAн =;"cosy(t)-aнsinv(t). Данные выра•
жения связывают дискретные значения импульсных . реакций •не
синхронного и синхронного каналов.
Реакцию g 2 (t) можно также представить рядом (3 .79), в кото- -
ром а" и~< заменены на a11,=g2(kЛt) и a1н = g2(kЛt). Спектраль-
ная плотность реакции g 2 (t) равна
""
к(.)
iу(t) ~В -iwkЛt(
11
)
2 !ffi =е
~не
ffi1 < ffi <:ffi2 ,
k=- "'
где В" имеют указанный выше смысл (3 .77) и связаны с а1" и
а 1k соотношениями:
a'=-2
-
Re[eiy(OB]· а: = -2- Jm[eiy(t>в],
k
Лt
k'
kЛt
k
из которых вытекает, что величина (a 1 k) 2.+ (i?1<) 2 не меняется с
течением времени (для всех k) .
Очевидно,
•
""
11= А I [( а~)2 +(а~)2] (А= const) .
k=- "'
kcf;O
Проделанный анализ показывает, что погрешность 11 на выходе,
корректора с коэффициентом передачи (3.74) не зависит от t, хо ,
тя форма импульсной реакции ,канала и ее преобразования Гиль
берта меняются с течением времени . Аналогичный вывод справед
лив и для произвольного по.линомного ,корректора с коэффициен-
том .передачи (3.27), поэтому минимизация 11 как выпуклой функ-
6*
Корре/(тор
Р.и,с. 3.27 . С-груктурная ,схема ,кор,рекции частотных характеристик
несинхронного, ,ка,нала
163
ции переменных а,/ и а,/' может выполняться на основе таких ал
горитмов, ,как метод сечений с использованием изображенного на
рис. 3.27 устройства [ 15].
•
,Генератор -сиг.нало.в ГС посылает .в канал б-им[Iульсы с пе,риодом Т =
= т2п/ ('<u2~w1), где т - целое число, выбираемое из условия, чтобы за время Т
переходный проце1:с в канале ,пра.кти.чески ок ончижя. На ,выходе · / преобраэо
.вателя Гильберта Н ·сиг.нал •совпадает ,по форме .с его ,вход,ным сигналом g2(t),
а .на .выходе II сигнал g2(t) являет,ся квадратурой (.преобразованием Гилыберта)
• входного си,гнала. Электронные ключи ЭК, управляемые генерато,ром тактовых
импульсов ГТИ, осуществляют выборку •сигналов g 2(t) и g2(t) ,в ,моменты .в,ре
мени kT/m, за и•склю'!ением k=O . У,средняющий индикатор И, подключенный
через сумматор к выходам ,квадрати '!ных детекторов Кд, . у,казывает ,вели'lи.ну
,i':- Для оптимальной коррекции характеристик ·несинхрон·ного ,канала необхсщи
мо миними.зировать показания индикатора И. ,В проце1:се наст,ройки один из ,ре
гулято:ров .a,h <должен оставаться ·неизмен.ным, в противном случае, установив
_а,=0 ,для всех k, 1полуqим 1']1=iO=min за с'!ет того, '!ТО !K(iw) 1=0.
iН епосредственная минимизация искажений полосовых кана
лов по импульсным реакциям. Обоснуем способ оптимальной кор
(рекции частотных характеристик полосовых ,каналов непосредст
rnенно ,по импульсной реакции ·канала ·без использования ее пре
V'бразования Гильберта [12].
Исходные данные: К1 (iw) и g1 (t) - коэффициент передачи и
импульсная реакция полосового синхронного . канала с ,граничными
частота:ми щ и w2 . Каска.дно с ,каналом включен полиномный кор
ректор с ,коэффициентом передачи (3.27). ОбозначИtм: К2 (iw) =
=K1 (i w)K(iw) -хоэффициент передачи; g2(t) - импульсная ре
акция системы «канал+корректор». Для оriтттмальной коррекции
необходимо, чтобы коэффициент r1ередачи K2(iw) реального .ка
на,ла наименее уклонялся от коэффициента передачи и,деального -
полосового синхронного канала Кз (iw) = С'е-iш,: (щ~ 1 w 1 ~со2) с
полосой пропускания Лw = w2-•W1 и импульсной реа,к,цией
gз(t)=c sin0,5Лщ(t-т) cos w1 +w2 (t - т)
(с=С'Л~),
О,5Лw(t-т)
2
,.
гдети
С1 - зщцанные постоянные.
В ,качестве меры уклонения Kз(iw) и K2(iw) выберем интег~
ш,
ращ,ную ,ква.цратичную погрешность 11 = J 11* (iw)11 (iw)dw,
где
ш;
'f}(iiffi) = K.2(iw)-Kз (iw) .
,Расширим диа,пазон [ w1, w2] до диапазона [ wi', w/], гр·анич
ные частоты wi' и w 2' которого вьiбираются исходя из следующих
требований: 1. Диапазон [ w1', w/] полностью охватывает полосу -
пропускания канала: wi'~w1; w/ ? w2; _ w/-w1' = wc?Лw =
=
w2-
,w 1; 2. w1/wc = n - любое целое число . В этом диапазоне
расомотри,м ~погрешность
164
.•'
,
(1)2
тj"= J11*(iro)1'J(iro)dro,
(3.80)
где 'У] (iro) имеет у,казанный выше смысл при условии, что Кз (iro)
за.дано в диапазоне [roi', ro2'] . Поскольку IK2(iro) 1 =0 ( ro1'::::;;
::::;; 1roi ::::;; ,ro1, ro2::::;; 1Iro l•::::;;'ro{),
,
(1)1
(1)2
,
·;:j= 1'J+р,- р= ~IКз(iro)l2dro+ SIК3(i,ro)l2dro= const.
Погрешности 'У] и ч отличаются на постоянную .р, не зависящую от
К2 (iro), поэтому В дальнейшем вместо 'У] используется Ч·
00
На основе равенства Парсеваля rj = :гс S[g2 (t)-gз (.t) ]2dt, где
-оо
-
(t)_-СsinО,5ffic(t- т)
.
,(t)
g3
-
----- cos(J) -т
-
О,5ffic (t - т)
о
[- с·,. ;
,
i(,+')]
С= ffic:гс, ffio=~(J)I (J)2 •
Свяжем rj со значениями коэффициентов ak,
Заменив в (3 .80) K(iro) его выражением (3 .27) , получим
,
•
q,
;;-= L A1tal+2 ~ Ak1 a1tщ+1-
k=O
k,l
q
-2
LB1ta1t+Q (k=1,2, ..., q,k=f=.l,l=1,2, ..., q-k),
k=O
-
,
(1)2
где !A1t= \ 1K1(iro) cpk (iro)l2d ro;
'.
1111
,
(1)2
Akl = Re s,1 K1(i ro)/2 (j)k (i ro) (j)Z+i (i ro) dro;
,
(1)2
Bk= Re S,K1(iro)K;(iro) cpk (iro)dro;
,
(1)2
Q= ~К(iro)к;(iro)dro.
(1)1
165
Выразим :;:j° через ~дискретные значения g 2 (t) и g3 (t). Для g 2 (t)'
справедливо разложение
00
(t)= '1 Ь sin0,5ffic[t-(kЛt+т)] COSffi' [t-(kЛt+т)]
g2
~ k 0,5ffic[t-(kЛt+т)]
·о
'
(3.81 )
k=-o o
ще bk = g2(kЛt+т), Лt = л/ffic.
Поэто,му К2 (iffi) и YJ (iffi) !можно записать в виде:
00
,,2 ,1ffi - --е
kе
"Vf")-;rt
- i(i), Е ь -f(!)kЛt
ffic
k=-oo
ri (i w) = ~ e-i (i),[(ь-С) +,~. ь,.-• 00 ,.•],
kcj=O
о
2
J
а;
СJмин
лz;-
2
2
---
1-
1
1
г
1
11.
14-
1•
1
..--/12 . __.,....--43
1l
___ _v__V---~~
1
1
1
1
1
1
1
1
1
1
1
1
о
2
J
6)
Рис. 3.28 . Области tдопу,стимых знаrqений
ча,ст,оты диок,ретизации сиr~нала с полос
ным оое-к1"1ром (а) и 11рафИ1к зависимости
минималЬ1но воз·мОIЖiной частоты диюкрети
зации от шкрины и положения спек11ра
сигнала (6)
166
что дает
~ = А[(Ь- с)2+ ktoo bk]
k,tO
(А= const) .
Таким образом, погреш
ность У], являясь выпуклой
функцией переменны х коэф
фициентов ak (k=O, I, 2, ...,
q), может быть представле- .
на как суммарный квадра
тичный эффект дискретных
значений импульсной реак
ции полосового канала без
использования преобразова
ния Гильберта. Проделан
ный анализ показывает, что
коррекция синхронного по
лосового канала по дискре_т
ным значениям его импульс
ной реакции, в принципе, не
отличается от аналогичной
коррекции низкочастотного
канала и может осущест
вляться с ПОМОЩЬЮ устрой
ства, изображенного на рис .
3.20, при условии, что часто
та ffic удовлетворяет выше-
указанным требованиям. Поскольку выбор частоты roc играет важ
ную роль и представляет самостоятельный интерес_, остановимся на
этом вопросе подробней.
Требования 1 и 2 эквивалентны выполнению неравенств
<йсS< Ю1, (S+1)ffic > Сй2,
(3.82)
где s=[ro1/ffic] - целая часть дроби ro1/roc. При этом ro'1=rocs;
ffi'2= roc (s + 1). Решение неравенства (3.82) дано на рис. 3.28а.
Заштрихованные области, соответствующие искомы:\1 значениям
roc, ограничены двумя серия,ми прямых:
Юс=-1 ~; ffic = -1
-
(~+l) (k=l,2, ...).
Лrо kЛrо_Лrо'k Лrо
,
«Разре шенные» значения roc, при ,которых справедливо разложе
ние (3.81), удовлетворяют не•равенству
-
1лroi.>~
>,-
1-
· (1+~) (k=O, 1,2, ... ,т),
(3.83)
k
(()
Лrо
1+k
Лrо
/
где ,т1 = [ ro1/ Лrо] - целая часть дроби ror/ Лrо, а «запрещенные»
значения ,roc, при которых разложение (3.81) неоправедливо, удов
летворяют неравенству
_1 _.~ <~<-
·-1 _(1+~)
l+kЛro Лrо 1+k
Лrо
(k=O,1,2, ..., т-1); -1
-(1 +~)>~ (k=m).
1+k
Лrо
Лrо
• Функция g2 (t) с ограниченным спектром имеет бесконечную
протяженность. Однако всегда можно выбрать такой интервал вре
мени Т, вне ,которого значения g 2 ( 1t) малы и •их мож·но отбросить
при заданной точности описания g2 (t) . В ЭТО!М случае ряд (3.81)
заменяется ·конечной суммой, число членов ,которой минимально
возможное при заданном Т, если roc опрещелSiется из выражещн1
ffiмии = 1+ ro1/Л ·ro
Лrо
1+т
(3 .84)
где т имеет указанный выше смысл, либо из выражения @мин =
=ro2/N, где N2= [ro2/Лro] - целая часть дроби ro1/Лro. Из этих вы
ражений, являющихся- нижней -границей неравенства (3.83), сле
дует, что Юми~Лrо (rог~оо) (рис. 3.286). При выборе
rомин согласно (3.84) для описания g2 (t) в виде ,конечной суммы
требуется минималь~ое число дискретных значений g2 (kЛt), от
считанных с ,максимальным ша,гом диакретизадии Лi=лJrомин -
В заключение отметим, что для функции g2 (t) нар,я,ду с выра
жением (3.81) справедливо также ,более общее выражение
167
гдеw' и w11 -
произвольные частоты, у1довлетворяющие неравенст•
вам w1 pE;'w 1 ~w1; w2~w11 ~w12.
3.6. :Коррекция интерференционных помех
в многопозиционных системах с интегральным
прие м ом
Системы с согласованными фильтрами
Схема - :многопозиционной системы с сог,ласованны,ми фильтра ~
ми изображена на рис. 3.29, тде Sk(.t) (k = 1, 2, ... , т) - набор
заданных рабочих сигналов со спектрами Sk (iw); К,; (iщ) - комп
лексный ,коэффициент передачи параметричеакого ·канала с ли-
1
1
1
1
1
1
L __________J
1J.{ ((J}
г-------,
L___ _____
1/f (цJj
2
г----- - --,
т
.L
____
· ____ _j
1/{r, ((J)
РУ
Рлс. 3.29. Многапози,ционная система с со гласо
ванными ,фильтра1ми
нейными искажениями; РУ - решающее устройство; 1V1(iw) (l = 1,
2, . .. , т) - ,ко.мпле15сные коэффициенты переда ч и согласованных
фильтров, реализованных по 1полиномной стру,ктуре:
q
'I'1 (iw)= ~ atO'\\,(iw) (l= 1, 2, . ; .,т);
'V=I
'\'C1>v(iw)(-v=l,2,•..:,q;1=1,2,
...,т)
--; эада н ные базисные
функции; а,С1)" - регулируемые пара,метры, с помощью которых до
стигается требуемый коэффициент передачи согласованных фильт
ров; N,; (t) - реализация · аддитивного шума со спектром N'т, (iw}.
При подаче на вход .канала сигнала (f)k (t) на 11- м выходе системы
в момент регистраrции t0 получим
q
Р1ц = I at!J Pi';),
где
168
v=I
(3.85) ✓-
Pkt) =
-
1-s
v~l)(i ro) [/(,; (i ro) Sk (i ro) +N1: (i ro)] ei (i) t. d ro;
2л:
Е
Е - частотное множество, охватывающее протяженность . спектра
сигнала на выходах системы.
,Качество системы оцени,м по · квщдрату нормы ~матрицы погреш
ностей на выходах системы
~11~ 11 IPI' - IPJII - ,,t/ P;,-r,,,J'- ,.t, (t,tc•t'' Pj)' - r,,)', (З.86)
где ,[р]'-матрица, составленная . из элементов rрт.1 (,k, l=1, 2, ... ,
m); [р] - заданная (еталонная) матрица, составленная из эле
.ментов рт.1 , ,которые необходимо получить на выходах системы.
Черта над выражением означает усреднение по всем шумовым
реа.лизация.м . .
С учетом (3.85) нетрудно видеть, что при заданных y(/Jv (iro) и
Sт. (iro) llri 11 - многомерная вьшу,клая вниз функция переменных
a(1Jv (v = 1, .2, ... , q; l = l, 12, ... , 1m), не содержащая неразреши
мых оврагов. Будем считать согласованные фильтры оптима.льны
·ми, если величина llri 11 минимально воз,можная. -Мини.му,м llri 11 нa-
d,i'l'J11
.
ходитсяизусловия --=0 (v=l,2, . .. ,q,
l=l,2, ... ,m) .
d a<l)
V
Эти соотношения являются исходными при расчетах оптимальных
зна·чений коэффициентов aUJ v.
Рассмотрим возможные реализации систем, минимизирующих
,l lri 11 на основе алгоритма послмовательной оптимизации (,метода
сечений) и алгоритма скорейшего спуска. Для реализации
_ метода сечений на выходах l = ·l, 2, ... , rm неОlбходимо включить
устройство, указывающее значение llri 11, что ,достигается, напри.мер,
с помощью изображенной на рис. 3.30 схемы. На вход ,канала
К1: (iro) подается пробный (зондирующий) сигнал, представляю
щий собой периодическую последовательность рабочих сигналов
S1(t), S 2 (,t), ... , Sm(t), сдвинутых относительно друг друга на ин- .
тервал Т [Т выбир_аетоя больше длительности каждого из ука
занных сигналов и достаточно ,большим, чтобы за время Т прояви
.лись статистические свойства шума N (t)]. Электронные ,ключи ЭК
производят одновременную выборху сигналов на всех выходах
1, 2, ... , т в момент времени t0, затем в ,момент времени t0 +Т,
iо + ·2т, ... , t0 + ('m - l)T, что дает на-боры импульсов с амплиту,да-
·ми р'н, р'21, р'з1 . .. p'mz (l= l, 2, ... , т). Синхронно с этими им
пульса.ми на вычитающее устройство подаются с генератора эта
.лонных импульсов ГЭИ импульсы с амплитудами pu, ,р21, ..., pm1
(l_: _ 1, 2, ... , т). Индикатор И, включенный на выхме сум 1мато
ра через ква~дратичнь!,.Й детектор Кд и интегратор , указывает ве
.личину llrill. Варьируя пос.JJедовательно .коэффициенты a<IJv, доби
.ваемся ,минимального показа•ния индикатора И, что в силу выпу-к-
169 .
/_
2
ру
1·
1·
И1·
1'
:
llqll 1:
L_ __
-----
-
-
_
__ ..J
P,!DC. 3.30 . Стру,кту,рная схема ус11ройс11ва .для ,аnрЕщеления llrill
лости и отсутствия оврагов соответствует безусловной .минимиза •
ции 11 1lll.
т
Для 111lll (3 .8 6) справедлива форма записи ll'Y)II = ~ 'Y)z, тде
l=I
Y)z= f (i a~Pi1'-Pkz)
2
Очевидно, что при заданных -vt1>(iffi) и
k=I v=I
S,i(iffi) 'У) 1 -взаимно независимые функции переменных а (~>.поэто
му можно настраивать каналы 1, 2, ... , т взаимно независимо, для
чего на выходе каждого канала включаются Кд, генератор и ин
дикатор, указывающий величину 'Y)z, по минимуму которой и ос у
ществляется настройка данного канала .
•
Минимизация 111l ll ,методом ~rрадиента требует одновременного
изменения всех коэффициентов ,шtn (v=l, 2, ... , q; 1=1, 2, ... ,
т) соответственно на величины, пропорциональные компонента '\f
градиента функции 111ll l и противоположные им по зна,ку . Гра
диент 1l1lll определяется выражением
т
q
;;'1'1= V ""л(l)a(l)
V'1
-'-, ;
_;;:,, .
'11
V'
l=I '11 =1
где 'л.t1 > - компоненты градиента;
-:;:;,tn - единичные векторы П{)
переменным;
т
л(1)=~ = 2~(р' -р )P(v) .
v
d a(l)
1,,J kl
kl_ kl
v
k=I
Техническая ,реализация системы с адаптацией no алгоритму скорейшего,
спуска изО16ражена -на ри,с. 13.311. На этом рисунке ,у казан лишь о.дин канал, 1110-
скольку все каналы аналогичны по конструюции н настраиваются .взаимно ,не-
J7()
зависимо. Как и для схемы рис. 3.30, на вход канала К ,:(iro) подаются перио
дически рабочие сигналы Sk(t). На выходах электронных ключей ЭК l-iro кана
ла получаем импульсы с амплитуда.ми Pkz<v> и ,p'kz, а :на ,выхода.х перем,ножите
лей - импулысы с .амплитусдами (.p'kz--()kz)Pkz<v> (v='l, 2, . .. , q; k='l, 2, ... , т).
V{(w}
,--------
-
-
-
------,
L_ _________ _______ __J
'% .f{,J)
г------------------,
ру
L_---------------
_J
1/f, (w)
г---- . -----
------,
1•L
т
Рис. 3.3 1. Стру,ктур:ная схе,ма ,у,с11ройс1'ва для ,на,ст•ройки оог ла,сова,н,ных
филы1рО1В .мног-апоз,щи,онной системы
Эти импульсы сум,мируются и у◊редня ются .в ,на,копительных устройствах У, .на
\Выходах которых ,получаем управляющие сигналы с амплитудами, пропорцио
нальными л(!)v, Управляющие ,сигналы изменяют -ко,эффициенты передачи ,регу
ляторов aU>v, в результате чего величина llri 11 ·минимизируется .методом скорей
шего -спуска. Опwсанная минимизация является ,безусло•вной, т. е. отыскивается
rлобалыный миниму,м llri ll, поскольку llrill - ,выпуклая функция, ,не содержащая
оврагов.
Адаптивные системы с корреляционным приемом
Многопозиционная система с .корреляционным приемом изо
бражена на рис. 3.32, где g, (t) ~ импульсная реа1щия парамет
рического канала с коэффициентом передачи К, (iw); ЧГ1 (,t) (l =
= 1,2,
. . ., т) - опорные сигналы, вырабатываемые опорными
генераторами . Каждый из опорных генераторов реализован в ви
де набора генераторов базисных сигналов v(IJ (.t) (v = 1, 2, ... ,
. q), выходы которых .через регулируемые аттенюаторы а<~> под_аны
на соответствующие сумматоры, поэтому
171
х !---------
~~
1/{{t} •
1
1
1
1
1
:
1
. L_J
Рис. 3.32. Много:rюзи,цио1шая СИСТt>Ма с КОр!реЛЯIЦИОННЫМИ
,IDриемнwка1ми
q
Ч'z(t)=1:atnvtl)(t)(l=1,2, ..., т).
V=I
Изменение коэффициентов atlJ позволяет ~получить нужную фор •
му сигналов Ч'z (t).
При передаче ,k-го сигнала Sk (t) на выходах интеграторов по
лучим
q
P1i1 1= :I at1J QkyJ; Qi'{) = J U1i (t) +N, (t)] yt0 (t) dt;
V=I
Et
t
f1i(t) = fер'(0)q,(t-e)dе,
-00
где Е 1 - множество, по которому ведется интегрирование (в част-
ности, Е 1 - ;множество точек отрез.ка [О, t0], i 0- .момент регист-
рации] .
_
По аналогии с предыдущим .качество системы оценим по ус~
редненному ·квадрату нор-мы ,матрицы погрешностей на выходах
интеграторов
11ri il = ll[p]'-:-[pJ II= k,ti (~
1
atl) QkyJ - pkzy,
(3.87)1
где [р]' - ,матрица принятых параметров р'1iz; [р] - эталонная
матрица; уср~днение ведется по всем шу,мовым реа,лизация,м 1•
Выражение (3.87) по форме не отличается от выражения (3.86).
т. е. при заданных Sk(t) и -y< 1)v (t) ll ri ll - выпуклая щшз фующшг
переменных a< 1)v , не содержащая неразрешимых оврагов. Поэта ~
му для минимизации ll ri ll воспользуемся вышеу,казанным методоl'lt
сечения и методом градиента.
'
Реализация метода сечений в системах с ,корреляционньн,1
.
1 ,Вопросы ,ста т истического усреднения ·в ада п тивных корректорах _ Iрассмот -:
.рены в (39).
172
приемом не отличается от реализации этого же :ме тода в систе-
1мах с согласованными фильтрами и осуществляется путем вклю
чения на выходах интеграторов устройства, определяющего вели -.
чину 111111 , которое 1по ~конструкции аналогично устройству, изобра-
женному на рис. 3.30 .
-
Градиентна,я система, использующая алгоритм скорейшего
спуска, приведена на рис. 3.33, где для простоты указан один
(l-й) -канал . Коэффициенты ,a(1Jv (v = 1, 2, ... , q) этой системы
изменяются на величины aл(1Jv, где
т
л<1> =~ = 2 '1 (р' -Pяz)Q(v).
v
d Cl_(l)
1.J
kl
kl·'
V
k=I
а - коэффициент пропорциональности. Все каналы системы иден
тичны по конструкции и настраиваются взаимно независимо.
Адаптация описанных систем производится по испытательно
му сигналу. Эту адаптацию ,можно осуществлять либо в переры
вах 1между сеансами связи, либо непосредственно в продессе пе
редачи инфор,мации, примешивая !Периодический испытательный
сигнал к рабочему сигналу на передаче и выделяя .мето1дом на
копления •этот сигнал на приеме .
-- -/
--- 2
l
1/{ (tl
г::---
--~
1
Z
1
.......,.---.....---т--'
1
1
1
1
,
l
Р,НIС. 3.33 . Стру,кту~р·ная схема ус'!'ройс'!)ва для ·наiс'I)ройк,и ге
нера:г()lров ош:~рных ,сиnналов .м,ногопозициоНJной с:wстемы
'
Системы, изображенные на рис . 3.31 и 3.33, осуществляют сов
местную минимизацию и - интерференционных (межсимвольных и
межканальных) помех, и аддитивных помех.
173
СПИСОК ЛИТЕРАТУРЫ
1. Зуховицкий С. И., Авдеева Л. А. Линейное и выпуклое програ,ммирование.
М.: Наука, 1964.
2. Кисель В. А. Некоторые вопросы расчета и ·настройки гарм-онических коррек
тор:ов по -сигналу. - В ,кн.: Методы математического моделирования и тео
рия электрических цепей. Киев: Институт кибернети-ки АН УССР, 1965,
·ВЫП. 6, ·с. 71-91.
З . Кисель В. А. А,нализ итерационного алгоритма настройки джжретного кор-
ректора. - В кн.: Теоретическая эле-ктроника. Львов: 1,966, вып. 1,
'С . 108~117.
4. Кисель В. ·А. О коррекции ча,стотных характеристик по импульсной реак
ции. - В ,кн. : Труды конференции, посвященной 70-летию изобретения ра
дио. Киев: Технiiка, 1966, ,с . 5-12.
5. Кисель В. А. Оптимальные алгоритмы настройки гармонических корректоров
1по ·минимуму 1квадратичной погрешности. - В кн .: Методы ,отбора и ,преоб
разования информации. Львов: Наукова думка, 1967, вып. 6, 'С . 71-86.
6. Кисель В. А. Дискретный -синтез корректирующих цепей. Автореф. дис. на
,с ои,ок. учен. степени канд. техн. нау1К. Одесса: '1967.
7. Кисель В. А., Одесский В. Я. Оптималыные алгоритмы настройки полином
ных корректоров. - В кн . : Вопросы электросвязи . Киев: Технiка, 1967,
с. 45-50.
8 : Кисель В. А. Оптимальные алГ'оритмы настройки дискретного корректора
по минимуму ,сум,мар ,ной абсолютной погрешности. - В ,кн.: Математическое
м·оделирование и теория эле'ктриче_ских цепей. Киев: Институт кибернетики
АН УССР, 1957, ,ВЫП. 5, с . 334-360.
9. Кисель В. А. Алгоритм настр:ойки гармонических корректоров ло импульс
ным реа,кциям ,полосовых ,каналов. - В кн.: Методы математического моде
лирования и теория электричеоких цепей. Киев: И1-11ститут кибернетики АН
УССР, 1967, .вып. 3, с. 3-38.
10. Кисель В. А. Оптимальные алг.оритмы настройки дискретных корректо-ров
,по мини,муму максимальной абсолютной погрешности. - В кн.: Теоретиче
'ская электротехника. Лыво1в: 1967, 'ВЫЛ. 4, с. 23-32.
11. Кисель В. А. Алгоритм настройки гармонических корректоров для несин
хронных каналов. - В кн.: Методы математического моделирования и тео
рия электричооких цепей. Киев: Институт ,кибернетики АН УССР, 1968,
вып. 2, с. 70-85.
12. Кисель В. А. Непосредственная кор ,рекция характеристик полосового канала
rю импульсной реакции. - В кн.: Труды учебных институтов ·связи. Л.:
1969, :вью. 44, с. 75-80.
13. А. с. 285063 (СССР). Устройство для настройки фазовых характеристик
четырех.полюсни.ков и ,каналов связи/Ки·сель В. А., Лев А. Ю . , Нудель
ман П. Я.
14. А, с. 292246 (СССР). Устройство для коррекции амллитудных и фазовых
искажений iканалов ·связи /Кисель В. А.
15. А. с. 291362 (СССР). У·стройство для на,стройки коооекторов по импульс-
ной реакции полосового несинхро'Нного канала/Кисель В. А.
16. А. с . 330572 (СССР). Корректор межсимвольных искажений/Кисель В. А.
17. А. с. 344594 (СССР). Фаз·овый корректор лолосо'ВЫХ каналов/Кн-сель . В. А.
18. Березин И. С., Жидков Н. П. Методы вычислений. Т. 1. М.: Наука, 1966.
19. Беркович Д. А., Лев А. Ю . Система ко-ррекции стандартных канало-в то
нальной чжтоты с а,втоматической настрой1юй . М.: Связь, 1972.
20. Ланнэ А. А. Оптимальный синтез линейных электричеоких цепей. М.: Связь,
1969 .
21. Ремез Е. Я. Осно·вы численных мет.адов чебышевского приближения. Киев:
Наукова думка, 1969.
22. Фадеев Д. К. , Фадеева В. Н. Вычислительные методы линейной алгебры .
М.: Физматгиз, 1960.
174
23 . Кловский Д. Д. Передача диокретных сообщений по радиоканалам. М.:·
Связь, 1969 .
124. Уайдл Д. Дж. Методы поиска экстремума . М.: Наука, 1967.
25. Bogert В. Р. Automatic Phase Equalizer. Pat. N 2908873. (USA), 1959.
26. Becker F. К., Holzman L. N ., Lucky R. W ., Port Е. Automatic Equalizatio11
for Digital Communication.-«Proc. of the IEEE», 1965, v. 53, N 1, р. 110-
112.
27. Di Toro М. J. Communication in Time-Frequency Spread Media Using Adap-
tive Equaliza'tion. - «Proc. of the IEEE», 1968, v. 56, N 1О, р. 1653-1675.
28. Boyd R. Т., Monds F. С. Adaptive Equalization for Multipath Chanпels. -
«Electroпics Letters», 1970, v. 6, N 17, р. 556-558.
29 . Chang R. W . Joint Optimisation of Automatic Equalizatioп and carrier
Acquisition for Digital Communication. -«BSTJ», 1970, v. 49, N 6, р. 1069-
1104.
30. Gerscho А. Adaptive Equalization of Highly Despersive Channels , for Data
Transmission.-«BSТJ», 1969, v. 48, N 1, р. 55-70.
31. Rupprecht W. Verallgem e iп erte Verzweigungnuetzwerke . zur Entzerrung von
Kaniileп fi.ir die Digitale Dateni.ibertragung.- «NTZ», Heft 6, S. 316-322.
32. Proakis J. G., Miller J. Н. An Adaptive Receiver for Digital Signaling thro-
ugh Channels with Intersymbol Interference. -
«IEEE, Trans. Information
Theory», 1969, v. IТ-15, N 4, р. 484 - 497.
33. Lucky R. W . Automatic Egualization for Digital Communication.- «BSTJ;>,
1965, v. 44, N 4, р. 547-588.
34. Lucky R. W . Techniques for Adaptive Equalization of Digital Communicatio:1
Systems.-«BSТJ», 1966, v. 45, N 2, р. 256-286.
35. Niessen С. W., Willim D. К. Adaptive Equalizer for Pulse Transmission. -
«IEEE, Trans. Commun. Technol.», 1970, v. 18, N 4, р. 377-395.
36. Нirch D., Wolf W. J. А Simple Adaptive Equa\izer for Efficient Data Trans-
mission. -«IEEE, Trans. Commun. Technol.», 1970, v. СОМ-18, N 1, р. 5-11.
37. Кисель В. А. Минимизация интерференционных mомех в цифровых каналах с
эхо -,сигнала-ми. - Радиотехника. 1973, No 10, <: . 28-3.5 .
38. Lucky R. W., Salz J., Weldon Е. J. Principles of Data Communication. New
York, Мс. Graw-Hill Boock Со ., 1968, р. 443.
39. Rudin Н. R., А Continuously Adaptive Equalizer for General-Purpose Commu-
nicatioп Channels.-«BSTJ», 1969, v. 48, N 6, р . 1865-1884.
40. Капа) L. Survey of Automatic Equalization. Iп: IEEE Computers and Com-
munications Conference. Rome, New York, 1969, р. 23-33.
41. Стоянов Г. К. Фазови коррекции на телефонните канали за передване на
данни. - В кн.: Пощенски телеграфии, телефонии и радиосъобщения. Со
фия: 1972, т. ,23, No 11, с. 2ы~253.
42 . Brownlie J. D., Groves К. An Experimental 4800 Ьit/s Adaptively-Equalized
Modern for Switched Telephoпe Connections.
,
!п: Proc. International Zurich Seminar on Digital Communications. Source
Encoding, Channel Encoding and Modulation, Digital Coшmunication Loops.
1974, р. Hl(l)-H(l).
43. Berland J. R ., Pentaux J. В. Methodes D'egalisation Automatique Pour Trans-
mi ssion de Donnees par Moderпs Utilisant une Modulation Liпeaire . -«L'Onde
electrique», 1975, v. 55, N 1, р. 4-8.
44 . Berland J. R ., Pentaux J. В. Chix et Definition d'un Egaliseur Automatiq11e
Adaptatif Pour Modern а 9600 Bitssec.
In: Proc. International Zurich Seminar оп Digital Communications. Source
Eпcoding, Channel Encoding and Modulation, Digital Communication Loop.s.
1974, р. Н5(!)-Н5(6) .
45. Рое W. R. Adaptive Equalization.
In: Proc. IEEE Conf. Decis. and Contr. Incl. 12-th Symp. Adapt. process.
Sап Diego, Calif., N. У. , 1973, р. 244-246.
46. Lucky R. W . The Status of Adaptive Equalizer Technology.
In: IEEE Sumposium Digest. 1970 Canadian Symposium оп Communications.
Montrea l, N. У., 1970, р. 103-104.
175
47. Schollmeier G., Koeth Н. Theoretica\ Limits for the Settling Time -of Adapti-
ve Equalizers and the Behaviour of the Practica\ Equa\izers. In: IEEE Jut.
Conf. Commun. Minneapolis, Minn __N _ У., 1974, N 4, р. 35D-1-35D4.
48. Sha R. Т., Tang D. Т. А New C\ass of Automatic Equa\izers. - «IВM, J. Res.
•
and Develop . », 1972, N 6, 16, р. 556-566.
•
• 49. Данилов Б. С., Штейнбок М; Г. Однополосная передача цифровых сигналов.
,М.: Связь, 1974.
•
50. Панкратов В. П. Фазовые искажения и их компен.сация в каналах ТЧ при
-передаче диск·ретных си,гналов. М.: Свя _зь, 1974.
Глава 4
ГАРМОНИЧЕСКИЕ КОРРЕКТОРЫ С ОБРАТНОЙ
СIЩЗЬЮ
-+-
4.1. Общие положения
По сравнению с полиномными корректорами без обратной свя
зи принципиально новыми возможностями обладают та,к называе-
,:
а)
oJ
РИJс. 4.1 . Ко·р;р1:Jктqры ,с обра11ной связью параv1лель.но!'о (а) и пос
ледО/Вательно,ю (б) ,в111д,ав
мые полиномные корректоры с обратной связью (рис. 4. ,1), коэф
фициенты передачи которых о п исываются выражениями:
q
~ СЧ1. (j)k (i ffi)
k=l
К1 (i w) = -------
q
1+~ Bk (j)k (i ffi)
k=l
(4.1)
где ak, Bk(iw) (k = I, 2, ... , q) и cp(iw) -.коэффициенты передачи
соответствующих узлов корректоров (a,k и Bk - вещественные).
Система с коэффициентом пере.дачи К1 (iw) устойчива, если годо-
q
граф вектора~ akcp 1,(iw) в комплексной · плоскости не охватываеr
k=I
176
точку (-1,0) (О:::;; lшl :::;;оо). Исходя из этого ,критерия для систе
мы с ,коэффициентом передачи К2(iш) получим, что она устойчива,
если годограф вектора -1-ср(iш) (k = l, 2, ... , q) не схватывает
μk
точку (- 1,0) (0:::;;lwi:::;;oo), .г,де щ - корни !Полинома 1+
q
+~ Bkxk.
k==I
В настоящей главе даются основы общей теории полиномных
. корр екто ров
с обратной связью. Главное внимание уделяется rap •
моническим корректорам ка,к находящим все большее применение
на практике (рис. 4.2). Эти ,корректоры по сравнению с ,коррек
торами без обратной связи при вдвое iМеньшей длине линии .за
держки обладают значительно большими корректирующими спо-
собностя.ми.
•
z-плоскость
а;
о)
I
Рис. 4.2. Га,р•м,он,и,чеокий ко:рректор с л~ростой ,свя.зью (а); ра,с
пол,ожение ·полюсов коэффициента пере;цачи ·кар1рекюра в Z-1П·ЛО
С•кости (б); корректор с кам:б.и1шрова"Н~ной обратной овязью (в)
Рассмотрим основные ти п ы ,корректоров с обратной св,язью.
Для корректора с простой обратной связью (рис. 4 . 2а) отводы с
коэффициентами передачи a1i (k = 0, 1, 2, . .. , п)
образуют пря
мую связь корре,ктора, отводы с коэ.ффициентами передачи Bk
(k=0,1,2,
. . . , п) - обратную связь. Коэффициент передачи
корректора равен
177
п
е-iu>плt}]a,keiu>kлt
к(iro) = ____k_=_O ___
_
п
1+~Bkе-iu>kлt
k=l
или 1в терминах z-лреобразования [2, 13, 14]
п
zn ~ a,kz-k
к(z) = ___
k=_ O
____
_
_
k_=_l _ _
_
п
п
(4.2)
1+~ Bk zk
ВпП(z - μk)
k=l
k=l
где z = e-iu>Лt;
Лt - время .задерЖ!КИ блока линии; у11,
иμ11,-
нули и полюсы К (,z). В дальнейшем ,множите.ль
zn, характеризующий постоянное запа.здывание, вносимое коррек
тором, не учитывается, поэтому
К(z) = Pi (z),
(4.3)
Р2 (z)
где
п.
п
Р1= r akz-k; Р2(z) = (+~ ~11,i.
k=O
k=l
Рассматриваемый ,корректор устойчив, если все полюсы μk ра•
циона.льной функции К (z) расположены в комплексной плоскости
z вне ,круга единичного радиуса, т. е. если все корни полинома
P2(z) по модулю больше единицы (рис. 4.26) [1, 2, 6, 13-16].
Схема гармонического корректора с комбинированной обрат
ной связью [1, 3] изображена на рис. 4.2в. Коэффициенты а'11, об- •
разуют прямую св~Язь корректора, эти же коэффИlциенты совмест~
но с ,коэффициентами В'11, образуют обратную связь. Коэффициент
передачи .корректора 1без учета множителя zn равен
п
~а;z-k
К(z)= _k_
= _O--
п
где В11,
1J Bkzk
k=O
определяются согласно
линейных соотношений:
-р~
-1
-
р~
а;
р;
р~
х
а;
р; р;
~~
р;~;р~
1р;р;~;...р~
,
а
-
п_
178
(4.4)
одной ИЗ нижеследующи х систем
-вп...:...
В2
(4.5)
В1
Во
-
1 а;а;
,
-
1- -во
-
ап
.__
1а;а;
~;
Bl
1а;а;
х~;
В2
(4.6)
а; а;
а;
~,
-
п_
в"
или
п
п
Bk=Lа;p;+k=I р;a;_k
i=O
i=O
(k=O, 1, 2, ... ; а~=Р~= 1; a~k=O).
Сопоставляя (4 .3) и (4.4), нетрудно видеть, что коэффициенты
передачи корректора с простой обратной связью и корректора с
комбинированной обратной связью .могут быть всегда уравнены
между собой, т. е. у,казанные корректоры еквиваленты по своим
потенциальным возможностям.
Схемы рис. 4.2, естественно, не исчерпывают всего многообра
зия корректоров с обратной связью. Тем не менее в настоящей
главе основное внимание будет уделено именно етим схемам, так
как они являются каноническими и обладают функциональной пол
нотой в том смысле, что позволяют моделировать .произвольные
рациональные функции от z с вещественными · коэффициентами,
удовлетворяющие условию физической реализации, при минималь
ном числе ре гуляторов СХ1< и ~k и минималь н ом числе блоков ли
нии задержки. Кроме того, они являются эквивалента,ми ,любой
дру,гой схемы -корректора с обратной связью.
4.2 . Расчет корректоров с обратной связью
по временнь,м и частотным характеристикам
каналов связи
Временная область
Ко:рректор, .ком1Пенсирующий искажения канала связи, прео·бразует им
пульсную реакцию .кана.ла .g 1(t) в импульсную реакцию идеального канала
sinffi"(t- т)
g3 (t) = С --'------'-
(i)c (t -
"t)
(С, "t - постоянные; Wc -
.граничная частота канала).
В термwнах z - преобразо:вания задача корректо,ра заключается в преобразо
,вании сигнала (дискретной импульсной реак ц ии)
т,
&(z)= Lakzk ( ak=g1 (kЛt), Лt=n/ffic]
в ·сигнал g3 (z) = 1 (постоянные С и "t не учитываются). Этот случай коррекции
практически .наиболее важный, п оэтому ограничимся расчетом корректоров с
обратной связью, предназначенных для преоб,разо,вания g1 (z) в gз(z) = 1.
179
Исходными данными к ра-счету являются ди,скретные значения · g 1 (kЛt) им
пульсной ·реаюции g1(t), т. е. коэффициенты а1,. полинома g 1(z). Очита-ем, что
полином -g1(z) удовлетворяет усло.вию коррек'I'ируемости (не содержит кор,ней,
по модулю ра'В'ных единице). Значения а1,. нумерую"Гся та,ким образо·м, Ч'I'Обы п 1
IJ)ав·нялось числу корней полинома g1(z), модуль которых меньше -еди-ницы, а
т 1 - чи-слу ,корней, модуль кото.рых ,больше единицы.
11(0:эффи.циент передачи корректора, преобразующего g 1(z) в g 3 (z) = 1, ра
.вен
К(z)=gз(z) = _1_ = Р1(z) •
g1 (z)
g1(z) Р2(z)
Т,ри;;иальное ,решение 1Поставленной задачи получим , положив
Р1(z)=1, }
Р2(z) = g1(z).
(4. 7)
Как упоминалось ранее, корректор с коэффициентом передачи (4 .3) удо,в
лет.воряет условию устойчивости, если 1\Се корни полИ1нома P2 (z) по ,модулю
больше единИ1цы. Полином g 1(z) в общем случае содержит ка ,к -корни, модуль
которых ,больше единицы, так и корни, модуль которых меньше единицы. В свя
зи с этим корректор, ра,с,считанный -согласно (4.7) , в . о'бщем случае не будет
устойчивым. Во из, бежение этого недостатка поступим следующим образом
{6, 16]. Факторизуем полином
.
. g1 (z) относительно единичной окружности ·
g 1(z)=P+,(z)P-(z), где P+(z) - полином по положительным степеням z, со
держащий корни полинома .g1 (z), по модулю большие единицы; P-(z) - поли
.нам •по отрицательным степеням z, ,со.держащий корни, ,по модулю меньшие
т1
n1
единицы: P+(.z)=~l1,.zk; P-(z)=~d1,.z -k. Фа,ктори·заr.щю -выполним так, что·бы
k=O
k=,0
~=1.
~
•Воз.ведем полином P-(z) .в отри.цателыную степень:
оО
[P-(z)]-I = ~ Dkz-k ,
k=O
где
1
Do=-' D k=
do
k-1
.
-+~D;dk-i(k*О,k=1,2,
,о i=O
.
.
.).
(4.8)
Ряд (4:8) сходится, так .как все корни nолинома P - (z) ,рас,положены в плоско
сти z внутри круга единичного •радиуса, поэтому , ог,ра.ничившись некоторым чи-с
лом членов ряда, пре.дстави,м 1[P - (z)]- 1 -в .виде полинома степени п:
п
[р-(z)]- 1= LDkz-k.
k=O
С учетом изложенного
п
~Dk!
k=O
K(z) =
+
р (z)
(4. 9)
Полученный коэффициент передачи - •соо11ветствует устойчивому корректору,
поскольку корни п олинома Р+ (z) по модулю большие единицы. Таким образом,
искомые значения а1,. и ~1,. определяются
.выражениями: ~1,. = l1,./l0 (k= 1, 2, ... ,
т1); a1,.=D1,. (k= _O, 1, 2, ... , п).
180
.)
Изложенный опособ ра:очета поз,воляет по равноотстоящим дискретным зна
чениям лм1Пуль-сной реакции ка,нала .ооределить коэффициент пер-едачи коррек
то.ра, прео.бразующего g1(t) 'В g 3(t), ,в принци1Пе, с любой степенью . точности.
Погрешность преоrбразования определяется погрешностью, которая возникает
при замене ряда (4.8) полиномом (4.9). Чем больше п (т.· е. чем больше число • J
блоков запаздывания корректора), тем меньше полрешность. Для вычи-сления
п
п,+п
по,r,решности находим полином g 2 (z)=P - (z) !nkz-k = ~b_kz-k, который ОIПИ -
k=О
k=O
сывает ди,скретный си,гнал на .выходе корректора при подаче .на его ,вход сигна
ла g1(z). Коэффициенты bk этого 1Поли,нома являют-ся дискретными значениями
выходного -сигнала кар.ректора при п_одаче на вход сигнала • g1 (t). Поэтому bk
ука-зывают погрешность (уклонение) си,nнала g 2 (t) относительно требуемого.
сигнала gз(t) для моментов времени kЛt.
Кор ,ректоры с ,простой и комбинированной обра11ной овязью эквивалентны, а
их каэффициенты .перещачи ра1вны ,меж,ду оо-бой, если а'k= akfao; Bk = ~k (~для
всех k). Восшол~,зооавши-сь (4.16), находим
~'n = Bn; -~,n-i = Bn-1-~'na'1;
~, n - 2=тBn - 2-~n-1a'1-~' na'2 и т. д. Эти ,выражения .позволяют по известным
ak и ~;. получить а' k и ~, 1<- Поэтому расчет ко.рректора с комби.ниро:ванной с,б
ратной связью за,меняем пе.рвона ,чально ра,счетом .корректора с простой обрат-
.
ной свявью, после чего lПереход,им к кор,ректору с ,комбинирова,нной О'братной
связью.
Изложенный спосо•б расчета связан с необходимостью вычислять корни по
•линома g1(z). Ниже дает-ся приближенный способ расчета, соглаено которому
коэффициенты ak и ~k определяю'!'ся из системы линейных урав·нений [б]. За
пишем выражение для g,(z) •в такой форм,е:
g1(z) = р+(z)р-(z) =
или
00
g1 (z) ~D11.z-k = р+(z).
k=O
p+(z)
(4. 10)
Считаем, что полишо м Р-(z) нормирован относительно свободного члена :
do = 11, поэтому Do= 1. ,Выражение (4.10) дает бесконечную систему уравнений,
которую ,разобьем .на .две системы уравнений.
Система уравнений 1
ат,
-
l-
т,
ат,
D1
аз
ат,
D2
х
(4.11)
а2 аз
l2
а1а2аз
l1
аоа1а2а3
·ат, _
_ Dm,_
lo
JiJJJИ [а]" Х [D]' = [[].
Система урав нею-1й 11
181
ао
щ
а2
ат,
D1
а-1 ао
щ
а2
ат,
D2.
а_2 а-1 ао
щ
а2
Dз
а-2 a_l ао
а1
а2
х
а-п,
а-2 а-1 ао
а1
а_п,
а-2 а-1 ао
i-
•••
.;
..
..,
-1,
а_п; J
или [a] X[D]=----,[a]' (~пустые места в матр-и,цах соответствуют нулям, которые
опущены для у,прощения формы запи,си).
,Р ешая систему уравнений II относительно [D], получим [D] = -{a]-
1
X[a]',
где [а]- 1 - матрица, ,обратная l[a] .
Для нахождения .неизвест.ных D" необходимо вычислить [а]- 1 . Бесконечные
матр ицы -обращаются неод·ноэна1чно, т. е. существует множество матриц, о'брат
ных [а]. Из этою ,множест ва нас интересует матрица [а]- 1, у1Довлет,воряющая
оrрани,чению : ,ря,ды, ооста1влен,ные ив строк и столбцов матрицы [а] - 1 , должны
быть а1бсолютно сход5rщими-ся . Наложеl!'ное ог,раничение соо т:вете11вует требова
нию физ!fчес-кой ,реаливуемости ра,оочитываемого ,корректора. - Мат,рица [а] имеет
обратную с учетом указанного ограничения, если полином g1 ( z) содержит в
ком:плеысной плоскости z п 1 корней .в,нутри кру,га единичного радиуса и т1
корней .вне едини,ч,ного .кру,га (~по числу нижних и верхних ,диагоналей .матри
цы [а]) . Со,гласно ,вышеоговоренному полином g1(z) удовлетворяет данному ус
ловию, п оэтому с истема уравнений II имеет ,решение, приводящее к физически
реализ уем ой схеме корре·ктора.
Вычисление [а]- 1 в силу ее бес-конечности связа.но с рядом трудностей ,и .не
может быть выполнено только линейными операциями . Заменим •поэтому ,беско
нечную ,систему уравнений II конечной ,с и,стемой ура,внений
-а0 а1 а2
ат,
-
л1-
а_1
a_l ао а1
а2
ат,
л2
а-2
!а_2a_lао
а1
ат,
лз
х
(4.12)
а_п,
a_l
ао
а1
а-n ,
а-1 ао
а-п,
а-п,
а-1ао
_ }::q
или [а]Х[л) = --j[с].
Размеры матрицы [a]-qXq ; q ,в ыбирается из условия q-;;,n .
•Решая (4.12), получим [л] = -l[ а] - 11[с] .
Элементы л,,_ матри:цы [л] являют,ся приближенными значениями коэфф и
циентов D,. . Степень ,при' ближения
определяет-е л вели'Чиной q; выбирая q доста :
точно большим, мож,но свести погрешность к любой ,наперед за,данной величине
lim Лk-+Dn . Это выраже н И(; справедливо, если g ;- (z) удовлетворяет вышеприве
денному условию . Определwв коэффициенты л,,_, находим значения l" согласно
(4.11), подставляя •вместо D• .коэффициенты "•·
Искомые значения а,. ,и ~. ,получим .из соотношений:
fik=lk/l0 (k=l,2, . .. , т1); CXk=Лk/l0 (k=l,2 , ... , п); а.0 =1/10 .
По из•вестным а. и ~ • .при ,необходимости определяем а',. и ~, •·
Пример 1. Пусть
sinffic (t+Лt)
siп ffic t
sinffic(t - Лt)
gl (t)= -О з --~-~ +о 85---+o,s -----
,
ffic (t+Лt)
'
ffic t
ffic(t- Лt)
(рис. 4.За) или g1 (z) =-0,Зz-1 +0,85 +0,5z.
182
6)
Рис. 4.3. Примеры искаженной (а) и откорректирован
ной (6) не п рерывн ы х им п ульсных реакци й
Требуется раосчитать .коэффициент .передачи корректора
а:о+а:1z- 1+а:2z- 2
К(z)=а= 1+~1z+~2z2
преобразующего g1(t) в gз(t)=sinIOJct!шct, g 3.(z) = !l .
Фа•кторизуем g 1(z) O11носительно единичной ,окружности: g1(z)=
= P-(z)P+,(z) =1 (, 1-0,Зz- 1 ) (1 +0,,5z), P- .(z) = 'l-0,3z- 1 ; P+(z) = 1+0,5z. Окоача
тельно ,получим ao= ll; а1 = 10,3; а2 = !0,09; 1~1 = 0,,5; ~2 = 0.
~Сигнал g2(z), .возни·кающий :на .выходе ,ра,с·очитанного корректора при пода-
че на его .вход сигнала g 1(z), ,равен g 2(z) = g 1(z)K(z) = '0,027z- 3 + '1. Си11нал
g2(t) имеет вид (рис. 4.36)
sinffic(t+3Лt)
sin ffic t
g2(t)=0,027---"-'--'---'--+
-
-
ffic(t+3Лt)
ffic t
и совпадает с g 3 (t) с точностью до ,2,7%. При записи g2(t) не учтено запа-з,ды
вание ,; = 2Лt.
1Вооnользу_ем,ся теперь спосо;бом nри,ближенного расчета коэффициентов а"
и ~k - Согласно (4.12)
[ 0,85 0,5]х[Л.11=[0,3],
-
0,3 0,85
л2
О
откуда нах одим л 1 = ·01292; л2 = 1,003 . Из системы (4.11) ~получим : lo= 0,9 -96; /1 =
= 0,5. В ,итоге а0 = 1,004; а 1 = ·0,:293; а2 = 0,1; В 1 = О,1501, что cOrBl[la,дaeт ,с анал,о
гичными значениями а 1,, и Bk, вычисленными ранее, с хорошей степенью точ
ности.
Оптималь.ные ,спосо,оы ,ра•счета, изложенные .в ,гл. 3 nрименителыно ,К кор-
ректорам без обратной связи, спра,ведли,вы и для корректоров с обратной
связью, если ,ра,счет 1произ1водить .в таком ,поряд,ке :
1. Опр~щеляем полином P 2 (z), как ,это указано выше.
:2. Выч,исляем коэффици-енты ak полинома P 1(z), пользуясь методикой рас
чета корректора без обратной свяви по ·ми,нимуму суммарной квадратичной,
суммар·ной а,бсолютной , суммарной обобщенной и т. д. логрешностям .выходного
сигнала (см. гл. 3). Коэффициенты ak раосчитываются iКа'к коеффициенты а_,.
корректора без обратной связи. При этом полином P1(z) (,с заменой а1,, на а_1,,)
.ра-ссматривает-ся ка-к к,00,ф;фициент ,передачи ,корректора (кар.ректора преддейст
вия), а mолином P-(z) - ,ка.к ,входной ,сиrг,нал этого ко,рректора .
Бели mo условиям расчета степень п полинома P1(z) и P2(z) ограничена и
n<m {m1-степень P+(z) ], то разбиваем P+(z) на два полинома P+(z) =
=P1+(z)P2+(z), где P 2+(z) - полином степени п, нее корни кото,рого по мо•ду
лю меньше корней .полИJнома P 1+(z) . Выlбираем ,в качестве P 2(z) полином
1
P 2(z) = - ,-, P 2+(z) [Во11 - с1юбод:ный член полинома P2+(z)]. Соста,вляем про-
Во
изведение
т 1-п
) Pt(z)р-(z)= ~ Aki.
О
k=- n,
183
Вычисляем - ко1эффи.циенты а1, полинома P 1(z), ра,с-сматри,вая ег,о ,как коэффи
циент передачи кор ,ректора без обратной связи, .ia вход которого посту,пает
си11нал с дискретными значения-ми А11..
Пример 2. Пусть g 1 (z) =iO,Зz- 1 + 1 +0,Зz (рис. 4.4а),
а,0= 1
1,0
91 (z)
a_1=D,J
а1=O,J
-2
-f
о
2 t/Лt
О 1 t//Jt
а;
Рис. 4.4. ЦрИJмеры дИlш~ретных .импулысных 1реаищий:
а) 1некоррек1'црава~н~ная •решюция; 6) ~реакция, откqр1рек
ти-рова,н,ная по 1крит1с1рию Чебьшnева
Определим а,,_ и /311. так, чтобы абсолютная погрешность уклонения выход
ного си11нала g 2 (z) от ,сигнала g 3 (z) = 1 приняла минимальное значение. С этой
целью .факториэуе.м g1 (z):
g1 (z)=0,9(1+ - 1
-
z)(1+-1
-z- 1). Выбираем P2(z)=1+- 1 z; /З,=J; -/32=
3
3
3
.
3
=0. Постоянный множитель 0,9 в расчете не учитывается. Коэффициенты ;а 1 и
а2, для которых максимум абсолютной погрешности ,е принимает минимально
возможное значение 0,023, равны соответственно 0,307 и 0,078. Сигнал g 2 (z) изо
бражен на рис. 4 .46.
Интерпо,ляционный расчет в частотной области
Пусть F(i,w) - заданная на отрезке {-wc; Wc] функция •с четным .модулем
и нечетным аргументом. Решим задачу : рас-считать гармонический корректор с
обратной .с,вязью та:к, ч'Dобы Lд;ЛЯ диа,пазона \ w \ ~ 'Wc выпол,нялось равенство
1
K(iu>)=F(iu>)= --
(_- ( 1u> 1,( u>c),
.
К1 1w)
(4. 13)
nде .под F(i.w) ,подразумевается функция, обратная коэффициенту передачи кор
ректируемо:го канала К1 (i,w). Естественно, равенство (4.13) для ,прош~вольных .
F (i,w) может .выполняться только в коне~чном числе точек отрезка [- wc, {J)c].
Поэтому в ~дальнейшем речь ,будет идти 01б интерполя:ции за,данной функции
F(i:ro) дробными тригонометричес,кими функциями K(iw).
Обозначим:
Wc
(!)v =v -
(v=0,1,2,.
п
., . п; n=q).
При расчете .целесообразно и-опользо:вать нормирова·нные значения <pv = <JJ v -
- vCfu (v=0, 1, 2, .. ., п), т. е. вместо фун,щии <p(.w) = argF.(iw) -целесообраз,но
п
184
использовать функцию ~(ffi) =<p((J))-(J)T, где T=<p((J)c)/(J)c, Фу,нкция
лет.воряет граничному у,словию <p(:(J)c) = '<p'(--.. . ;(J)c) =0, что у,меньшает
интер~поля.ции (при этом предполагается, что F ,(i(J)) непрерывна
[-\(!)с, (J)c]) •
Для узлQIБ ин'I'ер:поляции (J)v справедливо ,ра,вен,ство
iw kлt
,q}((J)) удов
по,греШН(}СТЬ
на -отрезке
ake v
(v=O, ±1, ±2, .. . , ±n),
(4. 14)
которое rпред,ста,вляет ,собой систему из · 2n+'1 линейных ура:внений , содержащих
п ,неизвестных Bh и n+ 'l ,неизвестных ah . Эта система значительно у,прощается,
вели воопользовать·ся следующим искуоств-енным приемом. У.множим лев у ю и
пра,вую ча·сти выражения (4.,14) на е-1wvлЛ 1, (л=О, ± 11, ±а, .. ., ±п)
и· пр·осу м
мируем по переменной v полу,ченные для каж:дог,о значения л уравнения
~'
[
~-iwkЛt] -iw'),,Лt
~F(iffiv) 1+k,,,Bkе v
еv
V=- n
k=I
~
'
~iwkЛt
=~
~CGke V
Х
v = -nk=O
-iw ллt
хе v (л=О,±1,±2, . . ,, ±n).
Знак ~, показывает, что крайние члены ,сум.мы (v = ±n) ,берутся с весом, рав
ным 0,5 .
Принимая .во :внима!jие тождест,во
i'e-iwv(k+л)Лt ={ О, k+л+О;
2n, k+л=О,
V=- n
получим две ,системы ,уравнений .
Система ,ура·внений 1
[
gn gп+I
gn-1gn
go
gi
Система ура:в.нений 2
n
1~'
gk=2n ~
V=- n
•
0
•
gn-!~ [Bil
rg_ Jl
• • •gп-2
В2
g_2
х.
=-
.
'
.
.
.
.
.
.
.
go
ВпJ
g_nJ
-
iw kЛt
еV
(k=O, ± 1, ±2, · · ·• ±n; g2n+k=gk; gn+k=g_ n+k).
,
(4.15)
(4. 16)
,Решение системы (4:1'6) дает ковффи,циенты Bh, по котс,рым с учетом (4.'15)
. ,найдем каэффиц11енты ,ah,
1Ра,с,очитанный изложенным :опособо.м корректор обеапечивает точное •воапро
изв-едение за.данной функции F (i(J)) в 2n+ll точках и ,приближенное воспроиз
ведение во в_сех остальных точках отрезка (-(J)c , Wc], Число блоков линии
задержки корректора rпри этом .равно п.
185
После .нахож,дения .ко•эффициентов ~1< следует проверить гар ,мони,ческий кор
ректор на устойчивость. С этой целью составляется хара·ктеристичесжий ,поли-
п'
ном P2(z)= L ~1izh (~o=l). Если корни P2(z) лежат в 1юмплек,сной плоскости
k=O
2 вне круга едини~ного радиу,са, корректор устойчив. В противном случае кор
ректор неустойчwв и заданная функция F (iw) не м,ожет ·быть ,в,ос·произ'Ведена
гармони"!еСJким корректором с обратной овязью.
~Коэффициент переда ·чи .корректора описывается выражением (4 .2), однако
множитель е- 1 wплt при составлении ура·в,нений (4.14) ,не учитывался. Кроме
того, ,ра,очет ·произ·вадился по нормированным значениям ер v. В силу этог,о
argK (iw) = argF,(iw )--<w-r-nЛtw, так как ар ,гумент функции F (i,w) воопроwзво
дится корректором ,с то"!ностью до линейного слагаемо,го -(nЛt+-r)w .
Расчет корректора по периодической последовательности
частотно-ограниченных сигналов 1
Укажем опособ ра,счета корректора с простой обратной ,связью по диокрет
ным з•начениям iiv си11нала gi(t) . Коэффициенты a1i (k= .1, 2, ..., п) находят,ся
из си:стемы ураВ'нений
a-(n-l) a-(n-2)
а_2 а_1 а0
К:rnффици,енты P1i ,находятся ло формуле
fik =bn/b0 (k=1,2, .. . , п),
х
где b1i аnределяем :из системы линейных соотношений
Ьп
ап
а_п a-(n-l)
а-2 а-1
-
an-l ап
а_п
а-(n-1)
а_2
ап-2 an-l ап
а_п
,,
~
а1
а2
ап а-п
ао
щ
ап-1 ап
(4. 18)
сч
х а:2
(4.19)
Gtn
-
Матрица, стоящая в правой части данного выражения, имеет размеры
.n+il хп+11 .
<Корректор, преобразующий gi(t) ·в cp 1(t), содержит п+ 1 011водов , a1i (k=
=0, ,1, 2, ... , п; ao=il) и п от.водов P1i (k='1, 2, ... , п).
,Раочет корректора, преобразующего g1(t) в cp 2 (t), ,производится анало,ги,ч-
1110. Такой корректор содержит n+l отв.адов a1i (k=O, 1, 2, ... , п; а0=·1) и п-1
от.водов ,P1i (k=1l, 2, ... , п-1) . Размеры матрицы, ,стоящей в правой
ча-сти вы-
1ражения (4 .' 19), ,в ,этом случа,е ,равны nxn+l.
[1ри· расqете корректора с обратной связью для п,рео'бразования g 1(t) в
1 О смысле используемых .в на,стоящем параграфе функций .и величин
см. гл. 2.
186
ip 3(t) или cp 4(t) пользуемся выражениями (4.17), (4..t ,8) и (4.19), осуществив
~~варительно слещуюll!,ую замену.: 1) в ,выражении (4.17) заменяем iiv на
aV; ~ В ВЫраЖеНИИ (4.19) Заменяем iiV ,на а V (V :- ПОЛОЖИТеЛЬ ·НОе) И ij_ V
на -av (v - .положительное)..
Корректоры, .раосчита,,н~~Iе согласжо предложенным опособам, осуществляют
преобразование й1(t) ил11 gi(t) в ,:Pi(t), cp2(t) или в ,:Рз(t), ip4(t) с точн,остью
до множителя Ьо .
Пример. Задан ·сигв:ю1 (рис. 4.5а)
Р.ис. 4.5 . Примеры периодических и,мпулыаных rреа ,к
ций:
а) ,некоррЕJкщро,ваш,ная •реакция; б) 011кор,реюиро
ва·нная а:~еахция
2
_
~_
1
ffic
gi(t)= 1,.. akср1(t- kЛt);,:р1(t)=5 sinWctcosec5 t;Лt= n/Шс,
k= -2
где ii- 2=~012; ii-1 = 0,5; iio= 1; ii1 =~0,3; ii2= 0,3 .
Необходимо ра-с-считать коэффициент передачи корректора с обратной
связью
2
~ ct11.ei(!)kЛt
k=O
K(iш)=
2
1 +L ~k e-i(!)kЛt
k=I
преобразующего й1(t) в cpi(t) (рис. 4.56).
• Составляем систему уравнений (4.17), решив которую получим а1 = -0,383;
а2 =0,391 . Из линейных соотношений (4.19) находим bo=l,232; bi=-0,423 ;
Ь2 = 0,562. Далее воDпользуемся (4.18): ~1 =-0,341; ~2=0,457. Ра-ссчитанный
корректор преобразует g1(t) в ip 1(t) с точностью до множителя Ьо= 1,232 .
187
4.3. Алгоритмы :компенсации ис:кажений сигналов
на основе :корре:кторов с обратной связью
Rорректоры с простой обратной связью
•Данные в г.л. 3 алгоритмы автоматической коррекции дискрет
ных и непрерывных сигналов пригодны дл ,я ,коМ~пенса ц ии искаже
ний с помощью корректоров без обратной связи, и их нельзя ис
пользовать в случае корректоров с обрапюй связью. Обусловлено
это тем, что обобщенная погрешность на выходе корректора с об
ратной связью не обладает свойством выпуклости относительно
коэффициентов ~h- Поэтому в настоящем разделе даются а.лгорит
мы ,коррекции сигналов с применением ,корректоров с обратной
-свя.зью. Изложение алгоритмов ведется для случая полной ,ком
пенсации 1эхо - сигналов, когда gз(z) = 1.
•
Алгоритмы коррекции сигналов, не содержащих преддействия
или последействия. Предположим, что сигнал g 1(z) не содержит
последействия:
о.
g1 (z)= L ahzk (ak=O; k>O; а0= 1),
k=- n
т. е. все корни полинома g1 (z) расположены в плоскости z внутри
круга миничного радиуса. Преобразование g1 (z) в gз (z) = 1 осу
ществляется схемой ,гармонического корректора (рис . • 4.6), для
которого ан =О (k>O); ао= 1; а-1 =- а-1ао; а_2 =-:- а- 1а-1-
-а-2ао, ... Из этих выражений вытекает простой алгоритм кор
рекции преддействия, включающий в себя еле.дующие операции:
1. Исходное состояние: ао = 1, ан = О (для всех ;k).
•
2. Меняя регулятор а-1, добиваемся равенства нулю сигнала
на выходе ,корректора для точки k=-,1, что дает _ а...:. 1 = -а_ 1 а0 .
Меняя регулятор а-2, добиваемся равенства нулю выходного сиг
нала для точки k = -2, в результате чего получим а_2 =
=-а-1а-1-а-2ао. Регуляторы а-з, а-4, ... , . а_ п ,
настраивают
ся аналогично.
Алгоритм всегда обеспечивает схqдимость процесса коррекции.
после однократного подбора коэффициентов a - k, если корни по
линома g 1 (z) по модулю меньше единицы. После окончания .кор
рекции получим К (z) = 1/g1 (z), где К' (z) - коэффициент переда
чи корректора преддействия (см. рис . 4.6) .
Рис. 4.'6 . Кор•рею::о,р предJдейс-гвия
оилнала
188
Рис. 4.7 . ~ор1рек-гор с обратной
овязью для ,ко:мпе,Н!сации после
дейст,в:ия сигнала
Рассмотрим теперь случай, когда сигнал g 1 (z) не содержит
т
пре,д.~действия: g1(z) = \" a11,zk (а11, = О; k<O; ао = 1), т. е . все кор
~
k=O
ни полинома g 1 (z) расположены вне круга единичного ра,диуса .
Преобразование сигнала g1 (.z) в g 3 (z) = 1 в этом случае целесо
образно осуществлять гармонически,м корректором (рис. 4.7), для
которого
f31t=~=а11, (k=1,2, ..., т);
(4.20)
.
ао
где К" (z) - коэффициент передачи корректора последействия:
К" (z)=--
1-
n
~ ~kzk
k=O
•
Алгоритм ,коррекции последействия требует выполнения та,КИ'<
-операций: от,ключение цепи обратной -связи и .под,бор . согласно
(4.20) значений коэффициентов передачи по отводам линии за
держки, после чего замыкание цепи обратной связи. Кроме ука
занного, возможен также алгоритм последовательной настройюr
регуляторов ~11,, выполняемый в такой последовательности:
1. Исходное состояние: В11,=О (~o = l) .
2 . Меняем значение коэффициента В1 до тех пор, пока выход-
1юй сягнал в точ,ке k= 1 не обратится в нуль, что дает Bi =а 1 /ас.
ИЗ]меняем затем значение ,коэффициента ,пер~дачи ,в 2 , добиваяс':>
равенства н ул ю выходного сигнала в точке k=2, в результате че•
го получим 1В2 = а2/ао. Аналогичным образам настраиваем регуля ~
торы Вз, В4, ... , Вп, добиваясь в каждом
случае равенства нулю
выходного сигнала для соответствующей точки.
Алгоритм последовательного подбора .коэффициентов Bk обес-
- печивает
сходимость процесса настройки, если все корни полино -
1п-i
мов g 1i (z) = I a11,zk (O::;;;i::;;;m-1) лежат вне .круга единичного
k=I
рмиуса. · В противном слу чае схема коррекJора в .пр оцессе на-
- стройки
возбуждается. Укажем на одно .и.остаточное условие вы
полнения наложенного ограничения. Если все значения ak поло
жительны и удовлетворяют неравенству
(4.21)
то все полиномы g1i (z) содержат только ,корни, по ,модулю боль
шие единицы [,17].
При выполнении (4 .21) настройка ,корректора путем последо
вательного подбора Bk всегда приводит ,к требуемому результату.
Естественно, для преобразования сигнала g1 (z), не содержащего
:nред1действия, в сигнал gз (z) = 1 ,можно использовать схему -кор-
189
ректора ,по рис. 4.6, ,для которой a-k = O, ,ао =;1, а1 = -а1ао, а2=
=- а1а 1 - а2ао, . .. Алгоритм коррекции последействия, вытекаю .,
щий из данных выражений, полностью аналогичен рассмотренно
му выше алгоритму коррекции преддействия.
Изложенные а.лгоритмы отличаются ,простотой, однако облает:,
их применения ограничена сигнала.ми, не содержащими преддей
ствия или последействия .
Общие алгорит.мы коррекции сигналов . Факторизуем сигнал
т
g((z) = ~ akzk , содержащий преддействие и послещействие, отно-
k= -n
сительно единичной окружности: g1 (z) = P+(z)P-(z). У•множим
о:,
g 1 (z) на некоторый pяJJ. Q (z) = L a_kz-k та,к, чтобы произведение
k=O
g2 (z) = g1 (z) Q (z) не содержа.ло отрицательных ст епеней :
т
.
g2 (z) = f bkzk, где g 2(z) - некоторый полином по положитель-
k=О
ным степеня.м z. Нетрудно видеть, что при сходящемся ряде Q (z)
обiязательно получим: Q (z) = 1/P-(z); g 2(z) = P +(z) . Таким обра
зом, если сигнал g 1 (z), содержащий пре.,щдействие и ,последейст
вие, преобразуется в сигнал ,без ,пред.действия g2 (z), то корни по- ·
линама g 2 (z) совпадают с корнями полинома g 1 (z), расположен.
ными вне круга единичного ра,диуса . Из сказанного вытекает ал
горитм коррекции произвольных сигналов [5-9], который вклю
чает два этапа : 1) преобразование сигнала g 1 (z) в сигнал без
пред.действия g2(z) = P+(z); 2) преобразование g2( ,z) в gз(z) = l.
Второй этап не вызывает ни.ка,ких затруднений, поскольку преоб
разование сигнала без пред.действия в сигнал ,gз (z) = •1 выполня
ется достаточно ,просто согласно изложенным алгоритмам. Оста
новимся поэтому подробнее на ,перво.м :этапе.
Преобразование g1 (z) в g2 (z) = P+(z) осуществляется коррек
тором без обратной связи, для которого ak = O (k>O), т . е . кор
ректором пред.действия . Укажем возможные способы коррекции
пре.ддействия в случае сигналов, содержащих и пред.действие, и
после.действие. Все способы, по существу, сводятся к коррекции
сигналов на отрицательной щискретной оси времени.
I способ. Исходное состояние: a- k= O (k= 1, 2, ...), ао= 1.
Первый шаг настройки: устанавливаем a(l)_k=-a-11 . (k= 1, 2, ... ) .
Второй шаг настройки: a( 2)-k = a(l)_k - a(l)_k (k = 1, 2, ...) . .
После i-го шага имеем aO)_k = a<i-l)_k - a<i- l)_k (.k = .1, 2, ...) или
K1(i) (z) = К1(Н) (z) ., - g2 -(i-J) (z); g2(H) (z) = g1 (z) К1(Н) (z), где
a(i)k - значение ,коэффициента передачи k-го отвода линии задерж
ки после i шагов настройки; a<i- l)_k
-
значение сигнала на выхо,
де настраиваемого корректора для точки - k после i-1 шагов на
стройки; K1(i)(z) - ,коэффициент ,передачи .корректора; g 2(i- 1)(z) -
сигнал на выходе настраиваемого корректора; g2- <i -l) (z) - пред.
действие сигнала g 2<i - l) (z), т. е. левая часть функции g2<i-lJ (z),
190
получаемая из g2<i - IJ(z) отбрасыванием свобмного члена, а так~
же ч.ленов с положительными степеня,ми z.
Изложенный способ является итерационно - разностны,м алго
ритмом коррекции ,преддействия сигнала при наличии последей
ствия.
Пример. Пусть ff1(z)=0,3z- 1 +1+0,4z. Пер .вый шаг: а( 1 )_ 1 = 0,3; а0 ( 1 )=1;
K1( 1 )(z) = 1 1-,0,Зz- 1 . Сwгнал gi1J(z) равен: g2( 1)(z)=g1(z)K1(1J(z)= - 0,09z-2 +
+I0,88+'4z. Второй ша .г: a( 2)_2 = i0,09; a( 2J_ 1=-0,3; a 0 (2J= :l; K1( 2J(z) = , l-0,Зz- 1 +
+0,•09z-2 ; gi2J(z)=0,027z- 3 +0,0З6z - 1+0,18·8+0,4z •И т. sд.
,Как ,ви,дно из примера, уже после 1втораг-о ша.га .на1стройки си,г.нал gi2J (z)
совпадает с истинным значением си.гнала g2(z) = •P+(z) = •0,86+0,4z с точ-
l}!остью 40/о.
I I способ. Этот способ заключается в многократном ис
пользовании алrорит,ма ·коррекции пред.действия для сигналов без
последействия. Ка,к указыва,лось выше, ,коррекция преддействия в
случае сигналов без последействия производится однократно. При
менение а,лгоритма коррекции преддействия в случае сигналов
прмдействия и последействия приводит к тому, что после одно
кратной коррекции из-за .мешающего в.лияния пос.ледействия !Пред
действие полностью не компенсируется. Поэтому .коррекцию сле
дует повторить. Число повторений определяется исходными иска"
жения,ми сигнало'в g1 (z).
I I I с,п о с об. Допустим, что на вход корректора преддействия
-
о
.
с ,коэффициентом передачи К' (.z) = ~akzk подается си.гнал
т
g 1 (z) = Lakzk. На выходе ,корректора получим сигнал g 2(z) =
-п
т
о
=g1 (z) К1 (.z) = I bkzk, где bk= I ak-lai , Обозначим через
•
-(п+п,)
i= -n,
11
-1
су,м.марную обобщенную погрешность: ri= У D(bk), где D(u) -
."- 1
k=-(n+n,)
произвольная выпуклая вниз функция переменной и = Ьk, Для
компенсации прещдействия необходимо минимизировать 'У]. По
грешность ri - выпуклая функция переменных ai, поэтому для
настройки корректора целесообразно применить алгорит-м после
довательной оптимизации или алгоритм скорейшего спуска. Кор
рекция преддействия согласно этим ал,горит,мам производится в
полной аналогии с ,компенсацией искажений дискретных сигналов
-с помощью -корректора без обратной связи ( см. гл. 3).
Осуществив .компенсацию преддействия [т. е. преобразование
g 1 (lZ) в g 2 (z) = P+(z)] согласно одному из описанных способов,
далее следует преобразовать сигнал P+(z) в сигнал gз (z) = •l . Для
этого необходимо последовательно с корректором преддействия
:включить корректор последействия (рис. 4.8). Такая схема, буду
чи эквивалентной общей схеме корректора без обратной связи,
.отличается от последней раздельной настройкой ,каж,дой из частей
191
Pwc . 4 .8 . Ка,ска~д,ное ,в'Ключение ~кqр,ректора пред1д~ЙС1)В.Ия ,и
,~ор,ре,ктара последействия
схемы (,корректора преддействи1Я и ,корректора последействия)
согласно изложенным алгоритма.м. При етом настройка коррек
тора преддействия осуществляется многократно [в зависимости от
искажений сигнала g1 (z)], а настройка ,корректора последейст
вия - сщнократно.
Очевидно, корре,~щию ,можно производить и в обратно~М поряд
ке, т. е. сначала от,корректировать . последействие, а затем 1пред
действие . Преобразование g2(.z) =P+(z) в gз(z) = 11 целесообраз
но выполнять корректором последействия с обратной связью (см,
рис. 4.7). Если включить последовательно, а затем объединить
СХ('jМЫ по рис. 4.6 и рис. 4.7, получим полную схЕ1му ,корр~ктора с
обратной связью (рис. 4.9), которая настраиваетоя следующю,1
образом:
•
:лг_г::-,. .d
~
Рис. 4..9 . Структу1рная • схема 1На1Стройк,и корIректора
с обра11ной связью
1. Исходное состояние: цепь обратной связи от,ключена ~н = О
(k=1l, 2, ... , п), что превращает корректор с обратной связью R
,корре.ктор пред.действия :
·2. Настраиваем цепи а-н (k=,1, 2, ... ) согласно описанным
алгорит,мам, добиваясь полной ,компенсации прмдействия си1гна
ла g 1 (z). Если настройка выполняется по III способу, использует
ся ключ К1л2, пропускающий только пред.действие си,гнала, анали
затор А и индикатор И, указывающий величину погрешности fl.
Цепи а-н настраиваются по ,минимальному показанию индикато
ра И на основе опти.мальных алгоритмов, изложенных в гл. 3.
192
3. Скомпенсиров_ав ,преддействие, .получим на выходе корректо
ра сигнал , содержащий только последействие, ,которое компенси
руется с использованием _ изложенных ранее алгоритмов .
Корректор с комбинированной обрат~ой связью
Остановимся на одной особенности расчета корректора с ком
бинированной обратной связью . Из (4.5) и (4.11) вытекает, что
при ао = 1 и ао= 1 коэффициенты в'k корректора , ,преобразующего
заданный сигнал g 1 (z) в g3 (z) = 1, ·равны
P~= ak (,?=1,2, ...,т),
(4.22)
где ak - дискретные значения сигнала g 1(z) . Условие а0 = 1 tдО ·
стигается нор,мировкой ak по отношению к ао . В етом сл у чае рас
чет ,корректора несколь.ко упрощается , так как требуется опреде
лить только коэффициенты a'k; значения , в\ полагаются равными
дискретным значени,ям последействия сигнала g1 (z).
Алгоритм коррекции , вытекающий из (4.22), включает следую
щие этапы:
1. Ра з мыка ем обратную связь корректора и устанавливае1м ко
эффициенты B'k согласно (4 .22), после ч_его замыкаем обратную
связь (цепи a'k предварительно отключаем: ·а'1<=0) .
2. Включаем и .настраиваем цепи a'k, добиваясь полной ком
пенсации преддействия выходного сигнала. Настройку a'k выпол
няем одним из способов I - III .
ОписаюJ.ЫЙ алгоритм лежит в основе опособа а~втомати,ческой ,коррекции
амплиту-дно-частотнь1х и фа-за-частотных ха-рактерпстик каналов провод1н6й свя
зи по их импуль-сным реакциям [1, 1.2] . Gпосо,б реализует-ся с ,помощью изобра
женного на рис. 4.1 О у,стройст,ва. Ген ерато-р ГС посылает в .канал ,после,дова
'rельность импульсов с периодом, превышающим длительность перехощного про
цесса .в канале и крат,ным ,периоду наивысшей частоты ка,нала. К орректор · .с
комбинированной обратной -связью преобразует импулысную реа ,кцию та·ким об
разом, чтобы она не содержала импульс-ав преддействия и .последейст,вия , что
свидетельствует о ком,пен-сации ам1плитудных и фа з авых и с кажений ка нала с вя-
7- 181
Рис . 4.1 О. А~в11оматический корр ект ор ча1ето11ны х
. характери~е-rик
·ка,нал ов связ и ,на оано.ве к ор;ре,к
т ора_ с ,коМiбини,р ава,н,ной о•qр атной овязью
193
зи. Для этого филь'!'ром Ф 1 -выделяют на приемном конце тактовую ча,стоту,
равную частоте среза ка,нала. Затем с помощью -блока БОИ выделяют основной
положитель·ный отечетный 1им1пульс , макси,Мум которого .совrпа.дает с .положи
телыным мак,оимумом та,кто,вой частоты, и испол~,зуют его для управления бло
ком настройки БН корректора . Мешающие имiпулысы ра,спределяю'Гся, и .каж
дый из регуляторов корректора на,страивается на минимум напряже.ния, при
ч~м, .в первую очередь, ключом ЭК 01брывае'ГСя обра'Гная связь в БН и регуля
торы цоои абратной связи ,на,страиваются путем сраJВнен,ия .на,пряжений, посту
пающих ·на вход корре,кт,ора, с напряжения,Ми, ~поступающими нз корректирую
щих -цепей. Поскольку опект,р сигнала настройки ог_раничен нижней частотой
среза полосо1вого ка1нала связи, на прием,ной стор<}Не wску,сст.вен,но доба,вляют
низкоча,стот.ные соста,вляющие, формируемые гребен!Чатым фильтром ГФ, -нели
нейным элемент-ом НЭ, ,фильтром Ф2 и ,блоком еогласова,ния фаз гармоник СФ.
Описанному устройству свойствен нмостаток, заключающийся
в том, что при больших искажениях сигнала g 1 (z) не всегда га
рантируется устойчивость ,корректора . В силу (4.22) ~после на
стройки и замыкания обратной связи коэффициент передачи кор-
т,
ректора равен R(z) = 1/1 + ~ . в\zk= 1/gi (z) (a'k=O), где
R.=1
gi (z) - полином, получаемый из g;1 (z) отбрасыванием членов с
отрицательными степеня, ми z.
Корректор с коэффициентом передачи R (z) устойчив, если все
корни й1 (.z) по модулю больше единицы. Это требование выпол
няется только при сравнительно небольших искажениях _ сигна
ла g1 (z), из чего следует, что в процессе настройки согласно опи
санному алгоритму корректор может возбудиться. В связи с эти,\1
при ,больших искажениях g 1 (z) настройку корректора целесооб •
разно производить по такому алгоритму:
1. Исходное состояние: цепи a'k и , в'k отключены: a'k= B'k=O
(,для всех k). Согласно (4.22) настраиваем цепи B'k•
2. Не замыкая обратной связи производим настройку .цепей
одним из способов I-III, добиваясь ·компенсации пред~ействи>I
сигна.ла на выходе ,корректора, после чего ~за-мыкаем обратную
связь. Поскольку цепи а\ настраиваются при от,ключенных цепях
В'1<, схема корректора в процессе настройки не воз-буждается. Од
нако в этом случае увеличивается время настройки корректора.
194
Данный алгоритм лежит в основе принципа действия устройст-
Хорректор
Р.ис. 4.11. Устрой~ст~во для на,ст,ройки кор,ректqр ·ов с
прямыми .и обратным-и свЯ1Зя-ми 1ра:зных типо1в
1
ва для настройки гар.монических корректоров с прямыми и ос-
ратными связями по импульсным реакциям ,каналов [9] (рис.
4.11). В это.м устройстве ФНС - формирователь низкочастотных
составляющих сигнала настройки; РС - регистр сд"ви,га; П
-
пе
реключатель; И - индикатор. Остальные узлы _совпадают по на
значению с аналогичными узлами устройства рис . 4.1 О. Основной
отсчетный импульс аа сигнала g, (z) с ВОН поступает на РС и че
рез отводы регистра управляет работой ЭК, осуществляющего
дискретизацию сигнала на выходе ,корректора. Индикатор в ·завп
симости от ,положения переключателя П указывает дискретные
значения сигнала на выходе корректора.
Для настройки корректора необходимо компенсировать им
пульсы преддействия и последействия выходного сигнала. С этой
целью, устанавливая П последовательно в положения 1, 2, ... , п,
настраиваем ,цепи обратной связи. Отключив обратную связь, на
страиваем uепи прямой связи, для чего П устанавлива ·ем в поло
жения О, -1, --2, .. . , --п !:!., вкдючая регу,ляторы ао, а,, ... , а.п,
добиваемся :нулевого показания индикатора за счет измененин
коэффициентов передачи соответствующих регуляторов. При боль
ших искажениях указанную ,компенсацию 1преiддействия необходи
мо повторить.
После настройки цепей ,прямой связи замыкаем цепи обратной
связи. Это исключает возможность возбуждения корректора, если
входной сигнал удовлетворяет усл0tвию ,корректируемости .
Устройство, изображенное на рис . 4 .11, является универса.ль
ны1м в том смысле, что оно пригодно и для настройки корректоров
с простой обратной связью. При этом первоначально по аналогип
с изложенным включаем и настраиваем цепи прямой связи, а за
тем настраиваем и включаем цепи обратной связи. На рис. 4.12
изображен пример осциллогра,ммы иакаженного сигнала (рис
4.12а) и сигнала, · откорректированного с помощью гармоническо
го корректора с обратной связью (рис. 4.126) .
5)
Ри,с. 4.12. Осциллопрам·мы нек0tрректи,рован·ной ( а) и отк(}р,ре.кти
·р,ава,н,ной (б) импулысной ;реа,кl!;ии
Экспериментальная проверка показала, что при малых искаже
ниях входных сигналов настройка коррект6ра с комбинированной
обратной связью требует меньше времени, нежели настройка ,кор-
7•
195
ректора с простой обратной связью. При больших искажениях по
ложение меняется , так как корректор с комбинированной обрат
ной связью в процессе настройки возбуждается. Поэтому перво
начально необходимо настроить цепи а,,, а затем - цепи
~"·
4.4. Синтез регулируемых фазокорректирующих
цепей с помощью линий задержки, охваченной
обратной связью
Анализ фазовой системы в комплексной плоскости
Гармонический корректор с обратной связью может быть ис
пользован для синтеза· регулируемых фазокорре,ктирующих цепей
с неизменной частотнонезависимой амплитудной характеристикой
[ 4] . Проанализируем эту возможность.
Рис. 4.13. Ои11пезатор фазовых ха 1ра•ктер:исти•к на
остове .ли,нии задержки с ое\рат,ной овязью
В терминах z -преобразования ,коэффициент передачи схемы,
изображенной Нс\ рис. 4.13, записывается в виде рациональной
функции от z
К(z)=
Вп+Вп_1z+Вп--2z2 + ••• +В1 z"-
1+ i"
1+В1z+В2Z2+ ...+Вп-1zn-l+Впz"
(4.23)
Полином Р 1 (z) отличается от .полинома Р2 (z) обратным по
ряд,ком следования коэффициентов -~,, (k=l, 2, . .. , п), т. е: P 1(z)
является транспонированным полиномом Р2 (z), ,поэтому если μ,,-
корни P 2 (z), а у,,~корни P 1(z), то y1i=l/μ,, (k = l, 2, ... , п).
Для устойчивости схемы необхощимо, чтобы 1 μ1i 1 > 1, следова
тельно, jy1, l <l (k=l, 2, . .. , п). Таким образом, нули и полюсы i
К (z) расположены в плоскости z соответственно внутри и вне
круга единичного радиуса (рис. 4.14а) .
Очевидно, Р1 (z) = z"P2 (z-1), P 2 (z-1) - инверсия P 2 (z). На
единичной окружности имеем
196
-i.
-,..._;;;
г)
Р.и,с. 4. 14 . Рааположение нулей и Jюлю~оs фазо,в,ой си
стемы в ком,плеканой .плоокости z
е-iwплtР1(iw) -
P2(i W)
где P1(iw)=P2(-iw) = P2*(iw), следовательно, IK(iw)\ = 1 дла
всех w,
п
~ B1i sinkwЛt
срп(w)= argK(iw)=-wnЛt-t-2arctg __k=_l ____
_
п
1-f-~B1icoskwЛt
k=l
[ индекс п при cpn ( w) •указывает на порядок системы, т. е. на число
блоков линии задержки] .
Из вышеизложенного вытекает, 1iто система с коэффициентом
пере.дачи (4.23) является фазовой, поэтому в дальнейшем будем
называть ее фазовым гармоническим ,корре!{тором.
На рис. 4.15а, б прИВЕ\дены фазовые характеристики
cp1(w)=-wЛt-t-2arctg BsinwЛt
.1 -f-Вcos(1)Лt
i97
!l(ш), ipail
-JбО
- JOO
-2 40
-18D
- 120
-6D
!l(w), граа
-JБО
О 0,2J o,J 0,7J 1 i,2J 1,5 f,7J r., .;/GJc
а}
-:юа
-2 4D
- {80
-120
-бD
о
-4
-J
-2
од 0,5 0,7J
f,25 f,J t,7J (,J/r., .;c
б)
0,2J 0,5 0,7J t
1,2J f,5 t,75 (,J/CJc
d)
Р.и1с. 4.15. Фазо-,частот,ные характер,ис1'ики (а, б) и
ха,рактер.ист1И1КИ ГВЗ (в) ,системы .п1:1рвс;го поря,дrка:
J-13=0; 2- i:\=0,3; 3-13=0,6; 4-(3=0,8; 5-13 =0,9; 6 - 13=
= - 0,3 ; 7-13= -О,6; 8-f3= - 0,8; 9-i:\= -0,9
гармонической системы первого порядка, а на рис . 4.15в - г руп
повое время распространения
-ri(ffi)=Лt[ P(P+coscoЛt) - l] .
.
1+ р2 +2P_cOS(t) Л f
Фазовые характеристики
и характеристики группового времени запаздывания
't2(ffi)= 2Лt _ _:___~----------- -
I
[ ВТ+2В~+В1(1+ ЗВ2)cos(1)лt+ 2В2cos2(1)лt
]
1+ ВТ+ В~+ 2В1(1+ В2) cos (1)/л t + 2в2cos_2ffiЛ t
гармонической системы второго порядка даны на рис. 4.16 и 4.17
для различных значений '\11 и у2.
'1(1, .;) граи
- 720
-ббО
-бОО
-- 540
-480
-420
- JбО
'-300
-240
- 180
- f?O
-50
о
0,5
1,5
Ри1с. 4. ,116. Фаза.вые ха,ра.<тери·сти,ки системы ,вторщ-о ,порядl!{а:
1-v,=0,6 e-i:rt/4, v,=О,б ei:rt/4; 2-v,=-0,6 е - i:rt/4 , v,= -0,б е i:rt/4 ;
з-v,=v, = 0,6; 4-v,=о,в е-i:rt/4 , v,=о,в ei:rt/4 ; s-v, =-O,B, v, =-О ,в .
От.метим основные свойства (f)п (ffi) и 'tn (ffi) . Обозначим
<vп(ffi) =cpn(ffi) +ffinЛt, тогда:
1, CfJn {ffi+kffic) = -cpn (kffic-ffi) {ffic=л./Лt).
2wc
2. S~п(ffi)dffi= О;
о
2w
-
.(CfJп_(ffi) d (1) = 2 ffic n Л..
о
3. сrп (k ffic) = О; CfJn (k ffic) =пл..
4.
_
't'n (k ffic + ffi) = 't'n (k ffic -ffi).
Установим зависимость cpn(ffi) и 'tn(ffi) от расположения нулей
и полюсов К (z) на комплексной плоокости z.
Для К (,z) (4.23) оправедлива форма записи
199
' l'(wJ
-в
-7
-б
-J
-4-
-J
О at 0,2 0,3 0,4 0,,5 qr; 0,7 0,8 0,8 1w/(,)c
Рис. 4.17. Характерлсти~и ГВЗ системы
вто:ро,го поряд,ка:
кривые 1- 5 даны для тех же значений, что ·и
• кривые 1-5 рис. 4.16; 6-у,=О,бi; v, =-0,бi;
7-у, =с:у,=О
п
п
п (l -y1tГ1 )
п (l -y1tZ-1 )
к(z)= zn k_~
_
-1
______
= zn_k_=
_ I_____
п
п
~пП(z --μ1t)
П(1- Ykz)
k=I
k=I
Образуем функцию
п
П(1-у~z- 1)
л
К(z) = zn k_=_I _
_
• ----
п
~п П (z-μ~)
где
(4.24)
(4.25)
μ~=μ1ie i ТJn; ')'~=')'1ieiТJn,
(4.26)
л
т . е. К (z) отличается от К (z) поворотом нулей и полюсов на угол
rpt.
С учетом (4.24) - (4.26) имеем
п
П(1-Ykeiлt(w+ТJ wc))
Л
•
Лt
•
k1
К(iw)=е-'wп е-'пriп_ =
_________
_
п
П (! -Yke-i Л 1 (w+ТJwc))
k=I
200
отк уда следу ет :
л
IК(iw)1= 1;
л
л
-
(/)п(w)= argК(iw)=-п11n:- wnЛt+(/)п(w+11wc);
л
't'n (w) = 't'n (w+11wc).
Рассмотрим частны е случаи.
л
1. 11 = 0 ,5 (поворот на 90°) : При этом 't'n(w) = 't'n(w+0,5wc) ,
Повернув вещественные нули и полюсы у1, у2, μ1 , μ2 системы вто
рого порядка на 90°, при ходим к с истеме с мнимыми нулями и по
люсам и (см. рис. 4.1 46). Характеристика группового времени р ас-
. простран ен ия
полученной системы отлич ается от хара,ктеристики
исхОiдной системы лишь сдвигом на 0,5wc (кривые 3 и б на рис.
4.17) .
.
•
л
2. 11 = 1 (~поворот на 180°). При этом
't'n( w)='t'n (1w+wc). По
ворот на 180° эквивалентен синтезу системы, нули и полюсы кото
рой являются зеркальным отображ ени ем н у.ле й и полюсов· исход
ной системы (считаем, что ,комплексны е ну ли и пол юсы образуют
сопряж е нные пары) (см . рис. 4.14в) . В рез у.,!I ьтате х аракт еристик а
гру1ппового времени сдвигается на wc, Примером мог ут • служить
кривые т 1 (w) рис. 4.15г .для отрицательных и положительных ,~ .
Наибольший практический интерес представляет случай , .когда
нули и полюсы, лежащие в верхней полуплоскости, поворачивают
ся на угол rin:, а нули и полюсы, лежащие в нижней полуплоско
сти, повара чиваются на угол - rin: (см. рис. 4.14г). Считаем, что
_ нули и полюсы не лежат на вещественной оси. Если на вещест
венной оси расположены нули и пqлюсьi четной степени кратности ,
то половина ну.лей и полюсов ~переходит в верхнюю полуплос
кость, а другая половина - в нижн·юю полу плоскость. Этот слу
чай рассмотрим на конкретном примере системы второго порядка .
Повернув соответствующим образам нули и полюсы этой системы
(см. рис . 4.15г), приходим к системе с характеристиками фазы и
А
_
_
А
группового времени cp(w) =cpl(w+il'.,wc) +ср1 (,w-лщс) ; т(w) =
е
.
:-т,(,w+Лwс) + т,(w-лwс), где л=ri+ - ; 0 = argμ 1 (в радианах) ;
-
п
ср1 (w) и 't'1 (w) - характеристики системы первого порядка, нуль и
плюс которой соответственно равны 1μ11 и l'Y 11- Например, ха •
рактеристика -группового времени запаздывания (,кривая 1 н а .
рис. 4.17) может быть получена как сумма ,кривых первого поряд
ка: 't'2 (w) = 't'1(w + 0,25wc) + 't'1 (щ-О,25wс), где л = 0,25, т1 (w) -
х арактерист_и ка системы первого порядка , полюс которо й раве н
1/ l'Y11 = 1,66 , а нуль равен l'Y1 I=0,6, т. е. т1 (w) является ,кривой на
рис. 4.15 для ~ =-0,6.
.
_
Аналогичным образом поступа ем и ~д ля систе м более высоког о
пор5Lдка . Это позволяет построить .фазовые х арактеристики и ха -
рактеристики группового времени распространения • для · сист_е м
8-181
20.1.
любого порЯJдка сложности и при любом расположении нулей и
полюсов системы, если известны характеристики систем первого
поряд,ка .
Проделанный анализ показывает, что положение всплеска груп
пового времени за,медления определяется величиной аргумента
комплексной пары ,корней, а величина всплеска - моду лем ,коr
ней . Чем ближе модуль корня к единице, тем - больше всплеск
группового времени замедления. _
Расчет фазовой гармонической системы
Фазовая гармоническая система используе1'ся либо для синтеза фазо,вых
хара'Ктеристшк, либо для коррею:щи фаза -частотных и,скажений тракта лередачи
систем связи. Рассм,отрим итерполя.ционный расчет ,га,рмонической ,си,стемы, ком
пенсирующей ,нелинейность _ заданной функции •'f,(ш). 1В этом случае .выполняется
равенство срn(,ш)+Ч'(Ф)=,ш,t ( l (i)l~шc=:rt/iЛt), 11де (рn' (ш) - фазовая характе
ристика корректо,ра; 't - результирующее гру;пповое время за,держlfи корректо
ра и кор,ректи,руемого о.бъекта. Очитаем, что Ч', (О) = '0.
Заменим 'f,(ш) · фу.нк,цией Ч' = Ч' (,ш )-(t)Ч'{шс) /шс, которая удовле11воряет
условию '!f, (,шс) =Ю и ха,раюеризует отклонение Ч'(,ш) от линейной функции.
Для компенсаци·и W((i)) не()бход.имо .вы1Полнить равен1С1'ВО !рn· (ш) =-Ч', (ш), ко
торое для конечного числа узлов интерполяции ,ш; преобразуется в систему урав
нений
iвksin[kwiЛt+ +Ч'(Wi)]= -siп+Ч'(Wi) (i=l,2, . .. , п). (4.27)
k=l
Результирующее гру1П11ювое время задерж·ки корректируемо•го объекта и
кqрректора равно . п-Лt+ Ч', (,шс)/шс.
Пре,щставляет · такж,е интерес .ра,очет фа,зового корректора, который в за
да,нных · точках· Шi од,но:времен,но компенсирует ка,к нелинейность фазовой харак
тери,стик,и Ч'(ш), так и .нерав.но.мерtность. гру,ппового времени ра,опространения
6(~) =d'l'j~)/d,(J) заданного объекта. Гjри этом фазовая характери:стика и ха
РiJ.Ктерист:ик::~ 11рупшовоrо •ВJремени ра 1опростра1нения кор·ре,ктора долж,ны удовлет
ворять · тр'вб'о'ваниям: •
!'1(Wi) ~:
1
.~'V (wi); }
.
_
(i=1,2, .•
'tп(ffii) = ...,..... 0(Wi)
п),
(4. 28)
.где ••
-
dЧJп(w) ·, B(w) = dW(w)
1t"n(ro)== dw
dW
Выра.жения (4.,28) ~позволяют составить систему уравнений :
2n.
[
1-
]
1-
)
1:Bksiп kwiЛt+2 Ч'(w;) = -siп2 Ч'(wi);
k=l
.
.
{~[
.,_][,_]
, l _Bk kЛt+ т е(со;) cos kw;Лt+2'l'(W;) =
k=l
(4.29)
•
1-
1-
=--
0(w;) cos -Ч'(W;) (i = 1,2, ... , п),
2
2
из которой находим искомые коэффициенты Bk- Суммарное труп,повое время
Зс!д~ржки кqр ректиру,емо,го . ~б_ъекта и, кар.ректора, рассчитан,ного согласно
(4.29), ,равно 2гьЛt+ 'f{l(i)c) /шс.
202
Примеj). Откорректируем фаза-частотную характеристику с н.ели-нейно·стью ·
-
л
:rt(!)
Ч'(u>)= -
sin -
.
Для этого ,воопользуемся корректором второго пор1rщка .
•
3
~
.
1
2
Выберем узлы интерполяции (i)1 =з Фе, W2= з(J)с , Составив И решив систему урав-
нений ТИIПа ·(4.27), получим В1 =-0,525; в~ = 0,149.
У.беди.мся, что ,ра·ооч.итанный корректор устойчив. С этой целью вычислим
корни μ 1 и μ2 ха -ра.ктерИ1стического полинома P2(z)= ,1- 0,525z+0,.149z2. Искомые
корни равны: μ1. = l,7'6+11,9i; μ2 = 11,76 - 1,9i, т. е. \μ1\=\μ 2 j>l, следовательно,
корректор устойчи,в.
Мак-симум суммарной хара'ктеристики Ч'(rо) +(1)2 (-w) , пrедставляющ~й собой
абсолютную .по;rрешность корректирования , ,не ~превышает 6 .
Фазокорректирующая система с неравномерным расположением .
ОТВОДОВ
На -рис. 4.1 8 из,о-бражена фа,зовая си.стема ,с .неравномерным ра,оположени ем
отвс;дав вдоль линии задерж~и. ~оэффи.циент пер -едачи системы рюзен
п
1+~
•
k=I
к(jffi) = e-IW't' -----
n
1+ ~ Bk e-iwtk
k=l
где t~ и t'k - время за,держ.ки, соответствующее k-му отводу линии; ,; ~ , !fipe,1
мя задержки в•tей ли.нии. Счет Вн .веде'l'ся от начала линии .к концу, счет q,.,,--;т-.
от конца линии к началу; аналогично t,. _
о'!'считьrвает,ся от · начала линии; а
t',. _
-
от конца линии.
Рис. 4.18. Фазовая ,система с нера,вномерным ~рас
положением ·О'!'В' Одов
Если В"= а,._ и tk = t'1<, то ,система будет фазовой, у -которой
1K(iffi)1=!,
п
~ Bk sinffifk
k=l
arg К (i ffi) = - ffiT +2arctg ___п ___
_
1 + ~ BkCOS(l)ik
k=I
•
8*
203
Выберем некоторое чи,сло Лt', ,на которое деля11ся .все t'h без о<:татка:
t-:;л t' ~ mk,
(4 .30)
,~,де mh - целое полож, ительное число; Лt'
-
наибольший общий делитель .чи
сел t' h- В результате прих,одим к гармонической <:wстеме с ра,вномерным ра,опо
ложением от,водов по длине линии зад,ержки с интервалом Лt' (,см . -рис. 4.13) :
Поэтому анализ гармо,нической <:и-стемы с неравномерным ,ра,аположением 011во
дов при <:оответс11вующем .вьгбо:ре Лt' ,может ,быть про•в-еден на основе анализа
сист-емы <: равномер ·ным ра'оположением отвод.о-в. Если деление (4.30) н.е явля
ет<:я точным, то а,нализ, ,естественно, ,будет приближенным .
Наряду с си-стемами, изображен.ными .на рис. 4.13 и 4.18, возможен та,кже
<:интез регулируемых фазовых ,систем на основе схемы, показанной на рис . 4.16,
которая бу,дет фазО1вой, если aq-i .= ~h (k=1, 2, ... , q); aq=l; cp*(iw)cp(iw)=l.
Нап_ример, в качестве 'блоко1в ,с ,коэффициента.ми переда•чи cp.(iw) можно исполь
зовать фазовые контуры любого порядка. Однако такие ,сис11емы : по универ•саль
.ности (функциональной полноте) устушают <:истемам, ,содержащим линию за
держ,ки, так как .фазовые характеристики контуров нелинейно за1висят от ча
стоты.
4.5. Специальные виды корректоров с обратной
связью
Синтез произвольных комплексных периодических функций
Свойства ·корректоров существенно меняются, если включить
в· · прямые и обратные связи те или иные добавочные четыреХ'по
л-юсники. Рассмотрим некоторые из этих воз,можностей.
• Особенность корректоров, реализованных по схеме рис. 4.2, в
том, что ,модуль и фаза их .коэффициента передачи, являясь пе-
Р.' 1
r IJ;,_1
_
,,,
Р.ис. 4.19. Синтезатор кoмrr.rre·к{,1:iыx периодических
фун~щий
рио,дическими функциями с периодом 2л/Лt, неизбежно обладают
соответственно симметрией первого и второго ро1да относительно
частот Wн, = kл/Лt (k = O, ± 11, ± 12, ... ) . Это свойство обуслов.лено
тем, что в выражениях (4.2) и (4.4) а,<, Bk, a'li и rB'li - веществен
ные числа. По этой причине корректоры рис. 4.2 нельзя исполь
зовать для ,пол у чения произвольных (не обладающих каким-либо
видом симметрии) комплексных периодических функций. Во из
бежание у,казанното недостатка включим в схему ,корректора
рис. 4 . 2а добавочные цепи прямой и обратной связи (рис. 4.19).
где Н - преобразователь J;ильберта. Коэффициент rпередачи полу
ченной системы описывается выражением
п
е-iu1пЛt~(л'+Нл")eiu1kЛt
·"-'
k
k
К(iW)=
----
-k=
_
O - --------
п
(4.31)
!+~(р~+Нр;)е-iu1kЛt •
k=O
•
или в терминах h-преобразования [7]
п·
п
Zn~ (Л~+Нл:)z-k
(л~+нл~)П[z - (v~+нv;)]
k=O
К (z) = -------
п
k=I
п
1+~(р~+Нр;)i
k=O
. ( Р~+нр~) П [z -( μ~+нμ;)1
k=I
где у'li +Н"у11k - нули, а μ'к +,Нμ"k - .полюс_ы К(z).
Система с коэффициентом передачи (4.31) устойчива, если
1μ~+Нμ;1= VIμ~12+1μ:12>1 (k= 1,2, ···, п)•
При по.мощи полученной системы можно моделировать произ •
вольные периО/дические ·комплексные функции частоты w для w >
>0. У этой системы ,модуль и фаза K(iw)--:- соответственно чет
ная и нечетная функции относительно w = O. Рассматриваемая
система - каноническая, так как позволяет получить требуемые
хара,ктеристики при минимальном числе регуляторов и преобра
зователей Гильберта.
Гребенч~тые . фильтры со ,смещенным положением зубьев частотной харак
теристики. Корректор с. простой обрат.ной связью (см. ,рис. 4.2а) широко ис
пользуется для синтеза рекурси-в.ных цифровых фильтров (накопителей) [! 8].
Основной не,достаток этих фильтров в том, .что их полосы ,проrпуока ,ния или за- •
держивания ,равномерно ра•ополагаются на ча,стотах Wn=kn/:Лt (k=O, ± 1,
±2, ... ) , что ограничивает их возможности. Поэтому синтезируем гребенчатые
филь'I'ры, зубья ,частотных ха,рактеристик .которых -смещены для положительных
частот (w>0) · _ ·на
произ•воль,ную величину w0, а для отрицательных частот
(w<О)- на
__: wo.
•
·•
Очевидно, что ,поставленная задача не .м-ожет быть решена • простой заме
ной .в ,выражени,и (4.2) ча-стоты w на w-.w 0 , та .к ,как эта заме•на приводит - к
фильтру, ,не удС1влетворяющему условию физической реализации, п-осколь·ку мо
дуль _и фаза е•го .коэффициента передачи . не обладают соответствующей симмет-
рией· относительно ,нул_евой ча-стоты.
•
•
Для решения поставленной за.дачи заменим в (4.12) ш на- Ш=Шо sign ш:
п
'\" а eiw 0kЛtsignw e- iwkЛt
, l..,1 n-k
k=O
К (i со)= __п
_________
l + ~ ~I , eiw 0kЛtsignw e-iwkЛt
k=I
Учитывая, что -енх=соs х+Н sin х (х - произволь-ное
разований приходим ,к ,выражению (4.31) , ,в котором
число), лосле ,преоб-
л~-k= an-kcosWokЛt, р~ = ~kcosWukЛt;
л~-k=an-ksinWokЛt, р; =
~ksiпWokЛt (k= 1,2,
.. ' п).}
(4. 32)
Та.ким образом, смещение зу,бьев ха,рактеристики фильтра при-в-одит к пере
счету коэффициентов переда•чи по отводам линии задержки ,с применением пре
образователей Гнль-берта. Это позволяет использовать .для ра•счета фильтров со
с.мещен,ными зубьями раз,нообразные методы, разработанные лрименнтельно к
обычны _м ,греб енчатым фильтрам с :несмещенными характеристиками .
Исходя из критерия устойчивости Найк•виста, нетрудно видеть, что пере
счет коэффициентов передачи по отводам , линии соглаоrо (4.32) .не нарушает
условий у,стойчиво,сти ,синтезирова ,нно.г.о ,фильтра .
Нули и ,полюсы фильтра со смещенными зу,бьями -связаны с нулями и полю
сами нсхо:дно,го фильтра соотношениями:
'\'~ =
'\'k cos со0Л t; '\'~ =
'\'k siп со0Л t;
μ~=
~tkcosWоЛt; μ;= μksinWоЛt.
Синтезированный фильтр, естественно, не является единственно возможным.
Используя приведенный в .на-стоящем параграфе .прием, мож•но получить до
статочно большое чис,ло а·налогичных фильтров, исходя из суще.ствующих схем
обычных гребенчатых фильтров с .несмещенными характери,стиками .
КQррекция полосовых каналов. Система , изображенная на рис
4.19, в силу функциональной полноты ее коэффициента передачи
(4.32) на пол у оси w>O (или w<O) пригодна для ,компенсацюr
исю::1жений полосовых каналов, если выбрать Лt=2n/(w 2 -w 1 ), гд е
w 1 и со 2 - нижняя и верхняя граничные частоты канала.
Вводя в (4 .31) обозначен.ия- л.k=Л.'1<+Нл.'' k , pk = p',,+Hp"1<, по
лучим
п
zn ~ ЛkZ-k
к(z) =
__
k_=O_ __
п
1+~ Pk~Zk
k=O
(4.33)
Для импульсной реа,кции полосового канала h-преобразование
т
.
•
имеетвидG1(z) =1:Akzk, где Ak= ak- H;,k, a"= g1(kЛt), ak=
__,
k=- n1
=g1 (kЛt) - дискретные значения импульсной реакции и ее пре
образования Гильберта.
Выражение (4.33) не отличается по форме от аналогичного
206
выражения (4.2), поэтому все способы расчета ,корректоров и ал
горитмы ,.компенсации искажений дискретных сигналов, изложен
ные в § 4 .2 и 4.3 настоящей главы ,применительно ,к низкочастот
ным ,каналам, остаются в силе и для ,полосовых каналов [7]. Пр ,r
этом необходимо принять во внимание, что операции с функцио
нальны м и числа м и P+HQ (Р, Q - действительные числа) не от
личаются от операций с комплексными числами P+iQ.
Корректоры с дифференцированием
в прямой и обратной связи
Для ,коррекции телевизионных (видео) сигналов -используютсн
гармонические корректоры с дифференцированными эхо-сигнала-
б}
Рис. 4.20. Корр.екторы с дифференци1рова,ние'А:
,в цепях !Прямой и ,об,ра11ной связи
ми, не сQдержащие обратной связи [ 19]. В этих корректорах вьr
сокая степень компенсации ,мешающих эхо-сИ'гналов достигается
207
при достаточно ,большом числе блоков запа·з.дывания линии зя
держки, . что усложняет конструкцию корректора и делает его
труднорегулируемым. От указанных недостат,ков свободен коррек
тор, схема которого изображена на рис. 4.20а [10]. В этом кор.
ректоре в це п ях пр ямой и обратной связи осущест вляется диф ф е
ренцирование корректируемо г о с и гнала , что повышает степен1:,,
компен са ции эхо - сигналов и упро щ ает процесс настройк и коррек
тора по пе ре ходной хара,ктеристике кана л а связи.
Коэффициент передач:1 ,корректора описывается . выражение:-.1
п
е-iшплt(схо+iСО)~СХ/,eiшkлt •
к(iсо)= -----~---
i,_= _I_____
п
(4.34)
1+iсо~Bkе-iш"лt
k=I
где сос=2л/Лt - ,граничная частота ,канала. Цепи ak служат д.ля
коррекции опережающих, цепи Bk - запаздывающих эхо-сигналов
(k=l,2,...,п).
Другой вид корректора с дифференциров анием в прямой и
обратно й связи изображен на рис . 4 .206 {11] . Его коэффициен т
пере.дачи описывается выражением (4.34) , если заменить а1, н а
a'k и B'k на Bk, где Bk связаны с a'k и B'k соотношения.ми (4.5)-
(4.7) .
В рассмотренных ·корректорах постоянная составляющая вы
_ ходного сигнала не меняется в процессе рег у лировки цепей пр»
мой и обратной связи, что является положительным свойством с
точки зрения конструкции телевизионного канала.
4.6. Экспериментальные исследования
и использование корректоров с обратной связью
Проверка ра,ботоепособн-ости 'Корректоров проводила,сь с помощью изо'бра
женных на рис. 4.10 и 4.11 устройств .на корректоре с о,братной связью ( см .
рис . 4.2) с 12 бл-сжами за1паздывания (п= , 12) . В корре·кторе использовалась
аналоговая линия -задерж'ки .на фазовых контурах .
Результаты эксперимента иллюстри•руются осцилло·граммами, приведенными
на ,рис. 4.2,1 и 4.22 .
Ои,пналы, ~подлежащие коррекции, изображены на рис. ·4.21а и 4 .22а; на
рис 4..216 и 4.'226 - с1и1г.налы .после однократной, а ,на рис. 4.,21в и 4.22в - пос
л•е дв укратн-ой на,стройки цеттей ан, компенсирующих преддействие сигнала п о
способу II (~с м. § 4.,3) . Я_ркие точки на инте,р,валах Л1 даны для уд()бства оцен
ки результа т о,в 1юррекции. :Выбор основ,ното отсt\.етного зна ,ч-ения и положени я
<> моментов дискретизации производился, как указано в § 2.2 гл. 2. Сигн·алы на
рис. 4.2 1 г и 4 .'22г ,получены после одно.кратной ластрой к и цепей обратной связи
~ k, ка'К опи,сано .в §4.3.
,Рисунки 4"21 и 4 .,22 отличаю-1,ся друrг ' р_т . друга различн1;>1ми И•скажениями
wсходноrо иекорректи·рова ,ино,го сигнала . Как видно из прнведенных осцилло
r,рам м, двук ратная .настройка цепей ан обеспечивает практически ~полную ком
пенсацию пр еддействия (с погрешностью 1- 3% по отношению к максимальн,о
му значению .вы:,юдноrо си~г,нала) . Общая сумма амплит уд мешающих эхо..сиг
налов (п.реддействия и посл•едействия) уменьшается · корректором более че,м в
ЮО раз.
208
-На
основе . ко,рректора, изображенного .на рис. 4.2в, ,в ОЭИС им . А. С. По
ло,ва в 1·951_.196'4 гг. был разра ,ботан !Гармонический корректор АИМ сИJг,налов
[1 ] ,и {12]. С ,помо,щью .этого корректора -впервые .в ССОР ,была достиг.нута ,устой
чивая 1ра·бота линии связи с дву,кратной фаэо·вой М:(Jlдуляцией при рекордной для
, указанных годов с1юрости ,передачи 6000 ,бит/с (в ста·ндарт.ном .канале ТЧ).
о)
г)
Рис. 4.21. ОощилJюгра•ммы, J!ЛЛЮС'I'р!llрующие •КОМ1Пен,саrцию [!ре!ДЩеЙ
С'11ВИЯ
tJ)
г)
Р,ис. 4.22. ПР'имеры, иллюс1.1ри1рующие ,работу .кор ·ректqра с обрат
ной ,ОВЯЗЬЮ
Корректор с обратной связью (см. рис. 4.2в) иопользоважя также в разра
ботке автоматизированного комплекса кор.ректирующих у,стройст;в (АК:У), пред-
209
назначенно,го для ко:ррек,щ:rи и,скажений ,каналов в . системах передачи )!анных .
Ком1J;лекс ком1Пенсирует искажения ча1стотных характеристик прямых и коМ:му
тиру,емых трактов, ,соста,вленных из ,ста 1нда рт.ных каналов тональной частоты ,
удовлетворяющих .рекомендациям МККТТ на телефонные ,каналы .для вторич
ного у~плотнения системами тональ·ноrо телеr,ра,фн•рования. Настройка .комплекса
ведется по опедиальным зощди·рующим (иопытательным) сигналам.
Ооновные .данные А,КУ:
количество переприемных уча,стков по НЧ
точность коррекции в диапазоне 400~3300
1
.Гц
по nвз
по фазовой ха,рактеристике
остаточно.м:у затуханию
автощ1тической на1стройки
IПО
время
время ручной ,настройки .
~
.6
(ка,налы ТЧ
.30 0-3400 Гц)
±ЗОО мкс
± '110°
± 11,5 дБ
30-40 с
5 мин
А!втоматич-еский коМIПлекс обеапечи,вает передаrчу сигналов с различными
видами модуляции .по каналам ТЧ с 6 переприемами при скоростях 4800 и
6200 .бит/с ,со оредней ,вероятностью ,ошибки порядка 2,4 ··1О - 5.
Наряду с вышеи:зложенным кар .ректор с обра'Г'НОЙ с-вязью ,иапользовался и
в высакоско·р·ос11ной аJI11паратур -е переда~чи данных, ра·ботающей ·в стан:да•ртн·ом ка
нале со скор -остью 9.600 битfiс (модуляция - однополоаная, число ,передаваемых
уровней - четыре).
СПИСОК ЛИТЕРАТУРЫ
1. А. с. 171026 (СССР). Устройство для корректирования а,мплитудно-им
пульсных модулированных сиrналов/Беркович Д. А., Кисель В. А.
2. Волгин Л. Н. Элементы теории управляющих машин . М.: Советское ра;що,
1962.
3. Кисель В. А. Дискретный синтез корректирующих цепей: Авrореф. дис. на
1ооиок. учен . ,степени rканд. техн. наук. Одеоса: 1967.
4. Кисель В. А. По·строение фа:зокорректирующих цооей с помощью линии за
держки , - Электросвязь. 1965, No 12, .с. 42-50.
5. Кисель В. А. Об одном алr.оритме настр .ойки гармонических 1юрректоров.
-
В кн.:. Труды учебных институтов евязи. Л.: 1966, вып. 30, с. 109-'116.
6. Кисель В. А. К раочету корректоров с . обратной связью по временным ха-
,рактери,ст.икам канала. - ИВУЗ. Радиоэлектроника. Киев: 1967, No 3,
с. 312-31.5 .
7. Кисель В. А. Алrорит,м настройки гармонических корректоров по импульс
ным реакциям ·· поло'совых канало,в. - В кн.: Мето:ды ,математическо-rо мо
делирования и теория электрических цепей. Киев: Институт кибернетики
АН УОСР, 1967, вып. 3, ·с. 3-38.
8. Кисель В. А. Алгоритм на~строЙlки корректо,ра для сигналов с произвольной
нумерацией дискретных значений. - В кн.: Электросвязь и .передача дан
ных. Киев: НТОrРЭС им. А. С. Лоnова, 1969, с. 2'11---'22 ·1 .
9. А. с. 291372 (СССР). У,стройство для на·стройки гармонических корректоров
с прямыми и обратными овязями по импульсной реакции/Кисель В. А.
10. А. с. 294267 (СССР). У1стройство для коррекции формы телевизионного сиг
нала/Кисель В. А.
11 . А. с. 287141 (СССР). У,стройс-лво для корректирования амплитудiно-импульс-
ных модулированных .сиrнало ·в/Кисель В. А.
\
12. А. с. 191643 (СССР). Опособ на,стройки линейных корректоров в каналах
~проводной овязи/Лев А. Ю . , Беркови.ч Д. А., Кисель В. А.
13. Ту Ю. Т. Цифровые и им,пулЬ<сные системы автоматическото управления .
·М . : Машино·строение, 1964.
14. Цыпкин Я. 3. Теория линейных им:пулнсных систем. М . : Госиздат физико
математической литературы, ·1963.
15. Schreiner К. Е., Funk Н . L., Hopter Е. Automatjc Distortion Correctioп fQr
.
_
Efficient Pulse Traпsmission.-«IВM, Journal of Research . and Development» ,
1965, v. 9, N 1, р. 20-30.
210
16. Di Toro М. J. Communication in Тime-Frequency Spread Media Using Adapti-
ve Equalization. -«Proc. of the IEEE», 1968,- v.
-56, N 10, р. 1653-1679.
17. Курош А. Г. Курс высшей алгебры. М.: Физматгиз, 1955, изд. 4. .
18. Финке,льштейн М . И. Гребенчатые фильтры. М.: Советс1юе радио, 1969 .
19 . Обзорная ,инфо•рмация о зарубежной технике связи . Радиосвязь, радио,в еща
ние, теле,видение, 1968, вып . 4.
Глава 5
СОВМЕСТНАЯ КОРРЕКЦИЯ СОБСТВЕННЫХ
И ВЗАИМНЫХ ИСКАЖЕНИЙ КАНАЛОВ
МНОГОКРАТНЫХ СИСТЕМ СВЯЗИ
-+--
5.1. Коррекция дискретных сигналов
в многократных системах
Общая постановка вопроса
Современные сиrтемы связи содержат в общем случае п ,кана
лов, ,каждый из ,которых характеризуется ,ка,к собственными ли
нейными искажениями, возникающими за счет неравно.мерности
частотных характеристик отдельных каналов, та,к и взаимными
(перекрестными или межканальными) искажениями, возникающи
ми за счет взаимной связи (влияния) ,каналов. Полиномные (в
частности, гармонические) .корректоры, теория ,которых изложенэ
в гл . 2-4, являясь одноканальными, компенсируют лишь собствен
ные искажения каналов и непригодны для одновременной компен
сации взаимных искажений. Поэтому рассмотрим расчет _ многока
нальных ,корректоров, компенсирующих искажения дискретных
(цифровых) сигналов, передаваемых одновременно по п ,каналам
системы. Воспольз у емся для этой цели z-преобразованием, .кото
рое, ,как -бу,дет видно из дальнейшего, алгебраизирует и ~предельно
упрощает весь процесс расчета, сводя его к несложным операциям.
Дискретные многоканальные корректоры без обратной с·в.язи
Ориентированный граф п-·канальной системы изображен на рис.
. 5. 1а [1]. Введем обозначения: g(ii)(z) (i= ,1, 2, .. . , п) - собствен
ные импульсные реакции, характеризующие собственные искаже
ния каналов; gUj)(z) (i=I= j; i, j = 1, 2, ... , п) - взаимные (пере
крестные или меж,канальные) импульсные реакции, характери
зующие искажения за счег взаимной связи каналов;
т
g(ii)(z)- , '°" ak(ii)zk (• • 12
-
рл 1)
,..
t, J=
,
,...,п;z=е
.
k=- n
Здесь g(ii)(z) - реакция, возникающая на выходе i--го .канала, з
211
Вх.1
-
-
-
-
-
-
-
ВЬIХ f'
Хю(l)
q"' (Z)
Вьlх 2'
xm{Z)
fШ(z)
Вх.п
_-;,,;а..----.-:.'---
Вь1х. п'
)(fn\z)
.
qtnl(z)
п-канальная система c§nJU.
п-канальный корректор
а;
г--- -r~ - -,
1
А1z
1
t'
1
1
2--+ ---- А / 2 ----2'
.2
1
1
1
1
•
tn
1
rz • L__ ~'.:..z ____J ;)о п'
б}
Рис . 5.1 , Г1ра,фы многока 1нальшой ,системы н ,много,ка,нальноrо кор
ректора (а); граф идеальн•ой ,мноюканалЬ"ной си•стемы .(6)
g(ij)(z) - реакция, возни.кающая на вых0~де j-го ,канала, если на
вход i -,го канала подано воздействие в виде функции Дирака б (t),;
при этом на вход j-го канала воздействие не подается.
Допустим, что на входы каналов системы связи поступают не
которые дискретные сигналы x<i)(z) (i = 1, 2, ... , п).
Сигналы
y(i)(z) (i= 1, 2, ... , п) на выхQДе ,каналов находятся из системы
линейных соотношений
или в ·компактной форме
[y]=[g]X[x],
(5.1 )
где [х] и [у] - матрицы-столбцы сигналов x<i>(z) и y((i)(z); [g]-
квадратная ,матрица дискретных импульсных реакций g(ij)(z). В
дальнейшем [х] и [у] называются матричными либо векторными
сигналами, а [g] - z-изображением .матричного коэффициента
передачи п - каналь-ной системы .
. 212
Идеальной назовем систему, у ,которой
iii) (z)= {A;/i ·(~=i_= 1.' 2: ... , п); .
(5.2)
О (t=l=J; t, J=l,2, ... ,n),
где Ai и ,t; - нек.оторые величины. В этом случае y<iJ (z) =
= A;z1ix(i)(z.) (i=I, 2, ... , п), · т. е. выходные сигналы совпадают
с входными с точностью до а,мплитуды и адвига во времени. Граф
идеальной системы изобр.ажен на рис. 5.16.
Матрицу с элементами (5.2) обозначим через Е. На выходе
идеальной системы имеем [у] =Е[х]. Если [g] =l=E, то многократ
ная система вносит искажения, поскольку [у] =l=E [ х] .· Задача кор •
рекции заключается в преобразовании векторного. сигнала [у] в
сигнал Е[х]. Для этой цели используем ,многокана,льный коррек
тор, чриентированный граф которого изображен на рис . 5.la ,кас
кадно с .многократной системой связи.
Пример двухканального ди_скретного .коррект_ора, реализован
ного на линиях задержки с регулируемыми отвода.ми, дан на рис.
5.2 [ 1, 6, 7]. Корректоры, у ·которых п> ,2, строятся по ана,логич,
ному принципу.
(11}
о(_2
(11)
ос,
O<U,} .
о
.
(ff}
с,1., .
Вых.t
Рис. 5.2 . Двухка,нальный г-а,рмоничесншй кор ,р-ектОiр ·без обра11ной
<JВЯЗИ
Обозначим через Юii) (z) собственные, а через к<ji) (z) (i=l=j)
взаимные (перекрестные) .коэффициенты передачи каналов кор 0
ректора:
213
J((ji)() ~ (ji)k(. •
I2
)•
Z=~CXkZ J,i= , ,...,n.
k=-n,
Укажем способ расчета, позволяющий опрмелить KUi)(z), т. е.
определить коэффициенты a"<ji> (j, i = 1, 2, ... , п; -n1~k ~m1)
по известным импульсным реакциям g(ij)(z) при условии, что ,кор
ректор преобразует [у] в Е [ х] . ВхQдн'ые и выходные • векторные
сигналы ,корректора связаны соотношением
'[ q] = [КJX[YJ,
(5.3)
где [q] - матрица-столбец сигналов q(i>(z) (i = .1, 2, . . . , п) на вы
ходах каналов корректора; [К] - z-изображение .матричного ко,
эффи:циента ,передачи корректора:
[Kl--; -[~(!:) ~z)_ •. •. •. ~(n,I) _(z~].
(5.4)
к<ln) (z) . . .J<.(nn) (z)
С учетом ('5.1) и (5.3) [q] = [К] Х [q] Х [х].
При неискаженной передаче [q] = Е[х], поэтому z-изображе
ние матричного коэффициента передачи дискретного ,многоканаль
ного корректора ,должно удов.летворять условию Е[х] = [К]>~
Х [,g] Х [х] или Е= [К] Х [g], откуда
.[К]=Е
[gГ1 ,
(5 .5)
где [gJ-1
-
матрица, обратная (g],.
,Систему связи с п каналами .можно ра<::сматривать ка,к неко
торый .линейный оператор с ,матрицей [gJ, который преобразует
векторный сигнал [х] в сигнал [у]. Корректор осуществляет об
ратное преобразование векторного сигнала [у] в сигнал Е[х], по
это,му ~матрица [К], описывающая ,корректор, обратна матрице
[g] с точностью до диагональной матрицы Е.
Согласно (5.4) и ('5.5)
к<ii>(z) = Лп(z) А./j
Л (z)
J
(5.6)
(i=l,2, ... ,n; j=l,2, ... ,n),
где Л (.z) - определитель матрицы
'[g]; Лji (z) - алгебраическое
дополнение елемента g(ij)(z). Та,ким образом, для нахождения ис
комых коэффициентов а1<<iЛ (.z) (i, j = 1, 2, . .. , п, -n1~k ~m1) не
обходимо проделать следующие операции: 1) вычислить и возвес
ти в степень - 1 полином ,Л (z); 2) перемножить л- 1 (z) и Лji (z) Х
XAjzlj_ Коэффициенты этих произведений являются искомыми зна
чениями a,/U>. Естественно, возведение .Л(z) в степень
- 1 следует
выполнить на окружности единичного радиуса I z 1 = 1 в ,комплекс
ной плоскости z, как ето рассмотрено в гл. 2. Такое возведение
может быть выполнено толь.ко в том случае, если Л (z) не содер
жит корней, по модулю равных единице, т. е. расположенных н
плоскости z на окружности единичного радиуса. Поэтому отсут ,
214
ствие в полиноме Л (z) у,казанных ,корней .является необходимым
и достаточным условием корректируемости многократной системы
свя.зи в строгом смысле.
При расчете ,корректора, преобразующего [у] в произвольный
заданный векторный сигнал l[b] с учетом требования отсутствия в
от,корректированной системе взаимных связей между кана.лами не
обходимо в выражении (5.5) за,менить Е на дижональную матри
цу Е 1 с элементами b(iJ (z) jx(i) (z), где ,b(i) (z) - элементы матрицы
[Ь]. Если z-изображение матричного ,коэффициента передачи кас
к31дного соединения ,многократной системы и ,корре,ктора должно
совпадать с заданной матрицей [Ко], z-изображение матричного
коэффициента передачи корректора находится из . выражения
[К] = [,g]-1[Ko].
Изложенный материал показывает, что при использовании
z-преобразования в совокупности с матричным исчислением рас
чет ,многоканального корректора по форме не отличается от рас
чета одноканальных корректоров, рассмотренных в гл. 2.
Корректоры с простой и взаимной обратными связями
Описанные многоканальные ,корректоры относятся к корректо
рам без обратной связи. Возможно также построение ,многока
нальных корректоров с обратн9й связь~. Пример двухканального
гармонического , корректора такого типа и его ориентированного
граф? ,дан на рис. ,5.3. Цепи
~ (i)"-
(k=1,2, ...,т;i,j=1,2)обра
зуют обратную связь корректора, цепи a1,,(ijJ (k = O, 1, 2, ... , т; i,
j = tl, 2) - прямую связь. Собственные и взаимные коэффициенты
передачи ,каналов корректора равны
т
~r4;лz- k
K(ii) (z) = _k_= _o _
___
_
Ро(z)
т
Р; (z)
1+~ ~ii) Zk
(i,j=1,2, ..., т).
k=l
В данном выражении не учитывается ~множитель zm, хара,ктери
зующий запаздьrвание, вносимое корректором . .
Приведем способ расчета многоканального ,корректора с об
ратной связью по известным импульсным реакциям g(ij)(z) (,i, j=
= '1, 2, ... , п). Значения К(iЛ(z)
найдем из выражения (5.6). В
этом выражении Л (z) - полином, содержащий ,ка,к .корни, модуль
которых ,меньше миницы, так и корни, ,модуль ,которых больше
единицы. Фа,кторизуем Л (z) относительно единичной окружности:
Л(z)=Л+(z)Л-(z); Л+(z)=_La+1,,z"-; Л-(z)=}:a-1,,z-"-, где
k
k
Л+(z) - полином, корни которого по .модулю больше единицы ~
Л-(z) - полином, ,корни которого по модулю меньше единицы.
Факторизацию выполним так, чтобы а0+= 1. Возведем_ Л-(z) в
степень - 1 и умножи1м полученный результат на Лj; (z). В качест
ве ,коэффициентов a1,,(ijJ берем ,коэффициенты ,полученного лроиз -
215
вых.1
1/0 {z)
- f-F[ (Z)
Вх. 1---.,-:;;._,,,,;~---~~-- Вых. 1
Вх. 2 ----..... .-""" ---- -;~~ .... ;:-- --Вы х. 2
-
t- r; (z}
Рис. 5.3'. ДвуХJка,налыный га~.мони"Iеакий
кюр1ректор с
обрат,ной овяэью (а) и его лраф (6)
ведения, а в ,качестве ,коэффициентов ~(i)k - коэффициенты a+k:
j3 <i)k = a+k (для всех k). Коэффициенты обратной связи для раз
ли;чных ,каналов .корректора одинаковы: Pi (z) = Л+. (z). Рассчитан ,
ный согласно изложенному приему корректор удовлетворяет усло
вию устойчивости, так как все .корни Pi (z) по модулю больше
единицы.
216
На рис. 5.4а у,казана схе.ма двухканального корректора со
взаимной обратной связью, а на рис. 5.46 дан е.го ориентирован
ный граф. Корректоры, изображе!Iные на рис. 5.За и 5 :4а, эквива-
лентны, если
(11)
-
7((11) (z) .
К (z)- Q(z)
,
( 12)
-
7((22) (z)Ю12) (z) . j
К (z)-
Q(z)
,
'
'
к(21) ( ) R(ll) (z) 7((21) (z)
к(22) (z) = 7((22) (z) ,
•
z=
· Q(z)
·
·
Q (z)
(5. 7)
т
где Q(z) = l - R(l2)(z)I021)(z); ю11) (z) = I a(l)kzk; R(12)(z) =
1
k=O
----------
.
-
,!
fl{z)
112!(z)
--- ----- ---
------,
1
:к120rzJ
1
~
L ____________ -1
а)
кr'0rzJ
Bx.t--t-------------.:.....;i-Bыx.1
Ри,с. 5.4. Двух;ка.налыный га~р,мон .ический .к<:)(р ·ректо,р с
.вза·и•мJНой обра'nной связью (а) .и е!10 nраф (б)
217
т
т
т
= I ~<1)kz'<;
ю21) (z) = L~k<2)zk;
j((22)(z) = ~ a(2)hzk .
Здесь
k=O
k=O
k=O
R_( 11)(z), Ю22)(z)-собственные, а R< 12)(,z) и Ю21 ) (z) - взаимные
коэффициенты передачи корректора рис. 5.4а.
Рассчитаем описываемый ,корректор, исходя из условия, что он
предназначен для .компенсации искажений в двухканальной сис
теме связи, хара,ктеризующейся дискретными импульсными реак
ЦИЯ~МИ g(ij)(z) (i, j= ,1, 2). Учитывая (5.6) и (5.7), после неслож•
ных преобразований получим
l((ll) (z) =
!
К(22) (z) =
___
g< 11) (z)
g<22) (z)
-(12)
g< 12) (z)
- (21)
g<21) (z)
К (z)=
-
11)
;К(z)=
-
(22) .
(5.8)
g< (z)
g (zJ
Данн.ые выражения позволяют определить искомые коэффи
циенты а< 1 )1<, а< 2)1<, 13< 1)1< и -13<2)1< по известным импульсным реа1щиям
g<ij)(z) (i, j=·l, 2).
Алгоритмы коррекции векторных дискретных сигналов
Обобщим алгоритмы, изложенные в г.л. 3 .применительно к
коррекции дискретных сигналов в сщнокана.льных системах, на
случай коррекции векторных сигналов и аддитивных помех в ,мно
гократных системах связи. Векторные сигналы на входе и выходе
многоканального ,корректора связаны соотношением (5.3). Степень
близости выходного сигнала [g] и некоторого заданног_о (эталон
ного) сигнала [с] оценим обобщенной нор.мой их разности ii;ill =
=ll[K X{[y]+[N]}-[c]II, или llrill=Lp(i)1<D(,q(i)1<_c(i)1<) , ,где
i,k
D (и) - выпуклая вниз функция, принимающая наименьшее зна
чение !При и = О; p(i)k - дискретный неотрицательный вес; q<i)h и
c<i)h -дискретные значения сигналов q(i)z и c(i)(e), образующих
векторные сигналы [q] и [с]; [,ij] - матрица ~помех на п входах.
Под оптимальной будем подразумевать ·коррекцию, в резуль-
тате которой достигается минимально возможное значение 11,;j"!f .
__
_ ,[q]
[К]
Допустим, что коррекция осуще-
ствляется многоканальным кор
ректором без · обратной связи, z-
изображение коэффициента пере
дачи которого описывается выра-
Рис. 5.5 . Общая ,структу~р,ная ,схема жением (5.4). Поскольку D (и) -
на.стройки 11юррек'I'о1ра
выпуклая вниз функция перемен -
ной U, а qh(i) В СИЛУ (5.3) И (5.4)
линейно за.висят от aUi)h, то IIYJII - выпу,клая вниз функция пере
менных aUi)h (j, i=1, 2, ... , п; -n 1 ~k~'m1). Поэтому минимиза-
ция llri 11 выполняется на основе структурной схемы рис. 5. 5 теми
218
же алгоритмами, при помощи которых :достигался .минимум сум
марной обобщенной погрешности на выходе одно.канального дис
кретного ,корректора (см. гл. 3). В етой схеме на выходе ~оррек-
тора включается устройство, регистрирующее величину ll 'l'J 11. Ре
гулируя [К] тем или иным алгоритмом, добиваемся получения
11:;j°llмин , что приводит к оптимальной коррекции векторного сигнала
{q] .
Согласно изложенному ,коррекция векторных сигналов фор
мально не отличается от коррекции «окалярных» сигналов, ,ка•<
это описано в гл. 3. Основное принципиальное отличие в том, что
во всех рассуждениях вместо скалярных величин (сигналов, ко
эффициентов передачи и т. д.) необходимо использовать соответ
ствующие векторы и ,матрицы.
Выше _ речь шла о ,корректорах без обратной связи. Остановим
ся теперь на алгорит,мах настройки мно г оканальных дискретных
корректоров с обратной связью. Основное внимание удели.м щвух
канальному ,корре~ктору со взаимной обратной связью как наибо
лее ,простому.
Представим двухканальный ,корректор состоящим из четырех
Г.::--------1Вых.1
r
if,,IZ)=I
l(орректир!Jемая
101"
1
система I
oim 1
art1 1
'
- ,к(/"щ
&1
~
1
1
-
1
J(орректир!/емая а)
система 1
lкrгz}z;
1
с/2!/
ml
/Выхz
L::: _
-
-
-
-
__
_
J
------- -,
_..,....___..,..._
1
1R(/21(z)
(1)1
1
1
_J
Рис. 5.6. Стру~ктурные схе,мы на,стройки прямых свя
зей (а) и обратных евязей (6) двухка,нального ,кор
ректора
219
-корректоров с коэффициентами передачи R(ij)(z) (i, j= ,1, 2). П~,и ~.
нимая во внимание (5.8), настройку каждого из корректоров
-Юij)(z) целесообразно производщъ . с,rrедующим •образом. Размы
каем обратную связь корректора . и , подаем воздействие б (t), на
пример, на вход .канала 1 коррек-тируемой системы связи (рис .
5 . 6а) . На вход ,канала 2 воздействие не подается. На выходе ка
нала 1 получим сигнал g 2<11 >(z) . О<;:уществляем настройку отв01до~:t
a< 1)k, добиваясь получения на выходе ,корректора R< 11 ) (z) сигна.ла
g2 (z) = 1. Подав на вход канала 2 воздействие б (t), получим на
выходе этого канала сигнал g< 22 >(z) (на вход канала 1 воздейст
вие не подается) . Осуществляем настройку a< 22 )k, добиваясь полу
чения на выхОlде корректора К (< 22 ) (z) сигнала g2 (z) = 1. Настрой -
ку производим на ·основе алгоритмов, описанных в г.л. 3. Для
удобства изображения цепи ~(l)k и ,~< 2)k на рис. 5.6а не показаны.
•
Для настройки Ю 12> (,z) замыкаем Оiдну обратную связь, ,как
указано на рис. 5.66, и подаем на вход ,кана.ла 1 воздействие о (t)
(на вход ,канала 2 воздействие не подается). Цепи a< 1>k, a< 2)k и ,~< 2>h
на рис . 5.66 не изображены.
Сигнал в точке А рис. 5.6 равен g 3 (z) =g<12)(,z) +R< 12)(z)g<11 )(z).
Настраиnае.м цепи ~(l)k, добиваяс·ь полной .компенсации си.гна.ла
g·з (z) (gз (.z) = 0), что дает к< 12) (z) =-g<12) (z)/I012)(.z).
Настройка R< 21 >(z) .производится аналогично.
Таким образом, подбор требуемых значений a(i)k и ~(i)k (i= 1, 2)
осуществляется достаточно просто, что и является основным
преимуществом корректора со взаимной обратной связью .
5.2 . Коррекция комплексного матричного
коэффициента передачи многократной системы связи
Исходные соотношения
Обоснуем возможность минимизации частотных искажений (мо
дуля и фазы) собственных: и взаимных (перекрестных) комплекс
ных коэффициентов передачи многократной системы [2, 3, 4, 5].
Под матричным ком~плексным коэффициентом передачи многократной си
стемы будем подразумевать ;к;вадратную ,матрицу следующего ·вида :
•
[G11(iffi) • • .G
. 1n.(1.· ffi.)],
[G] =
.
...
.
.
.
-
Gni (1 ffi)
.Gnn(i W)
где GJh(iw) при j=k являюrея собственными коэ.ффициентами передачи, при ·
j=l=k - взаимными коэффициентами передачи каналов системы (j, k= 1, 2; .. .
. .. , п) . Коэффициенты G;1<(iw) - некоторые ограниченные по модулю функции, от
личные от ,нуля тольк•о в ,полосе частот 0-wc; Wc - гра ,ничная частс>Та кана
лов.
На вход j-,го .канала посту,пает сигнал x;(t) .со спект.ральной плотностью
Х; (iw), ограниченной частотой Wc. Совокупность Х; (iw) (j= !, 2, ... , п) образуе т
• • задающий ,вектор (входной векторный сигнал)
220
На выходе j-1ro ка~нала ,возникает отклик y;(t) со опектральной плотность ю
Y;(i(J)) . Совокушность Y;(i(J)) (j='l , 2, ... , п) образует .выходной вектор
[У]= -[Yl ~i ffi)] ( / (t) 1<ffic) -
Yп (i ffi)
•
Векторы [У] ,и [Х] связаны соотношением ,[Y]=1[G]X[X]. Многократная система
не вно'сит искажений, если
Gn(iffi)=Bje- i(i)'tj(j=l,2, . •
..,п);
Gjk(iffi)=O (j=l=k; }, k=1,2, .. . ,
} ( / (() 1<ffic),
п)
(5. 9)
где В; - модуль коэффициента передачи; -т:;
-
.время задержки j-го канала .
В ,неискажающей · системе между каналами нет взаимной связи и .каждый ка,нал
представляет собой идеальный фильтр с граничной частотой (J)c, следо1вательно ,
саrналы y;[t) отличают-си от x;(t) тол~,iю а.м,плитудой и сдвигом ,во времени :
y;(f)=B;x;(t--т:;) (j=1, 2, . .., п).
Пос~юльку .реальные п-~ратные си1стемы не удовлетворяют условию ' неиска
женной передачи ('5 ..9), их характеристики ,необходимо корректировать, щля чего
иапольэуем м·ногока,нал1,1ный корректор с ма11рич:ным кам1пле1юным коэффицие,н-
том nередач;и
-
[Кн (i ffi) • • -К1п (i ffi)]
[К]= ....
.
.
.
.
'
_
Kn1(iffi)
-Kпп(iffi)
где KJk(iФ) - сабственные (j = k) и взаимные (j=l =k) коэффициенты передачи
ка.налов корректора (j, k=1, 2, ... , п) ,
,В случае регулируемых пол11номных корректоров собственные и взаимные
коэффициенты передачи являются ,обаб1денными лолиномами K;k (i(J)) =
т
= L a1<щ<p1(i(J)) (j, k= 1l, 2, .. ., п), где ai<i">- регулируемые к-оэффициенты, по-
1=1
зволяющие получить нужную форму K;я(i(J)); <p1(i(J)) (l=I, 2, ..., т) - система
бщнrсных функций . Пример регулируемого двукратного корректора дан на
рис. 5.7. Многокра11ные полиномные кор,ректоры (п>2) строят-си аналогичным
образом.
При подаче на входы корректора сигналов y;(t) (j= 1, 2, ... , п) на выхо.дах
возникают сигналы q;(t) (j= 1, 2, ... , п) со ,спектральными плотностями Q; (i(J)) ,
которые образуют вектор
[
Ql (i ffi)]
[Q) =
:
.
•
Qп(iffi) •
Очевидно, [Q]=[К]Х[У]. Обозначим ч•ерез [Р] матричный коэффициент передачи
каскадного включения многократной сист-е.мы и м,ногократного корректора
[Р11 (i ffi) •• •Р1п (i ffi)]
[К)Х[G]=[Р] =
.
.
.
.
.
.
.
.
.
.
,
.
Pn1(iffi)
,PnnOffi)
221
с<.(22)
2
Р.и-с. 5.7. Полином,ный д'В.у_х,ка,налыный
ко,р·ректqр
где
п
Pjk(iffi) = LKjv(iffi)Gvk(iffi).
'11;=1
Между [Q] .и [Х] существует
линейная связь: [Q] = (Р]Х[Х].
При неwскажеН!ной передаче
Q(iw) = вjxj e-i(J)tj .
(j=
=1, 2,
.. ., п),
где ВJ-множи
тель, характеризующий :осла~бле
ние сигнала XJ(iw); tJ-запаз
дьrва1ние этого •си·гнала. Из данно
·го ,выражения 'ВЫте·кает, что
{ В. e-i(J)tj
Pjk (i ffi) =
1О
(j =k= 1,2, ... , п),
(j=k;j,k=1,2, ..., п).
Для ,прастоты считаем, что
BJ-= 1, lJ=0 для всех ,[Х]. В этом
случае система являеТ'Ся ·неиска
жающей, если для лю'баго [Х] вы
полшяе'I'Ся ра1венство [Q] = (Х] .
Учитывая, что [Q] = (К]Х[1G]Х[Х],
1привед,енное услооие -мож1н-о запи
сать в :виде [Р]={К]X(G]=Е,
где Е - е~дин1~,Ч1ная матрица п-го
порядка, апИ!сываю щая .матриrч•ный
коэффициент пер1щач11 идеалЬ"ной
п-кратн-ой системы. Е~сли [G]-
неособенная ма'Гр,ица, то
(5, 10)
где [GJ- 1
-
матрица, обратная {G]. Требование
являет,ся .нео·бх-одимым и достаточным условием
системы в ,строгом смысле . Из (5.10) получим
неособенности матрицы [G]
корректируемости п-кратной
K(ik)(iffi)= -Лkj(iffi) /Л(iw) (j, k=l,2, .. . , п),
rде Л(iw~ - определитель матрицы ;[G]; ЛлJ(iw) - алгебраическое дополнение
элемента GUЧ(iw). Разложим правую · часть этого ,выраже,ния в обобщенный
ряд Фурье .в корректи.руемом диапазоне частот Iw1,;;;; Ыс в пр,едположении, что
qJ1(iw) - орто,гональные .на [-, (t)c, Ыс] фу,нюции
Бели этот ,ряд сходится, то, ограничив его некоторым членом т, приходим к об
общен•ному полиному, коэффициенты которого равны искомым знач·ениям
а1Uл>.
222
. Выпуклость и алrоритмы минимизации обобщенной нормы
матрицы поrрешиостей иа выходе миоrоканальиоrо корректора
• Условия неискаженной передачи в общем случае (т - .конеч
ное) выполняются лишь приближенно . Оценку степени приближе.
ния произведем по величине погрешности
п
111111= ~ 11jk,
(5.11)
j, h=l
где
( roc
~,.-1 J. L' (ro) 1Р1, (i ro)-1 l'dro U-k- 1, 2, ••• , п);
1 ГL2(w)JPj1i(iw)J2dw (j=i=k; j, k= 1, 2, ... , п).
t -roc
В этих выражениях 11jk (j=k) - суммарные ~квадратичные
уклонения собственных коэффициентов передачи Pj1i (j=k) от
единицы; 1']jk (j=i=k) - суммарные ,квадратичные уклонения взаим
ных ,коэффициентов передачи Pjh (j=i=k) от ну,ля; L2(w) - .задан
ная весовая- функция. Нетрудно видеть, что 1111 11 - ,квадрат нормы
матрицы ([P]-E)[L]:
11 ri 11 = ll([P]-E) [L]ll2 = 11 ([К] [G]-E) [L]/12,
где [L] - весовая матрица, представляющая собой щиагональную
матрицу п-го порядка, все элементы которой равны L(w) .
Выполним коррекцию так, чтобы величина llчll приня.ла мини •
мально возможное значение, что приведет ,к оптимальной · (в смыс
ле ,квадратичного критерия) ,компенсации и собственных, и взаим
ных коэффициентов · .передачи многократной системы . Проанали
зируем потрешность llч l l . С этой целью представим 1']jk в развер
нутом виде:
roc
п
т
2
f L2 (w) ~ Gvk(iw)~ aji")cp1 (iw) dw (j=i=k; j,k=I, 2, ... , п) ,
V=l
1=1
_ГL2(ш)lt!Gvk(iш) ia\iv)(j)z (iш)-112d(!) (j = k = 1, 2, ... , п) .
с
Правые части этих выражений являются уравнениями тп
мерных положительных парабол в rпространстве переменных а/М
(l=1,2, ..., т;j,v=1,2, ..., п),
т. е. 11j1<-выпуклые вниз
функции. Сумма выпу,клых функций также выпуклая функция, по
этому llчll - выпуклая вниз функция пере менных а/М (l= 1, 2, .. .
. . . , т; j, v= 1, 2, ... , п), имеющая единственный глобальный ,ми
нимум. Распространим полученный рез ультат на случай обобщен-
2,23
ной нормы ,матрицы погрешностей на выходе .многоканального
корректора, под .которой будем подразумевать выражение
JlμII = i,t=
1
W1i.JLгн (ffi) D [ t1
Gvk (i ffi) t1
a;i v) qJz (i ffi)-R1н (i ffi)] d ffi,
(5.12)
лде Lл,(ffi) и Wj1,,-неотрицательные весовые фующии _ и коэффи
циенты; Rjh (iffi) - заданные ,комплексные .функции, к ,которым не
обходимо приблизить собственные и взаимные ,коэффициенты пе
редачи каскадного соединения ,многократной системы и многока
нального ,корректора; Q - частотное множество, на .котором осу•
ществляется коррекция; D(u) - выпуклая вниз функция перемен
ной и. По существу, llμII - взвешенная нор.ма (!Погрешность) укло•
нения ,матрицы [Р] от заданной матрицы [,R], составленной из
элементов Rл,(iffi) . Если D(u) принимает наи,меньшее значение при
и = О, то минимизация выражения -(5.12) приведет к оптима.льно~"1
(в смысле обобщенной нор.мы) ,коррекции собственных и взаим
ных искажений многократной системы, в результате ,которой мат
ричный ,коэффициент передачи [Р] каскадного соединения сис
темы и корректора наилучшим образом (в смысле обобщенной
нормы) приближается к заданному (эталонному) матричному ко
эффициенту передачи [R].
Воспользовавшись результатами гл. 3, непосредственно полу
чим, что 11μII - выпуклая вниз функция в .многомерном пространст
вепеременных,щ<jv) (l= 1,2, ..., 1m; j,v = 1,2, ..., п). Для мини
мизации 11 μ 11 .можно воспользоваться разнообразными алгоритм·а
ми :поиска минимума функций многих переменных, о .которых речh
Xz(t}
2мс
Xz(t)
мк
Рис. 5.8 . Стру,кту~р,ные схемы ,на,стройк.и
.многока1нальнаго 1юр,рек.тора Jю ·общей по
греr111но1сти
шла в гл. 3. Эти методы
позволяют синтезировать
ряд корректоров, компен
сирующих оптимальным
образом (в смысле мини
мума ll μII, llri 11) искаже
ния многократных сис
тем . Рассмотрим некото
_
рые из таких корректо-
ров,
минимизирующих
норму llrill.
•
На рис. 5.8 изображена
структурная схема, в которой
МС - многократная система
связи; МК - многоканальный
корректор; Кд - квадратич
ные детекторы; И - усредняю
щий индикатор. Подадим пе-
'риодически на входы системы
сигналы x;(.t) (j=l, 2, ... , п) одинаковой формы, отличающиеся друг от друга
·только сдвигом во времени: x;(i)=x1 [t- (j- l)T] (j=l, 2, ..., п), где Т больше
времени переходных процессов в каналах системы . Длительность сигналов x;(t)
не должна превышать Т, а период повторения равен пТ. Форма сигналов выби-
224
рается таким образом ; чтобы модуль их спектральной плотности совп адал .:
L(w) (\w\ ~ !Wc),
п
На выхоiдаХ корректора име~м qJ(t)= I q; h(t), гsде q;h(t) - О'J\КЛИК j-го
k=l
!Канала на воздействие Xn(t), поданное 1на вход k-го rканала. Пр.и k=j q Jн(t)
характеризует собстве,1ные искажения j-то канала, при j=;l=k - и,скаж-ения за
счет .влияния k -го J!:анала ,на j-й канал. Сигналы q;n(t) (k= 1, 2, ... , п) .ра3нес•е
ны во времени относительно друг д р уга на Т подобно сигналам х" (t) (k= 1,
2, ... , п). Ках оговорено выше, величина Т выбирае'I'ся так, чтобы м,ежду си,гна-
лами q}l,(t) ,не было интерференции . ·
•
(В случае полной ,ком,пенсации собственных и взаимных искажений qJn(t) =
= x;(t) (k=j); q;п(t)= ,O (k=;l=j; j, k=I , 2, .. ., п).
Усредняющ ий индикатор И указывает вел ичин у 11'=
11jk =
s [qjj(t)- Xj(t)]2dt(k=j);
пТ
s Iqл"(t)i2dt
(k 4= j).
пТ
11
I 11\п, где
j,k =l
(5.13)
~При за1Пи1~и sданнаго выраж,ения учтено, что сигнал XJ(t) ра·вен нулю .пр и
наличии сигналов qJn(t) (k=;I= j), ,кроме того, учтен·о, что межiду си:гналами
qJп(t) (k=I , 2, ... , п) нет взаим1ной интерференции.
Опектральные плотности сигналов q;п(t) равны Li'(w)PJя(iw), где L 1.(w) -
спектр сиnнала xi(t). Воапольза:вавшись равенством Пар,севаля, нетрудно ви -
1
•
1
деть, что 11';п = 2л 11ih (j, k= 1l, с\!, ... , п), поэтому 11'= 2л 1111!! .
Таким образом, 11' -
выпуклая функция лер,еменнь1х .a1<ik) (l= I, 2, ... , т;
k, j = 1I, 2, ... , п). Для опти.малыной ,коррекции неdбходимо
минимизировать 11' ,
что целесообразно выiПолнить методом •с-ечений как наи6оле•е простым в смщле
технической реализа~ии . В силу выпукл,ости, а также ,в силу отсутствия :в функ
ции 11' неразрешимых ов·рагов, метощ сечений яв-ляется сходwщимся, т. е. мини
мизируя показания нндикатора И последовательной р,егулировкой коэффициен
тов a1<ikJ, мы ненз1бежно лри•ближаемся к .минималын.о .воз·можному значению т]',
что свидетельствует .о·б опти.мальной ком1пенсации соб'ственных и взаим.ных нс •
кажений п-кратной системы свsmи.
Наряду с вышеизложенным ,метмом .возможен также мета!.(
сов местной настройки коэффициентов azUk), сущность которого за-
п
ключается в еле.дующем. Представим ri в виде ri= ~ rJj, где rJj=
п
-
~ 'Y]jk,
k=I
i=l
При фиксированных j погрешности 'Y]jk ~ выпуклые функции
однихитехжепеременныхazU'v) (,l= 1,2, ... , т; v=1,2, ... , п)
(k - любое), следовательно, rJj - выпу1клая функция только пе
ременных a1<jv) (l= 1, 2, ... , т; v = 1, 2, ... , п). Для различных
j функции 'YJj взаимно независимы. Поэтому минимизация 'YJ сво
дится к раздельной мини.мизации функций 'Y]j (j= rl, 2, ... , п) ,
М,етод совместной ,на,стройки иопользова,н в j'\Стройстве для ,корр,еrкции ис
кажений двукратных систем с<вя,зи [4] (ри,с. 5.9). У1стройс'I'во содержит генера
тор си11нало13 ГС, выра,батывающий -на вых•адах J и 2 последовательности б-,им
пуль;сов со сдвигом на половину периоща сл•вдования, двукратную систему ,с·вя
зи ДС, д1ву:~rканальный корректор ДК, электронные ключи ЭК и индикаторы ,
указывающи,е. !jеличи,ны :
225
226
Р.ис . 5.1О. Автаматичесжий сrюр1рек1'ор Lд1ву1Юратных си
стем связи
где Лt =n /uJ c (uJ c - граничная ча ,стота каналов си,ст,емы) ; А
-
.некоторая по
стоянная . Ф ильтр Ф, генератор Г и делитель ча1стоты следования импульсов
ДЧ И <:i!уж ат для полу,чения .в,апомогательных импульсных последовательностей .
В результате .м инимизации ТJ1" и ТJ2", достигаемой регулировкой ДК, q11(t) и
q22 (t) п о фор м е ,прюближаются к иNoпулысным •реа.1щиям wдеального низкочастот
,1оrо ф ильтра Asiп ,uJc,(t)/uJct, а q12(t) и q21(t) - к ,нулю.
На ,р !!'С. ,5 .11О ~приведена схема автоматюческого \{Орректора дву,кратных си
стем связи (5). Генератор ЛС .вырабатывает испытателыные сигналы xi(t) и
x 2 (t) , а генераторы Г1 и Г2, у~правляемые блоком восстановления ,временнь1х
соотношений ВВС, - эталонные оигналы, с кот-орыми срав,ниваются сигналы .на
выходах двухканального корректора . К:орректор автоматически минимизирует
величину llrill, определяемую выражением (5 . 11). Регуляторы a1<iv> (l= l, 2 , .. .
. .. , т; j , v= 1, 2) м е няются со скоростями, пропорциональными по величине и про
тивоположными no на1правлению ком:rюн•ентам гра.диента llrill. Компоненты вы
числяются корреляторами С, которые управляют регуляторами az U v >. Настрой
ка ,регуляторов .производит,ся J:JO методу скорейшего спуска .
Автоматические многоканальные корректоры, у которых n>2, строятся п о
аналогии с корректором, ,изображенным - ,на ри1с. 5.1 О .
СПИСОК ЛИТЕРАТУРЫ
1. Кисель В. А. Многоканальные дискретные корректоры .
-
В кн.: Труды
учебных ,институтов связи . Л.: 1967, .вып. 35, •с . 81-90.
2. Кисель В. А. К:ом,пенсация искажений в системах двукратной овязи по ква
дратичному кр .итерию. - В кн . : Вопросы электросвязи. Киев: Технi-ка, 1971,
с. 67- 73.
3. Кисель В. А. Алгоритмизация. настрой.кн ,корректор·ов в системах многократ
•ной связи. - В кн .: Труды учебных институтов связи . Л. : 1970, вып . 51 ,
с. 95-·1 0 3.
4. А. с. 273292 (СССР ) . Устройство для настройки корректоров/Кисель В . А .
5. А. с. 350186 (СССР). Автоматический корректор двукратных систем свя
зи/Кисель В. А.
6. Ольшевский Н. Н . Приведенные частотные характеристики при двукратно й
фазовой •модуляции . - Электросвязь. 1968, No 8, .с. 39-43 .
7. Kettel Е. Ubertraguпgssysteme mit idealer Impulsfuпktion.-«Arch. Electr.
Ubertragung», 1961 , Н. 5, Band 15, S. 207- 214.
ОГЛАВЛЕНИЕ
Предисловие
Стр.
3
5
•Список Jщтературы .
Г л а в а 1. Условия отсутствия интерференционных помех в высокоско
ростных многоуровневых системах с частотно-ограниченными
каналами
6
1.1 . Задачи, решаемые в главе
.
.
.
.
.
.
.
6
1.2 . Передача сигналов по низкочастотным каналам. Оптимальные отсчет-
ные фильтры
8
Низкочастотные отсчетные фильтры
8
Оптимальный отсчетный фильтр для систем с натуральной дискрети-
зацией.......
11
Максимизация отношения сигнал/шум в отсч.етном фильтре
18
Минимизация межсимвольных помех для скоростей передачи выше
скорости Найквиста
22
1.3. Передача дискретных сигналов через полосовые системы
24
Отсчетность огибающей ,реакции полосовой системы
24
Оптимальный выбор несущей частоты
26
Разделение перекрывающихся реакций, спектр которых не содержит
нулевых частот
30
У слови я неискаженной передачи однополосного сигнала
38
Расширение теории передачи Найквиста .
41
Отсчетные фильтры и восстановление сигналов по их дискретным зна-
чениям.
42
Экспериментальное моделирование импульсных реакций отсчетных
фильтров
.
.
45
Использование преобразования Гильберта для скоростной передачи
дискретных сигналов
45
1.4. Минимизация ме?!{символьных помех в системах с интегральными ме-
тодами приема.
.
51
Системы с корреляционным приемом
51
Многоканальные корреляционные системы
56
Согласованная фильтрация
58
Многоканальные фильтровые системы
60
Выбор оптимального опорного сигнала в системах с корреляционным
приемом
63
Примеры синтеза опорных сигналов . . .
66
Выбор опорного сигнала в виде части рабочего сигнала
69
Синтез спектров сигн алов, ортогоналБных с временнь1м сдвигом
70
Список литературы .
.
.
.
.
.
.
.
.
.
.
71
Глава 2., Общая
теория гармонических корректоров
72
2. 1. Основньiе положения
72
2.2 . Дискретизация сигналов с ограниченным спектром
.
74
228
Оптимальное представление сигнала с ограниченным спектром усечен
ньщ р51дом Кqтельникова .
Выбор ос·н9вного отсчетного импульса
Критерий корректируемости канала по импульсной реакции
2.3. Аналитические _ методы расчета гармонических корректоров без обрат
ной связи·
Частотная ·область .
Временная . область
Расчет корректоров по последовательности импульсных реакций при их
вз аимной интерференции. Теоремы отсчетов для периодических частот-
но-ограниченных сигналов
.
2.4 . Особенности коррекции полосовых каналов по импульсным реакциям
Постановка за.дачи. Обобщенная теорема qтсчетов для сигналов с по-
лосным _ спектром . . .
Метод h - преобразования
Теоремы отсчетов для сигналов с полосным ограниченным по протя
женност1;1 дискретным· спектром
Список литературы
Гл а в а 3. Алгоритмы автоматической дискретной коррекции
3.1 . Задачи, решаемые при разработке алгоритмов коррекции
3.2. Итерационные алгоритмы коррекции на основе z-преобразования (кор
рекция дискретных сигналов на бесконечной оси времени) .
Общие сведения
Корре1щия сигналов в случае_ ма_лых_ фаза-частотных искажений
Итерационный алгоритм для произвольных фаза-частотных искажений
3 .3 . Корре1щия сигналов на конечном отрезке времени
Общий итерационный алгоритм
Простая итерация
.•
.
Одношаговый циклический алгоритм
Групповаярелаксация. . . . . . . . . .
3.4 . Оптимизация искажений на основе суммарных критериев
Суммарный квадратичный критерий . . . . . .
Суммарный абсолютный критерий . . .
Условия выпуклости суммарного обобщенного критерия . . . .
Минимаксный критерий близости дискрет~tых сигналов (критерий Че-
бышева)
•
Минимизация модуль:максимума интерференционных помех' в много-
уровневых дискретных системах связи . . .
3.5. Использование алгоритмов дискретной коррекции для минимизации
искажений частотных характеристик ~шналов связи
Каналы низкой частоты
Полосовые каналы .
.
.
.
.
3.6 . Коррекция интерференционных помех в многопозиционных системах с
интегральным приемом
.
.
.
.
Системы с согласованными фильтрами
Адаптивные системы с корреляционным приемом
Список _литературы
Гл а в а 4. Гармонические корректоры с обратной связью
4.1 . Общие положения
.
.
.
.
.
4.2 . Расчет корректоров с обратной ·связью по временнь1м и частотным ха
рактеристикам каналов связи
Временнаяобласть. . . . . . . .
Итерполяционный расчет в частотной области . . . . . . .
Расчет корре-ктора по периодической последовательности частотно-огра
ниченныхсигналов.........•
.
.
.
.
.
.
4.3 . Алгоритмы -компенсации искажений сигналов на основе корректоров с
обрат-ной связью
Стр.
74
77
80
80
80
83
96
102
102
105
107
111
JlЗ
113
115
115
116
121
124
124
127
129
131
131
131
136
143
146
149
155
155
159
168
168
171
174
176
176
179
179
184
186
188
229
Стр.
К:орректоры с простой обратной связью
188
К:орректор с комбинированной обратной связью
193
4.4 . Синтез регулируемых фазокорректирующих цепей с помощью линий за-
держки, охваченной обратной связью
196
Анализ фазовой системы в комплексной плоскости .
196
Расчет фазовой гармонической системы
202
Фазокорректирующая система с неравномерным расположением отводов 203
4.5 . Специальные виды корректоров с обратной связью
.
204
Синтез произвольных комплексных периодических функций .
204
К:орректоры с дифферен цированием в прямой и обратной связи
207
4.6 . Экспериментальные исследования и использование корректоров с об-
ратной связью
208
Список литературы
210
Г л а в а 5. Совместная коррекция собственных и взаимных искажений
каналов многократных систем связи
21l
5.l . К:оррекция дискретных сигналов в многократных системах
.
211
Общая постановка вопроса
.
.
211
Диокретные многоканальные корректоры без обратной связи
211
К:орректоры с простой и взаимной обратными связями .
215
Алгоритмы коррекции векторных дискретных сигналов .
218
5.2 . К:оррекция комплексного матричного коэффициента передачи много-
кратной системы связи
220
Исходные соотношения .
.
.
.
.
.
.
.
220
Выпуклость и алгоритмы минимизации обобщенной нормы матрицы по-
грешностей на выходе многоканального корректора
223
Список литературы
227
ИБ No 666
ВИТ.АЛИй АНДРЕЕВИЧ !(ИСЕЛЬ
Синтез гармонических корректоров
для высокоскоростных систем связи
РедакторВ.1(.Старикова
ХудожникВ.С.Федоров
Художественный редактор Р. А. 1( аз а к о в
Технический редактор Л. 1(. Гр а ч ев а
!(орректорР.М.Шишкова
Сдано в набор 30/VJ 1978 r.
Подп. в печ. 19/IV 1979 r.
Т-03782
Формат 60 Х 90/ 16
Бумага кн.-журн .
Гарни тура литерат.
Печать высокая
14,5 усл. печ. л. 15,59 уч . -изд. л. Тираж 1340 зкз .
Изд. No 17567
Зак. No 181
ЦенаIр.80к.
Издательство «Связь». Москва 101000, Чистопрудный бульвар, д. 2
Ти п ография издательства «Связь» Госкомиздата СССР
Москва 101000, ул. !(нрава, д. 40
ВНИМАНИЮ ЧИТАТЕЛЕЙ!
И зда т ельство !<Связь» в 1979 г . готовит к выпуску следу ющие книги:
Б е л я е в Б. В. Работоспособность химических источников тока.
М.: Связь, 1979 (IVкв.) - 10 л., ил. - 50 к.
Рассматриваются вопросы про е ктирования и экс п луатации химич ес ких
источников тока . Даются методы р асчета . и измер ен ия внутр е ннего сопро
тивления источников тока, закон о мерности разря да при ра злич ны х усло
виях его протекания, а также уравнения, определяющие разрядную емкост ь
и энергию.
Книга рассчитана на инж ен ерно- техн иче ских р аботнико в , з анимающих
ся и зуче ни ем и про ектирова нием химических источни ков тока.
Данилов Ю. В., Мурдасов А. Б., Фуртиков Г. В. При
меиение ЭВМ при проектировании ГТС. - М. : Связь, 1979 (III кв.) -
8,5л.,ил.- 45к.
,
Описывается ряд программ для ЭВМ, которые позволяют автомати зи
ровать этапы про е ктирования ГТС при составлении г е неральных схе м в
._
тех ническом проектировании. Применение предлагаемых методов на этапе
те]!:нического проектирования позволяет вычислить заказные спецификации ,
сметы и кроссировочные таблицы . Приводятся программы для на хожден и я
оптимальных местоположений ста нций и узлов.
Книга предназначена для инженерно -технических работников проект
ных организаций.
-Хал ин Ф . М. Адресно-кодовая .коммутация каналов связи. - М . :
Связь, 1979 (II кв.) - 10 л., ил. - 50 к.
Рассматривается - адресно - кодовый метод коммутации дискретных ка
налов связи как раз н овидность пространственно-временного метода . Опи
сываются принципы построения ад ресно-кодовы х . коммутаторов с поте
рями и без потерь. Проводится расчет краевых ис1{ажений сигналов в си
стеме коммутации. Излагаются способы коррекции сигналов и варианты
их использования в коммутационных системах . Приводятся различные ВЗ ··
рианты построения объединенных систем «уплотнение - коммутация» с
использованием ад р есио-кодового метода, приводится их сравнительный
анализ по объему оборудования и частоте следования импульсов в общем
и групповых трактах системы.
Предназначена для инженерно-т ехнических работников , занимающихсn
вопросами коммутации каналов.
Заказы н а эти книги индивидуальные по купатели оформляют на поч
товых открытках с указанием обратного адреса, учреждения и предприя
тия - гарантийными письмами. Книжные магазины принимаю:г заказы на
эти и зда ния юш т в е рды е, гарантированные за1,азы .
•
.,/