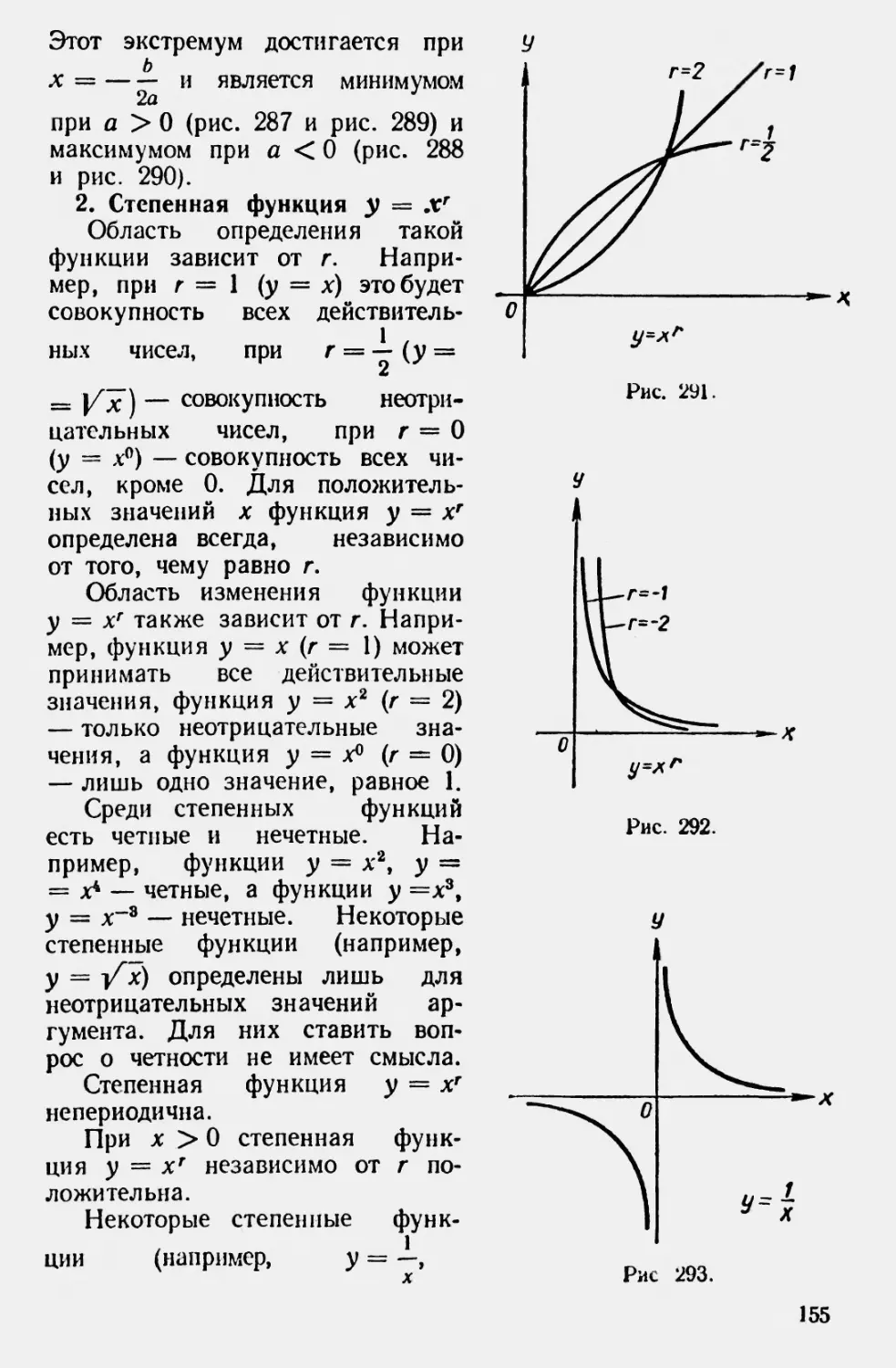
Similar
Text
Е. С. КОЧЕТКОВ
Е. С. КОЧЕТКОВА
Алгебра
и элементарные
функции
Учебное пособие
для учащихся 10 класса
средней школы
Под редакцией доктора
физико-математических наук О. Н. Головина
Утверждено Министерством
просвещения РСФСР
Издание 9-е
МОСКВА
«ПРОСВЕЩЕНИЕ»
1974
512 (075)
К 75
Эта книга, предназначенная для учащихся
10 класса, представляет собой вторую часть
учебника «Алгебра и элементарные функции».
В обеих книгах сохранена единая нумера-
ция глав, параграфов, рисунков и упражнений.
0661-175
* М 103(03)-74
ТРИГОНОМЕТРИЧЕСКИЕ
ТЕОРЕМЫ СЛОЖЕНИЯ
Расстояние между двумя точками плоскости.
Системы координат
§ 149
Каждая точка А плоскости характеризуется своими коорди-
натами (х, у). Они совпадают с координатами вектора ОА, выхо-
дящего из точки О — начала координат (рис. 216).
Пусть А и В — произвольные точки плоскости с координа-
тами (xj, уО и (х2,у2) соответственно (рис. 217). Тогда вектор АВ
имеет, очевидно, координаты (х2 — xit у2 — yt). Известно, что
квадрат длины вектора равен сумме квадратов его координат
(см. ч. I, § 92). Поэтому расстояние d между точками А и В,
или, что то же самое, длина вектора АВ, определяется из ус-
ловия
d* = (х2 — %i)a + (у2 — У1)’.
Отсюда
d = V(x2 — + (y2 — yt)a.
Полученная формула позволяет находить расстояние между
любыми двумя точками плоскости, если только известны коор-
динаты этих точек.
Каждый раз, говоря о координатах той или иной точки плос-
кости, мы имеем в виду вполне определенную систему коорди-
нат хОу. А вообще-то систему координат на плоскости можно
выбирать по-разному. Так, вместо системы координат хОу можно
рассмотреть систему координат х'Оу' (рис. 218), которая получается
в результате поворота старых осей координат вокруг
X X
Рис. 216.
Рис. 217.
3
Очевидно, что в системе
ординаты (cos a, sin а), a
наты (1, 0).
начальной точки О против часовой
стрелки на угол а. Если некоторая
точка плоскости в системе коорди-
нат хОу имела координаты (х, у),
то в новой системе координат х'Оу'
она будет иметь уже другие коор-
динаты (х', у').
В качестве примера рассмотрим
точку М, расположенную на оси
Ох' и отстоящую от точки О на
расстоянии, равном 1 (рис. 218).
координат хОу эта точка имеет ко-
в системе координат х'Оу' коорди-
Координаты любых двух точек плоскости А и В зависят от
того, как в этой плоскости задана система координат. А вот
расстояние между этими точками не зависит от способа задания
системы координат. Это важное обстоятельство будет существенно
использовано нами в следующем параграфе.
Упражнения
1024. Найти расстояния между точками плоскости с коор-
динатами:
1) (3, 5) и (3, 4); 3) (0, 5) и (5, 0); 5) (—3, 4) и (9, —17);
2) (2, 1) и ( —5, 1); 4) (0, 7) и (3, 3); 6) (8, 21) и (1, —3).
1025. Найти периметр треугольника, стороны которого за-
даны уравнениями:
х 4- у — 1=0, 2х — у — 2 = 0 и у = 1.
1026. В системе координат хОу точки М и N имеют коорди-
наты (1, 0) и (0, 1) соответственно. Найти координаты этих точек
в новой системе координат, которая получается в результате
поворота старых осей вокруг начальной точки па угол в 30°
против часовой стрелки.
1027. В системе координат хОу точки М и N имеют коорди-
/ 1 \
наты (2, 0) и I~ I соответственно. Найти координаты этих
точек в новой системе координат, которая получается в резуль-
тате поворота старых осей вокруг начальной точки на угол в 30°
по часовой стрелке.
4
Косинус суммы и рахмости двух углов
$ 150
В этом параграфе будут доказаны следующие две формулы:
cos (а + 0) = cos а cos 0 — sin а sin 0, (1)
cos (а — 0 ) = cos а cos 0 + sin а sin 0. (2)
Косинус суммы (разности) двух углов равен произве-
дению косинусов этих углов минус (плюс) произведение
синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для
простоты изложения предположим сначала, что углы а и 0 удов-
летворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2л:
0 < а < 2л, 0 < 0 < 2л;
2) а > 0.
Пусть положительная часть оси Ох является общей началь-
ной стороной углов а и 0 (рис. 219). Конечные стороны этих
углов обозначим соответственно через ОА и ОВ. Очевидно, что
угол а — 0 можно рассматривать как такой угол, на который
нужно повернуть луч ОВ вокруг точки О против часовой стрелки,
чтобы его направление совпало с направлением луча О А.
На лучах ОА и ОВ отметим точки М и N, отстоящие от
начала координат О на расстоянии 1, так что ОМ = ON = 1.
В системе координат хОу точка М имеет координаты (cos а,
sin а), а точка N — координаты (cos 0, sin 0). Поэтому квадрат
расстояния между ними равен:
d?{ = (cos а — cos 0)а + (sin а — sin 0)a = cos’ а — 2 cos а cos 0 4-
4- cos2 0 + sin2 а — 2 sin о
= 2(1 — cos a cos 0 —
При вычислениях мы воспользовались
sin2 ф 4- cos2 ф
Теперь рассмотрим другую систем;
получается путем поворота осей Ох и
часовой стрелки на угол 0. В этой
системе координат точка М имеет
координаты (cos (а — 0), sin (а — 0)),
а точка N — координаты (1, 0). По-
этому квадрат расстояния между
ними равен:
sin 0 4- sin2 0 =
sin a sin 0).
тождеством
= 1.
r координат ВОС, которая
Оу вокруг точки О против
<%— [cos (а —0) — 1 Ja4- [sin (а — 0) —
— 0 ]’ = cos’ (а— 0) — 2 cos (а — 0)4-
4-14-sin’(a — 0) = 2 [1 —cos (a—-0)J.
Рис. 219.
5
Но расстояние между точками М и N не зависит от того,
относительно какой системы координат мы рассматриваем эти
точки. Поэтому
di = dl
или
2(1 — cos a cos Р — sin а sin Р) = 2 П — cos (а — Р) 1.
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые
мы наложили для простоты изложения на углы а и р.
Требование, чтобы каждый из углов а и Р был неотрицатель-
ным, на самом деле не существенно. Ведь к любому из этих
углов можно прибавить угол, кратный 2л, что никак не отра-
зится на справедливости формулы (2). Точно так же от каждого
из данных углов можно вычесть угол, кратный 2л. Поэтому
можно считать, что 0 < a <Z 2л, 0 < р < 2л.
Не существенным оказывается и условие а > р. Действи-
тельно, если а < р, то Р >а; поэтому, учитывая четность функ-
ции cos х, получаем:
cos (а — Р) = cos (Р — а) = cos Р cos а + sin Р sin а,
что по существу совпадает с формулой (2).
Таким образом, формула
cos (а — Р) = cos а cos Р + sin а sin р
верна для любых углов а и р. В частности, заменяя в ней Р
на —Р и учитывая, что функция cos х является четной, а функ-
ция sin х нечетной, получаем:
cos (а + Р) = cos [а — ( —Р) ] = cos а cos ( —Р) + sin а sin ( —Р) —
= cos а cos Р — sin а sin р,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
1) cos 75° = cos (30°+ 45°) = cos 30° • cos 45°— sin 30° sin 45°=
K*3 KT i KT _ V~6 — KT
- 2 ‘ 2 2 2 ~ 4
2) cos 15° = cos (45° —30°) — cos 45° • cos 30°+sin 45° • sin 30° =
K~2 KT KT 1_ kt+kt
— 2 ' 2 2 ’ 2 — 4
Упражнения
1028. Вычислить, не пользуясь тригонометрическими таб-
лицами:
a) cos 17° • cos 43° — sin 17° • sin 43°;
6
6) sin 3° • sin 42° — cos 3° • cos 42®;
в) cos 29° • cos 74° 4- sin 29° • sin 74°;
r) sin 97° • sin 37° 4* cos 37° • cos 97°;
. 3 л . . 3 л
Д) COS — тг • cos---I- sin — л • sin —
' 8 " 8 8 8’
3 7 7 3
e) sin— л • sin — n — cos — л • cos —л.
5 5 5 5
(Л \
----a .
3
О
cos
Упростить выражения (№ 1029 — 1034):
1029.
1030.
1031.
1032.
1033.
cos (36° 4- a) • cos (24° — a) 4- sin (36° 4- «) • sin (a — 24°).
cos 2a 4- tg а • sin 2a.
cos (a 4~ P) 4~ sin a • sin p
cos (a — P) — sin a • sin В
cos (a — P) — cos a • cos p
cos (a -|- P) -|- sin a • sin p
1035. Вычислить: a) cos (a — P), если
2 . _ 5
cos a =------, sin p =------;
5 13
)° < p < 270°;
если cos a — 0,6;
90°
6) cos^
з / /о
— л < а<2л.
1036. Найти cos (a + Р) и cos (a — р), если известно, что sin a—
7 5
= —, cosp = —— и оба угла (а и Р) оканчиваются в одной и
той же четверти.
Вычислить:
1037.
1038.
1039.
cos
cos
cos
arcsin — 4- arccos —1.
3 3 j
Г . 1 /2
arcsin----arccos I
L з \ з
arctg ± 4- arctg (—2) 1.
Синус суммы и разности двух углов § 151
Полученные в предыдущем параграфе формулы для cos (а ± Р)
мы используем теперь при выводе соответствующих формул для
sin (а ± Р). Для этого придется воспользоваться формулами
приведения (см. ч. I, § 111).
7
Представим sin (а 4- 0) в виде:
sin (а 4- 0) = cos — (а + Р)|
После этого заметим, что
у-(а + Р) =(^-а)-р.
Следовательно,
sin (а + Р) = cos К у — aj — 0 j — cos cos 0 4-
4- sin sin 0 = sin а • cos ₽ 4~ sin 0 • cos а.
Итак,
sin (а 4- 0) = sina • cos04~sin0 -cosa. (1)
Синус суммы двух углов равен произведению синуса
первого угла на косинус второго плюс произведение
синуса второго угла на косинус первого.
Например,
sin 105° = sin (60° 4- 45°) = sin 60° • cos 45° 4-
+ sin45» • cos60" = Ц- Ц
Формула (1) представляет собой тождество, то есть равенство,
справедливое при любых значениях а и 0. В частности, оно
должно быть верным, если 0 заменить на — 0. В результате
такой замены мы получим:
sin (a — 0) = sin a • cos ( —0) 4- sin ( —0) • cos a =
— sin a • cos 0 — sin 0 • cos a.
Итак,
sin (a — 0) = sin a • cos 0 — sin 0 • cos a. (2)
Синус разности двух углов равен произведению сину-
са первого угла на косинус второго минус произведение
синуса второго угла на косинус первого.
Например,
sin 15° — sin (45° — 30°) — sin 45° • cos 30° — sin 30° • cos 45° =
V2 )/3 1 V2 _V& — V2
~ 2 ' 2 2 2 4
Упражнения
1040. Вычислить:
a) sin 19° • cos 26° 4- sin 26° • cos 19°;
6) sin 46° • cos 44° -j- cos 46° • sin 44°;
8
в) sin 61° • cos ЗГ — cos 61° • sin 31е;
г) sin 53° • cos 7° — cos 53° • sin ( —7°);
A) sin ( —15°) • cos 75° + cos 15° • sin 75°.
Упростить выражения (№ 1041 — 1047):
1041. cos (25° + a) • sin (15° —a) 4- sin (25° 4- a) • cos (15° —a).
1042. sin (96° —a) • cos (36° 4- a) — cos(96° — a) • sin (36° 4- a).
1043. sin (a 4- P) • cos (a — 0) — sin (a — 0) • cos (a 4- 0).
1044. ctg a sin 2a — cos 2a.
Ю45 s*n (a + fl) — cos a * sin fl
sin (a — P) + cos a • sin fl
1046 s*n — A) + cos a * s*n *
sin (a + P) — sin a • cos P
1047. sin (a ~ P)
* tga —tg0
1048. Найти sin la —если sin a = —0,8.
у з
1049. Найти sin (a 4-0) и sin (a — 0), если sin a = —cos0 =
V13 n . . n Л . о '
= — причем 0 < a < -h- < 0 < л.
1050. Найти sin (a 4- 0) и sin (a — 0), если известно, что
cos a = —, sin0 — —21, причем углы a и ₽ оканчиваются в
разных четвертях.
Вычислить:
1053.
(1 2 \
arcsin—Ь arccos —).
3 з/
Г 1 /2
1052. sin arcsin —|- arccosl-
I 2 \ 3
sin (arctg 3 — arctg 2).
1054.
sin arcsin
агссоз
2
2
Тангенс суммы и рааности двух углов
§ 152
Формулы для выражения синуса и косинуса суммы (разности)
двух углов через синусы и косинусы этих углов позволяют полу-
чить соответствующие формулы для тангенса и котангенса.
Действительно,
fg /а | 0) s’n + 0) sin а • cos 0 4- sin ft • cos а
cos (а 4- 0) cos а • cos 0 — sin а • sin 0
Предположим, что cos а и cos 0 отличны от нуля (это равно-
сильно тому, что tg а и tg 0 определены). Тогда, разделив
9
числитель и знаменатель последней дроби на cos а • cos Р, по-
лучим:
sin а • cos Р + sin Р • cos а
cos а * cos р — sin а • sin р
sin a • cos P 4- sin P • cos a
cos a • cos p _______ tg a tg p
cos a • cos P — sin a sin P 1— tg a • tg p’
cos a • cos P
Итак, если тангенсы углов a, 0 и a 4~ 0 определены, то
te(«+w~ + (1)
Тангенс суммы двух углов равен сумме тангенсов
этих углов, деленной на единицу минус произведение
тангенсов этих углов.
Пример:
Л
/ „ ч tg -т- + tg а
t { л , \ 4 1 &
tg т +а =---------—
\ 4 / Л
1 — tg у tg а
Заменяя в формуле (1) Р на ( —Р)
у = tg к является нечетной, получаем:
tg (a - и = « » + Ш <—Р>_ =----------,
l-tga-tg(-p) 1-f-tga-tgp’
tg(a —р) = tga~tgP,
l+tga.tgp
Тангенс разности двух углов равен разности танген-
сов этих углов, деленной на единицу плюс произведение
тангенсов этих углов.
Пример 1.
_ _ 1 + tg а
I —tga
учитывая, что функция
(2>
и
tg q — tg fi .
t — tga
1 4- tg а
Л
/ х tg — — tg a
, / Л \ 4
tg-------a =--------------
I 4 1 Л
K ' 1 4-tg— -tga
4
Пример 2. Пусть прямая у = ktx
угол а, а прямая у = k2x — угол р (рис. 220). Тогда угол ф между
этими прямыми будет равен ф = Р —а.
Предположим, что рассматриваемые прямые не перпендику-
лярны друг другу. Тогда тангенс угла ф существует и равен
tg Ф = tg (Р — a)
1 + tg р • tg а
Но tga = kc, tg Р = k2. Следовательно,
tg?= —•
1+М2
образует с осью абсцисс
10
Так, угол между прямыми
У = 7(^1 = 7) и у = Зх (й8 = 3)
определяется из условия
, 3-^
tg<p--------- = 1-
1 + з-7
Рис. 220.
Поэтому ф =
Формулы для котангенса суммы и разности двух углов можно
получить аналогично. Однако на практике эти формулы исполь-
зуются очень редко и поэтому приводить их мы не будем.
Упражнения
1055. Найти tg 105°, представив 105° в виде суммы 60° + 45°.
1056. Вычислить:
tgl3°+tg47° . tgl°- tg 46° .
' i — tg 13° • tg 47° ’ ' 1 + tg 1° • tg 46° ’
6) l-tg27°.tg33° . . 1 + tg 4° - tg 49°
’ tg 27°-J-tg 33° ’ 7 tg49° —tg4° ’
1057. Найти tg (a + p) и tg (a — p), если sin a = 0,6; cos P= — —
13
|— <а<л; л<Р< — л).
\2 2 /
1058. Найти tg (a + P) и tg (a — p), если sin a = — —; cos P =
5 13
причем оба угла (a и P) оканчиваются в одной и той же чет-
верти.
Вычислить (№ 1059—1061):
1059. tg (arctg 2 + arctg 3).
(1 2 \
arcsin—|- arccos —I.
3 3/
1061. tg [arcsin ( —7=^ + arccos ( —1/_У1.
L \ /3^ \ V 3 JJ
Найти угол между данными прямыми (№ 1062, 1063):
1062. у = х и у = -|х + 6.
1063. Зх — 2у = 6 и 2х + Зу — 7 = 0.
1064. Доказать, что прямые у = £tx + bt и у = k2x + b2
перпендикулярны тогда и только тогда, когда kik2 — —1.
11
Тригонометрнчеокне функции двойного угла
§ 153
Положив в формуле
sin (а + Р) — sin а • cos р + sin р • cos а
Р =а, мы получим:
sin 2а = sina • cosa 4- sina • cosa = 2 sina cosa.
Итак,
sin 2a = 2 sin a cos a. (1)
Синус двойного угла равен удвоенному произведению
синуса данного угла на его косинус.
Аналогично, положив в формуле
cos (a + Р) = cos a • cos Р — sin a • sin P
p = a, получим: cos 2a = cos a • cos a— sin a • sin a = cos2a — sin’a.
Итак,
cos 2 a — cos2 a — sin2 a. (2)
Косинус двойного угла равен квадрату косинуса дан-
ного угла минус квадрат синуса того же угла.
Точно так же, положив в формуле
tg(a + P)= ,IS° + 'tPR
1 — tg a • tg р
P = a, получим:
tg2“=-s^- ®
Тангенс двойного угла равен удвоенному тангенсу дан-
ного угла, деленному на единицу минус квадрат танген-
са того же угла.
Примеры. 1) Пусть sina = 0,6, причем угол а оканчи-
вается во 2-й четверти. Тогда cosa = —р41—sin2 a =
= — V1 — 0,36 = — 0,8.
Поэтому
sin 2a = 2 sina • cosa = 2 • 0,6 • ( —0,8) = —0,96;
cos 2a = cos2 a — sin2a = 0,64 — 0,36 = 0,28.
2) Пусть tga = 3. Тогда
tg2e__2j42_
6 1 —tgJa 1—9 В 4
Замечание. He следует думать, что двойной угол обяза-
тельно содержит четное число градусов или радианов: 20°; 60°;
4; 6 и т. д. Под двойным углом можно понимать любой угол.
Например,
12
и т. д., вообще, а = 2 • ~ Поэтому иногда доказанные выше
формулы полезно записывать в виде:
о . а а
sin а = 2 sin— • cos —:
2 2
9 Cl • 9 Ct
cos а = cos2-sin2 —;
2 2
2tgf
tga -----------
1-tg2T
Эти формулы выражают тригонометрические функции угла
через тригонометрические функции половинного угла.
Упражнения
1065. Известно, что sin a = 0,8, причем угол a
во 2-й четверти. Найти синус, косинус, тангенс
угла 2a.
1066.
чивается
Найти tg 2a и cos 2a, если известно, что
не в 1-й четверти и tga=-|-.
оканчивается
и котангенс
угол а окан-
1067. Найти cos а, если sin-^=0,1 и угол а оканчивается
в 4-й четверти.
1068. В какой четверти оканчивается угол а, если
а) sin a > 0, sin 2a > 0; в) sin a < 0, sin 2a > 0;
6) sin a > 0, sin 2a < 0; r) sin a < 0, sin 2a < 0?
1069. Вычислить:
tg22°30*
1 — tg222°30'’
1 — tg2 -
s 6
. л
tg6 6
a) sin22°30'.cos22°30'; в)
6) cos222°30'— sin222°30'; г)
1070. Доказать тождества:
а) (sin a + cos a)2 = 1 4- sin 2a;
6) cos4 a — sin4 a = cos 2a;
в) ctg a — tg a = 2 ctg 2a.
1071. Доказать, что для любого острого угла a
sin 2a < 2 sin a.
1072. В каких пределах может изменяться выражение
sin a • cos a?
Упростить выражения (№ 1073—1078):
1073. sin2 (p — 45°) — cos2 (P — 45°).
13
1074. sinf— — aVcosf—— al
\4 J \4 )
<075. ---?--------!---.
1 — tg a 1 4- tga
/ • a , a\ / . a a\
1076. (sin—(-cos— (sin----cos—.
\ 4 4J\ 4 4)
Доказать равенства (№ 1079, 1080):
1079. sin 10° • cos 20° • cos 40° = -.
8
лол * Л 2л 1 t я
1080. sin — - cos— = — tg—.
5 5 4 & 5
Ю77 tg (45° +
’ 1 - tga (45° +af
1078. sin — cos — cos a.
2 2
1081. Выразить sin a и cos a:
а) через sin — и cos —;
2 2
б) через sin-^;
в) через cos—.
Упростить выражения (№ 1082—1087):
• «on sin3 a-cig a tnOe /я , \ _ In \
1082. --—. 1085. sec —(- al • seel-al.
sin 2a \ 4 / \ 4 /
1083. (tga 4* etga) sin 2a. Ю86. * ~ .
1084. 2cos2a — cos2a. 1087. -1.~:s-in.2.0t-.
cos a — sin a
Вычислить (№ 1088—1091):
1088. tg(2arctg3). 1090. cos ^2 arcsin -1).
1089. tg ^2 arccos 1091. sin [2 arctg (—2)].
1092. Найти формулу общего члена арифметической про-
грессии, для которой Ui = cos 2ф; аг = cos2 <р.
1093. Доказать, что бесконечная геометрическая прогрессия,
у которой at = 4 sin <р, а2 = sin 2<р, является бесконечно убываю-
щей, и найти ее сумму.
Выражение sin а и cos а через тангенс
половинного угла § 154
При решении некоторых задач оказываются полезными сле-
дующие формулы:
14
1-tg27
Докажем их.
sin а = 2 sin J? • cos— =
2 2
„ . а а
2 sin — • cos —
2 2
а „а
sin* 2 — 4" cos2 T
2 2
a a
2 sin ~ • cos —
2 2
2 а
COS2 —
2
o а а
sin2 — 4- cos2 —
2 2
cos2 —
2
Тем самым доказана формула
и формула (2):
о а . 9 а
cos а — cos2------sin2 —
2 2
(1). Аналогично доказывается
а а
cos2 — — sin2—
2 2
sin2 — 4- cos2 —
2 2
cos2 — — sin2 —
2 2
cos2 —
2
. a a
sin2 — 4- cos2 —
2 2
n-tg’f
a
cos2 —
2
в том случае, когда cos & 0,
2
Формулы (1) и (2) верны лишь
или, другими словами, когда выражение tg у определено.
Пример. Найти sin а и cos а, если tg — = 2.
По формулам (1) и (2) получаем:
а
1 — tg2 —
cosa =---------—
1 +tg2 V
г,; = —0.6.
IS
Упражнения
1094. Найти sin а и cos а, если tg—= 5,
2
1095. Найти sin 2а и cos 2а, если
a) tga = —3; б) ctgа = 3.
1096. Дать тригонометрическое доказательство неравенства
1097. Доказать, что sin 2a и tga имеют один и тот же знак
(оба отрицательны, оба положительны или оба равны нулю)
при любом а.
Ct 1
1098. Известно, что tg — = —. Найти:
ь 2 2
а) sin4 a — cos4 a;
6) sin a • cosa • cos 2a.
Соотношения между тригонометрическими
функциями половинного угла и косинусом
целого угла § 155
Складывая и вычитая почленно тождества
1 = cos2 — -f- sin2 — 2 2
И , а . , a cosa = cos2 sin2 —, 2 2
получаем: 1 4- cos a= 2 cos2 —; 2 (1)
1 —cosa = 2 sin2—. 2 (2)
Эти две формулы очень часто используются для преобразо-
вания различных тригонометрических выражений. Кроме того,
они позволяют выразить синус и косинус половинного угла
через косинус целого угла:
cos-= ± д/1+ cosa- (3)
2 у 2
sin- = ± -шЛ-со5». (4)
2 V 2
Из последних двух формул, в свою очередь, вытекает тождество
tg- = ± у/i-cosa. (5)
2 у 1 4- cos a ’
16
Знаки (4- или —) перед радикалами в формулах (3), (4) и (5)
выбираются в зависимости от того, в какой четверти оканчива-
ется угол Если, например, у < л, то в формуле (4) нужно
взять знак плюс, а в формулах (3) и (5) — минус (синусы углов,
оканчивающихся во 2-й четверти, положительны, а косинусы
и тангенсы — отрицательны).
Примеры. 1) Найти синус и косинус угла 22°30'.
По формуле (4) получаем ( “ = 22°30', а
sin22°30' = -1/ 1 ~cos t5°
0,3827.
2
Знак + перед радикалом мы выбрали потому, что синус
угла 22°30' положителен.
Аналогично, исходя из формулы (3), получим:
cos 22°30' = -1/1 + cos 45° = 1^2 4- /2 _ ~ 0.9239.
/ 2 2
2) Найти tg—.
8
По формуле (5) получаем (у — а — jУ
-1/ 2~
V 24-/2
,/(2-/Т) (2-/2~) 2-/2
Г (2 4- / 2) (2 — /2) /4 — 2
= -2~]f2- = /2 — 1 0,4142.
/2
Упражнения
Доказать тождества (№ 1099—1102):
1099. 1 4- 2 cos 2а 4- cos 4а = 4 cos2 а cos 2а.
1100. 1 — 2 cos За 4* cos 6а = —4 sin2 — • cos За.
2
1101. 1 4-sin а = 2cos2(——-Y
\4 2/
1102. 1-sina = 2sin2f- —-1
\4 2/
1103. Упростить выражение 1~ s‘"-ct.
1 4- sin а
1104. Найти sin a, cos а и tg а, если известно, что cos 2а = —0,6.
17
1105. Найти sin у, cos-^и tg-^, если известно, что |cosa| =
= 0,6, причем угол а оканчивается во 2-й четверти.
1106. Найти tga, если sin 2a = —.
6 3
Вычислить:
1107. sin arccos 0,8
\2
1108. cos (— arcsin 0,6
I 2
1109. tg|j arcsin (— 0,8
1110. tg| arctg (— 0,75
Выражение тангенса половинного угла
через синус и косинус целого угла
§ 156
Тангенс половинного угла можно выразить через синус и ко-
синус целого угла с помощью формул:
tg- = —(1)
2 1 + cos а ' '
а = 1^0, а
2 sina
о „ sin а
Действительно, ------------
1 + cos а
а а
2 sin — • COS —
2 2а
= 1g 2*
а
2 cos2 —
2
Тем самым доказана формула (1). Аналогично доказывается и
формула (2).
Формулы (1) и (2) удобнее доказанной в § 155 формулы
tg - = ± 1 /* 1 ~ cos a, (3)
2 Г 1 -|- cos a
поскольку они не содержат радикала и, следовательно, не нужно
решать, какой знак должен стоять перед радикалом. Однако при
расчетах по формуле (3) достаточно знать лишь косинус угла а,
а при расчетах по формулам (1) и (2), помимо косинуса, нужно
знать и синус этого угла.
1
™ („ко sin 30° 2 1
Пример: tg 15 —----------------------------—
1 +cos 30° 1 + УЗ_ 2+Уз
2
2 — /3
= -------------— =2-/3 0,2679.
(2 + /3)(2-/з) Г
Упражнения
1111. Найти tg если известно, что sina = j^ и угол a
оканчивается не в 1-й четверти.
18
1112. Найти tga, если известно, что sin 2a =—0,8 и угол
2a оканчивается не в 4-й четверти.
1113. Доказать, что если синус и косинус угла 2a рацио-
нальны, то тангенс угла а также рационален.
Верно ли обратное утверждение?
Преобразование произведения тригонометрических
функций в сумму § 157
Сложив почленно тождества
sin (a 4- р) = sin a • cos p 4- sin P • cosa
и
sin (a — P) = sin a • cos p — sin P • cos a,
получим:
sin(a 4- P) 4-sin (a — P) = 2 sin a • cos P,
откуда
sin a • cos 0 = ~ (sin (a + 0) + s*n (a “ 0)1* (1)
Произведение синуса одного угла на косинус другого
равно полусумме синуса суммы и синуса разности этих
углов.
Например, sin 15° • cos 75°= ^-[sin (15° 4-75°)4-sin (15°— 75°) 1=
= - (sin 90° 4- sin (—60°)] = - Г1 —
2 2 | 2 I 4
Сложив почленно тождества
cos (a 4- 0) = cos a • cos P — sin a • sin P,
cos (a — P) = cos a • cos P 4- sin a • sin P,
получим:
cos (a 4- P) 4- cos (a — P) = 2 cos a • cos p,
откуда
cos a • cos p = у (cos(a 4- p) 4- cos(a — P)]. (2)
Произведение косинусов двух углов равно полусумме
косинуса суммы и косинуса разности этих углов.
Например, cos — л • cos — = — [cos (— л 4- — 4- cos (—л —
12 12 2 [ \12 12/ \12
л\1 1 Г 2 л] 1 Г 1 , Л1 1
-------- — cos — л 4- cos— = —--------Ь 0 =-----.
12/J 2 [ 3 2 J 2 L 2 J 4
Если из тождества
cos (a — Р) = cos a • cos Р 4“ sin a • sin P
19
вычесть почленно тождество
cos (а + Р) = cos а • cos Р — sin а • sin р,
то в результате получим:
cos (а — Р) — cos (а 4- Р) = 2 sin а • sin р,
откуда
sin а • sin Р = у [cos (а — р) — cos (а + Р)]. (3)
Произведение синусов двух углов равно полуразности
косинуса разности и косинуса суммы этих углов.
Упражнения
Вычислить, не пользуясь таблицами (№ 1114—1119):
1114. 2 sin 37°30' cos 7°30z. 1117. sin 52°30' sin 7°30'.
1115. sin 52°30' cos 7°30z. 1118. cos 75° cos 105°.
1116. cos 37°30' cos 7°30'. 1119. sin 45° sin 15°.
Данные произведения представить в виде сумм (№ 1120—
1127):
1120. sin 3° • sin 5°.
1121. sin 7° • cos 9°.
1122. cos 17° • cos 3°.
1123. sin (x 4- a) • sin (x —a).
1124. sin (x 4- a) • cos (x —a).
1125. cos (x 4-a) • cos (x —a).
1126. 4 sin 20° • cos 50° • cos 80°.
1127. 4 cos 15° • sin 20° • sin 40°.
Доказать тождества:
1128. 2 sin 2a sin a 4- cos 3a = cos a.
1129. sin a— 2 sin — 15°
\2
4- 15°
Преобразование суммы (разности) синусов
двух углов в произведение
§ 158
В предыдущем параграфе мы получили формулу
sin a • cos Р = -i- [sin (a 4* P) 4- sin (a — P) ]. (1)
Эта формула верна для любых значений аир. Пусть а и Р
таковы, что а 4- Р = х, а — р = у. Тогда а и Р найдутся как ре-
шение системы уравнений
a 4- р = х,
a — р = у.
20
Складывая эти уравнения почленно, получаем 2а = х 4- у. Вычи-
тая эти уравнения почленно, получаем 20 = х — у. Поэтому
г 2
В таком случае тождество (1) можно переписать в виде:
sin • cos - = — (sin x + sin у),
2 2 2
откуда
sin х + sin у —2 sin - cos . (2)
2 2
Сумма синусов двух углов равна удвоенному произ-
ведению синуса полусуммы на косинус полуразности
этих углов.
Заменяя в формуле (2) у на —у и учитывая, что sin (—у) =
= —sin у, получаем:
sin х —- sin у = 2 sin cos * + -. (3)
2 2
Разность синусов двух углов равна удвоенному про-
изведению синуса полуразности на косинус полусуммы
этих углов.
Примеры. 1) Сумму sin 75° 4- sin 15° легко вычислить без
таблиц, если использовать формулу (2):
. _с0 . • mo п • 75° 4-15° 75° —15°
sin 75 4- sin 15 = 2 sin ——— • cos----=>
2 2
= 2 sin 45°-cos 30° = 2- YJL -YL=-V6.
2 2 2
5 л
2) Разность sin —n —sin — легко вычислить без таблиц,
' 12 12
если использовать формулу (3):
5 я 5 я
.5 .я о . 12Я —12 12Я+ 12
sin— п — sin — = 2 sin------ • cos----=
12 12 2 2
= 2sin— • cos — = 2 • — • YA. — YA .
6 4 2 2 2
Упражнения
Вычислить (№ 1130 — 1135) без таблиц, используя формулы
для суммы и разности синусов двух углов:
ИЗО. sin 105° 4- sin 75°. 1131. sin 105° — sin 75°.
21
1132. sin — л 4- sin — л. 1134. cos— 4- sin - л.
12 12 12 12
1133. sin —л — sin —л. 1135. cos-—sin —л.
12 12 12 12
Упростить данные выражения (№ 1136, 1137).
1136. sinf— 4- o') 4- sin(-—al
\ 3 ) \з /
1137. sin f— 4-a^—sin(------al
\3 / k3 J
1138. Доказать тождества:
1 4- sin a = 2 cos2 [-— —1
\4 2/
1 — sin a = 2 sin2 (-— — 1
\4 2/
используя формулы для суммы и разности синусов двух углов.
Данные выражения (№ 1139, 1140) представить в виде про-
изведений:
П39. l_|_sina. 1140. /З- —2 sin a.
1141. Доказать, что синусы углов аир равны тогда и только
тогда, когда
a = ( —1)" 0 4- пл,
где п — некоторое целое число.
Преобразование суммы (разности) косинусов
двух углов в произведение § 159
Для суммы и разности косинусов двух углов верны следую-
щие формулы:
+ Л X + у X — у
cos v = 2 cos —cos-—;
л 2 2
Л • х + V • Х — у
COS X — cos V = — 2 sin —— sin-
J 2 2
(1)
(2)
Сумма косинусов двух углов равна удвоенному про-
изведению косинуса полусуммы на косинус полуразно-
сти этих углов.
Разность косинусов двух углов равна минус удвоен-
ному произведению синуса полусуммы на синус полураз-
ности этих углов.
Примеры. 1) cos 75° 4- cos 15° = 2 cos 75 15 • cos75 ~ 15 =
— 2 cos 45° • cos 30° = 2*11 -iZ =
2 2 2
22
5 я 5 я
o. 5 я o . 12Я+ 12 .12Я” 12
2) cos — л — cos — = — 2 sin------ sin-----=
12 12 2 2
= -2sin5-.sin^ = -2lCL.l = -^
4 6 2 2 2
Формулы (1) и (2) могут быть получены многими способами.
Докажем, например, формулу (1).
1-й способ. В § 157 была доказана формула
cos а • cos 0 = у Icos (а 4- 0) 4- cos (а — 0) ].
Полагая в ней а + 0 = х, а — 0 = у, мы и приходим к фор-
муле (1). Этот способ аналогичен тому, с помощью которого
в предыдущем параграфе была получена формула для суммы
синусов двух углов.
2-й способ. В предыдущем параграфе была доказана формула
Рп . а 4- 6 а —в
= 2 sin —— • cos--
2 2
Полагая в ней а = х 4- у, 0 = У 4- р
получаем:
sin (х 4- — 4- sin (у 4- — = 2 sin (^-+2 4- —V cos
\ 2/ V 2/ \ 2 2)
Но по формулам приведения sinlx 4- \ = cosx;
cosx 4- cosy =
= cos у; sin 4- = cos Следовательно,
= 2 cos cos что и требовалось доказать.
Формулу (2) мы предлагаем учащимся доказать самостоя-
тельно. Попробуйте найти не менее двух различных способов
доказательства!
Упражнения
Вычислить (№ 1142—1147) без таблиц, используя формулы
для суммы и разности косинусов двух углов:
1142. cos 105° 4- cos 75°.
1143. cos 105° —cos 75°.
1144. cos — л 4- cos — л.
12 12
11 5
1145. cos — л — cos —л.
12 12
1146. cos 15° — sin 15°.
1147. sin — 4- cos — л.
12 12
Упростить данные выражения (№ 1148, 1149).
1148. cos (— 4- 4- cos (-— a
\3 J \3
1149. cos
23
1150. Каждое из тождеств
sin а 4- cos а = У 2 sin (а 4-
sina — cos а = У 2 sin (а — у)
доказать не менее чем двумя различными способами.
Данные выражения (№ 1151 — 1154) представить в виде про-
изведений:
1151. УТ 4- 2 cos а. 1153. sin х 4- cos у.
1152. УЗ — 2 cos а. 1154. sin х — cos у.
1155. Упростить выражение sin21 a— — ] — cos2|a4- — )•
Разложить на множители данные выражения (№ 1156—1159):
1156. 1 4-sina—cosa.
1157. sina 4- sin (a 4- 0) 4- sin 0.
1158. cosa 4- cos 2a 4- cos 3a.
1159. 1 4- sina 4- cosa.
Доказать данные тождества (№ 1160—1163):
11 во. . sinct + sin3a e tg 2a.
cos a cos 3a
11 fi. sin (a 4-P)-f-sin (a — 0) _ .
cos (a 4-P) 4-cos (a — P)
1162. -sin(a + P)~si?-<.a_-Pl = -ctga.
cos (a 4- P) — cos (a — p)
П63. Sina-2sin2a4-sin3a = tg2a
cos a — 2 cos 2a 4- cos 3a
1164. Доказать, что косинусы углов а и 0 равны тогда
и только тогда, когда
a = ± ₽ + 2пл,
где п — некоторое целое число.
Преобразование суммы (разности) тангенсов
двух углов § 160
При решении некоторых задач бывают полезны следующие
формулы:
tg*-|-tgy-=-sin(*-M); (!)
cos х • cos у
. . sin (х — v) zrn
tg X — tg у =--i---(2)
COS X • cos у
Сумма тангенсов двух углов равна отношению си-
нуса суммы этих углов к произведению косинусов тех
же углов.
Разность тангенсов двух углов равна отношению
синуса разности этих углов к произведению косинусов
тех же углов.
24
Докажем, например, формулу (1). Имеем: tg х 4- tg у —
slnx , sin у sin х • cosy 4- cos x • sin у . .
=------1---- =-------L--- -- ; HO Sin% • COSy-j-COSX- SIH y =
cosx cosy cosx. cosy
= sin (x 4- у), поэтому tg x 4- tgy = самым форму-
cos x • cosy
ла (1) доказана. Аналогично доказывается и формула (2).
Пример. Доказать, что тангенсы углов а 4-пя
и Р =# 4- пл равны тогда и только тогда, когда эти углы раз-
нятся на угол, кратный л.
Пусть а и Р разнятся на угол, кратный л; тогда а = Р 4- пл,
где п — некоторое целое число. Но в таком случае
tga = tg (р 4- пл) = tg р.
Обратно, пусть tga = tgр. Тогда tga — tg Р = О и по фор-
муле (2)
sin (a — Р) = 0
cos а • cos р
Но это возможно лишь при условии, что sin (а — Р) = 0.
Как известно, синус обращается в нуль лишь для углов, крат-
ных л. Поэтому
a — р = пл,
а — р 4* пл,
что и требовалось доказать.
Упражнения
Вычислить (№ 1165—1168), не пользуясь тригонометрическими
таблицами:
1165. tg22°30' 4-tg67°30'. 1167. tg^n4-tg^n.
1166. tg 22°30'— tg 67°30'. 1168. tg||n —tg^n.
1169. Упростить выражение
tg a 4- tg P
tga — tgp ‘
1170. Данные выражения представить в виде произведений:
а) /З-tga; б) 1 4-tga.
1171. Найти условие, при котором котангенсы углов аир
равны между собой.
Доказать тождества:
П72. tg(^4-y-tg(^^ = 2tga.
25
1173.
1 + ctg 2a
1 — ctg 2a
Графики тригонометрических функций
кратных углов
§ 161
В главе V (часть I) мы показали, как строятся графики
тригонометрических функций у = sin х; у — cos х; у = tg х; у =ctgx.
Теперь мы рассмотрим вопрос о том, как строить графики три-
гонометрических функций кратных углов сох, где со — некоторое
положительное число*.
Для построения графика функции у — sin сох сравним эту
функцию с уже изученной нами функцией у = sin х. Предполо-
жим, что при х = х0 функция у = sin х принимает значение, рав-
ное у0. Тогда
у0 = sin х0.
Преобразуем это соотношение следующим образом:
Итак,
Уо =
. /со \
Уо = sin I — х01 — sin
\СО /
6)
sin[“(v)}
Следовательно, функция у = sin сох при х = — принимает то
со
же самое значение у0, что и функция у = sin х при х — х0. А это
означает, что функция у = sin сох повторяет свои значения в со
раз чаще, чем функция у = sin х. Поэтому график функции
у = sin сох получается путем «сжатия» графика функции у = sin х
в с» раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжа-
тия» синусоиды у = sin х вдвое вдоль оси абсцисс (рис. 221).
График функции у = sin-^- получается путем
соиды у = sin х в два раза (или «сжатия» в
«растяжения» сину-
у раза) вдоль оси х
(рис. 222).
Поскольку функция у = sin сох повторяет свои значения в со
раз чаще, чем функция у = sin х, то период ее в со раз меньше
периода функции у = sin х. Например, период функции у = sin 2х
равен ^- = л, а период функции у — sin равен = 4л.
2
•со — греческая буква; читается: омега.
26
-/
Рис. 221.
Рис. 224.
Аналогично строятся графики и других тригонометрических
функций кратных углов. На рисунке 223 представлен график функ-
ции у = cos 2х, который получается путем «сжатия» косину-
соиды y=cosx в два раза вдоль оси абсцисс. График функции
у = cos — (рис. 224) получается путем «растяжения» косинусои-
ды у = cos х вдвое вдоль оси х.
На рисунке 225 вы видите график функции у = tg 2х, полу-
ченный «сжатием» тангенсоиды у = tg х вдвое вдоль оси абсцисс,
а на рисунке 226 — график функции у = tgy, полученный «рас-
тяжением» тангенсоиды у = tg х вдвое вдоль оси х.
Упражнения
Построить графики данных функций (№ 1174—1181) и ука-
зать координаты точек пересечения этих графиков с осями коор-
динат. Определить периоды данных функций.
1174. y = sin-^-x. 1177. y = tgyX. 1180. y = cosyX.
1175. у = cos у х. 1178. у = ctgy х. 1181. y = ctgy.
1176. y = tg-x. 1179. y = sin-x.
3 3
1182. Определить периоды функций у = sin (тех) и у = tg ^-xj.
1183. Приведите два примера функций, которые принимают
все значения от —1 до 4-1 (включая эти два числа) и изме-
няются периодически с периодом 10.
1184*. Приведите два примера функций, которые принимают
все значения от 0 до 1 (включая эти два числа) и изменяются
периодически с периодом
1185. Приведите два примера функций, которые принимают
все действительные значения и изменяются периодически с пе-
риодом 1.
1186*. Приведите два примера функций, которые принимают
все отрицательные значения и нуль, но не принимают положи-
тельные значения и изменяются периодически с периодом 5.
Графики функций /= Л sin СОХ, у = A COS (ОХ,
у = Л tg сох, у = A ctg сох
$ 162
Пусть А > 0. Тогда если у = A sin со/ > 0, то значения этой
функции в А раз больше соответствующих значений функции
у = sin©/; если же у = A sinctf < 0, то значения этой функции
в А раз меньше соответствующих значений функции у = sin at.
Поэтому кривая у = A sin at получается путем «растяжения» кри-
вой у — sin сох в А раз в вертикальном направлении.
28
Рис 226.
Рис. 227.
Например, кривая у = 3 sin 2х (рис. 227) получается путем
«растяжения» кривой у = sin 2х в вертикальном направлении
втрое. Аналогично, кривая у = у sin 2х (рис. 228) получается пу-
тем «сжатия» кривой у = sin 2х в вертикальном направлении
втрое (или путем «растяжения» в
раза).
£
3
30
Рис 230
Рис. 232.
Аналогично строятся и графики функций у = A cos сох,
у = A tg сох, у = A ctgcox. На рисунке 229 представлен график
функции у = 3 cos 2х, на рисунке 230 — график функции у =
= — tg2x, на рисунке 231—график функции y = 3ctgx.
Если А <. 0, то для построения графика функции у = A sincox
предварительно следует построить график функции у = | А | sincox,
а затем отобразить его симметрично относительно оси х. На ри-
сунке 232, например, показано построение графика функции
у = —3 sin 2х. Аналогично строится график функции у =
= — tg 2х (рис. 233).
Отметим, что периоды функций у — A sin сох, у = A cos сох,
у = A tg сох, у = A ctg сох (А =# 0) не зависят от А.
У пражнения
Построить графики данных функций (№ 1187 — 1196) и ука-
зать координаты точек пересечения этих графиков с осями
координат. Определить периоды данных функций:
1187. у = sin Зх. 1190. У = 1 • 1 к\ — sin 2 к з/
1188. у — —3 sin 2х. 1191. У = — — cos 2х. 3
1189. у = sin Зх. 1192. У = —2 cos —. 2
2 Заказ 1159
33
1193.
1195. у = — -Mg2x.
1196. y=ltg(-il
1197.
у = — 2 cos (— Зл).
1194. у = 2tgy.
Приведите два примера функций, которые принимали
бы все значения от —- до + —, включая эти два числа, изменяясь
2 2
периодически с периодом —.
1198*. Приведите пример функции,
значения, по модулю большие чем 5, и
1
с периодом —.
5
которая принимает все
изменяется периодически
Графики тригонометрических функций
у = A sin (со (х 4- а) ], у — A cos (со (х 4- а) J и т. Д.
§ 163
Начнем с простого примера. Пусть нам требуется построить
график функции у =
функцию с функцией у — sin х, график которой мы уже умеем
строить. .
Пусть данная функция у = sin lx 4—) при х = х0
мает некоторое значение, равное у0. Тогда
Уо = sin 4-
Но в таком случае функция у = sin х должна принять
самое значение у0 при х — х0 4- —. Таким образом, все
ння, которые принимает функция у
функция у — sin х. Если х толковать как время, то можно ска-
зать, что каждое значение у0 функцией у = sin 4- у) принима-
ется на единицы времени раньше, чем функцией у = sin х. От-
I получается
оси абсцисс влево
сравним данную
приня-
то же
значе-
принимает и
3 7 л\
сюда вытекает, что график функции у = sin I х 4- — I
посредством сдвига синусоиды у = sin х по
на — (рис. 234).
Аналогично можно было бы построить
функций, как у = cos {х 4- j, у = tg (х 4- j
Заметим, что с подобными задачами мы уже сталкивались
в § 120, ч. 1, при построении графика функции
у = cosx = sin (х —).
и графики таких
и т. д.
34
принимает те
что и функция у = sin х, только с запаздыва-
получается по-
Если бы нам нужно было построить график функции у =
= sin(x— —), то рассуждения, аналогичные приведенным выше,
дали бы такой результат. Функция у =
же значения,
нием во времени (если аргумент х интерпретировать как время)
на у. Поэтому график функции у = sin
средством сдвига синусоиды у = sin х по оси абсцисс вправо на
у (рис. 235).
Аналогично можно было бы построить и графики таких функ-
ций, как у = cos
Теперь рассмотрим более сложные примеры. Пусть нам нуж-
но построить график функции
у — A sin 1о> (х + a) J.
Для этого сравним данную функцию с функцией
и т. д.
у = A sin их,
график которой мы уже умеем строить (см. § 162). Предполо-
жим, что функция у = A sin [со (х 4- а) | при х = х0 принимает не-
которое значение, равное у0. Тогда
у0 = A sin [<о (х0 -|- а) 1.
35
Это соотношение показывает, что функция у = A sin ах при
х = х0 4- а принимает то же самое значение у0. Поэтому все те
значения, которые принимает функция у = A sin [о (х 4- а) ], при-
нимает и функция у = A sintox. При этом каждое значение у0
принимается первой функцией на а единиц времени (если х тол-
ковать как время) раньше, чем второй функцией. Но это озна-
чает, что график у = A sin 1© (х + а) ] получается посредством
сдвига графика функции у = A since х по оси абсцисс влево на а.
Например, кривая у — 3 sin 21 х 4- —) получается посред-
ством сдвига кривой у = 3 sin 2х влево по оси абсцисс на —
(рис. 236). 4
Кривая у = — 3 cos 2 (х 4- — | получается посредством сдви-
I \ з / J
га кривой у = —3 cos 2х влево по оси абсцисс на расстояние —
(рис. 237). 3
Аналогично могут быть построены графики таких функций,
как у = A sin [<о (х — a) J, у = A cos [<о (х — а) ] и т. д. Они получа-
ются соответственно посредством сдвига графиков функций
у = .А sincox, у = A cos сох и т. д. вправо по оси абсцисс на рас-
стояние а.
На рисунке 238 (стр. 38) вы видите график функции у .=
= 3 sin
полученный посредством
сдвига графика
функции у = 3 sin 2х вправо по оси абсцисс на расстояние —.
4
На рисунке 239 представлен график функции у = — ctg 12 Ах —
— — ] , полученный посредством сдвига графика функции
у = — ctg 2х вправо по оси абсцисс на расстояние —.
Заметим, что период функции у = A sin Lo (х 4- а) ], как и пе-
риоды других аналогичных тригонометрических функций, не
зависит от а.
У пражнения
Построить графики данных функций (№ 1199—1205) и ука-
зать координаты точек пересечения этих графиков с осями коор-
динат. Определить периоды данных функций:
1199. а) у = sin 1 f 1 Л \ *+т); г) у = cos х ]; \ б/
б) у — sin / f л \ X ; < 4 / д) . / , Л \ у = + т; \ 4 /
в) у = cos / . л \ Iх + 6; е) / Л \
36
1200. у = 2sin I—fx + —1.
I 2 \ 3 I J
1201. у = — cosl — (x + — 'j 1.
2 L 2 \ 4 / j
§ 164
Графики функций у = A sin fax -f «)»
у = A cos (ox -|- а) и т. Д.
Пусть нужно построить график функции у = 3 sin (2х— 5)*
Представим эту функцию в виде y = 3sin 2
После
этого нетрудно понять, в какой последовательности следует вы-
полнять построение.
1. «Сжимая» синусоиду у = sin х по оси х вдвое, получаем
кривую у — sin 2х (рис. 240, кривая I).
2. Путем «растяжения» кривой у — sin 2х в вертикальном на-
правлении в 3 раза получаем кривую у = 3 sin 2х (рис. 240, кри-
вая II).
3. Смещая кривую у = 3 sin 2х вправо на расстояние в
единицы масштаба, получаем график функции у = 3 sin (2х — 5)
(рис. 240, кривая III).
Аналогично строится график функции у = A sin («х + а) и при
любых других значениях А,ш, а.
На том же принципе основано построение графиков функ-
ций у = A cos (их 4- а), у= A tg (wx ~Ь а), у = A ctg (сох+а). На-
. . 1 .
пример, для построения графика функции у = — t;
сначала представим ее в виде у = — tg 2 (х + —
з \ 6, j
1) «сжимая» тангенсоиду у = tg х по оси х вдвое,
график функции у = tg 2х (рис. 241, кривая I);
2) «сжимая»
в три раза,
вая II);
3) перенося
1
3
; после этого:
получаем
кривую у = tg 2х в вертикальном направлении
получаем кривую у = — tg 2х (рис. 241, кри-
3
лучаем график
ван III).
кривую у = tg 2х влево на расстояние по-
(рис. 241, кри-
3 -
функции у = —tg(2x
3 \
Рис 241.
40
У пражнения
Построить графики данных функций (№ 1206—1213) и ука-
зать координаты точек пересечения этих графиков с осями коор-
динат. Определить периоды данных функций. Каковы экстре-
мальные (то есть минимальные и максимальные) значения этих
функций?
1206. у = 2sin(3x — 2).
1207. у = 1 sin(3x — 3).
1208. y = 2sin(-x + —\
\3 3)
1209. у = 2cos(l —
\ 2/
Гармоническое колебание
1210. у = —-cos(3x + 2).
1211. у = -cosf—х----— \
1212. у = —
Л 3 \ 3 6/
1213. y = 3tg(—— 2х\
\ 4 /
§ 165
Пусть точка М (рис. 242) движется по окружности радиуса
А против часовой стрелки равномерно с постоянной угловой
скоростью о радианов в секунду. Если в начальный момент
времени (/ = 0) эта точка занимала положение Мо, определяемое
углом ф, то через t секунд она займет некоторое положение М,
определяемое углом + ф.
В то время как точка М движется по окружности, ее про-
екция Р на ось ординат совершает колебания вдоль диаметра
CD, достигая то наивысшего положения С, то наинизшего по-
ложения D. Чтобы математически описать это колебание,
выразим ординату точки Р через угол ф, угловую ско-
рость со и текущее время t. Отношение этой ординаты у к ра-
диусу окружности А является синусом угла, который обра-
зует вектор ОМ с осью х. Но этот угол в момент времени t, как
указано выше, равен ю/ + ф. Поэтому — = sin (о/ + ф), откуда
А
у = A sin (<о/ + ф). (1)
Формула (1) и представляет собой закон
колебания проекции точки М на ось
ординат. Колебания такого рода полу-
чили название гармонических колебаний.
Формула гармонического колебания
у— A sin (<о/ + ф) определяет у как функ-
цию времени t. Максимальное значение
этой функции равно, очевидно, А, а мини-
мальное (—А). Следовательно, все зна-
чения этой функции заключены между
—А и А. Поэтому А называется ампли-
тудой колебания.
41
Переменный угол со/ 4- ф называется фазой колебания.
Начальная фаза колебания <р всегда положительна и мень-
ше 2л.
Время Т, в течение которого точка М сделает один полный
оборот по окружности, называется периодом гармонического
колебания. В течение этого периода проекция Р точки М пройдет
дважды все свои возможные положения и возвратится в перво-
начальное положение. Исключение составят лишь предельные
положения С и D (см. рис. 242), каждое из которых точка прой-
дет один раз.
Посмотрим, как выражается период гармонического колебания
Т через амплитуду А, угловую скорость со и начальную фазу ф.
За время Т точка М пройдет путь со Т радианов. Но этот путь
вместе с тем равен длине окружности, то есть 2л радианам.
Поэтому о Т = 2л, откуда
(2)
р ___ 2л
со
Таким образом, период гармонического колебания обратно
пропорционален угловой скорости. Он не зависит ни от
амплитуды, ни от начальной фазы колебаний.
Период гармонического колебания (1) является периодом функ-
ции у = A sin (со/ + ф). Действительно,
A sin [со (/ 4- Т) + ф] = A sinf со (t 4- — ) 4- ф =
[ \ <о /
= A sin [со/ 4- ф 4- 2л ] = Л sin (со/ + ф).
Это можно было бы понять, конечно, и без выполненных пре-
образований. Ведь в момент времени / 4- Т точка Р возвращается
в то же самое положение, которое она занимала в момент вре-
мени /. А значения функции A sin (со/ 4- ф) представляют собой
ординаты точки Р.
Величину, обратную периоду колебания, принято называть
частотой колебания и обозначать буквой v*. Частота гармони-
ческого колебания (1) равна
1 СО /Q\
V = — = —. (3)
Т 2л
Эта величина показывает, сколько колебаний совершает точка
в течение одной секунды.
Угловая скорость со выражается через частоту v и период
колебания Т следующим образом (см. (3)):
о 2л
со = 2 л v = —.
Т
<о
Поэтому уравнение гармонического колебания (1) часто записы-
вают в виде:
у = Л sin (2л v/ 4- ф),
* v — греческая буква; читается: ню.
42
или
Упражнения
у = A sin
/ 2л, । \
(yf 7‘
1214. Для каждого из данных гармонических колебаний оп-
ределить амплитуду А, период Т, частоту v и начальную фазу <р:
а) у = — sin (3t -J- —\
л 2 к 4 J
б) у = 7 sin
(2/ + -);
к 6/
в) у = 3 cos 3t\
г) у = 2 sin (3 nt + 1).
1215. Какие числовые значения могут принимать амплитуда,
частота и начальная фаза гармонического колебания?
Построить графики данных гармонических колебаний (№ 1216,
1217):
1216. у = 3sin/2/+ — \ 1217. у= —sin (3t 4- —\
к 3/ л 2 к 5 )
1218. Какое влияние на график гармонического колебания
оказывают амплитуда и частота этого колебания?
Гармоническое колебание в электротехнике
§ 166
Электрический ток, которым питаются городские осветитель-
ные сети, является переменным током. Его величина / постоян-
но изменяется, совершая гармоническое колебание
/ = /osin^yZ 4-<р), (1)
где /0 — максимальное значение тока, Т — период колебания,
Ф — начальная фаза.
Выясним, в какие моменты времени ток достигает экстре-
мальной (то есть минимальной или максимальной) величины и
когда его величина обращается в нуль.
Как это следует из формулы (1), своей минимальной вели-
чины сила тока достигает при условии, что sin^-^/ — — 1.
Эго уравнение дает: ~t 4- Ф = л 4-2»л, откуда
t = т(п + А—
к 4 2л/
3 ф . 3 о
Если —- > —, или <р < — л, то первый момент минимума мож-
4 2л 2
но получить из формулы (2) при п ~ 0:
3 <р \
4 2л/
43
Если же у < у-, или ф > у и, то первый момент минимума
получается из (2) при п = 1:
* \ 4 2л /
Каждый последующий момент минимума наступает через Т
секунд после предыдущего момента минимума (докажите это!).
Своей максимальной величины ток / достигает при условии,
что sin
1. Это уравнение дает: у-/ ф = у -|-2лл,
откуда
(3)
t = т(п+ 1 — -JL’
\ 4 2л(
__ I . Ср Л *’
Если — > —, или ф < —, то первый момент максимума можно
получить из формулы (3) при п = 0:
= Т(- — -2-1
1 U 2л/
Если же у < или Ф > у, т0 первый момент максимума по-
лучается из (3) при п = 1:
ф
2л
это!).
тока I
Каждый последующий момент максимума наступает через Т се-
кунд после предыдущего момента максимума (докажите
Теперь выясним, в какие моменты времени величина
обращается в нуль. Для этого нужно решить уравнение
sin I — t -f- ф> = О,
которое дает
2л , .
— t 4- ф = пп.
откуда
Так,
если
t = .LIn_4\ (4)
2 \ л/
впервые величина тока станет нулевой в момент времени
I = -(1 — А
Ф<л, и в момент времени
1 = Ц
Ф л. Каждый последующий такой момент наступает через
если
т
— секунд после предыдущего (докажите это!).
44
Упражнения
1219. Знаете ли вы, какова частота колебания тока в ваших
осветительных сетях?
1220. В какие моменты времени величина у, изменяющаяся
по закону
принимает экстремальные (то есть минимальные или максималь-
ные) значения и когда она обращается в нуль?
1221. То же, что и в задаче 1220, для законов колебаний:
а) у — 2 sin
3/ 4- -
5,
/ R
б) у = 7 sin (2 / 4* — л
Преобразование выражения a sin х 4- b cos х
путем введения вспомогательного угла
$ 167
Лемм а. Если сумма квадратов двух действительных
чисел равна единице, то одно из этих чисел можно рас-
сматривать как косинус, а другое как синус некоторо-
го угла.
Другими словами, если а2 4- 62 = 1, то существует угол ф,
такой, что а = cos ф; b = sin ф.
Прежде чем доказывать эту лемму, поясним ее на следующем
примере:
+ 3 +± = 1.
\ 2 ] ^\2) 4^4
Поэтому существует угол ф, такой, что = cos ф; у = sin ф.
В качестве ф в данном случае можно выбрать любой из углов
30°, 30° ± 360°, 30° ± 2 • 360° и т. д.
Доказательство леммы. Рассмотрим вектор ОА (рис.
243) с координатами (а, Ь). По-
скольку о2 4- b2 = 1, длина этого
вектора равна 1. Но в таком
случае его координаты должны
быть равны cos ф и sin ф, где ф —
угол, который образует данный
вектор с осью абсцисс. Итак,
o=cos ф; b = sin ф, что и требова-
лось доказать.
Доказанная лемма позволяет
преобразовать выражение a sin х 4-
4- b cos х к более удобному для
изучения виду.
Прежде всего вынесем за скобки выражение У а2 4- Ь2:
(а , b \
|/^+FS,nX + /а* 4 Ь*' с03 /
п / ° \2 । I b V 1 о
Поскольку I . - - I 4-1 - | = 1, первое из чисел -т=-и
1 \Уа» + 6а / к^а24-6а/ Уа* + Р
Ь
- можно рассматривать как косинус некоторого угла ф,
У а2 4 ft2
а второе как синус того же угла <р:
а b
= COS ф, - --- = Sin ф.
)'а24Ь2 Уа2 + &
Но в таком случае _____________
asinx 4- bcosx = /а2 4 b2 (созфзтх 4мпфС05х) =
= )/a2 + b2 (* + ф).
Итак a sin х 4~ b cos х = У а2 4” b2 sin (х 4- ф)>
где угол ф определяется из условий
. Ь а
sin ф = ---—; cos ф = .
Примеры.
1) sinx 4 cosx = ]/2 s*nx + cos х) =
— У2(cos — sin х 4- sin — cosx) = У 2 sin Ix 4- — |.
4 4 / \ 4 /
Полученную формулу
sin x 4- cos x = У2 sin [ x 4- —)
\ 4 /
полезно запомнить.
2) Если одно из чисел а и Ь положительно, а другое отрица-
тельно, то выражение a sin х 4 b cos х удобнее преобразовывать
не к синусу суммы, а к синусу разности двух углов. Так,
3 sin х — 4 cos х = 1/9 4 16 ( 3- - sin х----*— cos х^ =
П9 4 16 /9 4 16 /
— 51 sin х • — — cosx • —5sin (х—ф),
где под ф можно подразумевать любой угол, удовлетворяющий
условиям: совф-Д sin<p = ^.
5 5
В частности, можно положить ф = arctg —. Тогда получим:
3
(4
х — arctg у
Упражнения
Преобразовать данные выражения (№ 1222 — 1229) путем вве-
дения вспомогательного угла:
1222. sin х 4 У 3 cos х. 1223. sin х — cos х.
46
1224. 3 sin x 4- 4 cos t.
1225. 4 sin x — 3 cos x.
1226. 5 sin x — 12 cos x.
1230. Какое наибольшее и
1227. —7 sin 2x — 24 cos 2r.
1228. 3 sin 3x + 2 / 2 cos 3r.
1229. sin 5x -j- cos 5x.
какое наименьшее значение может
принимать каждое из данных выражений:
а) 3 sin х 4- 4 cos х; г) 5 — 7 sin х — 24 cos х;
б) |3 sin х — 4 cos х|; д) ]/sin х — cos х;
в) —5 sin х 4- 12 cos х; е) /
' ' |sm х + cos х|
1231. Доказать, что уравнение
j/99 sin х — 49 cos х = 51
не имеет корней.
Построить графики данных функций (№ 1232, 1233):
1232. у = sin х 4- V 3 cos х. 1233. у = sin 2х — cos 2х.
Сложение гармонических колебаний
одинаковой частоты
§ 168
На практике (например, в электротехнике) часто приходится
иметь дело с колебаниями одинаковой частоты. Любые два таких
колебания можно представить в виде:
yi = At sin (со/ 4- фО; у2 = А2 sin (at 4- ф2).
Особый интерес представляет случай, когда начальная фаза пер-
вого колебания равна 0, а начальная фаза второго колебания
равна у-. Тогда yt = At sin to/; y2 = A2 sin f co/ 4* y-j = A2 cos co/.
Сумма таких гармонических колебаний равна:
At sinco/ 4- Аг coscoZ — j/" A2t 4- A?2 • sin (coZ Ф), (1)
где угол ф определяется из условий
А
л । + А2 •
sin =
____^2
]/д[+дГ;
cos ср =
(2)
Формула (1) показывает, что если два гармонических ко-
лебания имеют одинаковую частоту и фазы 0 и ,
то их сумма есть гармоническое колебание той же
частоты.
Амплитуда А суммарного колебания выражается через ампли-
туды At и А2 слагаемых колебаний по формуле
А =
а начальная фаза ф определяется из условий (2).
Пример. Найти амплитуду, частоту и начальную фазу
колебания у = sin 5/ — )/3 cos 5/.
47
Имеем: sin 5/ —У 3 cos 5/ = ]Z1 4- 3 sin (5/ 4- ф) — 2 sin (5/ 4- ф),
1 п 5л
причем sin ф = — ig-; соэф = Поэтому <р = — и, следова-
тельно, / с„\
sin 5t — )/3 cos 5/ = 2 sin (5/4-г
\ Э / 5
Амплитуда данного колебания равна 2, частота —, а начальная
5л 2л
сраза —.
Упражнения
Для каждого из данных гармонических колебаний (№ 1234 —
1237) найти амплитуду, частоту и начальную фазу. Построить
графики этих колебаний.
1234. у — sin 2/ — cos 21. 1236. у — 4 sin nt 4-3 cos nt.
1235. у = У 3 sin 3t 4- cos 3t. 1237. у = 7 sin t — 24 cos t.
1238. Докажите, что сумма двух произвольных гармоничес-
ких колебаний одинаковой частоты есть гармоническое коле-
бание той же частоты. Как определяются амплитуда, частота и
начальная фаза суммарного колебания через соответствующие
характеристики слагаемых колебаний?
1239. В мастерской установлены два двигателя. При включе-
нии одного из них каждая точка пола приходит в гармони-
ческое колебание с амплитудой 0,1 мм и частотой 1400 1/мин.
При включении другого каждая точка пола начинает совершать
гармонические колебания с той же амплитудой и частотой
1450 1/мин. Как будет колебаться пол при включении обоих
электродви гателей?
Доказательство тригонометрических тождеств
§ 169
Существует много различных способов доказательства триго-
нометрических тождеств. На конкретных примерах мы рассмот-
рим некоторые из этих способов.
Пример 1. Доказать тождество
cos а 4- sin а . / , л \ .,.
-----—— = tg а 4- — . (1)
cos а — sin а \ 4 )
1-й способ. Выражение, стоящее в левой части этого тождества,
преобразуем так, чтобы оно привелось к виду tg(a4--^j. Для
этого запишем cos а как sin 4*a ) • Тогда, используя форму-
лы для суммы и разности синусов двух углов, получим:
cosa 4- sina = sin (----(-a) 4- sma = 2sm a 4-----) • cos— =
\2 / \ 4/ 4
= /2"sin (a 4- -7);
43
cos a — sin a = sin (— -I- a । — sin a = 2 sin — • cos | a 4- -) =
\2 / 4 \ 4/
= У2 cos (a 4- — Y
\ 4 J
Поэтому
У 2 sin (a + —) . .
cos a + sin a = \ 4 / = tg/a -1).
cos a —sin a /Tcosfa^- — ' 4
2-й способ. Выражение tg (a + стоящее в правой части
cos a + sin a n
данного тождества, преобразуем к виду ------------. Для этого
cos a — sin a
воспользуемся формулой для тангенса суммы двух
л sin a
/ ~ \ tg a 4- tg — x t --------------+ 1
tg /a + —]= 4 tg a 4 1 cos a =
\ 4 / 1 - tg a tg 2L 1 - tg a ! _ -52п--в
4 cos a
углов:
sin a 4- cos a
cos a
cos a — sin a
cos a
cos a 4* sin a
cos a — sin a
Однако здесь необходимо сделать одно принципиально важное
л
/ ~ \ tg a 4- tg —
[ л \ 6 1 ь 4
замечание. Когда мы писали, что tg I« + — I = -------------, то
7 I- tga-tg-fL
4
фактически мы предполагали, что выражение tga определено,
то есть a ¥= у + пл. На самом же деле это предположение может
оказаться неверным. Поэтому случай, когда а = -у + пл, нужно
рассмотреть отдельно. В этом случае cos a = 0, и поэтому левая
часть данного тождества принимает вид:
cos a 4- sin a _ sin a _ ।
cos a — sin a —sin a
Правая же часть данного тождества при а = — + пл
обращается
в tg (a 4- — = tg f— л 4- пл). Но
\ 4 / \4 /
л есть период тангенса; сле-
довательно,
tg (a + 4) = ^Тл = — !•
\ 4 / 4
Таким образом, и при а =-------|- пл равенство (1)
справедливо.
Теперь можно считать, что данное тождество полностью до-
казано.
49
3-й способ. Выражения, стоящие в левой и правой частях
данного тождества, преобразуем к одному и тому же виду. Для
, cos а + sin ос
этого числитель и знаменатель дроби ------------ разделим на
cos а — sin а
cosa, предполагая сначала, что cosa =# 0. В результате получим:
cos a 4- sin a
cos a + sin a__ cos a __ I 4- tg a
cos a — sin a cos a — sin a 1 — tg a
cos a
Правую часть данного тождества преобразуем, используя
формулу для тангенса суммы двух углов:
л
. . tg a + tg —
tg a+ _________________i_ =.tgg + 1
\ 4 . , . « 1 — tga
I — tga • tg —
4
Сравнивая (2) и (3), получаем:
cos a 4- sin a . / л\
--------------------2— = tg a .
cos a — sina \ 4 /
Случай, когда cos a = 0, нужно рассмотреть отдельно, так же
как мы это сделали при рассмотрении способа 2.
П р и м е р 2. Доказать тождество
cos За • sin 5a — sin 2а = sin За • cos 5а.
(3)
Покажем, что разность между выражениями, стоящими в
левой и правой частях данного тождества, равна 0. Действи-
тельно, cos За • sin 5a — sin 2а — sin За • cos 5а =
= (cos За • sin 5а — sin За • cos 5а) — sin 2а =
= sin (5а — За) — sin 2а = sin 2а — sin 2а = 0.
Тем самым тождество доказано.
У пражнения
Доказать данные тождества:
1240. sin (a — В) о — = cos a • cos р. tg а — tg 0 tg т+а g т-а)
1241. — — sin 2 а. /л \ /л \ tg(j- +°J + ‘Цу- aj
1242. tg а sin (а + Р) + sin (а — Р) tg 0 sin(a + 0) — sin (а — 0)
1243. tg (а -f- 0) = 2 sin а • cos 0 — sin (а — 0) (sin a 4- cos a) cos P — (sin p 4- cos P) sin a
1244. cosa . / л a\ = tg 1 . ] 4- sin a \ 4 2 /
50
1245. .81п.<?£-+«) -cos(60°4-a) = ^T
sin (30° 4- a) 4- cos (60° 4- a) ' ® ’
1246. cos 4a • cos 6a — cos 10a = sin 4a sin 6a.
1247. —- tg 2 a sin 2 a =---------------------.
4 tg2 a — ctg-'a
Равенства, содержащие
выражения arcsfn a, arccos а и т. д.
§ 170
Пусть нужно доказать равенство
Q
arctg 2 4- arctg 3 = — л.
Прежде всего выясним, в каких пределах заключен угол
arctg 2 + arctg 3. Каждый из углов arctg 2 и arctg 3 больше 0 и
меньше А Поэтому
0 < arctg 2 4- arctg 3 < л.
А 3
Аналогичному неравенству удовлетворяет и угол—л:
4
А / 3
О < — л < л.
4
3
Таким образом, углы arctg 2 4-arctg 3 и — л находятся в интер-
4
вале от 0 до л. Но в таком случае для доказательства их ра-
венства достаточно показать, что равны их тангенсы. Имеем:
tg (arctg 24- arctg 3) =
tg (arctg 2) 4- tg (arctg 3)
1 — tg yirctg 2) • tg (arctg 3)
tg^-л = — 1.
4
2 4-3
1-2-3
Тем самым данное равенство доказано.
Заметим, что нахождение тех пределов, в которых заклю-
чена сумма arctg 24-arctg 3, является обязательным. Нельзя делать
з
вывод, что arctg 2 4- arctg 3 = — л, на основании только того, что
4
3
tg(arctg2 4- arctg3) = tg— л. Из равенства тангенсов двух углов
4
еще не следует, что равны сами эти углы. Однако если углы
заключены в пределах от 0 до л, то равенство их тангенсов
обеспечивает равенство и самих углов.
Упражнения
Доказать данные равенства:
1248. arctg у 4- arctgу = —.
51
1249. arctg 5 4- arctg -—_ д
5+ УЗ 6
1250. arcsin 0,6 4- arcsin 0,8 = —.
* * 2
5 12 120
1251. arccos-----arccos — = arccos —.
13 13 169
1252. arcsin 0,8 4- arccos — = —.
5 2
1253. arcsin 0,8 — arccos 0,6 = 0.
Тригонометрические уравнения
§ 171
В этой главе был получен ряд важных тригонометрических
тождеств. Сейчас на конкретных примерах мы покажем, как эти
тождества можно использовать для решения тригонометрических
уравнений.
Пример 1. Решить уравнение
tg-* + tg(y + х) = — 2.
Используя формулу для тангенса суммы двух углов, полу-
чаем:
Мт + Х) =
Л
tg — 4-tgx
4
л
1 — tg — • tg X
4
1 + tg X
1 — tg X *
Поэтому данное уравнение можно переписать в виде:
igx+4+Jii=-2.
1 — tgx
Обозначив tg х через у, мы приходим к алгебраическому урав-
нению
или
У (1 - У) 4- 1 4- У = -2 (1 - у),
откуда
у = ±/3.
Итак, либо tg х = и тогда х = — 4- пл, либо tg х — — ]/з
3
и тогда х = — у 4" где п и — любые целые числа. Обе эти
группы решений можно представить одной формулой
х = ± — 4- пл.
з
Ответ, х — ± — 4" п л.
3
52
П р и м е р 2. Решить уравнение
3 cos 2х = 1 sin х.
Представим cos 2х как cos2 х — sin2 х. Тогда данное урав-
нение можно записать в виде:
3 (cos2 х — sin2 х) = 7 sin х.
Заменяя cos2 х на 1 — sin2 х, получаем:
3(1 — 2 sin2 х) = 7 sin х.
Обозначая sin х через у, приходим к следующему квадрат-
1 3
ному уравнению: — бу2 — 7у 3 = 0, откуда у, = —; у2 =---------.
3 2
Вспоминая, что у = sin х, получаем: либо sin х = —, либо
з
sin х — — Но второе невозможно: синус любого угла по абсо-
лютной величине не превышает единицы. Поэтому sin х = —,
3
откуда х = (— 1)я arcsin у + пл, где п — любое целое число.
ПримерЗ. Решить уравнение
з
2 sin2 х 4- cos2 х = — sin 2х.
2
Представив sin 2х в виде 2 sin х cos х, придем к однородному
уравнению 2 sin2 х + cos2 х = 3 sin х cos х. Разделив обе части
этого уравнения на cos2 х, получим:
2 tg2 х + 1 = 3 tg х.
Отсюда
(tgx)j = 1, или х = — -f- пл;
4
(tg*)2 = у. или х = arctg у + кл.
Ответ. х = —4-пл, х = arctg— + Лл, где л и k— любые це-
4 2
лые числа.
П р и м е р 4. Решить уравнение
1 + cos х + sin х = 0.
Представим 1-f-cosx как 2cos2-|-, a sinx как 2 sin у cos у.
Тогда данное уравнение можно записать в виде;
2 cos2 — 4-2 sin — cos — — 0.
2 2 2
Поэтому
2 cos — (cos — + sin —= 0.
2 \ 2 2/
53
Отсюда
Поэтому
Зх = kit,
Если cos = 0, то — = 4- пл и, следовательно, х — л 4- 2лл.
Если cos — + sin у = 0 (однородное уравнение), то 1 4- tg у = О,
откуда tg — — — 1; — = —- 4- kn. Следовательно, х = —- 4- 2kn.
2 2 4 2
Ответ, х = п 4- 2пл: х = —- 4- 2ftn, где п и ft— любые
2
целые числа.
П р и м е р 5. Решить уравнение
cos 2х = cos 6%.
Перепишем данное уравнение в виде cos 2х — cos 6х = 0 и ис-
пользуем формулу для разности косинусов двух углов. В ре-
зультате получим:
о . 2х 6х . 2х — бх л
— 2 sin-----1---- sin------= О,
2 2
или 2 sin 4х sin 2х = 0.
В таком случае либо sin 2х = 0 и тогда 2х = т, х =-^ т, либо
sin 4х = 0 и тогда 4х = ftn, х — k. Обе группы корней можно
представить одной формулой х = — ft.
4
Ответ, х = — ft.
4
Пример 6. Решить уравнение
cos 4х cos 2х = cos 5х cos х.
Представим произведения cos 4х • cos 2х и cos 5х • cos х в виде
(см. § 157):
cos 4х cos 2х — (cos 6х 4- cos 2х);
cos 5х cos А'= ~ (cos 4-cos 4х).
Тогда данное уравнение можно переписать в виде:
Y (cos 6х 4- cos 2х) = (cos 6х 4- cos 4х).
cos 2х — cos 4х; —2 sin Зх • sin ( —х) = 0;
cos 2х — cos 4х = 0; 2 sin Зх • sin х = 0.
либо sin х = 0 и тогда х = пл, либо sin Зх = 0 и тогда
/гл
х = —. Очевидно, что обе группы корней можно за-
3
писать одной формулой х = — tn,
3
О л
твет. х — — т,
3
54
Пример?. Решить уравнение
tg Зх — tg х = 0.
Используя формулу для разности тангенсов двух углов, по-
лучаем: sin2x = q
COS Зх • COS X
откуда sin 2х =0, 2х = тп; х—-^т. Из этих значений х нужно
отбросить как посторонние те, при которых хотя бы одно из
выражений cos Зх и cos х обращается в нуль. Выражение cos х
обращается в нуль при х = — 4- kn. Поэтому из полученных
ранее значений х = — т остаются лишь значения х = тп. Выра-
жение cos3x обращается в нуль при условии, что Зх = — 4-пл,
2
или х = — 4- — k = — (2k + 1). Число (2k 4- 1) нечетное, а число 6
6 3 6
четное. Поэтому число 1 не может быть целым и, следова-
2ft I 1
тельно, значения х = —л не содержатся среди значений х = тп.
Таким образом, все числа вида х = тп являются корнями данного
уравнения.
Ответ, х = тп.
Примере. Решить уравнение
sin2 2х + sin2 х = 1.
Из тождества 1 — cos а — 2 sin2 — вытекает, что
2
• 2 1 — cos 4х . , 1 — cos 2х
sin2 2х =--------; Sin2 X — -----------.
2 2
Поэтому данное уравнение можно переписать в виде:
1 — cos 4х ,1 — cos 2х ,
2 2
откуда
cos 4х + cos 2х = 0.
Ого уравнение легко решается с помощью формулы для суммы
косинусов двух углов, из которой получаем:
2 cos Зх • cos х — 0.
Если cos х =0, то х— — + лл; если же cos Зх — 0, то Зх — — 4-
2 2
4- kn, откуда х = 4- k. Нетрудно понять, что вторая груп-
па корней (х = — 4- — А*) при k = Зл 4- 1 содержит в себе все
\ 6 3/
55
корни первой группы (х = — + лл ]. Поэтому ответ к данной
\ 2 /
задаче можно выразить одной формулой: х — — 4—Л.
6 3
П р и м е р 9. Решить уравнение
sin х — У 3 cos х =
Преобразуем выражение sin х —УЗ cosx,
ный угол (см. § 167): sinx— /3cosx =
i z---------Г 1
= 1/ 12 । ( |/ о V ----------- Sin X — _
1 1 +(| 3Чи* + (^з)! I-
= 2 I— sin х — 3 4 - 1 я -
введя вспомогатель-
COS X
sin л' — !/э cos x'j = 21 cos — sin х — sin — cos х
) \ 3 3
л • / Я\
— 2 sin х-----.
\ 3/
Теперь данное уравнение можно записать в виде:
2
откуда sin
2 sin (х--= 1,
\ 3/
л\ 1
х----1 = — и, следовательно,
3/ 2
х--? = (-1)^ + ил, X =+ (—1)п+ ля.
о О о О
Ответ. х = — + (— 1)" — 4- лл.
з 6
ПримерЮ. Решить уравнение
5 sin х — cos х =5.
Это уравнение в принципе можно решать тем же способом,
что и предыдущее уравнение:
1/26 I -737 sin х--- cos *| = 5,
\/26 V26 )
У 26 sin (х — <р) — 5,
где СО5ф — ———, sin ф = —-—,
/26 /26
или <р= arctg -g-.
Поэтому sin k-arctg Д= ,
\ Б 5/ /26
откуда x_arctgl = (_ir
arcsin -Lt- -|- nn;
6 5 v ' /26
x = arctg 1 + (— 1)" arcsin + ля.
66
Но в данном случае лучше использовать другой метод реше-
ния, который приводит к более простому ответу. Введем в рас-
смотрение новую переменную у = tg—:
2<g I 1- tg2| . ,
sin x ---------- _fo... cos x =--------—------—•
i + tg-Л > + 1 + 1б.Д • + >’
2 2
Тогда данное уравнение можно переписать в виде:
1°У 1 — у2 = 5
1 4- у2 1 4- у2
откуда
10у — 1 + у2 = 5 (1 + у2);
4у2 — 10у + 6 = 0;
1 3
У» = 1, Уг = -•
Вспоминая, что у = tg —, получаем:
(х\ л, /х\ . 3 . Л,
— = —|- пщ (— I = arctg —h 2kn.
2 /> 4 \ 2 /2 2
Следовательно, данное уравнение имеет две группы корней:
х = — + 2 лл и х = 2 arctg — 4- 2Ал,
2 2
где л и k — любые целые числа.
Желающие могут проверить, что ответы, полученные двумя
различными способами, выражают один и тот же результат.
Вводить новую переменную у = tg у можно лишь в том случае,
если заранее известно, что у ¥= у -|- пл, или х =# л + 2пл. Таким
образом, описанный способ решения уравнения a sin х + b cos х =с
может привести к потере некоторых корней, а именно корней
вида х = л 4- 2лл. Такие корни требуют специальной проверки.
Упражнения
Решить уравнения:
1254. tgx-tg(|-x)= 1.
1255. sin (— 4- —- sin х = Y 3 .
\3 / 2 2_
1256. cos (— — дс) — 0,5 sin х — .К3 cos х.
\6 ) 2
1257. cos 2х • cos х = sin 2х • sin х.
1258. sin а • cos (а 4- х) = cosa sin (а 4- х).
57
1259. cos(^ + xj
1260. tg3x-tgx = 1.
1261. sin 2x = 2 sin x.
1262. cos2x = 2sin2x.
1263. sinx • cosx = 0,25.
1264. sin x + cos — = 0.
2
1265. sin4 x + cos4 x = sin 2x.
1266. sin2 - — cos2 - = 0,5.
2 2
sin (-- — x । = 0.
\3
1267. sin4 - — cos4 - = 0,25.
2 2
1268. 5 cos 2x = V56 sin x.
1269. cos 2x = 2sin x— —.
2
1270. tgi.tg*-tg| + tgx
1271. tg2x = 3tgx.
1272. 4- -ILL = 2.
tg x tg 2x
1273. 2 sin2x=j/6sin2x—3cos2x.
1274. cos2 x + 4 sin2 x = 2 sin 2x.
1275. sin 2x 4- sin x • cos x = 2 cos 2x.
1276. cos 7x • cos 3x = cos 4x.
1277. cos 3x • cos x = cos 7x • cos 5.v.
1278. cos 2x ♦ cos 3x — cos 5x • cos 6x.
1279. sin x • sin 3x = sin 2x • sin 4x.
1280. sin 2x • cos 3x = sin 3x • cos 2x.
1281. cos (a 4- x) • cos (a — x) 4- sin2 x = 0,5.
1282. cos = 1 4- cos x. 1285. cos 2x = 1 4- sin x.
1283. 1 —cosx = sinx. 1286. 4(1 4-cosx)=3 sin2 у cos-^-.
1284. 1 4* cos x 4- cos 2x = 0. 1287. sin x 4- sin 3x = 0.
1288. sin x — sin 3x = 0.
1289. sin (30° 4- x) — sin (60° — x) = 1.
1290. cos 2x 4- cos 6x = 0.
1291. cos 2x — cos 6x = 0.
1292. cos (x —a) — cos (x — 0) — sin (0 —a).
1293. sin 3x = cos 2x.
1294. sin x 4~ sin 2x 4- sin 3x 4- sin 4x = 0.
1295. cos x — cos 2x = sin 3x.
1296. sin x 4- sin 3x 4- sin 5x = 0.
1297. tg 5x 4- tg 3x — 0.
1298. tg 5x = tg 3x.
1299. tg 4x = tg 2x.
1300. tg (a 4- x) 4- tg (a — x) == 0.
1301. tg| + tgx = tgl*.
1302*. tg x 4- tg 3x 4- tg 5x = 0.
1303. cos2x 4- 3cos2 - = 2.
2
58
13С4. sin2x 4 sin2 3x 4- — cos6x = 1.
2
. лд* •> , л • *> r* 3 —cos lOx
1305. cos2 x 4- 2 sin2 5x =-------.
2
1306. sin2 4x 4 7 cos2 6x 4 — cos 8x = 5.
2
1307. sinx — ]/3cosx = 1.
1308. ]/3 sin x 4 cos x = У2.
1309. sin 5x 4 |/3”cos 5x = 2 sin 7x.
1310. sinx—У7 cosx = 4^7.
1311. sinx±5°^ = 1/2?
cos 2x
1312. sin x — cos x 4 tg x = 1.
1313. 2 sin x — 5 cos x_4 2 tg x = _5.
1314. V Tsin x — KT cos x = / 3.
1315. sin 2x • tg x = 1.
1316. cos 4x 4 tg 2x = I.
1317. cos x • tg2 — = — —.
2 2
Графический способ решения тригонометрических
уравнений § 172
О графическом способе решения некоторых тригонометриче-
ских уравнений мы уже говорили в § 125, ч. I. Теперь, умея строить
графики тригонометрических функций кратных углов, мы можем
решать этим способом гораздо больше уравнений, чем прежде.
Но основная идея решения, конечно, остается той же самой.
Для примера рассмотрим уравнение
tgf =2-х.
Графики функций у = tg — и у — 2 — х (рис. 244) пересекаются
в бесконечном числе точек. Значит, данное уравнение имеет бес-
конечное множество корней. Найдем, например, наименьший
положительный корень х0. Этот корень является абсциссой точки
пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами
тангенсов (см. таблицы В. М. Брадиса, стр. 62). Выпишем значе-
X
— и
ния функций у = tg
окрестности
точки х = 1.2.
у = 2 — х в
2
59
X 1,2 1,3
'у асГ ьо | * 0,6841 0,7602
у == 2 — х 0,8000 0,7003
1 сч 7 * I сч 4-* —0,1159 0,0602
Как видно из этой таблицы, при переходе от значения к = 1,2
к значению х =1,3 разность tg у — (2 — х) меняет свой знак на
противоположный (с — на +). Значит, в нуль эта разность
обращается где-то между значениями 1,2 и 1,3. Следовательно,
с точностью до 0,1 х0 « 1,2 (с недостатком) и х0 «1,3 (с избытком).
Используя таблицу тангенсов, можно найти и приближенное
значение этого корня с точностью до 0,01. Для этого рассмот-
рим значение х = 1,25, являющееся средним значением чисел
1,2 и 1,3. При х = 1,25
tg-| « 0,7215,
2 — х = 0,7500.
Поскольку tg^-< 2 — х, то х0> 1,25 (см. рис. 244). Итак,
1,25 <х0< 1,30.
Теперь испытаем значение х — 1,28, которое близко к сред-
нему значению чисел 1,25 и 1,30. При х — 1,28
tg| 0,7445,
2 — х = 0,7200.
Теперь уже tg ~ >2—х. Значит (см. рис 244), х0 < 1.28.
Аналогично, рассматривая значение х =1,26, мы получили бы
tgy < 2—х и потому х0> 1,26. Значит,
1,26 <х0< 1,28.
Поэтому с точностью до 0,01
х0 « 1,27.
Если бы нужно было определить, какое это приближенное
значение (с недостатком или с избытком), то нам пришлось бы
сравнить значения tg и 2—х в точке х — 1,27.
Предлагаем учащимся сделать это самостоятельно.
Упражнения
1318. Найти наименьший положительный корень уравнения
с точностью до
1319. Найти
fg(2x — —^ = 2 — л-2
\ 3/
0,01.
корень уравнения
sin 2х = 1 — 4х
с точностью до 0,01.
Задачи на повторение
1320. Сколько действительных корней имеет каждое из дан-
ных уравнений:
a) sin х = 2х; в) tg ах = Ьх + с (6 ¥= 0);
б) sin х = г) cos 2х —
1321. Может ли тангенс суммы двух углов быть равен
сумме тангенсов этих углов? Если может, то в каком случае?
1322. Вычислить sin (а + 0) и cos (а — 0), если известно, что
sin а = , cos 0 — — , причем углы а и 0 оканчиваются
в одной и той же четверти.
61
1323. Вычислить sin 2a и cos 2a, если cosa= —-—г
а + b
(известно, что а > b > 0 и угол а оканчивается не в 1-й чет-
верти).
1324. Найти sin 4х, если известно, что tg х = 3.
Доказать тождества (№ 1325 — 1327):
1325. sin 200° • sin 310° 4- cos 340° • cos 50° =
1326. 16 sin 10° • sin 30° • sin 50° • sin 70° = 1.
1327. cos — 4- cos — л — —.
5 5 2
Упростить выражения (№ 1328, 1329).
1328. sin2 a —sin2 p
sin p cos a — cos P sin a
1329. ]/г14-81пф—У1—$1пф при а)0< ф<
б)у<Ф<3
1330. Разложить на множители:
cos2 4a 4- cos2 3a — sin2 2a — sin2 a.
Доказать тождества (№ 1331 — 1334):
I — sin a _ . 2 / л a\
1 + sin a \ 4 2 /
1 + cos a 4- cos 2a 4- cos 3a o
—-------—-------1----- = 2 cos a.
cos a + 2 cos2 a — 1
1 — sine a — cose a 3
i — sin4 a — cos4 a 2
1331.
1332.
1333.
1334.
a.
1335. Электрогенератор вырабатывает трехфазный ток:
Л = 4 sin (со/ + ф), /2 = /0 sin + ф 4- у nJ.
(4 \
<о/ 4- ф 4- — л .
3 у
Доказать, что в любой момент времени t
1336. Как связаны между собой углы а и Р, если
| sin а | = | sin Р |?
1337. Упростить выражение:
j/ sin2 a 4- cos 2a 4- 1
и проверить справедливость полученного результата при a — О
и a = л.
62
Решить уравнения (№ 1338 — 1351):
1338. 2 sin х sin 2х 4- cos Зх = 0.
1339. [cos2 х — sin2x| = !/=•
1340. sin x + cos x = cos2x .
1 — sin 2x
1341. 5 (sin x 4- cos x)3 — 13 (sin x 4- cos x) 4- 8 = 0.
1342. cos 3x — sin x = cos x — sin 3x.
1343. tg x — tg 2x — tg 3x + tg 4x = 0.
1344. у (sin4 x 4- cos4 x) 4- sin x cos x 4- sin2x cos2 x — 0.
1345. sin 2x 4- cos 2x 4- sin x cos x 4- 1 = 0.
1346. sin (cos x) = cos (sin x).
1347. cos2 x 4- cos2 2x + cos2 3x 4- cos2 4x = 2.
1348. cos 2x 4- tg x = 1.
1349. cos3 x sin 3x 4- sin3 x cos 3x = —.
4
1350. sin x sin 3x = 0,5.
1351. sin x 4- cos x 4- 2 sin x cos x = —1.
Решить системы уравнений:
1353.
1354.
sin x 4- sin у = 1,
1352.
sin x 4- sin у =)/ 2,
. л
x 4- у = -.
sin x sin у
cos x cos у
УЗ -1
4
£E±_L
4
1355.
1356.
1357.
’ . 3
sinx sm y = —,
4
tgxtgy = 3.
tgx4-tgy =
= /3 (/3-2),
I Л
x + у=т-
4
s_inx_ = y^
sin у
cos x 1
cos у УЗ
Из истории тригонометрии
§ 173
Слово «тригонометрия» греческого происхождения. В переводе на рус-
ский язык оно означает «измерение треугольников». Как и все другие разделы
математики, зародившиеся в глубокой древности, тригонометрия возникла в
результате попыток решить те задачи, с которыми человеку приходилось стал-
киваться на практике. Среди таких задач следует прежде всего назвать задачи
землемерия и астрономии.
В том, что тригонометрия относится к древним наукам, нас убеждает хотя
бы 1акой факт. Для предсказания момента наступления солнечного или лунного
затмения необходимо произвести расчеты, требующие привлечения тригономет-
рии. Весьма точно предсказывали затмения еще древне вавилонские уче-
63
ные. По-видимому, они уже владели элементарными тригонометрическими
понятиями.
Первые достоверно засвидетельствованные тригонометрические таблицы
были составлены во втором веке до н. э. Их автором был греческий астроном
Гиппарх. Таблицы эти до нас не дошли, но в усовершенствованном виде
они были включены в «Альмагест» («Великое построение») александрийского
астронома П големея. Таблицы Птолемея подобны таблицам синусов углов от 0°
до 90°, составленным через каждые четверть градуса. В «Альмагесте», в частно-
сти, есть формулы для синуса и косинуса суммы двух углов, содержатся также
элементы сферической тригонометрии*.
В средние века наибольшие успехи в развитии тригонометрии были до-
стигнуты учеными Средней Азии и Закавказья. В это время к тригонометрии на-
чинают относиться как к самостоятельной науке, не связывая ее, как прежде,
с астрономией. Большое внимание уделяется задаче решения треугольников.
Одним из самых примечательных сочинений по тригонометрии этого периода
является «Трактат о четырехугольнике» Насир Эддина (XIII век). В
этом трактате введен ряд новых тригонометрических понятий, по-новому дока-
заны некоторые уже известные результаты. Основные работы по тригонометрии
в Европе были выполнены почти на два столетия позднее. Здесь следует прежде
всего отметить немецкого ученого Региомонтана (XV век) Его главное
произведение «Пять книг о различного рода треугольниках» содержит достаточно
полное изложение основ тригонометрии. От наших нынешних учебников по
тригонометрии это сочинение отличается в основном лишь отсутствием удобных
современных обозначений. Все теоремы сформулированы словесно. После появ-
ления «Пяти книг» Региомонтана тригонометрия окончательно выделилась в
самостоятельную науку, не зависящую от астрономии. Региомонтаном составле-
ны также довольно подробные тригонометрические таблицы.
Развитие алгебраической символики и введение в математику отрицатель-
ных чисел позволило рассматривать отрицательные углы; появилась возмож-
ность рассматривать тригонометрические функции числового аргумента. Раз-
витие математики позволило вычислять значения тригонометрических функций
любого числа с любой наперед заданной точностью.
Существенный вклад в развитие тригонометрии внес Эйлер. Им дано
современное определение тригонометрических функций и указано на тесную
связь этих функций с показательными функциями (см. гл. VIII).
В настоящее время тригонометрические функции лежат в основе специаль-
ного математического аппарата, гак называемого гармонического анализа, при
помощи которого изучаются различного рода периодические процессы: колеба-
тельные движения, распространение волн, некоторые атмосферные явления и пр.
* Сферическая тригонометрия рассматривав! углы и другие фигуры не на
плоскости, а на сфере.
ПОКАЗАТЕЛЬНАЯ
И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
VIII
Степень положительного числа с положительным
рациональным показателем § 174
В главе IV (часть I) было дано определение степени поло-
жительного числа а с рациональным показателем г. Напомним
это определение.
Если число г — натуральное, то ат есть произведение г чисел,
каждое из которых равно а:
аг = а • а • ... • а. (1)
Если число г — дробное и положительное, то есть г — —, где
л
tn и п — натуральные числа, то
m
ZT ----------------------------------
ar = a =у ат.
(2)
Формулы (1) и (2) определяют степени любого положительного
числа а с любым положительным рациональным показателем г.
Если же показатель г является рациональным и отрицательным,
то выражение аг определяется как величина, обратная к а~г:
ar = -L. (3)
а~г
Здесь уже число —г положительно.
Наконец, если г — 0, то аг равно 1:
а° = 1. (4)
Формулы (1), (2), (3) и (4) определяют степень положи-
тельного числа а для любого рационального показателя г.
Для дальнейшего нам потребуются следующие две теоремы.
Теорема 1. Если число а больше 1, то из двух сте-
пеней этого числа с положительными рациональными
показателями больше та, показатель которой больше.
Доказательство. Пусть а > 1 и — > —, где т, п, р и
л q
q — натуральные числа. Покажем, что
ГП
р_
,Q
3 Заказ 1159
65
Действительно,
т р
Приведем эти корни к корням с одинаковыми
показателями:
7^ =
Так как — > — , то mqZ> пр. Поскольку а > 1, то отсюда выте-
n q
ruj /~------------------------- nq у
кает, что am9> anp, а потому и у amc> > у anp, или
m p
a > a .
Аналогично может быть доказана и другая теорема.
Теорема 2. Если число а больше нуля, но меньше 1,
то из двух степеней этого числа с положительными
рациональными показателями больше та, показатель
которой меньше.
Доказательство этой теоремы предлагаем учащимся провести
самостоятельно.
Примеры. 1) 1,4 < 1,5. Поэтому
2) 0,51 <0,52. Поэтому л0*51 <л0-52;
0,52
л \°’51 I л
4
4
Упражнение
1358. Какое число больше:
Степень положительного числа с положительным
иррациональным показателем
§ 175
В предыдущем параграфе мы напомнили, как определяется
степень аГ любого положительного числа а с любым рацио-
нальным показателем г. Теперь нам предстоит определить
степень ах положительного числа а с положительным
иррациональным показателем х. Мы начнем с рассмотре-
66
ния следующего частного примера: как следует понимать выра-
жение 3 ?
Выпишем десятичные приближения числа У~2 с недостатком:
1; 1,4; 1,41; 1,414; ... (1)
и с избытком:
2; 1,5; 1,42; 1,415;... (2)
Все члены этих последовательностей представляют собой
рациональные числа. А степень положительного числа с рацио-
нальным показателем нами уже определена. Поэтому мы вправе
рассмотреть последовательности:
31. 31,4. 31.41. 31.414.
З2; З1-5; 3|>42; 3'-4'5; **’ ’
(3)
(4)
Как известно,
1 < с/_2< Z2
1,4 < Z]/ 2< Z 1,5
1,41 < <У2< С 1,42
1,414 < ^У2< С 1,415
Поэтому, принимая во внимание теорему 1 из предыдущего
параграфа, естественно считать, что интересующее нас число
у = 3/2 удовлетворяет неравенствам:
З1 < у < З2
3’ 4 < у < З1’5
З1-4’ < у < З1-42
3>-414 < у < 3'.415
Можно доказать, что существует и притом только одно число а,
удовлетворяющее каждому из этих неравенств*. По определе-
нию это число а и принимается за З^2.
Рассмотрим еще один пример: как следует понимать выра-
жение — I ?
\ з /
* Доказательство этого факта выходит за пределы нашей программы и по-
тому здесь не приводится.
3* 67
По аналогии с первым примером рассмотрим последова-
тельности:
1 м /1x1.4
з/’ \3/ ’
И
1 \1 >41
3/ ’
1 XI ,414
(5)
иу /_LV'S /И1-42.
\з/ (з/ ; ’
/ 1 X1.415
\3/
(6)
Естественно считать, что интересующее нас число у = ("э/
удовлетворяет неравенствам (см. теорему 2 из предыдущего
параграфа):
1 \>.4
1 \I.41
] \ 1.415
1 X 1.414
Можно доказать, что существует и притом только одно
число р, удовлетворяющее каждому из этих неравенств. По
(1 9'
— 1 .
Рассмотрение представленных двух примеров приводит нас
к следующему определению.
Определение. Если а > 1, то степенью этого числа
с положительным иррациональным показателем х называется
число, которое больше всех степеней числа а с показателями,
равными десятичным приближениям числа х с недостатком, но
меньше всех степеней числа а с показателями, равными деся-
тичным приближениям числа х с избытком.
Если О < а < 1, то степенью этого числа с положительным
иррациональным показателем х называется число, которое
больше всех степеней числа а с показателями, равными десятич-
ным приближениям числа х с избытком, но меньше всех степеней
числа а с показателями, равными десятичным приближениям
числа х с недостатком.
К этому остается добавить, что для любого иррационального
числа х
Е = 1.
68
Степень положительного числа с отрицательным
иррациональным показателем
| 170
Если а > О и х — положительное иррациональное число, то
по определению
Г' =
а
Например,
° з V2 ' \ з / /_L\,<2
\ з /
Чтобы введенное определение было корректным, необходимо
показать, что дробь — в правой части равенства (1) имеет
ах
смысл при любых положительных а и х. Для этого нужно
доказать, что
ах 0.
Действительно, по определению степени с положительным ирра-
циональным показателем
ах' < ах < ах",
где одно из чисел х' и х" есть десятичное приближение числа х
с недостатком, а другое — соответствующее десятичное прибли-
жение этого числа с избытком. Числа х' и х" рациональные и
положительные. Поэтому ах' > 0 и ах" > 0. Но число, заключен-
ное между двумя положительными числами, само должно быть по-
ложительным. Поэтому ах > 0.
Итак, мы определили степень положительного числа с любым
действительным показателем. Степень отрицательного числа
с действительным показателем, вообще говоря, не определена.
Основные свойства степеней положительных
чисел с действительными показателями
§ 177
Степени положительных чисел обладают следующими основ-
ными свойствами:
1) ах • аУ = ах+>’, 3) (ab)x = ахЪх, 5) (ах)У = ахУ.
— = ах~У (~\Х = —
2) аУ ’ 4) \ ь / Ьх ’
Эти свойства были частично доказаны нами в главе IV (ч. I)
для рациональных показателей. На самом же деле они верны и
для иррациональных показателей. На доказательстве этого факта
мы не будем останавливаться.
69
Примеры.
= 5/Г-/2- = 5/2.
5^'2
Упражнения
Доказать тождества (№ 1359, 1360):
/з~
1359. (1 j'2 • 4 2- • 163 * * * * В * =
i9> 48 9271х 3 _
1360. ^-= . - =(6 • 210)Гз .
4 ПОЗ 6^27 V '
Упростить выражения:
1361. [(Узуз-]~2,/3.
-Л ГА-
1362. [(/8) 3]?6
Показательная функция и ее график
§ 178
Показательной функцией называется функция вида
у — ах,
где а — некоторое фиксированное положительное число.
Примером показательных функций могут служить функции:
У = 2- У = (ур У = (0,1)-.
В природе наблюдается целый ряд явлений, которые матема-
тически можно описать с помощью показательных функций.
Например, распад радия приближенно можно описать соотно-
шением
т (0 = т (0) • (0,9996)',
где т (0) — первоначальное количество радия в граммах, а т (I)—
то количество радия, которое останется через t лет после нача-
ла распада. По показательному закону изменяется также атмос-
ферное давление с изменением высоты.
70
В определении показательной t
функции у = ах указывается, что *
число а положительное. Объясняется
это тем, что степень отрицательного _
числа с произвольным показателем,
вообще говоря, не определена. 1
Среди всех положительных зна- -------------—------------
чений а следует особо выделить и
а = 1. При таком а функция у—ах
имеет вид у = 1 (рис. 245). Такая
функция не представляет особого Рис. 245.
интереса. Поэтому в дальнейшем,
говоря о показательной функции у = ах, мы всегда будем пред-
полагать, что а > 0 и а ф 1.
Перейдем к построению графика показательной функции.
В качестве примера на одном чертеже построим графики функ-
ций у — 2х и у = 10х, а на
другом — графики функций
/ 1 \х / 1 \Х ГТ
у = — и у = — . Для
Л \2/ У \10/
этого предварительно соста-
вим таблицы значений этих
функций. Для функций у=2х
/1 V
и у = I — в качестве зна-
\ 2 /
чений х выберем
X — 3 — 2 — 1 0 1 2 3
у = 2х 1 8 4 1 2 1 2 4 8
/ 1\х У~ \ 2) 8 4 2 1 1 2 ]_ 4 т 8 ...
—3, —2, —1, 0, 1, 2 и 3.
(1 \х
—) целесообразно выбрать
другие значения х, поскольку при х = ±2, +3 указанные функ-
ции принимают либо слишком большие, либо слишком
(1 \3 1
— =-------• Такие зна-
10/ 1000
чения у трудно зафиксировать на графике. Поэтому в данном слу-
чае в качестве значений х удобнее выбрать, например, такие
числа: -1, 0.1.
4 4 4 4 4 4
Соответственные значения у можно вычислить последовательно:
10° = 1.
1 ____________
104 .= = К |/Тб ^/3,1622^ 1,8;
2 I
10 4 = 10 2 = /16^3,2;
71
3 ______
10 4 = frio3 = К/1000 /31,6227 » 5,6;
101 - 10;
10" = -V^ — st; 0,6
L 1,8
и T. Д.
В итоге получается следующая таблица приближенных зна-
fl \-v
— :
X — 1 __3 4 1 I to — 2 4 0 2 4 2_ 4 со | 1 ...
У — 10х 0,1 0,2 0,3 0,6 1,0 1,8 3,2 5,6 10 ...
/ 1 V 10 5,6 3,2 1 ,8 1,0 0,6 0,3 0,2 0,1 ...
Используя составленные таблицы, можно в общих чертах
представить себе поведение рассматриваемых функций. Точные
графики функций у = 2х и у = 10х приведены на рисунке 246,
/1 \х /1 \х
а функций у = | —) и у = I —) на рисунке 247.
Рис. 246. Рис. 247.
72
Упражнения
1363. Используя график функции у = 2х, найти
_ Зу____!_____1
УЪ УУ у/2 ’ 2 J/2 ‘
При каких значениях аргумента эта функция принимает зна-
чения, равные 0,5; 0,9; 1,0; 1,8; 2,7?
/1 \*
1364. Используя график функции у = IttJ • найти
io-3; ^оДюТ; (1) °’7.
При каких значениях х эта функция принимает значения, раВ'
ные 0,5; 0,9; 1,0; 3,0; 5,0?
1365. Построить графики функций:
а) У = 2Г—*; в) у = 2'*>; д) у = 2х + 1;
б) у= 2-r+1; г)у = 2х—1; е) у = 2'1 х1.
1366. Построить графики функций:
а) у = И)*-2: в) y=(i)W; Л у = (|)’+й
«9У = (4)'+2; г)У=(1)'-2; e)y = (l)-W.
1367. На одном и том же рисунке построить графики функций
у = 3х и у = З'Л
Основные свойства показательной функции
§ 179
В этом параграфе мы изучим основные свойства показательной
функции
у = (1х. (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фик-
сированное положительное число, отличное от 1.
Свойство 1. Областью определения показательной
функции является совокупность всех действительных
чисел.
В самом деле, при положительном а выражение ах определено
для любого действительного числа х.
Свойство 2. Показательная функция принимает
только положительные значения.
Действительно, если х > 0, то, как было доказано в § 176,
ах >0.
73
Если же к < 0, то
а~х
где — х уже больше нуля. Поэтому а~х > 0. Но тогда и
ах =
— >0.
а~х
Наконец, при х = 0
ах = 1.
2-е свойство показательной функции имеет простое графичес-
кое истолкование. Оно заключается в том, что график этой функ-
ции (см. рис. 246 и 247) располагается целиком выше оси абсцисс.
Свойство 3. Если о> 1, то при х > о «Л> 1, а при
х < 0 ах < 1. Если же а < 1, то, наоборот, при х > 0
ах < 1, а при х < 0 ах > 1.
Это свойство показательной функции также допускает про-
стую геометрическую интерпретацию. При а > 1 (рис. 246) кри-
вые у = ах располагаются выше прямой у — 1 при х > 0 и
ниже прямой у = 1 при х < 0. Если же а < 1 (рис. 247), то, на-
оборот, кривые у = ах располагаются ниже прямой у = 1 при
х > 0 и выше этой прямой при х < 0.
Приведем строгое доказательство 3-го свойства. Пусть а > 1
их — произвольное положительное число. Покажем, что
ах > 1.
Если число х рационально) х = — 7О ах _ ап = у/~а™.
\ п Г
Поскольку а > 1, то и ат > 1, но корень из числа, большего еди-
ницы, очевидно, также больше 1.
Если х иррационально, то существуют положительные ра-
циональные числа х' и х", которые служат десятичными приближе-
ниями числа х:
х' < х < х".
Но тогда по определению степени с иррациональным показателем
ах' <ах < ах”.
Как показано выше, число ах' больше единицы. Поэтому и число
ах, большее, чем ах', также должно быть больше 1.
Итак, мы показали, что при а > 1 и произвольном положитель-
ном х
ах > 1.
Если бы число х было отрицательным, то мы имели бы
г 1
0х = ----,
а~х
74
где число —х было бы уже положительным. Поэтому а~х>1.
Следовательно,
а-*
Таким образом, при а > 1 и произвольном отрицательном х
ах < 1.
Случай, когда 0<а<1, легко сводится к уже рассмотрен-
ному случаю. Учащимся предлагается убедиться в этом само-
стоятельно.
Свойство 4. Если х = 0, то независимо от а ах = 1.
Это вытекает из определения нулевой степени: нулевая сте-
пень любого числа, отличного от нуля, равна 1. Графически это
свойство выражается в том, что при любом а кривая у — ах
(см. рис. 246 и 247) пересекает ось у в точке с ординатой 1.
Свойство 5. При а> 1 показательная, функция у = ах
является монотонно возрастающей, а при а < 1 — мо-
нотонно убывающей.
Это свойство также допускает простую геометрическую ин-
терпретацию.
При а > 1 (рис. 246) кривая у — ах с ростом х поднимается
все выше и выше, а при а < 1 (рис. 247) — опускается все ниже и
ниже.
Приведем строгое доказательство 5-го свойства.
Пусть а > 1 и х2 > х^ Покажем, что
ах>.
Поскольку х2 > х1г то х2 = Xi + d, где d — некоторое положи-
тельное число. Поэтому
ах* — = aXl+d — ах' = ах' (ad — 1).
По 2-му свойству показательной функции а*<>0. Так как d >0,
то по 3-му свойству показательной функции ad>\. Оба множи-
теля в произведении ax‘(ad — 1) положительны, поэтому и само
это произведение положительно. Значит, — ах> > 0, или ахг >
> а\ что и требовалось доказать.
Итак, при а > 1 функция у = ах является монотонно воз-
растающей. Аналогично доказывается, что при а <. 1 функция
у = ах является монотонно убывающей.
Следствие. Если две степени одного и того же по-
ложительного числа, отличного от 1, равны, то равны
и их показатели.
Другими словами, если
аь = ас (а > 0 и а 1),
то
b — с.
75
Действительно, если бы числа бис были не равны, то
в силу монотонности функции у = ах большему из них соот-
ветствовало бы при а > 1 большее, а при а < 1 меньшее значе-
ние этой функции. Таким образом, было бы или аь > ас, или
ab <z ас. Й то и другое противоречит условию аь = ас. Остается
признать, что b = с.
Свойство 6. Если az> 1, то при неограниченном воз-
растании аргумента х (х -> оо> значения функции у — ах
также неограниченно растут (у-*оо). При неограни-
ченном убывании аргумента х (х-+ — со) значения этой
функции стремятся к нулю, оставаясь при этом поло-
жительными (у-> 0; у > 0/
Принимая во внимание доказанную выше монотонность функ-
ции у — ах, можно сказать, что в рассматриваемом случае функция
у = ах монотонно возрастает от 0 до оо.
Есла0<а<;1, то при неограниченном возрастании
аргумента х (х-+ со) значения функции у = ах стремятся
к нулю, оставаясь при этом положительными fy->0;y>0).
При неограниченном убывании аргумента х (х-+ —со)
значения этой функции неограниченно растут (у-+со).
В силу монотонности функции у = ах можно сказать, что в
этом случае функция у = ах монотонно убывает от оо до 0.
6-е свойство показательной функции наглядно отражено на
рисунках 246 и 247. Строго доказывать его мы не будем.
Нам осталось лишь установить область изменения показатель-
ной функции у = ах (а > 0, а =# 1).
Выше мы доказали, что функция у = ах принимает только
положительные значения и либо монотонно возрастает от 0 до оо
(при а > 1), либо монотонно убывает от оо до 0 (при 0 < а < 1).
Однако остался невыясненным следующий вопрос: не претерпе-
вает ли функция у — ах при своем изменении каких-нибудь скач-
ков? Любые ли положительные значения она принимает? Воп-
рос этот решается положительно. Если а >0 и а=/= 1, то, каково
бы ни было положительное число у0, обязательно найдется х0,
такое, что
ах> = у0.
(В силу монотонности функции у = ах указанное значение х0
будет, конечно, единственным.)
Доказательство этого факта выходит за пределы нашей
программы. Геометрическая интерпретация его состоит в том, что
при любом положительном значении у0 график функции у = ах
обязательно пересечется с прямой у = у0 и притом лишь в одной
точке (рис. 248).
Отсюда можно сделать следующий вывод, который мы формули-
руем в виде свойства 7.
76
Свойство 7.
функции у = ах
положительных чисел.
изменения показательной
Областью
(а > 0, a^\) служит множество всех
Упражнения
1368. Найти
а) У = 2Х;
1369. Какие
1411 Уз-
области определения следующих функций:
6)У = (1У^- — 1
\Ю/
из данных чисел
„ 2
4) л 5;
2) (Из)2;
" ; В) у = —
О
больше 1 и какие меньше 1:
7) ( л У*41»001
\ 4 /
/л + 1\—ИГ
л \/1.0С1 .
1370. На основании какого свойства показательной функции
можно утверждать, что
1371. Какое число больше:
ч —/з" / 1 \—v~
а) л или —I ;
или
_2 \1 + ^6
. 3 /
г)
в)
или — ;
\3/
КГ или (/3)/У-2?
1372. Равносильны ли неравенства:
а) ах
-V ’ и 2х < х— 1?
В)
б) 5 х < б* и х- < х\ М<>/ \ i /
1373. Что можно сказать о числах х и у, если ах = аУ, где а —
заданное положительное число?
77
1374. 1) Можно ли среди всех значений функции у = 2х вы-
делить:
а) наибольшее значение; б) наименьшее значение?
2) Можно ли среди всех значений функции у = 21*1 выделить:
а) наибольшее значение; б) наименьшее значение?
Логарифм числа по данному основанию
§ 180
ла а по известным значениям
ва (1) в степень — (если толь
Алгебру иногда называют «арифметикой семи действий», же-
лая этим подчеркнуть, что, кроме четырех арифметических дей-
ствий (сложения, вычитания, умножения и деления), она рас-
сматривает также возведение в степень и два обратных к нему
действия.
Обозначим основание степени через а, показатель через х, сте-
пень через Ь. Тогда можно написать:
b = ах. (1)
«Пятое» алгебраическое действие — возведение в степень —
состоит в нахождении числа b по известным а и х. Эго действие
мы подробно изучили в главе IV (часть I), о нем говорилось так-
же в начале этой главы.
«Шестое» алгебраическое действие состоит в нахождении чис-
Ь и х. Возводя обе части равенст-
во х =/= 0), получаем:
।
= ЬХ.
Поэтому «шестое» алгебраиче-
ское действие легко сводится
к «пятому».
Теперь мы переходим к изу-
чению «седьмого» алгебраичес-
кого действия — нахождению
показателя х по известным зна-
чениям степени Ь и основания а.
Эта задача по существу состо-
ит в том, чтобы решить урав-
нение
ах = Ь, (2)
х где а и Ь — некоторые заданные,
а х — неизвестная величина.
Сразу же заметим, что данная
задача разрешима не всегда.
а
78
Если, например, в уравнении (2) число а положительно, а число 6
отрицательно, то это уравнение корней не имеет. Но если толь-
ко а и b положительны и а=/= 1, то оно непременно имеет и при-
том только один корень. Напомним, что график показательной
функции у = ах обязательно пересекается с прямой у = b и при-
том лишь в одной точке (см. рис. 249). Абсцисса точки пересече-
ния и представляет собой корень уравнения (2).
Корень уравнения (2) принято обозначать loga b (читается:
логарифм числа b по основанию а).
Логарифм числа Ь по основанию а есть показатель степени,
в которую нужно возвысить число а, чтобы получить число Ь:
а'°ва ь =- Ь.
Примеры.
1) 24 = 16, поэтому log2 16 = 4.
2) 2-3 = —, поэтому log2— = —3.
8 8
3) 6° = 1, поэтому log6 1 = 0.
С логарифмами мы сталкиваемся при решении целого ряда при-
кладных задач. В качестве примера рассмотрим следующую задачу.
Как мы знаем, распад радия приближенно описывается форму-
лой (см. § 178):
т (0 = т (0) • (0,9996)',
где т (0) — первоначальное количество радия в граммах, а т (0 —
количество радия (также в граммах) через t лет. Выясним, каков
период полураспада радия, то есть через сколько лет количество
радия уменьшается вдвое.
Искомое число лет t является корнем уравнения
т (0) • (0,9996)' = 0,5/п (0),
ИЛИ (0,9996)' = 0,5.
Поэтому
i ~ logo,9936
В дальнейшем мы научимся находить такие логарифмы с
помощью специальных таблиц, а пока нам придется принять на
веру, что
1°§0,9996 1600.
Таким образом, количество радия уменьшается вдвое примерно
через каждые 1600 лет.
Упражнения
1375. Данные равенства записать в виде логарифмических
равенств (например, З2 = 9 -> log3 9 = 2):
а) 22 = 4; в) 44 = 256; д) 2~2 = —;
4
б) З3 = 27; г) 53 = 125; е) З-4 = 1;
79
ж) 7° = 1; и) 83 =4; л) 8° = 1;
1
з)42=2; к) ^27 = 3; м) ^8 = 2.
1376. Проверить справедливость следующих равенств:
3)10^16 = 2; в) log5125 = 3; д) log31 = — 4;
cl
б) Iog3 243 = 5; г) log71 = —2; е) log10 1 = 0.
1377. Найти логарифмы следующих чисел по основанию 2:
4; 16; 32; 1; 0,5; 0,125; /2; 2/2.
1378. Найти логарифмы следующих чисел по основанию
1; 2; 8; 32; 0,25; 1; ~^=; /2; 4/2?
16 /2 Г
1379. Найти логарифмы следующих чисел по основанию 3:
3; 1; 27; 81; 1; —; /3; 3/3?
9 243 /3
1380. Найти логарифмы следующих чисел по основанию i:
О
1. 1.
3’ 27’
1381. Вычислить:
a) log2 (sin -yj;
б) log2(sinyj;
1382. Доказать тождество
1; 3; 27; -L; /3; -L.
81 V3 9^3
в) logs^g^);
г) log, (tg-1
1 / т
log„" (ат) = —.
п
Используя это тождество, вычислить:
a) log8 16; г) logjg 64; ж) k>gL ]25;
б) )og2 2/2; д) logg 27; з) log4(sin^;
в) log^y 1; е) ]о&7 243; и) log9(tg^.
1383. Используя основное логарифмичесиое тождество
а'огаь = Ь,
вычислить:
80
1) 2,og‘8; 4) 32loe’9; 7)3 з log‘8. Ю)/I}*08’6;
2)3"’=’’; 5) 8) 4:oe'7;
3) 2'’"'*'’; 6) 2~*,og-9) 9'”“‘'°; 12) (I)”2 12.
1384. Доказать, что при любом положительном a=h 1
loga(sin 1°) • loge(sin 2°)... loga (sin 89°) • logjsin 90°) = 0.
Логарифмическая функция и ее график
§ 181
Логарифмической функцией называется функция вида
У = loga к,
где а — некоторое фиксированное положительное число, отличное
от 1.
Формула у = loga х выражает то же самое, что и формула
аУ = х. (1)
Отсюда легко установить связь между логарифмической функцией и
показательной функцией
у = ах. (2)
Если показательная функция (2) описывает изменение степени в
зависимости от изменения ее показателя, то ввиду (1) логарифми-
ческая функция, наоборот, описывает изменение показателя сте-
пени в зависимости от изменения степени. Поэтому логариф-
мическая функция у = loge х называется обратной к показатель-
ной функции у = ах.
Формула (1) получается из формулы (2), если в последней пере-
менные величины х и у поменять местами. Отсюда следует, что
значения логарифмической функции у = loga х легко получить из
соответствующих значений показательной функции у = ах,
если то, что для показательной функции было у-ом, для лога-
рифмической функции рассматривать как х, а то, что для показа-
тельной функции было х-ом, для логарифмической функции рас-
сматривать как у.
Таблицы значений показательных функций у = 2х, у = 10х,
(1 \х / 1 \х
— 1 и у = I — 1 были составлены нами в§ 178. Используя
их, мы получаем таблицы (см. стр. 82) приближенных значений
функций:
у = log2 х, у = logi0x, у = log । х и у = log । х.
~2 1о
81
X £ 8 1 4 2 2 1 2 4 8 ...
10g2X —3 —2 —1 0 1 2 3 ...
log] X Г 3 2 1 0 —1 —2 —3 ...
X 0,1 0,2 0,3 0,6 1,0 1,8 3,2 5,6 10,0 ...
logic X — 1 CO | xr 1 __2 ~ 2 2 ~ 4 0 4 2 2 | W 1 ...
log] X io 1 3 4 2 2 £ 4 0 1 ~ 4 _2 ~ 2 CO | 1 —1 ...
Эти таблицы дают некоторое (хотя и весьма ограниченное)
представление о поведении рассматриваемых функций. В част-
ности, они могут быть использованы при построении графиков
этих функций.
На рисунке 250 вы видите графики функций у = log2 х и
у= 1о3ю х> а на рисунке 251—графики функций у = log] х и
~2
У = log] х.
10
Следует обратить внимание на следующее важное обстоятель-
ство. Когда х 0, то логарифмическая кривая у = \ogax не-
ограниченно приближается к оси ординат. Но оси этой она никогда
не достигает (см. рис. 250 и 251). Об этом не следует забывать при
построении логарифмических кривых.
82
Для сравнения графика логарифмической функции у = log„x
с графиком соответствующей ей показательной функции у = ах
обратимся к рисункам 252 (а = 2) и 253 [а = Как видно из
этих рисунков, графики логарифмической функции и соответст-
вующей ей показательной функции симметричны друг другу от-
носительно биссектрисы 1-го и 3-го координатных углов. Если,
например, рисунок 252 перегнуть по этой биссектрисе, то графики
функций у = 2х и у = log2 х наложатся друг на друга.
Упражнения
1385. Пересекается ли логарифмическая кривая у = logax:
а) с осью х; б) с осью у?
1386. Используя график функции у = log., х, найти логариф-
мы по основанию 2 чисел 0,5; 0,6; 0,7; 1,5; 2,3; 3,0.
Логарифмы каких чисел по основанию 2 равны 0,7; 0,8; 0,9;
1,0; 1,5?
1387. Исходя из графика функции у — log2 х, построить гра-
фики функций:
а) у = log., (х — 1); в) у = — log2 х; д) у = | log2 х |;
б) у = log2 (х + 2); г) у = log2 | х |; е) у = log2 (—х).
1388. Построить графики функций:
а) у = log । х; в) у = log^(x4-2); д) y=logjx|;
Т з" 3
б) у = log± (х — 1); г) у - I log^xI; е) у = log±(—х).
333
1389. На одном и том же рисунке построить графики функ-
ций
у = log3 X и у = log^x.
3
83
Основные свойства логарифмической функции
§ 182
В этом параграфе мы изучим основные свойства логарифми-
ческой функции
у = logex. (1)
Напомним, что под а в формуле (1) мы подразумеваем любое
фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения логарифмической
функции служит множество всех положительных чисел.
Действительно, пусть b есть произвольное положительное
число. Покажем, что выражение log06 определено. Как мы зна-
ем, loga& есть не что иное, как корень уравнения
а* = Ь. (2)
Если а и b — положительные числа, причем а =£ 1, то такое
уравнение по свойствам 2 и 5 показательной функции (см. § 179)
всегда имеет и притом только один корень. Этим корнем и является
Joga b. Следовательно, log„d в данном случае определен.
Покажем теперь, что если b < 0, то выражение loge Ь не оп-
ределено.
Действительно, если бы это выражение имело смысл, то оно
давало бы корень уравнения (2); в таком случае должно было бы
выполняться равенство
a'oga * = fe.
На самом же деле это равенство не выполняется, поскольку ле-
вая его часть представляет собой положительное, а правая —
отрицательное число или нуль.
Итак, выражение loga6 (а > 0, а 1) определено для всех
положительных значений 6, но не определено ни для какого от-
рицательного значения Ь, ни для b = 0. А это и означает, что
областью определения функции у = loge х является множество
всех положительных чисел.
1-е свойство логарифмической функции доказано. Геометри-
ческая интерпретация этого свойства заключается в том, что гра-
фик функции у = logax целиком расположен в правой полуплос-
кости, которая соответствует только положительным значени-
ям х (см. рис. 250 и 251).
Свойство 2. Областью изменения логарифмической
функции служит множество всех чисел.
Это означает, что выражение \ogax при различных значениях х
может принимать любые числовые значения.
Пусть Ь — произвольное действительное число. Покажем, что
существует число х, которое удовлетворяет условию
k)ga х = b. (3)
Тем самым и будет доказано свойство 2.
84
Соотношение (3) означает то же самое, что и соотношение
аь — к.
Число а — положительное. А степень любого положительного
числа с произвольным показателем всегда определена. Поэтому,
выбрав в качестве искомого значения х число аь, мы и удовле-
творим условию (3).
Свойство 3. При а> 1 логарифмическая функция
у = log„ х является монотонно возрастающей, а при
О < а < 1 — монотонно убывающей.
Пусть а > 1 и х2 > xt. Докажем, что
loge х2 > loge х(.
Для доказательства предположим противное: log„x2 < loga xt
или logex2 = logeXi. При a > 1 показательная функция у = а*
монотонно возрастает. Поэтому из условия logax2 <. Iognxt вы-
текает, что a’°gax« <z a,0Sax>. Но alosax« = х2, а'°?ах> = х,. Следова-
тельно, х2 < Хр А это противоречит условию, согласно которому
х2> Хр К противоречию приводит и другое предположение: logaxt=
= logax2. В этом случае должно было бы быть = alV>,
или Xi = х2. Остается признать, что
> loga*i-
Тем самым мы доказали, что при а > 1 функция у => logax яв-
ляется монотонно возрастающей.
Случай, когда а<1, предлагаем учащимся рассмотреть
самостоятельно.
3-е свойство логарифмической функции допускает простую
геометрическую интерпретацию. При а > 1 график функции у =>
= logax с ростом х все выше и выше поднимается (см. рис. 250),
а при а <. 1 он с ростом х все ниже и ниже опускается (см.
рис. 251).
Следствие. Если логарифмы двух чисел по одному и
тому же положительному основанию, отличному от 1,
равны, то равны и сами эти числа.
Другими словами, из условия
logax = logay (a > 0, a =/= 1)
вытекает, что
х = у.
Действительно, если бы одно из чисел х и у было больше дру-
гого, то в силу монотонности логарифмической функции одно из
чисел logax и logay было бы больше другого. Но это не так. Следо-
вательно, х = у.
85
Свойство 4. При х = 1 логарифмическая функция
у = logax принимает значение, равное нулю.
Графически это означает, что независимо от а кривая у =
= loga х пересекается с осью х в точке с абсциссой х = 1 (см.
рис. 250 и 251).
Для доказательства 4-го свойства достаточно заметить, что
при любом положительном а
а° = 1.
Поэтому logal = 0.
Свойство 5. Пусть а>1. Тогда при х>\ функция
У = logo* принимает положительные, а при 0 < 1 —
отрицательные значения.
Если же 0 < а < 1, то, наоборот, при х > 1 функция
у = logax принимает отрицательные, а при 0<х < 1 —
положительные значения.
Это свойство логарифмической функции также допускает прос-
тую графическую интерпретацию. Пусть, например, а > 1. Тог-
да та часть кривой у = logax, которая соответствует значени-
ям х > 1, располагается выше оси х, а та часть этой кривой, ко-
торая соответствует значениям 0<х<1, находится ниже оси х
(см. рис. 250). Аналогично может быть интерпретирован и случай,
когда а< 1 (рис. 251).
5-е свойство логарифмической функции является простым
следствием 3-го и 4-го свойств. Для определенности рассмотрим
случай, когда а > 1. Тогда по 3-му свойству функция у = logax
будет монотонно возрастающей. Поэтому если х > 1, то loga х >
> logal. Но по 4-му свойству loga 1=0. Следовательно, при
х > 1 loga х > 0. При х < 1 logax < loga 1, то есть logax < 0.
Аналогично может быть рассмотрен и случай, когда а < 1.
Учащимся предлагается разобрать его самостоятельно.
К рассмотренным пяти свойствам логарифмической функции
мы без доказательства добавим еще одно свойство, справедливость
которого наглядно отражается на рисунках 250 и 251.
Свойство 6. Если а > 1, то при х-> 0 значения
функции у= \ogax неограниченно убывают (у-*—<х>). Если
0 < a<z 1, то при х->-0 значения функции у = log„x не-
ограниченно возрастают (у-+оо).
У пражнения
1390. Найти области определения следующих функций:
а) у = log2 (1 + х);
6) у = log>_ (х2 + 1);
в) У = logio (4 + х2);
г) У = log5 (—х);
Д) У = log7 | х |;
е) у = log3 (х2 + х — 2);
ж) У = log0,5 <5х — х2 — 6);
з) у = log6 (х2 + х + 1).
86
1391. Для каких значений х в интервале 0 < х < 2л определе-
ны выражения:
a) log8 (sin х); в) log4 (tg х);
б) log3 (cos х); г) log5 (ctg х)?
1392. Что вы можете сказать о наибольших и наименьших
значениях функций:
а) У = log2 х; б) у = | log2 х | ?
1393. На основании какого свойства логарифмической функ-
ции можно утверждать, что
a) log10 5 > log10 4; б) log0>1 5 < logo,* 4?
1394. Какое число больше:
a) log25 или log2 6; в) log, 2 или log, 4;
з" з~
б) log51 или log5l; г) log, 4 или log, Ъ
х и — D —• О
1395. Решить относительно х неравенства:
a) log2x> log23;
б) logsx2> log. 4;
в) log±x> log±2;
3 3
Г) logj_ (Зх) < log^6;
Д) logic (*2 — 1) > logic (4x + 4);
e) logo.i (1 —x2) > logo(1 (2x + 2).
1396. Что можно сказать о числе а, если
a) log.,7 > logo 6; в) log,, 1 < loga
О £
б) logo 5 < logo 4;
0 logo 5 > О?
1397. Что можно сказать о числе а, если при любых значе-
ниях х
loge (х2 + 1) > loga *?
1398. Между какими последовательными целыми числами за-
ключены логарифмы:
a) log2 5; б) loga 8; в) logj 7; г) logj_ 9?
3 2
1399. Какие из данных чисел являются положительными и
какие отрицательными:
a) log25; в) log^ 5; д) log71; ж) log„4;
2* З"
б) log2^; г) log, 1; е) logn3; з) 1о§л 4?
3 12 Г
87
Логарифм произведения и частного
6 183
Теорема 1. Логарифм произведения двух положи-
тельных чисел равен сумме их логарифмов; точнее, если
числа а, х и у положительны и а =^= 1, то
loga (ху) = loga X + logay. (1)
Для доказательства этого тождества достаточно убедиться в
том, что
flloga(x0 =а^ах+}°еаУ. (2)
(Если степени одного и того же положительного числа, отличного
от 1, равны, то равны и показатели этих степеней.) Справедливость
формулы (2) установить очень просто, если воспользоваться опре-
делением логарифма. Имеем:
a^a^=Xyt
aWga x+logai, = aloga х . у = x . y
Отсюда вытекает формула (2), а стало быть, и формула (1).
Примеры.
1) log3 15 = log3 (3 • 5) = log3 3 + log3 5 = 1 4- log3 5.
2) Iog10 2 4- log10 5 = logjo (2 - 5) = log10 10 = 1.
Если числа x и у отрицательны, то формула (1) теряет смысл.
Например, нельзя писать
log2 К-8) • (-4) 1 = log2 (—8) 4- log, (-4),
поскольку выражения log2 (—8) и log, (—4) вообще не определе-
ны (логарифмическая функция у — log2 х определена лишь для
положительных значений аргумента х).
Теорема 1 справедлива не только для двух, но и для произволь-
ного числа сомножителей, то есть для любого натурального k и
любых положительных чисел х^, х2, .... xk:
logfl(*i • х2 • х3 • ... • xh) = logaxt 4- logex2 4- togax3 4-... 4- togaxft.
Теорема 2. Логарифм частного двух положи-
тельных чисел равен разности логарифмов делимого
и делителя.
Другими словами, если числа а, х и у положительны и
а 1, то
,Ogo ( у ) = 1<>ga Х ~ ,Og°У' (3)
Доказательство. Формула (3), очевидно, равносиль-
на следующей формуле:
toga у 4-loga У = logo X, (4)
88
которая получается из (3), если выражение logay перенести из
правой части в левую. Поэтому для доказательства формулы (3)
достаточно установить формулу (4). А эта формула легко выво-
дится из формулы (1):
log„ у 4- loga у = loge (у * у) = 1об<Л-
Примеры.
1) log3 у = log3 25 — log316.
2) log2 ЮОО — log2125 = log2 = log2 8 = 3.
Следствие из теоремы 2. Поскольку loga 1 = 0, то
logQ -j- = loga 1 — logQ b = — log,, b.
0
Таким образом,
iog(14=—iog(1
Логарифмы двух взаимно обратных чисел по одному
и тому же основанию отличаются друг от друга
только знаком.
Примеры.
log3 9 = — log31; log5 -h = — log5125
У J zb
и T. Д.
Упражнения
1400. Вычислить:
1) log62 + log63; 6) logi2 4 + logi2 36;
2) log2 3 -J- log2 4; 7) log5100 — log5 4;
О
3) log37 — 10g3l; 8) log64 + loge 9;
4) log10 40 4- logJ0 25; 9) logc 14- log6 1;
5) log100,18 — log10 180; 10) log0,i50 — log0>i0,5.
J401. Зная, что log102 « 0,3010, log103 « 0,4771, log105 « 0,6990,
найти логарифмы следующих чисел по основанию 10:
6; 15; -; 20; 1.
6 30
1402. Найти log102 и log105, если известно, что произведение
этих логарифмов приближенно равно 0,2104.
1403. Найти log2 (tg ф) и log2 (ctg ф), если известно, что
log2 (sin ф) « —0,1919; log2 (cos ф) « —0,1157.
89
1404. При каких значениях х выполняется равенство
log3 L(x + 1) (х — 1)] = log3(x + 1) + log3(x — 1)?
1405. При каких значениях х выполняется равенство
log, 2 = log, (х2 + 1) - log, (х« - Зх + 2)?
—- X ОХ -4- Z —
3 ’ 3 3
1406. На сколько log2(100a) больше log2-j-—?
1407. Как нужно изменить число, чтобы его логарифм изме-
нил знак на противоположный?
Логарифм степени и корня § 184
Теорема 1. Логарифм степени положительного
числа равен произведению показателя этой степени на
логарифм ее основания.
Другими словами, если а и х положительны и а =/= 1, то для
любого действительного числа k
logaxft = k\og(lx. (1)
Для доказательства этой формулы достаточно показать, что
а^а *k = ak (2)
Имеем:
, k
а*еа* * * * * * * * * х = хк,
ак^ах = (а^аху=Х\
Отсюда вытекает справедливость формулы (2), а стало быть,
и (1).
Заметим, что если число k является натуральным (k = п), то
формула (1) является частным случаем формулы
logfl(%i • х2 • ... • хп) = logax, + logax2 + ... + logaxn,
доказанной еще в предыдущем параграфе. Действительно, пола-
гая в этой формуле
х, = х2 = ... = хп = х,
получаем:
logaxn = п logax.
Примеры.
1) log325 = log352 = 2 log35;
2) log32^ = /3 log32.
При отрицательных значениях х формула (1) теряет смысл.
Например, нельзя писать log2 (—4)2 = 21og2 (—4), поскольку
90
выражение log2 (—4) не определено. Заметим, что выражение,
стоящее в левой части этой формулы, имеет смысл:
log2 ( —4)2 = log2 16 = 4.
Вообще, если число х отрицательно, то выражение logox2* опре-
делено, поскольку х2* > 0. Выражение же logex в этом случае
не имеет смысла. Поэтому писать
log^j х2А = 2k logax
нельзя. Однако можно писать
logfl х2* = 26 log,, | х | . (3)
Эта формула легко получается из (1), если учесть, что
Х2А = I X I 2*.
Например,
log3 ( —З)4 = 4 log31 — 3 | = 4 log3 3 = 4.
Теорема 2. Логарифм корня из положительного
числа равен логарифму подкоренного выражения, делен-
ному на показатель корня.
Другими словами, если числа а и х положительны, а #= 1 и
п — натуральное число, то
=- loge*.
п
£
Действительно, /х = х'*. Поэтому по теореме 1
£
logo Л = loga^" = - loga-X.
п
Примеры.
1) log,/8 = 1 log,8; 2) log, ^27 = | log, 27.
У пражнения
1408. Как изменится логарифм числа, если, не изменяя осно-
вания:
а) возвести число в квадрат;
б) извлечь из числа квадратный корень?
1409. Как изменится разность log2 а — log2 b, если числа а и Ь
заменить соответственно на:
а) а3 и 63; б) За и 3d?
1410. Зная, что log102 « 0,3010; log10 3 « 0,4771, найти лога-
рифмы по основанию 10 чисел:
8; 9; ^2; ^6; 0,5;
91
1411. Доказать, что логарифмы последовательных членов
геометрической прогрессии образуют арифметическую про-
грессию.
1412. Отличаются ли друг от друга функции
у = log3x2 и у = 2 log3 х?
Построить графики этих функций.
1413. Найти ошибку в следующих преобразованиях:
log2 4 = ,0&4’
О о
2 log.
( 1 \2 . 1 .
(з/ > 3’
1 _1^
9^3'
Переход от одного основания логарифмов к другому §185
Иногда оказывается полезным от логарифмов по одному ос-
нованию (например, а) перейти к логарифмам по другому осно-
ванию (например, с). В этом случае пользуются следующей фор-
мулой:
= (1)
При этом предполагается, что а, b и с — положительные числа,
причем а и с отличны от единицы.
Пусть, например, нам известно, что log10 2 ~ 0,3010; log10 3 ~
« 0,4771. Требуется найти log2 3. По формуле (1)
Iog23 = 1 58.
62 log,0 2 0,3010
Для доказательства формулы (1) воспользуемся основным
логарифмическим тождеством
а'°е« ь = Ь.
Если положительные числа равны, то, очевидно, равны и их лога-
рифмы по одному и тому же основанию с. Поэтому
1оаДа,о’а ь) = log. 6.
Но по теореме о логарифме степени
log.(a'°3a 6) = log. 6 • log. a.
92
Следовательно,
loga& • log,а = log,6,
откуда вытекает формула (1).
Если в формуле (1) в качестве с взять Ь, то получим:
= —1—.
log6 a logj а
Итак,
'Ofc »=!-!-• (2)
logd
Примеры.
1 л 1 1
°^32 ~ log., 32 ~ 5
10gi25 5 ~ 10& |25 — у
Упражнения
1414. Зная, что log 1о 2 ~ 0,3010 и log 10 3 « 0,4771, найти:
a) log3 2; б) log3 8; в) log312; г) log12 3.
1415. Доказать, что отношения
lofex н log* 2
tog3 х logA 3
не зависят от х.
1416. Доказать неравенства:
a) log25-h logs2>2; б) log, 4 + log41 < — 2.
7— О
1417. Изменится ли логарифм числа, если это число и основа-
ние логарифма возвести в одну и ту же степень?
Логарифмирование и потенцирование $ 186
Если некоторое выражение составлено из положительных
чисел посредством умножения, деления, возведения в степень и
извлечения корня, то логарифм всего этого выражения легко вы-
разить через логарифмы входящих в него чисел.
Пусть, например,
_ 132/йб
Л — _ •
/67 • 98
Тогда по теореме о логарифме дроби
log.x = log. (132 /140) - log. /67 • 98.
Теорема о логарифме произведения дает:
о ____ о _____
log.(132/140) = log. 132 + log. /140,
log. ^67?98 = log. i/67 + log. j/98.
93
Теперь, используя теоремы о логарифме степени и корня,
получаем:
loga 132-2 lOga 13, l0go /б7 = 1 loga 67,
э
о __ t 5 __ i
logfl/140 - 4 loga 140, loga /98 - 4 loga98.
d о
Таким образом,
loga X - 2 logo 13 + 4 loga 140 - 4 loga 67 - 4 loga 98.
6 DO
Переход от выражения к его логарифму называется логарифми-
рованием этого выражения.
Операция, обратная логарифмированию, называется потен-
цированием. Она заключается в том, что по логарифму некоторого
выражения восстанавливается само выражение. Поясним это на
следующем примере. Пусть
loga х - 2 loga 10 — 4 loga 7 — 3 ,Oga 3 + V ,Ogo 19‘
Z О
Прежде всего, используя теоремы о логарифме степени и корня,
можно записать:
2 log. 10 = log, 10* = log, 100,
ylog,7 = log.(7)^ = log./7;
3 log, 3 = log, 3» = log, 27,
1 log, 19= log, (19? = loggia
После этого loga x можно записать в виде logaх = 1°§д 160 —
— loga /7 — loga 27 + log„ •/19. Теперь, используя теоремы
о логарифме произведения и частного, получим:
log.* = (log, 100 + log, у 19) - (log,/r + log. 27^=
= log. (100 ^19) - log. (KT 27) = log.
27 У 7
Итак,
i „ u 100^19
logaX = loga ----------------------X—.
27V 7
Но если логарифмы двух положительных чисел по одному и тому
же основанию равны, то равны и сами эти числа. Поэтому
100/19
ЛС -— .
27/7
Упражнения
Прологарифмировать по основанию 10 следующие выражения
(№ 1418—1422):
94
1418. a) x = За7; в) х = а2 ab\
б) х = 15а363с7; г) х = a yf ab~.
б)
1420. а)
б)
1421. а)
б)
1422. а)
б)
В задачах № 1423—1426 найти х из данных уравнений:
1423.
а) 1о& х = loga 2 + loga 3; в) loge х = 2 iogd 8 — 4 loge 2;
б) loga х = loga 2 — loga 4; г) loga x = 3 loga 2 + 2 loge 2.
1424. a) log3x = 1 log^;
«3
6) log3x = -| log38 + log316;
в) log5x = A!£M Jog»?.
' 65 5 10
1425. a) log2 x = log2 a + n log2 (a + b) — - log2 (a — b);
n
;3& — |10g3a +
6) log3x =
B) log5x =
2
9 Г 1
— log5(a + &) + - 21og5a+ -log56 —
□ L
— 4(log5a — logs 6) — logs ° •
О
95
1426. a) 10& x = log0 sin Ф +11о& tg <p -1 log„ cos <p;
о о о
6) log2х = 1 +llog2tg^- —l|og2(l 4-tg2y 4-
Z Z Z \ Z J
+ |log2cos^.
Целая и дробная части числа
§ 187
Целой частью числа а называется наибольшее целое число, не
превосходящее а.
Целая часть числа а обозначается [а]. Например,(2,31 = 2;
10,165] =0; [5] = 5. Целая часть числа—4,7 равна—5. Ошибочно
было бы считать, что [ —4,7 ] = —4. По определению целая часть
числа а не должна превосходить а, но —4 > —4,7.
Аналогично
[ —5,791 = —6,
I —0,142] - —1,
( -л] = [ —3,14...] ~ —4.
Разность между числом а и его целой частью [а ] называется
дробной частью этого числа и обозначается {а}:
{а} = а — ]а ].
Например,
{2,3} = 2,3 — 2 = 0,3;
{0,165} = 0,165 — 0 =0,165;
{—5,79} = —5,79 — ( — 6) = 0,21;
{—0,142} = —0,142 — ( — 1) = 0,858.
Очевидно, что целая часть числа а может быть любым целым
числом: положительным, отрицательным или нулем. Дробная же
часть числа а всегда неотрицательна и меньше 1.
Любое действительное число а можно представить в виде суммы
его целой и дробной частей:
а = (a ] 4- {а}.
Например,
2,3 =2 4- 0,3;
0,165 = 0 4- 0,165;
—5,79 = —6 4- 0,21;
—0,142 =—1 4- 0,858.
Упражнения
1427. Данные числа представить в виде суммы их целых и
дробных частей:
2,01; л; 5; —2,37; —6,07; —7; —л.
96
1428. а) Изменится ли дробная часть числа, если к нему при-
бавить целое число?
б) Изменится ли целая часть числа, если к нему прибавить
правильную дробь?
Десятичные логарифмы и их свойства
§ 188
За основание логарифмов часто принимают число 10. Лога-
рифмы чисел по основанию 10 называются десятичными. Для
обозначения десятичных логарифмов обычно используют знак 1g,
а не log; при этом число 10, указывающее основание, не пишут.
Например, вместо logw105 пишут просто: 1g 105; вместо log10 2
пишут 1g 2 и т. д.
Десятичным логарифмам присущи все те свойства, которыми
обладают логарифмы при основании, большем 1. Например, де-
сятичные логарифмы определены только для положительных чи-
сел. Десятичные логарифмы чисел, больших 1, положительны, а
чисел, меньших 1, отрицательны; из двух положительных чисел
большему соответствует и больший десятичный логарифм и т. д.
Но, кроме того, десятичные логарифмы обладают и рядом специ-
фических свойств, которыми и объясняется, почему в качестве
основания логарифмов удобно выбирать именно число 10.
Прежде чем рассмотреть эти свойства, введем следующее
определение.
Целая часть десятичного логарифма числа а называется харак-
теристикой, а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а обозначается
как [1g al, а мантисса — как {1g а}.
Известно, например, что 1g 2 « 0,3010. Поэтому
[1g 21 = 0, {1g 2} « 0,3010.
Известно* также, что 1g 543,1 ~ 2,7349. Следовательно,
[1g 543,1 ] = 2, {1g 543,1} « 0,7349.
Точно так же из равенства 1g 0,005 « —2,3010 заключаем, что
[1g 0,0051 = —3, {1g 0,005} = 0,6990.
Теперь перейдем к рассмотрению свойств десятичных лога-
рифмов.
Свойство 1. Десятичный логарифм целого положи-
тельного числа, изображенного единицей с последую-
щими нулями, есть целое положительное число, равное
количеству нулей в записи данного числа.
♦ В дальнейшем мы научимся находить десятичные логарифмы положитель-
ных чисел по таблицам.
4 Заказ 1159
97
Например, 1g 1000 = 3,
lg 1 000 000 = 6.
Вообще, если
а = 1000 ... О,
/1
то а = 10" и потому
lg а = 1g 10" = п 1g 10 = п.
Свойство 2. Десятичный логарифм положительной
десятичной дроби, изображенной единицей с предшест-
вующими нулями, равен — п, где п — число нулей в за-
писи этого числа, считая и нуль целых.
Например, 1g 0,01 = —2,
1g 0,00001 = —5.
Вообще, если а = 0,000...01, то а == 10~" и потому
lg а = 1g 10~" — п 1g 10 = —п.
Свойство 3. Характеристика десятичного логариф-
ма положительного числа, большего 1, равна количеству
цифр в целой части этого числа без одной.
Примеры. 1) Характеристика логарифма 1g 75,631 равна 1.
Действительно, 10 < 75,631 < 100. Поэтому
1g 10 < 1g 75,631 < lg 100,
или
1 < lg 75,631 < 2.
Значит,
lg 75,631 = 1 + а,
где а — некоторая правильная положительная дробь. Но тогда
11g 75,631 ] = 1,
что и требовалось доказать.
2) Характеристика логарифма 1g 5673,1 равна 3.
Действительно,
1000 < 5673,1 < 10 000.
Поэтому
1g 1000 < 1g 5673,1 < lg 10 000,
или
3 < lg 5673,1 < 4.
Следовательно,
[lg 5673,1 ] = 3.
Вообще, если целая часть положительного числа а, большего
единицы, содержит п цифр, то
10"-‘ < а < 10".
98
Поэтому
1g 10я-1 < Ig а < 1g 10я,
или
п — 1 < 1g а < п.
Следовательно,
11g а] — п — 1.
Свойство 4. Характеристика десятичного логариф-
ма положительной десятичной дроби, меньшей 1> равна
— п, где п — число нулей в данной десятичной дроби
перед первой значащей цифрой, считая и нуль целых.
Примеры. 1) Характеристика логарифма 1g 0,0015 рав-
на —3.
Действительно,
0,001 <0,0015 <0,01.
Поэтому
1g 0,001 < 1g 0,0015 < 1g 0,01.
или
— 3 < lg 0,0015 < —2.
Значит,
lg 0,0015 = — 3 + а,
где а — некоторая правильная положительная дробь. Но в таком
случае
11g 0,0015] = —3.
2) Характеристика логарифма 1g 0,6 равна —1. Действительно,
0,1 <0,6< 1.
Поэтому
1g 0,1 < 1g 0,6 < lg 1,
или
—1 < lg 0,6 < 0.
Следовательно,
lg 0,6 = —14- а,
где а — некоторая правильная положительная дробь. Но в таком
случае
[1g 0,6] = -1.
Вообще, если первой значащей цифре правильной десятичной
дроби а предшествует п нулей (считая в том числе и нуль це-
лых), то
0,000...001 <а< 0,00...01.
п. п— 1
Поэтому
IgO.OOO... 001 < lgа < IgO.OO ...0,1,
п п—1
ИЛИ
—л < 1g а < — (л — 1).
99
Следовательно,
[lg л I = —п.
Свойство 5. При умножении числа на 10" десятич-
ный логарифм его увеличивается на п.
Действительно, по теореме о логарифме произведения
1g (а • 10") = 1g а + 1g 10" = 1g а + п.
Например,
1g (579,13 • 100) = 1g 579,13 + 2;
lg (16 • 1000) = 1g 16 + 3.
Перенос запятой в положительной десятичной дроби на п зна-
ков вправо равносилен умножению этой дроби на 10". Поэтому
при переносе запятой в положительной десятичной дро-
би на п знаков вправо десятичный логарифм увеличи-
вается на п.
Свойство 6. При делении числа на 10" десятичный
логарифм уменьшается на п.
Например, lg = 1g 1,57 — 3;
lg = 1g 0,63 - 2.
При переносе запятой в положительной десятичной
дроби на п знаков влево десятичный логарифм умень-
шается на п.
Например, 1g 0,3567 = 1g 35,67 — 2;
lg 0,00054 = lg 0,54 — 3.
Учащимся предлагается самостоятельно доказать эти утверж-
дения.
Есе доказанные до сих пор свойства десятичных логарифмов
относились к их характеристике. Теперь обратимся к мантиссе
десятичных логарифмов.
Свойство?.
ложительного
этого числа на
Действительно,
и отрицательном)
1g (а • 10") = 1g а 4- 1g 10" = lg а + п.
Но дробная часть числа не изменяется при прибавлении к нему
целого числа.
Перенос запятой в десятичной дроби вправо или влево равно-
силен умножению этой дроби на степень числа 10 с целым по-
казателем п (положительным или отрицательным). Поэтому при
переносе запятой в положительной десятичной дроби
влево или вправо мантисса десятичного логарифма этой
дроби не изменяется.
Например, (1g 0,0067} = {1g 0,67} = {lg 0,0000067}.
Мантисса десятичного логарифма по-
числа не изменяется при умножении
10" с любым целым показателем п.
при любом целом п (как положительном, так
100
Упражнения
1429. (Ус т н о.) Найти десятичные логарифмы чисел:
1; 10; 100; 1000; 10 000;
0,1; 0,01; 0,001; 0,0001; 0,00001.
1430. (Усти о.) Найти характеристики десятичных логариф-
мов чисел:
2,00; 57,38; 632,70; 3402,99;
0,17; 0,99; 0,023; 0,0100; 0,0003.
1431. Известно, что 1g 2 « 0,3010, 1g 3 « 0,4771.
Найдите характеристики и мантиссы следующих логарифмов:
a)lg6; б) 1g 15; в) 1g 32; г) 1g 30; д) Igl.
Таблицы десятичных логарифмов § 189
Для нахождения десятичных логарифмов составлены специаль-
ные таблицы. По ним, зная число х, можно с той или иной точно-
стью определить 1g х. Мы будем пользоваться «Четырехзначными
математическими таблицами» В. М. Брадиса. Они содержат значе-
ния десятичных логарифмов с точностью до 0,0001.
В § 188 было показано, что характеристики десятичных ло-
гарифмов легко находятся без таблиц. Поэтому в таблицах при-
ведены лишь мантиссы логарифмов. Рассмотрим несколько при-
меров нахождения логарифмов чисел по таблицам.
1) Логарифмы трехзначных целых чисел
Пусть, например, требуется найти 1g 456. Характеристика
этого логарифма равна 2. В таблице XIII на страницах 65—67
находим число, стоящее на пересечении строки с пометкой 45 и
столбца с пометкой 6. Это число 6590. Оно указывает на то, что
мантисса логарифма числа 456 приближенно равна 0,6590. Значит,
1g 456 « 2,6590. Аналогично находим 1g 238 ~ 2,3766, 1g 850 «
» 2,9294 и т. д.
2) Логарифмы одно- и двузначных целых чисел
Пусть, например, нужно найти 1g 5. Если число умножить на
100, то мантисса его десятичного логарифма не изменится. Поэтому
мантисса логарифма однозначного числа 5 равна мантиссе трех-
зиачного числа 500. По таблицам эта мантисса равна 0,6990. По-
скольку характеристика логарифма числа 5 равна 0, то 1g 5 ~
« 0,6990. Аналогично найдем 1g 3 « 0,4771 и т. д.
Если нужно найти логарифм числа 13, то для определения его
мантиссы достаточно число 13 умножить на 10. Мантисса логариф-
ма числа 130 равна 0,1139. Поскольку характеристика логарифма
числа 13 равна 1, то 1g 13 ~ 1,1139. Аналогично найдем 1g 75 ~
« 1,8751, 1g 64 « 1,8062 и т. д.
3) Логарифмы четырехзначных чисел
Вы, наверное, уже обратили внимание на то, что в правой ча-
сти таблицы XIII расположены числа, напоминающие поправки
101
к таблицам тригонометрических функций. Эта часть таблицы со-
держит поправки на четвертую цифру, что дает возможность вы-
числять логарифмы четырехзначных чисел. Пусть, например,
нужно найти 1g 2587. По таблице XIII найдем мантиссу трехзнач-
ного числа 258 и прибавим к ней поправку на число 7. В результа-
те мы получим мантиссу логарифма четырехзначного числа 2587.
Мантисса 1g 258 приближенно равна 0,4116, а поправка на 7 равна
0,0012 (в таблице вместо 0,0012 пишут просто 12). Поэтому мантис-
са логарифма числа 2587 равна:
,0,4116
0,0012
0,4128
Учитывая, что характеристика этого логарифма равна 3, получа-
ем окончательно 1g 2587 « 3,4128.
Аналогично
1g 9625 3.9832 1g 7718 = 3,8871
4- 0,0002 4- 0,0004
3,9834 3,8875
4) Логарифмы целых чисел, содержащих более четырех цифр
Если целое число содержит более четырех цифр, то его округ-
ляют так, чтобы все цифры, начиная с пятой, были нулями. Если
при этом пятая цифра меньше 5, то первые четыре цифры не изме-
няются. Если же пятая цифра больше или равна 5, то четвертую
цифру увеличивают на 1.
Например, 573 528 « 573 500, 36 289 « 36 290, 19 998 « 20 000,
7 425 538 « 7 426 000. Логарифмы исходных чисел приближенно
равны логарифмам чисел, полученных в результате округления.
Мантиссы логарифмов этих чисел легко найти по таблицам. На-
пример, мантисса логарифма числа 573 500 равна мантиссе логариф-
ма числа 5735 (при делении числа на 100 мантисса его десятичного
логарифма не изменяется). По таблицам находим эту мантиссу:
0,7586. Учитывая, что 1g 573 528 имеет характеристику 5, получаем:
1g 573 528 » 5,7586.
Аналогично получаем: мантисса логарифма числа 36 290 равна
мантиссе логарифма числа 3629, то есть 0,5598. Поэтому
1g 36 289 4,5598.
5) Логарифмы дробных чисел
Пусть, например, нужно найти 1g 803,24. Характеристика этого
логарифма равна 2 (целая часть числа 803,24 содержит 3
цифры). Мантисса этого логарифма равна мантиссе логарифма
числа 80 324 или приближенно мантиссе логарифма числа 80 320.
Из таблиц находим эту мантиссу: 0,9048. Значит, 1g 803,24
« 2,9048. Аналогично характеристика логарифма 0,0053 равна —3
102
(дробь 0,0053 перед первой значащей цифрой имеет три нуля,
включая нуль целых). Мантисса этого логарифма равна мантиссе
логарифма числа 530. Из таблиц находим эту мантиссу: 0,7243.
Следовательно, 1g 0,0053 ~ —3 -f- 0,7243 = —2,2757.
Упражнения
1432. Используя таблицы В. М. Брадиса, найти десятичные
логарифмы следующих чисел:
257; 301; 25; 99; 2; 3; 3796; 9999: 10 325;
267 398; 37 990 653; 263,56; 35,074; 2,9345; 0,002863; 0,000056.
1433. Используя таблицы В. М. Брадиса, вычислить:
log3 5; log» 17; logo,05 0,004.
Таблицы антилогарифмов§ 190
По таблице XIII можно находить не только логарифмы чисел,
но и числа по их логарифмам. Однако еще проще эта задача решает-
ся с помощью таблицы XIV (см. таблицы В. М. Брадиса, стр. 68—
70). Рассмотрим несколько примеров.
1) Найти число, логарифм которого равен 2,345. Не обращая
внимания на характеристику 2 этого логарифма, найдем число,
мантисса логарифма которого равна 0,345. Для этого в таблице XIV
отыскиваем строку с пометкой 34 и столбец с пометкой 5. На их
пересечении стоит число 2213. Это и есть (приближенно) значащая
часть искомого числа. Поскольку характеристика логарифма рав-
на 2, то целая часть искомого числа содержит три цифры. Зна-
чит, искомое число приближенно равно 221,3.
2) Решить уравнение 1g х = 0,7823. В таблице XIV отыски-
ваем число, стоящее на пересечении строки с пометкой 78 и столб-
ца с пометкой 2. Им оказывается число 6053. К нему прибавля-
ем поправку на 3, равную 4. В результате получаем 6057. Это
и есть значащая часть числа. Поскольку характеристика лога-
рифма числа х равна 0, целая часть числа х содержит одну циф-
ру. Поэтому х » 6,057.
3) Найти число, логарифм которого равен — 3,0576. Прежде
всего найдем характеристику и мантиссу этого логарифма:
—3,0576 = —4 + 0,9424. Следовательно, характеристика равна
—4, а мантисса 0,9424. Такой логарифм принято записывать в
виде 4,9424. Черта над цифрой 4 указывает, что характеристика
логарифма равна —4, а не 4. Теперь, не обращая внимания на ха-
рактеристику 4, найдем число, соответствующее мантиссе 0,9424.
Это число 8758. Поскольку характеристика логарифма искомого
числа равна —4, то это искомое число записывается в виде десятич-
ной дроби с четырьмя нулями перед первой значащей цифрой:
0,0008758.
ЮЗ
Упражнение
1434. Пользуясь таблицей антилогарифмов, решить следующие
уравнения:
a) 1g х = 0,3625; г) 1g х = —2,5440;
б) 1g х = 4,0002; д) 1g х = —3,0257;
в) 1g х = —0,3928; е) 1g х = —1,9994.
Таблицы десятичных логарифмов
тригонометрических функции§ 191
Логарифмы синусов малых углов (от 0° до 14°) приведены
В. М. Брадисом в таблице XV на страницах 71—72. Например,
чтобы найти
lg sin 8°47',
отыскиваем в этой таблице строку с левой пометкой 8°40' и
столбец с верхней пометкой 7'. На их пересечении стоит
число 1,1838 (характеристика 1 указана выше на пересечении
строки с пометкой 8°00' и столбца с пометкой О'). Значит,
Igsin 8°47' «1,1838 (или —1 + 0,1838 = —0,8162).
По таблице XV можно находить и логарифмы косинусов
углов от 76° до 90°. Пусть, например, нужно найти lg cos 77°34';
на пересечении строки с правой пометкой 77°30' и столбца
с нижней пометкой 4'стоит число 1,3331. Значит,
lg cos 77°34'«1,3331 (или —0,6669).
Для нахождения логарифмов синусов углов от 14° до 90°, а
также косинусов углов от 0° до 76° нужно пользоваться табли-
цей XVI, приведенной В. М. Брадисом на страницах 73—74. Здесь
углы чередуются через каждые 6'. Поэтому иногда приходится
учитывать поправки. Правило учета поправок таково:
если данный угол больше угла, приведенного в табли-
це, то поправка прибавляется для синуса и отнимает-
ся для косинуса; если же данный угол меньше угла,
приведенного в таблице, то, наоборот, поправка прибав-
ляется для косинуса и отнимается для синуса.
Примеры. 1) Найти Igsin 43°36'. В таблице XVI на пе-
ресечении строки с левой пометкой 43° и верхней пометкой 36'
стоит число 1,8386. Значит, Igsin 43°36' « 1,8386 (или —0,1614).
2) Найти Igsin 65°32'. На пересечении строки с левой помет,
кой 65° и верхней пометкой 30' (стр. 74) стоит число 1,9590. К это-
му числу нужно прибавить 1 — поправку на 2'. В результате по-
лучим: Igsin 65°32' « 1,9591 (или —0,0409).
3) Найти lgcos 1Г54'. На пересечении строки с правой по-
меткой 11° и нижней пометкой 54' стоит число 1,9906. Поэтому
lg cos 1Г54' « Г,9906 (или —0,0094).
104
4) Найти Igcos 5Г20'. Сначала находим Igcos 51°18', а затем
отнимаем от него поправку на 2'; Igcos 5Г18' ~ 1,7960; поправка
на 2' равна 3. Поэтому Igcos 5Г20' « 1,7957 (или —0,2043).
Логарифмы тангенсов углов от 0° до 14° (а также котанген-
сов углов от 76° до 90°) приведены в таблице XVII на страни-
цах 75—76. Логарифмы тангенсов и котангенсов углов от 14° до
76° находятся по таблице XVIII (стр. 77—78). Логарифмы тан-
генсов углов от 76° до 90°, а также котангенсов углов от 0° до 14°
содержатся в таблице XIX (стр. 79—80). Устройство этих трех
таблиц вполне аналогично устройству описанных выше таблиц
XV и XVI. Поэтому подробно на них мы останавливаться не будем.
Отметим только, что поправки учитываются для логарифмов
тангенсов углов так же, как и для логарифмов синусов углов,
а для логарифмов котангенсов углов — так же, как и для лога-
рифмов косинусов углов.
Упражнения
1435. Пользуясь таблицами логарифмов тригонометрических
функций, найти десятичные логарифмы следующих величин:
a) sin 12°17'; sin 3°29'; cos 77°47'; cos 88°19';
б) sin 48°38'; sin 60°46'; sin 85°57';
cos 4°ЗГ; cos 49°52'; cos 74°33';
в) tg3°49'; tg 13°23'; ctg80°29'; ctg 89°35';
г) tg 45°38'; tg 67°10'; tg 74°39'; ctg 31°2';
ctg 56°46'; ctg 7Г27';
д) tg 83°39'; tg 89°29'; ctg 0°17'; ctg 9°36'.
1436. Дать обоснование правила учета поправок при нахожде-
нии по таблицам логарифмов тригонометрических функций.
Действия над логарифмами
§ 192
Сложение логарифмов в особом пояснении не нуждается.
Поэтому мы ограничимся лишь приведением двух примеров:
3,0607 4,0380
+£,8701 +5,9927
3,0056 2,0449
1,9364 6,0756
Вычитание логарифмов целесообразно сводить к сложению.
Для этого логарифмы, перед которыми стоит знак —, преобра-
зуют так, чтобы этот знак сменился на знак +. Например,
—£5604 = —8 + 0,4396 = 8,4396;
—5,2967 = 5 — 0,2967 = 4,7033.
105
Так, выражение 2,0073 — 7,5604 — 5,2967 преобразуется в сумму:
2,0073
+8,4396
4,7033
5,1502
Умножение логарифма на число. Сначала умножаем на
число характеристику, а затем мантиссу логарифма и полученные
результаты складываем. Например,
5,6315 • 4 = — 20 + 2,5260 = 18,5260;
1,0501 • — 3 + 0,0751 = 3,0751;
3,7500 • (—0,5) = 1,5 — 0,3750 = 1,1250.
Деление логарифма на число. Если характеристика логарифма
неотрицательна, то деление его на число производится обычным
способом. Например, 8,024 : 4 = 2,006. Если же характеристика
отрицательна, то возможны два случая.
1) Отрицательная характеристика делится на делитель без
остатка. В этом случае характеристику и мантиссу делим на дели-
тель отдельно. Например,
15,6305 : 5 = 3,1261.
2) Отрицательная характеристика не делится на делитель
без остатка. Тогда прибавляем к ней столько отрицательных
единиц, чтобы полученное число делилось на делитель без остат-
ка; к мантиссе прибавляем столько же положительных единиц.
Например,
15608 : 4 = (—4 + 2,5608) : 4 = Т,6402.
Мы рассмотрели случаи, когда делитель есть целое число. Если
это не так, то предварительно логарифмы нужно представить в
обычном виде. Например,
+7102 : 2,3546 = —3,2898 : 2,3546 « —1,3971 =1,6029.
Деление логарифма на отрицательное число сводится к делению
на положительное число. Например,
3,6409 : ( —4) = — (3,6409 : 4) — (1,4102)=1 — 0,4102= 0,5898.
Упражнения
1437. Выполнить указанные действия над логарифмами:
а) Т.4792 +Т.5706 + 3,0056;
б) 1,0032 + 2,7368 + 3,9263;
в) 0,9329 — 1,2605 — 5,0060,
106
г) 1,0256- —-;
_ \ 3 /
д) 4,4437 • ( —0,2).
б) 3,0280 : -; в) 5,2709 : (— -Y
г) 2,4645 — 4,3839 + _б,0092 — 5,3973;
д) 1,2396 — 0,5974 — 2,9328.
Вычислить с точностью до 0,0001 (№ 1438, 1439):
1438. а) 2,0296 • 0,36;
б) ЗД728 • 5;
в) 7,2894 • 9,8;
1439. а) 2,6302 : 7;
t> \ з/
Примеры вычисления с помощью таблиц
логарифмов § 193
Пример 1. Пусть нужно вычислить
х_ 0.4752^sjn23go22>
tg85°13' |<239Х
Логарифмируя это выражение, получаем:
1g х - 21g0,475 + Igsin 38°22' — lg tg 85° 13' — -Mg239,3.
По таблицам логарифмов находим:
1g 0,475 « Т6767; lg sin 38°22' «7,7929;
lg 239,3 « 2,3790; lg tg 85°13' « 1,0774.
Поэтому
2 lg 0,475 «2 + 1,3534 = 7,3534;
— 1 lg 239,3 « — 0,4758=1,5242;
— Igsin 38c22' 2 ' 1,7929 _ 1,5858^ Yggjg.
3 3 3
— lg tg 85°13' « —1,0774 = 2,9226.
Следовательно,
1,3534
£5242
£,8619
2,9226
Igx^ 3,6621.
Итак, igx « 3,6621. Отсюда, используя таблицу антилога-
рифмов, получаем:
х « 0,004593.
107
Пример 2. Вычислить
х= V |/35 — у^ЗО.
Сплошное логарифмирование здесь невозможно, поскольку под
знаком корня 5-й степени стоит разность. В подобных случаях
вычисления ведут по частям: сначала находят у/35, потом у/ 30,
затем их разность и, наконец, корень 5-й степени из этой
разности.
1g У 35 = - 1g 35 « - • 1,5441 0,3860,
4 4
1/35^2,432,
1g }С/30 = - 1g 30 ♦ 1,4771 0,2462,
6 6
^30^1,763,
//35 — !6/30 « 2,432 — 1,763 = 0,669,
1g ///35- / 30 ~ Ig^'OW = llgO,669^1- Г,8254
Г,9651,
//з5 —у'ЗО « 0,9228.
"Упражнения
Вычислить с помощью таблиц логарифмов (№ 1440—1446):
1440. у 673,8. 1,842 1441 у6/< 2,5914 *Л°’0836 j443 у sin 32°14' ♦ 26,73* у 13,65 • ctg 2948' 1444 cos75°28' У 0,5 V tg2 70°16' • sin — 9
3.89-2 —0,1536 1442. • 0,924* 1445. -^51/2 + /3 —21/5. 1446. ~\/ ь/ Тдоосй 1 1/ tg— . 1 у cos 16 32 + у 1ь 1з
1447. Найти площадь 36,54 см и 59,02 см. треугольника со сторонами 67,28 см,
1448. Найти площадь треугольника со сторонами 238,4 см и
79,3 см, если угол между этими сторонами равен 37°23'.
Натуральные логарифмы
§ 194
Десятичные логарифмы для наших потребностей являются весьма удобны-
ми. Однако при изучении высшей математики более удобными оказываются
логарифмы по основанию е = 2,718281828... (см. § 134, ч. 1). Употребление
108
этих логарифмов позволяет значительно упростить большое количество математи-
ческих формул. Логарифмы по основанию е получаются при решении многих
физических задач и естественным образом входят в математическое описание
некоторых химических, биологических и других процессов. Этим и объясняется
их название «натуральные логарифмы».
Натуральный логарифм числа а обозначается 1п а. Сейчас имеются доста-
точно полные таблицы натуральных логарифмов.
Обоснование действий на логарифмической
линейке § 195
Известные нам свойства логарифмов позволяют довольно
просто обосновать правила действий, выполняемых с помощью
логарифмической линейки. В этом параграфе мы рассмотрим
два простейших действия — умножение и деление. Предварительно
покажем, как с помощью двух простых линеек можно производить
сложение и вычитание чисел.
Каждую из двух одинаковых по длине линеек АВ и CD
разобьем на 20 равных частей и отметим эти части на линейке
АВ у верхнего края, а на линейке CD у нижнего края
(рис. 254).
Пусть к числу 11 нужно прибавить число 5. Отметку 0 на
линейке CD установим над отметкой 11 линейки АВ (рис. 255).
Тогда под отметкой 5 на шкале CD будет находиться отметка
16 на шкале АВ. Эта отметка и показывает сумму чисел
11 и 5.
Теперь предположим, что от 18 нужно отнять 6. Над отметкой
18 на шкале АВ установим отметку 6 на шкале CD (рис. 256).
0 5 10 15 20
А В
С D
0 5 Ю 15 20
_______। .1 ।______
Рис. 254.
С D
0 5 10 15 20
-I---------Г-1-------Н--------Н------------1---------
5 Ю11 15 16 20
А В
Рис. 255.
109
C D
О 5 6 10 15 20
Г I I I I I I I I I I 1 I Г~Г ' I I I I I------'-----------1----------
t 2 3 4 5 6 7 8 9 10 111213 1415 1617181920
A В
Рис. 256.
Тогда под отметкой 0 на шкале CD будет находиться от-
метка 12 на шкале АВ. Эта отметка и показывает разность
чисел 18 и 6.
На этом простом принципе основано устройство логарифмиче-
ской линейки. Только здесь отметки изображают не числа, а
их логарифмы. Как известно, сумма логарифмов двух положи-
тельных чисел равна логарифму их произведения:
1g а 4- lg b = lg (ab),
а разность логарифмов двух положительных чисел — логарифму
их частного:
Iga — lg b= Ig-^-.
Поэтому если на линейках отмечать не сами числа, а их лога-
рифмы, то с помощью двух таких линеек (или шкал) можно будет
легко производить умножение и деление чисел.
Примем длину линейки за единицу. Цифрой 1 отметим на
ней точку, соответствующую числу lg 1 = 0; цифрой 2 — точку,
соответствующую числу 1g 2 ~ 0,3010; цифрой 3 — точку, соот-
ветствующую числу 1g 3 « 0,4771, и т. д. (рис. 257). Правая край-
няя точка будет при этом отмечена числом 10, что соответствует
числу 1g 10 = 1. В результате мы получим шкалу, которая назы-
вается логарифмической шкалой. С помощью двух таких шкал
можно производить умножение и деление чисел.
Пусть, например, нужно умножить 2 на 4. Отметку 1 на
шкале CD устанавливаем над отметкой 2 на шкале АВ (рис. 258).
Под отметкой 4 на шкале CD читаем отметку 8 на шкале АВ.
Эта отметка и показывает произведение чисел 2 и 4.
/ 2 3 4 5 6 7 8 910
1 I 1 I I I I I I
Рис. 257.
ПО
Рис. 258.
В
Рис. 259.
А
Аналогично производится деление. Пусть 9 нужно разделить
на 6. Отметку 6 на шкале CD устанавливаем над отметкой 9 на
шкале АВ (рис. 259). Под отметкой 1 на шкале CD стоит отметка
1,5 на шкале АВ. Эта отметка и дает отношение —.
Основные способы решения показательных
уравнений
§ 196
Показательными уравнениями называются уравнения, содержа-
щие неизвестную величину в показателе степени.
К таким относятся, например, уравнения 3х = 2х-1; 5х2-6—1 = О
и другие.
Показательные уравнения, так же как и тригонометрические,
в отличие от алгебраических (например, линейных, квадратных),
относятся к трансцендентным уравнениям.
Простейшим показательным уравнением является уравнение
ах = &, (1)
где а и Ь — данные положительные числа (а =/= 1), а х — неизвест-
ная величина. Такое уравнение имеет единственный корень х =
= loga6. Более сложные показательные уравнения часто сводятся
либо к алгебраическим уравнениям, либо к уравнениям вида (1).
Рассмотрим основные способы решения показательных урав-
нений на частных примерах.
I. Решить уравнение
5х~в = 515-2Ж.
Ill
Решение подобных уравнений основано на следующем свой-
стве степеней: если две степени одного и того же положитель-
ного числа, отличного от 1, равны, то равны и их показатели.
В данном случае это свойство степеней дает:
х — 6 = 15 — 2х,
откуда х = 7.
Проверка. При х = 7 5х-® = 5, 515-2* = 5. Значит,
х = 7 — корень данного уравнения.
Ответ, х = 7.
Аналогично решается уравнение
Действительно, 49х = (72)x =72х; = (7_1)ж* = 7~х*. Поэтому
72х = 7-х2, откуда 2х = — х2, или хг = 0, х2 = — 2. Проверка по-
казывает, что оба эти значения х удовлетворяют данному
уравнению.
Ответ. Xi = 0; х2 = —2.
По этому же принципу можно решать и показательное урав-
нение ах — Ь, если Ь есть целая степень числа а. Например,
если 3х = 27, то, представив 27 в виде 27 = З3, получаем
3х = З3, откуда х = 3.
II. Иногда путем введения новой неизвестной величины
показательное уравнение сводится к алгебраическому уравнению.
Пусть, например, нужно решить уравнение
4х 4. 2х — 6 = 0.
Обозначим 2х через у. Тогда 4х = (22)* = 2гх = (2х)2 = у2.
Поэтому данное уравнение сводится к квадратному уравнению
у2 + у — 6 = 0,
из которого получаем: ух = 2, у2 = —3. Но у = 2х. Значит, если
только данное уравнение имеет корни, то они должны удовле-
творять либо уравнению 2х = 2, либо уравнению 2х = —3. Первое
из этих уравнений имеет корень х = 1; второе же уравнение
корней не имеет, поскольку выражение 2х не может принимать
отрицательных значений. Итак, мы получили: х = 1.
Проверка. При х = 1
4х 4- 2х — 6 = 4l + 21 — 6 = 0.
Следовательно, х = 1 — корень данного уравнения.
Ответ, х = 1.
III. Решить уравнение
2х = 3х.
112
Разделив обе части данного уравнения на 3х (такое деление
/ 2
возможно, поскольку при любом х 3х >0), получим: (— =1.
Но 1 = j , поэтому х = 0. Проверка показывает, что это
действительно корень данного уравнения.
Ответ, х = 0.
Аналогично решается уравнение 52х = 73х.
Действительно, 52х = (52)х = 25х; 73х = (73)х = 343х. Поэто-
му данное уравнение можно переписать в виде
25х = 343х.
Отсюда, так же как и в предыдущем случае,
получаем: х = 0.
Упражнения
Решить уравнения (№ 1449—1454):
1449. а) 5х = 125;
б) 4х = 64;
в) 3х = 1;
' 81
г) 25х =
о
д) 2Х+3 = 32;
е) 8х = 16;
ж) 9-х=27;
з) /у = ^9?
и) 343;
к) /F • /3^ =36.
В) 5x4-1 _ 5<-i =24;
1452. а) 25-х =23х~3;
г) 2х • 5х = 0,1 • (10х-1 )5;
д) )/ -j/4х-н = (0,5)2~4х;
1453. а) 52х — 5х — 600 = 0;
б) 9 х —3х — 6 = 0;
в) 4х 4- 2Х+* = 80;
г) 2x’-6x-2,5 = 16 /2;
д) а(х-2) (х-3,= 1 (а > 0);
е) 52 • 54 • 5е.52х = 0.04-28.
г) 3х-1 + 3х-2 + Зх~3 = 13;
д) 7Х+2 + 4 • 7х-1 = 347;
е) 5x4-1 _|_ з. 5х-1 _6.5* _[_io= 0.
е) (0,25)2~х =
ж) К27х-*=^ 92-*;
з) ах+1 = у4ах~2 (а > 0);
и) 4^1= 64 • 2/Гр1;
к) 16 V^(0,25)5~^ =21'^7’'’
г) 3х + 9х-1— 810 = 0;
Д) 32/х—4-3/х+3 = 0;
. . . 2 5
е) 4 +-------------,
3 х —1 3 х-1
113
1455.
1456.
1457.
= 1,2; з) 9* * * * * * * * * х +6* = 4Х.
Г) 53*—7* — 5?* • 17 + 7* • 17 = О
ц) 3 • 2х = 2 • 3*;
е) 1-2х =5-3*;
ж) ах = Ьх (о > О, 6 > О).
1458. /5х-5У = 100’
(5х-1 + 5У-1 = 20.
1459. Г 1^49 = У~/<343,
(Зу=92х-у.
X /3V+1 , / 3\1—
ж) — + —
' \ 5 / \ 5 /
1454. а) 11* = 17*;
(1 \5х
—) ;
243/
в) 13* = 19~<*;
Решить системы уравнений:
3 • 2* 4- 2- 3>= —,
4
2*— Зу = ——.
4
(2х • Зу = 648,
}3* • 2у = 432.
(2х + Зу — 8 —,
9
2х • Зу= —.
9
Основные способы решения логарифмических
уравнений§ 197
Логарифмическими уравнениями называются уравнения, содер-
жащие неизвестные величины под знаком логарифма.
К таким относятся, например, уравнения
log2x = 5, logx (х — 1) = О
и т. д. Так же как и показательные, логарифмические уравнения
являются трансцендентными.
Простейшим логарифмическим уравнением является уравнение
logax = b, (1)
где а и Ь — данные числа, ах — неизвестная величина. Если а —
положительное и не равное единице число, то такое уравнение
имеет единственный корень
х = аь.
Решение более сложных логарифмических уравнений, как пра-
вило, сводится либо к решению алгебраических уравнений, либо
к решению уравнений вида (1). Поясним это на некоторых частных
примерах.
I. Решить уравнение
logx (х2 — Зх + 6) = 2.
По определению логарифма из этого уравнения следует, что
х2 = х2 — Зх + 6, откуда х = 2.
114
Проверка. При х = 2
l°gx (х2 — Зх 4- 6) = log2 (4 — 64-6) = log2 4 = 2.
Значит, х = 2 — корень данного уравнения.
Ответ, х = 2.
II. Решить уравнение
1g (х2 - 17) = lg (х 4- 3).
Решение подобных уравнений основано на следующем свой-
стве логарифмов: если логарифмы двух чисел по одному и тому же
основанию равны, то равны и сами эти числа. Из этого свойства
логарифмов вытекает, что если только данное уравнение имеет
корни, то они должны удовлетворять уравнению
х2 — 17 = х 4- 3,
откуда
Xj = 5, х2 = —4.
Проверка. При х = 5
]g (х2 — 17) = 1g 8; 1g (х 4-3) = 1g 8.
Значит, х =5 — корень данного уравнения. При х = —4 левая и
правая части данного уравнения не определены, поскольку
х2 — 17 = — 1 < 0 и х 4- 3 = — 1 <0. Следовательно, х = — 4
не есть корень этого уравнения.
Ответ, х = 5.
Рассмотрим еще одно уравнение
21g (х — 1) = 1 lg х5 — ig (2)
£
Выполним следующие преобразования:
21g(x-l) = lg(x-l)2,
5 1 |
у 1g х5—lg )zx = lg х2 — lg х2 = lg Y = lg xa.
x2
Таким образом, исходя из уравнения (2), мы пришли к урав-
нению
lg (х — I)2 = 1g х2.
Из него вытекает, что (х — I)2 = х2, или х = -i-. Но при
£
2
(3)
Х=Л
2
левая часть уравнения (2) не определена (х — 1 =
следовательно, данное уравнение не имеет корней.
Заметим, однако, что для уравнения (3) число ~ является
корнем. Таким образом, уравнения (2) и (3) не эквивалентны
друг другу. Это лишний раз говорит о том, что при решении лога-
115
рифмических уравнений необходимо делать проверку полученных
значений. Среди них часто оказываются «посторонние» корни.
III. Некоторые логарифмические уравнения сводятся к алге-
браическим уравнениям посредством введения новой неизвестной
величины. Если, например, в уравнении
log? х — 3 loggX — 10 = 0
log^ обозначить через у, то оно сведется к квадратному урав-
нению у2 — Зу — 10 = 0, откуда уг = —2, у.2 = 5. Вспоминая,
что у = log3x, получаем: если log3x =—2, то х — -i-; если же
log з х — 5, то х = 243.
Проверкой легко установить, что оба эти значения х удовлетво-
ряют данному уравнению.
Ответ. Xi = ; х2 — 243.
IV. Некоторые уравнения решаются путем почленного лога-
рифмирования. Пусть, например, дано уравнение
л,е*-| = ]00
Прологарифмируем это уравнение почленно:
lgx’cx~' = 1g 100,
(lg х — 1) lg x = 2.
Обозначая Igx буквой у, мы приходим к квадратному уравне-
нию
у2 — у — 2 = 0,
имеющему корни ух = —1, у2 = 2. Вспоминая, что у = 1g х, полу-
чаем: либо Igx = —1, и тогда х = 0,1; либо Igx = 2, и тогда
х = 100.
Проверка. При х = 0,1
igx-i = о, i-1-i = 0 д-2 = J_ = ЮО;
Л 0,01
следовательно, х = 0,1 — корень данного уравнения. При х = 100
х’8*-1 = юо2"1 = ЮО;
так что х = 100 — также корень уравнения.
Ответ. хх = 0,1; х2 = 100.
V. При решении некоторых логарифмических уравнений
оказывается полезным использовать формулу перехода от одного
основания логарифмов к другому:
]ogafe = l^.
logca
Решим, например, уравнение
log2 х + log3 х = 1.
116
Для этого от логарифмов по основаниям 2 и 3 перейдем к лога-
рифмам по основанию 10:
log, х log, Л =
Ь2 1g 2’ 63 1g з
Тогда данное уравнение примет вид:
1g* lg * _ j
lg2 lg3
откуда
1аХ = lg2‘lg3 =
ь Ig2-Hg3 lg 6
Поэтому
lg3 Itj з
л =10 !gC =(10,g2)’g6 =2Ig6.
При необходимости это значение х можно определить с помощью
таблиц логарифмов.
Проверка. При найденном значении х
2- lg 3\
П£<г )=_!_ !g2~ te3 _ lg3
J lg2 IgG
. lg* 1
lo&x=lil = i^-^10
Аналогично,
1g 6
log3x =
83 lg6
Поэтому
1og2x + 1оЬх = ^. + = И = !.
2 ® Igo lg6 I36 IgC
Значит, найденное значение х является корнем данного урав-
нения.
ig з
Ответ. x = 2g •
Рассмотрим еще одно уравнение:
log2 х 4- logx 2 = 2.
Поскольку
1
logx2 =------,
1®о2 *
то, обозначая log2 x через у, получаем:
У+-=2,
У
откуда у = 1. Следовательно, log2 х = 1 и х = 2. Проверка пока-
зывает, что х = 2 есть корень данного уравнения.
О т в е т. х = 2.
117
Упражнения
Решить данные уравнения (№ 1460—1465):
1460.
a) lg (lg х) = 0;
б) log2 [log3 (log4 x)] = 0;
в) logx_1 (x2 — 5x + 7) = 1;
г) logx2 — logx3= 4;
д) lg x = 3 — lg 5;
e) —!^L_ = 2;
1— lg 2
ж) 100’g <л+20> = 10 000.
1461. a) lg x = lg 2;
6) lg x = — lg 2;
в) log2 (x — 1) = log2 (x2 — x — 16);
r) 21g /Т = lg (15 — 2x);
д) 21g x = — lg (6 — x2);
e) 2le* =1;
lg(Sx-4)
7 x
Ж) 2 lOggX = — logg—.
4 □
1462. a) lg (0,5 + x) = lg 2 — lg x;
6) 0,51g(2x—1)= 1—IgVx—9;
в) lg(x + 6)-2 = llg(2x-3)-lg25.
1463. a) llg2x = l-^lgx;
6) --‘----1--------= 1;
' 5-lgx 1 + lgx
в) ------------|---------- 3;
5-41g(x+l) i+ig(x+i)
r) 0,1 lg4 x — lg2 x 4- 0,9 = 0.
1464. a) x*=x; в) 531gx = 12,5x; д) x= 10 ,-0’25,gx;
6) x,og‘x-2= 125; r)xlgx+2 = 1000; e) 0,lxIgx-2 = 100.
1465.
a) loge x + logx2 3=1; r) log5x + logx5 = 2,5;
6) log2x • log3x = log2 3; д) log3x 3 = (log33x)2;
в) log3 x + log5 x = log3 15; e) log16 x + logt x + log2x = 7.
Решить системы уравнений (№ 1466— 1469):
'«6. r9. 3’
1467 + У = 34,
Uog2* + log2y = 6.
1468. (5* — 36y = 0,
I4O°- ^6* — 25y = 0.
1469. P? = 4J’
|xlgy = 4.
118
Примеры графического решения показательных
и логарифмических уравнений
§ 198
Пример 1. Решить уравнение
2 х = 2х.
На одном и том же чертеже (рис. 260) построим графики
двух функций: у = 2 х и у = 2х. Эти графики пересекаются в двух
точках: А с абсциссой 1 и В с абсциссой 2. Поэтому данное урав-
нение имеет два корня: х = 1 и х = 2.
Пример 2. Решить уравнение
1g х — х.
Графики функций y = lgxny = x (рис. 261) не пересекаются
друг с другом. Поэтому данное уравнение не имеет корней.
Мы рассмотрели простейшие примеры. Уравнения, которые
получаются при решении практических задач, обычно значи-
тельно отличаются от таких «учебных» задач. Для их решения
наряду с графической иллюстрацией приходится обращаться и
к таблицам. Рассмотрим, например, такое уравнение:
log2x - 1.
Графики функций y = log2x и у = — (рис. 262) пересекаются
в одной точке, абсцисса которой заключена между 1 и 2. Поэтому
данное уравнение имеет один корень х0, который больше 1, но
меньше 2:
119
искомый корень х0 должен быть больше, чем 1,5 (см. рис. 262).
Теперь мы уверены, что
1,5 <х0 <2.
«Испытаем» точку х = 1,7 как одну из ближайших к средней
точке интервала (1,5; 2,0). При х = 1,7 получаем, используя табли-
цы В. М. Брадиса,
log2x = ’ALL — 0,76;
2 lg2
1^0,58.
120
Поскольку
log,1.7> jy.
искомый корень х0 должен быть меньше, чем 1,7 (см. рис. 262).
Следовательно,
1,5 <х0 < 1,7.
Поэтому с точностью до 0,1
х0 « 1,6.
Рассматривая точки интервала (1,5; 1,7), мы могли бы получить
и более точное значение корня х0. Попробуйте, например, само-
стоятельно получить приближенное значение х0 с точностью
до 0,01.
Упражнения
1470. Решить графически уравнения:
а) 2х = х + 2; в) 2х = л* 1 2; д) log3x =
б) 3х = Зх; г) log2 х = х — 1; е) log2 (х + 3) = 3 —х.
1471. Найти корень уравнения
2х = 2 — х
с точностью до 0,1.
1472. Найти наименьший корень уравнения
log2* = уХ
с точностью до 0,01.
Показательные и логарифмические неравенства
§ 199
Решение показательных и логарифмических неравенств основано на том,
что функции у = ах и у = loga х при а > 1 являются монотонно возрастающими,
а при 0 < а < 1 — монотонно убывающими.
Рассмотрим несколько примеров.
1) Решить неравенство
2х > 4.
Перепишем данное неравенство, представив 4 в виде 2е:
2х > 22.
Функция у = 2х является монотонно возрастающей. Поэтому большему значе-
нию этой функции соответствует большее значение аргумента. Следовательно,
х > 2.
2) Решить неравенство
3х’ —з* > 1
9
Перепишем данное неравенство, представив в виде 3-а :
З^-Зх > 3-2.
J21
Отсюда х2 — Зх > —2, или %2 — Зх + 2 > 0. Это неравенство выполняется при
х < 1, а также при х > 2 (ч. I, § 61).
3) Решить неравенство
log 1 (х— 1) > — 2.
Г
Представив — 2 как log j_ 25, перепишем данное неравенство в виде
5
log 1 (х — 1) > log ! 25.
s’ s'
Функция у = log 1 х является монотонно убывающей. Поэтому большему ana-
's
чению этой функции соответствует меньшее значение аргумента. Следовательно,
х — 1 < 25. К этому неравенству необходимо добавить еще неравенство х—1 >0,
выражающее тот факт, что под знаком логарифма может находиться только по-
ложительная величина. Таким образом, данное неравенство эквивалентно сис-
теме двух линейных неравенств
(х — 1 < 25,
— 1 > 0,
из которой получаем:
1 < х < 26.
Важно отметить, что если бы мы «забыли» учесть условие х — 1 > 0, то
пришли бы к неверному выводу: х < 26. В частности, в это «решение» входило
бы и значение х = 0, при котором левая часть исходного неравенства не имеет
смысла.
Упражнения
1473. Решить неравенства:
I / 1 \х*-х 1
а) Зг > в) 3* > 2; д) <-.
1474. Решить неравенства:
а) 1g (х + 1) > 1g (5 — х);
б) log ( (х — 7) > 4; в) log(2х — 6) < log , к.
~2 7 7
1475. Данные неравенства решить графически:
а) 2 х < 2х; б) log2 х > х — 1.
Из истории открытия логарифмов§ 200
Основная идея введения логарифмов основывается на формуле
ат - ап = ат+п (1)
и состоит в том, что умножение можно свести к более простому действию — сло-
жению. С идеей этой были знакомы еще математики древности. Общая формули-
ровка, эквивалентная правилу умножения (1), дана, например, в девятой книге
знаменитых «Начал» Евклида. Однако о логарифмах в древние времена
не могло быть и речи. Тогда еще не рассматривались степени с дробными и от-
122
рицательпыми показателями, да и сами отрицательные числа многим математи-
кам не были известны. Впервые дробные показатели использовал, по-видимому,
французский математик О р е з м (вторая половина XIV века). Но идеи Орезма
слишком опередили математику того времени, и трактат его был вскоре забыт.
Нулевой и отрицательный показатели появились в работе французского мате-
матика Ш ю к е (XV век). Введение в математику степеней с произвольными
действительными показателями подготовило почву для рассмотрения лога-
рифмов.
Первые логарифмические таблицы были составлены независимо друг от
друга шотландцем Непером (1550—1617) и швейцарцем Б ю р г и (1552—
1632). Характерно следующее высказывание Непера, которое он приводит в
предисловии к своим таблицам: «Я всегда старался, насколько позволяли мои
силы и способности, отделаться от трудности и скуки вычислений, докучность
которых обыкновенно отпугивает многих от изучения математики».
Таблицы Непера были в некоторых отношениях более совершенными, чем
таблицы Бюрги. Однако и они были неудобны для вычислений. Неперовские
логарифмы (Nep log х) определялись (в наших обозначениях) таким об-
разом:
107
Nep log х = 107 loge—,
где e » 2,7 (см. ч. I, § 134). В частности,
Nep log 1 = 107 log^ 107 =/= 0.
Такие таблицы не удовлетворяли и самого Непера. Вместе со своим почитате-
лем Бриггсом (1561—1631) Непер решил составить таблицы более про-
стых, десятичных логарифмов. Эти таблицы были изданы Бриггсом в 1624 году
уже после смерти Непера.
Наибольшее влияние оказали логарифмы на развитие астрономии. Успе-
хи мореплавания в средние века обусловливали большой спрос на астрономиче-
ские таблицы, составление которых требовало весьма сложных вычислений.
Использование логарифмических таблиц значительно облегчало и ускоряло эти
вычисления. По образному выражению французского математика Лапласа
(1749—1827), изобретение логарифмов, сократив работу астронома, продлило
ему жизнь.
Общее определение логарифмической функции и ее широкое обобщение
дал Леонард Эйлер.
Задачи на повторение
1476. Население города возрастает ежегодно на 3% по срав-
нению с предыдущим годом. Через сколько лет население этого
города увеличится в 1,5 раза?
1477. Одна бригада за месяц вырабатывает продукции в
1,1 раза меньше, чем другая бригада. Ежемесячно производи-
тельность труда первой бригады растет на 1%, а второй
бригады — на 0,7%. Через сколько месяцев первая бригада дого-
нит вторую по сменному выпуску продукции? Какая из бригад
даст больше продукции за полгода: первая или вторая?
1478. Вычислить:
а) 2410^3->; в) (y)1Og,2_3;
б) 231°е*5+4; г) ('iyog“4+2,
\ 5 I
123
1479. Построить графики функций:
а) у = I log2 * I;
б) у = log2 | х |; в) у = log2 ( —х).
1480. Решить уравнения:
a) (|/2)""2' = ^2; 6) 5>'" = (-1
2*
a) log I Л или
ГЗ
- - 1
11O1. наши iug2 *vo2 г Г Г .
1482. Не решая квадратного уравнения
log.,2x — 5 log2 х + 4 = 0,
доказать, что произведение его корней равно 32.
1483. Не решая данных уравнений, найти произведения их
корней:
a) 1g2 х + 1g х — 2 = 0;
б) 6 1g2 х + 1g х — 1 =0;
в) lg2 х — lg х + 1 = 0.
1484. Решить уравнение logx а = а (а > 1).
1485. Пользуясь таблицами десятичных логарифмов, найти:
a) log7 25; б) logi_ 1
з
1486. Что больше:
3 2
б) log! у или log( 1;
—. / — D
5 7 . .
1487. При каких значениях х в интервале 0 < х < 2л определе-
ны функции:
а) у = lg (sin х); б) у = sin (1g х)?
1488. Доказать, что уравнение
lg sin х = sin х
не имеет действительных корней.
1489. Сколько цифр содержат числа 2100 и 5200?
1490. Доказать, что функция у = lg (1 + х) является монотонно
возрастающей, а функция у = lg (1 — х) монотонно убывающей.
Решить уравнения (№ 1491—1499):
l\Igr?
7
1491. 5 • 32х—1 — 9v-0>5 = 9 х + 4 • 32х~2.
1492. 3 х + Зх+* -J- Зх+2 = 5*.
1493. 3 • 4х 4- 2 • 9 х = 5 • 6х.
1494. 57* = 75\
1495. 62х+4 = 28+х • 33х. ______
1496*. (/4+/15)'-(/4- 1/15)' =
1497. log2 (х — 1 )2 — logo,5 (х — 1) = 9.
1498. 5'8Х —З^-1 = 3’2*+» —б1**-1.
124
1499. log8 x + log2 x + log| x +... = 1
1500. He пользуясь таблицей логарифмов, найти lg 2 и lg 5,
если известно, что 1g 2 — 1g 5 « —0,3980.
1501. Доказать тождества:
log/» (log& д)
а) b = а\ б) a l°gz> ° = log6 а.
1502. Какое число больше, а или 6, если:
a) log2 а = log з b\ б) loga2 = log6 3?
1503. Выразить logaft х через loga х и log6 х.
1504. Доказать тождество
loga(b + )= — loga(b — /Ь2—i у
Решить уравнения (№ 1505—1507):
1505. 3 1g2 (х2) — 1g х — 1 = 0.
1506. 2 lg2 (х3) — 31g х — 1 = 0.
1507. 41og23 5х — 7 log3 15х + 7 = 0.
Решить системы уравнений (№ 1508, 1509):
3
3sin X . 3COS у — 3 lg sinx + lg sin у = lg—,
1508. L. ’ 1509. o 2
gsinxCOStf , ж . 3
Sin2 X + sin-y —
1510. Решить систему уравнений
= yt
yVZ — x?.
1511. Определить интервалы возрастания и интервалы убыва-
ния функций:
а) у = 2*2+4*+з
б) у = log2(8 + 2х — х2).
Решить неравенства (№ 1512—1514):
1514. (0,25)х~4
ФУНКЦИИ И ПРЕДЕЛЫ
IX
Постоянные и переменные величины.
Понятие функции
§ 201
С понятием функции мы уже неоднократно сталкивались.
В части I мы рассмотрели линейную, квадратную, степенную
и тригонометрические функции. Предыдущая глава была по-
священа изучению показательной и логарифмической функций.
Теперь нам предстоит сделать общий обзор того, что мы уже
знаем о функциях, и рассмотреть некоторые новые вопросы.
Наблюдая различные процессы, можно заметить, что величи-
ны, участвующие в них, ведут себя по-разному: одни из них изме-
няются, другие остаются постоянными. Если, например, в
треугольнике АВС вершину В перемещать по прямой MN, па-
раллельной основанию АС (рис. 263), то величины углов А, В
и С при этом будут непрерывно изменяться, а сумма их,
высота h и площадь треугольника будут оставаться неиз-
менными.
Другой пример. Если какой-нибудь газ сжимать при постоян-
ной температуре, то объем его (V) и давление (р) будут изменять-
ся: объем уменьшаться, а давление увеличиваться. Произведе-
ние же этих величин, как устанавливает закон Бойля — Мариот-
та, будет оставаться постоянным:
Vp = с,
где с — некоторая константа.
Все величины можно разделить на постоянные и переменные.
Переменные величины, участвующие в каком-либо процессе,
обычно изменяются не независимо друг от друга, а в тесной
N
Рис. 263.
связи друг с другом. Например,
сжатие газа (при постоянной темпе-
ратуре) приводит к изменению его
объема, а это, в свою очередь, обу-
словливает изменение давления газа.
Изменение радиуса основания ци-
линдра вызывает изменение площади
этого основания; последнее же при-
водит к изменению объема цилиндра
126
и т. д. Одна из главных задач математического изучения того
или иного процесса заключается в том, чтобы установить, как
изменение одних переменных величин влияет на изменение
других переменных величин.
Рассмотрим несколько примеров. Упомянутый выше закон
Бойля — Мариотта говорит, что при постоянной температуре
объем газа V изменяется обратно пропорционально давлению р:
V = —. Если известно давление, то по этой формуле можно
р
вычислить объем газа. Аналогично, формула S = яг2 позволяет
определить площадь круга S, если известен его радиус г. По
формуле 0= —а
можно найти
острый
угол прямоугольного
треугольника, если известен другой острый угол этого треуголь-
ника, и т. д.
При сравнении двух переменных величин одну из них удоб-
но рассматривать как независимую переменную, а другую — как
зависимую переменную величину. Например, радиус круга г
естественно считать независимой переменной, а площадь круга
S = лл2 — зависимой переменной величиной. Аналогично, давление
газа р можно считать независимой переменной величиной;
тогда его объем V = — будет зависимой переменной величиной.
Р
Какую же из двух переменных величин выбрать в качестве
зависимой и какую в качестве независимой? Этот вопрос
решается по-разному в зависимости от поставленной цели.
Если, например, нас интересует, к чему приводит изменение
давления газа при постоянной температуре, то естественно
давление принять за независимую, а объем — за зависимую
переменную величину. В этом случае зависимая переменная
величина V будет выражаться через независимую величину р
по формуле: V = —. Если же мы хотим выяснить последствия
Р
сжатия газа, то лучше объем рассматривать как независимую,
а давление — как зависимую переменную величину. Тогда зави-
симая переменная величина р будет выражаться через неза-
висимую переменную величину V по формуле р = -у. В любом
из этих случаев две величины связаны между собой так, что каж-
дому возможному значению одной из них соответствует вполне
определенное значение другой.
Если каждому значению одной переменной величины х каким-
либо образом поставлено в соответствие вполне определенное
значение другой величины у, то говорят, что задана функция.
Величину у при этом называют зависимой переменной величиной
или функцией, а величину х — независимой переменной величи-
ной или аргументом.
127
Для выражения того, что у есть функция аргумента х,
обычно используют обозначения: у = f (х), у = g (х), у = ф (х)
и т. д. (читается: игрек равно эф от икс, игрек равно же от икс,
игрек равно фи от икс и т. д.). Выбор буквы для обозначения
функции (/, g, ф) является, конечно, несущественным. Суще-
ственно лишь то, какую связь между величинами х и у
выражает эта буква.
Значение, которое принимает функция f (х) при х = а, обо-
значается [ (а). Если, например, f (х) = х2 + 1, то
/(1) = Г- -к 1 = 2;
f (2) = 22 + 1 = 5;
f (« + 1) = (а + I)2 + 1 = а2 + 2а + 2;
f (2а) = (2а)2 + 1 = 4а2 + 1
и т. д.
Упражнения
1515. Газ, находящийся под давлением в 2 атмосферы,
сжимается. Как изменяется при этом: а) вес газа; б) его объем;
в) его давление?
1516. По электрической цепи течет ток. С помощью реостата
мы изменяем сопротивление цепи. Изменяется ли при этом:
а) ток в цепи; б) напряжение тока?
1517. Вершина В треугольника АВС движется по окруж-
ности, диаметр которой совпадает с основанием АС этого тре-
угольника. Какие величины в этом процессе остаются постоян-
ными и какие изменяются?
1518. f(x) = ’-±1..
1 — х
Найти: a) f (0); б) / (а2); в) / (—V, г) f (sina).
\ а /
1519. Выразить f (2a) через f (а) для функций:
а) f (*) — sin х; б) f (х) = tg х; в) f (х) = х2.
Способы задания функций § 202
Задать функцию — это значит указать, как по значениям
аргумента отыскиваются соответствующие значения функции.
В школьном курсе математики мы привыкли к аналитическому
способу задания функции. При таком способе указывается фор-
мула, связывающая зависимую переменную величину (функцию)
с независимой переменной величиной (аргументом), например:
у = j/x, у = 1g х, S = яг2, V = — и т. д. Рассмотрим более
р
сложные примеры функций, заданных аналитически.
128
Пусть
х если г < О,
У ~~ [sin х, если х > О. (1)
Каждому значению х поставлено в соответствие вполне опре-
деленное значение у, причем при отрицательных значениях х
величина у находится по формуле у = х, а при неотрицательных
значениях х — по формуле у — sin х. Если, например, х = —2,
то у — х — —2; если х = -у, то у = sin у = 1 и т. д.
Не следует думать, что соотношение (1) определяет две функ-
ции. Речь идет лишь об одной функции у, которая при отрица-
тельных значениях аргумента х ведет себя как линейная функция
у = х, а при неотрицательных значениях аргумента х — как три-
гонометрическая функция у = sin х.
График рассматриваемой функции представлен на рисунке 264.
Рассмотрим еще один пример:
_ (х2, если х < 0, (2)
У ~ [з, если х > 0.
Это соотношение между величинами х и у также определяет
одну функцию. График ее представлен на рисунке 265. Стре-
лочка на прямолинейном участке указывает, что точка М не
принадлежит графику данной функции. Ведь согласно формуле (2)
при х = 0 величина у находится по формуле у = х2, а не по фор-
муле у = 3. Поэтому при х = 0 у также равен 0.
Предположим, что функция у задана посредством некоторого
выражения f (х), например: у = х2, у = tg х и т. д. Если при этом
не сделано никаких оговорок относительно того, в каких пре-
делах изменяются значения аргумента х, то мы будем считать,
что выражение f (х) задает нашу функцию при всех тех значе-
ниях х, при которых оно определено. Так, запись у — хг озна-
чает, что у = х2 при всех действительных значениях х.
Аналогично, запись у = 1g х означает, что у = 1g х при всех
положительных значениях х.
5 Заказ 1159
129
Помимо аналитического спо-
Рис. 266.
соба, на практике часто пользу-
ются графическим способом зада-
ния функций. Этот способ удобен,
когда задать функцию аналити-
чески довольно трудно (см., на-
пример, рис. 266). Кроме того,
при изучении многих процессов
мы пользуемся приборами, кото-
рые не могут говорить с нами на
языке формул. Однако с помощью
этих приборов мы получаем кри-
вые, по которым можно судить о
характере изменения одних вели-
чин в зависимости от изменения других величин. В медицине,
например, широко используются электрокардиографы. С помощью
этих приборов можно получать электрокардиограммы — кривые,
которые отражают изменение электрических импульсов, возни-
кающих в мышце сердца. Такие кривые помогают сделать правиль-
ные заключения о работе сердца.
Графический способ задания функции очень часто используется
в математике для иллюстрации тех или иных свойств функций.
При изучении некоторых процессов удобно пользоваться
также табличным способом задания функций. Метеорологи,
например, составляют таблицы выпавших осадков в различных
точках земного шара. Эти различные точки земного шара высту-
пают в данном случае в роли «значений аргумента», а количества
осадков — в роли «значений функции».
Упражнения
Г / \ fC0S если * < О,
1520. f (х) если х о
Найти:
а)/(_т); б)/Ш в)/(0);
.го. Г / \ П + х2, если х < 2,
1и21. f (х) |sjn х, если х 2.
Найти:
г) / (о2)-
а)/(у); б) /(«>. в) /(2-а*).
Построить графики следующих функций
—1, если х < —1,
х, если —1 < х < 1,
1, если х > 1.
(№ 1522—1525):
130
1523. у =
1524. у =
1525. у =
1,5х + 3, если х < О,
3 — 2х, если х > О.
х 4- 6, если х < —2,
х2 — х — 2, если | х |
О, если х > 2.
(2х, если х > О,
[1, если х < О.
< 2,
1526. Как по графику функции у — f (х) построить график
функции у = f (х) + с, где с — некоторое заданное число?
Ответ пояснить на примере функций:
а) у = — 4-2; б)у = — — 1; в) у = 2х 4- 1; г) у = Igx — 2.
X X
1527. Как по графику функции у = f (х) построить график
функции у = f (х 4- а), где а — некоторое заданное число?
Ответ пояснить на примере следующих функций:
п • ( п
1) y = sinfx—-
2) у = sin I х 4- —
4) y = cos(x4-yj;
5) y = tg(x — -JY
6) У = ctg p 4-7-)-
\ 4 /
1528. Как по графику функции у = f (x) построить график
функции у = Af (х), где А — некоторое заданное число?
Ответ пояснить на примере следующих функций:
1) у = 2х2; 3) у = —2х2; 5) у = —2cos х;
2) у = — х2; 4) у = 3 sin х; 6) у = — tgx.
3
1529. Как по графику функции у = f (х) построить график
функции у = | f (х) |?
Ответ пояснить на примере следующих функций:
1) у = | х2 — х — 6 |; 3) у = | cos х |;
2) у = | —6х2 4- х 4- 1 I; 4) у = | sin х |.
1530. Как по графику функции у = f (х) построить график
функции у = f (сох), где (о — некоторое заданное число?
Ответ пояснить на примере следующих функций:
1) у = sin 2х; 3) у = cos 1,5х;
2) у = sin у; 4) у = cos ~
5*
131
Рис. 268.
Область определения
н область изменения
функции § 203
Каким бы способом
ни была задана функция
у = f (х), рассматривая ее,
мы всегда имеем дело с
двумя множествами: мно-
жеством значений, кото-
рые может принимать ар-
гумент х, и множеством
значений, которые может
принимать функция у.
Например, для функции
у = 2х (рис. 267) множе-
ством всех значений, ко-
торые может принимать
аргумент х, является со-
вокупность всех действи-
тельных чисел, а множе-
ством всех значений, ко-
торые может принимать
функция у,—совокупность
всех положительных чисел.
Совокупность всех тех
значений, которые прини-
мает аргумент х функции
у = / (х), называется обла-
стью определения этой
функции. Совокупность
всех тех значений, кото-
рые принимает сама функ-
ция у, называется областью
изменения этой функции.
Например, областью
определения функции у =
= sin х (рис. 268) является
совокупность всех дей-
ствительных чисел, а об-
ластью изменения—сово-
купность всех чисел, за-
ключенных между —1 и 1,
включая эти два числа.
Для функции у = 1g х
(рис. 269) областью опре-
132
деления является совокупность всех положительных чисел, а
областью изменения — совокупность всех действительных чисел
и т. д.
Ранее мы изучали числовые последовательности. Члены любой
числовой последовательности можно рассматривать как возмож-
ные значения некоторой функции, определенной для натуральных
значений аргумента. Например, члены последовательности
1 I 1 1 1
’ 2 ’ 3 ’ 4 ’ “ ' ’ п. ’
. 1
являются значениями функции у = —, а члены последователь-
л
ности
1, —1, 1, —1,...
— значениями функции у = (—1)лИ. Каждую из этих функций
мы рассматриваем как функцию, определенную только для на-
туральных значений аргумента п. Вот почему иногда говорят,
что числовая последовательность есть функция нату-
рального аргумента.
Рассмотрим несколько более сложных примеров на нахожде-
ние области определения функции.
Пример 1. Найти область определения функции
у хг -J- 2х — 3 '
Эта функция определена для всех значений х, кроме тех,
при которых знаменатель дроби ха 4- 2х — 3 обращается в нуль.
Решая уравнение ха + 2х — 3 = 0, находим: хг = 1, ха = —3.
Поэтому областью определения данной функции является сово-
купность всех действительных чисел, кроме 1 и — 3.
Пример 2. Найти область определения функции
Корни квадратные определены только для неотрицательных
чисел. Поэтому область определения данной функции можно рас-
сматривать как совокупность всех значений х, удовлетворяющих
неравенству
2-^> 0.
3 — бх
Прежде всего выясним, при каких значениях аргумента х
числитель и знаменатель этой дроби положительны и при каких
отрицательны. Решая неравенство 2х — 4 >0, получаем х > 2.
Таким образом, при х > 2 числитель положителен; при х < 2
133
о
^222
2
<-zz//zzz//^zz/ZZz,
о 1
2
Рис. 270.
он, очевидно, отрицателен. Это от-
мечено на рисунке 270. Заштрихо-
_ ванная часть верхней числовой пря-
мой соответствует той области, в
которой он положителен, а незаштри-
хованная — той области, в которой
он отрицателен. Аналогично иссле-
дуется знаменатель 3 — 6х. Имеем:
3 — 6х >0;
3 > 6х;
6х <3;
. ]
х <—.
2
второй числовой прямой на рисунке 270
в которой знаменатель 3 — 6х положи-
2
Заштрихованная часть
соответств ует области,
телен, а незаштрихованная — области, в которой он отрицателен.
Из рисунка 270 видно, что оба выражения
знаменатель) имеют одинаковые знаки только при
2х______________________________4
Поэтому в этой области дробь----- положительна.
3 — бх
она обращается в 0. Следовательно, областью определения дан-
ной функции является совокупность действительных чисел,
удовлетворяющих неравенству
— < х < 2.
2
Пример 3. Найти область определения функции
. I 2х Л
(числитель и
— < х < 2.
2
При х = 2
Десятичные логарифмы определены только для положитель-
ных чисел. Поэтому область определения данной функции можно
рассматривать как совокупность всех значений х, удовлетворяю-
щих неравенству
2х
Выполнив вычитание в левой части этого неравенства, получим:
^-1 > 0.
ч_______(алйи.айа
0 1
Числитель этой дроби положителен при х > 1 и отрицателен
прих<1, а знаменатель положителен
прих >—1 и отрицателен при х<—1
(рис. 271). Поэтому дробь положитель-
на при х<—1 и при х>1. Все эти
значения х можно записать в виде
одного неравенства | х | > 1.
•1 О
Рис. 271.
134
Пример 4. Найти область определения функции
tg X
У= -—5-------
sin X — cosx
Во-первых, tg х не определен для х = -у + пл. Во-вторых,
данная дробь не определена для тех значений х, при которых
знаменатель обращается в нуль. Эти значения находятся из
уравнения sin х — cos х = 0. Это однородное тригонометрическое
уравнение. Деля обе его части на cos х (докажите, что это деление
возможно!), получим:
tg х = 1,
откуда
х — — -j-kn.
Итак, областью определения данной функции является сово-
купность всех действительных
п , я , ,
чисел, кроме-------|-лл и —)-лл,
где п и k — произвольные целые числа.
Теперь мы рассмотрим несколько примеров на нахождение
области изменения функции.
Пример 5. Как известно, линейная функция у — ах + b
при а Ф 0 принимает любые действительные значения. Поэтому
областью изменения этой функции является совокупность всех
действительных чисел.
Пример 6. Найти область изменения функции
у = № — 4х 4- 7.
Преобразуем квадратный трехчлен х2 — 4х + 7, выделив из
него полный квадрат: у = х2 — 4х + 4 + 3 = (х — 2)3 + 3.
Выражение (х — 2)2 принимает, очевидно, все неотрицательные
значения. Поэтому областью изменения данной функции является
совокупность всех чисел, больших или равных 3. Эту область мож-
но задать с помощью неравенства у 3.
Пример 7. Найти область изменения функции
у = sin х + cos х.
Представив данную функцию в виде
у = У 2 sin (х -|- —
(вспомните, как это делается), нетрудно понять, что область ее
изменения определяется неравенством
— У' 2 < у < У 2, или | у | < У 2.
135
Упражнения
Найти области определения функций (№ 1531—1566):
1531. 1532. y=2±i. z Зх—6 х2 — 9 х 3 1549. у = + 1550. у = 1g 2х — 5
1533. 5 1) — в 1551. у = 1g- *~5 . Л 62+х—ха
6х2 — х — 1
1534. 1535. Зх — 1 11 — 1552. У — tg —. X 1553. y = ctgnx.
Л х2 + X 4- 1 * у = У х — 1.
1536. у = У5— 10х. 1554. у = (sin лх)-1.
1537. у = У 1 — cos X. 1555 v == —С05Л
z )/3— 2 sin х' I
1538. 1539. 1540. 1541. у = ]/ sin х — 1. _ 91/х 1 5 1556 v = -
/3 + 2 cos х 1557 v= 1
у — х 1/ л. 1 . * У4 — х у = Ух2 + 2х + 4. у = Ух + У1—Х. ‘ Z /3 4- tgx‘ 1558 v = 1
sinX • COSA 1559 v = 1
sin x cos x 1560. у = ^-л+> ^O5X sin x — Уз cos x 1000 1 hfi 1 11 —
1542. у = Ух2 — 4х— 12.
1543. 1544. 1545. у = Г(1-*)(1 + 5х). у == log2 (х2 — 4х — 5). у = log( (— Зх2 — 7х — 2). з"
1 uv I • V —— e У 2 sin2 x — cos x 1562. y = 2-^. 1563. у = 3/л 4-3^.
1546. 1547. 1 / 2х — 4 у= V х+г V = 1/— Л~4 ' 2 — 1564. y = lg|6x — 8|. 1565. у — lg cos x.
1548. У= ]/- — 1. Г X 1566. y=lgtgx.
1567. (У с т н о.) Найти области изменения следующих функ-
б)
в)
г)
Д)
ции:
а) У = I sin х |;
у = cos2 х;
у = cos х — 1;
У = tg2 х\
у = sin2 х + cos2 х;
е)
ж)
з)
и)
у = cos х — sin х;
у = 3 sin х 4- 4 cos х,
у = 12 sin х — 5 cos х\
у = sin х • cos х.
136
1568. Найти области изменения функций:
а) у = (х — З)2 — 1; г) у = 5s,nx;
б) у = — (х + 2)2 + 5; д) у = х — | х |;
в) у = 2х2 — 28х + 96; е) у = sin4 х -ф cos4 х.
1569. Сравнить области определения функций:
а) у = х и у = 10Je*;
б) у — 2 1g х и у = 1g х2.
Построить графики этих функций.
Возрастание и убывание функций
§ 204
Функция / (х) называется монотонно возрастающей (или
просто возрастающей) в интервале а < х < Ь, если из условия
х2 > X! вытекает, что
При этом
/ (Х2) > f (X,).
а < хх < Ь, а < х2 < Ь.
Другими словами, функция называется монотонно возраста-
ющей в некотором интервале, если из двух произвольных значений
аргумента, взятых из этого интервала, большему соответствует
большее значение функции.
Например, функция у = sin х (см. рис. 268 на стр. 132) является
« л . л 3 _ ^5 7
возрастающей в интервалах —— < х < —, — л < —л, — л <
9
< х < — л и т. д. Функция у = 2' (см. рис. 267) является возра-
стающей на всей числовой прямой, функция у =
возрастает (рис. 272).
нигде не
Если функция у — f (х) монотонно возрастает в интервале
а < х < Ь, то график ее в этом интервале с ростом х поднимается
все выше и выше. Это, конечно, не
означает, что график «уходит» вверх
как угодно высоко. Например, гра-
фик функции у —--------- при положи-
тельных значениях х (см. рис. 273) под-
нимается с ростом аргумента все выше
и выше. Тем не менее он никогда не
перейдет и даже не дойдет до оси
абсцисс.
Функция у = f (х) называется моно-
тонно убывающей (или просто убываю-
137
щей) в интервале а < х < Ь,
если из условия х2 > xt
вытекает, что
Нх2)
При этом
а < хг < Ь, а < х2 < Ь.
Другими словами, функ-
ция называется монотонно
убывающей в некотором ин-
тервале, если из двух произ-
вольных значений аргумен-
та, взятых из этого интер-
вала, большему соответст-
вует меньшее значение фун-
кции.
Например, функция у =
— sin х монотонно убывает в
л , , 3
интервалах —< х < — я,
2 2
. / 1 Xх
т. д. Функция у = —
убывает на всей числовой прямой. Функция у = 2х нигде не убывает.
Если функция f (х) монотонно убывает в интервале а < х < Ь,
то график ее в этом интервале с ростом х опускается все ниже и
ниже. Это также не означает, что график «уходит» как угодно
далеко вниз. Учащимся предлагается самостоятельно построить
соответствующий рисунок.
Функции, которые в интервале а < х < b только возрастают
или только убывают, называются монотонными в этом интер-
вале.
До сих пор мы говорили об интервале а < х < Ь. Такой ин-
тервал включает в себя крайние точки х=аих=6и потому
называется замкнутым интервалом. Но в некоторых случаях гово-
рить о замкнутом интервале нехорошо. Неудобно, например,
говорить о поведении функции у = tg х в интервале
л л г, Л
—— < к < —. Ведь при х — ——
и х = эта функция вообще
не определена. Поэтому вместо интервала---------< х
Л
< — лучше го-
ворить
об
л
интервале ——
< х < — . Такой интервал не содержит
крайних точек х —-------и х = — и поэтому называется откры-
тым интервалом.
В дальнейшем нам придется говорить как об открытых, так и
о замкнутых интервалах. Однако в каждом из этих случаев
138
будет ясно, о каком интервале идет речь, и потому мы будем говорить
просто об интервалах. Отметим лишь, что замкнутый интервал
а < х < b обычно записывается в виде [а, 6], а открытый интервал
а < х < Ь — в виде (а, Ь).
Упражнения
Определить участки возрастания и участки убывания данных функций; построить графики этих функций (№ 1570—1585):
1570. 1571. у = х2 + Зх — 108. у = — х2 + Зх -Ь 4. 1578. 1579. у = | cos х |.
У х 2 ’
1572. у = |х2 + Зх— 101. 1580. у = sin2x.
1573. у — | —х2 + Зх + 41. 1581. у = cos —. л 2
1574. у = sin (х + — 1 \ 4 / 1582. у = lg(l + х).
1575. / л \ у = cosx . Л \ 6 / 1583. у = lg( 1 —X).
1576. у = ,е(Л + т} 1584. 5x4-4 у = X
1577. y = ctg (х — у! 1585. х4-1 У = Г х— 1
1586. функций: Определить участки возрастания и участки убывания
а) у = 23-6t; б) у = 5.
1587. Доказать, что сумма двух функций, монотонно возра-
стающих в некотором интервале, есть функция, монотонно воз-
растающая в этом интервале.
1588. Будет ли разность двух монотонно возрастающих функций
монотонно возрастающей функцией?
Экстремальные значения функции
§ 205
В этом параграфе мы изучим некоторые вопросы поведения
функции у — f (х) в интервале [а, 6]. При этом, конечно, мы будем
предполагать, что функция / (х) определена в каждой точке этого
интервала.
Наибольшее из всех тех значений, которые принимает функция
у = f (х) в интервале [а, Ь], называется ее абсолютным максиму-
мом, а наименьшее — абсолютным минимумом в данном интервале.
Например, для функции у = f (х), графически представленной
на рисунке 274, абсолютным минимумом в интервале [0, 7] является
значение f (0) = 1, а абсолютным максимумом — значение
/(6) = 5.
139
Наряду с абсолютным макси-
мумом и абсолютным минимумом
в математике часто говорят о ло-
кальных (т. е. местных) макси-
мумах и минимумах.
Точка х = с, лежащая внутри
интервала [а, 6], называется точ-
кой локального максимума функ-
ции у = f (х), если для всех значений
х, достаточно близких к с,
f W < f (с).
Значения функции
точках ее локальных
(D
у = / (х) в
максимумов
называются локальными максимумами этой функции. Например,
для функции у = f (х), графически представленной на рисунке 274,
точками локального максимума являются точки х = 2 и х = 6,
а самими локальными максимумами — значения
f (2) = 3 и f (6) = 5.
В точках х = 2 и х = 6 функция f (х) принимает значения, боль-
шие, чем в соседних точках, достаточно близких к ним:
/(2) >/(*);
Н6) >/(х).
Для функции у = f (х), графически представленной на рисун-
ке 275, точкой локального максимума будет, например, точка х = с.
Для всех х, достаточно близких к с,
(с).
так что условие (1) выполняется. Точка х = хх также является
точкой локального максимума. Для всех значений х, достаточно
близких к Xi, f (х) < f (хх), если х < хх, и f (х) = f (хх), если х > хг.
Следовательно, и в этом случае f (х) < f (xj. А вот точка х = х2
уже не будет точкой локального
максимума. Левее ее/(х) = f (х2),
но правее ее f (х) > f (х2). По-
этому условие (1)не выполняется.
Точках = с, лежащая внутри
интервала [а, Ь], называется точ-
кой локального минимума функ-
ции у = f (х), если для всех зна-
чений х, достаточно близких к с,
f (X) >f (с). (2)
Значения функции в точках ее
локальных минимумов называют-
140
ся локальными минимумами этой функ-
ции. Например, для функции у = f (х),
графически представленной на рисунке
274, точкой локального минимума яв-
ляется точка х = 3, а самим локаль-
ным минимумом — значение f (3) = 2.
Для функции, графически пред-
ставленной на рисунке 275, точкой
локального минимума будет, например,
точка х = х2. Для всех значений х,
достаточно близких к х2, f (х) = f (х2),
если х <x2,Hf (х) > f (х2), если х > х2.
Следовательно, условие f (х) > f (х2) вы-
Рнс. 276.
лолняется. Точка х = с, отмеченная нами выше как точка локаль-
ного максимума, является вместе с тем и точкой локального
минимума. Ведь для всех точек х, достаточно близких к ней,
/(*)=/(*),
и потому формально неравенство f (х) > f (с) выполняется.
Точки минимумов и точки максимумов функции f (х) назы-
ваются точками экстремумов этой функции. Значения функции
/ (х) в точках экстремумов называются экстремальными значениями
этой функции.
Рисунок 274 показывает различие между абсолютными и ло-
кальными экстремумами. Функция у = f (х), изображенная на этом
рисунке, имеет в точке х = 2 локальный максимум, который не
является абсолютным максимумом в интервале [0, 7|. Точно так
же в точке х = 3 эта функция имеет локальный минимум, не яв-
ляющийся абсолютным минимумом в интервале (0, 7].
Если абсолютный максимум функции у = f (х) в интервале [a, dj
достигается во внутренней точке этого интервала, то этот абсо-
лютный максимум является, очевидно, и локальным максимумом
(см., например, рис. 274 в точке х = 6). Но может случиться, что
этот абсолютный максимум достигается не внутри интервала [а, 6],
а в какой-нибудь крайней его точке (рис. 276). Тогда он не яв-
ляется локальным максимумом. Отсюда вытекает следующее пра-
вило для нахождения абсолютного максимума функции у — f (х)
в интервале [а, Ь].
I. Находим все локальные максимумы функции у = f (х) в дан-
ном интервале.
2. К полученным значениям добавляем значения этой функ-
ции в концах данного интервала, то есть значения f (а) и f (д).
Наибольшее из всех этих значений и даст нам абсолютный
максимум функции у = f (х) в интервале [а, Ь].
Аналогично находится и абсолютный минимум функции
у — [ (х) в интервале [а, 6].
Ml
у Пример. Найти все локальные
экстремумы функции у = № — 2х — 3.
" Каковы наибольшее и наименьшее зна-
. чения этой функции в интервале [0, 5)?
\ / Преобразуем данную функцию, вы-
\ . / делив полный квадрат:
-----—j-------4----—х у = х2 — 2х 4- 1 — 4 = (х — I)2 — 4.
\ । / Теперь легко построить ее график. Это
\ 1 / будет направленная вверх парабола с
\ j / вершиной в точке (1, —4) (рис. 277).
\ । / Единственной точкой локального экст-
lSJ-Z ремума является точка х = 1. В этой
। точке функция имеет локальный мини-
мум, равный —4. Чтобы найти наи-
тие. 277. большее и наименьшее значения данной
функции в интервале [0, 5], заметим,
что при х = 0 у = —3, а при х = 5 у = 12. Из трех значений —4,
—3 и 12 наименьшим является —4, а наибольшим 12. Таким
образом, наименьшее значение (абсолютный минимум) данной
функции в интервале [0, 5] равно —4; оно достигается при х = 1.
Наибольшее значение (абсолютный максимум) данной функции
в интервале [0, 5] равно 12; оно достигается при х = 5.
Упражнения
1589. Какие из известных вам функций на всей числовой
прямой:
а) совсем не имеют локальных экстремумов;
б) имеют ровно один локальный экстремум;
в) имеют бесконечное множество локальных экстремумов?
В упражнениях № 1590—1600 найти точки локальных экстре-
мумов и сами локальные экстремумы данных функций. Выяснить,
какие это экстремумы (максимумы или минимумы):
1590. у = (х — I)2 + 5. 1595. у = ! . 2 — cos х
1591. у = 3 —(х+ 2)2. 1592. у = 12х2 — х— 1. 1593. у = (х — 1)(х — 3). 1594. у = ? . 7 X2 -ь X + 1 1596. у = V х2 — 2х 4- 8. 1597. у = —х(х 4- 2а). 1598. у == sin (х —— 1 \ 4) 1599. у = cos(x 4- —1 1600. у = sin х 4- cos х.
Найти абсолютные экстремумы данных функций в указанных
интервалах (№ 1601—1603):
1601. у = —2х2 — Зх — 1 в интервале [ х ] <2.
1602. у = | х2 + 5х + 6 | в интервале [— 5, 4].
142
1603. у — sin х — cos x
в интервале
л
3
1604. Найти абсолютные
Nf-a.b)
экстремумы функции
M(a.b)
—©
У = (х — 3) (х - 5)
в интервалах:
а) 12, 3|; в) [4, 5];
б) [3, 4]; г) [2, 5].
Четные и нечетные
функции § 206
о
Функция у = f (х) называет-
ся четной, если при всех значе-
ниях х из области определения
этой функции
H-X) = f (X).
Примерами четных функций
могут служить хорошо изучен-
ные нами функции у = х2,
у = cos х, у = | х | и т. д.
Пусть точка М с координа-
тами (а, Ь) принадлежит гра-
фику четной функции у = f (х).
Тогда b — f (а). Так как функ-
ция f (х) четна, то и f ( —а) =
= f (а) = Ь. Но это означает, что
наряду с точкой М (а, Ь) гра-
фику функции у — f (х) должна
принадлежать и точка N с
координатами ( —а, Ь). Эти две
точки симметричны друг другу
относительно оси у (рис. 278).
Таким образом, какую бы
точку графика четной функции
мы ни взяли, на нем обяза-
тельно найдется точка, сим-
метричная первой относительно
оси у. Вот почему график чет-
ной функции представляет
собой линию, симметрич-
ную относительно оси ор-
динат (один из таких гра-
фиков показан на рис. 279).
Рис. 278.
143
Функция у — f (х) называется нечетной, если при всех значе-
ниях х из области определения этой функции
f(-x) = -f(x).
Примерами нечетных функций служат функции у = х, у = х3,
у = sin х и т. д.
Пусть точка Р с координатами (а, Ь) принадлежит графику
нечетной функции у = f (х); тогда b = f (а). Так как функция f (х)
нечетна, то f (—а) = —f (а). Поэтому f (—а) = — Ь. Последнее ра-
венство означает, что точка Q с координатами ( —а, —Ь) должна
принадлежать графику функции у = f (х). Итак, если точка Р
с координатами (а, Ь) принадлежит графику нечетной функции
у = f (х), то этому графику должна принадлежать и точка Q с
координатами (—а, —Ь) (рис. 280). Точки Р и Q симметричны
относительно начала координат (докажите это!).
Таким образом, какую бы точку графика нечетной функции мы
ни взяли, на нем обязательно найдется другая точка, симметрич-
ная первой относительно начала координат. Вот почему
график любой нечетной функции симметричен отно-
сительно начала координат (см., например, рис. 281).
Не следует думать, что всякая функция является либо чет-
ной, либо нечетной. Существует очень много функций, которые
нельзя отнести ни к четным, ни к нечетным. Так, например,
для функции / (х) = х + Xs имеем: f ( —х) = — х + х2. Ни одно из
двух тождеств f ( —х) = / (х) и f ( — х) = —f (х) не имеет места.
Следовательно, данная функция не является ни четной, ни не-
четной.
Кроме того, говорить о том, что функция у = f (х) четна или
нечетна, можно лишь в том случае, когда область определения этой
функции является симметричной относительно начала координат.
Это означает, что если функция определена при х = а, то
144
должна быть определена и при х =—а. В противном случае
сравнивать выражения f (х) и [ ( —х) не имеет смысла. Например,
функция у = 1g х определена только для положительных значе-
ний аргумента. Поэтому одно из выражений 1g х и 1g ( — х) на-
верняка не имеет смысла. Следовательно, говорить о том,
является ли логарифмическая функция четной или нечетной,
также не имеет смысла.
Упражнения
1605. (Усти о.) Среди данных функций указать четные и
нечетные:
1) у = х100;
2) у = х-3;
3) у = J/x;
4) у =/х;
5) у — х4 — 2х2 + 3;
6) у — х3 — 5х — 1;
7) у = sin (х2);
8) у = tgx 4- ctgx;
9) у = sin х 4- cosec х;
10) у = х4-sinx;
11) у = 2х 4- 2~*;
12) у = —;
X
13) у
X
1606. Какие из данных функций являются четными и какие
нечетными:
1) у= 10-*—10';
2) у = sin (—х);
3) у = cos (—х);
1607. Доказать, что сумма, разность, произведение и частное
двух четных функций являются четными функциями.
1608. Доказать, что произведение и частное двух нечетных
функций представляют собой четные функции.
1609. Может ли функция быть одновременно и четной и нечетной?
1610*. Что вы можете сказать о четности функции f (х), если
известно, что функция | f (х) |: а) четна; б) нечетна?
1611. Может ли монотонная на всей числовой прямой функция
быть: а) четной; б) нечетной?
1612. Как достроить график четной функции у = [ (х), если
он задан только при х > 0?
145
Периодические функции
$ 207
Функция у = f (х) называется периодической, если существует
число Т =£ 0, такое, что при всех значениях х из области определе-
ния этой функции
f(x + T) = f (л).
Число Т в этом случае называется периодом функции.
Периодическими являются, например, тригонометрические
функции у = sin х и у = cos х. Их период равен 2л. Примером
периодической нетригонометрической функции может служить
функция у = {х}, которая каждому числу х ставит в соответствие
его дробную часть*. Например, {3,56} = 0,56;{2,01} = 0,01 и т. д.
Если к произвольному числу х прибавить 1, то изменится лишь
целая часть этого числа; дробная же часть останется прежней.
Следовательно, {х + 1} = {х} и потому функция у = {х} является
периодической с периодом 1.
Из равенства f (х + Т) = f (х) следует, что все значения функ-
ции у = / (х) повторяются с периодом Т. Это находит свое отра-
жение и в графическом изображении периодических функций.
Так, например, в интервале [0, 2л] синусоида имеет ту же самую
форму, что и в интервалах [2л, 4л], [4л, 6л] и т. д. (рис. 282). На
рисунке 283 представлен график функции у = {х}. Периодичность
функции у = {х} обусловливает то, что график ее в интервале
[0, 1] имеет ту же самую форму, что и в интервалах [1, 2],
[2, 3] и т. д.
Если Т — период функции / (х), то 2Т, ЗТ, 4Т и т. д. также
периоды этой функции.
Действительно,
f (х + 27) = f [(X + 7) + 7] = f (х -I- 7) = / (x),
/ (x + 37) = f [(X + 27) + 7] = [ (x + 27) = f (x)
♦ О дробной части числа см. в главе VIII, § 187,
146
и т. д. Кроме того, периодом
функции f (х) можно считать и лю-
бое из чисел: —Т, —2Т, —ЗТ
и т. д. В самом деле,
f(x-T) = f [(х—Т) + Т] = f(x),
f (х - 2Т) = Д(х-2Т)+2Т] = Дх)
и т. д. Итак, если число Т есть
период функции f (х), то при лю-
бом целом п число пТ также пе-
риод этой функции. Поэтому всякая периодическая функ-
ция имеет бесконечное множество периодов. Например,
периодом функции у — sin х можно считать любое из чисел: 2л,
4л, 6л, —2л, —4л, а периодом функции у ={х} — любое из чисел
1, 2, 3, —1, —2, —3 и т. д.
Говоря о периоде функции у = f (х), обычно имеют в виду
наименьший положительный период. Так, мы говорим, что пе-
риодом функции у = sin х является число 2л, периодом функции
у = tg х — число л, периодом функции {х} — число 1 и т. д.
Следует, однако, иметь в виду, что наименьшего положитель-
ного периода у периодической функции может и не быть. Напри-
мер, для функции f (х) = 3 (рис. 284) любое действительное число
является периодом. Но среди положительных действительных
чисел не существует наименьшего. Поэтому и функция f (х) = 3,
имея бесконечное множество периодов, не имеет наименьшего
положительного периода.
Упражнения
Для каждой из данных функций (№ 1613—1621) найти наи-
меньший положительный период:
1613 y = sin2x. 1619. у = sin(3x——1
\ 4 /
1614. у = cos—. 1620. y = sin2x.
2
1615. y = tg3x. 1621. у = sin4х 4- cos4х.
1616. y = cos(l—2х). у
1617. у = sinxcosx.
1618. у = ctg -------j-------
О
1622. Доказать, что сумма и про-
изведение двух функций, периодиче-
ских с одним и тем же периодом Т, q
являются функциями, периодическими
с периодом Т.
1623*. Докажите, что функция у =
= sin х + (х), являющаяся суммой двух Рис. 284.
147
периодических функций у = sin х и у = (л), сама не является
периодической.
Не противоречит ли это результату предыдущей задачи?
1624. Как достроить график функции у = f (х), периодической
с периодом Т, если он задан лишь в интервале [О, Т]?
Обратные функции
§ 208
Каждому допустимому значению переменной величины х ра-
венство у = f (х) ставит в соответствие вполне определенное зна-
чение переменной величины у. Однако в некоторых случаях
соотношение у = / (х) можно рассматривать и как такое равен-
ство, которое каждому допустимому значению переменной вели-
чины у ставит в соответствие вполне определенное значение пере-
менной величины х. Поясним это на конкретных примерах.
Пример 1. Равенство у = 2х — 1 каждому значению у ста-
вит в соответствии следующее значение х: х — . Например,
при у = lx = 1; при у = 2х = 1,5; при у = Зх = 2 и т. д. По-
этому можно сказать, что равенство у = 2х — 1 определяет х
как некоторую функцию переменной величины у. В явном виде
эта функция записывается таким образом: х — у
Пример 2. Равенство у — 2х каждому положительному зна-
чению у ставит в соответствие следующее значение х: х = log2 у.
Например, при у = 1 х — log2l = 0; при у = 2х = log2 2=1;
при у = Зх = log2 3 и т. д. Следовательно, равенство у = 2х опре-
деляет х как некоторую функцию переменной величины у. В явном
виде эта функция записывается таким образом: х = log2 у.
Пример 3. При--------— < х < — равенство у = sin х каждо-
му значению у, заключенному в интервале от —1 до 4-1, ставит
в соответствие число х, равное arcsin у. Например, при у = — 1
х = arcsin (—1)= ——; при у = 0 х = arcsin 0 = 0; при у = -^=
2 ) 2
х = arcsin и т. д. Следовательно, равенство у = sin х
л _ л
при дополнительном условии, что —— < х < — ,
как некоторую функцию переменной величины у.
эту функцию можно записать следующим образом:
т.
определяет х
В явном виде
х = arcsin у.
Вообще, пусть, исходя из равенства у = / (х), по каждому
допустимому значению величины у можно восстановить одно
и только одно значение величины х. Тогда это равенство
148
определяет х как некоторую функцию от у. Обозначим эту функцию
буквой <р: х = ф (у).
В этой формуле у выступает в роли аргумента, а х — в роли
функции. Вошло в обычай букву х употреблять для обозначения
аргумента, а букву у — для обозначения функции. Поэтому ту
функциональную зависимость, которая обозначена буквой ф, мы
перепишем в виде:
у = Ф (х).
Так определенная функция у = ф (х) называется обратной по
отношению к функции
У = f (*)•
Примеры. 1) Исходя из равенства у = 2х — 1, мы получили
х = Поэтому функция у = является обратной к функ-
ции у = 2х — 1.
2) Исходя из равенства у = 2х, мы получили х = log2 у.
Поэтому функция у = log2 х является обратной к функции у = 2х.
3) Исходя из равенства у = sin х при---< х < мы по-
лучили х = arcsin у. Поэтому функция у = arcsin х является об-
ратной к функции у = sin х, рассматриваемой на интервале
л л
----< X < —.
2 2
Отметим, что область определения и область изменения функ-
ции у = f (х) и обратной к ней функции у = ф (х) как бы меня-
ются ролями. То, что для функции у = f (х) было областью опре-
деления, для обратной функции у = ф (х) становится областью
изменения, а то, что для функции у = f (х) было областью изме-
нения, для обратной функции у = ф (х) становится областью
определения. Так, например, для функции у = 2х областью опреде-
ления является совокупность всех действительных чисел, а
областью изменения — совокупность всех положительных чи-
сел. Для обратной к ней функции у — log2 х, наоборот, совокуп-
ность всех положительных чисел является областью определе-
ния, а совокупность всех действительных чисел — областью
изменения.
Для любой ли функции у = f (х) существует обратная функ-
ция у = ф (х)? Чтобы ответить на этот вопрос, рассмотрим два
примера.
Пример 1. Каждому значению у по формуле у = х2 соот-
ветствует два значения х; например, значению у = 1 соответст-
вуют значения х = +1 и х = —1; значению у = 4 соответствуют
значения х = 2 и х = —2 и т. д. Поэтому если функцию у = х2
рассматривать на всей числовой прямой (или при всех действи-
149
тельных значениях х), то она не будет иметь обратной функции.
Однако если эту функцию рассматривать только при положи-
тельных значениях х, то она будет обладать обратной функцией.
По значению квадрата положительного числа это число
восстанавливается однозначно. Обратную функцию в данном
случае можно записать в виде у = -j/ х.
Пример 2. Каждому значению величины у, заключенному
в интервале от—1 до 1, по формуле у = sin х соответствует
бесконечное множество значений х. Например, при у = 0 такими
значениями х являются 0, л, 2л, Зл и т. д.; при у = 1 х =
5 9
— л, — л и т. д. Поэтому если функцию у = sin х рассматривать
на всей числовой прямой (или при всех действительных значе-
ниях х), то она не будет иметь обратной функции. Если же эту
функцию рассматривать только при-----< х < -р то по значе-
ниям у значения х восстанавливаются однозначно. Следова-
тельно, при —< х < функция у = sin х имеет обратную
функцию у = arcsin х.
Нетрудно подметить то общее, что делали мы в обоих при-
мерах при нахождении функций, обратных к данным. Для каждой
из данных функций мы выделяли интервал, в котором она
является монотонной. Можно доказать общее утверждение: если
функция f (х) монотонно возрастает (или убывает) в
интервале [а, Ь], то при а < х<Ь существует обрат-
ная к ней функция.
У пражнения
В упражнениях № 1625—1628 найти функции, обратные к
данным. Указать области определения и области изменения
данных и обратных к ним функций:
1625. у = х3. 1626. у = log, х. 1627. у = 1^. 1628. у=х\х< 0).
Г 1 +*
1629. Доказать, что при а =# 0 функция, обратная к линейной
функции у = ах + Ь, есть функция линейная.
1630. Доказать, что функция, обратная к дробно-линейной
функции у = № — Ьсф 0), сама является дробно-линейной.
1631. Какому условию должны удовлетворять числа а, Ь, с и d,
чтобы дробно-линейная функция у = ах-~-- была тождественно
сх + d
равна обратной к ней функции?
Приведите несколько примеров.
150
1632. Существует ли функция, обратная к функции у =« cos к
в интервале:
а) —— < х < —; б) 0 < х < л; в) — < х < — л?
2 2 7 2 2
1633. Существует ли
интервале:
\ л . л
а)----<х<—;
2 2
1634. Существует ли
в интервале:
В
функция, обратная к функции у = tg х
б) 0 < х < л;
в) — < х < — л?
2 2
функция, обратная к функции у = {х}
1 1 ч
а) 0 < х < —; б)0<х<1; в)0<х<1; г)—<х<—?
2 2 2
Взаимное расположение графиков прямой
и обратной функции
§ 209
В этом параграфе мы рассмотрим вопрос о взаимном распо-
ложении графика функции у — f (х) и графика обратной к ней
функции у — <р (х). Для этого нам потребуется следующая лемма.
Лемма. Точки плоскости с координатами (а, b)u(b, а)
симметричны друг другу относительно биссектрисы
1-го и 3-го координатных углов.
Доказательство. Пусть точка Р имеет координаты
(а, Ь), а точка Q — координаты (6, а) (рис. 285). Опустим из этих
точек перпендикуляры на оси координат. В результате получим:
ОА = OD = а-, ОВ = ОС = Ь.
Перегнем чертеж по прямой ОМ — биссектрисе 1-го и 3-го коор-
динатных углов. Тогда ось у пойдет по оси х, так как Z. МОВ =
= Z_ МОС. Точка В совместится с точ-
кой С, поскольку ОВ — ОС, а ВР пой-
дет по CQ, так как через точку С можно
провести лишь одну прямую, перпен-
дикулярную оси х. А в силу того, что
ВР = СQ, точка Р совпадет с точ-
кой Q.
Таким образом, если перегнуть чер-
теж по биссектрисе ОМ, то точки Р
и Q совпадут. А это и означает, что
они симметричны друг другу относи-
тельно биссектрисы ОМ.
Лемма доказана.
151
Пусть теперь точка Р с коор-
динатами (а, Ь) принадлежит гра-
фику функции у — f (х). Тогда зна-
чению у = b равенство у = f (х)
ставит в соответствие значение
х = а. Но это означает, что точка
Q с координатами (Ь, а) должна
принадлежать графику обратной
функции у — <р (х).
Итак, если точка Р с коорди-
натами (а, Ь) принадлежит графику
функции у — f (х), то точка Q с
координатами (Ь, а) должна при-
надлежать графику обратной функ-
ции у = <р (х). Эти точки симмет-
ричны относительно биссектрисы 1-го и 3-го координатных углов.
Таким образом, какую бы точку Р на графике функции
у = f (х) мы ни взяли, на графике обратной к ней функции у = <р (х)
обязательно найдется точка Q, симметричная точке Р относи-
тельно биссектрисы 1-го и 3-го координатных углов. Вот почему
графики взаимно обратных функций симметричны друг
другу относительно биссектрисы 1-го и 3-го координат-
ных углов (см., например, рис. 286, на котором представлены
графики взаимно обратных функций у — 2х и у = log2 х).
У пражнения
На одном и том же чертеже построить графики данной и обрат-
ной к ней функций (№ 1635—1641):
1635. у = х2 (х > 0).
1636. у = — л"-Г 1.
Л 3
1637. у=(Х’еСЛНХ<°'
(2х, если х>0.
1638. у= 1/Г^х.
1639. у = J (0,5х -|- 2, если х>0,
|2х -|- 2, если х <; 0.
[х2, если х > 0,
1640. у = j
1 х3, если х < 0.
1641. y = sinxf--------— <х<— Y
\ 2 2 /
1642. Каковы особенности графика функции у = f (х), если эта
функция тождественно равна обратной к ней функции?
Ответ пояснить примерами (см., например, задачу № 1631).
Краткий обзор свойств и графиков
ранее изученных функций
§ 210
В этом параграфе мы дадим краткий обзор свойств и графиков
ранее изученных функций. При этом мы будем придержи-
ваться следующего плана: 1) область определения функции;
152
2) область изменения функции;
3) четность функции; 4) периодич-
ность функции; 5) интервалы
знакопостоянства; 6) нули функ-
ции, то есть те значения аргумен-
та, при которых функция обра-
щается в нуль; 7) монотонность
функции; 8) локальные экстремумы
функции; 9) поведение функции
вблизи «особых» точек (например,
функции у = — вблизи точки
х = 0).
Впрочем, порядок этот не яв-
ляется обязательным и в некото-
рых случаях для пользы дела
может быть смело изменен. От-
метим лишь, что осуществление
каждого пункта плана всегда по-
лезно сопровождать геометричес-
кой интерпретацией на графике ис-
следуемой функции.
1. Квадратная функция
у = ах2 + bx -\-с (a 0)
Эта функция определена для
всех значений х, так что областью
ее определения служит совокуп-
ность всех действительных чисел.
Графиком квадратной функции
служит парабола, вершина кото-
/ ь
рои имеет координаты------------,
\ 2а
---------1. При а > 0 парабола
направлена вверх (рис. 287), а
при а < 0 — вниз (рис. 288). Если
а > 0, то областью изменения
данной функции является
совокупность всех чисел, боль-
Ь* — 4ас
ших или равных--------—; если же
а < 0, то областью изменения
ее служит множество всех чи-
сел, меньших или равных
Ьг — 4ас
4а
Рис. 289.
153
Рис. 290
При Ь #= 0 функция у = ах2 4-
+ Ьх + с не будет ни четной, ни
нечетной, поскольку ни одно из
равенств
ах2 — Ьх + с — ах2 4- Ьх + с,
If (—х) = f (x)J
и
ах2 — Ьх 4- с = — (ах2 4* Ьх 4- с),
If (—х) = —f (х)1
не выполняется тождественно. При
Ь = 0 квадратная функция прини-
мает вид у = ах2 4* с и потому яв-
ляется четной функцией.
Данная функция непериодична.
Если дискриминант
d = Ь2 — 4ас
отрицателен, то функция не имеет нулей. В этом случае все ее
значения имеют один и тот же знак — знак коэффициента а (см.
рис. 289 для а > 0 и рис. 290 для а < 0). Если дискриминант d
положителен, то функция имеет два нуля:
— b— /б2 — 4ас „ — Ь + Уб2 —4ас
2а 2а
Если к тому же а > 0, то функция положительна при х < xt и
х > х2, а отрицательна при х^ < х < х2 (см. рис. 287). В случае,
когда d > 0, а а < 0, функция положительна при хх < х < х2,
а отрицательна при х <х1 и х > х2 (см. рис. 288).
Наконец, возможен и случай, когда d = 0. Тогда квадратная
функция имеет единственный нуль
При всех значениях х =/= — она сохраняет один и тот же знак —
знак коэффициента а.
В случае, когда а> 0, квадратная функция у = ах2 + Ьх + с
монотонно убывает при х < — — и монотонно возрастает при
к > — £ (см. рис. 287 и рис. 289). В случае, когда а < 0, она,
20 . ь л
наоборот, монотонно возрастает при х < — — и монотонно убывает
при х > — (см. рис. 288 и рис. 290).
Данная функция имеет единственный локальный экстремум
— 4ас
Уэкстр— — •
151
Этот экстремум достигается при
ь
х — — — и является минимумом
при а > 0 (рис. 287 и рис. 289) и
максимумом при а < 0 (рис. 288
и рис. 290).
2. Степенная функция у = хг
Область определения такой
функции зависит от г. Напри-
мер, при г = 1 (у = х) это будет
совокупность всех действитель-
1 .
ны.х чисел, при г = — (у =
2
= j/jc) — совокупность неотри-
цательных чисел, при г = 0
(у = х°) — совокупность всех чи-
сел, кроме 0. Для положитель-
ных значений х функция у = хг
определена всегда, независимо
от того, чему равно г.
Область изменения функции
у = хг также зависит от г. Напри-
мер, функция у = х (г = 1) может
принимать все действительные
значения, функция у = х2 (г — 2)
— только неотрицательные зна-
чения, а функция у = х° (г = 0)
— лишь одно значение, равное 1.
Среди степенных функций
есть четные и нечетные. На-
пример, функции у = х2, у —
= х4 — четные, а функции у ~х3,
у = х~3 — нечетные. Некоторые
степенные функции (например,
у — х) определены лишь для
неотрицательных значений ар-
гумента. Для них ставить воп-
рос о четности не имеет смысла.
Степенная функция у = х'
непериодична.
При х > 0 степенная функ-
ция у = хг независимо от г по-
ложительна.
Некоторые степенные функ-
, 1
ции (например, у = —,
155
3
•A «
у = x ) не имеют нулей, для дру-
гих же нулем является число 0 (на-
пример, для функций у = ]/~х~, у=х3
и т. д.).
Если число г положительно, то
при х > 0 степенная функция у = хг
монотонно возрастает (рис. 291). Если
же г отрицательно, то при х > 0 сте-
пенная функция у = хг монотонно
убывает (рис. 292).
Некоторые степенные функции,
например у — ха, у = xi, имеют локальный минимум в точке
х = 0.
Отметим еще поведение функций у —
1 1 <
— и у = — вблизи
X х*
точки
х = 0. Когда х стремится к нулю, оставаясь положительным,
функция у = — неограниченно возрастает. Когда же х стремится
к нулю, оставаясь отрицательным, она неограниченно убывает
(рис. 293).
Функция у = — при приближении х к нулю (как слева, так
X*
и справа) неограниченно возрастает (рис. 294).
3. Тригонометрические функции
Из тригонометрических функций мы рассмотрим лишь две
функции: у = sin х и у — tg х.
Областью определения функции у = sin х является совокуп-
ность всех действительных чисел, а областью изменения — сово-
купность всех чисел, заключенных в интервале 1—1,1] Функция
является нечетной и периодической с периодом 2л. В интервалах
2лл <х <л+ 2лл эта функция положительна, а в интервалах
я + 2лл < х<2л + 2лл отрицательна (рис. 295). При х=пп она
обращается в нуль. В интервалах — — + 2лл < л < —
4-2лл функ-
ция монотонно возрастает, а в
+ 2лл монотонно убывает.
интервалах -^-+ 2лл
3
х < — я 4-
2
156
Точки х — -—к- 2пл являются
2
точками локального максимума
функции у = sin х. В них она при-
нимает наибольшие значения,
равные 1. Точки х =----- 4- 2пл
являются точками локального
минимума. В них функция при-
нимает наименьшие значения,
равные —1.
Функция у = tgx определена
при всех значениях х, кроме
х = — 4- пл. Областью ее измене-
2
ния является совокупность всех
действительных чисел. Эта функция
нечетна и периодична с пери-
одом л (рис. 296). В интервалах пл
<ZX< — + пл она положи-
тельна, а в интервалах — — + пл < х < пл отрицательна. При
х = пл функция обращается в нуль. В каждом интервале, не
содержащем точек х = у+ пл, эта функция монотонно возрастает.
Локальных экстремумов функция не имеет. Когда значения х
неограниченно приближаются к — + пл, оставаясь меньше — + пл,
значения функции у = tgx неограниченно возрастают. Когда же
значения х неограниченно приближаются к---------Ь пл, оставаясь
больше этих значений, функция у — tg х неограниченно убывает.
4. Показательная функция у = ах (а>0, а =# 1)
Областью определения этой функции является совокупность
всех действительных чисел, а областью изменения — совокупность
всех положительных чисел. Функция не является ни четной, ни
нечетной. Не является она и периодической. При всех значениях
аргумента х эта функция положительна. При а > 1 показатель-
ная функция у = ах является монотонно возрастающей (рис. 297),
а при а < 1 — монотонно убывающей (рис. 298). Точек локаль-
ных экстремумов функция не имеет.
5. Логарифмическая функция у = logo* (а>0, а 1)
Областью определения этой функции является совокупность
всех положительных чисел, а областью изменения — совокупность
всех действительных чисел. О четности или нечетности этой функ-
ции говорить не имеет смысла. Функция не является периодиче-
ской. Если а > 1, то при х > 1 функция положительна, а
157
при х < 1 отрицательна
(рис. 299). Если же а < 1,
то, наоборот, при х > 1 функ-
ция отрицательна, а при
х < 1 положительна (рис. 300).
Единственным нулем лога-
рифмической функции яв-
ляется точка х = 1. При а > 1
эта функция является моно-
тонно возрастающей (рис.
299), а при а < 1 — монотон-
но убывающей (рис. 300). Ло-
кальных экстремумов функ-
ция не имеет. Если а > 1,
то при приближении х к ну-
лю функция неограниченно
убывает; если же а < 1, то
при приближении х к нулю
функция неограниченно воз-
растает.
Упражнения
По плану, описанному в
данном параграфе, исследо-
вать функции (№ 1643—1652):
1643. у = sin2 х.
1644. у = sin 2х.
1645. у = — |cos х|.
1646. у = sinfx----1
\ 4 /
1647. y = tg(x + у).
1648. у = х2 — 4х + 5.
1649. у = х2 + х — 7.
1650. у = 1 4- j — 2ха.
1651. у = х Ух.
1652. у = ^±5.
z 1 —х
Предел функции § 211
Прежде чем дать общее оп-
ределение предела функции, рас-
смотрим несколько примеров.
Пример 1. Пусть f (х) =« х2.
Если аргумент х пробегает ряд
значений, сходящихся к числу 2,
158
то функция / (х) будет пробегать ряд значений, сходящихся к числу 4. Это мож-
но заметить, рассматривая таблицу приближенных значений функции
|х’-4|:
X 1,96 1,97 1,98 1,99 2,00 2,01 2,02
х2 (приближенно) 3,84 3,88 3,92 3,96 4,00 4,04 4,0b
1 х2 — 4 | (приближенно) 0,16 0,12 0,08 0,04 0 0,04 0,08
Чем ближе значение аргумента х к 2, тем меньше абсолютная величина раз-
ности ха — 4.
В этом можно убедиться и строго математически, не обращаясь к таблич-
ной иллюстрации. Докажем, что, какое бы малое положительное число в
мы ни взяли, всегда можно указать такой интервал, содержащий внутри се-
бя точку х = 2, что для всех точек этого интервала буде! выполняться нера-
венство | ха — 4 | < е.
Действительно, неравенство | х2 — 4 | < 8 эквивалентно двойному нера-
венству
—8 < X2 — 4 < 8,
откуда получаем:
4 — е<ха<4 + е,
У4 — е < х < V4 + ё.
(Мы учитываем только положительные значения х, поскольку поведение функ-
ции у = ла нас интересует сейчас лишь вблизи точки л = 2.) _____
Итак, неравенство | х2 — 4 | < 8 выполняется в интервале У 4 — е < л <
< 1^4 + е, который содержит внутри себя точку х = 2.
Например, неравенство | х2 — 4 | < 0,1 (е = 0,1) выполняется в интервале
]/3,9 < х < J^4,1, или 1,98 < х < 2,02; неравенство | х2 — 4 | < 0,01(8= 0,01)
выполняется в интервале }z3,99 < х < 1^4,01, или 1,998 < х < 2,002.
Интервал (1^4—8, можно было бы построить и геометрически.
Пусть А есть точка графика функции у = ха с абсциссой х = 2 (рис. 301).
По обе стороны от этой точки проведем го-
ризонтальные прямые, отстоящие от А
на расстоянии в. Эти прямые пересекают
правую часть параболы у = х2 в
Рис. 300.
Рис, 301.
159
точках В и С. Опуская из них перпендикуляры на ось абсцисс,
получим отрезок В'С'. Этот отрезок и представляет собой интервал
(1^4—в, + е), который раньше мы получили алгебраически.
Итак, если значения аргумента х выбирать достаточно близкими к 2, то
значения функции у = ха будут как угодно мало отличаться от 4. Можно, на-
пример, добиться, чтобы выполнялись неравенства
I — 4 I < 0,001;
I х2 — 4 | < 0,0001
и т. д. Число 4 в таком случае естественно назвать пределом функции у = х2
при х, стремящемся к 2.
х2 — 9
Пример 2. Рассмотрим таблицу значений функции у =-------------- вбли-
х 3
зи точки X = 3.
X 2,94 2,96 2,98 3 3,02 3,04 3,06
о со 1 1 ’к 4 II 5,94 5,96 5,98 Функция не определена 6,02 6,04 6,06
При х = 3 наша функция не определена: числитель и знаменатель дроби
обращаются в нуль. Если же значения х выбирать достаточно близкими к 3
(но не равными 3), то соответствующие значения у будут сколь угодно близ-
ки к 6.
Не ограничиваясь табличной иллюстрацией, докажем этот факт строго ма-
тематически, а именно: покажем, что для любого положительного числа е,
как бы мало оно ни было, можно указать такой интервал, содержащий
точку х = 3, что всюду внутри него, за исключением самой точки х = 3,
будет выполняться неравенство
|у — 6| < е. (1)
Действительно, если х =£ 3, то
Поэтому неравенство (1) сводится к такому неравенству:
| х + 3 — 6 | < е,
или
| х — 3 I < в.
Последнее неравенство эквивалентно двойному неравенству
—е < х — 3 < в,
откуда получаем;
3 — 8 < X < 3 + 8.
Таким образом, неравенство (1) выполняется для всех значений х, заключенных
в интервале от 3 — е до 3 + е, кроме значения х = 3.
Если, например, мы хотим, чтобы значение у отличалось от 6 меньше, чем
на е= 0,01, то должны рассматривать значения х в интервале от 3—0,01 до
3 + 0,01, то есть в интервале (2,99; 3,01). Аналогично, при е= 0,001 мы полу-
чили бы интервал (3 — 0,001; 3 + 0,001), или (2,999; 3,001) и т. д.
160
Интервал 3 — е < х < 3 + е можно бы-
ло бы построить и геометрически. Это постро-
ение вполне аналогично тому, которое мы
делали при рассмотрении примера 1. Поэ-
тому мы ограничимся лишь тем, что приведем
соответствующий рисунок (рис. 302), пред-
лагая учащимся самостоятельно в нем разоб-
раться.
Итак, если значения аргумента х вы-
бирать достаточно близкими к 3, но не рав-
ными 3, то значения функции f (х) будут
сколь угодно мало отличаться от 6. Можно,
например, добиться, чтобы величина ] у —6 |
была меньше 0,1; 0,01; 0,001 и т. д. Не-
смотря на то что рассматриваемая функция
не определена при х = 3, естественно счи-
тать, что предел ее при х -> 3 существует и
равен 6.
Рассмотрев примеры, мы приходим к
следующему определению предела функции.
Число b называется пределом функции f (х) при х, стремящемся к а, если для
любого положительного числа е можно указать такой открытый интервал, со-
держащий точку х — а, что всюду внутри него, за исключением, быть может,
самой точки х= а, будет выполняться неравенство
। f (Х) _ b 1 < е.
Тот факт, что предел функции f (х) при х, стремящемся к а, равен bt записы-
вается следующим образом:
lim f (х) = b
а: .1
(читается: предел f (х) при х, стремящемся к а, равен Ь).
Например,
lim л2 = 4;
х -* 2
lim
х -
х2 — 9
зх — 3
= 6.
Упражнения
Исходя из определения предела, доказать следующие соотношения (№ 1653—
1658):
1653. lim (Зх + 5) = 5. х - о 1656. lim — — 2. X-l | х— 1
1654. lim уЛх = 2. х - 8 х2 —0,25 t 165о. lim __ 1. 1 х —0,5 X2 — X — 6 1657. lim — —5. х -* —2 х + 2 1658* lim 10х =1. х -*0
1659. Почему при нахождении пределов некоторых дробей (см., например,
упр. № 1655—1657) возможно сокращение этих дробей? Ведь то выражение,
на которое мы сокращаем, может обратиться в нуль.
6 Заказ 1139
161
Основные теоремы
о пределах функций § 212
(рис.
Прежде всего заметим, что не для
всякой функции у = f (х) существует
предел lim f (х). Так, например, при
Л х-а
х — значения функции у = tg х
£
303) или неограниченно растут
л \
при
< — I, или неограниченно убы-
Л\ г-,
при х > Поэтому нельзя ука-
вают
Рис. 305.
зать никакого числа Ь, к которому стре-
мились бы значения этой функции.
Другой пример. Пусть
{1 — х, если х < О,
О, если х = О,
—2— х, если х > 0.
График этой функции представлен на
рисунке 304. Когда значения аргумен-
та х приближаются к 0, оставаясь от-
рицательными, соответствующие значе-
ния функции стремятся к 1. Когда
значения аргумента х приближаются
к 0, оставаясь положительными, соот-
ветствующие значения функции стре-
мятся к —2. В самой же точке х*= 0
функция обращается в 0. Очевидно, что
указать одно какое-нибудь число, к ко-
торому стремились бы все значения у
при приближении х к 0, нельзя. Поэто-
му данная функция не имеет предела
при х 0.
Говоря в дальнейшем о пределе
функции, мы всегда будем предполагать,
что этот предел существует.
(Предположение о существовании
предела lim / (х) еще не означает, что
х -*а
этот предел совпадает со значением
функции / (х) в точке х = а. Для при-
мера рассмотрим функцию, график ко-
торой представлен на рисунке 305. Оче-
видно, что предел lim / (х) существует
х -♦ 0
и равен 1. Но в самой точке х = 0 функ-
ция принимает значение, равное 2. По-
этому в данном случае
lim /(х) ¥=/(0).
Если функция у 5= / (х) удовлетво-
ряет условию
lim f (х) = f (.?)
х -*а
162
то она называется непрерывной в точке х— а. Если же указанное условие не
выполняется, то функция f (х) называется разрывной в точке х= а.
Все элементарные функции (например, у = хл, у = sin х, у = tg х, у =
= tg2 х + tg х и т. д.) непрерывны в каждой точке, в которой они опре-
делены.
Функция у = f (х) называется непрерывной в интервале [a, ft], если она
непрерывна в каждой точке этого интервала. Например, функция у = tgx не-
л л]
прерывна в интервале — —, — , функции у = sin х и у = cos х непрерывны в
4 4 J
любом интервале и т. д.
Приведем без доказательства основные теоремы о пределах функций. Эти
теоремы вполне аналогичны тем, которые мы рассматривали (также без доказа-
тельства) ранее при изучении пределов числовых последовательностей.
1. Предел константы равен самой этой константе:
Пт с = с.
х -*а
2. Постоянный множитель можно выносить за знак предела:
Пт |й • f (х)] = k • lim/(x).
х-а х-*а
3. Предел суммы (разности) функций равен сумме (разности)
пределов этих функций:
lim [/ (х) ± g(x)| = Пт /(х) ± lim g(x).
х-»а х->а х-*а
4. Предел произведения функций равен произведению пределов
этих функций:
lim [/(х) • g(х)] = lim/(х). lim g(x).
x-ю х—а х-»а
5. Предел отношения двух функицй равен отношению пределов
этих функций, если только предел делителя не равен нулю:
limf(x)
lim = 7—^—- |Нт g (х) #= 0].
x->ag(x) Hmg(x) X-а
х-*а
Рассмотрим несколько типичных примеров нахождения пределов функций.
Пример 1. Найти
7х —5
hm ———.
х ч ь 10 4- 2х
По свойству пределов
_ lim(7x — 5) Hm7x—lim 5
lim 7*~5 _ x-5__________x-5 x-5
x™510 4- 2x lim(10 4-2x) lim 10 4-lim 2x
x-*5 x-*5
71imx — 5
x — 5___
10 + 21imx
x*5
7 - 5 — 5 30 3
10 4-2-5“ 20“ 2’
Пример 2. Найти
x2 —2x —3
,im —к—ГГ'
x - з x2 — 5x 4- 6
6*
163
При х -> 3 числитель и знаменатель данной дроби стремятся к нулю. Поэтому
непосредственное применение теоремы о пределе частного здесь невозможно.
Однако данную дробь можно сократить:
х2 —2х —3 (х~3)(х4 1) х+ 1
х2— 5х + 6 (х — 3)(х — 2) — х — 2’
После этого предел может быть легко найден:
lim
х - 3
х2 — 2х — 3 v x-f-1 3+1
—-------— = hm ------- =----
х- — 5х + 6 х - з х — 2 3—2
Пример 3. Найти
х - о * — х
Этот предел легко находится, если предварительно данную дробь сократить
на У х.
.. x+V7 VT + 1 о+1
lim ----— = lim —z----=-----= — 1.
х-0х—/х х-о/х—1 °—1
(Обратите внимание на следующую важную особенность, характерную для
рассмотренного примера. Когда мы говорим о пределе lim / (х), то обычно пред-
х - с
полагаем, что функция f (х) определена во всех точках, достаточно близких
х + X
к точке х = а. Однако функция -— определена лишь для положитель-
х — /х
н ы х значений х. Поэтому, рассматривая предел этой функции, мы фактически
предполагаем, что х -> 0, оставаясь все время положительным. В подобных
случаях говорят не просто о пределе, а об ооноспюроннем пределе. С аналогич-
ными примерами мы еще встретимся при выполнении упражнений к этому пара-
графу.)
Пример 4. Найти
X V1 + X — 1
Предел знаменателя дроби при х —> 0 равен 0. Поэтому непосредственное
использование теоремы о пределе частного здесь невозможно. Кроме того, дан-
ную дробь нельзя сократить, как мы делали это в примерах 2 и 3. В дан-
ном случае числитель и знаменатель дроби следует умножить на выражение
У1 +х + 1, сопряженное знаменателю дроби. В результате получим:
X = х(/1Ч-х + 1) = х(У 1 4- х+ 1) = + 1
уТ+х — 1 (|/Г+х—1МКГ+*+1) 1 + х —1
После этого данный предел находится легко:
lim 77т=т=---Г = lim(/1 + х + 1) = 1 + 1 = 2.
х-оУ 1 + х — 1 х~о
(Полагая, что ____
lim +х = 1,
х -о
мы тем самым используем свойство непрерывности функции у = УЛ + х :
lim/1 +х =/1 +0= 1.)
х -* 0
164
Пример 5. Найти
iim!2^_2
Х-4 х — 4
При х -> 4 числитель и знаменатель данной дроби стремятся к нулю. Поэто-
му применить теорему о пределе дроби нельзя. Преобразуем дробь, представив
знаменатель в виде произведения:
/7 — 2______/7—2__________1
х —4 “ (^7+2)(/7—2) "/7 + 2*
/7-21 11
Теперь получаем: lim-= lim--= -—- = —.
x->ix —4 х-4/х+2 24-2 4
Упражнения
Найти пределы (№ 1660—1675):
1660. lim (2х2 4- Зх — 5).
х 1
1668. lim -------7=-.
X -1 1 — V X
v X — 2
1669. lim — -------•
х - 16 1 v — 4
1662.
lim —------------
х о 2х2 — х — 1
2 lzx
1670. lim------—
— 3x
— 2x"
1663.
3x4-2
lim
х - 1 х2 — 4х 4- 3
.• Зхг4-5х —2
1664. lim —-------------.
х - —2 5х"4- 12л 4- 4
г 2x2 + 5х ~ 3
1665. h m -------------.
1 х2 — 6х — 7
1671. lim —===—
x с У x2 -j- 4 — 2
1672. lim -----7—•
х-зУ 2x 4- 10—4
1673. lim 1.
x -* I x — 1
— 3
2
1666. lim -—; -
х —2 1 - Y X 4- 3 •
,л«7 г Va + x — V'a
1667. hm------------------.
X -0 X
1674. lim
x -0
1675. lim
x -.0
Некоторые тригонометрические неравенства
и их использование при нахождении пределов § 213 * 1
В этом параграфе мы докажем некоторые тригонометрические неравенства,
которые будут играть важную роль в дальнейшем изучении функций.
1. Для любого острого угла х (выраженного в радианах)
sinx < х < tgx. (1)
Доказательство. Пусть на рисунке 306 ОА = OB = 1, Z АОВ = х
радианам, BD и АС перпендикулярны к ОА. Очевидно, что площадь треуголь-
ника О А В меньше площади кругового сектора О АВ, а площадь кругового сек-
165
Рис. 306.
тора О АВ, в свою очередь, меньше площади
треугольника ОАС. Но
• BD = ^BD-,
л • О А2 х .
^сект-ОАВ = 2ч Х ~ ~2 ’
5дОЛС= ~ • ОА • АС = АС.
Учитывая, что BD = sin х, АС = tg х, получаем:
1 . * 1
-sinx< — <-tgx,
график функции у = х расположен выше графика функции у=
откуда и вытекает неравенство (1).
Рисунок 307 служит графической иллюстрацией неравенства (1). В интер-
вале
= sin х, но ниже графика функции у = tg х.
Остановимся подробнее на неравенстве sin х < х. Мы доказали его в пред-
л
положении, что 0 < х < — . Но при таком предположении х и sin х положитель-
ны. Поэтому х = | х | и sin х = | sin х | и неравенствоsinx < х можно переписать
в виде:
| sin х | < | х |.
(2)
Это неравенство верно и для отрицательных значений х, заключенных в интер-
вале
, так как
| sin (—х) | = | —sin х | = | sin х |,
Перепишем неравенсгво (2) в виде:
1 sinx — 0 1 < | х |.
Если х стремится к 0, то | sin х — 0 |, будучи меньше | х |, тем более будет
стремиться к нулю. В частности, | sin х — 0 | может стать меньше 0,1; 0,0Г,0,001
и т. д. Вообще, какое бы малое положительное
число е мы ни взяли, всегда можно добиться,
чтобы выполнялось неравенство | sin х — 0 |<е.
Для этого нужно х выбирать в интервале (—е, е).
Но это означает, что
Jim sin х = 0.
А -♦ и
Предел синуса х при х-*О равен О.
(Поскольку 0 = sin 0, то полученный резуль-
тат по существу означает, что функция y=sin х
непрерывна в нуле, то есть при х = 0.)
2. Для любого острого угла х (вы-
раженного в радианах)
\ —cosx < х. (2>)
X
Действительно, 1 — cos л = 2 sin2 —. Но
166
л . х f _ . 2 X . X , X X
О < sin -^ < 1. Поэтому sin2 — < sin у. По доказанному выше sin — < —.
Итак, , л . о х . х х
1 — cos х = 2 sin- — < 2 sin — < 2 — = xt
что и доказывает формулу (3).
Если угол х острый, то х и 1 —cosx положительны. Поэтому х = | х |,
1 — cos х = | 1 — cosx Следовательно, неравенство (3) можно переписать в виде
| 1 — cos х | < ] х |. (4)
Это неравенство, очевидно, верно и при х < О, поскольку
| 1 — cos (—х) | = | 1 — cos х |; | —х | = | х |.
Из (4) вытекает, что
lim cos х = 1.
х -О
Предел косинуса х при х -> 0 равен 1.
Поскольку 1 = cos 0, то полученный результат по существу означает, что функ-
ция у = cos х непрерывна в нуле.
Отсюда, используя доказанную выше непрерывность в нуле функции у =>
= sin х, легко показать, что функции у =* sin х и у = cos х непрерывны в л ю-
б о й точке х. Попробуйте это сделать сами!
Упражнения
Найти пределы (№ 1676—1681):
1676. lim tgx. 1678. lim sin | — 4-х). 1680. lim tg | — 4-2х).
х-о х-о \4 ) х-о \3 )
х { л \
1677. lim cos —. 1679. lim sin 2x. 1681. lim cos ( — — x 1.
x->0 2 x-o x-o \2 /
1682. Доказать тождества:
a) lim sin (x + a) = sina; 6) lim cos (x +a) = cosa.
x -♦ 0 x - 0
1683. Для всех ли положительных значений х верны неравенства:
а) sin х < х; б) х < tg х?
1684. Докажите, что единственным корнем уравнения sin х = х является
n Sinx
Предел отношения -------- при х -> 0
X
§ 214
Докажем, что Цт _ i (1)
х-о х
Пусть х стремится к нулю, оставаясь при этом положительным. Тогда мож-
л
но считать, что 0 < х < — и потому, как было показано в § 213,
А
sin х < х < tg х,
причем все входящие в это неравенство выражения положительны.
Рассмотрим 1ри дроби:
sin х sin х sin х
----. ---- И -—.
sin X х tgx
167
При одинаковых числителях меньше та дробь, знаменатель которой больше.
Поэтому
sin х sin х sin х
sin х х tg х
или
sin x
1 >------- > cosx.
x
Умножим это неравенство почленно на —1. Знаки неравенства при этом изме-
нятся на противоположные:
sin x
Прибавив к каждой части этого неравенства 1, получим:
sin х
Но I — cos х < х (см. § 213). Поэтому
Л . sin х
sin х
Так как х > 0 и 1 —------> 0, то величины
sin х
1 —------- и х в последнем
х
неравенстве можно заменить их абсолютными значениями. В результате получим
I sin х
что можно, конечно, записать и в таком виде:
(2)
Неравенство (2) мы получили в предположении, что х > 0. Однако оно вер-
Л sin х
но и при х < 0, так как функция ------- четна, и, следовательно,
х
I sin (—х) j sin х j
I (— х) ’ х
_ I sin х I
Если х стремится к нулю, то, как видно из (2), ------— 1 ,будучи мевь-
I х |
ше | х |, тем более будет стремиться к нулю. Как бы мало ни было положительное
число е, всегда можно добиться, чтобы выполнялось неравенство
sin х
-----— 1 < е.
Для этого х нужно выбирать в интервале —в, е). Но это и означает, что
sinx
lim ------------------------------------ — 1.
х -0 х
Следствие. Поскольку при малых значениях х
sin х
-----= J
X
мало,
то можно написать приолиженное равенство
sin х
0.
Отсюда------- 1 и, следовательно, sin х х.
х
168
Итак, при малых значениях х
sin х х.
Это лишний раз подтверждает справедливость вывода, к которому мы при-
шли в § 113 главы V (часть I) при рассмотрении графика функции у = sin х при
малых значениях х.
Примеры: sin (0,01) % 0,01,
sin (0,04) % 0,04,
sin (0,07) « 0,07,
sin (—0,03) % —0,03.
Сравните эти значения с теми, которые приведены в таблицах В.М. Бра-
диса.
Примеры вычисления пределов
§ 215
В этом параграфе мы
шение
Пример 1. Натти lim
х о
вычислим несколько пределов, используя соотно-
V sinx
lim ----- = 1.
х -* о х
sin3x
Умножив числитель и знаменатель данной дроби на 3, получим:
sin Зх 3 sin Зх
х Зх
Обозначим Зх через у. Из условия х -* 0, очевидно, вытекает, что и у -> 0. По-
этому
.. sinЗх 3sin Зх 3sin у siny
lim ----= lim -------= lim ------ — 3 lim----= 3 • 1=3.
x-*o x x-o 3x у v-o у
Пример 2. Найти
sin tnx
lim --------------------------- (n 0).
x- 0 nx
Умножая числитель и знаменатель данной дроби на т и вводя новую пере-
менную у = тх, получаем:
, sin/nx /и-sinznx т sin y
lim -----= lim ---------= lim--------=
x -* 0 nx x - 0 n (nix) y-^Q ny
ni siny m m
= — lim ------= — • 1 = —.
H y^Q у n n
Пример 3. Найти
Используя тождестве
1 — cosx = 2 sin2 —
АЛ
получаем:
lim
х -* О
1 — cos X
X2
2 sin2
169
X
Введем новую переменную у = —.
Итак,
Тогда х = 2у и
1 - — COS X , 2 sin2 у 1 sin2y
lim lim _ ’ — lim , =>
x - 0 X2 y-0 (2y)2 2 y-0 y-
1 .. s'n У .. s>n У 1 t t 1
— lim hm । ’ 1 • 1 = —,
2 у-о у £-0 у 2 2
lim
х - О
1 — COS X
X2
£
2*
Отсюда, в частности, вытекает, что при малых значениях х
1 — cos х 1
х2 ~ 2 ’
или
1 е
1 — COS X » — х\
£
1 1 3
COSX 1 — ~"Х2.
2
Например,
cos (0,04) « 1 — • 0,0016 а 0,9992,
cos (—0,08) 0,0064 х 0,9968.
Сравните эти значения с табличными!
Упражнения
Найти пределы:
sin4x
1685. lim ——.
х-♦ о 2х
Л , sin 5х
1686. lim —------
х -* 0 6.V
Зх
1687. lim -------
Х-0 . х
Sin —
о
1688. Jim
х -*0 *
х—sin4x
1693. lim--------.
х-0 X
г K*4-sinx — Vx
1694. lim------:---------•
х-»л sinx
sin3x— sin 12x
1695. lim ------------:
x^0 lOx
.ЛОЛ г *8х
1690. lim -------.
х -* о х
169!. Нт
X - 0 Ьх
.. sin 5x4-sin 7x
1696. lim----------------.
X->0 X_
4
1697. lim /54-sinx-/5-sinx^
x-0 X
1698. lim + cos* ~
x-»o x2
170
1699. lim
cos Юх — cosx
4x2
. [ л
1 — cos — 4- x
1701. lim--------- —
л (5x + л)2
5
1700. lim
sin llx — 6x
5x
1702. lim
sin2 x — sin2 a
x2 — a2
x - О
x - 0
Из истории развития понятий функции
и предела § 216
До XVII века математика была наукой о постоянных величинах. Введение
переменных величин связано с именем французского ученого Декарта.
Его работы получили высокую оценку Ф. Энгельса, который говорил: «Пово-
ротным пунктом в математике была декартова переменная величина. Благодаря
этому в математику вошли движение и диалектика».
Термин «функция» появился в одной из работ немецкого ученого
Лейбница (1646—1716).
Понятие функции ученые XVII и XVIII веков вводили по-разному. Од-
ни определяли функцию как некое «аналитическое выражение», другие
связывали понятие функции с «произвольно начерченной кривой». Идею
соответствия, как единственную основу понятия функции, подчеркнул в
своем определении немецкий математик Дирихле (1805—1859). у есть функ-
ция от х, говорил он, если всякому значению х соответствует вполне опреде-
ленное значение у, причем совершенно неважно, каким именно способом уста-
новлено указанное соответствие. Еще до Дирихле идею соответствия выска-
зал основатель неевклидовой геометрии Николай Иванович Лоба-
чевский (1792—1856). Однако долгое время это оставалось незамеченным
в математике.
Привычное для нас обозначение функции у = f (х) принадлежит Эйлеру.
Определение предела впервые появилось в XVII веке. Зачатки теории
пределов можно обнаружить, например, в работах английского физика и
математика Исаака Ньютона (1642—1727). Однако математики XVII и
XVIII веков не ставили своей задачей построить стройную теорию преде-
лов. Эта задача была поставлена и решена лишь в XIX веке. Большая
заслуга в этом принадлежит французскому математику Коши (1789—1857).
Он развил теорию пределов и положил ее в основу построения одного из важ-
нейших разделов математики — математического анализа.
Задачи на повторение
Найти области определения функций (№ 1703 — 1706):
1703. у = ~|/±±2 -1 1704. у = 1g •
л У 2л — 4 Л ъх2 —2х—15
1705. у =-----!----. 1706. у = .
tgx4-clgx sinnx
Найти области изменения функций (№ 1707—1709):
1707. у = (—1)*. 1708. у=5 sin х—10 cos х 4- 1. 1709. y=10coyt«
1710. Функции f (х) и g (х) — монотонно возрастающие на всей
числовой прямой. Будет ли их произведение монотонно возрас-
тающей функцией? Ответ пояснить примерами.
171
1711. Доказать, что если функция f (х) периодична с перио-
дом тТ. а функция g (х) периодична с периодом пТ, где /и и л —
натуральные числа, то функции f (х) 4* g (х) и f (х) • g (х) перио-
дичны с периодом тпТ.
1712. Доказать, что функции у = ах и у = loga х (а > О,
а =/= 1) не являются периодическими.
Какое обобщение этого результата вы могли бы предложить?
1713. Используя тождество (подумайте, как оно получается!)
f(x\ = Л*)4-/(-*) , Дх)-/(-х)
доказать, что любую определенную на всей числовой прямой
функцию можно представить в виде суммы четной и нечетной
функций.
1714*. Доказать, что любую функцию f (х), определенную на
всей числовой прямой, можно единственным способом предста-
вить в виде суммы четной функции <р (х) и нечетной функции g (х):
/ (х) = <р (х) + g (х).
1715. Представить функцию у = 2х в виде суммы четной и
нечетной функций.
Исследовать функции (№ 1716—1721):
:. 1718. у=—
1719. у=/Т — cosx. 1721. у ={х}.
1716. у = /3 sinx 4- cosx,
1717. у — |x2 —2x —3|.
Найти пределы (№ 1722—1737):
x- Зх 4“ 2
1722. lim ——-----—.
x - I x 2 — 2x 4- 3
1723. lim —/2 —x
x - 0
1724. lim
a-^0
2x
x
1725. lim
x
1726. lim -------------
х - и X
__ f. sin 9х + sin 1 lx
172/. hm----------------
x -0 5x
f. sinx— tgx
h m -----------.
x - 0 X3
1 — cos X
lim ---------.
v-o x
1728.
1729.
1738.
Доказать, что для любых
1. 1720. у=6х24-х4~1.
sin ax
1730. lim ---.
x - о sin bx
1-701 1-
1731. lim ----.
X 0 tg bx
1-7QO Г tgx+tg2x
1732. hm ---------.
%-0 sin3x
733. Iim
x-0 (a + b)x
.. /1 -f-sinx — /1 — sinx
1734. lim-------------------------
x-0 tgx
1735. lim (~r~————\
X--O\sinx____ tgx /
.•70C* 1- sin x — /sin®
1736*. hm --------------—----.
x - a l<x — /a
1 — /sin X
173/* у = lim----- -
x-ZL /1 + cosx -
2
натуральных чисел rn и n
, xm — 1 m
lim — -----= —.
X - 1 xn — 1 П
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Равномерное и переменное движение по прямой.
Скорость и средняя скорость движения
§ 217
Из всех движений тел простейшим является равномерное движение по пря-
мой. Это такое движение, когда тело, не меняя направления, за любые равные
промежутки времени проходит пути одинаковой длины. Равномерно и прямоли-
нейно движутся на некоторых участках поезда, автомобили, пароходы, самолеты
и т. д.
Путь, проходимый телом при равномерном движении по прямой в единицу
времени, называется скоростью этого движения.
На практике мы часто имеем дело с неравномерным движением. Поезд, от-
ходящий от станции, сначала только «набирает скорость». За вторую минуту
своего движения он проходит путь, больший, чем за первую, за третью минуту —
путь, больший, чем за вторую, и г. д. Набрав определенную скорость, он идет
равномерно, проходя за каждую минуту пути одинаковой длины. При прибли-
жении к месту назначения поезд начинает сбавлять скорость, проходя за каж-
дую минуту путь, меньший, чем за предыдущую минуту. То же самое можно ска-
зать об автомобиле, пароходе и т. д.
В различные, но равные по величине интервалы времени тело, находящееся
в неравномерном движении, может проходить пути разной длины. Поэтому не-
равномерное движение (в отличие от равномерного) нельзя полностью охаракте-
ризовать длиной пути, пройденного в какую-нибудь единицу времени.
Часто неравномерное движение характеризуется средней скоростью за оп-
ределенный промежуток времени.
Средней скоростью движения ва время t называется отношение длины S пу-
ти, пройденного телом за время /, к этому времени:
s
ср
Для равномерного движения средняя скорость на любом участке пути сов-
падает со скоростью движения. Средней скоростью обычно характеризуется дви-
жение поездов. Например, экспресс Москва—Ленинград (расстояние 650 км)
находится в пути 6 ч, и потому мы говорим, что его средняя скорость равна:
Однако это не означает, что за каждый час экспресс проходит 108 км Например,
за первый час движения, когда поезд «набирает скорость», он проходит всего
лишь 80—90 км. В следующий час пройденный путь составляет примерно 130 км
В Бологом экспресс делает остановку, и потому за тот час, на который приходит-
ся эта остановка, экспресс проходит путь еще меньший, чем 80—90 км.
173
Из этого примера видно, что
средняя скорость не может служить
полной характеристикой неравно-
мерного движения.
Упражнения
1739. На рисунке 308 представ-
лен график движения поезда. На ка-
ких участках поезд шел равномерно
и на каких неравномерно? Когда он
делал остановку и на сколько ми-
нут? Найти среднюю скорость по-
езда за первые 4 часа.
С какой средней скоростью шел
поезд в течение четвертого часа дви-
жения?
1740. В интервале времени (0,/j)
км
поезд шел со скоростью vt —,
в интервале времени (^р /2) —со скоростью v2 —, в интервале времени (/2, t3) —
ч
км
со скоростью — и т. д., наконец, в интервале времени (tn_v tn) — со ско-
км
ростью vn —. Чему равна средняя скорость движения поезда в интервале
времени (0, /л)?
Закон движения.
Мгновенная скорость движения
§218
К более полной характеристике движения можно прийти следующим обра-
зом. Время движения тела разобьем на несколько отдельных промежутков
(/р 4)» (^2» G) и т- Д- (не обязательно равных, см. рис. 309) и на каждом из них
зададим среднюю скорость движения. Эти средние скорости, конечно, будут
полнее характеризовать движение на всем участке, чем средняя скорость за все
время движения. Однако и они не дадут ответа на такой, например, вопрос: в
какой момент времени в интервале от до /2 (рис. 309) поезд шел быстрее: в мо-
мент t\ или в момент
Средняя скорость тем полнее характеризует движение, чем короче участки
пути, на которых она определена. Поэтому один из возможных способов описа-
ния неравномерного движения состоит в задании средних скоростей этого дви-
жения на все более и более малых участках пути.
Предположим, что задана функция s (/), указывающая, какой путь прохо-
дит тело, двигаясь прямолинейно в одном и том же направлении, за время t от
6 ^2
tt t; tj tn
Рис. 309.
174
начала движения. Эта функция определяет вакон движения тела. Например,
равномерное движение происходит по закону
s (О = vtt
где v — скорость движения, свободное падение тел происходит по закону
где g — ускорение свободно падающего тела, и т. д.
Рассмотрим путь, пройденный телом, движущимся по некоторому закону
s (0, за время от t до t + т. К моменту времени t тело пройдет путь s (0, а к мо-
менту времени t + т — путь $ (/ + т). Поэтому за время от i до t + т оно прой-
дет путь, равный s (/ + т) — $ (0. Разделив этот путь на время движения т,
мы получим среднюю скорость движения за время от t до t + т:
s(/ + t)-s(Z)
VCp —
Предел этой скорости при т -> 0 (если только он существует) называется мгно-
венной скоростью движения в момент времени t\
v(t) = lim
т -♦ о
(1)
Мгновенной скоростью движения в момент времени t называется предел сред-
ней скорости движения за время от i до t + т, когда т стремится к нулю.
Рассмотрим два примера.
Пример 1. Равномерное движение по прямой
В этом случае s (/) = vtt где v — скорость движения. Найдем мгновенную
скорость этого движения. Для этого предварительно нужно найти среднюю
скорость в интервале времени от t до t + т. Но для равномерного движения
средняя скорость на любом участке пути совпадает со скоростью движения v.
Поэтому мгновенная скорость v (0 будет равна:
v(t) = lim v — v.
г -с
Итак, для равномерного движения мгновенная скорость (как и средняя скорость
на любом участке пути) совпадает со скоростью движения.
К такому же результату, конечно, можно было бы прийти и формально,
исходя из равенства (1).
Действительно,
/а г 5(/ + т)-5(/)
v(t) = lim --------------= lim
т -♦ о т т о
Р • (< + т) — V^t
1
V • т
«= lim ----= lim v = v.
т -*o x i ->o
Пример 2. Равноускоренное движение с нулевой начальной скоростью
и ускорением а. В этом случае, как известно из физики, тело движется по закону
f(0 =
at2
175
По формуле (I) получаем, что мгновенная скорость такого движения и (О
равна:
a (t 4- т)2 — at2
2
2т
а
х -* о т - о 2
v(t) = hm-------------= lim
т - 0 т т - О
at2 4- 2я/т 4- ат2 — at2 t 2q/t 4- ат2
= bm--------------------- = lim —
т - о 2т т -* о
(а \
at 4- — т = lim at 4~ lim — т.
Поскольку at не зависит от т,
lim at = at.
х - о
Кроме того,
1. о а а
пт — т = — lim т = -— • 0 = 0.
х - о 2 2 х - о 2
Поэтому
v (t) = at 4- 0 = at.
Итак, мгновенная скорость равноускоренного движения в момент времени
t равна произведению ускорения на время t. В отличие от равномерного движе-
ния мгновенная скорость равномерно ускоренного движения изменяется с течением
времени.
Упражнения
1741. Точка движется по закону $(/)= ц/+
at1
2
(s — путь
метрах,
в
время в минутах). Найти мгновенную скорость этой точки:
а) в начальный момент движения;
б) в момент времени /0.
1742. Найти мгновенную скорость точки, движущейся по закону $ (0 = t
(s — путь в метрах, t — время в минутах):
а) в начальный момент движения;
6) через 10 сек после начала движения;
в) в момент t = 5 мин.
1743. Найти мгновенную скорость 1ела, движущегося по закону s (/) = Vt,
в произвольный момент времени /.
Производная функции § 219
На протяжении всего школьного курса алгебры и элементарных функций
мы расширяли математические понятия, углубляли их, доводя до более общих,
более сложных понятий. То же самое нам предстоит сделать и в этом параграфе
Что представляет собой мгновенная скорость движения, определенная
в § 218?
Имеется некоторая функция $ (/), указывающая путь, пройденный телом за
время от 0 до t. Аргументу t дается некоторое приращение т, то есть вместо зна-
чения t рассматривается значение / 4- т ЗЙому приращению аргумента соот-
ветствует следующее приращение функции s (0:
$(* + т)-$(/).
176
Это приращение функции делится на приращение аргумента т
s(/ + т)-5(0
т ' '
и берется предел при т->0. Выражение
s(/ + t)-s(/)
т
можно рассматривать как «среднюю скорость» изменения функции s(t) в интер-
вале от t до t + т, а предел этого отношения при т->0 — как мгновенную ско-
рость изменения этой функции в момент времени t.
В приведенных выше рассуждениях функция s(t) представляла собой путь,
пройденный телом за время от 0 до t. Это обстоятельство накладывало на функ-
цию s(t) определенные ограничения. В частности, она должна была быть определена
только для неотрицательных значений аргумента t (ведь t — время), принимать
только неотрицательные значения (s — длина пути) и быть монотонно возрастаю-
щей (чем больше время тем больше пройденный путь). Теперь же мы обобщим
наши результаты на произвольные функции, вообще говоря, никак не связанные
с движением тел.
Пусть f (х) — произвольная функция. При фиксированном значении xQ
аргумента х эта функция принимает значение, равное f (х0). Дадим значению х0
приращение Дх0*, то есть вместо значения х0 рассмотрим значение х0 4- Дх0
Тогда функция f (х) примет значение f (х0 + Дх0) и, таким образом, получит
приращение Ду0**:
Ду0 = f (*о + Д*о) — / (*о)«
Отношение
ДУо = /(Хр +Дх0) —f(x0)
Дх0 Дхп
представляет собой среднюю скорость изменения функции /(х) в интервале от
х0 до хп + Д*о Эта средняя скорость зависит, очевидно, как от х0, так и от Дх0.
Устремляя теперь Дх0 к нулю, мы получим мгновенную скорость изменения
функции / (х) в точке х = х0:
ДУо р / (х0 4-Дх0) —/(х0)
hm -— = hm -----------------------
д%0 -*i Дхи дх0 -* с Д^о
(если, конечно, указанный предел существует). Для заданной функции f (х)
этот предел зависит от х0 и называется производной от функции f(x) в точке х =
= х0. Каждому значению х{, соответствует свое значение мгновенной скорости
изменения функции / (х). Поэтому предел (если только он существует)
/(х-Ь Дх) —/(х)
11 m --------------’
дх - и Дх
представляющий собой мгновенную скорость изменения функции f (х) в произ-
вольной точке х, можно рассматривать как новую функцию аргумента х Э1а но-
вая функция называется производной от заданной функции f (х).
* Выражение Дх0 читается: дельта икс нуль Эго одно нераздельное выра-
жение. Его не следует путать с произведением Д • х0.
** Ду, также нераздельное выражение. Его не следует путать с произведе-
нием Д • у0.
177
Часто в выражении «производная от функции f (х)» слово «от» опускают и
говорят просто «производная функции / (х)».
В математике используется несколько обозначений производной. Мы будем
пользоваться следующими обозначениями: у' и /' (х):
, Ау .. /(x-f-Дх) —/(х)
у = / (х) = lim — = lim ----------------------
Ах С Дх Ах -* О
Дх
Рассмотрим несколько примеров.
Пример 1. Найти производную функции / (х) = с, где с — некоторая
константа.
Имеем: f (х) = с, f (х + Дх) = с.
Ау
Поэтому Ду = / (х 4- Дх) — / (х) = с — с = 0 и, следовательно, — =
=±=о.
Дх
Таким образом,
Ду
у'= lim -— = lim 0 = 0.
Дх -* 0 Дх Дх -♦ о
Производная константы равна 0.
Пример 2. Найти производную функции / (х) = х.
Имеем:
/ (х) = х, f (х 4-Дх) = х + Дх.
Поэтому
Ду = / (х + Ах) ~ f W — (* +д*) = Ах.
Следовательно,
Ду Дх j
Дх Дх
Отсюда вытекает, что
у'= lim = lim 1=1.
Ах -♦ ( Дх Лх -♦ 0
Производная функции f(x)=x равна 1.
Пример 3. Найти производную функции / (х) = х2. Имеем:
/ (х) = х2, / (х + Дх) = (х 4- Дх)2.
Поэтому
Ду = / (х 4- Ах) — / (х) = (х 4- Ал)2— х2 = [х2 4~ 2х • Дх 4“ (Ах)2 ] — х2 =
= 2х • Дх 4- (Дх)'.
Значит,
Ду
-— = 2х 4- Дх.
Дх
Следовательно,
Ду
у'= lim -— = lim (2х-|-Дх) = lim 2х-}- lim (Дх) =
Дх •* 0 Дх Дх -* 0 Дх -»0 Дх -»С
= 2х -|- 0 = 2х.
Производная функции f (х) = х2 равна 2х.
В отличие от первых двух примеров здесь производная зависит от х.
Значение производной от функции f (х) при х — а обозначают /' (а). На-
пример, если / (х) = х2, то /' (х) = 2х и потому
f (0) = 2.0 = 0.
f (1) = 2 . 1 = 2.
178
Упражнения
1744. Найти производные следующих функций:
а) у = х + 1; в) у = (х + J)2; д) у = 1 — ха;
б) у = 2х2; г) у = 2 }Лх; е) у = х2.
1745. При нагревании тела его температура Т изменяется с течением вре-
мени t по закону Т = 0,4/2 (Т — температура в градусах, t — время в секундах).
Найти:
а) среднюю скорость изменения температуры тела за промежуток времени
от tx = 4 сек до = 8 сек\
б) мгновенную скорость изменения температуры тела в момент t = 5 сек.
1746. Ток / ампер изменяется с течением времени t по закону / = 0,5/а,
где t — число секунд. Найти скорость изменения тока в конце пятой секунды.
Дифференцируемые функции
§ 220
Производная функции у = f (х) в точке х определяется как предел
)' (х) => lim
Ах - О
/(х +Дх) —Дх)
Дх
Но пределы существуют не всегда. Точно так же не всегда существуют и произ-
водные. В качесгве примера рассмотрим следующую функцию:
/ (х) = I X |.
Покажем, что производная f (0) от этой функции при х = 0 не определена.
Действительно, по определению производной
,, г /(0 + Дх)-/(0) Ю + Дх|-|0|
/ (0) = lim -------------- = lim ----------!-----
дх -♦ о Дх Дх -♦ о
Дх
Дх
= lim
дх-*о Дх
|Дх|
1---L (1)
Если Дх стремится к нулю, оставаясь положительным, то
Iim
Дх - о Дх
(Дх>0)
Если же Дх стремится к нулю, оставаясь отрицательным,
тогда
| Дх | = Дх и тогда
то | Дх | = — Дх и
/х-*о Дх
(Дх<0>
Если бы предел в формуле (1) существовал, то он не зависел бы от того, как Дх
стремится к нулю. На самом же деле это не так. Но отсюда можно сделать лишь
тот вывод, что предел в (1) не существует.
Итак, для функции f (х) = | х | производная в точке х = 0 не определена.
Легко показать, что во всех остальных точках производная функции f (х) = | х |
существует и равна
f Ь
/(x)=L
если х > 0,
если х <0.
Предлагаем учащимся убедиться в этом самостоятельно.
179
Операция нахождения производной от
данной функции называется дифференциро-
ванием этой функции. Функция, имеющая
производную в точке х = а, называется
дифференцируемой в этой точке. Если
функция дифференцируема в каждой точке
некоторого интервала, то говорят, что она
дифференцируема в этом интервале. Напри-
мер, функция у = | х ) дифференцируема
в каждом интервале, не содержащем точки
х = 0; функция у = х дифференцируема
всюду.
(Можно доказать, что функция, разрыв-
ная в точке х = а (см. гл IX, § 212), не яв-
ляется дифференцируемой в этой точке. Та-
ким образом, дифференцируемыми мо-
гут быть только непрерывные функ-
ции. Однако не следует думать, что любая
непрерывная в точке х = а функция являет-
ся дифференцируемой в этой точке. Напри-
мер, функция у = | х | непрерывна в точке
х = 0, но, как показано выше, не дифферен-
цируема в этой точке. Существуют и более
убедительные примеры: функция может
быть всюду непрерывна, но нигде не диф-
ференцируема. Однако рассмотрение таких
функций выходит далеко за пределы нашей
программы.)
Упражнение
1747. Являются ли функции / (х) = |х |2
и 7 W — I л I3 дифференцируемыми в точке
х= 0?
Касательная к кривой
§ 221
До сих пор мы имели дело лишь с каса-
тельной к окружности. Касательной к окруж-
ности в заданной точке М мы называли пря-
мую, имеющую с окружностью одну и
только одну общую точку — точку М. Такое
определение годится не для всякой кривой.
Например, естественно считать, что прямая
АВ касается кривой MNP в точке М
(рис.310),хотя имеет с этой кривой не одну, а
две общие точки: М и Р. Прямая CD, наоборот,
имеет лишь одну общую точку с кривой
MNP — точку N. Однако считать ее каса-
тельной к кривой MNP в точке N было бы
совсем не естественно.
Чтобы определить касательную к про-
извольной кривой в точке М (рис. 311), возь-
180
мем на этой кривой еще одну точку Mt и проведем секущую Л4Л41. Если точку
! перемещать по данной кривой, неограниченно приближая ее к точке А1, то секу-
щая будет все время поворачиваться вокруг точки М, занимая последовательно
положения ММ1г МЛ12, Л1Л13 и т. д. Предельное положение А1А секущей и даст
нам касательную к кривой в точке Л4.
Касательной к кривой в точке М называется предельное положение секущей
MMlt когда точка М{, двигаясь по кривой, неограниченно приближается к точ-
ке М.
Нетрудно понять, что для окружности это определение эквивалентно тому,
которым мы пользовались до сих пор в геометрии (см. рис. 312).
Точка AIt, двигаясь по кривой, может неограниченно приближаться к точке
М с разных сторон. Например, на рисунке 313 точка М' приближается к М не
сверху, как на рисунке 311, а снизу. В этом случае мы имеем дело с другими
секущими: ММ', ММ", ММ"' и т. д., но их предельное положение то же са-
мое — MN.
Однако не исключена и такая возможность (см. рис. 314): в результате при-
ближения точки Л41 к точке М справа секущие МAfn ММ2, ММ3,... стремят-
ся занять одно предельное положение — MN, а в результате приближения точки
М' к точке А! с л е в а секущие ММ', ММ", ММ'",... стремятся занять другое
предельное положение — МР. В подобных случаях говорят, что кривая не имеет
касательной в данной точке.
Упражнения
1748. Что является касательной к прямой в произвольной ее точке?
1749. Имеет ли график функции у = |х| касательную в точке с абсциссой
а) —1;
б) 0;
В) 1?
1750. Существует ли касательная к графику функ-
ции у = | sin х | в точке х = л?
1751. Хорошо известно, как определяется угол
между двумя прямыми. А как бы вы определили
угол между двумя пересекающимися кривыми в
точке их пересечения (см. рис. 315)?
Рис. 315.
181
Геометрическое
истолкование
производной
§ 222
Пусть кривая KL, представ-
ленная на рисунке 316, есть гра-
фик функции у = / (х). Отметим
на ней две точки: М с коорди-
натами (х, у) и с координа-
тами (х + Дх, у -j- Ду). Проведем
отрезок МР параллельно оси
абсцисс. В треугольнике ММАР
МР = Дх, МХР = Ду. Поэтому от-
Ду
ношение — равно тангенсу угла
а, образованного секущей
Рис. 316. с гсь*0 абсцисс. При Дх -> О точ-
ка М остается неподвижной, а
Мг неограниченно приближается вдоль кривой к точке М. Секущая ММ±
все это время изменяет свое направление. Вместе с этим изменяется и угол а.
При этом
В пределе хорда займет положение касательной MN, образуя с осью абс-
цисс некоторый угол р. Очевидно, что при этом Р = lim а, и
Ах-* О
Но
tg р = lim tg а.
Ах -♦ о
. Ау
tg а = —•
Дх
Следовательно,
tgp = lim =у'.
Ах -♦ 0 Дх
Таким образом, производная функции
f(x) в точке х равна тангенсу угла на-
клона касательной к графику этой
функции в точке с абсциссой х.
Полученное соотношение между значе-
нием производной от функции / (х) в произ-
вольной точке х и угловым коэффициентом
касательной к кривой у = / (х) в этой точке
позволяет довольно просто составить уравне-
ние касательной. Поясним это на следующем
примере.
Пусть требуется найти уравнение каса-
тельной к параболе у = х2 в точке М с абсцис-
сой х = 2 (рис. 317). Искомая касательная
имеет уравнение у «= kx + b. Угловой коэффи-
циент k равен значению производной от функ-
ции у «= х2 в точке х = 2. Так как у = х2,
то у' = 2х. Поэтому k = 4. Следовательно,
касательная имеет уравнение у = 4х + Ь. Не-
известный коэффициент b можно найти из
182
условия, что касательная проходит через точку М параболы у = х2 с абсциссой
х = 2 (то есть через точку касания). Ордината этой точки равна 4. Подставляя
в уравнение у = 4х 4- 8х = 2. у = 4, получаем 4=8+6, откуда b = —4.
Итак, искомая касательная имеет уравнение у = 4х — 4.
Упражнения
1752. Написать уравнение касательной к параболе у = х2 в точке с аб-
сциссой:
а) —1; б) 0; в) +1.
1753. Под каким углом прямая х=3 пересекается с параболой у = х2?
1754. В каких точках прямая у = х пересекается с параболой у = х2?
Какие углы образуются в результате пересечения?
Вынесение постоянного множителя
за знак производной
§223
Пусть g (х) = а/ (х), где а — некоторое число, a f (х) — произвольная
дифференцируемая функция. Покажем, что функция g (х) также дифференци-
руема и
У (X) = af (х). (1)
Действительно,
й(х+ Лл-) — g(x} af (х -ф Дх) — af (х) f(x + Дх) — f(x)
------------------ = ----------------- = д----------------.
Дх Дх Дх
Так как функция /(х) дифференцируема, то предел отношения
/(хЦ-Дх) — /(X) Л A rzZv
-------------- при Дх->0 существует и равен f (х).
g(x + bx) — g(x)
Поэтому lim ------------------
дх - о Дх
также существует и равен af (х). Соотношение (1) доказано.
Постоянную величину можно выносить за знак производной.
Примеры.
(Зх)' = 3 • (х)' = 3 1 = 3;
(—5х2)' = —5 (х2)' = —5 • 2х = —10х.
Упражнение
1755. (У с т н о.) Найти производные следующих функций:
а) у = — х; X2 ж) у= — /3 х’;
X б) У = р г) у = У5 х; е) у = “ ч ^5 -1 а з) У- Л_ х\ 2/2
Производная суммы функций § 224
Теорема. Если функции и (х) и ® (х) дифференцируемы, то
их сумма w (х) = и (х) 4- ® (х) также дифференцируема, причем
w' (х) = и' (х) + v' (х).
183
(Производная от суммы д&ух функций равна сумме производных
от этих функций.)
Доказательство. Имеем:
Au1 (х) = w(x 4- йх) — w (х) =
«= |и (х + Ах) 4- v (х 4- Ах)] — lu (х) 4- v (х)] =
= |и (х 4- Дх) — и (х)) 4- lv (х 4- Дх) — v (х) ].
Поэтому
Аьу
Ах
ц (х 4-Дх) — и (х)
Дх
v (х 4- Ах) — v(x)
&.Х
Так как функции и (х) и v (х) дифференцируемы, то существуют пределы
и (х 4- Дх) — и (х)
lim ---------;--------- = и (х),
Дх - 0 Ах
о (х 4- Л*) — v(x) , , г
lim /-----— = V (х).
Дх * о Ах
Следовательно, существует и предел
&W
lim — = w' (х),
Лл -оДх
причем
w' (х) = и' (х) + V* (х).
Мы получили формулу для производной суммы двух функций. Аналогично
можно получить и формулу для производной разности двух функций
[и (х) — V (х)' j = и1 (х) — v’ (х).
Впрочем, ее можно вывести из формулы для производной от суммы, если выра-
жение и (х) — v (х) рассматривать как сумму и (х) + I—v (х) ] и использовать
теорему о вынесении постоянного множителя за знак производной. Предлагаем
учащимся разобраться в этом самостоятельно.
Отметим, что доказанная выше теорема верна для любого конечного числа
слагаемых:
(Wj 4- + ••• +ил)' = “S + + ••• + и л*
Примеры. Пусть / (х) = х2 + 2х — 5.
Тогда /' (х) = (х2)' + (2х)' - (5)' = 2х + 2 - 0 = 2л: + 2.
Аналогично,
(~3х2+ 5х + 7)' = (-Зх2)' + (5х)' + (7)' = —3 *2х + 5 • 1 + 0 = — 6х + 5.
Упражнения
Найти производные следующих функций:
1756. (Устно.)
а) у = 1 — х; г) у = 1 — Зх + 6х2; ж) у = х (1 — л);
б) у = х — х2; Д) у = 6 — Зх2£ з) у = (х + 1) (х — 1).
в) у — 2х + х~ —е) у = х —
1757. у = (х — 1) (х + 2). 1760. у = (3 — 2х) (х — 6).
1758. у = (х - I)2. 1761. у = Зх - 5 (1 - х) (1 - 2х).
1759. у = (2х — I)2 1762. у =(х — I)2 — (х + I)2.
184
Дифференцирование произведения двух функций $ 225
Пусть функция w (х) равна произведению двух функций и (х) и г(х);
w (х) = и (х) • V (х)
То же самое мы будем записывать короче:
W = и • V.
Предположим, что функции и и v дифференцируемы. Будет ли дифференцируе-
мым их произведение w? Имеем:
Ддо = w (х + Дх) — w (х) =
= и (х + V (х + Л*) — и(х) V (х).
Но и (х + Дх) — и (х) = Ди,
v (х + &х) — v (х) = Да
Отсюда
и (х + &х) = и 4- Aw,
v (х + Ах) = v + Д V.
Следовательно,
Адо = (и 4* Au) (v + Аг) — uv —
<= и • v + и • A v + Ди • v 4- Ди • Ди — и и =
= иД v 4- fАи 4- АиД v.
Поэтому
Ддо Дг Ди Ди
— = и — + v — + — Аг.
Дх Дх Дх Дх
При Ах -> 0 получаем:
и -> и;
v -> г;
Ди .
— -> и ;
Дх
Ди ,
— -> v .
Дх
Покажем что при Дх -> О Д v также стремится к нулю. Действительно,
Дг
Дг = — Ах -> г' • 0 — 0.
Дх
Таким образом,
Ддо
lim — = иг' 4- w'r 4- и' • 0 = uv' 4~ w г.
Ах о Ах
Итак, в рассматриваемом случае производная существует и равна:
(uv)' = u'v 4-<н>'«
Производная произведения двух функций равна произведению
производной от первой функции на вторую функцию плюс про-
изведение первой функции на производную от второй функции.
Примеры.
1) Найти производную функции у = (х 4- а) (х 4-Ь).
По правилу дифференцирования произведения
у' = (х + а)' (х 4- Ь) 4- (х 4- а) (х 4- b)' = 1 • (х 4- Ь) 4- (х 4- а) • 1 =
= 2x4- b
2) Найти производную функции у = (х 4- 1) (ха — 3).
185
Имеем:
У' = (% + 1)' (х2 - 3) + (х + 1) (х2- 3)'=
= (14-0) (х2 — 3) 4- (х 4- 1) (2х 4- 0) = Зх2 4- 2х — 3.
Упражнения
Найти производные следующих функций (№ 1763—1771):
1763. у = (х2 + 1) (3 — 5х2).
1764. у = 5х2 (х —х2).
1765. у = (х2 + х + 1) (х2 — х + 1).
1766. у = (1 — Зх + 7х2) (—5х2 — 1).
1767. у = х4.
1768. у = х2 (1 — х2).
1769. у = (2х — З)4.
1770. у = (х2 + ах)2.
1771. у = (х3— а) (х3 + Ь).
1772. Показать, что теорема о вынесении постоянного множителя за знак
производной (§ 223) является частным случаем теоремы о дифференцировании
произведения.
1773. Доказать тождество
(uvw)' = и'vw 4- uv'w + uvw'.
Используя его, найти производную функции у = (х + а) (х 4- Ь) (х -{- с).
Производная дроби § 226
Пусть и и v — некоторые функции аргумента х. Как, зная производные
/ , и
этих функций и и v , найти производную их отношения — в тех точках, в кото-
рых и не равно нулю? Да и вообще, существует ли эта производная?
Чтобы решить эту задачу, выполним следующие преобразования:
и (х 4- Дх) а(х) _ а 4- Да и
V (х 4- Дх) V (х) v 4- Д^ v
uu4~ t'Au — UV — U&U V&U — U&V
v(y Поэтому и (х 4- Ах) и (х) и(х4-Дх) и (х) Дх 4-Ду) ~ V2 v2 4- и Ди 1 ГДи Ди" А А -и — и• 4- и Ди Дх Дх
Поскольку функции и и v дифференцируемы, существуют пределы:
г Аи
hm — = и ,
Дх - о Дх
г Ау
hm — = и .
дх -> о Дх
Кроме того,
lim [и2 4- v Ди] = lim [ua 4- v — • Дх1 = u24- uu' • 0 = и3.
дх-*о Дх-о[ Дх J
186
Поэтому существует и предел
равный
и (X + и
t V (Х + &х) v (и
lim ---------—-----= —
Ах - о Дх' \ v
и у — uv
V2
Итак, если функции ии v дифференцируемы, то в тех точках,
и
в которых v отлично от нуля, отношение — также дифференци-
v
руемо и
(и\' _ и'р — пд'
V / ~ ®3
Примеры.
п /1 + * \'_(1 +*Y(1 -*)-(! +х)(1-*)' _
\1 — х / (1 — х)2
_1 • (1 -х) — (1 +*)(-!)__2
(1-х)2 ~(1-х)2’
Л V _ (1Гх-1 • (х)' 0 - х-1 • 1 _
\ X / X- X2 X2*
У пражнения
Найти производные следующих функций:
1774. 1 — г 1777. у = 2х2
У = 1 4-/ 1 — 7/
1775. 2х —3 1778. у = 5
У = 5 — 4х’ 6л' — 4
1776. X 1779. у = 5
У = х- — 1’ 6 — X
—7
,78°- * = aZlo?
Производная степенной функции
§ 227
В предыдущих параграфах мы уже рассматривали некоторые примеры на
нахождение производной от степенной функции у = хп при натуральном п. Так,
например, мы доказали, что (xz) = 1, (х2)' = 2х. Используя теорему о произ-
водной произведения двух функций, легко получить производные и любых дру-
гих натуральных степеней х. Например,
(x3)z = (х- • л)' = (x2)z • х + л2 • (х)' = 2х • х + х2 • 1 = Зх2;
(x4)z = (х3 • x)z = (x3)z • х -h x3 • (x)z = Зх2 • a 4- x3 • 1 = 4x3;
(x5)z — (x4 • x)' = (x4)z • x -j- x4 • (x)z = 4x3 • x -f- x4 • 1 = Бх4
и т. д. Нетрудно подметить общее правило для нахождения производной от функ-
ции у = хп при любом натуральном п.
Чтобы найти производную функции у = хп, нужно показатель
п взять коэффициентом, а у самого х показатель понизить на
единицу, то есть
(1)
187
Например,
(х10)' = 10х9, (x46)' = 45X44.
Рассуждения, которые мы проводили здесь в подтверждение справедливо-
сти формулы (1), являются лишь наводящими; за строгое доказательство этой
формулы их принять, конечно, нельзя. К формуле (1) мы еще вернемся в § 262,
где и дадим ее строгое доказательство.
Полученное нами правило нахождения производной от степенной функции
верно не только для натуральных, но и для любых показателей, то есть для ло-
бого действительного числа а
( ха У = аха-"! (х > 0).
Доказательство этой формулы выходит за пределы школьной программы
и поэтому здесь не приводится.
Примеры.
1) Пусть у = Тогда
у' = = (х-1)' = — 1 • аг1’1 = — х-2 = — (х =/= 0).
\ х / х2
2) Пусть у = /х. Тогда
Упражнения
Найти производные следующих функций (№ 1782—1788):
1782. (У с т н о.)
X 7 V 4. Ч 1 •
а) у = х7; г) у = —, е) У =
б)у=^-хЗ; д)у = х/£ ж)у = Х
в) у = — 2лЛ2 ;
—- 1 5х2“~" х 1
1783. у = У х 1785. у = у—# 1787. у =-----------.
х х
з у----— 1 7____Зх 4- х4
1784. у=У ЗхУ5х. 1786. у =-------------1788. у =---------------
х у 2х х у х
1789. Почему, приводя общую формулу
( ха У = аха’"1 ,
обычно оговаривают, что х > 0?
188
Производная многочлена
§ 228
Многочлен степени п имеет вид:
Рп (*) = °<+ а2хп-- + ... 4- о„_, х 4- ап,
где ап — свободный член, а а0, alf ..., ап_} — коэффициенты при хл,хл*1, .... х
(соответственно), причем а =£ 0. Такое выражение можно рассматривать
как сумму (п 4- 1) функций: апхп, а1хп~1, а^х”-2. , ап_} х, ап. Поэтому про-
изводная многочлена раьна сумме производных этих функций:
Р'п (х) = (асхпУ 4- (а1хп~1)' 4- (а2хп~2)' 4- - 4- (an~ixY + (anY-
Производная от ап, как производная от константы, равна нулю. Остальные
производные легко найти, используя то, что постоянный множитель можно вы-
носить за знак производной и при любом натуральном k (х*)' = Ах*-1. Таким
образом, получаем:
(at.xnY = g„(x")' = о,./!*"-1:
(GjX''-1)' = а, (х"-1)' =а} (п — 1)хл-2;
(оп-1Х)' = яп-! (х)' = ап.г;
WnY = 0-
Отсюда
(а,.хл 4- аухп-х 4- о2хл-2 4- ... 4- оп_,х 4- аяУ =
= «(лх',_1 4- ал(п — 1)хл-2 4- ... 4-Ол-г
Примеры.
1) (Зх2 — 5х — 7)' = 3 - 2х - 5 = 6х - 5;
2) (10xs — 4Х3 4- х)' = 10 - 6хэ — 4 • Зх2 4- 1 = 60xJ — 12х2 4- 1.
Упражнения
Найти производные следующих функций:
1790. у = 2х5 — х. 1794. у = (х3 —1 —2х) (х2—5).
1791. у = Зх7 — 6х — 4х: 4- 5х2 -р 17. 1795. у = (х74-х)2.
1792. у = — х3 — Зх2 4- бх — 100. 1796. у = (2х — бх*)3.
1793. у = 5 — 6х 4- 17х4.
Дифференцирование тригонометрических
функций § 229
Теорема 1. Производная синуса равна косинусу:
(sin х)' = cos х.
Доказательство. Пусть аргумент х получил приращение Ах. Тог-
да функция у = sin х получит приращение
Ay = sin (х 4- Дх) — sin х.
Преобразуем это выражение, используя формулу для синуса суммы двух углов:
Ду — sin х • cos Ах 4- cos х • sin Ах — sin х =
с= cos х • sin Дх — sin х (1 — cos Дх).
189
Учитывая, что 1 — cos Д х = 2 sin2
Отсюда
. . _ . , /Дх’
Ду = cos х sin Дх — 2 sinx sinx2 —
\ 2
а • a sin2 "V I
Ду sinAx Л , \ 2 /
— = cos х • — ----—2 sin х----------.
Дх Дх Дх
sin Дх
Мы знаем (гл. IX, § 214), что lim —------= 1. Исходя из этого, найдем
Дх - о Дх
Дх \
2 /
:---Обозначим
Дх
sin2
предел выражения
потому
sin2
Следовательно,
Дх \
. 2 /
lim ---------= lim
Дх-о Дх г-0 2г
Теперь из (1) получаем:
Дх
T
Дх
Sl‘n22
sin2
sin-г 1 sin г
lim---------------
2 г-о г
(1)
г. Тогда Дх = 2г и
lim sin z —
2-0
• 1-0 = 0.
£
2
sin2
— 2 sin x lim ----------
д* - с Дх
Ду sin Дх
(sinx) = lim —=cosx- lim —-------
Дх - 0 Дх Дх - 0 Дх
= cos х • 1 — 2 sin х • 0 = cos х.
Теорема доказана
Теорема 2. Производная косинуса равна синусу, взятому с
противоположным знаком:
(cos х) = — sin х.
Доказательство. Пусть аргумент х получил приращение Дх. Тогда
функция у = cos х получит приращение
Ду = cos (х + Дх) — cos х.
Преобразуем это выражение, используя формулу для косинуса суммы двух
углов:
Ду —
cos (х -f- Дх) — cos х = cos х • cos Дх — sin х sin Дх — cos x =
= —sin x sin Дх — cos x (1 — cos Дх) =
= — sin x sin Дх — 2 cos x sin2 f — 1.
Отсюда
Ay _
Дх
sin Дх
— sin x —------
Дх
• 2 /ДХ
s,n (т
2 cos x------
Дх
но
sin Дх
lim -------
Ax - о Дх
sin2 1
a lim ---------- =0.
Дх-U ДХ
190
Поэтому
Ду
(cos xY = lim -— = — sin аг - 1 — 2 cos х • 0 = — sin х.
Лх-сДх
Теорема доказана.
Примеры.
1) Найти производную функции у = a sin х 4- b cos х.
Имеем:
у' = (a sin х + b cos х)' = a (sin х)' + b (cos х)' = a cos х — b sin х.
2) Найти производную функции у = х sin х.
По правилу дифференцирования произведения двух функций получаем:
у' = (х sin х)г == х' sin х + х (sin х)' = sin х + х cos х.
Используя правило дифференцирования дроби, легко найти производные
функций tg х при х ф — 4- пл и ctg х при х У= пл.
Действительно,
sz /sin x V (sin x)r cos x — sin x (cos x)' — — о — \cosx / COS2 X cos x cos x — sin x (—sin x) cos2 x 4- sin2 x 1 — i , cos2 x cos2 x cos2 x , /cosx\' (cos xY sin x—cos x (sin x)' (ctgx)' - . = . - \ sin X / sin- X — sin x sin x — cos x cos x sin2 x + cos2 x 1 sin2x sin2 x sin2x’
Итак, (ctg x)' r-7- (X лл). sin- x
Упражнения
1797. Написать уравнение касательной к синусоиде у = sinx в точке с абс-
циссой:
Л л 3 л
а) х = 0; б) х = —; в) х = л; г) х = —; д) х л.
X *
1798. Написать уравнение касательной к косинусоиде у = cos х в точке с
абсциссой:
л 3 л
а) х = 0; 6) х = —; в) х = — л; г) х = —; д) х = л.
Найти производные следующих функций:
1799. у = 3 sin х 4- 2 cos х.
1800. у = 4 sin х — 5 cos х.
1801. у = —sin х 4- i cos x.
1802. у = — 0 sin х — 9 cos x.
1803. у = sin2 x.
1804. у = cos2 x.
1805. у = sin x • cos x.
1806, у = x2 sin x.
1807. у = X2 COS X.
1808.* у = cos2
1809. у = (5x 4- sin x) (x2 — cos x).
1810. y= (1 —2 sinx) (1 —3cosx).
191
1811. у = sin 2х.
1812. у = cos2x.
1813. у = (а 4- bx) sin х4- (с 4- dx) cosx.
sin х
1814. у =--------.
х
1815. у = sin^x 4- cos2 х.
1816. у = y'xsinx.
Дифференцирование функции f (ax + b)
3cosx
1817. у = ——
1818. у = sin I x
1819. y= cos
§ 230
В математике часто приходится иметь дело с выражениями вида f (ах + 6),
где f (х) — некоторая заданная функция. Так, при изучении гармонических коле-
баний рассматриваются функции типа sin (<ох 4- Ф). При решении различных
задач часто встречаются выражения вида 1g (ах 6), (х 4~ а)л и т. д. Большой
интерес представляет вопрос о дифференцировании подобных функций.
Пусть f (х) — некоторая функция, для которой мы можем найти производ-
ную. Как в таком случае найти производную функции ф(х), которая выражается
через f (х) следующим образом:
Ч>(*) = f (ах + Ь)?
По определению производной
,, . ф (х 4-Дх) — ф (х) )\а(х +&х)-\-b]—f(ax+Ь)
ф (х) = нт ------------------ = lim-------------;-------------
Дх - о Дх Дх - о Дх
f[(ax 4- b) 4- а • Дх| — / (ах 4- Ь)
= lim ------------------------------.
дх - о Дх
Обозначив ах 4- Ь через у, получим:
/(У + аЬх) — /(у)
Ф (х) — lim ----------------.
Дх -* о Дх
Умножим числитель и знаменатель этого выражения на число а:
/(у + аЬх) — /(у)
ф (х) = lim ----------------- • а.
Ах -* о аДх
Обозначив теперь аДх через h, получим:
,, . .. /(У + й)—/(У)
ф'(х)= hm ----------------
Л - о Л
(Поскольку Дх -> 0, то и h =аДх -> 0.)
• а.
„ .. /(у + Л) —/ У ,, , .
Но hm ---------------- == t (У)-
й -о h
Поэтому
ф' (х) = af (у)
Вспоминая, что у = ах 4- bt получаем окончательно:
ф' (х) = af (ах 4- Ь).
192
Итак,
[f (ах + &)]' = af' (ах 4- b). (1)
Число а есть производная функции ах 4- Ь. Поэтому равенство (1) можно
сформулировать таким образом.
Для нахождения производной выражения f(ax + b) достаточно
продифференцировать его по правилу дифференцирования выраже-
ния f(x) (с заменой в окончательном выражении х на ах + Ь)
и результат умножить на производную выражения ах + Ь (то есть
на число а).
Примеры.
1) |(2х 4- 1)1иГ = 10 (2х 4- I)9- (2х 4- 1)' = 10 (2jc 4- I)9 . 2=20 (2х 4- I)9;
2) (sin Зх)' = cos Зх • (Зх)' = 3 cos Зх;
Упражнения
Найти производные следующих фу
1820. у = (2х + З)5.
1821. у = (х + 7)3.
1822. у = (I — 5х)7.
1823. у = sin 4х.
1824. у = sin--.
5
1825. у = cos 6х.
1826. у = sin (2х — 3).
/л \
1827. у = cos I — — х 1.
й (№ 1820—1834):
1828. у — Л sin (сох -f- <р).
1829. у = A cos (<р — (ох).
1830. у = Зх sin 2х.
1831. у = 3 (х — 5)3 + 2 (1 — х)4.
1832. у = Зх sin 2х 4- 2х cos Зх.
1833. у = /2x4- 1-
1834. у = ^1 —х .
1835. Доказать, что I —-----
\сх 4- d
Понятие о второй производной.
Производные высших порядков § 231
Производная от производной у1 функции у называется второй производной
этой функции и обозначается у” или /" (х):
у" =(/)'; /"(*) = 1Г(*)Г
Рассмотрим несколько примеров.
1) Пусть у = Зх3 — 6х2 4- 7х — 1. По правилу дифференцирования мно-
гочленов
у' = (Зх1 — 6х24- 7х — 1)' = 9х2 — 12х 4- 7;
у" = (у')' = (9х2 — 12х + 7)' = 18х — 12
2) Пусть у = sin х. Тогда у = (sin х)' = cos х; у" == (cos х)' = —sinx.
7 Заказ 1159 193
3) Если у = — , то
у" == (ах)' = а.
Вторая производная у" функции у, так же как и первая ее производная у',
допускает простую физическую интерпретацию. Будучи производной от первой
производной у', она характеризует скорость изменения этой производной. Пер-
вая же производная у' характеризует скорость изменения функции у. Таким обра-
зом, у" характеризует «скорость изменения скорости изменения» функции у.
С подобным понятием мы уже сталкивались в физике. Изучая равноускоренное
движение, мы вводили понятие ускорения как изменения скорости движе-
ния в единицу времени. Это понятие как раз и характеризует скорость изменения
скорости движения. Поэтому, используя язык механики, можно сказать, что вто-
рая производная у" функции у есть ускорение, с которым функция у = f (х)
изменяет свои значения при изменении значений аргумента х.
Третья производная функции у = f (х) есть производная от второй произ-
водной этой функции. Она обозначается у"' или f'"(x) : у = (у")', /'"(*) =
= l/^WK- Аналогично, четвертая производная функции у = f (х) (обозначает-
ся yiv или /IV (х)) есть производная от ее третьей производной и т. д.
л- я производная функции /(х) иначе называется производной п-го порядка
(обозначается /((1)(х)). Например, третья производная иначе называется производ-
ной третьего порядка, четвертая производная — производной четвертого порядка
и т. д.
Примеры.
1) Для функции у = х2 4- х + 1 имеем:
у'= 2х 4-1;
У" = 2;
у'" = 0;
y,v = 0.
Очевидно, что все производные данной функции, начиная с третьей, равны
нулю.
2) Для функции у = sin х:
у' cos х;
у" = —sin х;
у"' = —cos х;
у IV= —(—sin х) = sin х;
V
у = COS X
и т. д.
Упражнения
1836. Найти ускорение тела, движущегося по закону s (/) = 2/3 5/а + 4t
($ — путь в метрах, t — время в минутах), в момент времени: a) t = 40 сек\
1837. Найти ускорение тела, движущегося по закону s = у t (s — путь в
метрах, t — время в минутах), в произвольный момент времени i.
Для данных функций найти производные всех порядков (1838—1843):
1838. у = (х + 2)3. 1840. у =х2 — х — 1. 1842. у = cos х.
1839. у = (2х — I)3. 1841. у =х*> 4-4*3 — 7ха. 1843. у = (1+х)100.
194
1844. Доказать, что для функции у — a sin х 4-6 cos х справедливо соотно-
шение y,v = у.
1845. Сколько раз нужно продифференцировать функцию у = (ха -f- 1)10э,
чтобы в результате получился многочлен 50-й степени?
1846*. Найти производную 100-го порядка от функции у = sin х cos3 х.
Выражение коэффициентов многочлена через значения
его производных § 232
Пусть
Р W = а0 4- агх 4- а2х2 4- а3х} 4- о^х4 4- ... 4- апхп.
Тогда
Р' (х) = 1 . 4- 2а2х 4- Заре24- 4а4х3 4- ••• ~Hianx п—'•
Р" (х) = 2 1 • аз 4- 3 • 2а/ 4- 4 • За4х2 4- • • -4* л (п — 1) опхп~2 .
Р'"(х) = 3 • 2 • 1 • аз 4- 4 • 3 -2а4х 4- ... -f- п (п — 1) (а —2)апхр-^
и т. д. Полагая в формулах (1), (2), (3) и (4) х => 0, получаем:
(1)
(2)
(3)
(4)
г (и) = 1 • za2,
Р'" (0) = I • 2 • Заз,
откуда
ао = Р (0),
Р'(0)
аг- j >
Р"(0)
°2 = 1-2’
Р"' (0)
°3 - 1 • 2 • 3 ‘
Продолжая этот процесс дальше, мы получили бы:
piv(0)
01 1 • 2 - 3-4’
a5=-pV<°) .
1 • 2 - 3 - 4-5
и т. д. Очевидно, что для любого натурального k
°k =
P(ft>(0)
1-2- 3- ... • Л’
(5)
где Р*(0) — значение /г-й производной многочлена Р (х) при х = 0.
Произведение 1 • 2 • 3 «... • k принято обозначать символом Л! (читается:
ка факториал). Поэтому формулу (5) можно переписать в виде:
pW(0)
к fel
(6)
Эта формула будет верна и при £= 0, если под выражением Р 01 (х) (нуле-
вой производной функции Р (х)) подразумевать просто функцию Р(х) и считать,
что 0! = 1
Формула (6) выражает коэффициент многочлена Р (х) при х* через значение
Л-й производной этого многочлена в нуле.
195
Поясним эту формулу на некоторых примерах.
Пример 1. Найти коэффициент многочлена (х 4- I)10 при х3.
Имеем:
Р (х) = (х + I)10;
Р' (х) = 10 (х + I)9;
Р" (х) = Ю • 9 (х + I)8;
₽"'(*) = Ю-9. 8(х4-1)7
Поэтому Р'" (0) = 10 • 9 • 8 • I7 = 720. По формуле (6) получаем:
Итак, коэффициент многочлена (х + D10 при хл равен 120.
Пример 2. Найти коэффициент многочлена (Зх — I)9 при ха.
Имеем:
Р (х) = (Зх — I)9;
Р' (х) = 9 (Зх — I)» • 3 = 27 (Зх — 1)8;
Р" (х = 27 . 8 (Зх — I)7 • 3 = 648 (Зх — 1)?.
Поэтому искомый коэффициент равен:
Р"<0) _ 648 • (- I)7 _
21 1-2 3 4‘
У пражнения
В задачах № 1847—1851 найти коэффициенты данных многочленов при ука-
занных степенях х.
1847. Р (х) = (х + 2)10 при х3. 1850. Р (х) = (х + а)9 при х4.
1848. Р (х) = (1 — х)40 при х2. 1851. Р (х) = (х + 1)" при х5 *.
1849. Р (х) = (2 — х)25 при х3.
1852. Определить степень многочлена Р (х) = (х + 2)л, если его коэффи-
циент при х2 равен 24.
Формула бинома Ньютона
§ 233
До сих пор нам были известны формулы для второй и третьей степени дву-
члена а 4- Ь :
(а 4- Ь)2 = а2 4- 2аЬ 4- Ь2,
(а 4- Ь)3 = а3 4- 3o2Z? 4- ЗдЬ2 4- Ь3.
В этом параграфе мы получим формулу для степени (а + Ь)п с произвольным
натуральным показателем п. Для этого рассмотрим многочлен степени п
Р (X) = (х 4- а)п,
где а — некоторое заданное число.
Свободный член этого многочлена равен Р (0) = ап. Для нахождения коэф-
фициентов при степенях х воспользуемся формулой (6) предыдущего параграфа.
Согласно этой формуле коэффициент при xk равен
Pk (0)
—-— , где Р*(0)— значение
я!
196
fe-й производной многочлена Р (х) при х = 0. Найдем это значение. Имеем:
Р(х) = (х + а)п;
Р' (х) = п (х 4- а)'1-1 ;
Р" (X) = П (п — 1) (X + й)"-2;
Р" (х) = л (л — 1) (л — 2) (X 4- а)"-3
и т. д. Очевидно, что k-n производная многочлена Р (х) равна!
Pk (%) = п (п — 1)(л — 2) ... (n — k 4- 1)(х + а)п~к.
Поэтому
Pk (0) = л(л — 1)(л — 2) ... (л — k 4- 1) fl"-ft .
Следовательно, коэффициент многочлена Р (х) при xk равен:
Р<ь’(0) л (л — 1) (л — 2) ... (л — fe 4-1)
k\ k\
Выражение
л(л —1)(л— 2) ... (п — fe+1)
fe!
принято обозначать (читается: це из эн по ка). Поэтому коэффициент много-
члена Р(х) при xk равен an~k . Например, коэффициент при х равен СП1 ап~~19
коэффициент при х2 равен С” ап~“ и т. д. Но в таком случае данный многочлен
можно представить в виде:
(х + а)п = ап + CJ, ап^х 4- ап~2хг 4- ... 4- С^~1ахп~1 4- Сяхя.
Полагая в этой формуле х = Ь, получим:
(а 4- bf = ап + С1п ап-Ч> 4- С2 а"-2624- ... 4- C'-'alF* 4- С"У». (1)
Отметим, что (k 4- 1) -е по счету слагаемое в разложении (а 4- Ь)п имеет вид:
C£a"-ft b* (Q<k < л).
Формула (1) называется формулой бинома* Ньютона, а коэффициенты
С[п, С2п, ... , , С”, участвующие в ней,—биномиальными коэффициен-
тами.
Пример.
(а 4- *)4 = а4 4- а3Ь 4- С2а262 4- CfaP 4- С*Ь*.
Но 11 1 — С© 1 . „ || СЧ СО СЧ СО • . • || со сч со сч со сч тГ | — тГ —1 II II II II хг V V V
* Формула (1) была строго доказана еще до Ньютона Якобом Бернулли
(1654—1705) — одним из членов семьи швейцарских ученых, давшей миру 11
видных математиков. Ньютону принадлежит идея о распространении формулы (1)
на случай дробных и отрицательных значений л. Эта идея широко используется
при решении многих задач высшей математики.
197
Поэтому
(а + ЬУ = а4 + 4й36 + 6а2&2 + 4а^ + ZA
Упражнения
1853. Вычислить:
а) С?; б) Cj?; в) С|; г) С®; д) Cfc е) С®.
1854. Исходя из формулы бинома Ньютона, получить формулы для кубов
суммы и разности двух чисел.
1855. Вычислить по формуле бинома Ньютона:
а) (К5-/2)4; б) (К6 + /2)4; в) (К6-/2-)5; г) (ГТо-уТ)5.
1856. Определить степень бинома (За — 2)л, если известно, что коэффициент
при а2 в разложении этого бинома равен 216.
1857. Доказать равенства:
а) сг' =с; = п; 6) СГ! = С* =
1858. Доказать тождество:
C^ = Chn.
п — k
k+r
1859*. Доказать, что число II10 — 1 делится на 100.
Об одном свойстве биномиальных
коэффициентов
§ 234
По определению
k л (л — 1) (л — 2)... (л — k + 1)
1 • 2 • 3- .... k
Умножив числитель и знаменатель этой дроби на
(л — k)(n — k — 1) ... 3- 2. h
(1)
получим:
л (zz — 1) ... (л — fe 4- 1) (п —(л — fe — 1)3 - 2 > 1
п~~ 1 .2-3.../г(л —/г)(л —/г —1)... 3. 2- 1
Таким образом,
л!
/г! (л — k)f
с‘ =——
п Л! (и — k)l
Эта формула справедлива для любых натуральных чисел л и /г, если только
п > k. В частности, заменяя в ней k на п — k, получаем:
л! л!
(2)
ft =
п (п — /г)! [л — (л — /г]! (л — /г)! /г! ’
Правые части равенств (2) и (3) равны; значит, равны и левые части:
(3)
ph____ —h
''п
(4)
Формула (4), выражая важное свойство биномиальных коэффициентов,
значительно упрощает их вычисление. Например, при возведении двучлена
198
a + b в 6-ю степень приходится вычислять ClQt с|, С%, С%, с|. По определе-
нию (см. формулу (1)):
4=7 = 6;
, 6-5
4=—2 = 15;
3 = LlLJ.=20.
6 1-2-3
Для вычисления й с| теперь нет необходимости представлять их по фор-
муле (1). Достаточно воспользоваться формулой (4) и уже полученными значе-
ниями:
<4 = ф4 = = 15;
4=4-5 = 4=6-
Отметим еще, что С£=1. Это вытекает непосредственно из определения
числа С";
с„ = и (л — 1) (п — 2)... 3 2 1 =
п 1 • 2 • З...(л — 2) (л — 1)л
Условимся считать, что С?п = 1. В результате такого соглашения формула
(4) оказывается верной не только для п > kt но и для п = k:
спп = (% = 1.
Упражнения
1860. Вычислить:
а) С10; б) С}|; в) С^р0; г) С36 .
1861. Известно, что С* = . Можно ли утверждать, что х = у?
1862. Решить уравнения:
а) Сх~2 + 2х = 9; б) ф? = х? — 13; в) С%~2 = с£.
/ 1 \12
1863. В разложении I а + — I найти коэффициент при о®.
( 1
1864. В разложении 12а — — I найти коэффициент при а4.
Применение формулы бинома Ньютона
к приближенным вычислениям
§ 235
Положив в формуле бинома Ньютона
(а + ЬГ = ап 4- 4 <F-lb + С2п ап—гЬ2 + ... 4- сфаб'’-1 4- 4^
а= 1, Ь = г, получим:
(1 -I- хГ = 1 4- 4x4-4** 4- - (1)
199
Если величина х мала, то величины х2, х3, ... , хп тем более малы. Поэтому если
в формуле (1) отбросить члены, содержащие х2, х3, ...» xnt то полученная в ре-
зультате формула
(1 + лГ«1 + ^х (2)
будет приближенной, причем ошибка такого приближения должна быть неболь-
шой. Поскольку С\ = л, формулу (2) можно переписать в виде:
(1 + х)п « 1 + их. (3)
Практически при малых значениях х формула (3) дает вполне удовлетворитель-
ный результат. В подтверждение этого приведем следующую таблицу для
случая х = 0,01.
\(1 4- *)" п >4 По фор- муле (3) Значение с четырьмя верными десятичными знаками
2 1,02 1,0201
3 1,03 1,0303
4 1,04 1,0406
10 1,10 1,1046
Формула (3) верна и для малых отрицательных значений х. Например,
(1 __ 0,02)6 « 1 — 5 • 0,02 = 0,9;
(0,93)2 = (1 — 0,07)2 1 — 2 0,07 = 0,86.
Формулу (3) мы получили для натуральных значений л. На самом же деле
ею можно пользоваться при любых действительных значениях л.
Например,
/ТТобз = (I 4-о,ооз)2 « 1• °-°°з= 1,о<Л5;
„ 1 i
Уо797"= (1 — 0,03)"з » 1 — — • 0,03 = 0,99;
’ о
^ = 0,98-’ =(1 — 0,02)-1 ~ 1 4-(—1)(—0,02) = 1,02;
’1 -1 -L 1
1 = 0,96 < = (1—0,04) 4 « 1 4-— • 0,04= 1,01.
/0,96 4
Упражнения
Найти приближенные значения следующих выражений:
1865. (1,04)3. 1871. V1,05. 187 7. /0,98’
1866. (1,001)10. 1867. (1,03)«. 1872. 1873. /0,95. У1703. 1878. 1 1,02 ’
1868. (0,99)3. 1874. ^6799- 1879. 1
1869. (0,98)4. 1875. /2 И/24- 0,97 ’ 1
1870. (0,97)5. 1876. (3/0Л8)4' 1880.
/4 —
Солй)3’
200
Применение производной
и нахождению участков
возрастания и участков
убывания функций § 236
С помощью производной легко найти
участки возрастания и участки убыва-
ния любой дифференцируемой функции.
Имеет место следующая теорема.
Теорема. Если производная
f (х) функции / (х) положительна
в интервале [а, Ь], то функция f (х)
монотонно возрастает в этом ин-
тервале. Если же производная от-
рицательна в этом интервале, то
в нем функция f(x) монотонно убы-
вает.
Доказательство этой теоремы выхо-
дит за пределы школьной программы.
Поэтому мы ограничимся лишь ее гео-
метрической иллюстрацией.
Производная функции у = f (х) при
х = х0 равна угловому коэффициенту ка-
сательной, проведенной к графику функ-
ции х = f (х) в точке с абсциссой х0.
Условие f (х) > 0 означает, что в рас-
сматриваемом интервале угловые коэф-
фициенты касательных положительны. Но
это возможно лишь в том случае, когда
углы, образованные касательными с по-
ложительным направлением оси х,—ост-
рые (рис. 318). Тогда график функции
У = f М с ростом х поднимается все
выше и выше. А это и означает, что функ-
ция у = f (х) монотонно возрастает.
Случай, когда в интервале [а, 6]
/' (х) < 0, рассматривается аналогично
Условие /' (х) < 0 означает, что угловые
коэффициенты касательных к графику
функции у = f (х) отрицательны. Но это
возможно лишь в том случае, когда
углы, образованные касательными с по-
ложительным направлением оси х,—тупые
(рис. 319). Тогда график функции у=/ (х)
с ростом х опускается все ниже и ниже.
А это и означает, что функция у = /(х)
монотонно убывает.
Пример. Определить участки воз-
растания и участки убывания функции
f (х) = х2 — 4х + 3.
Имеем: /' (х) = 2х — 4.
При х>2 f'(x) > 0, а при х<2 f'(x)<S).
Значит, функция /(х) = х2 — 4х + 3
при х>2 возрастает, а при х < 2 убы-
вает (рис. 320).
201
К такому же результату мы пришли бы, если бы исследовали данную функ-
цию путем выделения полного квадрата (см. рис. 320):
/ (х) — х2 — 4х 4- 3 = х2 — 4х 4 — 1 «= (х — 2)2 — 1.
Использование производной в данном случае легче и быстрее приводит к
решению задачи.
У пражнения
Определить участки возрастания ций: и участки убывания следующих функ-
1881. у = 3 4- 4х — х3. 1882. у = Xs —3x4-1. 1886. у = Зх2 4- х. 1887. у = /х3 — Зх.
1883. у = х* — 2х2 — 3. 1888. у = х 4- —. X
1884. у = х3 4- 6х3 — 15х 4- 2. 1889. у = sin х —х.
1885. у — х2 — 5 — 2х — вх3. 1890. у = х 4- cos х.
Доказать, что данные функции (№ 1891—1894) являются монотонными на
всей числовой прямой. Какие из них монотонно возрастают и какие монотонно
убывают?
1891. у = х3 — х2 4- х — 5.
б £
1893. у = у2 х — cosх.
1892. у = 6 — 6х — 2х3 4- Зх3.
л
1894. у =sin х ——х.
Определить участки возрастания и участки убывания следующих функций:
X " 4- 1 х2
1895. у =--------. 1896. у = — 4- cos х. 1897. у = sin2x — х.
X £
Применение производной к нахождению
локальных экстремумов функции В
§ 237
В этом параграфе мы покажем, как с помощью производной можно находить
локальные экстремумы дифференцируемой функции.
Теорема. Если точка, х=>а является точкой локального
экстремума дифференцируемой функции у => f(x)t то производная
f' (х) в этой точке обращается в нуль:
f (а) =0.
Доказательство этой теоремы выходит за пределы школьной программы,
поэтому мы ограничимся лишь ее геометрической иллюстрацией.
Пусть точка х = а является точкой локального максимума функции у =
= f (х) (рис. 321). Тогда касательная к графику этой функции в точке с абсцис-
сой а будет параллельна оси х. Угловой коэффициент этой касательной равен 0.
Но, как мы знаем, этот угловой коэффициент должен равняться [' (а) Следова-
тельно,
Г (а) = 0.
202
Рис. 322.
Аналогично интерпретируется случай, когда точка х = а является точкой
локального минимума (рис. 322).
Важно подчеркнуть, что полученное условие f'(a) = 0 относится лишь к
функциям, дифференцируемым в точке х = а. Вообще же функция может иметь
локальный экстремум в точке х •= а и будучи недифференцируемой в этой точке.
Взгляните, например, еще раз на кривую, представленную на рисунке 274
(стр. 140). Эта кривая служит графиком функции f (х), для которой точка х=3
является точкой локального минимума. Но эта функция при х = 3 не имеет про-
изводной (кривая в точке с абсциссой 3 не имеет касательной). Поэтому условие
/' (3) = 0 не выполняется.
Пример. Функция /(х) = ах24-6х + с имеет единственный локальный
экстремум в точке х =— —. В этом легко убедиться путем выделения из дан-
ного квадратного трехчлена полного квадрата (см. ч. I, § 49):
2 L . ( , b\2 Ь--4ас
сх2 + ^х + с = а хЧ--- ——----------.
\ 2а) 4а
/ ! ь\
Легко проверить, что /' I — — 1=0. Действительно, поскольку / (х) =
= ах2 + Ьх + с, то
/' (х) = 2ах + Ь
и потому
Естественно возникает вопрос: как, зная, что х= а есть точка локального
экстремума функции / (х), определить, какой экстремум она дает: максимум или
минимум?
Пусть при х < a f'(x) < 0, а при х > a f'(x) > 0. Тогда вблизи точки
х = а функция f (х) должна убывать в точках, лежащих левее а, и возрастать
в точках, лежащих правее а (рис. 322). В этом случае точка х = а является
точкой локального минимума. Если же при х < a f (х) > 0, а при х > а /'(х) <
< 0, то, наоборот, левее точки х = а функция / (х) будет возрастать, а правее
х = а убывать. В этом случае точка х = а будет точкой локального максимума
(рис 321).
Итак, если производная f (х) в точке х = а обращается в нуль,
а при переходе через эту точку меняет свой знак с «—» на «+>, то
точка а есть точка локального минимума функции f (х). Если про-
изводная f (х) в точке х = а обращается в нуль, а при переходе че-
рез эту точку меняет свой знак с «+> на «—», то точка а есть
точка локального максимума функции f(x).
203
Например, для функции f (х) = ах2±Ьх-}-с про-
изводная /'(х) = 2ах-{- b обращается в нуль при х =
b
. Предположим, что а > 0; тогда при х <
2а
b
< — — получим:
b
а при х > —
2а
2ах < — b,
2ах + b < О,
2ах > — b.
2ах + Ь > О.
> О, то при переходе через точку
Итак, если а
b
х =— — производная функции /(х) = ах2 Ьх +
+ с меняет знак с «—» на «-{-». Поэтому точка х =
b
= — — является точкой локального минимума этой
функции. К такому же результату мы приходили и
выражение
/ ^\2
а И+;г
\ 2а/
& — 4ас
4а
Учащимся предлагается самостоятельно с помощью производной рассмотреть
b
случай, когда а < 0, и убедиться, что тогда точка х = — — является точкой
локального максимума функции f (х) = ах2 + Ьх + с.
Не следует думать, что если /' (а) = 0, то точка х = а обязательно является
точкой локального экстремума. Например, для функции f (х) = х3 имеем f'(x)=
= Зх2, и поэтому f'(0) = 0. Но, как видно из графика этой функции (рис. 323),
точка х = 0 не является ни течкой локального минимума, ни точкой локального
максимума. Объясняется это тем, что в точке х = 0 производная /' (х) = Зх2,
обращаясь в нуль, не меняет своего знака. Как при х < 0. так и при х > 0 она
положительна.
Можно доказать, что если /' (а) — О и при переходе через точку
х = а производная f (х) не меняет знака («+> переходит в«+> или
«—> в «—то точка х — а не является ни точкой локального
минимума, ни точкой локального максимума.
Точки, в которых производная /' (х) функции / (х) обращается в нуль, на-
зываются стационарными точками, а значения функции в этих точках — ста-
ционарными значениями этой функции.
Упражнения
Для данных функций (№ 1898—1909) найти все локальные экстремумы.
По возможности выяснить, какие из них представляют собой локальные мини-
мумы и какие — локальные максимумы:
1898. у = 4х2 — 6х — 7.
1899. у = —Зх2 — 12х + 100.
1900. у = (а — х) (а — 2х)
1901. у = (1 — ах) (1 — 2х)
1902. у = 2х3 + 6х2 — 18х + 120.
1903. у = 2х3 — 6х2 — 48х — 17.
1904. у = Зх4— 4Х3.
1905. у = sin х + cos х.
1906. у=У 3 sin х — cos х.
1907. у = sin х + У^З cos х
1908. у = х5.
1909. у = sin2 х — cos2 х.
204
В задачах № 1910—1913 найти стационарные значения данных функций:
1910 у = х — sin х 4- cos х.
1911. у = 2х + sin х — cos х.
1912. у = 5 sin x-f-12 cos х— 13х
1913. у = sin* 1 2 х — cos х.
1914. Докажите, что функция f (х) = | х | имеет в точке х = 0 локальный
минимум. Удовлетворяется ли при этом условие /' (0) = 0?
1915. В конус вписан цилиндр наибольшего объема. Докажите, что радиус
2 1
этого цилиндра составляет — радиуса основания конуса, а высота — высоты
о «5
конуса.
Наименьшее н наибольшее значения функции
в заданном интервале
§ 238
В главе IX (§ 205) мы рассмотрели вопрос о том, как отыскивается абсолют-
ный минимум и абсолютный максимум функции f (х) в интервале [а, 6). Среди
всех локальных экстремумов и значений функции f (х) в концах интервала [а, д]
нужно выбрать наименьшее и наибольшее значения Они и даюг абсолютные эк-
стремумы. Однако в главе IX мы не могли решить вопрос о том, как находить
локальные экстремумы. Теперь же мы можем решить эту задачу
Для того чтобы найти абсолютный минимум и абсолютный максимум диф-
ференцируемой функции у=/(х) в интервале [a, 6], нужно:
1) из уравнения /' (х) = 0 найти все стационарные точки функции / (х) и,
выбирая те из них, которые попадают в интервал [а, Ь], определить стационар-
ные значения этой функции в данном интервале;
2) к стационарным значениям функции / (х) в интервале [а, Ь] добавить
значения этой функции в концах этого интервала, то есть f (а) и f (b)\ среди по-
лученных значений нужно выбрать наименьшее и наибольшее
И вновь, как и в § 237, следует подчеркнуть, что полученный результат
относится лишь к функциям, дифференцируемым в рассматриваемом интервале
[а, Ь]. Если же в этом интервале имеются точки, в которых исследуемая функция
не имеет производной, то эти точки следует рассмотреть особо. Абсолютный ми-
нимум или абсолютный максимум функции в интервале (а, Ь] может достигаться
в одной из таких точек (см. рис. 274 на стр. 140 в интервале [2, 6]).
Рассмотрим несколько примеров.
Пример 1. Найти наименьшее и наибольшее значения функции / (х) =
= х3 —Зх2 в интервале [1; 3].
Имеем: f (х) = х3 — Зх2, /' (х) = Зх2 — 6х. Из уравнения /' (х) — 0, или
Зх2 — 6х = 0, находим стационарные точки функции f (х): = 0, х2 = 2. В ин-
тервал (1,3] попадает лишь вторая точка. В ней функция принимает значение
/(2)=— 4. В крайних точках интервала [1, 31 имеем: f (1) = —2; / (3)=0.
Из трех значений / (2)= —4, f (1) = —2 и f (3) =0 наименьшим является—4,
а наибольшим 0.
Поэтому минимальное значение функции / (х) = х3 — Зх2 в интервале (1.3]
равно —4, максимальное 0. Они достигаются соответственно в точках х = 2 и
х= 3.
Пример 2. Найти наименьшее и наибольшее значения функции / (х) =
3
— х -J- sin х в интервале [а, &].
Имеем:
3
Т(х) = у + cos X.
205
Функция /' (х) положительна при всех значениях х. Поэтому f (х) монотонно
возрастает на всей числовой прямой. В таком случае в левом конце (х = а) ин-
3
тервала (а, Ь] эта функция должна принимать наименьшее значение — a -f- sin а,
£
3
а в правом конце (х = Ь) — наибольшее значение — b -|- sin b.
&
Упражнения
1916. Найти наименьшее и наибольшее значения функции у = х3—Зх в
интервалах: а) [—0,5; 0,5]; б) (—1,5; 2].
1917. Найти наименьшее и наибольшее значения функции у = sin х —
— УЗ cosx в интервалах: а) [ — л; 0]; б) 0; — .
х3 5
1918. Найти наименьшее и наибольшее значения функции у = ~— — х2 -f-
-f- 6х + 10 в интервалах: а) [0; 1]; б) [0; 2,5]; в) [0; 4].
Найти наименьшие и наибольшие значения данных функций в указанных
интервалах (№ 1919—1923):
1 Г л 1 Г л л 1
1919. у = —х— sinx в интервалах: а) 0; — I; б) ——; — I;
[л л 1
2’ "2J
л ч Г л л 1
1920. у = х — cos 2х в интервалах: а) — —; — ; б) [—л; л];
1-n.oi. L 2 2J
1921. у = х4 — 8х2 — 9 в интервалах: а) [—1; 1]; б) [0; 3]; в) [—3; 5].
1922. у = Зх4 — 4Х3 — 72х2 + 200 в интервалах: а) [—1; 1 ]; б) [—0,5; 3,5];
[—2; 5].
1923. у = 1 + 36х + 36х2 — 2х3 в интервалах: а) [—3; —1]; б) [—2];
[—10; 4].
В)
в)
в)
в)
V ; б) [—л; л];
5
2
Использование производных для исследования
дифференцируемых функций и построения
их графиков § 239
Использование производных значительно облегчает исследование дифферен-
цируемых, функций и построение их графиков. С помощью производной можно
установить интервалы возрастания и интервалы убывания функций, найти ста-
ционарные точки и локальные экстремумы. А это позволяет более точно построить
графики исследуемых функций.
В дальнейшем мы будем придерживаться следующего плана* исследования
функции у = f (х):
1) область определения функции;
2) поведение функции вблизи «особых» точек (например, функции у = —
вблизи точки х = 0);
3) четность функции;
* Эгог план лишь незначительно отличается от плана, описанного в § 210.
206
4) периодичность функции;
5) стационарные точки и локальные экстремумы функции;
6) интервалы возрастания и интервалы убывания функции;
7) нули функции, то есть корни уравнения f (х) = 0;
8) интервалы знакопостоянства функции;
9) поведение функции при неограниченном возрастании значений аргумента
(х -> оо) и при неограниченном убывании значений аргумента (х -> —оо);
10) область изменения функции.
Осуществление каждого пункта этого плана полезно сопровождать геомет-
рической интерпретацией, выполняя шаг за шагом построение графика исследуе-
мой функции.
В качестве примера рассмотрим функцию
у = х4 — 10х2 + 9.
1) Областью определения данной функции является множество всех дейст-
вительных чисел.
2) «Особых» точек (типа точки х = 0 для функции у = —эта функция не
имеет.
3) Функция четна, поскольку при любом значении х
(—х)4 — 10 (—х)2 + 9 = х4 — 10х2 + 9.
Это должно найти свое отражение и в графике функции. Он должен полу-
читься симметричным относительно оси ординат.
4) Рассматриваемая функция, очевидно, непериодична.
Вообще периодичность той или иной функции часто устанавливается путем
простого указания на периодические составляющие этой функции (например,
sin х, cos хит. п.). Данная функция подобных составляющих не имеет. Конечно,
это не может служить строгим доказательством непериодичности рассматривае-
мой функции. Поэтому мы еще вернемся к этому вопросу при рассмотрении
пункта 6.
(Впрочем, возможно и такое доказательство непериодичности. Если бы дан-
ная функция была периодической с периодом Т > 0, то при любом значении х
выполнялось бы равенство
(х + Т)4 — 10 (х + Т)2 + 9 = х4 — 10х2 + 9.
В частности, при х = 0 мы получили бы
Г4 — ЮГ2 4-9=9,
откуда Т = /10. Таким образом, в качестве периода может выступать лишь
число /10. Но, как мы знаем, периодические функции имеют бесконечно много
положительных периодов Получено противоречие. Следовательно, предположе-
ние о периодичности данной функции неверно.)
5) Стационарные точки функции /(х) находятся как корни уравнения /'(х)=
е= 0 В данном случае /'(х) = 4х3 — 20х; поэтому нам нужно решить уравнение
4х3 — 20х = 0.
Оно имеет три корня:
х1= 0;
л2=-/5:
х3 = /5?
Чтобы выяснить, какие из этих трех стационарных точек дают локальные эк-
207
стремумы и какие именно экстремумы (минимумы или максимумы), рассмотрим
поведение производной /' (х) вблизи стационарных точек. Имеем:
/' (х) = 4Х3 — 20х = 4х (х2 — 5).
Если х близко к нулю и х < 0, то оба сомножителя 4х их- — 5 отрицательны.
В этом случае f' (х) > 0. Если же х близко к нулю и х > 0, то множитель 4х
будет положительным, а множитель х2 — 5 — отрицательным. В этом случае
/' (х) < 0.
При переходе через точку х = 0 производная f (х) меняет знак с «+» на
«—» Поэтому точка х = 0 является точкой локального максимума функции у =
= х4 — 10х + 9.
Аналогично устанавливается (сделайте это самостоятельно ), что точки х =
=» —и х=)^5 являются точками локальных минимумов.
Теперь можно найти и сами локальные экстремумы. При х = 0 у= 9; при
х = ± У5 у = —16.
Итак, функция у = х4 —10х2+9 имеет один локальный максимум, равный 9
(он достигается при х = 0), и два локальных минимума, каждый из которых
равен —16 (они достигаются при х= —и х = 1^5). Это позволяет нам
208
отметить на координатной плоскости три точки графика нашей функции. Это
будут точки с координатами (0,9), (—} 5, — 16) и (р^б, —16), причем первая
из них служит геометрическим образом локального максимума, а остальные две—
геометрическими образами локальных минимумов данной функции (рис. 324, а).
6) Найдем интервалы возрастания и интервалы убывания рассматриваемой
функции. После исследования стационарных точек легко понять, что при — Уг5'<
< х < 0 и х > 4^5 эта функция возрастает, а при х < — /5 и 0 < х <
<р^5 убывает (см. рис. 324, а). Но это, конечно, можно доказать и строго, не
обращаясь к геометрической интуиции.
Действительно, производная
/' (%) = 4х (х2 — 5)
при — 4^5 <х<0их>/5 положительна, а при х < — /5и 0<х<
<рЛ5~отрицательна. А это и служит доказательством того, что выше мы подме-
тили, исходя из геометрических соображений.
Полученный результат, между прочим, доказывает (и притом вполне строго),
что функция у = х4 — 10х2 + 9 непериодична. Действительно, при х она
монотонно возрастает и, следовательно, значения ее не могут повторяться перио-
дически.
7) Нули данной функции находятся из уравнения
х4 — Юх2 + 9 = 0.
Оно имеет четыре корня:
хх = —3,
х2 — —1,
*з= !.
х4 = 3.
(Симметричность этих корней вполне понятна: ведь рассматриваемая функция
четна.)
Теперь мы можем отметить на плоскости координат еще четыре точки, при-
надлежащие графику нашей функции. Это точки оси х с абсциссами —3, —1.
1 и 3 (см. рис. 324, б).
8) Очевидно, что между любыми двумя соседними нулями функция f (х)
сохраняет свой знак постоянным*. Так, при —3 < х < —1 она принимает
либо только положительные, либо только отрицательные значения. Чтобы вы-
яснить, какие именно (по знаку) значения принимает наша функция при —3<
< х < —1, достаточно определить ее знак в какой-нибудь одной точке этого
интервала. В данном случае удобно выбрать х=—4^5—точку локального ми-
нимума. В ней, как было указано выше, функция принимает значение, равное
—16. Поэтому всюду в интервале —3 < х < —1 наша функция принимает от-
рицательные значения.
Аналогично можно установить (сделайте это самостоятельно!), что при —1 <
< х < 1 наша функция принимает положительные значения, а при 1 < х < 3 —
отрицательные значения. Что касается значения функции при |х| > 3, то все
они будут положительными.
9) При неограниченном возрастании х(х->оо) и неограниченном убы-
вании х (х —>— оо) значения функции у =х4 — 1 Ох2 + 9 неограниченно воз-
растают (у —> оо). Эгот факт является очевидным, поскольку с ростом х
величина х4 растет гораздо быстрее, чем Юх2. Возможно и такое объясне-
ние:
х4 _ Юх2 + 9 = (х2 — 1) (х2 — 9).
* Это «очевидное» утверждение может быть доказано и совсем строго. Одна-
ко доказательство выходит за пределы нашей программы.
209
Когда х —> оо или х->— оо, то каждый из сомножителей х2—1 и х2— 9
неограниченно растет. Поэтому неограниченно растет и их произведение.
10) Теперь нетрудно определить область изменения исследуемой функции.
Минимальное значение, равное — 16, функция принимает в двух точках: х =
— V5 и х = 5. Максимального значения она не имеет: при неограниченном
росте х (по абсолютной величине) неограниченно растут и значения функции.
Поэтому область изменения функции у = х4—10х2-f-9 определяется неравен-
ством у > — 16.
График функции у=х4—10х24-9 представлен на рисунке 324, в.
Упражнения
Исследовать данные функции (№1924— 1930) и построить их графики:
1924. у = х4 — 2х2 — 3. 1928. у = — х 4- sin х. J 2
1925. у=1(х^- 13х2 + 36). 1929. у = ¥$ cosx— 2х.
1926. у = х3 —9х. 1930*. у = sin2 х -j- 2 cos х -|- -j.
1927. у = х3 — Зх2 + 2.
Применение производной к графическому
решению уравнений
§ 240
Вопрос о применении производной к графическому решению уравнений мы
рассмотрим на примере уравнения sin х = х.
Для решения этого уравнения на одном и том же чертеже построим графики
функций у = sin х и у = х (рис. 325). Эти графики пересекаются в точке с абс-
циссой х = 0. Поэтому х = 0 есть корень данного уравнения.
Можем ли мы быть уверены, что других корней этого уравнения не су-
ществует? Может быть, вблизи точки х = 0 имеется еще какая-нибудь точка
пересечения графиков, которую мы просто не замечаем? Ведь нельзя же,
например, при выбранном на рисунке 325 масштабе «графически» убедиться,
что 0,01 не корень уравнения sin х = х. К тому же, если мы заглянем в три-
гонометрические таблицы, то обнаружим, что sin 0,01 « 0,01; sin 0,02 % 0,02;
sin 0,03 « 0,03, ... . Так что пока у нас нет оснований считать, что
х = 0 — единственный корень
у
Рис. 325.
уравнения sin х = х.
Чтобы разобраться в данном вопро-
се, заметим, что (sin x)z = cos х, а (х)'=1.
Для любого острого угла х cosx < 1.
„ Л л
Поэтому на участке 0 < х < — скорость
изменения функции у — х больше ско-
рости изменения функции у = sin х Но
в таком случае при 0 < х < —
функция
у = х будет всегда «опережать» функцию
у — sin х. Следовательно, никакое число
_ л
из интервала 0 < х < — не может слу-
жить корнем уравнения sin х = х. Тем
более не может быть корнем уравнения
210
и х> —, поскольку sinxc 1. Таким образом, данное уравнение не имеет по-
ложительных корней.
Если бы существовал отрицательный корень этого уравнения —а, то мы
имели бы sin (—а) = —а, откуда sin а = а. Но это означало бы, что уравнение
sin х =х имеет положительный корень х = а.
Получено противоречие. Значит, уравнение sin х = х не может иметь отри-
цательных корней. Остается признать, что число х 0 является единственным
корнем этого уравнения.
Упражнения
1931. Доказать, что
л
единственным корнем уравнения cos х — — — х
Л
является х = —.
£
Решить графически уравнения:
3
1932. sinx = — к — л. 1933. cosx = x — — л.
Исторические замечания
§ 241
Тот раздел математики, который изучает производные функций и их при
менения, называется дифференциальным исчислением. Это исчисление возникло
из решения задач на проведение касательных к кривым, на вычисление скоро-
сти движения, на отыскание наибольших и наименьших значений функций.
Отдельные результаты в дифференциальном исчислении были получены
уже давно. Однако до конца XVII века не удавалось выделить основных поня-
тий, лежащих в основе данного вопроса. Поэтому, хотя почва для создания нового
исчисления была подготовлена, исчисления, как такового, еще не было.
В систематической форме дифференциальное исчисление впервые было из-
ложено по-разному и независимо друг от друга Ньютоном и Лейбни-
цем. Ньютон изложил свои взгляды на новое исчисление в работе «Метод флюк-
сий и бесконечных рядов». Этот трактат был составлен около 1671 г., но вышел
в свет лишь в 1736 г. — уже после смерти автора. Первая печатная работа Лейб-
ница по дифференциальному исчислению относится к 1684 г.
Автором первого курса по дифференциальному исчислению был представи-
тель школы Лейбница французский математик Лопиталь (1661—1704).
Этот курс под названием «Анализ бесконечно малых» вышел в свет в 1696 г.
Современной трактовке дифференциального исчисления положил начало
Коши.
Термин «производная» был введен французским математиком Л а г р а н-
жем (1736—1813).
Задачи на повторение
1934. Найти значения производной от функции у = — х4 — 4х3 4- 16
в точ-
ках х = 0 и х = 2.
1935. Найти значения производной от функции у = (Зх + 5) (2ха — 1) в
точках х = —1 и х = 0.
1936. Найги значения второй производной от функции у = 5 sin х — 3 cos х
л л
в точках х= — и х == — —.
1937. Точка движется по закону s(0 = & ($ — путь в метрах, t—время
в секундах). В какой момент времени ее мгновенная скорость равна средней
скорости движения в интервале от \ = 13 сек, до t2 = 46 сек?
211
1938. Точка движется по закону s (Л = 15 — (5 — /) (3 — /) до тех пор,
пока ее скорость не обратится в нуль. Какой путь пройдет при этом точка?
1939. Одна точка движется по закону (I) = 13'4- f2, а другая — по за-
кону S2 (/) = 3/‘2 4- /, где s, и Sz — длины путей в метрах, t — время в секун-
дах. Найти скорости движения точек в тот момент, когда пути их равны.
1940. Найти уравнение касательной к кривой у = Зх^ 4" 2х 4- 5 в точке
пересечения этой кривой с осью ординат.
1941. Найти уравнение касательной к кривой у = вх3 —1 в точке пересече-
ния этой кривой с осью абсцисс.
1942. Какой угол образуется при пересечении прямой
соидой у = sin х?
1943. Какие углы образуются при пересечении прямой
5
X = —л
4
с сину-
с косинусои-
1
у=7
дой у = COS X?
1944. Найти координаты вершин парабол:
а) у = Зх2 — 6х + 7; 6) у = 2х2 + 8х — 3.
2 V2
\ 3 ~ х ./
1945. В
разложении
найти тот член, который содержит х4.
1946. Доказать тождество 1 -J- С1п 4- 4- ... 4- CJJ = 2п. (Указание.
В формуле бинома Ньютона положить а= b= 1.)
1947. Сколько рациональных членов содержит разложение (^2 4” У^З)100?
Исследовать функции и построить их графики (№ 1948—1955):
1 5
1948. у = —х4 —х2 4" 9.
IO Z
1949. у = 2х2 — х —1.
1950. у = х — х4.
1951. у = х 4" sin х.
1952. у = sin2 —.
’ 2
1953*. у = 0,5х2 4- cos х
1954. у = sin х (1 4- cos х)^_
1955*. у = 4 cos2 х — 4p/r3”sin х 4~ 5.
1956. Известно, что прочность балки с прямоугольным сечением прямо про-
порциональна ширине и квадрату длины сечения. Найти размеры сечения балки
наибольшей прочности, которую можно выпилить из круглого бревна, имеющего
диаметр в d сантиметров.
Найти производные следующих
1957. у== —1.
Л 2x4-5
1958. у = УЗ^х.
1959. y = (*-3P4-^4^J.
1960. у = sin2 2х cos
функций (№ 1957—1963):
1961. у = (х2 4- 1) cosx — (х2—l)sinx.
1962. у =-------------•
Щ х 4- cte х
1963. у = sin4 х 4- cos4 х.
1964. Доказать, что кривые у = cos2 х + sin 2х и у = —5х2 4~ Зх 4~ 1
касаются друг друга в точке х = 0. (Касание кривых в некоторой точке означает,
что они имеют общую касательную в этой точке.)
1965. В шар радиуса г вписан цилиндр наибольшего объема. Чему равен
этот объем?
1966*. Доказать, что биномиальные коэффициенты — числа целые.
КОМПЛЕКСНЫЕ ЧИСЛА
XI
Числовые поля
§ 242
Понятие числа прошло длинный путь исторического разви-
тия. В главе II (см. ч. I) мы рассказали о том, как от простейших,
натуральных чисел человек пришел к более сложным, действи-
тельным числам. Сейчас мы хотим вернуться к рассмотрению
этого вопроса. Но при этом нам придется несколько отступить
от того порядка, в котором исторически развивалось понятие
числа.
Одним из простейших числовых множеств является множе-
ство натуральных чисел
1, 2, 3, 4, 5, . . .
В нем всегда выполнимы два основных алгебраических дейст-
вия: сложение и умножение. Это означает, что, каковы бы ни бы-
ли натуральные числа тип, сумма их т 4- п, а также произве-
дение т • п являются непременно натуральными числами. При этом
соблюдаются следующие пять законов:
1) коммутативный закон сложения:
т + п = п 4- т;
2) ассоциативный закон сложения:
(т 4- п) 4- k = т 4- (п 4- fe);
3) коммутативный закон умножения:
т • п = п • т;
4) ассоциативный закон умножения:
(т • п) • k = т • (п • k\,
5) дистрибутивный закон умножения относительно сложения:
(т 4- п) • k = т • k 4- п • k.
Что касается вычитания и деления, то эти два действия в мно-
жестве натуральных чисел выполнимы не всегда. Так, ни одна
из разностей 3—5 и 2—2, а также ни одно из частных 3 : 5 и 7 : 4
нельзя выразить никаким натуральным числом.
213
Чтобы действие вычитания было выполнимым всегда, мно-
жество натуральных чисел нужно расширить путем присоеди-
нения к нему всех отрицательных целых чисел и нуля. В ре-
зультате такого расширения мы приходим к множеству всех,
целых чисел'.
. . . , —3, —2, —1, 0, 1, 2, 3, ... .
Числовое множество, в котором всегда выполнимы сложение
и умножение, подчиненные указанным выше пяти законам, а также
вычитание, называется кольцом. Таким образом, множество
всех целых чисел образует кольцо.
Расширив множество всех натуральных чисел до множества
всех целых чисел, мы добились тем самым, что действие вычита-
ния стало выполнимым всегда. Но деление по-прежнему оста-
лось, вообще говоря, невыполнимым. Чтобы устранить этот
пробел, нужно расширить и множество всех целых чисел.
Сделать это можно путем присоединения к нему всех обыкновен-
ных дробей, то есть чисел вида —, где т и п — произвольные
п
целые числа и п 0. В результате такого расширения мы по-
лучаем множество всех рациональных чисел. Как было показано
во второй главе, в этом числовом множестве всегда выполнимы
действия сложения, умножения, вычитания и деления (кроме
деления на нуль), причем первые два из них подчинены пяти основ-
ным законам сложения и умножения.
Множество чисел, в котором всегда выполнимы действия
сложения и умножения, подчиненные пяти основным законам,
а также действия вычитания и деления (кроме деления на нуль),
называется полем. Множество всех рациональных чисел
является простейшим числовым полем.
Уместно сразу же заметить, что множество всех иррациональ-
ных чисел поля не образует. Действительно, любое из четырех
действий (сложение, умножение, вычитание и деление) над ирра-
циональными числами может привести к числу рациональному.
Так, например,
]/2_+(-У2) = 0,
/2 -/2 =2
и т. д. А вот множество всех действительных чисел образует
поле. Как указывалось во второй главе, действия сложения,
умножения, вычитания и деления действительных чисел (кроме
деления на нуль) не выводят нас за пределы действительных
чисел, причем сложение и умножение подчинены пяти основным
законам.
Приведем еще один, более сложный, пример числового поля. Рассмот-
рим все действительные числа вида г -)- s К 2, где г и s — рациональные
числа. Пусть a-f- Ь)^2 и с -f- d 1^2 — произвольные два числа рассматри-
ваемого вида. Тогда
214
(a 4- b/Г) 4- (c + d/2) = 0 4-c) 4-04-<0/2?
(a4-b/2)-(c4- d/2)=(a —c)4-(& —d)/2,
(a4-Z>/2) -(c4- d/2) = ac4-ad/2 4- be/24- 2bd =
= (ac+ 2bd) 4- (ad 4- be) /2?
Предположим теперь, что число с 4-d )/2 не равно нулю. Тогда, очевидно, и
сопряженное ему число с — d 1^2 будет отлично от нуля (докажите это!). По-
этому можно написать:
a+bVT= (a4-&/2~)(c— dpT) (ас — 2М) 4- (6с — ad) /2~
с 4- d^2 (с 4- dV~2)(c — d/7) са — 2d3
ас — 2bd be — ad
= с3 — 2d3 + с3 —2d3 ' 2 ’
Как мы видим, каждое из четырех действий (сложение, вычитание,
умножение и деление) над числами вида г 4- s ]^2 приводит к числу того
же самого вида. Ясно также, что сложение и умножение всех этих чисел
подчинено каждому из пяти указанных выше законов. Поэтому совокуп-
ность всех чисел вида т 4- s У 2, где и г и s— рациональные числа, образует
числовое поле.
Упражнения
1967. Образует ли кольцо:
а) множество всех четных чисел;
б) множество всех нечетных чисел;
в) множество всех чисел, кратных некоторому числу р?
1968. Образует ли поле:
а) множество всех дробей со знаменателем 3;
б) множество всех дробей, знаменатели которых есть целые
степени числа 3?
1969. Докажите, что множество всех конечных десятичных дро-
бей образует кольцо, но не образует поле.
1970. Докажите, что любое числовое поле либо совпадает
с множеством всех рациональных чисел, либо содержит в себе это
множество.
1971. Докажите, что множество всех чисел вида а 4- b ]/~3, где
а и Ь — рациональные числа, является полем. Содержит ли это поле:
а) все рациональные числа;
б) все иррациональные числа;
в) все действительные числа?
Постановка задачи о расширении поля
действительных чисел. Комплексные числа
§ 243
Потребности математики уже давно указывали на серьезную
необходимость расширения поля действительных чисел. Как мы
знаем, в нем, помимо сложения, вычитания, умножения и де-
215
ления, выполнимо еще действие возведения в степень, представ-
ляющее собой не что иное, как многократное умножение. А вот
извлечение корней, то есть действие, обратное возведению в сте-
пень, выполнимо не всегда. Мы не знаем, например, какой смысл
можно придать выражениям у'—1, ]/ —16. Поэтому в поле
действительных чисел не разрешимы даже такие на первый
взгляд простые уравнения, как х2 + 1 = 0, х4 4- 16 = 0 и т. д.
Таким образом, мы приходим к необходимости расширить пом
действительных чисел путем присоединения к нему новых чисел так,
чтобы расширенное множество образовывало числовое поле, в кото-
ром всегда было бы выполнимо действие извлечения корней.
Окончательно эта задача была решена лишь вXIX столетии.
Посмотрим, какие же элементы должно содержать новое,
расширенное поле.
Прежде всего оно должно содержать все действительные числа.
Далее, в нем должно быть разрешимо уравнение х2 = —1, по-
скольку действие, обратное возведению в степень, в этом поле
выполнимо. Число, квадрат которого равен —1, принято обо-
значать буквой i и называть мнимой единицей. Итак, по определе-
нию числа i
i2 = —1.
Мы требуем, чтобы новое множество чисел было полем.
Поэтому наряду с действительным числом b и мнимой единицей i
ему должно принадлежать и их произведение Ы. Точно так же
вместе с действительным числом а и произведением Ы новому
числовому полю должна принадлежать и их сумма а + bi.
Таким образом, новое множество чисел должно содержать все
числа вида
а + Ы,
где а и b — произвольные действительные числа, a i — мнимая
единица. Эти числа мы назовем комплексными числами.
Число а принято называть действительной частью, а вы-
ражение Ы — мнимой частью комплексного числа а + bi. Число b
называется коэффициентом при мнимой части. Например, для
комплексного числа 2 + Зе действительной частью является
число 2, а мнимой — выражение Зг, коэффициент при мнимой
части равен 3. Для числа 0 — Зе действительной частью является
число 0, а мнимой — выражение — Зе; коэффициент при мнимой
части равен —3. Для числа 5 + Ое действительной частью яв-
ляется число 5, а мнимой — выражение Ое; коэффициент при мни-
мой части равен нулю.
Два комплексных числа считаются равными, если равны их
действительные части и коэффициенты при мнимых частях.
Другими словами,
а + bi = с + di
тогда и только тогда, когда а = с, b = d.
216
Как мы знаем, для неравных действительных чисел опреде-
лены соотношения «больше» и «меньше». Так, 5 > 4, 0 < 7 и т. д.
Для неравных комплексных чисел такие соотношения определить
невозможно. Нельзя, например, сказать, какое из двух чисел
больше: 2 4- 3i или 5 — 71, 0 + 2i или 0 + 4i и т. д.
У пражнения
1972. Что значит, что два комплексных числа а 4- Ы и с 4- di-.
а) равны друг другу; б) не равны друг другу?
1973. Найти действительные числа х и у из уравнений:
а) (х — у) 4- (Зх 4- у) i = 3 — 3i;
б) (х — 5у) 4- (2х — у) i = 6 4- 3i.
Сложение комплексных чисел.
Противоположные числа
§244
Определение. Суммой двух комплексных чисел а + Ы и
с 4* di называется комплексное число (а 4* с) 4- (Ь 4- d)i:
(а 4- Ы) 4- (с 4- di) = (а 4- с) 4- (Ь 4- d)i.
Другими словами, при сложении комплексных чисел их
действительные части и коэффициенты при мнимых частях
складываются.
Примеры.
1) (1 4- 0 4- (2 4- 30 = (1 4- 2) 4- (1 4- 3) i = 3 4- 4г,
2) (5 4- 60 4- (7 — 60 = (5 4- 7) 4- (6 — 6) i = 12 4- Oi;
3) (4 4- 90 4- ( -4 4- 0 = (4 - 4) 4- (9 4- 1) i = 0 4- 10i;
4) (3 - 70 4- (-3 4- 70 = (3 - 3) 4- (—7 4- 7) i = 0 4- 0i.
В области действительных чисел имеется число «нуль», при-
бавление которого к любому другому действительному числу не
меняет этого числа:
а 4- 0 = а.
В области комплексных чисел аналогичную роль играет
число 0 4* 0/. Действительно, каково бы ни было комплексное
число а 4- Ы,
(а 4- Ы) 4- (0 4- Oi) = (а 4- 0) 4- (Ь 4- 0) i = а 4- Ы.
Как мы знаем, два действительных числа а и —а, сумма
которых равна нулю, называются противоположными. По ана-
логии с этим комплексные числа а 4- Ы и —а — Ы также назы-
ваются противоположными.
Упражнения
1974. (У стн о.) Назвать комплексные числа, противополож-
ные данным:
а) 3 4- i; 6) 1 — 5i; в) —2 4- 0i; г) 0 4- 4i; д) 0 4- 0i; е) 7 4- i.
217
1975. Найти действительные числа х и у из уравнений:
а) (5х + ЗуО + (2у — xt) = 3 — i\
б) (2х — 50 + (7у 4- 2xi) = —12 + Зуг,
в) (х + ЗуО + /А у + 2x0 = 4 4- 8i.
Вычитание комплексных чисел § 245
Определение. Разностью двух комплексных чисел zt =
= а 4* bi и z.> = с 4- di называется такое комплексное число
г3 = х 4- yi, которое в сумме с г2 дает гг.
Другими словами, для комплексных чисел, так же как и для
действительных, равенство
2 з — Zi — z2
по определению означает то же самое, что и равенство
г3 4- z2 = zr.
Само по себе введенное нами определение не гарантирует, что
из каждого комплексного числа можно вычесть любое другое ком-
плексное число. Возможность такого вычитания и его однозначность
устанавливаются следующей теоремой.
Теорема. Для любых комплексных чисел Zi = а 4- Ы и
г2 = с 4- di разность z3 = zt — z2 определена и притом
однозначно.
Фактически нужно доказать, что существует и притом един-
ственное комплексное число г3 = х 4- yi, которое в сумме с za
дает zx:
(с 4- di) 4- (х 4- у0 = (а 4- bi). (1)
По определению суммы комплексных чисел:
(с 4- di) + (х 4- yi) = (с+ x) + (d +у) I.
Поэтому уравнение (1) можно переписать в виде:
(с 4- х) 4- (d 4- у) i = а 4- bi.
Два комплексных числа равны тогда и только тогда, когда
равны их действительные части и коэффициенты при мнимых
частях. Поэтому
(с 4- х = а,
[d + у = Ь.
Эта система уравнений всегда имеет и притом единственное решение:
х = а — с, у = Ь —d.
Поэтому существует и притом единственная пара действитель-
ных чисел (х, у), удовлетворяющая уравнению (1). Тем самым
теорема доказана.
218
По существу мы доказали, что
(а + bi) — (с + di) = (а — с) + (Ь — d)i.
Чтобы из одного комплексного числа вычесть другое,
достаточно это вычитание произвести отдельно для
действительных частей этих чисел и коэффициентов
при мнимых частях.
Примеры.
1) (5 + 60 — (3 + 7) = (5 — 3) + (6 — 7)4 = 2 - i-
2) (2 + 0 - (9 + 0 = (2 - 9) + (1 - 1) i = -7 + 00
3) (3 + 40 — (3 — 0 = (3 — 3) + (4 + 1) i = 0 4- 5i;
4) (7-0-(7-0 = (7-7) + (- 1 + l)i = 0 + 00
Упражнения
1976. Что выражает каждая из данных формул — определение
или теорему:
а) (а + Ы) + (с + di) = (а + с)+ (b + d) i\
б) (а + Ы) — (с + di) = (а —с) + (b — d) i?
1977. Найти действительные числа х и у из уравнений:
а) (0 + 3%0 — (10* + 2у0 = —5у + 30
б) (—Зу + 1 хО — (—Зх + 5yt) = — 2 + 120
в) х — 2yij — у + 6x1 j = 0 + 210
Умножение комплексных чисел § 246
Естественно потребовать, чтобы умножение комплексных
чисел а + Ы и с + di выполнялось так же, как и умножение дву-
членов с действительными коэффициентами, а именно:
(а 4- Ы) (с 4- di) = ас 4* adi 4- bci+bdi2= ас 4- (ad-\-bc) i 4- bdi2.
Но по определению числа i
i2 = —1.
Поэтому bdi2 = —bd и, следовательно,
(а 4- bi) (с 4* di) = (ас — bd) + (ad 4- be) i. (1)
Эта формула и кладется в основу определения произведения двух
комплексных чисел.
Определение. Произведением двух комплексных чисел
а 4- bi ис + di называется комплексное число (ас —bd) 4- (ad+bc)i.
Для того чтобы уметь умножать комплексные числа друг на
друга, формулу (1) помнить не обязательно. Нужно лишь знать,
что она дает такой же результат, как и простое умножение двучле-
нов а 4- bi и с 4- di с последующей заменой i2 на —1.
219
Примеры.
1) (2 4- 3t) (6 — 5i) = 12 — 10i + 18t — 15i2 = (12 + 15) +
4- (18 — 10) i = 27 4- 8t;
2) (4 + 0 (4 — 0 = 16 — 4t + 4i — t2 = (16 4- 1) 4- (—4 4-
+ 4) i = 17 4- Oi;
3) (1 4- i)2 = (1 + 0 (1 4- 0 = 1+ i + i + i2 = (1 - 1) 4-
+ 2t = 0 4- 21-
Как мы знаем, в области действительных чисел нуль обладает
тем свойством, что произведение его с любым другим действитель-
ным числом равно нулю:
а • 0 = 0.
Учащиеся без особого труда могут убедиться в том, что в множе-
стве комплексных чисел аналогичным свойством обладает число
0 4- 0t. Для любого комплексного числа а 4- bi
(а 4- Ы) (0 + 00 = 0 4- 0/.
Упражнения
Вычислить (№ 1978—1987):
1978. (5 4- 0 ( —2 4- 30-
1979. (3 4- 40 (6 — 50.
1980. (7 — 20 (3,5 — 0-
1981. (0,5 4- 0,20 (2 4- 30-
1982. (7 4- 402.
1988. Найти комплексное чис
(2 — 30 •
1983. (5 4- 0 (15 — 30-
1984. (—6 4- 2/) (11 4- 50-
1985. (0,5 4- 0 (I +_20-
1986. (/_2 —0 (/ 3-4-20-
1987. (/ 3 4- 50 (5 — У 2,1).
г из уравнения
= —1 — 5/.
Деление комплексных чисел
§ 247
В области комплексных чисел так же, как и в области действи-
тельных чисел, соотношение
г3 = (г2 Ф 0 4- 00
*2
понимается в том смысле, что z3 • z2 = zx.
Определение. Частным от деления комплексного числа
Zj на комплексное число z2 #= 0 4- Oi называется такое комплексное
число г3, которое при умножении на z2 дает
В области действительных чисел частное — определено для
ь
всех значений а и Ь, если только 6 =/= 0. Аналогично обстоит дело
и в области комплексных чисел.
Теорема. Частное -+ —
r c + di
определено и притом одно-
значно для всех комплексных чисел а + Ы и с 4- di, если
только с -{-di 1=0 4-
220
Доказательство. Нам нужно показать, чтоесли c-\-di^=
=£ 0 + Oi, то существует и притом единственная пара действитель-
ных чисел (х, у), удовлетворяющая уравнению
(х 4- yi) (с + di) = а 4- Ы. (1)
По правилу умножения комплексных чисел
(х + yi) (с 4- di) = (хс — yd) 4- (xd 4- yc)i.
Поэтому уравнение (1) можно переписать в виде:
(хс — yd) 4- (xd 4- yc)i = а 4- bi.
Два комплексных числа равны тогда и только тогда, когда рав-
ны их действительные части и коэффициенты при мнимых частях.
Поэтому
(сх — dy = а,
\dx 4- су = Ь. (2)
Вычислим главный определитель этой системы:
с
d
Д =
= с2 4- d2.
Поскольку с 4- di Ф 0 4- О», хотя бы одно из чисел end отлично
от нуля. Но тогда Д = с2 4~ d2 > 0. Следовательно, по правилу
Крамера (см. § 30, ч. I) система уравнений (2) имеет и притом
единственное решение:
х _ Дх _ ______с[_ ос 4-м
Д с2 + d2 с2 d2 *
|с а|
__Ду___ \d ____Ьс — ad
Д с2 + d2 с2 + d2
Итак,
а 4- Ы ас + bd .be — ad .
—— = ——--------1--------1,
c + di c2 + d2 c2 4- d2
Запоминать эту формулу не нужно; достаточно знать, как она
получается.
g__7/
Пример. Найти отношение-----------.
r r 2 — 3i
Пусть
Тогда
(х 4- yi) (2 — 30 = 9 — 7t,
2х 4- 2yt — 3xt — 3yi2 = 9 — 7i,
(2x 4- 3y) 4- (2y — 3x) i = 9 — 7i.
Отсюда
( 2x 4- 3y = 9,
(—3x -j- 2y = —7.
221
Решая эту систему, находим х = 3, у = 1. Поэтому
9 — 71
2 — 34
3 4"
Упражнения
1989. Что выражает каждая из данных формул — определение
или теорему:
а) (а 4- bi) (с + di) = (ас — bd) + (ad + be) i\
g. a + bi ac + bd jbe — ad
c + di c2 + d2 c2 d2
Вычислить (№ 1990—1992):
1990. 2±4. 1991.£±1. 1992.-^"01 .
1 + i 2 — i —4 +3Z
Доказать равенства:
1993. -—- = 134-4U 1994. L±l= 13 + 4t~.
3+ 4t —254-25t’ 3 —t 17 — 9i
Поле комплексных чисел
§ 248
Комплексным числам мы посвятили уже несколько параграфов. Но наши
рассуждения часто были нестрогими. Мы допустили (хотя и сознательно!) ряд
логических погрешностей, которые теперь нужно устранить.
Чтобы разобраться в этом, поставим перед собой такой вопрос: что значит
ввести в рассмотрение новые числа? Конечно, для новых чисел мы должны выбрать
какие-то обозначения. Например, комплексные числа мы обозначаем а 4е Ы.
Но главное не в этом. Главное в том, чтобы определить, как сравниваются эти
числа друг с другом, как производятся действия над ними (сложение, вычитание,
умножение, деление). Пока эти действия не определены, употреблять такие выра-
жения, как «сумма новых чисел» и «произведение новых чисел», мы не имеем
права.
А как мы вводили комплексные числа? Прежде всего (см. § 243) мы потре-
бовали, чтобы новое множество чисел содержало число, квадрат которого (то есть
произведение с самим собой) равен — 1. Среди уже известных нам действитель-
ных чисел такого числа не существует. Если оно и существует, то только среди
новых чисел. Но как же в таком случае мы могли говорить о произведении? Ведь
умножение новых чисел еще не было определено! Таким образом, уже определе-
ние мнимой единицы было математически некорректным. Об умножении новых
чисел мы говорили фактически и тогда, когда требовали, чтобы новое множество
чисел вместе с действительным числом b и мнимой единицей i содержало их про-
изведение bi. Далее, мы говорили о сумме а+ Ы, хотя сложение новых чисел
так же, как и умножение*, еще не было определено.
Вот почему наше изложение теории комплексных чисел нельзя признать ма-
тематически строгим. Но как же в таком случае ввести в рассмотрение комплекс-
ные числа? Ответ на этот вопрос дается ниже.
Комплексными числами называются числа, записываемые в виде а 4* bi, где а и
b — произвольные действительные числа, a i — некоторый символ.
Вводя обозначение а 4" bi, мы вовсе не связываем его с какой бы то ни было
суммой. Знак «4"» в выражении а 4" bi п о к а не является признаком сумми-
рования. Он входит просто как составная часть одного, не разделяемого на части
выражения а + Ы. Отметим также, что мы не требуем заранее, чтобы вы-
полнялось соотношение i2 = —1. Ведь пока что i — это просто символ, а не
число.
222
По определению а + bi = с + di тогда и только тогда, когда
а = с, b = d.
Сумма двух комплексных чисел определяется по формуле
(а + Ы) + (с + di) = (а + с) + (b+ d)i, (1)
а произведение — по формуле
(а + bi) (с + di) = (ас — bd) + (ad + bc)i. (2)
Разность двух комплексных чисел а+ Ы и с+ di определяется как такое
комплексное число, которое в сумме с с + di дает а + bi. Как было доказано
в § 245, это число существует и равно
то есть (а — с) + (Ь — d} i.
(о+ bi)-(c+ di)<= (а-с)+ (b - d) I. (3)
Частным от деления комплексного числа а + bi на комплексное число с + di
называется такое комплексное число, которое в результате умножения на с + di
дает а+ bi. В § 247 было доказано, что если с+ di 0+ 0g то частное от
деления а + bi на с + di существует и равно
а + Ы ac-\-bd . be — ad .
с + di с2 -|- d2 с2 -|- d2 *
Из приведенных выше четырех формул естественными на первый взгляд
кажутся лишь формулы (1) и (3). Другие же две формулы трудно понять с первого
взгляда. Вот почему мы начали с такого изложения теории комплексных чисел,
которое хотя и является нестрогим, но зато дает возможность понять, как можно
прийти к формулам (2) и (4).
Действия сложения, умножения, вычитания и деления над
комплексными числами приводят опять же к комплексным чис-
лам. Посмотрим, выполняются ли при этом те законы сложе-
ния и умножения, которые были присущи действительным
числам:
+ *2 = ?2 + zb
(21 4- Z2) + Z3 = 2i + (z2 + 23),
21^2 =
(Z1Z2) 23 = 21 (z2Z3),
(21 4- Z2) Z3 = 212 3 + 2,2 3.
Если мы покажем, что эти законы выполняются, то тем самым
будет доказано, что множество всех комплексных чисел обра-
зует поле.
Начнем с первого закона. Пусть 2Х = а + bi, г2 = с + di.
Тогда
zi + z2 = (а + &0 + (с + di) = (а + с) + (b + d) i,
z2 + zi = (с + di) + (a + bi) = (c + a) + (d + b) i.
Для действительных чисел коммутативный закон сложения,
как мы знаем, выполняется. Следовательно, а + с = с + а;
b + d = d + b. Поэтому комплексные числа zx + z2 и г2 + гх
имеют одинаковые действительные части и коэффициенты при мни-
мых частях. Но в таком случае они равны: Zi + г2 = z2 + гх.
Теперь обратимся к пятому закону. Пусть zx = а + bi, г2 =
= с + di, г3 = е + fi. Тогда гх + г2 = (а + с) + (b + d) i.
223
Следовательно,
(zx + z2) г3 = [(a 4- с) + (b + d)i] (e + fi) =
= [(a + c) e — (b + d) f] + [(a + c) f + (b + d) e] i =
= [(ae — bf) + (ce — df)] + [(af + be) 4- (cf 4- de)] i.
С другой стороны,
zx23 = (a 4- bi) (e 4- fi) = (ae — bf) + (af 4- be) i,
z2z3 = (c 4- di) (e 4- fi) = (ce — df) 4- (cf 4- de) i.
Поэтому
zxz3 4- z2z3 = [(ae — bf) 4- (ce — df)] 4- [(af 4- be) 4- (cf 4- de)] i.
Сравнивая числа (zx 4- z2) z3 и zxz3 4- z2z3, мы замечаем, что они
имеют соответственно равные действительные части и коэффи-
циенты при мнимых частях. Но в таком случае этим комплексные
числа равны между собой:
(zi 4- г2) z3 = 2iZ3 4- г2г3.
Мы доказали, что для комплексных чисел выполняются комму-
тативный закон сложения и дистрибутивный закон умножения
относительно сложения. Предлагаем учащимся самостоятельно
убедиться в том, что для комплексных чисел выполняются и все
остальные законы сложения и умножения.
Итак, множество всех комплексных чисел образует
поле.
Упражнение
1995. Образует ли поле совокупность всех чисел вида:
а) 0 4- bi, где b — действительное число;
б) а + at, где а — действительное число;
в) а + bi, где а и b — произвольные рациональные числа?
Геометрическое изображение комплексных
чисел
§ 249
Как известно (см. ч. I, § 44), действительные числа можно
изображать точками числовой прямой. При этом каждому действи-
тельному числу соответствует единственная точка числовой пря-
мой. Например, действительному числу соответствует точка А
(рис. 326), находящаяся справа от начальной точки 0 на рас-
стоянии в
8_______________С Д
г О V7 5
2
Рис. 326.
_5
2
единицы длины; дей-
ствительному числу —2 соответству-
ет точка В, находящаяся слева от
точки О на расстоянии в 2 единицы
длины; действительному числу ]/~2
224
соответствует точка С, находящаяся
справа от О на расстоянии в У 2 еди-
ниц длины. Обратно, каждой точке чи-
словой прямой соответствует вполне
определенное действительное число.
Например, точкам А и В (рис. 326) со-
5
ответствуют рациональные числа — и
—2, а точке С — иррациональное число
У%. Таким образом, множество всех
действительных чисел находится
во взаимно однозначном соответствии с множеством
всех точек числовой прямой.
Подобно тому как действительные числа можно изображать
точками числовой прямой, комплексные числа можно геометри-
чески представлять точками плоскости.
Каждому комплексному числу а 4- Ы поставим в соответствие
точку плоскости с координатами (а, Ь). Например, числу 2 + 31
поставим в соответствие (рис. 327) точку А с координатами
(2, 3), числу —1 + i — точку В с координатами (—1, 1), числу
4 + Qi — точку С с координатами (4,0), числу 0 — 2i — точку D
с координатами (0, —2) и т. д.
Каждая точка плоскости имеет определенные координаты.
Поэтому при выбранном соответствии каждой точке плоскости
будет отвечать некоторое комплексное число. Например, точке
А с координатами (2, 3) отвечает число 2 + 3i (рис. 327), точке В
с координатами ( —1, 1) — число ( —1 + I), точке С с координа-
тами (4, 0) — число 4 + Qi, а точке D с координатами (0, —2) —
число 0 — 2i. Но не может ли случиться так, что одной и той же
точке плоскости, например точке (а, 0), будут соответствовать
различные комплексные числа, например, + bti и а2 + b2 i?
Если бы было так, то мы имели бы:
а = аь 0 = b^,
оса2, 0 = Ь2.
Отсюда ах = а2, = Ь2. Но в таком случае числа аг + bti и
а2 + b2i были бы равны между собой.
Итак, каждому комплексному числу а + Ы соответствует одна,
вполне определенная точка плоскости, а именно точка с коор-
динатами (а, Ь). Наоборот, каждой точке плоскости (а, 0)
соответствует одно, вполне определенное комплексное число, а
именно число а + 0t. Таким образом, множество всех комп-
лексных чисел находится во взаимно однозначном соот-
ветствии с множеством всех точек плоскости.
С каждой точкой плоскости А можно связать вектор ОА,
выходящий из начала координат и оканчивающийся в точке А
(рис. 328). Поэтому комплексные числа допускают и другую
8 Заказ 1159
225
у| геометрическую интерпретацию. Каждое ком-
а ___ь плексное число а + Ы можно геометрически
интерпретировать как вектор ОА с координа-
} \ тами (а, Ь). Координаты вектора ОА при этом
‘—£—-J------— будут такими же, как и координаты точки А,
° ° х а именно (а, Ь). Очевидно, что такое соответ-
ствие между всеми комплексными числами
и всеми векторами плоскости, выходящими из
начала координат, является также взаимно
однозначным.
Рис. 328. Используя векторную интерпретацию комп-
лексных чисел, легко истолковать то опреде-
ление, которое мы приняли для суммы двух комплексных чисел:
(а + Ы) + (с + di) = (а + с) + (b + d) i.
Как известно, при сложении векторов их соответственные
координаты складываются. Поэтому если вектор ОА (рис. 329)
имеет координаты (а, Ь), а вектор ОВ — координаты (с, d), то
их сумма — вектор ОС — будет иметь координаты (а + с, b + d).
Этот вектор как раз и соответствует комплексному числу
(а + с) + (6 + d) i, которое является суммой комплексных чисел
а + Ы и с + di.
К сожалению, определение произведения двух комплексных
чисел
(а + Ы) (с + di) = (ас — bd) + (ad + be) I
не допускает такой простои интерпретации.
Упражнения
1996. Данные комплексные
кости:
а) 1 + г, в) —2 4- 3i;
б) 1 — i; г) —3 — 21;
числа изобразить точками плос-
д) 5 4- 01; ж) 0 4- 51;
е) —6 4- Of; з) 0 — 41.
1997. Какие комплексные числа
изображают на рисунке 330 точки
А, В, С, D и О?
1998. Дать геометрическую ин-
терпретацию формулам:
а) (1 4- 20 4- (1 -20 = 24-0/;
б) (3 — 404-(—14- 20=2 — 2/.
1999. Пусть точка М служит
изображением на плоскости комп-
лексного числа а 4- bi. Построить
на той же плоскости точки, ко-
торые изображали бы комплекс-
ные числа:
226
Рассмотрим отдельно все точки плоскости, лежащие на оси
абсцисс. Они имеют координаты (а, 0) и, следовательно, соот-
ветствуют комплексным числам вида а + Oi. Пусть аг + Oi и
а2 + Oi — два таких числа. Легко убедиться в справедливости
следующих соотношений:
(ах 4- Oi) 4- (^2 4- Oi) = 4" 4" Oi;
(th 4- Oi) — (а2 4- Oi) = (at — a2) 4- Oi;
(fli 4~ Oi) (o2 4- Oi) = 4- Oi;
21±^=^l + 0.-
02 4-Of a2
Эти соотношения показывают, что все комплексные числа вида
а 4- Oi, то есть числа с нулевыми коэффициентами при мнимых
частях, складываются, вычитаются, умножаются и делятся друг
на друга как соответствующие им действительные числа. Геомет-
рическое изображение этих чисел также совпадает с геометри-
ческим изображением соответствующих действительных чисел:
как те, так и другие представляются точками оси абсцисс. Это
позволяет нам не делать различия между комплексным числом
а 4- Oi и действительным числом а. Поэтому в дальнейшем мы
всюду вместо а 4* Oi будем писать просто а; в частности, 0 4-
4- Oi — 0. По этой причине ось абсцисс, на которой расположены
точки, соответствующие действительным числам, или комплекс-
ным числам вида а 4- Oi, называется действительной осью.
Теперь нам ясно, каким образом действительные числа входят
в совокупность всех комплексных чисел.
Точки оси ординат имеют координаты (0, 6) и потому соответ-
ствуют числам вида 0 4- Ы, то есть комплексным числам,
8*
227
действительные части которых равны нулю. Такие числа харак-
теризуются тем, что квадраты их отрицательны (если только Ь^О).
Действительно,
(О 4- bi)' « (0 + Ы) (0 4- Ы) = 0 + 0 • Ы + b • 01 — Ь3 =
= — + 0Z = —Ь\
В частности,
(0 + 09 = -1.
Когда комплексные числа еще не были введены в математику,
трудно было представить себе, что квадраты чисел могут быть
отрицательными. Поэтому комплексные числа вида 0 4- Ы полу-
чили название чисто мнимых чисел. В дальнейшем эти числа мы
будем обозначать не 0 4- bi, а просто Ы. Ось ординат, на которой
располагаются все чисто мнимые числа, называется мни-
мой осью.
Условимся в дальнейшем комплексное число 0 4* » обозначать просто I.
После такого соглашения мы можем говорить не только о каком-то символе I,
но и о комплексном числе i, подразумевая под ним число 0 4- /•
Как было показано выше, (0 4- О2 = —1 Поэтому
«3= —1.
Число I получило название мнимой единицы. Рассмотрим произведение про-
извольного действительного числа Ь на мнимую единицу I:
ь. i = (ь 4- оо (0 4- 0 = ь - о 4- ы 4- о - о/ 4- о - Р = о 4- ы.
Итак,
Ь • i = 0 4- Ы.
Этим и оправдывается принятое выше соглашение обозначать числа вида 0 4- W
просто Ы.
В § 248 мы говорили, что по определению а 4° bi есть просто особое обозна-
чение, а не выражение суммы чисел а и Ы. Ведь тогда мы еще не знали, что
представляют собой комплексные числа а и Ы\ тем более мы не могли знать,
как складываются эти числа. Теперь же мы знаем, что представляют собой ком-
плексные числа а и Ы и что представляет собой сумма двух комплексных чисел.
Поэтому теперь законно поставить вопрос: а нельзя ли выражение а 4* Ы
рассматривать как сумму двух чисел а и Ы? Для решения этого вопроса заметим,
что
а <= а 4- 0i,
ы = о 4- ы.
Поэтому сумма чисел а и Ы равна:
(а 4- 00 4- (0 4- ьо = (а 4" 0) 4* (0 4* Ь) I — а 4* Ы.
Это дает положительный ответ на поставленный выше вопрос. Комплексное число
а 4- Ы можно рассматривать как сумму двух комплексных чисел: действительного
числа а и чисто мнимого числа Ы.
Упражнения
2001. Что означает каждое из выражений:
а) комплексное число а 4- bi равно нулю;
б) комплексное число а 4- Ы не равно нулю?
2002. Найти действительные числа х и у из уравнений:
а) (х 4- у) 4- (х — у) i = 2 4- 41;
б) (х 4- у) 4- (х — у) i == 4/;
228
В) (X + у) + (х — у) i = 2;
г) (у + 2х) + (2у 4- 4х) i — 0;
д) (х 4- 1,5у) 4- (2х 4- Зу) i = 13/.
2003. Найти чисто мнимые числа и и о из уравнений:
а) и 4- iv = —3 4~ 2/; б) 5u — 6/о = —24 — 5/.
2004. Что можно сказать о двух комплексных числах, если
их сумма и разность одновременно представляют собой:
а) действительные числа; б) чисто мнимые числа?
2005. Вычислить:
а) [1(2 —О]2; б) [2/(3 —4/)]а.
2006. Доказать, что квадрат комплексного числа a 4- bi пред-
ставляет собой действительное число тогда и только тогда, когда
либо а = 0, либо b = 0.
Сопряженные числа. Практический способ
деления комплексных чисел § 251
Комплексное число a — Ы называется сопряженным к комп-
лексному числу a 4“ bi. Например, число 2 — 3/ является сопря-
женным к числу 2 4- 3/, число 5 + 4/ — сопряженным к числу
.5 — 4/, число —6/ (=0 — 6/) — сопряженным к числу 6/ (= 0 +
+ 6/) и т. д.
Пусть a — произвольное действительное число. Тогда
a = a + QI = a — Qi.
Поэтому любое действительное число равно своему сопряженному.
Верно и обратное утверждение: если комплексное число a + bi
равно своему сопряженному, то есть
a + Ы = a — Ы, (1)
то это число действительное. В самом деле, из (1) вытекает, что
Ь = —Ь или b = 0. Следовательно, a + bi = a + 0 • I = а, что
и требовалось доказать.
Таким образом, из всех комплексных чисел действи-
тельные числа (и только они) равны своим сопряжен-
ным числам.
Число а — Ы является сопряженным к числу а + Ы. Но чис-
ло а + Ы будет, очевидно, сопряженным к числу а — Ы. Таким
образом, числа а + bi и а — Ы являются сопряженными друг
другу. Поэтому они называются взаимно сопряженными комплекс-
ными числами. Очевидно, что любые взаимно сопряженные ком-
плексные числа а + bi и а — Ы изображаются на плоскости
точками, симметричными друг другу относительно действитель-
ной оси (см. рис. 331).
Произведение двух взаимно сопряженных комплекс-
ных чисел есть число действительное.
229
В самом деле,
•a*bl (а + bi) {а — Ы) =
। = а2 — (&i)2 = а2 — b2i2.
! Но i2 = —1. Поэтому
। (а + Ы) (а — Ы) = а2 + Ь*.
io л Доказанное свойство взаимно со-
j пряженных чисел позволяет до-
। вольно просто производить деление
! .. комплексных чисел. Пусть нужно най-
1 ти частное
Рис. 331.
а-±^ (c + di^O).
C-f-dl
Умножим числитель и знаменатель этой дроби на число с — di,
сопряженное знаменателю. В результате мы получим дробь, зна-
менатель которой будет действительным числом:
а+Ы _ (а + Ы)(с — di) _ (ас+М)+(6с—ad)4
с + di (с + di) (с — di) с3 -f- (Р
Теперь, используя дистрибутивный закон умножения относитель-
но сложения, получим:
e _J_ [ (ас 4- bd) + (be — ad) i] = 4-
c + di c2 + <p' ’ v c24-da c=‘4-da
В § 247 эта формула была получена иным путем.
Примеры.
.. 7 — < _ (7 — <) (3 —0 21 — 74 — 34 — 1 _ 20— 101 _ о _
' 3 + i ~ (3 4-0(3—0= 9 4-1 “ 10 1'
2 ) 1 +*' = (1 +') (!+') = 1 +21-1 = 2i_ = .
1 - 1 (1 -1) (1 + 0 1 + 1 2
Упражнения
2007. Назвать комплексные числа, сопряженные данным.
Изобразить данные и сопряженные к ним числа точками
плоскости:
а) 1 4- i\ б) 2 — 3i; в) 5; г) 4ц д) 0; е) 2i — 1.
Вычислить:
2008. Уз — / /з’+‘* 2012. 2 — &’ 4 + «’ 6 — 74 4 — i
2009. 42 + 24
3 + 5i ' 2013. 2 + < + —
2010. 7 — 24 _ 3 — 5/ < — 1 •
2 4- 71
2011. 1 2014. а — Ы .b — al — 1
Ь + а4 а + bl
230
Степени мнимой единицы
S 252
По определению первой степенью числа i является само число i,
а второй степенью — число —1:
i1 = t« = _1.
Более высокие степени числа I находятся следующим образом:
Is = • i = —1 • i = —i;
i* = (-з . i = _t-2 = i;
I5 = (!./ = i-
ie = i5 • i — i2 = —1
и т. д. Очевидно, что при любом натуральном п
iin = 1; i4n+‘ = t;
(in+2 __ _ J. (4n+3 _ ____J.
Например,
(125 (26 _ (124 + 1 (24+2 _ f (2 _ f | ],
(103 | (88 | (63 _ (100 | (1*0+2 (60 +3 | J ( _
Упражнения
Вычислить (Mb 2015—2020):
2015. i® + t‘e + i23 4-188 + i4e + t56.
2016. i8 4- 113 4- t23 4- i33 4-<43 + i53.
2017. i + i2 4- ia 4- i4 4- . . . + in (n > 4).
2018. i • t2 • i3 • i*. . . i*00.
2019. —
I3
2020. 1 — 1 4- -!-------L
/11 /41 /75 /1023 •
2021. При каком действительном значении а число 31я — 2ai2 4~
+ (1 — а) i + 5 будет:
а) действительным; б) чисто мнимым; в) равным нулю?
Извлечение корней квадратных
из отрицательных чисел. Решение квадратных
уравнений с отрицательными дискриминантами § 253
Как мы знаем,
I2 = -1.
Вместе с тем
(—1)8 = (_1 . i)« = (—J)». = — 1.
Таким образом, существуют по крайней мере два значения корня
квадратного из —1, а именно I и —i. Но, может быть, есть еще
какие-нибудь комплексные числа, квадраты которых равны —1?
231
Чтобы выяснить этот вопрос, предположим, что квадрат комп-
лексного числа а 4- Ы равен —1. Тогда
(а 4- Ы)2 -= —1,
а2 4- 2аЫ — Ь2 = — 1.
Два комплексных числа равны тогда и только тогда, когда равны
их действительные части и коэффициенты при мнимых частях.
Поэтому
(а2 — Ь2 = —1,
[ab = 0. (1)
Согласно второму уравнению системы (1) хотя бы одно из чисел
а и b должно равняться нулю. Если b = 0, то из первого урав-
нения получается а2 — —1. Число а действительное, и поэтому
а2 0. Неотрицательное число а2 не может равняться отрица-
тельному числу —1. Поэтому равенство 6 = 0 в данном случае
невозможно. Остается признать, что а = 0, но тогда из первого
уравнения системы получаем: —Ь2 = —1, b — ±1.
Следовательно, комплексными числами, квадраты которых рав-
ны —1, являются только числа i и —i. Условно это записывается
в виде:
= ±i.
Аналогичными рассуждениями учащиеся могут убедиться
в том, что существует ровно два числа, квадраты которых равны
отрицательному числу —а. Такими числами являются У a I
и — У a i. Условно это записывается так:
У—а = ± Уа1.
Под У а здесь подразумевается арифметический, то есть поло-
жительный, корень. Например, У 4 = 2, У 9 = 3; поэтому
У—4 = ±21, У—9 = ±3i и т. д.
Если раньше при рассмотрении квадратных уравнений с отри-
цательными дискриминантами мы говорили, что такие уравнения
не имеют корней, то теперь так говорить уже нельзя. Квад-
ратные уравнения с отрицательными дискриминантами имеют
комплексные корни. Эти корни получаются по известным нам
формулам. Пусть, например, дано уравнение х2 4- 2х 4- 5 = 0;
тогда
х1>3 = —1 ±/Т^5=—1 l±2t.
Итак, данное уравнение имеет два корня: = —14- 2i, х3 =
= —1 — 2t. Эти корни являются взаимно сопряженными. Инте-
ресно отметить, что сумма их равна —2, а произведение 5, так что
выполняется теорема Виета.
232
Упражнения
2022. (У с т н о.) Решить уравнения:
а) х« = —16; б) х2 = —2; в) За 2 = —5.
2023. Найти все комплексные числа, квадраты которых равны:
2024. Решить квадратные уравнения:
а) х2 — 2х + 2 = 0; б) 4х2 + 4х + 5 = 0; в) х2—14x4-74 =0.
Решить системы уравнений (№ 2025, 2026):
2025. (х 4- у = 6, 2026. (2х — Зу = 1,
|ху = 45. |ху = 1.
2027. Доказать, что корни квадратного уравнения с действи-
тельными коэффициентами и отрицательным дискриминантом яв-
ляются взаимно сопряженными.
2028. Доказать, что теорема Виета верна для любых квадрат-
ных уравнений, а не только для уравнений с неотрицательным
дискриминантом.
2029. Составить квадратное уравнение с действительными коэф-
фициентами, корнями которого являются:
a) Xi = 5 — i, ха = 5 + i; б) xt = 37, х2 = —31.
2030. Составить квадратное уравнение с действительными коэф-
фициентами, один из корней которого равен (3 — t) (2i — 4).
2031. Составить квадратное уравнение с действительными коэф-
32 _i
фициентами, один из корней которого равен ---
Двучленные уравнения 3-й степени
с действительными коэффициентами § 254
Так называются уравнения вида
ах8 = Ь,
где а и Ь — произвольные действительные числа, отличные от нуля.
Решение таких уравнений мы рассмотрим на некоторых част-
ных примерах.
Пример 1. Решить уравнение х3 — 8.
Перепишем данное уравнение в виде х3 — 8 = 0. Используя
формулу для разности кубов, получим: (х — 2) (х2 4- 2х 4- 4) = 0.
Если х — 2 = 0, то х = 2; если же х2 4- 2х 4- 4 = 0, то х = —1 ±
±]/TTZ4 = _l 1 ±У31.
Таким образом, данное уравнение имеет три корня:
xt = 2; х2 ——1—УЗ i; х3 = —1 +У1}1.
Действительным среди них является лишь один корень х = 2.
233
Пример 2. Решить уравнение— Ух3 = 4.
Умножив обе части этого уравнения на —2, мы придем к урав-
нению х3 = —8. Это уравнение принципиально не отличается от
ранее рассмотренного уравнения х3 = 8. Поэтому мы приводим
его решение без объяснений:
х3 + 8 = О,
(х + 2) (х2 — 2х_+ 4) = О,
Xi = —2; хг = 1 — i; х3 = 1 4- р^З I.
Пример 3. Решить уравнение -уХ3 = —2.
Умножив обе части этого уравнения на 3, получим х3 = —6,
откуда х3 + 6 = 0. Рассматривая число 6 как куб числа
разложим х3 4- 6 на множители:
(х3 4- 6) = (х 4- Уб) [х2 - Убх 4- (Уб-)2]-
Следовательно, либо х 4- у 6 = 0, либо х2 — У6 х 4- (У6 )2 = 0.
Первое из этих уравнений имеет корень хг = — У 6. Второе
уравнение дает:
х ± V (3/б)’-н;т)! ± з/б. v з‘
2>3 - 2 ~ 2
= (1 ±Уз1)
2
Итак, данное уравнение имеет три корня:
х, = —Уб;
X. = (I + V3i)
х, = ^-(1 -/3
&
Из этих трех корней лишь один представляет собой действительное
число.
Упражнения
Решить уравнения (№ 2032—2037):
2032. Зх3 = 81. 2034. х3 = 3. 2036. Зх3 = 2.
2033. х3 = —27. 2035. х3 = —5. 2037. —4Х3 = 1
2*
2038. Доказать, что сумма всех корней уравнения х8 = —4
равна 0.
2039. Найти произведение всех корней уравнения х3 = 6.
234
Двучленные уравнения 4-й степени
с действительными коэффициентами § 255
Так называются уравнения вида
ах4 = Ь,
где а и b — произвольные действительные числа, отличные от нуля.
Решение таких уравнений мы тоже рассмотрим на некоторых
частных примерах.
Пример 1. Решить уравнение х* = 16.
Перепишем данное уравнение в виде:
х4 — 16 = 0.
Левую часть этого уравнения разложим на множители:
х4 — 16 = (х2 — 4) (х2 4- 4) = (х 4- 2) (х — 2) (х2 4- 4).
Отсюда следует, что корнями уравнения х4 = 16 будут:
хх = —2, х2 — 2, х3 = 2i, хк = —21.
Действительными среди этих корней являются лишь два корня:
хх = —2 и х2 = 2.
Пример 2. Решить уравнение х4 = —16.
В множестве действительных чисел это уравнение не имеет
корней, так как четная степень любого действительного числа
неотрицательна. В множестве комплексных чисел это уравнение,
как мы сейчас покажем, имеет 4 различных корня.
Перепишем данное уравнение в виде:
х4 4- 16 = 0.
Выражение х4 4- 16 можно рассматривать как сумму квадратов
чисел х2 и 4. Дополнив эту сумму до точного квадрата, получим:
х4 4- 16 = х4 4- 16 4- 2 • 4 • х2 — 2 • 4 • х2 = (х2 4- 4)2 — 8х2.
Теперь используем формулу для разности квадратов двух чисел:
(х24- 4)2 — 8х2 = (хЧ-4 +Vвх2)(х24-4 — /8х^) =
= (х2 4-2/2 х 4-4)(х2 —2/2 х-]-4).
Итак,
х2 4- 16 = (х2 + 2/2"х 4- 4) (х2 — 2/2"х 4- 4).
Поэтому уравнение х4 = —16 можно представить в виде:
(х2 4- 2/2х 4- 4) (х2 — 2/2 х 4- 4) = 0.
Если х2 4- 2/Гх4-4 =0, то х1>2 = —/2 ±/2^4? или
х1 = -/^+ V2J,
а*2 = -/2-/2г,
235
если же л2 — 2|/'2х + 4 = 0, то х3>4 = У 2 ± )^2 — 4, или
х3 = У2-У21,
л4 = /2’ч-/Г/.
Мы получили четыре корня уравнения х4 = —16. Среди них
нет ни одного действительного корня.
Пример 3. Решить уравнение Зх4 = —6. Принципиально
это уравнение не отличается от предыдущего. Поэтому мы при-
водим его решение без объяснений:
х4 - —2.
х4 + 2 = х4 + (/2 )2 = х4 + (У 2 )2 +_2х2]/2 — 2х2У 2 =
= (х2 + У2 )2 — 2|/2х2 =
= (х2 +У2)2— (У8_х)2= (х2 + f 8 х + У2) (х2—У 8 х + У2).
Если х2 + У8~х + J/2 = 0, то
v _ ~У8± /(/8)2-4/2’_ - Ув ± K-2F2" _-У&± у’8 I
‘’2“ 2 ~ 2 2
Если же х2 — i^8x 4* У2 — 0, то аналогично получим:
_ У 8 ± 1^81
о,4 —
Таким образом, данное уравнение имеет четыре различных
корня. Среди них нет ни одного действительного корня.
Упражнения
Решить уравнения (№ 2040—2044):
2040. х4 = 81. 2042. х4 = 2. 2044. Зх4 = 5.
2041. х4 = —81. 2043. х4 = —3.
2045. Найти сумму всех корней уравнения х4 = 4.
2046. Найти произведение всех корней уравнения х4 = —7.
Тригонометрическая форма комплексных чисел
§ 256
Пусть комплексному числу а Ы соответствует вектор О А
с координатами (а, Ь) (см. рис. 332). Обозначим длину этого векто-
ра через г, а угол, который он образует с осью х, через <р. По опре-
делению синуса и косинуса:
а b
— = COS ф, — = Sin ф.
236
Поэтому а = г cos <p, b = г sin ф. Нов таком
случае комплексное число а + Ы можно запи-
сать в виде:
а 4- bi — г cos <р + ir sin q> = г (cos ф + i sin <p).
Как известно, квадрат длины любого век-
тора равен сумме квадратов его координат.
Поэтому г* = а2 + Ь2, откуда г = У а2 4- Ь2.
Итак, любое комплексное число в 4- Ы
можно представить в виде:
а 4- Ы — rfcoscp 4-Zsin ср), (1)
где г = у^а^+д2, а угол ср определяется из условия:
а
cos <р = -
т /а2 + ba
Такая форма записи комплексных чисел называется тригонометри-
ческой.
Число г в формуле (1) называется модулем, а угол ф — аргумен-
том комплексного числа а 4- bi.
Если комплексное число а 4~ bi не равно нулю, то модуль
его положителен; если же а 4- bi — 0, то а — b = 0 и тогда г = 0.
Модуль любого комплексного числа определен однозначно.
Если комплексное число а 4- bi не равно нулю, то аргумент
его определяется формулами (2) однозначно с точностью до угла,
кратного 2л. Если же а 4- bi = 0, то а — b = 0. В этом случае
г = 0. Из формулы (1) легко понять, что в качестве аргумента <р в
данном случае можно выбрать любой угол: ведь при любом <р
0 • (cos <р 4- i sin ф) = 0.
Поэтому аргумент нуля не определен.
Модуль комплексного числа г иногда обозначают | г |, а аргу-
мент arg г. Рассмотрим несколько примеров на представление
комплексных чисел в тригонометрической форме.
Пример 1. Записать в тригонометрической форме комплекс-
ное число 1 4- i.
Найдем модуль г и аргумент ф этого числа.
Следовательно, sin ф = -р=, cos ф = откуда Ф — ~ 4- 2лл.
Таким образом,
1 4- i = ]/2 cos 4* 2л л j 4- i sin 4- 2пл j |
237
Рис. 333.
Имеем:
где п — любое целое число. Обычно из беско-
нечного множества значений аргумента комплек-
сного числа выбирают то, которое заключено
между 0 и 2л. В данном случае таким значени-
л
ем является —. Поэтому
1 + / = У2 (cos — 4- i sin —
\ 4 4 /
Пример 2. Записать в тригонометриче-
ской форме комплексное число У Т — i.
г = У 3 + 1 — 2; cos <р — Kl, sin ф — —
п о Н
Поэтому, с точностью до угла, кратного 2л, ф = — л; следова-
тельно,
У 3 — I = 2 (cos — л + I sin — л\
\ 6 6 J
Пример 3. Записать в тригонометрической форме комп-
лексное число I.
Комплексному числу I соответствует вектор О А, оканчиваю-
щийся в точке А оси у с ординатой 1 (рис. 333). Длина такого век-
тора равна 1, а угол, который он образует с осью абсцисс, равен -у.
Поэтому
, л ... л
i = COS--Н Sin —
2 2‘
Пример 4. Записать в тригонометрической форме комп-
лексное число 3.
Комплексному числу 3 соответствует вектор ОА, оканчиваю-
щийся в точке оси х абсциссой 3 (рис. 334). Длина такого
Рис. 334.
вектора равна 3, а угол, который
он образует с осью абсцисс, равен
0. Поэтому
3 = 3 (cos 0 + I sin 0).
Пример 5. Записать в три-
чт тонометрической форме комплекс-
ное число —5.
Комплексному числу —5 соот-
ветствует вектор О А, оканчиваю-
щийся в точке оси х с абсцис-
238
сой —5 (рис. 335). Длина такого вектора равна 5, а угол, который
он образует с осью абсцисс, равен л. Поэтому
—5 = 5 (cos л + i sin л).
Упражнения
2047. Данные комплексные числа записать в тригонометриче-
ской форме, определив их модули и аргументы:
1) 2 + 2/Ti; 4) 12/ — 5; 7) 3t;
2) V 3 + t; 5) 25; 8) —2i;
3) 6 —6t; 6) —4; 9) 3i —4.
2048. Указать на плоскости множества точек, изображающих
комплексные числа, модули г и аргументы ф которых удовлетворяют
условиям:
1) г= 1, <Р = р
4
2) г = 2;
3) г < 3;
4) г<3; 7)0<ф<-^;
5) 2 < г < 3; 8) 0 < ф < л;
6) 9) 1 <г < 2,
10) 0<ф<^.
2049. Могут ли модулем комплексного числа одновременно
быть числа г и —г?
2050. Могут ли аргументом комплексного числа одновременно
быть углы ф и —ф?
Данные комплексные числа представить в тригонометрической
форме, определив их модули и аргументы:
2051*. 1 + cos а + i sin а. 2054*. 2 (cos 20° — i sin 20°).
2052*. sin ф + i cos ф. 2055*. 3 ( —cos 15° — i sin 15°).
2053*. —5 (cos 40° — i sin 40°).
239
Умножение и деление комплексных чисел,
заданных в тригонометрической форме § 257
Умножение и деление комплексных чисел удобнее выполнять, если эти числа
заданы в тригонометрической форме. Имеют место следующие теоремы.
Теорема 1. Модуль произведения двух комплексных чисел ра-
вен произведению их модулей, а аргумент — сумме их аргументов.
Доказательство. Пусть
?х = rt (cos фх 4- i sin фх), z2 - r2 (cos ф2 -f- < sin <p2).
Тогда
Zj • z2 = rr • r2 (cos <pj + i sin фт)(со5 <p2 4- i sin ф2) =
= fj • r2 (cos ф1 • cos ф2 4- i cos ф1 • sin ф2 4- i sin ф! • cos ф2 — sin ф1 • sin ф2) =
= rj • r2 [ (cos ф, • cos ф2 — sin ф] • sin ф2) 4-<(sin ф1 • cos ф2 4- cos ф1 • sin ф2) J;
HO
cos ф1 • cos ф2 — sin ф! • sin ф2 = cos (ф! 4- ф2Х
sin ф1 • cos <p2 4- cos ф, • sin ф2 = sin (ф1 4- Ф-Л
Поэтому
Z1Z2 = fir2 lcos (Ф1 + Ф2) -H Sin (ф1 4- ф2)].
А это и означает, что модуль произведения zt • равен произведению модулей
чисел Zx и г2, а аргумент произведения—сумме аргументов чисел zt и г2. Теорема 1
доказана.
Примеры.
2 (cos 130° 4- i sin 130°) • 3 (cos 230° + i sin 230°) = 6 (cos 360° 4- i sin 360°)=6;
6 (cos 47° + i sin 47°) • 4 (cos 13° 4- i sin 13°) = 20 (cos 602 + i sin 60°) =
= 2o(j + i = 10 + 10/3 i.
Отметим, что доказанная теорема справедлива для любого числа сомножителей,
то есть при любом л:
гх (cos фх 4-1 sin Фх) • ra(cos ф2 4-1 sin ф2) ... rn (cos фл 4- i sin фл) =«
= Г1 Га ••• rn (cos (ф1 + Фа 4- ... + Ф„) + i sin (Ф, 4- Фа 4- ... 4- Фл) 1-
В частном случае, когда все сомножители равны между собой, полу-
чаем:
[г (cos ф 4- i sin ф)Р = rn [cos лф 4- i sin лф].
Эта формула носит название формулы Муавра*. При г=* 1 она принимает
вид:
(cos ф + I sin ф)п =» cos лф 4~ i sin лф.
Теорема 2. Модуль частного двух комплексных чисел равен
частному модулей делимого и делителя; аргумент частного двух
не равных нулю комплексных чисел равен разности аргументов де-
лимого и делителя.
Доказательство. Обозначим частное от деления комплексного
числа zx « rt (cos фх + I sin фх) на комплексное число za = r2 (cos ф2+* sin ф^О
через г = г (cos ф 4- i sin ф). Тогда г =» или 2 • z2 = zx. Поэтому
Z2
г (cos Ф 4- I sin ф) • r2 (cos ф2 4- i sin ф2) =» гх (cos фх 4- i sin фх).
Производя умножение в левой части этого равенства, получаем:
rr2 [cos (ф 4- ф2) 4- / sin (ф 4- ф2)] = гх (cos фх 4- *sin фх).
Модули двух равных комплексных чисел, отличных от нуля, равны, а ар-
гументы могут отличаться лишь на угол, кратный 2л. Поэтому из последнего
♦ М у а в р (1667—1754) — английский математик.
240
равенства вытекает, что
ГГ2 = Ф + Фа ~ Ф1 3 2ЛЛ,
где п — некоторое целое число Следовательно,
—, ф = ф1 — ф2 + 2лл.
Г2
Аргумент любого комплексного числа, отличного от нуля, определен лишь
с точностью до угла, кратного 2л. Поэтому можно считать, что аргумент ф ком-
плексного числа г равен
Ф1—ф2.
Теорема доказана
Примеры.
2 (cos 150° +/sin 150°) 2
3(cos 105° +»sin 105°) ~ 3
(cos 45° 4- i sin 45°)
3 \ 2 2 /
2) cos (— 30°) 4- i sin (— 30°) = cos 30° — i sin 30° =
' cos 100° 4- i sin 100°
2 2
Упражнения
2056. Выполнить указанные действия:
a) 5 (cos 40q 4" i sin 40°) • 3 (cos 50° + I sin 50°);
6) 2 (cos 20°- 4- I sin 20°) • 7 (cos 100° + i sin 10СГ);
/л я '
В) 4 cos — 4- i sin —
\ О О j
(8 8
cos—л 4-1 sin ттл
15 15
2057. Вычислить:
7 7
cos — Л 4- » sin — Л
8 8
'2 2 \
cos— л 4~ ‘ sin — л I
. 3 3 /
/4 4 \
•2 cos—- л 4- / sin -- л).
\ 5 5 /
a)
б) (K34-O50;
в)
2058. Как изменяется модуль
умножения этого числа на:
а) /; в) 2/; д)
б) —/; г) —3/; е)
2059. Выполнить деление:
cos 130° 4-/sin 130°
а) ------------------;
cos 40° 4- / sin 40°
cos 130° — / sin 130°
6Г -------------------;
cos 40° 4- / sin 40°
2060. Как изменятся модуль
деления этого числа на: а) /; б) — /?
и аргумент комплексного числа в
результате
4;
-5?
—cos 100° +1 sin 100°
в)*------------------;
cos 40° — i sin 40°
2 (cos 107° +/sin 107°)
Г) 5 (cos 47° 4-i sin 47°) *
аргумент комплексного числа в
результате
и
Извлечение корней из комплексного числа § 258
Предположим, что корень степени п из комплексного числа г (cos ф 4-
4- I sin ф), отличного от нуля, существует и равен
р (cos 0 4“ / cos 0)*.
♦ р н 0 — греческие буквы, читаются соответственно: ро и тэта.
241
Рис. 336.
Тогда
[р (cos 0 -|- i sin 6)]л == г (cos <р + * sin ф)-
Используя формулу Муавра, получаем:
рл (cos п 6 + i sin п 0) = г (cos ф 4- i sin ф).
Модули двух равных комплексных чисел,
отличных от нуля, равны, а аргументы могут
отличаться лишь на угол, кратный 2л.
Поэтому
рл = г, л0 = ф + 2kn,
откуда
P = V7, в = £+“1,
V п
где k может быть любым целым числом. В част-
ности,
при k = 0 0 — —;
п
„ри» = 1
п п
ср 4л
при k — 2 0 = — + —;
п п
• • •••••.......• •
. < Л Ф 2(п —1)л
при k = п — 1 0 = — 4---.
п п
При k = л, л4-1> л 4- 2 и т. д будут получаться значения 0, отличающиеся
от написанных выше на углы, кратные 2л. Поэтому никаких новых комплексных
чисел эти значения k дать не могут.
Легко показать, что никаких новых комплексных чисел мы не получим и
при отрицательных значениях k.
Итак, если только корень степени п из комплексного числа
г (cos ф + < sin ф) существует, то он может принимать лишь следующие
п значений:
/ ф Ф
а0 = cos — 4- i sin —
*_______________________\ n n
n — l ф4-2л c
04 = ifr cos-----------4- i sin -
y \ n
Ф 4- 2 (n — 1) л
n
. . ф4-2(п-1)л
4-1 sin---------
n
Непосредственной проверкой легко установить, используя формулу Муавра,
что каждое из этих чисел удовлетворяет соотношению
ап = г (cos ф 4- i sin ф)
и потому является корнем л-й степени из комплексного числа
г (cos ф 4" * sin ф).
Таким образом, каждое комплексное кисло, отличное от нуля,
имеет ровно п корней п-й степени.
Геометрически все л значений корня л-й степени из комплексного числа
г (cos ф 4- i sin ф) изображаются точками, лежащими на окружности с центром
в начале координат, радиус которой равен (см., например, рис. 336, на
242
котором r (cos ф 4- i sin <p) = 1, n = 6). Если эти точки соединить последователь-
но прямолинейными отрезками, то в результате получится правильный
л-угольник.
Пример. Найти все значения корня 4-й степени из числа I.
л л
Представив I в виде I = cos — 4* sin — , найдем, что
4— , п л 2л
ней равны = 1, а аргументы ; — 4- —;
г 8 8 4
5 9 13 m
— л; — л; —л. Поэтому корнями 4-й степени из числа
8 8 8
л 4л
модули всех кор-
л 6л
Т + “" или
8*4
л
7:
i являются
числа:
Л л
cos — 4- i sin — ;
8 8
5 5
cos — л + i sin — л;
8 8
9 9
cos — л 4- i sin— л;
8 8
13 13
cos — л 4- i sin— л.
8 8
При желании, используя тригонометрические таблицы, эти корни можно
записать в более явном виде.
Упражнения
2061. Найти все значения данных корней:
а) ^3‘. в) j/T'« A) /cos 100° 4-t sin 100°.
б)уТ+7; г>
2062. Решить уравнения:
а) х6 = а (а — действительное число); б) х5 = I.
2063. Решить уравнение:
х44-^+*я + ^ + 1 = 0-
2064. Доказать, что все корни л-й степени из комплексного числа г можно
расположить так, что в результате получится геометрическая прогрессия. Найти
знаменатель этой прогрессии.
Алгебраическое уравнение п-й степени
§ 259
Наиболее полно элементарная математика рассматривает ал-
гебраические уравнения только двух степеней: первой и второй.
Эти уравнения имеют вид:
ах 4-д =0 (а =/= 0),
ах2 4- Ьх + с = 0 (а =# 0).
В области комплексных чисел любое алгебраическое уравне-
ние 1-й степени имеет ровно один корень, а любое алгебраиче-
ское уравнение 2-й степени — ровно два корня. В высшей алгебре
изучаются уравнения произвольных степеней.
243
Алгебраическое уравнение л-й степени имеет следующий вид:
Сох" + а^-* + агхп~2 + . . . 4- an_j х + ап = 0, (1)
где х — неизвестная величина, а а0, alt . . . , ап — заданные комп-
лексные числа, причем а0 =/= 0. Вопрос о существовании и коли-
честве корней такого уравнения долгое время являлся централь-
ным вопросом алгебры. В 1799 г. выдающийся немецкий математик
Гаусс (1777 — 1855) доказал следующую теорему: любое алгеб-
раическое уравнение п-й степени имеет хотя бы один
комплексный корень.
Это утверждение вошло в математику под названием основ-
ной теоремы алгебры*. После доказательства Гаусса
было предложено очень много других способов доказательства эгой
теоремы. Да и сам Гаусс предложил еще три доказательства.
Все существующие до настоящего времени доказательства этой
теоремы довольно сложны и потому не могут быть рассмотрены
в нашем учебнике.
Рассмотрим уравнение
(х —I)3 (х — 2) = 0.
Нетрудно понять, что оно имеет ровно два корня: 1 и 2. Однако
корни эти находятся в неравноправном положении. Множитель
х — 2, соответствующий корню 2, входит в левую часть уравне-
ния в первой степени, а множитель х—1, соответствующий
корню 1, — в третьей степени. Про корень 2 говорят, что он яв-
ляется простым корнем рассматриваемого уравнения, а про
корень 1 — что он является кратным корнем, точнее, корнем
кратности 3.
Основная теорема алгебры гарантирует существование хотя
бы одного комплексного корня алгебраического уравнения. Од-
нако, исходя из нее можно доказать, что любое алгебраиче-
ское уравнение п-й степени имеет ровно п комплексных
корней, если каждый корень считать столько раз, ка-
кова его кратность. При этом если корни уравнения (1)
равны хь х2, .... хп, то левая часть этого уравнения представ-
ляется в виде:
л0 (х — xj (х — х2) . . . (х — хп).
(Сравните с квадратным уравнением!)
Для уравнений 1-й и 2-й степени выведены общие формулы,
по которым можно находить корни этих уравнений. Так, напри-
мер, для уравнения ах2 + Ьх + с = 0 такой формулой является
формула
у —Ь ± Vb2 — 4ас
2а
* По мере развития алгебры изменялось и ее содержание. Современная ал-
гебра включает в себя настолько обширный материал, что сейчас указанную тео-
рему часто уже не считают основной теоремой всей алгебры.
244
Аналогичные формулы получены и для уравнений 3-й и 4-й
степени. Однако эти формулы слишком громоздки и потому здесь
не приводятся. Что же касается произвольных алгебраических
уравнений более высоких степеней, то для них, как показал
норвежский математик Абель (1802—1829), таких формул со-
ставить, вообще говоря, нельзя. Исчерпывающее решение вопроса
об условиях, при которых уравнение может быть решено в ра-
дикалах, дал выдающийся французский математик Эварист
Галуа (1811—1832).
Итак, точно решить алгебраическое уравнение степени выше
четвертой удается не всегда. Однако современная математика
располагает весьма эффективными методами приближенного
решения таких уравнений. Эти методы излагаются в книгах по
вычислительной математике.
Исторические замечания § 260
Первое упоминание о «мнимых* числах как о квадратных корнях из отрица-
тельных чисел относится еще к XVI веку. В 1545 г. итальянский ученый Кар-
дано (1501—1576) опубликовал работу, в которой, пытаясь решить уравнение
х3 — 12х+16=0, он пришел к выражению V—243. Через это выражение
представлялись действительные корни уравнения xv = х2 « 2; х3 = —4. Та-
ким образом, в работе Кардано мнимые числа появились как промежуточные
члены в вычислениях.
В 1629 г. голландский ученый Жирар (1595—1632) впервые высказал
утверждение, что всякое алгебраическое уравнение n-й степени имеет ровно п
корней. Строго доказать это ему не удалось. Как мы знаем, это сделал Гаусс
лишь в 1799 г. Однако важно то, что, высказав правильную гипотезу, Жирар
подчеркнул, что, помимо действительных корней, при этом нужно учитывать и
комплексные корни.
До середины XVIII века комплексные числа появляются лишь эпизодически
в трудах некоторых математиков. С середины XVIII века Даламбер, Эй-
лер и Лагранж с успехом используют функции комплексного аргумента
для решения некоторых задач гидродинамики. С помощью функций комплексно-
го переменного решаются задачи о составлении географических карт, а также ряд
чисто математических задач. К концу XVIII века были изучены все основные
свойства комплексных чисел. Эти числа становятся одним из сильнейших инстру-
ментов математики.
Однако математики XVIII века не понимали до конца природы комплексных
чисел. Они считали эти числа воображаемыми, лишенными всякого объективного
содержания.
Лишь в конце XVIII века, когда в математику прочно вошли векторы, ком-
плексным числам стало возможно дать простую геометрическую интерпретацию
и объяснить правила действий над ними. Впервые это сделал датчанин Вес-
сель (1745—1818). Интересно отметить, что Вессель не был специалистом-мате-
матиком. Его исследования о геометрическом истолковании комплексных чисел
долгое время оставались неизвестными и обратили на себя внимание лишь во
второй половине XIX века.
Полное признание математиками комплексных чисел началось лишь после
выхода в свет работ Гаусса.
Одним из самых замечательных достижений математики XVIII и XIX веков
явилось создание теории функций комплексного переменного. Э1а теория играет
сейчас одну из основных ролей в прикладной математике.
245
Задачи на повторение
2065. Может ли сумма квадратов двух чисел быть отрица-
тельной? Ответ пояснить примерами.
2066. При каком условии квадрат комплексного числа а + Ы
является чисто мнимым числом?
2067. В каком случае сумма и произведение двух комплекс-
ных чисел являются действительными числами?
Упростить выражения (2068—2073):
2068. (1 + О2 + (1 — О2-
2071.
2069. (1 + 08 + (1 — О3.
2072.
2070. (1 4- О4 + (1 —
2073.
!+?,!-?
1 — « 1 + i'
U+08 ] 3 + 2? ,j , ,
(l-?)4 i(6 —8«)
2 — i 1 — 2t
,4 + 3i 3 + 4i,
0,4(1— О8
Доказать тождества (№ 2074, 2075):
2074. (1 + О20 = — 2*°.
2075. (1 — 08о = 2151.
2076. Составить квадратное уравнение с действительными коэф-
фициентами, один из
а) (5 + 0 (/ - 3);
2077. Может ли
коэффициентами иметь корни 1 + i и 1 + 2t?
2078. Найти действительные числа х и у из уравнений:
х Зх — ty _ 7 + 5t g. у — ix _ 4 + j
2y — 5ix 12 — 8i ’ x + iy 4i—1"
2079. Найти чисто мнимые числа и и v из уравнений:
а) 5ц — 7ui = —7 + 5г, б) 2и + 3vi = 12 + 6/.
2080. Доказать, что для любых комплексных чисел и г2
корней которого равен:
б)-^±1.
i — 3
квадратное уравнение с действительными
Какую известную из геометрии теорему о диагоналях параллело-
грамма выражает это соотношение?
2081. Найти модуль и аргумент комплексного числа
(5 — 120 (3 — 40.
2082. Выразить модуль и аргумент комплексного числа через
модуль и аргумент сопряженного к нему числа.
2083. Представить в тригонометрической форме комплексные
числа:
а) 1 + i tg б) ”.
' 6 1 -Htga
246
2084. Точка плоскости А изображает комплексное число а 4- Ы.
Какое число изображает точка В, симметричная точке А отно-
сительно:
а) действительной оси;
б) мнимой оси;
в) начала координат?
2085*. На плоскости известно положение точки, соответст-
вующей комплексному числу г. Как с помощью циркуля и ли-
нейки отыскать на той же плоскости точку, соответствующую
комплексному числу —?
2>
2086. Доказать, что все корни п-й степени из комплексного
числа г (cos ф + i sin ф) геометрически изображаются как вершины
правильного л-угольника. Найти сторону этого п-угольника.
2087. Доказать, что сумма всех корней п-й степени из лю-
бого комплексного числа равна нулю.
2088. Вычислить:
(/з‘4-0‘°4-(/з"—О10-
2089. хг и х3 — корни уравнения х3 — 1=0. Чему равно
выражение
1 1 1
-----4------ 4-------?
\ *2 *2 Х3 Х3
МЕТОД МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ
Общие и частные утверждения.
Дедукция и индукция
XII
S 261
Все утверждения можно разделить на общие и частные.
Примерами общих утверждений являются утверждения:
1) в любом треугольнике сумма двух сторон больше третьей
стороны;
2) все числа, оканчивающиеся четной цифрой, делятся на 2
и т. д.
Частными являются, например, утверждения:
1) в треугольнике АВС (рис. 337) сумма двух сторон АВ и ВС
больше третьей стороны АС.
2) число 136 делится на 2.
Переход от общих утверждений к частным называется дедук-
цией. Дедукция очень часто используется в математике. Все об-
щие теоремы мы доказываем именно для того, чтобы затем ис-
пользовать их для решения различных частных задач.
Но наряду с этим в математике часто приходится от частных
утверждений переходить к общим. Например, рассматривая ариф-
метическую прогрессию
01, <?2> «3, • • • » аП' • • •
(см. ч. I, § 142), мы заметили, что
о2 = ох + А,
Оз = Oi + 2d,
о* = оЛ + 3d.
Исходя из этих частных формул, мы сделали вывод, что
при любом натуральном п
on = Oi + (л — 1) d.
Переход от частных утверждений к общим называется индук-
цией.
В В отличие от дедукции индукция
может привести как к верным, так и
/ к неверным результатам. Например,
/ рассматривая значения квадратного
трехчлена / (л) = л* 4- л + 41 при ма-
лых натуральных значениях л,
Рис. 337. можно заметить, что эти значения вы-
248
ражаются простыми числами (то есть числами, которые без
остатка делятся только на себя и на 1).
Действительно,
(1) = 43;
/ (2) = 47;
f (3) = 53;
f (4) = 61
и т. д. Напрашивается вывод, что при любом натуральном п зна-
чение выражения п2 + п + 41 является простым числом. Однако
вывод этот является неверным. Например, при п = 41
п2 + п + 41 = 412 + 41 + 41 = 41 (41 + 1 + 1) = 41 • 43.
Пусть некоторое утверждение справедливо в нескольких част-
ных случаях. Рассмотрение всех остальных случаев или совсем
невозможно, или требует большого числа вычислений. Как же
узнать, справедливо ли это утверждение вообще? Этот вопрос
иногда удается решить посредством применения особого метода
рассуждений, называемого методом математической индукции.
Этот метод мы рассмотрим в следующем параграфе.
В математике уже издавна используется индуктивный метод, основанный
на том, что то или иное общее утверждение делается на основании
рассмотрения лишь нескольких частных случаев. История, например, со-
хранила следующее высказывание Эйлера: <У меня нет для доказатель-
ства никаких других доводов, за исключением длинной индукции, которую
я провел так далеко, что никоим образом не могу сомневаться в законе,
управляющем образованием этих членов... И кажется невозможным, чтобы
закон, который, как было обнаружено, выполняется, например, для 20 членов,
нельзя было бы наблюдать и для следующих».
Веря в непогрешимость индукции, ученые иногда допускали грубые
ошибки. К середине семнадцатого столетия в математике накопилось немало
ошибочных выводов. Стала сильно ощущаться потребность в научно обо-
снованном методе, который позволял бы делать общие выводы на основании
рассмотрения нескольких частных случаев. И такой метод был разработан.
Основная заслуга в этом принадлежит французским математикам Паскалю
(1623 — 1662) и Декарту, а также швейцарскому математику Якобу Бер-
нулли (1654— 1705).
Упражнения
2090. Какие из данных утверждений являются общими и ка-
кие частными:
а) число 16 четное;
б) всякое число, оканчивающееся цифрой 6, четное;
в) синус любого угла по абсолютной величине не превышает 1;
г) синус угла 50° меньше 1;
д) десятичный логарифм числа —2 не определен;
е) отрицательные числа не имеют десятичных логарифмов?
2091. Числа 24 , 64, 104 делятся на 4. Можно ли на основа-
нии этого сказать, что любое число, оканчивающееся цифрой 4,
делится на 4?
249
2092. Синусы углов 45° и 60° иррациональны и
Можно ли из этого заключить, что синусы любых углов ирра-
циональны?
Метод математической индукции
§ 262
В основе метода математической индукции лежит следующий
принцип.
Некоторое утверждение верно при любом натураль-
ном п, если:
1) оно верно при п = 1
и
2) из справедливости этого утверждения при каком-
либо произвольном значении п = k(k> 1) следует, что
оно верно и при п = k 4-1.
Действительно, при п = 1 утверждение верно в силу 1). Да-
лее, 2 = 1 + 1, а потому в силу 2) утверждение верно при п — 2;
3 = 2+ 1, поэтому в силу 2) утверждение верно и при п = 3.
Вообще, любое натуральное число п может быть получено из 1
путем последовательного прибавления к нему единицы п — 1 раз.
При каждом таком прибавлении мы получаем натуральное число,
для которого рассматриваемое утверждение верно. Поэтому оно
верно и для натурального числа п.
Метод доказательства, основанный на использовании этого
принципа, называется методом математической индукции.
Рассмотрим несколько примеров.
Пример 1. Найти сумму
S = — + — + — +... + —!------.
л 1-2 2-3 3-4 п(п +1 )
Сначала найдем суммы одного, двух, трех и четырех сла-
гаемых. Имеем:
5 = 1;
1 1-2 2
5<=^ + г-з = ? + М:
3 1-2 2-3 3-4 3 12 4
111 11 11 1 4-1 = 1
4 +20 5
1-2 2-3 3-4 4 5
В каждом из этих случаев получается дробь, в числителе
которой стоит число слагаемых, а в знаменателе — число, на
250
единицу большее числа слагаемых. Это позволяет высказать ги-
потезу (предположение), что при любом натуральном п
1 1
--- 53 ---
1-2 2
п
п 4-1 ‘
Для проверки этой гипотезы воспользуемся методом матема-
тической индукции.
1) При п = 1 гипотеза верна, так как
2) Предположим, что гипотеза верна при п =* k, то есть
с____!__|_ 1 • *
5‘"Ь2 +
Докажем, что тогда
п = k 4- 1, то есть
5‘*‘ = Гг + Г5+- +
Действительно,
^й+1
k
2-3 ’ " ‘ k(k 4- 1) ft 4-1
гипотеза должна быть верной и при
1
k(k 4- О
4---------------
(ft 4- 1)(*4-2)
fe + 1
Л + 2
Но по предположению Sft =
Q _ k I
'"’ft + l ~
1_______
(k + l)(k + 2) *
* п
Поэтому
k2 + 2fe + 1
(k 4- D*
(ft4-l)(ft4-2)
(k 4-1) (k 4-2) (Л 4-1) (Л 4- 2)
= 1±2
k 4-2
Таким образом, исходя из предположения, что гипотеза Sn «=
верна при п = k, мы доказали, что она верна и при п = k 4- 1.
Поэтому формула
S = — 4- — 4- ... 4------1---= -2—
п 1-2 2-3 л (л 4- 1) л 4-1
верна при любом натуральном п.
Пример 2. Доказать, что л-й член арифметической прогрес-
сии равен
Яп = а1 + (л — О d>
где а! — первый член, ad — разность этой прогрессии.
Этот пример отличается от предыдущего тем, что строить гипо-
тезу здесь не надо, она дана. Нужно только доказать, что эта гипо-
теза верна.
Доказательство будем вести методом математической индук-
(1)
ции.
1) При п = 1 формула (1) имеет вид:
Я1 = alt
так что при п = 1 эта формула верна.
2) Предположим, что она верна при п = k, то есть
ак = Oj 4* (А —- 1) d,
251
и покажем, что в таком случае она должна быть верной и при
л = k 4- 1, то есть
п, 4* kd.
Действительно,
ak+t = ah + d = {01 + (k — 1) d] + d = at + kd,
что и требовалось доказать.
Оба условия принципа математической индукции выполняют-
ся, и потому формула (1) верна для любого натурального
числа п.
Пример 3. Доказать тождество
(cos а 4- i sin а)" = cos па + I sin па. (2)
1) При п = 1 обе части формулы (2) принимают один и тот
же вид, cos а 4- i sin а, так что при п = 1 эта формула верна.
2) Пусть она верна при п = k, то есть
(cos а 4" i sin а)к = cos ka 4- i sin ka.
Тогда
(cos a 4* i sin a)ft+1 = (cos a 4- i sin a)ft • (cos a 4- i sin a) =
= (cos ka 4- i sin ka) (cos a 4- i sin a) =
— (cos ka cos a — sin ka sin a) 4- i (cos ka sin a 4- sin ka cos a) =
= cos (ka 4- a) 4- i sin (ka 4- a) = cos (k 4- l)a 4- i sin (k 4- 1) a.
По это означает, что формула (2) верна и при п = k + 1.
Оба условия принципа математической индукции выполняются,
и потому формула (2) верна при любом натуральном п.
Пример 4. Доказать, что при любом натуральном п* (3)
(хп)' = лхп-1.
1) При п = 1 формула (3) принимает вид: х' = 1.
Это соотношение, как было доказано в главе X, верно. Значит, при п = 1 форму-
ла (3) верна.
2) Предположим, что она верна при п = k, то есть (хй)' = kxk~l, и, исходя
из этого, докажем, что она должна быть верна и при п = k + 1, то есть (хА+1)' =
•= (fc + 1) хй. Действительно, представляя хА+1 в виде хк • х н используя пра-
вило дифференцирования произведения, получаем:
(хй+1)' = (хй • х)' = (хй)' х 4- хй • (х)'.
Но по предположению (хй)' — кхк~\ к тому же х' = 1. Поэтому
(хй+1)' = kxk~* • х 4- х* • 1 = (k 4-1) хй.
Итак, оба условия принципа математической индукции выполняются, и потому
формула (3) верна при любом натуральном п.
Упражнения
Доказать тождества (№ 2093—2096):
1
2093. — 4- — 4- — 4- - 4------------------------ —-—.
1-3 3-5 5-7 (2л— 1) (2«4-1) 2л 4- 1
2094. -------- 4" • • 4“ ••• 4"----------- — ———
а{а 4- 1) (a4-l)(a4-2) (а4-л—1) (а-И) а(а4-л)
• Если х * 0; случай, когда х = 0, требует, строго говоря, специального
рассмотрения.
252
2095. I2 + 22 + З2 4-... + л2 = ?(”4-1)(2п + 1).
6
2096. I3 4- 2s 4- 3я 4-... 4- пя = +
2097. Вывести формулу общего члена геометрической про-
грессии.
2098. Доказать, что при любом натуральном п число л3 4* бл
делится без остатка на 6.
2099. На сколько частей делится плоскость л различными
прямыми, проведенными в этой плоскости через одну ее точку?
2100. Методом математической индукции доказать тождество:
о . Оя sin 2"+1 а
cos а • cos 2а • cos 4а... cos 2"а -----—.
2Л+1 sin а
Какой еще метод вы можете предложить для доказательства
этого тождества?
2101. Доказать, что при любом натуральном л и а —1
(1 4- а)п >14- па.
2102. Доказать, что при любом л с помощью циркуля и линейки
с заданной единицей длины можно построить отрезок длиной
в Уп.
2103. Доказать, что при любом натуральном л
I sin пх | < л | sin х |.
2104. Доказать, что при любом натуральном п
2105. Используя формулу задачи Хе 2104, найти производные следующих
функций:
(х__ 1 \5 / 2х2_1 \3
—-—1; б) у = I ———1;
2) у = sin32x;
4) у = (ха — Зх + 5)4; 6) у = (sin х — cos г)4.
Другой вариант метода математической индукции § 263
Некоторые утверждения справедливы не для всех натураль-
ных л, а лишь для натуральных л, начиная с некоторого числа р.
Такие утверждения иногда удается доказать методом, несколько
отличным от того, который описан в § 262, но вполне аналогич-
ным ему. Состоит он в следующем.
Утверждение верно при всех натуральных значениях
п>р, если:
1) оно верно при п=р (а не при л = 1, как было в § 262);
2) из справедливости этого утверждения при п = k,
где k >р (а не k > 1, как в § 262), вытекает, что оно вер-
но и при n — k + 1.
253
а2 Поясним это на следующем при-
Омере.
Доказать, что сумма Sn внутрен-
них углов любого выпуклого много-
угольника равна (л — 2) я, где п —
число сторон этого многоугольника*:
5„=(л-2)я. (1)
д
к Это утверждение имеет смысл не
Рис.338. для всех натуральных п, а лишь
для п ^>3. Поэтому метод, описанный
в § 262, здесь использовать нельзя. Однако можно исполь-
зовать другой вариант индукции, описанный на предыдущей
странице.
1) При п = 3 наше утверждение принимает вид: S 3 = я. Но
сумма внутренних углов любого треугольника действительно рав-
ная. Поэтому при п = 3 формула (1) верна.
2) Пусть эта формула верна при п = k, то есть Sh = (k — 2) я,
где k 3. Докажем, что в таком случае имеет место и формула
Sft+1 = (k 1) я.
Пусть AlAz ... АкАк+1 — произвольный выпуклый (k + 1)-
угольник (рис. 338). Соединив точки Дх и Ah, мы получим выпуклый
ife-угольник Д1Д2 ••• Аь-1АЛ. Очевидно, что сумма углов (k + 1)-
угольника Д1Д2 ••• ^k^k+i равна сумме углов 6-угольника
AtA2 ... Ак плюс сумма углов треугольника Но сумма
углов 6-угольника ДхД2 ... Ак по предположению равна (6 — 2) я,
а сумма углов треугольника ДхДдДд+х равная. Поэтому
Sft+1 = Sk + я = (6 — 2) я + я = (k — 1) я.
Итак, оба условия принципа математической индукции выпол-
няются, и потому формула (1) верна при любом натуральном л > 3.
Упражнения
2106. На сколько треугольников может быть разбит выпуклый
л-угольник своими непересекающимися диагоналями?
2107. Доказать, что при л > 3
2" > 2л + 1.
2108. При каких натуральных значениях л справедливо не-
равенство
2я > л2?
* Эго утверждение верно и для невыпуклых многоугольников, если, правда,
стороны их пересекаются только в вершинах. Мы же для простоты ограничиваем-
ся лишь выпуклыми многоугольниками.
254
Замечание и методу математической индукции
§ 264
Доказательство методом математической индукции состоит из
двух этапов.
1-й эта п. Проверяем, верно ли утверждение при п — 1 (или
при п — р, если речь идет о методе, описанном в § 263).
2-й этап. Допускаем, что утверждение верно при п = k, и,
исходя из этого, доказываем, что оно верно и при п — k + 1.
Каждый из этих этапов по-своему важен. В § 261, рассматри-
вая пример f (п) = п2 4- п 4* 41, мы убедились, что утверждение
может быть верным в целом ряде частных случаев, но неверным
вообще. Этот пример убеждает нас в том, насколько важен 2-й
этап доказательства методом математической индукции. Опустив
его, можно прийти к неверному выводу.
Не следует, однако, думать, что 1-й этап менее важен, чем 2-й.
Сейчас мы приведем пример, показывающий, к какому нелепому
выводу можно прийти, если опустить 1-й этап дока-
зательства.
«Теорема». При любом натуральном п число 2«+1
четное.
«Доказательство». Пусть эта теорема верна при п = k,
то есть число 2k 4- 1 четное. Докажем, что тогда число 2 (k 4- 1) 4* 1
также четно.
Действительно,
2 (Л 4- 1) 4- 1 = (2k 4- 1) 4- 2.
По предположению число 2k 4- 1 четно, а поэтому его сумма с
четным числом 2 также четна. Теорема «доказана».
Если бы мы не забыли проверить, верна ли наша «теорема»
при п = 1, мы не пришли бы к такому «результату».
ЗАДАЧИ НА ПОВТОРЕНИЕ ВСЕГО КУРСА АЛГЕБРЫ
И ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
2109. На одном складе а тонн угля, на другом b тонн. Еже-
дневно на оба склада поступает по с тонн угля. Через сколько
дней на первом складе будет угля в 2 раза больше, чем на
втором?
2110. Два крана, работая одновременно, наполняют сосуд
за 6 ч. За какое время наполняет сосуд каждый кран в отдель-
ности, если известно, что один первый кран наполняет сосуд на 5 ч
дольше, чем один второй?
2111. Поезд был задержан на 16 мин и нагнал опоздание на
перегоне 80 км, увеличив скорость на 10 км/ч по сравнению с обыч-
ной. Найти обычную скорость поезда.
2112. На вспашку поля один тракторист тратит времени в
1,2 раза больше другого, но на 3 ч меньше третьего тракториста.
Работая вместе, три тракториста вспахали поле за 4 ч. За сколько
часов может вспахать поле каждый из трактористов?
2113. Велосипедист совершил поездку из А в В и обратно.
Путь состоял из подъема, горизонтального участка и спуска.
На горизонтальном участке он ехал со скоростью 20 км/ч, на
спуске — 25 км/ч, а на подъеме — 15 км/ч. Из А в В велосипедист
ехал 2 ч 22 мин, а из В в А — 2 ч 14 мин. Определить
длину подъема и длину спуска, если горизонтальная часть пути
составляет 30 км.
2114. Два самолета вылетают одновременно навстречу друг
другу из городов А и В, расстояние между которыми равно
1800 км. Встреча между ними произошла через час после вылета.
Первый самолет прибыл в город В на 27 мин раньше, чем второй
в город А. Найти скорости самолетов.
2115. Один сплав состоит из двух металлов, входящих в отно-
шении 1 : 2, а другой содержит те же металлы в отношении
3 : 4. Сколько частей каждого сплава нужно взять, чтобы полу-
чить третий сплав, содержащий те же металлы в отношении
15 : 22?
256
2116. Два пешехода, находясь друг от друга на расстоянии
10,2 км, отправляются одновременно из пунктов А и В, двигаясь
по прямой АВ. Они встретятся через 1 ч 12 мин, если будут идти
навстречу друг другу, и через 6 ч 48 мин, если будут идти в одном
направлении. Найти скорость каждого пешехода.
2117. В шахматном турнире двое из участников выбыли, сы-
грав по пять партий каждый. Поэтому на турнире было сыграно
всего 38 партий. Сколько участников было в начале турнира?
Сыграли ли между собой выбывшие из турнира шахматисты?
2118. Пароход идет от Горького до Астрахани 5 суток, а от
Астрахани до Горького — 7 суток. Сколько времени будут плыть
от Горького до Астрахани плоты?
2119*. Два конькобежца выбегают одновременно: первый из
Л в В, а второй из В в Л — и встречаются на расстоянии 300 м
от А. Пробежав дорожку АВ до конца, каждый из них поворачи-
вает назад и встречает другого на расстоянии 400 м от В. Найти
длину дорожки АВ.
2120. Решить уравнения:
а) а2х — 1 = а 4- х;
б) ах = b — х‘,
. а (1 — bx) b 4- а2х ах (а2 4- Ь2),
а + b а — b а2 — Ь2
2121. Решить уравнения:
а) | 2х — 3 | = а-,
б) | 4 — 5х | = 18 — х |;
в)* |х+1|+|х-1|+|х-3| = 3 + х.
2122. (У с т н о.) Сколько решений имеет каждая из данных
систем уравнений:
а) (х — 2у — 0, г) (х — 9у — 0,
[Зх — у = 1; (0,5х — 4,5у = 2;
б) Г4х 4- 5у = 3, д) (2х — Зу — 5,
\2х — бу = 0; |4у — 6х = 7?
в) (х — 0,5у = 3,5,
\2х — у = 7;
2123. Решить системы уравнений:
а) ((а—1)х —у= 1,
|х 4- ау = а;
(2х — ау = а + 1»
(ах— 2у = 1;
х у
9 Заказ 1159
257
2124. Найти действительные решения систем уравнений:
а)
1 1 1
х у — 20’
ху = 20;
'№ — у2 = а,
х — у = Ь;
(х2 va
б) У+7 =3’
х 4- у = 2;
г)
х + у = а,
ху = Ь.
2125. Доказать неравенства:
а) _^±*_<_£_+_±_
1+а + 6 1 +д 14-Ь
б) а + 4Ь > 4 УаЬ
В) + iZ > + ' ;
b а у а у b
. а 4- bx* _ о г—
г) >2^аЬ
(а>0, 6> 0);
(а>0, 6> 0);
(а > 0, &>0).
2126. У продавца неточные весы (коромысла весов имеют
различные длины). Зная это, продавец отвешивает каждому по-
купателю половину товара на одной чашке, а половину — на
другой чашке весов, думая, что тем самым он компенсирует неточ-
ность весов. Прав ли он?
2127*. Доказать, что из всех треугольников с данным пе-
риметром Р наибольшую площадь имеет равносторонний тре-
угольник.
2128. Доказать, что для любого острого угла ф
tg ф + ctg ф > 2.
2129. Решить неравенство
х —6
1 — х
2130*. Для каких значений а неравенство
х2 4- ах — 2 _ о
□ TV
хг — х 4-1
удовлетворяется при всех значениях х?
2131. Решить уравнения:
а) х— 6 = 1 -4-]/" х — 1;
б) /х^Т 4- )/Зх4- 1 = 2;
в) ]/~х — 1 4- j/x — 4 = 3.
258
2132. При каких значениях а уравнение
(а — 3) х2 — 4х — 2а = О
имеет:
а) действительные корни;
б) действительные корни одного знака;
в) действительные корни разных знаков?
2133. Решить уравнения:
а) /(х —2)а = — (х — 2); в) /(х — 2)8 + ]/ (х — 4)2 = 2.
б) /(ха —х + I)8 = х8 — х 4- 1;
2134. Построить график функции:
У=/х2+/(х-1)8.
2135. Что больше:
а) 3е00 или 6300;
_ 3_ _ 3_
б) (2/3)2 или (3/2) 2;
_ _£ _2_
в) (2/21) 7 или (4/5) 7?
2136. Средний годовой процент прироста населения из года в
год остается постоянным. Если бы он увеличился на k%, то через
п лет численность населения была бы в два раза больше, чем при
нормальных условиях. Определить годовой процент прироста
населения.
2137. Найти косинус, тангенс и котангенс угла ф, если
5
sin ф = —.
г 13
2138. Найти синус, тангенс и котангенс угла ф, если
3
cos ф — — —.
2139. Найти синус, косинус и котангенс угла ф, если
tg<₽ = -р
2140. Найти синус, косинус, тангенс и котангенс угла
. 1
arcsin —.
3
2141. Найти синус, косинус, тангенс и котангенс угла
arccos ( — — \
\ 13/
2142. Найти синус, косинус, тангенс и котангенс угла
arctg (- (J.
9*
259
Доказать тождества (№ 2143—2147):
2143. 1/+ 1/1+е«= _ 2|cosec|а
г 1 + cos а r 1 — cos а
n 1 л л tg2 а + c^g2 а— 6 ,
2144. -——— -----------= cos 4а.
tg2 а + ctg2 а+ 2
("4" а) 1 + sin 2 а
2И5- \ = •
2146. 2 sin 5а sin За + cos 8а = cos 2а.
2147. а =tg»(---\
1 + sin а \ 4 2)
Упростить выражения (2148—2150):
2148.
1 — sin" а — cos0 а
1 — sin4 а — cos4 а
2149. ]/ j cos ср — у 1—C0S(p
2150. a) tg 1° • tg 2° • tg 3° • . . . • tg 89°;
6) lg tg 1° • lg tg 2° . . . • lg tg 89°.
2151. При каких значениях а данные уравнения имеют дей-
ствительные корни:
a) 1g2 х — 1g х + а = 0;
б) cos2 х + cos к + а = О?
2152. Числа а, 0 и у составляют арифметическую прогрессию
с разностью -у- . Доказать, что
tg а • tg 0 + tg 0 • tg у + tg у • tg а — —3.
2153. Доказать равенства:
a) tg 20° tg 40° tg 80° = /3;
6) sin 18° cos 36° == 0,25;
D) l~tg2 15° = /з~
1 + tg« 15° 2
2154. Вычислить:
a)* sin
arccos (—0,8) ;
6) sin (arctg2 + arcctg (—2)J;
в) tg (1 arcsin (—0,6) j.
260
2155. Проверить равенства:
a) arctg4- arctg у =
б) arcsin 0,8 — arccos 0,6 = 0.
Решить уравнения (№ 2156—2179):
2156. sin х — cos 2х = 2.
2157. sin х cos Зх = —1.
2158. cos 2x = sin x cos 2x.
2159. 2cos2x — 7sinx —5 = 0.
2160. = 0.
tg*
2162. У 3 cos x = — sin x.
2163. cos2x—3sinx cosx 4-1 =0.
2164. cos (cos x) = sin (sin x).
2165. sin x cos x = —-— cos2x.
/3
2166. cosx ctg2 — = —.
& 2 2
2161. 3sinx — 2cosx=6.
= —1.
2168. tgx — tg^y — xj
2169. 3 cos 4x = 7 sin 2x.
2170. 2 cos2 x + sin2 x = — sin 2x.
2
2171. cos 3x cos 5x = cosx cos 7x.
2172. sin2 2x + sin2 x = 1.
2167. sin4x =14- cos2x.
2175. cos2x 4- 3 cos2 — = 2.
2
2176. cos7x — sin5x =
= ]/3 (cos 5x — sin 7x).
я \ . я
— =sinx4-sin—.
3 / 3
л \ _
~
2173. sinx — T/3cosx = — 1.
2174. sin x — 4 cos x 4- tg x = 4.
Решить системы уравнений (№ 2180—2183):
2178. tg(.
= tgx + tgy.
2179. (tgx)C0SX=(ctgx)C0s*
2180*.
2181.
2182.
, 2л
x 4- у = —,
Л 3
14-/3
sm x 4- cos у = ——.
2Sin x + cos у_ ।
gSin2 x 4- cos2 у = 3
. , 1-/3"
sin x 4- cos у = ——»
VT
sin x • cos у = — —
^4
2183.
COS X cos у = —,
4
Ctg X ctg у = —4.
i 4
2184.
Является ли последовательность всех положительных
корней уравнения cos — = 0:
а) конечной; б) ограниченной?
261
2185. Крайние члены арифметической прогрессии равны 5
и 25. Найти два равноотстоящих от них члена, произведение ко-
торых равно 189.
2186. Найти четыре числа, из которых первые три состав-
ляют геометрическую прогрессию, а последние три — арифмети-
ческую; сумма крайних чисел равна 14, а сумма средних
равна 12.
2187. Арифметическая и возрастающая геометрическая про-
грессии имеют первые члены, равные каждый 2, и равные тре-
тьи члены. Второй член арифметической прогрессии на 4 боль-
ше второго члена геометрической прогрессии. Найти эти про-
грессии.
2188. Найти острый угол прямоугольного треугольника, ес-
ли известно, что его стороны образуют геометрическую про-
грессию.
2189. Дан правильный треугольник, сторона которого равна
а. В треугольник вписан круг, в круг снова вписан правиль-
ный треугольник, в треугольник — круг и так далее до беско-
нечности. Определить сумму площадей всех кругов и сумму длин
всех окружностей.
2190. Найти бесконечно убывающую геометрическую про-
грессию, если ее сумма равна 3, а сумма квадратов ее членов
равна 4,5.
2191. При каких значениях х числа 1g 2, 1g (2х — 1) и 1g (2х 4-
4- 1) образуют арифметическую прогрессию?
2192. Доказать, что log2 3 — число иррациональное.
2193. Вычислить:
a) log3/3- 27;
б) lg 1|-1g 150;
в) logntg^S
4
Д) - —5;
\ о )
\ O,0g _15
е) 2 2/2 .
Решить уравнения (№ 2194—2208):
2194. 2^ • 9х—2-63х~*4- 42х~‘ • 34х“2 = 0.
2195. 9х —2 2 = 2 — 32х-‘.
2196. 8х + 18х — 2 • 27х = 0.
2197. 3х — 50 • 2х = 5 • З2 - 2Г
2198*. (К2 + ИЗ Г+ (К/2 — /з)*= 4.
2199. lg (х + а) = 1g х + lg а.
2200*. x'gx’-3 = 100.
2201. 1g (Зх — 4) = lg (6х 4- 2) — 1.
262
2202. xloe‘x" + = 1.
X
2203. log! 4x — log312x = 1.
2204. lg2 x3 — 5 lg x2 + 1 = 0.
2205. Vlg ( 4ГГ + 2‘+/Г + 9992 ) = 2.
2206. 2x — lg (52r + 4x — 16) = lg 4х.
2207. log3- +log3x= 1.
2208. lg sin x = lg cos x.
2209. Вычислить:
a) log7 log7 7 Vl VI ’ в) log3 5 • log25 27;
2+ lg!6
6) 10 ; r) log^ b, если logad a = 4.
2210. Доказать, что уравнение lgcosx = cosx не имеет
корней.
2211. Что больше:
a) logg 2 или log23; б) у^0,01 или у^0,001 ?
2212. Найти все значения х, для которых
'6^44 >'s —4-
2213. Решить системы уравнений:
log2 (*У) = 5,
X 1
в)
а> log!
2
(log2 х-4- log2 у = 5,
llog2 (x2 + у2) = loga ЮН-3;
lg* • lg(*У) = 2,
lg- = 3;
у
г) |'J<27-l/t<2^ =1/128,
Ug (* + у) = 1g 40 — lg (х — у);
д) (5(lgyx + lgxy)= 26,
[ ху = 64.
263
2214. Световой луч, проходя через пластмассовую пластинку,
теряет своей интенсивности. Сколько таких пластинок можно
поставить на пути луча, чтобы при прохождении через них
потерялось не более — его первоначальной интенсивности?
2215. Построить графики функций:
а) у = I loga х |; б) у = log2 | х |; в) у = log2 | — х |.
2216. Найти области определения функций:
а) у = У — 5х2 4- 8х 4- 4;
б)
_____У*_____
Ух 4- 1 — V1 —х
ч 1
г) у=~^~
23x-l _ j
д’ у =
в) У =
2217. Доказать, что функция
е) у = lg (1,5 4- sin х 4- cos х).
/| I 2 г)а
/(х) — — - четная, а функ-
ция f(x) = lg нечетная.
1 —X
2218. Функция Дирихле определяется следующим образом:
D (х) = /0, если х рационально,
[1, если х иррационально.
а) Является ли эта функция четной?
б) Доказать, что эта функция периодична, причем любое рацио-
нальное число является ее периодом. Есть ли у этой функции наи-
меньший положительный период?
в) Доказать, что никакое иррациональное число не является
периодом данной функции.
2219. Доказать, что производная периодической функции является периоди-
ческой функцией. Привести примеры.
2220. Доказать, что производная четной функции есть функция нечетная,
а производная нечетной функции—функция четная. Привести примеры
2221. В каких интервалах существуют функции, обратные
данным:
а) У = tg(-J — -у); б) у = cos2х?
2222. На одном и том же чертеже построить графики данной
и обратной к ней функций:
а)у = 2х —1; б) у = 3*+1.
264
2223. Найти пределы:
ч х/х-З/З
a) hm ——-----
х-з /7 —/I
X3
б) Чг/ттг-;—1
, „ 1 — cos 2*
в) hm ——---------
х-.о Зх2
, sin (х + а) + sin (х — а)
г) lim -----------------------
х~о х
2224. Вычислить
х25 — 8х14 + Зх4 — 4ха — 10 при х = I.
2225. Доказать, что числа j-j-4 и являются противопо-
ложными.
2226. Выполнить указанные действия:
34
1 — i ’
В) (2 + 0(1 — 0.
' 3 — 21 ’
г) (2+i/^)3 + (2 — iV2 )’.
2227. Доказать, что кубы сопряженных чисел представляют
собой сопряженные числа.
2228. Найти действительные значения х и у из уравнений:
a) (Xi — у)2 = 6 — 8i + (х + iy)a;
б)
х—2 у—3
= 1 — 3t;
. i i 1
В) - + - + Т =
х у 6
2_____1_ + 5£
х у у'
2229. Показать, что произведение любых двух корней уравне-
ния х3 = 1 есть также корень этого уравнения.
2230. Вычислить
(1 + cos а + i sin а)л.
(Указание Воспользоваться формулой Муавра.)
2231. Показать, что если п кратно 3, то
/_1 + //3*\л /—1 — //3 \л= 2
\ 2 / \ 2 / "
2232. На плоскости даны две точки, соответствующие ком-
плексным числам: гх = хг + iyi и г2 = ха + iya. Где находится
точка, соответствующая числу (zt г2)?
А
265
2233. Выражение (cos ф -f- / sin ф)5 преобразовать двумя способами:, с по-
мощью формулы Муавра и с помощью формулы бинома Ньютона. Сравнивая
результаты, выразить sin 5ф и cos 5ф через sin ф и cos ф.
2234. Тело движется по закону s (/) =» /3 (s — путь в метрах, t — время
в секундах). В некоторый момент т сек его мгновенная скорость равна средней
скорости в интервале от сек до t% сек (fa > /t). Доказать, jto < т < t*
2235. Написать уравнение касательной к кривой у в точке с абсцис-
сой к = 4.
2236. Написать уравнения касательных к параболам у = х2 и у = (х — 2)1
в точке их пересечения.
2237. Найти производные следующих функций:
a) sin4 х\ в) cos6 (х — 1); д) (х2 + I)6;
б) cos3 2х; г) cos1 (2 — х); е) (3 — 2х)3.
2238. Тело совершает гармоническое колебание с амплитудой Д, частотой го
и начальной фазой ф. Найти скорость и ускорение этой точки
2239. Могут ли две разные функции иметь равные производные? Ответ по-
яснить примерами.
2240. Исследовать данные функции и построить их графики:
б) у = х6— 4х; г) у = cos х (1 -f- sin х).
2241. Пусть С* = Сгп. Доказать, что либо k = г, либо k = п — г.
2242. Доказать, что 1000-е производные функций (2х2 4- 7)100 и (7х2 4- 2)100
равны между собой.
2243. Пусть (х — 2)100 = аи 4- atx 4- аах2 4- ... 4- а10и х100. Найти:
Я) ^97»
Q До + + а2 + • ’ ' + °100»
в) + 2^2 4- Зав + • • • +
2244. Доказать, что квадрат суммы п чисел равен сумме квад-
ратов этих чисел, сложенной со всевозможными их удвоенными
попарными произведениями.
2245. Доказать, что если Т — период функции f (%), то при
любом натуральном п пТ — также период этой функции.
2246. Доказать тождество
lg (а,а2 . . . ап) = lg + lg а2 + . . . 4- lg ап
(fix > 0, аг > 0, . . . , ап > 0).
2247. Доказать, что при любом натуральном п sin nr и cos пх
выражаются рационально через sin х и cos х.
2248. Доказать неравенство
| Oi 4- аа 4- а8 4- ,.. + ап | < I Oj I 4- I а2 | 4- • . • 4- I оп |.
266
2249. Доказать тождество
)п радикалов
п я
= 2 cos--------
2Л+1
2+ V Ч + /2+... 4-/2 + у~2~
2250. Проверить справедливость неравенства
sin2na + cos2na < 1,
где п — натуральное число.
2251. Доказать, что производная суммы любого фиксированного числа диф-
ференцируемых функций равна сумме производных этих функций.
ОТВЕТЫ К УПРАЖНЕНИЯМ
ТРИГОНОМЕТРИЧЕСКИЕ ТЕОРЕМЫ СЛОЖЕНИЯ
VII
1024.
1) 1; 2)7; 3)5 /2; 4) 5; 5) 3 /65; 6) 25. 1025. 2 1/2 +^5 +3
1026.
б) -
1027. М (/3; 1); N (Д ; 0). 1028. а)
£
ЕЕ ; В) Е2. ; г) — ; д) Е2.; е) — 1. 1029. cos а. 1030. —. 1031. 0.
2 2'22 2
М
(л \ / л л \
а=£ — + лл I. 1033. 1 I а ± у + лл; 0=£ — + Лл I. 1034. tg а tg 0.
1035. а)24~5ГЯ 6 ЗКЗ+< 103(. & „ 204 Д/?-/5~
_ 65 _ 10 _325 325 _ 9 __
1038. Е5 ~i Е—. 1039. 4 . 1040. a) -Е2. ; б) I; в) —; г) Е3- ; д) Е3. .
9 5 ' 2 ' ' 2 ' 2 ' 2
1044. 1 (а лл). 1045. 1 1а =/= лл, 0 =/= — 4- kjij. 1046. tg а ctg 0.
1047. cosacos0^a — 4-лл, 0 =£ — + 6л j. 1048.—0,44-0,3 )z3, если л4-
4-2лл< а < у + 2ил; —0,4— 0,3 У 3, если ух4-2/гл< а< 2л4- 26л. 1049. О
и — Е3?. 1050. — — И — — . 1051. — (1 + /10). 1052. Е.15.~2. 1053. ЕЕ.
8 65 65 9 6 10
13 r- 1 16 56 56 16
1054. — . 1055. —2— /3. 1056. б) —— ; г) 1. 1057. — . 1058.—; —.
14 И 3 63 33 33 63
9 __ _ _____________ 1л.
1059. — 1. 1060. — (/2 4-/5). 1061. —2 /2. 1062. arctg—. 1063.—.
3 5 2
24 7
1065. sin 2а =—0,96; cos2а =—0,28. 1066. — —; — —. 1067. 0,98.
7 25
1068. а) В 1-й; б) во 2-й; в) в 3-й; г)
1 1
1072. От — — до 4- — ,
(а У= 45°4- 180° • л). 1078.
включая эти два
— sin 2а. 1081.
1 2
в 4-й. 1069. в) —; г)—/3.
2 3
числа. 1075. tg 2а. 1077. — -^- ctg 2а
а
б) sin а= 2 sin —
2
если
— л 4- 4лх < а < к 4- 4лх,
sin а =— 2 sin
sin2 — , если л4-
2
268
а 1 / пл\ /
4- 4пп < а < Зл 4- 46л; cos а = 1—2 sin2 —. 1082. — а — 1. 1083. 2 1а
2 2\ 2 / \
пл
т
(Л \
— 4- пк I
2 /
3 24 1
1088.----. 1089. — 1090. —. 1091
4 7 2
1087. cos а — sin а а^= — + пл I •
\ 4 /
4 7 84
>098. а)-; б)--. »03.
а=£ + 2пл j . 1105. 1^0,8, У 0,2 и 2, если 4- 4пл <
к Ал ] Ал
5
у л 4кл < а < Зл 4“ 4£х.
< а < л 4- 4лл; —1^0,8, — У0,2 и 2,
если
1106. 34-2 ^2 или 3 — 2 /2. 1107. /0,1. 1108. /О. 1109. - у.
1110. — —. 1111. —. 1112. — 2. 1114. 1+^2 . 1115. X3 +. £?-.
3 2 2 4
1116. X-3 + ^2 . 1117. У^2—1 . 1118. .У3~2.. . 1119. ^3—1 . 1126. — —
4 4 4 4 2
— sin 10° — cos 20° 4- sin 50°. 1127. cos 5° — cos 75° -|- cos 35’ — . 1130.
J/24-/3. 1131.0. 1132. EIL. 1133. 1134. 1^24-/3. 1135. 0.
2 2
1 Л
— 4- sin a = sin — 4- sin a = 2sin
2 6 -
— /7— /3? 1144. —K2-. 1145. — 1146. El2-. 1147. —E2.
2 2 2
\ л ( Л \ (
1139.
1143.
1151.
1142. 0.
2
. . . . л a\
4- cos a =2 cos — 4- cos a == 4cos — 4- ~ X
J \ 4 I \8 2 /
У2 4- 2 cos a = 2
. 11SS. — Й-
] \ 4 / \
---- cos 2a. 1156. 2 У 2 sin — • sin
2---2
— — cos2a. 1165.2/2^ 1166. —2.
2 6/ / л \
2 sin [ — —a
л л \ \ 3 I
a=/= — 4-лл, B=£—4-6л]. 1170. а) ------------ . 1184.
2 2 I cos a
л jx
7 ~"2t
[а л\
1158. 4cos 4~ T" Г cos
\2 6/
X cos
1169. S^±61
sin (a—p
I ЛХ
-|,g5 -
У= у (14-sin4x)—
один из примеров; другой укажите сами. 1186. у=
меров; другой укажите сами. 1215. Л>0, о>>0, 0< ф < 2л
5
1219. 50 герц. 1220. Минимальные значения при /=—4-
значения при t —— — 4- 4п;
5
3 '
при
один из при-
шли —Л < ф <л).
максимальные
4
t = - V +2п-
о
4n,
нулевые значения
13л 2пл
1221. а) Минимальные значения при /=——4-—— , i
ом о
л 2лл л пл
при t = —; 4-----J нулевые значения при /=— тт + 77 •
10 3 15 3
/ л\ / 4 \
I х—— 1. 1224. 5 sin 1*4- arctg — 1. 1225.
12\ . /
х—-arctg—-j. 1227. 25sin 12x 4- л 4- arctg —
1226.
максимальные значения
1222. 2 sin ( *+ —).
\ 3/
24\
7 J
1230. a) —5; 5;
269
б) 0; 5; в) — 13; 13; г) —20; 30; д; 0; у^2; е) минимальное значение —=-,
__________________________________________ л V
максимального не существует. 1234. А = у 2, w =2 , ф=——. 1236. Л=5,
4
arctg liJLJL 1255. 2пл.
3 1 1/ 5
w =«= л, (p=arctg —. 1254. arctg—--------+ пл;
4 2
л пл
1256. х — любое число. 1257. Т" + т- . 1258. пл.
6 3
л л пл
1259. — — 4-пл. 1260. —
4 8 ’ 4
л л пл . л
1261. пл. 1262. ± -г + пл. 1263. (—If — + — . 1264. (2п 4-1 )п; (—l)*+l —4-2/гл.
6 12 2 3
1 __ 2 1
1265. —((—Ifarcsin (р 3—1)4-пл]. 1266. ± л 4-2пл. 1267. ± arccos — +
2 о__________VTZ 3 л 4
4-(2п+ 1 )л. 1268. (—If arcsin -—LJJ 4-пл. 1269. (—If ~ + пл. 1270. 2пл.
д 10 6 "/* г>
2/гл— 2arctg 3. 1271. пл, ± “Г +/гл. 1272. Нет корней. 1273. arctg —-(- пл.
6 2
1 1 пл /гл
1274. arctg у 4- пл. 1275. arctg — + пл; — arctg 2 4- /гл. 1276. у ; у .
пл пл пл пл _ л пл
1277. —. 1278. —; —. 1279. —. 1280. пл. 1281. Если а = — 4-— ,
8 3 8 5 4 2
то х — любое
число, если
2л
± ~ + 4/гл.
о
1283.
1285.
1288.
1291.
л пл
— 4- —- , то
4 2
л
— 4- 2/гл.
2
1282. (2п 4- 1) л;
л 2
— 4- лл; ± — Л 4- 2/гл.
& О
1 . ПЛ
; :. 1287. —.
3 1 2
„ я пл я fen
; 150°4- 360°п. 1290. — 4- — ; — 4- — .
8 4 4 2
если а 4* 04- 2 пл, то
л 2пл
Ю + Т ’
л
— — 4-2/пл. 1296. — ;
4(2fe4-l).
х — любое число; если а =£
4- 2fen. 1303. ± arccos V -!7 ~~3 4- 2пл.
7л
— 4-2fen.
О
корней
нет.
2пл;
1284.
пл; (— 1)*+1 4- /гл.
6
л кл
пл\ — 4- — . 1289. 60°4- 360°п;
пл 4 2
у . 1292. Если а=Р4-2пл, то х — любое число;
л
1288. ±
2 arccos — + 4пл.
л л
х —— — 4“ а + 2/гл; х = — — 4~ Р + 2тл. 1293.
2 2
2пл л
— ; —Ь kn-
3 4
не равно
2
2пл л
— ; — 4- кл\ (2m 4- 1) л. 1295.
5 2 Лд
- 2 ....
± — 4- fen. 1297. —
3 пП 8
1299. — . 1300. Если
пл
8
л
-+
пл
" 3 ’
1298. пл.
пл
, то корней
„2 я
1304. — 4-—.
4 ~ 2
, где п
пл
а= —- , то
2л . 2_
3 ’
1 2 пл
2
1301. 2пл; ±
пл /гл
1305. — ; — . 1306. ± — arccos — 4- — . 1307. 4- 2пл;
6 4 12 7*6 2
нет.
4
л
2
1308.
"12 7’6
j- 4-2 пл; ~ 4-26л. 1309. у 4-пл; 4- ~ . 1310. 2arctg }^7 4- 2пл; (2/г 4- 1 )л.
л 7л
1311. + ”^ + 2/гл*
5 л
arctg у 4- 1314. у 4- 2лл;
пл л /гл 2л
181в- 7Г ’’ Т+ТГ- ,317-
2 8 2 3
если а»0; бесконечное множество, если а =/= 0; г) 3.
” 18 ’ 6 - •
л
1312. — 4- пл; (2k 4- 1) л. 1313.
4
— 2 arctg (4 4- /15)4- 2fen. 1315.
(2п+ 1)л;
л
± Т +лл.
4
4-2пл. 1318. 0,94. 1319. 0,17. 1320. а) 1; б) 1; в) 1,
1321. В том и
270
только в том случае, когда сумма этих углов кратна л и тангеноы_ их
существуют. 1322.
да — 6а/> +
“ (<> + 5)2
- - Ф . кч Ф
/2 +^6 .
4
24
!324. —
а) 2 sin— ; б) —2 cos —. 1330. 2 cos a cos 2а cos 5а.
Зл
/24-^6 1323 _ 4(a-fc)/at>
4 ' ' (а 4- Ь)г
1328. — sin (а 4- ₽) (р а 4- пл). 1329.
1338. -^4-лл. 1339.
1341.-^ 4-2лл; 2/гл.
2
2 ’ 2
л Зл л л
± — 4- лл; ± — 4-Лл. 1340. — — +пл; — — 4* 2лгл; 2Лл.
1342.
1346.
~ 8
л Лл лл л . л
лл; — 4- — . 1343. — . 1344. — — 4- пл. 1345. — 4-лл; — arctg — 4-Лл.
8 2 5 4 2
,, л л Лл л ш
Нет корней. 1347. — + лл; ~ + у ;
- 3 '
л тл . л
Го + Т- 7+*»•
5
Л ЛЛ Л Л л
1349. —4-—. 1351. —--|-лл;——- + 2Лл; л+2/лл. 1352. х =— + 2лл,
8 2 4 2 6
л
у= — — 2лл.
* 6
л л л
1353. х = — + 2лл, у = — — 2лл. 1354. х = — +(л+/72)л.
4 4 4
л л л л
У=— — 4- (л— т)л; х =— — 4-(г4-8) ”. У = ~ +(г—ь)л; х=— — 4- (k 4-I) п,
1 £ 1 £ *т IX
у= Y 4-(* — 0х=~ т 4-(s4-О”. У =^ + (8 — /)л. 1355. к =
4 4 12
= -7 4- (п 4- т) л, у = 4- (л—/л) л; х =— -7 4-(Л-Н)л, у=— 4-(fe — 1)п.
О d d d
1 1/3“ 1 pT
1357. cos x= — , cosy —— или cos x , cos y=— Д—- ; отсюда полу-
2^2 2 2
чается 8 групп решений.
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
VIII
1358.
2_ 6,5
а) б3 ; б) в) (4) ; г)
\ d /
/ip\5r
In/
1
1361. —. 1362. 2 4 ,
9
1368. а) х Ф 0; б) |х|>1; в) множество всех действительных чисел.
1369. Больше 1: 2), 5), 6), 7); меньше 1:
а = 1, то х и у — любые числа. 1377.
Г- 3
log22 /2 = -.
1
1380. log. ——
Г/3
(1 у^зГ*
—) ;
л )
1373. Если а 1, то х =у; если
lee. ^ = - Т:
г- 1 , 1 5
log, V 3 =— — ; log, —— = -
Т 2 2
1381. а) — I; б) 0; в) ± ; г) 0. 1383. 3) 243; 4) 81; 5) 7; 6) 1; 7) ; 8) 49;
\ 4 J \ 3 /
1_
2 ’
9) 100; 10) — ; 11) —; 12) 20 736. 1390. а) х >—1; б) множество всех чисел;
6 25
г) х < 0; д) х у- 0; е) х < —2; х > 1; ж) 2 < х < 3; з) множество всех чисел.
271
л 3 л 3
1391. а) 0 < х < л; б) 0< х< — ; — л < х < 2л; в) 0 < х < ; л<х< —л;
л 3
г) 0< х< —-; л < х < —• л. 1392. а) Ни наибольшего, ни наименьшего зна-
X л
чения функция не имеет; б) наименьшее значение функции равно нулю
(при х = 1), а наибольшего не существует. 1395. а) х > 3; б) | х | > 2;
в) 0 < х < 2; г) х > 2; д) х > 5; е) | х | < 1. 1396. а) а>1; б) а < 1; в) а >1;
г) а > 1. 1397. а > 1. 1398. а) 2 и 3; б) 1 и 2; в) - 2 и — 1; г) - 4 и ~3.
1400. 5) — 3; 9) — 3; 10) —2. 1403. —0,0762, 0,0762. 1404. х > 1. 1405. х< 1,
х > 2. 1406. На log2 10000. 1414. а) 0,6309; б) 1,8927; в) 2,2618; г) 0,4421.
1417. Нет. 1418. a) 1g 3 + 7 1g а; б) 1g 15 + 3 lg а + 3 lg b + 7 lg q в) ylgfl +
5 4 2 1 3
+ — lg b-, r) — lg a + — lg b. 1419. a) — (lg (a + ft) — lg (a—ft)]; r) — (Iga-
/ О и Z 0
3 1
— lg b — lg 2). 1420. a) — у lg cos <p; 6) — (lg 2 + 2 lg cos ф — 3 lg sin ф).
2 113 2
. „VC.- -O- 6) — lg3+ — lg 4 — — Iga — — lg ft;
О Ч О Я о
1 5
— (3 lg 5 + 7 lg m + 4 lg n). 1422. в) — (lg a — lg ft). 1423. a) 6; 6) 0,5; в) 4;
18 8
Ю/ST a(a + b)n 1 24
"/---fc ’ i/— r
ya — ft у a '
1421. а) — (lg ft -lg a— 31g 3); б)
О
В)
!8' “ ’ ’
32. 1424. а) 2; б) 16; в)
Г)
1»/a4fc5 . 1426. a) tg <р; б) 2 cos
и + b 2
в)
b\a—_W_.
a\a + ft)3’
л = 3 4-0,1415 ... ;
— 2,37’=—3 4-0,63; —7 = -7 4-0; — л =—4 4-0,8584... . 1431. a) lg 6 «
к 0 4- 0,7782; 6) lg 15 « 1 4-0,1761; д) lg ± «—24-0,9208. 1433. « 1,4651;
« 1,2894; « 1,8431. 1434. a) « 2,304; 6) « 10 000; в) «_£,4048; г) 0/102858;
д) «0,0009426; e) «0,01001. 1438. a) 1,2907; 6) 15,8640; в) 66,2361;
r)0,6496; д)0,7112. 1440. «186,5. 1441. «3,870. 1442. «—0,04146. 1443. «88.
1444. «0,3224. 1445. «1,617. 1446. «1,087. 1447. «1076 см*. 1448. «5738см'.
1 4
1449. г) — —; з) — ; к) 4. 1450. а) —4; в) 3; г) 7; —1; д) если а=1, то х—
любое, если а ф 1, то xi = 2, х2 = 3; е) 7. 1451. а) 3; б) 1; е) 2. 1452. б) 1;
г) ; е) 3; ж) ; к) 24. 1453. а) 2; б) 1; в) 3; г) 4; д) 0; 1; е) I; log3-y ; ж)0;
Z 1 о 4
3) log2 1+J^- 1454. а) 0; б) 0; в) 0; г) 0; д) 1; е) '^5^: ж) если
а ft, то х = 0; если а = ft, то х — любое. 1455. х —— 2, у = 0. 1456. х = 3,
несов-
д) 200;
1
78125’
1462. а) Г 00—1 ; б) 13; в) 14; 6. 1463. а) 10; 0,0001; б) 100; 1000; в) 9;
4
/ТО —1; г) 0,001; 0,1; 10; 1000. 1464. а) 1; — 1; б) 0,2; 125; в) 10;
г) 0,001, 10; д) /ТООбб; е) 0,1; 1000. 1465. а) 3; б) ; 3; в) 5; г) /5]
и
у = 4. 1457. х — 3, у = —2; х —— log29, y=log38. 1458. Система
*/“9~
местна. 1459. х = 3, у = 4. 1460. а) 10; 6) 64; в) 4; г) ~l7 —;
г о
е) 25; ж) 80; 1461. а) 2; б) у; в) 5; г) 5; д) /2"4- 1, /£-1; е) 4; ж)
/33—1 , ------ - -- - --- • ----- -........-
272
25; д) 1; е) 16. 1466. х=10/10, у= 1467. х = 2, у = 32; х = 32,
1UU / 10
х=-2, y = i 1469. * = 10, у = 4; х = 4,
уии
у=2. 1468.
у = 10. 1471. 0,6.
1472. 1,40. 1473. а) х>— 2; б) х > 3; в) х > log32; г) х < 1; х > 5;
д) х <— 1; х > 2. 1474. а) 2 < х < 5; б) 7< х <7 — ; в) х > 6. 1476. При-
мерно через 14 лет.
81
1478. а) — ; б) 2000; в)
1481. log2 7 — 3. 1483.
1
1484. аа . 1485. а) »
1477. Примерно через 8 месяцев; вторая бригада.
971/9" л пл
; Г) 0,02. 1480. а) (-1)" + ~ ; б) пл.
а) 0,1; б) в7т^» в) уравнение не имеет корней.
1
$<10’
1
1,6541; б) «0,6309. 1486. a) log, 3 ; б) logj 7 ’
/1\1е|- /1Мвг-
\5/ \7/
1491. Нет корней. 1492.
2
1487. а) 0 < х < л; б) х > 0. 1489. 31; 140.
lg 2
1g 13
Ig5—lg 3 ’
1493. 0; 1.
1494.
lg lg 7 — lg lg 5
lg7 — lg5
1495. 4. 1496.
’б У 44- К15
isos. |5О5.
logo х+ logfr* J<10
1497. 9.
1498. 100. 1499. 2.
1 Q _
1506.—z; 710.
V10
1502. a) b\ 6) b.
.SO’.
3 > r л л
— / 27. 1508. x =. пл, у — 2/гл; x = — -f- 2пл, у =—4-fen. 1509. Система не-
5 2 2
совместна. 1510. х = у=1. 1511. а) Возрастает при х >—2, убывает при
х <— 2; б) возрастает при 1<х<4, убывает при —2 < х < 1. 1512. —3< х <
<—2; х > 3. 1513. 0,01 < х < 10000. 1514. х <—4.
ФУНКЦИИ И ПРЕДЕЛЫ
IX
1518. в) При а = 0 и а
.----------------------------------------л 3
число), то f (2а) = 2f (а) V1 —(а); если — 2лл< а < — л 4- 2/гл,
если а = 0, и sin (а2), если
и 1 4- (2 — а2)3, если
не определено; при а «/= 0 и
а * 1
а +1 л л
----. 1519. а) Если —--h 2лл< а < •— + 2пл (п — любое
а— 1 2 2
f (2а) =- 2/ (а| К1 - /а (а). 1520. г) 1,
1521. ‘ ' П - л "
a) 1 4- б) 0; в) sin 2, если а = 0,
4
целое
то
а 0.
а »/= 0.
1534.
Совокупность всех действительных
1539.
1
< х < 4. 1542. х < — 2; х > 6. 1543.
5
1548. 0 < х < 1. 1550. 0 < х < —; х >
л
чисел. 1538. х — — 4-2лл.
— ~-<*< 1. 1547. х < 2;
5
2
3. 1552. х =/= 0; х ————-.
’ (2л 4-1) я
273
у + 2лл. 1568.
1
" 2
1569. б) См.
рис.
1* и 2*.
в) у > — 2; д) у < 0;
3
1570. При х < — —
возрастает. 1572.
Убывает
при х < — 5 и при
убывает,
3
- 2
3
при х > — —
< 2, возрастает
— 5 < х
3
~ 2
1
и при х > 2.
1576. Возрастает при
при
5
— —’ л + пл < х < — л 4~ пл. 1579. Возрастает в
6 6
держащем точки х = 2. 1581. Убывает при 4пл < х < 2л + 4лл; возрастает при
2л 4- 4/?л < х < 4л -f- 4/?л. 1584. Убывает в каждом интервале, не содержа-
х4- 1 2
щем точки х = 0. 1585. Указание. -----------= 1 4-------. 1586. а) Всюду
х — 1 х — 1
убывает; б) всюду убывает. 1588. Вообще говоря, нет. 1590. xmjn = 1, ут,п = 5.
1593. xmin = 2, Ут1п=— 1. 1597. хтах =— а, утах = °2• 1598. xmjn= —-~-4“2лл,
4
3
1600. xmin = —-7 ^ + 2^,
4
-. 1602.
8
6
каждом интервале, не со-
1601. —15;
функции 3) и
Ут1п —
0;
1)
42.
5), нечетные
нечетным. 1609.
и 2).
Един-
, 3
Уш in = ~ И *max =-7 Л + 2/гл, Утах = 1-
4
= — /2; хтах = ~ + 2/гл, утах = VT.
1603. —1^27 ^32~ *. 1606- Четные
Остальные функции не относятся ни к четным, ни к
ственной такой функцией является функция у =0. 1610. а) Функция f (х)
удовлетворяет условию f (— х) = ± f (х), причем одним значениям х может
соответствовать знак «+», а другим < —». В ©том случае относительно
четности функции f (х) нельзя сделать, вообще говоря, никаких выводов;
6) /(х) = 0. 1611. а) Нет; б)
_ л
1615. -
3
1625. у = |
1616. л. 1617. л.
(1
у] .
никаких
да; например, у=х3. 1613. л. 1614.
2л
1618. Зл. 1619.
1627. у =
у. 1620. л. 1621.
Данная и обратная к
4л.
л
Т
ней
274
функции совпадают. Области определения этих функций задаются неравен-
ством х Ф — 1, а области изменения — неравенством у =£ — 1. 1628. —
1632. а) Нет; б) да; в) нет. 1633. а) Да; б) да; в) да. 1634. а) Да; б) нет; в) да;
г) нет. 1660. 0. ‘ _
1666. — 2. 1667.
1661. — 10. 1662. 1. 1663. 4
2
1668. — 2. 1669. —. 1670.
4
1
1664.
2
3
8
1665. 0.
1671. 4. 1672. 4.
1673. —. 1674. 3.
4
1. Указание.
Ввести новую
1675. -------. 1677.
Зу а* 2
х /2
переменную у = -у. 1678. —g”.
X (sin х 4-cos х). 1685. 2. 1687. 9. 1688. 1.
л
переменную у = х — —. 1690. 1. 1692. — 10.
□
1
1696. 48. 1698. ——1700. 1. 1701. 0,02.
4 2
Указание. sin I + х) =
Указание. Ввести
—. 1695.
2 Гл
sin a cos а
---------, если
1694.
1702.
а
V2
2 х
новую
9
— 10’
а^О,
1, если а = 0. 1703. 2 < х < 7. 1704. — 3 < х < 0; 2<х< 5. 1705. х —•.
2
1706. Совокупность всех нецелых положительных чисел.
1708. 1—5)/"5<у<14-5К5Г 1709. 0.1 < у < 10. 1710. Вообще говоря,
нет. 1715. 2х = (2х-1 4-2-х-‘) 4-(2Л-‘— 2-*-’). 1722. 3. 1723. —4=г.
4 I' 2
12 1а
1724. —=-. 1725. — 1726. 0. 1727. 4. 1718. — —. 1729. 0. 1730. —.
Уа 3 2 Ь
а — а
1731. —. 1732. 1. 1734. 1. 1735. 0. 1736. cos а V -. 1737. 0.
b у sin а
ПРОИЗВОДИЛИ И ЕЕ ПРИМЕНЕНИЕ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
X
1741. a) v0; б) 4- at0.
1742. а) 0 м/мин-, б) — м/мин-, в) 75 м/мин.
1743. - J-r-. 1744. а) 1; б) 4х; в) 2(х4-1); г) —+ д) — 2х; е) Зх2.
2 у / I х
1745. а) 4,8 град/сек\ б) 4 град!сек,. 1746. 5 ампер/сек. 1747. Обе функции
дифференцируемы в точке х = 0. 1748. Эта же прямая. 1749. а) Имеет, у = — х;
б) нет; в) имеет, у = х. 1751. Угол между касательными к кривым в
точке их пересечения (см. рис. 3*). 1752. а) 2х +
4- у + 1 == 0; б) у = 0; в) 2х — у — 1 = 0. 1753.
л
— — arctg 6. 1754. В точке (0,0) под углом
— ив точке (1,1) под углом arctg 2— —.
4 4
1757. 2х+ 1. 1758. 2х—2. 1759. 8х—4. 1760. —4x-f-
+ 15. 1761. 18 —20х. 1762. — 4. 1763. — 20х3 4—4х.
1764. 5х2(3 — 4х). 1765. 4х» + 2х. 1766. — UOx3 +
275
4-45ха—24x4-3. 1767. 4х«. 1768. 2х(1—2х2). 1769. 8(2х—З)3.
X (2х 4- а). 1771.
1776.
2
(Ц-Х)2’
15
1780.
(X2 — 1)а’
70
~ (3 — Юх)2 '
_ J . 1786-
Зх/х
Юх4 — 1. 1791.
— 6 4- бвх3. 1794.
1770. 2(х24-ах) х
2
1775.
1781.
2(3х— 2)2’
3
(5-4Х)2
5
(6-хр
/45
1784. -2~тт
2 /х
—214-Зх4-5х4
2х2 И х
— Зх2 — 6х 4* 6
1779.
Зх2(2х3 — 5 4* а). 1774.
4х— 14х2
1777. ----------. 1778.
(1 — 7х)2
ad — be
---------- 1783. -----
(ex 4- d)2 4 у x
3 1
—- =-. 1787. 5 4-—. 1788.
2 У 2 х2У х х2
21х® — 36х» — 12х2 4- Юх. 1792.
5х4 — 21х2 — 2х 4- 10. 1795. 2х(хв 4-1)(7х« + 1)
1785.
1790.
1793.
1796. 24х2(1 — Зх4)2 (1 — 15х4). 1797. а) у = х; б) у = 1; в) у = — 1';' г) 4х —
— 4 У 2 у + (4 — л) = 0;
1804.
1809.
1816.
1821.
д) х 4- У — л = 0. 1803. sin 2х
— sin 2х. 1805. cos 2х. 1806. 2х sin х + х2 cos х.
(5 + cos х) (х2 — cos х) 4- (5х 4- sin х) (2х 4~ sin х). 1812. — 2 sin 2х. 1815. 0
1 . / л\
—-=- (sin х 4“ 2х cos х). 1818. cos х 4- — .
2 У х \ 4 /
6(х4-7)ь. 1822. — 35(1—5х)в. 1823. 4 cos4x. 1824.
1828. Лео cos (сох 4- ф). 1829. Аю sin (ф — сох). 1833.
1
б) 730 м/мин2. 1837.
1820. Ю(2х4-3)4
1 х
5 C°S 5
1
И 2x4- 1
1
1834. — о 1836. а) 18 м/мин2-,
3^(1 -х)2
1838. у' = 3 (х 4- 2)2; у" = 6 (х 4- 2); у'" = 6; у
= 6 (2х — I)2; у" = 24 (2х — 1); у'" = 48; у V
Г”
у"= — cos х; у'" = sin х; у
1846. — sin х 4- — sin Зх. 1847. 15 360. 1848. 780. 1849. — 2300 • 222.
4 4
IV V
= у ==... =0. 1839. у' =
V
= у =...=0. 1842. у =— sinx;
IV
= cosx, и далее все повторяется. 1845. 150 раз.
31°°
1851.
1855.
1859.
муле
что
п (п — 1) (л — 2) (п — 3) (п — 4)
—--------------------------L. 1852. 4. 1853. а) 10; г) 7; е) 6.
__120 _ _ _
а) 89 —28/10; б) 112 4-64/3; в) 176 /6 — 304 /2. 1856. 4.
Указание. II10 — 1 =(10-j-I)10—1; (1O4-1)10 разложить по фор-
бинома Ньютона.
биномиальные
1862.
Для полного
коэффициенты — числа
в) 5. 1863. 66. 1864.
0,99. 1877. 1,01. 1878.
б) 4;
1875.
убывает. 1882. При | х | < 1
— 1 < х < 0 и х > 1 возрастает,
решения
целые.
5120
~ 9 ‘
0,98. 1881. При х < 2 возрастает
убывает, при |х| > 1 возрастает,
а при х < — 1 и 0<х<1
задачи нужно доказать,
1860. а) 45; г) 630.
. 1865. 1,12. 1868. 0,97.
а) 3;
1871. 1,025.
при х > 2
1883. При
убывает. 1884. При х < — 5 и х > 1 возрастает, а при — 5 < х < 1 убывает.
л л
1885. Всюду убывает. 1889. При——4-2пл < х < — 4-2пл возрастает,
3 3
л 5 „ л 3
при — + 2/гл < х < — л 4- 2/гл убывает. 1890. При — 4~ 2лл< х<~~ л4-2лл
и 3 4 4
3 9
убывает, при — л 2/гл < х < — л 4“ 2/гл возрастает. 1891. Возрастает.
4 4
1892. Убывает. 1893. Возрастает. 1894. Убывает. 1895. При — 1 < х < 0 и
0 < х < 1 убывает, при | х | > 1 возрастает. 1896. При х < 0 убывает, а при
276
х > 0 возрастает. 1897. Всюду убывает. 1898.
37 а2
— — (минимум). 1900. — —
4 8
Минимум 110, максимум 174.
— 177, максимум 39. 1904.
(минимум). 1902.
1903. Минимум
Минимум — 1.
1905. Минимум — Y 2, максимум V2. 1906. Ми-
Нет локальных
экстремумов. 1910. 2пл + 1 и у + 2&л —1.
а) — 1,375; 1,375; б) —2; 2.
/3; б) — /3; 1. 1919. а)
л /Г
-
нимум — 2, максимум 2. 1908.
л
2
1916.
л V2
б) 8 ~ 2 ’
л Уз
~ 6 + 2 ’
рис. 5*.
1917. а)
л Уз
6 ~ 2 •
л
— 2;
2 *
в)
0;
/зг
6 ~ 2 ’
1926. См. рис.
1928. См.
рис. 5*. 1937. t = 31 сек. 1939. 25 м/сек и
37 м/сек. 1940. 2х—_у + 5=0. 1941. 6х— у—3=0.
л К 2
1942. у — arctg -у.
Iх Г
л — arctg -у. 1944. а)
1945. — х«.
9
1943.
(1.4);
4*.
. /3
arctg -у и
б) (-2, -11).
быть равна
3
(х-3)4’
1963. —sin4x.
1947. 51.
d
/3 ‘
1960.
1957.
1956.
Ширина должна
2
1958.
1
(2х + 5)2' ,аи°' 2/3^i ’ ,959‘ 3(Х~ 3)а“
1 X
2 sin 4х — — sin у. 1961. (1 + 2х — х2) cos х — (х + I)2 sin х.
277
КОМПЛЕКСНЫЕ ЧИСЛА
XI
1967. а)
6) либо
1973. а)
в) X = tt
Да; б) нет; в) да. 1968. а) Нет; 6) нет. 1972. а) а=с, b = d't
а =£ с, либо b d; возможно, конечно, что и а±с и b =£ d.
х = 0, у =— 3; б) х=1, у =— 1. 1975. а) х = ур у =— ~
2
1977. а) х =— 3,
= — (4 — /), гДе t — любое действительное число.
о
У
92 194 9
у = —6; б)х = ——, У = в)х = —2; у = -у 1978. - 13 + 13/.
1982. 33 4-56/. 1988. 1 —/. 1989. а) Определение; б) теорема. 1990. 2 4-2/.
3 4 ас
1991. 1993. Указание. Для доказательства пропорции —= —
5 5 b d
достаточно показать, что числа b и d отличны от нуля и ad = be.
1995. а) Нет; б) нет; в) да. 2001. а = b = 0; б) хотя бы одно из
чисел а и b отлично от нуля. 2002. а) х = 3, у =— 1; б) х = 2; у =— 2;
в) х==у = 1; г) х = /, у= — 2/, где t — любое действительное число;
д) равенство не выполняется ни при каких действительных значе-
ниях х и у. 2004. а) Действительные числа; б) чисто мнимые числа.
1 г-
2008. у(1 —/3 /). 2011. —/. 2014. —1 —/. 2015. 0. 2016. 0. 2017. 0, если
если п -~= 4k 4- 2; 1, если п = 4k 4- 3.
(1+0; б) ± —. 2024. а) 1 ±/.
п = 4/г; /, если п = 4k 4- 1 / — 1,
2018. — 1. 2019. /. 2023. а) ± —7=
У2
2029. а) о (х2 — Юх + 26) = 0. 2030. а (х2 + 20х + 200) = 0. 2031. а (2х2 — 14х+
+ 205) =0. 2032. 3; — (1 ± /Г i). 2033. — 3; (1 ± /з\). 2035. —J 5;
y(l±/3i). 2039. 2042. ± \ 2; ± у 2 ».
4/Т2(1±0 t/12(l±i) / л
2043. — —--~2045.0. 2046. 7.2047. 1) 4[cos — +
2 2 \ 3
л \ / л , . л \ г— II 7 \
4" /sin—]; 2) 21 cos—4-* sm — ; 3) 6)<2 cos — л 4-1 sin—л);
3 / \ б о / \ 4 4 1
12
4) 13 [cos (л — ф) 4-1 sin (л — ф], где ф== arctg—; 5) 25 (cos 0 4-/ sin 0);
5
3 3 \
2” ’ 2
3
5 [cos (л — ф) 4- * sin (л — ф) ]f где ф = arctg —. 2048. 2) На окружности
4
6)
9)
4 (cos л 4- / sin л);
л / n . л \ / 3 3\
7) 31 cos— 4- i sin— ; 8) 2 cos — л 4- / sin — л ;
\ 2 2J ' \ 2 2
радиуса 2 с центром в начале координат; 3) в круге радиуса 3 с центром
в начале координат; 5) в кольце между концентрическими окружностями
радиусов 2 и 3 с центром в начале координат, исключая эти окружности;
6) на луче, исходящем из начала координат и образующем с осью х угол
л
7’
2
а / а
2049. Только при г = 0. 2050. Могут, при ф = пл. 2051. 2 cos — I cos —
2 \ 2
а \
+ isin т}
а
если — л 4-< а < л4~ 4/?л; — 2 cos —
278
+ i sin
, если л + 46л < а < Зл + 46л. 2054. 2 (cos 340° 4- I sin 340°).
2055. 3(cos 195°+£sln 195°). 2050. a) 15i; 6) —7 + 7^3 l’, в) —24; г) 42.
i з _
2057. a) — -7 — i; б) 2« (1 4- К 3 /); в) 1. 2059. a) i; 6) cos 190° + i sin 190°.
4 u
2. 3, 4; 6) cos(—
\10
2 \
л + —- Ы H-
o /
2062. a) Ya (cos 4- i sin 6 = 0, 1,
\ 5 5 j
/1 2 \
+ fsinl —л+— fen), 6 = 0, 1, 2, 3, 4. 2066. При |а| = |6|^=0. 2069. —4.
2070. — 8. 2071. 0. 2073. — 21. 2076. a) a (x24~ 32x + 260) = 0; б) a (5x2 4-14x4-
+ 13) = 0. 2077. Нет. 2078. а) х = 2/, у =/, где t — любое действительное
число, отличное от нуля; б) х и у — любые действительные числа, не равные
нулю одновременно. 2083. б) cos(—2а) 4- i sin (—2а). 2088. 1024.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
XII
2099. 2л частей. 2101. При п = 1 утверждение верно. Пусть оно верно при
n = k. Тогда (1+а)*+‘ = (1 + а)* * (1 + а) > (1 + fai) (I + а) = l-f-ta-t-
-f-a-f-fea2— 1 +(fe+ 1)а 4- fta4 > 1 4-(fe -j- 1)а.
ЗАДАЧИ НА ПОВТОРЕНИЕ ВСЕГО КУРСА АЛГЕБРЫ
И ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
2117. 10 человек.
1
----если а =
а— 1
число: если а=1, то корней нет; в) нет корней.
3 4~ о
то корней нет; если а > 0, то х =—-—; б) —1, 2.
а2 — а — 1 1
У = —---------—; б) если а =£ ± 2, то х= ---------, у =
а2 — а 4- 1 2 — а
1 + 2t
2 ’
а — 2Ь
2109. Если а > 2Ь, то через ---- дней. Если а < Ь. то на первом складе
с
никогда не будет угля вдвое больше, чем на втором. 2110. 15 ч и 10 ч.
2111. 50 км/ч. 2112. 12, 10 и 15 ч. 2113. 10 км и 5 км. 2114. 1000 км/ч
и 800 км/ч. 2115. 9; 28. 2116. 5 км/ч и 3,5 км/ч.
2118. 35 суток. 2119. 500 м. 2120. а) Если а =/= ± 1, то х =
с=з — 1, то х — любое
2121. а) Если а < 0,
2а
2123. а) х=-------—,
а2— а 4- 1
1 а
;; если а = 2, то решении нет; если а = — 2, то х = t, у =
а 0 и а 1
б) х=4-
а — 2'
где t — любое число; в) при а = 0 и а = 1 нет решений; при
х = у = ;----. 2124. а) х = 5, у = 4 и х = — 4, у = — 5;
а I — a
442 л 1[а \
= —их = —. У = в) если то *=т т + &* •
о о о £ \О I
если b = 0, а а 0, то решений нет, если а = Ь = 0, то х = у
9 7
любое число. 2129. — < х < — 2130. — 1 < a < 2. 2131. а) 10; б)
4 z
2132, а) а < 1; а > 2; б) 0 < а < 1; 2 < а < 3; в) а < 0; а > 3. 2133. а) х <2;
б) х —любое действительное число; в) 2 < х < 4. 2135. 3<0° > 6300.
2
б) х = —, у =
□
1
У~ 2
t.
—. 2124. а) х = 5, у = 4 и х = — 4, у — —
а
2 1 {а
у = —; в) если b 0, то х = I — 4- Ъ
где t —
1; в) 5.
9
7
4
2
279
Указание. З’00 = (З2)300 = 9300. 2133. Если й>100(У2 — 1). то ежегод-
k— 100 (^2 — 1)
ный прирост населения составляет
процента. При
k < 100(72 —1) условия задачи противоречивы. 2137. Если угол ф оканчи-
вается
. м 12 5
в 1-й четверти, то со5ф = ~ tg<p = — если
12 х 5
четверти, то созф==——; tgqp=——. 2138. Если угол ф
угол <р оканчивается
во 2-й
оканчи-
вается во 2-й четверти, то sin ф = 4 4 Т 1гФ--т. если угол ф оканчи-
вается 2/2? 2148. в 3-й О « А 1 четверти, то 5 12 sin ф — 5 СЧ | со I II е- с с ГГ | 1О СЧ 1 2110. —; 3 3 £ сч 1
3 ’ _2 2/f ’ 3
' 13’ • 13’ 12’ 3/ пл\ /л — а =#= — ). 2149. 2 sin — 2\ 2 ) \ 4 ~5 /13’ Ф \ — М. 2150. а) 1 j/Тз1 ; б) 3’ 0. 2151. — 2‘ а <
1 б)— 2<д<—. 2154. а) 4 ,г— 3 /ОД); б) — —; । 5 В) _1_ — 3‘ л 2153. — 2 4- 2пл.
2157. Нет । корней. 2158. л 7 + пл л —; ~ + 2/гл. 2 2 2159. ( -1)л+1“ и - 4-
л
2162. — — + пл.
3
л
2160. ± — + пл. 2161. Нет корней.
3
2163.
arctg 2 4- /гл. 2164. Нет корней. 2165. — 4-пл; — 4-fen. 2167. —4-пл. /о Z
2168. пл; (— 1)п 1 пл л • arcsin у + 2 ’ 2*7®- 4 + пл<
— arctg <5 4" 1ОУ.
arctg 2 4- /гл. пл 2171. —. 2172. 4 л пл л — 4- — • 2173. — 4- 2пл; 6 3 6
л
т +
4
— 2/гл. 2174. (2л 4-1) л; arctg 4 4-/гл. 2175. £ arccos —— 4-2пл.
л л fen _ „ л „ л
2176. 12+ 24+'б‘ 2177‘ 2”Л; ~ у + 2/гл- 2178. пл< — ~ 4-*л.
2179. — 4-пл. 2180. х =--4-2пл, у = 2пл; х = 2 arctg (/3 4-2)4-
4 3 3
2л z г— \ л
-f- 2лл, у = — — 2 arctg (^3 + 2) — 2пл. 2181. х = (— 1)л — 4-
з о
2 л л л
у = ± -л4-2/гя; х = (-1)п+‘-4-пл, у = ± ~4-2/гл. 2182. х = (-1)” - 4-
3 О О О
4-пл; у = ± ~• л 4- 2fen; х = (— 1 )л+1 4- пл, у = ± ~ 4-21гл. 2183. х =
6 3 3
л л t л л
= — 4- (п + М У = — 4- (п — Л) я; х= — — 4- (п 4- /г) л, у = — —4-(п—fe) л.
3 3 3 3
25 15 9 3
2185. 9 и 21. 2186. 2, 4, 8, 12 или —, —, —, —. 2187. 2, 10, 18 и 2,
Л Л it L
280
6, 18. 218а arctg
2194. 1. 2195. у.
а
то х =------;
а— 1
9 1
2203. 7;-.
1 + /5 ла2 2ла .„„22
—Ч----. 2189. — -7=. 2190. 2, —, —,
2 9/3 3 9
2
2196. 0. 2197. ----. 2198. 2; —2. 2199. Если
lg3 — 1g 2
; при а < 1 корней нет. 2200. 100;
о _________ 1
2204. 10; /10. 2205. I. 2206. 4. 2207. 1; 3; —.
О
1 , 1
±-т=-. 2202. 1; —;
/10 2
2208.
а>1,
л
7 +
+ 2пл. 2212. х<—5. 2213. а) х = 4, у = 8; х =— 4, у = — 8;
б) х = 8, у = 4; х = 4, у = 8; г) х = 7, у = 3; х = — 7, у = — 3; д) х = 2,
у = 32; х = 32, у = 2. 2214. Не более 5 пластинок. 2216. в) 2 < х < 5; г) *+0
и —; д) совокупность всех неотрицательных чисел, кроме х =
3
= — + пл и х = — + fen. 2223. а) 9; б) 6; в) —; г) 2 cos а. 2226. а) 8+53/;
2 4 3
9
г) — 8. 2228. а) х = 1, у = 2; х = — 1, у = — 2; б) х = 0, у = 7; х=— у=18.
2 cos —
2
\П (cos —- + * sin “Г )• 2233. cos 5ф = cos6 ф — 10 cos3 ф sin2 ф 4-
\ 2 2 /
2230.
4- 5 cos'ф sin4 <pf sin 5ф = sin6 ф — 16 sin3 ф cos2 ф 4- 5 sin ф cos4 ф. 2235. x — 4 у 4-
4-4 = 0. 2236. 2x — у — 1=0; 2x -f- у — 3 = 0. 2237. a) 4 sin3 x cos x;
6) 6 sin2 2x cos 2x; в) — 5 cos4 (x — 1) sin (x — 1); r) 4 cos3 (2 — x) sin (2 — x);
д) 10x(x24-l)4; e) —6(3 — 2x)2. 2238. Лео cos (co/ 4- ф); — Ясо2 sin (со/ф)«
2239. Могут, например, х и х 4- 1. 2243. а) — 1 293 600; б) 1; в) —100.
ОГЛАВЛЕНИЕ
ТРИГОНОМЕТРИЧЕСКИЕ ТЕОРЕМЫ СЛОЖЕНИЯ VII
§ 149. Расстояние между двумя точками плоскости. Системы коор-
динат .........................„...................................... 3
$ 150. Косинус суммы и разности двух углов ............................. 5
§ 151. Синус суммы и разности двух углов ............................... 7
§ 152. Тангенс суммы и разности двух углов ............................. 9
§ 153. Тригонометрические функции двойного угла ................ • 12
§ 154. Выражение sin а и cos а через тангенс половинного угла .... 14
§ 155. Соотношения между тригонометрическими функциями поло-
винного угла и косинусом целого угла . 16
§ 156. Выражение тангенса половинного угла через синус и косинус
целого угла.......................................................... 18
5 15 7. Преобразование произведения тригонометрических функций
в сумму.............................................................. 19
§ 158. Преобразование суммы (разности) синусов двух углов в произ-
ведение ............................................................. 20
§ 159. Преобразование суммы (разности) косинусов двух углов в про-
изведение ........................................................... 22
§ 160. Преобразование суммы (разности) тангенсов двух углов .... 24
§ 161. Графики тригонометрических функций кратных углов .... 26
§ 162. Графики функций у = A sin сох, у = A cos сох, у = A tgcox, у =
= A ctg сох ......................................................... 28
§ 163. Графики тригонометрических функций у = A sin [со (х + а)|, у =
= Л cos [© (х + а)] и т д. ........................... 34
§ 164. Графики функций у = A sin (сох + а), у = A cos (сох + а) и т. д. 39
§ 165. Гармоническое колебание ........................................ 41
§ 166. Гармоническое колебание в электротехнике ....................... 43
§ 167. Преобразование выражения a sin х + b cos х путем введения
вспомогательного угла................................................ 45
282
§ 168. Сложение гармонических колебаний одинаковой частоты • • • 47
5 169. Доказательство тригонометрических тождеств ........ 48
§ 170. Равенства, содержащие выражения arcsin a, arccos а и т. д. ... 51
§171. Тригонометрические уравнения ............................. . 52
§ 172. Графический способ решения тригонометрических уравнений . 59
Задачи на повторение .......................................... 61
§ 173. Из истории тригонометрии ..................................... 63
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ VIII
§ 174. Степень положительного числа с положительным рациональным
показателем ..................................................... 65
§ 175. Степень положительного числа с положительным иррациональ-
ным показателем ................................................... 66
§ 176. Степень положительного числа с отрицательным иррациональ-
ным показателем ................................................... 69
§ 177. Основные свойства степеней положительных чисел с действитель-
ными показателями .................................................. —
§ 178, Показательная функция и ее график ........................ 70
§ 179. Основные свойства показательной функции .................... 73
§ 180 Логарифм числа по данному основанию ....................... 78
§ 181. Логарифмическая функция и ее график ........................ 81
§ 182. Основные свойства логарифмической функции .................. 84
§ 183. Логарифм произведения и частного ........................... 88
§ 184. Логарифм степени и корня .................................. 90
§ 185. Переход от одного основания логарифмов к другому ........... 92
§ 186. Логарифмирование и потенцирование ...................... 93
§ 187. Целая и дробная части числа ................................ 96
§ 188. Десятичные логарифмы и их свойства ...................... 97
§ 189. Таблицы десятичных логарифмов ............................ 101
§ 190. Таблицы антилогарифмов .................................... 103
§ 191. Таблицы десятичных логарифмов тригонометрических функций 104
§ 192. Действия над логарифмами ............................... . 105
§ 193. Примеры вычисления с помощью таблиц логарифмов ...... 107
§ 194. Натуральные логарифмы ..................................... 108
§ 195. Обоснование действий на логарифмической линейке ...... 109
§ 196. Основные способы решения показательных уравнений ..... 111
§ 197. Основные способы решения логарифмических уравнений • . • 114
283
$ 198. Примеры графического решения показательных и логарифми-
ческих уравнений ........................................... 119
§ 199. Показательные и логарифмические неравенства ............... 121
$ 200. Из истории открытия логарифмов............................ 122
Задачи на повторение....................................... 123
ФУНКЦИИ И ПРЕДЕЛЫ IX
§ 201. Постоянные и переменные величины. Понятие функции............ 126
§ 202. Способы задания функций ..................................... 128
§ 203. Область определения и область изменения функции ............. 132
§ 204. Возрастание и убывание функций .............................. 137
§ 205. Экстремальные значения функции .............................. 139
§ 206. Четные и нечетные функции ................................... 143
§ 207. Периодические функции ....................................... 146
§ 208. Обратные функции............................................. 148
§ 209. Взаимное расположение графиков прямой и обратной функций . . 151
§ 210. Краткий обзор свойств и графиков ранее изученных функций ... 152
1. Квадратная функция у = ах2 + Ьх + с (а 0)................. 153
2. Степенная функция у = хг ................................. 155
3. Тригонометрические функции .............................. 156
4. Показательная функция у = ах (а > 0, а =£ 1) ............ 157
5. Логарифмическая функция у = loga х (а > 0, а 1) ......... —
§211. Предел функции .............................................. 158
§ 212. Основные теоремы о пределах функций ......................... 162
§ 213. Некоторые тригонометрические неравенства и их использование
при нахождении пределов ............................................ 165
sin х
§ 214. Предел отношения ----- при .................................. 167
§ 215. Примеры вычисления пределов ................................. 169
§ 216. Из истории развития понятий функции и предела ............... 171
Задачи на повторение ..........................................
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§ 217. Равномерное и переменное движение по прямой. Скорость и
средняя скорость движения ..................................... 173
§ 218. Закон движения. Мгновенная скорость движения ................. 174
284
§ 219. Производная функции........................................ 176
§ 220. Дифференцируемые функции.................................. 179
§ 221. Касательная к кривой....................................... 180
§ 222. Геометрическое истолкование производной ................... 182
§ 223. Вынесение постоянного множителя за знак производной........ 183
§ 224. Производная суммы функций.................................... —
§ 225. Дифференцирование произведения двух функций ............... 185
§ 226. Производная дроби ......................................... 186
§ 227. Производная степенной функции.............................. 187
§ 228. Производная многочлена..................................... 189
§ 229. Дифференцирование тригонометрических функций ................ —
§ 230. Дифференцирование функции / (ах + Ь) ...................... 192
§ 231. Понятие о второй производной. Производные высших порядков . . 193
§ 232. Выражение коэффициентов многочлена через значения его про-
изводных ......................................................... 195
§ 233 Формула бинома Ньютона...................................... 196
§ 234. Об одном свойстве биномиальных коэффициентов .............. 198
§ 235. Применение формулы бинома Ньютона к приближенным вычисле-
ниям ............................................................. 199
§ 236. Применение производной к нахождению участков возрастания
и участков убывания функций....................................... 201
§ 237. Применение производной к нахождению локальных экстремумов
функции ...........................................................202
§ 238. Наименьшее и наибольшее значения функции в заданном интер-
вале ............................................................. 205
§ 239. Использование производных для исследования дифференцируе-
мых функций и построения их графиков ............................. 206
§ 240. Применение производной к графическому решению уравнений . . 210
§241. Исторические замечания..................................... 211
Задачи на повторение ......................................... —
КОМПЛЕКСНЫЕ ЧИСЛА XI
§ 242. Числовые поля ............................................. 213
§ 243. Постановка задачи о расширении поля действительных чисел.
Комплексные числа................................................. 215
§ 244. Сложение комплексных чисел Противоположные числа........... 217
285
§ 245. Вычитание комплексных чисел ................................. 218
§ 246. Умножение комплексных чисел.................................. 219
§ 247. Деление комплексных чисел . ................................. 220
§ 248. Поле комплексных чисел .......................................222
§ 249. Геометрическое изображение комплексных чисел................. 224
$ 250. Действительные и чисто мнимые числа ......................... 227
§ 251. Сопряженные числа. Практический способ деления комплексных
чисел............................................................... 229
§ 252. Степени мнимой единицы....................................... 231
§ 253. Извлечение корней квадратных из отрицательных чисел. Реше-
ние квадратных уравнений с отрицательными дискриминантами —
§ 254. Двучленные уравнения 3-й степени с действительными коэф-
фициентами ......................................................... 233
§ 255. Двучленные уравнения 4-й степени с действительными коэф-
фициентами ................................................... .... 235
§ 256. Тригонометрическая форма комплексных чисел .................. 236
§ 257. Умножение и деление комплексных чисел, заданных в триго-
нометрической форме ................................................ 240
§ 258. Извлечение корней из комплексного числа...................... 241
§ 259. Алгебраическое уравнение л-й степени ........................ 243
§ 260. Исторические замечания....................................... 245
Задачи на повторение ......................................... 246
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ XII
§ 261. Общие и частные утверждения. Дедукция и индукция ............ 248
§ 262 Метод математической индукции ............................... 250
§ 263. Другой вариант метода математической индукции ............... 253
§ 264. Замечание к методу математической индукции .................. 255
Задачи на повторение всего курса алгебры и элементарных
функций ...................................................... 256
Ответы к упражнениям ....................................... 268
Евгений Семенович Кочетков
Екатерина Семеновна Кочеткова
АЛГЕБРА
И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
10 класс
Редактор И. С. Михеев
Переплет художника А. С. Котлярова
Художественный редактор Е, Н. Карасик
Технический редактор В. Ф. Коскина
Корректор М. В. Голубееа
Подписано к печати с матриц 3/VII 1973 г. 60X90716-
Типографская №3. Печ. л. 18. Уч.-изд. л. 14,89.
Тираж 1900 тыс. (1—1 600 000) экз. Заказ 1159.
•
Издательство «Просвещение* Государственного коми-
тета Совета Министров РСФСР по делам издательств,
полиграфии и книжной торговли. Москва, 3-й проезд
Марьиной рощи, 41.
Саратовский ордена Трудового Красного Знамени
полиграфический комбинат Росглавполиграфпрома
Государственного комитета Совета Министров РСФСР
по делам издательств, полиграфии и книжной торговли.
Саратов, ул. Чернышевского, 59.
Цена 27 коп.
27 к.
Просвещение > 1974