НАУКУ —ВСЕМ!
Шедевры научно-популярной литературы (математика) • № 80
А. В. Жуков
ЭЛЕГАНТНАЯ МАТЕМАТИКА
Задачи и решения
Издание стереотипное
URSS
МОСКВА


ББК 22.1 о 22.130 22.1я73 74
Жуков Александр Владимирович
Элегантная математика: Задачи и решения. Изд. стереотип.
М.: Книжный дом «ЛИБРОКОМ», 2016. — 176 с. (НАУКУ — ВСЕМ! Шедевры научно-популярной литературы (математика). № 80.)
В настоящем пособии собраны задачи, которые привлекли автора своей эстетикой. Почему может нравиться та или иная задача? Что является источником красоты и элегантности в математике? Вот основной круг вопросов, обсуждаемых в книге. Изложение основано на большом количестве изящных примеров из области элементарной математики.
В книге представлены задачи, не требующие, за редким исключением, сложных выкладок или рассуждений. Они могут быть интересны школьникам средних классов, педагогам, а также всем любителям математики с минимальной математической подготовкой.
В оформлении макета использована компьютерная графика автора
Издательство «Книжный дом “ЛИБРОКОМ”». 117335, Москва, Нахимовский пр-т, 56.
Формат 62x90/16 Печ. л. 11. Доп. тираж. Зак. № АХ-796.
Отпечатано в ООО «ЛЕНАНД». 117312, Москва, пр-т Шестидесятилетия Октября, ПА, стр. 11.
ISBN 978-5-397-05431-7
© Книжный дом «ЛИБРОКОМ», 2012, 2016
20087 Ю 216194
9 785397 0
5431
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
URSS
E-mail: URSS@URSS.ru Каталог изданий в Интернете:
http://URSS.ru
Тел./факс (многоканальный): + 7 (499) 724 25 45
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или передана в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая фотокопирование и запись на магнитный носитель, а также размещение в Интернете, если на то нет письменного разрешения владельца.


Оглавление
Предисловие 5
Глава 1. Сквозь кристалл времени 7
1. «Смотри!» 7
1.1. Взгляд в прошлое 8
1.2. Невидимо — видимо 12
1.3. Очевидно для глаза — неочевидно для ума 13
2. Игры с числами 14
2.1. Сума сумм 14
2.2. Этюд на тему Пифагора 16
3. Блеск логики 22
3.1. Reductio ad absurdum 23
3.2. Существует ли объект? 25
4. Магия могущества 29
5. Ритмы в стиле жизни 31
Решения, ответы и комментарии 37
Литература 50
Глава 2. Почему нравится задача? 52
1. Сказочная фабула 52
2. Раскрепощенность фантазии 55
3. Парадоксальность 58
3.1. Острый взгляд математика 58
3.2. Граффити на полях 59
4. Радость озарения 63
5. Неожиданный ракурс 65
з


Оглавление
6. Великолепие миниатюр 67
6.1. В задаче всё должно быть прекрасно 67
6.2. Минимум средств 70
6.3. Обманчивая простота 70
7. Элегантные мотивы 71
7.1. Мотив натурального ряда 71
7.2. Мотив круга 74
7.3. Мотив симметрии 76
7.4. ZIP-мотив 79
7.5. Ансамбли задач 80
7.6. Мотив дополнения. 83
8. Математика факта 85
8.1. Гармония числа и формы 86
8.2. Три биссектрисы 89
8.3. Задача Брокара 91
9. Заигрывание интуиции 94
9.1. Veni, Vidi, Vici 94
9.2. Угадывание особого места 96
9.3. Предчувствие ответа 98
9.4. Интуиция воображения 100
9.5. Именованные задачи 105
9.6. Юмор 106
9.7. Остальные задачи 107
Решения, ответы и комментарии 109
Литература 145
Глава 3. Компьютер-числоскоп 150
1. Многоликая спираль 150
2. Алгоритм «стежок» 154
Решения, ответы и комментарии 158
Литература 161
О красоте, математике и не только 162
Поэт элегантной математики (2>. С. Горобец) Т. 166


Предисловие
Но еще немало протечет воды... пока школа, наконец, обнаружит, что математика может быть гуманитарной наукой и что ученики могут так же хорошо понимать Эйлера, как Платона и Гёте.
А. Шпайзер.
Из предисловия к книге Леонарда Эйлера «Введение в анализ бесконечных»
— Из всех видов туч я больше всего люблю отраженные.
— А я из всех видов рек — отражающие.
Владимир Казаков.
Набросок
Всех людей, знакомых со словом «математика», можно разделить на три категории. Их условно можно назвать: идеалисты, нигилисты и все остальные.
Идеалисты, естественно, склонны идеализировать то, чем они занимаются. «В мире нет места уродливой математике», — утверждал один из самых ярких представителей этой группы, прекрасный английский математик Годфри Харолд Харди (1877-1947). Однако его высказывание можно трактовать и так, что профессиона- лы-математики должны проявлять изысканность в выборе своих приоритетов и не заниматься чем попало, в изобилии наличествующем в их любимой науке.
«Математики, как французы: всё, что вы им говорите, они переводят на свой язык и это тотчас же становится чем-то иным», — шутил видный представитель лагеря нигилистов, прекрасный немецкий поэт Иоганн Вольфганг Гёте (1749-1832). Отчасти в этом виноваты сами математики, чрезмерно увлекающиеся формализ¬
5


Предисловие
мом, а отчасти — те упорные педагоги, которым судьба предоставила благоприятную возможность воспитывать убежденных нигилистов.
Все остальные, в том числе и автор этой книги, склонны воспринимать жизнь такой, какая она есть. Точно так же, как фотограф или художник, охотящийся за неожиданным сюжетом, ракурсом, игрой света и тени, автор книги из некоторого разнообразия доступных ему тем и сюжетов попытался выделить те, которые привлекли его своей эстетикой. Очевидно, взгляд автора сугубо субъективен, и читатели могут с ним не согласиться, а также дополнить собранную скромную коллекцию своими собственными впечатлениями и находками. Эту книгу следует воспринимать как приглашение к разговору на важную тему. Это заявка на большую работу! Хочется надеяться, что затронутая автором тема будет прирастать читательскими идеями, а книга будет переиздаваться, обогащаясь новым материалом.
О структуре книги
Большинство задач книги заимствовано из различных источников, указанных в списке литературы к каждой главе. В тех случаях, когда авторы задач известны, они указываются. Некоторые задачи оказались настолько привлекательными, что превратились в фольклор. Авторов «фольклорных» задач установить практически невозможно, однако мы будем благодарны всем, кто поможет нам сделать соответствующие уточнения.
В настоящей книге представлены задачи, не требующие, за редкими исключениями (они отдельно оговариваются в тексте), сложных выкладок или рассуждений. Они могут быть интересны школьникам средних классов и всем любителям математики с минимальной математической подготовкой.
Автор выражает искреннюю благодарность Вячеславу Викторовичу Произволову, Григорию Александровичу Гальперину и Игорю Федоровичу Акуличу, личное общение с которыми обогатило книгу интересными задачами, темами и сюжетами. Он благодарен также всем другим авторам, чьи задачи нашли отражения в настоящих заметках.


Глава 1
Сквозь кристалл времени
Я люблю обращаться к своей памяти: она вечно чего-то не помнит, и мне приходится всё сочинять заново.
Владимир Казаков. Созвездник
1. 	«Смотри!»
Ни один математик не мыслит формулами.
Альберт Эйнштейн
Любое произведение искусства представляет собой диалог с каждым стоящим перед ним человеком.
Г Гегель
Среди секретов, которым владеют художники, имеется и такой. Произведение искусства должно воплощать в себе не только то, что зритель видит непосредственно, но также и то, что угадывается, домысливается, «дочувствывается» наблюдательным созерцателем. Он должен испытать радость озарения, прикоснувшись к тайне, вольно или невольно припрятанной в художественном замысле произведения.
Этим изысканным секретом воздействия на аудиторию, несомненно, владели и древнеиндийские математики. Пожалуй, именно с их творчеством можно связать появление взгляда на математику как на особого рода искусство.
Сквозь кристалл времени
7


1. «Смотри!»
1.1. 	Взгляд в прошлое
Месяца месяцами сменялись до нас, Муцрецы мудрецами сменялись до нас,
Эти мертвые камни у нас под ногами Прежде были зрачками пленительных глаз.
Омар Хайям
В своем труде «Венец учения» (ок. 1150) индийский математик и астроном Бхаскара Ача- рья (р. 1114 - ум. позднее 1178) привел чертеж (рис. 1.1), под которым поставил подпись из одного единственного слова: «Смотри!».
Созерцая этот чертеж, мы убеждаемся, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна суммарной площади четырех таких треугольников плюс площадь маленького центрального квадрата с длиной стороны а - Ь, где а — больший, а b — меньший катет треугольника. Иными словами, если с — гипотенуза треугольника, то
с2 =4~ab + (a-b)2,
Полученный результат выражает знаменитое утверждение теоремы Пифагора: квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
В древнеиндийских математических текстах часто встречаются чертежи, под которыми написано только: «смотри!». На рис. 1.2 представлено еще одно доказательство теоремы Пифагора, придуманное индийскими математиками в этом стиле.
или с2 = а2 + Ъ2.
8
Глава 1


1.1. 	Взгляд в прошлое
Один и тот же большой квадрат разрезается на части двумя различными способами. Треугольники слева и справа — одни и те же, поэтому белый квадрат слева равновелик двум белым квадратам справа. Но левый квадрат построен на гипотенузе, а правые — на катетах треугольника.
В древнем китайском трактате «Математика в девяти книгах» (II в. до н. э.) приводится другой чертеж, доказывающий теорему Пифагора (рис. 1.3).
Ключ к доказательству теоремы приводится на рис. 1.4. На рис. 1.4а заштрихован квадрат, сторона которого равна гипотенузе с прямоугольного треугольника с катетами а и Ъ.
Рис. 1.3
*)
Рис. 1.4
Сквозь кристалл времени
9


1. «Смотри!»
Два заштрихованных прямоугольных треугольника с катетами а, b перемещаются в соответствии со стрелками на рис. 1.4а, в результате чего получается чертеж 1.46. Заштрихованная часть на зггом чертеже образует два квадрата со сторонами а и b — рис. 1.4в. Итак,
2 2 , г 2
с = а + b .
Рис. 1.5, воспроизведенный из древнекитайского трактата «Чеу- пей», также в стиле «Смотри!» доказывает тождество
2а2 + 2Ь2 = (а + Ь)2 + (а - Ь)2.
а Ъ
а
Ъ
Действительно, два заштрихованных квадрата площади 2а2 вместе с двумя белыми квадратами площади 2Ь2 составляют большой квадрат, к площади которого из-за наложения заштрихованных квадратов следует добавить площадь маленького темного квадрата в центре.
Традиция «Смотри !»-математики поддерживалась также в школе Пифагора (см. п. «Игра в числа» в этом разделе). Приведем еще несколько примеров классических задач, решение которых становится понятным из рассмотрения рисунка.
I Задача 1. {Эвклид, Предложение 1 Первой книги «Начала», III в. до н. э.). На отрезке АВ построить равносторонний треугольник.
Решение. См. рис. 1.6.
6 а
Рис. 1.5
10
Глава 1


1.1. 	Взгляд в прошлое
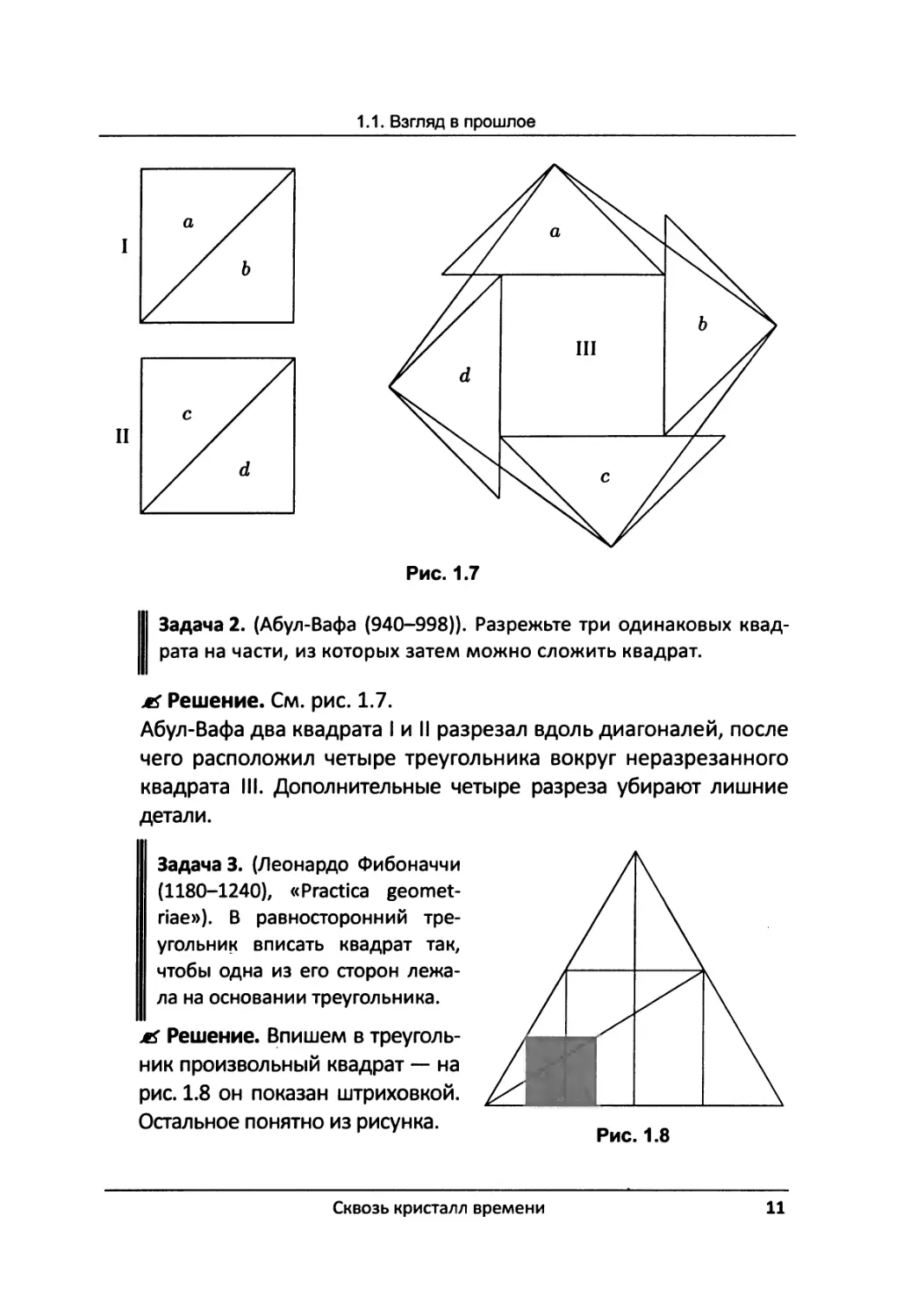
I Задача 2. (Абул-Вафа (940-998)). Разрежьте три одинаковых квадрата на части, из которых затем можно сложить квадрат.
jtS Решение. См. рис. 1.7.
Абул-Вафа два квадрата I и II разрезал вдоль диагоналей, после чего расположил четыре треугольника вокруг неразрезанного квадрата III. Дополнительные четыре разреза убирают лишние детали.
Задача 3. (Леонардо Фибоначчи (1180-1240), «Practice geomet- riae»). В равносторонний треугольник вписать квадрат так, чтобы одна из его сторон лежала на основании треугольника.
jtS Решение. Впишем в треугольник произвольный квадрат — на рис. 1.8 он показан штриховкой.
Остальное понятно из рисунка.
Рис. 1.8
Сквозь кристалл времени
11


1. «Смотри!»
1.2. 	Невидимо — видимо
Чем меньше мы видим, тем меньше воображаем.
Ж. Дюссо
Умение смотреть и видеть развивают геометрические задачи. Ответы на приведенные ниже упражнения можно найти в Решениях, ответах и комментариях (далее Комментариях) к разделу «Смотри!».
Q (М. Ахмеджанова, [1].) Разрежьте каждую из показанных на рис. 1.9 фигур на две равные части.
Рис. 1.9
Q (Мартин Гарднер, [2].) Докажите, что угол С на рис. 1.10 равен сумме углов А и В.
Q (К. Кохась, [3].) У ослика Иа-Иа есть 100 палочек. Докажите, что, сломав не более двух из них (ослик ломает палочки на две части), он может из всех палочек сложить прямоугольник.
12
Глава 1


1.3. Очевидно для глаза — неочевидно для ума
Q (JI. Смирнова, [4].) Из некоторых четырех палочек можно сложить четырехугольник, диагонали которого перпендикулярны. Докажите, что из этих же палочек можно сложить четырехугольник с двумя прямыми углами.
В (М. Панов, [5].) У Васи есть пластмассовый угольник (без делений) с углами 30°, 60° и 90°. Ему нужно построить угол в 15°. Как это сделать, не используя других инструментов?
£ (Р. Сарбаш, [6].) Как, не имея никаких инструментов, кроме ножниц, разрезать 2 бумажных квадрата площадью 9 и 16 квадратных единиц на прямоугольные куски, из которых можно составить квадратный лист площадью 25 квадратных единиц?
В (В. Произволов, [7, с. 10].) Два одинаковых бумажных выпуклых четырехугольника разрезали: первый — по одной из диагоналей, второй — по другой диагонали. Докажите, что из полученных треугольников можно сложить параллелограмм.
В (В- Произволов, [7, с. 11].) Три одинаковых треугольника разрезали по разноименным медианам. Сложите из полученных кусков один треугольник.
1.3. Очевидно для глаза — неочевидно для ума
Но легко ли зеркалу отражать красоту?
Владимир Казаков.
Построение
Психологи давно подметили интересный феномен: идея, не вызывающая сомнения при беглом взгляде на чертеж, порой сопряжена с непреодолимыми трудностями в ее осмыслении.
Сквозь кристалл времени
13


2. 	Игры с числами
Задача 1. (С. Фомин, [8].) Две пересекающиеся окружности вырезают из плоскости три ограниченные непересекаю- щиеся области. Докажите, что не существует окружности, делящей пополам площадь каждой из этих трех областей.
Согда смотришь на чертеж (рис. 1.11), утверждение этой задачи кажется очевидным. И всё же, как его обосновать? (Решение см. в Комментариях.)
2. 	Игры с числами
...Что числа дают опьянение такое же, как вино или звезды, они не знали...
Владимир Казаков. Ошибка живых
2.1. 	Сума сумм
Копите такое богатство, которое нельзя потерять.
Ж. Боссюэ
Задача 1. (Пифагор (V в. до н. э.)) Обоснуйте закономерность:
1 = 1 1+3=4 1 +3 + 5 = 9 1 +3 + 5 + 7= 16
В пифагорейской школе эта закономерность обосновывалась в стиле «Смотри!» математики: если к квадратной клетке последовательно при-
Рис. 1.12
14
Глава 1


2.1. Сума сумм
кладывать «гномоны» (уголки) из 3, 5, 7, 9, и т. д. клеток, то каждый раз общее количество клеток будет полностью заполнять квадрат (рис. 1.12).
Академик Андрей Николаевич Колмогоров (1903-1987) вспоминает, что обнаружив эту закономерность в возрасте пяти-шести лет, он испытал «радость математического „открытия"» [9].
Задача 2. (Никомах из Герасы (1-11 вв.))
Обоснуйте закономерность:
1 = 13 3 + 5 = 23 7 + 9 + 11 = З3
Задача 3. (Архимед (ок. 287-212 до н. э.)). Чему равна сумма квадратов л первых чисел натурального ряда:
12 + 22 + 32+... + и2?
jes У этой задачи имеется элегантное решение. Несмотря на то, что нас интересуют квадраты, давайте несколько «расширим горизонт», и вместо квадратов рассмотрим кубы:
13= 1
23 = (1 + I)3 = I3 + 3 • I2 + 3 • 1 + 1 З3 = (2 + I)3 = 23 + 3 • 22 + 3 • 2 + 1 43 = (3 + I)3 = З3 + 3 • З2 + 3 • 3 + 1
«3 = ((я - 1) + I)3 = (и - I)3 + 3 • (я - I)2 + 3 • (и - 1) + 1
(«+ 1)3 = и3 + 3 • л2 + 3 • л + 1.
Замечаем, что кубы, начиная с I3 и кончая п3, располагаются как в левой, так и в правой части этих равенств. Поэтому при сложении всех равенств кубы чудесным образом «растворятся» и останутся лишь квадраты и первые степени. Сложим:
(и + 1)3 = 3-(12 + 22+...+ я2) + 3 -(1 +2+...+ «)+ 1 •(«+ 1), откуда получаем
Сквозь кристалл времени
15


2. 	Игры с числами
1‘ н- 2г +...+ яг ■(" t !>1-fel.1?. - (1 + 2 +... + „) = +‘X2” * !> .
3 6
Этот способ «расширения горизонта» можно использовать для нахождения сумм других степеней последовательных натуральных чисел.
2.2. 	Этюд на тему Пифагора
Свойства чисел, известные сегодня, по большей части были открыты путем наблюдения и открыты задолго до того, как их истинность была подтверждена строгими доказательствами.
Леонард Эйлер (1707-1783)
Впервые таблица Пифагора примерно в таком виде, в каком мы ее находим на обложках ученических тетрадей, появилась в сочинении неопифагорейца Ни- комаха Геразского (I—II вв.). В его «Введении в арифметику» таблица выполнена в ионийской нумерации. По словам Никомаха, эта таблица восходит «к самому Пифагору».
Более древние таблицы умножения обнаружены в месопотамских глиняных табличках — их «возраст» около 5 тысяч лет.
Числа в каждой строке таблицы Пифагора образуют арифметическую прогрессию. Пожалуй, в этом нет ничего удивительного, ведь умножение натуральных чисел есть ни что иное, как многократное прибавление к накапливаемой сумме одного и того же слагаемого.
1
2
3
4
5
6
7
8
9
2
4
6
8
10
12
14
16
18
3
6
9
12
15
18
21
24
27
4
8
12
16
20
24
28
32
36
5
10
15
20
25
30
35
40
45
6
12
18
24
30
36
42
48
54
7
14
21
28
35
42
49
56
63
8
16
24
32
40
48
56
64
72
9
18
27
36
45
54
63
72
81
Рис. 1.13
16
Глава 1


2.2. Этюд на тему Пифагора
Таблица Пифагора симметрична относительно диагонали, ведущей из левого верхнего угла в правый нижний угол. Эту диагональ мы будем называть главной. Данное свойство — геометрическая иллюстрация свойства коммутативности умножения (от перемены мест сомножителей произведение не меняется).
Указанные два свойства, несмотря на всю их очевидность и простоту, бывают весьма полезными, когда приходится вручную выписывать таблицу Пифагора для большого количества множителей.
Цифры в первом столбце и последние цифры в девятом столбце таблицы Пифагора повторяют друг друга, но идут в обратном порядке. Может быть, нечто подобное наблюдается и у других пар столбцов? Так и есть, этим свойством обладают последние цифры 2-го и 8-го столбцов; 3-го и 7-го; 4-го и 6-го. Маленькое открытие: для произвольных двух цифр а и b последняя цифра произведения ab равна последней цифре произведения (10 - а)(10 - Ь). Пожалуй, и в этом тоже нет ничего удивительного, ведь разность чисел ab и (10 -я)(10 - Ь) делится на 10.
А вот некоторые факты, которые можно обнаружить лишь при более пристальном исследовании таблицы. На эти факты указывает Николай Иванович Авилов [10].
Назовем квартетом четыре числа таблицы Пифагора, расположенных в вершинах некоторого квадрата.
Оказывается, что если стороны этого квадрата параллельны диагоналям таблицы Пифагора, то суммы диагональных чисел квартета равны.
Если стороны квадрата параллельны сторонам таблицы, то равны произведения диагональных чисел квартета. Если при этом квадрат расположен симметрично главной диагонали таблицы Пифагора, то сумма всех чисел квартета — квадрат некоторого натурального числа.
Доказательства этих свойств просты и основаны на определении таблицы Пифагора, а именно: каждое число таблицы равно произведению номера строки и номера столбца, на пересечении которых оно стоит.
Таблицу Пифагора можно представить сколь угодно далеко продолженной вправо и вниз. Рассмотрим последовательность таблиц Пифагора размера п х п, где число п пробегает значения натураль-
Сквозь кристалл времени
17


2. 	Игры с числами
ного ряда 1, 2, 3, .... В следующих упражнениях требуется найти закономерность, которой подчиняются некоторые числовые свойства таблицы Пифагора в зависимости от величины п.
^Упражнения
Q Найдите выражение для суммы S(n) всех чисел пхп- таблицы Пифагора.
В По какому числовому закону образуется последовательность сумм чисел в «уголках» («гномонах») таблицы Пифагора, показанных на рис. 1.14?
Рис. 1.14
В Какой закономерности подчиняются суммы чисел на последовательных диагоналях таблицы Пифагора, показанных на рис. 1.15?
Далее мы подробнее остановимся на исследовании третьего вопроса этих упражнений. Ответы на первое и второе задания можно найти в Комментариях.
Итак, в нашем распоряжении имеется следующая последовательность чисел:
1, 4, 10, 20, 35, 56, 84, 120, 165, 220,...
18
Глава 1


2.2. Этюд на тему Пифагора
Какой закономерности она подчиняется?
Пока трудно сказать, поэтому продолжим экспериментировать с входящими в нее числами. Запишем строку чисел, каждое из которых является разностью двух соседних чисел исходной последовательности: 3, 6, 10, 15, 21, 28, 36, 45, 55, ... — здесь уже лучше обнаруживается регулярность. Чтобы она стала еще более зримой, рассмотрим новые разности, образованные каждыми двумя соседними числами этой новой последовательности: 3, 4, 5, 6, 7, 8, 9, 10,... — теперь закономерность проступила явственно!
Знание этой закономерности позволяет рассчитывать каждое число исходной последовательности, отправляясь от ее трех последовательных предыдущих членов (подумайте, как это можно осуществить). Мы приведем формулу, которая по номеру диагонали п позволяет сразу вычислить сумму стоящих в ней чисел:
р _ п(п + 1)(л + 2)
6 "•
Обоснование этой формулы приведено в Комментариях.
S Каталог схем
В завершение темы предлагаем поискать закономерности в следующем Каталоге схем (рис. 1.16, 1.17), имеющих непосредственную связь с таблицами умножения. Принцип составления этого Каталога, а также некоторые скрытые в нем закономерности обсуждаются в Комментариях. Мы гарантируем, что перед пристальным взором, исследующим «тайнопись» Каталога, предстанет целый «букет» замечательных свойств и загадок.
Поистине, многие математические факты можно открывать для себя «одними глазами».
Сквозь кристалл времени
19


Рис.1.16
<Уу -Ь. Лл) ?0 о 40 00 "J О» Ut ^ ы
о
о
о
о
о
сх
00
о
□
о
□
о
о о оо
999
С<
о<
-о-
о-
о
оо
о
®
о
°<
®
о
AV
о
оо
ООО
<х<
§о
оо
о
000
оо
<х<
0000
о
ООО
AV
<
®
о
о
ООО
AV
©
о
о
о оо о о о
X
о-
о □ оп
99999
с*
С*
-о-
СЬ
□ □ о о
X
о-
О
о
оо
о
о
&
&
о
©
о
©
о
©
о
&
&
о
&
&
о
&
&
о
©
о
2. Игры с числами


2.2. Этюд на тему Пифагора
12 13 14 15 16 17 18 19 20
XX
сх
©о
□ □□ 0о
х^х
®®с
эфсф*
©о
AVAV
о
®®
оо
□000 □ оо
®о
©О
□ □□□ Ооо
®®
о
00000
Оооо
□ □□□ о
ЛУ 6 66
®®0
И*
оооо
оооо
□ □□ о
© © оо
□□ 00 оооо
©о
©©
ООоо
®®0
шя*
*
©о
Щб
®о
®®о
XX
XXX
ООО
©о
□ □□ ООО
W
о vo
®о
AVAV
ООО
ООО
AVAV AV О
□ □□□ Ооо
ь
□ □□ о
66666
66
□ □□ 0о
®®0
ш*
©©©
о
V
AVAV
О
AVAV
ОО
оооо
оооо
оооо
®®0
®®о
W
оооо
XXX
®©
О
У&6
©о
66666
4466
©о
щ
00000
оо
©о
AVAV
ОО
00000
ооооо
□ ООО
□ оо
©о
©о
00оо
AVAV AV О
0<Ш>
Оо
;фсб
©о
©©©
О
00000
Ооо
□ □□ ООО
□□ 00 оооо
□ □□□ о
AVAV
ООО
ООО
©о
□ □□□ оооо
х^х
©о
фф*
©о
W
О О
®®
о
©О
®®о
S $ » $
®®0
□ □□□ оооо
Що
^х
оо
Рис. 1.17
Сквозь кристалл времени
21


3. Блеск логики
3. 	Блеск логики
Шесть ты мне тысяч послал, когда я просил их двенадцать.
Чтобы двенадцать ты дал, двадцать четыре спрошу.
Марк Валерий Марциал (ок. 40 - ок. 104).
Эпиграммы
Открытие красоты логических рассуждений по праву принадле- а жит древнегреческим математикам. Наиболее полно это открытие во¬
плотилось в знаменитых 13 книгах эвклидовых «Начал» (III в. до н. э.). Примечательно, что вторая
I книга этого многотомного труда посвящена разнообразным алгебраическим тождествам, изложенным на языке геометрических фигур. В книге чувствуется влияние более древних матема- Рис. 1.18 тических культур, в чём-то пере¬
кликающихся с творчеством математиков Древней Индии и Китая. Например, Предложение 4 второй книги «Начал» устанавливает алгебраическое тождество
(а + b)2 = а2 + 2 ab + Ь2
(сам Эвклид буквенной символикой не пользовался) на основе геометрической модели рис. 1.18. Бхаскара Ачарья в этом месте написал бы: «Смотри!», но Эвклид такого себе не позволяет - он достаточно подробно и скрупулезно объясняет, как доказываемое свойство следует из всех предшествующих определений, постулатов и теорем. В каноническом переводе «Начал» Д. Д. Мордухай-Болтов- ского [12] это обоснование занимает почти две страницы!
Отличительная черта изложения Эвклида — логическая строгость. Причем, когда созерцаешь весь величественный храм умозак-
а
Ь
22
Глава 1


3.1. Reductio ad absurdum
лючений, построенный на незатейливом фундаменте исходных предпосылок, удивляешься, насколько эта строгость органично вписывается в стройность и единство стиля, изящество основного канона.
Всё же, отдавая дань строгой логике в обосновании математических истин, не следует забывать, что слово теорема происходит от древнегреческого корня Оесоресо - рассматриваю. «Есть вещи, которые надо видеть для того, чтобы им верить, и есть другие, которым нужно верить для того, чтобы их видеть» — Пьер Буаст (1765-1824).
3.1. 	Reductio ad absurdum
Reductio ad absurdum — острейшее оружие математика. Это гамбит гораздо более тонкий, чем шахматный: шахматист может пожертвовать пешкой или даже фигурой, но математик предлагает в жертву всю партию.
Г. X Харди
Этим латинским названием (приведение к абсурду) иногда называют метод, больше известный школьникам как доказательство от противного.
II Задача 1. {Эвклид). Докажите, что количество простых чисел бесконечно.
jes Доказательство. Допустим, что 2, 3, 5, р — множество всех простых чисел и р — наибольшее из них. Рассмотрим целое число
q = 2-3-5-...-р +1
Оно не делится ни на одно простое число от 2 до р включительно. Но q > 1, и тогда либо q — само простое, большее р, или оно делится на простое число, большее р. Противоречие.
В истории науки известно немало примеров, когда с помощью метода Reductio ad absurdum делались важные математические открытия. Мы рассмотрим другую задачу, напрямую связанную с высказыванием английского математика Г. X. Харди (1877-1947).
Сквозь кристалл времени
23


3. 	Блеск логики
Задача 2. В двухходовых шахматах правила игры такие же, как и в обычных шахматах, за исключением того, что каждый из игроков по своему усмотрению может сделать один или два хода подряд. Докажите, что у начинающего игру существует непроигрышная стратегия.
Доказательство. Предположим, что начинающий обязательно проиграет. Тогда двойным ходом шахматного коня сначала на доступное ему поле шахматной доски, а затем обратно (например, КсЗ — КЫ), начинающий создает исходную позицию и передает обязанность начать партию своему противнику. В этом случае — по нашему предположению — противник должен проиграть. Противоречие.
Вы согласны с этим решением?
Следующая задача не только подкупает своей красотой, но и непостижимой загадкой: стоит ее условие лишь немножко подправить, как она тут же превращается в неприступную проблему...
Задача 3. Плоскость произвольным образом раскрасили в два цвета (в житейском варианте — белую скатерть каким-то образом залили чернилами). Докажите, что найдется отрезок длины 1, концевые точки которого имеют один и тот же цвет.
Доказательство. Предположим, что такого отрезка не существует. Рассмотрим произвольный равносторонний треугольник ABC с длиной стороны 1 на этой плоскости. По нашему предположению, цвет точек В и С должен отличаться от цвета точки А, но этого не может быть, поскольку В и С — концы единичного отрезка. Противоречие.
В сороковые годы прошлого века математики П. Эрдёш и Г. Хад- вигер сформулировали проблему, не решенную до сих пор:
It Найти наименьшее число цветов, которыми можно раскрасить I плоскость (в более общей постановке -- пространство) так, чтобы точки, отстоящие друг от друга на расстояние 1, оказались раскра- I шенными в разные цвета.
24
Глава 1


3.2. Существует ли объект?
В заключение приведем один пример из школьной практики. Семиклассники осведомлены, что в треугольнике против большей стороны лежит больший угол, и, наоборот, больший угол противостоит большей стороне. Через два года они узнают более точную связь между длинами сторон и ушами в треугольнике (теорему синусов, теорему косинусов), а пока они, естественно, выдвигают различные гипотезы. Одна из таких, на первый взгляд правдоподобных, гипотез состоит в том, что длины сторон треугольника пропорциональны величинам противоположных углов. Развеять это заблуждение помогает метод reductio ad absurdum. Действительно, если допустить такую пропорциональность, то в треугольнике с углами 30°, 60°, 90° стороны были бы пропорциональны числам 1,2,3, чего не может быть (почему?).
3.2. 	Существует ли объект?
Но это, но это
Далекое ГДЕ-ТО
Я всё же хочу отыскать.
Уолтер Де ла Мэр.
Где-то
Часто на вопрос, вынесенный в заголовок пункта, можно ответить утвердительно, предъявив объект для всеобщего обозрения.
Рассмотрим задачу современного математического композитора Игоря Акулича, участвовавшую в конкурсе журнала «Квант» в 2003 г.:
Задача 1. (И. Акулич, [13].) Все натуральные числа выписаны в порядке возрастания без разделителей. В результате получилась бесконечная последовательность цифр: 1234567891011121314... . Докажите, что для некоторого натурального N число, образованное первыми N цифрами этой последовательности, делится на 2003.
Отвечая на вопрос этой задачи, ученик 8 класса Бер Гуэта из города Беер-Шева (Израиль) просто взял и предъявил нужное число. Мы не будем его здесь полностью приводить, поскольку оно состоит из 1437 знаков, а опишем его словами. Начинается числовой гигант, естественно (это требуется по условию
Сквозь кристалл времени
25


3. 	Блеск логики
задачи), с цифр 1234..., замыкает же цепочку последовательность ...513514515. Пожалуй, найти этот объект без помощи компьютера было бы сложновато...
Особой прелестью обладают рассуждения, с помощью которых удается доказать существование какого-либо объекта, не предъявляя его. Например, если в двух клетках разместили трех кроликов, то ясно, что найдется клетка, где сидят двое ушастых. Это популярная иллюстрация логического рассуждения, именуемого принципом Дирихле по имени немецкого математика Петера Густава Лежёна Дирихле (1805-1859), который успешно использовал его в своих теоретико-числовых исследованиях. Довольно изящно этот принцип применили семиклассник Дима Бабичев (Россия) и член математического клуба Негев (Израиль) Ариэль Девис для решения обсуждаемой задачи Игоря Акулича.
я£ Вот их решение. Рассмотрим последовательность чисел
1,
(*) 1234567891,
1234567891... 12345678901234567891,
1234567891... 123456789012345678901234567891... 12345678901234567891,
Первое число последовательности равно 1. Каждое следующее число строится по алгоритму, указанному в условии задачи И. Акулича, а именно: последовательно выписываются числа натурального ряда до тех пор, пока не выпишется предыдущее число последовательности (*) (вверху повторяющиеся фрагменты чисел выделены жирным шрифтом). По принципу Дирихле, в последовательности (*) найдется два числа, дающие одинаковые остатки при делении на 2003 (здесь остатки — «клетки», числа — «кролики», причем «кроликов» гораздо больше, чем «клеток»). Разность этих чисел представляет собой число вида А-\0к и делится на 2003 без остатка. Так как степень 10 на 2003 не делится, то на 2003 делится число А, по своему способу построения удовлетворяющее всем условиям задачи. Оно и будет искомым.
26
Глава 1


3.2. Существует ли объект?
Ill Задача 2. Пусть а\лЪ — иррациональные числа. Может ли число аь III быть рациональным?
У этой задачи любопытная история. Положительный ответ на ее вопрос следует из глубоких теоретико-числовых исследований, связанных с решением в 1934 г. так называемой седьмой проблемы Гильберта [14]. Однако эта задача вместе со следующим необычным решением появилась на свет, когда российский школьник Гриша Гальперин (ныне профессор Восточно-Иллинойсского университета) предложил ее в 1969 году для Областной математической олимпиады.
Н2
gs Рассмотрим число V2 . Если оно рациональное, то ответ на вопрос задачи положительный для чисел a = V2, b = \J2.
Если же это число иррациональное, то возьмем а = у/2^, b = \J2. И снова получаем положительный ответ на заданный
вопрос, поскольку = 2. Итак, предъявлено две пары чи¬
сел а и Ь, одна из них удовлетворяет условию задачи (хотя мы и не знаем какая именно!).
А чтобы жюри не отклонило эту задачу по той причине, что никто такого решения на олимпиаде (да даже и не на олимпиаде!) не придумает, Гриша припас второе, более стандартное решение с логарифмами, на сей раз конструктивное.
jes Возьмем а = >/з , Ь = 2 log3 2, тогда
В первом решении мы так и не узнали, какие же числа надо брать в качестве а и Ъ (неконструктивность), а во втором построили эти числа «руками». Как видите, элегантность математики проявляется по-разному.
В качестве полезного упражнения придумайте схему неконструктивного рассуждения, использующего числа \/з (здесь его придется проводить не два раза, как с числами Л, а три раза).
Сквозь кристалл времени
27


3. 	Блеск логики
Задача 3. У подножия горы расположена келья монаха. В понедельник ровно в 9 часов утра монах начал подниматься по тропинке в гору и достиг ее вершины в 9 часов вечера. Переночевав на горе, в 9 часов утра следующего дня монах по той же тропинке начал спускаться вниз и ровно в 9 часов вечера достиг своей кельи. Докажите, что на тропинке существует место, в котором монах оказался в одно и то же время дня как при подъеме в гору, так и при спуске с горы.
Имеется изумительно красивое решение этой задачи. Представим, что ровно в 9 часов утра в один и тот же день по одной и той же тропинке в путешествие отправляется не один, а сразу два монаха: один из них поднимается в гору, а другой — спускается с горы. Ровно в 9 часов вечера каждый из них достигает своего конечного пункта: монах с низу оказывается на вершине горы, а монах с вершины — у ее подножия. Ясно, что существует момент времени, когда они встретятся на тропинке.
Какой прок от тех теорем существования, в которых не только не предъявляется искомый объект, но даже не указывается способ, по которому его можно найти или сконструировать?
Во-первых, лежащее в основе такой теоремы рассуждение, как правило, несет в себе мощный эстетический заряд и благотворно влияет на эмоциональное самочувствие решающего. А разве это плохо?
Во-вторых, в некоторых случаях факт, устанавливаемый теоремой существования, особенно если он подкрепляется дополнительной информацией о единственности существующего объекта, бывает принципиально важным для использования других, в том числе и конструктивных, методов. Поучительный пример на эту тему приведен в Комментариях.
^Докажем,
что существует объект
Q Точка. (В. Произволов, [7, с. 13].) На стол положили несколько одинаковых листов бумаги прямоугольной формы. Оказалось, что верхний лист покрывает больше половины
28
Глава 1


4. 	Магия могущества
площади каждого из остальных листов. Можно ли в таком случае воткнуть булавку так, чтобы она проколола все листы?
В Набор чисел. (XII Московская математическая олимпиада, 1949 г., [15].) Докажите, что если имеется 100 любых целых чисел, то среди них всегда можно взять несколько (или может быть одно), так, что в сумме они дадут число, делящееся на 100.
4. 	Магия могущества
Если одну и ту же проблему поставить перед представителями различных профессий, в чем-то необычную, нестандартную или незнакомую им всем, то математик с ней справится лучше.
Гуго Штейнгауз (1887-1972)
Древнегреческих ученых можно также считать первооткрывателями изумительной эффективности математики. И дело здесь даже не в пифагорейской концепции гармонии мира, основанной на числе. Математика оказалась действенным практическим инструментом, способным выручать в затруднительных ситуациях. В этом — еще один незаурядный аспект ее привлекательности.
Задача 1. (Фалес Милетский, ок. 625- 547 до н. э.).
Определить расстояние от берега до корабля на море.
ж$ От точки А вдоль берега откладывались два равных отрезка АС = CD, а от точки D — луч DE под углом ZADE = ZDAB, где В — корабль в море. На луче DE точка Е выбиралась таким образом, чтобы из нее точка В просматривалась на одной линии с точ-
Рис. 1.19
Сквозь кристалл времени
29


4. 	Магия могущества
кой С. Из равенства треугольников АСАВ = ACDE следует равенство расстояний АВ = DE. Длина расположенного на берегу отрезка DE измерялась непосредственно.
Задача 2. (Герон Александрийский, I в.). В точке А на побережье моря с прямолинейными очертаниями берега находится человек, а в точке В на этом же берегу вспыхнул пожар. По какому кратчайшему пути должен бежать человек к очагу возгорания, если сначала ему нужно добежать к морю, чтобы зачерпнуть воды?
В •
Рис. 1.20
Решение этой задачи весьма элегантно: нужно симметрично относительно берега отразить точку В — получим точку В' (рис. 1.21). Если теперь соединить точку А с точкой В' прямой линией, то точка пересечения этой линии с берегом определитточку С, в которой следует набрать воды для тушения пожара. Длина ломаной АСВ — кратчайшая. (Длина отрезка АВ' равна длине ломаной АСВ, а для любой другой точки D на берегу, отличной от точки С, длина ломаной ADB' больше длины отрезка АВ'.)
Задача 3. (Герон Александрийский, I в.). Через гору ABCD провести прямолинейный туннель, если даны его выходы В и D (рис. 1.22). На плане местности, пользуясь линейкой, это сделать легко. А как решить эту задачу практически, имея дело с реальной горой? Каждая из точек В и D скрыта от другой нагромождением камней и не может служить опорным ориентиром для прокладки направления коммуникации.
30
Глава 1


5. Ритмы в стиле жизни
Именно такая практическая задача стояла перед строителями туннеля через гору Кастро на острове Самос (родине Пифагора) в 530 г. до н. э. Древние строители справились с ней блестяще: при длине туннеля 1,3 км рассогласование в месте встречи (туннель прокладывался одновременно с двух точек В и D) составило не более 10 метров! Такой высокой точности можно было добиться только на основе точных расчетов. Автор замечательной книги [16] полагает, что в этих расчетах принимал участие сам Пифагор.
Дальнейшее обсуждение задачи Герона см. в Комментариях.
5. 	Ритмы в стиле жизни
Ритм — душа музыки.
А. 	Ремизов
Нет ничего более властного в жизни человеческого организма, чем ритм.
И. Павлов
Листая подборку старинных задач, невольно обращаешь внимание на то, что их сочинителям явно небезразличны сюжеты, обыгрывающие циклические процессы.
Согласно древней индийской легенде (ее возникновение датируется примерно началом нашей эры) изобретателю шахмат предложили запросить за придуманную им замечательную игру любую награду. Изобретатель оказался верен себе: «Положите на первую клетку шахматной доски одно зернышко, на вторую — два, на третье — четыре и так далее, складывая на каждую следующую клетку в два раза больше зерен, чем на предыдущую». Вопрос задачи-легенды касался общего количества зерен, которые запросил себе мудрец.
В чем неувядающая прелесть этого древнего шедевра? Причин, по-видимому, несколько: предельная простота алгоритма плюс красивый арифметический факт, приводящий к низвержению интуиции.
Если перевести условие задачи на математический язык, то мы имеем дело с последовательностью чисел, заданной рекуррентно:
Сквозь кристалл времени
31


5. Ритмы в стиле жизни
Яо Я/i 2 • tf/1-ь ^ 1,2, ...
Требуется найти сумму
х = #1 + <*2 + ... + 064= 1 + 2 + 22 + 23 + ... + 263.
Изящный трюк: умножаем эту сумму на 2 и замечаем, что 2 + 22 + 23 + ... +263 + 264 = (1 + 2 + ... + 263) + 264- 1,
то есть
2х = х + 264- 1,
откуда
х = 264 - 1.
Мы могли действовать и по-другому: прибавить к сумме 1 + 2 + ... + 263 единичку и насладиться зрелищем, как она постепенно слева направо сворачивает всю цепочку:
1 + 1 =2->2 + 2 = 4->4 + 4 = 8-> ...-» 263 + 263 = 2 -263 = 264.
Очень красивый факт: если к сумме первых последовательных степеней двойки прибавить единицу, то получится следующая степень двойки.
Но вернемся к регулярным процессам.
Задача 1. (Старинная задача арабского Востока). Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти 4 двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину собранных ею яблок, стражнику у второй двери — половину остатка, стражнику у третьей двери — половину нового остатка, и точно так же она отдала половину остатка стражнику у четвертой двери. У нее осталось 10 яблок. Сколько яблок она собрала в саду?
Просто поразительно — каким колоссальным поборам подвергается потребитель товара, если этот товар проходит длинную цепочку посредников.
В старинных задачах наряду с арифметической и геометрической прогрессиями встречаются числовые последовательности более общего вида.
32
Глава 1


5. Ритмы в стиле жизни
Задача 2. Торговка первому покупателю продала половину всех своих яиц и еще пол-яйца, второму — половину остатка и еще пол- яйца, третьему — половину оставшихся яиц и еще пол-яйца. У нее осталось 5 яиц. Сколько яиц у нее было первоначально?
Задача 3. (И. Ньютон, 1707). Некий торговец каждый год затрачивает на свою семью 100 фунтов, а оставшийся капитал увеличивает на одну треть. Через 3 года он обнаруживает, что его состояние удвоилось. Сколько денег у него было вначале?
Задача 3. (В. Д. Войтяховский, 1811). Веселый француз пришел в трактир с неизвестною суммою своего богатства, занял у содержателя столько денег, сколько у себя имел; из сей суммы издержал один рубль. С остатком пришел в другой трактир, где опять, занявши столько, сколько имел, издержал в оном также 1 рубль; потом пришел в третий и четвертый трактир, учинил то же, наконец, по выходе из четвертого трактира не имел ничего; спрашивается количество его денег.
В основе трех предыдущих задач лежит арифметико-геомет- рическая прогрессия, которая задается рекуррентным соотношением
хп+\ = ахп + Ь, п = 0, 1,2, ...,
где а и b — ненулевые константы. Если начальное значение х0 этой последовательности задано, то общий ее член может быть вычислен по формуле
|1-*л 1 ^ х„=а xQ+b- , п =1,2,...
1-я
Задача 5. (Франция, XVII в.). Трое имеют по некоторой сумме денег каждый. Первый дает из своих денег двум другим столько, сколько есть у каждого. После него второй дает двум другим столько, сколько каждый из них имеет. Наконец, и третий дает двум другим столько, сколько есть у каждого. После этого у всех троих оказывается по 8 экю. Сколько денег было у каждого вначале?
ж$ Как и некоторые из предыдущих задач, эта задача легко решается с конца. Однако нас больше интересует динамическая модель задачи. Обозначим jc1(0), х^\ х^0) начальные капиталы
Сквозь кристалл времени
33


5. Ритмы в стиле жизни
первого, второго и третьего человека. Тогда после первого шага процесса, то есть после завершения всех трех описанных в
условии операции, их новые капиталы xf
(I) v(i) v(i)
v2 >
ху'равны:
r(i)_4r(0)_4r(0)_4 (0)
= -2*fe>+6^0)-2J40>,
,(D
ДО
= -х
(0).
2
(0)
(1)
+ 7ж<°>.
Этот процесс легко вообразить себе продолжающимся далее. Для упрощения дальнейших записей нам удобно обратиться к формализму матричной алгебры. Прежде чем это сделать, дадим необходимые объяснения. Вектором-столбцом, или про¬
сто вектором х назовем тройку капиталов х =
на п-м шаге процесса задаются вектором
f у N Х{
. Капиталы
*1
х\
г(«)
2
, так что х0 =
*<°>
> xi =
хт
х2
г(л)
Л1
V -3 /
г(0)
\ /
V J У
и так далее.
Матрицей А назовем таблицу коэффициентов, использованных в правой части (1):
А =
4 -4-4'
-2 6 -2 -1 -1 7
Умножить первую строку (4-4-4) матрицы А на вектор х означает найти сумму попарных произведений соответствующих элементов:
4*1 - 4x2 - 4дг3 •
34
Глава 1


5. Ритмы в стиле жизни
Точно так же умножается вторая строка матрицы А на вектор х:
-2х| + 6х2 - 2*3
и третья строка:
-X| -X2 + 7х3
(по сути, здесь выписаны правые части соотношений (1) без указания номера шага процесса). В результате умножения матрицы на вектор получается вектор-столбец с тремя компонентами (координатами).
Таким образом общую рекуррентную схему исследуемого нами процесса в матричном представлении можно записать очень компактно:
хп Ахп_^ 9 п 1, 2,...
здесь в правой части равенства стоит произведение матрицы А на вектор .
Если расписать результат умножения матрицы А на вектор Ах покомпонентно (сделайте это самостоятельно), то можно заметить, что результат будет точно таким же, если сначала умножить матрицу А на матрицу А, а затем вновь полученную матрицу умножить на вектор х. Умножить матрицу А на соразмерную ей матрицу В означает следующее. Столбцы матрицы В представим как совокупность векторов. Умножать матрицу А на каждый из этих векторов будем по описанному выше правилу. Получающаяся при этом совокупность векторов составляет столбцы матрицы-результата.
Итак, обозначим
А2=АхА, А3=АхА2, ..., А"=АхА"~1.
С помощью новых обозначений легко выразить значение вектора х на л-м шаге процесса, зная его начальное значение х0 :
х„ = Лх,^ = А2хп_2 = А3^ =... = Ап70 .
Сквозь кристалл времени
35


5. Ритмы в стиле жизни
Конечно, даже матричная алгебра не спасает, когда нужно проводить конкретные расчеты, скажем, для больших значений п или для большого количества человек, раздающих друг другу деньги (в последнем случае размеры вектора х и матрицы А будут большими). Здесь на помощь приходят компьютеры.
^Упражнение
для тех, кто любит программировать
Предположим, что цвет каждой элементарной ячейки прямоугольника к х т отображает финансовое состояние некоторого банка страны. На каждом шаге итерационного процесса (скажем, ежедневно) банки обмениваются капиталами, из-за чего соответствующие им ячейки прямоугольника меняют цвет. Придумайте модели взаимодействия банков и изучите их поведение, написав соответствующую компьютерную программу. При некоторых модельных допущениях на экране монитора можно наблюдать красивые динамические узоры.
У* Утешение для тех, кто не любит программировать
В 1997 г. участники заочного конкурса, проводимого журналом «Квант», решали следующую задачу.
Задача 6. (А. П. Савин, [17].) В последовательности аь а2, а3,... число аг равняется 1799, а число а2 равняется 1828. Каждое из следующих чисел находится по закону
an +1
ап+1 “
ап-\
Чему равняется Oi997?
Кое-кто составил компьютерную программу расчета чисел заданной рекуррентной последовательности и сослался на результаты ее счета: а\997 = 1828. Однако признать корректным такое решение нельзя. Дело в том, что с абсолютной точностью компьютер умеет обрабатывать лишь целые
36
Глава 1


Решения, ответы и комментарии к главе 1
числа, а вот дробные числа, хотя и с достаточно высокой точностью, вычисляются им приближенно. Так, например, для числа а 1997 железный вычислитель может выдать результат 1,828 ООО ООО ООО ООО 0 • 103, гарантируя лишь 16 точных значащих цифр после запятой. Что располагается начиная с 17-го места после запятой и далее — для компьютера «покрыто мглой». В данном случае компьютер может лишь подсказать наблюдательному исследователю возможную закономерность, наличие же ее нужно обосновывать иным способом, например, с помощью алгебраических выкладок.
& Решения, ответы и комментарии
к главе 1«Сквозь кристалл времени»
Я в мыслях мысли сочиняю, Глазами трогаю ответ.
Владимир Казаков. Большая орда
К разделу 1 «Смотри!»
1.2. 	Невидимо-видимо
К упражнениям
Q См рис. 1.23.
Рис. 1.23
Сквозь кристалл времени
37


Решения, ответы и комментарии к главе 1
Q См рис. 1.24.
В Сначала пусть ослик сломает на две равные части любую палочку, из этих частей он составит вертикальные стороны своего прямоугольника. Из оставшихся палочек ослик сложит отрезок и разделит его пополам, если нужно, разломив посередине. Из полученных половинок он составит горизонтальные стороны прямоугольника.
Q Обозначим длины палочек х, у, z, м, а длины отрезков диагоналей сложенного из этих палочек четырехугольника а, Ь, с, d{рис. 1.25).
По теореме Пифагора,
х2 =а2 +Ь2, у2 =Ь2 +с29
z2 =с2 +d2, и2 = d2 +а2.
Отсюда видно, что если из палочек рис> ^25
с длинами х и z сложить катеты одного
прямоугольного треугольника, а из палочек с длинами у ни — катеты другого прямоугольного треугольника, то гипотенузы у этих треугольников будут одинаковыми. Совместив эти треугольники по гипотенузам, получим четырехугольник с двумя прямыми углами.
38
Глава 1


К разделу 1 «Смотри!»
Q Два возможных решения (без сомнения, есть много и других) приведены на рис. 1.26. Угол 15° отмечен дугой.
Рис. 1.26
В Квадрат 4x4 перегибаем пополам и отрезаем полоску 2x4 (рис. 1.27а). На эту полоску накладываем квадрат 3x3 и отрезаем полоску 1x2 (рис. 1.276). Из полученных «деталей» собираем квадрат 5x5 (рис. 1.27в).
о)
б)
Рис. 1.27
Сквозь кристалл времени
39


Решения, ответы и комментарии к главе 1
Q См. рис. 1.28.
В См. рис. 1.29.
1.3. Очевидно для глаза — неочевидно для ума
jss К задаче 1
«В решении используем почти очевидное соображение: если каждая из двух кривых делит площадь данной фигуры пополам, то они обязательно пересекаются. Предположим, что нужная окруж-
40
Глава 1


К разделу 2 «Игры с числами»
ность нашлась. Проведем прямую 0\02, пересекающую центры данных окружностей у\ и уь (рис. 1.30). Она делит площадь фигуры Г\ пополам. Но и у делит эту площадь пополам. Значит, внутри Г\ у у и у прямой 0\02 есть точка пересечения. Аналогично, у них есть точки пересечения внутри Гг и /3. Но окружность и прямая не могут пересекаться более чем в двух точках. Значит, такой окружности у быть не может» (С. Фомин, [8, с. 38].)
К разделу 2 «Игры с числами»
2.2. 	Этюд на тему Пифагора
& К упражнениям
Ц Выражение для суммы S(n) имеет вид:
S(n) = 1*(1 + 2 + ...ч-л)4-2*(1 + 24-...-1-л) + ... + и,(1н-24-...4-л) =
= (1 + 2 +... + й) • (1 + 2 +... + и) = (1 + 2 +... + «)2 =- (я + 1) .
4
В Суммы чисел в «уголках» образуют последовательность кубов натуральных чисел. Результат предыдущего упражнения позволяет вывести отсюда любопытное следствие: сумма кубов п последовательных чисел равна
-п2(п + 1)2.
4
В Сначала объясним, почему математики иронично относятся к психологическим тестам следующего содержания.
Пусть задана конечная последовательность чисел у\, у2, •••, уп- Психологические тесты предлагают найти закон, который лежит в основе образования заданной последовательности, и, исходя из этого закона, указать, каким должно быть следующее число уп+\ последовательности.
Сквозь кристалл времени
41


Решения, ответы и комментарии к главе 1
Докажем, что существует бесконечное количество различных многочленов Р(х), принимающих прих = 1,2,..., п значенияу\,уг, •••,уп■ Образуем многочлен (так называемый интерполяционный многочлен Жозефа Луи Лагранжа (1736-1813)):
г,.л .. (*-2Х*-3)...(х-и) , (*-1Х*-3)...(х-л)
(1-2)(1-3)...(1-«) (2-1)(2-3)...(2-п)
+ (лс-1Хх-2)...(лс-(я-1))
Ун (и - 1)(и - 2)...(и - (и -1))
(в числителе г-й по счету дроби отсутствует множитель (х - /), а в знаменателе — множитель (г-г)). Структура дробей здесь такова, что при х = i, i = 1, 2, ..., и, все дроби, кроме одной (а именно той, в числителе которой отсутствует множитель (х - /)), обращаются в нуль, а единственная уцелевшая дробь принимает значение 1. Таким образом, значения многочлена Цх) при х = i, i = 1, 2, ..., п равны соответственноyi,y2, ■■-,уп- Пусть
Р(х) = Цх) + G(x)(x- 1)(х-2)...(х- п),
где G(x) — произвольный многочлен. Очевидно, что в точках х = /, i = 1, 2, ..., и значения многочлена Р(х) совпадают со значениями в этих точках многочлена L(x), в остальных же точках многочлен Р(х) может принимать любые значения, что обусловлено произвольным выбором многочлена G(x).
Следовательно, условие психологического теста рассматриваемого типа с точки зрения математики некорректно, поскольку допускает любой ответ.
Обоснуем формулу
^ _я(л + 1Хя + 2) ^
6
для суммы чисел в п-й по счету диагонали, перпендикулярной главной диагонали таблицы Пифагора. Для этого воспользуемся методом математической индукции.
42
Глава 1


К разделу 2 «Игры с числами»
Очевидно, что при п - 1 формула (*) верна.
Предположим, она справедлива для некоторого натурального п = N, где N>1. Докажем, что в этом случае она будет справедливой также для N + 1. Имеем: ,
SN+\ =(N + \)-\ + N -2 + (N -l)-3 + ... + 2- N + l-(N + 1) =
= [N-\ + (N-l)-2 + (N-2)-3 + ... + l-N] +
+[1 + 2 + 3 + ... +N + (N + \)].
По предположению индукции, выражение внутри первой пары квадратных скобок равно
N(N + l)(N + 2)
6
а внутри второй пары квадратных скобок сумма равна
(N + IXN + 2)
2
Складывая эти две дроби, получаем
(N + \)(N + 2)(N + 3)
Sn+'~ 6 ’
что и доказывает утверждение.
& К упражнению «Каталог схем»
Сначала объясним принцип формирования Каталога.
Зададимся каким-нибудь натуральным числом т> 2, которое мы будем называть основанием. Числами-основаниями мы будем нумеровать столбцы Каталога. На приведенном в основном тексте рисунке число т пробегает значения от 3 до 20. Количество столбцов в Каталоге можно увеличивать.
Рассмотрим какой-нибудь конкретный столбец Каталога, скажем, с номером т = 10. Этому столбцу соответствует таблица Пифагора, показанная на рис. 1.13 (на ней изображены произведения чисел от 1 до 9).
Сквозь кристалл времени
43


Решения, ответы и комментарии к главе 1
Зададимся натуральным числом п < т. По числам пит создаются рисунки на пересечении строки с номером п и столбца с номером т. Пусть, например, п = 3.
Используя таблицу Пифагора, посмотрим, какие получаются цифры в разряде единиц результата при умножении каждой из цифр О, 1,2, 3,4, 5, 6, 7, 8, 9 на выбранное нами число 3. Изобразим сами цифры точками, а операцию умножения на 3 — стрелочкой, показывающей, чему равен результат (рис. 1.31):
6
5 о
о о
8
Рис. 1.31
В книге [11] подобные рисунки названы схемами умножения в 10-арифметике. Их можно также назвать ориентированными графами (ориентация задается стрелочками). Если стрелочки стереть, то получатся неориентированные графы — как раз те картинки (без указания цифр), которые приведены в Каталоге на пересечении строки с номером 3 и столбца с номером 10.
Такие картинки можно построить не только в 10-арифметике, но и в арифметиках с другим основанием: 3-арифметике, 4-арифметике и т. д. Следует только иметь в виду, что в арифметиках с основанием т роль цифр выполняют числа 0, 1,2,..., т - 1.
При исследовании Каталога возникает множество вопросов. Вот лишь некоторые из них.
Назовем кружок О «вишенкой», а схему () — «лимоном» .
В клетках главной диагонали Каталога количество вишенок подчиняется простой закономерности: 1, 2, 1, 2, 1, 2, .... Одна из этих вишенок изображает схему умножения цифры 0. А другая? В каких случаях появляется вторая вишенка?
Какие числа порождают лимоны на главной диагонали?
Что отличает фигурки в 7 столбце от фигурок в столбцах 6 и 8? Тот же вопрос — о фигурках в столбцах 10, 11, 12, а также в столбцах 13,14, 15.
44
Глава 1


К разделу 2 «Игры с числами»
В столбцах с каким номером фигурки не имеют черенков? Соответствующие им графы называются циклами — по каждому такому циклу можно пройти, вернувшись в исходную точку, при этом побывав в каждой вершине цикла только один раз.
Исследуем клетки Каталога на пересечении 4 строки и столбцов с номерами 7, 11, 13, 17, 19. Мы видим циклы из треугольников, квадратов, пятиугольников, шестиугольников и девятиугольни- ков. При этом ситуация, в которой одновременно встречались бы треугольники и пятиугольники, а также шестиугольники и квадраты, не наблюдается. С чем это может быть связано?
Назовем длиной цикла количество сторон у соответствующего многоугольника. Как связана длина цикла с номером столбца Каталога, в котором этот цикл обнаруживается?
Даже в столбцах с составным номером обнаруживаются циклы. В каких строках обнаруживаются циклы, если номера столбцов имеют составной номер?
Давайте подсчитаем, сколько в каждом столбце содержится клеток Каталога, где наблюдаются циклы. При этом буцем учитывать еще одну, не изображенную на рисунке строку Каталога, соответствующую цифре 1. В этой строке находятся только одни вишенки, причем количество вишенок в столбце с номером т равно т. Запишем эти числа внизу Каталога в соответствующем столбце. Получим последовательность чисел 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 4,... (счет ведется со второго столбца). Как связаны длины циклов в столбцах с выписанными числами? Для каждого т подсчитайте количество натуральных чисел, меньших т и взаимно-простых с т. Как соотносятся эти числа с выписанной выше последовательностью?
Обратим внимание на фигурки с черенками. Нам удобно будет опять учитывать ориентацию в графах. Для черенков эта ориентация легко восстанавливается по Каталогу, если учесть, что из каждой вершины графа обязательно выходит одна стрелочка (для цикла возможны два варианта ориентации). Сколько стрелочек может входить в вершину графа, расположенного на пересечении строки с номером а и столбца с номером ml Связано ли это число с наибольшим общим делителем чисел а и ml Можете ли вы предсказать, сколько вишенок, лимонов и других циклов может содержаться в конкретной клетке Каталога?
Сквозь кристалл времени
45


Решения, ответы и комментарии к главе 1
Восстановим ориентированный граф, соответствующий строке с номером 2 и столбцу с номером 16 Каталога (рис. 1.32).
С первого взгляда последовательность чисел 1, 9, 5, 13, 3, 11, 7, 15 на рис. 1.32 не обнаруживает никакой закономерности. Но давайте запишем эти числа в двоичном виде: 0001, 1001, 0101, 1101, 0011, 1011, 0111, 1111. Что получится, если мы отбросим правый разряд и прочитаем полученные двоичные числа справа налево, то есть 000, 001, 010, 011, 100,101,110, 111?
Зная подобные закономерности, можно предсказывать, как будут «вырастать деревья» — схемы умножения в 2т-арифметиках.
Исследование Каталога позволяет легко открывать многие замечательные факты теории чисел.
1 9 5 13 3 11 7 15
V V V V
2 Ю 6 14
12
0
о
К разделу 3 «Блеск логики»
3.1. 	Reductio ad absurdum
В приведенном на стр. 24 решении задачи 2 имеется весьма тонкая ошибка, на которую в своё время обратил внимание академик А. Н. Колмогоров ([18], стр. 123). Она обусловлена так называемым «правилом трёхкратного повторения позиции», принятом в шахматах: если некоторая позиция во время игры трижды повторяется, то объявляется ничья. В двухходовых шахматах ситуации до начала игры и после двукратного хода конём первого игрока (см. решение на стр. (27)) не идентичны, поскольку в процессе ходов
46
Глава 1


К разделу 3 «Блеск логики»
коня арбитры успели зафиксировать появление двух позиций. При дальнейшем двукратном повторении любой из них наступит ничья.
Можно ли, всё же, «спасти» задачу о двухходовых шахматах?
Автор превосходной книги «Шахматы и математика» Евгений Яковлевич Гик, из которой мы позаимствовали эту историю, предлагает организовать сеанс одновременной игры в двухходовые шахматы двух игроков на двух досках, в шторой один из игроков — назовём его А — играет с игроком Б одну партию белыми фигурами, а другую (с ним же) — чёрными. Причём белыми фигурами на второй доске А дублирует ходы партнёра белыми фигурами на первой доске, после чего дожидается ответа Б чёрными фигурами на второй доске, и точно так же ходит своими чёрными фигурами на первой доске. Ясно, что при такой организации игры какую-то из двух партий А не проиграет, что, по мнению автора книги [18], доказывает существование у начинающего непроигрышной стратегии. Однако это не так. Всё, что следует из приведенных рассуждений, сводится к утверждению: «Игрок Б играет не хуже самого себя» (причём неважно — двухходовые это шахматы, трёхходовые или обычные одноходовые).
Предложим другой вариант рассуждений reductio ad absurdum применительно к двухходовым шахматам.
Заметим, что шахматное «правило трёхкратного повторения позиции» избыточно: если игрок не может свести игру к ничьей, используя «правило троекратного повторения позиции», то у него не получилось бы свести игру к ничьей и в том случае, если бы соблюдалось правило двукратного повторения позиции. И наоборот: если у игрока имеется стратегия повторения одной и той же позиции, то, применив её несколько раз, он может повторить позицию не только дважды, но и трижды и вообще сколь угодно много раз.
Предположим, начинающий игру в двухходовые шахматы всегда проигрывает. Это означает, в частности, что он не может воспользоваться ни «правилом трёхкратного повторения позиции», ни правилом двукратного повторения позиции, если бы мы ему такое правило предоставили. Сделав ход конём «в поле и обратно», он передаёт право начинать партию своему сопернику, но уже при соблюдении правила двукратного повторения позиции. По предположению, соперник в этом случае тоже должен проиграть. Противоречие.
Сквозь кристалл времени
47


Решения, ответы и комментарии к главе 1
3.2. 	Существует ли объект?
& Поучительный пример из области вычислительной математики (см. стр. 28) Рассмотрим числовую последовательность {*„}, п = 1, 2, заданную рекуррентно: начальный член х0 этой последовательности — произвольное положительное число; остальные члены последовательности вычисляются по формуле:
( „ '\
1
х„ = — " 2
хп-1 +■
Xn-\J
(1)
где а — некоторое фиксированное положительное число.
Если бы нам было известно, что у последовательности (1) существует отличный от нуля предел, то мы смогли бы устремить п к бесконечности в обеих частях равенства (1), получив предельное соотношение
\( а х = —\ х + —
2 v х
Из последнего равенства следует х2 = а, или
х = у/а . (2)
Таким образом, если бы мы знали о существовании указанного
предела, то формула (1) служила бы прекрасным средством для при¬
ближенного вычисления квадратного корня из заданного числа а. Но как узнать, что у последовательности {х„} предел существует?
На этот вопрос дает ответ «чистая» теорема существования Карла Вейерштрасса (1815-1897). Она доказывается в стандартных курсах математического анализа. Применительно к нашему случаю ее можно сформулировать так:
Если числовая последовательность {*„} монотонно убывает:
*„+1 < (3)
и ограничена снизу:
х„> с (4)
(здесь л = 0, 1,2, ..., с — некоторая константа), то у этой последовательности существует предел х > с.
48 Глава 1


К разделу 4 «Магия могущества»
В качестве полезного упражнения предлагаем самостоятельно проверить выполнимость условий (3) и (4) для процесса (1).
Теорема Вейерштрасса устанавливает также существование предела монотонно возрастающей числовой последовательности, ограниченной сверху.
Поскольку предел числовой последовательности единственен, то формулой (2) правомерно пользоваться для вычисления предела последовательности (1).
& К упражнению «Докажем, что существует объект»
Q Точка. Можно. Для этого нужно воткнуть булавку в центр верхнего листа бумаги, так как этот центр, по условию задачи, принадлежит каждому из остальных прямоугольников.
В Набор чисел. Пусть дгь х2, ..., хюо — произвольный набор целых чисел. Образуем из них другой набор:
*|+х2, х,+х2+х} xt+x2+ ... +х|00.
Среди чисел нового набора встретится число, делящееся на 100 (и тогда составляющие его слагаемые будут искомыми), либо два числа, дающие при делении на 100 одинаковые остатки. Разность двух последних чисел делится на 100 и представляет собой сумму некоторых чисел исходного набора.
К разделу 4 «Магия могущества»
</ \ $ v sv v' 4 ' ^ ' <s ' Me . '' & < Ai'
К задаче 3
(задача Герона Александрийского)
Предположим, вокруг горы можно очертить прямоугольник KLMN так, как это показано на рис. 1.33 (сторона NK очерчивается частично). Измерив доступные элементы прямоугольника KLMN, несложно узнать величину недоступных для измерения катетов DP и РВ прямоугольного треугольника DPB, и, значит, тангенс угла
Сквозь кристалл времени
49


Литература к главе 1
DBP. Гипотенузы прямоугольных треугольники RDQ и SBK с тем же отношением катетов указывают искомые направления, по которым необходимо прокладывать туннель.
Рис. 1.33
На местности не всегда возможно очертить прямоугольник требуемых размеров. Герон Александрийский в своем сочинении «О диоптре» предлагает проводить систему взаимно перпендикулярных отрезков, примыкающих к контуру горы. Параллельный перенос построенных таким образом отрезков на стороны прямоугольника позволяет свести задачу к рассмотренному выше случаю.
Литература
к главе 1 «Сквозь кристалл времени»
1. Ахмеджанова М. Задача 1 // Квант. 2005. № 2. С. 24.
2. Гарднер М. Математические новеллы. М.: Мир, 1974. С. 419.
3. Задачи Санкт-Петербургской олимпиады школьников по математике / Сост.: К. П. Кохась и др. СПб.: Невский диалект, 2002. С. 12.
4. Смирнова J1. Задача 3 // Квант. 2000. № 6. С. 29.
5. Панов М. Задача 4 (7 класс) // LXV Московская математическая олимпиада, МЦНМО, 2002. С. 4.
50
Глава 1


Литература к главе 1
6. Сарбаш Р. Задача 3 // Квант. 2002. № 3. С. 26.
7. Произволов В. Задачи на вырост / Приложение к журналу «Квант». № 5, 2003. М.: Бюро Квантум, 2003, 128 с.
8. Фомин С. Задача М471 // Квант. 1978. № 9. С. 38.
9. Колмогоров А. Н. Математика — наука и профессия / Серия «Библиотечка „Квант"». Вып. 64. М.: Наука, 1988. С. 7.
10. Авилов Н. Сюрпризы таблицы умножения / Квант. 2000. № 2. С. 32-33.
11. ДынкинЕ. Б., Успенский В. А. Математические беседы. Изд. 2. Москва — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002. 260 с.
12. Эвклид. Начала. Кн. I-IV. ГИТТЛ. М. — Л., 1950. С. 64-65.
13. Акулич И. Задача 10 // Квант. 2003. № 5. С. 25.
14. БолибрухА. А. Проблемы Гильберта (100 лет спустя). М.: ЦНММО, 1990. 24 с.
15. Сборник задач Московских математических олимпиад / Сост. А. А. Леман.
М.: Просвещение, 1965. С. 141.
16. Волошинов А. А. Пифагор: союз истины, добра и красоты. М.: Просвещение, 1993.224 с.
17. Савин А. Я. Задача 15 // Квант. 1997. № 6. С. 20.
18. ГикЕ. Я. Шахматы и математика. М.: Наука, 1983. С. 17.


Глава 2
Почему нравится задача?
Задача должна быть такой, чтобы возникало желание ее решать.
В. 	Произволов
Задача безусловно элегантная, если она прошла испытание временем, как большинство задач, рассмотренных в первой главе. Это очень четкий и явственный критерий, но... он не вскрывает «скрытых пружин» элегантности, тех побудительных мотивов, которые, собственно, и делают задачу привлекательной.
Что же это за «скрытые пружины»?
1. 	Сказочная фабула
Для меня и, думаю, для большинства математиков существует другая реальность, которую я буду называть «математической реальностью».
Г. Харди. Апология математика
Сказка — ложь, да в ней намек — Добрым молодцам урок.
Русская народная поговорка
Трудно найти образованного человека, которому не была бы знакома старинная задача о волке, козе и капусте. Она была включена в рукописный сборник «Задачи для изощрения ума» ирландского ученого монаха Алкуина (735-801).
52
Глава 2


1. Сказочная фабула
I Задача. Крестьянину нужно перевезти через реку волка, козу и кочан капусты на лодке, вмещающей, кроме крестьянина, только одного из трех. Как перевезти их, чтобы коза не могла съесть капусту, I а волк — козу?
Конечно, среди любителей животных могут найтись те, кто прикармливает кровожадного волка. Но очень маловероятно, что среди них обнаружится крестьянин, озабоченный также выращиванием козы. И уж совсем невероятно, что этому отчаянному экс- тремалу захотелось бы на свою голову приключений, связанных с транспортировкой опасного груза. Описанная Алкуином ситуация, очевидно, сказочная. А вымысел всегда привлекателен, в какой бы форме он не выражался — в форме сказки или в форме задачи. А еще лучше, когда эти формы сплетены в одну...
^Задачи-сказки
Q На одном острове жили правдивые люди, которые всегда говорили правду, и лжецы, которые всегда лгали. Однажды трое жителей этого острова разговаривали.
Первый сказал: «Только один из нас лжец».
Второй сказал: «Только один из нас правдивый».
Третий сказал: «Вы оба лжецы».
Кто из них правдивый, а кто лжец?
Q (А. Жуков, [1].) В Зазеркалье водятся многоголовые, многорукие, многоногие существа. Существо считается умным, если количество его голов больше, чем суммарное количество ног и рук; сильным, если количество его рук больше, чем суммарное количество голов и ног; быстрым, если количество его ног больше, чем суммарное количество голов и рук.
Существуют ли в Зазеркалье гармонически развитые личности: умные, сильные, быстрые?
Q (А. Жуков, [2].) В лесу водятся крикливые пушистые зверюшки, среди которых имеются барабашки. Какого бы
Почему нравится задача?
53


1. Сказочная фабула
зверя ни взять, существует барабашка точно такой же крикливости и существует барабашка точно такой же пушистости (возможно, это один и тот же барабашка). Среди всех зверюшек одинаковой крикливости барабашки самые пушистые. Среди барабашек более крикливые являются более пушистыми. Следует ли отсюда, что среди всех зверюшек одинаковой пушистости барабашки наименее крикливые?
В [3] Правила приличия запрещают мужчине стоять в очереди перед женщиной. В очереди из ста человек первый мужчина. Докажите, что в этой очереди нет женщин.
В (А- Шаповалов). Житель страны Ш считается богатым, если его месячный доход выше ставки министра финансов, иначе — небогатым. Известно, что богатые женихи предпочитают небогатых невест. Докажите, что если доходы у всех разные, то можно установить такую ставку министру финансов, чтобы в стране стало поровну богатых мужчин и небогатых женщин.
В [4] «Некий хитрый лазутчик вознамерился проникнуть в стан неприятеля. Он искусно замаскировался в кустах и стал подслушивать, какой пароль говорят охране лагеря. Вот кто-то подходит, и часовой к нему обращается, называя число:
— Двадцать шесть.
Немного подумав, посетитель отвечает:
— Тринадцать, — и часовой его пропускает.
Вот еще кто-то появляется. Часовой к нему:
— Двадцать два.
Гость:
— Одиннадцать, — и проходит в лагерь.
„Ага!“ — осенило лазутчика. — „Секрет предельно прост!“ Он вылез из кустов и уверенной походкой направляется к охране.
— Сто, — говорит ему часовой.
54
Глава 2


2. Раскрепощенность фантазии
— Пятьдесят, — небрежно отвечает лазутчик. И тут же попадает в объятья охраны:
— Неправильно, три! Попался, голубчик!
В чем секрет пароля?»
2. 	Раскрепощенность фантазии
Но кто проникнуть мог во тьму, Где Духа молния родится?
Дж. Г. Байрон.
Паломничество Чайльд Гарольда
От полета фантазии авторов иных задач захватывает дух. «Оцените, какую работу необходимо совершить, чтобы завязать узлом стальной лом?» (задача предлагалась на V Московском турнире юных физиков в 1983 г.). Существует ли многогранник, неустойчивый на каждой своей грани? (Чего стоит одна только идея, ведь такой многогранник, если бы он действительно существовал, мог бы конкурировать с изысканнейшими проектами «вечного двигателя»!)
Но не только оригинальной постановкой вопроса поражают яркие задачи. Иногда восторг способен вызвать и нестандартный, неожиданный способ решения.
Задача 1. (Г. Гальперин). 17 биллиардных шаров, между которыми одинаковые промежутки, движутся один за другим с одинаковыми скоростями слева направо, а 19 таких же шаров, тоже с одинаковыми промежутками между ними, движутся один за другим справа налево с теми же одинаковыми скоростями. Сколько ударов произойдет в этой системе?
лх Решение. (Г. Гальперин). После столкновения два шара разлетаются в разные стороны. Можно об этом мыслить как о двух прозрачных шарах, которые просто обменялись своими номерами (предполагается, что вначале все они были пронумерованы). Итак, все шары прошли друг сквозь друга, то есть 17 шаров прошли сквозь идущих им навстречу 19. Значит, всего произойдет 17 • 19 = 323 удара.
Почему нравится задача?
55


2. Раскрепощенность фантазии
Одну и ту же работу можно выполнять по-разному. Например, суммировать натуральные числа от 1 до 100 можно так, как это делает компьютер по бесхитростной программе — бездумно перебирая слагаемые одно за другим. Но можно поступить иначе, последовав вдохновенному примеру юного Карла Фридриха Гаусса (1777-1855). Широко известна легенда о том, как маленький Гаусс несказанно удивил своего учителя, обнаружив замечательное свойство предложенного ему числового ряда:
1 + 100 = 2 + 99= ... = 50 + 51 = 101.
Этот факт позволил ему найти сумму 1 + 2 + ... + 100 практически мгновенно.
Как записать десятичную периодическую дробь 1,2333... в виде обыкновенной дроби? Можно попытаться вспомнить правило из учебного руководства1: «Чтобы обратить периодическую дробь в обыкновенную, надо в числителе записать разность между числом, стоящим до второго периода, и числом, стоящим до первого периода, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом». Впрочем, неизвестно, уцачной ли будет эта попытка — гораздо легче заметить, что если умножить число х = 0,0333... на 10, то получится число «почти» такого же вида, а именно:
1 Ojc = д: + 0,3.
Отсюда
стало быть,
__1_
*~30
2 37
1,2(3) = 1— + х = —. 10 30
Призовите на помощь немного фантазии, чтобы решить следующие упражнения.
1 Кремер Н. Ш., Константинова О. Г., Фридман М. Н. Математика абитуриентам экономических вузов. М.: ЮНИТИ, 2001. С. 12.
56
Глава 2


2. Раскрепощенность фантазии
У* Упражнения
Q (С. Дворянинов). Даны 10 чисел: 1,2, 3,10. Найдите сумму, состоящую из S суммы этих чисел по одному:
1+2 + ... + 10,
а также
S суммы произведений этих чисел по два:
1 х 2+ 1 х з + ... + 9 х ю,
а также
S суммы произведений этих чисел по три:
1 X 2 х з + 1 х 2 х 4 + ... + 8 х 9 X 10, а также ( и т. д.)
S суммы произведений этих чисел по девять: 1х2хЗх...х8х9+1х2хЗх...х8хЮ + ...+2хЗх...х9хЮ, а также
S произведения этих чисел
1 х 2 х з X ... X 8 х 9 X 10.
Q Упростите:
(x+y + zf-(x+y-zf- (х-у + z)3 - (-Х +у + z)3. Q [1] Решите уравнение х3 - Зх2 — Зле — 1=0.
Q [2] Решите уравнение (д: - I)4 +х4 = 7.
Q [3] Решите уравнение yfx + 1 = 5 - х2. В Вычислите
Почему нравится задача?
57


3. Парадоксальность
3. 	Парадоксальность
...а я при этом улыбался ее удивлению и удивлялся ее улыбке.
Владимир Казаков.
Набросок
3.1. 	Острый взгляд математика
Других людей восхищает тот факт, что они могут взять в математике даже простейшие вещи, которые применимы в их работе. На уроках труда токари очень гордятся своим знанием формул длины окружности и площади круга, хотя вряд ли могут сказать что-то определенное о том, откуда эти формулы взялись, а слово «трансцендентный» они вообще воспринимают как ругательное.
А. Браверман
Но не только сказочностью фабулы привлекает задача Алкуина о волке, козе и капусте. В ее условии описывается, казалось бы, безвыходная ситуация: то коза может съесть капусту, то волк козу, то на одном берегу реки, то на другом — перед крестьянином возникают сплошные проблемы. А в нагромождении проблем триумф рассудка воспринимается как некий ошеломляющий и, в силу этого — элегантный парадокс.
S Как бы поступили Вы в следующих житейских ситуациях?
В Врач прописал Вам таблетки двух сортов: А и В. Вы должны принимать две таблетки одновременно через каждые пол часа: одну таблетку сорта А и одну таблетку сорта В. Именно в таком сочетании, сортов и количеств лекарства, иначе для Вас могут наступить нежелательные последствия.
58
Глава 2


3.2. Граффити на полях
Но вот беда: когда осталось всего два приема, 4 таблетки перемешались (из них 2 таблетки сорта А и 2 таблетки сорта В). Различить же эти таблетки по внешнему виду совершенно невозможно. Что делать?
В (А. Блюфштейн, [1].) Вы собрались в отпуск и решили захватить с собой неразборную четырехметровую удочку. Вы бы не хотели ее сгибать или ломать, а железнодорожные правила запрещают провозить предметы длиной более 3 метров. Как же сдать ее в багаж?
В Известный испанский художник Сальвадор Дали (1904—1989) в своей книге «Моя тайная жизнь» описывает следующий эпизод из своей биографии: «Перед конкурсом на лучшую картину я заключаю пари, что стану победителем, нарисовав полотно таким образом, чтобы кисть ни разу не прикоснулась к поверхности холста. И мне действительно удается выполнить произведение на заданный сюжет... я получаю первую премию»2. В чем оказался секрет Сальвадора Дали?
3.2. 	Граффити на полях
Мы попросили изучавших впервые этот материал поделиться своим мнением в форме «граффити» на полях...
Часть замечаний позитивна, часть — негативна, ценность остальных равна нулю.
Р. Грэхем, Д. Кнут, О. Паташник.
Конкретная математика
В некоторой школе в некоторой библиотеке обнаружен задачник, на полях которого ученики оставили свои граффити. Ниже приведены фрагменты из этой книги вместе с пометками читателей, выделенные курсивом. Как вам представляется, есть ли в сопроводительных комментариях здоровое зерно?
2 Дали С. Моя тайная жизнь. Минск.: Попурри, 2003. С. 31.
Почему нравится задача?
59


3. Парадоксальность
1. Календарь из двух кубиков (Мартин Гарднер, [2].)
На каждой грани двух кубиков требуется разместить по одной цифре таким образом, чтобы из них можно было бы скомбинировать наборы: 00, 01, 02, ..., 30, 31. Первая цифра набора должна быть написана на грани одного кубика, а вторая — на грани другого. Можно ли это сделать?
Очевидно, что цифры 0, 1, 2 должны присутствовать на обеих кубиках. Но тогда, на оставшихся шести гранях кубиков разместить семь цифр 3, 4, 5, 6, 7, 8, 9 не удастся.
II 2. Что ближе?
Какое из чисел ближе к единице: правильная положительная дробь или дробь, обратная к ней?
Возьмем очень маленькую дробь, например, 1/10000. Ясно, что она будет ближе к 1, чем дробь, обратная к ней. Однако, если взять дробь, близкую к единице, например 9999/10000, или какую-нибудь другую такого же сорта, то еще надо посмотреть, что получится.
3. 	Выбежит или не выбежит? (В. Дубов, [3].)
Две прямолинейные аллеи парка пересекаются в его центре — точке О. На равном удалении от центра находятся две скамейки — в точках Ли В, также соединенных аллеей. На каждой скамейке сидит девочка, а собака Моська располагается ровно посередине между ними. Девочки одновременно встали и с одинаковой скоростью пошли по аллеям. Одна из них пошла по аллее ОА от центра, а другая — по аллее ВО к центру Рис. 2.1
парка. Собака в каждый момент времени занимает середину отрезка, соединяющего
двух девочек. Выбежит ли собака Моська за пределы аллеи АВ, пока одна из девочек будет двигаться к центру парка?
Уж наверняка выбежит, ведь отрезок ВО наклонен в сторону аллеи ВА, а продолжение луча ОА за точку А — наоборот, отворачивается от АВ.
60
Глава 2


3.2. Граффити на полях
4. Тот, кто был хуже, оказался лучше (П. Самовол, М. Аппельбаум, [4].) Два спортсмена соревнуются в точности стрельбы (точностью стрельбы называется отношение числа успешных выстрелов к числу использованных патронов). Вначале каждому спортсмену выдается ровно 40 патронов. Соревнование проходит в два этапа, причем на каждом этапе спортсмен может использовать любую отличную от нуля часть патронов. Может ли случиться так, что на каждом из двух этапов точность стрельбы первого спортсмена будет выше, чем точность стрельбы второго, но по общему результату соревнований точность стрельбы первого спортсмена окажется ниже точности стрельбы второго?
Если бы это произошло, то это было бы странно и несправедливо по отношению к первому спортсмену.
5. Доход, превышающий расход, который превышал доход ([5].) Один человек каждый месяц записывал свой доход и расход. Может ли быть так, что за любые пять идущих подряд месяцев его общий расход превышал доход, а в целом за год его доход превысил расход?
Если бы он был бухгалтером, то его уволили бы с работы.
6. Враги в парламенте (О. Бородин, [6].)
В парламенте у каждого его члена не более трех врагов. Можно ли разбить парламент на две палаты так, что у каждого парламентария в одной с ним палате будет не более одного врага? (Считается, что если А — враг В, то В — враг Л.)
Если бы у любого парламентария был только один враг, то каждую враждующую пару можно было бы легко развести по разным палатам. С двумя врагами — посложнее, а с тремя — ?.. Во избежание эксцессов пусть лучше сделают трехпалатный парламент.
^Упражнения
Q ([7].) На рис. 2.2а изображены графики трех линей- ных функций, а на рис. 2.26 — трех квадратичных функций.
Почему нравится задача?
61


3. Парадоксальность
Рис. 2.2
Могут ли это быть функции: в случае а)
у = ах + Ъ\
у - Ъх + с;
у = сх + а,
в случае б)
у = ах2 + Ьх + с;
у = сх2 + ах + Ь;
у = Ьх + сх + а!
В (77. Самовол, М. Аппельбаум.) Существуют ли две
различные функции у(х) и Дх), которые в каждой точке интервала (0; 1) принимают одинаковые значения у(х) = fix), х е (0; 1), но, тем не менее,
/(/(*))*>(/(*)) в каждой точке этого же интервала?
В ([8], 10-11 класс.) На плоскости дана парабола .у = х2 и окружность, имеющие ровно две общие точки: А и В. Оказалось, что касательные к окружности и параболе в точке А совпадают. Обязательно ли тогда касательные к окружности и параболе в точке В также совпадают?
62
Глава 2


4. Радость озарения
4. 	Радость озарения
Самая милая шу...
Половина ело...
Владимир Казаков
В понедельник 19 сентября (1994) я с утра сидел в своем кабинете... Внезапно, совершенно неожиданно, на меня снизошло озарение...
Эндрю Уайлс3
Попробуйте восстановить недостающие буквы (они отмечены точками) в названии геометрической фигуры:
К.А.Р.Т
Решение данной задачи приходит не в результате каких-либо логических умозаключений, оно появляется сразу, целиком.
Подобное озарение играет сольную партию в драме научных открытий.
Фалес Милетский (ок. 625-547 до н. э.) обнаружил, что у маленького человека и у величественной пирамиды есть одно общее свойство: способность отбрасывать пропорциональную своей высоте тень. Применив пропорцию к нахождению высоты пирамиды, Фалес несказанно удивил египетского царя Амазиса.
Другая ассоциация помогла Эратосфену Киренскому (ок. 276- 194 дон. э.) оценить длину окружности меридиана Земли в то время, когда еще многие его современники даже не подозревали о шарообразности нашей планеты. Эратосфен заметил, что в момент летнего солнцестояния тень, отбрасываемая в городе Александрии стержнем в центре полой градуированной полусферы (скафиса) составляет такую же часть окружности, что и длина меридиана между Александрией и городом Сиеной, где в этот момент Солнце находилось в зените. Расстояние между двумя городами Эратосфен определил по времени прохождения каравана верблюдов, что позволило ему оценить окружность Земли с поразительной точностью около 1 %!
3 Цит. по: Сингх С. Великая теорема Ферма. МЦНМО, 2000. С. 250.
Почему нравится задача?
63


4. Радость озарения
I Задача 1 (Я. Штейнер, 1833). На плоскости заданы две параллельные прямые и отрезок АВ на одной из них. Постройте середину отрезка АВ с помощью одной линейки.
Если не удается решить эту задачу сразу, постарайтесь вспомнить, какие факты вам известны о параллельных прямых, о фигурах, имеющих параллельные стороны. Наводящее указание к решению см. в Комментариях.
^ Тренировка ассоциативного мышления
В Изучите картину Сальвадора Дали (1904—1989) «Сон, навеянный полетом шмеля вокруг граната, за секунду до пробуждения (1944)». Почему на ней изображены последовательно возникающие из граната окунь, тигр, штык?
Q а) В квадрат вписан другой квадрат так, как показано на рис. 2.3. Докажите, что их центры совпадают.
б) На гипотенузе прямоугольного треугольника с катетами а и Ъ построен квадрат (рис. 2.4). Найдите расстояние от вершины прямого угла треугольника до центра квадрата.
64
Глава 2


5. Неожиданный ракурс
Q а) Дж. Дж. Сильвестр (1814-1897), 1893). Докажите, что если на плоскости задано п > 2 точек, не лежащих на одной прямой, то существует прямая, содержащая ровно 2 из данных точек.
б) На плоскости нарисовано п > 2 прямых, среди которых нет двух параллельных и не все пересекаются в одной точке. Докажите, что существует точка, в которой пересекаются ровно две прямые.
5. 	Неожиданный ракурс
Закон прозы: слова взрываются, если хотят. Другой закон прозы: даже если и не хотят.
Владимир Казаков.
Зиглинда
II Задача 1. Какие грузы можно взвесить с помощью гирь массами в 1, 2, 2г, 23, 2п, ... граммов (п — натуральное) и сколькими спо¬
собами?
& Испробовав небольшие значения п, несложно прийти к гипотезе, что с помощью набора гирь в 1, 2, 22, ..., 2” граммов можно взвесить любой груз массой от 1 до 2n+1 - 1 граммов. Причем, это можно сделать единственным способом. Действительно, если предположить, что существует два набора попарно различных гирь с равной суммарной массой:
2** +2*2 + ... + 2*' = 2mi + 2т* + ... + 2ш%
то наибольшая из степеней двойки в этом выражении всегда больше суммы степеней двойки в другой части равенства (см. п. 5 «Ритмы в стиле жизни» предыдущей главы). Противоречие. Сформулированную гипотезу сравнительно несложно доказать методом математической индукции. Однако совершенно неожиданный ракурс в решении этой задачи обнаружил Леонард Эйлер в 1750 г., о чем мы сейчас и расскажем.
Почему нравится задача?
65


5. Неожиданный ракурс
Рассмотрим произведение
ct(z) = (1+ z)(l + z2) (1 + Z4) (1 + z8)... (*)
Если раскрыть скобки и привести подобные члены, то получим выражение вида
a(z) = 1 + A \z + A2z2 + A3Z3 + ...
Здесь / получается как произведение каких-то одночленов z2m — не более одного из каждой скобки в (*), а коэффициент Ак выражает количество способов, которыми можно представить число к в виде суммы некоторых чисел из 1, 2, 22,..., 22т,....
Для вычисления коэффициентов Ак Эйлер записывает тождества
(1- z) (1 +z) = 1 -z2, (l- z2) (l +z2) = 1 -z4,
(l- z4) (l + z4) = 1 -z8,
Далее, перемножив и сократив на общие множители, получает (1 -г) ■ a(z) = 1, или
(1 -z)( 1 +A,z + A2z2 + A3z3 + ...)= 1,
1 -z + A\z — AiZ1 + A2z2 — A2z3 +A3Z3 - ... = 1,
откуда, приравняв коэффициенты при аргументе z многочленов в левой и правой частях последнего равенства, находит Аг = 1, Аг = Ai = 1, Л3 = А2 = 1 и вообще Д* = 1 для всех Лг. А это и означает, что всякий груз в целое число граммов можно взвесить гирями в 1, 2, 22,..., 2”,... граммов единственным способом.
II Задача 2. (С. Дворянинов, [1].) Числа х, у, z, t лежат в интервале (0; 1). Докажите неравенство:
yjx2 +(1-/)2 +\Jy2 +(1-дг)2 + ^z2 +(1-у)2 + ф2 +(l-z)2 <4
jtS Решение (I способ). Воспользуемся неравенством для положительных чисел а и Ь:
у]а2 +Ь2 <а + Ь .
66
Глава 2


6. Великолепие миниатюр
Применив его к каждому из радикалов в левой части доказываемого неравенства, получим, что она меньше, чем сумма
х +(1 — t) + у +(1 — х) + z +
+ (1 — j/) + f + (1 — z) = 4.
II способ. См. рис. 2.5 — длина периметра четырехугольника, вписанного в единичный квадрат, не превышает периметра квадрата.
6. 	Великолепие миниатюр
Всё точное — коротко.
Ж. Жубер
1,2, 3,4, 5, 6, 7, 8, 9, 10, 12? 11!
F. Le Lionnais
6.1. 	В задаче всё должно быть прекрасно
В числах — почти утренний смысл.
Владимир Казаков.
Дневник
Любители шахматных задач высоко ценят миниатюры — композиции, в которых задействовано малое количество шахматных фигур. В математическом фольклоре также существуют композиции, привлекающие короткой изящной формулировкой условия и элегантным решением.
1 -t t
Рис. 2.5
Почему нравится задача?
67


6. Великолепие миниатюр
Задача 1. (В. Произволов, [1].) На балу каждый кавалер танцевал с тремя дамами, а каждая дама — с тремя кавалерами. Докажите, что на балу число дам равнялось числу кавалеров.
* Решение. Определим число различных танцевальных пар. Если число кавалеров принять за к, то число пар было Зк, если число дам принять за т, то число пар было 3т. Так как 3к = 3т, то к = т.
Задача 2. (Э. Чезаро (1859-1906)). Докажите неравенство
(а+Ь)(Ь+с)(с + а)
где а, Ь, с — длины сторон произвольного треугольника. я£ Доказательство:
(а + b)(b + с)(с + а)
(а ЪЛ
Ь сЛ
1
(с аЛ
=
— + —
+
+
КЪ a ;
U ь)
1
U с)
+ 2>8.
abc
В этом решении использовано классическое неравенство:
^>2,
У х
где х, у — произвольные положительные числа. Последнее неравенство следует из эквивалентных ему неравенств
х2 + у2 > 2ху, (х-у)2 > 0.
В следующих упражнениях представлены задачи, в которых используется минимальное количество параметров.
У Упражнения
Один параметр
Q {Софи Жермен (1776-1831)). Докажите, что число пА + 4 составное при натуральном n > 1.
В (Г. В. Лейбниц (1646-1716)). Докажите, что если число п целое, то а) п5 - п делится на 5; б) п1 - п делится на 7.
68
Глава 2


6.1. В задаче всё должно быть прекрасно
Q Найдите наименьшее натуральное число п такое, что 2п — квадрат, а Зи — куб целого числа.
Два параметра
В Решите в натуральных числах уравнение х + у = ху.
В (77 Дьюдени, [2].) Найдите два различных натуральных числа, сумма квадратов которых была бы кубом, а сумма кубов — квадратом.
Три параметра
В Три разных натуральных числа таковы, что сумма любых двух из них делится на третье.
Докажите, что из этих чисел можно составить арифметическую прогрессию.
В Докажите, что
а Ъ с
а) если — = — то a = b = с;
b с a
б) если = — + — то (а + b)(b + с)(с + а) = 0.
a+b+c а b с
В (В. Сендеров). Целые числа х, у, z таковы, что ху +yz + zx = 1. Докажите, что число (1 + х2) (1 +У) (1 + z2) — точный квадрат.
В {Леонардо Пизанский (1180-1240)). Найдите рациональные числа х, у, z такие, чтобы каждая из сумм
x + y + z + x2, x + y + z + x2+y2, x + y + z + x2+у2+z2 была квадратом.
В (В. Произволов, [3].) Натуральные числа х и у таковы, что сумма ху+х+у дает квадрат целого числа. Докажите, что найдется натуральное число z такое, что каждая из семи сумм
xy + z, yz + x, zx + y, yz + y + z, zx +я z + x, xy + yz + zx, xy + yz + zx + x + y + z дает квадрат целого числа.
Почему нравится задача?
69


6. Великолепие миниатюр
6.2. 	Минимум средств
Мастера узнают по его инструментам.
Поговорка
Итальянский математик Лоренцо Маскерони (1750-1800) в работе «Le geometria del compasso» (Геометрия циркуля), Pavia, 1797, доказал, что всякая задача на построение, разрешимая с помощью циркуля и линейки, разрешима и с помощью только циркуля.
II Задача 1. (Л. Маскерони). Располагая только одним циркулем, разделите пополам отрезок, заданный своими концами — точками А и В (то есть постройте точку С на отрезке АВ такую, что АС = СВ).
Задачами построения с помощью одной только линейки, если заданы дополнительные фигуры на плоскости, занимался немецкий математик Якоб Штейнер (1796-1863) (см. п. 4. «Радость озарения»).
6.3. 	Обманчивая простота
Быть может, высший класс в математике — когда понять задачу может любой, но никто не в силах ее одолеть.
А. Сойфер
Известные сегодня факты — лишь крошечный островок в безбрежном океане неизведанного. Вот лишь маленькая пригоршня загадок из его набежавшей волны. Право же — их условия просты и прозрачны, понять их может любой...
1. (Э. Каталан (1814-1894)). Существует два последовательных натуральных числа, каждое из которых является степенью натурального числа с натуральным показателем, большим 1, например, 8 = 23; 9 = З2. Существуют ли другие пары таких последовательных натуральных чисел?
2а) Пара простых чисел с разностью 2 называется близнецами. Например, числа 3 и 5, 5 и 7, 11 и 13 - близнецы. Конечно или бесконечно количество близнецов?
70
Глава 2


7. Элегантные мотивы
26) Российским математиком Б.С. Стечкиным в 2003 году высказано предположение, что между каждой парой квадратов простых чисел найдутся близнецы:
4 < 5 < 7 < 9;
9<11<13<25;
25<29<31<49;
Верна ли эта гипотеза?
3. Натуральное число называется совершенным, если оно равно сумме своих собственных делителей. Например, число б совершенное, поскольку 6 = 1 + 2 + 3.
Существуют ли нечетные совершенные числа?
7. 	Элегантные мотивы
Здесь каждый звук, и близкий, и далекий, Таит всемирной музыки истоки.
Дж. Г. Байрон. Паломничество Чайльд Гарольда
Музыка есть бессознательное отношение души к арифметике.
Г Лейбниц
7.1. 	Мотив натурального ряда
Число дает стимул словам.
Владимир Казаков.
Дневник
Этот мотив начинает «звучать» уже в произведениях древних авторов.
Герону Александрийскому (I в.) принадлежит задача о бьющих из-под земли источниках, из которых первый заполняет бассейн за
Почему нравится задача?
71


7. Элегантные мотивы
один день, второй — за два дня, третий — за три дня... и здесь можно было бы поставить «и т. д.», но Герон ограничивается четвертым источником, который заполняет бассейн за четыре дня. В задаче спрашивается, за сколько дней заполнят бассейн все источники вместе.
Некоторую вариацию мотива натурального ряда можно услышать в древнеиндийской задаче (III—IV в.): среди прихожан храма второй жертвователь дал вдвое больше первого, третий — втрое больше второго, четвертый — вчетверо больше третьего — здесь тоже можно было бы поставить «и т. д.», но автор решил ограничиться четырьмя прихожанами, и спрашивает, сколько дал первый, если все вместе дали 132?
I Задача 1. (Бхаскара I, Индия, VI в.). Найти натуральные числа, дающие при делении на 2,3,4, 5,6 остаток 1, но без остатка делящиеся на 7.
л! Решение. Искомые числа должны представляться в виде 60и+1, а также 1т, где п, т — натуральные. Из равенства 60п+1=1т следует
60 п + 1 „ 4п + 1 т = = 8л + .
7 7
Последняя дробь — целое число, если 4n+l=lk, где к — целое, откуда
7к-1 , Ък — \ п= = к + .
4 4
Аналогично Зк- 1 = 4г, где г — целое, откуда
, 4r +1 г +1
к = = /• + .
3 3
Точно так же /-+1 = 35, где s — целое, откуда
г = 35- 1
Последовательно подставляя последнее выражение в предыдущие формулы, находим
к = 4s- 1; n = ls -2.
72
Глава 2


7.1. Мотив натурального ряда
Придавая различные натуральные значения s = 1, 2, 3, получим п = 5, 12, 19, ... и, соответственно, искомые числа вида 60л + 1:301, 721,1141,....
Можно ли обобщить задачу Бхаскары на другие числа натурального ряда? Очевидно, это можно сделать так: найти натуральные числа, дающие при делении на 2, 3, 4, 5, 1 остаток 1, и,
кроме того, делящиеся на р, где простое р > 2. Эта задача, как и в случае с р = 7, всегда имеет решение.
Задача 2. (Л. Ф. Магницкий, 1703). Найти число, которое s при делении на 2 дает в остатке 1,
S при делении на 3 дает в остатке 2,
✓ при делении на 4 дает в остатке 3,
S при делении на 5 дает в остатке 4.
Как можно обобщить эту задачу?
* Решение задачи Магницкого очень элегантное.
Прибавим к искомому х число 1, тогда оно поделится и на 2, и на 3, и на 4, и на 5. То есть х+ 1 = 60к, где к — целое, откуда х = 60к - 1 — ответ.
Прислушайтесь к мотиву в следующих упражнениях.
^Упражнения
□ (А. П. Савин, [1].) Однажды на лестнице я нашел странную тетрадь. В ней было написано сто следующих утверждений:
«В этой тетради ровно одно неверное утверждение».
«В этой тетради ровно два неверных утверждения».
«В этой тетради ровно три неверных утверждения».
...,
«В этой тетради ровно сто неверных утверждений».
Какое из этих утверждений верное?
Q (А. Жуков). Для какого наибольшего п существует набор из п чисел, среди которых
Почему нравится задача?
73


7. Элегантные мотивы
ровно одно число делится на п; ровно два числа делятся на п — 1; ровно три числа делятся нап- 2;
• • • >
ровно п чисел делятся на 1 ?
0(5. Брагин, [2].) Сколько существует таких групп из девяти последовательных четырехзначных чисел, что первое число делится на 10, второе делится на 9, третье — на 8, ..., девятое — на 2?
Q Пустьр\ = 2,р2 = 3,рз = 5,р4 = 7, — последова¬
тельные простые числа. Найдите натуральные числа, которые При делении на pj дают остаток 1;
При делении на р2 дают остаток 2;
• • • >
При делении на рп дают остаток п.
7.2. 	Мотив круга
Я очень сомневаюсь, что человеческая изобретательность способна загадать загадку, которую человеческая изобретательность не способна была бы разгадать.
Э.По
Этот мотив в задачах звучит также издавна — взять, хотя бы, теорему Пифагора, где на сторонах прямоугольного треугольника по кругу располагаются квадраты.
Кстати, почему именно квадраты?
Проведем из вершины прямого угла с
высоту на гипотенузу (рис. 2.6). Этот отрезок разделит исходный треуголь- Рис. 2.6
ник на два меньших, подобных ему и в сумме
74
Глава 2


7.2. Мотив круга
равновеликих ему. Отразим треугольники симметрично относительно сторон — получим чертеж, показанный на рис. 2.7, где по кругу располагаются прямоугольные треугольники, для которых
Si +S2 = Si,
В силу подобия треугольников можно записать
ка2 + kb2 = кс2,
откуда следует еще одно изящное доказательство теоремы Пифагора.
Эту идею Евклид распространил на произвольные подобные фигуры. В шестой книге его «Начал» содержится теорема:
Если на катетах а, b и гипотенузе с прямоугольного треугольника построены какие угодно подобные между собой фигуры площади Fa, Fb, Fc так, что катеты и гипотенуза являются сходственными отрезками этих фигур, то имеет место равенство:
Fa + Fb= Fc.
У По кругу, по кругу...
Q (В. Произволов, [4].) Точку Q в треугольнике соединили с вершинами. Оказалось, что образовавшиеся при этом углы подчиняются равенствам:
Z1 < Z2; Z3 < Z4; Z5 < Z6
(рис. 2.8).
Докажите, что точка Q — центр вписанной в треугольник окружности.
Рис. 2.8
Почему нравится задача?
75


7. Элегантные мотивы
с
Q Длины пяти последовательных сторон описанного около окружности шестиугольника равны а, Ь, с, d, е (рис. 2.9). Найдите длину шестой стороны.
Q Найдите сумму внутренних углов произвольного звездчатого пятиугольника при его вершинах (см. рис. 2.10).
QHa сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что их центры также образуют равносторонний треугольник.
7.3. 	Мотив симметрии
Голова у Ивана Ивановича похожа на редьку хвостом вниз; голова Ивана Никифоровича на редьку хвостом вверх.
Н. В. Гоголь
Повесть о том, как поссорился Иван Иванович с Иваном Никифоровичем
Закон отражений: отражений закон.
Владимир Казаков.
От головы до звезд
Красивый мотив симметрии проявляется в двух ипостасях: в условиях задачах и в способах их решений.
76
Глава 2


7.3. Мотив симметрии
Приведем примеры задач с симметрией в условии:
Задача 1. (А П. Савин, [6].) Доля блондинов среди голубоглазых больше, чем их доля среди всего населения. Верно ли, что доля голубоглазых среди блондинов больше, чем их доля среди всего населения?
Задача 2. (А. П. Савин, [7].) Круг и квадрат имеют одинаковые площади. В круг вписали квадрат, а в квадрат вписали круг. Что больше — площадь квадрата, вписанного в круг, или площадь круга, вписанного в квадрат?
Задача 3. Какое число больше: sin(cosx) или cos(sin х) ?
Задача 4. (Л. Эйлер (1707-1783)). Решите в рациональных числах уравнение Xх = /.
Решения задач, основанные на симметрии, также впечатляют своим изяществом.
Шахматисты любят рассказывать сказку об одном предприимчивом дельце (назовем его Мистер С), который с выгодой для себя заключил сделку с двумя именитыми гроссмейстерами. Суть его сделки состояла в следующем.
1) С каждым гроссмейстером Мистер С играет одну партию по почтовой переписке.
2) В случае выигрыша Мистер С получает 1000 долларов, в случае ничьей получает 500 долларов, а в случае проигрыша — сам платит 500 долларов.
Секрет его финансовой выгоды заключается в том, что с одним из гроссмейстеров Мистер С играет черными фигурами, с другим — белыми. А как играет — догадаться несложно.
Почему нравится задача?
77


7. Элегантные мотивы
Задача 5. ([8].) Двое мальчиков играют в такую игру: они по очереди ставят ладьи на шахматную доску. Выигрывает тот, при ходе которого все клетки доски оказываются побитыми поставленными фигурами. На битое поле ладьи можно ставить. Побитым считается также поле, на которое ставится фигура. Кто выигрывает в этой игре, если оба стараются играть наилучшим образом?
Решение. Выиграет второй мальчик, если он будет ставить свои ладьи симметрично ладьям первого мальчика относительно центра доски.
Всё же не следует чересчур уповать на симметрию. Поучительную историю на сей счет можно извлечь из следующей старинной задачи.
Задача 6. ([9].) Купец должен был отвесить двум своим покупателям по одинаковому числу фунтов товара; но его весы были неверны: одно плечо коромысла было короче другого. Для первого покупателя он положил груз на короткое плечо, а товар на длинное; для второго поступил наоборот. Выиграл или потерял торговец при таком взвешивании товара?
^Упражнения
Q ([10].) На листе бумаги расположены 2000 точек, яв- ляющихся вершинами правильного 2000-угольника. Двое игроков по очереди соединяют эти точки отрезками. За один ход разрешается соединить любые две точки так, чтобы проведенные отрезки не пересекались. Проигрывает тот, у кого нет хода. Кто выигрывает при правильной игре: начинающий
или его партнер?
Q {Мартин Гарднер, [11].)
Разделите фигуру, состоящую из 5 кругов (рис. 2.12), на две равные по площади части прямой линией, проходящей через точку Р — центр левого круга в нижнем ряду. рис. 2.12
78
Глава 2


7.4. ZIP-мотив
0(Л. Жуков, [12].) Существуют ли простые числа, которые можно представить в виде разности
аа...а-bb...b,
Ь цифр о цифр
где а, b — цифры, Ь> а.
И(С. Майзус, [13].) Найдите все простые числа р, для которых число 2Р + р2 тоже простое.
В Чему равны числа а и 6, если а процентов от b равно Ъ процентов от о?
7.4. 	ZIP-мотив
Сделай так, чтобы душа сначала вот так вот развернулась, а потом свернулась.
Фраза из фильма «Свадьба в Малиновке»
Словом zip в англоязычных странах называют застежку-мол- нию. Современные компьютерные технологии в это слово привнесли дополнительный смысл: сжатие информации («зазипо- вать» — сжать информацию с помощью программы-архиватора). И тот, и другой смысл вполне подходят к алгебраическим манипуляциям в следующих задачах.
У Упражнения
В Упростите выражение:
(,а + Ъ) (а2 + Ь2) (а4 + Ъ4) (а8 + Ь*) (а16 + Ьхь) (а32 + Ь32),
если известно, что а = b + 1.
В Докажите, что при любом а > 1 значение выражения
Почему нравится задача?
79


7. Элегантные мотивы
112 4
• + + — + г +
1 -а 1 + а 1 + а 1 + а
8
16
32
отрицательно.
Q Упростите выражение:
2п
2п
х ]( х
cos— COS
п-1
cos-
)П-2
cos-
Q Упростите выражение:
V2+V3 • V2+V2+WX х^2 + -у/2 + 72+^-^2-\/2 + 72 + 7з .
Q ([14], задача 6. С. 14). Докажите неравенство: ^/б + ^/б + ... + \/б +>/б + -\/б + ... +Тб <5.
7.5. 	Ансамбли задач
Вот, например, — нецелое мгновение; десяток таких мгновений составят нецелую минуту, а там, глядишь, и целый нецелый год наберется.
Владимир Казаков.
Набросок
К разряду элегантных, несомненно, можно отнести задачи, служащие идейным источником других задач.
1. 	Согласно древней китайской легенде, однажды отдыхавший на берегу император Ю (ок. 2200 до н. э.), увидел необычную черепаху. На ее панцире был нарисован квадрат с числами (числа изображались точками):
80
Глава 2


7.5. Ансамбли задач
6
1
8
7
5
3
2
9
4
Сумма чисел в каждой строке, в каждом столбце, а также в каждой из двух диагоналей такого квадрата одна и та же. Квадраты с подобными свойствами получили название магических. За многовековую историю их математические свойства удалось изучить достаточно хорошо, и сейчас известны способы построения магических квадратов произвольных размеров.
Ill Задача 1 [15]. Заполните квадрат 3x3 различными натуральными числами так, чтобы произведение чисел, стоящих в каждой его строке, в каждом столбце, а также в каждой из двух диагоналей было одним и тем же.
2. В 1202 г. Леонардо Пизанский по прозвищу Фибоначчи (1180-1240) опубликовал с виду ничем не примечательную задачу о кроликах. Из этой задачи выходило, что ежемесячная динамика численности пар кроликов такова: 1, 1, 2, 3, 5, 8, 13, ... . Члены этой последовательности получили название чисел Фибоначчи. История распорядилась так, что эти числа стали играть заметную роль в некоторых важных вопросах математики.
Выпишем рекуррентную зависимость последовательности Фибоначчи:
а\ “ а2 — 1’ an+1 = an-1 ап‘
Задача 2 (Канадская математическая олимпиада, 1969 г.). Найдите все строго возрастающие последовательности натуральных чи-
I сел а\, аъ в которых а2 = 2 и ап .т = ап • ат для всех натуральных /гит.
3. Наименьшее общее кратное НОК (п, т) и наибольший общий делитель НОД (п, т) двух произвольных натуральных чисел п и т связаны с числами пит замечательным соотношением:
НОК (п, т) • НОД (я, т) = п- т.
Почему нравится задача?
81


7. Элегантные мотивы
А нет ли аналогичного соотношения для суммы чисел?
II Задача 3. (С. Токарев, [16].) Натуральные числа пит таковы, что НОК (п, т) + НОД (п, т) = п + т.
Докажите, что одно из чисел п или т делится на другое.
4. 	Согласно так называемой «обобщённой теореме Фалеса» параллельные прямые MjKi, М2К2, М3К3, на сторонах угла отсекают пропорциональные отрезки (рис. 2.13):
мхм2 _ кхк2
М2М3 " К2КЪ *
В прелестном ансамбле с этим утверждением находится следующая задача.
Задача 4. (А. Аджанс, [17].) Дуги трёх окружностей лежат по одну сторону от прямой АВ, причём каждая из дуг имеет концы в точках А и В (рис. 2.14). Два луча, проведенные из точки В, пересекают эти дуги в точках Ml, М2, М3 и Kl, К2, КЗ соответственно. Докажите, что дуги на сторонах угла отсекают пропорциональные отрезки:
мхм2 кхк2 М2м3 ~ К2Кг '
М3 ' М2 ' м,
А
В
Рис. 2.13
Рис. 2.14
82
Глава 2


7.6. Мотив дополнения
7.6. 	Мотив дополнения
Чаньские монахи, пытаясь понять, что же представляет собой истинная тишина, истошно вопили в течение нескольких минут, поднимая криком окрестные деревни, а затем внезапно замолкали...
А. 	Маслов4
Чей-то голос чуть не прозвучал в тишине.
Владимир Казаков.
Импровизация
В древней восточной философии особое значение придавалось невысказываемому в поэзии, паузам в музыке и пустому пространству в изобразительном искусстве. Действительно, некоторую сущность иногда проще понять, обращая внимание не на нее, а на то, что ее окружает — ее дополнение.
Ill Задача 1. Продавец получил для продажи несколько пачек конвертов по 100 конвертов в пачке. 10 конвертов он отсчитывает за I 10 сек. За сколько секунд он отсчитает 90 конвертов?
jsSЗа 90 секунд? Но ведь можно и быстрее, ведь мы знаем, что в каждой пачке ровно 100 конвертов...
II Задача 2. (В. Произволов, [18].) Известно, что каждый угол выпуклого 12-угольника кратен 30°. Докажите, что все углы этого 12- угольника равны.
jes Рассмотрим дополнение к углам 12-угольника — его внешние углы. Поскольку их сумма равна 360°, то каждый из них равен 30°. Значит, и все внутренние углы 12-угольника равны.
Иногда выбор дополнения не столь очевиден. Не ясно, к чему дополнять, как представлять себе исходную конструкцию вложенной в другую, объемлющую конструкцию — да и какую именно? Умение разрывать путы обусловленного, раздвигать горизонты и выходить на новые неизведанные рубежи — великое искусство.
4 Чань-буддизм / Энциклопедия для детей. Религии мира. Т. 6. М.: Аванта+. С. 665.
Почему нравится задача?
83


7. Элегантные мотивы
Задача 3. (Региомонтан, 1436-1476). Докажите, что высоты треугольника пересекаются в одной точке.
jts Решение. Дополним исходный треу- N гольник ABC до объемлющего MNP таким образом, что MN || AC, PN || АВ, МР || ВС, причем стороны объемлющего треугольника проходят через вершины исходного (рис. 2.15). В новом треугольнике MNP точки А, В и С — середины сторон МР, MN и PN. Перпендикуляры в этих точках к сторонам треугольника MNP пересекутся в одной точке; вместе с тем для данного треугольника они будут высотами.
II Задача 4. (А. Зайчик). Могут ли числа АРК и КАР одновременно делиться на 49? (Здесь одинаковыми буквами обозначены одинаковые цифры, разными — разные, А Ф О, К Ф 0.)
* Решение. Рассмотрим дополнительное число КАРК:
КАРК = К • 1000 + АРК = КАР • 10 + К.
Если бы каждое из чисел АРК и КАР делилось на 49, то на 49 разделилось бы и число 999К, что невозможно.
S Упражнения
Q Какая из дробей больше: 99/100 или 100/101?
Q Современник Блеза Паскаля (1623-1662) рыцарь ка- валер де Мере однажды обратился к с своему именитому земляку с просьбой помочь в вычислениях. Сам де Мере был азартным игроком в кости и немного импровизировал. Желая разбогатеть, он придумал такие правила игры. На стол бросаются 4 игральных кости. Если при этом хотя бы один раз выпадает число 6, то де Мере выигрывает, а иначе проигрывает. Какова вероятность выигрыша де Мере?
р
Рис. 2.15
84
Глава 2


8. Математика факта
А
В
D
С
Рис. 2.16 Рис. 2.17
В {И. Акулич, [19].) На рис. 2.16а показан способ разрезания некоторого шестиугольника одной прямой линией на две равновеликие части. Однако если этот же способ применить к шестиугольнику, показанному на рис. 2.166, то в результате получатся не две, а три части. Придумайте способ разрезания шестиугольника на рис.2.166 одной прямой линией на две равновеликие части.
В (В. Произволов, [20].) Прямоугольники ABCD и KLMN имеют соответственно параллельные стороны и расположены так, как показано на рис. 2.17. Докажите, что площади четырехугольников ALCN и KBMD равны.
8. 	Математика факта
Рассуждая об эстетике математики, следует иметь в виду, что существует математика метода и существует математика факта.
В. 	В. Произволов
Некоторыми утверждаемыми в задачах фактами можно любоваться как красивым пейзажем, тонким рукоделием или великолепным творением живописца. В этом пункте мы ограничимся рассмотрением простейшей геометрической фигуры — треугольника.
Почему нравится задача?
85


8. Математика факта
8.1. 	Гармония числа и формы
Есть тонкие властительные связи Меж контуром и запахом цветка. Так бриллиант невидим нам, пока Под гранями не оживет в алмазе.
Валерий Брюсов. Сонет к форме
Треугольник — удивительный объект. Всего три отрезка, застывших в хороводе, а сколько математического таинства!
Взять, хотя бы, теорему синусов, которая на школьных уроках математики среди прочих теорем заучивается привычно и буднично. А ведь обратите внимание (обозначения см. на рис. 2.18) — в пропорциях
а _ b _ с sin a sin/? sin у
играет сама гармония и совершенство!
Рис. 2.18 Рис. 2.19
В изящном исполнении векторного формализма великолепно «играет» также теорема косинусов (рис. 2.19):
86
Глава 2


8.1. Гармония числа и формы
(с9с) = (а + Ь9а + Ь).
В геометрии треугольника существует огромное множество изумительных по красоте фактов. Ознакомление с ними не входит в задачи этой брошюры (см., например, [1, 2].) Всё же трудно удержаться, чтобы не привести парочку.
Рис. 2.20 Рис. 2.21
На рис. 2.20, 2.21 в одной точке внутри треугольника пересекаются три отрезка, каждый из которых соединяет вершину и какую-то точку противоположной стороны — это могут быть знакомые всем медианы, высоты, биссектрисы или же какие-то другие отрезки. На рис. 2.20 заданы длины составных частей, на которые разбиваются стороны треугольника, а на рис. 2.21 — длины составных частей, на которые разбиваются сами отрезки, при этом т\ + т2 = т, п\+п2 = п, к\+ к2 = к. Справедливы следующие соотношения:
Bl.^L.£l = \ щЖ' Чева (1648-1734)), а2 ^2 С2
—+ —+ —= 1 {Ж.Д. Жергонн (1771-1859)). т п к
Если окружность пересекает треугольник так, как показано на рис. 2.22, при этом отсекая от его сторон а, Ь, с по три отрезка, длины которых указаны на рисунке, то
а\Ь\С\ {а - аъ) {Ь - Ьъ) {с - с3) = афгсъ {а - ах) {Ь - Ь\) {с - с,).
Почему нравится задача?
87


8. Математика факта
Еще несколько фактов из серии: «Математика, ты — прекрасна!». Доказывать их совершенно не обязательно.
Факт 1. ([3].) Все четыре треугольника, заштрихованные на рис. 2.23, равновелики. Докажите, что три четырехугольника, не заштрихованные на нем, также равновелики.
Факт 2. (В. Произволов, [4].) Через точку О внутри равностороннего треугольника проведены прямые, проходящие через его вершины. В результате получились 6 треугольников, 3 из которых через один закрасили (рис. 2.24). Докажите, что если сумма площадей закрашенных треугольников равна половине площади равностороннего треугольника, то точка О лежит на одной из медиан треугольника.
88
Глава 2


8.2. Три биссектрисы
ФактЗ. {А. Заславский, [5]) (10 кл.). Докажите, что если тангенсы углов треугольника — натуральные числа, то они равны 1, 2, 3.
8.2. 	Три биссектрисы
Три феи, как три веселых мысли, кружились в феерическом танце.
Здесь мы приведем малоизвестное доказательство равенства двух треугольников по трем биссектрисам. Его автор — Игорь Акулич [7].
II Теорема. Если три биссектрисы одного треугольника соответственно равны трем биссектрисам другого треугольника, то эти треугольники равны.
лб Доказательство. Пусть треугольники и Д2 имеют соответственно равные биссектрисы. Назовем соответственными сторонами этих двух треугольников стороны, к которым проведены равные биссектрисы. Точно так же назовем соответственными углы этих треугольников, если из них выходят равные биссектрисы. Возможны лишь два (вообще говоря, не взаимоисключающих) случая:
1) все стороны одного треугольника не меньше соответственных сторон другого треугольника;
2) ровно одна сторона одного треугольника меньше соответственной стороны другого треугольника.
Рассмотрим случай 1). Если все соответственные стороны треугольников равны, то эти треугольники равны по третьему признаку равенства треугольников.
Предположим, что у треугольников имеются неравные соответственные стороны. Во-первых, заметим, что треугольники не могут быть подобными с коэффициентом подобия, большим 1. В противном случае биссектрисы этих треугольников также были бы подобными с коэффициентом подобия, большим 1, чего не может быть. Следовательно, у треугольников имеются неравные углы. Не умаляя общности, будем считать, что стороны треуголь-
Почему нравится задача?
89


8. Математика факта
ника Ai не меньше соответственных сторон треугольника Д2. Поскольку у треугольников Aj и Д2 имеются неравные углы, а сумма всех внутренних углов треугольников одна и та же, то в треугольнике Ai найдется угол cpi, меньший соответственного угла ср2 в треугольнике Д2. Если угол <pi в треугольнике Дх образован сторонами Pi, qb а угол ф2 в треугольнике Д2 образован сторонами р2, q2) то для длин биссектрис li, 12 этих углов имеем
2cos— 2cos—
'-тЧ- '-тН? 111
Р\ Я\ Рг Яг
Здесь мы воспользовались формулой
2 cos—
/=i Ь’ т
Р Я
связывающей длину биссектрисы I со значением угла ф, в котором она проведена, а также с длинами р и q образующих этот угол сторон треугольника.
У? Упражнение
Выведите формулу (2).
Вернемся к соотношениям (1). Так как
<р2<(/\, Р2<Р\, д2<Яи
то h<l\ — противоречие.
Итак, в рассматриваемом случае треугольники могут иметь только равные соответственные стороны.
Рассмотрим случай 2).
Без ограничения общности можно считать, что стороны а\, b\, ci треугольника Д1 соответственны сторонам а2, Ьг, с2 треугольника Дг, причем
90
Глава 2


8.3. Задача Брокара
(3)
Воспользовавшись еще одной известной формулой, связывающей длину биссектрисы с длинами сторон треугольника, имеем:
'i =v.
f
1
ч
/
1 —
L2 -b2c2
(6,+Ci)
(b2+c2) J
(4)
С учетом неравенств (3), из (4) следует 1а^ < — про¬
тиворечие.
Признак равенства треугольников по трем биссектрисам доказан.
8.3. 	Задача Брокара
В памяти моей сохранилось несколько расстояний.
Владимир Казаков.
Набросок
Существует ли треугольник, длины биссектрис которого равны трем наперед заданным числам 1а, 1Ь, 1С1 — Такую проблему в 1875 г. поставил французский математик Анри Брокар (1845-1922), хотя, возможно, этой задачей математики интересовались и раньше.
В 1994 г. румынские математики Петру Миронеску и Лаурен- тин Панаитопол в журнале «Mathematical Monthly» [6] привели решение задачи Брокара, основанное на теореме Брауэра о неподвижной точке. Здесь мы приведем другое решение, в идейном плане доступное старшеклассникам, хотя и требующее для полного обоснования некоторых фактов математического анализа. Автор этого решения — Александр Жуков [7].
Почему нравится задача?
91


8. Математика факта
Теорема. Для любых положительных чисел /ф 1Ы 1С существует единственный треугольник с биссектрисами, длины которых равны Ig, 1Ы 1с-
ms Доказательство. Воспользуемся известными равенствами, выражающими биссектрисы 1а, 1ь, 1с через соответственные стороны а, Ь, с треугольника, к которым они проведены:
И=Ьс
Ч =ас
11= аЪ
1 —
(Ь + с)2
(а + с)
1 —
(a + bf
Введя вспомогательные переменные %,rj,g ,р:
р = а + Ь + с,
Р
равенства (1) запишем в виде:
',2/,
1-2£
1-2 tj
2е „
— - =р
1-2?
(1)
(2)
(3)
92
Глава 2


8.3. Задача Брокара
/2(1-*)2 ,
Заметим, что вещественная функция <pt=— —х = гх +
1-2*
/V
+ (здесь / — вещественный параметр) на интервале
1 — 2л:
хе (0,1/2) непрерывная и монотонно возрастающая как сумма двух монотонно возрастающих и непрерывных на этом интервале функций. Значит, и обратная к ^функция/также непрерывная и возрастающая. Теперь равенства (3) можно записать так:
(t}
II
7 '
\1а
n = f
f \
t
12 ’ KLb )
(t Л
II
(4)
rp,et=p2^ijC
,, ~ а Ъ с a + b + с л
Поскольку £ +77 + <^ = — + — + —= = 1, получаем урав-
Р Р Р Р нение /(»/£)+/('/£)+/('/£) = 1. В его левой части стоит
возрастающая функция, при t-> 0 стремящаяся к 0, а при t -» оо — к 3/2. Значит, решение этого уравнения t - и существует и единственно. Зная и, из ( 4 ) находим £*, т}*, , затем на¬
ходим р* из соотношения р=Шй .
Наконец, в соответствии с (2), существуют единственные числа а, Ъ, с такие, что
Ъ = Т1.р„ (5)
с = д,р..
Почему нравится задача?
93


9. Заигрывание интуиции
Таким образом, по длинам гипотенуз 1Ф 1Ы 1С величины а, Ь, с определяются однозначно. Осталось лишь убедиться в том, что числа а, Ь, с удовлетворяют неравенству треугольника, то есть они действительно могут выражать длины сторон некоторого треугольника. Сначала заметим, что неравенству треугольника удовлетворяют числа 7,, д,. Поскольку они подчиняются неравенствам
0<£< —; 0</7< —; 0<$-< —
2 ' 2 ь 2
и равенству % + т] + д = \, то
'£+*= 1-6 >£,
;*+£=1-£>£,
£+£. =1-7, >7*.
Согласно (5), неравенству треугольника удовлетворяют и числа а, Ь, с. Теорема доказана.
9. 	Заигрывание интуиции
Предчувствие разоблачает тайны.
Валерий Брюсов.
Числа
9.1. 	Veni, Vidi, Vici
Трудно определить границу между тем, что мы вспоминаем сами, и тем, что само вспоминается.
Владимир Казаков.
Дневник
Ниже подобраны простые упражнения для устного счета. Попробуйте их одолеть, руководствуясь максимой римского императора Гая Юлия Цезаря (102-44 дон. э.): «Пришел, увидел, побе¬
94
Глава 2


9.1. Veni, Vidi, Vici
дил». После непродолжительного, но внимательного изучения условия заданий ответ у вас должен возникнуть как бы сам собой.
^Упражнения
В Угадайте хотя бы одно решение уравнений:
а) 6 =л:(л: + 1);
б) 2х2 -у2 = 1;
в) |2*-104 = 2;
г) х + - = 20,05;
д) Xу[у + у\[х = 30;
х + у + z = 9,
. 111,
е) i -+- + - = 1,
X у Z
ху + yz + zx = 27.
В (77. Самовол, М. Аппельбаум). Известно, что [*2+/+z2=l,
> х3 +х* + z3 =-1, x5+y5+z5=-1.
Чему равно х + у + z?
Как решались эти упражнения? Вероятно, где-то ассистировала память, где-то сработал «внутренний компьютер» для проверки результата, но ответ всегда возникал как бы сам собой, на уровне числовой интуиции. Однако, если бы вопрос к заданиям стоял так: «Найдите все решения уравнений», наша интуиция, скорее всего, оказалась бы беспомощной (см. Комментарии).
Почему нравится задача?
95


9. Заигрывание интуиции
9.2. 	Угадывание особого места
— Пух нашел Северный Полюс, — сказал Кристофер Робин. — Здорово, правда? Вот Земная Ось.
Пух скромно опустил глаза.
— Вот это? — спросил Иа.
— Да, — сказал Кристофер Робин.
— Значит, мы вот эту штуку искали?
— Да, — сказал Пух.
— Гм, — сказал Иа-Иа. — Ну что ж. Во всяком случае, дождя не было, — добавил он.
А. А. Милн.
Винни-Пух и все-все-все
Иногда интуиция оказывает услугу в угадывании особого места. Французскому схоласту Жану Буридану (1300-1358) приписывают рассказ об удивительном ослике. Этот персонаж («буриданов осел») мог безошибочно (причем — на любом расстоянии!) определять количество вкусной массы в произвольной охапке душистого сена. Предположим, на лугу в точках А и В имеются две такие абсолютно одинаковые охапки. Куда нужно поставить буриданово- го длинноухого эксперта, чтобы он не смог предпочесть одну из этих охапок другой? — Очевидно, в точку, являющуюся серединой отрезка АВ. Это и есть особое место в данной задаче. В других задачах особое место может быть иным.
Попробуйте угадать особое место в следующих задачах.
У Упражнения
Q ([1].) На сковородке лежат два квадратных блина так, как показано на рис. 2.25. Можно ли рассечь их одним прямолинейным разрезом на равные части каждый?
В Внутри выпуклого четырехугольника найдите точку М такую, чтобы длина всех отрезков, соединяющих М с вершинами четырехугольника, была наименьшей.
96
Глава 2


9.2. Угадывание особого места
D
.'А
В.*'''
АС Е
Рис. 2.26
0 «А вот еще такой непростой вопрос, — Поселенец был обуян жаждой созидания, и у него то и дело возникали вопросы. — Мне нужно соорудить две теплицы (рис. 2.26). Где мне выбрать точку С так, чтобы длина соединяющего верхушки теплиц провода (BD) была наименьшей?»
«Скажите, уважаемый, а одинаковыми ли должны быть склоны у ваших теплиц?»
«О, да! У каждой теплицы склоны одинаковы (АВ = ВС, CD = DE), но у разных теплиц они могут быть разными (не обязательно АВ = CD). Углы же склонов при основании всех теплиц одинаковые» ([2])
В (В. Произволов, [3].) В прямоугольнике вырезали дырку прямоугольной формы (рис. 2.27). Проведите прямую линию, которая разделит образовавшуюся фигуру (на рисунке она заштрихована) на две части равной площади.
В ([4].) На прямоугольную карту положили карту той же местности, но меньшего масштаба (рис. 2.27). Можно ли проткнуть иголкой сразу обе карты так, чтобы точка прокола изображала на обеих картах
Почему нравится задача?
97


9. Заигрывание интуиции
одну и ту же точку местности?
В Решите уравнение:
jx-2 1лг-3 Ьс-4 1х -2001 /лг-2000 I х-1999
V 2001 V 2000 V1999 “V 2 V 3 V 4
Всё же и здесь интуиция может только помочь угадать ответ. Но всегда ли он будет правильным? — Увы, ответить на последний вопрос интуиция бессильна (см. Комментарии).
9.3. 	Предчувствие ответа
Мой высокочтимый учитель Гаусс, бывало, часто в доверительной беседе высказывал мнение, что математика в гораздо большей степени наука для глаза, чем для уха.
Й. Ф. Энке
Предваряя свои знаменитые труды по теории чисел, Карл Фридрих Гаусс (1777-1855) указал, что толчком для его плодотворных исследований послужила одна «изумительная истина»:
«...Когда я в начале 1795 г. впервые принялся за исследование такого рода... я случайно наткнулся на одну изумительную арифметическую истину... и так как она не только показалась мне прекрасной, сама по себе, но и навела на мысль, что она связана и с другими выдающимися фактами, я со всей энергией взялся за то, чтобы выяснить причины, на которых она основывается, и получить строгое ее доказательство. После того, как это желание, наконец, осуществилось, прелесть этих исследований настолько увлекла меня, что я уже не мог их оставить» [5].
Предлагаем читателям открыть обнаруженный К. Ф. Гауссом замечательный арифметический факт, исследуя фрагменты компь-
98
Глава 2


9.3. Предчувствие ответа
ютерного фильма, который условно можно назвать «Танец маленьких чисел» (рис. 2.28):
В каждом кадре этого фильма изображены четыре квадрата, размеры которых зависят от значения параметра р, указанного под рисунком (для удобства созерцания на всех рисунках кроме последнего указаны линии квадратной сетки). Можно ничего не знать о происхождении этих кадров и, тем не менее, обнаружить закономерность,
Почему нравится задача?
99


9. Заигрывание интуиции
шторой подчиняются узоры внутри квадратов. Попробуйте обнаружить эту закономерность и предсказать содержание кадра для р = 41: будут ли там пустые квадраты, как при р = 3, 7, 11, 19, 23, или же внутри квадратов появятся узоры, как при р = 5,13, 17,29?
Подсказку своей интуиции вы можете проверить, прочитав ответ в Комментариях.
9.4. 	Интуиция воображения
Полет воображения — полет ангелов и молний.
А. Дюма-отец
Воображение — это умение видеть сквозь толщу стен.
Т. Уайдлер
Приведенные ниже упражнения мы рекомендуем решать так: сначала высказать предположение, которое кажется наиболее правдоподобным, а затем проверить свою догадку, либо воспроизведя решение (рекомендуется), либо заглянув в ответ.
Точки
Каждый видит не только то, что существует в действительности, но и то, что открывается с определенной точки зрения.
А. Дюма-отец
Q Можно ли расположить на плоскости 6 точек и соединить их непересекающимися отрезками так, чтобы каждая точка была соединена ровно
а) с 3 другими точками?
б) с 4 другими точками?
Q (Г. Гальперин, В. Сендеров, [7].) Могут ли 6 футболистов расположиться на футбольном поле так, чтобы каждый из них мог дать пас по земле ровно 4 другим?
100
Глава 2


9.4. Интуиция воображения
Q (М Гарднер, [8].) Внутри замкнутой кривой (рис. 2.29), заключено бесконечно много точек. Предположим, что мы выбрали из них наугад 1000 точек. Всегда ли на плоскости можно провести прямую так, чтобы она не проходила ни через одну из отмеченных точек и при этом разделила все точки на два подмножества по 500 точек в каждом?
В (Ф- Вайнштейн, [9].) Пусть М— конечное множество точек на плоскости, не принадлежащих одной прямой. Найдутся ли три точки множества М такие, что проходящая через них окружность не содержит внутри себя других точек множества Ml
У Точки и многоугольники
Воображение... взмывает ввысь на собственных крыльях, и, шныряя туда и сюда, вычерчивает причудливые линии, которые то и дело меняют свое направление.
И. Гёте
Q (Д. Калинин, [10].) Дана точка А и прямая /, не проходящая через точку А. На прямой отметили 4 точки и соединили каждую с точкой А. Могут ли все 6 треугольников, которые возникнут на таком чертеже, оказаться равнобедренными?
В Существует ли плоская
а) 6-звенная,
б) 8-звенная,
в) 2005-звенная ломаная, пересекающая каждое свое звено ровно один раз, причем во внутренней точке звена?
Почему нравится задача?
101


9. Заигрывание интуиции
В (А. Шаповалов, [11].) Существует ли 10-звенная плоская ломаная из условия предыдущей задачи, каждое звено которой пересекает другое звено под прямым углом?
Q (Т. И. Голенищева-Кутузова, Ю. Г. Кудряшов, [12].) Кролик, готовясь к приходу гостей, повесил в трех углах своей многоугольной норы по лампочке. Пришедшие к нему Вини Пух и Пятачок увидели, что не все горшочки с медом освещены. Когда они полезли за медом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть?
В Существует ли многоугольник, внутри которого можно указать точки, из которых ни одна его сторона не видна полностью?
SМногоугольники
Стены молча затворяют длину.
Владимир Казаков.
Большая орда
В {В. Произволов, [13].) Существуют ли два многоугольника, у которых все вершины общие, но у которых нет ни одной общей стороны?
В (С. Волчёнков, [14].) Существует ли шестиугольник, который нельзя разрезать одним прямолинейным разрезом на два четырехугольника?
В ([15].) Вершины четырехугольника Р лежат на сторонах четырехугольника Q. Может ли площадь Р быть больше площади Q1
В ([16].) Может ли так быть, что длины всех сторон одного треугольника меньше 1 см, длины всех сторон другого треугольника больше 100 м, а площадь первого треугольника больше площади второго?
102
Глава 2


9.4. Интуиция воображения
В ([17].) В квадрат вписывают окружности равных радиусов так, как показано на рис. 2.30. Зависит ли сумма площадей вписанных кругов от их числа?
0 ([18].) Можно ли в квадрат со стороной длины 1 поместить несколько непересекающихся кругов, сумма радиусов которых равнялась бы 1000?
У Фигуры
Форма — это тело, хранящее душу.
Чжуан Цзы
В Существует ли фигура, имеющая ровно два центра симметрии?
В (Н. Михайленко, [19].) Существует ли на плоскости такая ограниченная фигура, которую переводят в одну и ту же фигуру два различных преобразования: некоторый поворот на ненулевой угол и некоторый параллельный перенос, отличный от тождественного?
В ([20].) Существует ли фигура на плоскости, не имеющая ни осей симметрии, ни центра симметрии, но переходящая в себя после поворота вокруг некоторой точки на угол, меньший 360°?
В Ш- Б. Васильев, А. Г. Самосват, [21].) Существует ли такая фигура, что ею нельзя накрыть полукруг радиуса 1, а двумя ее экземплярами можно накрыть круг радиуса 1 ?
В ([22].) На двух одинаковых бумажных кругах художник нарисовал двух совершенно одинаковых драконов. На
Почему нравится задача?
103


9. Заигрывание интуиции
одном рисунке глаз дракона совпал с центром круга, а на втором не совпал. Можно ли второй круг разрезать на части так, чтобы из них можно было сложить тот же круг с тем же драконом, у которого глаз находится в центре круга?
Клетчатая плоскость
У абстракции больше всего форм выражения.
Е. Лец
Q (С. Беспамятных, [23].) Клетки бесконечного листа клетчатой бумаги раскрашиваются в 1000 цветов. Обязательно ли найдется прямоугольник, вершины которого лежат в центрах клеток одного цвета, а стороны идут параллельно линиям сетки — по вертикальным и горизонтальным прямым?
В (И. Акулич, [24].) На бесконечном во все стороны листе клетчатой бумаги в каждой клетке записано натуральное число, причем все натуральные числа встречаются по одному разу. Верно ли, что найдутся имеющие общую сторону две клетки, числа в которых различаются больше, чем на миллиард?
В (И. Акулич, [25].) Плоскость разделена вертикальными и горизонтальными прямыми на бесконечное число одинаковых квадратов. В каждом квадрате записано натуральное число, причем каждое число п записано ровно в п клетках (то есть всего на доске одна единица, две двойки, три тройки и т. д.). Для каждой пары соседних клеток подсчитывается разность (по абсолютной величине) между числами в этих клетках (соседними считаются клетки, имеющие общую сторону). Может ли наибольшая из этих разностей равняться 2?
104
Глава 2


9.5. Именованные задачи
9.5. 	Именованные задачи
Уж если давать облакам имена, то, конечно, не человеческие, а облачные.
Владимир Казаков.
Краткие сцены
Один из достаточных (post factum) критериев элегантности мы уже упоминали: задача элегантная, если она прошла испытание временем. Здесь мы обсудим другой критерий такого же сорта: задача элегантная, если она приобрела свое собственное имя. Этот феномен отмечают Г. А. Гальперин и А. К. Толпыго в книге «Московские математические олимпиады» ([1], с. 17): «Однако наиболее красивые... и оригинальные задачи олимпиады... получают... широкое распространение, превращаясь в математический фольклор; «знатоки» сразу вспоминают их по кратким специфическим названиям».
«Улитка» (Н. Н. Константинов, [1, с. 72]). Улитка ползет вперед (не поворачивая назад) с непостоянной скоростью. Несколько человек наблюдают за ней по очереди в течение 6 мин. Каждый начинает наблюдать раньше, чем кончает предыдущий, и наблюдает ровно 1 мин, причем замечает, что за эту минуту улитка проползла ровно 1 м. Доказать, что за б мин улитка сможет проползти самое большее 10 м.
«Игра в скалярное произведение» (Д. Б. Фукс, [1, с. 74]). Играют двое, один из них загадывает набор из целых однозначных чисел хъ х2,..., хп, как положительных, так и отрицательных. Второму разрешается спрашивать, чему равна сумма
аххх +а2х2+ ...+а„хп,
где а 1, а 2, а „ — любой набор чисел. Каково наименьшее число вопросов, за которое отгадывающий может узнать задуманный набор?
Почему нравится задача?
105


9. Заигрывание интуиции
«Гангстеры» (Н. Б. Васильев, [2].) 50 гангстеров стреляют одновременно. Каждый стреляет в ближайшего к нему гангстера (или в одного из ближайших, если несколько человек находятся на одинаковом расстоянии от него) и убивает его наповал. Найдите наименьшее возможное количество убитых. (Гангстеры — различные точки плоскости.)
9.6. 	Юмор
Чай удивительно отвлекает от мыслей, за что и ценится всеми мыслителями.
Владимир Казаков.
Окна
Математические задачи, как и всякое многоплановое отражение нашей жизни, не могут обойтись без сюжетов, способных вызвать улыбку и немножко поднять настроение.
Вот какую замечательную задачу придумала одна малышка [1]: «По одной стороне улицы бежало 10 зайцев, по другой — все остальные. Сколько зайцев бежало по улице?»
Задача 1. (М. Наумов, [2])
— Я сдаю жилплощадь по цене 10 центов, или 0,1 доллара, за квадратный метр, — объявила хозяйка обратившемуся к ней математику.
— Прекрасно, — обрадовался клиент, — но я хотел бы поселиться на этой жилплощади вместе со своей тещей.
— Ах, вот как! В таком случае ставка возводится в квадрат. Вы должны будете платить не 10, а 100 центов за квадратный метр.
— Но, позвольте! — возразил математик. — В таком случае вместо прежней цены 0,1 я должен буду платить всего лишь (ОД)2 = 0,01 доллара за квадратный метр!
Сколько же на самом деле должен платить математик?
106
Глава 2


9.7. Остальные задачи
I Задача 2. Докажите, что все положительные числа интересные.
л* Доказательство. Предположим противное. Тогда должно существовать наименьшее неинтересное положительное число. Ха! — Так ведь это чертовски интересно!
9.7. 	Остальные задачи
Если мы чувствуем поэзию непосредственно, зачем разбавлять ее словами, несомненно более слабыми, чем наши чувства?
X. Л. Борхес. Семь вечеров. Поэзия
Одна из классификаций животных, якобы восходящая к аргентинскому писателю Хорхе Луису Борхесу, состоит в следующем [1].
«Животные подразделяются на:
а) принадлежащих Императору;
б) бальзамированных;
в) прирученных;
г) молочных поросят;
д) сирен;
е) сказочных;
ж) бродячих собак;
з) включенных в настоящую классификацию;
и) буйствующих, как в безумии; к) неисчислимых;
л) нарисованных очень тонкой кисточкой на верблюжьей шерсти; м) и прочих;
н) только что разбивших кувшин; о) издалека кажущихся мухами».
Между этим списком и обсуждаемым в данной главе перечнем критериев, по которым, якобы, можно определять элегантность тех или иных задач, существует некий изоморфизм (взаимно-однознач¬
Почему нравится задача?
107


9. Заигрывание интуиции
ное соответствие). В подтверждение этому мы обязаны проиллюстрировать пункт м) вышеприведенного списка кое-какими задачами. Почему эти задачи приятные, симпатичные, вкусные и т. п.? — Мы не знаем. Они просто симпатичные, и всё.
S Прочие упражнения
Д([2].) Имеется несколько кувшинов, среди которых есть два кувшина разной формы, а также два кувшина разного цвета. Верно ли, что среди них найдутся два кувшина одновременно и разной формы, и разного цвета?
В ([3].) В магазин привезли платья трех разных фасонов и трех разных расцветок. Продавщица хочет выбрать для витрины три платья так, чтобы были представлены все фасоны и все расцветки. Всегда ли она сможет это сделать?
В ([4].) Десять человек пришли в гости в галошах. Уходили они по одному, и каждый надевал произвольную пару галош, в которую он мог влезть (то есть не меньшего размера, чем его собственная). Какое наибольшее число людей не смогло надеть галоши?
В ([5].) На некоторой вечеринке собрались 5 супружеских пар. Встречаясь, участники обменивались рукопожатиями (супруги, разумеется, друг другу руки не пожимали). Мистер Браун опросил всех участников, сколько рукопожатий сделал каждый из них. Все названные числа оказались различными. Сколько рукопожатий сделала миссис Браун?
В (С- Фомин, [6].) Назовем пузатостью прямоугольника отношение его меньшей стороны к большей (пузатость квадрата равна 1). Докажите, что как бы ни разрезать квадрат на прямоугольники, сумма их пузатостей будет не меньше 1.
108
Глава 2


Решения, ответы и комментарии
& Решения, ответы и комментарии
к главе 2 «Почему нравится задача?»
Образец диалога:
— Да?
-Да.
Владимир Казаков.
Дневник
К разделу 1 «Сказочная фабула»
jsS К задачам-сказкам
Q Любопытно социально-психологическое решение этой задачи, предложенное учащейся московской философской школы «Новый Акрополь»: «Мне кажется, что среди них был лишь один правдивый человек, который смог сказать правду в глаза, а не намекать, как другие — это был третий человек».
А вот решение того, кто верит в сказки:
Предположим, третий правдивый. Следовательно, первый и второй должны быть лжецами, но легко заметить, что именно в данной ситуации второй высказывает истину. Итак, третий — лжец, и среди первых двух имеется хотя бы один правдивый. Оба правдивыми они быть не могут, поскольку их высказывания противоречат друг другу. Следовательно, правдивый — второй, поскольку он высказывает истину, а первый и третий — лжецы. Легко проверить, что условие задачи в этом случае выполняется.
В Шуточный ответ: да, конечно, например, при количестве голов М = -3, количестве рук N= -4; количестве ног К = -5. Это же Зазеркалье!
Если быть серьезным и рассматривать только неотрицательные значения М, N и К, то легко показать, что гармонически развитых личностей в Зазеркалье не существует. Действительно, сложив три неравенства из условия задачи, получаем
Почему нравится задача?
109


Решения, ответы и комментарии к главе 2
M + N + K>2(M + N + K), а этого не может быть.
Q Да, следует. Если предположить противное, то среди некоторых зверюшек одинаковой пушистости найдется барабашка б и зверь 3, не являющийся барабашкой, причем менее крикливый, чем б. Пусть Б — барабашка одинаковой со зверем 3 крикливости. Тогда Б— более пушистый, чем 3, и, значит, Б более пушистый, чем б. Тогда Б более криклив, чем б и, значит, Б более криклив, чем 3. Противоречие.
Эта задача — сказочная переформулировка следующего утверждения: если среди всех тел равного объема наименьшую площадь поверхности имеет шар, то среди всех тел равной площади поверхности наибольший объем также у шара.
Q Если установить ставку министру финансов выше зарплаты всех жителей страны Ш, то разность d между количеством богатых мужчин и небогатых женщин будет отрицательным числом. Установим ставку министру финансов ниже зарплаты каждого жителя страны Ш, тогда разность d станет положительным числом. Теперь постепенно будем повышать ставку до тех пор, пока число d не станет равным нулю. В этот момент в стране Ш станет поровну богатых мужчин и небогатых женщин.
В Указание. Подсчитайте количество букв в числах, которые называет часовой.
К разделу 2 «Раскрепощенность фантазии»
К упражнениям
Q Рассмотрим многочлен
(х + 1)(лг + 2) • ... • (* + Ю).
Раскрыв скобки и приведя подобные члены, замечаем, что он равен произведению
1х2хЗх...х8х9*10
но
Глава 2


К разделу 2 «Раскрепощенность фантазии»
плюс сумма одночленов, в которых коэффициентом при х стоит сумма
1х2хЗх...х8х9+1х2хЗх...х8хЮ+... + 2хЗх...х9х10;
коэффициентом при х8 стоит сумма
1 х2+1 хЗ + ...+9х Ю;
коэффициентом при х9 стоит сумма
1 +2 + ... + 10;
коэффициентом при х10 стоит 1.
Положив х = 1, отсюда находим искомую сумму:
2 • 3 • 4-...-10 - 11- 1 = 39916799.
Q Обозначим данное выражение через и. Легко видеть, что если хотя бы одна из переменных х, у, z обращается в нуль, то и всё выражение равно нулю. Следовательно, и делится на xyz. Поскольку и — многочлен третьей степени, то и = Cxyz, где С — некоторая константа. Подставив значения х = у = z = 1, находим: и = С = 24.
В Указание. Исходное уравнение преобразуется к виду:
2хг - хг - Зх2 - Зх - 1 = 0, 2х3 = (х + I)3.
В Указание. Используйте замену переменных: х=_у+1/2.
В Возведем обе части в квадрат:
х + 5 = 52 - 2 • 5х2 + х4
и рассмотрим последнее равенство как квадратное уравнение относительно параметра 5. Корни этого уравнения:
^ 2x2+l±^(2*2+l) ~^(х4 ~х) 2х2+1±(2х + 1)
(1.2) - 2 ” 2 '
Почему нравится задача?
111


Решения, ответы и комментарии к главе 2
Далее осталось рассмотреть два квадратных уравнения относительно х:
10 = 2л:2 +1±(2дг + 1)
и отобрать из их решений те, которые удовлетворяют ограничению |х| < л/5.
Q Искомый предел х должен удовлетворять уравнению *=7277, откуда х = 2. Вопрос о существовании предела решается с помощью теоремы Вейерштрасса — см. Комментарий к п. 3.2. «Существует ли объект?» главы 1.
К разделу 3 «Парадоксальность»
3.1 Острый взгляд математика
&Z К упражнен иям «Как бы поступили Вы в следующих житейских ситуациях?»
Q Нужно все 4 таблетки разломать ровно пополам на левые и правые половинки, а затем принять сначала 4 левые половинки, а потом — 4 правые половинки.
Q Удочку следует разместить в чемодане. Его размеры можно подобрать так, чтобы удочка в нем не болталась, но уж с запасом хватит чемодана с квадратным дном размерами 3 х 3 м2.
Q Формально спор можно выиграть, нарисовав полотно ка- ким-либо инструментом, отличным от кисти, Однако великий маэстро пользовался именно кистью! Вот что Сальвадор Дали пишет в своих воспоминаниях: «И мне действительно удается выполнить произведение на заданный сюжет, с метрового расстояния набрызгивая кистью капли краски таким образом, что
112
Глава 2


К разделу 3 «Парадоксальность»
они образуют собой поразительную картину в стиле пуантилистов. Рисунок и колорит подобраны настолько удачно, что я получаю первую премию».
3.2. Граффити на полях
& Кзадйчам
Q Это возможно сделать благодаря трюку: с ролью цифры 9 на грани кубика вполне может справиться цифра 6. На гранях первого кубика можно расположить цифры 0, 1, 2, 3, 4, 5, а на гранях второго — цифры 0, 1,2, 7, 8, 9.
В Правильная дробь всегда ближе к 1, чем дробь, обратная к ней. Действительно, если а > Ъ > 0, то
- а Ъ .
1-т<—Ь
b а
поскольку
а b „ -+->2. b а
В Докажем, что собака Моська за всё время движения не выбежит за пределы аллеи АВ. Пусть в некоторый произвольный момент времени одна из девочек находится в точке Р, а другая — в точке Q, при этом АР = BQ (рис. 2.31). На стороне АО треугольника АОВ рассмотрим точку R такую, что AR = АР. Треугольник ROQ — равнобедренный и ZORQ = ZOAB, следовательно, RQ || АВ. Так как прямая АВ проходит через середину стороны PR треугольника PRQ, то она делит другую сторону PQ этого треугольника пополам. Итак, середина отрезка PQ располагается на отрезке АВ.
В Да, может, если распределение числа успешных выстрелов и числа патронов по этапам будет таким:
Почему нравится задача?
113


Решения, ответы и комментарии к главе 2
I этап
II этап
I спортсмен
Число успешных выстрелов
10
4
Число патронов
13
27
II спортсмен
Число успешных выстрелов
13
2
Число патронов
17
23
Задача допускает, например, следующее любопытное обобщение. Пусть каждому спортсмену выдают вначале 4п патронов, п > 10. Исследуемая ситуация возникает при таком распределении числа успешных выстрелов и числа патронов по этапам:
I этап
II этап
I спортсмен
Число успешных выстрелов
п
п-в
Число патронов
п + 3
Зп-З
II спортсмен
Число успешных выстрелов
п + 3
п- 8
Число патронов
л + 7
Ъп-1
Q Может. Например, если разности между доходами и расходами за каждый месяц года распределены так: 2, 2, 2, 2, — 9, 2, 2, 2, 2, — 9, 2, 2. Сумма любых пяти последовательных чисел выписанной цепочки отрицательна, а в целом за год сумма всех чисел положительна.
Q Построим разбиение парламента на две палаты, удовлетворяющее условиям задачи. Вначале распределим парламентариев по этим палатам произвольным образом. Если в какой-нибудь из палат у некоторого парламентария А будет не меньше 2 врагов, то число его врагов в другой палате не более 1. Поэтому после перемещения А в другую палату суммарное число пар врагов внутри палат уменьшится. Такие перемещения продолжим до тех пор, пока требуемое условие не будет выполнено.
jsS К упражнениям
Q Функции не могут изображаться показанными на рис. 2.2а, б графиками.
114
Глава 2


К разделу 3 «Парадоксальность»
В случае а) рассмотрим график с самым большим угловым коэффициентом. Пусть ему соответствует уравнение у = Ьх + с, так что b > с. Но, поскольку на рисунке он пересекает ось Оу выше, чем все остальные графики, то должно быть с > Ь. Противоречие.
В случае б) ветви парабол направлены вверх, поэтому а > 0; Ъ > 0; с > 0. Кроме того, все параболы пересекают ось Ох в двух точках, поэтому дискриминанты квадратных трехчленов должны быть положительными: а2 > 46с; Ь2 > Аса; с2 > АаЬ. Перемножив по-
Л Л Л ООО
следние неравенства, получаем а Ь с >64 а Ь с — противоречие.
В Такие функции существуют, например,
.К*) = М-1 и /(*)=•*-1.
Прид: е [0; 1] имеем _у(х) = f(x).
С другой стороны, для дг е [0; 1]
*(/(*)) = |*-1|-1=-*; Д/(*)) = (дг-1)-1=*-2.
Ни в одной точке интервала (0; 1) эти функции не совпадают.
В Обычно касание окружности, имеющий с параболой две общие точки, представляют себе так, как показано на рис. 2.32а. Но окружность может очень элегантно коснуться параболы, и пересекая ее — рис. 2.326. Именно так ведет себя по отношению к параболе у = х2 окружность
(х + 4)2 + (у - 3,5)2 = 31,25.
Рис. 2.32
Почему нравится задача?
115


Решения, ответы и комментарии к главе 2
Возможность проверить все технические детали мы предоставляем читателям. Правильный ответ на вопрос задачи: нет.
К разделу 4 «Радость озарения»
К задаче 1
Воспользуйтесь следующим свойством трапеции: точка пересечения ее диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Построения, которые можно осуществить, проводя лишь прямые линии, если уже начерчены либо две параллельные линии, либо параллелограмм, либо окружность, изложены в известной монографии швейцарского математика Якоба Штейнера (1796-1863) «Geometrische Konstruktionen, ausgefuhrt mittles der geraden Linie und eines festen Kreises» (Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга), Berlin, 1833.
jsS К упражнениям «Тренировка ассоциативного мышления»
Q а) Обсуждение задачи Дж. Сильвестра см. в [1, 3].
б) 	Между задачами п. а) и б) прослеживается аналогия: то, что в п. а) утверждается относительно точек, в п. б) переформулируется относительно прямых. Эта аналогия имеет глубокую подоплеку. В так называемой проективной геометрии она находит отражение в принципе двойственности: утверждение этой геометрии остается справедливым, если мы всюду поменяем местами слова «точка» и «прямая», соответственно поменяв местами выражения «лежит на» и «проходит через» и подобные им. Таким образом, с точки зрения проективной геометрии п. б) доказывать не нужно — достаточно лишь сослаться на принцип двойственности.
Проективная геометрия отличается от обычной евклидовой тем, что в ней две параллельные прямые пересекаются в бесконечно удаленной точке. Всевозможные бесконечно удаленные точки лежат на бесконечно удаленной прямой, равноправной с остальны¬
116
Глава 2


К разделу 6 «Великолепие миниатюр»
ми прямыми плоскости. Таким образом, условие попарной непараллельное™ прямых в п. б) всего лишь уточняет, что все заданные в условии задачи прямые попарно пересекаются в ограниченной части плоскости — аналог того, что все точки в п. а) также лежат в ограниченной области.
Идею принципа двойственности изложил французский геометр Жан Виктор Понселе (1788-1867) в своем «Трактате о проективных свойствах фигур» (1822). Дальнейшее обсуждение темы см. в [2, 4].
К разделу 6 «Великолепие миниатюр»
6.1. 	В задаче всё должно быть прекрасно
& К упражнениям
П л4 + 4 = (я2 + 2)2 - 4п2.
Далее используйте формулу разности квадратов.
Qa) п5-п = п(п2- 1)(и2+ 1).
Если п не делится на 5, то п имеет вид 5к + 1 или 5к ± 2. Соответственно и2 представимо в виде 25ЛГ2 ± 10&+ 1 или 25^ + 20А: + 4, то есть одно из чисел п2 - 1 или п2 + 1 делится на 5.
б) 	аналогично п. 2а).
Своеобразным обобщением результатов Лейбница в этом направлении является так называемая малая теорема Пьера Ферма (1601-1665): если числа пир взаимно просты и р — простое, то число пр - п делится на р.
В 23 • З2.
Q Заметив, что х ф 1, у Ф1, запишем исходное уравнение в виде
Число у может быть натуральным только тогда, когда х = 2, отсюда^ = 2.
Почему нравится задача?
117


Решения, ответы и комментарии к главе 2
Q Решение Г. Дьюдени: «Вообще мы можем взять числа вида 625w6 и 2 • 625т6» [2, с. 247].
QОбозначим числа в порядке возрастания а<Ь<с. Поскольку а + Ь : с, то а + Ь = с. Так как число а + с = 2а + Ъ делится на Ъ,
то 2а : Ъ, отсюда 2а = Ь, тогда с = За. Из чисел а, 2а, За можно со¬
ставить арифметическую прогрессию.
Q Указание:
1 + д: =xy + yz + zx + x =(х + z)(x + у),
1 + у2 = ху + yz + zx + у2 = (х + у)(у + z),
9 9
1 + z =xy + yz + zx + z =0> + z)(x + 2)•
В Леонардо Пизанский приводит один из возможных ответов:
Пусть z = х + у + 2т + \, где т = у]ху + х + у . Существует
бесконечно много пар натуральных чисел х, у, для которых число т является натуральным. Непосредственно проверяется, что при этих значениях все семь сумм условия задачи представляют квадрат целого числа:
yz+y + z = (y + m + I)2, zx + z+ x = (x + m + l)2, ху + z = (т + l)2, yz + x = (у + m)2, zx + у = (x + mf, xy+yz + zx = (x+y + m)2, xy+yz+zx + x+ y + z = (x+y + m + 1 )2. {Произволов В. Задача 5 // Квант. 2002. № 3. С. 21.)
118
Глава 2


К разделу 6 «Великолепие миниатюр»
6.2. 	Минимум средств
£$ К задаче!
Маскерони приводит 4 различных способа решения этой задачи. Рассмотрим один из них.
Сначала укажем способ удвоения отрезка (он будет использован в дальнейшем). Построим окружность с центром в точке В радиусом ВА (рис. 2.33).
От точки А раствором циркуля, равным радиусу ВА, отмечаем равные дуги AC, CD, DE. Таким образом строится диаметр АЕ построенной окружности, заданный своими концевыми точками А и Е, при этом АЕ = 2АВ.
Переходим к построению середины отрезка АВ.
С центром в точке А построим окружность радиуса АВ. С центром в точке Е построим окружность радиуса ЕА — пусть Ми М' — точки пересечения этих двух окружностей (рис. 2.34). Из точек М и М' как из центров проводим дуги окружностей радиуса МА = М'А - они пересекутся в точке X, расположенной в силу симметрии всей фигуры на прямой АЕ.
Докажем, что точка X — искомая. Действительно, равнобедренные треугольники АМХ и АМЕ подобны друг другу по двум углам, так что АХ: АМ = AM: АЕ =1:2. Отсюда АВ = 2 АХ.
А
Е
Рис. 2.33
Рис. 2.34
Почему нравится задача?
119


Решения, ответы и комментарии к главе 2
К разделу 7 «Элегантные мотивы»
7.1. 	Мотив натурального ряда
м ШШ | —и I шмжмттттшттттшшшшштттттм
& К упражнениям
Q Очевидно, что в тетради написано не более одного верного утверждения. Все утверждения не могут быть неверными, так как в противном случае последнее утверждение было бы истинным. Значит, верно лишь одно утверждение, а именно 99-е.
В Сначала рассмотрим случай п > 5. Поскольку ровно п - 1 число делится на 2, то среди п чисел не более одного нечетного. Следовательно, среди п - 2 чисел, делящихся на 3, не менее п - 3 чисел четных, то есть не менее п - 3 чисел должны делиться на 6. С другой стороны, по условию на 6 должны делиться ровно и - 5 чисел. Полученное противоречие говорит о том, что случай и > 5 невозможен. Набор из 5 чисел, удовлетворяющих условию задачи, возможен, например: 4, 5, 6, 12, 18.
В Пусть группа имеет вид
п, п + 1, п + 2, ..., п + 9.
Рассмотрим число п + 10.
Оно делится на 10, т. к. п делится на 10.
Оно делится на 9, т. к.
п+ 10 = (л+ 1) + 9,
а число п + 1 делится на 9.
Оно делится на 8, т. к.
п + 10 = (п + 2) + 8,
а число п + 2 делится на 8.
Оно делится на 2, т. к.
п + 10 = (и + 8) + 2, а число л + 8 делится на 2.
120
Глава 2


К разделу 7 «Элегантные мотивы»
Значит, и + 10 кратно всем числам от 2 до 10. Следовательно, п + 10 кратно НОК (2, 3,10) = 2520, т. е. и + 10 = 2520k.
Заметим, что все числа группы четырехзначные. Поэтому
1009 < п + 10 < 10 001, или 1009 < 2520&< 10 001,
откуца получаем к=\,2,3. Следовательно, имеется только 3 группы.
Эту задачу, предлагавшуюся на заключительном финальном соревновании турнира им. А. П. Савина в 2004 г., придумал шестиклассник Володя Брагин из г. Снежинска Челябинской области.
В Изложим способ решения этой задачи, восходящий к китайскому математику III в. Сунь-Цзы. Пусть
МММ
М~р\рг ... Рп, т1=—, т2 =—, ..., т„=—.
Р\ Рг Рп
Подберем вспомогательные целые числа уь у2, ..., у„ таким образом, чтобы каждое из чисел дуй, (/ = 1, 2, ..., п) при делении наpt давало остаток 1.
Обозначим
х0= \-т1у1+2-т2у2+... + п-т„уп.
Искомым будет любое число х, которое при делении на М дает такой же остаток, что и число х0.
Например, при п = 3 получаем:
Р\- 2, />2 = 3, рз = 5, М= 30, /«1 = 15, т2= 10, /и3 = 6.
В качестве вспомогательных чисел yt можно взять у\ = у2 = уг = 1, тогда *0 = 53.
Искомые числа: 23, 53, 83,... .
В общем случае справедлива так называемая китайская теорема об остатках:
Если целые числа к/, к2, К отличны от нуля и попарно вза¬
имно просты, то для любых целых чисел си с2, .... с„ существует целое число х, дающее остаток с, при делении на к, для всех i = 1, 2 п.
Почему нравится задача?
121


Решения, ответы и комментарии к главе 2
Для нахождения х по способу Сунь-Цзы следует найти числа
М= к\ кг... кп,
ММ М
Щ =~Г’ т2 =~, > •••> тп =~Г
кх к2 кп
и подобрать вспомогательные целые числаупу2, ..-,Уп таким образом, чтобы каждое из чисел д'/т, (г = 1, 2, ..., п) при делении на kt давало остаток 1. Число х будет давать такой же остаток при делении на М, как и число х0 = с, • т1у] + с2 • т2у2 + — + сп ■ тпу„ . Действительно, для каждого kt все произведения mjyj при j * i делятся на ki, а произведение дает остаток 1. Таким образом, при делении на ki число х0 имеет такой же остаток, что и при делении с, на к,. За подробностями отсылаем к стандартным курсам теории чисел (см., например, [3].)
7.2. 	Мотив круга
& К упражнениям «По кругу, по кругу...»
В Достаточно доказать равенства а = b = с для перпендикуляров а, Ь, с, опущенных из точки Q на стороны треугольника (рис. 2.35).
^Из неравенства Zl > Z2 следует а > Ъ\
^Из неравенства Z3 > Z4 следует b > с;
^Из неравенства Z5 > Z6 следует с > а.
^Из полученной цепочки неравенств следует требуемое равенство.
122
Глава 2


К разделу 7 «Элегантные мотивы»
с.
Рис. 2.36
Рис. 2.37
В Каждую сторону описанного шестиугольника представим в
виде совокупности двух касательных отрезков к окружности (рис. 2.36):
причем искомая длина шестой стороны равна а\ + е2.
Сложив равенства (1) с нечетными номерами и вычтя равенства с четными номерами, с учетом (2) имеем:
а\ + ег = а + с + е - b - d.
ВI способ. Введем обозначения углов, показанные на рис. 2.37. Тогда сумма углов внутреннего выпуклого пятиугольника равна
Г
U — flfj "f #2»
b = bl+b2,
* С = Cj + С2 9 d = dj “h d2 9 e-ex +e2.
(i)
По свойству касательных
(2)
Почему нравится задача?
123


Решения, ответы и комментарии к главе 2
л-а+л-р+л-у+л-8+л-е=
= 5 л - (а + /3 + у + 8+е).
С другой стороны, эта же сумма равна л • (5 - 2) = Ъл, поэтому а + Р + у + 8 + е = 2л.
Искомая сумма внутренних углов звездчатого пятиугольника при его вершинах равна
л - (а + е) + п - (/? + а) + л - {у + J3) + л - (8 + у) + л - (е + 8) =
= 5 л- 2(а + /3 + у + 8 + е) = 5л-4л = л.
II способ. Обойдем по контуру звездчатый пятиугольник, отправляясь от точки А (рис. 2.38а). Вектор, указывающий направление движения, при этом дважды повернется по часовой стрелке, заметая угол 4 л (рис. 2.386). Искомая сумма углов равна 5л - Ал = л.
Рис. 2.38
Q Авторство этой задачи иногда приписывается Наполеону Бонапарту, хотя Г. С. М. Кокстер и С. JI. Грейтцер в своей популярной книге [5, с. 79] отмечают, что «его знания геометрии являются сомнительными для такого подвига». Приведем решение задачи, следуя [5].
Пусть дан произвольный треугольник ABC и пусть на его сторонах внешним образом построены равносторонние треугольники ВРС, CQA и ARB. Сначала докажем, что окружности, описанные
124
Глава 2


К разделу 7 «Элегантные мотивы»
вокруг треугольников ВРС, CQA и ARB, пересекаются в одной точке F, называемой точкой Ферма (рис. 2.39).
А
Рис. 2.39
При повороте на 60° против часовой стрелки вокруг точки А точка R переходит в точку В, а точка С — в точку Q, то есть прямая RC переходит в прямую BQ, и, значит, угол между этими прямыми равен 60°. Пусть эти прямые пересекаются в точке F. Поскольку отрезок CQ из точек F и А виден под одним и тем же углом, то четырехугольник С FAQ — вписанный. Аналогично четырехугольник В FAR — вписанный, а, так как сумма углов ВРС и BFC равна 180°, то и четырехугольник PBFC — вписанный. Точка F является общей точкой окружностей, описанных вокруг треугольников ВРС, CQA и ARB.
Обозначим К, L и М центры окружностей, описанных вокруг треугольников ВРС, CQA и ARB. Так как
■S KL перпендикулярно FC;
•S LM перпендикулярно FA;
S МК перпендикулярно FB,
то по свойству углов с перпендикулярными сторонами углы KLM, LMK и MKL равны 60°, что и требовалось доказать.
Справедливы и другие любопытные факты. Треугольник KLM обозначим Т\. Двойственный к нему треугольник Т2 получим, если на сторонах треугольника ABC будем откладывать равносторонние треугольники не вовне, а вовнутрь. Оказывается [5], тре¬
Почему нравится задача?
125


Решения, ответы и комментарии к главе 2
угольник Т2 тоже равносторонний, центры треугольников Т\ и Т2 совпадают с центром тяжести исходного треугольника, а разность площадей треугольников Т\ и Т2 равна площади исходного.
7.3. 	Мотив симметрии
& К задачам
Q Верно.
В Площадь вписанного круга больше площади вписанного квадрата.
В cos (sin х) > sin (cos ;t).
В Задача подробно обсуждается в книге: Серпинский В. «О решении уравнений в целых числах». М.: Физматлит, 1961. С. 86-88. Приведем ответ из этой книги. Если х = у, то х (и, соответственно, у) — произвольное рациональное положительное число. Если х &у, например, у > х, то
п+1
I+A
nj
где п — натуральное число. Из этих формул, в частности, следует, что только для п = 1 мы получаем решение в натуральных числах.
В Если длины плеч коромысла находятся в отношении а: Ь,р — требуемый покупателями вес, q — вес товара, полученного первым покупателем, г — вес товара, полученного вторым покупателем, то
Р - а и г _ а
q b р b
Проданный купцом товар весит
b а
q+r=p-+p-=p a b
{ и „ \ 'о а
— + —
ка Ъ,
Но Ь/а+а/Ь > 2 , поэтому q + г > 2р.
126
Глава 2


К разделу 7 «Элегантные мотивы»
Подумайте, существует ли, всё же, у купца способ взвесить на своих неверных весах именно тот вес, который требуется покупателю.
J&S К упражнениям
Q При правильной игре выигрывает начинающий. Первым ходом он проводит самую большую диагональ 2000-угольника, а затем соединяет точки, симметричные относительно проведенной диагонали тем точкам, которые соединяет второй игрок.
В См. рис. 2.40.
В Поскольку в уменьшаемом и вычитаемом сумма цифр одинакова, то они имеют одинаковые остатки при делении на 9. Всякое число указанного вида делится на 9, и поэтому простым быть не может.
В Подходит только значение р = 3. Для простого р > 3 каждое из чисел 2Р +1, р2 -1 делится на 3, поэтому на 3 делится и число
2Р + р2 = (2Р +1) + (р2 -1).
В а и b могут быть любыми неотрицательными числами.
7.4. 	ZIP-мотив
& К упражнениям
В Несмотря на то, что произведение в условии задачи и так уже представляет собой довольно длинный «поезд», домножим его слева еще на один «вагон» — множитель (а - Ь), равный 1.
Работает «застежка-молния»:
Почему нравится задача?
127


Решения, ответы и комментарии к главе 2
(a-b)(a + b) = a2-b2;
{a2-b2)(a2 + b2) = a4-b4\
(a4-b4)(a4+b4) = a*-b*;
(а8-Ь*)(а* + Ь*) = а'6-Ь'6;
(а16 - Ь16)(а16 + Ь16) = а32 - Ь32;
(а32-Ь32)(а32+Ь32) = ам-Ь64.
В итоге получаем вполне «зазипованный» ответ.
Q Указание:
домножьте произведение на sin-^- и п раз воспользуйтесь формулой синуса удвоенного угла sin 2а =2 sinacosa.
В Указание: здесь «молния» застегивается справа.
В Заменим в конструкции
■^6+^/б" +...+
самую внутреннюю шестерку на большее число 9. Тогда 79 = 3,
V6+V9 =79 = 3 и т. д. — все квадратные радикалы последовательно, один за другим, «зипуются» в число 3. Точно так же, заменив самую внутреннюю шестерку в конструкции из кубических радикалов на большее число 8, «зазипуем» ее в число 2. Итак, исходная сумма радикалов не больше, чем число 2 + 3 = 5.
7.5. 	Ансамбли задач
& К задачам
В I способ.
Если взять любое число, отличное от 0 и 1, например 2, в качестве основания степени, а показателями степени сделать числа ка- кого-либо магического квадрата с постоянной суммой, то получен¬
ие
Глава 2


К разделу 7 «Элегантные мотивы»
ные числа образуют магический квадрат с одинаковыми произведениями.
II способ.
Пусть а и Ъ — различные простые числа. Составим две таблицы, показанные ниже:
1
а2
а
а2
а
1
а
1
а2
Ь
Ъ2
1
1
Ъ
ъ2
Ъ2
1
ъ
Поэлементно перемножив числа в соответствующих ячейках этих таблиц, получим искомый квадрат:
в
2.2 a b
а
а2
а Ь
Ь2
ab2
1
а2Ъ
QI способ.
Очевидно, ai = 1, а4 = «2 -2= «2 • «2= 4, и в силу монотонности последовательности аз = 3. Возникает гипотеза, что для любого натурального и справедливо равенство а„=п. Обоснуем ее методом математической индукции. Предположим, что гипотеза верна при всех п < Nддя некоторого натурального N> 1. Выведем отсюда, что она верна и при п = N. Возможны две ситуации.
а) Число N—составное, N = pq. Тогда aN = ам = ар ■ aq = pq = N.
б) Число N — простое. Тогда число N+ 1 составное, N+ 1 =st, причем s<N;t<N, поэтому aN+\ = as • а, = st = N+ 1.
Кроме того, по предположению индукции aN.\ = N- 1. В силу монотонности последовательности отсюда следует aN = N.
II способ.
Легко убедиться в том, что для натуральных п справедливо равенство а2„ =2". Поскольку в интервале ^2"_i;2"j располагается ровно 2"-1 - 1 чисел: 2"-1 + 1, 2я”1 + 2, ..., 2”- 1, то в силу монотонности последовательности эти числа равны соответственно
Почему нравится задача?
129


Решения, ответы и комментарии к главе 2
а2"-'+\’ а2”*'+2’ а2"-V В итоге получаем а„ = п. Действительно, в
этом случае равенство ап.т = а„ ■ ат выполняется.
Q Положим т = kd, п = Id, где d = НОД(я, т).
Тогда НОК(и, т) = kid и, значит, kid + d = kd + Id. Отсюда получаем, что (к - 1) (/- 1) = 0, то есть к- 1 или /= 1. Это означает, что либо т, либо п равно НОД (и, т). Следовательно, либо п делится на т, либо т делится на п.
В Проведя отрезки АМ\, АМ2, АМ3, АК\, АК2, АК3, запишем равенства вписанных в соответствующие дуги углов:
ZAMX В = ZAKXB, (1)
ZAM2 В = ZAK2B, (2)
ZAM3 В = ZAK3B. (3)
Из (1) и (2) следуют равенства
ZAMxM2 = ZAKxK2, (4)
ZAM2M} = ZAK2K3 (5)
соответственно. Значит, треугольники АМ\М2 и АК\К2 подобны по двум углам. Отсюда следует, что
М,М2 КХК2 АМ2 ак2
АМ2 ~ АК2 ’ М2МЪ ~ К2К3 ‘
Перемножив два последних равенства, получим требуемое.
7.6. 	Мотив дополнения
, Ш К упражнениям
В Вероятность невыпадения числа 6 при одном бросании кости равна 5/6. Вероятность того, что это событие повторится 4 раза подряд, равна
130
Глава 2


К разделу 7 «Элегантные мотивы»
5V
Тогда искомая вероятность противоположного к этому событию равна
:\4
-1
671
1296’
1
что больше —. Таким образом, придуманная де Мере игра оказалась для него выгодной, и он в многократных сеансах действительно стал выигрывать. Скоро, однако, это не понравилось его партнерам, и они перестали с ним играть.
Тогда де Мере придумал другую игру. Он предложил кидать два кубика 24 раза. Если при этом хотя бы раз сверху окажутся две пятерки, то де Мере выигрывает. В этом случае правила оказались неблагоприятными для де Мере, он стал проигрывать и в конце- концов, проиграв всё свое состояние, превратился в нищего.
В См. рис. 2.41.
Er-
IC
N
1
\
\
\
\
\
\
р Q
S R
\
\
\
\
/
/
/
/
/
/
/
/
/
/
/
/
Ч
- Л\
М
Рис. 2.41
D С
Рис. 2.42
Почему нравится задача?
131


Решения, ответы и комментарии к главе 2
Q В качестве дополнения в данной задаче можно выбрать прямоугольник EFGH (см. рис. 2.42). Поскольку площадь треугольника KQB равна половине площади прямоугольника KEBQ\ площадь треугольника BRM равна половине площади прямоугольника BRMF\ площадь треугольника MSD равна половине площади прямоугольника MSDG; площадь треугольника DPK равна половине площади прямоугольника DPKH, то площадь четырехугольника KBMD равна полусумме площадей четырехугольников HEFG и PQRS. Аналогично убеждаемся, что площадь четырехугольника ALCN также равна полусумме площадей четырехугольников HEFG и PQRS.
Следовательно, площади четырехугольников ALCN и KBMD равны.
К разделу 8 «Математика факта»
8.2. 	Три биссектрисы
& К упражнению Указание. Площадь треугольника, с одной стороны, равна
1
-pqsmp,
с другой стороны — равна
1 , • 9 1 i-9
— Dl Sin— + — <7/ Sin— .
2 2 2 2
Приравняв эти два выражения с учетом того, что
. . (р (D
sinfi> = 2sin—cos—,
2 2
получаем требуемый результат.
132
Глава 2


К разделу 9 «Заигрывание интуиции»
К разделу 9 «Заигрывание интуиции»
9.1. 	Veni, Vidi, Vici
& К упражнениям
Dа) Интересно, угаданные вами числа положительные или отрицательные?
г) Поскольку 20,05 = 20 +1/2, то jcj = 20 и хг = 1/20.
Д) toy} = И; 9} или {х-,у} = {1; 25}.
t) х = у = z = 3.
Обоснуем угаданное решение. Из второго уравнения системы следует xyz = 27. Тогда по теореме, обратной к теореме Виета, х, у, z являются корнями кубического уравнения
и3 - 9и2 + 27м -27 = 0, или (и-3)3 = 0.
Следовательно, х = у = z = 3 — решение единственное.
Q Несложно угадать следующее решение: значения двух неизвестных равны нулю, а значение третьего равно -1, так что
x+y + z = -1.
Однако без обоснования единственности это решение признать корректным нельзя — девиз Цезаря: «Veni, Vidi, Vici» здесь не проходит!
Заметим, что в силу первого уравнения системы каждое из неизвестных по модулю не превышает 1, поэтому
х + 1>0, д>+1£0, z + 1^0.
Сложив первое и второе уравнение системы, получаем
*2 (*+1)+у2 0>+1)+у2 Су+1) = о.
Это возможно лишь в том случае, когда каждое неотрицательное слагаемое в сумме равно нулю, следовательно, любое неизвестное может равяться только 0 или -1. Из последнего уравнения
Почему нравится задача?
133


Решения, ответы и комментарии к главе 2
системы следует, что значение -1 может принимать только одно из неизвестных, отсюда
Х+У + z = -1.
9.2. 	Угадывание особого места
■ш 'Ш-?т

8111
снениям
В А что, если соединить центры квадратов прямой линией?
Q А не будет ли особым местом точка пересечения диагоналей?
Обозначим через О точку пересечения диагоналей выпуклого четырехугольника ABCD, а через М — произвольную точку плоскости (рис. 2.43).
Согласно неравенству треугольника,
AM + МС >АС = АО + ОС
(знак равенства возможен, если точка М расположена на отрезке АС);
ВМ + MD >BD - ВО + OD
(знак равенства возможен, если точка М расположена на отрезке BD). Складывая эти равенства, получаем
AM + ВМ + СМ + DM >АО + ВО + СО + DO,
D причем равенство возможно, если
точка М совпадает с точкой О. Итак, точка О — действительно искомая.
С G Рис. 2.44
| Пожалуй, особым местом могла бы служить середина отрезка АЕ? Обоснуем эту догадку.
Из вершин В и D опустим пер- Е пендикуляры BFJlAE, DG1AE, BHLDG (рис. 2.44). Так как тре-
134
Глава 2


К разделу 9 «Заигрывание интуиции»
угольники ABC и CDE равнобедренные, то
FC = — AC; CG = — СЕ,
2 2
поэтому FG = АЕ/2 — величина постоянная (ведь отрезок АЕ фиксирован). Если точка С не лежит на середине отрезка АЕ, то один из подобных треугольников CBF, EDG больше другого — пусть, для определенности,
DG > BF,
и, следовательно, DH> 0.
Но тогда в прямоугольном треугольнике BHD имеем
BD > ВН = FG.
Если же точка С — середина АЕ, то точки D и Н совпадают, и, значит, в этом случае отрезок BD имеет наименьшую длину.
Q Особое место — прямая, проведенная через центр искомого прямоугольника и центр прямоугольника-дырки. Она делит образовавшуюся фигуру на две части равной площади.
0 Особое место — предельная точка сжимающего отображения прямоугольной карты в себя. Рассмотрим отображение f переводящее большую карту К0 в меньшую карту К\, каждой точке, изображающей некоторый пункт на карте ставится в соответствие точка, изображающая тот же пункт на карте К\. Обозначим через К2 образ карты К\ при этом же отображении и вообще положим
J[K^i) = = K„,n=l,2,... .
Прямоугольники К0, К\, К2, ...,Кп, ... имеют ровно одну общую точку, поскольку размеры прямоугольников стремятся к нулю. Эта точка и есть нужная точка прокола.
Q Особое место — число 2003. Изучая уравнение, можно заметить, что 2 + 2001 = 3 + 2000 = 4 + 1999 = 2003. Это наблюдение может подсказать следующую группировку членов уравнения:
Почему нравится задача?
135


Решения, ответы и комментарии к главе 2
х-2 /jc — 2001> f /jc — 3 f
200Т _V 2 Г V2000 ~V
■ 2000^1
/Е5_ [.
V1999 V
jc — 19991
= 0.
Далее можно заметить, что все выражения в скобках одного знака, и лишь при jc = 2003 они обращаются в нуль. Действительно, функция
/м
_ Ix — n jx-m _ V-m V «
при х>т>п>0 имеет отрицательную производную
1
1
y[m(x^nj yfn(x^m) на области ее определения, и f(m + n) = 0.
9.3. 	Предчувствие ответа
«Танец маленьких чисел»
£ S
При р = 41 внутри квадратов появятся узоры — см. рис. 2.45.
Общая закономерность такова. Если простое число р при делении на 4 дает в остатке 1, то узор появляется, если же остаток деления равен 3, то квадраты остаются пустыми.
Основу алгоритма «Танец маленьких чисел» составляют простые соотношения. Пронумеруем строки и столбцы квадратной таблицы числами от 0 до п. На пересечении /'-й строки и J-го столбца запишем
• I * I I I
Р-
Рис.
= 41 2.45
136
Глава 2


К разделу 9 «Заигрывание интуиции»
число к= i2 + j2. Далее, если число к делится на р, отметим соответствующую клеточку черным цветом, если нет — белым цветом. Вот и всё. Чести быть отмеченными удостаиваются те простые числа р, которые можно представить в виде суммы квадратов целых чисел.
Компьютерные эксперименты показывают, что «привилегированными» в отмеченном выше смысле оказываются лишь те простые р, которые при делении на 4 дают в остатке 1. Этот факт был известен еще Пьеру Ферма (1601-1665) и вошел в литературу под названием «Рождественской теоремы Ферма» [6].
(Написанную на Delphi программу, реализующую этот «танец», можно бесплатно переписать с сайта «Планета Математика» Московского детского клуба «Компьютер»: math.child.ru, раздел «Лаборатория», п. «Клеточные узоры»).
9.4. 	Интуиция воображения
& К упражнениям «Точки»
Q В обоих пунктах а) и б) ответ положительный — см. соответственно рис. 2.46а, б.
Q Да, могут, см. рис. 2.47.
Q Рассмотрим все возможные пары выбранных точек и через любые две точки проведем прямую. Вне замкнутой кривой, окружающей все точки множества, выберем точку А, не лежащую ни на одной из проведенных нами прямых. Проведем через А произволь-
А
а)
б)
ис. 2.46
Рис. 2.47
Почему нравится задача?
137


Решения, ответы и комментарии к главе 2
ную прямую. Поворачивая прямую вокруг точки по часовой стрелке, будем проходить одну за другой точки нашего множества (пройти одновременно через две точки множества прямая не может). После того, как «за кормой» окажется половина точек нашего множества, задача будет решена.
В Пусть А и В — две ближайшие точки из данного множества М. Третью точку С выберем так, чтобы величина угла ZACB была наибольшей. Так как АС > АВ, ВС > АВ, то величина угла ZACB не больше 60°. Легко видеть (рис. 2.48), что ZADB > ZACB для всех точек D внутри окружности (независимо от того, по какую сторону от АВ лежит D), поэтому ни одна из точек D не принадлежит М.
& К упражнениям «Точки и многоугольники»
В Могут (см. рис. 2.49). Треугольники ВАС, BAD, BAE, CAD, CAE, DAE равнобедренные.
А
Рис. 2.49
В Ответ в пунктах а), б) — существует, см. соответственно рис. 2.48а, б.
в) 	Такой ломаной не существует. Если бы такая ломаная существовала, то в каждой точке пересечения звеньев пересекалось бы по два различных звена. Но звеньев — нечетное количество.
138
Глава 2


К разделу 9 «Заигрывание интуиции»
Рис. 2.50 Рис. 2.51
Q Да, см. рис. 2.51.
В Да, могло — см. рис. 2.52. Буквой «Л» обозначены лампочки. В Да, существует, см., например, рис. 2.53.
л
Почему нравится задача?
139


Решения, ответы и комментарии к главе 2
& Купражнениям«Многоугольники»
Q Существуют, на рис. 2.54 один из таких многоугольников показан сплошной линией, другой — штриховкой.
Q Существует, см. рис. 2.55.
Q Может, см. рис. 2.56. На этом рисунке вершины четырехугольника ABCD лежат на сторонах четырехугольника A\B\C\D\.
Q Может. В качестве первого треугольника можно взять правильный треугольник с длиной стороны 0,5 см, а в качестве второго — равнобедренный треугольник с основанием 200 м и высотой 10”7м. Его боковая сторона больше половины основания, то есть тоже больше 100 м, а площадь равна 10~5 м2 и меньше площади первого треугольника, равной >/з/16 см2.
Q Не зависит.
Q Можно. Разобьем исходный квадрат на п2 квадратиков со стороной длины 1/и. В каждый квадратик поместим круг радиуса 1/2я, так что сумма радиусов всех п2 кругов равна л/2. Несложно подобрать п так, чтобы это число равнялось 1000.
140
Глава 2


К разделу 9 «Заигрывание интуиции»
Q Предположим, что существует фигура Ф, у которой есть ровно два центра симметрии — точки А и В. Тогда точка С фигуры, симметричная точке В относительно точки А, также является центром симметрии фигуры Ф, а это противоречит условию. Действительно, рассмотрим произвольную точку X е Ф (рис. 2.57). Пусть точка Xi симметрична точке X относительно точки А; точка Х2 — симметрична точке Xi относительно точки В; точка Хз — симметрична точке Х2 относительно точки А. Убедитесь самостоятельно в том, что точка Х3 симметрична точке X относительно точки С (последнее и означает, что точка С — ещё один центр симметрии фигуры Ф).
В Таких фигур существует сколько угодно. На рис. 2.58 показан круг, получающийся поворотом исходного круга (выделенного пунктиром) относительно точки Р по часовой стрелке. Его можно также получить параллельным переносом исходного круга на вектор ОО'.
В Да. Одна из таких фигур изображена на рис. 2.59.
В Существует, например, «пропеллер», показанный на рис. 2.59, при соответствующим образом подобранных размерах. Годится и такой вырожденный пример: из круга радиуса 1 с центром О выкалываются три точки — вершины равностороннего треугольника с центром О.
Рис. 2.58
Рис. 2.57
Почему нравится задача?
141


Решения, ответы и комментарии к главе 2
В Это возможно. Следует совместить изображение дракона на обоих кругах (рис. 2.60) и во втором круге вырезать часть, общую с первым кругом. Затем оставшийся после вырезания «серп» присоединить к этой части с противоположной стороны.
К упражнениям «Клетчатая плоскость»
Q Такой прямоугольник обязательно найдется. Рассмотрим горизонтальную полосу бумаги ширины 2N. Среди бесконечного количества столбцов этой полосы найдется 2 одинаково окрашенных столбца, причем в каждом из этих 2 одинаково окрашенных столбцов найдутся 2 клетки одного и того же цвета. Эти 4 клетки в совокупности и составляют вершины искомого прямоугольника.
В Верно, такие клетки всегда найдутся. Предположим, что это не так. Рассмотрим квадрат со стороной (109+ 1) клеток, в центре которого стоит число 1. Назовем «ходом» переход от одной клетки к другой через общую сторону. Заметим, что от центральной клетки квадрата можно дойти до любой его клетки не более, чем за 109 ходов. Так как числа в последовательно пройденных клетках различаются не больше чем на 109, то любое число в квадрате отличается от 1 не более, чем на 109 х 109= 1018, и по¬
де
Глава 2


К разделу 9 «Заигрывание интуиции»
этому не превышает 1018 + 1. С другой стороны, в квадрате всего (109 + I)2 чисел. А так как, по условию, все они различны, то наибольшее из них не меньше (109 + I)2 = 1018 + 2 • 109 + 1, а это больше, чем 1018 + 1. Противоречие.
0 Может. Соответствующая расстановка чисел понятна из приведенной ниже таблицы.
...
...
...
...
...
...
...
...
...
...
...
8
9
...
...
...
...
...
...
8
6
7
9
...
...
...
8
6
4
5
7
9
...
8
6
4
2
3
5
7
9
9
7
5
3
1
2
4
6
8
...
9
7
5
3
4
6
8
...
...
9
7
5
б
8
...
...
...
...
9
7
8
...
...
...
9
...
...
...
...
...
...
...
...
...
...
...
...
...
9.5. 	Именованные задачи
& К задаче «Улитка» Пусть а\ — первый наблюдатель; а2 — последний из всех наблюдателей, начавших следить за улиткой до того, как за ней кончил следить а\, а3 — последний из наблюдателей, начавший следить за улиткой до того, как за ней кончил следить а2, и т. д. Нечетные промежутки наблюдения аь а3, <з5,... между собой не пересекаются, так же как четные промежутки а2, а4, а6, ... не пересекаются между собой (иначе один из наблюдателей был бы выбран неправильно). Но любой из этих промежутков равен 1 мин, а весь интервал наблюдения составляет 6 мин. Поэтому как четных, так и нечетных промежутков не более 5. Отсюда число наблюдателей не больше 10, и, зна¬
Почему нравится задача?
143


Решения, ответы и комментарии к главе 2
чит, улитка проползла не более 10 м. Она проползет ровно 10 м в такой, например, ситуации: ползет улитка только тогда, когда на нее смотрит ровно один наблюдатель; остальное время она стоит.
£$ К задаче «Игра в скалярное произведение»
Достаточно одного вопроса, если второй задаст числа «1 = 1, я2 = ЮО, а3 = 1002, ..., а„ = ЮО2"-2 (или любой другой набор быстро растущих чисел).
& К задаче «Гангстеры»
Рис. 2.61
Заметим, во-первых, что в каждом убитом может находиться не более 6 пуль, а ровно 6 пуль может быть лишь в случае, когда его убийцы расположены в вершинах правильного шестиугольника и убитый находится в его центре. Убитый гангстер, назовем его А, и сам стреляет в одного из этих 6 убийц, назовем его В. Нетрудно показать, что если в А 6 пуль, то в В не больше 4-х. Поскольку было выпущено 50 пуль, а в каждом убитом не более 6 пуль, то убито не менее 9 гангстеров. Если убито ровно 9 гангстеров, то не меньше 5 из них убито шестью пулями. Но тогда должно быть еще 5 убитых гангстеров, а этого быть не может. Следовательно, убитых не меньше 10. Ситуация, в которой оказывается ровно 10 убитых гангстеров, изображена на рис. 2.61. Гангстеры разбиваются на 5 групп по 10 человек, и в каждой группе оказывается по 2 убитых.
144
Глава 2


Литература к главе 2
9.7. 	Остальные задачи
& К «прочим упражнениям»
Q Да, верно.
QHeT.
и
Q 4 рукопожатия. Так как все количества рукопожатий различны, то это могут быть только числа 0, 1, 2, ..., 8. Поэтому найдется человек, сделавший 8 рукопожатий, причем это не миссис Браун (иначе не нашлось бы человека, который бы сделал 0 рукопожатий). Пусть это будет мистер Смит. Поскольку его жена сделала 0 рукопожатий, то после удаления мистера Смита и его жены для оставшихся 4 пар будут выполняться все условия задачи. Снова удалим соответствующую пару супругов и т. д. Миссис Браун здоровалась только с каждым из удаляемых мужчин — всего 4 раза.
5. Пусть квадрат разрезали на п прямоугольников. Обозначим через ак большую, а через Ък — меньшую сторону к-го прямоугольника, к = 1,2, ..., п. Все величины а* не превышают 1, поэтому для суммы пузатостей имеем:
Ъ\ ь ъ
1—— + ...Н—— ^ +#2^2 *^* •••"*■ = ^ *
а\ а\ ап
Литература
к главе 2 «Почему нравится задача»
1. 	Сказочная фабула
1. Жуков А. Монстры Зазеркалья // Квант. 1996. № 4. С. 26.
2. Жуков А. Задача 5 // Квант. 2004. № 3. С. 25.
3. Задачи по математике, предлагавшиеся ученикам математического класса 57 школы. М.: МЦНМО, 2004. С. 17.
4. Живой фольклор // Квант. 2002. № 3. С. 43.
Почему нравится задача?
145


Литература к главе 2
2. 	Раскрепощенность фантазии
1. Шарыгин И. Ф. Математический винегрет. М.: Мир, 2002. С. 124.
2. Горячев Д., Воронец А. Задачи, вопросы, софизмы для любителей математики. Москва — Ижевск: РХД, 2000. С. 28.
3. Кордемский Б. А. Математические завлекалки. М.: ОНИКС, Альянс-В. 2000. С. 460.
3. Парадоксальность
1. Блюфштейн А. Задача 3 // Квант. 1993. 9/10. С. 53.
2. Гарднер М. Математические новеллы. М.: Мир, 1974. С. 414.
3. Дубов В. Задача 4 // Квант. 2003. № 4. С. 28.
4. Самовол П., Аппелъбаум М. Задача 2 // Квант. 2004. № 3. С. 25.
5. Васильев Н. Б., Гутенмахер В. Л., Раббот Ж. М., Тоом А. Л. Заочные математические олимпиады. М.: Наука, 1986. С. 105.
6. Бородин О. Задача М580 // Квант. 1979. № 8. С. 38.
7. Агаханов Н., Подлипский О. Математические олимпиады Московской области. 1993-2002. М.: Изд-во МФТИ, 2003. С. 31.
8. 25 Турнир Городов, весенний тур, 10-11 класс, основной вариант, задача 5 // [Электронный ресурс] www.turgor.ru/25/tumir25.php
4. Радость озарения
1. Кокстер Г С. М. Введение в геометрию. М.: Наука, 1966. С. 105-107.
2. Там же. С. 331-337.
3. Вокруг задачи Сильвестра // Квант. 1984. № 5. С. 21.
4. Щербаков Р. Н., Пичурин Л. Ф. От проективной геометрии — к неевклидовой (вокруг абсолюта). М.: Просвещение, 1979, 160 с.
5. Неожиданый ракурс
1. Дворянинов С. Задача 32 // Квант. 2005. № 2. С. 24.
6. 	Великолепие миниатюр
1. Произволов В. В. Задачи на вырост. М.: МИРОС, 1995. С. 5.
2. Дьюдени Г. 520 головоломок. М.: Мир, 1975. С. 66.
3. Произволов В. Задача М1799 // Квант. 2001. № 6. С. 19.
146
Глава 2


Литература к главе 2
7. Элегантные мотивы
1. Савин А. П. Задача 5 // Квант. 1987. № 7. С. 43.
2. Брагин В. Задача 4 // Квант. 2005. № 2. С. 22.
3. Бухштаб А. А. Теория чисел. М.: Просвещение, 1966. 384 с.
4. Произволов В. В. Задачи на вырост. М.: МИРОС, 1995. С. 62.
5. Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. М.: Наука, 1978. 224 с.
6. Савин А. П. Занимательные математические задачи. М.: ACT, 1995. С. 8.
7. Савин А. П. Задача 2 // Квант. 1984. № 6. С. 31.
8. Задача 5 // Квант. 1979. № 4. С. 37.
9. Горячев Д., Воронец А. Задачи, вопросы и софизмы для любителей математики. Москва — Ижевск: РХД, 2000. С. 16.
10. Задача 4 // Квант. 1981. № 7. С. 35.
11. Гарднер М. От мозаик Пенроуза к надежным шифрам. М.: Мир, 1993. С. 221.
12. Жуков А. Задача 2 // Квант. 2001. № 5. С. 27.
13. Майзус С. Задача 663 // Квант. 1981. № 1. С. 26.
14. LXV Московская математическая олимпиада. Окружной тур. Отчет. МЦНМО,
2002. 	80 с.
15. Кордемский Б. А. Математическая смекалка. М.: ГИФМЛ, 1963. С. 307-311.
16. XXI Российская олимпиада школьников по математике // Квант. 1995. №5. С. 47.
17. АджансА. Задача 4823 // «Математика в школе». 2005. № 3. С. 54.
18. Произволов В. Задача 5 // Квант. 2002. № 5. С. 23.
19. Акулич И. Задача 3 // Квант. 2002. № 2. С. 19.
20. Произволов В. Задача 5// Квант. 2003. № 2. С. 26.
8. Математика факта
1. Зетелъ С. И. Новая геометрия треугольника. М.: Учпедгиз, 1940. 96 с.
2. Мякишев А. Г. Элементы геометрии треугольника. М.: МЦНМО, 2002. 32 с.
3. Васильев Н. Б., Егоров А. А. Задачи Всесоюзных математических олимпиад // XVII Всесоюзная математическая олимпиада. М.: Наука, 1988. С. 88. Задача 363.
4. Произволов В. В. Задачи на вырост. М.: МИРОС, 1995. С. 59.
5. LXV Московская математическая олимпиада. М.: МЦНМО, 2002. С. 6.
6. Petru Mironescu, Laurentin Panaitopol. The Existence of a Triangle with Prescribed Angle Bisector Lengths // Mathematical Monthly. 1994, January. P. 58-60.
7. Жуков А., Акулич И. Однозначно ли определяется треугольник? // Квант. 2003. № 1.С. 29-31.
Почему нравится задача?
147


Литература к главе 2
9. 	Заигрывание интуиции
1. ЯщенкоИ.В. Приглашение на математический праздник. М.: МЦНМО; ЧеРо, 1998. С. 10.
2. Жуков А. Великий Решатель и Маленький Спрашиватель // «Математика». № 48. 1998, декабрь. С. 31-32.
3. Произволов В. В. Задачи на вырост. М.: МИРОС, 1995. С. 7.
4. Васильев Н. Б., Гутенмахер В. JI.t Раббот Ж. М., Тоом А. Л. Заочные математические олимпиады. М.: Наука, 1986. С. 137.
5. Гаусс К Ф. Труды по теории чисел. М.: Академия наук СССР, 1959. С. 14.
6. Стюарт Я. «Сказка о Рождественской теореме Ферма» // Квант. 1991. С. 12- 19.
7. Гальперин Г, Сендеров В. Задача 2 // Квант. 2004. № 6. С. 26.
8. Гарднер М. Математические новеллы. М.: Мир, 1974. С. 99-100.
9. Вайнштейн Ф. Задача М765 // Квант. 1982. № 9. С. 33.
10. Калинин Д. Задача 2 // Квант. 2002. № 5. С. 23.
11. Шаповалов А. Задача 35 // Сборник материалов пятого турнира «Математика 6-8» журнала «Квант». Кострома, 1999. С. 22.
12. Голенищева-Кутузова Т. И., КудряшовЮ. Г. Задача 2 (7 класс) // LXVII Московская математическая олимпиада. Задачи и решения. М.: МЦНМО, 2004. С. 3.
13. Произволов В. В. Задачи на вырост // Приложение к журналу «Квант» №5. 2003. С. 59.
14. Волчёнков С. Задача 1 // Сборник материалов заключительного этапа VII конкурса им. А. П. Савина «Математика 6-8» журнала «Квант». Иваново, 2001. С. 5.
15. XI Международная олимпиада «Интеллектуальный марафон»// Квант.
2003. 	№ 2. С. 55.
16. Васильев Н. Б., Гутенмахер В. Л., Раббот Ж. М., Тоом А. Л. Заочные математические олимпиады. М.: Наука, 1986. С. 105.
17. ГотманЭ.Г. Уравнения, тождества, неравенства при решении геометрических задач. М.: Просвещение, 1965. С. 21.
18. Задача 5 // Квант. 1979. № 10. С. 39.
19. Михайленко Н. А как вы думаете // Квант. 1982. № 1. С. 48.
20. Задача 4 // Квант. 1983. № 12. С. 31.
21. Васильев Н. Б., Самосват А. Г. Задача М937 // Квант. 1985. № 8. С. 40.
22. Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. М.: Просвещение, 1986. С. 143, задача 3.
23. Беспамятных С. Задача М750 // Квант. 1982. № 6. С. 20.
24. Акулич И. Задача 4 // Квант. 2002. № 6. С. 26.
25. Акулич И. Задача 20 // Квант. 2005. № 1. С. 27.
148
Глава 2


Литература к главе 2
9.5. Именованные задачи
1. Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. М.: Просвещение, 1986. 304 с.
2. Васильев Н. Задача 10. Конкурс «Математика 6-8» 1991-1992 гг. // Квант. 1991. № 12. С. 39.
9.6. Юмор
1. Рыжик В. И. 25 ООО уроков. М.: Просвещение, 1993. С. 214.
2. Наумов М. Такая задачка... // Квант. 2003. № 1. С. 15.
9.7. Остальные задачи
1. О классификации // Квант. 1987. № 6. С. 18.
2. Задача 2 // Квант. 1978. № 4. С. 39.
3. Задача 4 // Квант. 1978. № 10. С. 57.
4. Задача 1 // Квант. 1978. № 5. С. 35.
5. Живой фольклор // Квант. 2002. № 3. С. 43.
6. Фомин С. Задача М697 // Квант. 1981. № 8. С. 38.


Глава 3
Компьютер-числоскоп
Неизъяснимой полон красоты
Весь этот край, обильный и счастливый.
Дж. Г. Байрон.
Паломничество Чайльд Гарольда
Для большинства компьютер — занятная игрушка (увы, чаще всего «стрелялка»), для других, более серьезных пользователей — комфортабельная печатная машинка, а еще для кого-то — автоматизированный мольберт. Но мало кто знает, что компьютер прежде всего — это волшебный инструмент, способный распахнуть окно в загадочный мир математических виртуалий. Для тех, кто отважится на путешествие в этот мир, открываются невиданные пейзажи и причудливые формообразующие их законы.
Сейчас уже многие осведомлены о фракталах — радующих глаз прекрасных узорах, нарисованных компьютерами по математическим сценариям. Однако речь в нашей книге будет идти не о них. Хотя мы рассмотрим и не столь великолепные образцы компьютерной графики, но, тем не менее, дающие пищу уму и услаждение взору. Их легко воспроизвести на домашнем компьютере, зная азы программирования. Эта область математико-компьютерных исследований еще только начинает развиваться и сулит немало перспектив и сюрпризов для каждого, кто ею заинтересуется.
1. 	Многоликая спираль
Узоры из уравнений и фигур не уступают по красоте и причудливости узорам на морозном стекле.
В. Произволов
Американский математик польского происхождения Станислав Улам (1909-1984) еще на заре компьютерной эры провел замечатель¬
но
Глава 3


1. Многоликая спираль
ный эксперимент. Существует совершенно трогательная легенда о том, как находящийся на скучном совещании Улам ради забавы нарисовал на клетчатой бумаге числовую спираль (рис. 3.1).
37
36
35
34
33
32
31
38
17
16
15
14
13
30
39
18
5
4
3
12
29
40
19
6
1
2
И
28
20
7
8
9
10
27
21
22
23
24
25
26
Рис. 3.1
Затем закрасил клетки, в которых стояли простые числа. Хотя на рис. 3.2 закрашенные клетки еще не обнаруживают каких-либо геометрических закономерностей, но скучающий Улам на этом не остановился, он закрашивал клетки всё дальше и дальше, пока, наконец, перед ним явственно не проступили четкие структуры, давшие впоследствии название его творению «Скатерть Улама».
101
100
99
98
97
96
95
94
93
92
91
102
65
64
63
62
61
60
59
58
57
90
11
66
11
36
35
34
33
32
31
56
89
104
67
38
17
16
15
14
13
30
55
88
105
68
39
18
5
4
3
12
■1
54
87
106
69
40
19
6
1
2
11
28
51
86
107
70
41
20
7
8
9
10
27
52
85
108
11
42
21
22
23
24
25
26
51
84
109
72
43
44
45
46
47
48
49
50
III
110
73
74
75
76
77
78
79
80
81
82
111
100
11
98
97
96
95
94
93
92
91
Рис. 3.2
Компьютер-числоскоп
151


1. Многоликая спираль
Рис. 3.3
На самом деле Станислав Улам составил программу для одной из первых вычислительных машин MANIAC, позволившую нанести на придуманную им спираль около 65 тысяч чисел. Картина, которую впервые увидел Улам, показана на рис. 3.3. Здесь каждое простое число отмечено черной точкой, составное — белой. Четко видны загадочные «лесополосы» из простых чисел, располагающиеся по диагоналям.
А теперь зададимся естественным во¬
просом: что получится, если черным цветом отмечать не эти, а другие квадратики (при грубом разрешении — точки), соответствующие числам иного свойства. Например, те, где располагаются так называемые фигурные (они же многоугольные или полиномиальные) числа. n-Q по счету фигурное число 5-го порядка задается формулой
• При 5 = 3, как частный случай, получаются так называемые треугольные числа;
• при s = 4 — квадратные числа;
• при s = 5 — пятиугольные и т. д.
Давайте зафиксируем параметр s и посмотрим, как на спирали Улама располагаются 5-угольные числа:
5 = 3
s = 4
5 = 8
Рис. 3.4
Рис. 3.5
Рис. 3.6
152
Глава 3


1. Многоликая спираль
На этих рисунках четко прослеживаются регулярные структуры. А вот некоторые связанные с ними вопросы для исследования.
1. При каких значениях параметра s фигурные числа располагаются вдоль прямых линий, как на рис. 3.5?
2. Как зависит от параметра s количество «рукавов» спиралей? На рис. 3.4 (при 5 = 3) видно 17 «рукавов», а на рис. 3.6 (при 5 = 8) — 15 «рукавов».
3. Как зависит от параметра s ориентация «рукавов» спиралей? На рис. 3.4 «рукава» закручиваются по часовой стрелке, на рис. 3.6 — против часовой стрелки.
Отразите на спирали Улама числа, обладающие другими свойствами, например числа, делящиеся на 33. Какую картину вы при этом увидите?
Придумайте другие способы отражения натурального ряда на клетчатую плоскость. Вообще говоря, таких способов существует бесконечно много, но из них интерес представляют лишь в некотором смысле регулярные. Одним из таких способов, например, является алгоритм Георга Кантора (1845-1918) для нумерации клеток квадранта плоскости по диагоналям (рис. 3.7).
Как на таких структурах будут отражаться различные свойства чисел?
Рис. 3.8 иллюстрирует расположение квадратных (5 = 4) чисел при диагональной нумерации Кантора. Отчетливо видны два семейства линий. Что это за линии?
Вопросов здесь больше, чем ответов.
1
2
4
7
3
5
8
6
9
10
Рис. 3.7 Рис. 3.8
Компьютер-числоскоп
153


2. Алгоритм «стежок»
2. 	Алгоритм «стежок»
Творчество математика в такой же степени есть создание прекрасного, как творчество живописца или поэта.
Г. Харди.
Апология математика
Просто поразительно, как иногда сложность и разнообразие способны скрываться в невзрачной простоте. Еще одно подтверждение этому — незатейливый алгоритм «Стежок». Суть его состоит в следующем.
Нарисуем на бумаге в клеточку (это может быть обычная ученическая тетрадь) произвольный прямоугольник, ориентируя его по линиям сетки (рис. 3.9). На этом рисунке проставлена также нумерация вертикальных линий сетки — она нам пригодится в дальнейшем, хотя «вышивать» можно и без нее. Условимся нижнюю сторону прямоугольника называть пол, а верхнюю — потолок. В произвольном узле сетки на полу выбирается точка старта. На рис. 3.9 эта точка помечена стрелочкой. Во всех дальнейших наших иллюстративных примерах, если это не оговорено особо, точкой старта будет точка под номером 3.
После того, как точка старта выбрана, начинается математическая вышивка: последовательно по линиям сетки прокладываются стежки: вверх — вправо — вверх — вправо — ... — до тех пор, пока мы не упремся в потолок (рис. 3.10). Дальше срабатывает правило: «Нельзя идти вверх — иди вниз». Оно является частным случаем общего правила: «Нельзя идти в одну сторону — иди в противоположную» («Нельзя идти вправо — иди влево» и т. п.).
0 1 2 3 4 5 6 7 8 9 10 11 12 0 123456789 10 11 12
0123456789 10 11 12 0123456789 10 11 12
t t
Рис. 3.9 Рис. 3.10
154
Глава 3


2. Алгоритм «стежок»
Когда же остановиться? Заметим, что в точку, где вертикальная линия старта пересекает пол или потолок, стежок при горизонтальном перемещении может попасть как слева, так и справа. Так что не более чем после четвертого такого случая мы выйдем на ранее проложенный маршрут. В экспериментах, которые мы сейчас проведем, условимся оканчивать «вышивку» при наступлении первого такого случая, независимо от того, произошел выход на уже проложенный маршрут, или нет.
Всё, алгоритм описан, пора приниматься за дело.
На рис. 3.11 показан орнамент, вышитый по алгоритму «Стежок» в прямоугольнике 90 х 65 (90 столбцов и 65 строк).
Рис. 3.11
Пока что здесь трудно обнаружить какие-либо интересные закономерности, поэтому давайте уменьшим размеры исходного прямоугольника. На рис. 3.12 показан другой орнамент, выполненный в прямоугольнике 20 х 4.
Здесь видны две фигурки, напоминающие дерущихся каратистов.
“ч>
Сколько таких фигурок в прямоугольнике? — 5. Числа 20 (длина прямоугольника), 4 (ширина прямоугольника) и 5 между
Рис. 3.12
Компьютер-числоскоп
155


2. Алгоритм «стежок»
собой чудесным образом связаны. Оказывается, алгоритм «Стежок» — не просто игрушка, он демонстрирует нам свойства делимости чисел.
Давайте посчитаем, сколько вот таких элементов укладывается по длине и по ширине в орнаменте рис. 3.11.
Оказывается, 18 раз — по горизонтали, и 13 раз — по вертикали. Что это за числа? Как они связаны с числами 90 и 65?
Связь простая, если заметить, что наибольший общий делитель чисел 90 и 65 равен 5.
С высоты полученных знаний орнамент на рис. 3.13 уже не представляет собой математическую загадку (длина прямоугольника 91, ширина 65).
Итак, если размеры исходного прямоугольника не взаимно просты, то в орнаменте появляются какие-то повторяющиеся замысловатые фигуры.
А что следует ожидать в том случае, если размеры исходного прямоугольника окажутся взаимно простыми, как, например, для прямоугольника 92 х 65? Свою гипотезу вы можете проверить, заглянув в Комментарии.
Сравните теперь рисунки 3.14, 3.15, 3.16. Согласитесь, у них есть какая-то общность. Можно ли ее описать математически?
Рис. 3.13
156
Глава 3


2. Алгоритм «стежок»
nlri
ЧуИ|
Г Ж
гЧи*
ПИГт
AJ
(йвм(?
Длина: 90, ширина: 75, Длина: 59, ширина: 49,
точка старта: 1 точка старта: 1
Рис. 3.14 Рис. 3.15
Длина: 88, ширина: 73, точка старта: 3
Рис. 3.16
В завершение мы предлагаем подумать над такой задачей.
Задача 1. (А. Жуков; [1].) Кузнечики Петя и Вася соревнуются на беговой дорожке в виде ленты А. Мёбиуса (1790-1868), обустроенной следующим образом. Длинная гибкая полоска расчерчивается с двух сторон на сантиметровые деления так, как показано на рис. 3.17, после чего лента перекручивается, участки 0 и 1997 накладываются друг на друга и склеиваются. Кузнечики стартуют одновременно с пункта 1 в сторону увеличения нумерации, причем кузнечик Петя прыгает на 100 см вперед, а кузнечик Вася — на 150 см. Кто из них первым окажется в пункте с номером 1?
Первая сторона
0
1
2
1996
1997
1997
1996
1995
1
0
Вторая сторона Рис. 3.17
Компьютер-числоскоп
157


Решения, ответы и комментарии к главе 3
Вы не видите связи этой задачи с алгоритмом «Стежок»? Тогда давайте проследим за тем, как изменяется номер вертикальной линии сетки по мере прокладывания стежков. В качестве примера нам удобно будет использовать рис. 3.12. Стартуя с 3 точки на полу, мы затем попадаем в 7 точку на потолке, затем — в 11 точку на полу, затем ■— в 15 точку на потолке, затем — в 19 на полу — до сих пор мы двигались слева направо, и нумерация возрастала. После этого момента мы меняем направление движения, с 19 точки на полу мы переходим в 17 точку на потолке. Потом — в 13 точку на полу и т. д. Существенно здесь то, что переход с возрастания нумерации к убыванию произошел плавно — именно так, как это происходит на ленте Мёбиуса.
Оказывается, алгоритм «Стежок» моделирует метрику ленты Мёбиуса!
Предлагаем читателям исследовать и другие интересные свойства этого алгоритма. Примерные темы для исследований: классификация орнаментов, связь алгоритма с фигурами Лиссажу и другие. А любители прикладного искусства имеют прекрасную возможность приспособить получающиеся узоры не только для вышивания, но, разукрасив их, — для обустройства великолепных панно или кафельных мозаик.
& Решения, ответы и комментарии
к главе 3 «Компьютер-числоскоп»
Из всех ответов я выбрал бы не все.
Владимир Казаков.
Сцена-набросок
К разделу 2 «Алгоритм ,,стежок“»
На рис. 3.18 представлен орнамент в прямоугольнике 92 х 65, а на рис. 3.19 — в прямоугольнике 107 х 65. Оказывается, и между взаимно простыми числами существуют непростые взаимоотношения!
158
Глава 3


К разделу 1 «Алгоритм .стежок"»
Такими узорами можно вышивать тюль. Сравните также рис. 3.20 и 3.21, на которых показаны орнаменты в прямоугольниках 90 х 64 и 101 х 76.
Рис. 3.18
Рис. 3.19
Рис. 3.20
Рис. 3.21
MS К задаче 1
v 8 ' , i V - V' да йЖШ ШШШ8Ш
Номер пункта а, после i-то прыжка (/= 1, 2, 3, ...) кузнечика определяется по следующей формуле:
а, = а0 + / Д - Nk, если к — четное,
а, = (к + l)N - а0 - / Д, если к—нечетное,
(*)
где йо — номер пункта старта кузнечика (во = 1); N — максимальный номер пункта на ленте Мёбиуса (N= 1997); А — длина прыжка
Компьютер-числоскоп
159


Решения, ответы и комментарии к главе 3
кузнечика (для кузнечика Пети А =100; для кузнечика Васи А = 150); к = — индикатор возрастания или убывания нуме¬
рации пунктов при выполнении /-го прыжка (квадратные скобки здесь обозначают функцию «целая часть»: И — наибольшее целое число, не превосходящее х).
Решая совокупность (*) неопределенных уравнений в целых числах относительно целых неизвестных /, к при <я, = 1, находим для кузнечика Пети наименьшее натуральное значение /=1318 (при этом к = 65), а для кузнечика Васи соответственно / = 213 (при этом к= 15). Следовательно, кузнечик Вася первым окажется в пункте с номером 1.
Соотношения (*) оказываются весьма полезными при исследовании орнаментов алгоритма «Стежок». Если а0 задает номер стартовой точки для исходного прямоугольника размером N х А, то величина я„ вычисляемая по формулам (*), определяет номер точки на полу (для четных /) или на потолке (для нечетных /) при последовательной реализации алгоритма «Стежок», / = 1, 2, 3, .... Обозначим d — наибольший общий делитель чисел N и A, Ki — класс чисел из множества {0; 1; 2; ...; N], которые при делении на 2d дают остаток / или
2d -/, /=0,1,2 N.
Оказывается, тип орнамента полностью определяется классом Kh которому принадлежит стартовая точка а0. Свойства симметрии орнамента относительно вертикальных или горизонтальных осей также зависят от соответствующих классов. Например, в случае A = (2q+l)d (q — натуральное) симметричными относительно центральной горизонтальной оси оказываются орнаменты, стартовые точки которых принадлежат сопряженным классам Кр и Kd р ,
n 1 d +1
Р = 0, 1,
Если, к тому же, N = 2rd (г — натуральное), то каждый из этих орнаментов в отдельности симметричен относительно вертикальной оси.
160
Глава 3


Литература к главе 3
Литература
к главе 3 «Компьютер-числоскоп»
Алгоритм «стежок»
1. Жуков Л. Задача 2 // Конкурс в сети Интернет. Квант. 1998. № 2. С. 56


О красоте, математике и не только
(Вместо послесловия)
А если так, то что есть красота И почему ее обожествляют люди? Сосуд она, в котором пустота,
Или огонь, мерцающий в сосуде?
Николай Заболоцкий
Математика есть прообраз красоты мира. (И. Кеплер)
£$ Никто, не познав числа, никогда не сможет обрести истинного мнения о справедливом, прекрасном. (Платон)
162


О красоте, математике и не только
В математике есть нечто, вызывающее человеческий восторг. (Ф. Хаусдорф)
Любой предмет производит на нас впечатление лишь в той степени, в какой он затрагивает наш разум. (Л. Вовенарг)
£$ Хорошая задача будит не только наш разум, но и наши эмоции. (В. Произволов)
Решая задачу, мы в первую очередь должны заботиться о том, чтобы решение было правильным, особо не заботясь о красоте. Если решение получилось красивым — это подарок за все наши предшествующие труды. (И. Акулич)
£$ Воображение творит красоту. (Б. Паскаль)
Воображение более важно, чем знание. (А. Эйнштейн)
Человек, обладающий развитым воображением, получает доступ к огромному количеству удовольствий. (Д. Аддисон)
Я*) Прекрасно только то, что истинно, но не всё прекрасно, что истинно. (Д. Аддисон)
Свойство очаровываться миром нам открывает мир, какой он есть. (Е. Евтушенко)
Простота — одно из главных качеств красоты. (Д. Дидро)
Js£ Естественность и оригинальность — вот два качества, которые наиболее ценны в задачах. Кажется, что они друг другу противоречат, и всё же, когда они сливаются воедино, то это создает эффект математической красоты. (В. Произволов)
Гений также невозможен без вкуса, как характер без нравственности. (Ж. Нерваль)
163


Вместо послесловия
Гений — человек, способный решать проблемы, о которых вы и не знали, способом, который вам непонятен. (Ф. Кернан)
^Музыка, поэзия, математика — сколь родственны они. (Имре Мадач)
Поэзию следует искать не в сочетаниях слов, а в атмосфере, которую создают эти сочетания. (Э. Верхарн)
Поэзия - это разновидность вдохновенной математики. (Эзра Паунд)
£*} То, к чему приступаешь с усилием, часто получается плохим, а самое легкое — прекраснейшим. (С. Цвейг)
Добро нуждается в доказательствах, красоте они ни к чему. (Б. Фонтенель)
Ничто не прокладывает себе путь к душе более непосредственно, чем красота. (Д. Аддисон)
Если вы жаждете красоты — раскройте глаза. (У Сароян)
Красота красит и тех, кто созерцает ее. (А. Грин)
Красота расковывает души. (Д. Голсуорси)
Очень редко бывает так, что прекрасное вместе с тем и популярно. (И. Гёте)
Секрет элегантности в том, чтобы норковую шубу носить как простенькое пальтецо, а простенькое пальтецо — как норковую шубу. (П. Бальмен)
Того, кто видит красоту, не коснется дуновение зла: он чувствует себя в гармонии с самим собою и со всем миром. (И. Гёте)
164


О красоте, математике и не только
Математика владеет не только истиной, но и высшей красотой — красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. (Б. Рассел)
Красота — призрачная тень совершенства. {Т. Драйзер)
& Красота — это вечность, длящаяся мгновение. (А. Камю)


Поэт элегантной математики
Жуков Александр Владимирович родился 16 марта 1955 г. в г. Изяславе Хмельницкой области (Украина). После окончания средней школы в 1972 г. поступил на механико-математический факультет Московского государственного университета имени М. В. Ломоносова. После окончания университета в 1977 г. его распределили в Вычислительный центр СО АН СССР в Красноярске. В 1980 г. он был призван в кадры Вооруженных Сил СССР и начал службу в одной из противоракетных частей в Подмосковье, а закончил ее 18 лет спустя в 45-м институте Министерства обороны в звании подполковника. В этом институте Александр работал по теме искусственного интеллекта, поступил в адъюнктуру и окончил ее в 1990 г. защитой диссертации по указанной теме, став кандидатом технических наук. В 1998 г. он уволился из 45-го института и вышел в отставку по состоянию здоровья.
После этого Александр занялся «чистой» математикой, ее историей, стал литератором и педагогом от этой царицы наук. И тогда раскрылось редкое сочетание талантов Александра: глубокое владение геометрией и алгеброй, писательское мастерство, педагогическое умение увлечь математически ориентированную молодежную аудиторию и читательские круги решением широкой гаммы увлекательных и удивительных задач.
С 1998 г. Александр стал математическим журналистом, он вел рубрику для младших школьников в известнейшем в СССР и СНГ физико-математическом журнале «Квант». Несколько последних лет также вел подобную рубрику в журналах «Математика в школе» и «Математика для школьников». Был преподавателем в Московском детском клубе «Компьютер».
Хорошо известны научно-популярные книги, написанные Александром Жуковым (иногда в соавторстве). Это энциклопедия для детей «Математика» (в коллективе соавторов), книги «Изучаем
166


Поэт элегантной математики
Delphi», «Вездесущее число л», «Элегантная математика», а также «Прометеева искра: Античные истоки искусства математики» — к сожалению, уже последняя книга А. В. Жукова, содержащая научно-историческое исследование античных корней математики, ее органической связи с философией и поэзией древних элит. Наряду с книгами Александром написано много десятков научно-популярных обзоров, статей, заметок, подборок задач для журналов «Квант», «Домашний лицей», «Математика для школьников».
Нужно сказать, что большая часть примеров и решений в книгах Александра воспринимается нелегко. Это книги не для «среднего ума». Хотя в них есть нетрудные «изюмсодержащие» задачи, но все же в большинстве своем задания соответствуют, условно говоря, олимпиадному уровню сложности. Как мне представляется, эти книги предназначены в первую очередь амбициозной, элитарной «естественно-научной» молодежи, тем математическим альпинистам, кто, ступив на первую ступеньку и уверенно закрепившись, будет карабкаться к вершинам, не щадя времени и мозговых усилий. Конечно, для этого нужны особые природные склонности и ум. Однако ум и таланты, как известно, распределены в природе крайне неравномерно (в отличие от здравого смысла). Но без математической элиты не может развиваться цивилизованное общество. Отсюда потребность в элитарных математиках-педагогах, отбирающих, питающих и воспроизводящих высшие слои специалистов и творцов новых знаний в области точных наук. В нынешней России, в которой правит «золотой телец», книги А. Жукова работают еще и как фактор сопротивления централизрванному процессу оболванивания молодежи таблоидами, гламуром, попсой, пивом и прочими прелестями общества потребления — естественных тормозов на пути к новым научным знаниям.
Одним из принципов отбора задач с решениями у Александра были, по его собственным словам, «предельная простота алгоритма плюс красивый арифметический факт, приводящий к низвержению интуиции». Эта лаконичная, красивая и смелая формулировка не должна приводить к заблуждению: «предельная простота» вовсе не означает простоту в общем смысле. Здесь это словосочетание означает нахождение наименее сложного пути из всех возможных, а выбор такого пути зачастую совсем не лежит на поверхности. По¬
167


Поэт элегантной математики
исками последнего автор и занимается, взяв за руку своего типичного читателя, следя, чтобы он, спотыкаясь, не сбился с тропы, постепенно воспитывая свою элиту.
Очень украшает книги Александра ярко выраженное по всему тексту личное его отношение к ключевым объектам своих работ — числу щ геометрической фигуре, формуле, теореме и т. д.; оно сродни эмоционально-эстетическому отношению поэта к слову, фразе, размеру, образу стиха.
«Все окружности похожи» — это выражение писателя, по- моему, представляет собой блестящую по краткости и легкой ироничности максиму!
«Треугольник — удивительный объект, — пишет А. Жуков. — Всего три отрезка, застывших в хороводе, а сколько математического таинства!.. В геометрии треугольника существует огромное множество изумительных по красоте фактов...»
В связи с этими строками вспоминаю, как однажды позвонил Александру с просьбой помочь в решении одной задачи с треугольником из раздела «С» (повышенная сложность) заданий ЕГЭ (2008). Я не раз обращался к нему с подобными просьбами, и Александр уверенно решал любые задания — через 10-20 минут раздавался его ответный звонок и звучал голос: «Записывай!». Вот и на этот раз он мне сказал: «Твоя задача решается очень просто, если знать свойство углов педального треугольника». А я и понятия не имел, что это такое. Он объяснил: «Такой треугольник образуется внутри заданного треугольника, если соединить в последнем основания трех его высот. Отрезки этих высот являются биссектрисами углов при вершинах полученного педального треугольника». Вскоре выяснилось, что никто из преподавателей как наших подготовительных курсов, так и кафедры высшей математики также не слышал о «педальном треугольнике» (хотя некоторые из них могли решить предложенную задачу более длинным путем). Вообще, у меня сложилась уверенность, что Александр мог решить любую задачу из всей огромной области «элементарной математики».
Вспоминаю, что вскоре после нашего знакомства с Александром в 2004 г., которое состоялось после выхода его книги о числе п, я обратился к нему с вопросом, касающимся частоты встречаемости палиндромных слов (напомню, что это слова типа стоящих
168


Поэт элегантной математики
во фразе: Мэм, казак незаразен). Я обратил внимание на то, что более 90 % таких слов, да и целых фраз в русском и других языках, использующих алфавитное письмо, состоят из нечетного числа букв. Спросил Сашу, можно ли сей факт объяснить математически. Уже через пару дней он мне прислал построенную им математическую модель формирования палиндромных структур, которая включала в себя функцию «антье» (от франц. entier — целый). Формула Жукова в принципе объясняла возникновение ступенек при переходе от нечетного числа букв начиная с 1 к четным, и так до 7- 8 букв. Это наше совместное исследование (мое экспериментальное и его теоретическое) вошло потом как раздел в книгу «Новая антология палиндрома» (авт.-сост. Б. Горобец, С. Федин, М.: URSS, 2008; 2-е и 3-е издания (URSS, 2010, 2011) вышли под названием «А роза упала не на лапу Азора: Искусство палиндрома»). Считаю за честь для себя, что в том очерке имя А. Жукова стоит рядом с моим.
Для израильтян будет, наверное, небезынтересным узнать, что Александр сообщил о результатах математического исследования палиндромов своему другу Петру Самоволу, работающему в колледже в Беэр-Шеве (Израиль). Вскоре Петр прислал нам в ответ список из 170 слов-палиндромов иврита, найденных его школьниками, которые с энтузиазмом начали исследовать свой древнейший язык, по-видимому, впервые отыскивая в нем палиндромы. Оказалось, что слов с нечетным числом букв в иврите около 77 %.
Если сравнить книги Александра Жукова с книгами известнейшего классика популярной математики середины XX века Якова Перельмана, то последние, на мой взгляд, на порядок проще. Но вместе с тем при всей неоспоримой увлекательности, познавательной и образовательной ценности книг Я. Перельмана в них нет, по-моему, и десятой доли поэтичности книг А. Жукова, в которых едва ли не все главы пропитаны поэзией с изрядной долей философии и иронии, а также нередко самоиронии.
И еще. В книгах А. В. Жукова прослеживается поразительный отличительный признак — огромное число первоисточников, которые им цитируются не только в виде включенных в книгу задач и способов их решения, но и в качестве эпиграфов, помещенных почти перед каждым подразделом и даже перед многими отдельными задачами. Удачно подобранные эпиграфы сразу цепляют неожи¬
169


Поэт элегантной математики
данной, острой мыслью и помогают увлечь небезразличного читателя в омут математических абстракций, из которого всплывает истина, нередко совсем неожиданно. Вот лишь три примера эпигра- фов-цитат из произведений писателя Владимира Казакова, излюбленного литературного источника Александра Жукова: «Высоко над ним стояли числа, опираясь на рукояти из звезд»; «Стал считать и сбился на бесконечности»; «Четыре стены: первая, вторая и две третьих».
А вообще подобных примеров великое множество. Меня поражает знание Александром целого моря первоисточников, причем не только математических, но и поэтических и прозаических произведений авторов от древнейших времен до наших дней. Трудоспособность и эрудиция этого человека были необычайными.
В предисловии к 5-му изданию «Вездесущего числа л» Александр Жуков писал не без оттенка печали: «Число п— река, которая катила воды свои еще до того, как мы родились и пришли на ее берег. Налюбовавшись, мы уйдем с берега, а вода в реке будет уплывать все так же, ибо земных пределов у нее нет».
29 ноября 2011 г. он ушел с берега. Навсегда. Самый великодушный, элегантный и поэтичный математик своей страны.
Борис Горобец, профессор, член Союза писателей Москвы
15.02.12


Представляем Вам следующие книги:
Теория игр
/Шикин Е. В. От игр к играм. Математическое введение.
/Оуэн Г. Теория игр.
/Колесник Г. В. Теория игр.
/ Колесник Г. В. Управление производственными системами с распределенными правами собственности: Экономико-математический анализ.
/Жуковский В. Я. Введение в дифференциальные игры при неопределенности. Кн. 1-3. /Жуковский В. Я. Риски при конфликтных ситуациях.
/Жуковский В. Я. Кооперативные игры при неопределенности и их приложения.
/Жуковский В. Я, Жуковская Л. В. Риск в многокритериальных и конфликтных системах при неопределенности.
/Жуковский В. Я, Кудрявцев К. Я. Уравновешивание конфликтов и приложения.
/Смольяков Э. Р. Теория конфликтных равновесий.
Оптимизация /Галеев Э. М. Оптимизация: теория, примеры, задачи.
/Софиева Ю. Я., Цирлин А. М. Введение в задачи и методы условной оптимизации. •/Гороховик В. В. Выпуклые и негладкие задачи векторной оптимизации.
/Ковалев М. М. Дискретная оптимизация (целочисленное программирование).
/Ковалев М. М. Матроиды в дискретной оптимизиции.
/Балакришнан А. Введение в теорию оптимизации в гильбертовом пространстве. /Бондаренко В. А., Максименко А. Я. Геометрические конструкции и сложность в комбинаторной оптимизации.
/Понтрягин Л. С. Принцип максимума в оптимальном управлении.
Философия математики
/Вейль Г. О философии математики.
/Харди Г. Г. Апология математика.
/Реньи А. Диалоги о математике.
/Асмус В. Ф. Проблема интуиции в философии и математике.
/Светлов В. А. Философия математики.
Серия «Физико-математическое наследие: философия математики»
/Кутюра Л. Философские принципы математики.
/Фосс А. Сущность математики.
/Фрейсинэ Ш. Очерки по философии математики.
/Лаплас П. Опыт философии теории вероятностей.
/Флоренский П. А. Мнимости в геометрии.
Вычислительная математика и программирование
/Самарский А. А. и др. Задачи и упражнения по численным методам.
/Самарский А. А., Вабищевич Я. Я. Численные методы решения обратных задач математической физики.
/Самарский А. А., Вабищевич П. Я. Численные методы решения задач конвекции—диффузии.
URSS


Представляем Вам следующие книги:
Алгебра
s Чеботарев Я. Г. Основы теории Гклуа. В 2 кн. s Вейль Г. Классические группы. Их инварианты и представления.
/Фробениус Ф. Г. Теория характеров и представлений групп.
✓ Эйзенхарт Л. П. Непрерывные группы преобразований. s Бэр Р. Линейная алгебра и проективная геометрия.
sНикифоров В. А., Шкода Б. В. Линейная алгебра и аналитическая геометрия. s Шевалле К Введение в теорию алгебраических функций. s Уокер Р. Алгебраические кривые.
s Супруненко Д. АТышкевич Р. И. Перестановочные матрицы. s Киселев А. Я. Задачи и упражнения к «Элементам алгебры». s Золотаревская Д. И. Сборник задач по линейной алгебре. sКутищев Г. П. Решение алгебраических уравнений произвольной степени: Теория, методы, алгоритмы.
Серия «Физико-математическое наследие: алгебра»
s Чеботарев Я. Г. Введение в теорию алгебр. s Чеботарев Н. Г. Теория групп Ли. s Чеботарев Я. Г. Теория Гклуа. s Чеботарев Я. Г. Теория алгебраических функций. s Александров П. С. Введение в теорию групп.
sМаркус М., Минк X. Обзор по теории матриц и матричных неравенств. s Бохер М. Введение в высшую алгебру. s Млодзеевский Б. К. Основы высшей алгебры. s Шмидт О. Ю. Абстрактная теория групп.
Серия «Физико-математическое наследие: топология»
s Александров Я. С. Введение в теорию множеств и общую топологию.
✓ Мил нор Дж. Теория Морса.
sCmunpod Я. Топология косых произведений. sЛистинг И. Б. Предварительные исследования по топологии.
Теория вероятностей и математическая статистика
s Гнеденко Б. В. Курс теории вероятностей. s Гнеденко Б. В. Очерк по истории теории вероятностей. s Гнеденко Б. В. Математика и контроль качества продукции. s Гнеденко Б. ВКоваленко И. Я. Введение в теорию массового обслуживания. sИвченко Г. Я., Каштанов В. А., Коваленко И. Я. Теория массового обслуживания. ^Хинчин А. Я. Работы по математической теории массового обслуживания.
/Хитин А. Я. Асимптотические законы теории вероятностей.
/Хитин А. Я. Математические основания квантовой статистики. sCaamu Т. Л. Элементы теории массового обслуживания и ее приложения.
/Боровков А. А. Эргодичность и устойчивость случайных процессов.
/ Тактаров Я. Г. Теория вероятностей и математическая статистика.
URSS


Представляем Вам следующие книги:
Теория чисел
sOpe О. Приглашение в теорию чисел. sВейль А. Основы теории чисел. sВейль Г. Алгебраическая теория чисел.
/Понтрягин JI. С. Обобщения чисел.
/Хинчин А. Я. Т^и жемчужины теории чисел.
/Хитин А. Я. Цепные дроби.
/Парфенов И. И. Цепные дроби — ожерелье мехатроники.
/Ожигова Е. И Что такое теория чисел.
/Виноградов И. М. Особые варианты метода тригонометрических сумм. sКараиуба А. А. Основы аналитической теории чисел. sГельфонд А. О. Трансцендентные и алгебраические числа.
✓Яглом И. М. Комплексные числа и их применение в геометрии. sДеза Е. И. Специальные числа натурального ряда. sДеза Е. Котова JI. В. Сборник задач по теории чисел.
Серия «Физико-математическое наследие: теория чисел»
sДиофант Александрийский. Арифметика и книга о многоугольных числах. s Ферма П. Исследования по теории чисел и диофантову анализу.
^Дирихле П. Г. Л. Лекции по теории чисел. sДедекинд Р. Непрерывность и иррациональные числа.
^Ингам А. Э. Распределение простых чисел. s Берман Г. Н. Число и наука о нем: Общедоступные очерки. sЛандау Э. Основы анализа: Действия над числами. s Титчмарш Э. Ч. Дзета-функция Римана. sДэвенпорт Г. Высшая арифметика: Введение в теорию чисел.
•/Гельфонд А. О. Решение уравнений в целых числах.
Дифференциальные и интегральные уравнения
sФилиппов А. Ф. Введение в теорию дифференциальных уравнений.
✓Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. sЭльсгольц Л. Э. Дифференциальные уравнения. s Степанов В. В. Курс дифференциальных уравнений, у'Немыцкий В. ВСтепанов В. В. Качественная теория дифференциальных уравнений. s Краснов М. Л. и др. Обыкновенные дифференциальные уравнения. Сборник задач «Вся высшая математика» с подробными решениями. s Краснов М. Л. Интегральные уравнения. Введение в теорию.
✓Шалдырван В. А., Медведев К. В. Руководство по решению обыкновенных дифференциальных уравнений. Кн. 1,2. s Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений, i s Петровский И. Г. Лекции по теории интегральных уравнений.
✓Федорюк М. В. Обыкновенные дифференциальные уравнения.
✓Федорюк М. В. Асимптотика: Интегралы и ряды. s Федорюк М. В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений.
URSS


Представляем Вам следующие книги:
Математическая логика
/Колмогоров А. Я, Драгалин А. Г. Математическая логика: Введение в математическую логику.
/Колмогоров А. Я, Драгалин А. Г. Математическая логика: Дополнительные URSS главы.
/Драгалин А. Г. Конструктивная теория доказательств и нестандартный анализ.
/Фреге Г. Логика и логическая семантика.
/Гладкий А. В. Введение в современную логику.
/Гамов Г1, Стерн М. Занимательные задачи.
/ Карпенко А. С. Развитие многозначной логики.
/Карпенко А. С. Логики Лукасевича и простые числа.
/Карпенко А. С. Фатализм и случайность будущего: Логический анализ.
/Бахтияров К И. Логика с точки зрения информатики.
Серия «Физико-математическое наследие: основания математики и логика»
/ Чёрч А. Введение в математическую логику.
/Гудстейн Р. Л. Математическая логика.
/Бурбаки Я. Теория множеств.
/Хаусдорф Ф. Теория множеств.
/Френкель А. А., Бар-Хиллел Я. Основания теории множеств.
/Лебег А. Об измерении величин.
/Гейтинг А. Интуиционизм: Введение.
/Гильберт Д, Аккерман В. Основы теоретической логики.
s Пойа Д. Математика и правдоподобные рассуждения.
sЛакатос И. Доказательства и опровержения: Как доказываются теоремы.
Серия «Физико-математическое наследие: теория функций»
s Курант Р. Геометрическая теория функций комплексной переменной. s Привалов И. И. Субгармонические функции. s Бор Г. Почти периодические функции.
/Артин Э. Введение в теорию гамма-функций. s Князев П. Я Интегральные преобразования.
Дискретная математика
sXapapu Ф. Теория графов. sOpe О. 1}>афы и их применение. sOpe О. Теория графов.
sЕмеличев В. А., Мельников О. Я. и др. Лекции по теории графов. s Мельников О. И. Теория графов в занимательных задачах: Более 250 задач с подробными решениями. sМельников О. И. Незнайка в стране графов: Юным математикам и программистам. sМельников О. И. Обучение дискретной математике.
/Деза Е. Я., Модель Д. Л. Основы дискретной математики. s Панюкова Т. А. Комбинаторика и теория графов.
/Березина Л. Ю. 1)>афы и их применение.


Представляем Вам следующие книги:
Серия «НАУКУ — ВСЕМ! Шедевры научно-популярной литературы» СДт
Колмогоров А. Н. Математика — наука и профессия. |
Гашков С. Б. Занимательная компьютерная арифметика: Математика
и искусство счета на компьютерах и без них. URSS
Гашков С. Б. Занимательная компьютерная арифметика: Быстрые алгоритмы операций с числами и многочленами.
Гнеденко Б. В. Беседы о теории массового обслуживания.
Гнеденко Б. В. Беседы о математической статистике.
Гнеденко Б. ВХитин А. Я. Элементарное введение в теорию вероятностей.
Мизес Р. Вероятность и статистика.
Меннхен Ф. Некоторые тайны артистов-вычислителей.
Вильямс Дж. Д. Совершенный стратег, или Букварь по теории стратегических игр. Юдин Д. Б. у Юдин А. Д. Математики измеряют сложность.
Крэндалл Р., Померане К Простые числа: Вычислительные и криптографические аспекты.
/Пухначев Ю. В., Попов Ю. П. Математика без формул. В 2 кн.
'Супрун В. П. Математика для старшеклассников: Задачи повышенной сложности. /Супрун В. П. Математика для старшеклассников: Нестандартные методы решения задач.
'Супрун В. П. Математика для старшеклассников: Методы решения и доказательства неравенств. 367 задач с подробными решениями.
' Морду хай-Болтов ской Д. Д. Геометрия радиолярий.
/ Золотаревская Д. И. Теория вероятностей. Задачи с решениями.
✓Федин С. Н. Математики тоже шутят.
/Петров Н. Н. Математические игры.
/Пойа Д. Как решать задачу.
/Литвинов В. Н. Правильный пятиугольник: Геометрия, декоративное искусство, архитектура.
/Амелькин В. В. Дифференциальные уравнения в приложениях.
/Медведев Г Н. Участникам олимпиад и вступительных испытаний по математике.
Тел./фаис:
+7(499)724-25-45
(многоканальный)
E-mail:
URSS®URSS.ru
http://URSS.ru
Наши книги можно приобрести в магазинах:
«НАУНУ - ВСЕМ!» (и. Профсоюзная, Нахимовский пр-т, 56. Тел. (499) 724-2545) «Библио-Глобус» (и. Лубянка, ул. Мясницкая, 6. Тел. (495) 625-2457) «Московский дом книги» (м. Арбатская, ул. Новый Арбат, 8. Тел. (495) 203-8242) «Молодая гвардия» (м. Полянка, ул. Б. Полянка, 28. Тел. (495) 238-5001,
(495) 780-3370)
«Дом научно-технической книги» (Ленинский пр-т, 40. Тел. (495) 137-6019)
«Дом книги на Ладожской» (м. Бауманская, ул. Ладожская, 8, стр.1.
Тел. (495) 267-0302)
«Санкт-Петербургский Дом книги» (Невский пр., 28. Тел. (812) 448-2355) «Книжный бум» (г. Киев, книжный рынок «Петровка», ряд 62, место 8 (павильон «Академкнига»). Тел. +38 (067) 273-5010)
Сеть магазинов «Дом книги» (г. Екатеринбург, ул. Антона Валена, 12.
Тел. (343) 253-5010)


Уважаемые читатели! Уважаемые авторы!
Наше издательство специализируется на выпуске научной и учебной литературы, в том числе монографий, журналов, трудов ученых Российской академии наук, научно-исследовательских институтов и учебных заведений. Мы предлагаем авторам свои услуги на выгодных экономических условиях. При этом мы берем на себя всю работу по подготовке издания — от набора, редактирования и верстки до тиражирования и распространения.
URSS
Среди вышедших и готовящихся к изданию книг мы предлагаем Вам следующие:
^ sЖуков А. В. Прометеева искра: Античные истоки искусства математики.
V* sЖуков А. В. Вездесущее число «пи».
ВВ
mi
s Краснов М.Л. и др. Вся высшая математика. Т. 1-7. sКраснов М. Л.у Киселев А. И., Макаренко Г. И. Сборники задач «Вся высшая математика» с подробными решениями. s Тактаров Н. Г. Справочник по высшей математике для студентов вузов. у Боярчук А. К., ЛяшкоИ. //., Гай Я. Г., Головач Г. П. Справочное пособие по высшей математике (Антидемидович). Т. 1-5.
Т. 1. Введение в анализ, производная, интеграл.
Т. 2. Ряды, функции векторного аргумента. iS Т. 3. Интегралы, зависящие от параметра; кратные и криволинейные интегралы,
е? Т. 4. Функции комплексного переменного: теория и практика.
Т. 5. Дифференциальные уравнения в примерах и задачах.
/Босс В. Лекции по математике. Т. 1-16. Т. 1: Анализ; Т. 2: Дифференциальные уравнения; Т. 3: Линейная алгебра; Т. 4: Вероятность, информация, статистика;
Т. 5: Функциональный анализ; Т. 6: От Диофанта до Тьюринга; Т. 7: Оптимизация;
Т. 8: Теория групп; Т. 9: ТФКП; Т. 10. Перебор и эффективные алгоритмы;
Т. 11. Уравнения математической физики; Т. 12. Контрпримеры и парадоксы;
Т. 13. Топология; Т. 14. Теория чисел; Т. 15. Нелинейные операторы и неподвижные точки; Т. 16. Теория множеств: От Кантора до Коэна. s Босс В. Лекции по теории управления. Т. 1: Автоматическое регулирование. s Босс В. Интуиция и математика.
/Ивченко Г. ИМедведев Ю. И. Введение в математическую статистику. Статистика знает все. s Пантаев М. Ю. Матанализ с человеческим лицом, или Как выжить после предельного перехода: Полный курс математического анализа. В 2 т.
/Зуев Ю.А. По океану дискретной математики: От перечислительной комбинаторики до современной криптографии. В 2 т. sБоровков А. А. Теория вероятностей.
£.
&3
и
%ш\
—•л!
до
По всем вопросам Вы можете обратиться к нам: тел. -|-7 (499) 724-25-45 (многоканальный) или электронной почтой URSS@URSS.ru Полный каталог изданий представлен в интернет-магазине: http://URSS.ru
Научная и учебная литература