О. Г. Смоля нов
Е.Т.Шавгулидзе
КОНТИГОАЛЬНЫЕ
ИНТЕГРАЛЫ

УДК 513.015.7+517.988+519.216
Смолянов О. Г., Шавгулидзе Е. Т. Континуальны* интегралы. — М.:
Изд-во МГУ, 1990. —150 с —ISBN 5—211—00944—4.
Континуальные интегралы (интегралы Фейнмана) занимают одно нз
центральных мест в математическом аппарате теоретической физики и нахо-
находят все более широкое применение для решения разнообразных математи-
математических задач. В монографии дан обзор различных определений континуаль-
континуальных интегралов и соответствующих обобщенных мер на бесконечномерных
пространствах, установлены связи между ними, описаны свойства этих ин-
интегралов и классов интегрируемых функционалов. Приведены применения
континуальных интегралов при решении эволюционных уравнений (в частно-
частности, уравнения Шредингера), при исследовании дифференциальных н псевдо-
псевдодифференциальных операторов н в других задачах.
Для научных работников, специализирующихся по математической
физике.
Рецензенты:
доктор физ.-мат. наук В. Ю. Бенткус,
доктор физ.-мат. наук Р. А. Минлос
Печатается по постановлению
Редакционно-издательского совета
Московского университета
60&QJ0000—020
/ff 83—90
077@2)—90
5.4^211— 00944—4 © Смолянов О. Г., Шавгулидзе Е. Т.,
1990

ОГЛАВЛЕНИЕ
Предисловие 4
Глава I
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
§ 1. Цилиндрические подмножества векторных про-
пространств 8
■ § 2. Цилиндрические меры 14
§ 3. Мера Винера 24
§ 4. Квазимеры 31
§ 5. Гладкие меры, обобщенные меры и обобщен-
обобщенные функции 34
Глава II
РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ ИНТЕГРАЛОВ ФЕИНМАНА
§ 1. Интегралы Фейнмаиа как пределы конечнократ-
ных интегралов 37
§ 2. Два специальных класса функций, интегрируе-
интегрируемых по мере Фейнмана - 50
§ 3. Интегралы Фейнмана как аналитические про-
продолжения интегралов по гауссовским мерам . . 69
§ 4. Один важный класс функционалов, интегри-
интегрируемых по мере Фейнмана 85
§ 5. Определение интегралов Фейнмана прн помо-
помощи равенства Парсеваля и другие определения ин-
интегралов Фейнмана ......... 91
Глава III
ПРЕДСТАВЛЕНИЕ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕ-
УРАВНЕНИИ КОНТИНУАЛЬНЫМИ ИНТЕГРАЛАМИ
§ 1. Решение уравнения Шредннгера в конфигура-
конфигурационном пространстве 99
§ 2. Решение уравнения Шредкнгера в фазовом про-
пространстве 113
§ 3. Решение уравнения Шредингера с потенциалом
полиномиального вида четвертого порядка в беско-
бесконечномерном пространстве 137
§ 4. Решение уравнения Шредингера с потенциалом
полиномиального вида в конечномерном простран-
пространстве 143
Литература 147

Надо сегодня сказать лишь то, что уместно сегодня.
Прочее все отложить и сказать в подходящее время.
Гораций
ПРЕДИСЛОВИЕ
В книге рассматриваются- математические за-
задачи, возникающие при исследовании одного из центральных
объектов современной математической физики бесконечномер-
бесконечномерных систем, прежде всего квантовой теории, — континуального
интеграла (его наиболее важный для приложений и историче-
исторически первый вариант носит название интеграла Фейнмана;
именно ему и уделяется основное внимание в книге). Значение
континуальных интегралов определяется тем, что они позволя-
позволяют представить в «явном виде» решения различных задач, свя-
связанных с уравнениями, содержащими дифференциальные опе-
операторы с частными производными, и более общим образом —
псевдодифференциальные операторы. В частности, с помощью
континуального интеграла выражается ядро разрешающего
оператора задачи Коши для уравнения Шредингера как в ко-
конечномерном, так и в бесконечномерном случае (соответствую-
(соответствующие формулы, известные в конечномерном случае как форму-
формулы Фейнмана—Каца, а в бесконечномерном иногда называе-
называемые формулами Фейнмана—Каца—Нельсона, давно стали
классическими) '. Кроме того, интегралы Фейнмана «в фазо-
фазовом пространстве» естественным образом возникают при пред-
представлении бесконечномерных псевдодифференциальных опера-
операторов, действующих в пространствах функций и мер на беско-
бесконечномерном пространстве, и потому являются аппаратом, не-
необходимым не только для решения основных задач теории, на
и для самой их формулировки. Эффективность подхода, ис-
использующего континуальные интегралы, определяется сход-
сходством их формальных свойств со свойствами обычных интегра-
интегралов по мере (Лебега), что позволяет, экстраполируя на конти-
континуальные интегралы известные приемы интегрального исчисле-
исчисления, получить довольно развитый и гибкий формальный ап-
аппарат.
Несмотря на все это, положение, сложившееся в литературе
по континуальным интегралам, пожалуй, не имеет аналогов: с
одной стороны, огромное количество работ, написанных на так
1 В ситуации, которую мы называем конечномерной, речь идет об урав-
уравнении Шредннгера относительно функции конечномерного аргумента (оиа
зависит от «времени» и конечного числа пространственных координат); бес-
бесконечномерной мы называем здесь ситуацию, когда неизвестной является
функция бесконечномерного аргумента, что соответствует задачам, возни-
возникающим в квантовой теории поля; но и в первой — «конечномерной» —■
ситуации уравнение Шредингера может рассматриваться как уравнение Га-
Гамильтона для бесконечномерной гамильтоновои системы.

называемом физическом уровне строгости, довольно большое —
особенно за последние 10 лет — число публикаций в математи-
математических журналах — и почти полное отсутствие посвященных
континуальным интегралам математических монографий. Ко-
Конечно, основной причиной этого являются реальные математи-
математические трудности, возникающие при исследовании континуаль-
континуальных интегралов. Для того чтобы составить о них представле-
представление, достаточно заметить, что интеграл Фейнмана ' в фазовом
пространстве определяет преобразование Фурье; это преобра-
преобразование Фурье переводит функции в меры (определенные на
пространстве, сопряженном к тому, на котором определены
функции). Если это последнее пространство конечномерно, то
после отождествления мер с их плотностями определяемое так
Преобразование Фурье совпадет с классическим. Таким обра-
образом, теория интеграла Фейнмана — это бесконечномерный ана-
Йог классического гармонического анализа функций, опреде-
определенных на конечномерном евклидовом пространстве. Именно
математическими трудностями объясняется и то обстоятель-
обстоятельство, что в течение почти двадцати лет после появления (в вы-
вышедшей в 1948 году работе Фейнмана) концепции континуаль-
континуального интегрирования она воспринималась только как изящ-
Иый, но недостаточно понятный и в основном бесполезный спо-
способ переформулировки известных результатов. Еще в 1965 г.
Фейнман и его соавтор по книге «Квантовая механика и ин-
интегралы по траекториям» Хибс были вынуждены оправды-
оправдываться в том, что осмелились посвятить целую монографию
этому подходу к квантовой механике. Положение резко изме-
изменилось только в 1967 г., когда в работе Л. Д. Фаддеева и
В. Н. Попова с помощью континуальных интегралов был полу-
получен ранее неизвестный результат — проведено квантование ка-
калибровочных полей. Хотя примерно одновременно (и независи-
независимо) похожий результат был получен Брайсом де Виттом с по-
помощью традиционной операторной техники, именно простота и
естественность подхода Фаддеева—Попова, основанного к а ис-
использовании континуального интеграла, привела к тому, что
работа де Витта прошла незамеченной. Сейчас континуальный
интеграл стал стандартным орудием математической физики.
При этом в физических работах эти интегралы рассматривают
1 Понятие интеграла Фейнмана аналогично понятию интеграла по гаус-
совской мере (и является его непосредственным обобщением). Именно каж-
каждой неотрицательно определенной квадратичной форме В на векторном про-
пространстве Е соответствует гауссовская мера на двойственном пространстве
с преобразованием Фурье ехр(—В(х))\ совершенно аналогично каждой ве-
вещественной квадратичной форме BL на Е соответствует интеграл Фейнмана,
задаваемый «мерой Фейнмана» с преобразованием Фурье exp(i'Bi(x)); иног-
иногда, отказываясь в этом последнем определении от требования веществен-
вещественности, считают гауссовскую меру частным случаем «меры Фейнманах Та-
Таким образом, понятие интеграла Фейнмана определяет не единственны"; объ-
объект, а целый класс объектов; этим и объясняется использование термина
«интегралы» (а не «интеграл») Фейнмана.

теперь не как способ представления решений квантово-механи-
ческих уравнений, а как исходную конструкцию, заменяющую
эти уравнения (которые при этом вообще не вводятся). Это,
разумеется, не освобождает от необходимости придания кон-
континуальным интегралам точного математического смысла, а
также обоснования законности применения к ним «интеграль-
«интегрального исчисления», аналогичного обычному. Но именно такого
обоснования и не было до сих пор получено в математической
литературе для ситуаций, возникающих в реалистических мо-
моделях квантовой теории поля. В настоящее время, по-видимо-
по-видимому, существуют только две математические монографии, посвя-
посвященные интегралу Фейнмана. Одна из них — книга Альбеве-
рио и Хег-Крона [1] —даже в момент выхода A976 г.) пред-
представляла в основном чисто методический (или по крайней ме-
мере чисто математический) интерес. В ней рассматриваются ин-
интегралы Фейнмана от функций, являющихся преобразованиями
Фурье обычных счетно-аддитивных мер на бесконечномерном
пространстве; поэтому наиболее интересные для физики зада-
задачи оказываются вне рамок теории Альбеверио и Хег-Крона.
Следует также заметить, что в книге этих авторов не только
очень узок запас интегрируемых функций, но и само инте-
интегральное исчисление для интегралов Фейнмана развито явно
недостаточно. Еще одна математическая монография, в загла-
заглавии которой появляются слова «интеграл Фейнмана», — это
книга В. П. Маслова. Противоположная по характеру книге
Альбеверио и Хег-Крона, она содержит ряд глубоких ориги-
оригинальных идей и, в частности, новый подход к исследованию ин-
интегралов Фейнмана по пространству траекторий. Хотя все эти
идеи реализуются в ней применительно к конечномерной (но
зато, вообще говоря, нелинейной) квантовой механике, они
имеют смысл и могут быть применены и в бесконечномерном
случае, что может представить интерес в связи с квантовой
теорией струн. Часть этих идей — подходящим образом разви-
развитых — обсуждается ниже.
Основная цель предлагаемой монографии — дать математи-
математически корректное описание свойств интегралов Фейнмана в
случаях, близких к встречающимся в реалистических моделях
квантовой теории поля. При этом мы придерживаемся подхо-
подхода, провозглашенного И. Г. Петровским в предисловии к одной
из его книг: мы выбрали из теории континуальных интегралов
лишь несколько вопросов, но стремились изложить их доста-
достаточно полно. В книге рассматриваются, в частности, связи
между всеми известными в настоящее время определениями
интеграла Фейнмана; описываются довольно широкие классы
функционалов, интегрируемых по Фейнману (эти классы со-
содержат экспоненты от полиномов), и доказываются — при есте-
естественных для физических приложений ограничениях — форму-
формулы типа формул Фейнмана—Каца и Фейнмана—Каца—Нель-
Фейнмана—Каца—Нельсона о представлении решений уравнений типа Шредингера

континуальными интегралами. При этом рассматриваются как
уравнения, содержащие конечномерные операторы, так и урав-
уравнения с бесконечномерными (дифференциальными и псевдо-
псевдодифференциальными) операторами, а интегралы берутся как
по пространству траекторий со значениями в фазовом про-
пространстве, так и по траекториям со значениями в конфигура-
конфигурационном пространстве (собственно, только в последнем случае
Получаемые формулы естественно связывать не только с Фейн-
маном, но и с Кацем и Нельсоном; для случая фазового про-
пространства даже прототипы получаемых формул у Каца и
Нельсона не встречались).
Значительная часть результатов книги ранее с полными
доказательствами не публиковалась. Некоторые из этих ре-
результатов обсуждались с В. С. Владимировым, В. П. Масло-
Щым, Ю. М. Березанским, А. В. Углановым, А. Ю. Хреннико-
Хренниковым и А. М. Чеботаревым. Нам приятно выразить им свою
Глубокую благодарность.

ГЛАВА I
Предварительные сведения
§ 1. ЦИЛИНДРИЧЕСКИЕ ПОДМНОЖЕСТВА
ВЕКТОРНЫХ ПРОСТРАНСТВ
Пусть Ei и Е2— два векторных пространства
и Ь: EiXEz-^-R1, (xi, х2)<-*{Х\, х%У— билинейный функционал.
Пусть, далее, Y — непустое подмножество пространства Е2, а
X — векторное подпространство пространства Е\. Подмножест-
Подмножество А в X назовем У-цилиндрическим (или просто цилиндриче-
цилиндрическим, когда ясно, о каком Y идет речь), если существуют такое
конечное семейство (yi,...,yn) элементов из У и такое боре-
левское подмножество' В л-мерного евклидова пространства
Rn, что
п и ..., уп; В) =
= ЙХ, ({х, уг), (х, у2), .... (х, уп))<=В).
При этом будем говорить, что цилиндрическое множество
А (у\,..., уп', В) задается, или определяется, элементами у и ■■■
...,уп и борелевским множеством В (короче, набором (г/ь ..., г/п;
В)). Конечно, одно и то же цилиндрическое множество может
быть задано различными такими наборами. При фиксирован-
фиксированных у\,...,уп семейство %У1 Уп всех множеств вида А(у\,...
...,уп', В) представляет собой ст-алгебру подмножеств X.
Обозначим множество всех У-цилиндрических подмножеств
Од
X через Щ.у; очевидно, %Y— U U ЭС»» у • Рассмотрим не-
п^'»' Уп п
сколько примеров.
1. Пусть Ei=E2—Rn и Ь(хи х2) = (хи х2)п, где (•, •)„ — ска-
скалярное произведение в Rn, X=E[, Y=E2 и пусть е\,...,еп — ба-
базис в Rn. Тогда 31е, еп— это просто ст-алгебра всех борелев-
ских подмножеств в Rn.
2. Пусть S — множество, Х=Е\—линейное пространство
(некоторых) числовых функций, определенных на S, E2—E\* и
Y={fs: seS}, где для каждого seS /s — линейный функционал
на Еи определяемый так: fs(<P)=(P(s)- Тогда А е Шу в том и
1 Подмножество В топологического пространства Т называется борелев-
борелевским, если оно является элементом сг-алгебры, порожденной всеми замкну-
замкнутыми подмножествами Т.

только в том случае, когда существуют такие п элементов S\,...
...,sn множества S и такое борелевское подмножество В л-мер-
ного евклидова пространства, что Л={фе£ь (qp(si),...
...,q>(sn) )<=£}.
3. Чаще всего в дальнейшем будем рассматривать случай,
когда одно из пространств Еи Е2— локально выпуклое про-
пространство (ЛВП), а другое — ему сопряженное.
Итак, пусть Ei — ЛВП и Е2=Е/. В такой ситуации, как
обычно, положим b(xi, х2)=х2(Х[) (*2(#i)—эт0 значение ли-
линейного функционала х2^Е2 на элементе Х\^.ЕХ). При этом
множество AczXaEi является F-цилиндрическим (YaE2) в
том и только в том случае, если для некоторого n^N сущест-
существуют такие п линейных непрерывных функционалов q>i,..., ф„
на Е\, являющихся элементами Y, и такое борелевское подмно-
подмножество В /2-мерного евклидова пространства, что А{Х
Ф1(),,Ф„ ())}
Аналогично, если Е2 — ЛВП, ЕХ=Е2, мы будем полагать
Ь(хи х2)—Х\ (х2); в этом случае множество AczXczEi является
У-цилиндрическим (YczE2) в том и только в том случае, если
для некоторого n&N существуют такие п элементов У\,...,уп
множества Y и такое борелевское подмножество В л-мерного
евклидова пространства, что
Очевидно, что если YidY2, то всякое Урцилиндрическое
множество является и У2-Цилиндрическим (т. е. 3lva=>9tv,)-
Хотя вообще обратное неверно, справедливо следующее
Предложение 1.1. Если S(Y)—линейное подпро-
подпространство, порожденное в Е2 множеством Y, то всякое 3?{Y)-
цилиндрическое множество является и Y-цилиндрическим.
Доказательство. Пусть 3?(Y)-цилиндрическое множе-
множество задано набором (г/ь...,уп; В). Тогда существуют такие
bij^R1 и ya^Y (t=l, 2,..., л; /=1, 2,..., т), что для каждого
{ }
Поэтому
где L — линейное отображение евклидова пространства Rnm в
евклидово пространство Rn, переводящее элемент (kij) этого

пространства в элемент (^ЬгАо") пространства Rn. Из предло-
жения 1.1 вытекает, что если & = 2?{у\,..., уп)—векторное под-
подпространство, порожденное в Е2 семейством (г/ь..., у2), то
3ls? = 9ty, yn, так что если два различных семейства у\,.«.,уп
и Z\,..., zk элементов из Y порождают в Е2 одно и то же век-
векторное подпространство, то %Vi yn = Uz1 Zfe-
Предложение 1.2. Множество Жу всех У'-цилиндриче-
У'-цилиндрических подмножеств пространства X является алгеброй мно-
множеств.
Замечание 1. Вообще говоря, Шу не является ст-алгеб-
рой; в частности, сг-алгеброй не является описанная в приме-
примере 2 алгебра цилиндрических подмножеств пространства функ-
функций на S, если S бесконечно.
Предложение 1.3. Пусть, как и выше, 3?(Y)—линей-
3?(Y)—линейное подпространство, порожденное в Е2 множеством Y. Тогда
Л е 91У в том и только в том случае, если существуют боре-
левское подмножество В п-мерного евклидова пространства Rn
и линейное отображение L: X^*Rn, такие, что A=L~lB, причем
L непрерывно при наделении пространства X топологией
Доказательство. Пусть У-цилиндрическое множество
А задано набором (г/ь ...,г/п; В). Тогда A=L~lB, где непрерыв-
непрерывное линейное отображение L: (X, а(Х, S'(Y)))-+-Rn определя-
определяется так: L(x) = ((x, y{>,..., (х, уп>).
Пусть теперь A=L~1B, где В — борелевское подмножество
Rn, a L — непрерывное линейное отображение (X, а{Х, S(Y)))
в Rn. Тогда для каждого х^Х существуют такие числа- Xi(x)
(t=l, 2,..., л), что L(x) = (Xi(x), ...Д„(х)); в силу непрерывно-
непрерывности L существуют такие элементы у\ (i=l, 2,..., л) простран-
пространства 2?{Y), что Xi(x)=<x, yO для каждого i. Но это означает,
что Ле31вд; в силу предложения 1.1 отсюда следует, что
А%
у
Предложение 1.4. Для того чтобы подмножество АаХ
являлось У'-цилиндрическим, необходимо и достаточно, чтобы
существовали о(Х, 3?(Y))-замкнутое подпространство Хо про-
пространства X конечной соразмерности и борелевское подмноже-
подмножество В фактор-пространства Х/Х& такие, что А=Р0~1В, где
Ро — каноническое отображение X на Х/Хо. Подпространство
Хо называется образующим (или направляющим) подпростран-
подпространством множества А, а В — его основанием (в фактор-простран-
фактор-пространстве XI Xq).
Доказательство. Достаточность вытекает из предыду-
предыдущего предложения. Докажем необходимость. Пусть А—У-ци-
линдрическое подмножество X. Тогда в силу предложения 1.3
A=L~l(B), где В — борелевское подмножество Rn, a L — не-
непрерывное отображение (X, а(Х, 3?(Y))) в Rn. При этом мож-
10

но считать, что L(X)=Rn, заменяя в противном случае Rn на
L(X). Положим X0=kerL. Тогда Ро — каноническое отображе-
отображение X на Х/Хо, то существует такое взаимно однозначное отоб-
отображение г: X/Xg-^R71, что L=roP0. Поэтому, если положить Б=
=i~1B, будет справедливо равенство А=Р0~1В.
Таким образом, для алгебры Шу всех F-цилиндрических
подмножеств пространства X существует такое множество 3*
линейных отображений X в конечномерные линейные простран-
пространства, что А е Щ-у в том и только в том случае, если ЛеР''^р
для некоторого PeiF; здесь 3&р — ст-алгебра борелевских под-
подмножеств того конечномерного линейного пространства LP, в
которое Р отображает X. Кроме того, при этом выполняется
следующее условие (А): каковы бы ни были Р\, Р2^9>, суще-
существуют такое отображение Ръ^.3" и такие отображения Р31:
'■Lp^-^-Lf, и Р32'- Lp,-*~ LPl, что оказывается коммутативной
следующая диаграмма:
Рш
Как это вытекает из предложения 4.1, примером такого
множества 9" является совокупность канонических отображений
пространства X на всевозможные его фактор-пространства по
по замкнутым в топологии а(Х, S(У)) подпространствам ко-
конечной коразмерности (в этом случае для всех Ре^3, Р(Х) =
~Lp). Другим примером является множество
U {р (п; Уъ • • •. хп) :уи ..., уп£Е Y},
п—\
где для каждых n<=N и у\,..., уп^У Р{п; у\,...,уп)—отображе-
у\,...,уп)—отображение X в Rn, переводящее элемент х^Х в вектор {(х, i/i>,...
.... <х, yn>)<=Rn; отметим, что здесь Lp(n;i,l Уп) = Rn, причем,
вообще говоря, Р(п; ух уп) {X)=/=Rn.
Обратно, пусть задано некоторое множество £р линейных
отображений линейного пространства X в конечномерные ли-
линейные пространства, причем выполнено приведенное выше ус-
условие (А). Тогда (мы пользуемся введенными выше обозначе-
обозначениями) множество %*=={А\АаХ\ ЗРе#\ ЛеГ1/}
представляет собой алгебру подмножеств X, причем Щ. =ШУ,
где У — множество всех линейных непрерывных функционалов
на пространстве X, наделенном самой слабой среди топологий,
для которых непрерывны все отображения из clJ. Заметим, что
^= U %Р, где %Р = Р~1МР для каждого Р.
11

Отметим еще, что отображения рц, о которых говорится в
условии (А), не определяются, вообще говоря, однозначно; это,
однако, будет так, если все отображения из & сюръективны
(для всякого множества 9* линейных отображений X в конеч-
конечномерные линейные пространства, удовлетворяющего условию
(А), существует удовлетворяющее этому же условию множе-
множество Q сюръективных линейных отображений X в конечномер-
конечномерные линейные пространства, такое, что 31^ = 31 ).
Предположим теперь, что для всякого х^Х существует та-
такой элемент i/еУ, что <х, г/>=И=О (при этом порожденное Y-
замкнутое линейное подпространство пространства (Е2,о{Е2,Х))
совпадает с Е2).
Предложение 1.5. Для того чтобы множество AczX яв-
являлось Y-цилиндрическим, необходимо и достаточно, чтобы су-
существовали конечномерное линейное подпространство I про-
пространства X, непрерывный в топологии а(Х, 9?{Y)) проектор
Р в X, отображающий X на I, и борелевское подмножество В
пространства I, такие, что А=Р~1В.
Доказательство. Достаточность вытекает из предло-
предложения 1.3, поскольку в силу отделимости пространства (X,
о(Х, S'(Y))) (являющейся следствием тотальности множест-
множества Y) всякое его конечномерное подпространство также отде-
отделимо и потому изоморфно евклидову пространству соответ-
соответствующей размерности.
Необходимость следует из предложения 1.4. В самом деле,
пусть Хо— замкнутое линейное подпространство в Ха= (X,
а(Х, S'(Y))), имеющее конечную коразмерность, Ро — кано-
каноническое отображение Ха на Ха/Х0, ВА — борелевское подмно-
подмножество в Ха/Х0 и A=Pq~1Ba. Пусть, далее, ^i—линейное под-
подпространство пространства X, алгебраически дополнительное к
Хо. Тогда сужение Ро на Х\ (обозначим это сужение через Pi)
представляет собой взаимно однозначное непрерывное отобра-
отображение, обладающее в силу отделимости Ха/Х0 непрерывным
обратным; таким образом, Pt — изоморфизм Ху на XaIXQ. По-
Положим теперь P=Pi~lP0 и В=Рг1ВА. Тогда Р — непрерывный
проектор в Х„, отображающий Х„ на Хи В — борелевское под-
подмножество в Х{ и А=Р~1В.
Ниже будем использовать следующие обозначения. Если
Ж— семейство подмножеств некоторого множества, то симво-
символом о(Щ обозначаем ст-алгебру подмножеств этого множест-
множества, порожденную семейством Ш', вместо символа о(Шу) обычно
используем символ сту.
Предложение 1.6. Пусть YtсY, причем каждый элемент
из У является пределом некоторой последовательности элемен-
элементов из Yx в пространстве S{Y), наделенном топологией
a{S{Y), X). Тогда aY=oYl.
Доказательство. Поскольку Сту = стC1у), достаточно
установить, что Sfycray,; для этого в свою очередь достаточ-
достаточно показать, что каковы бы ни были ае/?1 и yczY,
12

(так как семейство всевозможных множеств такого вида по-
порождает алгебру Щ). Пусть для каждого п^М yneFi и уп-у-
-*~у при я->-оо. Тогда, как легко проверить,
А(у, (-оо, a))=U U П {* = <*. Уп)<а—~\,
так что А е aYl.
Далее будем сразу определять векторное пространство X и
множество У, не описывая предварительно пространств Ех и
£2; в том случае, когда У является частью X*, предполагаем,
что <х, у>=у{х) для всех х^Х и i/eF. Если Z{ и Z2 — вектор-
векторные пространства, то запись Zx gZ2 означает, что 1\—подпро-
1\—подпространство Z2.
ЛВП X назовем квазигильбертовым, если на нем сущест-
существует непрерывная норма, порождаемая скалярным произведе-
произведением XxX-*~R\ (хи лг2) —*■ <ДС1, х2>н-
Пусть У — квазигильбертово ЛВП, X=Y', p — непрерывная
гильбертова норма на Y, Н — гильбертово пространство, полу-
получаемое пополнением Y по этой норме, <р — каноническое вложе-
вложение У в Н, ф* — сопряженное вложение пространства И' в X.
В дальнейшем не будем различать элементы У (соответственно
Н') и их образы в Я (соответственно в X). Отождествив еще
обычным образом Н и Н', получим тройку пространств
Хш>Нш>У, где Y всюду плотно в гильбертовом пространстве
Я и Я всюду плотно в пространстве (X, о(Х, У)) (последнее
вытекает из инъективности отображения <р). Кроме того, если
hesH, y^Y, то ih, г/>н=/г(у) (И.(у) —значение h как элемента
из X на элементе i/gF).
Заметим теперь, что если Р — конечномерный ортогональ-
ортогональный проектор в Я, область значений 3?Р которого содержится
в У, то Р непрерывен в топологии, индуцированной в Я топо-
топологией а(Х, У).
Это вытекает из того, что если (г/ь.... уп)—ортогонормиро-
ванный базис в 3?Р, то для каждого элемента /Я
причем для каждого г/еУ отображение h>->-h(y), H-+R1 непре-
непрерывно в топологии а(Х, У). Поэтому он может быть продолжен
по непрерывности на все X; это продолжение снова обозначим
тем же символом Р. Пусть Q — множество всех отображений
X-^-Y, каждое из которых можно получить таким способом;
13

элементы из Q по-прежнему называем конечномерными орто-
ортогональными проекторами.
Предложение 1.7. Для того чтобы множество АаХ бы-
было Y-цилиндрическим, необходимо и достаточно, чтобы нашелся
такой конечномерный ортогональный проектор P^Q, что А =
=Р~1В, где В— некоторое борелевское множество из области
значений Jzfp этого проектора.
Доказательство, Достаточность вытекает из предложе-
предложения 1.5, поскольку каждый проектор из множества Q непреры-
непрерывен как отображение пространства (X, а(Х, Y)) в себя. Дока-
Докажем необходимость. Пусть А—F-цилиндрическое подмножест-
подмножество X, Хо — его образующее подпространство и В — основание
А в Х/Хо. Пусть, далее, Xх— ортогональное дополнение замк-
замкнутого подпространства Н[}Х0 пространства Я и Хо° — поляра
Хо в Y; покажем сейчас, что Хо = Хх.
Прежде всего, так как <h, г/>я=Му)=0, если
heaH(}X0 и #e=X°(crF), то
Х2с=(ЯПХ0)х. A.1)
Далее, поскольку ХоП(ЯП*о)х==(ЯП*о)П(ЯП*о)х={О}> под-
подпространство (HfiXoI- пространства X содержится в (некото-
(некотором) подпространстве этого пространства, алгебраически до-
дополнительном к подпространству Хо, и, следовательно,
dim^nX0)x<dimX/X0. A.2)
Но dim X0°=dim Х/Хо (поскольку (^о0)' изоморфно Х/Хо); от-
отсюда и из соотношений A.1) и A.3) вытекает, что
dim Хо = dim (Я (~| Х0)х = dim Х/Хо; A.3)
поскольку dimZ/Z0<oo, из A.1) и A.3) следует, что Хо°=
(Я*)х
()
Пусть теперь, как и в доказательстве предложения 1.5, Ро—
каноническое отображение X на Х/Х$ и ВА — борелевское под-
подмножество в Х/Хо, такие, что А=Р0~1В; пусть еще Ро — изо-
изоморфизм Х/Хо на Хо°, обратный к сужению Ро на Хо°, Р=РоРо,
и В=Р0ВА. Тогда А=Р~1В, причем PeQ, поскольку сужение
Р на Я является проектором Я на (ЯП-^о)х. Предложение 1.7
доказано.
§ 2. ЦИЛИНДРИЧЕСКИЕ МЕРЫ
Пусть Е — векторное пространство (над полем
вещественных чисел), G — подмножество алгебраического со-
сопряженного Е* к Е, Щ.а— алгебра G-цилиндрических подмно-
подмножеств Е, Т — ЛВП (над полем вещественных чисел).
Определение 1. Цилиндрической мерой на {Е, StG>
(короче, G-цилиндрической мерой) со значениями в Т назы-
14

аается функция v:$la-+-T, обладающая следующими свойст-
свойствами: A) множество ее значений ограничено в Т; B) каковы
бы ни были натуральное п и элементы gu ...,gn^G, сужение v
на а-алгебру %gl gn счетно-аддитивно.
Отметим, что цилиндрическая мера на (Е, Щв является
мерой (т. е. аддитивна на Шв)-
Функция f на Е со значениями в R1 или С называется G-ци-
G-цилиндрической, если справедливо равенство f(x)=y(gi(x),...
...,gn(x)), где n^N, ф — некоторая функция на Rn, a gi gne
eG. Если ф — борелевская функция на Rn (т. е. если она из-
измерима как отображение {Rn, $n) в (R1, &\)), то цилиндриче-
цилиндрическая функция f измерима относительно cr-алгебры 3lgl gn
(являющейся, напомним, подалгеброй алгебры всех G-цилин-
дрических множеств в Е), т. е. измерима как отображение
{Е, 9lgl gn) в {R1, <%\)\ такую цилиндрическую функцию на-
называем борелевской. Так как сужение G-цилиндрической меры
на каждую ст-алгебру Stglt...,gn счетно-аддитивно, то для боре-
левских G-цилиндрических функций имеет смысл понятие инте-
храла Лебега относительно числовой G-цилиндрической меры.
Интегралы от (числовых) функций по G-цилиндрическим мерам,
принимающим значения в ЛВП, не совпадающем с R1, будут
встречаться очень редко — только от ограниченных функций
я в предположении, что Т секвенциально полно; в этом случае
они определяются как пределы соответствующих интегральных
сумм; существование таких пределов вытекает из секвенциаль-
лой полноты Т.
Всюду далее, если не оговорено противное, предполагается,
что G — векторное пространство.
Пусть еще Т — комплексификация пространства Т, Щ.—
алгебра подмножеств пространства Е, содержащая алгебру
Ша, причем ЛВП Т секвенциально полно, v —мера (т. е. ад-
аддитивная функция множества) на Ш. со значениями в Т, при-
причем сужение v на Щ,а представляет собой цилиндрическую ме-
меру на (Е, %G) со значениями в Т.
Определение 2. Преобразованием Фурье меры v назы-
называется функция v : G~*-T, определяемая равенством
(интгграл оправа — это интеграл от ограниченной борелев-
борелевской G-цилиндрической функции по мере со значениями в Т).
Если Е — гильбертово пространство и / — каноническое изо-
изоморфное отображение Е на Е', то функция x<-+vH(x)s=v(Ix)
называется гильбертовым преобразованием Фурье меры v. Та-
Таким образом, если Е — гильбертово пространство, то гильбер-
гильбертово преобразование Фурье \н этой меры — функция на про-
пространстве Е, принимающая значения в Г и определяемая ра-
15

венством g vH(x)=\eii-x-z'>v(dz) ((•, •) — скалярное произведе-
Е
ние в Е).
Ниже будем пользоваться правилом замены переменных в
интеграле; согласно этому правилу, если X — множество, Ш—■
а-алгебра его подмножеств, ц — счетно-аддитивная мера
на Ш, F— измеримое отображение (X, Шх) в измеримое про-
пространство (Z, Шг) (-Z—множество, Щ.—а-алгебра его подмно-
подмножеств) и [iF-1 — образ уь при этом отображении, то
для всякой измеримой функции / на (Z, Шг); это равенство
означает, что стоящие в его левой и правой частях интегралы
существуют или нет одновременно и в том случае, если сущест-
существуют, равны.
Предложение 2.1. Если ц и v — две цилиндрические ме-
меры на (Е, Ша) со значениями в ЛВП Т, причем \i{g)=v{g) для
всех g^G, то jj,=v (т. е. цилиндрическая мера однозначно опре-
определяется по ее преобразованию Фурье).
Доказательство. В силу теоремы Банаха—Хана доста-
достаточно доказать теорему для случая, когда T=RK Действитель-
Действительно, пусть это сделано и ц и v — две цилиндрические меры со
значениями в ЛВП Т, обладающие совпадающими преобразо-
преобразованиями Фурье; тогда, каков бы ни был линейный непрерывный
функционал / на Т, f(\i{g))=f{v{g)) для всех g^G. Но функ-
функции gi-^-f(jj,(g)) и g*-+f(v(g)) являются преобразованиями
Фурье цилиндрических числовых мер 3iG э Л—> / (jj, (Л)) и StG э
^A—*f(v(A)) на (Е, Шв)', поэтому эти меры должны совпадать
(согласно принятому предположению). Это значит, что если
Ле8б, то f([i(A))==f(v(A)). Так как последнее равенство
верно для каждого /еГ, то в силу теоремы Банаха—Хана
fi(j4)=v(/l). Таким образом, для каждого А^Шв, V>(A)=v(A)y
т. е. jj, = v. Итак, пусть ц и v — две числовые (т. е. принимаю-
принимающие значения в R1) цилиндрические меры на (Е, Шс), причем
V-{8)—v(g) Для всех g^G. Предположим сначала, что E=Rnr
G — Rn (при этом алгебра Шв совпадает с а-алгеброй всех бо-
релевских подмножеств Rn), a v, ц счетно-аддитивны на Шв-
Для того чтобы доказать, что n(A)=v(A) для всех Ле310, до-
достаточно доказать, что n(V)=v(V) для каждого открытого ги-
п
перлараллелепипеда V, т. е. множества вида 11 (ak, bh), ak, bk e
g/}1. Пусть (ф„)—монотонно неубывающая последователь-
последовательность непрерывных функций на Rn, сходящаяся к индикатору
yv множества V (числовая функция ф на множестве X называ-
называется индикатором его подмножества Хи если ф(л:) = 1 при лге
ё.Х{ и ф(д;)=О при хфХх); такая последовательность, очевид-
16

но, существует. Если для каждого п \ фп <^v = j Фп Ф-. т0 п0
Теореме Лебега о предельном переходе под знаком интеграла
(или же по теореме Беппо—Леви)
Таким образом, для доказательства того, что \i=\, в рассмат-
рассматриваемой ситуации остается доказать, что \ <pn dv = \ cpn d\i
для каждого n^N. Докажем, что ^ ^ dv = J г|) d\i для каждой
финитной непрерывной функции на Rn (функция называется
финитной, если она обращается в нуль вне некоторого ограни-
ограниченного множества; очевидно, все функции последовательности
(фп) финитны). Пусть \j) :/?"->■/?• — финитная непрерывная
функция и V — гиперпараллелепипед, вне которого она обра-
обращается в нуль. Пусть, далее, (\|з„)—последовательность триго-
тригонометрических многочленов, сходящаяся к чр равномерно на
каждом компактном множестве. Тогда
■ j ty d\i = lim j г|з„ d\i = lim j tyn dv = ^ ip dv
Rn gi Rn Rn
(третье равенство справедливо потому, что jj,=v). Таким обра-
образом, для случая, когда E=Rn, G=Rn, предложение доказано.
Общий случай сводится к этому частному. Действительно, если
Ле^в, то существуют такие замкнутое в топологии о{Е, G)
векторное подпространство £\ пространства Е, обладающее ко-
конечной коразмерностью, и борелевское подмножество В (ко-
(конечномерного отделимого) фактор-пространства Е/Еи что А —
=Ф~1В, где Ф — каноническое отображение E~*-E/Ei. Поэтому
v=fi, если совпадают образы этих мер относительно канониче-
канонического отображения Ф (уЛ=^Ф-') (В) = (цФ~1) (S)=jj,S). Но
эти образы уФ-1 и |лФ-1 являются мерами на конечномерном
(отделимом) пространстве Е/Еи причем если g — линейный
функционал на Е/Е (так как последнее пространство конечно-
конечномерно, он обязательно непрерывен), то
Е/Ег Е
»в)(*)у(dx) = v(Ф*§) = (Г(O'g) = м^Ф (g)
(мы воспользовались формулой замены переменной).
Таким образом, преобразования Фурье мер уф и цФ совпа-
совпадают; следовательно (поскольку пространство Е}Е\ конечномер-
конечномерно), совпадают и сами эти меры; таким образом, совпадение
цилиндрических мер ц и v доказано.
17

Пример 1. Пусть b—Rn. Мера v на ст-алгебре борелев-
■ских подмножеств называется (невырожденной) гауссовской,
■если существуют такие симметричный определенный оператор
В в Rn (называемый корреляционным оператором меры v) и
элемент а^Дп, называемый математическим ожиданием (или
средним) меры v, что, каково бы ни было Ле^п,
—(В~1х—а,х—а)
(det Б — определитель матрицы оператора В в стандартном ба-
базисе). Преобразование Фурье (гильбертово) этой меры опреде-
определяется равенством
^ — (Вг.г)
v(z) = e 2
Действительно,
. (В~Чх-а),х-а)
Bя)"/2 (det S)I/2
если S — такое ортогональное преобразование Rn, что оператор
B\=S~lB~lS является диагональным (ниже мы обозначаем соб-
собственные значения оператора В с учетом их кратностей через
bk; из положительной определенности В вытекает, что bk>0 для
всех k; числа bk~l образуют последовательность собственных
значений оператора В~1), то (здесь и далее x=(xh) = (zk')=z'=
: = ^ e
^!1 J
= Bя)п/2 Пbke * = Bnf2 (detB)l/2e
= Bя)"/2 (det 5I/2e ' '* = Bя)"/2 (det B)i/2
18

Подставляя полученное выражение в правую часть предыду-
предыдущей цепочки равенств, получаем v.
Если Ех и Е2-—два вещественных векторных пространства,
G] и G2— векторные подпространства пространств EY* и Е2*,
f — линейное отображение £\ в Е2, непрерывное при на-
наделении пространств Ех и Е2 топологиями о(Еь Gi) и
а(Е2, G2), то прообразом (относительно этого отображения)
каждого С2-цилиндрического подмножества пространства Е2
является Gi-цилиндрическое подмножество пространства Е\.
Действительно, если Л = {хе Е2, (gk (х)) ей}ё Шв2 (Sefln>
Вп—о-алгебра борелевских подмножгств в Rn), то /~'Л = {хе
^ E1:((f*gk)(x))^B}^Ua1. Поэтому для каждой Gi-цилин-
дрической меры на Е{ можно определить ее образ при отобра-
отображении /—■ О2-цилиндрическую меру v/ на Е2, задаваемую ра-
равенством (vf-1) (Л) ^vif-^A)).
Предложение 2.2. При перечисленных предположениях
справедливо равенство
Доказательство.
£2 Я,
(частный случай этого предложения фактически использовался
при доказательстве предложения 2.2).
Пример 2. Из результата примера 1 и предложения 2.2
вытекает, что гауссовскую меру на Rn можно определить и ина-
иначе. Именно мера (на ст-алгебре $п борелевских подмножеств
пространства Rn) является (невырожденной) гауссовскои в
том и только в том случае, если ее преобразование Фурье v
определяется равенством v(x) = e , где В — по-
положительно определенный оператор в Rn, называемый корре-
корреляционным, а а — вектор из Rn, называемый средним значе-
значением меры v. На этом пути определение гауссовскои меры мож-
можно несколько обобщить так, чтобы не исключать случай, обыч-
обычно называемый вырожденным. Именно, мера v на 3§п назы-
называется гауссовскои, если ее преобразование Фурье определяет-
определяется равенством
где В — неотрицательно определенный линейный оператор в
Rn, a a — элемент из Rn (в этом примере мы отождествили Rn
19

и его сопряженное, так что фактически речь все время шла о
гильбертовом преобразовании Фурье; если бы отождествления
Яп и Rn* произведено не было, следовало бы считать В опера-
оператором в /?"*).
Пример 3. Если v — гауссовская мера на о-алгебре боре-
левских подмножеств Rn и / — линейное отображение Rn в Rk,
то борелевская мера на Rh, являющаяся образом меры v при
этом отображении, также гауссовская; это вытекает из предло-
предложения 2.2 и примера 2.
В частности, если v — гауссовская мера в Rn с корреляци-
корреляционным оператором В, имеющим ненулевое ядро kerS, и G— ор-
ортогональное дополнение в Rn этого ядра, то v является обра-
образом— относительно канонического вложения F: G-W?n— своего
сужения на G; иначе это можно выразить, сказав, что v сосре-
сосредоточены на G.
Для простоты считаем, что математическое ожидание меры
v равно нулю. Пусть при этом vG—(гауссовская) мера на G с
корреляционным оператором Вс, являющимся сужением В
на G (так как В*=В, то B(G) = G). Таким образом,
так как FBGF*=B. Поэтому, в силу предложения 2.1 {vGF~l) =
=v.
Пример 4. Пусть теперь, как и в начале параграфа, Е—
произвольное векторное пространство над полем вещественных
чисел, G — векторное подпространство его алгебраического со-
сопряженного. Цилиндрическая мера на (Е, Ща) называется га-
гауссовской, если существуют такие неотрицательно определен-
определенный симметричный билинейный функционал Ь на GxG и ли-
линейный функционал а на G, что v(g) = exp (ia(g) b(g, g)\-t
при этом функционал b называется корреляционным функцио-
функционалом меры v, a a — средним значением (или математическим
ожиданием) этой меры. Как и для конечномерного случая, об-
образом Сгцилиндрической гауссовской меры в пространстве Ех
(мы пользуемся сейчас обозначениями и предположениями,
приведенными перед предложением 2.2) при линейном отобра-
отображении f:Ei-*-E2 (непрерывном относительно топологий а(Е\,
Gi) и о(Е2, G2) пространств Ех и Е2) является С2-цилиндриче-
ская гауссовская мера в Е^. Оказывается, верно следующее
усиление формального обращения последнего утверждения: для
того чтобы G-цилиндрическая мера v на £ была гауссовской,
необходимо и достаточно, чтобы, каков бы ни был линейный
функционал g на Е, являющийся элементом пространства G,
образ vg меры v относительно отображения g:E-+Rl пред-
представлял бы собой гауссовскую меру на R1. То, что для гауссов-
20

<ской G-цилиндрической меры это действительно так, вытекает
из предложения 2.2. Докажем обратное.
Покажем сначала, что если все меры v/~'(feG)—гауссов-
ские, то, каковы бы ни были/i, fz^G, функция x*-*f\(x) -f2(x)
интегрируема. В силу неравенства Коши—Буняковского
J I /i W! I /2 (*) I dv < (j" (fL (x)f dv J (f2 (x)f dv
E ЕЕ
Но для k=l, 2
S)9dv=J t*vfj[(dt)<oo,
1/2
так как v/h — гауссовская мера на R1 (вырожденный случай
не исключается; вырожденная гауссовская мера на R1 — это
лросто нормированная мера, сосредоточенная в точке).
Определим линейный функционал а на G равенством:
^(существование (и конечность) a(g) вытекают из гауссовости
меры vg~l).
Определим далее билинейный функционал Ь на GXG равен-
равенством
Ь(gi. ft) = $ (ft(x)~a(gi))(g2(x)~a{g2)v(dx).
Конечно, он является неотрицательно определенным; действи-
действительно,
big, e) =
(заметим, что мера v заранее не предполагалась неотрицатель-
неотрицательной). Тогда гауссовская G-цилиндрическая мера на Е с корре-
корреляционным функционалом b и математическим ожиданием а
совпадает с исходной мерой. Чтобы в этом убедиться, доста-
достаточно найти преобразование Фурье исходной меры. Проделаем
соответствующую выкладку
e««<*>v (dx) = J eltvg-1 (dt) = e
E
Цилиндрические меры могут быть или не быть счетно-аддитив-
счетно-аддитивными на своей области определения, т. е. на алгебре цилиндри-
цилиндрических множеств (начиная с этого места, мы будем часто опус-
опускать явное указание на семейство функционалов, задающее ци-
цилиндрические множества). Оказывается, однако, что векторное
пространство, на алгебре цилиндрических подмножеств кото-
21

рого. задана цилиндрическая мера, можно расширить — с «со-
«сохранением алгебры цилиндрических множеств» — таким обра-
образом, чтобы мера стала счетно-аддитивной, причем это расшире-
расширение можно выбрать общим для всех цилиндрических мер. Точ-
Точный смысл сказанному придается определением и предложе-
предложениями, которые сейчас будут сформулированы. Вплоть до при-
примера 5 не предполагается, что G— векторное пространство.
Определение 2.3. Измеримым векторным простран-
пространством назовем пару (Е, 3fG), где Е— векторное пространство,
G— множество линейных функционалов на Е, разделяющее
точки из Е, Ща— алгебра G-цилиндрических подмножеств Е.
Определение 2.4. Говорим, что измеримое векторное
пространство (£2> 3Ig2) является расширением измеримого век-
векторного пространства (Еъ 3fGi), если существует такое инъек-
тивное отображение f:Ei-*~E2, что отображение *й(?2эЛ —►-
— Г" (А) является изоморфизмом Щ.Ог на Жв^ При этом f назы-
называем отображением, задающим рассматриваемое расширение.
Предложение 2.3. Для всякого измеримого векторного
пространства (Е, Шв) существует такое его расширение (Е,
3tg), что, какова бы ни была числовая G-цилиндрическая мера
v на Е, ее образ v/i относительно отображения f, задающего-
рассматриваемое расширение f : E-+-E, представляет собой счет-
счетно-аддитивную меру на (Е, 3%).
Это предложение вытекает из следующей теоремы.
Теорема 2.1. Пусть Е\ — векторное пространство, Gt —
некоторое множество линейных функционалов на Еь разделяю-
разделяющее точки, из Ей Тогда существуют векторное пространство Е2,
множество G2 линейных функционалов на Е2, разделяющее точ-
точки из Е2, и линейное отображение f: Ех-^-Е% представляющее-
собой гомеоморфизм пространства (Еи о(Еи S{GX)) на его об-
образ (Ez, o(E2, 2>(GZ)), такие, что какова бы ни была цилиндри-
цилиндрическая мера v на (Et, Ща), ее образ vf~l относительно f пред-
представляет собой счетно-аддитивную меру на (Е2, а(Е2, 2>(G2)).
Доказательство. Пусть S — базис Гамеля в S'(Gi);
обозначим через Е2 множество всех вещественных функций на
S, через G2 ■— множество всех линейных функционалов на Е2,
имеющих вид £23(pi-*(p(s) (seS), и определим отображение
f:Ei-+E2 следующим образом: если ifefi, то f(-ф)=ф(е£12),
где (p(s)=s(i|)) для каждого seS. Линейность и непрерыв-
непрерывность f очевидны; его инъективность является следствием того,
что G\ разделяет точки из Е\; то, что образ vf~' цилиндриче-
цилиндрической меры v является счетно-аддитивной (цилиндрической) ме-
мерой, вытекает из теоремы Колмогорова.
Предположим теперь, что v — счетно-аддитивная G-цилин-
G-цилиндрическая мера на векторном пространстве Е (как и ранее,
G — векторное подпространство алгебраического сопряженного-
к Е). Тогда ее можно продолжить на а-алгебру, порожденную
алгеброй Шв G-цилиндрических множеств, причем это продол-
22

зкение единственно. Далее, а-алгебру, порожденную G-цилин-
дрическими множествами, обозначаем символом cG и называем
G-цилиндрической а-алгеброй. С другой стороны, если \л —
счетно-аддитивная мера на а-алгебре og, to она однозначно
восстанавливается по своему сужению на алгебру %-g G-ци-
линдрических множеств. Поэтому из предложения 2.1 вытекает,
что мера ц однозначно восстанавливается по своему преобра-
преобразованию Фурье.
Отметим, что если Е — ЛВП, G=E' и v — счетно-аддитивная
мера на а-алгебре борелевских подмножеств пространства Е,
то она, вообще говоря, не восстанавливается однозначно по
•своему преобразованию Фурье; можно лишь утверждать, что
по преобразованию Фурье однозначно восстанавливается суже-
сужение v на алгебру Ше' и а-алгебру оЕ'. Выделить среди раз-
различных мер на о-алгебре борелевских подмножеств, обладаю-
обладающих одинаковыми преобразованиями Фурье, единственную
можно с помощью каких-либо дополнительных требований; на-
например, можно потребовать, чтобы выделенная мера была ме-
мерой Радона (т. е. чтобы ее значение на каждом множестве
можно было с любой степенью точности аппроксимировать зна-
значениями, принимаемыми ею на содержащихся в этом множест-
множестве компактах). Среди мер, определенных на а-алгебре борелев-
борелевских множеств и обладающих заданным преобразованием
•Фурье, существует не более одной меры Радона (хотя может
не существовать и ни одной).
Наша очередная цель — установление равенства Парсеваля.
Предположим теперь, что Е — ЛВП, Е' — его сопряженное, на-
наделенное какой-либо топологией, согласующейся с двойствен-
двойственностью между Е и Е', ц и v — счетно-аддитивные меры на о-
алгебрах а£, в Е и оЕ в Ег и функция (g, x)*-+g(x) измерима
относительно произведения а-алгебр оЕ и оЕ'- Тогда справед-
справедливо следующее равенство, называемое равенством Парсеваля:
Е'
(это означает, в частности, что обе его части имеют смысл).
Для доказательства достаточно заметить, что при принятых
предположениях существует интеграл | eis<-x'>v(dg)\i(dx), при-
Е'ХЕ
чем по теореме Фубини
j e*«(*>v (dg) \i(dx) = ^ v(x) [i(dx)
e'«*)v (dg) ц (dx) = J JI (g) v (dg).
Если для счетно-аддитивных мер равенство Парсеваля яв-
является теоремой, то для распределений на гильбертовом про-
23

странстве (определение этого термина сейчас будет приведено)
равенство Парсеваля служит для определения преобразования
Фурье (при этом именно справедливость равенства Парсеваля
для обычных счетно-аддитивных мер показывает, что такое
определение преобразования Фурье для распределений совпа-
совпадает— когда рассматриваемое распределение является обыч-
обычной счетно-аддитивной мерой — с определением преобразова-
преобразования Фурье для мер).
Перейдем теперь к описанию схемы, в рамках которой мож-
можно определить понятие распределения на ЛВП. Пусть Е — ве-
вещественное ЛВП, Е' — его сопряженное и наделенное тополо-
топологией, согласующейся с двойственностью между Е' и Е; пусть,
далее, &~(Е)—некоторое локально выпуклое пространство не-
непрерывных комплекснозначных функций на Е, содержащее
подпространство, состоящее из преобразований Фурье некото-
некоторых счетно-аддитивных мер на аЕ, причем множества Ш (яв-
(являющееся векторным пространством) тех мер, преобразования
Фурье которых являются элементами пространства £Г(Е), до-
достаточно для различения непрерывных ограниченных функций
на Е' (т. е. если / — такая непрерывная ограниченная функция
на Е', что для каждой меры [хеЯЛ, j fd[i — O, то /=0). &~(Е)-
распределением на Е называется линейный непрерывный функ-
функционал F :@~(Е)-*-С. Преобразованием Фурье распределения F
называется линейный функционал F на Ш, определяемый ра-
равенством: F(y)=F(v). В том случае, когда пространство 3JI со-
содержит все меры, сосредоточенные в одноточечных множествах,
преобразование Фурье можно считать функцией на Е'; значе-
значение этой функции Fv в точке у^Е' определяется равенством
Fv(g)—F(8g), где 6g — мера, сосредоточенная в этой точке. От-
Отметим еще, что так как 8g= [*>->• е*«<я)], то F<f(g)=F([x>~+ei8M]).
Следует подчеркнуть, что сейчас описана лишь самая общая
схема построения теории распределений на Е; в частности, из
принятых предположений отнюдь не вытекает, что по преобра-
преобразованию Фурье распределение определяется однозначно. Да-
Далее будет рассмотрен ряд реализаций этой схемы.
§ 3. МЕРА ВИНЕРА
Всюду далее, говоря о цилиндрических подмно-
подмножествах гильбертова пространства Я, предполагаем, если не
оговорено противное, что это — Я'-цилиндрические множества,
где Н! — сопряженное к Я пространство; при этом мы еще бу-
будем, как обычно, предполагать, что Я' отождествлено с Я (и в
связи с этим использовать также термин «Я-цилиндрическое
множество»). Сказанное относится и к терминологии, связан-
связанной с цилиндрическими функциями.
24

Итак, пусть Я— сепарабельное гильбертово пространство
(над полем вещественных чисел). Корреляционным оператором
гауссовской цилиндрической меры w на Я, обладающей корре-
корреляционным функционалом Ь, называется линейный оператор В
в Я, соответствующий функционалу b (это значит, что для всех
Х\, х2^Н должно выполняться равенство b(x\, х2) = (Вхи x2)).
Отметим, что в соответствии с только что сказанным мы счи-
считаем (отождествив Я' и Я), что функционал Ь определен на
НхН; фактически это означает, что мы рассматриваем гиль-
гильбертово преобразование Фурье. Из известного критерия счет-
счетной аддитивности произвольной неотрицательной цилиндриче-
цилиндрической меры в гильбертовом пространстве вытекает, что для
счетной аддитивности цилиндрической гауссовской меры необ-
необходимо и достаточно, чтобы ее корреляционный оператор был
ядерным.
Канонической гауссовской мерой на гильбертовом про-
пространстве называется гауссовская цилиндрическая мера v с ну-
нулевым математическим ожиданием, корреляционный оператор
которой является тождественным отображением. Если Р — ор-
ортогональный проектор в Я, dimР(Н)=п, А — борелевское под-
подмножество в Р(Н), то v(P-1(A)) = Bnyn/2 J e-{x'x)/2dx. В силу
только что сказанного, если гильбертово пространство беско-
бесконечномерно, эта мера не является счетно-аддитивной (так как
тождественное отображение бесконечномерного гильбертова
пространства в себя не является ядерным).
Пусть снова Я—сепарабельное гильбертово пространство
со скалярным произведением (•, •), В — положительно опреде-
определенный симметричный оператор в Я и пространство W2X=
=ш21([0, 1], Я) опредгляется так: ср<=1?У в том и только в том
•случае, если функция ср определена на [0, 1], принимает значе-
значения в Я, абсолютно непрерывна1, ф@)=0, и если существует
и конечен интеграл Я ||ф' (t)\\2dt. Равенство (ф, г|з) = Г (q/ (t)
"о о
ty'(t))dt определяет скалярное произведение в WV; всюду ниже
будем считать, что W2l наделено этим скалярным произведе-
произведением; относительно него оно является гильбертовым простран-
пространством.
1 Абсолютная непрерывность гильбертовозначной функции определяется
■совершенно так же, как и абсолютная непрерывность числовых функций.
Если пространство Н сепарабельно — что мы предполагаем, — то свойства
этих функций также оказываются аналогичными обычным. Для дальнейше-
дальнейшего можно принять следующее определение: функция f: [a, b] (а, bei?1)
называется абсолютно непрерывной, если существует такая интегрируемая
(по Бохнеру) функция g[a, b]->-Rl, что для всех te./?1 справедливо равен-
равенство /@ = Cg(t)dT + C.
25

Пусть еще v — гауссовская мера на W2\ обладающая нуле-
нулевым математическим ожиданием и корреляцион ф
налом Ь, определяемым равенством Ь(ф, г|з)=
о
существование последнего интеграла вытекает из неравенства
|Яр/@,'Ф'@К11^1111ф/@1111'Ф/@11 и того, что функция t^
-||ф'(ОН*11Ч)'(О11 интегрируема ввиду интегрируемости функ-
функций Л-Ч1<р'(ОИ2 и *-ЧЫ>'(ОН2- Пусть, наконец, СН=С([О, 1],
Н)—пространство всех непрерывных функций на [0, 1] со-
значениями в Н, наделенное нормой ||-|1с, определяемой, равен-
равенством ||cp||c = max||cp (t)\\H; относительно этой нормы оно явля-
является банаховым.
Мерой Винера на пространстве Сн с корреляционным опе-
оператором В называется С'н-цшшндрическая мера w на Сн, яв-
являющаяся образом гауссовской меры v на ш2' относительно ка-
канонического отображения фйУ2'-»-С2н, переводящего каждую
функцию, являющуюся элементом пространства w2l, в ту же
самую функцию, но рассматриваемую уже как элемент про-
пространства С([0, 1], Н).
Прежде всего, из этого определения вытекает, что мера Ви-
Винера с корреляционным оператором В является гауссовской
(так как ее преобразование Фурье имеет согласно предложе-
предложению 2.2, тот вид, который должно иметь пргобразование Фурье
гауссовской меры). Найдем теперь явную формулу для преоб-
преобразования Фурье меры Винера. Заметим прежде всего, что про-
пространство, сопряженное пространству Сн, можно описать так:
/еС'([0, 1], НLФ существует счетно-аддитивная Я-значная
мера V/ ограниченной вариации, такая, что Уф е Сн /(ф) =
= \(<p = (t}vf(dt)), где интеграл справа определяется как предел
интегральных сумм вида
(Ф (У. v/ (th, tk+1]), 0 = t0 < tL < . . . < tn+l = 1,
при
(существование такого интеграла можно доказать совершенно
так же, как доказывается существование интеграла Стилтьеса
от непрерывной функции по функции ограниченной вариации).
Далее, по предложению 2.2 w(f)=v(ty*f) (f^C'H), так что
J)'@, Wf)'(t))dt.
26

При этом непосредственно проверяется
(Ч>7) @ = J J v, (dg) dt = J v, ((т, 1 ]) dt.
О £ О
Поэтому
1 1
S(fl = exp(-$ Jmin(s, t)(Bvf(ds),vf(dt)))
о о
^эту формулу достаточно проверить для мер, каждая из кото-
которых сосредоточена в одной точке).
Это и есть та явная формула, которую мы хотели найти.
Приведем теперь еще два определения меры Винера (с кор-
корреляционным оператором В). С этого места предполагаем, что
корреляционный оператор этой меры является ядерным; как
будет видно из дальнейшего, ядерность корреляционного опе-
оператора является критерием счетной аддитивности меры Вине-
Винера. Обозначим через 5Г множество (линейных непрерывных)
функционалов на С([0, 1], Я), определяемое так:
fe^F^3fel[0, 1], f(<p)=<p(O(cpe=C).
Обозначим, далее, через w{ ^"-цилиндрическую меру, опре-
определяемую равенством (ниже gi^H, /ге[0, 1], щ, b^R1, i=\,
2,...,п, ty<t2<...<tn);
, 1], Я); (gh <р№))е=(аь bt); i = l, 2...я}) =
1
X
Bя)"/2 (<!(<„-<!) ... (tn-tn-i)I/2(b(g,., ft) ...b(gngn))l/2
n л i —•__?—ii .. —tlzl
al an
Теорема З.1. ^"-цилиндрическая мера w{ совпадает с су-
сужением на %&{С) меры Винера с корреляционным операто-
оператором В.
Доказательство. Достаточно проверить, что на SBEГ)
совпадают преобразования Фурье этих мер. Но обе эти ме-
меры — гауссовы (для меры w это было показано выше, а для
меры W\ это вытекает из также приведенного выше критерия
гауссовости цилиндрической меры, согласно которому для то-
того, чтобы SB {ЗГ) -цилиндрическая мера была гауссовской, до-
достаточно, чтобы всякий линейный функционал из SB(&~) пере-
переводил ее в гауссовскую меру на прямой; в рассматриваемом
случае, как можно показать с помощью прямого вычисления,
это действительно так). Поэтому для того, чтобы доказать
совпадение их преобразований Фурье, достаточно доказать,
27

что совпадают их корреляционные функционалы (математиче
ские ожидания обеих мер, очевидно, равны нулю). Но корреля
ционный функционал меры w{ определяется так: если gu
^ (т. е. £,(ф)=ф(/,)), то
ф). £2(ф)^i№р) = (Bgv g2)m\n(tl, t2)
(это равенство проверяется прямым вычислением с использо-
использованием приведенного только что определения wx). Таким обра-
образом, w{(g)=w(g) при g^3?(&~), что и требовалось.
Отметим еще, что с-алгебра, порожденная в Сн^-цилиндри-
ческими подмножествами, и, а-алгебра, порожденная С'я-ци-
линдрическими подмножествами, совпадают каждая с а-алгеб-
рой борелевских подмножеств; поэтому, так как ffi'i счетно-ад-
счетно-аддитивна (это еще предстоит доказать), то она однозначно
продолжается до меры на а-алгебре борелевских подмножеств;
так как мера w{ на %.& совпадает с мерой Винера w (с кор-
корреляционным оператором В), то и продолжения этих мер сов-
совпадают; именно поэтому определение меры Ш[ можно рассмат-
рассматривать как еще одно определение меры Винера. Отметим по-
попутно, что из сказанного вытекает еще один факт: именно, для
доказательства счетной аддитивности С//-цилиндрической ме-
меры Винера с корреляционным оператором В достаточно дока-
доказать счетную аддитивность ге сужения на алгебру ^"-цилиндри-
^"-цилиндрических множеств (проверьте это).
Продолжение (счетно-аддитивной) цилиндрической меры W\
на о-алгебру М борелевских подмножеств С([0, 1], Н) назы-
называется (борелевской) мерой Винера на С([0, 1], Н) (с корре-
корреляционным оператором В).
Прежде чем перейти к третьему определению меры Винера
(которое одновременно позволит нам установить ее счетную-
аддитивность), введем еще один объект. Пусть Ж — произве-
произведение счетного числа экземпляров пространства Н и \i — бо-
релевская мера на Ж, представляющая собой произведения
счетного числа экземпляров гауссовской борелевской меры vb
на Н с нулевым математическим ожиданием и корреляционным
оператором В. Так как оператор В ядерный, то каждая из мер-
сомножителей счетно-аддитивна; поэтому счетно-аддитивна на
полукольце подмножеств вида X {Аъ . . . , Ah) = {(hn) е Ж '■ hllh e
еД, &=1, 2, ...у} (Ак — борелевские множества в И) и
мера (хь определяемая для каждого такого множества равен-
/
ством \nl(X(Al, ... ,Aj))=\l vB(Ak). Следовательно, ее счетно-
k=\
аддитивное продолжение на порожденную этим полукольцом
о-алгебру (она совпадает с о-алгеброй борелевских множеств
в Ж) существует и единственно; это продолжение и является
тем самым произведением счетного числа экземпляров гауссов-
гауссовской борелевской меры, которое мы обозначили символом ц.
28

Пусть F — отображение некоторого подмножества G про-
пространства Ж в С(@, 1], Я), определяемое равенством
1
2 sin kt
(G — это подмножество тех элементов (*л:/г=0, 1, 2, ...) про-
пространства Ж, для каждого из которых ряд, фигурирующий в по-
последнем равенстве, сходится и определяет непрерывную функ-
функцию аргумента t, т. е. элемент пространства Сн). Покажем сей-
сейчас, что [j,(G) = l. Положим
п-\
и imn= max \smn(x)(t)\,
тогда
Я?
Ho
поэтому
k—m
tmn < max
у _£
n-\
Xk+1
R
k=m
n—m—\ m—l—l
SJ^+2SIS
/> хш)
j=m
u)u+
re—1
m—I—1
(Xj,
* /=.m
2y/2:
n—1
n—m—1 n—/—1
L
(trB)*
—+ 2(/i — m)
nr
(/J (/ +
— m \ 1/2
1/2
trfl.
re-\ 2" (
oo;
Следовательно, на подмножестве Ж полной меры \i исходный
ряд сходится равномерно; иначе говоря, множество G тех
29

{)Ж, для которых функция t^-F({xn)) (t) непрерывна, име-
<ет меру единица. Но если glt g2^@~, то
gi ((f (*)) @) £2 (F (x) @) Ф = —
я
Таким образом, корректно определено (на множестве полной
меры) линейное отображение F пространства Ж в СН', при этом
если А — ^"-цилиндрическое подмножество Сц, то F~lA — бо-
релевское подмножество в Ж. Поэтому можно определить
^"-цилиндрическую меру v в Сн как образ ц при отображении
F. Эта мера является гауссовской (это доказывается аналогич-
аналогично тому, как выше проверялась гауссовость меры Винера), и
ее корреляционный функционал совпадает с корреляционным
функционалом меры Винера (а математическое ожидание рав-
равно нулю). Поэтому v — это мера Винера.
Пусть Ео — гильбертово пространство, р — каноническая
гауссовская мера на Ео (гауссовская цилиндрическая мера с
тождественным корреляционным оператором и нулевым мате-
математическим ожиданием).
Будем говорить, что полунорма p:E0—*-R измерима относи-
относительно меры р, если для любого положительного е существует
такой ортогональный проектор Ро на конечномерное подпрост-
подпространство пространства Я, что для любого другого ортогонально-
ортогонального проектора Р на конечномерное подпространство, ортогональ-
ортогонального к проектору Ро, имеет место неравенство
Будем говорить, что норма II • || на пространстве Ео измери-
измерима, если она является измеримой полунормой относительно ме-
меры р.
Теорема 3.2. Если норма II • || измерима на пространстве
Ео и Е — пополнение пространства Ео по норме \\-\\, то мера р
порождает счетно-аддитивную борелевскую меру на простран-
пространстве Е с нормой 11-11, и, наоборот, если мера р порождает счет-
счетно-аддитивную меру на пространстве Е, то норма II ■ II измерима.
Доказательство можно прочитать в книге Х.-С. Го.
Пусть Н — гильбертово пространство со скалярным произ-
произведением (•, -)н и нормой || -\\н, еи ..., еп, ... — ортонормиро-
ванный базис в пространстве Н, Т — положительно определен-
определенный самосопряженный оператор Гильберта — Шмидта, удов-
удовлетворяющий равенству Ten—"knSn Vn (kn^R)- Отметим, что
тогда 1п>0 я
л=1
.30

Обозначим через Со ([О, t], Я) пространство всех непрерыв-
непрерывных отображений х:[0, ty+H (t>0), таких, что х(^)=0. Введем
норму 11-11 на пространстве С0([0, t], Я), полагая
|= max
для любых хеС0([0, t], Н). Пространство С0([0, t], Я) банахо-
банахово относительно нормы II ■ |(.
Обозначим через F линейное подпространство пространства
Со([0, t], Я), состоящее из всех отображений х:[0, t]-*~TH, для
которых почти всюду существует производная х'(т)еГЯ и вы-
выполнено условие
На пространстве F определим скалярное произведение, полагая-
(х,у)=((Т-1х'(т), T~xy'(x))Hdx.
Пространство F будет гильбертовым по отношению к скалярно-
скалярному произведению (,).
Если теперь положить E0=F, Е=С0(@, t], H), то норма ||-||
будет измерима, а мера р порождает счетно-аддитивную вине-
ровскую меру на пространстве С0([0, t], H).
§ 4. КВАЗИМЕРЫ
Введенное выше понятие цилиндрической меры
не охватывает конструкций, связанных с «мерой Фейнмана».
Чтобы включить и этот случай в рассматриваемую теорию,
вместо алгебры всех цилиндрических множеств рассмотрим ее
подалгебру, которую сейчас определим. Итак, пусть, как и рань-
раньше, Е — векторное пространство, G — некоторое векторное
пространство линейных функционалов на Е. Для каждого пе
ei\/ и каждого набора gu ..., gn^G элементов из G обозначим
символом Fgl...gn отображение E^>~Rn, определяемое так:
Fb---gn(x)=(gi(x)> ■ • • >8п(х))- Пусть, далее, ЯМ — алгебра под-
подмножеств Rn, определяемая так: Ле^п"<=>Л или Rn\A — огра-
ограниченное борелевсксе подмножество Rn. Обозначим, далее, че-
через 5tg,...gs алгебру множеств /*&!..«„(Ял), и пусть Ufo =
= U &«!• ••«„'» %в представляет собой алгебру подмножеств Е;
n.g,...en
ее элементы мы будем называть скалярно ограниченными G-ци-
линдрическими подмножествами пространства Е. G-цилиндри-
ческой квазимерой на W будем называть всякую меру v (т. е.
аддитивную функцию) на W, обладающую следующим свойст-
31

вом: каковы бы ни были n^N, gu ..., gn^G и ограниченное
борелевское множество BcRn, сужение v на о-алгебру подмно-
подмножеств множества Pgl...gn(B), состоящую из всех множеств вида
F7t---en(V)' гДе У — борелевское подмножество Rn, содержа-
содержащееся в В, счетно-аддитивно.
Но, будучи образом счетно-аддитивной меры ц, мера v так-
также счетно-аддитивна. Таким образом, доказана следующая
Теорема 4.1. ^"-цилиндрическая мера Винера на
С ([0, 1], Я) с некоторым ядерным корреляционным оператором
В счетно-аддитивна.
Отметим, что ядерность В и необходима для счетной адди-
аддитивности этой меры.
Пр и м гр 1. Пусть E=Rn. Квазимера v на URn называется
(невырожденной) квазимерой Фейнмана (классической), если
существуют такие симметричный положительно определенный
оператор В в Rn (называемый корреляционным оператором ква-
квазимеры v) и элемент a^Rn, называемый математическим ожи-
ожиданием (или средним) квазимеры v, что, каково бы ни было
ограниченное борелевское подмножество AcRn,
'112 f c-
v (А) = BяГ"/2 (det В)'112 f
i
*-я>.*-я)/2 dx
(как и выше, det В — определитель матрицы оператора В з
стандартном базисе). Для борелевского подмножества АаВп,
обладающего ограниченным дополнением Rn\Ay полагаем
v(A) = \—v(Rn\A).
Пример 2. Пусть снова E=Rn, причем размерность п чет-
четна. Симплектической квазимерой Фейнмана на Rn называется
квазимера v на /?", значение которой на каждом ограниченном
борелевском подмножестве AcRn определяется равенством
y{A)=[el(x'z) dxdz; ее значение на борелевском подмножестве
А
AczRn, обладающем ограниченным дополнением, определяется
равенством V(A) = \— v(Rn\A) [x, z^Rn, (x, z) =
Пример 3. Пусть Я — бесконечномерное гильбертово
пространство со скалярным произведением (•, •). Стандартной
квазимерой Фейнмана на Я называется Я-цилиндрическая ква-
квазимера \ф на Я, определяемая так: если Р — ортогональный
проектор Я на конечномерное подпространство Нп пространст-
пространства Я (dim#n=/z), и Л — ограниченное борелевское подмноже-
подмножество в Я„, то
1 А) = Bя)~ ~ \e~l ~ dx.
32

Сейчас мы опишем те цилиндрические функции, которые
можно интегрировать по G-цилиндрическим квазимерам. G-ци-
линдрическую функцию / назовем финитной, если f(x) =
=<p(gi(x), ..-, gn{x)), где gx, ..., gn^G и <р — финитная функ-
функция на Rn (функция на Rn называется финитной, если замыка-
замыкание множества тех точек из Rn, на которых значение ф отлично
от нуля, представляет собой ограниченное подмножество в Rn).
Интеграл от цилиндрической финитной борелевской функции по
цилиндрической квазимере определяется совершенно так же,
как и интеграл от цилиндрической борелевской функции по ци-
цилиндрической мере.
Обозначим через S)o множество всех финитных цилиндри-
цилиндрических функций f вида f(x)=<p(gx(x), ... gn(x)), где «р — фи-
финитные бесконечно дифференцируемые функции на Rn. \п=
= 1, 2, ...) (таким образом, (p—&>(Rn)). Непосредственно про-
проверяется, что каждая такая цилиндрическая функция является
преобразованием Фурье меры, сосредоточенной на подпростран-
подпространстве пространства G, порожденном функциями gi, ..., gn; в
том случае, когда эти функции линейно независимы, она обла-
обладает плотностью относительно меры Лебега на этом простран-
пространстве (порождаемой выбором элементов gu ..., gn в качестве
ортонормированного базиса); плотность является (конечномер-
(конечномерным) преобразованием Фурье функции ф. Это обстоятельство поз-
позволяет определить преобразование Фурье G-цилиндрической
квазимеры на Е. Именно преобразованием Фурье такой квази-
квазимеры v называется функция v на G, обладающая следующим
свойством: каковы бы ни были gu ..., gn^G, образующие ли-
линейно независимое семейство, и какова бы ни была функция
q<==2)(Rn), если Vze^R"
ф(;Г Zkgh)= )e dx1...dxn
то
I "vB zhgh) 5 B zhgh) dzt... dzh = j Ф(^ (хг), ...,gn (xn))dv.
Иначе говоря, преобразование Фурье определяется с помощью
равенства Парсеваля. Следует подчеркнуть, что не всякая ква-
квазимера обладает преобразованием Фурье в этом смысле. Стан-
Стандартная квазимера Фейнмана на Н преобразованием Фурье об-
обладает; оно определяется равенством
; и.*)
v(x) = e~ 2 . 2
1 (е*) — базис в Е, биортогональиый семейству g>: gs(er)=Ssr-
2 Преобразованием Фурье произвольной квазимеры можно — естествен-
естественным образом — определить как функционал на комплексификации простран-
пространства Н\ однако такое определение нам а дальнейшем не понадобится.
2 Зак. 273 33

Для цилиндрических квазимер имеют смысл конструкции,
описанные выше для цилиндрических мер. В частности, для
них естественным образом определяются образы при линейных
отображениях, которые оказываются связанными с операцией
преобразования Фурье той же самой формулой, что и приведен-
приведенная в предложении 2.2 предыдущего параграфа для цилиндри-
цилиндрических мер. В реальных задачах квазимеру Фейнмана удобна
задавать с помощью ее преобразования Фурье. В частности, ес-
если Е — векторное пространство, G — векторное подпространст-
подпространство его алгебраического сопряженного и Ъ — билинейный функ-
функционал на GxG, то G-цилиндрическая квазимера Фейн-
Фейнмана на Е с корреляционным функционалом b (и ну-
нулевым математическим ожиданием), это по определению
G-цилиндрическая квазимера w, преобразование Фурье
которой определяется равенством w(g)=exp(—ib(g, g)).
Аналогично определяется квазимера Фейнмана и с не-
ненулевым математическим ожиданием. Если Е — гиль-
гильбертово пространство, G=E'(=E), то вместо корреляцион-
корреляционного функционала удобно говорить о корреляционном операто-
операторе В, определяемом равенством (Вх, х)—Ь(х, х). Если Си—
=СA[0, 1], Н) и Сн'=(С([0, 1], Я))' —то же, что и в предыду-
предыдущем параграфе, то Сн'-цилиндрической квазимерой Фейнмана
на Сн с корреляционным оператором В (:#-»-#) называется
Сн'-цилиндрическая квазимера w на Си, корреляционный функ-
функционал которой определяется равенством w(f) = exp(—i f X
о
i
X \ min (s, t)\ vf (ds) vf (dt), где используются обозначения, совпа-
о
дающие с применявшимися в случае мгры Винера.
§ 5. ГЛАДКИЕ МЕРЫ, ОБОБЩЕННЫЕ МЕРЫ
И ОБОБЩЕННЫЕ ФУНКЦИИ
Пусть ц, — счетно-аддитивная мера на локаль-
локально выпуклом пространстве Е, А — борелевское подмножества
пространства Е, h — вектор из пространства Е. Будем говорить,
что число dh\x,(A) является производной по направлению h ме-
меры \i на множестве А, если
dhlx (A) = \im ± (\i (A+ th)-ii (А)).
Меру | на пространстве Е назовем производной меры \i по на-
направлению h и обозначим ее символами dh\i, если для любога
борелевского подмножества А пространства Е выполнено ра-
равенство
34

Ютметим, что если мера |j, счетно-аддитивна и для каждого бо-
релевского подмножества А существует производная dh\x,(A),
чо мера \i дифференцируема по направлению h.
Пусть Е, F — локально выпуклые пространства, находящие-
находящиеся в двойственности <.Е, F>, и их топология согласована с двой-
двойственностью.
Для каждой счетно-аддитивной меры ц на пространстве Е
определим ее преобразование Фурье |j,:.F->-C, полагая
Если мера |j, дифференцируема по направлению h и счетно-ад-
счетно-аддитивна, то имеет место равенство
Отметим, что если мера \i счетно-аддитивна на пространстве Е,
то функция [i:F-*-C будет непрерывна и ограничена.
Пусть М(Е) —некоторое линейное пространство мер на про-
пространстве Е с локально выпуклой топологией, находящееся в
двойственности с пространством Сь(Е):
где Сь{Е) — пространство всех непрерывных ограниченных
функций на Е.
Обозначим через М'(Е) топологически сопряженное про-
пространство к пространству М(Е), и его элементы назовем обоб-
обобщенными функциями. Легко видеть, что имеет место канониче-
каноническое вложение Сь(Е)^>М'(Е).
Аналогично определим пространства обобщенных функций.
Пусть &~(Е) — некоторое линейное пространство непрерывных
•ограниченных функций, наделенное структурой локально вы-
выпуклого пространства и находящееся в двойственности с про-
пространством М(Е):
V\ie=M(E),
где М(Е) — пространство всех счетно-аддитивных мер на про-
пространстве Е. Обозначим через &~'(Е) топологически сопряжен-
сопряженное пространство к пространству 3^(Е), а его элементы назо-
назовем обобщенными мерами.
Легко видеть, что существует каноническое вложение
(Е)9"(Е)
35

Точно так же определяют пространства обобщенных мер и
обобщенных функций на пространстве F.
Так как для любого A'ef функция е/,':£->-С, задаваемая
равенством ен-{х) = i (x, h'), принадлежит пространству Сь(Е),.
то можно определить преобразование Фурье для обобщенных
мер %^ЗГ' (Е):
|(А')= .!(«*-).
если пространство & (ей-) содержит подмножество {ен> '■ h' e F).
На пространстве М'(F) также можно определить преобра-
преобразование Фурье как сопряженное отображение
M'(F)r*M'(F)
к отображению
M(E)-+M(F), |i^jT.

ГЛАВА II
Различные определения интегралов
Фейнмана
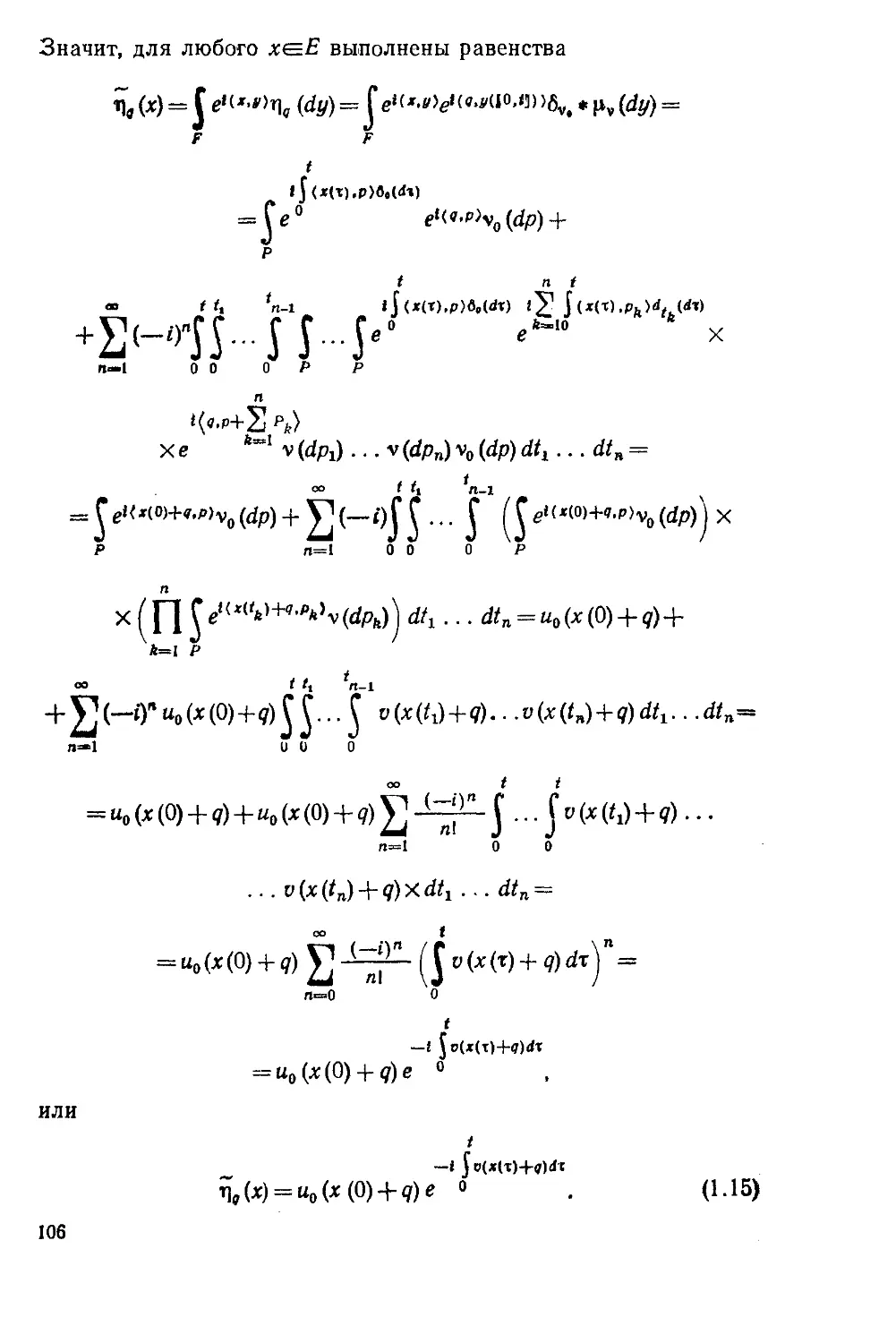
§ 1. ИНТЕГРАЛЫ ФЕЙНМАНА КАК ПРЕДЕЛЫ
КОНЕЧНОКРАТНЫХ ИНТЕГРАЛОВ
Пусть Е — сепарабельное банахово пространст-
пространство с нормой 11-11, Ео — линейное подпространство, плотное в Е,
Ь — вещественная квадратичная форма на Ео, Еп — последо-
последовательность конечномерных подпространств пространства Ео,
удовлетворяющих условиям:
1) Еп+х^зЕп,
2) для любого п сужение Ь на Еп не вырождено;
оо
3) линейное подпространство £«, = \J En плотно э Е.
Зададим на каждом Еп меру Лебега Кп и положим
„ = lim \ e 2 Kn (dx).
Рассмотрим функцию f:Eoc-+C, сужения на Еп которой измери-
измеримы по Лебегу и для них существуют пределы
/„(/) = lim \f(x)e 2 K(dx).
Определение 1.1. Скажем, что функция / интегрируема
по мере Фейнмана Фь1, если существует предел
при этом величину Фь'(/) назовем интегралом Фейнмана и обо-
обозначим через V f {х)ф\{йх).
Замечание 1. Мерой Фейнмана является обобщенная ме-
мера Фб1, определенная на пространстве всех функций, для кото-
которых определены интегралы Фейнмана. Отметим, что из свойств
(пределов следует линейность интеграла Фейнмана, поэтому это
.пространство функций будет линейным.
Замечание 2. Определение меры Фейнмана зависит от
выбора последовательности конечномерных подпространств Еп,
37

Пусть квадратичная форма Ъ удовлетворяет условиям:
А1) существуют подпространства Еол и Е0,2 пространства Ео и
неотрицательные квадратичные формы Ьи Ъъ на Ео, такие, что
А2) £o,ifl£o,2=O (замыкание берется в Е), Е0,\®Е0,2=Е;
A3) квадратичная форма a=bx + b2 невырождена и определяет
скалярное произведение (-, •) на Ео, причем пространство Ео—
гильбертово и подпространства £0,i и Е0>2 ортогональны между
собой;
А4) гауссовская мера цй, порожденная квадратичной формой а
(с нулевым средним), счетно-аддитивна на пространстве Е,
-т. е. норма II • II измерима в гильбертовом пространстве Ео.
Пусть также F — банахово пространство и существует двой-
двойственность <£,/•"> между пространствами Е, F, тогда существует
непрерывное отображение T:F-*-E, сопряженное к вложению
Е$-*~Е. Так как подпространство Ео плотно в пространстве Е,
то отображение Т инъективно.
Отметим, что в силу условия (А2) пространство Е являет-
является прямой суммой подпространств Еол, £0,2- Определим для
а>0 отображение 1а;Е-+Е, полагая
для любых Xie£0,i и
Пусть М — конечномерное подпространство пространства
Ео, удовлетворяющее равенству Л1= (Affl^o.i)® (^П^о.г) • На про-
пространстве задано скалярное произведение, индуцированное из
пространства Ео. Комплексификацию пространства М обозна-
обозначим через Мс. Аналитическое продолжение по параметру а на
С\{0} и С-линейное продолжение по переменной линейного опе-
оператора 1а обозначим через 1ас.
Лемма 1.1. Если р:Мс^-С — полином, то для любой точ-
точки xgM имеет место равенство
— ib(x) оо J—ib(x)
р(х)е2 =£р,(Ш)е2 , A.1)
где D — оператор дифференцирования по пространству М,
Pk — полиномы на пространстве Мс, определяемые равенством
\ Г/Г Г\\Ь О V™»™»-* *
■ JL X)W ■ Л #• ^) е ]dx
BЯ) 2 Af C C
A.2)
(N — размерность пространства М).
38

Доказательство. Положим А = I n . В силу свойств
'полиномов Эрмита имеем равенство
(х,х) оо (х,х)
р(Ах)е 2 =Y,Ph(iD)e 2 О-3)
fe=0
для любых точек х из пространства М, где
- — (*,*)
]dx. A.4)
Отметим, что если k больше порядка полинома р, то р* = 0.
Поэтому бесконечная сумма в равенстве A.1) имеет конечное
число ненулевых членов.
Обозначим через Ьс аналитическое продолжение квадратич-
квадратичной формы Ъ с пространства М на пространство Мс. В силу ра-
равенства (х, х)=—ibc(Ax) для любых хеМ и аналитичности
обеих частей равенства A.3) получим тождество
— ibc AсАх) со —ibcUCAx)
p{IcaAx)e2 " =Ер((/£г'Ш)е 2 " ' A.5)
для любых точек хеМ и любых чисел аеС\{0}. Положим
а = г— и Pk{y)=pk{Ay). Тогда равенство A.5) влечет равен-
равенство A.1), а формула A.2) следует из равенства A.4).
Обозначим через || • ||0 норму в пространстве Ёо, порожден-
порожденную скалярным произведением (•, •).
Наложим дополнительные ограничения на последователь-
последовательность конечномерных подпространств Еп, требуя выполнения
равенства Еп={Еп[\Еол)®{Еп?\Ео^) при любых п.
Предложение 1.1. Пусть р:Е-+С — полином порядка
m, |j, — счетно-аддитивная мера на пространстве F, удовлетво-
удовлетворяющая условиям
+ °o A.6)
при k=\, ..., т.
Тогда функция f:E-*~C, определенная равенством
39

будет интегрируемой по мере Фейнмана Фь1, причем
A.7)
— ib(Ty)
2
k=0 F
где
^
, D)kp(x)]va(dx). A.8)
Доказательство. Введем фактор-пространство /7П=
=F/EnL (E±={y^F:Yx^En <x, г/>=0}), проектор nn':F-+Fn и
ортогональный проектор я„ : Е0-+Еп в гильбертовом простран-
ве Ео. Двойственность <.Е, F> порождает двойственность
<£„, Fn). Скалярное произведение (•, ■) в Еп определяет изо-
изоморфизм /„:/*'гг*~Еп. Обозначим через \in образ меры \i_ в про-
пространстве Fn относительно отображения л/ и через ц-n образ
меры fi« в пространстве Еп относительно отображения \п. Имеет
место равенство
?» = (*•("«« Л- (!-9)
Нормы в пространствах F, Fn обозначим соответственно симво-
символами Ц-llf. H"llfn- В силу неравенства A.6) и оценки ||яп{/||/?п^
^ \\У\\р Vy^F для любого п выполнено неравенство
при й=1, ..., т.
Для каждого е>0 и любого натурального п определим меру
г\г,п на пространстве Еп, преобразование Фурье которой задано
в пространстве Еп и имеет вид Щ,п{х) — e~~^w. Оценка A.10)
влечет выполнение неравенств
для любых е>0 и натуральных п при k=l, .... m. Положим
Bя)
Bя)
X [[(Iе. „ x', D)p(Ic. я х)]е 2 l*'', A.12)
i el- el~
40

где N(n) — размерность пространства Еп, k—0, 1, ..., т. Из
леммы 1.1 и равенства Парсеваля следуют равенства
Отметим, что существование интегралов
- — ib(x')
2
следует из оценки A.11).
Переходя к пределу при е-»- + 0 в равенстве A.13) и учиты-
учитывая оценку A.10), получим
В силу равенства A.9) имеем
т
A.14)
fc=0 F
Из равенства A.12) следует
pk(y) = limpk.n(nnTy) VytEF, A.15)
где полиномы ри определены равенством A.8).
Учитывая A.14) и A.15), получим
т .
-—1Ъ(Ту)
pk(y)e 2 v(dy),
S F
что влечет равенство A.7) и интегрируемость функции / по ме-
мере Фейнмана Ф&1.
Определим линейное пространство РМ, как линейную обо-
оболочку в пространстве С(Е) всевозможных функций вида рц,
где р — полином на пространстве Е со значениями в С, а ц —
счетно-аддитивкая мера на пространстве F, удовлетворяющая
условию
41

для любых натуральных k, не превосходящих порядка полино-
полинома р, и jx — преобразование Фурье меры ц, определенное в
пространстве Е.
Теорема 1.1. Если функция f принадлежит пространству
РМ, то существует интеграл f f(x)Ol(dx).
Доказательство теоремы непосредственно следует из линей-
линейности интеграла Фейнмана и предложения 1.1.
Положим для каждого натурального п
— ib(x)-t{x,x)
Сп= lim \е2 dx.
г-Ы-0 „0
Возьмем произвольную функцию f:Ex-*-C, сужения на Еп ко-
которой измеримы по Лебегу и имеют пределы
1 "■'•' &{x,x)
/„(/)= Нт \f{x)e* dx.
Определение 1.2. Скажем, что функция f интегрируема
по мере Фейнмана Ф&2, если существует предел
E-+o Cn
при этом величину Ф*2(/) называем интегралом Фейнмана и
обозначаем через f f(x)<bl(dx).
Замечание. В определении предполагается, что квадра-
квадратичная форма Ь удовлетворяет условиям (А1) — (А4).
Для каждого г>1 определим открытое множество Ur в С,
полагая
U2 = {а е С: 1/г < | а | < г, 0 ■< arg а <С я/4}.
Через Ur будем обозначать замыкание множества Ur в С.
Введем пространство функций &~Ur, состоящее из всех функ-
функций у:Е-*-С, таких, что для каждой из них существует функ-
функция g:OaxE-*-C, непрерывная на UaxE, удовлетворяющая ра-
равенствам
g(\, x) = <p(*) Vxef,
g(a$, x) = g(P, /ax)Vxe£,
аналитичная по первому аргументу на множестве Ur при лю-
любом фиксированном значении второго аргумента из Е, имею-
имеющая непрерывную на множестве UrxE частную производную
£с/(а, х) и для которой также функция g(a, x) е-*И2 и
g<x,{a,x)e-zW При Ve>0 ограничены на пространствах UrXE и
42

соответственно. Функцию g называем продолжением
функции ф на множество UrXE.
Для каждой функции (p^@~Ur зададим число
= inf
6>0LVJ ■ '/ X£E
где g — продолжение функции ф на множестве VrxE.
Лемма 1.2. Если функция <р принадлежит пространству
3?~Ur, то для каждого натурального числа п определены поли-
полиномы
— ib(x)-e(x,x)
рп,к,г{х')= \е2 ф (•*)(*, x'fdx
на пространстве Еп при любом. е>0 и любом целом k>-0 и
имеют место оценки
JL
|Pri,ft,E (х')|< 2 2 1/^!|С;|/(ф)||х'1|о* A.16)
при Yx'^En, кроме того, для любых х'^.Еп и k^O существует
предел
pn,k(x')= limpn,k,e(x')
и выполнено равенство
' ~, х)(х, IciJLx')e~~^'dx, A.17)
Bя)
где g — продолжение функции ф на множество UrxE, а ска-
скалярное произведение (•, •) по аналитичности продолжается на
ЕпсхЕпс (Епс — комплексификация пространства Еп).
Доказательство. Возьмем число т, удовлетворяющее
неравенствам 0<т<я/4, и произвольное е>0. Пусть k — про-
произвольное неотрицательное целое число. Положим для любого
Е
I — Ь(х)-г(х,х)
qAx')=\ e 2 (х, x')kg(ei\ x)dx.
Обозначим через /(а) определитель матрицы, задаваемой в
произвольном ортонормированием базисе пространства Еп ли-
линейным отображением /а J£a : Еа-*-Еа. Функция / имеет анали-
аналитическое продолжение на множество С\{0}. Это аналитическое
43

продолжение также обозначаем символом /. Для любой точки
х'^.Еп и любого а>0 выполнено равенство
— Щ1ах)-еAах,1ах)
, x)(x, 1ах'Ге2 dx. A.18)
п
Ограниченность и непрерывность функции g{a, х)е ° на
VrXEn при любом 6>0 влечет непрерывность функции
— ibc(I^x)-e(I^x,I^x)
(ot£i\ х)(х, Icax')ke2 а а а dx
на множестве {e-ixt]r){\Ur при каждом фиксированном
а ограниченность и непрерывность функции ga(a, x)e "на
UrXEn при любом 6>0 влечет ее дифференцируемость на мно-
множестве (e-ixUr)(]Ur, откуда следует ее аналитичность. Кроме
того, эта функция будет постоянна при l/r<a<l/r в_ силу
{1.18), следовательно, она постоянна на множестве e~'xUr. По-
Поэтому
gx(x)= J(e \T>) I g{e ~, *)(*, Iе. (JL_x] x')k х
— ibC (Iе x)—e (Iе x, Iе x)
xe ° U ] ° U > ° U ' dx. A.19)
Переходя к пределу в равенстве A.19), получим
i — .. i — r -~(x,x)~eib(x)
pn,k,e(x') = J(e 4^ "'" * ^<v 'C ^" 2
iV(fi)
и в силу равенства Сп = J (е 4) Bя) 2 (Л/ («) — размерность про-
пространства Еп) имеем
я
4 x) v
Bя)
г (х.х)—кЩх)
X (х, Ict „х')е 2 dx. A.20)
44

Равенство A.17) следует из равенства A.20) при переходе к
пределу е-*-+0. Из равенства A.20) следует неравенство
\pn.k.e(x')\<\C'n\
Bл) 2
i —
X С \g(e *, x)\-\x, ICiJLx'\ki
V л
Применяя неравенство Коши — Буняковского, получим
.|р„.М(*')!< \С'п\( ~- f \g(e ~, х)\Ч~~(Х'Х)dxV X
\ Bя) 2 Еп )
v / . Г \(г 1 л r'1la*f>2 ' Hy\ 2 Л 91\
V Bя)"^" £n e /
Для любого 6>0 имеет место оценка
.Я 1 ,
4 v-U2 л 2
Af(ra)
Bя) 2
я
i — If»
[sup(|g(e * , x)\e-6M\')f \e2®We 2
Bя)^ En
<I[sup(|g(e 4 , x)|e-e'l*ll')]a I e26' x>\* \ia(dx),
x£E J
юткуда следует неравенство
.я 1
A.22)
'Возьмем в пространстве Еп ортонормированный базис 1\, ...
..., 1ы(п), такой, чтобы вектор / г л х' принадлежал бы линей-
е *
ной оболочке векторов еь бг в пространстве Епс, при этом пред-
предполагается, что вектор х'¥=0 фиксирован. Координаты вектора
Е обозначаем символами
45

Пусть х/, х2' — комплексные числа, удовлетворяющие равен-
равенству
Тогда имеют место равенства
.С ' II С '
е 4
откуда
ТС '\ 2 / 2/ 2 2ч
, 4
Следовательно,
— — (х,х
Bя) 2 £п
-j-oo -j-oo I 2 2
<~IU'lloft f f (*? + *«)e™ *' Vdxldxa=2*||*'|lo*.
2я J J
—OO —00
и, учитывая оценки A.21), A.22), получим неравенство A.16).
Обозначим через Mi (F) пространство всех счетно-аддитив-
счетно-аддитивных комплекснозначных мер на пространстве F, удовлетворяю-
удовлетворяющих соотношению
k_
; + оо, A.23>
где Сг — норма линейного отображения T:F-*-E0 (в простран-
пространстве Ео берется норма II-Но).
Предложение 1.2. Если функция f:F-*-C имеет вид f—
=ф-|я, где [I — преобразование Фурье меры ii^M{(F), а функ-
функция ф при некотором г>\ принадлежит пространству @~Ur, та
функция f интегрируема по мере Фейнмана Фь2 и имеет место
равенство
x)=j? $pk(y)\i(dy), A.24)
ft=O F
где
^\(e \ x)(x, ICiJLTy)iia(dx) A.25)-
4
и g — продолжение функции ф на множество Ur-xE-
46

Доказательство. Для любого натурального п и про-
произвольного е>0 имеют место равенства
f ei(x,x')e2 (f(x)dx =
ft=0
. —'*(*)—е(х.х)
) в2
I
—(x,x)—tib(x)
2 dx.
2 Еп
е A.26)
Последнее равенство следует из равенства A.20). Отметим так-
также, что сходимость ряда следует из оценки A.16) для любого
'Еп. Положим
— ib(x)-R(x,x)
<p(x)dx.
Из леммы 1.2 и равенства A.26) следует для любого е>0
оценка
оо ft
Н
Применяя равенство Парсеваля, получим равенства
— Щх)-е(х.х)
2 f()
откуда в силу A.26), A.16) и A.23) имеем
К
где
Рп,кЛх')=\ е2 Ф(*)(*. x'fdx.
К
Переходя к пределу при е->-+0 в равенстве A.27), получим
•».*(*')i*n <«**'). A-28)
47

где функции рп,к определяются формулой A.17). Положим
PnAx')=-^-Pn.k(x') Vx'<=Fn A.29)
k\Cn
и, заменяя интегрирование по мере ц,п на интегрирование по
мере ц, получим
\ A-30)
ft=0 F
В силу A.17) и A.29) следует соотношение
\xmpn,k{nnTy)=pk{y), A.31)
п~*оо
где функция pk определена соотношением A.25). Из равенств
A.30), A.31) и оценок A.27), A.23) вытекает
00
iim-i-/;</)=у; {
л fc=0 F
что влечет равенство A.24).
Пусть <PU= U <^"f/r.
Для каждого 6>0, удовлетворяющего соотношению
на пространстве ЗГИ определим норму U, полагая
i—
/в(Ф)=[ sup (er*'W'\g(e *,x)\
где g — продолжение функции <р. Зададим в пространстве
Mi(F) норму 1м равенством
оо k
k=0
Возьмем линейную оболочку LTM всех функций / из про-
пространства С(Е), представимых в виде /=фм-, где функция ср
принадлежит пространству &~U, a \i — преобразование Фурье
меры [I из пространства Mi(F). Для каждого 6>0, удовлетво-
удовлетворяющего условию A.32), введем на пространстве L&~M норму
|| • ||4, считая
где
48

а инфинум берется по всевозможным представлениям
Обозначим через &~МЬ пополнение пространства LMF относи-
относительно нормы || • ||в. Легко видеть, что имеет место включение
&~M6czC(E) и для каждой функции fe#~Me существуют после-
последовательности функций фпе#~и и мер yin^Mi(F), таких, что
=£ ФА
A.33)
A.34)
Теорема 1.2. Если функция f принадлежит пространств}/
&~МЬ, то она интегрируема по мере Фейнмана Фь2 и имеет ме-
место равенство
A.35)
п=1
и мер
где последовательности функций
удовлетворяют условиям A.33), A.34).
Доказательство. Пусть функция / принадлежит про-
пространству &~МЬ. Найдем последовательности функций фг»е#"£/
и мер \in^Mi(E), удовлетворяющие соотношениям A.33),
A.34). Из неравенства /(фл)<:Л(фл) и оценки A.16) следует,
что для любого е>0 и произвольного натурального п выпол-
выполнены неравенства
ibti\—Fir г\ ^_
q>k(x)n(x)(dx)
— Щх)—г(х,х)
m=0
— ib(x)-z(x,x)
ke* <pk(x)dx
т. e.
A.36)
Ф* (*)!**
49

Следовательно,
оо 1
С.Х) •—. /» — гй(ДГ)—£(Х,Х) _
Же. A.37)
1 оо 1
— ib(x)—г(х,х) х-~, р — ib(x)—E
В силу оценок A.34) и A.36) ряд в равенстве A.37) будет
сходиться равномерно при е>0, поэтому в равенстве A.37)
можно перейти к пределу при е->-+0, откуда следует
оо
1 ж'/гч гч 1 ,-, ~. ч A.38)
■Оценка A.36) влечет неравенство
1
•откуда в силу A.34) следует равномерная сходимость по па-
параметру п ряда из равенства A.38). Из предложения 1.2 сле-
следует, что для любого натурального k функция ц>кЦк интегрируе-
интегрируема по мере Фейнмана, т. е.
Следовательно, в равенстве A.38) можно переходить к преде-
пределу при га-^оо, откуда вытекает равенство A.35).
§ 2. ДВА СПЕЦИАЛЬНЫХ КЛАССА ФУНКЦИЙ,
ИНТЕГРИРУЕМЫХ ПО МЕРЕ ФЕЙНМАНА
Пусть Е — сепарабельное банахово пространст-
пространство с нормой 11-11, Ео — линейное подпространство, плотное в
Е, Ъ — вещественная невырожденная квадратичная форма на
Ео, определяющая на £0 скалярное произведение (-, •), отно-
относительно которого пространство Ео будет гильбертовым; кроме
того, предполагается, что F — банахово пространство, находя-
находящееся в двойственности <Е, F) с пространством Е, Еп — после-
последовательность конечномерных подпространство пространства
ЕОу удовлетворяющих условиям A) — C) из параграфа 1. Так-
Также полагаем, что гауссовская мера ць, порожденная квадра-
квадратичной формой Ь (с нулевым средним), счетно-аддитивна на
пространстве Е, т. е. норма ||-|| измерима в гильбертовом про-
пространстве Ео.
Обозначим через s&~\ класс всех непрерывных функций на
Е, представимых в виде
SO

где п — произвольное натуральное число, Pk (х) — однородные
непрерывные функции на Е, порядок однородности /*■ которых
удовлетворяет оценкам 0<4<:4, такие, что если /*>0, то для
любых хеЕ выполнено неравенство р*(х)>0, |х — преобразо-
преобразование Фурье счетно-аддитивной комплекснозначной меры \х^
eAf^F) и и(х) — непрерывная комплекснозначная функция
на Е, такая, что существует функция g:U0XE-+C (£70 — замы-
замыкание в С множества £/0={аеС: 0<arga<rt/4, а^=0}), удов-
удовлетворяющая равенствам
, x)=u(x) Vxi=E,
г(«Р, x)=g®, ax) Vx<=E, VPet70, Va>0,
аналитичная по первому аргументу на множестве UQ, при лю-
любом фиксированном значении второго аргумента из Е, непре-
непрерывная на ПоХЕ, для которой функции g(a, x)e-EH*l|2 при лю-
любом фиксированном е>0 ограничены на множестве О0хЕ.
Теорема 2.1. Если функция f принадлежит классу
mo функция f будет интегрируемой по мере Фейнмана Фь2.
Доказательство. Пусть
f(x)=u(x)v(x)e *
принадлежит классу s&~x иг — некоторое вещественное число,
большее 1. Тогда
при Vaei7r. Значит, функция f принадлежит пространству
&~Мь при некотором б>0 и в силу теоремы 1.2 она интегрируе-
интегрируема по мере Фейнмана Фь2.
Лемма 2.1. Если функция <р:R-*-C представила в виде
где п — натуральное число, р:С-*-С — полином степени, не пре-
превышающей 2/г—1, и а — комплексное число, удовлетворяющее
неравенству Rea<0, то существуют положительные числа е,,
С, такие, что будет иметь месте оценка
BЛ)
Доказательство. Функция
+ОО
Р _ Г ег<(т+Р)+о(т:+РJп+Р(т+Р)
51

определена и аналитична на С, кроме того, она постоянна на
R в силу равенства
+ОО +ОО
Г gi<(T+P)+o(xfpJ"+p(-t+P) d%= \ ет+ат2п+р(т) fa ф е £)(
—оо —оо
поэтому она будет постоянна на С, следовательно, для любого
«>0 имеет место равенство
2/г +оо 2/г 1 1
+
С e«t-e< 2п-1+а(х+Ш 2"-1 J"+p(-rW 2"-' ) ^Т. B.2)
—оо
Из условия Rea<0 следует, что существуют такие положитель-
яые е, Си что имеет место оценка
2п 1 1
_ е/ 2п+1 _(. Re [a (T _(. jgj; 2/г-1 Jп + р (т + 18* 2"-' )]< Сх + — Re at2"
2 B.3)
для любых /ei?. Положим
с =
+оо 2/г
ltx-et 2л—1
Из соотношений B.2), B.3) следует оценка B.1).
Лемма 2.2. Пусть g:R-+R — непрерывно дифференцируе-
дифференцируемая функция, удовлетворяющая равенству g(O) = l и ограни-
ограниченная вместе со своей первой производной, а0 — положитель-
положительное число, п —■ натуральное число, «р :#"->£ — непрерывно
дифференцируемая функция, удовлетворяющая условию q>'(x)¥=
¥=0 Vx^R", С — положительное число, f:Rn-^R — непрерывно
дифференцируемая функция, Q:Rn-+Rn — отображение класса
С1 и G:[0, ао]хЯп->-#" — отображение класса С2, такие, что
■будут выполнены соотношения G@, x)=x Vx^R",
S-[f(G(a, x))DetG'x(a, x)]
да
A+1
|f(G(a, x))DetG;(a, jc
A + 11*11)" '
-j-G(O, x)=Q(x).
aa
S2

Тогда имеет место равенство
-f- [ f(G(a, x))DetG'x(a,
да У
= J №<x), <f(x)g(<p(x)))'x)+f(x)gto(x))iT&(x)]dx. B.4)
.Доказательство. Из условий леммы следует, что
-f- f /(G(a, *))DetG»(<z, *)dx|o=0=
За J
[(f'W, Q(x)) + f(x)trQ'x(x)]dx=
) B.5)
"В силу теоремы Стокса
^ (^JWcb. B.6)
Учитывая равенство ёг(ф(х)) = 1 для любых x^Rn, удовлетво-
удовлетворяющих условию ф(х)=0, получим
J VII ф (*) II
. B-7)
•откуда в силу равенств B.5) — B.7) получим равенство B.4).
Лемма 2.3. Пусть С, at — положительные числа, п — на-
натуральное число, y)p:Rn-+R, f:Rn->-R, g:R-*-R — непрерывно
дифференцируемые функции, такие, что g@) = l, i|/(x)¥=0 Vxe
^:Rn, и функция g ограничена вместе со своей первой произ-
производной; кроме того, F:[0, ai]XRn->-Rn — отображение класса
С2, такое, что для любого ае[0, а{\ отображение F(a, •):#"-»-
--*-Rn является диффеоморфизмом класса С2, и выполнены со-
.отношения
~f(F(a, x))DetF'x(a, x)
53

^F(a, x) I \\f'(F(a, x))|||Det F'x(a, x
\f(F(a, x))| \\(F'x(a, x))-'|| | Det/^cc,
\f(F (a, *)
-f-Det К (a, x)
A
с
.A + 11*11)"
Пусть также для каждого aei[O, сч] существует ао, такое, что
отображения G(Aa, x)=F(a-{-Aa, F (а, х)),
(a, Г'(а, л;)), ф^^гр^ (a, x)), f, g
удовлетворяют условию леммы 2.2. Тогда имеет место равенство
д
да
Г f(F(a,
(a,x), g($(x))r(F(a,x)) +
f M> (*)) / (F (а, *)) ((^х (а, х))-1)* ^ (х)) Det £ (а, х) +
+ /(Z7(а, х)) g(гр(х)) ^- DetF'x(а, х) 1 dx. B.8>
ста J
Доказательство. В силу леммы 2.2 имеем равенства
-j- f f(F(a, x))DztFx(a, x)dx=
= —— \ /(G(Aa, x'))DetG^(Aa, x')dx'\Aa=,o=
*'), g(Ф (a:')) /* (xf) + f <x') g'(ф (x')) w'x(xr)) 4-
Учитывая равенства
'' l 1^1 (a, x)),
производя замену x=F~1(a, xl) и замечая, что
DetF^a, x) tr [ (~f)'(a, х)(^(а, x))-1l=^-Detf;(a, x),
получим равенство B.8).
54

Пусть t — положительное число, Q=Rn, (-, •)<? — скаляр-
скалярное произведение в Q, II-II? — норма в Q, 1и ...,/« — канони-
канонический ортонормированный базис в Q.
Обозначим через Е пространство всех непрерывных отобра-
отображений х:[0, t}-*-Q, таких, что x(t)=0. Положим Ес=С®Е (Ее
<zEc). Введем норму 11-11 на пространстве Е, полагая
|| х ||= max ||*(т)||,
0<«
для любых
Обозначим через Ео линейное подпространство пространст-
пространства Е, состоящее из почти всюду дифференцируемых отображе-
отображений х, удовлетворяющих условию
6
Определим на пространстве Ео скалярное произведение (-, •),
.полагая
(х, у)=^(х'(т), у'(т))с1т,
о
-и зададим функцию а(х) = (х, х). Обозначим через \ка гауссов-
скую меру, порожденную квадратичной формой а и нулевым
средним, на пространстве Е. Отметим, что она будет счетно-ад-
счетно-аддитивной на пространстве Е.
Зададим последовательность разбиений (to,■... , tk , ■ ■ ■
...,т#), @=T^<xf<...<т#-1<т#=/) отрезка [0, /], таких,
что
lim max |т^—т^ j =0.
Обозначим через EN линейное подпространство Е, состоящге дз
всех ломаных, гладких на @, /)\{^, ... , ^_i}.
Пусть @~0.\,с — класс аналитических функций на Qc=
=Cn(Qc=>Q), таких, что для любой функции w^g~QhC и лю-
любых положительных е, г существует такая константа Ci(e, r),
что для любых аь аг^С, qOy qu q2^Q, удовлетворяющих усло-
условиям
, |<x2i<2, 0<argOj<n/4, 0<argce,<n/4, lko|
выполнено неравенство
I w (q0 + al4l + a2q2)| < С, (е> г) e^<^< . B.9)
Определим отображение Ar.E-^E, полагая
t n
) = |[£ (х(тг), eh)f+lek dxv
55

Предложение 2.1. Пусть и — функция класса 9~Q\,c,
w : Ес-+С — аналитичная функция, такая, что для любого е>0
существует С>0, при котором
\Dhw(x)\^C[\h\\e\WB Vx, he=Ec B.10)
(Dh — оператор дифференцирования по направлению п); кро-
кроме того, k — натуральное число, для каждого l^2k (/^1) оп-
определен однородный полином pi: Q->/? степени I, причем
P2k(q)>0 Vg^O и P/(x)=f Pt(x(T))dx. Тогда для любого ре
о
е@, я/8£) существуют натуральное число m и положительные
числа ?, Cj C2fc, такие, что для любых Г\, ...,
выполнено равенство
г 1
г . * 1~-Р| ж-ч ,._ . ..■
ехр
J
Е
lie U I ^ п[(ЯЛ(х)) * + CtP,(x)]' +
11
t (JL _ $) 2kr~l J
(X)-CA J[ ((Рад (X)) 2* +[CtP, (X))
(PA (x))
+ ClPl(sAmx+e
L
J X
Л_р) _L
4 'x)Jfe J
X exp { *— e (Г P) Y] (x @),
О /=-1
60

t n
(
о /=i
XMfeeW )Amx(O)+x(O))w(ze ^ 'Л»х + х)|
+ J exp j/e \* I JJr,[P2fei
+ irzh [ P2k (icAnX + x) -
2fe—-1 J 2k
2fc } exp { _JL_
0 l=-l 0 I—I
x и ($Amx @) 4- x @)) w (гЛтл- 4- x) [xa (Лс) 4-
l . / л \
С ( P) Г I
4-i (e \ 4 / —1M da \ expiie
J J I
2^ «f--P)
x 2j ri t(P"fe ((A—a)r+a?e 4 )AmX +x)JA +
4-C,r/P/(((l—a)f4-are ^4 ')Лтх + 4]' +
x
((Ptfc ((A - a) r 4- are \ * I) Anx 4- x)Jfe +
г I
4- С,ггРг ((A - a) s + are
U
-+ie V4 / r2fe+1 (P2h ((A —a) r 4- are ^4 >) Amx + x) 2k) I x
57

Xexp{-—^-((l-aJr-ar/W" ^(x@), efqm+2-
o /=i
. /_я__ p\ 2m+l < n
U i) 2 J £|(*(т), ег)Гйт J X
0 /=1
X ехр{-(Р2Ь(/!тх + д;)-Р2й(д;)Lт+2} х
X {A4m* j [й \* i [ J] r, [(Ptfc(((I —a
2k~l t I—-») —
a) H- Ще \ * j) Лтх + x) *
(
-a) r + are U
-a) ? + are W j) Лтх + x)Jfe j —
} E
1=1
n „\ t n
б /=1
Xи ((A -a) r + are V * /) Amx @) + x @)) x
X ш(A—a) 5 +ape ^4 /Лтх + хI +
58

X
I
n -(A-а)Е+аЕ« U /)Bm+l) ^ {x(xi),el)fldxl
x
i fj--pjBm+l) »
X
о " 1=1
Bm + 1)^
^(())^]d ^±Lj(^(x(T)) ettf)d*} X-
о /=i
X ы((A— a)? + cc?e U ))Ax(O) + x(O))x
a(dx) B.11)
имеет место неравенство
| \ exp {fe4 4" £ r, [(Ptft (x)Jfc
E /
./_я_„\
й 4
\ {
E /=1
2ft—1 J 2k
[P2k(x)-C2
_
2h[P2k(x)-C2h £ ((P(x)) +CP(*)) ]2fe
Cexp(£|r,| 4fe). B.12)
Доказательство. Возьмем натуральное число т. Най-
Найдем такие положительные числа у, Сь .... Сг^, С2й+ь чтобы
функция
sx(а, х, ги ..., r2*+i) =
2ft-1 J J
a
I
j
2fe 1
59

была бы определена на пространстве [у/10, +oo)xEXR2k't'tr
кроме того, для любых ги ..., r2k+i^R, хеЯ, удовлетворяю-
удовлетворяющих P2k{Amx)>P2k{x), была бы аналитична на множестве
{i? : а>£/10} и аналитично продолжаема на множество
: |а|>5/10}, а также удовлетворяла бы оценке
2ft+1
(
(a, х, rlt ..., Г2/4-1)
2/Ц-1
(
1
2ft
Из оценок B.9), B.10), B.13) и равенства B.11) при т>;
> B£+1J получим оценку
, 2k— 1
i
+ ie
1
.iT
2fc
-h
Е
2ft+l
0 /=^1
г=1
где Со — некоторая константа. Из неравенства B.14) следует
оценка B.12).
Остается доказать равенство B.11). Для этого определим
отображения
Am,N:QN-+QN, FN:RXQN->QN,
полагая
при
60

Лп,лг(<71. • • ■. Ям):
N—\ n 2m+l
r
/,= 1
JV—1 n 2m+l
l=k J,=l /,=о
и зададим функции fN:QN-*~C, tyN:(f-+R, Pi,n:Qn-*-R A
^/^2^), g:R-+R, полагая
JV
N— 1
х exp | —
'=' 2 iv
2k—\ I 2k
Г Г"» у"» % ^ Г^ 9fe у"» Г^ / | ОЬ
61

Nn Nn
где <7 = (<7i, ..., qN), C(N) = Bn) 2 (-j-\ 2 . Отметим, что при
a>0 отображение F(a, •) : QN-*-QN является диффеоморфиз-
диффеоморфизмом класса С°°, кроме того, имеет место равенство
Det(i)'(a, ft, <,„)) =
W—1 2m
ХП
( ^^£
B.15)
поэтому
l \ (a, q))dq.
Так как функции /#, ifw, g' и отображение F^ удовлетворяют
условиям леммы 2.3, то для любых a2>ai>0 имеет место ра-
равенство
fN (FN (a2, </)) Det ((FN)'q(a2,
лг (/="* К, ?)) Det ((^>; (alt
l
(a2 — ai) da J j [((f л,)« (a2a + ax A — a),
о *w
-«Ml —a),
i v
+ fN (FN (a2a + ax A - a), q)) g (MpN (q)) X
X — (Det(FA)^(a2a4-a1(l— a), q))\ dq B.16)
((>)qn — каноническое скалярное произведение в QN).
62

Определим для каждого натурального N отображение
л?: E->QN, полагая
Для каждого х^Е будут выполнены равенства
Ига
N-+OO
UmC(N)fN(ZN(x))exp
B.17)
B.18)
(N-l)t \ ( (N-l)t
N—l
It \ I (l+l)t \ (It
)х(}х[
N
/= 1
2 iv
где
F(a, x) =
= f(x),
[B.19)
B.20)
B.21)
/ (x) = exp
** +ClP,(x)]' +
I 2k 1
ie
'2k
ier r2k+l {P.ik (x))lnk) и (x@))w(x). B.22)
В силу B.15)
J(a, ^ = bjn Det((^);(a, 1„(х))) =
t m
= exp
о ;=i
B.23)
кроме того,
Ф(
a, jt) = lim I
3 I
C(N)fN(FN(a, %N(x)))X

xexp
(N-l)t \ I (N-l)t
N
I N
2-L
N
i i
= / (x) exp ( 2— V (x @), в/)*и-« _
;i
t n
о /=i
и в силу B.17)
lira {{FN)q(a, ^(
n -
о l=i
t
aBm+l)
dT1jeh
1= 1
,2m+l
X
X(x(x),
]dx.
B.25)
Переходя к пределу в равенстве B.16) при jV-^»-oo и q=\N(x)
и учитывая равенства B.17) —B.19), B.23) —B.25), получим
a(dx)= J Ф(«1, x)J(a2, x)\ia(dx) +
*0
Г ф(ах
),

), x)D > _! - X
—a), х) + Ф(а2а + а1A— а), л:)£(ij?(л))X
X-
(a2a + ax(l— a), x)j|ie(djr). B.26)
В равенстве B.26) правая часть определена для
удовлетворяющих условию a2>ai>0, и постоянна относительно
этих переменных, кроме того, она аналитически продолжается
в комплексную область
и = {{а2, ctj):^, a,eC, |a2a + a1(l—a)|>y/10Vae [0, 1]},
следовательно, продолжение ее также будет постоянно в об-
области U. Возьмем это продолжение для
а = /т -*)
и, учитывая равенства B.20) — B.25), получим равенство
B.11).
Обозначим через S&~2 класс функций /: Е->С, представи-
мых в виде
2k t
где и — функция класса &~Qi, с, k — натуральное число,
Ръъ. '■ Q->~R — однородный полином степени 2k, удовлетворяю-
удовлетворяющий условию P2k(q)>0 Vq¥=0, pi : Q-+R — однородные поли-
полиномы степени I @<l<2k), w : Ec-*-C — аналитичная функция,
такая, что для любого е>0 существует С>0, при котором вы-
выполнено неравенство B.10). Отметим, что полиномы pi могут
тождественно быть равны нулю при l<2k.
Теорема 2.2. Если функция f принадлежит классу s&~2>
то она интегрируема по мере Фейнмана Фо2 и имеет место
равенство
-}-ОО 4-0°
J / (*) Фа (dx) = I ... I фх (Гх) . . . ф2А+1 (Г2*+1) X
—оо — с»
2k
X j exp {ie U '£ г, [(РЛ (х)Jk +C,Pf (x)]l
+ ieU гЛ [P2h (х)-СЛ £ ((P2h (х)Jk +С,Я, (х)) ! ]
i=\
i(JL _p) _L
+ ie 4 r2k+l (P2h(x)Jk } и (ix @)) w (ix) (ia (dx) drx ... dr2k+l, B.27)
3 Зак. 273 65

еде С\, .... Ctk+t — некоторые положительные константы,
t
Pi (*) = I Pi (x (x)) dx @ < / < 2Л),
О
irtr+i_re . 2 ав
, K2k,
+00 , . 1 2ft J62ft
<Pi(r,) = — \ e dr B.29)
2я J
— 00
при l=2k, 2Л+1.
Доказательство. Выберем такие же константы, как и
в предложении 2.1.
Обозначим через lN меру Лебега на пространстве EN. Легко
видеть, что подпространства Ец пространства Е конечномерны.
Положим
t
С (a, N)= §e ° KN{dx)
ири Rea<0.
Имеют место равенства
t
е-Ч-0 ■ Еи б
2/Ц-1
X ехр
X ехр [/ У] e^'Pi (х) 1 и (е^х @)) w(еЩ lN (dx). B.30)
В силу B.28), B.29)
-|-оо -|-оо
66
— 00 — 00

x Iexp {—И{х> (т)> х'(т))"dT+' 4 x
о
2fe-l J l
_i_ 2ft
2fe
ie 4 /-2*+i (P2ft (*)J* I y ('•* @))w (ix) K\ (dx) drt... dr2*+i
-J-oo
— OO —00
X J exp {-L 1в«Э J (x' (t), л:' (т)),
E °
EN
2ft-1 £'
2k J
_
' 1
l
+ ir2k+l (P2h (x)Jk j и (е'Эх @)) ш (в«Эх) Ял {dx) drt... dr2k+l =
exp {i
EN
{x)\ u(e^x{O))w{e^x)XN(dx). B.31)
Из оценок B.1), B.12) следует равенство
!
Й с(-!,ло
—оо —оо
3* 67

f
X \ exp | \ (x'(t), x'(x))odx-\-ie ' * ' x
I 2 J
t(JL—ei)
X(T), *(t)),dx + ieK*
,P, (x)]l + ie 4 r2fc x
2ft—1 J_ Jk_
X [P2fc W-C2fc £] ((P2ft (x)) 2* + ClPl (x)) l
if——б)
ie 4
if——б) —
+ ie 4 r2ft+1 (P2fc (x)) 2* j у (f (x @)))a> (ix) %N (dx) drx... dr2k+l
t(JL
Jexp Jie 4
2k~x
—oo —oo
fe Ч 4 r2fe [P2h (x)-C2fc JJ ((Pa(x))
— — t(—-p) —
+ C,P, (x)) ' ] 2* + ie 4 >«+, (P2fc (x)Jk ) u (/x @)) x
X w (ix) \ia (dx) drx... dr2k+i. B.32)
В итоге равенства B.30) — B.32) дают равенство B.27).
Следствие 1. Пусть pi,т : Q^>~R — последовательность
однородных полиномов степени / @<l^2k), равномерно сходя-
сходящаяся на ограниченных множествах при т-*-оо к pi: Q-*~R,
причем p2k,m(y)>0, p2k(y)>0 Vm, Vy¥=G; um — последова-
последовательность функций из класса 2TQ\, с, wm '■ Ес->С — последова-
последовательность аналитических функций, поточечно сходящихся к
функции u^3TQi,c и аналитической функции w : ЕС-*~С соот-
соответственно, таких, что для любых положительных е, г сущест-
существуют положительные числа С\(г), С2(е, г), при которых будут
выполнены неравенства
| Dhwm (х) | < Q (е) || А || ё^ Ух, he Ec,
I um (q0 + aiqi + сзд2) К С2 (е, г) е8*4+*4
для любых т; qo, Qu ?2^Q. cti, a.2^C, удовлетворяющих
l«1|<2, |a2|<2,
68

Тогда последовательность функций
2ft t
и функция
2k i
будут интегрируемы по мере Фейнмана Фа2 и имеет место ра-
равенство
венство
Доказательство непосредственно получается из оценок B.1),
B.12) и равенств B.11), B.27).
§ 3. ИНТЕГРАЛЫ ФЕЙНМАНА КАК
АНАЛИТИЧЕСКИЕ ПРОДОЛЖЕНИЯ ИНТЕГРАЛОВ
ПО ГАУССОВСКИМ МЕРАМ
Пусть Е — сепарабельное банахово простран-
пространство с нормой Ц-11, Ео — линейное подпространство, плотное
в Е, Ь — вещественная квадратичная форма на Ео, удовлетво-
удовлетворяющая условиям (А1) — (А4) из параграфа 1. Так же, как
в параграфе 1, введем гауссовскую меру ца на Е (см. (А4)) и
скалярное произведение (•, •) на Ео (см. (A3)). Пусть при
г>\
t/r = {oeC:l/2<|o|<r, 0<arg|a<jt/4}.
Для a>0 определим отображение 1а : Е-уЕ, полагая
для любых Xie£o, 1 и лг2е£0,2 (£о, ь Е0,2 — пространства, оп-
определенные в (А1)). Комплексификацию пространства Е обо-
обозначим через Ес. Определим отображения 1ас : ЕС->ЕС для
любого аеС\{0} как аналитическое продолжение по парамет-
параметру а на С\{0} и С как линейное продолжение по переменной
линейного оператора /а.
Определение 3.1. Скажем, что функция / интегрируема
по мере Фейнмана ФгД если при некотором г> 1 существуют
интегралы \ f (Iax) \ia (dx) для любых a^R, удовлетворяющих
неравенствам 1/г^.а^г, и непрерывная функция ср: ОГ->С,
аналитическая на множестве Ur, такая, что
69
Ф (o) = J

при любом a^R, удовлетворяющем неравенствам
'т
При этом величину ц(е ) называем интегралом Фейнмана »
обозначаем через ^ / (х) Ф? (dx).
Пусть F — банахово пространство и существует двойствен-
двойственность <Е, F> между пространствами Е, F. Зададим так же, как
в параграфе 1, отображение Т : F-*-Eo.
Лемма 3.1. Если р:Е-*~С — полином порядка гп, ц —
счетно-аддитивна» мера на пространстве F, то имеют место ра-
равенство
\р(х))>{х)]>а(йх)=Ъ)РЛУ)е »№) C.1)
Е ft=0 F
и неравенство
оо 1
Е | J Рн (У) е~ ~*(TyJ% (dy) | < (ц) (F) (J (p (x)f pa (dx))l/\ C.2)
k0 F F
| J
k=0 F
где
C.3)
Доказательство. Возьмем последовательность конечно-
конечномерных подпространств Еп пространства TF, удовлетворяю-
удовлетворяющих условиям:
1) для любого п Еп+\>Еп;
2) для любого п En=(Eni)EOi i)®(En(]EOt 2);
3) линейное подпространство Е00=[)Еп плотно в гильбертовом
пространстве Ео.
Для каждого натурального п в силу свойств полиномов Эр-
мита имеем равенство
1 со 1
х-(х.х) __ х-(х,х)
Р{х)е 2 =Y,Pkn(iD)e C-4>
для любых точек х из пространства Еп, где
Рк,п
Bя) 2 £„
n). C.5)
Заметим, что при k>m pfe, n=0, поэтому все слагаемые в бес-
бесконечной сумме из равенства C.4) с номерами, большими пг,
равны нулю.
70

Пусть пп ■ Eq-^-Еп — ортогональный проектор и
~^n=v°{nn°T)-K . C.6)
В силу равенства C.4) и равенства Парсеваля имеем
2 * . П _ / .#\ . 2
Bя) z *n R=t
я, учитывая равенство C.6), получим
1 оо
1
BЛ) 2 п
C.7)
Из равенств C.3) и C.5) следует
Pk(y) = limpkn{nn, Ту) C.8)
n-f-oa
для любого ^gF. Переходя к пределу при п-*-оо в равенстве
C.7) и учитывая равенство C.8), получим равенство C.1).
Из свойств полиномов Эрмита следует, что имеет место
равенство
)/ lPkJiD)e UPm,nWe 2 ]<** = 0 C.9)
для любого натурального п и любых целых неотрицательных
чисел т, k, не равных между собой, откуда получим равенства
X
— -g-lx.x) £, f —(х,х) _ -—(х.х)
Ef -z-{x,x) ъ~{х,х)
)е2 \pkn{iD)e 2 \*dx. (ЗЛО)
Для любых натуральных п и целого неотрицательного & поло-
положим
к
апри рк:Пф0 и а*, П==1 при pfe?rt=0. В силу неравенства Коши—
£уняковского и C.9), C.10) имеют место соотношения
<2л) 2 £п
71

Bл)
Bя)
Bя)
oo
'(У——
-W*)
]dx
и, учитывая (ЗЛО) и равенство Парсеваля, получим
V Bя) 2
C.11)
Переходя к пределу при п^»-оо в неравенстве C.11), в силу
C.8) получим оценку C.2).
Лемма 3.2. Пусть для каждого натурального я ряд
00
V а*,п(Яб,п^С) сходится и для любого е>0 существует такое
натуральное N, что для любых п, m>N выполнено неравенство
А=0
Тогда для каждого k существует предел
ah — lim uk,n,
сходится числовой ряд
и выполнено равенство
flM
C.12)
72

Доказательство. Из неравенства
оо
\Ctk,n — Clk,m\ < ]£ \uk.m—a.k,n\
следует, что для каждого k последовательность ak, n будет
фундаментальной, откуда вытекает существование предела
ак = lim ak.n.
C.13)
Докажем равномерную сходимость ряда V* пк,п при любом
натуральном п.
Возьмем произвольное положительное е. Из условия леммы
следует, что существует такое натуральное N, что для любых
натуральных п, m>N выполнено неравенство
C.14)
оо
Положим m=N+\. Из сходимости ряда V а*,т следует су-
ществование такого натурального К, что для любого натураль-
натурального k>K выполнено неравенство
IS"»
C.15)
В силу C.14) и C.15) для любого n>N и любого k>K вы-
выполнены неравенства
■Ч.п
/,»— aj<m)
i=K
fe.n—Ofe.ml +-|-<e,
откуда следует равномерная сходимость ряда V cik,n, что
в свою очередь влечет сходимость ряда V ак и равенство
C.12).
4 Зак. 273
73

Лемма 3.3. Если комплекснозначная функция f принадле-
принадлежит пространству 3?i{E, \ia) и ц — счетно-аддитивная мера
на пространстве F, то имеют место равенство
2 {ТУ'ТУ) Р№ C.16)
k=0 F
и неравенство
ft=O F
где
[ \f(x)\*\ia(dx))~,C.l7)
E
Ph (У) = -^- J f (x) dTyixa (fix). C.18>
E
Доказательство. Возьмем последовательность полино-
полиномов qn:E-*C, сходящуюся в пространстве 3?2{Е, \ia) к функ-
функции /. Для такой последовательности будет иметь место равен-
равенство
f / (х) (dr/ h. (dx) = Iim f qk (x) {dTyf ца (dx)
£
для каждого y^F и любого натурального п, или
P/i(y) = lim qk,n(y), C.19)
где
?fe.n (#) = ■ . ■ f Як (х) dru ft» (dx).
Из леммы 3.1 следует равенство
оо 1
qn(x)\y(x)\ia(dx)— V f<7n.fe(i/)^ z "' М-(d^) C.20)
для любых натуральных п.
Покажем равномерную сходимость ряда
C.21)
'.—0 ' F
по параметру п.
Возьмем произвольное положительное е. Так как последо-
последовательность полиномов qn фундаментальна в пространстве
74

3?2(E, (ia), то найдется такое натуральное число N, что для
любых п, m>N выполнено неравенство
I ИI (П (J I Чп (х)-Чт W12 ft. (dx))~ < е,
я
откуда,' учитывая равенство
Чп.к {У)—ЯтАУ) = (~,')Й f fan («)— 7т (*)) <*** ft, (<&)
Е
и неравенство C.2), из леммы C.1) получим неравенство
£ IIJ Чп.*Ш ^(ТУ'ТУ) »{dy)\-\ f wwr-r(r"rrt к^)||<
fc-0 F F
1
~(T*r%|e. C.22)
Для ряда C.21) выполнены все условия леммы 3.2, так как
для любого натурального п ряд C.21) сходится и выполнено
неравенство C.22), поэтому ряд C.21) будет сходиться равно-
равномерно.
Из равномерной сходимости ряда C.21) и равенства C.19)
следует, что в равенстве C.20) можно перейти к пределу при
л->-оо, что влечет равенство C.16).
В силу неравенства C.2) леммы 3.1 имеет место неравенст-
неравенство
| J
F
| J
ft=0 F
для каждого натурального п. Учитывая равномерную сходи-
сходимость ряда C.21) и равенство C.19), в неравенстве C.23)
можно перейти к пределу при n-voo, откуда следует оценка
C.17).
Предложение 3.1. Пусть г — вещественное число, боль-
большее единицы, q:Ur-E—>~C (Ur-E^EC) — бесконечно диффе-
дифференцируемая функция, такая, что для каждого п>0
\\gin)(Ica)\\e=32(E, ^)VaeZ72
и
ап (g) = sup \ \\g{n) (Icax)\\ \ia (dx) < oo, C.24)
кроме того, \i — счетно-аддитивная мера на F, такая, что
Ьп О*) = S ll^ll" IИ №< oo (fln (g) ф 0) C.25)
75

и
J\± li)<oO. C.26)
n=0
Пусть также f: Е-*-С — функция, определенная равенством
f(x)=g(x)n(x), где ц — преобразование Фурье меры ц. Тогда
функция f интегрируема по мере Фейнмана Фб3 и имеет место
равенство
- — ЩТу) 1Л ч ^32^
k=0 F
где
\ jl x) tfTy)k Va (dx). C.28)
Доказательство. Определим отображение [а* : F—>~E
для любого а>0 как сопряженное к отображению Ia : E-+E
относительно двойственности (Е, F>. Имеет место равенство
/аГ=Г/„*. C.29)
Из леммы 3.3 следует, что
f
E
f Vax) Va (dx) = f \ pk (a; /; y) e~ ^ {U>T1> ц (dy) C.30)
k^O F
для любого a^U2(]R, где
Pk (a, У) = -~^ Jgi!*x) dTy ца(dx). C.31)
я
Интегрируя по частям правую часть равенства C.31), по-
получим
?*(«, *)= ■**£-$8*Ч1аХ)AаТу)к1ъ№- C.32)
Для каждого целого неотрицательного & определим функцию
<7* : UrXE^-С, полагая
qh (a, у) = igi J g(») (/Sx) D Ту) ^a (dx). C.33)
Из оценки C.24) следует, что
^ afcte) C.34)
76

для Va^Ur, Vy^F, откуда следует непрерывность функции
Pk по первой переменной на множестве Ог и, учитывая анали-
аналитичность отображения о-*g(k)(l1x)(Ia'Ty)k, ее аналитичность на
множестве Ur также по первой переменной. Из оценок C.34),
C.25) и
-AСТу.1СТу)
\е 2 « « |^1
при VaeUr, Vy^F следует, что для любого aEPf
qh(a,
. C.35)
на множестве Ur и аналитична на множестве Ur.
Определим функцию ф : 0г->-С, полагая
(а*>а*)
Поэтому функция a-* \ gft(a, #)e 2 ц (d#) непрерывна
C-36)
Из оценок C.35) и C.26) следует равномерная сходимость
ряда в равенстве C.36), а так как каждое слагаемое является
непрерывной функцией на множестве Ог и аналитической функ-
функцией на множестве Ur, то функция ф также будет непрерывной
на множестве Ог и аналитической на множестве Ur. Из ра-
равенств C.30), C.29), C.32), C.33) и C.36) следует, что для
любого вещественного а, удовлетворяющего неравенствам
1/^^ имеет место равенство
откуда следует интегрируемость функции f по мере Фейнмана
Фь3.
Из равенства
Ян(е 4 , х) = рк(х)
в силу C.33) и C.28) и равенства C.36) следует равенство
C.27).
Для каждого г> 1 обозначим через #~£Л-°° пространство всех
функций g : E-+C, таких, что каждая из них имеет функцию
: Ur-E-+C (Ur-E^EC), бесконечно дифференцируемую на
,-Е относительно комплексного поля, такую, что для каждого
\\фп)Aа -)\\ е «#2(Е, \ха) VaG Ur
77
Т

и,
= sup f \Wn) (fcax)\\ ца (dx) < oo,
Функцию rf назовем продолжением функции £ на множество
Or-E.
Пусть L&M?— линейная оболочка всех функций f из про-
пространства С(Е), представимых в виде f=g\i,tAt функция g при-
принадлежит пространству 9U™, а ^— преобраэоМНИе Фурье
меры \i, счетно-аддитивной на пространстве F и такой, что
I" (ч, v) = J] -^(г + iJXW J ll^ii" ||ij (dy)<oo
(здесь г|) — продолжение функции g на 0,-Е). Зададим на
пространстве Ь&М™ норму Ц-llr00, полагая
Hfllr" = inf (/°° (Ч1, щ) + ... + Г (qn,
где п — произвольное натуральное число, пары (qn, \xn) удов-
удовлетворяют условию Iх (qk, \Лк), а инфинум берется по всевоз-
всевозможным представлениям
f =
Обозначим через tFM^° пополнение пространства. L^M^ по
норме \\-\\х.
Легко видеть, что пространство &М? вкладывается в про-
пространстве 3?! (Е, ц) и для каждой функции /„ s aFM? суще-
существуют последовательности функций gn^oFU'? и счетно-адди-
счетно-аддитивных мер р.п на F, таких, что
/ = £?»?» C-37)
п=1
Г(?„, ЦдХоо. C.38)
Теорема 3.1. £слы функция f принадлежит пространству
М?, то она интегрируема по мере Фейнмана Ф&3 ы «лгеег
место равенство
£ C.39)
последовательности функций qn e с^/УГ ы счетно-аддитив-
счетно-аддитивных мер \1П на F удовлетворяют условиям, C.37) и C.38).
78

Доказательство. Пусть функция / принадлежит про-
пространству g'U?. Найдем последовательности функций qn e
^.afUT и счетно-аддитивных мер цп на F, удовлетворяющих
соотношениям C.37 )и C.38).
Для каждого натурального п определим функцию ф„: Ur-*-
—*~С, полагая
где
?*.» («. У) = ~ J Ч>№ (&) (%Ту)к \ia (dx),
Е
a tyn — продолжение функции gn на множество Ог-Е. Из до-
доказательства предложения 3.1 известно, что функция фп непре-
непрерывна на множестве Ог и аналитична на множестве Ur для
любого вещественного а, удовлетворяющего неравенствам
1/г. Выполнено равенство
„ (/.х) ^а (dx) C.40)
и имеет место оценка
J ?*.» (а,
р
а
Из оценки C.41) следует неравенство
I Ф„ ИI </"(?». Ш.) C.42)
для любых аеОг.
Положим
C-43)
и=1
В силу C.42) и C.38) ряд в равенстве C.43) будет сходиться
равномерно на множестве Ог, поэтому функция ф будет опре-
определена и непрерывна на множестве Ог и аналитична на множе-
множестве Ur. Из равенства C.41) следует, что
ф(а) =
n=l £
значит, функция f интегрируема по мере Фейнмана Ф&3 и име-
<ет место равенство C.39).
79

Лемма 3.4. Если функция g принадлежит пространству
&"Ur, то для каждого целого неотрицательного k определена
функция pk : UTX.F-+C равенством
ph(a, y)=\$(a, x)(l£x, Ty)ky,a{dx), C.44)
я
где 1|з — продолжение функции g на множество ОгхЕ и имеет
место оценка
k
Vk\ I'(g) \\Ty\\o,
1
V (у) = Ы (J e2W ^
х<=Е, a(=Ur. C.45)
Доказательство. Из неравенства Коши—Буняковского
следует
(«, У)\ <((J 1*(«. *I2М<*х))~ J |(/&, Ty)|«*litt(dx))~. C 46)
Е Е
Для любого 6>0 имеет место оценка
f \Ща, x)\'vLa (dx)< [ sup _ (|Ф(о, x) I e-«')]2 f
откуда следует неравенство
(a, x)|Va(^X(/'WJ- C-47)
я
Возьмем в пространстве £о два вектора ей бг, таких, что
116x110=1, INI«=1. (ei, е2) = 0,
и существовали бы числа х/, х%, удовлетворяющие равенству
(здесь а, у — фиксированы и взяты из Ur, F соответственно).
Пусть М — линейная оболочка векторов в\, е% и х\, х2 — ко-
координаты вектора х^М в базисе еь е2 {х=х\е\-\-Х2е^, тогда
£
~ f
2л J
ike 2 dx =
+
J
CD +ОО 1_ 2 2
^ 2 *' *2 Лс^х«| х; |»+ I х^12)fc *1 2*,
2я
— 00 —СЮ
80

откуда, учитывая
получим
I , Ту) |2* pa (dx) < 2* k\ ir + Mrfk \\Ty\fok. C.48)
Из оценок C.46), C.47), C.48) следует C.44).
Обозначим через M2,r(F) пространство всех счетно-адди-
счетно-аддитивных мер |j. на F, удовлетворяющих соотношению
C.49)
К! \ Г I J
k=0
Предложение 3.2. Если функция f: E-+C имеет вид
f=g\x, где ц — преобразование меры n^M2,r(F), и функция g
принадлежит пространству 8P~Ur при некотором г>1, то функ-
функция f интегрируема по мере Фейнмана Фь3 и имеет место ра-
равенство
C.50)
где
Pk (У) = ^~ f * (? Т. х) (х, Iе * Ту? ца (dx) C.51)
i ° 4
«if — продолжение функции g на множество ОГХЕ.
Доказательство. Определим функцию ф : Ог-*-С, по-
полагая
(О* Г Г..,,- „wic
И *(а> х) {1*х> Ty)k ^а {dx) •*ш C52)
F Е
Из оценки C.45) леммы 3.4 следует, что
f J ^(а, *)(/Sx, ry)*jte(d*)l*(dy)|<2~■/*!/' (<?) J \\Ty\\
J ^(а, *)(/Sx, ry)jte(d*)l*(dy)|<2/*!/ (<?) J \\Ty\\\
F £
откуда в силу C.49) следует равномерная сходимость ряда из
C.52) на множестве Ог.
Так как каждое слагаемое в ряде из равенству C.52) явля-
является непрерывной функцией по а на множестве Ur и аналити-
аналитической функцией на множестве Ur, то функция ф также непре-
непрерывна на множестве Ог и аналитична на множестве Ur.
81

Так как для любого вещественного а, удовлетворяющего
неравенствам 1/г^.а^.г, выполнены равенства
Ф («) = J [ £ ^~ J('«*, Ту)" ц (dy)} фA, 1ах)ца(Лс) =
£ ft=0
= j" 1* ('«*) g У a*) ft. (<**) = J
то функция / будет интегрируема по мере Фейнмана Фь3 и
лмеет место равенство
откуда следует равенство C.50).
Для каждого б>0, удовлетворяющего соотношению A.32),
определим на пространстве &~Ur,t норму /'г, в, полагая
1
> = ( SUp О11*11' lih in. г\\\\(Ч o2eWn. Mv\\ 2
где if — продолжение функции g. Зададим на пространстве
M2,r(F) норму 1'м, 2, полагая
со _k_
' ли ■y/fel J '°
. Возьмем линейную оболочку LSTMr всех функций / из про-
пространства С(Е), представимых в виде f=gp, где функция g
принадлежит пространству &~Ur, а \у, — преобразование Фурье
меры ц из пространства M2,r(F). Для каждого б>0, удовлет-
удовлетворяющего условию A.32), определим на пространстве L&~Mr
норму II • П'г, *, полагая
где gi, .... gn^&~Ur, m, .... ^EAf!,r(F), а инфинум берется
по всевозможным представлениям
Обозначим через #"МГ, „ пополнение пространства L&~Mr по
норме 11-11'г,«. Легко видеть, что имеет место включение
2ГМт, t,(—C(E) и для каждой функции f^3TMr, e существуют по-
82

следовательности функций gn^&~Ur и мер A„еМ2,г(^), таких,
что
/ = £gnjln C.53)
Я
о*
Теорема 3.2. Если функция f принадлежит пространству
"rtt при некотором г>\ и некотором 6>0, удовлетворяющем
условию A.32), то функция f интегрируема по мере Фейнмана
<Db3 и имеет место равенство
оо
$/(*)ф|(Же) = 5] §gn(x)Vin(x)<$l(dx), C.55)
л=1
■где последовательности функций gn^8P~Ur и мер nn^M2ir(F)
удовлетворяют условиям C.53), C.54).
Доказательство. Пусть функция / принадлежит прост-
пространству 8ГМГ, (,. Найдем последовательности функций gn^&~Ur
и мер рп^М2,г(Р), удовлетворяющие соотношениям C.53),
C.54).
Для каждого натурального п определим функцию <fn : Ог-+
~>С, полагая
г, x)(tax, Ty)k
Ri J
fe=0
где $п — продолжение функции gn. В ходе доказательства
предложения 3.2 была получена оценка
оо k
| Фп (a) i < JJ 2~ -i- V (gu) ^ \\Ty\\* | ц„ | (dy),
k~0 F
т. е.
|фп(ОС)| ^1г,б(УпIм,г(\><п) C.56)
в силу l'(gn)^l'r,<i(gn), и_было доказано, что функция ф не-
-прерывна на множестве Ur и аналитична на множестве Ur.
Положим
Ф(а)=]^фп(а)- C-57)
Из оценок C.56) и C.54) следует равномерная сходимость
ряда из равенства C.57), что влечет существование и непре-
83

рывность функции ф на множестве Ur, а также ее аналитич-
аналитичность на множестве Ur.
Из равенства
Ф (а) = J ёп AаХ) Ца (IaX) V-a (dx
Е
для любых а, удовлетворяющих неравенствам 1/г^а^г, сле-
следуют равенства
<Р И = £ \ gn VaX) jln (/а*) ра {dx) - J / (/а
n=-I
откуда вытекают интегрируемость по мере Фейнмана
функции / и равенство
-T
C.58>
Из предложения 3.2 следует, что
г— "" ,
4 S^JI
ft=0
и, учитывая C.58), C.57), получим C.55).
Пусть теперь Ь — положительная квадратичная форма на
Ео. Обозначим через S# класс всех непрерывных функций на
Е, представимых в виде
где п — произвольное натуральное число, ц — преобразование
Фурье меры ц, принадлежащей при некотором г>1 простран-
пространству М2,r(F), и ph, и — функции на Е, удовлетворяющие тем
же требованиям, которые были введены для аналогичных,
функций при определении класса SSTi.
Теорема 3.3. Если функция f принадлежит классу
то функция f будет интегрируемой по мере Фейнмана Фь3.
Доказательство. Пусть
2
f(x) = u(x)Vi(x)e *-i
принадлежит классу 5^- Найдем такое число г>1, что мера.
84

будет принадлежать пространству М2, r(F). Так как для любых
0 выполнено неравенство
где /б — порядок полинома однородной функции, то функция
'2
будет принадлежать пространству #"£/,-, откуда в силу предло-
предложения 3.2 получим, что функция / интегрируема по мере Фейн-
мана Фь3.
§ 4. ОДИН ВАЖНЫЙ КЛАСС ФУНКЦИОНАЛОВ,
ИНТЕГРИРУЕМЫХ ПО МЕРЕ ФЕЙНМАНА
Пусть Q — гильбертово пространство со ска-
скалярным произведением (•, •)? и нормой Ц-ll?» ей ..., еп, ... —
ортонормированный базис в пространстве Q, Т — положитель-
положительно определенный самосопряженный оператор Гильберта—
Шмидта, удовлетворяющий равенствам Теп='кпеп. Отметим, что
тогда Хп>0 и \^Х„<Соо. Пусть также t — положительное
л=1
число.
Обозначим через Е пространство всех непрерывных отобра-
отображений х : [0, t\-+Q, таких, что x(t)=O. Введем норму ||-|| на
пространстве Е, полагая
= max \\x (т)||,
для любых ле£. Пространство Е будет банаховым относитель-
относительно нормы || • ||.
Обозначим через Ео линейное подпространство пространства
Е, состоящее из всех отображений х : [0, t]-*-TQ, принадлежа-
принадлежащих пространству Е, для которых почти всюду существует
производная х'(т)е7Ч2 и выполнено условие
На пространстве Ео определим скалярное произведение (•, •),
считая
i
{х, у) = \ (Т х' (т), Т у' (x))?dx,
о
85

и положим а(х) = (х, х). Пространство Ео будет гильбертовым
по отношению к скалярному произведению (•, •) и норма H-li1
будет измеримой в гильбертовом пространстве Ео, т. е. гауссов-
ская мера ц0, порожденная квадратичной формой а (с нуле-
нулевым средним), счетно-аддитивна на пространстве Е.
Скажем, что отображение р : Е-+Д принадлежит классу
Si&~P4, если
р(х)=р4(х, х, х, х) Vxf=E,
где Р4: ExExExE-^R — 4-линейное симметричное отображе-
отображение, такое, что для любых ненулевых ле£
Р4(х, х, х, х)>0 D.1}
существует число С4, ь для которого выполнено неравенство
Pt [х, х, х, х) <C4il \ (V £ (qn (т))в)^ dx D.2)
со
для любых х = V qn(-)en^E и существует число С
для которого выполнено неравенство
P4(x1, xa, x3, ^X^
Vxx, x2, x3, Хь,е.Е. D.3)
Обозначим через Ес комплексификацию пространства Е.
Скажем, что отображение /: Е-+С принадлежит классу SSTir
если оно представимо в виде
f(x) = eiP(x'>u(x) Vx€=E,
где р —отображение из класса ,S@~P4, а и:Ес-+С — непре-
непрерывное отображение, такое, что отображение а>-*ы(;е+аг/)*
Vx, y^E будет голоморфным на С и имеет место оценка
|| Щ,д
о е
Ve>0, Vxx, x2e^E,l
D.4>
oo
где в свою очередь ll<7lk«=][] q" Y q = I.qnen<=Q,
Теорема 4.1. Если функция f принадлежит классу
то она интегрируема по мере Фейнмана Ф<А
86

Доказательство. Пусть функция / принадлежит классу
, тогда она представима в виде
В свою очередь функция представима в виде
р(х)=Р4(х, х, х, х),
где Pi — линейная симметричная функция. Функцию р4 можно
продолжить на ЕсХЕсХЕсХЕс, продолжая по линейности ш>
каждому аргументу, а значит, также можно продолжить на
пространство Ес функции р и f. Обозначим эти продолжения
теми же символами.
Положим £/={аеС : 0^arga<n/4, а=^0} и определим функ-
функцию ф : U-уС, полагая
D.5>
Из оценки D.4) следует, что для любого компактного подмно-
подмножества Kali найдутся положительные числа С, е, такие, что
будет иметь место неравенство
|/(ох) |< Се
для любых д:е£ и а^К. Следовательно, функция <р будет не-
непрерывна на U, и так как для любого гладкого замкнутого-
контура yczU выполнены равенства
J Ф (a) da = J (J / (ах) ца (dx)j da = f (<J / (ax) da) ца (dx) = 0,
V V E E v
то функция ф будет аналитична на множестве
У0={аеС : 0<arga<n/4, a^O}.
Определим отображение А : Е-+Е, полагая
Для любой непрерывной ограниченной функции gn на Rn и
произвольного E>0 выполнено равенство
2Д<
dy1 . . . dyn =
87

„4 4
i!J
^ -»+*' --L.p>4__i_
2Д< 4 ' 32
X e fc=I *=' " "Ti x
n
(здесь уп+i = 0, xn+i = 0, A; = ^/n), откуда следует равенство
^(£, nJ, VP>0,
где
n=\ О
Пусть 0=^0, n/8<arga<n/4. Тогда для любого положительного
Э имеет место равенство
[ f (a, x) \ia (dx) =\f(ax + сфАх) х
e Ё
i з
X e 2 4>" 2 fia(^) D.6)
oo t
n=l x
■88

Определим функцию фа : i/i->C, полагая
— 3fl->c@)f| —^Bl{")+ —
В силу оценок D.2) — D.4) для любого компактного подмноже-
подмножества KczUx будет существовать такое положительное число С,
что для любых д:е£ и fi^K будет выполнено неравенство
Поэтому функция фа будет определена и непрерывна на U\ и,
кроме того, аналитична внутри области Ult так как для любого
гладкого замкнутого контура ve^i имеют место равенства
5 Ч>а(Р) dp = J (J / (ах + арАс) X
Е
J (J
Е V
PI[x(O)|t L р«В(х)+ 1
x e 4 "*W"*'» 2 ' " ' 2
Отметим, что для любых положительных С, е существует число
Со, такое, что выполнена оценка
для любого леЯ.
Так как функция фа постоянна на множестве {E: |E|>1/2,
argE=0} в силу D.6), то она будет постоянна на множестве
Uи следовательно, имеет место равенство
ф (а)= Г f (ах + е 16 аАх) X
-iJL —tJL -г —
-1-е 16|W0)||4|,--L e 8BlW+i_e 16 д,(х)
* 2 2
D.8)
для любых а=^0, n/8<arga<n/4. В силу оценок D.2) —D.4)
следует, что существует такое положительное число С, что вы-
выполнено неравенство
+
q
<g<^-j, D.9)
8 4 J
S Зак. 273 89

откуда следует, что существует предел
lim ф (а).
л
Значит, функция / интегрируема по мере Фейнмана Фа3.
Следствие 1. Пусть f — продолжение на пространстве
Ес функции из класса SST^ Тогда существует константа С, за-
зависящая от констант С4, С4,2, Ci(e), 6>0 из оценок D.2) — D.4),
такая, что выполнена оценка
I — i — я
\f(e *х+е 16
Кроме того, функция / интегрируема по мере Фейнмана Фа3 к
имеет место равенство
|/(e 4 х + е 16 Ах)х
1 ~ 1 Ч "
-— е 16 nwmn. -——к 8 R.izt д- — р 16
D.11)
Доказательство. Оценка D.10) следует непосредствен-
непосредственно из оценок D.2) — D.4). Из доказательства теоремы D.1)
следует, что функция / интегрируема по мере Фейнмана Фа3 и
\f(x)<J>l(dx)= lim Ф(а).
Поэтому, равенство D.11) следует из равенства D.8) и оценок:
D.7), D.9).
Теорема 4.2. Пусть р — функция из класса s@~P4, un :
:Ес-*-С — последовательность непрерывных отображений, та-
таких, что для любого натурального п отображение a>-*Un(x+
+ ау) Vx, y^E будет голоморфным на С и для каждого е>0
существует С!(е)>0, для которой выполнено неравенство
с(р(х1)+р(дг,)+||х1@I|2+||д!,@)||2+||х1(
Vхи х2^Е,
Vaj, a,E{aEC |a|<2, 0 < arg a < л.''4}, D.12)
90

кроме того, для любого х^Ес существует предел
u(x)=\imun(x)
и функция и: ЕС->С будет непрерывна, а отображение
ai-*u(x+ay)Vx, у^Е будет голоморфно на С. Тогда функции
fn—eipun, 1=ег/Ри интегрируемы, по мере Фейнмана Фа3 и имеет
место равенство
Г / (х) Ф3а (dx) = lim[fn (х) Ф3, (dx). D.13)
Доказательство. Переходя к пределу в неравенстве
D.12) при я-voo, получим для функции и оценку D.4). Следо-
Следовательно, функции /„, / принадлежат классу S&~4 и в силу тео-
теоремы 4.1 интегрируемы по мере Фейнмана Фо3. Из оценки
D.12) и следствия I теоремы 4.1 следует существование кон-
константы С>0, такой, что
г— г-3-я —1|*@I|4,,+—
\fn(e *x + e 16 Л)|<Се8 8
откуда в силу D.9) следует равенство
• — з
lim [fn(e 4 х + е 1б "Ах) х
— iJL —I— i "
- — e IS ||x(O)||Ea- — e » B,(*) + — « 1б »•(*>
X б 4 2 2
Xua(dx)=C/(e ~x + e ~**Ax)x.
е 16 |И0)||4(Г-е 8 р,(х)+ —в 1б ВЛх)
Хе 2 2 ХAа(Л),
что в свою очередь влечет в силу D.11) равенство D.13).
§ 5. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛОВ ФЕЙНМАНА
ПРИ ПОМОЩИ РАВЕНСТВА ПАРСЕВАЛЯ
И ДРУГИЕ ОПРЕДЕЛЕНИЯ ИНТЕГРАЛОВ
ФЕЙНМАНА
Пусть Е — сепарабельное банахово простран-
пространство с нормой ||-II, Ей — линейное подпространство, плотное в
Е, Ь — вещественная квадратичная форма на Ео, удовлетво-
удовлетворяющая условиям (А1) — (А4) из параграфа 1, F — банахово
5* 91

пространство и существует двойственность <Е, F> между про-
пространствами Е, F. Так же, как в § 1, введем гауссовскую меру
Но на Е (см. (А4)) и скалярное произведение (•, •) на Ео (см,
(A3)) и зададим отображение Т:F-*-Eo.
Обозначим через M(F) пространство всех счетно-аддитив-
счетно-аддитивных комплекснозначных мер на пространстве F и через М(Е) —
пространство всех функций Е, являющихся преобразованиями
Фурье мер из пространства M(F).
Зададим на пространстве M(F) норму \-\м, полагая
где ц — преобразование Фурье меры ц. Пространство М {Е) бу-
будет полным пространством относительно нормы \-\м-
Пусть #" —линейное пространство, состоящее из некоторого
семейства комплекснозначных функций, определенных на Е,
содержащее множество М(Е). Пусть также на линейном про-
пространстве &~ задана локально выпуклая топология, такая, что
вложение М(Е)->&~ будгт непрерывным.
Обозначим через ёГ' пространство всех непрерывных линей-
линейных функционалов на пространстве &~ (обобщенных мер).
Напомним, что в пространстве М(Е) содержатся функции
вида е^''У\ где у— произвольная точка пространства F, и, сле-
следовательно, определено преобразование Фурье обобщенных:
мер: для каждой обобщенной меры vef определяется функ-
функция v : F->C равенством
v(y) = v(el< ■■У>).
Наложим дополнительное ограничение на пространство &~г.
требуя плотность множества М(Е) в пространстве #".
Определение 5.1. Говорим, что на пространстве Е зада-
задана мера Фейнмана Ф&4, если существует обобщенная мера Ф&4
из пространства &"', удовлетворяющая равенству
для любых \x^M(F). Также говорим, что функция f:E-+C ин-
интегрируема по мере Фейнмана Фьа, если она принадлежит про-
пространству &~. Интегралом функции / назовем величину Фь4(Ь)
и обозначим через
Замечание. Определение меры Фейнмана Фь4 зависит
от выбора пространства функций &~.
92

Теорема 5.1. Обобщенная мера х из пространства 8Г' яв-
является мерой Фейнмана Фь4 тогда и только тогда, когда ее
преобразование Фурье имеет вид
v(y)=e
— ib(y)
E.2)
Доказательство. Пусть v—мера Фейнмана на про-
пространстве Е. Так как пространству M(F) принадлежит при
каждом j/ef мера Дирака бу, сосредоточенная в точке у и
то в силу E.1) имеем
- — ib(u') lb(y)
e 2 6ll(dy')=e 2 ,
что влечет равенство E.2).
И обратно, пусть обобщенная мера v из пространства ЗГ'
имеет преобразование Фурье вида E.2), тогда в силу равен-
равенства Парсеваля для любой меры ц из пространства M(F) вы-
выполнено равенство
ц, (dy\ = j v (у) [i (dy)=v (
F
откуда следует, что обобщенная мера v является мерой Фейн-
Фейнмана на Фь4.
Теорема 5.2. Если @"=М(Е), то существует мера Фейн-
Фейнмана Фь4, определенная равенством E.1).
Доказательство. Легко видеть, что равенство E.1)
определяет линейный функционал на пространстве #", поэтому
достаточно проверить его непрерывность. Для этого заметим,
что
для любого \i^M(F), т. е. |Ф&4(ц) |^'|ц|м, что влечет непре-
непрерывность.
Пусть L — конечномерное подпространство пространства F.
Обозначим через nL проектор из пространства Е в простран-
пространство Е/Ьх, где
Lx = {xeaE:VyeaL (х, у) = 0).
Лемма 5.1. Пусть р — полином на пространстве Е, пред-
ставимый в виде p=q°nL, где q — полином на пространстве
93

EjLx порядка т; ц — счетно-аддитивная мера на пространстве
F, m раз дифференцируемая по подпространству L и удовле-
удовлетворяющая условиям
$ «> E.3)
при &=1 пг; /=0, 1,..., т. Тогда существует счетно-адди-
счетно-аддитивная мера т) на пространстве F, такая, что
E.4)
для любого х^Е, и выполнено равенство
— ib(Tu)
/), E-5)
\
-t-Lb(Ty) °° -±.щту)
2 (й) ^ l( ^
где
Ph (У)=-7Г" ? К7*» - Ту' D) p V°i - *М «*» (dx)<
% е " е 4
Доказательство. Полином /? определяет дифференци-
дифференциальный оператор p(iD) m-порядка по подпространству L, а так
как пространство £/Lx конечномерно и мера |л m раз диффе-
дифференцируема по подпространству L, то определена мера т)=
=p(iZ))|x и из свойств преобразования Фурье следует равен-
равенство E.4).
Найдем последовательность конечномерных подпространств
Еп пространства £о,удовлетворяющих условиям A) — C) из § 1,
а также равенству Еп=(Ёп(]Е0Л)(В{Еп(]Е0Л), где подпро-
подпространства Ео,и Ео,2 определены в пункте (А1) из § 1.
Возьмем положительное е и некоторое натуральное п. Так
же, как в предложении 1.1, определим на пространстве Е меру
Яе,п(^е,п(*)!==е~8||дс|11)- Зададим меры т)п> ц„ на пространстве
Ео равенством
1\п=Ч°(Пп°ТГ1, E.7)
где яп — ортогональный проектор из пространства Ео в про-
пространство Еп.
Из соотношений E.6), E.7) следует оценка
(dx')<+co E.8)
при k=l, 2,...,m.
94

Из равенства Парсеваля следует
\е 2 K,n*4\n(dx')=—[ е2 е-*Ш" т\(х) их,
i Cn J
E
и в силу E.4)
2 »... *т> W^^J-Г />2 Р-В\\х\\г n(v\i,(v}Hr E.9)
J
п
где Л^(л) —размерность пространства Еп, а
С„= lim f e2
— Щх) ~
2
т 1
аналогично равенству A.13) получим равенство
\\.(x)dx=
п
где
()
jpuMe 2 Kn*Vn(dx% E.10)
£„
f I(/C^x' D)P(/Ci!*;]e 2
Bя) 2 £n e е E.11)
и существование интегралов
§ Pk,n(x')e 2 ' * Яе,„*М<&')
следует из оценки E.8).
Из равенств E.9), E.10) следует равенство
j i
^е 2 К,п*ЧпШ') =\ ^ рк,п(х')е 2 ХЕ,П* |*п(^')>
откуда, переходя к пределу при е-»- + 0, получим
- — Щх')
\ е 2 n ldx'\-
95

В силу равенств E.11) и E.6) имеет место равенство
Следовательно, можно перейти к пределу при n-^оо в равен-
равенстве E.12), что влечет равенство E.5).
Пусть функция / принадлежит пространству ^"Mr°° (см. § 3)
и представима в виде f=g\x., где функция g принадлежит про-
пространству £Гит, \i — преобразование Фурье счетно-аддитивной
меры \i на F, такой, что
(г+1Jп °п w I|! Ту ||Л'м'{dy) <
n=0
(здесь ijj — продолжение функции g на ОГЕ). Для каждой не-
непрерывной ограниченной функции ф: F-+C определим величину
Elj
где
На пространстве <УМ? определим преднорму /", полагая
C(/) = inf (f 4(gn, !*„
1
где инфинум берется по всевозможным представлениям
и пары (gni \in) удовлетворяют условию
п=-1
Обозначим через aFM?,c линейное пространство &М? с ло-
локально выпуклой топологией, порожденной семейством пред-
норм 1$, где ф пробегает пространство непрерывных ограни-
ограниченных функций на F со значениями в С. Легко видеть, что ис-
96

ходная топология на пространстве JFM? будет сильнее по-
последней топологии.
Лемма 5.2. Для каждого г>1 множество М(Е) плотно в
пространстве ^МТ,с-
Доказательство. Легко видеть, что достаточно пока-
показать, что любая функция f^^T.c, представимая в виде /==
=*ц- (p-nL), принадлежит пространству М(Е), где L — конечно-
конечномерное подпространство пространства F, nL — проектор из про-
пространства Е на пространство E/Lx, р — полином порядка m на
пространстве FfL^ и ц, —счетно-аддитивная мера на простран-
пространстве F, удовлетворяющая условиям
при k=l,...,m и m раз дифференцируемая по подпространству
L. Положим т)=р(Ш)ц. Так как мера ц m раз дифференцируе-
дифференцируема по подпространству L и полином р имеет порядок т, то ц^
JH (F). Из свойств преобразования Фурье следует, что
откуда получим, что функция / принадлежит множеству М(Е).
Теорема 5.3. Если &=<УМ!?,с, то существует мера
Фейнмана Фь\ причем, если функция f принадлежит простран-
пространству &М™с, то имеет место равенство
J fix) Ф1 (dx) = J / (х) Ф? (dx). E.13)
Доказательство. Пусть функция f принадлежит про-
пространству . eF7W"c. Тогда ее можно представить в виде
/=£ gjn. E-14)
n=l
где
f/"to». !*»)<«• E-15)
Положим
E.16)
—0 F
где
(i)k г
Е е * е "
97

Из теоремы 3.1 следует, что имеет место равенство E.13). В си-
силу E.16)' и E.15) имеет место неравенство
£"(*„, И»), E.17)
причем из теоремы следует, что неравенство E.17) выполнено
для любого представления вида E.14), откуда следует оценка
а значит, функционал Ф64 непрерывен.
Теорема 5.4. Если f^PM, то имеют место равенства
J f (х) Ol(dx)=J f (x) (bl (dx) - J / (*) Ol (dx) = J / (x) Ф*4 (dx).
Доказательство теоремы следует из утверждений теорем 3.1,
5.3, 1.1, 1.2.

ГЛАВА III
Представление решений дифферен-
дифференциальных уравнений континуаль-
континуальными интэгралами
§ 1. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА
В КОНФИГУРАЦИОННОМ ПРОСТРАНСТВЕ
Пусть Q —сепарабельное банахово простран-
пространство с нормой ||-||g, a — положительно определенная квадра-
квадратичная форма, определенная на линейном подпространстве Qo,
плотном в пространстве Q, задающая на Qo скалярное произ-
произведение (•, -)д, относительно которого пространство Qo будет
гильбертовым. Пусть также Р — банахово пространство, нахо-
находящееся в двойственности <Q, P> с пространством Q, и гаус-
совская мера ца, порожденная квадратичной формой а (с ну-
нулевым средним), счетно-аддитивна на пространстве Q, т. е. нор-
норма 11-11, измерима в гильбертовом пространстве Qo.
Определим на пространстве Да оператор Лапласса, порож-
порожденный скалярным произведением (•, -)а, полагая для каждой
дважды дифференцируемой функции и: Q-+C и любой точки
Q
где выражение tr(.,.) u"(q) в произвольном ортонормирован-
ном базисе /ь..., /„,... в Q представимо
£ п, /„)■
Скажем, что поставлена задача Коши для уравнения Шре-
дингера с потенциалом v : Q-+R, если задано уравнение Шре-
дингера
dU(tdlQ) =-f i<*\P(t, q)-iv(q)u(t, q) (a>0) A.1)
и начальное условие
и@, q) = uo(q) Vq^Q, A.2)
где «o:Q->C Решением задачи Коши для уравнения Шредин-
гера назовем функцию и: [0, +oo)xQ->-C, дифференцируемую
по t для любых t^[0, +oo), q^Q, для которой определено вы-
выражение. Aau{t, •) при любом te[0, +oo).
99

Пусть Тр : P~**Qo — сопряженный оператор к вложению Qo-+-
-*-Q, где пространство Qo рассматривается с гильбертовой то-
топологией, а пространства Q, Р находятся в двойственности
Обозначим через Ма(Р) пространство всех счетно-аддитив-
счетно-аддитивных комплекснозначных мер на Р, каждая из которых удовле-
удовлетворяет условию
j а (ТРР) ц (dP)< + оо. A.3)
р
Пусть t>0. Обозначим через Е пространство всех непрерыв-
непрерывных отображений х: [0, t]-*-Q. Введем норму ||-|| на простран-
пространстве Е, полагая
||х |]= max ||#(t)||?
для любого х^Е. Пространство Е будет банаховым относи-
относительно нормы || • ||.
Обозначим через Ео линейное подпространство простран-
пространства Е, состоящее из всех отображений х: [0, t]-*-Q0, принадле-
принадлежащих пространству Е, для которых почти всюду существует
производная /(t)gQo и выполнено условие x(t)=O,
), x'{x))adx<oo.
На пространстве Ео определим скалярное произведение (•, •),
считая
t
) = \{х'{х), y'{x))dx,
и положим Ь(х) = (х, х). Тогда пространство Ео будет гильбер-
гильбертовым по отношению к скалярному произведению (•, •) и нор-
норма || • || будет измеримой в гильбертовом пространстве £0. т. е.
гауссовская мера ць, порожденная квадратичной формой Ь (с
нулевым средним), счетно-аддитивна на пространстве Е.
Обозначим через F. множество счетно-аддитивных мер на
[О, t] со значениями в пространстве Р, имеющих ограниченную
вариацию. Множество F будет банаховым пространством с нор-
нормой II«/IIj?=|«/| ('[О, t]). Зададим двойственность <Е, F>, полагая
(х, у) = ^(х(т), y(dx))
о
для любых х^Е, y^F.
Сопряженное отображение Т: F->E0 к вложению Е0-*~Е име-
имеет вид
(Ту)(х)=ТР(у([О, х])) Vx<=[O,t]. A.4)
100

Обозначим через Жр наименьшую а-алгебру подмножеств
пространства F, порожденную алгеброй цилиндрических под-
подмножеств пространства F относительно двойственности <£, F>.
Предложение 1.1. Если v — счетно-аддитивная мера
на Р, то существует счетно-аддитивная мера [iv на а-алгебре
3£,р, удовлетворяющая равенству
F
+£ (-'г и ■ ■ ■ Т[ 5 • • • if{pA+■ ■ •+рл«) х
п=1 0 0 О Р Р
Xv(dPl) ...v(dpn)]dt1...dtn A.5)
s{8x — мера Дирака на [0, t]), сосредоточенная в точке те[0, t])
для любой ограниченной функции f : F—>-C, представимой в ви-
виде /=/0- Т, где /0 непрерывная функция на Еа.
Доказательство. Для каждого натурального п обозна-
обозначим через Dn л-мерный симплекс.
м определим вложение пп : DnxPn-*-F (Рп—Р х ... X Р), полагая
nn(tu ... , tn, ри ... , р„)
Так как для каждого х^Е отображение
DnxPn-+F:(tu ... , tn, p1( ... , рп) —
"-* (*. пп(к, ..., tn, р1у ... , Pn))=(x(t1), Pi) + . . .+{x(tn), pn)
непрерывно, то вложение яп будет измеримым относительно <т-
алгебры Жр (на пространстве DnXPn берется борелевская <т-
алгебра).
Мера Xn®v® — ®v является счетно-аддитивной на простран-
пространстве DnXPn (Ъп — мера Лебега на пространстве Rn). Следова-
Следовательно, мера \in,v—bn®vg) ... ®v)-ri^1 будет счетно-адди-
счетно-аддитивной на а-алгебре $F, имеет место равенство
A.6)
Из сходимости ряда
будет сходиться по вариации ряд V \in,v и определять счетно-
оо
аддитивную меру ^v=6 + V \in,v на а-алгебре X.
101

В гильбертовом пространстве Qo наименьшая а-алгебра, по-
порожденная цилиндрическими множествами, совпадает с а-ал-
геброй борелевских подмножеств, поэтому функция /0 будет из-
измеримой относительно этой а-алгебры, а значит, и функция f
будет измеримой относительно а-алгебры Жр. Так как она
ограничена, то она будет интегрируема по мерам fiv, ц„,у, и в
силу оценки A.7) и равенства A.6) имеем равенство
S f (У) ^ №=f @) + JT J f (у) m.v (dy).
F л=Л F
Учитывая равенства
=l\--- I J ••• J7(«n(*t, '■,•••, tn. plt..., Pn))X
0 0 0 P P
0 0 OP
X v(dpx) ... v(dpn)dtl ... dtn=
t U {n-i
= 1 \ • ■ ■ I \ • • • \ / (PA. + • ■ ■ + Prfit) x
J Л J J J ' "
0 0 OP P
X ^(dpj ... \(dpn)dt1 ... dtn,
получим равенство A.5)
Теорема 1.1. Если функции щ: Q-*-C, v : Q-+R
и0(q)=[ e*(«.P>v0(dp), v(g)=[ e'<«.p> v(dp),
v0, v — меры из пространства Ма(Р), то задача Коши для
уравнения Шредингера A.1), A.2) имеет решение, представи-
мое в виде
U(tt q)==(u(x@) + q)e ° <bl(dx). A8)
Доказательство. Положим
ia(T_D)i
Mdp) +
- - ia(Tnp)t
n=\ 0 0 OP P
102

-■И"
x e
*=1
4=2
— t 1
X
Из оценок
t t, Vi
v (dp,) ... v (dpn) v0 (dp) dtx ... dtn. A.9)
0 0 OP P
xe
X
Я=2 I =--« x
>v(dp1)...v(dpn)vo{dp)dt1...dtn
1 /.
0 0 0
я A.7) следует сходимость ряда в равенстве A.9). Имеет ме-
место равенство
_ J_
2
п=-1 0 0 0 Р Р
х
(р+Ер')) (f*-i-v-1'" 1ГрР)'п
х е *=2 '"ft х
X v (dPl) ... v (dpn) v0 (dp) dtt...dtn.
Сходимость ряда в равенстве A.11) следует из оценок
X
A.11)
оо op р
103

*=•!
X
X e
/=*
X
X v(dPl) ... v(dpn)v0(dp)dt1 ...dtn
x J ... Ja (Т
■It-
А=1
-^-(n+l)C ... f [я
я >
0 0 О
• •• ]v|(dpn)|v0|(dp)<
x
*=i
<
... |v|(dpn)|v0|(dp)<
+aG»)|vo|(dp).
В силу A.9), A.11) получим
д С
—— u(t, x)= \ ei<4-p-
р
-f io(V>'
n=l 0 0 О
X e *=2
X e
v (dPl) ... v (dpfl) v0 (dp) Лх ... dtn
n
t U 'n-l l (»•"+£ "ft)
*- (-
0 0 U
X e
-J-i-afrp(p+V Pft\) «-«,) -«-
x
104

x e 2 laiTp")in v {dpi) ... v {dpn) Vo(dp) dti
p p
+У1(—о*-1 с ii ••■ Сe
LA J J J
n=2 0 0 0
n n
xe ft=2 e *=3 '-* X
i
Xe 2 % (ф2) ... v (ф„) v0 (dp) dt, ... <йп j =
=-i-»Aa"(^, p)-iv(p)u(t, p), A.12)
откуда следует, что функция и является решением задачи Ко-
ши для уравнения Шредингера A.1), A.2), так как
в@, q) = le^'p\(dp) = uu(q). A.13)
Вложение п0: P-+F: р >tрб0 определяет меру ^ =уо-Ло~' на <т-
алгебре ЖР.
Положим
и •4(, = (p,Fv,*^v).
Для любой ограниченной функции f:F-*-C, измеримой относи-
относительно a-алгебры Ж*, в силу A.5) имеем
J f (У) К * V>v (dy) = J j" / (У1 + У г) 6v.
F F F
J j
F F
= J ($ /tii+pbo)vo (Ф)) Rv(rf*.) = I f ШVo (dp) +
F P P
00 i tv 'n-i ft
0 0 0 Al
Xvo(dp)dt1...dtn. A.14)
105

Значит, для любого х^Е выполнены равенства
Чв (*) = J еЧ*>1»цд (dy) = Гe'f*.»>е»««^«о.«!) >6V, * f*v (dy) =
n t
X
п-i oo о" р р
п
X е Hv (dpx)... v (dpn) v0 (dp) dtt... dtn =
oo t U '„.
S<-oJM
=1 0 0 0
(nj
n
x (
n=«l U 0 0
oo t t
n=l 0 0
или
106
X

Для каждого y^F положим
Функция / ограничена и измерима относительно а-алгебры
так как представима в виде f=fo°T, где/0:£0->-С : х-*-е
непрерывная функция в гильбертовом пространстве Ео. Кро-
Кроме того, для каждого у^Е вида y=p8Q+pi8ti + ...+pn6tn имеет
место равенство
~"*Ia(Vs'(E0-Tl)))dir ~Т^а(тР(р+ 2 pft))dT
f(y) = e ° =е ° '*<' =
х
откуда в силу равенств A.14), A.9) получим
и С <7)=S/(#)e!<«^0-">>6Vo*H^)=\e ^(Ф). A.16)
А £
Из определения 5.1 главы II следует, что
u(t, q)=l
Е
и, учитывая равенство A.13), получим A.8).
Замечание. Из соотношений A.9) — A.12) следует, что
функции u(t, •)> u'(t> *) принадлежат пространству ffl(Q) и
отображение t—+uf(t, ■) непрерывно в пространстве M(Q), от-
откуда получим, что решение задачи Коши для уравнения Шре-
дингера A.1), A.2), представленное в виде A.8), принадлежит
пространству С ([0, +оо), M(Q)).
Определим на пространстве Ma(Q) норму 1м,а, полагая
1м.а (v) = J (а (Трр) + 1) | v | (dp) Vvs=Ma(P).
р
Обозначим через lQlM норму на пространстве M(Q). Тогда
Iq,mG) = |v| (P) для любого veAf(P).
Обозначим через M'(Q), Ma'(Q) сильные сопряженные про-
пространства к пространствам M(Q), Ma(Q) соответственно и че-
через 1'м,а, 1'q,m нормы на пространствах Ma'(Q).
107

Отображение Ао : Ma(Q)-^-M(Q) : \>-+&av непрерывно в силу
равенства
J Vv(=Ma(P),
поэтому определено сопряженное к нему отображение Mr(Q)—>-
-*-ffla{Q), которое будет также непрерывно. Это отображение
также обозначаем через Да.
Поставим задачу Коши для обобщенного уравнения Шре-
дингера
ut
задавая начальное условие
£@)=ЬеЛ1'(<2) A-18)
и требуя Ц/)еМ'(О), —l(t)^Ma(Q). Отметим, что произведение
dt _
v для Vv^M(Q), V^M'{Q) определяется равенством v (v) =
= (vv) для любого vgM(^) и равенство A.17) понимается как
равенство элементов из пространства Ma'(Q).
Теорема 1.2. Если обобщенная мера v0 принадлежит про-
пространству M(Q) и функция v принадлежит пространству M(Q),
то существует решение t' [0. +°o)-*-M'(Q) задачи Коши обоб-
обобщенного уравнения Шредингера A.17), A.18) при £o=y(vo),
определяемое равенством
t
—г j»(*(T)+i7)dT
° A.19)
для любого u()
Доказательство. Из равенств A.19), A.14) следует ра-
равенство
A.20)
откуда получим оценку
11 @ (Р) I < I vo I (Q) I ^v I (Z7) (P) (P) = I v01 (Q) 114
Значит, при любом / обобщенная мера l(t) принадлежит про-
пространству M'(Q). В силу A.9), A.20), производя замену
108

получим
«7,Р)е 2 р Vo(dq)p(dp) +
t*l
п=1 у О О О Р Р
со , п со
(рB h)Y 2
i-e(r р)«-<[)
хе 2 р Mdq)v(dp])...v(dpn)p(dp)dtl...dtn =
е "~1 X
n=l Q 0 и б Я Р
X
:хЛ[... *» + (—О J j je'<*.p+p.>e ' 2 °(Гр
Q Р Р
, ( п
00 ^2 п—-1 '(^tP+^j Рь/
n=2 Q 0,0 О Р Р
л , п—1 п
k=l A«=2
X
)
vo(dq)v(dPl) . . . v(dpn)p(dp)dt2 . . . dtn =
Q P
-4-i6G'(»+p6(,))
2
109

vo(dq)v{dp)\iv(dy)—i ff f f в*<».»<1°.<1)+И-л>х
Q P P F
xvo(q)v{p)\v(y)
Q P P F
xe v
± it(t)(bJP)-tt(t)G°) = -Y i
~ E @ (p) = ~ i (A«S @) E-' ("E @) (p)
или
для всех peAfo(P). Откуда следует равенство A.17).
Теорема 1.3. Если функции и0, v принадлежат простран-
пространству Ma(Q), то решение задачи Коши для уравнения Шредин-
гера A.1), A.2) существует и единственно в классе С'([0,
+ оо), М(<Э))ПС([0, +оо), Ma{Q)) и представимо в виде A.8).
Доказательство. Существование решения следует из
теоремы 1.1. Остается доказать единственность решения.
Пусть «1 — решение задачи Коши для уравнения Шрединге-
ра A.1), A.2), принадлежащее классу
, +оо), M(Q))nC([0, +оо), Ma(Q)).
Положим
I j v(x(x)+g)dx
и(t, q) = u,{t,q)-l Щ(х@) + q)е ° ФЬ4(dx).
Тогда функция и будет решением уравнения Шредингера A.1),,
будет удовлетворять равенству ы@, <7)=0 Vq^Q и принадле-
принадлежать пространству
С1 ([0, + оо), М (Q)) П С ([0, + оо), Ма (Q)).
Пусть ^>0. Возьмем произвольную меру уо, принадлежащую
пространству M(Q). Из теоремы 1.2 следует, что существует
решение
g:'[0, +oo)-^iH
обобщенного уравнения Шредингера
~l(t) = -^i
at 2.
удовлетворяющее начальному условию
Определим функцию ф : [0, tQ]->-C, полагая q>(t)=l(t0—t) X
X (и, /, ■)) ПРИ ^[0. ^о]. Так как семейство векторов |(/) при
ПО

te[O, to] ограничено в пространстве М' (Q) и неС'([0, +оо),
t?(Q)), то имеет место равенство
lim £(>„-*-ДО (-J-(u(t + M, •)-«('. .))) =
яри t&[0, to], откуда следует равенство
At
l\m-L[l(t0-t-At)(u(t, .))~i(to-t)(u(t, •))] =
д*о Д<
-)) + (-|-6(<о-0)(«(Л •))• 0-23)
Из равенства A.21) следует
учитывая A.1), A.23), получим
Значит, ф(<о)=ф@). В силу A.22) имеем
т. е. 5u(<0, q)vo(dq) = 0.
Так как мера vo была произвольной, то из последнего равенства
следует, что u(t0, q)(Vq^Q) при всех tfo>O, что влечет равен-
равенство
t
iJo(*(T)+?)rfT
"i (<, <7) = \ «о (* @) + q)e'° <Ы (dx),
•откуда следует единственность решения.
111

Теорема 1.4. Если мера v0 принадлежит пространству
M(Q) и функция v принадлежит пространству Ma(Q), то реше-
решение задачи Коши для обобщенного уравнения Шредингера
A.17), A.18) существует и единственно.
Доказательство. Существование решения следует и»
теоремы 1.2. Докажем единственность.
Пусть £i — решение задачи A.17), A.18). Положим
J(()+e)
I(t) (w) = Ъ (t) И-1 [) w(x@) + q)e ° <b\(dx)\ v0 {dq)
Q
Тогда отображение t>-*t,(t) будет решением обобщенного урав-
уравнения Шредингера A.17), кроме того, будет выполнено равен-
равенство £@)=0.
Пусть ?о>О. Возьмем произвольную функцию и0 из про-
пространства Ma(Q). Из теоремы 1.3 следует, что существует ре-
решение и уравнения Шредингера
t, q)ivu(t, q),
удовлетворяющее начальному условию
н@, q)
и принадлежащее пространству
&([0, +оо), M(Q))nC([0, +oo), Ma{Q)).
В силу равенств A.24), A.25) имеем
-t, -))=~i (Aal(t))(u(t0-t,.))
-il(t)(vu(to-t,
-Lit(t)(Aau(t0-t, -))-i
откуда следует
т. е. в силу A.25) £(*о) («о)=О. Так как функция и0 из про-
112

странства Ma(Q) была взята произвольно, то из последнего
равенства следует, что £,(t)=0 (W>0). Значит, решение един-
единственно.
§ 2. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА
В ФАЗОВОМ ПРОСТРАНСТВЕ
Пусть Q, Р — банаховы пространства с норма-
нормами II-IIq II-Ир соответственно, находящиеся в двойственности
<Q, P>. Пусть также а — непрерывная вещественная функция
на пространстве Р.
Обозначим через Ма(Р) пространство всех счетно-аддитив-
счетно-аддитивных комплекснозначных мер на Р, удовлетворяющих условию
B.1)
•Функция а определяет псевдодифференциальный оператор а:
: Ma(Q)->-ffl(Q) (с символом а), полагая
B.2)
где Ma(Q)—фурье-образ пространства Ma(Q), M(Q)—фурье-
образ пространства M(Q), ц — произвольная мера из про-
пространства Ма(Р) и ц — ее преобразование Фурье
Пусть функция h : PxQ->-R представима в виде
h(p, 9) =
где v — счетно-аддитивная борелевская комплекснозначная ме-
мера на банаховом пространстве QXP. Определим псевдодиффе-
псевдодифференциальный оператор Идр: M(Q)->-M(Q) с ^Р-символом h, по-
полагая
o)v(d(qot dp0), B.3)
Г С
и псевдодифференциальный оператор ЯдР : М(Q)->-М (Q) с qp-
символом h, полагая
W (Я) =Ц е'«°+«'"°>/ (q + q0) v (dq0, dp,), B.4)
Q P
где / — произвольная функция из пространства M(Q).
113

Будем говорить, что поставлена задача Коши для уравнения
Шредингера с псевдодифференциальным оператором, имею-
имеющим qp-сишвол а—h, если задано уравнение Шредингера
dt , q)-ihqr>u{t, q) B.5)
и начальное условие
и (О, Я)=МЯ) V<?eQ, B.6)
где Uo^Ma(Q), V*>0 u(t, -)^Ma(Q). Аналогично определим
задачу Коши для уравнения Шредингера с псевдодифференци-
псевдодифференциальным оператором, имеющим р^-символ а—h, задавая уравне-
уравнение Шредингера
MLl , q)-ihPQu(t, q) B.7)
и начальное условие B.6).
Замечание. В случае, когда Q=P — Rn, a — полином на
пространстве Р и
h(p, q) = v(q) =
p
т. e. v = vi®6o F0 — мера Дирака на пространстве
Q, сосредоточенная в нуле) уравнения Шредингера B.5) и B.7>
приобретают одинаковый вид
^ia(~-f-)u(t, q)—iv{q)u(t, q),
dt \ i dq
где а — линейный дифференциальный оператор на простран-
пространстве Q=Rn с символом а, а v : Q-^-R — потенциал.
Обозначим через EQ, EP банаховы пространства измеримых
по Борелю ограниченных отображений из отрезка [0, t] в
странства Q, Р соответственно с нормами
5Q = .S,UP, H*q(t)Hq
ДЛЯ
\\Хр \\Вр = ^Р,
для Хр^Ер. Положим E=EpXEQ. Пространство Е состоит из
всех измеримых по Борелю ограниченных отображений из от-
отрезка [0, t] в пространство PxQ и норма \\(хР, Xq)\\e — \\xp\\e -\~
+ \\xq\\e задает на нем банахову структуру.
Обозначим через FQ, FP пространства счетно-аддитивных
мер на отрезке [0, t] со значениями в пространствах Q, Р соот-
соответственно, имеющих ограниченную вариацию. Пространства
114

Fq, FP будут банаховыми относительно норм |{/<з|<з=|г/а| ЦО,
t]) для yQ^FQ и \ур\р=\ур\ ([О, £]) для yP<=FP. Положим
F=FQxFP. Пространство F состоит из всех счетно-аддитивных
мер на отрезке [0, t] со значениями в пространстве QXP огра-
ограниченной вариации, и норма \\(yQ, ур)\\р=\уя\а+\ур\р задает
на нем банахову структуру.
Для каждого натурального п определим вложение nn'-DnX
X(QxP)n-+F, полагая
яп(к, .... tn, {qu ft), ..., (<7„, pn)) = (<7i, ЛN(,+ --. +(qn, Pn)\,
где /)„={(£ь..., tn) : t>-U>-U>-... >^n>0} — я-мерный симплекс
и 6Т — мера Дирака на [0, t], сосредоточенная в точке те
€=■[0, fl.
Обозначим через 5F наибольшую а-алгебру подмножеств
пространства F, содержащуюся в а-алгебре борелевских под-
подмножеств, инвариантную относительно сдвигов на векторы из
пространства F и умножения на число и такую, что для любо-
то натурального п вложение я„ измеримо в этой а-алгебре (в
пространстве DnX(QxP)n берется а-алгебра борелевских под-
подмножеств).
Предложение 2.1. Если у — счетно-аддитивная мера на
банаховом пространстве QxP, то существует единственная
счетно-аддитивная мера (Xv на а-алгебре BF, удовлетворяющая
равенству
П=1
t tl
0 6
, dPl) .
V.
6
. . л
г, л
Q P
'(dqn,
С Г
• \ w(i
Q P
dp»)]*
,«7i, Pi) 8,,
i • ■ • Л„,
+
B
.8)
для любой ограниченной функции f : F-*-R, измеримой относи-
относительно BF.
Предложение 2.1 доказывается аналогично предложению 1.1.
Для пары пространств ЕР, EQ определим двойственность
<ЕР, EQy, полагая
t
(xP, Уо) = ) {yQ(d%), xP(x))
0
для xps£P, yQ^FQ. Аналогично для пары EQ, Ер определим
двойственность <EQ, EP>, полагая
t
(xQ, Ур) = \ (хР(х), yQ{dx))
для Xq<=Eq, yP^FP. Двойственности <ЕР, FQXEQ, FP> задают
двойствелшость <Е, F) равенством
<(хР, xQ), (yQ, уР)У=<хР, yQy + <xQ, yP>
115

для Хр^Ер, xq^Eq, yQ^FQ, yP^FP. Цилиндрические подмно-
подмножества пространства F относительно двойственности (Е, F~> со-
содержатся в классе подмножеств BF.
Лемма 2.1. Если v — счетно-аддитивная мера на банахо-
банаховом пространстве QXP, то имеет место равенство
),xA
где h(p, q) = l e»<«.P.>'ei<?..P>v(d<70, dp0)
и xP, Xq — произвольные функции из пространств ЕР, EQ соот-
соответственно.
Доказательство. Отметим, что отображение
из пространства F в R является цилиндрической функцией от-
относительно двойственности (.Е, F), поэтому оно измеримо отно-
относительно а-алгебры BF. Следовательно, в силу предложе-
предложения 2.1
n=l 0 0 0 Q Р
Ue p Q '• " " '» v(d?!, dpj...v(dqn, dpn)Ы^...
-- Г
Г
n=l 0 0 0 ft^l Q P
n=l 0 0 0
x...h((xP(tn)), xQ{tn))dtl...dtn =
t -i\h(xp(x),x (x))dx
)n °
n=>l
откуда следует равенство B.9).
Предложение 2.2. £сли непрерывная функция а:
удовлетворяет неравенству
116

при любых ри Pi^P (С — некоторая положительная констан-
константа), функции h:PxQ-*-R, uo:Q-*-C представимы в виде
h(p, q) = §е'«7-Ро>е«Оо,р>у(^0, dp0), B.11)
4(dp0), B.12)
где v, va — счетно-аддитивные меры, ограниченной вариации на
пространствах QxP, P соответственно, удовлетворяющие усло-
условиям
ll\a(P)\\v\(dq, dp)< + oo, B.13)
j|a(p)||v0|(d/7)< + oo, B.14)
то решение задачи Коши B.5), B.6) существует и представи-
мо в виде
и (t, q) = J" e'<ff.p>e'«(pL {dp) + £ (—«)" 5 f ■ ■ • J
X
n=l Об О
n га n—1
2
/=*+,
y.v(dqu dpj) . . . v(dqn, dpn)v0(dp)] dtx . . . dtn. B.15>
Доказательство. Покажем, что при t>0 функция
u(t, •) принадлежит пространству Ma(Q).
Пусть t>0. Определим меру р* на a-алгебре борелевских.
подмножеств пространства Р, полагая для каждого борелев-
ского подмножества А пространства Р.
... ^ X
n=l 0 0 0
X
'PQP Q P
117

n— 1
х v (dqu dPl) ... v (d<7n, d/7n) v (dp)] df!... dfn, B.16)
где %a — характеристическая функция множества А. Из оцен-
оценки
00 t tt n-l fl
\ \ ' ' ' \ \\l'''l\ ^^ I p ~l / Pft X
n^=l 00 0 PQP QP fc=l
X |v|(d^, dp,)... \v\{dqn, dpn)|v0|(dp)l dtx... dtn^
|v|(Q, P))
n=0
следуют счетная аддитивность и ограниченность вариации ме-
меры pt. В силу B.10)
t ti fl-l
И1 [ШИ1И
00 0 PQP QP ft=l
(... \v\(dqn, dpn)\v,\{dp)\ dt,... << J|a(p)| |vo|(dp) +
-——
p
n
*=1 Q P
X
Q P
откуда следует принадлежность меры pt пространству Ма(Р).
Из равенств B.15), B.16) следует, что
u(t, q) = \
р
значит, u(t,
118

Так как
и (О, q)=le!«-i»vo(dp),
р
то функция и удовлетворяет начальному условию B.6).
Остается проверить равенство B.5). Имеют место равенст-
равенства
ди jt, g)
dt
t U 'n-i
С eг<*•P>
n=l 00 OPQP Q P
* n n n
v{dqu dpx) . . . \(dqn, dpll)v0(dp)dt1
n
-*-+^-ГШв1<' x
JИ
0 0 0 P Q P
n n n
] Ph)(t-U)+i ^ a(p+'^l Р/)(^_г-
2 *3 <*
n— 1
t dPl)...v(dqln dpn)X
xvo(dp)dt2... d/nj =i^a
p
— i Г f
Q P P
'- - i (?+?!.P+
n=2 Q^P 00 OPQP QP
n n n
ia(p+ 2 Pft)«-'«)+* 2 "(p+S P/)('h-x-'h>

9n, dpn)v0(dp)x
И—1
, x(dt2 ... dtn)v(dqlt dPl)"j =i Ja
p
— i f f f e*<«-ft>e«<»+»-P>v(d%. dpo)pt(dp),
Q P P
и в силу равенств B.2), B.3) получим равенство B.5).
Предложение. 2.3. tfi/сть а : P-+R, h : PXQ-+R, и0: Q-v
-»-С — непрерывные функции и v, vo — счетно-аддитивные
меры ограниченной вариации на пространствах QXP, Р соот-
соответственно, такие, что выполнены соотношения B.10) — B.14),
тогда решение задачи Коши B.6), B.7) существует и пред-
представило в виде
u{t, q) =
р
п п
i S Ш$$ ft1 fc1
0 0 0 Р Qil
п п
o)tn i 2 (^./=
...v(dqa, dpn)v0(dp)]dt1...dtn. B.17)
Доказательство. Принадлежность пространству Ma(Q)
функции u(t, •) при каждом ^0 и выполнение начального ус-
условия B.6) проверяются точно также, как и в предложении
B.2). Остается доказать выполнение равенства B.7). В силу
B.2), B.4) имеют место равенства
du(t, q)
dt
= f еН'-рЧа (р) eia^\ (dp) + \] (—i)n x
t h *n-i
И1ШИ (
00 0 P Q f Q P ft—1
n n n
320

n л
X e — '=" v (dqu dPl)... v (dqn, dpn) v0 (dp) dtx... dtn +
+П-ПИ•И; " -
00 0 P Q P Q P
n n n n
ле е "с X
X v (dft, dp^ ... v (d<7n, dpn) v0 (dp) d/2... dtn 1 =
oo t t.
[ 0
л n
и ^ Q P Q P *=1
л л
i 2 "(p+2 Pz)<'*_i-'ft)+'eo>)'n«2 w-p2 />
X efe=2 /=fe e *=' '=ft v (dqu dPl) ...v (dqn,
dpn) vo(dp)dt1... d*J—/Г J Je*<*^-*> (Je«<**..P>Vo(dp)) X
у p p
< f n
n-1
1
n=2 QP 00 OPQP
n n n n
л л
2 (/
Xeffl(p)'«e *=2 '=* v (d<72> dp2)... v (dqn, dpn) v0 (dp) dt, ... dtn) X
Xv(d<h, dpj^iauit, q)—ihpqu{t, q).
откуда следует равенство B.7).
€ Зак. 273

Введем отображение Т+ : F-*-EP, T~ : F-**EP, полагая
(T+(yQ, Ур))(х) = Ур([х, t]),
для любых те [0, t], yQ^FQ, yp^Fp. Обозначим через
FM(FP, EP) пространство всех отображений из пространства
FP в пространство борелевских комплекснозначных мер на Ер
ограниченной вариации, таких, что каждое отображение Ур~-*
<~*Ш:Р удовлетворяет следующим условиям:
1) sup \рвр\(ЕР)\
2) для любой ограниченной борелевской комплекснозначной
функции ф, определенной на банаховом пространстве Ер и та-
такой, что функции ф°Г+, ф°7"~ измеримы относительно а-алгеб-
ры &р, функция
q, Ур) = J еНхр^ ф (хР) \iyp (dxP)
измерима относительно о-алгебры £Sp{U '■ F-+C). Через @~(F)
обозначим пространство всех комплекснозначных функций /,
определенных на пространстве F=(FqXFp) и представимых
в виде
\ B.18)
где отображение уР~-\ку принадлежит пространству 3rM{FPr
Ер).
Для каждой функции f из пространства &~(F) определим
функцию T]a(f) : F-*-C, полагая
B.19).
где функция f и семейство мер \ку связаны соотношением
B.18).
Обозначим через M+(F) множество всех неотрицательных
счетно-аддитивных мер р, определенных на а-алгебре 38р, име-
имеющих ограниченную положительную вариацию и удовлетворя-
удовлетворяющих следующему условию: для каждого множества X из се-
семейства 38р существует множество А, принадлежащее семей-
семейству £F, такое, что Х^А и р(Л\Х)=0, где $f — наименьшая
а-алгебра подмножеств пространства F, содержащая все ци-
цилиндрические подмножества, порожденные двойственностью'
Е F
122

Каждая мера р из множества M+(F) задаст на пространст-
пространстве &~(F) полунорму
Отметим, что для каждого f^&~(F) функция r\a{f) огримнчгпм
и измерима относительно а-алгебры З&р, в силу раш'пспы
B.19) интеграл в равенстве B.20) конечен.
Легко видеть, что семейство полунорм (peAf+(F)) опргдг-
ляет на пространстве @~{F) локальную выпуклую топологию.
Пространство всех непрерывных линейных функционалов па
пространстве S?~(F) будем обозначать через &~'(F).
Для каждого хе£ определим функцию ех: F—>-C, полагая
у)
Лемма 2.2. Функции ех(х^Е) принадлежат пространству
(F) и линейная оболочка множества {ех: х^Е} плотна в
пространстве &~{F).
Доказательство. Пусть &Ер,Хр— мера Дирака на про-
пространстве ЕР, сосредоточенная в точке хР. Для каждого х=
= (хр, xQ)^E отображение Ург-+е1{ХA'Ур)8Ер>Хр принадлежит
пространству @~M(FP, EP), поэтому в силу равенства
., Чх'р.Уц) i{xQ,yp)
е 8Ep<Xp(dx'p)
функция ех будет принадлежать пространству &~(F).
Остается доказать, что линейная оболочка семейства функ-
функций ех(х^Е) плотна в пространстве $~{F). Пусть f^&~(F) и
мера р принадлежит множеству M+(F). Возьмем е>0. Так как
функция r\a(f) ограничена и измерима относительно а-алгебры
35f, то найдутся натуральное п, комплексные числа си, ..., ап
и попарно непересекающиеся множества Х{, ..., Хп из а-алгеб-
ры 38f, такие, что
jt B.21)
где %х — характеристическая функция множества X. Из при-
принадлежности меры р множеству M+(F) следует существование
множеств А\ Ап, принадлежащих а-алгебре Ж/?, таких, что
Ak>Xk, p(/4fe\X4)=0 при k=l, ..., п. Из оценки
\ak\ J \%Ak(y)~%xh(y)\
123

и неравенства B.21) имеем
га
% (f) (y)~J] «*Ч ^ | Р № < Т • B-22>
Так как мера р счетно-аддитивна и множества Ak (k—l, ...
..., п) принадлежат а-алгебре ЖР, то для любого k^n функ-
функцию %Ak можно приблизить цилиндрическими функциями с лю-
любой точностью относительно полунормы
В свою очередь ограниченные цилиндрические функции можно
приблизить с любой точностью относительно той же полунормы
линейными комбинациями функций ех(х^Е). Поэтому найдут-
найдутся такие комплексные числа Pi р* и точки Xi — {x\ip, *i, q),...
..., xi—{xit p, xit q), принадлежащие пространству Е, что будет
выполнено неравенство
51 И* £ч |т- B-23>
Положим
Из равенств
t f.a(x'p(x))dx
Q, yP)= Je ° e'('i>1"«^l('e>">) x
t
i fa
X 6£p, xP(dx'p) = e о e{Xp,XQ) (yQ, yP)
следует
41>ч)-=5>ч- B-24>
В силу B.22) —B.24)
124

B.25)
y) Ip (dy)
Значит, любую функцию f из пространства #"(.F) можно с про-
произвольной точностью приблизить относительно полунормы ур
линейными комбинациями функций ех(х^Е).
Пусть pi pk — меры из множества M+(F). Заметим,
что если меры рЛ, р" принадлежат множеству M+(F), то мера
Ро=р'+р" тоже будет принадлежать множеству M+(F), так
как для любого множества X из a-алгебры З&р найдутся мно-
множества А', А" из (т-алгебры $Р, такие, что А'>Х, А">Х,
р'(Л'\Х)=0, p"(i4"\X)=0, а значит, множество также будет
при А=А'{]А" принадлежать a-алгебре ИР и будут выполнены
соотношения ро(Л\Х)=р'(/4\Х) + р"(Л\Х)=О. Следователь-
Следовательно, мера p=pi+ ... +р*: будет принадлежать множеству M+(F).
Из оценок
(g)=l\ Ча (g) (У) I Pm № < S | Т|„ (g) (У) | | p | (dy) < Sp (g)
для любого g^@~(F) и m==l ft и неравенства B.25) сле-
следует, что
i
[ ) (
m—l m=l
при m=l, ..., k. Значит, линейные комбинации функций
ех(х<^Е) плотны в пространстве &~{F).
Вложение / пространства Р в пространство Е, задаваемое
равенством /(Р) = @, рЬ%), для каждой меры уо^М(Р) опреде-
определяет меру vo0/", счетно-аддитивную на борелевской а-алгебре
банахова пространства F. Для каждой пары хо^М(Р), ve
^M(QxP) свертка \i*(vo°j~1) мер |л„ и vo0/ будет счетно-
аддитивной мерой ограниченной вариации, определенной на
<г-алгебре <%Р. Обозначим через ^,v,vo,<7 линейный функционал
на пространстве &~{F), задаваемый равенством
Г*
tv,v0<7 if) = J Ф9 (У) Ла (/) (f/) ^v * (Vo »
для любой функции \^Э~(¥). Семейства множеств {/~'(Л):
:Ле1}, {ял^ЧЛ) :Ле=Х) («=1, 2, ...) совпадают с борелев-
ским a-алгебрами пространств Р, DnX (QxP)n соответственно,
поэтому вариация | ц,-*1 (vo0/) | меры <р?- |iv* (vo°/-1) будет при*
125

надлежать множеству М+{Е). Значит, линейный функционал
£a,v,vo,<7 непрерывен в силу оценки
I &,.v.v.., (/) I < J" I ч, (/) (у) | | щ • К • Г1) I (dy),
т. е. он принадлежит пространству &"'(F).
Обозначим через &~а{Е) пространство всех комплекснознач-
ных функций ф, определенных на пространстве Е, каждая из
которых ф представима в виде <р=|, где %(х)=£(ех) Vx^E и
ge^"'(F). Пространство &~а{Е) будет линейным пространством
и отображение из пространства &~'(F) в пространство &~а{Е),
задаваемое преобразованием Фурье ■£>-•■£, в силу леммы 2.2
будет линейным изоморфизмом. Определим на пространстве
ЗГ (F) сильную сопряженную топологию и зададим с помощью
отображения %*-*% локально выпуклую топологию на простран-
пространстве @~а(Е) так, чтобы это отображение было бы топологичес-
топологическим изоморфизмом. Обозначим через &~а'(Е) пространство
всех линейных непрерывных функционалов на пространстве
£Га{Е). Определим отображение f>-+f из пространства &~(F)
в пространство Та{Е), полагая f(i7=5(/) Y\^T'{F).
Квадратичные формы а+ : F-*~C, a~:F-*-C, задаваемые ра-
равенствами a+(yQ, yp)=<T+(yQ, yP), yQ>, a-(yQ, yp)=<T-(yQ,yP),
Уо>, являются измеримыми относительно а-алгебры <%р функ-
функциями. Функции g+: F-*~C, #>—e+(*>, g~~:F-+C, y-*eia W бу-
будут принадлежать пространству &~(F), так как имеют место
равенства
для любого у=(у<}, yp)^F. В свою очередь меры удовлетворя-
удовлетворяют оценкам
и для любой ограниченной борелевской функции ф на прост-
пространстве ЕР, для которой функции tp°T~, ср°Т+ измеримы отно-
относительно а-алгебры SSf, функции
g+ iy* Ур) = I ei{'W> Ф (хР) 6EpJ+y (dxP) =
= <р(Ту)е
126

е У'У
также будут измеримы относительно а-алгебры З&р.
Мерами Фейнмана Фа+, Фо~, порожденными квадратичны-
квадратичными формами 2а+, 2а~ соответственно, на пространстве F будем
называть «обобщенные меры» g+, g-^&~a'(E). Скажем, что
функция / : Е~*-С интегрируема по мере Фейнмана Ф4а+ (соот-
(соответственно Ф4а—), если она принадлежит пространству @~а(Е).
При этом величину g+(f) (соответственно §~(f)) назовем ин-
интегралом Фейнмана по мере Фд+^'о") и обозначим через
f / (х) Ф4а* (dx) (соответственно Г / (х) Фа- (dx)).
Лемма 2.3. Пусть а : P-+R, 'h : PXQ-+R, и0: Q-+C — не-
непрерывные функции и v, vo — счетно-аддитивные борелевские
неры ограниченной вариации на пространствах QXP, Р соот-
соответственно, такие, что выполнены соотношения B.10) — B.14).
Тогда для каждого q^Q имеет место равенство
х) — "о \х \У) т?) л
< i
i f a(*p(T))dT-i f ft(*P(T),XQ(»)+<?)^
P 0 i
x
Vx = (xP, xQ)e=E. B.26)
Доказательство. В силу равенств
1 \ a(x'p{i))dx
i
I Г a(xp(t))dx
_е 0 eUxp,yp) e
имеем
^ a,v,vo,i7 (X) = £o,v,v0i7 iex) ==
= \ *la (ex) % (yQ, Ур) И-v * (vT • Y~'
i
I Г а(хр{х)) dx
= e° \ep<eQ'e y \iv* (vo° y~l)(dy) =
127

г
if a(xp(x))dx
i HxVQ) i(xQ,yp+p6a) l(q,yp(W.i})+p)
v e e v0 (dp) щ (dy) =
( ()+7P p l(xp,
-e • \e ^ v(dp)je P
откуда в силу B.11), B.12) и леммы 2.1 получим равенство
B.26).
Теорема 2.1. Пусть a:P-*R, h:PXQ-*-R, uo:Q-+C —
непрерывные функции и \, \0 — счетно-аддитивные борелев-
ские меры ограниченной вариации на пространствах QxP, P
соответственно, такие, что выполнены соотношения B.10) —
B.14). Тогда решение задачи Коши B.5), B.6) существует и
представимо в виде
t t
I j а(жр(т)) dx-l j А(хр(т), xQ(x)+q)dx
« (t, q) - J «o (xQ @) + q)e ° ° Ф*а- (dx). B.27)
Доказательство. Из леммы 2.3 и определения интег-
интеграла по мере Фейнмана Фа- следует
t t
i f a(xp(x)) dx—l f ft(xp(T) ,
e о ° x
X Ф*" (dx) = ga- (la.v.v..?) = b.v.vb.
a (Ы =
F
t
ija(p(x))dT
= U \ e о e(Xp'VQ) 8EpT-y (dxP)) ■ q>, (у) щ, * (v0 о у-
F EP
EP
i
a(yp(\x,t1) dx
t(T y,yQ) l(q,yp([0,n))
e Q e
i [ai.yp(lx,n)+p)\dx l[(yq(d%),ypi.lx,t\)+p)
128

Из предложения 2.1 и равенства B.27) следует
u(t, q) =
оо
+Е (-
р
i U ln-\ n
Р Q P Q Р
(а.н2 pfe)
X e *-i v (dGt) dft) ... v (d<?n, dpn) v0 (dp)] dtx ... dtn,
и в силу предложения 2.2 функция u(t, q) будет решением за-
задачи Коши B.5), B.6).
Теорема 2.2. Пусть а : P-+R, h : PXQ-+R, и0 : Q-+C —
непрерывные функции и v, vo — счетно-аддитивные борелев-
ские меры ограниченной вариации на пространствах QXP, Р
соответственно, такие, что выполнены соотношения B.10)—•
B.14). Тогда решение задачи Коши B.6), B.7) существует и
представимо в виде
u{t, q) = juo(xa(O)^q) X
t t
г f a(xp(T))dt-i j Л(хр(т), JtQ(x)+a)<Ji
X e о ° Фа+ (d*). B.28)
Доказательство. В силу леммы 2.3 имеем
t
X
р р
Учитывая предложение 2.1, получим равенство B.17). Следо-
Следовательно, функция u{t, q) является решением задачи Коши
B.6), B.7).
Замечание 1. В работе Ф. А. Березина [34] предлага-
предлагалось искать решения задачи Коши для уравнения Шредингера
с псевдодифференциальным оператором и (/р-символом B.5),
B.6) в виде континуального интеграла
129

t t
С a(Xp(x— O))dx— I f h(xp(x—O),XQ(
)+0 0+0 у
t
I j <(jrQ)'(T).Jtp(T))<lT
и для уравнения Шредингера с псевдодифференциальным опе-
оператором с р^-символом а—h B.7) в виде континуального ин-
интеграла
i
i Г a(xP(x))dx
u(t, q) = ^uo(xQ
t t
—i f h{xp(.i),xq(x-Q)+q)dx —i Г ((XQ)'(T),xP(x))dx
x e °+° e °+° n(d^, dxP),
см. также работу [З].
Отметим, что в решениях этих задач, представленных формула-
формулами B.27), B.28), «сдвиг по времени» также проявляется
в квадратичных формах
t
ariyq, yp) = \{yQ(dx), уР([т, t])),
S
t
, yP([r, t])),
задающих меры Фейнмана Фа", Фс+.
Определим на пространстве Ma{Q) норму 1м,а, полагая
для любых р()
Замечание 2. Из равенства B.16) и оценок из доказа-
доказательства предложения B.2) следует, что решение задачи Коши
B.5), B.6), представленной в виде B.27), принадлежит прост-
пространству С'([0, +оо), M(Q))[]C{[0, +оо), Ma(Q)). Аналогично
проверяются в силу соотношений из доказательства предложе-
предложения B.3), что решение задачи Коши B.6), B.7), представлен-
представленное формулой B.28), также принадлежит пространству
С'([0, +оо), M(Q))pC([0, +сх>), Ma(Q)).
Обозначим символом Iq,m норму на пространстве M(Q)
(Iq,m(p) = \p\(P) VpeM(P)), символами M'{Q), Ma'(Q) силь-
сильные сопряженные к пространствам M(Q), Ma(Q) соответст-
соответственно, и символами I'q.m, I'm,а нормы на этих пространствах.
130

Отображение й : Ma(Q)->M(Q) : p—►dp непрерывно в силу
оценки
км (а, р)= \\а(р)\ |р| (ф)</«>аГр);
'р
следовательно, определено сопряженное к нему отображение
й': М'(Q)-+Ma'{Q), которое также будет непрерывно.
Из оценок
к,м (Ада, Р)< |v| (Q, Р) |р| (Я)< |v| (Q, P)Iq,mCp),
fg.« (£WPX M (Q, P)-/0!a.(P)
(напомним, что
Q P
следует непрерывность отображений Я,,р : M(Q)-+M(Q), Hpq
MQ)MQ) б
р р ,р ()() pq
(Q)(Q), значит, определены сопряженные отображения
H'qp:M'(Q)-+M'{Q), firpg:M'(Q)->M/(Q), и они непрерывны.
Поставим задачу Коши для обобщенного уравнения Шре-
дингера
-|-5W ='а'6@-&6@, B-29)
ы
задавая начальное условие
6(O)=5oeiH'(Q) B.30)
и требуя l(t)eM' (Q), —g^)eMa(Q) (производная берется
в слабой топологии на пространстве M'a{Q)). Аналогично ста-
ставится задача Коши для обобщенного уравнения Шредингера
jC B.31)
задавая начальное условие B.30) и требуя
5@ е Л?'(Q), -~Ut)^M'a
В силу включения Ма(Р)^.М(Р) и оценки
пространство Al'(Q) можно считать линейным подпространст-
подпространством пространства M'a(Q), так как множество Ma(Q) плотно
в M(Q), поэтому равенства B.29), B.31) определяются как
равенства векторов из пространства M'{Q).
131

Определим вложение а : М (Q)-*-M'(Q), полагая
«(Р) (/) = I f (Q) P (dq) V р е М (Q), V /
Q
Теорема 2.3. Если мера vo принадлежит пространству
M(Q), функция h : PxQ-^-R представима в виде
h{pt <7) = Jei<«"pV«-'">v(d<7l, dPl)
)) и непрерывная функция а : P-*-R удовлетворяет
соотношению B.10), то существует решение |: [0, +оо)^»-
*&-M'(Q) задачи Коши для обобщенного уравнения Шредин-
гера B.29), B.30) при |o=a(vo), задаваемое равенством
X
. I J .--■..
Q
t t
i f a(xp(x))dx—i f h(xP(,r),XQ^)+q)dx
xe° ° 4>*a-(dx)]vo(dq) B.32).
для любого u^M(Q).
Доказательство. Из равенства B.32) следует, что для
любого peAf (P) имеет место равенство
t t
i f a(gp({x, W)+p)dT i f <»Q(dx),yP([T,(l)+P>
Q F P
X ei(g'yP(i0^)+p)p(dp)iiv(dy) vo(d<7), B.33)
откуда получим оценку
|vol (Q) ll*»l (/0 iPl C) = Ivo| (Q) IHv
Значит, при любом ^0 обобщенная мера £(/) принадлежит
пространству iW'(Q). В силу B.33), производя замену
получим
n=\ 000 0 POP OP
132

л
X е R=I e
л—1
л л
2
X
л
X е
... v (dqn, dpn) р0 (dp) v0 (dq) dt[ ... d/n =
с г
< 'l 'л—1
'(«.p+S "^
n=l УОО 0 P Q p Q P
X e"»(p)'«-n (fl (p)
X v (
n) p (dp) v0
— О J ^ f ^e«<'
Q P Q P
x
X
'n.P> x
[... d<;+
.. .. ,dp1)p(dp) +
n=2 QOO 0
^ ' 2 a(
fc2
X
X
Xv(dqv dft) • • •
t
dpn) p0 (d/?) v0
P F
xel
133

•'ШИ-'1
Q P Q P F
x
X ^
= П @ (a P)~% @ (Л№Р) = i (S'g @) (p)-i (JkpKt)) (V)
для любого реМо(Р), откуда следует равенство B.29). По-
Положив £=0 в равенстве B.33), получим равенство B.30).
Теорема 2.4. Если мера vo принадлежит пространству
M(Q) и функция h : PxQ-*~R представима в виде
h{p, qf)=
ы непрерывная функция а : P-+-R удовлетворяет соотношению1
B.10), то существует решение |: [0, + оо)-*-M'(Q) задачи
Коши для обобщенного уравнения Шредингера B.30), B.31}
при £o=a(vo), задаваемое равенством
t t
ij a(xp(x))dx-l jft(*p(T),*Q(T)+i7)dt
о X
X<Dl+(d*)]vo(dflf) B.34)
любого u^M(Q).
Доказательство приводится аналогично доказательству тео-
теоремы 2.3.
Теорема 2.5. Пусть a:P->R, h : PxQ-^R, uo:Q-+C —
непрерывные функции и v, vo — счетно-аддитивные борелев-
ские меры ограничений вариации на пространствах QxP, P
соответственно, такие, что выполнены соотношения B.10) —
B.14). Тогда решение задачи Коши B.5), B.6) существует а
единственно в классе
С1 ([0, + с»), М (Q)) П С([0, + с»), Д, (Q))
ы представимо в виде B.27).
Доказательство. Существование решения следует из
теоремы 2.1, поэтому достаточно доказать единственность.
Пусть щ — решение задачи Коши для уравнения Шредин-
Шредингера B.5), B.6), принадлежащее классу
СЦ[0, +оо), M(Q))flC([O, +оо), Mu(Q)).
134

Положим
и (t, q) = и,.(t, q)— J u0 (xQ @) + q)x
t t
I J a{xP(x))dx-l j" Л(дгр(х),дго(т)+1?)Л
Xe ° ° Фа
Тогда функция и будет решением уравнения Шредингера B.5),
удовлетворять равенству и@, ?)=0 Vq^Q и принадлежать
пространству
С1 ([0, +оо, М(О))ПС([0, +оо), Ma(Q)).
Пусть <о>О и vo — произвольная мера из пространства Ма(Р).
Из теоремы 2.3 следует, что существует решение
обобщенного уравнения Шредингера B.29), удовлетворяющее
начальному условию £(O)=a(vo). Определим функцию <р: [О,
io]-*-C, полагая <p(t)=l{to—t)(u (t, •)) при *е [0, t0]. В силу
>B.5), B.29) выполнены равенства
= i{2'l{to-t))(u(t,
ihqpu(t, -))=0,
откуда следует равенство ф(^о)=ф(О), или
(/0> q)Vn(dq)=1@)(и(tn, -)) = Ш
Так как мера vo из пространства M(Q) бралась произволь-
произвольным образом, то будет иметь место равенство
и ((, q)= VqezQ, Vf>0.
Следовательно, {-сшсние единственно.
Теорема 2.0. Пусть а : P-+R, h : PxQ-^-R, Щ : Q-*-C —
непрерывные функции и v, vq — счетно-аддитивные борелев-
ские меры ограниченной вариации на пространствах QxP, P
соответственно, такие, что исполнены соотношения B.10) —
135

B.14). Тогда решение задачи Коши B.6), B.7) существует и
единственно в классе
С1 ([0, +оо), M(Q))nC([0, +°o), Ma(Q))
и представимо в виде B.28).
Доказательство проводится аналогично доказательству тео-
теоремы 2.5.
Теорема 2.7. Если мера v принадлежит пространству
M(Q), функция h : PXQ-+R представима в виде
h(p, 9)=Je'<«-">e'<«-P«>v(dflf1, dft) (vezM(Qx P))
и непрерывная функция а : P-*-R удовлетворяет соотношению
B.10), то решение задачи Коши B.29), B.30) существует и
единственно.
Доказательство. Существование решения следует иа
теоремы 2.3. Докажем единственность.
Пусть |i — решение задачи B.29), B.30). Положим
-J [ J
X
t t
i £ a{xplT))dT-l ^
xe° о
Тогда отображение ^-*g@ будет решением обобщенного урав-
уравнения Шредингера B.29), удовлетворяющее начальному усло-
условию '|@)=0.
Пусть /о>О и «о — произвольная функция из пространства
Ma(Q). Из теоремы 2.5 следует существование решения «
уравнения Шредингера B.5), удовлетворяющего начальному
условию ы@, q)=uo(q) и принадлежащего пространству
СЦ[О, +оо), M(Q))flC([O, +оо),
В силу равенств B.5), B.29) имеем
+1@
откуда следует
l(to)(u(O, -)) =
136

или g(^o)("o)=O. Так как функция и0 из пространства Ma(Q)
бралась произвольным образом, то имеет место равенство
Б@ = 0 (V*>0),
Следовательно, решение единственно.
Теорема 2.8. Если мера v принадлежит пространству
M(Q), функция h : PXQ-+R представима в виде
h(p, q)= J e»w-P>e'<«'P«> v(dft, dPi) (vezM(Q* P))
и непрерывная функция а : P-+R удовлетворяет соотношению
B.10), то решение задачи Коши B.30), B.31) существует и
единственно.
Доказательство проводится аналогично доказательству тео-
теоремы 2.7.
§ 3. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА
С ПОТЕНЦИАЛОМ ПОЛИНОМИАЛЬНОГО ВИДА
ЧЕТВЕРТОГО ПОРЯДКА В БЕСКОНЕЧНОМЕРНОМ
ПРОСТРАНСТВЕ
Пусть Q — гильбертово пространство СО ска-
скалярным произведением (•, •), и нормой ||-||9; еи ..., еп, ... —
ортонормированный базис в пространстве Q; Т — положитель-
положительно определенный самосопряженный оператор Гильберта—
Шмидта, удовлетворяющий равенствам Ten—hnln(kn^R), т. е.
векторы в\, ..., еп, ... являются собственными векторами ото-
отображения Т; h Лп, ... — соответствующие им собствен-
собственен
ные значения, удовлетворяющие оценкам Я,„>0, V Хп<0.
n»l
Пусть также Р : QxQxQxQ-^R— 4-линейное симметричное
отображение, такое, что для любых ненулевых qe.Q
Pt(q, q, q, q)>0, C.1)
существует число С4,i>0, такое, что для любых fl"
n-l
q, Я, Я, <7)<С4,,(£ &£)*". C-2)
и существует число С4,2>0, такое, что для любых qx, q2, q3, qt^Q
РЛЯи <72. Я: <74)<С4.2/Ы/(<72)/(<7з)/М, C.3)
где
Ц*) = (Р*(я, я, я, я)У<*.
кроме того, Р3 : QxQxQ-+R,P2 : QxQ-+R, Рг : Q-+R— 3-, 2- и 1-

линейные симметричные отображения, такие, что выполнены
для любых qu q2, <7з^<2 неравенства
1Л.071, Яш, ?зI<С3/(?1)/(?,)/(?3), C.4)
C.5)
C.6)
где С3, С2, Ci — константы, не зависящие от qu q2,
Определим функции Р : Q-+R, v : Q-*-R, полагая
= PAq, <7> Я, Я), C.7)
Я, Я, Я) + Рв(Я, Я, Я) + РЛЯ, Я) + РЛя) + Ро, C-8)
где ро — некоторое вещественное число.
Положим
Будем говорить, что поставлена задача Коши для уравне-
уравнения Шредингера, если задано уравнение Шредингера
-|"Ы(<, q) = ~iATu(t, q) + iv(q)u(t, q), C.9)
и @, d)=uo(q)—начальное условие. C.10)
Пусть t — положительное число. Пусть символы Е, Ео, Ес,
11-11, (-, •), a, ||-|lo,g обозначают те же объекты, что эти сим-
символы обозначали в § 4 главы II.
Обозначим через @~Qc класс аналитичных функций на
Qc=C®Q, таких, что для любой функции w из класса @~Qc и
любых положительных е, г существует такая константа
Сх(е, г), что для любых q0, qlt q2, hu h%e Q, a1( а,бС,
удовлетворяющих условиям
0 ^ arg at ^ —, 0 ^ arg a2 ^ я/4
4
выполнено неравенство
IDAwfa, + а1Я1 + a2q2) | < С, (е, г)/П
где символы Dh обозначают производную функции по направ-
направлению h.
Лемма 3.1. Если функция w принадлежит классу &~QC,
то для любых положительных е, г существует такая константа
138

С2(е, г), что для любых h, q0, qu <72eQ, «i, c^eС, удовлет-
удовлетворяющих
\\Qo\\a<r, ||Л||,<1,
Kl<2, |a2|<2,
выполнены неравенства
.e. C ,3)
Доказательство. Неравенство C.12) следует из нера-
неравенства C.11) и оценки
| £>*a>fa> + arfi + aifc) |< | Dhw@) | +
+ max (\DD((
Dhw (т (?0 + а^ + а2<72)) | + | a2Dg,Dhw (т (% + otfi 4-
Аналогично неравенство C.13) следует из неравенства C.12)
и оценки
max (\Dg.w(x(q0 + a1q1
tw (t {q0 + alql + a2q2)) \ + | a2Dg,w (x (q0 + a
Лемма 3.2. Если функция и0 принадлежит классу
то функционалы
t
i j v(q+x(x))dx
x~e° uo(x(O)+q),
t
i J v{q+x{x))dx
х-Дгг° uo(x(O) + q),
определенные на пространстве Е, интегрируемы по мере Фейн-
мана Фа3 и имеет место равенство
t
i j v(q+K(x))dx
t
i J v(q+x(T))dx
Qld C.14)
139

Доказательство. Положим
t
i j 1о@+*(т))-р<х(т)IЛ
g(q,x)=e°
Из оценок C.1) — C.13) следует, что для любых q, h, hu
•функционалы
t t
ifp(x(x))dx ifp(x(x))dr
e° g(q, x), e° Dhg(q, x),
t t
J
, x), e ° ATg(q, x)
принадлежат классу s@~P4 и в силу теоремы 4.1 главы II ин-
интегрируемы по мере Фейнмана Ф<Д
Возьмем монотонную последовательность бп>0, стремящу-
стремящуюся к нулю. Из оценок C.2) — C.13) следует, что для любого
фиксированного h^Q последовательность функционалов
удовлетворяет условию теоремы 4.2 главы II, поэтому имеют
.место равенства
t
I f p(x(x))dx
n-*oo On
t
g(q, x)\ia(dx) =
t
I jp(x(x))dt
? ° [g(Q + bnh, x)—g(q, x)]y,a(dx) =
p(x(x))dx
j p(())
= f e о lim -l-[g(q + bnh, x)~g(q,
J n-»oo 0n
t
j P(x(x))dx
0 Dkg(q, x)\ia(dx). C.15)
Аналогично в силу теоремы 4.2 главы имеют место равенства
t t
I f p(x(x))dx i f p(x(r))dx
D<h \ e ° Dhlg (q, x) ^ (dx) = [ e о Dhi Dh,g (q, x) [ia (dx),
J C.16)
140

t
t f p(x(x))dx
. x)\ia(dx). C.17)
Из равенств C.15) — C.17) следует равенство C.14).
Теорема 3.1. Если функция и0 принадлежит классу &~Qc,
то задача Коши C.9), C.10) имеет решение и, представимое
в виде
t
I J v(q+x(x))dx
u(t, q) = $e° uo(q + x @)) Ф^ (dx). C.18)
Доказательство. Положим
t
i t v(q+ax(x)) dx
wt (t, q, a) = J e о u0 (q + x @)) pa {dx),
E
t
J
°
a ij o(G+ox(t)) dx
q, a) = JJ-^-A(ef ы0(q + ax@)))
t
I j o(<?+ax(T))dT
t
j 0(<?+x(T))dT
для любых f>0, i/eQ, aeC, удовлетворяющих неравенствам
#0 0<</4
141

Так как функционалы
t
t
I J v(g+x{x))dx
интегрируемы по мере Фейнмана Фа3, то функции
a-*wt{t, q, a), a-*w2{t, q, а)
будут непрерывны на множестве
Г п 1 Jj
и аналитичны на множестве
п
, O^arga^
4
Из свойств меры Винера цо следует, что функция a>i пр»
а>0 является решением уравнения
—-w^t, q, a)=^-Ar®1(f, q, а) + 1и(Я)ха^, q, a) "C.19)
от л
с начальным условием lim©1(f, q, a) = uo(q). Поэтому при a>0
Из свойств аналитических функций следует, что равенство
C.19) будет иметь место также для всех а, принадлежащих
множеству ы0- Значит,
■—ЩЦ, Я, e~T) = wt(t, q, е'Ь, C.20)
lim w^t, q, e^) = uo(q). C.21)
<-*+o
Из леммы 3.2 следует равенство
w2(t, q, e^) =-i-Aa»1(<, q, e ^) + iv{q)Wl{t, q, e~). C.22>
112.
Из равенства u{t, q) = w1(t, q, e 4)в силу C.20) — C.22) получив
равенства C.9), C.10).
142

§ 4. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА
С ПОТЕНЦИАЛОМ ПОЛИНОМИАЛЬНОГО ВИДА
В КОНЕЧНОМЕРНОМ ПРОСТРАНСТВЕ
Пусть Q=/?n, (•, •)<? — скалярное произведение
в Q, II "IU — норма в Q, р\ : Q->/? — полином степени, не пре-
превышающей 21—1, и рч: Q-*-R — однородный полином степени
21, удовлетворяющий неравенству
0 V?eQ\{0}.
Пусть также
где п2=± 1.
На пространстве Q поставим задачу Коши для уравнения
Шредингера
£ ibu(t, q) + iv(q)u(t, q) D.1)
(A — оператор Лапласа в Rn), задавая начальное условие
и @, </) = «„(</). D.2)
Пусть t — положительное число. Обозначим через Е про-
пространство всех непрерывных отображений х : [0, t]-*-Q, таких,
что x(t)—0. Введем норму ||-|| на пространстве Е, полагая
|| х ||= max ||х(т)|!.
Vxe£.
Обозначим через Ео линейное подпространство пространства
Е, состоящее из всех отображений х : [0, t] ->-Q, принадлежа-
принадлежащих пространству Е, имеющих всюду производную x'{t) и
удовлетворяющих условию
t
с'(т), х' [x))qdx<oo.
Обозначим через &~Qo, с класс аналитических функций
на Qc=Cn(Q^Qc), таких, что для любой функции их класса
eye^FQo, с и любых положительных е, г существует такая кон-
константа Ci(e, r), что для любых
Qo> Qi< Яъ< "i>  ^ У' ^i» ^2^=^»
удовлетворяющих условиям
О ^ arg аг < я/4, 0 sc: arg а, ^ л/1

выполнено неравенство
| DhiDh,w (q0 + «ад + сзд2) | <Q (e, г) е*М>Ш\ D.3)
где символы Dn обозначают производную функцию по направ-
направлению h.
Лемма 4.1. Если функция w принадлежит классу &~Qq,c,
то для любых положительных е, г существует такая константа
^(е, г), что для любых а\, а^С; q0, qi, q2, h^Q, удовлетво-
удовлетворяющих
\\Яо\\,<г,
l«iK2, |о, К 2,
выполнены неравенства
| Dbw (q0 + al9l + агЯг) | < C2 (e, r) e^<^<, D.4>
I w (q0 + axqx + aA) \ < C2 (e, г) е^чЛ>ШЪ. D.5>
Доказательство леммы 4.1 аналогично доказательству лем-
леммы 3.1.
Теорема 4.1. Если функция и0 принадлежит классу
&~Qo,c, то задача Коши D.1), D.2) имеет решение и, предста-
вимое в виде
t
t J v(q+x(x))di
= ^e° uo(q+x @)) ф£ (dx). D.6>
Доказательство. Из определения интеграла Фейнмана
следуют равенства
lim lim Г
~th_ii-*0 e-»+ol
u(t, q)= lim lim Г X
max\ththii0 +ol (ЛГ+1)"
kZN+l L Bn) 2
п ti
•-"■
х-^н—\--ie ^ ■■ ■■■ x
].

« lim lira Г ■ Г ' X
im lira Г ■ Г
«"+' L Bя) 2 ° (П
D.7)
+ /t» (9 + qN) e *
X "o(9o+ 9)] Afo • • • dqNdt
' + u0(q)
(to = 0, tN+i=t, 0<tt< .
Учитывая равенства
Ды(^, o)= lim lim x
B-+O <^+»)" N+l
Bя) 2 f] ^k-<fc-l
f ... \
Q
X f ... \e *=' " e2 *-'* x
Q Я
X A(e ft=> uo(
(9)« (t, q) = lim lim -i— — x
X
A'+l
г 2 "(^«k-iX'k-'ft-i)
X e k=l u0 (q0 -{ q) dq0 . . . dqx,
! 15

в силу следствия 1 теоремы 2.1 главы II и оценок D.3) — D.5)
получим равенство
t
"{t-q)=Я \iAu {t''q)+iv {q)"{r> q)]dt'+"°(<?)>
о
причем функция т«—• — iAu (т, q) + iv (q) и (т, q) будет непрерывна
на [0, t] при любом q^Q, откуда в свою очередь следует, что*
функция и, задаваемая равенством D.6), является решением
задачи Коши D.1), D.2).
Заключительные замечания. Здесь мы называем некоторые
направления исследований, связанные с теорией континуаль-
континуальных интегралов, но не нашедшие отражения в книге.
1. Исследование континуальных интегралов от функций, оп-
определенных на (супер) многообразиях и, возможно, принимаю-
принимающих значения в супералгебре.
2. Применение континуальных интегралов при квантовании
гамильтоновых систем со связями, в том числе при квантова-
квантовании калибровочных полей.
3. Применение континуальных интегралов в теории пред-
представлений (супер) групп.
4. Исследование связи континуальных интегралов с теорией
Фейнмана — Маслова функций от некоммутирующих операто-
операторов.
5. Применение континуальных интегралов в спектральной
теории операторов.
6. Исследование асимптотик континуальных интегралов.
7. Связь континуальных интегралов с теорией перенормиро-
перенормировок.
8. Применение нестандартного анализа в теории контину-
континуальных интегралов.
9. В настоящее время довольно популярны квантовомехани-
ческие модели, при построении которых используются вместо
(обычных) полей вещественных или комплексных чисел поле
р-адических чисел или другие нетрадиционные поля (или коль-
кольца). Пока не ясно, насколько полезно в этих ситуациях приме-
применение континуальных интегралов.
Ни одно из этих направлений в настоящее время ни в какой
мере нельзя считать завершенным; таким образом, в действи-
действительности мы перечислили возможные направления дальней-
дальнейших исследований.

ЛИТЕРАТУРА
I. Книги
1. Albeverio S., Hoegh-Krohn R. Mathematical theory of Feyn-
tnan path integrals. Lecture notes in math. Berlin. Springer, 1976.
2. Берез и н Ф. А. Метод вторичного квантования. М.: Наука, 1986.
3. Б е р е з и н Ф. А., Шубин М. А. Уравнение Шредингера. М.: Наука,
1984.
4. Боголюбов Н. Н., Ширков Д. В. Введение в теорию кванто-
квантованных полей. М.: Наука, Ш76.
5. Васильев А. Н. Функциональные методы в квантовой теории по-
поля и статистике. Л.: Изд-во ЛГУ, 1976.
6. Глимм Дж., Джаффе А. Математические методы квантовой фи-
физики. Подход с использованием континуальных интегралов. М.: Мир, 1984.
7. С г е е n M. В., Schwartz J. H., W i 11 e n E. Superstring theory.
Cambridge Univ. Press, 1987.
8. Г о X.-C. Гауссовские меры в банаховых пространствах. М.: Мир,
1979.
9. Далецкий Ю. Л., Фомин С. В. Меры и дифференциальные урав-
уравнения на бесконечномерных пространствах. М.: Наука, 19)83.
10. Ефимов Г. В. Проблемы квантовой теории нелокальных взаимо-
взаимодействий. М.: Наука, 1986.
11. Exner P. Theory of open systems. Дубна, 1985.
12. И ци кс он К-, Зюбер Ж.-Б. Квантовая теория поля. Т. 1, 2. М.:
Мир, 1980.
13. К а ц М. Вероятность и смежные вопросы в физике. М.: Мир, 1965.
14. Конопле в а Н. П., Попов В. Н. Калибровочные поля. М.: Нау-
Наука, 1980.
15. Мае лов В. П. Комплексные цепи Маркова и интеграл Фейнмана
для нелинейных систем. М.: Наука, 1976.
16. Попов В. Н. Континуальные интегралы в квантовой теории поля
и статистической физике. М.: Атомиздат, 1976.
17. Р а й д е р Л. Квантовая теория поля. М.: Мир, 19.87.
18. Рид М., Саймон Б. Методы современной математической физи-
жи. Т. 2. М.: Мир, 1978.
19. Simon В. Functional integration and quantum physics. N. Y.: Aca-
Academic press, 1979.
20. С л а в н о в А. А., Фаддеев Л. Д. Введение в квантовую теорию
калибровочных полей. М.: Наука, 1978.
21. Рамаджараман Р. Солитоны и инстантоны в квантовой теории
поля. М.: Мир, 1985.
22. Р а м о н П. Теория поля. Современный вводный курс. М.: Мир, 1984.
23. С о к о л о в А. А., Тернов И. М., Жуковский В. Ч., Бори-
с о в А. В. Калибровочные поля. М.: Изд-во МГУ, 1986.
24. Фейнман Р., Хибс А. Квантовая механика и интегралы по тра-
траекториям. М.: Мир, 1968.
25. Фейнман Р. Статистическая механика. М.: Мир, 1984.
26. Фейнман Р. Взаимодействие фотонов с адронами. М.: Мир, 1975.
27. Фейнман Р. Квантовая электродинамика. М.: Мир, 1964.
28. Functional integration. Theory and applications. N. Y., London, Ple-
Plenum Press, 1979.
29. Feynman path integrals//Lecture notes in physics. 1979. N 106.
30. Ш в а р ц А. С. Квантовая теория поля и топология. М.: Наука,
1989.
147

2. Статьи
31. Алимов А. Л. О связи между континуальными интегралами ш
дифференциальными уравненнями//Теоретическая и математическая физика.
Ш-72. Т. 2, № 2. С. 182—189.
32. Алимов А. Л. Представление решения краевой задачи в виде кон-
континуального интеграла//3аписи ученых семинаров ЛОМИ. 1974. Т. 42.
С. 6—11.
33. Алимов А. Л., Буслаев В. С. О континуальном интеграле для
параболического уравнения второго порядка//Вестн. ЛГУ. Сер. математика.
1972. № 1. С. 5—14.
34 Березин Ф. А. Континуальный интеграл по траекториям в фазо-
фазовом пространстве//УФН. 1980. Т. 1.32, вып. 3. С. 497—548.
36. Блохинцев Д. И., Барбашов Б. М. Применение функциональ-
функциональных интегралов в квантовой механике и теории поля//УФН. 1972. Т. 106,
вып. 4. С. 593—615.
36. W a t а п a b e H. Path integral for some systems of partial differen-
differential equations//Proc. Japan Acad. Ser. A. 1984. V. 60, N 3. P. 86—89.
37. Гельфанд И. М., Ми и л ос Р. А. Решение уравнений квантован-
квантованных полей//ДАН. 1954. Т. 97, № 2. С. 209—ЯЫ.
38. Гельфанд И. М., Яглом А. М. Интегрирование в функциональ-
функциональных пространствах и его применения в квантовой физике//УМН. 1956. Т. 11,
№ 1. С. 77—114.
39. Далецкий Ю. Л. Континуальные интегралы, связанные с опера-
операторными эволюционными уравнениями//УМН. 1962. Т. 17, № 5. С. 3—115.
40. Далецкий Ю. Л., Стремский В. В. Фейнмановские интегралы
для уравнения Шредингера в функциональных производных//УМ'Н. 19№.
Т. 24, № 1. С. 191—192.
41. Далецкий Ю. Л., Фомин С. В. Обобщенные меры в функцио-
функциональных пространствах/ДГеория вероятностей и ее применения. 1965. Т. 10,.
№ 2. С. 329—343.
42. D e w i 11 - М о г е 11 e С. Feynman's path integrals. Definition without
limiting procedure//Comm. Math. Phys. 1972. V. 28. P. 47—67.
43. Евграфов М. А. Об одной формуле для представления фунда-
фундаментального решения дифференциального уравнения континуальным интег-
ралом//ДАН. 1970. Т. 191, № 5. С. 979.-982.
44. J о n s о n G. W., L a p i d u s M. L. Generalized Dysonseries, genera-
generalized Feynman integral and Feynman operational calcu!us//Mem. Amer. Math.
Soc. 1986. N 351. P. 1—78.
45. Jon son G. W. The equvalence of two approaches to the Feynman
integral//J. Math. Phys. 1982. V. 23, N 11. P. 2090—2096.
46. Jonson G. W., S с о u g D. Noteson the Feynman integral. Ill: The
Schrodinger equation//Pacific J. Math., 1983. V. 105. P. 321—358.
47. Ho K. Wiener integral and Feynman integral//Proc. 4th Berkoley
Symp. Math. Stat and Probability. 1961. V. 9. P. 227—238.
48. Cameron R. H. A family of integrals serving to connect the Wie-
Wiener and Feynman integrals//J. Math, and Phys. 1960. V. 39, N 2. P. 126—140.
49. Cameron R. H., Storvick D. A. Some Banach algebras of ana-
analytic Feynman integrable functionals//Lecture Notes in math. 1980. N 798.
P. 18—67.
50. Cameron R. H., Storvick D. A. Analitic Feynman integral so-
solutions of an integral equation related to the Schrodinger equation//J. Analy-
Analyse Math. 1980. V. 38. P. 34—66.
51. Kac M. On a distribution of urtain Wiener functionals//Trans. Amer.
Math. Soc. 1949. V. 66. P. 1—13.
52. Ктитарев Д. В. Формула Фейнмана в фазовом пространстве для
одного класса систем псевдоднфференциальных уравнений/Матем заметки
1987. Т. 42, № 1.С. 40—49.
53. Ктитарев Д. В. Формула Фейнмана для систем псевдодифферен-
псевдодифференциальных уравнений в бесконечномерных пространствах//Вестн. Моек ун-та.
Сер. 1. Математика. Механика. 1988, № 2. С. 76—78.
148

54 Майков Е В. т-гладкие функционалы и интегрирование в функ-
функциональных пространств ах//УМН. 10F3. Т. 18, № 3. С. 243—244.
55 Майков Е. В. т-полиномы и т-аналитические функционалы//ДАН.
1964. Т. 156, № 5. С. 10126—1028.
56 Маслов В П, Чеботарев А. М. Континуальный интеграл по
ветвящимся траекториям//УМН. 1979. Т. 34. Вып. 5. С. 237—238.
57. Маслов В. П., Чеботарев А. М. Обобщенная мера в контину-
континуальном интеграле Фейнмана//Теоретическая и математическая физика. Т. 28,
№ 3. С. 29-1—307.
58. М а с л о в В. П., Чеботарев А. М. Скачкообразные процессы и
их применение в квантовой механяке//Итоги науки. Совр. проблемы мате-
математики. 1978. № 15.
59. Маслов В. П., Шишмарев И. А. О Г-произведении гипоэллип-
тических операторов//Итоги науки. Совр. проблемы математики. 1976. № 8.
С. 137—197.
60. М е н с к и й М. Б. Теоретико-групповой вывод интеграла по путям//
//ТМФ. 1983. Т. 57, № 2. С. 217—231.
61. См о л янов О. Г. Бесконечномерные псевдодифференциальные опе-
операторы для мер и квантование по ШредингеруУ/Третья международная
Вильнюсская конференция по теории вероятностей и математической стати-
статистике. Тезисы докладов. 1981. Т. 2. С. 165—166.
62. С м о л я н о в О. Г. Бесконечномерные псевдодифференциальные опе-
операторы и квантование по Шредингеру//ДАН. 1982. Т 263, № 3. С. 558—
561.
■63. С м о л я н о в О. Г., Хренников А. Ю. Центральная предельная
теорема для обобщенных мер на бесконечномерных пространствах//ДАН.
1985. Т. 281, № 2. С. 279^-283.
614. С м о л я н о в О. Г., Ш а в г у л и д з е Е. Т. Различные определения
меры Фейнмана и связи между ними//Четвертая международная Вильнюс-
Вильнюсская конференция по теории вероятностей и математической статистике. Те-
Тезисы докладов. 1985. Т. 3.
65. S m о 1 у а п о v О. G., S h a v g u 1 i d z e E. T. Some properties and
application of Feynman measures in the phase space Proc. of the Fourth Vil-
Vilnius Conference. 1987. V. 2. P. 595—608.
66. Смол янов О. Г., Шавгулидзе Е. Т. Преобразование Фурье
и псевдодифференциальные операторы в суперанализе//ДАН. 1989. Т. 299,
№ 4. С. 816—820.
67. Смол янов О. Г., Хренников А. Ю. Алгебра бесконечномер-
бесконечномерных псевдодифференциальных операторов//ДАН. 1987. Т. 292, № 6. С 1310—
1314.
68. С м о л я н о в О. Г., Ш а ч г у л и д з е Е. Т. Представление решений
линейных эволюционных супердифференциальных уравнений второго порядка
континуальными интегралами//ДАН. 1989. Т. 309, № 3. С. 545—549.
69. С м о л я н о в О. Г., Шавгулидзе Е. Т. Представление решений
эволюционных супердифференциальных уравнений континуальными интегра-
лами//УМН. 1967. Т. 42, № 4. С. 130—131.
70. Угланов А. В. Об одной конструкции фейнмановского интеграла/^
//ДАН. 1978. Т. 243, № 6. С. 1400—1409.
71. Угланов А. В. Фейнмановские меры со знаконеопределенным кор-
корреляционным оператором//ДАН. 1982. Т. 262, № 1. С. 37—40.
72. Feynman R. D. Space-tim approach to nonrelativistic quantum me-
chanics//Rev. Mod. Phys. 1948. V. 20, N 2. P. 367—387.
73. F e у n m a n R. D. Mathematical formulation of the quantum theory
of electromagnetic iteration//Phys. Rev. 1950. V. 80. P. 440.
74. Feynman R. D. An operation calculus having applications in quan-
quantum electrodinamics//Phys. Rev. 1951. V. 84. P. 108—128.
75. Nelson E. Feynman integrals and the Schrodinger equaUon//J Math.
Phys. 1964. V. 5, N 3. P. 332—343.
76. Чеботарев А. М. Аппроксимативно полные множества обобще-
обобщений меры Фейнмана//ДАН 1988. Т. 298, № 1. С. 52—57.

77. Чеботарев А. М. Достаточные условия регулярности скачкооб-
азных марковских процессов//Теория вероятностей и ее применения. 1988.
. 33, № 1. С. 25-39.
78. Владимиров В. С, Волович И. В. Суперанализ. I. Диффе-
гнциальное исчисление//ТМФ. 1984. Т. 59, № 1. С. 3—27.
79. Хренников А. Ю. Математические методы неархимедовой физи-
я//УМН. 1990. Т. 45, вып. 4 B74). С. 80—110.
80. Хренников А. Ю. Функциональный суперанализ//УМН. 1988.
. 43, вып. 2. С. 872—914.
Замечание к списку литературы. Полная библио-
эафия работ по континуальным интегралам должна была бы
асчитывать несколько тысяч наименований, и составление та-
эй библиографии — это самостоятельная задача, которую мы
еред собой не ставили. Мы включили в список литературы,
э-первых, те работы, которые цитируются в тексте, во-вторых,
:е известные нам книги на русском языке, в которых есть
эстаточно обширные разделы, посвященные описанию конти-
уальных интегралов или их применениям, и, в-третьих, рабо-
ы, в которых рассматриваются вещи, близкие к тем, о кото-
ых идет речь в книге. Наконец, мы включили несколько ра-
эт, которые давно считаются классическими. Отметим еще,
го большие списки литературы по континуальным интеграладМ
:ть в книгах 1 и 11.
Работы, имеющиеся в сборниках 28 и 29, мы, естественно,
гдельно в список литературы не включили.

Научное издание
СМОЛЯНОВ Олег Георгиевич
ШАВГУЛИДЗЕ Евгений Тенгизович
КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ
Зав. редакцией Н. М. Глазкова
Редактор Л. А. Николова
Художественный редактор Л. В. Мухина
Технический редактор Г. Д. Колоскова
Корректоры Л. А. Айдарбекова, Т. С. Миля,

ИБ № 3655
Сдано в набор 12.03.90.
Подписано в печать 22.01.91.
Формат 60X90/16 Бумага тип. № 2
Гарнитура литературная. Высокая печать
Усл. печ. л. 9,5 Уч.-изд. л. 9,44
Тираж 1640 экз. Заказ 273 Изд. № 1271
Цена 2 р. 80 к.
Ордена «Знак Почета» издательство Московского уни
103009, Москва, ул. Герцена, 5/7.
Типография ордена «Знак Почета» изд-ва МГУ.
119899, Москва, Ленинские горы