Современные основания общей теории систем - Портер У.А.

Author: Портер У.А.
Tags: регулирование и управление машинами, процессами математика инженерия инженерное дело издательство наука главная редакция географической литературы математическая кибернетика теория систем
Year: 1971
Similar
Контроль динамических систем
Теория управления движением. Линейная система
Динамическое программирование и современная теория управления
Динамическое программирование и современная теория управления.
Text
                    У. HUP Т Е Р
СОВРЕМЕННЫЕ ОСНОВАНИЯ ОБЩЕЙ
ТЕОРИИ СИСТЕМ
Перевод
Э. «Л. НАППЕЛЬБАУМА под редакцией С. В. ЕМЕЛЬЯНОВА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1971
6Ф.6.5 П.60
УДК 62-52
Современные основания общей теории систем, Порт ер У.» перев. с англ., изд-во «Наука», Главная редакция физико-математической литературы, М., 1971, 556 стр.
Книга Портера убедительно доказывает адекватность и широкие возможности аппарата функционального анализа для решения задач общей теории систем, позволяющей с единой точки зрения рассматривать такие различные системы, как дифференциальные, импульсные, гибридные, а также системы с распределенными параметрами. Подробно излагаются основные понятия и результаты функционального анализа, наиболее пригодные для теории систем. Развитый аппарат позволяет с различных точек зрения исследовать вопросы структуры линейных систем. Последняя глава посвящена решению задач оптимального управления для ситуаций. в которых эти задачи могут быть сформулированы как задачи поиска вектора с минимальной нормой, принадлежащего заданной области гильбертова или банахова пространства.
Илл. 67. Библ. 224 назв.
William A. Porter
The University of Michigan
MODERN
FOUNDATIONS OF SYSTEMS
ENGINERING
The Macmillan Company, New York Collier-Macmillan Limited, London
ОГЛАВЛЕНИЕ
От редактора русского перевода................................... 5
Введение......................................................... 7
0.1. Задачи математического моделирования..................... 8
0.2. Подход теории функциональных пространств................ 12
Глава 1. Функциональные пространства............................ 14
1.1.	Множества............................................... 14
1.2.	Метрические пространства................................ 24
1.3.	Линейные пространства................................... 42
1.4.	Банаховы пространства................................... 58
1.5.	Гильбертовы пространства................................ 75
1.6.	Литература к главе 1.................................... 95
Глава 2. Преобразования......................................... 96
2.1.	Функции................................................. 96
2.2	Линейные преобразования................................ 112
2.3.	Однородные системы первого порядка..................... 141
2.4.	Неоднородные системы первого порядка................... 162
2.5.	Некоторые преобразования, связанные с линейными динамическими системами........................................... 181
2.6.	Литература к главе 2..................................... 194
Глава 3. Структура линейных систем............................. 195
3.1.	Линейные функционалы..................................... 195
3.2.	Некоторые примеры использования линейных функционалов 214
3.3.	Сопряженные и присоединенные преобразования.............. 235
3.4.	Каноническое представление линейных систем............... 252
3.5.	Различные режимы поведения стационарных систем ....	277
3.6.	Некоторые задачи, связанные со структурой системы . . .
3.7.	Литература к главе 3................................... 315
Глава 4. Геометрические методы решения задач оптимального управления..................................................... 316
4.1.	Некоторые геометрические понятия....................... 321
4.2.	Решение задачи 1 для случая преобразований единичного ранга 337
4.3.	Решение задачи 1....................................... 363
4.4.	Обобщение задачи о минимизации усилий.................. 391
4.5.	Литература к главе 4................................... 413
Приложение	1.	Метрические	пространства..................... 415
Приложение	2.	Разложение	Фурье............................. 428
Приложение 3.	Вычисление матриц перехода..................... 440
Приложение 4.	Уравнения n-го порядка........................ 447
Приложение 5.	Канонические формы............................ 469
Приложение 6.	Дополнение к вопросу о единственности......... 488
Приложение 7.	Обращение линейных преобразовании............. 500
Приложение 8.	Задачи с подвижным концом..................... 508
Приложение	9.	Системы с распределенными постоянными........ 519
Литература.................................................... 546
Среди разнообразных основных тенденций развития теории управления в настоящее время все большую популярность приобретает одна, связанная с попытками поставить и разрешить классические задачи теории в наиболее общем виде. Такая тенденция не является следствием малооправданного стремления к «наукообразию», а вызвана насущными потребностями сегодняшнего дня. Во-первых, сама задача управления стала пониматься более широко — появились работы по исследованию процессов управления в биологических, физиологических, экономических и организационных системах. А во-вторых, даже в привычной сфере применения классической теории, в задачах управления технологическими объектами появились новые задачи, требующие иного подхода к математическому моделированию. В то же время успе хи классической теории управления в слишком большой степени зависят от удачно выбранной исходной модели объекта (который всегда удавалось раньше описать системой обыкновенных или конечноразностных уравнений), обладающей целым рядом специальных свойств (грубость, управляемость наблюдаемость и т. п.), вытекающих из некоторых неявных предположений, навязанных спецификой довольно узкого класса традиционных объектов. Для многих новых задач эти рамки оказались узкими, а попытка их расширить привела к появлению нескольких вариантов новой теории (которую чаще всего называют общей теорией систем), обобщающих классическую, освобождающих ее от некоторых неявных допущений и открыто постулирующих те из них, которые не удается отбросить. Один из таких вариантов, или, вернее, первый шаг на пути его создания, и представлен в этой книге.
Создавая свой вариант общей теории систем, Портер пошел по самому осторожному пути. В качестве основного языка теории он выбрал аппарат теории нормированных функциональных пространств, вполне естественный даже и для классических исследований. К тому же его эффективность в рамках теории управления уже была установлена несколькими исследованиями конкретного характера (теория систем с распределенными параметрами, статистическая динамика систем управления, функциональные методы теории оптимальных систем). Портер же попытался целиком переложить на этот язык два крупных раздела классической
6	ОТ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
теории управления: теорию линейных систем и теорию оптимального управления. Попытка эта не вполне увенчалась успехом. В теории линейных систем оказались рассмотренными в основном структурные вопросы, а в оптимальной теории — ситуации, в которых критерий качества может быть представлен в виде нормы соответствующего (банахова или гильбертова) пространства, а объект управления линеен. Однако изучение функционального анализа людьми, занимающимися управлением, полезно само по себе, а изучение предлагаемых Портером вопросов углубит понимание теории управления и у тех, кого пока еще не слишком заботят проблемы создания общей теории. (Сошлюсь хотя бы на то, что книга позволяет ясно почувствовать зависимость сложности решения задачи оптимизации от степени гладкости критерия качества.) Поэтому книгу можно всячески рекомендовать советскому читателю.
С. В. Емельянов
ВВЕДЕНИЕ
В этом введении не упоминается ни один из результатов, составляющих цель данной книги. Мы хотим сейчас лишь набросать общую картину, которая позволит читателю все время чувствовать перспективу дальнейшего развития событий. Обойдем мы и чреватые затруднениями попытки дать явное определение понятия «система». Вместо этого мы будем опираться на общепринятое или интуитивное представление о системе, которое заложено в индивидуальном опыте каждого из нас. Сама возможность такого подхода и составляет одну из граней общей теории систем, предопределяющих ее важность. Действительно, нам удается обнаружить идеи и методы теории систем в таких, на первый взгляд, совершенно несвязанных областях знания, как теория синтеза вычислительных машин, исследования человеческой нервной системы, вопросы управления ракетами, в различных социальных и биологических задачах.
Для целей настоящей книги достаточно рассматривать систему как некоторый «черный ящик», у которого имеется набор доступных для наблюдения входов и выходов. Его поведение подчиняется некоторому физическому закону. Величины, характеризующие поведение системы, часто оказывается удобно разделять на следующие категории: (а) внешние (возмущающие) воздействия — внешние стимулы, оказывающие влияние на поведение системы; (б) выходные переменные (или реакции), описывающие те аспекты поведения системы, которые представляют интерес для исследования, и (в) вспомогательные переменные, которые нельзя отнести ни к первой, ни ко второй категориям. На схеме рис. 0.1 клеммы, на которые подаются внешние воздействия (так называемые входы), показаны стрелками, направленными к системе. Выходные сигналы системы показаны стрелками, направленными от нее. Вспомогательные переменные, если таковые имеются, скрыты внутри самого «ящика».
Технические и научные аспекты исследования систем обычно охватывают широкий спектр вопросов, таких, как определение законов, предопределяющих поведение системы по наблюдениям происходящих в ней физических явлений; изучение математической модели, приближенно описывающей физическую систему; вопросы математического синтеза системы с заданными свой-
ствами; вопросы физической реализации результатов математического синтеза. Из только что перечисленных четырех групп задач в этой книге рассматриваются лишь те, которые связаны с проблемами анализа и синтеза при известной математической модели. С точки зрения теории «черного ящика» математическая
модель должна позволить определять реакцию системы и (или) ее вспомогательных переменных на заданные внешние воздействия. А так как различным целям лучше соответствуют разные методы описания систем (т. е. различные типы математических моделей), то не удивительно, что существует и много разных подходов к общей теории систем. Займемся теперь выяснением возможных причин, заставляющих исследователя остановиться на том или ином подходе.
0.1. Задачи математического моделирования
Одна из возможных целей математического моделирования связана с желанием разобраться с качественной точки зрения в свойствах и поведении систем вообще, и в этом случае нам необходимо такое описание, которое позволило бы получить принципиальную модель, охватывающую как можно более широкий класс реальных систем. Ясно, что в определенной степени каждый разумно выбранный метод описания позволяет расширить наши представления и наше понимание задач общей теории систем. Вторая задача математического моделирования состоит в количественном изучении определенного, ограниченного класса систем. В этом случае желательно «скроить» метод описания систем «по мерке» интересующего нас класса, даже за счет потери полной общности такого представления. Наконец, третья цель, с которой часто приходится сталкиваться, определяет выбор описания системы соображениями, связанными со стремлением воспользоваться некоторым конкретным методом анализа. Естественно, каждое конкретное описание системы в определенной степени удовлетворяет или не удовлетворяет каждой из этих целей.
Популярность большинства математических методов, используемых в теории систем на сегодня, можно объяснить их успехом в достижении одной из этих целей. В качестве иллюстрации справедливости этого утверждения рассмотрим два подхода, наиболее часто используемых при анализе систем с «сосредоточенными параметрами» (т. е. систвхМ, описываемых обыкновенными дифференциальными или интегральными уравнениями) *). Если рассматриваемые системы линейны и стационарны, то классический метод их исследования базируется на преобразованиях Лапласа или Фурье и описывает системы с помощью их передаточных функций. Такой метод описания идеально подходит для исследования линейных стационарных систем, заданных дифференциальными уравнениями, так как метод интегральных преобразований позволяет построить для этих уравнений аналог — алгебраические уравнения, после чего формулировка и решение многих задач анализа и синтеза упрощаются. Именно этим и объясняется огромный объем литературы по методам анализа и синтеза этого типа, опубликованной за последние 20 лет. Многие попытки распространить метод интегральных преобразований на более широкий класс систем не увенчались успехом, так как основная слабость этих методов связана с теми относительными трудностями, с которыми приходится сталкиваться при применении их к анализу нелинейных и нестационарных систем. Поэтому метод интегральных преобразований можно считать типичным примером аппарата, пригодного для исследования весьма ограниченного класса систем, но в то же время успешно решающего задачи, которые связаны с этим классом.
Чрезвычайно модный сейчас в технических кругах метод параметров состояния позволяет описывать поведение систем во временной области. Такой подход теснее связан с физической природой системы и позволяет глубже проникнуть в ее суть, чем это удается сделать методом передаточных функций. Этот метод описания систем позволяет с единой точки зрения рассматривать как линейные, так и нелинейные, как стационарные, так и нестационарные системы, хотя решение нелинейных задач остается по-прежнему трудным. Этот подход создает к тому же естественные предпосылки для формулировки некоторых задач оптимизации.
Слабость обоих подходов состоит в первую очередь в том, что описание системы в обоих случаях слишком тесно связано с конкретной физической природой ее поведения. А это затрудняет восприятие ее общих или абстрактных свойств. Этой фразой мы хотим сказать, что при обоих подходах основное внимание обращается на реакцию системы на определенное внешнее воздействие, а
*) Точнее сказать, систем, вся совокупность переменпых которых (т. е. внешних воздействий, выходных величин и внутренних переменных) может быть представлена конечномерной векторной функцией времени. (Прим, ред.)
не на некоторый класс таких воздействий. Кроме того, многие физические системы в рамках одного из этих подходов описываются со значительным трудом. Примерами таких «трудных» систем могут служить системы с распределенными параметрами, термодинамические системы и многие другие.
Рассмотрим теперь две конкретные задачи теории систем, которые будут положены в основу рассуждений всего введения.
Пример 1. В качестве простого примера, часто встречающегося
в механических и электрических системах, рассмотрим задачу, исследовавшуюся X. Д. Блоком*). На рис. 0.2 показана единичная

Рис. 0.2. Механическая система.
масса, подвешенная на стержне и испытывающая воздействие некоторой силы P(Z). Функция x(t) описывает смещение массы из ее первоначального равновесного состояния в момент времени t, а через & обозначено восстанавлива ющее усилие, развиваемое стержнем и действующее на массу. Если пренебречь трением, то движение системы описывается уравнением
+	= (1)
Мы специально воспользовались здесь рукописным к тому у нас несколько причин. Предположим, что мы пытаемся определить $ экспериментально. Если положить, что восстанавливающая сила стержня обладает гистере-
зисом, то диаграмма смещение — напряжение, показанная на рис. 0.3, представляет собой типичный результат определения $ при изменяющемся х. Если во время опыта
увеличивать х от х0 до х^ затем уменьшать его до х2, вновь увеличивать до х3 и вновь уменьшить до х^ то соответствующая точка в плоскости (х, вычертит траекторию от Ро до Р19 от Рх до Р2, ..., от Р7 до Ро. Заметим, что значение силы f хотя и зависит от х, но не является функцией лишь х. В самом деле, если х равно, например, то, как показано на рис. 0.3, & может принимать по крайней мере четыре различных значения, а в действительности этих значений может быть много больше,— все зависит от характера последовательности событий, приведших к тому, что х стало равным Определить не поможет и рассмот
♦) Н. D. В 1 о с k, Periodic Solutions of Forced Systems Having Hysteria us, IRE PGGT, 423-31 (Dec. 1960).
рение dxldt, dPxIdt2 и т. п. Наконец, еще более ясно, что & нельзя рассматривать как функцию t, не меняющуюся при изменении программы нагрузки. Это позволяет заключить, что не есть функция одной или нескольких переменных и что уравнение (1), следовательно, не есть дифференциальное уравнение в принятом смысле этого слова. Но, с другой стороны, если функция x(t) задана на промежутке времени 0 t Т, то f можно рассматривать как функцию t на том же промежутке. В частности, если
Рис. 0.3. Явление гистерезиса.
x(t) задано для всех t 0, то на этой полуоси задано и f. Таким образом, & является некоторым отображением функции x(t) в Другую функцию [^(х)](/).
Пример 2. В этом примере мы обратимся к изучению системы, схематически показанной на рис. 0.1, обозначив через хъ ..., хт входные воздействия, а через уъ ..., уп выходные величины. Вместо того чтобы рассматривать входные воздействия как некоторые функции времени или некоторые временные ряды, определим m таких классов допустимых входных воздействий Хь... ..., Хт, что каждый входной сигнал я. окажется членом одного из этих классов X., i = 1, 2, ..., т.
Определение допустимости входного воздействия обычно базируется на физических или инженерно-конструкторских соображениях. Например, Хх может состоять из функций времени, определенных на промежутке	b, и таких, что каждая из них
обладает следующими общими свойствами: (а) все элементы Х\ ъ
интегрируемы с квадратом, т. е. \x2(t)dt< оо; (б) все элементы а
Ад должны быть непрерывны; (в) все элементы Хг не превосходят по абсолютному максимуму некоторой фиксированной постоянной;
(г) все элементы должны быть вида z(t) " sin (пл/), где п рационально. Аналогичным же образом обычно удается установить, что и выходные сигналы также должны быть элементами некоторых функциональных классов. В связи с этим саму систему можно рассматривать как некоторое отображение класса входных сигналов в множество классов выходных сигналов или некоторое соответствие между ними.
Исследователя систем обычно интересует широкий круг вопросов, которые можно сжато сформулировать, воспользовавшись представлением системы, показанной па рис. 0.1. Например, задача оптимизации в типичном случае принимает следующий вид: при заданной цели работы системы и заданном критерии ее качества найти конкретное множество входных сигналов в пределах допустимых классов	Xw, которые обеспечат
не только выполнение поставленной цели, но и приведут к достижению максимального качества.
0.2. Подход теории функциональных пространств
Два примера из § 0.1 типичны для задач, стоящих перед исследователями систем. Изучение этих примеров, а также других, с которыми мы столкнемся позже, показывает, что естественный метод представления большинства систем состоит в том, чтобы рассматривать их как некоторое соответствие между элементами классов входных и выходных сигналов. Такой подход, по необходимости, требует использования аппарата теории функциональных пространств (грубо говоря, множеств, элементами которых служат функции). В математике вопросы исследования и применения этого аппарата объединяют под названием «функциональный анализ». Хотя в этой книге функциональный подход к исследованию систем занимает главное место, это не исключает возможности использования методов, связанных с параметрами состояния или передаточными функциями и интегральными преобразованиями.
Хотя функциональным анализом математики усиленно занимаются уже не менее пятнадцати лет, методы функционального анализа проникли в теорию систем практически после 1960 года. Быстрый рост популярности этого подхода к решению задач теории систем можно объяснить не только тем, что он позволяет формулировать эти задачи более широким (а следовательно, и менее приближенным по отношению к физическому прототипу) образом, но и тем, что использование языка функционального анализа позволяет яснее понять суть даже классических результатов. И хотя пока еще не ясно, почему это так, мы ограничимся здесь замечанием о том, что этот подход к решению задач теории систем позволяет освободиться от влияния конкретной природы каждой за
дачи. Другими словами, многие из результатов этого подхода сохраняют свой смысл для самых разных систем, будь они системами с распределенными параметрами, цифровыми, нелинейными или биологическими. Естественно, что результатам, полученным в абстрактной постановке, необходимо придать затем конкретную форму, сочетающуюся со смыслом решаемой физической задачи.
Для того чтобы добиться целей, преследуемых в этой книге, эффективным образом, мы не можем не познакомить читателя с основными понятиями различных разделов функционального анализа. Поэтому первые параграфы этой книги представляют собой введение в разделы, позволяющие свободно обсуждать задачи теории систем на языке функционального анализа. В связи с тем. что мы рассматриваем систему как устройство, преобразующее пространство входных сигналов в пространства выходных величин, мы прежде всего возьмемся за изучение таких пространств. Именно этому и посвящена вся глава 1. А так как объем книги ограничен, то мы отбросили все попытки украсить этот материал пространными примерами из практики искусственных систем.
В первых двух параграфах главы 2 мы познакомимся с элементарными свойствами отображений одного функционального пространства в другое. Затем мы переносим наше внимание с абстрактных вопросов на более конкретные и в оставшейся части этой главы рассматриваем свойства линейных динамических систем. Мы надеемся, что к концу главы 2 читатель почувствует, что он может довольно свободно формулировать задачи теории систем на языке функционального анализа. Остальная часть этой книги представляет собой некий сплав теории и ее применений. Обращаем специальное внимание читателя на то, что приложения к книге содержат дополнительный материал к ее основному тексту.
В заключение нам хочется отметить, что многие идеи и методы этой книги впервые используются в теории систем. Для того чтобы обеспечить их усвоение, мы старались постоянно использовать геометрические и интуитивные представления. Например, нам потребуется определить такие понятия, как расстояние между двумя элементами функционального пространства, их величину (длину), угол между ними. При этом мы обязательно воспользуемся эквивалентными определениями для векторов обычного трехмерного пространства в качестве моделей, позволяющих представить себе образную картину для этих более абстрактных понятий. Очень часто полезно рисовать для каждого такого определения некоторую элементарную диаграмму.
На этом мы заканчиваем наше введение, посвященное философии, целям и структуре настоящей книги. В последующих главах нам остается лишь облечь плотью столь торопливо набросанную схему.
ГЛАВА 1
ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
Эта глава посвящена ряду математических вопросов, которые будут положены в основу остального материала книги. Такой подход, при котором математические основания теории изложены в одной главе, позволит нам собрать в одном месте большинство определений, терминов и понятий, которыми мы будем пользоваться в дальнейшем. А так как наши отправные посылки не слишком определенны (см. введение), то эта глава позволяет читателю к тому же «залатать дыры» там, где это окажется необходимым, обращаясь к дополнительной литературе. (В конце этой главы мы порекомендуем некоторые из книг по каждой из затронутых тем.)
Каждый раз, когда в книге идет речь о подготовке математического аппарата, чрезвычайно важно установить прочные связи между математикой, с одной стороны, и физическими явлениями, стимулирующими ее развитие в данном направлении, — с другой. С этой целью читателю следует постоянно помнить о модели системы со многими входами и выходами, символически представленной на рис. 0.1. Во введении мы уже условились о том, что такую систему удобно рассматривать как объект, устанавливающий определенное соответствие между двумя функциональными пространствами — пространством входных и пространством выходных сигналов. Прежде чем приступить к исследованию таких соответствий, мы изучим в этой главе сами функциональные пространства.
1.1.	Множества
Теория множеств и операций над множествами является потенциально полезным аппаратом исследования в большинстве инженерных дисциплин с достаточно развитым математическим аппаратом. В связи с важностью теории множеств мы приведем здесь краткий перечень наиболее часто используемых теоретико-множественных обозначений. Изложение не будет строгим, так как мы предполагаем, что каждый читатель интуитивно знаком с понятием множества. В настоящем контексте мы будем представлять себе множество как некоторую совокупность, систему или собрание объектов и элементов, объединенных в единое целое в соответ-
ствия с некоторым правилом. Например, мы говорим о множестве всех целых положительных чисел, о множестве всех рациональных чисел на вещественной прямой, о множестве всех точек на комплексной плоскости.
Если элементами множества являются другие множества, мы будем говорить о «классе» множеств вместо множества множеств. Однако мы не собираемся закреплять значения слов «элемент», «множество» и «класс» раз и навсегда. Например, мы можем рассматривать вещественную прямую не как множество вещественных чисел, а как некоторый объект, как элемент другого множества, и говорить тогда о множестве всех прямых на плоскости.
Второе интуитивное понятие теории множеств — это понятие «принадлежности». Если х принадлежит множеству А (т. е. х — элемент множества Л, или х содержится в множестве Л), то мы будем обозначать это х ЕЕ Л. Кроме того, удобно пользоваться обозначением х Л в случае, когда элемент х не принадлежит множеству Л. На понятии принадлежности базируется и понятие эквивалентности множеств. Взаимосвязь между этими двумя понятиями устанавливается с помощью следующей аксиомы.
Аксиома эквивалентности. Два множества А и В называются эквивалентными (или равными), А = В, тогда и только тогда, когда они состоят из одних и тех же элементов; другими словами, они эквивалентны тогда и только тогда, когда из х ЕЕ Л следует, что х ЕЕ В, и наоборот.
Например, если Л — множество корней уравнения х2 — 6х + 8 = 0, а В = {2,4}, то Л = В. Если Л и В не равны, то мы пишем, что A В. Другим важным понятием является понятие подмножества.
Определение А. Каковы бы ни были множества А и В, А называется подмножеством В (что записывается как А cz В) тогда и только тогда, когда из х ЕЕ Л следует, что х ЕЕ В.
Обозначим через В множество всех футбольных команд Большой десятки, а через Л — все команды этих городов, играющие в первой лиге. Тогда Л с В. Одним из следствий приведенного выше определения является то, что утверждение Л cz В не исключает возможности Л = В, В порядке уточнения понятия подмножества мы станем называть множество Л собственным подмножеством множества В (A CZ В) тогда и только тогда, когда Л cz В и Л '=£= В. Если Л cz В (или Л CZ В), то можно утверждать, что В cz Л (или В Z) Л), и говорить, что В включает в себя множество Л.
В дальнейшем нам удобно будет пользоваться символом логического следования (импликации) => . Пусть р и q — некоторые высказывания; тогда р => q означает, что из р следует q (т. е. если р истинно, то истинно и q). Точно так же символом о обозначается двусторонняя логическая импликация, или логическая
эквивалентность. Она обозначает, что высказывания, объединяемые этим символом, логически эквивалентны и что из любого из них следует второе. Этот символ обычно читают как «тогда и только тогда, когда» или «эквивалентно».
Из приведенных выше аксиомы и определения вытекают следующие очевидные свойства операции включения:
(1)	AQA, каково бы ни было А;
(2)	A CZB и В А А = В;
(3)	А с В иВсСн>АсС.
Интересно отметить, что свойства (1) и (2) можно объединить в едином утверждении: A =	Это замечание
указывает на удобный путь доказательства эквивалентности множеств. А именно один из способов доказательства эквивалентности множеств и состоит в том, чтобы не просто пересмотреть все их элементы, а доказать, что каждое из них является подмножеством другого.
Для описания множества в дальнейшем мы станем пользоваться двумя естественными методами. Во-первых, мы можем просто перечислить все его элементы, заключив их в фигурные скобки. Так, А = {1, 4,7} означает, что А — это множество, элементами которого служат 1,4 и 7. Чаще же мы будем вводить множество, указывая свойство, позволяющее определить, принадлежит ли любой элемент этому множеству или нет. В этом случае мы станем пользоваться так называемым коллективизирующим обозначением:
А = {х:р(х)},
где р(х) есть некоторое высказывание или уравнение, описывающее свойства всех элементов множества А. Это читается следующим образом: множество А состоит из всех элементов х, обладающих свойством р(х) *).
Например, рассмотрим множество {1,2,3,4,5} - {х: х— целое число, удовлетворяющее неравенству 1 х 5}. Аксиома эквивалентности гарантирует единственность множества, определенного таким образом. Приведем еще один пример второго определения множества:
{ + 1, ±3, +5, ...} = {п: п — нечетное число}.
Мы часто будем стараться сократить наши обозначения. Так, вместо последнего обозначения мы могли бы воспользоваться следующим: {п: п нечетно}. В дальнейшем мы всегда будем добиваться наибольшей краткости, не идущей вразрез с требованиями ясности и однозначности.
*) Для которых р (х) истинно. (Прим, перев.)
Поскольку нам часто придется сталкиваться с этим, мы введем специальные обозначения для различных подмножеств вещественной прямой. Если а и b — два вещественных числа, а < Ь, то в качестве стандартных мы будем использовать следующие обозначения:
[а, Ы	=	{%' а х	Ъ},
(а, Ь]	=	{х\ а < х	Ь},
[а, Ь)	=	{ х: а х	<	Ь},
(а, Ь)	= {х: а < х	<	Ъ}.
Выписанные выше множества мы будем называть отрезком с началом в а и концом в Ь; промежутком, открытым в а и замкнутым в Ь; промежутком, замкнутым в а и открытым в Ь, и интервалом с концами в а и Ь, соответственно.
Другим часто используемым множеством является пустое множество, обозначаемое символом 0 и определяемое условием 0 = = {х: х=^= х]. Но так как не существует такого х, которое удовлетворяло бы условию х =[= х, то ясно, что множество 0 не содержит элементов. Из аксиомы эквивалентности немедленно следует, что все пустые множества эквивалентны между собой. Кроме того, из определения А следует, что для любого множества И,
Алгебраические операции над множествами. Представляется вполне естественным и даже нужным научиться строить новые множества из тех, которыми мы уже располагаем. Для того чтобы избежать определенных логических трудностей, мы во всех последующих утверждениях будем неявно предполагать, что все рассматриваемые там множества являются подмножествами некоторого всеобъемлющего множества, которое обозначается символом Й. В зависимости от ситуации мы будем менять нашу точку зрения на то, что мы подразумеваем под универсальным множеством Й. Например, говоря о множествах вещественных чисел, мы примем, что й — это /?, множество всех вещественных чисел. Изучая же множество комплексных чисел, мы будем считать, что й — это С, множество всех комплексных чисел. Иными словами, мы всегда будем предполагать, что такое универсальное множество й имеется в нашем распоряжении, и мы вольны выбирать его соответственно потребностям конкретной ситуации.
Геометрическая интерпретация зачастую позволяет легче представить себе множества и операции над ними. С этой целью мы можем представить Й в виде прямоугольника на плоскости, а элементы й — точками, попавшими в этот прямоугольник. При такой интерпретации множества могут изображаться различными областями прямоугольника, а это в свою очередь позволяет строить диаграммы, позволяющие проиллюстрировать различные операции
над множествами или отношения между ними. Например, если Л и В — это два множества из £2, то диаграмма на рис. 1.1 описывает ситуацию, в которой А является подмножеством В (мы рассматриваем здесь множества как совокупность всех точек, принадлежащих области, ограниченной соответственной замкнутой кривой). Такие графические иллюстрации положений теории множеств часто называют диаграммами Венна.
Впоследствии нам окажутся полезными следующие четыре простые теоретико-множественные операции. Первой из них является операция объединения, иллюстрируемая диаграммой на рис. 1.2.
Определение Б. Каковы бы ни были множества А и В. объеди-
Рис. 1.1 А содержится в~Я. пением А и В называется множество
A(JB = {я: х ЕЕ А или х ЕЕ В}.
Рис. 1.2. Объединение А и В.
Таким образом, во время «объединения» множеств мы собираем в единое множество Л (J В все элементы, принадлежащие либо Л, либо В. Смысл этой операции следует из рис. 1.2, на котором множество A|J5 состоит из точек заштрихованной области.
Теорема А. Каковы бы ни были множества А и В, A cz В тогда и только тогда, когда A (J В = В.
Доказательство. Справедливость этой теоремы очевидна из диаграмм рис. 1.1 и 1.2. Однако нам кажется полезным привести и формальное доказательство. Пусть A U В=В. Если х^А, то х^А JZ? = ~ В и, следовательно, хеВ. Отсюда А ст В. Предположим теперь, что А се В. Если х е A (J В, то либо х е А, либо хСЕВ. Но если х^А, то хЕЕ В, так как А ст В. Отсюда A|J5 ст В. В то же время из определения Б сразу следует, что В ст A (J 5, и значит, A (J В =В. Очевидное следствие из теоремы А состоит в следующем: каково бы ни было множество А, А II А = = А и 0J А = А.
Второй основной теоретико-множественной операцией является операция пересечения, результат которой обозначается через ЛП#. Пересечением двух множеств называется совокупность общих для них элементов.
Определение В. Каковы, бы ни были множества А и В, пересечением А и В называется множество
А П В = {х: х А и хеВ}.
Диаграмма на рис. 1.3, где элементы A Q В представлены точками заштрихованной области, мо- * жет служить иллюстрацией этого определения.
Теорема В. Каковы бы ни были множества А и В, Асе В тогда и только тогда, когда A Q В = А.
Диаграмма на рис. 1.3 не оставляет сомнений в справедливости этого утверждения. Формальное доказательство теоремы практически повторяет доказательство теоремы А, и мы предоставляем его читателю. Очевидными следствиями теоремы Б являются следующие утверждения, справедливые для произвольного множества А: во-первых, А Г) А = А и, во-вторых, 0 П А = 0.
Определение Г. Каковы бы ни были множества А и В, разностью А и В называется множество
А\В = {х: х £Е А и х В}.
Смысл этого определения уточняется рис. 1.4. Заштрихованная область на этой диаграмме содержит точки множества А\В.
Во время вычитания множеств из А отбрасываются лишь точки, принадлежащие А П В.
Теорема В. Каковы бы ни были множества А и В, А СЕ В тогда и только тогда, когда А\В = 0.
Доказательство. Если A cz В, то для всех х ЕЕ А х е В и, следовательно, А \ В = 0. Если же А \ В = 0,
Рис. 1.4. Разность А и В. то не существует элемента х такого, что х (= А и х В. А это значит, что из х £= А следует, что хЕЕ В, а значит, A cz 5. Ясно, что для любого множества А :А \ А = 0 и 0\А = 0.
Последней из этих простейших операций является операция дополнения. Дополнение множества А обозначается через А' и состоит из всех элементов, не принадлежащих множеству А. Поскольку мы рассматриваем только те элементы, которые образуют
20
Вл. i. фуййциойалЬнё1е пространства
множество Я, то формально определить А' можно следующим образом.
Определение Д. Дополнением А' произвольного множества А называется множество
А' = {х\ х А).
Диаграмма на рис. 1.5 (где А' заштриховано) иллюстрирует это определение.
Четыре простейшие операции объединения, пересечения, вычитания и дополнения отнюдь не являются независимыми. Например, простое сравнение определений Д и Г сразу позволяет установить соотношение
А' - Я \ А между дополнением и разностью. А отсюда сразу можно получить утверждения 0' = Я и Я' = 0. Поль
зуясь этим же соотношением, нетрудно получить, что
(Л')' = Я \ (Я \ А) = А.
Изученные простейшие теоретико-множественные операции можно объединить в более сложные несколькими естественными способами. В нижеследующей теореме мы приведем семь полезных теоретико-множественных тождеств. Они используются настолько часто, что их целесообразно отметить специально.
Теорема Г. Каковы бы ни были множества А, В и С, каждое из которых есть некоторое подмножество универсального множества Я, имеют место следующие равенства'.
(1)	A и (в и 0 = И и в) и с,
(2)	лп (В л С) = (Л п В) n С,
(3)	а и (В п С) = (л и в) л (Я U С),
(4)	WUQ = (л Л Л)им Л С),
(5)	(Л и ву = Л' л в’,
(6)	(Л л ву = Л' и в',
(7)	A cz В & В' Л'.
Доказательства этих полезных тождеств мы оставляем читателю в качестве упражнений. Следует отметить, что некоторые из этих утверждений можно доказать, не прибегая к понятию «при-
надлежпости». Например, можно показать, что утверждение (6) следует из утверждения (5), если в последнем заменить А и В на А' и В', соответственно, и перейти к дополнениям обеих сторон равенства.
Утверждения (1) и (2) легко обобщить на случай п множеств. Действительно, повторное применение указанных тождеств показывает, что множества
(j A = и A U • • • U Л,
i=l
n Ai = А, П А2 П . • . п Ап i 1
можно образовать из объединений и пересечений, соответственно, взятых в произвольном порядке, и что это не приведет к неоднозначности. В некоторых случаях мы воспользуемся множеством индексов, состоящим из возможных индексов рассматриваемых множеств.
Определение Е. Пусть I — некоторое множество индексов, и пусть каждому i ЕЕ I соответствует некоторое множество А.. Тогда объединением множеств А. называется множество
U А{ = {х: найдется / СЕ 7 такое, что хЕ^А^}, is Г
а пересечением множеств А. — множество
П Ai = {х\ для всех i^I, xfEE. AJ.
Если характер множества индексов I очевиден, то эти обозначения безопасно упростить и писать |J . А. и А.. Если же класс {A.: i е/} состоит из некоторой последовательности множеств, т. е. из Аь А2,..., то их объединение и пересечение мы будем обозначать символами [J £,х А. и П^А., соответственно. Для полноты отметим следующее обобщение предыдущей теоремы. (Равенства (3) и (4) следующей теоремы известны в литературе как теоремы Моргана.)
Теорема Д.
(1)	а и ( П Вг) = П (А и В),
ief г&1
(2)	А п ( и Bt) = и М n Bi),
iG-Г
(3)	(и А)' = A A'i,
iE=I	ief
(4)	( П A) = U A'i.
г&Г	iel
При изучении различных соотношений между теоретико-множественными операциями можно обнаружить, что для доказательства одного и того же соотношения имеется несколько путей. При этом сообразительность и опыт доказывающего играют зачастую более важную роль, чем какие-либо формальные процедуры. В качестве иллюстрации рассмотрим теоретико-множественное тождество (A (J В) \ С — (А \ С) (J (В \ С). Из импликации х ЕЕ (A(JB)\C => xE(A'j^) и х С следует, что либо я ЕЕ А, либо х ЕЕ В и х С. Если хЕ А и х С, то х Е= (А \ С) и, следовательно, х ЕЕ (А\ C)|J(B \ С). Точно так же, если х е В, и х С, то ясно, что х£ (A \C’)U(B\Q. Отсюда (A(J£)\ \С С (А \ C)U(B\C). Для того же, чтобы доказать обратное отношение, предположим, что я Е: (А \ C)|JCS \ С). Тогда либо х (= (А \ С), либо х £Е (В \ С). Если х ЕЕ (А \ С), то zE А и
С, а значит, х Е: A (J В, и так как х С, то х s (A (JB)\C и (А \ C)U(fi \ Q с (AJB) \ С и т. д.
Второй и более простой способ доказательства использует теорему Г, а именно: AUB\C = (Аи#)ПС" = ПС") U С® U С") = = (А \C)U(B\C).
Декартовы произведения. Рассматривая в дальнейшем системы со многими переменными, мы убедимся в полезности понятия декартова произведения множеств (или просто произведения множеств). Это понятие выросло из понятия декартовой системы координат, применяемой в аналитической геометрии. Читатель помнит, что двумерная декартова система координат определяется двумя прямыми на плоскости, расположенными под прямым углом относительно друг друга, причем за начало отсчета (нуль) на каждой прямой выбрана точка их пересечения. Положение любой точки z на плоскости определяется значениями ее двух ортогональных проекций на каждую из этих осей. Иными словами, z = (х, г/), где х — координата по первой оси, а у — по второй.
Одно из важнейших геометрических свойств заключается в том, что если zt = (xx, z/j) и z2 = (х2, у2) — некоторые точки на плоскости, то
Z1 = z2 4=> хг = х2 и уг = у2.
Если перейти на более строгий язык, то множество {а, Ь} называется упорядоченной парой и обозначается через (а, Ь), если оно принадлежит некоторому классу, для которого справедлива следующая аксиома.
Аксиома упорядоченных пар. Каковы бы ни были упорядоченные пары (а, Ь) и (с, d), (а, b) = (с, d) тогда и только тогда, когда а = с и Ъ = d.
Предположим теперь, что Yr и У2 — два непустых множества. По аналогии с декартовым представлением комплексной плоскости введем следующие определения.
Определение Ж. Каковы бы ни были множества Yr и у2, декартовым произведением Yx X У2 будем называть множество
У1 X У2 = {(У1, У2 ): У16 Л и у2<= У2).
Другими словами, множество У! х Y2 представляет собой совокупность всех упорядоченных пар {(уп у2)}, таких, что уг е Е=У1, a y2(EiY2. Несмотря на произвольный характер множеств Y1 и У2 иногда оказывается полезным представлять себе Yr и У2 так же, как мы представляем себе декартову систему координат на плоскости.
Определение произведения двух множеств естественно обобщается на случай п множеств. Например, если УА, У2,..., Уп — непустые множества, то их декартовым произведением Yr х У2Х... ... X Yn называется множество всевозможных упорядоченных п-ок (уц у2, ..., уп), таких, что у<^У{ при любом значении индекса i. Если все У$ являются копиями одного и того же множества У, то их произведение обозначается Уп. Например, через R1 можно обозначать R, прямую вещественных чисел, через R2 — вещественную плоскость, а через R3 — множество всех упорядоченных троек вещественных чисел, лежащее в основе классической аналитической геометрии трех измерений.
В качестве второго примера вспомним о системе со многими переменными, схема которой изображена на рис. 0.1. Вводя в рассмотрение множества X = х ... X Хт и у == ух х ... ... X Уп» мы сразу убеждаемся в том, что эту систему можно считать устанавливающей соответствие между множествами X и У, а не между классами {%<} и {У^, что было бы сложней. После введения новых множеств не остается серьезных причин, по которым системы с несколькими переменными и с одной переменной нужно изучать порознь.
Используя упорядоченные n-ки, мы часто называем yi z-й координатой п-ки, а У{ i-м координатным множеством.| Если 2 = (Ун •••, Уь •••» Уп) Er. YtX ... X Yn = Z, то у{ часто называют проекцией Ина множество Yt. Аналогично множество У{ можно назвать проекцией множества Z на его z-e координатное множество.
Все элементарные теоретико-множественные операции легко обобщить на декартовы произведения множеств. В дальнейшем мы будем неявно предполагать, что новое универсальное множество имеет вид произведения координатных универсальных множеств. Нижеследующая теорема содержит три примера полезных теоретико-множественных тождеств относительно декартовых произведений.
Теорема Е. Каковы бы ни были множества А, В и С,
(1)	Л х (Z?UQ - (л X 5) и (Л X С),
(2)	А X (В П С) = (Л X В) П (Л X С),
(3)	Л X (В \ С) =- (Л X В) \ (Л X С).
Доказательство (1). Если (х, у) €~Л %(B(JC), то х Л и i/G GE/?|JC. Тогда yEzB или у 6= С, так что (х,у)Е= ЛхВ или (х, у) ее €= Л х С. Поэтому (х, у) £ (Л X В) (J (Л х С) и Л х C#U0 <= с (Л	X 5)и(Л	X С).	Если же	(х, у) S (Л X В) ЩЛ	X С), то
(х, у)	е л X В или (х, у)ЕА	х С. Это	значит, что	х ё= А,
а у	В или у	е С.	Другими	словами,	у ЕЕ B\JC и	(х, у) ЕЕ
ЕЕ А	X (В J С),	так	что (А	х В) [J (А	х С) £ А х	(В (J С),
откуда А х (#UQ = G4 х В)|J(А X С).
Упражнения
1.	Пусть Q — множество {1, 2}. На этом множестве можно построить четыре подмножества. Выпишите их. Сколько подмножеств содержится в множестве Q - {1, 2,	и}?
2.	Докажите теоремы Б и Г до конца.
3.	Убедитесь в справедливости следующих теоретико-множественных тождеств:
(а) (б) (в)	A U (Л П В) = А = А П (Л U В), (Л и Л) \ С = (Л \ С) и (В \ с), Л \ (В и с) - (Л \ В) \ с.
4. Множество Л Д В = (А \ В) (J (В \ Л) называют разностью множеств А и В. Докажите, что
(а)	А А (В Д С) = (Л Д В) Д С (ассоциативность),
(б)	Л П (В А С) = Л П В Д Л р| С (дистрибутивность),
(в)	лив = лдвдлия,
(г)	Л Д В = Л Д Л п
симметр ической
5. Докажите утверждения (2) и (3) теоремы Е.
6. Представьте цилиндр с радиусом основания г и высотой h в виде произведения множеств.
1.2. Метрические пространства
В § 1.1 мы познакомились с основными понятиями и терминологией, необходимыми для эффективного изучения операций над абстрактными множествами. Хотя у всех этих понятий есть много интересных применений, понятие «множества» становится для нас особенно полезным лишь после того, как ему придается определенная структура. Множество, наделенное определенной структурой, т. е. множество с установленными соотношениями между
его элементами или операциями над ними, называют «пространством». Структуру же множества чаще всего можно отнести к числу геометрических либо алгебраических структур.
В этом параграфе мы введем понятие расстояния, которое по своей природе является геометрическим. Расстояние между двумя точками х и у на вещественной прямой определяется числом \х — г/|. В двумерном пространстве расстояние между двумя упорядоченными парами zY = (xj9 yY) и z2 = (х2, у2) обычно определяется по формуле {(хх — х2)2 И (У1~ */г)2 }'/2- Не представляет труда обобщение понятия расстояния на случай трех или большего числа измерений.
При изучении систем общего вида нам окажется необходимым ввести понятие расстояния, распространяющееся и на абстрактные множества. Элементы множеств и сами множества, которые будут интересовать нас больше всего,— это функции времени или временные последовательности. Введение расстояния в таких множествах не так очевидно, как в только что приведенных геометрических примерах. В качестве естественных кандидатов на формулу для расстояния между двумя функциями u^t) и u2(t) можно предложить следующие:
ь
max | (t) — и2 (0 |,	\ | Hi (0 — и2 (0 | dt
^[а, Ь]	а
или
[ 3 lwi Gk) u2(^k)]2"| •
В системах же со многими переменными для определения расстояния между упорядоченными n-ками и = (un ..., ип) и v = (vl9 ... ..., vn) зачастую пользуются и такими сложными выражениями, как
к Ъ	2/р П	2/ У
[(2 5 I uj (0 "" V3 W |Р^) (2 2	(^i) *" I •
L ;=1 a	1 j=k+l	'
Сложность приведенных выражений подсказывает, нам, что, прежде чем пользоваться конкретными формулами, было бы неплохо разобраться в элементарных свойствах понятия расстояния. Метрическое пространство (понятие, которое будет определено позже) — это всего-навсего некоторое непустое множество, для которого определено (в соответствии с некоторыми правилами) понятие расстояния между его элементами. Если теперь исследовать понятие геометрического расстояния и попытаться сформулировать его основные свойства в специальной аксиоме, то мы,
по-видимому, довольно естественно придем к следующему определению.
Определение А. Пусть X — некоторое непустое множество, Расстоянием или метрикой в X называется вещественная функция *) р пары элементов X такая, что если х, у, z (= X, то выполяются следующие три условия:
(1)	р(х, у) > 0, и р(х, у) = 0 <=> х = у (свойство тождественности),
(2)	р(х, у) = р(у, х) (симметричность),
(3)	р(я, у) р(я, z) + р(у, z) (неравенство треугольника).
Число р(х, у) и есть то расстояние, которое нам понадобится, а три условия, выписанные в определении, известны под названием аксиом метрического пространства. Недолгое размышление позволяет признать, что эти аксиомы суммируют фундаментальные свойства, которых интуитивно ожидаешь от понятия расстояния.
Определение Б. Метрическое пространство представляет собой совокупность двух математических объектов: некоторого непустого множества X и некоторой метрики р, определенной в X,
Элементы X называют точками метрического пространства (X, р). Каждый раз, когда это не может привести к путанице, мы будем обозначать метрическое множество (X, р) тем же символом X, который используется и для обозначения множества точек, лежащих в его основе. Однако ни в коем случае нельзя забывать, что метрическое пространство — это не просто некоторое непустое множество, а непустое множество с определенной в нем метрикой.
Определить метрику р в множестве X можно не единственным образом. На самом деле, часто оказывается, что на одном и том же непустом множестве можно задать несколько метрик. Использование различных метрик приводит к созданию различных метрических пространств. Очень важно полностью освоиться с аксиомами определения А. С этой целью рассмотрим несколько примеров метрических пространств, каждый раз обращая специальное внимание на то, насколько естественным здесь оказывается выполнение каждой из этих аксиом.
Пример 1. Для любых точек х, у вещественной прямой R метрику можно задать по формуле
р(*. у) = к - И
♦) Здесь автор допускает определенную логическую непоследовательность, пользуясь понятием функции, которое он определит лишь в главе 2. (Прим, перев,)
Легко проверить, что все три условия нашего определения здесь не нарушены:
(1)	р(*.	у)	=	|* —	у|	=	= у>
(2)	р (х,	у)	=	| х —	у	| =|	—	(у — х) | = | у — х |	=	р(у,	х),
(3)	Р (х,	у)	=	I X —	у I	=	|	(х	— Z) + (z — у) К	| X	—	Z	| +
+ |z —у| = pk.	z)	+	p(z, у).
Метрику |гг — у\ называют естественной метрикой в R, Если противное специально не оговорено, то множество R в качестве метрического пространства предполагается имеющим эту метрику.
Пример 2. Если С — множество всех комплексных чисел z = а + /&, то одна из подходящих метрик может определяться по формуле
р (*!> Z2) = {(zx - z2) (Zi - z2))*/. = |zx _ z2|.
Эта метрика считается для С естественной, и читателю в качестве упражнения 3 предлагается самому убедиться в том, что для нее выполнены все три аксиомы определения А.
Пример 3. Напомним, что Rn (или Сп) — это множество вещественных (или комплексных) упорядоченных n-ок х =
..., хп), у = (уп у2, ...» уп)‘ Множество Rn (или Сп) можно преобразовать в метрическое пространство, вводя метрику
pk. у) = {S k< - yt I2/’-
Очевидно, что первая и вторая аксиомы метрического пространства здесь выполняются. Доказать третью тоже несложно, но мы отложим это на некоторое время для того, чтобы привести более общее доказательство. Указанная метрика для Rn (или Сп) называется евклидовой, а пространство Rn (или Сп) с такой метрикой называется евклидовым пространством и обозначается через Еп.
Для того чтобы лишний раз подчеркнуть сказанное выше, приведем пример, показывающий, что метрику можно вводить далеко не единственным образом. Читатель может убедиться в том, что следующие функции также могут быть метриками для множества Rn:
п
рак. у) = S ki -г/il.
г=1
п
Рзк. у) = S ^ki	г =
i=l
При исследовании физических систем мы часто будем проявлять гибкость в выборе метрики. Такая гибкость очень полезна, так как позволяет выбрать метрику, наиболее подходящую для данной конкретной ситуации или упрощающую некоторые детали исследования.
Пример 4. Гильбертовым пространством 12 называется множество всех последовательностей вещественных чисел х =	х2, ...
ео
..., Xi, ...) таких, что 'ряды 2 l^il2 сходятся. Для этого прост-г=1
ранства расстояние определяется по формуле
°°	у,
Р (*- у) = { S I xi - Ui I2} • г«1
Доказательство того, что определенная так функция является метрикой для 12, приведено в примере 4 в § 1.4.
Прежде чем переходить к пятому примеру, рассмотрим множество A CZ В, где А — некоторое непустое ограниченное множество. Прилагательное ограниченное означает, что найдется такое Xq€~R, что для любого х S А :| х |	х0. Но если множество А
ограничено сверху числом х0 < оо, то у А должна быть верхняя грань (supremum или sup), т. е. число х ЕЕ R такое, что хЕЕА=$> => х^х, и при этом не существует другого числа, удовлетворяющего тому же условию и в то же время меньшего х. В этом и состоит формулировка «аксиомы полноты». Компактное изложение основных свойств множества действительных чисел можно найти, например, в главе 2 книги Тейлора [А82]. Аналогично, число у называется нижней гранью (infimum или inf) множества А, если у больше или равно произвольной миноранте множества А (минорантой называется любое число у0 такое, что х е А ==> х у0). Для того чтобы формализовать все эти определения, введем следующие обозначения.
ОпределениеВ. Пусть А — некоторое ограниченное подмножество множества R, Тогда через inf (А) обозначается элемент х ЕЕ R, являющийся нижней гранью множества А, а через sup (А) обозначается его верхняя грань.
У множества А может быть и наибольший элемент, обозначаемый через max (А), т. е. такой элемент этого множества, который больше или равен всем остальным элементам того же множества. Разницу между max (А) и sup (А) легче всего уяснить на примере множества [0,1), для которого sup А = 1, a max А не существует, так как число 1 не принадлежит множеству. На самом деле, если sup А Е А, то max А = sup А. Аналогично выглядит и разница между min А (минимальным элементом множества А) и нижней гранью inf А. Понятия верхней и нижней гранен оказываются
полезными и потому, что они всегда существуют, что несправедливо для максимума и минимума.
Пример 5. Обозначим через С (а, Ъ) множество всех непрерывных вещественных функций, определенных на промежутке [а, Ь]. Естественной метрикой *) для этого множества считается функция
рСг, у) = sup I х (/) — y(t) I,
про которую говорят, что она однородна. Из определения ясно, что р(ж,	я) > 0 и что р(я, у) == 0	(t) у (/) при всех
t €= la, 6]. Более того,
|x(Z) — z(0| = | [х (0 — y(t)] + Iy(0— z (011 <
< | x(t) — y(t) | + | y(t) — z(0 |<sup|z(/) — у(0|4- sup| y(t) — — z(0 | = p(*. !/) + p(y, z).
Переходя к верхней грани, в левой половине получим р(аг, z) < р(х, у) + р(у, z),
что и доказывает справедливость в данном случае всех аксиом метрического пространства.
Последний пример показывает, с какими метрическими пространствами мы будем в основном сталкиваться в последующих главах. Хотя элементы пространства С(а, Ь) кажутся гораздо сложнее элементов' пространства Еп, очень важно, что метрика вводится здесь так же просто и удовлетворяет тем же аксиомам, что и в Еп.
Поскольку метрическое пространство во многих смыслах получено в результате обобщения абстрактных свойств Е2, то разумно ожидать, что большинство из понятий, связанных с расстоянием и определенных для Е2, удастся перенести и на более общий случай. Первыми из таких понятий, которые мы введем, пользуясь терминологией метрических пространств, будут понятия шара (шаровой окрестности), диаметра множества и расстояния между точкой и множеством.
Определение Г. Пусть X — некоторое метрическое пространство, x^Ei X, иг — некоторое положительное вещественное число. Тогда подмножество Sr(xQ) = {х: хЕХ,и р(гг, я0) < г} называется открытым шаром радиуса г с центром в точке х0.
♦) Здесь функция 8 (t) = | х (Z) — у (/) | может достигать своего минимума в точках а или Ь. В этом случае,заменив max на sup, мы убедимся в том, что
sup е (t) = sup 8 (/) + sup 8 (0 = sup 8 (0
[a, b] [a, b) (a, b] (a, b)
п, следовательно, выбор конкретного типа промежутка здесь безразличен.
Точно так же замкнутым шаром с центром в точке х0 мы будем называть множество, отличающееся от Sr(x0) только тем, что в последнее добавлено множество точек, для которых р(гг0, х) = г.
Рис. 1.6. Шаровые окрестности в пространствах Е1 и Е'2
Эти определения согласуются с более простым понятием окрестности. Для иллюстрации на рис. 1.6 показаны окрестности для Е1 и Е2.
В качестве более сложного примера рассмотрим шаровые окрестности в пространстве С (а, Ь)(с естественной метрикой). Пусть
Рис. 1.7. Шаровая о крестность в пространстве С (а, Ь).
/о — функция, непрерывная на интервале (а, Ь). На рис. 1.7 изображен шар Sr(f0), т. е. открытая шаровая окрестность /0. Шар Sr(f0) состоит из всех функций fEEC (а, Ь), графики которых не выходят за пределы заштрихованной области с центром /0 и шириной 2г по вертикали.
С понятием шаровой окрестности множества непосредственно связано понятие радиуса множества.
Определение Д. Пусть А—некоторое множество в метрическом пространстве X. Верхняя грань расстояния р (ж, у) между всевозможными парами точек хиуЕА называется диаметром множества А и обозначается символом diam (А):
diam (А) = sup {pta, х2): xv х2ЕЕ А}.
Для A CZ R, очевидно, справедливо отношение diam(A) — = sup (А)— inf (А), т. е. diam (А) —это длина наименьшего промежутка, содержащего (А целиком. В пространстве R2 diam (А) равен диаметру наименьшего круга, содержащего А. В Я3 diam (А) в два раза больше радиуса наименьшего шара, содержа-
щего А. И вообще, в любом метрическом пространстве для шаровой окрестности А = 52(х0): diam (4)	2г.
Подмножества метрических пространств с конечными диаметрами называют ограниченными. Например, ограничен замкнутый промежуток 0 х 1. То же самое справедливо и относительно квадрата или n-мерного куба. С другой стороны, полупрямая х
0, вещественная прямая или пространство Еп могут служить примерами неограниченных множеств.
Определение. Е. Пусть X — некоторое метрическое пространство иАсХ.ах^ЕХ. Тогда расстоянием между точкой xQ и множеством А называется число
р(х0; Л) = inf {р(х0, a): aS Л}.
Расстояние р(х0; А) можно определить также как радиус наибольшей шаровой окрестности xQ, не пересекающейся с А. Интерпретация р(х0; 4) в пространствах Е1, Е2 и Е3 очевидна.
Упражнения
1.	Пусть X — некоторое множество. Для х, у £= X определим функцию р, такую что р (х, х) = 0, а р (х, у) = 1 для любых х =/= у. Докажите что X с такой метрикой является метрическим пространством.
2.	Пусть X — некоторое метрическое пространство с метрикой р. Определим новую функцию р' (х, у) выражением
.	р(®.у)
Р (*•-У) =Г+Р (*,,/)•
Докажите, что р' может быть метрикой в X и что 0 р' < 1.
3.	Доведите до конца доказательство в примере 3. Убедитесь в том, что функции ра и рз из примера 3 удовлетворяют аксимомам метрического пространства.
4.	Пусть А — некоторое подмножество метрического пространства X. Убедитесь в том, что diam (4) >0 и что при х ЕЕ X: р (х; Л) < + °°*
5.	Пусть ..., Хп — некоторый класс метрических пространств с метриками pt, ..., рп, соответственно. Покажите, что р = max {pj у,)} и р = ^7=1 Р< являются допустимыми метриками для пространства — произведения X = Хх X Ха X ... X Хп.
6.	(а) Покажите, что если множества Л и В не пусты и Л С 5, то diam(A)^ diam (В).
(о) Докажите неравенство diam (Л (J В) diam (Л) + diam {В).
Сходимость в метрических пространствах. Ряды и их сходимость играют важную роль во многих областях анализа и во многих технических приложениях. Поэтому полезно исследовать эти понятия в их наиболее абстрактной форме. Прежде всего отметим, что последовательность вещественных чисел
{^п} = {^1» Х2' •••» Хп> •••} называют сходящейся, если существует такое вещественное чис-
ло х (называемое пределом последовательности), что для произвольного заданного е 0 пайдется некоторое положительное целое число такое, что п п0 ==> |	— х | < е. Это условие
означает, что для достаточно больших п число хп должно оказаться достаточно близко к х. В этом случае часто пользуются обозначениями хп -+х, lim хп -- х или говорят, что хп стремится
П-+ОО
ИЛИ СХОДИТСЯ К X.
Эти определения можно обобщить па случай произвольных метрических пространств.
Определение Ж. Пусть {хп} — некоторая последовательность точек метрического пространства X. Если для каждого е 0 можно найти такое число nQ, что п	р <
< е, то говорят, что {хп} сходится к х.
Большинство из основных свойств, связанных со сходимостью на вещественной прямой, переносятся и на произвольные метрические пространства. Для справочных целей мы сведем наиболее привычные примеры к следующей теореме.
Теорема А. Пусть {хп} — некоторая последовательность точек метрического пространства X.
(1)	Если {хп} сходится, то всякая подпоследовательность {znfc} сходится к той же точке.
(2)	У последовательности {.гп} не может быть более одного предела.
(3)	Если {хп} сходится, то множество чисел {р(хп, 0)} для любого Q GE X ограничено.
(4)	Сходимость {zn} не зависит от конечного числа любых членов.
Доказательство. Утверждение (1) очевидно, так как если p(zn, х) < е при п^>п0(е), то справедливо и р(яп/£, х) < е при > и0 (е). Для того чтобы доказать утверждение (2), предположим, что хп-+х и хп -+у. Воспользовавшись аксиомой метрического пространства, получим, что р(х, у)^р(х, хп) + + Р (^п, У) < 6 при достаточно больших п. А так как х и у фиксированы, а е — произвольное положительное число, то неравенство может быть верным, только если р(я, у) =0, т. е. если х = у. Утверждение (4) очевидно, а доказательство (3) мы оставляем читателю в качестве самостоятельного упражнения.
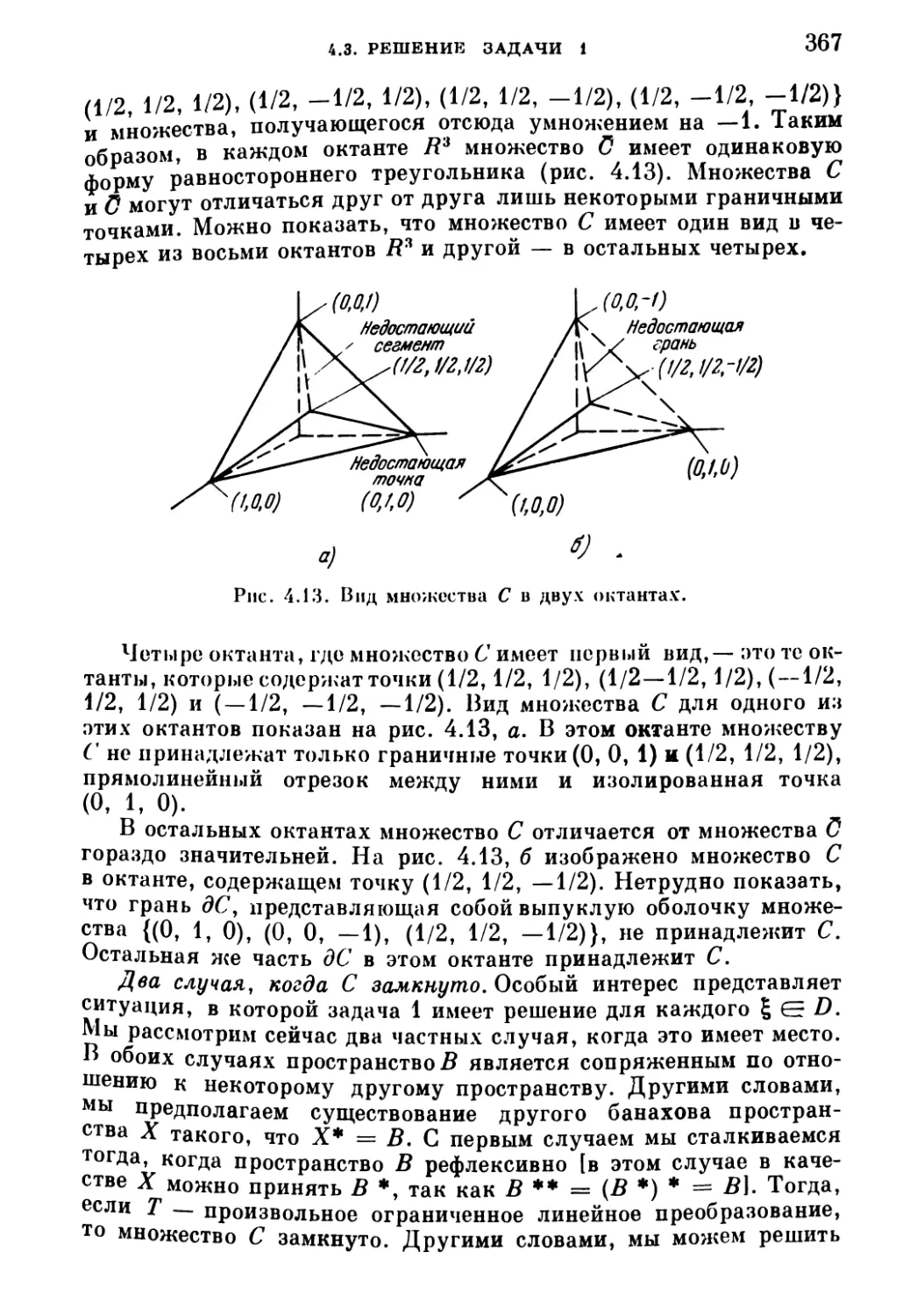
Для того чтобы лучше разобраться в понятии сходимости, рассмотрим два примера.
Пример 6. Пусть х* = {xj,..., х£}, k = 1, 2, ...,— члены сходящейся последовательности в Еп с обычной евклидовой метрикой. Если
lim р (х, хк) = О,
Где х = (хх, ...» хп) — фиксированный элемент £п, то
Lj-1
при к —>оо. Отсюда следует, что (х* — xj)2 ->0 при /=1,..., п и к ->оо, и, следовательно, сходимость в этом пространстве имеет покоординатный характер.
Пример 7. Рассмотрим вопросы сходимости в пространстве С(а, Ь). Пусть некоторая последовательность {тп} элементов С(а,Ь) сходится к х. Это значит, что
sup | х (t) — хп (t) | -> 0 при П->оо, t
т. е. для каждого е^>0 найдется некоторое натуральное число п0 = п0(е) такое, что
sup | x(t) — хп (01 < е для всех п п0(е). I
Отсюда | x(t)— xn(t)\ < е при всех п > п0(е) и всех t G (а, Ь). Но из этого следует, что последовательность {xn(t)} сходится к функции x(t) равномерно. Справедливо и обратное: если xn(t) сходится к x(t) равномерно, то р(хп, х) —>0. Именно поэтому указанная метрика в С(а, Ь) называется равномерной.
Определение 3. Точка xQ называется точкой сгущения (или предельной точкой) множества Л, если из точек этого множества, не совпадающих с xQ, можно построить бесконечную сходящуюся последовательность, пределом которой является х0.
Смысл этого определения очевиден: оно утверждает, что точки множества А группируются около х0. Однако читатель не должен слишком быстро проходить мимо определений такого рода. Ведь приведенное определение не утверждает, что точка х0 принадлежит множеству А. Так, у последовательности {1, 1/2, 1/3, ...} вещественных чисел предельной точкой является число 0. Более того, 0 —это единственная предельная точка этой последовательности. У промежутка |0,1) число 0 является предельной точкой, принадлежащей этому множеству, а число 1, хотя и является предельной точкой, но ему не принадлежит. Более того, каждое вещественное число х, 0 < х < 1, также является предельной точкой этого множества.
Определение И. Каждая точка множества А, не являющаяся точкой сгущения этого множества, называется изолированной.
Для^множества {1, 1/2, 1/3, например, точка 0 является единственной предельной точкой множества. Все же остальные его точки считаются изолированными.
Из этих определений следуют две теоремы, используемые, правда, многими авторами в качестве определений точки сгущения и изолированной точки.
Теорема Б. Для того чтобы точка xQ была точкой сгущения множества А, необходимо и достаточно, чтобы каждый открытый шар с центром в точке х0 содержал кроме х0, по крайне мере, еще одну точку множества А.
Сделаем еще одну попытку уточнить это понятие. Пусть А — некоторое множество в метрическом пространстве X. Если х G= А и является предельной точкой А, то каждая шаровая окрестность х должна содержать, по крайней мере, еще одну точку А, т. е. по крайней мере одну точку множества А \ х. Другими словами, при любом х: $г(х)П(А \х) =f=0. Аналогичные рассуждения приводят к следующей теореме.
Теорема В. Для того чтобы точка xQ была изолированной точкой множества А, необходимо и достаточно, чтобы нашлась такая шаровая окрестность Sr(xQ) этой точки, что Sr(x) П А = = Ю-
Неподготовленного читателя разница между понятиями предела и предельной точки зачастую может поставить в тупик. На вещественной прямой, например, последовательность {1, 1, ... ..., 1,...} сходится к своему пределу 1. Однако точка 1 не является предельной, так как члены этой последовательности не отличаются от ее предела (а этого требует определение). Таким образом, у последовательности может быть предел и не быть предельных точек. Обратно, мы убедимся впоследствии, что множество точек, образующих последовательность, может иметь предельные точки, а сама последовательность сходиться при этом не будет. Взаимоотношения между этими понятиями устанавливаются в следующей теореме.
Теорема Г. Если сходящаяся последовательность элементов некоторого метрического пространства содержит бесконечное число различных членов,то ее предел является и предварительной точкой множества элементов, составляющих эту последовательность.
Доказательство. Пусть {хп} — некоторая сходящаяся последовательность с пределом х в метрическом пространстве X. Пусть х не есть предельная точка множества членов последовательности. Это предположение означает, что имеется некоторый открытый шар Sr(x) с центром в х, не содержащий других членов последовательности, кроме х. Однако х есть предел нашей последовательности, и потому все хп при п nQ должны принадлежать 5г(я), и, значит, все они должны совпадать с х. Но это означает, что последовательность содержит лишь конечное (не более nQ + 1) число различных членов, что противоречит условию теоремы.
Мы уже выяснили, что предельные точки некоторого множества А не обязательно принадлежат самому этому множеству. Если
добавить к множеству Л все его предельные точки, то мы построим новое множество, которое называют замыканием множества А и обозначают через А.
Определение К. Пусть А — некоторое подмножество заданного метрического пространства. Обозначим через А другое подмножество этого же пространства, которое назовем замыканием множества А. Тогда точка х0 принадлежит А, если либо %0(==А, либо существует последовательность точек х1?	•••
..., хп, принадлежащих множеству Л, и таких, что limzn = х0.
п-*оо
Например, если А — открытый шар единичного радиуса 4 = {z: p(z, 0) < 1}, то А — замкнутый шар того же радиуса: А = {z: p(z, 0) < 1}.
Последнее определение можно было бы сформулировать еще и так: для того чтобы точка х0 не принадлежала А, необходимо и достаточно, чтобы существовала шаровая окрестность точки х0, не пересекающаяся с множеством А.
Упражнения
7. (а) Воспользовавшись неравенством треугольника, докажите утверждение (3) теоремы А.
(б) Покажите, что если {хп} и {уп} сходятся, и хп -► х, а уп -► у, то Р уп) — о (х, у).
8. Убедитесь в справедливости следующих теоретико-множественных тождеств: (a)	(б) М<^М\ (в) Q = Q; (r)Q = Q; (д) Af\Af С
(е) MQAcMHiV.
Замкнутые и открытые множества. В математическом анализе большую роль играют также и понятия замкнутого и открытого множеств. Действительно, на эти понятия опираются теория меры, теория интегрирования и топология. В дальнейшем мы убедимся, что оба эти понятия тесно связаны между собой. Более того, многим утверждениям относительно открытых множеств соответствуют двойственные утверждения относительно замкнутых множеств, и наоборот.
Определение Л (открытое множество). Произвольное подмножество G метрического пространства X называется открытым, если для каждой точки х из G существует некоторое положительное вещественное число г такое, что Sr (х) С G.
Другими словами, каждый элемент открытого множества можно сделать центром некоторого открытого шара, состоящего исключительно из точек этого же множества. Грубо говоря, множество открыто, если каждая из его точек лежит «внутри» множества, а наше определение как раз и уточняет смысл понятия «внутри». На вещественной прямой множество, содержащее всего одну точку, не открыто, так как каждый открытый промежуток с'центром в этой точке содержит элементы,не принадлежащие этому множеству.
Точно так же нельзя считать открытым и подмножество [0,1) вещественной прямой, так как точка 0 из этого интервала обладает тем свойством, что всякий открытый промежуток с центром в этой точке содержит точки, не принадлежащие [0,1); точки, лежащие слева от 0, например. Если отбросить точку 0, то полученный в результате ограниченный интервал (0, 1) оказывается открытым.
ТеоремаД. В любом метрическом пространстве X пустое множество 0 и все пространство X являются открытыми множествами.
Доказательство. Для того чтобы доказать, что множество 0 открыто, нужно показать, что каждая точка из 0 может быть центром некоторого открытого шара, содержащегося в 0. Но так как 0 не содержит никаких точек, то последнее условие выполняется автоматически. Что же касается X, то, как мы помним, это — универсальное множество, и оно, очевидно, открыто, так как любая сфера, построенная около любой точки X, не может содержать точек, не принадлежащих X.
Определение М (замкнутое множество). Произвольное подмножество F любого метрического пространства X называется замкнутым, если оно содержит все свои предельные точки.
Грубо говоря, множество F замкнуто, если ни одна из его точек не приближается сколь угодно близко к точкам, лежащим за пределами F. Множество из единственной точки на вещественной прямой является замкнутым, так как у этого множества нет предельных точек, а следовательно, это множество содержит все свои предельные точки. Точно так же замкнуто и всякое множество, содержащее лишь конечное число точек. Промежуток [0,1), как подмножество на вещественной прямой, не замкнут, так как точка 1 является для него предельной и в то же время ему не принадлежит. Добавив недостающую точку 1, мы получим замкнутый промежуток [0,1].
Теорема Е. В любом метрическом пространстве Q пустое множество 0 и само пространство й замкнуты.
Доказательство. Пустое множество не имеет предельных точек. Значит, оно содержит все свои предельные точки и, следовательно, замкнуто. Полное пространство Q содержит всевозможные точки, следовательно, оно автоматически содержит и предельные точки, а значит, оно замкнуто.
Следующая теорема устанавливает связь между замкнутыми и открытыми множествами.
Теорема Ж. Пусть X — произвольное метрическое пространство. Некоторое его подмножество F замкнуто <£=> его дополнение F' открыто.
Доказательство. Предположим вначале, что F замкнуто, и покажем, что в этом случае F' открыто. Если F' = 0, то оно
открыто, и, значит, можно предположить, что F' не пусто. Пусть х есть некоторая точка из F'. Так как F замкнуто, то х не принадлежит F и не является его предельной точкой. Но если это так, то существует открытый то ар с центром в точке х\ Sr(x), который не пересекается с F. Другими словами, всегда найдется открытый шар Sr(x) с центром в точке .г, целиком содержащийся в F'. Но так как х — это любая точка F', то F' открыто.
Предположим теперь, что F' открыто. Единственная возможность, при которой F оказывается незамкнутым, заключается в том, чтобы F' содержало предельные точки F. Но этого не может быть, так как если F' открыто, то каждая из точек этого множества является центром некоторой открытой сферы, не пересекающейся с F, и, значит, ни одна из них не может быть предельной точкой для F.
Логическое построение этого доказательства весьма типично для теоретико-множественных доказательств.
Теорема 3. Пусть X — некоторое метрическое пространство. Тогда
(1)	объединение любых открытых множеств из X открыто]
(2)	пересечение любого конечного числа открытых множеств из X открыто]
(3)	объединение любого конечного числа замкнутых множеств из X замкнуто]
(4)	пересечение любых замкнутых множеств из X замкнуто.
В силу теоремы Ж два последних утверждения теоремы 3 следуют из утверждений (1) и (2). Доказательство же этих утверждений мы оставляем читателю. Примеры
Ю1 = Д(а--^-, & +	0 = Д(п, оо),
П (a, b +	= (a, fe]
п=1\	п <
показывают, что пересечение счетного числа открытых множеств может быть замкнутым, открытым, либо ни тем, и ни другим. Аналогичное утверждение относительно объединения счетного числа замкнутых множеств можно получить, переходя к дополнениям.
Что же касается понятия замыкания, то здесь имеются следующие связи. Пусть X — некоторое метрическое пространство, и Л — некоторое множество из X. Тогда
(1)	А замкнуто А = Л»
(2)	А — наименьшее замкнутое множество, содержащее Л; другими словами, А содержится в любом замкнутом множестве, содержащем и Л;
Рис. 1.8. Множество, его граница и его внутренность.
(3)	А совпадает с пересечением всех замкнутых множеств, содержащих А.
Для моделей только что введенных понятий выберем в качестве универсального множества комплексную плоскость. На рис. 1.8 множество А ограничено сплошной линией там, где граничные точки принадлежат А. Множество А отличается от Л тем, что к последнему нужно добавить еще и все его предельные точки. Внутренность множества А состоит из точек множества Л, за исключением его граничных точек. Для уточнения последнего утверждения необходимо определить понятия внутренности множества и его границы. Это совсем нетрудно.
Пусть X — произвольное метрическое пространство, содержащее множество Л. Элемент Л называется внутренней точкой Л, если он служит центром некоторого открытого шара, целиком содержащегося в Л.
Определение Н. Внутренностью Л, т. е. 1п1(Л), называется множество всех внутренних точек этого множества. Другими словами,
int (Л) = {х: х ЕЕ А и Sr(x) cz Л при некотором г}.
Внутренность множества обладает следующими свойствами:
(1)	int (Л) — открытое подмножество Л, содержащее любое открытое подмножество Л (т. е. внутренность Л — это наибольшее из открытых подмножеств Л);
(2)	Л открыто 44 Л int (Л);
(3)	пН(Л) совпадает с объединением всех открытых подмножеств Л;
(4)	int (Л) = ЦЛ7)]'.
Определение О. Точка х некоторого подмножества А метрического пространства X называется граничной точкой этого подмножества, если любая открытая сфера с центром в этой точке пересекается как с А, так и с А'. Множество всех граничных точек А называется его границей и обозначается bnd (Л). Другими словами, bnd (Л) = A Q (Л').
Из определения границы Л и свойства (4) внутренности множества сразу следует, что для произвольного множества Л
А = int (Л) (J bnd (Л).
Упражнения
9.	Пусть X — некоторое метрическое пространство. Покажите, что любые две различные точки X могут быть разделены открытыми сферами в следующем смысле: если хну — две различные точки X, то существуют две открытые сферы с центрами в х и у, такие, что они не пересекаются между собой.
10.	Пусть X — некоторое метрическое пространство, и пусть {г} — подмножество X, содержащее лишь одну точку. Покажите, что его дополнение {х}' открыто. Покажите также, что А открыто всегда, когда А — конечное подмножество X.
И. Пусть X — некоторое метрическое пространство, a Sr (х) — открытый шар в X радиусом г, с центром в точке х. Пусть А — некоторое подмножество X с диаметром, меньшим г, и пусть оно пересекается с Sr (х). Докажите, что A CI $г (х).
12.	Опишите внутренность каждого из подмножеств вещественной прямой, перечисляемых ниже: множество целых чисел; множество рациональных чисел; множество иррациональных чисел; (0, 1); [0, 1]; [0, 1) U И» 2). Сделайте то же самое для следующих подмножеств комплексной плоскости: {z: | z | < 1}; {z: | z | < 1}: {z: Im (z) = 0}; {z: Re (z) рационально}.
13.	Пусть А и В — два подмножества некоторого метрического пространства X. Докажите, что
(a)	int (Л) U int (В) С int (Л J В);
(б)	int (Л) П int (В) = int (Л П В).
Приведите примеры двух подмножеств А п В вещественной прямой таких, что int (Л) (J int (В) =/= int (Л J В).
14.	Пусть X — некоторое метрическое пространство. Обобщите результат задачи 9, доказав, что можно разделить любую точку и замкнутое множество, ее не содержащее, в том смысле, что если х — некоторая точка, a F — некоторое замкнутое множество, не содержащее г, то найдется пара непере-секающихся открытых множеств Gx и С2 таких, что х €= G\ и F CZ С2.
15.	Пусть X — некоторое метрическое пространство, а Л — подмножество X. Пусть г — предельная точка Л. Покажите, что каждый открытый шар с центром в х содержит бесконечное число различных точек Л. Воспользуйтесь этим результатом для того, чтобы показать, что любое конечное подмножество X замкнуто.
16.	Пусть X — некоторое метрическое пространство, а Л — его подмножество. Докажите, что
(а)	(Л)' = int (Л)';
(б)	Л = {х: р (х; Л) = 0}.
Полные пространства. В теории последовательностей вещественных чисел рассматривают последовательность {яп }, обладающую тем свойством, что для каждого е 0 всегда найдется целое число 7V0(e) такое, что для любых m, NQ выполняется неравенство | хт — хп | < е. Эту последовательность называют последовательностью Коши. Указанное свойство является не только необходимым, но и достаточным для сходимости в R (а также и в С). Однако в произвольном метрическом пространстве условия Коши может быть недостаточно для установления факта сходимости. Определение П данного параграфа позволяет выделить из всей совокупности те метрические пространства, для которых критерий Коши сохраняет свою силу. Но прежде всего формализуем понятие последовательности Коши.
Определение II. Последовательность {хп} элементов произвольного метрического пространства X называется последовательностью Коши, если для каждого е 0 существует такое целое 7V(e), что р(хт, хп) < е при любых т, п, N (е).
Рассмотрим теперь произвольную сходящуюся последовательность {хп} с пределом х, где х и все хп принадлежат метрическому пространству X. По определению понятия сходимости для каждого е 0 существует такое число No, > что при п^ NQ: р(хп, х) < е/2. Отсюда, в силу неравенства треугольника в метрическом пространстве, р(хт, Хп) р(ят, х) 4- р(хп, х) < ъ при т, п^> Nq. Итог этим рассуждениям подводит следующая теорема.
Теорема И. Пусть X — произвольное метрическое пространство, Если некоторая последовательность {zn}CZ X сходит.-сч к некоторому пределу х ЕЕ X, то это — последовательность Коши,
К сожалению, обратная теорема неверна: последовательность Коши не обязательно должна сходиться. Оказывается, в некоторых метрических пространствах удается найти последовательности Коши, которые не сходятся ни к какому элементу этого же пространства. В качестве примера рассмотрим прежде всего пространство (0,Ц. Последовательность {1/п}, очевидно, является последовательностью Коши, однако точка 0 (к которой сходится эта последовательность в более широком пространстве) исходному пространству не принадлежит, и потому эта последовательность не сходится.
Далее, пусть X — метрическое пространство, состоящее из всех рациональных чисел с метрикой р(хх, х2) = | хг — х2 I. В этом пространстве последовательность {хп}, где хп = (1 4- 1/п)п, является последовательностью Коши. Но в то же время она сколь угодно близко приближается к иррациональному числу е, которое не принадлежит X, Таким образом, эта последовательность в рассматриваемом пространстве не сходится.
Трудности, с которыми мы сталкиваемся во всех таких примерах, связаны с тем, что понятие сходящейся последовательности зависит не только от характера самой последовательности, но и от структуры пространства, элементами которой она образована. Другими словами, нельзя говорить, что последовательность сходится сама по себе; нужно еще, чтобы она сходилась к некоторой точке рассматриваемого пространства. Если это пространство обладает такими свойствами, что теорема, обратная теореме И, справедлива, то мы для такого пространства используем понятие «полное».
Определение Р. Если в некотором метрическом пространстве X любая последовательность Коши сходится к некоторому пределу {принадлежащему X), то пространство X называется полным.
В заключение этого параграфа мы рассмотрим пример, который позволит довольно хорошо разобраться в том, с помощью каких рассуждений можно установить полноту метрического пространства. Этот пример поможет также установить некоторые дополнительные факты, которые время от времени могут оказаться полезными. Мы хотим также обратить внимание читателя на приложение 1, примыкающее к материалу этого параграфа, а также заметить, что содержание каждого из имеющихся в этой книге приложений ничуть не менее важно, чем основной материал.
Пример 8. Рассмотрим сначала пространство Сд(а, Ъ) вещественных непрерывных функций. Пусть {я:п} — некоторая последовательность Коши из Сп(а, Ь). Это значит, что для каждого е 0 найдется некоторое целое п0, такое что при r/i > и и > > Щ
sup I хп (0 — хт (0 | < е.
В частности, если зафиксировать t — /0, то числовая последовательность {^п(^о)}^-1 оказывается последовательностью Коши. Поскольку пространство R полно, то найдется такое вещественное х(/0), зависящее от £0, что
I (U — х (t0) I 0 при П-+ОО.
Аналогичные рассуждения для каждого t из промежутка (л, Ь) позволяют нам построить некоторую вещественную функцию х ~ = x(t). Остается только доказать, что х принадлежит CR и что в Cr хп > х.
Но при 7П, п TIq
I (0	^ш(0 | < е
при всех t из (а, Ъ). Полагая тп —> оо, получим, что
1^.(0— *(0| < е
для каждого /, и, следовательно, sup |я„(0 — x(t) | е для п п0.
Таким образом, мы показали, что для каждого е > 0 найдется такое целое г?0, что ||.г„ — хЦ С к, если т? >/г0, т. е. что последовательность {/„} сходится к .г в смысле метрики CR. Другими словами, вопрос о том, «сходится ли каждая последовательность Коши из Сц», мы свели к вопросу вида: «если некоторая последовательность из Cr сходится, то обязательно ли ее предел принадлежит Сд?», или к следующему: «если последовательность {хп} непрерывных функций равномерно сходится к некоторой функции х = x(t), то обязательно ли эта функция непрерывна?» Ответить на последний вопрос нетрудно. Так, с помощью не равенства треугольника мы можем для любых tQ из (я, Ь) и
произвольного п получить соотношение
| x(t)— x(t0) I < I x(t)— xn(t0) I + I x„(t0)— xn(t) I + I xn(t) — x(t0) |.
Поскольку мы рассматриваем случай равномерной сходимости, то первое и третье слагаемые в правой части можно сделать меньшими е за счет выбора достаточно большого п. Поэтому при достаточно большом и фиксированном п
I ^0) | < 2е -|- | xn(t) ^n(^o)l*
Но так как функции хп непрерывны, то найдется такое б О, что если | t — t0 | <6, то | x(t) — x(t0) | < Зе. Это значит, что x непрерывна в точке /0, а так как значение t0 произвольно, то функция х непрерывна на всем отрезке (а, Ь). Доказательство полноты пространства комплексных непрерывных функций получается из предыдущего, если заменить фразу «так как пространство R полно» на фразу «так как пространство С полно».
Упражнения
17.	Докажите, что любое замкнутое подмножество некоторого полного пространства также является полным пространством.
18.	Докажите, что каждая последовательность Коши ограничена. Рекомендация: выберите некоторое е > 0 и некоторое N и покажите, что если г max {е, р (х, xN), ..., р (xN_r хп)}, то при всех п р (xn, xNj < г.
19.	Пусть {iSn} — некоторая последовательность замкнутых шаров X такая, что 5n+i CL Sn для любых п. Докажите, что если X полно, а радиус Sn стремится к нулю при п —> оо, то пересечение Sn не пусто и состоит из единственной точки.
20.	Докажите, что пространство Е4 полно. Рекомендация: используйте факт покоординатной сходимости в Е” и полноту пространства R.
21.	Рассмотрите вопрос о точечной и равномерной сходимости последовательностей {хл} и {уп} в С (0, 1), где
*n(*) = *n>	*G[0, 1],
t* + nt
yn(t) =	i е [0,1].
Постройте графики некоторых из этих функций. Какая из этих последовательностей является последовательностью Коши?
1.3.	Линейные пространства
В предыдущем параграфе мы показали, что незначительное обобщение понятия расстояния позволяет ввести метрику в целом ряде важных функциональных пространств, которые могут представить интерес и для инженера. В частности, если потребовать, чтобы расстояние удовлетворяло лишь определению А § 1.2, то, проявляя определенную сноровку при выборе метрик, мы сможем рассматривать пространства Я, С, Rn и С(а,Ь) как примеры более общего метрического пространства. В частности, каждая теорема,
справедливая для абстрактного метрического пространства, автоматически оказывается справедливой и для каждого из этих конкретных пространств.
Совершенно ясно, однако, что понятие расстояния не исчерпывает всех структурных свойств конкретных пространств, перечисленных выше. Действительно, в каждом из этих пространств определена операция «сложения» его элементов, не зависящая от его метрики. В настоящем параграфе мы покажем, что в том случае, когда от понятия «вектор» не требуют слишком многого, каждое из этих конкретных пространств можно считать примером абстрактного линейного пространства, которое в свою очередь получается в результате абстрактного обобщения свойств обычного трехмерного евклидова пространства, хорошо знакомого читателю.
В последующем нам придется пользоваться множествами вещественных или комплексных чисел, используя их элементы в качестве сомножителей при элементах исходных функциональных пространств. Буквы греческого алфавита (а, (3, у, ...) мы будем использовать для обозначения скалярных множителей, а буквы х, у, z, ..., как и раньше, — для обозначения элементов множества X. Более того, мы будем предполагать, что (а) имеется правило, позволяющее сопоставить каждой паре элементов хну пространства X некоторый третий элемент ZEE X, называемый суммой элементов а: и у и обозначаемый через х + у, и (б) имеется правило, позволяющее сопоставить кажому элементу j Е X и каждому скаляру а некоторый элемент и ЕЕ X, называемый произведением х на скаляр а и обозначаемый через ах.
Определение А. Множество X называется линейным пространством*), если на X определены операции сложения и умножения на скаляр, удовлетворяющие следующим условиям:
(1)	х + у — у + х для любых х и у из X;
(2)	(х + У) + z = х -I- (у + z) для любых х, у и z из X;
(3)	существует некоторый элемент О Е X (называемый нулем) такой, что х + 0 = х для любого х ЕЕ X;
(4)	для любогохЕХ найдется такой элемент у ЕЕ X (элемент, противоположный х), что х 4- у = 0;
(5)	i*x = х для любого х Ez X;
(6)	а(Ря) = (аР)а; для любого х ЕЕ X и любых а и Р;
(7)	(а 4- Р)я = ах 4- P# для любого х Ez X и любых а и Р;
(8)	а(х + у) = ах 4- ау для любых х, у Е X и любого а.
Линейное пространство называется вещественным или комплексным в зависимости от того, вещественны или комплексны скалярные коэффициенты. Преимущество использования термина
*) В русской математической литературе линейные пространства также часто называют векторными. (Прим, ред.)
«скаляр» состоит в том, что позволяет нам одновременно рассматривать как вещественные, так и комплексные линейные пространства. Элементы линейного пространства называют векторами. Отметим, что всякое комплексное линейное пространство автоматически оказывается и вещественным линейным пространством.
Аксиомы определения линейного пространства в неявном виде предполагают наличие еще четырех дополнительных свойств. Эти свойства, перечисленные в условиях .теоремы А, настолько тесно связаны с понятием линейности, что в дальнейшем мы будем рассматривать их как часть основного определения.
Теорема А. Во всяком линейном пространстве X
(1)	пулевой элемент единствен-,
(2)	каждому элементу соответствует единственный противоположный-,
(3)	для каждого х & X справедливо равенство Ох — 0;
(4)	элемент у = (— l)z является противоположным по отношению к любому х ЕВ X.
Доказательство. Поскольку эта теорема впервые предоставляет возможность использовать сформулированные выше аксиомы линейного пространства, мы докажем ее довольно подробно. Существование по крайней мере одного нулевого нуль-вектора (нулевого элемента пространства) гарантируется определением А(3). Предположим, что в пространстве R имеются два нуль-век-тора: 0х и 02. Полагая х = 0х и 0 = 02 в определении А (3), получим
01 + 02 = 0Р
В то же время, полагая х = 02 и 0 = 0х, в силу того же определения имеем
02 + 0х = 02.
Сравнение первого и второго соотношений с учетом аксиомы А (1) приводит к равенству 0х = 02, что и требовалось доказать.
Существование по крайней мере одного противоположного элемента для каждого элемента линейного пространства гарантируется определением А(4). Предположим, что некоторому элементу х соответствуют два обратных элемента: уг и у2. Прибавляя элемент у2 к обеим сторонам равенства х + уг = 0 и используя определения А (2) и А (3), получим, что
!/г + (* + У1) = (Уг + *) + У1 = 0 + {/! = у„
Уг + {х 4- У1) = у2 4- 0 = у2.
Следовательно, yt ~ y2i что и требовалось доказать.
Рассмотрим, наконец, элемент Ох 4- 1х. Используя определения А(7) и А (5), находим
Ох + Iх = (0 + 1)я = 1х = х, Ох 4- 1я = Ох 4- х.
Отсюда х = Ох 4* х- Прибавляя к обеим частям этого равенства элемент у, обратный х, мы найдем, что
о = X 4- у =(0х 4- *)+ У = Ох 4-(х 4- у) = Ох 4- 0 = Ох, откуда 0 = Ох. Пусть, наконец, у =(— 1)х. Тогда для суммы х 4- У имеем
х 4- у = 1х 4“ (—1)я = (1—1)х = Ох = О, откуда следует, что у — элемент, противоположный х, что и требовалось доказать.
Читатель, наверное, уже заметил, что в этой теореме мы использовали символ 0 в двух смыслах. Например, в выражении 0х=0 первый нуль означает нулевой элемент множества скаляров, а второй — нулевой элемент линейного пространства. К счастью, из контекста всегда ясно, в каком смысле мы используем этот символ в каждом из конкретных случаев.
Доказав предыдущую теорему, мы можем теперь обозначать элемент, противоположный х, через — х. Существование противоположных элементов позволяет ввести операцию вычитания. По определению, разностью х — у двух элементов х и у называется сумма элемента х и элемента, противоположного у, т. е. —у. Это определение согласуется с тем, как вводится операция вычитания в арифметике.
Рассмотрим теперь несколько конкретных пространств и посмотрим, удастся ли нам определить на них операции, подчиняющиеся аксиомам линейного пространства.
Пример 1. Пространство R. Множество вещественных чисел является вещественным линейным пространством, в котором операции умножения на скаляр и сложения определены обычным для этого множества образом. Нулевым вектором в этом пространстве оказывается число нуль. Отметим, однако, что если допустить, что скаляры могут быть и комплексными, то множество R уже не будет линейным пространством. Таким образом, не каждое вещественное линейное пространство оказывается и комплексным линейным пространством.
Пример 2. Отрезок [0,1]. Множество вещественных чисел 0 х 1 не есть линейное пространство, если сложение и умножение на скаляр определить естественным образом, так как всякое число х 1/2, будучи умноженным на 2, дает число, не принадлежащее отрезку [0,1].
Пример 3. Пространство С(а, Ь). Элементами этого множества служат функции x(t), непрерывные в промежутке а t Ъ. Определим в этом множестве операции сложения и умножения на скаляр обычным образом. Иными словами, если я, у ЕЕ С(а, Ь), то х + + У — это функция, значение которой в каждой точке t определяется как x(t) y(f):
(х + y)(t) = x(t) X y(t).
Аналогично определяется и операция умножения на скаляр:
(*!/) (/) = Ху (/).
Ясно, что х + у и Хх — непрерывные функции на промежутке и, следовательно, они принадлежат С (а, Ь). Нулевым элементом этого пространства является функция, значение которой равно 0 при каждом t [а, Ь]. Проверку всех аксиом определения А мы оставляем читателю.
Пример Пусть Р — множество всех полиномов с вещественными коэффициентами, определенных на замкнутом промежутке [0,1]. Если линейные операции интерпретировать здесь обычным образом, т. е. как обычное сложение двух функций и умножение функции на вещественное число, то Р — это вещественное линейное пространство. Его нулевым элементом является нулевой полином.
Пример 5. Пусть для каждого положительного целого числа п определено подмножество Рп множества Р, состоящее из полинома, тождественно равного нулю, и всех полиномов со степенью, меньшей п. По отношению к операциям, определенным на Р, пространства Рп являются вещественными линейными пространствами.
Пример 6. Множество Rn всех вещественных n-ок является вещественным линейным пространством, если операции сложения и умножения на скаляр определить следующим образом. Пусть я, У & Rn, и пусть х = (хь х2. ..., хп) и у = (i/p у2,..., Уп)- Тогда
X + у = (х-L + ух, Х2 + у2,..., Хп 4- у„), ах = (а^, ая2,..., ахп).
Отметим, что при п = 3 операции векторного сложения и скалярного умножения в /?3, определенные в примере 6, совпадают (при условии, что мы отождествляем вектор (хх, х2, х3) с направленным отрезком прямой, соединяющим начало координат с точкой (хъ х2, х^) с обычными правилами «параллелограмма» и «подобия» элементарной математики.
Теперь, после того как мы познакомились с понятием линейного пространства, а также с некоторыми конкретными примера
ми таких пространств, нам будет нетрудно обнаружить ряд дополнительных свойств пространств этого рода.
Определение Б. Пусть М — некоторое непустое множество элементов линейного пространства X. Множество М называют линейным подпространством (многообразием) X, если М также является линейным пространством.
Это определение эквивалентно условию, согласно которому все суммы, разности и произведения на скаляры элементов М оказываются также элементами этого множества. Поскольку —х = — (—1)#, то это в свою очередь эквивалентно условию, требующему, чтобы М было замкнуто относительно операций сложения и умножения на скаляр. По аналогии с определениями, введенными раньше, линейное подпространство М называется собственным линейным подпространством пространства X, если его элементы образуют собственное подмножество X. Нулевое пространство {0} и само пространство X всегда являются подпространствами X. Нетрудно видеть, что пересечение произвольной совокупности подпространств X является подпространством X.
Возвращаясь к рассмотренным выше примерам, мы видим, что Рп — это подпространство Р для каждого положительного п и, более того, Р есть подпространство С[0, 1]. Легко выяснить, что в линейном пространстве R3 собственными подпространствами являются следующие:
Ml = {(*!, 0 0)}, М2 = {(0, х2, 0)}, М3 = {(0, 0, я3)},
М4 = {(0, х2, я3)}, Мь = {(^, 0, я3)},ЛГв = {(л?!, х2, 0)}, где отличный от нуля член может принимать любое вещественное значение.
Пусть имеется несколько элементов	некоторого ли-
нейного пространства X. Элемент у, удовлетворяющий условию
У = ад + ... +
также принадлежит X. Мы будем называть у линейной комбинацией векторов лгх,..., хт, а скаляры аь..., ат — коэффициентами этой линейной комбинации.
Определение В. Пусть X — некоторое линейное пространство и пусть {^х,...,	— некоторое непустое множество из
X. Множество {а^, ..., £гп} называется линейно зависимым, если найдутся такие коэффициенты ах,..., ат, не равные все тождественно нулю, что арГх 4- ... + <%тхт = 0.
Если множество {^р..., яш} не отвечает этому определению, то его называют линейно независимым. Перефразируя определение В, мы можем утверждать, что множество {т1?	.г7П} линейно
независимо, если равенство arxY + ...+ <хтхт 0 справедливо лишь в том случае, когда все = ос2 = ...= ат = 0.
Если линейная комбинация
ал + ••• + ал = О
(и, по крайней мере,одно из чисел аь..., aj не равно нулю), то совершенно очевидно, что
ал + ... + ал + Ozj+1 + ...+ Оагт = О
(и при этом по крайней мере одно из чисел аь ..., ат не обращается в нуль). Если, например, не равен нулю коэффициент afe, то
Все эти свойства суммируются следующей леммой.
Л е м м а А. Если некоторое подмножество {a^, ..., xk} линейно зависимо, то линейно зависимо и всякое более широкое множество {□?!, ..., хп}, п > к. Элементы хъ ..., хк линейно зависимы тогда, когда один из них может быть представлен в виде линейной комбинации остальных.
Про множество векторов {хг, х2, ..., яп} говорят, что на него натянуто линейное пространство М или что оно определяет линейное пространство М, если каждый вектор из М может быть представлен в виде линейной комбинации векторов хх, ..., хк. Другими словами, в этом случае для каждого вектора у из М найдутся такие скаляры ап ..., afe, зависящие, вообще говоря, от у, что
У = ал + ... + ahxk.
А так как в линейном пространстве новые элементы можно определять, образуя линейные комбинации из уже существующих, фиксированных элементов, то идея пространства, натянутого на векторы, открывает один из эффективных путей построения подпространств. Для уточнения этой идеи мы введем следующее формальное определение.
Определение Г. Обозначим через S = {^х, ..., хп} некоторое непустое множество линейного пространства X. Множество L(S) называется линейным подпространством, натянутым п
на S, если	; х = 2 аЛ» aj произвольные скаляры^.
То, что L(S) является линейным подпространством X, не вызывает сомнений. В действительности же L(S) — это такое подпространство X, которое должно содержаться в любом подпространстве X, содержащем S. Другими словами, L(S) — это наименьшее из линейных подпространств X, содержащих S. Подпространство L(S), очевидно, натянуто на S. Однако если мно
ж ест в о S линейно зависимо, то, как мы увидим, L(S) можно натянуть и на некоторое собственное подмножество S.
Рассмотрим теперь два подпространства иМ2, М19 М2С1Х. Множество
Ei= {z:	У, х s мъ у G М2}.
называется суммой множеств Мг и М2 (записывается: Е = Мг + 4- М2). Так как Мх и М2 являются подпространствами, то, очевидно, подпространством будет и множество Е. Обобщая эту идею, мы будем говорить, что Е представляет собой сумму множеств М (i = 1,..., п) (чт0 записывается как Е =	если каждое
х ZE Е можно представить в следующем виде:
п
ж=2жь	i = l,...,n.
i=l
Для приложений наибольшее значение имеет прямая сумма подпространств. В этом случае необходимо добавить еще и требование единственности такого представления.
Определение Д. Пусть X — некоторое линейное пространство, и пусть М.. i = 1, ..., п. — его линейные подпространства. Если каждый элемент х некоторого множества Е CZ X можно единственным образом представить в виде
х = хх + х2 + ... 4- хп. х. (ЕЕ Af., i = 1, 2, ..., n,
то про пространство Е говорят, что оно является прямой суммой подпространств, что символически записывается как Е = М± ф ф М2 ф ... ф Мп или. короче, как Е = ф.Мг]	—
Центральную роль в этом определении играют слова «единственным образом», поскольку однозначность такого представления, как мы увидим, требует, что подпространства М. не пересекались между собой.
Теорема Б. Пусть некоторое линейное пространство X является суммой двух подпространств Мг и М2. так что X = Мх 4-4- М2. Тогда для того, чтобы X было прямой суммой этих подпространств. необходимо и достаточно, чтобы Мг Г] М2 = {0}.
Доказательство. Предположим, что X - Мг ф М2 и что оба подпространства Мг и Af2 содержат один и тот же элемент и =/а0. Тогда для каждого элемента х (Е: X. который можно представить в виде
X = у + z. у мъ z е м2.
возможно и другое представление:
х = (у — и) 4-	+ и)» У ~ и Мг. z 4- и ЕЕ М2.
очевидно, отличное от первого. Таким образом, если и =/= 0, для
элементг1 х мы не можем гарантировать единственности представления, а следовательно, сумма М\ и М2 не может быть прямой.
Предположим теперь, что каждый элемент х ЕЕ X представим в виде
х == у + z, i/G М1? z М2
и что Q М2 = {0}.
Для того чтобы выяснить вопрос о единственности выписанного выше представления, предположим, что существует еще и второе представление, т. е. что
X = у 4- Z = У! + Zb у, У! <= Мг, Z, zx е м2.
Вычитая тогда одно представление из другого, мы увидим, что у —	= z1 — z, у — е М1Ч z1 — z М2,
где вектор в правой части принадлежит подпространству а вектор в левой части —подпространству М2. Но так как единственным общим элементом этих подпространств является нулевой Мг А М2 = {0}, то обе стороны последнего равенства должны обращаться в нуль, и, следовательно, у = у± и z = z1? что и доказывает единственность представления.
Условие X = Mt ф М2 часто выражают следующими словами: «для пространства X существует декомпозиция на подпространства Мг и М2». Несмотря на то, что подпространства М\ и М2 имеют общий нулевой элемент (этот элемент является общим вообще для всех линейных пространств), их считают непересекающимися. Условия декомпозиции линейного пространства на три или несколько подпространств рассматриваются в упражнении 7.
Работая с линейными пространствами, читатель сталкивается с тремя различными, хотя и похожими операциями над множествами: декартовым произведением, объединением и суммой. Для иллюстрации различия между этими операциями рассмотрим подпространства М1 = {(я, 0)} и М2 = {(0, у)}. По определению Mi ф М2 = Я2, в то время как множество Мг (J М2 состоит лишь из тех точек Я2, которые принадлежат координатным осям Н2. Что же касается множества М1 X М2 - {х, 0, 0, у}, то оно, естественно, является некоторым подпространством 7?4. Для различения всех этих операций может оказаться полезным соотношение Мг ф М2 = ЦМХ и М2)-
У пражнения
1.	Пусть х, у и z — линейно независимые векторы. Справедливо ли утверждение, согласно которому линейно независимы и векторы х у, у z и z + х?
2.	Каждое из следующих условий определяет некоторое подмножество вещественного линейного пространства R3 всевозможных точек х = (хх, х«,
х3) вещественных чисел: (a) хх — целое; (б) хх = 0 плп хч = 0; (в) xt + 2хг = -= 0; (г) X! + 2x2 = 1. Какие из этих подмножеств являются подпространствами Я3?
3.	Каждое из нижеследующих условий определяет некоторое подмножество вещественного линейного пространства С [—1, 1] всевозможных непрерывных вещественных функций у = f (х), определенных на интервале [—j, 1]: (a) f дифференцируемы; (б) f — полиномы третьей степени; (в) / — четные функции в том смысле, что / (—х) = / (х) при всех х; (г) /—нечетные функции в том смысле, что / (—х) = —f (х) при всех х; (д) / (0) = 0; (е) f (0) = 1; (ж) / (х) > 0 при всех х. Какие из этих подмножеств являются подпространствами С I—1, 1]?
4.	Покажите, что пространство С [—1, 1], введенное в предыдущем упражнении, является прямой суммой подпространств, определенных условиями (в) и (г). (Рекомендация: учтите, что / (х) = [/ (х) + / (—х)]/2 + [/ (х) — -/ (—х)/2.)
5.	Пусть х, у, и и v — некоторые векторы из Я4, а М п N — подпространства Я4, натянутые на {х, у} и {и, г} соответственно. В каком из перечисленных ниже случаев Я4 = М ф N?
(а)	X = (1, 1, 00), и = (0, 1, 0, 1),	у = (1, 0, 1, 0), v= (0, 0, 1, 1);
(б)	х = (_1, 1, 1, 0), и = (1, 0, 0, 0),	у = (0, 1, -1, 1), р = (0, 0, 0, 1);
(в)	х = (1, 0, 0, 1), и = (1, 0, 1, 0),	у = (0, 1, 1, 0), v = (0, 1, 0, 1).
6.	Пусть X — множество, состоящее из шести векторов (1, 1, 0, 0), (1,0,1,0), (1,0, 0,1), (0,1,1,0), (0,1,0, 1), (0, 0,1,1) пространства Я4. Найдите два различных максимальных линейно независимых подмножества X. (Максимальным линейно независимым подмножеством множества X называется такое линейно независимое подмножество Y с X, которое становится линейно зависимым каждый раз, когда к У добавляется любой вектор из X, еще не принадлежащий У).
7.	Пусть некоторое линейное пространство X представляет собой сумму подпространств Мъ ..., Мп (п > 2). Покажите, что X есть прямая сумма этих множеств тогда и только тогда, когда М{ не пересекаются (с точностью до нулевого элемента) с подпространством, натянутым на все остальные Mj. Последнее условие, очевидно, предполагает, что каждое Mi не пересекается с любым другим Мj. Однако обратное утверждение ложно. Это можно показать, убедившись в том, что в Я3 можно найти такие три подпространства Мх, Мг и Мз, что Q Мч = Мх Q Мз — Мч Г) Мз = {0}, но М, П (М2 + А7з) #= {()}.
Размерность и базис. Среди шести первых примеров вещественных векторных пространств, приведенных в этом параграфе, пространство R3 является наиболее знакомым. А решение задач в пространстве R3 показало, что кроме уже введенных понятий оказываются полезными еще и некоторые другие. В этом разделе мы собираемся рассмотреть понятия системы координат и размерности. Возможность распространить эти крайне наглядные понятия на случай произвольного линейного пространства естественным и продуктивным образом кажется нам весьма обнадеживающей.
Преследуя эту цель, мы будем опираться на наши нынешние представления о линейной зависимости и о множестве векторов, на которое можно натянуть некоторое пространство. В двух леммах, следующих ниже, мы попытаемся в качестве первого шага уточнить содержание определения Г.
Лемма Б. Пусть {хг, ..., хп, у} — элементы некоторого линейного пространства. Если вектор у принадлежит линейному многообразию L(xt, ..., zn), то Ь(хг,..., .хп) содержит и линейное многообразие Ь(хг, ..., хп, у).
Включение у (= Цхъ ..., хп) предполагает, что у можно представить в виде линейной комбинации {ггх,..., хп}. Отсюда следует, что если z представимо в виде линейной комбинации {zx, ..., хп, у}, то оно представимо и в виде линейной комбинации {zx, ..., хп}. Ио это значит, что z ЕЕ Цх^ ..., z7l) и, следовательно, Ь(хъ ...
хп) Z) Цхъ..., хп, у).
Л е м м а В. Каждый элемент множества {xj}, линейно зависимый от совокупности остальных элементов множества, можно отбросить, не меняя при этом линейного многообразия, натянутого на множество.
Доказательство. Пусть, например, вектор хг линейно зависит от векторов х2, х3, ... Тогда хг ЕЕ Цх2, х3, ...). В соответствии с леммой Б отсюда следует, что
Е^х^, х2, ..., Хп} (_Цх2,..., Хп}.
Но, с другой стороны, очевидно, что
Е(х2,'... Хп) CZI •^'(^'1»	•••»
откуда следует, что
//(Zj, х2, ..., хп) = Ь(х2,..., хп).
Определение Е. Пусть множество {zx,..., zn} состоит из элементов некоторого линейного пространства X. Это множество называется базисом некоторого подпространства М, если Ь(*х, хп) = М и {zx, ..., хп} — линейно независимое множество.
Каждый элемент х GE М может быть представлен в виде некоторой линейной комбинации zx, ..., хп, и это представление обычно называют разложением х по базису {zx, ..., хп}. Нетрудно видеть, что при принятых предположениях коэффициенты разложения по базису определяются для каждого х & М однозначно. Действительно, если бы мы могли написать для вектора х два разложения
z = axzx + a2z2 + ... + anzn,
* = Pl*l + ₽2*2 + ••• + ₽п*п,
то, вычитая одно из другого, мы получили бы, что
О = («1 — Pi)^i + (а2 — Рг)^ + ... + (ап — Рп)яп«
Но так как векторы ..., хп, по определению, линейно независимы, то отсюда следует, что
ai = Pi, а2 ~ 02» ...»	= Рп-
Эти единственным образом определяемые числа ах, а2, ..., ап называются координатами вектора х по базису {хх}.
Для того чтобы распространить эти понятия на произвольные непустые конечные или бесконечные множества векторов из X, мы должны условиться, что произвольное множество называется линейно независимым, если линейно независимо его любое непустое конечное подмножество. В противном случае оно называется линейно зависимым. После этого незначительного обобщения понятия линейной зависимости мы можем утверждать, что произвольное (и не обязательно даже счетное) линейно независимое подмножество {rra} некоторого линейного пространства X является базисом подпространства М, если каждый вектор этого подпространства единственным образом представляется в виде некоторой (конечной) линейной комбинации векторов {ха}.
Можно показать, что у каждого векторного пространства имеется базис. Это — нетривиальный результат. Множество вещественных чисел можно рассматривать как линейное пространство, в котором существует такое подмножество вещественных чисел {жа}, что любое вещественное число х может быть представлено в виде
х = 2VaXa’
где va — рациональные числа, а под знаком суммы находится лишь конечное число слагаемых, не обращающихся в нуль. Более того, хл должны быть линейно независимыми в том смысле, что любая конечная сумма Svarra, где все va рациональны, может обращаться в нуль тогда и только тогда, когда все va = 0. Но так как число возможных^произведений каждого фиксированного ха на рациональный множитель счетно, то число различных ха базиса обязательно должно быть несчетным (для R этот базис называют базисом Гамеля).
Рассмотрим теперь линейное многообразие Ар, натянутое на совокупность векторов ха, где а =/= 0. Ясно, что таким образом мы получим несчетное число различных подпространств Ар пространства Л. В частности, мы уже доказали существование несчетного
множества различных подгрупп ♦) пространства R, каждая из которых содержит несчетное множество элементов!
Один из важнейших результатов введения понятия базиса линейного пространства состоит в том, что после определения базиса линейные операции над элементами этого пространства, которые по началу были совершенно абстрактными, становятся обычными линейными операциями над скалярами, т. е. над координатами векторов по заданному базису. Для того чтобы проиллюстрировать эту мысль, выберем в пространстве X некоторый базис {^х, ..., хп}. Тогда, если х и у — произвольные элементы X, то
х = ад + а2х2 + ... + апхп,
У ~	•••Ч- Рп.З'п*
В силу аксиом сложения для линейных пространств
X + у = (at + Р1)^1 + (а2 4- 02)*2 4- ...4- (ап 4- ₽п)*п,
а если 1 — произвольный скаляр, то
кх = (Xajxx + (Ха2)а:2 + ...+ (2ап)хп.
Если в некотором линейном пространстве X удается найти п линейно независимых векторов, и при этом любые (п + 1) векторов этого пространства линейно зависимы, то число п называют размерностью пространства X, а про само это пространство говорят, что оно n-мерно. Линейное пространство, в котором можно найти произвольно большое число линейно независимых векторов, мы станем называть бесконечномерным.
ТеоремаВ. Если X — произвольное линейное пространство размерности п, то в нем существует некоторый базис, содержащий ровно п векторов. Более того, любые множества п линейно независимых векторов такого пространства являются для него базисом.
Доказательство. Пусть ех, е2,	еп -— некоторое множество
п линейно независимых векторов заданного n-мерного линейного пространства X. Пусть х — произвольный вектор этого пространства. Тогда множество (п + 1) векторов
{х, е2, е2, ...» еп}
линейно зависимо. Другими словами, существует такая линейная комбинация
aox +	... + апеп = О,
в которой по крайней мере один из коэффициентов а0, ах, ..., ап
♦) G называется подгруппой Я, если О ЕЕ С и если х — у EG для любых х и у EG.
отличен от нуля. Нетрудно убедиться в том, что а0 не равен нулю. Действительно, если бы это было не так, то у нас получилось бы, что векторы е2, ...» еп линейно зависимы, что невозможно по условиям теоремы. Тогда обычным образом, т. е. разделив все это уравнение на а0 и перенеся все члены, кроме первого, в правую часть, мы убедимся в том, что х может быть представлен в виде некоторой линейной комбинации векторов е2, ...» еп. Но х — произвольный вектор пространства X. Поэтому векторы в!, е2, ..., еп образуют базис этого пространства.
Следующая теорема завершает нынешнее направление рассуждений о свойствах конечно-мерных линейных пространств.
Теорема Г. Пусть X — произвольное линейное пространство. Если в X имеется некоторый конечный базис Вг = {е<} = = {en	из п элементов, то любой другой базис этого прост-
ранства В2 = {Д} также конечен и содержит ровно п элементов.
Доказательство. Доказать конечность В2 можно от противного и это нетрудно. Поэтому здесь мы займемся лишь более трудной задачей и покажем, что если В2 конечно и
Вг =" {/,} = {А, /2,	/т},
где т — некоторое положительное целое, то т и п равны. Поскольку пространство X натянуто на {е$}, то элемент Д может быть представлен в виде некоторой линейной комбинации е„ а множество
: {Л»	^2» •••, ^п} линейно зависимо. Следовательно, один
из векторов ei, например eio, является линейной комбинацией остальных элементов S^. Вычеркнем eio из и получим в результате этого новое множество S2 — {Д, ех, ..., е^-и е<о+1, ...» еп}. Пространство X по-прежнему можно натянуть на S2, а значит, множество S3 = {Д, Д, eif ..., eit+i, ..., еп} линейно зависимо. Но так как Д линейно независимы, то один из элементов е{ должен оказаться линейно зависящим от остальных элементов S3. Этот элемент мы можем снова отбросить и получить в результате новое множество, на которое натягивается X. Продолжая этот процесс далее, мы увидим, что нельзя выбросить последние ei раньше, чем будет исчерпан запас Д, так как в противном случае оставшиеся Д оказались бы линейными комбинациями тех, которые заменили е{ в Sk, а это противоречит предположению о линейной независимости Д. Таким образом, ясно, что п т, т. е. что п не может быть меньше т. Однако если и Д поменять ролями, то точно такими же рассуждениями можно показать, что п т, откуда и вытекает, что п = т.
Из изложенного следует, что если в пространстве X существует конечный базис, то число векторов этого базиса совпадает с размерностью X.
Что касается бесконечно-мерных пространств, то аналогичное утверждение содержится в следующей теореме.
ТеоремаД. Пусть X — некоторое линейное пространство. Если Вг = {е<} и В2 = {fj} — два произвольных базиса X, то Вг и В2 содержат одинаковое число элементов, т. е. между их элементами можно установить взаимно однозначное соответствие.
В заключение этого параграфа мы попытаемся проиллюстрировать, хотя бы частично, факт огромного многообразия возможных линейных пространств. Эти примеры содержат исключительно полезные и часто используемые в технических и научных приложениях классы функций. Все эти классы имеют очень много общего, и именно эту общность мы и подчеркиваем в данной главе, переходя на более высокий уровень абстракции.
Пример 7. Простейшим примером линейного пространства может служить Нп. Определения операций сложения и умножения на скаляр для этого пространства приведены в примере 6 этого параграфа. По определению 0 = (0,..., 0) и — х = (— ?i,..., — £п)« Нетрудно проверить и справедливость для этого пространства всех восьми аксиом линейного пространства.
Размерность Вп равна п. Для того чтобы доказать это, положим ех = (1, 0, ..., 0), е2 =" (0, 1, 0, ..., 0), ..., еп = (0, 0, ..., 0, 1). Если х = (£п ..., £п), то ясно, что х —	+ ...+ £пеп. Таким
образом, множество ei, ...,еп порождает все пространство Вп и в то же время линейно независимо, так как + ... + апеп = = (<%!, ..., ап) = 0 тогда и только тогда, когда все а равны нулю. Отсюда следует, что е1У ...» еп образуют базис в Rn.
1 Особенно привлекательный вид имеют линейные многообразия в пространстве R3. Пусть х± GE Rn. Одномерное многообразие Мх = является прямой, направленной вдоль xY. Точно так же, если хи х2 ЕЕ Rn и линейно независимы, то М2 = Цхх, х2) представляет собой плоскость, содержащую хг и х2. Читатель легко может убедиться в справедливости этих утверждений для пространства R3.
Пример 8. Обозначим через Сп множество всевозможных п-ок х = (£п ..., £п) комплексных чисел. Нетрудно видеть, что Сп — комплексное n-мерное линейное пространство. Как и раньше, нетрудно убедиться в] том, что п векторов et = (1, 0, ..., 0),... ..., еп = (0,0,..., 1) образуют базис Сп. Элементы Rn принадлежат Сп. Однако Rn не есть подпространство Сп, так как если а комплексно, а х принадлежит Rn, то ах принадлежит Crt, но не обязательно принадлежит Rn (например, iet = (i, 0, ..., 0) не принадлежит Rn).
Однако множество Сп можно рассматривать и как вещественное линейное пространство (с вещественными скалярами). Для такого пространства один из возможных базисов составляют векторы {е1ч ..., еп, ier, ... ien}, а значит, его размерность становится равной 2п, вместо прежней п. Но, как правило, Сп рассматривают как комплексное пространство,
Пример 9. Множество С(а, Ь) непрерывных функций, определенных на промежутке [а, Ы, является линейным пространством (см. пример 3 § 1.3). Пространство С(а, Ь) бесконечномерное. Пусть ^о(0 =	= *П' п =	Ясно, что все х0, хи хп при-
надлежат С(а, Ь). Но это множество элементов линейно независимо, как бы велико ни было п, так как в соответствии с хорошо известным свойством полиномов выражение а0 + a±t + ...+ anfn обращается в нуль для всех t из некоторого промежутка а t b только в том случае, когда а0 = аг = ...= ап = 0. Это показывает, что С(а, Ь) не может быть конечномерным.
В качестве подпространства С(а, Ь) мы можем рассматривать множество Рк всех полиномов относительно t со степенью не выше к. Это линейное многообразие, очевидно, натянуто на систему функций {1, t, £а, ..., £*}. Отсюда следует, что это множество образует базис Ph, и, значит, Ph является (к + 1)-мерным пространством.
Другим базисом для линейного многообразия Рк может служить множество
Pq ~ аоо> Pi “ аю
Рк = Яко + akLt + ... + ahht\
где матрица (а,ц) невырождена (т. е. ни одно из не равно нулю). Для доказательства этого заметим, что невырожденность матрицы (ац) гарантирует возможность выразить Г через р0, ..., pk. Но это значит, что t* (= А(р0, •••» Рп)» откуда следует, что	tk) cz
с Цр°, ..., рк). Соотношение же Цр0, ..., pk)^L(tQ, t, ..., tk) очевидно. Поэтому оба линейных многообразия могут лишь совпадать.
Пример 10. Пусть / — некоторая аналитическая функция комплексной переменной z, определенная в единичном круге |z| < 1. Класс всех таких функций образует комплексное линейное пространство, если / + g и а/ определить обычным образом. Это пространство, конечно, бесконечномерно. В качестве возможного подпространства упомянем о классе всех функций /, для которых /(0) = 0.
Пример 11. Пусть функция x(t) является комплексной функцией вещественной переменной t и обладает тем свойством, что x(t), x'(t) и x"(t) определены и непрерывны на замкнутом промежутке [а, Ы. Множество всех таких функций образует линейное пространство по отношению к обычным операциям сложения и умножения на скаляр. Его часто обозначают через С3 (а, Ь). Оно бесконечномерно.
В качестве его подмножества можно рассматривать = {х : £ GE С3(0, л) и x”(t) + x(t) - 0}. Размерность Пг равна двум. Одним из базисов подпространства Ях могут служить функции
{еЛ е“к}, а другим — функции {sin t, cos t). Интерес представляет и другое линейное многообразие Н2 = {#(0: #(0 ЕС2(0, л), х(0) = гг(л) = 0}. Оно бесконечномерно, поскольку содержит бесконечное линейно независимое множество {sin nt, п = 1, 2,
1.4. Банаховы пространства
Для предыдущих параграфов мы отбирали материал, преследуя две цели. Во-первых, нам нужно было ввести понятия, определения и обозначения, необходимые для эффективного изучения вопросов, которые мы будем рассматривать в дальнейшем. А во-вторых, мы надеемся на то, что за это время читатель освоился с абстрактной точкой зрения, для которой главное — это сами понятия или операции, вне связи с их конкретными проявлениями.
Конечно, теорию метрических и линейных пространств можно было бы изложить гораздо глубже, чем это сделано здесь. Однако,
имея в виду те приложения, которым посвящена эта книга, мы по-
прежнему станем придерживаться тактики постепенного прогресса.
Для изучения теории систем первостепенную роль играет теория банаховых и гильбертовых пространств. Значение этих пространств становится по-настоящему понятным лишь тогда, когда мы переходим к исследованию линейных операторов или линейных функционалов, заданных на этих пространствах. В настоящем параграфе мы ограничимся лишь рассмотрением общих свойств этих пространств, а вопросы, связанные с более глубоким их анализом, а также с приложениями, отложим до последующих
глав.
Для успешного обобщения геометрических представлений на случай абстрактных пространств нам необходимо, среди прочего, не только измерять расстояния между элементами (что достигается введением метрики), но и измерять размеры или величины самих элементов. Введение соответствующего понятия приводит нас к рассмотрению теории нормированных линейных пространств, а точнее говоря, к теории банаховых пространств. Мы начнем со следующих определений.
Определение А. Линейное пространство X называет-
ся нормированным, если существует некоторое правило, ставящее в соответствие каждому элементу хЕХ некоторое вещественное число (которое называют нормой элемента х и обозначают через ЦгЦ). Это правило должно удовлетворять следующим условиям (аксиомам нормированного пространства):
(1) || х ||	0 и ||х|| — 0, тогда и только тогда, когда х — 0,
(2) 11х + леи,+ Ы>
Неотрицательное вещественное число || х || можно рассматривать как длину элемента х. Правило, позволяющее определять ||х||, является некоторой вещественной функцией, определенной на элементах пространства. Поэтому иногда мы будем говорить о |х|| как о норме, заданной наХ. Вектор х, длина которого равна единице, называется нормированным. Нормировать можно каждый ненулевой вектор у (другими словами, всегда найдется такое число X, что, умножив у на это число, мы получим вектор единичной длины). В самом деле, решая уравнение ||Xi/|| = 1 относительно X, мы получим
Поскольку в нормированном линейном пространстве для измерения расстояния между элементами и для измерения их длины нужно пользоваться одним и тем же масштабом, естественно определить на этом пространстве метрику с помощью соотношения.
р(х, у) = Цх - J/||.
Легко показать, что это определение расстояния удовлетворяет всем аксиомам метрического пространства. Проверку этого мы оставляем читателю в качестве упражнения. Если воспользоваться метрикой, порожденной нормой, то определение понятий предела и сходимости приобретает следующий вид:
х = lim xno lim ||хп — х|| = 0. П-*СО	П-*ОО
В связи с этим сходимость в нормированном линейном пространстве получила название сходимости по норме. В дальнейшем мы всегда будем неявным образом предполагать, что в любом нормированном линейном пространстве используется метрика, порожденная нормой, если только специально не оговорено противное.
Еще одно свойство нормы, вытекающее из аксиом нормированного пространства, заключается в следующем:
Ы - hll<k - j/ll.
Для того чтобы доказать это утверждение, заметим, что х = = (х — у) + У- Но в соответствии с определением А(2) отсюда || х || ^|1х — 1/|| + || у ||. Перенося второе слагаемое из правой части в левую, мы как раз и получим требуемое неравенство. Более сильное неравенство, вытекающее из предыдущего, можно получить, заметив, что
IЛ - kl - М = 11(-1)(х -у)| = к - л.
что вместе с предыдущим результатом даст
Ikll - ИИ КЬ-!/11-
Определение Б. Банаховым пространством называет ся нормированное линейное пространство, полное относительно метрики р(х, у) = ||х — у\\, порожденной его нормой.
Банаховым пространством В, очевидно, является линейное пространство, элементы которого х имеют длину ||х(|, удовлетворяющую ^нескольким простым геометрическим свойствам, как раз и сформулированным в аксиомах нормированного пространства. В метрике р(х, у) = ||х — уЦ все последовательности Коши сходятся^к соответствующим точкам пространства В. Поскольку каждое нормированное линейное пространство можно рассматривать как некоторое метрическое пространство, все понятия сходимости, предельной точки, открытого и замкнутого множеств, границы и внутренности, введенные в § 1.2, сохраняют свою силу и для нормированных линейных пространств.
Рассмотрим теперь некоторое линейное пространство X, на котором определены две нормы Ц и || ||2. Мы будем говорить, что эти две нормы эквивалентны, если любая последовательность из X, сходящаяся по норме || |х, сходится по норме || ||2, и наоборот. Так как для определения предельных точек единственным понятием, которым нужно пользоваться, является понятие сходимости, то любое множество S, считающееся открытым (или замкнутым) в множестве X с нормой || ||п необходимо будет открытым (или замкнутым) и в пространстве X с эквивалентной нормой Ц |2. Справедливо и обратное утверждение.
Т^е о р е м а А. Для того чтобы две нормы [ |х и || ||2, определенные на линейном пространстве X, были эквивалентны, необходимо и достаточно, чтобы существовали такие постоянные а, Ь > 0, что
J^lli || ^Цг Ь | я|1»
каково бы ни было х Ez X.
Эта теорема служит прямым следствием утверждений, сделанных выше, и ее доказательство мы оставляем читателю. Читателю нетрудно догадаться также, что из теоремы А вытекает еще и неравенство (1/Ь)||х||2	|| ^Ik ^(1/а) ||х||2, которое должно выпол-
няться для любых х G= X. Отсюда следует симметричность определения эквивалентности. Прежде чем переходить к примерам в банаховых пространствах, мы сформулируем без доказательства одну теорему, выделяющую два особых свойства нормированных линейных пространств конечной размерности. Доказательство этой теоремы можно найти в любой из книг, цитируемых в конце этой главы.
ТеоремаБ. Каждое нормированное линейное пространство конечной размерности полно. Все нормы конечномерного пространства эквивалентны.
Рассмотрим теперь несколько наиболее часто встречающихся банаховых пространств, в каждом из которых линейные операции (сложение и умножение на скаляр) определены либо покоординатно, либо поточечно, в зависимости от того, что кажется в каждом случае естественней. Обозначения, используемые в этих примерах, нужно рассматривать как стандартные для соответствующих пространств.
I Пример}}.. Простейшими банаховыми пространствами являются пространства Я и С, пространства вещественных и комплексных чисел. Норма числа х в этом случае определяется соотношением ||ж|| = |ж|, где |я| — абсолютное значение х. Метрика, порождаемая такой нормой,согласуется стой, с которой мы познакомились в примерах 1 и 2 § 1. 2. Оба эти пространства по отношению к данной норме являются полными, и, значит, они оба банаховы. Подмножество [0,1] нормировано и полно, но не является линейным, а значит, и не может быть банаховым.
|Пример 2. Как мы увидим в примере 3, линейные пространства Вп и Сп всевозможных n-ок х = (xv х2, ..., а^), образованных из вещественных или комплексных чисел, позволяют построить бесконечное множество различных банаховых пространств. Норма в этом пространстве может быть определена, например, следующим соотношением:
и=(3|х,1>У'’. i—1	'
Метрика р(х, у) = |я — у|, порожденная этой нормой, согласует ся с той, которую мы рассматривали в примере 3 § 1.2. Веществен ные и комплексные евклидовы пространства, определенные таким образом,‘ в предыдущих параграфах обозначались через Е". И те и другие пространства полны, а следовательно, и банаховы.
В данном и последующих примерах мы рассматриваем пространства, элементами которых являются n-ки скаляров, скалярные последовательности и скалярные функции. Сами же скаляры могут быть вещественными либо комплексными числами. В дальнейшем необходимо все время помнить, что мы допускаем обе эти возможности, если только специальным образом не оговорено обратное. Более того, мы не будем даже пользоваться специальными обозначениями для того, чтобы отделить вещественный случай от комплексного. Если же каждый из этих случаев требует особого подхода, то мы отметим это, указав, например, что речь идет о «комплексном пространстве».
Пример 3. Пусть р — некоторое вещественное число, такое что 1 р < оо. В качестве стандартного мы будем пользоваться обозначением 1р(п) для пространств, образованных из Rn и Сп путем введения нормы
п /
Иг11 = (31х<г)1Р-i=l 7
Так как евклидово пространство, очевидно, является специальным случаем 1р(п) при р = 2, то мы часто будем пользоваться для него обозначением 12(п) вместо принятого ранее обозначения Z?n. Нетрудно показать, что введенная выше норма действительно удовлетворяет аксиомам нормированного пространства. Неравенство треугольника ||х± + х2 ||^||^i|| + ||*2|| в этом случае оказывается эквивалентным неравенству Минковского (о котором речь пойдет дальше в этом параграфе) для конечных сумм, а именно:
[21С. + п.гГ<[||Ы’Г+[21п,1’Г.
Доказательство полноты /р(п) мы оставляем читателю.
Пример 4. Рассмотрим теперь обобщение пространств 1р(п) на случай бесконечной размерности. Пусть р — по-прежнему некоторое вещественное число, такое, что 1 р оо. Обозначим через /р пространство всех бесконечных скалярных последовательностей
таких, что 2°1_11 хп |Р <С 00, с нормой
kl = (3 knl) •
п=1
Пространства 1р действительно банаховы. Неравенство Минковского из примера 3 справедливо и для бесконечных сумм, а это значительно упрощает проверку того, что введенная выше норма удовлетворяет аксиомам нормированного пространства.
Следующие два примера относятся к предельным случаям 1Р и Zp(n), возникающим при неограниченном увеличении р.
Пример 5. Как и в примере 3, мы начнем с линейного пространства всевозможных скалярных n-ок х = (Ж|, х2, ..., хп). Однако норму теперь определим уже по-другому, а именно:
Цг|| = max {|xL I, |ar2|, .... |xn|}.
В результате мы получим банахово пространство, обычно обозна
чаемое через /«.(п). Такое обозначение объясняется тем, что
max {| Xi |} = lim [2 I xt I”)>Р-р-*°° 4=i	'
Для того чтобы выяснить, почему это так, рассмотрим вкратце случай п = 2. Итак, пусть х — (х,, х2) есть некоторая упорядоченная пара вещественных чисел. Без какой-либо потери общности мы можем предположить, что и 0. Если хх ~ xz, то
lim ||х|| = lim (2х2)1/р = хг = ||.г ||«, р—>оо	р—*оо
а если ^<^£2» т0
lim ||х|| = lim (г?-f-X2)Vp= lim +1]*?) =
р—>оо	р-*оо	р->оо L\ /	-I /
Г/Гт р	11/р
= lhn[( — I +1	*2 = Хг = ||х||оо*
р->оо L\ *2 /	J
Пример 6. Рассмотрим теперь, как и в примере 4, линейное пространство всех ограниченных скалярных последовательностей х =	х2, •••' хп}- По аналогии с примером 5 определим в нем
следующую норму:
Ml = sup | хп |. п
Полученное в результате банахово пространство мы будем обозначать через Zoo- Как и в примере 5, можно показать, что норма, введенная в Zoo, является пределом нормы для 1Р при р -> оо. Действительно, можно показать, что
suPl^nl = Ит 1 l'm(|x1|p + . . . + | хп |р)1/р]. п	п—*оо р-»оо
Обозначим теперь через с множество всех сходящихся последовательностей. Легко показать, что с представляет собой замкнутое линейное подпространство Zoo и потому само является некоторым банаховым пространством. Другим банаховым пространством того же семейства может служить подмножество с, обозначаемое с0 и содержащее всевозможные сходящиеся последовательности с нулевым пределом.
Элементами банаховых пространств в первых шести примерах были скалярные n-ки либо скалярные последовательности, а отличались они друг от друга нормами. В физических же приложениях пространства функций обычно столь же важны, как и пространства последовательностей. Банаховы функциональные
пространства бесконечно разнообразны, и в следующих трех примерах мы познакомимся с тремя наиболее важными их них.
Пример 7. Пусть Т — произвольное непустое множество, а В(Т) — класс всевозможных вещественных или комплексных ограниченных функций х, определенных на Т. Если положить
||х|| = sup |х (01, гет
то В(Т) становится нормированным линейным пространством.
Заметим, что 1^ — это частный случайВ(Т), где Т есть множество всевозможных положительных целых чисел. В тех же случаях, когда Т принимает вид некоторого промежутка [a, i], мы будем писать вместо В(Т) В[а, Ь]. Доказательство полноты пространства В(Т) мы оставляем читателю в качестве самостоятельного упражнения.
Пример 8. Пространство С(а, Ъ) непрерывных скалярных функций, определенных в промежутке [а, Ь], с нормой
11/11 = sup 1/(01
представляет собой замкнутое подпространство В[а, Ы и, следовательно, является банаховым пространством. (Замкнутость пространства С устанавливается теоремой, утверждающей, что предел любой равномерно сходящейся последовательности непрерывных функций является непрерывной функцией. Эта теорема рассматривается в примере 7 § 1. 2.). Полнота С(а, Ь) доказана в примере 8 § 1.2.
Функциональные пространства. Обозначим через Сь(а, Ь) пространство непрерывных скалярных функций, определенных на промежутке [а, Ы, с нормой
ь И = $ |х(0\dt. а
Ясно, что последнее выражение определяет некоторую норму на соответствующем множестве, и, значит, пространство Сь(а, Ь) может считаться линейным и нормированным. Однако, в отличие от пространства С(а, Ь) из примера 8, пространство С£(а, Ь) не полно. Для того чтобы показать это наиболее простым образом, рассмотрим последовательность {а;п} из СЦО, 2), определенную следующим образом:
х =	о<«1.
' I 1,
Легко показать, что эта последовательность является последовательностью Коши относительно интегральной нормы, введенной
выше, и сходится она к ступенчатой функции (О, 0<<<1,
не принадлежащей 2). [Между прочим, приведенная последовательность не является последовательностью Коши в смысле равномерной нормы на С(0, 2).]
Рассмотренный пример показывает, что для построения некоторого банахова пространства с интегральной нормой нам нужно начать с множества, которое по крайней мере достаточно широко для того, чтобы включать кусочно-непрерывные функции. К сожалению проблему полноты пространства не удается решить таким простым путем. Одна из возникающих при этом трудностей связана со свойствами интеграла Римана. Суть этой трудности состоит в том, что оказывается возможным построить на некотором промежутке последовательность {zn} скалярных функций, каждая из которых интегрируема по Риману, а их предел х недостаточно гладок для того, чтобы гарантировать существование от него интеграла Римана.
Для того чтобы обойти это препятствие, была введена новая, более сильная форма интегрирования, а именно интеграл Лебега. Интеграл Лебега и интеграл Римана совпадают на классе функций, интегрируемых в смысле Римана. Поэтому для наших целей удобно рассматривать интегрирование по Лебегу как обобщение интегрирования по Риману. При интегрировании по Лебегу множеством меры нуль называется любая совокупность точек, занимающая на оси вещественных чисел область, длина которой равна нулю. Всякое множество, содержащее лишь счетное число точек, может служить примером множества меры нуль. Любая функция, равная нулю, всюду, кроме множества меры нуль, имеет интеграл Лебега, равный нулю. Одной из таких функций является функция Дирихле z, определенная на некотором промежутке [a, fe| следующим образом:
z(0 — )1, если t рационально,
|0, если t иррационально, £ ЕЕ [а, &].
Ее интеграл Лебега равен нулю.
Ясно, что если две функции х и у отличаются друг от друга лишь на множестве меры нуль, то функция |х — у| будет отлична от нуля тоже лишь на множестве меры нуль, и, следовательно, ее интеграл Лебега должен быть равен нулю. Поэтому, если для введенной нормы мы собираемся сохранить свойство ||я — у|| = О О <=> х = у, то нем придется считать равными (или, строго говоря, эквивалентными) любые две функции, отличающиеся друг от друга лишь на множестве меры нуль.Это допущение не только приемлемо
с инженерной точки зрения, но и свидетельствует о хорошем математическом вкусе.
Пример 9. Обозначим через Lp(a, Ь), 1 р оо, пространство скалярных функций, определенных и интегрируемых (в смысле Лебега) на промежутке [а, &], с нормой
Г С о 11/р
||/|| = [$|/(0|pd*] • Lu
Для 1 < р < оо справедливо неравенство Минковского
ь	ь	, Ъ	,.
гР	'll/Р гр	'll/р ГР «	11/Р
fSi/o)+?(оМ <ы/(0|₽л] +[Jif(or^J , La	La	La
откуда следует, что ||/ + g|| ^ ||/|| + ||g||- Справедливость других аксиом нормированного пространства очевидна, а мы уже знаем, что с помощью аппарата современной теории интегрирования можно показать, что £р(а, Ь) полно. Таким образом, пространство £р(а,Ь) является банаховым.
Как и в примерах 5 и 6, можно найти интерпретацию и для предельного случая р ->оо. Легко показать, что для каждого конечного промежутка [а, Ы пространство /?(а, b)CZLp (а, Ь), 1^р<С < оо. Более того, если х GE В(а, &), то ||х||р —^supf | x(t) | при р -^оо. Если же пространство В(а, Ь) несколько видоизменить, исключив из него неинтегрируемые функции и добавив к нему функции, ограниченные всюду, за исключением множества меры нуль, и ввести на этом более широком пространстве норму
||я||	ess sup {|я(/)| : / €Е [а, Ы},
где существенной верхней гранью (ess sup) называется наименьшее из значений М, для которого \x(t)\^M лишь на множестве меры нуль, то вместо обозначения В(а, Ь) мы будем пользоваться символом b).
Для того чтобы построить теорию пространств Lp на строгом фундаменте, совершенно необходимо разбираться в современных теориях меры и интеграла. Однако, к нашему счастью, основные свойства пространств Lp и основные результаты, их касающиеся, могут быть усвоены и использованы и без разбора всех этих тонкостей. В последующем мы станем по-прежнему рассматривать все встречающиеся нам интегралы, как будто бы они были римановыми. А читатель может чувствовать себя в полной безопасности, зная, что при подходящей интерпретации все эти результаты могут быть получены совершенно строго.
Обсуждение. Если не считать нескольких разрозненных замечаний, то материал предыдущих параграфов совершенно не
мотивирован с точки зрения возможных технических приложений. Теперь же мы продвинулись уже настолько, что небольшое отступление, касающееся физических прототипов банаховых пространств из приведенных примеров, кажется нам весьма и весьма своевременным. Рассмотрим непрерывную систему с входной переменной и, выходной переменной х и импульсной характеристикой W. В любой момент времени t эти три функции связаны уравнением
t X(t)=^W(t,s)u(s)ds,	t>t0.	(1)
to
Поскольку уравнение (1) описывает обычный двухполюсник, а также разнообразные механические системы (находящиеся в состоянии покоя в момент t — tQ), то мы оставляем на совести каждого читателя построение простейшей физической задачи, для которой это уравнение может служить моделью. Обозначим через tf некоторое время, tf Zo, а через т — интересующий нас интервал г = Uo, Z/L Более того, мы будем предполагать, что наибольший интерес представляет конечный момент tf. Переписав уравнение (1) для этого момента времени, мы получим соотношение
ь
х (tt) = \ W (tf, s) и (s) ds.	(2)
to
Из множества широко распространенных физических ситуаций, отвечающих этому случаю, упомянем лишь две. Пусть функция и описывает расход горючего; точнее говоря, в момент времени t расход горючего равен | u(t) |. Ясно, что в этом случае суммарный расход горючего за время г в точности определяется выражением $| u(0|dt = || uh-
В подобных случаях естественно рассматривать уравнение (2) как определяющее некоторое преобразование над элементами функционального пространства L^x).
Второй, не менее распространенный класс проблем связан с задачей управления системой при ограниченных управляющих воздействиях. Например, в системе управления ракетой-носителем и может обозначать угловое отклонение оси реактивного двигателя от номинального направления. Попятно, что в этом случае величина и должна быть все время достаточно малой, а мерой и может служить
М» = sup|u(0|.
1ST
В этом случае естественно предположить, что допустимые управляющие воздействия должны принадлежать пространству Loo (Г).
Итак, мы убедились в том, что при исследовании непрерывных систем естественно возникает необходимость обращаться к функциональным пространствам Ьр(х). Аналогичные пространства последовательностей игракИт столь же важную роль при изучении поведения дискретных (или импульсных) систем. Рассмотрим, например, множество o' = {£0,	..., ^,..., tf} и множество входных
величин X = {и: u(tk),	состоящее из скалярных функ-
ций дискретного аргумента (времени), определенных на о*. Если обозначить через Zp(cr) пространство X, на котором определена норма
blip = tel u(M|p)1/P, ' а	'
то дискретная двухполюсная система с входным сигналом х и выходным сигналом у, удовлетворяющая уравнению
/
*(М = 2W(tht})	(3)
5=0
является дискретным аналогом системы, описываемой уравнением (1).
Для того чтобы сделать аналогию с непрерывным случаем более явной, заметим, что дискретное «топливо», доставляемое входной величиной, очевидно, измеряется числом
3l“(^)i = hli» о
а его пиковые значения — числом
max {| и(^)| } = ЦиЦоо.
Таким образом, банаховы пространства /р(о*), Lp(r), 1 р оо, и С(а> Ь) оказываются естественным аппаратом исследования поведения динамических систем. И это впечатление по мере разворачивания материала этой книги будет только укрепляться.
Неравенства для ^-пространств. Для использования аппарата теории банаховых пространств 1Р и Lp необходимо иметь хотя бы поверхностное знакомство с некоторыми стандартными неравенствами. Как и раньше, мы будем рассматривать вещественный и комплексный случаи одновременно.
Теорема В. Если х, у S Lp(a, Ь), то х + у €= Lp(a, Ь), 1 р 00 • Если р > 1, то Lp(a, b) С b).
Доказательство. Пусть х и у — произвольные элементы Lp(a, b). Разобьем промежуток 1а, Ы в соответствии с отношением
А - {/: 1x^)1 <1^)1}, В = [а, Ы \ А.
Тогда для t Е= А
I *(<) + у(0 |” < [| x(t) | + | y(t) Цр < 2” | y(t) |
и, следовательно,
^|x(t) + y(z) |”dz<2Р $|р(0|рл<4-оо. Л	А
Аналогично можно показать, что интеграл | x(t) +	ко-
нечен и, следовательно, х + У G Lp(a, b). Для того, же, чтобы показать, что Lp(a, b) CZ ЛДа, Ь), произведем разбиение промежутка [а, Ы в соответствии с правилом
С = {/: |х(0| < 1}, D = [a,b] \ С.
Интеграл | x(t) | dt, очевидно, сходится, а сходимость (существо-с
вание) интеграла | x(t) | dt следует из того факта, что |х(/)|р D
|z(0! пРи t ЕЕ D и что х ЕЕ Lp (а, Ь).
Предположим теперь, что р 1. Число д, удовлетворяющее соотношению 1/р + i/q = 1 (т. е. q = р/(р — 1)), называется показателем, сопряженным к р. Для доказательства следующей теоремы нам понадобится лемма, относящаяся к свойствам сопряженных показателей.
Лемма А. Для произвольных неотрицательных г и s S R, г 0,	0, и произвольных сопряженных показателей р и q спра-
ведливо неравенство
(r)VP(s)V.<^ + ^_ .
Доказательство. Рассмотрим функцию
ф(х) -хЛ — ах, 0 < х < оо,
при 0 < а < 1. Ее производная ф'(^) = а(^а“х — 1) положительна при 0 < х< 1 и отрицательна при х > 1. Поэтому максимум ф достигается строго в точке х =1. Из неравенства ф(х) ^ф,(1) = = 1 — а следует, что хЛ ах + (1 — а) при всех х 0. Пусть г и $ положительны. После подстановки х — r/s получаем

Умножая обе стороны неравенства на s и полагая, что а == 1/р, а1 — а = 1/у, мы получим, что
Это неравенство подавно справедливо, когда одно из чисел г или s или оба они вместе обращаются в нуль. На этом доказательство леммы заканчивается.
Следующая теорема устанавливает справедливость неравенств Гельдера для сумм и интегралов.
Т е*о р е м а Г. Пусть р удовлетворяет неравенствам 1 <Zp < < оо, и пусть q = р/(р — 1). Тогда для произвольных элементов-х = ($!, ..., хп, ... ) е I? и у = (ух, ... уп, ...) GE lq справедливо-соотношение
s I I < [21	1’Г • [21 ГТ=1 х 1 1 s !•
Точно так же для произвольных х Lp(x) uyE Lq(x) справедливо соотношение
$ I х (0 у (01 dt < [51 х (0 |p]1,p. I у (01’]v’ = |ММ
Доказательство. Поскольку эта теорема становится сразу тривиальной, когда х или у оказываются нулевыми элементами, мы рассмотрим здесь лишь нетривиальный случай. Образуем для х ЕЕ £Ари?/Е Lq новые элементы а = х/|| х|| и Р = у! ||у||. Положив в предыдущей лемме s = | a(t) |р и г = | Р(£) |д, получим
Отсюда следует интегрируемость произведения оф (а следовательно, и произведения ху). Проинтегрировав это выражение в промежутке т и замечая, что
$|a(t)|pdt = l = $|p(f)|’df, t	т
мы получим
$|a:(OP(0|d*<4r + T = 1-т
Из этого неравенства и из определения а и Р немедленно следует неравенство Гельдера для интегралов. Неравенство Гельдера для сумм устанавливается точно таким же образом.
Теорема Д. Пусть х и у — произвольные элементы пространства 1Р (или Lp). Тогда при 1 р < оо
I»+ v 1 = [s I 1’Г’ < [21 I’]+ [21 1"Г =111+1 я 1  или
p + y|=[5l®(O + y(0l₽^]VP<
<|$|г(/)|рл]1,р+[!;к(0|р^1/'’= kll + hll-
Доказательство. Рассмотрим вначале Zp:
к 4-dp = Sk 4- i/i l₽ = S(ki + !d-ki 4- Уг Нс i	i
< 21 ;ci I • I хг 4- У г I”’1 + 2I Уг I • I xi 4- Уг I”’1-
i	i
Используя далее теорему Б для сумм (|хх 4 J/i|p'1» •••, l^n + + Уп1р~1, •••), играющих роль элементов lq, получим
к 4- dr <(И 4- hll) к 4- 1/1Г’.
Разделив последнее неравенство на |х 4- мы и получим требуемый результат. Аналогичным образом доказывается и та часть теоремы, которая относится к элементам Lp. Последняя теорема этого раздела приводится здесь без доказательства, лишь для возможных справок.
Теорема Е (неравенство Йенсена). Если О < р < q, то
г	i
Одно из следствий неравенства Йенсена состоит в том, что для О < р < q мы можем установить следующие включения:
ZiCzZpCl/^C.Co^^CZZoo.
Нетрудно построить примеры, показывающие, что каждое из этих включений является собственным.
Некоторые потенциальные применения. В заключение этого параграфа рассмотрим несколько типовых задач теории систем, в которых использование банаховых пространств приносит ощутимую пользу. Воспользуемся уравнениями (1) и (3) в качестве моделей для системы с одним входом и одним выходом. Обозначим через Bt и В2 такие банаховы пространства, в которых рассматриваемая система каждому элементу и <ЕЕ Вг (входному сигналу)
ставит в соответствие некоторый выходной сигнал хЕЕ52-Это соответствие мы будем обозначать х = F(u). Располагая аппаратом теории банаховых пространств, мы можем сформулировать следующую простую задачу теории чувствительности.
Обозначим через й и Z = F(u) некоторую эталонную совокупность входного и выходного сигналов, а через и — некоторую другую входную величину, мало отличающуюся от й. Другими словами, пусть и = й -j- би, где норма || би|| мала. Если входному сигналу и соответствует выходная величина х — X + бх [т. е. х = X + бх = F(fi + би)], то
бх - F(fi + би) - F(u).	(4)
Пусть рассматриваемая система аддитивна, что справедливо для систем, описываемых уравнениями (1) или (3). Тогда F(fi + би) = = F(U) + F(6u) и уравнение (4) преобразуется к виду
бх = F(6u).	(5)
Подходящей мерой чувствительности системы представляется отношение || бх|| /1| би|| при условии, что би =/= 0. Если же нас интересует «чувствительность» системы к вариациям входного сигнала в некоторой е-окрестности эталонного сигнала й, то более подходящей мерой чувствительности было бы число
s^p.®:6“+0)-
До сих пор все наши рассуждения не требовали уточнения характера пространств и В2- Если исследуемая система описывается уравнением (1) и Bt = Lp(a, b), a W(tf, t) ЕЕ Lq(a, б), то, используя неравенство Гельдера, мы можем установить справедливость следующей последовательности неравенств:
ь	ь
бж| = | \ PF(f/,s)6u(s)ds|< ( |TF(tz,s)|-|6M(s)|ds< fo	to
/ /	1/q / /	\1/P
S)\<ds) ( jj	=(||W||Q)(||6u||p),	(6)
fo	/о
откуда сразу следует, что S ^|| J¥||g. (Позже мы увидим, что на самом деле это неравенство следует заменить равенством.) Точно так же для дискретной системы, описываемой уравнением (3), при BY = 1р(а) и W(tf, tr) ЕЕ lq (о) аналогичный результат выглядит следующим образом:
I &х| с (31 w (tf, . (216u (tk) |”)1/p = (IIW ||Q) (II 6u ||p). (7) a	a
Здесь важно отметить, что использование абстрактного понятия расстояния позволило одновременно охватить весь диапазон возможностей 1Р и Lp, 1 р < оо, избежав при этом необходимости вычислять сложные интегралы и суммы, связанные с изучением конкретных систем. Использование понятий нормы и окрестности позволило сосредоточить все наше внимание на самой сути задачи, а не на вычислительной специфике, с нею связанной.
Наша вторая задача также относится к гипотетическим системам, описываемым уравнениями (2)или(3). Так же, как и в задаче теории чувствительности, мы обозначим соотношение между входным и ЕЕ В и выходным x(tf) ЕЕ R сигналами с помощью уравнения х — F(u). Пусть £ ЕЕ R — некоторая фиксированная точка. Мы сейчас попытаемся ответить на вопрос, существует ли такой сигнал ЕЕ Ви который одновременно удовлетворяет соотношению = £ и минимизирует критерий качества системы ||х||. Другими словами, мы хотим выяснить, имеется ли элемент с минимальной нормой в классе допустимых входных сигналов, который система связывает с выходным сигналом x(tj) = £. Судя по разнообразию возможных физических интерпретаций понятия нормы в пространстве входных сигналов (например, расход топлива, пиковая амплитуда, энергия и т. п.), эта задача может служить прототипом для одного чрезвычайно важного класса задач теории оптимизации (которая подробно изучается в главе 4).
Для того чтобы решить поставленную задачу, мы вернемся прежде всего к доказательству леммы А. Отметим, что в соотношении (r)1/p (s)1^ < (г/р + s/q) равенство имеет место тогда и только тогда, когда г = s. Эта однозначность сохраняется на протяжении всего доказательства теоремы Г и приводит к тому, что для каждого х 6= 1Р равенство в первом соотношении в формулировке теоремы Г возможно в том и только в том случае, когда компоненты вектора у G= lq с точностью до некоторой постоянной к 0 определяются однозначно из условий
| Xi |р - к\yi |«, i = 1, 2, ..., Л’> 0.
Точно так же для каждого х ЕЕ. Lp знак равенства во втором соотношении в формулировке теоремы Г оказывается справедливым тогда и только тогда, когда функции у (= Lq удовлетворяют соотношению
|х(0 |р = к I y(t)\q, Л>0, /ет.	(8)
Ясно, что до тех пор, пока 1/р + 1/q = 1, эти числа играют в приведенных соотношениях двойственную роль.
Ограничимся теперь рассмотрением системы, описываемой уравнением (2), и предположим, что W(tfl s) ЕЕ LQ. Уравнение
8)	утверждает, что входной сигнал с единичной нормой, максими-ирующий выходной сигнал, определяется по формуле
и (Z) = sign [W (tf, /)1	-уц.?-— •
IIй II
Поэтому оптимальным управляющим воздействием является единственное скалярное кратное этого сигнала, удовлетворяющее конечному условию x(tf) — £.
Для изучения систем со многими входами и выходами приходится прибегать к помощи декартовых произведений банаховых пространств. Для иллюстрации этого утверждения предположим, что {Bt: i 1, ..., п} есть некоторое множество банаховых пространств, а В - Bt х ... Вп — обычное декартово произведение пространств из этого множества. Конечно, хотелось бы, чтобы и само В в этом случае было банаховым пространством. Произведение В является линейным пространством относительно естественного определения опграций сложения и умножения на скаляр. Поэтому остается лишь решить вопрос об определении нормы на пространстве В и выяснить вопрос о полноте этого пространства. Обычно ни то, ни другое не представляет особого труда. Более того, существующая гибкость выбора нормы позволяет исследователю приспосабливать характер нормы к конкретным условиям рассматриваемой задачи.
В качестве иллюстрации рассмотрим вектор х = (х^ ..., хп) ЕЕ 6= В. Обозначим через || норму, определенную на В^ Вектор, составленный из норм, ц (х) — (II^ilk, •••» ||*n||n) является, очевидно4 вполне определенным элементом Rn. Обозначим через | | любую норму, определенную на Rn. Тогда функция | |, определенная на В условием
И = In (*)l, х 6= в,	(9)
может служить нормой для пространства /?. Например, если | | — это норма, принятая для 1р (п), то
п i/p
|х| = (s пигГ *</>< i 1
Упражнения
1.	Пусть А и В — подмножества банахово го пространства X, Обозначим через А + В множество всех элементов х вида х = а + Ь, где а£ Л, а b е В. Покажите, что если А или В открыты, то открыто и Л -j- В. При-ведите пример двух замкнутых подмножеств А, В С В таких, что А + В не замкнуто.
2.	Пользуясь примером 8 § 1.2 как моделью, докажите полноту пространства В (т) пз примера 7. Докажите полноту пространства Zp.
3.	Пусть X — n-мерное пространство с базисом {q, ..., еп]. Для каждого iS X найдутся скаляры {оц (z), an (z)}, однозначно определяющие
разложение х по базису ..., еп}. Другими словами, эти скаляры удовлетворяют соотношению х = щ (х) е*. Пусть | | обозначает некоторую норму для Rn (или С71). Покажите, что функция
I х | = | [аг (х), ..., ап (х)][, х е X,
может служить нормой для X. Покажите, что в конечномерных пространствах сходимость по норме и по координатная сходимость эквивалентны.
4.	Убедитесь в том, что функция | |, определенная в уравнении (9), является нормой для В. Для Bt = Lpi (a, b), i----- 1, ..., к, и В[ ~ i = к 4- 1, ..., и, выпишите эту норму подробно.
5.	Проверьте следующие утверждения.
(а)	Пространство со замкнуто в с, а пространство с замкнуто в 1^.
(б)	Если рассматривать как подмножество то его замыканием служит с0. (Заметим, что это следует из факта замкнутости с0 в i^.)
(в)	Пространство 1Р плотно в Z^. (Множество Е в метрическом пространстве X называется плотным, если Е = X.)
(г)	Обозначим через М одномерное пространство с, натянутое на вектор (1/2, 2/3, 3/4, ...). Тогда с = с0 ф М.
6.	Пусть некоторое банахово пространство В представляет собой прямую сумму линейных подпространств М и N, так что В = В ф N, Если z = х + у является единственным представлением вектора z из В в виде суммы двух векторов х и у из М и N соответственно, то новую норму на линейном пространстве В можно определить с помощью выражения || z||' = || х|Ц-+ IIУ ||- Докажите, что это действительно норма. Пусть В' — линейное пространство В, на котором определена эта новая норма; докажите, что пространство В' банахово при условии, что М и N замкнуты в В.
7.	Пусть N — некоторое нормированное линейное пространство. Докажите, что U является банаховым пространством тогда и только тогда, когда множество {х\ ||х||<1} полно.
1.5.	Гильбертовы пространства
Банаховы пространства, изученные в параграфе 1.4, можно рассматривать как нечто большее, чем просто линейные пространства, для которых определено подходящее понятие длины вектора. Важным геометрическим понятием, которого нам пока недостает, является понятие скалярного (или внутреннего) произведения двух элементов. В этом параграфе мы познакомимся с абстрактным скалярным произведением и покажем, к каким важным выводам можно прийти, пользуясь этим понятием.
Рассмотрим вещественное трехмерное евклидово пространство £3. Вектором, или элементом, Е3 служит упорядоченная тройка х = (хх, х2, х3) вещественных чисел, а норма в этом пространстве задается выражением
k II = (l*il2 + hl2 + Нз!2)1'’.
В элементарной векторной алгебре скалярное (внутреннее)
произведение х и другого вектора p=(j/i, Уг, Уз) определяется *) следующим образом:
<х, у> = XjP! + х2у2 + ХзУз-
В связи с этим норма в Е3 может быть выражена через скалярное произведение
ЦхЦ2 = <х, х>.
В пространстве Е3 определен еще и угол 0 между векторами х и у. Его значение можно найти из уравнения
<х, У) -= ||х|| . ||у И cos 0.
В частности, векторы х и у считаются ортогональными, если <х, у)=0, и коллинеарными, если <х, у> — + ||я|| • ||у|(. В комплексном пространстве Е3 скалярное произведение двух векторов х = = (xi, х2, х3) и у ~ (уп у2, уз) можно определить (см. пример 2 § 1.4) с помощью выражения
<х, у> = хгух + х2у2 + х3у3,
где черта над компонентами указывает на то, что берутся комплексно-сопряженные числа. Это понадобилось для того, чтобы обеспечить совпадение обычной нормы и нормы, задаваемой скалярным произведением
<х, х) — ЦхЦ2.
Так как <х, у> в комплексном пространстве уже не всегда вещественно, то очевидно, что в общем случае нам не удастся уже ввести понятие угла между х и у. Тем не менее условия <х, у> = 0 и <х, у> = = +Их1Н|у|| по-прежнему определяют ортогональность и коллинеарность векторов, соответственно, и эти понятия оказываются столь же полезными, как и в вещественном пространстве.
Используя все эти идеи как некоторую стартовую площадку, сформулируем основное определение скалярного произведения в абстрактном линейном пространстве.
Аксиомы скалярного произведения. Пусть X — некоторое комплексное линейное пространство. Правило, ставящее в соответствие каждой паре элементов х, у £ X некото
*) В литературе не существует единого установившегося правила для обозначения скалярных произведений. В элементарных работах чаще всего пользуются обозначением z-y, а в более сложных — обозначением (х, у). Выбор обозначения] <z, у>, принятого в этой книге, диктуется материалом последующих глав, где сложность многих выражений заставляет использовать множество различных скобок, что могло бы привести к путанице в отсутствие специального символа для обозначения скалярного произведения.
рый скаляр (х, у}, называется скалярным произведением, если выполняются следующие условия:
(1)	у) = (у, х>, закон коммутативности;
(2)	(я, у + z) = <х, у) 4- <^г, z>, закон дистрибутивности;
(3)	<Хх, у> = X <х, j/>, каково бы ни было комплексное X;
(4)	<х,	0, где <х, х) = 04=>х = 0.
Как и при определении линейного пространства, из аксиом (1), (2), (3) и (4) непосредственно вытекают некоторые дополнительные соотношения. С доказательства их мы и начнем. Рассмотрим три элемента х, yt и у2 пространства X. Используя сначала аксиому (1), затем аксиому (2) и, наконец, аксиому (3), построим следующую цепочку равенств:
<У1 + У21 Я> = <Х, У! + у2> = <Я, У!> + <Я, у2> = <f/lt Ж> + <у2, X).
В результате в дополнение к аксиоме (2) мы получим следующее соотношение:
(2')	<1/а4-!Л>, *> = <У1,я> + <Уг,
Точно так же с помощью аксиом (1), (3) и (4), использованных именно в этом порядке, мы можем построить другую цепочку равенств:
<ж, Ху> = <Ху, х} = X <у, х) = X (х, у), которая позволит нам получить следующее дополнение к аксиоме (3):
(3')	<ж, Ху> = Х<я, у>.
Наконец, воспользовавшись аксиомой (2), мы найдем, что
0> = <ж, 0 + 0> = {х, 0) + <я» о>, откуда
, 0> = 0 = (0,.г>
для любого х€Е:Х.
Определение А. Комплексное линейное пространство X называется предгильбертовым (или пространством со скалярным произведением)*), если на нем определена некоторая комплексная функция, удовлетворяющая аксиомам скалярного произведения.
Наш опыт работы с пространством Е'Л позволяет надеяться, что в произвольном предгильбертовом пространстве скалярное произведение можно будет использовать для построения нормы. В частности, функция [{х, кажется вполне подходящим кандидатом для роли нормы. В данном случае интуиция нас не обманывает, и мы покажем, что так выбранная функция действительно
*) Заметим, что при таком определении не исключается случай, когда пространство X вещественно.
удовлетворяет всем аксиомам нормы. Например, из равенства
<ая, otz> = У"| а |а <я, я> = | а | У х)
следует справедливость для этой нормы третьей аксиомы. Первая аксиома является простой переформулировкой аксиомы (4) скалярного произведения. Для ‘ доказательства второй аксиомы нам понадобится следующая теорема.
Теорема А (неравенство Коши). Пусть х и у — некоторые элементы предгильбертова пространства X. Тогда
Рис. 1.9. Скалярное произведение.
Доказательство. Геометрическое подтверждение этого соотношения приведено на рис. 1.9. Начнем, с того, что выберем произвольные х и уЕ^Х и произвольный скаляр X. Тогда
<х + Ху, х + Ху> = <х, х> + Х<х, у > + X <у, х> +
+ IM2 <У> У>>0.
Предположим, далее, что ЦуЦ =£= 0 (в противном случае окончательный результат был бы очевидным), и выберем X так, чтобы
л __ ~<М>
Тогда предыдущее неравенство, справедливое для произвольного X, принимает вид
/т „ч _	_ <.т, у) <у, а;> I <ж, у) |2
7 \У>уУ <у,у> +1<!/.г/>|2
что в свою очередь сводится к следующему:
тч _ I <•*, У> I2 _ I У> I2 . I <ж, У> I2	о
’’ 7	<У,У>	<У,У>	<У,У>
или в конце концов к следующему соотношению:
*> <у, У) > | <х, у> |2 <4 Ц аг|.| у || > I <х, у >|.
Теперь мы в состоянии завершить проверку того, что [(х, х)\ч действительно может служить нормой для X.
Теорема Б. Пусть X — некоторое предгильбертово пространство. Тогда
||гг|| = [<х, я)]1/’
является нормой, определенной на X. Более того, для произвольных х, у Е справедливо следующее правило параллелограмма:
||* + </1М к-!/||2 2 ||х|М- 2 II yf.	(1)
Правило параллелограмма легко доказать, выписав выражения в левой части равенства через скалярные произведения:
|| X + у II2 + II X — у II2 = (х + у, х + уУ + <х — у,
X— уУ = <х, хУ + (х, уУ + <у, хУ + <*/, уУ +
+<г, ху — <х, уУ — (у, хУ + <!/. УУ 2<х, х> + 2<у, уУ = 2|М12 + 2||У|Р.
Теперь, после того как мы достаточно хорошо познакомились с понятием скалярного произведения, переход к понятию гильбертова пространства кажется вполне естественным.
Определение Б (гильбертово пространство). Линейное пространство X называется гильбертовым, если оно является предгильбертовым пространством и полно отно сительно нормы, порождаемой своим скалярным произведением.
Эквивалентное определение: гильбертовым называется любое банахово пространство, в котором норма порождена каким-нибудь скалярным произведением. Многие авторы включают в эти определения дополнительное требование бесконечномерности, сохраняя название евклидово пространство для любых конечномерных гильбертовых пространств. Однако для целей этой книги нам нет никакого смысла различать эти два случая.
Рассмотрим теперь несколько конкретных примеров гильбертовых пространств. Мы немедленно убедимся в этом, что с большинством из них мы уже хорошо знакомы. Для того чтобы подчеркнуть, что гильбертово пространство как банахово пространство имеет вполне определенную норму, а как метрическое пространство — вполне определенную метрику, мы каждый раз будем выписывать норму и метрику, задаваемые введенным скалярным произведением.
Пример 1. Пространство 12 (п). Если х = (хг, ..., хп) и у = = ( j/i,..., уп) — два вектора в пространстве 12 (и), то естественно следующее определение скалярного произведения:
п
<х, //> = S xiy-i-
г=1
Обычные норма и метрика в 12 (п) определяются тогда соотношениями
п®и=(2 i=l
п	7>
р (®. у) = II®+у11 = (S l®i - yd2) ’•
Пример 2. Пространство /2. Для пространства 12 скалярное произведение векторов
X -- (хп х2, хп, ...) и у—- (yt, у2,	уп...)
естественно определить следующим образом:
оо
<®. У> = 2 ХпУп-
Выпишем также обычные норму и метрику для этого пространства
II® 11 = к®,®»'7- (2 ki 12)л>
i=l
во	7
p(®,y) = ll®4-!/|| = (2 l®i-J/il2) •
i=l
Пример 3. Пространство L2 (а, Ь). Пусть х (t) и у (0 — две функции из пространства L2 (а, Ь). Тогда в качестве скалярного произведения в этом пространстве мы выберем функцию
ь
<®, У) = ^x(t)y(t)df. а
Естественные норма и метрика в L2 (а, Ь) задаются соотношениями
Ь	7
||®||== 1<®,®)Г7, = |$|®(012л| \ а
ь	7з
р(х,у) = ||®-1/||= |$|ж(0 -</(Z)|2dz] . а
Скалярные произведения, выбранные в этих примерах, казались естественными по отношению к функциональным пространствам, на которых они определялись. Однако эти определения скалярных произведений ни в коем случае не являются единственно
возможными. Для того чтобы проиллюстрировать широкий простор, существующий в выборе скалярных произведений, нам достаточно будет всего одного примера.
Пример В пространстве L2 (а, Ь) зачастую удобно ввести скалярное произведение несколько более общего вида, чем рассмотренное в примере 3. Пусть р (0 — некоторая функция р (0 > 0, определенная на интервале (а, 6). Тогда вполне законным скалярным произведением может быть функционал
ъ
<Х,У) = н (0 МО#(0 dt-
а
В этом случае ь	7
а
И
р (*, у) = к - у II = и (О I * (О - у (0 Pd<]Л • а
Пространство L2 (а, Ь) с определенным таким образом скалярным произведением мы будем обозначать через L2 (а, Ь; р). Каждому новому р (0 при этом будет соответствовать новое гильбертово пространство.
Поскольку каждое гильбертово пространство является в то же время и банаховым, определения и различные свойства сходимости и других метрических свойств, содержащиеся в предыдущем параграфе, непосредственно переносятся на случай гильбертовых пространств. Отметим также, что при р = 2 неравенства Гельдера вырождаются в неравенство Коши — Шварца. Что же касается неравенства Минковского, то оно, естественно, сохраняет свое значение и для конкретных гильбертовых пространств.
Нам представляется чрезвычайно важным в полной мере уяснить доказательство таких свойств, как неравенство Коши — Шварца, в абстрактной постановке. Для того чтобы подчерк-утьэту мысль, ознакомимся с конкретными формами, принимаемыми неравенством Коши — Шварца в каждом из четырех примеров гильбертовых пространств, рассмотренных ранее. В абстрактном виде: | <х, у > | ^ |х|| • ||у||. Конкретные его формы определяются следующим образом.
1.	В пространстве 12 (п) с элементами х = (х^ ..., хп) и у = = (У1. •••, Уп)
к*.</>1 = 13	ы8]л[3 ij/i г]А-
i 1	1=1	i=l
2.	В пространстве 12 с элементами х *= (xv хп) и у —'(уи ... ...» Уп, )
1<я,у>1 = | S xiSi |< |S I®! i2]z|S I Vi l2]7 • г=1	г=1	г—1
3.	В пространстве Ь2 («» Ь) с элементами х = х (t) и у — у (/)’ /£[а, Ь]
ь	ь	ъ
а	а	а
4.	В пространстве Ь2 (а, Ъ\ р) с элементами х -- х (t) и у --= у (0, £<=[«, Ь]
ъ
<х> у> I = | $ и (О * (0 у (0 dt |’ < а
ь	7 Ь	7
<[$p(O|x(0|4t] ’[$р(0 1Н0 I2 dt] ’. а	а
Таким образом, в любом гильбертовом пространстве гарантировано существование неравенств или равенств такого рода.
Закон параллелограмма открывает еще одну интересную сторону взаимоотношений между банаховыми и гильбертовыми пространствами. В любом гильбертовом пространстве скалярное произведение можно выразить через норму с помощью следующего тождества:
<х,у> = 4_fl® + ylFH*-y|l3 + ^ +W-ik-wll2}. (2) которое можно сразу проверить, представив выражение в правой части через скалярные произведения.
Теорема В. Пусти В — некоторое комплексное банахово пространство, норма которого удовлетворяет закону параллелограмма \уравнение (2)1 и на котором определено с помощью уравнения (2) скалярное произведение. Тогда В является гильбертовым пространством.
Доказательство теоремы В мы оставляем читателю в качестве самостоятельного упражнения. Эта теорема помогает уяснить, почему нельзя построить гильбертовы пространства из любых банаховых пространств и, в частности, из пространств 1Р и Lp при Р 4= 2.
Ортонормальные множества. В начале этого параграфа мы спе циально подчеркивали сходство, существующее между банаховыми и гильбертовыми пространствами. Однако для многих технических
приложений различия, связанные с существованием скалярного произведения и понятия ортогональности, играют существенную роль. В следующих разделах мы займемся исследованием некоторых наиболее важных свойств, выделяющих гильбертовы пространства из общего класса банаховых пространств.
Обозначим через {хх, ..., хп} некоторое множество элементов гильбертова пространства II. Матрица G (хп ..., хп), определенная следующим образом:
<Tt, Xi)... <.ТЬ Хп)
<х2, хх> . . . (х2, хп)
(7 (хх,..., хп) —
^1) • • •
называется матрицей Грама этого множества. Определитель этой матрицы, соответственно, называется определителем Грама и обозначается через Дп.
Теорема Г. Множество элементов {хх, ..., хп} гильбертова пространства Н линейно зависимо тогда и только тогда, когда его определитель Грама обращается в нуль.
Доказательство. Предположим, что множество {xp ...» хп} линейно зависимо. Тогда существует такой набор скаляров (из которых не все равны пулю), что
aiXi + ... + апхп = 0.
Вычисляя скалярные произведения каждой из сторон этого ра* венства с векторами хх, ..., хп, мы получим следующую систему уравнений:
«1 <*ь *1> + ••• +	*п>	0,
0&1	'I' •••	%п) ~~
Если рассматривать ah как неизвестные этой системы п линейных уравнений, то для существования некоторого нетривиального решения (ар ..., ап) необходимо, чтобы определитель Дп обращался в нуль.
И наоборот, если Дп - 0, то у этой системы найдется некоторое нетривиальное решение (ар ..., ая). Переписав системы уравнений в виде
п
<^Xi,2 <*/9^ = 0,	4 = 1,...,п,
;=1
мы видим, что умножение i-ro уравнения на щ с последующим
сложением всех таких произведений приводит к равенству
п	п
<2 «л. 2 «л)* = 12а^ | = °.
откуда следует, что 2C=i оц^г = 0, что и доказывает линейную зависимость исследуемого множества.
Следствие. Ранг матрицы, Грама равен размерности линейного многообразия (хх, хп). Если =/= 0, то не равен нулю и определитель Грама для любого подмножества {хх, ..., хп}.
Доказательство, Поскольку из равенства Дп = 0 следует, что множество {хх, ..., хп} линейно независимо, то линейно независимым должно быть и любое подмножество {хх, ..., rrfc}, следовательно, определитель Грама этого подмножества также не обращается в нуль. Доказательство первой половины утверждения мы оставляем читателю.
Определение В. Два элемента х и у произвольного гильбертова пространства Н называются ортогональными, если (х, у> = 0.
Утверждение «х ортогонально у» часто символически записывают в виде х_[_у. Поскольку <х, у) = <у, х>, то справедливо соотношение х | у <=> у I х. Ясно также, что х | 0, каково бы ни было х, а равенство <х, х) = ЦхЦ2 показывает, что 0 — это единственный вектор пространства, ортогональный по отношению к самому себе. Более того, легко проверить справедливость теоремы Пифагора, принимающей в абстрактном пространстве следующий вид:
I * + у II2 = || X (|2 + || у О2 & X 1 у.
Определение Г. Пусть S — некоторое непустое подмножество гильбертова пространства Н. Множество S называется ортогональным, если для любой пары х, y€zS таких, что х=^у, х У- Если, кроме того, || х|| — 1 для каждого х Ez S, то множество S называется ортонормальным.
Лемма А. Каждое ортонормальное множество линейно независимо. Если х ортогонально любому элементу множества {хх, ... ...,zn}, тох— ортогонально линейному многообразию L(xv ..., хп).
Доказательство. В матрице Грама ортогонального множества от нуля отличны лишь элементы главной диагонали: || тх ]}2, ... ...,||znt Следовательно, Ап^И^1(|2,11д:2||2-----||2:п||2 =/=0, и потому, в силу теоремы Г, исследуемое множество линейно независимо. Если <х, х^ — 0, i — 1,..., п, то для каждого у ЕЕ L (хх, ..., хп)
п
У = 2 aiXi’
1=1
и значит, п
<Х, уУ = 3 <*, *<> = О,
1=1
что и завершает доказательство.
В пространстве Еп утверждения леммы А становятся очевидными. Мы советуем читателю построить для себя картину (или по крайней мере мысленную картину), иллюстрирующую этот и каждый из последующих результатов. Переключим теперь наше внимание на задачу построения ортогональных множеств.
Пусть X = {а?!, ..., xh} — произвольное конечное множество линейно независимых векторов, и пусть L (х^ ..., xk) — линейное многообразие, натянутое на множество X. Зададимся вопросом, нельзя ли всегда найти такое ортонормальное множество £’={е1, ..., еп}, которое могло бы служить для L базисом. Ответна этот вопрос оказывается положительным. С помощью одного метода, известного под названием процесса ортогонализации Грама-Шмидта, из любого множества линейно независимых векторов {^} можно построить множество взаимно ортогональных векторов {в{}. Этот процесс представляет самостоятельный интерес и сводится к следующему. Положим
У1 = Xi
и определим у2 с помощью формулы
2 <уъ yi>
Другим словами, пусть у2 равняется х2 минус его проекция на Тогда <1/2> У1) — 0- Аналогичным образом определим и третий элемент у3 множества. Пусть
у = х _ <х*	7, _ <х^
У3 3 <УЪ уг> У1 <У2, ?/2>
т. е. пусть у3 равняется х3 минус его проекция на плоскость, образованная векторами yt и у2. Очевидно, что
<Уз, У1> <Уз, У2>	0.
Предположим теперь, что векторы у2, у]_г (j <; к) уже определены таким образом. Положим у; равным Xj минус его проекция на подпространство L (уу2, • Vj-i):
V? <ЖГ Vi>
Ясно, что yj ортогонален к ух, уу_х). Кроме того, yj не может быть нулевым вектором, так как в противном случае xj оказался бы линейно зависящим от у^ у2, ...» уj-i, а следовательно, и от ух, Уг» •••» У/-2» </-1» что вытекает из определения у^г. Продолжая это рассуждение далее, мы в конце концов установим, что линейная зависимость Xj от ух, у2, ..., у j-x приводит к линейной зависимости Xj от хх, х2, ...» Xj_x, а это противрречит нашему исходному условию, согласно которому исходные векторы хх, х2, ..., xh линейно независимы. Таким образом, мы убедились в том, что описанный процесс позволяет построить множество из к ненулевых векторов, обладающих свойством взаимной ортогональности.
Далее, векторы {yj} можно нормировать, получив в результате множество {ej}. Сам процесс построения свидетельствует о том, что каждый вектор можно представить в виде некоторой линейной комбинации Xj и, наоборот, каждый вектор Xj выражается в виде некоторой линейной комбинации eit В связи с этим, очевидно, L(Xj,x2, ..., xn)—L (ех, е2, ..., ek). Продолжая процесс далее таким же образом, мы придем в конце концов к следующей теореме.
Теорема Д (Г рама — Шмидта). Если X = {xi} — некоторое конечное или счетное множество векторов гильбертова пространства Н, то существует такое ортогональное множество У = {^}, что L (X) = L(Y).
Пример 5. Рассмотрим подмножество 5 = {еъ е2, ...» еп} пространства /2 (и), в котором ei — это n-ка с единицей на i-м месте и нулями на остальных местах. Очевидно, S в этом пространстве является ортонормальным множеством. Аналогично, если еп — это последовательность, n-й член которой равен 1, а все остальные — нулю, то множество {ех, е2, ..., еп} ортонормально в Z2.
Пример 6. Пусть X — вещественное пространство Е\ Рассмотрим следующее множество векторов: хх = (ах, 0, 0), х2 = (аг» &2» 0) и х3 — (яз» &з, ^з)- Построим на его базе ортогональное множество, пользуясь процедурой Грама — Шмидта. Для этого прежде всего положим
J/х Л = («1» 0, 0),
Затем, по аналогии, положим
и = г — <Хз’ ?/|> » — <Жз’ уз> и 3 <yi> yi> <У«» Уг>
У* = («з, Ь„ с3) -	(Д1, 0, 0) -	(0, Ь2, 0) = (0, 0, с3).
Другое ортогональное множество можно построить, если принять ух = х3. Для простоты анализа мы конкретизируем исходное
множество, приписав для начала численные значения его буквенным координатам. Итак, пусть
хх = (1, 0, 0), х2 - (1, 4, 0), х3 - (1, 2, 2).
Положим, далее,
" ^3 — (1 > 2, 2),
^ = (1,4, 0) - 7Т<1+^_(1, 2, 2).
Последнее уравнение приводит к следующему виду второго вектора:
Уг (0, 2, - 2).
Наконец, пусть
». = (I. 0. 0) - 4ТТ(0. 2, -2) - r-,;^(1, 2, 2), или
f/з = 4-<8’ ~2- ~2)-
Ортогональность этих векторов нетрудно установить непосредственно.
Пример 7. Рассмотрим теперь множество S — {1/2, cos t, sin t, cos 2Z, sin 2t, ..., cos nt, sin nt, ..., }. Легко показать, что в вещественном пространстве L2 (—я, л; р), где р (t) = 1/л, множество S является ортонормальным. Напомним, что скалярное произведение в таком пространстве определяется выражением
п
1 С
<Х, у> = — у X (0 у (/) dt.
Теория и применения ортонормальных множеств представляют собой одну из наиболее плодотворных областей прикладной математики, физики и техники. Именно к этой области относится и хорошо известная теория рядов и интегралов Фурье. В приложении 2 теория ортонормальных множеств развивается в этом направлении.
Ортогональная декомпозиция. Пусть х — некоторый фиксированный элемент гильбертова пространства И. Обозначим временно через Мх пространство всех векторов, ортогональных фиксированному вектору х. Из леммы А следует, что Мх — обязательно некоторое векторное пространство. Мы утверждаем, что Мх еще и замкнуто. Для того чтобы убедиться в этом, предположим, что у — некоторая предельная точка множества Мх. Но тогда существует
последовательность упЕ=Мх, которая сходится к у. А так как
<а-, у> = lim <.г, уп> = О,
71—>ОО
то и у€ЕМх.
Определение Д обобщает эти рассуждения.
ОпределениеД. Пусть S — любое непустое множество векторов из Н. Мы говорим, что у ортогонально S, и записываем это y_\_S, если у ортогонально х, yj_x. каково бы ни было х из S. Множество всевозможных векторов, ортогональных S, обозначается через и называется ортогональным дополнением множества S.
Отметим следующие факты, вытекающие из этого определения.
Л е м м а Б. Если S и Т — два непустых подмножества Н, то
(1)	{О}1 -- II, ll '	{0},
(2)	S П 51 = {0},
(3)	S CZ Т => 51 Z) Г1,
(4)	S С S’*"*" [где определяется как
(5)	S1 — замкнутое линейное подпространство Н,
(6)	S11 является наименьшим замкнутым линейным подпространством Н, содержащим S.
Доказательство. Доказательство утверждений (1) — (4) очевидно, и мы оставляем его читателю. Для того чтобы доказать утверждение (5), заметим, что из того, что у eS1, следует, что у GE Мх для каждого zES. Поэтому
П{МХ}, xes
т. е. S является пересечением замкнутых подпространств, а значит, и само — некоторое замкнутое подпространство.
Рассмотрим теперь утверждение (6). В силу (5) 5“L1 = есть некоторое замкнутое линейное подпространство, которое в соответствии с утверждением (4) содержит S. Обозначим через М наименьшее замкнутое линейное подпространство Н, содержащее S. Тогда S11 Z) М.
Попытаемся теперь выяснить, из каких же элементов состоит М. Так как М — некоторое линейное подпространство и содержит к тому же S, то оно, очевидно, должно содержать все конечные линейные комбинации элементов S. Из-за того, что М замкнуто, оно должно содержать и все пределы последовательностей, составленных из элементов того же вида. Но, с другой стороны, легко проверить, что это последнее множество является замкнутым линейным подпространством, содержащим S. Поэтому М — это множество всевозможных векторов х = lima:n, где хп — не-71-*ОО
которая конечная линейная комбинация векторов из S.
Но отсюда следует, что если у 51, а х = lim хп — произ-71—*ОО
вольный вектор из М, то (х, у) = lim < хп, у) =0, так что п-»оо
у GE М1. В силу утверждения (3) М1 С 51, откуда и следует, что МЛ = S1' Таким образом, S и замкнутое подпространство, им порожденное, имеют одинаковое ортогональное дополнение.
Собирая полученные факты воедино, мы сведем утверждение (6) к следующему.
Лемма В. Если М — замкнутое линейное подпространство Н, то М11- = М.
Доказать эту лемму можно непосредственно, но это заняло бы довольно много места и потребовало бы определенных усилий. В то же время гораздо более простое доказательство опирается на теорему Хана — Банаха, с которой мы познакомимся в § 3.2. В связи с этим мы предпочитаем отложить доказательство леммы В до изучения этой теоремы (упражнение 12 § 3.2).
Прежде чем переходить к доказательству следующей теоремы, исследуем вкратце введенные выше понятия на примере трехмерного евклидова пространства Е3, Если отожествить вектор х = = (хх, х2, х3) из Е3 с направленным отрезком прямой, соединяющим начало координат с точкой (хх, х2, х3), то ясно, что (одномерным) подпространством, натянутым на вектор х, является вся эта прямая, заданная двумя своими точками. Аналогично (двумерное) подпространство Е3, натянутое на векторы х = (агх, х2, х3) и у = (ух, у2, i/з),— это плоскость, проведенная через три точки с координатами (0, 0, 0), (хь х2, х3) и (уь у2, у3). Более того, мы знаем, что каждый вектор из Е3 может быть представлен совокупностью своих координат вдоль осей х, у и z соответственно. И вообще говоря, мы можем осуществить аналогичную декомпозицию каждого вектора из Е3 относительно любых трех взаимно ортогональных векторов Е3. Точно так же мы можем выбрать любую плоскость L, проходящую через начало координат, а затем разложить любой вектор из Е3 в сумму векторов, один из которых принадлежит L, а другой — ортогонален L. Другими словами, Е3 = L ф L1. (Таким образом, мы видим, что по отношению к прямой сумме определяет то, что осталось в £3, а значит, используемое название «ортогональное дополнение» вполне оправдано.)
Имея в виду тот факт, что наше абстрактное определение гильбертова пространства было рассчитано на то, чтобы впитать в себя все «существенные» свойства Е3, естественно ожидать, что если Н — некоторое гильбертово пространство, a L — его линейное подпространство, то пространство Н удастся представить в виде Н = L ф [Л. Поскольку при любых L L Q — {0}, то нам остается получить ответ на единственный вопрос: охватывает ли L ф все Н или нет? Очевидно, это то же самое, что спросить:
можно ли каждый вектор х из Н записать в виде х = у + z, где I/ £ a z Е Если не требовать, чтобы подпространство L было замкнутым, то можно построить примеры, дающие отрицательный ответ на этот вопрос. Что же касается замкнутых линейных подпространств, то для них справедлива следующая теорема.
Теорема Е (о проекциях). Пусть L — некоторое замкнутое линейное подпространство И. Тогда каждый вектор х из Н однозначным образом может быть представлен в виде суммы х = у + z, где у ЕЕ L, a z ЕЕ А1 (вектор у называется проекцией х на L),
Доказательство. Однозначность такого представления доказывается тривиальным образом. В самом деле, если
я = I/ + z, у ЕЕ L, z ЕЕ ZA, х = у' + z', У' ЕЕ L, z' ЕЕ L\
.— два возможных представления х, то вектор у — yf = z — z' одновременно принадлежит и L, и L\ а в силу утверждения (2) леммы Б это значит, что у' — у = 0 = z' — z.
Итак, как уже отмечалось выше, достаточно показать, что Н = L ф /А. Но если равенство М = L ф L1 справедливо, то L ЕЕ М и /А CZ М, откуда М^ЕЕ L и ЕЕ L\ так что М1 = = {0}. Следовательно, М^1- = Н, и нам остается только доказать, что множество М замкнуто (после чего мы сможем воспользоваться леммой В).
Предположим, что х — некоторая предельная точка из М. Тогда найдется такая последовательность {хп} из М, что хп -> х. Но каждое хп можно представить в виде хп = уп + zn, где уп ЕЕ L, zn ЕЕ L-Е Так как
%п %in || 2 ~ || (Уп Ут) (zn %т) || 2 “
= || Уп — Ут II2 -И II Z„ — Zm ||2 > || уп — ут ||а,
то {Уп} — последовательность Коши в линейном пространстве L, И в силу замкнутости L уп~+ у ЕЕ L. Аналогично zn -> z ЕЕ Однако в этом случае из равенства
kn - (у -г Z) II2 = Й уп - у II2 + II zn - Z ||2
следует, что х = lim хп = у + z, значит, х GE М, что и требова-п->оо
лось доказать.
Замечание 1. Теорема о проекциях, без сомнения, несет в себе информацию об одном из самых важных свойств гильбертовых пространств. Его значение мы по-настоящему почувствуем только впоследствии. Здесь же мы хотим лишь подчеркнуть, что правильно будет рассматривать гильбертово пространство как банахово
пространство с нормой, достаточно «хорошей» (т. е. порождаемой скалярным произведением) для того, чтобы обеспечить состоятельность и полноценность теоремы о проекциях.
Замечание 2, Теорема о проекциях может быть положена в основу одного полезного метода доказательства эквивалентности двух замкнутых подпространств L и М. Предположим, что уже известно, что L CZ М. В этом случае L — М тогда и только тогда, когда из условий х & М и х | L следует, что х = 0. В частности, если S есть некоторое множество векторов из Н и если из условия <х, s> = 0 при любых s £= 5 следует, что х = 0, то замыкание линейного многообразия L (5), натянутого на 5, совпадает с ZT.
Замечание 3. Пусть М — некоторое замкнутое линейное подпространство Н. Теорема о проекциях гарантирует существование для каждого х GE Н такого единственного вектора у GE М (проекции х на 7W), что х-уЕ М±. Мы рекомендуем читателю самому доказать, что у удовлетворяет соотношению
IIх - у К Ях - т II,
где т — произвольный элемент М. И наоборот, если у ЕМ удовлетворяет этому условию, то у = у'. Это значит, что проекцию х на М можно охарактеризовать как такой вектор из М, который ближе всего к х.
Замечание 4. Обратим наше внимание еще раз на проблемы, сформулированные в обсуждении (см. стр. 66). Примем, что для непрерывной системы, описываемой уравнением (2), или дискретной системы, описываемой уравнением (3) из § 1.4, функции W (tf, t) или W (tf, tn) являются элементами гильбертовых пространств L2 (а, Ь) и 12 (а) соответственно. Обозначим через Н то из этих пространств, которое нам понадобится (в дальнейшем мы не будем делать различия между дискретным и непрерывным случаями). Тогда уравнения, описывающие наши системы, могут быть представлены в следующем виде:
х = <u>, и>.	(3)
Рассмотрим теперь некоторый фиксированный элемент | ЕЕ R. Для системы, описываемой уравнением (3), найдем такой элемент G Я, что
| = <1Р, и>	(4)
и одновременно его норма минимальна на множестве всех элементов, удовлетворяющих условию (4). Эта простая задача теории оптимального управления может быть решена практически сразу. Действительно, ее решение имеет вид
и । = kw.	(5)
где скаляр к определяется соотношением
к =	(6)
Для того, чтобы убедиться в том, что это управляющее воздействие действительно оптимально, нам достаточно было бы в рассуждениях предыдущего параграфа положить р = 2. Другое доказательство сводится к следующему. Разложим Н в прямую сумму
Н = L (w) ф М (w).
Тогда для каждого и (= Н справедливо однозначное представление
и = Ui + и2,
где их (= L (ш), и2 | иг. Заметив теперь, что
<U>, U> = <1Г, Uj + u2> = UY) + (a;, u2> = (w, ur) + 0
и что ||u|| = ||Will + IIu2||, получим
Ы<14
Поэтому, если можно было бы найти такое и е L (и;), которое удовлетворяло бы условию (4), то это управляющее воздействие и было бы оптимальным и %. Уравнения (5) и (6), очевидно, определяют такое управляющее воздействие. Для большей ясности выпишем в развернутом виде решение этой задачи для непрерывной системы. Ее управляющее воздействие в момент времени t ЕЕ tf) должно определяться выражением
МО = 5 [ '$ I (th S) I» ds]’1 w (tf, t). fo
Решением же дискретного варианта этой задачи должно быть управляющее воздействие, удовлетворяющее в момент времени ЕЕ о уравнению
udM = 5 [31W (tf, Ы I’]'1 W (tf, tj. (J
Задача, сформулированная и решенная таким образом, является всего-навсего простейшим прототипом того, что обычно называют проблемой управления с минимальным расходом энергии. Использование термина «энергия» в сочетании с гильбертовыми пространствами является следствием того, что энергия,
выделяемая током i на сопротивлении Я, определяется по формуле
ь
R § i2 (t) dt = R (i, i). a
В главе 4 мы увидим, что некоторые сложные примеры задач управления с минимальным расходом энергии могут исследоваться практически так же просто, как и в этом примере.
Произведения гильбертовых пространств. Новые гильбертовы пространства можно построить по уже имеющимся, образуя декартовы произведения. Если {Н^ — некоторое конечное множество гильбертовых пространств, то множество Н =HlxH2 X... ... X Нп проставляет собой линейное пространство, для векторов которого обычным образом определены операции сложения и умножения на скаляр. Если х =	х2, ,,,, хп) и у = (yt, у2, ...
..., Уп) — Два элемента Н, то скалярное произведение на Н можно определить с помощью выражения
п
у> = 2 <*>> У1><»	(7)
i=l
где через <#., у.) обозначено скалярное произведение векторов х. и у. из пространства Н., Определенное таким образом скалярное произведение называют естественным.
Проверка того, что естественное скалярное произведение удовлетворяет аксиомам скалярного произведения, не представляет никакого труда. Норма, порождаемая в Я, очевидно, принимает следующий вид:
п
1=1
а неравенство Коши — Шварца преобразуется к виду
Для того чтобы показать, что по отношению к естественному скалярному произведению пространство Н полно, заметим, что если {х', ..., х\ ...} есть некоторая последовательность Коши, то из соотношения
п
hm-zp||2= 2к1т-^Р112<е», n,p>N0,	(8)
1—1
следует, что
||а£* — х?||. < е, i = 1, п, п, p>N0, и что составляющие последовательности также представляют собой последовательности Коши. Но так как составляющие пространства Н. полны, то последовательности {х?}, i = 1, ..., п, должны сходиться к пределам i = 1, ..., п. Цоэтому, переходя к пределу при р -> оо в уравнении (8), получим, что
п
Ь’п-2||а = ЗкГ-<М,<еа, m>N0,
что справедливо при любом г, начиная с некоторого NQ (е). А это значит, что хп -> (.гп ..., 7П) 6Е Н.
Предложенное определение скалярного произведения на декартовом произведении гильбертовых пространств ни в коем случае нельзя считать единственно возможным. В упражнениях мы познакомимся с несколькими другими возможными определениями, которые часто оказываются полезными для приложении.
Упражнения
1.	Пусть и {yj} — два произвольных конечных множества в гильбертовом пространстве Н. Докажите, что при произвольных скалярах {aj и {pj} справедливо уравнение
<2^- 3 <хда>-
i	j	ij
Пусть H — конечномерное пространство с базисом {ej. Покажите, что скалярное произведение произвольных элементов х = и у = 2pjej из Н полностью определяется как скалярное соотношение
<®, У> = 2
V в котором ktf = <q, еу>.
2.	Обозначим через < , > скалярное произведение, определенное на некотором линейном пространство X. Покажите, что
<х, у> = <х + у, х + уУ — <х — у, х — уУ,
если X вещественно, и что
У> — <х + у, х +'!/> — <х — у, х — уУ +
+ < [<*+ х + iy> — <х — iy, х —
если X комплексно. Покажите, что если <я, хУ — 0 для х (= М, где М — некоторое линейное подпространство X, то для всех у GE М справедливо соотношение (х, уУ — О.
3.	Докажите теорему В при условии, что В — это вещественное банахово пространство.
4.	Пусть х, у, z и со — четыре элемента гильбертова пространства Н. Покажите, что
||X- z|H|y-w|) <k- !Z||-h-w|| + ||у- z || • || х — со ||,
В каком случае выписанное неравенство переходит в равенство?
5.	Пусть {яр ..., агп} — некоторое линейно независимое множество в Н. Определим в виде
<яь л> . . . <xi, агп_1> х,
Ч’п =	’
<хл, Х1> • . . <ТП, хп
Покажите, что <i|'n,	= 0, если к < п, и что <ipn, хп> Лп - определи-
телю Грама этого множества. Покажите также, что <фЛ, фп> = АП_1АП.
Наконец, установите, что функции
XI е1"ИИ’	/ = 2-"л’
образуют ортонормальное множество, на которое можно натянуть L (xv... • • • ♦ Xft).
6.	Завершите доказательство леммы Б.
7.	Пусть S — любое непустое множество Н. Покажите, что
1.6. Литератора к главе 1
Материал главы 1 охватывает широкий круг математических вопросов, а наше изложение, по необходимости, было ограниченным как по тематике, так и по глубине изложения. Поэтому мы обращаем внимание читателя на приложения 1 и 2, относящиеся к материалу этой главы, на которые мы время от времени ссылаемся в других главах книги. Кроме этих приложений, читатель может обратиться к множеству прекрасных учебников, относящихся к тем или иным затронутым здесь вопросам.
Часть материала глав 1 и 2 наппсана под сильным влиянием великолепного учебника Симмонса [А.77]. Кроме того, по своему уровню и по выбору материал этой главы тесно связан с книгами Колмогорова и Фомина [А.49], Шилова [А.76] и Вулпха |А.93|. На аналогичном уровне написаны книги Фридмана [А.30], Гер цел я и Трэлли [А.32], Гильдебрандта [А.40] и Индрптца [А.44], но они освещают другие возможности применения. Несколько на более высоком уровне находятся полезные монографии Ахиезера и Глазмана [А.2], Дьедоппе [А.21], Данфорда и Шварца [А.22, А.23], Люстерника и Соболева [А.56], Рисса и Секефальви-Надя [А.72], Тейлора [А.83] и Хилле и Филлипса [А.41].
В качестве дополнительной литературы по более широким вопросам, примыкающим к материалу §§1.1 и 1.2, можно рекомендовать вводные книги Андерсопа и Холла [А.4], Арнольда [А.6], Бартла [А.9] и Курнатовского (А.54]. По вопросу о линейных пространствах дополнительно следует прочесть книги Халмоша [А.35], Мирского [А.62], Неринга [А.64] и Столла [А.81]. О банаховых и гильбертовых пространствах можно прочесть не только в общих монографиях, цитированных выше, но и в книгах Банаха [А.8], Халмоша [А.36], Лорха [А.57] и Натансона [А.63]. Если же читатель захочет полнее ознакомиться с теорией интеграла Лебега, то ему следует обратиться к книгам Халмоша [А.37], Хартмана и Минусинского [А.39], Колмогорова И Фомина [А.50], Натансона [А.63], Рудина [А.73] и Уильямсона [А.94].
ГЛАВА 2
ПРЕОБРАЗОВАН И Я
2.1. Функции
Понятие функции лежит в основе всего анализа. В своей наиболее привычной форме — это некоторое правило, связывающее элементы одного множества вещественных чисел с элементами другого. Например, формула у = х3 описывает функцию или функциональное соотношение. На самом же деле мы понимаем это равенство как некоторое правило, утверждающее, что с каждым вещественным числом х мы связываем другое вещественное число, а именно э?. Этот процесс или эту формулу (возведения в третью степень), определяющие характер такой связи, мы и называем функцией. Конечно, описать функцию с помощью простого явного алгебраического выражения удается лишь в очень незначительном числе случаев. Некоторые из функций, не описываемых такими формулами, встречаются настолько часто, что для них построены высокоточные таблицы и придуманы специальные стандартные названия, например sin х или 1g х.
В главе 1 мы пользовались понятием функции, не затрудняя себя строгим определением. Ведь когда речь идет о временных последовательностях или функциях времени, часто удается обойтись одними интуитивными представлениями. Однако для того, чтобы рассматривать систему как некоторую функцию, нам понадобится совершенно строгое определение. Определение, которым мы будем пользоваться, представляет собой лишь незначительное обобщение классического определения, очерченного в первом абзаце этой главы.
Определение А. Пусть X и Y — произвольные непустые множества. Соответствие f, связывающее с каждым элементом х, принадлежащим некоторому подмножеству Dj множества X, некоторый элемент у EY, называется функцией, отображающей X в Y. Подмножество D f CZ X, на котором эта функция определена, называется областью определения функции. Подмножество Rf CZ.Y, состоящее из точек, соответствующих некоторым х G= Df, называется областью значений этой функции.
Например, оценки участникам соревнования по гимнастике можно рассматривать как некоторую функцию, связывающую оп-
ределенное вещественное число с выступлением каждого участника. Здесь X может обозначать множество людей, занимающихся гимнастикой, Df — множество гимнастов, участующих в данном соревновании, Y — множество вещественных целых чисел 0
п 100, a Rf — множество всех выставленных оценок. В качестве второго примера предположим, что X — это множество всех квадратов на плоскости, а У — это множество расположенных на той же плоскости окружностей. Мы можем определить функцию у ~ / (х), потребовав, чтобы правило / связывало с каждым квадратом х (Е: X окружность у Е: У, в него вписанную. В этом случае Df = X к Rf = Y.
В определении А фигурируют три математических объекта: два непустых множества и правило, связывающее каждый элемент некоторого подмножества X с единственным, однозначно определенным элементом у&У. Символическая запись /:Х->У задает функцию с правилом /, областью определения Df CZ X и областью значений Rf CZ У. Такое обозначение оказывается полезным, поскольку оно выделяет все существенные составляющие понятия функции, как сложного математического объекта, и подчеркивает, что центральную роль здесь играет правило /. Если из конкретного контекста ясно, каковы множества X и У, или если нет никакой необходимости в явном виде указывать, что это за множество, то обычно запись /: X -> У сокращают и пользуются лишь символом /. При этом говорят тоже только об / (не упоминая множества X и У). В других случаях удобней пользоваться обозначением х -> f (х).
Элемент у множества У, связанный функцией / с элементом х е Df, называется образом точки х. Если J/ЕУ и у = f (х), то элемент х называют прообразом точки у. У каждого элемента х ЕЕ Df должен быть единственный образ у ~ У. В то же время у каждого у е У может быть и несколько прообразов. Естественным обобщением понятия образа элемента является понятие образа множества элементов.
Определение Б. Пусть задана некоторая функция f: X-> У. Для каждого подмножества А из Df подмножество В = {у ЕЕ У : / (х) для некоторого х из А} называется образом А, определяемым функцией f. Мы записываем это в виде R = f (А), чтобы показать, что В — это образ множества А.
Функцию часто называют отображением, преобразованием или оператором. Все эти термины кажутся оправданными в том смысле, что функцию можно считать переводящей некоторую точку х €= Df в точку / (х) ЕЕ У. Аналогичным же образом можно считать, что подмножество A CZ Df переводится в подмножество В CZ Rf с помощью отображения / (А) = В. Для графического представления этих идей зачастую полезна диаграмма, показанная на рис. 2.1.
Нам удалось успешно определить понятие функции, не прибегая к графическим представлениям. Но так как кривые и графики являются частью нашего интуитивного наследия, то интересно было бы посмотреть, какое место занимают они в рамках развиваемой абстрактной схемы.
Определение В. Пусть f: X Y. Подмножество Gf = = {(#, У): У €= f (х), х ЕЕ Df} множества X X Y называется графиком f.
Рис. 2.1. Функция как преобразование/
Определение В часто полезно рассматривать как исходное определение функции. Предложение «функцией называется некоторое множество упорядоченных пар, в котором нет двух различных пар с одинаковыми первыми координатами», очевидно, проще определения А и в то же время содержит ровно столько же информации. С этой новой точки зрения функция и ее график неразличимы.
Все эти понятия иллюстрируются рис. 2.2. Заметим, что если X и Y — множества, a Gf — некоторое заданное подмножество X X Y, то Gf может служить графиком некоторой функции /: X -> Y только в том случае, если, каково бы ни было х ЕЕ Df, в подмножестве Gf найдется один и только один элемент вида (х, у). Или если говорить более вольно, Gf может служить графиком некоторой функции /: X —> Y только в том случае, если для каждого xEDj «вертикальная» прямая, проходящая через х, пересекает Gf лишь в одной точке.
Две функции / и g называются совпадающими, если их области определения одинаковы и для каждого х из этой общей области определения / (х) = g (х). В терминах их графиков функции / и g совпадают тогда и только тогда, когда эквивалентны множества Gf и Gg. Функция /: X -> Y, у которой Df X, называется
отображением X в У. Этим мы хотим подчеркнуть, что / (X) cz ст У. Если же на самом деле / (X) = У, то / называют отображением X на У *). В обоих случаях множество У называют множеством (или пространством, если это соответствует действительности) возможных значений, а множество / (х) — просто областью значений. Таким образом, для накрытия (так еще называют сюръективное отображение) множество возможных значений и область значений совпадают.
Рис. 2.2. Функция как множество упорядоченных пар.
Определение!1. Функция f: X -> У называется взаимнооднозначной, если из равенства f (х)	/ (х') следует, что х = х',
каковы бы ни были х и х' из Df.
Таким образом, функция /: X -> У взаимно однозначна, если для каждого yEzlij найдется только одно х ЕЕ D f такое, что / (я) = У- Если функция f: X -+Y одновременно является накрытием и взаимно однозначной **), то для нее можно определить обратное отображение /-1: У —X, связывающее с каждым у из У тот единственный элемент х из Df, для которого / (х) = у (существование и единственность такого х гарантируются взаимной однозначностью / и тем, что / (х)	у). Другими словами,
f~l (у) -- х- Ясно, что описанная процедура определяет функцию отображающую У в X, в соответствии с определением А. Если же в качестве основного принять определение «функции» через подмножество упорядоченных пар, то У”1 — это просто-напросто множество таких упорядоченных пар (у, х) 6= У X X,
*) Такое отображение называют еще сюръективным. {Прим. редЕ
**) Такое отображение иногда называют еще биективным или наложением. {Прим, ред.)
для которых (х, у) ЕЕ С геометрической точки зрения функция /: У -> X есть обратная в том и только в том случае, когда для каждого у из У «горизонтальная» прямая (в X X У), проходящая через у, пересекает Gf только в одной точке. Уравнение х ~ У"1 (у) получается в результате решения уравнения у = / (х) относительно х точно таким же образом, каким выражение х ~ = In у является результатом решения уравнения у = ех относительно х.
Определение Д. Пусть / — некоторая взаимно однозначная функция с областью определения Df CZ X и областью значений Rf = У. Если Gg = {(у, х) ЕЕ Y X X: (х, у) ЕЕ Gf}, то g — взаимно однозначная функция с областью определения У и областью определения Rg = DfEL X. Эта функция g называется обратной по отношению к функции / и обозначается через У"1.
Новичкам часто трудно не запутаться в разнице между функцией и ее значениями. С этой точки зрения о функции лучше всего думать как об отображении или графике. Значением функции в точке х CZ Df служат элемент у = у (х) CZ Rf. Так, говоря о пространстве С (а, Ь), мы можем утверждать, что х ЕЕ С (а, Ь), если ее значения в точке /ЕЕ [а, Ы задаются, например, уравнением х (/) = t2. Однако во многих случаях единственная возможность определить функцию состоит в том, чтобы выписать все ее значения {У (х)} по мере того, как х пробегает область определения Df. Функция У: X -> У называется постоянной, если имеется такая фиксированная точка I/ ЕЕ У, что У (х) = у, каково бы ни было х ЕЕ Df. Функция У: X -> У называется тождественной (на X) и обозначается через I (или 1Х), если f (х) = х, каково бы ни было хе х.
Композиция функций. Рассмотрим две функции t -> х и х -> у, значения которых задаются следующими формулами:
х (/) = 2л/ — 5,	/Е [0, tf],
у (/) = sin х,	х ЕЕ [ — оо, сю].
Из этих двух функций можно построить их композицию, т. е. образовать третью функцию t -> у вида
у (/) = sin (2л/ — 5), /ЕЕ [0, /у].
Этот простой пример композиции двух функций должен подготовить нас к обсуждению более общего случая.
Определение Е. Пусть ft X -> У и g: У -> Z суть функции, для которых Df = XuDg = Y. Композицией функций fug называется отображение, связывающее с каждым элементом хЕ X элемент z = g [f (х)] ^Z, Эта новая функция обозначается через h = gf - X Z.
Другими словами, в композиции функций элемент х е X отображается с помощью / в некоторый элемент f (х) е У, а этот, уже в свою очередь, отображается в z = g [f (я)] G= Z. Функция h: X -> Z является, таким образом, композицией функций /: Х->У и g:Y Z для каждого хЕ X и h{x) = g [f (х)], как это и показано на рис. 2.3.
Заметим, что два отображения, фигурирующие здесь, не вполне произвольны, поскольку множество У, содержащее область значений первой функции, должно быть одновременно и областью определения второй. И вообще говоря, произведение (композиция) двух отображений имеет смысл только тогда, когда область значений первого из них содержится в области определения второго (или если предполагается, что первая функция сужена таким образом, что ее областью определения считается лишь множество A CZ Df, для которого справедливо соотношение / (4) = Rf Г| Г| D б). В композиции gf мы всегда будем считать первым отображением функцию /, а вторым — g.
Понятие композиции двух функций можно распространить на случай любого конечного числа функций. В любом случае область значений каждой функции, участвующей в композиции, должна содержаться в области определения последующей функции. Как отмечалось выше, для функций, которые являются взаимно однозначными и накрытием, можно определить обратные. Обращаясь к случаю сложных функций (результатов композиции), мы можем следующим образом перефразировать определение Д.
Пусть функции /: X -> У и g'.Y-+X заданы. Функция / называется обратной по отношению к g, а функция g — по отношению к /, если g [f (z)l х и f [g (у)] ---= у, каковы бы ни были х Е- Df --- Rg и у ЕЕ Dg =- Rf. В этом случае функции / и g называют взаимно обратными и говорят, что они обратимы. Пусть i: X X и j :Y -> У — тождественные функции, определенные на Df и Dg соответственно. Тогда утверждение «/: X -> У и g: У->Х— взаимно обратные функции» эквивалентно следующему: «g/ = i и fg = j»t
Докажем теперь, что все эти предложения действительно эквивалентны утверждению, что обе функции / и g взаимно однозначны и являются накрытиями. Предположим, что эти предложения верны и что / (jq) = / (х2) для некоторых хг и х2 €= Df. Тогда хг = g [f (jq)] = g [f (x2)] = x2, и, следовательно, / — взаимно однозначная функция. Для того чтобы показать, что f — это накрытие, предположим, что у G Rf- Тогда g (у) EF Df и / I# (*/)1 = У- Поэтому, если положить х — g (у), то у = / (х), и, следовательно, / — это накрытие. Обе эти функции можно затем поменять ролями, так как определения обратных функций симметричны по отношению к ним. Поэтому функция g: Rf-+ Df также взаимно однозначна и является накрытием.
Выше мы доказали необходимость взаимной однозначности и сюръективности (в противном случае нам удастся определить У"1 лишь на Rf) функции /: X -> Y для того, чтобы у нее существовала обратная. Нетрудно показать, что это условие является и достаточным. Более того, можно показать, что функция g: Y
X определяется единственным образом.
Пример 1. Пусть X = {j:0	а У = R, т. е. совпа-
дает с пространством вещественных чисел. Определим / с помощью соотношения / (х) = х2 для любых х(Е:Х. В этом случае ясно, что эквивалентным определением было бы / = {(я, у): у = х2 и х ЕЕ X}. (Так задается график / в соответствии с определением Г.)
Ясно, что областью значений / (х) этой функции является замкнутый промежуток 0 у 4. Более того, функция / определяет взаимно однозначное отображение X на / (X) и, следовательно, имеет обратную функцию У'1. Нетрудно видеть, что функция У"1 определена на промежутке 0 у 4 и связывает каждое у с положительным значением своего квадратного корня.
Точно такое же соответствие х -> х2 задает функцию, определенную на х = {х\ —	со значениями из Y = R.
Однако теперь g (X) представляет собой промежуток 0 у 1, а область значений обратного отображения g'1 является собственным подмножеством X.
Формула х Ух, очевидно, не задает функции, определенной на промежутке — 1 х 1.
Пример 2. «Функцией Дирихле» называется отображение У пространства R в /?, удовлетворяющее условию:
.	__ [1, если х рационально,
I \х) — |0, если х иррационально.
Пример 3. Для каждого х из [0, 1] уравнение ех (У) = f (х) определяет функцию ех, отображающую С (0, 1) в пространство комплексных чисел (функцию ех часто называют «значением в точке х»).
Если Е — некоторое подмножество метрического пространства X, то уравнение р (х; Е) = inf {р (х, у): у G Е} задает вещественную функцию х-+р(х,Е), определенную на X.
Пример 4. В системах, использующих цифровые элементы, важную роль играют операции «квантования по времени» и «экстраполяции». Напомним, что через В (т) мы обозначаем класс ограниченных скалярных функций, определенных на т (см. пример 7 из § 1.4). Пусть а = {^: к — 1, ..., и}, где tk < — некоторое упорядоченное подмножество [а, Ы. Тогда, если х ~ = В (a, b), a Y = В (о), то операцию «квантования по времени» можно описать некоторой функцией, отображающей X в Y и определенной для каждого х е= X условием
(Sx) (/R) - х (^), t* <= а.	(1)
Аналогичным образом, экстраполяция нулевого порядка (или запоминание) — это преобразование С из Y в X, определенное условием
(Су) (0 = у (tk), t G Un, Zk+1l, tk e a,	(2)
для каждого у EE Y.
Пример 5. Преобразование Т: С (0, 1) -> С (0, 1) можно определить, потребовав, чтобы образом / из С (0, 1) при действии Т была функция, значение которой в точке / ЕЕ [0, 1] равняется
(s) ds. Другими словами, Tf — это элемент пространства о
С (0, 1), определенный условием
t (T/)(0 = $/(s)ds,
О
Точно так же / -> (dldt)f — это преобразование пространства Сп (0, 1) функций с п непрерывными производными в пространство Сп-Х (0, 1).
Теория интеграла Лебега как раз и занимается расширением области определения отображения <р, первоначально задававшегося интегралом Римана на пространстве С (0, 1):
i q>(/) = $/Wdz’ о
на более широкий класс функций. Этот более широкий класс Lx (0, 1) включает, например, функцию Дирихле, о которой мы уже говорили выше.
Пример 6. Обозначим через W (/, s) квадратную матрицу n-го порядка, каждый элемент которой Wa (t, s) принадлежит
пространству В (т X т) (иными словами, (/, s) определены и ограничены для любых t, sGEt). Пусть для начала т = [а, 61, X = LPi (а, b) X ... X LPn (а, 6). Многомерная система с входным сигналом х = (хъ ..., rrn) ЕХ и выходным сигналом у = (у и •••» Уп) S X описывается уравнением
t
y(t) = (Fx)(t) = \W(t, s)x(s)ds, t(=[a, 6],	(3)
a
и может быть отождествлена с функцией F: X -> X. В любой фиксированный момент времени f Е т значение у (/') выходного сигнала системы принадлежит Rn и соотношение
tr
у (f) = Тх = § W (f, s) х (s) ds	(4)
а
определяет новое отображение Т: х -> Rn.
Получить дискретные аналоги уравнений (3) и (4) нетрудно. Полагая] т = о и X = lPx (о) X ... X 1Рп (о), мы получим функцию F = X -> X, значение которой в момент tk СЕ о определяется по формуле к
(Fx) (t^) = 2 W Gic» 0)^(0)»	(5)
j=0
а отображение T:x-+Rn задается следующим уравнением:
к
=	(6)
j=0
где точка ЕЕ а считается фиксированной.
Предложенные два способа описания многомерных систем являются основополагающими, и к этому примеру мы еще будем неоднократно возвращаться в дальнейшем по мере изложения материала нашей книги.
У пр ажнения
1.	Пусть функция /: А -> В задана, и пусть X и Y — некоторые подмножества А. Докажите, что
(а)	/ (х и У) = f (X) и f (У);
(б)	/ (х п У) с f (X) n f (У);
(в)) если функция /: А В взаимно однозначна, то / (X П У) = / (X) Q
2. Пусть / определяется уравнением / (х) = х2 — 1. Постройте график этой функции, а также ее области определения и значений для множества А = {х: | х | < 1}. Является ли функция / взаимно однозначной?
3.	Обозначим через А множество положительных вещественных чисел. Для каждого a ЕЕ А обозначим через fa: R —> А функцию, заданную соответствием fa (х) = ах, X G Я, а через ga: А R — функцию, заданную соответствием йа (*) = logax, X А. Докажите, что для каждого а е А функции fa: R -> А и ga: А -> R взаимно обратны.
4.	Пусть функция /: [—1, 1 ] -> R задается соответствием f (х) = = arcsin х, х ЕЕ [—1, 11» и пусть функция g: R -► [—1, 1] определяется равенством g (х) = sin х, х е R- Докажите, что эти две функции не взаимно обратны.
5.	Напомним, что два отображения /: X -* У и g: X —* У считаются совпадающими (что записывается как / = g), если для каждого х из X справедливо / (х) = g (х). Пусть /, g и h — три отображения некоторого непустого множества X в самого себя. Покажите, что композиция (произведение) преобразований удовлетворяет свойству ассоциативности в том смысле, что / (^) = (/*) ь-
6.	Пусть X — некоторое непустое множество, и пусть f и g — взаимно однозначные отображения X на себя. Покажите, что fg взаимно однозначное отображение X на себя и что (fk)"1 = g"*1/'1-
7.	Предположим, что начальные состояния двух цепей, схемы которых показаны на рис. 2.4, задаются условиями q (0) = д0 и i (0) = io, где q — заряд на емкости. Опишите соотношения —» ез и ез -* е4 в виде функций.
Если е2 ЕЕ С (0, оо), то что можно сказать об областях значений этих функций? Если две цепи связаны между собой так, что ез = е3, то описывается ли новая цепь функцией ei —► е3, получающейся в результате композиции двух исходных функций? Изменится ли ответ, если принять, что i0 = 0, 7о = 0? Какое неявное допущение с точки зрения физики содержится в понятии композиции функций?
8.	Пусть о = Кк’» к = 1, 2, ...}, и пусть 1Г (о) — банахово пространство {х = (х (^), ..., х (^.),...); 2а х № I < °°}- В системе, рассматривающейся в этой задаче (рис. 2.5), импульсный элемент С, осуществляющий операцию
Рис. 2.5.
«квантование по времени», и «экстраполятор» S (см. пример 4) соединены друг с другом через первую из цепей упражнения 7. Можно ли такую систему описать композицией соответствующих функций? Какова область значений полученной сложной функции?
9.	Пусть / — некоторое отображение множества X в множество У. Для каждого подмножества Е множества У обозначим через f~l (Е) подмножество X, определенное условием
Г1 (Е) - {х е X: f (х) е Е}.
Пусть А и В — подмножества У. Докажите следующие утверждения:
(а)	Г1М\В) = Г1(Л)\Г1(В);
(б)	Г1 (А П В) = ГЦА)‘ П Г1 (В);
(в)	Г1 (A U В) = ГЦА) U Г1 (В).
Множество /-1 (Е) называется прообразом Е для отображения /. Обратите внимание на то, что соответствие Е -* /-1 (Е) всегда является вполне определенной функцией, отображающей пространство подмножеств У в пространство подмножеств X. Эта ситуация совершенно непохожа на ту, с которой связаны наши первые попытки использования символа Z"1 для обозначения обратной (в точке) функции, которая в общем случае может и не существовать. Однако если для / существует обратная функция, то для любого множества Е GZ У множество /-1 (Е) является образом Е в силу Z"1, независимо от того, в каком смысле мы понимаем символ /"х.
10.	Пусть X и У — два непустых множества, и пусть / отображает X в У. Если А и В — подмножества X и У соответственно, то покажите, что
(a)	ft"1 (В) С2 В и /Г1 (В) = В выполняются для всех В тогда и только тогда, когда / — накрытие;
(б)	A О Z”1/ (Л) и Л = f"1/ (Л) справедливы для всякихтогда и только тогда, когда / взаимнооднозначно;
(в)	f (А! П А2) = f (AП f (Л2) справедливо для любых Аг и Л2 тогда и только тогда, когда / взаимно однозначно.
И. Пусть через S обозначена операция съема данных из примера 4. Пусть S определена на пространстве С (0, 1), ах принадлежит области значений S. Из чего состоит множество 5”1 (х)?
Непрерывные функции. С понятием «непрерывности» мы впервые сталкиваемся уже в классическом анализе. Рассматривая условие или условия, которым должна удовлетворять функция для того, чтобы ее можно было назвать непрерывной в точке гг0, мы приходим к необходимости строго сформулировать следующее утверждение: функция / непрерывна в точке гг0, если / (х) мало отличается от / (гг0), как только х оказывается достаточно близко к х0. Но что такое «мало отличается» и что такое «достаточно близко»? Оказалось, что вместо того, чтобы устанавливать какой-то эталон степени близости, гораздо удобнее потребовать, чтобы, какой бы степень близости / (х) и / (xQ) мы ни выбрали, ее все равно можно было бы добиться, выбрав х достаточно близким к гг0. В строгой формулировке функция /: R —> R называется непрерывной в точке XqEER, если, каково бы ни было е>0, всегда найдется такое S > 0, что, как только \х — гг0| < д, справедливым оказывается и неравенство |/ (х) — / (х0) | < е.
Для теории систем наибольший интерес представляют функции, отображающие одно метрическое пространство в другое. Нижеследующее определение является естественным обобщением обыч-
\
ного определения непрерывности на случай, когда функция задана и принимает значения в соответствующих метрических пространствах *).
ОпределениеЖ. Пусть XuY — метрические пространства с метриками pj и р2, соответственно, и пусть / отображает X в Y. Тогда функция / называется непрерывной в некоторой точке х0 из X, если выполняется одно из следующих эквивалентных условий:
Для каждого е > 0 существует такое б > 0,чторг (х, xQ) < < 6р2 (/(*),/W) < е-	с
(2) Для каждого открытого шара о£ (/ (гг0)) с центром в точке f (х0) найдется некоторый открытый шар (rr0) с центром в точке х$ такой, что f (5g (r0)) cz Sz (f (#0)).
Первое из этих условий является очевидным обобщением нашего исходного определения, в то время как второе оказывается более удобным для доказательства некоторых теорем. Мы предлагаем читателю самому убедиться в эквивалентности условий (1) И (2).
Теорема А. Пусть XuY — метрические пространства, и пусть f: X -+Y. Функция / непрерывна в точке xQ€= X тогда и только тогда, когда / (хп) —>/ (х0) при хп —>х0.
Доказательство. Предположим сначала, что функция / непрерывна в точке xQ и что {хп} — такая последовательность элементов X, что хп —>-гг0. Нужно показать, что / (хп) -+f (х0). Обозначим через Sz (f(xQ)) некоторый открытый шар с центром в точке / (х0). Поскольку функция / непрерывна, то существует такая открытая сфера 5g (rr0) с центром в точке гг0, что / (5g (х0)) с: cz Se (f (xQ)). Но хп ->я0, и, значит, все хп, начиная с некоторого N, п^ N, попадают внутрь 5g (xQ). А поскольку / (5g (х0)) <zz 5£ (/ (х0)), то все / (хп) при п > N оказываются внутри 5£ (/ (*о))- Это и доказывает, что / (хп) ->/(я0).
Для доказательства необходимости предположим, что функция / не непрерывна в точке х0. Тогда найдется такой открытый шар 5е (/ (х0)), что образ любой открытой окрестности с центром в х0, полученный отображением /, не будет содержаться в ней. Рассмотрим последовательность открытых шаров S± (х0), 51/, (х0),... ..., S1/n (х0), .... Построим такую последовательность {хп}, что Хп (Е. 51/п (дг0) и / (хп) €£ Sz (f (х0)). Ясно, что хп сходится к а / (хп) не сходится к / (гг0). А это значит, что если / не непрерывна, то из хп ->х не следует, что / (хп) -+f (хп).
Отображение одного метрического пространства X в другое называется непрерывным на X, если оно непрерывно в каждой
*) Отметим, что наиболее общее понятие непрерывности функции формулируется в терминах топологического, а не метрического пространства. (Прим, ред.)
точке X. Точно так же, если X и Y — метрические пространства и /: X то / непрерывна на X тогда и только тогда, когда хп -+х =Ф / (хп) —>/ (я), каково бы ни было х ЕЕ X. Таким образом, непрерывное отображение одного метрического пространства в другое — это такое отображение, которое сохраняет свойства сходимости.
Другим понятием, очень полезны^ для прикладных задач, является понятие равномерной сходимости. Читатель мог заметить, что в определении непрерывности функции в точке х() мы требовали, чтобы при любом 8 > 0 всегда можно было найти такое б > 0, что (ц (хр х0) < б => р2 I/ (х), / (х0)| < е0. Совершенно ясно, что б зависит от е. Не менее ясно, что в общем случае б должно зависеть и от дг0. Если же функция /: X ->У непрерывна на пространстве X, и если для каждого е мы можем найти такое б, которое одновременно удовлетворяет всем условиям во всех точках пространства (и в этом смысле не зависит от х0), то функцию / называют равномерно непрерывной. Строгая формулировка понятия равномерной непрерывности выглядит следующим образом.
Определение 3. Если X и Y — метрические пространства с метриками рх и р2 соответственно, то отображение f: X ->У, Dt = X, называется равномерно непрерывным, если для каждого е > 0 всегда найдется такое б > 0, что рх (х, х) < < 6 «=> р2 (/ (х), / (#')) < е, каковы бы ни были х, х' ЕЕ X.
Очевидно, всякое равномерно непрерывное отображение является непрерывным. Вещественная функция /, определенная на всей оси вещественных чисел R с помощью уравнения / (х) = = 2х, равномерно непрерывна. Но уже функция g, определенная на R соотношением g(x) = х2, непрерывна, но не равномерно непрерывна.
Один важный тип равномерно непрерывного отображения, который часто встречается на практике, получил название изометрии.
Определенней. Если X и Y — метрические пространства с метриками и р2 соответственно, то отображение X в Y называется изометрией (или изометрическим отображением), если рх (х, х') = р2 (/ (х), f (х')), каковы бы ни были х, х' ЕЕ Df. Если такое отображение существует для случая Df = X и Rf = Y, то мы говорим, что X изометрично Y.
Совершенно ясно, что изометрия является взаимно однозначным отображением. Если X изометрично Y, то точки этих пространств могут быть приведены во взаимно однозначное соответствие таким образом, что расстояние между парами соответствующих точек одинаково как в одном, так и в другом пространствах. На самом деле, мы часто рассматриваем изометрические пространства как идентичные.
Например *), пусть {еп },?Li — некоторый ортонормальный базис (сепарабельного) гильбертова пространства Н. Равенство Парсеваля^показывает, что преобразование, ставящее в соответствие каждому х из Н последовательность его коэффициентов Фурье {уп}, является изометрией Н в 12.
Пример 7. 11усть X — некоторое банахово пространство, и пусть /: X —> R определяется уравнением
/ U) = И-
Воспользовавшись неравенством (см. § 1.4)
I/ (*) - / (*n)l = I (М - к ID I < к - *4 найдем, что норма должна быть непрерывной функцией. Например,
—> X	|| Хп || —► || X ||.
На самом деле норма даже равномерно непрерывна.
Пример 8. Пусть X — некоторое банахово пространство. Рассмотрим две последовательности хп ->1И уп -+у. Из соотношений II (хп + Уп) — (* + у)|| = II (Хп — х) + (уп — г/)|| <
< ||*п — *1 + D'/п — У|| мы непосредственно найдем, что
*п + Уп + У-
Следовательно, операция сложения непрерывна.
Пример 9. Пусть у — некоторый фиксированный вектор в гильбертовом пространстве Н. Отображение х -> (гг, уУ непрерывно.
Пример 10. Функция точечной оценки eto (х) = х (Q (см. пример 3) является непрерывным отображением метрического пространства С (0, 1) в метрическое пространство С комплексных чисел. Заметим, что если {хп} — последовательность из С (0, 1), сходящаяся к ж, то при п —> оо
sup |хп(/) — я(/)| —>0.
В частности,
| Хп (U Х (^о) |
а это значит, что efo (х^ -+eto (х).
Аналогичным образом читатель может убедиться в том, что функция, отображающая хЕЕС (0, 1) в функцию y(t) = § x(s)ds, является непрерывным отображением С (0,1) в С1 (0,1). С другой
*) См. приложение 2.
стороны, функция Дирихле в каждой своей точке не^вляетсй непрерывной.	/
Определение К. Пусть функция / отображает метрическое пространство X в метрическое пространство р. Про функцию / говорят, что она удовлетворяет условию Липшица, на множестве S CZ Df, если существует такой вещественный скаляр О < М < ос, что
Р2 U (*), / (!/)) < Мр! (х, у),
каковы бы ни были х, у Ez S. Если М < 1, то отображение / называют сжимающим.
Если / удовлетворяет условию Липшица на некотором множестве S, то мы называем функцию / липшицевой, а вещественный скаляр М — постоянной Липшица для /. Точная верхняя грань постоянных Липшица для / называется нормой Липшица для этой функции и обозначается через |/|s- Если вид множества и без того ясен, то индекс 5 можно отбросить. Итак, в соответствии со строгим определением
|/|s = sup (р2 (/ (х,), / (х2))/р (хр х2): хп х2 S 5).
В этом случае, когда X и Y — банаховы пространства, это выражение можно преобразовать к виду
|/|s = sup {||f (xj — / (x2)|lIllx, — x2||: xlt x2 e 5}.
Функция, отображающая одно банахово пространство X в другое Y, называется ограниченной на множестве S, если существует такая постоянная с > 0, что
и (х)!|<с||х|1.
каково бы ни было х е S.
Теорема Б. Пусть S — линейное подпространство банахова пространства X. Если / — некоторая липшицева функция, определенная на S и принимающая значения из банахова пространства Y, то
(1) из / (0) = О следует, что / на S ограничена;
(2) / на S равномерно непрерывна.
Утверждения этой теоремы очевидны из соотношения
в/ (х) -/(y)|<|/|s • II X - у||.
И в самом деле, утверждение (1) получается отсюда сразу, если положить у = 0, а утверждение (2) является прямым следствием определения 3 при 6 = e////s.
Однако если не учитывать утверждения теоремы Б, то понятия непрерывности, ограниченности и липшицевости в остальном независимы. В качестве иллюстрации этого рассмотрим функцию
j- Ц —> Д. где / (х) = ах + Ь, а =f= 0, Ь 0. Функция / удовлетворяет условию Липшица и |//= |а|, но она не ограничена в окрестности х = 0. Точно так же функция х ->х2, определенная на В, непрерывна, но она не является ни равномерно непрерывной, ни липшццевой, ни ограниченной. Наконец, функция, определенная на 1П = [0,1] с помощью соответствия х ->х2, равномерно непрерывна, но не удовлетворяет условию Липшица.
Упражнения
12.	Пусть / — некоторое отображение метрического пространства X в метрическое пространство У. Докажите эквивалентность следующих утверждений:
(а)	/ непрерывно;
(б)	У-1 (G) открыто в X, если только множество G открыто в У;
(в)	/-1 (F) замкнуто в X, если только множество F замкнуто в У;
(г)	для каждого подмножества ЕС У / (£) = / (£). (Здесь, как обычно, чертой сверху обозначена операция замыкания множеств в X или У.)
13.	Пусть X и У — метрические пространства, а / — некоторое отображение X в У. Если У — постоянная функция, то покажите, что У непрерывна. Используйте этот пример для того, чтобы показать, что непрерывное отображение не обязательно должно обладать свойством, согласно которому образ каждого открытого множества должен быть открытым.
14.	Рассмотрим систему с входным сигналом и и выходным сигналом х описываемую (в момент времени выражением xi (h) = \ W (Zi,T) и (т) dx.
t
Предполагая, что\ W2 (/j, т)с/т<оо, рассмотрим эту систему как некоторую •’о
функцию, определенную на L2 (0, t) и принимающую вещественные значения. Покажите, что эта функция непрерывна. Если xQ — некоторая фиксированная точка в произвольном гильбертовом пространстве Я, то непрерывна ли функция У (х) = <х, х0>, х ЕЕ Я? Является ли опа равномерно непрерывной?
15.	Определите, какая из перечисленных ниже функций равномерно непрерывна па открытом единичном промежутке (О, 1): 1/(1 — х); sin х; sin (1/х); х'!*, хя. А какая из них равномерно непрерывна на открытом промежутке (О, ее)?
16.	Пусть У и g — функции, отображающие метрическое пространство X в себя, причем Df = X. Пусть f и g непрерывны на X. Покажите, что, каковы оы ни были произвольные скаляры а и 0, функции аУ + 0$ и fg непрерывны. Докажите также непрерывность на X полиномиальной функции
h (х) = /п (х) +	(х) + . . . + ai/ (х) + аох, хе X
17.	Покажите, что функция f: 12 -* Л, определенная нах= (хп х2,...)С Е ° помощью правила
/(«)=2
(где суммирование S' распространяется па все индексы, для которых |х,(^ 1), непрерывна, но не ограничена на любом шаре с радиусом, большим 1.
18.	Пусть функции /, g и h описывают схемы о граничите л я/о дно пол у-периодного выпрямителя и двухполупериодного выпрямителя/характеристики которых показаны на рис. 2.6. Если каждая из этих фу нкшш определена на С (0, й), то каковы соответствующие области возможных значении? Какая
из этих функций непрерывна, равномерно непрерывна, удовлетворяет условиям Липшица? На каких подмножествах каждая из этих функций взаимно однозначна? Опишите множества /-1 (z), g~* (z) и Л”1 (z), если z выбрано подходящим образом.
19.	Повторите упражнение 18 для функций F и G (рис. 2.7), приближенно описывающих явление гистерезиса, и для более реалистичной модели & из § 0.1.
 Линия задержки
Рис. 2.8.
20.	Во многих реальных системах при передаче сигналов происходит запаздывание во времени. Опишите звено чистого запаздывания (рис. 2.8) (время запаздывания равно т) как некоторую функцию, определенную на (0, ti).
2.2. Линейные преобразования
В этом параграфе мы сосредоточим наше внимание на одном специальном классе функций, определенных на линейных пространствах. Что же касается того, что свойства и представления линейных преобразований (так называются эти функции) играют
важную^роль почти на всех стадиях анализа, то это станет ясно по мере\1акопления новых фактов. Теория линейных преобразований мЬжет быть развита на самых различных уровнях, каждый из которых характеризуется своей степенью глубины, общности и требует своей математической подготовки. Наше изложение будет достаточно абстрактным для того, чтобы мы могли с пользой употреблять понятия, определенные в главе 1, и в то же время достаточно конкретным для того, чтобы его легко было связать с конкретными физическими задачами.
Линейные преобразования обычно обозначают заглавными буквами. Значение некоторого преобразования А в точке х (или, как обычно говорят, результат преобразования А вектора х) обозначают через А (х) или Ах.
Определение А. Пусть X и Y — два линейных пространства с общим множеством скаляров, и пусть А: X -+Y есть некоторая функция, определенная на X и принимающая значения из Y. Функция А называется линейным преобразованием X eY, если она обладает следующими свойствами:
(1) A (xt + х2) = Axl + Ах2 для любых xt. х2 е= X.
(2) А (ах) = аАх для любых х ЕЕ X и а.
В соответствии с этим определением мы называем линейным преобразованием такую функцию, которая отображает одно линейное пространство в другое и обладает свойствами аддитивности (1) и однородности (2). Линейное преобразование некоторого линейного пространства X в себя (Y = X) называется (линейным) оператором, определенным на X. Если же Y — это множество скаляров, то А называют линейным функционалом, определенным на X.
Пусть А — некоторое линейное преобразование X в У. Выясним, что может следовать из справедливости гипотезы аддитивности (1). Прежде всего, мы видим, что
А (0) - А (0 + 0) - А (0) + А (0), и, следовательно, А отображает нулевой вектор своей области определения в нулевой вектор своей области значений. Аналогичным же образом для любого х ЕЕ X
0 - А (0) - А (х — х) - А (х) + А (—х), откуда следует, что А (—х) = — А (х). Так как А (пх) = А (х + х + ... + х) == А (х) + А (х) + ... + А (х). то легко видеть, что А (пх) = пАх. если только п — положительное и целое число. Так как
А (— пх) = А (п (—х)) nA (—х) = — пЛ (х),
то последнее утверждение справедливо и для отрицательных целых чисел. Далее, из A (х)=А [п (1/п)х] = 1пА (1/и) ху следует, что Л[(1/п)х] = (1/п)Лх, и, наконец, если r=mln—любое рациональное число, то	/
А (гх) = а(п-^- xj = nA х^ = гА^х).
Возникает естественный вопрос: а не получается ли так, что любая аддитивная функция, определенная на линейном пространстве, автоматически оказывается и линейной? Недолгое размышление показывает, что если X комплексно, а относительно А предполагается, что оно лишь аддитивно, то этого еще недостаточно для того, чтобы утверждать, что А линейно. Действительно, функция	преобразующая вектор из одномерного комплексного
линейного пространства С в комплексно-сопряженный, обладает свойством аддитивности и тем не менее не является линейным преобразованием. Отрицательным может быть ответ и в том случае, когда X вещественно, но причина этому гораздо более тонкая. В настоящее время мы ограничимся лишь утверждением, что даже в простейшем из вещественных линейных пространств — в R — имеется много аддитивных функций, не являющихся линейными преобразованиями. Заинтересовавшийся читатель найдет необходимые ссылки и краткий анализ причин этого в книге Боаса [А.И, стр. 108].
В том случае, когда А определено лишь на некотором подпространстве X, мы, как обычно, обозначим через DA область определения А. Обратим внимание читателя на то, что определение А требует, чтобы DA всегда было некоторым линейным подпространством линейного пространства X. Область значений А обозначим через НА и определим условием RA -- {у: у ~ Ах, tEDa}. Символом Na обозначается нуль-подпространство (или ядро) преобразования А:
Ал = {х\ х ЕЕ Da, Ах — 0}.
Легко видеть, что NА — это некоторое линейное подпространство X.
Теорема А. Пусть /1 — некоторое линейное преобразование с областью определения DA CZ X и областью значений RA CZ Y (где X uY—линейные пространства). Тогда RA—линейное подпространство Y.
Доказательство. Пусть у19 у2 GE RA, и пусть а — некоторый скаляр. Нам нужно доказать, что ух + Уг и «Ух принадлежат Ra. Но так как ух ЕЕ 7?л, то должен существовать такой вектор Ti GE DЛ, что Axv = z/р Точно так же должен существовать и вектор х2 СЕ Т)А такой, что Ах2 Уг- Однако преобразование А
ЛйнейноХи, следовательно, А + х2) = Ахг + Ллг2 = уг + J/г, a A (axj) ^аЛ^ = az/p так как хх + хг СЕ DA и €= DA, и т. д.
В § 2.1\мы познакомились с понятием непрерывности, и это понятие, очевидно, без всяких изменений можно перенести на нынешнюю ситуацию. Однако мы с самого начала хотим подчеркнуть, что 'непрерывность преобразования Л: X -+Y — это непрерывность по норме. Другими словами, мы считаем преобразование Л непрерывным в точке zE Л, если || Ахп — Ах|| —► 0 каждый раз, когда {#п} — некоторая последовательность из X такая, что ||л:п — х[| ->0, в отличие от общего случая, где непрерывность определяется сначала «в точке», а затем уже для всего пространства «в целом». Следующая теорема показывает, что для установления непрерывности линейного преобразования «в целом» достаточно выяснить его непрерывность в произвольной единственной точке.
Т е о р с м а Г>. Если Л — линейное (или просто аддитивное) преобразование X в Y и если Л непрерывно в некоторой точке xQ G= X, то А непрерывно и в любой точке х ЕЕ X.
Доказательство. Если хп—>х, то хп — х + х0 и, следовательно, Л (хп — х + £0) -> AXq. Однако из-за аддитивности Л имеем Л (хп — х + я0) = Ахп — Ах + Лх0, и, значит, из хп ->х следует, что Ахп —>Лх.
Второе замечание, касающееся понятия непрерывности, состоит в том, что любое аддитивное отображение Л некоторого вещественного банахова пространства X в любое банахово пространство Y однородно, если оно непрерывно. Действительно, вспомним, что аддитивная функция, определенная на линейном пространстве, была однородной, если коэффициент г рационален. Если же г — это некоторое заданное иррациональное число, а {гп} — последовательность рациональных чисел, сходящаяся к г, то гпх — гх|| = ||XT|| • | гп — г | —> О и в силу непрерывности Л: гпАх = - Л (гпх) ->Л (гх). Однако так как гпАх, очевидно, сходится к г Ах, то Л (гх) = г Ах, и, значит, Л однородно при любых вещественных г.
Напомним определение ограниченного преобразования.
Определение Б. Пусть А — некоторое преобразование определенное на X и принимающее значение из Y, где X и Y — банаховы пространства. Преобразование А называется ограниченным, если найдется такая константа М, что || Лх|| Л/ЦхЦ, каково бы ни было х ЕЕ: X.
Читателю нужно не забывать, что || Ах | — это норма в пространстве Y, в то время как ||х|| — это норма в пространстве X. Для большей ясности в связи с этим иногда полезно будет пользоваться в такой ситуации нижними индексами. Так, вместо только что выписанного неравенства мы могли бы написать, что
Если А — некоторое линейное ограниченное преобразование, то, как легко видеть, из ограниченности любого множества X' CZ X следует и ограниченность множества-образа А (X')' = Yf CI Y. Мы только что убедились в том, что каждая непрерывная аддитив-ная функция является и линейным оператором (у. е. обладает и свойством однородности). Следующая теорема проливает дополнительный свет на взаимосвязь между различными свойствами линейных преобразований.
Теорема В. Пусть X и Y — банаховы пространства, а Л — преобразование X в Y. Тогда /I ограничено в том и только в том случае, если А непрерывно.
Достаточность. Пусть А: X —> У, и пусть А не ограничено. Тогда существует такая последовательность {хп}, что для каждого п
||Лх„||>п||хп||.
Построим далее новую последовательность, положив хп — = хп / п|| хп ||. Ясно, что х’п ->0, поскольку || х'п || = 1/п. Но, с другой стороны,
II ^хп II = I А	II хп 11^ | = Л||д. || * II А.Хп || ^> 1,
и, следовательно, ||Ахп|| не сходится к ||А0|| при п ->оо. Поэтому А не может быть непрерывным в начале координат, что противоречит условию теоремы.
Необходимость. Пусть преобразование А аддитивно и ограничено. Тогда || Ах|| < М\\х||. Если хп -+х, то || Ахп — Ах\\ = = || А (хп — x)j| Af||xn — х ||, и, следовательно, Ахп ->Ах, что и завершает доказательство нашей теоремы.
Следующая теорема подводит итог всему тому, что мы пока узнали.
Т е о р е м а Г. Пусть X и Y — банаховы пространства, и пусть А: X -+Y. Тогда, если А линейно, то следующие условия для А эквивалентны между собой:
(1)	А непрерывно',
(2)	А непрерывно в начале координат*,
(3)	существует вещественное число М > 0 такое, что || Ах ||	Л/||х||, каково бы ни было х S X;
(4)	если (0) = {х: ||х||	1}, то его образ А (0)] является
ограниченным множеством в У.
Па самом деле, при доказательстве этой теоремы не приходится пользоваться свойством полноты пространств X и У; вполне достаточно, чтобы они были нормированы и линейны. В § 2.1 мы ввели понятие нормы Липшица, распространяющейся на произвольную функцию, отображающую одно метрическое простран
ство в другое. Для линейных преобразований это определение нормы Липшица превращается в следующее.
Определение В. Пусть X и Y — нормированные линейные пространства, и пусть А — некоторое ограниченное линейное преобразование X в Y. Наименьшее число М. для которого неравенство ||4х||, М ||х||х справедливо при всех х^Х. называется нормой А и обозначается через |] А |.
В соответствии с этим определением вещественное число || А || таково, что
ll-kllx,
каково бы ни было х 6Е X. Более того, для каждого е > 0 найдется такое х'. что
||Лх'II, > (II4 1 - 8)||х'||х.
Нетрудно показать, что приведенное определение эквивалентно следующему:
М11 = sup {Ц (x)J„: hllx < !}•
Если же X не есть ядро преобразования, то из-за однородности А предыдущее определение сводится к следующему:
Mil = sup {М (*)k kllx = i}-
С помощью теоремы Б мы найдем, что множество всех оценок для А сверху эквивалентно множеству радиусов всех замкнутых сфер с центрами в начале координат, содержащих А(8г (0)). Это позволяет получить еще одно новое определение нормы А:
||4 || = inf {К: К > 0 и ||4 (х)|| К ||х||х для всех х}.
Из последнего определения сразу следует, что
М (х)1„ <МНх||х>
каково бы ни было х GE X. Все эти замечания доказывают эквивалентность следующих формул:
|| 41|= sup || Аг ||,
||х||^1
М||=«ир ММ,
II» 11=1
Выше мы пользовались нижними индексами при символах норм для того, чтобы подчеркнуть зависимость определения || А Ц от определения || ||х и || |(, (как известно, на каждом линейном пространстве можно определить много различных норм). И в точности так же, как изменение нормы приводит и к изменению
характера пространства X или У, так и выбор новой нормы Цх|| порождает новую норму оператора А. В следующем параграфе мы убедимся в том, что функция || А || удовлетворяет аксиомам нормированного пространства, а значит, наша терминология является оправданной.
Прежде чем идти дальше, приведем примеры некоторых линейных преобразований.
Пример 1. Легко убедиться в том, что функция Т (см. пример 5 §2.1)
t
(Тх) (t) = х (s) ds, а t Ъ, а
определяет непрерывный линейный оператор в С (а, Ь). Аналогичным же образом преобразование
ь ф (я) =	(/) dt,
а
отображающее Lx (а, Ь) в 7?, ограничено и линейно. Ядро ф бесконечномерно. Например, если 6 л, а а — л, то условию ф (х) = 0 удовлетворяет бесконечное множество {х\ х (/) — = sin nt, cos nt, n = 1, 2, ...} линейно независимых функций.
Пример 2. Функционал точечной оценки et9 (х) = х (t0) (см. примеры 3 и 10 § 2.1) является непрерывным комплексным линейным функционалом, определенным на С (0, 1). Новым здесь является лишь утверждение о его линейности, которое вытекает из того, что
Z(, (ах + Ру) = (ах + Ру) (t0) = ах (t0) + Рг/ (<#)• Непрерывными линейными функционалами были и функции, рассматриваемые в примерах 4, 6 и 9 § 2.1.
Пример 3. Стационарная линейная система с одним входом и одним выходом в пространстве преобразований Лапласа описывается соотношением У ($) = II (s) X ($), где II ($) — передаточная функция системы, X ($) — преобразование Лапласа входного сигнала, а У ($) — преобразование Лапласа выходного сигнала системы. При доказательстве линейности операции «умножения на II ($)» легко подметить те же этапы, что и при доказательстве справедливости принципа суперпозиции для линейных систем.
Пример 4. Пусть X — пространство всех вещественных чисел, определенных на промежутке 0 t < оо и таких, что функция х (/) интегрируема и lim |х (/) | < Ае*', где а < оо. Функция t-*oo
L, заданная соотношением
со
(Z/)(.s) = $e-’'/(OdZ, о
представляет собой линейное преобразование, отображающее X в пространство комплексных функций комплексной переменной.
Следующие три примера теспо связаны с задачами теории систем различных типов. Поэтому мы рассмотрим эти типовые задачи довольно подробно.
Пример 5. Вся техническая литература может служить убедительным свидетельством того, насколько важны линейные преобразования в конечномерных пространствах. Так, в механике многомерные соотношения между нагрузками и напряжениями могут быть описаны (по крайней мере в приращениях) с помощью линейных преобразований в Еп. При проектировании систем управления и навигации сигналы различных датчиков и измерительных приборов, описывающие движение тела в некоторой системе координат, связанной с этими датчиками, необходимо преобразовать так, чтобы они определяли движение в обычной системе координат. И такое преобразование координат, как правило, является линейным. На самом деле, список различных возможных применений теории линейных преобразований настолько внушителен, что теория матриц в большинстве технических дисциплин играет не менее важную роль, чем основы математического анализа.
В настоящем примере мы считаем, что X = Y = Нп, и рассматриваем преобразование А, описываемое вещественной матрицей Га*у] размерности (п х п), преобразующей вектор х = = (£1» •••> tn) в вектору = (т]1т	1];) по правилу
п
ni=Saijih i =	(1)
>=1
Поскольку кх =	..., Цп), то из уравнения (1) и очевидного
равенства
п	п
2 «{AS/ = ^ (3
следует, что Лкх — кЛх. Столь же просто убедиться и в том, что преобразование А аддитивно. Таким образом, А — линейное преобразование. Так как Нп конечномерно, то мы сразу устанавливаем, что преобразование А непрерывно.
В § 1.4 мы видели, что на Нп можно определить множество различных норм. В частности, для х = (£х,	£п) нормой может
служить функция
15.1’]V’,
Где р — произвольное число, 1 р < оо. Для того чтобы показать на примере, что норма А действительно зависит от выбора норм в областях определения и значений, мы порознь рассмотрим три различных случая.
Для простоты мы будем во всех этих случаях предполагать, что в области определения и в области значений выбираемые нормы одинаковы.
Случай!: (п) -> (п), Цж]! =	&|. Число || А в явном
виде вычисляется по формуле п
|A|i = “ах 3 J i=l
Другими словами, норма преобразования А при условии, что этот оператор действует в 1Х (п), равняется максимальной из норм в 1г (п) вектор-столбцов матрицы [а^].
Случай 2: 12 (п) -> 12 (п), ||а:||2 = [У"=11 |2]7«. Норма ||А||2, порожденная нормами 12 (п), определяется выражением
II ||г = ^шах>
где Хтах — наибольшее собственное значение матрицы В = А*А. Более подробно о собственных числах мы поговорим в следующей главе.
Случай 3:	(n) -+1оо(п). В этом случае норма вектора х из
Rn определяется по формуле ||хЦ» = max Норма А, порожденная такой нормой (мы обозначим ее через ||4||оо), определяется выражением п
ЦЛЦоо = max 2 |аиI• i j=l
Таким образом, если рассматривать А как оператор в 1^ (п), то норма Л равняется максимальной в 1Х (п) из норм среди всех вектор-строк матрицы [aiyl.
Результат, относящийся к случаю 3, можно получить без каких-либо трудностей. Попутно мы познакомимся при этом с одним конструктивным приемом, который оказывается часто полезным при вычислении нормы ограниченного оператора. Для начала напомним, что
||Л||оо= sup IIAxjoo-II
Пусть преобразование Л характеризуется матрицей [<х<у] и у = = Ах, где x = (^lt |п), а у = (т]1. •••> Пп)- Пусть координаты
i - 1, п, вычисляются по формуле (1), тогда
п
j=l
Но так как ||у||оо = maxf{|ni|). т0 «« сразу находим, что
Mxk = hk =max|t]iKmax 2l«ul • 11}I-’	1 j=i
Однако если ЦхЦ» = 1, то ясно, что 1< 1, каково бы ни было /. Учитывая этот факт в предыдущем неравенстве, мы видим, что
|| Л Ц» = sup ||Лх||<тах 2 |<*м | • Нх11оо=1	j=l
Предположим теперь, что J I достигает своего максимума при i = к, и построим вектор с координатами
О, если akj = О,
Lj£2_L ? ссли а 0,	/ = 1, 2, . . ., п.
Ясно, что ||s°||oo = 1 и что, более того,
Sa/cj£j= 2 lawl-;=1 ;=1
Поэтому вектор х° обращает полученное неравенство в равенство
п	п
||Лж°||ов = 2 lawl = max 2 |а;;|, ;=1	1 j=l
что и завершает наши вычисления.
Пример 6. В § 1.4 мы обращали внимание читателя на системы, цепи и механизмы, преобразующие входной сигнал х в выходной сигнал у в соответствии с правилом
1 y(s) = ^k(s,	0<ssg:l.
о
В этом случае при t = 0 система находится в состоянии покоя [*/ (0) = 0]. Через к (.9, t) обозначена импульсная характеристика
(или функция Грина) этой системы. Если х £=. С (О, 1), а к (5, t) — функция, непрерывная на квадрате 0^5, t 1, то, как нетрудно видеть, функция у, определенная при 0	1 этим
выражением, также непрерывна. Если мы обозначим это преобразование символом у = Тх, то Т будет отображать С (0, 1) в себя. Легко убедиться в том, что оператор Т линеен в С (0, 1), так как из равенств
1	i
IT (л + '-2)1 (•’) - $ * (•’. 0 1'1 (/) + '-2 (/)] <и = $ к (S, I) л (0 dt + о	о
1
+ t)x2(t)dt = (T.ri)(s) + (Г.г2)(>-) = (7’х1 + Тхг) (s) О следует, что
Т (xt + х2) = Тхк -|- Тх2>
Кроме того, для любого скаляра а
Т (ах) = аТх.
При вычислении нормы Т мы предположим, что в пространствах входных и выходных сигналов используется обычная норма я|] = supo^t^j |х(1)|. Тогда из неравенства
11 1
| § k(s, t)x (t) dt I | &(.<?, t) I • I x (t) I dt ^sup I x (t) I § I k(s, t) | dt 0	*	0	z	0
мы сразу можем найти
i	i
[|7\r||= sup I k(s, t) x (t) dt \ <|x| sup t)\dt.
OC8<1 I Q	I o^s^l 0
Отсюда следует, что
i
|| T|| sup | k(s, t)\dt. oCsCi о
В действительности же можно показать [А.56, стр. 83], что
1
ЦТ||= sup J|к(s, t)\dt.
OCS^l Q
Между примером 6 и случаем 3 предыдущего примера есть определенное сходство, которое станет яснее, если переформулировать задачу, рассмотренную в примере 5, пользуясь несколько отличной терминологией. Действительно, будем рассматривать векторы х = (51, ...» 5п) пространства (п) как функции, ото-
бражающие множество {1, 2, ..., п} в R. Норма вектора (функции) х — это равномерная норма. Матрицу [ац] теперь естественно рассматривать как некоторую вещественную функцию, определенную на «прямоугольнике» 1 i, / п. Тогда значение оператора определяется интегралом произведения [а^]х, и мы
показали уже, что норма этого оператора равняется максимуму Zj-норм вектор-столбцов [аи].
Точно так же функцию к (s, t) можно рассматривать как матрицу с бесконечным (счетным) числом столбцов и строк, а векторы С (0, 1) — как последовательности (xt) с бесконечным числом чле"
Рис. 2.9. Механическая система.
нов. При этом Z-й координатой xt должно служить значение функции х (t) в точке t. В этом смысле пример 6 можно рассматривать как обобщение случая 3 из примера 5.
Во всех этих эвристических замечаниях мы не стремились к особой строгости. Здесь, однако, полезно будет сказать, что этим
двум примерам, а также и многим другим, с которыми нам придется еще встретиться, можно придать необходимую строгость, если воспользоваться методами современной теории интегриро
вания и рассматривать встречавшиеся выше операторы как частные случаи одного абстрактного оператора. Мы советуем читателю самому попытаться продумать другие аналогии между непрерывными и дискретными явлениями, с которыми мы уже столкнулись или столкнемся в будущем.
Пример 7. Рассмотрим простую систему с пружиной и демпфером, схематически изображенную на рис. 2.9. Она описывается уравнениями
МхЫ (0 + /хО) (0 + кх (0 - у (0, t0 < t,
*(1) (/0) =- xj, (t„) xt
В этом примере мы займемся исследованием функции х -> у, определенной этими уравнениями *). Для несколько большей общности мы будем рассматривать преобразование у = Lx, заданное уравнениями
у (0 = ап (0 х(п) (0 + . • • + «1 (О Х(1) (/) + а0 (/) X (0,
(^о) —1	» • • • > x(t0) = хо.
♦) Здесь через обозначена к-я производная х по времени t, причем х(о)(0 полагается равным х (0.
При изучении преобразования L мы будем пользоваться функциональным пространством Сп (а, &), которое образуется всевозможными функциями, определенными на промежутке [а, Ы, непрерывными и п раз дифференцируемыми на этом промежутке, с нормой
п
||х||= 2 sup I xw (t) |. 1=0 f
Нетрудно видеть, что для Сп (а, Ь) справедливы все аксиомы нормированного пространства. Например, если х, у G= Сп (а, &), то, каково бы ни было / = 0, 1, ..., п,
|	(I) + У0) (О I < I (01 + 1 у(}) (0 j < sup I хО) (О I + sup | у0) (О I
и, следовательно,
sup (t) +	(0| sup (J)| + sup \ у(Я (Z) [.
Суммируя по индексу / обе стороны приведенного соотношения, мы получим неравенство треугольника. Более того, можно показать, что пространство Сп (а, Ь) банахово.
То, что оператор L определен и линеен на пространстве Сп(а, &), не вызывает никаких сомнений. Ядро L состоит из всех решений дифференциального уравнения n-го порядка Lx = 0. Обычная теорема существования (см. теорему А из приложения 4) утверждает, что у этого уравнения ровно п линейно независимых решений хг, ..., хп (которые иногда называют собственными движениями системы). Отсюда можно заключить, что ядро L представляет собой линейное многообразие L (xt1 ..., хп). Для того чтобы доказать, что оператор L ограничен, введем обозначение dk = sup |	(t) |, к = 0. 1, ..., и, и а = шах {«!, ..., ап}. Тогда,
если у = Lx, то
п	п
1<М0|-1*да(0К /с=о	/с=о
а 2 I х^ (<) | ^ а 2 SUP I(0 I — ® IIх
к=0	к=0
и, следовательно, [| ?/|| — sup | у (t) ]	<21|х||.
Поскольку =/= 0, то отображение L не взаимно однозначно, а потому и не обратимо. Однако область определения L можно сузить таким образом, чтобы L стало взаимно однозначным. Пусть X — банахово пространство следующего вида:
X — {х: х Сп (а, &), х (а) = х(1) (а) = ... = х(п-1) (а) — 0}.
Тогда в силу второй теоремы существования решений дифференциальных уравнений (см. теорему Г из приложения 4) существует всего одно значение х С X для каждого у G С (а, Ь) такое, что I/ == Lx. Другими словами, в этом случае CZ С (а, Ь) и для каждого у G С (а, Ь) в X найдется всего один прообраз. Учитывая соотношение Ск (a, b) С С (а, Ь) и определение L, мы видим, что
= С (а, Ь). А это значит, что оператор L обратим, если его область определения ограничена пространством X.
Оператор, обратный L, помогает установить связь между материалом этого примера и материалом примера 6. Рассмотрим частный случай. Пусть
у (0 = (Lx) (t) =	(0.
Интегрируя дважды и меняя порядок интегрирования, мы получим
1	и	t
x(t) = ^du^y (s) ds =	— О У (s) ds.
0	a	a
Введем обозначение
f (* ~ 0
ft(LS) = {	0
t
тогда
ъ x(t) = y(s)ds, a
и у преобразуется в х оператором того же типа, что и рассматривавшийся в примере 6.
* Пространство линейных преобразований *). Обозначим через X и Y два линейных пространства, а через L (X, У) — множество всевозможных линейных преобразований X в У. Как мы видели в примере 1, с каждым линейным преобразованием A: Rn ->Rn можно связать некоторую матрицу [ам1. Аналогичным образом в примере 2 каждое ядро к (.$, /), непрерывное по обоим своим переменным в квадрате а	Ь, можно связать с некоторым
линейным оператором Т: С (0, 1) -> С (0, 1). Наше множество L (X, У), по определению, содержит все эти операторы.
В L (X, У) можно ввести линейные операции. Пусть X и У — два линейных пространства с одинаковыми скалярами. Пусть А и В — это два преобразования из множества L (X, У).
♦) Звездочкой помечены разделы, чтение которых не обязательно для того, чтобы понять остальной материал главы 2. При желании читатель может пропустить этот материал.
Определим их сумму Т = А В следующим образом:
Тх -= (А + В)х — Ах + Вх, х ЕЕ X.
Определим также операцию умножения на скаляр Т = кА с помощью следующего соотношения:
Тх - (ХЛ)х = кАх.
Легко доказать, что введение этих определений преобразует множество L (X, Y) в некоторое линейное пространство. Нулевое преобразование (т. е. нулевой элемент этого линейного пространства) 0 определяется условием 0 (х)	0, а преобразование — Т
условием (— Т) (х) = — Т (х). Другими словами, мы доказали сейчас следующую теорему.
Теорема Д. Пусть X и Y -— два линейных пространства с одинаковыми полями скаляров. Тогда множество всех линейных преобразований X в Y само является линейным пространством по отношению к только что определенным операциям сложения и умножения на скаляр.
Введенное ранее определение композиции двух функций справедливо, в частности, и для линейных преобразований. Так, если Л Е А (У, Z), а В Е А (X, У), то произведение АВ есть преобразование X в Z, удовлетворяющее условию
(АВ)х - А (Вх), хЕЕХ.
Нетрудно убедиться в том, что АВ также линейно и, значит, принадлежит L(X, Z). В частности, если X = У = Z, то, как мы установили только что, при А и Be^L (X, X): АВ ЕЕ L (X, X). Легко видеть, что это произведение обладает свойствами ассоциативности
А (ВС) = (АВ) С.
Более того, так определенное умножение связано со сложением через дистрибутивные законы
Л (В + С) = АВ + АС и
(А + В) С = АС + ВС,
а с умножением на скаляр с помощью соотношения а (АВ) - (аА) В = А (аВ).
Доказательство всех этих фактов не составляет никакого труда. В качестве иллюстрации приведем простую цепочку выкладок,
доказывающих один из законов дистрибутивности:
|(Л + В) С] (х) = (А + В) (С (х)) -
= А (С (х) + В (С (х)) = (АС) (х) + (ВС) (х) = (АС + ВС) (х).
Обращаем особое внимание читателя на то, что в принятых предположениях свойство коммутативности (АВ ~ ВА), вообще говоря, отсутствует. Например, матрицы размерности (п ?< п), каждая из которых отображает Вп в /?'\ не коммутативны. Рассмотрим еще один пример. Выберем X С (а, 1>) и введем два оператора:
1
у (s) = (Ar) (х) = stx (t) dt о
и
z (s) = (Вх) (s) — sx (s).
Тогда
i	t
ABx = st-tx (t) dt = t2x (t) dt, о	0
1	t
В Ax = s^stx (t) dt = s2 § tx (t) dt, о	о
и, следовательно, AB =/= BA.
До сих пор мы говорили только об одном конкретном элементе L (X, X), а именно о нулевом преобразовании 0. Второе, почти тривиальное преобразование — это тождественное преобразование /, определяемое условием I (х) = х. Заметим, что Z =/= 0 <=> О X =^= {0} и что
Al = IA = 4,
каково бы ни было А е L (X, X). Если а — любой скаляр, то умножение на скаляр а можно рассматривать как линейное преобразование а/, так как
(al) (х) = al (х) = ах.
В теореме Ж мы покажем, что если преобразование А(=еЬ (Х,Х) невырождено, то существует и линейно А"1, и, следовательно, A~l^L(X, X).
Определение Г. Линейное пространство X называется алгеброй, если в нем определена операция, ставящая в соответствие каждой упорядоченной паре (х, у) элементов X некоторый третий элемент X, обозначаемый через ху и называемый произведением х на у, и если эта операция удовлетворяет следующим
аксиомам:
(1)	(ху) Z = X (yz),
(2)	х (у + z) = ху + xz,
(3)	(х + у) Z = XZ + yz,
(4)	(а*) (РУ) = (аР) (ху).
Во всех этих аксиомах нужно считать, что х, у и z — это произвольные элементы X. а а и 0 — произвольные скаляры. Ал-гебру называют вещественной или комплексной в зависимости от того, комплексно или вещественно поле скаляров.
Если в алгебре X существует такой элемент i, что ix = xi — = х, каково бы ни было х е= X, то i называют единицей алгебры, и этот элемент обязательно единствен. Если ху = ух, какова бы ни была пара (т, у), то соответствующая алгебра называется коммутативной. Если Хо — это некоторое подмножество алгебры X, такое, что каждый раз, когда (х, у) принадлежат Хо, туда же попадают и х + У, ах и ху где а — некоторый скаляр, то XQ называют подалгеброй алгебры X. Другими словами, подалгеброй называется подпространство, которое само по себе является алгеброй.
Из этих определений и заме’ лий, предшествовавших определению алгебры, следует, что множество L (X, X) — алгебра. Более того, в этой алгебре есть единица, а именно оператор 7, определенный условием 1х = х. В общем случае алгебра L (X, X) не коммутативна.
* Нормированные пространства линейных преобразовании. Итак, мы установили, что множество L (X, У) всевозможных линейных преобразований, отображающих линейное пространство X в линейное пространство У, само является некоторым линейным пространством. Пусть пространства X и У банаховы. Тогда для всех ограниченных преобразований из L (X, У) мы уже определили понятие нормы оператора. Это двоякое употребление термина «норма» подсказывает нам, что существует возможность построения на базе подмножества всех ограниченных преобразований из L (X, У) некоторого нормированного линейного пространства. Но для этого нужно проверить выполнимость некоторых дополнительных условий.
Обозначим через 0 (X, У) множество всевозможных непрерывных (и, следовательно, ограниченных) линейных преобразований нормированного линейного пространства X в нормированное линейное пространство У. Если A GE 0 (X, У), то функция || А || (см. определение Б) удовлетворяет всем акиомам нормированного пространства. В самом деле, предполагая, что X =/= {0}, мы получим:
(1)	1|А|] = sup||X||=1 ||Лх|| > 0 (что очевидно); если || А |( = 0, то Ц Ах|| = 0, каково бы пи было х, для которого ||а:|| = 1. Но в
силу однородности А отсюда следует, чть Ах = 0, каково бы ив было х вообще, и, значит, А = 0.
(2)	ЦМ|| = sup||M = i ||ХАх|| = | М supi,,!-! ||Ах) = |Х|.|Л
(3)	||А + В\\ = supn,!!»! ||(Л + В)х|< sup,х। = 11| Ах\\ +
+ sup|,j,i ||Вх|| = IIЛII + ||ВЦ.
Таким образом, мы частично доказали следующую теорему.
Теорема Б. Если X и Y — нормированные линейные пространства, то множество 0 (X, Y) всевозможных непрерывных линейных преобразований X в Y само по себе представляет нормированное линейное пространство по отношению к поточечным линейным операциям и норме, порожденной X и Y. Более того, если пространство Y банахово, то банахово и пространство 0 {X, Y).
Доказательство. Мы уже показали, что 0 (X, Y) — нормированное линейное пространство, и нам остается только доказать, что если пространство Y полное, то полно и 0 (X, У). Другими словами, нам нужно показать, что если {Ап} — некоторая последовательность Коши из 0 (X, У), то она сходится к некоторому преобразованию из 0 (X, У).
Итак, пусть {Ап} — некоторая последовательность Коши из 0 (X, У). Если х есть произвольный вектор из X, то из того, что ЦАт((х) -Ап (х) || = || (Ат — Ап) (х)1С||Лт-ЛпЦ.Цх||, еле-дует, что последовательность {Ап (х)} представляет собой последовательность Коши в У. А так как пространство У полное, то найдется некоторый вектор из У (мы обозначим его через А (х)) такой, что Ап (х) -> А (х). Но это и определяет отображение А из X в У.
Является ли это отображение линейным? Поскольку А (хг + + х2) = lim Ап (xt 4- х2) = lim Ап (хг) + lim Ап (х2) и А (ах) = -lim Ап (ах) = a lim Ап (х) — аА (х), то ответ на этот вопрос, очевидно, должен быть положительным. В завершение доказательства нам остается только показать, что А непрерывно и что Ап ->Л по норме, определенной на 0 (х, у). Замечая, что нормы членов последовательности Коши в нормированном линейном пространстве должны образовывать ограниченное множество чисел, мы получим, что
|| 4 (х)|| =Ц lim Ап (х)|| = lim||An (х)||< sup (|| АпЦ-||х||) = = (sup || 4n||)||х||, откуда следует, что А ограничено, а следовательно, и непрерывно. Остается только доказать, что || Ап — А|| ->0. Зададимся некоторым е > 0 и обозначим через п0 некоторое положительное целое число такое, что т, n^nQ=S> || Ат — Ап|| < е. Существование такого числа гарантируется свойствами произвольной
последовательности Коши в нормированном пространстве. Если ||х|| < 1 и т, п> п0, то
II лт (х) - Ап (х)|| = II (Ат - Лп) (х)|| < II Ат - Ап||-||х|| <
^п|| < Е*
Теперь мы воспользуемся одним классическим приемом, сводящимся к тому, что т фиксируется, а п устремляется к бесконечности, в результате чего || А т (х) — Лп (х) || -►-|| А т (х) — А (х)||, откуда и следует, что || Ат — А (х)|| е для любых т nQ и всех х, для которых ||х||	1. Это непосредственно и доказывает
что || А т — Л || е для всех т п0, что и требовалось доказать.
Как и раньше, мы можем распространить все эти результаты на случай, когда областью определения преобразования и областью его значений служит одно и то же нормированное линейное пространство. Мы будем называть непрерывное линейное преобразование X в себя просто ограниченным линейным оператором в X и будем обозначать нормированное пространство ограниченных линейных операторов в X через 0 (X) (а не через несколько более сложное 0 (X, X)). Теорема Е показывает, что 0 (X) — банахово пространство, если только X — банахово пространство. Пусть А и В — два оператора из 0 (X). Выше мы определили их композиции АВ и В А. Покажем теперь, что
цлвцсрнвц.
Это утверждение легко доказывается следующими соотношениями:
|| АВх|| = || А(Вх) || < |( А || • || Вх || < || 4 || • || 51| • ||х ||.
В предыдущих параграфах мы показали, что в любом банаховом пространстве операции сложения и умножения на скаляр совместно непрерывны. Если 0 (X) — банахово пространство, то можно заключить (используя неравенство, приведенное выше), что совместно непрерывна и операция умножения преобразований. Другими словами, если Ап и Вп ->В, то АпВп -+АВ.
Это вытекает непосредственно из следующих соотношений:
|Л„ВП - АВ|| = ||АП (Вп -В) + (Ап - А) ВЦ
<||4П|.||ВП — ВЦ +||АП - АЦ.ЦВЦ.
Если пространство X нетривиально (X =1= {0}), то тождественное преобразование I является единицей для 0 (х) и
Ц/Ц = sup {||/ (х)||: ||х|| < 1} = sup {||х||: ||х|| < 1} = 1.
Если Т — некоторое преобразование, определенное на X, принимающее значения из У и являющееся взаимно однозначным
накрытием, то Т называется невырожденным (несингулярным) или обратимым. Если Т к тому же и линейно, то преобразование, ему обратное, обладает еще и следующими дополнительными свойствами.
Теорема Ж. Пусть Т — некоторое линейное преобразование с Dt = X и RT = Y, где X и Y — нормированные линейные пространства. Тогда:
(1)	Г'1 существует и ограничено в том и только том случае, когда найдется такая постоянная т > 0, что т || х||	|| 7\г||, ка-
ково бы ни было X ЕЕ X*,
(2)	если утверждение (1) справедливо, то ||71“1||^ 1/ттг;
(3)	если Т"1 существует, то оно линейно.
Доказательство. Для того чтобы доказать утверждение (2), предположим, что уг, y2EEY. Тогда уг = Тхх и у2~ Тх2, где хг = = Т-^ух и х2 = Но так как (уг + у2) = Т + х2), то мы получим, что 71-1 (j/i + у2) =	+ #2 = Т~гУ1 4- Т~ху2. Точно так
же равенство tyi = Ткхг предполагает, что	=
= ^Т~1у1, так что преобразование Т”1 аддитивно и однородно. Для того чтобы доказать утверждение (1), заметим, что для m > О при условии, что ти||х||	|| Гх||, Тх = 0=$>х = 0, и,следовательно,
Т взаимно однозначно. Более того, если 71-1 существует, то у = Тх эквивалентно х — Т~гу. Поэтому тпЦ дг|| (| Тх^ =>
|| у || => ||7’“1г/(|	1/т| у ||, каково бы ни было у из Нт, служащей
областью определения преобразования Т^1. А отсюда уже в силу теоремы В следует, что преобразование Т”1 непрерывно.
Обратно, если Т~г существует и ограничено, то для всех у = = Тх ЕЕ Rt справедливы соотношения
k II = ГЛ/II < IIТЛЬШ = ГЛ-11 ^11..
так что условия теоремы выполняются, и m =
Другими словами, если Т линейно, ограничено снизу (т. е. 771IIxll II Тх\\) и Rt Y, то Г"1 существует и принадлежит Р (У, X). Для дальнейшего обсуждения этого вопроса мы отсылаем читателя к приложению 7.
Выяснить возможность обратимости преобразования, как правило, совсем не просто. Однако следующая теорема дает нам одновременно и критерий существования ограниченного обратного преобразования, и вычислительный метод, позволяющий аппроксимировать это обратное преобразование.
Теорема 3. Если X — некоторое банахово пространство и Г Е Р (X), причем ||Т||^ а<1, то преобразование, обратное (I — Т), ограничено и удовлетворяет условию
||(Z-T)-lKTLr.
Более того, ряд
оо
(Г — Т)"1 = 2 тп
п=0
в Р (X) равномерно сходится к левой части этого равенства.
Доказать эту теорему нетрудно, и мы предоставляем читателю возможность сделать это самому. В упражнениях 7—10 к § 2.5 мы убедимся, что она даст нам полезный метод изучения систем с обратной связью.
* Проекции. В этом разделе мы лишь вкратце остановимся на двух линейных преобразованиях специального вида. Эти преобразования заслуживают особого внимания потому, что они тесно связаны с изучением структуры линейных пространств и, кроме того, знакомство с ними обогатит наше понимание этой структуры. Первое из этих преобразований называется проекцией. С понятием проекции мы в неявном виде уже познакомились в § 1.3 в связи с изучением прямых сумм линейных многообразий, и мы начнем сейчас как раз с этого.
Напомним, что линейные подпространства {Мг, ..., Мп} разлагают линейное пространство X в некоторую прямую сумму X = М ф ... ф Мп, если каждый хЕЕ X можно единственным образом представить в виде х = хх 4- ... + хп, где М^. Это разложение может быть использовано для того, чтобы определить функции Pj, удовлетворяющие условиям
Р^х = Xi, i = 1, ..., и,
каково бы ни было х ЕЕ X. Эти операторы, очевидно, линейны и удовлетворяют соотношениям
ЛР;. = о,
Р? = РЪ f =
Z = px + ... +Pn.
Область значений каждого из операторов Р| — это соответствующее подпространство М}. Ядром оператора Р| служит подпространство X Q (Другими словами, NP. = Мх ф ... ф Л/^ф Ф ^{+i© Мп.)
Определение Д. Линейный оператор Р в X называется проекцией если Р2 = Р. Если область значений Р равна М, то Р называется проекцией X на М.
Легко показать, что если Р — проекция, то
X - RP ф Np.
В самом деле, поскольку каждый элемент х X может быть пред
ставлен в виде
х = Рх + (I - Р)х
и Рх S Rp, то нам нужно показать лишь, что (Z — Р)х е Np и что Rp П Np — 0- Следующая последовательность равенств
р I(Z - Р) (*)] = (Р (Z — Р)1 (я) = (р - рэ) (я) = (Р - Р) (*) =
= 0 (х) =0
доказывает, что (Z — Р) (х) принадлежит #Р, а значит, NP и RP позволяют натянуть на себя все X. Для того чтобы убедиться в том, что Хр и RP не пересекаются, нам нужно только заметить, что если Р (х), принадлежащий RP, принадлежит и NP, то Р (Р (х)) = = 0 и, следовательно, Р (х) = Р2 (х) = Р (Р (х)) = 0. Это доказывает, что X = RP © NP, и, следовательно, Р — действительно проекция х на RP.
Аналогичным же образом можно определить и проекцию Q пространства X на NP. Ясно, что Q = I — Р, так как если Р — некоторая проекция на X, то уравнение
Q2 = (Z - Р)2 = (I - Р) (Z -’Р) = Z- P- P+P2 = Z- P = (?
показывает, что и Q — проекция, а мы знаем, что Р есть проекция на Яр, когда I — Р — проекция на NP. Сделаем еще одно дополнительное замечание. Если М\ — некоторое заданное линейное подпространство X, то существует, вообще говоря, множество подпространств М2 таких, что X = Мг © М2. Поэтому наверняка должна существовать проекция Р на М2, но эта проекция не определена однозначно до тех пор, пока не выбрано подпространство М2. (Читатель легко может убедиться в этом на частном примере R2.)
До сих пор мы ничего не говорили о непрерывности. Рассмотрим проекцию Р в банаховом пространстве X. Если Р непрерывно, то ядро ДОр, будучи ядром непрерывного линейного преобразования, должно быть замкнуто (см. упражнение 1). Но так как область значений Р представляет собой одновременно и ядро Z — Р и это второе преобразование также непрерывно, то замкнутым должно быть и RP. Справедливость этого взаимно обратимого утверждения доказывается в следующей теореме.
Теорема И. Каждая непрерывная проекция Р, действующая в банаховом пространстве X, определяет два замкнутых линейных подпространства RP и NP таких, что RP ф NP = X. И обратно, каждая пара линейных замкнутых подпространств М и N таких, что М ф N = X, определяет некоторую проекцию Р, для которой RP = М и NP = N.
В общем случае неверно было бы утверждать, что у каждого замкнутого линейного подпространства М банахова пространства X имеется непрерывная проекция, принимающая значения из М. Трудность здесь заключается в том, что для М может не найтись замкнутого линейного многообразия АГ, дополнительного по отношению к М. Кроме того, может оказаться, что М ф N не замкнуты, хотя М и N замкнуты (см. замечание 1 из § 3.2).
В том случае, когда пространство X гильбертово, задач, связанных с декомпозицией X, не возникает. В самом деле, вспомним, что в соответствии с теоремой Г из § 1.5 у каждого замкнутого линейного подпространства М имеется некоторое замкнутое дополнение, а именно 7И1, такое, что X = М ф М-L. Для гильбертовых пространств мы безо всякой неоднозначности можем ввести понятие ортогональной проекции.
Определение Е. Пусть Н — гильбертово пространство. Линейный оператор Р называется ортогональной проекцией в Н, если Р есть проекция, a Rp | ЛГр. Если М — некоторое замкнутое подпространство Н, то проекция Р с Rp = М и Np = = называется ортогональной проекцией Н на М.
Ортогональные проекции играют важную роль в изучении общей структуры линейных операторов. Сейчас же мы не будем исследовать свойств этих проекций дальше, хотя и поговорим об этом в упражнениях.
* Изоморфные и конгруэнтные пространства. Для того чтобы оправдать необходимость введения следующего определения, рассмотрим вкратце один пример линейного пространства X. Пусть векторы из X — это упорядоченные пары (£, ц) вещественных чисел. Сложение и умножение на скаляр определены в X следующими правилами:!
(£1- П1) + (1г, Пг) = 011 + *12, Е’ + 5г). X (g, л) = (Ц, Ц),
где X вещественно. Недолгие размышления показывают, что в этом случае все аксиомы определения А из § 1.3 удовлетворяются, и, следовательно, X — действительно линейное пространство. Но так как раньше мы уже сталкивались с пространством R х R = = R2, то естественно задать вопрос, а не «эквивалентны» ли пространства X и 7?2? Специалист по теории множеств немедленно воскликнул бы: «Ну, очевидно же!» Однако остальные из нас не могут не чувствовать некоторого скептицизма. Оба эти пространства линейны, и нам интуитивно кажется, что для эквивалентности пространств необходима и «эквивалентность» определения операций сложения и умножения на скаляр, а в данном случае этого нет. Поэтому мы говорим, что эти пространства различны. Но насколько различны? Безусловно, не настолько, насколько
различны, скажем, (' (0, 1) и В самом деле, X и Вг отличаются друг от друга лишь совершенно тривиальным аспектом. Так, если определить отображение Т : X -► Н2 с помощью следующего условия:
т (£, Т]) = (Т), 5),
мы сразу увидим, что Т линейно, взаимно однозначно и накрывает Я2. Более того, любое «утверждение теории линейных пространств», справедливое в Я2, с помощью Т переводится в некоторое истинное утверждение относительно X. Например, сразу можно утверждать, что X двумерно и что его базис может состоять из векторов Г-1 (0, 1) = (1,0) и Г-1 (1,0) = (0, 1). Короче говоря, линейное пространство X можно получить из линейного пространства Я2 с помощью простого переименования его точек. Естественно, что такое изменение считается совершенно тривиальным, особенно если учесть, что при изучении линейных пространств мы, в конце концов, вообще не интересуемся конкретным характером их векторов. С другой стороны, если для получения X из Я2 приходится менять больше, чем просто «язык», то это отразится на структуре Я2 как линейного пространства, и такое изменение уже нельзя считать тривиальным.
Предыдущие рассуждения показывают, что нам следует считать два линейных пространства X и Y «эквивалентными», если у них идентичны структуры. А так как все наши определения и свойства линейного пространства берут свое начало из определений операций сложения и умножения на скаляр, то это возможно тогда и только тогда, когда найдется некоторое взаимно однозначное отображение Т пространства X на У, которое сохраняет сложение
Т + х2) = Тхх + Тх2.
С формальной точки зрения это приводит к следующему определению.
Определение Ж. Два линейных пространства X и Y (с одинаковым полем скаляров) называются изоморфными, если существует некоторое взаимно однозначное линейное преобразование, отображающее X на У. Такое преобразование называется изоморф измом.
С точки зрения этого определения пространства X и Я2, рассматривавшиеся выше, изоморфны с изоморфизмом Т, преобразующим (5, ц) в (ц, ^). Первоначальная путаница возникла из-за того, что тождественное преобразование I, отображающее пару (5» ц)» как элемент X, в (£, т|), как элемент Я2, хотя и взаимно однозначно, биективно и однородно, но не является аддитивным:
I ((51, Т]1) + (5г, Пг)) = 1((Л1 + Пг, + 5г)) =
= 011 +	51 + 5г) = Oil, 51) + 012, 5г).
в то время как
* ((£ь П1)) + ((5г, П2))	П1) + (5г» Пг)-
Преобразуя приведенное выше определение, мы утверждаем, что для изоморфных пространств с изоморфизмом Т, Dt = X, Rt = У, существует Г-1. А вследствие линейности Т и Т-1 отображение Т сохраняет свойства векторного сложения и умножения на скаляр, т. е. если и х2 соответствуют уг и у2, то у\ + у2 соответствует Х\ + х2, а аух соответствует а^. Кроме того, если X изоморфно У, а У изоморфно Z, то X изоморфно Z.
В качестве упражнений мы предлагаем читателю самому убедиться в правильности следующих предложений:
(1)	Если X и Y изоморфны и конечномерны, то dim X = dim У.
(2)	Если dim X = dim У < оо, то X и У изоморфны.
(3)	Если X и У изоморфны с изоморфизмом Т, а М — некоторое линейное многообразие в X, то Т (М) — линейное многообразие в У. Более того, каждое линейное многообразие N из У имеет вид N = Т (Af), где М — некоторое единственное линейное многообразие из X.
Теперь, после того как мы договорились считать идентичными любые два изоморфных линейных пространства, естественно встает вопрос об «эквивалентности» метрических пространств. Вспоминая, что метрическое пространство — это просто множество X с определенной в нем метрикой р, и поступая аналогично тому, как мы поступали с линейными пространствами, мы убедимся в том, что изоморфизмами «метрических пространств» должны быть изометрии (см. определение; II из § 2.1). Точнее говоря, мы называем метрические пространства {X, рх} и {У, р2} изометрическими, если существует некоторое (необходимо) взаимно однозначное отображение Т пространства X в пространство У такое, что
Р1 (*1. х2) = р2 (Тх2, Тх2),
каковы бы ни были xl9 х2 ЕЕ X. Ясно, что если пространства X и У изометричны, то изометрия Т переводит любое метрическое свойство пространства X в аналогичное свойство пространства У, и обратно. Чтобы привести лишь один пример (но типичный), покажем, что У полно, если полно X. Доказательство этого утверждения несложно. Если {уп} — некоторая последовательность Коши, то из-за взаимной однозначности и сюръективности Т существует единственная последовательность {хп} из X, для которой Тхп = уп. Но так как Т — изометрия, то последовательность {.тп} в пространстве X — это последовательность Коши. Поэтому хп —> х из X, и равенство
р2 (Уп, Тх) = Pi (хн, х) показывает, что уи Тх Е Y.
Мы советуем читателю самому показать, что изометрия сохраняет свойства замкнутости или открытости и другие метриче-ческие свойства *).
Рассмотрим теперь пару банаховых пространств X и Y. В каком случае их можно считать эквивалентными? Поскольку каждое из них еще и линейное пространство, то нам нужно, чтобы X и Y были изоморфными в качестве таковых. Кроме того, каждое из них еще и метрическое пространство. Поэтому нужно, чтобы X и Y были и изометрическими, но так как метрическая структура банахова пространства но вполне независима от его структуры как линейного пространства (условия ||Хх|| -- |Х|*||х|| и ||х
+ ||У|| связывают между собой, например, понятия расстояния, умножения на скаляр и сложения), то нам нужно потребовать, чтобы X и Y были изометричны относительно того же отображения, которое устанавливает и их изоморфность. Другими словами, мы условимся считать банаховы пространства X и Y идентичными, если существует некоторый изометрический изоморфизм Г, отображающий X на К, или, более подробно, взаимно однозначное линейное отображение X па У, для которого
II *i — т2|| --- || Tty — 7X211.
каковы бы ни были хг и х2 ЕЕ X. Беглый обзор определений банахова пространства показывает, что такое отображение Т действительно сохраняет структуру банаховых пространств X и У, и наше интуитивное представление об эквивалентности банаховых пространств находит свое отображение в понятии изометрического изоморфизма **).
Наконец, рассмотрим случай двух гильбертовых пространств X и У. Естественно, что мы не решились бы отождествлять между собой пространства X и У, если бы они не считались идентичными в качестве банаховых пространств (т. е. не были бы изометрически изоморфными). Но в то же время тождество
<*. у> == 1/4 {||х + у|Р - II* - г/ll2 + II* иГ - II* - г/П показывает, что любое линейное отображение, сохраняющее норму, автоматически сохраняет и скалярное произведение. А так как вся внутренняя структура гильбертова пространства определяется его скалярным произведением, то становится ясным, в чем состоит «изоморфизм гильбертовых пространств». Два гильбертовых пространства X и У со скалярными произведениями <,>х и <,>2 могут считаться идентичными, если существует такое
*) Замкнутость и открытость — это, вообще говоря, топологические свойства. (Прим, ред.)
••) Два изометрически изоморфных банаховых пространства обычно называют конгрувнтными.
взаимно однозначное отображение Т пространства X на У, для которого
х2\ = \ Тхц Тх2х/2, хг, х2 ЕЕ X, или (хотя с первого взгляда это условие и кажется более слабым) klk = II Мг-
Короче говоря, гильбертовы пространства X и У эквивалентны, если они изометрически изоморфны.
Подводя итоги, мы можем сказать, что если обобщить понятие изоморфности так, чтобы оно обозначало идентичность структур, то изоморфизмом метрических пространств является изометрия, изоморфизмом линейных пространств — несингулярное (сюръективное) линейное преобразование, а изоморфизмом банаховых (гильбертовых) пространств — несингулярное (сюръективное) линейное преобразование, обладающее одновременно свойствами изометрии. Перейдем теперь к некоторым примерам использования понятий этого параграфа. Дополнительные примеры можно найти среди упражнений.
Пример 8. Напомним, что два вещественных (или комплексных) полинома р (t) а0 Ч art + ... 4-	и q (t) —
— Ро + Pi^ 4' ••• 4- Pn-U71"1 называются равными в том и только в том случае, когда	i — 0, 1, ..., п — 1. Таким образом,
преобразование 7, отображающее р в n-ку вещественных (комплексных) чисел (а0, ах, ..., an-i), вполне определено и является взаимно однозначным отображением пространства вещественных (комплексных) полиномов (п — 1)-й степени в линейное пространство Нп (Сп) вещественных (комплексных) n-ок. Преобразование Т линейно и сюръективно, так что пространство Рп вещественных (комплексных) полиномов степени не выше (п — 1)-й изоморфно Rn (Сп).
Пример 9. Пусть Н — некоторое сепарабельное гильбертово пространство, и пусть	— некоторая ортонормальная по-
следовательность в П (см. приложение 2). Мы уже видели, что каждое х из II может быть представлено в виде оо
•Г ~ 71—-1
где ап = <х, еп> и I ап |2 = ||*||2- Более того, если у = = ^^=1 Pn^n—это другой вектор из II, то для того, чтобы х=у, необходимо и достаточно (в силу линейной независимости е,) равенство ал -- 0n, п =-= 1, 2, ... Таким образом, х из 11 однозначно определяет вектор (ап а2» ...) из /2, и нетрудно убедиться
в том, что это соответствие линейно и взаимно однозначно. В то же время, если (alt a2, ...) — произвольный вектор из /2» то РЯД ai^i сходится в Н (так как последовательность усеченных сумм есть последовательность Коши). Таким образом, мы можем заключить, что пространство Н изоморфно /2. Равенство Парсеваля Sn | <х, еп) | 2 =- ||х||2 показывает к тому же, что это соответствие еще и изометрическое. Поэтому каждое сепарабельное гильбертово пространство изометрически изоморфно (конгруэнтно) пространству /2-
Упражнения
1.	Докажите, что ядро каждого линейного преобразования замкнуто.
2.	Приведите примеры неограниченных операторов с замкнутыми и незамкнутыми ядрами.
Указание. Постройте какое-нибудь декартово произведение замкнутых (незамкнутых) линейных пространств. Определите линейное преобразование на произведении.
3.	Рассмотрите линейное пространство R2. Убедитесь, что каждый из операторов, выписанных ниже, является линейным и накрывает R2.
(а)	7\ [(gj, £2)1 = (a£i’l а^)» где а — некоторое вещественное число. Результат воздействия 7\ заключается в умножении каждого вектора из R2 на скаляр а.
(б)	— (?2, £i)- Т2 отражает R2 относительно диагонали хх - х2.
(в)	Т3 [(^, |2)1 " (L 0). Т3 проектирует R2 на ОСЬ Хр
(г)	Т4 Kli, £2)] = (0, g2). Т4 проектирует R2 на ось х2.
Покажите, что этим операторам соответствуют следующие матрицы:
'а 0 1
.0 aj ’
(а)
'0 Г
1 oj ’
(б)
4	0 го	о
0	0 J ’	0	1
(В)	(Г)
4.	Пусть N — произвольное нормированное линейное пространство. Покажите, что всякое линейное преобразование некоторого конечномерного пространства X в N непрерывно.
Указание. Выберем в X некоторый базис е2, ..., еп}. Произвольный вектор х из X может быть однозначно записан в виде
Х — а1А + а2е2 + ••• +
Отсюда мы найдем, что А (х) = avA (ei) + а2Л (е2) + ... + ап4 (еп). Воспользуйтесь тем фактом, что сходимость в X обязательно должна быть покоординатной.
5.	Пусть N — некоторое конечномерное линейное пространство размерностью п > 0, и пусть {q, е2, ..., еп} — один из базисов этого пространства. Каждый вектор из N можно однозначно представить в виде
х =	+ а2е2 + ... + апеп.
Если Т — это взаимно однозначное линейное преобразование W на (п), задаваемое условием Т (х) = (ах, а2, ..., с^), то в силу результата упражнения 4 преобразование Т~1 непрерывно. Докажите, что непрерывно и преобразование Т.
Указание. Если Т не] непрерывно, то для некоторого е > 0 найдется такая последовательность {уп} из N, что уп -> 0, а ЦТ (уп)|| > е. Обозначим через хп вектор уп ЦТ (i/n) ||. Ясно, что zn -> 0 и что ЦТ (zn) || = 1. Подмножество, состоящее из всех векторов единичной нормы, компактно (см. приложение 1), и у последовательности {Т (zn)} найдется подпоследовательность, сходящаяся к некоторому вектору единичной нормы. Теперь остается лишь воспользоваться непрерывностью преобразования Т“1.
6.	Обозначим в этом упражнении через Н некоторое гильбертово пространство, в котором заданы замкнутые подпространства {Afj}, служащие областями значений соответствующих ортогональных проекций Докажите следующие утверждения:
(а)	Произведение PiP2 является проекцией тогда и только тогда, когда РХР2 = Р2Рг. Областью значений проекции Р±Р2 служит замкнутое подпространство Мх П ^2*
(б)	Два подпространства Мх и М2 ортогональны тогда и только тогда, когда РХР2 = Р2РХ = 0.
(в)	Любая конечная сумма Р = Рг + ... 4-Рп является проекцией в том и только в том случае, когда PtPj = 0, i =/= /, т. е. когда подпространства {М^. i = 1, ..., п} попарно ортогональны. Область значений проекции Р — это подпространство М ~ Мх ф ... ф Мп.
(г)	Разность Р = PY — Р2 двух проекций может быть проекцией в том и только в том случае, когда М2 CZ Мх. Область значений проекции Р представляет собой ф М2.
7.	Линейное преобразование Т линейного пространства на другое линейное пространство Y является изоморфизмом тогда и только тогда, когда удовлетворяется одно из следующих эквивалентных условий:
(а)	Ядро NT преобразования Т состоит из одного 0.
(б)	Существует линейное преобразование Т пространства Y на X такое, что Т' Т п ТТ' являются тождественными операторами в X и Y соответственно.
(в)	Т (5) является базисом У, если только S =	— это некоторый
базис в X.
Докажите это.
8.	Напомним, что каждая функция f (z), аналитическая в круге | z | < 1, может быть разложена в ряд Тейлора
оо
/(г)=2«пл 1ч<1. о
Этот ряд равномерно сходится в каждом из замкнутых кругов | z | R <1. Обозначим через Н2 множество всех тех аналитических функций / (z), для которых их коэффициенты Тейлора квадратично-суммируемы:
оо
21»пР<~.
о
Докажите, что
(а)	Н2 — линейное пространство;
оо
(б)	</,g> = 2апьп (/=2a«zn’ f=^ibn^n)> о
(в)	преобразование, отображающее / (z) = anzn из Яа в последовательность (а0, аь ...), является изометрическим изоморфизмом, отображающим Н2 в 12. В частности, Н2 — это (сепарабельное) гильбертово пространство.
(г)	Постройте в Н2 некоторое полное ортонормальное множество.
9.	Пусть [л,	— некоторый замкнутый промежуток, а р (/) — произ-
вольное положительная функция, определенная на [я, Ь]. Тогда £2 (а» и) изометрически изоморфно Ь2 (0, 1). Докажите это. показав сначала, что / -* //ц — это изометрический изоморфизм, отображающий Ь2 (а, Ь; р) на Lz(a, b). Затем покажите, что отображение Т, где
(Т/) ($) =	У (а 4- (Ь - я) «*?), О < s < 1,
также является изометрическим изоморфизмом, отооражающим L2 (а, Ь) па L2 (0, 1).
10.	Система, символически показанная на рис. 2.10, я, осуществляет скалярнозначное умножение одного сигнала, зависящего от времени, на другой и описывается уравнениями
.	( а (О и (0.	* >
1 I 0,	t < to.
Какие условия нужно наложить на множитель а (/) для того, чтобы систему можно было рассматривать как некоторый оператор в L2 (т) или I (т) (в предположении, что /0 ЕЕ т)? Линеен ли этот оператор? Определите липшицеву норму этого оператора, если а (/) — t/V\ + /2,( t ЕЕ т, а пространство входных и выходных сигналов есть В (— оо, сю) (см. пример 7 из § 1.4).
Рис. 2.10. Три физические системы.
И. На рис. 2.10, б показана схема стандартного ЯС-контура с переменной емкостью С (t) = 1 + Z2, t ЕЕ [0, &]. При каких условиях эту систему можно рассматривать как линейный оператор в С (0, Ъ) или Ь2 (0, &), если выходным сигналом здесь считается напряжение на активном сопротивлении, входным — напряжение источника питания и если начальный заряд на емкости q (t0) полагается равным д°?
12. Система, показанная на рис. 2.10, в — это простая линия задержки • Другими словами, здесь х (t) = и (t — т). Для функционального пространства ограниченных синусоид, определенных на (— ею, оо), исследуйте линейность этой системы п определите норму оператора, ее описывающего.
2.3. Однородные системы первого порядка
В § 2.2 мы обратили особое внимание на преобразования, определенные в примерах 6 и 7. Это внимание вполне заслужено, поскольку эти два примера охватывают характеристики широкого класса систем. В оставшейся части этой главы мы отложим на время изучение общих свойств функций и пространств и сосредоточим внимание на изучении двух специфических классов систем, входящих в общий класс, очерченный в этих двух примерах.
Дифференциальные уравнения представляют собой классическое средство математического описания таких физических устройств, как электрические цепи, механизмы и систем]»! вообще. Это, безусловно, известно читателю. В более поздний период появление цифровых вычислительных машин в качестве активных элементов привело к широкому употреблению конечноразностных уравнений для целей математического моделирования. В связи с этим совершенно ясно, что материал *нескольких разделов, следующих ниже, представляет интерес и сам по себе. Переходя к изучению этого материала на настоящей стадии знакомства с общей теорией систем, мы получим также и двоякую возможность: с одной стороны, укрепить наше понимание теории преобразований и функциональных пространств, а с другой стороны, построить большое число физических примеров, к которым мы сможем обращаться в последующем.
В дифференциальном исчислении производная функции / GE С [а, Ы определяется как предел при h —>0 отношения
+	 М + *е|«,Ц.
Этот предел называется, соответственно, правой, производной/ в точке t, если h > 0, и левой производной, если h < 0. Если же эти два предела равны, то мы говорим, что у / есть производная в точке L В последующем для обозначения производной / в точке t мы на равных правах будем использовать символы / (0, (df/dt) (0 и (d/dt) / (0.
При исчислении конечных разностей мы рассматриваем непосредственно частное и не устремляем h к нулю. В этом случае мы определяем разностный оператор, обозначаемый через Дл, с помощью соотношения
А„/(0 =	+	, t, t + /»Е [а, Ь].	(1)
Нетрудно показать, что оператор линеен. Приведем четыре важных свойства этого оператора:
= cbhf (0,	(2)
Ah[/(t)+ g(01 = Ah/(Z) + Ahg(i),	(3)
А,. [/ (0 g (01 = [A/J (Ok(0 + f(t + h)-[&hg (01.	(4)
f (0 ~l g(O\/(Q-/(')\g(')
hL*(0 J g(t)g(t + h) •	[)
В приложениях, относящихся к динамическим системам, дей-ствующим непрерывно, т. е. к системам, в которых независимая
переменная t непрерывна, сигналы и реакции на них описываются функциями времени. В системах же, действующих дискретно (импульсных или цифровых), сигналы описываются временными последовательностями либо принимают значения лишь в дискретные моменты времени. Определение разностного оператора на временных рядах очевидно.
Пусть т — некоторый вещественный временной интервал, содержащий подмножество а ={*о> Ь» •••>	•••} такое, что > О*
Если функция / (/) определена на т, то / определено и на o', и образом / (о) является множество точек {/(£&)}. Это множество представляет собой временной ряд / = (/ (/0), / Gi)» •••♦ / (fy)» •••)• Разностный оператор можно определить на этой последовательности. В самом деле, положим hk —	— tk, тогда
- v1	(6)
После такой модификации определения разностного оператора мы можем распространить все приведенные выше формулы и на случай временных последовательностей.
В оставшейся части этого параграфа мы будем заниматься теорией систем, описываемых дифференциальными или конечноразностными уравнениями первого порядка следующего вида:
=	(0 + ---«1п(0хп(0,
:	:	:	t е т
dx (t)
= ап1 (0 xL (t) + . . . + апп (t) хп (0
в непрерывном случае и
А*У1 GO = an (М Уг (*/с) + • • • + Яш G/c) Уп (М>
ЬкУп (М = «м У1 (tk) + . . . + ann (tk) yntk
в дискретном случае. Здесь мы пользуемся терминами «дискретный случай» и «непрерывный случай» для того, чтобы определить характер независимой переменной, действующей в системе, а не для того, чтобы ограничить каким-либо образом непрерывность коэффициентов axj и функций Xj.
Системы, описываемые уравнениями первого порядка такого типа, называются нормальными. В упражнениях к этой главе и в приложении 4 показывается, что к нормальному виду с помощью стандартной и легко выполнимой замены переменных можно привести дифференциальные и конечноразностные уравнения гораздо более общего типа. Поэтому результаты, полученные при
изучении нормальных систем, можно непосредственно перенести на более широкий класс систем.
В последующем независимую переменную, какова бы ни была ее физическая сущность, мы станем называть «временем» и обозначать через t или tk. В общем случае коэффициенты ац могут быть функциями времени. В этом случае нормальная система называется нестационарной (или с переменными параметрами). Если же оказывается, что коэффициенты а^ от времени не зависят, то нормальную систему называют стационарной (или системой с постоянными параметрами).
При построении теории систем нормального вида существенную пользу приносит введение векторно-матричных обозначений. Помимо обычных векторно-матричных операций в Rn нам потребуется ввести производную от матрицы, конечную разность матриц, интеграл матрицы и т. п. Эти определения имеют совершенно естественный вид. Пусть А = [ai7l — некоторая нестационарная матрица. Тогда, по определению,
т- =	(MJ.
Аналогичным образом вводятся определения интеграла и суммы матриц:
t	i
A (s) ds = aij (s) ds] , о	о
n	n
2 (^к)= [ 2 av (mJ • fc=l	R=1
Дифференциальное и конечноразностное матричные исчисления совершенно аналогичны соответствующим исчислениям для вещественных функций, хотя здесь и имеется несколько важных отличий. Из только что приведенных определений следует, что если А (0 и В (t) — две квадратные матрицы, зависящие от непрерывного времени, а С (tk) и D (tk) — квадратные матрицы, зависящие от дискретного времени, то
Г л । А? /Л] (О । dB (t)
~dt + В = "ST" + "dF" ’
Д/с [С (М + D (ffc)] = A/jC (tk) + &kD (tk),
А(ДВ)(0=	+	8
Ait \C (t„) D (Ml = (AkC (Ml D (tk) 4- C (Mi) [A.D (Mb (8)
Но так как умножение матриц в общем случае не коммутативно, здесь становится важным порядок сомножителей. Например, если у матрицы A (t) есть обратная A"1 (t), то
47=°=4 <Л-1Л) = А +Л-1 м Чг и, значит,
= - А'1 (0	А-1 (0.	(9)
Точно так же, если матрица С (t^) не вырождена ни при ни при ^Лг+1» то
о = д^ дне чм с’(М1 - [Д^с-1 (Ml с со + C4W
и, следовательно,
дкс-1 со = с-1 (^0 [ д,с (Ml с-1 (М.	(10)
Эти формулы аналогичны формуле [dx~l!dt) = — ж-2 (dxldt) элементарного анализа, но не могут быть упрощены до этого вида, если только матрица А не коммутирует, скажем, с матрицей dAldt.
Теоремы существования и единственности для дифференциальных систем. Рассмотрим сначала системы, поведение которых в момент времени G г ::= [а, Ы описывается дифференциальным уравнением
^- = A(t)y(0;	y{t0)=l, 0toer.	(11)
Здесь у = (ух, ..., yn), g = (gp ..., gn), а через А = [ai7] обозначена квадратная матрица n-го порядка. Нам необходимо ввести дополнительные предположения относительно свойств элементов aij матрицы А, и для начала мы предположим, что ai;- GE С (т) — классу функций, непрерывных на т. В этом случае мы будем называть матрицу А непрерывной. Интегрируя обе части уравнения (И), мы можем представить его в эквивалентной форме:
t
y(t)=l + \A(s)y(s)ds, t(=r.	(12)
G
Всякий вектор, удовлетворяющий любому из этих уравнений, называется решением уравнения (или траекторией системы). Значение решения в точке ГЕ г при условии, что у (tQ) = £, мы будем обозначать через у (t, £, t0),
ТеоремаЛ. Пусть матрица А непрерывна на т. Тогда для каждых tQ, t ЕЕ т и ||£|| < оо существует единственное решение уравнения (И).
< Доказательство, Для того чтобы упростить выкладки, договоримся обозначать через |(	|| любую норму, определенную на
Яп, а через ||А (£)] — соответствующую норму матрицы A (t), рассматриваемой как некоторое отображение на Rn (см. пример 5 из § 2.2) Пространство X считаем произведением {С (т)]п.
Познакомимся теперь с одним методом, часто используемым для доказательства теорем существования и единственности,— со знаменитым и фундаментальным методом последовательных приближений, принадлежащим Пикару. Для этого рассмотрим последовательность (векторных) функций, индуктивно определенных следующим образом:
Уо(0 = В, Моет,
t
J/1 (0 - В 14 Л (*)y»(s)ds, to
:	;	аз)
f
Уп+1 (0 = В + $ л (s) уп (s) ds, п = 0, 1, 2, . . ., to
где мы воздержались (временно) от использования развернутого обозначения у (f; £, t0). Нижние индексы в уравнениях (13) указывают на различные этапы индуктивного процесса вычисления (а не на различные компоненты вектора). Такое двойное использование индексов практикуется на протяжении всего этого параграфа, если не возникает опасность их смешения.
Нам надо показать, что последовательность векторных функций {yj} равномерно сходится к некоторой функции у (£) при всех t €= т. Если это удастся, то нам придется доказать, что функция У (0 удовлетворяет уравнению (12), а затем уже — что функция у (t) является единственным решением этого уравнения. Легко показать, что каждая из итераций Пикара уп представляет собой некоторый элемент пространства X, которое в качестве произведения конечного числа банаховых пространств само является банаховым. Поэтому, если бы мы могли показать, что итерации Пикара образуют последовательность Коши, то полнота пространства X гарантировала бы нам, что уа^уЕЕХ.
Из интегральных рекуррентных соотношений (13) мы находим
t
УппЩ — M0 = ^(s)|y„(s)- yn-i(s)\ds, п>1.	(14)
to
Введем для удобства обозначение Т siipT||/l (т)|| и определим Дп+i (0 = || Уп+i (О Уп (О II-
Тогда, вычисляя норму обеих сторон равенства (14) и используя легко проверяемое соотношение t	t
|$4(s)y (s)ds[<$||4(s)|| • ||j/(s)||ds, t0	1q
мы найдем, что
t Д» (Z)< A $ Дк_! (s) ds. to
Однако для к = 1 из уравнения (13) следует, что t
Го
С помощью несложного процесса дедукции мы найдем из уравнения (14)
Дпн (0 = I Упп (0 - Уп (/) И< и(* ~ fo)r' « = 0,1,2,... (15)
Располагая теперь этим неравенством, мы можем показать, что последовательность {уп} является последовательностью Коши по отношению к выбранной норме. Доказательство этого факта выглядит следующим образом:
р—1
Уп+р (О Уп (О = 2 [.Уп+i+i (0 Уп+j (0L
2=0
что позволяет самому читателю убедиться в справедливости для t х следующих неравенств:
р—1	р—1	п+У+1
Ц</п+р (О Уп (0 || S ^n+;+i (0	2 НИ I /^| 1
2=0	2=0	' ~ '
||^||[Л«-/о)]п+1 у1 [Л(е—*>)]' <-Н11^(*-'’)Г+1рХп1Т^ /М
----(iT+iji---Д /!	(п + 1)| — ехР 1-1 (« - i0)l-
(16)
Таким образом, мы доказали сходимость рассматриваемой последовательности на любом конечном интервале, а это позволяет заключить, что уп (0 -^у (0 при п —>оо. Остается лишь показать, что у (0 единственно и, конечно, что у удовлетворяет уравнениям (11) или (12).
Предположим, что, на самом деле, уравнению (11) удовлетворяет некоторая функция z, т. е. что
= A (t) z (t), z(t0) = i, r0, zer.
Вычислим разность между z (0 и (п + 1)-й итерацией последовательности Коши, рассматривавшейся выше:
t	t
Z (0 — Уп+1 (О =$4 (S) [z (s) — yn (s)] ds = §4 (s) [z (s) — yn+1 (s)] ds+ to	t0
t
+ § 4 (s) [i/n+i (S) — yn(s)]ds, zer.
Тогда используя соотношения, полученные ранее, мы видим, что
IIZ (0 — Уп+1 (01|< $ || A(S) | • || z (s) — yn+l (s) || ds + J (t —t0) Дп+а. to
Теперь нам понадобится результат следующей леммы.
Лемма А. Если функция у G С (tQ, tf) и f ЕЕ Lx (f0, tf) удовлетворяют неравенству
t
| У (t) I < м [1 4- k $ IУ (О I • I/ (О I dt], t е= [f0, tf], to
то справедливо и неравенство
| у (Z) | < Af exp {fcdf 51/(01^}- *>*о-
I,
Пусть в рассматриваемом случае
М(0|1 = 1/(01,
И(0-Уп+1(011 = 1уЮ|.
M = ±=A(tf-t0)AMi(t). а
Тогда в силу только что сформулированной леммы
IIZ (О — Уп+1 (0II < A (tf — t0) Дп+2 exp {J || A (s) |]ds}.	(17)
to
Но так как Дп+2 ->0 при и ->оо, a {yn+1 (t)} сходится, то на основании неравенства (17) уп равномерно сходится к z. Заметим, что, по определению, z — это произвольное решение уравнения (И). Но последовательность {уп}, будучи последовательностью Коши, сходится всегда к единственному пределу. Поэтому z — это единственное решение уравнения (И), и итерации Пикара сходятся к этому решению.
В предыдущих рассуждениях мы упустили из виду два факта, про которые легко забыть, но которые необходимо выяснить, прежде чем двигаться дальше. Прежде всего, поскольку решение у €Е X непрерывно, уравнение (12) можно продифференцировать и получить из него уравнение (11), откуда следует, что dx/dt также принадлежат X. И вообще говоря, гладкость dxldt определяется гладкостью матрицы А. Кроме того, нам необходимо доказать лемму А, что совсем несложно.
Доказательство леммы. Умножим обе стороны первого неравенства на /(0 |:
t
|У (01 • (/(01<ЛГ |/(0|[1+Л$ |у(01 • I/(О|Л].
to
St
\у (t) f (0 I Л. Тогда предыдущее не-to
равенство цожно интерпретировать следующим образом:
у(0<л/|/(0| [1 +М01. или
Интегрируя обе части, находим t
In (1 +kv(t))<kM$ |/(0 |Л.
to
откуда
t	t
l+A:$|/(0y(O|^<exp[fcAf$|/(t)|d/]. to
Но в силу исходной гипотезы t
to
что в сочетании с предыдущим дает
t
\y(t)\<Mexp \кМ $|/(01 di.
Приведенный результат является всего лишь одним из обширного числа фактов, относящихся к проблеме существования решений задачи Коши (задачи с заданными начальными условиями). Действительно, предположения теоремы А гораздо сильнее того, что требуется, и в качестве примера типичных обобщений мы сформулируем еще две теоремы без доказательств.
Теорема Б. Пусть А — матрица, норма которой |р4|| 6=	(т). Тогда уравнению (И) удовлетворяет некоторая
единственная абсолютно непрерывная*) векторная функция у такая, что у (t0) = £.
Замечание 1. В теореме Б предполагается использование интеграла Лебега, а об уравнении (И) считается, что оно удовлетворяется на т почти всюду. Читатель с элементарными познаниями теории меры легко видоизменит предыдущее доказательство так, чтобы получить этот более общий результат. Важно специально отметить, что даже при нынешних довольно слабых условиях, наложенных в теореме Б на вид матрицы А, единственное решение у уравнения (11) по-прежнему остается элементом пространства X.
Для того чтобы указать на другую возможность обобщения, обозначим через р — (рх, ..., pR.) Л-мерный вектор параметров. Пусть А (/, р) есть некоторая функция t и р, определенная на (к + 1)-мерном пространстве т х v, где v — некоторая открытая шаровая окрестность вектора р0.
Т е о р е ма В. Если функция A (t, р) непрерывна по р и удовлетворяет условиям теоремы Б по t на т х v, то уравнение
(t; t,, t0, н) = А (*, н) У (*; £, <0. и).
у (*0; *0> и) = t, н) е т х и,
имеет единственное решение, непрерывное по всем параметрам рх, ..., pfc и t для любого tQ S т и р GE U.
В частности, параметрами р могут быть начальные условия, задаваемые в точке t0. Поэтому решение у (£; £, t0) должно быть непрерывным и по £. В самом деле, если {ик} есть некоторая последовательность параметров из U и ик —то решения уравнения (11) У (<; £, t0, uk) -+у (t; £, to, и).
Мы показали, что для каждого £ Ez Rn существует единственное решение уравнения (И). Обозначим через х множество всех таких решений и займемся исследованием его свойств. Ясно, что множество к представляет собой линейное пространство. (Читатель в качестве упражнения может доказать, что если yv у2 ЕЕ х, т. е.
*) Грубо говоря, это функция, представимая неопределенным интегралом некоторой функции из
являются решениями этого уравнения, а ах и а2 — произвольные скаляры, то вектор atyY + &2У2 Еп.)	.	•• г.
Теорема Г. П одпространство х является п-мерным.
Доказательство. Для того чтобы доказать n-мерность подпространства х, необходимо построить какое-нибудь множество линейно независимых векторов z/x, уп такое, что каждый вектор J/i Е х и любой г/ 6= х можно представить в виде линейной комбинации {yt}. Обозначим через {tj множество п линейно независимых постоянных векторов из пространства Rn. Тогда в соответствии с теоремой существования для любого /0Et найдется п однозначно определенных решений {уг Zo)} уравнения (И) таких, что z/i (Zo) = Доказательство того, что эти решения образуют базис подпространства х, мы начнем с того, что покажем, что векторы {у^ (/;	/0)} образуют линейно независимое множе-
ство в 7?п при каждом t ЕЕ т. Если бы это было не так, то необходимо нашлось бы п скаляров {cj, среди которых есть и ненулевые, таких, что по крайней мере при одном t ЕЕ: т
п
У (/ ) = 2 СгУг ’ Si’ *о) = 0. г=1
Однако определенная таким образом функция у является решением уравнения (И). Если у (f) = 0, то у (/) — 0 при всех t Е_- т, так как нулевой вектор удовлетворяет уравнению (И) и нулевым начальным условиям в точке f, а решение уравнения (И) при каждом начальном условии должно быть единственным. Но отсюда следует, что
п	п
У (^о) = 2 Ci^i (^0’ Si? *о) = 2 CiSi = 0, i=l	i=l
а это противоречит предположению о нелинейной независимости векторов Следовательно, множество {jZi (^; Si» М} линейно независимо при любых Е т.
Если же у (/; £, /) есть произвольное решение уравнения (11), определенное на т, то поскольку натягивают на себя все пространство возможных начальных условий, существуют (единственные) постоянные c-t такие, что
п
? = S <&•
i=l
Но функция
11
У (0 ~~ 2 ^i^i Sb ^о)
г=1
является решением уравнения (11) на т и принимает в точке t0 значение £, а значит, в силу единственности решений задачи Коши оно должно быть равно у (t; £, t0):
п
У ^о) = 2 с1Уь Go! Сь ^о)« г=1
Таким образом, каждое решение у уравнения (И) представимо в виде (единственной) линейной комбинации {^}, и, значит, множество {у{ (t)} образует базис пространства х.
Фундаментальные матрицы решений. Матрица Ф(0, каждый из п столбцов которой образует один из векторов некоторого базиса {z/i (t\	f0)} пространства х, называется фундаменталь-
ной матрицей решений уравнения (И). Матрицу Ф (t) можно называть также фундаментальной матрицей ядра х. Простая проверка легко показывает, что
Ф (0 А (0 Ф (0, Ф (f0) = Z при всех t е т. (18) Так выглядит матричное дифференциальное уравнение, соответствующее уравнению (И), определенному на т. Здесь через Z обозначена матрица, образованная векторами начальных условий играющих здесь роль столбцов. Если соответствуют обычному координатному базису в Rn, то Z = /.
В теории систем фундаментальные матрицы играют важную роль. Для последующих ссылок мы отметим сейчас некоторые из их основных свойств.
Теорема Д. Обозначим через |Ф (0| определитель фундаментальной матрицы Ф (0 решений уравнения (11). Тогда
п
-*-|ф(0| = [3 а«(0]|Ф(0| г=1
или, в интегральной форме,
t п
| Ф (<) | = | ф (<0) ехр	2 аи («)ds} •
U 1=1 «п
[С величиной 2ji=1 аи (0 в теории матриц сталкиваются очень часто, и поэтому для нее ввели специальное название. Ее называют следом матрицы А (0 и обозначают через tr (А).]
Доказательство. Доказательство, которое мы предлагаем построить читателю, базируется на двух следующих фактах:
(1) d \ Ф (0 | /dt представляет собой сумму определителей, образованных в результате замены элементов одной строки | Ф (01 на их производные.
(2) Столбцы Ф (0 представляют собой решения уравнения (11).
Доказательство состоит в упрощении определителей, полученных на первом этапе, с помощью (2).
Следствие. Для того чтобы матрица Ф (0 была фундаментальной матрицей решений уравнения (11), необходимо и достаточно, чтобы (1) Ф (t) = A (t) Ф (0 при всех t GF. т;
(2) | Ф (0 | =/= 0 при всех t е т.
И необходимость, и достаточность выписанных здесь условий (1) и (2) непосредственно вытекают из определения и теоремы Д. Матрица, вектор-столбцы которой являются линейно независимыми элементами пространства [С (т)]п, может иметь определитель, тождественно равный нулю на промежутке т. Например, это справедливо для матрицы
t t2
В(/)= о о
на любом вещественном интервале т. Смысл сформулированного следствия как раз и состоит в том, что равенство определителя нулю невозможно, если эти векторы представляют собой решения уравнения (И).
Теорема Е. Если Ф (0 — некоторая фундаментальная матрица решений уравнения (11), а Н — произвольная невырожденная матрица, то Ф (0Я есть новая фундаментальная матрица решений уравнения (11). Более того, каждая фундаментальная матрица решений уравнения (И) может быть представлена в виде такого произведения с некоторой невырожденной матрицей Н.
Доказательство, Если Ф (0 — некоторая фундаментальная матрица решений уравнения (11), а Я — произвольная постоянная невырожденная матрица, то
[ф (О Я1 = ф (0 н = а (0 ф (0 н = а (0 [ф (Z) Я], t е т,
и, следовательно, матрица Ф (0Я есть решение матричного уравнения (11). Но так как
|(Ф (0 Я] | = |Ф (0|.|Я| ^0,
то матрица Ф (0 Я и должна быть фундаментальной.
Обратно, если Фх (0 и Ф2 (0 — две фундаментальные матрицы, то теорема утверждает, что существует некоторая постоянная невырожденная матрица Я такая, что Ф2 (0 = Фх (0 Я. Для того чтобы показать это, положим Ф'1 (0 Ф2 (0 = Т (0. Тогда Ф2 (0 = фг (0	(0. Дифференцирование этого равенства дает
Фа(0 = Фх(0У(О+ФхТ(0.
Это уравнение, используя (11), можно переписать в виде
А (0 Ф2 (0 =- Ф, (/) 4 (0 4 А (0 Ф, (0 т (0.
Но так как Ф2 (0 = 4^ (0 Тх (0, то
ФД0 Т(0 = О, а это значит, что 4* (0 - 0, и, следовательно, Т (0 = II — const. К тому же, поскольку Фх (0 и Ф2 (/) невырождены, то невырожденной должна быть и матрица II.
Замечание 2. Если потребовать только, чтобы Ф2 (0 была некоторой матрицей решений, то Я может оказаться и вырожденной. Отметим еще, что если Ф (0 есть некоторая фундаментальная матрица решений уравнения (И), а Я — некоторая постоянная невырожденная матрица, то матрица ЯФ (0, вообще говоря, не является фундаментальной матрицей этого уравнения.
Наконец, две различные однородные системы не могут иметь одинаковых фундаментальных матриц, поскольку из уравнения (И) следует, что А (0 = Ф (0 Ф"1 (0. Таким образом, Ф (0 однозначно определяет А (0, хотя обратное и неверно. Выше нам было удобно избегать развернутых обозначений Ф (0 Z, t0) для фундаментальной матрицы, удовлетворяющей начальному условию Ф (0; Z, t0) Z. В этом разделе мы обратим особое внимание на свойства фундаментальной матрицы, соответствующей координатному базису в пространстве начальных состояний.
Определение А. Обозначим через Ф (0 t0) фундаментальную матрицу решений уравнения (И), удовлетворяющую условию Ф (0, 0) = I. Эту матрицу мы будем называть матрицей перехода для системы (И).
Термин «матрица перехода» объясняется тем, что
у (0 £, 0) = Ф(0 t0)^ ter.	(19)
Таким образом, матрица Ф (0 t0) отображает начальные условия У (0) — £ в текущее состояние системы у (0 £, t0) для каждого t €= т. Кроме того, легко видеть, что если Фх (0 — фундаментальная матрица, удовлетворяющая условию Фх (0) — Я, то
Фх (0 = Ф (/, t0) И.	(20)
Замечание 3. Важное значение имеют два следующих свойства матриц перехода:
Ф (0, 0) Ф (0, 0) = Ф (0, 0), 0, 0, 0 е т, (21) Ф (0, 0)-1 - Ф (0, 0).
Доказательство справедливости этих утверждений мы оставляем читателю.
Замечание 4. Уравнение (19) можно интерпретировать двумя способами, каждый из которых может оказаться полезным. Во-первых, его можно считать характеризующим линейное преобразование Ф: Rn ->х, где (Ф£) (/) = у {t\ £, Zo), по мере того как t пробегает т, а во-вторых, его можно рассматривать как параметризованное множество {Ф (Z, £0):	преобразований, оп-
ределенных на Rn.
Пример. В качестве иллюстрации к предшествующему материалу рассмотрим линейную однородную систему	•<
xf (t) -= A (t) х (О,
где А (0 — матрица *)
4(0 =
-2 - ef '
.е~‘	1 .
Непосредственной подстановкой читатель может убедиться в том, что этому уравнению удовлетворяют два вектора:
г e^cost 1	г — e^sin Г|
= I sin < J ’	= L е* cos t J ‘
А так как фх (0) = col [1, 0] и ф2 (0) = col [0, 1] **), то мы приходим к выводу, что матрица Ф (£), вектор-столбцами которой служат фх и ф2, удовлетворяет условиям
Ф(0 - А (О Ф (О, Ф(0) - 1.
Если матрица А постоянна, то Ф (Z, tQ) можно найти, подставляя в выражение для Ф (Z) разность t—t0 вместо t. В нашем случае матрица А непостоянна, и нам придется пойти на дополнительные хитрости. Опираясь на тождество Ф (f, tn) Ф 0) — Ф (t, 0), мы найдем, что Ф (/, /0) = Ф (Z, 0) Ф”1 (/0, 0). Нетрудно убедиться в том, что если
re2t cos t
Ф(г,О) = t . , '	' I sin t
— e^sinT e* cost.
то
г e~2t cos t
е~* sin t e-'cost
*) Пример заимствован из работы [А.95], стр. 343.
**) Так автор обозначает вёктор-столбцы с координатами 1 и 0 или 0 и 1 соответственно. (Прим, ред.)
Отсюда непосредственным вычислением найдем, что
Ф(Мо) =
'ё* cos t е* sin t
— е** sin t "I г	е~*° cos t0
e* cosfj * I — e”2f°sinf0
e_/osin Zo cos tQ
re(-2/-2Zo)COS (t — Zo)
Le(r2fo)sin (t — tQ)
— e<2*-'o)sin (t — f0)"l £<*-*•) cos (t — e0) J
Упражнения
1.	Обозначим через f (t) функцию Л”1 [/ (/) — f (t — Л)]. Покажите, что уравнения (4) и (5) сохраняют свою силу после замены Д^ на V^.
2.	Пусть Eh — оператор сдвига: Eh f (t) = f (t + h). Покажите, что Д/i = h~' (Eh - I), Vh = h-i (I - Eh) и Ah = Vh.
3.	Определяя по индукции целые степени Дл и Eh (например, Д£ / (t) = Ah [A”-1 / (()]). покажите, что Д£ = h~3 (E3h — 3E% + 3Eh — I).
4.	Пользуясь обозначением (jj) = nV [(fc — n)l fc|], покажите, что если п — некоторое положительное целое, то
Д^(0 = Л-п 2 Q(-l)n-^y(t).
Указание. Воспользуйтесь формулой бинома Ньютона.
5.	Пусть f (t) = с1, где с — некоторое положительное вещественное число. Воспользуйтесь результатом упражнения 4 для того, чтобы показать, что
Д£с« = Ъгпс1

Отметьте, что эта сумма представляет собой развернутое выражение для (<Л — 1)п и что, следовательно, предыдущий результат можно переписать в виде
t	t
6.	Проверьте, что | А (з) у (s) ds | < || A (s) || • || у (s) ||. 6	о
Указание. Воспользуйтесь нормами из уравнения (4) для доказательства частного случая, а также фактом эквивалентности всех норм, определенных на конечномерных пространствах.
7.	Завершите доказательство теоремы Д и ее следствия. Убедитесь в справедливости замечания 2.
8.	Рассмотрим матричное дифференциальное уравнение
Х =
L2
У
Х = АХ.
Покажите, что = col (—to\ <0^) и х2 = col (е3^ f°^), е3^ <0Ь являются решениями этого дифференциального уравнения. Покажите также, что
Ф (/, Ч =
е-0-М	e3(f-fe)“
е-(*-М e3(f-fe)
есть фундаментальная матрица решений этого уравнения.
Теоремы существования и единственности траекторий дискретной нормальной системы. Интересно отметить, что все результаты предыдущего раздела, без каких-либо исключений, находят себе эквивалент в теории дискретных нормальных систем. В этом разделе мы строго сформулируем и докажем наиболее важные из этих параллельных утверждений. В начале этой главы мы уже говорили о том, что разностный оператор Д можно определить как оператор, действующий на функцию / (f), tfEiX, либо как оператор, действующий на временной ряд / (tk), tk€E<j. Для большей ясности в этом разделе мы будем говорить лишь о разностных операторах в пространствах временных последовательностей.
Линейная нормальная дискретная система описывается уравнением
Д/с У (h) — A (tk) у (tk); у0 (t0) — £, tk е tf»
(22)
представляющим собой, по сути дела, некоторое рекуррентное соотношение. Действительно, если вспомнить определение оператора Дк, то станет ясно, что уравнение (22) можно переписать в другом виде:
У (^♦i)	1-^ 4~ hkA (Ml У (М» У (М —	(23)
В результате мы получили рекуррентную формулу для вычисления последовательности {у (М), Л = О, 1,... На самом деле многие авторы даже предпочитают это второе выражение в качестве основной формы описания дискретной линейной системы. Наше исследование таких систем мы начнем с доказательства следующей теоремы.
Теорема Ж. Пусть A (tk) — квадратная матрица порядка п, определенная для = {£0> М •••» М •••}• Тогда существует единственная последовательность вектор-столбцов {У (М}> удовлетворяющая уравнению (22).
Доказательство. Определим векторы у (tk) следующим образом. Пусть
V («•) =>о-
Тогда, поскольку у (/к+1) = [Z + hkA (/k)l у (/k), то последовательность
У1 = У (*х) = I/ + h0A (t0)]y0,
У2 = И + М = IZ + htA (rj] [Z + h0A («о)]уо
определяет решение, удовлетворяющее условиям теоремы. Для .доказательству единстренности предположим, что условиям теоремы удовлетворяет и последовательность {zfc}. Но тогда
zo ~ Уо»
Z1 = [Z + М (1о)]Уо = У1,
2П=	. . .	= Уп»
и, значит, эти последовательности идентичны, а решение уравнения единственно. Читатель, без сомнения, согласится, что приведенное доказательство много проще доказательства аналогичной теоремы для дифференциального уравнения.
Замечание 5. Если A (tk, р,) — некоторая последовательность • квадратных матриц, каждая из которых непрерывна относительно вектора р = (р1? ..., рй) при любом	то решение у (tk,
Уо» ^о» И) уравнения (22) непрерывно относительно р. В самом деле, для каждого tk: у (tk; у0, /0, р) есть конечное произведение матриц, каждая из которых непрерывна по р и, следовательно, может дифференцироваться по р по стандартным правилам дифференцирования матриц.
Теорема 3. Пространство н решений уравнения (22) п-мерно. Если матрицы {[/ + hkA (/fc)J: tk^a} невырождены, то любой базис {фД из к порождает векторы {ф; (^)}, линейно независимые при всех tk GE о.
Доказательство. Мы уже убедились в том, что уравнение (22) имеет для каждого начального условия у (t0) = £° в точности одно решение, каково бы ни было £° е Rn- Выберем в качестве базисного множества единственные решения ф1 (tk), ..., фп (tk), удовлетворяющие начальным условиям ф^ (t0) = е\ где {ej} — координатный базис пространства Rn. В соответствии с результатом теоремы Ж базис {ф; (^)} вполне определен. Предположим теперь, что при некотором tk GE o' векторы, составляющие это мно-- жествр^ линейно зависимы. Другими словами, пусть найдется такой набор скаляров ..., ап), среди которых не все равны нулю, что
•	«1Ф1 («») + ... + апфп (h) = 0-	(24)
Но так как все удовлетворяют уравнению (22), то
Ф^и) = (Z + Ak-M (tk_i)} ф/(«к-1), / = 1.....
и после подстановки этого выражения в уравнение (24) Мы получим
п	п
2	17 + Лк-хЛ (/к-х)] <р' (tk-х) = |7 + Лк-хЛ (Гк-х)1 2 Л-i) = 0.
j=l	J=1
Из условий теоремы следует, что матрица [I + hkA (/fc-x)l невырождена.
Поэтому
п	п
2 a-itf (М = о=» 2	(Z*-1) = °-
>=1	}=1
Повторяя этот процесс по индукции, мы придем в конце концов к тому, что
п	п
2 а,ф>(г0) = 2 «Л = °-j=l	j=l
Однако это невозможно, так как векторы ej линейно" независимы. Это противоречие доказывает линейную независимость ф*7 (ffc) при всех tk (Е о*.
Для того чтобы показать, что любое решение z (tk) уравнения (22) есть некоторая линейная комбинация {ф;}, заметим, что при любом tk решение z (tk) есть вектор принадлежащий Rn. А так как ф' (fk), ..., фп (tk) представляют собой п линейно независимых векторов из Rn, то они образуют базис Rn, и, следовательно, существуют скаляры ах, ..., ап такие, что
п
2 («к) = 2 ai4>} (tk)-;=i
Все входящие в это равенство последовательности удовлетворяют уравнению (22). Поэтому
п
z (^/с) =	+ Л/с-14 (£fc-i)l 2 (^-1) = [/ “И Л/с-14 (£fc_1)] 2 CLj(f* (tf/f-1),
Z=1 и, следовательно, n
2 (^/c-1) = 2	(^-1)’
;=i
По индукции нетрудно доказать, что во все предшествующие или
последующие моменты tk о 71
z(/R) = 2 а/И(М Для любого tk ЕЕ о, (25) ;=1
что и требовалось доказать.
Замечание 6. На первый взгляд кажется, что для условия невырожденности матрицы [I + hkA (fk)] при всех tk ЕЕ о* нет параллелей в теории нормальных непрерывных систем. Однако в теореме 3 из § 2.2 показано, что если hk^A (^)|| < 1, то [I 4-+ hkA (£jf)l невырождена. При малых hk это условие автоматически выполняется. В некотором нестрогом смысле в непрерывном случае роль h играет дифференциал dt. Условия теоремы А как раз и гарантируют тот факт, что ||4 (0||Л — бесконечно малая величина, и, значит, автоматически удовлетворяют гипотезе невырожденности матрицы [Z + </ф4|||. Мы упомянули здесь об этом в основном для того, чтобы освежить память читателя.
В качестве конкретного примера уравнения (25) предположим, что Ф (tk, t0) есть матрица, /-м столбцом которой служит вектор ф* (t0)ej. Тогда, если z (t0) = z°, то
z (tk) = Ф (tk, t0) z\	(26)
и матрица Ф (ffc, tQ) удовлетворяет матричному конечноразностному уравнению
Q = Л (tk) Ф (^, tQ), Ф (tQ, t0) = I. (27)
Свойства матрицы Ф (tk, t0). Без всякого сомнения, читатель интуитивно предполагает, что матричная последовательность Ф (tk, t0) и матричные функции Ф (tk, tj) должны играть в теории дискретных нормальных систем такую же роль, как и матрица перехода в теории непрерывных нормальных систем. В этом разделе мы попытаемся выяснить, до какой же степени это правильно. Отметим, что с помощью простого сдвига независимой переменной наши предыдущие рассуждения показали бы, что последовательность {Ф (tk, tj)} при любом	является решением
уравнения
А/сФ (tk, = A (tk) Ф (tk, t}y, Ф (t}, tj) = 1, tjG a. (28)
В частности, отсюда следует, что
Ф (0+i> tj) = (Z + hjA (£>)] Ф (tj, tj) — [Z + h/А (fj)l, tj <T.
(29) Отсюда нетрудно получить полугрупповое свойство:
Ф (h, tj) ®(t}, k) = Ф (tk, ti), tk, tj, ti e or. (30) В частности,
ф (tk, tj) = Ф"1 (tj, tk), tk tj e T.
(31)
Любая матрица Ф (tk), образованная линейно независимыми решениями уравнения (22), называется фундаментальной матрицей решений этого уравнения. В частности, матрицей перехода системы мы будем называть матрицу Ф (tk, i0).
Замечание 7. Если матрица [I + ^А (^)] вырождена при каком-то	то Ф (^, t0) вырождена при tk > и уравнение
(31)	справедливо лишь при tk, tj < Если любой из аргументов уравнения (30) превышает то это уравнение верно лишь при Так же как и в непрерывном случае, можно показать, что любую фундаментальную матрицу решений уравнения Ф (tk) можно представить в виде Ф (tk) — Ф (^, Q Я, где матрица Н невырождена.
Итог всем этим утверждениям подводится в следующей теореме.
Теорема И. Пусть A (tk) — некоторая квадратная матрица порядка п, определенная на о*, и пусть матрица [7 + + hkA (£fc)] невырождена на о*. Тогда матрица Ф (ffc, Q, удовлетворяющая уравнению (28), является единственной, невырожденной и удовлетворяет уравнениям (29) — (31). Единственное решение у (tk, £,£0) уравнения (22), удовлетворяющее условию У ^о) = может быть представлено в виде у (tk; £, tQ) = = ф (tK, t0) I.
Упражнения
9.	Рассмотрите дифференциальное уравнение второго порядка ^(0+p(')^-(0 + 9(0x(t) = 0-	(а)
Воспользуйтесь заменой переменных уг (t) = х (t) и у2 (t) = (dx/dt) (t) для того, чтобы свести уравнение (а) к эквивалентному виду
0	1 1 [уНО!
dt Lzmoj L—<?(*) — р(о г LmoJ *	u
Рассмотрите проблему задания начальных условий при этом преобразовании.
10.	Распространите результат упражнения 9 на случай уравнения dnx (t) dxn~x (t)
—^ + an(t)-^rr' + ...+«n(fl*(0=0.	(в)
Пользуясь результатами данного раздела, докажите, что пространство решений уравнения (в) представляет собой n-мерное линейное многообразие.
11.	Пусть у удовлетворяет скалярному уравнению у (^+1) — — а (tk) у (tk) =0, где a (tk) > 0. Покажите, что у (tk) = exp [u (^)j, где и удовлетворяет уравнению и (^+i) — и (tk) = In [а (/*)]•
12.	Сведите уравнение в конечных разностях
Л^х(1 ) + «1 ('/.) Дн «к) + «г «к) ® 0к) = 0
к эквивалентной нормальной форме с помощью метода, аналогичного использованному в упражнении 9.
13.	Нарисуйте символическую схему вычислительного устройства, моделирующего дифференциальную систему
Л (t) = А (0 х (0, х (Го) == £.
Объясните, как с помощью этой модели можно вычислить матрицу Ф (t, t0). Конкретизируйте все это для системы, описанной уравнением (б) из упражнения 9. Постройте аналогичную схему на линиях задержки для уравнения (22).
14.	Рассмотрим систему
91 (0 = 9i (0. 9i (0) = 0.
У1(0 = —У1(0,	у2(0)=1.
Покажите, что итерации Пикара сходятся к вектору решения (sin Г, cos t).
15.	В этой задаче необходимо обобщить теорему А на один класс нелинейных уравнений. Пусть (г0, £) — некоторый фиксированный элемент пространства Я71*1, а /: Я71*1 —» Яп — некоторая векторная функция, удовлетворяющая условию Липшица и ограниченная в некоторой окрестности S:
$ = {(*, у): к-Го К а,	*ея, уеяп}.
Если || f (S) | < Af, то покажите, что система дифференциальных уравнений
9 (0 = f (Г, У (О)» У (Го) =5, t е т, имеет на интервале
т = {г: 11 — Го I < « = min {«» Ъ/М}} единственное решение.
Указание. Видоизмените метод Пикара для этой ситуации.
16.	Как следствие упражнения 10 докажите, что /-я итерация Пикара yj принадлежит окрестности решения у, определяемой следующим соотношением:
|y(O-yi(OI<yff^ е“к. <ег.
А (/ + 1)1
где К — липшицева норма / на множестве S.
17.	Динамическая система называется устойчивой, если для каждого б > 0 найдется такое е > 0, что Ц х (t0) || < б «=> | х (0 || < 8 для любых t > tQ, и асимптотически устойчивой, если она устойчива и если х (/) —• 0 при t -♦ оо. Покажите, что уравнение (И) описывает устойчивую систему тогда и только тогда, когда норма |Ф (t, tQ) || при t Ro» °°1 ограничена, и соответствует асимптотически устойчивой системе в том и только в том случае, когда, кроме того, Ц Ф (Г, Го) II 0 ПРИ г -* оо.
2.4. Неоднородные системы первого порядка
Однородные системы, изучавшиеся в § 2.3, играют важную роль на протяжении всей книги. В этом же параграфе мы доводим выбранный план изучения до своего претворения, переключившись на исследование возмущенных, или неоднородных, систем. Здесь так же, как и в § 2.3, на равных правах мы будем рассматривать как непрерывный, так и дискретный варианты задачи.
Итак, рассмотрим возмущенную (или неоднородную) дифференциальную систему, описываемую уравнением
t (0 = А (О X (0 + / (0, х (tQ) - g, t, tQ е т. (1)
Предполагается, что матрица А обладает теми же свойствами, что и в § 2.3. Как нетрудно видеть, уравнение (1) отличается от уравнения (И) из § 2.3 только наличием члена (/— п)-мерного вектор-столбца возмущающих воздействий, определенных на т. Решение уравнения (1), если таковое существует, мы будем обозначать через xf £, t0).
Сам факт существования и единственности xf (/; £, t0) можно установить в качестве одного из следствий теорем А и Б из § 2.3. Введем для этого расширенную матрицу
где через F (t) обозначена квадратная диагональная матрица порядка п с компонентами / (t) по главной диагонали. Обозначим, далее, через z (t) = col \z± (0, ..., z2n (0] 2п-мерный вектор-столбец, который служит решением однородной дифференциальной системы
i (0 = A (t)z (0, z (f0) = z°, t е т.	(3)
При выполнении весьма слабых условий, сформулированных в предыдущем параграфе, решение этого уравнения z существует и единственно при произвольном z°. Пусть z° = col (£, 1, ..., 1). Тогда, если z (t) разбить на два n-мерных вектор-столбца zL (t) и 2ц (0: z (t) = (zi (t), zn (0), то из уравнений (2) и (3) получим
(0 = А (0 zt (0 + F (0 zn (0, Zl (t0) = g,	(4)
zn(0 = 0, zn(Q =col(l,... ,1),	(5)
причем эти уравнения определены на т. Решение уравнения (5) очевидно; zn(0 = col(l, ..., 1) для Подставив этот результат в уравнение (4) и воспользовавшись определением матрицы F (0, мы найдем, то F (t)zn (0 = / (0. Но это значит, что Zj (0 удовлетворяет уравнению (1), а отсюда следует, что все результаты относительно существования и единственности решений уравнения (11) из § 2.3 можно очевидным образом перенести на решения уравнения (1).
В соответствии со сказанным можно сформулировать следующую теорему.
Теорема А. Пусть A (J) — квадратная матрица п-го порядка, a f (t) — п-мерный вектор-столбец, и пусть $ И(0^<оо	||/ (01|dt < оо. Тогда существует единствен-
ный вектор Xj (t; g, t0) такой, что xf (f0; g, t0) = g, a Xf (t; g, t0) удовлетворяет уравнению (11) при всех tE^x. Если A(t)*) непрерывным образом зависит от некоторого параметра р (возможно, векторного), то при каждом t ЕЕ Трешение xf (t; g, t0) также непрерывно по р.
Замечание 1. Если (т) — обычное пространство интегрируемых на х функций, то из того, что ||/ (£)|| ЕЕ Ьг (т), следует, что каждая из Д (t) ЕЕ Lr (т), i — 1, 2, ..., п. В связи с этим условия теоремы А можно было бы эквивалентным образом перефразировать, потребовав, чтобы норма|| А (£)|| была ограничена на т, а / (0 е Щ (Т)Г.
После того, как мы установили, что Xf (/; g, t0) существует, попытаемся определить общий вид этого решения. На это время мы договоримся считать, что матрица A (t) и вектор / (t) непрерывны на т. Читатель, владеющий аппаратом современной теории интегрирования, без всякого труда может изменить последующие утверждения и прийти в результате к более общим выводам*
Воспользуемся хорошо известным методом вариации параметров (Лагранжа) и попытаемся получить решение в виде xf (0	t0) = Ф (t, t0)y (t; f). Здесь x (t), у (t) и Ф (t, t0) предпо-
лагаются непрерывными и дифференцируемыми функциями, причем их первые производные тоже считаются непрерывными; Ф (t, tQ) представляет собой матрицу перехода для уравнения (1) при условии, что / (t) = 0. Заметим с самого начала, что для того чтобы решение xf удовлетворяло начальным условиям, необходимо, чтобы у (tQ, /) = g.
Итак, подставив предполагаемое выражение для X; в уравнение (1), получим
ф (t, t0) у (t,f) + Ф (t, t0) у (0 /) = А (0 Ф (t, t0) у (0 /) +
+ ф (t, t0) y(f,f) = А (0 Ф (0 t0) у (0 /) + / (0.
Отсюда
Ф (t, t0) у (f, f) = / (0, t e x.
Но так как матрица Ф (t, t0) невырождена при всех iG т, то у (t; /) = Ф'1 (t, t0) / (0, t S x,
*) Или / (z). (Прим, ped.)
или, после интегрирования этого уравнения с учетом того, что y(t0, n =
to
А так как xf (t; £, t0) — Ф (t, t0) у (<; /), то мы нашли, таким образом, решение уравнения (4) в виде
xt (<; Z, t0) = Ф (МоК + J Ф (t, t0) Ф’1 (••?, «о) f (®) ds, Мо, s (= т. (6) to
Используя этот результат и свойства матрицы перехода, мы можем сформулировать теперь следующую теорему.
Теорема Б. Если уравнение (1) удовлетворяет условиям теоремы А, а матрица Ф (£, £0) есть матрица перехода соответствующего однородного уравнения, то решение уравнения (1) можно представить в виде одной из следующих эквивалентных форм:
t
Xf {t- t0) = Ф (t,	+ Ф (t, t0) J Ф-1 (s, t0) f (s) ds =
to t
=Ф (t, t0) £4- J Ф (/, s) /(s) ds = to
t
=Ф (?, и £ + Ф 0, tQ) f Ф Go. s) / (s) ds, s, t, tQ e T.
to
На этом этапе уместно сделать несколько замечаний относительно содержания теоремы Б. Совершенно ясно, что Xf (t; g, Jo) представляет собой суперпозицию двух членов. Первый из них, Ф (*> ^о)£> описывает решение уравнения (1) при условии, что / (t) равно нулю на всем т, а £ произвольно. Второй описывает решение уравнения (1) при условии, что £ = 0, а / (£) £= [Z/X (т)]п, и в остальном произвольно. Эти два слагаемых часто называют свободным и вынужденным движениями неоднородной системы.
Рассмотрим теперь поведение системы, у которой входной сигнал / (t) имеет следующий вид:
/ю =
о,
о,
т<*<т + Ат, т + Ат^ t.
В соответствии со свойствами матрицы перехода мы получим следующую последовательность равенств:
Ф(Мо) J Ф Go. s)/(s) ds = Г
= Ф(г,т)Ф(т, f0) [ j Ф (10,х)Ф (г, s)f(s) ds] =
= Ф(«,т)[ J ф(т,«)/(«)(й].	(7)
т
Введем обозначение
r-t-Дт
Л= j Ф(Т,«)/(5)Ж.	(8)
Тогда суммарная реакция системы примет следующий вид:
G. &> ^о) — |
Ф(М.К,
0<«<т,
(9)
Ф(Мо)£ + Ф(М)Л. T<t,
где Дт предполагается малым, а т + Дт = t. Решение (9) уравнения (1) можно представить в другом эквивалентном виде:
(Ф(М.К.	0<i<T,
®' (<; С’<о) = { Ф (*ЛИС + Ф Go. т) А], т < t. (10)
Из этих соотношений следует, что реакция системы на начальное условие £ и импульсноподобный входной сигнал / (t) мало отличаются друг от друга. Действительно, в уравнении (9) входное воздействие /т играет как бы роль второго начального условия, которое добавляется в момент времени т, не нарушая влияния первого. В уравнении же (10) реакция системы представлена в виде решения однородного уравнения с начальным условием £ при t < т и £ + Ф (f0, т)/т при t > т.
Рассмотрим теперь поведение неоднородной векторной конечноразностной системы
М (М = A (tjy + / Gk), у Go) = 0, е от. (11)
Здесь, как и в уравнении (2), можно ввести расширенную квадратную матрицу A (tK) порядка 2п и преобразовать уравнение (И) в однородное. После этого мы сумеем воспользоваться условиями теоремы 3 из § 2.3 о существовании и единственности решения однородного уравнения и показать, что^ уравнение (11) имеет един-
i.l. ЙЁОДЙОРОДЙЬГЕ СИСТЕМЫ ЙЕРЙОЁО ПОРЯДКА
ственное решение. На этом этапе мы оставляем все детали доказательства на совести читателя, а сами попытаемся найти решение все тем же методом вариации параметров. Как и раньше, через Ф (^, £0) мы будем обозначать матрицу перехода однородного аналога уравнения (И). Для удобства предположим, что матрица Ф Gk» ^о) на & невырождена.
Обозначим через у (^) некоторое решение уравнения (И) и попытаемся определить такую векторную последовательность и (/к), что
У (^к) = Ф Gk» *о) 1(' Gk> ^о)*
Применив оператор Afc к обеим частям этого равенства, получим
&кУ (^к) = 1^кФ Gk» и Gk» ^о) 4” Ф Gk+1> ^о) t^ku Gk> ^о)5 =
= A (tk) Ф t.) + Ф Gk+1, t0) [Aku (^, f0)L
С учетом уравнения (11) отсюда находим
Л Gk) Ф (tk, tQ) и (tk, tQ) -г / (tk) = A (tk) Ф (tk, t0) +
4" Ф (^к+1» ^о)	(^к» ^о)1»
и, следовательно,
/ Gk) = Ф Gk+1» ^о)	(^к» *о)1-
Если предположить, что ни одна из матриц [Z + hkA (^)l невырождена, то у матрицы перехода всегда найдется обратная, и, следовательно,
Afcu (tk, t0) = Ф 1 Gk+i> t0) f (tk),
u (^k+1) = u (^k) 4“ ЬкФ 1 (£fc+i, t0) / (tk) =
= u (tk) + АкФ Go» ^k+i) / Gk)*
Выписывая эти соотношения подробно и используя условие у (£0) = 0» получим
и (М = о,
u (tx) = Л0Ф (f0, tr) f (£0),
и (*а) = Л0Ф (tQ, / (t0) + ЛХФ (t0,	/ (^),
к	к—1
и (^к) = S ^<-1Ф Go» ^i) / (^i-1) = 2 ^>Ф Go» ^’+1) / (0)« i=0	j =0
Этот результат приводит к следующей теореме.
Теорема В. Пусть A (tk) — квадратная матрица п-го порядка, и пусть матрицы [I + hkA (^)l определены и невырождены
на множестве ст = {f0, tv ..., tn}. Тогда конечноразностное уравнение
&1сУ (М = А (^к) У (^) + / (^к), У (^о) — 0, h <= o', имеет единственное решение — векторную последовательность вида
к—1
У (*к) = Ф Gk, М 2 Go» ^+1) / G/)»	^к£= °*	(12)
;=0
Замечание 2. Прежде всего заметим, что решение (12) можно представить в другом виде:
У Gk+1) =	+ ЛЛЛ Gk)I У Gk) + W Gk) —
~ Ф Gk+1» ^к) У Gk) 4" ^к/ (^к) ~
= Ф Gk+1, ^к) l£/Gk) 4“ Н (^к) / (^к)], Н (tk) = Л/j Ф (^к, ^к+1)-
Последнее выражение часто используют в качестве эквивалентного определения дискретной динамической системы. Далее, воспользовавшись полугрупповым свойством (30) из § 2.3, мы увидим, что утверждение теоремы В этого параграфа можно переписать в виде
к—1
y(tk)= 2 МФл.'м)/ (Ъ)-	(13)
j=0
При доказательстве теоремы В мы опирались на предположение о невырожденности матрицы Ф (tk, t0) на а, и это предположение играло существенную роль. Проверка справедливости этого предположения, а также доказательство следующего следствия могут быть получены довольно неизящным, но простым способом, использующим уравнение (11) как простое итерационное соотношение.
Следствие. Векторное конечноразностное уравнение
&ky (tk) -= A (tk) у (^) + / (tk), у (t0) = 5,	(14)
определенное на О', имеет единственное решение у, задаваемое на о* формулой
к—1
У< h *о) = Ф (*к, *о) £ 4“ З^Л^к» ^)/(0)»	(15)
>=i
Если матрица Ф (tK, tQ) действительно невырождена, то мы можем переписать уравнение (15) иначе, вынеся за скобку общий множитель Ф (tfc, t0).
Пример 1. Рассмотрим электронную цепь и ее линейный эквивалент, показанные на рис. 2.11. Предположим, что в момент
б)
Рис. 2.11. Схемы: а) триггер; б) эквивалентная линейная модель.
£0 = 0 все емкости разряжены. Тогда рассматриваемую систему можно описать уравнением
Г ii (О'] г — а — 1 Г Xl — dJ L z2(t)
' е ~
I	^>0,
L i2(t)j L — с где а = (Я0Н Rp) (7?х + Т?2) СХД, 6 = R, (Ro + Rp) (\&, с = R^R0 + ЯР)С2Д,	d = (R.R.'+^R^ R.RJ С2Д,
е = Ro (7?! + Я2) Сх\,	f = Тго^АД,
А = RqR1R2 + RqR\Rp + RqRzRp + Вводя обозначения
= - 4- (а + d Н- /(я - d)a + 46с), = - 4- (а + d - /(а - d)« + 46с),
мы можем записать матрицу перехода в виде
г ФН(М) Фц(М) 1 Ф(М)Ч. Ф41М Фа2(«, s) J ’
где
Фп (М) = (Хх - X,)-11 - (а + Х2)	+ (а + XJ ,
Ф21 (*, *) = (Хх - X,)"1 {Ь~1 (а + Хх) (а + Ха)’[ех <*-*> -
Ф12 (М) = (Хх - ХзГЧ- Ь (^) - ех’('-*)]},
Ф22 (*• 5) = (Хх - ХзГМ(а + *1) e*'(t~6) - (а +	ех’('-8)].
Пример 2. Рассмотрим поведение системы общего вида из трех масс, которая в ньютоновой механике описывается системой дифференциальных уравнений второго порядка *)
“ тЛ1	'«12	'«13 '	'Z1 '		/11	L /12	/13	11			
^21		^23	a-2	+	/21	/22	/23	i*2	+		
_тз1		гпзз.	_ ^3 _		, /31	. /32 Ли	/33 _ &12	??- 1— w H w	X1		’/1(0
					+	i	^22 ^32	^23 ^33 _	1 <N CO 	J	=	/2(0 L/s(0
Мы будем предполагать, что все массы тп^, все коэффициенты трения и все коэффициенты упругости не зависят от t. Прежде всего перепишем эти уравнения в матрично-векторной форме:
МЛ (0 + Ft (0 -4- Кх (0 = / (0,	(16)
где М = [wul, F = [/и] и К = [fcij]
Воспользовавшись процедурой, намеченной в упражнениях 9 и 10 § 2.3, мы можем привести уравнение (16) к нормальному виду. Для этого мы будем рассматривать в качестве координат не только положения масс, но и их скорости. Итак, пусть щ = и и = = (ух, у2, у3). Тогда уравнение (16) можно заменить на систему.
0 = и (0 + It (0 - Iv (0 + Ох (0 = 0, Mv (0 + Ft (t) + 0у (0 + Кх (0 = / (0, t е т.
Вновь воспользовавшись преимуществами векторно-матричных обозначений, получим
Г 0:Z 1 Г у(0 1 Г—/:0 I Г У (t)~] Г 0 1
[ "м\ F J L X (0 J + [ б Т К J I. х (0 J = [ f (0 J •	(17)
Будем считать матрицу
LM\F J
*) Этот пример заимствован из § 9.2 книги Хафмана (R. L. Half та п, Dynamics, v. II, Addison-Wesley Reading, Mass).
невырожденной. Очевидно, что это так, если невырождена матрица М, Читатель легко может убедиться в том, что
 О I I Г1 Г — M'lF ! М~1 
___I_	_ __________I_____ L I | °
(18)
Умножая уравнение (17) на эту матрицу, мы получим
z(t) = Az (/) + Ви (/),	(19)
где и = (0, /), z = (и, х), В — матрица из уравнения (18), а А имеет следующий вид:

(20)
Так простым и очевидным способом нам удалось свести общую систему дифференциальных уравнений второго порядка к нормальному уравнению первого порядка. В качестве конкретного
Положение равновесия
Рис. 2.12. Система с массами, пружинами и амортизатором.
примера рассмотрим систему, показанную на рис. 2.12. Эта система двух масс удовлетворяет следующим уравнениям движения:
' т1 0 1 Г £г (/)' 0 т2 £2 (/)
где / (Z) отображает действие внешних сил, направленных вправо. В своей эквивалентной нормальной форме эти соотношения
После окончательного приведения
к стандартной форме мы
Рис. 2.13. Позиционная следящая система второго порядка.
получим уравнение (19), в котором матрица А имеет вид
		Г /	-/	2к	— к "	
		mi	mi	ГП1	7721	
А =	(-1)	1 m2	/ m2	— к Ш2	2k ТП2	(21)
		-1	0	0	0	
		_ 0	-1	0	0	
Пример 3. Рассмотрим теперь позиционную следящую систему, схема которой показана на рис. 2.13. Пусть поведение
этойЛсистемы характеризуется следующими физическими парамет-рамй
— постоянной двигателя, fel — постоянной вращающего усилия, Ац — коэффициентом передачи, к2 — постоянной потенциометра, А'— коэффициентом усиления усилителя, J — моментом инерции (приведенным к валу), R — сопротивлением обмотки,
/ — коэффициентом вязкого трения (приведенного к валу). При фиксированном ir и нулевых начальных условиях (при t = t0) поведение этой системы описывается уравнениями
et (t) = А к, 1ег (t) - 0Р (01 = Hi (t) + лд (t), T (t) = J0O (t) + /9o (t), 0p (0 “ *300 (0*
Вводя обозначения
Акъкзк^	k2 (fR . 7 \ T Ak2ki
a° ~ —TR~ ' a' = Тп[-Ъ +кф k=~!R'
мы можем привести эти уравнения к следующему виду:
0 (0 -F аД (0 + аД (0 = Л0. (0, 0О М = 0О (/0) = 0.
Последнее уравнение с помощью замены переменных (t) = 0О (t) и (0 = 0о (0 можно представить в нормальной векторно-матричной форме:
-Х2 (0.
’ 0 1
_ — ао
Г^х(01 . ГО
-aj [мо.
к

Матрица перехода для этой системы имеет вид Ф12 (0 ^о) Ф22 (^» ^о)
Ф (/, t0) =
’фи Ф21	^о)
где
Фи (*. to) = CiC-'X'-'») sin [<о (/ — t0) —	,
Ф12 (t, t0) =	sin [co (t — f0) 4-,
Ф21 (t, t0) = cse-bi'-'»> sin co (t — Zo), Фм t0) =	sin [co (t —t0) + i|?a]
+	/(«1-6)2 + (02	.	\	.-(О
с1 = —й—- С*=И -------------й-----> 4'1= tgi — ,
С., =	,	СО = </0 — Ь2,	115, = f <т-1
со	а — b
ап	у си
,	О = — .
•’со	2
Замечание. Читатель, без сомнения, уже заметил, что ни один из рассмотренных примеров не приводит к конечноразностным уравнениям. Это, естественно, не должно означать, что в природе редко встречаются физические системы дискретного характера. Наобдрот, имеются многочисленные примеры дискретных динамических систем, описывающих явления, дискретные по самой своей природе. Именно так обстоит дело с цифровыми вычислительными машинами и цифровыми системами управления. В других системах непрерывные физические явления приобретают дискретную форму при квантовании по величине или по времени. Например, в радиолокационной станции слежения импульсного типа информация о расстоянии до цели снимается дискретно, с частотой повторения импульсов. С помощью дискретизации мы могли бы свести к конечно-разностному виду и каждое из уравнений трех предыдущих примеров. А так как импульсные системы с точки зрения приложений образуют важный класс систем, то мы специально остановимся на основных связях между дискретными, импульсными и непрерывными системами.
Импульсные системы. При математическом моделировании физических систем часто оказывается необходимым несколько обобщить уравнения (1) и (14). Точнее говоря, может возникнуть ситуация, при которой поведение линейной динамической системы удобнее описывать уравнениями следующего вида *)з
dtx (t) = A (t) х (t) + В (t) и (f), х (/0) = 5, t S v,
у (t) = C (t) x (t) + D (t) и (0,	t e v.	(22)
Здесь вектор и = (un ..., um) описывает независимые входные воздействия, влияющие на поведение системы; вектор у=(у1,... ..., Уп) — независимые наблюдаемые выходные величины, а вектор х = fo, ..., хг) — некоторое минимальное множество внутренних переменных (не обязательно единственное), которых достаточно для описания динамики системы. Размерности матриц 4, В, Си Д, естественно, таковы, чтобы выписанные уравнения имели смысл.
Сходство между непрерывными и дискретными системами позволяет надеяться, что с помощью разумного выбора обозначений нам удастся практически одинаковым образом описывать поведение как одних, так и других. В уравнениях (22) мы сделали первый шаг в этом направлении. Поскольку множество а дискретно, то функцию х, определенную на а, можно без каких-либо разночтений обозначить через х (Z), t а. Точно так же никаких
♦) Примеры систем, требующих использования математических моделей такого более общего вида, приведены в приложении 4.
сомнении не возникает и при использовании обозначения
I Д,лг (0 = h? [х (Zk+1) — X (/*)], t = e a,
вместо символа (th), которым мы пользовались ранее. Поэтому, если v = т, то под символом dt мы будем понимать дифференцирование, а если v = О’, то будем считать, что он обозначает разностный оператор dt = &t. Таким образом, про систему, описываемую уравнениями (22), нельзя сказать, дискретна она или непрерывна, до тех пор, пока не определено v. Но как только мы ука-жем, что представляет собой область V, так система, описанная уравнениями (22), станет вполне определенной.
На рис. 2.14 приведена схема системы, описанной уравнениями (22), построенная с точки зрения концепции черного ящика. По
u(t)
D(t)

u(t)\
\
J yW
c(t)
___________J
Рис. 2.14. Типичная многомерная система.
очевидным причинам мы называем матрицу D матрицей передачи, а матрицы В и С — матрицами входных и выходных ограничений соответственно. Если в рассматриваемой системе имеются один вход и один выход, то матрица В представляет собой некоторый вектор-столбец, а матрицы С и D — вектор-строки. В общем случае мы будем называть систему, описываемую уравнениями (22), многомерной, а в том случае, когда у нее всего один вход и один выход,— одномерной.
Покончив со всеми предварительными замечаниями, перейдем непосредственно к изучению импульсных систем. Нашей целью будет не просто показать, что непрерывная система с импульсным элементом (осуществляющим квантование сигнала по времени) может быть представлена в виде дискретной системы, а скорее установить роль импульсных систем в качестве двусторонних связей между системами с непрерывным и дискретным временем.
Для начала предположим, что дискретное множество о представляет собой некоторое подмножество промежутка т. Обозначим через X класс всевозможных функций, определенных во всех точках т, а через Y — класс всевозможных временных рядов, определенных на о. Тогда, если о С т, а через S обозначена операция квантования по времени или дискретного съема сигнала,
то S — это линейное преобразование 5:Х->У, определенное следующим соотношением:	I
(Sf) (t) =
f (tjc), EzS, 0,
С физической точки зрения это преобразование описывает поведение дискретно срабатывающего ключа при условии, что ключ замыкает контакты мгновенно в моменты времени i Е а. Операция экстраполяции нулевого порядка, с которой мы познакомились в примере 4 из § 2.1, также полезна для изучения импульсных
Рис. 2.15. Системы с эквивалентными соотношениями вход — выход.
систем, и мы будем считать, что она описывается линейным преобразованием С, отображающим Y в X условием
(Су) (0 = у (0), t е [*/, ^+1),
где t ЕЕ т, a ЕЕ (J.
Для того чтобы конкретизировать стоящие перед нами задачи, рассмотрим две системы, схематически представленные на рис. 2.15. Непрерывная и дискретная системы считаются эквивалентными, если они осуществляют идентичные преобразования входных сигналов, поступающих на клеммы Л, в выходные величины, снимаемые с клемм В. Совершенно ясно, что импульсный элемент можно включить справа от клеммы Л, а выходной импульсный элемент заменить на цепочку последовательно соединенных импульсного элемента и экстраполятора первого порядка, и что при этом эквивалентность двух систем не будет нарушена.
Для того чтобы аналитически сформулировать понятие эквивалентности дискретных и непрерывных систем, предположим, что
дискретная динамическая система описывается уравнениями:
j	(£/с) = A х (t^) + В (£k) и (^),
I	(23
I У (М = С (М i (М + D (h)lb (M> ffc S <5, а непрерывная динамическая система — уравнениями
± (0 = A (Z) х (t) + В (0 й (/), t G т,	(24)
y(t) - С (t) х (t) + D (t) й (t),
где^через й (t) мы обозначили функцию (Си) (/). Решим теперь нашу^задачу, естественным образом распадающуюся на две части.
Задача 1. Можно ли для каждой непрерывной системы, описываемой уравнениями (24), построить такую дискретную систему, описываемую уравнениями типа (23), для которой значения у и у на о совпадают, какова бы ни была функция и, определенная на а?
Поскольку функция и = 0 является допустимым входным воздействием, то из условия у (t) = у (t) при t е а мы сразу получим, что при t €= о: С (t) х (Z) должно равняться С (£) х (/). Чтобы обеспечить это равенство, достаточно выбрать С (£) = (5С')(0 и показать, что при этом обеспечивается равенство х (/) = (5х) (£). Для этой цели удобно воспользоваться соотношениями
И-1
х (0 = ф (t, t0) X» 4- ф (t, t0) 2 Л,Ф (t, t^) в (tj) и (t}),	t e 5,
(25) t
x (t) = Ф (t, ta) a:0 -f- Ф (t, to) $ Ф (t0, s) В (s) a (s) ds, t£=x.
to
Эквивалентность x (t) и f (/) на а при и = 0 и всевозможных х° и Zo требует выполнения условия
Ф (th tk) = Ф (tj, 4), tj, tk (= a.
Но Ф (tk, t0) = П jZj (/ + hkA (Zk)], что в свою очередь определяет матричную последовательность {Л (tk)}. Приравнивая значения вынужденной реакции систем в моменты времени tOi ..., /к,... и полагая й (t) = и (tk) при t G Um ^+iL нетрудно показать, что выходные величины систем совпадают на а тогда и только тогда, когда
#/С4 1
hkB(tk)= 5 Ф (tk+1, s) В (s) ds, к = 0,1, 2,...
*к
Таким образом, для непрерывной системы, описываемой уравнениями (24), эквивалентная дискретная система однозначн ) определяется соотношениями
C(tk)=C(tk),
В jc) = D
к
(26)
I <|с+1 &(М=	$ Ф(^+1, ’) В (s)ds].
*к
Задача, обратная задаче 1, может быть сформулирована следующим образом.
Задача 2. Можно ли для каждой дискретной системы, описываемой уравнениями (23), определить такую непрерывную систему, которая была бы ей эквивалентна в том смысле, что при каждом и (t), определенном на о, выходные величины обеих систем совпадали бы на а?
Эта задача значительно сложнее первой. Из уравнений (23) и (24) ясно, что для того, чтобы найти такие матрицы А и В, которые обеспечивали бы равенство суммарной реакции х непрерывной системы на а значениям £ (^), достаточно выбрать произвольные матрицы С и D, принимающие на о значения С (^) и D (tk).
Лемма. Пусть задана некоторая дискретная линейная система с матрицей перехода Ф (tj, tk). Предположим, что Г (t) представляет собой некоторую невырожденную дифференцируемую матрицу, для которой
|Г(0Г(0-Ч<т(0€=Мт),
Г (tk) = Ф (tk, Zo), А = 0, 1, 2, ...
Определим Ф (t, s) как произведение Г (t) Г-1 (s), и пусть А (<) — = Г (<) Г (О-1. Тогда матрица Ф (t, t0) является матрицей перехода для дифференциальной системы
i (t) = A (t) х (f)
Ф (0, h) = Ф (О, tk), j, А = 0, 1, 2, ...
Доказательство. Пусть матрица Г (t) удовлетворяет условиям леммы, и пусть
Ф (t, з) = Г (О Г (s)'1.
Тогда
ф = Г (0 Г-1 (0 = Г (0 Г-1 (0 Г (0 Г-1 (0 =
I	= Г (0 Г-1 (ОФ (*, S).
Более того,
Ф (/, t) = г (г)Г-1 (о = I.
Таким образом, матрица Ф (t, s) служит матрицей перехода рассматриваемой системы, и, значит, наша лемма доказана.
С самого начала мы отмечали, что выбор матрицы Г (0 неоднозначен. Существует много способов построения ее, но мы расскажем здесь лишь об одном.
Если задано конечноразностное уравнение (th) = = А (^) $ (£к) или, что то же, матрица перехода дискретной системы Ф /0) = П1~о U + Л^Л то матрицу перехода непрерывной системы можно сконструировать в соответствии с уравнением
Ф (t, t9) = (Z + (t - tk) A («*)] Ф (tk, t0), t e
Очевидно, что Ф (t, t0) является непрерывной функцией t на всем т и удовлетворяет условию Ф (^, /0) = Ф (^, £0), каковы бы ни были €= а. Более того,
Ф (t, и = A (tk) Ф («ь f0) == A (tk) u + (t- tk) A	t0),
а это последнее равенство описывает нестационарную систему с матрицей коэффициентов
а (0 = A (tk) И + (t + tk) А (го]-1, t е [г*, t e a.
К сожалению, такая матрица А (0 не непрерывна (хотя лемма и не требует непрерывности матрицы Л, справедливость этого свойства была бы желательной), поскольку, переходя в полученном выражении к пределу справа и слева от мы получили бы, что
Л G /с) — Л (tic) Ф (^, £fc+i), VA (it) = A (tm).
Тем не менее это не может помешать нам использовать найденную матрицу Ф (t, s) и, пользуясь равенством матриц С и Z), найти такую матрицу В (0, которая обеспечит эквивалентность систем.
Упражнения
1.	Рассмотрим линейную динамическую систему, описываемую уравнением (22). Обозначим через Н зависящую от времени матрицу, определяющую преобразования в канале пассивной обратной связи:
и (0 = Н (t) ytf) + v (0, t е v.
Предполагая, что ЦП (0 Н (t) ||< 1, igo, приведите уравнения замкнутой таким образом системы к стандартному виду (22).
2.	Повторите упражнение 1 для системы с активной обратной Связью
и (0 = Z (0 + v (0, t €= v,’
atZ (t) = Н (t) + у (0, t е v.	I
Указание. Здесь вместо х нужно рассматривать пару (я, z).
3.	Обозначим через х п £ два возможных набора внутренних переменных некоторой линейной динамической системы. Поскольку взаимосвязь х -> у между внешними переменными не может измениться из-за выбора той или иной математической модели (внутренних переменных), то и та и другая система уравнений будут иметь следующий вид:
dtx (t) = A (/) х (0 + В (0 и (0, t е V,
У (0	=	С	(0 х (Z) + D (0 и (0,	t е v,
dt A(t)	=	a	(z) f (0 + в (/) и (z),	t е v,
У (t)	=	С	(0 f (0 + D (t) и (0,	t е V.
Предположим, что К —	это	такая матрица, для которой существуют одно-
временно К (0, К1 (0 и К (0 при всех fgZ), и что векторы внутренних переменных связаны между собой соотношением
f (t) = К'1 (0 х (0.
Покажите, что в этом случае для непрерывной системы выполняются соотношения
Ф (/, 0 = К"' (t) Ф (Z, 0 К (0,
A (0 = К'1 (0 А (0 К (0 - К'1 (0 К (0,
В (0 = К'1 (0 В (0,
С (0 = С (0 К (0,
каковы бы ни были t. s £ т, п что эти соотношения сохраняют свою силу и для дискретных систем, если X”1 (0 заменить на X"1 (Zfc+1), а К (t) на
4.	Электромеханическая система типичного громкоговорителя описывается следующими дифференциальными уравнениями:
di (I)	dx (/)
V Hi (t) +U =
m + kx (/) — Ui (t) =0,
где через v, x и i обозначены приложенное напряжение, механическое смещение и ток в обмотке катушки, соответственно. Приведите эту систему уравнений к неоднородной системе первого порядка. Предполагая, что R/L = 6, a U*!mL = 10, постройте решение уравнений как функцию остальных параметров. Пользуясь этим результатом, постройте зависимость х и i от v.
2.5. 1^>Е0БРА30ВАНИЯ, СВЯЗАННЫЕ С ЛИНЕЙНЫМИ СИСТЕМАМИ 181 2.5. Некоторые преобразования, связанные с линейными динамическими системами
В §§ 2.3 и 2.4 мы выяснили некоторые важные свойства линейных динамических систем. В данном параграфе мы найдем для них новую интерпретацию с точки зрения теории линейных преобразований.
Рассмотрим уравнения (22) еще один раз. Как и раньше, обозначим через Ф (/, s), t, s ЕЕ v, матрицу перехода для этой системы. В системе с дискретным временем множество а упорядочено (т. е. tj^ <Z tj), в связи с чем можно определить новую функцию [Z], где
[£] = шах {ft: t^t}.
Другими словами, U] = й тогда и только тогда, когда t 6= ^+1]. Пользуясь этой функцией и уравнением (15), мы, очевидно, можем представить реакцию дискретной системы и -> х с помощью следующего соотношения:
[П-1
хи (t; I, м = ф (t, М Е + 2 V, *м)в (h) и (Ч), t е б,- (1) ;=0
или, в невырожденном случае,
[П-i
Хи (Ч I, Ч) = Ф (t, t0) | + ф (t, t0) 2 (to, tjn) В (tj) и (tj), (2)
>=0
где t пробегает все а. Аналогичные соотношения можно выписать и для системы с непрерывным временем:
t
=Ф(Мо)£ + Ф(*> t0)^(t0,s)B(s)u(s)ds,	(3)
6)
где t пробегает т. И в том и в другом случае взаимосвязь между входным и выходным сигналами и -> у определяется дополнительным соотношением
У (t) = с (0 xu(t; I, <0) + D (t) и (0, t S v.
Для простоты мы будем предполагать, что D = 0, а С = I, ос-тавляя незначительные модификации последующих утверждений, необходимые для получения более общего результата, на совести самих читателей.
Уравнения (2) и (3) можно рассмотреть с той точки зрения, которую мы приняли при изложении материала § 2.2. Для этого обозначим через I (о) векторное пространство всевозможных вещественных функций, определенных на о. Обозначим еще через Um (о) декартово произведение т пространств I (о):
Um (а) = I (<*) X I (о) X ... X I (о) (т раз).
Рассмотрим сначала вынужденную реакцию системы, описываемой уравнением (2). Для каждого и из Um (о) теорема В из § 2.4 гарантирует существование единственного вектора хи (/; О, /0), определенного на о и удовлетворяющего уравнению (2). Определим на Um (о) некоторое линейное преобразование, потребовав, чтобы образ и совпадал с этим х:
[П-i
(Fu)(t) = xu(t-,O,to) = 2 w (t’tfiultj),	(4)
7=1
где
W (t, tj) = hi Ф (t, t^) В (tj).
Здесь через (Fu) (t) обозначен образ элемента и е Um (о) в момент времени i £ а. Совершенно ясно, что F вполне определено и что область значений F принадлежит пространству Um (о). Если принять, что о конечно, то пространство Um (о) будет конечномерным, а преобразование F — ограниченным по отношению к любой норме, заданной на Um (о). Наконец, понятно, что F описывает вынужденное движение рассматриваемой дискретной системы в том смысле, что и функция F, и сама система преобразуют внешнее воздействие и в одинаковые выходные величины х. Все эти соображения объединены в следующей теореме.
Теорема А. Вынужденное движение каждой линейной динамической системы с дискретным временем можно представить как некоторое (ограниченное, если о конечно) линейное преобразование F одного банахова пространства в другое.
При решении многих задач управления нас интересуют значения выходной величины системы лишь в какие-то конкретные моменты времени. В этом случае система преобразует элементы пространства Um (<з) входных воздействий в некоторый n-мерный вектор с вещественными координатами, определяющий выходной сигнал системы в какой-то момент времени £ О'. А это побуждает нас рассматривать систему как некоторое линейное преобразование в Rn, т. е. как некоторое отображение Fa, заданное условием
FqU — (Fu) (41) >
где момент времени ta фиксирован и принадлежит о. Ясно, что параметр ta определяет целое семейство отображений {Fo}. Обратно, эти отображения позволяют вычислять значения выходных величин на любом подмножестве Е CZ а и, в частности, в своей совокупности определяют и само F. Из всего этого вытекает справедливость следующего утверждения.
Следствие. Вынужденное движение каждой линейной динамической системы с дискретным временен можно описать семейством {Fa\ ta ЕЕ о} ограниченных линейных преобразований Fa, каждое из которых определено на Um (о) и принимает значения из Rn. Исходное множество о, на котором определены входные воздействия, является для этого семейства множеством индексов. Преобразование Fa преобразует входную функцию в целом в значения ta — импульсов выходных величин.
Возвратимся теперь к уравнению (3). Вспомним для начала, что матрица Ф (t, s) предполагается непрерывной на квадрате т X т, а матрица W (t, s) = Ф (t, s) В (s) — ограниченной на т X т, если только на т ограничена матрица В ($). Займемся изучением вынужденных движений системы, описываемой таким уравнением. Обозначим через £р(т) (1 р оо) обычное банахово пространство функций с интегрируемой (по Лебегу) р-й степенью на промежутке т = к0, ^]. Через Um (т) мы обозначим декартово произведение
Um (т) = Lr (т) X ... X Ьг(х) (т раз).
Определим на Um (т) преобразование F, потребовав, чтобы образ х каждого элемента и е Um (т) определялся соотношением
t
(Fu) (t) = zu(f;0, tQ) =	(t,s)u(s) ds.	(5)
to
Таким образом, мы снова обозначаем через (Fu) (t) значение образа элемента и е= Um (х) в момент времени Е т. Но так как х непрерывно, а каждая функция, непрерывная на т, ограничена, то нетрудно проверить, что
х ЕЕ 1С (т)]п CZ Un (т),
где через С (т) мы обозначили обычное банахово пространство функций, непрерывных на т. Итак, F представляет собой линейное преобразование, определенное на Um (х) и принимающее значения из С* (х) = С (х) X ... X С (т), и, в частности, является линейным отображением в Un(t). Более того, воспользовавшись одним методом, с которым мы познакомимся позже в этом же параграфе, мы смогли бы показать, что если т конечно, то F, рассматриваемое как некоторое отображение пространства Um (х) (с подходящей
нормой) в пространство Сп(т) или ип (т), с любой подходящей нормой, определенной в них, ограничено. Все эти результаты сведены в следующую теорему.
Теорема Б. Вынужденные движения любой непрерывной линейной динамической системы можно описать некоторым {ограниченным при конечном т) линейным преобразованием F, отображающим одно банахово пространство в другое.
Пусть нас интересуют лишь значения выходных величин системы в конкретные моменты времени (в этом случае система преобразует элементы пространства входных воздействий в п-мер-ные векторы с вещественными координатами, определяющие состояние выходной величины системы в момент времени ta (ЕЕ т). Тогда систему можно рассматривать как некоторое линейное преобразование в 7?п, т. е. как отображение Fa, определенное условием
=.(Fu) (U,
где ta принадлежит т и фиксировано. Ясно, что при таком подходе F определяет целое семейство отображений {Fa}. И обратно, значение этих отображений позволяет выяснить значения выходных величин на любом подмножестве Е СЕ т и, в частности, определить само F. В связи с этим справедливо следующее утверждение.
Следствие. Вынужденное движение любой линейной динамической системы с непрерывным временем можно описать некоторым семейством {Fa: ta G т} ограниченных линейных преобразований Fa, каждое из которых определено на Um (т) и принимает значения из Rn. Основное множество т, на котором определены входные сигналы, служит для этого семейства множеством индексов. Отображение Fa преобразует весь входной сигнал системы в целом в значение выходного сигнала в момент времени ta.
Замечание 1. В главе 1 и в первых двух параграфах этой главы мы старались донести до сознания читателей мысль, согласно которой системы любых типов следует рассматривать как отображения одного функционального пространства в другое и что разбивать системы на различные классы по их физическим признакам не только не обязательно, но часто и вредно. Материал этого параграфа лишний раз подтверждает эти мысли. Действительно, изучение уравнений (1), (2) и (3), а также теорем А и Б и их следствий доказывает, что линейные динамические системы с непрерывным или дискретным временем отличаются друг от друга только такой второстепенной технической деталью, как выбор базового функционального пространства.
Замечание 2. Выше мы всюду предполагали, что множество т ограничено, а множество о конечно. Вводить эти ограничения не
2.5. ПРЕОБРАЗОВАНИЯ, СВЯЗАННЫЕ С ЛИНЕЙНЫМИ СИСТЕМАМИ 185 обязательно, они не связаны с существом дела. Однако на данном этапе они позволяют обойтись без понятия устойчивости.
Замечание 3. В явном виде мы исследовали лишь вынужденные режимы работы системы. Тем не менее режим свободного движения также можно рассматривать как линейное преобразование Ф: Rn -> Un (0), определенное для каждого £ ЕЕ Rn соотношением
(Ф£) (0 = ф (t, t0) I, t e V.	(6)
Иными словами, свободный режим работы системы можно описать с помощью параметризованного семейства {Фа: iaE v} линейных операторов в Rn, определенных условием
Ф<Л = Ф Q £, ta е v.
В этих рамках нетрудно найти модель и для реакции системы. Определим расширенное пространство входных воздействий V (как для непрерывного, так и для дискретного случаев) следующим образом:
V = RnxUm (v).
Тогда элементы V имеют вид и = (£, и), а преобразование 5, определенное на V, задается условием
(Sv) (t) = [5 (L и)] (t) = Ф (t, tQ) I + (Fu) (t), t G= v, и, очевидно, линейно, вполне определено и ограничено, если только ограничено F. Другим возможным описанием суммарного движения системы может служить параметризованное семейство {Sa; ta (= v}, где
Sav = Sa (£, и) = Ф (ta, i0) £ + (Fu) (ta), ta e v.
Гибридные системы. К теоремам А и Б мы подошли в результате непосредственного наблюдения за поведением систем, описываемых линейными дифференциальными или конечноразностными уравнениями первого порядка. Однако сформулированные в них выводы сохраняют свою ценность и для гораздо более широкого класса динамических систем. В этом разделе мы займемся исследованием системы, составленной из нескольких взаимосвяз-ных непрерывных и дискретных подсистем (см. рис. 2.16). Всякое такое объединение подсистем с дискретным и непрерывным временем, связанных между собой линейными устройствами связи (импульсными элементами или экстраполяторами), мы будем называть гибридной системой.
На рис. 2.16 символом и = (иъ ..., иг) обозначен некоторый элемент декартова произведения U = [I (а)]г, а через v = (у1?... ..., и3) — элемент декартова произведения V = [Ах (т)Р. Вектор х = (х1ч ..., хс) принадлежит произведению X = [Z (<т)]с, а вектор
у = (z/1? ..., yd) — произведению Y = [Z/X (x)]d. Режимы свобод* них движений двух подсистем рассматриваются как преобразования Фх: Rc -> X и Ф2: Rd -> У, определенные аналогично тому, как это делалось в уравнении (6). Точно так же функции F и G определены уравнениями, аналогичными уравнениям (4) и (5)
Рис. 2.16. Гибридная система.
соответственно. Учитывая операцию экстраполяции первого порядка С: X -> У, мы предположим, что поведение системы в целом описывается следующими уравнениями:
Ге]—1
х (s) = Ф1 («, t0) + 2	(«♦ 0«) Bi (Ч)и (h)’ se3> (7)
j=0
t
у (0 = Фг (4, t0) уо + $ Ф,(tf Р) В2 (Р) [у (Р) + (Сх) (Р)] dp, tex, (8) to
или, что то же;
х (s) = (Фр:0) (s) +	(«). S е а,	(9)
У (О = (Ф2«/°) (0 + {Gv) (4) + (GCx) (4), tG т. (10)
Если обозначить через г° = (х°, у°) (= Rn = Rc X Rd суммарный вектор начальных условий, то из уравнений (9) и (10) можно получить, что режим свободных движений системы описывается следующими соотношениями:
х (s) = (Ф|Х°) (s),	s£ а,	(И)
у (/) = (ссФр*) (<) + (Ф2у°) (0, t е т.
Стремясь к большей компактности, определим на т матрицу ф8 to) с помощью соотношения
Ф3(/,/0) = $Фа(«,Р)Ва(Р)СФ1(Р,/0)йр, /ЕТ. (12) to
Тогда, если 0 (г; tQ) — матрица следующего вида:
(Di (s, tn) О
в<г;‘">= [ф.(М.) ф.«.<•)] r = (s-‘)eoXT’ <13>
то режим свободных движений системы, описывавшейся уравнениями (11), можно представить в виде линейного преобразования
0: Rn-*-X'<Y, где
(0z°) (г) = 0 (г; t0) z°, г = (s, /) Е о X т. (14)
Аналогичным образом можно описать и вынужденный режим движения гибридной системы. Для этого в уравнениях положим z° = 0 и найдем
х (s) = (Fu) (s),	а,
у (t) = (GCFu) (t) + (Gv) (0, t e t. Изменив уравнение (12) так, чтобы оно приняло вид i
ф3(м>) = $ фа(«,Р)5а(Р)ф1 (Р.м а₽, /ет, t}e ч мы можем показать, что
И-1
(GCFu) (t) = Л;Ф3 (t, tj+1) (tj) U (tj), H
Пользуясь матрицами
Wi (s, tj) = hj(&i (s, tj+j) (tj),	s, tj s о
W2 (t, p) = Ф2 (t, p) B2 (p),	t, p e=
W3 (t, tj) = A/D3 (t, tj^) Bi (tj),	(t, tj) EE
(9) и (10)
(15)
(16)
(17)
(18) а,
уравнения (15) и (16) можно переписать в более компактном виде: [8]-1
x(s)= 2 1^1(«,Ми(0)>	(19)
[П-1	t
2 ^(t.^u^-h Jir2(Z,p)y(3)d3, t^x. (20) J=O	to
Эти соотношения показывают, что гибридную систему, схема которой изображена на рис. 2.16, можно описывать точно так же, как и непрерывные или дискретные системы. Ее режим вынужденных движений можно представить себе как некоторое преобразование Т, отображающее элементы (u, v) банахова пространства U X V в элементы (х, у) е= X X Y:
[Т (и, i?)I (г) = [я ($), у (J)], г = (s, t) е о X т, (21) в соответствии с уравнениями (19) и (20) по мере того, как г = = (s, t) пробегает прямоугольник (а X т). Так как режим свободных движений уже был описан преобразованием 0 [см. уравнение (14)], то суммарную реакцию системы можно отождествить с преобразованием (0, Т): Rn X U X	X У, где
[(0, Т)] (z°, и, 0] (г) = (02°) (г) + [Т (и, р)] (г), г Ео X т. (22)
Выбирая фиксированные точки ra - а X т, мы можем построить параметризованное семейство преобразований из Rn X U X V в Rn.
Непрерывность в многомерных системах. Мы уже видели, что произведение двух банаховых пространств, с определенными на них нормами, также является банаховым пространством. Например, можно принять, что
|(i*, у)|| = max {||4 М|},
||(М, р)|| = (Мр + «№, !</><«>.
Из этих примеров ясно (а на самом деле это верно для любой нормы, определенной на декартовом произведении), что последовательность (un, ип) из U X V сходится к (u, v) G U X V по норме, определенной на U X У, тогда и только тогда, когда ип -> и и vn -> v в U и У, соответственно. Этот же факт можно выразить и другими словами, сказав, что два вектора (и, и) и (u', v') мало отличаются друг от друга в пространстве U X У в том и только в том случае, когда и мало отличается от и' в t7, a v мало отличаатся от v в У.
Рассмотрим теперь преобразование, определенное уравнением (20). Поскольку х = Fu, а у = G (и -|- Сх) = Gv + GCFu, то ясно, что преобразование Т линейно. Например, вектор X (u, v) = = (Хи, Хи) отображается с помощью Т в вектор со следующими компонентами:
F (X, u) - XFU - Кх,
G (Хи) + GCF (Хи) = ХСи J KGCFu = Ху, откуда следует, что
ТХ (U, V) = КТ (U, и).
При этом мы воспользовались тем фактом, что преобразования р. и х, С: X -> V и G: V -> Y линейны. Если, кроме того, эти преобразования еще и ограничены, то ограничено и преобразование Т. В самом деле, если (un, vn) ЕЕ U X V сходится к (u, v) G G U X V, то
ип -> и,
Уп У
и в силу непрерывности F\ С и G
Fun -> Fu,
G (vn + CFun) -> G (p + CFu), откуда
т (un, Vn) -+ T (u, v).
Таким образом, ясно, что ограниченность преобразования, описывающего гибридную систему, является следствием ограниченности преобразований, представляющих каждую ее подсистему. А это побуждает нас заняться выяснением вопроса, при каких же условиях эти преобразования ограничены. (Этот вывод можно обобщить на случай разомкнутой системы из сколь угодно большого конечного числа подсистем. Однако случай замкнутой системы из нескольких подсистем требует дополнительного исследования. Трудности этого исследования можно почувствовать, взявшись за решение упражнений 7 и 11 этого параграфа.)
Напомним, что две нормы || || и || ||', определенные на некотором пространстве X, считаются эквивалентными в том случае, когда существуют такие постоянные 0 а (3, что а |х|	|х|'
0||я|| для всех х е X. Предположим теперь, что || и || ц — это две эквивалентные нормы, определенные на некотором пространстве X, а | | и | |' — две эквивалентные нормы, определенные на другом пространстве У. Если А есть некоторое линейное отображение X в У, то
||Ля|| ЛфЦ для всех х ЕЕ X, тогда и только тогда, когда при любых х Е X
Другими словами, ограниченное линейное преобразование одного банахова пространства в другое остается ограниченным, если в этих пространствах ввести эквивалентные нормы.
В частности, если X = Хх X ... X Xn, a Y = х ... ... хУт — декартовы произведения пространств, то для того, чтобы доказать ограниченность некоторого линейного преобразования А, переводящего X в У, достаточно выбрать любую подходящую пару норм. Это соображение приводит к дополнительному
упрощению вычислений, необходимых для того, чтобы доказать ограниченность преобразования сложной системы. Обозначим через Ах = у = (у1, ..., ут) е= Y образ вектора х = (хх, ... ..., хп) из X. Тогда преобразование А ограничено, если
max {UloDC-M [ max {hill}]-i<i<n
Другими словами, линейное преобразование А: X -> Y ограничено тогда (и только тогда), когда ограничено каждое из преобразований Ар X -> Yj (j = 1, 2, ..., тп), где
Ajx = у,.
Рассмотрим теперь преобразование G (см. схему на рис. 2.16). Для v = (р1? ..., рв) ЕЕ V j-я компонента вектора Gv ЕЕ Y определяется по формуле
t 8
(Gjv) (0 = $ 2 ^V’k) , ₽) (₽) dp, 1 < i < d, to K=1
где через (t, (3) обозначен элемент на пересечении /-го столбца и А-й строки матрицы W2 (*, |3). Преобразование G ограничено, если ограничено каждое из Gji V -> Yj, что в свою очередь следует из неравенств
t
| $И^’к)(г,Р)1МР) dp|
to
где в левой части неравенства — норма в пространстве Yj, а через обозначена норма принятая в
Дальнейшее продвижение невозможно, если не конкретизировать пространства входных воздействий V, что в свою очередь требует привлечения физических соображений. Например, нам может понадобиться изучить поведение непрерывной системы G, на которую действуют входные сигналы v с максимальной дифференцируемостью или минимальной интегрируемостью. В первом случае мы будем считать, что V — это С1 X ...X С1, а во втором, что это х ... X Lv Но, что еще хуже (если мы стремимся к максимальной общности), иногда встречаются ситуации, в которых приходится рассматривать входные воздействия и = (р1? ..., ив), для компонент которых нельзя найти однородных требований, в результате чего V может представлять собой декартово произведение С, С1, ..., Сп, а также различных пространств Lp. Наконец, физическими соображениями диктуется и выбор норм (а следовательно, и пространств Yj), по которым будет оцениваться вектор выходных величин у = Gv.
Проиллюстрируем наш метод на одном конкретном примере* Пусть Fx = F2 = ... = F8 = Lp (tQ, b), где p фиксировано (1 p <" оо). Тогда можно установить достаточные условия, которым должны отвечать функции И1;Л)(г, 0) и матрицы W2(t, 0), для того, чтобы гарантировать ограниченность преобразования G. Это, конечно, будет зависеть и от выбора норм для пространств Yj. Учитывая, что ик €= Lp (/0, Ь), мы потребуем от PF^’r)(Z, 0), чтобы они принадлежали пространству LQ(Z0, 0) при каждом так как это гарантирует интегрируемость произведения (Z, 0) ик (0). (Здесь i/p+ 1/q = 1, как обычно; при р = оо, q = 1, и наоборот.) Введем еще более сильное предположение: примем, что И?’” (t, s)^Mjk, т. е. что все эти функции ограничены на прямоугольнике k0, b] X По, Ь]. Тогда с помощью неравенства Гельдера мы установим, что
t	t
I $	(t, P) vk (P) dp I < $ MJk I vk (p) I dp <
to	to
b
<$^IMP)|dp<34bll. 0
где
,	если l^£<^oo,
I M если q = oo, a IPfcll — норма в Zp(/0, 6). Таким образом, норма функции t
$ W2'к) (t, 0)	(0) d0 в пространстве не превосходит М|| vk j|, где
о
М = max {М
Подводя итог, мы можем сказать, что если элементы матрицы W2 ограничены, то G —- это ограниченное линейное преобразование, отображающее V = Lp (£0, b) X ... X Lp (£0, Ь) в пространство Zoo(*o, b) X ... х £оо(*о, Ь).
Упражнения
1.	Обладает ли матрица 0 (г, г0) из уравнения (13) обычными полугруп-повымп свойствами и свойствами обращения, полученными для матриц
2.	Проверьте формулу для (GCFu) (е), приведенную в уравнении (17).
3.	Пусть А (/, р) — некоторая переменная матрица, непрерывным образом зависящая от параметра р. Пусть р — это номинальное значение р, а соотношение A (t, р) = A (t, ji) + dp// (t) описывает функциональное поведение 4 в окрестности {dp: || dp [| < /с}, где к мало. Найдите общий вид
возмущений в преобразованиях Ф, Фд, F и Fa в окрестности JT для системы * (/) = л (/, р) х (/) + в (о и (/), t е т.
Выясните, являются ли нормы ЛФ, 6Фа, 6F и dFe, как функции, определенные на соответствующем гильбертовом пространстве, подходящими и содержательными мерами чувствительности системы к вариациям ц в частном случае, когда А и Н — диагональные матрицы.
4.	Обозначим через и В2 множества функций, определенных для некоторых множеств моментов времени v. Обозначим через / отображение Вх в В2, а через — произвольную точку v. Пусть значения функции у = fu при t > tf полностью определяются числом
У (?) = (/“) («')
и значениями функции и при t > t', каково бы ни было и е Bv Тогда ото-бражение / мы будем называть причинным. Докажите причинность поведения линейной динамической системы
dtx (0 = А (0 х (0 + В (0 и (0, t е v,	(23)
у(0= С (t) х(0 + D (t) и (0
как для непрерывного, так и для дискретного случаев, где	если
v = а, и dt = d/dt, если v = т. Причинна ли гибридная система, рассматривавшаяся в этом параграфе?
5.	Отображение f из упражнения 4 мы будем называть физически реализуемым, если для всякого 6 v значение
у (О = (/“) («')
не зависит от того, какие значения принимает и при t > f. Выясните вопрос о физической реализуемости отображения (23). Является ли физически реализуемой гибридная система, рассматривавшаяся в этом параграфе? Если нет, то при каких условиях она станет физически реализуемой?
6.	Вернемся еще раз к линейной динамической системе, описывающейся уравнением (3). Пусть т — это промежуток ^, ес], и пусть преобразование Fb определяется соотношением
tb
Fbau = С Ф (tb, s) В (а) и (0 ds.
*а
Покажите, что суммарная реакция системы удовлетворяет уравнению х (tc) - Ф М * (ta) = Ф (tc, t ь) Fba и + Fcbu
при каждом th ЕЕ т.
В остальных упражнениях мы рассматриваем одноконтурную систему, схема которой показана на рис. 2.17. На этой схеме приведены следующие преобразования: F: Вх -♦ В2, описывающие внутреннюю реакцию фиксированного объекта управления; G: Bi -♦ Вх и L: В2 Вх, описывающие поведение компенсаторов, и К: В2 —* В2 и J: В2 -► В3, описывающие выходные ограничения. Символы Вх, В2 и В3 обозначают банаховы пространства. Для описания поведения системы в целом нам понадобятся следующие переменные: и — входной сигнал системы, х — полезный выходной сигнал системы, — наблюдаемый выходной, сигнал системы, ез — внутренняя координата
(состояние) системы, e2 — входной сигнал объекта управления, g и ц — внешние возмущения, действующие на систему.
7.	Пусть М = LJ. и пусть преобразования (I + MFG) и (Z + FGM) обратимы. Покажите, что
et = (Z + MFGV1 [u + g -
e3 = (I + FGM)-1 \FG (u + g) + ц].
Пусть задача выбора компенсаторов М = LJ и G состоит в том, чтобы в отсутствие помех (g = 1] = 0) сохранить между входным сигналом и полезным выходным сигналом соотношение, характеризующее объект управления (е3 = Fu). Покажите тогда, что
G = (I — MF)-1.	(24)
8.	Пусть все рассматриваемые преобразования линейны и ограничены. Покажите, что если \\FGM |, || МF Ц и ||Filf || меньше 1, то из того, что
(а) следует
(б)
(в) (г) (д)
Указание. Воспользуйтесь теоремой Е из § 2.2 для того, чтобы установить обратимость преобразований, а затем освободитесь от знаменателей. Заметим, что если ограниченные операторы грубо определять как операторы устойчивых систем, то эти результаты напоминают хорошо известные достаточные условия устойчивости. (Дальнейшие соображения в этом направлении можно найти в работах (Б.105, Б.106, Б.123].)
9.	Постройте метод синтеза, позволяющий реализовать выражение (24) для преобразования G, основанный § 2.2).
10.	В отсутствие внешних возмущений система описывается уравнениями ё3 = Fu и ёг = и — Мё3. Пусть g = т] = 0, и пусть характеристики объекта изменились: F -♦ F + 6F. Покажите, что с точностью до приращений первого порядка возмущения де3 и значений ё3 и ёи соответственно, удовлетворяют уравнениям
б*! = [Z — MF] {-МЪРи + g - MnJ,
бс3 = [Z - FM\ \bFu + F (I - MF)~4 + Tj.
И. Предположим, что преобразование F обратимо, и пусть М* = XF*1 где 0 < X < 1. Что можно сказать о возможности снижения чувствительности системы с помощью обратной связи? (Какая взаимосвязь существует между снижением чувствительности и коэффициентом усиления G?)
G = (I - MF)~\
(I + FGM)"1 = (Z - FM),
(I + MFG)'1 = (I - MF).
(I + FGM)~lFG = F.
I - M (I + FGM)~'FG — I — MF.
Рис. 2.17. Одноконтурная система.
на разложении Неймана (теорема Е из
2.6 Литература к главе 2
В §§ 2.1 и 2.2 мы продолжали заниматься теми же вопросами, что и в главе 1. Поэтому книги, которые мы предлагали как литературу к главе 1 в целом, способствуют пониманию содержания и этих двух параграфов. Но так как в главе 2 одним из основных математических методов служит теория матриц и определителей, то мы добавим к предыдущему списку еще книги Айткена [А.1], Айерса [А.7], Кука [А.17], Гоффмана и Кунце [А.42] и Перлиса [А .66]*). Дополнительные примеры и результаты из теории интегральных уравнений можно найти в книгах Трикоми*{А.87] и Вольтерра [А.92].
Теории дифференциальных и конечноразностных уравнений посвящено множество отличных книг. Этим же вопросам посвящены и специальные главы нескольких справочных пособий общего характера. Мы можем порекомендовать специализированные монографии Веллмана [А.10], Коддингтона [А.15], Каплана [А.4G] и [А.47], Миллера [А.61], Понтрягина [А.68] и Шпигеля [А.80]. На несколько более высоком уровне написаны книги Коддингтона и Левинсона [А.16] и Лефшеца [А.55]. Богата и литература об уравнениях в конечных разностях. В первую очередь здесь можно порекомендовать книги Гольдберга [А.34], Миллера [А.59] и Ричардсона [А.70]. Читателю следует также прочесть приложения 3 и 4, развивающие материал §§ 2.3 и 2.4.
Среди многих книг, посвященных приложениям или излагающим другой подход к решению аналогичной задачи, наиболее близки к теме §§ 2.3 и 2.4 работы Ту [А.86] и Задэ и Дезоера [А.95]. Более классичны монографии Брауна [А.13], Горовитца [А.43], Джури [А.45], Куо [А.53], Пешона [А.67], Ту [А.85] и Цыпкина [А.89].
В остальных главах мы будем заниматься в основном линейными системами. Однако следует заметить, что многие задачи теории нелинейных систем можно рассматривать как естественное обобщение материала главы 2. В частности, работы Сандберга [Б.105—Б.109], Зеймса [Б.123], [Б.124], Минти [Б.84—Б.86], Браудера [Б.15—Б.17] и Зарантонелло [Б.125], [Б.126] образуют внушительную теорию нелинейных систем (сошлемся еще на работы Анселоне [А.5], Кронина [А.18], Красносельского [А.51], [А.52], Саати и Брауна [А.74] и Вайнберга [А.91]).
*) Па русском языке можно порекомендовать еще книги Ф. Р. Гантмахера «Теории матриц», 1967, «Наука» и Р. Боллмана «Введение в теорию матриц», 1969, «Наука».
ГЛАВА 3
СТРУКТУРА ЛИНЕЙНЫХ СИСТЕМ
Глава 2 показала нам со всей очевидностью, что между неведением линейных динамических систем и свойствами линейных преобразований в банаховых пространствах существует тесная и глубокая связь. На примерах § 2.5 мы смогли убедиться в том, что некоторые типичные системы могут описываться ограниченными линейными преобразованиями, отображающими одно декартово произведение пространств Lp или 1Р в другое. Эта информация не может не радовать, так как теперь мы уверены в том, что наши усилия, затраченные на изучение абстрактных понятий главы 1, не напрасны и уже приносят свои плоды, позволяя по-новому подойти к задаче математического моделирования систем.
Однако если бы задача специалиста по общей теории систем состояла лишь в математическом моделировании изучаемых им систем, то это техническое достижение, безусловно, было бы слишком поверхностным. В действительности дело обстоит совсем не так. Как правило, чаще всего оказывается, что математическое моделирование системы — это всего лишь первый шаг, ведущий к изучению более глубоких задач теории чувствительности, оптимального управления, устойчивости, синтеза или фильтрации. В оставшейся части этой книги мы будем преследовать именно эти цели.
По мере того, как от ответа на вопрос: «А что такое линейные динамические системы?» мы переходим к решению более интересной задачи, связанной с выяснением того, как можно использовать этот ответ, мы естественным образом приходим к необходимости исследования структурных свойств линейных преобразований. В §§ 2.1 и) 2.2 мы накопили уже немало сведений по этому вопросу. Данная глава продолжает развивать эту тему и доводит до частичного завершения изучение тех понятий, которые жизненно необходимы для решения наших основных задач.
3.1.	Линейные функционалы
За исключением тождественного преобразования и нулевого преобразования, линейный функционал представляет собой наипростейшее из всех возможных линейных преобразований. А поэтому изучать его структурные свойства проще, чем свойства
линейных преобразований более общего вида. В этом параграфе мы изучим линейные функционалы достаточно подробно. Впрочем, не следует думать, что мы делаем это исключительно для того, чтобы «размяться» перед исследованием более общих преобразований. Изучение линейных преобразований полезно и само по себе, а теория линейных функционалов окажется весьма полезным аппаратом для целого ряда последующих применений.
Определение А. Линейным функционалом *) называется линейное преобразование, отображающее область определения X (некоторое нормированное линейное пространство) в пространства К^скаляров, связанных с X.
feglMbi уже выяснили, что пространства К (т. е. R или С) представляют собой одномерные банаховы пространства. Поэтому каждый функционал является некоторым элементом пространства L (X, К) линейных преобразований X в К. Если линейный функционал / к тому же и ограничен, то / ЕЕ р (X, К) — пространству* всех ограниченных линейных преобразований X в К.\
Пространства L (X, К) и р (X, К) в современном анализе играют столь значительную роль, что стало обычной практикой вводить для них специальные обозначения. К сожалению, пока не удалось еще договориться об общепринятых обозначениях для этих пространств. Однако часто пользуются символами X' для обозначения L (X, К) и X* для обозначения Р (X, X), и именно их мы и примем для оставшейся части этой книги. Таким образом X* представляет собой (полное нормированное) линейное подпространство Xх, состоящее из всевозможных ограниченных линейных функционалов, определенных на X. По причинам, которые станут очевидными позже, пространство X* называется сопряженным или двойственным по отношению к пространству X. Элементы / ЕЕ X* называются вещественными или комплексными в зависимости от характера используемого множества скаляров.
Поскольку множество скаляров образует банахово пространство, все свойства линейных преобразований, установленные ранее, распространяются и на функционалы. Для конкретности мы приведем резюме этих свойств для пространства X*.
Свойства линейных функционалов.
(1)	/ (х, 4- х2) =7/ (хг) + / (х2), хп хг S X;
(2)	У/ (ах) = a f (х) для всех х е X и для любых скаляров а;
(3)	/ (хп) -► / (х) при хп -> х, хп е X;
(4)	|/ (х) | М Ы для всех х S Х^и некоторого М[^ 0;
(5)	|/|= sup |/(х)| = sup |/(х)|.
____________м-1	IMK1
*) Термин «функционал» берет свое начало в теории интегральных уравнений, где’он использовался для того, чтобы иметь возможность различать функцип]в’элементарном’смысле этого слова, т. е. определенные на некотором множестве чисел, от функций (или функционалов), определенных на множестве функций.
Подчеркнем, в частности, что X* представляет собой банахово пространство независимо от того, является ли X банаховым или нет. Для того чтобы убедиться в том, насколько часто нам приходится сталкиваться с линейными функционалами, рассмотрим следующие примеры.
Пример 1. Обозначим через х = (^1? хъ х3) элемент евклидова пространства Е3. Тогда любая линейная комбинация /0 (х) --= = o^Xi + &211 * * * * * * * Х2 + «э^з представляет собой некоторый линейный функционал. Но так как	определяет скалярное произ-
ведение вектора xQ = (ах, а2, аз) и вектора х, то функцию /0 (х) можно представить как {х, х0). Изменяя вектор х0, мы можем построить целое семейство функционалов, определенных на 7?8, вида /а (х) = (х, ха). В соответствии с неравенством Шварца
i	i
и, следовательно, функционал /0 ограничен и имеет норму
l/oll^(Sl«ila),/*. г
Нетрудно видеть, что приведенная выше оценка сверху на самом деле является точной, т. е. в ней знак неравенства следует заменить на знак равенства.
Пример 2. Пусть X = Ь2 (0, 1), и пусть / (х) = ^х Этот функционал ставит в соответствие каждому х е X некоторое вещественное число (его среднее значение). Поскольку в соответствии с неравенством Шварца
11	1	V»
| / (х) | = | § х (t) dt |	§ | х (t) | dt	[ § | x (t) |2dZ]	oo,
0	‘	о	о
то ясно, что функционал f (x) ограничен, и его норма не больше единицы. Воспользовавшись определением <х, у) = я У
мы сможем записать / (х) в виде <#, 1>. В общем случае скаляр-
ное произведение fn (х) = (х, h), где h ЕЕ Ь2 (0, 1), представляет собой некоторый линейный функционал, определенный на Ь2 (0, 1).
Пример 3. Пусть X = С (а, 6), и пусть tQ — произвольная фиксированная точка из промежутка [а, &]. Соотношение
f (х) = х (/0)
определяет один из элементов X*, как это показано в примере 10 из § 2.1. Функционал того же типа, но более общего вида
определяется соотношением
ь /(* *) = \x(s)dg ($), а
где g есть произвольная функция ограниченной вариации, определенная на промежутке [а, Ы, а интеграл понимается в смысле Стильтьеса. Если читатель незнаком с‘ интегралами Стильтьеса, то ему полезно знать, что в том случае, когда функция g имеет непрерывную переменную g', последний интеграл можно переписать в виде
ъ
/ (г) = j X (s) g' (s) ds, a
где этот интеграл является уже интегралом Римана.
Пример 4. Пусть X = Z2, и пусть а = {ап} есть некоторый элемент Za. Определим / с помощью соотношения
оо
/(*) S= <х,а> = 2
г=1
где х = {£п}. Неравенство Шварца показывает, что выписанный выше ряд сходится, а / принадлежит X* и имеет норму, не превосходящую (2i | а, I2)1/’.
В примерах 1, 2 и 4 нам удалось представить линейные функционалы в виде некоторых скалярных произведений. Более того, каждый функционал типа скалярного произведения полностью характеризуется всего лишь одним вектором. Действительно, функционал /о определяется вектором х0, a fh — вектором А*). Эти два свойства функционалов распространяются на ситуацию гораздо более общего вида. Однако для начала мы сосредоточим наше внимание на гильбертовых пространствах.
Пусть у — некоторый фиксированный вектор гильбертова пространства Н. Рассмотрим функционал /у, определенный на Н с помощью скалярного произведения: fy(x) = {х, у). Легко видеть, что функционал fy линеен, так как
+ ^2) = (^1 4" ^2» УУ = УУ 4" ^2» УУ = /у (^1) + /у и
/„(ах) = <ах, у) = а<х, у> = а/„ (х).
Более того, используя неравенство
 I /у (х) I = I х, V I <Н-М«
*) Для того чтобы доказать это, достаточно заметить, что если Л, k G Я, а / (х) = <х, А> = <z, /с>, то <z, h — ку = 0, каково бы ни было х 6 Я. Выбирая х = h — /с, мы получим || h — к ||2 = 0 =4- h = к.
мы убедимся в том, что функционал непрерывен и, следовательно, е Я*. Отсюда следует также, что ||/J	||г/||.
Мы можем даже показать, что ||/J| = ||у||. Действительно, если у = 0, то справедливость этого утверждения очевидна. Поэтому предположим, что у 0, и выберем х0 = у/||у||. Но тогда
|/v(^o)l = -L7^LL=hll.
а так как |хо|| = 1, то мы и доказали это утверждение.
Мы показали попутно еще и то, что каждое значение у из Н определяет некоторый функционал из Я*. Соотношение ||/J| = = ||у|| показывает, что соответствие у -> fy определяет взаимно однозначное отображение Я в Я*, сохраняющее норму. Следующая теорема показывает, что это отбражение является к тому же еще и накрытием.
Теорема А. ПустьН — некоторое гильбертово пространство, и пусть / — произвольный функционал из Н*. Тогда в пространстве Я найдется такой единственный вектор и, что
/ (*) = <*. U>,
каково бы ни было х из Н. Более того, ||/|| = ||и||.
Доказательство. Рассмотрим прежде всего ядро Nf функционала /. Если Nf = Н, то / (я) = 0 при всех ЕЕ Я, а так как / (х) = (х, 0> = 0, каково бы ни было я ЕЕ Я, то вектор и = О выполняет требуемую функцию характеризации функционала /. Как мы уже убедились ранее, Nf представляет собой некоторое замкнутое подпространство Я, и поэтому мы для удобства можем представить Я в виде прямой суммы Я = Nf ф Nf~, что всегда возможно в силу утверждений теоремы о проекциях. Тогда произвольное значение х ЕЕ Я, х Nf допускает представление
х = z + w, z е Я/*, w е Nt, z =/= 0.
Но / (х) = / (z) + / (w) = f (z) = a 0. Определим теперь хг как z/a; в результате находим / (zj = 1. Пусть у £ Я — совершенно произвольный элемент пространства Я, причем / (у) = |3. Тогда
о = / (у) - 0/ (*1) = Цу - ₽^1), так что
у — (3^ = и\ ЕЕ Nf, или
У = pXj + Шр
Таким образом, каждое у является суммой некоторого вектора, принадлежащего Nf, и другого вектора, принадлежащего одномерному пространству, натянутому на хг. Отметим при этом, что
Xi | wv Следовательно,
<у, *i> = РЫ2’
а так как 0 = / (у), то имеем
где и = ^/И2.
Вспомним теперь, что у вполне произвольно. Это позволяет заключить, что / и функционал fu идентичны. Однако мы уже ранее видели, что \\fv\\ =||и|| и что если fu = fr, то и = г. Следовательно, вектор и является единственным вектором из Я, удовлетворяющим условию / = /и. Кроме того, ||/|| = ||и||, что и требовалось формулировкой теоремы.
Только что доказанная теорема содержит исключительно важную информацию о структуре абстрактного гильбертова пространства. Например, мы знаем теперь, что функционалы из примеров 1, 2 и 4 исчерпывают все возможности ограниченных линейных функционалов, определенных на соответствующих пространствах. И вообще говоря, совокупность отображений	у>, где
у ЕЕ Н и фиксировано, в точности совпадает с множеством всевозможных линейных функционалов, определенных на любом гильбертовом пространстве Н.
Другое важное следствие этой теоремы относится к структуре пространства Н*. Напомним, что если В — некоторое нормированное линейное пространство, то множество jB* всевозможных ограниченных линейных функционалов, определенных на Я, всегда является банаховым пространством. В самом общем случае о структурных свойствах В* мы вряд ли можем сказать нечто большее. Но дело обстоит много проще, когда пространство В оказывается еще и гильбертовым, Н. В этом случае мы можем утверждать, что отображение у fv сопряженно-линейно, т. е.
/l/t+1/i = /1/1 “Ь /у«>	/°ч/ = *fy-
Оба эти соотношения непосредственно вытекают из определений. Например, равенства
fay (х) = <х, ау> = а О, У> = afv (х) доказывают сопряженную однородность отображения у	fу.
Определим теперь на Я* X Я* функцию (,), потребовав, чтобы
(fx, fy) - <У, *>•
Так как каждое / СЕ Я* имеет вид /и при некотором и СЕ Я и так как вектор и, удовлетворяющий этому условию в Я, единствен,
такое определение функции (,) непротиворечиво, и, следовательно, мы действительно определили на Н* X Н* некоторую комплексную функцию. Мы утверждаем еще, что функция (,) на самом деле определяет скалярное произведение в Я*. Однако прежде чем доказать это, заметим, что в соответствии с выводами теоремы А норма ограниченного линейного функционала fv совпадает с нормой его характеристического вектора у из Я, т. е. что
II/JI = и
где ||/vll — операторная норма функционала. Но отсюда следует, что скалярная норма fy совпадает с операторной нормой этого функционала, и, значит, пространство Я* с определенным на нем скалярным произведением (,) полно и, следовательно, представляет собой гильбертово пространство.
Осталось лишь доказать, что функция (,) удовлетворяет всем аксиомам скалярного произведения. Но, в самом деле,
(/х. + /х.. fv) = <У- xi + х»> = <У- ж1> + <У,	= (/х„ fy) + (/х.. /у),
(а/х. fv) = (/jx. fv) = <У’ ат> а <У< х> = «(/х. /у).
(/х, fy) = <У, х> =	,У>	(/у. /х).
(/х> /х)=	х = о=^ fr = о.
Итог всем этим результатам подводится в следствии, сформулированном ниже.
Следствие. Если Я — некоторое гильбертово пространство, то гильбертовым является и сопряженное пространство Н*. Скалярное произведение в Н* определяется по формуле
(fx> fv) = <У> х>>
и норма fy, определяемая этим скалярным произведением, совпадает с прежним выражением нормы этого функционала как нормы линейного преобразования, определенного на Я.
Это следствие можно было бы сформулировать еще и по-другому. Обозначим через Н() гильбертово пространство, построенное следующим образом. Векторы Яо обязательно должны принадлежать Я. Сумма двух векторов х и у из Яо совпадает с суммой векторов х и у в Я. Однако, произведение вектора х на скаляр Л в Яо определяется не так, как в Я, а как соответствующее произведение х на X в Я. По-другому определено в Яо и скалярное произведение <,>0:
У>о = <*Л *>•
В этом случае сформулированное выше следствие утверждает, что сопряженное к Н пространство Я* изометрически изоморфно гильбертову пространству Яо*).
Поэтому мы можем отождествить Но и Я*. Наконец, совершенно ясно, что те же самые рассуждения в равной степени применимы и к гильбертову пространству HQи приведут к доказательству изометрической изоморфности HQ и Н. так как пространства Н и Яо образованы в точности теми же самыми векторами с теми же самыми алгебраическими операциями и отличаются лишь определением скалярного произведения, в котором нужно сделать перестановку порядка переменных, то пространства Н и По обычно не различают между собой. Если договориться об этом, то мы сможем утверждать, что каждое гильбертово пространство Н является самосопряженным, т. е. Я* = Н.
Перейдем теперь к исследованию содержания всех этих утверждений на примере некоторых конкретных гильбертовых пространств.
Пример 5. В пространстве 12 (п) n-мерных векторов скалярное произведение двух векторов х = (£п ..., gn) и у = (Л1., •••» Лп)» а, следовательно, и наиболее общий ограниченный линейный функционал /, определяется выражением / (х) = <х, у> = Более того,
П/ll2 =
Последний результат можно доказать непосредственно. Векторы — 1, где = (0, 0,..., 0,1, 0, ...,0), образуют в 12 (п) базис. Поэтому, если х = (gx, ..., %п) £= h (и), то х = ^7=1 Пусть теперь / — некоторый линейный функционал, определенный в 12 (п), и пусть /(^) = т]р Тогда
/(*) = /	= S lit fa) = ЗВгп» =	y>,
i	i	i
где
У = fai....Пп)-
Пример 6. Точно таким же образом, как и для пространства 12 (п), можно показать, что наиболее общий ограниченный
*) Заметим, что пространство Яо является зеркальным отображением Н и что, по аналогии с ситуацией на комплексной плоскости, пространство Яо заслуживало бы названия пространства, сопряженного Я. Поэтому наше следствие можно интерпретировать как утверждение того, что пространство, сопряженное (в смысле двойственности банаховых пространств) Я, совпадает с (геометрически) сопряженным пространством Яо. Заметим еще, что если гильбертово пространство Я вещественно, то между Я и Яо нет никакой разницы.
линейный функционал в /2 имеет вид
оо
/ (х) = <х, у) = 2
{“1 причем оо ll/ll2 = kF-i=l
Пример 7. В пространстве L2 (0, 1) наиболее общий ограниченный линейный функционал имеет вид
1 /(*) = §x(t)y(t) dt, о
а его норма
1 ll/lla = JI</(*) |2Л.
о
Пространства, сопряженные некоторым конкретным банаховым пространством. Возможность представления линейного функционала в виде скалярного произведения гарантирована лишь для гильбертовых пространств. Однако часто весьма привычную форму принимают линейные функционалы, определенные и на других конкретных пространствах. Наш следующий пример как раз и посвящен подробному исследованию линейных функционалов, определенных на одном конкретном банаховом пространстве.
Пример 8. Каждый ограниченный линейный функционал /, определенный на пространстве с0, имеет вид
00
/(®)=ЗЬтц, * =
i=l где
оо
(пьП2,..-)е/х и ||/||=2hol-
4=1
Доказательство. Если (тц, ц2, •••) G llt то для каждого х = = (£1»	•••) из cQ справедливо условие
sup I Ы = 1И1 < °°» и, следовательно,
П	71	ОО
i«l	i=l	i=l
Отсюда вытекает, что оо	оо
122 I’M, i=l	i=l
и, значит, функция /, определенная на с0 выражением
/ (*) = 2 х = (Si, Sa,...) е с0, 1=1
ограничена и имеет норму
Кроме того, ясно, что функция / линейна.
Для того чтобы показать, что норма / в действительности равна 2Г£=1|т1г|, достаточно убедиться в том что для каждого 8 > 0 найдется такой вектор х = (^, £2, ..«)из с0 с ||лг||	1, что|/ (х) |^>
> J’ili | r]i j — 8. Но так как | rji | < оо, то существует такое целое число п0, что
оо
2 I’M <8-
i=n0
Обозначим через х = (£х, £2, •••) вектор, координаты которого определены следующим образом:
£< =
MJ	л • А О
-•	, если ть^О, .
Т].	’	I» >	’
0, в противном случае.
»^о»
Ясно, что х ЕЕ с0 и оо	и»	оо
/ (*) = 2 Sint = 2 I m I > 2 I ’ll I -8-i=l	i=l	i=l
Остается лишь доказать, что если / — ограниченный линейный функционал в с0, то в всегда найдется такой вектор (гц, ц2, ...), что
f(x) = Fspii,
каково бы НИ было X = (£х, £2, •••) со- ДЛЯ ЭТОГО положим rji = / (^i), где Xi и определяется следующим условием:
xL - (о,	0, 1, 0, ...),
в соответствии с которым все его координаты, за исключением i-й, равны 0. Если у вектора х = (Еп £2, •••» 5п» 0, ...) лишь конечное число ненулевых координат, то ясно, что / (х) = У&Лр Зафиксируем теперь целое число п и определим вектор х = = (hi» Ь, ...) с помощью условий
li =
' h( I
0, в
если 0,
i = 1, 2, .. . , п,
противном случае.
Мы найдем тогда, что
П	п
г=1	г=1
Но так как число п произвольно, то можно заключить, что 00 и> следовательно,
(тц, Т)2» •••) €= 1\-
Наконец, если вектор х = (£п £2, ...)€= с0 и задан, то положим яп = (11» 5г» • ••, U» 0» 0» •••)» ГДО п = 1, 2, ... Ясно, что хп с0. Но если задаться еще и е^> 0, то всегда найдется такое п0, что | 5i| <С е ПРИ г > я0, и следовательно,
k—M = suP|£iKe i>n
каждый раз, когда п п0. Другими словами, в пространстве с0 хп -+х. Пользуясь непрерывностью /, можно утверждать, что /(*n)	Но, с другой стороны, f (хп) = j'"=i Si-Hi и, как
П	00
легко видеть, при п -► оо: У, £<т]4 —> У, Поэтому
г=>1	г=1
оо f (*) = S г=1
что и требовалось доказать.
Пример 8 характерен для ситуации, существующей во многих знакомых банаховых пространствах. Подытожим полученный результат для наиболее интересных с точки зрения потенциальных приложений банаховых пространств.
Теорема Б. Пусть 1	< оо, и пусть Up + 1/g = 1.
Тогда, если f — некоторый линейный функционал, определенный на пространстве Lp(t), то существует единственный элемент
у е Eq (т), такой, что
f (*) = fv (х) = J х (0 У (0 т
причем норма функционала f равна норме у, как элемента пространства Lq (т):
Этот результат подтверждает целесообразность называть Lq пространством, сопряженным пространству Lp. Точнее говоря, сформулированная только что теорема утверждает, что отображение f -+fу является линейной изометрией между Lp и Lq.
Аналогичный результат для пространств, составленных из последовательностей, сформулирован в теореме В.
Теорема В. Пусть 1 < р оо и Ир + Hq = 1. Если / — некоторый линейный функционал, определенный на пространстве 1Р, то существует такой единственный элемент y€Elq, что
оо f(x)=fu(x) = 3 Мк» fc=i
гдех = (&,	...) и и = (т]п r]h, ...), причем ||/u|| = || и||, =
= &il
Замечание 1. Если р = q = 2, то наши результаты справедливы для гильбертовых пространств Ь2 (т) и 12. так как l2 (п) Q /г» то теорема В справедлива также и для пространства 12 (п). В этом случае функционал имеет вид / (х) =
Приведенные теоремы сохраняют свою справедливость и в том случае, когда р = 1. В этой ситуации уравнение 1/р + 1/q = 1 подсказывает, что Lx =	и = Zoo- Эти предположения,
действительно, оказываются верными. Так, каждый ограниченный линейный функционал /, определенный на LY (т), имеет норму
/(*) =tv (х) = p(W) dt, где
уе£оо(т) И 1/1 = 11^1100 = ess sup |p(t)|.
Аналогично норма ограниченного линейного функционала в 1г определяется по формуле
00
/ (*) = fy (X) = 2 X U, ...)<= /1,
где
У = (Пп Пг» ••• и принадлежит /оо» причем
|/| = kl» = sup | Till, i
(Доказательство того, что Гг = практически повторяет рассуждения примера 8).
Таким образом, теоремы Б и В оказываются истинными для значений р, лежащих в пределах 1	< оо. Но что удивитель-
но (а часто и очень неприятно), так это то, что обе эти теоремы несправедливы для случая р = ос. Тот факт, что каждый вектор у = (т]1? т]п, ...) из /оо определяет некоторый линейный функционал в /х, норма которого совпадает с || у||оо, приводит к неравенству
ОО	00
13 IBil) (sup и. D-i=l	i=l
Если теперь зафиксировать z = (gx, ...,	...) в /х, а вектору у
позволить меняться в /оо» то отображение, преобразующее у в число является некоторым ограниченным линейным функционалом в /оо. Другими словами, ZxCZ /оо- Однако это включение в данном случае оказывается собственным, т. е. в недостаточно векторов для того, чтобы охарактеризовать все ограниченные линейные функционалы, определенные на /оо- Аналогично обстоит дело и с пространством (т), для которого Lx 6= L^.
Представляется полезным отметить, что такая патология не наблюдается в конечномерном случае. Другими словами, 1Х (и) двойственно /оо (и), и, следовательно, соотношение [1Р (и)] * = = lq (и) справедливо при 1 р сю. Причина этого состоит в том, что /оо (ц) конечномерно, или, что эквивалентно, все линейные функционалы в /оо (и) ограничены.
Наконец, заметим еще, что если 1 < р оо, то 1 < q оо, и теорема Д (соответственно, Е), примененная к пространству Lq (соответственно, /q), показывает, что Lp (соответственно, 1Р) двойственно к Lq (lq). В чисто символическом виде: Lp = Lp и /р = = /р, если только 1 <С Р <С 00• Предыдущее замечание показывает также, что [1Р (п)] ** = 1р (п) при 1 р оо. Таким образом, при 1 < р оо пространства lp (n), lp и L9 рефлексивны (см. § 3.3).
Для читателя с более полной подготовкой утверждения двух последних форм могут быть сформулированы следующим, более общим образом.
Теорема Г. Пусть 1 р оо, и пусть Ир + Hq = 1. Тогда, если / — некоторый ограниченный линейный функционал, определенный на банаховом пространстве Lp (т, р,) всевозможных измеримых функций, определенных на т и таких, что |/(£)|р, р интегрируемо на этом промежутке, то существует такой единственный элемент у (Е~ Lq (т, р). что
f(x)=fy (х) =
причем
ЛА,1 = Ы, = |•
Пространство BV. Прежде чем переходить к следующему примеру, мы остановимся вкратце на изучении свойств одного важного банахова пространства — пространства функций ограниченной вариации. Обозначим через {^,	^п-х} некоторое под-
множество точек промежутка [а, Ь]. где а = tQ ... < tn = Ь. а через v — соответствующее этому подмножеству разбиение [а, 6]. Тогда для каждой функции /, определенной на [я, &], можно найти число
п—1
l/k= 3l/('i+i)-/(Mi-i=0
Если через Q обозначить множество всевозможных разбиений про- ” межутка [а, 6], то вариация функции на этом промежутке определяется следующим соотношением:
var (/) = sup | / |v.
[a,b] vEQ
Если varta>bj (/) оо, то про функцию / говорят, что она имеет ограниченную вариацию.
Сейчас у пас нет ни времени, ни желания исследовать этот класс функций сколько-нибудь подробно. Однако мы перечислим здесь некоторые из важнейших свойств этих функций. Во-первых, заметим, что если функция / неубывающая (т. е. / (/J	/ (/2)
при^1 < f2l, то var[a,b] (/)=/(&)—/ (а). Аналогично, если / — невозрастающая функция, то уаг[а>ь] (/) -- /(«)—/ (Ь). Во-вторых, если функция / дифференцируема на промежутке [а, Ь]. то
ь var(/) = j|/' [а.Ь] а
и если / — ступенчатая функция (т. е. / постоянна всюду, за исключением конечного числа точек, где она претерпевает скачок), то
[а.Ь]
где суммирование происходит по всем точкам разрыва /0. Очевидно, вариация постоянной функции равна нулю, а соотношения var (а/) = | ос | var (/), [а.Ь]	[а.Ь]
var(/ + g)<var (/) 4- var(g)
[а.Ь]	[а.Ь]	[а.Ь]
справедливы для любых скаляров а и произвольных функций / и g ограниченной вариации.
Другими словами, пространство BV 1а, Ы всевозможных функций ограниченной вариации, определенных на промежутке [а, 6], представляет собой линейное пространство. Более того, если не принимать во внимание того факта, что равенство нулю var[a, ь] / означает постоянство функции /, то «вариационный оператор» удовлетворяет на ВV [а, 61 всем аксиомам нормированного пространства. Этот незначительный изъян можно исправить, потребовав, например, чтобы каждая функция / 6= BV [а, 6] удовлетворяла еще и условию / (f) = 0 для некоторого фиксированного f ЕЕ [а, 6]. К эквивалентному результату можно прийти, если считать эквивалентными в BV [а, 61 две любые функции, отличающиеся друг от друга лишь на постоянную. В этом смысле любая постоянная функция оказалась бы эквивалентной тождественному нулю и пространство BV [а, 6] стало бы нормированным линейным пространством, состоящим из классов эквивалентности.
Пространство LY (а, Ъ) можно погрузить в пространство BV[а, 61. Делается это следующим образом. Каждой функции /' ЕЕ (а, Ь) ставится в соответствие функция /, где
t a
Это правило, очевидно, определяет некоторое линейное преобразование (а, Ь) в BV [а, 61. Можно показать, что такое преобразование сохраняет норму. Другими словами, можно показать, что
var (/) =||Г [|х, [а.Ь]
Однако неверно было бы утверждать, что каждую функцию / ЕЕ BV [а, 6] можно построить таким образом.
Для того чтобы показать существование другого подмножества BV [а, Ь], воспользуется знакомой (хотя и чисто формально) дельта-функцией Дирака *). Обозначим через 6 (t — th) обобщенную функцию, определенную следующими условиями:
6 (t — t^) = 0, t =/= tk ЕЕ [а, 6],
^+е
j 5(t — tk)dt = 1,	e>0.
'k-'
Обозначим, далее, через о = {tk} такое подмножество (а, Ь), для которого th <С tk+19 а через а = (ах, а2, ...) — некоторый вектор из Zx. Обозначим через ga функцию
г
Тогда функция ga (Z), определенная выражением
/ ga (0 = J ga (s)ds, а
представляет собой ступенчатую функцию с разрывами в точках множества o’, претерпевающую в этих точках скачкообразное приращение Ь {ai}. Более того, вариация ga определяется по следующей формуле:
var(ga) = ||<х|| = 2l«i I-[a.b]	i
В связи с этим становится ясным, что пространство (a, b) и линейные пространства обобщенных функций аналогичного типа естественно считать собственными подпространствами BV [а, 6].
Теорема Д. Каждый линейный функционал f в пространстве С (0, 1) можно представить интегралом Стилътьеса
1
/(х) = ^x(t)dg(t), хе С(0,1), о
где g (t) — некоторая функция ограниченной вариации на [0, 1], причем || / Ц равна полной вариации g на этом промежутке.
♦) Эту дельта-функцию можно строго определить лишь в рамках теории обобщенных функций. Заинтересовавшийся читатель может обратиться к нескольким прекрасным руководствам ([А.29], [А.75] или [А.95], например).
Из приведенных примеров совершенно ясно, что рассматривавшиеся там функционалы, определенные на банаховых пространствах, весьма похожи на функционалы в гильбертовых пространствах. В приведенных примерах каждый функционал /п, определенный на X, образуется в результате выбора некоторого элемента из какого-то вспомогательного пространства U и операции fu (х) = (я, м>, где символ <,> обозначает операцию того же типа, что и скалярное произведение, которая каждый раз, естественно, принимает вид, подходящий к конкретному рассматриваемому случаю и типу пространства X.
Пространства X* и U находятся во взаимно однозначном соответствии, т. е. для всякого и G U найдется свой соответствующий функционал /и = из X*, и наоборот. Более того, поскольку \\fu (х)||	||н||, то у соответствующих и и /и — одинаковые
нормы. Если переименовать все и, использовав для этого соответствующие /и, в результате чего / (х) окажется равным (я, />, то исчезнет необходимость и в явном упоминании вспомогательного пространства U. В этом случае пространство X*, будучи пространством операторов, должно состоять из элементов вида (,/>. Однако в последующем зачастую проще представлять себе X* как пространство, образованное элементами / и обладающее операцией (,>.
Обсуждение. Исследуем взаимосвязь между X и X* более подробно. Мы знаем, что если / есть некоторый фиксированный вектор из X*, то отображение х -+f (х) линейно:
/ («Л + а2я2) = ad (*i) + «г/ (дг2).
Более того, оно ограничено:
II/ (*) II < ИЛ-И для всех е х.
Предположим теперь, что Д и /2 являются элементами пространства X*, a Oj и а2- некоторые скаляры. Напомним, что если рассматривать X* как пространство линейных преобразований, определенных на X и принимающих значения в поле скаляров, то в нем автоматически определяются естественные алгебраические операции. Так, по определению, через ахД + «2/2 мы обозначили линейный функционал, определенный на X, и преобразующий вектор х из X в о^Д (х) + а^Д (я):
(а1Д + а2/г) (*) =	(х) + а<>/2 (х).
Мы знаем, кроме того, что этот функционал также ограничен, а следовательно, представляет собой элемент X*.
Задумавшись на секунду, мы сразу поймем, что если в этом последнем уравнении фиксировать х и менять Д принадлежащие X*, то отображение / ->/ (х) будет тоже линейным.
Это заключение можно сформулировать более конкретным образом. Мы договорились уже обозначать через <х, /> вещественные (или комплексные) скаляры / (х). Тогда <,> представляет собой некоторую функцию, определенную на X х X* и принимающую значения из поля скаляров. Эта функция билинейна:
(ВД + а2а:2, /> = Ox /> + а2<х2, />.
<х, aJi 4- О2/2> = ах < х, А > + а2 (х, f2~>
и обладает свойствами скалярного произведения, о чем мы уже упоминали выше. В последующем мы будем свободно заменять обозначение / (х) на <х, />. Тот факт, что символ <,> приобретает новый смысл, если пространство X гильбертово (а сама функция — новые свойства, например, <х, у> = \У, я>), не вызывает никаких затруднений, если мы не будем забывать о контексте, в котором он используется. В то же время такое обозначение чрезвычайно удобно по многим причинам. Например, исходное определение X* как пррстранства ограниченных линейных функционалов, определенных на X, наводит на мысль, что пространство X в некотором смысле более фундаментально, чем пространство X*. Однако в каждом конкретном примере банахова пространства, который мы рассматривали до сих пор, пространство X* оказалось таким же фундаментальным банаховым пространством, как и X. Действительно, пространство Lq ничуть не менее важно, чем пространство Lp, и пространство Zoo заслуживает изучения ничуть не в меньшей степени, чем пространство 1Х. Обозначение <х, /> ставит векторы пространств X и X* в равные права, и по одной этой причине оно заслуживало бы предпочтения перед обозначением / (я). Однако за использование символа (я, /> говорит не только это. Рассмотрим утверждение, согласно которому каждое / из X* есть некоторый ограниченный линейный функционал, определенный на X. В наших новых обозначениях утверждение об ограниченности функционала / имеет вид
| (я, /> I ||/|| • каково бы ни было х Gz X.
Это соотношение, безусловно, напоминает неравенство Коши — Шварца, полученное для гильбертовых пространств. Однако это неравенство справедливо для каждого / из X*, так что, фиксируя х из X, мы получим, что
| \Х, /> | ^ ||яЦ • (|/||, каково бы ни было / ЕЕ X*.
Таким образом, каждое х из X задает с помощью операции <х,> некоторый ограниченный линейный функционал, определенный на X*. В символической форме записи это означает, что X CZ X**,
Таблица 3.1
X	X*	Вид функционала	Норма Функционала
4(п) ^2	j. МО, 1) £р(0, 1) (1 < р < оо) МО, 1) 1р (1<РО) h ' £(0, 1)	Z2(n) ^2 £2(0, 1) ь9(0,1) ^(0,1) 1я loo {j : j (t) ограничена на [0,1]}	п <*. />=2$л 1 00 <х, />=2м< 1 1 <ж,/> = ^z(t)/(0rff 0 1 <*,/> — 0 1 <z, /> = \x(t)f (t)dt 0 00 <*, />=3^i 1 00 <®, />=S^i 1 1 <*,/> =5® (')<*/(*) 0	il/l = (Shii2),;’ 1 0 /с	W’ и/|=()|/(01’л; 0 ||/|| = esssup|/(t)| 0«<l 1 ц/11 = зир|^| i 11/11= vary) [«. b]
3.1. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
где X** — (по определению) банахово пространство, сопряженное к X*. Это утверждение мы более подробно рассмотрим в § 3.3.
Наиболее полезной чертой гильбертовых пространств является то, что в них определено понятие ортогональности. Поэтому вполне естественно попытаться ввести в каком-нибудь виде это понятие и в теорию банаховых пространств. Действуя по аналогии, назовем векторы х ЕЕ X и / ЕЕ X* ортогональными, если <х, /> = 0. Дальнейшее развитие этой*идеи мы отложим до § 3.2, однако здесь сразу же отметим одну трудность, вытекающую непосредственно из этого определения. Естественно, что мы надеемся на то, что вектор / из X* не окажется ортогональным всем векторам X, если только это не нулевой вектор пространства X*. Аналогично хотелось бы предполагать, что если х X и ортогонально всем / СЕ X*, то х 0. Первое предположение оказывается верным, так как утверждение \х, f> — 0, каково бы ни было х е X, совпадает с утверждением / (я) = 0. Справедливо и второе утверждение. Однако для того, чтобы установить это, нужно показать, что для всякого ненулевого вектора х пространства X существует некоторый ограниченный линейный функционал /, определенный на X и не обращающийся в нуль на х. Это утверждение в свою очередь основывается на теореме Хана — Банаха (теорема В из § 3.2) (и на самом деле может рассматриваться как ее эквивалентная формулировка). Как мы увидим далее, эта теорема представляет собой центральный результат теории банаховых пространств.
Результаты этого параграфа подытоживаются в табл. 3.1.
На нестрогом языке эта таблица помогает прийти к выводу о том, что каждый функционал <, /> полностью характеризуется единственным элементом /. Обратно, каждый элемент / полностью определяет некоторый функционал < ,/). Пространства {(,/)} и {/} находятся во взаимно однозначном соответствии и оба являются банаховыми пространствами, для которых |]<, />[| = ]]/||.
3.2. Некоторые примеры использования линейных функционалов
В § 3.1 мы рассматривали линейные функционалы, определенные на абстрактном нормированном пространстве X, установили, что X* всегда образует банахово пространство, и обнаружили, что пространства X и X* связаны между собой каноническим образом с помощью билинейной формы < , ). Тем не менее в наших рассуждениях имеется зияющая брешь. Хотя для тех конкретных банаховых пространств (Lp, Zp, С), которые мы уже рассматривали, удалось выяснить существование непустого множества ограниченных линейных функционалов, не обращающихся тождественно в нуль, мы не показали еще, что аналогичное множество можно построить и для произвольного банахова пространства.
Априори нет ничего невозможного в том, что в заданном банаховом пространстве X не удастся определить ни одного ограниченного линейного функционала, не обращающегося тождественно в нуль. В этом случае наше пространство X* состояло бы из одного нулевого вектора. Одной полноты линейного метрического пространства X еще недостаточно, чтобы гарантировать условие X* =/= {0} *). Основная теорема этого параграфа, однако, показывает, что этого не может быть, если метрика X порождена определенной в этом пространстве нормой (т. е. если X — некоторое банахово пространство). Значение этой теоремы определяется не только тем, как она используется в этом параграфе, но и той первостепенной ролью, которую она играет на протяжении всей главы 4.
В последующих параграфах нам необходимо будет строить ограниченные линейные функционалы, обладающие определенными специальными свойствами. В большинстве случаев трудность решения этой задачи определяется тем, что рассматриваемое банахово пространство бесконечномерно. Во всяком конечномерном нормированном пространстве каждый линейный функционал автоматически ограничен (см. упражнение 4 из § 2.2), и следовательно, здесь не возникает задачи обеспечения непрерывности выбранного линейного функционала. Для того чтобы избежать необходимости доказывать, что каждый функционал /, интересующий нас в данной задаче, ограничен, естественно попытаться найти способ свести требование ограниченности / на X к требованию ограниченности / на некотором подпространстве X, Иначе говоря, мы надеемся, что удастся определить функционал / на некотором подпространстве X, а затем доказать, что / можно непрерывным и линейным образом продолжить на все пространство X. Именно этого плана мы не будем придерживаться.
Определение А. Пусть Xn X, Ух и Y — нормированные линейные пространства, и пусть А± и А — линейные отображения Лх: Хх ->УХ и А:Х~уУ. Отображение А называется линейным продолжением отображения Av если ХхС X, Ух cz Y и Ахх = Ах при х е Хх. Отображение А называется линейным продолжением Лх, сохраняющим норму, если, кроме того, ||Л| = = И ill-
Теорема А. Пусть М — некоторое подпространство банахова пространства X, и пусть / — некоторый линейный функционал, определенный и ограниченный на М. Тогда функционал / имеет единственное линейное продолжение на М, сохраняющее норму.
*) Достаточно понятный пример можно найти в статье Картера: S. С а г-t er, American Mathematical Monthly, 69, No. 7, 638—640 (Aug.— Sept. 1962).
Доказательство. По условиям теоремы существует такая постоянная С 0, что | / (х) |	С||т||, если только х ЕЕ М. Пусть
х0 — заданный вектор из М. Тогда в М найдется такая последовательность векторов {яп}, что ||xn — хЦ ->0. Но так как
I / Un) — / Um) I = I / Un — *m) | < фп — *m|»
то последовательность {/ (яп)} представляет собой последовательность Коши в пространстве скаляров, и, следовательно, она сходится к некоторому скаляру а. Докажем теперь, что значение а зависит лишь от х$ и не зависит от конкретного вида аппроксимирующей последовательности {сп}. Предположим, что {хп} — другая последовательность векторов из М, также сходящаяся к х0. Пусть lim / (х'п) = 0. Тогда
I / (Хп) f (^п) I	(ll^n Ц + ||*о	^п||)
и, следовательно,
| ₽ — а К lim С (|| хп — х0|| + ||я0 — хп ||) = 0. п—юо
Таким образом, мы доказали возможность однозначного определения функционала F на М, полагая F (х) = lim / (хп), где {хп} — любая последовательность векторов М, сходящаяся к х. Если х принадлежит М, то к х сходится, например, тривиальная последовательность, каждым членом которой является х, так что на М функционал F совпадает с /. Если х, я'(ЕЕ М, хп -+х и хт -> -+х , то последовательность {хл + хт) сходится к х 4- я', и, следовательно,
F(x + x') lim/Un + *п) lim / Un) + lim/Un) = F (x) + F (x'). Аналогичным образом можно доказать и однородность функционала F. Наконец, если х е М и хп -+х, то
|F (х) I = limI/Un) КlimС||жп|| = С||х||, п	п
что позволяет установить ограниченность функционала F, норма которого не превосходит С.
Предположим теперь, что существует какое-то другое ограниченное линейное продолжение F' функционала / на М. Пусть х е М. Тогда, выбирая хп 6= М, ||гп — х|| -> 0, мы видим, что непрерывность функционала F' гарантирует нам равенство
F' (х) = lim F (х) = lim / (хп) =• F (х), п	п
доказывающее, что F = Fr. Единственность линейного продолжения, таким образом, доказана.
Рассмотрим теперь другую ситуацию, в которой решить задачу продолжения столь же легко.
Теорема Б. Пусть банахово пространство X представляет собой прямую сумму замкнутых подпространств М и N. Тогда каждый ограниченный линейный функционал, определенный на М, имеет ограниченное линейное продолжение, определенное на X. Это продолжение оказывается единственным, если потребовать, чтобы оно было тождественно равным нулю на элементах пространства N.
Доказательство. Условия теоремы означают, что каждое х S X единственным образом разлагается в сумму х = у + z, Где у (= м, a z (= N. Если оба функционала F и F' являются продолжениями одного и того же функционала/, определенного на М, и каждый из них обращается в нуль на элементах пространства N, то F (х) = F (у + z) = F (у) + F(z) = / (у) = F' (у) = /' (х). Та-ким образом, если линейное продолжение /, обращающееся в нуль на N, существует, то оно единственно. Оператор проектирования X на М вдоль N определяется условием Р (х) = у, где х =-- у + z, у ЕЕ М, z N. Напомним (см. § 2.2), что если М и N замкнуты, то оператор Р ограничен. А это в свою очередь показывает, что композиция F fP представляет собой некоторый ограниченный линейный функционал, определенный на X и обращающийся в нуль на элементах подпространства N. А так как на подпространстве М оператор Р вырождается в тождественный, то функционал F является линейным продолжением /.
Следствие. Если X — некоторое гильбертово пространство, а М — подпространство X, то каждый ограниченный линейный функционал, определенный на М, имеет ограниченное линейное продолжение на X.
Доказательство. В силу утверждения теоремы А заданный функционал можно продолжить на М. Но с помощью теоремы о проекциях мы можем представить пространство X в виде прямой суммы М ф N, где N — ортогональное дополнение М. Тогда утверждение следствия непосредственно вытекает из результата теоремы Б.
Замечание 1. Предыдущее следствие нетрудно доказать и непосредственно. Так, если / есть некоторый ограниченный линейный функционал, определенный на М, то (поскольку М образует гильбертово пространство) найдется такой вектор у ЕЕ М, что / (х) = {х, у), каково бы ни было х ЕЕ М. Определяя F (х) как
У) Для всех х ЕЕ X, мы найдем ограниченный линейный функционал F, являющийся продолжением функционала / на X. Заметим, что ||F|| — ||z/|| = ||/|| и что F обращается в нуль на элементах дополнения М.
Если бы для каждого замкнутого подпространства банахова пространства существовало дополнение, позволяющее представлять
его в виде прямой суммы, то предыдущая теорема решила бы всю проблему продолжения. Однако это не так даже для относительно простых пространств Lp. Основная причина такого положения состоит в том, что для банаховых пространств несправедлива теорема о проекциях. Дальнейшие подробности по этому вопросу можно найти у Мюррея [Б.87] и Дэя [А.20, стр. 120].
Перейдем теперь к основной теореме этого параграфа.
Теорема В (Хана — Банаха). Пусть М — некоторое собственное подпространство нормированного линейного пространства X, и пусть f — некоторый линейный ограниченный функционал, определенный на М. Тогда функционал f можно продолжить до ограниченного линейного функционала fQ, определенного на всем пространстве X, такого, что ||/0|| = ||/||.
Формулировка теоремы Хана — Ванаха обманчиво проста. Ее значение частично объясняется тем, насколько полезна она для доказательства других теорем. В качестве иллюстрации этого докажем следующую теорему, базирующуюся на теореме Хана— Банаха.
Теорема Г. Если линейное пространство X нормировано, а х0 есть ненулевой вектор пространства X, то существует такой функционал / из X*, что / (х0) = ||х0|| и ||/|| = 1.
Доказательство. В гильбертовом пространстве теорему Г можно было бы доказать непосредственно. Действительно, пусть / (х) = <х, уУ, где у = 1о/||Хо||. Тогда ||/|| = Jj/|| = 1, а / (x0) = = ||х0||. Не более сложно и настоящее доказательство теоремы Г. Поскольку xQ предполагается не равным нулю, то на можно натянуть одномерное пространство L (х0). Векторы из L (х0) имеют вид ая0, где а — некоторый скаляр. Определим функционал / на L (т0), потребовав, чтобы / (ая0) = оф:о||. Ясно, что функционал / линеен и что
11/11 = sup |/(ж)|= sup Iа|-||х0|| = 1. 1И|=1	Цахо||=1
xeL(xo)
Доказываемое утверждение получается теперь как прямое следствие теоремы Хана — Банаха.
Замечание 2. Рассуждения в конце § 3.1 вместе с теоремой Г показывают, что если пространство X банахово и ему соответствует двойственное пространство X*, то билинейная форма <,), связывающая эти два пространства, обладает следующими свойствами:
(1) Если <х, /> = 0, каково бы ни было х СЕ X, то / == 0;
(2) Если (х, /) = 0, каково бы ни было / £= X*, то х = 0.
Другими словами, единственным вектором пространства X (или X*), ортогональным всем векторам пространства X* (или X соответственно), является нулевой.
Замечание 3. Заметим, что теорема Хана — Банаха не требует полноты пространства X. В своей книге Банах доказывает более сильную теорему, чем сформулированная выше. Он показывает, что если X — некоторое линейное пространство, М — линейное подпространство X, а/ —линейный функционал, определенный на М и мажорируемый на М полунормой р:
I/ U) I Р (х) ПРИ всех
то для / существует линейное продолжение F, определенное на X, причем F по-прежнему мажорируется р. (Полунормой на линейном пространстве X называется неотрицательная функция, удовлетворяющая следующим условиям:
Р (х + у)<р (х) + X, X, р (Ьх) = |Х|р (аг).
Теорема, сформулированная выше, является частным случаем этой более сильной теоремы, где роль р (х) играет СЦхЦ; С — норма f на М).
Нынешнее направление исследований мы завершим следующей теоремой.
Теорема Д. Пусть М — некоторое линейное подпространство банахова пространства X. Тогда, если вектор х0 ЕЕ X находится на положительном расстоянии d от М, то существует такой ограниченный линейный функционал f, определенный на X, что / обращается в нуль на элементах подпространства М, f(x0) = 1 и И/ll = l/d.
Доказательство. Если пространство X гильбертово, то для него возможна ортогональная декомпозиция X = М ф Af-L и х0 можно единственным образом представить в виде х0 = yQ + + z0, где y0€z М, z0 ЕЕ и z0 =^= 0. Нетрудно видеть, что функционал
/ (х) = <Х, Zo>, Zo =	,
обладает требуемыми свойствами. Для доказательства общего случая рассмотрим множество Af0 векторов х вида х = у -|- ах0, где у пробегает множество М, а а — множество скаляров. Множество MQ образует линейное подпространство X, и так как d > 0, то представление х = у + ах0 является однозначным. Действительно, если’у = ах0 = у' + а'х0, то (а — а') х0 = у — у1 ЕЕ М. А так как х0 М, то отсюда следует, что а — а' = 0 и у = у'. Определим функционал /, потребовав / (х) = а. Функционал / определен на1 Мо и линеен, / (х) =0 на М, / (х0) = 1. А так как И=|у + axj| = ||a||-jy/a + х0|| > | а| d, то (х)|| = |\х | < |И|/с/>
таК что [/||	1/d. С другой стороны, в соответствии с определением
расстояния между вектором и линейным подпространством должна существовать такая последовательность {уп} векторов М, что lim ||yn — rr0|| -- d. Но тогда | / (уп — я0) I = f (*о) = 1 <
— х0|, и> следовательно, 1 d||/|, или ||/(| 1/d. Это показывает, что [/[ = 1/d. Остается только воспользоваться теоремой Хана — Банаха и продолжить построенный функционал / на X.
Двойственные множества. В гильбертовых пространствах существование ортонормального базиса создает условия для построения разложений Фурье (см. приложение 2). В банаховых же пространствах понятие ортогональности отсутствует, однако введение ортонормального базиса приводит к таким внушительным последствиям в прикладных задачах, что нам не хотелось бы отказываться от этого понятия без борьбы. Теорема Хана — Банаха как раз и является средством, позволяющим распространить многие свойства разложения Фурье на случай банаховых пространств.
Теорема Е. Обозначим через {яр ..., zn} некоторое линейное независимое множество элементов банахова пространства X. Тогда в X* существует такое линейное независимое множество {/1- •••. tn}, что
fi (xj) = бу, i, j = 1, n.
Доказательство. Обозначим через линейное подпространство, натянутое на {х2, хп}. Совершенно ясно, что вектор хх находится на положительном расстоянии от Мг. Но в силу теоремы Д существует такое Д е= X*, что Д (xj = 1 и / (ЛД) = 0. Повторяя этот процесс для каждого хь мы построим множество {/1» •••» /п}> обладающее требуемыми свойствами.
Теорема ЯС Обозначим через (Д, ..., /п} некоторое линейно независимое подмножество X*. Тогда существует такое линейно независимое подмножество {xY, .... rrn} пространства X, что
h (xj) = i, t = t •••. «•
Доказательство. Если пространство X рефлексивно, то теоремы Е и Ж утверждают одно и то же и нужно лишь X и X* поменять местами.
В общем же случае мы докажем эту теорему индукцией по п. Если п = 1, то Д =Д 0 и существование xY из X, для которого /х (xi) = 1» является тривиальным фактом. Предположим теперь, что п 1 и что теорема уже доказана для случая п = 1. Тогда мы доказали существование векторов	пространства X,
удовлетворяющих условию Д (у^ = 1 и Д (yj) = 0, если i =f= j (i, / = 1, 2, ..., n — 1). Обозначим через 5 множество всех таких х Gz X, что
А (х) = А (я) = ••• = /п-i (х) ~ 0.
Тогда для любого zEX вектор х — ^^Г/Д (х) ух принадлежит S. Поэтому, если бы функционал /п тождественно обращался в нуль на 5, то для каждого х ЕЕ X
п—1	п—1
/(*) = / ([х~ 2 fi (х) yi\ + 3 fi (ж) yi) =
= /(ЗА(^)у*) = (2/(уоа)(*)-
Это показывает, что /п =	/ (уО fi линейно зависит от Д, ...
..., fn—±. Однако этот результат противоречит условию, и мы можем заключить, что найдется такой вектор уп S 5, что /п (уп) = 1. Но поскольку уп (= 5,
fi (Уп) = 0, i — 1, 2, ..., 71 — 1, то, полагая
xi = yi — fn (уд Уп, i = 1, 2, ..., 71 — 1,
%n Уп, мы получим fi (xj) = i, j = 1, 2, n.
Линейная независимость xt следует отсюда непосредственно.
Определение Б. Пусть S = {*«} CZ X и S+ = {/J CZ ClX* обозначают линейно независимые множества. Если Д (ху) = = £>ij, h f = 1» 2, ..., то множества S и S* называются двойственными по отношению друг к другу.
Пусть множества S = {хг} и 5+ = {Д} двойственны друг другу. Для каждого а: из L (S) существует единственное множество скаляров {а;} такое, что
i
Прямое вычисление с учетом линейности функционалов Д показывает, что
h (х) = h (2 а‘х‘) = За^ = Л>> j = ' i	i
Это позволяет переписать разложение х в виде x==^xi<xffi>, xEL(S).
i
Аналогично для каждого / ЕЕ L (5+) существует представление
/=2Л^ь/>, /e=L(5+).
Если пространство X гильбертово, а множество S служит для X ортонормальным базисом, то S = S+, и оба эти разложения приводят к обычным разложениям Фурье. В тех случаях, когда опасность путаницы невелика, мы будем обозначать множество, двойственное множеству 5 = {^!, •••» яп}, через = {х+, ..., Хп}.
Пример 1. Рассмотрим случай Х ЕП и примем, что S — = {.Гр ..., £п} есть некоторый базис в Еп. (Здесь через Xi мы обозначаем вектор-столбцы с вещественными координатами.) Тогда каждый вектор х X допускает представление
х = 9С1х1 + ... + апхп, где а; вещественны. Для того чтобы определить S+, построим подпространство, натянутое на {х2, ...» хп}, а затем найдем нормаль ег к этому многообразию. Тогда	= 0 при i = 2, ..., пи
=f= 0. Изменяя длину вектора мы построим такое что <Xi, #!> = 1 и <Xi, х^ = 0, i = 2, ..., п. Повторяя этот процесс, мы будем каждый раз вычеркивать новые элементы множества S и таким образом построим множество
S	{^1, • • •» *Гп } •
Другой метод построения множества 5+ состоит в том, чтобы из вектор-столбцов образовать матрицу Е. Поскольку множество {xt} линейно независимо, то матрица Е не вырождена. Читатель без труда убедится в том, что строки обратной матрицы Е~х образуют двойственное множество 5+.
Диадные обозначения. На этом этапе полезно познакомиться с удобным формальным аппаратом, опирающимся на диадные обозначения. Для этого в уже принятые обозначения нужно внести две небольшие поправки. Во-первых, будем обозначать число / (х) через </, х>, а не через <х, />, хотя для комплексных пространств последнее и удобней. Во-вторых, нам нужно придать дополнительную окраску тому смыслу, который мы вкладываем в символ <и>. В дальнейшем мы станем связывать символ > с векторами, а символ < с функционалами. В связи с этим </, х) формально читается как функционал </, действующий на вектор и). В качестве иллюстрации обозначим через и> некоторый вектор-столбец, а через (v оператор умножения на некоторую вектор-строку. Тогда в с и = (£i,	£л) и v = (гц, ..., Tjft) операция <г>, и) определяется
обычным образом:
к
Заметим, однако, что, определив и и) как вектир-строку и вектор-столбец соответственно, мы получили возможность приписать
определенный смысл и выражению п > <г. Теперь в соответствии с общепринятыми правилами

•hi, • • •
ЦП I
-£/cTii
SiTlc'
t. e. определяет матрицу. Но все матрицы размерности к х к являются линейными преобразованиями в 0 (Я\ RK). Поэтому А = и><г? есть некоторый линейный оператор Л:	->
определенный следующим условием
п
Ах = и) (у. х) = и (2 Лixi\» г=1	'
где х = (хц ..., xh) — произвольный вектор из R*. Область значений оператора А одномерна и представляет собой линейное подпространство Rk. натянутое на вектор и.
Если же X и Y — линейные пространства общего вида, то выражение
Л = е)«.
где / <= X*, а	интерпретируется как линейный оператор
Л Е Р (X, У), у которого 7?а = Ь(е)С Уи который для любого х ЕЕ X определяется условием
Л (х) = е></, х>.
Оператор Л = е)</, очевидно, линеен и ограничен. Оператор Л называют диадой первого ранга.
Рассмотрим теперь линейно независимые множества Е =
= {ех, ..., еп}СУ и F= {Д, ..., fn} CZ X*. Оператор Ле 0 (X. Y), обозначаемый через
п
л = 2
г=1
и определяющийся условием
Ах = CiXA, ,г> + ... 4- en></n, х>, X,
называется диадой n-го ранга. Легко видеть, что оператор А линеен и ограничен, если ограничены функционалы Д, ..., /п. Областью значений диады Л служит линейное многообразие Ra = L (е15 ..., еп) CZ Y. Определить диаду n-го ранга можно следующим более общим способом.
Определение В. Пусть X и Y — линейные пространства. а множества {et, ..., еп} CZ Y и {Д, ..., /п} CZ X* линейно независимы. Тогда, если квадратная матрица невырождена.
то преобразование Л: X -+Y:
п а = 2 ei> аи <h> 0=1
определяемое уравнением
п
Ах ~ 2 ei> aij\1v
г, .i—1
называется диадой ранга п.
Областью значений А является RA = L (elt еп). Диада А линейна и ограничена (если функционалы из F ограничены).
Пример 2, Предположим, что пространство X n-мерно, а его базис образуют векторы ех, е2, ...» ^п» которым соответствует двойственное множество е* , е£, е*. Если у — произвольный вектор из X, то можно представить его с помощью разложения Фурье в виде
У =	» £/> + ^Х^» £/> + ... + enX<£» £/>.
Замечая, что тождественный оператор определяется условием Ly = г/, мы можем записать этот оператор через диады в следующем виде:
I “	+ ... + епУ^еп-
Таким образом, любой базис S пространства X и множество ему двойственное, могут использоваться для разложения тождественного оператора.
Операторы конечных рангов. Каждый линейный оператор А с конечномерной областью определения DA имеет конечномерную область значений RA. Действительно, если Е = {еп ..., еп} есть какой-то базис DAi то на векторы {Aelt ..., Аеп) можно натянуть Ra. Если оператор А невырожден, то эти векторы образуют базис RA. Ясно, что обратное утверждение неверно, так как у любого функционала, определенного на L2, область значений одномерна, а область определения бесконечномерна. Аналогичным же образом, у диады ранга п (см. определение В) — бесконечномерная область значений и конечно- или бесконечномерная область определения. Преобразования с конечномерными областями значений называются преобразованиями конечного ранга.
Теорема 3. Каждое линейное преобразование конечного ранга может быть представлено как диада такого же ранга.
Доказательство. Рассмотрим преобразование А: X —>У. Поскольку Ra CZ Y n-мерна, то в RA существует базис,который мы обозначим через Е = {е7}, / — 1, ..., п. Для каждого х ЕЕ X
А (х) ЕЕ В а и, следовательно, допускает разложение
А (х) = с1е1 + cze2 + ... + спеп	(1)
по векторам базисного множества. Коэффициенты ej являются функциями х, и потому их можно обозначить через Cj (х). Поскольку преобразование А линейно, то
А (кх) — кА (х) — ^(ж) ег -I- ... -| ксп (х) еп и
Л (жх + ж2) lq (ж^ + q (ж2)] ei + ... + kn (q) + сп (ж2)1 еп.
Более того, непрерывность преобразования А, если таковая имеет место, предполагает и непрерывность cj (ж). Таким образом, нам удалось показать, что cj (ж) представляют собой линейные функционалы, определенные на X, А это значит, что, используя диадные обозначения, мы можем вместо Cj (х) написать (/;, ж), где </> — подходящий функционал из пространства X*. Подстановка этого результата в уравнение (1) дает
п
Ах = 2 «i> <Л> *>, 1=1
что” и доказывает сформулированную теорему.
Замечание 4. Функционалы Д линейно независимы в X*. Действительно, предположим, что
п
2 ад - о.
i=i
Выберем тогда хг & X так, чтобы А (ж{) = q. Тогда, очевидно, fj (xi) = fiij и» следовательно,
п
о=2 <ы(х,) = <ъ.
3=«1
Замечание 5. Диадное представление преобразования конечного ранга не единственно, поскольку базисное множество {q, ..., еп) для области его значений можно выбирать произвольным образом. Рассмотрим тот случай, когда X —- гильбертово пространство ff. Функционалами fj ЕЕ Я* служат скалярные произведения с векторами fj Е: Н. Обозначим через М линейное подпространство, натянутое на векторы (/х, ..., /п). Как показывает замечание 4, это многообразие п-мерно.
Представим пространство II в виде ортогональной суммы пространства М и его дополнения М-L. По определению каждый вектор h ЕЕ М1 ортогонален подпространству М. Другими словами,
Рис. 3.1. [Некоторые подпространства, определяемые линейным преобразованием.
<Л, /> = 0 для всех h (= М-L и всех / s М. В частности, для каждого h СЕ Af-L вектор h | /; (/ = 1,	п). Поэтому М^- CZ Na-
Кроме того, если х (= Na> то
п
0 = Л(х) =2 *{></«,*>•
1=1
Но в силу независимости	еп} все </b Z; 0, и, значит,
г СЕ АГ-L. Таким образом, для преобразования Л - 2?el ядроА'д £(Л, ...,/п)1, что позволяет схематически представлять себе оператор А так, как это показано на рис. 3.1.
Замечание 6. Поскольку М и Ra n-мерны, то преобразование А должно взаимно однозначным образом отображать М на 7?д. А это значит, что отображение А должно быть несингулярным.
Замечание 7. Обозначим через Е = {еъ ..., еп} и F = = {/и •••» /п} произвольные базисы в RA и М соответственно. Тождественный оператор в Ra можно представить в виде
п
= ei> <~ei> i=l
а тождественный оператор в М — в виде п
;=1
Из очевидного соотношения IrAIm = А находим п	п	п
А = (2 *<> <4) А (2 fj> <fi) = 3 «<> «** Af,» i«=l	'	4=1	J» i=l
Полагая atj = (e*, Afj), i, j = 1, ..., n, мы получим разложение A в виде
4=2
i. j=l
Матрицу скаляров [а^1 называют матрицей А относительно базисов Е и F и обозначают через [Л]Е, f или просто через [Л], если выбор базисов очевиден. (Если Е = F, то используют запись [Л]Е.)
Элементарные задачи управления с минимальным расходом энергии. Рассмотрим преобразование Т: Н ~^Rn^ отображающее некоторое гильбертово пространство Н на Rn. Из замечания 6 следует, что для каждого £ GE Яп существует единственный вектор ЕЕ М = JVt, для которого Ти% = £. Рассмотрим любой прообраз и Н вектора £. Существование ортогональной декомпозиции Н = М ф Nt гарантирует возможность однозначного представления и в виде следующей суммы:
и = Ui + U2, Ui G М, ЕЕ Nt-
Цепочка равенств
£ = Ти = Т (-р ^2) = Ти^ -|- Т U2 = Тих 4-0
и замечание 6 доказывает, что иг = и*. Более того, ортогональность и и2 доказывает, что ] иЦ2 = | 12 -р || и^Ц2, и поэтому вектор является к тому же еще и прообразом £ ЕЕ Rn с наименьшей нормой.
Эта простейшая задача играет ключевую роль при решении довольно сложных задач минимизации расхода энергии. Прежде чем переходить к рассмотрению различных ответвлений этой задачи, выясним, как подойти к проблеме вычисления вектора и%. Предположим, что преобразование Т уже представлено в виде
п
«<></«.
1=1
где {*i> ...» еп} — некоторый базис в Rn.
Из предыдущих рассуждений ясно, что, каково бы ни было заданное £ £= Яп, вектор и^ G: М = L (Д, ..., /п) и, значит, должны существовать такие скаляры {сс£}, что
п
«ч = 2
1=1
Точно так же, поскольку $ Rn и {ej образует базис в Я", существует единственное множество {Э<} скаляров таких, что
п
^=2 м-
Воспользуемся теперь предполагаемым представлением преобразования Т и получим
п	п	п	п п
I = 2 piCi> = [2	</i] [S <*///>] = 2 2	</i, fj> е».
Поскольку векторы {е<} линейно независимы, то п ’=1
Обозначая через 0 вектор-столбец (Рх, 0П), через а — вектор-столбец (ах, ап) и через & — матрицу, элементами которой служат /;>, мы придем в эквивалентной матричной формулировке
Р = &а.
Пример 3. Рассмотрим линейную динамическую систему, описываемую уравнением
£ (П = А (0 х (0 + В (0 и (0, t Е т.	(2)
Найдем такой элемент и, который преобразует вектор (х(0), 0]е Е X т в вектор [х (0), 0] Е Rn X т и минимизирует при этом функционал m 0
7(u) = 2 $ lui(s)lads-
1=1 i9
Рассматриваемую систему в фиксированный момент времени 0 можно столь же успешно описать и преобразованием, отображающим Rn х U в Rn и задаваемым соотношением
5
х (*/) = (Фх«) (t/) + (Fu) (tf) = Ф (tf, i0)	$ Ф (tf, S) В (s) и (s) ds.
t/
Задача, сформулированная выше, очевидно, эквивалентна задаче отыскания элемента и Е [Ьг (0» 0)1 = U с минимальной нормой и удовлетворяющего условию
5
g = Ти = £ Ф (0, s) В (s) и (s) ds,	(3)
t9
гце
5 = х(0)-Ф(0,0) х°.
Область значений преобразования Т, очевидно, принадлежит /?п. Воспользуемся координатным базисом этого пространства (другими словами, выберем базис, образованный векторами = (1, 0,	0), е2 = (0, 1,0, ..., 0) и т. д.) и обозначим через (s)
элемент на пересечении j-го столбца и /-й строки матрицы W (s) = - Ф (t„ s) В (s). Тогда, очевидно, уравнение (3) можно переписать в виде
п /т \
I = Ти = 2 е, (2 J Wi} (s) и} (s) ds) .
>=1 /о
Определив на U функционалы
А(«) = 5 [з Wtf («)“/(«)]<&» i =
to >=1
мы можем представить преобразование Т в виде
п т = 2 <ч> <л. i=l
До сих пор мы пользовались конечномерностью пространства Вп лишь для того, чтобы переписать уравнение (3) в более удобном для наших целей виде. Теперь, следуя описанной выше процедуре, мы можем решить и саму задачу. Прежде всего вычислим матрицу f. Поскольку frij =	/у>, то в этом примере
Ч
& (tt, t0) = J W (s) W*(s) ds = Ф (th s) В (s) B*(s) Ф*(гм s) ds, (4) G	/о
где через И7* обозначена матрица, сопряженная и транспонированная по отношению к И7. Более того, поскольку базис {е4} ортонормален, то
₽ = £ = * (<у) - Ф (t„ t0)	(5)
Заметим, еще, что
М0 = 2 «i/i(0 = W*(/)a, tEt.	(6)
Решая уравнения (5) и (6) совместно и принимая во внимание, что a = У’1 (tf, tQ) р, мы приходим к искомому решению
(0	*о) [х^Д-Ф^,	(7)
Пример 4. В качестве второго примера рассмотрим дискретную динамическую систему, описываемую уравнением
\tx (t) ----- А (fy х (t) + В (t) и (fy, t ЕЕ o’.
Как и раньше, поставим перед собой задачу отыскания управляющего воздействия, определенного на множестве o’ = {fy,..., fy}, переводящего вектор (х0, fy) в вектор (xf, tf) и минимизирующего при этом критерий качества
т [t]-1
i=l j«=0
Сходство с предыдущим примером значительно облегчает решение этой задачи. Если через l2 (o’) обозначить гильбертово пространство всех функций, определенных на а, со скалярным произведением
а
то, принимая, что пространством входных (управляющих) воздействий служит U — [12 (о)Г со скалярным произведением
<и, р> = 2 Sui(*?yi(o)> u,ve-u, i=l а
мы видим, что нынешняя задача полностью аналогична рассмотренной в примере 3. Легко проверить, что в данном случае матрица & вычисляется по формуле
К,]-1
Я*/Л) = 2 /i’O(G,Ui)B(U5*Ga)O*(//t	(8)
а минимизирующее управляющее воздействие и^ можно найти из соотношения
u;(fy)=B*(fy)O*(fy, fy+OF^fy, fy) (fy)~<l> (fy, fy) ^1, fy e or. (9)
Пример 5. Для того чтобы проиллюстрировать полученные результаты для более сложной постановки, вернемся к случаю гибридной системы, схема которой представлена на рис. 2.16. Обозначим через г = (5, fy некоторый фиксированный момент времени из o’ х г, и пусть z° = (х (s0), у (fy)) и J = (х (sfy, у (tf)) суть фиксированные векторы из Вп. Нужно найти вектор W = (u, г), переводящий z° в ? и минимизирующий при этом
функционал тх [•]—1	1 j »h
j(“.^)=2 2fii।w>wi4+S 31v><t)i4dx-i=l j=0	*• j=l
Учитывая уравнения (18), (19) и (20) из § 2.5, мы видим, что достаточно решить задачу минимизации J (и, v) при дополнительном ограничении
5 = Т (и, v),
где g = ? — 0 (гр r0) z°, а Т определено уравнениями (19) и (20) § 2.5. Если положить, что U — IL2 (*о, 0)1т‘» а И = [Z2 (сг)1гп\ то J (и, v) в точности совпадает с нормой на U х V, и, значит, этот пример ничем в принципе не отличается от предыдущих двух.
Используя матрицы, определенные в уравнении (18) § 2.5, вычислим компоненты матрицы f (гр г0):
& 13 (rh го)
&22 (rh го)
(10)
Эти компоненты имеют следующий вид:
[•/]—1
& 11 (rh го) = 2	(*/»	0)>
>=0
1
^*1а(грГ0) = 2	(s/» 0)	(^/> ^')»
j=o
^21 ('•у; Го) = 2 1^3 Gn М ^1*($/> fy)> j=0
^22 (гр r0) = W2 (h, s) W* (h, s) ds.
Тогда, если ввести матрицу
^3*(sz,s) W^(th t)
размерности m x n, то искомое решение записывается, как и раньше, в виде
(uc (s), Vi (t)) = W* (r; r0) -1 (rz; r0) [z'O (77, r0) z°],
r = (s, 0 €E о XT.
Обсуждение. Решение задач, связанных с минимизацией нормы и рассмотренных в этом параграфе, может служить еще одной наглядной иллюстрацией преимуществ описания систем в функциональных пространствах. Для того чтобы подчеркнуть это, заметим, что основная задача полностью решена в абстрактной форме и что в примерах нам пришлось не отвечать на вопрос: «А каково же решение?», а лишь решать более простую задачу выяснения, как же выглядит уже полученное общее решение в различных конкретных условиях.
Простая задача минимизации нормы в гильбертовом пространстве позволяет получить гораздо более общий результат, чем это кажется с первого взгляда. В последующих параграфах мы увидим, что ряд внешне более сложных задач можно свести к нынешней за счет соответствующего выбора гильбертова пространства.
По отношению же к нынешней теме исследования естественно задать себе вопрос: а нельзя ли обобщить постановку этой задачи оптимизации на случай банаховых пространств? Обсуждение в § 1.4 предлагает нам одну интересную с прикладной точки зрения задачу. Пусть Т: В -> R -— линейное преобразование одного банахова пространства в другое. При фиксированном £ R найти и ЕЕ В, обладающее минимальной нормой и удовлетворяющее условию 5 — Ти. Решение этой задачи действительно много сложнее решения тех задач, что рассматривались выше. Нахождению его и посвящена большая часть главы 4.
Упражнения
1.	Пусть X — n-мерное банахово пространство. Покажите, что X* также п-мерно. Если S = {zi,..., хп} — базис в X, то покажите, что 64 = {х+, ..., х*} образует базис в X*.
2.	Обозначим через F множество {(0, 0,1), (0,1,1), (1,1,1)}, а через Е — множество {(1, 0, 0), (1,1,0), (0, 0,1)}, и пусть A: R3 -♦ Я3определяется соотношениями
ЛД = А (0, 0, 1) =- (2, 3, 5),
Л/2 = А (0, 1, 1) = (1, 0, 0),
Л/3 = А (1, 1, 1) = (0, 1, -1).
Вычислите матрицы [Л ]Е, [Л ]F и [Л]£ F,
3.	Пусть множество ..., еп} образует базис в Е”. Оператор проектирования, определенный соотношениями х — £1^ + ... + £псп, Ах -	+
+ ••• + tmem^ где m < и, имеет область значений R А размерности m < п. Как выглядит тогда [Л]£?
4.	Пусть множество 5 = [т1.хп} образует базис гильбертова про-
странства X. Для каждого Л : X -» X введем [Л] матрицу Л относительно S (в этом случае a^j = <zt, Лхр). Покажите, что соответствие Л —>|Л| взаимно однозначно отображает fi (X, X) на 0 (Еп, Еп).
5.	Пусть А и В -- линейные операторы, а а н 0 — скаляры. Покажите, ЧТ° (а) |аЛ + рВ| = а [Л| + Р |5],
(б	) [0] = нулевой матрице,
(в	) [71 = [б01, r i
(г	) [ЛЯ] = [Л] [5],
(д	) [Л”1] = [Л]”1, если только Л"1 существует.
6.	Пусть Л е 7/ (X, У), а В е L (У. %)• Пусть при определении [Л1 и [5] используется базис 5 для У. Покажите, что утверждение (г) из упражнения 5 сохраняет свою силу и в этой более общей постановке.
7.	Обозначим через Р — {хр ..., хп} и S =	...» хп} два базиса] для
X, а через С — матрицу [С\Д где
п
Xfc = 2 cJkxj' А: — 1, . . . ;=1
Покажите, что для Л £ А(Х, X) матрицы [Л]р, [Л]8 и С связаны между собой соотношением
[Л1р= С~1 [Л]8 С.
8.	Обозначим через det ([Л]) определитель матрицы Л. Напомним, что определитель обладает следующими основными свойствами:
det ([/]) = 1,
det ([Л] [5]) = det ([Л J)-det ([5]), det ([Л])ф0 <=> [Л I невырождена.
Используя эти свойства и результат упражнения 7, покажите, что для оператора А конечного ранга и любых базисов S и Р dot ([Л]8) = det ([Л]р). В связи с этим определитель оператора Л
det [Л 1 = det ([Л ]s)
вполне определен и не зависит от выбора S. Покажите также, что единствен и не зависит от выбора базиса характеристический полином оператора Л, задаваемый формулой
А (К) = det (Л - Х7).
9.	Пусть Л — некоторый линейный оператор в X. Ранее мы определили ранг Л (обозначаемый через р (Л), как размерность области значений Л). Аналогично определим дефект оператора Л, обозначаемый через v (Л), как размерность его ядра. Если X конечномерно, а Л и В GE L (X, X), то покажите, что
(а)	р (Л) + v (Л) - dim (X),
(б)	р (Л -|- 5)<р(Л) F р (5),
(в)	р(ЛВ)<пнп{р(Л), р (/?)},
(г)	V (АВ) < v (Л) + V (5),
(д)	р (АВ) = р (ВА) -- р (Л), если В невырождена,
(е)	АВ =--- 0 => р (Л) 4- Р (В) Ч <liin (X),
(ж)	v (АВ) max (V (Л), v (В)}.
10.	Докажите, что матрица [</{, /р] невырождена тогда и только тогда, когда множество (Д, ..., fn} линейно независимо.
И. Обозначим через Л: В -* R преобразование банахова пространства В р банахово пространство 5, задающееся соотношением
п
я = 2 е;>
Hl
Покажите, что NA = Uf-. Предположим, что tq, w2, ...» ип G В, а матрица Q = [</j, ыр] невырождена. Обозначим через S линейное подпространство В, натянутое на {мь ..., wn). Докажите, что пространство В разлагается в прямую сумму
в = Na ф S,
т. е. что В = Na + 5, Na f]S= {0}, и что проекция В на NA вдоль S непрерывна.
1S.	Покажите, что если М — некоторое подпространство гильбертова пространства, то м11 = м.
Указание. Обратите внимание на то, что теорема Д утверждает, что если S есть некоторое подпространство банахова простанства В, то для того, чтобы вектор х из В принадлежал 5, необходимо и достаточно, чтобы f (х) в 0, где / — любой функционал, обращающийся в нуль на элементах подпространства S.
13.	Возвратимся еще раз к задаче минимизации расхода энергии, рассматривавшейся в этом параграфе. Обозначим через W*: Rn -♦ (NT)-^ любую изометрию Rn на (ЛГг)-^. Докажите, что композиция TW* представляет собой некоторую невырожденную матрицу и что оптимальное управляющее воздействие определяется по формуле
= w* (TW*)^,	(11)
каково бы ни было £ €: Яп- Заметим, что в примерах 3 и 4 такая изометрия сводилась к умножению на матрицу В* (s) Фф (tf, s).
14.	Сосредоточим наше внимание на примере 3 настоящего параграфа, положив: т = Ra, tc], W* — отображение, определенное в упражнении 13, а g = [х (tc) — Ф (;с, ta) х (fo)]. В духе упражнения 6 из § 2.5 определим
г
Докажите, что
[(/И^]-1 (x(tc) - Ф (tc, tb) х (tb) = [(FW")‘ ]-* [r (te) - Ф (tc, ta) x (ta)],	(12)
каково бы ни было €= т.
Указание. Воспользуйтесь выражением для управляющего воздействия из уравнения (11) и покажите, что
X (tb) = Ф (tb. ta) Г (ta) +	I(FI7*)« ]-• [r (tc) - Ф (te, ta)x
Затем умножьте это уравнение па Ф (te, 1Ь) и воспользуйтесь тождеством
Ф (te, tb) = (™‘)еа - (™*)b-
15.	Заметьте, что уравнения (7) и (11) в совокупности указывают на возможность управления системой, описываемой уравнением (2), в результате введения контура мгновенной обратной связи согласно закону
(0 = В* (t) Ф* (tf, t) jr-i (tf, t) [x (tf) - Ф (tf, t) x (Г)],	t e t.
Постройте принципиальную схему физической реализации этого закона,
Вернитесь к одному из конкретных примеров § 2.4 и проработайте упражнение для этого частного случая.
16.	Получите результаты, аналогичные результатам упражнений 14 и 15, для систем из примеров 3 и 4 этого параграфа.
Примечание, В упражнениях 14 и 15 мы предполагали, что матрица & (tf, t) обратима при всех t е т. В § 3.6 мы убедимся, что это не всегда так. Однако обсуждение этого вопроса мы пока отложим.
3.3. Сопряженные и присоединенные преобразования
Для того чтобы продвинуться дальше в изучении структуры линейных систем, нам понадобятся понятия сопряженного и присоединенного преобразований. Эти понятия не только приближают нас к цели настоящего исследования, но и оказываются полезными в целом ряде прикладных инженерных задач. Так, граничные задачи, возникающие в прикладных проблемах микроволновой техники или теории электромагнитного поля, могут служить конкретным примером, в котором понятие присоединенного оператора играет важную роль. В качестве другого приложения можно указать на терминальную задачу наведения. В пространстве присоединенных операторов были решены некоторые из первых задач управления ракетами (см. упражнение 8).
В главе 4 мы увидим, что ввести понятие сопряженного преобразования необходимо, если мы хотим обобщить нашу задачу о минимизации нормы из § 3.2 на случай банаховых пространств. Наконец, непосредственная польза от введения понятия присоединенного преобразования состоит в том, что в § 3.4 оно позволит получить две удобные канонические формы описания линейных систем.
Второе сопряженное пространство. Теорема Хана — Банаха показывает, что для каждого банахова пространства существуют нетривиальные ограниченные линейные функционалы. Другими словами, эта теорема утверждает, что сопряженное пространство всегда^содержит и другие векторы, кроме нулевого. В частности, не только нулевой вектор содержит и пространство X**, двойственное по отношению к банахову пространству X*. Многие элементы пространства X** мы уже нашли. В самомТделе, для каждого х из Хкмы установили, что отображение / —/> представляет собой некоторый линейный функционал, определенный на X*. Это вытекает из неравенства
К*, />КЖ1 *ех,/ех*,
и того, что функция <,> линейна по своей второй^переменной. Обозначим, временно эту функцию через так что,^по определению, Fx (j) = <х, /> для каждого /, принадлежащего X*. Ясно, что, по мере того как х пробегает X, соответствующий функционал
Fx пробегает X**, а предыдущее неравенство показывает, что I р* (/) I < k II»
если норма / в X* не превосходит 1. Но в то же время теорема Г из § 3.2 гарантирует существование такого вектора / из X* с единичной нормой, что Fx (/) = |х||. Поэтому
И«Й = k II-
Таким образом, мы убедились в том, что отображение х F х представляет собой изометрию, отображающую X в X**. Это преобразование к тому же и линейно. Действительно, если хи х2ЕЕ X, а и а2 — скаляры, то
(/) =- (ед + «2*2, /)	/> + а2\^2» /> =
=	(/) + а2^х. (/) = (ai^x! + a2FX2) (/).
Так как / является произвольным вектором пространства X*, то отсюда следует, что
FaiX^a^Xt = &1Fxt «2^xt*
Короче говоря, преобразование х -+FX представляет собой изометрический изоморфизм, отображающий пространство X на некоторое (замкнутое) подпространство X**. Или, говоря обычным языком, пространство X (как банахово пространство) не отличается от некоторой части пространства X**. Если теперь отождествить каждый вектор х из X с его образом Fx в X** (т. е. с функционалом <z,», то мы можем утвержать, что ХсХ**, и рассматривать каждое х из X как какой-то функционал на X*.
Этот результат позволяет прийти к полезному следствию, для чего нужно подробнее рассмотреть уравнение ||z|| — Их II- Вспоминая определение нормы линейного функционала, определенного на банаховом пространстве, мы видим, что член в правой части этого уравнения имеет следующий вид:
Их 11= sup \Fx(f) ||/||<i,/gx*
Однако по определению Fx (/) — это просто (х, f), и мы получили другую возможность вычисления нормы вектора х в пространстве X:
||х|1= sup |<х, />|.
II/ 1Ю, /ех»
Это уравнение в точности двойственно определению нормы элементов в пространстве X*:
||/||= sup |Сг, /?|.
||х||<1.
Естественно ожидать, что соотношение включения X CZ АЛ** на самом деле не является собственным и что пространство, двойственное X*, совпадает с X. Для X = Lp(0, 1), где 1 < р оо, мы убедились в том, что это правильно: ограниченные линейные функционалы, определенные на Лр, можно отождествить с векторами пространства Lq(\lp + 1/q = 1), а ограниченные линейные функционалы, определенные на Lq,— с векторами пространства Lp.
Следующее определение разбивает всю совокупность банаховых пространств на «хорошие» пространства и «плохие».
Определение А. Банахово пространство X называется рефлексивным, если отображение хF х накрывает X**, т. е. если X** - X.
Мы уже видели, что каждое гильбертово пространство является рефлексивным и что этим же свойством обладают и пространства 1Г, и где 1 р оо. Тем не менее следующий пример показывает, что не каждое банахово пространство рефлексивно.
Пример 1. Пространство с0 не рефлексивно.
Напомним, что пространство с0 образовано из всех векторов х = (51, 5г, •••), У которых lim = 0. Норма в этом пространстве определяется соотношением ||х|| = supJ^J. Пространство, сопряженное к с0, можно отождествить с Zx. Точнее говоря, между с* и Zx существует изометрический изоморфизм, и это отображение связывает каждое / Е с некоторым единственным вектором У = (Лх, Лг, •••) из 4- Обратно, каждое у ЕЕ Zx однозначно определяет функционал /, принадлежащий с*. Это соответствие между /иг/ устанавливается соотношением
00
/(*) = 3 SiHi. i=l
справедливым для каждого х = (gn g2, ...) из с0 и каждого У = (Лп Лг, •••) из 119 причем
|/1=1Н = 21ч.ь г=1
Нам известно также, что пространство I* можно отождествить с Zoo. Но очевидно, что каждая последовательность скаляров (51, 5г, •••), сходящаяся к 0, должна быть ограниченной, а это значит, что с0 Q Zoo- В то же время не менее ясно, что не все ограниченные последовательности сходятся к нулю, так что отношение включения Zo CZ Zf< является собственным. Другими словами, если X — с0, то, как мы убедились, второе сопряженное пространство X** — (X*)* — Z* — Zoo не эквивалентно X.
Поскольку отображение х —> Fx из X в X** является изометрией, то область значений этого отображения замкнута в X**. Проверим это утверждение для пространства с0 непосредственно, показав, что пространство с0 представляет собой замкнутое подпространство /©с. Доказательство этого факта несложно. В самом деле, если члены хп = (Й, £?, ...) образуют некоторую последовательность векторов пространства с0, сходящуюся к вектору х ~ (Si, 5и» •••) из с0 CZ /л, то, по определению нормы пространства /эо, для каждого е > 0 найдется такое т], что
supl^-SiKy
для всех и т]. В частности, |	| < е/2 для i = 1, 2, ...Но
так как последовательность !•£,...) сходится к пулю, то можно указать такое /0, что |£?|<е/2, как только z0. Отсюда
+ т=в
при	Это означает, что последовательность скаляров
(51, 5а, ••• ) сходится к нулю, и, следовательно, вектор х принадлежит пространству с0.
В нижеследующей теореме мы перечислим наиболее распространенные банаховы пространства, обладающие свойством рефлексивности.
Теорема А. Рефлексивным является каждое из банаховых пространств, перечисленных ниже:
(1)	любое конечномерное пространство у
(2)	любое гильбертово пространствОу
(3)	лебеговы пространства Lp при 1 < р оо,
(4)	пространства последовательностей lpt 1 р оо.
Сопряженные и присоединенные операторы. Понятие присоединенного оператора ♦) играет исключительно важную роль во многих областях анализа. А функциональные понятия, введенные выше, помогут нам определить, что же такое сопряженные и присоединенные операторы. Для начала рассмотрим два нормированных линейных пространства X и У и некоторый линейный оператор А: X -+Y.
Пусть / е У*. Тогда / (у) определено для каждого у ЕЕ У, а значит, в частности, и для каждого у = Аху где z Е X. Другими словами, композиция /А отображает X в поле скаляров. Обозначим композицию /А через g.
Поскольку композиция g образована из двух линейных преобразований, то этот функционал линеен. Более того, поскольку
♦) В советской литературе он иосит название (гильбертового) сопряженного.
оператор А ограничен, то |g(x)| = |/ (Лх) | <	<|/||-ИН4
и, следовательно, функционал g линеен и ограничен на X с нормой И^И'ИИ- Другими словами, g(=X*.
Но это показывает, что соответствие f g = fA определяет отображение У* в X*. Это отображение также линейно, ибо если /х и /2 ЕЕ У* и (Xi и <х2 — произвольные скаляры, то
(aji + «г/г) А = «1 (АЛ) + а2 (/2Л).
Обозначим это отображение через А*, так что, по определению, для каждого / из Y* справедливо уравнение A*f = /А. Переписывая приведенное выше неравенство, получим, что
1(4*/) (х)| = |/(Лх)|<1ИНИН4
Следовательно, функционал Л*/ имеет форму
Но так как / ЕЕ У* произвольно, то мы можем заключить, что А* — ограниченное линейное преобразование, определенное на У* и принимающее значения из X*. Ограниченное линейное преобразование А*: У* задаваемое условием А*/ = g = /А, называется преобразованием, сопряженным относительно преобразования А.
Заметим, что нам не пришлось потребовать,чтобы А накрывало У, для того, чтобы определить А*. При фиксированном / из У* композиция А*/ представляет собой ограниченный линейный функцио
нал, определенный на X. Его значения в точке х из X определяются условием (А*/) (я) = / (Лл:) (см. по этому поводу рис.3.2).
Важнейшие свойства сопряженного преобразования подытожены в следующих двух теоремах.
Теорема Б. Преобразование А* ограничено и линейно, причем 1| А ♦] = || A J.
Доказательство. Учитывая замечания, сделанные выше, мы должны лишь доказать, что ||А*Ц > |Л||.
Однако, по определению нормы ||А||, для каждого е > 0 найдется такой вектор х0 GE X с ||z0|| = 1, что |Ал:0||	||А|| — е. Если
же Ах0 = yQ (= У, то теорема Г из § 3.2 гарантирует нам сущест
Рис. 3.2. Линейное преобразование и преобразование, ему сопряженное.
вование такого функционала /Е У*, что / (г/0) = ||g0|l и il/ll *• Поэтому (Л*/) (я0) = / (Axq) = f (yQ), и, следовательно, ||A*f |> ^>||Л||— е. А так как норма / равна 1, то это означает, что норма И*11 > МИ - г, и поскольку е выбиралось произвольным, то норма ||Л*|| должна быть не меньше ||Л||.
Теорема В. Сопряженные преобразования обладают следующими свойствами:
(1)	0* - 0,
(2)	(Аг + Л2)* - Л! + Л;, Л, е ₽ (X, У),
(3)	(аЛ)* = аЛ*.
Если Л"1 существует, ограничено и определено на У, то (4) (Л'1)* = (Л*)’1.
Наконец, если Y X, то
(5) 7* = I,
(6) (Лхл2)* = л;л1, Ai е Р (X, X).
Доказательство. Доказать первые три утверждения просто. Например,
[(аЛ)*/] (х) =- / [(аЛ) х\ = а/ (Ля) = а (Л*/) (я) = [(аЛ*) /1 (я),
и, следовательно,
(аЛ)*/ = (аЛ*) / и (аЛ)* — аЛ*.
Для того чтобы доказать четвертое, предположим, что Л-1 ЕЕ ЕЕ Р (У, X). В этом случае у преобразования Л-1 есть сопряженное —(Л'1)*, определенное на X* и принимающее значения из У*. Зафиксируем некоторое / из У* и для всех у = Ля ЕЕ У получим
(Л-г)* (Л*/) (//) - (Л*/) (Л"М (Л*/) (х) = / (Лх) - / (у).
Поскольку каждое у ЕЕ У имеет вид у - Ля для некоторого яЕ X, то функционал (Л~1)*Л*/ согласуется с функционалом /, а так как функционал / Е У* выбирался произвольно, то отсюда следует, что (Л"1)*Л* представляет собой оператор, тождественный в У*.
Аналогичным же образом для g S X* и я €= X
[Л* (Л"1)* gl (я) - [(Л"1)* gl (Ля) -- (Л’1)* g (у) = g (А-'у) -
=• g (х),
откуда Л* (Л-1)* g - - g, и, следовательно, преобразование Л* (Л-1)* определяет тождественный оператор в X*.
Но из уравнений
(Л"1)* Л* = 7у, Л* (Л"1)* = 7у
следует, что преобразование Л* является обратным по отношению к (Л-1)*, что и доказывает утверждение (4) нашей теоремы.
Для того чтобы доказать утверждение (6), заметим, что
ЦЛ ХЛ2)*1 (х) = / (А,А2х) = (Л1/) (Л2х) = (A\A*J) (х), и, следовательно,
(ЛЛ2)* (/) - (АХ) (/).
Для обозначения скаляра / (х) мы уже пользовались символом (х, f), где л: и / принадлежали соответственно некоторому нормированному линейному пространству и пространству, ему сопряженному. В этих обозначениях наше определение Л* приобретает вид
<х, Л*/> = (Лх, />,	х<=Х, f^Y*,
пригодный в случае, когда линейное преобразование Л: X ->У ограничено. Если же Л есть некоторый оператор в X (т. е. если Y — X), то сопряженное преобразование Л* представляет собой оператор, определенный в X*. В частности, если X = Я, т. е. если наш оператор определен в некотором гильбертовом пространстве, то каждый оператор Л Е Р (Я, Я) однозначно определяет некоторый оператор Л* Ер (Я*, Я*).
Мы уже видели, что пространство Я* можно отождествить с гильбертовым пространством Яо, образованным из пространства Н в результате переопределения операции скалярного умножения и изменения порядка следования переменных в формуле скалярного произведения. Эквивалентное утверждение состоит в том, что соответствие у определенное условием
У/ = fv(x) = <х, fvy,
представляет собой сопряженно-линейную изометрию из Я на Я*, т. е. каждый ограниченный линейный функционал, определенный на Я, имеет вид fy при некотором у ЕЕ Я, а отображение у -+fy обладает следующими свойствами:
/ki+J/? fill I /l/г»
/х»/ =
ll/»l = hll-
В вещественном гильбертовом пространстве Яо — Я, и отображение у -+fy, действительно, линейно, так что Я* и Я невозможно различить, а Л* можно рассматривать как некоторый оператор в Я. В более сложных случаях эта ситуация оказывается чрезвычайно полезной, и, чтобы использовать ее, мы введем в рассмотрение один новый оператор.
Пусть оператор Л Е Р (Я, Я) задан. Зафиксируем у е Я. Тогда по определению оператора Л*, сопряженного к Л, Л^ЕЕЯ*, и, значит, в силу теоремы о представлении ограниченных
линейных функционалов, определенных на Н, найдется такое единственное z (ЕЕ Я, что
A*fv = Л-
Другими словами, мы установили существование вполне определенного соответствия ->z между пространством Н и им же. Обозначим это соответствие через А*у = z, чтобы показать зависимость z от у. Преобразование А* отображает Н в Н, и, более того, А* е Р (Я, Н). Для того чтобы доказать это, найдем прежде всего другое представление оператора А*.
Мы утверждаем, что A представляет собой единственный вектор из Н, удовлетворяющий условию
<Ах, у} = (х, А*у), каково бы ни было х (ЕЕ Н.
Тот факт, что А*у действительно удовлетворяет этому уравнению при любых х ЕЕ Я, следует из равенства
fy {Ах) = {A*jv) (х) = fz (х), z = А*у.
Единственность же вектора А*у (ЕЕ Я вытекает из того, что если бы вектор z' ЕЕ: Я удовлетворял уравнению
<я, А*у} = (Ая, уУ — \х, z') при всех я (ЕЕ Я, то
<я, А*у — z'> — О при всех х ЕЕ Я,
так что z' = А*у.
Теперь не представляет никакого труда доказать, что оператор А* линеен и ограничен. Действительно,
<*, Л* («1У1 + а2у2)> = (Ах, щ + а2у2> =
= а/Лх, {/!> + «2<Лх, у> = fy(x, А&) + fy <х, Л*у2> =
= <х, Л1А*У1 + а2А^у2),
откуда в силу единственности вектора A* (aj/i + а2у2) следует, что оператор А* линеен и
I <*. А*у) I = I (Ах, у) | с ЦЛ^НМ < И1И1И-
Это показывает, что
M*i/|| = sup |<х,Л^>|<МН1/|1. хеН И<1
и, следовательно, оператор А* ограничен. (На самом деле, из уравнения
A*fv = Л, z А*у,
вытекает, что соотношение со /w является изометрией. А так как |Л *| = |Л|, то на самом деле ||А*|| = ||А||. Доказать линейность Аф можно еще и по следующей схеме: у -+A*fy = fz -^z.)
Наконец, прежде чем подводить итоги полученных результатов, выясним характер отображения Л ->Л*, преобразующего 0 (Я, Н) в само себя. Рассмотрим следующую цепочку равенств:
<х, (4 -г В)*уУ = <(4 + В) х, у) = (Ах, j/> + (Вх, у} =
= А*у + В*у>, (х, (а,	= <(а4) х, j/> + а (Ах, у> =
= а(х, А* у У = (х, а.А*уУ и
(х, (АВ)*у)У = ((АВ) X, уУ = (Вх, А*уУ (г, В^А^у).
Поскольку каждое из них справедливо при всех х Н, то мы доказали следующую теорему.
Теорема Г. Пусть Н — некоторое гильбертово пространство. Тогда каждому оператору А (Е 0 (77, Н) соответствует единственный оператор	(77, 77), удовлетворяющий лю-
бому из следующих условий:
(1) А*у есть единственное z ЕЕ 77, для которого A*fv = fz\
(2) А*у есть единственное z GE 77, для которого (Лх, у> = = <х, z> при всех х е 77.
Соответствие между А и Л* подчиняется следующим правилам
(1)	О* = 0, /* = 1;
(2)	(4 + В)* = 4* + В*, (аЛ)* = <24*;
(3)	(45)* = 5*4*;
(4)	1)4,11 = ||4||.
Если гильбертово пространство А вещественно и, следовательно, И* можно отождествить с Н, то А * совпадает с преобразованием Л*, сопряженным с Л.
Оператор Л* называют присоединенным *) относительно Л. Теорема Г утверждает, что у каждого ограниченного оператора в гильбертовом пространстве Н имеется свой присоединенный ♦♦) оператор Л* и что переход к присоединенным операторам сохраняет нормы и суммы, меняет порядок перемножения и является сопряженно-однородным. Тривиальные операторы 0 и 7 являются самоприсоединенными в том смысле, что операторы, присоединенные относительно них, совпадают с самими этими операторами.
Из предыдущего ясно, что операторы Л* и Л*, сопряженные и присоединенные по отношению к ограниченному линейному оператору Л, логически совершенно различны. Тем не менее мы отбросим обозначение Л* для присоединенного оператора и станем
♦) Этот оператор называют еще гильбертовым сопряженным.
*♦) Если А: —> Нч есть ограниченное линейное отображение между различными гильбертовыми пространствами, то сопряженное отображение А*:	порождает отображение Лф: Нч -♦ которое тоже называют
присоединенным.
пользоваться обозначением Л* для обоих этих преобразований, что согласуется и с общепринятой практикой. Когда это будет необходимо, мы для ясности будем говорить «присоединенный оператор /1*» или «сопряженный оператор Л*», чтобы уточнить конкретный смысл, приписываемый символу А* в рассматриваемой ситуации. Поскольку присоединенный оператор определен лишь для (ограниченного линейного) отображения гильбертова пространства в само себя, то такое двойное использование символа А* может вызвать путаницу лишь в том случае, когда оператор А определен в некотором комплексном гильбертовом пространстве. Как правило, читателю следует понимать символ Л* как преобразование, сопряженное Л, если только понятие присоединенного оператора тоже имеет смысл. В последнем случае Л Е Р (Я, //), и символ Л* всегда будет обозначать оператор, присоединенный к Л.
Пример 2. Обозначим через некоторую ортонормальную систему в гильбертовом пространстве /2. Каждый элемент х /г единственным образом представляется в виде
оо
*=Sa«en, ап = <^еп>. 1
Определим на 12 оператор сдвига S с помощью соотношений
оо	оо
8х = 2 ®п«п+1, где X = 2 лпеп. П=1	П=1
Построим теперь оператор 5*, присоединенный к S. Если
оо
у — S мп, п=1
ТО
оо	оо	оо оо
уУ = <Хцвп+1, 2	= 3 S	) •
71=1	71=1	71=1 /£=1
А так как
(	k = п + 1,
^^71+1 •	| z-v
[О	в остальных случаях,
то предыдущее сводится к виду
<5’ЯГ, (/> = ajpz + «2₽3 + •••
Однако нетрудно видеть, что последнее выражение представляет
3.3. СОПРЯЖЕННЫЕ И ПРИСОЕДИНЕННЫЕ ПРЕОБРАЗОВАНИЯ 245 собой скалярное произведение вектора х и вектора z с координатами (р2» Рз, •••)• Другими словами, вектор z имеет вид где е0 понимается как нулевой вектор. Зто позволяет прийти к выводу, что 5* отображает у — УГРл в вектор S*y = J?
Если же говорить на языке системы координат, то оператор S отображает вектор х с координатами (ап а2, ...) в вектор Sx с координатами (0, at, a2, ...), а оператор 5* отображает вектор х в вектор S*x с координатами (а2, а3, •••)•
Предыдущие рассуждения ясно показывают (и мы оставляем на совести читателя строгое доказательство этого факта с помощью разложений Фурье), что операторы S*S и 55* совершенно различны. В самом деле, оператор 5*5 преобразует вектор х с координатами (an a2, ...) в вектор, координаты которого были сначала сдвинуты на одно место вправо, а затем — на одно место влево, и, значит, оператор 5*5 является тождественным в /2. Но в то же время оператор 55* преобразует тот же вектор х в другой, координатами которого служат (0, а2, а3, ...). Другими словами, оператор 55* отображает одномерное подпространство L (ех), натянутое на е19 в 0 и является тождественным на ортогональном дополнении L (ej.
В общем случае мы не можем утверждать, что оператор в гильбертовом пространстве коммутирует со своим присоединенным оператором. Операторы Л, для которых ЛЛ* = Л*Л, называют нормальными. Такая терминология объясняется тем, что именно это условие необходимо для того, чтобы гарантировать возможность диагонального представления заданного оператора (см. § 3.4).
Пример 3. Любая матрица [a^l размерности п х п определяет некоторый оператор в конечномерном банаховом пространстве. В частности, матрица [a^l определяет некоторый оператор Л в гильбертовом пространстве /2 (п). В этом случае, если х = = (5i> L» • ••, £n) S к (^), то Лх представляет собой вектор у = = 611, П2, •••, Пп), гДе
п
=	' =1,2,
3=1
Если z = (ylt уг, •••, Yn) k. («), то
<Ax,z) = <у,х>	= Sri (ЗМ/
i	i j
Обозначим через матрицу присоединенного оператора Л*. Тогда
\Ах, z> /х, 4*z) -=	a*T>).
i j
Сравнивая между собой два последних уравнения, мы видим, что а,* = aji, т. е. матрица А* является транспонированной по отношению к матрице, сопряженной А.
Отсюда следует, что самоприсоединепными операторами в 12 (п) являются именно такие операторы, матрицы [а1;] которых удовлетворяют условию аи = Например, в двумерном гильбертовом пространстве 12 (и) самоприсоединенными операторами служат лишь те, у которых матрицы имеют вид
/а т\ \т ₽/’
где аир вещественны, а у комплексно. В вещественном гильбертовом пространстве /2 (п) матрицы самоприсоединенных операторов должны быть симметричными относительно главной диагонали, аи = ац.
Пример 4. «Непрерывным» аналогом предыдущего примера может служить оператор Фредгольма, определенный на L2 (0» 1) с помощью соотношения
1
(Ах) (/) = § К (s, t) х (s) ds. о
[При этом мы, естественно, предполагаем, что его ядро К (s, t) ведет себя достаточно хорошо, чтобы выписанный интеграл сходился для каждого х из L2 (0, 1). Это имеет место, например, если ядро К (s, t) ограничено в квадрате О О, t 1.J Если у = Ах и z 6= L2 (0, 1), то
1
< Ах, z> = <у, z> = § у (t) z (t) dt = о
ii	ii
= § z (t) ( § К (s, t) x (s) ds] dt = § x (s) ( § К (s, t) z (t)dt)ds. 0	0	0	0
Из этого уравнения следует, что присоединенный оператор А* преобразует z GE L2 (0, 1 ) в функцию
1
(A*z) (/) = (f, s) z (s) ds. о
Таким образом, присоединенный оператор по-прежнему принадлежит к классу операторов Фредгольма, а его ядро получается из ядра оператора А за счет «сопряженного транспонирования».
У самоприсоединениых операторов типа Фредгольма ядра удовлетворяют условию К (s, t) = К (t, s).
Пример 5. Рассмотрим теперь линейную динамическую систему с непрерывным временем и определим ее с помощью матрицы перехода
х(<) = (Фх°)(0 + (Ги) (0 =
t
= Ф (Мо) *° + $ Ф («. ®) в (s)и (s)z <= т [л0’ М • to
Выберем в качестве области определения этого преобразования F пространство [£2 (t)] = а в качестве его области значений — пространство [Л2 (т)]п = Я2. Тогда для каждого у Е Я2 мы получим ♦)
Ч	t
<У, Fu} = у (J), J Ф (/, $) В (s) и (s) dsj dt = t0	tn
4 t
= S S В U ds & ~ to *•
4 t
= j J [5* (s) Ф* (t, s) у (/), и ($)] dsdt, to to
где через Ф* (t, s) обозначена матрица, присоединенная относительно Ф (t, s)t как оператора в Еп. Использовав условия перемены порядка интегрирования, мы получим, что
Ч Ч
(yf Fu} = f £ [Я*($) Ф*(/, s) у (£), и (s)] dt ds = <F*y, u>, to 8
где F* определено на H2 соотношением
Ч (Fy)(s)= В* (8)Ф*	s ?r.
s
В этих же рамках можно привести еще несколько примеров. Например, зафиксировав f Ет, мы можем рассмотреть и преобразование Т: Нх -+Еп, определенное соотношением Ти = (Fu)(t').
*) При изучении многомерных систем часто оказывается полезным обозначение [g, т]] = J7=i Si’ll» которым мы и воспользовались здесь.
Для £ С: Еп справедлива следующая цепочка равенств:
Ги> = [Ц ф (f, $) В (S) и (s) ds] =
<0
Г
= $ [ё, Ф s) В ($) и ($)] ds =
/о
Г
= $ [В’ ($) Ф* (Г, S) и ($)] ds = <Г£, и>, to
где преобразование, сопряженное Т, задается уравнением
(T*l)(t) =5*(/)Ф*(Г, 0 g, Jet.
Для того чтобы рассмотреть дискретный аналог этого примера, положим
И7 (tin tj) ~ (бс> 0+1) В (tj)
и зафиксируем t'^ Ео*. Рассмотрим преобразование 7\: IIх -+Еп1 где
[4]-
>0
a Ht -- {1г а' = {t: t GE о, t < 4}.
Для произвольного £ GE En можно получить соотношение
К]-1
<^Ги>= 2	tj) I, и (/;)].
;=0
Поэтому 7*, сопряженное с Т, определяется условием
(Г*& (tj) hjB* (tj) Ф* (/„ 0+1) tj е а.
Замечание 1. Понятие сопряженного преобразования чрезвычайно полезно и для материала § 3.2. Рассмотрим, например, преобразование Т: X ->У. Обозначим через 5 -- {ev ..., сп} некоторый базис для У. Тогда, воспользовавшись декомпозицией тождественного оператора в У в виде
iv = 2 ei>(
i=l
с помощью следующей цепочки уравнений:
Тх — 1у Тх = 2 ei>	= 2 ei>
1=1 1=1
мы можем доказать, что функционалы {ft	i ~ 1, ...» п}
образуют множество, позволяющее привести Т к диадной форме
п т = 2 ^><л. 1=1
В задачах минимизации расхода энергии из § 3.2 важную роль играла матрица = 1<Л, fj)], связанная с преобразованием Т. Но так как Д — Г*е+, то ясно, что
</i, Л> = <ГМ,ГЧ> = <еГ, (ТГ) е*>, i, j = 1, . . п.
Поэтому, если обозначить через Е матрицу, i-й строкой которой служит вектор е), i ~ 1, ..., п, то прямым перемножением легко проверить, что
f = ЕТТ*Е*.
В частности, если множество S образовано из координатных векторов Rn, то Е = I и 3* = ТГ*.
Замечание 2. У отображения Ф, определенного на Еп с помощью соотношения Ф£ = Ф (f, t) есть присоединенное Ф*ц = = Ф* (f, 0т]. Матрица присоединенного оператора Ф* (f, t), как функция t, обладает некоторыми интересными свойствами, которые становятся ясными из следующей цепочки уравнений:
=|4Ф" <''< =
=-[—Ф-1^.	t') Ф-1 (/, z')* =
= —Ф* (/', t) [Л (t) Ф (Z, Г)]*Ф* (f, t) = —А* (/) Ф* (t', t).
Другими словами, если две матрицы Ф (£, t0) и Y (t, /0) определены условиями
<Ь (t, t0) = А (0 Ф (Z, t0), Ф (/0, /0) = /,	(1)
Т (/, /0) - -Л* (0 V (t, /0), V (/0, t0) - I,	(2)
У* («, /0) -- Ф-1 (/, 70) - Ф (t0, t).
Поскольку для каждого t ЕЕ t справедливо равенство
V* (/, /о) Ф Q - /, ясно, что столбцы Чг (/, /0) движутся в пространстве Rn как
функция от t таким образом, чтобы в любой момент они образовывали множество, двойственное по отношению к столбцам матрицы Ф(£,£о). Систему, описываемую уравнением (2), часто называю1) присоединенной по отношению к системе, описываемой уравнением (1).
Упражнения
1.	Рассмотрим свободное движение системы как отображение (Ф£) (t) = = Ф (t, t0) & пространства Е* в [£2 (t0, t/)]m. Покажите, что Ф* определяется соотношением
к
(Ф*у) = I Ф%?, t0) у (s) ds. у е [£2 (to, t/)]n.
to
2.	Обозначим через С операцию формирования, определенную в уравнении (2) примера 4 § 2.1. Если С рассматривать как отображение 12 (о) L2 (т), то покажите, что С* определяется следующим образом:
ffc+i (С*у)(<л)= § y(s)ds,
3.	Убедитесь в том, что матрица перехода системы ± (t) — A (t) х (t), где
. Г 2 , 1
— e2/”r° sin (t — to)
ez“z° cos (t — to)
Покажите, что матрица перехода T (t, t0) присоединенной системы связат а с матрицей Ф (t, t0) соотношениями V (t, t0) = [Ф”1 (t, t0)l* = Ф* (t0, t).
4.	Обозначим через <2/ следующее линейное преобразование:
(^x)(t) = Щ — A(t)x (t), t е [to, t/].
Оператор SB не ограничен в \Lz (to, ty)n]. Тем не менее покажите формально, что если S3* определить как
= -y(i)-A* (0 У (t), t e [to, ty],
и обозначить через <,> обычное скалярное произведение в [L2 (t0, ty)ln, то
<у, 5?х> - <Я*у, Х> = [у (0. ® (0]//.	(3)
где через [,] обозначено скалярное произведение в Еп.
5.	Положите в примере 5 В (s) = I. Преобразование F, заданное соотношением
t
х (t) = (Fu) (t) = Ф (t, з) и (s) ds. t G [to, tj,
to
e
имеет вид
e2Z“/o cos (t — to) ef”2fo sin (t — to)
Ф (I, to) =
(4)
имеет сопряженное F*, где tj q (0 = (F*y) (t) = \ ф* <*• О V (»)d»- ‘6 [U Г/J. i
Воспользовавшись замечанием 2, покажите, что q удовлетворяет дифференциальному уравнению; ь
q (t) = — Л* (0 q (0 — у (0, q (*о) = \ Т (Zo, *) У (*) <Ь. Zo
6.	Пользуясь разложением Д* [у* («*),*(*»)] =[Дку(М. «(**)] + [У (Г*+1). Д^Ф*)], докажите, что
N— 1	N—1
3 лк[ДкУ(«к).^к)]-1У(^).®«к)1т- 3 МУ(*к+1).Дк*(*к)1-т	т J
Перегруппировав члены, докажите также, что N-1 2	(Zfc)i Я (f/c)] =
тп N-1
= [У («*).»(**-!)]£- 2 Му(‘к). тп
7.	Обозначим через G оператор, заданный следующим соотношением: (бз) (tfc) = Ak® (tk) — A (tk) х (tk), tk e <T. Если <u, v> = У*"1 ft* [u (t), v (tk)l, то воспользуйтесь уравнением (4) и докажите, что
<у, Gxy — <G*y, х> = [у (tK), х («It-Plj*, где, по определению,
(В*у) (tk) = [ft;11 + А* ((*)] у (tk) - ft;1 у (t^).
Заметим, что G определено на a = {tm1 ..., tN}, в то время как G* определено на a' = {tm_v ..., Обозначим через Ф (fk, Zo) и V (Zfc, t0) матрицы перехода систем, описываемых соответственно операторами G и G*. Покажите,
'Е('*-1.<о)ф(<г«1)= I.
Если Ajt |Л* (Zfc) |< 1, то воспользуйтесь разложением [/ + h^A* (Гм)Ji - I - htA^ (tf) - ft« [Л* (Zt)J« + ..
чтобы показать, что присоединенная система приближенно описывается уравнением
Д*уОм) = -Л*(<#)у(«»_1).
8.	Опишем движение ракетной системы следующим векторным дифференциальным уравнением:
* (0 = / k к),и (/), d, i е ко. tf].
где X =	....тп), / = (Д..../п) и и == (Up ...» ип). Пусть вектор (й, .г)
обозначает некоторую номинальную пару (управление — траектория), удовлетворяющую поставленным терминальным условиям х (tf) = S (t ) = 5* Предположим, что внешние возмущения вынуждают ввести коррекцию du управляющего воздействия. Разложите оператор нелинейной системы в ряд относительно точки (й, 7) и выведите уравнение в вариациях
Л* (0 = A (t) Ъх (0 + В (t) Ъи (0, t е Ro, */Ь
Обозначим через 1] ЕР такой вектор, что [bx (tf), rjl может служить полноценной мерой точности системы. Воспользуйтесь результатомВупражнения 4, чтобы определить характер такого корректирующего регулятора.
Указание. Заметьте, что (Ldx) (0 = (Вби) (0; выберите у такое, что 1/(ь) = Т]. См. также книгу Цзяня [А.88].
9.	Покажите, что каждое замкнутое подпространство рефлексивного банахова пространства само является рефлексивным банаховым пространством.
3.4. Каноническое представление линейных систем
В этом параграфе мы доведем до завершения нынешнее направление теоретических исследований, получив в результате три различных канонических представления линейных преобразований. В § 3.2, например, мы уже убедились в том, что преобразования конечного ранга можно разложить по произвольному базису области значений. Понятно, что свойства каждого преобразования не должны зависеть от выбранного базиса. Однако кажется весьма вероятным, что в одних координатах структура преобразования будет представлена гораздо более выпукло, чем в других.
Кроме того, более или менее очевидно, что трудно было бы ожидать существования единой канонической формы представления всех линейных преобразований. В самом деле, естественно предположить, что каноническое представление линейных преобразований конечного ранга должно отличаться от канонического представления тех линейных преобразований, которые не обладают этим свойством. Точно так же мы выяснили, что некоторые специальные классы преобразований имеют особенно простую структуру и что на другие преобразования это свойство не распространяется. Изучение всех этих вопросов с самых общих позиций далеко выходит за рамки нашей книги. (Этим в действительности и занимается современная математика.) Поэтому мы ограничимся здесь тем, что познакомимся с основными идеями, позволяющими сформулировать и понять некоторые более общие результаты.
Инвариантные многообразия. Обозначим через А: X -> X некоторый линейный оператор, определенный на линейном про
странстве X. Линейное подпространство М CZ X называется инвариантным по отношению к оператору А, если А (М) CZ М, т. е. если для каждого х (=Е М справедливо соотношение Ах (ЕЕ М. Очевидными примерами инвариантных многообразий могут служить все пространство X в целом, ядро оператора Na и его область значений 7?д.
Если М представляет собой собственное подпространство X и инвариантно по отношению к оператору А, то сужение оператора А на область определения М можно рассматривать как оператор, определенный на одном М. Другими словами, в этом случае мы можем игнорировать преобразования оператором А тех векторов, которые не попадают в М. Если М и N — собственные подпространства X такие, что X М ф АГ, и оба эти подпространства инвариантны по отношению к А, то о пространствах М и N говорят, что они приводят оператор А. Эта возможность представляет значительный интерес, поскольку она позволяет заменить изучение оператора А в целом исследованием его сужений на подпространства М и N. При этом нам остается только надеяться, что эти сужения окажутся операторами какого-нибудь особенно простого типа.
В конечномерных пространствах информация об инвариантности некоторого подпространства по отношению к какому-то оператору позволяет прийти к конкретным выводам относительно характера матричного представления этого оператора. Конкретнее, пусть М CZ X есть некоторое m-мерное подпространство, инвариантное по отношению к оператору А. Пусть само пространство X n-мерно, a N — это такое (и — тп)-мерное подпространство, что X = М ф N, В общем случае подпространство N не должно быть инвариантным по отношению к А. Тогда справедлива следующая теорема.
Теорема А. Если М — некоторое т-мерное инвариантное подпространство оператора А, определенного на X, то в X существует такой базис 5, что оператор А может быть представлен матрицей [А ]3, у которой в левом нижнем углу размерности (п — т) х т все элементы равны нулю.
Доказательство. Обозначим через S' = {дг1? ..., хт} и S" = = {хт+1, ..., хп} соответственно базисы в М и N. Тогда множество S = (хи •••♦ хп} образует базис для X в целом. Поскольку подпространство М инвариантно по отношению к А, то Axj G= S L (5"), / = 1, ..., т. По определению двойственного базиса <я£, уУ = 0 для каждого у G L (S') и i = т + 1, п. А это значит, что
= <4» Axj) = 0, i = т + 1, ..., n, j = 1, m, что и требовалось доказать.
Очевидное следствие из теоремы А состоит в том, что если оба подпространства М и N инвариантны к оператору А, то матрица
[Л], должна иметь вид
М1,=
• А 0 •
. "о” л’’ J ’
где	и Л2 — блочные матрицы размером (т х т) и (п — т) х
X (п — т) соответственно. И вообще, если обозначить через {Afj, i = 1, .... р) некоторую совокупность подпространств пространства X, для которых Х = АЛ ф ... ®MV, a Mi ъ X Q инвариантны по отношению к A, i = 1, ..., р, то существует такой базис S пространства X (образованный подбазисами Si пространств Mt, i = 1, 2, ..., р), что
г АI ° о I л,
L о |...i
0 1
-6"
где каждая матрица Ab i = 1, 2, ..., р, описывает воздействие оператора А на подпространство Построение множества S и проверку последнего вывода мы оставляем читателю.
Одним из наиболее важных типов инвариантных подпространств являются одномерные, т. е. подпространства вида М = L (х), где х — некоторый фиксированный вектор. По определению инвариантного подпространства, если М инвариантно по отношению к А, то
Ах = Хх, х =/» О, где X — некоторый скаляр. Такой вектор х называется характеристическим или собственным вектором оператора А, а соответствующий скаляр X — характеристическим или собственным числом оператора А.
Рассмотрим теперь некоторый базис {хх, х2, ...» хп} для пространства X и обозначим через матрицу оператора А относительно этого базиса. Если мы говорим, что некоторое комплексное число X представляет собой собственное число оператора А, то это значит, что существует такой вектор х = Ум =/= О, что Ах = Хх. А это в свою очередь эквивалентно утверждению о том, что следующая однородная система уравнений
(ац — X) 04 + а12а2 + ••• + flinan = О,
®nlal + ап2^2 + ... + (&ПП — X) ап = О
имеет нетривиальное решение относительно неизвестных а{. Из элементарной алгебры известно, что это возможно тогда и толь-
3.4. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 255 ко тогда, когда определитель*) det [4 —X/] этой системы обращается в нуль. Заметим теперь, что этот определитель представляет собой полином степени п относительно X. Его называют характеристическим полиномом оператора А и используют для получения следующего критерия: комплексное число X является собственным числом оператора А тогда и только тогда, когда X есть нуль характеристического полинома этого оператора. Это приводит нас к теореме Б.
Теорема Б. Каждый линейный оператор в конечномерном комплексном линейном пространстве имеет по крайней мере одно собственное число.
Доказательство. Учитывая предыдущие замечания, мы должны показать, что у характеристического полинома оператора есть некоторый корень. А это следует из фундаментальной теоремы алгебры, утверждающей, что у каждого полинома с комплексными коэффициентами имеется по крайней мере один комплексный корень.
Прежде чем двигаться дальше, заметим, что теорема Б далеко не элементарна. Для ее доказательства нам пришлось опереться на один из наиболее глубоких фактов относительно множества комплексных чисел, и, на самом деле, у нас нет другого выхода, так как характеристическим полиномом линейного оператора в некотором конечномерном пространстве может быть любой полином р (X) — Хп 4- «хХ71-1 + ... 4- ап. (Действительно, рассмотрим, например, оператор в некотором n-мерном пространстве, матрица которого имеет следующий вид:
О	1	0	0“
0	0	10
1
-	®П-1	• • • “	-
Таким образом, наша теорема логически эквивалентна фундаментальной теореме алгебры.)
Заметим еще, что предположение о комплексном характере пространства X имеет принципиальное значение. В самом деле, у матрицы
ГО - 1 ’
_ 1	0
в вещественном двумерном пространстве нет собственных чисел,
•) Здесь уместно вспомнить ^см. упражнение 8 из § 3.2), что этот определитель зависит лишь от оператора и не зависит от базиса, использованного для его вычисления.
так как ее характеристический полипом не обращается в нуль на вещественных X.
Если А есть линейный оператор, определенный на конечномерном линейном пространстве, то спектром оператора Л, обозначаемым через в (Л), называют подмножество множества комплексных чисел, состоящее из собственных чисел оператора Л. Мы уже видели, что комплексное число Л принадлежит o' (Л)} тогда и только тогда, когда определитель оператора Л — X/ оказывается равным нулю. А это в свою очередь эквивалентно утверждению о сингулярности оператора Л — X/. Другими словами, о (Л) состоит из таких X, при которых оператор Л — X/ необратим.
Мы знаем уже, что если А есть некоторый оператор в п-мер-ном пространстве, то множество o' (Л) не пусто и состоит не более чем из п различных точек. Это общее утверждение является наиболее сильным из всех, которые можно сделать, так как если Хц Х2, ..., Хт — произвольное множество комплексных чисел, то ясно, что диагональная матрица, имеющая на главной диагонали только эти числа, будет иметь спектр {Хх, Х2, ..., Хт}. Такой же спектр будет и у треугольной матрицы, если на ее главной диагонали размещены все те же Хр Таким образом, у совершенно различных операторов может быть одинаковый спектр.
Предположим теперь, что Л —- это некоторый линейный оператор в комплексном конечномерном пространстве X.
Лемма А. Собственные векторы Хц х2, ..., хт оператора Л, соответствующие различным собственным числам Хх, Х2, ..., Хт, линейно независимы.
Доказательство. Предположим, что векторы ..., хт линейно зависимы и что среди них существует некоторое максимальное линейно независимое подмножество хъ ..., Xj.x (мы перенумеруем векторы, если это потребуется). Кроме того, пусть справедливо соотношение
Yixi + у2я2 + ... + уух, = О
между j собственными векторами оператора Л, в котором по крайней мере одно у, скажем Yi» отлично от нуля. Применяя к этому соотношению оператор Л, мы получим, что
Y1X1X1 + У2^2*2 + ... + YA;*; = 0.
Умножая первое из уравнений на Ху и вычитая произведение из второго уравнения, получим
Yi (^i xi + Тг (^2 — х2 + ••• ~Ь YJ-i Aj-i М xi-\ ~ 0. По векторы х1У ..., X}-! линейно независимы, поэтому все коэффициенты
Yi (X! — ХД, ..., Y)-i (^>-i
должны обращаться в нуль. Однако условие ух — Ху) = О противоречит нашему предположению о том, что Yi =#0 и =f= =f= Kj, а значит, наше допущение о линейной зависимости между Гх, Х2, ..., Xj ложно.
Прямым следствием из леммы А является утверждение о том, что если у оператора А имеется п различных собственных чисел, то существует такой базис хх, х2, ...» хп, по отношению к которому матрица этого оператора диагональна. В самом деле, если в качестве базиса X выбрать собственные векторы А , то лемма А гарантирует нам правомочность такого выбора, а для каждого х — lE.aixi из % мы будем иметь
4х = 2ai^Xi = i	i
и, значит, по отношению к такому базису хх, х2, ..., хп оператор А характеризуется матрицей
Хх 0 . . . О О Х2 ...
Таким образом, если все п собственных чисел оператора различны, то мы можем выбрать п таких линейно независимых векторов хх, х2, •••» хп, что преобразование х в направлении х{ оператором А сводится к умножению на Хр
Замечание 1. Линейный оператор А в п-мерном пространстве называется простым, если у него имеется полный набор из п линейно независимых векторов. Другими словами, оператор является простым, если матрица этого оператора может быть приведена к диагональной форме. Мы только что убедились в том, что операторы с различными собственными числами Хх, ..., Хп являются простыми. Однако это условие ни в коей мере не является необходимым. Например, у тождественного оператора I имеется всего одно собственное число, X = 1, но его матрица тоже диагональна (а именно, единичная), независимо от выбора базиса.
Обозначим через А (X) = (X — Хх)Р‘(Х — Х2)р» ... (X — Xm)Pm характеристический полином оператора А, Здесь все Хх, ..., Хш различны и 2у pj = п. Кратность р} корня Ху называют алгебраической кратностью собственного числа Ху, j = 1, ..., т. Для каждого Ху оператор А — Ху/ вырожден, а его ядро натянуто на собственные векторы, соответствующие этому собственному числу. Размерность ядра (т. е. его дефект) оператора (4 — Ху/) называется геометрической кратностью собственного числа Ху. С учетом предыдущих замечаний совершенно ясно, что простыми оказываются
9 У. Портер
только те операторы, у которых алгебраическая и геометрическая кратности каждого собственного числа одинаковы.
Для того чтобы иметь возможность сравнивать между собой эти кратности, рассмотрим в духе примера 3 из § 3.3 два оператора в двумерном пространстве с матрицами
У обоих операторов — всего одно собственное число, X = 1. В качестве упражнения читатель может убедиться в том, что оператор Т не является простым.
Функции операторов. Пусть линейное пространство X представляет собой прямую сумму X -- Х± ф Х2ф...фХп линейных подпространств {XJ. Напомним, что в § 2.1 мы определили оператор проектирования пространства X на подпространство Х{ как линейное преобразование, удовлетворяющее условиям:
Р& = 0,	х S X *v	i j;
Ргх = х, х GE ХР
Заметим что P{Pj — 0, если i =f= j, Р* = и что сумма Рх 4 + Р2 + ••• + Рп представляет собой тождественный оператор в X. Более того, Xt = Р{ (X) служит областью значений оператора Рр
Предположим теперь, что dim (X) = тг, и пусть А есть некоторый простой оператор в X. Мы утверждаем, что тогда в X можно единственным образом определить семейство {Р*} операторов проектирования, обладающее следующими свойствами:
PiPj = 0, если /=/=/,	(1а)
Ел = /,	(1б)
i
А =	(1в)
i
где — собственные числа оператора А. В самом деле, поскольку оператор А является простым, то мы можем выбрать в X базис {^i, е2, ..., ен), состоящий из собственных векторов А. Тот факт, что
образуют базис в X, означает, что X = L (ех) ф L (е2) ф ... ...ф L (еп), а это в свою очередь эквивалентно утверждениям (1а) и (16), если обозначить через Рг операторы проектированиях на
Уравнение (1в) эквивалентно системе из п уравнений вида Ав{	Наконец, если {(^} — некоторое другое множество
из п операторов проектирования, определенных в X и обладающих свойствами (1а) и (16), то х =~QX (X) ф Q2 (Х)ф... ф(?н (X).
Отсюда следует, что каждое Qi =/= 0 и что на самом деле dim Qi(X) = 1. Кроме того, из условия
А =
i
при некоторых скалярах следует, что
п
AQjx=^ HiQt) (Qjx) = HjQjx, i=l
и, следовательно, скаляры {рг} являются лишь перестановкой собственных чисел {ХД оператора А, а операторы Q — операторами проектирования на соответствующие собственные подпространства L (е^ = Pi (х). Это доказывает единственность семейства {Pi} операторов проектирования, порождаемых простым оператором А.
Получить каноническое представление для операторов Pi нетрудно. Действительно,
Pi ~	(4-
и матрица (по отношению к базису {е2, е2, ..., еп}) состоит из одних нулей, за исключением г-го элемента на главной диагонали, равного 1. Уравнение (1в) приобретает тогда вид
А 2 ei/^i (4
1=1
и утверждает, что матрица А диагопальна.
Если оператор А является простым, то предыдущее спектральное представление А или, что то же, представление А с помощью диагональной матрицы относительно базиса {^, е2, еп} позволяет рассматривать «функции» оператора А. Если к — положительное целое число, то степень Л* можно определить по индукции с помощью соотношения Л*141 = A (Л*), к = 1, 2, ... Для простого оператора Л из уравнения (1в) прямым вычислением получим
п	п
л* = 2 (мкл = 2	<4.
1=1	i=l
Аналогичным образом, для любого полинома
N
4 (2) = 2 akzlc
К=0
оператор
N
Я>(Л)= 2 а*4*
к=о
допускает спектральное представление
t (4) = 3 Ф (М pi = 3 Ф (М i	i
Если оператор А обратим [т. е. если 0 б (Л)], то совершенно ясно, что А1 можно представить в следующем виде:
А-1 = 2хг‘Л.
i
Другими словами, матрица оператора А1 относительно базиса {е2, •••» еп} остается диагональной, а ее главную диагональ образуют числа {Х^1,	•••» Х^1}. На самом деле, если / (z) — произ-
вольная функция комплексной переменной, аналитическая в некотором открытом множестве, содержащем спектр простого оператора А, то можно показать, что функция / (Л) вполне определена (например, с помощью рядов Тейлора) и
/М) = 2/(МЛ = 2^>/(^) <£.
i	i
Заметим еще, что спектральное представление позволяет легко вычислять спектр функций от оператора А. В самом деле, для функций z -> zn, z ф (z) и z -> z-1 из самого вида спектрального представления следует, что спектры операторов Ап, ф (Л) и Л"1 равны соответственно [о (Л)]п, ф [о (Л)] и [о (Л)]"1. И вообще, если / — некоторая функция, для которой выражение / (Л) имеет смысл некоторого оператора, то *)
о [/ (Л)] = / [а (Л)],
где множество в правой части, но определению области значений /, имеет вид
/[а (Л)1 = {v: v = / (X), X е а (Л)}.
Нормальные операторы. До сих пор мы пользовались лишь тем фактом, что пространство X линейно. Предположим теперь, что X = Н, т. е. что в X определено скалярное произведение, ко
*) Это уравнение может служить формулировкой теоремы о спектральных отображениях, которая, будучи более или менее тривиальной для простых операторов, сохраняет свою справедливость и для операторов, не являющихся простыми.
торое позволяет рассматривать его как конечномерное гильбертово пространство. Мы по-прежнему можем использовать понятие инвариантного линейного подпространства относительно оператора А, определенного на Я, а так как пространство Н конечномерно, то оно обязательно замкнуто и, следовательно, является подпространством И. В бесконечномерном случае легко видеть, что если М есть некоторое инвариантное линейное подпространство оператора Л, то его замыкание М является инвариантным подпространством А. По аналогии с алгебраическим случаем мы будем говорить, что инвариантное подпространство М оператора А приводит Л, если М1- также инвариантно по отношению к Л.
Легко построить примеры, показывающие, что инвариантные подпространства оператора не обязательно его приводят. Например, рассмотрим гильбертово пространство 12 векторов (<хп а2,...), для которых У5° |afc |2<^оо, и оператор сдвига S, определенный на этом пространстве (см. пример 2 из § 3.3). Подпространство, состоящее из векторов вида (0, 0, а3, ...), инвариантно относительно S, но не приводит оператор S. Действительно, М± состоит из векторов вида (ап <х2, 0, ...), и понятно, что образ (0,	а2,
О, ...) такого вектора в силу S не обязательно принадлежит М±.
Соотношение <Лх, у> = <х, Л*у> между оператором Л и присоединенным оператором Л* показывает, что подпространство М инвариантно относительно Л тогда и только тогда, когда M-L инвариантно относителшо Л*. Пусть Л (М) CZ М; тогда из предыдущего соотношения следует, что если у | М, то для всех х е М справедливо А*у | х, и, значит, Л* (JfT)J-CZ Мк Обратно, если М± инвариантно относительно Л*, то М = (Afl)-L инвариантно относительно (Л*)* = Л.
Данное рассуждение показывает, что подпространство М приводит оператор Л в том и только в том случае, когда оно инвариантно одновременно относительно Л и Л*.
Рассмотрим теперь оператор Л, определенный в конечномерном гильбертовом пространстве Н, Предыдущие результаты показывают, что матрица Л, по крайней мере для простых операторов, может быть приведена к диагональному виду за счет подходящего выбора (не обязательно ортогонального) базисаЯ. Если мы воспользуемся далее процедурой Грама — Шмидта и построим ортонормальный базис {j/j, у2, ..., уп}, то, как нетрудно видеть, относительно этого базиса матрица оператора Л будет треугольной. Как показывает теорема В, это утверждение сохраняет свою силу и в том случае, когда относительно оператора Л не предполагается, что он простой.
Теорема В. Пусть} А —некоторый линейный оператор в конечномерном комплексном гильбертовом пространстве Н,
Тогда в Н существует такой ортонормальный базис {хп х2, хп), что по отношению к нему матрица А имеет вид
Xj	Я12	а13	•	 •
0	X,	а23	а2п
0	0	Х3	&3п
. 6	б	0	
Диагональными элементами Х2, ..., этой матрицы служат собственные числа оператора А, повторенные столько раз, какова их кратность как корней характеристического полинома А (т. е. какова их алгебраическая кратность).
Доказательство. Нам нужно доказать лишь первое утверждение. Второе вытекает непосредственно из того, что определитель треугольной матрицы равен произведению ее диагональных элементов.
В силу теоремы Б у оператора А есть собственное число Xj, а следовательно, и единичный собственный вектор х2:
Ахх =
Обозначим через многообразие А(х2) и рассмотрим ортогональное дополнение Н2 = Н^-. Оно представляет собой снова конечномерное гильбертово пространство. Если приводит А, то Н2 инвариантно относительно А, и мы имеем полное право рассматривать оператор А как оператор в Н2. Воспользовавшись теоремой Б для сужения оператора А на Н2, мы получим вектор х2 | хг и Х2 такие, что Ах2 = к2х2. Однако не обязательно приводит А, поэтому вместо этого оператора рассмотрим оператор Р2А, где Р2 проектирует Н па Н2. Этот оператор действительно оставляет пространство Н2 инвариантным, и, следовательно, мы можем найти Х2 и х2 | X} такие, что
Р = ^2*^2 •
Поэтому найдется некоторый скаляр аг2 такой, что
^4^2 ~ ^12^1 ~Ь 2*^21 *^2 1	» II *^21| =
Далее рассмотрим пространство Н3 — L (х1ч х2)-^ и оператор Р3А, определенный на Н3, где Р3 проектирует Н на Н3. Теорема Б гарантирует существование таких Х3 и х3 ЕЕ Н3, что
Р= ^3*^3’ II *^3 |1 =
А так как (7 — Р3) Ах3 принадлежит L (х19 х2), то
(7 Рз) Ах3 = о^|з^д + &23х2,
з 4 КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 263 и, следовательно,
Ах3 =	+ ^3^3» Х3 _1_ Х1> х2 И 1*3 || =
Продолжая подобным образом, мы и придем к утверждению теоремы.
Теорема Г. У линейного оператора А в Н возможна диа* зональная матрица относительно некоторого ортонормального базиса Н в том и только в том случае, когда А коммутирует с А*,
Доказательство, Если матрица А диагональна относительно некоторого ортонормального базиса, то это справедливо и относительно оператора Л*, а факт коммутативности двух диагональных матриц тривиален. Отсюда условие А А* ~ А*А является необходимым.
Предположим теперь, что А А* = А* А, Мы можем также предположить, что матрица А треугольна. Тогда матрица оператора А* имеет вид
Ч, 0 0 ... О '
^2 0 ... О а13 а23 ^3	• • •	’
_ aLn a2n a3zi • • •	.
и прямые расчеты показывают, что при перемножении двух таких матриц все элементы, кроме диагональных, обращаются в нуль.
Достаточность условий нашей теоремы можно доказать, заметив еще, что если А А* = А*А,тоАх = кх предполагает равенство А*х = кх и, следовательно, пространства Н1, У/2, //3, ... (в соответствии с теоремой В) приводят оператор Л; и, значит, вводить скаляры а/;- не надо.
Оператор А в произвольном гильбертовом пространстве называется нормальным, если он коммутирует со своим присоединенным оператором. Теорема Г утверждает, что нормальные операторы в конечномерных гильбертовых пространствах —это именно те операторы, которые могут быть представлены диагональными матрицами относительно каких-либо ортонормальных базисов {е1? е2, ..., еп}. Если оператор А в конечномерном гильбертовом пространстве Н нормален, то ортонормальный базис {еп е2, ...,еп} для Н можно построить из собственных векторов А. Обозначив через оператор проектирования Н на L (et), мы получим, что PiPj = 0 при I =£ j, Pf = Pi и, как и раньше, ”=i Pt = I. Однако в нынешней ситуации у операторов есть дополнительное свойство: Р\ = Pit В самом деле, если х = (хг, х2, ..., хп)
и у = (У1, у2, •••» Уп), то <х, Pty) = {PiX, уУ = <Xj, У(У = = <x1Pi у), что эквивалентно утверждению о попарной ортогональности подпространства L (ej. Как и раньше, мы можем представить А с помощью операторов Pt в виде А =	или в диад-
ных обозначениях, заменив оператор Pi на
Другими словами, с нормальным оператором А мы связываем спектральное семейство {Р/} операторов проектирования, обладающее следующими свойствами:
Р* = Р1 = р;, ЛР> = 0, если i=£f,	(2а)
2л = д	(2б)
i
A = 2i^pi-	(2в)
i
Уравнением (2в) мы будем определять спектральное разложение оператора А.
Предоставляем читателю доказать самостоятельно, что если {(\} — некоторое другое семейство операторов проектирования, удовлетворяющее уравнениям (2а), (26) и (2в), со скалярами {p,t}, то {nJ представляет собой простую перестановку скаляров {Xf}, a Qi совпадают с соответствующими Р;. Обратно, легко видеть, что если {Pt} есть семейство операторов проектирования, удовлетворяющее условиям (2а) и (26), то уравнение (2в) определяет некоторый нормальный оператор А в Я, каковы бы ни были скаляры Хп Х2, ...
До сих пор наше изучение нормальных операторов шло по тому же направлению, что и для простых операторов, и оба эти класса казались бы совершенно идентичными, если бы не внешне безобидный факт, согласно которому Pi = Pf. Но в этом и кроется коренное отличие, позволяющее привязать поведение оператора А к метрической структуре пространства Я, чем мы теперь и займемся. Отметим прежде всего, что из уравнения (2в) следует справедливость для каждого вектора х из Н соотношения Ах = =	и, следовательно, для каждого у GE Н
(Ах, уУ =	У/> = <PiX, У>'
i	i
Переходя к комплексно-сопряженным величинам, мы получим
(А*у, ху = (Ах, уУ =	<,У, ptx> =
i
= 3 М (^1%) уУ =	• (3)
Это свидетельствует о том, что {PJ служит спектральным семейством операторов проектирования и для оператора А* и, более того, спектр А* является комплексно-сопряженным по отношению к спектру А: о (А*) = о (А). В частности, отсюда следует, что спектр нормального оператора веществен тогда и только тогда, когда оператор А является самосопряженным, т. е. когда А*= А.
Возвращаясь к уравнению (2в) еще раз, мы видим, что
II4х||2 = <4х, Ах) =	2М/®) =
= 2 <РгХ, Р.х) = 31 м |3 • II1Г-	(4)
V’	i
А это показывает, что если оператор А нормален, то || А || равен радиусу спектра этого оператора:
||А|| = max {| X |: X G а (А)}.
Замечание 2. Оператор U, для которого U*U = I = £7£7*, называют унитарным. Из этого определения следует, что всякий унитарный оператор является нормальным, а из уравнения (4) вытекает, что нормальный оператор оказывается унитарным тогда и только тогда, когда || Е7х|| = ||х||, каково ’бы ни было хЕН. Это в свою очередь возможно в том и только в том случае, когда а (£7) лежит на окружности единичного радиуса.
Замечание 3. Назовем самосопряженный оператор А положительным (будем символически изображать это как А 0), если его спектр лежит па полуоси неотрицательных чисел. Если оператор А положителен, то для любого х Е= Н
(Ах,Х) = 2^<РЛ Х> ='^1^i<Pix, Ptx)
I	i
и, следовательно, <Ая, х) > 0. Обратно, если А есть некоторый самосопряженный оператор, для которого (Ах, х) 0 при всех х G= Н, то
0< (АР ^х, PjX) = Tki^Pi (PjX), PjX) = ЧЗД
и, следовательно, все X; 0. Поэтому положительными операторами являются те самосопряженные операторы, для которых квадратичная форма (Ах, х) неотрицательна.
В частности, для любого оператора В положительным является оператор А = В*В, поскольку (Ах, х) = (В*Вх, х) = || Вх||2. Обратно, если А >0 и, следовательно, в его спектральном разложении
п ?
4=2 к.Р,
все неотрицательны, то у каждого из этих собственных чисел единственным образом определяется положительный вещественный квадратный корень и
(5 ^'Pi] (3 ^'Pj) = (3 rt'Pi) (3	=
^^’i'PiPi =^UPi = A.
ij
Таким образом для положительного оператора А определяется квадратный корень А’/», спектральное разложение которого имеет следующий вид: A't* = У\ ХУ* Нетрудно видеть, что условия А'/» > 0 и (А1/*)2 = А определяют этот квадратный корень однозначным образом. Другими словами, если В2 А и 5 ^0, то В должно совпадать с оператором У{Х’/’Р
Замечание 4. С помощью спектрального разложения А = = УТ=1ХгРг нормального оператора А нетрудно построить некоторое функциональное уравнение. Так, для функции фп (X) = = Хп (п > 1) имеем ф (А) = Ап, по определению Ап, и фп (А)*Х X фп (Л) = АП*АП = А *пАп = АпА*п =фп(Л)ф„(А)ф, так что оператор фп (А) снова нормален. Кроме того, поскольку проекции Pi попарно ортогональны, то
(П	\ 71	П	П
Змл =3 х?л = 3 t,.(мл-
i—1	/	г=1	г—1
Полагая, кроме того, А0 = /, мы получим ф0 (А) = I — ^{Pi ~
У1Ф0 (XJ и можно заключить, что для любого полинома ф (z) =	оператор ф (А) = У?ацАп имеет спектральное
разложение
1|)(Л) = St (МЛ-
г
Этот последний результат отражает элементарный факт, состоящий в том, что если А — некоторая диагональная матрица, то ф (А) (где ф (z) — произвольный полином) вновь является диагональной матрицей, и ее элементы на главной диагонали имеют вид t (М, t (М- •••< t (М).
Замечание 5. Зная спектральное разложение оператора ф (А), мы можем вычислить его норму. Действительно,
II t (Л) х ||2 = <-ф (Л) х, (Л) ху = <S t (ХО Л*, 31 (М Pfly> =
i	J
= 31 (X;) w7) p^ = S11 (Xj) i2 • ii p,x и2 <
i;	i
<max1(X;) |2ЗИЛ*||2 = max1(X;) |2- ||i||2.
’	i	<
5.4. каноническое Представление линейных систем 2Ь7 Выберем теперь к таким образом, чтобы max |i|) (XJ | ~ |Ч? (М I и у = Phx =f= 0. Тогда
h М) у II2 = 21 * (М I2 • II pip^ II2 ~ 11 I2 • h II2-г
Таким образом, для любого полинома ф (X) оператор ф (А) имеет норму
||ф (А)|| - sup {|ф (X) |: ХеЕо(А)}.
Заметим, что этот результат можно было бы получить, воспользовавшись следующим соображением: из-за того, что ф (А) =-= у{ф (XJ Pi, спектр оператораф (А) образуется числамиф (XJ, ... ...,ф (Хп), но, как мы уже видели, норма каждого нормального оператора совпадает с радиусом его спектра.
Замечание 6. В качестве последней иллюстрации использования спектрального разложения нормального оператора исследуем область численных значений W (А) такого оператора. При этом W (А) определяется как область значений квадратичной формы (Ая, х), принимаемых на единичной сфере в Н:
Ж (Л) = {(Ах, х>:||х||= 1}.
Если А = JiXiPi и оператор А нормален, то для всякого х с [| я:|| = = 1
(Ах, х) =	*> = SilЛММ.
£	i
2im2 = M2 = i-i
Другими словами, {{Ах, х)} принадлежит выпуклой оболочке множества {Хх, Х2, ...» Хп}. Обратно, если X = 5\очХ| (о^	0,
У|а£ = 1) принадлежит выпуклой оболочке множества {Хг, Х2, ... ..., Хп}, то х можно положить равным ^г^е^ В этом случае Iх Г = Ха« = 1 и
(Ах, х) = {^а/'Ае^^а/'е^ = 2а«‘аУ%	е;> =^-
г	j	i
Это позволяет прийти к выводу о том, что если оператор А нормален, то W (А) представляет собой выпуклую оболочку спектра оператора А.
В качестве примера читатель может показать, что оператор U в трехмерном евклидовом пространстве с матрицей
'О 0 11 1 О О _0 1 0_
относительно естественного базиса явлется унитарным и что спект-
ром его служат три кубических корня из 1. Для этого оператора
W (А) представляет собой равносторонний треугольник, вершинами которого служат указанные корни. Для контраста укажем,
что мы
ГО О’ матрица Т = L Q в двумерном евклидовом пространстве со спектром а (Т) =
определяет оператор единичной нор-
= {0}, и его область W (Т) представляет собой круг радиуса V2 с
центром в начале координат.
Канонические представления. При изучении линейных систем
часто полезными оказываются три конкретных представления соответствующих линейных преобразований. Представление первого типа, на которое мы и обратили наше внимание прежде всего,— это спектральное представление нормальных операторов в гильбертовых пространствах. Для нормальных операторов в конечномерных гильбертовых пространствах спектральное представление приведено в уравнении (1) этого параграфа. Аналогичный результат имеет место и для каждого ограниченного нормального оператора, определенного в некотором бесконечномерном гильбертовом пространстве. Однако получение этого более общего результата предполагает некоторое знакомство с теорией меры. Поэтому мы не включили его в эту книгу. Заинтересовавшийся читатель найдет в приложении 5 некоторые сведения по этому вопросу, и в том числе формулировку теоремы об общем спектральном представлении ограниченных нормальных операторов.
Вторым достаточно полезным типом представления является жорданова каноническая форма, пригодная для любого линейного оператора, определенного на произвольном (не обязательно гильбертовом) конечномерном линейном пространстве. Для простых операторов эта жорданова форма представления совпадает со спектральной. Если же рассматриваемый оператор не является простым, то жорданово представление можно рассматривать как наилучшее приближение к диагональной форме.
Для конкретности рассмотрим оператор А. в Rn с различными собственными числами {Х17 ..., Хт}, где т п. Пусть собственное число £ о (А) имеет алгебраическую кратность pj и геометрическую кратность qj. Тогда с каждым Ху связано некоторое подпространство Xj размерности pj, инвариантное по отношению к оператору А. С Aj связаны еще и qj линейно независимых собственных
3.4. КАНРНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 269 векторов, каждый из которых принадлежит подпространству Xj. Подпространства {X;} разлагают X, т. е. X = Хг® Х2 ф ... .. фХш. Теперь у нас имеются две возможности.
Если Pj == qj, то собственные векторы, соответствующие собственному числу Хд образуют базис пространства Xj. В этом случае оператор Aj, являющийся сужением оператора А на Хд— простой и, следовательно, матрица этого сужения диагональна. Если pj > Qj, то собственные вектора, соответствующие собственному числу 1;, образуют лишь частичный базис пространства Хд и матрицу Aj нельзя привести к диагональному виду. Теорема Жордана гарантирует существование таких векторов {е^: i ~ ^+1, ... ...» Pj}, которые, будучи добавленными к собственным векторам {е^: i = 1, 2, ..., qj}, образуют базис Ej = {ед, ..., ejP.} для пространства Xj. Более того, матрица Л; по отношению к этому базису имеет вид
Л 0	:
О
=
t
L(?>+ столбец _
<—	+ 1)“я строка. (5)
Множество Ej называется жордановым базисом Хд а матрица [Л— жордановой матрицей.
Для того чтобы получить жорданово каноническое представление оператора Л, построим сначала жордановы базисы Ед ; = 1, связанные с каждым из различных собственных чисел kj&f (Л). Жорданов базис Е для всего пространства X определяется как объединение этих базисов: Е = [JjEj =
270	гл. з. структура линейных систем
= {е?ц, ...» ^ipp • ••» ет,рт}- Читатель без труда убедится в том, что в матрице[А]Е ненулевые элементы могут входить лишь в диагональные блочные матрицы
[А]е =
(6)
Другими словами, главная диагональ матрицы [AJe образована числами {Aq, ..., кт}, каждое из которых повторяется столько раз, какова его алгебраическая кратность. Первая наддиагональ (сверху и справа от главной) состоит из нулей и единиц в пропорциях, определяемых соотношениями между алгебраической и геометрической кратностями каждого из собственных чисел. Например, оператор с характеристическим полиномом Д (X) = (X — Ах)3 х X (31 — А,2) (А, — А3) может иметь одну из следующих трех жорда-новых форм:
rXi 1	0	0	0~
О	Xi	1	О	О
О	0	Xi	О	О
О	0	0	Аз	О
0	0	0	0	Аз-
Ai 0 0 0 Оп
О	Ai 1	О	О
О	0	Ai	О	О
О	0	0	Аз	О
О	0	0	0	Аз-
rAi 0 0 0 0~i
О А] О О О
О 0 Ai О О
О 0 0 Аз О .0 0 0 0 Аз-
Последняя каноническая форма представления, на которой мы остановимся в этом параграфе, называется полярным представлением *). Рассмотрим произвольное гильбертово пространство ZZ, n-мерное гильбертово пространство Еп и линейное преобразование Т: Н -> Еп. Центральный результат, относящийся к полярным представлениям, содержится в теореме Д.
Т е о р е м а Д. Пусть Т — некоторое линейное преобразование Т: Н -+Е'1. Тогда существуют такое ортонормальное множество {^i, ..., en}CZ Еп, такое ортонормальное множество {Д, ..., /п} CZ CZ Н и такие неотрицательные вещественные скаляры {щ, ...рп}, что
п
Т = 2 q> Hi </i.	(7)
1=1
Доказательство, Предположим, что Т может быть представлено в указанном виде. Несложный расчет показывает, что преобразова-
♦) Объяснение этого термина можно найти в приложении 5.
з 4. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 271 ние, сопряженное с Т, может быть представлено в виде
п
(8) 1=1
Воспользуемся ортонормальностью множества {/J и найдем непосредственно из уравнений (7) и (8)
и i=l
Теперь совершенно ясно, что скаляры {н?} должны образовывать спектр оператора ТТ*, а элементы {ej должны служить собственными векторами ТТ*.
Эти вводные замечания подсказывают, как можно найти векторы {е;} и {fj} и скаляры {р^}, удовлетворяющие условиям теоремы. Для любого Т\ Н ->Еп образуем ТТ*, представляющее собой некоторый неотрицательный самоприсоединенный оператор в Еп. В связи с этим все его собственные числа Xlt Х2, ..., Хп (каждое из которых повторяется столько раз, какова его алгебраическая кратность) должны быть положительными. Оператору ТТ* соответствует определенное множество ортонормальных собственных векторов е2, ..., еп. Можно предположить, что X; перенумерованы таким образом, что сначала идут все ненулевые собственные числа. Пусть тогда Х;- > 0 при j = 1, 2, ..., к и Х;- = 0 при / = == к + 1, ...» п. Определим последовательность {/J следующим образом. При 1 i к положим Д = X“1/aT*ef; /к+1 положим равным любому единичному вектору, ортогональному к линейному многообразию L (Д, ..., fk); fM положим равным любому единичному вектору, ортогональному к ..., /л+1), и т. д. Поскольку Т*ег = 0 при i = Z- + 1, п, то, множество {/i}, определенное таким образом, удовлетворяет условию
Z-A/.	j 1, 2, П.	(9)
Ясно, что описанный процесс позволяет (хотя и не обязательно однозначно) для каждого линейного преобразования Т: Н -+Еп определить ортонормальное множество {ej}CZ Еп и множество {Л}СГЯ, а также множество неотрицательных скаляров {Xi/2}. Остается лишь показать, что эти множества удовлетворяют условиям теоремы. Прежде всего, из-за ортонормальности множества {еп} мы можем представить тождественное преобразование в Еп в виде
7J
I —	& i / \^i •
Но тогда уравнение (7) является следствием уравнений
(п	\	п	п
S J г “ 2 «<>	</i-
i=l	/	i«l	i=l
Ортонормальность множества {/{} доказывается соотношениями
<А, //> = < VAT*ei,	=	е,>=(Х^)-‘/.ХКеье,> =
= 6ib i = 1, . . . , n,
после чего справедливость теоремы Д становится очевидной.
Полярное представление уравнения (7) содержит в себе значительную информацию о преобразовании Т. Ранг Т оказывается равным числу ненулевых элементов Область значений преобразования Т представляет собой линейное многообразие, натянутое на элементы Д, соответствующие ненулевым Более того, || Т || — = шах {рч} (см. упражнение 7). г
Полярное представление преобразования Т единственно, если в спектре ГГ* нет кратных собственных чисел. Если же некоторые из собственных чисел ТТ* кратны, то в выборе базисных множеств для собственных подпространств всегда имеется неоднозначность. Короче говоря, разложение (7) однозначно с точностью до поворотов в собственных подпространствах. Следует особо отметить, что вычисление этого канонического представления возможно лишь в простейшем из двух пространств, связанных с Г, а именно в Еп. В самом деле, в этом случае 7Т* есть матрица, а элементы {в{} — n-мерные векторы. Векторы более общего гильбертова пространства {fa} выражаются через как показано в доказательстве, приведенном выше.
Замечание 7. Все описанные канонические представления имеют общие черты. Все они относятся к линейным преобразованиям конечного ранга и существенным образом зависят от характера спектра и собственных подпространств некоторого оператора. Но если пренебречь этой общностью, то все три представления взаимно независимы друг от друга, и их следует рассматривать как совершенно различные. Спектральное представление нормальных операторов обычно вводится в рамках функционального анализа и зависит от структуры гильбертова пространства, вида присоединенного оператора и свойств коммутативности этих операторов (в этом случае конечномерность пространств не играет никакой роли и не фигурирует в формулировке основной теоремы). Напротив, жор-дановы канонические формы всецело принадлежат линейной алгебре. Возможность ее использования существенным образом зависит от конечномерности пространства, но совершенно не зависит от его метрической структуры, т. е. от характера нормы или вида
3.4. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 273 скалярного произведения, определенных на нем. Полярное каноническое представление сохраняет смысл и для преобразований, а не для операторов. В этом случае необходимо, чтобы соответствующие пространства были гильбертовыми. Обобщение полярного представления на случай бесконечномерных пространств, осуществляемое в приложении 5, ясно показывает, что по своему духу полярное представление подобно спектральному представлению нормальных операторов.
Поскольку дополнительные сведения о спектральном представлении нормальных операторов содержатся в приложении 5 и упражнениях, а жорданона каноническая форма используется в § 3.5, то сейчас мы непосредственно перейдем к использованию полярного представления. Рассматриваемый пример покажет нам, что с помощью полярного канонического представления можно глубоко разобраться в структуре интересующего нас преобразования.
Пример. Рассмотрим еще раз задачу о минимизации расхода энергии, поставленную и решенную в § 3.2. Вспомним прежде всего некоторые определения евклидовой геометрии.
Рассмотрим подмножество D2 вещественного пространства Е2, определенное следующим образом:
D2 = {(*1, х2) =	ос2|а2): а® + а® = 1).
где и р,2 — фиксированные скаляры, отличные от нуля. Нетрудно показать, что 1)2 — это эллипс с центром в начале координат и с главными осями, расположенными вдоль естественных координатных осей. Действительно, для каждого вектора (xv x2)EzD2
я?/Н® + Я2/Н2 = а? + а? = 1.
Последнее уравнение есть хорошо знакомое уравнение эллипса.
Определить обобщенный эллипсоид в пространстве Еп можно следующим естественным образом. Пусть {еп ..., еп} — некоторый ортонормальный базис Еп, и пусть {цр ..., рп} — некоторое множество вещественных скаляров. Тогда множество Dn определяется условием
х: х= 2 еь 2 а® = 1 <=1 1=1
(10)
и называется эллипсоидом. Главные оси этого эллипсоида направлены вдоль одномерных подпространств L (ех), ..., L (еп). Если п = 2 и q = (1,0), а е2 = (0, 1), то Z)n, очевидно, совпадает с множеством Z)2, определенным ранее.
Рассмотрим теперь линейное преобразование Т: Н -> Еп. Полярное каноническое представление этого преобразования имеет
/
ВИД	/
п
г =	(Н)
г=1
Предполагая, что pf =/= 0, i = 1, ..., п, находим, что подпространство М = (Дгт)1 совпадает с линейным подпространством
Обозначим через dUM множество
dUM = {и: иеМ, ||и|| = 1}.
Поскольку множество {ft} ортонормально и образует базис М, то легко проверить, что предыдущее определение дUm можно заменить следующим эквивалентным:
{п	п
u: и = 3 ®i/i, 3 «? = 1 •
i=l	г=1
С геометрической точки зрения dUM представляет собой сферу, лежащую в А/, с центром в начале координат и единичным радиусом. С помощью уравнения (И) мы найдем тогда, что
{п	п
У' У = 3 ei	2^ = 1-
i=l	г=1
Сравнивая определения множеств T(dUM) и Z)n, мы убедимся в том, что преобразование Т отображает сферу единичного радиуса М в некоторый эллипсоид из Еп.
Теперь можно представить себе преобразование Т с чисто геометрической точки зрения. Векторы {е^ ..., еп} — это главные оси эллипсоида Dn. Скаляры {р*} — это «коэффициенты растяжения» в направлениях этих главных осей. Поскольку || Т || = max {р{}, то нормированное преобразование Т должно иметь вид
(п	\
2^>МА .	(12)
г=1	J
где 0 pi = р{/1| Т ||	1, i = 1, ..., п. Значения р{ могут ис-
пользоваться в качестве меры эксцентриситета этого преобразования. В силу линейности преобразования Т каждое множество adUM, «подобное» единичной сфере, преобразуется Т в множество aZ)n, подобное исходному эллипсоиду.
Пусть g = Еп, и пусть мы снова рассматриваем задачу отыскания такого элемента и? с минимальной нормой, который удовлетворял бы условию g = Тш. С принятой здесь геометрической точки зрения эта задача эквивалентна отысканию множества aZ)n,
ЗА. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 275 содержащего & с последующим определением однозначного прообраза 5 среди элементов ад Um- Полярное представление преобразования Т позволяет подойти к решению этой задачи непосредственно. Если обозначить через преобразование, отображающее 5 в и; для каждого £ЕгЕп,то из того, что область значений Т+ должна совпадать с М, а композиция ТТ+ должна быть тождественным оператором в Еп, непосредственно следует соотношение
п
Г+ = ЗЛ>-^<е;.	(13)
1=1 н
Это и есть решение задачи минимизации расхода энергии в явном виде.
Для того чтобы наметить этапы вычисления полярного представления преобразования, описывающего какую-либо физическую систему, рассмотрим электромеханическую систему, символически изображенную на рис. 2.13. В примере 3 из § 2.4 мы уже вычислили уравнения движения и матрицу перехода этой системы. Примем эти результаты в качестве отправной точки. Обозначим через Т преобразование, отображающее Н = L2(tQ, tr) в Е2 и определяющееся условием
Ч
Ти = Ф (tf, s) В ($) и (s) ds.
Мы уже видели, что преобразование 71*: Е2 Н представляет собой умножение на переменную матрицу В* (/) Ф* (t}, t). В нынешнем примере В — это вектор-столбец (0, к), и, следовательно, непосредственным вычислением можно убедиться в том, что
7’7’* =
у Ф (tf, s) В (s) B*(s) (b*(th s) ds = to
^11 ^12
Gl ^22
где
/у	/у
^11=	б/2Ф12 (tf, s) ds *, ^12 =	б/2Ф12 (tf, s) Ф22 (ifi s) ds \
to	to
4	'k
^21 == б/2Ф22 (£/,$) ®12 G/» $) ds*, t22 — ^^2Ф22 (tf i s) ds. to	to
Компоненты матрицы Ф (t, t0) в явном виде были определены в примере 3 из § 2.4. Поэтому совершенно ясно, что матрицу ТТ* можно вычислить в явном виде для любого интервала По, tf].
Кроме того, можно легко найти спектр оператора /7* и ортонормальное множество его собственных векторов.После этого полярное представление выписывается непосредственно, и решение задачи завершено.
Упражнения
1.	Пусть операторы А и В нормальны и АВ* = В*А. Покажите, что А + В и АВ тоже нормальны. (Более глубокий результат того же типа можно найти в работе (A.23J па стр. 934.)
2.	Пусть 6 £п — некоторый фиксированный вектор, преобразование Т: Н —» Е'1 определяется уравнением (11), a = <ef, £>, i = 1, ..., w. Воспользуйтесь уравнением (13) для того, чтобы показать, что минимальная энергия, необходимая для попадания в определяется выражением
3.	Обозначим через К некоторый оператор в гильбертовом пространстве Еп. Пусть X/ 0 (К) — некоторая точка спектра, и пусть ей соответствует собственный вектор е$. Обозначим через К' = К + возмущенный оператор К. Если норма || 8К || мала, то собственные векторы К' и его спектр мало отличаются от собственных векторов и спектра оператора К соответственно. Покажите, что
6Х. =	б/Се.>, i = 1,... ,п.
Получите зависимость между вариациями {б^} и дК.
Указание. Подставьте в уравнение (К — X,/)	= 0 значения К + ЬК
вместо К, Xf + 6Xf вместо Хг и + 6ef вместо и воспользуйтесь тем фактом, что (К — Хг/) = 0.
4.	Для преобразования из уравнения (13) норма || Т || = max {pf} представляет собой всего лишь одну из нескольких мер операторного «коэффициента растяжения». Рассмотрим объем Vn наименьшего гиперпараллелепипеда, содержащего эллипсоид Dn. Очевидно,
^=2Гк=2(1Ь»У/’.
i	' i
Используя результат упражнения 3, покажите, что если Vn =/= 0, то вариация бРп, вызванная изменением 6Х, удовлетворяет уравнению
уп	\	£ «**<> •
5.	Обозначим через а некоторый параметр матрицы A (t, а) из примера 3 § 3.2. В соответствии с теоремой Б из § 2.1 преобразование Т из этого примера непрерывно зависит от а, если этим свойством обладает А (/, а). Воспользуйтесь результатом упражнения 4, чтобы исследовать чувствительность преобразования Т к изменениям а.
6.	Пусть матрица Q (t) при любом t (Е т положительно определена, самоприсоединенная и непрерывна но t. Докажите, что функция <х,
определенная на векторах [Z2 (т)1п соотношением
<*» 3/>q = ^ [*(*)» Q(*)y(s)]ds,
может служить скалярным произведением.
7.	Докажите, что для преобразования Т из уравнения (8) справедливо П Г || = max {pf}.
Указание. Воспользуйтесь для этого равенством
|| Т* з-1|2- Сг, ТТ*ху
и тем фактом, что
II Т || = || Т* ||.
3.5. Различные режимы поведения стационарных систем
В приложении 3 мы покажем, что матрица перехода системы
х (/) = Ах (/), fGT,	(1)
где Л — пе зависящая от времени матрица, может быть записана в виде
Ф (t, tQ) = exp [Л (t - Q], t, t0^x.
Используя канонические формы представления матрицы Л, мы можем существенно уточнить это выражение. В результате найдем разложение матрицы перехода Ф, позволяющее получить полезные сведения о поведении стационарных систем.
Прежде всего, допустим, что матрица Л — простая. Тогда множество 5 = {е1? ..., еп} собственных векторов Л образует базис в 7?п, и с помощью этого базисного множества, а также множества, ему двойственного, матрицу Л можно представить в виде
п
А = 2
1=1
Напомним, что в § 3.4 мы установили, что если / (z) — произвольная функция, аналитическая в некотором открытом круге, содержащем спектр оператора Л, то функция оператора / (Л) представима в следующем виде:
п
/(Л) = 2	(2)
и, в частности,
п
exp [ A (t — /0)] = У, et) exp [А,; (/ — /0)] <4-	(3)
1=1
Из уравнения (3) мы непосредственно получаем следующее выражение для свободного движения стационарной системы:
п
X (0 = S Ci > exp [X; (i — /0)] <4, «°>, t > t0.	(4)
i=l
Инвариантные подпространства матрицы А (в этом случае это собственные подпространства) будем называть режимами системы. Тогда функция а7- (/) = exp [Xj (t — £0)]	х°> описывает по-
ведение системы в /-М режиме. Уравнения же (3) и (4) описывают соответственно спектральное (порежимное) разложение матрицы перехода и свободное движение стационарной системы.
Замечание 1. Из уравнения (3) следует, что каждый режим систем возбуждается независимо от остальных. Иными словами, интенсивность возбуждения i-ro режима определяется непосредственно выражением (et, х°> и не зависит от значений (ек, х°> при к =f= i. Если начальное значение х° принадлежит некоторому подмножеству режимов, то траектория системы остается в этом подмножестве при всех t tQ. Другими словами, если для какого-нибудь / скалярное произведение , х°> = 0, то коэффициент при ej остается равным нулю при всех t tQ.
Траектории в фазовом пространстве. Траекториями в фазовом пространстве (или фазовым портретом движения системы) называют изображение свободного движения дискретной или непрерывной системы в пространстве Кп. Все результаты и все замечания § 2.4 приобретают особенно простой вид, если перевести их на язык фазовых траекторий. Для упрощения изложения рассмотрим сначала частный случай, когда матрица А вещественна и имеет размеры (2 х 2), собственные числа {Хр Х2} и собственные векторы {ev ^2}, которые также вещественны.
Случай 1 (узел). Предположим, что Хх и Х2 отличны от нуля, имеют один и тот же знак и
Ы<М	(5)
Пусть для начала
<0, Х2 < 0.
Поскольку движение такой системы в каждом режиме пропорционально exp [Xi (t — /0)], то ясно, что с ростом t движение в каждом из режимов приближает выходную величину системы к началу
координат. Поскольку Х2 < Хх < 0, то отношение амплитуд движения в каждом из режимов, равное
<g21 О . СХр [	(/—/р) ]
(е+, £> * ехр [Л1 (г — /о)] ’
стремится к нулю по мере того, как t ->оо. Поэтому траектория системы асимптотически приближается к режиму ег по мере движения к началу координат. Фазовый портрет поведения такой системы называется устойчивым узлом и показан на рис. 3.3. Если же вместе с (5) имеют место неравенства
^>0, Х2>0,
то фазовые траектории системы остаются теми же, что и раньше, но движение по ним идет в обратном направлении. Соответствующий фазовый портрет называют неустойчивым узлом (рис. 3.4).
Рис. 3.3. Устойчивый Рис. 3.4. Неустойчивый Рис. 3.5. Устойчивый узел узел, X, <	< 0. узел, Х2 >	> 0.	= Х2 < 0.
Наконец, если Хх = Х2, а векторы ег и е2 по-прежнему линейно независимы, то фазовые траектории такой системы вырождаются в в прямые. Для случая устойчивого узла соответствующий фазовый портрет показан на рис. 3.5.
Случай 2 (седловая точка). Предположим, что собственные числа и Х2 имеют разные знаки. Для определенности примем, что
Xj < 0 < Х2.
В этом случае движение в первом собственном подпространство
устойчиво, а движение во втором собственном подпространстве неустойчиво. По своей форме фазовые траектории напоминают гиперболы, а движение вдоль этих траекторий направлено к началу координат вдоль первого собственного подпространства и от него — вдоль второго. Про такой фазовый портрет (рис. 3.6) принято говорить, что на нем имеется сед-
L(ez)
Рис. 3.6. Седловая точка, X] < 0 <
ловая точка.
Случай 3 (комплексные собственные числа). Случай комплексных собственных чисел достаточно интересен для того, чтобы исследовать его подробно. Пусть Хх = ах + + /со j — комплексное собственное число матрицы А. Поскольку коэффициенты характеристического полинома вещественны, то собственным числом матрицы А должно Х2. быть и Х2 = ai — /сох- Собст-
венные векторы ег и е2, соответствующие Хх и Х2, также комплексны. Очевидно, их можно выбрать так, чтобы они были комплексно-сопряженными. Обозначим их символами
*1 = 1*1 + 71*2,
*2 = 1*1 — 71*2,
где Нх и 1*2 — вещественные линейно независимые векторы. (Если бы это было не так, то q и е2 оказались бы зависимыми.) Нетрудно показать, что комплексно-сопряженными будут и двойственные векторы ?х и е2.
Для того чтобы найти эти двойственные векторы, положим
+ 1 , . 1 + 1 .1
*1 =—Vl+j—V2,	*2 =— 3’1 —7 — ^2-
Воспользовавшись свойством дистрибутивности скалярного произведения и четырьмя соотношениями
<4, ф=6и, *,/ = 1,2,
читатель без труда убедится в справедливости следующих четырех
скалярных соотношений, связывающих между собой векторы U., vv р2 И V2:
Н1> = !>	<^2. Н1> = °-
<РР ц2> = 0,	<v2, р2> = 1.
Отсюда следует, что = pt и г2 — р2- Теперь у нас имеются четыре уравнения:
ri == Ш + /М-2»	ei ~ {Hi + /На)»
е2 = Pi — /р2,	«2 = 4"	— /Иг >•
Пользуясь этими обозначениями, читатель может проверить, что для любого х° свободное движение в системе описывается уравнением
х (Z) =	<е|, ж0) exp (/ — /0)1 + е2> <е£, х°> ехр Щ (t — t0)],
которое приводится к виду
х (t) = exp [ах (t — Q] (<wt, xQ) cos сох/ + <p2, z°> sin co^) щ + 4- exp [ax(/ — /0)| ((^2, x") cos (ох/ — <pt, x") sin cox0 p2.
В эквивалентной полярной форме:
х (t) = exp [ax (t — f0)l [у cos (co^ — ф) щ — у sin (co — ф)р21, где параметры у и Ф определяются условиями
у cos ф = <Pi, я°>, у sin ф — <р,£, xQ).
Последний из сомножителей в квадратных скобках представляет собой суперпозицию двух гармонических движений в направлениях рх и ц2. Амплитуда и фаза этих колебаний зависят от начальных условий, я0. При ах = 0 каждая из фазовых траекторий оказывается логарифмической спиралью и про соответствующий фазовый портрет говорят, что на нем есть фокус. -Если ах <4 0, то движение по этим тра- к екториям направлено к началу координат, и такой фокус (рис. 3.7) называют устойчивым. Если же ах > 0, то движение направлено в обратную сторону, и такой фокус называют неустойчивым (рис. 3.8). Наконец, если ах = 0, то каждая траектория образует замкнутую кривую, и фокус системы вырождается (рис. 3.9).
Рис. 3.7. Устойчивый фокус, Re (1)	0.
в центральную точку
Общий случай. Рассмотрим матрицу А размером (п х и) и не будем обязательно предполагать, что она простая. Тогда из изложенного в § 3.4 следует, что можно найти такой базис Е = {ер ... ..., еп}, который позволит привести матрицу Л к ее жордановой канонической форме, которую мы обозначим через J А = [Л]#. Понятие функции матрицы не требует, чтобы матрица Л была
Рис. 3.8. Неустойчивый
фокус, Re (X) > 0.
Рис. 3.9. Центральная точка, Re (X) = 0.
простой. Поэтому нам нужно лишь рассмотреть вопрос о том, к каким вычислительным различиям приводит разница между простыми матрицами и матрицами общего вида. Обозначим через уи элемент на пересечении г-го столбца и ;-й строки матрицы, и пусть
п
а = 2
г,}=1
Тогда нетрудно показать, что матрицу / (Л) можно представить в виде
п
/(А)= 2 ei>rij<6j, ij=l
где через обозначен элемент на пересечении f-ro столбца и /-й строки матрицы f(JA). Таким образом, мы свели нашу задачу к вычислению функций от жордановых матриц.
Рассмотрим жорданову матрицу J, у которой ненулевыми могут быть только элементы диагональных блочных подматриц J — = diag [J1?..., Jp](cm. уравнение (7)из§3.4). Из-за того, что матрица / имеет квазидиагональный вид, функция / от матрицы J оказывается того же типа, и что / (J) == diag [/ (<7\), ..., / (Jp)l (мы сове
туем читателю убедиться в этом на примере полинома от матрицы). Поэтому наша задача сводится, в конце концов, к вычислению функций от элементарной жордановой блочной матрицы. Ключ к решению этой задачи содержится в утверждениях теоремы А.
Теорема А. Пусть / — некоторая функция, аналитическая в некоторой открытой окрестности X, а матрица D — элементарная жорданова блочная матрица ранга р. Тогда / (Z?) есть верхняя треугольная матрица вида
О
fW
Доказательство этой теоремы мы оставляем читателю в качестве упражнения. В частности, заметим, что
t . . .
exp {Dt} = exp (Kt)
Случай 4 (вырожденные узлы). Для того чтобы завершить изучение фазовых портретов, начатое в § 3.4, рассмотрим двумерный случай, для которого базисные векторы {е1? е2} в R2 таковы, что А приводится к жордановой форме. Тогда в силу уравнения (6) exp [A (t — Zo)] = егу exp [X (t —	+ (t — tQ) ej] +
+ e2y exp [X (t — Z0)l < e2 .
Поэтому, если z° ЕЕ/?2, то свободное движение системы описывается суммой
х (t) = аг (/)*! + а2 (0 е2, где
а1 (М = ехР (t — QI <**»	+ (t — t0) < е2, xQy,
а2 (t) — exp [X (t — Zo)] < e2 , x°>.
Предположим, сначала что X >0. Очевидно, изменяя знак разности t—tOi мы осуществляем зеркальное отображение в фазовой плоскости. Поэтому достаточно рассмотреть случай положительных t — tQ. Если(^ 7 я°>= О, то мы получаем две траектории,
Рис. 3.10. Устойчивый вырожденный
узел.
Рис. 3.11. Неустойчивый вырожденный узел.
направленные вдоль eL к началу координат. Если в нуль обращается <е*, х°>, то
«1(0 = G — *о) <^2+, Х°У exp [X (t — t0)], «2 (t)'= (е2 , х°> exp [X (t — £0)j.
При t = tQ траектория лежит на оси е2. Но по мере увеличения t изображающая точка начинает приближаться к оси ev приходя в начало координат асимптомически вдоль этой оси. Теперь легко завершить построение фазового портрета этой системы (рис. 3.10).
Если X > О, то фазовые траектории системы можно получить зеркальным отображением фазового портрета для случая X < О, направив движение по этим траекториям в обратную (т. е. от начала координат) сторону (рис. 3.11). Про соответствующие фазовые портреты говорят, что на них имеются соответственно устойчивый и неустойчивый узлы.

L (ez)
Рис. 3.12. Вырожденный Рис. 3.13. Вырожденный узел, Хх ~~ О-узел, Xt = 0, Ха < 0.
Наконец, случай, в котором одно из собственных чисел равно нулю, можно изучить, опираясь на материал предыдущих параграфов. В самом деле, если Xj = 0 и Х2 =/= 0, то из уравнения (4) следует, что
х (О = ^iX**» я°> + ^2> ехР 1^2 (* ~	, *°>, t > Не-
соответствующий фазовый портрет показан на рис. 3.12 для случая Х2 0. Если Х2 0, то направление стрелок нужно поменять на обратное.
Если Xj = Х2 = 0, то либо
х (0 =	, *°> + ^Х**» *°>»
и каждая точка на фазовой плоскости является точкой равновесия, либо
х (О - в1>[<еГ, х°> + /<е2+, х°>] + е2><е2+, я°>
п движение происходит по прямым, параллельным е2. Все точки на прямой {е2 , являются в этом случае точками устойчивого равновесия (рис. 3.13).
Замечание 2. Графическое обобщение метода фазовых траекторий на случай, когда размерность пространства больше двух, непродуктивно. Но это не означает бесполезности обобщения идей, заложенных в этом методе. Основы такого обобщения заложены в замечании 1, если добавить еще, что движение в каждом из отдельных режимов можно рассматривать как отдельную фазовую траекторию, а суммарное движение представлять себе как суперпозицию всех отдельных траекторий.
Понятия и свойства, введенные и изученные в этом параграфе, открывают широкое поле для разнообразных применений. В настоящий момент мы рассмотрим всего два примера, иллюстрирующих различные свойства линейных преобразований.
Пример 1. Рассмотрим однородную дифференциальную систему, описывающуюся уравнениями
*i(0 1	Г1
х2 (О J	L(X
aj . Г*1 (Ml = Г 1
1 J Lx2(0j ’ Lj;2(^0)J L *2 J
Определить собственные числа матрицы А нетрудно. Они имеют следующий вид: == 1 + а и Х2 — 1 — а. Матрица перехода Ф (£, ^о) = ехР W (t — Z0)J для такой системы вычислена в упражнении 6 данного параграфа. Полученный там результат можно записать в виде
1 Г 1 1
4
ф (t — tQ) = у exp [Хх (t — «о)1
I 1	1 —1
+ у exp[X2(Z — f0)] [_4	!
в чем читатель легко убедится, подставив эту матрицу в исходное дифференциальное уравнение. Решение х (£; х°, Zo) может быть записано в виде
ж (Z; .г°, t0) =
1
exp [М (t — /0)1	+ яф + exp [X2 (t — t0)J («« —
exp (t — Q] (zj + *°) 4- exp [X2 (t — Z0)l ( — 4 + a*)
Пример 2. Рассмотрим стационарную однородную дифферен-циальную систему
'*1 (О
-я2 (0-*
-15
-24
121 ГЛ(Г)1
19-J
В приложении 3 мы выясним, что матрица ехр [4 (Z — Zo)] — = Ф (t — t0) имеет следующий вид:
Г 9 -61	Г -8 61
Ф(*-*о) = exp(Z-tQ) [12 _8J +exp[3(^-Q][_12 gJ .
Читатель может проверить, что Ф (0) = /, а Ф (t — tQ) удовлетворяет исходному дифференциальному уравнению. Для того чтобы получить тот же результат методом спектрального разложения, нам нужно прежде всего найти собственные векторы q и е2 матрицы этого уравнения. Нетрудно убедиться в том, что собственные числа матрицы А равны 1 и 3. Для того чтобы найти q,
Р"'"'" У'”ВВС“Г-16 121 ГО] М-МН>-[_24 18JIJ - [ о J 
Его решение имеет вид ег к col (3, 4), где к — произвольный скалярный множитель, который можно положить равным единице. Аналогичным образом найдем е2 = col (2, 3).
Двойственные векторы и е2 должны быть вектор-строками. Пусть е{ = («» 0). Тогда из условия	= 1 мы получим
За 4р. =. 1, а из условия <4, е2) =0— 2а 4-30=0. Решение этой системы уравнений относительно а и 0 дает
= о, - 2).
Аналогичным образом можно показать, что
е2 = (- 4, 3).
Спектральное разложение матрицы А должно иметь вид
<^i> et, и, следовательно,
л = [^].(1).[3,
Г 2 1
-21 + I , -(3)-[—4, 31 = L О J
г 9	Г —8 61	Г—15 121
= L12 -8- +31-12 9-1 = 1-24 19-1
Кроме того, в данном конкретном случае матричная функция ехр [4 (t — /0)1 = 2X1 ехр Щ (Z — <0)1 <е-
принимает следующий вид:
1‘ 3 1
ехр [A (t — Q] = ехр (t - t0) [ J. [3, -2] =
Г2 1 - 3
= exp[3(i —10)]
3] = exp (t — t0)
’ 9
-12
—6 '
-8 -
+ exp[3(/ — Q]
’ -8 6‘
--12 9-
Оба эти результата подтверждают полученные ранее выводы. Если начальное условие работы системы имеет вид х (Q = col (а:?, х^), то проекция ее траектории на первый режим описывается уравнением
<Х х (0> = (ei, X (t0)> ехр IX, (t — Q] =
= ехр (t — Q {Зх? — 2x°t},
а на второй режим — уравнением
<4, X (0> = <4, * (Q> exp IX2 (t — f0)l =-
= exp [3 (t — tQ) {—	+ 3^2).
Поэтому суммарная траектория системы выглядит следующим образом:
х (/)> 4- х (0> = exp (t — tQ) (Зх° — 24) X
Xcol (3, 4) 4' exp [3 (t — Z0)l (— 44 + 34)-col (2, 3),
что совпадает с выражением для Ф (t — tQ) х (tQ). Поскольку в этом случае оба собственных числа вещественны и положительны, то фазовый портрет свободного движения системы представляет собой неустойчивый узел.
Замечание 3. Дискретная система, определенная на множестве а = {^о*	•••>	•••} уравнением
Д/ х (t) А (/) х (f), t s o', называется стационарной, если матрица Ф (/л+1, th) = [Z 4~ 4- hkA (/*)], th Go, постоянна. Л так как
К
ф(<ь'о)=	+
j=o
то ясно, что матрица перехода стационарной системы Ф /0) — = [Ф («1. Ulk.
Рассмотрим случай, когда матрица А простая и имеет спектр о (Л) = {\, ..., %п}. Отсюда сразу следует, что жорданова форма матрицы Ф (t19 Zo) = [Z 4“ ЛЛ] имеет вид Уф = diag [(1 4~ MJ, ... ..., (1 4~ Мп)]. Обозначим через {Xj скаляры, для которых = = h-1 In (1 4- MJ, i = 1, ..., п (через In х здесь обозначен натуральный логарифм х). Так как th — t0 = kh, то нетрудно проверить, что
(Уф) =ехр[Уф(//с *<>)],
где Уф = diag Щ, ..., Таким образом, если собственные векторы матрицы Л' совпадают с собственными векторами матрицы Л, и спектр матрицы Л' получается из о(Л) с помощью отображения X/ -> Xj, то мы можем записать:
Ф (t, t0) = [I 4- hAp-'o) = exp [A'(t - Q], t, t0 G 0,	(7)
как в дискретном, так и непрерывном случаях. Значит, рис. 3.1 — 3.11 справедливы и для дискретного случая (после дискретизации времени в соответствии с о).
Вынужденное движение. Из замечания 3 следует, что вынужденное движение некоторой стационарной системы описывается уравнением
t
(Fu)(t) = exp[A(t-t0)] Jexp[A(Z0 — s)] Bu (s)ds, t(=3,
если она непрерывна, и
(П-i
(Fu)(t) =ехр[Л (/ — /(1)| 2 PXPl/1(/o -«>)! Ниц,), lEi,
J=o
если она дискретна.
Здесь матрица В не зависит от /, а ее столбцы обозначаются через Ьт. Рассмотрим сначала случай одномерного входного сигнала , когда Ви (t) =	(0. Положим /0 = 0 и предположим,
что матрица А простая. Воспользовавшись спектральным представлением матрицы ехр (At), мы получим следующие уравнения:
л	t
•<(J) = ЗЛ'	з,- + Je х<3 <«*, 6t> щ (s) ds] , I £t, (8)
И
n	г	[/1-1	1
#(/) =	^°/ +	^1? u (M »	1^5, (9)
i=l	L	j=0	J
где через {^i}i обозначено множество собственных векторов матрицы А. Таким образом, при любом t реакция системы х (t) по-прежнему представляет собой некоторую линейную комбинацию различных режимов системы. Однако на этот раз динамика изменения коэффициентов этой линейной комбинации сложней, чем было раныпе. Интенсивность возбуждения z-го режима, вызванного входным сигналом uv (t), описывается соответственно выражениями
/
ex»f bL) е~х*я (s) ds, i GE т, о
[П-i
еЧ <е*, ЪГУ 2
;=0
при любых tEEv, причем эти члены пропорциональны постоянной определяющей проекцию Ь± на ось из базиса {£*}.
Выражения, приведенные выше, подсказывают следующие выводы:
1.	Независимо от вида bt реакция каждого режима не зависит от реакций остальных режимов. Другими словами, степень
10 У. Портер
возбуждения каждого конкретного режима не зависит от степени возбуждения всех остальных режимов.
2.	Если вектор Ьг ортогонален любому из собственных подпространств систем (т. е. (г*, &> = 0), то на движение в этом собственном подпространстве uY (t) (независимо от его вида) не оказывает никакого влияния.
3.	Из утверждений (1) и (2) следует, что в том случае, когда оба вектора и xQ принадлежат некоторому инвариантному подпространству Л, движение системы происходит только в этом подпространстве при всех t t0.
Все эти результаты естественным образом обобщаются на случай многомерного входного сигнала. В этом случае В — постоянная матрица размерности (п X т) со столбцами ..., Ьт, а и == = [t/j (/), ..., ит (/)] — обычный элемент декартова произведения пространств. Рассмотрим весовую матрицу Z (t) = Ф (£0, t) В (t). Если предположить, что матрица А простая, то мы сразу получим, что
и
= Ф(/о-0/?= 1^> ехр |Х; (/0 —/)] ?.}в, iev.
i = l
Это уравнение можно значительно упростить, если ввести еще две новые матрицы. Обозначим через Л (/0 — t) диагональную матрицу с элементами ехр [X,- (/0 — 0L i = 1, ...» и, на главной диагонали:
Л (zo ~ 0 = diag {ехр [Хх (/0 — /)], ..., ехр [Хп (/0 — 01},
а через Н — матрицу со столбцами е19 ..., еп:
Нетрудно видеть, что матрица Н невырождена (поскольку ... ..., еп линейно независимы) и что в матрице , ей обратной, строками служат двойственные векторы е*, ..., е*\
Кроме того, очевидно,
ехр [Л (£0 — 01 = ЯЛ (/0 — 0 Я-1, t е v.
Все это позволяет утверждать, что
z (0 = ф (/0 - 0 Я = Я л (/о - 0 я1/?, t е V.
Лоома записи справедлива и в более общем случае, если Эта изменить в соответствии с выводами теоремы А относи-тельно жордановых канонических форм.
Поскольку вынужденное движение можно описать одним из следующих двух уравнений:
х (/) = НА (t - to) и-1 \ НА (t0 — s) 1Г1Ви (s) ds, 11= т,
It]—1
X (I) - НА (t - to) JI-1 2 (to - t) H~lBu (tj), t G 3, ;=o
которые сразу приводятся к виду
t
.> (I) = II jj Л (I - s) H lBu (s) ds, t (= X,
Io
[']-!
X (t) = H 2 A (/ — tj) H-'Bu (tj), t e 3, /о
то мгновенное воздействие /с-го входного сигнала Uk (t) на движение в i-м режиме определяется значением элемента на пересечении t-й строки и /с-го столбца матрицы Н1В (равного постоянной
и весовой функцией ехр [%/ (/0 — a)J. Таким образом, столбцы матрицы Я”1 В играют роль постоянных, связывающих фиксированные входные сигналы с различными режимами, а ее строки связывают различные входные сигналы с фиксированными режимами. Суммарное воздействие представляет собой интеграл (или сумму) мгновенных воздействий, взвешенных матрицей А (/0 — t).
Если для матрицы А не существует диагональной канонической формы, то картина получается не столь простой. Здесь через А (/0 — t) приходится обозначать экспоненту от жордановой формы А, а это значит, что она образована диагональными жордано-выми блоками. Однако рассматривая каждое полное инвариантное подпространство как некоторый режим, мы можем распространить предыдущее утверждение и на этот более общий случай.
В завершение этого параграфа рассмотрим подробно один конкретный пример.
Пример 3. Для цепи, изображенной на рис. 3.14, контурные уравнения Кирхгофа имеют вид
- /?Л,
Rih —	+ (Ri +
Эти уравнения можно привести к виду
dii / /6 * .	. (. । / 1 \	\
d7 = (77r)'* + 'd '-2+fcW’
di^ (Hi .	//6 + /^ .
~dt	— у1'2-
Обозначим через х (/) вектор-столбец Ux (/), г2 (01 и приведем
Рис. 3.14. Простая цепь.
последние уравнения к нормальному виду
£ (0 = Ах (t) + Ьи (/), х (tQ) = xQ, где матрица А и вектор Ь:
/?1	-
Л1 )
/?1 Hl -I /?2
/>2	^2
' ~ А Д 0 )'
не зависят от I.
Для большей конкретности предположим, что = 30, R2 = 6, Lv = ЮЛ и L2 = 9Л. Читатель без труда убедится в том, что в этом случае собственными числами матрицы А являются = —2 и Х2 = — 5. Соответствующие собственные векторы этой матрицы имеют вид
а векторы, им двойственные,
Определив эти величины, мы можем выписать выражение для матрицы перехода системы:
ф (t, io) = ехр [Л (f - /о)] = S ei> ехР l^i (t — Ml <4-
Подставляя полученные численные значения, мы видим, что ф(<, <0) = ft 4)>ехр[-2(/ _	т)+(и’ -1)?х
Г Г /Л . \ , / /1 О	2 \
Хехр [-5 (t - Z0)l , -у).
Нетрудно вычислить матрицу Н, столбцами которой служат ех и с.,, и матрицу, ей обратную (ее строками служат е* ие2+). Определив A (t, /0) соотношением
ехр [—2(t — tQ)]	О
О ехр [—5 (t — £0)]J ’
A(U0) = [
читатель может убедиться в том, что Ф (/, tQ) можно представить и в виде Ф (/, /0) = НА (t — /0) Н~1. Для этого конкретного примера
Ф(/, 1п) =
1
Л”
То
-1
ехр [~2(t — ^)]
О
ехр [-5 (Z - /0)]
О
£" 5
2_
3 J
В качестве еще одной возможности рассмотрим параметризованное семейство функционалов {g', t^x} в Яп, определенных следующими уравнениями:
<g',	= охр [-2 («-/„)] [е;, Cl = (| Ci + у ехр [-2 (Z - Q],
'4- С = ехр [-5 (t - /0)] [еь, =	_ |^ехр[-5 (Z - i0)].
Через эти функционалы матрицу Ф (t, t0) можно представить в следующем виде:
Ф (/, /0) =	( g[ + е2> ( g'2t t<=zX'
Легко определить и вынужденное движение этой системы. Дейст-вительно,
/
(Fu) (t) = \\(t, s) H-^bu(s) ds. to
Учитывая принятые выше численные значения параметров и кож кретный вид вектора Ь, можно переписать это выражение в виде
(Fu) (0 =
1	15 е ехр[— 2{t — s)]
I -da о
о
ехр [—5 (t — $)]
Г11
15
L 9 j
и (s) ds.
Если обозначить через F1 преобразование, определяемое условием F* и = (Fu) (/), и воспользоваться функционалами
</'Р = 44ехР I—2<z - •’)]и (х)ds’
^0 t
</£, = 1Г eXP I —5 ~ *’) 1 U dS' t(=X' t.
to F* можно записать в диадных обозначениях:
F* = Hl > < Л + ш > < А-
Если v (/) = (х", л-j, и (<)), то суммарную реакцию Т системы можно описать уравнением
{Tv) (/)	(Фх») (0 ! {Fu) {t)
exp[-2(/-Z0)]
О
ехр[-5(/ — /0)]
ехр [ -2 (Z
О
О
ехр[—5{t — s)]
1
1.3
1
*- 9 -J
и (s) ds
О
Вводя функционалы и определенные в 7?а х U с помощью уравнений
<Л'р y> = <g;, •т°> + </'1, U>, (ЕТ, <^2’ Р> = <?'2> Т°> +	Z Т>
3 5 РАЗЛИЧНЫЕ РЕЖИМЫ ПОВЕДЕНИЯ СТАЦИОНАРНЫХ СИСТЕМ 295 эту реакцию в момент времени t можно представить также в виде Т* — Hi/ </г{ -[-	(^2, t Gt,
или, используя численные значения параметров, в виде
+ \ <'*Р [ — 2 (Z — .<) | и (я) rf*} Ч-to
3
16
-1
'ехр [—5 (/ — /0)1 X
х [(¥} х°т ~ (т) *?]+4 $ехр 1 ~5 ~s) 5 u •
На этом этапе мы можем затронуть один вопрос, представляющий значительный практический интерес. Заметим, что х (t) = — Gi(0» Ч (0), а точки в каждом из контуров можно определить непосредственно но результатам, полученным выше, приняв
h (/) = ((1,0), *(/)),
Ё2 (0 = ((о, 1), X (/)).
Этот факт можно использовать как орудие для дополнительных расчетов. В качестве иллюстрации определим уг (t) (рис. 3.14):
1/1(0 = Лаё3(/) = Я2((0, 1), x(t)) =
= б [(|{ехр [-20- U] [(у)	+
+ 1У ехР I ~2 (/ — -s')| и (s) t/s) -to
+4" ^ехр н5 и—«)1"
to
Действительно, если поведение некоторой физической системы описывается нормальной системой уравнений, то поведение всех внутренних координат такой системы можно определить через ре-шэние этой системы, вычисляя соответствующие скалярные произведения.
Упражнения
1.	Определить собственные числа и собственные векторы матрицы
Какие ограничения нужно наложить на к и h для того, чтобы собственные числа матрицы были вещественны? Вычислите ехр (Mt).
2.	Обозначим через N наддиагональную матрицу n-го порядка вида
Г о 1 0 ... 0 1 \	0
N=
* \ i о о
Вычислите N2, N3, ..., и покажите, что А'п-1 — 0. Пусть / ($) есть некоторая функция, аналитическая в некоторой окрестности точки $ — X и допускающая в этой окрестности разложение в ряд Тейлора
оо
/(»)= 3 п=0
(s-K)ndnf
J п п as
Обозначим через D жордапову элементарную матрицу D = А/ + Л. Непосредственно убедитесь в том, что / (D) полностью определяется первыми п членами этого ряда.
3.	Обозначим через / ($•) некоторую функцию, аналитическую в круге, содержащем спектр матрицы А размерности (пХп). Можно показать, что если все собственные числа матрицы А простые, то
/ (А) = р-i [r0Z + М + ... +
где через и обозначен определитель Вандермонда
1 .........1
......
v= ч ...........К
I ...........
a Vk отличается от v лишь тем, что в нем (к + 1)-я строка v заменена на вектор (/ (Aj), ...» / (Ап)]. Воспользуйтесь этим представлением для того, чтобы проверить результаты первых двух упражнений.
4.	Обозначим через А матрицу
-/2	/2 I
3-2/2 -3 + 2/2" J
Покажите, что = — 1 и А2 = —2. Покажите двумя различными способами, что
ерх (Л0 = ё
2—2/2
3—2 /Т
,-2t
2 /2 — 1 - /2 ‘
2 /2^3 2 — /2 _
5.	Обозначим через А матрицу
Покажите, что = 1 + а и Х2 = 1 — а. Вычислите двумя различными методами функцию ехр [Л (t — /о)].
6.	Одно из отличий дискретных систем от непрерывных заключается в том,* что в первом случае свободное движение может привести в начало координат за конечное число шагов. Это происходит только тогда и только тогда, когда матрица Ф(^, t0) оказывается вырожденной. Исследуйте соответствующую ситуацию.
7.	Обозначим через А некоторую фиксированную нормальную матрицу, все собственные числа которой	простые, причем <0, i =
= 1, ...» п. Построите такое множество дискретных моментов времени {/(, /2,...,tn}, что Ф(/п, /0) будет равным нулю и каждое из чисел {|| Ф(^-, /0) ||: = 1,2, ..., п} минимально.
8.	Для стацпонарной системы из уравнения (8) примем, что, х° = 0, tQ = — оо и и (t) = е^. Убедитесь, что в этом случае
и	+ I
[U (/)]-! X (0 = 2 «i I - •	(Ф)
Воспользуйтесь этим выражением для того, чтобы предложить геометрическую интерпретацию частотных характеристик стационарных систем. Изучите конкретную систему Dny (/) + aJl_lDn~l у (/) + ... + аоу (t) = и (t). Выпишите частотную характеристику этой системы, воспользовавшись разложением ее передаточной функции на простейшие дроби. Сравните полученное выражение с выражением (♦), предварительно приведя уравнение системы к нормальному виду первого порядка. Выясните в частности, чему соответствуют полюсы и нули передаточной функции.
9.	Рассмотрим векторную систему первого порядка
Л (0 = Ах (t) + bu(t), t е т,
у (0 = <с, х (0>,	(♦)
которая является обычным (см. приложение 4) эквивалентом уравнения
z(n) (0 +	+ ... + aQXl (t) = и (0, t e T.	(♦♦)
(Здесь b — (0, 0, ..., 0, 1) и c = (1,0, ..., 0).) Предположим, что в том п другом случаях функция и определяется входным сигналом 0 и сигналом линейной обратной связи
и (/) = 0 (0 — кхх (/) = 0 (/) — к <с, х (0>, t е т.
Для уравнения n-го порядка это означает, что и (t) нужно заменить на 0 (t), а а0 на л0 к. Покажите, что для нормальной системы первого порядка изменение и -* 0 приводит к преобразованию
А —> А' = А — к [ЬУ <е].
Покажите, что полюсы передаточной функции нового уравнения n-го порядка при любых значениях к совпадают с собственными числами матрицы А. Покажите, как можно использовать метод корневого годографа, обычно применяющийся для анализа устойчивости уравнений n-го порядка, для того, чтобы определить спектр А' как функцию к.
10.	Рассмотрим систему, описываемую уравнениями (♦) и (♦♦), цр|( услов и, что к = 1, а b = (0,	0, 1). Покажите, что если с
= (^о» •••» cn-i)» то характеристический полином А' имеет вид
р (к) = X + (Дп-1 + сп-1) к 1 + ... + (а 1 -f- ci) к + (ао + со).
Докажите, что для каждого множества (о0, ...» ап-1) коэффициентов уравнения (»♦) можно найти такие значения скаляров (с0,	сп_1), что спектр А' сов-
падет с заданным (Xi, ...» кп}. Комплексные собственные числа могут быть лишь комплексно-сопряженными парами.
И. Пусть матрица А простая, и пусть вещестгенные части всех ее собственных чисел отрицательны. Докажите существование таких скаляров К > 0 и р < 0, что
|| ехр [Л (Z — /„)] || < К ехр [р (Z — Zo)|.
Справедлив ли этот результат, если матрица А не простая?
12.	Пусть A (t) = At + Аг (/)» где Л, удовлетворяет условиям упражнения 11, а || Аг (01 €=	(0, оо). Докажите, что существуют такие скаляры
М > 0 и р < 0, что || Ф (/, £0)|1 < М ехр [р (t — /0)j.
Указание. Покажите сначала, что
t
И Ф (/, 1и) КК- ехр [р(/- Zo)] [1 + J ехр [р (/<, - >•)]-|| .12 (л) ||.||Ф (s, /0) Ids ], Jo
и воспользуйтесь леммой Л из § 2.3.
3.6.	Некоторые задачи, связанные со структурой системы
В этом параграфе мы займемся решением некоторых задач, связанных с исследованием линейной динамической системы, описываемой уравнениями
dtx (/) — A (t)x (/) + В (t) и (/), t ei v,	(1)
и
у (0 С (/) х (/) + D (/) и (/), t е V.	(2)
Здесь мы воспользовались формальными обозначениями, введенными в § 2.5, и потому эти уравнения описывают как дифференциальную систему (v = т и dt = dldt), так и конечноразностную систему (v = о и dt --- Af). Для конкретности мы используем дифференциальную систему как основу для исследования. Понятно, что аналогичными свойствами должны обладать и дискретная, и гибридная системы. Однако детали, связанные с переходом к системам этого типа, мы оставляем читателю.
В упражнении 3 из § 2.4 мы познакомились с понятием эквивалентности систем, удовлетворяющих уравнению (1). Это упражнение играет важную роль для материала настоящего параграфа, и поэтому, прежде чем двигаться дальше, мы рассмотрим вкратце ситуацию, возникающую в этом упражнении. Исследуем для начала
простую однородную систему
х (/) = A (t) х (/).	(3)
Обозначим через К (t) любую матрицу, невырожденную на т, а через i (t) — вектор, связанный с х (t) соотношением
х (0 = К (0 х (t).	(4)
Естественно, возникает вопрос, существует ли такая однородная динамическая система, решением которой служит х (Z), и если существует, то каким уравнением она описывается? Получить ответ на эти вопросы нетрудно, так как, дифференцируя уравнение (4) по /, подставляя результат в уравнение (3) и объединяя подобные члены, мы убедимся в том, что х удовлетворяет однородной системе вида
х (/) = A (/) х (/),	(5)
где А (/) определяется по формуле
А (/) = К-1 (t)A (t)K (t) - К-1 (/) К (I).
Преобразование х (/) — К (/) х (Z) устанавливает взаимно однозначное соответствие между решениями уравнений (3) и (5).
Из сказанного следует, что с помощью простого преобразования координат линейную динамическую систему можно описать уравнениями различного вида. Но в то же время чувствуется, что все эти различные описания системы в некотором смысле эквивалентны между собой. Для того чтобы придать этим «ощущениям» строгий смысл, введем следующее определение.
Определение А. Две однородные динамические системы, описываемые уравнениями (3) и (5) соответственно, называются эквивалентными, если существует такая матрица К (Z), что
(1)	К (I) и К (/) определены на v,
(2)	supv || К (/) II < оо, supv |( К-1 (/)]] < ОО,
(3)	X (?) = А-1 (/) X (/), t е V.
Условия (1) и (3) естественным образом вытекают из вступительных замечаний к этому параграфу. Что же касается условия (2), то оно включено для того, чтобы гарантировать сохранение устойчивости решений х (t) и # (Z) относительно преобразования К (/). Очевидно, конкретный вид нормы, используемый в условии (2), не имеет никакого значения.
Определение эквивалентности двух систем можно обобщить и на случай неоднородных динамических систем. Рассмотрим две неоднородные динамические системы:
х (t) = А (/) х (t) + В (Z) и (t), t G= v,
У (t) = С (t) x(t) +D (t) и (0, t e v,	(6)
и /
X (/) - А (/) х (/) + В(1) и (/),	/EV,'
(7) у (/) = С (Z) х (Z) + Ь (/) и (/), t V.
Определение Б. Две линейные динамические системы, описываемые уравнениями (6) и (7) соответственно, называются эквивалентными, если при любых и (/) справедливо равенство у (/) = у (t) на v , а х (t) и $ (/) эквивалентны (в смысле определения А) при условии, что и (/)	0.
Замечание 1. Рассмотрим обычную задачу теории черного ящика, в котором и и у — внешние воздействия и выходные величины, соответственно. При этих предположениях определение Б задает условия эквивалентности выбора х и х внутренних переменных, описывающих поведение системы. Пользуясь результатами, полученными ранее, читатель может убедиться в том, что эквивалентность систем, описываемых уравнениями (6) и (7), соответственно, предполагает справедливость следующих матричных соотношений *):
Ф (/, т) = К-1 (/), Ф (/, т) К (т),
А (/) = к-1 (О а (/) к (/) - к-1 (/) к (/), t е v,
B(t) = К-1 (J) В (t),	(8)
с (о = с (/) к {/).
Собственные системы. Сейчас мы подробно покажем, к чему может привести использование полярного разложения (теорема Д из § 3.4) для преобразования линейной динамической системы. Полученные результаты будут зависеть только от свойств линейного преобразования Т : В -> Rn, определенного на произвольном гильбертовом пространстве Н и принимающего значения из Rn. Это позволит нам интерпретировать получаемые результаты в равной мере для непрерывных, дискретных и гибридных систем.
Определение В. Обозначим через Т линейное преобразование Т : Н -> Rn, допускающее полярное представление в виде
п
т = 2 е1 > Hi <f i-
г=1
Преобразование Т называется собственным, если ни одно pz, i — 1, ... ..., п, не равно нулю.
Так как все отображения Н в Rn допускают полярное представление, то из этого определения следует, что собственными преобра-
♦) Определения А и Б, а также уравнения (6), (7) и (8) сохраняют свою силу и для аналогичных дискретных систем, если / £ а и если Я"1 (/) заменено на X-1 (Z/f+i) и К (/) па К (tk).
яб НЕКОТОРЫЕ ЗАДАЧИ, СВЯЗАННЫЕ СО СТРУКТУРОЙ СИСТЕМЫ 301 зованиями мьт называем те и только те преобразования, которые накрывают Вп.	__
Рассмотрим для начала объект, у которого D (/) и С (') = = I. Не проведя никакого различия между отдельными системами, обозначим через F : Н —> В и Ф : Ru —> В преобразования, описывающие вынужденное и свободное движения системы, соответственно. Та^, для любого и^Н и x°(=Rn реакция х системы в момент времени t€Ey определяется выражением
х (/) - (Ф.г«) (/) ь (Fu) (/), /ev.	(9)
В последнее время среди специалистов по теории линейных динамических систем большим вниманием пользуется проблема управляемости.
Определение Г. Линейная динамическая система называется управляемой (на, v), если для каждого вектора (,т°, /0) существует такое управляющее воздействие и Н и такой момент времени ia<EEv, что
*о) = о.
Другими словами, управляемой мы называем такую систему, которую, по прошествии достаточно большого времени, всегда можно перевести из произвольного начального состояния в начало координат. Определим преобразование Та : Н -> Rn с помощью условия Таи = (Fu) (/а), где а иЕН. Взаимосвязь между понятиями собственной системы и управляемости вскрывается в следующей лемме.
Лемма А. Линейная динамическая система называется управляемой тогда и только тогда, когда существует такое taEEv, что преобразование Тл собственно.
Доказательство. Поскольку на множестве v матрица Ф (ta, /0) невырождена и соответствующее преобразование накрывает Rn, вектор £ == (I) (1а, /0) xQ можно считать произвольным при произвольном выборе вектора х°. Из условия 0 — ли(1а; х°, /0) = - (I)(^a»^o) I’ следует, что управляющее воздействие и должно удовлетворять соотношению Таи = — Jj. По так как вектор £ произволен, то это условие удается выполнить тогда и только тогда, когда область значений Та охватывает все пространство Вп. В свою очередь, это возможно в том и только в том случае, когда преобразование Та является собственным.
Если ввести понятие управляемости так, как это сделано в определении Г, то использование слова «управляемость» может показаться лингвистически неоправданным. Действительно, технические термины, использующие в качестве корневого слова «управление», наводят на мысль о целенаправленном воздействии на систему. В то же время согласно определению, приведенному выше, понятие управляемости оказывается, по сути дела, связанным лишь
со структурой системы и не связано с самим процессом управления. Доказательство леммы А дополнительно подчеркивает^ это обстоятельство, так как в нем показано, что, хотя определение В и содержит строгое утверждение о структуре определенного класса линейных дискретных, непрерывных и гибридных/динамических систем, для которых в любой момент времени t описывающее их преобразование накрывает Яп, определение Г,/ по существу, утверждает, что если это преобразование действительно является накрытием, то предпочтительней пользоваться термином «управляемая система», а не терминами «система, описываемая собственным преобразованием или накрытием».
Лемма Б. Преобразование Т: И -> Rn является собственным тогда и только тогда, когда матрица ТТ* невырождена.
Поскольку скаляры {ц,} в полярном представлении Т являются положительными значениями квадратных корней из собственных чисел матрицы ТТ*, то справедливость этой леммы очевидна. Из-за своей простоты она представляет удобный способ определения ранга преобразования Т. Например, для линейной непрерывной динамической системы
± (/) = А (/) х (/) + В (/) и (/),	(10)
присоединенная матрица такова, что
ТХ = J Ф (G, .9) в (.<?) В* ($) Ф* (/а, s) ds.
Аналог последнего выражения для случая дискретных систем (г->з) выглядит следующим образом:
ПаЬ-1
2 ^Ф(^.0)В(/Л1)К*(<Л1)ФЧ/а,/у). >0
И в том и в другом случаях вычисление матричных произведений очевидно, если определены матрицы перехода соответствующих систем.
В следующей теореме мы сосредоточим наше внимание на линейных динамических системах с непрерывным временем, описываемых уравнением (10). Предположим дополнительно, что элементы {bjj : i 1, ..., п; ] — 1, ..., m} матрицы В и элементы {aif- i, f — 1, ..., п} матрицы Л но крайней морс (n —1) раз дифференцируемы. Обозначим символом X линейный дифференциальный оператор, определенный на промежутке т с помощью соотношения
(Хх) (t) = х (t) — A (t) х (/), /Ет.
Преобразование Та определим, как и раньше:
\
Тли А(Ти) (ta) = $ Ф («а, S) в (S) и (.S-) ds, t0, t е Т.
\
Теорема А. Если ранг преобразования Та меньше п, то для каждого фиксированного момента времени Za €Е т совокупность столбцов п матриц
B(t), (ХВ) (/),	(^в) (/)
лежит в подпространстве с размерностью, меньшей п.
Доказательство. Пусть ранг преобразования Та меньше п. Другими словами, пусть преобразование Та не собственно. Спектр матрицы ТаТ* содержит нуль, или, иначе говоря, существует такое ненулевое ХбЕ /Г, что Та X = 0. В рассматриваемом конкретном случае это значит, что существует такое ХгЕ Лп, что
В* (/)Ф* t) X - 0,
Напомним теперь, что в § 3.3 мы показали, то Ф* (ta, t) = 'К (/, ta) — матрице перехода присоединенной системы, и что вектор Ф (/) = = Ф* (/a, I) к удовлетворяет уравнению
ф (/) + А* (Оф (/) = 0, /ЕТ.
Но в силу непрерывности ф и В из уравнения
В* (/) ф (/) = 0, t(=x, следует, что
°=4м ю = Ё* ю w(о=
=- /?* (/) 1|, (/) - /?* (?) a* (z) 4 (Z) -
= (A* (Z) - /?♦ (Z)X* (z)l ф (z) = {(ХВ) (Z)]* ф (z), zer.
Так как ф =/= 0, то на этот вектор в любой момент времени t натягивается некоторое одномерное подпространство Вп. Приведенные выше соотношения показывают, что все вектор-столбцы матриц Н (/), (ХВ) (Z),..., (Х"~ХВ) (/) принадлежат ортогональному дополнению линейного многообразия L (ф (/)), что и доказывает теорему А, сформулированную выше.
Следствие. Если матрицы А и В не зависят от t, то для неуправляемой системы ранг матрицы
[В, АВ, А2В, ..., Ап-'В]
рамером (п X тп) должен быть не больше п — 1.
Так как для стационарных систем ХВ = АВ, то это следствие Непосредственно вытекает из утверждения теоремы А. Если столбцы
матрицы В не удовлетворяют условиям теоремы А/ то про них говорят, что это столбцы общего вида. Такая терминология связана с изучением импульсной характеристики системы /
W (/, $) = Ф (г, $) В ($) - Ф (/, Zo) Т* (/0, J) В ($).
Если столбцы матрицы В не общего вида, то по крайней мере одна строка матрицы Т* (Zo, s) В (s) состоит из одних тождественно равных на т нулю элементов, и, следовательно, на соответствующий столбец матрицы Ф (£, £0) нельзя оказать никакого влияния.
Замечание 2. До сих пор мы исследовали лишь вполне конкретную дифференциальную систему с одинаковыми коэффициентами усиления по всем выходным величинам (т. е. с х = у). Однако для того, чтобы учесть влияние канала прямой связи и роль выходных коэффициентов усиления, в предыдущие рассуждения необходимо внести незначительные изменения. В частности, для того чтобы учесть входные ограничения, достаточно заменить преобразование Та на Т'л = С (ta) Та. Что же касается канала прямой связи, то его роль можно учесть, рассматривая систему как некоторое отображение, преобразующее вектор [и (/а), и} в у (ta) согласно правилу
У (<а) = D (ta) и (ta) + Тли.
Соответственно в леммах А и Б преобразование Та нужно заменить на D (fa) ф Тл. В этом случае матрица ТаТ*л заменяется матрицей 1\ТЛ | D (/а) 7?* (/а). Другие изменения основного результата этого раздела станут ясны при анализе в упражнении.
Замечание 3. Линейный объект называется полностью наблюдаемым на промежутке Ио, t'], если по значениям его выходных величин на этом промежутке можно однозначно восстановить начальное состояние системы xQ в предположении, что и (t) = 0. Так как матрица перехода системы в уравнении (1) невырождена при всех /, то полная наблюдаемость объектов, у которых С (t) = /, является тривиальным фактом. В более общем случае объекты, описываемые уравнениями (1) и (2), полностью наблюдаемы в том и только в том случае, когда отображение СФ : /Г' — > L™ (/), описываемое соотношением
(СФ £) (0 = с (/) Ф (*, /оН, является собственным.
Из равенств
fu
3 «. НЕКОТОРЫЕ ЗАДАЧИ, СВЯЗАННЫЕ СО СТРУКТУРОЙ СИСТЕМЫ 305 следует, чтА
\	(С’ф)*у = ( Ф*(«, t0) C*(s) у (s) ds
и что объект с выходными ограничениями С полностью наблюдаем в том и только в том случае, когда матрица
\ tf
(С’Ф)*СФ = $ Ф*(з, /0) С* (s) С (з) Ф (з, /0) ds
невырождена.
Разделяющиеся системы. В некоторых случаях систему /г-го порядка можно рассматривать как некоторую совокупность невзаимодействующих систем более низкого порядка. Например, представим матрицы и векторы из уравнения (1) в следующем виде:
х (0 = col (24 (/), ni (0) =
— col (п. (Z), •••»	(0» %Л+1 (0» •••» %n (0)»
л (/)
^11 (0 j ^12 (0
Й21 (t)\~A22(t)
ZGT,

_^n_k (0
/ЕТ,
где квадратные матрицы Лп и Л22 имеют размерности (к X к) и (п — к) X (п — к) соответственно, а матрица В ь имеет размерность (к X т). С учетом этих обозначений уравнение (1) можно переписать в следующем виде:
(0 =	(t) Х1 (t)	Л12 (0 Хц (0 + &к (0 u (0, t ЕЕ т,
(11)
(0 - Л22(0п(0 -М22(/)п,(0-| b,n.jt(0/4(Z), /ЕТ.
Если Л21 ~ 0, то вторую систему можно исследовать независимо от первой. Если, например, матрица Вп_к = 0, то вторая система находится в свободном режиме. Если, кроме того, Л12 также тождественно равно нулю, то и поведение первой системы не зависит от поведения второй, и всю систему в целом можно представить как две независимые системы.
Определение Д. Линейная динамическая система, описываемая системой уравнений (И), с матрицами А 12= 0 или Л21= 0 на множестве т, называется разделяющейся. Если Л21 (соответственно А = 0 и Вп-к (соответственно Bk) = 0, то такую систему называют однородно разделяющейся.
Другими словами, если можно найти преобразование координат х (t) = К (t) х (0, удовлетворяющее определению Б и приводящее уравнения линейной динамической системы ювиду (11), где 421 = 0 или 4]о = 0, то соответствующая система называется разделяющейся. Если же, кроме того, в уравнении, где матрица перекрестных членов (421 или Л12) тождественно равна нулю, нет членов, содержащих внешние воздействия, то такая система называется однородно разделяющейся. В соответствии с этим определением вынужденное движение однородно разделяющейся системы определяется характеристикам^ некоторой динамической системы более низкого порядка. Более того, вынужденное движение такой системы происходит в некотором собственном подпространстве Вп. Это следует из уравнений (И), где при Л21 = 0 и Вп_к 0 вынужденное движение полностью определяется уравнением
xL (0 = А п (0^ (/) + Л12 (0-гы (0 4- Bk (0 и (0, t Ет,
и целиком принадлежит подпространству L (сп ..., е1() пространства 7?п. Другими словами, внешнее воздействие и оказывает влияние лишь на первые к компонент вектора х.
Как указывалось выше, если в момент времени /а вынужденное движение линейной динамической системы не описывается некоторым собственным преобразованием, то внешнее воздействие может изменить лишь некоторое подмножество {Фп ..., Ф/{} столбцов матрицы Ф (£, t0). В связи с этим можно предположить, что если ранг преобразования Та меньше п, то соответствующая система может оказаться однородно разделяющейся.
Теорема Б. Обозначим через Та значение переходной характеристики вынужденного движения я инейной динамической системы, описывающейся уравнением (10), в момент времени ta. Если ранг Та равен к <; п, то эта система однородно разделяема в промежутке [/0, Za|.
Для того чтобы доказать эту теорему, достаточно лишь найти подходящее преобразование координат, разделяющее систему. Таких преобразований можно предложить несколько. Первое из них, которое мы будем рассматривать, использует фундаментальную матрицу К (/) Ф (t, /0). Так как матрица Ф (/, /0) невырождена и удовлетворяет условиям определения А в любые конечные моменты времени, то ясно, что ее можно использовать как матрицу преобразования координат:
х (t) = Ф (t, t0) i (0, zer.
В соответствии с уравнением (8) вектор х (0 удовлетворяет линейному дифференциальному уравнению, в котором матрицы А (0
и В (0 определяются следующим образом:
\ В (t) = [Ф (t, Zo)]-1 В (t),
А (/) - [Ф (/\ МГ1 А (0 Ф (t, t0) - [Ф (/, г0)НФ (/, /0), /ет.
Но так как матрица Ф (/, t0) должна удовлетворять матричному однородному дифференциальному уравнению, то отсюда следует, что
А (0 = 0.
Если же учесть еще и условия теоремы Б, то становится ясно, что
матрица В имеет следующий мечанию 2):
вид (см. абзац, предшествующий за-
Z(0
/GET,
(/) -*=
где Z (t) — ненулевая блочная матрица размерности (к X п). Обозначим через zh i = 1, А, i-ю строку матрицы Z (t). Преобразованная дифференциальная система имеет теперь вид
[*г(£), u(t)], i = 1, . . . , к, /Gt,
0, I = к 1, . . . , n, t GE т,
и, следовательно, очевидным образом однородно разделяема, что и требовалось доказать.
Идея использования фундаментальной матрицы Ф (/, tQ) для преобразования переменных позволяет легко доказать теорему Б. Кроме того, из нее следует, что введение любого базиса, разлагающего пространство Rn в момент времени tEix на линейное многообразие L (Ф! (Z), ..., Фй (Z)) и его дополнение, приведет к тому же результату. Это и в самом деле так. Например, в основу искомого преобразования координат можно положить условия, обеспечивающие общность вида столбцов матрицы В (Z). Для того, чтобы избежать ненужных осложнений, ограничимся рассмотрением систем с одним входом.
Теорема В. Система, описываемая уравнением (1), однородно разделяема тогда и только тогда, когда вектор b не является вектором общего вида.
Цля систем с одним внешним воздействием вектор b является вектором общего вида по отношению к Л, если векторы
ь> (/) = ь (/), М/) - - Л (/)	(/) | ЬА1(/) (/ - 2,	п),
линейно независимы при любом tт. Предположим, что по отношению к А вектор b есть не вектор общего вида. Примем для конкретности, что векторы (t), ..., Ьь (I) линейно независимы, а векторы 6fc+1, ..., Ьп (t) являются линейными комбинациями
векторов Ь± (0, bk (0 при любом t€Ex. Прежде чем переходить к доказательству теоремы, сформулируем следствий, которое мы докажем одновременно с теоремой.	/
Следствие. Матрица К, разделяющая систему, образуется из векторов-столбцов Ъ1Ч ..., рп ..., рп-л* ректоры рр ...
выбираются произвольно и должны лишь (обеспечивать невырожденность матрицы К на т.
Доказательство. Сформулированные выше теорему В и ее следствие мы докажем методом непосредственной проверки. В соответствии со следствием положим
Используя понятие двойственных векторов, мы можем записать К1 в виде
Так как bp= — Ab^-^-bj-v или bj-^ bj-\-Abj^ то ясно, что
г t t t t I
_ I II i
r	t	I	t	t	t	t
= (b., -I- Ab,), (b3 -)• Ab.,).(bk + Abk_,), bk, pb. . . , [Vfc
-	I	I	1	I	I	I	.
Отсюда
AK - К =
Г t t	t .	t .	t .
= - b„	. . . ,	- bk, (Abk	- bk),	(Лр1 - PJ, .	. .	, (ЛРП-к - pn_k)
. I I	I	I	I
Если теперь воспользоваться заменой переменных х = = К~г (t) х, то преобразованная система примет вид
х (t) = [К~1 (0 А (0 К (0 - К-1 (0 К (0] х (0 + K-\t) bu(t).
в
соответствии с предыдущим мы найдем, что
к строк,
где а. = [bj, (Abk — bh)] (/ = 1,	— элементы матрицы
L — имеют вид 1^ ~~ lb*, (ЛР; — Р,)] (i = 1, j = 1, ... ...,7г — &), а элементы матрицы N : пц = [р/, (Лр,— Р;)|. Более того, поскольку bY = b, то ясно, что
К"1 b = со!(1, 0,	0).
Наконец, последнее соотношение показывает, что при хг = = col (xi, ...» xk), х2 = col (д7Л+1,..., хп)
Я2 (О = N (t) х2 (£),
Xi (/) = М (/) х± (/) + L (t) х2 (t) + tiU (0,
что и доказывает теорему В. (Через М здесь обозначена матрица с размерами (к х к), занимающая верхний левый угол матрицы К'1 А К - К^ 'К.)
Пример 1. Рассмотрим сначала систему второго порядка *)
Прежде всего находим
и, следовательно, b2 = 2Ь. Значит, эта система разделяющаяся. Полагая рх = col (1, 0), мы построим К в виде
*) Примеры 1 и 2 заимствованы с разрешения автора из книги: A. R. Stubberud, Analysis and Synthesis of Linear Time-Variable Systems, Univ, of Cal. Press, Berkeley, 1964, гл. 6.
Легко показать, что
0 - Г
1 1
и, следовательно, ГО - 1
1 1
К1 А К =
1 11 Г—2 — 2'
-1 0 =	0-1
 - 3 - г
2	0
0 - 1
1 1
г
-1
1
о
Если х — Ку, то
*1
xt.
’-2-2
О - 1
1'
О
и(/)
й после разделения: х2= — x2t х2 = х2 (0) е~1 и хх = — 2хг + + [х2 (0) е~1 + и (t) 1, причем второе уравнение также решается без какого-либо труда.
Пример 2.
'У1 (0 ‘ у» (0
_£/з (0 -
- (1 + е-‘) - 1	0‘
(1 + Зе1)	0 - 1
- Зе-'	0	0.
(0 ”
Уг (О
-Уз (0 -
4" — 1 и (t).
е~1
01
Как и раньше,
= col (0, — 1, е'),
Ьз —
о-
- 1
О
-+(!+«') +1	О’]
(1 + Зе-')
+ Зе-'
г 01
-1 +
е*'_
- О -
О
— е~‘
г- 1 е~‘
— е-'
•- 1 -е~‘
- 1 -
1 4-е-' - 2е-‘
О + 1
О О
Так как &з = &2 — то рассматриваемая система разделяется. Выберем Pi = col (0, 0, 1). Тогда
	г 0 - 1 0-1
K(t) =	1	1 . 1 О i ь* 1 1 о Л. JL О О 1	
к =	0	0 — е~1 с~1 0
	Г	( —10-
Х‘(/) =	-1	0 0 g-2t — е 1	е-1 1
Далее читатель без особого труда может вычислить матрицу Н (/) = К"1 (t) A (t) К (t) — К"1 (t) к (/) и убедиться в том, что
О 1
Н(Г) = -1-1
о
о
1-
0 е~!
а
Отсюда
-Z1-хг
т, (/)' х., (/)
1 -О е~' J 1*3 (0.
1-
0 u(t), О
-
о
-1 о
1
- 1 о
И, следовательно, рассматриваемая система разделяется на две:
и
(0 = e-f х3 (О
*1 (О
Xj (i)
О 0]	Г1'
- 1 - 1] + [о
[и(0 + х3 (/)].
Стационарный случай. Подводя итог изложенному в данном па-раграфе, рассмотрим стационарную систему с простой матрицей А.
Для большей конкретности предположим, что первые к векторов
= Ь,
^2 == — АЬ±^
Ьк = (-1)АЬк_г = (-1)*-^Ь
линейно независимы, а все остальные векторы из этой последовательности зависят от {Ьр bh}.
Поскольку мы условились, что матрица А простая с собственными числами {X.} и собственными векторами {uf}, i = 1, n, то у матрицы А существует спектральное представление А = — / ?=i	> Ч Нам известно, что из-за того, что к < п,
векторы дх, bk принадлежат некоторому ^-мерному инвариантному подпространству относительно А. Однако все инвариантные подпространства А натянуты на какие-нибудь подмножества множества собственных векторов этой матрицы. Для удобства мы предположим, что эти собственные векторы перенумерованы таким образом, что на множество {е1? eh} натягивается подпространство, содержащее {61? ..., Ьк}. Другими словами, мы будем предполагать, что линейные многообразия L (ех, ..., eh) и Ь/{) идентичны.
При построении матрицы К мы, как и раньше, выберем в качестве первых к столбцов этой матрицы векторы {6Х, ..., bh}. Выбирать остальные столбцы мы будем несколько менее произвольным образом. Точнее говоря, выберем для них собственные векторы eh+l, ..., еп. Ясно, что матрица
ft ft t '
К- — by,..	в|с+1 > • • • i
j • • •»
II i -
левы рождена.
В том случае, когда система стационарна, замена переменных х — Ку приводит к дифференциальному уравнению
ytf) = К-'АКу (С + К-'Ъи (О-
Из изложенного ранее следует, что
АК = — 62, . . ., — Ьк,—	• • .Дп^п
так что прямым перемножением можно показать, что К'1АК =
О
1, О о
О —	^-+11
о -[0^11
о
О — [Ь^, i’k+i) I
j О
I О
о ! 
Как и раньше, К~~ГЬ = col (1, 0,	0). Таким образом, рас-
сматриваемая система приведена к очень простому виду. Важно отметить, что это разложение требует знания лишь собственных векторов elf ..., еп матрицы А.
Упр ажнения
1.	Пусть С — некоторая матрица размерности (n X п). Может ли преобразование Та, описанное в замечании 2, быть собственным, если преобразование 7\ не собственно? Может ли понижаться ранг преобразования Та (соответственно Та) по мере увеличения промежутка [f0, fa]? Может ли быть собственным преобразование Га, если этим свойством не обладает Та? Приведите простые примеры, иллюстрирующие каждый из ответов. Изменятся ли эти ответы, если С — матрица размерностью (п X тп)?
2.	Покажите, что система
4 (0 = -Л* (0 q (0 - С* (0 и (0, t (Е ТМ	(*)
Л (t) = В* (0 q (0 + D* (0 v (0, t s Т,
формально является присоединенной по отношению к системе, описываемой уравнениями (1) и (2). Какие граничные условия нужно наложить при этом на функции и (0 и v (0?
Указание. Обратитесь к упражнениям 4 и 5 из § 3.3. Выясните, какая аналогия с точки зрения понятий управляемости и наблюдаемости существует между линейной и присоединенной системами.
3.	Выведите для стационарной дискретной динамической системы аналог теоремы А.
4.	Обозначим через х = Ти преобразование, описывающее систему с двумя входами и = (ип и2). Совершенно ясно, что найдутся два преобразования Тх и такие, что
Ти ~ Тхих + Т2и2,
каково бы ни было и. Если оба эти преобразования собственны, то всегда ли этим свойством обладает и Т? А если оба эти преобразования не собственны? Какое минимальное условие, накладываемое на 7\ и Т2, гарантирует собственность преобразования Т?
5.	Предположим, что две подсистемы связаны между собой так, как это показано на схеме гибридной системы (рис. 2.16 из § 2.5). Объясните взаимосвязь между управляемостью и наблюдаемостью каждой из этих подсистем и всей системы в целом.
6.	Получите условие разделяемости стационарной системы, воспользовавшись порежимным представлением системы (уравнения (8) и (9) из § 3.5). Что можно сказать о понятии наблюдаемости в стационарном случае?
7.	Покажите, что если A (t), t GE т,— произвольная квадратная матрица, удовлетворяющая условиям теоремы существования А из § 2.4, а Я — стационарная матрица таких же размеров, то дне системы
/ (/) - А (/) х (/), у (t) - Ну (/), / е т,
на любом конечном т эквивалентны.
Указание. Воспользуйтесь заменой переменных К (/) = Ф (/, /0) X Хехр|Я (Z—/0)1» ZGt, и тем фактом, что /(А) и А коммутируют друг с другом.
8.	Покажите, что если матрица А периодическая [т. е. если A (t + (о) = = А (/), / т) с периодом <о, то матрица Ф (Z + со) является фундаментальной матрицей уравнения (3), если только фундаментальной матрицей служит и Ф (/). Покажите, что матрицу Ф (/, /0) в этом случае можно представить в виде Ф (Z, /0) = М (Z) ехр [В (Z — /0)] Л/-1 (z0), где М (Z) — периодическая и невырожденная матрица.
Указание. Воспользуйтесь результатом упражнения 7. Покажите, что если матрица В приведена к жордановоп форме, то матрица М определяется однозначно.
9.	Предположим,что в результате теоретических исследований задачи синтеза, мы пришли к выводу о целесообразности конструирования системы Ln (Я, Z) х (Z) = Mq (Я, Z). Однако значения параметров п и q вынуждают нас воспользоваться приближенной системой Lm (Я, t) х (/) = и (Z), где m = = п — q. Предложите подходящие принципы решения задачи такого приближенного синтеза.
Указание. Приведите уравнение системы к нормальному виду и воспользуйтесь возмущением вектора внешних воздействий для того, чтобы выделить q режимов системы. Затем воспользуйтесь заменой переменных, разделяющей систему.
10.	В упражнениях к § 3.4 мы ввели понятие объема Vn = 2Пг^я1 рг«, связанного с полярным представлением системы, в качестве меры чувствительности этой системы. Если преобразование Т не собственное, то при некотором i: р, = 0, и, следовательно, Уп= 0. В связи с этим обсудите возможность использования искусственного объема Vn = 2П™ л (а + |хг) (где а > 0, но мало), в качестве меры управляемости системы.
11.	Обозначим через S постоянную матрицу
5-	:	0	•• о
s~	\i
_ — а$	0	0 _
размерности (п X п). Покажите, что всегда можно найти такие скаляры р = (р0, pn-i), что у матрицы S' = S — ЦО, ..., О, 1)> <р] спектр о (Л) = {Xlt ...» Хп} произволен, если только не считать, что комплексные числа могут входить в него лишь комплексно-сопряженными парами.
Указание. Воспользуйтесь заменой переменных с матрицей Т из приложения 4 и результатом упражнения И к § 3.5. Можно показать, что Р = = Т-’а, где а определяется как раз в этом упражнении.
12. Докажите, что если b — вектор общего вида по отношению к произвольной матрице Л, то существует такое уравнение канала обратной связи р (/) = 9 (/) — |а, х (/)], где а (а0, ..., а,^), что матрица Д’ — А — [Ь>«х] может иметь любой подходящий спектр а (Л') =-	..., А,п}.
Указание. Прежде всего воспользуйтесь матрицей К из данного параграфа для того, чтобы привести матрицу Л к виду, какой показан в последнем уравнении параграфа. Затем преобразуйте переменные так, чтобы получить матрицу типа 5, и, наконец, воспользуйтесь результатами предыдущего упражнения.
13. Рассмотрите упражнения 14, 15 и 16 к § 3.2. Покажите, что закон управления можно реализовать даже в том случае, когда (//, /) вырождается на некотором подынтервале [fy fy] С т.
Указание. Воспользуйтесь уравнением (12) из § 3.2 и покажите, что вектор lx (tf) — Ф (fy, t) х (/)] всегда принадлежит области значений преобразования & (tf, /). В связи с этим вместо (tf, /) можно воспользоваться подходящим левым обратным преобразованием.
3.7. Литература к главе 3
В качестве общей литературы к материалу §§ 3.1, 3.2 и 3.3 можно поре комендовать монографии Ахиезера и Глазмана [А.2], Дьедонне [А.21], Данфорда и Шварца [А.22], Халмоша [А.36], Люстерника и Соболева ]А.56]. Лорха [А.57], Рисса и Секефальви-Надя [А.72], Ниренберга [А.65] и Тейлора |А.83]. Дополнительный материал к § 3.3 содержится также в приложении 5 к этой книге.
Диадными обозначениями пользуется Фридман [А.30], Гертцель и Трэл-ли [А.32] и Задэ и Дезоер [А.95]. В последней из только что упомянутых книг излагается также материал § 3.5 и части § 3.6. Информацию о жордаповых канонических формах читатель может найти у Халмоша [А.35], Хоффмана и Кунце [А.42], Неринга [А.64] и Столла [А.81]. Мы можем порекомендовать также статьи Хохштадта [Б.48] и Фрейма |Б.36].
Вопросы, затронутые в § 3.6, рассматриваются частично в книгах Ту [А.86] и Задэ и Дезоера [А.95] и в статьях Калмана [Б.50], [Б.51], Крпндлера и Сарачлка [Б.64], Маркуса и Ли |Б.77] и Стабберуда [Б.113]. Задача минимизации расхода энергии решалась также Калманом [Б.53], Балакришнаном [Б.9], Куо [Б.69], Портером [Б.99] и Ту [А.86].
ГЛАВА 4
ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ РЕШЕНИИ ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Класс технических и математических задач, которые называют «задачами оптимального управления» *), очень широк и многообразен. Такое многообразие находит свое отражение в первую очередь в самом факте существования целого ряда методов, каждый из которых пригоден для решения одной или нескольких задач этого класса. В настоящей главе мы будем рассматривать оптимальные задачи лишь одного конкретного типа и связанные с такими задачами методы их решения. Важность задач рассматриваемого типа определяется тем воздействием, которое они оказали на развитие теории линейных систем управления, а также и тем, насколько тесно они связаны с задачами оценки и фильтрации полезных сигналов. Эта глава по самой своей сути теоретическая, и потому для того, чтобы оправдать необходимость изучения изложенного здесь материала, важно с самого начала выяснить, в каком соотношении находятся рассматриваемый класс задач и задачи физического характера. Имея это в виду, мы, прежде чем переходить к математическим деталям, рассмотрим одну важную область применения результатов, которые будут получены ниже.
Задачи управления и наведения космических аппаратов являются достойной областью применения результатов современной теории управления. Для успешного решения этих задач приходится учитывать взаимодействие различных явлений, совершенно различных по своей природе, а задача конструирования системы, которая сможет осуществить обычную программу полета, представляется весьма сложной. В этой главе нас не будут интересовать задачи наведения или управления движением «в большом». Мы будем рассматривать здесь лишь задачи управления возмущенным, верньерным поведением системы (рис. 4.1). При этом в качестве рабочей гипотезы мы примем, что в окрестности номинального закона наведения или номинальной траектории связь малых изменений в сигналах на выходе датчиков, в положении
*) В этой главе мы следуем работе [Б.100], и я хотел бы воспользоваться настоящей возможностью для того, чтобы поблагодарить Дж. II. Уильямса за ценную помощь при выполнении этой ранней работы и за конструктивную критику материала этой главы.
исполнительных устройств и в траектории движения аппарата описывается линеаризированными уравнениями его динамики. Точнее говоря, рассмотрим динамическую систему, которая при каждом t > «о описывается уравнением
i (О = / (•* (0, и (/), /), х (?0) = х°.	(1)
Вектор х = col (х19 ..., хп) содержит достаточно координат для того, чтобы отразить поведение физической системы, а вектор
Рис. 4.1. Задача наведения летательного аппарата.
и = col (un ..., ип) описывает всю совокупность внешних воздействий, оказываемых на систему. Через / (х (t), и (£), t) здесь обозначена вектор-функция х (t), и (t), t с компонентами {/f (х (/), и (О» 0}Л Вектор (й, X) обозначает некоторое априори фиксированное внешнее воздействие на систему и соответствующее ему решение уравнения (1). Во многих случаях в качестве вектора (й, х) выбирается одно из решений оптимальной задачи. Однако пока нам достаточно того, что вектор (й, X) зафиксирован заранее.
Утверждение о том, что (й, X) есть некоторая номинальная пара управление — траектория, но означает, что система, на вход которой подано воздействие й, действительно будет двигаться по траектории х. На самом деле вектор (й, X) описывает лишь математическую идеализацию. Неточности в отработке й, внешние возмущения, неопределенности в вычислении / (х, u, t) и всевозможные помехи, действующие на систему,— все это приведет к неизбежным отклонениям от номинальной пары (й, X). Обозначим через (би, бх) отклонение действительной пары (и, х) от номинала (и, х). Другими словами, пусть (би, бх) = (и, х) — (Й, X). Тогда, предполагая, что (би, бх) мало и что функция / (X, й, t) достаток-
но гладкая по отношению к (й, я), с помощью стандартного разложения в ряд Тейлора вблизи точки (й, £) найдем, что (би, бх) удовлетворяет в первом приближении уравнению
б* (0 = А (0 6xj(/) + В (/) би (0, бх (М = бх°. (2)
Здесь элементами на пересечении i-й строки и /-го столбца матриц А (/) и В (/) служат частные производные dfjdxj и dfjduj соответственно, вычисленные в точке (й, х). В связи с этим всякое исследование поведения системы наведения в достаточно малой окрестности номинальной траектории естественным образом приводит к необходимости исследования непрерывных и (или) дискретных линейных динамических систем.
С практической точки зрения задача теперь состоит в том, чтобы выбрать такое би, которое вызвало бы нужное изменение бх (например, свело бы бх к нулю). Чаще всего эту задачу желательно было бы решить оптимальным в некотором смысле образом. Например, хотя критерий выбора (и, х) может быть чрезвычайно сложным, конечность запасов рабочего тела на борту космического аппарата может потребовать такой стратегии управления малыми отклонениями, которая минимизирует некоторый функционал J от би.
Например, если обозначить через би; (/), t ЕЕ [/0, ^/1 мгновенный расход рабочего тела в /-м исполнительном устройстве, то функционал
if т
jt(Su) = 2 1б,ъ(01^
/о
описывает суммарный расход рабочего тела на управление би. В других случаях может оказаться предпочтительным минимизировать энергию управляющих воздействий би:
г tf ™	'17
•’> J—1
а не расход рабочего тела. Очень часто физические исполнительные устройства обладают характеристиками насыщения, что накладывает пиковые ограничения на характер управляющих воздействий. В связи с этим при исследовании нас может интересовать и максимальная амплитуда
•/3(6u) = max { sup |би7(/)|}
всей совокупности управляющих воздействий. Наконец, если суммарная тяга реактивного двигателя ограничена (как это и бы-
ГЛ. 4. ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ 319 вает в «плазменных» или «ионных» двигателях), а функции {6иД описывают направления тяги, то пиковая мгновенная тяга определяется функционалом
т
/4(6и)= sup I 2 1быИ<)|2]/", IJ
и при выборе би этот функционал является естественным критерием оптимальности.
Во всех четырех перечисленных выше случаях рассматривавшиеся функционалы можно считать нормами, определенными на подходящем банаховом пространстве. В связи с этим мы можем теперь, не делая никакого различия между дискретными, гибридными или непрерывными системами (хотя последние и легли в основу нашего иллюстративного примера), поставить следующую задачу теории оптимального управления.
Задача 1. Пусть В nD — два банаховых пространства, и пусть 7’ — ограниченное линейное преобразование, определенное на В и принимающее значения из D. Для каждого £, принадлежащего области значений 71, найти такой элемент иЕ-. В, который удовлетворяет условию
& = Ти
и минимизирует при этом критерий качества
J (и) = Ци||.
Задача 1 очевидным образом обобщает на случай банаховых пространств задачу о минимизации расхода энергии из § 3.2, сформулированную там для гильбертовых пространств. Для каждого £ из области значений Т рассмотрим множество Г”1 (5) всех прообразов Как мы могли уже убедиться ранее, исследование этого множества представляет несомненный интерес. Содержит ли это множество элемент с минимальной нормой? И если содержит, то является ли такой элемент единственным? Наконец, если и на этот вопрос можно ответить утвердительно и если обозначить через Т+ Z единственный минимальный прообраз вектора £ из области значений преобразования Т, то какими характеристиками обладает функция Т+, определенная указанным выше образом, и, точнее говоря, как вычислять ее значения?
Трудности, связанные с необходимостью такого обобщения, нельзя недооценивать. Рассмотрим, например, систему с одним (скалярным) управляющим воздействием, отображающую гильбертово пространство Н в R в соответствии с соотношением
£ = </, и), и^Н.
Если	фиксировано, то прообраз % с минимальной нормой
единствен и может быть определен в явном виде. Напротив, если В — произвольное банахово пространство и /	В*, то прооб-
раз £ ЕЕ /? по отношению к / с минимальной нормой в В не обязательно существует, и даже если его существование доказано, то неясно, является ли такой элемент единственным. Два последующих примера иллюстрируют эти положения.
Пример 1. Обозначим через С множество всех вещественных комплексных непрерывных функций, определенных на промежутке 0 t 1 и обращающихся в нуль при / = 0. Нетрудно видеть, что С есть замкнутое подпространство обычного банахова пространства непрерывных функций, определенных на [0, 1], и, значит, само является банаховым пространством. Обозначим через Т некоторое преобразование (линейный функционал), определенное на и 6= С с помощью соотношения
1
Ти = и (t) dt, о Тогда
1Ж sup I м (0 I = ||м||
и, следовательно, || Ти ||	1. Отсюда следует, что если и £= С и
удовлетворяет условию Ти = 1, то 1 = | Ти |	|| и ||. Но в то же
время нетрудно проверить, что
inf {Ц и || : Ти = 1} = 1
и что эта нижняя грань недостижима. Действительно, для каждого и S С единичной нормы найдется такое 6 > 0, что j и (t) | < < 1/2, если 0 t 6, и, следовательно,
в	1
| Ти\ = |$«(l)clt + ^u(Z)d/|	S + (1 -S)-1 = 1 =4’<1-
0	8
А это позволяет заключить, что вектор (число) 1 не имеет минимального прообраза по отношению к Т.
Пример 2. Обозначим через В плоскость, в которой определена норма
II х II = I I + I х2 |» если х = (xn z2).
Определим на В линейное преобразование Т формулой
Тх = х± + z2.
Совершенно ясно, что || Т || = 1 и, следовательно, любое х е В такое, что Тх = 1, имеет норму не меньше 1. А это значит, что минимальным прообразом 1 по отношению к преобразованию Т может служить любой из векторов (0, 1) или (1, 0).
Короче говоря, функции минимизирующей усилие и связанной с Г, может не существовать либо из-за отсутствия, либо благодаря перепроизводству минимальных прообразов. А так как эти трудности возникают даже для таких простейших преобразований, как функционалы, рассматривавшиеся в примерах 1 и 2, то очевидно, что нам необходимо обнаружить их источник. Поэтому нам обязательно нужно разобраться в геометрических свойствах банаховых пространств. Этим мы займемся (попутно с определением Г4-для преобразований Т единичного ранга) в §§ 4.1 и 4.2.
После того как с этими подготовительными исследованиями будет покончено, мы сумеем непосредственно перейти к решению общей задачи 1. Обобщения этой основной задачи приведены в § 4.4 и приложении 8. Возможности применения общей теории иллюстрируются в примерах и упражнениях на протяжении всей главы и приложений 8 и 9. Обзор относящейся сюда литературы составляет часть § 4.5.
4.1.	Некоторые геометрические понятия
Для решения задач теории оптимального управления необходимо привлечь некоторые понятия геометрической природы. При этом читатель убедится в том, что большинство абстрактных определений получается в результате очевидных обобщений различных утверждений о свойствах множеств пространств R2 и R3. Эту интуитивную связь мы будем постоянно подчеркивать, используя плоскостные или трехмерные диаграммы каждый раз, когда нам покажется, что это может принести пользу.
Первые несколько понятий имеют смысл в любом линейном пространстве X с приданным ему (вещественным или комплексным) полем скаляров К. Обозначим через Q и S два подмножества пространства X. Векторная сумма подмножеств Q и S определяется с помощью соотношения
Q + 5 = {х\ х = q + s, s G S, qE (?}.
В частности, если xQ ЕЕ X, то множество
х0 + Q = {я: я = я0 + д, де <2}
называется переносом подмножества Q вдоль х0. Скалярное произведение aS множества S и скаляра а ЕЕ К определяется
следующим образом:
aS = {х: х = as, s Ez S}, или в более общем виде: если К' — любое подмножество К, то множество K'S определяется условием
K'S = {х: х — as, a ЕЕ К',	5}.
Определение Л. Пусть S — некоторое подмножество X, и пусть Е = {а: |а| 1, a £= К}. Тогда множество S называется
(1)	симметричным, если S = (—1) S;
(2)	уравновешенным, если ES CZ S;
(3)	поглощающим, если для каждого х Ez X найдется такое в >* О, что ах ЕЕ S, если 0 < | а [ е.
Поскольку а = —1 принадлежит множеству Е, то все уравновешенные множества симметричны и содержат 0. Для поглощающих множеств можно предложить следующее эквивалентное определение: множество S является поглощающим, если для каждого х ЕЕ X найдется такое |3 > 0, что х ЕЕ aS, если / а Р. Отметим еще, что по определению каждое поглощающее множество
Рис. 4.2. Множества S, S(J (—5) и ES.
должно содержать 0. На рис. 4.2, а в пространстве R2, показано множество S, которое не является ни симметричным, ни уравновешенным. На рис. 4.2, б изображено множество S (J (— 5). Заметим, что множество S (J (— S) симметрично, но не уравновешенно. Наконец, на рис. 4.2, в показано множество ES.
Совершенно ясно, что пересечение нескольких уравновешенных множеств также является уравновешенным множеством. Уравновешенной оболочкой множества S мы будем называть пересечение всех уравновешенных множеств, содержащих S. Нетрудно показать, что уравновешенная оболочка любого множества S в точности совпадает с множеством ES.
Прямолинейным отрезком, соединяющим две точки х и у G X, называется множество всевозможных точек вида kx + (1 — X) у, где 0	1. Это множество мы будем обозначать через [ж: у]л
Открытым на концах прямолинейным отрезком (х: у) мы будем называть то же множество, но из которого выброшены конечные’точки х и у (т. е. О < X < 1). Очевидным образом определяются и множества [я: у) и (х: у]. Теперь мы можем дать еще одно определение поглощающему множеству. Множество S называется поглощающим, если S содержит прямолинейные отрезки любого направления. Другими словами, для поглощающего множества S при каждом z G X найдется такое у =/=» 0, что [0: у] CZ [0: z] Г|5.
а)	б)
Рис. 4.3. Множество и его выпуклая оболочка.
Определение Б. Множество S в пространстве X называется выпуклым, если при х, у €= S [х: у] CZ S.
Совершенно ясно, что каждое подпространство выпукло. Простые вычисления показывают, что выпуклым является и любой перенос выпуклого множества. Точно так же выпукло и пересечение любого числа выпуклых множеств. Однако уже объединение нескольких выпуклых множеств не обязательно должно быть выпуклым. Поскольку само X выпукло, то семейство всех выпуклых множеств, содержащих некоторое заданное множество S CZ X, не пусто. Пересечение всех членов этого семейства называется выпуклой оболочкой множества S и обозначается через Sc. Ясно, что Sc представляет собой минимальное выпуклое множество, содержащее S. Произвольное множество 5 и его выпуклая оболочка показаны на рис. 4.3. Следующая теорема подытоживает некоторые дополнительные свойства выпуклых множеств.
Теорема А. Пусть X — линейное пространство. Тогда (1) для каждого подмножества S CZ X его выпуклая оболочка задается следующим образом:
Sc = |х: х =	оц > 0,;
(2)	если S выпукло, а а и 6 положительны, то aS + 65 = == (а 4- р) $;
(3)	если подмножества S и Q не пусты, а X и у — некоторые скаляры, то (Х5 -f- yQ)c = KSC + yQc\
(4)	если подмножества S и Q не пусты, то (S (J Q)c = = и {[х: у] : X е Sc, у е <?с}.
Доказательство теоремы А мы предлагаем читателю в качестве упражнения. В теореме Б мы исследуем некоторые элементарные свойства выпуклых мно-
жеств в банаховом пространстве.
Теорема Б. Пусть S — некоторое подмножество банахова пространства В. Тогда
(1) если S выпукло, то выпуклы и его замыкание S, и его внутренность
Рис. 4.4. Внутренность 5 выпукла.
int (5);
(2) если S открыто, то открыто и Sc.
Доказательство. Напомним, что операции сложения и умножения на скаляры обладают свойством непрерывности. Другими словами, если хп -> х и уп -> у, то (хп + уп) -> (х + у) и ахп -> ах. Это соображение сразу показывает, что для любых подмножеств S и Т пространства В справедливы соотношения
5 + Тс=(5 + Т),
aS cz (aS).
Множество S выпукло тогда и только тогда, когда aS + (1 — — a) S CZ S, каково бы ни было 0 < а < 1. Поэтому, если S выпукло, то
aS + (1 - а) 3 cz (aS + (1 - а) 5) cz S,
а значит, выпукло и S.
Для того чтобы решить вопрос о выпуклости внутренности выпуклого множества S, выберем х и у £= int (5). Для этих точек можно найти две такие сферические окрестности (рис. 4.4), что
{zG5:||z-x||<8}CZ5,
{z G В: || z - у || < е} CZ S.
Если o)o — это некоторая точка открытого отрезка (х: у), то для некоторого О <С a <Z 1 справедливо соотношение оэо = а х + + (1 — а) у. Теперь достаточно показать, что если || со — <х>0 || <
< е то со ЕЕ Но это следует из тождества
G) = (1 — а) (у + о) — о)о) + а {х + со — <оо)
Рис. 4.5. Множество и его функционал Минковского.
и того факта, что у + w — w0 и х + со — оэо принадлежит S, Наконец, утверждение (2) является следствием утверждения
(1). В самом деле, если множество S открыто, то соотношение S (Z Sc предполагает, что int (5) = 5 CZ int (5С). Но в силу утверждения (1) int (5Г) выпукло, а так как Sc— наименьшее выпуклое множество, содержащее 5, то Sc (Z CZ int (5С), и, следовательно, Sc открыто.
Определение В.
Пусть X — некоторое линейное пространство, aS — некоторое поглощающее выпуклое множество. Функция р,
значение которой в точках х ЕЕ X определяется соотношением
р (х) = inf {X > 0: х i— А, 5},
называются функционалом Минковского *) для множества S.
Это определение можно интерпретировать следующим образом. Пусть х — любая точка пространства X, Одномерное подпространство L (х) пересекает границу dS множества S в некоторой точке у (рис 4.5). Тогда х = р (х) у. Другими словами, р (х) определяет, насколько нужно растянуть (или сжать) множество S, чтобы точка х оказалась на его границе dS,
Тот факт, что множество S поглощающее, гарантирует что р (х) определено и конечно при любом х ЕЕ X, Отметим еще, что уравнение р (х) =0 отражает тот факт, что весь луч {ах\ а > 0} принадлежит S, В частности, если пространство X нормировано, а S — некоторое ограниченное множество (т. е. если числа || z Ц при образуют ограниченное подмножество на оси вещественных чисел), то уравнение р (х) =0 выполняется в том и только в том случае, когда х = 0.
Теорема В. Пусть S — некоторое выпуклое поглощающее множество в линейном пространстве X. Тогда
(1)	р (0) =0, р (kx) = кр (х), если к >> 0;
<2)	Р (х + у) < р (х) + р (у),
') Или опорной функцией. (Прим, ред,)
а если множество S к тому же и уравновешенное, то
(3)	р (М = I I р (*)>
каков бы ни был скаляр X.
Доказательство. Так как О G S, то утверждение р (0) = 0 очевидно. Для того чтобы доказать вторую часть утверждения (1), выберем некоторое х ЕЕ X и некоторый фиксированный скаляр X > 0. Тогда
р (kx) = inf {а > 0: кх ЕЕ а5} = inf {0% >0: Хя ЕЕ 0X5} = = X inf {0 >0: х (ЕЕ 05} = Хр (я).
Для того чтобы доказать утверждение (2), зафиксируем х и у ЕЕ X и предположим, что х ЕЕ а5, а у ЕЕ 05. Тогда х + у G= aS + + 05 = (а + 0) 5, так что р (х + у) а + 0. Но отсюда Р (# + У) inf {а + 0: х S а 5} = р (х) + 0 и, наконец, Р (х + у)< р (х) + р (у).
Если множество 5 уравновешенно, то (X/1 X |) х ЕЕ 05 тогда и только тогда, когда х ЕЕ 05. Поэтому
p(U) = inf{a>0: Ьеа5} = inf{|X|р>0: уц|1|ж e₽|X|<s}= = |X|inf{p>0: А-а:е^} = |МР(*).
что и завершает доказательство нашей теоремы.
Неотрицательная функция р, удовлетворяющая условиям (2) и (3), называется полунормой. Теорема В утверждает, что если множество 5 выпукло, уравновешенно и является поглощающим подмножеством пространства X, то его функционал Минковского является полунормой. Справедливо и обратное утверждение: каждая полунорма служит функционалом Минковского некоторого выпуклого уравновешенного поглощающего множества 5 (см. упражнение 4). Если f есть линейный функционал, опреде-ленный|на X, то функция р (х) = |/[(я) |'определяет полунорму р на X.
Нетрудно сообразить, что нормой является просто некоторая полунорма, обращающаяся в нуль лишь на нулевом векторе. В любом банаховом пространстве полунорма оказывается нормой, если она служит функционалом Минковского некоторого выпуклого уравновешенного, поглощающего и ограниченного множества. Обратное же утверждение, как показывает упражнение 10, неверно. В нашей последней теореме о функционалах Минковского мы познакомимся с несколькими дополнительными свойствами этого функционала.
Теорема Г. Пусть S — некоторое выпуклое поглощающее множество банахова пространства В. Обозначим через р функцио-
нал Минковского для S и обозначим через подмножество (х: р (я) < 1}, и черев S2 — подмножество {х\ р (х)	1}. Тогда
(1)	р (х) < 1, если только х <=~ S и из неравенства р (х) < 1, следует, что xES;
(2)	int (5) CZ CZ S CZ S2 CZ
(3)	S = Sx, если S открыто, и S = S2, если S замкнуто;
(4)	если p непрерывен, mo Sr = int (S) и S2 = g;
(5)	функционал p непрерывен в том и только в том случае, когда О е int (5).
Выпуклое множество V CZ X называется конусом с вершиной в начале координат, если для каждого х е V ах СЕ V, каково бы ни было а > 0. Другими словами, конус V содержит все полупрямые {ах-. а>0}, проходящие через начало координат и любую точку конуса. Множество Vo называется конусом с началом координат в точке у G X, если множество — у + Vo является конусом с вершиной в начале координат. Если V — конус с вершиной в начале координат, то из того, что х, у GE V, должно следовать, что ах + pjy €= V, каковы бы ни были а, |3 > 0. Читатель без особого труда докажет это сам. Более того, если S — произвольное выпуклое множество, то множество V = С7а>0	(«5) явля-
ется наименьшим конусом с вершиной в начале координат, содержащим множество S.
Изучение выпуклых множеств на плоскости показывает, что в них важную роль играют «угловые» точки. Действительно, треугольник полностью определяется своими тремя вершинами, а четырехугольник — четырьмя. Если изучить эту ситуацию более подробно, то мы увидим, что «угловые» точки определяют множества в том смысле, что эти множества являются выпуклыми оболочками множества «угловых» точек. Более того, угловые точки можно определить как единственные точки множества, не принадлежащие ни одному прямолинейному отрезку, целиком принадлежащему этому же множеству. В результате обобщения этих соображений мы получим следующее определение.
Определение Г. Точка х выпуклого множества S называется экстремальной точкой S, если не существует ни одного открытого отрезка (у : z), содержащего х.
^Другими словами, точка х S S называется экстремальной точкой S, если из соотношения
х = ay + (1 — a) z, 0 < а < 1, следует, что х = у = z. На плоскости треугольник, прямоугольник и круг обладают тем общим свойством, что они являются выпуклыми оболочками своих множеств экстремальных точек. (Экстремальными точками круга являются точки, лежащие на ограничивающей окружности.) В то же время замкнутая верхняя полуплоскость, хотя, безусловно, и выпукла, не имеет
экстремальных точек, а следовательно, и не располагает этим свойством.
Теорема Д (Крейна — Миль мана). Если множество S выпукло и бикомпактно *) в банаховом пространстве В, то в S существуют экстремальные точки. Более того, S представляет собой замыкание выпуклой оболочки множества своих экстремальных точек.
В связи с этим, если х S 5, то х можно с произвольной точностью приблизить суммами вида £.а..г., где 2. а. = 1, а. > О, xt — экстремальные точки S.
Теоремой Крейна — Мильмана, очевидно, можно воспользоваться для решения задачи отыскания некоторого «малого» подмножества выпуклого бикомпактного множества, которое определяло бы его полностью. У этой теоремы есть и другое важное применение. Теорема, сформулированная и доказанная Алаоглу **), утверждает, что в некоторых топологиях единичная сфера С7* в двойственном пространстве 5* для банахова пространства В бикомпактна. А так как С7* очевидным образом выпукло, то из теоремы Крейна — Мильмана следует, что С7* представляет собой замыкание (в соответствующей топологии) множества его экстремальных точек. Это значит, что мы совершенно неожиданно добиваемся следующего выигрыша. Если Е — банахово пространство, у единичной сферы которого нет экстремальных точек, то такое Е не может быть двойственным никакому банахову пространству. Например, пространства е0 и Lx (т) не могут быть двойственными какому-нибудь банахову пространству, а следовательно, и не могут быть рефлексивными.
Пример. Экстремальными точками единичной сферы U в Zco служат те точки х = (ab а2, ...), у которых | а. | = 1, i = 1, 2, ...
Доказательство. Прежде всего отметим, что экстремальные точки единичной сферы в любом банаховом пространстве должны иметь единичную норму. В самом деле, если || х || < 1, то найдется такой скаляр а > 1, что норма вектора ах по-прежнему меньше единицы и
х=f1 - -9°+4-(а'г)>
так что х содержится в отрезке (0; ах) = U.
*) См. приложение 1.
**) Хотя в этой книге мы и не говорим о «топологиях», все же мы время от времени будем формулировать важные результаты, которые нельзя доказать, не зная теории топологических пространств. Наличие нескольких хорошо написанных учебников (см., например, [А.54], [А.58], [А.77], [А.83] и [Б. 104]) поможет обойти эту трудность, а обратиться к их помощи во время повторного чтения этой книги, пожалуй, полезно. Между прочим, теорему Алаоглу можно найти в § V.4.1 книги [А.22].
Поэтому, в Zee экстремальные точки должны иметь вид х = = («1, а2, •••)» где SUP I ai I = Остается показать, что х — экстремальная точка тогда и только тогда, когда ни одно а. не удовлетворяет неравенству | а. | < 1. Доказать необходимость этого условия нетрудно. Например, если | ах | < 1, то ах не является экстремальной точкой единичного круга на комплексной плоскости, и поэтому найдутся такие комплексные числа рх =f= Yi с мо" дулем, не превосходящим 1, и такое число 0 < А < 1, что
«1 =	+ (1 — х) Yi-
Полагая
у = (Р1, а2, аз, •••),
z = (Yi, “2, а3, ...),
МЫ получим, ЧТО X = ку + (1 — к) ZVLy=pZ^U.
Для того чтобы доказать достаточность, предположим, что | ccf | = 1 при всех /, и пусть х = ку + (1 — A) z для некоторого О < X 1 и z, y^U. Пусть, например, у = (тн, Лг, •••), a z = (£х, £2, ...). Тогда ах — Цх + (1 — к) £. Так как ах должно быть экстремальной точкой единичного круга на комплексной плоскости, то это равенство позволяет утверждать, что т]х = Si* Аналогичным образом доказывается, что т]. = £., i = 2, 3, ..., а отсюда следует, что у = z. А это значит, что х должно быть экстремальной точкой U.
Свойства отделимости. Обозначим через X некоторое линейное пространство, а через L — некоторое собственное подпространство X. Перенос М — х0 + L подпространства L вдоль х{} назовем линейным многообразием *). Прежде всего заметим, что такое задание линейного многообразия ни в коем случае не является единственным. Действительно, если М = xQ L и z Е М, то для каждого I ЕЕ L z + I = xQ + I + (z — xQ), а так как z — х0 е L, то ясно, что М с тем же успехом можно представить в виде переноса вдоль z: М = z + L. В пространстве R2 линейным многообразием может быть либо точка, либо прямая (не обязательно проходящая через начало координат). В пространстве же R3 линейными многообразиями могут служить плоскости, прямые и точки.
Про подпространство L пространства X говорят, что его коразмерность {фактор-размерность) равна к, если найдется к линейно независимых элементов хх, ..., хк из X таких, что они не принадлежат L, а на множество {х^ ..., xh, L} натягивается пространство X. Если фактор-размерность L равна 1, то подпространство L называется максимальным. Другими словами, подпростран
*) В другой терминологии множества М называют плоскостями, сохра няя для них название гиперплоскостей в том случае, когда L максимально* (Прим, ред.)
ство L максимально, если в пространстве X не существует собственного подпространства L' такого, что L CZ L’. В пространстве R2 максимальными подпространствами служат прямые, проходящие через начало координат, а в пространстве Л3 — плоскости, проходящие через эту же точку. В любом гильбертовом пространстве максимальным является ортогональное дополнение линейного подпространства, натянутого на х, где х — любой элемент, принадлежащий Н.
Теорема Е. Ядро любого ненулевого линейного функционала в X является максимальным подпространством. Обратно, каждое максимальное подпространство пространства X служит ядром некоторого линейного функционала, определенного в X.
Доказательство. Пусть L Е X имеет фактор-размерность, равную 1. Тогда существует такое у Е X, что у L и на {у, L} натягивается X. Каждое х Е X однозначным образом можно представить в виде х = ay + Z, где а — некоторый скаляр, a I Е L. (Единственность такого представления следует из того, что X представляет собой прямую сумму L п линейной оболочки, натянутой на у.) Теперь мы можем определить в X линейный функционал, потребовав, чтобы
/ (х) ~ а, если х ~ ay + I.
Совершенно ясно, что функционал / линеен, а / (Z) = 0 тогда и только тогда, когда Z Е А, и что f (у) = 1. Таким образом, вторую часть сформулированной теоремы можно считать доказанной. Что же касается ее первой части, то положим теперь, что / =f= 0 — некоторый произвольный линейный функционал, определенный в X. Ядро этого функционала представляет собой линейное подпространство, и наша задача состоит лишь в том, чтобы показать, что фактор-размерность этого подпространства равна 1. Пусть у' Е X такое, что / (у') =/= 0. Тогда элемент у = y'/f (у) обладает тем свойством, что / (у) = 1. Но отсюда следует, что X натягивается на {у, N/}, так как если х Е X и а = / (х), то
х — ay Е Nf и
X = (х — ау) + ау.
Следствие 1. Если L — некоторое линейное подпространство X фактор-размерности к, то существует к линейно независимых функционалов Д, ..., fh, определенных в X и таких, что
к L = П NVl.
Доказательство этого следствия мы предоставляем читателю в качестве упражнения.
Перенос максимального подпространства называют гиперплоскостью. Для повышения эффективности вводимой терминологии гиперплоскостями (проходящими через начало координат) называют и сами максимальные подпространства. Операции с гиперплоскостями облегчает следующее следствие.
Следствие 2. Если f — не равный нулю функционал, определенный на X, а а — произвольный скаляр, то множество f (х) = а} представляет собой гиперплоскость. Обратно, каждая гиперплоскость М, не содержащая точку 0, может быть представлена в виде М = {х: f (х) = 1}, где функционал f выбирается единственным образом и f =/= 0.
Доказательство. Из теоремы следует, что гиперплоскости в X представляют собой переносы ядер линейных функционалов! определенных в этом пространстве, и, следовательно, имеют вид {х: f (х) = а}. Для доказательства единственности такого представления заметим, что если / и g — линейные функционалы и {х: f (х) = 1} = {х: g (х) = 1} = М, то / и g идентичны.
Замечание 1. Если М — некоторая гиперплоскость, проходящая через начало координат банахова пространства В, то из того, что М CZ М(Z В, следует: М = М или М = В. Можно показать, что подпространство М замкнуто в том и только в том случае, когда функционал /, соответствующий М, ограничен. Таким образом, каждый раз, когда гиперплоскость замкнута, ей соответствует ограниченный функционал, и наоборот.
Полезно рассмотреть конкретный пример в вещественном пространстве X = У?2. Если и — любой вектор, принадлежащий В2, то множество Мо, где
Мо = {х: f (я) = и) = 0}, представляет собой прямую, проходящую через начало координат и нормальную к и (рис. 4.6). Поэтому, если хг Мо, то гиперплоскость
М = {хг z: zE MQ} = х± Мо представляет собой прямую, параллельную Мо. Очевидно, М делит В2 на две открытые полуплоскости	и S2. Из рис. 4.6 яс-
но, что если х ЕЕ 5Х, то х можно представить в виде
х — т + ки, т ЕЕ М, к >> 0.
Аналогично, если у ЕЕ 6’2» то У молено записать в виде
у = т + Ли, т ЕЕ М, к <; 0.
Поэтому полупространства Sx и S2 можно определить условиями: = {х- / (х) > a}, S2 — {х: f (х) < а},
гДв / — линейный функционал f (х) = (х, и>, а а = /(zrx) = (х^ и>
Этот результат, полученный для двумерного пространства, без труда переносится на более общий случай. Если М = = {х: f (х) = а} — некоторая гиперплоскость в вещественном пространстве X, то каждое из множеств
{х:/(т)<а}, {х:Цх)>а}, {х: f (х) < а}, {x:f(x)^a}
выпукло и называется полупространством, определяемым М, Если X — В — банахово пространство, а функционал / непрерывен, то М замкнуто и пер
Рпс. 4.6. Разбиение R1 на полупространства.
вые два из этих полупространств открыты, а вторые два — замкнуты.
Будем говорить, что множество S лежит по одну сторону гиперплоскости М, если S целиком содержится в одном из четырех полупространств, определяемых М. Если S лежит по одну сторону М и S П М = 0, то мы будем говорить, что S лежит строго по одну сторону М. Два множества S и Q пространства X называются разделяющимися некоторой гиперплоскостью М,
если они принадлежат противоположным полупространствам, ограниченным этой гиперплоскостью. Поэтому М разделяет Q и S, если f (х) а при х ЕЕ S и f (х) а, при х ЕЕ Q,
В § 3.2 мы привели теорему Хана — Банаха (теорема В) в ее аналитической формулировке. В том виде она решала вопрос о продолжении линейных функционалов, определенных на некотором
подпространстве, на все пространство в целом, причем это расширение должно было сохранять некоторые свойства или удовлетворять части их. Теорема Хана — Банаха, однако, имеет еще и две геометрические формулировки, позволяющие лучше почувствовать ту важную роль, которую она играет в современном анализе. Для полноты картины мы приведем теперь все три эквивалентные формулировки этой теоремы.
Теорема Ж (теоре маХана — Банаха в аналитической формулировке). Пусть X — некоторое линейное пространство, L — подпространство X, а р — полунорма, определенная в X. Если / — линейный функционал,
определенный в L, такой, что
|/(*)Кр(*), x^L,
то / имеет линейное продолжение J на пространство X, удовлетворяющее условию | / (х) | р (х), каково бы ни было хЕ%>
Теорема 3 (теорема Хана — Банаха в геометрической формулировке). Пусть S — некоторое открытое выпуклое множество в (вещественном или комплексном) банаховом пространстве В, и пусть N — некоторое линейное многообразие, не пересекающееся с S. Тогда существует замкнутая гиперплоскость М, которая содержит N и не пересекается с S.
ТеоремаИ (теорема Хана — Банаха об отделимости). Пусть S и Q — два выпуклых множества в вещественном банаховом пространстве В. Тогда, если int (S)=£0u int (5) р| Q = 0, то существует замкнутая гиперплоскость М, которая разделяет S и Q.
Мы не собираемся вдаваться в подробности доказательства эквивалентности этих формулировок (см. по этому поводу упражнение 8), но все же сделаем несколько дополнительных замечаний. Во-первых, обратим внимание на то, что для геометрической формулировки существенно, чтобы S было открытым. Например, в В2, если S представляет собой объединение открытой верхней полуплоскости и точки (1, 0), a Q — начало координат, то разделяющей гиперплоскости вообще не существует.
Следствие. Каждое замкнутое выпуклое множество Q является пересечением всех замкнутых полупространств, содержащих Q.
Доказательство. Достаточно показать, что если х Q, то найдется такое полупространство Н, содержащее Q, что х И. Но это следует из теоремы о разделимости, так как по условию должна существовать открытая сфера S с центром в х, не пересекающаяся с Q.
Пусть А — некоторое открытое множество, и пусть М — гиперплоскость. Множество М называется опорным для А (точнее говоря, опорной гиперплоскостью множества Л), если A GZ {х*. / (х) а} либо A CZ {х\ / (х)	а}, и A f] М =/= 0.
Неформально говоря, М называется опорной гиперплоскостью А, если их пересечение не пусто, и А лежит по одну сторону М. Замкнутое выпуклое множество с непустой внутренностью называется выпуклым телом. Выбирая Q = {х0}, где х0ЕЕдА, и S ~ int (4), мы убедимся в том, что из теоремы об отделимости следует такой важный результат: для каждой граничной точки некоторого выпуклого тела существует замкнутая опорная гиперплоскость, проходящая через эту точку.
На рис. 4.7 показано выпуклое тело в У?2. Иногда полезно представлять себе функционал /, определяющий опорную гиперпло
скость, как нормаль к выпуклому телу, направленную наружу в точке касания с опорной гиперплоскостью. На самом деле, иногда удобно даже называть / нормалью к опоре. В самом общем случае через заданную точку опоры можно провести несколько опорных гиперплоскостей. На рис. 4.7 у точки имеется целый конус нормалей к опоре. Кроме того, одна опорная гиперплоскость может
проходить и через несколько граничных точек тела. Из рис. 4.7 ясно, что если две различные граничные точки лежат на одной и той же гиперплоскости опоры, то в силу выпуклости множества этой же опорной гиперплоскости должен принадлежать и весь сегмент, ограниченный этими точками.
Комплексные пространства *). Пусть задано некоторое комплексное линейное пространство X. Из него всегда можно выделить соответствующее вещественное линейное пространство Хо, приняв в качестве векторов Хо векторы X, а умножение на скаляры определив лишь для вещественных чисел. При этом некоторые понятия (например, понятие выпуклого множества) определяются в Хо так же, как в X. Однако для ряда других понятий это неверно. Например, каждое подпространство пространства X является и подпространством Хо, в то время как обратное утверждение уже неверно. Для того чтобы подпространство М пространства Хо оказалось еще и подпространством X, необходимо и достаточно, чтобы iM CZ М. Аналогично уравновешенное множество из Хо не обязательно должно быть уравновешенным в X.
Переход от X к Хо отражается и на других понятиях. Если пространство X n-мерпо, то пространство Хо имеет размерность 2п. Поэтому, если множество {с1? е2, ..., еп} образует максимальный набор векторов, линейно независимых в X, то аналогичное максимальное множество векторов, линейно независимых в Хо, имеет уже вид {elt е2, ..., en, ielt ie2t ..., ien}. Это широко известно для примера плоскости, представляющей собой одномерное комплекс
*) Этот раздел при первом чтении можно опустить.
ное пространство X (натянутое на 1) или двумерное пространство Хо (натянутое на 1 и Z).
Любой линейный функционал, определенный на X, остается линейным и на XQ. Однако линейный функционал /, определенный на Хо, не обязательно будет линейным функционалом, если считать, что он действует в пространстве X. Поскольку векторы X и Хо одинаковы, при таком переходе сохраняется свойство аддитивности /, но для сохранения его однородности необходимо ввести дополнительные ограничения. Последнее замечание следует рассмотреть подробнее. Пусть / — линейный функционал, определенный на X. Тогда для каждого х G= X / (х) представляет собой некоторое комплексное число, и мы можем обычным образом выделить его вещественную и мнимую части, построив таким образом пару вещественных функционалов /0 (х) и g0 (я), где
/ (*) = /о U) 4- *£о (Д х G X.
Подобным образом мы определим /0 и £0 для каждого ^£Х0, причем оба они могут принимать лишь вещественные значения. Мы утверждаем также, что оба эти функционала линейны в Хо. Действительно, если х, у £= Хо, то
/ (* + у) = /о (х -I- у) 4- igo (х + у).
/(*)+/ (у) = I/о (*) 4- /о (г/)1 + i teo (*) + go (f/)L
в силу определения /0 и g0, а также из-за аддитивности /, требующей равенства вещественной и мнимой частей обеих сторон этих уравнений. Итак, /0 и gQ аддитивны. Далее, для всякого вещественного скаляра а справедливы равенства
/ (ах) = /0 (ах) 4- ig0 (ах),
а/ (х) = [а/0 (х)1 4- i [ag0 (х)], и потому
/о (ах) = Re / (ах) = Re af (х) = а/0 (х),
go (ах) = Im / (ах) = Im af (х) = ag0 (х),
что доказывает однородность функционалов /0 и g0 в пространстве Хо. Наконец, заметим, что между /0 и g0 существуют следующие соотношения:
— go (х) = i/o (х) = if (х) = / (ix) = /0 (ix) 4* ig0 (ix), откуда следует, что
go (х) = —/0 (ix),	/0 (х) = go (х) = go (ix).
Это значит, что из / при переходе в Хо получается на самом деле всего лишь один линейный функционал. Действительно,
соотношение
/ (*) = /о (*) — ifo
определяет комплексный функционал в X, и мы предоставляем читателю возможность самостоятельно доказать, что / аддитивен и однороден по отношению к комплексным скалярам.
Теорема К. Пусть X — некоторое комплексное линейное пространство, а Хо — порожденное им вещественное линейное пространство. Тогда существует взаимно однозначное соответствие f <-> /0 между линейными функционалами, определенными в X, и линейными функционалами, определенными в XQ. Это соответствие определяется формулой
/ (*) = /о U) — if о
Если X = В — банахово пространство, то нормировать Во можно просто, потребовав, чтобы норма х в Во совпадала с нормой х как элемента В. Пространство BQ, очевидно, полно. Более того, если хп -> 0 в Во, то из-за того, что || ixn\\ = [ хп ||, мы можем утверждать, что и ixn -> О в Во. Следовательно, функционал So (#) = tfo непрерывен, если только непрерывен /0. А это вместе с тем фактом, что комплексная функция непрерывна тогда и только тогда, когда непрерывны ее мнимая и вещественная части, показывает, что / £= В * тогда и только тогда, когда /0 (= BQ *.
Наконец, хотя по-настоящему теорема об отделяемости формулируется лишь в вещественном банаховом пространстве, ее можно с помощью несложного приема сформулировать и для комплексного пространства, заменив комплексное В на порожденное вещественное Bq и решая задачу отделения в Bq. В результате получается вещественный линейный функционал /0, отделяющий заданные множества, или, что то же, комплексный функционал /, вещественная часть которого по-прежнему решает задачу разделения.
Теорема Л (теорема Хана — Банаха об отделении в комплексном пространстве). Пусть S и Q — два выпуклых множества в комплексном банаховом пространстве В, и пусть у множества S — непустая внутренность. Тогда, если Q не пересекается с int (S), то существует такое f ЕЕ В*, что
sup Re/ (х) inf Re/(j;).
xes	xeQ
Упражнения
1.	Покажите что (а) пересечение уравновешенных множеств уравновешенно; (б) пересечение выпуклых множеств выпукло; (в) произвольный перенос выпуклого множества выпукл; (г) уравновешенная оболочка S совпадает с ES. Приведите пример двух выпуклых множеств, объединение которых не рыпукло,
2.	Пусть S и Q — Два подмножества банахова пространства В. Покажите,* что S + Q открыто, если только открыто S.
3.	Докажите теорему А.
4.	Пусть р — некоторая полунорма в линейном пространстве X. Если S = [х: р (х) < 1}, то покажите, что S — выпуклое, поглощающее и уравновешенное пространство. Покажите, что р есть функционал Минковского для S.	л
5.	Докажите, что единичная сфера любого банахова пространства выпукла, уравновешенная и поглощающая.
6.	Опишите экстремальные точки единичной сферы в L^a, Ь). Покажите, что у единичной сферы в <?0 нет экстремальных точек. Покажите, что экстремальные точки единичной сферы в С (0, 1) представляют собой функции постоянного модуля, равного 1. Как выглядят экстремальные точки единичной сферы в L (0, 1)?
7.	Докажите следствие 1 теоремы Е.
8.	Докажите, что из теоремы И следует теорема 3.
Указание. Пусть Q представляет собой линейное многообразие, порожденное N. Перенесем эти множества так, чтобы в силу теоремы И существовал функционал / G В* такой, что /	и / (N) с. Из того же, что
О N, выведем, что ядро / удовлетворяет условиям теоремы 3.
9.	Пусть множество S выпукло, а М — некоторая гиперплоскость. Покажите, что из S Q М = ( следует, что S лежит строго по одну сторону от М.
Указание. Пусть М — {.г: / (х) — а}, и пусть xv х2 (= S и такие, что / (rq) < а < / (х2). Найдите значения / на сегменте fа?! : х2] CZ S.
10.	(а) Пусть р — полунорма в банаховом пространстве В. Покажите, что множество {х: р (х)	1} ограничено в том и только в том случае, когда
для некоторой постоянной с > 0
р (х) > 41X || при всех х ЕЕ В.
(б) Из (а) следует, что если множество {х: р (х)	1} ограничено, то р
на самом деле является нормой в В. Покажите, что обратное утверждение неверно.
Указание. Пусть А — ограниченный оператор в гильбертовом пространстве, и пусть А взаимно однозначно неплотно в области своих значений, но не обратимо. Рассмотрите тогда р (х) = || А х ||.
4.2. Решение задачи 1
для случая преобразований единичного ранга
Как указывает заголовок этого параграфа, мы собираемся сейчас решить задачу 1 при упрощающем предположении, согласно которому область значений преобразования Т одномерна. Однако в § 4.3 мы выясним, что аппарата, развитого в настоящем параграфе, почти достаточно для того, чтобы решить задачу 1 в ее наиболее общем виде. Поэтому при изучении нынешнего частного случая мы намереваемся быть предельно подробными.
Для того чтобы в явном виде поставить решаемую задачу, мы будем рассматривать (без какого-либо ущерба для общности) вещественное банахово пространство В, пространство В*, ему сопряженное, и поле вещественных скаляров R. Преобразование Т считается линейным; его областью значений служит R, и оно определяется с помощью билинейной формы (,), порождаемой В и
В*. Возможны два случая. Во-первых, входные сигналы системы могут принадлежать пространству В, а следовательно, преобразование Т определяется правилом
Ти = <и, />, и е В,	(1)
где f (Е В* является некоторым фиксированным функционалом, определяющим (и в то же время определяющимся) Т. Но, с другой стороны, если входные сигналы системы отождествляются с элементами пространства Z?*, то преобразование Т задается правилом
Tf = <п, />,	/ е 5*,	(2)
в котором и Ez В является фиксированным элементом, определяющим и определяющимся Т.
На самом же деле второй случай содержится в первом. Действительно, напомним, что для каждого иЕ В существует некоторое u** G= 5** такое, что
О, /> - </, и**>,	(3)
каково бы ни было f Ez В*. Положив и** вместо и и заменив В на В*, а В* на В**, мы приведем второй случай к первому. Более того, если В рефлексивно, то задачи первого типа содержат в себе и задачи второго типа, поскольку каждому u** $= В** соответствует некоторое и ЕЕ В, для которого справедливо соотношение (3) (т. е. В** = В, если пространство В рефлексивно). Одна и та же подстановка в этом случае определяет два типа задач.
Существование минимального элемента. Рассмотрим сначала преобразование из уравнения (2). Без потери общности (см. упражнение 1) можно предположить, что || и | = 1. Попытаемся выяснить, существуют ли в В* элементы, удовлетворяющие условию Tf = 1 и одновременно минимизирующие ||/||. Поскольку для каждого / 6= В*
|<U, />|<|1Н	(4)
то ясно, что для каждого прообраза 1 Е Л должно быть || /1| > 1. Однако следствие (см. теорему Г из § 3.2) из теоремы Хана — Банаха утверждает, что для каждого и с В с нормой || и || = 1 существует такое f ЕЕ В*, что|| /1| = 1 и
<и, /> = 1.
Поэтому для Т: В* -> R можно определенно утверждать, что решение задачи 1 о минимизации нормы действительно существует. (Мы оставляем в качестве упражнения практически тривиальную проверку предположения о том, что допущения || и || = 1 и £ = 1 не сужают постановки задачи.)
В том же случае, когда Т: В -> R и преобразование описывается уравнением (1), нам не удается прийти к столь же категорическим результатам. Видоизменяя предыдущие рассуждения (теперь нам нужно предположить, что Ц /|| = 1) на этот случай, мы приходим к импликации Ти = 1 => || и ||	1. Это неравенство
вместе с неравенством
Ти <= <и, /) < sup | <u, f) | = || f || = 1	(5)
II u ||=1
показывает, что проблема существования прообраза 1 е R, обладающего минимальной нормой, эквивалентна задаче о том, достигает ли функционал / своей верхней грани на единичной сфере в В или же не достигает.
Если банахово пространство В произвольного вида, то функционалы, определенные на В, могут как достигать, так и не достигать своей верхней грани на единичной сфере в этом пространстве. С некоторыми примерами этого типа мы познакомимся в следующем параграфе. Однако если пространство В рефлексивно, то каждый функционал / ЕЕ /?* достигает своей верхней грани на единичной сфере. Другими словами, в этом случае существует такое и G= В, что || и || = 1 й / (и) = || / || (см. упражнение 2), так что для рефлексивных пространств наша упрощенная версия задачи 1 всегда имеет по крайней мере одно решение *).
Гораздо большей глубиной отличается обратный результат: если каждый ограниченный линейный функционал, определенный на В, достигает на единичном шаре своей верхней грани, то пространство В рефлексивно. Этот факт был установлен Р. Ч. Джеймсом [Б. 49]. Итог этому разделу мы подводим в следующей теореме.
Теорема А. Задача 1 имеет решения для каждого преобразования единичного ранга, определенного в банаховом пространстве В, тогда и только тогда, когда пространство В рефлексивно.
Прежде чем закончить изучение вопросов существования, сделаем еще одно последнее замечание. Преобразование Т отображает единичный шар из В в некоторое множество, содержащее 0. Это множество выпукло и вместе с £ обязательно содержит и — Однако хорошо известно, что выпуклыми подмножествами множества вещественных чисел могут быть лишь отрезки. Поэтому образом единичной сферы в силу Т может быть лишь один из отрезков
) Читатели, знакомые с литературой по топологии, рекомендованной выше, заметят, что этот же результат можно было получить и по-другому. дСЛИ пространство В рефлексивно, то его единичный шар слабо компактен. л поэтому отображение и -♦ <и, /> представляет собой некоторую вещественную непрерывную функцию, определенную на бикомпактном множестве, и, следовательно, достигает своего максимума.
(— || Т || : || Т ||) или [— || Т || : || Т ||]. Наконец, мы уже отмечали, что задача 1 имеет решения при заданном Т в том и только в том случае, когда Т достигает своей верхней грани. Объединяя все эти соображения в одно целое, мы получим следующий критерий: если преобразование Т определено на Ви его ранг равен 1, то задача 1 для этого Т имеет решение в том и только в том случае, когда образ единичного шара из В для Т замкнут.
Единственность минимального элемента. Вопрос о единственности решения задачи 1 более сложен, чем вопрос о его существовании. Прежде всего введем некоторый стандарт на используемые
дальше обозначения. Будем обозначать через U = {х е В\ || х || < 1} замкнутый шар единичного радиуса в В. Границей dU, очевидно, является множество dU — {х В : || х || = 1}. Внутренность U, а именно int (Z7) = {х ЕЕ ЕЕ В:\\ я:|| < 1}, будем называть открытым единичным шаром. Большинство важных свойств банахова пространства в той или иной мере связано с характеристиками его единичного шара. Например, мы уже имели возможность убедиться в том, что вид шара имеет непо-
Рис. 4.8. Множество U для X = 1р (2), р = 1, 2 и оо.
средственное отношение к вопросу о том, может ли это пространство быть двойственным по отношению к какому-либо другому банахову пространству. Напомним еще, что (см. упражнение 5 к § 4.1) U всегда выпуклое, поглощающее и уравновешенное, и что норма представляет собой функционал Минковского на единичном шаре.
Прежде чем переходить к более общим аспектам этого раздела, рассмотрим форму U для одной довольно простой ситуации. Предположим, что В — вещественное линейное пространство Я2,
в котором определена норма
II * IIp = (l“i 1р + I «2 |р),/Р. х = (av a2) е Я2,
где р меняется в диапазоне 1 р оо. На рис. 4.8 множество U изображено для случаев р = 1, 2 и оо. Если р = 1, то U — прямоугольник с вершинами (1, 0), (0, 1), (— 1, 0) и (0, — 1). По мере роста р от 1 до бесконечности соответствующее множество U расширяется от этого прямоугольника до прямоугольника с вершинами (1, 1), (1, — 1), (— 1, — 1) и (— 1, 1), проходя попутно через стадию окружности при р = 2. (На том же рисунке пунктиром ориентировочно показан случай р = 1/2. Поскольку соответствующее множество не выпукло, то правило треугольника не может иметь места, и, значит, функция || Д./а не может быть нормой.)
Даже на этом простом примере легко заметить, что у единичного шара могут быть как плоские границы, так и угловые граничные точки. При этом оказывается, что банаховы пространства, у единичных шаров которых нет плоских участков границы, обладают определенными полезными свойствами. В связи с этим целесообразно выделить их в особый класс, что и делается с помощью следующего определения.
Определение А. Пространство В называется строго выпуклым, если dU не содержит прямолинейных сегментов.
Другими словами, пространство В строго выпукло, если каждый открытый сегмент (х : у), соединяющий между собой некоторую пару несовпадающих точек dU, состоит исключительно из точек, норма которых меньше единицы. В теореме Б перечисляются несколько эквивалентных определений понятия строгой выпуклости пространства.
Теорема Б. Следующие свойства банахова пространства В эквивалентны между собой:
(1)	В строго выпукло.
(2)	Из [| хг + х21| = || хг || + || х21| следует, что х± = Кх2, или х2 = kxr для некоторого А, 0.
(3)	Каждая точка dU является экстремальной точкой U.
(4)	Для каждого / ЕЕ 5*, не равного нулю тождественно, существует по крайней мере одно xEU такое, что / (х) = || /||.
(5)	Каждая опорная гиперплоскость U пересекает U не более чем в одной точке (а значит, строго в одной точке).
(6)	Каждое выпуклое множество К из В содержит не более одного минимального элемента (другими словами, имеется не более одного вектора х ЕЕ К, удовлетворяющего условию || х ||	|| z ||,
каково бы ни было z (ЕЕ К).
Доказательство. Пусть В строго выпукло, и пусть х± и х2 удовлетворяют условию
II Ъ + х2 II = || Х± || + II х21|.
Предположим, что хг =/= 0 и х2 0. Тогда для доказательства (1) =>(2) достаточно показать, что если 0 а 1, то
11апА-+
II ИИ v 7 1Ы| II
поскольку это верно только при ^/1 хх || = х2 /|| х21|. Проверка же этой гипотезы не составляет никакого труда (см. упражнение 4).
. Докажем теперь, что из утверждения (2) следует утверждение (о). JTIycTb х ЕЕ dU задано, и пусть х = ay + (1 — a) z, где у
а 0 < а < 1. Тогда, в силу неравенства треугольника, нормы у и z равны 1, но
II аУ + (1 - a) z || = 1 = || ау || + || (1 - а) z ||,
и, следовательно, в силу (2) необходимо, чтобы
ay = X (1 — a) z или (1 — а) z = Kay, где К > 0. Если справедливо первое из предположений то
0 < а = || ау || = || К (1 — a) z || = К (1 — а)
и, следовательно, у = z. Точно так же второе предположение приводит к тому, что у = z, а это значит, что х — экстремальная точка U.
(3)	(4). Предположим, что 0=^/Е S* и что =/= х2 принад-
лежит U и удовлетворяет условию / (xj = ||/|| = / Сг2). Положим х = 7г (zi + #2). Но в этом случае х е U и f (х) = = 7г/ (*i) + х/2 / (ъ) = II / II» откуда следует, что
И/ll-	=1/1,
Это показывает, что х е= dU и в то же время принадлежит сегменту (л?! : х^ CZ U. Следовательно, х не может быть экстремальной точкой U, что противоречит утверждению (3).
(4)	=> (5). Если Н есть опорная гиперплоскость для U, то Н имеет вид Н = {х : / (х) = 1}, где / ЕЕ В*, и можно предположить, что
Re / (х)	1, х ЕЕ U.
Применив / к единичному вектору х [(/ (я))/1/ (х) |], получим, что || / Ц 1. Это неравенство на самом деле должно быть равенством, так как пересечение Н и U обязательно не пусто и содержит по крайней мере одну точку х. Если же г/ Е Я Q U, то / (у) = 1 = = || /1| и у s U. Но в этом случае в силу утверждения (4) у = х, (5) => (6). Пусть К — некоторое выпуклое множество из В.
Очевидно, если 0 Е Я, то минимальным элементом служит 0, так что можно предположить, что
1 = inf{||z||: zE К}
Если U — единичный шар В, то ясно, что int (С7) =/= 0, int (U) П К = 0, и, следовательно, по теореме об отделимости существует гиперплоскость Н, разделяющая U и К, Множество минимальных элементов К в точности совпадает с множеством U П К, а это множество содержится в U Q К, которое, в силу предыдущего утверждения, содержит не более одного вектора.
(6)	=> (1). Если хг и х2 ЕЕ U и : х2\ СЕ dU, то выпуклое множество К =	: х2] содержит более одного элемента, если только
не равен х2.
Замечание 1. Заметим, что в (4) мы не утверждаем, что каждый функционал /, определенный на В, достигает своей верхней грани на границе единичного шара. Мы утверждаем лишь, что если это так, то возможно лишь строго в одной точке. Аналогичным образом строгая выпуклость пространства в утверждении (6)
не гарантирует существования минимального элемента в К, а гарантирует лишь единственность его. Таким образом, понятие строгой выпуклости существенным образом связано с вопросами единственности.
После того, как мы выделили в особый класс банаховы пространства, на границе единичного шара которых нет плоских областей, мы сосредоточим наше внимание на вопросе существования угловых точек. Поскольку угловая точка — это точка, через которую проходит несколько опорных плоскостей, то мы воспользуемся следующим определением.
Определение Б. Банахово пространство В называется гладким, если каждой точке dU соответствует в точности одна опорная гиперплоскость U.
Свойства гладких пространств подытоживается следующей теоремой.
Теорема В. Следующие свойства банаховых пространств В эквивалентны между собой:
(1)	Пространство В гладко.
(2)	Для каждого 0 х ЕЕ В существует не более одного j ЕЕ В* такого, что || /1| = 1 и / (х) — || х ||.
(3)	В каждой точке х (ЕЕ dU существует предел
е-0	8
каково бы ни было z ЕЕ В. Более того, каждый раз, когда G определено, этот предел есть линейная вещественная функция z с единичной нормой.
Доказательство. По определению, Н является опорной гиперплоскостью U в точке х ЕЕ dU, если U опирается на Я и содержит х. Если воспользоваться нашими прежними методами характеризации гиперплоскостей, то это эквивалентно утверждению: существует такое fEEB*, что
(a)	Re / (2)	1 при всех г ЕЕ U.
(б)	/(х) = 1/
Но утверждение (а) эквивалентно утверждению {/1|	1, и,
следовательно, между гиперплоскостями Н, на которые опирается U в точках х, и векторами / ЕЕ £7*, для которых / (х) = || х ||, существует взаимно однозначное соответствие. Отсюда же следует эквивалентность утверждений (1) и (2). Эквивалентность утверждений (2) и (3) доказывается в приложении 6.
Воспользовавшись теперь утверждением (2) теоремы В и утверждением (4) теоремы Б, мы покажем, что свойства строгой выпуклости пространства и его гладкости практически двойственны. Обозначим через £7* единичный шар В*. Теорема Б утверждает, нто каждому G (ЕЕ В** соответствует не более одного / (ЕЕ £7*,
для которого G (/) = || G ||, в том и только в том случае, когда В* строго выпукло. Но так как В можно считать подпространством В**, то из того, что В* строго выпукло, следует, что для каждого х ЕЕ В имеется не более одного / ЕЕ U*, для которого / (х) = || х ||. Другими словами, в общем случае условие гладкости В слабее условия строгой выпуклости 5*, и эти два условия эквивалентны ДРУГ другу» если В рефлексивно. Подводя итог, мы можем утверждать, что если В** = В, то каждый функционал, определенный на В (или на 5*), достигает своей верхней грани в U (или С7*) не более чем в одной точке в том и только в том случае, когда В строго выпукло (или В гладко). Короче, говоря, если пространство В рефлексивно, то В гладко (строго выпукло) тогда и только тогда когда В* строго выпукло (гладко).
На этом этапе полезно ввести следующую терминологию. Если 0 =/= / е 5*, то вектор х ЕЕ U называется экстремалью f, если х удовлетворяет условию / (х) = || / ||. Ясно, что норма каждой экстремали / равна 1. Но тогда теорема Б утверждает, что для каждого / G В* имеется не более одной экстремали в том и только в том случае, когда В строго выпукло. Аналогичным образом, если 0 =f= х CZ В, то элемент / ЕЕ U* называется экстремалью х, если / удовлетворяет условию / (х) = || х ||, а теорема В утверждает, что для каждого х ЕЕ В существует не более одной экстремали в 5* тогда и только тогда, когда В гладко.
Замечание 2. Если х Е: В, то теорема Хана — Банаха гарантирует существование по крайней мере одной экстремали / в В*. Соответственно, если пространство В рефлексивно, то каждому О =f= / ЕЕ В* (0 =/= х ЕЕ В) соответствует единственный элемент В (5*) в том и только в том случае, когда В строго выпукло (В* гладко). Наконец, если В рефлексивно, строго выпукло и гладко, а через х (/) обозначена единственная экстремаль х (/) в 5* (5), то экстремальная функция должна обладать следующими операционными свойствами:
(а)	х = т~й Для всех 0=/=>хЕЕВ\
(б)	для всех
(в)	(kx) = х, каким бы ни был комплексный скаляр X.
Мы уже могли убедиться в том, что в любом банаховом пространстве каждому х =f= 0 соответствует по крайней мере одна экстремаль / (= С7*, а максимальная информация об /, которой мы располагаем, состоит в том, что норма / равна 1. Эту информацию можно несколько расширить.
Теорема Г. Пусть х =/= О принадлежит В и фиксировано. По крайней мере одна из экстремалей х является экстремальной точкой U*,
Доказательство этой теоремы существенно зависит от изучения топологических свойств пространства В. В самом деле, множество С* = {/ СЕ U*- / (х) = || х ||} является непустым, выпуклым и (слабо) замкнутым подмножеством £/*, а следовательно, оно должно быть (слабо) бикомпактным. Из теоремы Крейна — Мильмана тогда следует, что в С* имеется экстремальная точка / . Легко показать, что на самом деле /0 является экстремальной точкой U*. Действительно, если /0 = а/ -|- (1 — а) g, где 0 < а < <1 й / и gG С/*, то
II х II = /о (х) = af (х) + (1 — а) g (х) <
С а | / (х) | + (1 - а) | g (х) |< а || х || + (1 - а) ||х||,
откуда следует, что / (х) = | / (х) | = || х || и g (х) = || х ||. Другими словами, в этом случае /0 принадлежит (/ : g) С С* и, следова-тельно, / = g.
Эта теорема утверждает также следующее: если пространство В рефлексивно, то каждое ср ЕЕ В* достигает своей верхней грани на U в некоторой экстремальной точке U (и, следовательно, является собственным только в том случае, когда не каждый вектор dU является экстремальной точкой С7, т. е. если пространство В не строго выпукло).
Экстремали в некоторых конкретных банаховых пространствах. В § 4.3 мы убедимся в том, что нахождение экстремалей составляет один из основных этапов решения основной задачи оптимизации. Оставшаяся часть этого параграфа посвящена тому, что для последующих ссылок мы определяем, какой характер приоб-
ретает эта операция в некоторых пространствах, имеющих важное значение для приложений. Однако, поскольку абстрактное решение задачи может быть найдено и без этой конкретной инфор
мации, некоторые читатели могут при первом чтении пропустить этот раздел и сразу перейти к § 4.3.
Среди широко распространенных банаховых пространств, с
которыми мы сталкивались в предыдущих параграфах, пространства с0, 1Г и Zqo и соответствующие функциональные пространства С (т), Lr (т) и Loo (т) не являются ни строго выпуклыми, ни гладкими. Но по другую сторону барьера мы имеем пространства Lp и 1<р<оо, которые одновременно обладают свойствами
гладкости и строгой выпуклости. Этими же свойствами обладает и любое гильбертово пространство. Поскольку эти пространства имеют более приятные геометрические свойства, то мы начнем наши примеры именно с них.
Пример 1. Lp (а, Ъ) и 1р при 1 < р < оо. Если X — одно из этих пространств, то для х GE X с || х || = 1 соотношение Ф> | ^ || ф ||, где фЕЕХ*, в точности совпадает с неравенством Гельдера. В § 1.4 было отмечено, что в этом соотношении равенство достигается в том и только в том случае, когда х специальным
и единственным образом связано с ср (иначе говоря, если х является экстремалью ф). В самом деле, если ф = (фп <р2> •••) £= lq есть некоторый непрерывный линейный функционал, определенный на Zp, где Ир 4- 1/q = 1, то ф = (фп <р2, •••) S Zp/где
фк =
О,
если
ф* / МУ'1 I фк I \ ||ф|| /
если
ф* = 0,
Фи =h 0,
где через фь обозначены числа комплексно-сопряженные фд. Если мы рассматриваем вещественные пространства, то это выражение упрощается и принимает вид
Ф» = ||ф||(1“®>8’8п 1фк1'|ф*1?-1»
где функция sign [ф J принимает значение +1, если фл > 0, и —1, если фл <0, и равна нулю, если ф& = 0.
Аналогичным образом, если ф е Lq (а, Ь) — некоторый функционал, определенный на Lp (а, Ь), где 1/р + Mq = 1, то ф — экстремаль ф и принимает в точке t ЕЕ [а, Ы значение, определяемое условием
ф(0 =
о, Ф(0 flф«)I |ф(01\ 11Ф11 /	’
если ф (t) = 0, если ф (t)	0.
Так же как и для пространства последовательностей, переход к вещественным пространствам позволяет свести это выражение к виду
ф (0 = II Ф ll(w) sign [ф (01- I Ф (0 Г’1, t [я, Ы.
Без всякого труда можно проверить, что определенные таким образом функции удовлетворяют необходимым условиям. Например, легко убедиться в том, что
ь	ь
IIФII = [ IФ Ю |р dt]1,P = II ф	[ jj I ф (0 I dt] Vp .
а	а
Однако 1/р + 1/д = 1 <4 р (q — 1) = д ФФ (1/д) (q/p) = (Д/q) X X (q — 1), и, пользуясь этими двумя эквивалентными формами, мы сразу получим, что || ф || = 1. Более того,
ъ
< ф. ф>=|1 Ф IF1-’* I ф (0 1Р(’-”^ = || ф ||(1-” -|| ф ||«= ||ф ||,
4.2. СЛУЧАЙ ПРЕОБРАЗОВАНИЙ ЕДИНИЧНОГО РАНГА 347 и значит, определенные выше ф действительно являются экстремалями ф.
Пример 2. 1Р (и), где р = 1 или оо. Эти пространства могут служить примерами пространств, не обладающих свойством строгой выпуклости. Напомним, что пространство (п) рефлексивно и что [Zx (и)]* = Zoo (л). Если ф = (фп ..., фп) е Zoo (п), то
II Ф || = max {| <рх |,	| <рп ]},
а для х = («1, .... хп) е li (п) п
И = ЗМ-
1=1
В обоих случаях нетрудно найти необходимые условия, которым должны удовлетворять экстремали. В самом_ деле, если Ф€= Zoo (и), то компоненты любой экстремали ф = (фр ..., фп) е GE Zx (п) должны удовлетворять условию
фк = assign [фк], где
ад 0, к = 1, ..., п,
ал = 0, если | фА [ =/= || ф ||,
п
S х* = 1-
К=1
Другими словами, если из множества {+* = 1» •••> п), гДе et — i-й координатный вектор пространства, выбрать такое подмножество {е]}, что
< Ф > = || Ф ||, то любая экстремаль ф должна представлять собой некоторую выпуклую комбинацию {ei} (т. е. ф должно быть одним из единичных векторов выпуклой оболочки {^}).
Интерес представляет и обратная ситуация, в которой х — == (#1> ...» яп), а ф = (фп ..., фп) является экстремалью х. В этом случае
[signal, — ( — 1 ^фк^1, xfc=0.
Достаточность этих условий проверить нетрудно. В самом деле, поскольку | фд |	1 во всех случаях и | фд|< 1 для всех к в том и
только в том случае, когда х = 0, то мы сразу видим, что || х 1| = 1.
Но с другой стороны,
<я, s> = 2a;i<₽i =	=
и наша проверка закончена.
На рис. 4.9 показаны экстремальные условия для Zr(2) и Zoo (2). Отметим, что подмножество S = {х: xt = 1; — 1 < х2 < 1} поверхности единичного шара представляет собой плоскую область.
Рис. 4.9. Единичный шар для (2) и (2).
Функционал (1, 0) ЕЕ (2) определяет общую опорную гиперплоскость для точек и одновременно является единственной экстремалью для всех точек У угловых точек х = (1, 1) и х = = (1, —1), напротив, имеется целый конус опорных функционалов, а именно множество А = {<р: <р = а (1, 0) + (1 — а) (0, 1), 0 < а < 1}. И обратно, каждый элемент является экстремалью для (1, 0) GE Zr (2) и определяет одну из опорных гиперплоскостей, проходящих через эту точку. Более того, элемент (1, 1) ЕЕ Zoo (2) является единственной экстремалью для любой точки А. Отметим еще, что U имеет лишь четыре экстремальные точки: (1, 0), (0, 1), (— 1, 0) и (0, —1). В этом можно убедиться на глаз. Поэтому для того, чтобы найти экстремали ср Е: loo (2), необходимо исследовать лишь его значения в этих четырех точках.
Пример 3. Lp (а, Ь) при р = 1 или оо. Пространства Lx {а, Ь) и Loo (а, Ь) можно рассматривать как предельные случаи пространств Lp (a, b), 1 < р < оо. Напомним, что Loo (а, Ь) — это множество всех (измеримых по Лебегу) функций, таких, что
II х ||оо = ess sup | х (t) | < oo.
Пространство, сопряженное к L1{a, b), совпадает c (a, b). Поэтому мы можем поставить перед собой задачу характеризации экстремального соотношения, отображающего L± (а, Ь) в Loo (а, Ь),
Если х е (а, Ь), то нетрудно видеть, что каждая экстремаль £ S L<„ (а, Ъ) должна принимать в точке t еЕ [а, &] значения X (/), удовлетворяющие условиям:
f sign [*(<)], если х (/) =/□ О, [|2(<)|^1, если £(t) = 0.
В самом деле, из этих условий сразу следует, что || £ || = 1 и что ь	ь
<ж, £} = x(t) sign [х(0] dt = |ж(0 \dt = ||а:||. а	а
Хотя каждое х S (а, Ь) имеет по крайней мере одну экстремаль х Е= Loo (а, Ь), обратное утверждение неверно. В качестве
Рис. 4.10. Две функции, принадлежащие (а, Ь).
примера рассмотрим две функции Д и /2 G (а, Ь), графики которых показаны на рис. 4.10. У функции /2 имеется экстремаль h, где
_ (l/(tz — h) при L < t < t2, i | о	в друГИХ случаях,
а у функции /j экстремали вообще нет. В самом общем случае, если мера М (t) множества т = {£ ЕЕ [а, Ы: / (0 ЕЕ || /1|} отлична от нуля, то функция
(1/т(х) при
/ (^) — I о в друГИХ случаях является экстремалью /.
Пример 4. Другим нетривиальным примером нерефлексивного банахова пространства, не обладающего строгой выпуклостью, может служить пространство С (т). Если т есть замкнутый промежуток [а, Ь], то
||.т||= sup | х (/) I = max |я(0|, ^ЕС[а, fe],
*е[а, Ь]	te[a, Ь]
и единичный шар С [а, Ы состоит, очевидно, из всевозможных непрерывных функций х, значения которых удовлетворяют
неравенству —	(t)	1, tEix (рис. 4.11). Отметим, что у еди-
ничного шара С [а, Ь] имеются в точности две экстремальные точки, а именно постоянные функции х (t) = 1, t СЕ_т, и х (t) = — 1, t е т.
Для того чтобы исследовать экстремали х ЕЕ (а, Ь), принадлежащие С* [а, Ы, рассмотрим множество S = {t ЕЕ [а, Ь]: х (t) = || х ||}. Поскольку каждая непрерывная функция, определенная на любом замкнутом ограниченном промежутке, достигает своей верхней грани, то множество S не пусто. Если положить th ЕЕ S, а через g обозначить ступенчатую функцию
Г 0,	CL t t j£,
gid* 1) — I sign (г (Ml.
TO var (gk) = IlgJ = 1 и, более того, [а, 6] ь
g*) = 5	=|®(М I = 1И1-
a
т. е. экстремалью х служит единичная дельта-функция с особенностью в tk.
Если множество S содержит более одной точки, то ему соответствует несколько экстремалей. Например, если S = {^, ...,£л}, а {#i> •••> ёп} — ступенчатые функции, определенные предшествующими выражениями при условии, что к пробегает значе-
I ния от 1 до тг, то экстремалями х служат не только все
|	।	такие но и все их выпук-
1	•	лые комбинации. Наконец,
а.	&	если мера S отлична от нуля,
Рис. 4.11. Множество U для С [а, Ь]. то экстремали можно построить, интегрируя функции из Ьг (а, Ь). Например, если х совпадает с функцией/2из рис. 4.9, то любая функция Lr (а, Ь), удовлетворяющая условию ||g|| = 1 и условиям
g (О > 0, g (t) = о,
t е ki, U»
t G [д, Ь] \ Ri, £3],
является экстремалью x.
Поскольку пространство С [а, Ь] не рефлексивно, то отсюда следует, что в С* [а, Ь] имеются функционалы, не достигающие своей верхней грани на поверхности единичной сферы С [а, &]. В качестве примера приведем функционал, определенный с
помощью соотношения
7>	г
/ (х) = \ х (t) dt — \ х (t) dt, х^С [а, Ь].
о	7.
Легко показать, что |!/||^1, но в то же время условия sup | х (t) |	1 и / (z) = 1 предполагают, что
х (t) - 1,	0<К 1/2,
x(t) = - 1,	1/2 <	1,
и, очевидно, эта функция не принадлежит С (а, Ь). Но в то же время функционал
/ (z) = я (/) dt о
достигает своей верхней грани в единственной точке — постоянной х (t) = 1.
Экстремальные задачи в произведениях пространств. В первых четырех примерах мы сосредоточили внимание на изучении тех элементарных функциональных пространств, с которыми чаще всего приходится сталкиваться во время исследования систем с одним входом и одним выходом. Однако изучение многомерных систем заставляет нас интересоваться не этими элементарными пространствами, а скорее конечными или бесконечными декартовыми произведениями таких пространств. В качестве примера рассмотрим гибридную систему, схема которой показана на рис. 2.16 (см. § 2.5). Мы уже видели, что эту систему можно представить некоторым линейным преобразованием Т: В -> D одного банахова пространства в другое, причем В, например, можно рассматривать как любое из произведений вида
в = X • • • х 1Рз(б) X LPt+1(x) X ••XLPm(т).
Если все pj удовлетворяют условию 1 < pj < оо, то В является декартовым произведением строго выпуклых рефлексивных пространств. Поэтому естественно задать себе вопрос, а как определить норму на этом декартовом произведении таким образом, чтобы все необходимые свойства пространств-сомножителей автоматически переносились и на пространство В?
Оправдывая наши усилия необходимостью изучения многомерных систем, рассмотрим пространство В =	В., представ-
ляющее собой конечное произведение банаховых пространств i = 1, ..., п. Предположим, что норма, принятая на В, сохра-
352 ГЛ. 4. ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ няет свойства сходимости в том смысле, что если хк есть некоторая последовательность хк = (х\, ..., хкг) ЕЕ В, и такая, что х* я0, то я*Z = 1, 2, ..., м. К аналогичным результатам приводит и условие, согласно которому проектирование В на подпространства В., i = 1, 2, п, должно быть непрерывным. Если эти условия выполнены, то для каждого х = (х1ч ..., хп) ЕЕ В вектор / = (Д,... ..., /п), где /. s В*, i = 1, ..., п, задает с помощью формулы
п
<•*,/> = 2 <xi> /i> i=l
некоторый ограниченный линейный функционал /, определенный на В. И обратно, можно показать, что каждое f ЕЕ В* может быть представлено в таком виде, а следовательно, В* =	. Про
такие нормы говорят, что они сохраняют топологию произведения.
Предположим теперь, что В = ПР=1 В. есть конечное произведение банаховых пространств, наделенное некоторой нормой, сохраняющей топологию произведения. Тогда пространство В рефлексивно в том и только в том случае, когда рефлексивно каждое подпространство В.. Но, с другой стороны, пространство В не наследует строгой выпуклости от пространств-сомножителей В( для столь широкого класса норм, определенных на произведении. (Действительно, вещественная прямая обладает свойством строгой выпуклости, а уже плоскость, рассматриваемая как произведение вещественной прямой на себя, позволяет определить много норм, не обладающих строгой выпуклостью. Например, строгой выпуклости нет у 1± (2) и (2), порожденных 7?2.)
Но хотя сохранить строгую выпуклость и труднее, чем рефлексивность, две следующие теоремы перечисляют несколько норм для произведений, позволяющих получать строго выпуклые пространства.
Теорема Д. Пусть Вх, ..., Вп -— нормированные линейные пространства. Определим для х ~ (лгх, ..., хп) S Bi = = В норму | | с помощью формулы
= lkiir)/P. i<p<oc.
где через || я. || обозначена норма х.в В.. Тогда
(1)	пространство В с нормой | | строго выпукло в том и только в том случае, когда строго выпуклым является каждый из сомножителей Bt, i = 1, ..., п (по отношению к его собственной норме);
(2)	если ф S В*, то ф = (ф, ..., фп), где ф. ЕЕ В., i = 1, ..., п,
и
/ "	_ 1/9
|ф| = (3 ll<PilN > i=l '
Up 4-1/5 = 1;
(3)	если В строго выпукло, <р = (<рп (р„)ЕВ* и q>f есть экстремаль <р. G Вt, i = 1, п, то экстремаль G В функционала <р определяется по формуле
ф = («1Ф1, а2ф2> • • •> апфп),
где

I ф. || (9—1)
ТфТ/
(4)	если каждое из В. рефлексивно и гладко, то этими же свойствами обладает и В, а экстремали X ЕЕ каждого х = (х1? ...
хп) ЕЕ В определяются по формуле
X = (^1^1, [^2^2> • • •»
где [3. = (|| х. ||/1 z|)(p-1), a xi S В* являются экстремалями для x.t В., i = ‘ 1, п.
Доказательство этой теоремы приводится в приложении 6. Следует отметить, что утверждение (4) по отношению к утверждению (3) является двойственным. Все возможные принципиальные трудности, связанные с этой теоремой, проистекают, вероятнее всего, от ее длины, а не от глубины содержащихся в ней утверждений. Вот почему полезно, по-видимому, проиллюстрировать ее содержание на конкретном примере.
Пример 5. Как уже бывало раньше, мы хотим обосновать этот пример необходимостью рассматривать гибридную систему из § 2.5. Для конкретности (но не поступаясь при этом особенно общностью) предположим, что у этой системы два дискретных и два непрерывных входных сигнала. Другими словами, предположим, что
и = (^i, а2) £ lpi (a) X 1Р2 (о) = В± X В2,
V = (рх, р2) е LPi (т) X LPi (т) = В3 X В4.
Предположим еще, что рассматриваются вещественные пространства и что 1 < р. <z оо, а 1/р. + i = 1, i = 1, 2, 3, 4, причем все пространства-сомножители строго выпуклые и гладкие. Более того, мы будем считать, что можно воспользоваться результатами примера 1.
12 У. Портер
Если в пространстве В = П^1В1 определена норма из теоремы Д при некотором 1 < р < оо, т. е. если
|(U„ и„ 1>„ »,) I , II u, f + II и, II" + I Г, I” + II 1’1"’ =
L а	7	а
то норма любого ср = (фь ср2, <р3, ср4) е В*, срг ЕЕ , имеет вид
I ф I = II Ф1 II’ + || Ф2 II’ + II ФЗ II’ + || Ф. ll’l1Z’= I IS I Ф1 1”)’/” +
+ (S । фз (м + QI Фз (о I’’ dt)4/4a + ЦI ф> (о Г1 dt У'4']''4 •
Более того, воспользовавшись утверждением (3) теоремы Е (см. далее), мы можем в точности указать метод вычисления единственной экстремали <р (= В для каждого <р ЕЕ В*. Согласно этому методу первый шаг заключается в вычислении | <р | по формуле, приведенной выше. После того как это сделано, вычисление скаляров af = (II IK | ф| не представляет никакого труда. Компоненты же искомой экстремали должны удовлетворять соотношениям
ф;(0 = ||Ф. ||<1-’j> sign [ср; (<)] • | Ф; (t)	, i = 1, 2, 3, 4,
где t пробегает множества о либо т. При этом вектор
Ф (/, s) = [а^ ($), а2ф2 (5), «зфз (*), а4ф4 (Oh (*, 0 т х о,
оказывается полностью определенным.
Вторая норма для конечного произведения пространств, которую мы хотим отметить особо, представляет собой некоторое видоизменение первой нормы.
Теорема Е. Пусть В — декартово произведение нормированных линейных пространств Вi = 1, п, и пусть [а^] есть некоторая положительно определенная симметрическая матрица размерами (n X и), каждый элемент которой неотрицателен. Тогда функция
*-м = (. 3 МЫ-Ы)‘А
является нормой для х = (хп ..., хп) В, определенной на В. Более того,
(1) пространство В строго выпукло (рефлексивно) в том и только в том случае, когда каждое из пространств-сомножителей В I = 1, п, строго выпукло (рефлексивно);
Р(2) если ф = (фп •••, Фп) S то норма ||| ф|[| преобразования ф определяется по формуле
III т III = ( S ЫчМ-Ы) ’•
i. >1
где через [feij обозначена матрица, обратная [а^];
(3) если ф. G Bi — экстремаль ф* е В* , i = 1, ...» п, то Ф GE В( — экстремаль ф GE Z?*) — определяется по формуле
ф = (<Х1Ф1, а2фа, . . оспфп),
где aj = (111ФЦ1)"1 (2i*=i йо1|ф/1|) » а чисЛ0 III Ф III вычисляется по формуле, приведенной в пункте (2);
(4) если каждое из пространств В. рефлексивно и гладко, то % Ez В*, а экстремаль х ЕЕ В определяется по формуле
% = (^1^1 >	• • •» ^п^п)>
где 6. = (||| л: Щ)"1 (J”=i a.j || ху||), а число HI х HI вычисляется по формуле, приведенной в пункте (2).
Замечание 3. Совершенно ясно, что всякая диагональная матрица с положительными элементами на главной диагонали удовлетворяет условиям теоремы Е, и, следовательно, ею можно воспользоваться для того, чтобы определить строго гладкую норму на произведении пространств. Не менее просто построить разнообразные недиагональные положительно определенные матрицы с неотрицательными элементами. Например, если D — это произвольная матрица размерами (п X п) с неотрицательными элементами, то матрица А = DD* состоит из неотрицательных элементов и неотрицательно определена (А 0). (Получить из А положительно определенную матрицу можно простым добавлением е/, где е > 0.)
Однако утверждения теоремы Е неверны для произвольной положительно определенной матрицы. Убедимся в этом на примере. Пусть
Читатель может убедиться в том, что спектр этой матрицы состоит из точек 1/2 и 5/2 и, следовательно, матрица А является положительной. Положим, далее, в произведении В X В х = (z, — z) и
у = (z, z), где z ЕЕ В и имеет норму, равную 1. Тогда
III *2 III = 4 к II2 - b II2 - h II2 + 4II* II2 = II2II2 =1.
Ill У III2 = 4ll2 II2 - IIz II2-II2II2’1 4hll2 -1.
Однако ч	ч
III * + У III2 = III (2z, 0) |||а = 4II 2z II2 = 4 • 4IIz II2 = 6> так что
НИ + у 111 = /ё>2 = 111 *111 + III у III-
Поэтому матрица А не определяет нормы в пространстве В X В.
Экстремали в пространствах векторных функций. Рассматривая системы одного и того же типа (т. е. системы, в которых все переменные являются либо временными рядами, либо функциями непрерывного времени), мы можем воспринимать задачи, связанные с декартовыми произведениями пространств, и с другой точки зрения. Например, рассмотрим вещественную систему с непрерывным временем и входными воздействиями и = (и19 ..., un), определенными на промежутке т. Пусть норма в пространстве входных сигналов задается выражением
771 л	V
Н = [2) 1«ч(0 Rj ”•
В соответствии с предыдущим мы знаем, что и можно рассматривать как некоторый элемент произведения n£Li Lp (т), на котором, согласно теореме Д, определена соответствующая норма. Однако, не изменяя значения выписанной выше нормы, мы можем преобразовать выражение в правой части так, что
rfl'™	l/р |Р -1VP
ii“ii= [щЗ|мо1р И ’
Т 1=1
Данное выражение подсказывает, что соотношение t ЕЕ т, можно рассматривать как некоторое отображение т на Zp (тп). Другими словами, мы можем считать, что и есть некоторая векторная функция, принимающая значения и (t) Gz Яп, причем ее норма определяется выражением
г т	'll/р
lu(0|p = [Sl«<(0 rj -
В этом случае скалярная функция t -> | и (/) | принадлежит L (т), норма которого имеет следующий вид:
||и|| = Ц|и(0Г^]1/Р,
что согласуется с первой формулой.
Векторным функциям посвящена обширная математическая литература (см., например, главу 3 книги [А. 41]). Большинство привычных операций со скалярными функциями, таких, как дифференцирование, интегрирование и сложение, естественным образом обобщаются на случай векторных функций. В главе 2, во время изучения конечных семейств дифференциальных и конечноразностных уравнений первого порядка, мы познакомились с некоторыми элементарными возможностями такого обобщения. Мы не хотим утверждать, что в более общей ситуации такие обобщения не связаны с некоторыми трудностями. Однако здесь мы удовлетворимся тем, что подытожим результаты, которые представляют наибольший интерес для наших собственных целей.
Обозначим через X некоторое банахово пространство, а через т — промежуток вещественной прямой. Через х (•) мы будем обозначать функцию т-> X, ставящую в соответствие каждому t е т единственный вектор х (Z) е= X. Символ | | призван обозначать норму, определенную для пространства X. Поэтому | х (t) | — это скаляр, а | х (•) | —это некоторая функция, отображающая т в множество вещественных скаляров.
Определение В. Пространство Lp (X, т) состоит из таких функций *) х (•), отображающих хвХ, что | х (t) [р сй]1/р< т
< ОО.
Пространство Lp (X, т) становится банаховым, если ввести в нем нормы
к(-)Цр=	,	1<д<оо,
т ИЛИ
II х (-)оо II = ess sup I х (t) |, p = oo.
jtartt ^ак и в пространствах Lp скалярных функций, для строгого опреде-интог Элементов Ьр (X, т) необходимо воспользоваться обобщенной формой с кяи/)ИР°^аНИ^‘ Если пространство X сепарабельно, то каждое х (•) вместе ттетппт?1?М ' Должно образовывать скалярную функцию <х (•), />, удов-как ряющую Условиям измеримости для скалярных пространств Lp. Так же не стп ДЛЯ пР°стРанств скалярных функций, пространство Lp (х, т) состоит тике И3 ФУинДнй» сколько из классов эквивалентности, хотя на праймы оез особых опасностей можем и забыть про это различие.
Нетрудно показать, что если 1 < р < оо и пространство X рефлексивно, то рефлексивно и Lp (X, т). Более того, сопряженное пространство Lp (X, т) совпадает с пространством Lg (X,* т), где 1/р + Hq = 1.
Норму If ||	1 р < оо, можно рассматривать как резуль-
тат композиции нормы для X с нормой для Lp (т). Интерес представляет и вид функционалов, определенных на Lp (X, т). Воспользуемся обозначением (д;, для обычного билинейного соотношения между X и X*. Обозначим билинейное соотношение между элементами х (•) Е Lp (X, т) и / (•) Е Lg (X*, т) через {х (•), / (-)^ и будем определять их выражением
<>(•),/(-)>=$
т
В данном контексте интерес представляют три различных вида экстремальных функций. Во-первых, для каждого х Е X мы имеем экстремаль (единственную, если пространство X гладко) X Е X*. Во-вторых, каждому а Е L^(t) соответствует экстремаль (единственная, если 1 < р < оо) а Е Lq (т), где 1/р + Hq= = 1. Если предположить, что мы знаем, как вычислять эти две экстремали, то следующая теорема объясняет, как построить третью экстремаль, а именно х (•) Е Lg (X*, т) элемента х (•) Е Е Lp (X, т).
Теорема Ж. Пусть х (•) Е Lp (X, т) и произвольно. Тогда любая экстремаль i (•) Е Lg (X*, т) должна иметь вид
где 1 Р < 00 и 1/р + Hq = 1.
Для ясности еще раз подчеркнем, что через X (Z) обозначена экстремаль в X* для х (t) Е X; функция | х (•) | является элементом пространства Lp (т), а | х	(т) и СЛУЖИТ экстре-
малью этой функции. Число (|х(‘)|)(0 является значением функции \х (•) | в момент времени t Е т. Допуская определенную неточность в обозначениях, мы будем впредь писать, что
x(t) = \x~(t | •#(£), £ЕТ, вместо более правильного, но несколько более длинного обозначения в формулировке теоремы.
Что же касается самого доказательства этой теорему, то прежде всего отметим справедливость неравенств
О(-). /(•)>=$
т
1^(01. |/(0di<k(-)l!p-ll/(-)L
при любых х (•) = Lp (X, т) и / (•) (= Ц (X*, т). Зафиксировав х (•), мы сразу заметим, что последнее неравенство справа справедливо в том и только в том случае, когда | / (•) | е Lq (т) отличается от экстремали | х (•) | С Lv (т) лишь скалярным множителем. В то же время первое из приведенных выше неравенств справедливо тогда и только тогда, когда / (/) е X* пропорционально экстремали х (t) G X при каждом t & т (как и обычно, с точностью до множества меры нуль). Поэтому, если || / (-)1к	1 и
«*(•), /(•)» = I* (•)»₽,
то /(•) должно иметь тот вид, который указан в формулировке теоремы.
Следствие. Пространство Lp (X, т) строго выпукло (гладко), если X строго выпукло (гладко) и 1 < р < оо.
Доказательство, Поскольку гладкость X гарантирует единственность X (t) и | х (•) |, то отсюда следует, что я (t) единственно, и, следовательно, Lp (X, т) гладко. Если же X строго выпукло, то X* гладко, откуда следует гладкость LQ (X*, т), что и доказывает строгую выпуклость пространства Lp (X, т).
Выше мы пользовались довольно сложными обозначениями. В связи с этим нам кажется полезным проиллюстрировать введенные понятия на примере менее абстрактном.
Пример 6. На протяжении всего этого примера пары (г, s) и (р, q) обозначают сопряженные индексы (т. е. 1/г + 1/$ — = Ир + \lq = 1), а через X обозначается вещественное п-мер-ное пространство 1Г (п), на котором определена обычная (см. примеры 1 и 2) норма | |гдля случая, когда 1^г<оо. Вместо того чтобы пользоваться довольно запутанным обозначением Lp (1Г (п), т), мы будем обозначать это пространство всевозможных конечных векторных функций т—> 1Г (п) с определенной на нем нормой
1И1р = |r ^|1/Р, X^Bp,r,	l^r^oo,
т
просто через Вр>г.
Выше мы уже отмечали, что пространства Вр,г и Bqt8 для 1 < г, р < сю идентичны. Полезно набросать схему вычисления экстремалей элементов ВР,Т, принадлежащих Bq,r. Из примера 2 для 1 г о° мы знаем, что единственной экстремалью £ Е /2 (п) служит элемент £ ЕЕ Z8 (п), 1/г + 1/s = 1, вычисляемый по формуле
1 = 1? Гг> (11, .... In), L = Sign [Ы . I Ii
Для того чтобы воспользоваться утверждениями теоремы Ж, на помним, что в примере 1 мы установили, что для z ЕЕ Lp (т
экстремалью является элемент	\lp-\-llq = 1, следую-
щего вида:
2 (О = II2 Up_р)sign [z(0] • / z (0|(р-1), , t Et
Располагая этими формулами, мы можем вычислить и экстремаль ф ЕЕ Bqi3 элемента х (ЕЕ Вр,г. Воспользовавшись для этого теоремой Ж, получим
M) = k(0lr1-r)MO. •. ,Ш
(0 = sign [Xi (0] I xt (0	t e T,
I ^t) |r = [g | x (01? dljllp](1-p) I X (0 |'p-1) T
и, наконец,
х(О = (М)10М). <Et.
Но так как найденные выражения довольно сложны, то полезно проверить справедливость результата, выписанного выше. Прежде всего заметим, что
<(#, ж) = <.т (£), х (£)> dt = | х (t) (х (/), х (£)> dt,
где
МО, х(0> = |х(О|М2 1М0Г = 1* (0 k 1=1
Подстановка второго выражения в первое показывает, что
«X, х» = $ I |г • | X (0 \rdt = $ || rr II'1-1» . | X (0 I? dt = || X ||р. т	г
Но так как известно, что «х, х» = ||х||, то остается лишь показать, что ||i|| = 1. Для того чтобы убедиться в этом, докажем сначала, что |£ (0|3 =\| я (0|г> что следует из цепочки равенств, выписанных ниже:
/ п	\ 1/в
। а (о |,=। а х7?) io । • । х (0 (,=। хТо |г • । х (01'1-’) .(si	i •) =
1=1
n	,
= ix70|r.|x(0i'1-r)-(3ki(Oir)1' =
4=i	z
= I x7) |r . I x (0 IM . IX (0 1Г11 = IM) L
Но теперь
||х || = g I i (О I? dt\i/9 = [$ (| ® (0 Jr)’ dt]llq =
= [($ к (0 |?df)1/₽](1"p) IX (t) \^-»dt]llq,
а так как q (р — 1) = Р и 1/<7 = (Р ~ Wp> то мы сразу убеждаемся в том, что ||i|| = !•
Пример 7. Для приложении интерес представляет и предельный случай р, г = 1. Договоримся рассматривать В^, г как пространство всевозможных n-мерных векторов х (t) = [хг (t), ... ..., хп (Ob с нормой
Ы» = sup{(x(0|r}, .-re-Boo.
Тогда можно показать, что если и = 1, то 2?*г =	==
= ^оооо и Bptl = BqtOO. Пространства ВЬг и ВРэ1, 1 р, г < < оо, не являются гладкими. Поэтому экстремали в соответствующих сопряженных пространствах не должны быть единственными. Эти пространства исследовались Гриммеллом [Б. 43], которому удалось вывести для этих экстремалей уравнения, их определяющие.
, Элемент х ЕЕ В^^:
х (t) = (х± (£), ..., хп (/)), t е т,
является экстремалью элемента х ЕЕ Вх г:
X (О = (*1 (t), хп (0), t G т, если он удовлетворяет следующим условиям:
1.	Если 5 — 1, то
(t) =	(t) sign (/)], Z СЕ r, i -= 1, ..., /г,
где ki («) >0, f e T, i - 1, ..., zi, 7U />•; (t) И, t S т и ki (t) = 0 каждый раз, когда | x-t (t) | <C max/{|.r, (t) |}.
2.	Если 1 < s <Z oo, Vs -|- г/г ~= 1, to
i-i (0 = M (Z) | xt (t) |,,/s sign [х; (<)], t S t, i = 1, 2, ..., n, где
n	1/s
M(0 = [Si^(0ir] ls.
3.	Если 5 = OO, TO
xi (0 = sign [xt (/)], если Xi (t) =f= 0, | Xi (t) |	1,	если xt (t) = 0,
У п р аж йен и я
1.	Обозначим через и- минимальный элемент Т~1 (£). Покажите, что является минимальным элементом Т~1 (Л£).
2.	Воспользуйтесь теоремой Хана — Банаха для того, чтобы показать, что если пространство В рефлексивно, то для каждого f & В* существует такое и В, || и || = 1, что f (и) = || / Ц.
3.	Докажите, что каждое гильбертово пространство Н строго выпукло и гладко. Докажите, что экстремалью х ЕЕ Н служит т = х/||х||.
4.	Доведите до конца доказательство теоремы Б, показав, что из (1) следует (2).
Указание. Перегруппируйте члены в выражении || [а|| лг2||*1 + (1 — а)||х1||х2]|| и воспользуйтесь неравенством треугольника.
5.	Пусть С есть некоторое выпуклое множество в банаховом пространстве В, и пусть | ЕЕ 6С. Покажите, что множество всех нормалей к Св точке 5, направленных наружу, образует конус. Покажите, что конус образуют и экстремали элемента х Е: В.
6.	Покажите, что пространство L2 (X, т) является гильбертовым, если только гильбертово пространство X. Проиллюстрируйте это на примере X = 12.
7.	Рассмотрим три банаховых пространства: В — Lp(a, с), В{ — Lp (а, Ь) иВ2 = Lp (b, с), где а b с, 1 < р < сю. Убедитесь в том, что пространство В можно рассматривать как произведение Вг и В2, если вектор £ — (х19 х2) рассматривать как функцию
/п _(»>('). 'е|МЬ х( >~ 1*2(0. с]
и если определить в В норму согласно теореме Г. Из этого результата получите» что если Т Е: Lq (т) является экстремалью х ЕЕ Lp (t), то экстремалью любого «куска» х служит соответствующий «кусок» х.
8.	Рассмотрим систему, в которой выходная величина х связывается с входным воздействием следующим соотношением:
I
х (/) = Ж (t, .s) и (.s) ds, t 0.
о
Рассматриваемая система работает по двухступенчатому принципу, в связи с чем ее критерий качества имеет следующий вид:
/(«) = [ jj |u (s)|’/* rf,]2P/3 + [ ( Ц (,) I u (,v) |« dv]P/2 , 0	/1
где p (/) > 0 при всех f >0 u 1 < p < ю. Найдите единственное управляющее воздействие м, удовлетворяющее условию х (/2)	5 и минимизирующее
при этом J.
Указание. Воспользуйтесь результатом упражнения 7.
9.	Обозначим через В банахово пространство Вг X В2, в котором определена норма
III (U1. u2) III = 1 (|| U1II, |Ы|)|,
где символом ||	|| обозначены нормы в Вг и В2, а символом | | — норма
в В2. Обозначим через I/, иг и С73 единичные шары в этих пространствах.
Покажите, что
или что, другими словами,
U 23 {(мх, 112):	1/2 G (1 - a) U2, 0 а < 1}.
Покажите что если ||| (up и2) |1| = II Ui II + II и2 ||, то справедливо обратное отношение включения. Приведите пример, в котором обратное отношение включе-пия не имеет места.
10.	Обозначим через В пространство Ц (/•. (п), т) из примеров (> и 7. Дру-гими словами, пусть
_ п
х = (xi ,... ,xfl) GE В.
Покажите, что В* ~	(/2 (и); т) и
что
II / II = sup

/
Покажите, формуле
что экстремали i tz В*
элемента х fe В определяются по
х(1)
1^(0 I ’
x(/)=tO,

для / е т, где
4.3. Решение задачи 1
После того как мы ознакомились с содержанием §§ 4.1 и 4.2, мы готовы к решению задачи 1. На протяжении всего этого параграфа мы будем обозначать через В и D банаховы пространства, а через Т — ограниченное линейное преобразование, отображающее В на D. Обозначим через U и д0 единичный шар В и его границу соответственно, а через С -- Т (U) - образ U в D при преобразовании Т. Граничное множество для С будем обозначать через дС. Элементарные свойства множества С подытоживаются в лемме А.
Лемма А. (а) Множество С представляет собой выпуклую уравновешенную окрестность 0 в пространстве D\
(б) С П дС С Т (dU)\
(в) Множество С замкнуто в том и только в том случае, когда дС Q Т (dU).
Доказательство. Выпуклость и уравновешенность множества С следуют сразу из линейности преобразования Т и определения
множества С. Поскольку 7’ является накрытием, то из теоремы об открытых отображениях (см. приложение 7) вытекает, что Т ([/) содержит некоторый шар, подобный единичному шару для пространства jD, и, значит, С является окрестностью нулевого элемента D. Для того чтобы доказать утверждение (б), предположим, что £ = С Г) дС. Тогда £ ~ Ти для некоторого ueeU . Более того, если X > 1, то Си, следовательно, Ku Е: U. Но это значит, что ||и||>1/Х, а так как X произвольно, то ||и||^>1. Поэтому IeT (dU) *). Наконец, если С замкнуто, то дС = С П дС и, в силу (б), дС С Т (dU). И обратно, условие дС CZ Т (dU) га-рантирует, что дС CZ Т (U) = С, так что С должно быть замкнутым.
Замечание 1. Легко построить пример, показывающий, что в общем случае отношение, обратное отношению включения (в), не имеет места. Например, пусть В — трехмерное евклидово пространство, и пусть Т есть линейное преобразование, отображающее В на двумерное евклидово пространство и заданное формулой
Т (л^, х2, х3) = (хп х2).
Тогда
U = [(xn x2l х3): | a:i |2 + кг |2 + | ^212 < И и
т (U) = С = [(Л, х2):|х1|2 + |х2|2< 1].
Вектор (0, 0, 1) принадлежит dU, в то время как его образ (0, 0), безусловно, не является граничной точкой С.
Л е м м а Б. Если £ €= дС, то каждый прообраз £ имеет норму не меньше 1.
Доказательство. В силу леммы А замыкание С представляет собой выпуклое тело. Поэтому, если £ ЕЕ дС. то существует такое фЕЙ*, что
Re <£» ф> > Re <т], ф>,
каковы бы ни были т] ЕЕ С. Но так как множество С = Т (U) уравновешенно, то отсюда следует, что
Re <5, ф> | {Ти, ф> | = | <u, Г* ф> | при всех и ЕЕ U.
Находя верхнюю грань по U для правой части этого неравенствав получим, что
Re <5, ф> >ЦТ *<рЦ.
♦) Утверждение (б) можно было бы доказать еще, заметив, что поскольку Т отображает открытые множества в открытые, то Т [int (£7)] должно быть открытым подмножеством С, а следовательно, int (С) с Т [int (Z7)J, откуда следует, что С Q дС С Т (dU).
Отсюда же следует, что если и В отображается в g, то
М-Il Т *ф||> Re <u, Т *Ф> = Re <g, ф>>|| Т * ф||
и, значит, || u|| > 1.
Воспользуемся обозначением Т 1 (£) для множества всех прообразов D. Наша следующая теорема показывает, в каких случаях в множестве T~l (£) существует минимальный элемент.
Т е о р е м а А. Пусть g ЕЕ дС. Тогда для того, чтобы в множестве	имелся минимальный элемент, необходимо и до-
статочно, чтобы % £Е С.
Доказательство. Если	П дС, то 7 1 (5) содержит ка-
кой-то элемент U, а так как £ (ЕЕ: дС, то из леммы Б следует, что у этого элемента минимальная норма. И обратно, предположим, что и^ представляет собой минимальный элемент 71-1 (£). Из факта однородности Т следует, что аи? должен быть минимальным элементом 77-1 (а£), каково бы ни было а > 0. По если а < 1, то а£ е С и, следовательно, имеет прообраз с нормой не больше 1. Отсюда ||аиг||	1. А так как а произвольно, то ||^||	1. Сле-
довательно, ЕЕ dU и £ = ЕЕ С.
Следствие 1. 77-1 (5) содержит минимальна элемент для каждого D в томи только в том случае, когда С замкнуто.
Доказательство. Если в множестве T~l (£) имеется минимальный элемент, то, каково бы ни было £ ЕЕ D, в силу теоремы А каждое £ GE dU принадлежит и С. И обратно, предположим, что С замкнуто и что р является функционалом Минковского для С. Если 5=/=0 принадлежит D, то нетрудно показать, что [/>(£)] t= дС f) С, откуда в силу теоремы А для элемента 1р (£)]-1£ су-ществует минимальный прообраз, а значит, минимальный прообраз имеется и у
В теореме А и ее следствии 1 мы выделили ключевые составляющие вопроса о существовании решения задачи 1. Под этим углом зрения легко понять наши предыдущие результаты, касавшиеся преобразований единичного ранга. Более того, соображения, высказанные после формулировки теоремы А в § 4.2, имеют удивительное сходство с нынешним вопросом о существовании решения задачи 1.
Наш первый пример показывает, что даже для простейшей физической системы множество С может иметь очень интересный характер.
Пример 1. На рис. 4.12 показана упрощенная схема системы с тремя интеграторами и ключами. Предположим, что входными сигналами этой системы служат непрерывные функции, а нас интересуют лишь значения выходных величин {лг1э х2, х3} в момент времени t = 1. Если предположить, что в начальный момент времени выходные сигналы всех интеграторов равны нулю, то ясно, что эту систему можно описать линейным преобразованием
Тх С (0, 1) ->7?3. Для того чтобы определить Т, нам остается только задаться законом переключений в системе. Предположим, что средний ключ переключается всего один раз в момент t = 1/2, изменяя полярность входного сигнала с плюса на минус. Нижний
Рис. 4.12. Простейшая линейная система.
ключ переключается трижды в моменты времени {1/4, 1/2, 3/4}, причем в начальный момент времени он подает входные сигналы с положительной полярностью.
Обозначим через х (а> &) характеристическую функцию промежутка (а, 6] и введем в рассмотрение три функции: Д = х (°» !)♦ /г = Х(О, 1/2) -Х(1/«,1) и /з = Х(0,	1/4)-Х(1/4,1/4) +-
+ Х(1Л, 3А)— ХС'Л. !). каж
дая из которых имеет ограниченную вариацию и может быть использована для определения следующих функционалов на С (О, 1):
1
Д (и) = (и, /х> = и (s) ds, нееС (0, 1), о
1/1	*
/г(и) =	/а) — u(s)ds — ( u(s)ds, и ЕЕ С (0, 1),
о	Vi
7<	V»
/з (и) = <и, /з) = ( и (s) ds — ^u (s) ds +
0	Vi
V.	1
+ и (s) ds — и (s) ds, и EEC (0, 1).
V»	’/4
Пользуясь этими определениями, мы можем представить преобразование, производимое системой, в виде
з
т = 2 «<> <м i=l
где {е1? е2, е3} образуют координатный базис в R3.
Замыкание множества С = Т (U) для этой системы имеет вид выпуклой оболочки совокупности точек {(1,0,0), (0,1, 0), (0, 0, 1),
(1/2, 1/2, 1/2), (1/2, —1/2, 1/2), (1/2, 1/2, -1/2), (1/2, -1/2, —1/2)} и множества, получающегося отсюда умножением на —1. Таким образом, в каждом октанте R3 множество О имеет одинаковую форму равностороннего треугольника (рис. 4.13). Множества С и О могут отличаться друг от друга лишь некоторыми граничными точками. Можно показать, что множество С имеет один вид в четырех из восьми октантов R3 и другой — в остальных четырех.
Рис. 4.13. Вид множества С в двух октантах.

Четыре октанта, где множество С имеет первый вид,— это те октанты, которые содержат точки (1/2,1/2, 1/2), (1/2—1/2, 1/2), (--1/2, 1/2, 1/2) и ( — 1/2, —1/2, —1/2). Вид множества С для одного из этих октантов показан на рис. 4.13, а. В этом октанте множеству С не принадлежат только граничные точки (0, 0, 1) и (1/2, 1/2, 1/2), прямолинейный отрезок между ними и изолированная точка (О, 1, 0).
В остальных октантах множество С отличается от множества С гораздо значительней. На рис. 4.13, б изображено множество С в октанте, содержащем точку (1/2, 1/2, —1/2). Нетрудно показать, что грань дС, представляющая собой выпуклую оболочку множества {(0, 1, 0), (0, 0, —1), (1/2, 1/2, —1/2)}, не принадлежит С. Остальная же часть дС в этом октанте принадлежит С.
Два случая, когда С замкнуто. Особый интерес представляет ситуация, в которой задача 1 имеет решение для каждого £ GE D. Мы рассмотрим сейчас два частных случая, когда это имеет место. В обоих случаях пространство В является сопряженным по отношению к некоторому другому пространству. Другими словами, мы предполагаем существование другого банахова пространства X такого, что X* = В. С первым случаем мы сталкиваемся тогда, когда пространство В рефлексивно [в этом случае в качестве X можно принять В *, так как В ** = (В ♦) * = BJ. Тогда, если Т — произвольное ограниченное линейное преобразование, то множество С замкнуто. Другими словами, мы можем решить
задачу 1 для любого линейного ограниченного преобразования Т' определенного на В, независимо от характера его области значе" ний, если только В рефлексивно, а Т является накрытием. И обратно, если задача 1 имеет решение для любого линейного ограниченного преобразования (и, в частности, для преобразования единичного ранга), то результат Джеймса, о котором упоминалось ранее, показывает, что пространство В должно быть рефлексивным. Все это позволяет нам сформулировать новое следствие из теоремы А.
Следствие 2. Задача 1 имеет решение для каждого ограниченного линейного (сюръективного) преобразования, определенного на В, в том и только в том случае, когда пространство В рефлексивно.
Во втором случае, о котором мы будем говорить ниже, условие «пространство В рефлексивно» можно заменить дополнительными условиями, накладываемыми на преобразование Т и простран' ство D. В этом случае необходимо, чтобы существовало такое банахово пространство Y, что /)	У*. Обозначим через 5: Y X
некоторое ограниченное линейное преобразование, отображающее Y в X. Тогда S * есть ограниченное линейное преобразование, отображающее В в D, как это и требуется в задаче 1. (Читателю может оказаться полезным построить диаграммы связей между множествами для этого случая.) Но если S определено на всех элементах У, взаимно однозначно и отображает У на некоторое замкнутое подпространство X, то множество С = S * (17) CZ CZ D - У* должно быть замкнутым. Таким образом, мы доказали еще одно следствие.
Следствие 3. Пусть S — взаимно однозначное ограниченное линейное преобразование, отображающее У на некоторое замкнутое подпространство X. Тогда задача 1 всегда имеет решение для преобразования Т = S*, т. е. для всякого % D ~ У* найдется прообраз и^ЕЕ В = X* элемента £ при преобразовании Т — S*, обладающий минимальной нормой.
Строгое доказательство следствий 2 и 3 вновь заставляет нас прибегать к топологическим соображениям. Как и всюду в подобных случаях, мы ограничимся лишь наброском соответствующего доказательства, останавливаясь подробно лишь на оценке полученного результата.
Доказательство. Стандартный способ доказательства того, что некоторое преобразование отображает замкнутые множества в замкнутые множества, состоит в том, что сначала выясняют бикомпактность области определения этого преобразования, а затем основываются на том факте, что непрерывное отображение бикомпактного множеств должно быть бикомпактным. Известно, что если только В не конечномерно, то множество U не является бикомпактным в топологии, порождаемой нормой этого простран
ства Однако может оказаться, что U бикомпактно в другой топологии для В. Поэтому, если U слабо компактно (поскольку Т остается непрерывным при введении в В и D соответствующих слабых топологий), то множество С оказывается слабо бикомпактным в D. А каждое множество, замкнутое в слабой топологии, замкнуто и в топологии, порождаемой нормой. Наконец, для того чтобы U было слабо бикомпактным, необходимо и достаточно, чтобы пространство В было рефлексивным, так что следствие 2 доказано.
Ранее мы уже упоминали о том, что единичный шар в пространстве, двойственном любому банахову пространству, слабо ♦ бикомпактен (теорема Ллаоглу). Это позволяет сразу получить утверждение следствия 3. Точнее говоря, при его доказательстве мы пользуемся следующими фактами: если S есть некоторое ограниченное линейное преобразование банахова пространства Y в банахово пространство X, то преобразование 5*, ему сопряженное, отображает У* в X*. Отображение 5* непрерывно в слабых ♦-топологиях пространств X* и У*. Поэтому, если через U обозначить единичный шар в X*, то множество 5* (С7*) слабо ♦-бикомпактно в У* и, следовательно, замкнуто в У* по отношению к топологии, порождаемой нормой. Но если S взаимно однозначно и имеет замкнутую область значений, то согласно теореме Б из приложения 7 множество 5* (£7*) содержит множество, кратное единичному шару в У*.
Наконец, из следствия 2 непосредственно вытекает, что если пространство В конечномерно, то у задачи 1 всегда имеется решение. К аналогичному результату мы приходим, если D конечномерно, a S взаимно однозначно. В этом случае следствие 3 гарантирует существование решения задачи 1 для каждого 5	У*.
Характер оптимального управления. Теперь, после того как мы установили необходимые и достаточные условия существования решения задачи 1, наше внимание должно быть сосредоточено на попытках более конкретного описания множества дС Г) С и получения уравнений, описывающих решения задачи 1. Как и в § 4.2, будем обозначать через f ЕЕ В (х (Е В*) экстремали или множества всех экстремалей элемента / е В* (х Е В).
Теорема Б. Пусть ф Р*, и пусть множество 7*ф не пусто. Тогда справедливо следующее теоретико-множественное соотношение: Т (Е С Q дС. И обратно, каждое % Е С П дС может быть представлено в виде Т (Т*ф), для некоторого ф е D*, для которого множество Т*ф не пусто.
Доказательство. Пусть ф D* задано, и пусть 7*ф соответствует экстремаль и^. принадлежащая D. Предположим, что /	Ясно, что С, и, следовательно, нам остается до-
казать, что ее дС. С этой целью заметим прежде всего, что каж
дый вектор ц ЕЕ С можно представить в виде ц = Ти, где и ЕЕ U, и, следовательно,
Re<T], <р> = Re (и, Г*фХ|]7’*ф|| = <мФ, Г*Ф> =	Ф>.
Другими словами, функционал ф достигает своего максимального значения на С в точке £ф, что вместе с тем фактом, согласно которому любой линейный функционал отображает открытые множества в открытые множества, показывает, что не может принадлежать внутренности С. А это и доказывает, что {Т (Г*ф): ф ЕЕ е Z)*} СЕ С П дС\
Для завершения доказательства нужно показать, что если 5 CZ С р) дС, то каждый максимальный прообраз существование которого гарантируется теоремой Л, может быть представлен в виде Г*ф, где ф Е= 79*. Но так как £ ЕЕ ОС, а у С имеется внутренность (выпуклое тело), то можно выбрать вектор ф так, чтобы
Re<£, Ф>>И*ф||.
С другой стороны, принадлежит С и, следовательно, £ — Ти, где и ЕЕ £7, так что
|| Г*ф|| > Re <u, 7*ф> Re <Е, ф>.
Эти два неравенства вместе доказывают, что (£, ф) вещественно и что
<и, г*ф> -- <£, ф> ~ |1 г*ф||.
А так как и е U, то отсюда следует, что и представляет собой экстремаль Т*ф и, значит, £ ~ Ти ЕЕ {Т (7*ф): ф ЕЕ D*}.
Взаимосвязь между £ и ф уточняется следствием 1.
Следствие 1. Если £ G С[}дС, mo £ — Т (Г*ф) для некс-гпорого ф ЕЕ D* в том и только в том случае, когда это определяет одну из опорных гиперплоскостей к С в точке £.
Доказательство. Доказывая теорему Б, мы показали, что если ф определяет опорную гиперплоскость к С в точке 5» то Т (Т*ф) = %. И обратно, если вектор ф ЕЕ Z)* удовлетворяет условию Т (Г*ф) = то для каждого и ЕЕ U
Re (Ти, ф> - Re (и, Т*ф> < || Т*ф|| - <Т*ф, Г*ф> - <£, ф> и, следовательно, гиперплоскость
{п: <ль ф> = <£, Ф>}
является опорной по отношению к С и проходит через точку
Следствие 2. Пусть £ ЕЕ Q С, и пусть ф определяет гиперплоскость к С в точке £. Тогда Г*ф достигает своей верхней грани на U. Обратно, если для некоторого ф ЕЕ D* функционал
Т*<р достигает на U своей верхней грани, то у множества Т 1 (ЕФ) имеется минимальный элемент, каково бы ни было S Т (Т*ф).
Доказательство. Если ф определяет опорную гиперплоскость для С в точке В, то из доказательства теоремы Б следует, что у r*<p имеется экстремаль. И обратно, если Г*ф не пусто при некотором <р GE D*, то в соответствии с теоремой Б Т (Т*у) CZ С f) дС. А отсюда по теореме Л у каждого е Т (7'*ф) имеется минималь-
ный прообраз.
Замечание 2. Если пространство В рефлексивно или если выполняются условия следствия 3 теоремы А, то, комбинируя
Рис. 4.14. Линейная система второго порядка.
утверждения теорем А и Б, мы убедимся в том, что у 71”1 (£) имеется минимальный элемент, каково бы ни было £ Gz D. Каждый такой минимальный элемент должен иметь вид ~ р (5) где ф — некоторая направленная наружу нормаль к С в точке [р	а Т*ф — некоторая экстремаль Т*ф. Если же в по-
следнем случае пространство Y рефлексивно, то ф можно рассматривать как элемент У, а не как элемент/)* = (У*)*. Аналогичным образом мы можем заменить Г* на его сужение на У, т. е. на S. Определяя для элементов X экстремали, принадлежащие В = X*, мы, вместо того чтобы находить их для элементов X** и получать результаты в пространстве X*, сможем представить искомые минимальные элементы в виде = р (£)(5ф).
С помощью теоремы Б и ее следствий нам удалось свести задачу оптимального управления к задаче построения опорных гиперплоскостей для выпуклых множеств и вычислению экстремалей в банаховых пространствах. Для того чтобы проиллюстрировать это на примере конкретной ситуации, рассмотрим физическую систему, для которой множество С замкнуто.
Пример 2 (Гриммелл [Б. 431). Мы уже видели, что самые разнообразные простые динамические системы описываются целиком или частично дифференциальными уравнениями второго порядка. На рис. 4.14 показана схема аналогового устройства, моделирующего систему, описывающуюся уравнениями
Для того чтобы добиться в этом примере абсолютной конкретности, выберем для параметров системы следующие численные значения: а = 1/2, b = —1/2, с =1/2, d = — 1/2, е = 1, / = 1, g = 1 и h = —1. В этом случае уравнения (1) можно переписать в следующем эквивалентном виде:
Г xi (О
L хъ (0 .
VaG-M ^2 G — ^о)
*/2 G М
1 _1/2(/_/о)_
xi Go) 1
X2 Go) J
+

1 -l/2 (t - S)J ' [1
1
-1
(S)
U2 (s)
(2)
Для того чтобы исследовать задачу оптимального перехода [xi Go), х2 Go)l -Н*! (fy), х2 G/)b достаточно решить задачу £ = = Ти, где и (0 = Iи± (0, и2 (Ob t S Go> Ob £ = (£i, £2),
41 ’ _ -1/а х/з
Ла- -х/г —Оа
1 Х/а G 0)
х/а G 0) I xi (0) । l + OaG-QJ Ъа G/)J
xi Go) I \ -х’а Go) J '
а Т — линейное преобразование, отображающее и в R2 согласно правилу
G1 ио
— (S —/0) r«i(s)
4	*	/ X И5
1 J Liz2(s) J
(3)
Критерий оптимальности, который мы собираемся здесь использовать, был выбран на основании энергетических соображений, уже излагавшихся ранее. Предположим, что речь идет о некоторой механической системе, и функции иг и и2 описывают мгновенные расходы топлива. Однако, максимальный расход топлива
чаще всего ограничен величиной просвета управляющего клапана либо диаметром линии подачи топлива. Другими словами, расход топлива в таких системах имеет характеристику насыщения. Во время проектирования регулятора такое насыщение следует принимать во внимание. Даже в нашем простейшем примере насыщение может быть самого различного типа.
Случай 1. Рассмотрим сначала ситуацию, в которой иг и и2 описывают подачу топлива от независимых источников питания, а насыщение наступает при одинаковом значении*) подачи для обоих источников. Если же суммарные запасы топлива каждого из источников сами по себе не ограничены, то в качестве критерия оптимальности естественно выбрать функционал
J (ц) = sup max {| иг (/) |, | иа (Г) |}.
Без особого ограничения технического содержания задачи можно потребовать, чтобы и и2 были измеримыми. Тогда J (и) совпадает с нормой вектора (un п2), рассматриваемого как элемент пространства В^^ (см. пример 7 к § 4.2 для случая п = 2). Поэтому задачи оптимального управления и задачи о минимизации нормы прообраза 1- для отображения Т:	идентичны
с математической точки зрения.
Для того чтобы воспользоваться методами этого параграфа, выясним прежде всего характеристики нашего преобразования и его области определения. Пространство В^ оо не рефлексивно, но мы знаем, что оно является сопряженным по отношению к банахову пространству Blfl. Если в качестве S выбрать преобразование В2 —вида
г 1	От г Ф11
J • 1ф,]’	w
где ф = (фь ф2)	У?2, то нетрудно показать, что Т = S*. Более
того, S накрывает некоторое замкнутое подпространство В1А, а именно многообразие, натянутое на столбцы матрицы S.
Таким образом, на основании следствия 3 из теоремы А мы можем заключить, что множество С = Т (U) замкнуто. Воспользовавшись правилами вычисления экстремалей, содержащимися в примере 7 из § 4.2, мы видим, что вектор (un и2) является экстремалью 5ф, если
(t\= JsignI<p11,	Ф1=£°>
U1 1|«1(01<1.	Ф1 = (М(=Ро,Ы.	5)
_МО = sign [(Zo — Оф! + ф2], t s [/0, tf].
*) Разумный выбор переменных часто позволяет свести более сложные ограничения к этому виду.
Случай 2. Предположим теперь, что щ и и2 — это мгновенные расходы подачи топлива, поступающего из одного источника, и что для рассматриваемой системы роль ограничивающего фактора играет суммарный мгновенный расход (производительность источника). В этом случае в качестве критерия оптимальности разумно выбрать функционал
J (и) = sup ( | «I (<) I + | «2 («) I )-
Этот функционал совпадает с нормой вектора (ир и2) как элемента пространства 5оо, 1- Поэтому с математической точки зрения задача оптимального управления — это задача минимизации нормы для отображения Т: B^i —>Я2.
Мы убедились ранее в том, что ^оо, i является сопряженным по отношению к пространству и что S, определенное раньше, можно рассматривать как линейное преобразование Я2 -^Я1оо, причем Т* = S. Тогда, воспользовавшись следствием 2 из теоремы А, мы видим, что образ единичного шара в 5ooi, замкнут. Учитывая форму S и результаты примера 7 из § 4.2, находим, что вектор (мп w2) является экстремалью 5ф, если
_ fsign
"l() I 0,
(G) fsign 1<ра Н-(<0 — <) qjil, t^[t0,tt]\E, “m’l о,	les,
где
Е = {/(= [<0) tj: |Ф1| >| <р2 + (t0 - 0Ф1|)
Поскольку множество С замкнуто, то вид дС можно установить, вычисляя значения {Т (5ф): ф ЕЕ Я2}. В данном примере такие расчеты не представляют труда. Множества С для обоих случаев (при tQ = 0 и tf = 1) изображены на рис. 4.15.
Полезно разобраться до конца во всех этапах определения управляющего воздействия с минимальной нормой. В качестве конкретного примера рассмотрим ситуацию, в которой целью служит точка £ = (23,—8). Поскольку вид дС определен явно, то можно без труда найти, в какой точке луч, соединяющий начало координат с пересекает дС. С точностью до четвертого знака координаты этой точки пересечения имеют вид — (0,946, —0,329) в случае 2 и - (1,450, —0,500) в случае 1.
Для случая 2 внешняя нормаль к С в точке имеет вид ф = “ (1, —0,329). Используя уравнение (4), мы находим, что
<*»(')-[ _,_10329 ]. <е[0,ц.
Теперь, вычисляя экстремаль мы сумеем найти и прообраз обладающий минимальной нормой. А так как £ = 24,9£", то, умножая уравнение экстремали на 24,9, мы найдем в результате
Рис. 4.15. Два образа единичного шара.
а) Случай 1: К - {(£„ &г):	— 1,5= -0,25 (&, + 1)’},
L - {(£•„	- 1, 0}.
б) Случай 2: И - {(£,.	- 1,5 = -0,5 (fc, + I)2},
J {(51, 5г)= 5i - 1 = -0,5$.
прообраз £ с минимальной нормой. Таким образом, получается следующий вектор управляющих воздействий:
их (0 = 24,9, wa(0_ 0 при 0<f <0,671,
Ui (/) = 0,	п2(0 = —24,9 при 0,671 </<1.
Для случая 1 внешняя нормаль к С в точке % имеет вид ср = — 4,1. Отсюда следует, что
(5ф)(0 = [ _4* + 1 ], «еЮ, 1],
и так как | — 16|', то оптимальное управление для этого случая определяется условиями:
их (/) = 16 для 0 t 1;
16
-16
для Qi^zt <0,25,
для 0,25 <<<1.
На этом решение нашей задачи оптимального управления заканчивается. •
Пример 2 позволяет подметить несколько важных черт решения задачи 1. Из рис. 4.15 следует, что у множества С могут быть как плоские участки границы, так и угловые точки. Плоский участок для случая 1 возникает из-за того, что нормали ф = (0,1), порожденной 5, соответствует функционал с неединственной экстремалью (см. уравнение (5)). Преобразование Т отображает множество {5 (0,1)} в прямолинейный отрезок L. Однако легко показать, что минимальный прообраз для каждой точки L не единствен. На стыке множеств R и L имеется целый конус внешних нормалей к С. Для каждого ф = (фг, Ф2) из этого конуса, где ф! =£= 0, справедливо соотношение ф2 +	— ^/)ф1 > 0. В со-
ответствии с уравнением (5) это значит, что оптимальное управление для таких конечных условий единственно.
Такая неопределенность не является какой-либо особенностью системы из примера 2. В упражнении 1 вы познакомитесь со второй системой, у которой внешняя нормаль к дС в некоторых точках неоднозначна, хотя оптимальное управление для соответствующих конечных условий и остается единственным. В других же точках дС имеется всего одна внешняя нормаль, а соответствующее оптимальное управление все же не единственно.
С первого взгляда неединственность оптимального управления, наблюдаемая во многих случаях, кажется неприятной. Однако с технической точки зрения подобную неопределенность можно только приветствовать, так как она обеспечивает определенную гибкость выбора управляющего воздействия, дополнительную степень свободы, которую, возможно, удастся использовать для решения некоторой другой операционной задачи, например для уменьшения степени захода характеристик в некую конкретную область пространства состояний системы. Возникающую неопределенность можно к тому же и устранить, потребовав минимизации некоторого второстепенного критерия качества, определяющегося такими факторами, как простота управляющего устройства, ширина полосы пропускания для канала передачи сигнала или чувствительность системы к ожидаемым возмущениям. Конструктор системы может также с пользой для дела использовать эту неопределенность и для того, чтобы попытаться минимизировать неизбежную разницу между математической моделью, используемой при оптимизации,1 и действительным поведением физической системы.
Пример 3. Рассмотрим систему, входные сигналы которой имеют вид и = (un u2, u3), где — вещественные измеримые функции, определенные на промежутке т = По, /у]. Предположим, что поведение этой системы можно описать линейным преобразованием Т: В2,2 Ио» ->ЛП и что это преобразование непрерывно и накрывает некоторое подпространство Нп. Предположим еще, что на и наложены следующие ограничения: при
всех / ЕЕ т | (О I 1 ’ I (О | и
Для того чтобы определить, может ли рассматриваемая система осуществить заданный переход в пространстве состояний, надо решить задачу оптимального управления с критерием оптимальности вида
J (u) = max {а (и), b (и)}, а (и) = sup [maxduJOl , IMOIJL
Ъ(и) =
Можно показать (см. Гриммелл [Б. 43]), что для этой задачи каждый переход можно осуществить оптимальным способом.
Читатель в качестве упражнения может убедиться в том, что экстремали 7*ф имеют вид
M1 ~ {sign (/)],
и9 (t) = \
! [sign 1 (Г*ф)2(01,
w3 (О — с (^**ф)г (/),
1»
2»
/е 1/0,01, где через (Г*ф)| обозначена /-я компонента Г*ф, а
в то время как с определяется из соотношения
3
to 1=1
Для облегчения решения мы советуем читателю рассмотреть век-
/ = (Л, /2» /з),
где
(О,
h(t)= t
— sign (t)],
-у sign |(T*<P)2(Z)1,
t S [/0. M \ £i-
tf= \ ^2,
I tE E%,

Если eq (u) и a2 (u) определяются уравнениями
3 г
“1(“) = S Vi(Z)wi(0^,
к	Ei
то О, 7*ф> = ax (u) + a2 (и). Теперь остается показать, что на множестве всевозможных п, таких, что J (и) = sup [max {их (/), 1&:
и2 (0}1» определенное выше и максимизирует ах (п), а на мно-
жестве всевозможных п, для которых t I ui (0 |2d£ = 1, это же t0
и максимизирует а2 (и).
К вопросу о единственности решения задачи 1. Задачу 1 особенно удобно решать в гильбертовом пространстве. В этом случае у множества С в любой его граничной точке имеется единственная внешняя нормаль, а у множества Т"1 (§), каково бы ни было 5 £ имеется единственный элемент. В связи с этим, естественно, возникает вопрос, а существуют ли такие банаховы пространства и (или) такие линейные преобразования, которые обладали бы аналогичными приятными свойствами?
Прежде чем попытаться ответить на этот вопрос, перечислим еще раз возможные типы неединственности, возникающие в ситуации, описанной в теореме Б. Во-первых, каждой § ЕЕ С f) П дС может соответствовать более одной внешней нормали. Во-вторых, для каждой внешней нормали ф в точке § элементу 7*ф может соответствовать несколько экстремалей (и обратно, может оказаться, что Г*ф1 = 7*ф2, хотя ф! =/= ф2). Наконец, две различные экстремали 7*ф могут преобразовывать Т в один и тот же элемент С р| дС. Мы хотим показать, что все эти неопределенности можно систематически устранять, сужая область определения В.
Прежде всего отметим, что множество 7“1(g) прообразов £ замкнуто и выпукло. В связи с этим, если пространство В строго выпукло, то это множество не может иметь более одного минимального элемента (см. по этому поводу теорему Б из § 4.2), что подводит нас к следующей теореме:
Пусть В строго выпукло, и пусть £ 6= С Q дС. Тогда единственный минимальный элемент Т~х (5) имеет вид при некотором ф £= р*. Другими словами, если в этом случае в некоторой точке £ £= С р) дС существует несколько различных внешних нормалей к С, например фх и ф2, т0 либ° Т* Ф1 = ^*Фг» либо Т =£ ф Т (Г*ф2)- (На самом деле в упражнении 6 мы покажем, что последняя из этих возможностей не может реализоваться.)
Следует отметить, что предположение о строгой выпуклости пространства В в некотором смысле оказывается и необходимым. Точнее говоря, если потребовать, чтобы для каждого преобразования Т, определенного на В (и имеющего замкнутую область значений), множество Т~г (5) имело не более одного минимального элемента для каждого 5, то пространство В должно быть строго выпуклым. В самом деле, сформулированное только что требование означает, что каждый линейный функционал, определенный в В, достигает своей верхней грани в U не более чем в одной точке, а это эквивалентно утверждению о строгой выпуклости пространства В.
Располагая этим предварительным результатом, мы без особого труда можем доказать теорему В *).
Теорема В. Пусть пространство В рефлексивно, строго выпукло и гладко. Пусть D, Т и С определяются так же, как и раньше, и пусть р есть функционал Минковского для С. Тогда для каждого % D существует единственный элемент ф£ ЕЕ Z)*, для которого уравнение
=	= р£)Т^
определяет единственный прообраз £, обладающий минимальной нормой, функционал ф^ однозначно определяется равенством ||фя|| = 1 и одним из двух следующих условий:
(!) <П> Фе> С (р <5. ф?> при всех Т) Е= С,
(2)	И*чМ = [р (5)]-1 <£, Ф5>.
(Если пространство В комплексное, то условие (1) нужно за-менять на
(1)Re 0b Фе> < [р (5)]"1 Re <5, Фб>.)
Во аналогии с уже решавшейся в гильбертовом пространстве задачей птимизации (т. е. задачей минимизации энергии) мы будем называть иногда «дачу из теоремы В задачей о минимизации усилий.
Доказательство, Пусть и ф2 — две внешние нормали к С, проходящие через точку £ ее дС Г) С. Тогда из условия строгой выпуклости пространства В имеем
Т^Фх =	Т*ф2.
Но так как пространство В гладко, то можно найти экстремали для обеих сторон этого равенства и получить, что
ф1~2 ф2^ И*ф1|| “ ||Т*Ф2||
Утверждения теоремы вытекают теперь из условия ||ф|| = 1 и того факта, что Т* взаимно однозначно.
Рис. 4.16. Составляющие теоремы В.
На рис. 4.16 схематически представлена ситуация, описанная в теореме В, для частного случая двумерного пространства. Для простоты графического представления область значений представляется здесь в виде гильбертова пространства. В связи с этим мы смогли изобразить ф^, внешнюю нормаль к С в точке = = [р (£)]“Ч в D, не как элемент D*. Все обозначения на рис. 4.16 очевидны, за исключением, пожалуй, N — ядра функционала ф^.
Хотя теорема В и определяет преобразование Г* вполне корректно, это определение неявным образом использует понятие ф^. Для того чтобы получить в условиях теоремы В явную формулу для Т*, нам придется исследовать отображение £	ф^,
воспользовавшись с этой целью функцией К:В*-+В, похожей на сопряженную, которая определяется через экстремали выражением
ЛГ(/) =11/17, /;е5*.
Таким образом, каждому / функция К ставит в соответствие его экстремаль, а затем восстанавливает норму исходного элемента. Учитывая свойства экстремалей, нетрудно показать, что К (X/) = = КК (J) при всех Л и что </,	= Ц/||а.
Рассмотрим теперь функцию J: D* -+-D, где J = ТКТ*. Другими словами, рассмотрим функцию
7(ф)	ФЕО*.	(7)
Лемма В. Функция J сопряженно-однородна, взаимно однозначна, сюръективна и ограничена.
Доказательство. Сопряженная однозначность J [т. е. J (Кх) = = XJ (я)] унаследована этой функцией от однородных Т и Т* и сопряженной однородности К. Ограниченность преобразований Т и Г* гарантирует и ограниченность J. Поскольку g =	J (фО
описывает отображение ф? £ единичной ’ внешней нормали в точку ее ' пересечения' с дС, то нетрудно1 видеть, что это преобразование является накрытием (сюръективным). В упражнении 3 мы выясним еще, что преобразование] J взаимно однозначно и даже монотонно:
0^ <Ф1 “ Ф2, ^Фх — «7ф2> ПРИ всех Фп Фз S 7?*.
Поскольку J ограничено, взаимно однозначно и сюръективно, то существует преобразование J-1. Это обратное преобразование понадобится для того, чтобы по-новому описать Г+.
Следствие 1. Если все условия теоремы В выполнены, и преобразование J определено уравнением (7), то псевдообратную функцию Т* можно представить в виде
Т* = kt*j-\
Доказательство. Пусть Е -О и произвольно. Из теоремы В мы знаем о существовании единственного элемента ф^ с единичной нормой, удовлетворяющего условию
в =
Воспользовавшись определением J, мы можем переписать это равенство в виде
А так как для вещественных X преобразование J однородно, то отсюда следует, что
т. е. ф^, удовлетворяющее уравнению В = / (фд,)» должно быть кратным ф^. Доказательство следствия заканчивается, если заметить, что из ф5 = J-1^ следует
В = J (J^B) = ТКТ*/-1 = Ти?, а отсюда совершенно тривиально вытекает
= КТ*/-1^ = Г+В.
Разница между теоремой В и ее следствием заключается в основном в характере акцентов. В теореме В нас интересует в основном вопрос вычисления числа р (£) и опорной гиперплоскости к С, проходящей через точку [/? G дС. В следствии же нас занимает лишь вычислительная задача обращения оператора J. Нестрого говоря, теорема В позволяет определять Г* по точкам, в то время как ее следствие определяет эту функцию глобально.
Пример 4. В большинстве примеров, рассматривавшихся в книге, мы имели дело с системами с непрерывным временем. Воспользуемся сейчас представившейся возможностью и лишний раз отметим, что все результаты этой главы столь же пригодны и для дискретных или гибридных систем. Вернемся еще раз к гибридной системе, показанной на рис. 2.16 § 2.5. Для простоты рассмотрим некоторый фиксированный момент времени t' ЕЕ (= а П т и сосредоточим наше внимание на преобразовании Т: : В —> Вп, где значения Т в точке (u, и) ЕЕ В определяются условием
у) = Т (w, и), где
Р']-1
х 2 G»G) u (^)>
[Г]-1	г
5=0	t0
Матрицы Wlt W2 и W3 определены уравнениями (18) из § 2.5.
Линейное пространство В образовано векторами
& = /р, (о) х ... X lVl (3) х LPM (т) х ... X LPm (Т))
и на нем определены естественные правила сложения и умножения на скаляры. Предположим, что 1 <	< оо, / = 1, пг, и что
на В согласно теореме Д из § 4.2 определена норма. В этом случае пространство В оказывается строго выпуклым и рефлексивным. Пространство D (а следовательно, и D*) идентично Еп. Сопряженное преобразование Т* отображает Еп в В*. Его значения определяются произведением аргумента на матрицу И7*, элементы которой в момент (s, t) задаются условием
W* (t', г) =
....о...
r = (8,t)EiXl
где s, t t'.
Дли большей конкретности рассмотрим частный случай, уже исследовавшийся в примере 5 к § 4.2 (т = 4, I = 2). Для каждого (р = (Фи Фг» Ф»’ Ф«) е Е" определим
(Г*ф) («, 0 = И7* (f; s, г)ф, (s, ()ЕО X т.
Норму и экстремаль этого вектора (т. е. Г*ф) можно вычислить с помощью прямых методов, описанных в примере 5 § 4.2. Поскольку преобразование Т корректно определено, то это же можно сказать и о J. На самом деле, нельзя не отметить, что, за исключением трудностей, связанных с обращением J (или, что то же, с отысканием ф^), решение задачи о минимизации нормы, полученное выше, совершенно ясно.
Замечание 3. Условия теоремы В, наложенные на область определения преобразования, достаточны для того, чтобы обеспечить единственность ф; и при любом и любом (сюръективном) преобразовании Т. Что же касается конкретных Г, то может оказаться, что единственны либо ф^, либо ш (либо и то и другое), хотя область определения Т не строго выпукла и не гладка. Например, предположим, что у каждого функционала, определенного в области значений 71* (или, может быть, в области значений 19), имеется единственная экстремаль. Тогда очевидно, что уравнение (7) корректно определяет функцию J и Г*ф1 и Г*ф2 могут быть прообразами £ €= дС в том и только в том случае, когда Уф1 Лр2. В упражнении 3 мы убедимся в том, что || Т*ф1|| — —	^*Ф2\ откуда следует, что Г*ф2 служит экстремалью
7’*ф1, а так как этот элемент единствен, то значит 7’*ф1 -= Т*ф2. В упражнении 4 содержатся примеры единственности без строгой выпуклости и гладкости области определения.
Несколько последних замечаний. Для усвоения результатов этого параграфа могут оказаться полезными следующие соображения.
Замечание 4. С помощью следствия к теореме В легко получить решение задачи 1 в гильбертовом пространстве. Поскольку в любом гильбертовом пространстве экстремаль х имеет вид X = = л/ЦхЦ,„ то отсюда следует, что функция К оказывается тождественной, J сводится к оператору ТТ* и, следовательно,
Г* = KT*J-1 = Т* (7Т*)-1, что согласуется с результатами, полученными ранее.
замечание 5. Заметим еще, что при выводе мы попутно показали, что ||Г+ (£)|| = р (5). А так как функционал Минковского непрерывен по 5, то мы убеждаемся в том, что минимальное усилие, связанное с каждым £ ее D, есть непрерывная функция £. оэтому, если два вектора и £2 из D мало отличаются друг от
друга, то это же можно сказать и о нормах ut и и2 их минимальных прообразов, порожденных Т.
Замечание 6. При решении задачи 1 мы явным образом не упоминали о понятии управляемости. Однако оценить ту роль, которую играет это понятие для нынешнего класса рассматриваемых проблем, не представляет особого труда. Для конкретности мы будем говорить, что система Т: В D управляема по норме в том и только в том случае, когда каждому £ ЕЕ преобразование Т ставит в соответствии некоторый прообраз и (= В. Из леммы Л (а точнее говоря, из теоремы об открытых отображениях) очевидно, что система управляема по норме тогда и только тогда, когда Т является накрытием. Интересное следствие из этого факта состоит в том, что если Т компактно*), то для того, чтобы система оказалась управляема по норме, необходимо и достаточно, чтобы D было конечномерным. Это утверждение непосредственно вытекает из того, что множество С оказывается бикомпактным, если компактно Т, а бикомпактные окрестности начала координат встречаются лишь в конечномерных пространствах. Другими словами, свойства бикомпактности и сюръективности несовместимы для преобразований бесконечного ранга. Этот результат играет важную роль в приложении 9.
Замечание 7. Приведенное решение задачи 1 пригодно для управления по разомкнутому принципу. В самом деле, для того чтобы воспользоваться этими результатами, нужно прежде всего определить подходящее	Далее, теоремы Б и В позволяют
построить оптимальное управляющее воздействие, после чего остается только подать его на вход системы, и система будет вести себя оптимальным образом. Достаточно определить £ Е: D, и о поведении системы не нужно никакой дополнительной информации. Однако в автоматическом управлении широко признаются преимущества использования обратной связи для целей управления системой, и ею пользуются всякий раз, когда это оказывается возможным. Короче говоря, нам хотелось бы иметь правило, которое в каждый момент времени t позволяло бы определять и (/) — мгновенное значение управляющего воздействия для нашей системы — по х (Z) — мгновенному значению выходных величин этой системы. Более того, это правило должно приводить к тому же оптимальному управлению, что и управление по разомкнутому принципу.
Такое правило, если его удается найти, называется оптимальным законом управления, а результат синтеза этого закона, или его физическая реализация, называется оптимальным регулято-
♦) Линейное преобразование называется компактным (вполне непрерывным), если оно преобразует любое ограниченное множество в множество, замыкание которого бикомпактно. (Прим, ред.)
пом. Теоретические оптимальные законы управления существуют практически всегда. Их существование предопределяется частично причинно-следственным характером рассматриваемых систем (см. упражнение 4 к § 2.5). В некоторых случаях, вроде классического «релейного» закона управления объектом второго порядка в режиме слежения (см. работу [Б.98], эти законы имеют очень простой вид. Однако в большинстве нетривиальных ситуа-
ций получение оптимальных законов управления в явном виде — очень трудная задача.
В упражнениях 14 и 15 к § 3.2 мы выяснили, что оптимальные регуляторы можно синтезировать и при решении задачи о минимизации энергии. Более того, линейность Тт, характерная для решения этой задачи в гильбертовом пространстве, переносится и на этот регулятор. Аналогичный результат мы получим в упражнении 9 для случая задачи о минимизации усилий. Поскольку в банаховых пространствах Т¥ нелинейно, то неудивительно, что нелинейным оказался и оптимальный регулятор. Но если не говорить о самых общих результатах, то к задаче о синтезе опти
мального закона управления лучше подходить по-новому в каждом конкретном случае.
Упражнения
1.	(Уолтц [Б.116J). Для системы, изображенной на рис. 4.17, покажите, что матрица перехода этой системы имеет следующий вид:
г 1 а — /0) 1
ф(Мо) = [о 1 J» Мо6т>
Если т = [0, 2] и все = 0, кроме Ьп (/) = 1 —- t при t ЕЕ fO, 1],
Рис. 4.17.
(0 =-(/— 1) (2 - <) при геи, 2], b22(f) = t—i при tell, 2J, то покажите, что
1	2
X! (2) = (1 — Z) U1 (/) dl, х2 (2) = (Z — 1) и2 (/) dt.	(»)
о	1
13 У. Портер
Пусть уравнения (♦) определяют преобразование Г, отображающее В = = Lqo (°’ 2Л» т- е- ^оо, 2С « = 2, в D = Я2. Покажите, что Т является накрытием и С = Т (U) представляет собой квадрат
С = = (Xi, з2) е Я2: | I < 4“ ; * = 2}
и замкнуто.
Указание, Обратитесь к результатам упражнения 10 к § 4.2.
Найдите оптимальное управление для каждого из элементов = (0,8; 0,6) и = (0,5; 0,5). Единственны ли они?
2.	(Уолтц [Б.116]). Рассмотрим систему, описывающуюся уравнением ± = Ах + Ви, х (0) = 0, где х (t) =	(Z), х2 (Z), х3 (Z)], и (Z) = [ui (Z), и2 (t),
и3 (Z)], а Л и В матрицы вида
Л =
О 1 О
О 0 1 ООО
	*11 (Z)	*12 (0	*13 (Z)
В(/) =	0	*22 (Z)	*23 (0
	0	0	*33 (/)
при t ЕЕ [0, 3]. Пусть элементы этих матриц равны нулю всюду, кроме *ii W = 1 — * при t е [0, 1], 612 (Z) = — 3 (t — 1) (2 — t) (3 — t) и b22 (Z) -= 3 (Z - 1) (Z - 2) при t e [1, 2], bl3 (Z) = 1/2 (t - 2) (3 - z)2, *23 (Z) = — (Z — 2) (3 — Z) и b33 (Z) = (Z — 2) при Z (E [2, 3]. Покажите, что уравнения
i
xi (3) = (1 — s)ui (s) ds,
0
2
x2 (3) = 3 (.<? — 1) (2 ~ s) u2 (s) ds, i
з
хз (3) = (s — 2) из (.*?) ds
2
описывают систему как некоторое линейное преобразование на Я3. Если В =	(12 (3); [0, 3]), то покажите, что С = Т (U) представляет собой замк-
нутый куб
с = {(®1,	и)е«’: |х{ I < 4- , i = 1. 2, з].
Покажите также, что: (а) для £, принадлежащих граням куба С, оптимальное управление не единственно; (б) для £, совпадающих с вершинами этого куба, внешние нормали хотя и не единственны, но определяют единственное оптимальное управляющее воздействие; (в) для 5» лежащих на ребрах куба, не единственны ни внешние нормали, ни оптимальные управляющие воздействия. (Заметьте, что в (в) неопределенность в всегда возникает на одних и тех же промежутках.)
3	Докажите, что функция J из уравнения (5) взаимно однозначна.
Указание. Так как из того, что = /ф2, следует, что <ф! — фз, /ф1 “ __/ф2> = 0, то достаточно показать, что это равенство можно представит» в виде	____
(||Уф1||-||Г*ф2||)а + ||Т*ф1||(||Т*ф2||- <Тфф2, Т*Ф1»+	____
+1| Т*ф2 И (II ^*Ф1 II “	. Т*фа» = 0.
Воспользуйтесь строгой выпуклостью и гладкостью В, чтобы показать, что отсюда следует равенство Ф! = фа.
4. (Уолтц [Б.116]). Пусть Т, есть линейное преобразование, отображающее Lqq (0, 1) в R2 согласно правилу u
1 ГА г 1 — $ Т“ = Н 1
и (s) ds, и е (0,1).
о
Покажите, что в множестве С = Т (U) имеются угловые точки {zfcO/a»!)}» но нет плоских граничных участков. Пусть А — линейное преобразование, отображающее (h (2); [0, 1)) на R2 согласно условию
р Г1 — s О Ли = Н о о
ds, и£В.
Покажите, что множество С = A (U) не имеет ни угловых точек, ни плоских участков границы. Покажите, что в обеих системах оптимальное управляющее воздействие единственно.
5/Пусть В, D, Т, С и р определены, как в теореме В. Покажите, что функционал р представляет собой норму D, эквивалентную данной.
Указание. Для 0 =/= g G Р и X > р (g) имеем g ЬТ (U) =» || £ ||< X || Т || => «Фр (g) > (|| 7’Ю"1||5||. Используйте также факт замкнутости множества С.
6. Обозначим через пространство D, на котором согласно упражнению 5 определена норма | £ | = р (g). Покажите, что Di строго выпукло (гладко), если этими свойствами обладает В.
Указание. Заметьте, что | g | = || T*g|| при любых S6Z)i и что T+gi+ + е Г-1 (51 + 6г), так что
II т* (51 + 5з) II < IIГЧ1 + Т4а II < IIТЧ1II + II г+5аII и, следовательно,
151 + 5а | = | Ъ | + | 5а| =>|| ГЧ1 + ТЧг II = IIГЧ11| + J Т+5а ||,
откуда следует строгая выпуклость В => T+gi = Х7*Ца при некотором X > 0. Это же в свою очередь предполагает, что gx = Xg2 => строго выпукло. Для того чтобы доказать строгую выпуклость и гладкость в случае, когда строго выпукло и гладко Ви воспользуйтесь фактом взаимной однозначности отображения g — ф*.
7. Пусть — это строго выпуклое и гладкое пространство из упражнения 4, a g е дС. Покажите, что экстремаль g' 6= элемента g равна ф^.
Указание. Воспользуйтесь определениями,
<а>	<5; Г> = 1С| = р(0 = 1;
(б)	| v I - зиРлеС <п,{'> = suPuet/ <в, r»v> = I r*V 1 = 1.
Заметьте, что этот результат приводит к новому определению псевдообратного оператора:
8. Обозначим через fo, хп] линейно независимое подмножество векторов банахова пространства В. Среди элементов подмножества Q = f (xt) = at, i = 1, 2,	n}, где alt an — фиксированные скаляры, най-
дите элемент с минимальной нормой. Эта задача представляет собой простейший вариант «проблемы моментов» (см. [Б.1]).
Указание. Пусть через {elt ..., еп) обозначен координатный базис Rn, и пусть 5: Rn —* В определяется условием
п
s — 3
i=i
Покажите, что	S*f = g, где 5 = (ах, ..., ап), и воспользуйтесь
затем результатами теорем А и Б.
9. Рассмотрим линейный оператор и —» х, определяемый соотношением х = Ти = Ф (tf, s) В (s) и (s) ds, где uG-B, В — строго выпуклое гладкое и рефлексивное банахово пространство, а Т накрывает Вп. Для некоторого t G [*<>* */) определим" операторы F(U = \ Ф (tf, s) В (s) и (s) ds и G[U = = Ф (tf,~s) В (s) и (s) ds, отображающие В в Rn. Если обозначить через Bi множество	г (s) = а, $£ [f0, f]}, а через В* — {x GE В: x (s) =
= 0, s GE Ro> то пространства Вi и В* строго выпуклы, гладки и рефлексивны (см. упражнение 7 к § 4.2), и можно естественным образом отождествить В с произведением ВX В*. Покажите тогда, что можно однозначным образом записать:
(а)	Ти = FjUi GjU^, ui^ В^, U2 В^, и GE
(б)	т*Ф = (^^ф),<реяп.
Воспользовавшись результатами упражнения 7 к § 4.2, покажите, что
(в)	Г*ф = (а^ф, а2В*ф), ф е Вп, «2 — скаляры;
(г)	Уф = Рг^ф + р2/2ф, Ф С Rn, Pi, Р2 — скаляры,
где
/ф = |7Лф|Т(75ф),
лф=и;<ри,(7^),
Лф = ||Сгф||Сг (Сгф) и
Р1 = «I о ГФф 1 / II F\v ||, р2 = а || ГФф II / II ||.
Используя свойства линейных динамических систем, покажите, что если
X (tf) = Ф (tf, t0) X (to) = J (ф), то
(Д)	х (tf) - Ф (tf, tx) х (tx) = p2/2 (Ф),
(e)	x (tj) — Ф ((j, t0) x (f0) e P^ (ф)
и, следов ательно,
(ж)	(*/)-ф <*/’*> ®(<)1 = г+1* «/)- ф <*/»*>) ^Wl’
причем последнее условие выполняется на всем промежутке (t, </|. Другими словами, нелинейная функция
и (t) = [г (</) - Ф («/, t) х (<)]
описывает мгновенную обратную связь, которую нужно ввести для синтеза регулятора замкнутой системы, минимизирующей усилие.
F 10. (Гриммелл [Б.43]). В процессе синтеза системы, которая должна заставить объект управления выполнять заданную ему конкретную задачу, мы можем столкнуться с вопросом о выборе конструкции регулятора, позволяющего минимизировать некоторый функционал, зависящий как от пикового значения расхода топлива, так и от его суммарного потребления. В качестве примера рассмотрим объект, работающий как двойной интегратор, т. е. объект, поведение которого описывается преобразованием и —> g согласно правилу
и (t) dt.
t0
В качестве критерия оптимальности выберем функционал
J (и) = sup еет
*0
где т = [£0, /у]. Можно показать, что J (•) определяет для (т) норму, эквивалентную обычной норме этого пространства (т. е. норме ||u|| = sup<ex | и (t) |).
Отсюда следует, что этот объект можно переводить из любого начального состояния в любое конечное оптимальным образом. (Другими словами, мы утверждаем, что существуют оптимальные управляющие воздействия для любого д.) Покажите, что оптимальные управляющие воздействия, соответствующие экстремалям Г*ср, для ср, = (0,8; 1), фа = (0,4; 1) и ф3 = (0,1; 1) имеют следующий вид:
/	0,384, 0,0 </<0,552,
щ(/) =	0, 0,552 </<1,948,
(—0,384, 1,948 </< 3.
, ч ( 0,408, Ut(t)={ о, и3 (0 = 0,25;
0 </<1,45;
1,45 </<3;
0 < / < 3.
Указание. Пусть G (и) = ^(Г*ф) (0 и (/) dt. Тогда экстремали можно найти, заметив, что для любого заданного скаляра й = supfex | и (/) | G (и) ока-ппи8еТСЯ наиболыпим, если положить, что | и (/) | = й при тех значениях /, ри которых | Т*ф (/) । «достаточно» велико, и и (/) = 0 при остальных зна-чгжт? #?Ричем уровень, при котором и (/) становится отличным от нуля, 0 ^ыбРать тек, чтобы мера множества, на котором и (/) не равняется w	₽авна (1 — й)/й. После этого G (и) нужно выразить через й
и наити максимум полученного выражения.
И (Гриммелл [Б.43]). Выпишите линейное преобразование, связанное с работой в промежутке [f0, fy] системы, описываемой дифференциальным уравнением
’*1(0'		0 10 0		®1 (0		0 0	0			
*з(0		0 0 0 0		x»(t)		1 ° 4"		‘“1(0-	
	—				+			U2 (0	
*»(0		0 0 0 1		xs(0		0 0 0		-“з(0-	
*4(0		0 0 0 0		Я4(0		1 0 I т			
В качестве критерия оптимальности поведения системы выберем функционал
J (и) =
[sup (max {| Ui (l) |, | m (t) [})]» +
(/) рл)7*.
Можно показать, что этот критерий оптимальности соответствует норме банахова пространства, удовлетворяющего условию следствия 3 из теоремы А. Покажите, что для поставленной задачи оптимальные управляющие воздействия имеют вид
ui (t)=
ci
sign [ф1 («о—'0+фз].
г 1	1
ut (t)= / 2, 8ч'А 8'8П1’P* (/0 - о + Ф‘1>
L \С1 “Г с2' J
-“Нйй к1’
(ф1 + Ч>2) । (ф2 + ф«)
2	2
где
«1= j (|ф1('о—О + ф»| + |ф»(*о—0 + ф||)Л.
/(* Г„ (ф1Ч-фв) , (Ф» + Ф1) ]’
с« ” \ J [ ~ 0	2	-------2 J dtJ
<•
(Ф1. ф2. Фз. Ф«) G Rn.
Указание. Запишите <и, Т*<р> =	^(^*Ф/) (0 и (0 dt. Воспользуй-
тесь подходящими неравенствами для каждого из интегралов, а затем неравенством Шварца для получающейся суммы.
4 4 Обобщения задачи о минимизации усилий
Рис. 4.18. Задача наведения с ограничениями.
После того как нам удалось строго сформулировать и полностью решить задачу 1, мы можем переключить наше внимание на некоторые варианты ее, часто встречающиеся на практике. В качестве иллюстрации рассмотрим еще раз систему наведения космического аппарата, уже упоминавшуюся во введении к этой главе. В обозначениях этого введения векторы (#, й), (х, и) и (бя, би) = (х, и) — (3, й) описывают, соответственно, эталонную и реальную пары траектория — управление, а также пару возмущений траектории и управления.
Хорошо известно, что на выбор программы движения при выполнении некоторой цели запуска оказывают влияние соображения, связанные с тепловой нагрузкой аппарата, предельными скоростями маневрирования, перегрузками, возникающими при полете, ветровыми возмущениями и условиями безопасности полета. Каждый из этих факторов накладывает определенные ограничения (см. рис. 4.18), которые, по-видимому, принимаются во внимание при выборе номинальной пары (з,й). Но так как нарушение одного или нескольких ограничений может иметь для запуска самые
губительные последствия, то критерий [оптимальности выбора би должен быть чувствительным не только к величине би, но и ко всем этим факторам. Поскольку же степень нарушения указанных ограничений может быть оценена величиной бх, то естественно поставить задачу (мы обобщим ее в дальнейшем в задаче 2), в которой требуется, чтобы управление би удовлетворяло условию бх (tf) = g, минимизируя одновременно с этим функционал вида
J(u) =
т
2 |би3(<)|рл
J=1
(Если р = 2, то этот функционал можно рассматривать как взягую с одинаковыми весами сумму среднеквадратичного
отклонения бх от х и среднеквадратичного значения энергии, израсходованной верньерными двигателями.)
Используя эти замечания как физическую основу для дальнейшего исследования, мы поставим в этом параграфе несколько задач оптимизации, которые внешне выглядят сложнее задачи 1. Однако в каждой из них разумный выбор функциональных пространств и (или) линейных операторов позволяет свести эти сложные по виду задачи к задаче 1. Поскольку основной интерес в этих задачах связан для нас с выявлением в них постановки задачи 1 в ее замаскированной форме, то мы упростим технические детали, ограничившись рассмотрением задач типа минимизации усилий. Кроме того, мы воспользуемся еще и тем фактом, что Т* наиболее эффективно определяется в гильбертовом пространстве, а потому в наших примерах мы будем использовать именно эту ситуацию. Однако большинство из полученных здесь результатов поддаются обобщению того же типа, что и полученные в § 4.3, и теми же методами, которые использовались в этом параграфе.
В дальнейшем через 5, Вг и В2 мы всегда обозначаем строго выпуклые рефлексивные банаховы пространства, а через D — просто банахово пространство. Первые два обобщения задачи 1 довольно незначительны.
Задача 1(a). Пусть В, D, Т и g определяются так же, как в задаче 1, и пусть й есть некоторый фиксированный вектор из В. Найти управляющее воздействие и из В, удовлетворяющее условию Ти = g и минимизирующее функционал
J (и) = ||и - й||.
Те о р.е м а А. Задача 1(a) имеет в точности одно решение, а именно вектор
ик = Т+(£ — Ти) + и.
Доказательство. Совершенно ясно, что Т отображает гЦ в Обозначим через и любой прообраз g для отображения Т. Тогда из соотношения Т (и — й) = g = Тй следует, по определению Т+, что
||U - й|| > ||Г (£ - ТйЦ = (ие - й||.
Следовательно, и% есть решение задачи 1(a), а так как последнее неравенство является строгим при условии, что (и — й) не равно Т* (g — Тй), то ясно, что и% является единственным решением этой задачи.
Второй вариант задачи 1, который мы будем называть задачей 1(6), состоит в минимизации функционала ||Fu|| при соблюдении условия Ти = g. В этой задаче предполагается, что преобразование F линейно, ограничено и отображает пространство В в Вг.
Кроме того, нам понадобится наложить на F некоторые добавочные ограничения. Из наших предыдущих результатов мы знаем, что единственное решение будет существовать для каждого g g D в том случае, когда: (1)| и\ =||Fu|| является некоторой нормой для В, (2) пространство В рефлексивно, и (3) это пространство строго выпукло относительно новой нормы.
Первое из только что перечисленных условий выполняется в том и только в том случае, когда преобразование F взаимно однозначно. Поскольку
И <1ИН14
то наши нормы оказываются сравнимыми. Если же {В, | | } есть некоторое банахово пространство, то следствие из теоремы о замкнутых графиках (приведенной в приложении 7) показывает, что эти две нормы должны быть эквивалентными (т. е. для некоторого а > 0: а||м||	и|), что в свою очередь свидетельствует о рефлек-
сивности пространства {В, | |} всякий раз, когда рефлексивно пространство {В, || || }. Поэтому для выполнения условий (1) и (2) необходимо (и, очевидно, достаточно), чтобы преобразование F было ограничено снизу:
\\Fu\\ >> а ||и|| при всех и В.
Наконец, легко видеть, что при любом F пространство В оказывается гладким по отношению к норме | и | = ||Fuj| (при условии, конечно, что исходное В гладко по отношению к своей норме). Если F взаимно однозначно, то новая норма сохраняет и свойство строгой выпуклости. Таким образом, ограниченность снизу преобразования F является необходимым и достаточным условием сохранения строгой выпуклости, гладкости и рефлексивности пространства В. А это в свою очередь означает, что F должно быть ограниченным линейным преобразованием, для которого существует обратное и которое отображает В на банахово пространство Br = F (В). В связи с этим строгая формулировка задачи 1(6) имеет следующий вид:
Задача 1(6). Пусть F — некоторое взаимно однозначное ограниченное линейное преобразование В в Вг. Для каждого | ЕЕ D найти единственный вектор tu ЕЕ 5, удовлетворяющий условию Ти ~= g и минимизирующий при этом функционал J (и) = ||Fu||.
ТеоремаБ. Единственным решением щ* задачи 1(6) служит
u^Pf(1)F-^F^(Vx\)Y
Pf (£) есть функционал Минковского для множества
CF= {Ти: ||FW|| < 1},
а т] — единственный вектор из D* единичной нормы, удовлетворяющий условию
<5,	= И*’*7,*4
Доказательство. Поскольку преобразование F является взаимно однозначным и накрытием, то для него существует F-1, и это второе преобразование также ограничено и линейно. Отсюда следует, что (см. теорему В из § 3.3) преобразованию F* соответствует некоторое ограниченное обратное преобразование, причем (У?*)-1 = (F”1)*. Заметим теперь, что соотношения
J М = ||Fu|| = | v |,
Ти = (TF-1) (Fu) = (TF-1)»,
где » = Fu, справедливы при любом и G= В. Но в этом случае ясно, что задача 1(6) в точности совпадает с задачей 1, где TF"1 было заменено на Т в качестве интересующего нас преобразования. Поэтому на самом деле теорема Б есть не что иное, как теорема В из § 4.3, в которой осуществлена эта подстановка.
Наше следующее обобщение исходной задачи как раз и составляет цель этого параграфа. Для того чтобы подчеркнуть его важность, мы припишем ему название: задача 2.
Задача 2. Обозначим через F и Т некоторые ограниченные линейные преобразования, определенные на В и принимающие значения из Вх и D, соответственно. Для произвольного £ ЕЕ D найти элемент, минимизирующий функционал
J (и) =	+ И
и принадлежащий множеству Т-1 (£) CZ В всевозможных прообразов для Т.
В такой постановке задачи 2 предвосхищается дальнейшее развитие событий, которое покажет, что такой минимальный элемент действительно существует и единствен. Во время исследования задачи 2 нам понадобится определение графика преобразования. Если F отображает В в Вх, то графиком F называется множество
В (F) = {(и, и): и = Fu, и е В},
т. е. графиком преобразования называется такое подмножество произведения В X В19 в котором ордината и каждого элемента связана с его абсциссой соотношением v = Fu. Основные положения, имеющие отношения к теме нынешнего исследования, сведены в лемму А.
Лемма А. Определим в В X Вх операции сложения и умножения на скаляр обычным образом*.
(un У1) + (и2, р2) = (их + и2, рх + У2), a (u, v) = (аи, av).
Тогда
(а)	пространство В X Вх является строго выпуклым рефлексивным банаховым пространством, если на нем определена норма
Il(u, < = и + и2;
(б)	множество В (F) представляет собой некоторое замкнутое подпространство В X В и, следовательно, также является строго выпуклым рефлексивным банаховым пространством*,
(в)	если G: В (F) -> D есть преобразование, задающееся соотношением
G (и, Fu) = Ти, и €= В,
то G линейно и ограничено.
Доказательство. Утверждение (а) следует из теоремы Д § 4.2 и того факта, что произведение конечного числа рефлексивных пространств рефлексивно. Для того чтобы доказать утверждение (б), заметим прежде всего, что В (F) наследует свойство строгой выпуклости от 5 X В19 а так как всякое замкнутое подпространство рефлексивного пространства также рефлексивно (см. упражнение 9 § 3.3), то нам остается доказать только, что В (F) замкнуто в В X Bl. Но это следует из того очевидного факта, что (ип, Fun) ->• (и, v) тогда и только тогда, когда
ип —>и,	Fun—+v,
и непрерывности преобразования F. Наконец, утверждение (в) основывается на том, что ||G (и, Fu)\\ = ||Tu|| и что
ИМсйЛ • Н<11Л(Мг+ИМ2),/‘ = И|1 • 1(«» W
Необходимость доказательства леммы А вытекает из того, что в задаче 2 ищется вектор (и, Fu), принадлежащий В (F) и такой, что G (и, Fu) = £, а функционал
J(u)=l|u||2 + ||Ful|2 = ||(u,Fu)||2
минимален. Другими словами, задача 2 ничем не отличается от задачи 1, но в ней вместо основного преобразования Т*. В ->• D нас интересует преобразование G*.B(F)^D. Как только мы установили это, мы можем сформулировать и теорему В.
Теорема В. Задача 2 имеет единственное решение и $ для любого D, совпадающее с абсциссой вектора G+ (|) из В (F).
Необходимо обратить внимание на то, что теорема В не дает в явном виде решения задачи 2, а лишь сводит эту задачу к задаче вычисления функции G+. Однако несмотря на то, что вычисление может быть сопряжено с большими трудностями, теорема В на самом деле представляет большой шаг на пути решения задачи 2, так как она направляет наше внимание на конкретные вопросы построения соответствующих гиперплоскостей и экстремалей.
Замечание 1. Процедуру сведения задачи 2 к задаче 1 можно рассматривать под несколько другим, хотя и очень полезным углом зрения. Введем в пространстве В новую норму | | соотношением
I«I = (М2 + ИИ2)’4
и будем обозначать это новое пространство через В. Тогда пространство В должно унаследовать от В и свойства строгой выпуклости, рефлексивности и гладкости. Задачу 2 можно теперь переформулировать и потребовать найти такое иЕЕБ, для которого Ти = £ и которое минимизирует | и |. Это уже, очевидно, задача типа 1.
Замечание 2. Последняя точка зрения немедленно наводит нас на мысль о том, что задачу 2 можно сформулировать в предельно общем виде, определив на В х Вг любую норму, обеспечивающую рефлексивность и строгую выпуклость этого произведения (см. теоремы Д и Е из § 4.2). Если функционал J (и) совпадает с нормой пространства В (F), порожденной любой приемлемой нормой, определенной на В X 2?х, то наша задача автоматически сводится к задаче 1. Например, задача о минимизации усилий, в которой
7(и) = |1Мр + ИМр. 1<р<~, или
j (и) = au II и И4 4- а12 II и II • || Fu || + аг11| и || • || Fu || + ам || Fu ]|2,
эквивалентна задаче 1. Наконец, совершенно ясно, что задача 1 содержит еще и тот случай, когда функционал J (и) имеет вид
п /(и)=2иир. i=0
где Ft: В В} — некоторое заданные преобразования.
Функция Сг+. Вычисление G+ является нетривиальной задачей. Рассмотрим для начала частный случай, в котором пространства В и В± являются гильбертовыми, Н и Н1. Легко убедиться в том, что выражение
<(U1, vx), (u2, Р2)> = <wx, w2> + <1>X, l?2>
определяет^скалярное произведение в Н х Нх. В силу леммы А пространство Н X Нх полно относительно нормы, порожденной этим скалярным произведением. А отсюда следует, что Н X Нг и следовательно, Н (F) — график F в Н X Нх — также являются гильбертовыми пространствами.
Решение задачи 1 в гильбертовом пространстве было получено в результате сужения преобразования Т на ортогональное дополнение ядра этого преобразования. Это сужение не сингулярно, и преобразование, ему обратное, отображает любое £ из области значений Т в его прообраз с минимальной нормой. Этот же подход оказывается плодотворным и в нынешней ситуации, и мы построим ортогональное дополнение ядра G.
С этой целью заметим прежде всего, что ядро G, которое мы будем обозначать через Ng, имеет следующий вид:
Ng = {(и, Fu): и е АГГ}.
Так как для любого и Н справедливо соотношение G (и, Fu) = = Ти, то отсюда следует, что и N в том и только в том случае, когда (и, Fu) е NG-
Лемма Б. Обозначим через Q и М ортогональные дополнения ядер преобразований G и Т, соответственно. Тогда
Q = {(и, Fu): (I + F*F) и е М}.
Доказательство. Доказательство леммы Б содержится в следующей цепочке равенств:
Q = {(и, Fu): (и, Fu) | (и, Fu) при всех v ЕЕ NT} =
= {(и, Fu): <u, р> + {Fu, Fu) = 0, и ее NT} =
= {(и, Fu): {и, и) + {F*Fu, р> =0, и е NT} =
= {(u, Fu): <(/ + F*F)u, и) = 0, и NT] = = {(и, Fu): (I + F*F)u е М}.
Замечание 3. Иногда удобно рассматривать множество абсцисс элементов Q. Это множество мы будем обозначать через S. Из утверждения леммы Б ясно, что S задается одним из следующих эквивалентных образов:
5 = {и: (и, Fu) е Q} = {и: (Z + F*F) и СЕ М} = = {и: и = (I + F'F)-1»,	= (I + F*F)-XM.
При этом мы воспользовались фактом обратимости преобразования (Z -f- F*F). Этот факт следует из того, что преобразование положительно и, следовательно, спектр (/ + F*F) не должен содержать 0 (см. приложение 5).
Теперь мы в состоянии окончательно описать процедуру вычисления G+ для случая гильбертовых пространств.
Теорема Г. Единственное решение и^ задачи 2 для случая гильбертовых пространств определяется формулой
=	+ Г F)’1 Т V
где (р — единственный вектор из D*, удовлетворяющий условию
g = Т (I + /’♦/’)-1Т*ф.
Доказательство. С учетом только что введенных обозначений, вспоминая о решении задачи 1, мы сразу видим, что для (z^, Fu^) справедливо:
(1)	(*Ч, Fu^)^Q,
(2)	G(u^ Fut) = Z*
Но в силу леммы Б (и^, Рщ) Ez Q в том и только в том случае, когда и^ = (I + F+F)-1», где v Ez М. Ясно, что v однозначным образом определяется через ис. А так как Т+ представляет собой взаимно однозначное преобразование, отображающее ZJ* на М, то v = Т+ф для некоторого единственного вектора ф Е/)*. Так как по определению, G (и^ Fu$) = Ти^ то справедливость теоремы Г очевидна.
Теорема Г лишний раз подтверждает высказанное ранее утверждение о том, что основная разница в решениях задач 1 и 2 носит чисто вычислительный характер. Например, в задаче 1, если D = Rn, то векторы {/f}, встречающиеся в полярном каноническом разложении Т, образовывали в М готовый базис. В задаче 2 при D = Rn приходится вычислять базис для S. Например, базисом в S может служить множество {gf = (/ + F*F)“У/}. К сожалению, в общем случае получить явные выражения для преобразования, обратного (I + F*F), не удается и элементы {gf} приходится получать в качестве решений уравнений Д = = (Z + F*F)gh i = 1, ..., п. Впрочем, эта трудность имеет чисто вычислительный характер, и ее легко преодолеть с помощью вычислительной техники. Некоторые из вычислительных методов будут упомянуты ниже.
Пример 1. Обозначим через Q (/) и R (/) квадратные матрицы порядка п и т соответственно. Пусть они ограничены и положительно определены при каждом t СЕ т = k0, tf\. Определим гильбертово пространство HQ (т) как класс функций L% (т), на котором задано скалярное произведение
к
<х, y>Q = $ Iх ($), Q (s) у ($)] ds,	x,y^HQ (т).
t0
Аналогичным же образом можно определить гильбертово пространство HR (т) как множество функций L™ (т), на котором
задано скалярное произведение ь
<u, 1>>R = \ 1“ («). R(s) V (s)J ds, weHr (т). to
В упражнении 6 к § 3.4 мы уже доказали, что определенные таким образом пространства Hq (т) и HR (т) действительно являются гильбертовыми.
Рассмотрим линейную динамическую систему, у которой реакция x(t) на входное воздействие u(t) определяется уравнением
t
х (t) =	(t, s) В (s) и (s) ds, t^x.	(1)
*0
Одна из часто встречающихся задач оптимального управления состоит в том, чтобы найти управляющее воздействие и, переводящее систему из состояния (Zo, х0) в состояние (//, х/), минимизируя при этом критерий качества
G	h
J (и) = \ [u (s), It (s)u(s)] ds 4- \ [#($), Q ($) х ($)] ds.
Io	to
Если обозначить через F линейное преобразование, описанное в уравнении (1), и положить х0 = 0, а х/ = g, то эта задача, очевидно, эквивалентна задаче минимизации функционала
/(w) = J/’uJq + ||и||н
при выполнении условия
В = Ти,
где Т определяется уравнением (1), в котором t = tf. Но так как теперь все свелось к задаче типа 2, то решение нашей проблемы можно найти, воспользовавшись теоремой В.
С преобразованием Т мы уже имели дело раньше. В качестве упражнения читателю следует убедиться в том, что преобразование F*, присоединенное к F, принимает (для пространств Hq (т) и Hr (т)) вид
t.
(F*y) (0= J R-\t) Я*(0 Ф* (*, 0 Q (S) У (S) ds. (2) to
В следующем примере мы покажем, что уравнений (1) и (2) достаточно для того, чтобы задать (I + F*F)~1T^, и завершение решения задачи отложим до той поры.
Вычисление G+ для банаховых пространств. Рассмотрим подробно решение задачи 2 в банаховом пространстве. Обозначим прежде всего через Б пространство В с определенной на нем новой нормой
|«| =(И + ИО’Л.
которая, очевидно, эквивалентна исходной норме, определенной на В, так что ограниченные линейные функционалы, определенные на Л и на В, должны быть одинаковыми. При этом, естественно, норма |/| элемента / ЕЙ* не обязательно должна совпадать с нормой ||/||, в которой / рассматривается как элемент пространства В*. Лемма А утверждает, что пространство Б строго выпукло, гладко и рефлексивно, если только этими свойствами обладают пространства В и ВР В упражнении 1 мы покажем, что экстремаль х , соответствующая элементу х из В, определяется по формуле
, М(х) X = г I » и
где
М (х) = || .г || 7 ч-11^ и* (^),	(4)
а через X и Fx обозначены обычные экстремали элементов пространств В и Вх соответственно. Более того, преобразование М является взаимно однозначным, сюръективным и сохраняет норму, причем М (кх) = КМ(х) (см. упражнение 2).
При этих обозначениях задача 2 состоит в том, чтобы найти единственный вектор и = принадлежащий Б и такой, что Ти = g, а норма | и | минимальна. В соответствии с решением задачи 1 существует такой единственный вектор т] из В*, что hll = 1. а
и5 = рс(^)(Гт1)',	(5)
где pG (£) — функционал Минковского для множества Cg-
CG = {1 = Ти:\и\^1}.
Вектор ц определяется из условий ||ц|| = 1 и
<£, П> =|Г*т]|.	(6)
Обозначим через К: Б* -> В преобразование, определенное на элементах В* с помощью соотношения
*(/) = 1/1/'.
где через /' обозначена экстремаль элемента / ЕЕ В* относительно нормы | |, определенной на В. Рассмотрим далее преобразование J: В* -> В, соответствующее соотношению
J(T]) =|Г*1]|Т(Т*Т1)', лес*.	(7)
Ясно, что J = ТКТ* и что J отображает элементы ц Е- D* в некоторый век\ор пространства D, отличающийся лишь скалярным коэффициентом от вектора g е dCG, для которого вектор т] определяет опорную гиперплоскость. Из уравнения (5) следует, что
g = Ти^ = pG ф Т (Г*Т])' = pG (g) | Г*Т] Г1 /Т],
и следовательно,
Т1 =|TM[pG(g)]-V-1g, gezD,	(8)
что вместе с уравнением (5) дает
G4 =	I е= D,	(9)
причем это последнее выражение можно рассматривать как явную формулу для G+.
Заметим, что если F = 0, то | Т*т] | = ||F*r]||, так что вектор т], найденный из уравнения (6) с учетом нормирующего условия JtiII = 1, оказывается как раз той самой внешней нормалью <р к С = CG в точке с которой мы привыкли иметь дело раньше. Кроме того, в этом случае принадлежащие В экстремали элементов В* принимают свой обычный вид, так же как и функции J и К.
Добавление к условиям задачи 1 нового преобразования F не только вызывает трудности, связанные с построением множества CG, что нетрудно было предвидеть, но и определяет еще два дополнительных осложнения. Наиболее существенное из них связано с вычислением преобразования К. Заметим, что преобразования К и М позволяют находить экстремали: первое — в пространстве В для элементов Л*, а второе — в пространстве Л* для элементов В, и в то же время сохраняют норму. Поскольку пространство В строго выпукло и гладко, то отсюда следует, что преобразование К является обратным по отношению к М.
Интересно рассмотреть вопрос о возможности вычисления преобразования К в явном виде. Наиболее простой нетривиальный частный случай возникает, по-видимому, тогда, когда В и Вг являются гильбертовыми пространствами Н и Нг соответственно. В этом случае экстремали вычисляются согласно правилу Я = #/|l4 и» значит, преобразование М приобретает следующий вид:
М (х) = ||ф +	(7Г) =(I + F*F)x.
Но так как преобразование (Z + F+F)-1 может быть записано в явном виде лишь с помощью рядов, то, вероятнее всего, нам не стоит особенно надеяться на вычисление К каким-нибудь Другим методом, кроме как с помощью рядов.
Покажем теперь, что вариант задачи 2, относящийся к случаю гильбертовых пространств, является частным случаем только что
402	ГЛ. 4. ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАД^4
/
полученных результатов. Переписав уравнение (5) в/виде и^МЭДТсПГ1*^). '
мы сразу получим, что
Ъ. =, (I +	[pG (ЭД Г*Т] р Г*Т] ].
Сравнение этого результата с выражением из теоремы Д и подстановка соотношения Т+ = Т* (ТТ*)-1 показывают, что нам нужно лишь доказать справедливость для некоторого <р ЕЕ D соотношения
(7Т*)Ф = pG® | Пт]
Но так как преобразование (ТТ*) взаимно однозначно и обратимо в D, то это последнее утверждение является очевидным.
Поэтому совершенно ясно, что решение задачи 2 в банаховом пространстве, содержащееся в уравнениях (3)—(6), охватывает, как этого и следовало ожидать, и решение той же задачи в гильбертовом пространстве, и общее решение задачи 1. Более того, тот факт, что преобразование М даже в относительно простом случае гильбертовых пространств не удается обратить без помощи вычислительной техники, показывает, что в лучшем случае мы можем надеяться на получение итеративного метода вычисления М~\ Развивать этот вопрос далее мы здесь не будем.
Наконец, рассмотрим задачу вычисления | T*v\ | как функции т]. Определение
I Г*ц I = sup I <u, Т*ц> 1= sup —।Т Т1>' "	|и|=11Х	1/1 ueB (||и|р + Ии||2),/.
дает нам один подход к решению этой задачи. Два других подхода содержатся в лемме В.
Лемма В. Для каждого ц из R*
а)	|Г*ц|2= inf И*п-^*/2||2 + ||/2||2,
б)	|Т*т]|2 = <^(Т*т]), Т*х\).
Второе из этих утверждений является следствием того факта, что
К	= I ПI
Pg
Доказательство утверждения (а) содержится в упражнении 3.
Обсуждение задачи 2 мы закончим, подводя итог полученным результатам в заключительной теореме.
Т е о р e\f а Д. Единственное решение и^ задачи 2 определяется по формуле
и*=КТ*
где — единственный вектор из D* с нормой ||т)| = 1, который удовлетворяет одному из следующих двух эквивалентных условий:
(1) =
(2)	<5, Л> = I I,
а К1 = М отображает В на В* и определяется уравнением (4). Что касается чисел pG (£) и \ Т* т||, то их можно вычислить, пользуясь следующими выражениями:
pG(B) = (ll"d2 Ч-ИМТ*.
pG (g) = inf {х> 0:
.sup _.!<“» г*11>1 |; , иен, (|| и J2 + || Fu |p)V.
|Т*Т]|2= <ЛГ(7’*г]), 7’*q>,
|Т*т]|2= sup || 7*4- /’*/а||2 +1| /21|2.
Множество CG = {Ти: ||и||2 +||Fu||2	1} выпукло, уравновешенно
и является в D слабо компактной окрестностью 0. Через каждую его граничную точку проходит строго одна опорная гиперплоскость.
Видоизменения задачи 2. Как нетрудно видеть, те изменения, которые мы вносили в задачу 1, получая задачи 1(a), 1(6) и 2, можно комбинировать, расширяя тем самым область применения основных результатов. Здесь мы рассмотрим две типичные задачи. Первая из них аналогична задаче 1(6).
Задача 2(6). Пусть В, Вг и В2 — заданные банаховы пространства, a Fq: В -> В2 и F: В -> Вг — ограниченные линейные преобразования, причем Fq предполагается также взаимно однозначным и сюръективным. Найти такой единственный вектор и % из В, который удовлетворял бы условию Ти = £ и в то же время минимизировал бы функционал
j (и) = IM2 +	.
Воспользовавшись точно такими же рассуждениями, как приведенные перед постановкой задачи 1(6), мы увидим, что перечисленные выше ограничения, наложенные на вид преобразования
Fo, являются как необходимыми, так и достаточными для того, чтобы пространство В оставалось рефлексивным, /трого выпуклым и гладким после того, как на нем определится новая норма |u| =	(и). Поэтому задача 2(6) имеет единственное решение
для каждого £ ЕЕ D и
где pFo — функционал Минковского для множества
Cf.= {Tu:||F0< + M2<1},
а г| ЕЕ D* — единственный элемент с нормой = 1, для которого
(£, т]> = sup —= | Т*т]|. ueBt(||Fo< + ||Fu|pf> 1	"
Наконец, здесь через (2"*т])' обозначен вектор В, удовлетворяющий условиям:
а)	Иоио||2 + ||^о||2 = 1;
б)	<и0, Г*Т]> = |Г*Т]|.
Решение и % можно получить, сводя задачу 2(6) к задаче 2. Действительно, подстановка v = FQu приводит к уравнениям
j (и) = ИГ + 11^0-МГ
Ти = (TFQ~')v.
В этих обозначениях задача 2(6) идентична задаче 2. Опустим подробности этого перехода и отметим лишь, что теорема Д, очевидно, остается в силе с учетом необходимых поправок. Функция М принимает теперь вид
м (X) = Ио* II Fo* (+ || Fx || F* (F?),
а роль аналога последней формулы для | Т*т] I2 играет соотношение
sup----|<Ц’Г*П>|	= inf (IIТ*!]- F’o'1 ^/2II2 + ||/2II2)7*.
uen. (HoulP + II^IP)7* , *VI	"	"
Настоящее направление исследований достигает своего апогея в задаче 2(a).
Задача 2(a). Пусть F — некоторое ограниченное линейное преобразование, отображающее В в В1У Т — ограниченное линейное преобразование, отображающее В в D, и пусть й, у и £ — заданные векторы из В. Вг и D соответственно. Найти в пространстве
в такое и, Что Ти = £, а функционал
J(u)=h-^||a + ||Fu-^||2
достигает своего минимума.
При анализе задачи 2(a) мы воспользуемся графиком В (F) преобразования Fв произведении пространств В х^и уже определенным преобразованием G: В (F) -+D. Пусть w = (й, #). После очевидного изменения обозначений оказывается, что в задаче 2(a) мы ищем такое w = (и, Fu) из В (F), которое удовлетворяет условию G (w) = и минимизирует при этом произведение || w — — w|j2. Но если w^B (F), то, как нетрудно видеть, формулировка, приведенная выше, в точности соответствует постановке задачи 1(a), в которой 5, Т и й заменены соответственно на В (F), G и wJ, и, следовательно, воспользовавшись решением этой более ранней задачи, мы убедимся в том, что формула
(и^ Fu;) = G+ (g - Gw) + (й, Рй)
определяет единственное решение задачи 2(a).
Если же w не принадлежит В (F) (т. е. если у Рй), то воспользоваться результатами решения задачи 1(a) нельзя. Но зато легко видеть, что задача 2(a) по-прежнему имеет единственное решение. Действительно, обозначим через М подмножество произведения В х В, где
= {(u, Fu) - (й, у): G (и, Fu) = |},
т. е. пусть М является переносом G"1 (£) — (й, у) замкнутой линейной оболочки G-1 (£). Очевидно, что замкнуто и выпукло, а так как В х В строго выпукло и рефлексивно, то в М существует единственный элемент (u0 — FuQ) — (й, у), обладающий минимальной нормой. Другими словами, в В имеется единственный вектор uQ, для которого Ти0 = £ и
J (uo) = II («о» Fu)o — (й> 2/)||2 =
= min {|| (u, Fu) — (и, у)||2: G (и, Fu) = £} =
= min {J (и): Ти = 5}.
Мы доказали таким образом часть теоремы Е.
Теорема Е. Задача 2(a) всегда имеет единственное решение и1- Если у — Fa, то это решение определяется выражением
(и^, Fu$ = G*(l--Tv) + (a, $).
, О
произвольны, то и^ должно удовлетворять соотношению
(и^, Fи$ = G* (£ — Ти) -|- (й, FU),
Если же В = Н и BY = Н1 — гильбертовы пространства
где через (ц, Fu) обозначены ортогональные проекции (й, у) на H(F).
Доказательство. Нам остается только доказать ту часть теоремы Е, которая касается случая гильбертовых пространств. Прежде всего отметим, что wQ = G+ (5 — Тй) + (#, Fti) — (й, Q) должно принадлежать МБолее того, (u, Fft) — (й, у) должно быть ортогонально к G+ (£ — Тй) 6= Н (F), и, следовательно,
<М2 = IIG+ (В - Тй) + (й, Ffy) - (й, у)||2 =
= || G+ (5 - П) ||2 +1| («, Рй) - («, у) ||а. (10)
Кроме того, если и GE Н удовлетворяет условию G (u, Fu) = |, то вектор (и, Fu) — (fy, Fti) отображается с помощью G в (£ — — Тй), и, следовательно,
||(u,Fw)-(«, ffc)||>|]G+(g - П)||.
Поэтому из равенства G (и, Fu) = £ следует, что
(и, Fu) - (й, $) ||2 = || (и, Fu) - (в, Ffi) + (й, Гй) - (й, $) ||2 =
= || (и, Fu) - (й, Рй) ||2 +1| (й, Рй) - (й, $) ||2 >
> || G+ (g - Тй) ||2 +1| (й, Рй) - (й, $) ||2. (И)
Наконец, уравнения (10) и (И) показывают, что wQ является наименьшим элементом М %, что и завершает доказательство теоремы.
Проектирование на Н (F). Пусть оператор V, действующий в гильбертовом пространстве ИХ Нх, определяется соотношением
V (и, v) = (— v, и), (и, v) GE Н х ЯР
Очевидно, что V является линейной изометрией, отображающей Ях Нг в НгХ Я.
Лемма Г. Ортогональное дополнение Я (F) в Я х Нг задается соотношением
н (f)l = VH (F*).
Доказательство. Обозначим через (х, у) произвольный элемент Н (F)-L. Тогда для каждого и е Н
° = <(я, у), (и, Fu)} = <2Г, u> + <у, Fu} =	+ F*y, и},
откуда следует, что х = — F*y и что
(я. у) = (— F*y, у) = V (у, F*y).
Таким образом, (х, у) е VH (F*), и, следовательно, Н (F)' CZ О ул (F*). Обратно, если (х, у) (Z VH (F*), то
Н X = Н (F) ф VH (F*).
Однако для любого (u, Fu) справедливо соотношение (u, Fu) | v), и, значит, (— F*v, v) ЕЕ Н (F)1. Следовательно,
VH (F*) cz II (F)-L, и лемма доказана.
Одно из следствий этой леммы состоит в том, что ортогональное разложение пространства Нх Нх может быть, например, задано в явном виде с помощью формулы
Нх Нг = Я(П ф УЯ(Г*).	(12)
Эта формула будет полезна при определении ортогональной проекции Р пространства Н X Нг на Н (F). Для того чтобы вычислить эту функцию, обозначим через (й, у) е Н X Нх произвольный вектор. Тогда с учетом уравнения (12) можно утверждать, что для него существует однозначное разложение вида
(й, &) = (#» Ffi) + V (иъ F*^) = (ft, Fu) + ( — F*ult иг) =
= (и — F*u^ Fu + yJ.
Из этого равенства можно получить два других:
й = и — F*иъ у = Fu Ц- Ui.
Применив к обеим сторонам последнего равенства преобразование F* и воспользовавшись полученным результатом для того, чтобы исключить из первого равенства F*ux, получим
Ь=(1 + F*F)-'[&+ F*y].	(13)
Аналогичным образом нетрудно показать, что иг должно удовлетворять уравнению
и, - (I + FF*)"1 [у - Fu].
Но так как вектор (ft, Fu) полностью определяется значением ft, то уравнения (13) достаточно для того, чтобы определить проекцию Н X Нх на II (F). Простейшая проверка полученного результата состоит в доказательстве соотношения
(ft, Fft) J_ [(й, у) — (ft, Fft)] для всех (#, й) е Н х Hi-
Все эти рассуждения вместе с описанием преобразования G+, содержащимся в теореме Г, сводятся к теореме Ж.
Теорема Ж. Единственное решение и % задачи 2(a) в гильбертовом пространстве определяется выражением
ик = (/ + F*F)-' (Гт) + й + F*y\
где т] — единственный вектор из D, удовлетворяющий условию t = F*F)~l (Т+ц + й + F*y).
Замечание 4. Совершенно ясно, что формулировка задачи 2(a) охватывает и формулировку задачи 2 (й = у = 0), задачи 1(a) (# = 0, F = 0) и задачи 1 (й = Q =0, F = 0) в качестве частных случаев. А это приводит к тому, что теорема Ж сводится в этих случаях к теоремам Г, А и В (§ 4.3) соответственно. Так, если й = $ = 0, то и % определяется по формулам
и^ = (I + F*F)-1T+r],
I - Т (I + F'F)-1 (Т+ц).
Если у = 0 и F = 0, то
и? = Т+т] Р й,
^ = T(T+ri+u) = ri + Tu, т. е.
и^ =	(£ - Тй) + й.
Наконец, если й = 0, у --- 0 и F — 0, то и^ определяется из соотношений
^ = Т(ГЛ) = т1.
Пример 2. Рассмотрим теперь несколько видоизмененную задачу, поставленную в примере 1. Примем обозначения этого примера и добавим к ним еще символ х = Fu, обозначающий вынужденную реакцию системы, и символ z, обозначающий суммарную реакцию. Нас будет интересовать теперь задача перевода системы из начального состояния (tQ, zQ) в конечное (fy, zf) с одновременной минимизацией функционала
tj
J (и) = J [z (s) - & (s), Q (s) (z (s) - v (s))] + to
-|- [u(s) — u(s), R(s) (u(s) — u(s))] ds, где u G Яд (t) и v G Hq (t) — произвольные, но фиксированные элементы. Поскольку z и х связаны между собой соотношением
z (0 = Ф {t, t0) Z0 + X (0, t (= [f„, fy],
то ясно, что = z (tf) — Ф (tf, tQ)zQ является искомым элементом области значений. Введем переменную
но = V (0 - Ф (0 Uz0> i е [<о> 01,
ь,ь. ОБОБЩЕНИЯ ЗАДАЧИ О МИНИМИЗАЦИИ УСИЛИЙ 409 и воспользуемся определениями норм в гильбертовых пространствах Hr (т) и Hq (т) для того, чтобы записать функционал J (и) в более простом виде:
J (u) = h - $ II2 + II и - й II2 = || (и, Fu) - (й, &) ||«.
После того как этот важный шаг сделан, можно с помощью ряда очевидных операций получить искомое решение задачи. Если обозначить через р элемент й + F*y, то (см. уравнение (2) из примера 1) в данном случае р удается вычислить в явном виде по формуле
Р (0 = й (0 + J 7?"1 (0 Я* (0 Ф* (s, 0 Q (s) & (s) ds, t e Ro, to
Из утверждений теоремы Ж ясно, что искомое решение задачи зависит от обращения оператора (j + F*F). В самом деле, если й есть единственное решение уравнения (I -j- F*F) и = р, то в силу теоремы Ж и линейности всех преобразований ц является единственным элементом, удовлетворяющим уравнению
£ = Т (I + F*F)-1T+n + Тй.
Но так как Т и Т+ определены корректно, то задача сводится к об" ращению преобразования (I + F*F) — на этот раз на области значений Т+. В соответствии с леммой Б для вычисления (I
/г*^+1 на области значений Т+ достаточно решить уравнение
(I + F*F) u — v	(14)
при произвольных V е М.
Совершенно ясно, что изменения, внесенные в скалярные произведения при определении Hr (т) и Hq (т), не меняют характера множества Nt- В то же время множество М = Nt зависит от вида этих скалярных произведений. Легко убедиться в том, Что для пространства Hr множество М задается следующим соотношением:
М = {»• v (s) = R-1 (s) В* (s) Ф* (t0, s)c, с (=Rn,s(= Ro, 0]}.
Если q = pUt т0 уравнение (14) сводится к виду
и = v — F*q, v GE М.
Используя уравнение (14) и выражение для В*, приведенное в при-мере 1, мы приходим к уравнениям
и (/) = В1 (0 В* (t) ф* (t0, t) с-
Ч
- Вт1 (0 В* (0 Ф* (/0> 0 J Ф* (s, t0) Q (s) q (s) ds, (15) t t
q (t) = J ф (t, т) В (t) u (t) ds to
для каждого с. Обозначив через a (t) вектор
'/	1
а (0 = с — \ Ф (s, tQ) Q (s) q (s) ds =а(£0)-|- f Ф (s, t) Q (s) q (s) ds, J	Jo
to	to
мы можем записать и (t) в виде
и (t) = В"1 (0 В* (0Ф* (tQ, t) а (0.	(16
Рассмотрим далее вектор X (0 = Ф* (tQ, 0 а (0. Воспользовавшись тем, что Ф* (tQ, t) = Т (t, tQ), где ¥ (t, tQ) — матрица перехода для сопряженной системы, получим
t.) = — А* (0 ¥ (t, tQ), Ч (/0, tQ) = I.
С учетом этого из уравнений (15) находим
X (0 = Ф* («0, 0 к (<0) + Ф* (/0, 0 J Ф’ (s, t0) Q (s) q (s) ds = 4
= Y (t, i0) к (t0) + Y (t, t0) J Y (tQ, s) Q (s) q (s) ds, 4
откуда непосредственно следует, что X (0 должно удовлетворять следующему дифференциальному уравнению:
X (0 = — Л* (0Х (0 + Q (t)q (0, X (t0) = Хо. Аналогично из уравнений (15) и (16) следует, что q (0 удовлетворяет уравнению д(0 = А (0 q (0 + В (0 и (I) =
= A (t)q (0 + В (0 Я"1 (0 В*(0 X (0, q(t0) = 0. Таким образом, в конечном счете мы получили 2п линейных дифференциальных уравнений
q (0 = A(t) q(t)+B (t) B~l (0 В* (t)k (t), q (i0) = 0, MO = Q q (0 - A* (0 к (0, к (f0) = Xo,	(1 ’
LA. ОБОБЩЕНИЯ ЗАДАЧИ О МИНИМИЗАЦИИ УСИЛИЙ 411 решение которых определяет X (t), что в свою очередь с учетом выражения и (t) = Л"1 (0 5* (t) X (t) определяет и (t).
Теперь нельзя упустить из виду тот важный факт, что Хо ЕЕ Rn по-прежнему остается произвольным вектором. В самом делее просмотрев еще раз приведенный вывод, мы заметим, что произвольность выбора с была перенесена затем на выбор Хо, а в конечном счете — и на выбор и. Эта произвольность, естественно, устраняется, как только принимается во внимание краевое условие Ти = %. В нашем нынешнем примере это особенно просто, так как £ = Ти = (Fu) (tf) = q (tf), и, следовательно, X о должно быть выбрано таким, чтобы решение уравнений (17) удовлетворяло конечному условию q (tf) =
Возвратимся, наконец, к исходной задаче об оптимальном переводе системы из состояния (tQ, zQ) в состояние (tf, Zf). В этом случае £ = z (tf) — Ф (tf, t^z^. Функция й выбирается равной й, если (й, Q) ЕЕ Н (F), и находится из уравнения (I + F*F) fy = = р в противном случае. Если (й, ф) ЕЕ Н (F), то у (tf) = Тй вычисляется сразу, так как у (tf) = у (tf), а оптимальное управляющее воздействие определяется по формуле
uQ(t) = R-1 (t) В* (t) X (t) + fy (t),
где X (t) является решением уравнений (17) при
g (/,) = z (<,) - Ф (fz, «0) z0 - у (tf), g(<o)=O.
На этом рассмотрение нашего примера можно считать закон-ченным.
Упражнения
1.	Докажите (не заглядывая в приложение 6), что уравнение (3) определяет экстремаль элемента В*, принадлежащую В.
Указание. Проверьте неравенство
ПИ«II <У. У> + II Fx II <Fy, Fiy ] I < (|| X IP + Их IP)1/’ (|| у IP +1| Fy Ц»)*/-
и воспользуйтесь им для того, чтобы показать, что функционал х’ =М (х)/| х | принимает в точке х значение |х| и имеет в В* норму, равную 1.
2.	Убедитесь в том, что отображение М из’упражнения 1 сохраняет нор-МУ* Другими словами, покажите, что это преобразование взаимно однозначно, сюръективно и что М (Хх) = ХМ (х).
3.	В этом г упражнении нужно набросать доказательство части (а) леммы В Аннулятор L" В* подпространства L Q В определяется t как L° =
U' fy = 0, каково бы ни было х Е L}. Очевидно, что в гильбертовом пространстве L° = гД. Покажите, что L° является замкнутым линейным подпространством В*. ' Покажите, что аннулятор графика В (F) С В X В
представляет собой множество
B(F)° ={(-F*/, /): feB*}.
Поскольку В (F) само по себе есть некоторое банахово пространство, то для него существует двойственное пространство. Покажите, что В (F)* можно определить как множество векторов (компонентов) вида
<лХ = (/1. /2) + В (F)° = {(/1 - ft 4- ffr e B*}
с нормой
I (C/2) II = infjll /! - /’/; IP + II /2 + f, IP)’A
>2eB2
такие пространства в [A.83] или в [А.22] называются производными). В связи с этим простой расчет
<G (u, Fu), т)> - <(u, Fu), (Т*т] -	/2)>, f\ e
показывает, что G*t] представляет собой комножество (Т*т), 0).
4.	Пусть Н и Нх — гильбертовы пространства, D — банахово пространство, а Т и F — ограниченные линейные преобразования, определенные в Н и принимающие значения в D и Hi, соответственно. Предположим, что Т сюръективно, и найдем для произвольного £ (Е D элемент У-1 (5), минимизирующий функционалы
(a)	Jx (и) = || и |р — <u, t>0>,
(б)	Л (u) = Ии |Р - <Fu, z0> + || и |р - <и, и0>,
где у0 G Я, z0 £ и фиксированы. Пусть Нх = Н и оба пространства являются вещественными, и пусть (F + F*) > ml, тп > 0 (см. приложение 5). Найдите элемент Т-1 (£), минимизирующий функционал
(в)	Л(и) = ||Ги|Р+ <u, Fu>.
Указание. Ji (и) = | и — “2"	— |“4” j • Если F = VR — полярное
представление F (см. приложение 5), то
Л (и) = | Ru - 4 V*z j2 +1 и - 4- vo f - 4" IH IP + lly*z Pl-a
Л(и)=ИС-‘г|Р+|г|»,
где G = [(F + /’*)/2]'/> и и = Gv.
5.	Пусть T — линейное преобразование, отображающее В в Rn и такое, что
Ти = С Ф (Гр s) В (з) и (a) ds.
Укажите конкретные условия, которым должен удовлетворять элемент f-i (g),	£ Яп, минимизирующий функционал
г к ™	12/Р1 Г ({ КП
J(u) = U 2 I и. (t) |”-Л]	+ U 2 I u, (t) |*л] .
to г=1	to 1=1
Указание. Рассмотрите график тождества.
6.	В упражнениях 14 и 15 к § 3.2 решение задачи о минимизации энергии было представлено в виде закона управления замкнутой системой. Можно ли перенести этот же подход на решение задачи 2(a) этого параграфа? В чем здесь дополнительные вычислительные трудности? Постройте структурную схему синтезированной системы.
4.5. Литература к главе 4
Подробное резюме этой главы можно составить, просмотрев формулировки доказанных здесь теорем. В этих заключительных заметках мы хотим лишь осветить те аспекты затронутого вопроса, которые кажутся нам наиболее важными, и упомянуть вкратце относящуюся сюда литературу.
Центральную роль в этой главе играет § 4.3, в котором формулируется и решается основная задача оптимизации. Аппарат, используемый для решения задачи 1, основан на теореме Хана — Банаха, теореме об открытых отображениях и на различных геометрических свойствах банаховых пространств. В качестве общей литературы по всем этим вопросам можно рекомендовать книги Симмонса [А.77], Робертсона и Робертсона [Б.104], Тейлора [А.83], Ниренберга [А.65] и Хилле и Филлипса [А.41]. Не менее важны книги Бур-баки [А.12], Дея [А.20], Келли, Намиока и др. [А.48], Кларксона [Б.27], Клея и др. [Б.58], Эгглстоуна [А.24] и Данфорда и Шварца [А.22].
В общем и целом мы можем с удовлетворением отметить, что результаты этой главы достаточно компактны и ясны, и нетрудно понять, чем это вызвано. Конкурирующие методы, например принцип максимума (см. [А.69]), вариационные методы (см. [А.31], [А.26], [Б.53] и [Б.13]), методы программирования (см. [Б.96], [А.97]), и другие (см. [А.25], главу 6 [А.56], [А.91], [Б.2], [Б.18], [Б.19],[Б. 83]) обычно относятся к задачам конкретного динамического характера, например, с их помощью рассматривают системы, описы-ваемые^ дифференциальными уравнениями, и на равных основаниях (по крайней мере в теории) изучают как линейные, так и нелинейные системы. Напротив, при нынешнем подходе с самого начала предполагается линейность системы и конкретный тип критерия качества (он должен быть типа нормы), но зато допускается гораздо большее разнообразие в типах рассматриваемых систем. Такое видоизменение аналитической ситуации позволяет воспользоваться мощным аппаратом, о котором уже говорилось выше. Короче говоря, в этой главе рассматривается другой класс задач, чем те, которые ?аД??1ются Решению стандартными методами (см. дополнительно [А.98], 1А.14]ДА.67],[А.74],[А.86],где приводятся другие применения этих методов).
В этой главе упор делается на линейные системы любого типа, и в том чи-ле на гибридные семейства дифференциальных и конечноразностных систем, оторые можно и следует рассматривать как конкретные элементы абстрактен) множества. Для того чтобы усилить это утверждение, мы покажем в приложении 9, что результаты этой главы позволяют с тем же успехом решать и обп6ЧУ 0ПтимизаЦии системы с распределенными параметрами. Эти и другие оощения требуют, по-видимому, лишь искусства в построении подходящих паховых пространств и в вычислении экстремалей.
Материал этой главы представляет собой развитие работы [Б.100], а также работ [Б.101] и [Б.102]. Интерес представляют и некоторые другие статьи, и мы вкратце упомянем о них здесь. В работе Ахиезера и Крейна [Б.1] ставится задача, аналогичная сформулированной в упражнении 7 к § 4.3. Полученный в этой работе результат использовался для решения коп-кретных задач оптимизации сначала Красовским [Б.61], [Б.62], а затем Куликовским [Б.65], [Б.66], [Б.67], [Б.68]. Аналогичные исследования проводились Ньюстадтом [Б.90], [Б.93], Ридом [Б.103] и Антосиевичем [Б.З]. Задачи оптимального по быстродействию релейного управления решались, начиная с Бушау [Б.20], Веллманом, Гликсбергом и Гроссом [Б.12], Гамкре-лидзе [Б.38], Ла Саллем [Б.71], Халкиным [Б.44], Соннеборном и Ван Флеком [Б.112] и Фальбом [Б.34] (см. также работы [Б.77], [Б.57], [Б.73], [Б.74] и [Б.91]).
Относящиеся к общей теории технические приложения рассматривались ^)азными авторами. Прикладной характер носят книги [А.14], [А.67], [А.74], А.86], [А.88], [А.96], [А.97] и [А.98]. Полное впечатление от технической литературы по этому вопросу можно получить из статей Флюгге-Лотц и Мароаха [Б.35], Кадцоу^ [Б.26], Лэдда и Фридленда [Б.70],4 Стабберуда [Б.113], Уонхэма и Джонсона [Б.121], Кранца и Сарачика [Б.60], Атанса ГБ.4], [Б.5], Атанса, Фальба п Лакосса [Б.6], [Б.7], Уолтца [Б.116], Медича [Б.81], [Б.82], Балакришнана [Б.9], Портера [Б.99], Нахи [Б.88], Куо [Б.69], Гриммелла [Б.43] и многих других. 1	ь,
В большинстве приложений приходится решать одну или несколько чисто «вычислительных» задач. Так, в задаче 1 необходимо найти единичную внеш» нюю нормаль и чисто р (£). (В случае минимизации усилий вместо этого можно вычислить J-1 или (Т*Т)-1 в гильбертовом пространстве). В задаче 2 стоит вопрос об обращении оператора К (или оператора (/ + F*F), если пространство гильбертово). Эти вычисления могут быть выполнены с помощью нескольких существующих алгоритмов, но здесь еще много нерешенных проблем. Полезной общей литературой по этим вопросам могут служить книги [Б.46], [Б.114], [Б.55], (А.97] и [А.74]. Мы рекомендуем читателю работы Хо [Б.47], Ньюстадта [Б.89], Итона [Б.29], Харви [Б.45], Бабунашвили (Б.8], Гильберта [Б.39], Фаддена [Б.33], Барра [Б.10], Балакришнана [Б.9], Басса и Веббера [Б.И], Фридленда [Б.37], Грэхэма [Б.42], Уолтца [Б.116], Брайсона и Дэнхэма [Б.18], [Б.19], Кнудсена [Б.59], Куликовского [Б.66], [Б.67], Ли [Б.72], Медича [Б.80] и Паевонского [Б.94], [Б.95].
В некоторых из этих работ решается задача оптимизации быстродействия (см. приложение 7) или задача синтеза замкнутых систем (см. замечание 7 к § 4.3). В большинстве же случаев само заглавие работы достаточно четко определяет ее содержание.
В гильбертовых пространствах псевдообратное преобразование линейно, и его вычисление предполагает обращение линейных положительно определенных операторов (а именно ТТ* или (I + F*F) в задачах 1 и 2, соответственно). Некоторые методы такого обращения описаны Альтманом [Б.2] и Канторовичем (Б.55) (см. также Балакришнан [Б.9]). Вывод уравнения Рикарди из § 4.4 получен Куо [Б.69], но может быть получен и вариационными методами (см. работу Калмана [Б.53]).
ПРИЛОЖЕНИЕ 1
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Приложение 1 представляет собой краткую сводку основных понятий теории счетных множеств, теории сепарабельных пространств и теории компактных множеств. Первый из этих вопросов включен для полноты картины, остальные два играют важную роль в приложениях 2 и 5. Полученные здесь результаты используются также в главах 3 и 4.
Счетные множества. Предположим, что множества А и В содержат конечное число элементов и что мы хотим установить, одинаково это число для каждого из множеств или нет. Очевидное решение этой задачи заключается в том, чтобы подсчитать число элементов в каждом из них. Другими словами, мы должны будем поставить в соответствие каждому элементу соответствующего множества одно из целых чисел 1, 2, 3, ... Наибольшее из использованных целых чисел называется (кардинальным) числом элементов в множестве. Однако на наш вопрос можно ответить и без пересчета элементов множества. Например, пусть А есть следующее множество букв латинского алфавита:
А = {а, Ь, с, d, е},
& В — некоторое множество греческих букв:
В = {а, р, у, б, е}.
Если из элементов этих множеств составить таблицу
Л : д [& | с | d | g
В : а | 3 | т | б |"е ’
то, не подсчитывая числа элементов в каждом из них, мы сразу увидим, что число элементов А и В одинаково. Что же наиболее характерно для этого метода сравнения множеств? В нем каждому элементу одного множества ставится в соответствие один и только один элемент второго множества, и, наоборот, с каждым элементом второго множества оказывается связанным один и только один элемент первого множества.
Основная сила этого на первый взгляд тривиального метода сравнения заключается в том, что им можно пользоваться и в тех случаях, когда сравниваемые множества бесконечны. Например,
если через N обозначить множество всех положительных чисел, а через М — множество чисел вида 1/п, то второй метод сравнения сразу показывает, что число (в каком-то смысле этого слова) элементов множеств N и М одинаково. Для того чтобы убедиться в этом, достаточно образовать из этих множеств следующую таблицу:
N: 11 2 | 31 4...
1172|7з|74... ’
в которой в одну пару сведены числа п из N и т из М. Итак, нам удалось установить эквивалентность этих двух множеств, не отвечая на вопрос, а каково же абсолютное число элементов в каждом из них.
Любые два множества А и В называются эквивалентными в том и только в том случае, когда существует некоторое правило, определяющее взаимно однозначное соответствие между их элементами, т. е. если каждому д Е Л соответствует в точности одно i Е 5, и наоборот. Читатель сам может убедиться в справедливости следующих простых предложений.
(1)	Каждое множество эквивалентно самому себе.
(2)	Каковы бы ни были множества Л и В, если А эквивалентно В, то и В эквивалентно А.
(3)	Каковы бы ни были множества Л, В и С, если А эквивалентно В, а В эквивалентно С, то и Л эквивалентно С.
Определение А. Множество называется бесконечным тогда и только тогда, когда его элементы можно привести во взаимно однозначное соответствие с элементами его некоторой собственной части. Всякое множество, не являющееся бесконечным, называется конечным.
Для того чтобы проиллюстрировать основную мысль, на которой покоится это определение, рассмотрим множество N = — {1, 2, 3, ...} положительных целых чисел. Множество N кажется безусловно «больше» множества {2, 4, 6,...} всех четных положительных целых чисел, так как второе из них является собственной частью первого. Однако если мы имеем дело с бесконечными множествами, то нельзя забывать, что наш критерий эквивалентности зависит от существования какого-нибудь взаимно однозначного соответствия между элементами множества (а не от того, является ли одно собственной частью другого или нет). Что же касается взаимно однозначного соответствия между элементами рассматриваемых множеств, то его роль может играть следующее
1, 2, 3, ..., п, ...,
2, 4, 6, ..., 2п, ...,
где каждому положительному целому числу из верхней строки д вится в соответствие некоторое четное положительное целое Главное удвоенному верхнему), стоящее непосредственно под ним. А следовательно, эти множества нужно считать эквивалентными.
В качестве второго примера мы можем показать, что «число» квадратов (1,4,9,16, 25, ...) оказывается равным числу положительных целых. Справедливость этого утверждения очевидна из следующей таблицы:
1, 2, 3, 4, ...,
I2, 22, З2, 42, ...
Для того чтобы избавиться от непри-ятного ощущения, вызванного преды- _____________________ !
дущими примерами, наводящими нас	— v---------7
на мысль о существовании какой-то	В
аномалии в множестве целых чисел,	Рис. П1.1.
рассмотрим теперь рис. П1.1.
Обозначим через А множество точек, образующих гипотенузу, а через В — множество точек, образующих горизонтальный катет треугольника. Несмотря на то, что катет В очевидно короче, как отрезок прямой, гипотенузы А, между элементами этих множеств можно установить взаимно однозначное соответствие, проектируя А на В. Таким образом, как и в предыдущих примерах, мы вновь столкнулись с множеством, эквивалентным своему собственному подмножеству. Ясно, что никакое конечное множество не может быть эквивалентным своему собственному подмножеству. А значит, этим странным явлением мы обязаны бесконечности множества А.
Определение Б. Множество А называется счетным, если оно эквивалентно множеству положительных целых чисел. Если множесто конечно или счетно, то его называют не более чем счетным.
Из этого определения следует, между прочим, что множество счетно, если его элементы можно упорядочить в бесконечную последовательность. Счетным множествам посвящено много интересных и важных теорем. Здесь же для экономии места мы ограничимся лишь следующими.
Теорема А. Каждое множество содержит не более чем счетное подмножество. Любое подмножество не более чем счетного множества не более чем счетно.
Доказательство. Поскольку для конечных множеств оба ут-верждения этой теоремы абсолютно тривиальны, то допустим, что множество А бесконечно. Счетное подмножество А можно образовать, последовательно выбирая элементы из множества А и^ну-меруя их aif i = 1, п, ... Получающееся таким образом подмножество находится в очевидном соответствии с множеством
целых чисел. Если множество А не более чем счетно, a Z?CZ Л, то элементы множества В можно перенумеровать в таком порядке, какой задается исходным отображением множества целых чисел на множество А.
Теорема Б. Объединение конечного числа не более чем счетных множеств не более чем счетно.
Доказательство. Пусть множества А = {ап а2, ...} и В = = {bi, 62, •••} счетны. Тогда множество A (J В также счетно, потому что из его элементов можно образовать последовательность ах, л2, &2, • ••, 0П, Ьп, ... Для того чтобы доказать, что объединение п счетных множеств, где п — положительное целое число большее 1, счетно, достаточно воспользоваться методом индукции и только что доказанным результатом для случая п = 2.
Теорема В. Объединение счетного семейства не более чем счетных множеств счетно.
Доказательство. Обозначим через Аг = {а^, 0<2, i = 1,2,... ..., п, ..., элементы счетного семейства не более чем счетных множеств. Рассмотрим следующую таблицу:
а11	Я12	fl13 “	> 0ц	Як,-5
а21 1 /	0 22	028	Я2!	Я2->
i / 0;н	032	0ДЗ		035
	0J2	0ДЗ	044	045
rt51	052	rt53	051	055
Элементы этой таблицы можно упорядочить в последовательность, как показано стрелками. Ясно, что при этом ни один элемент не оказывается забытым. Итак, эта процедура позволяет упорядочить множество (J < Ai в последовательность. Если все А^ взаимно не пересекаются (т. е. если А{ Q Aj = 0, i =/= j), то эта процедура позволяет установить взаимно однозначное соответствие между множеством (J < и множеством целых чисел. Если же у множеств {Л J есть общие элементы, то достаточно договориться о том, что при построении нашей последовательности мы должны выбрасывать все элементы, когда-либо уже встречавшиеся ранее.
Теорема Г. Множество рациональных чисел счетно.
Доказательство. Каждое рациональное число может быть'пред-ставлено в виде р/g, где р — целое, ад — целое положительное число. Предположим, что эти числа взаимно несократимы. При
пишем каждому рациональному числу индекс | р | + q. Упорядочим далее множество рациональных чисел в порядке возрастания этих индексов. При этом числа с одинаковыми индексами упорядочиваются по своей абсолютной величине, а среди равных по абсолютной величине чисел первым ставится отрицательное. Построенная таким образом последовательность начинается следующим образом:
—11—11—22—11—33 0. ~~~ ’2’	1’1’	3’3’	1’1’
—1	1	—2	2	—3	3	—4	4
Т" ’ *4" ’	3’3’	2’2’	1’1*'*'
Возможность построения такой последовательности и доказывает утверждение теоремы.
К настоящему времени у читателя может возникнуть необоснованное представление, что все бесконечные множества счетны. Ответ на этот вопрос дает следующий пример несчетного множества.
Теорема Д. Следующее множество вещественных чисел {х: х ЕЕ R и 0	< 1} = [0,1] несчетно.
Доказательство. Предположим, что между множеством целых чисел и множеством вещественных чисел, заключенных между 0 и 1, существует некоторое взаимно однозначное соответствие. Представим вещественные числа из указанного промежутка с помощью бесконечных двоичных дробей. Тогда предполагаемое существование взаимно однозначного соответствия позволяет построить бесконечную таблицу примерно такого вида:
1 <-> 0,000000 ...
2<, 0, 011001 ...
3<^0,001101 ...
п <->0,1011100.. .
И если предположение о счетности множества [0, 1] верно, то в эту таблицу должно войти каждое число из этого множества.
Определим теперь число х е [0, 1] следующим образом. Рассмотрим главную диагональ построенной указанным образом таблицы из двоичных дробей. Предположим теперь, что у х в п-м
двоичном разряде имеется нуль, если в этом разряде у n-го числа таблицы имеется 1, и единица, если у n-го числа — нуль. Построен-ное’таким образом число’ж отличается’от n-го числа в таблице значением своего n-го разряда, а значит, это число не попало в указанную таблицу. Отсюда следует, что наше исходное предположение неверно, и, значит, рассматриваемое множество не счетно.
Теорема Е. Множество алгебраических полиномов с рациональными коэффициентами счетно.
Доказательство этой теоремы мы предоставляем читателю в качестве упражнения, подсказав, что множество Рп полиномов с рациональными коэффициентами степени не выше п счетно и что можно представить в виде объединения счетного семейства множеств Рю = (J“=i Рп-
Сепарабельные пространства. Подмножество Е всех рациональных чисел множества R всех вещественных чисел обладает тем важным свойством, что каждый элемент R может быть представлен как предел некоторой последовательности элементов Е. Другими словами, замыкание множества Е; Е= R. Это свойство получило название свойства плотности множества рациональных чисел в множестве R. Переведем теперь понятие плотности на язык теории метрических пространств.
Определение В. Множество S элементов метрического пространства X называется всюду плотным (или плотным в X), если S = X.
Согласно определению К из § 1.2 равенство S = X означает, что каждое х 6= X можно представить в виде х = lim хп9 где хп ЕЕ S, или что для каждого х GE X и е > 0 всегда можно найти такое х’ ЕЕ 5, что р (ж, х‘) < е. Это определение не исключает и того случая, когда X представляет собой некоторое подмножество более широкого метрического пространства.
Определение Г. Метрическое пространство называется сепарабельным, если оно содержит в себе некоторое счетное всюду плотное подмножество.
Большинство пространств, рассматривавшихся в качестве примеров в главе 1, сепарабельны.
В пространстве Rn каждый вектор можно представить в виде предела последовательности векторов с рациональными компонентами. Векторы же с рациональными компонентами в силу теоремы В образуют счетное множество. Таким образом, пространство Rn сепарабельно. Сепарабельность пространства Za можно установить следующим образом. Прежде всего, если х = (gx, £а, ...) есть некоторый элемент пространства Za, то последовательность
Iя должна сходиться, и, следовательно, выбрав число п
достаточно большим, мы мошем добиться того, чтобы величина V£° |£fc |2 была сколь угодно малой. Другими словами, мы можем сколь угодно точно аппроксимировать заданный вектор х другим вектором вида
Хп - (&n U U 0, ...).
В вещественном пространстве 12 все £. вещественны, и, следовательно, их можно аппроксимировать рациональными А это приводит к аппроксимации заданного вектора х некоторым другим вектором из Z2, у которого только конечное число отличных от нуля компонент, каждая из которых к тому же рациональна. Это последнее подмножество Z2 счетно, и, значит, мы можем утверждать, что Z2 сепарабельно. Для комплексного пространства Z2 доказательство сепарабельности совершенно аналогично.
Точно таким же способом читатель может показать, что множество Роо (а, Ь) всех полиномов с рациональными коэффициентами, определенных на промежутке (а, &), плотно в метрическом пространстве Роо (я, Ь) всех полиномов, определенных на (а, Ь) (с обычной метрикой). Теорема Вейерштрасса утверждает, что любую функцию х & С (а, Ь) можно представить с помощью последовательности полиномов, равномерно сходящихся к х. Если же в эту последовательность подставить аппроксимирующие элементы множества (а, Ь), то мы получим, что множество Р^ всюду плотно в С (а, Ь).
В завершение наших заметок о сепарабельности приведем еще две общие теоремы. 11
Теорема Ж. Каждое подпространство X' сепарабельного метрического пространства X сепарабельно.
Доказательство. Для каждого хп ЕЕ S мы выберем такое Уп G X' (если’ оно существует), что р (хп, у*) < 1/Л. Множество {Уп} всех таких элементов обозначим через SR. Заметим, что счетно и что SR CZ X’. Аналогично S' = |Jk Sk является счетным подмножеством X'.
Для того чтобы показать, что множество S' плотно в X', выберем для произвольного е > 0 такое А, что 1/А < е/2. Поскольку множество S плотно в X, то существует такое хп Gz5, что для произвольного х ЕЕ X' справедливо соотношение р (хп, х) < 1/к. Но отсюда следует существование такого у* Е= S', что р (у*» хп) > 1/А:. Теперь с помощью неравенства треугольника
Р (Уп, р (у*, Ял) 4- р (Хп, х) < 2/к < 8
мы легко устанавливаем плотность множества S' в Х\ а значит, и сепарабельность X'.
Теорема 3. Если некоторое всюду плотное подмножество X' метрического пространства X сепарабельно, то сепарабельно и X.
Доказательство, Пусть А есть некоторое счетное всюду плот-ное подмножество X'. Для каждого	и е^>0 (в силу то-
го, что X’ Bwojiy плотно в X) найдется такое х' GE X', что р (х, х’) < е/2. По так как А всюду плотно в X', то существует такое х" ЕЕ А, что р (xf, х") < е/2. А отсюда следует, что р (х, x")<Z е, и из произвольности е следует, что множество А всюду плотно в X.
Компактные пространства. Известна важная теорема Больцано — Вейерштрасса: в каждой бесконечной ограниченной последовательности вещественных чисел содержится некоторая сходящаяся подпоследовательность. Если А есть произвольное ограниченное подмножество R, то в соответствии с теоремой Больцано — Вейерштрасса мы можем утверждать, что любая последовательность, образованная из элементов множества А, содержит некоторую сходящуюся подпоследовательность. Но в то же время, если множество А не ограничено, то можно выбрать такую расходящуюся последовательность его элементов, никакая подпоследовательность которой не будет сходиться. Таким образом, пространство R обладает тем свойством, что в нем ограниченность множества эквивалентна факту существования сходящихся подпоследовательностей последовательности, образованной из элементов этого множества.
Но так как это справедливо относительно многих свойств оси вещественных чисел, то попытка переноса свойства Больцано — Вейерштрасса на случай произвольных метрических пространств сопряжена с определенными трудностями. Понятие компактности, намеченное в первом из наших определений, позволяет выделить в отдельную группу те пространства, которые обладают свойством Больцано — Вейерштрасса.
Определение Д. Подмножество А метрического пространства X называется компактным, если каждая бесконечная последовательность элементов А содержит некоторую сходящуюся подпоследовательность, предел которой принадлежит А, Если этим свойством обладает само X, то пространство X называется компактным,
Яспо, что компактным является любое множество с конечным числом элементов, так как в любой бесконечной последовательности, составленной из его элементов, один из них должен повторяться бесконечное число раз, а это автоматически обеспечивает нас бесконечной сходящейся последовательностью.
Теорема И. Каждое компактное множество ограничено.
Доказательство, Обозначим через А некоторое неограниченное множество. Для любого г > 0 выберем некоторое Е Л и заметим, что в силу’ неограниченности А это множество не может содержаться в шаре S2 (х±) радиуса гл с^ центром в xv Поэтому
всегда найдется такое х2 е Л, что р (х2, хг) > г. Неограниченность А гарантирует нам теперь существование	лежащего
вне шаров (х^ и S2 (х2). Повторяя этот процесс, мы построим бесконечную последовательность элементов А, никакая подпоследовательность которой не может быть сходящейся. А это означает, что множество А не может быть компактным, и, следовательно, теорема доказана.
В отличие от того, что наблюдается в пространстве /?, утверждение, обратное теореме И, в общем случае неверно, т. е. нельзя утверждать, что всякое ограниченное замкнутое подмножество произвольного метрического пространства компактно. Для того чтобы раз и навсегда выяснить это, рассмотрим следующий пример.
Пример 1. Единичный шар S — {х: ||х| — 1} пространства 12 может служить примером замкнутого ограниченного множества, не являющегося компактным. В самом деле, элементы
ег = (1, 0, 0, ...),
е2 = (0, 1, 0, ...)
образуют бесконечное подмножество 5 такое, что р (е.,	2
при i =f= j, и, следовательно, эта последовательность {еп} не может содержать какой-нибудь сходящейся подпоследовательности. Однако в пространстве 12 имеются и компактные подмножества, например множество Q, элементы которого х = (х1? х2, ..., хп, ...) е= ЕЕ 12 удовлетворяют условиям
I К — . I К ’ • • • ’ IХп I (4") ’ • • •
Т е о р е м а К. Каждое замкнутое ограниченное подмножество конечномерного нормированного пространства компактно.
Доказательство. Обозначим через п размерность пространства X, а через S — некоторое замкнутое ограниченное подмножество X. Если ввести в X некоторый базис {х1? ..., .гп}, то каждый элемент множества S оказывается связанным с вектором («1..., ап) дп с помощью разложения этого элемента
и
X = 2 i=l
по заданному базису. Обозначим через A., i = 1, ..., и, множество всех значений, принимаемых f-м коэффициентом этого разложения по мере того, как х пробегает S. Поскольку множество
ограничено (см. теорему Б из § 1.4), то можно показать, что ограничены и АГ Более того, каждая бесконечная последователь
ность {хк} элементов S порождает некоторую бесконечную последовательность и в каждом из Аi = 1, п. Сходящаяся подпоследовательность последовательности может быть построена следующим образом. Выберем в А1 любую сходящуюся подпоследовательность последовательности {ocj}. Обозначим ее через (ai }. Соответствующая последовательность {л^'} элементов S порождает некоторую бесконечную последовательность {а2 } элементов А 2. Выберем из нее некоторую сходящуюся подпоследовательность {сс2 }. Соответствующая последовательность {xh } элементов S по-прежнему бесконечна, и ее первые два коэффициента из Ai и А2 сходятся. Повторяя описанный процесс п раз, мы получим подпоследовательность исходной последовательности, сходимость которой порождается сходимостью в координатных пространствах.
Определение Е. Пусть А — некоторое подмножество метрического пространства X, и пусть е>0. Множество В CZ А называется е-сетью для множества А, если для каждого а ЕЕ А существует такое ЬеВ, что р (&, а) < 8.
Другими словами, множество В представляет собой е-сеть для множества Л, если в В имеется достаточно точек для того, чтобы сферические окрестности диаметром е всех точек В полностью покрыли множество Л. Каждое множество представляет собой свою собственную е-сеть. Если у множества Л при любом е > 0 существует конечная е-сеть, то Л называют вполне ограниченным. Совершенно ясно, что каждое вполне ограниченное множество к тому же и ограничено.
Теорема Л. Для того чтобы множество полного метрического пространства было компактным, необходимо и достаточно, чтобы оно было замкнутым и вполне ограниченным.
Доказательство. Необходимость условий этой теоремы, доказываемая здесь в первую очередь, не нуждается в предположении о полноте пространства. Предположим, что при некотором 8 > 0 для компактного множества не найдется е - сети. Тогда для хгееА мы сможем найти такую точку х2 ЕЕ А, что
Р (^i, *2) >е.
Точно таким же образом мы сможем найти и множество {х±, ..., хп} CZ Л, для которого р (xit Xj) е при i =/= j. В противном случае это множество было бы е-сетью для множества Л. Продолжая этот процесс по индукции относительно индекса п, мы построим бесконечную последовательность {л^}, для которой р Xj) > е при i =/= j и в которой, следовательно, нельзя выделить сходящейся подпоследовательности. Но это значит, что множество Л не может быть компактным, и, следовательно, вполне ограниченность множества является необходимой.
Предположим теперь, что при некотором е > 0 у множества А существует конечная е-сеть. Для удобства положим, что ех = 1. В этом случае конечное число шаровых окрестностей единичного радиуса покрывает множество А. Обозначим через {хп} некоторую бесконечную последовательность точек Л. Тогда одна из упомянутых выше окрестностей, назовем ее 5, содержит бесконечное множество точек из {.гп}. Выберем теперь в {тп} подпоследовательность {ггп}, отбрасывая члены, не попавшие в Точки хп, принадлежащие образуют последовательность, и для удобства мы их перенумеруем как 4°,	••• хп\ ...
Выберем далее е2 = 1/2. Отталкиваясь теперь от построенной подпоследовательности {т^} и рассуждая таким же образом, мы увидим, что некоторый шар S2 радиуса 1/2 содержит бесконечную подпоследовательность х(*\ т22),	..., порожден-
ную первой из подпоследовательностей. Этот процесс можно повторять бесконечное число раз, выбирая каждый раз подпоследовательность, содержащуюся в некотором шаре Sn радиуса
— 1/тг, п = 1, 2, ...
Выбранные таким образом подпоследовательности могут быть упорядочены в следующую таблицу:
„(1)	„(1)	„а»	(1)
	•тг ,		. .. , хп ,
4”.		г<2) ^3 >	т(2) . . . , ,
I?1.	г(з) х2 ,	~(3) •*-3 »	Г(3) ...» Л П ?
г-?’,		т(")	т(п) • • • » Хп 1
представляет собой подпоследовательность
В ней каждая строка порожденную предыдущей строкой. Кроме того, последовательность в n-й строке обладает тем свойством, что все ее элементы содержатся в некотором шаре радиуса 11п.
Воспользуемся теперь классическим «диагональным методом», а именно построим последовательность из точек, лежащих на главной диагонали нашей таблицы
JD ~(2)	Дп)
^1 » *Л/2 » • • • »	» • • •
Эта последовательность является подпоследовательностью исходной Последовательности,и для любых тп и р > п справедливы
соотношения
p(T(m\fl)<4- » Р(1(Л«)<Т>
где а — центр шара Sn. Поэтому
р (Хт\ 4₽)) < р (4Г \ а) + р (д, Х(рР)) <	.
Рассматриваемая последовательность является последовательностью Коши и, следовательно, в силу полноты пространства X сходится, что и доказывает теорему.
В качестве иллюстрации к этой теореме воспользуемся тем фактом, что каждое замкнутое ограниченное подмножество п-мер-ного банахова пространства может быть погружено в достаточно большой гиперкуб (т. е. в такое множество точек, координаты которых по произвольному базису ограничены по величине). Если такой куб разбить на меньшие кубики с диагональю длиной то вершины этого куба образуют конечную е-сеть для исходного множества, а значит, это множество компактно.
Конечная е-сеть множества Q из примера 1 может быть построена, например, следующим образом. Выберем число п так, чтобы (1/2)п < е/2. Каждому х = (xlt г2, ...) ЕЕ Q поставим в'со-ответствие точку х' = (х19 х2, ..., хп, 0, 0,...). Тогда
(ОО	/ 00	\ ’/•
<(s(4T) <dr-п-|-1	/ \n-H 7 /
Множество Q' всех таких х' принадлежит конечномерному пространству. Но в силу неравенства треугольника всякая конечная е/2-сеть для множества Q' будет е-сетыо для множества Q.
Этот пример подсказывает нам следующее следствие теоремы Ж.
Следствие. Для того чтобы подмножество М полного метрического пространства X было компактным, необходимо и достаточно, чтобы для каждого е > О существовала компактная ь-сеть множества М.	F
При изучении конкретных пространств условия компактности не всегда оказываются простыми. Пространство С (а, Ь), играющее центральную роль при изучении линейных динамических систем, может служить хорошей иллюстрацией того, как для установления компактности' приходится привлекать специальный аппарат. Для того4 чтобы сформулировать основную теорему для этого пространства, нам понадобятся два новых понятия. Функции из множества М — {х (t)} называются равномерно ограничен*
ными, если существует такая постоянная а > 0, что|х(/)|<^'а при всех t и всех х ЕЕ М. Функции х из множества М называются равностепенно непрерывными, если для каждого е > 0 существует такое 6, что | х (^) — х (*2) | < е при каждых | /2 — tr | < 6 и всех х М. Следующий критерий компактности множеств пространства С (а, Ъ) принадлежит Арцеля (Arzela).
Теорема М. Для того чтобы подмножество М пространства С (а, Ь) было компактно, необходимо и достаточно, чтобы функции х из множества М были равномерно ограничены и равностепенно непрерывны.
Литература
Составляя это приложение, автор опирался в основном на содержание главы I работы [A.63J и §§ 3.6—3.8 работы [А.93]. Мы отсылаем читателя также к работам [А.4], [А.6], главам II — IV работы [А.77], главе III работы [А.21], главам I и II работы [А.50], главе I работы [А.56] и главе II работы [А. 83].
РАЗЛОЖЕНИЕ ФУРЬЕ
В этом приложении мы займемся вопросом, безусловно знакомым читателю. В самом деле, разложение Фурье играет важную роль в механике, теории поля, термодинамике, теории систем управления с распределенными постоянными и вообще всюду, где систему можно описать с помощью обыкновенных дифференциальных уравнений или уравнений в частных производных. Здесь же мы познакомимся с абстрактной теорией разложения Фурье. Такое изложение свободно от конкретных расчетов и подчеркивает внутреннюю элегантность основной идеи. Кроме того, это приложение дает читателю дополнительную возможность поупражняться в абстрактной математике.
Теорема А. Пусть S = {еп е2, ..., еп} есть некоторое конечное ортонормальное множество элементов гильбертова пространства И, и пусть х — некоторый вектор пространства Н. Тогда
п
(1)	21<^>12<И2.
г=1
п
(2)	(х — 2 ei> ei^ I ej при Любом j.
Доказательство. Первое утверждение можно доказать с помощью вычислений, аналогичных использованным для доказательства неравенства Шварца:
п	п	п
Iх — S <x>ei>ei	Г =	<^х—	2	<х,е,>еьх—	2	==
U 1=1	i	1=1	j=l
n	n
= <z, Z> — 2 O’> ei> \A ei> — 2 vc> ei'> ei> + i=l n n
+ SS <X, <?i> <r, ep <eb ep,
г 1 j=l
откуда в силу ортонормальности S получим п
о<№- 3io,ei>p.
\
Для того чтобы доказать второе утверждение, заметим, что
п	п
— 3 <Х> ei> ei] ’ е>/ = <-Х’ ei> ~ S <а;> ffi> <eb е/> =
= <х, tj> — <*, ер = 0.
Совершенно ясно, что неравенство (1) с геометрической точки зрения можно интерпретировать как утверждение о том, что сумма квадратов компонент некоторого вектора в различных взаимноперпендикулярных направлениях не превосходит квадрата величины самого вектора. Это первая теорема, хотя и довольно ограниченного содержания, намечает путь для дальнейших исследований разложения Фурье. В дальнейшем нам остается только расширить применимость этого результата.
Теорема Б. Пусть L — замкнутое линейное подпространство, натянутое на ортонормальное множество S — {е^ ..., еп, Тогда для^каждого zEL
п
(1)	ж = lim 2 еЕ ei,
П-ЮО j—1
n
(2)	Ikll2 — lim 2 I <z’^i> I’-
п-юо i=1
Доказательство. В соответствии с доказательством леммы Б из § 1.5, каждое х GE L может быть представлено в виде предела последовательности {хп}, в которой каждое хп представляет собой некоторую (конечную) линейную комбинацию {ej}. Поэтому для каждого е > 0 найдется такая линейная комбинация X=i а^, что
п
|х— 2 atei| <е-
Более того, согласно определению нормы
|х ~~ 2 ai«i |* = <(х — 2 a.ei, х — 2	=
*	г	j
= <х, z> 4- 2®ia> <ei( в/> — 2ai <*> ei> — Sa< <ei> х> = i,j	г	г
= № — S«ici — 2аА + 21а41*»
Где ci —{х, q>; мы воспользовались тем фактом, что <q,	= 6^.
Последнее выражение можно переписать в виде
р —2ал|Г = кГ + 3(сА —®ici —ai5i—+aiai) —
-S^i = kll2-3Rila+3l«i-^l2-i	i	i
Заметим теперь, что правая часть этого уравнения принимает наименьшее значение	при аг =	q. Поэтому
п	п	п
°<иа-	s	ы2=|®-	Sciei|2< h- s «лГ<в’»
г=1	г=1	i=l
а так как е произвольно, то
п	п
X = lim 3 ciei = lim S ei> ег-n-кю i=1	n—oo i=1
Кроме того, из неравенства следует, что
п
lim 3l<a:'ei>l2 = lla:ll2-
n-woi=1
что и требовалось доказать.
Следствие (неравенство Бесселя). Пусть S = {q} есть любое не более чем счетное ортонормальное множество гильбертова пространства Н. Тогда для каждого х из Н
г
Доказательство. Если множество S конечно, то утверждение этого следствия эквивалентно утверждению теоремы А. Если же S бесконечно, то рассмотрим замкнутое линейное подпространство L (q, q>, • ••» • ••)• Согласно теореме о проекциях каждое х е Н однозначным образом представляется в виде
х = у + z, у е ь, z Е
Но в соответствии с теоремой Б
п
IIУ В2 = lim 3 |<У»е1> I2»
П-»ОО i—1
а т\к как при всех i (z, е4> = 0, то это можно переписать в виде
\ п
\	= Иш 2 I <*. ei> Г-
Доказываемое утверждение следует теперь из того, что
\	М2=М2+1№-
Замечания. Скаляры <х, е,> называют коэффициентами разложения Фурье вектора х по множеству (бц е2, еп, В дальнейшем мы будем пользоваться символом для обозначения операции lirn^—*оо i=i*
Заметим, что, доказывая неравенство Бесселя,_ мы в действительности обнаружили, что вектор х принадлежит L в том и только в том случае, когда || х ||2 = ^£11 (х, е{> |2.
Отметим еще, что неравенств0 Шварца | \<х, у) I < || XII • II у II можно получить из неравенства Бесселя, рассматривая ортонормальное множество, состоящее из единственного вектора у/|| у (|.
Полнота ортонормальных множеств. Семейство 5 ортонормальных векторов пространства Н называется полным, если S не может содержаться в некотором более широком ортонормальном множестве *). А это, очевидно, эквивалентно требованию, чтобы единственным вектором Я, ортонормальным всем векторам S, был вектор 0. Если Н есть евклидово пространство Еп, то любое множество п ортонормальных векторов является полным. В любом бесконечномерном гильбертовом пространстве полное ортонормальное множество по необходимости бесконечно. Легко видеть, что может существовать много бесконечных семейств ортогональных векторов, не являющихся полными. Следующая теорема, которую мы не будем доказывать, показывает, что наше определение является содержательным.
Теорема В. Каждое гильбертово пространство содержит некоторое полное ортонормальное множество.
Обычное доказательство этой теоремы позволяет утверждать нечто большее, а именно, что если 5 есть любое множество ортонормальных векторов Н, то существует полное ортонормальное множество S', содержащее S, т. е., короче говоря, любое ортонормальное множество можно расширить до полного.
Специально подчеркнем, что эта теорема не утверждает, что полное ортонормальное множество счетно. Однако мы можем показать, что любые два полных ортонормальных множества из Н
*) Заметим, что это понятие полноты отличается от того, с которым мы познакомились в § 1.2. Смысл термина «полный» каждый раз ясен из контекста, и такая двузначность не вызовет никакой путаницы.
равномощны. А это вместе с теоремой В показывает, что с каждым гильбертовым пространством Н естественным образом связывается некоторое кардинальное число а. Это число а естественно/назы-вать размерностью (гильбертова) пространства Н. Мы уже ввели понятие размерности векторного пространства. Поэтому/полезно отметить, что если размерность пространства Н в любо^< из этих двух смыслов конечна, то значения этих размерностей равны между собой. В общем же случае эти два понятия не Тождественны друг другу. Действительно, можно показать, что гильбертово пространство никогда не может иметь счетной размерности в смысле определения теории векторных пространств, в то время как у широкого класса гильбертовых пространств полные ортонормальные множества счетны. Для того чтобы избежать связанной с этой неэквивалентностью путаницы, договоримся называть «размерностью» значение параметра, введенного ранее (в рамках теории векторных пространств). Второе из этих понятий нам понадобится относительно редко, и мы будем упоминать о нем как о «гильбертовой размерности», если нам будет это необходимо.
Мы будем изучать полные ортонормальные множества лишь в том частном случае, когда они не более чем счетны. С формальной точки зрения мы'основываемся на следующем определении *).
Определение А. Гильбертово пространство Н называется сепарабельным, если оно содержит полную ортонормальную последовательность.
Предшествующие примеры'позволяют предположить, что в сепарабельном гильбертовом пространстве каждое ортонормальное множество конечно либо счетно. Легко доказать, например, сепарабельность пространства 12. В последующем мы [познакомимся и с другими подходящими примерами.
Теорема Г. Пусть Н — сепарабельное гильбертово пространство, и пусть S = {в|} — ортонормальное множество элементов Н. Тогда следующие утверждения являются эквивалентными:
(1)	множество'S полно]
(2)	из х \ S следует, что х = 0;
(3)	для каждого х из Н:х =	<я, e^ef,
(4)	для каждого х из Н: [х ||2 =	| (х, ег) |2;
(5)	Н есть замыкание линейной оболочки L (5) натянутой на q.
Доказательство. Для доказательства этой теоремы достаточно показать, что из каждого предыдущего утверждения вытекает последующее, а из’утвержденияv(5) вытекает^утверждение (1).
♦) Можно показать, что это определение не противоречит определению Г из приложения 1.
/Д _х (2). Если х S и х 0, то х S, и, следовательно, S является собственным подмножеством последовательности
U Но это противоречит утверждению (1) о полноте множества s\
яА........................................
<fx — 2j<x’ei>ei’e>Z = ЬшО —2 (х,е{>еьеЛ =0 \	Z П-*ОО 4	i=1	z
при / = 1, 2, ..., и, следовательно, согласно утверждению (2) х — <х, e^yei = 0. (Отметим, что мы воспользовались здесь свойством непрерывности линейного произведения. См. упражнение 14 к § 2.1.)
(3) => (4)	(5).J См. теорему Б, ее следствие и второе заме-
чание на стр. 431.
(5) => (1). Если утверждение (1) неверно, то в Н найдется такой вектор х 0, что он ортогонален 5, и, следовательно, L (5). Но это значило бы, что L (S) является собственным подпространством II, что противоречит утверждению (5).
Учитывая свойство (3), нам кажется естественным называть полную ортонормальную последовательность {^} в сепарабельном гильбертовом пространстве Н базисом этого (гильбертова) пространства. (Мы просим читателя не путать это определение базиса с уже введенным в теории векторных пространств. Это раннее определение предполагает, что каждое хеН может быть представлено в виде некоторой конечной линейной комбинации et.) Уравнение (3) называют разложением Фурье вектора х относительно базиса {cj. Важность утверждения (4), называемого равенством Парсеваля, подсказывает хотя бы тот факт, что из него тривиально следует неравенство Бесселя и что оно сводится к теореме Пифагора в случае, когда размерность II равна 2.
В завершение этого приложения приведем два примера из области математической физики. Во всех случаях строгое изучение функциональных пространств и, властности, полноты их ортонормальных множеств требует привлечения современной теории меры и интегрирования. По так как на протяжении всей этой книги мы старались не предполагать у читателя этих знаний и так как все эти тонкости никоим образом не касаются существа изучаемых примеров, то читатель может рассматривать все встречающиеся ниже интегралы как римановы.
Пример 1. Обозначим через L2 [0, 2л] ^гильбертово пространство всех интегрируемых с квадратом ^функций, определенных на промежутке [0, 2л]. Напомним, что в этом пространству
скалярное произведение и норма имеют следующий вид:
о	/
0 /
Легко убедиться в том, что функции einl, где ,
п — 0, ч-1, ч- 2, ... ,
взаимно ортогональны в Ь2, так так
einte~intdi = < п
т=^п, т =п.
Если же определить функции {еп; п = 0, ±1,±2, ...} с помощью условия еп (/) = егп</]/г2л, то множество 5 — {еп} является для Ь2 ортонормальным. Для каждой функции / из Ь2 скаляры
cn = <f, en) = -^=.^f(t)e-intdt /2л J
представляют собой классические коэффициенты Фурье этой функции. В этом конкретном пространстве неравенство Бесселя принимает следующий вид:
оо	2п
3 l*n|a< $ 1/(01^ п=—оо	о
Теорема Д утверждает, что множество {еп} полно.
Теорема Д. Если функция / интегрируема и
с2п • t
\ f(x)e~'ntdx = O, 7i = 0, +1, ±2,..., то f = 0.
Доказательство. Предположим сначала, что / непрерывна на промежутке [0, 2л] и что для некоторого я0 (0 <ZxQ <Z 2л) / (хо) 0. Тогда найдется такой замкнутый промежуток [х0 — б, х0 + б], что / (я) > у/(я0) во всех точках этого промежутка. Но теперь легко убедиться в том, что функции
Тц (х) = [1 + cos (х — xQ) — cos d]n
обладают следующими свойствами:
(1)	Ап (%) суть линейные комбинации экспонент;
(2)	rk(z) > 0 при х А;
(3)	если 0<6'<6 и А'= [ж0- 6', х0 + 6'], то Тп (х) -*• оо равномерно относительно А';
(4)	I Тп (х) |	1 вне промежутка А.
Согласно свойству (1) и условиям теоремы
0= { f(x)Tn(x)dx= } f(x)Tn(x)dx +	§ f (х) Tn(x)dx.
о	А	[о, 2rt]\A
Но в соответствии со свойством (4) второй интеграл справа не превосходит 2л sup х | / (х) |, а значит, первый из интегралов должен быть ограниченным, что противоречит условию (3). Аналогичные рассуждения показывают, что в точке £0 функция / не может быть и отрицательной. Поэтому / (х) = 0 при 0 < х 2л. А в силу непрерывности / (х) отсюда следует, что / тождественно равно нулю на промежутке 0 х 2л.
Предположим теперь, что / — произвольная интегрируемая функция, для которой / {x}einx dx = 0, п = 0, ±1, +2. Пусть (t)dt = F (х). Интегрируя по частям, мы убедимся в том, что 2л
$ F(x)einxdx = 0, п = ±1,±2,... о
Поэтому, если 2<0 = J F(x)dx, то функция F (х) —Ло непрерывна и ортогональна функциям e~irtx при всех и. Но тогда согласно первой части доказательства
F(x) - Ао = 0,
а это значит, что неопределенный интеграл от / представляет собой постоянную. Интуитивно ясно (впрочем, это можно и строго доказать), что это возможно лишь в том случае, когда / отлична °т нуля лишь на множестве точек меры нуль, т. е. если рассматривать эту функцию как элемент пространства Ь2 [0, 2л], то
Следствие. Множество тригонометрических полиномов всюду плотно в пространстве [0, 2л].
В силу этой полноты неравенство Бесселя можно усилить до равенства Парсеваля:
оо	2л
3 кп|а= $ I/WM-п=—оо	0
Кроме того, теорема Д утверждает, что полнота множества {еп} эквивалентна утверждению о том, каждое / из Разложимо в ряд Фурье:
/W = "i^nl0oC’‘em<-
Необходимо подчеркнуть, что это разложение нельзя интерпретировать как утверждение о том, что выписанный ряд поточечно сходится к исходной функции. Напротив, гильбертовы пространства являются полными по отношению к нормам, порожденным скалярными произведениями, и в этом случае, если вектор /л из L2 определяется как
71 мо = -4=- 3 ^,п/, к=-П
то сходимость последовательности {fn} к вектору/нужно понимать в том смысле, что
ll/n - пн 0.
Эту ситуацию часто выражают словами: «/а сходится к / в среднем». Для того чтобы придать нашей теории определенную общность, мы рассмотрим теперь два примера, аналогичных примеру 1.
Пример 2. Рассматриваемые в этом примере три различных множества порождаются решением следующего дифференциального уравнения второго порядка:
41/ & 4]+* wх & = -wт w. z е т’ (*)
с соответствующими краевыми условиями. Каждое из этих множеств является полным ортонормальным базисом для гильбертова пространства (т; г), где г (t) > 0, £ ЕЕ т, а скалярное произведение вычисляется по формуле
<х, У> = $ г (0 х (0 У (0 dt> Х,у ^L2 (т; г). т
Прежде всего рассмотрим полиномы Эрмита, где по определению = 1,	(t) = 2t, h2(t) = 4t2 — 2, ..., а полином общего
вида определяется по формуле
МО = (-1)^’41*"'’!’ *еи-~,оо].
функция Л„ удовлетворяет уравнению (*), если р (/) = е''2, q (t) = 0, г (/) = е~‘*
и = 2п, п = 1, 2, ... Нормированные полиномы Эрмита />„(/) = (2’1п! |<л)-'/К(0. «е 1- 00, 00], образуют полный ортонормальный базис пространства А2 (—оо, оо; в **)•
Рассмотрим далее полиномы Лагерра, где	— ^+1,...,а
!. = «' £.1‘“<г'1.
Эти функции также удовлетворяют уравнению (*) на промежутке [О, оо], по теперь
p(/) = Ze-‘, g(/) = 0, г (£) = е"‘
И
= п, п = 1, 2, ...
Нормированные полиномы Лагерра <pn (Z) = (1/n!)Zn (Z), п = О, 1, ...» образуют ортонормальный базис пространства.
Наконец, полиномы Лежандра
fn(t) = |1[/2-1]п; п = 0,1,2,..„
удовлетворяют уравнению (♦) на промежутке I—1, 1] при
р (Z) = Z2 — 1, q (Z) =0, г (<) = 1, t е= I—1, И.
а параметр X принимает значения
кп = п (п + 1), п = О, 1, 2, ...
После нормировки <pn (Z) = (2nw!)-1/n (<), п — О, 1, ..., эти функции также образуют полный ортонормальный базис пространства Ь2 (-1, 1).
Пример 3. Рассмотрим прямоугольник А = {(£, s): t е= [а, Ь]. sGlc, й]}сЯ2 и множество S всех функций, определенных (и измеримых) на прямоугольнике А, таких, что
<1 ь
S S । / (^*s)	ds < ОО .
с а
Это множество превращается в гильбертово пространство, если определить на нем скалярное произведение
d Ь
<f,g> = Wf(t,x)g(t,s)dtds.
Множество {фп} ортонормально, если <ф„, ср7П> = 0 при п =/=> т и d Ь
|1<Рп||2 = § $ | фп (М) I2 = 1, П = 1,... с а
Разложение Фурье любой функции / Е Я по полному ортонормальному базису {фг} должно иметь вид
оо
/(м) = S ci<Pi (<•«)• г=0
где = </, <Pi>.
Без потери общности предположим, что а -- с ~ — л, а Ь = d = л. Тогда функции
Z, cos mt, sin mt, cos ns, sin ns, ..., cos mt• cos ns, sin mt-cos ns, ..., cos mt-sin ns, sin mt-sin ns, ..., m, n — 1, 2, ..., образуют полный ортогональный базис Я. Попарную ортогональность этих функций легко проверить. Читатель также может убедиться в том, что
|! 1 || = 2л,	|| cos mt || = || sin mt l| = }/Г2л,
|| cos mt *cos ns || = |( sin mZ-cos ns || = || sin zn^sin ns || = л. Ряд Фурье для / Ez Я можно записать в следующем компактном виде (см. главу 7 работы [А.84]):
оо
/(Z,s)= 2 cmnexp[i(mt + ns)], m,n=—оо где я я
Стп=(4"я2)§ S /(С«)ехр[— i (mt + ns)]dtds, т,п = 0, +1, + 2,...
Упражнения
1.	Пусть {et} и {/J — две ортонормальные последовательности в пространстве Lz (а, Ь), и пусть ||— Л |р< 1. Докажите, что последовательность {^} полна в том и только в том случае, когда полна последовательность {/J.
2.	Убедитесь в ортонормальности нормированных полиномов Эрмита, Лагерра и Лежандра. Покажите, что эти функции действительно удовлетворяют дифференциальному уравнению (♦).
3.	Постройте нормированные полиномы Эрмита, воспользовавшись алго-питмом ортогонализации Грама — Шмидта в пространстве £з (—оо> оо; **) множества {1, 6	•••» *п» •••)•
4.	Перепишите уравнение Лагерра в виде
(0 + (1 - О У' (0 + Ьу (0 = 0» t е [о, оо].
Предположите, что решение этого уравнения имеет вид степенного ряда по и покажите, исследовав уравнение для индексов, что если X = 1, 2, 3, ... ...» п, ...» то решением этого уравнения будут служить полиномы степени 1,2,3, ...» п, ... соответственно.
5.	Разложите функции /(/) = id, tе[-1, и,
1,	»e[o, i],
в ряд по полиномам Лежандра.
6.	Покажите, что функция / (/, s) = ts, (t, s) G {—я, л] [—-я, я}, может быть представлена следующим двойным рядом Фурье:
Kt, ,о=4 2 (_i)w*n	nt .
т,п=1
Литература
См. также JA.19J, главу 5 книги [А.44] и главу VI книги [А.21].
ВЫЧИСЛЕНИЕ МАТРИЦ ПЕРЕХОДА
В главе 2 мы показали, что матрицы перехода играют центральную роль в динамике систем первого порядка, описываемых линейными дифференциальными уравнениями и (или) линейными уравнениями в конечных разностях. Тех математических свойств этих матриц, которые получены нами в § 2.3, достаточно для теоретических целей. Однако при попытке использовать полученные теоретические результаты в физических задачах оказывается необходимым вплотную заняться задачей конкретного численного расчета матрицы перехода системы. В этом приложении мы наметим некоторые из путей, позволяющих вычислять эти матрицы в явном виде.
Матрицу перехода системы можно найти путем решения на машине дифференциального уравнения, которому она удовлетворяет. В большинстве случаев вычисления на цифровых или на аналоговых машинах обеспечивают точность, согласующуюся с точностью задания значений параметров системы. Заметим, что в процессе доказательства теоремы А из § 2.3 мы получили попутно и вычислительный алгоритм для нахождения матрицы перехода. Мы говорили о методе последовательных приближений Пикара, каждый шаг которого строго определен и который может быть использован для построения последовательности *). сумма членов которой равномерно сходится к искомой матрице перехода.
В обоих случаях системы дифференциальных уравнений решаются одним и те же способом, независимо от того, стационарна система или нет. С теоретической точки зрения подобное разграничение не только бесцельно, но и нежелательно. Однако в стационарном случае у системы с точки зрения вычислений имеются особые свойства, на которые мы сейчас и обратим внимание. Все
♦) При этом уравнение (13) из § 2.3 нужно преобразовать к виду t
Фо (t, tQ) = 7, Ф: (z, to) = I + A (s) Фо (s, to) ds,..., Фп (t, to) = to t
= I + A (s) Фп_х (e, t>) ds. 10
эти специальные свойства косвенным образом вытекают из утверждений теоремы А.	-
Теорема А. Матрица перехода Ф (t, t0), удовлетворяющая уравнению
Ф (t, tQ) = АФ (t, t0), Ф (*о, U = Z, t S т, (1) еде матрица Л не зависит от времени на множестве т, может быть представлена в следующем виде:
Ф (t, t0) ехР И — t0)}, t, t0 S т.	(2)
Матричная функция ехр {А (t — t0)} определяется с помощью ряда ехр {A (t — t0)} = Z + A (t —10) + .. ., Ч-°) + • • • ,t0 G T,
(3) равномерно сходящегося на любом конечном промежутке.
Доказательство. Используя стандартные неравенства для норм в правой части соотношения (3), мы получим, что
|]ехр {A (t - t0)}||<2 —= ехР{|| 4||(t - to)}, t,t0ST, г=0
(4) а это значит, что уравнение (3) вполне корректно определяет матричную экспоненциальную функцию и что этот ряд абсолютно сходится на любом конечном промежутке т. Абсолютная сходимость правой части уравнения (3) позволяет дифференцировать его почленно. В результате имеем: 4exp{A(t-t0)} = A-bA3(t-t0)+...+	+ . .. =
= А {I + А (/ - /0) + . . . +	} = А ехр {A (t - t0)}.
А так как ехр {0} — 7, то ясно, что матричная экспонента удовлетворяет уравнению (1), что и заканчивает доказательство.
Но хотя сумма в правой части уравнения (3) сходится равномерно в любом конечном промежутке, из неравенства (4) ясно, ч™ скорость этой сходимости зависит от произведения скаляра II А I и длины промежутка т. Приведенное в теореме А представление матрицы перехода в виде бесконечного ряда имеет тот недостаток, что такая форма представления не замкнута. Но, несмотря на этот недостаток, указанное представление позволяет обнаружить основные свойства матричной экспоненциальной функции.
(1) (2) (3) (4)
Теорема Б. Пусть А, В и Т — три квадратные невырожденные матрицы. Тогда матричная экспоненциальная функция обладает следующими свойствами: еТВТ~' ^A(/+s) = gA^As-
[eAq-i = е-АГ
e(A+B)t _ eAteiit тогда и только тогда, когда АВ = В А,
(5)	eAt определена для — оо оо;
(6)	del [еА] =et,A *).
Доказательство. Свойство (3) следует из свойства (2), если $ положить равным —t. Свойство (5) вытекает из доказательства теоремы А. В справедливости свойства (1) можно также убедиться, подставив в уравнение ряд, определяющий матричную экспоненциальную функцию. Для того чтобы доказать свойство (2), заметим, что
во	во	ОО	. и j
ехр|Л11Мр|Л,|=(2^)(2^)= 2 1^, k=o	j=o	k,j=o
что справедливо из-за абсолютной сходимости всех рядов. Меняя порядок суммирования при п = j + к, мы получим, что
оо	. п
ехр {At\ ехр [Л«] = 2 (Лп) (А-2 (п _1|.|	=
n=0 К j=0 '	11	'
= S А (<п+,)П' = ех₽
71=0
Наконец, свойство (4) можно также проверить, подставляя соответствующие ряды в обе стороны равенства, а свойство (6) вытекает из теоремы Д § 2.3.
Замечание 1. Матричная экспоненциальная функция оказывается настолько полезной для исследования матриц перехода стационарных систем, что было бы неестественным не попытаться аналогичным образом описать матрицу перехода нестационарной системы. Если нас интересует уравнение x (t) = A (t) x(t), то естественное обобщение теории для стационарного случая заключается в том, чтобы определить матрицу
t
В (t) = § A (s) ds, to
♦) Символом tr А обозначается сумма элементов матрицы Л, стоящих на главной диагонали. (Прим, ред.)
выяснить, а не удовлетворяет ли исходному Но, как легко видеть, ответ на этот отрицательным. В самом деле, дифференци
а затем попытаться уравнению матрица вопрос должен быть
руя ряд
ев
почленно, мы сразу увидим, что ехр {В (<)} = ехр A (r)dx} удовлетворяет исходному дифференциальному уравнению только в том случае, когда матрицы В (t) и (dBldt) (t) коммутативны или, что то же, если коммутативны матрицы A (t) и А (т)й(т).
В общем случае матрица перехода разлагается в ряд, известный под названием ряда Неймана, члены которого зависят от интегралов А (/):
t	t	fi
Ф (t, t0) = 14- $ A (t) dr + J A (tx) [J A (r,) drj dTx + ... to	fo	fo
Как и раньше, если матрица А не зависит от Z, то этот ряд превращается в матричный ряд Тейлора:
Ф(* — Zo) = ехр{Л (Z —<0)} = 2 ~~ ~io)/C. к«о
Замечание 2. Замкнутое выражение для матричной экспоненциальной функции может быть получено несколькими способами. В § 3.5, например, для того чтобы получить такое представление, мы пользуемся инвариантными подпространствами матрицы А. Для решения этой задачи можно прибегнуть и к помощи преобразований Лапласа. Полагая t0 = 0, мы видим, что преобразование Лапласа уравнения (1) имеет вид
— Л] Ф (5) = Z,
где через Ф ($) = 55 [Ф (£, 0)], как обычно, обозначено преобразование Лапласа матрицы Ф (£, 0). Поэтому отсюда следует, что (если s не совпадает с собственным числом матрицы А)
ф ($) = [$Z _ Л]-1.
Элементы этой последней матрицы представляют собой обычные Дробно-рациональные функции, и к тому же
ехр {ЛО = Я"1 {[sZ - Л]-1}.
Использование преобразований Лапласа для определения матриц перехода хорошо отражено в главе 5 книги Заде и Дезоера[А.95| и главах 2 и 3 книги Ту[А.86], и поэтому мы не станем останавливаться на этом вопросе (см. еще работы Хохстадта [Б.48], Веллмана [А.10], Фрейма [Б.36] и Каплана [А.46], [А.47]).
Использование матричной экспоненциальной функции может служить примером того, как дополнительная информация о системе (а именно о стационарности матрицы А) позволяет воспользоваться специальным приемом для вычисления матрицы перехода системы. В качестве второго примера рассмотрим теорему В из § 2.3. Предположим, что матрица A (Z; в) зависит от параметра е следующим образом:
А (£; е) = Аг + еЛ2 (t)t f £т.
Поскольку матрица А непрерывным образом зависит от 8, то теорема В из § 2.3 утверждает, что и матрица перехода Ф (t, £0; в) является непрерывной функцией 8. Сделаем более сильное предположение, согласно которому эта матрица может быть разложена в степенной ряд:
оо
Ф(Мо; е) = 3 е'ФДМо).	(5)
7=0
Для того чтобы определить матрицы {Ф; (t, t0): t, tQ e т, / = 0, 1...}, мы подставим правую часть уравнения (5) в обе стороны уравнения
Ф (t, tQ; 8) = A (Z, в) Ф (t, £0; в), Ф (Zo, /0, в) = I. (6) Приравнивая коэффициенты при одинаковых степенях 8 по обе стороны знака равенства, получим следующую систему дифференциальных уравнений:
Фо (0 ^о) = АФ0 (^» *о),	Фо Go> *о) = Д
Фх (t, Q = 4^ (*, t0) + А2 (0 Фо (0 tQ),	Ф^о, tQ) = о,
•: : (?)
ф„ (t, Zo) = афп (t, tQ) + а2 (t) Ф,,-! (t, t0),	ф„ (Zo, t0) = о,
Но так как матрица А не зависит от времени, то эти уравнения можно Jрешать поеледовател ьно. 11 анример,
t
ф1 (Л Q = $ ехР {^1 (t — •*>)} 42 (.s) охр {At (s — t0)}, t, tQ (= т. t.
Если параметр e мал, то правую часть уравнения (5) можно оборвать, оставив всего несколько первых членов, достаточных для получения аппроксимации Ф(£, tQ; е) допустимой точности.
Упражнения
1.	Воспользовавшись преобразованиями Лапласа, покажите, что для матриц
Г1 01	1-1-15 —12’1
-41 = [з 1J’	-1» = L—24 -19.1
справедливы соотношения
г* 0~1	г Г 9 ~61 а* Г— 8 6]
ехр {Ait} = t t . ехр ~е [12 -8.1 +е [- 12 в}
\_OIC € J
С помощью нескольких членов разложения из уравнения (3) попытайтесь получить этот же результат для ехр {Л^}.
2.	Из неравенства (4) ясно, что для каждой матрицы А существуют такие постоянные М и ц, что Цехр) A(t — f0)}|| < М ехр [ц (t — f0)] при всех t и?0£т. Воспользовавшись этим свойством и предполагая, что || Л 2 (0 || G (т), исследуйте сходимость ряда в уравнении (5).
Рис. П3.1. Позиционная следящая система и ее принципиальная схема.
3.	На рис. П3.1 схематически показана позиционная следящая система второго порядка и ее эквивалентная структурная схема. Убедитесь в том, что передаточная функция такой системы имеет следующий вид:
0(.)	АКт
Вт{») ~ <** + '1Т + Акт) 
Воспользовавшись переменными хг = 0 и х2 = 0, преобразуйте уравнения этой системы в векторное уравнение первого порядка Л = Ах, где х = (хх, х2). Предположив, что АКт = 2, а Г = х/з, покажите, что
, ,	Г2^' —«**	1
2е-._г J.
Показанную на рисунке систему можно рассматривать как систему управления ориентацией спутника. При этом двигатель нужно заменить на пропорциональное реактивное исполнительное устройство. Если ЦТ = 0, а АКт = e 4, то покажите, что матрица перехода такой системы ориентации имеет вид
cos 2t
2sin 2t
— sin 2t cos2«
- ^Л₽ИС‘ П3.2 показано электрогидравлическое исполнительное уст-р ство. Уоедитесьв том,что характеристическое уравнение этой разомкнутой
системы имеет следующий вид:
(s + т) (s2 + 2&>ns + (D3) = О,
где т = (rp + Rl) / L, (on = к/М, а £ = В/2^кМ. Предположив, чтс т = 2, соп = F3Hg= 2//3, покажите, что корнями этого уравнения являются (—1, — 2, —3). Воспользовавшись переменными хг = Xv, х2 = Xv и
Усилитель* цепь Магнит Динамина Коэффициент Плунжер намагничивания	нлапана усиления
клапана
Плунжер ^''Вытесняющая площадь А
Рис. П3.2. Электрогидравлический клапан и его принципиальная схема.
х3 = преобразуйте уравнение этой системы в векторное уравнение первого порядка Л = Ах, где х = (я,, х2, х3). Покажите, что правая строка матрицы перехода ехр {At} этой системы состоит из элементов
[ехр {Л/}]п = Зе~* — Зе-2* + е“зГ,
[ехр	еj — 4е-а<+
[ехр {Л/}]и = — ~2~е * 4- е-а< — (”2~) е^*’
Покажите также, что вторая строка матрицы ехр {А О является производной по времени от первой и что третья равна производной по времени от второй, т. е. что [ехр {ЛObi = (<W0 [ехр {Л0]ц и т. д. •).
♦) Эта задача подсказана содержанием § 4.4 книги R. N. Clark’a «Introduction to Automatic Control Systems», Wiley, N. Y., 1962. Оттуда же с разрешения автора заимствован и рис. П3.2.
УРАВНЕНИЯ «ГО ПОРЯДКА
В этом приложении мы займемся изучением дифференциального оператора n-го порядка
Ln (D, t) = ап (t)Dn + an-iWZ)"-1 + ... + а0 (0, t G= т (где через обозначен оператор /‘-кратного дифференцирования), и дифференциальными уравнениями n-го порядка вида
Ln (D, t)x (0 = u(t),	t(=x.	(1)
В тех случаях, когда конкретный порядок п оператора Ln(D, t) не играет существенной роли, мы будем отбрасывать соответствующий индекс.
На протяжении всего этого приложения мы будем предполагать, что ни в одной точке промежутка т коэффициент ап (/) =j= 0. Это гарантирует нам, что исследуемое уравнение все время ведет себя как дифференциальное уравнение n-го порядка. Так как ап (/) не обращается на т в нуль, то обе стороны уравнения (1) можно разделить на ап (t). Поэтому в настоящем приложении мы воспользуемся эквивалентной операцией, предположив, что во всех случаях ап (/) = 1 на т.
Оператор L (D, J), очевидно, линеен. В качестве области определения оператора L(D, t) обычно берут пространство Сп(т), где С1(т) = С(т), а Сп (т) определяется условием Сп (т) = = {я: х, Dx, ..., Dn~x х существуют и непрерывны, a Dnx Д (т)}. Таким образом, L(D, t): Сп (т) -> Lr (т). Ниже мы покажем, что это отображение сюръективно.
Для того чтобы преобразовать уравнение (1) в векторное дифференциальное уравнение первого порядка, необходимо ввести новую систему переменных. Классический прием здесь состоит в том, что в качестве новых переменных выбирают производные х, т. 0,
г/((0 = а:(0,	t<=X,
= Dx(l),	t<=T,
:	(2)
I/,l_1(0 = Dl-«j:(0,
У At) = D'-'xlt), t^x.
Дифференцируя все эти уравнения, получим
Dyi (0 = у2 (0,
Dy2(t) = ys(t),
Dyn-i(t) = yn(t,) (gt,
Dyn(t) = Dnx(t),
Последнее из этих уравнений можно отождествить с уравнением n-го порядка (1), для чего его нужно разрешить относительно Dnx (t). В новых обозначениях
Dnx (t) = — aQ (t)x (t) — ax (t)Dx (t) — ... — (tyD^x (t) + + и (0 = — a0 (t)yt (0 — at (t)y2 (0 — ... — ап_г (t)yn (0 + + и (0, t (= x.
Заменяя правую часть последнего уравнения выписанным выше выражением, видим:
Jtyi(0=lM0» «Gt,
Dyn-i(t) = yn(l),
Dyn (0 = — а0 (0 у! (0 — ах (0 у2 (0 — . .. — an_x (0 уп (0 +
и (0, t	х.
Эту систему уравнений первого порядка нетрудно переписать в виде одного векторно-матричного уравнения:
Dy (0 = A (t)y (0 + епи (0, I е т,	(3)
где у = col (</!, ..., уп), еп = col (0, ..., О, 1), а матрица А имеет размеры (п х п) и в момент времени i G т принимает следующий вид:
ГО 1 0 ... О т
4(0 =
«о (0 • • • ^n-i (0
т. е. в Л (/) от нуля отличны лишь элементы на верхней наддиагонали, где они равны 1, и в нижней строке, где они последовательно равны — aQ (/), — (/), ..., —an-i (0- Таким образом, дифференциальное уравнение n-го порядка (1) эквивалентно (после замены
переменных (2)) нормальной системе уравнений первого порядка (3) с матрицей А вида (4).
Для того чтобы эффективно воспользоваться этой эквивалентностью, пересмотрим в новом свете результаты §§ 2.3 и 2.4. Начнем со случая однородного уравнения, когда и = 0. Для систем, описывающихся уравнением (3), мы показали (см. теоремы А и Б из § 2.3), что при выполнении не слишком жестких условий, накладываемых на вид матрицы Л, для каждого £ такого, что || £ || < оо, и любых t и t0 ее т существует единственный вектор У (£;	^о)» удовлетворяющий на т уравнению системы, а также
условию
У	(*oi ^о) ~ £ = С°1 (£1» •••> £п)*
В частности, в момент времени tQ компоненты этого вектора удовлетворяют условиям
У1	(^о) ~ С1» Уъ ('о) =	» •••» Уп о) ~
Легко видеть, что если у является решением уравнения (3) с матрицей Л из уравнения (4), то первая компонента этого вектора Уг = х служит решением уравнения (1). В самом деле, из уравнения (2) ясно, что Dyn (/) — Dnx (£), а так как последнее из уравнений системы (3) имеет вид Dyn (t) = — aQ (t)yt (t) — ar (t)y2 (£) — — ... — an_x	то отсюда следует, что Dnx (t) =
= ,— a0 (t)x (t) — av (t)Dx (t)—... — an (t)x (t), и, значит, решение уравнения (3) удовлетворяет и уравнению (1). Не менее очевидно и обратное утверждение, и, значит, множество всех решений {х< (0} уравнения
L (Z), I) xt (t) = 0, t е т,	(5)
и множество всех векторов {у (£)}, удовлетворяющих уравнению
Dy (/) = Л (t)y (г), t (= т,	(6)
отображаются одно в другое с помощью преобразования (2). Принимая во внимание начальные условия, порожденные преобразованием (2), приходим к следующей теореме.
Теорема А. Преобразование координат (2) определяет изоморфизм между решениями уравнений (5) и (6). Этот изоморфизм отображает функции, удовлетворяющие уравнению (5) и начальным л условиям х (t.) = U Dx (tQ) = £2, ..., Z)n-1 x (t0) = £n, в вектор г/, удовлетворяющий уравнению (6) с начальными условиями У (Q = g = col (gx, gn).
Такое отождествление компонент вектора с функцией и ее производными высшего порядка с физической точки зрения чрезвычайно привлекательно. Если х — некоторая физическая вели-чина, например смещение какого-то органа механизма, то для
15 У. Портер
описания условий, в которых находится этот механизм, или его состояния необходимо задать не только х, но и его скорость Dx и его ускорение Z)2#. Отметим еще, что для того, чтобы по решению векторного уравнения найти функцию х, решение уравнения п-го порядка, достаточно вычислить скалярное произведение векторов у и = (1, 0, ..., 0). Более того, Dx определяется как скалярное произведение у и = (0, 1, 0, ..., 0), а (ГЯх) (/) = [е7«, у (£)].
Описанный способ преобразования уравнения n-го порядка в n-мерное векторное дифференциальное уравнение первого порядка никоим образом не является единственным. В действительности в более сложных ситуациях (о которых речь пойдет ниже) более удобным оказывается другой метод. Однако пока мы будем предполагать, что для перехода от уравнения n-го порядка к векторному уравнению первого порядка и наоборот мы все время используем преобразование переменных (2).
Следствие. Ядро оператора Ln (D, t) п-мерно.
Доказательство. Это следствие вытекает из утверждений теоремы Г § 2.3 и теоремы А. Для доказательства обозначим через (pi (0, • ••? фп (0 линейно независимые решения векторного уравнения (3). Матрица
Ф(0 =
’Фи (0
-Фн1(0
Ф12 (О ... Ф1п(0‘
Фп2 (0 ... фпп (0-
t Gt,
является фундаментальной матрицей решений этого уравнения. Верхняя строка матрицы Ф (/), т. е. срп, ..., срп1, представляет собой набор решений (^, ..., хп) уравнения (5). Остальные строки матрицы Ф являются производными этой строки. Линейная независимость столбцов {cpi}i предопределяет и линейную независимость функций {zj}n. Поэтому размерность ядра Ln (0, t) не меньше п. Однако если бы существовало (п + 1)-е линейно независимое решение, то его можно было использовать для того, чтобы построить (п + 1)-е линейно независимое решение векторного уравнения (6), что противоречит утверждению теоремы Г из § 2.3.
Обозначим через S = {zji некоторое множество линейно независимых решений уравнения (5). Тогда S образует базис ядра оператора Ln (0, /). Более того, матрица
Xi (J)	х2 (t)	... хп (0
Dx1(t)	Dx2(t)	...Dxn(t)
.	(t) Dn~xx2 (0 . .. Dn~\cn (t).
I Et,
является фундаментальной матрицей уравнения (6). Из рассуждений § 2.3 ясно, что при всех t €= т определитель det Ф (t)	0.
в частном случае, рассматриваемом здесь, определитель матрицы ф (/) называется вронскианом оператора L„ (D, t) относительно базиса S и обозначается через W (хх, ..., х„). Вронскиан представляет собой некоторую функцию t, определен на промежутке т, и при фиксированных {хх, ..., хп} его значение в любой момент времени t обозначается через W (х1( ..., хп] (/).
Теорема Б. Для того чтобы п решений xlt ..., хп уравнения Ln (D, t)x = 0 на некотором промежутке т были линейно зависимыми, необходимо и достаточно, чтобы
W(xlt .... хп) (t) = О, ГЕТ.
Более того, вронскиан удовлетворяет уравнению t
W(xt.......rn)(0 = W(xlt...,x„)(f0){exp rjax(s)ds]}, t^x.
1 L/o
Доказательство. Поскольку уравнение W (rn ..., xn) (/) = 0 — это то же, что уравнение det Ф (t) = 0, то для любой фундаментальной матрицы решений первая часть этой теоремы является следствием теоремы Г из § 2.3. Второе утверждение вытекает из теоремы Д того же параграфа и того факта, что для интересующей нас матрицы частного вида из уравнения (6) след матрицы 4(0 совпадает с —аг (t).
Теорема В. Пусть (<рх, ..., фп) — п функций, имеющих непрерывные производные п-го порядка в промежутке т, и пусть W (<рх, ..., <рп) (t) =/= 0 на х. Тогда существует единственное однородное дифференциальное уравнение п-го порядка (с коэффициентом ап при старшей производной Dnx, равным 1), для которого эти функции образуют фундаментальную систему. Это уравнение имеет вид
(-1)”
ТУ (я, фь W (фь .
^V- = o.
Фп)
(7)
Доказательство. Вронскиан W (х, <рх, ..., (рп) представляет собой определитель матрицы, первая строка которой образована элементами х, фх, срп, а последующие являются производными
предыдущих, причем в последней строке оказываются производные п-го порядка. Прежде всего, ясно, что W (ф^ фх, ..., фп) = 0 v =	•••> п), так как в этом случае два столбца определителя
оказываются одинаковыми. Разложение числителя дроби в левой части уравнения (7) по элементам первого столбца показывает, что уравнение (7) — это дифференциальное уравнение п-го порядка, а коэффициент при Dnx равен как раз (—1)н W (фх, ..., фп), и, значит, коэффициент при D"x в уравнении (7) в точности равен 1.
оскольку W (фх, ..м фн) 0, то отсюда следует, что функции
Ф1, ..., фп образуют для этого уравнения фундаментальную систему. Единственность полученного решения следует непосредственно из того факта, что соответствующие векторы ф^ с компонентами Фи» Ф21» •••» фщ однозначно определяют матрицу коэффициентов, порождаемую этим уравнением системы. А так как между линейными векторными уравнениями первого порядка и линейными уравнениями n-го порядка существует взаимно однозначное соответствие, то это и доказывает утверждение теоремы.
Обозначим через Ф (/, t0) матрицу перехода уравнения (3). Свободная реакция этого уравнения определяется по формуле
У (t) = Ф (С tQ)l, t е т.
Но так как первая компонента вектора у описывает решение однородного уравнения (1) (с начальными условиями типа D*x = при t = £0), то
п
х(О = [е1,Ф(«,«о)^ = 2 Фи(Мо)&, «Gt, (8) ;=1
где х (t) — решение однородного уравнения (1) (п (/) = 0). Из рассуждений, сопровождающих следствие из теоремы А и теорему Б, очевидно, что' множество {ф|;} также однозначно определяется условиями
Ln(D, <о)=О, «ет,
(«0. «0) = &jk, i, к = 0,1,.. ., n — 1.
Неоднородные уравнения. Так же как и для однородного уравнения, установленное соответствие между уравнениями (1) и (3) позволяет свести исследование уравнения (1) к конкретизации результатов, полученных для неоднородных систем первого порядка. Основной результат этого раздела мы сформулируем в теореме Г.
Теорема Г. Пусть множество {фи (/, /о)}? определено из условий (9). Тогда решение неоднородного уравнения (1) задается формулой
п	t
(«; Uo) = S Ф1 i (t, «0) ёг + $ Ф1п («, s) и (s) ds. (10) 1=1	f0
Доказательство. Эту теорему мы докажем с помощью теоремы о решении неоднородных дифференциальных систем общего вида. Общее решение уравнения (3), согласно этой теореме, имеет вид
i
=ф(«, t0)l+^<D(t,s)enu(s)ds, (St.
«.
Первая компонента вектора уп как раз и есть искомое решение х. Эту компоненту можно выделить в явном виде, вычислив соответствующее скалярное произведение
(t; С, U = к. Уи (*; С, «о)1, t е т.
Проделав эту операцию с формулой для уп, мы получим t
= [е, Ф(/,/0)В1 I- $le1,a>(/,s)en]u(.s-)ds, (Gt.
G»
В соответствии с предыдущим замечанием [en Ф (Z, /0)£1 имеет требуемый вид. Более того, непосредственным вычислением читатель убедится в том, что
кх, Ф (/,	= <pln (t, s), t (= т;
и, следовательно, утверждение теоремы доказано.
Функция ф1п (/, $) играет достаточно важную роль, чтобы заслужить особое наименование. Обычно ее обозначаю! к (/, $) и называют «функцией Грина», или «весовой функцией» дифференциального оператора Ln (D, t). Основные свойства этой функции подытожены в теореме Д.
Теорема Д. При каждом фиксированном $е=т функция k (t, s) обладает следующими свойствами:
(1)	=0, а = 0,1,..., га-2;
ЛП-1
(2)	,_, = 1;
(3)	L (D, I) к (i, s) = 0, i е т;
(4)	к (^ 5) единственна при t, s ЕЕ т.
Доказательство. Все эти утверждения непосредственно вытекают из определения фп(/, $).
Замечание. Если множество {фх, ..., <рд} образует базис пространства решений для однородного уравнения с оператором ь (Z), /), но не является нормальным, то описанная выше процедура отличается тем, что теперь нужно пользоваться det [ф (ОФ"1 ($)1, где Ф (/)—фундаментальная матрица решений Уравнений (3), образованная из {фх, ..., фп}. Однако существует такая невырожденная постоянная матрица Я, что Ф (t) = dh /	и» следовательно, Ф"1 ($) = Я^Ф”1 (s, Zo), так что
Ф (ОФ"1 (0 = ф (/, tQ)H [Я-хФ-1 (s, tQ)] = Ф (/, 0, и теорема Д справедлива и в этом случае.
Читателю полезно будет также убедиться в том, что
1
иг (ф1,..., фп) (s)
Ф1	(s). .	• Фп (s)	
п- Ф1	2(s).	..фГ(«)	(Н)
Ф1	(0-	• • фп(0	
Упражнения
В этих упражнениях мы будем иметь дело с уравнениями n-го порядка в конечных разностях:
Дп* + ап-1 дП-1а: ('/<) + ••• + «» (Мх (*k) = “ Ofc)’	е G,
(12)
Д<Г Go)	~ о, 1, .. ., п — 1,
1.	Приведите уравнение (12) к стандартному виду эквивалентного векторного уравнения первого порядка, аналогичного уравнению (3).
2.	Какова размерность пространства решений однородного варианта уравнения (12)? Выпишите свободную реакцию этой системы в виде, аналогичном формуле (8).
3.	Выпишите полную реакцию уравнения (12) в форме, аналогичной формуле (10). Каковы свойства весовой функции этого решения?
4.	Постройте функциональную схему коммутаций аналоговой вычислительной машины, моделирующей уравнение (3), включая начальные условия. Разработайте аналогичную дискретную модель для уравнения из упражнения 1.
Другие векторные уравнения первого порядка. Замена переменных, описанная в уравнениях (2), ни в коем случае не исчерпывает всех существующих возможностей преобразования уравнения (1) в эквивалентное векторное уравнение первого порядка. В тех случаях, когда приходится иметь дело с дифференциальными уравнениями вида
Ln (Z), t) х (t) = Mq (ZJ, t) и (0, t G t,
где
n
Ln (D, t) = 3 a}(t) Di, an(i) = l, j=0
9
/£=0
(13)
(14)
предпочтительнее осуществлять такой переход совсем другим путем. Для того чтобы хорошо разобраться в том, чем это объясняется, заметим, что если класс допустимых входных воздействий,
которому должна принадлежать функция и (Z), требует, чтобы всех его элементов производная #-го порядка была кусочнонепрерывной [т. е. и е Cq (т)], то можно просто определить новую функцию /, потребовав, чтобы
/ (Z) = Mq (£>, Z) и (Z), t е т,
и воспользовавшись / в качестве внешнего воздействия, приступить к преобразованию исходного уравнения тем же способом, что и раньше. Однако требование ^-кратной дифференцируемости функции и не только довольно ограничивающее с математической точки зрения, ноифизически не оправдано. В самом деле, поскольку то ясно, что система, описываемая уравнением (13), является по своей природе «низкочастотной» и что любое и, по крайней мере кусочно-непрерывное, вызовет однозначную, вполне определенную реакцию х. Более того, уже с чисто вычислительной точки зрения невыгодно использовать в системе всю предысторию u (Z), а также все ее высшие производные, если таковые вообще существуют. На самом деле, нам требуется эквивалентное векторное уравнение первого порядка с векторным входным сигналом, зависящим лишь от и (Z).
В качестве первого шага к более общему случаю рассмотрим сначала уравнение
D3x (Z) + a2D2x (t) + atDx (Z) + aQx (Z) = и (Z), Z e r. (15)
To, что мы собираемся сейчас сделать, совпадает с процедурой, которой мы воспользуемся в этом более общем случае. Прежде всего переведем все высшие производные х в правую часть уравнения и проинтегрируем его п раз. Таким образом мы получим последовательность уравнений, справедливых для всех Z GE т: D4 (0 = w (0 - a2D2x (0 - aj)x (t) - аох (0,
t
Dzx (0 = _ a^Dx (0 — axx (0 + ^ [ — a^x (т) 4- и (т)] dx 4- kit t	a
Dx(0 = — a2x(t) 4- axa:(a) 4- ^ [—a0;r(r)4-u(r)]dT4-fcij da4-&a,
L	0	a
= J {“ агх (3) + §[— axa:(a) + ^(— aox(x) 4-
4- и (r)) dr 4- &i] da 4~ ^2} d₽ 4* A3»
где через klf k2 и k3 обозначены соответствующие постоянные интегрирования. Определим теперь три новые переменные
непосредственно из этой системы уравнений. Л именно пусть t	3
X (t) = ZX (0 = 5 (— аах (?) + ахх (а) + а
4-	— аох (т) + и (т)1 da. 4- кг} d? 4- ка,
t	а
z2 (0 = <hx (а) 4-^[ —a0z(T)4-w(T)]dT4-*i}d<x+ *s, t
z3(0 =§[ —«•*(*) 4- H(T)ldT + M
Продифференцировав каждое из этих уравнений по разу, мы получим
*1 (0 = — а^х (0 4- z2 (t), t е т,
za (0 = — <hx (0 4- z3 (0, ( E т, z3 (0 = — аох (t) + и (0,	t G= т.
Так как х = zlt то
ii(t)= -a2z1(0 4-z2(i), (бт, МО = — aiM0+ МО, <et, M)=-<Vi(O + “(0.
Если положить, что z = col (zlt z2, z8), b = (0, 0, 1), a
Г — аг 1 04
A' = — ax 0 1
— a0 0 0
(16)
(17)
то получится векторное уравнение i (t) = A'z (t) 4- bu (t)> Матрица А' напоминает матрицу Л, получающуюся при замене переменных (2), но эти матрицы не идентичны. В первом случае (см. уравнение (4)) матрица Л имела вид
ГО 1	О']
Л= 0	0	1
— (Ll —
Эта разница очень важна, так как хотя = х, но остальные переменные имеют другой вид: z2 = Dx + агх и z8 = D*x 4- ахх. Поэтому, если у = (х, Dx. D2x), то мы имеем соотношение z = Ту3
где матрица Т имеет следующий вид:
Г1 0 0"|
о
1
Т —	1
#1 ^2
Легко видеть, что
•— d2 ।	2
— ^1 + а2
О О'
1 о
— а2	1 _
и что А' = ТАТ~\ и, следовательно, эти два метода перехода первого порядка связаны между собой преобразованиями координат z = Ту, у Т~Ч. Для того чтобы по виду вектора z определить координату Dx, мы с помощью предыдущего соотношения сразу можем предложить формулу Dx = [е2, T^z] = [(—а2, 1, 0), z]. Аналогично получаем, что D2x = [е3, T"1z]=	1), z].
Эти соотношения понадобятся нам позже.
Рассмотрим теперь дифференциальное уравнение третьего порядка с постоянными коэффициентами
D3x +	+ <hDx + aQx = b3D3u + b2D2u + bxDu + b^u, (18)
где для экономии места мы не показывали в явном виде зависимость переменных от t. Оставляя в левой части лишь старшую производ
ную и интегрируя полученное уравнение п раз, мы получим следующую систему уравнений:
D3x = — a2D2x — avDx — aQx 4- b3D3u, 4- b2D2u 4- ^Du 4- bou,
D2x = — a2Dx — aYx 4- b3Dau 4- b2Du + b±u 4- § [— aoa?4“&ou14-^i>
Dx= — a2x+b3Du+b2u 4-ЭД — a1^4-b1u4- §(—Яот4-Ьон)+&1]+&2,
(19)
— b3u 4~ — u2x 4~ b2u 4~
+ [— a±x 4“	4“ (— aQx 4“ bQu) 4- ^i] 4- ^2} 4- ^3,
где к. — постоянные интегрирования. Руководствуясь теперь видом этих уравнений и предшествующим примером, мы введем новые переменные:
t
2з (0 = § I— ($) + bQu ($)] ds 4-t
z2 (Z) =^[ — a1x(s)+ ^4(5) 4- 23(s)]ds4- k2, t
zi (0 = [ — a2x (s) -f- b2u (s) + z2 (s)] ds — k3.
t^x, tex.
(20)
Другими словами, пусть х	=	b3u + zi	и	пусть
*1 (0 =	—	а2х	(0	+	b2U (/)	+	Z2	(/),	*
z2 (0 ~	—	aix	(О	+	^iu (О	+	23	(z),	г е Т,
Z3 (0 =	—	«0^	(0	4“	« (0>
откуда (заменяя х на Ъ3и + *i) получим
Z1 (0 = — «2*1 (О -I- *2 (0 + (fc2 — «2^з)« (О» t Т, *2 (0 ~ — «1*1 (О 4" *3 (0 4" (^1 и^Ъ^И (/), / Е Т)
Из (0 = — «0*1 (0 + (&о — «0&з)« (0,	* S т-
Полагая далее z = col (zx, z2, z3), мы видим, что
z(t) = A'z(t) + bu(t),	JET, 1
rr(O-M(O + [^i,*(Oh	*er, J
где
Таким образом, нам удалось свести исходное операторное уравнение к неоднородному векторному дифференциальному уравнению. Значение искомой переменной х можно найти теперь из решения этого уравнения и значения входного сигнала с помощью пассивного «считывания», сводящегося к вычислению скалярного произведения решения неоднородного векторного уравнения и вектора
Читатель, вероятно, заметил, что переход от уравнений (16) и (18) к их векторной форме привел к одинаковым матрицам А' системы (см. уравнения (17) и (22)). Но этого можно было ожидать, так как однородное уравнение Ln (Z), t) = 0 оставалось в обоих случаях одним и тем же. Обобщение этого метода на случай операторов более высокого порядка очевидно, а его результаты можно предугадать по виду матрицы Л и вектора b для уравнения третьего порядка.
Процедура перехода, описанная уравнениями (19), основана ни последовательном интегрировании исходного уравнения, приводящем к понижению на каждом шаге порядка оставшихся переменных. Если коэффициенты исходного уравнения зависят от времени, то процедура перехода, по сути дела, остается все той же, с той только разницей, что на каждом шаге нужно вносить определенные изменения в результат. Например, при интегрировании
слагаемое btDx приводится к следующему виду:
'	l<
\ bt (s) х (s) ds = bi (s) x (s) — bi (s) и (s) ds,
io	'°	!•
а не просто к btx, как было бы в стационарном случае.
В качестве конкретного примера рассмотрим дифференциальное уравнение
Dsx (Z) = (t + 2)D2x (Z) + t2Dx (Z) + (Z + l)x (Z) +
+ Z3D3u (Z) + Du (Z) + и (Z), Z S t. (23)
Читатель без труда убедится, что трехкратное последовательное интегрирование приводит к следующей системе интегральных уравнений:
D2x (Z) = (Z + 2) Dx (Z) -j- (Z2 - 1) x (Z) + t3D2u (Z) — 3z2Z)u (Z) + t
4- Itu (Z) + [(1 — s)x (s) — 6u (s)] ds ki,
Dx (I) = (Z + 2) x (Z) + t3Du (Z) — 6Z2u (Z) + ((32 — 2) x (3) +
+ 19pu (3) + [(1 — s) x (s) — 6u (s)| ds 4- kt) d) + k.2,
t	a
X (Z) = Z’u (Z) + J ((a + 2) X (a) - 9a2u (a) + J {(32 - 2) x (3) 4-з
4- 19.3u (3) 4- J [(1 - «) x (s) -	(s)] ds I- ki} d) f- кг) da k3.
Теперь, как и в предыдущем примере, мы можем ввести новые переменные t
23 (t) = [(— s 4- 1) х ($) — би ($)] ds + t
z2 (0 = |($2 — а) ($) + 19su (s) |- zx ($)] ds + k2,
zi (0 =4 l(s 4- 2) X (s) — 9s2u (s) 4- z2 (.9)1 ds 4- k3 и получить соотношения
x (Z) = zx (Z) 4* t3u (0
и
z3 (Z) = (—Z 4- 1)X (Z) - 6u (Z),
(0 = (Z2 — 2)x (Z) 4- 19Zu (Z) 4- Z8 (Z), Zx (Z) = (Z 4- 2)X (Z) - 9Z2u (Z) 4- Z2 (Z)
или, исключая х из системы уравнений и переписывая результат в векторно-матричной форме, соотношения
z (t) = A (t) z(t) -f- fe (t) и (0, | x(0 = «3u(0 + [e1, z(i)], J
(25)
где
A (I) =
1 O' 0 1 , 0 0.
5(0 =
/4 4- 2/3 - 9/»
Ze — 2Z3 + 19Z — h + t3 — 6
• (20)
t + 2
i2-2
Присоединенный оператор. В этом разделе через Ln мы обозначаем дифференциальный оператор из уравнения (1), а через X — связанный с ним дифференциальный оператор, для которого
(Ху) (0 - у (0 - А (I) у (0, t S т,	(27)
где А определяется формулой (4). В упражнениях к § 3.3 мы отметили уже, что оператор X*, определенный соотношением
(X*z) (0 = z(t) + A* (t)z (0, t S t,	(28)
с формальной точки зрения является присоединенным для оператора X в том смысле, что
t	t
$ [2 (S), т (S)l ds - $ l(2*z)(S), y(s)]ds = [y(t), z(0]t (29) to	to
Обозначим компоненты вектора z через ..., zn. Тогда, приравнивая (28) нулю, мы видим, что присоединенная система распадается относительно координатного базиса на следующую систему уравнений:
Zi(t) = aQzn(t), ^2 (0 = ^izn (0 zi (0> Z3 (О = ^2zn (0 Z2 (0»	>
(30)
zn (0 ---- fln-l (0 Zn-1 (0« 4
Эту систему уравнений первого порядка можно преобразовать в единственное уравнение n-го порядка. Для этого подействуем на Л-е уравнение этой системы оператором (—l)*-1#*"1. Сложив все получающиеся таким образом уравнения, найдем
(—V)nDnzn (0 + (- iy-W1 [ап^ (t) zn (01 +...
.. . + (-1) D [ax (0 zn (0| + a0 (0 zn (0 = 0.	(31)
В соответствии с уравнением (31) оператор Л* (D, t) определяется из условия
п
^(Р,«)=2(-1)^<(«).	(32)
Из уравнения (31) следует, что описанный процесс Л-кратного дифференцирования после приведения подобных членов приводит к дифференциальному уравнению n-го порядка, так что оператор L* (D, t) действительно является дифференциальным. В качестве самостоятельного упражнения читатель может убедиться в том, что коэффициенты этого дифференциального оператора имеют вид
<(/)- S ( кк_Аок-1[ак(1)],	(33)
k=i	Х Z
а сам оператор можно записать в другой, эквивалентной форме:
71
^: (£>,/)= 2^(0^.	(34)
г-0
Как в той, так и в другой формах мы делаем неявное предположе ние о том, что коэффициенты aj оператора Ln (D, t) принадлежат Cjiy), j = 0, 1, ..., п — 1, так как только в этом случае все указанные производные действительно существуют.
Легко проверить, что оператор Ln является присоединенным к оператору Ln практически в том же смысле, в каком оператор 55* присоединен к оператору Ж. Читатель может убедиться в том, что если Мк определить из условия
Мк = akDk,
ТО к /к\ м^(-1)‘2 L «Г’о*	(35)
а=0 Х
в том смысле, что
5 U (s) (Мkv) (s) ds — 5 V (s) (Mk и) (s) ds	Ek (u, v) |J‘,
to
где Eh (u, v) |{*
есть остаточное краевое условие. Воспользовавшись тем фактом, что
п
Ln = 3
к=о
мы найдем, что из уравнения (35) следует уравнение (34).
Другой вывод этого уравнения опирается на свойства операторов # и <2*. Введем обозначения
G
<u, v>i = и (tf) v (tf) ds, to
G	G n
<*, y>n = $ [4"0. Hs)l d>l = J '£ixi(s)Ui(s)ds t*	to i=l
и заметим пока, что в соответствии с видом матрицы А выражение <z, может быть разложено относительно координатного базиса следующим образом:
G
<2,	{2Х (tf) [Xi (tf) — Xa (tf)] + . . . +
to
+ Zn_x (s)[fn-l (s) — xn (s)] + Zn (s) iG^il (s)} ds.
Но так как хг = x.-±, i = l,	1, то отсюда следует, что
\2, «^/п = <2n, LnX}/i.
Таким же способом можно показать, что в соответствии с видом матрицы Л*
{X*z, X) = <L„zn, хх)х + П (xlt zx) |tl.
Но тогда из уравнения (29) следует, что
<v, Z„u>x — <L*i>, u> = П (и, и) It.	(36)
Граничное условие П (и, v) 11 получило название билинейного конкомитанта Лагранжа. Оно эквивалентно граничному условию из уравнения (29) и может быть вычислено разложением этого выражения по некоторому базису либо с помощью суммы (и, v) |Мы предоставляем читателю самому убедиться в том, что п k—1
п (и, и) = 2 3 (-1)’ (ZT I raj) (D*-1” и) = k=Q a=0
= [pax] и + Jva2] Du — uD [va2\ +
+ [ря3] D2u — D [ua3] Du 4- D2 [va3] и +
4- [uaol D'-'u - D [ va0] D^u 4- ... 4- (- I)”'1/)”"1 [ya0] u.
Это выражение нужно вычислить в конечных точках /0 и Zx.
\	УРАВНЕНИЯ Л-ГО ПОРЯДКА^	463
\
Общая формулировка. Окончательный результат этого приложения приведен в теореме Е.
ТеоремаЕ. Любое дифференциальное уравнение Ln (D, t) == = Mq (D, t) можно привести к эквивалентной векторной форме первого порядка
х (Z) = k, z (Z)] + (-l)nfe* (t)u (t),
z (t) = A {t)z (t) + b (t)u (t), (Gt.
Здесь z (t) = col (zj (Z), zn (/)); b* (Z); a* (Z) — коэффициенты присоединенных операторов Ln (D, Z) и Mq (D, Z) соответственно, а матрица A (Z) и вектор b (Z) имеют следующий вид:
J(Z) =
(-!)%:_! (o i... o' о . о
(-l)ao(Z)	0 ... О
"(-I)2"
(11)—
(-1)п+а« +(-i)V0
Доказательство этой теоремы мы вновь оставляем читателю в качестве самостоятельного упражнения.
Отметим, что если порядок q оператора Mq (D, t) меньше порядка п оператора Ln (D, t) по крайней мере на единицу, то 0 и входной сигнал не попадает непосредственно на выход системы. Другими словами, в этом случае х (/) зависит лишь ОТ Z (t).
Пример, В качестве иллюстрации использования этой теоремы можно привести уравнение из последнего примера к его канонической форме, воспользовавшись присоединенными операторами. По виду L3 (Z), t) х = D*y + (- t - 2) D2x + (- t2) Dx + 4" (— t — 1) x мы найдем
L* (D, z) x (Z) = (-1)я2)3х (Z) + D2 [(- Z -2) x (Z)l + D U2x (Z)] + + (- Z -1) x(Z)
ИЛИ
L* (D, f)x = - D3x (Z) - (Z + 2) D2x (Z) + (Z2 - 2) Dx (Z) + + (Z — 1) x (Z).
Аналогичным образом
M* (Z>, 0 и (/) = -t3D*u (0 - 9Z2£2u (0 - 19; Du (t) — 6u (;).
Вычисление элементов A (£) и b (t) с помощью теоремы E приводит к уравнениям (26).
Начальные условия. Дифференциальные уравнения вида Ln(D, t) х = 0 обычно сопровождаются начальными условиями для х и его п — 1 производной. Поэтому для того, чтобы пользоваться приведенной формой z (Z) = Л (/) z (/), нам нужно научиться преобразовывать исходные начальные условия, заданные в виде £ = = col (х (/0), х (£0),..., я71"1 (;0)), в условия для z (;0). Для этого надо разрешить уравнения преобразования переменных относительно z (Z) и выразить z (£0) через £. Интересующее нас преобразование переменных имеет вид
si —
Z1 = (—1)"ап-131 + з2,
zm = (—l)m'"+1a*_mz1 + zm+1, m = 1, . . m — 1,
zn = (—l)1aoz1.
Решая его относительно zm, получим
zi = Хч ^2 = ^1	\	1)
Zm+i = Zm — ( —	ГП = 1, . . ., Ш — 1,
— %п-1	(	1) ^1^.
Теперь мы можем разрешить его относительно zm и получить результат, зависящий от х и его п — 1 производной, подставляя каждое из полученных уравнений в последующее. Приведем несколько первых результатов:
Zi = ж,
z2 = i —(—Ifan-iZ,
z3 = i -	- (-1)”-^*-.^.
Это преобразование можно записать в векторной форме:
z (0 = Ту (Z),
где матрица Т, очевидно, треугольна. В частности, в момент t = = t0
*(Z0) = Tg.
Многомерные системы. На протяжении всего этого приложения мы предполагали, что исследуемое дифференциальное уравнение n-го порядка имеет только одно входное воздействие. Однако поскольку рассматриваемое дифференциальное уравнение линейно, то принцип суперпозиции позволяет аналогичным образом рассматривать и системы с несколькими входами. В случае нескольких входных воздействий исходное дифференциальное уравнение принимает вид
i
Ln Z) # (Z) = 3 Мqx (D, t) U* (Z), t (EE T,
k=i
где Mqk (D, t) и Uk (Z), к = 1,..., Z, — операторы типа (14) и k-e внешнее воздействие на систему соответственно.
Для того чтобы привести это уравнение к векторной форме, каждое из этих входных воздействий нужно рассматривать в отдельности. В результате мы получим систему векторных дифференциальных уравнений первого порядка
zk (Z) = A (Z) zh (Z) + bh (t) uk (Z), к = 1,..., Z,
xk (Z) = [d, zk (/)] + (-l)n&nb (Z) uk (Z), к = 1,..., Z,
где через Xk обозначено решение исходного дифференциального уравнения, в котором все входные воздействия, за исключением Uk, тождественно равны нулю. Воспользовавшись принципом суперпозиции, мы получим
Z (Z) = A (Z) z (0 + В (Z) и (z), t е= т,
х (Z) - D (Z) z (0 + С (Z) и (Z), Z е т, где
i
fc=l
I
x W = 3 xk (Z),
Jc=l
а В — матрица, построенная из вектор-столбцов {bk}:
Аналогичным образом можно преобразовать и систему из т уравнений типа (1) или (13). Поскольку отличия между всеми этими случаями сводятся в основном к отличиям в обозначениях, мы
удовлетворимся всего одним примером.
Пример. Рассмотрим систему с двумя входами и тремя выходами, описывающуюся уравнениями
У1 — t2y2 + (t + 1) у'я— у“л -= tx\ + Хг + х,,	(37)
t3y”i. + Уз~ Уз + 2t/3 — уг = + 2) хх + tx2,	(38)
ty'i — Уз + Уз =	+ х2.	(39)
Каждое уравнение такого типа можно интегрировать п раз, где п — порядок старшей производной соответствующего уравнения. Воспользовавшись интегрированием по частям, мы получим в ре-зульте t	Я
У1 $ I S L а2^2 +	+
+ j (2^1/21 2i/3 — хг — х2) ds &ц j da /с121 d$ -|~ ^13 — 0, Уз + t3yi +	+ J {— Ф2У1 — Уз — 2^3 + 2x2 +
+ [ (6s — 1) yt — (s + 2) xj ds + A:aiJ d[i + fc22 = 0, t
Уз —	(У\ — Уз + "Ь хз) ^3 + ^3i = 0*
Введем следующие переменные: t
Zl = (2&/2 — %Уз ~~ Х1 — Хз} ^3 +
S2 = [— 32Z/2 + (3 + 1) Уз + Х1 + 211 ^3 + ^12»
z3 =	+ z2) d$ + &1з»	>
z4 = [(63 — 1) У1 - (3 + 2) 2q] d$ + /са1,
з5 =	— y2 + 2y3 + 2x2 + s4) dft + 7c22- .
(40)
(41)
(42)
(43)
ПроДифФеРенциРовав УРавнсиия (43)> мы получим
Zj == 2iy2 2у3 xt x3t
z3 = — t2y3 + (t 4- 1) y3 + xt + zlt
Z3 = tXi 4” Zj,
Z4 = (6/ — 1) У! — (t 4- 2) Xi, z'6= — (>12У1 — У2 + 2Уз 4- 2.r2 4- z4,
(44)
ze = yi — У2 4- xi 4- x2-
Теперь уравнения (40), (41) и (42) можно переписать в виде
У1 = — z3,
4- У2 = - Z5 4- <*2,
(45)
— <Pi 4- Уз — ~ zt-
Эта система линейных уравнений имеет единственное решение в том и только в том случае, когда определитель ее коэффициентов не обращается в нуль на промежутке < t < t3. А так как
1
0 04
det
1 О
О 1
= 1=0,
то мы получаем единственное решение У1 = - 23,
Уг = t3z3 — z5 4- tx2,
Уз= <zs ze-
(46)
Подставляя уравнения (46) в (44) и приводя полученный результат к векторно-матричной форме, мы видим, что
zi '
za
Z3
Z4
Z5
" z6 -
-0 0	2Z(/34-l)	0	-2t
1 0	+ t 4-1)	0	t2
0 1	0	0	0
о о	— (6г — i)	о	о
0 0 -1 (t2 4- 6f 4- 2) 1	1
0 0 - (P + 1)	0	1
-1 1
+ -(i4-2) 0 0
(47)
Уравнение (47) имеет канонический вид. К требуемому типу относится и преобразование (46). Совершенно ясно, что подобный переход удается провести в том и только в том случае, когда определитель коэффициентов при старших производных в каждом из уравнений не обращается в нуль на интересующем нас промежутке времени. Это требование эквивалентно условию ап (0 =/-=/=0 на г для случая одного уравнения.
У п'р а ж н е н и е
Воспользовавшись описанным методом, приведите уравнения
У'" + бу” + у' + бу = О, у (0) -- 1, у' (0) - у" (fl) = О к векторной форме первого порядка. Покажите, что решение полученного векторного уравнения имеет вид
col [(Зе-' — Зс-2' + е-8'), (—Зе-' + бе-2' — Зе-3'), (Зе-' - 12е-2' + 9е"3')].
Каково решение исходного уравнения?
ПРИЛОЖЕНИЕ Г>
КАНОНИЧЕСКИЕ ФОРМЫ
В § 3.4 мы занимались в основном вопросами, связанными со структурой линейных преобразований конечного ранга. Сейчас мы постараемся обобщить некоторые из результатов этого параграфа па случай линейных преобразований бесконечного ранга. Точнее говоря, мы займемся здесь вопросами, связанными с приводящими подпространствами нормальных операторов и полярными каноническими формами линейных преобразований.
Для того чтобы оправдать необходимость изучения ограниченных операторов в бесконечномерных гильбертовых пространствах, рассмотрим достаточно подробно оператор М «умножения на х», действующий в />2 (0, 1). Оператор М преобразует функцию / ЕЕ L2 (0, 1) в функцию Mf = g, где g — xj (х). Ясно, что оператор М ограничен и что || М || = 1.
Прежде всего заметим, что у оператора М нет собственных чисел. В самом деле, уравнение Mf = Kf эквивалентно следующему:
1
0 = \\Mf-U\^=^\x-M2\f^)\2dx, о
и поэтому справедливо лишь в том случае, когда функция / (х) почти всюду равна нулю, т. е. когда функция / представляет собой нулевой вектор L2 (0, 1).
В частности, Mf = 0 выполняется только в том случае, когда / = 0, и, следовательно, преобразование М взаимно однозначно. Однако в отличие от ситуации, возникающей в подобных случаях в конечномерном пространстве, этот факт еще не гарантирует обратимости оператора М. При любом О X 1 область значений оператора М — X/ не содержит функции, тождественно равной единице, и, следовательно, для оператора М — X/ не существует обратного, определенного на всех элементах пространства Ь2 (0, 1).
Мы уже видели, и это можно тривиальным образом проверить, что присоединенный оператор М* определяется следующим усло-
(М*/) (х) = xf (х).
Другими словами, оператор М является самосопряженным. Вос ользовавшись этим, мы можем теперь показать, что множество
X, при которых оператор М — XI не имеет обратного, в точности совпадает с единичным промежутком 0 X 1. Если же комплексное число X не принадлежит этому промежутку, то существует такое е > 0, что
| X — х | > е при всех х GE [0, 1], и, следовательно, для всех / ЕЕ Ь2 (0, 1)
1
Л(М - U)/||2 = 5 I {х - X)/(х) |2d.r >e2||/||2. о
Поэтому, сслиХе=£ [0, 1], то оператор М — М ограничен снизу. Атак как оператор М является самосопряженным, то отсюда следует, что у оператора М — М существует ограниченный обратный оператор, определенный на всех элементах Ь2 (0, 1). (См. упражнение 11 (а).)
В связи с этим возникает идея определить спектр оператора А как множество комплексных чисел X, при которых оператор А — XZ не имеет ограниченного обратного оператора. В конечномерных пространствах все операторы ограничены. Поэтому нынешнее определение о (А) согласуется с приведенным ранее.
Мы показали выше, что оператор М является самосопряженным и что o' (М) = [0, 1]. А что можно сказать о диагональном представлении этого оператора? В конечномерных пространствах для таких операторов существовало представление	исполь-
зующее две группы характеристик оператора: его собственные числа Хг- и проекторы Рь проектирующие исходное пространство на соответствующие приводящие подпространства оператора. А так как у оператора М нет собственных чисел, то нам трудно надеяться на то, что мы сможем построить аналогичное представление оператора М. Вспомним, однако, что даже в случае конечномерных пространств наиболее важную роль играет семейство {Pj} проекторов. Другими словами, если мы можем найти любое семейство попарно ортогональных самосопряженных проекторов, составляющих в сумме оператор тождественного преобразования, и любое множество {ХД комплексных чисел таких, что А = то это должно значить, что Хг- суть собственные числа оператора А, a — операторы проектирования на соответствующие собственные подпространства этого оператора. Все это, естественно, заставляет нас попробовать отыскать для М семейство операторов проектирования или, что то же, найти разложение пространства Л2(0, 1) в прямую сумму замкнутых подпространств, каждое из которых приводит оператор М.
Для пространства Ь2 (0, 1) найти такое разложение нетрудно. Действительно, если промежуток [а, р] есть некоторое собственное
подмножество промежутка [0, 1], то совокупность S = S (а, ₽) элементов £2 (0, 1)» обращающихся в нуль вне [а, 0], может служить приводящим подпространством для оператора М. Единственное что нам нужно доказать, это то, что подпространство S замкнуто. Замкнутость же S следует из того факта, что оператор умножения на характеристическую функцию [а, 0] (т. е. отображение	₽)•/) определяет самосопряженный оператор про-
ектирования, область значений которого в точности совпадает с 5 (а, ₽)•
Из всего этого следует, что если 0 = а0 <	< ... < ап-1<
< ап = 1 определяет некоторое разбиение промежутка [0, 1], то
Л2 (0, 1) = S (а0, «0 ф S (а„ а2) ф ... ф5 (an_lt ап),
и правая часть этого соотношения определяет разложение пространства Л2 (0, 1) в прямую сумму попарно ортогональных подпространств, каждое из которых приводит М. Если через Pt обозначить оператор проектирования L2 (0, 1) на S а:), то эти операторы образуют семейство проекторов требуемого типа. Уравнение ЛГ =	означало бы теперь, что оператор М на
каждом из подпространств S (a/.j, af) совпадает с точностью до постоянного множителя с тождественным оператором, а это, очевидно, неверно. Однако в некотором смысле слова это приближенно правильно, так как если — некоторая фиксированная точка из промежутка [а^, af], то для каждого /f G S af) справедливо неравенство
ai
ai-i
и, следовательно,
Отсюда следует, что если / = G Лг (0» 1), то
о (м | м 2 Plf - S w |Г=IS (м - pif I*=
=IIS pi (М - хо /12 = 2II рг (Л/ - ХО 7 ||а С 2II pif II2 = Н / II1.
1 Де *) е = maxi (oq — a^). А так как / есть произвольный элемент
Заметьте, что при этом мы воспользовались коммутативностью операторов Р и М (см. упражнение 1).
пространства Л2 (0, 1), то мы можем заключить, что
|м -	(1)
Другими словами, мы показали, что оператор М является равномерным пределом последовательности операторов уже встречавшегося типа, с той лишь небольшой разницей, что область значений операторов проектирования уже не является одномерной. Итак, нам удалось добиться искомой диагонализации оператора М.
Прежде чем переходить к изучению более общей ситуации, нужно привести результаты, полученные ранее, к более удобному виду. Для этого определим Е (X), где	1, как оператор проек-
тирования Ь2 (0, 1) на подпространство 5 (О, X). В этих обозначениях
Pi = Е (at) — Е (а/_х),
а если % (О, Л) — характеристическая функция промежутка [О, X], то
£(Х)/ = х(0, *)Л /ел2(0, 1),	(2)
и, в частности,
х
=	/,gez2(0,1).	(3)
О
Заметим теперь, что <£* (X) /, />, как неопределенный интеграл от функции | / (х) |2, представляет собой некоторую вещественную-функцию с ограниченной вариацией на промежутке [0, 1] (на самом деле она даже абсолютно непрерывна). Поэтому нижеследующее тождество полярного типа
<£ (X) /, g> = 4' W + £)•/ + *>- <Е (X) (/ -£),/-£> + + i <Е (X) (/ 4- ig), / + ig> ~ i <Е(X) (/ -ig),f- ig,} показывает, что (Е (X)/, £> представляет собой комплексную функцию ограниченной вариации на промежутке [0, 1].
Посмотрим теперь на соотношение (1) с двух различных точек зрения. Прежде всего, заменяя в нем Р[ на соответствующие выражения с £j, мы получим для любого набора значений X| ЕЕ- lotj-i, aj
II М - 2х,- [Е (аг) - Е (а,.-,)] |) < в
при единственном условии, наложенном на разбиение промежутка: max; (az —	= е. Это утверждение можно записать более
компактным образом соотношением М = X dE (К), где мы вое-
льзовались очевидной аналогией с определением обычного ин-П0Грала Стильтьеса. Определение выражения в правой части этого соотношения содержится в неявном виде в наших предыдущих рассуждениях. Читается оно точно так же, как обычное определение интеграла от функции / (X) = X по функции ограниченной вариации, с той лишь разницей, что абсолютные значения теперь нужно заменить нормами, а функцию X—>£* (X) рассматривать как принимающую значения в пространстве операторов. Во всяком случае, для наших настоящих целей достаточно интерпретировать уравнение М = Jx dE (X) как сокращенную форму записи более сложного утверждения о разбиениях и их максимальной длине.
Другая, совершенно эквивалентная точка зрения на уравнение (1) вытекает из того, что его следствием является неравенство (<м/, £>-ЗМЛ,/. g> 1<е||/||-к||,
i
где / ng Е Ь2 (0,1). Ив этом неравенстве мы в неявном виде предполагаем существование некоторого разбиения 0 = а0 <	<...
...< ап= 1, причем yt е [аг_1? aj и е = maxf (af — af_J. Перепишем последнее неравенство с учетом определения оператора Е\
| <м/, g> - 3{<£ (а.) /, g> - <£(«i-О/, g>} I <8II/I|.||g||, i
а это приводит нас к следующей теореме:
Значение (обыкновенного) интеграла Стильтьеса
1
j*W) /, g> о
функции j (К) = X по функции Х-» <£ (X) /, g> с ограниченной вариацией в точности равно комплексному числу {Mf, g), т. е.
1
<M/,g> = $Xd<£’(X)/,g>, о
Преимущество второго подхода состоит в том, что он не предполагает введения никаких новых понятий, а интерпретация и доказательство соответствующих утверждений опираются исключительно на материал классического анализа. Для оператора М мы, конечно, могли бы очень быстро прийти к последнему уравнению с помощью формулы (3):
1	1	х
<ЛГ/, g> = Jl/(XjdA, = $Xd($/(X)^)dX),
0	0	0
у%Вам понадобились бы лишь определения операторов М и 4 I ) и классическое утверждение о сведении интегралов Стиль-rLeca к обычный.
При этом подходе мы используем тот факт, что интеграл
1
\<p(K)d(E(K)f, g> О
существует для всех функций ф (X), непрерывных на промежутке [0, 1], и, в частности, для любых полиномов. Предоставляем читателю самостоятельно показать, что если ф (X) = anX7t, то
1
0HW. g>= ^(X)d<£(X)/,g>.
О
Отметим, что эта формула является естественным определением Ф (М) для любой непрерывной функции ф.
Заметим еще, что
1	1
IIMf ||2 = <М/, М/> = $ М <Е (X) /, М/> = $ X2 d (Е (X) /, />,
О	о
так как х
<2? (X) /, Mf) = § / (х) xf (х) dx, о
или, в более общем виде, если ф есть некоторый полином, то
1
||^(M)/||2 = $|i|)(X)|2d<£(X)/,/>. О
Мы предоставляем читателю доказать, что отсюда следует:
hwu= sup к (х) I=hk
Хео(М)
где норма в правой части соотношения является обычной нормой банахова пространства С (а (М)) функций, непрерывных на а (М).
Найдем теперь решение нашей задачи для любого самосопряженного оператора А в гильбертовом пространстве Н. Спектр а (Л) оператора А определим точно таким же образом, каким мы сделали это для оператора М. Поскольку оператор А самосопряжен, то а (Л) представляет собой некоторое замкнутое ограниченное подмножество вещественных чисел (см. упражнение 10(6)). Теорема о спектральном разложении утверждает тогда, что существует спектральное семейство операторов {Е (X)}, определенных для любых вещественных X и обладающих следующими свойствами:
(1)	Е (А) есть оператор проектирования па Я;
(2)	оператор Е (А) непрерывен справа, т. е. || Е (А + е) — - Е(Х) ||-> 0 ПРИ е —* 0+;
(3)	2?(А,)=0 при А < min о (Л); Е (А) = I при А max о (Л);
(4)	Е (А) Е (р,) = Е (А), если А < р,.
Более того, справедливо соотношение А = A dE (А) или, что то же, в терминах обычных интегралов Стильтьеса:
<л/,$> = $ Xd<£(X)/,g>,
0(A)
||Л/||2= $ A2d <£(%)/,/>.
о(А)
Кроме того, как и раньше, мы можем представить функцию оператора А как интеграл от соответствующей численной функции, и это может быть сделано для каждой функции ср2 С (а (Л)). В этом случае для каждой непрерывной функции ср будет справедливо равенство || ср (Л) || = supxeo(A) | ср (А) |. В частности, норма самосопряженного оператора равна его спектральному радиусу:
|| Л || = max {|А |: А е сг (Л)}.
Для нормального оператора Л общего вида эта ситуация по существу остается такой же, но теперь мы сталкиваемся с чисто технической трудностью, связанной с тем, что спектр о (Л) может теперь быть любым замкнутым ограниченным подмножеством плоскости комплексных чисел. А это отражается в том, что спектральное семейство оператора Л теперь оказывается зависящим от двух переменных, а представление Л мы получаем уже в виде двойного интеграла от z = х + iy по в (Л).
Однако в тех случаях, когда оператор Л является унитарным (А*А = I = ЛЛ*), его спектр о (Л) является подмножеством единичного круга (упражнение 10(6)), и мы приходим к декомпози-ции А = ег0 dE (0), где £*(0) есть спектральное семейство на промежутке 0^0^ 2л.
Сделаем еще одно замечание. Спектральное семейство заданного оператора однозначно определяется этим оператором. Напри-меР, если имеются два семейства {Е (А)} и {£(А)} и оба они описывают самосопряженный оператор Л в определенном выше смысле, то для любого полинома ф (А)
$ * (*)d <Е (X) /, g> = <1|> (Л) /, g> = $ i|> (X) d (F (X) /, g>.
Но это условие вместе с нормирующими условиями (2) и (3), накладываемыми на Е и £, означает, что <£ (А) /, g> — 7Л(А) /, g>, а так как g и / совершенно произвольны, то Е (А) = F (А).
Упражнения
1. Пусть А есть некоторый оператор в гильбертовом пространстве а М есть некоторое подпространство Н. Обозначим через Р оператор проектирования Н на М. Тогда для того, чтобы подпространство М было инвариантным относительно А , необходимо и достаточно, чтобы PAP = Р. Воспользуйтесь этим по отношению к Л*, чтобы доказать, что М приводит А в том и только в том случае, когда операторы Р и А коммутативны.
2. Обозначим через М оператор умножения на х в пространстве £2 (О, 1), и пусть R есть некоторое инвариантное подпространство М. Тогда R = %eL2 для некоторого измеримого подпространства Е промежутка [0, 11.
Указание. Пусть еп (х) = хп (п 0). Наименьшее замкнутое поди ре странство £2, содержащее каждое еп, совпадает с L* (0, 1).
Пусть Р есть оператор проектирования £2 (0, 1) на R. Докажите, что (a) R есть (замкнутое) линейное подпространство, натянутое па векторы Реп;
(б)	если ф = Ре0, то Реп = еп [т. е. что (Реп) (х) = хп ф (я)] (воспользуйтесь для этого коммутативностью операторов Ри М); если р =^q апеп, то Рр = рф;
(в)	если {Рп/ есть некоторая последовательность полиномов, сходящаяся в £2 к ф, то Ррп -► Рф = ф и (рп — ф)> ф —» 0, так что ср2 = ф;
(г)	докажите, что Реп G %е‘ ^2 (п > 0), где Е = {х £ [0, 1]: ф (х) = 1}, так что R С ^2- Заметим теперь, что если /	£2 и / | Я, то f | Рел
и / | еп -— Реп, так как еп — еп(р обращается в нуль на Е и f обращается в нуль на £'. Поэтому f = 0 и R = 7Е-£2.
Компактные операторы. Читатель, наверное, заметил, что во время перехода от спектрального представления нормальных операторов в конечномерных пространствах к вопросу об аналогичном представлении операторов в бесконечномерных пространствах мы перешли от конечных сумм к их естественным аналогам, интегралам Стильтьеса, минуя не менее естественный с первого взгляда промежуточный этап — бесконечные суммы. Изучение операторов в конечномерных пространствах позволяет выдвинуть, казалось бы, естественную гипотезу о том, что каждый нормальный оператор может быть представлен в виде	причем этот ряд
должен сходиться по норме. Однако мы знаем, что это не так, по крайней мере для оператора М, а вообще говоря, и для любого оператора, не имеющего собственных чисел. Если A где Ei — попарно ортогональные операторы проектирования, сумма которых дает I (EiEj = 0, i =/= /; У t Et = I), то для f = Erf справедливо соотношение Af = Krf. Поэтому возникает необходимость исследовать условия, которым должен удовлетворять оператор для того, чтобы его спектр состоял из одних собственных чисел и чтобы множество этих чисел было не более чем счетно (см. упражнение 6). Это приведет нас к понятию компактного оператора, изучением которого мы сейчас и займемся.
Из приложения 1 следует, что множество М метрического пространства X называется компактным, если из каждой носледова-
тельности frj элементов М можно выделить некоторую сходящуюся последовательность {^}, предел которой принадлежит М. В конечномерном пространстве каждое замкнутое ограниченное множество компактно. Однако мы знаем, что в бесконечномерном пространстве это уже не так. Например, мы знаем, что единичный шар в пространстве 12 не компактен.
Возвращаясь к задаче изучения операторов, заметим, что если оператор А представляет собой любое ограниченное линейное преобразование, то А должен отображать ограниченные множества в ограниченные. В самом деле, из неравенства || х ||< М следует, что || Ах || М || А 1|. Наше определение компактного оператора потребует много большего. Нам удобно будет называть множество относительно компактным, если компактно его замыкание.
Определение А. (Ограниченный линейный) оператор А в банаховом пространстве называется компактным, если он отображает ограниченные множества в относительно компактные.
Каждый линейный оператор конечного ранга компактен, так как он отображает любое ограниченное множество в некоторое ограниченное множество конечномерного пространства. В бесконечномерном же пространстве имеется, вообще говоря, множество операторов, которые являются ограниченными, но не компактны. Одним из примеров таких операторов может служить тождественный оператор. Тождественный оператор в 12 отображает единичный шар S пространства Z2 в множество, не являющееся относительно компактным, а значит, этот оператор не может быть компактным.
Из приведенного определения следует, что если оператор А компактен, то для любого оператора В компактны и произведения АВ и В А. Действительно, если S есть некоторое ограниченное множество, то этим свойством обладает и В (S), а значит, его образ в силу А относительно компактен, и, следовательно, АВ отображает ограниченные множества в относительно компактные. Аналогичным же образом, множество A (S) относительно компактно, а так как непрерывное отображение компактного множества компактно (доказательство этого утверждения несложно), то В РЧ(£)) = (ВA) (S) также относительно компактно.
Это замечание показывает, что если dim Н = оо, то 0 принадлежит спектру каждого компактного оператора в Н. Действительно, если 0 а (А), а оператор А компактен, то А-1А = I, и, следовательно, Н <^оо.
Теперь мы подготовлены к тому, чтобы сформулировать спектральную теорему для компактных нормальных операторов.
Теорема А. Пусть А есть некоторый компактный нормальный оператор в Н.
Тогда
(1)	а (Л) состоит из не более чем счетного множества собственных чисел, каждое из которых имеет конечную кратность *);
(2)	если множество и (4) счетно, то его единственной предельной точкой является 0;
(3)	существует такая ортонормальная последовательность собственных векторов {фг} оператора А, где фг- соответствуют собственному числу что для каждого х СЕ Н справедливо разложение Фурье
ОО	00
Ах = 2 < Ах> ф>> Ф« = S bi <х> Ti> Ф«> 1=1	1=1
оо	оо
Л’г- = 2 <А*х, <р;> = 2 М <*, Ф<> Фь 1=1	1=1
(4)	последовательность {ср/} в пространстве Н является полной в том и только в том случае, когда 0 не является собственным числом оператора А, т. е. тогда и только тогда, когда Ах =^= 0 при х =/=> 0.
Этой теореме можно придать форму, аналогичную остальным результатам этого приложения, если заметить, что оператор Eh определенный из условия
Eix = <а:, ф{><рь
является оператором проектирования на Н. Более того, х | JLEjX при j =/= / и для каждых х и у GE Н
Ах = 2^i <*» ф«>ф{ = ^ЪЕгХ, (Ах, у) = 2^i (EiX, у), г	i	i
Последнее уравнение выражает (Ах, у) в виде интеграла Стильтьеса от функции / (X) = X по функции (Е (X) х, у), претерпевающей скачок (Е}Х, у) в каждой точке X = Xf и равной в остальном пространстве постоянной. Если 0 не есть собственное число оператора А и {ф/} образуют базис пространства Н, то 2/^ = 11 первое из уравнений отражает тот факт, что А = ^°° Х<2?|» ПРП" чем этот ряд сходится по норме оператора
N
|л-2мМ-° при
1=1
*) Собственное число X оператора А имеет конечную кратность, если множество {х: Ах = кх} конечномерно.
Пример 1. Рассмотрим линейный оператор A: l2 —> L, определенный следующими уравнениями:
оо
Ух = S i = 1, 2,	(4)
R=1
где У == Уъ х = (xi> X2V..) е Ч и у = Ах. Нетрудно показать, что в таком виде можно представить любой линейный оператор в 12. Воспользовавшись неравенством Коши — Шварца, мы видим, что
оо
М11<(2мТ-	(5)
i» 3
Если правая часть этого неравенства конечна, то такой оператор Л компактен, что мы сейчас и докажем.
Прежде всего отметим, что сходимость указанной двойной суммы означает, что для каждого е 0 найдется такое N, что
( 2 Ki2 )/!<е-г, j=n
Поэтому, если обозначить через AN преобразование А^х = у, определенное условиями
п
„ _ 2 аихь 1 = •••> ", У'1 ~ 3=1
О, г = п 1,
ТО || А - А n || < е. Следовательно, область значений оператора An образует е-сеть для области значений оператора А. Однако поскольку область значений оператора А конечномерна, то этот оператор компактен и, согласно следствию к теореме Л приложения 1, компактна и область значений оператора А.
Пример 2. В качестве второго примера рассмотрим линейный оператор К в L2 (а, Ь), значение которого в момент t ЕЕ [л, Ы определяется по формуле
ь
(Кх) (t) = s)x(s)ds, x^L2(a, b). a
пРеДполагается равномерно непрерывным на квадрате т«’>. а’ Другими словами, для каждого в > 0 можно найти такое 0 > о, что
I* (<i, в) — к (t2t s)| < в, se [а, &],
(6)
если | tr — /2 | < 6. С помощью неравенства Коши — Шварца Л1Ь| легко докажем теперь, что для любого х ЕЕ Л2 (а, Ь)
ь	’А
|(/Сг)(«) К1И|[§|k(t, s)|2ds] ,	(7}
а
\(Кх) (/J - (Кх) (/2)| < || х || [[* (/г, s) - k (/2, $) |2 ^|’Л	((S)
Из неравенства (8) следует, что для каждого х ЕЕ Ь2 (а, 6) Кх есть некоторая непрерывная функция, и, по мере того как х пробегает некоторое ограниченное множество, получающееся множество функций Кх оказывается равностепенно непрерывным. Неравенство (7) показывает, что это множество еще и ограничено. Поэтому согласно теореме Арцела образ К (S) любого ограниченного множества S Q L2 (а, b) относительно компактен в С (а, 6). Но так как равномерная сходимость гарантирует и обычную сходимость, то множество К (S) должно быть компактным в L2 [а, 6], и, следовательно, оператор К компактен.
Замечание. Условие непрерывности весовой функции к ни в коей мере не является необходимым условием компактности оператора К в L2. Оператор Т неопределенного интегрирования
t	1
(Tf) (t) = $ j (s) ds = fc (s, t) f (s) ds, /SZ2 (0, 1), 0	0
f 1,
= f<s, является компактным, хотя его весовая функция к, очевидно, нс непрерывна.
До сих пор нам не удалось показать,^что спектр оператора должен быть непуст. А это, очевидно, необходимое условие содержательности большинства наших результатов, полученных выше. В завершение этого раздела устраним отмеченный дефект.
Пусть Т есть некоторый оператор, и пусть для
R\ (t) = (Г — XZ)"1. Согласно результатам упражнения 10(6) мы получим тогда, что
II Ях (ПК (IM-II т ни,	|М>11Л,	(9)
а из упражнения 9(в) следует, что
09
Ях (Л - Ях. (Л = Ях. (Л 2 (* “ х«)(г)п - Ях. (Т) =
О
оо
= Ях.(Л2(^-^)пЯх.(Л"-
Отсюда
II /?х (Г) - Лх. (ПII < II Ях. (Л II {(1 ~ I * - *о I • Рх. (П Г - 1} < СI х - хо I -I) Ru (Т) IP (1 - | к - Хо1 .ц ях, (Г) ||)-Ч (10)
Зафиксируем р и к, не принадлежащие а (Т). Умножая тогда тождество
Т - р/ (Г - kl) - (р - к) I сначала слева на (Г), а затем справа на Ri (Г), мы получим (Г) - Ях (Т) = ^-k)R^T)R^T).	(11)
Теорема Б. Если Н {0}, а Т (Ez Р (Н), mo а (Т) не пусто.
Доказательство. Если о (Т) пусто, то оператор Яр. (Т) определен во всей комплексной плоскости. Однако согласно неравенству (9) он обращается в нуль при | X | —> оо и, в соответствии с неравенством (10), зависит от % непрерывным образом. Зафиксируем х и у s Н и рассмотрим комплексную функцию
Фх, у (М = <Пу (^) УУ*
Непрерывность Я> (Т), вместе с уравнением (И), показывает, что функция аналитична во всей плоскости. А так как 0 при | X | -> оо, то эта функция также ограничена во всей плоскости. Но отсюда, согласно теореме Луивилля, (pXtV постоянна и, следовательно, тождественно равна 0. Так как это верно для любых у, то нулевым вектором должна быть функцияЯ> (Т) х, а поскольку х произвольно, то оператор ЯЛ(Т) должен быть нулевым. Но в этом случае I = R\ (Т) (Т — XZ)= 0, что противоречит утверждению о том, что Н =j= {0}.
У пражнения
В этих упражнениях мы все время считаем, что А — некоторый компактный оператор в гильбертовом пространстве.
3.	Докажите, что любой отличный от нуля элемент о (4) является собственным числом А.
Указание. Выберите 0 =/= 1 С о (4) и предположите, что существует такая последовательность {хп}, что ||xn|| = 1 и Ахп — Кхп —> 0. Выберите затем из {4^} некоторую сходящуюся подпоследовательность. Воспользуйтесь соотношением хпк = (1/1)[4 хПк — (АхПк — 1хп/с)] —> 1Ду, завершающим доказательство.
4.	Докажите, что каждый компактный самосопряженный оператор имеет по крайней мере одно собственное число.
Указание. Воспользуйтесь для этого фактом равенства нормы самосопряженного оператора и его спектрального радиуса.
5#	Докажите, что каждое собственное подпространство компактного оператора конечномерно.
16 у. Портер
Указание, Заметьте, что если это не так, то в таком собственном подпро* странство можно построить бесконечное ортонормальное множество собственных векторов.
6,	Докажите, что если а > 0, то компактный оператор А может иметь не больше конечного числа собственных векторов, соответствующих X ЕЕ ЕЕ б (Л), для которых | X | > а.
Указание, Предположите справедливость обратного и придите к противоречию. Эта задача эквивалентна доказательству того, что единственной предельной точкой о (Л) может быть 0.
Полярное представление|оператора. Между операторами в гильбертовых* пространствах и комплексными числами можно провести много полезных аналогий. Например, мы уже отмечали в этой связи полезное понятие положительного оператора. Мы называем самосопряженный оператор А положительным, если неотрицательна квадратичная форма (Ах, х). Тривиальным следствием спектрального представления такого оператора является то, что у него имеется квадратный корень Л1/2, определяемый условиями Л1/2 >0и (Л1/2)2 = А. Этот факт позволяет определить положительный оператор и другим образом: оператор А является положительным в том и только в том случае, когда А = В*В для некоторого оператора В. Это проясняет аналогию между присоединенным оператором и комплексно-сопряженным числом.
Эти соображения наводят на мысль, что, возможно, существует разложение оператора на его «вещественную» и «мнимую» составляющие. Более того, разумно предположить тогда, что БеЛ = = 1/а (Л + Л*), a Im Л = х/а i (Л — Л*). Ясно, что при этом
А = 4 (4 + 4’) + i [4 i (А - 4*)] , [4(4 + 44 = 4(4 + 4-), [4Ч4-4-)]’ = [4ч4-4-)].
Таким образом, мы видим, что если Л — произвольный оператор, то для него существуют такие самосопряженные операторы В и С, что Л = В + iC, Это соотношение предполагает, что Л* = = В — iC и 2В = А + Л*, а также 2iC = А — Л*. Другими словами, операторы В и С однозначно определяются оператором Л.
Каждое комплексное число z может быть записано в полярной форме: z = rei9. А так как г = (zz)'^, то можно ожидать, что оператору Л будет соответствовать некоторый положительный оператор,— на самом деле это будет оператор (Л*Л)*'«. Что касается множителя ei9, то, заметив, что e~iQ-ei9 = 1, мы можем рассчитывать на то, что удастся найти такой унитарный оператор V, что
Л = 7(Л*Л)’\
Как будет показано ниже, дело обстоит почти именно так. Однако вначале нам потребуется одно определение.
Определение Б. Оператор Т в Н является изометрией, если {Тх, Ту) = {х, у) для всех хи у ЕЕ Н. Оператор Т называется частично изометрическим, если он является изометрией на ортогональном дополнении своего ядра.
Легко видеть, что оператор Т является изометрическим тогда и только тогда, когда преобразование Т сохраняет нормы Тх = = || х || для всех х G Н (см. упражнение 13 (а)). Отметим еще, что равенство <х, у) = {Тх, Ту) = {Т*Тх, у) при всех х, у G Н эквивалентно утверждению Т*Т = I. А отсюда следует, что изометрический оператор Т является и унитарным в том и только в том случае, когда он отображает Н на себя. В последнем случае каждое я из Я можно представить в виде Ту, где у удовлетворяет соотношениям
ТТ*х = Т (Т*Ту) = Ту = х, ТТ* = I.
Стандартным примером изометрического оператора, не являющегося унитарным, является оператор одностороннего сдвига в Z2. Теперь мы подготовлены к тому, чтобы построить полярное представление ограниченного оператора.
Теорема В. Пусть А — некоторый оператор в Н. Тогда существуют такой частично изометрический оператор R и такой положительный оператор V, что А = VR.
Доказательство. Как мы уже видели, оператор R должен быть равен (А*А),/». Но если R выбран таким образом, то найти V не так уж трудно. Действительно,
||Я< = (7?Ч х) = (А*Ах, х) = (|А^|2,	(12)
а это показывает, что изометрическое отображение Vo можно определить на области значений оператора R следующим образом. Для у = Rx положим VQy — Ах. Теперь нам нужно лишь убедиться в том, что это определение однозначно в том смысле, что если у может быть представлено двумя способами, как у = Rx± и у = Rx2, то векторы Ахг и Ах2 идентичны. Но это следует из уравнений
\\Rxt - Лг2|| = [Я (^ - я2)|| =	- Аяа||.
С помощью того же тождества можно показать, что если у = = limnZ?xn принадлежит замыканию области значений R, то векторы Ахп сходятся к некоторому вектору z. Это позволяет расширить оператор Уо на множество R (Я), полагая VQy = z. А так как
М - lim ||Яяп(( = lim ||Axn|| = ||z||,
то отсюда следует, что оператор Уо остается изоме трическим и осле расширения на эту более широкую область определения.
Наконец, обозначим (Я(Я))-Ь через Нг и договоримся,что оператор V принимает на элементах Нг значение 0, совпадая с Vo на элементах RH. Совершенно ясно, что оператор V частично изометричен на Я и для любого х е Я
VRx = Vo (Rx) = Ах, что и доказывает теорему.
Следствие. Если оператор А обратим, то А = VR, где оператор R положителен, а оператор V унитарен.
Доказательство. Это утверждение следует из того, что если оператор А обратим, что он ограничен снизу, т. е.
[Лj;||	С||^, при всех х €= Я.
Поэтому согласно неравенству (9) этим же свойством обладает и оператор R. А так как оператор R самосопряженный, то это значит, что он обратим (см. упражнение 11а)). Но тогда V = ЛЯ"1, т. е. представляет собой произведение двух обратимых операторов, а следовательно, и сам является обратимым.
В § 3.4 мы получили каноническое диадное представление оператора конечного ранга. Обобщим теперь это представление на случай компактных линейных преобразований.
Теорема Г. Пусть Т есть некоторое компактное линейное преобразование, отображающее HY в Н2. Тогда существуют такие положительные скаляры {А,п} и такие ортогональные последовательности в Н1и {еп} в Н2, что
оо
Т = 3 еп fn
1 в том смысле, что
N
ПШо|Т-Зеп>Хп</| = 0.
Доказательство. Несколько видоизменив доказательство теоремы Я, мы можем показать, что Т можно записать в виде Т= VR, где Я = (Г* Г)1/», а Г* — преобразование, присоединенное относительно Т. В этом соотношении Я есть некоторый положительный оператор в Нг, а V — ограниченное линейное преобразование, отображающее Нг в Я2 и обладающее следующими свойствами:
Vy = Тх, если у = Их,
Vy = 0, если у^ области значений Я.
Ясно, что поскольку преобразование Т компактно, то компактен и оператор Я. Поэтому согласно спектральной теореме,
справедливой для оператора R,
оо
1?Г = 2^п fn)fn,
1
где через кп обозначены отличные от нуля собственные числа оператора Н (повторяющиеся в этой сумме столько раз, какова кратность каждого из них), а через {/п} — соответствующая последовательность собственных векторов.
Но так как
Я/П = ХП/П, Хп>0,
то /п = R (X'Vn). а отсюда следует, что еп = Vfn образуют ортонормальную последовательность в Н2:
<еп, ет> = <F/n, F/m> = <T(^7n), T№fm)> =
= In Ы <fn, T*Tfmy = V tf </n, R*fm> =
=	(Jn i hmf m ) ®nm-
Наконец,
oo	oo
Tx = VRx = V (3 (xn, fn> fn) =	<x, /n> en.
1	1
Упражнения
7.	Пусть S — оператор одностороннего сдвига в Z2 (см. пример 2 из § 3.3). Воспользуйтесь фактом сходимости геометрической прогрессии ^j° Хп к пределу (1 — X)-1 при всех |Х | < 1 для того, чтобы показать, что каждая точка открытого круга | X | < 1 является собственным числом оператора S*.
8.	Если А есть некоторый оператор, то А обратим в том и только в том случае, когда обратим оператор Л* (см. доказательство теоремы В из § 3.3). Воспользуйтесь этим утверждением для того, чтобы показать, что для всякого А спектр о (Л*) = о (Л).
9.	(а) Как мы видели, пространство 0 (Я) ограниченных операторов в гильбертовом пространстве Н является банаховым. Если оператор Л G 0 (Я) имеет норму || Л || < 1, то
«+р	n-f-p	°°
12	< 2 Зии* =1М1|п(1-цлг\
n	к=п
а это показывает, что частичные суммы ЛА’}1°> образуют в 0 (Е) некото-что° последовательность Коши. Поэтому всегда найдется такое В G 0 (Я),
П	09
В= lim У Лк = У
Покажите, что В (I — А) = I = (I - А) В и что, следовательно, Ак = = (/ — Л)-1. Заметим еще, что || (7 — Л)-1!! < У^°||Л ||А = (1 — || Л Ц)-1.
(б)	Покажите, что если Т есть некоторый оператор, то оператор (Т — — 17) обратим при всех | 1 [ > |1 Т ||.
Указание, Перепишите Т — к! в виде —1 (7 — l-1?) и воспользуйтесь утверждением (а). Это показывает, что а (Т) содержится в замкнутом круге с центром в начале координат и радиусом, равным || Т||, и что, в частности, а (Т) есть некоторое ограниченное подмножество комплексной плоскости. Отметим еще, что || (Т — 17)-11| < (| 11 — || Т Ц)-1 при всех |1| > || Т ||.
(в)	Покажите, что множество а (Т) замкнуто, где Т — некоторый оператор.
Указание, Достаточно доказать, что дополнение а (?) открыто. В свою очередь для этого достаточно доказать, что если оператор Т — 107 обратим, то найдется такое е > 0, что Т — М обратим при всех 1 из множества | 1 — 10 | < е. Для того чтобы доказать это, нужно записать
Т - 17 = Т - 107 - (1 - 10) I = (Т - 10Т) {7 - (1 - 10) (Т - 107)-1} и воспользоваться результатом упражнения 10 (а).
10.	(а) Воспользуйтесь уравнениями (И) и (12) и результатом упражнения 9(6) для того, чтобы показать, что спектр оператора одностороннего сдвига в Z2 совпадает с замкнутым единичным кругом.
(б)	Пусть Н есть некоторое гильбертово пространство с некоторым ортонормальным базисом {еп}^о« Определим на Н оператор двустороннего сдвига U с помощью условия
Uen = вп+ь и = 6, ±1, ±2, ...
Покажите, что оператор U унитарен и что для него a (U) — единичный круг.
11.	(а) Пусть Л есть некоторый оператор в Я, и пусть Л ограничен снизу:
|| Л х [| > m ||Я|| при всех х С Н
для некоторого тп = 0. Покажите, что Л взаимно однозначен и что область значений Л замкнута.
(б)	Для любого оператора Л R (Л)-*- = N (Л#). Покажите, что область значений может быть плотной в том и только в том случае, когда присоединенный оператор также взаимно однозначен.
(в)	Если оператор Л нормален, то || Л*х|| = || Л х || при всех х 77. Покажите, что оператор Л обратим в том и только в том случае, когда он ограничен снизу.
(г)	Покажите, что если Л = Л*, то а (Л) есть некоторое подмножество вещественной оси.
Указание. Воспользуйтесь тождеством
|Х — X I • 1И12 = I <М - *)	*> — <*. М — X) г>| < 2 [(Л — X) х|| -I X ||.
(д)	Покажите, что если оператор U унитарен, то а (77) является некоторым подмножеством единичного круга.
Указание. Воспользуйтесь утверждением (в) и неравенством треугольника
II (U - X) X || >| II Ux II - II Хх III = I (1 - I X I) . И-
(е)	Покажите, что если Л = Л*, то оператор Л может быть положительным в том и только в том случае, когда <Лх, х> > 0 при всех х & Н.
(ж)	Пусть А есть некоторый оператор. Мы называем число X приближенным собственным числом А, если существует такая последовательность /л } векторов с единичной нормой, что || (4 — X) хп || —> 0. Воспользуйтесь утверждением (в) для того, чтобы показать, что если А нормально, то а (А) состоит исключительно из приближенных собственных чисел оператора А и только из них.
12.	(а) Пусть А есть некоторый оператор в Я. Покажите, что А нормален в том и только в том случае, когда
|| Ах || = || А*х || при всех х е Н.
Указание.
|| Ах ||2 —1| А ||2 = < Ах, Ах> — < А*х, А*х>.
(б)	Предположим, что оператор А нормален. Но тогда нормален и оператор А — V, и, следовательно, || (4 — 1Z) х || = || (4* — V) х || при всех х G Н. Покажите, что если х есть некоторый собственный вектор 4, соответствующий собственному числу X, то х является и собственным вектором оператора 4*, соответствующим собственному числу X.
(в)	Покажите, что если оператор 4 нормален и Ах = Хх, А у = ру, причем л =/= р, то х I у.
Указание. Исследуйте разность <4х, у> — <х, 4*у>.
(г)	Покажите, что если оператор 4 нормален, а множества Afx = {х ЕЕ Н: Ах = \х} представляют собой собственные подпространства 4, то ЛГХ приводят 4 и попарно ортогональны.
13.	(а) Покажите, что следующие условия, налагаемые на оператор Т9 эквивалентны между собой:
(1) ||Тх|| = ||х || при всех хЕН\
(2) <Тх, ТуУ = <х, у> при любых х, у G Н.
Указание. Убедитесь в справедливости тождества
4<Тх,Т7/> = <Г(х + 2/),Т(х + 2/)>^<Т(х^-2/),Т(х-2/)> +
+ i <Т (х + ly), Т (х + iy)> - I <Т (х - 1у), Т(х- 1у)у.
(б) Покажите, что если оператор Т частично изометричен в Я, то Т*Т представляет собой оператор проектирования Я на ортогональное дополнение ядра оператора Т. И обратно, всякий оператор, у которого Т*Т является оператором проектирования, частично изометричен.
Литература
См. также главы IV и V книги [А.1], главу XI работы [А.21], главы IV и V [А.56], работы [А.57] и [А.72], а также главу IV книги [А.83].
ПРИЛОЖЕНИЕ fi
ДОПОЛНЕНИЕ К ВОПРОСУ О ЕДИНСТВЕННОСТИ
Некоторые из теорем § 4.2 приводились без доказательства для того, чтобы не мешать усвоению материала. Однако эти теоремы играют важную роль в практических приложениях, а так как их доказательства имеются не всюду, то мы решили привести их в этом приложении. Для простоты мы разбили теоремы D иЕ § 4.2 на несколько более мелких в надежде, что так разобраться в их доказательстве легче.
Начнем с доказательства теоремы В из § 4.2 (которую мы называем здесь теоремой А).
Теорема А. Следующие свойства пространства В эквивалентны между собой:
(1)	Пространство В гладко.
(2)	В каждой точке dU имеется не более одной (а значит, ровно одна) опорной гиперплоскости для U.
(3)	Функционал х -> ||л|| имеет производную (в смысле Гато) в каждой точке dU, т. е.
||х 4-ez[| — ||х||	ч
11 m	у——11 = G(x, z)
e->0	8
существует для всех х ЕЕ U и z ЕЕ В. Более того, b (х, z) есть некоторая вещественная линейная функция z с единичной нормой, если только она определена.
Доказательство. Эквивалентность условий (1) и (2) уже была установлена в § 4.2.
Зафиксируем теперь х ЕЕ dU и предположим, что предел, определяющий Ъ (x, z), существует при каждом z ЕЕ В. Покажем, что Ъ (х, z) определяет на В некоторую вещественную линейную функцию с единичной нормой. Согласно теореме Хана — Банаха х обладает экстремалью, т. е. существует такое / ЕЕ В*, что / (х) = 1 = ||/||. Зададимся некоторым z ЕЕ В. Тогда при е > > 0 имеем
|х + ez| > |/(х + ez) I = I 1 + в/ (z) |,
|х — ez|| С If (х — ez) | = | 1 — е/ (z) |,
и, следовательно,
[[ х + ez || — 1	11 + е/ (z) | — 1
8^8	’
Дж — eg||— 1	11 — е/ (z) | — 1
— е	—8
Теперь с помощью обычного правила Лопиталя мы убедимся в том, что предел выражения в правой части существует и имеет следующий вид:
lim |1+п/(*)|-,£ = Re f (z)< 11
Воспользовавшись этим результатом и предположением о существовании G(x, z), получим
G (х, z) Re/ (z),
G(x, z) < Re/(z).
Так как z произвольно, то отсюда следует, что G (х, z) = Re / (z) является вещественной линейной функцией z, норма которой не превышает 1. Из определения G очевидно, что G (х, х) = 1, а это значит, что преобразование z ->G(x, z) определяет вещественный линейный функционал с единичной нормой. Это доказывает последнее утверждение теоремы. Более того, мы попутно доказали и импликацию (3) => (1), заметив, что предыдущие рассуждения показывают, что у любого линейного функционала с единичной нормой, принимающего на элементе х значение 1, вещественная часть совпадает с G (х, z). Поэтому соотношения /, g s U*, f (х) = = g (х) = 1 гарантируют нам, что Re/ = Reg, а это, в свою очередь, означает, что / = g (см. теорему Ж из § 4.1), а значит, пространство В гладко.
Предположим, что В гладко, и пусть х ЕЕ dU, a z ЕЕ В и заданы. Покажем, что предел, определяющий G (х, z), существует. В самом деле, ||х + ez Цесть выпуклая функция вещественной переменной е, так как при 0 < а < 1
IIх + [ае + (1 — а) т)1 z|| = ||а (х + ez) + (1 — а) (х + t]z)|| < < а || х 4- ez]| + (1 — а) Ц х + t)z|.
Поэтому согласно известным положениям теории выпуклых функций (см., например, работу Красносельского и Рутицкого [А.511) У этой функции в точке е = 0 имеются правые и левые производные, причем
а = lim Н~ег1|-1И! < iim |l5~.g£jLr..ll5_H = ь. e->0+	8	e-H)t	8
Нам достаточно показать, что а = b.
Но согласно условиям теоремы для каждого е 0 существует такое единственное /е из В* с единичной нормой, что/е (х + ez) = = II х + ez ||. Пусть / = /0. Мы утверждаем, что Ъ = f (z). Для того чтобы доказать это, заметим, что множество {/е} в качестве подмножества слабо ^-компактного множества 17* имеет предельную точку g ЕЕ £7, и, следовательно, мы можем выбрать последовательность сходящуюся к нулю таким образом, что (у) g (у) для каждого у ЕЕ В. Но так как
/е (*) = Ik + Н — б/. (z),
то отсюда следует, что g(x) = ||х|| = 1, и, следовательно, в силу единственности / мы получим, что g = f. Снова воспользовавшись единственностью /, мы получим, что из равенства
л
И^+ezll — /е(2)
следует:
1	> Ik + ezS — tf* (z)l-
Воспользовавшись этим неравенством и тем фактом, что норма / равна 1, мы получим, что
о< Re' Ь + ег!!-/(* +М = h + ez||-l _ Rey /2) = 6	в
II	X + 8Z Ц — &f (z) — 1
= Re J-----Ц—L—-------+ Re (/«(z) - / (z)) < Re (/. (z) - / (z)).
Отсюда следует, что b = Re / (z). Точно таким же образом мы можем доказать, что а = Re / (z), что и завершает доказательство импликации (1) => (3).
Теорема Б. Пусть	Вп — нормированные про-
странства, каждое из которых строго выпукло. Определим для х = (xj,..., хп) еП^ норму | | с помощью условия
И= (31ЫР) .
1=1
где через ||^|| обозначена норма в Вг. Тогда пространство В = нормой{ | строго выпукло. И обратно, если для пространства В существует некоторая норма, обеспечивающая строгую выпуклость, то каждое из пространств-сомножителей (с порождаемыми там нормами) должно быть строго выпуклым.
Доказательство. Прежде всего покажем, что функция | (действительно определяет на В норму. Ясно, что эта функция подо-
жительно определенная и абсолютно однородная, так что нам остается проверить лишь справедливость неравенства треугольника. Но если х = (х»...,х^ъу = (t/p..., уп) принадлежат В, то
п 1/ п 1/
। х+у । = (з	+У1 г )1/р < (з di ъ II+и yi ||)рУР <
< (2 11р)1/₽ + (2II IlT = k I+h h где последнее неравенство есть неравенство Гельдера (для 1Р (п)) относительно векторов
Для того чтобы доказать строгую выпуклость такого пространства-произведения, предположим сначала, что В = В± х В2 есть произведение двух сомножителей. Выше мы приводили несколько эквивалентных определений строгой выпуклости, и среди них одно, согласно которому каждое х ЕЕ В с единичной нормой должно быть экстремальной точкой единичного шара U пространства В. Точнее говоря, для каждого х, у которого |х| = 1, условия х— Т	~ 1 и I z I ~ 1 должны означать, что х = у = z.
Покажем теперь, что каждое х = (хх, х2) ЕЕ В с единичной нормой является экстремальной точкой единичного шара или, что то же, что если (х1? гг2) = г/2 (уъ у2) + Ч2 (z1? z2) и
|(У1, y2)l=(killp + hani/p = i.
I(zi, z2)| = (bxir + ll^n^ = 1,
a (У1, Уг) 4s (zi» z2), то ( (яр x2) | строго меньше 1. Здесь возможны два случая.
Случай 1. Предположим, что = ||zj( и Ы = ||z2||- Тогда I хг) |₽ = | -у- (У! + Zx) |Р+ || -у- (у» + z2) | <с
< [4- <н и. ।+bi |)]р+[4- <ь ।+в]’=। г+1 » г -1 • так как не могут одновременно удовлетворяться оба равенства у± = zi и Уг = z2. А это вместе со строгой выпуклостью пространств и В2 означает, что не могут одновременно выполняться условия
Ь + zill = IIj/iII + |lzill и ||у2 + М = W + Ы-
Случай 2. Предположим, что (||г/1||, ||t/2||) и (||zj, ||z2||) — два раз-ичных вектора из В2. Как ивестно, пространство В2 с определенной на нем р-нормой строго выпукло. Поэтому р-норма суммы этих
двух векторов строго меньше суммы их р-норм:
1(1^11 +11^ 11)р + (1Гг/2» + Ь2||т<
< (|| Ух ||Р + II2/2 nVp + (II г1 II” + II Mp)vp = 2.
Отсюда
I (Ъ, ^2) I = (| 4"	||₽+ 11Г ||Т
< {[4- (W + Ь: 11)]Р + [4- (II II + IIz а И)] ТР =
= 4-[(h1|| + b1||)p + (h2ii нм)р11/р<1-
Воспользуемся теперь методом индукции и предположим, что сформулированная выше теорема справедлива для произведения но более п — 1 пространств-сомножителей. Пусть В = Ц{яв1В<. Тогда в соответствии со сделанным предположением пространство п—1
Bl= n*i i=l с определенной на нем нормой n—i	i/р
| (^1> ^2» •••> хп-1) | = ( 2 II3'» 1|Р) i=l
строго выпукло. Но теперь с алгебраической точки зрения В ~ = В1 X Вп, и если х S В, то
п—1
klp- 2 killp + knir = |(^, *2,...»^n-or + knir, г=1
т. е. определенная на В норма является р-нормой, определенной на произведении двух пространств, каждое из которых строго выпукло. Этот результат и результат, полученный для случая п = 2, доказывают сформулированную теорему по индукции.
Отметим, что условие строгой выпуклости пространств-сомножителей является необходимым для того, чтобы их произведение с определенной на нем указанной выше нормой было строго выпуклым. Так, если х, у s В, то
|^ + !/| = |(0,...,0,х,0, ...,0) + (0, ...,0,у,0,...,0)|<
О,...,0)1+ 1(0,...,О, у,0...0)1	= |x| + |j/|,
и неравенство превращается в равенство в том и только в том случае, когда х = ку или у = кх при некотором X 0.
В частности, положив р = 2, мы увидим, что введение евклидовой нормы
п
| (#1» х2, . . . , Хп) | = ^2 llxi||aj
делает пространство В строго выпуклым. Следующий результат показывает, что последнее утверждение можно несколько обобщить.	f
Теорема В. Пусть пространства Ви В' определены так же, как и раньше, и пусть есть некоторая положительно определенная симметрическая матрица размером (п х п), каждый элемент которой неотрицателен. Тогда функция
п
х III х III = ( 3 aiA Xi IHl-fyllj
определяет на В норму, обеспечивающую строгую выпуклость этого пространства. Обратно, если для каждой такой матрицы [а^] эта функция задает норму, превращающую пространство В в строго выпуклое, то строго выпуклыми являются и все сомножители Bi (по отношению к заданным на них нормам).
Доказательство. Пусть х = (хх,	хп) принадлежит В.
Обозначим теперь через х тг-мерный вектор [xJI,..., ||xn||). Тогда, обозначая через [, ] обычное скалярное произведение в вещественном тг-мерном гильбертовом пространстве, мы видим, что нам требуется доказать, что функция
*->|||*||| = [Ах, хР’
является нормой для В. По условиям теоремы матрица А положительно определенная, и, значит, [Ах, х] > 0, причем это неравенство переходит в равенство тогда и только тогда, когда х = 0. Поэтому II х HI >> 0, если только х =/= 0.
Кроме того, ясно, что ||| кх ||| = / X | • ||| я||| для всех комплексных скаляров X. Наконец, если у = (уг, у2^-^ Уп) €= В, то
IIIх + у III’ = j IIxt + Vi II• IIx) + У) IK
<2^(11М + Ш1) (1КИ + Ш) =
= Smm-IKII + 2	+	=
= |||x|||’ + 2lAz, y] + |||yup. Воспользуемся теперь тем фактом, что у любой положительной матрицы имеется единственный самосопряженный квадратный корень, и с помощью неравенства Шварца для n-мерного пространства
получим, что
I [Ах, у] |2 = | [Л'/гх, А'^у] |2^ [А'^х, A'^xJ (Л'ау, А'Ьу[ —
= [Ах, х[ [Ау, у] = ||И||а-|1Ы|2-Таким образом,
III * + у III2 < III х IIIя + 2 III х III. Ill у III + III у III2 = (1(1 x HI + III у III)2, а это неравенство окончательно доказывает, что указанный функционал может быть нормой для пространства В.
Заметим, наконец, что, доказывая неравенство треугольника для нормы в пространстве В, мы использовали неравенство треугольника в каждом из пространств Bt и неравенство Шварца для тг-мерного пространства. Поэтому, если х, у В и Щ х + уЦ] --= III Ml + III У И1> то llri + У*1 = ИМ + IIMl для каждого i, а век-торы А'!2х и A'/fy линейно зависимы. Но так как матрица Л, а следовательно, и Л1/2 обратимы, то второе условие гарантирует и линейную зависимость векторов х и р, Но отсюда следует линейная зависимость векторов х и у пространства В, а следовательно, и строгая выпуклость пространства В с нормой |||	|||.
Обратное утверждение доказывается с помощью теоремы Б, где нужно положить р = 2, а матрицу [а^] сделать единичной.
Теорема Г. Пусть В =	где все В { строго выпуклы,
и пусть норма вектора х = хп), принадлежащего В, задается выражением
п hl = fSkillT. 1<р<--4=1	7
Если Ф есть некоторый ограниченный линейный функционал, определенный на В, то существуют такие функционалы ЕЕ В г, i = 1,..., п, что
п
<р> = 2 <®ь ф<>-i=l
Более того,
Доказательство, Тот факт, что каждый ограниченный линейный функционал ф, определенный на В, можно представить в виде
<Х, ф> =	<Pi>>
Где фг е хорошо известен. Поэтому мы докажем лишь второе из утверждений теоремы.
Пусть х е В. Тогда
\<х, ф>| = [3<хь <p>IKSl<a:i» ф<>1<
<ЗЫНЫ< (3 МР)1,Р (3 hili’)17’, так что
Для того чтобы доказать обратное неравенство, обозначим через ф< экстремаль*) элемента ф^, принадлежащего В^ и положим, что х = (аь ф{,..., апфп), где
«i = (а-1 IIФ111)’~\ а = (3II Ф| 11’)1/’«
Тогда
Iх 1Р = 3II «<ф| If = 3 а? = аР(1-,) 3II фЛр(’_1) = а~’ 3II Ф< F = 1 > i	i	i	i
и, значит, норма такого х равна 1. Наконец,
<®. ф> = 2 <<=ЧФ* (ф|> = 3°Ч11ф||1 = aw3hill’ =	= «•
i	г	г
А отсюда следует, что|ф| > а, что и доказывает второе утверждение теоремы.
С л е д_с т в и е 1. Пусть В и ф определены так же, как и выше. Если ф4 есть экстремаль функционала фь определенного на Вь то экстремаль ф функционала ф имеет следующий вид
Ф = (а^, а2ф2, . . . , оспфп), где
= (а"11| Ф11|)9-\	а = (3II «Pi II’)17’-
Следствие 2. Если каждое В{ к тому же рефлексивно и гладко, то экстремаль X элемента х = (хх, х2,..., хп) пространства В задается условиями
% = (Р1^»1 ?2^2» • • • » Рп^п)»
) Напомним, что экстремалью Ф функции ф, определенной на строго выпукломбанаховом пространстве В, называется единственный вектор х рз о единичной нормы, удовлетворяющий условию <z, Ф> = || Ф ||.
где
Pi = (p-1kiS)”-1, 3 = (3killp)1/₽. ' i '
а через обозначены экстремали элементов х{ в пространствах В{.
Доказательство. Поскольку = (В*)* и В* строго выпукло, то мы можем воспользоваться теоремой Г и показать, что сопряженное пространство Ц-В* с определенной на нем нормой
i
изометрически изоморфно пространству В, на котором определена соответствующая р-норма. Поэтому каждое я из В можно рассматривать как некоторый функционал, определенный на ПХ*, и следствие 2 доказывается с помощью следствия 1.
Теорема Д. Пусть В — Ц*=1 В{ строго выпукло, а норма на нем задана так же, как и в теореме Б. Пусть, кроме того, Ф = (фх» ф2>---> фп) есть некоторый ограниченный линейный функционал, определенный на В. Тогда
III я> III’ = (Ж-М Wl/''.
где матрица [6^1 обратна [ai;L
Доказательство. Введем х= (хх, х2,..., хп) s В и ф = (фп ф2,..., Фп) и обозначим через z и ф соответственно тг-мерные век-торы (jxj||, ||х2||,..., |гп|) и (Ы’Ы,---. ||фп[|)- В этих обозначениях
Hhlll2 = Saijhill-hj|| = Мя, г],
i. 3
где через [, ] обозначено обычное скалярное произведение в вещественном тг-мерном гильбертовом пространстве. Но
К®, ф>| = iShi- Ф1>|с3к*ь <Pi>I<Shill-hill-
i	i	i
Нетрудно видеть, что последнее выражение равняется [£, ф] и, следовательно, может быть вычислено по формуле
[г, <р] = [А-' аА'Ъх, ф] = [А,/?.г, Л-’/гср]
^||А’/^Ц-ЦЛ-’/гфЦ = [Ах,	ф],/а.
Отсюда следует, что ||| ф |||а < [ Д^Ф, Ф1 = 2м Мф|1Н1ф/11» гДе(М — матрица, обратная матрице А = (а{}).
Пусть теперь х, (= Bi есть экстремаль функционала ф,:
Ы =1.	<*i. ф!> = Ы’
и пусть х = (TiXj, г2х2, . .., Тпхп), где
Xi = У1 2 ЬИII Ф> И> X = (2 ЬИII xi II • IIxi Г }	i.i
Тогда
НИН2 = ЗМ*|1НИ11 = 3ai;TiY; ==
ij	i.3
= т-22аи (2 Ыф*1|) (2 bn II ф« l) =
= У2 2 Ыф/1Н|ф»И2а<Аг = i,*,l	j
= r22 ^hill-hitll = r2; r2 = i» i. к
где мы воспользовались фактом ортогональности i-й строки А к Z-й строке В при i =f= I. Кроме того,
<х, ф> = г12<тл, ф1> = 'г12'МФ111 = i	i
i i
и, следовательно, ||<р|| у» что в сочетании с результатом первой части теоремы показывает, что ||ф|| = у.
Следствие 1. Пусть В и Ф определены так же, как и в теореме Д, а есть экстремаль элемента ф{ из В{, Тогда экстремаль ф функционала ф, определенного на В, задается условием
ф = (Т1Ф1, Т2Ф2, • • • ,ТпФп), где
Xi = г-1 2 ьи II ф^ II» х = 2 Ьи II ф< Н ф> I-г
Следствие 2. Если, кроме того, каждое пространство В{ гладко и рефлексивно, то экстремаль S элемента х = (Xi,..., яп) пространства В определяется по формуле
X =	6^, • . . , ЪцХц),
где
6i = 6-x 2«ijlkilk	s = 3 «и hi II-IIИ-
i	i.i
В качестве еще одного примера методов построения экстрема, лей мы докажем теорему Е.
Теорема Е. Пусть пространства В± и В2 строго выпуклы гладки и рефлексивны, и пусть F есть некоторое ограниченное линейное преобразование, отображающее Вг в В2. Обозначим через В пространство Ви на котором определена норма
И = (k II2 + IIW'’-
Тогда пространство В строго ьыпукло, гладко и рефлексивно, причем В* = В*, а экстремали х' элементов х пространства В задаются формулой
х>__ ||М* + И*И*(^) (II т IP + Иг IP)1/1	’
где черточки над символами обозначают экстремали в соответствующих пространствах Вг и В2.
Доказательство. Поскольку F ограничено, то
И2<|1М2<ИМ2 = И2<(1 + И112)11<
и, следовательно, норма | | эквивалентна исходной норме пространства Bv Поэтому у пространств В и Вг одинаковые ограниченные линейные функционалы и, в частности, пространство В рефлексивно. Обозначим теперь через В (F) график F в пространстве Br X В2. Ясно, что отображение (х, Fx) —^х определяет (линейную) изометрию В (F) на В. Но так как произведение В± X В2 (с очевидной нормой) строго выпукло (согласно теореме Б), то должен быть строго выпуклым и его изометрический прообраз В. Свойство гладкости также сохраняется при изометрии, и любое подпространство гладкого пространства также гладко, так что нам осталось лишь доказать гладкость произведения Вг X В2.
Согласно теореме Г этого приложения пространство, двойственное Вг х В2, можно отождествить с пространством пар (Д, /2) ЕЕ Е 5* х В2, на котором определена норма
II(/ь /8)1-(ll/iir + IIM2)7’-
А так как по условиям теоремы пространства В* и В2 строго выпуклы, то в соответствии с утверждениями теоремы Г строго выпукло и пространство (5Х х В2)*, что эквивалентно гладкости пространства Bi х В2.
Наконец, положив М (х) =-||а:|к 4- |F.r||F* (Fx), мы увидим,
<х, М(я)> =||а:||<а:, «> +1|Fx|| <Fx, Fx) = |х||2 + Ц/агЦ2 = |х|2.
Теперь для любого у ЕЕ В
Ку, м ю> | = |И <у, «> +|M<4 ^KlklHMI -h|Fxj.||Fy|;< (И2 + ИО* (И +1W* = k I • I у I •
Другими словами, функционал ф(я) = М (я)/|я| принимает на х значение |х| и имеет норму вВ*, равную 1. Поэтому он является экстремалью элемента х пространства В.
Замечание. Из приведенного доказательства следует, что \М (х)| =-- |2-| при каждом х из В и что преобразование М накрывает В*. Кроме того, преобразование М антиоднородно:
М(Кх) = |Xx|(Xz)' =	= XM(z).
Наконец, М взаимно однозначно, так как из равенства
I х k' М (^) = м (у) = I у \у' следует, что
И ЧТО	1*1=11/1
X = I х |х" = I х| (| х) х'У = | у I (|у ] у')' = у.
Если X и Y — конечномерные линейные пространства, а Т — некоторое преобразование, отображающее X в У, то на вопрос об обратимости Т ответить нетрудно. А именно преобразование 5, отображающее У в X и удовлетворяющее условию, согласно которому TS и ST суть тождественные операторы в X и У соответственно, существует в том и только в том случае, когда преобразование Т взаимно однозначно и отображает X на У. Но если ввести понятие линейности, то на вопрос об обратимости однозначно ответить нельзя, если только не удается доказать теорему, согласно которой любое преобразование, обратное Т, линейно. Другими словами, нам нужно доказать, что для преобразования Т существует обратное линейное преобразование тогда и только тогда, когда Т обратимо.
Если же, кроме того, предположить, что пространства X и У нормированы, а преобразование Т является ограниченным и линейным и отображает X в У, то мы сталкиваемся с дополнительной неопределенностью в вопросе об обратимости преобразования Т. Однако и эта неопределенность разрешается теоремой, согласно которой любое линейное преобразование, определенное на конечномерном нормированном линейном пространстве, автоматически ограничено. Короче говоря, для конечномерных банаховых пространств вопрос: «Имеется ли для ограниченного линейного преобразования Т некоторое обратное ограниченное и линейное преобразование?» оказывается эквивалентным гораздо более простому вопросу: «Является ли преобразование Т взаимно однозначным и сюръективным?»
Рассмотрим ситуацию, в которой X и У считаются произвольными банаховыми пространствами, а Т — линейным и ограниченным преобразованием, отображающим X в У. Ясно, что для существования у Т обратного преобразования необходимо, чтобы Т было взаимно однозначным и сюръективным. Эти условия также достаточны для того, чтобы обратное преобразование было линейным. Но удивительнее всего то, что эти условия гарантируют также и ограниченность обратного преобразования; другими словами, если Т — некоторое ограниченное линейное преобразование, отображающее X на У, и Т взаимно однозначно, то для Т существует ограниченное линейное обратное преобразование. Эта тео
рема принадлежит Банаху и наряду с теоремой Хана — Банаха считается одним из самых мощных инструментов функционального анализа. Вместо того чтобы доказывать этот результат, сформулируем несколько более общую теорему, из которой предыдущий результат получается в виде следствия.
ТеоремаА (об открытых отображениях). Пусть X и Y — банаховы пространства, и пусть Т — ограниченное линейное преобразование, отображающее X на У. Тогда отображение Т открыто, т. е. если G есть некоторое открытое множество из X. то открыто и множество Т (G) из Y.
Прежде всего отметим, что условия теоремы требуют, чтобы оба пространства X и Y были полными и чтобы преобразование Т было сюръективным. Сформулированная теорема оказывается неверной, если не выполнено любое из этих условий (см. упражнение 1). Эту теорему можно сформулировать и иначе, утверждая, что любое ограниченное преобразование с замкнутой областью значений преобразует множества, открытые в области определения этого преобразования, в открытые множества его области значений. Еще одна эквивалентная формулировка этой теоремы состоит в следующем: если Т накрывает Y. а через U х и Uv обозначены единичные шары в пространствах X и Y соответственно, то существует такая положительная постоянная а > 0, что aUyCT (Ux). Другими словами, существует такое а > 0, что если у s Y и ||у|| а, то уравнение Тх = у имеет по крайней мере одно решение х. у которого	Или, на менее
формальном языке, если преобразование Т является накрытием, то Т не может отображать «обширные» множества в «незначительные». Поясним на примере, что мы имеем в виду. Оператор Т в Е3 вида
Т (хп х2. х3) = (хи х2. 0), очевидно, не накрывает Е3. и это отражается в том, что он отображает шар
{(Х1, х2, х3) : I Xi I2 + | Х2 j2 + | х3|2 < 1), «обширное» множество по нашему определению, в «незначитель-ное» множество — круг
{(Хр х2. 0): I Xil2 + |х2 I2 < 1}.
Заметим, однако, что если Т рассматривать как отображение Е3 в Е , где Т (хп х2. х3) = (хп х2), то Т становится накрытием, и это приводит к тому,что открытое множество{(хх, х2. х3): | Xif2+ | х212 + и £2 f2 1} из Е3 отображается на открытое же множество
Глубину этой теоремы можно почувствовать из одного перечисления ее следствий.
Следствие 1. Пусти Т есть некоторое взаимно однозначное линейное преобразование, отображающее банахово пространство X на банахово пространство Y. Тогда для Т существует ограниченное линейное преобразование, ему обратное.
Доказательство. Поскольку Т взаимно однозначно и сюръективно,™ существует такое линейное преобразование S, отображающее Y в X, что ST и TS суть тождественные операторы в пространства X и Y соответственно. Более того, так как согласно предыдущей теореме преобразование Т отображает открытые множества на открытые множества, то прообраз (для S) каждого открытого множества в X должен быть открытым множеством в Y. Но это означает, что преобразование S непрерывно, а так как непрерывность линейного преобразования эквивалентна его ограниченности, то S ограничено.
Замечание 1. Следствие! показывает, что любое взаимно однозначное ограниченное линейное преобразование с замкнутой областью значений оказывается автоматически ограниченным снизу, т. е. (Тх|| > к Ы для некоторого к > 0. И обратно, как нетрудно видеть, если Т ограничено снизу, то оно имеет замкнутую область значений и взаимно однозначно.
Заметим еще, что теорема утверждает, что всякий отличный от нуля ограниченный линейный функционал, определенный на X, является открытым отображением. Например, если (р G В* и U = {х G= В : И < 1}, то ф (U) является открытым множеством в поле скаляров.
Для того чтобы сформулировать следующее следствие, нам нужно ввести несколько новых понятий. Пусть X — некоторое линейное пространство, и пусть функции j и 112 определяют на X нормы. Эти нормы мы называем сравнимыми, если одна из них мажорирует другую, т. е. если для некоторого положительного к справедливо одно из условий:
1И11 НЬ при всех х х
или
11^2 к Цх^ при всех х Ez X.
Например, нормы
|х||г = sup {х (t): t е= [0, 11} и
i
1И|а= Г$|х(0|мЯ,/!
Lo
являются сравнимыми на линейном пространстве X функций, непрерывных на единичном промежутке.
Нормы || Ji и || ||2 называют эквивалентными на X, если существуют такие положительные постоянные к± и к2, что
И1 < Иг < *2 kill ПРИ всех х&
Таким образом, две нормы, определенные на X, считаются эквивалентными в том и только в том случае, когда последовательность Коши в смысле одной нормы является последовательностью Коши И в смысле другой (т. е. если ||xn — мало тогда и только тогда, когда мало jxn — Если Две нормы || |L и ) [2 экивалентны на X то нормированное пространство {X, || |j} является полным в том и только в том случае, когда полно нормированное пространство {X, || |2}. А так как в предыдущем примере пространство {Х,||||1} полно, а пространство {Х,||||2} не полно, то эти две нормы не могут быть эквивалентными на X. Следствие 2 показывает, что только таким образом, по сути дела, можно построить сравнимые, но не эквивалентные нормы.
Следствие 2. Пусть X есть некоторое линейное пространство, и пусть функции || и J ||2 задают на X сравнимые нормы. Тогда, если оба нормированных пространства {X, Ц и {Х,|| ||2} являются полными, то нормы || [j и || ||2 эквивалентны на X.
Доказательство. Предположим для определенности, что ЦхЦ^ Л Иг при всех х Е X. Обозначим через Хх и Х2 пространство X с определенными на нем нормами || , или (| ||2 соответственно. По условиям следствия тождественное преобразование i: Х2 —> Хг ограничено. А так как это преобразование, очевидно, взаимно однозначно, линейно и накрывает Хп а пространства Хг и Х2 являются банаховыми, то согласно теореме об открытых отображениях у i есть ограниченное преобразование, обратное i и отображающее Хх на Х2. Другими словами, для всех i Е Xj
при некоторой положительной постоянной I, а именно это и требовалось доказать.
Замечание 2. Напомним, что каждая норма, определенная на векторном пространстве X, порождает в X систему открытых множеств (т. е. топологию X). Предыдущее следствие утверждает, что если пространство X является банаховым относительно двух различных норм, а система открытых множеств, порожденная одной из них, содержит систему открытых множеств, порожденную Другой, то эти две нормы должны в действительности порождать одну и ту же систему открытых множеств.
Если векторное пространство X конечномерно, то любые две нормы, определенные на X, эквивалентны друг другу, так что пане эквивалентных норм возможна лишь для пространств. Доказать первое из этих утвер
ждений не просто. Его доказательство основывается на том, что если II || есть некоторая норма для X, то|| хп(( ->0в том и только в Том случае, когда каждая из координат хп сходится к нулю в поле скаляров. Действительно, стоит это показать, как сразу станет
ра сравнимых, но бесконечномерных
понятным, что последовательность элементов X может быть сходящейся только в одном смысле, а отсюда уже нетрудно видеть, что это предопределяет эквивалентность двух любых норм, определенных на X.
Следствие 3 (теорема о замкнутом графике). Пусть Т есть некоторое линейное преобразование, определенное на банаховом пространстве X и принимающее значение в банаховом пространстве Y. Тогда для ограниченности Т необходимо и достаточно, чтобы из
(а)	гп->х, хп(=Х,
(б)	Тхп-+у, y^Y,
следовало у — Тх.
Доказательство. Если преобразование Т ограничено, то из хп -> следует, что Тхп -^Тх, и, следовательно, если справедливо и условие (б), то у = lim Тхп = Тх, так что необходимость условий этой теоремы для ограниченности преобразования Т является тривиальной.
Обратно, предположим, что условия этой теоремы (а) и (б) выполнены. Полагая тогда, что
IKx, у)| = max {Н, IM), X е X, y^Y, мы построим банахово пространство X х Y. Множество G(T) = {(х, Тх):х^Х},
очевидно, является линейным многообразием в X X Y, и согласно сделанным предположениям множество G (Т) к тому же и замкнуто. Действительно, если (х, у) GE X X Y есть некоторая предельная точка G (Т), то для некоторой последовательности {хп} из X
Ц(хП1 Тхп)—(х, у)||—>0,
а это эквивалентно утверждению о том, что хп—>х в X, Тхп-+у в Y.
Поэтому, воспользовавшись условием (б), мы получим, что у = = Тх, и, следовательно, (х, у) = (х, Тх) GE G (Т).
Определим теперь линейное преобразование Ф, отображающее банахово пространство G (Т) на X, согласно условию
Ф (х, Тх) = х.
Очевидно, что Ф взаимно однозначно, и, следовательно, в соответствии с утверждением следствия 1 ограничено и преобразова
ние Ф-1. Заметим теперь, что неравенство
отражает и тот факт, что преобразование ф: (х, Тх) Тх ограничено и отображает G (Т) в У. Это позволяет заключить, что композиция фФ-1 = Т также ограничена, что и требовалось доказать.
Замечание 3. Множество G (Т), рассматривавшееся в предыдущем доказательстве, называется графиком преобразования Т. Доказанное следствие утверждает, что для того, чтобы линейное преобразование, отображающее одно банахово пространство в другое, было ограниченным, необходимо и достаточно, чтобы его график был замкнутым подмножеством произведения X х У, что, очевидно, и оправдывает название этой теоремы.
Теорема о замкнутом графике предоставляет в наше распоряжение весьма полезный критерий, позволяющий решить вопрос об ограниченности линейного преобразования Т, определенного в банаховом пространстве X. В самом деле, преобразование Т ограничено, если условия хп —>0 и Тхп -+у гарантируют нам, что у — 0. Заметим, однако, что для того, чтобы мы могли пользоваться этим критерием, необходимо, чтобы областью определения Т было все пространство X. Например, дифференциальный оператор
строго определен на линейном многообразии С (0, 1). У него замкнутый график, но он не ограничен (см. упражнение 2).
Только что изложенные соображения могут быть использованы для доказательства следующей теоремы.
Теорема Б. Пусть Т — некоторое ограниченное линейное преобразование, отображающее банахово пространство X в банахово пространство У. Пусть, кроме того, Т взаимно однозначно и имеет замкнутую область значений. Тогда преобразование Т* отображает У* на X*.
Доказательство. Согласно предположениям и теореме об открытых отображениях преобразование Т ограничено снизу:
Ц7’ггЦ ajxj при всех я ЕЕ X, где а — некоторая положительная постоянная. Нам нужно показать, что если / s X* задано, то / принадлежит области значений преобразования Т*.
Но согласно приведенному неравенству отображение Тх -> (х) строго определено, ограничено и линейно. В самом деле, если Тх ~ Ту, то х = у (так как Т взаимно однозначно). Поэтому
/ (х) = / (у), и неравенство
доказывает ограниченность этого преобразования. Согласно теореме Хана — Банаха мы можем теперь расширить это преобразование на все пространство Y (с сохранением его линейности и ограниченности) и получить таким образом некоторый вектор Ф Е У*. Тогда для любого х е= X
(Тх, <р> = <р (Тх) = / (х) = (х, fy,
а это значит, что / принадлежит области значений Т*, а точнее говоря, что / = Т*ф.
Замечание 4. Справедливо и утверждение, обратное только что доказанному. Другими словами, если Z* отображает К* на X*, то Т является взаимно однозначным и имеет замкнутую область значений. Доказательство этого основывается на том, что
(а)	если область значений Т* всюду плотна, то Т взаимно однозначно:
(б)	если область значений Т* замкнута, то этим же свойством обладает и область значений Т.
Для того чтобы доказать утверждение (а), заметим, что при Тх = 0 для всех ф ЕЕ У* справедливо соотношение
О = <Гх, ф> = <х, Т*ф>.
А это значит, что х, рассматриваемое как некоторый линейный функционал, определенный на X*, обращается в нуль на всюду плотном подмножестве X*, и, следовательно, х = 0 (согласно следствию из теоремы Хана — Банаха).
Доказательство утверждения (б) можно найти на стр. 488 монографии [А.22] или в главе IX книги [А.77].
У п р аж пени я
1.	Обозначим через М оператор «умножения на х» в £2 (0, 1): (Mf) (х) = xf(x), few, 1).
Тогда М определен на банаховом пространстве и отображает его на нормированное пространство. Покажите, что отображение М не является открытым.
Указание. Предположим, что М (U) ZD a U при некотором а > 0, где U — единичный шар пространства Lz (0, 1), и покажем, что отсюда следует, что ах/ \\Мх || Е U, если только 0=/=х£Е U. Покажите, что это невозможно, так как отсюда следует, что область значений М совпадает со всем £2 (0, 1) в целом.
2.	Пусть X есть подмножество С (0, 1), состоящее из тех функций х, производные которых х' непрерывны. Тогда X есть линейное многообразие в С (0, 1), и мы можем определить преобразование Т на X, положив Тх == = х' для х Е X. Покажите, что график Т замкнут и в то же время преобразование Т не ограничено.
Указание. При доказательстве первой части заметьте, что если	—» О
И хп^у, ТО	t	1
(s)ds-»^i/(s)ds.
о	о
Для доказательства второго утверждения мы рекомендуем рассмотреть функции хп (t) = tn.
3.	Теорема о замкнутом графике выше была доказана с помощью следствия 1. Покажите, что с помощью теоремы о замкнутом графике можно доказать, что каждое взаимно однозначное и сюръективное ограниченное преобразование является обратимым.
В этом приложении мы попробуем обобщить оптимальную задачу, рассматриваемую в главе 4, где предполагалось, что цель управления £ е D и преобразование Т: В -+D фиксированы и известны. Во многих физических задачах, однако, такое предположение нереально, и цель приложения <8 как раз и заключается в том, чтобы найти несколько полезных возможностей ослабления этих условий, не нарушая при этом радикальным способом методов решения классической задачи.
Воспользовавшись обозначениями главы 4, сформулируем прежде всего центральную задачу этого раздела.
Задача 3. Обозначим через {Tt: t ЕЕ v} некоторое параметризованное семейство ограниченных линейных преобразований, определенных на В и принимающих значения в D. Требуется определить элементы и S В, £ Z) и / Е v, минимизирующие функционал J (u, t, £f) на заданном классе векторов (и, t, и удовлетворяющие дополнительным ограничениям:
(a)	h — Ttu = 0, / Е v;
(б)	||и||</с;
(в)	(I/, t) = 0, i = 1, 2,.. , 771, t €= V.
Разумный выбор функционала J (u, t, и ограничений {г^} позволяет, как легко видеть, сформулировать на базе задачи 3 широкий класс более мелких задач. В этом приложении мы займемся случаями, аналогичными известной задаче Больца (см. книгу [Б.13]). В этих примерах основной упор делается на применение понятия псевдообратного преобразования как орудия решения этих более общих задач.
Прежде чем двигаться дальше, напомним формулировку теоремы, решающей задачу минимизации с обычными ограничениями.
Теорема А. Обозначим через /(x^..., хп) целевую функцию, экстремум которой нужно найти *). Пусть заданы еще
♦) Точка х метрического пространства X называется точкой локального экстремума функционала /, если /(£)>/ (^) или / (7)	/ (х) во всех точках
х некоторой окрестности f £ X. Эту же точку мы называем точкой условного локального экстремума, если одно из этих условий выполняется на пересечении некоторой окрестности х и множества точек, удовлетворяющих указанным условиям.
г независимых ограничений типа
g} (хх,..., Хп) = о, / = 1,..., г< п.
Предположим, что функция	хп) по крайней мере дважды,
дифференцируема в некоторой точке X = (2Х,..., £п). Тогда, если точка X является локальным экстремумом / (х) при заданных ограничениях, то необходимо, чтобы существовали такие скаляры ...» ^п), чтобы функция г
J* = f(X}, . . . , хп) -j- 2	(^х» • • • »^n)
;=i
имела безусловный локальный экстремум в точке X. Если же, кроме того, для z = (zn..., zn) выполняется условие
п
Sart.(ыли<0), i,j=l 1 J х
а также условия
о. г х
то этого достаточно для того, чтобы гарантировать существование условного экстремума X в точке f.
Замечание 1. Если X является безусловным экстремумом функционала J* (х), то X должно удовлетворять п + г уравнениям
-^=0,	i = i,...,n,
g}(£) = 0,	/ = 1....г,
с п 4- г неизвестными (хъ..., Хп, Хх,..., Хг).
Замечание 2. Если обозначить через Н матрицу с элементами.
ha = /а I . i, 7 = 1»• • •, п, 3 dxidxj\x
а через Vxg — вектор (dpldx,..., dg/dxn), то достаточное условие имеет следующий вид:
[z, Hz] > 0
для всех z = (zx,..., zn), удовлетворяющих уравнению
г] = 0.
Доказательство теоремы А вместе с геометрической интерпретацией множителей Лагранжа можно найти в книге [Б. 13] (см. еще работу Као [Б.56]).
Задача За. Пусть В и D -— фиксированные банаховы пространства, v — некоторое подмножество множества вещественных чисел, a {Tt: t у} — параметризированное семейство ограниченных линейных преобразований, отображающих В в D. Требуется определить элементы и е В и t s v, минимизирующие функционал J (и, t) = g (£n 0 + IIM2 относительно заданного класса векторов (u, t) и удовлетворяющие при этом дополнительным ограничениям
(a)	h — Ttu = 0,
(б)	(ёь 0 = 0, i = 1, 2,..., т*).
Замечание 3. Если множество v состоит из единственной точки t = /0, а функции g, , фт тождественно равны нулю, то эта задача сводится к| задаче 1 главы 4.
Предположим теперь, что существуют оптимальные (^, £0), которые вместе с функцией й решают задачу За. Зафиксировав (fo 7), мы увидим, что J (gb 7, и) отличается от (иЦ2 лишь на постоянную величину. Но согласно условию (а) оптимальное й является решением уравнения
lt=Ttu, t=~t,
с минимальной нормой. А так как для каждого t S v функция Tt определяется обычным образом, то оптимальное управление можно отыскать, воспользовавшись формулой
й = Щ, t = t.
Подставляя это выражение в условие задачи За, мы сведем ее к задаче минимизации функционала
J (&, О = g (&, 0 +1 ЛЪIIя, (0 Ь) е v xD,
с одновременным выполнением условий
(£ь 0=0» * = !»•••> т < dim (D).
Если D = Вп, то эта последняя задача имеет вид обычной задачи на отыскание условных экстремумов, и для ее решения можно воспользоваться теоремой А.
Пример. Управление гибридной системой, схема которой изображена на рис. 2.16 § 2.5, может служить хорошим примером задачи За. Пусть г0 = ($0, £0)игх = ($/» 0) обозначают фиксированные векторы в v = o’ X т, и пусть z (г/) = (у (sy), х (tf)) есть некоторый элемент Rn. В терминах формулировки задачи За
*) Если dim D < оо, то предполагается, что т < dimD.
рассмотрим два ограничения:
(z (г0)) = z (го) = О,
^2 (z (Г/)) = [z (Г/), Z (гу)1 — 1=0,
которым нужно удовлетворить одновременно с ограничением Z (Г/) = И (и. *>)] (rf) = Tf (и, V),
попутно минимизируя функционал
J[(u, 1>)1 =||Z/-z||a+2[“(**). “(Sfc)l + J ly(s), y(s)]<fc =
= ||Z/ - + !(«*» y)lla- (!)
Для того чтобы решить эту задачу, запишем преобразование Tf в его каноническом полярном виде (предположив для удобства, что щ =^= 0): п
Tf =	(2)
1=1
Тогда псевдообратное преобразование для Tf имеет вид
п
?! — Hi1
1=1
а отсюда сразу следует, что
||(й, i>)||a = ||r;z(r/)la = [z/, E^Ezf],
где матрица Л = diag [цх,..., pnL & Е — матрица, i-й строкой которой служит вектор i = 1,..., п. Таким образом, задача этого примера сведена к задаче минимизации функционала
J = \\zf-42 + [Zb E*A~*Ezj]
при условии, что
[Z/, Zf] - 1 = 0.	(3)
Решая эту последнюю задачу так, как это предписывает теорема А, мы построим функционал
= Ь/ - *11а + [zh E^Ezf] + Ml 2/1-1},	(4)
а приравнивая нулю градиент J* по Zy, получим
V2/* = 2zf - 2z +- 2E*X~2Ezt + 2Xz, = 0	(5)
ИЛИ
[(1 + X) I + Е*Лг2Е] zf = z,	(G)
где X выбирается так, чтобы удовлетворить условию (3). Положим Ezf = Р и Ёъ = у. Тогда уравнение (6) сведется к следующему:
[(1 + X) Z + А"2] р = у.	(7)
Но так как матрица (1 X) I + А“а diag [(1 + X + ...,(14 ХЦ Цп2)], то ее особые точки легко найти. Кроме того, поскольку Е* — Е~х (напомним, что множество {Ci}? ортонормаль-но), мы получим, что
1 - [zy, zj - [Е^р, Е_10] = IP, р],	(8)
и, таким образом, поставленная задача сведена к исследованию относительно простых соотношений (7) и (8).
Замечание 4. Если из функционала J [(u, v)l [см. уравнение (1)] выкинуть член ||zy — z|2, то уравнение (7) примет вид
Д-ар = _ хр,	(9)
a J [(и, г)] сведется к функционалу J [(u, v)] = [р, А-2 р], так что искомое Р является единичным собственным вектором матрицы А“2, соответствующим наименьшему собственному числу этой матрицы. Поэтому искомое решение имеет вид и = (1/pJ/j, где fj — любой из функционалов в представлении Ту, соответствующий наибольшему элементу {щ}Г.
Замечание 5. Задача, рассматривавшаяся в этом примере, типична для целого класса задач, к решению которых можно подходить по-разному. Для того чтобы убедиться в том, что ее можно рассматривать как один из вариантов задачи 2а из § 4.4, отождествим Hi с Еп. Для упрощения обозначений положим к = (u,. v). Кроме того, обозначим через Tf преобразование F, а через Н (Tf) будем обозначать график этого преобразования. Воспользовавшись тем, что Zf = Tfk, установим, что функционал
J [(и, г)] = J (к) из уравнения (1) можно переписать в виде J (к) = || Tfk - z |« + В fell2 = И (fe, Т,к) - (к, Tfk) ||а + II (к, к, z, Z) ||2, где через (к, Tfk) обозначена ортогональная проекция элемента k0, z) на линейное подпространство Н (Tf).
Преобразование G: Н (Тf) -> Еп, задаваемое соотношением
G (к, Tfk) = Tfk. к е Я1, позволяет переформулировать задачу из рассмотренного примера как задачу отыскания элемента
<о = (к, Tfk) f= Н (Tf), минимизирующего функционал
11“ - “II2 при условии, что
|’G.o||2 - 1.
В практических ситуациях, где ресурсы энергии, расходуемой на управление, ограничены, вполне может оказаться, что решение любой из задач минимизации расхода энергии потребует управления, энергия которого превышает максимальные возможности имеющихся физических источников. Предвидя такую возможность, очень важно решить, как же оптимальным образом расходовать имеющиеся ресурсы энергии для достижения поставленной задачи управления. Здесь сразу в глаза бросаются несколько возможностей. Мы можем допустить произвольное время попадания или произвольные конечные условия или то и другое вместе, добиваясь лишь минимизации «слабого» критерия качества типа
J(u) = н-М2 + Н12-
В нашей следующей задаче предполагается, что время попадания и конечное состояние системы фиксированы, а требуется лишь наилучшим образом распорядиться имеющимся ограниченным запасом энергии.
Задача 36. Обозначим через у некоторый заданный элемент пространства D, а через Т: В -+D — обычное ограниченное линейное преобразование. Требуется найти такой элемент и ЕЕ В, который минимизирует функционал
J (и)	7и||,	(10))
удовлетворяя при этом ограничению
||и|| < Л.
Нетрудно показать, что множество
К= {у - Ти:
замкнуто и выпукло. Поэтому (с учетом того, что пространство I) строго выпукло и рефлексивно) в нем имеется единственный э и мент с минимальной нормой. Другими словами, существует такое-
и ЕЕ В. норма которого не превосходит к. Оно и минимизирует J (и), и, значит, задача 36 всегда имеет решение. Из определения Т+ следует, что О Е К в том и только в том случае, когда || Т+ 11^к. Следовательно, вектор £ решает задачу 36 в том и только в том случае, когда || Г+£|| к.
Если (I Г+£ [ = к, то любое и ЕЕ В с нормой, не превышающей А, удовлетворяющее условию
О = £ — Ти,
должно совпадать с Г+£, и в этом случае задача 36 имеет единственное решение. Если же (| Т+£|| < к. то для любого г, принадлежащего ядру преобразования Т и имеющего норму не большую, чем А: — || Г+£||, вектор
*>+ ГЧ
является решением задачи 36.
Рассмотрим теперь более подробно случай | Г+£ [ > к. Для удобства предположим, что В = Я, где Н — некоторое гильбертово пространство, a D = Е11. Обозначим через кС множество векторов вида кх. где х £ С. Тогда очевидно что
кС = {х: х = Ти, ЦиЦ к}.
Нам удобно будет воспользоваться каноническим представлением .преобразования Т;
п
т= S*i>F4</i-
1=1
Из примера, рассмотренного в § 3.4, ясно, чтомножество кС можно представить в виде
кС = |х: х =	S a?C&2}.	(11)
i=i	i=i
Кроме того, определим скаляры Plt..., рп так, чтобы
п
1=1
Ортонормальность множества {е<}1 гарантирует тогда справедливость равенств
- Ти? = | (Pi - HiOti) |2 = i(₽i - НЛ)2,
и значит, нам удалось свести задачу, сформулированную в гильбертовом пространстве, к обычной задаче на условный минимум. Задача. Среди векторов
а = col («и..., а„), удовлетворяющих условию
]а, а] к2, найти элемент, минимизирующий функционал
10 — Ла, 0 — Ла],
где Л = diag [щ,..., pj, a 0 = col (0t. 0n).
Поскольку 5 £ kC9 то нам нужно рассматривать лишь те векторы I, которые удовлетворяют условию [а, а] = к2. С помощью единственного множителя Лагранжа X мы можем получить следующее необходимое уёловие для оптимального решения этой задачи: функционал
J (а) = [р — Да, Р — Да] + А’1 ([а, а] — 1)
должен достигать в точке а своего минимума. Но так как все встречающиеся здесь величины вещественны, а матрица А самосопряженная, то градиент функционала (а) вычисляется по формуле
VaJ* (а) = 2 {- Ар + (X/ + А2) а}.
Наша задача сводится таким образом к отысканию таких скаляров an, X, что
a = [X/ + AV1 р,	(12)
[а, а] = к.
Матрица [XZ + А2] диагональна и потому легко обратима. В самом деле, сразу ясно, что
[XZ + А2]'1 = diag I..., (X +	(13)
Поэтому при фиксированном Р
|а’а1(Х)=2(гтЬУ-
i—l \ А» -f- Pj J
Если
[ а, а 1 (0)< Л, то
Если же то	[а, а] (0) = к,
||Т^| = к.
Поэтому для нас представляет интерес единственный случай [а, а] (0) > к.
Поскольку функция [а, а] (Z) монотонно убывает вместе с Z и [а, а] (X) -> 0 при X -> оо,
то ясно, что X, решающее уравнение (13), всегда существует, а значит, всегда существует и решение задачи 36.
В качестве последнего варианта задачи 3 упомянем класс задач на максимальное быстродействие.
Задача Зв. Обозначим через {Tt\ t ЕЕ v} обычное семейство ограниченных линейных преобразований, определенных на В и принимающих значения в D. Требуется найти и ЕЕ В, минимизирующее функционал
J (0 = t.
среди множества элементов, удовлетворяющих ограничениям
(a)	I (t) - Т tu = 0,
(б)
Предположим сначала, что цель управления зафиксирована во времени (т. е. £ (/) = £) и что зависимость Tt от t имеет следующий характер. В пространстве В, образованном функциями, определенными на v, обозначим через Bt замкнутое линейное подпространство, удовлетворяющее соотношению
Bt = {х ее В: х ($) = 0, $ > f}.
Обозначим через Pt оператор проектирования В на Bt (Pt можно вычислять с помощью умножения на характеристическую функцию промежутка [£0, fj, где tQ есть наименьший элемент v). Теперь мы можем предположить, что семейство {TJ имеет следующий вид:
Ttu = TPtu, и ЕЕ В.	(15)
При этих условиях множество Cf, определенное равенством ct = TtU>
расширяется с увеличением t (см. упражнение 1), т. е. Ctl cz Ct2, если только < t2.
Предположим теперь, что при каждом t > t0 > tQ преобразование ft сюръективно. Функционал ||Т7£||, очевидно, монотонно
убывает с увеличением t. Задача Зв, как легко видеть, эквивалентна отысканию наименьшего t Ev такого, что = к. Пусть этот наименьший элемент множества v равен Между двумя задачами нахождения элемента и Е= 771 (£), который
(а)	минимизирует и удовлетворяет ограничению t = tu
(б)	минимизирует t и удовлетворяет ограничению ||н|| = к, существует естественное соотношение двойственности. А именно вектор (или множество векторов) ьь = Т\ £ определяет решение обеих задач сразу.
Если мы попытаемся ослабить ограничения, наложенные на постановку задачи Зв, то нам придется рассматривать много частных случаев. Отметим прежде всего, что совсем не обязательно, чтобы существовало такое / Е V, что £ е Ct. В упражнении 2, например, мы столкнемся с ситуацией, когда Ct при любых t е v остается внутри некоторого фиксированного ограниченного множества. Более того, в упражнении 3 мы увидим, что если Tt не имеет характера, описываемого уравнением (15), то множество Сг может даже сжиматься с увеличением Наконец, если наша цель £ меняется со временем, то может оказаться, что функция ||	(t) |
обладает очень странными свойствами (см. по этому поводу упражнение 5).
Упражнения
1.	Обозначим через В банахово пространство функций, определенных на промежутке [0, //]. Покажите, что Bt = {х Е В: х (s) = 0, s > tj представляет собой замкнутое линейное подпространство В. Покажите, что Ut — единичный шар в Bt — с увеличением t расширяется. Если Г: В — D, то покажите, что Ct = Т (Ut) также расширяется с увеличением t. Приведите пример, в котором Ct} = С1з, хотя < fc.
2.	Рассмотрим скалярную динамическую линейную систему, описывающуюся уравнением
t
х (t) = е~* х (0) + е-/+8 и (s) ds. о
Пусть вынужденная реакция такой системы определяет отображение £^(0, t) на R. Покажите, что множество С/ монотонно расширяется с ростом f, но никогда не выходит из промежутка [—1, 1].
3.	Рассмотрим скалярную динамическую систему, описывающуюся уравнением
ti
х (ti) = Ttiu = ехр [X (ti — .$)] и (s) ds, X < 0. о
Пусть
Н = Lz (m; 0, t), где m — весовая функция и m (t) = ехр [20/J, t Е [0, fj. Рассматривая 18*
Ttt как линейное преобразование, отображающее Н в покажите, что норма || Тц || монотонно убывает с увеличением fa при Р > 0 и монотонно возрастает при Р 0. Покажите также, что норма преобразования
G
х (t\) = Т\х = е'Хв и (s) ds о
пут любых р является неубывающей.
4.	Предположим, что Т( фиксировано, а пространства В и D из задачи Зв являются гильбертовыми и что множества Ct = TUf, t v, представляют собой эллипсы. Мерой расширения Ct с увеличением t от fa до fa может служить величина изменения собственных чисел Т/Тр Покажите, что если через !<(/) обозначено z-e собственное число этой матрицы, то уравнение
X. (fa) - X. (fa) + [е., Т (Pt. - Pt) Т%], I «= 1, .. . п,
с точностью до членов первого порядка малостп описывает изменение Xj с t. Через Pt здесь обозначен оператор ортогонального проектирования Н на Я/.
Указание. Воспользуйтесь результатом упражнения 3 к § 3.4.
5.	Положите для системы из упражнения 2 х (0) = 0 и возьмите в качестве В пространство L^/O, t). Определите функцию 5 (fa) «= х (fa), для которой | (fa) || монотонно убывает, монотонно возрастает или колеблется относительно некоторой заданной кривой.
ПРИЛОЖЕНИЕ 9
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПОСТОЯННЫМИ
В большинстве рассмотренных выше примеров изучался класс систем с сосредоточенными параметрами, поведение которых описывается совокупностью обыкновенных дифференциальных и (или) конечноразностных уравнений. Однако на самом деле все физические системы по своей природе распределены в пространстве. Поэтому естественно ожидать, что более тщательное изучение физических законов, определяющих поведение таких систем, приведет к построению математических моделей, опирающихся на дифференциальные (конечноразностные) уравнения в частных производных (разностях). Более того, в таких разнообразных физических объектах управления, как дистилляционная колонна, химический или ядерный реактор, сложная система кондиционирования воздуха и непрерывная печь, в системах с сжимаемыми или упругими исполнительными органами, пространственное распределение энергии препятствует описанию их с помощью моделей с сосредоточенными параметрами. В связи со всем этим не удивительно, что задачи, относящиеся к системам с распределенными параметрами, занимают все более значительное место в литературе.
Конечно, на этих нескольких страницах невозможно осветить все вопросы теории таких систем. Поэтому, учитывая селективный характер нашего изложения, мы заранее договоримся не затрагивать ни уравнений в частных разностях, ни нелинейных моделей. При этом мы увидим, что теория систем с распределенными параметрами хорошо укладывается в рамки той же аксиоматической теории, которая использовалась на протяжении всей книги для изучения систем с сосредоточенными параметрами. Но, конечно, не обходится и без некоторых различий, в основном в используемых функциональных пространствах. Однако по мере дальнейшего изложения мы увидим, что задачи теории систем с распределенными параметрами — это всего лишь задачи, решаемые на бесконечномерных функциональных пространствах, неоднократно Уже рассматривавшихся ранее.
Математическая модель. Математические модели больших распределенных систем могут быть довольно разнообразными. Однако в большинстве конкретных приложений встречаются некоторые общие черты, и перед тем, как перейти к детальному изложению
методов исследования, нам кажется полезным познакомиться с некоторыми из этих факторов, а также с основными обозначениями, используемыми далее.
Независимые переменные для системы с распределенными параметрами обычно включают время t и конечномерный вектор пространственных переменных (ах, ...» ап). Диапазон изменения времени мы будем обозначать через т, а через й обозначим подмножество Rn (или Сп), для которого пространственные переменные имеют смысл. Иногда й зависит от и в этом случае мы будем обозначать эту область через й/, t СЕ т. Множество
А = {(/, а): а = (ах, . . ., ап) е Qf, /G т} описывает интересующий нас диапазон изменения независимых переменных.
Зависимые переменные образуют некоторое конечное множество {тр i = l, . . ., т} скалярных функций, определенных на множестве Д. Эти переменные должны удовлетворять определенной системе дифференциальных уравнений в частных производных внутри множества Д и некоторым граничным условиям — на границе дД. Уравнения в частных производных и граничные условия определяются динамикой рассматриваемой системы. Внешние воздействия для такой системы могут быть распределены на й и (или) вдоль границы этой области. Мы будем называть систему с распределенными параметрами строго определенной, если знания внешних воздействий, граничных условий, соответствующих начальных условий и самих уравнений в частных производных оказывается достаточным для того, чтобы однозначно определить поведение системы.
В качестве иллюстрации рассмотрим линейное уравнение второго порядка с одной независимой пространственной переменной а и одной зависимой переменной х\
4* 2a122ja + a22^a 4“ ЯХо;Г/ 4~	4“ а00% = /»	(0
в котором мы не показываем явно зависимость функций {aty, /, х} от вектора (/, а), а нижние индексы указывают на дифференцирование по соответствующей переменной, например:
д2х (t, a) .	__ л
,	(t, a) G A.
UCL Ot ’	\ >	/
Кроме внешнего воздействия /, фигурирующего в (1), на систему могут действовать и граничные внешние воздействия. Например, если й = [а, Ы, то типичное граничное воздействие на систему имеет следующий вид:
х (t, а) =	(t), x(t, b) = h2(t),	(2)
Наконец, если т =	</1, то типичные начальные условия сис-
темы имеют вид
X (t0, а) = Х° (а), xt(t0, а) =.г*(а), аей. (3)
Во избежание путаницы сделаем несколько дополнительных замечаний относительно граничных и начальных условий. Уравнения (2) нужно всегда понимать в смысле сокращенной записи более строгих условий
lim х(/, а) = Л1 (0, Iim х(/» а) = /га (0»	1 е т-
а-*а+	а—*Ь_
Точно так же уравнения (3) должны заменять более строгие условия
limх (t, а) = я0 (а), lim.(t, а) ^^(а), аЕ й. о	о
Другими словами, граничные и начальные условия следует понимать в смысле пределов х при стремлении к соответствующей точке изнутри А.
Нам нужно установить некоторые основные требования, предъявляемые к гладкости различных встречающихся функций. В соответствии с видом уравнения (1) ясно, что решение х, если оно существует, должно иметь производную первого порядка по t и производную первого и второго порядка по а. Более того, эти функции после умножения на соответствующие коэффициенты должны сочетаться с элементами функционального пространства, выбранного для внешних возмущений /. Аналогичные условия накладываются и на функции х\ hv и h2. В частности, эти функции должны быть непрерывными и взаимно согласующимися, т. е. для того, чтобы функция х была непрерывной, необходимо, чтобы
xQ (а) = hx (0), xQ (b) = h2 (0).
Хотя уравнение (1) выглядит довольно просто, оказывается, что с его помощью, как это ни странно, удается описать многие чрезвычайно важные в практическом смысле системы. Читатель, возможно, уже угадал в нем такие уравнения, как уравнение колебаний струны (xti = Л:аа + /), уравнение теплопроводности
= а2хаа 4- /), телеграфное уравнение (хаа — a2xtt = 0) и уравнение Лапласа в различных его формах. Эти и многие другие классические примеры математических моделей физических систем, подпадающих под общую схему уравнения (1), с большой глубиной исследовались в целом ряде отличных монографий (см., например, [А.271, [А.291, [А.601 или [А.901). Несколько
в другом направлении развивались работы других авторов (такие, как [Б.24]. [Б.110], [Б.117] и [Б.118]), в которых рассматри-
ваются задачи управления, постановка которых мотивируется следующими двумя примерами.
Пример 1. Рассмотрим методическую печь, схематически показанную на рис. П9.1 *). В эту печь непрерывно подается со скоростью v полоса одно-
родного материала, причем для Рис. П9.1. Методическая печь. этого используется транспортное устройство с переменной скоростью. Температуры зон I п // печи обозначаются через Д (£, а) f и Д (Д а) соответственно. Пространственный диапазон изменения переменных (а, 0) имеет следующий вид:
Q ={(а, 0): аеЮ, 1], 0 (= [0, h]}.
Температуры Д, Д и скорость подачи полосы v являются регулируемыми переменными.
Рассмотрим сначала ситуацию, в которой полоса тонка, а распределение температур в печи пространственно однородно в обеих ее зонах (т. е. Д = Д = /). Температуру нагрева х (t, а) подаваемого материала можно приближенно описать с помощью уравнения
xt (t, а) = [Lxaa (f, а) + v (/) ха (t, а) + а [я (Z, а) — / (t, а)], (4)
где р, — коэффициент теплопроводности, а а — некоторая постоянная, пропорциональная теплопроводности поверхности материала. Если же подаваемая полоса достаточно толста, а Д и Д не зависят от а, то уравнение, описывающее внутреннее распределение температуры в полосе в направлении 0, имеет вид
Xt (t, р) = ЦХрр (t, р)
с граничными условиями х (t, 0) = Д (t) и х (t, h) = Д (t). И в том и в другом случаях, для того чтобы полностью поставить задачу, необходимо определить начальные условия работы системы.
Пример 2. Во многих космических аппаратах с аэродинамическим управлением движения при возвращении в атмосферу необходимо использовать абляционную теплозащиту, позволяющую
*) Рисунки 119.1 и П9.2 заимствованы с разрешения автора из главы «Управление системами с распределенными, параметрами» книги П. К. Ч. Уонга «Advances in Control Systems», vol. 1, Academic Press, N. Y., 1964.
| Изоляция
| Абляционный / материал (
предохранить аппарат от разрушающих воздействий аэродинамического разогревания. При этом нужно обеспечить такую точность управления скоростью и ориентацией аппарата, которая гарантировала бы нам, что скорость нагревания абляции ни на одном участке фазы входа в атмосферу не превышает предельно допустимого значения.
На рис. П9.2 схематически представлен одномерный вариант задачи абляционной защиты. Одна поверхность (а 0) абляционного сляба изолирована, а другая (а = 0) подвергается нормированному тепловому воздействию /. Обозначим через х (t, а) температуру сляба в первый момент входа в атмосферу, а через tL — момент времени, в который х (f,0) достигает температуры плавления х^. Изменение температуры сляба в период, предшествующий на
I
I II I II '| I I I I I f(t)
Рис. П9.2. Абляционный сляб.
чалу плавления, описывается тогда уравнением теплопроводности
xt (Л а) = р.т0 а (/, а), х (/0, а) = xQ (а)
с граничными условиями
з’И*, 0) = у/(0,	ха(/, t) = 0,
В момент tx поверхность сляба начинает плавиться, и мы будем предполагать, что расплавившийся материал немедленно уносится аэродинамическими силами. Обозначим через q (t) глубину эрозии, вызванной этим процессом, в момент времени t tlt Тогда температура оставшегося теплозащитного слоя по-прежнему подчиняется уравнению теплопроводности, но с другими начальными:
q (^) = 0, х (G, а) = х (^, а), и граничными условиями:
*(*, П (0) = pZllf (0 —	(*, п (0) = / (0.
хЛ (/, I) = 0, где к, р и L — соответственно теплопроводность, плотность и теплота плавления материала слоя.
Метод разделения переменных. Очень часто с помощью метода разделения переменных дифференциальное уравнение в частных производных удается свести к эквивалентной системе обыкновенных дифференциальных уравнений. Поэтому, прежде чем переходить к решению примеров, нам кажется полезным ознакомиться с этим методом в его общих чертах.
Сделаем это на примере уравнения (1), в котором / = 0. Предположим, что это уравнение (вместе с заданными для него граничными и начальными условиями) имеет решение х следующего вида:
х (t, а) = А (а) Т (/),	(*, а) е Д,
где А и Т — скалярные функции одной переменной. Подставляя это выражение в уравнение (1) и разделив его на х (t, а), мы получим новое уравнение:
flll (у-) + 2/712 ф)	+ <*10 (у J + Л01 (д-J + Лоо = 0, (5)
где, например,
Т' _ rp—idT А _____
У ~ 1 dt ’ ~А ~ Л ~dz •
Это уравнение справедливо в области (f, a) Д. Но если аи и а10 не зависят от а, а22 и я01 не зависят от С а12 = 0 и а00 (/, а) = = Лоо (0 + Лоо (а), то уравнение (5) можно переписать в виде
Т" Т'	(А А \
ап у- + Дю у + flJo = — у + aoi у + аоо) ‘
Левая часть этого уравнения не зависит от Z, а правая часть — от а. Поэтому обе части должны быть постоянными, и при некотором скалярном X уравнение (5) оказывается эквивалентным системе двух обыкновенных дифференциальных уравнений
вцТ* Н” <^Т’ + ciwT = XT,	t Е. т,	(6)
л-22 ^ Ч- л01^4 + QoqA = — ХЛ, а Е	(7)
Если мы хотим, чтобы функция х удовлетворяла другим дополнительным условиям, то необходимо ввести соответствующие ограничения, накладываемые на Т и А, Без существенной потери общности (см. упражнение 1) предположим, что в уравнении (2) fx = /2 = 0. Эквивалентные граничные условия для А имеют вид
А (а) - А (Ь) = 0.
(8)
Для того чтобы решить теперь исходную задачу, необходимо найти значения {Хп}, при которых уравнение (7) с граничным условием (8) имеет решение {Лп}, а уравнение (6) — соответствующее решение {Тп}. После этого остается построить линейную комбинацию ^СпАпТп полученных решений, которая удовлетворяет уравнению (1) и должна удовлетворять заданным начальным условиям системы.
К этой задаче мы еще вскоре вернемся. Пока же отметим, что условия, наложенные па коэффициенты {«^}, можно ослабить следующим (довольно очевидным) способом. Если выполняются условия:
(1)	существует такое преобразование переменных 0 = 0 (/, а) и у = у (/, а), якобиан которого не обращается в нуль ♦) на Д и для которого
(2)	получающееся дифференциальное уравнение в частных производных имеет вид
^11^33 + ^22rYY 4-	+ ftoi^Y +
(3)	функции Ьп и fe10 не зависят от у, функции Ь22 и 601 не зависят от 0, а (0, у) = bjo (0) + &оо (?) на Д, то существуют два обыкновенных дифференциальных уравнения второго порядка, каждое из которых содержит некоторый параметр и которые в совокупности эквивалентны уравнению (1).
Что касается условий (1) и (2), то можно показать (см., например, стр. 45 работы [Б.96]), что если коэффициенты {«0} имеют непрерывные производные второго порядка, то уравнение (1) всегда можно привести к одной из следующих канонических форм:
(1)	при «12 — апа22 0 — к гиперболической форме:
.т33 — х„ +	+ b01.rY 4- Ъ^х = 0;
(2)	при «12 — ^ия22 — 0 — к параболической форме:
^33 + ^ю^З + ^oi^y 4“ Ь^х = 0;
(3)	наконец, при «12 — а1Ха22 < 0 — к эллиптической форме:
*зз 4- rYY 4- 610z3 4- 601ty 4- Ь^х = 0.
В том случае, когда {«0} зависят от (t, <х), уравнение (1) может иметь разный вид в разных областях множества Д в зависимости от значения «i2 — ап«22 в этой области. С другой стороны, если уравнение в частных производных второго порядка
*) Это условие гарантирует обратимость такого преобразования. • Портер
имеет более двух независимых переменных, то можно привести примеры уравнений, которые не удается привести к подобным каноническим формам даже в сколь угодно малой области. Однако уравнение второго порядка самого общего вида, но с постоянными коэффициентами можно привести к каноническому виду, независимо от числа его независимых переменных (см., например, стр. 7 книги [А.90]).
Все это совсем не гарантирует выполнения условия (3). Более того, приведение к канонической форме совсем не обязательно должно быть полезным для отыскания подходящего преобразования переменных. Поэтому метод разделения переменных с практической точки зрения помогает лишь в тех случаях, когда рассматриваемое уравнение случайно (а это бывает с удивительной регулярностью) имеет подходящий вид.
Задача Штурма — Л иу вилл я. Основное различие между обыкновенными дифференциальными уравнениями и уравнениями в частных производных заключается в краевой задаче, сформулированной в уравнениях (7) и (8). Так как эта задача возникает в связи с разделением переменных, а ее граничные условия порождаются граничными условиями исходного дифференциального уравнения в частных производных, то она может принимать различный вид. Для того чтобы ознакомиться с этими важными вопросами, достаточно (см. упражнение 2) рассмотреть дифференциальный оператор второго порядка
(£г)(«) = ^[р(«)^]-9 («)«(«).	-
в котором р и q — вещественные непрерывные функции, определенные на [a, fel, и р ($)	0. Краевая задача типа Штурма —
Лиувилля состоит в отыскании нетривиальных решений уравнения
(Lz) (s) Хр ($) z (s), s е [я,	(9)
удовлетворяющих граничным условиям
Ui (z) = aLz (а) + a2z (а)	a3z (b) a4z (b) = 0,
u2 (z) = ₽xz (a) + p2z (a) + 03z (0 + p4z (b) = 0,	(W)
очевидно, включающим и более простое условие z (а) = z (b) = 0. Рассматривая эту задачу как задачу о собственных числах оператора L, мы сразу поймем, что такие решения не обязательно должны существовать для каждого X.
Можно показать (см. [Б.28], § 6.3 [А.44], § 9.1 [А.84] и [Б.122]), что если граничные условия удовлетворяют требованиям согласованности, то решение задачи Штурма — Лиувилля существует и, более того, эту задачу можно свести к задаче с интегральным оператором. Другими словами, в этом случае существует
некоторая функция Грина G (t, s) такая, что если
ь
z(t) = ^G(t, s)p(s)z(s)ds, tela, ft],	(11)
a
to z удовлетворяет также и уравнениям (9) и (10). В упомянутых выше работах (см. также упражнения 4 и 5) детально исследуются свойства функции Грина и методы ее построения. Для нас же здесь важно только то, что G (t, s) — G (s, t), s, t €E la, Ы, и что функция G равномерно непрерывна по обеим ее переменным. Поэтому линейный оператор у —> z из уравнения (11) самосопряжен и компактен в пространстве L2 (а, Ь) (см. пример 2 из приложения 5).
Эти два последних замечания позволяют сделать очень важные выводы:
(1)	Существует счетное множество собственных чисел {XJ с единственной предельной точкой в нуле. Множество { (	| }
имеет максимум.
(2)	Из собственных функций оператора у -> z можно построить полный ортонормальный базис {ej пространства L2 (а, Ь). (В нынешних условиях х | у => 0 = ^ах (s) у (s) р (s) ds.)
Кроме того, нетрудно показать, что
(3)	если q ($) > 0, sE [а, &], то Кп > 0, и
(4)	если / имеет непрерывные производные второго порядка и удовлетворяет условию /(а) = / (Ь) = 0, то ряд
оо
/(•>)= S/n«n(s),	/„ = </,₽„>
П=1
равномерно и абсолютно сходится.
В приложении 2 мы рассматривали полные ортонормирован-ные множества в гильбертовых пространствах. Теперь мы просим читателя обратить особое внимание на пример 2 из этого приложения. Сравнение с уравнением (9) ясно показывает, что полиномы Эрмита, функции Лагерра и полиномы Лежандра получаются в результате решения той или иной задачи Штурма — Лиувилля. Например, если
9 (5) = 0» р (s) = ехр {—$2},	р ($) = ехр { $2}
и й == — оо, 6 — оо, то
= 2п, п = 1, 2, . . .,
И ЯВЛЯЮТСЯ ноРмиРованными полиномами Эрмита.
Построение решения. Предположим, что нам удалось найти со ственные числа {Ап} и ортонормальные собственные векторы
{Лп} для уравнения (7) с граничными условиями (8). Используя эти значения {Хп}, мы можем тогда построить для уравнения (6) множество решений {Гп}, каждое из которых (так как это уравнение второго порядка) содержит два неопределенных параметра. Каждая из функций xn (t, а) = Тп (t) Ап (а), п = 1, 2, . . , удовлетворяет уравнению (1) и заданным граничным условиям. То же самое справедливо и относительно функции
оо
*(*,«) = 2 Tn(t)An(a)	(12)
П=1
при условии, что этот ряд сходится и что его можно дважды дифференцировать почленно по Z и а.
Для того чтобы определить теперь искомое решение однородного уравнения, неопределенные параметры в правой части уравнения (12) нужно выбрать так, чтобы решение удовлетворяло начальным условиям
00
3 Go) (а) = (а)>	&],	(13)
П=1
оо
*Go,*) =	<хе[О1.	(14)
п=1
Если х° и я1 (=£2(0, 6), то полнота ортонормального базиса {Лп} гарантирует возможность представления этих функций в виде следующих рядов:
00
*° («) = ^СпАп (а), Сп = <х°, А„>,	(15)
00
X1 (а) = ^СрАп (а), сп = <х1, Лп>.	(16)
П=1
Приравнивая друг другу соответствующие ряды, мы можем теперь определить и все неопределенные параметры решения (12).
Однако пока что мы полностью обошли молчанием один очень важный вопрос, а именно вопрос о сходимости ряда в уравнении (12) и его почленной дифференцируемости. А здесь могут возникнуть затруднения, связанные, например, с тем, что ряды (13) и (14) должны сходиться в La, а функция из уравнения (12) должна иметь производные второго порядка по обеим переменным. Однако можно показать (см., папример, § 9.7 [А.84]), что если решение х существует, непрерывно на А и удовлетворяет граничным и начальным условиям, то х можно представить в виде ряда (12)-
Другими словами, каждый раз, когда физические соображения позволяют установить существование решения, мы можем получить правильный результат с помощью формальных манипуляций с рядами, хотя с математической точки зрения наши действия и могут казаться недостаточно оправданными.
После того как мы научились находить решения однородной задачи, мы можем прибегнуть к очевидному формальному методу отыскания решения неоднородного уравнения. Если неоднородная часть уравнения / определена (измерима) на Д и
ъ tf
$ $ I f (*> а) |2^ doc < оо,
a t9
то на этом множестве ее можно представить (см. пример 3 к приложению 2) в виде следующего ряда:
оо
f(t, а) = 3“n(zMn(a),	(0 = </(<>• )Мп>, п = 0,1,... (17)
71=2
Повторяя заново все этапы процесса разделения переменных, мы выясним, что скаляры {Хп} и ортонормальный базис {Лп} определяются теперь так же, как и раньше. Функции {Гп} должны удовлетворять уравнениям
(0 Гп (t) + д10 Т'п (0 + (<& (f) - Xn) Тп (t) = ип (t), t f= [«о, «/], n = 1, 2, . .
с начальными условиями {Tn (Zo), Tn (£<>)}, определенными, как и раньше, в результате сравнения рядов (13) и (14) с рядами (15) и (16). И снова можно показать, что каждый раз, когда у исходной задачи имеется строго определенное решение, описанный формальный метод приводит к правильным результатам.
Полученным результатам полезно придать следующий вид. Обозначим через А бесконечную матрицу, у которой ненулевыми являются лишь элементы блочных матриц размером (2x2), расположенных вдоль главной диагонали. Эти блочные матрицы имеют следующий вид *):
Г/|1 Г 0	1	1
Minn —	/ 1 а ч	z ч , п = 1,2,..., t е [*0, ^/1 •
L —(aJo(O—^п)	- «io(*)J
) Поскольку случай, когда ап из уравнения (18) обращается в нуль, нужно исследовать отдельно, мы без потери общности полагаем теперь, что «и e 1*
Обозначим, далее, через и бесконечномерный вектор и = (0, и1? 0, и2, . . ., 0, ип, 0, . . .).
Тогда всю систему уравнений (18) можно описать единственным векторным уравнением вида
z (t) = А (Г) z (t) + и (0, z (tQ) = z°, t k0, tf], (19) причем
Z2n~l ко) ~ ко), Z2n ко) ~ ко), П ~ 1, 2, ...
Обозначим через Ф бесконечную матрицу, удовлетворяющую уравнению
Ф (t, to) = A (t) Ф к, to), Ф ко, to) = I.
Тогда решение уравнения (19) с формальной точки зрения можно представить в виде t
z (0 = ф к,^о) z ко) +$фк, s)u(s)ds, t^[to, tf]. (20)
Наконец, обозначив через о бесконечный вектор следующего вида: о (а) = {Л, (а), 0, Л2(а), 0, О, Лп(а), 0, ...},	(21)
мы сможем записать решение х неоднородного уравнения в виде
х (t, а) = [со (а), Z (£)] = S ®П (а) zn (0.	®) <= А •
П=1
Пример 3. Для того чтобы проиллюстрировать все эти вопросы на конкретном примере, рассмотрим подробно уравнение диффузии с дополнительными условиями
(a)	xt (t, а) = й2яаа к, а) + / (t, а), t > tQ, a €= (а, Ь),
(б)	х (t, 0) = х (t, Ь) = 0, t > to,	(22)
(в)	х (0, а) = xQ (а), а е (0, Ь).
В этом случае уравнения (6) и (7) принимают следующий вид:
Л" (а) + М (а) = 0, а е (0, Ь),	(23)
Т (t) + кЧТ (t) = 0, t > to,	(24)
где граничные условия для первого из них: А (0) = А (Ь) = 0.
Для того чтобы определить Л, нужно решить задачу о собственных числах уравнения
Л" (а) + U (а) = 0, Л (0) = Л (Ь) = 0.	(25)
Легко показать, что нетривиальные решения этого уравнения
имеются только в том случае, когда
=	« =	(26)
и что эти решения пропорциональны функциям
Л(«) ==	n = l,2,...,ae[0, Ь],	(27)
образующим ортонормальный базис пространства Ьг (О, Ь). Точно так же функции {?’„}, представляющие собой решения уравнения (24) при указанных значениях параметров Хп, очевидно, должны быть пропорциональны функциям
Тп («) = ехр	п = 1, 2, . . .
Поэтому умноженная на произвольный скалярный коэффициент функция
хп (t, а) = Тп (t) Ап (a), п = 1, 2, . .	(Z, а) ЕЕ А, (28)
удовлетворяет однородному уравнению (22) и граничным условиям (б).
Для того чтобы завершить формальное решение однородного варианта уравнения (22), мы построим функцию
x(t, a) = %Спхпу, a),	(/,а)еД,	(29)
П=1 автоматически удовлетворяющую заданным граничным условиям при любых скалярных {£„}. Для того чтобы удовлетворить затем и начальным условиям, нужно, чтобы
оо
*n(a)	26’плп(«);
71-—1
и, значит, Сп представляли собой коэффициенты Фурье функции я0, разложенной по ортонормальному базису {Лп} пространства £2(0, Ь):
__ъ
Сп = <z°, Ап} = j/'у ^°(a)sin (Xn2a)da, п = 1, 2, . . . (30) о
Формальное решение, построенное для уравнений (29) и (30), удовлетворяет, таким образом, граничным и начальным условиям однородного уравнения. Остается показать, что соответствующая бесконечная сумма сходится и что ее предел достаточно гладок для того, чтобы у него существовали частные производные
первого порядка по t и второго порядка по а внутри Д и сохранялась непрерывность на границе этого множества. Для рассматриваемого примера хорошо известно (см. стр. 173 [А.90]), что если я0 (Ъ) = я0 (0) = 0 и функция z° кусочно-непрерывна, то полученный ряд удовлетворяет сформулированным выше требованиям и действительно определяет свободное движение системы (22).
Переходя к вычислению вынужденного движения системы, нам нужно прежде всего вычислить по формуле
___ ь
Wn(0 = </(«, •),	=	J/G.^sin^dx, *>*0,	(31)
7 о
скалярные функции {un}, а затем воспользоваться ими, чтобы составить бесконечную систему уравнений
Д. (0 = -	(0 + «п (0. П = 1, 2......t > t9,
Тп (/о) = сп = <х°, Лп>, п = 1, 2, . . .
Бесконечная диагональная матрица А в этом случае, очевидно, имеет следующий вид:
А = diag [— &2ХП, —. . J,
а поэтому матрица перехода Ф соответствующей системы бесконечного порядка выглядит следующим образом:
Ф (/, s) = diag {ехр [— (t — $)],..., ехр [— №кп (t — $)],....}, J, s > tQ.	(32)
Обозначая через z, z°, со и и соответствующие бесконечномерные векторы
z(0 =(Л(0,	т2(0, • • м	тп (0,	.	..),	]
2° = (Сх, с2,	..., сп, ..	.),	I
(О (а) = (Л! (а),	А2 (а), . .	Ап (а),	.	.	.),	а е 10, Ы, I (33)
u (t) = (ux (0, U2 (£), . . ., ип (Z), .	.	.),	t >	tQ,	J
мы можем записать суммарную реакцию системы в следующем виде:
I
z (Z) = Ф (t, t0) z° 4- § Ф (t, s) и (s) ds, t > t0, ' „ <34>
«) -- [u(a),z<01 = 2(Ma)2n<()I (I.
71=1
Вспомним теперь, что в § 4.2 мы определили пространство векторных функций ЬР(Х*, т). Выберем в качестве X пространство Zp, 1 р, <оо. Тогда мы можем рассматривать Ф как матрицу линейного преобразования, отображающего пространство 1Р в Lp (Zp; т) согласно правилу
(Фг0) (t) = Ф (Z, tQ) z°, z° е Zp, t e T.
Обозначим по аналогии через Фл линейное преобразование, отображающее пространство 1Р в пространство ZP', согласно правилу
ф^0 = Ф (Zk, tQ) z°, z° е Zp.	(35)
С помощью уравнения (32) мы без какого-либо труда покажем, что каждое из этих преобразований ограничено.
Вынужденное движение системы можно рассматривать как линейное преобразование F, отображающее пространство Lp (Z^; т) в само себя в соответствии с уравнением
i
(Fu) (/) = §Ф (Z, s) и (s)ds, Zo, ZEE?, to
или, если зафиксировать Z,— как линейное отображение Fh с той же областью определения, но областью значений, совпадающей с Zp, и удовлетворяющее условию
Fku = § Ф (Z/c, $) и (s) ds.	(36)
to
Преобразования F и Fk также ограничены.
Диаграмма, изображенная на рис. П9.3, помогает подвести итог сказанному. Вынужденная реакция физической системы с распределенными параметрами представлена здесь как некоторое линейное преобразование х = Fu, отображающее одно пространство функций нескольких переменных Вх в другое такое же пространство В2- С помощью уравнения (17) мы можем ввести линейное преобразование Jf = и, определенное на и принимающее значения в Вг (бесконечномерном пространстве векторных функций). Уравнение (19) определяет другое линейное преобразование z = Fu, отображающее Бг в другое бесконечномерное пространство векторных функций В2. Наконец, уравнение (21) определяет отображение Kz = х пространства В2 в В2.
Приведенные выше соображения показывают, что F = KFJ и если преобразования К и J обратимы, то справедливо и соотно
шение F = K^FJ-1. Это свидетельствует о существовании естественной гибкости в выборе математических моделей системы. Выше мы нигде не говорили о нормах соответствующих пространств, но читателю должно быть совершенно ясно, что, например, постановка задачи о минимизации нормы из главы 4 в настоящих условиях не может вызвать никаких затруднений.
Задачи оптимального управления системами с распределенными параметрами. Возвращаясь к вопросам, затронутым в главе 4, мы должны отметить, что полученные там результаты сохраняют свою силу и для преобразований с бесконечномерными
Рис. П9.3. Формальная модель системы с распределенными параметрами.
областями значений. В соответствии с последними замечаниями предыдущего раздела мы видим, что методы главы 4 можно использовать для решения задач оптимального управления системами с распределенными параметрами. И действительно, общность этих методов оставляет нам лишь необходимость конкретизации соответствующих этапов решения для конкретных примеров.
Рассмотрим задачу оптимального управления системой, описываемой уравнением диффузии. Аналогичные задачи рассматривались в нескольких работах, уже упоминавшихся выше. Полезным источником других результатов может служить диссертация Фами [Б.32].
Итак, рассмотрим систему, описываемую уравнением (22), со следующими изменениями. Мы будем предполагать, что воздействовать на систему можно и на границе области Д, т. е. что ее граничные условия имеют вид
х (t, 0) = hL (/), X (t, b) = h2 (z), t G (to, th).
Более того, будем предполагать, что внешние воздействия, влияю-щие на поведение системы, состояние которой принадлежит Д, могут быть двух типов: обычное распределенное воздействие, заданное на всем Д, и конечное число воздействий {gx, . . ., gm}, сконцентрированных в определенных фиксированных простран
ственных точках {а, : 0 < ах < . . . < ат < В}. С математической точки зрения это означает, что неоднородную часть / уравнения (22) нужно заменить на функцию
т
2s(a~сч)£»(О. (<,а)еД.
i=l
Перебирая в различных комбинациях функции
{/, ^1, ^2, £1, • • •» £т}
в качестве управляющих и (или) возмущающих воздействий, мы смогли бы сформулировать множество различных задач управления. Если для функций
/, g = (gl, • • gn), h = (hl, h2> и *
определить подходящие банаховы пространства By, Bgi Bh и Вж, то из-за линейности уравнения (22) мы получили бы, что каждая из задач на минимизацию нормы, поставленная в главе 4, получает содержательную формулировку и для этой системы. А так как механизм решения этих задач аналогичен рассматривавшемуся выше для конечномерного случая, то нам кажется достаточным сосредоточить свои усилия на решении простейшей задачи, а именно задачи о минимизации энергии.
Линейность уравнения диффузии позволяет иногда довольно просто решать сложные задачи оптимизации. Простейшая фундаментальная задача предполагает наличие одного лишь распределенного воздействия / (в этом случае g = 0 и h = 0). Воспользовавшись обозначениями, введенными на рис. П9.3, введем гильбертово пространство как пространство всех функций, определенных на А и обладающих конечной нормой, порожденной скалярным произведением
h ь
<х, у) = х (£, а) у (£, а) dt da, х, у Нх. k о
Поскольку функции {Аа} образует некоторый ортонормальный базис пространства Л2 (0, Ь), то формула Парсеваля показывает, что (почти) для всех t ЕЕ По, £/<1 множество {ип} из уравнения (31) удовлетворяет условию
оо	ь
SI (/) I2 = (|К [/ (t, a)	t е Ro, M •
n=0	' £
Поэтому, обозначая через Ях пространство L2 (Z2; t<o. Zj), мы видим, что для и е Нг из уравнения (33) следует:
hL =1/1й-лл 1	XI1
Другими словами, отображение J, определенное на рис. П9.3, сохраняет норму (т. е. является линейной изометрией).
Это замечание показывает, что можно переформулировать поставленную задачу в терминах преобразования F. Для этого нужно определить вектор х* выражением
= (z*, . . ., z£, . . .), zKn = <z*, Лп>, n = 1, 2, . . .
После этого мы можем определить вектор £ = 12 согласно уравнению (35) в виде
£ = Ф (£k, tQ) z°.
(Заметим, что г-я компонента £. вектора £ имеет вид
li = Z- — ехр [— н. (tk — zo)] Z®, i = 1,2, . . .)
Пользуясь этими определениями, мы можем теперь сформулировать исходную задачу как задачу построения прообраза элемента £ GE Н2 = Z2 для Р из уравнения (36), обладающего минимальной нормой. После того как эта задача будет решена, оптимальное управление / можно вычислить по правилу / = J'1 и*.
Сформулированная задача, очевидно, сводится к определению псевдообратного преобразования относительно Fk. А как это делать, известно. Во-первых, заметим, что
Fk : 1%	1*2 (Z2; т)
ппедставляет собой преобразование следующего вида:
(Ffcx) (t) = Ф* (Zo, t) х, х l2t t £= [Zo, ZjJ,
так что оператор FkF* в l2 определяется бесконечной матрицей
FKFt = $ Ф (tk, s) Ф* (Zk, s) ds,	(37)
*0
которая в нашем случае диагональна,
FhF* = diag [уг, у2, . . ., уп, . . .1,
гдб
fj = § ехр [— 2/гХ (<к — s)J ds = {1 — ехр [ — 2k2kj (Zk — /0)|}/2Л%, °	(38)
Для случая гильбертовых пространств F% можно определить с помощью полярного представления Fhi вычислением которого мы теперь и займемся. Обозначим через {et} обычный координатный базис пространства Z2, через р. — скаляры i = = 1, 2, . . и через {gf} — ортонормальные векторы пространства L2 (Z2, т) для которых
Si (0 = Hi1 еХР 1“	ei* *	=	2, . . .
Тогда полярное представление Fh имеет следующий вид:
i=l
Замечание 1. Отметим, что преобразование Fh компактно. Объединяя уравнения (26) и (38), мы сразу увидим, что
|in ~ Ь/ 2лАп,
и, следовательно, спектр (FftFfc)v’ не только дискретен, но и имеет предельную точку в нуле. Вследствие этого рассматриваемая система неуправляема в том смысле, что для нее не каждый ограниченный элемент области значений имеет некоторый ограниченный прообраз для F. Другими словами, преобразование F^ нельзя считать ограниченным. Однако это не мешает нам построить неограниченное преобразование F$ и определить, на каких элементах Е /2 норма конечна *).
Совершенно ясно, что искомое обратное преобразование может быть представлено в виде
оо
*) Псевдообратные преобразования в гильбертовых пространствах, не обладающие свойством сюръективности, более аккуратно рассматриваются ivr^tk °Ав Шетлера («The Operator Theory of the Pseudo Inverse», Journal of Math. Analysis and Appl. 10, 1965) и докторской диссертации Вотруба («On beneralized Inverses and Singular Equations in Functional Analysis», Univ, of Michigan, Ann. Arbor, 1964).
Предыдущее замечание о скалярах {р,} показывает, что при 7-> оо р^-^оо, что и порождает неограниченность преобразования Fj. Кроме того, нетрудно видеть, что
имеет конечный прообраз из L2 (Z2; т) согласно Fk в том и только в том случае, когда
оо
1=1
Замечание 2. Рассмотрим теперь систему, описываемую уравнением диффузии с граничными условиями Лх, = 0 и управляющим воздействием вида
т f(t,a) =	(<* — °Ч)gt (0> (*> а) е А-
1=1
С физической точки зрения это означает, что мы ограничили возможность внешнего воздействия на систему пространственными точками {а.}. Это физическое ограничение (см. работу Фами [Б.32]) вызывает в математической модели лишь появление матрицы входных коэффициентов (нестрого говоря, размером (сю X т))
^11* • • ^im
В = ъп1. . . ь.
элементы которой
ьп)=	, j = l.....т, п = 1, 2, ...
Уравнение (34) принимает теперь вид
t
z (t) = Ф (/, t0) 4- 5 Ф (*» s) (s) ds, t > tQ, (39) ^0
где
g = (gl, • • •, gm) И Ф определены в уравнении (32).
Совершенно ясно, что значение вынужденной реакции системы (39) в момент t --= th определяет линейное преобразование Т: \Ltt0,	Сопряженное преобразование Т* имеет вид
(Т*Х) (0 - я*Ф* (<k, Z) х, /еро, /*],	Хе/2,
и можно показать, что ТТ* определяет бесконечную недиагональную матрицу, типичный элемент которой имеет следующий вид:
m
(2T.)d.
Снова оператор ТТ* компактен, и его обращение осложняется не только недиагональностью, но и замечанием 1. Однако в своей области значений Тт можно, как обычно, представить в виде
7’+ “ Т* (ТТ*)”1.
Замечание 3. В завершение нашего обзора методов управления системой, описывающейся уравнением диффузии, рассмотрим случай, когда управляющие воздействия возможны лишь на границе множества Д. В этой ситуации все функции /, gu ... . . . , gm полагаются тождественно равными нулю, а системой из примера 3 можно управлять лишь с помощью граничных условий
х (£> 0) = hr (£), х (t, b) = h2 (/), t EE (^o» th)*
Как и ранее, будем искать решение х в виде
оо
.t(Z, а) = ^Тп(1)Ап(л), 71=1
где множество {Лп} определяется из уравнений (27). Интегрируя выражение
__ь
= ]/"а) Лп(а)йа о
по частям дважды, мы можем формально получить следующий результат:
тп (!) = _ тп (0 + 2-^	(0 - (-1)"Л8 (01, п = 1, 2,...,
Определим, как и раньше, вектор г и матрицу Ф. Это позволит нам ввести еще и матрицы N и М:
1
1
1
N = (ооХ2)
Г
-1 1
-1
И
.г	Г 2 л/с2	2пл/с2 1
M = diag[-3r,...,-T5-,... | .
Теперь значение вынужденной реакции системы в момент времени tt можно рассматривать как значение линейного преобразования G : [L2 (<о, ^)1а —> ^2, удовлетворяющего условию
Gu = § Ф (fk, s) MNu (s) ds, и [Za (£0, ^)]2. to
Вид преобразования G* очевиден, а оператор GG* в 12 определяет бесконечную матрицу с типичным элементом
(GG*)mn-
{О,	если т + п нечетно,
“ ехр [ ~	+	(*k~zo)]}. если т + п четно.
Таким образом, вновь можно сформулировать задачу о переходе xQ (а) -> xf (а) с минимальной затратой энергии, и эту задачу удается решать обычным способом.
Эти замечания и последующие упражнения завершают наше изучение систем с распределенными постоянными. В добавление к уже упоминавшимся источникам укажем еще на статьи [Б. 12], [Б.21 - Б.23], [Б.ЗО], [Б.31], [Б.42], [Б.71], [Б.76], [Б.78], [Б.79], [Б.115], [Б.117 — Б.120], которые могут быть полезными читателю.
У пражнения
1.	Предположим, что граничные условия для уравнения (5) имеют вид ж (t, 0) = Pi (0, х (t, I) = р2 (t), t e т, где функции p-j и рг имеют производные первого порядка, соответственно, Pi и р^. Определим функцию у выражением
У (‘. а) = Н1 (0 + (а/0(Н2 (0 -	(0J. («. а) € А-
Покажите, что подстановка
х (t, а) = у (t, а) + V (t, а)
позволяет свести эту задачу с неоднородными граничными условиями к задаче с нулевыми граничными условиями, но с другой неоднородной частью.
2.	Предположим, что функция не обращается в нуль на [а, Ь]. Покажите, что дифференциальное уравнение
апУ' + аыУ' + аооУ = ~^У
может быть приведено к виду
ГруТ + ЯУ = —Ьгу-
Указание.
t
р (0 = ехр | аю (s)/aii (s) ds j, r (t) = p (t)/an (I), Я (t) = r (t) aoo (<).
Л
3.	Покажите, что дифференциальный оператор L из уравнения (9) с формальной точки зрения является самосопряженным (см. уравнение (36) из приложения 4) и даже строго самосопряженным на промежутке [а, Ь], если каждые х и у из области определения оператора L удовлетворяют граничным условиям (р (/) [х' (/) у (t) — х (t) у' (0]}д = 0.
В следующих трех упражнениях мы непосредственно займемся задачей Штурма — Лиувилля, поставленной в уравнениях (9) и (10) этого приложения.
4.	Обозначим через х и у р&ъ нетривиальные функции среди элементов ядра оператора L, удовлетворяющих условиям U1 (x(a)] = 0 и U2 fу(Ь)] = 0 соответственно. Убедитесь, что функция А = р [ху' — х'у] постоянна на [а, &].
Указание. Обратите внимание на то, что
X (ру'У — у (ps’Y = [р (ху' — ух')]' = 0.
5.	Предположим, что функция А из упражнения 4 отлична от нуля, и определим функцию G выражениями
/ — X (t) у (»)
I -------------^4->	1 < S,
G (I, х) = !
] — X (s) у (t)
I—р?—’	s<*
Покажите, что
(а)	функция G удовлетворяет граничным условиям при t = а и t = Ъ\
(б)	функция G непрерывна при t = $;
(в)	производная Gt претерпевает скачок в точке t = s величины —i/p (s)9 т- е. Gt(s^	(г, s) = 1/р (s);
(г)	LG = 0 на обоих промежутках [а, $] и [s, Ь];
(д)	если у (t) = G (/, s) L (s) ds, то Ly = h и у удовлетворяет граничим условиям при t = а и t = b.
6» Рассмотрим задачу теплопроводности в отсутствие источников тепла:
(t, a, р) = хаа (г, а, р) + хрр (/, а, р),	«, а, р) е А»
определенную на прямоугольнике А = {(f, а, 0): / > £о,О<а<я,О<Р< < Ь}. Предположим, что граничные условия этой задачи имеют следующий вид:
х (t, 0, 0) = х (t, а, Р) = х (t, а, 0) = х (t, а, Ь) = 0.
Покажите, что скаляры [lm,n (ил/я)2 + (тл/Ь)2; т, п = 1, 2, ...] позволяют разделять переменные в системе. Воспользовавшись в качестве образца для подражания примером 3 из приложения 2 и приложением 9, постройте свободную и вынужденную реакции этой системы.
7.	Покажите, что вынужденная реакция системы из замечания 3 может быть представлена в виде
t	t
х (f, ot) -- Gi (t — s, ct) hi (s) ds -|- G2 (t — s, ct) h2 (s) ds,
ht	t0
где Gi (t — s, ot) == G2(t — s, b — а) и
• / пла Г / плк \2 “I
Gt (t — «. a) = 2 2jlrt	(“Г"J exp |_“ V ~J ~
n=l
8.	Покажите, что вынужденная реакция системы из замечания 2 может быть представлена в виде
7И t
X (*, ot) = 2 $ W ар' s) Ip (s) ds'
P=1 to где
Д Г f плк \2	1 f nnct 4 fnnctp\
iy(ot,otp,/,s) = 2	/ S)J Sink“b/ sin(-b) ‘
?i=i
9.	Рассмотрим систему, описываемую уравнением диффузии, при условии, что управляющими воздействиями могут служить все функции /, g = = (£п gm) и h = (ht, hi) одновременно. Покажите, что если управляющее воздействие (/, g, h) вызывает переход системы из состояния х° (а) в состояние х* (а) и имеет минимальную норму, то
/ = ХА. Е-^, g = Т*Е~% h = G*E~%
где 6 = z (tk) - Ф (tk, t0) z (t0), а E = FkFk + TT* + GG*.
10.	(См. работу Фами [Б.32].) Рассмотрим систему, описывающуюся уравнением
дх (f, ot)	д2х (t, a)
di =к' И&
(t, а) е д,
с дополнительными условиями
х(^0, а) = О, а е й = [о, &], дх (t, 0)
—Lp = 72[x(t,0)-v(t)],	tG[te,ti],
Эх (t, Ь)
9а ~и’
1 ё [te, ti].
Здесь у2 есть некоторая постоянная, а зависящая от времени функция v (t) связана с управляющим воздействием и (t) обыкновенным дифференциальным уравнением первого порядка
dv (t)
dt- - -	(t) = и w, t e [to, ti],
в котором о2 — некоторая постоянная. С физической точки зрения эта математическая модель описывает процесс одностороннего нагрева металла. Покажите, что собственные числа соответствующего преобразования имеют ВИД	z	к.
f / ос
Sn (ot) = cosjPn 11 ——Д, осе [О, Ъ], л = 1,2,...,
а состояние х системы описывается соотношением
t
К (t — s, а) и (s) ds,
*0
в котором ядро К (т, а) имеет вид
оо
к (т. 0() = 2 [ Сп ехР {-	+ Dn ехР <— WV6)2 ТИ.
П=1
где Сп и Dn — вполне определенные скаляры. Пользуясь этим результатом, покажите далее, что динамику изменения состояния системы можно описать следующим образом:
00
*«.«) = 2 Лп(0^п(а).
71=1
Воспользуйтесь развитыми выше методами для того, чтобы решить в этих условиях задачу минимизации энергии.
И. (См. работу Фами [Б.32].) Рассмотрим критерий качества вида
ь
о
где функция Р (t, а) ограничена, строго положительна и измерима. Покажите, что разложение Фурье функции Р (t, а) / (t, а) по полной ортонормальной системе функций
{q’7l — У'2/b sin (пл/b) а}
[О, Ь] имеет следующий вид:
= 2 dnW<Pn(«).	Х[0, 6],
71=1
где
оо
dn(0 = (l//26) 2 {um (О	п = 1,2....
m=l
b
un (t) = V2/b / (Г, a) sin (пл/b) a da, n = 1, 2,..., о b
Cn (0 = V'2/b P (f, a) cos (лл/Ь) a da, л = 0,1, 2,,
о и
C_n(0 = Cn(0,	л = 1,2....
при всех t G [*0, *1). Воспользовавшись теоремой Парсеваля, покажите, что приведенный выше критерий качества можно представить в эквивалентной форме
1 С /(/) = J(u) = “A hW. pWM(01ds»
1*0
где Р — бесконечная симметрическая матрица, типичный элемент которой
Итп W = (V/26)	<0 - Ст.п «»•	< 6 [to. hj.
12. (См. работу Фами [Б.32].) Рассмотрим систему, описывающуюся уравнением диффузии (22) с нулевыми начальными условиями х° (a) = 0. Предположим, что критерий качества для этой системы имеет вид
tib	цъ
ла=4" §	। / <*>a) i*rfa at+4~ $ 5	* xi i* ***dt<
t,0	t о 0
где P и Q — ограниченные, строго положительные и измеримые функции, а Xf — реакция системы, находящейся под воздействием управления /. Определим у (t) как
У (0 = Р (О и* (0,
где Р (t) удовлетворяет условиям упражнения 11, а u* (t) является оптимальным управляющим воздействием, и* (t) = (и* (0,	(0, ...). Тогда у (0
удовлетворяет векторному обыкновенному дифференциальному уравнению второго порядка
р (0 = [-Л* + Q (0 (?-i (0 + Q (0 Л?-* (0] у (0 +
+ К? (0 Q-1 (0 Л* + Q (0 Л^-i Л* + Q (0 Р-i (0] у (0,
для которого бесконечная матрица Q (0 связана с Q (tt а) так же, как Р (0 связано с Р (f, а), а‘ матрица Л определяется уравнением (19). Покажите, что если Р = Q = I, где Z — тождественная матрица, то п-я компонента вектора
оптимальных управляющих воздействий вычисляется по формуле и* (/) = [[*! - 'о!-1 (ех₽	(*1 - «о)} +
п	+ [2 (пЛл/*)2]-1 ехр {-(nfcn/6)2 (tl- t)}]gn
и всех t GE Ro» *1) и Достаточно больших п. Здесь — это n-й коэффициент Фурье конечного состояния х1 (а) в разложении по системе функций /ф (а) = У2/Ь sin (пл/Ь) а}.
13. (См. работу Фами [Б.32].) Пусть Р = Q — I (I — тождественная матрица). Покажите, что оптимальное управляющее воздействие /♦ (t, а) удовлетворяет обратному уравнению диффузии
(,.4S4.
Дифференцируя это уравнение дважды и подставляя в уравнение (22а), покажите, что /♦ (t, а) удовлетворяет дифференциальному уравнению в частных производных четвертого порядка
А. Книги учебного характера
1.	Aitken А. С., Determinants and Matrices. Oliver and Boyd, Edinburgh, and Interscience, New York, 1956.
2.	A x и e з e p H. И., Г л а з м а н И. М. Теория линейных операторов в гильбертовом пространстве. Гостехиздат, М,— Л., 1950.
3.	А х и е з е р II. И., Кройн М. Г., О некоторых вопросах теории моментов. Харьков, 1938.
4.	Anderson К. W. and II а 1 1 D. W., Sets, Sequences, and Mappings: The Basic Concepts of Analysis. Wiley, New York, 1963.
5.	AnseloneP.M., Ed., Nonlinear Integral Equations. University of Wisconsin Press, Madison, 1964.
6.	Arnold B.H., Intuitive Concepts in Elementary Topology. Prentice-Hall, Englewoon Cliffs, N. J., 1962.
7.	Ayres F., Jr., Schaum’s Outline Series Theory and Problems of Matrices. Schaum, New York, 1962.
8.	В a n a c h S., Theorie des Operations Lineaires. Chelsea, New York, 1925. [Украинский перевод: Б а н a x С., Курс функщонального ана-л!зу. «Радянська школа», Киев, 1948).
9.	В а г t 1 е R. G., The Elements of Real Analysis. Wiley, New York, 1964.
10.	Bellman R., Introduction to Matrix Analysis. McGraw-Hill, New York, 1960. [Русский перевод: Веллман P., Введение в теорию матриц. Изд-во «Наука», М., 1969 г.]
11.	В о a s R. Р., Jr., A Primer of Real Functions. The Mathematical Association of America, 1960.
12.	Bourbaki N., Elements de mathematique, Livre VI, Espaces vec-toriels topologiques. Hermann et Cie, Act. Sci., et Ind., 1189, 1229, Paris, 1953, 1955. [Русский перевод: Бурбаки H., Топологические векторные пространства (Элементы математики). ИЛ, М., 1959].
13.	Brown W. М., Analysis of Linear Time-Invariant Systems. McGraw-Hill, New York, 1963.
14.	Chang S. S. L., Synthesis of Optimum Control Systems. McGraw-Hill, New York, 1961. [Русский перевод: Чанг III. С. Л., Синтез оптимальных систем автоматического управления. Изд-во «Машиностроение», М., 1964.)
15.	С о d d i n g t о n E. A., An Introduction to Ordinary Differential Equations. Prentice-Hall, Englewood Cliffs, N. J., 1961.
16.	С о d d i n g t о n E. A. ann Levinson N., Theory of Ordinary Differential Equations. McGraw-Hill, New York, 1955. [Русский перевод: КоддингтонЭ. А., Левинсон II., Теория обыкновенных дифференциальных уравнений. ИЛ, М., 1958.]
17.	Cooke В. G., Infinite Matrices and Sequence Spaces. Macmillan, London, 1950.
18.	С г о n i n J., Fixed Points and Topological Degree in Nonlinear Analysis. Mathematical Survey No. 11, American Mathematical Society, Providence, R. I., 1964.
19.	D a v i s II. F., Fourier Series and Orthogonal Functions. Allyn and Bacon, Boston, 1964.
20	Dav М. М., Normed Linear Spaces. Springer-Verlag, Berlin, 1962.
21	Dieudonne J. A., Foundations of Modern Analysis. Academic Press, New York, 1960. [Русский перевод: Дьедонне Ж., Основы современного анализа. Изд-во «Мир», М., 1964.]
22	Dunford N. and Schwartz J. T., Linear Operators. Part I. General Theory. Interscience, New York, 1958. [Русский перевод: Дан-фо p д IL, III в a p ц Дж., Лппейпые операторы. Общая теория. ИЛ, М., 1962.[
23.	Dunford N. and Schwartz J. T., Linear Operators. Part II. Spectral Theory: Self-Adjoint Operators in Hilbert Space. Interscience, New York, 1963. [Русский перевод: Данфорд II. и III в а р ц Дж., Линейные операторы. Спектральная теория. Самосопряженные операторы в гильбертовом пространстве. Изд-во «Мир», М., 1966.]
24.	Eggleston Н. G.. Problems in Euclidean Space: Application of Convexity. Perga mon, New York, 1957.
25	ЭльсгольцЛ. Э., Вариационное исчисление. Гостехиздат, М., ’ 1952.
26.	ЭльсгольцЛ. Э., Качественные методы в математическом анализе. Гостехиздат, М., 1955.
27.	Epstein В., Partial Differential Equations — An Introduction. McGraw-Hill, New York, 1962.
28.	Fox L., Numerical Solution of Ordinary and Partial Differential Equa tions. Pergamon; Adison-Wesley, Reading, Mass., 1962.
29.	F r i e d m a n A., Generalized Functions and Partial Differential Equations. Prentice-Hall, Englewood Cliffs, N. J., 1963.
30.	Friedman B., Principles and Techniques of Applied Mathematics. Wiley, New York, 1956.
31.	Г e л ь ф а н д И. M., Ф о м и н С. В., Вариационное исчисление. Физматгиз, М., 1961.
32.	G о е г t z е 1 G. and Т г а 1 1 i N., Some Mathematical Methods of Physics. McGraw-Hill, New York, 1960.
33.	Gray J. F., Sets, Relations and Functions. Holt, Rinehart and Winston New York, 1962.
34.	G о 1 d b e r g S., Introduction to Difference Equations. Wiley, New York, 1961.
35.	Halmos P. R., Finite-Dimensional Vector Spaces. Van Nostrand, Princeton, N. J., 1958. [Русский перевод: ХалмошП. P., Конечномерные векторные пространства, Физматгиз, М., 1963.]
36.	Н а 1 ш о s Р. R., Introduction to Hilbert Space and the Theory of Spectral Multiplicity. Chelsea, New York, 1957.
37.	Ilaliuos P. R., Measure Theory. Van Nostrand, Princeton, N. J., 1950. [Русский перевод: X а л м о ш И. Р., Теория меры. ИЛ, М., 1953.]
38.	Н а г d у G. Н., Littlewood J. Е., and Polya G. Inequalities. Cambridge University Press, New York, 1952. [Русский перевод: X a p-Д n \*9 Г Л иттл ьвуд Дж. E., Полна Г., Неравенства, ИЛ,
39.	Hartman S. and М i k u s i n s k i J., The Theory of Lebesque , Measure and Integration. Pergamon, New York, 1961.
40.	H i 1 d e b r a n d F. B., Methods of Applied Mathematics. Prentice-HaP’ Englewood Cliffs, N. J., 1952.
41-	Hille E. and P h i 1 1 i p s R. S., Functional Analysis and Semi-Groups. American Mathematical Society, Providence, R. I., 1957. [Русский перевод: Хилле Э., Филлипс Р., Функциональный анализ
49 хт полугруппы. ИЛ, М„ 1962.]
^•Hoffman К. and Kunze R., Linear Algebra, Prentice-Hall, Englewood Cliffs, N. J., 1961,
43.	Horowitz I. M., Synthesis of Feedback Systems. Academic Press, New York, 1963.
44.	I n d r i t z J., Methods in Analysis. Macmillan, New York, 1963.
45.	Jury E. I., Sampled-Data Control Systems. Wiley, New York 1958. [Русский перевод: Д ж у p и Э., Импульсные системы автоматического управления. Физматгиз, М., 1963.]
46.	Kaplan W., Ordinary Differential Equations. Addison-Wesley, Reading, Mass., 1958.
47.	Kaplan W., Operational Methods for Linear Systems. Addison-Wesley, Reading, Mass., 1962.
18. Kelley J. L., N a m i о k a I., and co-authors, Linear Topological Spaces. Van Nostrand Co., Princeton, N. J., 1963.
49.	КолмогоровА. H., Фомин C.B., Элементы теории функций и функционального анализа, вып. 1. Моск, ун-т, М., 1954.
50.	К о л м о г о р о в А. Н., Ф о м и н С. В., Элементы теории функций и функционального анализа, вып. 2. Моск, ун-т, М., 1960.
51.	Красносельский М. А., Рутпцкий Я. Б., Выпуклые функции и пространства Орлича. Физматгиз, M.J 1958.
52.	Красносельский М.А., Топологические методы в теории нелинейных интегральных уравнений. Гостехиздат, М., 1956.
53.	Кио В. С., Analysis and Synthesis of Sampled-Data Control Systems. Prentice-Hall, Englewood Cliffs, N. J., 1963.
54.	Kurnatowski K., Introduction to Set Theory and Topology. Per-gamon, Oxford; Addison-Wesley, Reading, Mass., 1962.
55.	L e f s c h e t z S., Differential Equations: Geometric Theory. Interscience, New York, 1963. [Русский перевод: Л e ф ш e ц С., Геометрическая теория дифференциальных уравнений. ИЛ, М., 1967.]
56.	Люстерник Л. А., Соболев В. И., Элементы функционального анализа. Гостехиздат, М.— Л., 1951.
57.	Lorch Е. R., Spectral Theory. Oxford University Press, New York, 1962.
58.	Mendelson B., Introduction to Topology. Allyn and Bacon, Boston, 1962.
59.	Miller K. S., An Introduction to the Calculus of Finite Differences and Difference Equations. Holt, Rinehart and Winston, New York, 1960.
60.	Miller K. S., Partial Differential Equations in Engineering Problems. Prentice-Hall, Englewood Cliffs, N. J., 1953.
61.	Miller K. S., Linear Differential Equations in the Real Domain. Norton, New York, 1963.
62.	Mirsky L., An Introduction to Linear Algebra. Oxford at the Clarendon Press, 1955.
63.	Натансон И. П., Теория функций вещественной переменной. Гостехиздат, М.— Л., 1950.
64.	N е г i n g Б. D., Linear Algebra and Matrix Theory. Wiley, New York, 1963.
65.	Nirenberg L., Functional Analysis. Lectures given in 1960—1961, New York University.
66.	Perlis S., Theory of Matrices. Addison-Wesley, Reading, Mass., 1952.
67.	P e s c h о n John, Ed., Disciplines and Techniques of Systems Control. Blaisdell, New York, 1965.
68.	Понтрягин Л. С., Обыкновенные дифференциальные уравнения. Изд-во «Наука», М., 1965.
69.	П о н т р я г и и Л. С., Болтянский В. Г., Гамкрелид-зе Р.В., Мищенко Е. Ф., Математическая теория оптимальных процессов. Изд-во «Наука», М., 1969,
7Л	R ichar dson С. Н., An Introduction to the Calculus of Finite Dif-ferences. Van Nostrand, Princeton, N. J., 1954.
74	r i r h tmy er R. D., Difference Methods for Initial-Value Problems. 71 • Inl^ience: New York, 1958.
72	Riesz F. and Sz-Nagy B., Functional Analysis. Frederick Ungar, New York, 1945. [Русский перевод: РиссФ., Секефаль-в п-Н а д ь Б., Лекции по функциональному анализу. ИЛ., М., 1954.1
73.	Rudin W., Principles of Mathematical Analysis. McGraw-Hill, New York, 1953.
74.	S a a t у T. L. and В r a m J., Nonlinear Mathematics. McGraw-Hill, New York, 1964.
75.	Schwartz L., Theorie des distributions, Tome II. Publication de L’Institut de Mathematique de L’Universite de Strasbourg, Hermann, Paris, 1959.
76.	Шилов Г. E., Введение в теорию линейных пространств. Гостехиз-дат, М.— Л., 1952.
77.	Simmons G. F., Introduction to Topology and Modern Analysis. McGraw-Hill, New York, 1963.
78.	Sneddon I. N., Elements of Partial Differential Equations. McGraw-Hill, New York, 1957.
79.	Соболев С. Л., Некоторые применения функционального анализа в математической физике. Изд-во Ленингр. ун-та, Л., 1950.
80.	Spiegel М. R., Applied Differential Equations. Prentice-Hall, Englewood Cliffs, N. J., 1958.
81.	Stoll R. R., Linear Algebra and Matrix Theory. McGraw-Hill, New York, 1952.
82.	T а у 1 о r A. E., Advanced Calculus, Ginn, Boston, 1955.
83.	T а у 1 о r A. E., Introduction to Functional Analysis. Wiley, New York, 1958.
84.	T о л с т о в Г. П., Ряды Фурье. Гостехиздат, М.— JI., 1951.
85.	Той J. Т., Digital and Sampled-Data Control Systems. McGraw-Hill, New York, 1959.
86.	To u J. T., Modern Control, McGraw-Hill, New York, 1964.
87.	T r i с о m i F. G., Integral Equations, Interscience, New York, 1957.
88.	T s i e n H. S., Engineering Cybernetics. McGraw-Hill, New York, 1954. [Русский перевод: Цзянь Сюэ-сэнь, Техническая кибернетика. ИЛ., М., 1956.]
89.	Цыпкин Я. 3., Теория линейных импульсных систем. Физматгиз, М., 1963.
90.	Тихонов А. Н., Самарский А. А., Уравнения математической физики. Гостехиздат, М., 1953.
91.	Вайнберг М. М., Вариационные методы исследования нелинейных операторов. Физматгиз, М., 1954.
92.	V о 1 t е г г а V., Theory of Functionals and of Integral and Integrodifferential Equations. Dover, New York, 1959.
93.	By лих Б. 3., Введение в функциональный анализ. Физматгиз, М., 1966.
94.	W i 1 liamsonJ. Н., Lebesque Integration. Holt, Rinehart and Winston, New York, 1962.
L. A. Z a d e h and C. A. D e s о e r, Linear System Theory. McGraw-Hill, New York, 1963. [Русский перевод: ЗадеЛ., Д e з о e p Ч., 0 Теория линейных систем. Изд-во «Наука», М., 1970.]
J9. Bellman R., Dynamic Programming. Princeton University Press, Princeton, N. J., 1957. [Русский перевод: Веллман P., Динамическое программирование. ИЛ, I960.]
97. Hadley G., Nonlinear and Dynamic Programming. Addison-Wesley, Reading, Mass., 1964. [Русский перевод: Хедли Д., Нелинейное и динамическое программирование. «Мир», М., 1967.]
98. Merriam С. W., Optimization Theory and the Design of Feedback Control Systems. McGraw-Hill, New York, 1965. [Русский перевод: Мерриам К., Теория оптимизации и расчет систем управления с обратной связью. «Мир», М., 1967.]
Б. Статьи, монографии, доклады и труды конференций
1.	Ахиезер Н. И., Крей и М. Г., О некоторых вопросах теории моментов. Харьков, 1938.
2.	Altman М., Approximation Methods in Functional Analysis. California Institute of Technology, Mal07c Notes, 1958—1959.
3.	A n t о s i e w i c z II. A., Linear Control Systems. Arch. Rational Meeh., Anal., 12, 313—324, 1963.
4.	A t h a n s M., Minimum-Fuel Control of Second-Order Systems with Real Poles. Fourth Joint Automatic Control Conference, Minneapolis, Minnesota, Preprints by A.I.Ch.E., 232—240, 1963.
5.	A t h a n s M., Time-, Fuel-, and Energy-Optimal Control of Nonlinear Norm-invariant Systems. IEEE Trans. Autom. Control, AC-8, No. 3, 196— 202, July 1963.
6.	A t h a n s M., F a 1 b P., and L а с о s s R., On Optimal Control of a Self-Adjoint System. Lincoln Laboratories, Massachusetts Institute of Technology, Report No. MS-709, 1962.
7.	A t h a n s M., F a 1 b P., and L а с о s s R. T., Time-Optimal Velocity Control of a Spinning Space Body. AIEE Trans. Appl. Ind., 82, 1963.
8.	Б а б у н а ш в и л и T. Г., Синтез линейных оптимальных систем. ДАН СССР, 155, № 2, 295—298, 1964.
9.	В а 1 a k г i s h n a n A. V., An Operator Theoretic Formulation of a Class of Control Problems and a Steepest Descent Method of Solution. J. SIAM Ser. A: Control, 1, No. 2, 1963.
10.	В a r r R. O. and Gilbert E. G., Some Iterative Procedures for Computing Optimal Controls. Proceedings IFAC Conference, London, England, June 1966.
11.	Bass R.W. and Webber R. F., On the Synthesis of Optimal Bang-Bang Feedback Control Systems with Quadratic Performance, to appear Trans, IEEE, GAC.
12.	В e 1 1 m a n R. E., G 1 i с к s b e r g I., and G г о s s 0. A. On the «Bang-Bang» Control Problem. Quart. Appl. Math., 14, 11—18, 1956.
13.	Bliss G. A., Lectures on the Calculus of Variations. University of Chicago Press, Chicago, 1946. [Русский перевод: Блисс Г. А., Лекции по вариационному исчислению. ИЛ., М., 1950.]
14.	Block Н. D., Periodic Solutions of Forced Systems Having Hysteresis. IRE, PGCT, 423-431, 1960.
15.	Browder F. E., The Solvability of Nonlinear Functional Equations. Duke Math. J., 30, 557-566,1963.
16.	В г о w d e r F. E. Remarks on Nonlinear Functional Equations. Proc. Nat. Acad. Sci. U. S., 51, 985-989, 1965.
17.	В г о w d e r F. E., Continuity Properties of Monotone Nonlinear Operators in Banach Spaces. Bull. Amer. Math. Soc., 70, 551—553, 1965.
18.	В г у s о n A. E. and D e n h a m W. F., A Steepest Ascent Method for Solving Optimum Programming Problems. J. Appl. Meeh., 29, Ser. E, No. 2, 247-257, 1962.
19.	Bryson A. E. and D e n li a m W. F., The Solution of Optimal Programming, Problems with Inequality Constraints. IAS Paper No. 63—78, IAS Annual Meeting, New York, January 1963.
20.	Bushaw D. W., Optimal Discontinuous Forcing Terms, Contributions tn the Theory of Nonlinear Oscillations, Vol. IV. Princeton University Press, Princeton, N. J., 1958, pp. 29—52.
21	БутковскпйА. Г., Оптимальные процессы в системах с распределенными параметрами. Автомат, и телемех. 22, № 1, 1961.
22.	Б у т к о в с к и й А. Г., Принцип максимума для оптимальных систем с распределенными параметрами. Автомат, и телемех., 22, № 10, 1961.	„
23.	БутковскийА. Г., Оптимальное управление системами с распределенными параметрами. В сб. «Оптимальные системы. Статистические методы», Изд-во «Наука», М., 1965.
24.	БутковскпйА. Г. и Лернер А. Я., Об оптимальном управлении системами с распределенными параметрами. Автомат, и телемех., 21, № 6, 682—691, 1960.
25.	Cater S., Note on a Theorem of Day. Amer. Math. Monthly, 69, No. 7, 638—640, August — September 1962.
26.	CadzowJ.A., A Study of Minimum Norin Control for Sampled-Data Systems. Proceedings of the Joint Automatic Control Conference, Troy, N. Y., June 1965.
27.	Clarkson J. A., Uniformly Convex Spaces. Trans. Amer. Math. Soc., 4, 396-414, 1936.
28.	D о 1 p h C. L., The Structure of Linear Operator Theory in Hilbert Space for Engineers and Physicists. Department of Mathematics, University of Michigan, Ann. Arbor, Michigan, Vols. I and II, 1964.
29.	E a t о n J. II., An Iterative Solution to Time-Optimal Control. J. Math. Anal, and Appl., 5, 329—344, 1962; Errata and Addenda. J. Math. Anal, and Appl., 9, 147—152, 1964.
30.	Егоров А. И., Об оптимальном управлении процессами в распределенных объектах. ПММ, 27, № 4, 688—696, 1963.
31.	Е г о р о в А. И., Об оптимальном управлении процессами в некоторых системах с распределенными параметрами. Автомат, и телемех., 25, № 5, 613-623, 1964.
32.	Fahmy М., A Solution Technique for a Class of Optimal Control Problems in Distributive Systems. Doctoral Dissertation, University of Michigan, Ann. Arbor, 1965.
33.	F a d d e n E. J., Computational Aspects of a Class of Optimal Control Problems. Doctoral Dissertation, University of Michigan, 1965.
34.	F a 1 b P. L., Infinite Dimensional Control Problem: On the Closure of the Set of Attainable States for Linear Systems. J. Math. Anal, and Appl., 9, No. 1, 12—22, August 1964.
35.	F 1 u g g e - L о t z I. and Marbach H., The Optimal Control of Some Attitude Control Systems for Different Performance Criteria. Trans. ASME, Ser. D; J. Appl. Meeh., 85, 165-176, 1963.
36.	Frame J. S., Matrix Functions and Applications, Part I — Part V. IEEE Spectrum, March — July 1964 issues.
37.	Friedland V., The Design of Optimal Controllers for Linear Processes with Energy Constraints. Melpar Technical Note 62/2, March 1962.
38.	Гамкрелидзе P. В., Теория оптимальных по быстродействию процессов в линейных системах. Изв. АН СССР, сер. матем., 22, № 4, 449-474, 1958.
39.	Gilbert Е. G., An Iterative Procedure for Computing the Minimum of a Quadratic Form on a Convex Set. Presented at First International Conference on Programming and Control, USAF Academy, Colorado, 1965.
*0» Гельфанд И. M., Фомин С. В., Вариационное исчисление. Физматгиз, М., 1961.
Goodson R. Е., Optimal Control of Systems with Distributed Parameters. 1965 J ACC Conference Proceedings.
42.	G г a h a m R. G., A Steepest-Ascent Solution of Multiple-Arc Vehicle Optimization Problems. Report No. TDR-269 (4550-20-3), Contract No. AF 04(695)-269, Aerospace Corporation, El Segundo, California, December 1963.
43.	G r i m m e 1 1 W. G., The Existence and Representation of Solutions to a Class of Linear Optimal Control Problems. Ph. D. Thesis, University of Michigan, Ann. Arbor, 1965.
44.	H a Ikin H., A Generalization of LaSalle’s «Bang-Bang» Principle. J. SIAM Ser. A: Control, 2, No. 2, 1964.
45.	H a r v e у C. A., Synthesis of Time-Optimal Control for Linear Processes. Honeywell Report No. U-RO6325 (1964), Honeywell Corporation, Minneapolis, Minn.
46.	Hestenes M. R. et al., Computing Methods in Optimization Problems. A. V. Balakrishnan and L. W. Neustadt, Eds., Academic Press, New York, 1964.
47.	H о Y. C., A Successive Approximation Techniques for Optimal Control Systems Subject to Input Saturation. J. Basic. Eng., 84, Ser. D., No. 1, 33-40, 1962.
48.	Hochs tad t H., Laplace Transforms and Canonical Matrices. Amer. Math. Monthly, 71, No. 7, 728-735
49.	J a m e s R. C., Characterizations of Reflexivity. Studia Math., 23, 205— 216, 1963/64.
50.	К а лиан P. E., Об общей теории систем управления. В сб. «Теория дискретных, оптимальных и самонастраивающихся систем», Труды I Международного конгресса ИФАК, Изд-во АН СССР, М., 1961.
51.	Kalman R. Е., Н о Y. С., and Narendra К. S., Controllability of Linear Dynamical Systems. Wiley, New York, 1963.
52.	Kalman R. E., Mathematical Description of Dynamical Systems. J. SIAM, Ser. A: Control, 1, No. 2, 1963.
53.	Kalman R. E., The Theory of Optimal Control and the Calculus of Variations, Mathematical Optimization Techniques. University of California Press, Berkeley, pp. 309—331, 1963.
54.	Канторович Л. В., Функциональный анализ и прикладная математика. УМН, 3, № 6 (28), 89-185, 1948.
55.	Канторович Л. В., Крылов В. И., Приближенные методы высшего анализа. Физматгиз, М., 1959.	:
56.	Као R. С., Geometric Interpretation of LaGrange Multipliers. Rand Report No. T-2713, AD No. 298197, The Rand Corporation, Fenruary 1963.
57.	Кириллова Ф.М.,0 предельном переходе в решении одной задачи оптимального регулирования. ПММ, 24, № 2, 277—282, 1960.
58.	К 1 е е V. et al., Convexity,Proceedings of Symposia in Pure Mathematics, Vol. VII. Seventh Symposium of American Mathematical Society, Providence, Rhode Island, 1963.
59.	Knudsen H. K., An Iterative Procedure for Computing Time-Optimal Controls. IEEE Trans. Autom. Control, AC-9. No. 1, 23—30, January 1964.
60.	К r a n c G. M. and Sarachik P. E., An Application of Functional Analysis to the Optimum Control Problem. Trans. Amer. Soc. Meeh. Engrs., Basic Engineering, 85, 1963.
61.	Красовский H. H., К теории оптимального регулирования. Автомат, и телемех., 18, № 5, 960—970, 1957.
62.	Красовский Н.Н.,К теории оптимального регулирования. ПММ, 23, № 4, 625-639, 1959.
63.	К г е i n d 1 е г Е., Contributions to the Theory of Time-Optimal Control. J. Franklin Inst., 275, No. 4, April 1962.
64.	К r e i n d 1 e r E. and Sarachik P. E., On the Concepts of Controllability and Observability of Linear Systems. PT GAC, AC-9. No. 2<
April 1964, 129—136; Errata: IEEE, GAC, AC-10, No. 1, January 1965
65	К u 1 i к о w s к i R., On Optimal Control with Constraints. Bull. Polish ’ Acad. Sci. (Ser. Tech. Sci.), 7, 285-294, April 1959
66	Kulikowski R„ Concerning the Synthesis of the Optimum Nonli-’ near Control. Bull. Polish Acad. Sci. (Ser. Tech. Sci.), 7, 391—399, June
67	KuiikowskiR., Synthesis of a Class of Optimum Control Systems. ’ Bull. Polish Acad. Sci. (Ser. Tech. Sci.), 7, 663—671, November 1959.
68.	Kulikowski R., Optimum Processes and Synthesis of Optimum Automatic Control Systems with Non-linear Invariable Elements. In Proceedings of the International Federation of Automatic Control Congress, Moscow, 1960, p. 473.
69.	Kuo M. G., The Application of Functional Analysis to Solve a Class of Linear Control Problems. Doctoral Dissertation, University of Michigan,
Ann Arbor, 1964.
70. Ladd H. 0., Friedland B., Minimum Fuel Control of a Second-Order Linear Process with a Constraint on Time-to-Run. Trans. ASME, Ser. D., J. Appl. Meeh., 86, 160—168, 1964.
71. LaSalle J. P., The Time Optimum Control Problem. Contributions to the Theory of Nonlinear Oscillations, Princeton University Press, Princeton, New Jersey, 1960, Vol. 5, pp. 1—24.
L e e E. B., Mathematical Aspects oi the Synthesis of Linear Minimum Response Time Controllers. ORE PGAC, 283—289, 1960.
Lee E. B., On the Domain of Controllability for Linear Systems Subject to Control Amplitude Constraints. IEEE Trans. Autom. Control, AC-8, 172-173, April 1963.
L e e E. B. and Markus L., Optimal Control for Nonlinear Processes. Archive for Rational Mechanics and Analysis, 8, No. 1, 36—58, 1961.
72.
73.
74.
75.	Лурье К. А., О методе Гамильтона — Якоби в вариационных задачах с частными производными. ПММ, 27, № 2, 255—264, 1963.
76.	Лурье К. А., Задача Майера — Больца для кратных интегралов и оптимизация поведения систем с распределенными параметрами. ПММ. 27, № 5, 842-853, 1963.
77.	Markus L. and Lee Е. В., On the Existence of Optimal Controls, Paper No. 61-JAC-2, J ACC, 1961.
78.	McCausland I., On Optimum Control of Temperature Distribution in a Solid. J. Electron. Control, 14, 655, 1963.
79.	McCausland I., On-Off Control of Linear Systems with Distributed Parameters. PhD Dissertation, Department of Engineering, Cambridge University, Cambridge, England, 1963.
80.	M e d i t c h J. S., Synthesis of a Class of Linear Feedback Minimum Energy Controls. IRE PGAC, 376—378, 1963.
81.	Meaitch J. S., On Minimal Fuel Satellite Attitude Controls. Fourth Joint Automatic Control Conference, Minneapolis, Minnesota, preprints by A. I. Ch. E., 558-564, 1963.
82.	M e d i t c h J. S., On the Problem of Optimal Thrust Programming for a Lunar Soft Landing. Presentation 1964 Joint Automatic Control Confe-I®nce» Stanford, California.
83.	M и x л и н С. Г., Проблема минимума квадратического функционала. Гостехиздат, М.— Л., 1952.
Q^MintyG. J., Monotone (Non-Linear) Operators in Hilbert Space. Duke Math. J., 29, 341—346, 1962.
Minty G. J., On a «Monotonicity» Method for the Solution of Nonli-1041 ^9630П9 in B&nach S₽ace8‘ Proc* Nat. Acad. Sci. U. S., 50, 1038—
86.	М i n t у G. J., On the Solvability of Nonlinear Functional Equations of Monotonic Type. Pacific J. Math., 249—255, 1964.
87.	Murray F. J., On Complementary Manifolds and Projections in Spaces Lp and lp. Trans. Amer. Math. Soc., 41, 138—152, 1937.
88.	N a h i N. E., Two Classes of Optimum Linear Systems. Presentation 1964 Joint Automatic Control Conference, Stanford, California.
89.	Neustadt L. W., Synthesizing Time-Optimal Control Systems. J. Math. Anal, and Appl., 1, 484—492, 1960.
90.	Neustadt L. W., Minimum Effort Control Systems. J. SIAM, Ser. A: Control, 1, No. 1, 16-31, 1963.
91.	Neustadt L. W., The Existence of Optimal Controls in the Absence of Convexity Conditions. J. Math. Anal, and Appl., 7, 110—117, 1963.
92.	Neustadt L. W., Discrete Time Optimal Control Systems. В книге LaSalle J. P. and Lefschetz S.. Eds., International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, Academic Press, New York, 1963.
93.	Neustadt L. W., Optimization, a Moment Problem and Nonlinear Programming. J. SIAM, Ser. A: Control, 2, No. t, 33—53, 1964.
94.	P a i e w о n s k у В., Synthesis of Time-Optimal Control for Linear Systems. A.R.A.P. (Princeton, N. J.) Tech. Memo 62—4, 1962.
95.	P a i e w о n s k у В., Time-Optimal Control of Linear Systems with Bounded Controls. В книге: L a S a 11 e J. P. and L e f sc he t z S., Eds., International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, Academic Press, New York, 1963, pp. 333—365.
96.	Петровский И. Г., Лекции об уравнениях в частных производных. Гостехиздат, М., 1953.
97.	Phelps R, R., Uniqueness of Hahn — Banach Extensions and Unique Best Approximation. Trans. Amer. Math. Soc., 95, 238—255, 1960.
98.	Понтрягин Л. С., Болтянский В.Г., Гамкрелидзе P. В., Мищенко Е.Ф., Математическая теория оптимальных процессов. Изд-во «Наука», М., 1964.
99.	Porter W. A., A New Approach to a General Minimum Energy Problem. 1964 J ACC Conference, Stanford, California, June 24—26, 1964.
100.	P о г t e г W. A. and Williams J. P., Minimum Effort Control of Linear Dynamic Systems. August 1964, Tech. Report 5892-20-F, Contract AF 33(657)-! 1501.
101.	Porter W. A., Williams J. P., A Note in the Minimum Effort Control Problem. J. Math. Anal, and Appl., 1965, No. 3.
102.	P о г t e r W. A. and Williams J. P., Extensions of the Minimum Effort Control Problem. J. Math. Anal, and Appl., 1965, No. 4.
103.	Reid W. T., Ordinary Linear Differential Operators of Minimum Norm. Duke Math. J., 29, 591-606, 1962.
104.	Robertson A. P. and Robertson W., Topological Vector Spaces. Cambridge University Press, Cambridge, 1964. [Русский перевод: Робертсон А., Робертсон В., Топологические векторные пространства. Изд-во «Мир», М., 1967,]
105.	Sandberg I. W., On the £2 Boundedness of Solutions of Nonlinear Functional Equations. Bell System Tech. J., 43, No. 4, 1581—1818, July 1964.
106.	Sandberg I. W., Conditions for the Causality of Nonlinear Operators Defined on a Function Space, to appear in Quart. Appl. Math.
107.	Sandberg I. W., A Note on the Application of the Contraction-Mapping Fixed-Point Theorem to a Class ot Nonlinear Functional Equations. SIAM Review, 7, No. 2, 199—204, April 1965.
108.	Sandberg I. W., On the Properties 01 Some Systems that Distort Signals. Bell System Tech. J., Part 1, 42, 2033—2047, 1963; Part 2. 43, 91—112, January 1964.
~ Sandberg I. W. and В ones V. E., On the Properties of Nonlinear integral Equations That Arise in the Theory of Dynamical Systems. Bell System Tech. J., 43, November 1964.
-ил Sa к a w a Y., Solution of an Optimal Control Problem in a Distributed-
11	parameter System. IEEE Trans. Autom. Control, AC-9, No. 4, 420—426, October, 1964.
Ill	СиразетдпновТ. К., К теории оптимальных процессов с распределенными параметрами. Автомат, и те л смех., 25, № 4,463—472, 1964.
112.	Sonneborn К. М. and Van V 1 е с к F. S., The «Bang-Bang» Principle for Linear Control Systems. J. SIAM, Ser. A: Control, 2, No. 2, 151-159, 1965.
113.	S t u b b о r u d A. IL, Minimum Energy Control of a Linear Plant with Magnitude Constraint on the Control Input Signal. 1965 JACC Conference Proceedings.
114	Todd J., Ed., Survey of Numerical Analysis. McGraw-Hill, New York, ’ 1962.
115.	Tung F. and Wang P. К. C., Analysis of Linear Distributed Systems with Random Parameters and Inputs. J. Franklin Inst., 275, No 5, 381 — 391, May 1963.
116.	Waltz F. M., Minimum Peak Amplitude Control. Doctoral Dissertation, University of Michigan, 1965.
117.	W a n g P. К. C., Control of Distributed Parameter Systems. Chapter in «Advances in Control Systems»,Vol. I, Academic Press, New York, 1964.
118.	Wang P. К. C., Optimum Control of Distributed Parameter Systems with Time Delays. IEEE Trans. Autom. Control, AC-9, No. 1, January 1964.
119.	Wang P. К. C. and Bandy M. L., On the Stability of Equilibrium of a Diffusion System with Feedback Control. IEEE Trans. Autom. Control, 1964, No. 2.
120.	W a n g P. К. C. and Tung F., Optimum Control of Distributed-Parameter Systems. Trans. ASME, J. Basic. Eng., 67—79, March 1964.
121.	W о n h a in W. M., and J о h n s о n C., Optimal «Bang-Bang» Control with Quadratic Performance Index. Trans. ASME, Ser. D., J. Appl. Meeh., 86, 107—115, 1964.
122.	Y о s i d a K., Lectures on Differential and Integral Equations. Interscience, New York, I960.
123.	Z a m e s G., Functional Analysis Applied to Nonlinear Feedback Systems. IRE PGGT, 392-404, 1963.
124.	Z a m e s G., Realizability for Nonlinear Feedback. IEEE Trans. Gir-cuit Theory, 2, No. 2, 186-194, Juno 1964.
1—Z	a r a n t о n e 1 1 о E. II., Solving Functional Equations by Contractive Averaging. U. S., Army Math. Res. Center, T. S., R160, 1960.
1-6.	ZarantonelloE. H., The Closure of the Numerical Range Contains the Spectrum. University of Kansas, Department of Mathematics, Technical Report No. 7, July 1964.
У. Портер
Современные основания общей теории системы
М., 1971 г., 556 стр. с илл.
Редактор Е. П. Маслов
Техн, редактор И. Ш. Аксельрод
Корректоры Т. С. Плетнева и Л- С. Сомова
Сдано в набор 2/XI 1970 г.	Подписано
к печати 15/III 1971 г. Бумага 60X90’/м Физ.-печ. л. 34,75 Условн. печ. л. 34,75.
Уч.-изд. л. 35,15. Тираж 8500 экз.
Цена книги 2 р. 64 к. Заказ № 1504
Издательство «Наука»
Главная редакция физико-математической литературы. Москва В-71, Ленинский проспект, 15.
2-я типопрафия издательства «Наука». Москва, шубинский пер., 10.