Ю.Н. Мальцев,
А.С. Кузьмина
ИЗБРАННЫЕ ЛЕКЦИИ
ПО ГЕОМЕТРИИ
ТРЕУГОЛЬНИКА
И ЧЕТЫРЕХУГОЛЬНИКА

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
"АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ"
Ю.Н. Мальцев, А.С. Кузьмина
ИЗБРАННЫЕ ЛЕКЦИИ
ПО ГЕОМЕТРИИ ТРЕУГОЛЬНИКА
И ЧЕТЫРЕХУГОЛЬНИКА
Учебное пособие
Барнаул 2016

УДК 514.112.3(075)
ББК 22.151.01я7
М215
Мальцев, Ю.Н.
Избранные лекции по геометрии треугольника и четырехугольника : учеб¬
ное пособие / Ю.Н. Мальцев, А.С. Кузьмина. Барнаул : АлтГПУ, 2016.
99 с.
ISBN 978-5-88210-834-1
Рецензенты:
Э.К. Брейтигам, доктор педагогических наук, профессор АлтГПУ;
К.О. Кизбикенов, кандидат физико-математических наук, доцент АлтГПУ;
Е.В. Журавлев, кандидат физико-математических наук, доцент АлтГУ
Учебное пособие написано на основе лекций, которые авторы читали в те¬
чение многих лет учащимся старших классов гимназий и лицеев г. Барнаула,
Алейска, а также студентам-математикам АлтГПУ.
Пособие состоит из трех разделов. В первом разделе излагается алгебраиче¬
ский подход к решению большого класса задач по геометрии треугольника. В
частности, предложен некоторый общий метод к доказательству определенно¬
го вида геометрических неравенств. Второй раздел посвящен изложению как
классических результатов, так и недавно опубликованных результатов (в ос¬
новном, в журнале "Forum Geometricorum") по геометрии четырехугольника.
В третьем разделе собран целый ряд задач для самостоятельного решения,
многие их которых сопровождаются подробными указаниями.
Пособие предназначено для учащихся старших классов, учителей средних
школ, а также для студентов и преподавателей математических факультетов
высших учебных заведений.
Рекомендовано к изданию редакционно-издательским советом АлтГПУ 23.06.2016 г.
ISBN 978-5-88210-834-1
© Алтайский государственный
педагогический университет, 2016

Предисловие
На протяжении последних 30 лет преподаватели математических факульте¬
тов АлтГПУ и АлтГУ участвуют в организации и проведении математических
олимпиад, математических боев в школах г. Барнаула и Алейска, а также в
подготовке учащихся старших классов к участию во Всероссийских конкурсах
исследовательских работ “Старт в науку” (МФТИ, г. Москва), “Шаг в буду¬
щее” (Баумановский госуниверситет, г. Москва), “Первые шаги” и др. Эта ра¬
бота сопровождается еженедельными занятиями на математических кружках,
на которых в течение года изучаются не только стандартные олимпиадные те¬
мы по математике, но и разделы олимпиадной математики, отсутствующие в
литературе на русском языке, опубликованные, например, в журналах “Forum
Geometricorum”, “Crux Mathematicorum”.
В течение последних лет студентам-математикам АлтГПУ читаются кур¬
сы “Элементарная математика” и “Методика работы со школьниками, прояв¬
ляющими повышенный интерес к математике”, на которых излагаются до¬
полнительные разделы элементарной геометрии: 1) алгебраический подход
к доказательству геометрических неравенств (фундаментальное неравенство
треугольника и его следствия); 2) классические результаты по геометрии че¬
тырехугольника и недавние результаты Жосевссона по геометрии некоторых
важных типов четырехугольников (см. [32] [44]).
В связи с этим возникла необходимость систематизировать материал и сде¬
лать его доступным не только ученикам средних школ и студентам, но и учи¬
телям средних школ, а также преподавателям вузов, интересующихся элемен¬
тарной геометрией.
Отметим, что нумерация утверждений и рисунков, а порой и обозначения
в каждом параграфе свои.
Авторы благодарят рецензентов, сделавших ряд ценных замечаний при под¬
готовке рукописи к печати.
3

ГЛАВА 1
Фундаментальное неравенство треугольника
Рассмотрим произвольный треугольник АВС. Пусть a, b, c длины его сто¬
рон и p, R, r полупериметр, радиусы описанной (около Л ABC) и вписанной
(в ЛАВС) окружностей соответственно. В настоящей главе мы докажем, что
a, b, c корни следующего уравнения третьей степени:
x3 — 2 px2 + (p2 + r2 + 4Rr)x — 4 pRr = 0.
Таким образом, треугольник АВС однозначно определяется своими парамет¬
рами p, R, r. Отметим, что эти числа p, R, r не являются a’priori произволь¬
ными. Именно, справедливо неравенство Эйлера (см. [11]):
R > 2 r.	(1)
Далее, в 1851 г. Е. Роше (E. Roushe) доказал, что параметр p также нахо¬
дится в определенных пределах, зависящих от R и r (см. [10, 11, 49]):
2R2 + 10Rr — r2 — 2(R — 2r)/R2—2Rr < p2 <	(2)
< 2R2 + 10Rr — r2 + 2(R — 2r)/R2 — 2Rr,
или
(p2 — 2R2 — 10Rr + r2)2 < 4R(R — 2r)3.	(2')
Следуя статье [49], мы будем называть неравенство (2') фундаменталь¬
ным неравенством треугольника («the fundamental triangle inequality»).
Интерес к нему появился в связи с публикацией В. Блундоном в 1965 1966 гг.
работ [20, 21], а также выходом в свет книги [11] молдавских математиков
В. Солтана и С. Мейдмана в 1982 году. В книге [11] приводятся многочислен¬
ные приложения неравенства (2) для доказательства неравенств в геометрии
треугольника. В последние десятилетия в журналах «American Mathematical
Monthly», «Crux Mathematicorum» регулярно появляются задачи (на неравен¬
ства в треугольнике), алгоритм решения которых предполагает хорошее зна¬
ние статей [20, 21], а также книг [10, 11, 47]. Цель настоящей главы изложить
доказательство неравенства (2) и привести многочисленные приложения это¬
го неравенства к решению трудных олимпиадных задач на геометрические
неравенства.
§ 1. Симметрические многочлены и формулы Виета
Многочлен f (x,y,z) от трех переменных x, y, z называется симметри¬
ческим, если при любой перестановке переменных x, y, z он остается неизмен¬
ным, т.е. f(x,y,z) = f(y,x,z) = = f (y,z,x) = f (x,z,y) = f (z,x,y) = f(z,y,x).
4

Например, многочлены Sk = xk + yk + zk, где k = 1,2,... являются симмет¬
рическими. Выделим среди всех симметрических многочленов следующие три
многочлена: о\ = x + y + z, о2 = xy + xz + yz, о3 = xyz. Назовем их элемен¬
тарными симметрическими многочленами. Справедлива следующая
теорема.
Теорема 1. Любой симметрический многочлен от x, y, z можно предста¬
вить в виде многочлена от и\, о2, о3.
Доказательство. Заметим, что
si = x + y + z = 0\,
s2 = x2 + y2 + z2 = (x + y + z)2 — 2 (xy + xz + yz) = of — 2o2,
S3 = 01S2 — 02S1 + З03 = of — З01О2 + З03,
s4 = o1s3 — o2s2 + o3s1 = 04 — 4^2^2 + 2 of + 4o1o3.
Более того, справедлива следующая формула Ньютона:
sk = Oisk—1 — 02sk—2 + 03sk—3
при k > 3.
Действительно,
O1sk—1 — O2sk—2 + O3sk—3
-(xy + xz + yz)(xk—2 + yk—
(xk + yk + zk) + xyk—1
= (x + y + z)(xk 1 + yk 1 + zk 1) —
2 + zk—2) + xyz(xk—3 + yk—3 + zk—3)
+ xzk 1 +yxk 1+yzk 1 + zxk 1 + zyk 1 —
xk 1y
xy
k 1
yk 1z zk
y
xyzk 2 xk 1 z
k2
xzyk 2 -
k2
xk 2yz
t—9	t_1	t_9
xzyk 2	xzk	1 xk 2yz
xyzk	2 = xk - yk - zk = sk.
Так как s1, s2, s3 выражаются в виде многочленов от o1, o2, o3, то, исполь¬
зуя метод математической индукции, получаем, что sk выражается в виде
многочлена от o1, о2, o3 (с целыми коэффициентами).
Обозначим далее через O(xky(zm) симметрический многочлен с наимень¬
шим числом членов, одним из слагаемых которого является xky(zm. Назовем
O(xky(zm) орбитой одночлена xky(zm. Например, O(xyz3) = xyz3 + yzx3+
+xzy3 и O(xky0z0) = sk. Тогда при k = l: O(xkyf = O(xk)O(xf — O(xk+i) =
= sks; — sk+i и O(xkyk) = - [s| — s2k] . Далее, если m < k, m < l, то O(xky(zm) =
= (xyz)m • O(xk—my(—m) = о” • O(xk—my(—m). Из этих равенств следует, что
орбиты одночленов выражаются в виде многочленов через элементарные сим¬
метрические многочлены o1, o2, o3.
Произвольный симметрический многочлен от x, y, z всегда представляет¬
ся в виде суммы орбит одночленов, умноженных на коэффициенты. Следова¬
тельно, любой симметрический многочлен от x, y, z можно представить в виде
многочлена от о1, о2, о3. Теорема доказана.	■
5

O(x3y) = a\a2 - 2of - СГ1СТ3,
- 20103,
Например,
O(x2y) = 0102 - З03,
3y
O(x2y2)
O(x3y2) = 01 o2 - 2о2оз - 0203,
s4 = 04 - 40202 + 2a2 + 40103,
O(x3y3) = 03 + З03 - 3010203,
O(x4y4) = 04 - 4010203 + 4a2a3 + 2a2a3-
В книге [3] приведены многочисленные приложения теоремы 1.
Пусть f (x) = a0x3 + a1x2 + a2x + a3 произвольный многочлен с действи¬
тельными коэффициентами (a0 = 0) и а1, a2, а3 его корни. Тогда
f (x) = ao(x - a1)(x - a2)(x - a3) = a0(x3 - («1 + a.2 + «3)x2 + («102 + «103 +
0.20.3)x — «10203).
Приравнивая коэффициенты при соответствующих степенях, получим, что
«1 + «2 + 03
O1O2 + «1«3 + O2O3
a^a3
01
ao ”
—2
ao
03
ao
(3)
Равенства (4) называются формулами Виета (для многочленов степени
три). Используя введенные ранее обозначения, получим, что 01(a1,a2,a3) =
	1, 02(a1,a2,a3) = — и 03(a1, a2, a3) = 3. Из теоремы 1 следует, что
ao	ao	ao
для любого симметрического многочлена f(x,y,z) его значение f(a1,a2,a3)
a1 a2 a3
является многочленом от —, —, —. Это замечание мы будем многократно
ao ao ao
использовать в дальнейшем.
§ 2. Уравнение для сторон треугольника
Фиксируем обозначения. В треугольнике ABC положим a = BC, b = AC,
c = AB, a = ABAC, в = AABC, 7 = AACB, p = — + ^ + C полупериметр,
S площадь ABC и R, r радиусы описанной и вписанной окружностей
треугольника ABC соответственно (см. рис. 1).
Пусть также I центр вписанной окружности и O центр описанной
окружности, A1, B1, C1 точки касания вписанной окружности со сторонами
треугольника. Тогда AC1 = AB1, BC1 = BA1, CA1 = CB1 и
a = BC = BA1 + CA1 = BC1 + CB1 = (c - AC1) + (b - AB1) = b + c - 2AC1.
6

Откуда следует, что AC\
b + c
2
а
tg 2
a
- = P
а
sin —
	2_
а
C0S2
a. Следовательно,
r
p — a
Далее, по теореме синусов
аа
a = 2R sin а = (4 sin — cos—)R.
Из последних двух равенств следует, что
sin2 — =	;		 и cos2 —
2	4R(p — a)	2
а
ar
а
a(p — a)
4Rr
Поэтому
или
Итак, a
1
2 a 2 a
sin2 —+ cos2 —
2 2
ar	a(p — a)
4R(p — a) +	4Rr
a3 — 2pa2 + (p2 + r2 + 4Rr)a — 4pRr = 0.
корень многочлена
x3 — 2px2 + (p2 + r2 + 4Rr)x — 4pRr = 0.
Аналогично доказывается, что и остальные длины сторон b, c тоже являются
корнями этого многочлена. Из этого следует, в частности, что треугольник
ABC однозначно определяется своими параметрами p, R, r.
По формулам Виета имеем, что
a + b + c = 2p,ab + ac + bc = p2 + r2 + 4Rr, abc = 4Rrp.
Используя теорему 1 предыдущего параграфа, получаем, что произвольный
симметрический многочлен от a, b, c можно выразить в виде многочлена от
2p, p2 + r2 + 4Rr и 4pRr. В частности,
7

a2+b2 + c2 = (a+b+c)2 — 2 (ab+ac+bc) = 4p2 — 2 (p2+r2+4Rr) = 2(p2—r2 —4Rr),
a3 + b3 + c3 = <j\(a, b, c)3 — 3<7i(a, b, c) ■ ^(a, b, c) + 3аэ(а, b, c) =
= 8p3 — 3 - 2 - p - (p2 + r2 + 4Rr) + 3 - 4pRr = 2p(p2 — 3r2 — 6Rr),
1	1	1	a + b +	c 2p 1
ab	ac	bc abc 4pRr	2Rr
(a + b)(a + c)(b + c) = 2p(p2 + r2 + 2Rr).
Числа p, R, r не являются произвольными. Справедлива следующая тео¬
рема Эйлера.
Теорема 1. Квадрат расстояния между центрами вписанной и описанной
окружностей треугольника ABC равен R2 — 2Rr (см. рис. 2).
Доказательство. Рассмотрим рис. 2.
Здесь / - центр вписанной окружности, O - центр описанной окружности,
Ai - точка пересечения биссектрисы A/ с описанной окружностью, MN -
диаметр описанной окружности, проходящий через точки / и O. Тогда М/ ■
/N = A/ ■ /Ai и M/ = R — /O, /N = R + /O, A/ = —^ . Угол ZB/Ai =
sin2
а в	a
— + — (как внешний угол ДВ/A) и ZCBAi = — = ZCAAi. Поэтому ДВ/Ai
a
является равнобедренным (BAi = /Ai). По теореме синусов BAi = 2Rsin—.
r	a
Поэтому (R — /O)(R + /O) = R2 — /O2 = 	^ * 2Rsin — = 2Rr. Откуда
sin —	2
2
следует, что /O2 = R2 — 2Rr. Теорема доказана.	■
Следствие 1 (неравенство Эйлера). R > 2r.
Заметим, что если R = 2r, то / = O и B/ = A/ = R, т. е. треугольник B/A
а в
является равнобедренным. В частности, = и а = в. Аналогично доказы¬
8

вается, что а = 7, т. е. Л ABC правильный треугольник. Легко проверить
справедливость обратного утверждения. Итак, доказано:
Следствие 2. В треугольнике радиус описанной окружности равен диамет¬
ру вписанной окружности тогда и только тогда, когда треугольник явля¬
ется равносторонним.
§ 3. Фундаментальное неравенство треугольника
В предыдущем параграфе мы доказали, что произвольный треугольник од¬
нозначно определяется числами p, R и г, при этом R > 2г. Докажем, что p
находится в некотором сегменте, концы которого являются функциями от R и
г. Для этого сначала опишем все треугольники, у которых радиус описанной
окружности равен R, а радиус вписанной окружности равен г, где R и г про¬
извольные положительные числа такие, что R > 2г. Пусть d = VR2 — 2Rr.
Рассмотрим окружность радиуса R с центром в точке O (см. рис. 1). Пусть
M произвольная точка такая, что MO = d. Проведем окружность радиуса
г с центром в точке M.
Поскольку d + г < R, то меньшая окружность лежит внутри большей.
Пусть TS диаметр большей окружности, проходящий через точку M, A
произвольная точка большей окружности и AB, AC касательные, прове¬
денные из точки A к меньшей окружности и касающиеся ее в точках L, K
соответственно. Докажем, что BC тоже касается меньшей окружности. Пусть
а = ABAC и AQ хорда большей окружности, проходящая через точки
A и M. Тогда AQBC = а, TM • MS = (R — d)(R + d) = R2 — d2 = 2Rr =
га
= AM • MQ =	а • MQ. Откуда следует, что MQ = 2R sin — = TQ. Следо-
sin 2 2
вательно, треугольник QBM является равнобедренным и AQBM = AQMB.
9

а
Так как ZQBC = — = ZBAQ, то ZCBM = ZABM и BM биссектриса уг¬
ла ZABC, т. е. меньшая окружность касается стороны BC и, следовательно,
является вписанной в треугольник ABC.
Выше приведенное рассуждение доказывает следующие утверждения:
1) при R > 2r (т. е. при d = \/R2 — 2Rr > 0) существует бесконечно мно¬
го треугольников, для которых R радиус описанной окружности, а r
радиус вписанной окружности (при R = 2r треугольник является пра¬
вильным и стороны его равны R\/3);
2)	числа R и r являются соответственно радиусами описанной и вписан¬
ной окружностей некоторого треугольника тогда и только тогда, когда
R > 2r.
Выясним далее, в каких пределах может изменяться полупериметр тре¬
угольника с фиксированными параметрами R и r. Для этого рассмотрим рис. 1
§3. Считая, что вершина A находится в верхней полуплоскости относительно
диаметра TS, получим, что треугольник ABC однозначно определяется дли¬
ной отрезка x = AM, где R — d < x < R + d, d = VR2 — 2Rr = OM. Имеем,
что AL = p — a (см. § 2) и
p = (p — a) + a = AL + a = V x2 — r2 + a = V x2 — r2 + 2R s
/	 а а /	 r
= v x2 — r2+4R sin — cos — = v x2 — r2+4R—
'/x2—r2
4Rr.
2
2
= V x2 — r2 (1+	2“)
Построим график функции p = p(x) на сегменте [R — d, R + d]. Поскольку
x4 — 4Rrx2 + 8Rr3
имеем, что p(x) =	 	, то производная p(x) обращается в нуль
	x3yx2 — r2
в точках xi = y/2R(R — d) и x2 = y/2r(R + d). Так как
x
p(R — d) = p(x2) = J 2R2 + 10Rr — r2 — 2(R — 2r) V R2 — 2R"r
и
p(R + d) = p(x1) = \! 2R2 + 10Rr — r2 + 2(R — 2r) V R2 — 2R"r,
то, учитывая знаки функции p'(x) в интервалах (R—d, x1), (x1,x2) и (x2, R + d),
получим, что в точках R — d и x2 функция p(x) достигает своего наименьшего
значения, а в точках R+d и x1 своего наибольшего значения. Следовательно,
график функции p(x) имеет вид, приведенный на рис. 2.
Итак, доказан следующий результат.
Теорема 1. Числа p, R, r однозначно определяют треугольник ABC, при
этом R > 2r и
2R2 + 10Rr — r2 — 2(R — 2r)VR2 — 2Rr < pi2 <	(4)
< 2R2 + 10Rr — r2 + 2(R — 2r)VR2 — 2Rr.
10

Из доказательства теоремы 1 следует, что при фиксированных числах R, r
(R > 2r) параметр p2 наименьшее значение
2R2 + 10Rr - r2 - 2(R - 2r) JR2 - 2Rr
достигает для равнобедренного треугольника ABC (см. рис. 3),
а наибольшее значение
2R2 + 10Rr - r2 + 2(R - 2r) J R2 - 2Rr
параметр p2 достигает для равнобедренного треугольника A1B1C1 (см. рис. 4).
Как уже отмечалось ранее, неравенства (4) были доказаны в 1851 г. Е. Роше.
Неравенства (4) можно переписать в виде:
(p2 - 2R2 - 10Rr + r2)2 < 4R(R - 2r)3.	(5)
Неравенство (5) называется «фундаментальным неравенством треуголь¬
ника» (см. [49]).
Следствие 1. Для произвольного треугольника выполнены неравенства
27r2 < 16Rr
5r2 < p2 < 4R2 + 4Rr + 3r2 <
27
R2
4
11

3V3r < p < - -R.
При этом каждое неравенство превращается в равенство тогда и только
тогда, когда треугольник является правильным.
Доказательство. Имеем, что
2R2 + 10Rr - r2 + 2(R - 2r) VR2—2Rr =
= — (R — 2r — VR2 — 2Rr)2 + (4R2 + 4Rr + 3r2) < 4R2 + 4Rr + 3r2 и
2 R2 + 10Rr — r2 — 2(R — 2r)VW—2RT =
(R — 2r — VR2 — 2Rr)2 + 16Rr — 5r2 > 16Rr — 5r2.
При этом в этих неравенствах достигаются равенства только в случае, ко¬
гда R = 2r или когда исходный треугольник является правильным (см. след¬
ствие 2 § 2).
27
Так как R > 2r (следствие 1 § 2), то 16Rr—5r2 > 27r2 и 4R2 + 4Rr + 3r2 <	R2.
Следствие доказано.	■
Следующее неравенство доказано В. Блундоном в 1965 г.
Следствие 2 (см. [20, 21]). Для любого треугольника справедливо неравен¬
ство
p < 2R + (3V3 — 4)r.
Доказательство. Учитывая теорему 1 § 3, достаточно проверить, что
2R2 + 10Rr — r2 + 2(R — 2r) VR2—2Rr < (2R + (3V3 — 4)r)2,
или
(R — 2r) VR2 — 2Rr < R2 + (6V3 — 13)Rr + (22 — 12V3)r2.	(6)
12

Если исходный треугольник правильный, то r
R
2 и
p = ^2- = 2R +(3V'3 - 4)r.
Иначе R — 2r > 0 и, так как
R2 + (бУ3 — 13)Rr + (22 — 12V3)r2 = (R — 2 r)(R — (11 — 6V3)r),
то неравенство (6) равносильно неравенству
/R2 — 2Rr < R — (11 — 6V3)r.
Возведем в квадрат левую и правую части последнего неравенства:
R2 — 2Rr < R2 — (22 — 12V3)Rr + (229 — 132V3)r2.	(7)
Так как 20 — 12\/3 < 0 и 229 — 132у/3 > 0, то неравенство (7) верно. Таким
образом, следствие доказано.	■
§ 4. О двух методах доказательства геометрических неравенств
Рассмотрим треугольник ABC и вписанную в него окружность (см. рис. 1).
Тогда, полагая BAi = BCi = x, CAi = CBi = y, ABi = ACi = z, получим,
что a = BC = x + y, b = AC = y + z, c = AB = x + z. Подстановка a = ж + y,
b = y + z, c = x + z называется подстановкой Рави (Ravi substitution [29]).
Приведем примеры, иллюстрирующие ее применение. Приведем сначала дру¬
гое доказательство неравенства Эйлера (см. § 2, следствие 1).
Пример 1. Для любого треугольника ABC справедливо неравенство R > 2r.
13

Решение. Так как площадь S треугольника ABC вычисляется по формулам
S =	= pr = = у/p(p — a)(p — b)(p — c), то R =	, r = — и неравенство
R > 2r равносильно неравенству abc >
	, или abc > 8 (p
p
— a)(p — b)(p — c).
Положим a = x + y, b = y + z, c = x + z. Тогда p
искомое неравенство примет вид
a + b + c
2
x + y + z и
(x + y)(y + z)(x + z) > 8xyz.
Последнее неравенство следует из следующих трех очевидных неравенств:
x + y > 2^xy, y + z > 2^yz и x + z > 2\fxz.	■
Пример 2. Пусть a, b, c - длины сторон произвольного треугольника. Тогда
справедливо неравенство
a2b(a — b) + b2c(b — c) + c2a(c — a) > 0.
Решение. Положим a = x + y, b = y + z и c = x + z. Тогда
a2b(a — b) + b2c(b — c) + c2a(c — a) = 2(xy3 + x3z + yz3 — xyz(x + y + z))
2 2 2
,y	x z
= 2xyz(-—|	1	x — y — z) > 0,
zyx
2
2
2
z2
|	x — y — z -
x
2
2
2
y2	y2	x2	x2	z2	z2	y2	x2
так как	+ z > 2\ — • z,	+ y > 2W — • y,	+ x > 2\ — • x и	1	+
z	V z y	у y x	V x	z y
(^- + z^ + ^x + y^ + ^z_ + ^ — 2(x + y + z) > 0.
Второй метод доказательства неравенств в геометрии основан на следу¬
ющем замечании. Предположим, что нам необходимо доказать неравенство
g(x,y,z)	,
-г-)	т рациональная дробь от перемен-
h(x,y, z)
ных x, y и z такая, что g(x,y,z) и h(x,y,z) симметрические многочлены,
а a,b,c длины сторон треугольника ABC. Согласно § 1 § 2 многочлены
g(x, y, z) и h(x,y, z) можно представить в виде многочленов от и\ = x + y + z,
и2 = xy + xz + yz, a3 = xyz, следовательно, их значения g(a, b, c) и h(a, b, c)
можно выразить через параметры p, R, r треугольника ABC. Далее приме¬
няем неравенства, связывающие параметры p, R, r (см. § 3, теорема 1, след¬
ствие 1, следствие 2).
Проиллюстрируем этот метод решением следующих нетривиальных задач.
В 2005 г. в журнале [23] была опубликована задача № 3087.
f (a, b, c) > 0, где f (x,y,z)
14

Пример 3. Пусть a, b, c - длины сторон треугольника ABC и R, r - соот¬
ветственно радиусы описанной и вписанной окружностей для Л ABC. До¬
казать, что
R a + b b + c a + c
3	• — >	1	1	:— > 6.
r c	a	b
(8)
В одном из следующих номеров того же журнала [24] было опубликовано
R	a	b
решение этой задачи, основанное на нетривиальном неравенстве — > — +—,
r	b	a
доказанным в [47].
Предложим свое решение, основанное на утверждениях, ранее доказанных
в § 1 § 3.
Решение. Рассмотрим разность
a + b b + c a + c\	a2b + b2a + b2c + c2b + a2c + a2c
	+	+ ^- I - 6 =	;	6:
cab
(a + b + c)(ab + bc + ac) — 3abc
abc
abc
6
(a + b + c)(ab + bc + ac) — 9abc
abc
2p(p2 + r2 + 4Rr) — 36pRr	2p (p2 + r2 — 14Rr)	p2 + r2 — 14Rr
4pRr
4 pRr
2Rr
При доказательстве мы воспользовались равенствами a+b+c = 2p, abc = 4pRr
и ab + ac + bc = p2 + r2 + 4Rr. Так как p2 > 16Rr — 5r2, то имеем
a + b b + c	a + c\	^	16Rr — 5r2 + r2 —	14Rr	2r(R — 2r)	R — 2r ^
c + a +	b J	>	2Rr	2Rr	R >	'
a + b b + c a + c R — 2r
Таким образом,	1	1	;— > 6 + ■
cab
R	/a + b b + c a + c4
r	V c + a + b
R
> 6. Далее,
з • R.
r
= з • R
r
((a + b + c)(ab + ac + bc) — 3abc)
abc
2 • p(p2 + r2 + 4Rr) — 12pRr	R
4pRr	r
p2 + r2 + 4Rr — 6Rr
2Rr
6R2 — p2 — r2 + 2Rr 6R2 — 4R2 — 4Rr — 3r2 — r2 + 2Rr
2Rr	>	2Rr
2R2 — 2Rr — 4r2	R2 — Rr — 2r2 (R + r)(R — 2r) ^
2Rr	Rr	Rr	>
так как R > 2r и p2 < 4R2 + 4Rr + 3r2.
Итак, доказан следующий результат.
15

Теорема 1. Для любого треугольника справедливы неравенства
3 . R > з R	_ (R + r)(R	— 2 r) > a + b	+ a +	c + b+_c	>	g + R — 2 r >	g
r ~ r	Rr	~ c	b	a	~	R ~
При этом выполняется равенство (хотя бы в одном неравенстве) тогда и
только тогда, когда треугольник является правильным.
Наш метод позволил нам не только найти новое решение выше приведенной
задачи, но и существенно усилить неравенства (8).
В 1961 г. на международной математической олимпиаде была предложена
следующая задача (см. [14, с. 43]):
Пример 4. Доказать, что для любого треугольника справедливо неравен¬
ство
a2 + b2 + c2 > 4V3S,
(9)
где a, b, c, S - соответственно длины сторон и площадь треугольника.
Это неравенство было впервые доказано в 1919 г. работе [50]. В 1937 г.
П. Финслер и Г. Хадвигер в работе [26] усилили неравенство (9), доказав, что
a2 + b2 + c2 > 4^3S + (a — b)2 + (a — c)2 + (b — c)2.	(10)
Недавно румынские математики Ц. Лупу и К. Похоате в работе [46] обоб¬
щили неравенство (10), доказав, что
a2 + b2 + c2 > 4S
3 + 4-4—^
4R + r
+ (a —
b)2 + (a — c)2 + (b — c)2.
(11)
Покажем далее, что на самом деле справедливо следующее усиление нера¬
венства (11).
Теорема 2. Для произвольного треугольника ABC с длинами сторон a, b, c
и площадью S справедливо неравенство
a2 + b2 + c2 > 4S\J3 + - r2r + (a — b)2 + (a — c)2 + (b — c)2.	(12)
Доказательство. Рассмотрим разность
a2 + b2 + c2 — (a —	b)2	—	(a — c)2	—	(b — c)2 =	2(ab + ac +	bc) —	(a2 + b2 +	c2).
Согласно § 2, ab + ac + bc = p2 + r2 + 4Rr и a2 + b2 + c2 = 2(p2 — r2 — 4Rr).
Значит, a2 + b2 + c2 — (a — b)2 — (a — c)2 — (b — c)2 = 2(ab + ac+bc) — (a2 + b2 + c2) =
= 2(p2 + r2 +4Rr) — 2(p2 — r2 — 4Rr) = 4r(r + 4R). Так как S = pr, то искомое
неравенство эквивалентно следующему неравенству
I	R — 2r
4R + r > pJ 3 + —r— .	(13)
16

Согласно теореме 1 § 3 p2 < 2R2 + 10Rr — r2 + 2(R — 2r) VR2 — 2Rr. Поэтому
искомое неравенство (13) будет доказано, если мы докажем, что
(4R + r)2 > (2 R2 + 10Rr — r2 + 2 (R — 2r) VR2—2& )(з + R - 2M . (14)
Введем новую переменную t = —. Согласно неравенству Эйлера t > 2. Деля
r
левую и правую части неравенства (14) на r2, получим, что (14) равносильно
неравенству
16t2 + 8t + 1 > (2t2 + 101 — 1 + 2(t — 2) Vt2 — 2t) (^3 +	,
или
16t3 + 8t2 +1 > (4t — 2)(2t2 + 10t — 1) + (4t — 2) • 2 • (t — 2)Vt2 — t.
Раскрыв скобки в последнем неравенстве и приведя подобные слагаемые, по¬
лучим неравенство, равносильное (14)
(t — 2)(8t2 — 12t + 1) > 2(t — 2)(4t — 2)Vt2 — 2t.	(15)
Если t = 2, то R = 2r и согласно § 2 исходный треугольник является пра¬
вильным. В этом случае (12) превращается в равенство. Пусть t > 2. Тогда
неравенство (15) равносильно неравенству
(8t2 — 12t + 1)2 > 4(4t — 2)2(t2 — 2t),
которое после приведения подобных можно переписать в виде
16t2 + 8t + 1 = (4t + 1)2 > 0.
Теорема доказана.
Замечание 1. Используя аналогичные методы, можно усилить неравен¬
ство (12), доказав, что для произвольного треугольника справедливо нера¬
венство
a2 + b2 + c2 > 4S
'	R2 — 4r2
3 + —
+ (a —
b)2 + (a — c)2 + (b — c)2.
Пример 5. В теории неравенств хорошо известно неравенство Несбит¬
та (Nesbitt’s inequality, [29]): для любых положительных чисел a, b, c спра¬
ведливо неравенство
a b c	3
Т	I	I	т > —.
b+c a+c	a+b	2
Интересно уточнить это неравенство, если a, b, c длины сторон треуголь¬
ника. Оказывается, справедлив следующий результат.
17

Теорема 3. Для любого треугольника выполняется неравенство
3( R — 2r
2 V + 9R - 2r
a b c 3	(R — 2r)(2R + r)
< b + c + a + c + a + b < 2 + 2(2R2 + 3Rr + 2r2)
< 2.
Доказательство. Имеем, что
a
b + c
+
bc
		1	T
a + c a + b
a3 + b3 + c3 + 3abc + (a2c + a2b + b2a + b2c + ac2 + bc2)
(a + b)(a + c)(b + c)
(a2 + b2 + c2)(a + b + c) + 3abc
(a + b)(a + c)(b + c)
Согласно результатам § 2, a2 + b2 + c2 = 2(p2 — r2 — 4Rr), (a + b)(b + c)(a + c) =
= 2p(p2 + r2 + 2Rr), abc = 4pRr. Следовательно,
a b c	2p • 2(p2 — r2 — 4Rr) + 12pRr	4r2 + 6Rr
b + c a + c a + b	2p(r2 + r2 + 2Rr)	p2 + r2 + 2Rr.
Далее, согласно следствию 1 § 3 имеем, что
16Rr — 5r2 < p2 < 4R2 + 4Rr + 3r2.
Поэтому получаем, что
— (4r2 + 6Rr)	—(4r2 + 6Rr)
(16Rr — 5r2) + 5r2 + 2Rr < p2 + r2 + 2Rr
<
— (4r2 + 6Rr)
2
4r2 + 6Rr
(16Rr — 5r2) + r2 + 2Rr
33
или —|—
2 2
R	2r
b + c
b
+
b
(4R2 + 4Rr + 3r2) + r2 + 2Rr ’
c	4r2 + 6Rr
a + c a + b
2
4R2 + 6Rr + 4r2 ’
(R — 2r)(2R + r)
9R - 2r
(R — 2r)(2R + r)
2R2 + 3Rr + 2r2
^	..	.	_	^ 3
’	+	+ alb < 2 + 2(2R2 + 3Rr + 2r2)
b + c a + c
2R2 — 3Rr — 2r2
2R2 + rRr + 2r2
. Так
< 1 , то
a
<
3 +	(R — 2r)(2R + r) < 3+1 =2
2	+ 2(2 R2 + 3Rr + 2r2)	2 + 2	.
Теорема доказана.	■
Пример 6. Пусть f (ж) - непрерывная функция, определенная на интервале
[0, то) и для любых чисел a > 0, в > 0 таких, что a + в = 1 справедли¬
во неравенство (для любых неотрицательных чисел xi, x2): f (axi + вж2) <
< af (xi) + ef (x2) (см. рис. 2, где ж = axi + вх2). Тогда функция f (x) назы¬
вается выпуклой вниз (см. [15, С. 294]). Известно, что если функция f (x)
имеет непрерывную производную f;(x), а также конечную вторую произ¬
водную f"(x), которая неотрицательна на [0, то), то f (x) - выпуклая (вниз)
функция (см. теорему 2 [15, С. 299]).
18

Рис. 2
Это утверждение дает нам способ проверки выпуклости функции, имеющей
вторую производную. Справедливо следующее утверждение.
Предложение 1. Пусть f (x) - выпуклая (вниз) функция, определенная на
[0, <xi). Тогда для любых чисел оц > 0, ..., ап > 0 таких, что оц + • • • + ап = 1,
n > 2 и для любых неотрицательных чисел x\,...,xn справедливо неравен¬
ство (Йенсена)
f (aixi +	+ о.пхп) < af(xi) +	+ o.nf {xn).	(16)
Доказательство. Воспользуемся методом математической индукции. При
n = 2 неравенство (16) следует из определения. Сделаем предположение ин¬
дукции об истинности неравенства (16) при n = k, докажем, что оно верно
при n = k + 1. Пусть xi,...,xk+i	произвольные неотрицательные числа,
а1,... , ak+i произвольные положительные числа такие, что ai + • • • + a^+i =
1. Тогда
f (aixi + • • • + ak+ixk+i) =
= f aixi + • • • + a k—ix k — i + (ak + ak+i)
akxk
■ + ■
ak+i
< aif (xi) + • • • + ak—if (xk—i) + (ak + ak+i)f
ak + ak+i ak + ak+i
akXk	,	ak+i
■ + -
ak + ak+i ak + ak+i
xk+i	<
xk+i <
< aif (xi) + ^ • ^+ak—if (xk—i) + (ak+ak+i)	f (xk) +			f (xk+i)
ak + ak+i	ak + ak+i
= aif (xi) + • • • + akf (xk) + ak+if (xk+i).
Предложение доказано.	■
В частности, для выпуклой (вниз) функции f (x) справедливо неравенство
f ^xi + • • • + xn^ < f(xi) + • • • + f (xn)
19

Рассмотрим функцию f (x) = xm, где m > 2. Поскольку при x е [0, <х) мы
имеем, что f"(x) = m(m — l)xm-2 > 0, то f (x) выпуклая (вниз) функция. В
частности,
xi+x2+x3\ m	xm+xm+xm
, < .
3	)	-	3
Интересно исследовать последнее неравенство для случая, когда x1 = a, x2 = b,
x3 = c длины сторон треугольника. Точнее, найдем оценки снизу и сверху
для разности
am + bm + cm	fa + b + Дm
33
при m = 2, 3.
Справедливы следующие результаты.
Теорема 4. Для любого треугольника справедливо неравенство
2
8	,	a2 + b2 + c2	fa + b + c
9r(R — 2r)  	3	—
- 8R(R—2r)-
(17)
Доказательство. Имеем, что
a2 + b2 + c2 fa + b + c\ 2 2 (p2 — r2 — 4Rr) 4p2
39
2 p2 — 6r2 — 24Rr	2(p2 — 3r2 — 12Rr)
9
9
Из следствия 1 § 3 следует, что
16Rr — 5r2 — p2 — 4R2 + 4Rr + 3r2.
Поэтому имеем
a
3 + b3 + c3	(°±|±£)2 = 2(P2 — 3r2 — 12Rr) -
3
9
28
— -(4R2 + 4Rr + 3r2 — 3r2 — 12Rr) = - R(R — 2r)
У	9
+ b3 + c3	/о + 6 + Л = 2(p2—3r2—i2Rr) > 2(i6Rr—5r2—3r2—12Rr)
3	9	9
3
- r(R — 2r).
9
Теорема доказана.
По теореме 4 если
"3 + b3 + c3	fa + b + c'
^a+|+c^2, то о - -r(R — 2R) - 0 и
33
R = 2r. Согласно § 2 исходный треугольник в этом случае является правиль¬
ным.
3
3
и
20

Теорема 5. Для любого треугольника справедливо неравенство
52
— V3r2(R — 2r) <
а3 + b3 + c3	/а + b + c
3
3
<
23^3
R2(R — 2r).
Доказательство. Согласно § 2 a3+b3+c3 = 2p(p2 — 3r2 —6Rr). Следовательно,
a3 + b3 + c3 /а + b + c\ 2p(p2 — 3r2 — 6Rr) 8 3 2p
3	I 3	) =	3	27P =27
— T^p3 = 2p (5p2—27r2—54Rr).
3V3,
3
Из § 3 следует, что 3\/3r < p < —— R и 16Rr — 5r2 < p2 < 4R2 + 4Rr + 3r2.
Поэтому
а3 + b3 + c3 — (аЛ^±Лу < | • Mr(2or2 + 20Rr + 15r2 — 27r2 — 54Rr) =
= ^R(R — 2r)(10R + 3r) < ^R(R — 2r)(10R + 3R) = 23V5R2(R — 2r).
9	9	2	9
Далее найдем оценку снизу. Имеем
а3 + b3 + c3	7 а + b + c4 3
3
(^+3+^) = §(5p2 — 27r2 — 54Rr) >
2	52
> — ^ 3'^3 • r(5(16Rr — 5r2) — 27r2 — 54Rr) = — v3r2(R — 2r).
52
Теорема доказана.
Замечание 2. Если
а3 + b3 + c3	(а + b + c
3
52
3
то непосредственно из
теоремы 5 следует, что 0 < — \/3r2(R — 2r) < 0 и R = 2r. Согласно § 2
9
в этом случае исходный треугольник является травильным.
Рассмотрим далее рис 3. Здесь Ci точка касания вписанной окружности со
стороной AB. В § 2 мы доказали, что AC1 = p — а, где p = —+ ^ + . Следова-
2
1
а
tg 2
1 + cos а
тельно, p—а = r	а = = r^/  	, а = 2R sin а = 2R\J(1 — cos а)(1 — sin а)
1 cos а
p =(p — а) + а = r • < —+	+ 2Ra/(1 — cos а)(1 + cos а).
V 1 — cos а
Возведя левую и правую части этого равенства в квадрат, получим, что
4R2 cos3 а — 4R(R + r) cos2 а + (p2 + r2 — 4R2) cos а + (2R + r)2 — p2 = 0.
Аналогично доказывается, что cos в, cos 7 тоже являются корнями многочлена
4R2x3 — 4R(R + r)x2 + (p2 + r2 — 4R2)x + (2R + r)2 — p2 = 0.	(18)
3
9
3
и
21

Согласно формулам Виета (см. § 1) получаем, что
cos а + cos в + cos 7 :
R + r
cos а cos в + cos а cos 7 + cos в cos 7 =
cos a cos в cos 7 =
Из последнего равенства следует, что:
p2 + r2 — 4R2
4R2	’
p2 — (2R + r)2
4R2	'
(19)
1)	треугольник ABC является прямоугольным тогда и только тогда, когда
p = 2R + r;
2)	треугольник ABC является тупоугольным тогда и только тогда, когда
p < 2R + r;
3)	треугольник ABC является остроугольным тогда и только тогда, когда
p > 2R + r.
П
Предположим далее, что в треугольнике ABC два угла не превосходят —.
П	П	П 11
Пусть а < —, в <77	и а >	в. Тогда 7	>	— и cos а > —, cos в >7,	cos а < cos в
^оо	3 22
и cos 7 <	. Рассмотрим график функции
f (ж) = 4R2x3 — 4R(R + r)x2 + (p2 + r2 — 4R2)x + (2R + r)2 — p2.
Так как cos 7 < - < cos а < cos в, то из разложения
f (x) = 4R2(x — cos y)(x — cos а)(ж — cos в)
22

следует, что на промежутке [cos 7, cos а] функция f (x) неотрицательна. В
частности,
f (1) = 4R2 • 1 - 4R(R + r) • 4 + (p2 + r2 - 2R2) • 1 + (2R + r)2 - p2 =
3	p2
= 2(R + r)2 - ~2 ^ 0,
т. е. p < /3(R + r).
Итак, доказано:
п
Предложение 2. Пусть в треугольнике ABC два угла не превосходят —.
Тогда
Р < /3(R + r).
В 2004 г. в журнале [22] была предложена следующая задача.
п
Пример 7. Пусть в треугольнике ABC два угла не превосходят —. Дока¬
зать, что
a
2 + b2 + c2 < 6R2(cos а + cos в + cos у).
Решение. Поскольку a2 + b2 + c2 = 2(p2 — r2 — 4Rr) (см. § 2) и, кроме того,
cos а + cos в + cos 7 :
a2
R + r
R
(см. (19)), то искомое неравенство равносильно
неравенству 2(p2 — r2 — 4Rr) < 6 • R2 •
R + r
R
p2 < 3R2 + 7Rr + r2. Из
предложения 2 следует, что p2 < 3(R + r)2 = 3R2 + 6Rr + 3r2. Так как 2r < R,
то p2 < 3R2 + 6Rr + 3r2 < 3R2 + 7Rr + r2.	■
Выше приведенная задача делает правдоподобным следующее предположе-
п
ние: пусть в треугольнике два угла не превосходят — и n натуральное число,
тогда
' + bn + cn < 2n—1 • 3nRn(cosn—1 а + cosn—1 в + cosn—1 7).
3/3,
(20)
При n =1 мы получаем известное неравенство p < R (см. § 3), при n = 2
пример 7. К сожалению, мы не знаем ответа на эту гипотезу в общем случае.
Приведем доказательство справедливости этой гипотезы при n = 3,4.
Имеет место следующий результат.
п
Теорема 6. Пусть в треугольнике два угла не превосходят —. Тогда спра¬
ведливо неравенство
’ + b3 + c3 < 12/3R3(cos2 а + cos2 в + cos2 7).
(21)
a
a
23

Доказательство. Используя равенства (19) и тождества из § 2, получаем,
что
cos2 a+sin2 в+cos2 7 = (cos a+sin в+cos 7)2-2(cos a cos в+cos a cos 7+cos в cos 7)
R + r \2 2(p2 + r2 — 4R)	1
R
4R2
= —^ (—P2 + r2 + 4Rr + 6R2).
2R2
Таким образом, неравенство (21) равносильно неравенству
p(p2 — 3r2 — 6Rr + 3^3pR) < 3V3(6R3 + 4R2r + Rr2).	(22)
Согласно предложению (2) p < \/3(R + r). Следовательно, имеем
p(p2 — 3r2 — 6Rr + 3^3pR) < V3(R + r)[3(R + r)2 — 6Rr + 3^3R-V3(R + r)] =
= 3^3(4R2 + 7R2r + 3Rr2).
Для доказательства искомого неравенства (22) достаточно проверить, что
3V3(4R3 + 7R2r + 3Rr2) < 3^3(6R3 + 4R2r + Rr2),
или 3Rr + 2r2 < 2R2. Последнее неравенство справедливо, поскольку имеем
(R — 2r)(2R + r) > 0. Теорема доказана.	■
Тем самым наша гипотеза (20) справедлива при n = 3. Для проверки ис¬
тинности неравенства (20) при n = 4 необходимо выразить а4 + b4 + c4 и
cos3 a + cos3 в + cos3 7 через параметры p, R, r.
Предложение 3. Для любого треугольника справедливо равенство
а4 + b4 + c4 = 2[(p + r)2 — 2r2 — 4Rr][(p — r)2 — 2r2 — 4Rr].
Доказательство. Имеем, что
а4 + b4 + c4
= (а2 + b2 + c2)2 — 2(a2b2 + a2c2 + b2c2) =
(а2 +	b2	+	c2)2	— 2	[(ab + ac +	bc)2	— 2abc(a + b + c)]	=
= (a2 + b2 + c2)2 — 2(ab + ac + bc)2 + 4abc(a + b + c) =
4(p2 — r2 — 4Rr)2 — 2(p2 + r2 + 4Rr)2 + 4 ■ 4pRr ■ 2p =
= 2 [(p — r)2 — 2r2 — 4Rr] [(p + r)2 — 2r2 — 4Rr] .
Предложение доказано.
Предложение 4. Для любого треугольника справедливо равенство
cos3 a + cos3 в + cos3 7
4R3 + 12R2r + 6Rr2 + r3 — 3p2r
4R3
24

Доказательство. Из § 1 и из равенств (19) следует, что
cos3 а + cos3 в + cos3 7 = (cos а + cos в + cos y)3-
— 3(cos а + cos в + cos y)(cos а ■ cos в + cos а ■ cos в + cos в ■ cos y) +
+ 3 cos а cos в cos y =
R + r\ 3	„ R + r p2 + r2 — 4R2
R
3
1
R
4R2
+ 3 ■ 4R2 [P2 — (2R + r)2]
= — |4R3 + 4r3 + 12R2r + 12Rr2 — 3Rp2 — 3Rr2 + 12R3—
4R3 1
— 3rp2 — 3r3 + 12R2r + 3p2R — 12R3 — 3Rr2 — 12R2r] =
= -^(4R3 + 12R2r + 6Rr2 + r3 — 3p2r).
4R3
Предложение доказано.	■
Справедливо следующее утверждение.
п
Теорема 7. Пусть в треугольнике ABC два угла не превосходят Тогда
справедливо неравенство
a4 + b4 + c4 < 72R4(cos3 а + cos3 в + cos3 y).	(23)
Доказательство. Подставим в левую и правую части неравенства (23) вы¬
ражения через p, R, r согласно предложениям 3, 4. Получим равносильное
неравенство
((p—r)2—2r2—4Rr)((p+r)2—2r2—4Rr) < 9(4R4+12R3r+6R2r2+R3r—3p2Rr),
или
((p — r)2 — 2r2 — 4Rr)((p + r)2 — 2r2 — 4Rr) + 27p2Rr <	(24)
< 9(4R4 + 12R3r + 6R2r2 + Rr3).
Так как по предложению 2 имеем p < \/3(R + r), то
((p — r)2 — 2r2 — 4Rr)((p + r)2 — 2r2 — 4Rr) + 27p2Rr <
< [(V3R+(V3— 1)г)2—2r2—■4Rr][(V3R+(V3+1)r)2—2r2—■4Rr]+27Rr-3(R+r)2 =
= 9R4 — 8r4 + 16R2r2 + 93R3r + 65Rr3.
Для доказательства неравенства (24) достаточно проверить, что
9R4 — 8r4 + 166R2r2 + 93R3r + 65Rr3 < 36R4 + 108R2r + 54R2r2 + 9Rr3,
или 112R2r2 + 56Rr3 < 27R4 + 15R3r + 8r4. Последнее неравенство можно
переписать в виде неравенства (R — 2r)(27R3 + 69R2r + 26Rr2 — 4r3) > 0,
истинность которого очевидна. Теорема доказана.	■
Следующая задача была предложена на математической олимпиаде в Ве¬
ликобритании в 1967 г. (см. [4, § 13]).
25

Пример 8. Доказать, что для произвольного треугольника справедливо нера¬
венство
cos2 а + cos2 в + cos2 7 > —.
4
Решение. При доказательстве теоремы 6 мы заметили, что
2	2 п 2	6 R2 + 4 Rr + r2 — p2
cos2 а + cos p + cos2 7 =		.
2 R2
6 R2 + 4Rr + r2 — p2	3
Значит, искомое неравенство равносильно	—г	> -, или
2 R2	4
9R2 + 8Rr + 2r2 > 2p2.	(25)
Согласно следствию 1 § 3 имеем, что 2p2 < 2(4R2 + 4Rr + 3r2). Поэтому
(9R2 + 8R + 2r2) — 2p2 > (9R2 + 8Rr + 2r2) — 2(4R2 + 4Rr + 3r2) =
= R2 — 4r2 = (R — 2r)(R + 2r) > 0
и неравенство (24) доказано.	■
Пример 9 ([4]). Доказать, что для любого нетупоугольного треугольника
справедливо неравенство
sin а + sin в + sin 7 > cos а + cos в + cos 7.
Решение. Поскольку sin а = —, sin в = —, sin 7 = — и, кроме того,
у	2R’ в 2R’ Y	2R ’ Р	’
(cos а + cos в + cos 7)
R + r
R
(см. равенства (19)), то искомое неравенство равносильно неравенству
a + b + cR + r	„	/ч
—2r—> —^, или p > R + r.	(26)
По условию исходный треугольник не является тупоугольным. Поэтому cos а > 0,
cos в > 0 и cos 7 > 0. Следовательно,
p	p2 — (2R +r)2	0
cos а cos в cos 7 =		 > 0,
4R2
p > 2R + r>R + r
и неравенство (26) доказано.
26

§ 5. О некоторых неравенствах для длин сторон треугольника
Рассмотрим произвольный треугольник ABC и фиксируем для него следу¬
ющие обозначения: положим R, r радиусы описанной и вписанной окружно¬
стей треугольника ABC соответственно, I центр вписанной окружности,
O центр описанной окружности треугольника ABC, d = IO, a = BC,
a = ABAC (см. рис. 1).
В работе [18] доказана следующая интересная теорема (автор работы [18]
отметил, что равенства в условии теоремы 1 достигаются для некоторых видов
равнобедренных треугольников).
Теорема 1. Для треугольника ABC справедливы неравенства:
(4) 8R2 — 8Rr — 4r2 — 8R\/R2 — 2Rr < a2 < 8R2 — 8Rr — 4r2+8RVR2 — 2Rr.
Доказательство. Рассмотрим рис. 1. Используя неравенство треугольника,
имеем, что
Рис. 1
R ’
AO — IO < AI < AO + OI.
a
Поскольку ABAI = —, то AI =
OI2 = R2 — 2Rr. Следовательно,
r
, то AI = 	a. По
. a •
sln2
По теореме 1 § 2 настоящей главы
R — \/ R2 — 2 Rr <
r
< R + / R2 — 2 Rr,
. a
sln2
27

или
К1 Ч1 -Rr <а< 1 . + -1|.
Из неравенств (27) следует, что
1
2
R
2 r
R
а 1
_	1 —- —W 1 — -	< sin2- <-	1 — - + А 1 —	.
22
R
2r
R
(27)
(28)
гл	2 а 1	-2 а	10-2 а
Откуда, исходя из равенств cos2— = 1 — sin2 — и cos а =1 — 2sm2 —,
получаем, что
V2 L r Г 2r	а V2 L r Г 2r
ТV1 + R — V1 — R<cos2 <TV R+ V1 — R (29)
r	2r	r	2r
R О/1 — R <cos а < R + V1 — R.
Поскольку sin2 а = 4 sin2 — • cos2 —, то, используя неравенства (28) и (29),
имеем, что
2r	r2	2r о	2r r2	2r
2 — R	— R— Ч1 — R	<sin2 а	< 2 — R — R	W1 — R.
По теореме синусов a = 2R • sin а. Следовательно,
8R2 — 8Rr — 4r2 — 8RRR2 — 2Rr < a2 < 8R2 — 8Rr — 4r2 + 8RRR2 — 2Rr.
По теореме 1 § 2 настоящей главы d = \/R2 — 2Rr. Поэтому четвертое
неравенство из условия теоремы 1 можно переписать в виде:
4((R — d)2 — r2) < a2 < 4((R + d)2 — r2).	(30)
Авторам настоящего пособия удалось доказать более точные оценки (сверху
и снизу) для a2. Справедлива следующая теорема (см. [45]):
Теорема 2. Для произвольного треугольника ABC справедливы неравенства:
(1) если 2r < R < (R + 1)r, то
4((R — d)2 — r2) < 16R2r2 (R(R+)2d—4 r2 < a2 < 16R2r2< 4((R + d)2 — r2)
(2) если (R + 1)r < R, то
4((R — d)2 — r2) < 16R2
2 (R + d)2 — r2
(R + d)4
< a2 < 4R2 < 4((R + d)2 — r2).
и
r
28

Для доказательства теоремы нам потребуется следующая лемма.
Лемма 1. В треугольнике ABC центр описанной окружности O лежит
внутри вписанной окружности тогда и только тогда, когда 2r < R < (\/2 + 1 )r.
Доказательство. Известно, что d = л/R2—2Rr и 2r < R (см. § 2). Более
того, центр описанной окружности O лежит внутри вписанной окружности
треугольника ABC тогда и только тогда, когда d2 < r2. Последнее неравенство
равносильно неравенству
R2 — 2Rr — r2 < 0, или (R — (V2 + 1)r)(R + (V + 1)r) < 0.
Таким образом, центр описанной окружности O лежит внутри вписанной окруж¬
ности в том и только в том случае, когда 2r < R < (\/2 + 1)r.	■
Теперь мы можем приступить к доказательству теоремы 2. Заметим, что
мы не только докажем неравенства из условия теоремы 2, но и покажем, что
эти неравенства дают более точную оценку квадрата стороны треугольника,
чем неравенства (30).
Доказательство теоремы 2. Фиксируем два числа R и r, такие, что
2r < R. Рассмотрим окружность радиуса R и с центром в точке O. Пусть
MN диаметр этой окружности и I точка на MN, такая, что IO = d =
= VR2 — 2Rr (см. рис. 2).
Возьмем произвольную точку A на окружности и проведем касательные AB
и AC к окружности радиуса r с центром в точке I. В книге [11] доказано, что
отрезок BC также касается этой окружности и, более того, все треугольники,
для которых R и r являются радиусами описанной и вписанной окружностей
29

соответственно, получаются таким образом (см. также § 3). Пусть x = |AI|.
Тогда можно считать, что |MI| < x < |IN|, т. е. x е [R — d; R + d] (см.
§ 3). Пусть ABAC = а и С\ проекция точки I на AB. Тогда |ACi| =
= Vx2 — r2 = xcos , |ICi| = r = xsin . Следовательно,
а a	r \/x2 — r2
a = 2R sin a = 4R sin cos = 4R — •
2	2	x x
4Rr
Vx2 — r2
т. е. a2(x) =
16R2r2
(x2 — r2). Исследуем поведение функции a2(x) на сег-
(2r2 — x2) и ее корнем
менте [R — d; R + d]. Имеем, что (a2(x))' = —
x
на промежутке (0; то) является число x0 = \/2r, при этом (a2(x))' < 0 при
x > x0 и (a2(x))' > 0 при 0 < x < x0. Значит, в точке x0 функция a2(x) имеет
максимум. Рассмотрим, далее, следующие случаи.
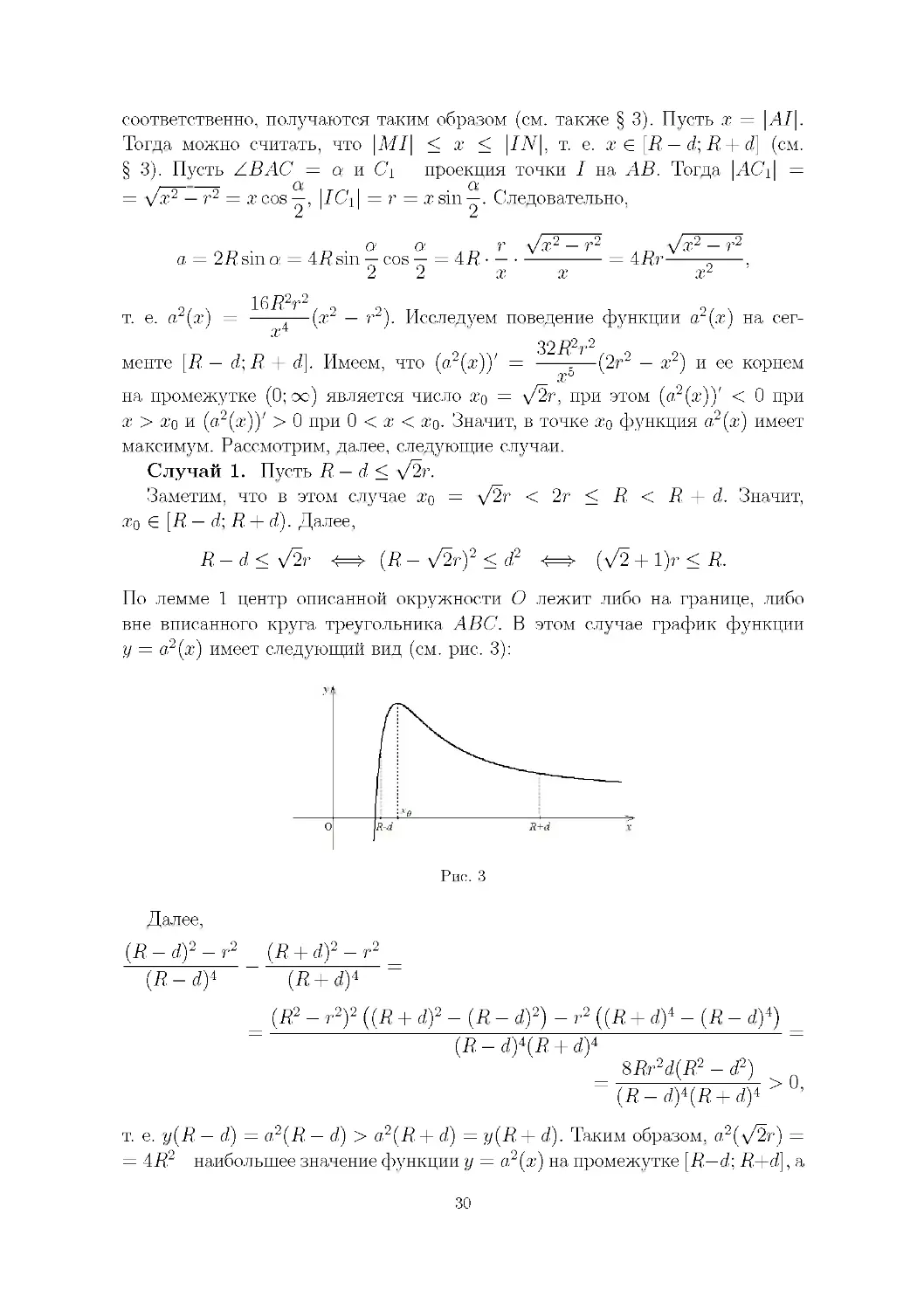
Случай 1. Пусть R — d < \/2r.
Заметим, что в этом случае x0 = \/2r < 2r < R < R + d. Значит,
x0 е [R — d; R + d). Далее,
R — d < V2r	(R — V2r)2 < d2	(V2 + 1)r < R.
По лемме 1 центр описанной окружности O лежит либо на границе, либо
вне вписанного круга треугольника ABC. В этом случае график функции
y = a2(x) имеет следующий вид (см. рис. 3):
Далее,
(R — d)2 — r2
(R — d)4
(R + d)2 — r2 _
(R + d)4	=
(R2 —	r2)2	((R +	d)2	— (R —	d)2)	—	r2	((R + d)4 —	(R	— d)4)
(R — d)4(R + d)4
8Rr2d(R2 — d2)
(R — d)4(R + d)4
> 0,
т. е.	y(R — d)	=	a2(R — d)	>	a2(R + d)	=	y(R + d).	Таким образом, a2(V2r)	:
= 4R2 наибольшее значение функции y = a2(x) на промежутке [R—d; R+d],
x
4
x
2
а
30

a2(R + d)
16R2r2 ((R + d)2 - r2)
наименьшее значение функции y = a2(x)
(R + d)4
на этом же промежутке. Итак, мы доказали, что при R > (\/2 + 1)r справед¬
ливы неравенства
16R2r
2 2(R + d)2 — '
(R + d)4
< a2 < 4R2
где d2 = R2 — 2Rr.
Покажем теперь, что эти оценки лучше неравенств (30). Поскольку R >
> (V2 + 1)г, то мы имеем, что R2 — 2Rr — r2 > 0. Поэтому получаем, что
(R2 — 2Rr — r2) + 2Rd > 0. Последнее неравенство эквивалентно неравенству
4R2 < 4((R + d)2 — r2). Далее, (R — 2r) + d > 0, так как R > 2r. Также,
поскольку R > 2r, мы получаем, что
(R — 2r) + d > 0 —^ 2Rr< (R + d)2 —^ 4R2r2 < (R + d)4 —^
4R2(R + d)2 — (R + d)4 < 4R2((R + d)2 — r2).
Последнее неравенство эквивалентно неравенству
(R2 — d2)2(R + d)2 — r2(R + d)4 < 4R2r2((R + d)2 — r2),
так как R2 — d2 = 2Rr. Это доказывает, что
4((R — d)2
— r2) < 16R2r2
(R + d)2 — r2
(R + d)4
Итак, мы показали, что
4((R — d)2
— r2) < 16R2r2
(R + d)2 — r2
(R + d)4
< a2 < 4R2 < 4((R + d)2
r2)
при R > (^2 + 1)r.
Теперь рассмотрим случай 2.
Случай 2. Пусть R — d W2r.
По лемме 1 условие R — d > \/2r означает, что центр описанной окружности
O лежит внутри вписанного круга. Так же, как это было сделано в первом
случае, можно показать, что a2(R — d) > a2(R + d). Тогда график функции
y = a2(x) имеет следующий вид (см. рис. 4):
Это означает, что при R > \/2r + d неравенства
16R2r2
(R + d)2 — r2
(R + d)4
< a2 < 16R2r2
(R — d)2 — r2
(R — d)4
(31)
выполняются. Наконец, сравним оценку (31) с оценкой (30). Поскольку R > 2r,
то мы имеем, что (R — d)4 < 16r4 < 4R2r2. Наконец,
(R—d)4 < 4R2r2	4R2r2((R—d)2 — r2) < 4R2r2(R—d)2—r2(R—d)4
31

4R2r2((R -	d)2	-	r2)	< (R2	-	d2)2(R -	d)2	-	r2(R -	d)4
,(R - d)2 - r2
16R2r2(
< 4((R + d)2 - r2).
(R - d)4
Заметим, что a2(R - d) = 4((R + d)2 - r2) в том и только в том случае, когда
треугольник ABC является правильным. Далее, докажем, что
4((R - d)2 - r2) < 16R2r2(R(R+d-4r2.
Действительно, справедливо неравенство (R - 2Rr) + d > 0. Поэтому
(R - 2Rr) + d > 0	(R + d)2 > 2Rr
^ 4R2(R + d)2 - (R + d)4 < 4R2((R + d)2 - r2) ^
^ (R2 - d2)2(R + d)2 - r2(R + d)4 < 4R2r2((R + d)2 - r2) ^
4((R - d)2 - r2) < 16R2r'
, (R + d)2 - r2
(R + d)4 '
Таким образом, мы показали, что оценка (31) точнее оценки (30). Заметим,
4((R - d)2 - r2) = 16R2r
>2 9 (R + d)2 - '
(R + d)4
тогда и только тогда, когда треугольник ABC является правильным. Итак,
нами доказано, что
4((R - d)2 - r2) < 16R'
>2 2(R + d)2 - '
(R + d)4
a2
< 16R2r2 (R(r-}2d)4 ^ < 4((R + d)2 - r2)
при 2r < R < (\/2 + 1)r. Это завершает доказательство теоремы 2.
32
что

ГЛАВА 2
Геометрия четырехугольника
Цель настоящей главы изложить доказательства некоторых важных об¬
щих свойств выпуклых четырехугольников, а также привести различные ха¬
рактеризации некоторых типов выпуклых четырехугольников. Многие резуль¬
таты, приведенные в этой главе, взяты из недавних работ шведского матема¬
тика М. Жосевссона (см. [32] [44]).
§ 1. Основные свойства выпуклого четырехугольника
и метрические соотношения в нем
Теорема 1. Пусть ABCD - выпуклый четырехугольник. Тогда середины
его сторон являются вершинами параллелограмма, стороны которого па¬
раллельны диагоналям четырехугольника ABCD.
Доказательство. Рассмотрим рис. 1, где M, N, P, Q середины сторон AD,
Рис. 1
AB, BC и CD соответственно. В треугольнике ADC отрезок MQ является
средней линией, параллельной AC и равной половине AC. Аналогично отре-
AC
зок NP равен —и параллелен диагонали AC. Следовательно, отрезки MQ и
AC
NP равны	и параллельны. Рассматривая треугольники ADB и BDC, до-
DB
кажем аналогично, что отрезки QP и MN равны и параллельны между
собой. Следовательно, MNPQ параллелограмм, стороны которого парал¬
лельны диагоналям четырехугольника ABCD. Теорема доказана.	■
Следующие два результата являются хорошо известными, но для полноты
изложения приведем их с доказательством.
Теорема 2. Выпуклый четырехугольник ABCD является вписанным в окруж¬
ность тогда и только тогда, когда ZA + ZC = п.
33

Рис. 2
Доказательство. Пусть четырехугольник ABCD является вписанным в окруж¬
ность (см. рис. 2). Тогда угол ZA равен половине дуги DCB, а угол ZC равен
^	360°
половине дуги DAB. Следовательно, их сумма ZA + ZC равна = 180°.
Докажем обратное утверждение. Пусть ZA + ZC = 180°. Опишем окруж¬
ность около треугольника ADB. Пусть Ci точка пересечения прямой CB с
этой окружностью (см. рис. 3). Если C = C1, то считая, например, что точка
C1 лежит внутри отрезка CB, получим, что ZA + ZC = ZA + ZC1 = 180° и
ZC1 = ZC + ZCDC1. Противоречие.
Случай, когда точка C1 лежит вне отрезка CB, рассматривается аналогич¬
но.
Теорема доказана.	■
Следующий хорошо известный результат принадлежит французскому ин¬
женеру Г. Питоту (1725 г.) и швейцарскому математику Я. Штейнеру (1846 г.)
(см. [39]).
Теорема 3. Пусть ABCD - выпуклый четырехугольник и a = AB, b = BC,
c = CD и d = AD. В четырехугольник ABCD можно вписать окружность
тогда и только тогда, когда a + c = b + d.
34

Рис. 4
Доказательство. Пусть в четырехугольник ABCD можно вписать окруж¬
ность (см. рис. 4). Обозначим через P, Q, R, S точки касания окружно¬
сти сторон AD, AB, BC, CD соответственно. Так как отрезки касательных
к окружности равны, то AP = AQ, PD = DS, RC = CS, BR = QB и
а + c = AQ + QB + CS + SD = BR + RC + AP + PD = b + d.
Докажем обратное утверждение. Пусть в выпуклом четырехугольнике ABCD
суммы длин противоположных сторон равны, т. е. а + c = b + d. Пусть I точ¬
ка пересечения биссектрис углов ZBAD и ZADC (см. рис. 5). Рассмотрим
окружность с центром в точке I, касающуюся сторон AB, AD и DC. Пред¬
положим, что она не касается стороны BC. Проведем касательную BC1 (мы
считаем, что окружность находится внутри четырехугольника; случай, когда
часть окружности лежит вне четырехугольника, рассматривается аналогич¬
но). Пусть P, Q, R, S точки касания отрезков AD, AB, BC\ и C\D соот¬
ветственно и x = AQ = AP, y = QB = BR, z = RC\ = C\S, t = SD = PD.
Тогда а = x + y, d = x +1 и а +1 + z = x +1 + y + z, а + c = x + y +1 + z + CCi =
= x + t + b = b + d. Откуда следует, что y + z + CC\ = b и по неравенству
треугольника BC\ + CCi > BC. Противоречие.
Теорема доказана.	■
Для изложения дальнейшего материала фиксируем обозначения. Пусть ABCD
35

выпуклый четырехугольник, AB = a, BC = b, CD = c, DA = d, AC = p,
BD = q,	ZDBA =	Si,	ZDBC =	S2,	ZA	= a,	ZC	= 7,	ZB	=	S,	ZD = A,
a + b + c + d
K и L середины диагоналей AC и BD соответственно, p1 = -
полупериметр, S площадь четырехугольника ABCD (см. рис. 6).
2
Имеет место следующая теорема Бретшнейдера (или согласно [2] вто¬
рая теорема косинусов).
Теорема 4. Справедливо равенство
p2q2 = a2c2 + b2d2 — 2abcd cos(a + j).
Доказательство. По теореме синусов имеем, что 	— = —^—, 	—
sin Si	sin a sin S2
dc	dc
_q_
sin y
. Откуда следует, что sin S1 sin S2 =	2 sin a sin y = 2 (cos a cos y—
q2
q2
a2 + d2 — q2	c2 + b2 — q2
— cos(a + y)). Так как cos a =			, cos y =	22	, то
2ad
2bc
sin S1 sin S2 = —2
q2
! + d2 — q2	c2 + b2 — q2
2ad
2bc
— cos(a + y) =
= cos S1 cos S2 — cos(S1 + S2).
Заметим далее, что cos S1
: + q2 — d2
b2 + a2 — p2
cos S =	. Поэтому
2ad
, cos S2
q2 + b2 — c2
2qb
и cos(S1 + S2)
dc
2ab
! + d2 — q2 c2 + b2 — q2
2ad
2bc
— cos(a + y)
a
2 +	q2	—	d2	q2	+	b2	—	c2	b2	+ a2	—	p2
2aq
2qb
2ab
или pi2q2 = a2c2 + Ь2—2 — 2abcdcos(a + y).
Теорема доказана.
a
a
a
36

Следствие 1 (теорема Птолемея). Для произвольного выпуклого четы¬
рехугольника ABCD (см. рис. 6) справедливо неравенство pq < ac + bd. При
этом pq = ac + bd тогда и только тогда, когда четырехугольник ABCD
является вписанным в окружность.
Доказательство. По теореме 4 имеем, что
p2q2 = a2c2 + b2d2 + 2 abcd — 2abcd(1 + cos(a + 7)) =
= (ac + bd)2 — 2abcd(1 + cos(a + 7)) < (ac + bd)2.
Откуда следует, что pq < ac + bd. При этом pq = ac + bd тогда и только
тогда, когда cos(a + 7) = —1, т. е. а + у = 180°. Согласно теореме 2 последнее
условие равносильно тому, что четырехугольник ABCD является вписанным
в окружность. Следствие доказано.	■
Следствие 2. Пусть M - произвольная точка окружности, описанной око¬
ло правильного треугольника ABC. Тогда один из отрезков MA, MB, MC
является суммой остальных.
Доказательство. Рассмотрим рис. 7. Пусть a = AB. По теореме Птолемея
имеем, что a ■ AM = a ■ CM + a ■ MB. Откуда следует, что AM = MC + MB.
Следствие доказано.	■
Следствие 3 (теорема Помпею). Пусть M - точка, лежащая вне окруж¬
ности, описанной около правильного треугольника ABC. Тогда из отрезков
AM, BM и CM можно составить треугольник.
Доказательство. Следует из теоремы Птолемея.	■
Согласно [2] следующий результат называется первой теоремой коси¬
нусов.
Теорема 5. Справедливо равенство
a2 = d2 + b2 + c2 — 2dc cos A — 2bc cos 7 + 2db cos(A + y).
37

Доказательство. Рассмотрим векторы AD, DC, CB и BA (см. рис. 6). Их
сумма равна нулю. Следовательно, BA = —(AD + DC + CB). Вычислим
скалярный квадрат вектора BA:
a2 = BA • BA =
= AD • AD + DC • DC + CB • CB + 2AD • DC + 2DC • CB + 2AD • CB =
= d2 + b2 + c2 — 2dc cos A — 2bc cos 7 + 2db cos(A + j),
т. к. угол между векторами AD и DC равен п — A, угол между векторами DC
и CB равен п — 7, а угол между векторами AD и CB равен 2п — (A + 7).
Теорема доказана.	■
Следующая теорема принадлежит Л. Эйлеру.
Теорема 6. Пусть K, L - середины диагоналей AC и BD соответственно
четырехугольника ABCD (см. рис. 8). Тогда KL2 =	(a2+b2+c2+d2—p2 — q2).
Доказательство. Рассмотрим векторы u = AD, v = DC, w = CB, z = AB,
p = AC, q = DB (см. рис. 8).
Тогда P + KL + 2
z и KL
z
p + q
2
. Откуда следует, что
KL2 = KL-KL
z^z+
p • p + 2p • q + q • q
4
-2 z-'p+q
2
a2+p2^
.p^q
+—2	z^p—z^ q.
Далее,
z • p
z • q
p^q
ap • cos (ABAC) = a • p •
qa • cos(AABD) = q • a •
(u + v)q = u • q + v •q =
a2 + p2 — b2	a2 + p2 — b2
2ap	2
q2 + a2 — d2	a2 + q2 — d2
2qa	2
d2 + q2 a2
d^q(—1)^^t-+cq•
a2 — d2 — q2 + c2 + q2 — b2
c2 + q2 — b2 _
2cq
a2 + c2 — d2 — b2
2
2
38

2	p2 + q2
a2 +	+
+
Следовательно, KL2
d2 - a2 - q2 _ a2 + b2 + c2 + d2 - p4 - q2
2	=	4
a2 + c2 - d2 - b2
+
b2 - a2 - p2
+
. Теорема доказана.
2
Следствие 4. Для любого выпуклого четырехугольника справедливы нера¬
венства
a2 + b2 + c2 + d2 > p2 + q2
(см. рис. 6). При этом a2 + b2 + c2 + d2 = p2 + q2 тогда и только тогда, когда
середины диагоналей совпадают.
Доказательство. Следует из теоремы 6 и неравенства KL2 > 0.	■
Следствие 5. Для выпуклого четырехугольника ABCD справедливы нера¬
венства
d2 + b2 - 2ac < p2 + q2 < d2 + b2 + 2ac.
Доказательство. Рассмотрим рис. 9, где P середина AD. Тогда PK =
2
PL = — (как средние линии треугольников ADC и ADB). Из неравенства
a + c	PL - PK
треугольника имеем, что KL < PK + PL = —-— и KL >
(если a > c). Следовательно,
теорему 6, имеем, что
22
2
KL2
(a + c)2
2
Учитывая
<
! + b2 + c2 + d2 - p2 - q2	a2 + b2 + 2ac
<
444
или b2 + d2 - 2ac < p2 + q2 < b2 + d2 + 2ac. Следствие доказано.	■
Отметим интересное неравенство, полученное при доказательстве следствия 5:
a + c
KL
2
Для выпуклого четырехугольника ABCD введем обозначение полупери-
a + c + b + d
метра (см. рис. 6): pi =			 . Справедлив следующий удивительный
результат.
2
c
2
ac
ac
a
39

Теорема 7. S2 = (pi — a)(pi — b)(pi — c)(pi — d) — abcd cos2 ^	•
ad sin — bc sin 7
Доказательство. Рассмотрим рис. 6. Имеем, что S =			1		— и
2
g2 = a2 + d2 — 2ad cos — = b2 + c2 — 2bc cos 7.
Откуда следует, что 2S = ad sin — + bc sin 7 и
— bc cos 7,
! + d2 — b2 — c2
ad cos —
4S2 = (ad)2 sin2 — + (bc)2 sin2 7 + 2abcd sin — sin 7
(a2 + d2 — b2 — c2)2
(ad)2 cos2 — + (bc)2 cos2 7 — 2abcd cos — cos 7.
Складывая соответственно левые и правые части последних двух равенств,
получим, что
4S2 +
(a2 + d2 — b2 — c2)2
= (ad + bc)2 — 2abcd(1 + cos(— + 7))
= (ad)2 + (bc)2 — 2abcd cos(— + 7) = (ad + bc)2 — 4abcd cos2
— + 7
2
S2
(ad + bc)2	(a2 + d2 — b2 — c2)2
16
abcd cos2
— + 7
2
/ — _|_ 7 \
(pi — a)(pi — b)(pi — c)(pi — d) — abcd cos2 f —2— ).
a
и
или
4
Теорема доказана.	■
Для вписанных в окружность четырехугольников получаем следующий ана¬
лог формулы Герона.
Следствие 6 (теорема Брахмагупты). Если четырехугольник является
вписанным в окружность, то S2 = (pi — a)(pi — b)(pi — c)(pi — d).
Доказательство. Действительно, в этом случае
— + 7
2
90° и cos
— + 7
2
0.
Следствие 7. Если четырехугольник является описанным около окружно¬
сти, то
S2
abcd sin2
— + 7
2
40

Доказательство. Так как a + c = b + d (см. теорему 3 § 1 главы 2), то
a + b + c + d	2	2 ( a + Y
pi =			= a + c = b + d и S2 = c • d • a • b — abcd cos2
2
= abcd sin2
a + y
2
Следствие 8. Если четырехугольник является вписанным в окружность и
описанным около окружности, то S2 = abcd.
Доказательство. Следует из следствия 7 и того, что
a + y
2
90°.
Следствие 9. Для произвольного выпуклого четырехугольника справедливо
равенство
2 p2q2	(a2 + c2 — b2 — d2)2
= 1 16 '
Доказательство. Из теорем 4, 7 следует, что
2
16S2 = 16(pi — a)(pi — b)(pi — c)(pi — d) — 16 abcd cos2 ^ —+Y ^
4 p2q2 = 4a2c2+4b2d2—8abcd cos(a+Y) = 4a2c2+4b2d2+8abcd— 16abcd cos'
a + y
2
Вычитая из левой части (правой части) первого равенства левую часть (соот¬
ветственно правую часть) второго равенства, получим, что
16S2 — 4p2q2 = 16(p1 — a)(p1 — b)(p1 — c)(p1 — d) —4(ac+bd)2 = —(a2 — b2+c2 — d2)2.
Следствие доказано.	■
Теорема 8. Пусть выпуклый четырехугольник ABCD является вписанным
2	(ac + bd)(ad + bc) 2	(ac + bd)(ab + cd)
в окружность. Тогда p2 =					, q2 =		— 	.
ab + cd	ad + bc
Доказательство. Поскольку y = 180° — a, то по теореме косинусов имеем,
q2 = a2 + d2 — 2ad cos a, q2 = b2 + c2 + 2cb cos a.
Откуда следует, что q2(cb+ad) = a2cb+d2cb+b2ad+c2ad = (ac+bd)(ab+cd), т. е.
q
2	(ac + bd)(ab + cd)	2	(ac + bd)(ad + bc)
,2 —	 Аналогично доказывается, что p2 =
ab + cd
ad + bc
Теорема доказана.
Из теоремы 8 следует еще одно доказательство теоремы Птолемея.
Следствие 10. Если четырехугольник является вписанным в окружность,
то pq = ac + bd.
что
41

Доказательство. Имеем, что p2q2
(ac + bd)2(ad + bc)(ab + cd)
(ab + cd)(ad + bc)
(ac+bd)2,
т. е. pq = ac + bd.	■
Из теоремы 8 следует, что в классе всех четырехугольников, около которых
можно описать окружность, каждый четырехугольник однозначно определя¬
ется длинами своих сторон (указанных в фиксированном порядке).
Теорема 9. Пусть выпуклый четырехугольник со сторонами a, b, c, d вписан
в окружность радиуса R. Тогда
1)	S2
2)	R2
(ad + bc)(ac + bd)(ab + cd)
16R2	;
(ac + bd)(ab + cd)(ad + bc)
16(pi - a)(pi - b)(pi - c)(pi - d), г е Pl
a+b+c+d
2
Доказательство. Рассмотрим рис. 6. Имеем, что S = -Р- +	Р = Р^
4R 4R	4R
adq bcq	q(ad + bc)
Jr + Jr =	Jr
и аналогично S
^(ab + cd)(ad + bc) и
-. Откуда немедленно следует, что
S2 = pq
16R2
2	(ac + bd)(ab + cd)(ad + bc)
R =	16S2
(ac + bd)(ab + cd)(ad + bc)
16(pi - a)(pi - b)(pi - c)(pi - d)'
Теорема доказана.
Автором следующей теоремы является И. Ньютон [16].
Теорема 10. Пусть в четырехугольник ABCD можно вписать окружность.
Тогда центр этой окружности и середины диагоналей лежат на одной пря¬
мой.
Доказательство. Если четырехугольник ABCD является параллелограм¬
мом, в который можно вписать окружность, то ABCD ромб и центр вписан¬
ной окружности совпадает с серединами диагоналей. Пусть в четырехугольни¬
ке ABCD есть хотя бы одна пара противоположных непараллельных сторон,
например, AB и CD (см. рис. 10). Пусть также M середина диагонали AC,
N середина диагонали BD и точка O центр вписанной окружности. Дока¬
жем, что
Samb + ScdM = SaBN + ScnD
Действительно,
Saob + Socd = 2 Sabcd.
samb + scdm
Sbna +Sncd
2 Sabc
2 Sabd
+
+
2 Sacd
t;Sbcd
2 sabcd,
Sabcd
42

Soab + Socd = 2(AB + CD)R,
где R радиус вписанной в четырехугольник окружности.
Поскольку
(AB + BC + CD + AD)
2
AB BC CD AD
sabcd = —2 • R +—2~ • R +—2~ • R +—2~ ^ R
и AB + CD = BC + AD, то SOAB + SOCD = 1SABCD. Итак, точки M, N, O
принадлежат множеству T, состоящему из точек L, находящихся внутри че¬
тырехугольника и удовлетворяющих условию Slab +Slcd = Sabcd = const.
Покажем, что T множество точек некоторой прямой. Для этого докажем две
Лемма 1. Пусть Ax + By + C = 0 - уравнение некоторой прямой на плос¬
кости и M(x0,y0) - некоторая точка плоскости. Тогда расстояние от M до
прямой равно
|Axo + Byo + C |
VA+P '
леммы.
Доказательство. Сначала заметим, что вектор n = (A, B) перпендикулярен
прямой. Действительно, пусть (xi,yi), (x2,y2) две различные точки на пря¬
мой. Тогда Axi + By1 + C = 0 и Ax2 + By2 + C = 0. Откуда следует, что
A(x2 — x1) + B(y2 — y1) = 0 и вектор (x2 — x1,y2 — y1) параллельный прямой
является перпендикулярным вектору n = (A, B) (ибо их скалярное произве¬
дение равно нулю). Пусть (x',y')	координаты основания перпендикуляра,
опущенного из точки M(x0, y0) на нашу прямую. Тогда вектор (x0 — x', y0 — y')
параллелен n = (A,B). Следовательно, их скалярное произведение равно
(x0 — x')A + (y0 — y')B = |n| • d • cos ф,
43

где d искомое расстояние и угол ф равен 0 или п. Поэтому
d = -- (Axo+Byo-(Ax'+By')) = -- (Ax0+By0+C) = ,	(Ax0+by0+C).
|n|	|n|	v A2 + B2
Лемма доказана.	■
Из доказательства следует, что прямая делит плоскость на две полуплос¬
кости: в одной из них значения Ax + By + C > 0, в другой Ax + By + C < 0.
Лемма 2. Пусть AB и CD - два непараллельных отрезка. Тогда геометри¬
ческое место точек M, удовлетворяющих условию Sabm + Smcd - посто¬
янная величина, содержится на некоторой прямой.
Доказательство. Пусть точка M удовлетворяет условию леммы и Sabm+
+Smcd = e. Воспользуемся методом координат. Пусть C начало координат,
точка D находится на оси OX. Тогда D(0,m), A(a,b), B(c,d), где b = d.
Уравнение прямой, проходящей через точки A и B, имеет вид
(d — b)x + (a — c)y + (b — d)a + b(c — a) = 0.
Следовательно,
Samb + Smcd = e =
y0 ■ m	y/(d —	b)2 + (a — c)2	| (d —	b)x0 + (a —	c)y0	+	(b	—	d)a + b(c — d) |
=	2	+	2	^(d — b)2 + (O—cf
где (x0,y0) координаты точки M. Откуда следует, что
my0 + | (d — b)x0 + (a — c)y0 + (b — d)a + b(c — d)| = 2e.
Ввиду выше приведенного замечания, можно считать, например, что
(d — b)x0 + (a — c)y0 + (b — d)a + b(c — d) > 0.
Следовательно, M лежит на прямой
(d —	b)x	+	((a —	c)	+ m)y + (b —	d)a +	b(c	— d) — 2e =	0.
Лемма доказана.	■
Доказательство теоремы 10 следует из леммы 2.	■
Приведем далее другое доказательство формулы Брахмагупты для пло¬
щади вписанного в окружность четырехугольника, основанное на формуле
Герона для площади треугольника.
Пусть ABCD вписанный в окружность четырехугольник. Если вписан¬
ный четырехугольник является параллелограммом, то он прямоугольник
(см. рис. 11), в котором р'
a + b + a + b
2
a + b, p' — a = b, p' — b = a
44

Рис. 11
и S = ab = \f(p' — a)(p' — b)(p — c)(p' — d). Таким образом, в этом случае
формула Брахмагупты справедлива.
Будем считать далее, что, например, стороны DC и AB (см. рис. 12) не
являются параллельными и M точка пересечения прямых DC и AB. Пусть
a = AD, b = CD, c = CB, d = AB, xi = MD, yi = MA, x2 = MC,
y2 = MB и A = —. Треугольники MDA и MCB являются подобными, так
как ZADC + ZcBm = 180°, ZMDA = ZCBM, ZBAD + ZMCB = 180°,
ZMAD = ZMCB.
n	xi y i a
Следовательно, — = — = — = A и x1
У2 X2 c
(d + bA)A	_ (b + dA)A Ис
1 — A2	i 1 — A2
комая площадь S четырехугольника ABCD равна разности S2 — S1, где S2
площадь треугольника MCB, а S1 площадь треугольника MDA. По фор¬
муле Герона	Si	=	V/Pi(pi — xi)(pi — yi)(pi	—	a),	где pi =	Xi—У	a, а	S2
= VP2 (P2 — x2)(p2 — У2)(Р2 — c), где P2 = ^ + Уу + °
2
Заметим, что pi = Ap2,
Pi — xi = A(p2 — У2), pi — yi = A(p2 — X2), pi — a = A (pi — c). Поэтому
S = S2 — Si = S2 — A2S2 = (1 — A2)S2 =
= Vp2(1 — A)	• (p2	—	x2)(1 + A) •	(p2	—	y2)(1 + A)	• (p2 —	c)(1 —	A).
xi + yi + b + d + c d + b + c(1 — A)	d + b + c(1 — A)
Далее, p2 =			=	, p2(1—A) = —	-
d+b+c—a
2”
, p2 — x2 =
2(1 — A)
d — b + c(1 + A)
2(1 + A)
(p2 — x2)(1 + A)
2
d+a+c—b
2 ,
b + c(1 + A) — d	b + a + c — d	d + b + c(A — 1)
p2—y2 =	, (p2— y2)(1+A) = 	Л	, p2 — c =
2(1 + A)
2(1 — A)
45

и (p2—c)(1 —Л) = d + Ь + a—-. Следовательно, S = \/(p' — a)(p' — b)(p — c)(p' — d),
где p
a + b + c + d
Выше приведенное доказательство опубликовано в работе [30].
Следующий результат был доказан в работе [37].
Теорема 11. Выпуклый четырехугольник ABCD является прямоугольни¬
ком тогда и только тогда, когда его площадь S равна S =	(a2 + c2)(b2 + d2),
где a = AB, b = BC, c = CD, d = AD.
Доказательство. Пусть ABCD прямоугольник. Тогда a = c, b = d и
1
S = ab = -v/(a2 + a2)(b2 + b2).
Докажем обратное утверждение.
Пусть S2 =	(a2 + c2)(b2 + d2). Рассмотрим рис. 13. Тогда
„	ad sin a	bc sin y	ab sin в	dc sin <5
S = —r + —7r-L = —^- + —^—
2S = -[ad sin a+bc sin p+ab sin в+dc sin 5] < -(ad+bc+ab+dc) = —(a+c)(b+d).
При этом равенство выполнено тогда и только тогда, a = в = Y = 5 = 90°.
Так как (a + c)2 < 2(a2 + c2) и (b + d)2 < 2(b2 + d2), то S2
(a2 + c2)(b2 + d2)
и
>
4
1 2 2 (a +c)(b +d)
>	(a + c)2(b+d)2 и S >
1o	4
является прямоугольником, т. е. a = в
доказана.
. Откуда следует, что четырехугольник
= p = 5 = 90° и a = c, b = d. Теорема
46

§ 2. Бимедианы четырехугольника
Пусть ABCD выпуклый четырехугольник, длины сторон AB, BC, CD,AD
которого равны a, b, c, d соответственно и AC = e, BD = f (см. рис. 1).
Пусть M,N,R,S середины сторон AB,BC,CD и AD соответственно.
Отрезки MR и NS называются бимедианами четырехугольника ABCD (см.
[40]).
В дальнейшем нам понадобится следующая вспомогательная лемма.
Лемма 1. Пусть AiBiCiDi - параллелограмм. Тогда
AC + BD = 2(AiB? + ADf)
(сумма квадратов диагоналей параллелограмма равна сумме квадратов его
сторон, см. рис. 2).
Доказательство. Пусть ZBiAiDi = а. Тогда по теореме косинусов полу¬
чим, что BiD2 = AiB2 + AiD2 — 2AiBi • AiDi cos a, AiCi = AiB2 + AiD2+
+2AiBi • AiDi cos а. Сложив соответственно левые и правые части этих ра¬
венств, имеем AiCf + BiD2 = 2(AiBi + AiDf). Лемма доказана.	■
Справедливо следующее утверждение.
Лемма 2. MNRS - параллелограмм.
47

Доказательство. Средняя линия MN треугольника ABC параллельна AC
AC .
и равна ——. Аналогично отрезок Ко является средней линией треугольни-
AC
ка ADC. Поэтому отрезок KS параллелен AC и равен ——. Следовательно,
MNKS параллелограмм, стороны которого параллельны диагоналям четы¬
рехугольника ABCD и равны их половинам. Лемма доказана.	■
Пусть m = NS и n = МК. Из лемм 1 2 следует, что
^	„2 а. С
2 | 2
m + n
2 d
ci f
e2 + f2
2
или e2 + f2	=	2(m2 + n2).	Поскольку	e2	+	f2	>	2ef, то	m2	+	n2	> ef. Итак,
справедлива следующая теорема.
Теорема 1. Пусть m,n - длины бимедиан и e, f - длины диагоналей выпукло¬
го четырехугольника. Тогда m2 + n2 > ef, при этом равенство выполняется
тогда и только тогда, когда e = f.
Теорема 2. В выпуклом четырехугольнике ABCD диагонали перпендику¬
лярны тогда и только тогда, когда a2 + c2 = b2 + d2.
Доказательство. Пусть p угол между диагоналями AC и BD, u = BO,
v = CO, w = OD, z = OA, где O точка пересечения диагоналей AC и
BD (см. рис. 1). Тогда по теореме косинусов a2 = u2 + z2 — 2uz cos p, c2 =
= v2 + w2	— 2vw cos p,	b2 = u2 + v2 +	2uv cos p, d2 = z2 + w2 + 2zw cos p,	т.	е.
a + c	= u + v + z	+ w — 2(uz + vw) cos p,
b2 + d2 = u2 + v2 + z2 + w2 + 2(vu + zw) cos p.
Отсюда следует, что a2 + c2 = b2 + d2 в том и только в том случае, когда
cos p = 0 и p = 90°. Теорема доказана.	■
Рассмотрим параллелограмм MNKS (см. рис. 1). Если бимедианы МК и
2	2 f f 2
NS перпендикулярны, то из теоремы 2 следует, что	= ( — j +
( f\2
+ 1 — 1 , т. е. e = f. Верно и обратное утверждение: если e = f, то бимедианы
МК и NS перпендикулярны (и MNKS является ромбом). Итак, доказана
следующая теорема:
Теорема 3. В выпуклом четырехугольнике диагонали равны тогда и только
тогда, когда бимедианы перпендикулярны.
Теорема 4. Площадь S выпуклого четырехугольника ABCD (см. рис. 1)
равна
S	= — у/ e2f2 — (m2 — n2)2,
где e, f - длины диагоналей и m, n - длины бимедиан четырехугольника ABCD.
48

Доказательство. Ранее мы уже отмечали, что S2 = — (4e2/2 — (а2 + с2 — b2
16
По теореме косинусов имеем, что
2 е2 + /2	2 e /
т =т + т — 2 • ^ • 2cos ?,
а2 + с2 = и2 + v2 + z2 + w2 — 2(uz + vw) cos
b2 + d2 = u2 + v2 + z2 + w2 + 2(vu + zw) cos ^
(см. обозначения в доказательстве теоремы 2). Отсюда следует, что
а2 + с2 — b2 — с2 = —2(u + w)(v + z) cos ip = —2е/ cos p
1
m2 = |(e2 + /2 + a2 + c2 — b2 — d2).
Аналогично
n2 = ^(e2 + /2 + b2 + d2 — a2 — c2).
Поэтому 4(m2 — n2) = 2(a2 + c2 — b2 — d2), 4(m2 — n2)2 = (a2 + c2 — b2 — d2)2 и
S2 = -(e2/2 — (m2 — n2)2). Теорема доказана.
При доказательстве теоремы 4 мы вычислили длины бимедиан. Именно,
справедливо следующее следствие.
11
Следствие 1. т2 = -(e2+/2+a2 + c2 — b2 — d2), n2 = -(e2 + /2 + b2+d2 — a2 — c2).
По лемме 1 имеем, что	e2	+ /2	= 2(m2	+	n2),	т. е.	(m2	—	n2)2 + 4m2n2	=
.2 + /2 \2	/ „2	/2 \2	(„2 I /2 4 2 ^2 „,2
. Откуда следует, что m2n2—
2
22
^ e2 — / 2Y
2n2—
l 4 )
e2/ 2
m2 - n
4
4
16	4
S2. Итак, доказана
16	16	4	4	4	’
Теорема 5. Площадь S выпуклого четырехугольника ABCD с длинами диа¬
гоналей e, / и длинами бимедиан m, n находится по формуле
S =4 / m2n2 —
2	л2 \ 2
e2 — /2 2
и
Следствие 2. S = mn тогда и только тогда, когда e = /.
Введем в выпуклом четырехугольнике ABCD следующие обозначения: a =
= ZCAD, в = ZBAC (см. рис. 3).
d2)2) .
2
49

Тогда по теореме косинусов получаем, что cos а
e2 — a2 _ b2	а2 — d2 - f2
и cos(a + в) = -			 . Из тождества
d2 — e2 - c2
2 ed
cos в
2ea	2 ad
(cos a cos в — cos(a — в))2 = (1 — cos2 a)(1 — cos2 в)
следует тождество
cos2 a — cos2 в — cos2 (a — в) — 2 cos a cos в cos(a — в) = 1.
Подставив в него вместо cos a, cos в и cos(a — в) выше приведенные выраже¬
ния, получим, что
e2f2 (а2 — b2 — c2 — d2 — e2 — f2) — (a2 — b2 — c2 — d2)(a2c2 — b2d2) —
—e2(a2 — d2)(b2 — c2) — f2 (a2 — b2)(c2 — d2) = 0.
Таким образом доказана следующая теорема Эйлера [40].
Теорема 6. Для любого выпуклого четырехугольника ABCD с длинами диа¬
гоналей e,f и длинами сторон a, b, c, d справедливо равенство
e2f2 (a2 — b2 — c2 — d2 — e2 — f2) — (a2 — b2 — c2 — d2)(a2c2 — b2d2) —
—e2(a2 — d2)(b2 — c2) — f2(a2 — b2)(c2 — d2) = 0.
§ 3. Ортодиагональные четырехугольники
Выпуклый четырехугольник ABCD называется ортогональным, если
его диагонали AC и BD перпендикулярны [35].
Цель настоящего параграфа изучение различных свойств таких четырех¬
угольников.
Имеет место следующая теорема.
Теорема 1. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда AB2 — CD2 = BC2 — AD2.
50

Доказательство. Опустим из вершин D и B на диагональ AC перпендику¬
ляры DX и BY соответственно (см. рис. 1). Используя теорему Пифагора,
получаем следующие равенства:
AB2 = AY 2+YB2,CD2 = DX2+XC2,BC2 = CY2+YB2,AD2 = DX 2+AX2.
Откуда следует, что
AB2 + CD2 - BC2 - AD2 = AY2 + XC2 - AX2 - CY2 =
= (AY - AX)(AY + AX) + (XC - CY)(XC + CY) =
= -XY • (AY + AX) - XY • (XC + CY) =
= -XY • (AX + AY + CX + CY) = -XY • 2AC.
Диагонали AC и BD являются перпендикулярными в том и только в том
случае, когда XY = 0. Последнее равенство равносильно условию AB2+
+CD2 = BC2 + AD2. Теорема доказана.	■
Замечание 1. Другое доказательство теоремы 1 можно получить с помо¬
щью того факта, что площадь S четырехугольника ABCD вычисляется по
формулам
AC Rn	1
S =	2 sin p = p/4AC2 • BD2 - (AB2 + CD2 - BC2 - AD2)2,
где p - угол между диагоналями (см. следствие 9 в § 1). Следовательно,
p = 90° тогда и только тогда, когда AB2 + CD2 - BC2 - AD2 = 0.
Пусть P точка пересечения диагоналей AC и BD выпуклого четырех¬
угольника ABCD. Тогда справедлива следующая теорема.
Теорема 2. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда ZPAB + ZPBA + ZPCD + ZPDC = 180°.
51

Рис. 2
Доказательство. Рассмотрим рис. 2. Пусть р угол между диагоналями
AC и BD. Тогда р = ZPDC + ZDCP = ZPAB + ZPBA и 2р = ZPAB+
+ZPBA + ZPDC + ZPCD. Следовательно, р = 90° тогда и только тогда,
когда ZPAB + ZPBA + ZPCD + ZPDC = 180°. Теорема доказана.	■
Опустим из точки P перпендикуляры PK, PL, PM и PN на стороны
AB,BC,CD и AD соответственно (см. рис. 2). Имеет место следующий ре¬
зультат.
Теорема 3. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда проекции точки P пересечения диагоналей
на стороны четырехугольника лежат на одной окружности (другими сло¬
вами, четырехугольник KLMN является вписанным в окружность).
Доказательство. Рассмотрим рис. 3.
Четырехугольники ANPK, KPLB, LPMC и DMPN являются вписанны¬
ми в окружности, поскольку суммы противоположных углов в них равны 180°.
Следовательно, ZNAP = ZNKP, ZPKL = ZPBL, ZPCL = ZPML и
ZPMN = ZPDN. Таким образом, имеем ZLMN + ZLKN = ZLMP+
+ZPMN + ZLKP + ZPKN = ZPCB + ZCBP + ZPAD + ZPDA. По тео¬
реме 2 четырехугольник ABCD является ортодиагональным тогда и только
52

тогда, когда ZPAB + ZPBA + ZPCD + ZPDC = 180°. Последнее равенство
равносильно равенству ZLMN + ZLKN = 180°, т. е. тому, что четырехуголь¬
ник KLMN является вписанным в окружность. Теорема доказана.	■
Пусть m,n длины бимедиан выпуклого четырехугольника ABCD. В § 2
настоящей главы мы доказали, что 2(m2 — n2) = ±(AB2 — BC2 + CD2 — AD2).
Из теоремы 1 § 3 следует, что четырехугольник ABCD является ортодиаго¬
нальным тогда и только тогда, когда длины его бимедиан равны, т. е. m = n.
Следствие 1. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда длины его бимедиан равны.
Теорема 4. Пусть ABCD - выпуклый четырехугольник, P -точка пересе¬
чения его диагоналей и m2,m2,m3,m4 - длины медиан, исходящих из верши¬
ны P в треугольниках ABP, BCP, CDP и DAP соответственно. Четырех¬
угольник ABCD является ортодиагональным тогда и только тогда, когда
m2 + m| = m2 + m4.
Доказательство. Пусть a,b,c,d длины сторон четырехугольника ABCD
(см. рис. 4) и x = PC, y = PB, z = PD, w = PA. Тогда (m2+m2) —(m2+m|) =
w2 + y2 a2 x2 + z2 c2 z2 + w2 d2 y2 + x2 b2	(d2 + b2) — (a2 + c2)
=	2 T+	2	1	2	+T 2	+T =	4	.
По теореме 1 § 3 четырехугольник ABCD является ортодиагональным то¬
гда и только тогда, когда a2 + c2 = b2 + d2. Последнее равенство равносильно
равенству m2 + m2 = m2 + m4. Теорема доказана.	■
Пусть R2,R2,R3 и R4	радиусы описанных окружностей треугольников
ABP, BCP, CDP и ADP соответственно, р угол между диагоналями AC и
BD четырехугольника ABCD. Пусть также h2,h2,h3 и h4 длины высот,
исходящих из точки P треугольников ABP, BCP, CDP и ADP соответ¬
ственно (см. рис. 4). Тогда по теореме синусов a = 2R2 sin р, b = 2R2 sin p,
c = 2R3 sin p, d = 2R4 sin р, т. е., другими словами, (a2 + c2) — (b2 + d2) =
= 4 sin2 p(R2 + Щ — R2 — R2). Следовательно, a2 + c2 = b2 + d2 в том и только в
53

том случае, когда R2 + Щ — R — Щ = 0. Итак, используя теорему 1, получаем
следующее следствие.
Следствие 2. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда R2 + Rj = Щ + R4, где R2, R2, R3 и R4 -
радиусы описанных окружностей треугольников ABP, BCP, CDP и ADP
соответственно, P - точка пересечения диагоналей AC и BD.
Площадь Si треугольника ABP вычисляется таким образом: Si
wy sin р
=			. Отсюда
2а •h
i=
1
j
h2	w2y2 sin2 р
Аналогично
w2 + y2 — 2wy cos р
w2y2 sin2 р
1 1
о + г
sin2 р
2 cos р
wy sin2 р
1
h3
1
h2
h\
11
-2 +	2
x2	z2
11
— +	;
y2	x2
1 1
о + о
Откуда следует, что
1 1
hi + h3
1 1
h2 + h4
1
wy
Поэтому (hi+hf) -( hi+4
Итак, нами доказано следующее следствие
1
2 cos р
sin2 р
1
xz sin2 р
2 cos р
sin2 р
1
xy sin2 р
2 cos р
sin2 р
wz sin2 р
1
+	+
xz
— + —) • (-
xy wz
2 cos р
sin2 р
тогда и только тогда,
когда р
90°
1
y
w
1
w
z
Следствие 3. Выпуклый четырехугольник ABCD является ортодиагональ¬
ным тогда и только тогда, когда—2+ -л = л + -л, где h1,h2,h3 и h4 - длины
h2i
h23
h2
hf
высот, исходящих из точки пересечения диагоналей AC и BD в треуголь¬
никах ABP, BCP, CDP и ADP соответственно.
§ 4. Свойства выпуклых четырехугольников,
описанных около окружности
Пусть выпуклый четырехугольник ABCD является описанным около окруж¬
ности, а = AB, b = BC, c = CD, d = AD, e = AC, f = BD, р угол между
диагоналями AC и BD и M точка пересечения диагоналей (см. рис. 1).
Тогда справедливы следующие утверждения.
54

Теорема 1. Площадь S описанного выпуклого четырехугольника ABCD вы¬
числяется по формуле:
1
S =2 V(-f )2 - (ac — bd)2.
Доказательство. По следствию 9 из § 1 площадь выпуклого четырехуголь¬
ника вычисляется по формуле S =	4(ef)2 — (a2 + c2 — b2 — d2)2. Посколь¬
ку a + c = b + d для четырехугольника, описанного около окружности, то
a2 + c2 — b2 — d2 = 2(bd — ac). Следовательно, S = 1 / 4(-f )2 — 4(bd — ac)2 =
1
= —\/(ef )2 — (ac — bd)2. Теорема доказана.	■
Теорема 2. Следующие условия для описанного выпуклого четырехугольни¬
ка ABCD эквивалентны:
(1)	ABCD - воздушный змей, т. е. a = b,c = d или a = d,b = c;
(2)	ac = bd;
(3)	диагонали AC и BD перпендикулярны;
(4)	S = -^, где S - площадь четырехугольника ABCD.
Доказательство. Докажем последовательно следующие импликации: (1) ^
(4), (4) ^ (3), (3) ^ (2), (2) ^ (1).
Пусть четырехугольник ABCD является бумажным змеем. Тогда имеем,
-f
что a = b,c = d, т. е. ac — bd = 0. По теореме 1 § 4 получаем, что S = —.
Итак, проверена импликация (1) ^ (4).
-f	-f
Если S = —, то sin p = 1, поскольку S = -4-sin р. Поэтому диагонали AC
и BD являются перпендикулярными. Таким образом, доказана импликация
(4) ^ (3).
55

Пусть диагонали AC и BD перпендикулярны. Тогда получаем, что S =
ef	ef 1
= sin р =	=	(ef )2 — (ac — bd)2. Откуда следует, что ac = bd, т. е.
нами доказана импликация (3) ^ (2).
Докажем, наконец, импликацию (2) ^ (1). Пусть a + c = b + d = M
и ac = bd = N. Тогда пары чисел a, c и b, d являются корнями уравнения
t2 — Mt + N = 0. Следовательно, либо a = b, c = d, либо a = d, c = b, т. е.
ABCD является бумажным змеем (см. рис. 2). Теорема доказана.	■
Рассмотрим окружности, вписанные в треугольники ABM, BMC, CMD и
AMD (см. рис. 3). Будем полагать, что их радиусы равны т\,т2,т3 и т4 соот¬
ветственно.
Рис. 3
Лемма 1. Пусть в треугольнике ABC радиус вписанной окружности ра-
а
вен т, полупериметр равен p, ABAC = а и BC = a. Тогда т = (p — a) tg .
Доказательство. Положим AC = b, AB = c. Пусть также I центр вписан¬
ной в треугольник ABC окружности. Рассмотрим рис. 4.
56

Видим, что ZBAI = - и а = BL + LC = BK + CN = (c — AK) + (b - AK).
c + b — а
Откуда следует, что AK =			= p — а. Из прямоугольного треугольника
AKI имеем, что
2
r	а
	= tg —. Лемма доказана.
p — а	2
Справедлив следующий критерий бумажного змея.
Теорема 3. Четырехугольник ABCD, описанный около окружности, явля¬
ется бумажным змеем тогда и только тогда, когда ri + r3 = т2 + r4 (см.
рис. 3).
Доказательство. Положим x = AM, y = DM, z = CM, t = BM, ZCMD =
= р. Из леммы 1 следует, что
ri + Тз =
t + x — а
р
■ tg2 +
z + y — c
р
■ tg2
t + x + z + y — а — c
р
tg 2,
2
2
2
Т2 + Т 4 =
t + z — b
1
—Р +
tg 2
x + y — d
1
t + z + x + y — b — d
1
2
2
Р
tg 2
2
Р '
tg 2
По условию а + c = b + d. Кроме того, используя неравенство треугольника,
получаем, что x + t > а и z + y > с. Поэтому t + x + z + y — а — c =
= t + z + x + y — b — d > 0. Следовательно, ri + r3 = r2 + r4 в том и только в том
случае, когда
, Р
tg2
1	t Р
р, т. е. tg
tg	2
g 2
1 и р = 90°. По теореме 2 § 4 условие
р = 90° равносильно тому, что четырехугольник ABCD является бумажным
змеем. Теорема доказана.	■
Замечание 1. Можно доказать, что четырехугольник ABCD является бу¬
мажным змеем тогда и только тогда, когда т1тз = т2т4 (см. [44J).
Пусть ABCD четырехугольник, являющийся вписанным в некоторую
окружность и описанным около некоторой окружности радиуса т. Пусть так¬
же ZBAD = а, ZCDA = в и I центр вписанной окружности (см. рис. 5).
57

Тогда ZBCD = 180° - a, ZABC = 180° - в, ZABI = 90° - , ZICD
(
= 90°-—. Поскольку AD = r
вычисляется по формуле:
\
11
a + в
Vs 2 'g V
, то площадь треугольника AID
(
Si = S (Л AID) = -
11
~a +	в
ltg2 'g2)
r2	1	в	r2 a в
Аналогично S2 = S(ЛAIB) = — у—a + 'g 2J , S3 = S(ЛВВС) = - tg - + tg 2
/
S4 = S^CID) = —
ника ABCD равна
a
tg 2 +
1
S = Si + S2 + S3 + S4 = —
/3
tg 2
/
2
—
tg2
. Следовательно, площадь S четырехуголь-
(a/2)	sin(a/2)
■ +
(a/2)	cos(a/2)
+ ■
1(в/2)
+
\
a 2
0 в
2+Т^в
+ 2'g 2
tg2
sin^/2)
= 2r2
cos(2/2)
+ ■
1
sin a cos в
Напомним, что a = AB, b = BC, c = CD, d = AD. Известно, что S =
= pr, где p = —+—+—+—. Из следствия 8 § 1 следует, что S2 = abcd. Таким
образом,
2
S2 = abcd = p2
: 4r4
1 1
sin a	sin в
4abcd
(a + b + c + d)2'
2
2
2
cos
2
r
2
2
r
и r =
58

Следствие 1. Пусть ABCD - четырехугольник площади S, вписанный в
некоторую окружность и описанный около некоторой окружности радиу¬
са г. Тогда S > 4г1 2.
Доказательство. Поскольку 0 < sin а < 1, 0 < sin в < 1, то
S
2 г2
1 1
sin а	sin в
> 2г2(1 + 1)
4г2,
причем S = 4г2 тогда и только тогда, когда а = в = 90° и ABCD квадрат.
Следствие доказано.	■
Следствие 2. Пусть ABCD - четырехугольник площади S, вписанный в
некоторую окружность и описанный около некоторой окружности радиу¬
са г с центром в точке I. Тогда площадь S этого четырехугольника равна
AI ■ IC + BI ■ ID.
Доказательство. Для доказательства следствия рассмотрим рис. 5. Имеем,
что
гггг
AI sin(a/2),ID	sin(e/2),IB	cos(e/2),IC	cos(a/2).
Следовательно,
S
2г2
1
+2r2-
sin а
1
sin в
+-
sin(a/2) ■ cos(a/2) sin(e/2) ■ cos(e/2)
2
2
г
г
AI ■IC+BI ■ID.
Следствие доказано.	■
В геометрии треугольника известна следующая теорема Эйлера: для произ¬
вольного треугольника ABC квадрат расстояния d между центрами описан¬
ной и вписанной окружностей равен R2 — 2Rr, где R,r радиусы описанной
и вписанной окружностей. Это утверждение можно переписать в виде:
1 1 _ 1
R — d + R + d г
В этом виде теорема Эйлера имеет аналог для четырехугольников, вписанных
в некоторую окружность и описанных около некоторой окружности. Справед¬
лива следующая теорема Фусса.
Теорема 4. Пусть ABCD - четырехугольник, вписанный в окружность с
центром в точке O и имеющей радиус R, и описанный около окружности с
центром в точке I и имеющей радиус г. Пусть также d = OI. Тогда
1 , 1 _ 1
(R - d)2 + (R + d)2 = г2.
59

Доказательство. Рассмотрим рис. 6, где F, E точки пересечения с описан¬
ной окружностью прямых AI и CI соответственно.
а + j
Пусть а = ZDAB, j = ZDCB. Тогда —-— = 90°, ZFCE = ZFAE = 90°
и FE диаметр описанной окружности. Существует прямоугольный треуголь¬
ник, в котором гипотенуза CA равна CL + KA (см. рис. 7). Его площадь равна
r(AK + CL) _ CI ■ IA
2 = 2 .
Так как (CL + KA)2 = CI2 + IA2, то r2(CI2 + AI2) = CI2 ■ IA2, т. е.
1
1
1
+ ■
r2	IA2 IC2
IO медиана треугольника FIE. Следовательно, d2 = OI2
-R2 и FI2 + IE2 = 2(d2 + R2). Поскольку AI ■ FI = CI ■ IE = (R - d)(R + d),
FI2 + IE2
2
1
FI2
1
IE2
j. Поэтому
1
+ -
1
AI2	(R2 - d2)2’ CI2	(R2 - d2)2'
1 _ FI2 +	IE2	_	2(d2 + R2) _(R - d)2 + (R + d)2
Г2 = (R2 -	d2)2	=	(R2 - d2)2 = (R - d)2(R + d)2	~ (R - d)2	' (R + d)2'
Теорема доказана.	■
Замечание 2. Данное доказательство теоремы Фусса принадлежит Ж.Салазару
(см. [48]).
60

Согласно [52] следующее неравенство было доказано Герасимовым и Коти
в 1964 году.
Следствие 3. Пусть четырехугольник является вписанным в окружность
радиуса R и описанным около окружности радиуса г. Тогда \/2r < R.
Доказательство. По теореме 4 § 4
1 11,
jR-df +(RTd)2 = Г2’ ГДе d расСТ°-
яние между центрами описанной и вписанной окружностей. Следовательно,
2r2 =
(R2 - d2)% (R2 - d2)^ R2
R2 + d2
R2
и \/2r < R; при этом R = к/2r тогда и только тогда, когда центр описанной
окружности совпадает с центром вписанной окружности. Следствие доказано.
Пусть ABCD четырехугольник, описанный около окружности (см. рис. 8).
Обозначим через e,f,g,h длины отрезков касательных, через p, q, S длины
диагоналей и площадь четырехугольника ABCD (см. рис. 8). Пусть также
r и I радиус и центр окружности, вписанной в четырехугольник ABCD,
а = ZDAB, y = ZDCB.
Предложение 1. Справедливо равенство:
2 efg + fgh + ghe + ehf
r =	.
e + f + g + h
Доказательство. Поскольку
c, AB • AD. CB • CD.	(e + f)(e + h).	(f + g)(g + h).
S =	sin a+	sin y =	sin a+	sin y
О	О'	О	О	1
а
и sin
а
cos
2	\/ r2 + e2’	2	-\/r2 + e2
• Y
sin
'Jr2 + g2’
Y
cos
r2 + g-
'Jr2 + g2
S = (e + f )(e + h)er + (f + g)(g + h)gr
r2 + e2
r2 + g2
r
e
r
g
то
61

С другой стороны, площадь S равна сумме площадей треугольников AIB, BIC, CID
и AID. Следовательно,
s = £ + Dl + И±еУт + (i±3l + (l±hr = (е + f + g + h)r.
2 2 2
Откуда получаем, что
(e + f) (e + h)e	(f + g) (g + h)g
2
r2 + e2
■ + ■
r2 + g2
e + f + g + h,
2 efg + fgh + ghe + ehf
r2 =			;	. Предложение доказано.	■
e + f + g + h
Следствие 4. Пусть ABCD - четырехугольник, описанным около окруж¬
ности радиуса г. Тогда его площадь S вычисляется по формуле
S = V(e + f + g + h)(efg + fgh + ghe + hef),
где e, f,g,h - длины касательных, указанных на рис. 8.
В работе [27] доказан следующий результат.
Предложение 2. Пусть ABCD - четырехугольник, описанным около окруж¬
ности. Тогда длины его диагоналей равны
Р = \j f+h ((e + g)(f + h) + 4fh ),q = J	((e + g)(f + h)+4eg),
где e, f, g, h - длины касательных, указанных на рис. 8.
Доказательство. Рассматривая треугольник ABD и применяя теорему ко¬
синусов, получаем, что q2 = (e + f )2 + (e + h)2 — 2(e + f )(e + h) cos а. Поскольку
a	e
cos —
2	\fr2 + e2
то
2 a	2e2	2e2(f + e + g + h)
cos a = 2 cos	1 = —z	T- — 1 = 		—	—	— — 1
2	r2 + e2	(e + f )(e + g)(e + h)
согласно предложению 1 § 4. Следовательно,
2	,	,.-,2	4e2(e + f + g + h)	f + h..	..	.	.
q =(2e + h + f )2	2	■	- = —■—((e + g)(f + h) + 4eg).
e + g
e + g
Аналогично вычисляется p. Предложение доказано.	■
Продолжим изучать зависимость между основными параметрами четырех¬
угольника, описанного около окружности. Итак, пусть ABCD четырехуголь¬
ник, описанный около окружности, W, X, Y, Z точки касания окружности
сторон этого четырехугольника (см. рис. 9). Пусть также k = WY, l = XZ,
\ = Z.CIX, g = ZXIB. Справедлив следующий результат.
62

Предложение 3. (см. [34]). Длины отрезков WY и XZ равны соответ¬
ственно
k _ 2(efg + fgh + ghe + hef)	^ _ 2(efg + fgh + ghe + hef)
//(e + f )(g + h)(e + g)(f + h)	//(e + h)(f + g)(e + g)(f + h)
где e, f,g,h - длины касательных, указанные на рис. 8.
Доказательство. Рассмотрим треугольник IYW. По теореме косинусов мы
получаем, что k2 _ 2r2 — 2r2 cos(2A + 2ц) _ 2r2(1 — cos(2(A + ц))). Посколь-
+ f . \ g	1 — tg2 Ц	r2 — f	2tg ц
ку tg ц _ -, tg A _ -, cos 2ц _ _	_ 2 + f2, sm 2ц
2rf
r
cos 2A
r2 + f2
sin 2ц sin 2A _ 2r2 •
r
r2 — g2
r2 + g2,
1 + tg2 ц
sin 2A
1 + tg2 ц	r2 + f2
2rg	k2
- —	2, то — _ 1 — cos 2ц cos2A +
(f + g)
2
r2 + g2
2r2
(r2 + f2)(r2 + g2)
. Откуда следует, что
k2 _ 4r4	(f + g)2
k	41	(r2 + f 2)(r2 + g2).
Из предложения 1 § 4 имеем, что
r2 + f2 _ (e + f)(f + g)(f + h) „ „2 , „2
e+f+g+h
и r2 + g2
(g + e)(g + f )(g + h)
e+f+g+h
Поэтому
k2 _ 4r4•
k
(f + g)2(e + f + g + h)2
(e + f )(f + g)(f + h)(e + g)(f + g)(g + h) ’
2(efg + fgh + ghe + hef)
(e + f )(g + h)(e + g)(f + h)
Аналогично доказывается второе равенство. Предложение доказано.
или
63

Следствие 5. Пусть a = e + f,b = f + g,c = g + h,d
k
четырехугольника ABCD (см. рис. 8 и 9). Тогда =
h + e - длины сторон
Доказательство. Из предложения 3 § 4 следует, что
k
1
Следствие доказано.
(e + h)(f + g)
(e + f )(h + g)
Следствие 6. Длины отрезков WY и XZ равны тогда и только тогда, когда
четырехугольник ABCD является бумажным змеем, т. е. a = b,c = d или
a = d,c = b.
Доказательство. Если ABCD бумажный змей (см. рис. 9), то равенство
WY = XZ следует из того, что треугольник ADC получается из треугольника
ABC симметрией относительно диагонали AC. Докажем, что если WY =
XZ, то четырехугольник ABCD является бумажным змеем. Из предыдущего
следствия имеем, что ac = bd. Поскольку четырехугольник ABCD описан
около окружности, то a + c = b + d. Откуда следует, что a2 + c2 = b2 + d2,
a2 — b2 = d2 — c2, a — b = d — c, (a — b)(a + b) = (d — c)(d + c). Если a = b, то
d = c и утверждение доказано. Если a — b = 0, то a + b = d + c. Учитывая,
что a + c = b + d, получаем, что b — c = c — b, т. е. b = c и a = d. Следствие
доказано.	■
Пусть четырехугольник ABCD является описанным около окружности.
Сохраняя все предыдущие обозначения, вычислим угол р между отрезками
WY и XZ (см. рис. 11). Пусть w = ZYWB,x = ZZXB,y = ZDYW,z =
= ZDZX, P точка пересечения отрезков WY и XZ, M точка пересечения
64

продолжения сторон AB и CD, если прямые DC и AB не параллельны (если
п
DC || AB, то y = w = — и y + w = п). Тогда y + w = п. Аналогично x + z = п.
Из четырехугольников BWPX и DYPZ следует, что 'т + р+x+ZCBA = 2п и
y + z + р + ZCDA = 2п. Складывая левые и правые части последних равенств,
получаем, что
(y + w) + (x + z) + 2р + ZC BA + ZC DA = 4п.
Ранее мы доказали, что площадь S четырехугольника ABCD вычисляется по
следующей формуле:
S = Vabcd • t
( ZCBA + ZCDA\
2
.
Следовательно, S = Vabcd • зт(п — р) = \/abcd • sin р и sin р
Учитывая следствие 4 § 4, получаем, что
S
V abcd
sin р
V(e + f + g + h)(efg + fgh + ghe + hef)
V(e + f )(f + 9)(9 + h)(h + e)
где e, f, g, h длины касательных, указанные на рис. 8. Таким образом, дока¬
зано следующее утверждение.
Предложение 4. Пусть четырехугольник ABCD является описанным око¬
ло окружности, WY и XZ - отрезки, соединяющие точки касания (с окруж¬
ностью) противоположных сторон, р - угол между WY и XZ (см. рис. 11).
Тогда
sin р
V(e + f + g + h)(efg + fgh + ghe + hef)
V(e + f )(f + g)(g + h)(h + e)
где e, f,g,h - длины касательных, указанные на рис. 8.
Следствие 7. Пусть четырехугольник ABCD является описанным около
окружности, WY и XZ - отрезки, соединяющие точки касания (с окруж¬
ностью) противоположных сторон. Отрезки WY и XZ являются перпен¬
дикулярными тогда и только тогда, когда четырехугольник ABCD можно
вписать в окружность.
Доказательство. Ранее мы заметили, что ZCBA+ZCDA = 2п — 2р. Откуда
п
следует, что р = — тогда и только тогда, когда ZCBA+ZCDA = п. Следствие
доказано.	■
Следствие 8. Пусть четырехугольник ABCD является описанным около
окружности, WY и XZ - отрезки, соединяющие точки касания (с окружно¬
стью) противоположных сторон. Четырехугольник ABCD можно вписать
в окружность тогда и только тогда, когда
(e + f + g + h)(efg + fgh + egh + ehg) = (e + f )(f + g)(g + h)(h + e),
где e, f, g, h - длины касательных, указанные на рис. 8.
65

Доказательство следует из следствия 7 и предложения 4 § 4.
Пусть четырехугольник ABCD является описанным около окружности ра¬
диуса r с центром в точке I. Имеет место следующий результат.
Предложение 5. Пусть четырехугольник ABCD является описанным око¬
ло окружности (см. рис. 12). Тогда справедливы следующие равенства:
. A _ jefg + fgh + ghe + hef . B _ jefg + fgh + ghe + hef
81П2=	(e + f)(e + g)(e + h) ’Sm 2 _	(f + e)(f + g)(f + h) ’
. C _
SmY_V (g + e)(g + f )(g + h)
efg + fgh + ghe + hef . D
Sln 2
efg + fgh + ghe + hef
(h + e)(h + f)(h + g) ’
где e, f,g,h - длины касательных, указанные на рис. 12.
Доказательство. Рассмотрим треугольник WZI. По теореме косинусов име-
4e2r2
так как ZZIW _ п — ZA,
1, что WZ2 _ 2r2 — 2r2 cos ZZIW
Ae
cos ZZIA _ — cos A и cos —
2	r2 +
ет, что r2 + e2 _
1
e+f+g+h
r2 + e2
=. Из предложения 1 § 4 сразу следу-
.2 _ц ,2 _ (e + f )(e + g)(e +h) 4 WZ2 _ 4e2. efg + fgh + ghe +hef
(e + f )(e + g)(e + h)
A _ 2 WZ efg + fgh + ghe + hef
sin
2 e
(e + f )(e + g)(e + h)
Аналогично доказываются остальные равенства. Предложение доказано. ■
Следствие 9. Пусть четырехугольник ABCD является вписанным в неко¬
торую окружность и описанным около некоторой окружности (см. рис. 13).
Тогда его площадь S вычисляется по формуле:
S _(e + f + g + h)(/ejgk,
где e, f,g,h - длины касательных, указанные на рис. 13.
66

Доказательство. Рассмотрим рис. 13.
A r
Поскольку AA + АО
C
п и tg — = -, tg — = -, то r2
2 e 2 g
fh. Значит, r4 = efgh и S
a + b + c + d
= (e + f + g + h)<4efgh. Следствие доказано.
2
2
r
r
r
= eg. Аналогично
(e + f + g + h) =
Следствие 10. ([42]). Пусть четырехугольник ABCD является описанным
около некоторой окружности и вписанным в некоторую окружность (см.
рис. 13). Тогда
A	bc B cd О ad D ab
tg2=	Odd tg¥= ab, tg¥= Cb, tg¥= Tc
где a = AD, b = CB,c = CD, d = AD.
Доказательство. Рассмотрим рис. 12. По теореме косинусов a2+d2-2ad cos A -
a2 + d2 - b2 - c2 „
. По-
BD2 = b2 + c2 + 2bc cos A. Откуда следует, что cos A ■-
скольку a + c = b + d, то (a — d)2
2(ad + bc)
Значит, cos A
ad bc
(b — c)2	и	a2	+ d2	— b2	—	c2	=	2(ad	— bc).
ad + bc
Далее,
tg A =
11 — cos A
1—
1 + cos A л
1 +
ad - bc
ad + bc
ad — bc
ad + bc
Остальные равенства доказываются аналогично. Следствие доказано.
Замечание 3. Заметим, что
A
sin —
A
tg 2
tg2 2 + 1
bc	A
	-	—, COs —
ad + bc	2
tg A + 1
1
ad
ad + bc’
67

. B
sin —
dc	B
—	- , cos —
ab + cd 2
ab
ab + cd
Теорема 5. ([52]). Пусть четырехугольник ABCD является описанным око¬
ло окружности радиуса r и вписанным в окружность радиуса R (см. рис. 6).
Тогда справедливы неравенства:
rf2	If A B B C CD D A\
~R - 2 ( sin^cos^ + sln^cos^ + sln^cosY + slnYcos^ ) - 1
Доказательство. Согласно следствию 8 § 1 площадь S четырехугольника ABCD
„	^—;	a + b + c + d	2\/ abcd
равна S = v abcd = = r ■			, то r =	-		. Далее,
ad • DB bc • DB	(ad + bc) • DB	>—-—;
S = S(AABD) + S(ADCB) = ——	1	= 4—	= Vabcd.
4R
4R
4R
tt	2	(ab + dc)(ac + db)
По теореме 8 § 1 DB2 = 		—		. Отсюда, таким образом,
ad + bc
ленно получаем, что
немед-
R
1	(ad + bc)(ab + cd)(ac + db)
4
abcd
8f2abcd
rf2 _
R	(a + b + c + d)^ (ab + cd)(ad + bc)(ad + bc)
Поскольку —+—+—+— > fabcd и —+— > fabcd (неравенство Коши), то
f2r
8f2abcd
2\/abcd
R	4УоШ^(ab + cd)(ad + bc) ■ ‘^fabcd	\Д—ьТЩ—^ГЬс)
A B	B	C	C D	D A
Положим T = sin — cos	+ sin —	cos	+ sin — cos	+ sin — cos —.	Докажем,
2 2	2	2	2 2	2 2м	’
что
2\/ abcd
< 1T < 1.
■\J (ab + cd)(ad + bc)	2
0	ZC	n	ZA	ZD	n	ZB
Заметим, что	=	, 	=	, и воспользуемся замечанием 3.
’ 2	2 2	2	2	2	J
Имеем, что
A	B	B	C	C	D	D	A
T = sin — cos	+ sin — cos	+ sin — cos	+ sin — cos — =
2	2	2	2	2	2	2	2
bfac + c\fbd, + dfac + aojbd,	('/ab + к/~сЗ)(к[—Л + '/bc)
у/ (ad + bc)(ab + cd)
■\J (ad + bc)(ab + cd)
68

ab + Vcd 4	ad + Vbc	4
Поскольку			> v abcd и			> v abcd, то
T
2
4\/ abcd
у/ (ad + bc)(ab + cd)
T	2—abcd
Откуда следует, что — >	. Далее докажем, что 1 < 2.
2	(ab + cd)(ad + bc)
ab + cd !	!—— ! 2	- ab ■ \/ cd
Поскольку			> 2 abcd, то 2(ab+cd) > ( ab+ cd)2 и 2 > —-	.
2	ab + cd
Аналогично доказывается, что —2 > —. + =-. Откуда следует, что 2 > T.
ad + bc
Теорема доказана.	■
Из теоремы 5 следует второе доказательство неравенства Герасимова Коти.
Следствие 11. ([32, 52]). Если четырехугольник ABCD является описан¬
ным около окружности радиуса r и вписанным в окружность радиуса R, то
R > —2r.
§ 5. Геометрия трапеции
Трапеция четырехугольник, имеющий пару параллельных противопо¬
ложных сторон. В частности, параллелограмм мы будем считать трапецией.
Фиксируем следующие обозначения для произвольного выпуклого четырех¬
угольника ABCD (рис. 1):
Рис. 1
Предложение 1. Четырехугольник ABCD является трапецией тогда и
только тогда, когда sin A ■ sin C = sin B ■ sin D.
Доказательство. Пусть четырехугольник ABCD является трапецией. Если
DC I AB, то sin D = sin(n — A) = sin A и sin C = sin(n — B) = sin B.
Откуда следует, что sin A ■ sin C = sin B ■ sin D. Если же AD || BC, то sin A =
= sin(n — B) = sin B, sin D = sin(n — C) = sin C и sin A ■ sin C = sin B ■ sin D.
Обратно, предположим, что sin A ■ sin C = sin B ■ sin D и, например, отрезок
AD не является параллельным отрезку CD. Тогда продолжения сторон AD
и BC пересекаются, например, в точке M (см. рис. 2).
69

Рис. 2
Пусть ZC'i = п — ZC и ZD\ = п — ZD. Тогда ZA + ZB = п — ZM = ZC1+
+ZD\, ZA — ZCi = ZDi — ZB, sin A • sin Ci = sin B • sin Di, cos(A — Ci) =
= cos(D1 — B) = cos(B — D1) и, следовательно, cos A • cos C1 = cos B • cos D1.
Поэтому cos(A + C1) = cos(B + D1) и ZA + ZC1 = ±(ZB + ZD1) + 2пк для
некоторого целого числа к. Если ZA + ZC1 = ZB + ZD1 + 2пк, то 2ZA =
= 2ZD1 + 2пк и ZA = ZD1 + пк. Поскольку ZA < — и ZD1 = п — ZD < —,
то k = 0 и ZA = ZD1 = п — ZD, т. е. DC || AB. Если же ZA + ZC1 =
= —ZB — ZD1 + 2пк, то 2ZA = —2ZB + 2пк и ZA + ZB = пк = п — ZM < п;
противоречие. Предложение доказано.	■
Предложение 2. Четырехугольник ABCD является трапецией тогда и
только тогда, когда cos A + cos D = cos B + cos C = 0.
Доказательство. Если AB || CD, то ZD = п — ZA, ZC = п — ZB и cos A+
+ cos D = cos B + cos C = 0. Обратно, пусть выполняются условия cos A =
A +D A — D B +C
= — cos D и cos B = — cos C. Тогда cos—-— • cos—-— = 0 и cos-
BC
2
AD
ZA ZD
2
п
2 + пк для
cos	= 0. Если, например, cos	=0, то
некоторого целого числа к и ZA = ZD+п+2пk; противоречие. Следовательно,
A + D
cos	=0 и ZA + ZD = п + 2пк < 2п. Откуда следует, что ZA + ZD = п
и CD || AB. Предложение доказано.	■
Предложение 3. Четырехугольник ABCD является трапецией (с парал¬
лельными сторонами AB и CD) тогда и только тогда, когда ctg A + ctg D =
= ctg B + ctg C = 0.
Доказательство. Если AB | CD, то ZD = п — ZA, ZC
cos^ — A)
(п — A)
ctg A, ctg C
cos^ — B)
sin^ — B)
п — ZB и
: — ctg B.
Откуда следует, что ctg A + ctg D = 0 и ctg B + ctg C = 0. Докажем обратное
утверждение. Пусть ctg A + ctg D = ctg B + ctg C = 0. Тогда cos A • sin D+
+ sin A • cosD = 0 и sin(A + D) = 0. Откуда следует, что 0 < ZA + ZD =
= пк < 2п, где к некоторое целое число, т. е. к = 1 и CD || AB. Предложение
доказано.	■
70

Предложение 4. Четырехугольник ABCD является трапецией (с парал-
A D
лельными сторонами AB и CD) тогда и только тогда, когда tg — • tg — =
B C
= tg 2 ^tg 2 = L
Доказательство. Если AB Ц CD, то ZD :
. . D п A
п — ZA и — = — — —. Поэтому
A
A D sinA
tg 2 ^tg T = ~
C0S 2
sm	— — —
cos — — —
= 1.
Аналогично доказывается, что tg — • tg — = 1. Докажем обратное утвержде-
A D B C
ние. Пусть tg — • tg — = tg — • tg — = 1. Предположим, что сторона AB не
параллельна CD. Тогда из равенства (ZA+ZD)+(ZB+ZC) = 2п следует, что,
A D A D
например, ZA + ZD > п и ZB + ZC < п. Далее, sin — • sin — = cos — • cos —
A + D	B + C 0 A + D п
и cos	 = 0. Аналогично cos	 = 0. Значит, 	 =	+ пк и
2 2 ’22
B + C п	/ л / r\
—-— = —+пп, где к, n некоторые целые числа. Следовательно, ZA+ZD =
= п + 2пк и ZB + ZC = п + 2пп < п; противоречие. Предложение доказано.
Предложения 1 4 описывают выпуклые четырехугольники, являющиеся
трапециями, на тригонометрическом языке. Далее мы предлагаем другие кри¬
терии того, что четырехугольник является трапецией. Для этого напомним,
что отрезок, соединяющий середины противоположных сторон четырехуголь¬
ника, называется бимедианой (см. [36]).
Имеет место следующее утверждение.
Предложение 5. Четырехугольник ABCD является трапецией (с парал¬
лельными сторонами AB и CD) тогда и только тогда, когда одна из его
бимедиан делит его площадь пополам.
Доказательство. Если четырехугольник ABCD является трапецией, то ис¬
комой бимедианой является бимедиана MN, соединяющая стороны AB и CD
(см. рис. 3). Действительно, пусть DK высота трапеции. Тогда S(ABCD) =
DC + AB
2
• DK и
DC AB
S (AMND) = 2	2 • DK = 1 S(ABCD).
Для доказательства обратного утверждения рассмотрим рис. 4. Пусть MN
бимедиана четырехугольника, T1 = S(AAMD),T2 = S(ADMN),T3 = S(ANMC)
71

лк	и
Рис. 3
и T4 = S (ЛMCB). По условию T + T2 = T3 + T4. Поскольку MN является ме¬
дианой в треугольнике DMC, то T2 = T3. Следовательно, T = T4. Поскольку
AM = MB, то длины перпендикуляров, опущенных из точек D и C на AB
равны, т. е. CD || AB и ABCD является трапецией. Предложение доказано.
Предложение 6. Пусть ABCD - выпуклый четырехугольник. Отрезок AB
параллелен отрезку CD тогда и только тогда, когда площади треугольников
APD и BPC равны (P - точка пересечения диагоналей AC и BD).
Доказательство. Отрезок AB параллелен отрезку CD тогда и только тогда,
когда длины перпендикуляров, опущенных из точек D и C на AB, равны.
Последнее условие равносильно равенству площадей треугольников ABD и
ABC (так как у них общее основание AB), а равенство указанных площадей
равносильно равенству площадей треугольников APD и BPC. Предложение
доказано.	■
Пусть ABCD выпуклый четырехугольник (см. рис. 5). Обозначим также
Рис. 5
S = S^DPC), T = S^APB),U4 = S(AAPD),U2 = S(APSB).
Предложение 7. Четырехугольник ABCD является трапецией тогда и
только тогда, когда S^ADC) • S^ABC) = S^DBC) • S^ABD).
72

Доказательство. Имеем, что
(S+U1)(T+U2) = (S+U2)(T+U1) ^ SU2+U{T = SV1+V2T ^ (S-T)(U2-U1) = 0.
Последнее условие равносильно тому, что S = T или U2 = U1. Условие U2 =
= U1 по предложению 6 равносильно тому, что DC Ц AB. Условие T = S по
предложению 6 равносильно тому, что BC || AD. Предложение доказано. ■
Заметим, что в произвольном выпуклом четырехугольнике U1U2 = ST (см.
рис. 5). Это следует из того, что
гт DP ■ AP . гт CP ■ BP .	„ DP ■ CP .	^ AP ■ BP .
U1 =			sin f, U2 =			sin f, S =			sin f, T =			sin f,
где f = ZCPB. Рассмотрим площадь K четырехугольника ABCD. Имеем,
что
K = S + T + U1 + U2 = S + T + 2^ST + U1 + U2 - 2 vST =
= (Vs + VT)2 + (U1 + U2 - 2Vu1U2) = (Vs + VT)2 + (W -VV)2,
так как U1U2 = ST. Откуда следует, что K > (VS + VT)2, причем K =
= (VS + VT)2 тогда и только тогда, когда U1 = U2. Последнее условие по
предложению 6 равносильно тому, что AB | CD и четырехугольник ABCD
является трапецией с параллельными сторонами AB и CD.
Введем для выпуклого четырехугольника ABCD следующие обозначения:
a = AB,b = BC,c = CD,d = AD, E,F основания перпендикуляров, опу¬
щенных из точек D и C соответственно на сторону AB, e = AC, f = BD,
x = AE, J точка пересечения прямых DC и AB, X = ZCJB и h = CF (см.
рис. 6).
Тогда по теореме Пифагора получаем, что
e2 = h2 + (x + c cos X)2,
f2 = (a — x)2 + (h — c sin X)2,
b2 = h2 + (a — c cos X — x)2,
d2 = x2 + (h — c sin X)2.
Откуда следует, что
e2 + f2 = 2(h2 + x2) + c2 + a2 — 2hc sin X + 2x(c cos X — a),
73

b2 + d2 = 2(h2 + x2) + a2 + c2 — 2hcsin A — 2ac cos A + 2x(c cos A — a).
Следовательно, (e2 + f2) — (b2 + d2) = 2ac cos A.
Предложение 8. Пусть ABCD - трапеция, не являющаяся параллелограм¬
мом, AB || CD и a = AB = c = CD. Тогда
2	ad2 — cb2 2	ab2 — cd2
e = ac +	, f2 = ac +	.
a c	a c
Доказательство. Рассмотрим рис. 7, a = ZDAB,j = ZDCB.
Рис. 7
По теореме косинусов имеем следующие равенства: f2 = b2 + c2 — 2bc cos 7,
e2 = a2 + b2+ +2ab cos 7. Откуда следует, что
f2a + e2c = ab2 + ac2 + a2c + b2c = (a + c)(b2 + ac).
Аналогично f2 = a2 + d2 — 2ad cos a и e2 = d2 + c2 + 2cd cos a. Исключая из
последних двух равенств cos a, получаем, что
f 2c + e2a = a2c + d2c + d2a + c2a = (a + c)(d2 + ac)
2	1 /,2	,2	d2a — b2c
e2 =	(b2c — d2a + ac(c — a)) = ac +	.
c — a	a — c
Аналогично
f2(a2 — c2) = (a + c)(b2 + ac)a — (a + c)(d2 + ac)c = (a + c)(b2a + a2c — d2c — ac2),
или
.2	1	2	,2	b2a — d2c
f2 =	(b2a — d2c + ac(a — c)) = ac +	.
a—c	a—c
Предложение доказано.	■
Предложение 9. В четырехугольнике ABCD стороны AB и CD парал¬
лельны тогда и только тогда, когда e2 + f2 = b2 + d2 + 2ac, где e = AC, f =
= BD, b = BC,d = AD, a = AB и c = CD.
74

Доказательство. Если e2 + f2 = b2 + d2 + 2ac, то, предполагая, что пря¬
мая AB не является параллельной прямой CD, и применяя теорему косинусов
к Л JAD, Л JAC, AJBC, AJDB, получим, что e2 + f2 — b2 — d2 = 2ac cos A =
= 2ac (см. рис. 6). Откуда следует, что A = 0; противоречие. Докажем обратное
утверждение. Если AB || CD, то, предполагая, что a > c, по предложению 8
§ 5 получим, что
2	ad2 — cb2 2	ab2 — cd2
e2 = ac +	, f = ac +	,
a c	a c
или
Если a
e2 + f2
4 f2
e
2ac + a(b2 + d2) - c(b2 + d2)
2 ac + b2 + d2.
a-c
c, то четырехугольник ABCD является параллелограммом и b
= 2(a2 + b2) = b2 + d2 + 2ac. Предложение доказано.
d,
Предложение 10. Пусть P - точка пересечения диагоналей трапеции ABCD,
не являющейся параллелограммом (см. рис. 7). Тогда
AP
a
a+c
ac +
ad2	cb2
a-c
, CP
c
a+c
ad2 - cb2
ac +
a-c
Доказательство. Рассмотрим треугольники APB и DPC. Они являются
подобными, так как ZCAB = ZACD и ZDBA = ZCDB. Следовательно,
-. Откуда следует, что AP(a + c) = ae, или
AP
e AP
AP
a
	e
a+c
a
a+c
ad2 - cb2
ac +
a-c
Аналогично
CP
c
a+c
ac +
ad2	cb2
Предложение доказано.
ac
75

ГЛАВА 3
Задачи для самостоятельного решения
Задача 1. Построить (с помощью циркуля и линейки) четырехуголь¬
ник ABCD, если известны длины сторон и угол между прямыми BC и AD.
Задача 2. Доказать, что середины сторон выпуклого четырехугольника
являются вершинами параллелограмма.
Задача 3. Доказать, что два выпуклых четырехугольника, имеющие об¬
щие середины сторон, равновелики.
Задача 4. Пусть ABCD прямоугольник. Доказать, то для любой точ¬
ки M плоскости справедливо равенство MA2 + MC2 = MB2 + MD2.
Задача 5. В четырехугольнике ABCD AB = AD, ZACD = ZBCA,
ZBAD = 140°, ZBEA = 110°, где E точка пересечения диагоналей. Найти
угол р = ZCDB.
Указание. Рассмотрим рис. 1.
Пусть a = AB = AD, b = BC, c = CD, u = BE, v = ED, 5 = ZBCE.
Тогда ZABD = ZBDA = 20°, ZBAE = 50°, ZEAD = 90° и a = v cos 20°. По
u	a	v cos 20°	u	b
теореме синусов имеем, что -
v, = sin 50° =
vc
sin 50°	sin 110°	sin 110°
так как CE биссектриса угла ZBCD в треугольнике BCD. По теореме
b
sin р
синусов c - sin(110° — 5)
Откуда имеем, что
sin р
sin р
sin(110° — 70° + р) sin(40° + р)
sin 50°.
sin р = sin 50° • sin(40° + р) = cos 40° • sin(40° + р)
и р = 50°.
^(sin(80° + р) + sin р)
76

Задача 6. Внутри выпуклого четырехугольника ABCD найти точку X,
такую, что величина XA + XB + XC + XD имеет наименьшее значение.
Указание. Рассмотреть точку пересечения диагоналей.
Задача 7. Пусть M произвольная точка окружности, описанной око¬
ло треугольника ABC, и не совпадающая с его вершинами. Пусть x,y,z
длины перпендикуляров, опущенных из точки M на стороны BC, AC и AB
соответственно. Доказать, что — = —|—, где a = BC, b = AC, c = AB.
x y z
Указание. Рассмотрим рис. 2.
Пусть u = MB,w = MA,v
vc + bu. Далее, Si
MC. По теореме Птолемея имеем, что
x—	yb
aw = vc + bu. Далее, S1 = S(ABMC) = —, S2 = S(AAMC) = —,
zc	uv—	wvb	uwc
S3 =	S(ABMA)	= —.	Поскольку Si	= —, S2	= —, S3 =	—,	где R
uv4	wv	Ruw
радиус описанной окружности, то x = ——, y = ——, z = ——. Следовательно,
2R	2R 2R
b	c	b ■ 2R	c ■ 2R	2R bu + cv	2Raw	2Ra	a
y	z	wv uw	w uv	wuv	uv	x
Задача 8. Пусть a, b, c, d последовательные длины сторон четырехуголь¬
ника площади S. Доказать, что S <	+	+
2
2
Задача 9. Пусть a, b, a, d длины сторон равнобокой трапеции. Доказать,
что квадрат диагонали равен a2 + bd.
Задача 10. Пусть ABCD четырехугольник, вписанный в окружность
радиуса R и центром в точке O. Пусть h1,h2,h3,h4 длины расстояний от
точки O до сторон AB, BC, DC и AD соответственно и r1,r2 радиусы впи¬
санных окружностей в треугольники ABC и ADC соответственно. Доказать,
что r1 + r2 = h1 + h2 + h3 + h4 — 2R.
Указание. Рассмотрим рис. 3.
77

Пусть AB = a,BC = b,AC = n, r1,p1 радиус вписанной окружности и
полупериметр треугольника ABC. По теореме Птолемея имеем, что
„ b	a	n n	a	b a	b	n
R • 2 = 0 ^ 2 + 1 ^ 2 ,R ^ 2 = 2 ^ 2 + 1 ^ 2,R ^ 2 = h ^ 2 + h ^ 2.
Далее,
2S(AABC) = 2p1r1 = ah1 + bh2 + nh0.
Откуда следует, что 2p1(r1 + R) = (a + b+n)(h0 + h1 + h2) и R+r1 = h0 + h1 + h2.
Рассмотрим рис. 4.
Рис. 4
Пусть r2 и p2 радиус вписанной окружности и полупериметр треугольни¬
ка ADC, d = AD, c = CD. Тогда 2p2 = n + d + c и 2S(AADC) = 2p2r2 =
= dh4 + ch3 — h0n, т. е. (n + d + c)r2 = dh4 + ch3 — h0n. По теореме Птолемея
n d c	n d c
имеем, что h4 = h0 + R из четырехугольника AH4H0O, R = h3 + h4 из
2
2
2
d
2
2
2
четырехугольника H4DH3O, —h3 = — h0 + — R из четырехугольника OH0H3C.
Складывая левые и правые части равенств
Rn = dh3 + ch4, Rd + h0c = h3n, cR + dh0 = nh4,
получим, что
R(n + d + c) = c(h4 — h0) + d(h3 — h0) + n(h3 + h4).
Откуда следует, что (R + r2)(n + d + c) = c(h3 + h4 — h0) + d(h4 + h3 — h0)+
+n(h3 + h4 — h0) = (c + d + n)(h3 + h4 — h0) и R + r2 = h3 + h4 — h0. Таким
78

образом, (R + ri) + (R + r2) = (ho + hi + hi) + (Нз + h4 — h0) = hi + h2 + Нз + h4
и ri + r2 = hi + h2 + h3 + h4 — 2R.
Задача 11. Пусть ABCD выпуклый четырехугольник, M, N середины
диагоналей AC и BD соответственно. Доказать, что:
(1) MN < |AD — BC|;
(2) MN2
! + b2 + c2 + d2 — e2 — f2
где a,b,c,d длины сторон, а e,f
длины диагоналей четырехугольника ABCD;
ef
(3) S =— sin tp, где S площадь четырехугольника ABCD,p угол между
прямыми AC и BD;
(4)	S <
(5)	S <
e2 + f2;
4	;
a2 + b2 + c2 + d2
4	.
a
Задача 12. Пусть ABCD трапеция, BC верхнее основание, AD
нижнее, а M и N середины диагоналей AC и BD соответственно. Доказать,
что MN
AD — BC
2
Задача 13. В четырехугольнике ABCD углы B, C, D являются тупыми.
Доказать, что диагональ AC больше диагонали BD.
Указание. Рассмотреть окружность с диаметром AC.
Задача 14. Пусть точка O центр окружности, вписанной в четырех¬
угольник ABCD. Доказать, что ZAOB + ZCOD = 180°.
Задача 15. Пусть ABCD трапеция, вписанная в окружность, и
диаметр этой окружности. Доказать, что AC >
AD + BC
2
AD
Задача 16. Пусть ABCD прямоугольник, длины сторон которого рав¬
ны a и b. Найти описанный около ABCD прямоугольник наибольшей площади
(a + b)2
и доказать, что эта площадь равна -—	.
Задача 17. Пусть треугольник ABC является правильным и точка M
не принадлежит окружности, описанной около треугольника ABC. Доказать,
что существует треугольник, длины сторон которого равны AM, BM и CM.
Указание. Воспользоваться теоремой Бретшнейдера.
Задача 18. В ромбе ABCD угол A равен 60°. На сторонах AB и BC
взяты точки K и M соответственно так, что AK = BM. Доказать, что тре¬
угольник KMD является правильным.
79

Задача 19. Пусть ABCD выпуклый четырехугольник и P,S,R,Q
точки пересечения биссектрис углов данного четырехугольника (см. рис. 5).
Доказать, что точки P, S, R, Q лежат на одной окружности.
Указание. Заметить, что ZASD
а + 5	р + 7
п —	и ZBQC = п
2
Задача 20. В выпуклом четырехугольнике ABCD ZABC = ZBCD =
= 120° и d2 = а2 + b2 + c2, где а = AB, b = BC, c = CD, d = AD. Доказать,
что в четырехугольник ABCD можно вписать окружность.
Указание. Докажем, что а + c = b + d. Пусть M точка пересечения
сторон AB и CD (см. рис. 6).
Тогда MB = MC = b и по теореме косинусов d2 = (а + b)2 + (c + b)2 —
— (а + b)(c + b) = а2 + b2 + c2 + ab + bc — ac. Поскольку d2 = а2 + b2 + c2, то
ac = b(fl + c) и (а + c — b)2 = (а + c)2 — 2b^ + c) + b2 = (а + c)2 — 2ac + b2 =
= a2+b2+c2 = d2, т. е. d = ±(fl+c—b). Если d = —(а+c—b), то d = b—(fl+c) < b;
противоречие. Таким образом, d = а + c — b, или а + c = b + d.
Задача 21. Пусть ABCD трапеция с основаниями BC и AD, а MN
отрезок, параллельный основаниям и делящий площадь пополам. Доказать,
а2 + c2
где а = BC, c = AD (см. рис. 7).
что его длина x равна
Указание. Пусть S площадь трапеции ABCD. Тогда высота трапе-
SS
ции MBCN равна	, высота трапеции AMND равна	. Высота тра-
а + x
пеции ABCD, с одной стороны, равна
2S
а + c
x + c
с другой стороны, она равна
80

Рис. 7
S S
+
a + x x + c
Задача 22. В четырехугольнике ABCD BC = 1, ZA = ZB = 120° и
ZB = 90°. Найти AD.
Задача 23. Четырехугольник ABCD вписан в окружность с центром в
точке O. Пусть P точка пересечения диагоналей AC и AD, а U,V центры
описанных окружностей около треугольников ABP и CPD соответственно.
Доказать, что либо точки U,O,P,V лежат на одной прямой, либо четырех¬
угольник OUPV является параллелограммом.
Рис. 8
Указание. Если AB || CD, то ABCD равнобокая трапеция и точ¬
ки U, O, V, P лежат на серединном перпендикуляре к AB.
Пусть AB и CD пересекаются в некоторой точке. Проведем через точку P
прямую t, параллельную прямой AB (см. рис. 8). Пусть а = ZAPB. Тогда
ZBAP = ZBDC = а и прямая t является касательной к окружности, опи¬
санной около треугольника PCD. В частности, прямая PV перпендикулярна
прямой t. С другой стороны, точки U и O лежат на серединном перпендику¬
ляре к AB. Следовательно, UO || PV. Аналогично UP || OV.
Задача 24. Пусть четырехугольник ABCD вписан в окружность с цен¬
тром в точке O и Gi,G2,G3,G4 точки пересечения медиан треугольников
ABC, BCD, ACD, DAB соответственно. Доказать, что точки Gi,G2,G3,G4
лежат на одной окружности.
Указание. Выберем декартову систему координат на плоскости так, что¬
бы центр описанной окружности O являлся началом координат, а ось OX
81

была параллельна стороне AD. Можно считать также, что радиус описанной
окружности равен единице. Рассмотрим рис. 9.
Тогда
Gi
cos в + cos y — cos a sin a + sin в + sin y
3	’	3
cos a + cos в + cos y sin a + sin в + sin y
G3
G2 ,	,
2 '	3	’	3
cos y sin y + 2 sin a	cos в 2 sin a + sin в'''
3
3
22
Далее, G\G2 = cos a, GiG3 =
4
3 ’
3
)■
sin03 — a)
, G1G4
2
sin(Y — a)
2
3
2
(y — в)
и G2G3 = 3
(a + в)
2
, G3G4 =
. Если положить Л = ZG\G2G3 и
в— a
p = ZGiG4G3, то, используя теорему косинусов, имеем, что cos p = cos
a — в
и cos Л = — cos —-— = — cos p. Откуда следует, что p + Л = 180°.
Задача 25. Пусть A, B, C, D точки в пространстве, такие, что никакие
три из них не лежат на одной прямой, и пусть AC • BD = AB • CD + AD • BC.
Доказать, что эти точки принадлежат одной окружности.
Указание. Воспользуемся методом координат. Выберем декартову систе¬
му координат так, чтобы A(—1, 0,0), B(u, v, 0), C(1, 0,0), D(x, y, z) и Q(0, a, 0),
где Q центр окружности, описанной около треугольника ABC (см. рис. 10).
Тогда равенство AC • BD = AB • CD + AD • BC после преобразований
можно записать в виде (a — at — 2y)2 = ((t + 1)2 — 4x2)(a2 + 1), или
(t — 2ya — 1)2 + 4(a2 + 1)z2 = 0,
где t = x2+y2+z2. Откуда следует, что z = 0, t = 2ya+1 и x2 + (y — a)2 = a2 + 1.
82

Рис. 10
Задача 26. Пусть в четырехугольнике ABCD сумма двух противополож-
п	п
ных углов равна—, т. е. ZA + ZC = — (см. рис. 11). Доказать, что AB2 - CD2+
+AD2 ■ BC2 = AC2 ■ BD2.
Указание. Рассмотрим инверсию плоскости с центром в точке B относи¬
тельно окружности достаточно большого радиуса R (см. рис. 11).
Пусть A’, C’, D’ - образы точек A, C, D соответственно. Тогда ZA’D’B =
= ZA и ZBD’C’ = ZC. Следовательно, ZA’D’C’ = П и треугольник A’D’C’
является прямоугольным. По теореме Пифагора (A’C’)2 = (A’D’)2 + (C’D’)2.
R2	R2	R2
Поскольку A’C’ = AC -R	,A’D’ = AD	-R	, C’D’ = CD	R	,
J	BA ■ BC	BA ■ BD	BD ■ BC
то AB2 ■ CD2 + AD2 ■ BC2 = AC2 ■ BD2.
Второе решение этой задачи следует из теоремы Бретшнейдера.
Задача 27. Четырехугольник ABCD является вписанным в некоторую
окружность Si и описанным около окружности S2. Доказать, что отрезки, со¬
единяющие точки касания противоположныхсторон четырехугольника ABCD
с вписанной окружностью, перпендикулярны.
Указание. Рассмотрим рис. 12 и инверсию плоскости относительно окруж¬
ности S2.
Используя известные свойства инверсии, получаем, что вершины A, B, C, D
четырехугольника ABCD перейдут в точки A’, B’, C’, D’ соответственно, ко¬
торые являются (в свою очередь) серединами отрезков KN, KL, LM и MN
83

соответственно (K, L, M, N это точки касания окружности S2 сторон четы¬
рехугольника ABCD). Окружность Si перейдет в окружность, проходящую
через точки A, B', C, D'. Поскольку A, B', C', D' середины сторон четырех¬
угольника KLMN, то четырехугольник A'B'C'D' является параллелограм¬
мом, вписанным в окружность. Значит, A'B'C'D' это прямоугольник, сто¬
роны которого параллельны диагоналям KM и LN. Следовательно, отрез¬
ки KM и LN перпендикулярны.
Задача 28. Доказать, что прямые, соединяющие последовательно центры
квадратов, построенных на сторонах параллелограмма ABCD и примыкаю¬
щих к нему извне, образуют также квадрат (см. рис. 13).
Указание. Рассмотрим рис. 13.
Рис. 13
Через O1,O2,O3,O4 обозначим центры квадратов, построенных на сторонах
AB,BC,CD и AD соответственно. Рассмотрим комплексные числа а = AB,
п . . п	а • £
в = AD и £ = cos —+г sin —. Тогда AOi =	,
4	4	v2
AO4 =
в • £
V2
■ и O1O4 = AO4—
84

fie 1 — ae	ae	@£
-AOi
. Далее, O1B = a	— , BO2 = — и O1O2 = O1B+
2 2 2
+BO2 = a ( 1	+ ——f=. Для решения задачи достаточно показать, что
22
вектор O1O2 получается из вектора O1O4 поворотом на 90°, т. е. O1O2 = O1O4•
в--1 — ae	в- — ae2	- в-
^Ч/Г" "2 = V- = Ч1 — —l) + —2 = O1O2.
i. Имеем, что O1O44 -
Задача 29. Пусть противоположные стороны выпуклого четырехуголь¬
ника ABCD при продолжении сторон попарно пересекаются в точках P и Q
(см. рис. 14). Доказать, что середина отрезка PQ середины диагоналей AC и
BD лежат на одной прямой.
Замечание. Приведенный результат принадлежит выдающемуся немец¬
кому математику К. Гауссу (1777 1855) (см. [16]).
Указание. Пусть p =	, q =	. Рассмотрим систему материальных
AP	C Q
точек (B, 1), (B, 1+ p + q), (P,p), (P,pq), (Q, q) и (Q,pq) и найдем центр тяже¬
сти этой системы двумя различными способами. Пусть точки M, N середины
отрезков AC и BD соответственно. Центр тяжести трех материальных точек
(B, 1), (P, p) и (Q, q) находится на пересечении отрезков AQ и PC, т. е. в точ¬
ке (D, 1 + p + q). Поэтому центр тяжести системы из четырех материальных
точек (B, 1), (P,p), (Q,q) и (B, 1 + p + q) находится в точке (N, 2 + 2p + 2q).
Рассмотрим шесть материальных точек: (B, 1), (B, 1 + p + q), (P,p), (P,pq),
(Q, q) и (Q,pq), и найдем центр тяжести этой системы. Для этого заметим,
что центр тяжести двух точек (P, pq) и (Q,pq) находится в точке (R, 2pq) и,
значит, центр тяжести всей системы расположен на прямой RN. С другой
стороны, искомый центр тяжести совпадает с центром тяжести следующей
системы материальных точек: (P,p + pq), (Q, q + pq), (B, 1 + p) и (B, 1 + q).
AB
Поскольку p = ——, то центр тяжести точек (P,p + pq) и (B, 1 + q) совпа-
AP
дает с точкой (A, (p + 1)(q + 1)). Аналогично центр тяжести точек (B, 1 + p)
и (Q, q + pq) совпадает с точкой (C, (p + 1)(q + 1)). Поэтому искомый центр
85

тяжести это середина отрезка AC, т. е. точка (M, 2(p + 1)(q + 1)). Откуда
следует, что точки M, R, N лежат на одной прямой.
Задача 30. Доказать, что в четырехугольнике, который можно описать
около окружности, середины диагоналей и центр вписанной окружности ле¬
жат на одной прямой.
Указание. Воспользуемся следующим общим утверждением, доказан¬
ным в книге [13]: Пусть М0 определенная точка выпуклого n-угольника
A1A2 ... An и B1C1,... , BnCn отрезки на сторонах A1A2, ... , AnA1 соответ¬
ственно. Тогда геометрическое место внутренних точек М этого многоугольни¬
ка, для которых сумма площадей треугольников MB1C1, MB2C2, ..., MBnCn
равна S^MoBiCi + S^MoBC + ... + S^MoBncn, является отрезком прямой, про¬
ходящим через точку M0.
Задача 31. Диагональ вписанного в окружность четырехугольника делит
его на два треугольника. Доказать, что сумма радиусов окружностей, вписан¬
ных в эти треугольники, не зависит от выбора диагонали.
Указание. Пусть дан четырехугольник ABCD и O центр окружно¬
сти, описанной около этого четырехугольника, а h1, h2, h3, h4, h0 длины пер¬
пендикуляров, опущенных на на AD,AB,CB,CD и BD соответственно (см.
рис. 15).
Обозначим через т1 радиус вписанной в треугольник ABD окружности, по¬
ложим также а = ZBAD, в = ZABD, j = ZBDA. Тогда cos a+cos в+cos 7 =
R + ri
= —-— (см. главу 1). Поскольку h0 = R cos a, h1 = R cos в, h2 = R cos j,
R
то R + r1 = h1 + h2 + h0 (по теореме Карно). Аналогично из рассмотре¬
ния треугольника BCD следует, что R +	т2	=	h3	+ h4	—	h0,	где	т2	радиус
окружности, вписанной в треугольник BCD. Откуда следует, что т1 + т2 =
= h + h2 + ft-3 + h4 — 2R.
Задача 32. Пусть ABCD четырехугольник, вписанный в окружность и
A1,B1, C1, D1 центры окружностей, вписанных в треугольники BCD, CDA,
DAB и ABC соответственно. Доказать, что A1B1C1D1 прямоугольник.
86

Указание. Заметим, что если I и O центры вписанной и описанной
окружностей некоторого треугольника PQT и D точка пересечения биссек¬
трисы PI с описанной окружностью, то QD = TD = ID (см. рис. 16).
Вернемся теперь к нашей задаче. Рассмотрим рис. 17.
Обозначим w AD = 2а, w AB = 2p,w BC = 2j,-^ CD = 25. Пусть
также M и N середины дуг BC и CD соответственно. Тогда точка Di лежит
на AM, Bi на AN и Ai точка пересечения BN и MD. Согласно замечанию
п а
MD1 = MB = MC = MA1. Поскольку ZAMD = а, то ZMA1D1 = — — —.
п в	Y + 5
Аналогично ZNA1B1 =	— . Так как ZNA1D =	, то
11 2 2 1 2 ’
ZD1A1B1 = iso- — (п — а
п в y + 5 а + в + y + 5 п
2 — 2 2 = 2 = 2.
Задача 33. Около окружности с центром в точке O описан четырехуголь¬
ник ABCD. Доказать, что ZAOB + ZCOD = 180° (см. [12]).
87

Задача 34. Доказать, что положительные числа p, R, r являются полу¬
периметром, радиусами описанной и вписанной окружностей соответствен¬
но прямоугольного треугольника тогда и только тогда, когда p = 2R + r и
R > r(V2+ 1).
Задача 35. Доказать, что для любого треугольника справедливо неравен¬
ство
а4 + b4 + c4 > 16S2,
где а, b, c длины сторон, а S площадь треугольника.
Задача 36. Доказать, что среди всех четырехугольников данного пери¬
метра квадрат имеет наибольшую площадь.
Задача 37. Пусть O точка пересечения диагоналей выпуклого четырех¬
угольника ABCD. Доказать, что для произвольной точки M плоскости четы¬
рехугольника выполняется следующее неравенство: OA + OB + OC + OD <
< MA + MB + MC + MD.
Задача 38. Доказать, что у всех ромбов, вписанных в данный прямоуголь¬
ник, острые углы одинаковые (ромб считается вписанным в прямоугольник,
если на каждой стороне прямоугольника лежит по одной вершине ромба).
Указание. Доказать, что тангенс половины острого угла такого ромба
равен частному длин сторон прямоугольника.
Задача 39. В трапеции сумма углов при большом основании равна 90°.
Доказать, что расстояние между серединами оснований этой трапеции равно
расстоянию между между серединами ее диагоналей.
Указание. Достроить трапецию до прямоугольного треугольника.
Задача 40. Пусть трапеция описана около окружности. Доказать, что
прямая, соединяющая точки касания оснований, и прямая, соединяющая точ¬
ки касания боковых сторон, проходят через точку пересечения диагоналей.
Указание. Воспользоваться методом координат.
Задача 41. Построить квадрат ABCD (с помощью циркуля и линейки),
если известны точки P,Q,R, S, лежащие соответственно на сторонах AB, BC,
C D, AD и не совпадающие с его вершинами.
Указание. Провести прямую, перпендикулярную SQ и проходящую через
точку P.
Задача 42. Длина высоты равнобедренной трапеции равна h, а боковая
сторона видна из центра описанной окружности под углом а. Доказать, что
7 2 а
площадь трапеции равна h ctg —.
Задача 43. Пусть ABCD выпуклый четырехугольник. Описать около
него квадрат.
88

Указание. Пусть A1B1C1D1 искомый квадрат (см. рис. 18).
Тогда Di принадлежит окружности с центром в точке O1 и с диамет¬
ром AD. Пусть P точка пересечения этой окружности и диагонали D1B1.
п
Тогда ZDO1P = —. Аналогично В1 принадлежит окружности с центром в
точке O2 и с диаметром CB. Пусть Q точка пересечения этой окружности
п
и диагонали D1B1. Тогда ZCO2Q =	.
Задача 44. Пусть треугольник ABC не является прямоугольным. Дока¬
зать, что следующие условия эквивалентны:
(1)	треугольник ABC остроугольный;
a3	b3	c3	q
cos3 a + cos3 в + cos3 7	’
(3)
■ +
+ ■
cos a cos в cos 7
abc
> 0;
(4) ——г > a cos3 a + b cos3 в + c cos3 7.
4 R2
Указание. Воспользоваться равенствами:
4prR
—c	(a cos3 a + b cos3 в + c cos3 y) =
4 R2	'	'
— R(sin 2a • cos2 a + sin 2в cos2 в + sin 2y cos2 7) =
4R2
pr R	sin 4a + sin 4в + sin 4y
=	—	sin 2a + sin 2в + sin 2y +
R 2	2
= R3 (p2 — (2R + r)2),
abc	2R sin a	2R sin в 2R sin 7
+	^ +	=	+	TT- +
cos a cos в cos 7 cos a	cos в	cos 7
4prR
= 2R(tg a + tg в + tg 7) = p2 _(2R + r)2
89

a3	b3	c
■ +	тт; +
3 в	cos3 '
333
cos3 a	cos3 в	cos3 y
: 8R3(tg3 a + tg3 в + tg3 y)
8R3 sin3 a	8R3 sin3 в	8R3 sin3 y
	1	— +		 =
cos3 a	cos3 в	cos3 y
_ 8 r3 8pr(p2r2 - 3R2(p2 — (2R + г)2))
= 8R	(p2 - (2R + г)2)3
Используя фундаментальное неравенство треугольника, заметить, что
p2r2 - 3R3(p2 - (2R + г)2) > 0.
Задача 45. Пусть p, q длины диагоналей параллелограмма (p > q) и a
его острый угол. Доказать, что площадь параллелограмма равна
2
p2 - q
,2
• tg a.
Задача 46. Доказать, что сумма квадратов расстояний от вершин квад¬
рата до любой точки, взятой на описанной около него окружности, равна 8R2,
где R радиус этой окружности.
Указание. Пусть ABCD квадрат и S точка, лежащая на окружности,
описанной около данного квадрата. Центром масс системы материальных то¬
чек 1A, 1B, 1C, 1D является центр O этой окружности. Следовательно, момент
инерции вычисляется следующим образом: Js = SA2 + SB2 + SC2 + SD2 =
= J0 + (1 + 1 + 1 + 1)SO2 = OA2 + OB2 + OC2 + OD2 + 4R2 = 8R2.
Задача 47. Зная в четырехугольнике ABCD длины всех сторон и диаго¬
налей, найти расстояние от вершины A до середины Z отрезка, соединяющего
середины диагоналей.
Указание. Пусть a = AB, b = BC, c = CD, d = DA, e = AC, f =
= BD. Центром масс системы материальных точек {1 A, 1B, 1C, 1D} является
точка Z. Момент инерции вычисляется таким образом: Ja = a2 + e2 + d2 =
= Jz+4AZ2. С другой стороны, Jz = -(a2+b2+c2+d2+e2+f2). Следовательно,
AZ2 = 16 (3(a2 + d2 + e2) - (c2 + b2 + f2)) .
Задача 48. Пусть около четырехугольника ABCD можно описать окруж¬
ать, Q середина CD, M точка
ресечения AB и MQ. Доказать, что
ность, Q середина CD, M точка пересечения диагоналей и L точка пе-
AL _ 4ADу
LB = vBCy .
Указание. Пусть a = AD, b = CB, x = AM, y = CM, u = MD и v = BM.
a	x	u
Поскольку треугольники AMD и BMC подобны, то — = — = —. Разместить
b	v	y
в вершинах C и D единичные массы, а в вершинах A и B соответственно мас¬
сы m и n так, чтобы центр масс Z[mA, nB] = L. Это означает, что —— =
LB
n
= —. При таком выборе масс центр масс всей системы {mA,nB, 1C, 1D} ле-
m
жит на LQ. Выберем m так, чтобы Z[mA, 1C] = M. Откуда следует, что
90

m = —, Z[nB, 1D]
x
M, n
u
v
AL
LB
и
n
m
ux
v —
a
b
2
Задача 49. Середина каждой стороны параллелограмма соединена с вер¬
шинами, принадлежащими противоположной стороне. Доказать, что отноше¬
ние площади образовавшегося восьмиугольника к площади параллелограмма
1
равно —.
6
Указание. Рассмотрим рис. 19.
Параллелограмм ABCD составлен из 8 треугольников, имеющих площадь,
равную площади треугольника BOK. Полученный в результате построения
восьмиугольник, составлен из 8 треугольников, имеющих площадь, равную
OA
площади треугольника PQO. Поскольку PO = —- (P центр тяжести тре-
KO
3
угольника BLK) и OQ = —(Q точка пересечения диагоналей в паралле¬
лограмме MBCN), то Sopq = -Sobk.
6
Задача 50. Доказать, что если сумма средних линий выпуклого четырех¬
угольника равна его полупериметру, то четырехугольник параллелограмм.
Задача 51. Углы ZA и ZC ромба ABCD равны —. На AB и CB взяты
соответственно точки K и M так, что AK = BM. Найти углы треугольни¬
ка DKM.
Указание. Используя теорему косинусов, докажите, что KD = KM =
= MD.
Задача 52. Из вершины B прямоугольника ABCD опущен перпендику¬
ляр BK на диагональ AC. Точки M и P середины отрезков AK и DC.
Доказать, что ZBMP является прямым.
Указание. Воспользуемся методом координат.
Пусть вершины прямоугольника имеют координаты: A(0, 0), B(0, a), C(1, a),
D(1, 0). Тогда K
о 2 + a2
1 + a2’ 1 + a2
MB
2a + a
2(1 + a2)’ 2(1 + a2)
MP
и MB • MP = 0.
2(1 + a2) 2(1 + a2)
Задача 53. Пусть ABCD выпуклый четырехугольник, а угол между
a
a
a
91

прямыми AB и CD, a = AB, b
CD. Пусть также M середина BC, а N
середина AD. Доказать, что MN2 = (a2 + b2 + 2ab cos a).
Указание. Воспользуемся векторной алгеброй. Имеем, что AB + BM—
—NM — AN = 0, MC — DC — ND + NM = 0. Откуда следует, что NM =
AB + DC
MN'
2
2 AB + DC AB + DC	a2 + b2 + AB ■ DC a2 + b2 + 2ab cos a
2
2
2
4
Задача 54. Пусть A,B,C,D произвольные точки плоскости такие, что
A,	B, C не лежат на одной прямой и точка D лежит внутри угла ABAC. Дока¬
зать, что AD ■ BC < AB ■ DC+AC ■ BD, причем AD ■ BC = AB■ DC+AC■ BD
в том и только в том случае, если точки A, B, C, D принадлежат одной окруж¬
ности.
Указание. Рассмотреть инверсию плоскости с центром в точке A от¬
носительно окружности достаточно большого радиуса. Окружность, описан¬
ная около треугольника ABC, перейдет в прямую. Рассмотреть образы точек
B,	D, C при этой инверсии.
Задача 55. Пусть в четырехугольнике ABCD противоположные сторо¬
ны AB и CD, AD и BC взаимно перпендикулярны. Доказать, что диагона¬
ли AC и BD тоже перпендикулярны.
Задача 56. Пусть четырехугольник ABCD разбит прямой MN, пересе¬
кающей его стороны AB и CD на два четырехугольника AMND и BMNC
(см. рис. 20).
Пусть P,Q, R точки пересечения диагоналей четырехугольников AMND,
MBCN и ABCD соответственно. Доказать, что P,Q,R лежат на одной пря¬
мой (см. [17]).
Задача 57. Доказать, что для любого треугольника справедливы равен¬
ства (a, b, c, длины сторон треугольника, R, r радиусы описанной и вписан¬
92

ной окружностей этого треугольника, p полупериметр этого треугольника,
а, в, y углы данного треугольника):
(1)	а2 + b2 + c2	= 2(p2 — r2 — 4Rr);
(2)	а3 + b3 + c3	= 2p(p2 — 3r2 — 6Rr);
(3)	а4 + b4 + c4	= 2((p + r)2 — 2r2 — 4Rr)((p —	r)2	—	2r2 — 4Rr);
(4)	а5 + b5 + c5	= 2p(p4 + p2(—10r2 — 10Rr)	+	5r4	+	40R2r2 +	30Rr3);
(5)	cos а + cos в + cos y =
R + r
R ;
1
(6) cos2 а + cos2 в + cos2 y = ц-тл (4Rr + 6R2 + r2 — p2);
2R2
(7) cos3 а + cos3 в + cos3 y = ^-^((2R + r)3 — 3p2r) — 1;
(8)	cos4 а + cos4 в + cos4 y :
(p4 — 2(4R2 + 4Rr + 3r2)p2 + (4R2 — r2)2 +8R(R + r)(R2 + 3Rr + r2)).
Задача 58. Пусть в треугольнике ABC два угла не превосходят —. Дока¬
зать, что p < \/3(R + r).
п	п	п
Указание. Если, например, положить, что а < —, в < ^, то y > —
и cos а > -, cos в > - и cos y < -. Поскольку числа {cos а, cos в, cos y}
являются корнями многочлена
f (ж) = 4R2x3	— 4R(R	+ r)x2	+	(p2	+ r2 — 4R2)x +	(2R	+ r)2 —	p2	= 0,
то f
1\	3(R + r)2 — p2
2
0.
Задача 59. Пусть в треугольнике ABC два угла не превосходят —. Про¬
верить справедливость следующей гипотезы при n = 1, 2, 3,4, 5 :
an + bn	+	cn	<	2n—1	•	3n	•	Rn (cosn—1	а + cosn—1 в + cosn—1 y) .
2
Задача 60. Доказать, что если в трапеции равны диагонали, то трапеция
равнобедренная.
Задача 61. Доказать, что внутренние биссектрисы параллелограмма об¬
разуют прямоугольник, диагонали которого параллельны сторонам паралле¬
лограмма.
Указание. Рассмотрим рис. 21.
93

Ясно, что четырехугольник MNPQ является прямоугольником. Далее, ME =
= AM = PC = PF. Следовательно, четырехугольник MECP является па¬
раллелограммом и, кроме того, MP || EC.
Задача 62. Каждая диагональ выпуклого четырехугольника делит его
площадь пополам. Доказать, что этот четырехугольник является параллело¬
граммом.
Указание. Заметить, что диагонали четырехугольника делятся точкой
пересечения пополам.
Задача 63. Два равнобедренных прямоугольных треугольника приложе¬
ны друг к другу так, как показано на рисунке 22.
Доказать, что середины сторон четырехугольника ABCD являются верши¬
нами квадрата.
Задача 64. В параллелограмме ABCD взята точка P такая, что ZABP =
ZADP. Доказать, что ZDAP = ZDCP.
Задача 65. Из всех параллелограммов данной площади найти тот, у ко¬
торого большая диагональ минимальна.
Указание. Пусть a,b длины сторон параллелограмма площади S и а
его острый угол. Тогда квадрат его большей диагонали равен
a2 + b2 + 2ab cos а = (a — b)2 + 2ab(1 + cos a) = (a — b)2 + 2S —+	> 2S.
sin a
Равенство достигается, если параллелограмм является квадратом.
Задача 66. Пусть P,Q,R точки, лежащие вне треугольника ABC и
удовлетворяющие условию ZPAC = ZRAB = X, ZRBA = ZCBQ =	,
94

ZBCQ = ZACP = 5 (см. рис. 23). Доказать, что прямые AQ,BP и CP
пересекаются в одной точке.
Указание. Пусть P' точка пересечения прямых AC и BP. Применяя
теорему синусов к треугольникам AP'P, PP'C, ABP и BPC, доказать, что
AP'	sin 5 sin(a + Л) c
=		 •	—. Затем применить теорему Чевы.
P'C	sin Л sin(5 + y) a
В работе [51] отмечается, что данный результат был доказан К.Ф. Якоби в
1825 г.
Задача 67. Пусть ABCD трапеция, BC верхнее основание, AD
нижнее основание, а M и N середины диагоналей AC и BD соответственно.
Доказать, что MN
AD - BC
2
95

Библиографический список
[1]	Адамар, Ж. Элементарная геометрия. Часть 1 / Ж. Адамар. - Москва : Учпедгиз,
1948.
[2]	Асталов, Н. Теория косинусов для четырехугольника / Н. Асталов, А. Жуков // Квант.
- 2002. - № 2.
[3]	Болтянский, В. Симметрия в алгебре / В. Болтянский, Н. Виленкин. - Москва : Наука,
1967.
[4]	Зарубежные математические олимпиады. Выпуск 17. - Москва : Наука, 1987. - (Биб¬
лиотека математического кружка).
[5]	Зетель, С. Новая геометрия треугольника / С. Зетель. - Москва : Учпедгиз, 1962.
[6]	Малышев, И. Клумбовый четырехугольник / И. Малышев // Математика в школе. -
2016. - № 3. - С. 50-53.
[7]	Мальцев, Ю. Избранные лекции по алгебре и геометрии / Ю. Мальцев, Е. Мальцева,
Т Пайсон. - Барнаул : Изд-во АлтГУ, 2006.
[8]	Мальцев, Ю. Избранные лекции по математике / Ю. Мальцев, Е. Мальцева, Е. Жу¬
равлев. - Барнаул : Изд-во АлтГУ, 2004.
[9]	Мальцев, Ю. Избранные олимпиадные задачи по математике : учеб. пособие / Ю.
Мальцев, Е. Мальцева, Е. Журавлев. - Барнаул : Изд-во АлтГУ, 2007.
[10]	Мальцев, Ю. Олипиадные задачи по математике: Реши + Если = Силен / Ю. Мальцев,
А. Саженков. - Барнаул : День, 1994.
[11]	Мейдман, С. Тождества и неравенства в треугольнике / С. Мейдман, В. Солтан. -
Кишинев : Штиинца, 1982.
[12]	Прасолов, В. Задачи по планиметрии : в 2 ч. / В. Прасолов. - Москва : Наука, 1986.
[13]	Соминский, И. О математической индукции / И. Соминский, Л. Головина, И. Яглом.
-	Москва : Наука, 1967.
[14]	Морозова, Е. Международные математические олимпиады / Е. Морозова, И. Петраков.
-	2-е изд. - Москва : Просвещение, 1968.
[15]	Фихтенгольц, Г. Курс дифференциального и интегрального исчисления / Г. Фихтен-
гольц. - Москва : Физматгиз, 1962.
[16]	Шклярский, Д. Избранные задачи и теоремы планиметрии / Д. Шлярский, Н. Ченцов,
И. Яглом. - Москва : Наука, 1967.
[17]	Энциклопедия элементарной математики : Т. 4 : Геометрия. - Москва : Гос. изд-во
ФМЛ, 1963.
[18] Birsan, T. Bounds for Elements of a Triangle Expressed by R, r, and s / T. Birsan // Forum
Geometricorum. - 2015. - Vol. 15. - P. 99-103.
[19]	Bottema, O. Geometric Inequalities / O. Bottema, R. Djordjevic, R. Janie, D. Mitrinovic,
P. Vasic. - Groningen : Wolters - Noodhoff, 1969.
[20]	Blundon, W. Inequalities associated with the triangle / W. Blundon // Canada Math. Bull.
-	1965. - Vol. 8. - P. 615-626.
96

[21]	Blundon, W. Problem E1935 / W. Blundon // Amer. Mat. Monthly . - 1966. - Vol. 73. -
P. 1122.
[22]	Crux Mathematicorum -	2004.	- V.	30.	- №	8. -	P.	519	(problem	№	2887).
[23]	Crux Mathematicorum -	2005.	- V.	31.	- №	7.
[24]	Crux Mathematicorum -	2006.	- V.	32.	- №	8.
[25]	Dospinescu, G. An elementary proof	of Blundon’s	inequality /	G.	Dospinescu // Journal of
inequalities in Pure and Applied Math. - 2008. - Vol. 9. - № 4. - P. 1-3.
[26]	Finsler, P. Einige relationen im Dreiek / P. Finsler, H. Hadiwger // Comm. Mat. Helv. -
1937. - Vol. 10. - P. 316-326.
[27]	Hajja, M. A condition for circumscriptible quadrilateral to be cyclic / M. Hajja // Forum
Geometricorum. - 2008. - Vol. 8. - P. 103-106.
[28]	Hoehn, L. A new formula concerning the diagonal and sides of a quadrilateral / L. Hoehn
// Forum Geometricorum. - 2011. - Vol. 11. - P. 211-212.
[29]	Hojoo, L. Topics in inequalities - theorems and techniques / L. Hojoo // Olympiad training
materials. - 2007. - P. 1-69.
[30]	Hess, A. A highway from Heron to Brahmagupta / A. Hess // Forum Geometricorum. -
2012.	- Vol. 12. - P. 191-192.
[31]	Hess, A. On circle containing the incenters of tandential quadrilaterals / A. Hess // Forum
Geometricorum. - 2014. - Vol. 14. - P. 389-396.
[32]	Josefsson, M. A new proof of Yun’s inequality for bicentric quadrilaterals / M. Josefsson //
Forum Geometricorum. - 2012. - Vol. 12. - P. 79-82.
[33]	Josefsson, M. Angle and circle characterizations of tangenial quadrilaterals / M. Josefsson
// Forum Geometricorum. - 2014. - Vol. 14. - P. 1-13.
[34] Josefsson, M. Calculations concerning the tangent lengths and tangency chords of a
tangential quadrilateral / M. Josefsson // Forum Geometricorum. - 2010. - Vol. 10. -
P. 119-130.
[35]	Josefsson, M. Characterizations of orthodiagonal quadrilaterals / M. Josefsson // Forum
Geometricorum. - 2012. - Vol. 12. - P. 13-25.
[36]	Josefsson, M. Characterizations of trapezoids / M. Josefsson // Forum Geometricorum. -
2013.	- Vol. 13. - P. 23-35.
[37]	Josefsson, M. Five proofs of an area characterization of rectangles / M. Josefsson // Forum
Geometricorum. - 2013. - Vol. 13. - P. 17-21.
[38]	Josefsson, M. Maximal area of a bicentric quadrilateral / M. Josefsson // Forum
Geometricorum. - 2012. - Vol. 12. - P. 237-241.
[39]	Josefsson, M. More caracterizations of tandentials quadrilaterals / M. Josefsson // Forum
Geometricorum. - 2011. - Vol. 11. - P. 65-82.
[40]	Josefsson, M. Properties of equidiagonal quadrilaterals / M. Josefsson // Forum
Geometricorum. - 2014. - Vol. 14. - P. 129-144.
[41]	Josefsson, M. Similar metric characterizations of tangential and extangential quadrilaterals
/ M. Josefsson // Forum Geometricorum. - 2012. - Vol. 12. - P. 63-77.
97

[42]	Josefsson, M. The area of a bicentric quadrilateral / M. Josefsson // Forum Geometricorum.
-2011. - Vol. 11.-P. 155-164.
[43]	Josefsson, M. The diagonal point triangle revisited / M. Josefsson // Forum Geometricorum.
- 2014. - Vol. 14. - P. 381-385.
[44]	Josefsson, M. When is a tangential quadrilateral a kite? / M. Josefsson // Forum
Geometricorum. - 2011. - Vol. 11. - P. 165-174.
[45]	Maltsev, Yu. An improvement of Birsan’s inequalities for the sides of a triangle / Yu.
Maltsev, A. Kuzmina // Forum Geometricorum. - 2016. - Vol. 16. - P. 81-84.
[46]	Lupu, C. Sharpening te Hadwiger - Finsler inequality / C. Lupu, C. Pohoata // Crux
Mathem. - 2008. - Vol. 34, № 2.
[47]	Mitrinovic, D. Recent advances in geometric ineualities / D. Mitrinovic, J. Pecaric,
V. Volenec. - Netherlands : Kruwer Acad. Publ., 1989.
[48]	Salazar, J. Fuss’s theorem / J. Salazar // Math. Gazette. - 2006. - Vol. 90. - P. 306-307.
[49]	Svtran, D. Non-euclidean versions of some classical triangle inequalities / D. Svrtan,
D. Veljan // Forum Geometricorum. - 2012. - Vol. 12. - P. 197-209.
[50]	Weitzenbock, R. Uber eine Ungleichung in der Dreiecksgeometric / R. Weitzenbock // Math.
Zeitschrift. - 1919. - Vol. 5. - P. 137-146.
[51]	Vickers, G. Reciprocal Jacobi triangles and the McCay cubic / G. Vickers // Forum
Geometricorum. - 2015. - Vol. 15. - P. 179-183.
[52]	Yun, Z. Euler’s inequality revisted / Z. Yun // Math. Spectrum. - 2008. - Vol. 40. - P.119¬
121.
98

Содержание
Предисловие	3
ГЛАВА 1. Фундаментальное неравенство треугольника	4
§ 1. Симметрические многочлены и формулы Виета	 4
§ 2. Уравнение для сторон треугольника	 6
§ 3. Фундаментальное неравенство треугольника	 9
§ 4. О двух методах доказательства геометрических неравенств 	 13
§ 5. О некоторых неравенствах для длин сторон треугольника	 27
ГЛАВА 2. Геометрия четырехугольника	33
§ 1. Основные свойства выпуклого четырехугольника и метрические соотношения
в нем 	 33
§ 2. Бимедианы четырехугольника 	 47
§ 3. Ортодиагональные четырехугольники	 50
§ 4. Свойства выпуклых четырехугольников, описанных около окружности ....	54
§ 5. Геометрия трапеции 	 69
ГЛАВА 3. Задачи для самостоятельного решения	76
БИБЛИОГРАФИЧЕСКИЙ СПИСОК	96
99

Учебное издание
Мальцев Юрий Николаевич
Кузьмина Анна Сергеевна
ИЗБРАННЫЕ ЛЕКЦИИ ПО ГЕОМЕТРИИ
ТРЕУГОЛЬНИКА И ЧЕТЫРЕХУГОЛЬНИКА
Учебное пособие
Подписано в печать 29.06.2016 г.
Объем 6,2 п.л. Формат 60x84/16.
Бумага офсетная. Гарнитура Times New Roman.
Тираж 100 экз. Заказ № 52.
Отпечатано в ФГБОУ ВО
"Алтайский государственный
педагогический университет"
656031, Барнаул, ул. Крупской, 139а,
тел. 8(3852)38-84-59.