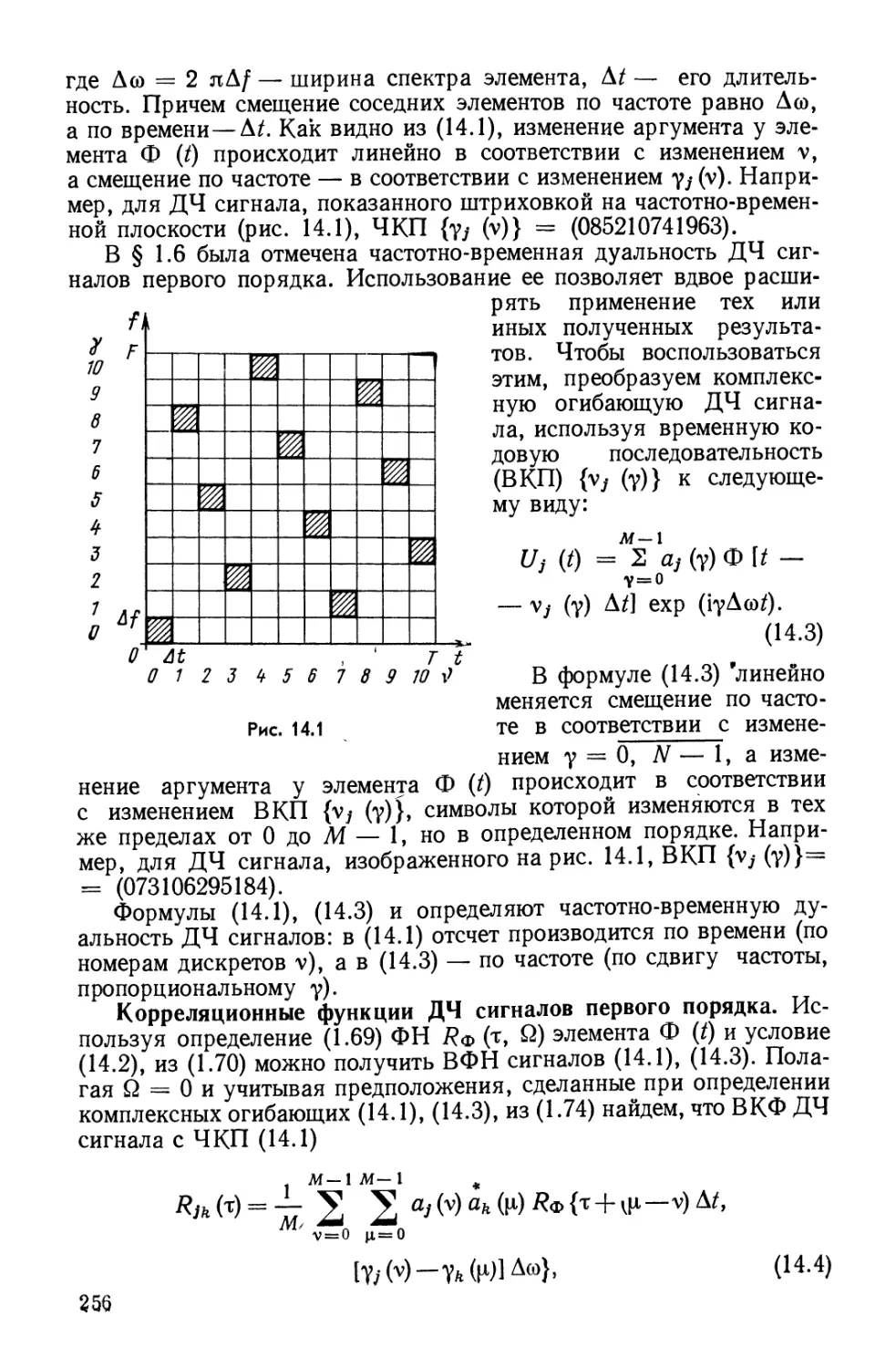
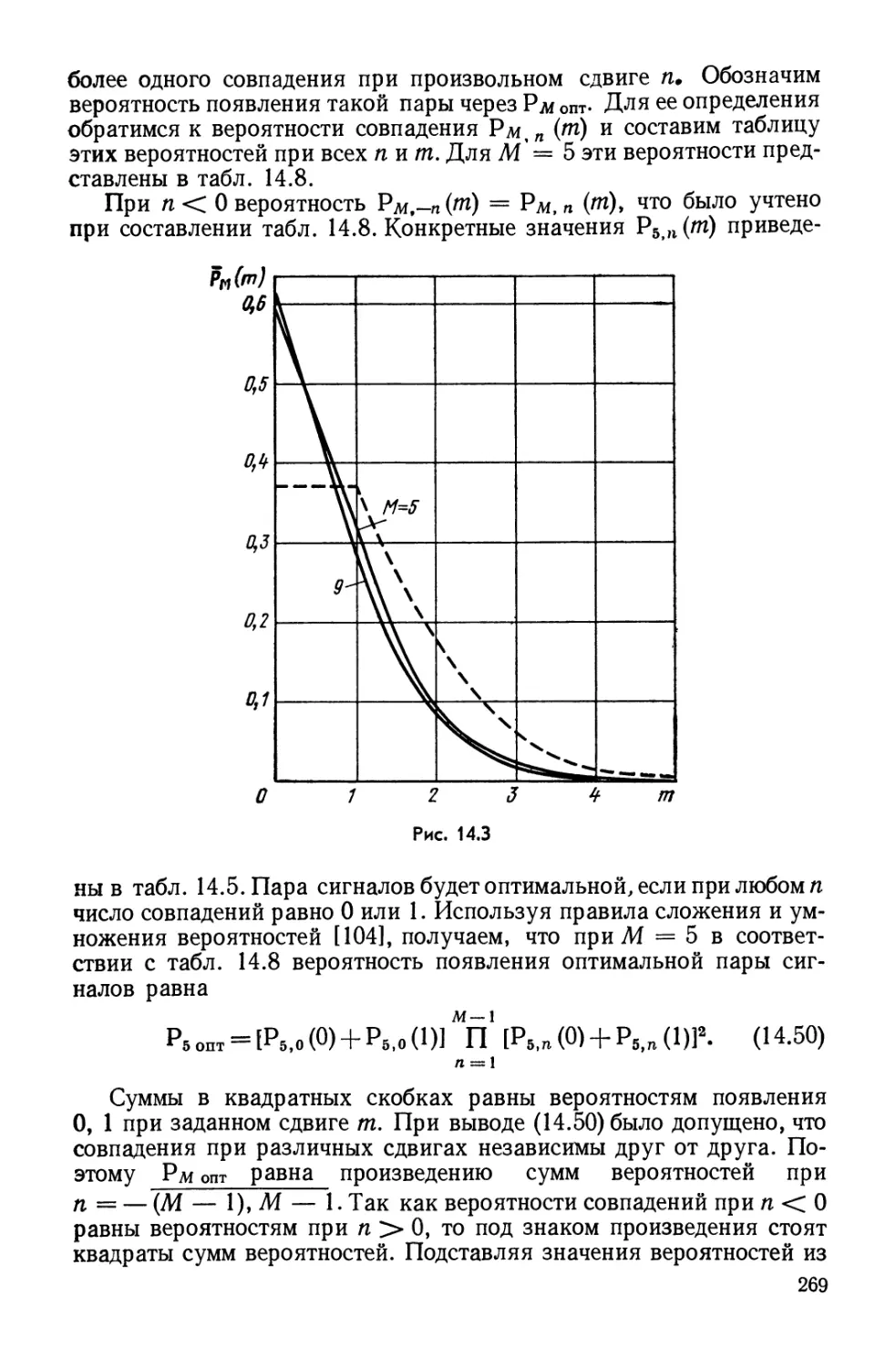
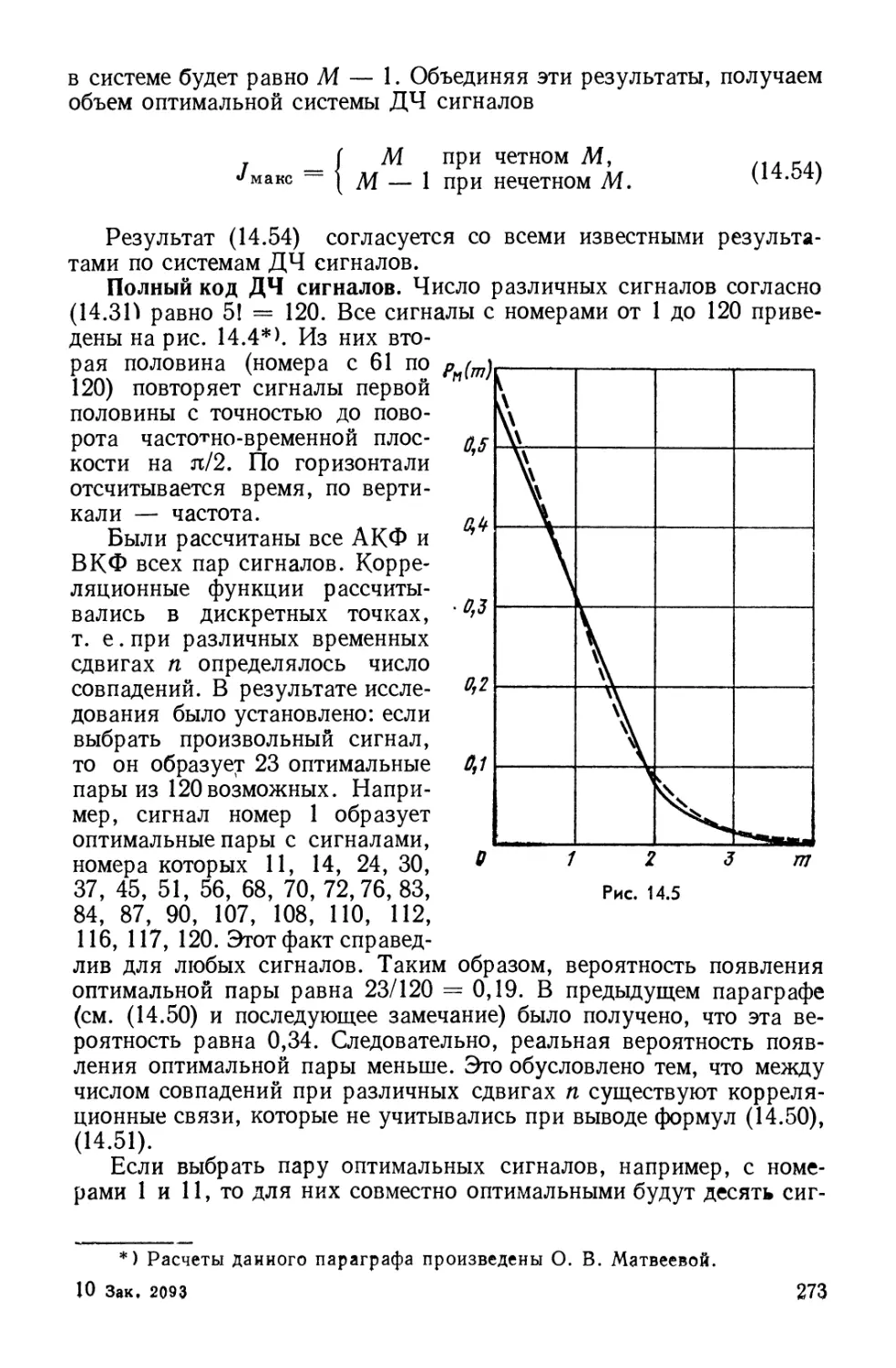
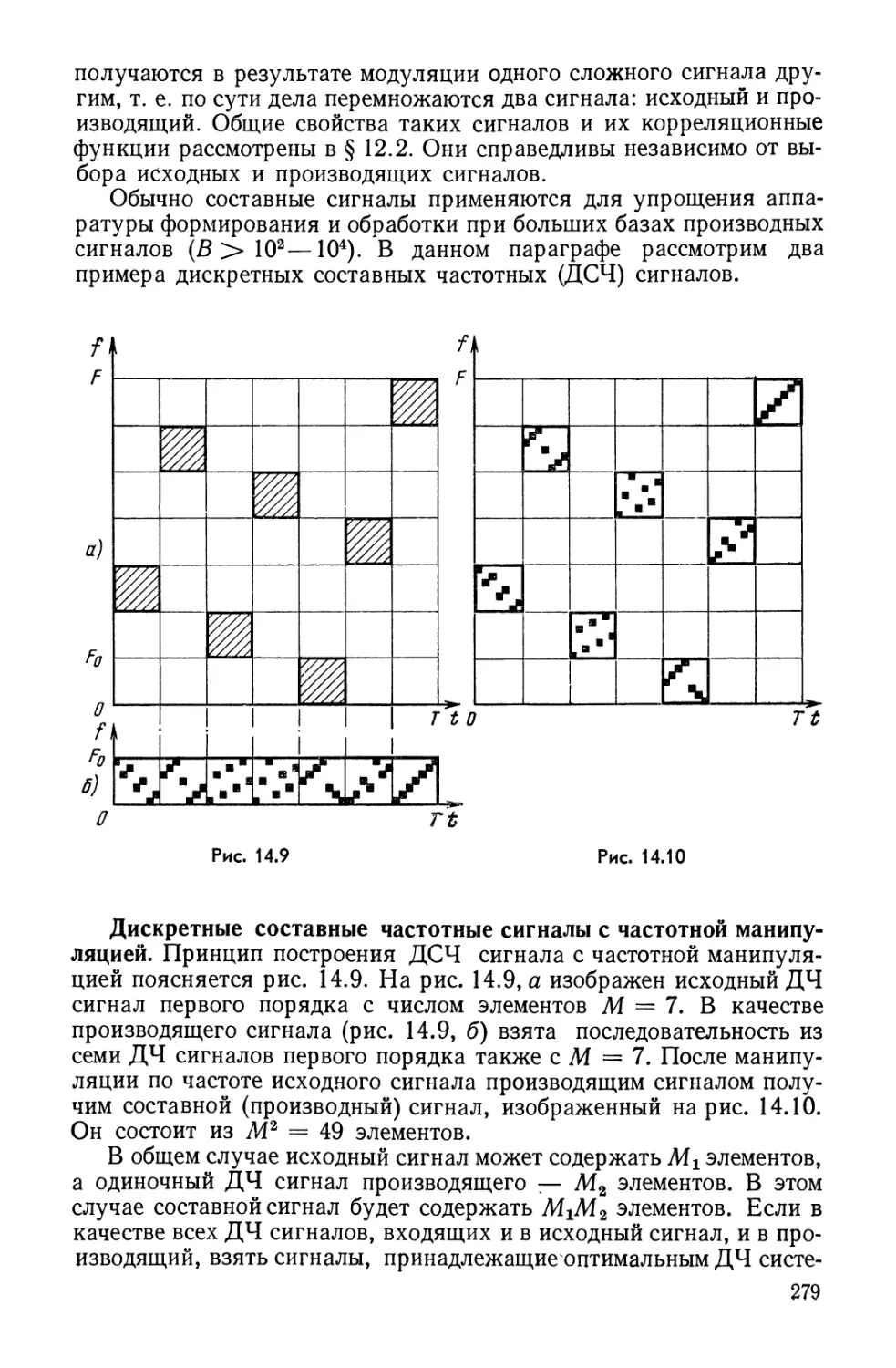
Text
Л. Е. ВАРАКИН
Теория
систем
сигналов
Москва «Советское радио» 1978
УДК 621.391
Варакин Л. Е. Теория систем сигналов. М., «Сов. радио»,
1978, 304 с.
На основе методов комбинаторики, теории групп,
теории чисел, общей и статистической радиотехники
разработаны основы общей теории систем сигналов. Определены
свойства полных произвольных и двоичных кодов, а также
взаимосвязи между числом блоков и корреляционными
свойствами систем сигналов. Исследовано большое число различных
систем сигналов: дискретных фазоманипулированных,
частотных, дискретных частотных и дискретных составных
частотных. Рассмотрено применение систем сигналов для
повышения помехоустойчивости и кодового разделения абонентов
в синхронных и асинхронных системах передачи информации.
Книга предназначена для научных работников,
инженеров и аспирантов радиотехнических специальностей, может
быть использована студентами вузов.
Рис. 76, табл. 34, библ. 242 назв.
Редакция литературы
по вопросам космической радиоэлектроники
ИБ № 339
Леонид Егорович Варакин
ТЕОРИЯ СИСТЕМ СИГНАЛОВ
Редактор Н. К. Калинина
Художественный редактор Н. С. Ш е и н
Обложка художника Б. К. Шаповалова
Технический редактор А. А. Белоус
Корректор Η. Μ. Давыдова
Сдано в набор 13.10.77 Подписано в печать 23.02.78 Т-01305
Формат 60X90/16 Бумага типографская № 2
Литературная гарн. Высокая печать.
Объем 19,0 усл. печ. л., 19,38 уч.-изд. л.
Тираж 8300 Зак. 2093 Цена 1 р. 60 к.
Издательство «Советское радио», Москва, Главпочтамт, а/я 693
Московская типография № 4 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии. Ц. innnifunfr торговли
Москва, И-41, Б. ПереясЛ
30401-039
046(01)-78
39-78
© Издательство «Советское радио», 1978 г.
Памяти мамЫ
Предисловие
С каждым годом появляются новые радиотехнические системы,
использующие радиоволны для передачи и приема информации, для
обнаружения объектов и измерения их параметров, для
автоматического управления различными аппаратами и т. д. В свою очередь,
требования, предъявляемые к надежности передачи информации,
точности измерения параметров объектов, быстродействию
управления, непрерывно растут, радиотехнические системы становятся
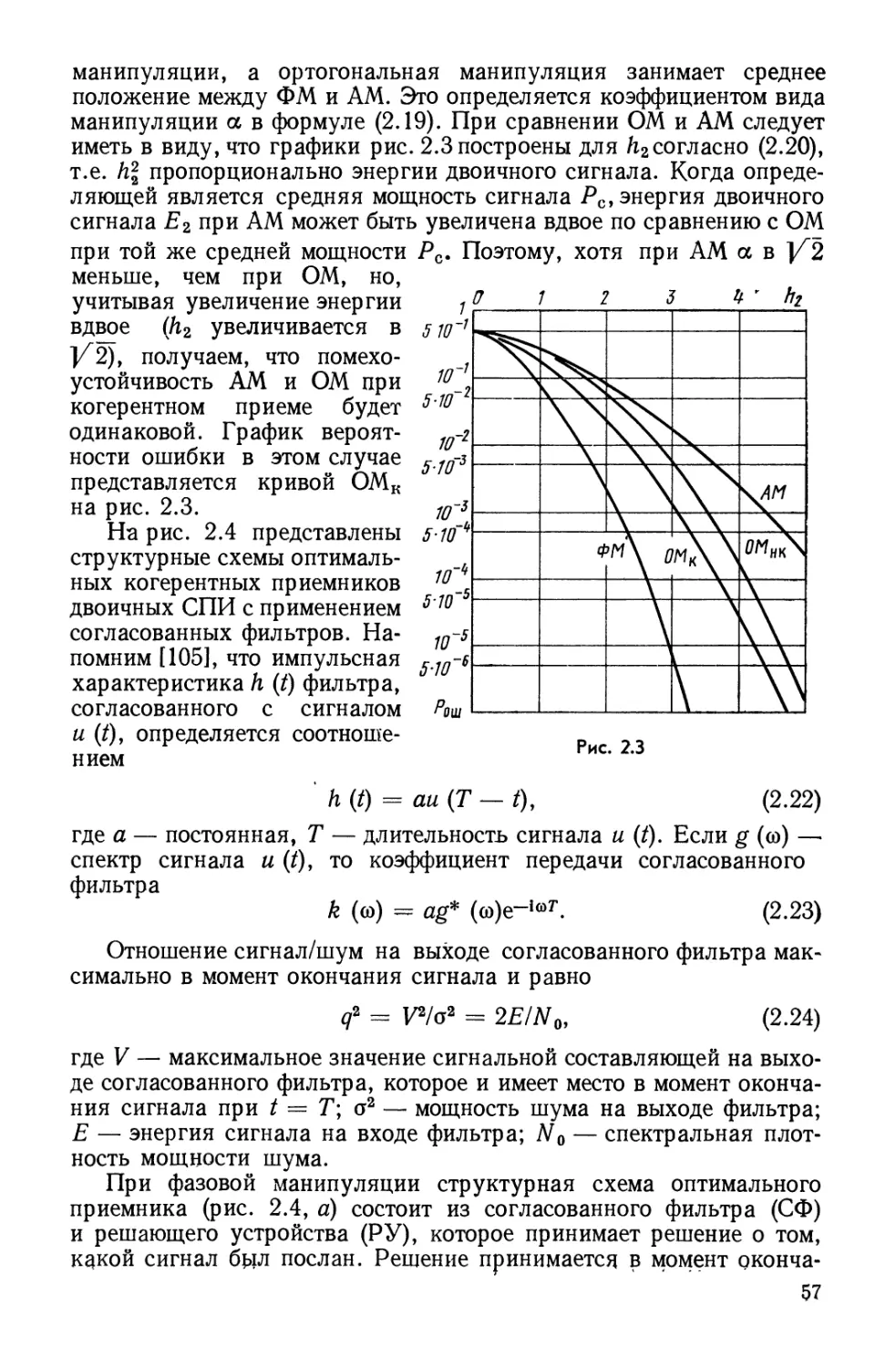
более сложными, и многие из них содержат большое число
различных радиоэлектронных средств. Кроме того, растет число
источников и потребителей информации в той или иной системе. Поэтому
появление новых радиотехнических систем требует расширения
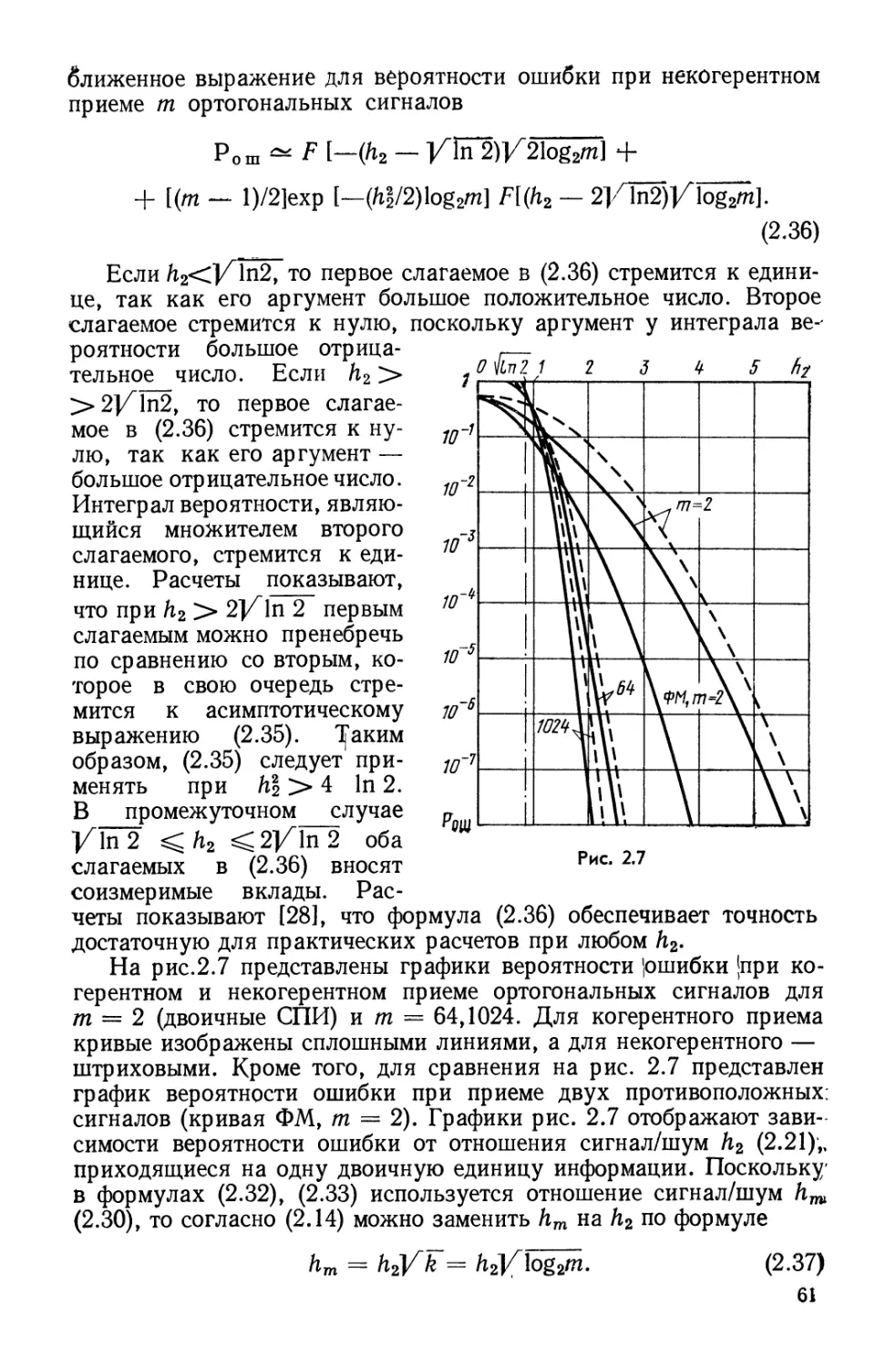
диапазонов радиочастот (или просто частот).
Если к тому же учесть, что в настоящее время все диапазоны
частот практически уже заняты существующими системами, то
становится ясно, что проблема распределения частот и выделения из
них новых весьма серьезна. Многочисленные прогнозы развития
радиотехнических систем убеждают, что в будущем эта проблема
станет еще острее. Следовательно, необходимо эффективнее
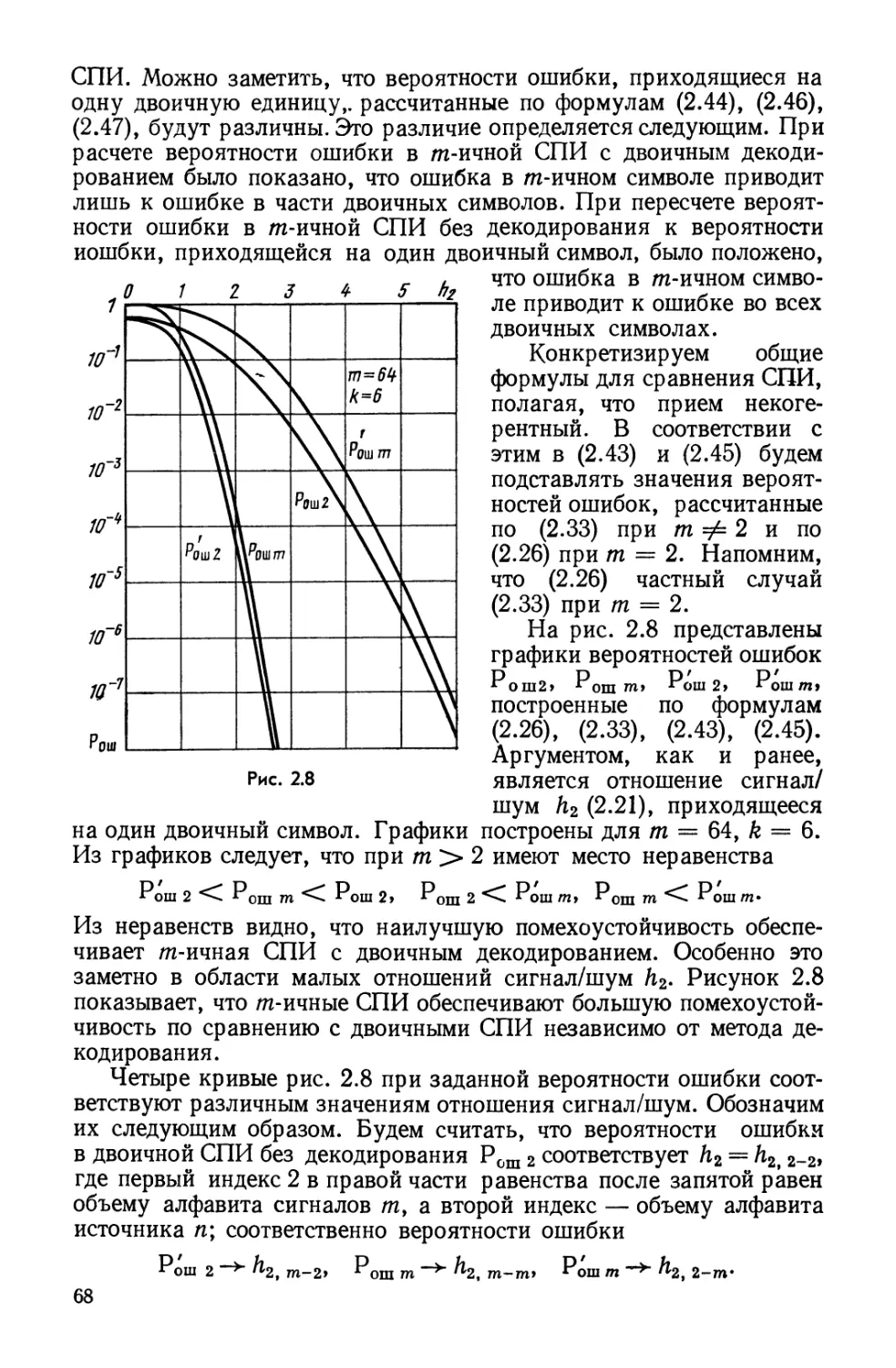
использовать диапазоны частот с максимальной плотностью
радиоэлектронных средств на единицу полосы частот. Но при этом возникает
другая проблема — электромагнитная совместимость различных
радиоэлектронных средств (абонентов), работающих в общей
полосе частот, отведенной для данной радиотехнической системы. Одним
из способов повышения эффективности использования диапазона
частот с учетом электромагнитной совместимости является
применение кодового разделения абонентов, работающих асинхронно в
общей полосе частот.
Асинхронный принцип передачи информации применяют, когда
невозможно регламентировать работу абонентов во времени. До
середины 60-х годов в асинхронных системах использовался метод
частотного разделения информации различных абонентов —
каждому выделялся свой частотный диапазон. Но так как число
свободных диапазонов уменьшалось, а станций (абонентов) —
увеличивалось, то стало очевидно, что частотное разделение не может
обеспечить растущие потребности радиоэлектроники. Именно
поэтому с середины 60-х годов начали применять кодовое разделение
(разделение по форме сигналов).
3
При кодовом разделении абонентов более экономично
используется частотный диапазон, отведенный для данной
радиотехнической системы, состоящей из многих абонентов. Такие системы
получили название асинхронных адресных систем (ААС), поскольку
информация каждого абонента «снабжается» адресом — сигналами
данного абонента. Число абонентов в ААС обычно велико, и требуемое
число сигналов так же велико, по крайней мере не меньше числа
абонентов. При выборе сигналов для ААС необходимо учитывать
взаимные помехи между абонентами,поэтому выбор сигналов нужно
производить так, чтобы минимизировать взаимные помехи, т. е.
обеспечить наилучшую электромагнитную совместимость. Это
возможно только в том случае^ если известны алгоритмы построения
используемых сигналов и их свойства.
В настоящее время ААС с кодовым разделением применяются
в различных наземных, спутниковых и других системах связи, в
системах командного радиоуправления и управления воздушным
движением и в некоторых других. Можно предположить, что такие
ААС будут использоваться шире, так как частотные диапазоны
практически неизменны, а число различных радиотехнических систем
непрерывно растет. Кодовое разделение может быть использовано
и для решения некоторых задач в общей проблеме электромагнитной
совместимости различных радиотехнических систем
(навигационных, локационных, связных, космических, управления и др.).
Свойства ААС во многом определяются свойствами применяемых
в них сигналов. В большинстве случаев сигналы конкретной ААС
подчиняются единому правилу или алгоритму построения, который
выбирается исходя из требований к ААС. Такой системный подход
к сигналам ААС является основой для определения систем сигналов.
Система сигналов — это множество сигналов, объединяемых
единым правилом построения, которое определяет как индивидуальные,
так и совместные характеристики сигналов. Индивидуальные
характеристики сигнала являются функциями его структуры по 'времени
и частоте, спектра, распределения энергии сигнала на частотно-
временной плоскости, автокорреляционных свойств. Совместные
характеристики зависят от индивидуальных характеристик и кроме
того являются функциями структуры системы сигналов в целом,
совместного использования частотно-временной плоскости,
взаимокорреляционных свойств. Таким образом, правила построения
систем сигналов, структурные и корреляционные свойства являются
зависимыми друг от друга. От перечисленных характеристик зависят
также и параметры радиотехнических систем, в которых
используются системы сигналов. Исследованиям зависимостей между
алгоритмами построения, структурными и корреляционными
свойствами сигналов, образующих системы, посвящена теория систем
сигналов.
Теория систем сигналов — это совокупность законов,
определяющих правила построения систем сигналов, их структурные и
корреляционные свойства, особенности применения в радиотехни-
4
ческих системах. Те или иные законы выявляются при обобщении
результатов исследований систем сигналов.
Теория систем сигналов использует методы общей
радиотехники, статистической радиотехники, теории сложных сигналов,
теории кодирования, теории линейной и нелинейной селекции сигналов,
теории групп, комбинаторики, теории чисел.
Естественно, что технически грамотно проектировать ААС с
кодовым разделением можно только при развитой теории систем
сигналов, поскольку все характерные особенности подобных ААС
определяются сигналами. Необходимость в такой теории возникла
недавно. Первоначально к системам сигналов не предъявлялось
особых требований, так как ААС только начинали развиваться и не
были подробно исследованы даже принципы их построения. Однако
при анализе условий работы ААС и исследовании их характеристик
было выяснено, что системы сигналов следует тщательно выбирать,
так как это позволяет улучшить характеристики ААС. Оказалось, что
при проектировании ААС с кодовым разделением возникает ряд
проблем, решение которых определяется свойствами систем
сигналов.
В данной книге поставлены, обсуждены и решены многие
наиболее важные проблемы теории систем сигналов. Решение этих проблем
основано на результатах многолетней работы автора в области
проектирования ААС с кодовым разделением абонентов. Так как
кодовое разделение основано на применении сложных сигналов, то
данная книга является логическим продолжением книги «Теория
сложных сигналов» (М., «Сов. радио», 1970). Основной материал
книги составляют работы автора и доклады, сделанные на
Всесоюзных сессиях НТОРЭС им. А. С. Попова, на четырех конференциях
«Проблемы оптимальной фильтрации» и научно-технических
конференциях Московского ордена Трудового Красного Знамени
электротехнического института связи и Всесоюзного заочного
электротехнического института связи.
Автор выражает искреннюю признательность проф., докт. техн.
наук В. И. Тихонову за всестороннюю поддержку и помощь. Автор
благодарен рецензентам—проф., докт. техн. наукЮ. С. Лёзину и
проф., докт. техн. наук Г. И. Тузову за ряд доброжелательных
критических замечаний, способствовавших улучшению книги.
Все замечания и пожелания автор просит направлять по адресу:
Москва, Главпочтампт, а/я 693.
Основные условные обозначения
Aj(t)
В
Во
Aj={ajn} — кодовая
последовательность
огибающая сигнала
комплексная
амплитуда элементарного
сигнала, символ
кодовой
последовательности
база сигнала
база элементарного
сигнала
Е, Ej — энергия произвольного
и /-го сигналов
F,Fj,Fq,Fc — ширина спектра
произвольного сигнала,
/-го сигнала,
элементарного сигнала,
ширина спектра
сообщения
Pay FK — ширина абонентской
полосы частот,
ширина полосы частот
канала связи
Fw F,
0(ω), Gj((o)
A2. h\, A*,
hi, Aj», A*,,
/-■
ширина спектра
исходного сигнала и
производящего сигнала
F(x) — интеграл вероятности
частота
спектр комплексной
огибающей
произвольного сигнала, /-го
сигнала
спектр
произвольного сигнала, /-го
сигнала
амплитудный спектр
сигнала
отношение сигнал/шум
в общем случае,
отношение сигнал/шум,
приходящееся на
двоичный и на m-й сигнал
(символ)
полное отношение
сигнал/шум в многока
но
OW.
&зан!
/mW
J
К
k
» ^исп
*(ω)
L
L(x)
a
/амакс
Μ
Μ2{χ}
η
нальнои системе
передачи информации, при
линейном разделении,
нелинейном
разделении, адаптивной пере-
Даче
- импульсная
характеристика
согласованного фильтра
- модифицированная
функция Бесселя
нулевого порядка, т-го
порядка
■ объем системы
сигналов
порядок дискретного
частотного сигнала
- число двоичных
единиц в дискретном
сообщении
• коэффициенты
занятости и использования
канала
- коэффициент передачи
согласованного
фильтра
- число сигналов в
классе, объем класса
число абонентов в
системе передачи
информации
- число каналов
- число сигналов,
обладающих свойством χ
число мешающих
абонентов
число активных
абонентов, максимальное
число активных
абонентов
• число элементов в
дискретном частотном
сигнале
второй центральный
момент случайной
величины X
m1{x}
mk {χ}
Ν
N0, Νπ
- объем алфавита, число
манипулируемых
параметров сигнала
- первый начальный
момент случайной
величины х, ее среднее
значение
- k-й начальный
момент случайной
величины X
- число элементов
дискретного сигнала,
число символов фазо-
манипулированного
сигнала
- спектральная
плотность мощности
белого шума и помехи с
равномерным спектром
.V(/), N(0)) — спектральная
плотность мощности
произвольной помехи
η (t) — помеха
Рс> ^п — мощность сигнала,
мощность помехи
^п вых — мощность помехи на
выходе
согласованного фильтра
^ош» — вероятность ошибки,
^ош ср» средняя и
максимальней макс ная вероятности оши"
бок
Рот л» — вероятность ошибки
Р0шд ПРИ приеме сигнала с
помощью линейного
согласованного
фильтра, с помощью
дискретного
согласованного фильтра
вероятность
правильного приема,
вероятность ложной тревоги
■ основание
манипуляции
активность абонента
■ число пораженных
элементов в сигнале
отношение сигнал/шум
на выходе
согласованного фильтра при
действии белого шума,
произвольной помехи
скорость передачи
информации
отношение сигнал/
шум, приходящееся
на элементарный
сигнал
> Λπτ
прав» ^лт
Ра
Q
£Я-
Ч\
R,Rm,R{b) ■
RfdSLKC
Rjh
Rjh (τ, Ω),
R) (τ, Ω), -
Rj(r), Rj(Q)
Пк (τ, Ω)
S(<o)
отдельные значения
корреляционных
функций
максимальный
боковой пик
корреляционной функции
коэффициент
корреляции между /-М и
k-u сигналами
комплексная
огибающая взаимной
функции
неопределенности (ВФН),
комплексная огибающая
взаимной
корреляционной функции (ВКФ)
комплексная
огибающая функции
неопределенности (ФН),
автокорреляционной
функции (АКФ), частотно-
корреляционной
функции (ЧКФ)
взаимная функция
неопределенности
спектр комплексной
огибающей
элементарного сигнала
(элемента)
комплексная
огибающая производного
сигнала
■ длительность сигнала
длительность
двоичного сигнала, т-ичного
сигнала
■ время
запаздывание v-ro
элементарного сигнала
U(t), Uj (/) — комплексная
огибающая произвольного
сигнала, /-го сигнала
- произвольный сигнал,
/-й сигнал
- максимальное
значение сигнала на выходе
согласованного
фильтра
■ комплексная
огибающая μ-го
производящего сигнала
• напряжение на входе
согласованного
фильтра
эффективная ширина
спектра сигнала
вес кодовой
последовательности
7
S£(0-
Т
Ь —
u(t),uj(t)
V
v(t)
^эфф ·
W
W0=2nFo — ширина спектра
элементарного сигнала
Ψj — у-й сигнал Уолша
w(x), w(x,y) — одномерная и
двумерная плотности
вероятности
Ζ — значение комплексной
огибающей на выходе
согласованного фильт-
тра
ζ — значение
корреляционного интеграла
А7· — матрица комплексных
амплитуд
β — отношение
абонентской полосы частот
к ширине спектра
сообщения
Г; — частотная матрица
γ — число активных
абонентов на единицу
полосы частот
γ; — символ частотной
кодовой
последовательности /-го сигнала
Δ/, Δω — сдвиг по времени и
частоте между соседними
элементарными
сигналами
τ|2, η™ — выигрыш по мощности
в двоичной и т-ичной
системе
θν — начальная фаза v-ro
элементарного сигнала
Θ; (/) — медленно меняющаяся
фаза сигнала
Λ — число элементов в
произвольном сигнале
σ2 — дисперсия шума на
выходе
согласованного фильтра
σ^ — дисперсия числа
активных абонентов
σ^ — дисперсия
корреляционной функции
τ — запаздывание
Φ (t) — комплексная
огибающая элементарного
сигнала, форма элемента
φ (ω) — фазовый спектр
сигнала
φ (t, m) — весовая функция
Ω — доплеровская
частота
Основные сокращения
ААС — асинхронная адресная
система
АКФ — автокорреляционная
функция
ВКФ — взаимокорреляционная
функция
ВР — временное уплотнение и
разделение абонентов
ВФН — взаимная функция
неопределенности
ДАСФ — дискретно-аналоговый
согласованный фильтр
ДСФ — дискретный
согласованный фильтр
ДСЧ — дискретный составной
частотный сигнал
ДЧ — дискретный - частотный
сигнал
КИМ — кодовая импульсная
модуляция
КР — кодовое уплотнение и
разделение абонентов
КФ — корреляционная функция
ЛСФ
MAC
МКФ
МЛЗ
мцс
РТС
САС
СПИ
ΦΜ
ФН
ЧКФ
ЧР
— линейный согласованный
фильтр
— многоканальная
автономная система
— многоканальный фильтр
— многоотводная линия
задержки
— многоканальная
централизованная система
— радиотехническая
система
— синхронная адресная
система
— система передачи
информации
— фазоманипулированный
сигнал
— функция
неопределенности
■— частотная
корреляционная функция
— частотное уплотнение и
разделение абонентов
Раздел I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИЕМА
СИСТЕМ СИГНАЛОВ
Глава 1
СИГНАЛЫ, СПЕКТРЫ, КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
1.1. Сигналы и спектры
Сигналом называется изменяющаяся физическая величина,
отображающая сообщение. Сигнал иу являющийся функцией времени
/, записывается в виде и = и (/).
Множество сигналов щ (/), определяемое единым правилом
построения, называется системой сигналов. Таким образом, система
сигналов определена, если известно правило построения сигналов.
Правило построения можно записать в любом виде, важно только,
чтобы оно было едино для данной системы. (Более подробно этот
вопрос рассмотрен в § 1.3.) Номер сигнала указан в виде индекса /.
Если число сигналов в системе равно /, то можно пронумеровать
сигналы натуральными числами от 1 до / и обозначить / = 1, /.
Число J назовем объемом системы сигналов.
Будем рассматривать сигналы конечной длительности. Такие
сигналы называются финитными. Обозначим длительность /-го
сигнала через Τ и допустим, что длительности всех сигналов системы
одинаковы.
В дальнейшем будем рассматривать сигналы, которые можно
представить в следующем виде:
uj (t) = Aj (/)cos [ω0/ + θ, (/)], (1.1)
где Aj (t) — огибающая, ω0 — несущая частота, θ7· (/) — медленно-
меняющаяся часть фазы сигнала. Допустим, что со0 не зависит от
номера сигнала и одинакова для рассматриваемой системы сигналов.
Представлению (1.1) соответствует радиочастотный сигнал. Так
как в книге рассматриваются реальные сигналы (которые можно
сформировать и обработать), то все функции времени и параметры
правой части (1.1) известны в детерминированном или в
статистическом смысле.
Когда сигнал задан в общем виде Uj (t) и правая часть (1.1) не
известна, то необходимо воспользоваться преобразованием
Гильберта [104] и найти сопряженный сигнал uj (/). В этом случае
огибающая
Aj(t)=VuUt) + iif(t)
9
и фаза
eJ(/) = o0/ + ei(/)=arctg
Uj(t)
φ)
Ajft)
δ) 1
И»
а ! ! ι !
в)
о
0j(t) |
3Ϊ
о
Ui(t)
г)
ι
Если функция Θ^ (/) непрерывная и имеет непрерывную первую
производную, то мгновенная частота сигнала ω (t)y по определению,
равна первой производной фазы θ^ (t)> т. е. ω7 (ή = ω0 + θ/ (/).
В дальнейшем θ^ (/) будем называть просто фазой сигнала. Она
может содержать постоянную составляющую θ70, называемую
начальной фазой, линейную составляющую Δω7·/ и нелинейную
составляющую Θ7·Η (/), т. е. θ7· (/)=
= θ^Η(/) + Δω7./+θ7.0.
Сумма ω^ = ω0 + Δω7·
является несущей частотой /-го сигнала,
ψ а Δω7· — частотным сдвигом /-го
сигнала. Обычно Δω7· <ξ^ ω0.
На рис. 1.1, α показан фазома-
нипулированный сигнал (ФМ),
состоящий из четырех радиоимпуль-
^ сов с одинаковой несущей частотой,
но с различными начальными
фазами. На рис. 1.1, б и β представ-
"^ лены его огибающая Aj (t) и фаза
θ7· (/). Огибающая постоянна на
интервале длительностью Г, а
фаза равна двум значениям О
или π.
"*Γ Если несущая частота сигнала
со0 = 0, то такой сигнал является
видеочастотным. На рис. 1.1, г
изображен видеочастотный сигнал
Uj (t) — последовательность
положительных и отрицательных прямоугольных импульсов,
полученный из ФМ сигнала рис 1.1, α при условии, что со0 = 0. Так как
знаки импульсов видеочастотного сигнала определяются
начальными фазами импульсов радиочастотного сигнала, то по аналогии
с радиочастотным сигналом видеочастотный также называется фазо-
манипулированным сигналом.
Спектр сигнала Uj (t) определяется преобразованием Фурье
ι Ι
η
I
Рис. 1.1
g,(<a)= J и,(/)е-'»'Л.
(1.2)
Спектр является функцией угловой частоты ω = 2π/, где / —
линейная частота. (В дальнейшем ω и / будем называть просто
частотой.) Бесконечные пределы интегрирования соответствуют общему
случаю. При определении спектра финитного сигнала необходимо
10
учитывать его расположение на оси времени /. Спектр может быть
представлен в виде N
&И=1&И|е1ф'(">,
гДе \ёз (ω) I — амплитудный, а φ/ (ω) — фазовый спектр сигнала
и, (ή.
Ширина спектра. Спектр финитных сигналов имеет бесконечную
протяженность, поэтому единого определения ширины спектра не
существует. В зависимости от целей исследования ширину спектра
сигнала находят по-разному (см., например, [25]). В дальнейшем
ширину спектра будем определять так, чтобы, во-первых,
максимально упрощать математические преобразования и, во-вторых,
правильно отображать суть решаемой задачи. Такой подход
оправдан тем, что для сигналов, входящих в одну систему, любое
достаточно разумное определение ширины спектра будет правильно
отображать спектральные свойства каждого сигнала и системы сигналов
в целом.
Ширину спектра /-го сигнала будем обозначать Fj. Ширину
полосы частот, занимаемую системой сигналов, обозначим FCRCT. Если
все спектры имеют одинаковую ширину и занимают одну и ту же
полосу частот, то FCV[CT = F9 где F — ширина спектра одиночного
сигнала. При различной ширине спектров FCWCT = /^акс —
максимальной ширине спектра. Если с изменением номеров сигналов
их спектры смещаются по частоте, определение FcliCi: должно
учитывать такое смещение.
База сигнала — произведение ширины спектра сигнала на его
длительность
В = FT, (1.3)
где F — ширина спектра /-го сигнала, т. е. F = Fj. По
предположению, сделанному ранее, все сигналы системы имеют одинаковую
длительность Т. База системы сигналов определяется аналогично
(1.3):
При /^сист = F база £Сист = В- Сигналы с В <1 1 называются
простыми, а с В >> 1 — сложными. Особое значение имеют сложные
сигналы с В > 1.
Энергия сигнала и частотно-временная плоскость. По
определению, энергия /-го сигнала
оо оо
Е}= J «ϊ(0#=™ J |^(ω)Ι'Λ». (1.5)
— ОО —ОО
Используя обратное преобразование Фурье
оо
U){t) = ~L· J &Ие,в/Ж>.
11
из (1.5) находим, что
Ε Г
оо оо
~^ЦиЛП §J ИеШ dW = Ц"1 (*) 8i (/) *l2nft df at. . (1 -6)
Из (1.6) следует, что энергия сигнала Ej — это средневзвешенное
значение произведения сигнала на его спектр. Усреднение
(интегрирование) производится по времени / и по частоте /. Весом является
экспонента ехр (ί2π//). Подынтегральное выражение в интеграле
(1.6) в некоторой точке с координатами /, / представляет собой
значение энергии, приходящейся на
площадь, равную dfdt, и характеризует
плотность распределения энергии на
частотно-временной плоскости (/, /).
Это дает возможность наглядно
проанализировать энергетические свойства
сигналов, особенно сложных.
У финитных сигналов спектр gj (/)
располагается по всей оси частот от —оо
до + оо, поэтому множитель Uj (t)gj (/)
тождественно равен нулю только вне
полосы О^/^Г, |/|<оо. Таким
образом, можно утверждать, что
энергия финитного сигнала распределена в
этой полосе.
Обычно большая часть энергии
сигнала сосредоточена в некоторой
полосе частот. Обозначим через F ширину такой полосы частот,
внутри которой сосредоточена большая часть заданной энергии, а вне
этой полосы — меньшая, которой можно пренебречь. Определенную
таким образом ширину полосы частот F будем считать шириной
спектра сигнала. В этом случае можно полагать, что энергия сигнала
сосредоточена в прямоугольнике со сторонами Τ по оси времени / и F
по оси частот /. Назовем этот прямоугольник базисным. Очевидно,
что для передачи сигнала с допустимой точностью необходимо иметь
канал с полосой частот шириной F и время передачи Т.
Для анализа распределения энергии сигнала на
частотно-временной плоскости можно непосредственно использовать (1.5),
представив интеграл в виде суммы интегралов по временным или
частотным интервалам:
/ = 2 J Ηΐ{ήάί=ζΣ^ I \SjH\2dcot (1.7)
Ej =
где интегрирование производится по неперекрывающимся
интервалам (tkt tk + Tk) или (ωη, ωη + 2nFn), а суммирование
обеспечивает получение полной энергии сигнала. Выражение (1.7) позво-
12
ляет отдельно рассматривать части сигнала (или части спектра) и
находить распределение энергии этих частей.
На рис. 1.2 приведен пример распределения энергии сигнала на
частотно-временной плоскости (/, /). Спектр сигнала сосредоточен
около несущей частоты /0 и располагается от /0 — F/2 до /0 + FI2.
Характерно, что весь сигнал по времени разделен на четыре части
и каждая занимает свою часть полосы частот, отведенной для
сигнала в целом.
Заметим, что рис. 1.2 имеет качественный характер, поскольку
для финитных сигналов, как было отмечено ранее, энергия
распределена в полосе 0^/^Г, |/|<оо, а для частей сигнала — на
интервалах (4, 4 + Tk). Другие примеры распределения энергии
сигналов на частотно-временной плоскости будут приведены в
дальнейшем.
Топографическое изображение распределения энергии сигнала
на частотно-временной плоскости наглядно выделяет те части
сигнала и его спектра, от которых в основном зависит энергия сигнала.
Во многих случаях использование частотно-временной плоскости
позволяет выделить и основные структурные особенности сигналов,
т. е. выделить «главные» с энергетической точки зрения элементы
сигнала.
1.2. Классификация сигналов
Число известных различных сигналов и систем сигналов
непрерывно растет. Это может привести к трудностям в определении [их
общих свойств и принципиальных различий. Поэтому здесь
уместно произвести классификацию сигналов и систем с целью
выяснения единства и различия как известных систем сигналов, так и
полученных в будущем. Классификация позволит объединить системы
сигналов с одинаковой структурой, выделить основную
классификационную единицу (совокупности сигналов), определить общие
свойства различных сигналов, имеющих одинаковые структурные
свойства. Кроме того, она позволит выработать единую
терминологию, так как существующая терминология имеет некоторые
неточности.
Классификация, приведенная в данном параграфе, вряд ли
удовлетворит всех исследователей, но она может быть в дальнейшем
усовершенствована.
Как было отмечено в § 1.1, по значению базы В сигналы делятся
на простые и сложные. Простые сигналы исследованы весьма
подробно и основные сведения о них можно найти, например, в [84,177].
Сложные сигналы также исследованы обстоятельно, и многие
известные результаты можно найти, например, в [3, 14, 15, 25, 99,
138, 162, 175, 191, 192].
По характеру изменения параметров сигналов во времени их
можно разделить на модулированные и манипулированные сигналы.
Под модулированными сигналами будем понимать такие, у которых
13
огибающая и фаза в (1.1) являются непрерывными функциями
времени. Поясним это определение. Непрерывность огибающей и фазы
обеспечивает отличие модулированных сигналов от манипулиро-
ванных. Параметры манипулированных сигналов изменяются
скачками, т. е. в течение некоторого интервала времени параметры
остаются неизменными; а затем мгновенно принимают другие
значения и т. д. На рис. 1.1 был приведен пример манипулированного
сигнала.
Классификации по базе и характеру изменения сигналов во
времени определяют тот или иной сигнал глобально и не дают
возможности судить о структуре сигнала более детально. Такая
возможность имеется, если перейти к классификации сигналов по виду
элементов, из которых они состоят.
Классификация сигналов по элементам. Каждый сигнал можно
представить в виде суммы некоторых известных сигналов. Такое
представление возможно при разложении исходной функции в ряд
по ортогональным функциям. Для сигнала {и (t) разложение имеет
следующий вид:
где ek (t) — ортогональные функции, удовлетворяющие равенству
?М0еж(0*={£ П*И1фт> (1-9)
Joo ( EQ при k = m,
Е0 — энергия ортогональных функций ek (/), одинаковая при всех
номерах. Коэффициенты разложения uk определяются исходным
сигналом и (/) и находятся умножением (1.8) на ет (/) с
последующим интегрированием с использованием соотношения (1.9). В
результате получаем
оо
щ=±- ^ u{t)%{t)dt. (1.10)
— 00
Из (1.10) следует, что коэффициенты разложения при
произвольных k определяются сигналом и ортогональной функцией ek (t).
Функции ek (/), удовлетворяющие условию (1.9), образуют систему
ортогональных функций (ek (/)}. Выбирая иную систему
ортогональных функций {е£ (/)}, получим другие коэффициенты
разложения ll'k.
В общем случае разложение (1.8) содержит бесконечное число
слагаемых. Но можно ограничить число слагаемых правой части
(1.8), если допустить, что сигнал представляется не точно, а с
некоторой ошибкой. При этом выбор системы ортогональных функций
{ek (/)} имеет большое значение, так как можно найти такую
систему, которая при заданном числе слагаемых в (1.8) обеспечит
наименьшую ошибку. Выбор системы ортогональных функций {ek (t)}
в свою очередь определяется характером исходного сиггнала и (/)
14
ej(t)k
a)
S)
Формулы (1.8)—(1.10) принципиально позволяют разложить
любой сигнал по любой системе ортогональных функций. Однако
наибольшее лрактическое значение*имеет разложение сигнала и (/)
по простым функциям ek (/), которые будем называть элементарными
сигналами или просто элементами. При таком разложении
некоторого сложного сигнала по более простым функциям можно,
во-первых, наглядно представить
структуру сигнала и, во-вторых,
использовать его как основу при
создании аппаратуры формирования
и обработки сложных сигналов.
Более того, можно заранее выбрать
систему элементов, из которых и
следует создавать сигналы. Число
выбранных элементов (объем
системы элементов) может быть
конечным, а сигналы будут отличаться
только своими наборами
коэффициентов uk. При этом число
слагаемых в (1.8) не превышает объем
системы элементов и элементы не
обязательно должны быть
ортогональными, хотя такое условие
всегда желательно. Наиболее часто
на практике используются
частотные элементы, временные (или
дискретные) элементы и частотно-
временные (или дискретные
частотные) элементы. Рассмотрим, чем
характеризуются сигналы,
представляемые в виде таких
элементов, и дадим их классификацию.
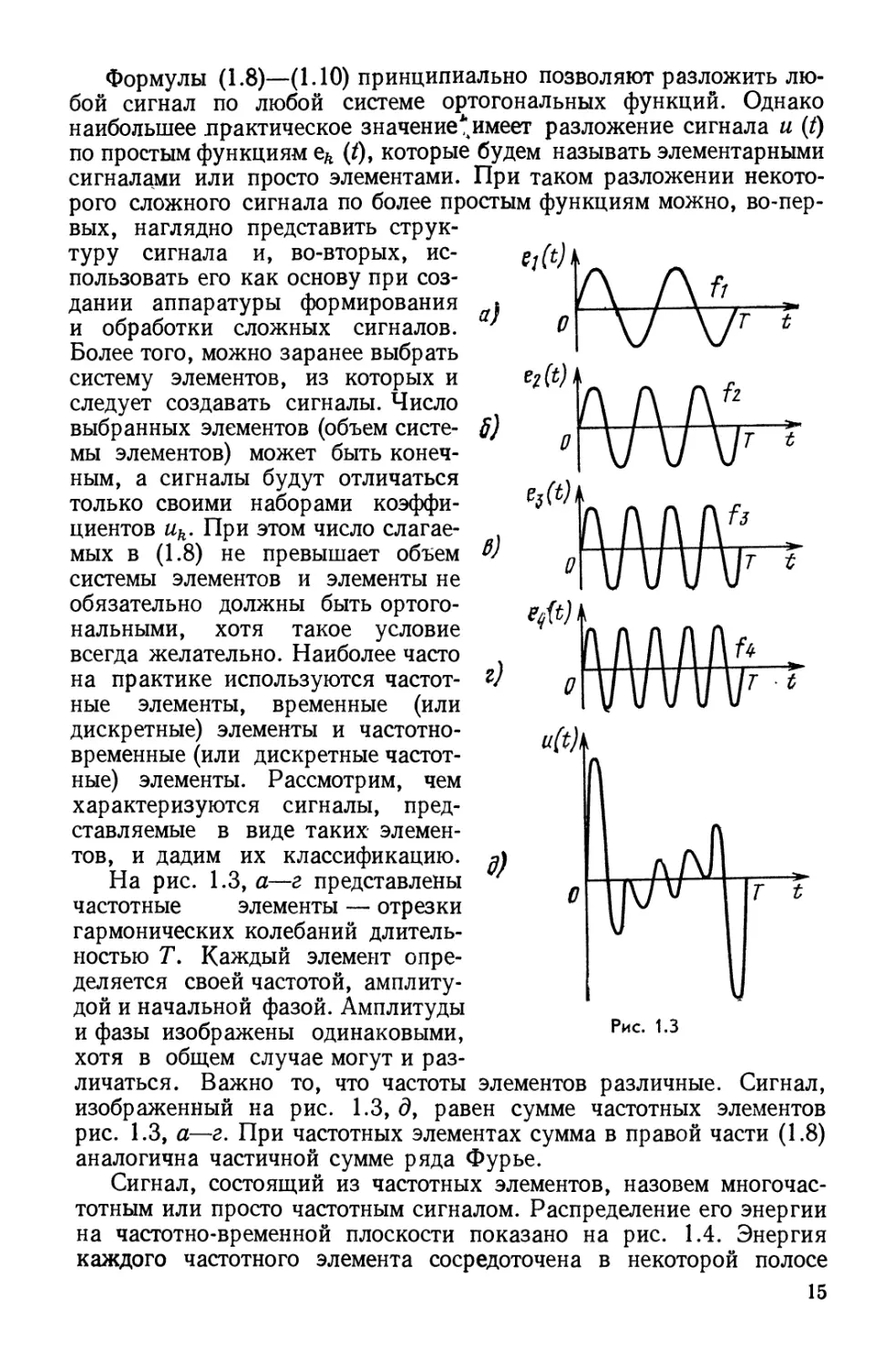
На рис. 1.3, а—г представлены
частотные элементы — отрезки
гармонических колебаний
длительностью 7\ Каждый элемент
определяется своей частотой,
амплитудой и начальной фазой. Амплитуды
и фазы изображены одинаковыми,
хотя в общем случае могут и
различаться. Важно то, что частоты элементов различные. Сигнал,
изображенный на рис. 1.3, д> равен сумме частотных элементов
рис. 1.3, а—г. При частотных элементах сумма в правой части (1.8)
аналогична частичной сумме ряда Фурье.
Сигнал, состоящий из частотных элементов, назовем
многочастотным или просто частотным сигналом. Распределение его энергии
на частотно-временной плоскости показано на рис. 1.4. Энергия
каждого частотного элемента сосредоточена в некоторой полосе
15
г)
д)
Рис. 1.3
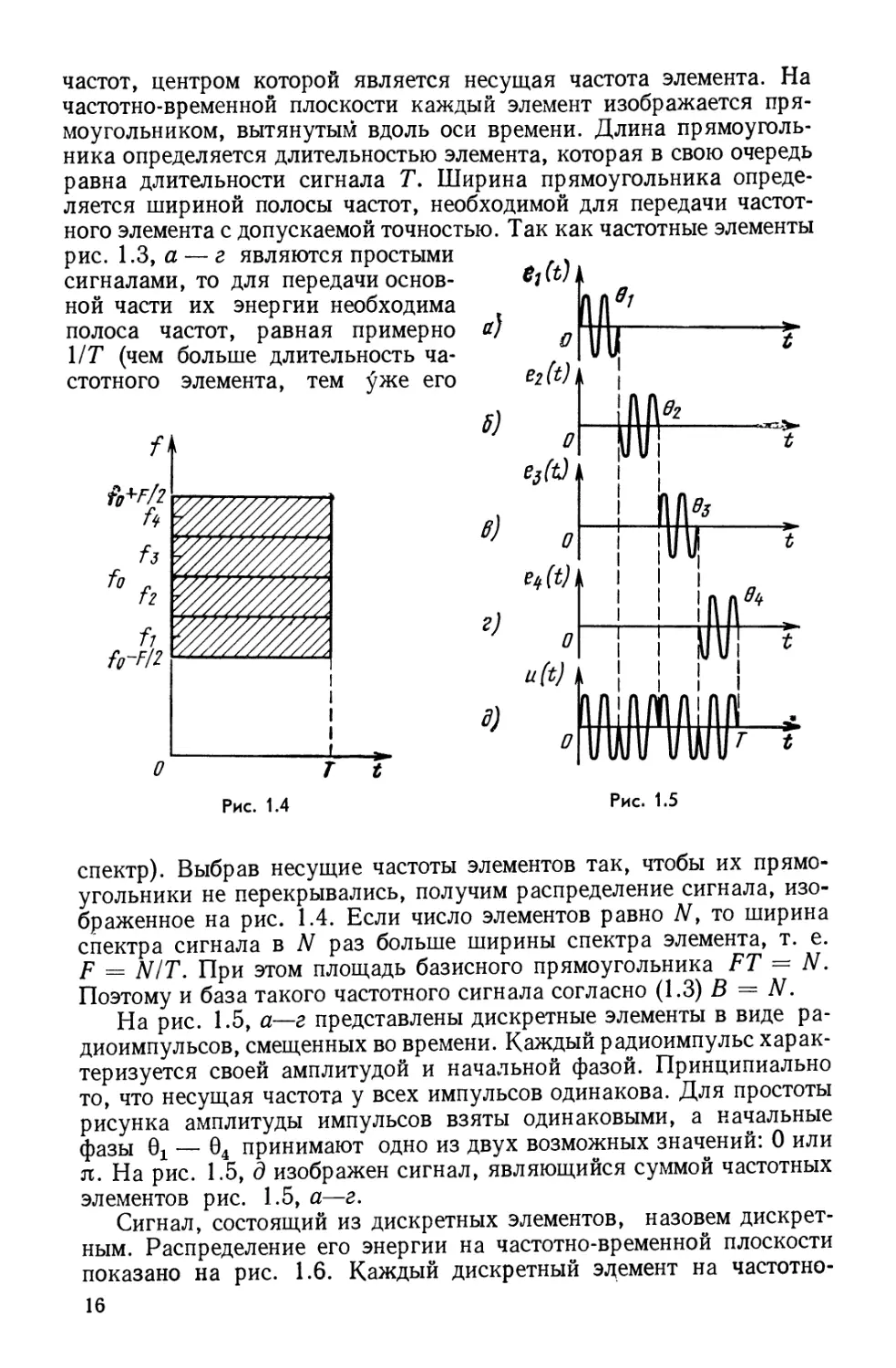
частот, центром которой является несущая частота элемента. На
частотно-временной плоскости каждый элемент изображается
прямоугольником, вытянутым вдоль оси времени. Длина
прямоугольника определяется длительностью элемента, которая в свою очередь
равна длительности сигнала Т. Ширина прямоугольника
определяется шириной полосы частот, необходимой для передачи
частотного элемента с допускаемой точностью. Так как частотные элементы
рис. 1.3, α — г являются простыми
сигналами, то для передачи
основной части их энергии необходима
полоса частот, равная примерно й)
\1Т (чем больше длительность
частотного элемента, тем уже его
δ)
в)
г)
3)
Рис. 1.4
Рис. 1.5
спектр). Выбрав несущие частоты элементов так, чтобы их
прямоугольники не перекрывались, получим распределение сигнала,
изображенное на рис. 1.4. Если число элементов равно Ν, то ширина
спектра сигнала в N раз больше ширины спектра элемента, т. е.
F = ΝΙΤ. При этом площадь базисного прямоугольника FT = N.
Поэтому и база такого частотного сигнала согласно (1.3) В = N.
На рис. 1.5, а—г представлены дискретные элементы в виде
радиоимпульсов, смещенных во времени. Каждый радиоимпульс
характеризуется своей амплитудой и начальной фазой. Принципиально
то, что несущая частота у всех импульсов одинакова. Для простоты
рисунка амплитуды импульсов взяты одинаковыми, а начальные
фазы θχ — θ4 принимают одно из двух возможных значений: 0 или
π. На рис. 1.5, д изображен сигнал, являющийся суммой частотных
элементов рис. 1.5, а—г.
Сигнал, состоящий из дискретных элементов, назовем
дискретным. Распределение его энергии на частотно-временной плоскости
показано на рис. 1.6. Каждый дискретный эдемент на частотно-
16
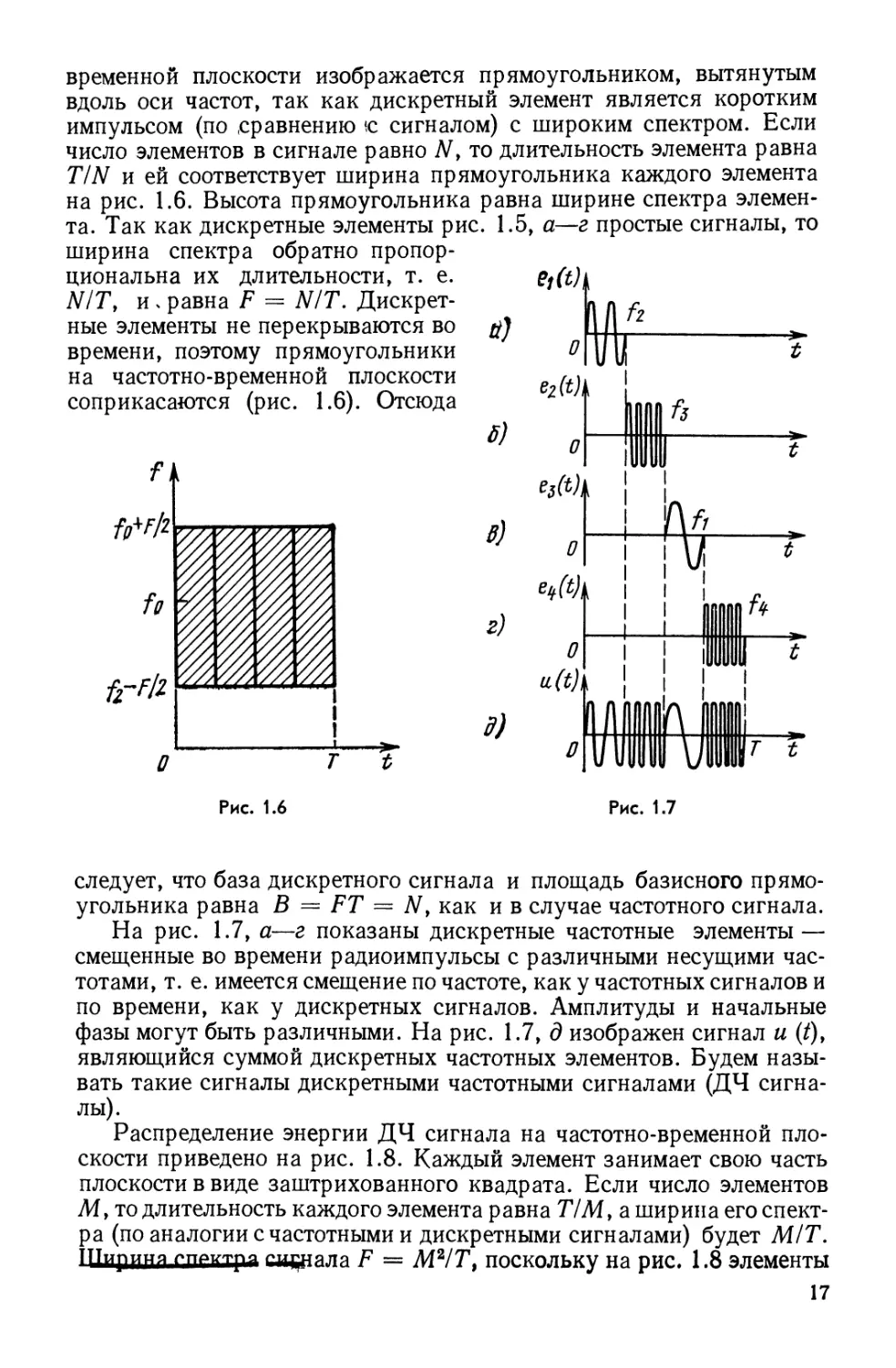
временной плоскости изображается прямоугольником, вытянутым
вдоль оси частот, так как дискретный элемент является коротким
импульсом (по сравнению <с сигналом) с широким спектром. Если
число элементов в сигнале равно N, то длительность элемента равна
TIN и ей соответствует ширина прямоугольника каждого элемента
на рис. 1.6. Высота прямоугольника равна ширине спектра
элемента. Так как дискретные элементы рис. 1.5, а—г простые сигналы, то
ширина спектра обратно
пропорциональна их длительности, т. е.
N/T, и . равна F = N/T.
Дискретные элементы не перекрываются во #]
времени, поэтому прямоугольники
на частотно-временной плоскости
соприкасаются (рис. 1.6). Отсюда
δ)
в)
fl-Fll
г)
9)
Рис. 1.6
Рис. 1.7
следует, что база дискретного сигнала и площадь базисного
прямоугольника равна В = FT = Ny как и в случае частотного сигнала.
На рис. 1.7, а—г показаны дискретные частотные элементы —
смещенные во времени радиоимпульсы с различными несущими
частотами, т. е. имеется смещение по частоте, как у частотных сигналов и
по времени, как у дискретных сигналов. Амплитуды и начальные
фазы могут быть различными. На рис. 1.7, д изображен сигнал и (/),
являющийся суммой дискретных частотных элементов. Будем
называть такие сигналы дискретными частотными сигналами (ДЧ
сигналы).
Распределение энергии ДЧ сигнала на частотно-временной
плоскости приведено на рис. 1.8. Каждый элемент занимает свою часть
плоскости в виде заштрихованного квадрата. Если число элементов
Μ, то длительность каждого элемента равна TIM, а ширина его
спектра (по аналогии с частотными и дискретными сигналами) будет М/Т.
. ацнала F = MVT, поскольку на рис. 1.8 элементы
17
fk
fo+F/2
fo
m
no частоте не перекрываются. База сигнала^ = FT = Λί2. При
этом сигнал занимает l/Λί* часть базисного прямоугольника.
Таким образом, по используемым элементам сигналы можно
разделить на три больших вида: частотные, дискретные и дискретные
частотные сигналы.
Когда элементы сигнала обладают или различными амплитудами,
или (и) фазами, т. е. элементы сигнала манипулированы по
амплитуде или (и) по фазе, то сигнал
является или амплитудно-манипулирован-
ным (AM), или (и) фазоманипулиро-
ванным (ФМ).
Если рассматриваются сигналы
одного вида, то нет необходимости
подчеркивать вид сигнала.
Например, если рассматриваются
дискретные сигналы, то дискретные сигналы
с фазовой манипуляцией (ДФМ)
можно называть просто фазоманипули-
рованными сигналами (ФМ). Такое
сокращенное название сигналов
будет использоваться тогда, когда оно
не будет приводить к
неопределенности.
Составные сигналы. Элементы сигнала не всегда простые —
они могут быть и сложными. Сигналы, составленные из сложных
элементов, будем дополнительно называть составными, а в обозначение
сигнала будем вводить*букву «С». Например: ДСЧ сигнал —
дискретный составной частотный сигнал. Отметим, что часто составные
сигналы состоят из различных элементов.
frf/*\
Г
Рис. 1.8
1.3. Классификация систем сигналов
В § 1.1 система сигналов была определена как множество
сигналов, объединяемых единым правилом построения. Рассмотрим это
определение более детально. Правило построения системы сигналов
может быть записано в виде ряда высказываний, которые определяют
последовательность вычислений всех сигналов системы.
Последовательность вычислений некоторых величин (функций) является
характерной чертой алгоритма вычисления этих величин (функций).
Поэтому рассмотрим возможные алгоритмы построения сигналов.
Алгоритмы построения сигналов. Сигнал Uj (t) является функцией
времени / и номера/, поэтому в любой алгоритм должны входить и/,
и /. Анализируя различные алгоритмы и сигналы, можно убедиться
в том, что ί и / могут входить в алгоритм двояко. Во-первых, сигнал
Uj (t) может быть функцией параметров, являющихся функциями t
uj (t) » Χ [α (t, /), β (f, /), ...],
18
где X — общее обозначение алгоритма, α (t, /), β (t9 j) — параметры,
являющиеся функциями ί и /. Алгоритмы этого вида назовем
параметрическими.
Во-вторых, сигнал Uj (t) может быть функцией всех предыдущих
сигналов или части их:
Щ (/) = Xity-ft-m (/), ..., Uj.k (/)],
т. е. Uj (t) является функцией т предыдущих сигналов, отстоящих на
k номеров от /, причем 1 < έ < /п и ft, m могут быть функциями /.
В предельном случае k = 1, т = j — 2. При этом tij (t) зависит от
всех предыдущих сигналов. Алгоритмы этого вида назовем
рекуррентными. Значения ky m являются параметрами этого алгоритма.
Возможны и рекуррентно-параметрические алгоритмы, которые
являются объединением предыдущих алгоритмов:
uj (t) = X [а (/, /), β (ί, /), ...; щ^.т (t)y ..., uj.k (/)).
Алгоритмы могут быть как детерминированными, так и
статистическими. В первом случае все параметры, определяющие алгоритм,
являются детерминированными величинами (функциями). Во
втором случае часть или все параметры могут быть случайными
величинами (функциями) и определяться соответствующими законами
распределения вероятностей.
При определении алгоритма подразумевается, что области
существования (определения) его параметров заданы и каждому
алгоритму однозначно соответствуют области существования его
параметров. При изменении области существования параметров возникает
другой алгоритм. Следовательно, алгоритм позволяет построить
единственное множество сигналов.
Класс сигналов. Множество, состоящее из всех сигналов,
построенных с помощью единого алгоритма, называется классом
сигналов. Понятие класса'является ключевым при классификации
систем сигналов. Во-первых, в класс входят только те сигналы,
которые можно построить с помощью выбранного алгоритма.
Во-вторых, в класс входят все возможные сигналы, которые можно
построить при данном алгоритме. Это означает следующее: если
алгоритм задан или выбран, то, изменяя последовательно параметры
по их областям существования, получим все возможные сигналы.
Для примера рассмотрим класс дискретных фазовых сигналов
(ДФМ сигналы). Каждый сигнал характеризуется числом элементов
и манипуляцией начальной фазы элементов. Положим, что число
элементов равно N', а число различных фаз т. Выберем следующий
алгоритм построения сигналов: фаза каждого элемента принимает
одно из т значений. В этом случае класс включает в себя сигналы,
состоящие из N элементов и отличающиеся друг от друга по
крайней мере фазой хотя бы одного элемента. Задание конкретных
значений N и т полностью определяет класс.
Система сигналов. Допустим, что в соответствии с некоторым
алгоритмом построен класс сигналов. Выберем из этого класса с по-
19
мощью заранее определенного правила некоторое множество
сигналов. Правило выбора сигналов из класса определяется
требованиями, предъявляемыми к* свойствам множества, которое
необходимо найти. Правило выбора связывает сигналы данного множества
в единое целое. Такое множество и будем называть системой сигналов.
Таким образом, любую систему сигналов можно построить
следующими методами. Первый заключается в том, что, применяя
алгоритм построения класса, а затем правило выбора сигналов из
класса, находим систему сигналов с заданными свойствами.
Естественно, что совокупность алгоритма построения класса и правила
выбора является правилом или алгоритмом построения системы.
Может оказаться, что этот алгоритм известен, тогда второй метод
заключается в том, что система сигналов строится непосредственно
в соответствии со своим алгоритмом. Следовательно, система
сигналов — это множество, сигналы которого вычисляются с помощью
единого алгоритма.
Из отмеченного следует, что для построения системы сигналов
с заданными свойствами необходимо найти или алгоритм ее
построения, или алгоритм построения класса и правило выбора сигналов из
класса. Именно эти задачи и являются центральными в теории
систем сигналов. В дальнейшем приведен ряд частных решений для
различных классов сигналов.
Любая система сигналов является подклассом своего класса
и поэтому обладает общими свойствами класса. Зная свойства
класса, можно предсказать некоторые свойства систем, которые входят
в него. Поэтому исследование свойств классов сигналов имеет
большое значение для анализа и синтеза систем сигналов и нашло
отражение в третьем разделе книги.
Классификация систем сигналов. По характеру изменения
сигналов во времени системы сигналов можно разделить на
модулированные и манипулированные. Первые состоят из модулированных
сигналов, вторые — из манипулированных.
По виду элементов, используемых для построения сигналов,
системы сигналов можно разделить на три вида: частотные,
дискретные и дискретные частотные системы.
Они состоят из соответствующих сигналов.
Каждый вид систем сигналов делится на классы, а классы —
на подклассы или системы. Изучению свойств классов и систем
сигналов и их алгоритмов построения в основном посвящена данная
книга.
1.4. Комплексная огибающая сигнала и ее спектр
Радиосигнал >(1.1) содержит быстроменяющийся множительта
виде косинусоиды, в аргумент которой входит несущая частох
ω0 = 2π/0. Соответственно спектр (1.2) этого сигнала состоит из двув
частотных полос, сосредоточенных около частот со0 и —ω0. При
20
теоретических исследованиях целесообразно для упрощения
промежуточных математических операций «освободить» сигнал и его
спектр от несущей частоты со0. Это можно осуществить при
введении комплексной огибающей сигнала. Однако комплексная
огибающая сигнала и ее спектр позволяют не только упрощать
математические операции, но также дают возможность более наглядно
представить свойства сигнала. Поэтому в большинстве случаев
исследования сигналов заканчиваются тогда, когда изучены свойства
комплексной огибающей и ее спектра.
Комплексная огибающая радиосигнала и} (t) (1.1) определяется
как
*М0 = |г/И01е|в'<*>, (1.Ц)
где модуль | Uj (t)\ = Aj (t) является огибающей сигнала tij (t).
Переход от комплексной огибающей к сигналу осуществляется с
помощью следующей формулы:
uj(t) = Re Uj (Oe1*·*, (1.12)
где Re — действительная часть.
На рис. 1.1, г была изображена комплексная огибающая ФМ
сигнала рис. 1.1, а. Она представляет собой последовательность
прямоугольных видеоимпульсов и является действительной
функцией времени. Это обусловлено тем, что начальные фазы импульсов
ФМ сигнала принимают одно из двух значений 0 или π. В общем
случае комплексная огибающая содержит и действительную, и мнимую
составляющие (см., например, [25]), но всегда является
видеосигналом, чем и объясняется переход к ней от радиосигнала.
Спектр комплексной огибающей
оо
0,(ω)= j Uj(t)e-i°>tdt. (1.13)
— оо
Комплексная огибающая сигнала находится согласно обратному
преобразованию Фурье
оо
— оо
Спектр комплексной огибающей можно представить в виде
<?,(ω) = |0,(ω)|β1φί(ω>,
где | Gj (ω) | — амплитудный, а Φ; (ω) — фазовый спектры.
Спектр сигнала gj (ω) и спектр его комплексной огибающей
Gj (ω) связаны соотношением [25, 170]
gj (ω) = 0,5О; (ω — ω0) + 0y5Gj (ω + ω0),
где * — знак комплексной сопряженности.
Так как комплексная огибающая Uj (t) — видеосигнал, то
спектр Gj (ω) расположен в области видеочастот.
21
Энергия сигнала и комплексная огибающая. Подставляя в (1.5)
выражение (1.1), получаем
оо оо
£' = Т J \υι-®\*ά* + γ J \UJ(t)\2cos2iti>ot+Qj(0]dt.
— оо —оо
Для сигналов, у которых | θ' (ή | макс^Юо» второе слагаемое много
меньше первого и им можно пренебречь. В результате имеем
выражение для энергии сигнала через модули комплексной огибающей
и ее спектра
оо оо
Ej=Y J \Uj(t)\*dt = -±-- J |G;.(cD)|2dco. (1.15)
Рис. 1.9
Поскольку | Uj (t)\2 = Uj (t)Uj (t)y то, заменяя второй
множитель согласно (1.14) и подставляя полученное произведение в (1.15),
находим
^·="^г J ί ^*(0 ό^°°)β""Ιω'rf/t dco="i" J J ^*w ό^ ^>e"^,2Jlf'rf/rf^·
— OO —00
(1.16)
Подынтегральное выражение в (1.16) так же, как и в случае
радиосигнала (см. (1.6)), характеризует распределение энергии
сигнала на частотно-временной плоскости. Поскольку
комплексная огибающая является видеосигналом, то базисный
прямоугольник, на котором распределена основная часть энергии сигнала,
будет расположен так, как это показано на рис. 1.9, а. Базисный
прямоугольник рис. 1.9, а получается из базисного прямоугольника
рис. 1.2, при смещении последнего вниз по частоте на величину
/0, чему и соответствует переход от радиосигнала с несущей
частотой /0 к его комплексной огибающей. (Деление базисного
прямоугольника на квадраты на рис. 1.9, а не изображено.) Аналогично
могут быть получены базисные прямоугольники комплексных
огибающих из базисных прямоугольников исходных радиосигналов.
22
Площадь базисного прямоугольника равна FT, где F — ширина
спектра комплексной огибающей сигнала, совпадающая с шириной
спектра сигнала, а Г — длительность комплексной огибающей
сигнала, равная длительности сигнала.
В зависимости от того, как расположен спектр радиосигнала
относительно несущей частоты, расположение базисного
прямоугольника на частотно-временной плоскости может быть иным, чем это
изображено на рис. 1.9, а. Если спектр радиосигнала расположен
несимметрично относительно частоты /0, то базисный прямоугольник
будет несимметричен относительно оси времени (рис. 1.9, б).
В дальнейшем будем использовать изображение базисного
прямоугольника в первом квадранте частотно-временной плоскости, как
представлено на рис. 1.9, б, поскольку это не будет приводить к
ошибкам.
1.5. Корреляционные функции сигналов
Оптимальный прием сигналов осуществляется с помощью
согласованных фильтров или корреляторов (см., например, [3, 7, 25, 93,
99, 105, 139, 162, 166, 170, 191, 192]). Напряжения на выходе таких
устройств описываются корреляционными функциями. В
зависимости от того, согласован или не согласован сигнал с фильтром,
имеется ли дополнительное доплеровское смещение несущей
частоты сигнала, корреляционные функции имеют различные
представления.
Взаимная функция неопределенности (ВФН) двух сигналов с
номерами / и k согласно определению [25] выражается через
комплексные огибающие сигналов и через их спектры следующим образом:
оо
Rih{%'Q)=zVT% f Uj(t)Uh(t-r)eiatdt=
— оо
оо
= i4^i С>-Й)Мсо)е.*Мсо, (1.17)
— оо
где τ — сдвиг одного сигнала относительно другого по времени,
Ω — доплеровский сдвиг частоты, Ej, Eh — энергии /-го и &-го
сигналов соответственно. Если энергии сигналов Ej = Ek = Ε, то
оо
^(τ,Ω) = ^- j Uj(t)Uk(t-x)e™dt=
*— ©о
оо
= —Ь" Г G>-Q)Gft (ω) βίωτ <ίω. (1.18)
23
ΒΦΗ (1.17), (1.18) является комплексной огибающей напряжения
на выходе фильтра, согласованного с k-м сигналом, когда на его
входе действует /-й сигнал с доплеровским сдвигом частоты Ω. Если
обозначить это напряжение через rJk (τ, Ω), то аналогично (1.12)
имеем
О* (τ, Q) = ReRjk(x, Ω)^τ. (1Л9)
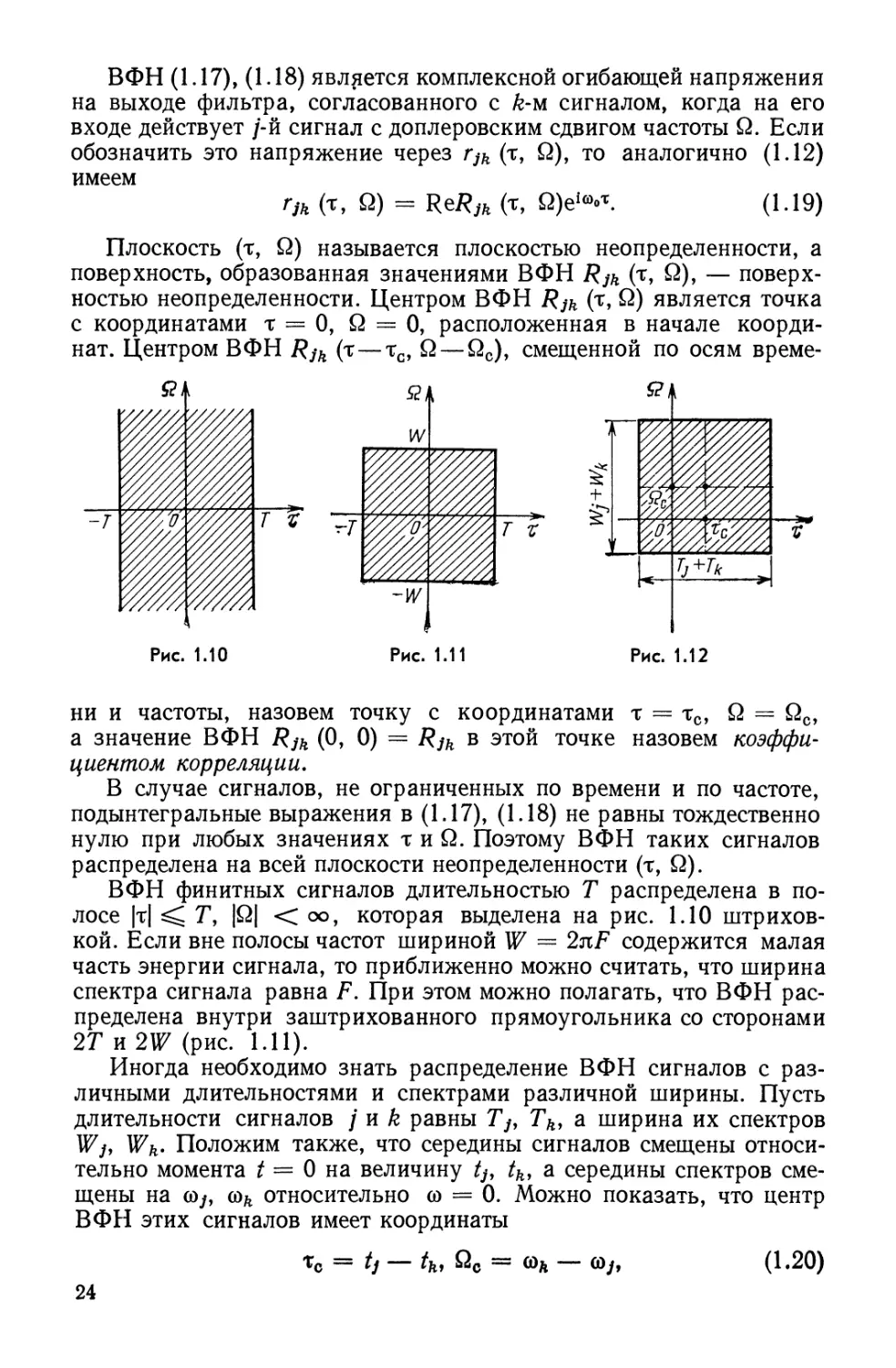
Плоскость (τ, Ω) называется плоскостью неопределенности, а
поверхность, образованная значениями ВФН Rjk (τ, Ω), —
поверхностью неопределенности. Центром ВФН RJk (τ, Ω) является точка
с координатами τ = О, Ω = 0, расположенная в начале
координат. Центром ВФН RJk (τ—tc, Ω — Ω0), смещенной по осям време-
Рис. 1.11
Рис. 1.12
ни и частоты, назовем точку с координатами τ = тс, Ω = Ω0,
а значение ВФН RJk (0, 0) = RJk в этой точке назовем
коэффициентом корреляции.
В случае сигналов, не ограниченных по времени и по частоте,
подынтегральные выражения в (1.17), (1.18) не равны тождественно
нулю при любых значениях τ и Ω. Поэтому ВФН таких сигналов
распределена на всей плоскости неопределенности (τ, Ω).
ВФН финитных сигналов длительностью Τ распределена в
полосе |τ| ^ Τ, |Ω| < оо, которая выделена на рис. 1.10
штриховкой. Если вне полосы частот шириной W = 2nF содержится малая
часть энергии сигнала, то приближенно можно считать, что ширина
спектра сигнала равна F. При этом можно полагать, что ВФН
распределена внутри заштрихованного прямоугольника со сторонами
2Г и 2W (рис. 1.11).
Иногда необходимо знать распределение ВФН сигналов с
различными длительностями и спектрами различной ширины. Пусть
длительности сигналов / и k равны Tj, Tk, а ширина их спектров
Wjy Wk- Положим также, что середины сигналов смещены
относительно момента t = 0 на величину /,·, tk> а середины спектров
смещены на ω7·, coft относительно ω = 0. Можно показать, что центр
ВФН этих сигналов имеет координаты
tc = tj — tk, Ω0 = ωΑ — ω^,
(1.20)
24
а стороны прямоугольника, в котором ВФН распределена, имеют
длину Tj + Tk и Wj + Wk (рис. 1.12). Координаты центра
определяются как среднеарифметические значения границ
прямоугольника по соответствующим осям.
Взаимокорреляционная функция (ВКФ) является сечением
ВФН при Ω = 0. Полагая Ej = Ek = Ε, Ω = 0, из (1.18) получаем
оо
— оо
оо
=~L· J 0;ИМ<о)е^Ло. (1.21)
— оо
Функция неопределенности (ФН). Если фильтр согласован с
сигналом, т. е. / = k, то из (1.18) получаем определение ФН
оо
— оо
оо
= — Г Gj((u—Q)GJ((u)ei^d(o. (1.22)
— оо
Автокорреляционная функция (АКФ) — сечение ФН при Ω = 0.
Полагая Ω = 0, из (1.22) находим
оо оо
^(τ)==ΐ j υΛΦΑΙ-χ)άί=^ j |G,((D)Pe«««d(D.(1.23)
— оо —оо
Из этого равенства (1.23) видно, что АКФ является
преобразованием Фурье энергетического спектра комплексной огибающей
сигнала..
Частотная корреляционная функция (ЧКФ) — сечение ФН при
τ = 0. Полагая τ = 0, из (1.22) получаем
оо оо
Rj{Q)=~k J \Uj(t)\^^dt = 1^ JG,(<»-Q)G,(<»)<fo. (1.24)
— оо — оо
Из первого равенства (1.24) следует, что ЧКФ является
преобразованием Фурье квадрата огибающей сигнала.
Максимум и симметрия корреляционных функций. В целом
функции (1.17), (1.18), (1.21)—(1.24) называются как было отмечено
ранее, корреляционными функциями (КФ). Известно [25], что макси-
25
мум КФ имеет место лишь при / =* k и τ = О, Ω = 0, т. е. только
в центре ФН (или АКФ етЧКФ). Максимум равен
Rj (0, 0) = Rk (О, 0) = 1, (1.25)
а
|Λ/Λ(τ,Ω)|/^<1,|Λ(τ,Ω)|τ^ο<1. (1.26)
Свойство симметрии КФ заключается в том, что
Rjk(-x, -Ω) = Rjk(x, Q)e"*. (1.27)
Из (1.27) следует, что
\Rjk(-x, -Q)\ = \RJh(x, Ω) Ι, (1.28)
\Rj(-xy-Q)\ = \Rj(xiQ)\, (1.29)
Rj (-^) = Rj W, Я, (-Ω) = Я, (Ω). (1.30)
Объем и среднеквадратические значения ВФН и ФН. Известно
(см., например, [223]), что объем, заключенный между
поверхностью, описываемой квадратом модуля ВФН, и плоскостью
неопределенности (или просто объем ВФН), равен единице, т. е.
оо
-^fJ|fyft(-t,Q)|WQ = l, (1.31)
— оо
и не зависит от формы и номеров сигналов. Полагая / = k, имеем
более известный результат: объем ФН также не зависит от формы
сигнала и равен единице, т. е.
оо
— ^\Rj{x,Qi)fdxdQ = \. (1.32)
— оо
Формулы (1.31), (1.32) позволяют найти эффективные значения
ВФН и ФН. Обозначим эти значения через /?/*эфф и Rjъφφ· Полагая,
что ВФН и ФН приближенно распределены на прямоугольнике
(см. рис. 1.11), и обозначая W = 2л;/7, согласно (1.31), (1.32) можем
записать, что R2Jk Эфф4/7Г = R2j9^FT = 1.
Отсюда находим
^эфф=^#1эфф=:::^7эфф= 1/2V FT. (1.33)
Из (1.33) видно, что чем больше база сигнала, тем меньше
среднеквадратические значения. Формулы (1.31)—(1.33) имеют большое
принципиальное значение.
Интегральные равенства. В теории сложных сигналов известен
ряд интегральных равенств (см. например, работы [4,22, 25, 29, 99,
153, 223]), которые позволяют находить различные оценки КФ. Из-
26
вестно, что для четырех сигналов с номерами /, β, /, т имеет Место
соотношение [223]
оо
Rmi К, Ωχ) Rjh К, Ωχ)= ^j RM (τ, Ω) RJm(τ, Ω) e' ^-* t) dxdQ.
— оо
(1.34)
Из (1.34) можно получить ряд интегральных равенств [22, 25].
Умножая обе части (1.34) на ехр (—ίζχχ), интегрируя по хг и
используя свойства дельта-функции, получаем
оо
j RmiЫ, Ω!)RJh (ть ΩΟ e-'«· dx1=
— oo
00
= j tffti (τ,ζ) R,m (τ, ζ) е-"* dx. (1.35)
— oo
В дальнейшем индекс 1 будет опущен.
Из формулы (1.35) можно найти частные интегральные
равенства. Рассмотрим их.
а). Положим / = & = /, ζ = 0.
Имеем
оо оо
§ \R(τ,Ω) |2dx= ^\R (τ) |2e~ia* dx. (1.36)
00 —OO
Средняя мощность модуля ФН в сечении Ω = const является
преобразованием Фурье от квадрата АКФ. Равенство (1.36) можно
найти в [4], а его использование для определения частичного объема
ФН в [29].
б). Положим / = /n, k = /, ζ = 0.
Имеем
] | Rjk (χ, Ω) |2 dx = J Rj(x) Rh (x) e~ «* dx.
— oo ^oo
в). Положим / = /η, k = /, 2 = Ωχ = 0.
Имеем
] |ЯЛ(т)|»Л= ] *,(τ)&(τ)Λ. (1-37)
— ОО —ОО
Из (1.37) следует, что среднее значение квадрата модуля ВКФ
сигналов с номерами / и k равно среднему значению произведения их
АКФ. Интегральное равенство (1.37) приведено в работе [153], где
даны и некоторые оценки ВКФ.
27
Обозначим квадраты эффективных значений ВКФ через
— оо
оо
Я?»ФФ=~ j Ι^(τ)Ντ, (1.38)
— оо
где Τ — длительность сигнала, a q = / или q = &. Используя
неравенство Буняковского—Шварца, из (1.37) получаем
Я/£эфф ^ #;эфф#Ьэфф· (1.39)
Из (1.39) следует, что для уменьшения эффективного значения
ВКФ необходимо уменьшать эффективные значения АКФ.
Отметим, что переход от (1.34) к (1.35) был совершен путем
умножения на ехр (—ιζ^) и интегрированием по xv Если умножить
обе части равенства (1.34) на ехр (izQJ и проинтегрировать по Ωχ,
то можно получить интегральные равенства, аналогичные (1.35)—
(1.38), но для частотных сечений. В этом случае также можно найти
оценки, аналогичные (1.39).
Корреляционные функции (1.17)—(1.34) справедливы для любых
сигналов. В следующих параграфах данной главы показано, какие
особенности имеют корреляционные функции сигналов того или
иного вида.
1.6. Дискретные частотные сигналы
В § 1.2 было отмечено, что по виду используемых элементов
сигналы можно разделить на частотные, дискретные и дискретные
частотные сигналы. Из определения дискретных частотных (ДЧ)
сигналов следует, что они должны обладать свойствами частотных и
дискретных сигналов (см. например, рис. 1.3—1.8). Действительно,
как будет показано в дальнейшем, это имеет место. Более того,
формулы для комплексных огибающих и корреляционных функций
частотных и дискретных сигналов могут быть получены достаточно
просто из соответствующих формул для ДЧ сигналов. По этой
причине сначала рассмотрим ДЧ сигналы.
Свойства ДЧ сигналов позволяют использовать их во многих
радиотехнических системах. Это объясняется, во-первых, тем, что
они позволяют более просто реализовать большую базу β, так как
число каналов пропорционально Υ В, а не базе, как в случае
дискретных или частотных сигналов. Во-вторых, они позволяют
получить лучшую помехоустойчивость относительно некоторых
видов организованных помех, что будет рассмотрено более подробно
в дальнейшем. Все это и обусловило то внимание, которое при-
28
влекают к себе ДЧ сигналы (см., например, [6, 7, 25, 65, 68, 75,
77, 117, 118, 131, 166]).
Порядок дискретных частотных сигналов. ДЧ сигналы являются
последовательностями элементов (элементарных сигналов),
смещенных по времени и по частоте. Например, на рис. 1.7 изображен
ДЧ сигнал, у которого на каждой временной позиции расположен
один элемент, несущая частота которого отличается от несущих
частот других элементов. На рис. 1.8 представлено распределение
энергии такого сигнала на частотно-временной плоскости.
В некоторых случаях необходимо применять ДЧ сигналы, у
которых на каждой временной позиции расположено К элементов с
/ 1 J · · О · ■ N
Рис. 1.13 Рис. 1.14
различными несущими частотами. Распределение энергии такого
ДЧ сигнала при К = 2 показано на рис. 1.13. На каждой временной
позиции расположено два элемента.
Число элементов К на одной временной позиции будем называть
порядком ДЧ сигнала. В соответствии с этим на рис. 1.7, 1.8
приведен ДЧ сигнал первого порядка, а на рис. 1.13 — ДЧ сигнал
второго порядка. Когда порядок ДЧ не оговаривается, это означает, что
рассматривается ДЧ сигнал первого порядка.
Комплексная огибающая и спектр ДЧ сигнала первого порядка.
На рис. 1.14 представлено распределение произвольного ДЧ сигнала
первого порядка. Длительность сигнала равна Г, ширина его
спектра F. Число временных позиций и элементов равно N, а число
частотных полос Λί. В общем случае ΜφΝ. Для общности положено,
что длительность элемента Т0 меньше сдвига по времени At между
соседними элементами. По этой же причине допущено, что ширина
спектра элемента F0 меньше сдвига по частоте между элементами
Δ/ = Δω/2π. Обозначим номера элементов через ν, причем ν =
- 1, N.
29
Сдвиг по времени v-fo элемента относительно начала KoopAHHaf
равен
fv = (ν— 1)Δ/. (1.40)
Сдвиг несущей частоты v-ro элемента относительно частоты ω0
равен
ω/ν = (Υ/ν— 1)Δω, (1.41)
где γ/ν — целочисленная функция индексов / и v, a /, как и ранее,
обозначает номер сигнала. Функция γ/ν определяет закон частотной
манипуляции ДЧ сигнала и изменяется от 1 (минимальное значение)
до Μ (максимальное значение).
Обозначим комплексную огибающую v-ro элемента через f//v (t).
С учетом запаздывания v-ro элемента во времени на величину U
(1.40) и сдвига по частоте на величину ω/ν (1.41) комплексная
огибающая ДЧ сигнала первого порядка запишется в следующем виде:
*М0= 2S Uiv[t-(v-l)At}exp{i(yfv-l)A<»[t-(v-\)At]}.
v= l
(1.42)
Представим комплексную огибающую v-ro элемента в виде
произведения комплексной амплитуды α/ν (комплексная величина, не
зависящая от времени) на функцию Φ/ν (t), определяющую форму
этого элемента, т. е. пусть
ί//ν (0 = fl/νΦ/ν (0 = I flyvl texp (ίθ/ν)1 Φ/ν (<). (1.43)
Комплексная амплитуда aJV определяет амплитудную манипуляцию
| α/ν I и (или) фазовую манипуляцию θ/ν, а функция Φ/ν (t)
определяет «манипуляцию по форме». Для простоты будем называть
Φ/ν (0 формой v-ro элемента. Подставляя (1.43) в (1.42), имеем
*М0= Σ fl/v*['-(v-l)A/]exp{i(v/v-l)A0[/—(ν-1) Щ.
ν= 1
(1.44)
В общем случае ДЧ сигналы первого порядка могут отличаться
друг от друга амплитудами |α/ν|, фазами θ/ν, формами элементов
Φ/ν (t), сдвигами частот, определяемых γ/ν. Каждый из
приведенных параметров определяется своей матрицей-строкой, которую
будем называть кодовой последовательностью. Манипуляция по
амплитуде описывается амплитудной кодовой последовательностью
\Aj\ = (\ail\,...,\aIN\), (1.45)
манипуляция по фазе — фазовой кодовой последовательностью]
Θ, = (ΘΛ, ..., 0,w), (1.46)
30
манипуляция по частоте — частотной кодовой последовательностью
Г, = (Тл, ...,Y;w), (1.47)
манипуляция по форме — элементной кодовой последовательностью
Ф, = (ФЛ, ...,Ф,·*). (1.48)
Одновременная манипуляция по амплитуде и фазе описывается
матрицей-строкой
Aj = (од, ..., ajN), (1.49)
которую назовем амплитудно-фазовой кодовой последовательностью.
В тех случаях, когда используется манипуляция только одного па-
Рис. 1.15
раметра, матрицы-строки (1.45)—(1.49) будем называть просто
кодовыми последовательностями.
Спектр комплексной огибающей v-ro элемента согласно (1.13)
описывается формулой
00
G/v(co)= (J Uh{t)e-mdt. (1.50)
— оо
Соответственно спектр комплексной огибающей ДЧ сигнала
первого порядка равен сумме спектров его элементов, т. е.
N
Gj(®)= 2 G/νΙω—(γ/ν —1)Δω]βχρ[—i(v—1)ωΔ/]. (1.51)
v=l
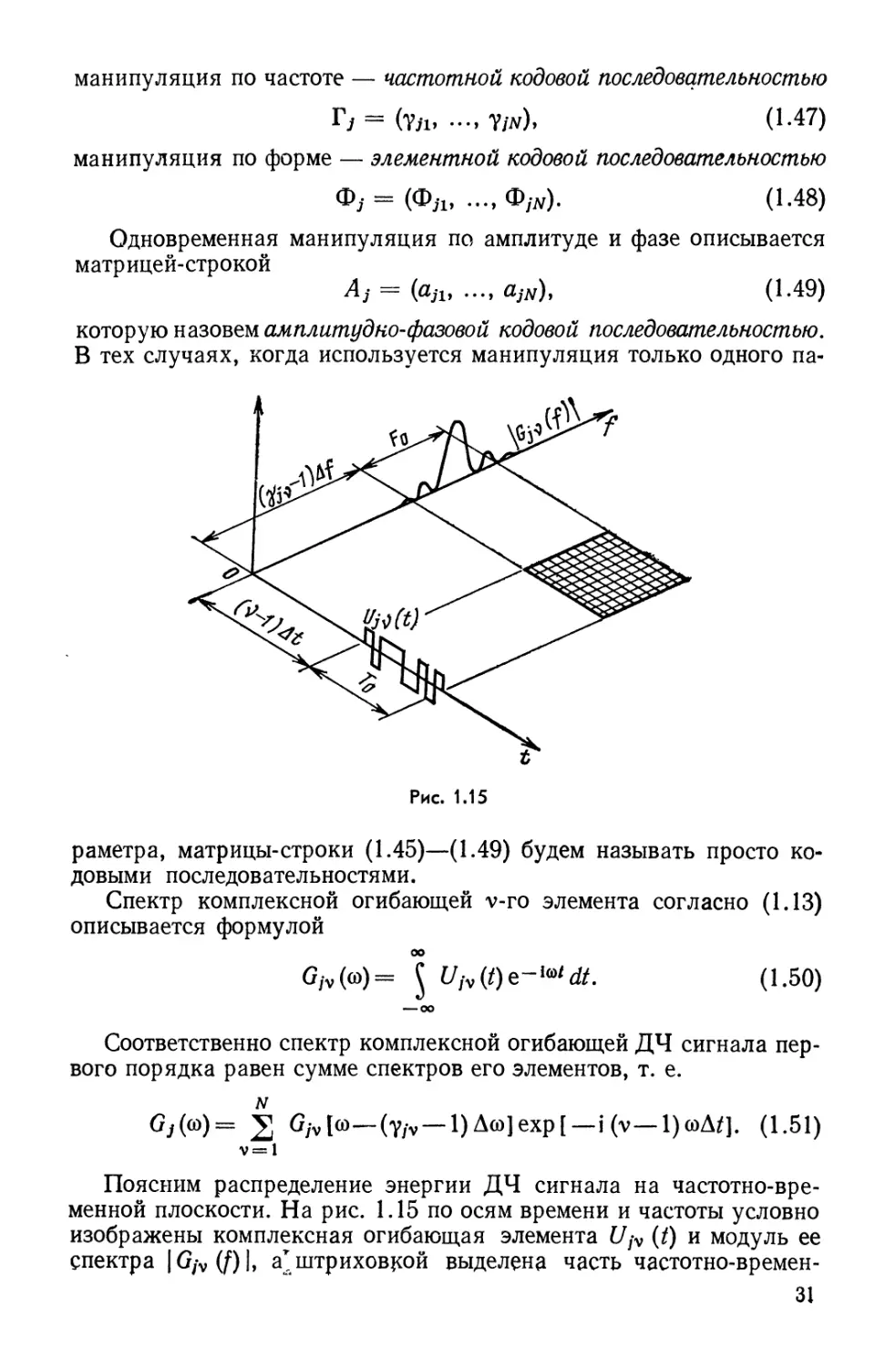
Поясним распределение энергии ДЧ сигнала на
частотно-временной плоскости. На рис. 1.15 по осям времени и частоты условно
изображены комплексная огибающая элемента f//v (t) и модуль ее
спектра |G/V(/)I, а'штриховкой выделена часть частотно-времен-
31
ной плоскости, на которой сосредоточена основная доля энергии
элемента. Запаздывание по времени согласно (1.40) равно (ν— l)At,
а смещение по частоте согласно (1.41) (γ/ν — 1)Δ/. Последовательно
переходя от элемента к элементу, можно найти распределение
энергии всего сигнала на частотно-временной плоскости. Пример такого
распределения приведен на рис. 1.14.
В общем случае длительность элемента Т0 может отличаться
от интервала между соседними элементами по времени At. Точно
так же и ширина спектра элемента F0 может отличаться от сдвига
сигнала по частоте Δ/. Будем считать, что Т0 ^ At, F0 ^ Δ/, т. е.
элементы не перекрываются по времени и частоте. В этом случае
согласно рис. 1.14 длительность сигнала и ширина его спектра
равны
T = (N- l)At + Г0, F = (Μ - 1)Δ/ +F0. (1.52)
В тех случаях, когда At = Т0 и Δ/ = F, имеем:
T = NT0y F = MF0. (1.53)
База сигнала согласно (1.3) при выполнении равенства (1.53)
равна
В = FT = MNB0J (1.54)
где
В0 = F0T0 (1.55)
— база элемента. Таким образом, база сигнала в MN раз больше
базы элемента. Если в качестве элемента взят простой сигнал с
В0 = 1, то из (1.54) имеем:
В = ΜΝ; (1.56)
при Μ = N получаем
В=М\ (1.57)
что и было отмечено при кратком описании ДЧ сигнала первого
порядка в § 1.2.
Определим долю используемой площади базисного
прямоугольника, которую обозначим через ε. Из рис. 1.14 следует, что она равна
ε = NBJB.
Подставляя в это выражение значение базы элемента В0 (1.55),
заменяя базу В согласно (1.52), полагая, что Μ > 1 и N > 1, и
отбрасывая малые более высокого порядка, получаем
ε ~ Яо/МЯомакс, (1.58)
где /?омакс = Δ/Δ^ — максимальная база элемента. Если В0 <g
С ^омакс и Μ > 1, то доля используемой площади базисного
прямоугольника мала.
Среди различных методов выбора элементов самым простым
является такой, при котором все элементы имеют одинаковую форму,
Φ/ν (0 = Φ}(ί). (1.59)
32
При этом комплексная огибающая ДЧ сигнала первого порядка
согласно (1.44)
*М0= Σ aiv<S>j[t-(v-\)At]exp{i(yiv-l)A(o[t-(v-.\)At]}J
(1.60)
а ее спектр в соответствии с (1.51)
N
<3;И= 2 α/νδ^ω—(γ/ν— 1)Лсо]ехр[ — ί(ν— 1)ωΔ/],(1.61)
ν = 1
где
οο
Sj (ω) = J Φ^ (0 exp (—mt)dt (l .62)
—СЮ
— спектр формы элемента.
Сравнивая попарно между собой выражения (1.44) и (1.51), (1.60)
и (1-61), можно заметить, что они имеют много общего. Например,
в (L60) аргумент у комплексной огибающей v-ro элемента
определяется сдвигом по времени, а в (1.61) аргумент у спектра
комплексной огибающей этого же элемента — сдвигом по частоте.
Аналогично в фазовых множителях (экспоненты в (1.60), (1.61)) сдвиг по
времени в (L60) заменяется сдвигом по частоте в (1.61). Такая
общность указанных выражений не является случайной, а определяется
структурой ДЧ сигналов первого порядка. Свойства взаимности
частотных ή временных соотношений у ДЧ сигналов назовем
частотно-временной дуальностью. Использование частотно-временной
дуальности очень часто позволяет существенно уменьшить объем
исследований при решений задач.
Корреляционные функции ДЧ сигналов первого порядка.
Подставляя в формулу (1.17) комплексные огибающие /-го и &-го ДЧ
сигналов первого порядка, определяемых согласно (1.42), и
производя преобразования, получаем ВФН этих сигналов:
«л(*.0)= 2 Σ Ρ**[τ-(ν-μ) Δ/, Ω +(γ/ν - γ*μ)Δω] eie* (τ' Ω)>
ν==1 μ= 1
(1.63)
л:де множитель
p=VEivEklx/EjEk ; (1.64)
Ejy Ek — энергии /-го и &-го сигналов, определяемые согласно (1.15);
£/v, Ek\i — энергии v-ro элемента /-го сигнала и μ-го элемента &-го
сигнала; индекс
Z = /ν, k\x (1.65)
33
некоторая комбинация индексов /, v, k, μ, причем ν, μ = 1, Ν,
ы сигналов; ВФН элементов с индек-
оо
Г Uiv(t)Ukll(t-x)e™dt; (1.66)
j9k — 1, /, a J — объем системы сигналов; ВФН элементов с
индексом Ζ
/?ζ(τ,Ω):
2VEhE*
фазовый множитель
&ζ (τ, Ω) = (γ*μ — 1)Δωτ + (ν — 1)ΔίΩ — (ν — μ)(γ*μ— 1)ΔωΔ/.
(1.67)
Из (1.63) видно, что ВФН ДЧ сигналов первого порядка равна
сумме ВФН элементов, из которых эти сигналы состоят, причем в
(1нГ%М~\
Рис. 1.16
(1.63) суммирование производится по всем индексам ν, μ. Чтобы
знать, как происходит такое суммирование, рассмотрим
распределение ВФН Rz (·) на плоскости неопределенности (τ, Ω).
Из (1.63) следует, что центр ВФН Rz (·) смещен по времени на
величину (ν — μ)Δ/ и по частоте на (γ^μ — γ/ν)Δω. Распределение
ВФН около центра определяется формами элементов, их
длительностями и шириной их спектров. На рис. 1.16 положение центра
отмечено точкой, штриховкой выделена прямоугольная область,
внутри которой сосредоточена ВФН Rz (·)· Ширина
прямоугольника по времени согласно рис. 1.12 равна сумме Тф + Tohll = 27,<ь
а по частоте — Ψφ + W0kn = 2TJ76, так как длительности
элементов и ширина их спектра у различных сигналов могут быть
разными. (Напомним, что W0 = 2nF0.) Такое распределение
соответствует общим свойствам ВФН двух сигналов (рис. 1.12).
Если элементы удовлетворяют условиям (1.53), то положения
центров определяются пересечением линий, образующих сетку на
рис. 1.17 (узлами сетки). ВФН Rz (·) распределена в прямоуголь-
34
нике, выделенном штриховкой. Стороны прямоугольника по
времени и частоте равны 2М = 2Т0 = 2T/N и 2Δω = 2№0 = 2W/M
соответственно. Из рис. 1.17 видно, что каждая Rz (·) может
перекрываться не более, чем с четырьмя соседними Rz (·)· Конечно,
такое положение справедливо приближенно. При решении
конкретных задач вопрос о взаимном перекрытии ВФН Rz (·) должен быть
уточнен в соответствии с условиями решаемой задачи.
Обычно требуется, чтобы ВФН RJk (τ, Ω) имела минимально
возможные значения. Для этого необходимо синтезировать такие
сигналы, у которых все возможные ВФН Rz{·) не перекрываются.
В настоящее время известен ряд сигналов [46, 68], удовлетворяющих
этому требованию, однако общее решение такой задачи не известно.
Пусть энергия сигналов и элементов равны между собой, т. е.
Ej = Ek = Ε и EfV = Ekn = EQ. Из (1.64) получаем, что р =
= EJE = UN и не зависит от индексов суммирования в (1.63).
Допустим, что элементы /-го и k-το сигналов имеют одинаковую
форму, т. е. имеет место равенство
Φ (0 = Φ/ν (0 = Φ*μ (ή. (1.68)
Обозначим ФН формы Φ (t) через НФ (τ, Ω). Согласно (1.22) имеем
оо
#Φ(τ,Ω) = — Γ Φ(ί)Φ(ί—т)е""Л. (1.69)
2£ф J
— оо
В этом случае ВФН ДЧ сигнала первого порядка согласно формулам
(1.43), (1.63)—(1.69) описывается следующей формулой:
χ Ν Ν
/?#(τ,Ω)=-2 2 α/νβ*μβφ[τ—(ν—μ)Δί, Ω + (γ/ν— 7*μ) Δω] χ
ν== 1 μ== 1
xexp[iez(r,Q)]. (1.70)
Отметим, что формула (1.70) справедлива при выполнении условия
нормировки комплексных амплитуд.
2 И/vl2 = Σ Κμ|2=ΛΛ (1.71)
V = 1 μ= 1
Дискретные частотные сигналы произвольного порядка. Как
было отмечено ранее, ДЧ сигналы порядка К содержат на каждой
временной позиции по К элементов, т. е. имеют N временных
элементов, состоящих в свою очередь из К частотных элементов. Такой
сигнал можно трактовать как сумму К ДЧ сигналов первого
порядка, элементы которых не перекрываются. Пример ДЧ сигнала
второго порядка приведен на рис. 1.13.
Обозначим элементы, стоящие нау-й временной позиции,
номером κν, причем κ = 1, /С, ν = 1, N. Запаздывание элементов по
35
времени определяется формулой (1.40), а сдвиг по частоте
аналогично (1.41)
·ω/κν = (γ/κν — 1)Δω, (1.72)
где γ/κν — целочисленная функция индексов /, κ, ν.
Обозначая через ί//κν (t) комплексную огибающую κν-го эле-
мента* находим комплексную огибающую ДЧ сигнала порядка К;
Uj(t)= Σ Σ ί//κν^-(ν-1)Δ^χρ{ι(ν/κν-1)Δω[/-(ν-1)Δ/]}.
v=i κ = ι
(1.73)
Введя комплексную амплитуду α/κν = |α/κν| exp (ίθ/κν) и
форму Φ/κν (0» аналогично (1.44), получаем
N К
Uj(t)= Σ Σ β/κνΦ/κν^-(ν-1)Δ/]6χρ{ί(γ/κν-1)χ
V=lX=l
ΧΑω[ί~ (ν—1)Δ/]}.
(1.74)
В общем случае ДЧ сигналы произвольного порядка могут
различаться между собой амплитудами |α/κν|, фазами θ/κν,
сдвигами частот, пропорциональными γ/κν, формами элементов Φ/κν (t).
Изменения указанных параметров определяются следующими
прямоугольными матрицами:
матрицей амплитуд
матрицей фаз
матрицей частот
матрицей форм
\А,\ =
а/и,..., а
ilN
ajKV ·-» ajKN
[вг-
θ/ιι θ/
IN
Γ; =
Φ,
Θ/Κ1, ..., djf,N
V/ii· ···· V/iw
V/кр ·"' Y/kw
Φ/ιι,·.., Φ/uv
Φ/ΚΙ» -".Φ/ΚΛ/
(T.75)
(1.76)
(1.77)
(1.78))
36
Подставляй определение комплексной огибающей ДЧ сигнала
(1.73) в формулу (1.13) и обозначая спектр κν-го элемента через
G/MV (ω) = J i//KV (f)e-'«'df, (1.79)
— οο
получаем спектр комплексной огибающей /-го сигнала
0/(ω)= Σ Σ G/κνΙω—(γ/κν —1)Δω]βχρ[ —i(v —1)ωΔ/]. (1.80)
ν=1 κ=1
Согласно (1.80) спектр ДЧ сигнала представляется суммой
спектров элементов сигнала (1.73).
Когда сигнал состоит из элементов одинаковой формы, т. е. имеет
место равенство Φ/κν (0 = Φ7· (0» аналогичное (1.59), то
комплексная огибающая ДЧ сигнала и ее спектр получаются из формул
(1.73), (1.80) и имеют следующий вид:
*Μ0=Σ Σ Α/κνΦ,^-^-ΟΔΊβχρΟίγ/κν-ΙΪΧ
ν=1κ=1
χ Δω [/-(ν -1) At]}, (1.81)
^И=Ц Σ <*!**$№ — (?/*ν —1)Δω]βχρ[ —i(v — 1)ωΔί], (1.82)
ν = 1 κ=1
где S7- (ω) определяется согласно (1.62).
Распределение энергии ДЧ сигнала произвольного порядка по
сути не отличается от распределения для сигнала первого порядка
(см. рис. 1.13).
Подставляя в формулу (1.17) комплексные огибающие/ -го и &-го
ДЧ сигналов К порядка (1.73) и производя необходимые
преобразования, получаем ВФН этих сигналов
Rjk (τ, Ω) = 2 Σ Σ Σ PRyΐχ-(ν -ν) At>Ω+
ν = ΐ κ=1 μ = ΐ χ = ΐ
+ (7/κν — γ^χμ) Δω] exp [ΐΒγ (τ, Ω)], (1.83)
где
p=VElwEkXil/EJEk\ (1.84)
Ej, Ek — энергии /-го и &-го сигналов, определяемых согласно
(1.15); JB/kv» Бы». — энергии κν-го и χμ-го элементов этих сигналов;
Y = jxv, £χμ; (1.85)
Ry (·) — ВФН κν-го элемента /-го сигнала и χμ-го элемента &-го
сигнала
оо
RY(x, Ω) = l f ϋΜ (t) UkKVi (t - τ) е1шЛ; (1.86)
— οο
37
фазовый множитель
εγ (τ, Ω) = (γ*κμ — 1)τΔω + (ν — 1)ΩΔ/ — (ν — μ) Χ
Χ (γ*κμ - 1)ΔωΔί. (1.87)
Если элементы /-го и &-го сигналов не перекрываются по
времени и по частоте, то они взаимно-ортогональны. Пусть Ej = Ek =
= Ε, a EJHV = Екк\\, = E0. При этом Ε = ΝΚΕ0 и в формулах
(1.83), (1.84) коэффициент
ρ = 1ШС. (1.88)
Если при этом элементы имеют одинаковую форму, то ВФН (1.83)
приобретает следующий вид:
ν к ν к
Rjk(XjQ) = — 2 2 2 2 α/*ναΑχμ£φ[τ—(ν —μ)Δ/,
ν = 1 κ=1 μ=1 χ = 1
(γ/κν — γ^χμ) Δω] exp [iey (τ, Ω)]. (1.89)
Отметим, что (1.89) справедлива при выполнении условия
нормировки
Σ Σ Κ*ν|2= 2 2 le^l'-wt (1.90)
ν = 1 κ= 1 μ=1 χ = 1
Полагая в (1.73)—(1.90) К = 1, получаем формулы для
дискретного частотного сигнала первого порядка.
1.7. Частотные и дискретные сигналы
Формулы, описывающие комплексные огибающие, спектры и
корреляционные функции частотных и дискретных сигналов, получим
из соответствующих формул для дискретных частотных сигналов.
Частотные сигналы. Полагая в (1.42), (1.51), (1.60), (1.61) Δ/ =
= 0, γ/ν = ν, получаем комплексную огибающую частотного
сигнала при различных формах элементов
^ (0 = Σ tf/v (0 exp [i (ν -1) Δω/] (1.91)
ν=1
и ее спектр
Gy(cD)= 2 G/v[<D-(v-l)Aa>]; (1.92)
v = l
комплексную огибающую при одинаковых формах элементов
Vj (ή = Φ7· (0 2 fl/v exP Π (ν— J) Δώ'1 ί1 ·93>
ν = 1
38
и ее спектр
N
Gj (ω) = 2 α/ν δ^ω — (ν ~ 1) Δω]. (1.94)
ν=1
Из (1.91)—(1.94) видно, что частотные сигналы представляют
собой суммы элементов Ujv (t) с различными несущими частотами.
Длительности элементов Т0 равны длительности сигнала Г.
Исследованию свойств частотных сигналов посвящены работы [6, 7, 25,
69, 99, 191].
Дискретные сигналы. Полагая в формулах (1.42), (1.51), (1.60),
(1.61) Δω = 0, получаем комплексную огибающую дискретного
сигнала при различных формах элементов
Uj(t)= 2 ί//ν[*-(ν-1)Δί] (1.95)
и ее спектр
G7(co)= 2 G/v(a>)exp[ —i(v —1)ωΔί]; (1.96)
ν=1
комплексную огибающую при одинаковых элементах
Uj(t)= 2 α»Φ,[ί-(ν-1)Μ] (1.97)
ν = 1
и ее спектр
Gj((o) = Sj(<u) 2 fl/vexp[ — i(v— 1)ωΔ/]. (1.98)
ν=1
Из (1.96)—(1.98) видно, что дискретные сигналы являются
последовательностями элементов ί//ν (ή, сдвинутых относительно друг
друга по времени. Исследованию дискретных сигналов посвящено
много работ (см., например, [3, 7, 15, 25, 99, 136, 156, 162, 183, 192,
210]).
Сигналы со смещением по частоте. Полагая в (1.42), (1.51) W = l,
At = 0, γ/κν = / и отбрасывая индекс ν = 1, получаем
комплексную огибающую
Uj (t) = Ux (/)ехр [i (/ — 1)Δωί] (1.99)
и спектр сигнала
Gj (ω) = d [ω — (/— 1)Δω] (1.100)
со смещением по частоте, который является частным случаем
частотного сигнала. В (1.99), (1.100) иг (t) — комплексная огибающая
первого сигнала, не имеющего частотного сдвига. Такие сигналы
называются также сигналами с. частотным сдвигом или частотно-
смещенными. Отметим, что такие сигналы имеют особый смысл толь-
39
ко при рассмотрении систем сигналов [25, 47, 198] когда / = 1, У.
Если они рассматриваются отдельно, то частотный сдвиг (/— 1)Δω
может быть отнесен к несущей частоте. При этом форма всех
сигналов определяется комплексной огибающей Ux (t).
Частотно-временная дуальность частотных и дискретных
сигналов. Дуальность ДЧ сигналов приводит к дуальности частотных и
дискретных сигналов. Сравним попарно выражения (1.91) и (1.96),
(1.92) и (1.95). Формула (1.91) определяет комплексную огибающую
частотного сигнала, а формула (1.96) — спектр комплексной
огибающей дискретного сигнала. Из сравнения этих формул видно, что
структурно они имеют одну и ту же форму, но все временные
зависимости заменяются частотными, а частотные зависимости —
временными. Точно такой же вывод следует из сравнения (1.92) для
спектра комплексной огибающей частотного сигнала с (1.95) для
комплексной огибающей дискретного сигнала.
Аналогичное заключение можно сделать, сравнивая попарно
формулы (1.93) и (1.98), (1.94) и (1.97). Причем, в случае
одинаковых элементов частотно-временная дуальность сравниваемых
сигналов выделяется особо заметно, так как Фу (t) и Sj (ω) связаны
между собой преобразованием Фурье (1.62), а суммы в (1.93), (1.98)
совпадают с точностью до знака в показателях экспонент.
Из частотно-временной дуальности частотных и дискретных
сигналов следует, что эти сигналы должны обладать одинаковыми
свойствами «с точностью до поворота частотно-временной плоскости
на π/2». Поэтому, если определено то или иное свойство для одних
сигналов, оно может быть перенесено на другие сигналы с заменой
частотных зависимостей на временные и наоборот.
Спектры кодовых последовательностей. Было отмечено, что
суммы правых частей (1.93), (1.98) совпадают с точностью до знака
экспонент с заменой Δω на Δ/ и ω на t. Комплексные амплитуды α/ν
определяют амплитудную и фазовую манипуляции в частотном(1.93),
(1.94) и дискретном (1.97), (1.98) сигналах. Для таких сигналов
амплитудная и фазовая манипуляции определяются матрицами-
строками аналогично (1.49)
AJ = {я/v} = fan* afr ···> α/")> (1.101)
которые в этом случае будем называть, как было отмечено ранее,
кодовыми последовательностями. Обозначения последовательностей
Aj = {α/ν} идентичны и будут использоваться в зависимости от
необходимости. Соответственно суммы из (1.93), (1.98)
Ηj (ή = 2 а* exP[i (v —!) Δω/1' (I Л 02)
v=l
#,(ω)= Σ Ял>ехр[—i(v—1)A*dJ (1.103)
40
назовем спектрами кодовых последовательностей частотного и
дискретного сигналов. Спектры кодовых последовательностей
подробно исследованы в [25]. Обозначим
Δωί = ξ, Δ/ω = ζ. (1.104)
При этом из (1.102), (1.103) получаем
НЛЪ)= Σ */νβχρ[1(ν-1)ξ], (1.105)
Ηj (9 = Σ α/ν exp [ - i (ν-1) ζ]. (1.106)
ν=ι
Спектры (1.105), (1.106) являются периодическими функциями
с периодом 2π. По (1.105), (1.106) можно определить комплексные
амплитуды исходных кодовых последовательностей. Используя
обратное преобразование Фурье, находим:
для частотного сигнала
л
α/ν = ~έΓ j^(l)exp[-i(v-l)|]d|; (1.107)
для дискретного сигнала
л
α/ν = -£- J Η, (ζ) exp [i (ν-1) ζ] άζ. (1.108)
— Л
Формулы (1.105)—(1.108) позволяют производить анализ и
синтез частотных и дискретных сигналов без учета формы элементов,
т. е. структурно.
Корреляционные функции частотного сигнала. Положим в (1.63)
Δ/ = 0, Т0 = Ту γ/ν = vh γ*μ = μ. Β результате получаем ВФН
частотного сигнала
*Α(τ,Ω)= Σ Σ Ρ«ζ[τ,Ω + (ν-μ)Δω]βχρ[ίβζ(τ)], (1.109)
где ρ, Ζ, Rz(-) определяются согласно (1.64)—(1.66). В
соответствии с (1.67) фаза
εζ (τ) - εζ (τ, 0) = (μ — 1)Δωτ. (1.110)
Когда энергия сигналов Ε}· = Ek = Ε и элементов EiV = £,*μ=£,(),
то из (1.109) имеем
Ял(*,0) = -|*-2 2Rzl%>® + (v-V)b<»]™Vli*z{x)]. (1.111)
41
Если элементы не йерекрываются, то в (1Л11)Е0/Ё = ΐ/ΛΛ При
этом сигналы состоят из элементов одинаковой формы, т. е. имеет
место равенство (1.59) и из (1.71), (1.111) имеем
Ν Ν
Rjk{XjQ) = ±. J J «/ν^μ/?φ[τ,Ω + (ν-μ)Δω]6χρ[ίεζ(τ)1.
(1.112)
ν=1μ=1
Рассмотрим структуру ВФН частотного сигнала О·^)· Из
формулы (1 109) ввдно, что ВФН Rih (τ, Ω) является суммой ВФН
^ r J ч элементов /?ζ(·)> центры
которых лежат в точках τ = 0,
Ω = —(ν — μ)Δω. Обозначим
λ = ν-μ. (1.113)
w
-τ
-w
Рис. 1.18
Г %
При этом координаты центров
ΒΦΗ#ζ(·) есть τ = 0, Ω =
= —λΔω. Центр одной из ВФН
Rz(-) выделен точкой на рис. 1.18
в предположении, что λ > 0.
Поскольку и ν, и μ изменяются
от 1 до Ν, то согласно (1.113) λ
изменяется от —(Ν — 1) до
(Ν—1), т.е. λ=— (Ν—Ι), (Ν—1).
Центры ВФН Rz (·)
совпадают с узлами сетки,
образующимися при пересечении
оси Ω с линиями Ω = —λΔω.
Линии Ω = —λΔω/λ = — (Ν — 1), (Ν — 1), назовем разностными
линиями. Учитывая пределы изменения λ, находим, что число
разностных линий равно 2Λ/* — 1. Число слагаемых в (1.109) при λ =
= const равно
Νι = Ν — \λ\. (1.114)
Если элементы удовлетворяют условию (1.53), т. е. имеют
спектры одинаковой ширины W0 = Δω, то ВФН Rz (·) с λ = const
распределена в полосе | τ | <1 Τ, —(λ + 1)Δω < Ω < —(λ — 1)Δω
с центром в точке ΐ = 0, Ω = —λΔω. Такое распределение
выделено штриховкой на рис. 1.18.
На разностной линии ВФН
Rz Ιτ, Ω + (ν — μ)Δω] = Rz>(r)
(1.1115)
является ВКФ, поскольку Ω + (ν — μ)Δω = 0. В (1.115) индекс
Ζ' =/v, k(v — λ). 0-16)
42
Допустим, что спектры элементов не перекрываются и они
обладают равными энергиями. При этом на разностной линии Ω =
= —λΔω суммируется Νχ ΒΚΦ. Из (1.111) имеем
ι Ν
Rjk(x, _λΔω)=-±- ^ Rz>(t)exp[i*z(r)]. (1.117)
ν = λ+ 1
Когда формы элементов одинаковы, т. е. имеет место равенство
(1.59), после преобразований (1.112), (1.117) получаем
Rjkfa — λΔω)-=*—£φ(τ) ^ α/ν a*(v_Mexp[i (ν— λ— 1)Δωτ].
ν=λ+1
(1.118)
Отметим, что в (1.118) входит АКФ Ra> (τ) элемента, которая не
зависит от индекса суммирования и поэтому вынесена за знак суммы.
Сумма состоит из слагаемых, в каждое из которых входит
произведение комплексных амплитуд/-го и &-го сигналов. Равенство (1.118)
включает в себя условие нормировки (1.71), которое должно
выполняться для кодовых последовательностей всех сигналов.
Используя распределение ВКФ (1.115) с λ = const около
разностных линий, представим ВФН частотного сигнала (1.109) в
следующем виде:
RJh(x,Q)= "Σ tfkfrQ), (1.119)
λ = _ (Ν—\)
где
/?/Λ(τ,Ω)= 2 ρ£ζ'(τ.Ω + λΔω)βχρ[ϊβζ(τ)]. (1.120)
В полосе )τ| < Γ, —(λ + 1)Δω < Ω < —λΔω суммируются
две группы ВФН (1.115) с «соседними» значениями λ, а именно с λ
и с λ+l. Общее число слагаемых будет равно Νχ + Νχ+\.
Корреляционные функции дискретных сигналов. Положим в
формуле (1.63) Δω = 0. В результате получаем ВФН дискретного
сигнала
*м (τ. Ω)= Σ Σ Ρ^ζ[τ-(ν-μ)Δ/>01βχρ[Ιβζ(0)1, (1.121)
ν=1μ=1
где Ζ, ρ, Rz (·) определяются согласно (1.64)—(1.66), а фаза εζ (Ω)
β соответствии с (1.67) равна
εζ (Ω) = εζ (0, Ω) = (ν — 1)ΔίΩ. (1.122)
Когда равны энергии сигналов Ek = Ек = Ε и энергии
элементов £/ν = Ek», = Ε0j то из (1.121) получаем
Ν Ν
Rjk(τ, Ω)=-ψ ^ Σ Rzίτ-(ν-^) Δί> Ωι εχρiie*ш- (1Л23)
ν=1μ=1
43
При выполнении условия (1.53), когда длительности элементов
Т0 = TIN и не перекрываются, EJE = UN. Если сигналы состоят
из элементов одинаковой формы, то из (1.70), (1.123) имеем
j Ν Ν
Rjk (τ, Ω) = — ^ 2 α» «*μ #φ h—(ν —μ) Δ/, Ω] exp [ίεζ (Ω)].
ν=1μ=1
(1.124)
Сравнивая (1.124) с (1.112), можно заметить, что структура этих
формул одинакова, а основное отличие заключается в изменении
зависимости ВФН Rz (·) от разности λ = ν — μ (1.113). В (1.112)
эта разность входит в частотный
аргумент Ω, в (1.124) — во вре-
W
-т
-W
ш
ш
ш
ш
ш
щ
ш
ш
ш
ш
ш
щ
τ ζ
Рис. 1.19
рис.
при
менной τ. Такое свойство
формул (1.112) и (1.124)
объясняется частотно-временной
дуальностью частотных и дискретных
сигналов. Поэтому
представляется, что корреляционные
свойства дискретных сигналов будут
такими же, как у частотных,
с той лишь разницей, что
изменяются роли осей τ и Ω
плоскости неопределенности.
Центры ВФН элементов
Rz (·) согласно (1.121)
расположены в точках τ = λΔί, Ω = 0,
где λ = ν —μ (1.113). На
1.19 положение центра выделено точкой. ВФН( дискретов
λ = const распределяются в полосе
(λ— 1)Δί<τ<(λ+ 1)Δ/, |Ω[<№
около разностной линии τ = λΔί, что отображено штриховкой на
рис. 1.19. (В общем случае указанная полоса не ограничена по
частоте из-за финитности элемента, т. е. | Ω | < оо. Поэтому ограничение
полосы |Ω| <; W является приближенным.) Сравнивая рис. 1.18 и
и 1.19, замечаем, что все частотные зависимости заменены
временными, а временные частотными.
Как и в случае частотных сигналов, число разностных линий
равно 2Ν — 1, а число слагаемых в (1.121), (1.123) при λ = const
будет Νλ (1.114).
Допустим, что элементы удовлетворяют условию (1.53), т. е.
не перекрываются. Вдоль разностной линии τ = λΔί из (1.124)
получаем
ι Л
/?^(λΔί, Ω) = -ί-#φ(Ω) 2 ****:<v-Mexp[i(v-l)A*Q].
(1.125)
44
Формула (1.125) отличается от (1.118) тем, что в нее входит ЧКФ
/?ф (Ω) формы элемента вместо АКФ R& (τ) из (1.118). Кроме того,
в показателе экспонент частотные и временные параметры
поменялись местами.
Используя распределение ВФН элементов (рис. 1.19), можно
представить ВФН дискретного сигнала в виде (1.117), где
R%(r,Q) = 2 РЯ*'(т—λΔ/,Ω)βχρ[ίεζ(Ω)]. (1.126)
В полосе λΔί < τ < (λ + 1)Δί, | Ω | < W суммируются две
группы ВФН с соседними значениями λ. Общее число слагаемых
равно Νλ + Νχ+\.
Связь между корреляционными функциями и спектрами кодовых
последовательностей. Из всех форм записей корреляционных
функций частотных и дискретных сигналов особое значение, как будет
показано в дальнейшем, имеют (1.118) и (1.125). Докажем одно
интегральное равенство, связывающее эти корреляционные функции
со спектрами кодовых последовательностей (1.105), (1.106) [25, 37].
Для частотного сигнала имеем
R}k(x, -λΔω)= **>(T)e~'*" X
X \ Hj(% + x)Hk(l)e-^dl, (1.127)
—π
для дискретного сигнала
Rjh(KAi,Q) = I^L j Я,«-у)/гк(С)е«*#, (1.128)
—π
где
* = Δωτ, у = ΔίΩ, (1.129)
a Hj (ξ), Hk (ξ) определяются согласно (1.105), a Hj (ζ), Hk (ζ) —
согласно (1.106). В справедливости равенств (1.127), (1.128) можно
убедиться, подставив вместо спектров кодовых последовательностей
их определения (1.105), (1.106). Это можно доказать непосредственно.
Докажем равенство (1.127),
*
Подставив в (1.118) вместо α/ν, ан (ν-λ) их определения согласно
(1.107). После простых преобразований имеем
Rjk(r, -λΔω) = -^-ЦЯДУЯНУ X
— π
Xexp[ifo—Alg-g, —λ*—*)] 2 exp[iv(—ξι + ξ,+ *)№<&·
ν = λ+1
45
Поскольку во внутренней сумме слагаемые с номерами ν > N и
ν < λ + 1 равны нулю, то можно расширить пределы
суммирования до бесконечности. Тогда
RJk(r, _λΔω)=^|^- J|#,(У#*(Ы Χ
—я
X exp[i (ξχ—λ|2— %—λχ—χ)] χ
χ 2 βφΐΐν (-ξι+ & + *)]<&<&· (1-130)
Но
2 βίνζ = 2π ^ δ(ζ—2πν), (1.131)
где δ (λ:) — дельта-функция. Так как на интервале (—π, π)
содержится одна дельта-функция, из (1.130) получаем
ЯФ (τ) "
Rjk (τ,- -λΔω) = _^L j j Я,- (У Я, (ξ2) X
— π
ХехрПйх—Я^-Ь-и-^бС-Ех + Ь + ^^х^-
Используя фильтрующее свойство дельта-функции, получаем (1.127).
Аналогично доказывается (1.128).
Корреляционные функции сигналов со смещением по частоте.
Подставляя выражение для частотного сигнала (1.98) в определение
ВФН (1.18) и обозначая ФН комплексной огибающей Ux(t) как
оо
/?ф (τ, Ω) = — f Ux (t) Uj. (t—τ) eliit dt, (1.132)
2E J
— 00
получаем ВФН сигнала со смещением по частоте
Rjk (τ, Ω) = /?Ф [τ, Ω + (у — *)Δω] exp [i (k — 1)Δωτ]. (1.133)
Таким образом, ВФН таких сигналов с точностью до фазового
множителя совпадает с ФН (1.132), смещенной по оси Ω на величину
(/ — &)Δω.
46
Глава 2
СИСТЕМЫ СИГНАЛОВ И ПЕРЕДАЧА ИНФОРМАЦИИ
2.1. Системы передачи информации
Системы передачи информации (СПИ) служат для передачи
сообщений от одного абонента к другому. Сообщения могут быть
дискретными и непрерывными. Дискретные сообщения представляют
собой последовательности символов, причем число различных
символов конечно. Примерами дискретных сообщений могут служить
телеграфные сообщения, телекодовые и т. д. Источники
информации, которые создают дискретные сообщения, называются
дискретными. Непрерывные сообщения представляют собой непрерывные
функции времени. Источники информации, которые создают
непрерывные сообщения, называются непрерывными. Примерами
непрерывных сообщений могут служить речь, музыка, значения
некоторого параметра, изменяющегося во времени, и т. д.
СПИ, предназначенные для передачи дискретных сообщений,
называются дискретными или цифровыми, а СПИ, предназначенные
для передачи непрерывных сообщений, — непрерывными или
аналоговыми.
Каналы, в которых передаются дискретные сообщения,
называются дискретными, а каналы, в которых передаются непрерывные
сообщения — непрерывными. Передача непрерывных сообщений
возможна и в дискретном виде. Для этого необходимо непрерывные
сообщения источника непрерывной информации превратить в
дискретные и по каналу будут передаваться дискретные сообщения,
т. е. канал будет дискретным.
Замена непрерывных сообщений дискретными всегда
производится с заданной точностью. Для этого следует разложить
непрерывное сообщение в ряд (1.8) по ортогональным функциям, т. е.
представить сообщение S (/) в следующем виде:
S(t)= f Sn<Pn(t), (2.1)
/l=— оо
где Sn — коэффициенты разложения, φη (/) — ортогональные
функции, образующие систему ортогональных функций. Две
функции (или два сигнала) называются ортогональными, если они
удовлетворяют интегральному соотношению (1.9)
\ <Pn(0<Pm(0^= _ ' (2.2)
Здесь Еп — энергия функции (сигнала) φη (/). Определение (2.2)
справедливо для любых систем ор1гогональных функций, как огра-
47
ничейных по времени (финитных), так и для имеющих бесконечную
протяженность. Коэффициенты разложения находятся согласно
равенству (1.10)
00
sn = 77 J s^Vn(t)dt. (2.3)
— 00
Если система ортогональных функций состоит из комплексных
функций φη (/), то разложение записывается, как и при
вещественных функциях, в виде (2.1), а условие ортогональности и
коэффициенты разложения определяются так:
г° /^ * /л Л4. ί ° при n^=m, /0 ..
\ <Pn(t)<Pm(t)dt^\ n * (2.4)
00
5» = ·^· j S(/)9n(0*. (2.5)
— оо
Сравнивая (2.3), (2.5) с определением корреляционных функций,
например, с (1.21), можно видеть, что коэффициенты разложения
Sn являются коэффициентами корреляции между сообщением 5 (/)
и функциями φη (/).
ι Ряд (2.1) в общем случае содержит бесконечное число членов.
Задаваясь требуемой точностью, всегда можно оставить конечное
число членов разложения, отбросив те, которые мало влияют на
(2.1). При этом получаем
5(/)-5х(/)= 2 Sn<Pn(t)> (2.6)
«=/1!
В (2.6) число членов ряда равно п2 — пг + 1. Будем считать, что
оно конечно. Величина среднеквадратической ошибки
■-\/~22.ΊγΙ*
[SiO-SiWpdi (2.7)
определяется отброшенными членами разложения (2.1). Выбором
п2 и пх можно обеспечить, чтобы ε < езад, где езад — заданное
значение среднеквадратической ошибки.
Представление (2.6) означает, что сообщение S (/) с заданной
степенью точности полностью определяется конечным набором
коэффициентов разложения Sn. Затем необходимо заменить конечный
набор коэффициентов разложения Sn конечным набором символов,
которые необходимо передавать по дискретному каналу.
Выбор системы ортогональных функций и метода перевода
коэффициентов разложения в символы определяется свойствами сооб-
48
щенйя и требуемой точностью его воспроизведения. Например; беж/
спектр сообщения ограничен по ширине Fc, то целесообразно с
практической точки зрения представлять его в виде ряда Котел ьникова,
в котором
{ή= sin2nFc(t-nM) (2.8)
а Δ/ = l/2/v Функцию φη (/) называют функцией отсчетов, При
этом сообщение S (/) заменяется последовательностью отсчетов Snr
которые следуют друг за другом с интервалом Δ/. Производя
квантование отсчетов по амплитуде, получаем конечное число различных
значений Sn. При квантовании по амплитуде возникает ошибка
квантования, которая тем меньше, чем больше уровней
квантования. Исходя из требуемой точности воспроизведения сообщения
можно найти необходимое число уровней квантования. После
квантования получаем, что сообщение определяется конечным набором
квантованных отсчетов. Заменяя тот или иной квантованный
отсчет своим символом, получаем возможность передавать
непрерывное сообщение в виде дискретного.
При иных свойствах сообщения может оказаться более
целесообразным с практической точки зрения другое разложение по
ортогональным функциям. Например, если разбить сообщение на
отрезки длительностью Г, то на каждом отрезке сообщение S (/),
можно представить в виде ряда Фурье, в котором
φη (/) = exp [\{2nntlT)\. (2.9))
Экспонента (2*9) является периодической функцией с периодом!
Т. Кроме упомянутых, известно большое число других систем
ортогональных функций, многие из которых нашли применение в СПИ*
Следует отметить, что системы ортогональных функций широко
используются в математике для решения различных задач.
Ортогональные функции, используемые в СПИ для передачи сообщений
будем называть ортогональными сигналами. Соответственно
совокупности таких сигналов являются системами ортогональных сигналов.
Применение систем ортогональных сигналов для представления
непрерывных сообщений в виде рядов является одним из примеров
применения систем сигналов в СПИ. Из (2.2), (2.4) следует, что
сигналы таких систем должны удовлетворять единственному условию,
ортогональности.
Многоканальные системы передачи информации. Необходимость,
обмена информацией между многими абонентами привела к
построению многоканальных систем передачи информации. Каждая
многоканальная СПИ работает в своем диапазоне частот, который
определяется ее назначением. Абоненты, входящие в многоканальную»
СПИ, работают в общей полосе частот, в пределах которой каждому
из них предоставляется канал для передачи информации.
Образование многоканальной СПИ из многих абонентов может
быть осуществлено двумя методами объединения абонентов. Один.
49*
йЗ них назовем централизованным объединением, а другой —
автономным. При централизованном объединении обмен информацией
между двумя абонентами производится через центральные станции
(ЦС на рис. 2.1, α и б). При передаче информации на большие
расстояния от абонентов одной зоны она сначала объединяется в
собственной центральной станции (ЦСХ и ЦС2 на рис. 2.1, а), затем
посылается по линии в ЦС другой зоны, после чего разделяется по
абонентам этой зоны. На рис. 2.1, α стрелками показан путь
прохождения информации между абонентами Αυ и А2и· Назовем
подобные многоканальные СПИ многоканальными централизованными
линейными системами (МЦЛС). К МЦЛС относятся радиорелейные
линии, радиотелеметрические системы и др.
Рис. 2.1
Централизованное объединение абонентов может быть
использовано и для обмена информацией между абонентами внутри одной
зоны (рис. 2.1, б). При этом требуется : одна ЦС. Стрелками на
рис. 2.1, б изображен путь! прохождения; информации между
абонентами Aj и Ak. Из рис. 2.1, б видно, что (Передача информации
осуществляется по радиусам-векторам, выходящим и входящим в
центральную станцию. По этой причине подобные многоканальные
СПИ можно назвать многоканальными централизованными
радиальными системами (МЦРС). Примерами МЦРС являются системы
радиосвязи гражданских служб, системы управления воздушным
движением, системы командного радиоуправления и др.
В тех случаях, когда не будет отмечаться линейность или
радиальность, многоканальные СПИ с централизованным уплотнением будем
называть многоканальными централизованными системами (МЦС).
Другим методом объединения абонентов является автономный,
при котором абоненты обмениваются информацией
непосредственно друг с другом (рис. 2.1, в). При этом нет необходимости в
центральной станции. Подобные СПИ назовем многоканальными
автономными системами (MAC). Примерами MAC являются системы
низовой радиосвязи (войсковой, сельской), системы командного
радиоуправления и др.
МЦС позволяет устанавливать более эффективный обмен
информацией между многими абонентами, лучше использовать
отведенные полосы частот и время. Однако наличие ЦС делает МЦС более
уязвимыми по сравнению с MAC, так как выход из строя ЦС при-
50
водит к выходу из строя всей МЦС. Наличие ЦС во многих случаях
усложняет СПИ в целом и увеличивает ее стоимость. Кроме того,
в некоторых случаях в соответствии с тактико-техническими
требованиями применение ЦС просто невозможно. По этим причинам
МЦС и MAC будут органически дополнять друг друга при создании
Единой автоматизированной системы связи (ЕАСС).
Следует отметить, что в некоторых случаях многоканальные
СПИ могут быть построены как с централизованным объединением
абонентов, так и с автономным. В таких случаях метод объединения
должен осуществляться с учетом тактико-технических и
экономических требований. Кроме того, возможно совместное применение
и централизованного, и автономного объединения.
Методы уплотнения и разделения каналов и абонентов. В
зависимости от назначения, каждой СПИ выделяется некоторый
диапазон частот, который в дальнейшем называется общей полосой
частот (общей для всех абонентов). Использование общей полосы
частот абонентами определяется методами уплотнения (размещение
спектров сигналов всех абонентов в общей полосе) и разделения
(выделение сигналов абонента). Поскольку тот или иной метод
уплотнения однозначно определяет метод разделения (обратное также
справедливо), то в дальнейшем будем классифицировать методы
уплотнения и разделения по методам разделения.
Возможны три метода разделения информации различных
абонентов, передаваемой по выделенным для них каналам. Метод
частотного разделения (ЧР) (см., например, [98]) заключается в том,
что каждому, абоненту отводится своя абонентская полоса частот
(частотный канал) в пределах общей полосы частот системы. При этом
абонентские полосы частот не перекрываются, но сигналы
абонентов перекрываются во времени. Метод временного разделения (ВР)
[98] заключается в том, что каждый абонент работает в свой
абонентский интервал времени (временной канал), в течение которого
другие абоненты информацию не передают. Спектры абонентов
занимают всю общую полосу частот и полностью перекрываются.
Метод кодового разделения (КР) заключается в том, что разделение
осуществляется по форме сигналов, которые использует тот или
иной абонент, причем абоненты работают в общей полосе частот
в одно время.
Первым нашло применение частотное разделение, так как оно
было известно раньше других методов и достаточно просто
реализовалось практически. Развитие импульсных методов модуляции
привело к появлению временного разделения. Внимание к кодовому
разделению было привлечено работой Костаса в 1959 г. [202].
Однако следует отметить, что основы разделения информации по
форме сигналов (основы линейной селекции) были развиты Д.В.
Агеевым в 1935 г. [1].
СПИ с частотным и временным разделением исследованы
весьма обстоятельно. Созданы методы расчета и проектирования таких
СПИ, хотя до настоящего времени проводятся исследования по их
51
усовершенствованию. Иное положение имеет место в случае СПИ
с кодовым разделением. Поскольку кодовое разделение основано на
различии сигналов, то построение таких СПИ и их характеристики
определяются выбором сигналов и их свойствами. Обычно число
абонентов достаточно велико, поэтому выбор сигналов для СПИ
с КР сводится к определению систем сигналов с заданными
свойствами. Развитие СПИ с КР и привело к исследованиям в области
теории систем сигналов, основные результаты которой будут
изложены в дальнейшем.
СПИ с КР являются адресными системами, так как сигналы або-
'нента выполняют роль его адреса. Адресные СПИ можно разделить
на два класса — синхронные адресные системы (САС) (см.,
например, [176, 211]) и асинхронные адресные системы (ААС) (см,
например, [56, 60, 62, 78, 106, 112]). Первые используются в основном
при централизованном объединении абонентов, а вторые — при
автономном.
В САС передачи информации осуществляется таким образом, что
переносчики информации удовлетворяют условию ортогональности
(2.2), т. е. если /-й и k-й абоненты используют сигналы tij (t) и uk (t)
со спектрами gj (ω) и gk (ω), то при j φ k имеют место равенства
J uj (t)uk (t)dt = 0, (2.10)
—00
00
I Si («Oft (ω)ίίω = 0. (2.11)
—00
Отметим, что условия ортогональности (2.10), (2.11) являются
частными случаями линейной независимости сигналов. Если
соблюдается равенство (2.10), то выполняется и (2.11). Если сигналы
линейно-независимы, то они разделяются без взаимных помех. На
практике обычно используются ортогональные сигналы.
Поскольку при временных смещениях ортогональность
нарушается, то для обеспечения ортогональности необходимо иметь
синхронизацию по времени. Таким образом, в САС передача
информации различными абонентами осуществляется ортогональными
сигналами при условии временной синхронизации между ними.
Наличие синхронизации приводит к тому, что в САС взаимные помехи
не возникают.
Следует отметить, что в СПИ с ЧР взаимные помехи
принципиально существуют всегда, так как сигналы с конечной длительностью
имеют бесконечно протяженные спектры, а разделительные фильтры
пропускают с конечным ослаблением все частоты. По этим двум
причинам часть энергии сигнала произвольного канала в СПИ с ЧР
попадает в любой канал, создавая взаимную помеху. Выбором
сигналов (уменьшением «внеполосных» излучений) и фильтров
(повышением ослабления вне полосы пропускания), размещением
каналов по частоте можно уменьшить взаимные помехи до допустимого
52
малого уровня. При этом можно считать, что приближенно условие
ортогональности (2.11) выполняется.
В ААС равенства (2.10), (2.11) не имеют места, поэтому в таких
системах существуют взаимные помехи между абонентами, которые
иногда называются «шумами неортогональности» [62]. Из-за
взаимных помех число одновременно работающих абонентов в ААС при
той же- помехоустойчивости будет меньше, чем в синхронных. Но
при построении ААС нет необходимости в обеспечении
синхронизации абонентов по времени и по частоте. Это является существенным
преимуществом ААС перед синхронными системами, особенно в тех
случаях, когда невозможно обеспечить временную синхронизацию
абонентов, разбросанных на большой территории, по этой причине
ААС и получили развитие.
В САС и ААС для обеспечения работы большого числа абонентов
необходимо иметь, по крайней мере, такое же число различных
сигналов. Поскольку сигналы нельзя выбирать произвольно, то
для таких СПИ необходимо использовать системы сигналов с
определенными свойствами. Выбору систем сигналов и посвящен в
основном дальнейший материал. Решение вопросов выбора систем
сигналов во многом определяется назначением СПИ и ее
характеристиками. Основными характеристиками СПИ являются
помехоустойчивость и эффективность. Под помехоустойчивостью СПИ
подразумеваем ее способность противостоять помехам, а под
эффективностью— использование-общей полосы частот, времени и
мощности передатчика.
Поскольку любые СПИ состоят из каналов (в предельном случае
из одного), то сначала необходимо рассмотреть помехоустойчивость
и эффективность одного канала, т. е. одноканальной СПИ. Сделаем
это на примере дискретной СПИ, предназначенной для передачи
дискретных сообщений.
2.2. Дискретная система передачи информации
На рис. 2.2 представлена структурная схема дискретной СПИ#
Источник информации (ИИ) создает дискретную информацию в виде
последовательности символов 5V. Положим, что число символов
конечно, т. е. ν = 0, η — 1. Совокупность символов^ 5ν, ν =
= 0, η—I называется алфавитом источника, an—объемом этого
алфавита. Если η = 2, то алфавит является двоичным, а если η > 2 —
то многозначным или я-ичным. Соответственно при η = 2 символы
называются двоичными, а при η > 2 — я-ичными.
Кодер (кодирующее устройство К) преобразует ;я-ичный
алфавит источника в /n-ичный алфавит, т. е. заменяет символы Sv
символами δμ. Как осуществляется такое преобразование, будет
объяснено в дальнейшем. Совокупность символов εμ, где μ = 0, т — 1,
называется алфавитом кодера, а т — объемом этого алфавита. Если
т = 2, то символы εμ и алфавит являются двоичными, а если т > 2,
53
то m-ичными. Отметим, что в общем случае т Φ η и возможно,
т> η или т < п. Если т = я, то 5ν = $μ. При этом необходимость
в кодере отпадает.
Передатчик (ПЕР) каждый символ δμ однозначно преобразует
в сигнал ί/μ, τ. е. осуществляет процесс модуляции, усиления
мощности и излучения. Совокупность сигналов и^, μ = 0, т — 1, как
было отмечено ранее, называется алфавитом сигналов.
Соответственно число т является также и объемом алфавита сигналов.
В канале (КАН) на сигнал ίΐβ (t) действует помеха η (/).
Предположим, что она является флюктуационной аддитивной помехой
в виде нормального случайного стационарного процесса с нулевым
средним и с равномерной спектральной плотностью мощности Ν0.
Такая помеха называется также белым шумом.
\ии
РН
к
\щ
ПЕР
ЩкйГ
X
—>
ЛР
х>
дк
Щ
ПИ
Рис. 2.2
На входе приемника (ПР) действует сумма сигнала и помехи
χ (t) = и^ (/) + η (/). Приемник анализирует χ (t) и принимает
решение о том, какой сигнал был передан, и в соответствии с принятым
решением выдает символ δμ. Если s^ = δμ, то осуществлен
правильный прием, если δμ Φ δμ, то при принятии решения была совершена
ошибка из-за помехи на входе приемника. Декодер (декодирующее
устройство ДК) преобразует символы δμ в символы 5V, которые
затем поступают на вход получателя информации (ПИ). Отметим, что
если т = я, то необходимость в декодере отпадает.
Из описания СПИ, структурная схема которой приведена на
рис. 2.2, следует, что основные различия между всевозможными
СПИ с точки зрения передачи и приема информации определяются
объемом алфавита источника η и сигналов /п. В зависимости от
значения т СПИ можно разделить на двоичные СПИ (т = 2) и
/п-ичныеСПИ (т > 2). В данной главе рассмотрим и сравним
двоичные и /n-ичные СПИ.
Скорость передачи информации. Положим, что она равна Я бит.
Длительность двоичного символа Т2 в двоичной СПИ и скорость
передачи информации связаны соотношением
Я = 1/Г2. (2.12)
Положим, что в /n-ичной СПИ, в которой используются m
символов, объем алфавита m определяется как
т = 2*, (2.13)
где k ~ целое положительное число. Допустим, что символы на
выходе источника информации равновероятны. Согласно общим
54
Положениям теорий информации [162, 171, 190] каждый /п-ичный
символ переносит k = log2/n двоичных единиц, т. е. /n-ичный символ
эквивалентен кодовой последовательности из k двоичных символов.
Так как длительность двоичного символа Т2 = 1/J?, то длительность
m-ичного символа
Тт = кТг = kIM = log2/n/J?. (2.14)
Соответственно длительности двоичных и m-ичных сигналов
будут Т2 и Тт.
Помехоустойчивость двоичных СПИ. Помехоустойчивость
дискретных СПИ характеризуется вероятностью ошибки Рош. Она
зависит от применяемых сигналов и метода приема. Сначала
предположим, что осуществляется прием полностью известных сигналов.
Это означает, что все параметры сигнала известны в точке приема,
т. е. известны его форма, амплитуда, частота, задержка во времени
и начальная фаза. Когда известна начальная фаза, то прием
называется когерентным. Неизвестным является только то, какой сигнал
находится на интервале наблюдения. Определение номера сигнала
является задачей приемника. Оптимальный приемник минимизирует
вероятность ошибки.
Если известны все параметры сигналов, за исключением
начальной фазы, то прием называется некогерентным.
Рассмотрим сначала когерентный прием. В двоичных СПИ для
передачи информации используются два сигнала: и0 (/) и иг (/).
Вероятность ошибки при когерентном приеме (распознавание двух
сигналов) определяется следующим равенством (см., например,
[162, 171]):
Р0Ш=1-/ЧЯ), (2.15)
где интеграл вероятности
χ
F(x) = —!— Г e-**'2dz, (2.16)
— оо
а аргумент
Я = V[(E0 + EJ/2N0](l-X)f (2.17)
Ε0ί Ег — энергии сигналов и0 (/), иг (/) соответственно, а
λ = —j— ГиоЮМОЛ. (2.18)
о
Коэффициент λ с точностью до постоянной совпадает с
коэффициентом корреляции сигналов и0 (/), их (/) (ср. с определением (1.21)
при τ = 0). В зависимости от значения коэффициента корреляции
между сигналами λ может принимать различные значения и
согласно (2.15), (2.17) вероятность ошибки будет различна.
Рассмотрим случаи, наиболее интересные с практической точки зрения.
55
В случае равенства энергий сигналов, максимум Η будет при
Минимуме λ, которая в точности равна коэффициенту корреляции
с минимумом—1 при противоположных сигналах: и0 (t)= — иг({).
Обозначая энергию двоичного сигнала через Е2 = Е0 = Еъ из
(2.17), (2.18) получаем Η = Υ~2Ε2/Ν0.
При передаче двоичной информации противоположными
сигналами различие между сигналами обеспечивается фазовой
манипуляцией (начальная фаза принимает два значения, разность между
которыми равна π). Поэтому такой метод передачи получил название
фазовой манипуляции (ФМ). Иногда он называется методом
фазовой телеграфии.
Если сигналы ортогональны, а энергии их равны, то из (2.18)
имеем λ = 0, а из (2.17) получаем H=]fE2/N0. Метод передачи
двоичной информации с помощью ортогональных сигналов назовем
ортогональной манипуляцией (ОМ). Часто этот метод называется
частотной телеграфией, когда ортогональность сигналов
обеспечивается сдвигом их несущих частот. Но это частный случай
ортогональности сигналов.
Если один из сигналов тождественно равен нулю, например,
их (ί) ξξΟ, то из (2.17), (2.18) получаем λ=0, Я = VE2/2N0. Этот
случай называется амплитудной манипуляцией (AM) или «пассивной
паузой».
Объединяя три результата для ФМ, ОМ и-AM при когерентном
приеме, запишем вероятность ошибки Рош (2.15) в следующем виде:
Рош= 1-F(ah2), (2.19)
где а — коэффициент вида манипуляции (а=]/"2 при ФМ, α = 1
при ОМ, α = 1/J/2 при AM); h2 — отношение сигнал/шум,
приходящееся на одну двоичную единицу информации
h2 =УЩШ0, (2.20)
Е2 — энергия двоичного сигнала. При ФМ и ОМ энергию двоичного
'сигнала можно заменить через среднюю мощность сигнала Рс
следующим образом: Е2 = РСТ2 или согласно (2.12) Е2 = PJJI.
Заменяя Е2 в (2.20), в соответствии с приведенными равенствами имеем
/*2 = УКтЖо = VPJMNZ (2.21)
На рис. 2.3 представлены графики зависимости вероятности
ошибки Р0ш от отношения сигнал/шум h2. Кривая ФМ соответствует
фазовой манипуляции, кривая ОМк—ортогональной манипуляции
при когерентном и ОМнк при некогерентном приеме, кривая AM —
амплитудной манипуляции.
Наилучшей помехоустойчивостью обладает двоичная СПИ с
фазовой манипуляцией, так как при одном и том же значении
отношения сигнал/шум h2 вероятность ошибки будет меньше, чем в других
случаях. Наибольшая вероятность ошибки будет при амплитудной
56
манипуляции, а ортогональная манипуляция занимает среднее
положение между ФМ и AM. Это определяется коэффициентом вида
манипуляции α в формуле (2.19). При сравнении ОМ и AM следует
иметь в виду, что графики рис. 2.3 построены для /г2 согласно (2.20),
т.е. hi пропорционально энергии двоичного сигнала. Когда
определяющей является средняя мощность сигнала Рс, энергия двоичного
сигнала Е2 при AM может быть увеличена вдвое по сравнению с ОМ
при той же средней мощности
меньше, чем при ОМ, но,
учитывая увеличение энергии
вдвое (/ι2 увеличивается в
Υ2) у получаем, что
помехоустойчивость AM и ОМ при
когерентном приеме будет
одинаковой. График
вероятности ошибки в этом случае
представляется кривой ОМк
на рис. 2.3.
На рис. 2.4 представлены
структурные схемы
оптимальных когерентных приемников
двоичных СПИ с применением
согласованных фильтров.
Напомним [105], что импульсная
характеристика h (t) фильтра,
согласованного с сигналом
и (/), определяется
соотношением
Поэтому, хотя при AM α в Υ2
7 2 δ Ur hz
5W~
10~
510~ι
10
5-10~
70"
5W~
-3
10
510
гош
ФМ\ ом\ \
\AM
0MhN
Рис. 2.3
h (t) = au(T — /), (2.22)
где a — постоянная, Τ — длительность сигнала и (/). Если g (ω) —
спектр сигнала и (/), то коэффициент передачи согласованного
фильтра
k (ω) = ag* (cu)e-iiu7\ (2.23)
Отношение сигнал/шум на выходе согласованного фильтра
максимально в момент окончания сигнала и равно
φ = l/2/σ2 = 2Ε/Ν0, (2.24)
где V — максимальное значение сигнальной составляющей на
выходе согласованного фильтра, которое и имеет место в момент
окончания сигнала при / = Г; σ2 — мощность шума на выходе фильтра;
Ε — энергия сигнала на входе фильтра; NQ — спектральная
плотность мощности шума.
При фазовой манипуляции структурная схема оптимального
приемника (рис. 2.4, а) состоит из согласованного фильтра (СФ)
и решающего устройства (РУ), которое принимает решение о том,
кзкой сигнал был послан. Решение принимается в момент оконча-
57
ния сигнала, который фиксируется синхронизатором (на рис. 2.4
это условно показано вертикальной стрелкой). По принципу
действия РУ при ФМ является пороговым, причем значение порога равно
нулю. При ортогональной манипуляции оптимальный приемник
(рис. 2.4, б) состоит из двух согласованных с сигналами uQ (t) и
иг (/) фильтров СФ0 и СФХ соответственно. Решающее устройство
принимает решение по максимальному значению напряжения на
выходе обоих каналов.
Оптимальный приемник при AM совпадает по схеме с
оптимальным приемником для ФМ (рис. 2.4, а), но порог в РУ должен быть
V/2.
Рис. 2.4
-*@-* ·=" "*0*
Гх~
[грс
■~*н
Рис. 2.5
Оптимальные приемники можно построить с использованием
корреляторов. При этом каждый согласованный фильтр на
структурных схемах рис. 2.4 заменяется соответствующим коррелятором
(рис. 2.5). Коррелятор состоит из перемножителя (х), интегратора
(И) и генератора опорного сигнала (ГОС). Опорный сигнал с
номером μ полностью совпадает и по форме, и по всем параметрам с
сигналом ί/μ (/), Напряжение на выходе коррелятора
ζ = j* x (t)u (t)dt,
0
(2.25)
где χ (t) — напряжение на его входе, и (t) — опорный сигнал.
Коррелятор и согласованный фильтр эквивалентны с точки
зрения приема информации и обеспечивают одинаковую
помехоустойчивость.
При некогерентном приеме начальная фаза неизвестна и
является случайной величиной. Наибольшая помехоустойчивость имеет
место при передаче двоичной информации ортогональными
сигналами. Вероятность ошибки при некогерентном приеме двух
ортогональных сигналов выражается следующей формулой [162, 171]:
Рош = 0,5ехр (—0,5ftl)f
(2.26)
где /ι2 определено формулами (2.20), (2.21). Зависимость
вероятности ошибки Рош (2.26) от отношения сигнал/шум h2 была
представлена на рис. 2.3 кривой ОМнк. Из сравнения ОЛЦ и ОМнк рис.2.3
58
Ьидно, tifo помехоустойчивость при когерентном и некогерентноУ
приеме двух ортогональных сигналов отличается незначительно.
Потери в отношении сигнал/шум при некогерентном приеме
относительно когерентного при Рош=10"3 составляют^ 1,2 дБ и
уменьшаются с ростом /ι2.
Структурная схема оптимального некогерентного приемника
приведена на рис. 2.6. Он состоит из двух каналов, в каждом из
которых есть согласованный фильтр и детектор огибающей (Д).
Решающее устройство принимает решение
по максимальному значению огибающей
на выходах каналов в момент окончания
сигнала.
Помехоустойчивость ш-ичных СПИ.
При передаче информации алфавитом
сигналов, объем которого т > 2, и
когерентном приеме наибольшую
помехоустойчивость обеспечивают симплексные
(или равноудаленные, или
трансортогональные) сигналы [97]. Такие сигналы обладают интересным
свойством. Если произвольный сигнал трактовать как точку в
/n-мерном пространстве, то симплексные сигналы соответствуют
вершинам m-мерной геометрической фигуры — симплекса. Вершины
максимально и одинаково удалены друг от друга, т. е. симплексные
сигналы максимально отличаются друг от друга, что является
причиной максимальной помехоустойчивости. Из-за максимального
отличия по форме коэффициент корреляции таких сигналов,
определяемый аналогично общей формуле (1.23) при τ = О,
£^Н*рП->
Ufo^M д |—»
РУ
г
Рис. 2.6
оо
at
(2.27)
не зависит от номеров / и k и равен
RJh = R = —Щт - 1).
(2.28)
При т. > 1 коэффициент корреляции R мало отличается от нуля
и поэтому ортогональные сигналы, у которых R = 0, обеспечивают
почти такую же помехоустойчивость, что и симплексные сигналы.
Если все коэффициенты корреляции равны между собой, т. е. Rjk =
= R, то доказано следующее равенство для вероятности ошибки
с равными коэффициентами корреляции [64, 97].
Рош (Am, R) = Рош {hmV\ - R, 0),
(2.29)
где отношение сигнал/шум, приходящееся на один m-ичный сигнал,
hm = VPcTJN0,
(2.30)
59
fm — длительность m-ичного сигнала, Р0ш (^m> R) — вероятность
ошибки при отношении -сигнал/шум hm и коффициенте корреляции
^,аР0Ш (hmVl — Rt 0) — вероятность ошибки при ортогональных
сигналах. Выражение (2.29) показывает, что помехоустойчивость
при равнокоррелированных сигналах будет такой же, как и при
ортогональных, но с измененным отношением сигнал/шум, равным
hmVl — i?. Для симплексных сигналов (2.28) равенство (2.29)
приобретает такой вид:
Рош (ftm, -Щт - 1)) = Рош (hmVm/(m-l), 0). (2.31)
При т > 1 множитель т/(т — 1) ~ 1 и ортогональные сигналы
обеспечивают такую же помехоустойчивость, что и симплексные.
Поэтому будем рассматривать помехоустойчивость при передаче
информации т ортогональными сигналами.
При когерентном приеме т ортогональных сигналов вероятность
ошибки определяется отношением [171]:
оо
Рош =1—7= f ^t2/2[F{t+V2hm)]m~ldtt (2.32)
— оо
где F (х) — интеграл вероятности (2.16).
При некогерентном приеме т ортогональных сигналов [171]
Pom=l-^e-(<2 + 2^)/2/0(K2/zm/)(l-e-^/2)m-i^ (2.33)
о
где /0 (х)—модифицированная функция Бесселя нулевого порядка.
Интегралы в (2.32), (2.33) в элементарных функциях не
выражаются, но они достаточно подробно табулированы и графики их
можно найти в [64]. Отметим только, что при больших т различие
между когерентным и некогерентным приемом незначительно.
При отношении сигнал/шум hm ^> 1 известны приближенные
формулы [157]:
для когерентного приема из (2.32)
Poni-(/n-l)[l-F(/im)]; (2.34)
для некогерентного приема из (2.33)
Рош - [(т - 1)/2]ехр (-ВД. (2.35)
При т = 2 из (2.32), (2.33) получаем точные равенства (2.19)
(а = 1) и (2.26). В работе [28] показано, что формула (2.35)
обеспечивает малую погрешность, если hJn > 4£ 1п2, что эквивалентно
неравенству h\ > 4 In 2. В этой же работе получено более точное при-
60
ёлиженное выражение для вероятности ошибки при некогерентном
приеме т ортогональных сигналов
Рош ~ F [—(hz - V\P2)V2\og2m] +
+ [(т _ 1)/2]ехр l-(h22/2)\og2m] Fl(h2 - 2l/Tn2)/tofom].
(2.36)
Если /ι2<)Λη2, то первое слагаемое в (2.36) стремится к
единице, так как его аргумент большое положительное число. Второе
слагаемое стремится к нулю, поскольку аргумент у интеграла
вероятности большое
отрицательное число. Если h2 >
>2yln2, то первое
слагаемое в (2.36) стремится к
нулю, так как его аргумент —
большое отрицательное число.
Интеграл вероятности,
являющийся множителем второго
слагаемого, стремится к
единице. Расчеты показывают,
что при h2 > 2}/Ίη 2 первым
слагаемым можно пренебречь
по сравнению со вторым,
которое в свою очередь
стремится к асимптотическому
выражению (2.35). Т|аким
образом, (2.35) следует
применять при h2 > 4 In 2.
В промежуточном случае
]/ΊιΓ2 <ft2 <2]Лп"2 оба
слагаемых в (2.36) вносят
соизмеримые вклады.
Расчеты показывают [28], что формула (2.36) обеспечивает точность
достаточную для практических расчетов при любом /ι2.
На рис.2.7 представлены графики вероятности '(Ошибки (при
когерентном и некогерентном приеме ортогональных сигналов для
т = 2 (двоичные СПИ) и т = 64,1024. Для когерентного приема
кривые изображены сплошными линиями, а для некогерентного —
штриховыми. Кроме того, для сравнения на рис. 2.7 представлен
график вероятности ошибки при приеме двух противоположных:
сигналов (кривая ФМ, т = 2). Графики рис. 2.7 отображают
зависимости вероятности ошибки от отношения сигнал/шум /ι2 (2.21),,
приходящиеся на одну двоичную единицу информации. Поскольку
в формулах (2.32), (2.33) используется отношение сигнал/шум Нш
(2.30), то согласно (2.14) можно заменить hm на /ι2 по формуле
(2.37)
61
Рис. 2.7
hm = h2Vk = /i2l^log2m.
Соотношение (2.37) позволяет рассчитать вероятности ошибки
при любом т как функции'/г2. Отметим, что выбор h2 в качестве
аргумента при сравнении вероятностей ошибок с различным т
является наиболее обоснованным, так как h2 содержит основные
энергетические и информационные характеристики СПИ: мощность
сигнала на входе приемника Яс, которая пропорциональна мощности
передатчика; спектральную плотность мощности шума N0 и
скорость передачи информации М.
Из графиков рис. 2.7 видно, что с увеличением объема алфавита
т помехоустойчивость /n-ичной СПИ растет, так как при h2 = const
вероятность ошибки уменьшается. Поскольку /n-ичные СПИ
обеспечивают большую помехоустойчивость при h2 = const, то они дают
возможность передавать информацию с заданной
помехоустойчивостью (Рош = const) и при меньшем значении отношения
сигнал/шум h2. Из рис. 2.7 следует, что при Рош = const требуемое
значение /г2 тем меньше, чем больше т. Тем самым /n-ичные СПИ
обеспечивают выигрыш в отношении сигнал/шум по сравнению с
двоичными СПИ. При постоянных значениях N0 и Я выигрыш в
отношении сигнал/шум h2 эквивалентен согласно (2.21) выигрышу в
мощности сигнала Рс. Будем называть его выигрышем по мощности.
Таким образом, /n-ичные СПИ являются более
помехоустойчивыми, чем двоичные, а при заданной вероятности ошибки
обеспечивают выигрыш по мощности, поэтому применение в СПИ алфавитов
с объемом т>2 имеет практическое значение.
- Преимущество /n-ичных СПИ перед двоичными известно давно
[97]. Оно полностью согласуется с общими положениями теории
информации [190]. Отметим, что приведенный результат (рис. 2.7)
по сути подтверждает основную теорему Шеннона [190] о
пропускной способности канала. Однако в настоящее время известно лишь
несколько примеров СПИ с алфавитами, объем которых т > 2
[11, 135, 184, 214]. Многочисленные исследования в теории
кодирования не привели пока к реальной возможности создания СПИ с
большими алфавитами.
Таким образом, /n-ичные СПИ имеют преимущество перед
двоичными, но пока что не получили широкого распространения. Очень
часто в качестве основной причины слабого развития /n-ичных СПИ
указывают на техническую сложность реализации оптимальных
приемников. Действительно, при передаче информации с помощью
сигналов оптимальный когерентный приемник должен содержать т
каналов, в каждом из которых должен быть свой согласованный
фильтр и решающее устройство, которое принимает решение по
максимальному напряжению на выходе одного из т каналов.
Некогерентный приемник содержит дополнительно детекторы
огибающей. Однако ссылки на сложность технической реализации
/n-ичного приемника с т > 2 вряд ли можно считать
убедительными, так как известны примеры реализации более сложных устройств,
например, ЭВМ на больших интегральных микросхемах.
Попробуем выяснить, почему /n-ичные СПИ с большими т не
62
получили широкого распространения. Рассмотрим рис. 2.7. Во-
первых, существенное увеличение т приводит к небольшому
уменьшению требуемого значения отношения сигнал/шум· Особенно это
заметно при сравнении /n-ичных СПИ и двоичной СПИ с ФМ.
Например, если задана Ρ 0ш=10"4, то при т = 1024 необходимо иметь
h2 = 1,6, а при /п = 2и ФМ h2 = 2,6. Проигрыш составляет 4 дБ.
Следует отметить, что действительно при т = 1024 сложность
реализации возрастает существенно, хотя выигрыш по мощности не
велик. Во-вторых, из сравнения графиков рис. 2.7 можно заметить,
что выигрыш по мощности существенно уменьшается при
увеличении объема алфавита /п. По мере роста объема алфавита т = 2k no
показательному закону требуемое значение h2 уменьшается слабее
стремясь при т -> оо к некоторому пределу. Это предельное
значение h2 получило название порогового значения /ι2π0ρ» а явление,
имеющее место в СПИ при h2 = /ι2ΠΟρ> называется пороговым
эффектом. Как будет показано в следующем параграфе, /ι2πορ ~
= У In 2. Это пороговое значение отмечено на рис. 2.7 штриховой
линией. Таким образом, можно сделать вывод, что применять
алфавиты очень большого объема с т > 1000 вряд ли целесообразно
с практической точки зрения, так как выигрыш по мощности растет
медленно, а сложность технической реализации с увеличением числа
каналов оптимального приемника по показательному закону (2.13)
возрастает очень быстро.
В-третьих, из рис. 2.7 следует, что при ft2< /*2пор=УТЙ2
вероятность ошибки Рош с увеличением т стремится к единице. Это
является еще одним свойством порогового эффекта. Если отношение
сигнал/шум меньше порогового значения, то /n-ичные СПИ так же,
как и двоичные, не могут обеспечить надежной передачи информации
и переход к алфавитам с т > 2 имеет практическое значение
только в том случае, если отношение сигнал/шум больше порогового
значения. Но при этом и двоичные СПИ обеспечивают
удовлетворительную помехоустойчивость приема информации.
Таким образом, отмеченные три причины слабого внедрения т-
ичных СПИ в свою очередь являются следствием порогового
эффекта при передаче информации алфавитами большого объема.
Поскольку выбор объема алфавита имеет большое значение при
проектировании СПИ, рассмотрим пороговый эффект более подробно.
2.3. Пороговый эффект в m-ичных системах передачи
информации
Теорема Шеннона и идеальное кодирование. Шеннон показал
[190], что пропускная способность канала передачи информации
C = FKlog2(l + PcAPni), (2.38)
где FK — ширина полосы частот, отведенной для передачи
информации, PQ — мощность сигнала, Ρ щ — мощность шума. Для белого
6^
шума с равномерной спектральной плотностью мощности N0
мощность шума
Рш = №*. (2.39)
При условии, что Рс < Яш, заменяя в (2.38) логарифм первыми
членами ряда Тейлора и используя (2.39), получаем [22]
С = Pc/N0 In 2. (2.40)
Условие Яс < Яш не является ограничивающим, поскольку
правая часть (2.40) определяет максимальную пропускную способность,
что следует из неравенства In (1 + χ) ^ χ.
Согласно теореме Шеннона [190], если скорость передачи
информации Μ меньше пропускной способности канала С, т. е. если Я<С,
то можно так закодировать информацию, что вероятность ошибки
(будет сколь угодно малой величиной. Если же Мт > С, то
вероятность ошибки резко возрастает, т. е. можно считать, что она
стремится к единице. Для получения сколь угодно малой вероятности
♦ошибки при Я < С необходимо использовать алфавиты сигналов
/большого объема. Шеннон [190] предложил использовать алфавиты
«сигналов, выбранных случайно. Назовем СПИ с такими сигналами
'идеальной /n-ичной СПИ.
Таким образом, значение Μ = С является пороговым между
двумя состояниями идеальной /n-ичной СПИ. Выясним, чему
соответствует такой порог с точки зрения отношения сигнал/шум.
Полагая Я = С, из (2.40) получаем
PJMN0 = In 2. (2.41)
Левая часть равенства (2.41) есть h\ согласно (2.21), а правая —
его пороговое значение. Поэтому пороговое значение отношения
сигнал/шум в идеальной /n-ичной СПИ равно
/ι2πορ = 1/ΊΊΓ2. (2.42)
Если h2 > /*2пор> то> увеличивая объем алфавита /п, можно
сделать вероятность ошибки сколь угодно малой величиной. Однако
•если h2 < /ι2πορ» το применение сложного кодирования не приведет
к надежной передаче информации.
В идеальной /n-ичной СПИ прием сигналов должен
осуществляться когерентно. Однако последнее обстоятельство не имеет
особого значения, что можно показать, рассмотрев/n-ичную СПИ, в
которой передачи информации осуществляется т ортогональными
сигналами. Доказано (см., например, [64]), что пороговое значение
^2 пор не зависит от того, когерентный или некогерентный прием
имеет место. В [64] показано, что при когерентном и некогерентном
приеме т ортогональных сигналов пороговое отношение сигнал/шум
совпадает с пороговым отношением в идеальной /n-ичной СПИ.
В работах [21, 28] рассмотрены особенности порогового эффекта при
некогерентном приеме т ортогональных сигналов. Результаты
отмеченных работ позволяют считать, что при т > 2 /n-ичные СПИ ς
64
ортогональными сигналами реализуют помехоустойчивость
идеальной СПИ. При этом m-ичные СПИ обеспечивают выигрыш по
мощности по сравнению с двоичными СПИ. Однако выигрыш по
мощности в m-ичных СПИ сопровождается требованием расширения
полосы частот, необходимой для передачи информации, как это будет
показано в следующем параграфе. Поэтому перейдем к сравнению
двоичных и m-ичных СПИ по мощности и по требуемой полосе
частот·
2.4. Сравнение двоичных и m-ичных систем передачи
информации
При сравнении двоичных и m-ичных СПИ необходимо иметь в
виду, что объем алфавита источника я и объем алфавита сигналов
m могут быть не равны между собой. Поэтому в зависимости от
соотношения между ними применяются различные методы
декодирования символов εμ в символы Sv. С этой точки зрения двоичные
СПИ можно разделить на два класса: двоичные СПИ без
декодирования или просто двоичные СПИ (т = я = 2); двоичные СПИ с
я-ичным декодированием (т = 2, я > 2).
> К первому классу относятся СПИ, в которых двоичные символы
источника информации взаимно независимы и используются
получателем информации независимо друг от друга. Примером
двоичной СПИ может служить командная радиолиния управления, в
которой каждый двоичный символ поступает по своему адресу. Ко
второму классу относятся СПИ, у которых последовательность
двоичных символов на выходе приемника преобразуется в я-ичные
символы. Примером двоичной СПИ с я-ичным декодированием может
служить двоичная СПИ, в которой непрерывная информация
передается с помощью двоичной кодовой импульсной модуляции (КИМ),
называемой некодированной КИМ [64].
В двоичной СПИ с я-ичным декодированием при заданной
скорости передачи информации Л длительность двоичных сигналов
удовлетворяет равенству (2.12). Если один я-ичный символ заменяет
собой k двоичных единиц, то согласно (2.13) я = 2k. Будем полагать,
что в дальнейшем равенство η = т имеет место. Такие СПИ будем
называть двоичными СПИ с m-ичным декодированием.
(Аналогично, т-ичные СПИ можно разделить на два класса:
m-ичные СПИ без декодирования или просто m-ичные СПИ (т =
= я > 2); m-ичные СПИ с двоичным декодированием (т > 2,
η = 2).
К первому классу относятся СПИ, у которых получатель
информации непосредственно использует m-ичные символы. Например,
при передаче непрерывной информации путем дискретизации по
времени и квантовании по уровню каждый m-ичный символ может
быть непосредственно преобразован в квантованный отсчет. Такой
метод передачи информации называется m-ичной или кодирован-
65
ной КИМ [64]. Ко второму классу относятся СПИ, в которых каждый
m-ичный символ преобразуется в последовательность из k двоичных
символов. Примером m-ичной СПИ с двоичным декодированием
может служить командная радиолиния управления, в которой для
повышения помехоустойчивости применяется укрупненный
алфавит сигналов, или СПИ, в которой передача информации
осуществляется с помощью двоичной КИМ.
Сравнение двоичных и m-ичных СПИ всех классов следует
производить с учетом получателя информации. С этой точки зрения
двоичные СПИ без декодирования и m-ичные СПИ с двоичным
декодированием эквивалентны, так как в обоих случаях на входе
получателя информация представлена в виде двоичных символов. При
сравнении таких СПИ необходимо сравнивать вероятности ошибки,
приходящиеся на один двоичный символ. Точно так же для
получателя информации двоичные СПИ с m-ичным декодированием и т-ич-
ные СПИ без декодирования эквивалентны, так как в обоих случаях
на входе получателя информация представлена в виде m-ичных
символов. В таких СПИ необходимо сравнивать вероятности ошибки,
приходящиеся на один m-ичный символ. Перейдем к сравнению
двоичных и m-ичных СПИ.
Сравнение по мощности. Общий метод сравнения двоичных и т-
ичных СПИ заключается в том, чтобы найти выигрыш по мощности
в m-ичной СПИ при равных вероятностях ошибок [64, 171].
Сначала произведем сравнение двоичной СПИ без декодирования
с m-ичной СПИ с двоичным декодированием. Основы такого
сравнения приведены в [64]. В m-ичной СПИ с двоичным декодированием
источник информации создает информацию в виде двоичных
символов со скоростью Я. Кодер последовательно разбивает двоичные
символы на кодовые последовательности из k двоичных символов.
Согласно (2.13) число различных кодовых последовательностей m = 2k.
Затем кодер каждую кодовую последовательность преобразует в т-
ичный символ, который передается соответствующим сигналом.
Назовем кодовую последовательность, соответствующую переданному
сигналу, исходной. В приемнике восстанавливается m-ичный
символ, который затем преобразуется в кодовую последовательность
из к двоичных символов. Эту кодовую последовательность назовем
восстановленной.
В случае правильного приема переданный и принятый т-ичные
символы совпадают, что приводит к совпадению исходной и
восстановленной кодовых последовательностей во всех символах. Если
произошла ошибка в приеме m-ичного символа с вероятностью Р0Шт»
то переданный и принятый символ не совпадут. (Индекс т
подчеркивает, что вероятность ошибки относится кт-ичному символу.) Из-за
симметричности канала на выходе приемника может появиться
равновероятно любой из т — 1 остальных m-ичных символов, которые
назовем ошибочными. В результате восстановленная кодовая
комбинация равновероятно может быть любой из m — 1=2* — 1
ошибочных кодовых комбинаций. При этом исходная и восстановленная
66
кодовые комбинации отличаются друг от друга, причем отличие
сводится к тому, что часть символов или все символы в этих кодовых
последовательностях при позиционном сравнении (по номерам)
будут различны. Но некоторые символы могут совпадать, даже если
произошла ошибка. Этот факт необходимо учитывать при расчете
вероятности ошибки, приходящейся на один двоичный символ. Эта
вероятность согласно [64] равна
Р'ош2 = 0,5т (т - 1)^Ρ0ΌΙτη. (2.43)
Обозначим ошибку при приеме двоичного символа в двоичной
СПИ через Р0Ш2- Приравнивая вероятности ошибки в двоичном
символе двоичной СПИ без декодирования и m-ичной СПИ с
двоичным декодированием Р0Ш2 = Рошг и подставляя в (2.43), имеем
Р0Ш2 = 0,5т (т - Ц-Фошт. (2.44)
ν Таким образом, если имеет место равенство (2.44), то двоичная
СПИ без декодирования и m-ичная СПИ с двоичным декодированием
эквивалентны с точки зрения равенства вероятностей ошибки в
одном двоичном символе. Вероятности Р0Ш2 и Р0Шт определяются
или формулой (2.32), или (2.33) при т = 2 и т Φ 2.
Основы сравнения m-ичных СПИ без декодирования и двоичных
СПИ с т-ичным декодированием можно найти в [ 171], где
вычисляется вероятность ошибки, приходящаяся на один m-ичный символ.
Пусть Рош 2 — вероятность ошибки при приеме двоичного символа
в двоичной СПИ с m-ичным декодированием. Вероятность
правильного приема одного двоичного символа равна 1 — Рош 2, а
вероятность правильного приема k двоичных символов равна (1 — Рош 2)*,
так как она равна вероятности того, что все k символов приняты
правильно. Поэтому вероятность ошибки при приеме k двоичных
символов (одного m-ичного символа)
Рошт= 1-(1-Р0ш2)*. (2.45)
Вероятность ошибки при приеме /π-ичного символа в т-ичной
СПИ обозначим, как и раньше, через Р0Шт· Приравнивая
вероятности ошибок, приема k двоичных единиц двоичной и m-ичной СПИ
Рош /я«'= Р0ш т !и подставляя в (2.45), получаем
1-(1-Рош2)* = Рошт. (2.46)
Таким образом, если имеет место равенство (2.46), то двоичная
СПИ с m-ичным декодированием и т-ичная СПИ без декодирования
эквивалентны с точки зрения равенства вероятностей ошибки при
приеме одного m-ичного символа (k двоичных единиц). Если Рош 2 <
< 1, то из (2.46) находим
Рош2-/гФошт. (2.47)
Формула (2.47) определяет эквивалентную вероятность ошибки,
приходящуюся на одну двоичную единицу информации в m-ичной
67
СПИ. Можно заметить, что вероятности ошибки, приходящиеся на
одну двоичную единицу,, рассчитанные по формулам (2.44), (2.46),
(2.47), будут различны. Это различие определяется следующим. При
расчете вероятности ошибки в m-ичной СПИ с двоичным
декодированием было показано, что ошибка в m-ичном символе приводит
лишь к ошибке в части двоичных символов. При пересчете
вероятности ошибки в m-ичной СПИ без декодирования к вероятности
иошбки, приходящейся на один двоичный символ, было положено,
О ι ? 3 ί S h что 0Шибка в /я-ичном симво-
/ ле приводит к ошибке во всех
двоичных символах.
Конкретизируем общие
формулы для сравнения СПИ,
полагая, что прием
некогерентный. В соответствии с
этим в (2.43) и (2.45) будем
подставлять значения
вероятностей ошибок, рассчитанные
по (2.33) при т Φ 2 и по
(2.26) при т = 2. Напомним,
что (2.26) частный случай
(2.33) при т = 2.
На рис. 2.8 представлены
графики вероятностей ошибок
*ош2> готту Рош 2, Гоши»
построенные по формулам
(2.26), (2.33), (2.43), (2.45).
Аргументом, как и ранее,
является отношение сигнал/
шум h2 (2.21), приходящееся
на один двоичный символ. Графики построены для m = 64, k = 6.
Из графиков следует, что при m > 2 имеют место неравенства
Рош 2 < Р0ш m < Рош 2, Рош 2 <С Рош ту Р0ш т < Рош /я·
Из неравенств видно, что наилучшую помехоустойчивость
обеспечивает /n-ичная СПИ с двоичным декодированием. Особенно это
заметно в области малых отношений сигнал/шум /ι2. Рисунок 2.8
показывает, что /π-ичные СПИ обеспечивают большую
помехоустойчивость по сравнению с двоичными СПИ независимо от метода
декодирования.
Четыре кривые рис. 2.8 при заданной вероятности ошибки
соответствуют различным значениям отношения сигнал/шум. Обозначим
их следующим образом. Будем считать, что вероятности ошибки
в двоичной СПИ без декодирования Рсш 2 соответствует h2 = /ι2| 2-2»
где первый индекс 2 в правой части равенства после запятой равен
объему алфавита сигналов /п, а второй индекс — объему алфавита
источника п\ соответственно вероятности ошибки
Рош 2 —*■ "2, т-2> Рош т ""*" ^2, тп-тпу Рош т ~* "2, 2-т·
68
Отношения
η2 = ΛΙ. 2-2/ΛΙ. m-2, 4m = ΑΙ. 2-w/Al, m-m (2.48)
определяют выигрыш по мощности /n-ичных СПИ перед двоичными.
Отношение η2 характеризует выигрыш /n-ичной СПИ с двоичным
декодированием относительно СПИ без декодирования, а Т1т-выи-
грыш /n-ичной СПИ без декодирования относительно СПИ с т-
ичным декодированием. Выражения (2.48) показывают, во сколько
раз мощность сигнала (или отношение сигнал/шум) в /n-ичной СПИ
должна быть меньше мощности сигнала (отношения сигнал/шум)
в двоичной СПИ при одной и
той же вероятности ошибки. ^,
Выразим в явном виде
отношения х\чу г\т как функции т
или k [20]. Рассмотрим сначала
η2. Подставляя в (2.44)
вероятности ошибки (2.26), (2.35) с
заменой Л2 на /ι2,2_2 и /i2| m_2 5
соответственно и учитывая, что
в (2.35) hm = /ι2ι m-2Vky
логарифмируем полученное равен- *
ство. После преобразования
находим, что j
h\, m-2k = ΑΙ. 2-2 + 1Π (2-χ/η).
(2.49) f
Заменяя т согласно (2.13) и
преобразуя (2.49) с учетом
обозначения (2.48), получаем' ; j ^ 7 9 /Г
η2 = Ml + 2hi22„2ln2k-4-1. Рис 2.9
(2.50)
Аналогично из равенства (2.47) следует [26]:
r\m = k{\ + 2/i2-,V2[ln (2* - 1) - In k]}'\ (2.51)
Если & = 1, то η2 = ηm = 1.
На рис. 2.9 представлены кривые, построенные по (2.50), (2.51)
в зависимости от к при двух значениях h2> 2_2 = 2; 4. С ростом k
выигрыш /n-ичных СПИ растет, причем, чем больше /ι2| 2_2 (меньше
вероятность ошибки в двоичной СПИ без декодирования), тем больше
этот выигрыш. С ростом т и k выигрыш по мощности уменьшается
и при больших т стремится к предельному значению. При больших
my\2~r\m. При т ->- оо кривые Рош г и Рош m стремятся к пределу,
определяемому пороговым значением отношения сигнал/шум /ι2πορ =
= νΊη 2. Поэтому при т ->■ оо А2| т_2 = /ι2ι т-т = j/Ίπ 2, а
"2, 2-го — ^2,2-2·
69
/
/Л
/
/
/
/ У
/ /у
l
ι/
Ι/
/ ι
Ι
....
4j/U,2pS
/Чг
Чт
f>z,z-z
Ίί
I
=2
ι"
Следовательно, предельное значение η2 = Лт в соответствии с
(2.48) и сделанными значениями равно
η*, = lim.T]2 = lim r\m=hl, 2-2 (1п2)-\ (2.52)
W->oo W->oo
Из (2.52) видно, что чем больше выигрыш по мощности /п-ич-
ной СПИ, тем больше отношение сигнал/шум в исходной двоичной
СПИ.
Сравнение по полосе частот. Выигрыш по мощности /п-ичных
СПИ перед двоичными приводит к расширению полосы частот,
занимаемой сигналами m-ичной СПИ. Чтобы оценить проигрыш по
частоте m-ичной СПИ перед двоичной, допустим,что ширина этой
полосы частот равна ширине полосы частот Fmi занимаемой т
ортогональными сигналами. Положим, что
Fm = am/Tm, (2.53)
где Тт — длительность m-ичного сигнала, а — постоянная
величина, равная примерно 0,5—2, зависящая от метода определения
ширины спектра и не меняющаяся для систем сигналов,
принадлежащих к выбранному классу. Формула (2.53) справедлива для всех
известных сигналов. Например, для системы ортогональных
сигналов в виде функций отсчета постоянная а = 0,5, а для системы
сигналов в виде экспонент (2.9) а = 1.
Полагая т = 2 (k = 1) и используя (2.14), получаем ширину
полосы частот, занимаемую двоичной СПИ:
F% = 2аЯ. (2.54)
Используя соотношения (2.13), (2.14), находим
Fm = aM2kk-x.
Проигрыш /n-ичной СПИ по частоте по сравнению с двоичной
равен
ζ = FJF2 = 2*-Чг\ (2.55)
Зависимость (2.55) приведена на рис. 2.9. Отметим, что при
й=1ий = 2£=1. Это означает, что четверичная СПИ (k = 2,
т = 4) не проигрывает двоичной по частоте, а в то же время имеет
выигрыш по мощности в полтора-два раза. При больших k
проигрыш по частоте ζ растет чрезвычайно быстро по показательному
закону. При k > 5 — 6 проигрыш по частоте растет гораздо быстрее
выигрыша по мощности.
2.5. Выбор объема алфавита сигналов
Из результатов, полученных в данной главе, следует, что
переход от двоичных СПИ к m-ичным с практической точки зрения
целесообразен, когда объем алфавита т не будет чрезмерно
большим. Такой вывод является результатом следующих фактов:
70
1)/п-ичные.СПИ обеспечивают существенный выигрыш по
мощности по сравнению с двоичными, если только отношение
сигнал/шум, приходящееся на один двоичный символ, больше
порогового значения;
2) с увеличением объема алфавита выигрыш по мощности
уменьшается;
3) с увеличением объема алфавита проигрыш по частоте растет
по показательному закону (2.55);
Кроме этого, отметим, что:
4) число каналов т оптимального приемника с ростом т растет
по показательному закону (2.13);
5) расширение полосы частот, занимаемой каналом, при
увеличении объема алфавита требует более широкополосных мощных
выходных каскадов передатчика, антенн, входных каскадов
приемника, что усложняет техническую реализацию m-ичных СПИ
по сравнению с двоичной;
6) увеличение полосы пропускания фильтров в выходных
каскадах передатчика и приемника приводит к принципиальным
потерям мощности сигнала [33, 114].
Отмеченные факты не позволяют однозначно определить
оптимальный или близкий к нему объем алфавита сигналов для любых
СПИ. При решении этого вопроса необходимо учитывать
конкретные требования, предъявляемые к проектируемой СПИ. Однако
в случае линейного обмена мощности на полосу частот,
занимаемую СПИ, можно дать рекомендации по выбору объема алфавита.
Действительно, при пороговом приеме, когда А2 не намного боль-
ше Λ2πορ = У In 2, между мощностью сигнала, скоростью передачи
информации и спектральной плотностью шума выполняется
соотношение (2.41), которое перепишем так: Я = PJNQ In 2. Для
увеличения скорости передачи информации Я необходимо увеличивать
Рс, причем зависимость между Я и Рс линейная. Но Я можно
трактовать как минимальную полосу частот, которую может
занимать СПИ. Отсюда и следует линейный обмен полосы частот на
мощность.
По этой причине в качестве критерия сравнения
эквивалентности выигрыша по мощности и проигрыша по частоте возьмем
линейный обмен мощности на полосу частот. Обозначим через β
отношение
β = η/ζ, (2.56)
где η = η2 или η = х\т.
Если β > 1, то выигрыш по мощности больше проигрыша по
частоте. Если β< 1, то выигрыш по мощности меньше проигрыша
по частоте. Значение β = 1 примем в качестве сравнения. Из
формул (2.50), (2.51) и рис. 2.9 следует, что при hi, 2-2 > 1 и
относительно небольших k отношения η2 ~ r\m ~ k. Подставляя это
значение η в (2.56) и заменяя ζ согласно (2.55), получаем
β = /рг-**-1). (2.57)
71
Отношение β = 1, если k = 2*-Vft. Решение этого уравнения
соответствует точке пересечения кривой ζ е прямой k> изображенной
штриховой линией на рис. 2.9. Исходя из полученного решения,
можно сделать вывод, что величина k должна быть меньше или равна
6, т. е. объем алфавита т ^ 64. С уменьшением отношения
сигнал/шум А2} 2_2 абсцисса точки пересечения ζ с η смещается влево,
т. е. k и т уменьшаются. Например, при А2} 2_2 = 2 максимальное
k = 4; 5, т. е. т = 16; 32. И, наконец, при малых й2, 2_2 следует
применять четверичную СПИ, которая обеспечит выигрыш по
мощности и не проигрывает двоичной СПИ по частоте.
Таким образом, для повышения помехоустойчивости передачи
дискретной информации на фоне флюктуационных помех с
ограниченной спектральной плотностью целесообразно применять алфавиты
(системы) ортогональных сигналов небольшого объема. Выбор
объема должен производиться с учетом технических и экономических
требований, предъявляемых к СПИ.
Глава 3
СИНХРОННЫЕ АДРЕСНЫЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
3.1. Линейное уплотнение и разделение абонентов
В § 2.1 были определены методы уплотнения и разделения
каналов и абонентов в многоканальных системах передачи информации
с частотным (ЧР), временным (ВР) и кодовым (КР) разделениями.
СПИ с КР можно разбить на два класса: синхронные адресные
системы (САС) и асинхронные адресные системы (ААС). В данной
главе будут подробно рассмотрены синхронные адресные системы и
будет произведено их сравнение с системами с частотным и
временным разделением.
В САС передача информации осуществляется таким образом, что
переносчики информации удовлетворяют условиям
ортогональности (2.10), (2.11). Это обеспечивается выбором сигналов и
синхронизацией их во времени. Как было отмечено в § 2.1, и частотное, и
временное разделение удовлетворяют этим условиям
ортогональности и поэтому они также являются синхронными. Таким образом,
частотное, временное и кодовое разделения абонентов (каналов)
основаны на использовании ортогональности переносчиков
информации. Поскольку ортогональность сигналов (или функций)
является частным случаем линейной независимости сигналов (функций),
то при общем описании и сравнении указанных методов разделения
будем условно называть их линейным разделением. Естественно,
что при линейном разделении (уплотнении) тракты передатчика и
72
приемника должны быть линейными, так как при нелинейных
трактах условия ортогональности (2.10), (2.11) будут нарушены и в
результате появятся взаимные помехи между абонентами
(междуканальные помехи).
На рис. 3.1 представлены структурные схемы передающего и
приемного устройств СПИ с линейным разделением и
централизованным объединением абонентов. Информация от источников ИИ
поступает на канальные модуляторы, где LK — число каналов.
В /*-м канальном модуляторе переносчик сообщения — опорный
канальный сигнал tij (t) модулируется сообщением Sj (t) так, что
на выходе канального модулятора канальный сигнал Vj (t) является
ии
Канал 1
Канал Lk
Μ
Οι
• · ·
EKJ
УУ
г-Д ¥_f-J
М»И—' T—npr~H
a)
Канал 1
ПР\—^
УР
-H/4I ^И.
V A N '
—И
^-^ —
Cz I
*;
Рис. 3.1
функцией времени t и сообщения SJy т. е. о/ (ί) = uj (t, Sj (t)).
При временном и кодовом разделении для обеспечения
ортогональности канальных сигналов vj (t) необходима синхронизация всех
опорных сигналов. Это обеспечивается синхронизатором Сх. Сигналы
с выходов канальных модуляторов уплотняются устройством
уплотнения УУ и образуют так называемый групповой сигнал, который
поступает в передатчик ПЕР, где переводится в требуемый диапазон
частот, усиливается по мощности, а затем излучается.
Устройство уплотнения выполняет роль сумматора канальных
сигналов. Поэтому групповой сигнал
/=1
(3.1)
Суммирование производится по всем источникам информации,
хотя некоторые из них могут и не передавать информации в момент
наблюдения L
Приемное устройство состоит из приемника ПР, который
оптимально обрабатывает групповой сигнал и выделяет сигнал
синхронизации. Выделенный групповой сигнал поступает на устройство
разделения УР, где групповой сигнал разделяется на канальные
73
сигналы. Канальные сигналы поступают на входы канальных
демодуляторов Д. Сигнал синхронизации или синхросигнал
выделяется синхронизатором С2, который управляет ритмом работы
канальных демодуляторов. Информация с выходов канальных
демодуляторов поступает к получателям информации ПИ. Отметим,
что структура приемника ПР определяется принятым методом
модуляции несущего колебания групповым сигналом.
Поскольку методы модуляции несущего колебания групповым
сигналом хорошо известны, то рассматривать их не будем.
Устройство разделения при ЧР является набором частотных
разделительных фильтров, при ВР — набором временных
селекторов. При кодовом разделении функции разделения выполняют
канальные демодуляторы. Структура канальных демодуляторов
определяется методами передачи информации. Предположим, что
информация передается в виде дискретных сообщений. При этом
канальные демодуляторы являются приемниками дискретных
сообщений. Структурные схемы оптимальных канальных демодуляторов
при приеме дискретных сообщений совпадают со структурными
схемами оптимальных приемников (см., например, рис. 2.4, 2.6).
Их свойства были достаточно подробно описаны в гл. 2, поэтому
будем считать, что свойства отдельного канала в многоканальной
СПИ известны, и перейдем к рассмотрению особенностей, которые
вносит совместная работа многих абонентов.
Активность абонентов. Каждый абонент, передавая информацию
другому абоненту, занимает некоторый канал в общей полосе
частот. Для характеристики занятости канала вводят коэффициент
занятости [62]
*зан = Ит -^5-, (3.2)
7набл->«> 'набл
где Тнабл — интервал наблюдения; Тзан — суммарное время
занятости канала. В (3.2) усреднение производится по одному
абоненту. Естественно, что величина &зан будет иметь смысл, если
СПИ содержит однородные абоненты. В этом случае усреднение
по реализации будет эквивалентно усреднению по ансамблю
абонентов.
Во время занятия канала абонент в большинстве случаев не все
время передает информацию, например, в системе телефонной
связи. В радиотелеметрической системе информация от некоторых
датчиков может не существенно изменяться в течение определенного
времени (параметры объекта остаются практически неизменными).
В этом случае можно считать, что абонент не передает существенной
информации и ситуацию целесообразно характеризовать
коэффициентом использования канала [62]
*исп = Пт If*-, (3.3)
Гнабл-*°° /зан
где Тинф — суммарное время передачи информации.
74
В целом абонент характеризуется своей активностью, которую
обозначим через ра и определим как ра==^зан^исп· Подставляя сюда
(3.2), (3.3), находим
pa = lim 1я*. (3.4)
Гнабл-*00 Унабл
Из (3.4) следует, что активность абонента равна отношению
суммарного времени передачи информации к времени наблюдения
при неограниченном увеличении последнего. Поэтому активность
абонента есть вероятность передачи информации в некоторый момент
времени. Активность абонента определяется видом системы, в какую
он входит (или, наоборот, система определяется абонентами,
которые ее составляют). В зависимости от типа СПИ активность абонентов
может меняться в широких пределах от долей процента до единицы.
Подчеркнем, что в большинстве случаев ра <^ 1.
Так как ра — вероятность того, что абонент в данный момент
времени является активным, т. е. передает информацию, то 1 — ра —
вероятность того, что он не передает информацию. Вероятность того,
что в данный момент времени активными являются 1а абонентов
определяется биномиальным законом, который записывается в
следующем виде [104]
P(la) = C[«p'°(l-pa)L«-\ (3.5)
где биномиальный коэффициент Cl — число сочетаний из LK
по /a; LK — число каналов в СПИ, равное максимальному числу
активных абонентов. Среднее значение активных абонентов по
определению [104]
Та = PaL*, (3.6)
а дисперсия
*1 = Ра О - Pa) U. (3.7)
При ра <^ 1 дисперсия числа активных абонентов о\ ~ paL.
Отношение
ОаК = V(l-Pa)'PaL«. (3.8)
Когда ра < 1, afla ~ WpaLK.
Если произведение paLK > 1, то отношение οα/ϊα < 1. Из
соотношения (3.6) следует, что la/LK = ра.
Помехоустойчивость при линейном разделении. Ранее было
отмечено, что при линейном разделении канальные сигналы Vj (t)
являются ортогональными. Условие ортогональности для сигналов
VJ (0> vk (ή согласно (2.2), (2.10) имеет следующий вид:
J I 0 при ]¥=k.
75
В соответствии с методами оптимального приема момент принятия
решения должен соответствовать моменту окончания сигнала.
Так как канальные сигналы взаимно-ортогональны (3.9), то в
момент принятия решения помех от других сигналов не будет.
Действительно, поскольку оптимальный демодулятор выполняет как
основную операцию вычисления корреляционного интеграла (2.25), то,
заменяя в (2.25) χ (i) на групповой сигнал υ (t) (3.1), а и (t) на vk (t),
согласно (3.9) получаем, что на выходе &-го демодулятора в момент
принятия решения будет составляющая с номером k. От канальных
сигналов с номерами / Φ k на выходе k-το демодулятора в момент
принятия решения напряжения равны нулю.
Поскольку при линейном разделении взаимных помех нет, то
принципиально ЧР, ВР и КР обеспечивают одну и ту же
помехоустойчивость при условии, что средняя мощность передатчика
ограничена и задана. При этом на каждый канал приходится 1/LK часть
мощности передатчика. Помехоустойчивость приема информации
произвольным абонентом при линейном разделении определяется
отношением сигнал/шум
h* = PcT/LKNQ = h20/LKy (3.10)
где Рс — мощность сигнала на входе приемника, N0 —
спектральная плотность мощности шума на входе приемника, Τ —
длительность сигналов, переносящих информацию, а А§ определяется
по (2.21) или (2.30) в зависимости от того, передается информация
двоичными или m-ичными сиволами. Произзедение РСТ определяет
энергию группового сигнала на входе приемника за время Т.
Из (3.10) следует, что отношение сигнал/шум делится между
всеми абонентами одинаково. Это означает, что при любом
разделении все абоненты одинаково используют мощность передатчика и
время, отведенное для передачи информации. Это будет
справедливо, если все абоненты одновременно передают информацию. Однако
число активных абонентов 1а может быть намного меньше общего
числа абонентов LK в СПИ, что определяется активностью абонентов
ра. Обозначим через η отношение используемой части мощности
передатчика к полной. Назовем η коэффициентом использования
мощности. Если каждому абоненту выделяется 1/LK часть мощности
передатчика, то коэффициент использования мощности
η = /«Α„. (3.11)
В соответствии с (3.6) среднее значение η = ра и чем меньше
активность абонентов, тем меньшая часть мощности передатчика
будет использована. Как улучшить использование мощности
передатчика, будет рассмотрено в данной главе.
Аналогично можно доказать, что в СПИ с временным разделением
при малой активности абонентов недостаточно используется
время, отведенное для передачи информации. Можно показать, что при
76
идеальном ВР среднее значение коэффициента использования
времени ν равно ν = ра, а при реальном ВР ν == /?α/κ, где κ —
коэффициент реального использования времени одним абонентом.
Коэффициент κ учитывает необходимость «защитных» временных
интервалов между каналами и обычно κ ~ 1,5—2.
Точно так же при малой активности абонентов плохо
используется общая полоса частот в СПИ с ЧР. Поскольку уже в настоящее
время существуют большие трудности в распределении диапазонов
частот между различными радиотехническими системами, то вопрос
об эффективном использовании частот является одним из главных
при проектировании СПИ. (Отметим, что существуют
предложения по введению платы за использование частот, т. е. за «выход
в эфир», как, например, производится оплата потребляемой
электроэнергии.) Учитывая важность эффективного использования частот,
рассмотрим этот вопрос более подробно.
Использование общей полосы частот. Если число активных
абонентов /а, а ширина спектра каждого передаваемого сообщения
Fc, то суммарная ширина спектра всех передаваемых одновременно
сообщений laFc. Допустим, что ширина общей полосы частот канала
FK. Обозначим через μ коэффициент использования общей полосы
частот или просто коэффициент использования частот:
μ = WFr. (3.12)
В дискретных СПИ ширина спектра передаваемого сообщения
равна скорости передачи информации Μ и поэтому коэффициент
использования частот можно рассчитывать по следующей формуле:
μ = IJIIF*. (3.13)
Максимальное значение μΜδκο == 1» так как общая полоса частот
используется полностью. Кроме коэффициента использования
частот (3.12), (3.13), большое значение имеет другой показатель —
число активных абонентов, приходящихся на единицу полосы частот
7 -^макс/Л (3.14)
где 1а макс — максимальное число активных абонентов, которые
могут одновременно работать в общей полосе частот шириной FK,
равное числу каналов в СПИ. Обычно у измеряется числом
активных абонентов, приходящих на полосу частот шириной в 1 МГц,
т. е. в абон/МГц. Сравнивая (3.12) и (3.14), замечаем, что
μ = yFcUlauABv (3.15)
При идеальном частотном разделении каждому абоненту
отводится абонентская полоса частот, ширина которой Fa равна ширине
спектра передаваемого сообщения, т. е. Fa = Fc. При этом ширина
общей полосы частот FK должна удовлетворять соотношению FK =*
77
= la маКс^с· Если число активных, абонентов 1а равно
максимальному значению 1а макс, то из (3.12), (3.14) получаем
μ4Ρ = μΜ&κο = 1» ?чр = ?макс = MFC. (3.16)
Можно также показать, что при идеальном временном и кодовом
разделении μΒΡ = μκρ = 1» ?вр = γκρ = MFC = ММ.
Например, пусть при КР используются сигналы с базой В = FKT =
= FJM. При такой базе можно выделить систему ортогональных
сигналов объема /аМакс = В. Полагая все абоненты активными,
получаем 1а = /аМакс = FJM или laM = FK. Поэтому из (3.13)
получаем μκρ = 1.
Однако реально общая полоса частот при ЧР будет
использоваться хуже по двум причинам. Первая заключается в том, что
в большинстве СПИ ширина абонентской полосы Fa существенно
больше, чем ширина спектра передаваемого сообщения Fc.
Обозначим их отношение через
β = Fa/Fc. (3.17)
Величина β зависит от типа СПИ, стабильностей частот
передатчика и гетеродина приемника, стабильностей резонансных частот
фильтров, избирательности фильтров, величины доплеровского
сдвига по частоте и некоторых других факторов. Например, в
малоканальных радиорелейных линиях β а* 100, в
радиотелеметрических системах β = 33, в системах низовой УКВ радиосвязи
β = 12,5; 6,25.
Ширина общей полосы частот при ЧР равна
^к == *а макс·» а> (u.lo)
где /аМакс — максимальное число активных абонентов при ЧР.
Заменяя в (3.12), (3.14) FK согласно (3.17), (3.18), получаем, что при
реальном ЧР
μ4Ρ = ljla Μακοβ»
(3.19)
Тчр = ϊ/β/ν
Естественно, чем меньше β, тем лучше используется общая полоса
частот. Минимальное значение β = 1. При этом
^ЧР = Бамако Ϊ4Ρ = MFC = Тмакс-
Если все абоненты будут активны, то μ4ρ = μΜβκβ = 1'.
Из формул (3.19) следует, что чем больше β, тем хуже
используется общая полоса частот при ЧР. При КР многие перечисленные
факторы, обусловленные частотными нестабильностями,
оказывают гораздо меньшее воздействие на работу СПИ, так как все
сигналы заранее располагаются в общей полосе частот. Поэтому
чувствительность СПИ с КР ко многим рассогласованиям будет меньше,
78
чем у СПИ с ЧР. В результате при КР общая полоса частот будет
использоваться лучше, чем при ЧР.
Вторая причина, из-за которой общая полоса частот при ЧР
используется плохо, заключается в том, что число активных
абонентов 1а обычно много меньше максимального числа /аМакс> т· е·
/а//амакс < 1. Это имеет место, когда активность абонентов мала.
Среднее значение коэффициента использования частот (3.19) равно
μ4Ρ=Ί[β//βΜαΚοβ. (3.20
Подставляя в (3.20) среднее значение числа активных абонентов
1а согласно (3.6), получаем
μ4Ρ = Pa/β· (3.21)
Следовательно, чем меньше активность абонентов ра и больше
β, тем хуже используется общая полоса частот.
Таким образом получается следующее. При ЧР ширину общей
полосы частот необходимо выбирать из условия одновременной
работы L абонентов (3.18), а использоваться будет в среднем только
ее часть, равная μ4ρ. С ростом максимального числа активных
абонентов, которым должны быть предоставлены каналы связи,
ширина общей полосы частот растет, а ее использование может быть
малоэффективным. Именно поэтому и существует проблема
использования малой активности абонентов для увеличения максимального
числа активных абонентов и общего числа абонентов в СПИ.
Проблема повышения эффективности СПИ при малой активности
абонентов получила ряд интересных решений, которые можно найти в
обширной литературе по проблеме сжатия данных и статистического
уплотнения. В следующем параграфе рассмотрим метод,
позволяющий использовать все каналы при частотном разделении. Назовем
его адаптивным частотным уплотнением и разделением абонентов.
3.2. Адаптивное частотное уплотнение и разделение абонентов
Предположим, что активность
абонентов мала, т. е. ра < 1. Как
было показано в предыдущем
параграфе, при жестком закреплении
частотных каналов за каждым
абонентом эффективность
использования общей полосы частот будет
низкой. Чтобы повысить эффективность,
можно использовать адаптивное
частотное уплотнение и разделение
абонентов. Оно заключается в том,
что частотные каналы не
закрепляются за одним абонентом, а
предоставляются активному абоненту.
Именно такой метод используется в
телефонии. Допустим, что общее число
абонентов в системе J намного
больше числа частотных каналов L.
Согласно (3.6) среднее число активных
абонентов
Τα-Ρα^. (3.22)
Зная статистику сообщений,
передаваемых абонентами, т. е.
активность абонентов, можно выбрать
число каналов L в СПИ следующим
образом: положить L равным среднему
числу активных абонентов 1а т. е.
L — Та. При этом среднее значение
коэффициента использования частот
согласно (3.20) равно
μΑ4Ρ-1/β, (3.23)
79
где индекс А обозначает адаптивность первых, если β > 1, то μΑ4ρ < 1.
данного метода. Из (3.23) следует, β числ актйвных
что в среднем использование-общей абонентов ' / больше среднего зна-
полосы частот не зависит от актив- — а ν Μ
^ чения Ι» — L, то некоторым або-
ности абонентов и определяется толь- нентам «е буд'ут выделены^ каналы
ко коэффициентом β (3.17). Если для передачи информации и они
β = 1, то μΑ4ρ = 1, т. е. будет мак- должны стоять на очереди для пере-
симально. Число активных абонентов Дачи сообщений. Во многих СПИ
на ^πΗΗΗττν ттпттпгы оттпепеляется Aon- это можно Допустить, но в некоторых
на единицу полосы определяется фор- нельзя> и тогда нужно предоставлять
мулой (3.19), т. е. 7дчр — 1/Р^с· каждому абоненту свой частотный
Таким образом, адаптивное ча- канал, т. е. применять жесткое рас-
стотное разделение позволяет повы- пределение каналов, которые при
сить эффективность использования ра < 1 будут использоваться плохо,
общей полосы частот. Отметим, что От указанных недостатков свободен
такой метод нашел применение в си- метод адаптивного кодового уплот-
стемах низовой радиосвязи. Однако нения и разделения, который
расой обладает двумя недостатками. Во- смотрим в следующем параграфе.
3.3. Адаптивное кодовое уплотнение и разделение абонентов
При кодовом уплотнении и разделении абонентов общая
полоса частот и время, отведенное для передачи информации,
используются полностью, так как при КР можно применять сигналы,
ширина спектра которых равна ширине общей полосы частот F =* FK,
а длительность равна длительности двоичной единицы Τ = \Ш.
Полагая Л = FCJ получаем Τ = 1/FC. База таких сигналов
В = FT = F/Fc. (3.24)
При малой активности абонентов полное использование общей
полосы частот и времени при КР можно получить за счет
увеличения максимального числа абонентов, имеющих доступ к каналу
связи. При этом необходимо применять автоматическую
регулировку уровня (АРУ) группового сигнала. Назовем такой метод
адаптивным кодовым уплотнением и разделением абонентов. Он
сводится к тому, что мощность передатчика делится поровну между
всеми активными абонентами.
Помехоустойчивость. Обозначим, как и ранее (см. (3.10)) через
hi отношение сигнал/шум по мощности для группового сигнала.
Поскольку мощность передатчика распределяется на 1а активных
абонентов, то отношение сигнал/шум для одного канала при
адаптивном КР будет равно
hi = hllla. (3.25)
Отношение сигнал/шум (3.25) выражается через сигнал/шум
при линейном разделении (3.10) следующим образом
h\ = hU«/la, (3.26)
где LK — число каналов в СПИ с линейным разделением, например,
при ЧР. Зависимость hpjhn как функция отношения /a/LK представ-
80
лена на рис. 3.2. Она показывает, .что если число активных
абонентов 1а в САС с адаптивным КР меньше числа каналов LK в СПИ
β ЧР, то помехоустойчивость САС будет выше, а если la > LK,
то ниже. Если^/д не намного превышает LK, то и снижение
помехоустойчивости будет малым. Определим пределы изменения
помехоустойчивости при условии, что среднее число активных абонентов
1а = LK. При этом общее число абонентов в системе / согласно
(3.22) будет равно
/ = JjPa = LJpa. (3.27)
При активности абонентов ра <£ 1, J > LK. Дисперсия числа
активных абонентов согласно (3.7) равна ol = ра (1 — ра) J. При
ра < 1, ol ~ ρ J = /~'= LK. Отношение σα/Ία~ l/V la = 1/]/Ι7
и при LK > 1 это отношение мно- л и
го меньше единицы. Это означает, А —
что отклонения 1а от своего
среднего значения Та будут малы.
Поэтому расчет САС можно
производить, исходя из среднего
значения числа активных
абонентов. Полагая la = LK,
получаем с точностью до малых
более высокого порядка, что
среднее значение т{ {hi} = Ал.
Поскольку 1а меняется со временем,
то в некоторые интервалы
времени помехоустойчивость будет
лучше, а в некоторые хуже.
Например, пусть la = L„ = 400.. В этом случае σα = 20. Если
биномиальный закон (3.5) аппроксимировать нормальным
законом распределения со средним значением 7а = 400 и дисперсией
ol = 400, то с вероятностью 0,997 число активных абонентов не
выйдет за пределы интервала (7^ — 3σα, Га + 3σα), т. е. 340 < 1а <
< 460. При этом отношение IJLK меняется в пределах от 0,85
до 1,15. Пусть Ал == 2,6, что соответствует вероятности ошибки при
когерентном приеме противоположных сигналов . Рот = 10"~4
(рис. 2.5). Используя график рис. 3.2 получаем, что Ад меняется
в пределах 2,4—2,8. Такому изменению Ад соответствует изменение
вероятности ошибки от 5 · 10~4 до 5 · 10~5, что можно признать
несущественным. Подчеркнем, что именно в этом проявляется так
называемая «эластичность» адресных систем — изменение числа
активных абонентов перераспределяется по всем абонентам, а в
результате изменение .помехоустойчивости каждого из них
незначительно.
Поскольку можно рассчитывать САС по среднему числу
активных абонентов, то лри 1а — LK общее число абонентов в САС
81
1,05
0,95
ПО
0,8
0,9 1,0
Рис. 3.2
случае аа
V кИк
с адаптивной КР определяется формулой (3.27). Чем меньше
активность абонентов, тем больше J по сравнению с LK, т. е. САС с
адаптивной КР имеет неоспоримое преимущество и перед СПИ с ЧР
с жестким закреплением каналов, и перед СПИ с адаптивным ЧР
как по эффективности использования общей полосы частот, так и по
числу абонентов на единицу полосы. Действительно, μκρ = 1,
поскольку ширина спектров используемых сигналов равна ширине
общей полосы частот. Число абонентов на единицу полосы частот
можно найти, полагая 1а = L = В. Подставляя в (3.14) значение
Ι = δ и заменяя базу В согласно (3.24), получаем γΑΚρ = VFC,
т. е. в среднем число активных абонентов на единицу полосы
соответствует идеальному частотному разделению, когда каждый канал
занимает полосу частот Fa = Fc. Поскольку в реальных СПИ с ЧР
ширина абонентской полосы Fa > Fct то всегда Yakp > 7чр.
Следовательно, САС с адаптивным КР реализует потенциальные
возможности линейного уплотнения и разделения абонентов. '
Требования к системе сигналов. Так как база сигналов В равна
L, то из (3.27) имеем, что объем системы сигналов J = В/ра. При
ра < 1 объем системы сигналов J > В. Например, если ра = 0,025,
то J = 40 В. Подобные системы сигналов, объем которых много
больше базы, назовем большими системами.
Известно, что число ортогональных сигналов равно базе, но
число различных ортогональных систем может быть весьма велико.
Поскольку нельзя выбрать все сигналы взаимно-ортогональными,
то в результате неортогональности сигналов при принятии решения
возникает взаимная помеха. Оценим ее значение и определим
уменьшение помехоустойчивости.
Положим, что произвольная пара сигналов имеет
взаимокорреляционную функцию (ВКФ) в точке принятия решения (коэффициент
корреляции), равную
RJk = α/β, (3.28)
где α — некоторая постоянная величина, причем |α] ^ 1. Выбор
такой зависимости определяется следующими соображениями.
Обычно среднеквадратическое значение ВКФ равно, ~ 1/]ЛВ, что будет
подробно рассмотрено в дальнейшем. Такое значение соответствует
усреднению ВКФ по всем временным сдвигам. Когда временного
сдвига нет, можно найти определенное число сигналов,
удовлетворяющих условию (3.28). Допуская, что взаимные помехи
суммируются по мощности, можно показать, что мощность взаимной помехи
будет равна 1а (аЕ/В)2. Суммируя мощность шума на входе
решающего устройства и мощность взаимной помехи, получаем
отношение сигнал/помеха в САС с адаптивным КР
h\n = hW + 2h\*4aB-% (3.29)
Полагая la — Та — LK = 5, перепишем (3.29) в виде
h\n = AV(1 + 2/ι^β-1). (3.30)
82
Из (3.30) находим условие, при котором можно пренебречь
взаимными помехами: 2hl^2B~1 < 1 или В > 2/ιΧα2. Например, если
В = LK = 400, a ha = 2,6 и |а| = 2, то неравенство выполняется,
т. е. 400 > 55, /iln c^h\n взаимными помехами можно пренебречь.
Из проведенного исследования следует, что применение
адаптивного КР совместно с АРУ группового сигнала позволит лучше
использовать полосу частот, время и мощность передатчика, чем
традиционные СПИ с ЧР или с ВР, и увеличить общее число
абонентов в системе. Рассмотренный принцип построения САС с КР
требует применения АРУ группового сигнала. Если можно
несколько снизить помехоустойчивость приема информации, то иногда
целесообразно перейти к нелинейному КР с жестким (пороговым)
ограничением сигнала. При этом отпадает необходимость в АРУ.
3.4. Нелинейное кодовое уплотнение и разделение абонентов
Совместное применение жесткого ограничения группового
сигнала и линейного кодового разделения сигналов составляет суть
нелинейного кодового уплотнения и разделения абонентов
(нелинейного КР). Оно было предложено в работе [161]. В дальнейшем
нелинейное КР исследовалось рядом авторов (см., например, [87]),
-»
[г
J
У9
>К""
(j
'ί I
Рис. 3.3.
но в основном рассматривалась помехоустойчивость относительно
взаимных помех (так называемые шумы нелинейного
преобразования). Лишь в работе [113] был произведен учет собственных шумов
приемника, но полученные результаты не позволяют достаточно
просто и наглядно сравнить нелинейное КР с линейным КР или ЧР.
По этой причине была исследована помехоустойчивость САС с
нелинейным КР с учетом как взаимных помех, так и шумов
приемника.
На рис. 3.3 представлена структурная схема САС с нелинейным
КР, где показаны элементы, относящиеся к одному /-му каналу.
Информация от источника в виде двоичных единиц Sj = ±1
поступает на модулятор. На второй вход модулятора поступает
опорный сигнал. В качестве опорного сигнала можно взять видеочастот-
83
ный дискретный фазоманипулированный сигнал. Он описывается
согласно (1.101) кодовой последовательностью Aj = (ап, ..., aJny
..., αίΝ), состоящей из N символов ajn = ±1. С выхода
перемножителя снимается кодовая последовательность
Vj = (^я> ···» tyn» ···> u/jv), символы которой vjn = 57·α7·η.
Очевидно, что ujn = ±1. На выходе устройства уплотнения (УУ)
имеем групповой сигнал Угр, равный сумме канальных сигналов.
Предполагаем, что все сигналы синхронны, что обеспечивается
синхронизатором Сх. Поэтому элементы группового сигнала имеют
ту же длительность, что и элементы канальных сигналов.
Амплитуда элементов группового сигнала равна
vn = vjn+ 2 vmn = Sjajn+ 2 Smamn.
Слагаемое vjn — Sjajn выделено потому, что при передаче символа
Sj знак этого слагаемого имеет значение для определения самого
символа Sjy в то время как сумму можно считать случайной
величиной.
В ограничителе производится предельное или жесткое
ограничение группового сигнала. Амплитуда элемента на выходе
ограничителя определяется согласно известному правилу
х [ ι приип>0,
1 —1 при ι>η<0.
Кодовая последовательность X =* (х1у ..., χηι ..., χΝ). На входе
канала (КАН) имеем сигнал χ (ή, состоящий из прямоугольных
импульсов длительностью TIN и (^амплитудами хп. На выходе
канала имеем колебание у (ή = YPcx(f) + π (ί), Pc — мощность
сигнала на входе приемника, а п (/) — нормальный стационарный
случайный процесс с нулевым средним и с равномерной
спектральной плотностью мощности N0.
В качестве оптимального демодулятора взят коррелятор,
состоящий из перемножителя (X), интегратора (И) и решающего
устройства (РУ). Ритмом работы коррелятора управляет
синхронизатор (С2). На структурной схеме рис. 3.3 показан только /-й
демодулятор·
На один из входов перемножителя поступает колебание у (/),
на другой — опорный дискретный фазоманипулированный сигнал
с кодовой последовательностью Aj = (ajly .... а3пу ..., Аш).
Положим, что опорные сигналы и соответственно кодовые
последовательности синхронны. Допустим, что передача двоичных символов
осуществляется противоположными сигналами. При этом решающее
устройство является пороговым с нулевым порогом.
84
Помехоустойчивость. Положим, что априорные вероятности
появления символов Sj = ±1 равны 0,5. Напряжение на выходе
интегратора
τ
Ъ = \У (0 А, (/) Я, (3.31)
о
где Aj (t) — опорный сигнал с кодовой последовательностью Aj.
Заменяя у (t) = VPcx (t) + η (t) и обозначая
τ
d = VPc\x (t) A j (t) dt, (3.32)
о
τ
h = J η (t) Aj (t) dt, (3.33)
о
получаем
z. = d + h. (3.34)
Величина ζ7· является случайной, так как и d, и А —
случайны. Первая из-за жесткого ограничения группового сигнала,
вторая — из-за действия шума. Можно показать, что среднее
значение и дисперсия величины d, определяемой ограничением
группового сигнала, равны:
Щ {d} = VTCT V2ln (/β-1), (3.35)
Μ2 {d} = PCT2 [1 — 2/π (la — l)]/N ~ PCT2/N. (3.36)
Из (3.35), (3.36) видно, что среднее значение случайной величины
d уменьшается как 1/γΊα— 1, а среднеквадратическое значение —
как Ι/yN. Их отношение
m1{d}/M2{d} = V2N/n (la— 1) (3.37)
тем больше, чем больше Nl(la — 1) = Β/(ία — 1), т. е. чем больше
отношение базы сигнала к числу мешающих абонентов.
При выводе формул (3.35), (3.36) было положено, что случайная
величина d является нормальной, поэтому она полностью
характеризуется своими средним значением и дисперсией. Перейдем к
определению статистических характеристик и функции распределения
случайной величины h. Так как по предположению η (t) —
случайный нормальный процесс с нулевым средним и с равномерной
спектральной плотностью мощности Af0, то h — нормальная
случайная величина, а ее среднее значение и дисперсия равны:
mx{h) = 0, Μ2{/ι} = 0,5#07\ (3.38)
Так как zj (3.34) является суммой двух нормальных случайных
величин d и ή, то она сама есть нормальная случайная величина.
Ее среднее значение согласно (3.35), (3.38) равно
а = m1{zJ} = шг{а}л+ mx{h} = VFCT УШ (la - 1), (3.39)
85
а дисперсия согласно (3.36), (3.38) приближенно равна
σ2 ~ М2 {zj} = М2 {d} + М2 {/ι} = PCT2/N + 0,5W07\ (3.40)
Вероятность ошибки согласно (2.19) будет
Рош = F(- V2hH)y (3.41)
где Ан — отношение сигнал/помеха на аходе решающего
устройства при нелинейном КР. Его квадрат равен
Α& = α2/2σ2 =
2Ν
hi
π(/β—1) 2Щ + Ы '
(3.42)
где согласно (3.10) /ι§ = PCT/N0 — отношение сигнал/шум на
входе приемника, а РСТ — энергия группового сигнала на его входе.
Напомним, что N — число элементов в сигнале, и можно полагать,
что N = В — базе сигнала.
Зависимость вероятности
ошибки Р0ш (3.41) от /ih
представлена на рис. 2.3 кривой
ФМ (необходимо положить
h2=hHy
При Ν » 2/ι§ из (3.42)
получаем
2,5
2,0
1,5
1,0
0,5
К
РагО
"ХГ
X
.05
У\
Aft ~2&*/π(/β-1), (3.43)
а при Щ > N
h2H ~ 2Ν/π(Ια — 1). (3.44)
0,5 1,0 1,5 2,0 2,5 hn
Рис. 3. 4.
нелинейного
уплотнения и
Сравнение
и линейного
разделения. С увеличением
расстояния между
передатчиком и приемником
отношение h\ уменьшается. Поэтому с практической точки зрения
наибольший интерес представляет случай, когда h\ < Ν, т. е. случай
малых отношений сигнал/шум. Сравним полученный результат
(3.43) с тем, какой имеем в линейных СПИ. Напомним, что в
линейной СПИ с ЧР или с КР, но без АРУ группового сигнала
отношение сигнал/шум согласно (3.10) hh = h20/LKy а при КР и
наличии АРУ в соответствии с (3.25) h\ = hllla. Сравнивая эти
значения отношения сигнал/шум со значением (3.43), замечаем, что
ЛЬ ~ 2h%/n ~ 2h%LJnla. (3.45)
Таким образом, при жестком ограничении группового сигнала
и при малом отношении сигнал/шум h\ имеем проигрыш в
отношении сигнал/помеха в 2/π раз (—2 дБ) по сравнению с системой с АРУ,
но зато имеем выигрыш в 2LJnla раз по сравнению с линейной сис-
86
темой. Чем больше LK//a, т. е. чем меньше активность абонентов,
тем больше выигрыш.
Следует напомнить, что этот выигрыш получается только при
малом отношении сигнал/шум hi. При этом линейная СПИ вообще
будет неработоспособной, но может оказаться, что и наличие
жесткого ограничения не намного улучшит дело. На рис. 3.4
показаны зависимости /ia, /ih, Нл как функциикл =
Н0/У^Ькприактивности абонентов ра = 0,05, т.е. LJla = 20. Кривые показывают, что
если /1л < 2,5, то нелинейное КР, действительно, обеспечивает
выигрыш в помехоустойчивости. Этот выигрыш тем больше, чем меньше
Ал. Но по абсолютному значению величина Ан такова, что в СПИ
может быть обеспечена передача информации с довольно частыми
ошибками (Рош> Ю~3). Поэтому жесткое ограничение следует
применять в СПИ, к которым не предъявляются требования
передачи информации с малой ошибкой или возможно обнаружение
и исправление ошибок.
Из рис. 3.4 видно также, что САС с КР и АРУ всегда обеспечивает
выигрыш в помехоустойчивости. Именно поэтому можно
рекомендовать построение синхронных СПИ с применением КР и АРУ·
Глава 4
АСИНХРОННЫЕ АДРЕСНЫЕ СИСТЕМЫ ПЕРЕДАЧИ
ИНФОРМАЦИИ
4.1. Кодовое уплотнение и разделение абонентов
в асинхронных адресных системах
Многоканальные автономные системы (MAC) передачи
информации служат для обеспечения обмена информацией между
абонентами, когда по некоторым причинам нельзя применять
централизованное объединение абонентов. Такими причинами могут быть
размещение абонентов на большой территории, случайность
размещения абонентов, большие скорости движения абонентов, небхо-
димость обеспечения большей надежности и живучести по
сравнению с многоканальными централизованными системами (МЦС) и
т. д.
В этих случаях MAC может быть только асинхронной по времени,
так как осуществить синхронизацию в перечисленных случаях
практически невозможно. По этой причине в MAC нашли
применение только частотное уплотнение и разделение (ЧР) и кодовое
уплотнение и разделение (КР).
При ЧР, как это было отмечено ранее, каждому абоненту
отводится свой частотный интервал (абонентская полоса частот) в
пределах общей полосы частот [98, 159]. В этом случае передатчики и
87
приемники пары абонентов, ведущих обмен информацией, должны
быть настроены на частоты выделенных интервалов. Поскольку
другие абоненты в этих частотных интервалах не работают, то прием
информации осуществляется без взаимных помех. Максимальное
число активных абонентов в системе равно общему числу абонентов
и определяется как отношение ширины общей полосы частот FK
к ширине абонентской полосы Fa, т. е. ЬцР = FJFa.
Если все абоненты работают одновременно, а ширина
абонентской полосы Fa равна ширине спектра передаваемого сообщения
FCJ то согласно (3.16) μ4ρ = 1 и отведенная полоса частот
используется полностью. При этом число абонентов нз единицу полосы
максимально и равно учр = VFC (3.16).
При ЧР реальная ширина абонентской полосы F > Fc. При
этом в (3.17) коэффициент β > 1. Кроме того, при малой активности
абонентов число активных абонентов 1а намного меньше
максимального числа активных абонентов в системе /аМакс> т· е· 'аС
С ^амакс- ПРИ э™м из формул (3.19) следует, что μ4Ρ <t μΜ&κο =1»
а γ4ρ С Тмакс = 1/^с» т· е. в СПИ с ЧР общая полоса частот
используется плохо.
С увеличением числа абонентов возникают серьезные трудности
распределения полосы частот между ними. Следует заметить, что
с некоторых пор число абонентских полос в большинстве диапазонов
частот много меньше числа возможных абонентов. Для увеличения
числа абонентов в системе связи целесообразно переходить к
кодовому разделению.
Кодовое разделение основано на том, что каждому абоненту
выделяется свой (абонентский) алфавит сигналов (или кодовых
последовательностей), с помощью которого он передает информацию.
Разделение возможно потому, что сигналы различных абонентов
существенно отличаются по форме. При таком способе разделения
передаваемая информация снабжается адресом, роль которого
играют выделенные сигналы. Наличие адресов позволяет реализовать
асинхронный режим совместной работы многих абонентов. По этой
причине MAC с КР получили название асинхронных адресных
систем (ААС) передачи информации.
Началом исследований по кодовому уплотнению и разделению
можно с полным основанием считать работу Д. В. Агеева [1],
опубликованную в 1935 г. В этой работе даны основы теории
линейного разделения, осуществляемого при использовании линейно-
независимых сигналов. При линейном разделении нет взаимных
(междуканальных) помех. При кодовом разделении в ААС имеют
место взаимные помехи, которые явгляются следствием
одновременной работы абонентов в общей полосе частот. Однако при кодовом
разделении можно так выбрать параметры сигналов, что уровень
взаимных помех будет сколь угодно малым, т. е. обеспечить
заданную помехоустойчивость.
Работа [1] осталась мало замеченной, так как она намного
опередила требования техники того времени. Для обеспечения асинх-
88
ронной связи достаточно было использовать частотное разделение,
при котором каждому абоненту отводился свой частотной канал.
После второй мировой войны оказалось, что диапазоны частот
не беспредельны и частотное разделение не в состоянии обеспечить
асинхронную радиосвязь с подвижными объектами. По этим
причинам были начаты разработки первых ААС. Одна из них —
радионавигационная система «Лоран» [219]. В дальнейшем было
опубликовано несколько работ (например, [230]), но особого интереса они
не вызвали. Внимание специалистов к ААС привлекла работа Кос-
таса [202], в которой были отмечены основные особенности таких
систем, в том числе и электромагнитная совместимость
широкополосных и узкополосных СПИ. Затем появился ряд работ, в
которых рассматривались как теоретические вопросы ААС, так и
вопросы технического проектирования [9, 56—59, 62, 78, 96, 127,
149—151, 187, 193, 196, 198, 203, 204].
В это время было предложено большое число различных ААС,
таких как «Phantom», «RADA», «RADAS», «RACEP» и др.,
предназначенных для работы как в наземных, так и в спутниковых
системах связи. Этот период можно считать началом освоения ААС,
так как их преимущества были очевидными,а недостатки казались
несущественными. Появилось большое число работ, основные
результаты которых нашли отражение в многочисленных обзорах и
книгах [116, 120, 137, 217].
Со временем определились недостатки ААС. Это привело к
ослаблению внимания к ААС и соответственно к сокращению числа
публикуемых работ. Однако в последнее время вновь наблюдается
усиленное внимание к ААС [79, 86, 106, 112, 125, 128, 129, 131,
145, 192, 197, 218, 221, 224, 226, 227]. Среди обычных наземных и
спутниковых ААС особое внимание привлекает применение
кодового разделения для 'решения проблем управления воздушным
движением (УВД) и электромагнитной совместимости. В настоящее
время ААС находят все более широкое применение, и области их
применения, несомненно, будут расширяться.
Как отмечалось ранее, ААС основаны на использовании кодового
уплотнения и разделения абонентов (КР). При этом требуемое
для ААС число сигналов равно произведению числа абонентов
на число сигналов в алфавите (полагаем, что все абоненты
используют алфавиты одинакового объема). Минимальное число сигналов
равно числу абонентов. Если число абонентов в ААС велико, то выбор
сигналов является главным вопросом при разработке ААС. Решению
этого вопроса посвящена в основном данная книга. Поэтому перейдем
к рассмотрению кодового разделения.
Основы кодового разделения абонентов в ААС. Обозначим через
LK число абонентов в ААС, а число активных абонентов, ведущих
передачу информации в рассматриваемый момент времени, через
1а. На вход приемника одного из абонентов, принимающих
информацию, поступают сигналы от I = 1а — 1 мешающих абонентов,
создающих взаимные помехи, и полезны^ сигнал от активного абонен-
89
та, который передает информацию данному абоненту. Когда I > 1,
то / ~ 1а.
Рассмотрим влияние взаимной помехи на помехоустойчивость
передачи полезной информации. В данном параграфе используем
энергетическое определение взаимной помехи, которое позволяет
наглядно выяснить основные особенности приема информации
на фоне взаимной помехи [78].
Пусть ширина общей полосы частот равна FK. Допустим, что
ширина спектра всех сигналов в ААС равна ширине общей полосы
частот. Предположим, что все активные абоненты создают на входе
выделенного /-го приемника сигналы одинаковой мощности Рс.
В этом случае мощность полезного сигнала будет Яс, а мощность
взаимной помехи 1РС. Допустим, что спектральная плотность
мощности взаимной помехи постоянна в пределах общей полосы частот
NU=IPC/FK. (4.1)
Предположим, также, что число слагаемых во взаимной помехе
/ > 1. Поэтому можно допустить, что взаимная помеха по своим
статистическим свойствам приближается к нормальному
случайному процессу. Таким образом, сделанные предположения позволяют
считать в первом приближении взаимную помеху нормальным
случайным процессом с равномерной спектральной плотностью
мощности (4.1).
При передаче и приеме дискретной информации
помехоустойчивость когерентного и некогерентного приема полностью
определяется отношением сигнал/шум, приходящимся на одну двоичную
единицу (2.21). Заменяя в формуле (2.21) N0 на Wn(4.1), возводя
в квадрат и опуская индекс 2, получаем
h2 = BIU (4.2)
где
B = FKT = FJi = FJF0 (4.3)
— база сигнала, приходящаяся на одну двоичную единицу. Из (4.2)
следует, что для обеспечения надежной передачи информации
(/ι2 > 1) необходимо, чтобы база В была много больше числа
мешающих абонентов /, т. е. чтобы отношение ИВ <^ 1. При передаче
информации с заданной помехоустойчивостью при h = const, формула
(4.2) позволяет найти требуемое отношение ИВ. Из (4.2) следует,
что при заданном числе активных абонентов 1а = I + 1
увеличение отношения сигнал/взаимная помеха возможно только за счет
увеличения базы В. Чем больше требумая помехоустойчивость, тем
больше должна быть база В. Это объясняется тем, что с
увеличением базы (с увеличением ширины спектра сигналов при постоянной
скорости передачи информации Я) уменьшается спектральная
плотность помехи Νπ (4.1). Принципиально увеличение базы В
позволяет получить сколь угодно высокую помехоустойчивость
приема информации в ААС,
90
При когерентном приеме, как было отмечено ранее, различай^
три возможные метода передачи двоичных символов: двумя
противоположными сигналами (фазовая манипуляция — ФМ), двумя
ортогональными сигналами (ортогональная манипуляция — ОМ) и
пассивной паузой (амплитудная манипуляция AM).
Вероятность ошибки Рош при когерентном приеме двоичной
информации определяется формулой (2.19). График зависимости
вероятности ошибки от h приведен на рис. 2.5.
Подставляя значение h (4.2) в (2.19), получаем для ФМ
Рош = F (-У2Щ (4.4)
для ОМ
Рош = F(-VW>. (4.5)
При AM коэффициент α в (2.19) равен 1/2, но при этом Νη в два раза
меньше, так как число суммируемых сигналов в среднем равно Z/2,
поскольку половина сигналов не передается. Помехоустойчивость
ОМ и AM одинаковы и определяются формулой (4.5). Отметим, что
при ОМ система сигналов в ААС должна иметь объем J = 2L, а при
AM J = L. Данное преимущество AM было отмечено в [56].
Однако при AM необходимо устанавливать пороговый уровень, не
равный нулю. Флюктуации порогового уровня могут существенно
снизить помехоустойчивость AM.
При некогерентном приеме двух ортогональных сигналов
вероятность ошибки Рош определяется формулой (2.26). Подставляя
(4.2) в (2.26), получаем
Рош = 0,5ехр(-Д/2/). (4.6)
Если информация передается m-ичными символами, то
основные соотношения (4.1), (4.2) не изменяются. При этом база /п-ичных
символов В = FTm. Отношениз сигнал/помеха /ι2, отнесенное к т
двоичным единицам, следует рассчитывать по формуле (4.2).
Используя полученное значение Л, вероятность ошибки можно
рассчитывать по известным формулам (2.32), (2.33).
Из соотношения (4.2) следует, что увеличивая базу В, всегда
можно добиться требуемого отношения сигнал/взаимная помеха.
Однако при этом не учитывается собственный шум приемника.
Рассмотрим влияние шума на снижение помехоустойчивости.
Допустим, что, кроме взаимной помехи со спектральной
плотностью Νπ (4.1), действует шум, являющийся нормальным
стационарным случайным процессом с равномерной спектральной
плотностью Ν0. В этом случае результирующая спектральная плотность
равна Nn + N0, а отношение сигнал/помеха согласно (2.21)
/ι2 = PcT(Pcl/F + No)-1. (4.7)
Преобразуя полученное соотношение и обозначая отношение
сигнал/шум hi = PCT/N0 = PJJZN0 (2.21), из (4.7) получаем
А» = (11В + 1/AJ)-1. (4.8)
91
Предельное значение h2 при В -> оо равно h\, т. е. предельное
значение помехоустойчивости ААС определяется шумом.
Из соотношения (4.8) можно найти допустимое число
мешающих абонентов при заданной помехоустойчивости (задано требуемое
значение К) и для определенного уровня шума (известно значение
/ι0). Преобразуя (4.8), находим, что
hHIB = 1 - hVhl (4.9)
График зависимости (4.9) представлен на рис. 4.1. Если шума
нет (N0 -> 0, /ι* -> оо), то lh2/B = 1 и относительное число
мешающих абонентов ИВ = 1//ι2, что совпадает с результатом,
получаемым из формулы (4.2). При
увеличении шума и /ι2 = const
допустимое число мешающих
абонентов уменьшается; а
при h = h0 оно равно нулю,
т. е. заданная
помехоустойчивость может быть
реализована, если нет взаимных
помех.
Из рассмотрения основ
кодового разделения
абонентов следует, что
помехоустойчивость ААС относительно
взаимных помех полностью
О 0,2 о,ь 0,6 h2/h* определяется отношением
базы сигналов к числу актив-
Рис; 4·1 ных абонентов (4.2).
Увеличивая базу сигналов, можно
всегда получить требуемую помехоустойчивость или
приблизиться к предельной. Однако при постоянной скорости передачи
информации увеличение базы сигналов означает расширение их
спектров, что приводит к увеличению общей полосы частот ААС. При
этом возникает вопрос, на сколько эффективно используется общая
полоса частот в ААС. Перейдем к рассмотрению этого вопроса.
Эффективность использования общей полосы частот в ААС.
Как и ранее, использование общей полосы частот будем
характеризовать коэффициентом использования частот μ (3.12), (3.13) и числом
активных абонентов на единицу полосы частот γ (3.14). Используя
определение базы сигналов (4.3) ,и заменяя F в (3.12), получаем
μκρ = IJB. Так как 1а = I + 1, а при 1а > 1 имеем 1а ~ I,
то в соответствии с формулой (4.2)
μκρ= 1//ι2 = Ι/Β. (4.10)
Из полученного соотношения следует, что эффективность
использования общей полосы частот тем выше, чем меньше требуемое
92
0,8
0,6
0Л
0,2
отношение сигнал/взаимная помеха Л2. Поскольку отношение
сигнал/взаимная помеха (4.2) уменьшается с ростом числа
мешающих абонентов, то чем больше число активных абонентов, тем лучше
используется общая полоса частот. Величина h определяет
вероятность ошибки. Чем она больше, тем меньше вероятность ошибки.
Таким образом, ААС целесообразно применять в тех случаях, когда
не требуется высокая надежность (или высокое качество) передачи
информации, а чцсло абонентов должно быть большим.
Сопоставляя μκρ (4.10) с μ4ρ (3.19) и заменяя 1а (3.19) его
средним значением Та = paL4V согласно (3.6), находим, что соотношение
μκΡ/μ4Ρ Равно:
μκρ/μ4Ρ = β(Ρα/*2)Λ (4.11)
где β = FJFC9 см. (3.17), ра — активность абонентов. Если
μκρ/μ4ρ>1> то ААС лучше использует общую полосу частот,
чем СПИ с ЧР, а если μκρ/μ4ρ<1» т0 — хуже. Равенство
/ι2 = β/ρα определяет границу, на которой эффективность обеих
систем одинакова. Из (4.11) следует, что чем больше отношение
β/ρα, тем большее преимущество имеет ААС. При малой активности
абонентов (ра < 1) ААС всегда будет лучше использовать общую
полосу частот. Это позволяет увеличить максимальное число
активных абонентов в системе.
Число активных абонентов, приходящихся на единицу полосы
частот, согласно (3.14) равно γ = /аМакС/Л гДе ^амакс —
максимальное число активных абонентов, имеющих возможность
одновременно передавать информации. Задавая качество передаваемой
информации, т. е. задавая величину отношения сигнал/взаимная
помеха /ι2, полагая согласно (4.2) I = B/h2 и выражая базу сигналов
В через отношение F/FG (4.3), получаем
7кр = Тмакс^'2* (4.12)
где 7макс = l/Fc- Так же, как и в случае соотношения (4.10), чем
меньше требований предъявляется к качеству передаваемой
информации (чем меньше /ι2), тем больше будет число активных абонентов
на единицу полосы. Сопоставляя (4.12) с соотношением для γ4ρ
(3.19), находим их отношение
γκΡ/γ4Ρ = β^2· (4.13)
Если β > /ι2, то ААС обеспечивает большее число активных
абонентов, чем СПИ с ЧР.
Сравнение существующих СПИ с ЧР с ААС показывает, что ААС
в большинстве случаев лучше использует общую полосу частот.
Преимущество ААС будет тем больше,чем меньше активность
абонентов. Кроме того, преимущество ААС возрастает, если не
требуется высокого качества передачи информации. Поэтому КР более
перспективно для СПИ среднего качества, например для СПИ
низовой радиосвязи [38].
93
4.1. Корреляционные и статистические свойства
взаимной помехи
При анализе кодового разделения в предыдущем параграфе
относительно применяемых сложных сигналов было сделано лишь
одно предположение, что ширина спектра сложного сигнала
должна быть равна ширине общей полосы частот. Поскольку выполнить
это условие можно достаточно просто, то может создаваться
впечатление, что в А АС с кодовым разделением применимы любые
системы сигналов. Однако детальное исследование вопроса выбора
систем сигналов показывает, что различные системы сигналов
обеспечивают различную помехоустойчивость. В то же время в
формулу (4.2), кроме ширины спектра, не входят иные свойства систем
сигналов. Такое различие между результатом (4.2) и влиянием
свойств систем сигналов на помехоустойчивость объясняется двумя
основными допущениями, которые были сделаны при выводе
формулы (4.2): во-первых, предполагалось, что взаимная помеха
нормализуется, и во-вторых, что ее спектральная плотность в общей полосе
частот равномерна. Однако и то, и другое предположение могут
не выполняться, что в значительной мере определяется свойствами
используемой системы сигналов. Для выяснения влияния свойств
систем сигналов на помехоустойчивость ААС с кодовым
разделением перейдем к корреляционному определению взаимной помехи,
основы которого приведены в работе [56]. Обобщение
корреляционного метода определения взаимной помехи и выбор сигналов для
ААС дан в [31].
Корреляционное определение взаимной помехи. Рассмотрим
работу приемника &-го абонента. Если LK — число абонентов в ААС,
то k = 1, LK. Поскольку выделение информации происходит на
выходе приемника, определим характеристики сигнала и взаимной
помехи на выходе. Допустим, что информация передается двумя
противоположными сигналами и осуществляется когерентный
прием. Оптимальный приемник k-vo абонента состоит из согласованного
фильтра и решающего устройства (см. рис. 2.4, б). На входе
приемника действует сумма полезного сигнала (последовательность
сложных сигналов, манипулированных последовательностью
информационных символов) и взаимной помехи, которая в свою очередь
является суммой мешающих сигналов. Нормированное напряжение
на выходе согласованного фильтра будет равно сумме
автокорреляционных функций (АКФ) от полезных сигналов и
взаимокорреляционных функций (ВКФ) от мешающих сигналов.
По определению (1.23) АКФ k-vo сигнала
Rk (τ) = ^ j Uk (t) Uk (t-τ) dt, (4.14)
— 00
94
а ВКФ /-го и &-го сигналов с равными энергиями (1.21)
R* W ~ j Uj (t) Uh (t-x) dt. (4.15)
— оо
Решающее устройство принимает решения в момент окончания
полезных сигналов, т. е. полагаем, как и ранее, что в приемнике
есть синхронизатор, который обеспечивает синхронный отсчет
информации.
Если на входе фильтра действует только. полезный сигнал,
то значение напряжения на его выходе в момент принятия решения
(момент отсчета) равно ±1, поскольку оно равно максимальному
значению АКФ с учетом знака передаваемого информационного
символа. При действии /-го мешающего сигнала значение ВКФ
в момент отсчета равно Rjk (τ), где τ — произвольное значение
аргумента, |τ|^Γ. При непрерывной передаче информационных
символов /-м абонентом в момент отсчета напряжение будет равно
Vjh = ljRjk(t - tj) + HRjk(x - tj - T)y (4.16)
где ξ;, ξ/ = ± 1 — случайные величины, определяемые знаками
ийформационных символов; tj — случайный сдвиг во времени
начала работы /-го абонента. Таким образом, величина Vjk
случайна из-за случайности информационных символов и случайного
сдвига во времени начала работы /-го абонента.
Пронумеруем номера мешающих абонентов так, чтобы / = 1, I.
Взаимная помеха в момент отсчета есть сумма напряжений вида
(4.16):
Vko= 2^=2 1% Rjk (*-*/) + 6/ Rjk (τ-tj-T)]. (4.17)
Индекс «с» означает, что Vkc соответствует одному из возможных
сочетаний мешающих абонентов, число которых определяется
биномиальным коэффициентом С[ .
Обозначим через Rjk произвольное значение Rjk (τ — tj), т. е.
Rjk 6 Rjh (τ — tj)- Так как tj — случайная величина, то и Rjk —
случайная величина. Аналогично, Rjk 6 Rjk (τ — h — Τ).
Поскольку Rjh (τ — tj) и Rjk (τ — tj — Τ) имеют одни и те же
значения, что и Rjk (τ), но только в различные моменты времени, то
Rju 6 Rjk (τ) и Rjk ζ Rjh (τ)· С учетом принятых обозначений,
из (4.17) получаем:
Пв-2 (tjRjk+liRh)· (4.18)
/«1
Величина VhG — случайная, так как, во-первых, она сумма
случайных величин Vjh и, во-вторых, сумма случайного числа
слагаемых по различным сочетаниям. Таким образом, случайная
величина Vkc> взаимная помеха в момент отсчета, представляет собой
функцию следующих случайных величин:. 1) числа (мешающих
95
абонентов /; 2) номеров мешающих абонентов (различных сочетаний
Cl ; 3) информационных символов ξ7·; 4) момента начала работы
абонента tj.
Для выяснения влияния взаимной помехи Vkc на
помехоустойчивость в дальнейшем будет определена вероятность ошибки,
которая является функцией Vhc и, следовательно, функцией
перечисленных случайных величин. Отметим их основные
характеристики.
Число мешающих абонентов /, так же как и число активных
абонентов, определяется биномиальным законом распределения
P(t) = ClL/a (l-Pa)LK-'. (4.19)
Поскольку Vhc является функцией /, то и ее плотность
вероятности будет функцией случайной величины /. Поэтому все возможные
функции от Vkc необходимо усреднять по I. В соответствии с
известными результатами [104] среднее значение функции / (VhG)
определяется равенством:
ш1{/(^с)}=2Р(0п11|/
S (IjRjk+VR'fi)
(4.20)
где символ / под тх означает усреднение по /. В общем случае такое
усреднение произвести довольно трудно, так как слагаемые в (4.18)
имеют различные функции распределения. Для простоты, когда
в окончательные расчетные формулы I будет входить в явном виде,
будем подразумевать под I ее среднее значение! = paLK — 1 в
соответствии с (3.6). Основанием для этого является то, что среднее
значение суммы случайного числа одинаково распределенных
случайных величин равно произведению среднего значения числа
слагаемых на среднее значение случайной величины [104].
Относительно изменения номеров мешающих абонентов следует
заметить, что все возможные сочетания равновероятны. Поэтому
вероятность появления какого-либо сочетания равна 1/с£ ·
Информационные символы 1 и —1, по предположению,
равновероятны. Поэтому их плотность вероятности
w (ξ) = 0,5 [δ (ξ + 1) + δ (ξ - 1)], (4.21)
где δ (χ) — дельта-функция.
Относительно момента начала работы абонента будем
предполагать, что tj распределено равновероятно на интервале (—Г, Т).
Такое предположение справедливо потому, что если ВКФ от /-го
мешающего сигнала попадает на момент отсчета, то ее смещение
не превышает 2Г.
Прежде чем перейти к определению плотности вероятности
взаимной помехи, остановимся на корреляционных и статистических
свойствах ВКФ.
Корреляционные и статистические
свойства ВКФ. Обозначим плотность
вероятности случайной величины
Rik как wR (χ). Хотя сама ВКФ
Rjk (τ) является детерминированной
функцией времени, но из-за
случайной задержки tj ее отсчетное значение
Rjk — случайная величина. Так
как ВКФ с различными номерами
отличаются друг от друга, то их
функции распределения и моменты
также будут различны. Сначала
найдем функцию распределения и
моменты при непрерывном определении
ВКФ (4.15). При этом будем
предполагать, что ВКФ действительная
функция.
Как было отмечено, величина Rjk
случайна потому, что из-за
случайной задержки tj ВКФ Rjk (τ)
попадает на момент отсчета
произвольно. Для определения случайной
величины Rjk надо предположить, что
аргумент ВКФ принимает
произвольные значения на отрезке [—Г, Т].
Поскольку tj равномерно
распределена внутри отрезка [— Г, Т],
то плотность вероятности случайной
величины τ
П/2Г при,,,<Г,
tW [О при |*| > Т. '
Случайные величины Rjk и τ
связаны функциональной
зависимостью
Rjh = Rjk(T). (4.23)
Поэтому для нахождения
плотности вероятности wR (χ)
необходимо воспользоваться общим правилом
определения плотности вероятности
функции случайной величины [104].
Поскольку обратная функция τ =
= Φ (Rjk) неоднозначна, то
плотность вероятности будет равна сумме
плотностей вероятности от каждого
однозначного участка функции
τ = φ (Rjk)· Пусть таких участков
будет μ. Согласно [104] имеем
wr? (х) =
Rjh v '
= Ι>τ[φμ(*)]ΙφμΜΙ> (4-24)
μ
где φμ (χ), φ^ (χ) — обратная
функция и ее производная на μ-м участке
однозначности. Используя (4.22), из
(4.24) получаем
%*<*> =
— 2|Ф|1М1. (4-25)
2Т
μ
Найдем v-й начальный момент
случайной величины Rjk. По
определению
mv {RJb} =
<jk
(χ) dx. (4.26)
Подставляя в (4.26) функцию
распределения (4.25) с учетом участков
однозначности, получаем
2Г^ S
μ+1
,{Rjk} =
I
*ν|φμ(*)μ*, (4.27)
где χ и *„_ι_ι границы μ-го участка
однозначности. Напомним, что в
интегралах (4.26), (4.27) аргумент χ
соответствует случайной величине
Rjk. Поскольку Rjk и τ связаны
функциональной зависимостью (4.23),
то можно перейти к новой
переменной τ в интеграле (4.27). При
этом пределы интегрирования
преобразуются в τ , τ ,ρ что
определяется обратной функцией τ = φ(*);
произведение | φ' (χ) | dx = dx,
поскольку άτ/dx = φ' (*); степень
= R^k (τ). Β результате п
mv {Ъъ} =
1 χΊΤμ+Ι
μ τμ
Суммируя, находим, что
mv {Rjk} =
Τ
= ^$ *7*w*·
олучаем
(4.28)
(4.29)
-Τ
Полученная формула (4.29) позволяет
находить моменты случайной
величины Rjk по детерминированной
ВКФ RJk (τ).
97
Найдем теперь закон
распределения случайной величину и ее
моменты при дискретном определении
ВКФ. Пусть ВКФ определена в
дискретных точках при значениях
τ = λΔ/, λ — целое число. Если
;-й дискретный фазоманипулирован-
ный сигнал определяется кодовой
последовательностью (1.93) Aj =
= (aju ..., α/ν, ..., ajN), где N —число
символов ajVy ν = ί,"Ν, a k-и
сигнал — кодовой последовательностью
Ак= (flw, ..., а^9 ..., akN), то ВКФ
таких сигналов в точках τ = λΔ/
определяется соотношением (1.125),
которое для λ > 0 и λ < 0 записьь
вается так:
Rjkfr) =
ajvak,v-h
ί 1 *
при λ>0,
! iV+λ
— 2 α/να*,ν-λ
*ν ν=1
при λ<0.
(4.30) ·
Поскольку дискретный сигнал
имеет конечное число различных
градаций символов α·ν (в простейшем
случае ФМ сигналов ajv = ± 1),
то ВКФ Rjk (λ) также имеет конечное
число различных значений. Поэтому
для определения случайной
величины Rjk достаточно найти
вероятности, с которыми она принимает то
или иное значение. ВКФ имеет всего
2N + 1 значение, но из них два
крайних равны нулю тождественно.
Так как при непрерывной передаче
информации последний нуль одной
ВКФ совпадает с первым нулем
ВКФ, запаздывающей на 2Г
относительно исходной, то будем
учитывать только первый нуль, т. е.
считать в каждой ВКФ 2N боковых
пиков. Каждый из боковых пиков
данной ВКФ имеет равную
вероятность 1/2 N попасть на момент
отсчета, если данная ВКФ попадает на
этот момент. Пусть κ^ (q) — число
появлений данного значения Rjh =
= q. Тогда вероятность появления
данного значения Rjk равна
В соответствии с определением
[104] v-й начальный момент
mv {Rjk} =
= Σ iviPRih (?*)> (4·32)
где суммирование производится по
всем /. Подставляя (4.31) в (4.32),
получаем
mv {#**} ^
= ^2??*7fcM. (4,33)
Переходя от суммирования по i
к последовательному суммированию
значений ВКФ, находим
mv {RJh} =
2Ν
Κ = -(Ν-\)
%(ЙяЧк(йда (4.31)
Таким образом, v-й начальный
момент случайной величины Rjh при
дискретном определении ВКФ
пропорционален сумме значений ВКФ,
взятых в v-й степени. Суммирование
в (4.34) производится по всем λ,
при которых Rjh (τ) не равна
тождественно нулю.
Плотность вероятности взаимной
помехи при приеме противоположных
сигналов. Обозначим произведения
в (4.18)
i)jk-ljRjk,
ч;*=*;*;*. (4·35>
Поскольку плотность вероятности
случайных величин ξ^, ξ.' определена
формулой (4.21), то, используя
определение плотности вероятности
произведения двух случайных величин
[104], получаем
«VW =
= 0,5 [wRjh (-χ) + wRjk (x)]. (4.36)
Плотность вероятности wn.. (х) яв-
ляется четной функцией. Так как
ij и £/ статистически независимы, то
статистически независимы и
случайные величины t)jk и r\jk. Поэтому
w , (х) = wn (х). Из-за четности
плотности вероятности (4.36) срец-
98
нее значение mx {r\jh} = 0, а
дисперсия и четвертый момент
случайной величины r\',k по определению,
с учетом формул (4.29), (4.36) равны:
оо
σ/*= ί *2t%jkMdx =
— оо
оо
2Т
j* RJk(x)dx, (4.37).
— Г
M47ft= J X*W^ (X)dx =
— oo jA
oo
= f x*wR (x)dx =
Плотности вероятности случайных
величин &jk определяются
следующим образом [104]:
= оъс Λ/ή шц (окс У η χ). (4.46)
Плотность вероятности случайной
величины Ζη с найдем, используя
характеристическую функцию. Пусть
случайной величине ejh соответствует
характеристическая функция
θ . (υ)= J we, (x)eiOXdx. (4.47)
ejh
Разложим ее в ряд по моментам:
2Т
] Rfk(x)dt. (4.38) = 2
— Τ
Подставляя (4.35) в (4.18),
запишем взаимную помеху в следующем
виде:
/
^с= 2 (rUfc + Л/л)· (4.39)
/==1
Среднее значение взаимной
помехи m1 {Vkc} = 0, а ее дисперсия
М2 {Vftc} «
= 2 Σ <ft = 2/ajc> (4.40)
/ = 1
где среднеарифметическое
1 /
°L = T% °]k. (4.41)
* /=ι
Произведем нормировку
случайных величин в (4.39). Обозначим
Zftc = Vftc/OfccV«, (4.42)
еул = Лул/алс Vrt, (4.43)
η = 2Л (4.44)
При этом
ι
Zkc= Σ («Jfc+ «/*). (4.45)
/-=ι
a m1{2fcc} = 0f M2 {Zkc} = 1.
= 1
m~o (aftc)mnm/2m!
>;*<*
™lc2 "Mc24
t)«z
υ*—...
(4.48)
Нечетных моментов нет, так как
плотность вероятности случайной
величины Ζ& с является четной функцией.
Поскольку характеристическая
функция суммы независимых
случайных величин равна произведению
характеристических функций ела*
гаемых [104], то
θ*„»= π θ»»=
bftc
/=1
7ft
^a|c24
(4.49)
Используя обычные методы при*
ближения [104] и полагая для
простоты, что Mmi/fc = 0 при m > 4,
получаем
β**<°>-
-σ»/2 ,
~ е-^ (ί + (Vftc/24n) о*), (4.50)
99
а плотность вероятности
(4.51)
где Я4 (.ν) — многочлен Эрмита
четвертого порядка,
+ 3
" ι = ι \ one I
(4.52)
а коэффициент эксцесса yjk
определен следующей общей формулой
[104]:
γ = (ЛУо4) — 3. (4.53)
Из (4.52) следует, что γ& с
является средневзвешенным значением
коэффициента эксцесса для данного
сочетания абонентов, причем
слагаемое в квадратных скобках
определяет смещение.
Плотность распределения
взаимной помехи при приеме
ортогональных сигналов. Плотность
распределения (4.51) была получена при
условии, что осуществляется прием
противоположных сигналов. Кратко
остановимся на тех особенностях,
которые имеют место при приеме
ортогональных сигналов.
Предположим, что все абоненты осуществляют
передачу информации при помощи
двух ортогональных сигналов.
Рассмотрим взаимную помеху на выходе
одного из согласованных фильтров
fe-ro абонента, если на его входе
действуют сигналы от / мешающих
абонентов. Используя такой же метод
определения взаимной помехи, что
и при передаче информации
двумя противоположными сигналами
(см. формулу (4.17)), можем записать
взаимную помеху в момент отсчета
при передаче ортогональных
сигналов в виде [43]
/
'Ас:
Σ ν»-
= Σ КЯ/.*(*-0) +
/ = ι
+ (1-ΘΛ/ι*(τ-0) +
+ (1-Е')Д/1*(*-0--Л]. (4.54)
В этом выражении в отличие от
(4.17) информационные символы ξ,
ς' = 1,0 с вероятностями, равными
1/2. Когда ξ = 1, то 1 — ξ = 0, а
когда ξ = 0, до 1 — ξ = 1. Поэтому
квадратная скобка в (4.54) содержит
также два слагаемых, как и в (4.17).
Индексы /о и Д у ВКФ в (4.54)
соответствуют двум ортогональным
сигналам /-го абонента, которые
служат для передачи информационных
символов «0» и «1». В общем случае
ВКФ с индексами j0k и j±k не равны
тождественно друг другу, как в
случае противоположных сигналов. Это
является основной причиной
отличия взаимной помехи (4.54) от (4.17).
При противоположных сигналах
исходная плотность распределения
(4.36) симметрична относительно
начала координат. А это означает, что
все нечетные моменты взаимной
помехи (4.17) равны нулю. При
ортогональных сигналах плотность
распределения произвольной ВКФ
может и не быть симметричной.
Поэтому ее нечетные моменты могут
быть и не равны нулю.
Следовательно, их необходимо учитывать при
определении плотности
распределения взаимной помехи (4.54).
Поскольку при разложении плотности
распределения основное значение
среди нечетных моментов имеют
первый начальный момент ( или
среднее значение) и третий центральный
момент, выражаемый через
коэффициент асимметрии, то имеет смысл
рассматривать только эти нечетные
моменты. Однако для большинства
В КФ среднее значение тождественно
равно нулю, и лишь для немногих
мало отличается от нуля. Поэтому
положим, что среднее значение ВКФ
равно нулю и будем учитывать
только третий центральный момент.
Используя тот же метод [31],
который был применен для определения
плотности вероятности (4Г51),
можно показать, что плотность
вероятности нормированной взаимной
помехи Zk с = Vk с/У" <*и с (4.42), где
Vh с определено согласно (4.54),
100
представляется следующим
выражением:
wZhc(x)-
V2"
2π [
1 + -~ Н3 (х)+
+ S:^W + -^-^ew], (4.55)
24/г
72/г
где
°ic =
Л / =
Σ °h (4·56)
/ = ι
aftc = — 2 ocjh(^^-)\ (4.57)
1 vi / QJk \A ,
7ftc=— 2j Vjft — +
л / = ι \ σ^ο /
+ 3
Л у = 1 \ ^hc
Ojk
— 1
, (4.58)
вестный метод нахождения
плотности вероятности модуля суммы двух
независимых взаимно
перпендикулярных векторов [104]. Обозначим
модуль взаимной помехи pftc =
= I Vkcl-
Он равен
9hc=VZlc + Yl
key
(4.60)
где ZfcC, Yhc — независимые
случайные величины, законы распределения
которых определяются формулой
(4.55). Плотность вероятности
модуля рис определяется общим
соотношением [104J
2π
w
(Pftc)=Pfcc J wZk (Pkccostp) χ
kc
XwZh (Pfccsinq>)dq>, (4.61)
так как wv — w7
rkc
'he
Заменяя в
(4.55) аргумент х на pfcccoscp и
pfccsinp, подставляя полученные
выражения в (4.61) и производя
интегрирование, получаем:
коэффициенты асимметрии a,jk
определяются согласно общей формуле
[104]
α = Μ3/σ3, (4.59)
а коэффициенты эксцесса yjk
согласно (4.53); #з (*), #4 (*),
#в (х) — многочлены Эрмита. Из
формулы (4.56) следует, что σ| с
является среднеарифметическим
значением дисперсий σ% ΒΚΦ
мешающих абонентов; из формулы (4.52)
видно, что аи с является
средневзвешенным значением коэффициентов
асимметрии ауь; из формулы (4.58)
видно, что Yfcc является смещенным
средневзвешенным значением
коэффициентов эксцесса γ^.
При когерентном приеме
ортогональных сигналов знание
плотности вероятности (4.55)
мгновенного значения взаимной помехи
достаточно для расчета
помехоустойчивости. При некогерентном приеме
необходимо иметь плотность
распределения модуля взаимной помехи.
Для ее определения используем из-
/ ч - Pic/2
^(Pfec)^Pfec e
H-g *№*>>+
(Pftc)
, (4.62)
где многочлены
ваФ) = ей) ρ4 - б ρ2 + б,
Be (Ρ) = (?/β) Ρ6 ~ (45/4) ρ4 +
+ 45 ρ2 —30. (4.63)
Второе и третье слагаемое в
квадратных скобках (4.62) определяют
отличие закона распределения
w(Phc) 0T релеевского. Чем они
меньше, тем меньше отличие. Отметим,
что коэффициент асимметрии а&с
входит в (4.62) в виде квадрата, т.е.
любая асимметрия исходного
распределения (4.55) приводит к
увеличению различия между
распределением (4.62) и релеевским.
101
4.3. Выбор систем сигналов для асинхронных адресных
систем
С первого появления сложных сигналов и их применения в
радиотехнических системах исследователи интуитивно представляли,
что применяемые сигналы должны обладать «хорошими»
корреляционными свойствами, т. е. обладать «малыми» боковыми пиками
АКФ. При этом смысл «малых» боковых пиков сводился к тому, что
они должны быть как можно меньше, т. е. стремиться к нулю.
При развитии ААС, помимо требований к АКФ, возникли те же
требования и к ВКФ, т. е. боковые пики ВКФ должны быть малыми.
Однако исследования многих систем сигналов и предельные свойства
систем сигналов убеждают в том, что получить «нулевые» ВКФ
невозможно. Поэтому сразу же возникает вопрос о том, каким
образом следует уменьшить ВКФ. Ответить на него можно только в том
случае, если выяснить, как влияют боковые пики ВКФ на
помехоустойчивость приема информации. Решение этого вопроса позволит
сформулировать правило выбора систем сигналов: следует выбирать
ту систему сигналов, которая обеспечивает максимальную
помехоустойчивость. Основные правила выбора систем сигналов
сформулированы в работе [31]. Для обоснования их сначала определим
вероятность ошибки.
Вероятность ошибки при приеме противоположных сигналов.
Вероятность ошибки при приеме информации k-м абонентом и при
данном сочетании мешающих абонентов определяется следующим
выражением:
Рош*о=Р{Пс>1>= J Whc(x)dx, (4.64)
1
где wyhG (х) — плотность вероятности случайной величины Vhc.
Поскольку все сочетания равновероятны, то вероятность
ошибки для &-го абонента при усреднении по всем сочетаниям равна
%
Рош h = πΐχ {Рош ftc} = —j— 2 рош и с· (4-65)
CLK c=l
Из (4.64), (4.65) следует, что
оо
Рош л = $ wVh(x)dx,
1
а
Ч c==1
(4.66)
(4.67)
т. е. плотности вероятности усредняются.
102
Вероятности ошибки Рош h в общем случае могут быть
различными для разных номеров k. Назовем средней вероятностью
ошибки среднеарифметическое всех Рош h:
Рош^-^-i Р«ш*. (4-68)
Определенную таким образом среднюю вероятность ошибки
можно принять за основу правила выбора системы сигналов, которое
сформулируем так; лучшей является такая система сигналов,
которая обеспечивает меньшую среднюю вероятность ошибки. Выразим
среднюю вероятность ошибки Рош через параметры системы
сигналов. Используя (4.42), из (4.64) получаем:
00
Рош*с=Р{^с><7/,с}= $ wZkc(x)dx, (4.69)
Яке
где
<fko=UohoVn (4.70)
является отношением сигнал/взаимная помеха по напряжению.
Подставляя (4.51) в (4.69), получаем
Ponlftc~ l-F(qkc) + ^-(qlc-3qkc) L_. (4.71)
где интеграл вероятности F (qkc) определяется формулой (2.16),
Поскольку при qkc > 1 для F (qkc) можно использовать
асимптотическую формулу [104]
F{qh0)~l - ' е-**'/2, (4.72)
У 2π qkc
то из (4.71) находим, что
Рош,с ~(l—F (qhc)) [1 + (ykc/24n) (q*kc - 3qL)l (4.73)
Из выражения (4.51) видно, что ykc Φ 0 приводит к отличию
Wzkc (χ) от нормального закона распределения. По этой же
причине Pomfcc (4.73) отличается от 1 — F (qkc).
Правило выбора систем сигналов при нормализации взаимной
помехи. Если ykc = 0 или настолько мало, что второе слагаемое
в (4.73) много меньше единицы, то из (4.73) следует:
е-?1с/2
PQmkc=l-F(qkc)c*y=^. (4.74)
В соответствии с (4.65) при усреднении по всем сочетаниям,
находим:
г1
^ Т 2 л
1 к ρ — <7£с/2
р— -гг Σ те· (4·76)
Lk c==i
Так как a]k (4.37) могут быть различными, то могут быть
различными и ale (4.41), и qkc (4.70). Определим условия, при которых
минимизируется Рош k. Обозначим
σία = σΙ + Δσίο· 6ftc = AoIJg] . (4.76)
Определим среднюю дисперсию &-го абонента как
c1l
1 к
СГ~ ^ «/с (4-77)
При этом
Lk c=l
2 Δσ|ο = 0, 2 6ас = 0. (4.78)
с = 1 с=1
Полагая, что 8kc < 1, т. е. отклонение дисперсий а|с мало,
из (4.70) приближенно находим:
qkc ~qk(l- bkJ2 + Зб|с/8), (4.79)
где
Як = VokVn. (4.80)
Подставляя (4.79) в (4.75) с точностью до малых более высокого
порядка, получаем
Pomk~(l-F(qk))i 1+ ^- 2 δίΛ (4.81)
Первый множитель определяет вероятность ошибки как функцию
средних значений а\ (4.77) и qk (4.80), а второй определяет
увеличение вероятности ошибки за счет различия в дисперсиях а|с.
Поскольку б|с > 0, то для уменьшения Р2шл необходимо уменьшать
различия между дисперсиями а|с. Минимум ошибки будет в том
случае, если а|с = о%. Отметим также, что влияние 2^1с на Рош k
с
тем больше, чем больше qk, т. е. чем меньше требуемая вероятность
ошибки. Из (4.81) следует, что если ql^kc < 1/2(6 ftc < V^oln),
то вторым слагаемым во втором множителе можно пренебречь.
При этом
P0Blh~l-F Ы· (4-82)
104
Из приведенного условия следует, что с ростом η (числа
слагаемых во взаимной помехе) влияние 8kc на Рош k уменьшается.
Если же 8kc = О, то (4.71) безусловно переходит в (4.82). Таким
образом, при прочих равных условиях необходимо уменьшать
разброс дисперсий ale и стремиться привести их к среднему значению
σ|. Согласно определениям (4.37), (4.77) имеем
(4.83)
ьк с- 1
Рассматривая все сочетания элементов ojk, /= 1, LKt k Φ /,
можно выяснить, что элемент a)k повторяется Ciri-2 раз. Поэтому
Следовательно, а% является среднеарифметическим значением
дисперсий ВКФ с номерами jkf где k = const, / = 1, L — 1.
Аналогично, производя усреднение по k, т. е. определяя
среднюю вероятность ошибки (4.68), можно найти, что она
минимизируется, если разброс между а% стремится к нулю, т. е. а% совпадает
со среднеарифметическим значением
--dbriS*- (4·85)
Величину σ2 назовем дисперсией системы. Обозначая через
q = VaVn (4.86)
tip и а\ ->■ σ2 будем иметь
Рош - 1 - F (q). (4.87)
Полученные результаты позволяют сформулировать правило
выбора системы сигналов: при условии нормализации взаимной
помехи необходимо выбирать систему сигналов с наименьшей дисперсией
σ2. Если дисперсии системы равны, то лучше та система, у которой
меньше разброс дисперсий ВКФ ofk-
Мерой разброса является величина
LK LK
ζ= Σ Σ (Δσ^)2, (4.88)
k = 1 / = 1
где Δσ/^ = α% — σ2. Формула (4.88) может быть получена так же
как сумма 2 δ/ с в выражении (4.81). Таким образом, если дисперсии
с
системы равны, то лучше та система, у которой ζ меньше.
Правило выбора систем сигналов, когда распределение взаимной
помехи отличается от нормального. Сначала предположим, что все
105
ВКФ обладают одинаковыми дисперсиями, т. е. а% = ой. β этом
случае из (4.73) имеем
VomKo<*(l-F(q))[l + -ξ£ (tf4 - З?2) ] , (4.89)
где q определяется формулой (4.85), a ykc согласно (4.52)
Y*c=i] Тл/'. (4<9°)
Производя усреднение по Ёсем сочетаниям и абонентам, получаем
Рош - [1 - F (q)] [1 + (у/24п) (q* - 3f)],> (4.91)
а коэффициент эксцесса системы
^К LH
y=[Lk(Lh-\)]-i 2 Σ Υ/*· (4·92)
*= 1 /= 1
Чем меньше γ, тем меньше средняя вероятность ошибки.
Полученные результаты позволяют сформулировать правило выбора
Рис. 4.2
системы сигналов: при равенстве дисперсий систем необходимо вы*
бирать систему сигналов с наименьшим коэффициентом эксцесса.
Сравнение двух систем сигналов. Сравним две системы
дискретных фазоманипулированных сигналов с числом символов N = 64
[31]. Первая система (У) основана на кодовых последовательностях
Уолша (см. гл. 12), которые являются строками матрицы Ада-
мара. Вторая система (П) является производной системой сигналов
(см. также гл. 12), кодовые последовательности которой
получались при помощи посимвольного умножения кодовых
последовательностей Уолша на производящую кодовую последовательность
(рис. 4.2). Последняя была выбрана из условия малости боковых
пиков АКФ. Были подсчитаны все ВКФ обеих систем (в дискретных
точках) и определены дисперсии и коэффициенты эксцесса. Для
системы У σ2 = 7,8 · 10~3, у = 20. Для системы Πσ2 = 7,7 · Ю"3,
у = 0,64. Разница между дисперсиями очень мала, а коэффициенты
эксцесса сильно отличаются. Это объясняется тем, что ВКФ системы
У имеют боковые пики гораздо больше, чем ВКФ системы П. Была
рассчитана средняя вероятность ошибки. Для расчета
использовалась формула (4.92), приведенная к следующему виду:
Pmtxll-F ((7)1(1 +fid),
где μ = γσ2/24, d = φ — 3<Д a q определяется формулой (4.86).
На рис. 4.3 приведены полученные зависимости Рош от q для обеих
106
систем. Сплошной линией показана зависимость 1 — F (q)y
соответствующая нормализации взаимной помехи. Из рис. 4.3 видно,
что система Π (с меньшим коэффициентом эксцесса) обеспечивает
меньшую вероятность ошибки, чем система У. Если вероятность
ошибки
помеха
10
-5
в отношении
сигнал/взаимная
2 4 q
ош- iv , проигрыш
относительно 1 — F (q)
для системы У составлял 1,7 дБ'
а для системы Π — 0,172 дБ.
Из проведенного сравнения
следует, что реальные системы
сигналов дают вероятность
ошибки больше, чем в случае
нормализации взаимной помехи.
Увеличение вероятности ошибки (или
проигрыш в отношении
сигнал/помеха) существенно зависит от выбора
системы сигналов. Следовательно,
выбор систем сигналов для ААС
имеет практическое значение.
Вероятность ошибки при
приеме ортогональных сигналов и
правило выбора систем сигналов.
Рассмотрим некогерентный прием
двух ортогональных сигналов [43]. Вероятность ошибки в общем
случае определяется следующей формулой [162]:
10"'
10~5
яг*
10 ° Υ
10'
1-7
ю ' μ
Рпш
Г ^^Ч
h
l·
'
\\ 1
L
VI
V
1 \\
Рис. 4.3
Pom=5dZ1^2(Z1,Z2)dZ2,
о zx
(4.93)
где Ζχ, Ζ2 — огибающие согласованного и несогласованного
каналов оптимального приемника. (Когда передается один из
ортогональных сигналов, то один из каналов оптимального приемника
(рис. 2.8) является согласованным с ним, а другой —
несогласованным.) Двумерная плотность вероятности w2 (Zly Z2) равна
произведению одномерных, так как Zx и Z2 статистически независимы,
поскольку сигналы и фильтры ортогональны. Одномерная
плотность вероятности в несогласованном канале определяется
выражением (4.62); в согласованном канале плотность вероятности также
определяется по (4.62), но с введением среднего значения, равного
нормированному значению сигнала.
Из (4.93) видно, что вероятность ошибки зависит от
вероятности превышения огибающей в несогласованном канале уровня
Z2. Как следует из (4.62), вероятность превышения величиной pkc
некоторого уровня определяется в значительной мере
коэффициентом эксцесса yk0 и квадратом коэффициента асимметрии а|с.
Поскольку при существенных значениях pkc многочлены (4.63)
положительны, то второе и третье слагаемое в квадратных скобках (4.62)
будут увеличивать вероятность превышения величиной р&с заданного
107
уровня. Это приведет к увеличению вероятности ошибки. Производя
последовательное усреднение вероятности ошибки по всем
сочетаниям и по всем абонентам, можно показать, что в первом
приближении средняя вероятность ошибки определяется квадратом
коэффициента асимметрии системы
«2= L ' η Σ Σ^ (4·94)
и коэффициентом эксцесса у (4.92). При этом правило выбора
системы сигналов формулируется следующим образом: при
прочих равных условиях необходимо выбирать систему сигналов с
наименьшим квадратом коэффициента асимметрии системы, или с
наименьшим коэффициентом эксцесса системы, или с наименьшими
обоими коэффициентами.
О выборе сигналов при действии мощных взаимных помех.
Сформулированные правила выбора систем сигналов справедливы
при условии, что мощности мешающих сигналов между собой равны
и равны также мощности полезного сигнала. Конечно, случай
равных мощностей на практике не встречается, но если мощности
мешающих и полезного сигналов имеют небольшой разброс
относительно некоторого среднего уровня, то можно считать, что
сформулированные ранее правила выбора систем сигналов будут
справедливы. На практике довольно часто встречаются случаи, когда
мощности одного или нескольких мешающих сигналов во много раз
больше мощности полезного сигнала.
Рассмотрим особенности выбора систем сигналов, которые имеют
место в этом случае. Положим, что мощность полезного сигнала
ΡCi а мощность мешающего сигнала Яп. Мощность сигнальной
составляющей на выходе согласованного фильтра в момент принятия
решения (отсчета) пропорциональна Яс, а мощность мешающей
составляющей PnRfk (τ), где Rjk (τ) — ВКФ полезного fe-ro сигнала
и /-го мешающего. Величина τ определяется смещением ВКФ
относительно момента отсчета. Отношение сигнал/помеха на выходе
будет равно
Α»(τ) = Ρ0/ΡπΛΪΛ(τ). (4.95)
Оно зависит от τ. Наименьшее отношение сигнал/помеха будет равно
<£ин = /УЯпЯ2макс, (4.96)
где Ямакс = шах | Rjk (τ) | — максимальное значение \RJk (τ) |.
Очевидно, что всегда необходимо уменьшать максимальные боковые
пики. Отсюда следует правило выбора сигналов, образующих
систему: при прочих равных условиях необходимо выбирать сигналы,
у которых максимальные пики ВКФ минимальны.
Если максимальные пики ВКФ уменьшены до среднеквадратаь
ческого уровня Ojh = σ, то среднее отношение сигнал/помеха
будет равно
φ ε» PQIPuo\ (4.97)
JOB
Например, если σ2 = 1/2FT, то
q* = (Pc/Pn)2FT, (4.98)
где FT = В — база сигнала. Для дискретных фазоманипулиро-
ванных сигналов σ2 = 1/2Ν, где N — число элементов. Для таких
сигналов
φ = {Ρ,!Ρη)2Ν. (4.99)
Из формул (4.98), (4.99) следует, что увеличение базы сигнала
увеличивает φ и может компенсировать уменьшение отношения PJPn
при увеличении Ри.
Из (4.96), (4.98) можно найти условия, при которых
сформулированные правила будут справедливы. Как следует из материалов
гл. 2, для надежного приема информации отношение сигнал/помеха
на выходе согласованного фильтра должно существенно превышать
единицу. Поэтому, если мощность помехи такова, что <$ин ^ 1,
то можно считать систему передачи информации неработоспособной.
Полагая в (4.96) ^ин ^ 1, получаем следующее условие
Ус Амакс
Аналогично из (4.98) находим условие
-^ >2/Т. (4.101)
При этом линейные методы обработки сигналов не могут обеспечить
надежного приема информации и поэтому необходимо переходить
к нелинейным методам обработки сигналов и применению
специальных сигналов. Все это более подробно рассмотрено в следующей
главе.
Глава 5
ОСНОВЫ ФИЛЬТРАЦИИ МОЩНЫХ ПОМЕХ
5.1. Классификация помех
В предыдущих трех главах была исследована
помехоустойчивость различных систем передачи информации (СПИ) при дей»
ствии двух видов помех. Во-первых, рассматривалось воздействие
помехи в виде нормального стационарного случайного процесса
с равномерной спектральной плотностью мощности. Типичным
представителем такой помехи является собственный шум приемника.
Было показано (см, гл, 2), что помехоустойчивость приема инфор-
т
мации при действии такой помехи полностью определяется
отношением сигнал/шум (2.20); (2.30), которое зависит только от энергии
сигнала Ε и спектральной плотности мощности шума Ν0 и равно
h2 = E/N0. Это отношение выражается через отношение сигнал/шум
на выходе согласованного фильтра q2 равенством q2 = 2й2, так как
согласно (2.24)
<72=~. (5.1)
No
Для надежного приема информации необходимо, чтобы q2 > 1.
Например, если q2 = 20, то вероятность ошибки при когерентном
приеме информации будет равна 10"4—10"5 (см. рис. 2.3).
Во-вторых, в предыдущих главах рассматривались взаимные
помехи, называемые также системными. Было показано, что
применение сложных сигналов и кодового разделения абонентов
позволяет успешно бороться со взаимными помехами, если база сигнала
много больше числа мешающих абонентов (4.2) и взаимные помехи
по мощности не выходят за определенные пределы (4.100), (4.101).
Если же взаимные помехи существенно превышают полезный сигнал
по мощности, то при линейной обработке сигналов СПИ не будет
работоспособной. Такие взаимные помехи будем называть мощными.
Кроме мощных взаимных помех, возможно воздействие мощных
организованных помех, предназначенных для подавления
радиотехнических систем (см., например, [13, 130]).
Воздействие мощных организованных и взаимных помех
существенно зависит от их мощности. Если спектральная плотность
мощности помехи описывается функцией Ν (ω), то средняя
мощность помехи равна
Pu = -^]ff(^)(bJJN(f)df. (5.2)
о о
Если интеграл в (5.2) сходится (имеет смысл), то мощность
помехи равна некоторой конечной величине. Помехи такого рода
будем называть помехами с ограниченной (постоянной) мощностью.
При этом Ри = const. Некоторые виды мощных организованных
помех нельзя отнести к помехам с ограниченной мощностью,
поскольку у таких помех спектральная плотность мощности постоянна
в пределах полосы частот, которая намного шире ширины спектра
сигнала. Будем называть их помехами с ограниченной спектральной
плотностью. К таким помехам относится заградительная шумовая
помеха [13]. Помехоустойчивость приема информации при
воздействии помех с ограниченной спектральной плотностью мощности
не зависит от формы сигналов и полностью определяется отношением
сигнал/помеха q2 = 2E/NU (5.1)t где Νπ — спектральная плотность
мощности помехи. Для повышения помехоустойчивости необходимо
применять алфавиты с объемом т > 2. Поскольку
помехоустойчивость при воздействии таких помех подробно рассмотрена в гл. 2,
J10
ίο в дальнейшем помехи с ограниченной спектральной плотностью
не будут рассматриваться.
Иное положение существует при приеме информации на фоне
помех с ограниченной мощностью, у которых Рп = const. В этом
случае помехоустойчивость будет определяться не только энергией
сигналов, но и их структурой, и некоторыми параметрами.
Отметим, что наиболее важным параметром, определяющим
помехоустойчивость при действии помех данного рода, является база
используемых сигналов (1.3) В =* FTf
где F — ширина спектра сигна- f
л а, Т — его длительность. F
По своим
частотно-временным свойствам помехи с
ограниченной мощностью можно
разделить на сосредоточенные,
узкополосные, импульсные и
структурные. fn
Сосредоточенными помехами
называются такие, у которых
ширина спектра Fn совпадает
с шириной спектра сигнала
(сигналов) F, т. е. Fn = F и помеха
полностью перекрывает спектр q tn Τ ϊ
сигнала. Узкополосными
помехами являются такие, у кото- Рис· 5·1
рых Fn < F. В свою очередь
импульсные помехи определяются тем, что их длительность Ти < Т.
Структурными помехами называются такие, структура которых
подобна структуре используемых сигналов, т. е. помехи состоят
из тех же элементов, что и сигналы, но отличаются параметрами
манипуляции. К структурным помехам относятся все взаимные
или системные помехи, а из организованных — имитационные и
ретранслированные. f
На рис. 5.1 представлена частотно-временная плоскость (/, t)>
на которой для примера изображены дискретный частотный (ДЧ)
сигнал первого порядка (наклонная штриховка), узкополосная
помеха (сплошная горизонтальная полоса), импульсная помеха
(сплошная вертикальная полоса), структурная помеха
(вертикальная штриховка). Относительно сосредоточенной помехи
предположим, что она полностью перекрывает базисный прямоугольник
как по частоте, так и по времени.
Отметим, что повышению помехоустойчивости радиотехнических
систем вообще и СПИ в частности относительно помех с
ограниченной средней мощностью всегда уделялось большое внимание*
Первыми работами, в которых было показано преимущество систем
со сложными сигналами при воздействии сосредоточенных помех,
являются [167, 195]. Исследованию воздействия различного рода
помех и сравнению помехоустойчивости радиотехнических систем
111
с простыми и сложными сигналами посвящено большое число работ
(см., например, [6, 7, 16, 25, 27, 78, 94, 123, 124, 126, 157, 158, 166,
171] и др.). Перейдем к рассмотрению фильтрации помех,
указанных ранее. Сначала рассмотрим прием отдельных элементов
произвольного сигнала.
5.2. Оптимальный прием элемента сигнала
Обратимся к рис. 5.1. Он характеризует распределение энергии
сигнала и помех на частотно-временной плоскости. Для случая,
изображенного на рис. 5.1, сигнал и помехи совпадают только в
одном элементе, т. е. та или иная мощная помеха поражает один
элемент сигнала. В общем случае число пораженных элементов
случайно. Если оно мало, то этот факт можно использовать для
уменьшения воздействия помехи на сигнал в целом, т. е. реализовать
различие между частотно-временными структурами сигнала и помех.
Чтобы выяснить особенности приема сложных сигналов с учетом
структурных свойств, предварительно необходимо рассмотреть
прием элемента сигнала при воздействии различных помех.
Оптимальный прием элемента при воздействии нормального случайного
процесса осуществляется либо с помощью согласованного фильтра,
либо с помощью коррелятора. Так как оба эти устройства
эквивалентны с точки зрения помехоустойчивости, то будем рассматривать
прием с помощью согласованного фильтра.
Сигнал на выходе согласованного фильтра. При приеме
информации производится отсчет напряжения на выходе согласованного
фильтра в момент окончания сигнала (в момент принятия решения).
При рассмотрении приема элемента также будем интересоваться
напряжением в момент окончания элемента.
Максимум сигнальной составляющей на выходе согласованного
фильтра в общем случае будет в момент окончания сигнала
V = УШ, (5.3)
где Ε — энергия сигнала; Η — постоянная фильтра, определяемая
следующим образом (см., например, [25]):
H^±]\k{a)\4a = 2^\k(J)\*df. (5.4)
о о
В формуле (5.4) k (ω) — коэффициент передачи согласованного
фильтра (2.23), а постоянная а = ΥΗΙΕ.
Для элемента максимум сигнальной составляющей на выходе
согласованного с ним фильтра (элементного согласованного фильтра)
согласно (5.3) равен
V0 = VEJT0, (5.5)
где Е0 — энергия элемента; Н0 — постоянная фильтра,
определяемая в соответствии с (5.4).
112
Для пояснения постоянной фильтра Н0 (или Я) рассмотрим
следующий пример. Предположим, что элемент обладает
равномерным амплитудным спектром шириной F0 в пределах полосы частот.
В этом случае элементный согласованный фильтр будет иметь
постоянный в этой полосе модуль коэффициента передачи /С0. В
соответствии с формулой (5.4), получаем
#0 = 2KIFQ. (5.6)
Если амплитудный спектр элемента (сигнала) и модуль
коэффициента передачи отличаются от равномерных, то при заданном
максимальном усилении фильтра, равном /С0, постоянная фильтра
пропорциональна полосе частот шириной F0.
При подстановке (5.6) в (5.5) находим, что
V0 = KoVZEjo, (5.7)
т. е. максимум сигнальной составляющей на выходе элементного
согласованного фильтра пропорционален коэффициенту усиления
фильтра. Аналогичное соотношение можно найти и для V (5.3).
Сосредоточенная шумовая помеха. Предположим, что шумовая
помеха является нормальным случайным процессом с равномерной
спектральной плотностью мощности Nn в пределах полосы частот
шириной F0. Согласно (5.2) Яп==^п^о» т· е· спектральная плотность
мощности помехи
Nn = PJF0. (5.8)
Для помех с ограниченной средней мощностью Рп = const
увеличение ширины спектра приводит к уменьшению спектральной
плотности мощности Nu. Это является основной причиной
повышения помехоустойчивости при действии организованных помех с
ограниченной плотностью и при действии взаимных помех (4.1).
Мощность помехи на выходе произвольного фильтра по
определению [162] равна
Рпвы,-]Щ)\Щ)\Ч- (5.9)
о
Подставляя в (5.9) N (/) = Νηπ используя (5.4), получаем
Λζβηχ = ^π#0/2. (5.10)
Отношение сигнал/шумовая помеха по мощности на выходе
элементного согласованного фильтра (элементное отношение сигнал/
шумовая помеха) равно
Я1ш = -^— = 4г-· (5Л1)
*П ВЫХ Ш ^П
Заменяя энергию сигнала согласно формуле Е0 = Яс^о» а ^п
согласно (5.8), находим, что
qim = lJ3-2B0, (5.12)
"π
где
B0 = F0T0 (5.13)
113
— база элемента. Если вместо Ё0 в (5.12) подставим базу сигнала
5, то получим отношение сигнал/помеха для полного сигнала.
Формула (5.13) замечательна тем, что она показывает основное
преимущество сложных сигналов (В0 > 1) перед простыми (В0 = 1)
[167]. Чем больше база элемента (сигнала), тем больше отношение
сигнал/помеха, т. е. сильнее подавляется помеха с ограниченной
мощностью.
Узкополосная помеха. Пусть узкополосная помеха на входе
является гармоническим колебанием, а ее мощность равна Рп.
Эффективное значение будет УРЮ а амплитуда V2FU. После
прохождения через согласованный фильтр с коэффициентом усиления
/С0 амплитуда помехи станет Vy = К0 У"2ЯП. Соответственно
мощность помехи на выходе будет- Рп вых у = КЬРП- При этом
элементное отношение сигнал/узкополосная помеха согласно (5.5), (5.6)
будет равно
д§у = —¥1—=£±2В0. (5.14)
*п вых у "п
Таким образом, и при действии узкополосной помехи имеем
выигрыш в отношении сигнал/помеха в В0 раз.
Импульсная помеха. На входе действует импульсная помеха
в виде радиоимпульса с амплитудой Ци и длительностью ти.
Мощность в импульсе или импульсная мощность Ри = i/J/2, а средняя
мощность источника помехи Рп = Яити/Тп, где Гп — период
повторения импульсов. Можно показать [25], что максимальное
напряжение на выходе согласованного фильтра в момент отсчета при
действии импульсной помехи с ти < Т0 равно Уи = aGR ]/2Яс, где
а = YHJEq, Gh = ί/ΗτΗ/2 — спектральная плотность импульсной
помехи. После простых преобразований получаем, что мощность
помехи на выходе равна РПвыхи = HIUI%1 = 2Ри#0Ти.
В этом случае элементное отношение сигнал/импульсная
помеха равно
<7§и = VIIРп вых и - (2ЯС/РИ). (ГДИ)2. (5.15)
Если положить, что ти ex. 1/F, то из (5.15) получаем
ηΙ^ψ-ΒΙ (5.16)
т. е. выигрыш в отношении сигнал/помеха пропорционален Во.
Однако этот результат получен для импульсной мощности Ри.
Поскольку средняя мощность равна Pn = P^jTm то из (5.15)
находим, что
qlM = (2PjPu)(TV%mTn). (5.17)
Если период повторения Ти = Г0, F0 ~ 1/ти, то из (5.17) имеем
^ = ^Ζο=-^2βο· (5.18)
114
Таким образом, выигрыш в отношении сигнал/помеха
пропорционален базе В0.
Сравнение действия помех. Будем считать, что средняя
мощность источника помехи ограничена. Это означает, что средняя
мощность помехи на входе приемника также не может превышать
некоторого предельного значения. Поэтому при сравнении действия
трех рассмотренных помех положим, что в формулах (5.12), (5.14),
(5.18) средняя мощность помехи Рп = const. Из отмеченных
формул следует, что при PjPn = const выигрыш в отношении сигнал/
помеха, равный отношению qbl{PJP^j, пропорционален базе
элемента В0 (в общем случае пропорционален базе сигнала В). Таким
образом, при заданной средней мощности подавление различных
помех за счет увеличения базы примерно одинаково и
пропорционально базе. Подобные результаты, полученные иным методом,
приведены в [157, 158].
Если отношение PjPn С #о> то необходимо увеличивать
энергию сигнала, т. е. составлять сигнал из большого числа элементов
и осуществлять накопление элементов.
5.3. Накопление элементов
Предположим, что сигнал состоит из Л элементов. Если
действуют помехи, отличающиеся от нормального случайного
стационарного процесса с равномерной спектральной плотностью мощности
(«белый» шум), то различные элементы сигнала могут быть
поражены помехами по-разному: одни элементы могут быть поражены
сильнее, другие слабее. Поэтому элементные отношения сигнал/
помеха для различных элементов будут различными. При этом
возникает вопрос, как оптимальным образом принимать сигнал
при действии подобной нестационарной и коррелированной
помехи. Чтобы упростить решение задачи, предположим, во-первых,
что элементы сигнала не перекрываются или по частоте (частотные
сигналы), или по времени (дискретные сигналы), или и по частоте,
и по времени (дискретные частотные сигналы). Это означает, что
элементы взаимно-ортогональны. Неперекрывающиеся элементы
можно оптимальным образом обрабатывать с помощью
элементных согласованных фильтров. Сигнальные составляющие на выходе
элементных согласованных фильтров из-за ортогональности
элементов также будут ортогональны. Во-вторых, предположим, что
составляющие на выходах элементных согласованных фильтров
статистически независимы. Такое предположение будет иметь место, если
помехи являются нормальными случайными процессами из-за орто*
тональности элементов. В случае воздействия иных помех их
возможной коррелированностью можно пренебречь.
При сделанных предположениях прием каждого элемента
характеризуется своим элементным отношением сигнал/помеха.
Подробно вопрос 00 обработке элемента рассматривался в предыдущем
115
параграфе. После обработки элементов в отдельности необходимо
определить, как производить суммирование (накопление)
напряжений с выходов элементных согласованных фильтров. Предположим,
что осуществляется прием с полностью известными параметрами.
При этом прием элементов и накопление будут когерентными.
Считая накопление когерентным, остается выяснить, с какими
весовыми коэффициентами необходимо суммировать напряжения с
выходов элементных согласованных фильтров. Сначала рассмотрим
случай линейного накопления, когда эти напряжения суммируются
непосредственно без весовых коэффициентов.
Линейное накопление. Обозначим через zm напряжение на
выходе элементного согласованного фильтра с номером т в момент
окончания элемента. Оно равно сумме сигнальной составляющей
Vm и помеховой составляющей \т, т. е.
Zm = Vm + lm. (5.19)
Положим, что среднее значение помехи тх {?т} = 0, а ее
дисперсия М2 {1т} = От- При этом среднее значение величины (5.19)
mi {zm} = Vm> а ее дисперсия М2 {гт} = σ^. Элементное отношение
сигнал/помеха равно
q%m = VUaln. (5.20)
При линейном накоплении на выходе накопителя в момент
окончания сигнала имеем
т=\
где
δ=2 ξ«· (5.23)
реднее значение (5.21) т1 {г} = V, а дисперсия
M2{z}= 2 °™ = о\ (5.24)
/π— 1
Равенство (5.24) справедливо при статистической независимости
случайных величин £т, что было предположено ранее. Обычно это
имеет место на практике в большинстве случаев. Отношение
сигнал/помеха на выходе линейного когерентного накопителя равно
^y2/(J2 /£у У / ^<ш ($.25)
Проиллюстрируем формулу (5.25) на простом примере.
Положим, что все сигнальные составляющие равны F9, а дисперсия
т
(5.21)
(5.22)
помехи принимают два значения σ§ и σ?, причем будем считать,
что σ? > σ§. Предположим, в Q элементах действует помеха
с дисперсией σ?, а в оставшихся Л — Q — помеха с дисперсией
σ§. Соответственно элементные отношения сигнал/помех а (5.20)
равны ql = Уо/σο и #? = Уо/σ!. Так как ^f < #§, то обозначим
<7макс = А^о- Подставляя введенные значения в (5.25) и преобразуя,
получаем
<72/<72макс = [1 + (Q/Λ) {qllq\ - \)Y\ (5.26)
На рис. 5.2 кривыми 1, 2 представлены графики зависимости
(5.26). Кривая 1 соответствует значениям ql = 1, q\ = 0,1, т. е.
отношение <7о/<7? = Ю, а кривая 2 — значениям ql = 1, q\ = 0,01,
0 β 2 W 0,6 0,6 β/Λ
Рис. 5.2
т. е. отношение qllq\ = 100. Из рассмотрения этих кривых следует,
что с появлением элементов, на которые воздействует мощная
помеха, суммарное отношение сигнал/помеха резко падает. С
увеличением Q/Λ суммарное отношение сигнал/помеха стремится
к своему предельному значению, равному q2 = Aq\, а графики
Л 2 на рис. 5.2 — к значению q\/ql. При Q = 0 отношение
?2/?2макс = 1.
Формула (5.26) получена при условии, что суммарная дисперсия
(мощность) более сильной помехи увеличивается пропорционально
Q, т. е. амакс = Qcrf, где а\ = const. Положим теперь, что
постоянной является суммарная дисперсия а!Макс мощной помехи,
т. е. положим af маКс = const. При этом дисперсия, приходящаяся
№ один элемент, равна
σ| = σ? макс/Q (5.27)
117
и уменьшается с ростом Q. Обозначая
q\ мин = Vo/0\ Макс, (5.28)
из (5.26) получаем
<№кс = Π + (Q/Λ) {qllq\ mhhQ - Ι)]"1. (5.29)
Формула (5.29) справедлива при Q = 1, Л, так как при Q->- О
дисперсия (5.27) а\ ->■ оо. При Q = 0 отношение q2/qlaKc = 1,
по определению. Положим <7?мин = Ю"2, ?о = 1» а Л = 10.
Отношение <7о/?мин = Ю2. При этих данных кривая 3 на рис. 5.2
представляет график зависимости (5.29). Как видно из этого
графика, распределение помехи по элементам не имеет особого
значения, так как отношение сигнал/помеха (5.29) остается
практически постоянным и малым, а кривая 3 по сути дела прямая линия.
Кривые 1, 2, 3 были рассчитаны для случая, когда мощная
помеха имела превышение по мощности в 10—20 дБ, т. е. такую
помеху нельзя признать чрезмерно мощной. Но даже в этом случае
наличие мощной помехи вызывает резкое уменьшение суммарного
отношения сигнал/помеха. Если мощная помеха станет более
сильной, то возрастет ее влияние на уменьшение суммарного
отношения сигнал/помеха.
Резкое уменьшение суммарного отношения сигнал/помеха на
начальном участке кривых 1, 2 (рис. 5.2) обусловлено появлением
пораженных элементов, которые в общую сумму (5.21) вносят
основную долю шумов с большой мощностью. Естественно, что если
отказаться от линейного накопления и суммировать напряжения с
выходов элементных фильтров с весовыми коэффициентами, то можно
уменьшить влияние пораженных элементов на суммарное отношение
сигнал/помеха. Очевидно, что чем меньше элементное отношение
сигнал/помеха, тем с меньшим весом оно должно входить в общую
сумму. Это случай оптимального линейного накопления. Подобная
задача решена в теории разнесенного приема (см., например, [89,
171]). Воспользуемся известными результатами.
Оптимальное линейное накопление. При когерентном весовом
накоплении величин (5.19) имеем
т= 1
где срт — весовые коэффициенты, а
νφ=2<Ρ".νΜ, (5·31)
т=\
£ф=2ф,Дпг (5-32)
118
Среднее значение т1 {ζ} = 1/φ, а дисперсий аналогично (5.24)
равна
Μ,{ζ} = σ$= 2 Ф«^«· (5·33)
m=l
Величина
<72 - ν£/σ* (5.34)
является отношением сигнал/помеха на выходе когерентного
весового сумматора. Подставляя (5.31) и (5.33) в (5.34), получаем
\m=l / / т=\
В соответствии с отмеченным ранее, необходимо определить
веса фт, которые максимизируют отношение сигнал/помеха q2
(5.35). Эта задача имеет следующее решение [89]. Преобразуем
числитель в (5.35) и используем неравенства Коши—Буняковского:
(2 «р»у™У=(Σ — ψ» σ„Υ< 29" Σ φ«σ"- (5·36)
\m=t / \w=l am / /я=1 m=l
где в первую сумму правой части (5.36) входят элементные
отношения сигнал/помеха (5.20). Равенство в (5.36) возможно в том
случае, если Vm/om = cpmam. Отсюда получаем условие
максимизации числителя в (5.35):
<Pm = VJo*n. (5.37)
Таким образом, чтобы получить максимум числителя в (5.35),
необходимо выбирать весовые коэффициенты пропорционально
сигнальной составляющей и обратно пропорционально дисперсии
(мощности) помеховой составляющей на выходе элементного
согласованного фильтра.
Максимизация числителя в (5.35) влечет за собой
максимизацию отношения сигнал/помеха, так как при замене числителя
согласно (5.36) получаем, что знаменатель в (5.35) сокращается.
Полагая, что условие максимизации (5.37) выполняется, окончательно
получаем
<72=2е (5-38)
w = l
В этом случае отношение сигнал/помеха равно сумме
элементных отношений сигнал/помеха. Поясним равенство (5.38) тем же
простым примером, что и при линейном накоплении. Допустим, что
в Q элементах из Л элементное отношение сигнал/помеха равно
q\, а в Л — Q элементах q% и q\ <^ ql- Подставляя значения q%, q\
в (5.38) и преобразуя полученное выражение, находим
Wm« - 1 ~ (О/А) (1 - tf/tf). <5·39)
119
где <72макс = Л^о- Зависимость (5.39) изображена на рис. 5.2
прямой 4 для отношенияk q\lq\ = 10. При Q = Л q2/q2
яУяЬ
wiyjiL т j^i/x win^JJ-icnriTi Ч 0'Ч1 — 1W* Axpri v^ — л л. Ч 'Ч Макс — τ Г τ О»
т. е. q2 = Aq\. С уменьшением отношения q\lq\ отношение (5.39)
стремится к следующему пределу:
<72/<72макс = 1 - Q/Λ. (5.40)
График зависимости (5.40) изображен на рис. 5.2 прямой 5.
Если положить постоянной суммарную мощность помехи а\ макс,
то, используя (5.27), (5.28), из (5.39) получаем
qVql
1-(Q/A) (1-<7?mhhQ/<7*)·
(5.41)
График зависимости (5.41) для значений ql/q\MnH = 100,
Л = 10 представлен кривой 6 на рис. 5.2. Она лежит между
прямыми 4 и 5.
/ГШГУ7 7
г*0—HZSI—Sh
L . . · · · ·
Канал А ^_^
'Т_1 ^ΤΖ-Π-ΧΙ ^Mt ι
r*i
/ \l/
ί—»
^r >
1 L /ίκ J
ζ
Рис. 5.3
Адаптивный приемник. В соответствии со сделанными ранее
предположениями относительно оптимального приема отдельных
элементов и полученными результатами по оптимальному линейному
накоплению на рис. 5.3 представлена структурная схема приемника.
Он является адаптивным, так как подстраивается под помеху,
максимизируя отношение сигнал/помеха (5.38)*
Адаптивный приемник состоит из Л каналов по числу элементов*
Каждый канал представляет собой последовательное соединение
элементного согласованного фильтра, каскада стробирования,
линии задержки и усилителя с регулируемым коэффициентом
усиления. Элементный согласованный фильтр (СФ) осуществляет
оптимальный прием элемента. Если элементы не перекрываются по
частоте, то он состоит из полосового фильтра и фильтра,
согласованного с элементом в выделяемой полосе частот. Так
осуществляется селекция по частоте. В момент окончания элемента в каскаде
стробирования производится отсчет напряжения на выходе
согласованного фильтра. Импульс отсчета (строб-импульс) поступает
от синхронизатора, который на рис. 5.3 не показан. Отсчет
напряжения на выходе элементного согласованного фильтра в момент
окончания элемента эквивалентен селекции элемента во времени,
поскольку в этом отсчете сосредоточена вся информация об элементе
120
с точки зрения оптимального приема. Отсчет с помощью линии
задержки смещается во времени так, чтобы отсчеты были совмещены
друг с другом в момент окончания сигналов. Отсчеты с выходов
всех каналов поступают на анализатор каналов (АК), который
производит анализ отсчетов и на основе анализа определяет
значения весовых коэффициентов срт (5.37). В соответствии с
полученными значениями срт в усилителях устанавливаются коэффициенты
усиления, пропорциональные срт. Поэтому на выходах усилителей
уровни отсчетов будут пропорциональны слагаемым cpmzm, а на
выходе сумматора получим сумму ζ (5.30), в которую слагаемые
входят с весовыми коэффициентами (5.37).
Вычисление весовых коэффициентов срт требует знания как
сигнальной составляющей V, так и дисперсии помехи о2т, хотя в
процессе приема элементов известны только величины zm = Vm + £m
(5.19). Относительно Vm можно предположить, что они известны.
Но даже и при этом необходимо находить оценки σ^ по измеренным
значениям гт. Отметим, что определение оценок дисперсии помехи
а1г является статистической задачей и заслуживает отдельного
глубокого исследования. Не решая этого вопроса, будем полагать,
что весовые коэффициенты срт определены.
Помехоустойчивость адаптивного приемника (рис. 5.3) зависит
от отношения числа пораженных элементов Q к общему числу
элементов Л (рис. 5.2). Повышение помехоустойчивости основано
на селекции пораженных элементов и уменьшении соответствующих
весовых коэффициентов. Адаптивный приемник производит
селекцию по частоте, времени и форме элементов. Селекция по частоте
и времени осуществляется элементными согласованными фильтрами,
которые согласованы с элементами с учетом несущей частоты этих
элементов. Селекция по времени обусловлена отсчетом напряжения
на выходе элементного согласованного фильтра в момент
окончания элемента.
Число элементов сигналаЛ может быть выбрано, исходя из
условия повышения помехоустойчивости, и в общем случае может
не совпадать с числом элементов, из которых сигнал сформирован.
Поясним это. Обратимся к рис. 5.1. Допустим для простоты, что
базисный прямоугольник разбит на Μ частотных полос (каналов) и
на Μ временных полос (каналов). Число полученных лрямоуголь-
ников равно Λί2. Если в каждом из них расположен элемент сигнала,
то число элементов равно Λ = Μ2. При этом и число каналов в
адаптивном приемнике также М2. Если действует узкополосная помеха
(жирная горизонтальная полоса на рис. 5.1), то число
пораженных элементов равно Λί, а отношение Q/Λ = 1/М.
Точно такое же положение будет и в случае действия
импульсной помехи (жирная вертикальная полоса на рис. 5.1), и в случае
помехи в виде ДЧ сигнала первого порядка (вертикальная
штриховка). Если используется ДЧ сигнал первого порядка (наклонная
штриховка) с числом элементов А = М, то при действии тех же
помех в соответствии с рис. 5.1 отношение Q/Λ = 1/М-
121
Допустим теперь, что осуществляется прием частотного сигнала
(см. рис. 1.3, 1.4), состоящего из N частотных элементов. Этот
сигнал занимает весь ба'зисный прямоугольник. Для оптимального
приема с оптимальным накоплением такой сигнал надо представить
не в виде частотных элементов, а в виде элементов, занимающих
отдельные частотно-временные прямоугольники согласно рис. 5.1.
Число таких элементов Л может быть и не равным АЛ Точно такое же
положение будет и в случае приема дискретного сигнала.
Из сравнения приема дискретных, частотных и дискретных
частотных сигналов следует, что адаптивный приемник будет наиболее
простым для дискретных частотных сигналов.
Квазиоптимальное линейное накопление. Вычисление весовых
коэффициентов срт (5.37) требует определения дисперсии ат и
сигнальной составляющей Vm, если последняя неизвестна, по отсчету
гт на выходе элементного согласованного фильтра. Можно
предложить квазиоптимальное определение весовых коэффициентов,
при котором нет необходимости находить отдельно оценку ат.
Положим, что Vm известно, и будем находить оценку величины Рт =
= Vm + От, равной средней мощности m-го отсчета. Образуем
весовой коэффициент срт следующим образом:
СРт = VJ(Vm + °2m). (5.42)
В этом случае согласно (5.20), (5,35) отношение сигнал/помеха
будет равно
φ-
А
т=\
А
Σ<&(ΐ+<&)-2
(5.43)
Проиллюстрируем полученную формулу на том же простом
примере, для которого были найдены формулы (5.39). Положим,что
ρ Q каналах элементное отношение сигнал/помеха равно q\, а в Л —
— Q каналах — q2Qy причем q\ <^ q\. Подставляя эти значения
в (5.43) и учитывая, что q2 макс = Aq20t получаем
Н4('-^)Г1Н[,:}5-Й
(5.44)
Зависимость (5.44) при различных отношениях q\lq\
изображается кривыми, которые близки к кривой 6 на рис. 5.2. Отметим,
что структурная схема приемника с квазиоптимальным
накоплением совпадает со схемой приемника, изображенного на рис. 5.3.
Сравнение оптимального и квазиоптимального накопления.
Из рассмотрения графиков рис. 5.2 можно сделать следующие вы-
роды.
1. Оптимальное и квазиоптимальное накопление при числе
пораженных элементов Q < Л всегда обеспечивает выигрыш в
отношении сигнал/помеха по сравнению с линейным накоплением» Этот
№
ШНЭ-
НШЭп
I · · ·
Канал Л
I °^ 1 II
4сф\
Рис. 5.4
выигрыш имеет наибольшее значение при малом числе пораженных
элементов и тем больше, чем больше мощность помехи,
действующей на пораженных элементах.
2. Если мощная помеха воздействует на все элементы (Q = Л),
то любое накопление обеспечивает одно и то же отношение сигнал/
помеха.
3. С увеличением мощной помехи отношение сигнал/помеха при
оптимальном и квазиоптимальном накоплениях стремится к
значению, определяемому формулой (5.40) (кривая 5 на рис. 5.2). Эта
формула характеризует приемник, в котором каналы с малым
элементным отношением сигнал/помеха q\ (с большой помехой) просто
отключаются от сумматора.
Структурная схема такого при- Канал 1
емника совпадает со схемой
приемника, изображенного на
рис. 5.3, с той разницей, что
усилители превращаются в
ключи: или пропускают отсчеты в
сумматор, или не пропускают.
Нелинейный приемник.
Реализация оптимальных и
квазиоптимальных приемников в
соответствии со структурной схемой,
представленной на рис. 5.3, требует определения структуры
анализатора каналов (АК). Иногда вместо АК и усилителей с регулируемым
коэффициентом усиления в каждом канале используют ограничители
[6, 7, 66, 186], которые подавляют мощные помехи, но вносят
потери в остальные каналы. При действии шумовых помех в виде
нормального случайного стационарного процесса потери
составляют примерно 2 дБ [102, 185]. Наличие ограничителя в канале
с согласованным фильтром приводит к тому, что такой канал
является оптимальным фазовым обнаружителем сигнала [104, 185], так
как ограничитель устраняет все амплитудные изменения, в том
числе вызванные мощной помехой.
На рис. 5.4 приведена структурная схема одного из возможных
нелинейных приемников [6, 7]. На входе приемника стоит
широкополосный полосовой фильтр, полоса пропускания которого не
меньше ширины спектра сигнала F. Следующий за ним ограничитель
предназначен для ограничения возможных импульсных помех.
Уровень ограничения должен устанавливаться по эффективному
значению суммы сигнала и помех. Затем спектр сигнала разбивается
на Л неперекрывающихся полос. Каждый канал состоит из
полосового фильтра с полосой пропускания FQ = F/A. Напряжения
с выходов полосовых фильтров поступают на «жесткие»
ограничители, которые подавляют возможные узкополосные помехи.
Напряжение с выходов ограничителей поступает на согласованный
фильтр. Так как такой приемник подавляет мощные
узкополосные и импульсные помехи, то он подавляет любые мощные
123
помехи, действующие в тех или иных элементных
прямоугольниках на частотно-временной плоскости. При шумовых
помехах такой приемник близок к оптимальному фазовому
обнаружителю.
5.4. Фильтрация сосредоточенных помех
В § 5.2 было рассмотрено воздействие шумовой помехи,
действующей на произвольный элемент сигнала. Обратимся к
воздействию сосредоточенной шумовой помехи, полностью перекрывающей
спектр всего сигнала.
Сосредоточенная помеха с равномерным спектром,
Предположим, что сосредоточенная шумовая помеха является нормальным
стационар^ш случайным процессом с равномерной спектральной
плотностью мощности Νπ в пределах полосы частот сигнала
шириной F. Если мощность помехи Яп, то ее спектральная плотность
мощности аналогично (5.8) равна
Nn = PJF, (5.45)
а отношение сигнал/помеха на выходе согласованного фильтра
аналогично (5.12) будет
q2==JjL2B) (5.46)
где В = FT — база сигнала. Как при одном элементе, так и в
случае сигнала в целом, чем больше база, тем больше отношение сигнал/
помеха φ на выходе по сравнению с отношением сигнал/помеха
Яс/Яп на входе. Поэтому с ростом базы сигнала подавление
сосредоточенной помехи увеличивается.
Сосредоточенная помеха одинаковым образом действует на все
элементы сигнала. Если они обладают равными энергиями, то
элементные отношения сигнал/помеха q%, (5.20) равны между собой.
В результате оптимальным накоплением будет линейное, поскольку
весовые коэффициенты (5.37) также равны между собой,. И в этом
случае набор каналов (рис. 5.4) сводится к одному фильтру,
согласованному с сигналом.
Отношение сигнал/помеха q2 (5.46) пропорционально
отношению сигнал/помеха PJPn на входе приемника. Кратко поясним,
чем определяется отношение PJPn. Мощность сигнала Рс на входе
приемника определяется мощностью передатчика Япер, создающего
полезную информацию, КНД антенн передатчика Dnep и
приемника Ζ)πρ, расстоянием до передатчика гпер, условиями
распространения радиоволн. В свою очередь мощность помехи Рп на входе
приемника определяется мощностью передатчика Яцерт
создающего помеху, КНД его антенны Dnep п, КНД антенны приемника
в направлении передатчика помехи Ьпрп, расстоянием до него
124
гперп и условиями распространения радиоволн. Полагая, что
условия распространения радиоволн одинаковы, имеем
^с *пер £*пер ^пр / гпер π^ν /с лп\
Ρ η *пер π £*пер π ^пр π \ гпер /
где ν зависит от среды, в которой распространяются радиоволны.
Для свободного пространства ν = 2. При использовании УКВ
следует полагать, что ν = 4. Из (5.47) видно, что отношение Рс/Рп
включает в себя основные технические и пространственные
характеристики системы передатчик—приемник—передатчик помехи.
Величины правой части (5.47) определяют стоимость и во многом
эффективность системы передачи информации и системы
разрушения информации. Таким образом, отношение PJPn имеет большое
практическое значение при разработке радиотехнических систем.
В зависимости от отношений параметров, входящих в правую
часть (5.47), и, особенно, от гпер п/гпер, отношение Рс/Ри может
быть весьма различным, в том числе много меньшим единицы. Если
гПерп/^пер изменяется, то и PJPn изменяется, но более резко.
Расчеты показывают, что отношение Рс/Рп может достигать
значений — (10—120) дБ.
Из формулы (5.46) следует, что если даже PJPn <C 1, то величина
<72, которая определяет помехоустойчивость приема информации
(q2 = 2/ι2), может быть сделана существенно больше единицы.
Например, пусть Рс/Рп= 0,1, а В = 100. Согласно (5.46) имеем
q2 = 20. При этом прием информации будет осуществляться с
вероятностью ошибки Рош ~ Ю-4 — Ю-5, т. е. достаточно надежно.
Следовательно, увеличивая базу используемых сигналов В, можно
достигнуть заданного значения ф. Напомним, что в гл. 4 были
приведены соотношения (4.98), (4.99), аналогичные (5.46),
полученные для случая воздействия взаимных помех.
Совместное воздействие помех и шума. Используя сложные
сигналы с большими базами, можно «извлекать» сигналы из-под
помехи, во много раз превосходящей сигнал по мощности. Предел
увеличения этой способности определяют собственные шумы
приемника (см., например, [25]), у которых спектральная плотность
мощности постоянна и равна N0 и практически не изменяется с
изменением полосы пропускания.
Можно показать [25, 27], что при воздействии сосредоточенной
помехи с мощностью Яп и собственного шума приемника со
спектральной плотностью N0, отношение сигнал/помеха на выходе равно
qlu = q* Рш/Рд П = Рс 2В, (5.48)
где q2 = 2E/N0 — отношение сигнал/шум; Яш = N0F — мощность
собственного шума, попадающего в полосу пропускания,
шириной F. Если Рш > Яп, то <7шп ^ <72, а если Яш <С Рю то с
собственным шумом приемника можно не считаться. При этом <7шп (5.48)
совпадают с q2 (5.46).
125
Из проведенного исследований видно, что помехоустойчивость
при воздействии сосредоточенных помех определяется отношением
PJPn и базой используемых сигналов. Отметим, что полученный
результат справедлив при двух условиях — сосредоточенная
помеха является нормальным случайным процессом и обладает
равномерной спектральной плотностью. Во многих случаях эти условия
не выполняются, например, при действии мощной структурной
помехи. В этих случаях помехоустойчивость в значительной мере
определяется подобием и различием структур сигнала и помехи, т. е.
тем, как подавляются отдельные элементы сигнала помехой.
Сосредоточенная помеха с неравномерным спектром. Допустим,
что помеха является стационарным случайным процессом с
неравномерной спектральной плотностью мощности Ν (ω). В этом случае
коэффициент передачи согласованного фильтра определяется
следующим выражением (см., например, [18, 25, 105, 1621):
к{(д)=С-^-е-'шТ, (5.49)
ν Ν(ω) ν ;
где с — постоянная; g (ω) — спектр сигнала. При равномерной
спектральной плотности Ν (со) = Ν0 формула (5.49) переходит
в (2.23). Отношение сигнал/помеха при этом определяется
выражением
π J Ν (ω) }
ο
Β [25] приведены результаты исследований изменения
отношения сигнал/помеха (5.50) при изменении спектра сигнала и спектра
помехи. С точки зрения постановщика помехи необходимо так
подстраивать помеху,, чтобы имело место равенство Ν (со) = Ъ \g (ω) |,
где Ь — постоянная размерная величина. Это равенство определяет
характер оптимального воздействия помехи: сильнее подавлять
те спектральные составляющие сигнала, которые переносят большую
часть энергии сигнала. Если помеха имеет резкий пик в своем
спектре, то согласно (5.49) усиление согласованного фильтра в области
частот пика резко снижается и в этой области частот согласованный
фильтр становится режекторным и исключает эту мощную часть
помехи. Здесь имеется полная аналогия между оптимальным
накоплением с весовыми коэффициентами (5.37) и согласованным фильтром
(5.49). Весовой коэффициент (усиление фильтра) пропорционален
сигнальной составляющей (по напряжению) и обратно
пропорционален мощности помехи.
В свою очередь любой «провал» в спектре помехи позволяет
согласно (5.49) увеличить усиление согласованного фильтра и тем
самым повысить отношение сигнал/помеха (5.50). Поэтому система
поставщик помехи — приемник находится в динамическом
равновесии только тогда, когда и спектр сигнала, и спектр помехи
равномерны. При этом ни одна из сторон не получает дополнительного
126
выигрыша в повышении (понижении) помехоустойчивости из-за
неравномерности спектра. Точно такой же результат следует нз рас·
смотрения кривых рис. 5.2, которые сходятся в точке Q = Л, т. е.
когда помеха действует на все элементы. Особенно показательно
сравнение прямых 3 и 4. Прямая 3 характеризует снижение
помехоустойчивости, если помеха воздействует на Q элементов, а в
приемнике не принято специальных мер по защите от мощных помех
и накопление в приемнике линейное, Если приняты меры по
защите от мощных помех в виде оптимального накопления (прямая 4),
то это обеспечивает существенный выигрыш в помехоустойчивости.
И только в точке Q = Л этого выигрыша нет. При этом выигрыш
в помехоустойчивости согласно (5.46), (5.48) можно обеспечить
только за счет увеличения базы сигнала.
Если помеха не является стационарной, то сначала
целесообразно рассматривать ее воздействие на элементы сигнала, а затем
учитывать результаты накопления. При этом для приближенных
расчетов достаточно формул § 5.2, 5.3. Для более точных расчетов необ*
ходимо использовать методы, рассмотренные s [18].
5.5. Фильтрация узкополосных и импульсных помех
При действии мощных узкополосных и импульсных помех
адаптивный приемник (рис. 5.3) будет обеспечивать оптимальный
прием. Помехоустойчивость определяется числом пораженных
элементов и элементным отношением сигнал/помеха. Отношение сигнал/
помеха на выходе адаптивного приемника определяется общей
формулой (5.38). Так как при действии узкополосных или импульсных
помех элементные отношения сигнал/помеха принимают два
значения (или близкие к ним), то для расчетов отношения сигнал/помеха
q2 можно использовать формулы (5.39)—(5.41), (5.44). Элементные
отношения сигнал/помеха определяются согласно (5.12), (5,14)
(5.18).
Если узкополосные помехи попадают на границы между
соседними частотными полосами, то число пораженных каналов при
расчете необходимо удваивать. При действии мощных помех надо такг
же учитывать попадание помехи в соседние каналы из-за отличия
частотных характеристик полосовых фильтров от прямоугольных.
Оценим количественно помеху в соседнем канале. Допустим, что
ширина спектра элемента F0 = 2/τ0, где τ0 — длительность
импульсов, из которых составлен элемент. В качестве полосового фильтра
возьмем пятикаскадный резонансный усилитель. Оптимальная
полоса пропускания на уровне 0,7 равна Δ/π = 0,67/τ0 [162].
Отсюда следует, что Δ/π = 0,35F0. Пусть частотная расстройка
между соседними каналами Δ/ = 2/τ0 = F0. При этом
относительная расстройка α = Δ//(Δ/π/2) ~ 6. Частотная характеристика
пятикаскаднопх резонансного усилителя описывается выражением
£ (а) = (1 + а2)-5/2. При а = 6 ослабление & ~ —80 дБ. Следо-
вательно, если помеха меньше 60—70 дБ, то с ней можно не
считаться.
При действии импульсных помех необходимо учитывать как
возможность их попадания на границы соседних элементов, так и
наложение фронтов мощных импульсов на соседние элементы. И в том,
и в другом случае число пораженных элементов увеличивается,что
необходимо принимать во внимание при расчетах.
Отметим, что результаты § 5.3 и выводы данного параграфа
по подавлению узкополосных и импульсных помех были получены -
при условии статистической независимости помех в различных
каналах. В тех случаях, когда помехи в различных каналах корре-
лированы, конечные результаты будут зависеть от степени
коррелированное™ помех.
5.6. Фильтрация структурных помех
Как было отмечено ранее, структурные помехи — это такие,
структура которых подобна структуре используемых сигналов.
Очевидно, что в случае дискретных или частотных сигналов
структурные помехи полностью перекрывают сигнал на
частотно-временной плоскости. Поэтому по своему воздействию они будут близки
к сосредоточенным помехам и отношение сигнал/помеха будет
определяться формулой (5.46). Естественно, что в случае мощных
структурных помех (Яп > ВРС) СПИ с дискретными или с частотными
сигналами не будут работоспособными.
Иное положение будет при использовании ДЧ сигналов. Число
элементов сигнала, пораженных помехой, случайно и определяется
вероятностью совпадения элементов сигнала и элементов помехи.
Например, совместное расположение синала и структурной помехи
на рис. 5.1 соответствует одному совпадению.
Рассмотрим ДЧ сигналы первого порядка. У них число элементов
Μ = ]^В. Пусть Q — число элементов сигнала, пораженных
элементами помехи, т. е. число совпадений элементов сигнала и помехи.
Если отбросить пораженные элементы, то согласно (5.40) отношение
сигнал/помеха будет равно
<72 = ?5акс (1 - Q/M) = <7£акс (1 - Q/VB), (5.51)
где <7макс = Mql, а ^ — элементное отношение сигнал/помеха.
Величина Q, как было отмечено, случайная. Определим ее
закон распределения. Допустим, что сигнал задан, т. е. Μ
элементов сигнала некоторым образом распределены по М2
непересекающимся областям частотно-временной плоскости. Поскольку
рассматривается ДЧ сигнал первого порядка, то в каждом столбце и в
каждой строке содержится только один элемент сигнала. Так как
помеха является структурной, то можно предположить, что и для нее
справедливо распределение элементов по столбцам и строкам
частотно-временной плоскости, Для определенности будем рассматривать
совпадение элементов сигнала и помехи по столбцам. Допустим, что
элемент помехи может равновероятно занимать любое положение
в столбце. Следовательно, вероятность появления элемента помехи
в данном элементном прямоугольнике столбца равна l/Λί. Поэтому
вероятность совпадения элементов сигнала и помехи ρ = 1/Af, а
вероятность несовпадения 1 — ρ = (Μ — 1)/Λί. Соответственно,
вероятность Q совпадений в Μ столбцах определяется биномиальным
законом [104]
Ρ (Q) = C%pQ (1 - p)"-*f (5.52)
где См — число сочетаний из Μ по Q. Подставляя в (5.52) значение
ρ = l/Λί, получаем
ρ (Q) = см(М — l)M-Q/MM. (5.53)
Если Μ > 1, т. е. ρ = 1/Af <C 1, то (5.52) асимптотически
аппроксимируется законом Пуассона [104]
P(Q) ~ 1/eQl (5.54)
Из (5.52), (5.54) следует, что наиболее вероятны следующие
случаи: во-первых, ни одного совпадения элементов (Q = 0, Q! = 1)
и, во-вторых, одно совпадение (Q = 1, Q! = 1). Соответствующие
вероятности приблизительно равны е-1 = 0,37.
Найдем среднее значение и дисперсию отношения
сигнал/помеха (5.51). Среднее значение по определению равно
? = т, {<?2}. = qlll- (l/Λί) mi {Q}], (5.55)
а дисперсия
σ* = М2 {92} = (q*/M*) M2 {Q}. (5.56)
Так как случайная величина Q распределена по биномиальному
закону (5.52), то ее среднее значение πΐχ {Q} = Мр = 1, а
дисперсия М2 {Q} = Мр (1 — ρ) = (Λί — 1)/Λί. Подставляя эти
значения в (5.55), (5.56), находим
ф = д1(\- l/Af)f (5.57)
σ| = (ί40/Λί2)(1 — 1/Λί). (5.58)
Среднее значение (5.58) свидетельствует о том, что
определяющим в (5.52) является одно совпадение. Из (5.58) следует, что
с ростом Μ дисперсия уменьшается как l/Λί2, а отношение a /q2 ~
~ l/Λί.
Таким образом, при действии структурной помехи на ДЧ сигнал
в среднем будет поражен один элемент. Если этот элемент
исключить, то отношение сигнал/помеха изменится незначительно, т. е.
СПИ будет вполне работоспособной. Если на ДЧ сигнал действует
μ структурных помех, в среднем их действие проявится в том, что
уменьшение отношения сигнал/помеха будет пропорционально
1 — μ/Λί, если μ С Λί. Следовательно, и в этом случае СПИ
останется работоспособной.
129
S.7. Радиотехнические системы, инвариантные к комплексу
помех
Инвариантными к воздействию
помех называются такие
радиотехнические системы (РТС),
помехоустойчивость которых не изменяется
(или меняется слабо) при резком
изменении мощности помех. Понятие
инвариантности РТС неоднократно
обсуждалось в литературе [106, 115].
Известны примеры СПИ,
инвариантных к действию некоторых помех.
Например, в работе [115] приведена
схема адаптивного приемника,
инвариантного к действию
узкополосных помех, имеющего структурную
схему, близкую к структурной схеме
приемника, представленного на
рис. 5.4, при использовании
частотных сигналов.
В связи с необходимостью
построения различных РТС (передачи
информации, радиолокационных,
радиоуправления и др.),
инвариантных к действию комплекса помех,
большую роль в развитии теории
таких систем играют работы, в
которых исследуются вопросы приема
сигналов на фоне неизвестных помех
(помех с неизвестными свойствами).
Круг проблем, которые решаются в
подобных работах, получил название
«синтез систем при априорной
неопределенности». Методы решения
подобных задач рассматриваются в
большом числе работ (см., например,
[16, 104, 188]).
Особое значение имеют системы,
инвариантные к действию мощных
помех, поскольку линейные методы
обработки сигналов не позволяют
успешно бороться с такими
помехами. Наиболее распространенными
помехами, предназначенными для
подавления РТС, являются
сосредоточенные шумовые, узкополосные,
импульсные, структурные, т. е. те,
которые были рассмотрены в данной
главе. Можно предполагать, что
этот комплекс помех будет наиболее
распространенным и в будущем.
Результаты исследований,
приведенные в данной главе, по
помехоустойчивости РТС к комплексу
перечисленных ранее помех позволяют
высказать ряд рекомендаций по
определению структуры
инвариантной РТС и по выбору сигналов.
130
1. Помехоустойчивость РТС при
воздействии сосредоточенных
шумовых помех с равномерной
спектральной плотностью мощности не зависит
от типа используемых сигналов. Она
полностью определяется базой
сигналов и отношением мощности
сигнала и помехи. Для повышения
помехоустойчивости необходимо
увеличивать базу сигналов.
2. Помехоустойчивость при
действии мощных помех с
неравномерным распределением энергии на
частотно-временной плоскости может
быть увеличена с помощью
адаптивного приемника (рис. 5.3) по
сравнению с помехоустойчивостью
линейного приемника. Адаптивный приемник
будет близок к инвариантному, так
как его помехоустойчивость при
малом числе помех слабо зависит от
мощности помех (рис. 5.2).
Адаптивный приемник учитывает различие
между структурами сигнала и помехи
на частотно-временной плоскости.
3. Помехоустойчивость РТС при
действии узкополосных и импульсных
помех и с использованием
адаптивного приемника (типа
представленных на рис. 5.3, 5.4) слабо зависит
от структуры сигналов и будет
зависеть в основном от реализации таких
приемников. Реализация
адаптивного приемника (рис. 5.3) будет
наиболее простой в случае ДЧ сигналов
первого порядка, так как их
структура наиболее полно отвечает
принципу работы адаптивного приемника.
4. Помехоустойчивость РТС при
воздействии мощных структурных
помех существенно зависит от типа
используемых сигналов.
Инвариантными системы будут только в случае
ДЧ сигналов первого порядка.
5. При прочих равных условиях
ДЧ сигналы первого порядка имеют
преимущество перед другими
сигналами, поскольку, во-первых,
обеспечивают большую помехоустойчивость
при действии структурных помех и,
во-вторых, позволяют проще
реализовать адаптивный приемник.
6. Возможность фильтрации
мощных структурных помех с
применением ДЧ сигналов и адаптивных
приемников позволит решить проб-
Лему электромагнитной совместимо- случаях тем больше, чем больше база
сти однотипных РТС. сигналов, то для построения РТС,
7. Помехоустойчивость РТС при помехоустойчивых относительно ком-
воздействии комплекса помех за- плекса помех, необходимо приме-
висит как от базы сигналов, так и от нять системы сложных сигналов,
их структурных свойств. Поэтому Именно этим и объясняется повышен-
выбор системы сигналов имеет су- ный интерес разработчиков совре-
щественное значение. Поскольку вы- менных РТС к системам сложных
ягрыш в помехоустойчивости во всех сигналов.
Глава 6
ОСНОВНЫЕ МЕТОДЫ ОБРАБОТКИ СИСТЕМ СИГНАЛОВ
6.1. Оптимальная и квазиоптимальная линейная обработка
сигналов
Как следует из материала предыдущих глав, свойства
современных систем передачи информации во многом определяются
характеристиками и свойствами применяемых систем сигналов.
С точки зрения теории и техники основными характеристиками и
свойствами систем сигналов являются следующие:
— объем системы сигналов и база сигналов;
— структурные свойства сигналов (вид элементов и их
расположение на частотно-временной плоскости);
— корреляционные свойства сигналов (ВКФ и АКФ, их
характеристики);
— возможность быстрой смены сигналов;
— простота устройств формирования и обработки, малые
габариты и масса.
Требования к объему системы сигналов и базе сигналов, к
структурным и корреляционным свойствам были подробно рассмотрены
в предыдущих главах. Кроме того, эти свойства систем сигналов
и их характеристики будут исследованы во втором и в третьем
разделах книги. В данной главе кратко рассмотрим основные методы
обработки систем сигналов с учетом их структурных свойств. Среди
различных методов обработки сложных сигналов, которые нашли
отражение в многочисленных книгах, обзорах, статьях (см.,
например, [2, 3, 6, 7, 19, 24, 71, 95, 99, 105, 137, 139, 152, 156, 162, 166,
192, 194]), будем рассматривать только те, которые позволяют
осуществлять быструю смену сигналов и являются относительно
простыми. При этом не будут затронуты методы, пригодные для обработки
единственного сигнала, например, с использованием дисперсионных
или гранатовых линий задержки.
Методы формирования и обработки систем сигналов полностью
определяются классом систем. Классификация систем сигналов
131
была приведена в § 1.3. Из-за требования быстрой смены сигналов
в СПИ в основном применяются системы манипулированных
сигналов. Системы модулированных сигналов практически не
используются из-за сложности или невозможности быстрой смены. Среди
манипулированных применяются и дискретные частотные, и
частотные, и дискретные системы сигналов. Поскольку создание
аппаратуры обработки связано с преодолением больших технических
трудностей, чем при создании аппаратуры формирования, то в
дальнейшем будем рассматривать только методы обработки.
Применение сложных сигналов усложняет аппаратуру
формирования и обработки. Чем больше база сигналов, тем труднее
изготовить такую аппаратуру. Однако такие сигналы, как было показано
в предыдущих главах, имеют неоспоримые преимущества перед
простыми. Поэтому несмотря на возрастающую аппаратурную
сложность, они находят применение в современных РТС и будут
применяться в системах будущего. Следовательно, проблема разработки
простых методов формирования и обработки систем сложных
сигналов весьма актуальна. Ее решение зависит как от нахождения
таких методов, так и от широкого применения цифровых и
аналоговых интегральных микросхем. Достижения микроэлектроники,
развитие цифровых методов обработки сигналов [10, 80, 81, 107],
опыт проектирования РТС со сложными сигналами и с применением
интегральных микросхем позволяют утверждать, что эта проблема
разрешима.
Оптимальный прием. Известно (см., например, [105. 162], гл. 2),
что оптимальный приемник при воздействии на его вход суммы
χ (t) = и (t) + η (t) известного сигнала и (t) и нормального белого
шума η (t) должен вычислять значение корреляционного интеграла
(2.25). Это значение вычисляется или коррелятором, или
согласованным фильтром. В последнем случае напряжение на выходе
согласованного фильтра равно
τ
ν (τ) ==kQ$x (t) u (t — x) at, (6.1)
τ
где k0 — постоянная величина; τ — временная задержка. При τ = 0
имеем ζ = υ (0)/k0, т. е. (6.1) и (2.25) совпадают с точностью до
постоянной. Функция v(x) (6.1) является ненормированной
корреляционной функцией χ (t) и и (/).
Согласованный фильтр является пассивным фильтром, его
импульсная характеристика (2.22) — зеркальное отображение сигнала,
а коэффициент передачи (2.23) — комплексно-сопряженный спектр
сигнала. Согласованный фильтр, как и всякий пассивный фильтр,
инвариантен относительно задержки сигнала во времени, т. е. на
сколько изменится задержка сигнала на входе фильтра, на столько
изменится и задержка отклика фильтра (6.1). Поскольку χ (/) =
= и (t) + η (t), то отклик фильтра υ (τ) содержит АКФ сигнала
и (t) независимо от задержки сигнала. Это — свойство
инвариантности согласованного фильтра относительно задержки. Но для при-
132
нятия решения о наличии сигнала (см. § 2.2) надо знать момент
окончания сигнала, т. е. необходимо измерить задержку по
принятому сигналу.
Коррелятор является параметрической системой и его называют
активным фильтром. Напряжение на выходе коррелятора во
времени изменяется следующим образом:
ν
ζ (/', τ) = Ι χ (t) u (t — τ) at. (6.2)
о
Если τ = 0, а /' = Г, то ζ (Г, 0) = ζ (2.25). Из сравнения (6.1)
и (6.2) следует, что напряжение на выходе коррелятора совпадает
с напряжением на выходе согласованного фильтра с точностью
до постоянной лишь в случае f = Τ, т. е. при окончании отрезка
интегрирования. Во все остальные моменты времени напряжения
тождественно не равны. В выражении (6.2) задержка τ для
рассматриваемого отрезка интегрирования является постоянной величиной.
Поэтому при τ Φ 0 величина ζ (Γ, τ) не содержит максимума АКФ.
Следовательно, для нормальной работы коррелятора необходимо
измерять задержку τ и уменьшать ее до нуля. Таким образом,
коррелятор, в отличие от согласованного фильтра, не будет
инвариантным относительно задержки сигнала.
Квазиоптимальный прием. В гл. 2 были приведены структурные
схемы оптимальных когерентных и некогерентных приемников для
приема двоичной и /n-ичной информации. При когерентном приеме
допускалось, что сигналы известны полностью, а при
некогерентном — с точностью до начальной фазы. В обоих случаях
предполагалось, что задержка сигналов известна, это и позволяло
правильно определить момент отсчета информации (момент принятия
решения). Момент определялся синхронизатором.
Однако в большинстве случаев в начале сеанса передачи
информации задержка сигнала неизвестна и ее необходимо измерить,
а затем ввести в решающее устрйство. Оценка времени задержки
может быть получена только из передаваемого сообщения, т. е.
из последовательности передаваемых сигналов. Поскольку на входе
приемника, кроме сигналов, имеется помеха, то оценка времени
задержки может случайным образом отличаться от истинного значения,
т. е. оценка будет содержать ошибку. Это приведет к ошибке в
определении момента отсчета, что в свою очередь снизит
помехоустойчивость приема. Точно так же дело обстоит с измерением частоты
сигнала. Поэтому приемники, в которых измерение параметров
сигналов производится по принимаемым сигналам, принято [162]
называть квазиоптимальными.
Общие принципы и методы измерения времени задержки сигнала
и сдвига по частоте хорошо изучены в радиолокации (см., например,
[25, 105, 162, 170, 171, 224]). При измерении времени задержки
в СПИ наблюдаются следующие особенности. Во-первых, при
передаче информации сигналы следуют непрерывно друг за другом
в течение длительного интервала времени, а в радиолокации в боль-
133
шинстве случаев со значительной, скважностью. В результате при
измерении времени задержки по последовательности сигналов,
переносящих информацию в СПИ, необходимо учитывать влияние
боковых пиков АКФ и ВКФ на характеристики измерения времени
задержки. Во-вторых, при передаче информации на вход
приемника поступает случайная последовательность сигналов,
образующих алфавит источника, а в радиолокации используется только
один сигнал. Так как сигналы, переносящие информацию, следуют
непрерывно друг за другом с периодом, равным длительности
сигналов Г, то сумма откликов всех согласованных фильтров
(см. рис. 2.4, 2.6) будет содержать центральные пики АКФ всех
сигналов, следующих с тем же перидом Т. Поэтому для измерения
времени задержки необходимо объединять (суммировать) отклики
всех согласованных фильтров [95]. При этом в промежутках между
центральными пиками соседних АКФ будут суммироваться боковые
пики АКФ и ВКФ на выходах всех согласованных фильтров, что
увеличивает время измерения задержки.
При корреляционном методе приема квазиоптимальный
приемник должен иметь устройство поиска сигналов по времени задержки.
В соответствии с принятым алгоритмом приемник перестраивает
генераторы опорных сигналов, чтобы задержка опорных сигналов
совпала с задержкой принимаемых сигналов. Необходимость в
блоке поиска определяется неинвариантностью корреляторов
относительно времени задержки.
Отметим, что, используя основные положения теории
измерения параметров сигналов и теории передачи сообщений, можно
составить схемы квазиоптимальных приемников как когерентного,
так и некогерентного методов приема сигналов. Однако при этом
остается неясным, насколько оптимален в целом весь
квазиоптимальный приемник. Это особенно важно знать при совместном измерении
нескольких параметров по принятому сообщению, например,
задержки и доплеровского сдвига по частоте. Для решения поставленного
вопроса необходимо использовать методы статистической
радиотехники с учетом характера изменения передаваемых сообщений и
измеряемых параметров. Поскольку измеряемые параметры входят
нелинейно в принятые сигналы, то теория приема сигналов в этих
условиях получила название теории нелинейной фильтрации.
Именно эта теория позволяет определить структуру квазиоптимального
приемника при измерении нескольких случайных параметров,
характер изменения которых определяется некоторыми
стохастическими дифференциальными уравнениями. Наибольшее значение она
имеет при определении структуры квазиоптимального приемника
для приема сигналов с неизвестным временем задержки и
неизвестным доплеровским сдвигом по частоте. При этом схемы
квазиоптимальных приемников содержат устройства слежения как за
временем задержки сигналов, так и за их несущими частотами, сложным
образом взаимосвязанных друг с другом, и с информационным
каналом (см., например, [3, 163, 166]).
134
Независимо от сложности в любом случае квазиоптимальный
приемник содержит согласованный фильтр или коррелятор, или их
комбинации. И согласованный фильтр, и коррелятор в соответствии
с (6.1), (6.2) являются линейными устройствами. По этой
причине согласованный фильтр (2.22), (2.23), (6.1) иногда называют
линейным согласованным фильтром, чтобы отличить его от
дискретного согласованного фильтра, который также будет рассмотрен в
данной главе.
6.2. Линейные согласованные фильтры
Линейные согласованные фильтры являются пассивными
фильтрами, их параметры не изменяются во времени. Структура
пассивных фильтров определяется элементами сигнала (импульсной
характеристикой фильтра). Пассивные методы обработки можно
разделить на три основные вида: частотный, временной,
частотно-временной.
При частотном методе произвольный сигнал представляется в
виде последовательности частотных элементов (элементарных
функций, смещенных по частоте). В общем случае вид этих элементов и
их расположение по частоте определяются преобразованием Фурье
исходного сигнала. В частном случае формирования сигнала из
частотных элементов он является частотным (см.§ 1.2).
Согласованные фильтры, построенные в соответствии с частотным методом,
являются многоканальными фильтрами (МКФ) [7, 19, 95, 99],
каждый канал которых выделяет соответствующую полосу частот
сигнала и производит необходимую оптимальную обработку этой
части сигнала.
При временном методе сигнал представляется в виде
последовательности элементов во времени, например, в виде прямоугольных
импульсов или в виде функций отсчета. Последние соответствуют
разложению сигнала в ряд Котельникова. Поэтому согласованный
фильтр, соответствующий временному представлению сигнала,
строится на основе многоотводной линии задержки (МЛЗ).
Частотно-временной метод обработки сложных сигналов основан
на представлении сигналов в виде элементов, разнесенных как во
времени, так и по частоте. Он объединяет, как это следует из
названия, частотный и временной методы. Согласованный фильтр
содержит ряд частотных каналов и многоотводную линию задержки (или
набор линий).
Частотный метод целесообразно применять для обработки
частотных сигналов, временной — для обработки дискретных
сигналов, частотно-временной — для обработки дискретных частотных
сигналов. Рассмотрим эти методы более подробно.
Частотно-временной метод обработки дискретных частотных
сигналов. ДЧ сигналы были подробно рассмотрены в § 1.6.
Комплексная огибающая ДЧ сигнала первого порядка определяется форму-
135
лой (1.44), а ее спектр .(1.51). Для простоты рассмотрим случай,
когда все элементы имеют одинаковую форму. При этом
комплексная огибающая и спектр определяются формулами (1.60), (1.61).
Коэффициент передачи согласованного фильтра определяется
формулой (2.23). Подставляя в (2.23) спектр ДЧ сигнала (1.61),
получаем
k (ω) = k0 Σ Ι αν I exp (
v=l
Канал Ν
Ι1Η>4ΙΗι
Канал J
H1H>-*HH
Канал 1
EH>-4Zh4J
Рис. 6.1
ίθν) S [ω — (γν — 1) Δω] Χ
χ βχρ {- ίω [Τ - (ν - 1) At]}, (6.3)
где комплексная амплитуда элемента av = \av\ exp (ίθν), спектр
элемента определяется преобразованием Фурье (1.62), а индекс f
в (1.61) не принят во внимание.
Как следует из (6.3),
согласованный фильтр должен состоять из
N каналов, входы которых
суммируются. Каждый канал —
прототип каждого элемента
сигнала (1.61). По сравнению с
(1.61) имеются некоторые
различия, которые определяются
формулой (2.23). Во-первых,
комплексная амплитуда каждого
канала (6.3) комплексно
сопряжена по сравнению с
комплексной амплитудой av элемента в
сигнале (1.61). По этой причине
канал должен содержать усилитель с коэффициентом усиления
| av | и фазовращатель, который создает сдвиг фаз равный — θν
или 2π — θν.
Во-вторых, АЧХ каждого канала определяется комплексно-со-
*
пряженным спектром элементарного сигнала S (ω), смещенного
по частоте на ту же величину (γν — 1) Δω, что и соответствующий
элемент сигнала. Обычно элементарные сигналы (1.59) имеют сим-
*
метричную форму. В этом случае согласно (1.62) S (ω) = S (ω) и
АЧХ каждого канала согласованного фильтра будет совпадать со
спектром элементарного сигнала (1.62).
В-третьих, если задержка каждого элемента в ДЧ сигнале
(1.61) составляет (ν — 1) At, то в согласованном фильтре задержка
соответствующего элемента согласно (6.3) равна Τ — (ν — 1) At.
Следовательно, первые элементы сигнала задерживаются в
согласованном фильтре больше, чем последние, что полностью
соответствует общим свойствам согласованных фильтров [105].
На рис. 6.1 представлена структурная схема линейного
согласованного фильтра, предназначенного для обработки ДЧ сигнала
первого порядка. Сигнал с выхода предыдущих каскадов приемника
(с усилителя промежуточной частоты (УПЧ)) поступает на МЛЗ.
136
Число отводов линии, включая начало, равно числу элементов N.
Общая задержка в линии (N — I) At = Τ—'At. Если ширина
спектра сигнала F, то полоса пропускания МЛЗ должна быть не
меньше F. Напряжение с каждого отвода поступает в канал, которщ
*
состоит из полосового фильтра с АЧХ \S [ω — (γν — 1) Δω] | и с
частотным смещением (γν — 1) Δω, усилителя с коэффициентом
усиления | αν | и фазовращателя φ, обеспечивающего сдвиг фаз
— θν или 2π — θν. Число каналов равно N. Выходы всех каналов
поступают в сумматор. Структурная схема рис. 6.1 полностью
соответствует коэффициенту передачи (6.3).
Кратко остановимся на основных элементах структурной схемы
рис. 6.1. Многоотводные линии задержки, нашедшие наибольшее
применение в согласованных фильтрах, могут быть магнитострикцион-
ными, кварцевыми или электрическими. Магнитострикционные
линии задержки являются ультразвуковыми и основаны на
распространении ультразвуковой волны в звукопроводе. Преобразование
радиоколебаний в ультразвуковые производится с помощью
специальных преобразователей, использующих магнитострикционный
эффект. Подробный обзор работ по таким линиям дан в работе
[19]. Отметим только, что магнитострикционные линии задержки
характеризуются большим затуханием (45—75 дБ), низкой
центральной частотой (порядка 0,5—3МГц), небольшой полосой
пропускания (не более 0,5 МГц), относительно малым числом отводов
(порядка 102) и большим временем задержки (до десятков
миллисекунд). Таким образом, магнитострикционные линии задержки
наиболее пригодны для обработки длительных, но относительно
узкополосных сложных сигналов. С помощью магнитострикционных
линий были реализованы первые согласованные фильтры для фазо-
манипулированных сигналов. Существенным недостатком таких
линий является большое затухание, из-за которого согласованные
фильтры становятся чрезмерно громоздкими.
Кварцевые линии задержки (см., например, [52, 93, 139]) также
являются ультразвуковыми и основаны на распространении
ультразвуковой волны в звукопроводе, которым является монокристалл
кварца. Возбуждение ультразвуковых колебаний основано на
использовании пьезоэлектрического эффекта, причем в многоотводных
линиях задержки используются поверхностные волны. Кварцевые
линии задержки характеризуются большим затуханием (70—80 дБ),
относительно большой центральной частотой (примерно 10—
20 МГц), большой полосой пропускания (порядка 5—10 МГц),
относительно малым числом отводов (порядка 30—64), относительно
малым временем задержки (до 50 мкс). В соответствии с этими
данными кварцевые линии задержки наиболее пригодны для обработки
относительно коротких, но широкополосных сложных сигналов.
Большое затухание является существенным недостатком таких
линий. Кроме того, относительно большая центральная частота
приводит к довольно жестким требованиям к фазовым рассогласованиям
137
в таких линиях 141, 52, 53], что имеет особое значение в ААС, когда
каждый абонент должен иметь возможность устанавливать связь
с произвольным абонентом. Применение кварцевых линий позволяет
относительно просто получать ДЧ сигналы с базами порядка 300—
500 [52].
Электрические линии задержки являются обычными LC-фильтра-
ми и представляют собой последовательное соединение стандартных
звеньев. Эти линии являются видеочастотными, т. е. их полоса
пропускания расположена между нулевой и некоторой другой
частотой, зависящей от числа звеньев в многоотводной линии задержки.
Ширина полосы пропускания многоотводной линии не превышает
0,5—1 МГц, длительность задержки 50—100 мкс, т. е. база сигналов,
которые могут обрабатываться согласованным фильтром с такими
линиями, не превышает 102 [19]. В этом отношении электрические
линии задержки уступают магнитострикционным и кварцевым. Но
они обладают и существенными преимуществами: малым затуханием,
большими допусками на рассогласования, большой надежностью
и относительно малыми габаритами. — Эти преимущества являются
причиной применения электрических линий задержки в
согласованных фильтрах.
Вопросы применения электрических линий задержки в
согласованных фильтрах были подробно исследованы [19, 44]. Следует
отметить, что поскольку полоса пропускания таких линий
сосредоточена в области видеочастот, то обработка сигналов возможна либо на
нулевой, либо на несущей частоте, не выходящей из пределов
полосы пропускания. В последнем случае несущая частота расположена
в области видеочастот. Для краткости этот случай будем называть
приемом на видеочастоте, а первый — приемом на нулевой частоте.
Основные принципы оптимального приема на нулевой частоте и
видеочастоте можно найти, например, в работах [6, 7, 105, 222],
пример сжатия ФМ сигнала на видеочастоте приведен в [6]. При
использовании электрических линий задержки для обработки сложных
сигналов возникает ряд вопросов по упрощению оптимальных и
получению более простых квазиоптимальных схем, определению
пределов применимости электрических линий задержки,
определению допусков на параметры сигнала и фильтра, сопряжению
согласованных фильтров на многоотводных электрических линиях
задержки с другими фильтрами для увеличения базы сигнала. Выбор
той или иной МЛЗ зависит от требований к СПИ. Полосовые
фильтры должны формировать требуемую частотную характеристику.
Полоса пропускания таких фильтров приблизительно равна ширине
спектра одного элемента, т. е. FIN (1.53), а N — число различных
элементов. Более подробно требования к фильтрам будут
рассмотрены при описании многоканальных согласованных фильтров для
обработки частотных сигналов. К усилителям и фазовращателям
предъявляются требования обеспечения необходимого усиления и
сдвига фаз в полосе частот шириной FIN при малых амплитудно-
частотных и фазочастотных искажениях.
138
Многоканальные согласованные фильтры при частотном методе
обработки частотных сигналов. Частотные сигналы определяются
формулами (1.91), (1.92). При одинаковых элементах имеем (1.93),
(1.94). Коэффициент передачи согласованного фильтра для
частотного сигнала может быть получен из выражения (6.3), если
положить задержку Δ^ = 0, γν = ν:
k((u) = k0 2 Ι «ν I е"
ν=ι
Μν§[ω—(ν— l)Aco]e-iu)r.
(6.4)
Канал N
HlhDHZ
Канал V
H>4Z
Канал 1
φ
*u
Рис. 6.2
Структурная схема многоканального согласованного фильтра
приведена на рис. 6.2. Обозначения те же, что и на рис. 6.1
Полоса пропускания каждого фильтра примерно равна FIN, a N —
число элементов в сигнале и
число каналов в фильтре. Задержка,
равная 7\ в множителе ехр (—ίωΓ)
в данном случае принципиального
значения не имеет, так как она
всегда обеспечивается реальными
полосовыми фильтрами.
Многоканальные согласованные
фильтры можно применять для
обработки не только частотных
сигналов, у которых частотная
структура выражена явно. Как
известно из теории рядов Фурье, любой
сигнал, удовлетворяющий
некоторым общим условиям, обычно
имеющим место в радиотехнике, можно приближенно представить
конечной суммой гармоник. Для радиочастотного сигнала следует
суммировать только те гармоники, которые проходят через
линейную часть приемника (смеситель, УПЧ). Согласованный фильтр
при таком представлении сигнала будет многоканальным.
При построении многоканальных согласованных фильтров
большое значение имеет АЧХ полосовых фильтров, которая в свою
очередь определяется спектром элемента (1.62). Во многих случаях
элементы являются простыми сигналами. Например, если элемент
является прямоугольным радиоимпульсом, то его форма Фп (0 = 1
при |/|< 772 и фп(/) = 0 при |/| >772. Соответственно (1.62),
спектр
Sn(<o)=(rsin^)/(if). (6.5)
Согласно (6.5) АЧХ полосового фильтра должна быть вида
| sin (co772)/((o772) |. По этому поводу следует заметить, что такая
АЧХ не реализуется с помощью цепей с постоянными параметрами.
Поэтому возникает вопрос о замене подобной АЧХ более просто
реализуемой. Одним из наиболее простых фильтров, удовлетворяю-
139
щих этому условию, можно считать фильтр с несколькими
одиночными контурами с одной и той же резонансной частотой при слабой
связи между ними. Частотная характеристика такого фильтра
приближается к гауссовой. В этом случае необходимо решить, как
следует выбирать полосу такого фильтра и какие искажения получит
сигнал и его АКФ.
АКФ частотного сигнала определяется формулой (1.112) при
Ω = 0. ВФН элементов (1.69) /?φ[τ, (ν — μ) Δω] будут
перекрываться при спектре элемента в виде (6.5). Эти ВФН зависят от
модуля разности номеров | ν — μ |. Можно показать, что если Δω =
= 2π/Τ, то
ι sin [π (ν-μ) (1-| τ Ι/Γ)]
|£Φ[τ, (ν—μ)Δω]| =
π (ν—μ)
(6.6)
Из формулы (6.6) следует, что с ростом | ν — μ | ВФН элементов
уменьшается обратно пропорционально этой разности. Начиная
с | ν — μ | ^ 3, влияние ВФН (6.6) на АКФ частотного сигнала
становится малым и практически их можно не учитывать.
Если элемент является гауссовым радиоимпульсом, т. е.
Фг = F0T exp (- nFl?), (6.7)
то его спектр
5Г (ω) = Τ exp [— π (ω/№0)2], (6.8)
где W0 = 2Fn0 характеризует ширину спектра элемента (и
полосу пропускания полосового фильтра) на уровне ехр (— π/4) ~
си 0,46. В этом случае ВФН элементов
*Φ[τ,(ν-μ)Μ=βχρ{--^[^τ»+£^]}. (6.9)
Как и в случае прямоугольного элемента, вес функций #ф с
ростом | ν — μ | падает, причем при больших | ν — μ| более резко,
что определяется вторым слагаемым в экспоненте формулы (6.9).
Изменение R<p зависит от величины F0. Ее приближенный выбор
может быть сделан следующим образом. Чтобы АКФ сигнала с
гауссовой срезающей функцией не отличалась намного от АКФ сигнала
с прямоугольной срезающей функцией, надо обеспечить, во-первых,
примерно равное изменение Ro от | ν — μ | в обоих случаях и, во-
вторых, приблизительно одинаковую форму #ф(т)для одних и тех
же ν — μ. Строгое определение оптимального значения F0
достаточно сложно. Однако оказывается, что оба условия имеют место с
точностью, достаточной для практических целей, если
F0 - (1,2 - 1,5) Δ/ = (1,2 - 1,5)/Т. (6.10)
Если F0 в формулах (6.7), (6.8) выбирается в соответствии с (6.10),
то АКФ сигнала с гауссовой срезающей функцией будет мало
отличаться от исходной, причем уровень боковых лепестков может
стать даже меньше. Что касается сигнала, то согласно формуле
140
(1.93) он будет иметь уже не прямоугольную форму, а гауссову.
При этом равномерность огибающей сигнала будет несколько
хуже, чем в случае прямоугольной формы.
Частотный метод, как было отмечено ранее, представляется
наиболее целесообразным при формировании и обработке
широкополосных частотных сигналов с малой длительностью. Согласно формуле
(6.10) длительность сигнала определяется шириной полосы
пропускания избирательного усилителя F0. Обычно эта величина
ограничена. Наименьшее значение F0 может быть 5—10 кГц при значении
несущей порядка сотен килогерц и единиц мегагерц. При этом
максимальная длительность сигнала будет равна 100—200 мкс.Большие
длительности вряд ли можно получить с помощью простых
канальных фильтров. С другой стороны, число каналов примерно равно
базе F/Δ/ ~ FT = В. Практически фильтр с числом каналов
больше 100 представляет достаточно сложное устройство. Как
показывают исследования рассогласований в многоканальных фильтрах,
изготовление и настройка многоканального согласованного фильтра
с числом каналов больше 100 — серьезная техническая задача.
Поэтому применять многоканальные фильтры целесообразно при
В < 100 и Т<100 — 200 мкс. Нижняя граница длительности
сигнала определяется максимально возможной шириной полосы
пропускания канального фильтра. Чем она больше, тем большую
полосу частот при той же базе будет занимать сигнал.
Многоканальные фильтры позволяют достаточно просто получать большие
полосы частот. Если ширина полосы пропускания канала порядка
0,5—1 МГц, то при 20—30 каналах ширина спектра сигнала будет
10—30 МГц. Длительности сигналов при этом примерно равны 1 —
2 мкс. Обычно в СПИ длительности информационных символов
много больше. Поэтому многоканальные фильтры в большинстве
случаев используются как один из элементов комбинированных
фильтров, осуществляющих частотно-временную обработку.
Согласованные фильтры с многоотводными линиями задержки
при временном методе обработки дискретных сигналов. Дискретные
сигналы определяются формулами (1.95), (1.96). Если элементы
имеют одинаковую форму, то необходимо пользоваться формулами
(1.97), (1.98). Коэффициент передачи согласованного фильтра,
предназначенного для обработки дискретных сигналов, можно получить
из (6.3), полагая Δω = 0. В результате имеем
k (ω) = k0S (ω) Χ
Ν
Χ Σ |αν| exp (— ίθν) exp {— ico [Τ — (ν — 1) Δ/]}. (6.11)
Структурная схема соответствующего согласованного фильтра
приведена на рис. 6.3. Обозначения те же, что и на рис. 6.1, 6.2.
В данном случае имеется только один полосовой фильтр с частотной
характеристикой S (со), который может быть расположен как на
141
Канал N
Канал V
входе согласованного фильтра (как это показано на рис. 6.3). так
и на его выходе. Число отводов МЛЗ, включая начало, равно Ν,
общая задержка равна (Ν — 1) At = Τ — At Полоса пропускания
МЛЗ дожна быть равна ширине спектра сигнала F. Центральная
частота МЛЗ должна совпадать с несущей частотой сигнала на
входе фильтра. Усилители и фазовращатели должны обеспечивать
необходимое усиление и сдвиг фаз в полосе частот, равной ширине
спектра сигнала F, и не вносить заметных амплитудно-частотных и
фазочастотных искажений.
В качестве МЛЗ можно применять, как было отмечено ранее,
магнитострикционные, кварцевые и электрические линии задержки.
Применение электрических линий
задержки для обработки
радиочастотных сигналов имеет свои
особенности, так как полоса
пропускания таких линий
сосредоточена в области видеочастот.
Для обработки радиочастотных
_^ сигналов с помощью
видеочастотных фильтров необходимо
перенести сигналы в область
видеочастот. При когерентной обработке
сигнала на нулевой несущей
частоте радиочастотный фильтр
заменяется видеочастотным согласно
структурной схеме рис. 6.4, я,
а при некогерентной обработке —
согласно структурной схеме рис. 6.4, б [105]. Эти структурные
схемы содержат умножители, генераторы гармонических колебаний с
частотой, равной частоте сигнала, согласованные фильтры (СФ),
квадраторы (Кв) и сумматор Σ. Генераторы опорных сигналов при
когерентном приеме создают гармоническое колебание cos ω0^, где ω0 —
несущая частота сигнала на входе радиочастотного фильтра; при
некогерентном — два квадратурных гармонических колебания
cos ω0( и sin ω0(. Согласованные фильтры выполняются по
структурной схеме рис. 6.3. Они являются в данном случае
видеочастотными, и в них можно использовать электрические линии задержки.
Границы применимости многоотводных электрических линий
задержки (МЭЛЗ) определены в [19].
МЭЛЗ составляется из стандартных звеньев (безотводных линий
задержки). Для увеличения базы сигнала, обрабатываемой с
помощью МЭЛЗ, необходимо использовать звенья, обладающие наиболее
равномерной АЧХ и наиболее линейной ФЧХ. Неравномерности
АЧХ звеньев приводят к существенному уменьшению полосы
пропускания МЭЛЗ, т. е. к уменьшению базы обрабатываемого сигнала.
Предел увеличения базы обрабатываемого сигнала определяют
рассогласования между сигналом и фильтром. Для МЭЛЗ, как
показали исследования по рассогласованиям, он равен 5 · 102—103.
142
Рис. 6.3
Однако результаты экспериментов и расчеты показывают, что этот
предел будет примерно 100—200 из-за неравномерности АЧХ.
Комбинированные методы обработки. Как следует из
предыдущего материала, согласованные^фильтры на многоотводных
электрических линиях задержки (СФМ) и многоканальные
согласованные фильтры (МКФ) относительно просты в изготовлении и
настройке, но позволяют обрабатывать сигналы с малыми базами (В <100).
Причем СФМ обладают относительно малой полосой (F ^ 1 МГц)
при времени задержки (длительности сигнала) Τ ^ 100—150 мкс,
а МКФ — относительно большой полосой (F ~ 1—30 МГц), но
малой длительностью сигнала (Т ^ 1—20 мкс). В соответствии с
такими свойствами представляется естественным объединить МКФ
и СФМ, т. е. использовать комбинированный метод обработки, ко-
hosu)0t φ
Ш ПП
SiVCUgt
Χ
ШФ
ЦКд
δ)
Рис. 6.4
торый должен сочетать широкую полосу частот, присущую
частотному методу (МКФ), относительно большую длительность,
присущую временному методу (СФМ), и простоту изготовления,
настройки и эксплуатации обоих методов.
При построении комбинированных схем обработки,
соответствующих таким методам, главную роль играет соотношение полос
пропускания МКФ и СФМ. Когда полосы равны, существенного
увеличения базы получить нельзя, но из-за уменьшения числа
отводов у МЭЛЗ базу все-таки можно увеличить. Такой случай назовем
случаем равнополосных фильтров. Большой интерес представляет
случай, когда полоса МКФ много больше полосы СФМ, т. е. случай
разнополосных фильтров. Отметим, что будем рассматривать прием
квазидетерминированного сигнала (со случайной начальной
фазой). В настоящее время известно большое число комбинированных
схем (см., например, [164]). Остановимся на двух из них.
Структурная схема оптимального приемника с равнополосными
фильтрами приведена на рис. 6.5. С выхода МКФ напряжение
поступает на два квадратурных канала, состоящих из перемножителя,
СФМ и квадратора (Кв), Напряжения с квадраторов поступают на
сумматор. Представленная схема является накопителем для
квазидетерминированного сигнала [105]. Принцип работы такой схемы
известен (см. рис. 6.4), поэтому останавливаться на нем не будем.
143
База обрабатываемого сигнала равна произведению базы
частотного сигнала, обрабатываемого МКФ, на базу дискретного сигнала,
обрабатываемого СФМ. В целом сигнал является дискретным
составным сигналом.
На рис. 6.6 представлена структурная схема
квазиоптимального приемника с разнополосными фильтрами. Пусть ^мкф» ^сфм —
полосы пропускания МКФ и СФМ. Если число каналов равно N, то
^мкф ^Л/^сфм. (6.12)
Каждый канал приемника рис. 6.6 совпадает с приемником рис. 6.5,
начиная от МКФ. Вся полоса частот, занимаемая сигналом, делится
r^|3^-^/i]-^^
МКФ
G0SU)ot
SlTlCugt
^Х
Э\СФЩ-Ц
Рис. 6.5
Канал 1
Кб
]! $C0SU)jt
^sincutt
чх
ШП\
ЦКд
Канал N\
гИХ
ЯЩ
Tcos ωΗ t
Кб
x}--^Q--^F
Рис. 6.6
на N полос, каждой соответствует свой канальный полосовой фильтр.
Частоты ωχ, ..., ωη, ..., ω^ удовлетворяют равенству
ωη = ωλ + (η — 1) Δω, Δω = 2nF/N.
(6.13)
Напряжения с такими частотами формируются генератором сетки
частот, который на схеме не показан. Хотя общая база сигнала равна
А/Бсфм, сжатие сигнала определяется только базой МЭЛЗ (т. е.
величиной /?Сфм), так как в каждом канале выделяется огибающая
и устраняется фазовая структура.
Рассмотренные в данном параграфе методы нашли широкое
применение на практике. Используя их, можно найти большое число
различных конкретных схем обработки сигналов.
6.3. Дискретный согласованный фильтр
Дискретный согласованный фильтр (ДСФ) является цифровым
(дискретным) устройством обработки непрерывных (аналоговых)
сигналов. Подробно принцип действия ДСФ и его
помехоустойчивость рассмотрены в работах [2, 17, 45, 70, 74, 91, 112, 192].
Принцип действия ДСФ основан на квантовании непрерывного
колебания (рис. 6.7, а) по времени и по амплитуде. Квантование
144
по времени осуществляется с интервалом, который определяется
структурой используемых сигналов и требованиями к общей ошибке.
Например, если используются дискретные фазоманипулированные
сигналы с длительностью элементов Δ/, то интервал квантования по
времени обычно выбирается равным Δ/ или At/2 [74].квантование
по амплитуде осуществляется на два уровня + 1 и — 1 (рис. 6.7, б).
Поскольку ДСФ имеет регистр сдвига, работающий с двумя
уровнями 1 и О, то двустороннее квантованное колебание (рис. 6.7, б)
необходимо превратить в одностороннее (рис. 6.7, в). Дискретная
часть ДСФ производит цифровую
обработку (когерентное
накопление с учетом фазовой структуры
сигнала) одностороннего
колебания (рис. 6.7, в).
Структурная схема ДСФ
приведена на рис. 6.8. Непрерывное
радиочастотное колебание с выхода
линейной части приемника с
помощью умножителя переводится в
область видеочастот, проходит
через фильтр нижних частот и
поступает на первое решающее
устройство (1 РУ)*. Напряжение на
входе I РУ имеет вид, изображенный
на рис. 6.7, а. Первое решающее
устройство состоит из
двустороннего ограничителя и каскада совпадения «1». В I РУ производится
квантование (дискретизация) сигнала по времени и по амплитуде
ва два уровня 1 и 0. Напряжение на выходе I РУ изображено на
рис. 6.7, в. Как следует из принципа работы I РУ, оно принимает
решение о знаке непрерывного колебания в момент отсчета.
Генератор тактовых импульсов определяет момент отсчета и управляет
работой ДСФ в целом, определяя синхронность работы каскада
совпадения и регистра сдвига (RG). Регистр сдвига выполнен на D-
триггерах и является дискретной линией задержки. С каждым
тактом выборочные значения продвигаются на единицу времени
задержки, равную интервалу квантования по времени, Регистр сдвига
представляет собой последовательность триггерных ячеек, каждая из
которых имеет два выхода: 1 (прямой) и 0 (инверсный). Производя
сложение в сумматоре напряжений с различных выходов
триггеров, можно получать различные импульсные характеристики ДСФ,
т. е. согласовывать его с различными сигналами. ДСФ рис. 6.8
согласован с дискретным фазоманипулированным сигналом, кодовая
последовательность которого есть 0 10 1 1. Напряжение с выхода
0
VJL/
x'i ^
1 '
/
0
1
0
1
δ)
г
—**
в)
Рис. 6.7
* Второе решающее устройство является обычным решающим
устройством, расположенным на выходе оптимального приемника и принимающим
решения об информационных символах.
145
сумматора может использоваться обычным образом. При
когерентном приеме двух противоположных сигналов оно непосредственно
должно поступать на второе решающее устройство. При
некогерентном приеме на каждый сигнал должно приходиться два
квадратурных канала, выполненных по структурной схеме рис. 6.8, но
с двумя опорными колебаниями cos ω0ί и sin ω0^.
Свойства ДСФ имеют много общего со свойствами обычного
линейного согласованного фильтра (ЛСФ) (2.23). Что же касается
особых свойств, одно из них заключается в том, что напряжение на
выходе ДСФ не является АКФ сигнала, которая имеет место на
выходе ЛСФ. На рис. 6.9 представлена ненормированная АКФ сигнала
Баркера с числом символов N = U (тонкая линия) и напряжение
на выходе ДСФ (толстая линия). Напряжение на выходе ДСФ от-
1РУ
-Их
τ
COSUgt
1 ι *c-~
щ%
Рис. 6.8
личается от напряжения на выходе ЛСФ не только своей
дискретной структурой, но и формой: уровень боковых пиков иной и
имеется значительная постоянная составляющая (штриховая линия).
Это объясняется тем, что основным элементом ДСФ является
регистр сдвига. Даже если на входе приемника не будет сигнала, то
и тогда на выходе ДСФ будет определенная постоянная
составляющая (в данном примере она равна 6, если на входе ДСФ нули).
Для конкретных сигналов напряжение на выходе ДСФ нетрудно
просчитать. При этом можно показать, что изменение уровня
боковых пиков не превосходит величины п/В, где η — число
одинаковых символов, расположенных друг за другом, В — база сигнала,
равная числу символов. Например, для Λί-последовательностей
п = 1°§2 Вис увеличением В отличие между АКФ и
напряжением на выходе ДСФ уменьшается.
Помехоустойчивость ДСФ. Сделаем следующие предположения
[17, 45, 70]. Допустим, что осуществляется когерентный прием
дискретного фазоманипулированного сигнала с числом символов
N = В и энергией Е. Информация передается с помощью фазовой
манипуляции, т. е. противоположными сигналами. Положим, что
шум является нормальным случайным процессом с равномерной
спектральной плотностью мощности Ν0. Каждый импульс сигнала
принимается оптимально, что требует синхронизации генератора
тактовых импульсов.
Для определения вероятности ошибки Рош д при приеме с
помощью ДСФ необходимо знать закон распределения напряжения
146
на его выходе в момент отсчета. Как было отмечено ранее, ДСФ
производит квантование (дискретизацию) сигнала по амплитуде и по
времени и выносит решение о знаках выборочных значений.
Полученная выборка принимаемого сигнала вписывается в регистр
сдвига. Так как интервал дискретизации по времени равен длительности
импульса сигнала, а полоса входных устройств согласована с этим
импульсом, то выборочные значения некоррелированы, а в силу
нормального распределения шума и независимы.
Вероятность правильного приема каждого импульса ФМ
сигнала, энергия которого в В раз меньше энергии всего сигнала,
согласно (2.19), (2.20) равна
'-'(/£)·
(6.14)
где интеграл вероятности F (х) определяется согласно (2.16).
Когда сигнал полностью впишется в регистр сдвига, в сумматоре
ДСФ складываются В независимых выборочных значений с
вероятностями правильного приема ρ (6.14) и с вероятностью ошибки 1 — р.
Вероятность Ρ (k) того, что из В значений ровно k будет принято
правильно, описывается биномиальным законом (3.5)
Р (ft)
cBva
Ρ)
B—k
(6.15)
где С J — число сочетаний из В по k. Ошибка будет иметь место,
если более половины символов ФМ сигнала приняты с ошибками,
т. е.
|Д=22с!р*(1-р)
k = 0
B—k
(6.16)
Формулы (6.14), (6.16) позволяют найти точное значение
вероятности ошибки. При больших базах, когда В > 1, а именно такой
случай представляет наибольший интерес, можно найти приближен-
147
ные формулы, которые позволяют достаточно просто определить
Рошд. Известно [104], что при большом числе слагаемых
биномиальный закон (6.15) нормализуется и принимает вид
•й-тв"!-^} <6Л7)
где среднее значение и дисперсия случайной величины χ равны
а = Вр, σ* = Βρ(\—ρ). (6.18)
При больших В вероятность /7 ^ 0,5 согласно (6.14). В этом
случае (6.17) мало отличается от (6.15). Так как число правильно
принятых выборочных значений и напряжение на выходе ДСФ
после фильтрации постоянной составляющей с точностью до
постоянного коэффициента связаны соотношением υ = χ — 0,55, то
распределение величины υ аналогично (6.17), но со средним значением
т„ = Вр— 0,5. (6.19)
Учитывая (6.17)—(6.19), получаем выражение для вероятности
ошибки
р_,- | .*»*- 1-'[У»1$£щ\ <«»)
При увеличении базы В вероятность ошибки Рошд
увеличивается и достигает максимального значения при В -»■ оо.
Используя приближенное представление интеграла" вероятности [104]
и заменяя ρ согласно этому представлению, получаем
р—а"-'(/-5г)· (6·2,)
Если прием сигнала производится линейным согласованным
фильтром, то согласно (2.19), (2.20) вероятность ошибки равна
р»л-1-*(|/|^). (6-22)
Сравнение выражений (6.21) и (6.22) показывает, что
увеличение вероятности ошибки Рошй в ДСФ эквивалентно
максимальным потерям в отношении сигнал/шум в π/2 раз, т. е. на 2 дБ [17,
45, 70].
Вероятность ошибки при некогерентном приеме с помощью ДСФ
и β->-οο определяется следующим выражением [45, 70]:
Pomn-0,5exp(-Jy. (6.23)
148
При линейном согласованном фильтре согласно (2.20), (2.26)
имеем
Рошл^0,5ехр(-^-). (6.24)
Из сравнения (6.23) и (6.24) следует, что максимальные потери
не превышают 2 дБ.
Исследование помехоустойчивости ДСФ при воздействии
гармонической помехи [70] показывает, что она значительно ухудшается
по сравнению с помехоустойчивостью линейного согласованного
фильтра.
Квазиоптимальный ДСФ. Помехоустойчивость ДСФ,
построенного согласно структурной схеме рис. 6.8, зависит от времени
прихода сигнала, так как необходима синхронизация по тактовой
частоте, с которой размещены импульсы в сигнале. В этом смысле
ДСФ не инвариантен относительно времени прихода сигнала. Вы-
зывано это тем, что коэффициент передачи фильтра нижних частот
согласован с одиночным импульсом сигнала. Такое согласование
резко изменяет форму импульса, из прямоугольного превращает
его в треугольный. Поэтому если нет синхронизации генератора
тактовых импульсов с момента прихода импульсов ФМ сигнала, то
это приводит к значительному увеличению Рош д, а когда тактовые
импульсы совпадают с разрывами фазы ФМ сигнала, то прием
сигнала вообще невозможен.
Для того, чтобы ДСФ был инвариантен относительно времени
прихода сигнала, необходимо расширить полосу фильтра нижних
частот. Это приводит к дополнительным потерям в
помехоустойчивости. Поэтому необходимо строить ДСФ, имеющие небольшие
дополнительные потери. Такой ДСФ в дальнейшем будем называть
квазиоптимальным. Можно построить несколько различных
квазиоптимальных ДСФ. Рассмотрим две наиболее простые схемы [70].
Метод построения квазиоптимального ДСФ заключается в том,
что полоса фильтра, которая в дальнейшем предполагается
прямоугольной, расширяется приблизительно в два раза и равняется
Δ/ = 2/Δ/, где Δ^ — длительность импульса ФМ сигнала. Это
приводит к уменьшению среднего значения отношения сигнал/шум в I
РУ и времени корреляции шума на выходе фильтра нижних частот
приблизительно в два раза (τκ = 0,5Δ/). Последнее позволяет
удвоить объем независимых выборок и получить небольшие потери в
помехоустойчивости.
Используя этот метод, можно построить квазиоптимальный ДСФ
по схеме рис. 6.8, расширяя полосу фильтра нижних частот до
Af=2/At и удваивая тактовую частоту генератора тактовых
импульсов и число ячеек в регистре сдвига. Этот же принцип можно
реализовать по двухканальной схеме. В этом случае вместо одного
регистра используются два с тем же числом ячеек и с той же тактовой
частотой, что и на рис. 6.8, но тактовые импульсы на регистры
подаются со сдвигом на пол такта.
149
В работе [70] показано, что. в среднем квазиоптимальный ДСФ
проигрывает оптимальному в отношении сигнал /шум 1 дБ.
Поскольку последний в свою очередь проигрывает 2 дБ ЛСФ, то средние
потери в квазиоптимальном ДСФ составляют примерно 3 дБ.
Максимальные потери в квазиоптимальном ДСФ [70] равны 4,5 дБ.
Рис. 6.10
щЩ£]
I
л.
3Z
Πι
I
Канал 1
6.4. Дискретно-аналоговый согласованный фильтр
Принцип действия дискретно-аналогового согласованного
фильтра (ДАСФ) [181, 182] поясняется рис. 6.10. Непрерывное колебание
χ (t) (тонкая линия) квантуется по времени и каждое выборочное
значение запоминается на
интервале квантования. Тем самым
непрерывное колебание заменяется
дискретно-аналоговым (толстые
линии на рис. 6.10), причем
имеется дискретность по времени и
«аналоговость» по амплитуде. Для
обработки такого колебания
необходимо иметь в первую очередь
дискретно-аналоговую линию
задержки (ДАЛЗ), которая должна
работать следующим образом.
В ячейках памяти в течение
интервала квантования должны
храниться выборочные значения,
которые были записаны в начале
этого интервала. В следующий такт
каждое выборочное значение
должно быть переписано в
последующую ячейку памяти. Таким
образом, с каждым новым тактом
информация дискретно (как и в
обычном регистре) продвигается
вдоль ДАЛЗ. Описания различных
ДАЛЗ можно найти в работах
[8, 122, 134, 182].
На рис. 6.11 приведена
структурная схема ДАСФ, построенная
в соответствии с описанным
принципом работы. ДАЛЗ состоит из
ключей (Кл) и ячеек памяти (П). Назначение ключей — перенос
информации с предыдущей ячейки памяти на последующую. Ритмом
работы ДАСФ управляет генератор тактовых импульсов (Г).
Импульсный модулятор преобразует непрерывное колебание в
дискретно-аналоговое в соответствии с рис. 6.10. С выхода каждого отвода
ДАЛЗ (с выходов ячеек памяти) напряжения поступают, как и в
150
ШХБ
п2
Пн
Канал 1
Канал N
LbM>*04J
z\*
Рис. 6.11
обычных согласованных фильтрах, на усилители и фазовращатели,
а затем суммируются в сумматоре. Отметим только, что
помехоустойчивость ДАСФ практически такая же, как и
помехоустойчивость линейных согласованных фильтров.
6.5. Активные фильтры
Активные фильтры или
корреляторы являются устройствами с
переменными параметрами. Активный
фильтр, общая структурная схема
которого представлена на рис. 6.12,
может иметь несколько
корреляционных каналов, состоящих из
умножителей (X) и интеграторов (И).
Необходимым элементом активного
фильтра является генератор опорных
сигналов (ГОС). При приеме
сигналов с неизвестной задержкой
активный фильтр имеет также
синхронизатор (С), который обеспечивает
поиск сигнала по времени (измерение
задержки сигнала) и слежение за
задержкой сигнала при его
изменении. Синхронизатор состоит из
устройства управления (УУ), которое
управляет ритмом работы активного
фильтра, устройства поиска (УП) и
устройства слежения за задержкой
(УСЗ). Решающее устройство (РУ)
принимает решение в конце
интервала анализа о наличии сигнала
и педедает его в блок управления
синхронизатора. Интересные
примеры активных фильтров можно
найти в работах [2, 90, 156, 166, 169].
Особенности построения
активных фильтров определяются в
первую очередь процедурой поиска
сигнала во времени, т. е. измерением
задержки [154, 156, 165, 166].
Устройство поиска может быть однока-
нальным (последовательный поиск),
многоканальным (параллельный
поиск) и комбинированным
(малоканальным с последовательным
поиском в меньших позициях) [95].
Одноканальное устройство
поиска. В этом случае активный фильтр
имеет только один корреляционный
канал, который состоит из одного
умножителя и одного интегратора.
Возможны различные процедуры
поиска, среди которых самая
простая — последовательный перебор.
При такой процедуре поиска
производится анализ одного
разрешаемого элемента — интервала по времени.
Если сигнал обнаружен, задержка
измерена, то поиск прекращается.
Если сигнал не обнаружен, то
анализируется следующий разрешаемый
интервал. Ширина разрешаемого
интервала определяется
длительностью центрального пика АКФ сиг-
Канал 1
Г? С—Π
Канал]
Кана η Ν
ГОС
\УСЗ
Ж
ж
РУ
УУ
J
Рис. 6.12
нала и необходимой точностью
синхронизации. Если время анализа
одного интервала Га, интервал
наблюдения Гн, разрешаемый интервал ΔΓ,
то число разрешаемых интервалов
равно Μ = ΤΒ/ΔΤ и максимальное
время поиска
Гпмакс = МГа = ГнГа/А7\ (6.25)
Как показывают исследования,
если истинное значение задержки
равномерно распределено на интер-
151
вале наблюдения, то среднее значение
времени поиска равно
7\1 = МГа/2 = ГнГа/2АГ, (6.26)
т. е. в два раза меньше. Из (6.25),
(6.26) следует, что время поиска
уменьшается с уменьшением ширины
интервала наблюдения. Поэтому
всегда имеет большое значение
априорное уменьшение этого интервала,
например, с грубым определением
задержки сигнала по его части [169].
Многоканальное устройство
поиска. Оно состоит из η
корреляционных каналов (рис. 6.12). Положим,
что n—M/k и является целым
числом. Каждый канал анализирует k
разрешаемых интервалов методов
последовательного перебора.
Максимальное время поиска равно
ГПмакс = ^а=Л1Га/л. (6.27)
В данном случае время поиска по
сравнению с последовательным
поиском (одноканальное устройство)
уменьшено в η раз. Если число
каналов η равно числу разрешаемых
интервалов М, т. е. к = 1, то
максимальное время поиска минимально
и равно времени анализа одного
разрешаемого элемента
^пмакс = ^а· (6.28)
Комбинированное я-канальное и
/я-шаговое устройство поиска.
Алгоритм работы такого устройства
существенно отличается от
алгоритмов работы двух предыдущих
устройств. Он заключается в следующем
[95]. На первом шаге весь интервал
наблюдения Гн разбивается на η
подынтервалов, каждый из которых
анализируется одним каналом в
течение времени Га. На первом шаге
грубо определяется задержка
сигнала с точностью Δ/χ = ΔίΜ/η.
После этого все каналы на втором
шаге анализируют выбранный
интервал, на котором грубо обнаружен
сигнал, шириной А/х и т. д. Так как
число каналов η и шагов т связаны
соотношением
Μ = пт, (6.29)
то максимальное время поиска
^п макс = тТ& =
= (\пМ/\пп)Та. (6.30)
По сравнению с (6.27) имеем
некоторое уменьшение времени
поиска, но при этом ухудшаются
характеристики обнаружения сигнала.
Сравнение активных фильтров.
В качестве наиболее грубого
критерия сравнения можно взять
произведение числа каналов на время
поиска. В одноканальном и
многоканальном устройствах эта величина
одинакова и равна МТЛ. Поэтому
для уменьшения времени поиска
необходимо увеличивать число каналов,
т. е. усложнять активный фильтр.
В многоканальном устройстве
поиска (при большом числе каналов)
и в комбинированном (п-канальном
и m-шаговом) сложность активного
фильтра возрастает из-за
увеличения числа каналов и усложнения
генератора опорных сигналов. В
результате весь фильтр значительно
усложняется. При этом некоторый
выигрыш в произведении числа
каналов на время поиска объясняется
ухудшением помехоустойчивости.
С практической точки зрения
целесообразнее использовать
многоканальное устройство поиска при
числе каналов, не превышающем числа
ячеек регистра, формирующего
дискретный сигнал. Тем не менее
наибольшее применение нашло одно-
канальное устройство из-за простоты
его структуры. Однако для
уменьшения времени поиска необходимо
переходить к многоканальным
устройствам.
152
Глава 7
РЕАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ РАДИОТЕХНИЧЕСКИХ
СИСТЕМ СО СЛОЖНЫМИ СИГНАЛАМИ
7.1. Помехоустойчивость приема сложных сигналов
с идеальными корреляционными функциями
В главах 4, 5 было показано, что применение сложных сигналов
позволяет повысить помехоустойчивость СПИ относительно
взаимных (структурных) и организованных помех. Однако реальная
помехоустойчивость будет ниже потенциальной по ряду причин.
Снижение помехоустойчивости происходит при вхождении в синхронизм
и приеме информации. Причинами снижения помехоустойчивости
при вхождении в синхронизм являются увеличение числа
разрешаемых элементов по дальности и скорости с увеличением базы сигналов
и боковые пики автокорреляционных функций (АКФ)
используемых сигналов. Кроме того, помехоустойчивость снижается из-за
аппаратурных рассогласований, которые будут сказываться как
при вхождении в синхронизм, так и при приеме информации. И,
наконец, имеется принципиальное ограничение увеличения
помехоустойчивости из-за снижения мощности генераторов при
значительном расширении спектра сигналов [33, 114]. Сначала рассмотрим
помехоустойчивость приема сложных сигналов при идеальных АКФ.
Обнаружение сложных сигналов с неизвестной задержкой.
Известно [12, 170], что при обнаружении сигнала с неизвестной
задержкой на фоне белого шума помехоустойчивость определяется
отношением сигнал/шум на выходе согласованного фильтра и числом
разрешаемых элементов по задержке. Длительность разрешаемого
элемента примерно равна длительности основного пика АКФ
сигнала. Чем больше число разрешаемых элементов, тем ниже
помехоустойчивость, так как увеличивается число ложных превышений
порога.
Иное положение имеет место при обнаружении сигнала с
неизвестной задержкой на фоне флюктуационной помехи с ограниченной
средней мощностью. В этом случае согласно (5.9) отношение
сигнал/помеха на выходе согласованного фильтра растет с
увеличением базы сигнала. Поэтому при обнаружении сложных сигналов,
у которых база много больше единицы, помехоустойчивость имеет
тенденцию, с одной стороны, возрастать с увеличением базы сигнала
из-за увеличения отношения сигнал/помеха, а с другой —
уменьшаться из-за увеличения числа разрешаемых элементов. В работе
[27] были рассмотрены вопросы обнаружения сложных сигналов
с неизвестной задержкой и измерения задержки при идеальных АКФ.
В данном параграфе приведены основные результаты [27].
Примем для простоты дискретную модель изменения задержки,
т. е. положим, что задержка сигнала во времени принимает ряд ди-
153
скретных значений. Число таких значений определяется отношением
интервала наблюдения* Тн к ширине центрального пика АКФ,
равного примерно 1/F, где F — ширина спектра сигнала. Положим, что
интервал наблюдения равен длительности сигнала 7\ т. е. Тн = Т.
-Число разрешаемых элементов по задержке будет равно Λίτ =
= T/(l/F) = Ву т. е. базе сигнала. В данной главе будем
рассматривать прием сигнала со случайной начальной фазой. Поэтому
оптимальный некогерентный приемник обнаружения и измерения
должен состоять из согласованного фильтра, детектора огибающей и
решающего устройства (порогового устройства).
Решающее устройство при обнаружении сигнала с неизвестной
задержкой работает по правилу, изложенному в [12]. Если
напряжение на выходе согласованного фильтра превышает порог на
интервале наблюдения, то принимается решение «сигнал есть», если
не превышает — «сигнала нет». Помехоустойчивость в этом случае
определяется вероятностью правильного обнаружения Рправ и ве_
роятностью ложной тревоги Рлт, которые выражаются следующим
образом [12]:
*прав = -I У* *лто/ О *право)> \'·4
Рлт= 1-(1-Рлто)в, (7.2)
где Рправ о — вероятность правильного обнаружения сигнала при
том дискретном значении задержки, где сигнал есть; Рлт 0 —
вероятность ложной тревоги при произвольном дискретном значении
задержки, т. е. вероятность ложного превышения порога.
Обозначим порог через V0, а его относительное значение через Ъ = VJV,
где V (5.3) — максимум сигнальной составляющей на выходе
согласованного фильтра. Отношение сигнал/помеха q2 на выходе
согласованного фильтра определяется формулой (5.1). При действии
помехи с ограниченной мощностью отношение сигнал/помеха
определяется формулой (5.46), при совместном же действии помехи
и собственного шума — формулой (5.48). Выражение (5.48) запишем
в следующем виде:
<72 = (2ЯС/РП) (1 + NoFPn1) -'В. (7.3)
Предполагая, что сигнал обладает идеальной АКФ без боковых
пиков, имеем [12]
оо
Рправ о = [ * ехр ( -^±£) /о (zq) dz, (7.4)
bq
где IQ (χ) — модифицированная функция Бесселя нулевого
порядка. Аналогично
P„o-Jzexp(--^)dz==exp(--^-). (7.5)
bq
154
Как видно из формул (7.1) —(7.5), вероятности Рправ и Р*лт
зависят от базы В двояко: с увеличением базы растет отношение
сигнал/помеха q и увеличивается показатель в (7.1), (7.2). Сначала
исследуем воздействие одной помехи. В этом случае из (7.3) при
NQ = 0 получаем q2 = ρβ, где ρ = 2РС/РП. Подставляя эти
выражения в (7.4), (7.5), а затем в (7.1), (7.2) и устремляя В -*■ оо,
находим [27], что пределы lim ΡπραΒ =1 и lim Рлт = 0. Это озна-
В-*оо £-оо
чает, что рост отношения сигнал/помеха с увеличением базы сигнала
оказывает большее влияние на помехоустойчивость, чем увеличение
числа разрешаемых элементов.
При совместном воздействии помехи и шума увеличение базы
приводит к тому, что помехоустойчивость будет определяться в
основном шумом. При В ->- оо и Рлт 0 Φ 0 вероятность правильного
приема (7.1) будет стремиться к единице, что объясняется
правилом работы решающего устройства. Вероятность ложной тревоги
приближенно определяется следующим образом [27]:
Рлт <*> В ехр [- γ2 (Ι — δβ"1)], (7.6)
где γ = &0/J/2", 8 = PnT/Nm. При больших базах вероятность
ложной тревоги растет пропорционально базе.
Обнаружение сложного сигнала с измерением неизвестной
задержки. В этом случае решающее устройство работает по правилу,
изложенному в [170]. Если напряжение на выходе согласованного
фильтра на интервале наблюдения не превышает порога, то
принимается решение «сигнала нет», если же оно максимально при каком-
либо дискретном значении задержки и превышает порог, то
принимается решение «сигнал есть» с этим значением задержки.
Вероятность ложной тревоги выражается соотношением (7.2).
Поэтому все сказанное ранее относительно нее справедливо и при
измерении задержки.
Вероятность правильного обнаружения [170]
оо
РПрав=| zexp (-г-^)/„И)[1 -ехр (-Щ*-1 dz, (7.7)
bq
где весовую функцию φ (ζ) = [1 — ехр (— Ο,δζ2)]^""1 можно
аппроксимировать единичным скачком. Момент скачка ζ0 =
= Vе! In (В — 1). При этом φ (ζ0) = е-1 = 0,37. Таким образом
φ (ζ) равна: 0 при ζ < ζ0, 1/е при ζ = ζ0 и 1 при ζ > ζ0. Пусть
действует только помеха. Так как φ пропорционально базе, то при
больших базах максимум обобщенного релеевского закона
распределения соответствует значению аргумента, равному У~рВ. Нижний
предел в интеграле (7.7) равен b VpB. Если скачок функции
φ (ζ, В) имеет место при значениях, меньших нижнего предела у
155
интеграла (7.7), то Рправ должно быть близко к единице.
Следовательно, если выполняется неравенство ЬУ рВ > У 2 In (В — 1),
то Рправ -*■ 1. Если удовлетворяется обратное неравенство, то
^прав -*- 0· Поэтому при любых b и ρ всегда можно выбрать
такое В, чтобы это неравенство выполнялось, так как 1η (β — 1)
растет медленнее, чем В. Следовательно, НтРправ=1. Когда
действует только шум, то аналогично предыдущему случаю можно
утверждать, что Рправ-*- 1» если q> Υ2 In (В — 1), что следует
из интеграла (7.7). Положив q = ]/2 In (В — 1), получаем В ~
~ exp (q2/2).
Рассмотрение помехоустойчивости при совместном воздействии
помехи и шума в случае измерения задержки практически не
отличается от рассмотрения помехоустойчивости при обнаружении
сигнала, поскольку максимальное значение базы определяется
вероятностью ложной тревоги (7.6) [27].
Таким образом, при обнаружении сложного сигнала на фоне
флюктуационной помехи с ограниченной средней мощностью и
измерении его задержки помехоустойчивость асимптотически растет
с ростом базы сигнала, несмотря на увеличение числа разрешаемых
элементов. Ограничение роста помехоустойчивости определяется
собственным шумом приемника с ограниченной спектральной
плотностью мощности. Допустимая база сложного сигнала
определяется по заданной вероятности ложной тревоги и резко зависит от
отношения сигнал/шум.
7.2. Помехоустойчивость приема сложных сигналов
с реальными корреляционными функциями
Как известно [56, 78, 95, 170, 183], применение сложных
сигналов позволяет повысить разрешающую способность и точность
измерения дальности и скорости в радиолокации, осуществить кодовое
разделение многих абонентов в радиосвязи. Однако наличие боковых
пиков у функции неопределенности (ФН) реальных сложных
сигналов приводит к увеличению неоднозначности при совместном
измерении дальности и скорости, к увеличению времени вхождения
в синхронизм. Поэтому при выборе или при синтезе сложных
сигналов в процессе проектирования радиотехнических систем
исследователи всегда старались найти сигналы с малыми боковыми пиками ФН
(иногда такие сигналы называют сигналами с хорошими
корреляционными свойствами). Обычно боковые пики ФН, даже если они
малы, могут существенно отличаться друг от друга по величине. При
этом необходимо определить: влияние боковых пиков на
характеристики обнаружения сигналов и измерения их параметров;
правило уменьшения боковых пиков, чтобы улучшить эти
характеристики, а также найти условия малости боковых пиков. Кроме того,
всегда желательно иметь приближенные соотношения, позволяю-
156
щие хотя бы грубо оценить ухудшение характеристик обнаружения
и измерения иь-за наличия боковых пиков.
Приближенное решение задачи по определению влияния
боковых пиков на характеристики обнаружения сложных сигналов
приведено в работе [26]. Поскольку и в радиолокации, и в радиосвязи
обнаружение сигналов сопровождается измерением их параметров
(задержка во времени, сдвиг несущей частоты и т. п.), то необходимо
определять влияние боковых пиков на характеристики обнаружения
сложных сигналов и измерения их параметров. Результаты этого
исследования опубликованы в работе [36] и приведены в данном
параграфе.
Основные определения и предположения. При обнаружении
сигнала и измерении его параметров колебание на входе приемника
может быть или шумом (помехой) или суммой сигнала и шума
(помехи). Предположим, что на вход приемника воздействует шум
в виде нормального стационарного случайного процесса с нулевым
средним и с равномерной спектральной плотностью мощности N0.
Допустим, что сигнал представляет собой последовательность
сложных сигналов одинаковой формы, длительность которых Τ равна
длительности периода повторения. Пусть энергия каждого сигнала
равна Е, а ширина его спектра F. Предположим, что параметры
сигнала — задержка τ и доплеровская частота Ω могут изменяться
дискретно. Пусть задержка изменяется с шагом 1/F равновероятно
на интервале шириной Т. Число дискретных значений задержки
Мх = В. Аналогично, пусть доплеровская частота изменяется
с шагом 2п/Т на интервале шириной W = 2nF^. Число дискретных
значений частот Mq = FaT. Общее число дискретных точек Μ =
= MxMq.
Определим структуру оптимального приемника. При сделанных
предположениях относительно доплеровской частоты он будет
многоканальным, причем число каналов равно числу дискретных
значений доплеровских частот М&. Допустим, что начальная фаза
сигнала является случайной величиной, равномерно распределенной
на интервале (0,2π) и в то же время постоянной для наблюдаемой
последовательности сложных сигналов. В этом случае каждый
канал должен состоять из согласованного фильтра для сложного
сигнала, когерентного накопителя и детектора огибающей [105].
Напряжения с выходов детекторов всех каналов поступают на
решающее устройство, которое выбирает максимальное отсчетное значение
огибающей (отсчет) из всех значений, превысивших порог. Уровень
порога определяется заданной вероятностью ложной тревоги,
которая зависит только от шума. Решающее устройство определяет
координаты максимального отсчета на плоскости (τ, Ω) и выдает
эти координаты в качестве оценок задержки и доплеровской
частоты.
Характеристиками процесса обнаружения сигнала и измерения
его параметров являются вероятность правильного обнаружения
сигнала с оценкой его параметров и вероятность ложной тревоги.
157
От свойства сигнала и его ФН завиоит только вероятность
правильного обнаружения. Поэтому в дальнейшем рассматривается именно
эта вероятность.
В общем случае боковые пики ФН обуславливают
статистическую зависимость всех Μ отсчетов. Учет этой зависимости сильно
усложняет задачу. Поэтому целесообразно определить условие,
при котором можно пренебречь статистической зависимостью
отсчетов на том основании, что обычно боковые пики ФН
существенно меньше единицы. Чтобы найти такое условие, рассмотрим два
коррелированных отсчета.
Обозначим через Rm отсчет ФН R (τ, Ω) в некоторой
дискретной точке на плоскости (τ, Ω), т = 1, Μ. При накоплении μ
сложных сигналов отсчет сигнальной составляющей на выходе
накопителя vm будет равен
vm — умакс^т> (7-8)
где максимальное значение амаКс = k0\iE с постоянной k0. В этом
случае дисперсия шума записывается в виде
σ2 = 0,5kfyEN0, а отношение сигнал/шум φ = 2Εμ/Ν0. Возьмем
два произвольных отсчета напряжения на выходе накопителя,
обозначая их χ и у, а соответствующие им сигнальные составляющие υη
и vk, причем υη, Ok определяются согласно (7.8) при т = η и т = k.
Обозначим коэффициент корреляции случайных нормальных
величин хиу через р. Значение ρ совпадает с боковым пиком R (τ, Ω),
координаты которого на плоскости (τ,Ω) равны разностям между
координатами отсчетов χ и у по времени и частоте.
Совместная плотность вероятности отсчетов хиу
записывается следующим образом [104]:
w (х, у) = (2πσ V\ — ρ2)"1 χ
exp {- 0,5σ-2 (1 - ρ2)"1 [(χ - vnf -29{χ- υη) {у - vk) +
+ Q/-vh)*]}. (7.9)
Если р = 0, то w (ху у) = w (x) w (у) и случайные величины
становятся независимыми, что является характерным для
нормальных случайных величин [104]. При этом линия уровня,
определяемая уравнением w (χ, у) = const, является окружностью. Если
ρ Φ 0, то это приводит, во-первых, к уменьшению множителя
σ2 (1 — ρ2), и, во-вторых, к изменению формы линии уровня,
которая превращается в эллипс. Чтобы снизить уменьшение (1 — р2),
необходимо иметь р2 <£ 1. Например, если положить ρ = 0,3, то
множитель уменьшится на 0,1 своей величины. Можно показать,
что отношение модуля разности между величиной оси эллипса
(большой или малой) и диаметром окружности к диаметру
приближенно равно 0,5р. Следовательно, если 0,5р <^ 1, то с изменением
формы линии уровня можно не считаться. Например, если ρ = 0,3,
то Δ6 = 0,15.
158
Таким образом, если боковые пики ФН Rm ^ 0,3, то
практически функция распределения (7.9) будет мало отличаться от
произведения w(x) w(y), т. е. в этом случае отсчеты χ и у можно считать
статистически независимыми. Аналогичный результат был получен
при исследовании влияния малого коэффициента корреляции
(ρ ^ 0,3) на вероятность превышения определенного порога хотя
бы одним отсчетом. Оказалось, что если ρ ^ 0,3, то отсчеты можно
считать статистически независимыми. Считая условие /?т^0,3
выполненным, будем полагать в дальнейшем отсчеты статистически
независимыми.
Вероятность правильного обнаружения. Согласно общему
методу [170] можно показать, что эта вероятность в соответствии с
принятыми допущениями определяется следующей формулой:
оо
Рправ = ί И> (0 ξ (0 Л, (7.10)
и
где Η — относительный порог; плотность вероятности максимума
сигнальной составляющей и шума
И0='ехр(-^^)/о(/<7); (7.11)
весовая функция
ЛГ— 1
1(0= Π \{t,rm); (7.12)
т=\
частная интегральная функция распределения
t
ξ(/, r) = \wr{z)dz. (7.13)
о
Плотность вероятности модуля бокового пика и шума wr (ζ)
определяется формулой (7.11), в которой t надо заменить на z, a q на
гт = Я\ Rm |. Если боковые пики ФН Rm = 0, вероятность
правильного обнаружения определяется известной формулой [170]
оо
РправО = 1И0<Р(0^ (7.14)
Η
где весовая функция φ (0 = Π — ехР (— 0,5Р)]М-1.
Наличие боковых пиков приводит к отличию весовой функции
ξ (t) от весовой функции φ (t). Весовая функция φ (t) по своей
структуре близка к единичному скачку, смещенному относительно
начала координат на величину t0 = V2 In (Λί — 1), поскольку она
является произведением Μ — 1 сомножителей вида ср0 (/) =
= ι _ ехр (— 0,5/2). которые равны 0 при t = 0 и стремятся к 1
при *->■ оо. Если гт = 0, то ξ (ί, 0) = φ0 (0 и ξ (t) = φ (t). Когда
rm > 0 частная интегральная функция распределения сместится
159
вправо относительно φ0 (t). Поэтому весовая функция ξ (t) также
сместится вправо относительно весовой функции φ (t). Поскольку
w (t) l(t)<w (t) φ (t) при любых t, то Рправ < Рправ о- Равенство
возможно только в случае Rm = О, Λί = 1, Λί — 1.
** Используя свойства весовой функции ξ (t), можно оценить
допустимое значение максимального бокового пика. Допустим, что
имеется один боковой пик, значительно больший, чем все
остальные, и величина которого равна \Rm\ = #МакС· Выделим из
весовой функции ξ (0 функцию ξ (ί, гмакс), где гмакс = qRMaKC, т. е.
запишем ξ (t) = ξ (t, гмакс) ξ_χ (t). Допустим, что все остальные
боковые пики имеют весовую функцию ξ_χ (t) ~ 1 в том интервале
значений t, где ξ (t, гмакс) существенно отличается от нуля. В этом
случае можно считать, что ξ (t) ~ ξ (t, гмакс). Чтобы влиянием
максимального бокового пика можно было пренебречь, необходимо
иметь ξ (t, гмакс) ~ 1 на том интервале, где плотность вероятности
w (t) существенно отличается от нуля. Ширина такого интервала
с практической точки зрения для w (t) (7.11) при q > 1 примерно
равна 6, так как при этом w (t) (7.11) близка к нормальной функции
распределения [104]. Точно также ширину плотности вероятности
wr макс (t) можно считать примерно равной 6. Поэтому боковой пик
Rmukc практически не окажет влияния на Рправ> если разность
q — гмакс ^ 6. Отсюда получаем, что значение максимального
бокового пика должно удовлетворять неравенству i?MaKC ^ 1 —6/^.
Например, если q = 8,6, то RMSLK(y < 0,3. Отсюда следует, что q
должно быть по крайней мере больше 6, так как иначе боковой пик
начнет оказывать серьезное влияние на уменьшение Рправ·
Максимизация вероятности правильного обнаружения.
Допустим, что имеет место следующее условие
Λί—1
Σ ^=Qp=const. (7.15)
Максимум вероятности правильного обнаружения (7.10) при
условии Qp = const, как показано в работе [36], будет при
равенстве боковых пиков, т. е. при rm = const. Такой результат
является естественным и следует из характера решаемой задачи. Чем
больше rm, тем правее сдвигается частная интегральная функция
распределения ξ (t, rm). Если допустить, что один из боковых пиков
станет неравным всем остальным, то весовая функция ξ (t)
раздвоится на ξ_! (t) и ξ (ty гмакс). Функция ξ_χ (t) относительно ξ (t)
сместится влево, а ξ (t, гмакс) вправо. Чем больше гмакс, тем больше
сместится вправо ξ (t, гмакс) и тем меньше будет вероятность
правильного обнаружения Рправ> поскольку при больших значениях
''макс именно этот боковой пик будет уменьшать вероятность
правильного приема. Поэтому для увеличения Рправ наД° уменьшать
гмакс- Но так как условие (7.15) ограничивает минимальное
значение боковых пиков, то необходимо стремиться делать их равными.
160
Условие (7.15) позволяет определить уровень боковых пиков при
Qp = const. Полагая \Rm\ = R = const, согласно (7.15) находим:
R = lVp/(M — Ι)]1*, (7.16)
где Vp = Qp/qp. Отметим, что решение R = const не зависит от
значения степени ρ в формуле (7.15). Поэтому необходимо
уменьшать разброс боковых пиков относительно среднестепенного
значения (7.16) и уменьшать это значение.
Оценка вероятности правильного обнаружения. В соответствии
с полученным результатом имеем Рправ макс < ^прав о> гДе
Рправ макс — максимальная вероятность правильного обнаружения
при условии равенства боковых пиков | Rm | = R = const:
Рправ макс = ]*> (О ί ί ζ exp [- 0,5 (ζ2 + q2R2)} X
я (о
Χ Ib(zqR)dz)M-4U (7.17)
полученная из (7.10)—(7.12), (7.16), а Рправо определяется
формулой (7.14). Выражение (7.17) позволяет найти оценку вероятности
правильного обнаружения при заданном значении R. Можно
показать, что максимальная вероятность правильного обнаружения
приближенно равна
Рправмакс ^ Рправ о U - 0,5 (Λί - 1) q2S (?) #2], (7.18)
где S (q) = 0,5?2ехр (— 0,5?2) [1 — ехр (— Ο,δ?2)]"1.
Из формулы (7.18) следует, что увеличением q можно добиться
уменьшения влияния боковых пиков на Рправ, так как функция
S (q) при q > 1 определяется в основном экспонентой ехр (— 0,5?2),
т. е. слагаемое 0,5 (М — 1) q2S (q) R2 может быть сделано сколь
угодно малым по сравнению с единицей. Следовательно, если модули
боковых^пиков близки к своему среднему значению, то увеличивая
отношение сигнал/шум можно уменьшить влияние боковых пиков
на вероятность правильного обнаружения.
7.3. Помехоустойчивость приема сложных сигналов при
неидеальной синхронизации по времени и частоте
Если время задержки сигнала и его несущая частота медленно
изменяются при передаче информации, то один из методов приема
заключается в том, что в состав обычного оптимального приемника
вводят измеритель времени задержки и измеритель частоты, которые
измеряют соответствующие параметры и вводят их в оптимальный
приемник. Такой метод приема называется квазиоптимальным
[82, 162]. Измерители осуществляют синхронизацию по времени
и частоте между принятым и опорным сигналами и являются
синхронизаторами. Процесс синхронизации сопровождается ошибками.
161
Будем рассматривать только случайные ошибки, которые
возникают из-за действия шума, причем будем полагать эти ошибки
малыми. Ошибки при измерении времени прихода сигнала и его
частоты приводят к рассинхронизации по этим параметрам и в
конечном счете снижают помехоустойчивость приема информации.
Исследованию помехоустойчивости квазиоптимальных приемников
посвящено значительное число работ (см., например, [5, 82, 83, 162]
и др.), однако в большинстве из них рассматриваются различные
случаи квазиоптимального когерентного приема. На практике
часто используется квазиоптимальный некогерентный прием. При
этом необходимо оценить снижение помехоустойчивости при
совместной рассинхронизации по времени и частоте для произвольных
сигналов, найти условия, при которых ошибки по времени и
частоте можно рассматривать независимо друг от друга, определить
влияние формы сигнала на помехоустойчивость квазиоптимального
приемника. Данный параграф посвящен решению сформулированных
задач для случая квазиоптимального некогерентного метода
приема двоичной информации при совместной рассинхронизации
повремени и частоте [34, 35].
Вероятность ошибки. Допустим, что информация передается
двумя равновероятными ортогональными сигналами. Пусть Ε —
энергия сигналов. Предположим, что шум является случайным
нормальным стационарным процессом с нулевым средним и с
равномерной спектральной плотностью мощности Ν0. Оптимальный приемник
при известном времени задержки сигнала и известной несущей
частоте состоит из двух каналов, каждый из которых представляет собой
последовательное соединение согласованного фильтра и детектора
огибающей (рис. 2.6). Решающее устройство выбирает максимальное
значение на выходе детекторов огибающих. Каждый фильтр
согласован со своим сигналом. Так как сигналы ортогональны, то
ортогональны и фильтры. Поэтому шумовые составляющие на выходах
фильтров в совпадающие моменты времени некоррелированы.
Поскольку шум на входе и на выходе фильтров является нормальным
случайным процессом, то шумовые составляющие на выходах
фильтров в совпадающие моменты времени независимы. В результате
огибающие на выходах детекторов также будут статистически
независимы в совпадающие моменты времени.
При рассинхронизации по времени (ошибка равна τ) и по
частоте (ошибка равна Ω) в момент принятия решения, который
определяется синхронизатором, огибающая на выходе согласованного
канала определяется огибающей функцией неопределенности (ФН)
передаваемого сигнала \R (τ, Ω)| (1.22), а огибающая на выходе
несогласованного канала — огибающей взаимной функцией
неопределенности (ВФН) μ (τ, Ω) = Rjk (τ, Ω) (1.18). Независимо от
значений τ, Ω шумовые составляющие на выходах фильтров
остаются некоррелированными в совпадающие моменты времени.
Следовательно, огибающие в момент принятия решения будут также
статистически независимыми, как и при τ = Ω = 0, Поэтому плох·
162
Яость вероятности огибающих на выхоДах детекторов описываются
законами Релея—Раиса, у которых сигнальные составляющие рав-
ны | R (τ, Ω) I и Ι μ (τ, Ω) |. Отметим, что R (0, 0) = 1, а μ (0, 0) = 0.
Обозначим отношение сигнал/шум в информационном канале
h = VWU. (7.19)
В соответствии с отмеченным можно показать, что вероятность
ошибки при рассинхронизации равна
Рош (*» Ω) = exp [- Λ2 (Я2 + μ2)] Χ
00
Χ j ζ2 exp (— 0,5ζ2) /0 (/2 hRz) Χ
ο
οο
Χ j t exp (— 0,5ί2) Ι0 (V2 Αμ/) dfcfe, (7.20)
где # = |Я(т, Ω)|, μ = |μ(τ, Ω) |. При τ = Ω = 0, R = 1, μ = 0,
вероятность ошибки определяется известной формулой (2.26) Р0ш=
= Рош (0, 0) = 0,5 ехр (- 0,5Л2).
Плотность вероятности и статистические характеристики
ошибок по времени и частоте. Напомним основные результаты теории
оценок параметров сигнала [25, 170] применительно к совместному
измерению времени задержки сигнала и частоты. Предположим, что
измеритель является оптимальным, т. е. обеспечивает минимальные
в среднеквадратическом смысле ошибки при совместном измерении
времени и частоты. При достаточно большом отношении сигнал/шум
на выходе измерителя
Я = УЩ^Ж, (7.21)
где Еаш — эквивалентная энергия сигнала в измерительном
канале, совместная плотность вероятности ошибок τ, Ω при
некогерентном приеме приближенно определяется следующим выражением
135, 170]:
w2 (τ, Ω) = k exp I2q2 | R (τ, Ω)|], (7.22)
где k — постоянная, а интегрировать надо в пределах
центрального пика ФН, так как при предположении φ > 1 ошибки малы.
Представим центральный пик | R (τ, Ω) | поверхностью второго
порядка [25]
\R (τ, Ω)| = 1 + /?;τ + #£Ω + 0,5/?;ττ2 +
+ ΛίοτΩ + 0,5#ωΩΩ2, (7.23)
где τ ^ 0, Ω > 0, а частные производные взяты в точке τ = Ω = 0.
Выражение для ФН при τ< 0 и Ω<0 можно найти из (7.23),
используя свойства симметрии ФН относительно осей τ, Ω [25].
Для ЧМ сигналов с четным законом изменения частоты и для
дискретных ФМ сигналов смешанная производная Rxq = 0 [25]. При
163
условии RZq = 0 ошибки τ и Ω статистически независимы. Поэтому
рассматривать будем сигналы, у которых Rtq = 0. Кроме того для
сигналов с прямоугольной огибающей Rq = 0, для ЧМ сигналов
Rx = 0 с точностью до малых высокого порядка, а для ФМ
сигналов RTX = 0. Таким образом для ЧМ сигналов с четным законом
изменения частоты
|1? (τ, Ω)|= Ι +0,5#;'ττ2 +
+ 0,5#£ωΩ2, (7.24)
а для ФМ сигналов
| R (τ, Ω) Ι = 1 + Rxr + 0,5#£ΩΩ2. (7.25)
Подставляя (7.24) в (7.22), получаем, что для ЧМ сигналов
ошибки τ и Ω распределены по нормальному закону, а их дисперсии
равны [25, 170]
ох = (2?21 R;x Ι)"1 ah = (2?21 %Ω \)~\ (7.26)
Для ФМ сигналов при подстановке (7.27) в (7.23) получаем,
что ошибка τ распределена по экспоненциальному закону с
дисперсией [162]
a; = (VI*;ia)-\ (7.27)
а ошибка Ω распределена по нормальному закону с дисперсией
(7.26). Из (7.26), (7.27) следует хорошо известный результат: чем
больше \R%\ (или |/?ΪτΙ) и |/?ωω|, тем выше точность измерения
времени и частоты при q = const.
Увеличение частных производных \RT\ или \RXX\ означает
уменьшение длительности центрального пика ФН, т. е. при этом
необходимо увеличить базу (или широкополосность) используемых
сигналов. Таким образом увеличение базы сигналов при Τ = const
повышает точность измерения времени.
Средняя вероятность ошибки. В работе [35] показано, что если*
ВФН имеет малые боковые пики в окрестности центра (τ = 0,
Ω = 0), то ее влиянием на вероятность ошибки можно пренебречь.
Такому условию удовлетворяют сигналы, у которых боковые пики
около центра плоскости неопределенности меньше \lY~B, где В —
база сигнала. Полагая μ = 0, из (7.20) находим, что вероятность
ошибки
Рош (^ Ω) = 0,5 exp (- 0,5/i21R (τ, Ω) |2). (7.28)
Средняя вероятность ошибки при усреднении по τ и Ω согласно
определению равна
оо
х ошср Л Рош (τ, Ω) а», (τ, Ω)άτάΩ, (7.29)
—оо
где w2 (τ, Ω) совместная плотность вероятности ошибок τ и Ω.
Интегрирование следует производить по области определения
центрального пика ФН.
164
Относительно центрального пика ФН предположим, то он
симметричен относительно осей τ, Ω. Это имеет место, как было
отмечено ранее, для ФМ сигналов и ЧМ сигналов с четным законом
изменения частоты. При этом ошибки τ и Ω статистически независимы,
а модуль центрального пика ФН может быть записан в виде
| R (τ, Ω) Ι = 1 - (Ι τ |/τ0)ν - (| Ω |/Ω0)\ (7.30)
где | τ | ^ τ0; | Ω | ^ Ω0. Для сигналов с прямоугольной
огибающей λ = 2. Для ФМ сигналов ν = 1, для ЧМ сигналов ν = 2.
При таком представлении центрального пика ФН интегрировать
в (7.29) необходимо в пределах (— τ0, τ0), (— Ω0, Ω0). Совместная
плотность вероятности ошибок τ и Ω, при условии, что они малы,
определяется формулой (7.22).
Подставляя (7.22), (7.30) в (7.29), интегрируя и нормируя,
получаем [34], что средняя вероятность ошибки приближенно равна
Рош ср ^ 0>5 ехр (— 0,5/ι2) (1 — /ι2/2<72)~(ν+λ)/νλ =
= Рош (1 — /ι2/2<72)~(ν+λ)/νλ· (7.31)
Из (7.31) следует, что средняя вероятность ошибки не зависит
от ширины центрального пика ФН по времени и частоте, так как
в это выражение τ0 и Ω0 не входят. Таким образом, средняя
вероятность ошибки при оптимальном измерении времени задержки и доп-
леровской частоты не зависит от базы используемых сигналов.
Поскольку форма центрального пика ФН (7.30) зависит от показателей
ν и λ, то и средняя вероятность ошибки зависит от формы
центрального пика, но зависимость эта слабая, так как отношение h2/2q2 ^
ίξ 0,5. При этом из (7.31) приближенно имеем
Рошср ^ Рош (1 + [(ν + λ)/νλ] (h2/2q2)}. (7.32)
Например, для ФМ сигнала ν = 1, λ = 2, а (ν + λ)/νλ = 3/2.
Для ЧМ сигнала ν = λ = 2, а (ν + λ)/νλ = 1. Обычно h2 < q2.
Поэтому различие в форме центрального пика сказывается слабо.
Следовательно, средняя вероятность ошибки практически не
зависит от формы сигнала и его базы, а определяется только
отношениями сигнал/шум на выходах информационного и измерительного
каналов. Поэтому для повышения помехоустойчивости
некогерентного квазиоптимального приема необходимо увеличивать отношение
сигнал/шум на выходе обоих каналов. Чтобы ошибки при
синхронизации сказывались слабо, необходимо иметь q2 > Λ2.
7.4. Помехоустойчивость приема сложных сигналов при
рассогласованиях
Любые аппаратурные рассогла-
вания приводят к снижению
помехоустойчивости. Исследованию
влияния рассогласований на снижение
помехоустойчивости приема сложных
сигналов посвящено большое число
работ, например, [19, 44, 88, 99,
155, 162, 172 и др.]. В большинстве
165
перечисленных работ
рассматривались рассогласования при приеме'
радиолокационных сигналов. В
меньшей степени этот вопрос исследован
для СПИ и особенно для ААС.
Поэтому в данном параграфе по
материалам [41, 52, 53] рассматриваются
рассогласования в ААС.
Следует отметить, что влияние
аппаратурных рассогласований на
характеристики ААС иное, чем в
других системах передачи информации.
Обычно, если рассогласования малы,
то потери из-за них можно
компенсировать увеличением энергии
излучаемого сигнала. В ААС, в первую
очередь, необходимо обеспечивать
помехоустойчивость относительно
взаимных помех, которая
практически не зависит от излучаемой энергии
сигналов, а определяется числом
активных абонентов и базой сигналов
согласно (4.2). Поэтому потери в
ААС из-за рассогласований можно
компенсировать только
уменьшением числа активных абонентов при
постоянной базе сигналов.
Здесь рассматриваются только те
рассогласования, которые
образуются между излучаемыми сигналами и
фильтрами в оптимальном
приемнике. Все остальные характеристики
оптимального приемника считаем
идеальными, поскольку
рассогласования по таким характеристикам
рассмотрены достаточно подробно
[180]. При исследовании
рассогласований необходимо учитывать, как
они влияют на общие характеристики
ААС. В зависимости от назначения
ААС такими характеристиками
могут быть или максимальная, или
средняя вероятность ошибки.
Когда задана максимальная
вероятность ошибки Рош макс» то в ААС при
любом сочетании номеров абонентов
вероятность ошибки не должна
превышать Рош макс· Выбор
максимальной вероятности ошибки в качестве
характеристики ААС справедлив для
асинхронных адресных систем
передачи данных, команд и т. п., т. е. для
таких ААС, в которых передача
информации должна происходить с
вероятностью ошибки, меньшей
Рош макс· Если при передаче
информации ошибка в одном символе слабо
влияет на передаваемую информацию
(например, при цифровых методах
передачи речи), то целесообразнее
в качестве характеристики ААС
использовать среднюю вероятность
ошибки Рошср· При такой
характеристике ААС гарантируется, что
независимо от сочетания номеров
абонентов передача информации
будет происходить в среднем с
вероятностью ошибки Рош ср, хотя
возможны случаи, когда истинная
вероятность ошибки будет больше средней.
Исходные соотношения.
Допустим, что абонент осуществляет
оптимальный прием двух ортогональных
сигналов. Оптимальный приемник
(рис. 2.6) состоит из двух
согласованных фильтров, детекторов огибающих
и решающего устройства.
Обозначим комплексные
огибающие сигналов через Ux if) и U2 (t).
Комплексная огибающая
нормированного напряжения на выходе &-го
согласованного фильтра при
действии на его входе /-го сигнала
определяется взаимокорреляционной
функцией (ВКФ), которую определим
следующим образом:
*Λ*φ(τ)=——— X
2 У EjC Ещ
оо
X J ί/д, (0 #*ф (*—τ) Я, (7.33)
— ОО
где Ej — энергия сигнала, / = 1,2;
k = 1,2. В индексы ВКФ введены
символы «с», «ф», которые
подчеркивают, что первый множитель в
подынтегральных выражениях (7.33)
соответствует сигналу, а второй
фильтру.
Когда рассогласований нет, то
в момент принятия решения (τ = 0)
значения АКФ | Ric ιφ (0) I =
= 1#2с2ф(0} I = 1, а значения ВКФ
I Ric 2ф (0) I =|#2с 1ф(0) | = 0, так как
сигналы по определению
ортогональны в усиленном смысле (по
огибающим). При ортогональных сигналах
фильтры так же будут ортогональны
в усиленном смысле, т. е. \R ιφ2φ(0)| =
= Ι#2φΐφ(0)| = 0, где ВКФ
согласованных фильтров определяются
по (7.33), но с заменой в
подынтегральном выражении комплексной
огибающей сигнала и ее спектра на
импульсную характеристику и
коэффициент передачи фильтра. При
согласовании ВКФ сигналов и
фильтров совпадают. В реальных ААС все-
166
гда есть рассогласования, поэтому
значения АКФ в момент принятия
решения меньше единицы, а значения'
ВКФ больше нуля. Рассмотрим
общий случай, когда сигналы и
фильтры рассогласованы между собой,
т. е. |Д101ф (0)| < 1,|Я2С2ф(0)| <
^ х> I А1С2ф (0)1 >0, | А2С1ф (0)|>
> о.
Поскольку рассогласования
имеют одинаковые статистические
характеристики для всех сигналов и
фильтров, то достаточно рассмотреть
прохождение одного сигнала совместно
с помехой. Допустим, что на входе
приемника действует первый сигнал
с комплексной огибающей Ux (t)
и взаимная помеха, относительно
которой предположим, что она
является нормальным стационарным
случайным процессом с
равномерной спектральной плотностью N0.
Обозначим λ = 1 — | #ιΟιφ(0) J, μ =
■= Ι Λιοίφ (0) Ι, Ρ = Ι £ιφ 2φ(0)|, где
λ = λ (|) определяет потери в
«согласованном» канале, μ = μ (ξ) —
неортогональность между первым
сигналом и вторым фильтром, а р =
= ρ (ξ) — коэффициент корреляции
между шумовыми составляющими на
выходе фильтров в один и тот же
момент времени. Аргумент ξ
определяется рассогласованиями. Когда их нет
ξ = 0 и соответственно λ = μ =
= ρ = 0. В дальнейшем будем
рассматривать только случай, когда
ρ = 0. Так как будет исследован
[41, 52] согласованный фильтр на
многоотводной линии задержки
(МЛЗ), то условие ρ = 0 естественно,
поскольку для обоих каналов
используется одна и та же линия
задержки.
Определение λ и μ.
Конкретизируем сигналы. Как показывают
исследования, одним из
перспективных типов сигналов для ААС
являются дискретные частотные
сигналы. Описание ДЧ сигналов
приведено в § 1.3. Из всего многообразия
ДЧ сигналов рассмотрим только
сигналы первого порядка, у которых
число элементов N равно числу
различных частот М. Для простоты
предположим, что элементы
являются радиоимпульсами с одинаковыми
энергиями и начальными фазами, а
их спектры прямоугольны и не
перекрываются. Обозначим через Δω
расстройку по частоте между соседними
спектрами и положим, что их
ширина также равна Δω. Через ω0
обозначим среднюю частоту
сигнала. Положим, что задержка т-го
элемента по времени равна tjm =
= (Pjm — 1) Δ/, где / — номер
сигнала, pjm — временная кодовая
последовательность, т — номер
спектра, а задержка между
соседними элементами равна Δ/ =
= 2 π/Am.
Одним из методов формирования
и обработки ДЧ сигналов является
применение формирующих и
согласованных фильтров на МЛЗ
(см. гл. 6), причем в каждом фильтре
используется одна МЛЗ. В качестве
МЛЗ можно применять кварцевые
ультразвуковые линии задержки.
Наиболее существенным источником
рассогласования в кварцевых
линиях задержки является различие в
фазовых скоростях распространения
ультразвуковой волны. Это
обусловлено рядом технологических причин.
В результате, задержки между
отводами в различных кварцевых МЛЗ
различны. Если при согласовании
задержка между отводами должна
быть равна А/, то в реальных линиях
эта величина различна, хотя для
данного экземпляра и постоянна.
Используя (7.33), можно найти
значение модуля
взаимокорреляционной функции при рассогласовании
(ВКФР) ДЧ сигналов в момент
принятия решения [52]:
|Дю*ф(0)| =
1 /"Ίϋ м
="77ΐ/ Σ Σ amfln cos(t|?w—t|?n),
M V m=\л«1
(7.34)
где
am=(s'mn,zm)/nzm,
ψΐϊΐ=(ωο + ω7η)Δ/2τ;
Zm = [Pi(m)-l](a-P)f k=*\\
Zm = Pi (m)—p2 И + [Pi (rn) — 1] a—
-[ρ2(/η)-1]β, * = 2.
Случайные величины α и β,
определяющие изменение задержки в
формирующем и согласованном
фильтрах соответственно, обусловлены
различными фазовыми скоростями
в кварцевых МЛЗ. Допустим, что
а и β — независимые нормальные
случайные величины с нулевы-
167
ми средними и с дисперсиями
М2 {α} = Μ2 |β} = σ|. Введем
также параметр φ = ω0Δ/, равный
количеству периодов радиочастоты в
одном элементе, умноженному на
2 π.
Максимальная вероятность
ошибки. В работе [52] показано, что в
случае кварцевых МЛЗ можно не
учитывать неортогональность из-за
рассогласований. Такой вывод
объясняется тем, что максимальное
значение модуля | /?1С2ф (0) I ПРИ
рассогласованиях определяется суммой
функций вида (sin*)/*, нули которых
смещаются друг относительно
друга. Уменьшение АКФ I Якяф (°) I
происходит из-за нарушения
когерентности между косинусоидальны-
ми слагаемыми.
Полагая μ = 0, можно показать
[52], что вероятность ошибки
Рош(а, Р) = 0,5ехр[-0,5Л2(1-Д)2]=
=0,5 ехр [—0,5Л21 R (α, β) |2], (7.35)
где | R (α, β) | = #1с1ф (0) |
определяется выражением (7.34). Если
рассогласования малы, можно
считать ат~1. Пренебрегая сот по
сравнению с со0, из (7.34) находим
|*(α, β)Ι2=
= [sin20,5M(p (α—β)] χ
χ [Μ2 sin2 0,5φ (α—β)]-1. (7.36)
Минимум \R (α, β)[2 достигается при
α = амакс, β = — осмакс, если
Мфамакс < π. Следовательно,
максимальная вероятность ошибки
равна
Рош макс =0,5 ехр (-0,5А2ИН), (7.37)
где минимальное отношение сигнал/
взаимная помеха равно
h2 -ft* 3ίη2ΜφαΜ&κο t7 ооч
'мин . . (/.όο)
M2sin2(paMaKc
В качестве примера рассмотрим
следующие линии [52]. Первая
линия: зедержка между отводами равна
Δτ = 0,8 мкс; полная задержка
Тф = 50,4 мкс; средняя частота
/о = ω0/2π = 20 МГц; ширина
полосы пропускания Δ/Π = 10 МГц;
число отводов (включая начало)
N = 64. Для такой линии параметры
168
ДЧ сигнала: Δ/ = 2,4 мкс, число
импульсов Μ = 22, ширина
спектра F= Ml Μ = 9.1 МГц, база
В = М2 = 484, φ = 3 . 10*. Вторая
линия: Δτ = 0,8 мкс; Тф = 24,8 мкс;
/о = 20 МГц, Δ/π = 10 МГц; N =
= 32. Параметры сигнала для
второй линии: At = 1,6 мкс; Μ = 16,
F = 10 МГц; В = М2 = 256,
φ = 2 . 102.
Расчеты приведенные для обеих
линий [52], показывают, что в ААС,
работа которых характеризуется
максимальной вероятностью ошибки,
следует применять кварцевые
линии с σφ<4 * Ю-5.
Средняя вероятность ошибки.
Обозначим через ξ = α — β. Так
как α и β — нормальные случайные
величины, то и ξ — нормальная
случайная величина с нулевым средним
и с дисперсией σ| = 2 aj,.
Вероятность ошибки (7.35) запишем в
следующем виде:
Рош(6) =
= 0,5 ехр [—0,5Л*|/?(Э|а]. (7.39)
Средняя вероятность ошибки по
определению равна
оо
Рошср- J Рош(1)И1)<*1· (7.40)
— ОО
Подставляя в (7.40) выражение
(7.39), записывая w (ξ) в виде
нормального закона распределения,
заменяя | R (ξ) | согласно (7.36) с
учетом обозначения ξ = α — β,
производя приближенное интегрирование
и отбрасывая малые высокого
порядка, можно найти следующее
приближенное выражение для средней
вероятности ошибки [41]:
Ponicp^0,5[2F(w)-l]X
X ехр(—0,5А2) + 1— F(u), (7.41)
где и = 2π/Μφθξ, F (и) —
интеграл вероятности (2.16). Когда h
увеличивается, то, начиная с
некоторого Лкр, средняя вероятность
ошибки не зависит от h и
определяется так:
Рошср^!-^"). (7.42)
При больших и величина /гкр с^ и.
Рассмотрим пример. Пусть
средняя вероятность ошибки Рош ср <
< 10-*. При этом /ίκρ с** 4,7.
Полагая /ικρ ^ и, из формулы и =
=*Ύ2π!Μφσφ определяем допустимые
значения σφ: для первой линии
σφ ~ 1,5 * Ю-4, а для второй σφ~
~ 3 · Ю-4. Сравнивая эти
требования по допустимому значению σφ
с требованиями при оценке ААС по
максимальной вероятности ошибки,
замечаем, что критерий средней
вероятности ошибки является менее
жестким, так как допустимые
значения σφ могут быть примерно на
порядок больше.
7.5. Определение числа активных абонентов
в ААС с учетом рассогласований
Максимальное число активных
абонентов в ААС, как было показано
в гл. 4, определяется заданной
вероятностью ошибки или
эквивалентным отношением сигнал/взаимная
помеха и базой используемых
сигналов. Из-за аппаратурных
рассогласований допустимое число активных
абонентов уменьшается. Определим
приближенно допустимое число
активных абонентов в ААС с учетом
рассогласований. Как и в
предыдущем параграфе, будем предполагать,
что каждый· абонент осуществляет
некогерентный прием двух
ортогональных сигналов с помощью
согласованных фильтров на
многоотводных кварцевых линиях задержки.
Основным источником рассогласований
будем считать различие в фазовых
скоростях ультразвуковых волн в
различных экземплярах линий
задержки, т. е. различие по времени
задержки.
Приближенно число активных
абонентов / определяется по
заданному отношению сигнал/взаимная
помеха h2 выражением (4.2)
/ = M2/h2t (7.43)
где М2 = В — база ДЧ сигнала;
Μ — число его импульсов.
Вероятность ошибки при
рассогласованиях определятся формулой
(7.39) и зависит от отношения
сигнал/взаимная помеха
hl = h2\R(l)\\ (7.44)
где \R (ξ)|2 определяется согласно
(7.36) при | = α — β. Если задана
вероятность Рош (|), то задано и h\.
Подставляя (7.44) в (7.43), получаем
1=№\Ж1)?1Ц. (7.45)
Когда I = О,
/Ш2 = 1, то / =
= /макс — M2/h%. Обозначая
отношение ///макс через ν, из (7.45)
находим
1*(6)1
(7.46)
Аппроксимируя | R (ξ) |2
параболой, т. е. | /? (ξ) I2 = 1 - (ξ/ξ0)2,
где ξ0 = 1,1π/Μφ, можно найти [53],
что плотность вероятности случайной
величины ν описывается выражением
«ι(ν) = [2π(1— ν)]""1/2σ-1χ
xexK~^)+26(v)hf(T)]
(7.47)
при 0 < ν < 1, а σ = Μφσφ/"|/^
Среднее значение
v"= [2F (1/σ)- 1] (1 -σ2) +
+Υ2/πσ exp (—1/2σ2), (7.48)
а дисперсия Μ2 {ν} = 2α4.
Следовательно, с уменьшением
рассогласований среднее значение"
увеличивается, а дисперсия уменьшается.
Расчеты, проведенные для двух
кварцевых линий предыдущего
параграфа, показывают, что если
допустить уменьшение среднего числа
активных абонентов на 10%, то для
первой линии σφ должно быть не
большее Ю-4, а для второй линии —
не более 2 · 10~4. Отметим, что
такой же порядок допустимых
рассогласований приведен в предыдущем
параграфе, но он был получен из
определения средней вероятности
ошибки.
Раздел II
ОБЩАЯ ТЕОРИЯ СИСТЕМ СИГНАЛОВ
Глава 8
КОМБИНАТОРНЫЙ АНАЛИЗ СИСТЕМ СИГНАЛОВ
8.1. Комбинаторика и теория систем сигналов
В § 1.1 системы сигналов были определены как совокупности
сигналов, объединяемых единым алгоритмом построения. Другими
словами, система сигналов — это подмножество некоторого
множества сигналов, элементы которого (сигналы) выбираются из
элементов множества в соответствии с принятым алгоритмом или
правилом выбора (построения). В соответствии с классификацией,
приведенной в §1.2, 1.3, система — это подкласс некоторого класса
сигналов. Исходным множеством является соответствующий класс
сигналов, из которого производится выбор подкласса или системы.
Большое значение в теории систем сигналов имеют исследования
упорядочения сигналов системы, выбора сигналов при некоторых
ограничительных условиях и т. д., т. е. исследования проблемы
перечисления элементов конечного или счетного множества. В свою
очередь эта проблема является основной проблемой
комбинаторного анализа или комбинаторики [132]. Комбинаторика тесно
связана с теорией вероятностей, высшей алгеброй и теорией чисел.
Применение методов комбинаторики в теории систем сигналов
позволяет определить объем системы сигналов, обладающей тем
или иным свойством или ограничением. Для того, чтобы перейти к
определению объема произвольной системы сигналов, напомним
основные правила комбинаторики.
Основные правила комбинаторики. Комбинаторика основана на
априорных рассуждениях и следующих двух правилах, по своей
природе являющихся определениями, которые «скорее нужно понимать,
нежели доказывать» [132].
Правило суммы. Если объект А может быть выбран т
способами, а объект В другими η способами, то выбор «или Л, или Л» может
быть осуществлен т + η способами. Следует отметить, что выборы
А или В являются взаимно исключающими, т. е. нет возможности
выбрать оба объекта одновременно. Методом математической
индукции правило суммы распространяется на произвольное число
объектов. Правило суммы в комбинаторике эквивалентно правилу
сложения вероятностей для несовместимых событий (правило сложения
см., например, в [104]).
Правило произведения. Если объект А может быть выбран т
способами и после каждого из таких выборов объект В в свою оче-
170
редь может быть выбран η способами, то выбор «А и β» в указанном
порядке может быть осуществлен тп способами. Правило произве-
деления также распространяется на произвольное число
объектов. Правило произведения в комбинаторике эквивалентно
правилу умножения вероятностей как для зависимых, так и для
независимых событий (правило умножения см., например, в [104]).
Объем класса манипулированных сигналов. Проиллюстрируем
применение одного из правил, а именно правила произведения, для
нахождения объема класса манипулированных сигналов. Как
следует из классификации манипулированных сигналов (§ 1.5), класс
включает все сигналы данного рода с заданными основаниями
манипуляций и заданными порядками. При конечных основаниях и
порядках объем класса конечен, т. е. он содержит конечное число
сигналов данного рода. Любая система сигналов является подклассом
какого-нибудь класса или в предельном случае самим классом.
Поэтому, если известны свойства класса, то могут быть известны и
свойства системы сигналов. По этой причине, как уже было отмечено,
класс является основной классификационной единицей и
исследование свойств классов имеет большое значение. Исследование свойств
классов и наиболее важных подклассов сигналов—цель данной
книги.
Допустим, что класс определяется т манипулированными
параметрами и основания манипуляции равны рь I = 1, т. Назовем
основанием манипуляции класса величину
т
Р= ΓίΡι. (8.1)
/ = ι
Формула (8.1) получена при использовании правила
произведения. Действительно, если один параметр (объект) можно выбрать
рг способами, а второй — р2 способами, причем независимо от
выбора первого параметра, то оба параметра совместно можно
выбрать р!р2 способами. Например, если основание амплитудной
манипуляции рг = 2 (|α/κνΙ = #ι или а2)> а основание фазовой
манипуляции равно р2 = 4 (θ/κν = θχ или θ2, или θ3, или θ4),
то, выбирая совместно и амплитуду, и фазу, имеем 8 способов
(αχθχ, ^02, αχθ3, агв4у a2Ql9 а2&2> #20з> Яг^)· Таким образом, имеем
8 элементов, которые отличаются между собой амплитудами и (или)
фазами. Применяя последовательно правило произведения к т
параметрам (объектам), получаем формулу (8.1).
Если каждый элемент выбирается одним из ρ способов (8.1),
то число различных сигналов в классе (объем класса),
отличающихся хотя бы одним элементом, равно
L = р», (8.2)
где N — число элементов. Формула (8.2) получена также на
основе применения правила произведения,так как ρ способами можно
выбрать и первый элемент, и второй, ... и N-и, что равно
произведению N сомножителей, каждый из которых равен р, т. е. ρΝ (8.2).
171
Каждый класс манипулированных сигналов по определению
содержит все сигналы с .заданными основаниями манипуляции и
заданными порядками. В теории кодирования классы называются
полными кодами [111]. Если основание манипуляций класса ρ = 2,
то такой класс будем называть полным двоичным кодом, а если
ρ > 2, то полным произвольным кодом.
8.2. Дискретные частотные сигналы произвольного порядка
Комплексная огибающая ДЧ сигнала порядка К определяется
выражением (1.73). Такой сигнал состоит из N временных
элементов, каждый из которых является суммой К частотных элементов.
По частоте имеется Μ возможных значений частот элементов.
Поэтому максимально возможное число частотных элементов не может
превышать Λί, т. е. для К имеем неравенство 1 ^ К ^ Λί. Пример
распределения энергии элементов на частотно-временной плоскости
был приведен на рис. 1.8.
Объем класса ДЧ сигналов порядка К. Обозначим через
Рам — основание амплитудной манипуляции, а через ром —
основание фазовой манипуляции. При этом амплитуда и фаза
каждого элемента ДЧ сигнала согласно (8.1) может быть выбрана р0 =
= РамРфм способами. К частотных элементов по частоте
занимают/С позиций из Λί. Так как порядок расположения элементов на
К позициях не имеет значения, то размещение К элементов
является сочетанием К элементов из Μ [132], или /С-сочетанием. Число
таких сочетаний равно биномиальному коэффициенту
q$= ■,.,;; ^. - ад
Ml
К\ (Μ-К)\
Амплитуда и фаза каждого /С-сочетания согласно формулам
(8.1), (8.2) может быть выбрана (рамРфм)* способами.
Поскольку имеется См /С-сочетаний из Λί, то число различных
выборов каждого временного элемента (основание манипуляции класса)
в соответствии с правилом произведения равно
ρ = рМ. (8.4)
Используя (8.2), находим объем класса ДЧ сигналов порядка К:
U = (рМ)". (8.5)
В случае ДЧ сигналов первого порядка (К = 1) См = Λί и из
(8.5) имеем
Lx = (poM)N. (8.6)
В этой формуле Λί является основанием манипуляции по частоте.
Объем L/c зависит от четырех параметров: /С, р0> Λί, N. С
ростом Μ и N объем L/c увеличивается монотонно, а при изменении
К он достигает максимума L/cMaKC ПРИ некотором оптимальном зна-
172
чении Копту которое зависит от значения р0. Найдем Κ0ΏΎ и
макс*
Обозначим
yK=±\gLK. (8.7)
Из (8.5) имеем
Ук = КЫРо+ЫС%. (8.8)
Поскольку логарифм — монотонно возрастающая функция, то
максимум ук макс имеет место при том же значении /С0Пт> что и
Ьк макс Из (8.8) следует, что- при р0 = 1, ук = lg См и
ί/кмакс = lgC^f/21, где [а:] — целая часть *, т. е. /Сопт =
= Λί/2. С увеличением р0 оптимальное значение /С0Пт растет.
Поскольку 1 ^К^,МУ то для /Сопт имеем неравенство Λί/2 ^
Если Λί > 1, то биномиальный коэффициент См (8.3) можно
заменить следующей асимптотической формулой:
CJ& ~ 2" K2/SM ехр [— (2/С — Λί)2/2Λί]. (8.9)
Формула (8.9) соответствует замене биномиального закона
распределения нормальным законом со средним значением Λί/2 и
дисперсией Λί/4. Подставляя (8.9) в (8.8), получаем
ук ~ К lg р0 + Λί lg 2 - [(2/С - Λί)2/2Λί] lg e +
+ lg У2/Ш: (8.10)
Производная
Ук = lg Ро - 2 (2/С - Λί) Λί"1 lg e. (8.11)
Приравнивая нулю производную (8.11) и решая полученное
уравнение, находим
ΚΟπτ = 0,5Λί(1-+0,51ηρ0). (8.12)
Из (8.12) следует, что с ростом р0 растет /Сопт· Очевидно, что
/Сопт макс не может превысить Λί, так как К^М. Подставляя
(8.12) в (8.10), с точностью до малых более высокого порядка
получаем
У К макс ^ Λί Χ, (8.13)
где
χ = lg 2 + 0,5 lg р0 + (lg p0)2 (8 lg е)"1. (8.14)
Можно показать, что при изменении р0 от 1 до 16 величина χ
меняется практически линейно от 0,3 до 1, т. е. при этом χ ^ 1.
Следовательно, у к макс <С Μ при указанных пределах изменения р0.
Подставляя (8.13) в (8.7) и переходя к LK, имеем:
U макс С* 10""* < 10"".
173
Оценка максимального объема класса ДЧ сигнала позволяет
утверждать, что объем'достигает больших значений. Например,
при Μ = N = 10 имеем ЬКмакс < 10100.
Сравнение объемов ДЧ сигналов различных порядков. Из
формул (8.5), (8.6) находим отношение
LKILX = (р^М^См)". (8.15)
Так же как и Lk (8.5), отношение (8.15) зависит от четырех
параметров. Увеличения Ν, Μ приводят к монотонному возрастанию
LkILx. При изменении К имеет место максимум при К = /Сопт
(8.12). Если положить р0 = 2, то /С0Пт — 5, а N'1 lg (WLJ ~
~ 2. Отсюда имеем Ьк!Ьл ~ 102ЛГ.
Используя приближенное значение (8.15), находим отношение
L/C максах ^ (10«* Ρο^Λί"1)^. (8.16)
Выражение (8.16) дает верхнюю оценку отношения Lk^kJLx,
т. е. истинное значение L*-MaKc/£j будет меньше того, которое
получится в правой части (8.16). Для точных расчетов необходимо
вычислять (8.15) при всех значениях К и находить максимум.
Сравнение объемов ДЧ сигналов и дискретных сигналов. ДЧ
сигнал располагается на частотно-временной плоскости, занимая
полосу частот шириной F = F0M (1.52), где F0 — ширина спектра
элемента сигнала, и отрезок времени Τ = NT0 (1.51), где Т0 —
длительность элемента. Согласно (1.53) база ДЧ сигнала равна
В = MNFqTq. Для сравнения ДЧ и дискретных сигналов по
объему предположим, что в качестве элементов используются простые
сигналы и база F0T0 = 1. В этом случае В = MN. При такой базе
число элементов в дискретном сигнале равно базе В. Полагая, что
амплитудная и фазовая манипуляции каждого элемента
производятся с теми же основаниями ρ дм и ром, т. е. р0 = рдмром, то
в соответствии с формулой (8.2) объем класса дискретных сигналов
будет равен
£д = Р? = рГ· (8.17)
Из формул (8.5), (8.17) находим отношение
LKILn = (Cbli%-K)». (8.18)
Если отношение См/р№~~к > 1, то объем LK класса ДЧ
сигналов порядка К больше объема £д класса дискретных сигналов;
если См/р(?~к < 1, то 1д> Lk- Для ДЧ сигналов первого
порядка имеем отношение Λί/ρο1-1. Если р0 = 2, то отношение
Μίρο"1<1 при ЛГ>2, а если р0>2, то М/ро~1 < 1 при
Μ > 1. Таким образом, объем класса ДЧ сигналов первого порядка
174
при Λί > 2 всегда меньше объема класса дискретных сигналов.
Перейдем к сравнению объемов при произвольном К. Отношение
г=—^— = — />£с£=— 10**, (8.19)
рм-к рм?о м рм
где у к определено формулой (8.8). Максимум ук согласно (8.12)
имеет место при /Сопт и равен в соответствии с (8.13) Мх9 где χ
из (8.14). Поэтому
гмакс ^ lC'/pf = (Ю-/р0)^. (8.20)
Следовательно, если отношение 10*/р0< 1, то zMaKC < 1 и
объем класса дискретных сигналов больше объема класса ДЧ
сигналов. Например, если р0 = 16, то согласно (8.14) χ = 1 и из
(8.20) имеем zMaKC <1.
Отметим, что сравнение объемов частотных и ДЧ сигналов даст
те же результаты, что получены в данном параграфе, так как
частотные и дискретные сигналы дуальны с точностью до поворота на
π/2 на частотно-временной плоскости (см. § 1.7). Другие
комбинаторные свойства систем ДЧ сигналов будут приведены в гл. 14.
8.3. Сигналы с двоичной амплитудной манипуляцией
В некоторых случаях используются сигналы с двоичной
амплитудной манипуляцией, при которой некоторый элемент сигнала
излучается или не излучается. Тогда последовательности элементов
ставится в соответствие двоичная кодовая последовательность,
состоящая из единиц и нулей. При этом обычно полагают, что 1
соответствует излучению элемента, 0 — не излучению.
Объем класса. Пусть для сигнала отведено N позиций п о
времени (частоте), т. е. он может состоять из N элементов,если нет
амплитудной манипуляции. Допустим, что AM такова, что сигнал
состоит из η элементов. Число сигналов, отличающихся хотя бы
одним элементом, определяется сочетанием η элементов из Ν, т. е.
L0 (η) = CnN. (8.21)
Каждый элемент может быть манипулирован по фазе с основанием
манипуляции р0. Кроме того, в случае ДЧ сигналов каждый
временной элемент может состоять из К частотных элементов. Поэтому
из-за ФМ и ЧМ объем класса увеличивается. В случае ДЧ
сигналов порядка К согласно формуле (8.5) и комбинаторному правилу
произведения имеем
Lk (η) = (PoCfi)" U (η) - (РоСмУ α. (8.22)
В случае ДЧ сигналов первого порядка (К = 1) из (8.22) получаем
U (п) = фоМ)п Си. (8.23)
175
Для дискретных или частотных сигналов Μ = 1 и из (8.23)
находим
L (п) = pnoCnN. (8.24)
Из сравнения формул (8.21), (8.24) еледует, что общей формой
является
L* (п) = р»С%, (8.25)
где основание манипуляции ρ = р0См для ДЧ сигналов порядка
К, ρ = PqM для ДЧ сигналов первого порядка, ρ = р0 для
дискретных (частотных) сигналов с фазовой манипуляцией, ρ = 1 для
дискретных (частотных) сигналов без фазовой манипуляции.
Если ρ = 1, то максимум L* (п) имеет место при η = [Ν72].
Если ρ > 1, то оптимальное значение η при котором L* (п)
максимально, определяется аналогично тому, как это было сделано в §8.2,
и равно согласно (8.12)
яопт = (N/2)11 + (1пр)/2]. (8.26)
Подставляя это значение в (8.25) и используя метод § 8.2
(формула (8.13), (8.14)), получаем максимальное значение объема
произвольного класса
L* (я)макс ^ 10"*, (8.27)
где χ определяется формулой (8.14). Оценку сверху для L* (п)
можно найти, используя тождество
(ρ + ι)" = pn + chpN~l +... + dS-y» + .··
... + 1. (8.28)
Так как Сы~п = Слг, то из (8.28) имеем неравенство
L* (л) = рпСЪ < (р + 1)". (8.29)
Сравним объем класса сигналов с амплитудной манипуляцией
с объемом класса без амплитудной манипуляции. Согласно (8.2)
объем класса без амплитудной манипуляции равен L = pN. Деля
(8.26) на pN, получаем
L* (n)/L = CnN/pN~«. (8.30)
При любых N и η увеличение основания манипуляции ρ ведет
к росту знаменателя в (8.30). Следовательно, начиная с некоторых
ρ объем L будет больше объема L* (я).
8.4. Сигналы с заданным числом блоков
Известно [30], что корреляционные свойства сигналов зависят
от числа блоков в них. Блок — это последовательность элементов
с одинаковыми значениями манипулированных параметров.
Например, если рассматривается дискретный ФМ сигнал с двумя зна-
176
чениями фазы 0 и π,το блок — последовательность элементов,
имеющих фазу 0 или π. Границами между блоками являются скачки
фазы. На рис. 8.1 изображен дискретный ФМ сигнал, состоящий из
9 элементов и 5 блоков.
В общем случае для сигнала, состоящего из N элементов, число
блоков Μ может изменяться от одного (все элементы одинаковы)
до N (каждый элемент отличается от соседних), т. е. μ = 1, N.
Обозначим длину блока через ην, ν = 1, μ. Имеем тождество
S nv = N.
ν=1
(8.31)
Определим число сигналов с одинаковым числом блоков.Если
сигнал состоит из μ блоков, то число границ между блоками равно
μ— 1. Эти границы тем или иным образом можно расставить на
N — 1 позиции, так как число таких позиций равно числу границ
между N
элементами'сигнала. Если порядок
размещения границ между блоками
не имеет значения, то число
таких размещений равно
числу сочетаний из N — 1
элементов по μ — 1, т. е.
1
о
-1
\
Ь
if
ЛЧ9
*J*
tz
*S
tjtt
I0fo) = C#=i. (8.32)
Рис. 8.1
Учтем теперь манипуляцию элементов блоков. Пусть основание
манипуляции р. В этом случае первый блок может быть выбран
одним из ρ способов. Второй блок может быть выбран одним из
оставшихся ρ — 1 способов. Третий блок и все остальные могут быть
выбраны также ρ — 1 способами, т. е. всеми ρ способами, за
исключением того, который был использован в предыдущем выборе. На
основании комбинаторного правила произведения манипуляция
увеличивает число сигналов (8.32) с одним и тем же числом блоков в
ρ (ρ—1)ν-χ раз. Таким образом, число сигналов с заданным
числом блоков равно
^(μ) = Ρ(Ρ-ΐ)μ-,ε»ζ1,.
Если ρ = 2, то имеем [40]
Μμ)
2С#:
(8.33)
(8.34)
Объем класса равен ρΝ (8.2). Если просуммировать все
значения L (μ), где μ = 1, Ν, то получим объем класса. Поэтому имеем
тождество
2 p(p-l)»C»Nz\=PN· (8.35)
177
При р = 2 правая часть (8.35) равна 2Ν, а левая часть [132]
2 Σ С%-\ =2 ΝΣ°ν-ι =2-2w-» = 2^
Точно так же можно проверить (8.35) и для других р.
При Ν > 1 справедлива следующая асимптотическая формула
для Ζ,(μ) (8.34) [40]:
L (μ) ~ 2" Κ2/π (JV — 1) exp [— 2 (μ — μ0)2/{Ν — 1)], (8.36)
где
μ0 = 0,5 (Ν + 1). (8.37)
Сумма всех L (μ) при μ0 — Δμ ^ μ <; μ0 + Δμ равна [40]:
μ0 + Δμ
5(μ,Δμ)= 2 £(μ) ~2" ^(2Δμ/]/Ίν-1)--ΐ], (8.38)
μ = μ0-Δμ
где F (α:) — интеграл вероятности (2.16).
Если 2Δμ < Υ Ν — 1, то, разлагая F {χ) в ряд по малому
аргументу [104], получаем
5 (μ, Δμ) ~ 2" |/"2~2Δμ [π (Ν — Ι)]-1/2 = 2^L (μ0), (8.39)
где L (μ0) находится из (8.36) при μ = μ0.
Глава 9
ПОЛНЫЙ ПРОИЗВОЛЬНЫЙ КОД
9.1. Алгебраические свойства полного кода
Как было определено в гл.л8, класс или полный код состоит из
всех последовательностей,отличающихся хотя бы одним элементом.
Объем класса согласно (8.2) равен ρΝ, где ρ — основание
манипуляции, N— число элементов. В частном случае, когда N = 1,
класс вырождается в алфавит объема L = р.
Исследование корреляционных свойств класса полного кода
имеет большое значение для изучения свойств систем сигналов,
являющихся подклассами данного класса. Оно существенно
упрощается, если учитывать алгебраические свойства полного кода,
который является группой. Перейдем к рассмотрению этого вопроса.
Группа и ее свойство. Допустим, что имеем некоторое множество
объектов или элементов. Обозначим объекты через а, Ь, с, ...
Определим на множестве бинарную операцию — однозначную функцию
178
двух переменных. Обычно операцию обозначают или как умножение
ab = с, или как сложение а + b = с.
Группой называется (см., например, [92, 121]) множество, на
котором определена бинарная операция и выполняются
следующие аксиомы.
1. Замкнутость. Операция может быть применена к любым двум
элементам группы, в результате чего получается элемент группы.
2. Ассоциативность. Для любых трех элементов группы а, Ь
и с имеет место ассоциативный закон, т. е. a (be) = (ab) с или
я + (Ь + с) = (а + Ь) + с. Ассоциативный закон означает, что
порядок выполнения операции несуществен и скобки не обязательны.
3. Нейтральный элемент. Существует нейтральный элемент еу
который не изменяет результата операции, т. е. ае = а или а + е =
= а для любого а.
Если операция называется умножением, то нейтральный элемент
называется единицей, обозначается 1 и определяется из уравнения
\а — а\ = а. Если операция называется сложением, то
нейтральный элемент называется нулем, обозначается 0 и определяется из
уравнения 0 + α = α + 0 = α.
4. Обратный элемент. Существует обратный элемент а такой, что
аа = е. При умножении обратный элемент обозначается яг1 и
определяется из уравнения аст1 = сгга = 1. При сложении обратный
элемент обозначается —та и определяется из уравнения а + (— а) =
= (— а) + а = 0.
Кроме перечисленных аксиом, элементы группы могут
удовлетворять коммутативному закону, т. е. ab = Ъа или а + b = b + а.
В этом случае группа называется коммутативной или абелевой.
Все рассматриваемые в дальнейшем группы коммутативны.
В теории групп большое значение имеет теорема о нейтральном
и обратном элементах [121].
Теорема. Группа обладает единственным нейтральным элементом
и каждому элементу группы соответствует единственный обратный
элемент.
Доказательство, а) Допустим, что в группе два нейтральных
элемента е и е'. Тогда имеем тождество ее' = е = е*, т. е.
нейтральные элементы совпадают. Следовательно, в группе один
нейтральный элемент, б) Допустим, что у элемента а имеется два обратных
элемента а и а'. Имеем равенства а = еа = а'аа = а!е — а\ т. е.
обратные элементы совпадают.
Примеры групп.
1. Аддитивная двоичная группа. Состоит из элементов 0 и 1.
Операция сложения определена по модулю 2 (mod 2), т. е. а +[Ь =
S3 с (mod 2), где == — знак сравнения. Числа а и b сравним по
mod ρ, т. е. а = Ъ (mod p), если
а = ЯФ + г, b = q2p + r, (9.1)
где ql9 q2 — любые целые числа; г — остаток, О^г^р—1.
Операция сложения в группе определена табл. 9.1.
179
Нейтральным элементом является 0, обратным элементом к О
является 0, а обратный к 1 является 1, так как 1 + 1=2 = 0
(mod 2).
2. Мультипликативная двоичная группа. Состоит из элементов
1 и —1. Операция умножения в группе определена табл. 9.2.
Нейтральным элементом является 1, обратным элементом к 1
является 1, а обратным к — 1 является — 1. Из сравнения табл. 9.1,
9.2 видно, что они имеют много общего. Если заменить элемент 0
на 1, элемент 1 на — 1, а операцию сложения по mod 2 на
умножение, то табл. 9.1 переходит в табл. 9.2. Это свойство сохраняется
и при р-ичных группах.
Таблица 9.1 Таблица 9.2
Θ
0
1
0
0
1
1
1
0
X
1
—1
1
1
—1
—1
—1
1
3. Аддитивная р-ичная группа. Она состоит из ρ элементов
0, 1, ..., ρ — 1. Операция сложения определяется по mod p и для
ρ = 5 приведена в табл. 9.3.
Нейтральным элементом является 0, а обратными являются:
для 0 элемент 0, для 1 — 4, для 2—3, для 3—2, для 4—1.
Обратными элементами являются те, которые дополняют элемент до 5 или 0,
так как 5 ξ= 0 (mod 5).
4. Мультипликативная р-ичная группа. Она состоит из
элементов Ь0у Ь1у ..., 6ρ_! вида
Ьп = exp (in 2π/ρ). (9.2)
Таблица 9.3 Таблица 9.4
Θ
0
1
2
3
4
0
0
1
2
3
4
1
1
2
3
4
0
2
2
3
4
0
1
3
3
4
0
1
2
4
4
0
1
2
3
180
X
bo
bi
Ьг
Ьз
bt
bo
bo
by
b*
b8
bi
bi
by
b*
b3
bi
bo
b2
b2
b3
bi
bo
bx
b3
h
bi
bo
bi
b*
bt
bi
bo
b,
&2
b3
Операция умножения определяется следующим равенством
ЬпЬт = exp [i (η + т) 2π/ρ] = bn+m. (9.3)
Следовательно, умножение элементов Ьп и Ьт изоморфно сложению
индексов пит, входящих в показатели экспонент. Табл. 9.4
определяет операцию умножения.
Из сравнения табл. 9.3 и 9.4 следует, что индексы у элементов
Ьп табл. 9.4 образуют табл. 9.3. Нейтральным элементом является
b0j а обратными элементами те, которые дополняют показатель
степени до величины, кратной'2π. Обратным к Ь0 является Ь0, гдля
Ъг — 64, Для Ь2 — Ь39 для Ъъ — Ьъ для 64 — Ьг.
5. Мультипликативная комплексно-сопряженная р-ичная
группа. Она состоит из элементов b0y bly ..., Ьр_г (9.2), но операция
умножения определяется следующим образом:
ЬпЬ*т = exp (in2n/p) exp (— \m2nlp) = exp (i (n — m) χ
Χ 2π/ρ) = 6n.m, (9.4)
где * — знак комплексной сопряженности. Из (9.4) следует, что
комплексно-сопряженное умножение соответствует вычитанию
индексов. Но разность
η — m = l (mod p),
где 0 <! Ι ^ ρ — 1, т. е. разности η — m можно привести к значе-
*
ниям 0, ρ — 1, а элементы ЪпЪт к Ъх.
В табл. 9.5 даны разности η — т для ρ = 5, приведенные к
значениям 0,4. Например — 2 + 1=4 (mod 5). Согласно табл. 9.5
в табл. 9.6 приведены правила комплексно-сопряженного
умножения согласно (9.4).
Так как Ь0 — нейтральный элемент, то Ь0 = Ь0. Из табл. 9.6
видно, что элемент bnbm расположен среди элементов Ъь I =
= 0,р-1.
Таблица 9.5 Таблица 9.6
*
®
bo
*
Ьг
к
*
ь3
к
bo
bo
ь»
b3
Ьг
Ьг
Ьг
Ьг
bo
bt
b3
Ьг
Ьг
Ьг
Ьг
bo
bi
b3
b3
b3
ь*
Ьг
bo
bi
bi
bt
b3
b*
Ьг
bo
θ
0
—1
—2
—3
—4
0
0
4
3
2
1
1
1
0
4
3
2
2
2
1
0
4
3
3
3
2
1
0
4
4
4
3
2
1
0
181
Таблица 9.7 6. Полный р-ичный код. Он
является группой, так как если в нем
определить бинарную операцию, то он будет
удовлетворять всем четырем групповым
аксиомам. Определение бинарной
операции зависит от представления
элементов (сигналов) полного кода.
Покажем это на примере.
Положим ρ = 3, а N = 2. Объем
полного кода L = З2 = 9, т. е. он
содержит 9 сигналов (элементов).
Каждому сигналу может быть поставлена в
однозначное соответствие кодовая
последовательность, представляющая запись
ее номера в р-ичной системе
счисления. При ρ = 3 алфавит состоит из элементов 0, 1, 2. В табл. 9.7
приведены номера кодовых последовательностей и их запись.
Представление кодовых последовательностей в виде,
представленном в табл. 9.7, обусловливает выбор в качестве бинарной
операции посимвольное сложение по mod ρ = 3. Например, сумма
элементов 5 + 6 = 2, так как
,12
•(mod3),
Номер
последовательности
0
1
2
3
4
5
6
7
8
Последовательность
0 0
0 1
0 2
1 0
1 1
1 2
2 0
2 1
2 2
02
в связи с тем, что 3 = 0 (mod 3). Таблица 9.8 представляет полную
таблицу сложения при ρ = 3, N = 2 для кодовых
последовательностей табл. 9.7.
По табл. 9.8 проверим все групповые свойства полного кода.
Замкнутость имеет место, так как все элементы табл. 9.8
принадлежат полному коду. Ассоциативность проверяется непосредственно.
Например, (5+ 6)+ 4 = 2 + 4 = 3. С другой стороны, 5 + (6 +
+ 4) = 5 + 1=3. Нейтральным элементом является 0, и для
каждого элемента имеется единственный обратный элемент, который
в сумме дает 0. Следовательно, полный код является группой.
Если символы кодовых последовательностей представить в виде
(9.2), то в качестве бинарной операции над элементами полного кода
следует взять посимвольное умножение согласно соответствующей
таблице умножения элементов Ъпу η = 0, ρ — 1. При этом индексы
у получаемых элементов будут соответствовать таблице сложения,
аналогичной табл. 9.8.
Разложение группы по подгруппам. Если часть группы обладает
свойствами подгруппы, т. е. у нее выполняются все четыре
групповые аксиомы, то она называется подгруппой. Очевидно,
нейтральный элемент подгруппы должен совпадать с нейтральным элементом
группы, иначе группа должна была бы содержать два нейтральных
элемента, что невозможно. В общем случае, все подгруппы^имеют
182
Таблица 9.8
Θ
0
1
2
3
4
5
6
7
8
0
0
1
2
3
4
5
6
7
8
1 ΐ
1
2
0
4
5
3
7
8
6
2
2
0
1
5
3
4
8
6
7
3
3
4
5
6
7
8
0
1
2
4
4
5
3
7
8
6
1
2
0
5
5
3
4
8
6
7
2
0
1
6
6 j
7
8
0
1
2
3
4
5
7
7
8
6
1
2
0
4
5
Ι з
8
8
6
7
2
0
1
5
3
4
один и тот же нейтральный элемент. Согласно четвертой аксиоме
подгруппа должна содержать все свои обратные элементы.
В качестве примера рассмотрим табл. 9.8. Из этой таблицы
сразу же можно выделить подгруппу, состоящую из элементов 0, 1,2.
Можно также выделить подгруппы из элементов 0, 3, 6; 0, 4, 8;
О, 5, 7.
Подгруппы имеют большое значение в теории групп, так как
они позволяют разлагать группы на более простые структуры.
Например, если использовать подгруппу 0, 1,2, то разложение группы
(полного кода) с ρ = 3, N = 2 имеет вид
О 1 2
3 4 5 (9.5)
6 7 8.
Перейдем к разложению группы G по подгруппе Η в общем
случае. Обозначим элементы группы G через g*0, gly ..., gL-i, где
L = pN — объем группы. (В теории групп объем L называется
порядком группы.) Элементы подгруппы Η обозначим через /г0, Къ ...,
..., /i/_i, где / — объем или порядок подгруппы. Положим
h0 = е. Составим упорядоченную таблицу элементов группы
следующим образом. В первую строку поместим элементы подгруппы,
причем она начинается с нейтрального элемента. Каждый элемент
подгруппы появляется в строке один раз. Первым элементом
второй строки может быть любой элемент группы, не входящий в пер-
183
вую строку. Остальные элементы.получаются в результате
выполнения принятой операции/например, при умножении (сложении) всех
элементов подгруппы на первый элемент строки. Аналогично
образуются и все остальные строки, до тех пор, пока в таблицу не войдут
все элементы группы. Такое представление группы дается
следующей таблицей, причем в качестве групповой операции взято
умножение:
h0 = е hx h2 ... Λζ_ι
giK = Si gJh gih2 ... «Ά-ι
g^O = g2 gJh glhi ... g2hi-!
gm-lh = gm-i gm-A gm-l k2 ... gm-iki-!. (9.6)
Из (9.6) следует, что число строк равно /п, а число столбцов
равно /. Число элементов в (9.6) равно 1т. С другой стороны, число
элементов в группе равно L. Поэтому
L = 1т. (9.7)
В общем случае порядок подгруппы делит порядок группы
(теорема Лагранжа).
Совокупность элементов в строке называется смежным классом,
а элемент, стоящий в первом столбце строки — образующим
смежного класса. Для разбиения (9.6) известен ряд теорем; основными
являются ниже следующие [121].
Теорема 1. Два элемента g и g' группы G принадлежат одному
и тому же смежному классу по подгруппе Η в G тогда и только
тогда, когда произведение gg' принадлежит Н.
Теорема 2. Каждый элемент группы G принадлежат одному
и только одному смежному классу по подгруппе Н.
Число различных разбиений группы по подгруппам весьма
велико [138]. Среди различных разбиений отметим только одно,
которое назовем натуральным. Заменим последовательности их
номерами в р-ичной системе счисления и положим, что объем подгруппы
/ = р", (9.8)
причем 0 ^ η <; N.
Если L = ρΝ, то / делит L и число смежных классов (включая
саму подгруппу) согласно (9.7) равно
т = р^-я. (9.9)
Расположим все элементы группы в порядке их номеров:
О 1 2 ... / ... рп— 1
рп р"+1 р" + 2 ... рп + j ... 2рп—1
kpn kpn+l kpn+2 ... kpn + j... (k+l)pn— 1
pN—pn pN—pn+1 pN—pn+2 ... pN—pn+j ... pN— 1. (9.10)
184
Пример такого разбиения был дан в форме (9.5). Оно позволяет
представить все сигналы через сигналы с номерами 0, 1, 2,..., рп — 1,
р", 2рпу ..., (ρΝ~η—1) ρ". Всего необходимо знать рп + ρΝ-η
сигналов вместо ρΝ. Наименьшее число будет при η = [Ν72].
Из (9.10) следует, что при любом ρ совокупность элементов 0, 1,
2, ..., рп~1 является подгруппой.
9.2. Ортогональность полного кода
Среди различных свойств полного кода следует отметить его
ортогональность, определение которой будет приведено в данном
параграфе. Ортогональность позволяет достаточно просто
находить статистические характеристики корреляционных функций
полного кода.
Упорядочим последовательности полного кода. Поставим в
соответствие каждой кодовой последовательности Aj = (α7ΐ, ..., α^)
(1.101) число /, записанное в] р-ичном счислении/ причем / =
=0, L— 1, а объем полного кода L= рп (8.2). Представим полный
код в виде матрицы π&:
πρΝ·-
^01
202
ап
а11
а
а г
л
а
12
In
а
J η
ClQN Cl\N ... CifN
.. flL-1. 1
. #L-1, 2
. «L — 1, N
(9.11)
Каждая кодовая последовательность является столбцом
матрицы п%. Всего столбцов L, а строк N. Каждый столбец получается
из предыдущего вписыванием снизу 1, а первый столбец (а01, ао2 ...
а0лг) = 0 0 ... 0 — состоит из N нулей. Например, при ρ = 3
имеем следующие матрицы:
и ЛГ = 1, 2, 3
π! = |0 1 2|,
П2 =
π§ =
0 0 0 1112 2 2
0 12 0 12 0 12
000000000111111111222222222
0001 1 12220001 1 1 2220001 1 1222
012012012012012012012012012
(9.12)
В соответствии с правилом построения и примерами (9.12)
матрицу π&+ι можно представить в символическом виде
следующим образом:
π5ν+ι
0 1
1
πρΝ
(9.13)
Здесь верхняя строка содержит столько символов 0, 1 и ρ — 1,
сколько содержится столбцов в матрице ηβ. Из приведенных
185
примеров (9.12) и символической записи (9.13) видно, что каждая
строка матрицы πρΝ содержит целое число периодов. Число
периодов я-й строки равно ρ"-"1, η = 1, N. Длина периода равна
Рассмотрим суммы вида
S(n,fc) = 2 а1п®а&, (9.14)
где ® — знак операции в группе. Суммы (9.14) при пфк можно
разбить по наименьшим периодам. Пусть k > п. Тогда Qk < Qn и
S(n,fc)= Ц 2 α*ι®** =
m>=0 L / = "#£ J
ρ*-1_ΐΓ (m+l)Qk Ί
= Σ \aJn Σ α* · (9·15)
m=0 [_ l = mQk J
Здесь α7·η вынесен за знак внутренней суммы, так как за период
Qh символ ctjn остается постоянным и меняется только при
изменении т. Окончательное выражение для 5 (я, k) можно найти, если
конкретизировать операцию. Возьмем в качестве символов символы
мультипликативной комплексно-сопряженной группы (9.2), (9.4).
В этом случае внутренняя сумма в (9.15) равна
{m+\)Qk (mfl)Qi
Σ Ъ*= Σ βχρ(ί*,2π/ρ)=0. (9.16)
Сумма экспонент в (9.16) за период равна нулю, поскольку она
содержит одинаковое число экспонент вида ехр (Ю), ехр (ί2π/ρ), ...
..., ехр (ik2n/p), ..., exp(i (ρ — 1) 2π/ρ). Если внутренняя сумма
в (9.15) равна нулю, то и вся сумма
S (/!,*)= 2 aJn®<*jh=0> (9.17)
/=о
т. е. строки матрицы π& ортогональны. Если положить η = k и в
качестве символов ajn взять символы мультипликативной
комплексно-сопряженной группы, то сумма S (я, п) = L, так как каждое
слагаемое суммы равно единице. Объединяя эти результаты, имеем
О при η φ k,
при n = k.
S(n,£)={°
Из периодичности строк матрицы лу (9.11) следует, что
S(n) = L^ajn=0. (9.19)
ISb
Точно т&к же доказывается, что среднее Значение произведений
любого числа несовпадающих строк матрицы (9.11)
S(n,k9...,u)= 2 tyn®flyfc® —®flJu=0· (9·20)
/=ο
9.3. Корреляционные функции полного кода
Корреляционные функции в дискретных точках. В гл. 1 были
подробно рассмотрены корреляционные функции (КФ) различных
сигналов. В большинстве случаев КФ внешне отличаются
значительно. Однако, если рассматривать значения КФ в некоторых
дискретных точках частотно-временной плоскости, то их можно привести
к одной форме, которая оказывается полезной в исследованиях.
Начнем с ВФН ДЧ сигнала порядка К (1.89). Положим τ =
= (ν — μ) Δ/, Ω = (γ*χμ — γ/κν) Δω, обозначим
λ = ν — μ, ξ = γΛχμ —γ/κν. (9.21)
Допустим, что произведение ΔωΔ/ = 2π. В этом случае фаза в
(1.89) ε (τ, Ω) == 0 (mod 2π). При сделанных допущениях из (1.89)
получаем
ν
μ=ν —λ
Υ*χμ=ν/κν+&
Суммирование в (9.22) производится по всем ν,
удовлетворяющим первому уравнению в (9.21), а пределы изменения μ
определяются решениями второго уравнения (9.21).
Для ДЧ сигналов первого порядка при тех же допущения из
(1.70) получаем
яЛм=-^ 2 *'***»· (9·23)
ν
μ = ν — λ
νΛμ^Υ/ν + δ
где λ = ν — μ, а ξ = γ*μ — γ/ν.
В случае частотных сигналов при τ = 0 из (1.118) имеем
#7*(-λ) = -ξ- J «/νά*.ν-λ. (9.24)
а для дискретных сигналов при Ω = 0 из (1.125) получаем
**(λ)~ 2 α/ν^.ν-λ. (9.25)
ν-λ+ι
187
Сравнивая выражения (9.22)—(9.25), замечаем, что с точностью
до постоянной их можно представить в следующей общей форме:
ν
В дальнейшем при исследовании статистических характеристик
КФ большое значение будет иметь число слагаемых в (9.26). Оно
зависит от режима работы радиотехнической системы. При
периодическом излучении одного и того же сигнала, а также при
последовательном излучении различных сигналов друг за другом число
слагаемых неизменно. С точки зрения характеристик оба эти
случаи одинаковы. Поэтому такие режимы работы будем для краткости
называть периодическими. Максимальное число слагаемых при
периодическом режиме равно N. Для частотных и дискретных
сигналов периодические КФ определяются из (9.24), (9.25) при λ = 0.
Если излучается единственный сигнал или КФ не
перекрываются, то такие режимы будем называть для краткости
апериодическими. В этом случае число слагаемых зависит от взаимного смещения
(сдвига) кодовых последовательностей Aj и Ak. Для частотных и
дискретных сигналов сдвиг равен λ. Когда λ = 0, число слагаемых
в КФ равно Ν, когда λ = ± 1, число слагаемых N — 1, когда
λ = ± 2, число слагаемых N — 2, т. е. в общем случае при сдвиге
λ число слагаемых равно N — λ, λ = 0, ± (Ν — 1).
Групповые свойства корреляционных функций. Допустим, что
элементы α/ν иа^ принадлежат некоторому алфавиту А из ρ
элементов. Пусть алфавит А является мультипликативной комплексно-
*
сопряженной группой. В этом случае произведение а^а^ согласно
примеру 5 в §9.1 является элементом группы Л, т. е.
α/νβΛμ = яте, (9.27)
где т является одним из значений 0, ρ — 1 и некоторой функцией
от /, ky ν, μ, т. е.
/и = φ (/, К ν, μ). (9.28)
Подставляя (9.27) в (9.26) и отбрасывая индексы /, &, ν, μ,
получаем
«=72fl«. (9-29)
m
В (9.29) суммирование производится по всем т (9.28), число
слагаемых равно я, причем 0 ^ η ^ N. Последовательность Ат =
= {ат}, состоящая из η символов, является одной из
последовательностей полного кода объема рп. Поэтому сумма
W=j\ am (9.30)
т
188
является одной из возможных сумм полного кода. Сумма W (9.30)
называется весом кодовой последовательности. Число всех весов
W равно ρΝ, но число разных весов будет гор аздо~ меньше.
Поскольку вес (9.30) и значение КФ (9.29) связаны соотношением
R = WIN, (9.31)
то знание распределения весов полного кода позволяет определить
статистические характеристики КФ. Перейдем к определению
распределения весов полного кода.
9.4. Распределение весов полного кода
Максимальное число различных весов. Как и ранее, будем
полагать, что число различных символов в кодовой
последовательности равно /?, а число символов равно η <; N.
Последовательности, имеющие равное количество одинаковых символов, имеют
одинаковый вес W (9.30). Определим максимально возможное число
разных весов кодовых последовательностей. Задача нахождения
максимального числа весов сводится к задаче определения числа
размещения η одинаковых объектов по ρ ячейкам [132]. Ее решение
таково. Представим все объекты в виде последовательности,
состоящей из единиц. Границы между ячейками обозначим через 0,
число таких границ равно ρ — 1. Например, для η = 9 и ρ = 3
имеем одну из возможных последовательностей 1110 11110 11,
т. е. в первую ячейку попадает 3 объекта (имеем три символа 0),
во вторую — 4 объекта (имеем четыре символа 1), в третью—2
объекта (имеем два символа 2). Общее число объектов в
последовательности из единиц и нулей равно η + ρ — 1. А число разных
размещений определяется числом сочетаний ρ — 1 нулей из η + ρ — 1
объектов. Следовательно, максимальное число разных весов равно
Lw==Cn+p—\ = Cn_j-p—1· (9.32)
При η > ρ — 1 из (9.32) можно получить следующую приближенную
формулу
Lw ~ пР-Ч(р — 1)!. (9.33)
Число последовательностей с равным количеством одинаковых
символов. Оно определяется числом сочетаний из п0 символов 0,
пг символов 1, ..., пр_1 символов ρ—1. Такое число сочетаний
вычисляется согласно полиномиальной формуле [132]:
κ= - , (9.34)
П0\ Пг\ ... Alp-i!
причем должно выполняться равенство
/=о
а некоторые из tij могут быть равны и нулю.
189
Модуль веса. Формула (9.32) определяет максимально
возможное число разных весов.-Однако на самом деле их будет меныиедак
как некоторые последовательности, имеющие разное число
одинаковых символов, дадут равные веса. Формула для расчета числа
весов в этом случае неизвестна. Дело еще более усугубится при
переходе к модулям весов.
Если символы ат являются комплексными величинами, т. е.
/θ„
Ат=|Ат|еЧ
(9.36)
где \ат\ — модуль, а 0т — фаза, то вес (9.30) является
комплексно-сопряженной величиной
^=2lflm|C0SeTO+i2|flm|smeTO.
(9.37)
Модуль веса W по определению равен
W
1=/[1'а
m I C0S 6m
+
21 am I sin 0Л
(9.38)
Число разных значений модуля | W | будет меньше числа весов
W> по крайней мере, по следующей причине. Если у одной
последовательности W = а + \ЬУ то равные модули будут иметь
последовательности с весами, равными а — \b, b + ш, b — ш. Для
иллюстрации рассмотрим примеры.
Распределение модуля веса. Допустим, что ρ = 3, а п = 4.
Объем полного кода согласно (8.2) равен рп = З4 = 81.
Максимальное число весов согласно (9.32) равно С\ = 15. В табл. 9.9
приведены условные номера комбинаций символов χ от 1 до 15, сами
комбинации, число таких комбинаций κ (9.24) и значения модулей
весов \W\.
Τ аблида 9.9
X
1
2
3
4
5
6
7
8
Комбинация
0, 0, 0, 0
0, 0, 0, 1
0, 0, 0, 2
0, 0, 1, 1
0, 0, 1, 2
0, 0, 2, 2
0, 1, 1, 1
0, 1, 1, 2
κ
1
4
4
6
12
6
4
12
Ι \π\ Ι
4
2,65
2,65
2
ι Ι
2
2,65
ι |
*
9
10
11
12
13
14
15
Комбинация
0, 1, 2, 2
0, 2, 2, 2
ι, ι, ι, ι
1, 1, 1, 2
1, 1, 2, 2
1, 2, 2, 2
2, 2, 2, 2
κ
12
4
1
4
6
.4
1
\w\
1
2,65
4
2,65
2
2,65
4
Сумма всех κ равна объему кода 81. Модули \W\ рассчитаны
для символов ат = Ьт, где Ьт определяется согласно (9.2). Из
(9.2) следует, что \ат\ = 1.
190
Как видно из табл. 9.9, имеется всего 4 различных модуля —
1; 2; 2,65; 4. Вероятность появления модуля веса \W\ равна
(9.39)
где числитель равен сумме всех κ с данным | W |. В табл. 9.10
приведено распределение модулей весов | W |.
Из табл. 9.10 следует, что при ρ = 3 определенному модулю
| W\ соответствует определенное значение κ. Например, если| W\ =
= 2,65, то κ=4. В общем
случае такое соответствие не
имеет места. Можно
показать, что если ff = 4, η = 4,
то для | TJP | = 2 значения κ
равны 12 и 4.
}W\
1
2
2,65
4
Таблица 9.10
Σκ
36
18
24
3
Ρ (\W\)
0,445
0,222
0,296
0,037
На рис.9.1 изображен
закон распределения Ρ (| W |)
для η = 10, ρ = 3* [51].
Нормализация. Проводить
непосредственные расчеты
вероятностей Ρ (| W\) при
больших η весьма
затруднительно. Поэтому
целесообразно иметь приближенный закон распределения, который можно
найти, используя нормализацию слагаемых веса W (9.37).
Обозначим
*c=2lflm|cosew, zs = 2lamlsin9w. (9.40)
т т
В этом случае
W=zc + 'izs, \W\=VW+%. (9.41)
Каждая сумма в (9.40) при η > 1 состоит из большого числа
слагаемых. По предположению, \ат\ = 1. Допустим также, что
ΘΓ/1 — случайная величина, равномерно распределенная на отрез-
* График рис. 9.1 рассчитан В, В, Житковымт
т
ке [О, 2π]. При таком допущении величины гс и zs равны сумме
большого числа случайных величин (синусоид со случайными
фазами) и плотность вероятности величин zc и zs должна
стремиться к нормальной. Среднее значение zc, zs равно нулю, а дисперсия
в соответствии с общими правилами [104]
σ2 = я/2. (9.42)
С учетом отмеченного нормальный закон распределения для zq,
zs имеет вид [104]:
w (гс) = w (zs) = w(z) = -j= e-2'·"1. (9.43)
у ПП
Расчеты показывают, что законы распределения zc и zs
близки к нормальному закону (9.43).
Если предположить, что величины zq, zs статистически
независимы, то модуль | W\ (9.31) должен быть распределен по закону
Релея [104]:
w(\W\)=*№-e-lWl4\ (9.44)
η
На рис. 9.1 кривая изображает закон Рэлея (9.44). Как видно
из этого рисунка, распределение \W\ можно считать релеевским
весьма приближенно. Отличие объясняется в основном тем, что
величины zc и zs не являются статистически независимыми.
Многочисленные расчеты показали, что даже если распределения гс
и zs близки к нормальному (9.43), распределение \W\ может в
большей степени отличаться от релеевского.
9.5.. Распределение корреляционных функций
Переход от весов к корреляционным функциям. Он
определяется формулой (9.31). Если считать, что вес W — случайная величина
с плотностью вероятности щ (W), то плотность вероятности КФ
в соответствии с общими правилами [104] будет равна
w (R) = Nw± (NR). (9.45)
Если ввести
Re = гсШ, Rs = zs/N, (9.46)
где zc, zs определены формулами (9.40), то согласно (9.43),
(9.45) имеем
»(Rc,n)--£=.e-*,**/'\ (9.47)
a w (Rs, n) получается из (9.47) после замены индекса С на 5.
Аналогично для модуля \R\ из (9.44), (9.45) получаем
штп) = ^1Ше-"2|«,'/'\ (9.48)
п
192
В аргументы плотностей вероятностей (9.47), (9.48) введен
параметр п. Это сделано потому, что в дальнейшем будет
производиться суммирование по η слагаемых вида (9.47), (9.48).
Периодические корреляционные функции. При периодическом
режиме на выходе согласованного фильтра имеет место
периодическая КФ. В случае дискретных или частотных сигналов, как было
отмечено ранее, в исходных формулах (9.29), (9.30) число слагае-
W(RC)
мых равно N. Полагай η = Ν,
из (9.47), (9.48) получаем
в,(Яс, Ν) = УШе-"*с>
w(\R\, N)=2N\R\ е-м*1". (9.49).
Апериодические
корреляционные функции. При
апериодическом' режиме работы число
слагаемых η в (9.29), (9.30)
изменяется от нуля до Ν, что
соответствует изменению сдвига λ
в (9.24), (9.25). Отметим, что
число слагаемых η = N
возможно только один раз при
λ = 0, в то время как число
слагаемых η<Ν появляется
дважды: при сдвиге вправо (λ > 0)
и влево (λ<0). Поэтому
значения КФ с я < N встречаются
дважды.
Рассмотрим следующую модель для исследования
апериодических КФ. Допустим, что момент наблюдения попадает
равновероятно на один из 2Ν отсчетов КФ. Обозначим через w (R\ n) плотность
вероятности случайной величины R' при числе слагаемых в сумме,
равном я. Если R' = Re, то w (Rc> n) определяется формулой
(9.47), а если R' = \ R | — то формулой (9.48). Найдем вероятность
того, что R' = R0y где R0 — некоторое фиксированное значение.
Значение R0 может появиться или при η = N с вероятностью
(1/2Ν) w (R0, Ν), или при η = N — 1 с вероятностью (Ι/Ν) Χ
X w (R0y N — 1) ..., или при η = k с вероятностью (l/N) w (R0, k),
или при η = 1 с вероятностью (l/N) w (R0, 1). Отметим что при
п<С N перед w (R0, η) имеется множитель l/N, так как п< N
встречается дважды, как было отмечено ранее. Поскольку
перечисленные события несовместимы, то согласно правилу сложения
вероятностей вероятность появления R' = R0 равна сумме
перечисленных вероятностей. В общем случае вероятность появления
некоторого значения /?' в апериодической КФ равна
193
Формула (9.50) позволяет находить функцию распределения
апериодических КФ, если известны w OR', η). Для примера на рис. 9.9
сплошной линией изображен закон распределения величины Re
(9.47) при N = 10. Штриховой линией показан нормальный закон
распределения с дисперсией, равной среднему значению дисперсий
слагаемых в (9.50) (можно показать, что эта кривая соответствует
закону (9.47) с η = Ν/2). Из сравнения кривых-рис. 9.2 следует,
что закон распределения (9.47) отличается от нормального (он
имеет большие значения на краях и в центре).
9.6. Статистические характеристики полного кода
Статистические характеристики периодических корреляционных
функций. Периодическая КФ, как было отмечено ранее,содержит
N слагаемых, т. е. (9.26) можно записать в следующем виде:
1 £,
Rjh = — 2, fl/v α*μ = я* (μ)· (9·51)
V = l
Назовем /ι-м начальным моментом Rjk величину
L-l L-1 μ0+//-1
•=w22 Σ ъы <9·52>
/=0 &=0 μ = μ0
1
где L = ρΝ — объем полного кода; суммы по / и k с множителями
1/L означают усреднение периодических КФ по всем
последовательностям полного кода, а сумма по μ с множителем 1/Ν означает
усреднение но сдвигам.
Заменяя в (9.52) КФ на вес согласно формуле (9.31), получаем
m»=idnj2 Σ Σ *№· <9·53>
/=r0 &=0 μ=μ0
Зафиксируем / и μ0, положив их постоянными. При изменении k
получаем все возможные веса, сумма которых не будет зависеть от
/, k и μ0. Поэтому справедливо следующее равенство для тп (9.53):
™»=~ 2 w'=τ Σ *>* ω· <?.w)
/=const
μ0 = const
т. е. необходимо каждый вес возвести в п-ю степень,
просуммировать и разделить на LNn. Подставляя в (9.54) определение (9.51),
получаем
194
mn = TT77 2 Ζ β/ν α*μ =
£=o\v=i /
μ = ί(ν)
1
1 L-l Γ W , Π Γ Ν # "Ι
Λ«υ La=i J l_v = i J
Полагая п = 1, из (9.55) находим среднее значение
L-1 N л N L—\ m
(9.55)
т1==7лГ Σ Σ fl/vfljfev = Ζ/ν Σ α/ν Σ ^ν· (9'56)
^=:0V=1 V=l k = 0
Но сумма по k равна нулю в соответствии с (9.19). Поэтому
среднее значение тх = 0. Поскольку тх = 0, то второй начальный
момент т2 совпадает со вторым центральным моментом М2 = σ2, τ. е.
L-\ N * ^ *
°2=i Σ Σα/α ^α Σα/ν α*ν· (9·57)
L^2 , "η -.
&=() α=1
Выделяя сумму по έ, имеем
AT Ν
1
LW2 ^
α = ΐ ν =
v = l
L—1
^v 2 а^а^ Σakvukat
(9.58)
*=o
Согласно (9.18) сумма по & равна 0 при ν Φ а и равна L при
ν=α. В этом случае в двойной сумме по α и ν необходимо учитывать
только слагаемые с α = v. В результате имеем
N
1
№
2ia/vi2·
(9.59)
V=l
Так как ранее было предположено, что символы ajv принадлежат
к символам вида (9.2), то |α7·ν|2 = 1 и
σ2 = l/N. (9.60)
Отметим, что второй центральный момент (9.60) не зависит от
объема алфавита (основания манипуляции) ρ и полностью
определяется числом символов N в кодовой последовательности.
Статистические характеристики апериодических
корреляционных функций. Определим я-й начальный момент апериодических
КФ следующим образом
^-άΰΣΣ *Σ **(μ)· (9·61)
/=0 * = 0 μ=-(//-1)
Здесь усреднение по μ производится на интервале шириной 2АЛ
Так же, как и в случае периодических КФ, среднее значение тх =
= 0. Поэтому рассмотрим только т2 = М2 = σ2.
195
Основное отличие начальных моментов апериодических КФ (9.61)
от периодических КФ (9.52) заключается в определении самой КФ.
В случае периодических КФ число слагаемых в (9.51) всегда
постоянно и равно N. Это число не зависит от сдвига μ. В случае
апериодических КФ, как было отмечено ранее, число слагаемых равно
Ν — μ, так как
ι Ν
RSk(P) = jf Σ α***.ν-μ· (9·62)
ν = μ+1
Определение (9.62) можно подставить в (9.61) и произвести
суммирование. Но можно применить и другой прием [37], используя
спектр кодовой последовательности (см., например, (1.106)). Из
(1.128) при Ω = 0 и λ = μ имеем
Rjk (μ) = -^ J Ηj (χ) Hk (χ) e"" dx. (9.63)
—π
Обратимся теперь к сумме μ в (9.61). Поскольку RJk (μ) ξ» 0
при Ι μ Ι ^ Ν, το
*Σ *&<μ)= Σ #7* (μ)· (9·64>
μ= — (Ν— 1) μ==—οο
Определим дисперсию σ2 из (9.61) при η = 2 следующим образом
/ = 0 & = 0 μ=—οο
Подставляя (9.63) в (9.65), получаем
Λ L—\ L—\ οο π
2A/L2 Δι Ad Ad (2π)2#« JJ J w AW
/=0 &=0μ = — οον ' —π
Преобразуя, получаем
L-1L-1 , π
2NL*
:Hj(y)Hk(y) J ^{x~u)dxdy. (9.66)
Χ j
μ= —οο
В теории обобщенных функций известно равенство:
2π
196
1_
τ;
μ=—οο μ —— οο
^ β4«= ^ δ(2 + 2π^), (9.67)
где δ (ζ) — дельта-функция. Заменим сумму экспонент в (9.66)
согласно (9.67). При интегрировании на интервале (— π, π) только
один член суммы дает результат, отличный от нуля. Используя
фильтрующее свойство дельта-функции, находим
1 L-1
ι ж-
ъ Σ Σ ττ ji^wn^wi2^. $щ
2Лз_
/=0*=0 _π
Подставляя в (9.68) выражение для спектра кодовой
последовательности (1.106) и производя интегрирование, окончательно
получаем
*=ΈϊΠβΙΣΣ,Σ Σ Σ 2 ***«*»'«»«»«". (9.69)
где символ
ίΐ при а — β = λ — ν,
η (9.70)
10 во всех остальных случаях. '
Меняя местами порядок суммирования, перепишем (9.69) в
следующем виде:
Ν_ Ν^ Ν [Ν vL-\ irL—l
' δαβλν. (9.71)
δαβλν = L
шу ΣΣΣΣΙΣ w» IIΣ a^akv
α = 1β=1 λ==1 ν=1 L / = o JL/5=o
В соответствии с условием ортогональности (9.18) сумма по /
равна нулю при α Φ β и равна L при α = β. Аналогично сумма по
k равна L только при λ = v. Таким образом
Ν Ν
2 Σ σ· (9·72)
2W3 £2
α=ΐ λ=1
Так как двойная сумма равна N2L29 то окончательно имеем
[37, 50]
σ2 = 1/2ЛЛ (9.73)
По поводу полученного результата заметим следующее.
Во-первых, σ2 (9.73), так же как и σ2 (9.60), не зависит от ρ и полностью
определяется длиной последовательности N. Во-вторых, дисперсия
апериодических КФ вдвое меньше дисперсии периодических КФ.
Докажем этот результат, используя в качестве исходного дисперсию
(9.60). Рассмотрим внутреннюю сумму по μ в (9.61) при η = 2 и
выразим ее через веса WJk (μ)
π *Σ *?*ω=·55τ *Σ ψ№· (9-74)
μ«-<#-1) μ=-(//-1)
При дальнейшем усреднении по / и по k квадраты модулей весов
WJk (μ) будут заменены их дисперсиями. Дисперсия веса W со-
197
гласно (9.31) и (9.60) равна N, т. е. длине последовательности. Если
длина последовательности равна η ^ Ν, то и дисперсия веса будет
равна п. Но при апериодических КФ число слагаемых, входящих
в ее определение, изменяется с изменением μ. При μ=0 оно равно
Ν, при μ = ± 1 оно равно N — 1 и т. д. При μ = ± (Ν — 1)
оно равно 1. Поэтому с учетом последующего усреднения по / и к
сумму (9.74) можно представить так:
±. J #/W)=^-^ + 2(JV-l) + 2(tf-2) + ... + 2] =
μ=—(Ν—\)
=M1+2+-+iN-2)+{N-l)+ihw- (9·75)
Подставляя (9.75) в (9.61) при η = 2, приходим к результату
(9.73).
Глава 10
ПОЛНЫЙ ДВОИЧНЫЙ КОД
10.1. Распределение корреляционных функций
Полный код с основанием манипуляции ρ = 2 назовем полным
двоичным кодом. Хотя он является частным случаем полного
произвольного кода с ρ > 2 и для него будут справедливы все
результаты гл. 9 (при ρ = 2), отдельное исследование такого кода
имеет большое значение по следующим причинам. Во-первых,
многие применяемые системы сигналов являются двоичными —они
позволяют широко использовать цифровую технику для
формирования и обработки. Во-вторых, для полного двоичного кода получены
некоторые дополнительные результаты, которые для ρ > 2
в настоящее время не получены.
Исследование некоторых свойств полного кода можно найти в
работах [37, 85, ПО, 111, 121, 138, 160, 205, 229]. Интересные
закономерности двоичных систем сигналов, близкие к свойствам полного
кода, отмечены в работах [141, 142].
Периодические корреляционные функции. Положим, что
двоичный алфавит является мультипликативной двоичной группой, т. е.
состоит из символов 1 и — 1. Поэтому символы α/ν кодовых
последовательностей равны 1 или— 1. Периодическая КФ, как было
отмечено в гл. 9, содержит постоянное число слагаемых в своей сумме.
Пусть оно равно N. Произведение a^ahVL при любых /, k, ν, μ равно
или 1, или — 1. Вес кодовой последовательности (9.30) в таком
случае равен разности между суммой 1 и суммой — 1.Пусть число 1 в
198
Q, так как всего сла-
(10.1)
N, то
сумме (9.30) равно Q, а число — 1 равно N
гаемых в (9.30) N. В результате вес
W = 2Q — N,
причем Q = 0, N. Если Q = 0, то W = — N, если Q
W = N. Шаг изменения веса равен 2. В соответствии с (9.31) КФ,
если она содержит N слагаемых, выражается следующим образом:
д = Г/Л/ = (2Q — ЛО/ЛЛ (10.2)
Число кодовых последовательностей, имеющих данный вес,
т. е. заданное число 1, находится как число сочетаний из N
элементов по Q и равно С%. Из (10.1) имеем равенство С$ = C%'*{N+W).
Общее число кодовых последовательностей согласно (8.2) равно 2N.
Вероятность появления кодовой последовательности с данным
весом, т. е. с заданным значением КФ, равна [ПО]
ρ (ψ) = C°/{N+W) 2~N. (10.3)
Распределение (10.3) является биномиальным. Следует
учитывать только, что вес изменяется с шагом, равным 2. Так как КФ и вес
связаны соотношением (10.2), то распределение (10.3) однозначно
определяет распределение КФ.
Апериодические корреляционные функции. Распределение
апериодических КФ можно найти, используя распределение (10.3).
Апериодические КФ содержат число слагаемых η = Ν — λ, где
λ — сдвиг. Заменяя N на η в C%MN+W\ находим число
появлений данного веса при произвольном периоде
κ (Wy n) = С™2, (10.4)
причем \W\ ^ п.
При η = N распределение весов (10.4) совпадает с (10.3).
Перейдем к следующему значению η = N— 1. При такой длине
объем полного кода равен 2Ν—1, но число последовательностей
остается равным 2Ν. Это приводит к тому, что каждая
последовательность повторяется дважды. В результате каждый вес при η =
= N — 1 встречается вдвое чаще, чем согласно формуле (10.4).
При η = N — 2 объем полученного полного кода равен 2Ν-2 =
= 2^/4 и в результате каждый вес встречается в 22 = 4 раза чаще,
чем согласно формуле (10.4). Например, при N = 4, ρ = 2
матрица п\ (9.11) имеет следующий вид:
п\ =
• · -У
1 ____ 1 1 1 1 _____ 1 1 1
1111 —1 —1 —1 —1
(10.5)
199
Здесь каждый столбец встречается один раз. Если отбросить
верхнюю или нижнюю строку, что эквивалентно η ■» N — 1, то в
оставшейся матрице каждый столбец встретится дважды. Если отбросить
две строки или сверху, или снизу, то в оставшейся матрице каждый
столбец встретится в четыре раза чаще по сравнению с
первоначальной матрицей и т. д.
Помимо увеличения числа появления данного веса, с
уменьшением η следует учитывать также, что при п<С Ν КФ имеет два
значения: одно при η = N — λ, а другое при η = — (Ν — λ).
Хотя конкретные значения могут быть различными, получаемые при
этом полные коды с L = 2^~λ одинаковы. В результате
необходимо удвоить число появлений заданного веса. Таким образом,
в общем случае, если \п\ = Ν — λ и λ^Ο, то величину (10.4)
необходимо умножить на 2λ · 2 = 2λ+*.
Далее поступим следующим образом. Умножим значения
£>(л+^)/2 (Ю.4) на соответствующий множитель 2λ+ι и
просуммируем те значения 2λ+1 C{n~*~W)/2> у которых вес W
одинаков. Поскольку, общее число слагаемых равно (2N — 1)2^, то,
разделив полученную сумму на этот нормирующий множитель,
получим вероятность появления данного веса W в апериодической
КФ. Для большей наглядности в табл. 10.1 приведены значения
соответствующих биномиальных коэффициентов и их множители.
После умножения каждого биномиального коэффициента на
соответствующий множитель суммирование необходимо производить
по столбцам, а полученные суммы разделить на (2N — 1) 2N.
Структура табл. 10.1 такова, что ее можно достаточно просто
построить и рассчитать. Например, в табл. 10.2 приведены результаты
для N = 8.
На рис. 10.1, а вертикальными линиями показано
распределение вероятностей Ρ (Ц7), приведенное в табл. 10.2 в последней
строке. На рис. 10.1, б вертикальными линиями представлено
распределение весов, близких к Ν9 в более крупном масштабе. Кривые
рис. 10.1, а и б изображают нормальный закон распределения
•<г>-&'-""■ (,α6)
с дисперсией οψ = Ν/2. Такая дисперсия веса кодовой
последовательности соответствует дисперсии апериодической КФ (9.73).
Из рис. 10.1 видно, что наибольшие отклонения распределения
вероятностей ρ (W) от нормального закона имеют место в центре и на
краях. Хотя такими отклонениями в некоторых случаях
пренебрегать нельзя, но в большинстве случаев можно считать
распределение весов нормальным с плотностью вероятности (10.6). Переходя
от весов к значениям КФ, получаем
w (Ry= уШе-"*\ (10,7)
200
~н
О
ι I
то
Cf
S
со
Η
Γ*
>
ι
•
—
ю
**
со
<N
о
τ
CN
1
со
1
"*
1
1
7"
I
1
1
,
Множн
тель
<< I
J
\ъъ
ко
o55
^
о
(
— —
ι ι
1
1
©55
О
CM
^H
•
* ι
I
I
ιΟιΟ
0
ч*ю
°
сою
О
•
ОЮ
О
■*■
I
^.
CM
*?
1
55; |
*·*
О
СОч*
О
(N^
о
гНч*
О
O^l
о
тЭЧК.
со
1
^
1СМ
t
1
^ 1
«со
о
ея«
О
ιΗΟΪ
©ее
CN
1
^.
см
с?
1
^ |
см см
о
г1СЯ
о
©ея
О
_«
1
^
см
°?
1
^ 1
—
;—i
—ι
1-11-1
О
—
—
* 1
см
^н
1
й:|
а 10.2
лиц
то
Η
00
г*.
со
Ю
СО
CS
о
τ
CN
I
со
I
I
ю
I
со
I
I
oo
1
-
^
00 00
00 CO
CM ~
00 00 CM
CM ^ 00
^ о «*
00 00 CO
со о oo oo
ю см см см
о о см со
tf со σ> ю
о о см со
t^ со o^ ю
~ ~ CM
о о см со
Tf со о^ ю
CO Q 00 00
ю см см см
Tf О ^F
00 00 CO
00 00 CM
см ^ со
00 CO
CM ~н
00 00
^
-
Результаты
расчета
~
со
^
^
00
о
00
CM
CM
CM
00
00
со
00
CM
00
00
CM
CM
00
о
^
^
со
*f
TO
2
2
0,0002
0,004 |0,001
©
ρ*
00
1 см
,o
°Ί
со
!°
©1
00
©Ί
со
° 1
00
О
со
о
° 1
00
CM
о
° 1
о
° 1
о
о
о
©Ί
Вероятность |0,0002
201
Формула (10.7) позволяет достаточно просто учитывать боковые
пики КФ при расчете характеристик СПИ со сложными сигналами.
Значения вероятностей Ρ (W) можно записать в аналитическом
виде, используя табл. 10.1. Например, для четного N вес W = 0
встречается
(ЛГ--2)/2
S„ = 2"
-2k+lckk
+сГ
(10.8)
P(w)
Ι
/
1
1
I
1
г
0,15
0,1
0,05
ΓΝ
\
\
\
Λ
\
\
N=
-8
-6
-Ϊ -2 0
a)
2 Ϊ
Рис. 10.1
6 W 5 6 7 W
δ)
раз, а для веса W = ± 1 имеем
Лг=1
(10.9)
Аналогично можно получить аналитические представления и для
других S.
10.2. Статистические характеристики
Дисперсия. Из материала гл. 9 и § 10.1 следует, что среднее
значение КФ равно нулю, а дисперсия σ2 = 1/2 N (9.73). Расчеты,
проведенные для различных систем сигналов, показали, что их
дисперсии близки к дисперсии полного кода.
В табл. 10.3 приведены данные для систем дискретных фазо-
манипулированных сигналов двух подклассов, которые будут
более подробно рассмотрены в дальнейшем: системы Уолша (У) и
производной системы (П). Число последовательностей равно числу
символов N и указано в первом столбце табл. 10.3. Например, для
системы У—16 N=16 и т. д. Производная система для определен-
202
ного N была получена из системы Уолша путем посимвольного
перемножения каждой последовательности на производящую
нелинейную последовательность [31, 32] с тем же N.
Таблица 10.3
Тип системы
сигналов
У—16
П-16
У—32
П—32
У—64
П—64
Предельное средне-
квадратическое
значение
0,177
0,177
0,125
0,125
0,0885
0,0885
Среднеквадратическое
значение системы
сигналов
0,173
0,171
0,128
0,123
0,0885
0,088
Коэффициент
эксцесса
системы сигналов
6,33
0,35
4,5
0,64
20
0,64
^макс
15
9
31
17
63
25
Во втором столбце табл. 10.3 приведено предельное
среднеквадратическое значение σ = l/]/"2iV, а в
третьем—среднеквадратическое значение реальных систем. Сравнивая результаты второго и
третьего столбцов, видим, что они близки.
Четвертый момент. Определим четвертый момент т4
апериодической КФ согласно (9.61), полагая я=4. Так как среднее значение
тг = 0, то т4 = М4 [104] и
м*=шу1 Σ ς' r*m- '<10Л°)
L /=0£=0μ^—(Ν— 1)
Используя ту же методику, что и для определения дисперсии
апериодической КФ в § 9.6, можно показать [37], что
М4 = (2Ν3 — 2Ν2 + Ν)/2Ν\ (10.11)
Определим^ коэффициент эксцесса как
γ = Μ4/σ4 —3. (10.12)
В соответствии с (9.73), (10.11) находим:
γ=1— 4/Λ^ + 2/Ν2. (10.13)
Предельное значение γ = 1 при N -+ <х>. Таким образом,
предельное значение коэффициента эксцесса полного кода больше
нуля. Положительное значение коэффициента эксцесса
свидетельствует о том, что исследуемая функция распределения должна быть
«обострена» в области малых значений R относительно нормального
закона (должна быть больше при малых R) и иметь большие
значения на краях (при R -> ± 1). Обращаясь к рис. 10.2, замечаем,
203
что характер распределения вероятностей ρ (W) соответствует
положительному значению коэффициента эксцесса γ. Таким образом,
можно считать, что характер распределения вероятностей при
различных N будет близок к
представленному на рис. 10.2.
Если ввести переменную χ =
= log2 N т. е., N = 2*, то
γ = 1 — 22~* + 21-2*. (10.14)
Зависимость (10.14) приведена
на рис. 10.2. Точками снизу вверх
отмечены значения у для N = 2,
3, 4, рассчитанные
непосредственно. Звездочками слева направо
отмечены значения γ для
производных систем П-16, П-32, П-64,
приведенные в четвертом столбце
табл. 10.3. Как видно из'рис. 10.2,
Рис. Ю.2 * коэффициент эксцесса
производных систем" близок к γ (10.14), но
все же меньше, что является, несомненно, достоинством таких
систем сигналов по сравнению с системами Уолша, у которых
V» 1.
10.3. Средняя спектральная плотность мощности полного кода
Определим среднюю спектральную плотность мощности полного
кода следующим образом:
ОМ = \Н(х)\*=±^Шх)\\ (10.15)
гд Я/ (х) — спектр кодовой последовательности, см., например,
(1.103). Используя (1.103), находим
°w=t Σ Σ 6'(μ~ν) Σ* "*"'·" (10Л6)
ν=1μ-1 /=0
Согласно свойству ортогональности (9.18) сумма по / равна L
только при ν == μ. Следовательно,
G^iVL^, (10.17)
т. е. средняя спектральная плотность мощности полного двоичного
кода не зависит от частоты. Отметим, что формула (10.17) соответст-
204
7
0,8
0,6
ОЛ
0,2
О
-0,2
-Ο,ϊ
-0,6
-0,8
— 1 П
S У
* Г
вует кодовым последовательностям. При переходе к спектрам
сигналов следует учитывать энергетический спектр одиночного импульса
\Ga (#)|2. При этом энергетический спектр сигнала будет равен
\Ga(x)\*G(x) = N\Gw(x)\2.
10.4. Произвольная система сигналов
Выберем из полного кода с N = const произвольным образом
L0 кодовых последовательностей. Такая система является
выборкой из полного кода. Пронумеруем все КФ и обозначим номер
каждой через / = 1, Lo. Каждая КФ имеет свою дисперсию of и
коэффициент эксцесса уг.
Обозначим выборочное среднее дисперсии системы L0 через σ§.
Оно равно
°1=
7τ2σ'· (10·18>
/-1
[Среднее по различным выборкам
L2
ш1{а1}=^-Ут1{а!1 (10.19)
Но т1 {of} = σ2 = 1/2Ν> поскольку по определению 1/2Ν —
дисперсия полного кода, усредненная по всем сочетаниям кодовых
последовательностей. Следовательно, т1 {σ§} = σ2, т. е. среднее по
различным выборкам совпадает с дисперсией полного кода.
Дисперсия выборочного среднего
L2
M,{a»=-VJ?M,<tf>. <10·20)
Можно доказать, что Ms {σ^} = М4 (10.10), так как тх = 0.
Поскольку М4 определен согласно (10.11), το Μ2 {σ/} ~ 1/А/2.
Из (10.20) имеем
М2 {of} ~ \IL\N*. (10.21)
Отношение среднеквадрэтического значения выборочного
среднего к его среднему значению равно
УЖЩ/Щ {σ0} = 2/L0. (10.22)
Таким образом, с увеличением Lq — числа сигналов в системе
разброс дисперсии системы σ% относительно своего среднего
значения, равного 1/2W, уменьшается. Следовательно, значение 1/2Ν
является предельным для всех систем сигналов.
205
Глава 11
ОПТИМАЛЬНОЕ ЧИСЛО БЛОКОВ И СИСТЕМЫ СИГНАЛОВ
11.1. Гипотеза об оптимальном числе блоков
Поиск и синтез одиночных сигналов и систем сигналов с
«хорошими» АКФ и ВКФ были начаты относительно давно и
продолжаются до настоящего времени (см., например, [15, 23, 25, 39, 55,
99, 119, 131, 136, 142, 146, 179, 183, 199, 207, 210]). Под «хорошими»
АКФ и ВКФ подразумеваются такие функции, экстремальные или
максимальные пики которых малы. Сигналы с такими АКФ и ВКФ
условно будем называть оптимальными. Среди оптимальных
сигналов содержатся и минимаксные [3, 162], у которых максимальные
пики минимальны.
Наибольшее количество сведений в настоящее время известно
о дискретных фазоманипулированных сигналах. Это объясняется
тем, что такие сигналы позволяют использовать наиболее простые
методы формирования и обработки, в особенности цифровые методы.
Сравнение различных оптимальных ФМ сигналов и систем сигналов
показало [30], что они обладают одним интересным свойством: число
блоков μ точно или приближенно равно
μ0~0,5(# + 1), (ИЛ)
где N — число элементов ФМ сигнала, а блок —
последовательность одинаковых элементов (см. § 8.5). Это свойство подтверждается
большим числом примеров как одиночных оптимальных ФМ*
сигналов, так и систем ФМ сигналов, рассматриваемых в данном
параграфе. Такое свойство позволяет высказать гипотезу: оптимальные
ФМ сигналы следует искать среди множества ФМ сигналов, кото-
рые удовлетворяют условию μ ~ μ0.
В свою очередь, высказанная гипотеза позволяет утверждать,
что число оптимальных сигналов при заданном N может быть
большим. Действительно, из общего числа различных ФМ сигналов,
равного 2Ν, можно найти много сигналов с μ ~ μ0. Кроме того, эта
гипотеза позволяет утверждать, что методы синтеза оптимальных
ФМ сигналов могут быть основаны на отборе из всех сигналов
наилучших с μ ~ μ0. Перейдем к доказательству необходимости
выполнения условия (11.1).
Связь между спектром фазоманипулированного сигнала и
числом блоков. На рис. 8.1 приведена комплексная огибающая ФМ
сигнала U (t) (действительная функция времени — видеосигнал).
Число импульсов (элементов) N, все импульсы имеют одинаковую
длительность Δ^, т. е. длительность сигнала Τ = ΝΔί. Амплитуды
импульсов равны ± 1, что соответствует значениям фазы ФМ сиг-
206
нала 0 или π. Моменты коммутации фазы (нули комплексной
огибающей ФМ сигнала)
tm = z(m)M, (11.2)
где ζ (т) — целочисленная функция аргумента т = О, μ.
Функция ζ (т) принимает выборочные значения от ζ (0) = 0 до ζ (μ) =
= N в зависимости от кодовой последовательности ФМ сигнала
Например, для сигнала рис. 8.1 N = 9, μ = 5, a z (m) принимает
значения 0, 2, 3, 6, 8, 9.
Спектр комплексной огибающей ФМ сигнала записывается в
следующем виде:
G(o)=J-
ιω
1+2*2 (-l)»'exp(-ic<„) + (-l)nexp(-icug
m = l
(Π
1.3)
поскольку спектр единичного скачка есть l/ίω. Вводя обозначение
ωΜ = χ (11.4)
и используя (11.2), из (11.3) получаем
G(x) = — [ΐ+2μ"Σ (— l)*expl—iz(m)x] + (— lV*exp(— \Nx)
(11.5)
Энергетический спектр согласно определению и формуле (11.5)
запишем так:
10{х)?=Ж>1Шх)1г, (Ц.6)
где
|<2μ (χ) |2 = 1 + {—l)*cosNx +
+ 2*2 (— l)mcosz(m)x+2 2 (— l)*+mcos[N—z(m)]x +
m*l m = l
+ 2*%*±\-l)^exp{-i[z(m)-z(k)]x} (11.7)
m = l k=l
— периодическая функция с периодом 2π, который соответствует
периоду по частоте, равному 2n/At согласно (11.4). Рассмотрим
некоторые особенности спектров ФМ сигналов.
Эффективная ширина спектра. В работе [47] было отмечено, что
с увеличением числа нулей происходит смещение спектра
комплексной огибающей ФМ сигнала в область более высоких частот.
Имеется в виду смещение той части спектра, в которой сосредоточена
основная часть энергии сигнала, поскольку принципиально спектр
ФМ сигнала тождественно не равен нулю (за исключением
множества точек с мерой нуль) на всей оси частот, Для определения смеще-
207
ния спектра можно использовать понятие эффективной ширины
спектра №Эфф (см., например, [3, 177]), которая определяется
соотношением
Win** Jj ω2|0(ω)|Μω / ξ |0(ω)|2Λο. (11.8)
.—οο / —οο
В случае ФМ сигналов интеграл в числителе расходится и
определение (11.8) не имеет смысла. Но учитывая, что основная часть
энергии ФМ сигнала сосредоточена между первыми нулями
(ω = ±2π/Δ/), то бесконечные пределы интеграла в числителе можно
заменить на ± 2π/Δ/. Переходя к переменной χ (11.4) и учитывая,
4to|G(*)|2 — четная функция, а интеграл в знаменателе (11.8)
равен 2πΝΑί, определим эффективную ширину спектра №μ9φψ
комплексной огибающей ФМ сигнала с μ блоками следующим
образом:
2π
01.9)
№μ Эфф =
1
nN (At)'
-$*2|0(*)|Μ*.
Подставляя (11.6) в (11.9), получаем
μ »φφ —
πΝ (At)2
2π
(11.10)
т. е. при таком определении №μ9ψφ пропорциональна интегралу
от периодической функции (11.7) за период 2π. После
интегрирования находим
W?
μ эфф
Ν (Δί)2
(2μ—1), а №μ,φφ
(11.11)
Следовательно, чем больше блоков имеет ФМ сигнал, тем больше
№μ9φφ. В табл. 11.1 приведены значения ψμ эфф для нескольких
ФМ сигналов,
существенно отличающихся друг от
друга по своей структуре.
В первой строке табл.
11.1 приведены данные
для прямоугольного
импульса длительностью Τ =
= NAt, имеющего всего
один блок (μ = 1). Чем
больше Ν9 тем меньше
№μ=ΐ3φφ. Этот пример
соответствует ФМ
сигналу, имеющему наимень-
шее число блоков. Во вто-
208
Вид ФМ сигнала
Прямоугольный
импульс
Меандр
Оптимальный
Идеальный
Τ
Число
блоков
μ
1
N
(Ν+\)/2
а бл и ца 11.1
Эффективная
ширина спектра
WH эфф
2IAtV~N
(VT/A/)x
χίΛ—i/sw
2/At
2/At
рой строке табл. 11.1 приведены данные для ФМ сигнала,
имеющего наибольшее число блоков μ = N. Этот ФМ сигнал
(меандр) представляет последовательность знакопеременных
импульсов. Для меандра lim ψμ Эфф= V~8/At, что является максимальным
значением ψμ Эфф. В третьей строке приведены данные для
оптимального ФМ сигнала,у которого μ = μ0 = (Ν + 1)/2. Для такого
сигнала №Дэфф в два раза меньше максимального. Таким образом,
эффективная ширина спектра оптимальных ФМ сигналов лежит
примерно на середине между значениями, соответствующими двум
крайним значениям для прямоугольного импульса и меандра. В
последней строке приведено значения эффективной ширины спектра
идеального (гипотетического) сигнала, состоящего из N импульсов,
энергетический спектр которого совпадает с энергетическим
спектром одиночного импульса длительностью At:
|G.(*)|» = tf|S(*)|», (И.12)
где энергетический спектр одиночного импульса
| s (х) |2 = [2 (Δ/)2/*2] (1 — cos x). (11.13)
Множитель N в правой части"(11.12) получен из условия равенства
энергий. Подставляя (11.12), (11.13) в (11.9), находим №и = 2/Δί,
что совпадает с эффективной шириной спектра оптимального ФМ
сигнала. Отметим, что АКФ идеального сигнала вообще не имеет
боковых пиков. Поэтому совпадение №μ3φφ для идеального и
оптимального сигналов имеет большое принципиальное значение и
является подтверждением высказанной ранее гипотезы о том, что у
оптимальных ФМ сигналов число блоков μ должно быть близко к μ0.
Квадратическое отклонение между энергетическими спектрами
идеального и оптимального сигналов. АКФ любого сигнала
полностью определяется его энергетическим спектром (1.23).
Энергетический спектр идеального (гипотетического) ФМ сигнала, АКФ
которого не имеет боковых пиков, определяется выражениями
(11.12), (11.13). Чем ближе энергетический спектр произвольного
ФМ сигнала к энергетическому спектру идеального сигнала, тем
меньше будет отличаться АКФ произвольного сигнала от АКФ
идеального сигнала (см., например, [25]). Сравнивая энергетические
спектры этих сигналов (11.6), (11.7), (11.12),(11.13), замечаем, что
они имеют общие множители 2 (Affix2 и периодические множители,
определяющие структуру сигналов. Поэтому в качестве критерия
приближения произвольного ФМ сигнала к идеальному можно
использовать квадратическое отклонение
2π
г-де δ (Ν, μ) - —ί— Γ Δ2 (χ) dx, (11.14)
A(x) = \QA*)\2-\Q»(x)\\ (Π.15)
IQH(*)I2 = W (1— cos*). (11.16)
209
Функция \QH(x)\2 (11.16) определена согласно (11.12), (11.13).
Подставляя в (11.15) правые части выражений (11.7), (11.16) и
выделяя постоянные составляющие, можем записать Δ (л;) в следующем
виде
АХ = А — В(х), (11.17)
где А — постоянная величина, равная
А = Ν — 2μ + 1, (11.18)
а В (χ) — периодическая функция, не содержащая постоянных хю.
ставляющих:
B(x) = Ncosx + ( — l)vcosNx + 2 2 cosz(m)x +
μ-1
+ 2 2 (— 1)μ+Λ cos [Ν—ζ (m)]x +
+ 2^^(-\Г+кехр{-1[г(т)-2(к)]х). (11.19)
m=»l *«1
m φ k
Подставляя последнее слагаемое в виде суммы косинусоид, имеем
μ-1
B(x) = Ncosx + (—l)»cosNx + 2 2 (—1)ШХ
m=l
μ-1
Xcosz(m)x + 2 2 (— W+mcoslN —z(m)]x +
+ 4^2 ^ (—l)1 cos [z(m) — z(m—l)]x. (11.20)
/=*1 m^H-1
Общее число гармоник в (11.20) равно
J = 2 μ + (μ — 1) (μ — 2)/2. (11.21)
Если μ > 1, το J ~ μ2/2. Представим (11.20) в следующем виде:
Ν
В(х)= 2 aqcosqx, (11.22)
где
*α« 2 6α;· (" -23)
/-ι
— амплитуда q-и гармоники, a bqj = ± 1. Знак определяется
фазой (0 или π) косинусоиды с частотой q из суммы (11.20). При
записи (11.20) в виде (11.22) выполняется условие
2 Λβ/· (11.24)
210
Подчеркнем, что некоторые aq могут быть тождественно равны
нулю в том случае, если в сумме (11.20) нет составляющих на
соответствующих частотах q.
Подставляя (11.22) в (11.17), а (11.17) в (11.14) и интегрируя,
получаем
δ(Λ^μ) = А2 + В, (11.25)
где
в= 4-2^· (1L26)
Величина А (11.18) зависит только от N и μ, а В — от структуры
сигнала (от вида функции г (т)). Поэтому найти значение В можно
только для конкретного сигнала. Однако, если предположить, что
сумма (11.23) образуется слагаемыми, знаки которых
равновероятны, то можно найти среднее значение В и, следовательно, δ (Ν,μ).
Будем считать, что bqj = 1 или —1 равновероятно. В этом случае
среднее значение тг {bQJ} = 0, а дисперсия М2 {bgj} =tl.
Поскольку по определению среднего значения
Γ(Ν9 μ) = щ {δ (Ν, μ)} = Л2 + mi {В}, (11.27)
а
mi {В} = {|ш1 {а\} = ± J М2 {ад} =||/,, (11.28)
<7=1 <7=1 <7=1
то подставляя (11.28) в (11.27) и используя (11.18), (11.21), (11.24),
находим, что
δ (W, μ) = (Ν - 2μ + Ι)2 + (μ - 1) (μ - 2) /4 + μ. [(11.29)
Обозначая
λ = μ/Ν9 α = Ι/Ν, φ (λ) = δ (Ν, μ)/Ν\ (11.30)
перепишем (11.29) в следующем виде:
φ (λ) = (1 — 2 λ + α)2 + (λ — α) (λ — 2 α)/4 + αλ. (11.31)
Если Ν ->■ οο , то величина α -^ 0. При этом
φ (λ) = (1 — 2 λ)2 + λ2/4 = (17/4) λ2 — 4λ + 1. (11.32)
Минимум функции (11.31) имеет место при значении
λ = λ0 = (1 + α)/2,125 + α/34. (11.33)
При больших N значение λ0->- 1/2,125 ~ 0,5. Такое λ0 согласно
(11.30) соответствует значению μ ~ Ν/2> что практически совпадает
с величиной μ0 (11.1). В окрестности минимума функция φ (λ)
меняется слабо. Это означает, что оптимальное значение μ не
обязательно должно точно совпадать с μ0. Отметим также, что точное
равенство μ = μ0 возможно, если А = 0.
211
Таким образом, если число блоков в ФМ сигнале близко к μ0
(11.1), то отличие энергетических спектров идеального и реального
сигналов будет наименьшим в статистическом смысле. Это означает,
что такие ФМ сигналы должны быть оптимальными.
В работе [30] рассмотрено большое число различных
оптимальных сигналов и показано, что все они удовлетворяют условиям
(11.1). К таким сигналам относятся сигналы Баркера, минимаксные
периодические последовательности (М-последовательности,
последовательности Лежандра и Якоби), минимаксные апериодические
последовательности с амплитудной манипуляцией и др. Примеры
указанных последовательностей можно найти в работах [3, 14, 15,
23, 25, 105, 136, 156, 162, 183]. Условию (11.1) удовлетворяют и
известные системы ФМ сигналов, обладающие хорошими
взаимокорреляционными функциями (ВКФ).
Известные системы ФМ сигналов (кодовых
последовательностей). Системы Уолша. Эти системы подробно будут рассмотрены
в гл. 12. Можно показать, что все кодовые последовательности
Уолша имеют различное число блоков, изменяющееся от 1 до Ν, т. е.
μ = 1, N. Как следствие этого, кодовые последовательности
Уолша имеют ВКФ с большими боковыми пиками. По этой причине
система Уолша непосредственно используется редко, но она служит
основной для построения производных систем с хорошими
корреляционными свойствами.
Производные системы. Они образуются умножением символов
кодовой последовательности системы Уолша на одну и ту же кодовую
последовательность (производящую) с хорошей АКФ. Впервые
такой метод был предложен в работе [135], где использовалась
следующая производящая кодовая последовательность 111 — 1 — 1
—1111 — 111 — 1 1 1 — 1 с N = 16 μ = 8, т. е. μ ~ μ0 =
= 8,5. В результате была получена производная система, кодовые
последовательности которой обладали АКФ и ВКФ с меньшими
боковыми пиками по сравнению с последовательностями Уолша. В
работе [30] приведены значения μ для последовательностей из [135].
Величина μ для различных последовательностей меняется мало.
Среднее значение μ = 8,5 и совпадает с μ0 (11.1), а среднеквадра-
тическое значение мало и равно σμ = 0,5. В работах [154, 183]
приведена производная система с иной производящей
последовательностью: 1 — 1 — 1 — 1 1 — 1 1 — 1 1 — 1 — 1 1 1 — 1 1 1 с N=16
и μ = 11. Соответствующие значения μ и их характеристики
приведены в [30] и равны μ = 8,5, σμ = 2,1. В этом случае значения μ
имеет большой разброс. В работе [30] приведены значения μ для
системы с производящей последовательностью вида 11 — 111
— 1 — 1 1 — 1 1 — 1 — 1 — 1 — 111 с N = 16 и _μ = 9,
которая нелинейна [25]. Для этой последовательности μ — 8,5
и σμ = 1,5, т. е. среднеквадратическоегзначение лежит посередине
между σμ для последовательностей в работах [135, 154, 183]. В [30]
приведены также значения μ для нелинейной производящей после-
212
довательности вида 11111 — 1 — 111 — 11 —1—11 — 1
— 1 — 1 — 1 — 11 — 11 — 1 1 1 1 — 1 1 1 — 1 — 1 —lc
N = 32 и μ = 16. Среднее значение μ = 16,5 совпадает с μ0
(11.1), а среднеквадратическое значение σμ = 2,5.
Таким образом, применение производящих
последовательностей с μ ~ μ0 дает систему последовательностей, у которых μ
также близко к μ0, в то время как у системы Уолша μ пробегает
все значения от 1 до N. Это и объясняет тот факт, что производные
системы работ [42, 135, 154, 183] имеют лучшие корреляционные
свойства, чем системы Уолша. Точно так же системы с нелинейными
роизводящими последовательностями лучше систем Уолша.
Данные табл. 10.3 подтверждают это. Как видно из таб,л. 10.3,
среднеквадратические значения ВКФ у обеих систем примерно
одинаковы, но коэффициент эксцесса существенно меньше у
производных систем. Поскольку при уменьшении коэффициента эксцесса
«хвосты» функции распределения боковых пиков ВКФ
уменьшаются^ уменьшаются и максимальные боковые пики (последний
столбец табл. 10.3).
Таким образом, приведенные характеристики систем сигналов
свидетельствуют о том, что лучшими (оптимальными) являются
системы, у которых число блоков всех кодовых последовательностей
примерно равно μ0 (11.1). Отметим также, что зависимость
корреляционных свойств сигналов от μ, когда μ близко к μ0, должна быть
слабой. Это особенно видно на примерах известных систем ФМ
сигналов [30]. Поэтому представляется возможным синтезировать
оптимальные ФМ сигналы, отбирая из случайных
последовательностей символов + 1 и —1 те, которые удовлетворяют критерию
близости μ κ μ0. Перейдем к примерам случайных сигналов.
Случайные ФМ сигналы. Для получения случайной
последовательности двоичных символов первоначально была использована
таблица десятичных случайных чисел [109]. Десятичные цифры
были разделены на две группы и цифры 0, 1, 2, 3, 4 в дальнейшем
заменялись ца 1, а цифры 5, 6, 7, 8, 9 — на — 1. Начало
последовательности бралось наугад и в десятичной записи имело вид
3276745035 ... [109 с. 306, 26 строка сверху]. Строки случайных
цифр записывались последовательно друг за другом. Была
составлена последовательность из 403 символов, которые были разбиты
на 13 последовательностей из 31 символов [30].
Среднее значение μ = 16,3 [30], а μ0 = 16. Разброс μ около μ0
невелик, среднеквадратическое значение σμ ~ 2,6. Наименьшие
значения ненормированного бокового пика АКФ VMSLKC = 6 и
соответствуют последовательностям с μ = 16; 17, т. е.
последовательностям, у которых μ или равно μ0, или близко к нему. Следующее
значение VMaKC = 7 соответствует последовательностям с μ =
= 14; 15, т. е. и для этих последовательностей μ близко к μ0. На
рис. 11.1 представлена общая картина распределения VMSiKC/N
в зависимости от λ = μ/Ν, где Ν = 31. Значения VMSlKC/N приведены
213
Ν
в [30] и на рисунке показаны кружками. Через наименьшие значения
VmslkJN для данных λ проведена штриховая линия, которая имеет
вид параболы с вершиной, близкой к λ ~ 0,5, т. е. при μ ~ μ0.
Если сравнить ход штриховой линии рис. 11.1 с функцией φ (λ)
(11.31), то можно заметить одинаковый
характер изменения этих функций
вблизи вершины. Таким образом,
действительно оптимальные
последовательности среди случайных необходимо
отбирать в первую очередь среди тех,
у которых μ ~ μ0. Однако условие
μ ~ μ0 является необходимым, но не
достаточным, так как есть
последовательности [30], у которых μ = μ0, но
^макс велико. Тем не менее отбор
последовательностей с μ = μ0 позволит
иметь большое число оптимальных
последовательностей и значительно сократить машинное время при
минимизации максимальных боковых пиков АКФ.
4*
0,1
\
\
о о
о
. °
1
о
Г /
/
/
0,2
0,4 0,6
Рис. 11.1
Рассмотрим пример системы
случайных ФМ сигналов [61],
состоящей из 10 сигналов с N = 63.
Сигналы выбраны так, чтобы
удовлетворялось неравенство для числа
блоков: μ0 — Δμ < μ < μ0 +
+ Δ μ, где μ0 = 32 в соответствии
с (11.1), а Δμ = 4. В результате
28 < μ < 36. Система из 10
случайных двоичных последовательностей
получена следующим образом. В
качестве источника случайных
двоичных последовательностей
использовался датчик случайных чисел
ЭВМ, вырабатывающий
последовательность 0 и 1 с равными
вероятностями появления. Далее в ЭВМ из
непрерывной двоичной
последовательности выбирались отрезки по
63 символа, вычислялось число
блоков каждого отрезка и отбирались
последовательности,
удовлетворяющие указанному ранее неравенству.
С помощью ЭВМ рассчитывались
АКФ и ВКФ десяти
последовательностей [61]. По результатам расчета
вычислялись законы распределения
ненормированных боковых пиков V
АКФ и ВКФ системы. Дисперсия
случайной величины У,
распределенной по нормальному закону (10.6),
равна Ν/2, т. е. в рассматриваемом
случае равна 31,5. Для случайной
системы, приведенной в [61], имеем:
дисперсия АКФ равна 29,2;
дисперсия ВКФ равна 29,6, т. е. отличие
от дисперсии нормального закона
мало. Коэффициенты эксцесса равны
соответственно 0,7 и 1, т. е. близки
к коэффициенту эксцесса полного
двоичного кода (10.13). Сравнение
дискретных распределений [61] с
нормальным законом распределения
показывает, что они в целом достаточно
близки. Отличия примерно такие
же, как и для распределения полного
кода (рис. 10.1, а). Следовательно,
рассмотренная случайная система
сигналов является «типичной» или
«средней» системой из полного
двоичного кода в том смысле, что она
обладает средними характеристиками
полного кода.
Рассмотренные в данном параграфе примеры и приведенное
доказательство достаточно наглядно характеризуют необходимость
поиска сигналов с μ ~ μ0. Перейдем к доказательству того, что
у сигналов с μ^μ0 вероятность появления экстремальных пиков
АКФ меньше, чем у других сигналов [42].
214
11.2. Вероятность экстремальных пиков и оптимальное число
блоков
Сформулировать задачу определения вероятности
экстремальных боковых пиков можно, рассмотрев процесс образования
произвольной КФ. Он заключается в следующем. При некотором сдвиге
КФ содержит η слагаемых, где 1 < η ^ N. Кодовые
последовательности, образующие КФ, содержат μχ и μ2 блоков. КФ,
имеющую η слагаемых, можно трактовать как некоторую кодовую
последовательность, имеющую μ блоков. При этом такая
последовательность имеет вес W = W (μ), являющийся функцией числа
блоков μ, а КФ имеет значение R = W (μ)/Ν = R (μ). Процесс
образования КФ иллюстрируется
диаграммой (рис. 11.2).
Каждый переход диаграммы
(рис. 11.2), за исключением
перехода W в R, неоднозначен. Как
будет показано в дальнейшем, при
v*W
н^7
W R Ρ(*\μνμζ)
Рис. 11.2
Рис. 11.3
заданных μχ и μ2 можно получить несколько различных значений μ.
Точно так же одно и то же μ может привести к различным весам W.
Поэтому каждый такой этап целесообразно с точки зрения
исследования характеризовать соответствующими вероятностями. В
итоге исследования всех узлов диаграммы (рис. 11.2) необходимо
получать условные вероятности появления того или иного значения КФ
при условии, что исходные кодовые последовательности имеют число
блоков, равное μχ и μ2 соответственно.
После того, как будут получены итоговые условные
вероятности, необходимо сравнить их с соответствующими вероятностями для
сигналов с произвольным числом блоков. На рис. 11.3 сплошной
линией изображена плотность вероятности для полного кода.
Если для последовательностей с числом блоков μχ и μ2, близким или
равным оптимальному μ0 (11.1), плотность вероятности
экстремальных (максимальных) значений (штриховая линия на рис. 11.3)
меньше плотности вероятности для полного кода, то из этого
следует, что вероятности экстремальных боковых пиков КФ будут
наименьшими при μ^μ0 (11.1).
Таким образом, вся задача в целом разбивается на три этапа:
1) определение вероятности образования последовательности с μ
блоками, если исходные содержали μχ и μ2 блоков; 2) определение
вероятности перехода μ блоков в вес кодовой последовательности
215
W\ 3) определение вероятности экстремальных значений и их
сравнение. Решение этой задачи приведено в [42]. Перейдем к
рассмотрению каждого этапа, начиная со второго.
11.3. Число блоков в кодовой последовательности и ее вес
|Границы веса. Пусть кодовая последовательность имеет N
символов и μ блоков. Символами являются 1 и —1. Все
последовательности с числом блоков μ можно разделить на две группы,
равные по численности. К первой отнесем последовательности,
которые начинаются с 1, т. е. с положительного блока. Назовем
последовательности этой группы прямыми. Ко второй группе отнесем
последовательности, которые начинаются с —1, т. е. с
отрицательного блока. Последовательности этой группы назовем обратными.
Будем сначала рассматривать только прямые последовательности.
Учесть обратные последовательности достаточно просто.
Введем ряд обозначений. Пусть Q+ — число символов 1 в кодовой
последовательности, a Q~ число символов — 1. В соответствии
с этим имеем следующие равенства для общего числа символов
и для веса кодовой последовательности:
N = Q+ + Q~, (11.34)
W = Q+ — Q-. (11.35)
Обозначим через μ+ число положительных блоков, через μ~ —
число отрицательных блоков, причем
μ = μ++ μ". (11.36)
Найдем границы для веса W, если кодовая
последовательность имеет μ блоков. Если имеется μ+ положительных блоков, то
число 1 должно быть или равно μ+, или быть больше μ+, τ. е.
должно выполняться неравенство μ+ ^ Q+. С другой стороны, если
последовательность имеет μ~ отрицательных блоков, то
минимальное число —1 равно μ~, а соответственнно максимальное число 1 не
может превышать разности Ν~— μ"", т. е. должно выполняться
неравенство Q+ < Ν — μ"". Объединяя оба неравенства, имеем
μ+<<3+< W —μ~. (11.37)
Из (11.34), (11.35) находим
Q+ = (ψ + N)/2, Q- = (Ν— W)I2. (11.38)
Подставляя значение Q+ (11.38) в неравенство (11.37) и
преобразуя, получаем
2μ+ _ N < W < Ν — 2μ". (11.39)
216
Между μ+ и μ~ имеется следующая взаимосвязь. Так как
положительные и отрицательные блоки чередуются, то при четном μ
в соответствии с (11.36) имеем
μ+ = μ~ = μ/2, (11.40)
а при нечетном μ и для прямых последовательностей μ+ = μ~" + 1,
μ+ = (μ+1)/2, μ- = (μ-1)/2. (11.41)
Подставляя значения (11.40) в (11.39), получаем для четных μ:
—(Ν — μ)< Ψ < Ν — μ. (11.42)
Подставляя (11.41) в (11.39), получаем для нечетных μ:
— (Ν — μ+1)<№<# — μ+1. (11.43)
Напомним, что вес кодовой последовательности W изменяется
с шагом, равным двум. Неравенства (11.42), (11.43) определяют
границы изменения веса, если последовательность имеет μ блоков.
Число кодовых последовательностей с заданным весом.
Обозначим число последовательностей с весом W и числом блоков μ
через L(W \ μ). Найдем это число с помощью следующих рассуждений.
Разбить кодовую последовательность на μ блоков при весе W
означает, что символы 1 числом Q+ разбиты на μ+ блоков, а символы—1
числом Q" разбиты на μ" блоков.
Естественно, что при разбиении последовательности должны
выполняться равенства (11.34), (11.35). Разбиение последовательности
на некоторое число блоков подробно рассмотрено в § 8.5. Число
таких разбиений определяется формулой (8.56). Так как разбиение
последовательности на μ блоков состоит в разбиении Q+ на μ+блоков
и в разбиении Q~ на μ~ блоков, то в соответствии с комбинаторным
правилом произведения и формулой (8.56) число прямых
последовательностей с заданными W и μ равно
Ln„(W№ = c£z\<%-Z\· (11-44)
Формула (11.44) справедлива только для прямых
последовательностей. Можно показать, что для обратных последовательностей
справедлива следующая формула:
LrtiWWt^CfzlCfczl (П.45)
Объединяя оба результата (11.44), (11.45) и заменяя Q+ и Q~
согласно (11.38), окончательно получаем искомое число
— W)/2 —1 +
— W)/2 —1 Cfo+V)/*-!. (11.46)
Для значения μ = 1 вес W =± N и L (N/1) = L (—Ν/1) = 1.
217
Число последовательностей L (μ) с числом блоков μ для
двоичных последовательностей определяется формулой (8.58). Очевидно,
что сумма по всем весам кодовых последовательностей
ΣΜ1Ημ) = Ι(μ)=26»=1. 01-47)
w
Относительная частота появления последовательности с весом
uf, если производится выбор из всех последовательностей с числом
блоков μ, равна отношению L{W\\x)IL (μ). Назовем это
отношение условной вероятностью появления веса W при данном μ и
обозначим
Ρ(^|μ) = L(W\^)/L (μ). (11.48)
Из (11.46) следует, что Ρ (— W | μ) ='Р (W | μ).Γ Поэтому
условное среднее равно нулю. Максимум распределения (11.48)
соответствует значению W=0 при четном N и W = ± 1 при нечетном N.
В табл. 11.2 приведены значения L (Ψ\μ) (11.46) для W^O,
поскольку L(W\\x) = L(—№|μ). Табл. 11.2 соответствует
N = 8. Суммы (11.47) даны в нижней строке с учетом значений
(11.46) для отрицательных весов (значения при W > О удваиваются).
При μ = 1 L (W\\) = 1. При Ν !Ξ> 1 распределения
вероятностей Ρ (W\ μ) можно аппроксимировать равномерными, полагая
Ρ (№\μ) = Ι/κ, где κ — число весов с заданным μ. Для N = 8 и
κ = 5 Ρ(№|μ) = 0,2. В работе [54] приведено распределение
вероятности Ρ (№|μ) для N = 16.
Таблица 11.2
W
0
2
4
6
8
Сумма
μ
1
1
2
2
2
2
2
2
14
3
8
8
8
1
42
4
18
16
10
70
5
18
16
10
70
6
18
12
42
7
6
4
14
8
2
2
Из неравенств (11.42), (11.43) и табл. 11.2 следует, что чем
больше μ, тем меньше область возможных значений веса кодовой
последовательности W, т. е. меньше уровень КФ R. Следовательно, чтобы
КФ обладала малыми боковыми пиками необходимо иметь ее
кодовую последовательность, которую назовем производной, с
максимально возможным числом блоков μ.
218
11.4. Число блоков в производной кодовой
последовательности и вероятность экстремальных пиков
Допустим, что исходные кодовые последовательности имеют
μχ и μ2 блоков. Определим вероятность появления μ блоков в
производной последовательности, которая получается при
перемножении исходных символов.
Рассмотрим сначала первую исходную последовательность. Она
имеет μχ блоков. Границы между блоками могут располагаться на
N — 1 позиции (столько «стыков» между N символами имеется в
сигнале). Число границ равно μχ— 1. Обозначим границы между
блоками через 1, а свободные позиции через 0. В таком случае
позиционная последовательность содержит μ1 — 1 символов I и N —
— μχ символов 0. В совокупности всех последовательностей с μχ
блоками символ 1 равновероятно может занимать любую N — 1
позицию. Поэтому вероятность появления символа 1 на некоторой
позиции в первой позиционной последовательности равна
Ριι = (μι-1)/(ΛΤ-1). (11.49)
Соответственно вероятность появления символа 0 равна
Рог = (Ν - μχ) / (Ν - 1). (11.50)
Для второй позиционной последовательности имеем вероятность
появления 1
Ρΐ2 = (μ2-№-1) (И.51)
и вероятность появления 0
Ρο2=(Ν-μ2)/(Ν-\). (11.52)
Производная позиционная последовательность является
результатом посимвольного сложения по mod 2 исходных позиционных
последовательностей. Например, если N = 5 и исходные
позиционные последовательности имеют вид 0 0 11 и 0 1 0 1, причем μχ =
= \*>г = 3, то производная позиционная последовательность
определяется так:
8 о? о J^002)· (п·53)
0 110
При этом производная последовательность имеет три блока, так как
μ — 1 = 2.
Из примера (11.53) следует, что символ 1 в производной
позиционной последовательности появляется, если или в первой
последовательности имеется 0, а во второй 1, или в первой имеется 1, а во
второй 0. Символ 0 в производной позиционной последовательности
будет тогда, когда в обеих последовательностях имеются или 0,
219
или 1. Следовательно, вероятность появления 1 в производной
позиционной последовательности равна
Pi = Р01Р12 + РпРо2> (11.54)
а вероятность появления 0 равна
Ро = ΡοιΡο2 + Р11Р12. (П-55)
Подставляя (11.49) — (11.52) в (11.54), (11.55), получаем
_jw—μι) 0*2—!) + (#—μ2)(μι— ΐ) /ц 56)
^ (лг-i)* ' к ' }
Ό = (Ν—μι) (W — μ2) + (μι— 0 (μ2— 0 /ц 57)
^° (W-1)2 ' \ · >
Если μχ = μ2, то
2(^)^-1) (^-μι). + (μι-ΐ).
^ (#—1)2 ^° (Л/-1)2 ν ;
Если производная кодовая последовательность имеет μ блоков,
то ее позиционная последовательность содержит μ — 1 символов 1.
Найдем вероятность того, что позиционная последовательность имеет
μ — 1 символов 1 и N — μ символов 0. Эта вероятность
определяется биномиальным законом (см., например, (3.5)):
Ρ(μ_1) = ^-1ρΓ'ρδ'-μ. (11-59)
В начале главы были отмечены интересные свойства сигналов
с числом блоков, близким к оптимальному значению (11.1). Поэтому
целесообразно рассмотреть случай, когда обе последовательности
имеют число блоков, близкое к (11.1). Для этого положим μχ = μ2.
Среднее значение μ и дисперсия биномиального закона (11.59)
равны 1104]:
μ _ 1 = (Ν - 1) plf σ* = (Ν - 1) Ριρ0. (11.60)
Подставляя в (11.60) значения вероятностей (11.58), получаем
μ2(]ν-μι)(μι-1)
r N—\ V
g2 2 (уу—μι)(μι—1)[(уу—μι)2+(μι—ι>η Π1
μ (Ν—1)3 ' \ · '
Рассмотрим сначала среднее значение (11.61). Можно показать,
что максимум μΜαΚ0 имеет место при
μχ = (Ν + 1)/2 (11.63)
и равен
μΜ&κο = (^+ 1)/2. (11.64)
220
То, что максимум μ имеет место при значении μχ (11.63),
совпадающим с (11.1), имеет принципиальное значение, которое будет
объяснено несколько позже.
Дисперсия (11.62), как показывает анализ, слабо
изменяется около значения μχ (11.63) и приближенно равна
σ* ~ (Ν — 1)/4. (11.65)
При большом N
биномиальный закон (11.59) достаточно
точно аппроксимируется
нормальным законом [104]. На
рис. 11.4 представлены два
нормальных закона с
различными средними значениями:
Ичиакс (сплошная линия) и μ <
<μΜαΚ0 (штриховая линия). Так
как дисперсия изменяется мало, то разница между графиками
(рис. 11.4) определяется в основном средними значениями. Из
графиков рис. 11.4 следует, что вероятность Ρ {μ > μ0} того, что μ
больше некоторого значения μ0, всегда больше для [Гмакс· Эт° м^к_
/о β /^макс
Рис. 11.4
рад
0,12
0,70
0,08
0,06
0,04
0,01
Ss/λ
^
* N
1 Л
1 £_
L-XT"
ч
δ
Lr-Z
12*
s N^O4^4
N=32
2
J
12 16
Рис. 11.5
20
24
28 RN
221
Симальное значение имеет-место тогда, когда число блоков в исходной
послеловательности оптимально (11.63). Как было отмечено в конце
§ 11.3, что чем больше μ, тем меньше область возможных значений
веса Wy тем меньше уровень КФ. Но выбор числа блоков μχ = μ2 =
= μ0 (11.1) обеспечивает наибольшую вероятность получения
максимальных значений μ, т. е. наибольшую вероятность малых КФ.
Поэтому вероятность экстремальных пиков минимальна.
Следовательно, число блоков μ0 (11.1), действительно, является
оптимальным.
На рис. 11.5 изображены функции распределения боковых пиков
Ρ (R/μ) при различном числе блоков μ для W=32 [54]*. По оси
абсцисс отложены значения ненормированных боковых пиков RN.
Чем ближе число блоков μ к оптимальному значению (11.1), тем
больше вероятность малых боковых пиков и меньше вероятность
больших боковых пиков. При числе блоков μ = 16, т. е. наиболее
близком к (11.1), вероятность максимальных боковых пиков минимальна.
Таким образом, расчеты [54] подтверждают, что оптимальные
сигналы должны иметь число блоков, близкое к (Ν + 1)/2.
* Графики на рис. 11.5 рассчитаны Г. Г. Моисеевой.
Раздел III
СИСТЕМЫ СИГНАЛОВ
Глава 12
СИСТЕМЫ ДИСКРЕТНЫХ СИГНАЛОВ
12.1. Системы Уолша
Среди различных систем дискретных сигналов наибольшее
распространение получили системы дискретных фазоманипулирован-
ных сигналов. У таких сигналов огибающая постоянна и это
позволяет излучать сигналы с максимальной энергией (при
ограниченной пиковой мощности). В данной главе рассмотрены системы
дискретных фазоманипулированных сигналов. Наибольшее внимание
уделено системам с двоичной фазовой манипуляцией, или просто
системам ФМ сигналов. В меньшей степени рассмотрены системы
с р>2, которые будем называть системами многофазных
сигналов. Среди систем ФМ сигналов многие образованы на базе систем
Уолша. Поэтому данный параграф посвящен их рассмотрению.
Матрицы Адамара и системы Уолша. Системам Уолша и их
применению посвящено большое число работ (см., например, [49, 108,
176,178, 192, 212]). Существуют различные и адекватные
определения систем Уолша. Для исследования систем Уолша с точки зрения
их корреляционных свойств целесообразно использовать матрицы
Адамара [103, 121].
Матрицы Адамара определяются следующим символическим
равенством:
#2# =
Ην Ην
Ην —Ην
(12.1)
где Ην — матрица Адамара порядка N (число строк равно числу
столбцов N), a Hzn — матрица Адамара порядка 2Ν. Полагая
#! = 1, из (12.1) получаем следующие матрицы порядка 2,4, 8:
Ш-
1 1
1 —1
(12.2)
Я4=
1 1
1 —1
1 1
1 —1
1 1
1
— 1
— 1
(12.3)
223
я« =
(12.4)
Используя (12.1), можно найти матрицы Адамара для любого
N = 2тх где т — целое число. Матрицы Адамара известны не только
порядка N = 2W, но и других значений N [103, 121]. В основном
известны матрицы Адамара порядка кратного 4. В [103] приведены
матрицы Адамара для N < 103 и кратных 4.
Матрицы Адамара удовлетворяют уравнению
НмНм
М,
(12.5)
где Ην — транспонированная матрица Адамара; I — единичная
матрица [121]. В (12.5) используется обычное произведение матриц.
Матрица порядка 2Ν может быть получена путем применения
прямого (или внешнего) произведения матриц [108]. Если Ην и
Нм—матрицы Адамара порядков^ и Λί, то прямое произведение
Нм®Нм=
/in Ял
Л19Ял
циМ ">12пМ ... Ιϊ\νΗμ
/г21Нм к21Нм ... Ιι>2νΗμ
h-N\ Ηм hN^HfA . .. h>NN Ht
Μ
(12.6)
где hjk — элементы матрицы Ην- Β (12.6) каждый элемент
умножается на все элементы матрицы Ям по правилу умножения матрицы
на скаляр. Порядок матрицы Ην ® Ям равен произведению ΝΜ.
Из (12.6) следует, что матрица
Η2ν = Я2 ® Ην-
(12.7)
Формула (12.7) соответствует символическому равенству (12.1)·
В качестве кодовых последовательностей системы Уолша можно
брать строки или столбцы матрицы Адамара. Число кодовых
последовательностей равно порядку матрицы N. Следовательно, объем
системы Уолша равен N. Обозначать системы Уолша будем
следующим образом: например, У-8, где цифра равна объему.
Обозначим /-ю кодовую последовательность Уолша как {№/},
а ее я-й символ через Wy (n). Уравнение (12.5) определяет
ортогональность кодовых последовательностей Уолша, т. е. выполняется
равенство
224
N^Wj(n)Wk(n)-
/ι=0
\N
при / φ k,
при j=k.
(12.8)
Мультипликативно-двоичное представление кодовых
последовательностей Уолша. Для символов последовательностей Уолша
используется следующее мультипликативно-двоичное представление
(см., например, [49]):
s
2
w=0
2 «/<->!>]
где
W,(/i)=(-l)
S = log2tf-l,
(12.9)
(12.10)
[χ] — целая часть χ, aj (m) — двоичное представление номера
последовательности /. В формуле (12.9) / = 0, N — 1, η = 0, N — 1.
Рассмотрим пример. Пусть N = 8 для матрицы Адамара (12.4).
В табл. 12.1 приведены формулы для определения показателя
степени Wj (ή) при / = const и сами последовательности.
/
0
1
2
3
4
5
6
7
т
0
0
1
0
1
0
1
0
1
1
0
0
1
1
0
0
1
1
2
0
0
0
0
1
1
1
1
Показатель степени
0
η
[я/2]
п+ [л/2]
[/г/4]
п+ [/г/4]
[/г/2] + [/г/4]
п+ [п/2] + [/г/4]
Таб
лица
12.1
η
0
1
1
— 1
1
—1
1
—1
1
—1
2
1
1
—1
—1
1
1
—1
— 1
3
1
—1
—1
1
1
—1
—1
1
4
1
1
1
1
—1
—1
—1
—1
5
1
—1
1
—1
—1
1
— 1
1
6
1
1
—1
—1
— 1
—1
1
1
7
1
—1
—1
1
~1
1
1
— 1
В первом столбце табл. 12.1 приведены номера
последовательностей / в десятичном счислении, а в трех последующих столбцах —
в двоичном счислении. Номера двоичных символов т расположены
в порядке возрастания разрядов слева направо так же, как в сумме
показателя степени в (12.9). В пятом столбце приведены формулы для
нахождения показателя степени, который равен сумме слагаемых
вида Ы12т]. Напомним определение целой части [д:]:если χ = q +
+ г, где q — целое число, 0 ^ г ^ 1, то [х] = q. Число слагаемых
в сумме равно числу единиц в двоичном представлении числа /.
Для / = 0 вся сумма равна 0, для / = 1 сумма равна первому
слагаемому [п/2°] = [п] = я, для / = 2 сумма равна второму
слагаемому [/г/21] = [п/2] и т, д. Вычисляя показатель степени для каждого
225
η и возводя —1 в получаемую, степень, получаем все символы
\V/ (я), которые приведены в последующих столбцах табл. 12.1,
Сравнивая полученные кодовые последовательности (строки
табл. 12.1, состоящие из 1 и —1) с кодовыми последовательностями
матрицы (12.4), замечаем, что они идентичны.
Групповые свойства. Система Уолша является группой [108,
212]. Доказательство следует из представления (12.9). Произве-
дение
Wj(n)Wk(n) = (-l)m=° . (12.11)
Сумма uj (т) + ak (т) = ах (/п), где {аг (т)} — некоторая
последовательность, принадлежащая тому же полному коду с N = const,
что и последовательности {а7- (т)} и {ak (m)}. Следовательно,
произведение W/ (п) Wft (η) = Wz (n)
является последовательностью
Уолша. Для примера в табл, 12.2
приведена таблица умножения
для системы Уолша У-8.
В табл. 12.2 / и k — номера
последовательностей Уолша,
упорядоченных в соответствии с табл.
12.1. Произведение двух
последовательностей Уолша дает новую
последовательность Уолша.
Например, если / = 6, k = 5, то в
результате умножения получается
последовательность с номером 3. Из
табл. 12.2 следует, что
нейтральным элементом является
последовательность с номером / = 0,
состоящая из одних единиц, а обрат*
ными элементами являются сами
элементы.
Так как система Уолша
является подклассом полного
двоичного кода с объемом L = 2N и в то же время она является группой,
то она есть подгруппа полного кода. В результате полный
двоичный код может быть разложен по системе Уолша в соответствии
с (9.6). Например, пусть N = 4. Полный код имеет объем 24 = 16.
Пронумеруем все последовательности полного кода номерами от 0
до 15. Последовательности Уолша имеют номера 0, 3, 5, 6. Одно из
возможных разложений полного кода имеет следующий вид:
0 3 5 6
12 4 7
15 12 10 9
14 13 J1 8, (12.12)
226
/
0
1
2
3
4
5
6
7 |
Ί
"аб
лица
12.2
1 *
0
0
1
2
3
4
5
6
7
1
1
0
3
2
5
4
7
6
2
2
3
0
1
6
7
4
5
3
3
2
1
0
7
6
5
4
4
4
5
6
7
0
1
2 |
3
5
5
4
7
6
1
0
3
2
6
6
7
4
5
2
3
0
1
7
7
6
5
4
3
2
1
0
На
J
О
ρ-
3 '6
U 2
\LRTbi67
Й (15.12) верхняя строки представляет собой систему УолШД*
а остальные строки — смежные классы. В соответствии с
классификацией систем сигналов каждая строка — подкласс полного кода.
Выбор образующих определяет свойства подкласса. Более
подробно этот вопрос будет рассмотрен в следующем параграфе. Число
смежных классов, включая систему Уолша, равно 2N/N. Так как
Ν=2η, где η — целое число, то число смежных классов равно 2Ν-η.
Число блоков. На рис. 12.1 приведены кодовые
последовательности У-8, упорядоченные по числу блоков μ, a μ = 1, N.
рис. 12.1 справа указаны число блоков μ
и номер последовательности / в
соответствии с табл. 12.1. Для системы Уолша
Характерно то, что число блоков в после*·
довательностях изменяется от 1 до iV.
В соответствии с результатами гл. 11
система Уолша должна обладать плохими
корреляционными свойствами, так как у
большинства последовательностей число
блоков далеко от оптимального (11.1).
Это подтверждается тем, что большинство
АКФ и ВКФ последовательностей Уолша
имеют большие боковые пики (см.,
например, табл. 10.3). Более подробно этот
вопрос будет рассмотрен в следующем
параграфе.
Спектральные свойства. Известно [47],
что спектры сигналов Уолша сдвинуты
относительно друга друга по частоте. Сдвиг
можно характеризовать как положением
максимума спектральной плотности мощности, так и эффективной
шириной спектра (11.8). Качественно оба метода дают один и тот
же результат. Графики спектров сигналов Уолша приведены в
работе [47]. Формула (11.11) определяет эффективную ширину
спектров через число блоков μ. Чем больше μ, тем больше сдвиг
спектра.
Если обратиться к спектру кодовой последовательности (1.98),
то можно показать, что спектр кодовой последовательности с μ = 1
имеет максимум при χ = 0, а спектр кодовой последовательности
с μ = N имеет максимум при χ = π. Оба эти максимума равны N.
Соответственно, максимум спектральной плотности мощности
равен Ν2. У остальных последовательностей максимумы спектров
лежат между значениями χ = 0 и χ = π.
При исследовании спектральных свойств системы Уолша
целесообразно использовать двоичное (или диадное) упорядочение
кодовых последовательностей [108]. Это показано в табл. 12.3.
В первом столбце табл. 12.3 дан номер последовательности k
в десятичной системе счисления, а в трех последующих — в двоич-
227
ПДЩЪе"
Рис. 12.1
ной системе. Кодовые noc^eAOBatetfbHocTH {bk(n)} содержат Младший
разряд справа, а число символов в них равно log2 N. В пятом
столбце указано число блоков μ, а в шестом—номер /-строки матрицы Ада-
мара, приведенной в табл. 12.1. Используя последовательности
{bh(n)}y можно представить спектр кодовой последовательности
Нк (х) (1.98) в следующем виде*:
ffk(x)=U [l+(—l)6fe(n)exp( —12-л:)]
(12.13)
л=0
где S определено (12.10). Подставляя последовательности {bk (ή)}
кодовых последовательностей
Уолша; число блоков в та-
в (12.13), можно найти спектры
Таблица 12.3
ких последовательностях
приведено в пятом столбце
табл. 12.3.
Сигналы Уолша рис. 12.1
имеют много общего с
тригонометрическими функциями.
Особенно это видно при
сравнении положений нулей
спектров сигналов Уолша и
нулей спектров
тригонометрических функций. Общность
между ними подчеркивалась
неоднократно [47, 49, 108,
178]. В отличие от
тригонометрических функций,
сигналы Уолша позволяют широко
и просто использовать цифровую технику при формировании и
обработке, что делает их весьма перспективными. Возможен даже
полный перевод всех каскадов радиотехнических систем, включая
мощные каскады передатчиков, на работу в дискретном режиме,
вплоть до излучения сигналов Уолша [178].
Как было отмечено ранее, корреляционные свойства систем
Уолша нельзя признать удовлетворительным. Но на базе систем
Уолша можно строить производные системы сигналов, которые
обладают хорошими корреляционными свойствами. Перейдем к
рассмотрению производных систем.
k
0
1
2
3
4
5
6
7
bk(n)
0
0
0
0
0
1
1
1
1
η
1
0
0
1
1
0
0
1
1
2
0
1
0
1
0
1
0
1
μ
1
2
4
3
8
7
5
6
/
0
4
2
6
1
5
3
7
12.2. Производные системы сигналов
Производным сигналом называется сигнал, который получается
в результате перемножения двух сигналов. В случае дискретных
сигналов перемножение должно осуществляться поэлементно или,
* Формула (12.13) была выведена Г. О. Биревой.
228
как чаще называют, посимвольно. Система, составленная из про*
изводных сигналов, называется производной.
Среди производных систем особое значение имеют системы,
построенные следующим образом. В качестве основы используется
некоторая система сигналов, корреляционные свойства которой не
вполне удовлетворяют требованиям к КФ,но которая обладает
определенными преимуществами с точки зрения простоты формирования
и обработки. Такую систему будем называть исходной. Затем
выбирается сигнал, который обладает определенными свойствами.
Такой сигнал будем называть производящим. Умножая производящий
сигнал на каждый сигнал исходной системы, получаем
производную систему. Производящий сигнал следует выбирать так, чтобы
производная система была действительно лучше исходной, т. е.
чтобы она обладала хорошими корреляционными свойствами.
Эмпирически такой метод был предложен в [96, 135]. В работе
[135] используется система Уолша (код Рида—Мюллера), каждый
сигнал которой умножается на один и тот же заранее выбранный
производящий сигнал. В результате получена новая система
сигналов, у которой боковые пики ВКФ в среднем меньше, чем у
исходной системы. В [135]' построена только одна система, а
относительно производящего сигнала отмечено, что его
автокорреляционная функция (АКФ) должна иметь относительно малые боковые
пики. В [96] для построения системы сигналов используется
длинная Λί-последовательность, из которой вырезаются
неперекрывающиеся сигналы (сегменты) меньшей длины. Какой должна быть
длина сегмента в [96] не указано. Несмотря на кажущееся сильное
различие между приведенными методами, они основаны на одном общем
интегральном свойстве ВКФ. Для начального подтверждения этого
факта отметим, что вырезание сегмента из М-последовательности
означает умножение ее на производящий сигнал в виде
прямоугольного импульса с длительностью, равной длине сегмента.
Теоретическое обоснование такого метода было дано в работах
[32, 48], а сравнение исходных и производных систем — в [30, 31].
Перейдем к исследованию производных систем сигналов.
Корреляционные функции производных сигналов. Комплексная
огибающая производного сигнала Sm (0 равна произведению
комплексных огибающих исходного сигнала Um (t) и производящего
сигнала 1/μ (/), т. е.
Sft (f)= Um (0 νμ (ή. (12.14)
ВФН сигналов S& (t) и Sn (t) по определению, согласно (1.18),
(1.20) равна
оо
^(τ'Ω)=-2ΐ7 J S»(QSZ(t-T)exp{iQf)dt=
— оо
оо
= тЩ- J Um(QUn(t-x)Vv(i)Vv(t-x)exp(mdt. (12.15)
— ОО
229
Здесь Es —энергия производных сигналов (12.14):
00
Es = y J \S»m(t)\*di. (12.16)
— оо
Полагаем, что Es одинакова для всех сигналов (12.14). Вводя в
(12.15) дельта-функцию*
оо
δ(/)=— Γ exp(itx)dx, (12.17)
— оо
получаем
оо
QZ (τ> Ω>= "W JJ u* W U» С ~τ)exP W ^ &) ^ (ίι-τ) χ
— оо
оо
χ δ ft—О Л#! =-^ (Τ £/m (0 &n (/—τ) exp (—utf) at χ
— оо
оо
X f Γμ ft) Vv ft—τ) exp [i (x+Ω) tt] dtx dx. (12.18)
— oo
ВФН сигналов — сомножителей правой части (12.14) — равны:
00
/?гоп(т,Й)=У- j t/m(0£u*—r)exp(iifc)#, (12.19)
— оо
оо
/?μν(τ,Ω)=1^· Γ V№(OVv(/—τ)βχρ(ίΩί)Λ, (12.20)
— оо
где £а> £V — энергии сигналов Um {t) и νβ (t), определяемые
соотношениями, аналогичными (12.16). Используя (12.19), (12.20),
из (12.18), находим
F Ε °°
Qiw(T>Q)=_^Jl j /?mn(T,-jf)l?№V(T,* + Q)dx. (12.21)
Еп Εν
— оо
Положим Ω = 0. Тогда ВКФ
ЕГ7Е
QZ W = -^- J Rmn (τ, -χ) Λμν (τ, x) dx. (12.22)
* Данный метод впервые предложен Б. А. Фогельсоном.
230
Если μ = ν, то, обозначая АКФ /?μμ = Rv, из (12.22) получаем
— σο
Если т = я, то, обозначая АКФ Rmm = #£/> получаем
Qmn W - -^^- J Rmn (τ, -*) /?v (τ, χ) dx. (12.23)
Q(r)= "у Γ /?ί/(τ,-^)^(τ,^)^. (12.24)
π£5 J
Соотношения (12.22) — (12.24) позволяют определять оценки
ВКФ и АКФ производных сигналов. Отметим, что в (12.22) —
(12.24) интегрировать необходимо на интервале (обозначим его
ширину через Ф), где подынтегральные выражения отличны от нуля.
Используя неравенство Буняковского — Шварца, из (12.22) —
(12.24) получаем
π^5 |/ Φ Φ
Qm^)<-~- \/\\Rmn^-x)?dx\ \Rv(x,x)\*dx\ (12.26)
ntS ψ Φ Φ
Q (τ) < -^- -l/S | Ru (τ, -*)|2 d* $ | Rv (τ, *)|2 dx. (12.27)
nEs f φ φ
Оценки (12.25) — (12.27) во многом зависят от соотношения
ширины ВКФ исходных и производящих сигналов вдоль оси допле-
ровских частот, т. е. от значения Ф. Широкополосный производящий
сигнал соответствует получению производной системы сигналов из
системы Уолша, а узкополосный производящий сигнал — системе,
состоящей из сегментов Λί-последовательности. В данном параграфе
рассмотрен случай широкополосного производящего сигнала, а
случай узкополосного производящего сигнала — в следующем
параграфе.
Широкополосный производящий сигнал. Пусть исходные и
производящие сигналы имеют одинаковую длительность Τ и = Ту=Т
и различные по ширине спектры. Обозначим ширину спектра
исходных сигналов через Fu, а производящих сигналов — через Fv,
причем положим, что Fv > Fu- Пусть все сигналы имеют
прямоугольные огибающие, а | V\ = 1. Тогда EuEv/Es —Т/2.
Допустим, что ВФН исходных и производящих сигналов
равномерно распределены на плоскости (τ,Ω).Тогда среднеквадратические
значения ВФН согласно (1.33) равны
oRmn = l/2VFu Τ, σο = 1/2 VFV Т. (12.28)
231
Так как Fv > /4/, то ширина ВФН исходных сигналов по оси Ω
меньше ширины ВФН ^производящих сигналов и поэтому Φ =
= 4 nFu. Заменяя в (12.25) | Rmn (τ, — χ) | и | #μν (τ, χ) | их средне-
квадратическими значениями, получаем
QSL (τ) < σ* ^_L = — 1 ίFJL . (12.29)
Из неравенства (12.29) следует, что значения ВКФ производных
сигналов при произвольном аргументе τ меньше или равны 0,5 χ
X yFu/Fv- Это означает, что и максимальные пики ВКФ будут
меньше этого значения. Следовательно, для уменьшения максимальных
пиков ВКФ необходимо увеличивать ширину спектра производящего
сигнала. Такой результат является следствием предположения о
равномерном распределении боковых пиков ВФН производящих
сигналов на плоскости (τ, Ω) в пределах полосы частот ± Fy. Из (12.29)
следует, что метод перемножения сигналов приводит к уменьшению
боковых пиков ВКФ производных сигналов, если только база
производящих сигналов FyT больше базы исходных сигналов
настолько, что VFvT> FuT.
Это объясняет результат работы [135], где в качестве исходных
сигналов использовались сигналы Уолша с шириной спектра Fu ^
~ \1Т и длительностью импульсов TINу N—число импульсов в
сигнале (в [135] N = 16). Производящий сигнал выбирался по АКФ.
Потвидимому, ФН выбранного производящего сигнала в работе
[135] обладала малыми боковыми пиками, также как и его АКФ.
Уменьшение максимальных пиков ВКФ. Соотношения (12.22) —
(12.27) позволяют обосновать метод уменьшения максимальных
пиков ВКФ. Допустим, что ВФН исходных сигналов занимают
полосу Ф, ширина которой по оси частот мала. Так, например, если
исходные сигналы близки к простым (FuT ~ 1), то Φ с*. 4 π/Τ.
Можно допустить, что вне этой полосы ВФН исходных сигналов
стремятся к нулю. В этом случае из неравенства (12.25) — (12.27)
следует, что необходимо как можно сильнее уменьшать значения
ФН производящего сигнала в той полосе, где сосредоточены ВФН
исходных сигналов. Если в соответствии с (12.29) для получения
Qmi <S 1 имеет место неравенство
Fv » F^ (12.30)
то полоса частот шириной Φ = 4 nFu будет узкой по сравнению
с шириной ФН производящего сигнала по оси частот. Причем эта
полоса Φ является центральной временной полосой [29]. Поскольку
в узкой центральной временной полосе боковые пики близки к
боковым пикам вдоль оси времени τ при Ω = 0, то в качестве
производящего сигнала следует выбирать такой, у которого АКФ имеет
минимальные боковые пики. Естественно, что при этом должно
выполняться условие (12.30).
?32
Таким образом, чтобы правые части неравенств (12.25) —
(12.27) были уменьшены, необходимыми и достаточными условиями
являются выполнение неравенства (12.30) и малость боковых пиков
АКФ производящих сигналов. Левые части неравенств (12.25) —
(12.27) представляют мгновенные значения ВКФ и АКФ при
различных τ, причем эти неравенства дают верхнюю оценку указанных
функций. Изменяя τ, можно пройти все боковые пики, в том числе
и максимальные. Поэтому (12.25) — (12.27) включают оценки и
максимальных боковых пиков. Следовательно, уменьшение правых
частей неравенств (12.25) — (12.27) приведет к уменьшению
максимальных боковых пиков ВКФ.
N46, μ=9
τ t
а)
N=32, μ=16
шиш
Τ t
δ)
Α/=54,/ί=32
шшшшш
шин шиш hi
\T t
6)
Рис. 12.2
Выбор производящих сигналов. Из предыдущего материала
следует, что выбор производящих сигналов определяется рядом
факторов, в том числе и исходной системой. Если сигналы исходной
системы широкополосные, то производящий сигнал может быть
широкополосным и иметь малые уровни боковых пиков ФН, близкие
к среднеквадратическому значению (12.28). Если же сигналы
исходной системы узкополосные, то достаточно выполнения
неравенства (12.30) и требования малости боковых пиков АКФ.
Возьмем в качестве исходной систему Уолша. В этом случае
производящие сигналы должны быть широкополосными (12.30) и иметь
хорошие АКФ. Кроме того, производящий сигнал должен иметь
столько же элементов, что и исходные сигналы, т. е. число элементов
N = 2ky где k — целое число. Этим условиям в целом удовлетворяют
нелинейные последовательности [25]. Поскольку основным· является
требование малости боковых пиков АКФ, то в классе нелинейных
последовательностей были отобраны наилучшие сигналы с числом
элементов N=16, 32, 64. Эти сигналы показаны на рис. 12.2. На
рис. 12.2 указаны также значения числа блоков μ для каждого про-
233
изводящего сигнала. Они .близки к оптимальному значению μ0 =2
= (Ν + 1)/2 (11.1). Это и является необходимым условием
получения хорошей АКФ с малыми боковыми пиками.
Свойства производной системы. Объем производной системы равен
объему системы Уолша N. С помощью ЭВМ были рассчитаны все
КФ большого числа производных сигналов. Оказалось, что системы,
производящие сигналы которых изображены на рис. 12.2, являются
типичными. Статистические характеристики таких производных
систем (П)были приведены в табл. 10.3, причем там же для сравнения
даны характеристики систем Уолша (У).
Ρ(ν),
0,3
0,2
Р,1
о*
L
1
bju
1
1
N.
Lfa
ι Ю"
7
О
_ 0
i
\
| '
I
N
ν
'—
N=16
||
4 6 8 ю и т ν
Рис. 12.3
Из табл. 10.3 следует, что среднеквадратические значения КФ
обеих систем близки к значению \lY2N (9.73), а коэффициенты
эксцесса различаются значительно. Для производных систем
коэффициент эксцесса гораздо меньше коэффициента эксцесса систем
Уолша. Оценим увеличение вероятности ошибки из-за наличия
коэффициента эксцесса. Их формул (4.86), (4.91) следует, что увеличение
вероятности ошибки приближенно пропорционально множцтелю
а = 1 + γ/24 ^ι3σ4. Полагая σ2 = 1/2JV, а число η =*Υ*Ν, получаем
а = 1 + у УМ6. При N = 64 для системы Уолша а ~ 27, а для
производной системы а ~ 2. Следовательно, вероятность ошибки
при использовании системы Уолша будет на порядок выше, чем
в случае производной системы.
Большое значение коэффициента эксцесса систем Уолша
объясняется наличием больших боковых пиков КФ. Для таких систем
ненормированное значение максимального пика VM8LKC = N — 1»
а нормированное RM&KC = 1 — VN. Значения УМакс приведеньп
234
в пятом столбце табл. 10.3. Отметим, что для производных систем
максимальный пик близок к утроенному среднеквадратическому
значению. Имеем
7макс - 3 Vm, Ямакс ^ 3/К2ЛГ. (12.31)
Для N = 16 Умакс ^ 9, для N=32 7макс ~ 12, а для N = 64
VMaKC = 17. Данные пятого столбца табл. 10.3 близки к этим
значениям.
На рис. 12.3 вертикальными линиями представлен закон
распределения Ρ (V) ненормированных значений КФ V для N = 16,
кривые характеризуют нормальный закон распределения w (V)
(10.6) с заменой W на V. Сплошные вертикальные линии
соответствуют системе Уолша, а штриховые — производной системе.
Краевые участки функций распределения изображены более крупно,
чтобы подчеркнуть существенное различие между законами
распределения систем Уолша и производных систем,
Из данного параграфа следует, что производные системы обла-
дают лучшими корреляционными свойствами, чем системы Уолша.
12.3. Сегментные системы
Сегментными назовем системы, образованные из Сегментов
(отрезков) Λί-последовательностей. Сегментная система является
производной, так как выделение сегмента из М-последовательности
эквивалентно применению узкополосного производящего сигнала —
простого сигнала с прямоугольной огибающей, длительность
которого равна длительности сегмента.v
Одной из первых работ, в которой указывалось применение
сегментных систем, была [96]. Λί-последовательность, с числом символов
W=217—1 = 131071, разбивалась на неперекрывающиеся сегменты
с длиной N0 = 63 символам. Было получено 2080 сегментов, из
которых с помощью ЭВМ было отобрано L=1000 сегментов, ВКФ
которых не превышали 0,25. Однако в работе [96] нет методики
определения чисел N, N0, LQ и не установлена их взаимосвязь с ВКФ.
Подчеркнем, что с ростом Ν, Ν0κ L выбор хороших сегментов может
оказаться неразрешимой задачей даже для современных ЭВМ. По
этой причине перешли к аналитическому изучению сегментов Λί-
последовательностей. Работы [200, 215, 225] посвящены нахождению
моментов распределения сумм символов в сегментах ш*и весов.
Результаты этих работ показывают, что функции распределения весов
могут быть сильно асимметричны и иметь большие «хвосты», что
приведет к увеличению боковых пиков ВКФ. Однако методика
определения N9 N0y L также не была найдена.
В работе [32] на основе общих свойств производных сигналов
были определены некоторые соотношения для N, N0, L длинных
сегментов (N0>V~N). Отметим также работы [146, 148], в которых
приведены результаты многочисленных расчетов на ЭВМ»
835
Данный параграф является развитием работы [32] и посвящен
исследованию и объяснению корреляционных свойств сегментов,
определению оценок ВКФ сегментов различного вида (как
неперекрывающихся, так и перекрывающихся), определению зависимостей
между N9 N0, L. Основные полученные результаты были
подтверждены с помощью расчетов на ЭВМ и приведены в работе [48].
Основные соотношения. Обозначим комплексную огибающую
исходного сигнала как U (t), а огибающую производящего сигнала
как V (t). Допустим, что
| U (0 | = 1 при 0 < t < Г, (12.32)
V (t) = 1 при 0 < t < Т09 (12.33)
а вне указанных отрезков | U (t) | = 0 и V (t) = 0. Кроме того,
допустим, что длительность производящего сигнала Т0 меньше
длительности исходного сигнала Т, т. е. Т0<Т. Назовем р-м
сегментом производный сигнал вида
sp (o= u(t + у v(t), (12.34)
причем в соответствии с (12.33) Sp(t) расположен на отрезке [0, Т0]
и вырезается из исходного сигнала на отрезке [tp, tp + Т0].
Последовательность сегментов {Sp}y ρ = 1, L, образует систему
сигналов.
ВФН сегментов Sp (t) и Sq (t) согласно (1.18), (1.20)
записывается в следующем виде:
оо
Qpq{x,Q)=-±- j Sp(t)Sq(t-x)txp(itlt)dt, (12.35)
— ОО
где Es — энергия сегментов, а * — знак комплексной
сопряженности. Подставляя в (12.35) выражение (12.34) и используя метод,
рассмотренный в предыдущем параграфе (введение дельта-функции),
получаем:
QPq (τ, Ω) =
оо
= Ρ f Ru (τ + tP — tqy x) exp (—ixtp) Rv (τ, — χ + Ω) dx,
(12.36)
где ФН исходного и производящего сигнала
оо
Ru(x,Q) = —— Г U(t)U(t—τ) exp(iΩ/)Λ, (12.37)
2£у J
— ОО
оо
Λν(τ,Ω) = —— Г V (t)V(t—τ)exp(iQ<)Л, (12.38)
2EV J
— оо
ρ = Eu£v/nEs, (12.39)
236
a Ευ, Εν — энергии этих сигналов. Полагая Ω = 0, из формулы
(12.36) получаем ВКФ:
оо
QPq (τ) = Ρ j Ru (τ + tp— tv x) exp (—ixtp) Rv (τ, — χ) dx.
(12.40)
Отметим особенности полученного выражения. Значение ВКФ
при заданном τ определяется интегралом от произведения частотных
сечений ФН исходного и производящего сигналов (Ru и Rv), а
также экспоненты ехр (—i xtp). Из-за того, что разным сегментам
соответствуют различные сдвиги tpy то ВКФ зависит как от значения tp
в показателе экспоненты, так и от разности tp — tq в ФН Ru.
Поскольку для ρ Φ q разность tp — tQ φ 0, то положения
центров ФН, где Ru = 1 и Rv = 1, не совпадают. Более того, так как
| Rv | φ 0 лишь при | τ К Т0, то если tp — tq> T0, центр ФН
Ru не попадает в полосу, занимаемую ФН Rv- Это означает, что в
подынтегральном выражении (12.40) Ru не достигает своего
максимального значения, равного единице. Сегменты с tp—tq^T0 будут
неперекрывающимися. Причем если tp — tq > Т0, то назовем сегменты
разнесенными, а с tp — tq = Т0 примыкающими. Если tp — tq <
< Т0, то сегменты будут перекрывающимися.
Из (12.40) получает, что
оо
Смаке<Ρ J \Ru(t + tp-iq,x)\ \Rv(t, -x)\dx, (12.41)
—оо
т. е. определенное таким образом максимальное значение ВКФ
зависит только от разности tp — tq. Следовательно, максимальные
значения ВКФ сегментов с tp— tQ = const зависят лишь от одной
полосы ФН Ru.
Корреляционные свойства неперекрывающихся сегментов.
Анализ корреляционных свойств таких сегментов произведем на
основе формулы (12.40), учитывая, что исходным сигналом является
Λί-последовательность. Сначала рассмотрим разнесенные сегменты,
у которых разность задержек между соседними больше длительности
сегмента, т. е. tp — tq > Т0. При этом центральный пик ФН Λί-
последовательности Ru не попадает на ФН производящего сигнала
Rv, т. е. ВКФ Qpq (τ) при различных τ определяется произведением
ФН Ru в области слабой корреляции (где \Ru\ С 0'и ФН Rv.
Частотное сечение ФН Rv для производящего сигнала (12.33)
им.еет следующий вид (см., например, [25], с. 74):
*ν(τ, -*)- L 2^ r°%[-i^(l+^)]. (12.42)
2
237
При данном τ Rv (τ, — χ) максимальна при χ = О, а максимум
равен 1 — |τ|/Т0 < 1. Вблизи максимума (в области |χ|< π/Τ0)
Rv(t> — ^меняется медленно, а затем становится затухающей
знакопеременной функцией. Исходя из такого характера Rv (τ,— χ)
можно предположить, что основной вклад в интеграл (12.40) вносит
та часть подынтегрального выражения, которая сосредоточена в об·
ласти \х\ < π/Τ0. Основанием для такого предположения является
асимптотическое свойство интеграла (12.40) при То-*- Т. Полагая
tp = tq = 0 и Т0 = Т, из (12.40) должны иметь тождество
со
/?ι/(τ)=Ρ J Ru(r, х) Rv (τ, — χ) dx, (12.43)
—οο
т. е. произведение pRv (τ, — л;) выполняет роль дельта-функции
δ (#), что дает в правой части Ru (τ, 0) = #α(τ).
Это, действительно, так, потому что при Т0 = Τ можно
полагать Т0 ->■ оо, поскольку сигнал U (t) (12.32) вне отрезка [0, Т]
тождественен нулю. Из определения дельта-функции следует
равенство
со
Р.1Х(Т> - х) dx = 1. (12.44)
—со
Так как при Т0> Τ величина ρ = Τ/2π, то дельта-функция
pRv (τ, — х) имеет эквивалентную ширину 2 π/Τ0. Отсюда следует,
что основной вклад в интеграл (12.40) вносит часть
подынтегрального выражения в области \х\ <! π/Τ0. Для случая Т0< Τ
приближенно можно полагать, что Rv (τ, — χ) = 1 при \х\ ^ π/Τ0
и Rv (τ, — л;) = 0 при \х\ > π/Τ0. Используя такое приближение,
а затем неравенство Буняковского — Шварца, из (12.40) получаем
π/Γ,
Qpg (τ) ^ ρ J Ru (τ + tp —tq9 x) exp (— ixtp) dx <
-я/г,
Г -Я/Г,
Интеграл под квадратным корнем пропорционален квадрату
эффективного значения Ru (τ + tp — tq, x) при усреднении на
отрезке [—n/TQ, п/Т0]. Функции неопределенностей Λί-последова·
233
'гелыюстей характерны тем^ что ойи имеют области слабой
корреляции, близкие к равномерным. Поэтому можно полагать, что
π/Γ,
-£■ J \Ru(r + tp^-tq,x)\*dx~
-π/Γ,
2π/τ0
2π/τ0
где правая часть (12.46) — квадрат эффективного значений при
усреднении по области частот на отрезке [—2π/τ0, 2 π/τ0], а τ0 —
длительность одиночного импульса М-последовательности, причем
τ0 = TIN. Обозначая максимальное эффективное значение боковых
пиков Ru, из (12.45) находим
Qpq(x)~p^.Ru. (1147)
I о
Поскольку при Т0 < Τ из (12.39) имеем ρ = 772π, а отношение
Т/Т0 = #/#0, то
Qp<z (τ) - /?α^/Λ/0. (12.48)
Известно (см., например, [25, с. 118], что максимальное
эффективное значение при усреднении на отрезке [—2π/τ0, 2π/τ0] равно
Ru = \lVTR. (12.49)
Подставляя (12.49) в (12.48), имеем
QPQ (τ) ~ КЛГ/К2^0 = αΐ/#/ΛΤ0, (12.50)
где α = l/l/"2. Отметим, что при выводе формулы (12.50) нигде не
была оговорена длительность сегмента Т0 = Ν0τ0. Следовательно,
оценка (12.50) приближенно справедлива как для длинных сегментов
(Nq>YN/2), так и для коротких (Nq<YW2). Выясним, какие
особенности имеются при длинных и коротких сегментах»
При коротких сегментах отрезок интегрирования [ — π/Γ0,
π/Τ0] в (12.45) расширяется и точность приближения левой и
правой частей приближенного равенства (12.46) увеличивается, т. е.
оценка (12.50) становится более точной. Однако при этом
Qpg (τ) меньше величины, которая в свою очередь больше единицы»
Так как Qpq макс (τ) < 1, то полученный результат свидетельствует
о том, что среди коротких сегментов обязательно будут такие, у
которых уровень ВКФ будет соизмерим с единицей.
При Ν0 > У Ν/2 значения ВКФ меньше единицы. Поэтому при
таком выборе длины сегмента можно быть уверенным, что ВКФ
будут малыми. Однако с ростом Ν0 уменьшается отрезок интегри-
239
рования в (12.45). В этом случае эффективное значение Ru -*
->- R (τ + ^р— tq). Следовательно, для уменьшения значений
ВКФ необходимо так выбирать М-последовательность, чтобы ее
АКФ имела малые боковые пики.
Рассмотрим теперь примыкающие сегменты, у которых tp —
— tq = TQ. При этом центральный пик ФН Ru попадает на
границу ФН Rv. Поскольку на границе ФН Rv мало отличается от
нуля, то вклад центрального пика ФН Ru в значения ВКФ Qpq (τ)
будет мал и его можно не принимать во внимание. Поэтому и для
примыкающих сегментов можно использовать оценку (12.50). Число
таких сегментов (т. е. число сигналов в системе) будет равно
L = Ν/Ν0. (12.51)
Обычно из условий применения системы сигналов задается либо
максимальное значение, либо эффективное значение ВКФ сигналов
(либо то, и другое вместе). Поэтому полагая, что Qpq (τ) ^ Q =
= const, из (12.50) и (12.51) имеем
N0 = aVW/Q. (12.52)
L = QVWa. (12.53)
Например, если Ν =_ 131071 (длина М-последовательности в [96]),
a Q = 0,25, α = 1//2, тоЛ/0 = 1020, a L = 127. Если же Q = 0,1,
тоЛ/0 = 2550, al = 51.
Корреляционные свойства перекрывающихся сегментов. Для
перекрывающихся сегментов разность задержек tv — tq = Т0 —
— ΔΓ, где ΔΓ = ΑΝτ0 > 0. В этом случае из формулы (12.40)
получаем:
оо
Qpq (τ) = Ρ ί Ru (τ+Γ0 — ΔΓ, χ) exp (—i xtp) Rv(r, — χ) dx.
(12.54)
При τ= — TQ + ΔΓ сечение ФН Ru есть Ru (0, χ) = Ra (χ) =
= sin (πΤ/2)/ (π772). Центральный пик этого сечения с
максимумом, равным единице, будет гораздо уже, чем центральный пик се*
чения Rv {—T0 + ΔΓ, х). Поэтому пределы интегрирования
в (12.54) можно положить равными — π/Τ и π/Τ, а в этих
пределах все множители в подынтегральном выражении считать
постоянными. Значения первого и второго множителя в (12.54) равны
единице (имеются в виду модули), а значение третьего согласно
формуле (12.42) равно отношению ΔΓ/Γ0. Обозначая Qpq (—T0 +
+ ΔΓ) как Q0, из (12.54) находим
Q0 = ρΔΓ2π/Γ07 = ΔΤ/Γ0 = Δ#/#0. (12.55)
При выводе формулы (12.55) было учтено, что согласно (12.39) ρ =
== 772π. Следует отметить, что результат (12.55) является есте-
240
ственным, так как если два произвольных сигнала имеют AN оди-
наковых символов (один в конце, а другой в начале),то их ВКФ
будет иметь по крайней мере один пик, равный отношению AN/N0.
Следовательно, этот пример еще раз подтверждает, что принятый
метод обеспечивает получение оценок с приемлемой точностью.
Для определения допустимого перекрытия сегментов положим,
что значение Q0 равно Q, которое определяется согласно (12.40).
В этом случае имеем
AN = QN0 = a V~N. (12.56)
Если заданы Q = Q0 и Ν, то длительность сегментов
определяется формулой (12.52), а число сегментов будет равно
L = N/(N0—AN) = Q ΫΈΐα (1 — Q), (12.57)
т. е. по сравнению с (12.53) увеличилось в (1 —Q)"1 раз. Например,
если N = 131071, то npnQ = 0,25, α = \[γ~2 число сегментов L =
= 170, а при Q = 0,1 оно равно L = 57. Следовательно,
перекрытие сегментов увеличивает их число при том же значении ВКФ.
Оценка максимальных боковых пиков. Для получения более
точной оценки максимальных боковых пиков ВКФ сегментов было
использовано циклическое свойство М-последовательностей,
заключающееся в том, что сумма по mod 2 двух одинаковых Λί-последо-
вательностей, сдвинутых относительно друг друга, является той же
Λί-последовательностью, но имеющей иной сдвиг во времени
(см., например, [25, с. 222]). Из этого свойства следует, что сумма
двух сегментов Λί-последовательности является сегментом той же
Λί-последовательности, но с произвольным сдвигом.
ВКФ сегментов Sp (t) и Sq (t) в дискретных точках τ = /ητ0
согласно определению имеет следующий вид:
N0-m-l
QP,im) = ~ 2 Sp(n)Sq(n + m), (12.58)
где Sp (n), Sq (n) — кодовые последовательности соответствующих
сегментов. Используя циклическое свойство сегментов,
сформулированное ранее, из (12.58) получаем
где St (n) = U{ (n) — /-й сегмент Λί-последовательности длины
N о —т.
Назовем весом сегмента сумму правой части (12.59);
W(N9N09l9m)= 2 *МЛ)· (12·6°)
241
Таким образом, оценка максимальных боковых пиков ВКФ
сегментов сводится к определению максимального веса WMaKc (N,
N0, I, т) = W (N). Решение этой задачи эквивалентно
нахождению максимального бокового пика среди всех АКФ,
соответствующих Λί-последовательности и ее циклическим сдвигам. Дей^
ствительно, если обозначить через Ruj (m) АКФ
Λί-последовательности со сдвигом /, а / =-- О, N — 1, то по определению
N—m — \ N — m—l+l
NRui(m)= 2 U(j + n)U(j + n + m)= 2 u(n) =
/1 = 0 n = l
N — m — l
= Σ £ΜΌ· (i2.6i)
л = 0
Длина сегмента Ui(n) равна Ν — т. При изменении / от 0 до
N — 1 индекс / также пробегает все эти значения, но только в ином
порядке. Поэтому при таком изменении / правая часть (12.61) даёт
веса всех сегментов длиной N — /п. В свою очередь изменение т
от 0 до N — 1 определяет все сегменты с длиной, изменяющейся от Μ
до 1. Это свойство АКФ Λί-последовательностей было использовано
для определения максимального веса W (N).
С помощью ЭВМ было найдено, что для N > 15
W (N) = И^макс (Ν, N0, U т) < 1,261/77. (12.62)
Приведенный результат подтвержден многочисленными
расчетами для различных Λί-последовательностей. Подобная оценка,
полученная для АКФ с помощью ЭВМ, приведена также в [140].
Это дает основание предполагать, что оценка (12.62) справедлива для
произвольных N. Используя (12.62), из (12.59) получаем верхнюю
оценку максимальных боковых пиков ВКФ сегментов Λί-последо-
вательностей
QMaKC<l,26]/F/W0. (12.63)
Эта оценка примерно в 1,77 раза превышает приближенную
оценку (12.50), т. е. в этом случае коэффициент α = 1,26. Следует
отметить, что верхняя оценка (12.62) встречается очень редко. Для
большинства рассмотренных ^-последовательностей W {N)<yN, т. е.
Q ~ VWN0, (12.64)
что в У2 раз превышает оценку (12.50). При этом коэффициент а =
= 1. Расчет длины сегментов, их перекрытия и числа сегментов
при использовании оценок (12.63), (12.64) следует вести по формулам
(12.52), (12.56), (12.57) с учетом значения коэффициента а.
Примеры расчета длинных сегментов. Приведем характеристики
двух систем сигналов, являющихся сегментами
Λί-последовательностей с числом символов N = 255 (характеристический
многочлен х8 + х? + х? + х+ 1)и N = 511 (характеристический много-
242
член χ* + χ* + 1). Предварительно были определены все веса
произвольных сегментов, в результате чего уточнены коэффициенты а.
Оказалось, что для Λί-последовательности с N = 255 коэффициент
α ~ 0,81, а для ^V = 511 α ~ 1,06. Для заданных Q (при W=255,
Q = 0,4 см. табл. 12.4, а при N = 511, Q = 0,3 см. табл. 12.5)
и уточненных коэффициентах α по формулам (12.52), (12.56), (12.57)
были вычислены длина сегментов Л/0,.их перекрытие AN и число
сегментов L. Эти величины приведены в табл. 12.4, 12.5 на первых
строках. Затем в соответствии с полученными Ν0 и AN исходные Λί-
последовательности разбивались на сегменты, причем с
произвольным началом первого сегмента.
С помощью ЭВМ были найдены ВКФ сегментов. Оказалось, что
значения ВКФ не превосходят заданного значения Q.
α
0,81
0,71
1,00
1,26
Т.
' No
33
28
40
51
а б лица 12.4
AN
11
11
16
20
L
12
15
И
8
Таблица 12.5
« 1
1,06
0,71
1,00
1,26
No
80
54
76
96
AN
24
16
23
29
L
9
14
10
8
На строках 2, 3, 4 табл. 12.4, 12.5 приведены значения N0y
AN, L для α, соответствующих приведенным ранее оценкам:
а = 0,71 = 1/"|/"2 соответствует оценке (12.50), а = 1 — оценке
(12.64), а = 1,26 — верхней оценке (12.63). Как видно из табл. 12.4,
12.5, расчетные значения N0, AN, L первых строк лежат между
значениями, соответствующими α = 0,71 и α = 1,26. Таким
образом, расчет характеристик сегментов по формулам (12.52), (12.56),
(12.57) при α = 0,71 и α = 1,26 укажет границы, в пределах
которых будут лежать характеристики сегментов. Поскольку а = 1
близко к среднеарифметическому значению указанных а, то расчет
характеристик при α = 1 даст результаты, близкие к реальным.
Поэтому для расчетов следует выбирать коэффициент α = 1.
12.4. Циклические системы
Циклические перестановки.
Допустим, что имеются две кодовые
последовательности {Л (ν)} и {В (ν)},
где ν—номер элемента. Положим, что
ν = О, N — 1 и символы этих
последовательностей Л (ν), В (ν)
принадлежат мультипликативной
комплексно-сопряженной р-ичной
группе. Если ρ > 2, то будем называть
сигнал многофазным. Кодовым
последовательностям {Л (v)J, {В (ν)}
можно поставить в однозначное
соответствие кодовые последовательности
{а (v)}» {^ (v)} символы которых
α (ν) и Ь (ν) принадлежат
аддитивным р-ичным группам. Как следует
из материала гл. 9, образование К Φ
сводится к перемножению символов
*
Α (ν) и β (ν), где * — знак
комплексной сопряженности, с последующим
суммированием. При переходе к сим-
волам a (ν), b (ν) ΚΦ определяется
через разности этих символов по
mod /?.
Для построения системы
сигналов, которые исследуются в данном
параграфе, выберем кодовые
последовательности {a (v)}, {b (v)},
обладающие следующим циклическим
свойством: разность по mod/?
кодовой последовательности {α (ν)} и
ее циклической перестановки
{α (ν + μ)} является другой
циклической перестановкой {α (ν +
+ λ)} исходной кодовой
последовательности, т. е.
{α (ν)} - {α (ν + μ)\ = {α (ν + λ)},
(12.65)
где λφΟ Ηλφμ (mod/?).
Циклические перестановки получаются так:
исходная кодовая
последовательность {α (ν)}, где ν = О, N — 1,
продолжается периодически, т. е.
записывается в виде бесконечной
последовательности ... a (N — 2),
a (N - 1), а (0), а (1) ... α (ν),
..., α (μ), ..., α (Ν - 2), a (W-1),
а (0), а (1) ...
Исходная последовательность
{α (ν)} начинается с символа а (0)
и заканчивается символом a (N —
— 1). Циклическая перестановка
{α (ν + μ)} начинается с символа
α (μ) при ν = 0 и заканчивается
символом α (μ + N — О при ν =
= N — 1.
Аналогично (12.65) определяется
циклическое свойство
последовательности {b (v)}, а именно:
{Ь (ν)} - {Ь (у + μ)} = {6 (ν +
+ λ)}. (12.66)
Равенства (12.65), (12.66)
выполняются для ^-последовательностей
[25] в соответствии с аддитивно-
циклическим свойством и для
последовательностей, построенных по
правилу
α (ν) = αν (mod p), (12.67)
где α — первообразный корень
уравнения ** — 1 = 0 [63],
ρ = м + 1 (12.68)
244
и является простым числом, ν =
= 0, N — 1. Для последовательностей
вида (12.67) имеем
α (ν) - α (ν + μ) = αν (Ι — αμ)>
μ= 1, Ν — 1. (12.69)
Так как α — первообразный
корень, то 1 = α° = α и поэтому
αμ φ. 1 при μ = 1, Ν — 1.
Следовательно, 1 — αμ ξ α\ где λ ^ μ,
и из (12.69) имеем
α (ν)—α(ν + μ) = αναλ=
=αν+λ = α(ν + λ), (12.70)
что и определяет равенство (12.65).
Циклические системы. Пусть
последовательности {α (ν)} и {b (ν)}
обладают циклическим свойством
(12.65), (12.66). Циклическая система
состоит из последовательностей
{с/(ν)), где / = 0, Ν— 1, символы
которых определяются равенством
cj (ν) = α (ν) — b (v + /),
(12.71)
ν =0, Ν—1. Каждая
последовательность циклической системы равна
разности между последовательностью
{α (ν)} и циклической перестановкой
{Ь (ν + /)}, т. е.
[с; (ν)} = {a (v)} - {b (v + /)}.
(12.72)
Можно доказать, что
последовательности системы (12.72) являются
симплексными. Отметим, что
циклические системы являются
производными, так как4'система
последовательностей {р (ν + /)} является
исходной, а последовательность
{α (ν)} — производящей. В данном
параграфе приведены результаты
[73]. Некоторым вопросам
построения циклических систем и расчету их
корреляционных функций
посвящены работы [141, 228].
Корреляционные функции
циклических систем. Поскольку
символы Cj (v) последовательностей
{cj (v)} относится к
мультипликативной группе, то
взаимокорреляционная функция (ВКФ) определяегся
в соответствии с (9.2), (9.4), (9.25)
следующим образом:
j W-λ-Ι
Φ*(λ) = — Σ ехР
2π
Χ
X[c7-(v + X)-cft(v)]J. (12.
73)
Отличие (12.73) от (9.25) заключается
в пределах суммирования. Это
изменение не имеет принципиального
значения, но более удобно при
исследовании.
Используя свойства образующих
последовательностей {a (v)), {b (ν)}
(12.65), (12.66) и определение
(12.71), запишем
Cj (ν + λ) — ck (v) = α (ν + λ) —
- b (ν + / + λ) - α (ν) +
+ b (ν + k) == α (ν, λ) —
- 6, (ν, λ, /, Q (mod ρ), (12.74)
где α (ν, λ), b (ν, λ, /, /г) —
некоторые циклические перестановки
образующих последовательностей.
Тригонометрическую сумму
правой части выражения (12.73) можно
представить в виде тройной суммы,
используя метод И. М. Виноградова
[63]. Такое усложнение позволяет
найти оценки правой части (12.73)
Итак, имеем:
М—\ Ν-λ~\ Ν—\
Χ
**<*>-£ Σ Σ Σ
ν=0 η = 0 ρ=0
χ exp Ji — [сj (v + λ) -ck (ν)]J χ
ΧβχρΓί-^(ν-η)]. (12.75)
Правые части (12.73) и (12.75)
равны [73].
Оценки корреляционных
функций. Обозначим периодическую ВКФ
образующих последовательностей
(12.74)
ом^-тг Σ ехр
Ν ν = 0
I'
2π
Ρ
Χ
χ [α (ν + λ)-6 (ν)]}, (12.
76)
а периодическую ВФН
Χ
Q λ, ρ)=— 2 ехР * :
# ν=ο Ι Ρ
χ[β(ν + λ)-&(ν)]}βχρ(ί^,
(12.77)
где ρ определяет дискретные
значения доплеровской частоты.
Оценки КФ (12.75) будем находить
отдельно для ρ = 0 и ρ Φ 0. Модуль
части суммы (12.75),
соответствующей ρ = 0, удовлетворяет
следующему неравенству:
\Ν—\
(Ν
rv ~ * ( 2π
-λ)Ν-*\ 2 exp i [cj(v+
I v=o I P
+ X)-ch(v)]\ \< max |<3(λ)|,
) | λ
(12.78)
где максимум обеспечивается
перебором всех λ = 0, N—1 и выбором
максимального значения.
Неравенство (12.78) объясняется тем, что
согласно (12.74) разность cj (ν +
+ λ) — си (λ) равна разности двух
образующих последовательностей с
различным сдвигом между ними.
Одно из значений | Q (λ) | при
изменении λ = 0, N — 1 совпадает со
значением левой части (12.78).
Для оставшейся части суммы
(12.75) при рф 0 получаем]
Ν — Ι Ν—λ—\ tf-l
^Σ Σ Σεχρ
ν=0 η=0 ρ=1
r7IC,(v
+
2πρ Τ
i — (ν~Ή) <
+λ)—cfe(v)]|expl·
г ι Ν~ι
< max [ Q (λ, ρ) |
λ, ρ
Ν-λ-1
Χ
η = 0
. (12.79)
Множитель в квадратных
скобках правой части неравенства (12.79)
245
не зависит от выбора образующих
последовательностей. Обозначим его
р=1 Ι η=ο ч ' |
(12.80)
Для тригонометрической суммы
(12.80) при Ν ^ 6 известна оценка
И. М. Виноградова* [63. с. 51]
β<1ηΛΤ-Χΐη(2[|-]+ΐ) = 8.
(12.81)
Используя (12,78) — (12,81),
находим оценку модуля максимальных
боковых пиков
#максМ<тах|<2М| +
λ
+ max\Q(X, ρ) ι 6. (12.82)
λ, ρ
Для построения системы
минимаксных сигналов (у которых
максимальные пики минимальны) необходимо,
чтобы периодические ВКФ и ВФН
образующих сигналов имели малые
боковые пики. В общем случае
регулярного метода построения таких
сигналов нет.
Для двоичных М-последователь-
ностей (р = 2) известен метод Голда
[201, 208, 209], позволяющий
выбирать пары образующих М-последова-
тельностей. Этот метод основан на
выборе последовательностей в
соответствии со свойствами многочленов.
Известно [25, 121], что каждой М-
последовательности длины N =
= 2п — 1, где η — некоторое целое
число, соответствует свой
неприводимый многочлен степени п.
Неприводимым называется такой многочлен,
который не может быть представлен
в виде произведения многочленов
с меньшими степенями. Каждому
корню многочлена степени η может
быть поставлен в соответствие
элемент поля Галуа GF (2п) (кодовая
последовательность полного кода
длины η за исключением элемента,
состоящего из одних нулей). Всего не-
* Впервые эту оценку
тригонометрической суммы использовал
для расчета корреляционных
функций В. Н. Власов,
нулевых элементов имеется 2п — 1
Корень а, все степени которого а0,
а1, а2, ..., а* = а0 дают
различные элементы поля, называется
первообразным или примитивным
[63, 121]. Неприводимый многочлен,
одним из корней которого является
примитивный элемент поля,
называется примитивным. В соответствии
с методом Голда образующим М-
последовательностям должны
соответствовать примитивные
многочлены, корнями которых являются α~ν
для первой и (а2* + г) ~ν для второй
последовательностей, где / — любое
целое число, взаимно-простое с п.
Выбираются такие
последовательности достаточно просто с помощью
таблиц неприводимых многочленов [121].
Если ^-последовательности выбраны
по методу Голда, то их ВКФ
являются трехуровневыми, т. е.
принимают только три значения [208,
209]:
Q(X) = JQa = V2/iV-l/JV. (12.83)
Вероятности появления этих
значений равны
Рх = 1/2 — 1/2 N,
Р2 = 1/4 + 1/4JV - 1/T/8JV,
Р3 = 1/4 + 1/4 N+1/УШ. (12.84)
Периодические ВКФ циклической
системы могут принимать только
значения (12.83), причем вероятности
(12.84) соответствуют случаю
усреднения по всем ВКФ всех циклических
перестановок. Дисперсия
периодических ВКФ по определению равна
(1 + 4/N)/N cz l/N, что совпадает
с полученным ранее результатом
(9.60) для полного кода. Отметим, что
максимальные боковые пики для
полного кода можно оценить по
формуле в то время как (12.83)
дает значения Т/2/У#с- 1,41/У#,
в два раза меньше.
Таким образом, оценка первого
слагаемого в (12.82) дается
максимальным значением (12.83), равным
"Ϋ2/Ν+1/Ν.$ \Щ показано, что мак.
246
симум модули периодической ВФЙ
max | Q (λ, р) I <
λ, p
<(23/2n~1iV-1/2 + iV-1)1/2-
~ 0,94Λ^~1/4. (12.85>
Подставляя в (12.82) оценки
'(12.83), (12.85), находим оценку
максимальных пиков ВКФ циклической
-системы*:
(λ)<
-<УЩ+ 1/# + 0,94δ/>/Й. (12.86)
Пример расчета. Для трех
значений N = 31,127,511 найдены
оценки максимальных боковых пиков
ВКФ циклических систем.
Результаты расчета приведены в табл. 12.6.
Как видно из табл. 12.6, оценки
'Ямакс (λ) достигают больших значе-
<ний и существенно превышают утро-
ценное среднеквадратическое значение
3/"1/2Л^· Это объясняется тем, что
эти оценки пропорциональны 1/j/W.
-На самом деле максимальные пики
Таблица 12.g
N
31
127
511
с<
СУ
Ε
0,59
0,134
0,059
Q
с<
СУ
СО
Ε
0;39
0,28
0,20
с<
а
мак
βί
0,935
0,74
0,61
Ρ
со
0,37
• 0,18
0,09
будут меньше. Были рассчитаны все
АКФ и ВКФ циклической системы
для N = 31 [73]. Образующие М-по-
следовательности строились на
основе примитивных многочленов
/а (*) = ** + * + 1 И fb (X) =
= χ$+χ* + χ? + χ + 1.
Многочлену fa (x) соответствует
последовательность {α (ν)} с начальными
условиями — 11 — 1 11,
многочлену fb (x) — последовательность
{b (v)}. Нормированное значение
максимальных боковых пиков
удовлетворяет неравенству /?Макс Μ <
< 0,42, что близко к значению
3/Т/2ЛГ = 0,37 табл. 12.6.
Ϊ2.5. Системы многофазных сигналов
Многофазные сигналы
рассмотрены в ряде работ (см., например, [25,
99, 174, 216J). В данном параграфе
приведены результаты исследований
систем многофазных сигналов [67, 72]
с числом фаз ρ > 2.
Оценки корреляционных
функций многофазных сигналов.
Положим, что в дискретном многофазном
сигнале число различных фаз равно
р, а фазы принимают значения
Qj (ν) = (2nr/p) aj (v). (12.87
Числа г и ρ — взаимно-простые
ν — номер элемента, ν = 0, N — 1
aj (v)-fi символ /-й кодовой последо
вательности {aj (v)}.
ВКФ сигналов / и к по определе
нию (9.25) записывается следующим
образом:
Подставляя в (12.88) определение
(12.87), находим
Ν
ν = 0
2яг
exp \ i — χ
Ρ
вен
где
X[aj(v + X)-ah(v)]\. (12.89)
Модуль максимального пика ра-
/Wc = (lWWc, (12.90)
/макс = тах |/,Λ(λ)|, (12.91)
/, k, λ
1
Ν—λ-1
Λ^(λ)=— Σ «ρ0[»πν+λ)-
Μ ν = 0
-eft;(v)]>. (12.88)
ΛΛ-λ-1
IjhW = 2 βχρ{ΐ[θ7·(ν+λ)-
ν = 0
-'θΛ(λ)]}. (12.92)
Максимальный боковой пик
будет минимальным, если максимальное
значение /Макс минимально, т. е.
* Формула (12.86) найдена Л. Н.
Волковым.
max | IJk (λ) Ι
/, ft, λ
amin.
(12.93)
247
Система минимаксных сигналов,
удовлетворяющих условию* (12.93),
неизвестна. Приведем найденные
системы, близкие к минимаксным. При
решении этой задачи используем
неравенство, полученное в теории
чисел [63] для оценки модуля
тригонометрической суммы. Пусть целое
число N > 6 и функция Φ (ν)
такова, что при некоторой Δ > 0 и
любом а = 1, N—1 справедливо
неравенство
П
ίν-1 / а
Σ Φ (ν) ехр ί i 2π — ν
<Δ.
(12.94)
В этом случае имеет место
следующее неравенство:
Ν-λ-ΐ
Σ φ(ν)
ν = 0
<
N-l
Σ φ(ν)
ν = 0
Δδ,
(12.95)
где δ определяется согласно (12.81).
Полагая
Φ (ν) = ехр
. 0 {θ, (ν + λ)
θ* (λ)]},
замечаем, что в
(12.92), (12.95)
(12.96)
соответствии с
/;#)!<
#-1
Σ фм
ν=ο
+ Δδ. (12.97)
Оценка первого слагаемого
сверху равна Δ согласно (12.94), что
объясняется характером Φ (ν) (12.96).
Поэтому
I Ijh W I < Δ (1 + δ). (12.98)
Неравенство (12.98) позволяет
свести (12.93) к следующему
условию. Так как δ (12.81) не зависит от
фазовой кодовой последовательности
{θ7· (ν)}, то для уменьшения правой
части неравенства (12.98) необходимо
определить такую последовательность
{Qj (v)}, у которой Δ минимальна.
Можно указать следующее
решение этой задачи.
Обозначим фазовую кодовую
последовательность, равную разности
фазовой кодовой
последовательности /-го сигнала и циклически
сдвинутой фазовой кодовой
последовательности fe-го сигнала, через
{θ,*(ν, λ)} = {θ,(ν + λ)}-{θΛ(ν)}.
(12.99)
Соответственно фаза разности
равна
θ,Λ(ν, λ) = θ/(ν + λ)-θΛ(ν). (12.100)
Введем ненормированную
периодическую АКФ последовательности
(12.99):
JV-1
Μμ>= Σ βχρ{ί[θ,(ν + λ + μ)-
ν = 0
-τθ*(ν + μ)-θ,(ν + λ) + θ*(ν)]}.
(12.101)
Выразим квадрат левой части
неравенства (12.94) через АКФ VQ (μ).
В соответствии с (12.94), (12.96)
имеем
ι/ΐ2= Σ Σ βχΡ{ί[θ,(ν+λ)-
ν = 0 η = 0
-θ*(ν)-θ,(η + λ) + θΛ(η)]}Χ
Xexp|"i2n-J-(v—η)1. (12.102)
В Двойной сумме (12.102) собе*
рем вместе слагаемые, для которых
выполняется сравнение
ν = η + μ (mod N). (12.103)
В результате получим
\ι?=ν+ Σ ^θ(μ)6χρ(ί2π7Γμ}
(12.104)
Если Vq ^) = V = const, то сумма
Σ М^)ехр(*2"^] =
-V^exp(i2»f^-V.
(12.105)
Если V = — 1, то в соответст*
вии с (12.104), (12.105)
|/| = УлГ+Т. (12.106)
Для V = 0 из (12.104) получаем
|/| = УЖ (12.107)
Из (12.105) следует, что для
уменьшения I / |а необходимо иметь
248
периодические АКФ с
положительными боковыми пиками.
В соответствии с (12,90) —
(12.92), (12.98), (12.106), (12.107)
для N > 1 имеем оценку для ВКФ
/?мако<(1/У^)(1 +«). (12.108)
Пример системы. Неравенству
(12.108) удовлетворяет система
кодовых последовательностей {aj (v)},
символы которой определяются из
сравнения второй степени:
aj (ν) = / ν2 + cxv + c0 (mod N),
(12.109)
где /= 1, N— 1 — номер
последовательности; cl9 c0 — целые числа
ν = 0, Ν—1; Ν — простое число.
Например, при N = 11, сг = с0 =
= 0 имеем
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
4
8
1
5
9
2
6
10
3
7
9
7
5
3
1
10
8
6
4
2
5
10
4
9
3
8
2
7
1
6
3
6
9
1
4
7
10
2
5
8
3
6
9
1
4
7
10
2
5
8
5
10
4
9
3
8
2
7
1
6
9 4
7 8
5 1
3 5
1 9
10 2
8 6
6 10
4 3
2 7
(12
1
2
3
4
5
6 ·
7
8
9
10
.110)
Каждая строка (12.110)
является кодовой последовательностью
{a/ (v)}. Для систем (12.109) при
р = апериодическая АКФ (12.101)
каждой последовательности имеет
нулевые боковые пики. Следовательно,
для систем (12.109), (12.110) справед--
лива оценка (12.108)·
Большие системы многофазных
сигналов. В работе [72] приведены
методы построения систем
многофазных сигналов, объем которых
L > N. Положим в (12.87) ρ = Ν,
т. е.
W=-^~MV>· (12Л11)
где г и N — взаимно-простые числа.
Определим символы aj (v) кодовых
последовательностей через сравнение
и-й степени:
η
aj (у) = 2 cjsVs+cxv+
s = 2
+ c0(moaN), (12.112)
где Cjs = 0, Ν—1 не равны нулю
одновременно; съ с0 — произволь-
ные целые числа: ν = 0, N — 1;
η < Ν\ Ν — простое число; / —
номер сигнала. Символы aj (v) лежат
в классе наименьших
неотрицательных вычетов по модулю числа N.
Любые две последовательности,
определяемые сравнением (12.112),
отличаются друг от друга хотя бы
одним из коэффициентов cj8, причем
все CjS не равны нулю одновременно.
Поэтому максимальный объем
системы
1 = #я-1—1. (12.113)
Свойства систем сигналов
зависят от тех ограничений, которые
могут быть предъявлены к
коэффициентам Cjs. В работе [72] этот воп-
Таблица 12.7
Коэффициент
Объем
системы
Оценки ВКФ
п = 2; Cj2 = l,N—l
п>3; Cjn=l,N— 1; cjf/I-i = 0
остальные Cjs = 0,N—1
п^Л—четное:
Ι 0,Ν—1 при четных s;
JS I 0 при нечетных s
Ν—Ι
(N—l)Nn~3
Νη/2_χ
ι+β
Vn
<->■$
<->#
249
рос рассмотрен подробно. Приведем строках приведены данные систем
окончательные результаты в виде большого объема или больших си-
табл. 12.7 (см. [72], табл. 1). стем. Как следует из оценок ВКФ
На первой строке табл. 12,7 при- табл. 12.7, увеличение объема си-
ведены данные системы (12.109) объ- стемы приводит к ухудшению кор-
ема N — 1, а во второй и третьей реляционных свойств.
Глава 13
СИСТЕМЫ ЧАСТОТНЫХ СИГНАЛОВ
13.1. Системы частотных сигналов
Огибающая частотных сигналов. Как было показано в § 1.4,
частотные сигналы дуальны к дискретным сигналам с точностью
до поворота частотно-временной плоскости на π/2. ЭтсГозначает, что
все временные соотношения заменяются на частотные, а частотные
на временные. Например, дискретные фазоманипулированные
сигналы обладают прямоугольной огибающей, но их амплитудные
спектры могут быть неравномерными. Примеры спектров дискретных ФМ
сигналов можно найти в [25, 105]. В свою очередь, частотные ФМ
сигналы будут иметь равномерный амплитудный спектр, но
огибающая таких сигналов будет иметь глубокую амплитудную модуляцию.
Амплитудная модуляция огибающей в большинстве случаев
нежелательна, так как приводит к дополнительным энергетическим
потерям. Поэтому при простом применении принципа дуальности
и переносе свойств дискретных сигналов на свойства частотных
полученные частотные сигналы могут не удовлетворять требованиям
практики. В результате всегда необходимо применять меры по
улучшению огибающей частотных сигналов, т. е. по уменьшению
нежелательной амплитудной модуляции.
Рассмотрим частотные сигналы с одинаковыми элементами.
Комплексная огибающая таких сигналов определяется согласно
(1.93), а ее спектр согласно (1.94). Изменяя нумерацию элементов,
имеем следующие формулы для комплексной огибающей и ее спектра:
ϊ/,(0=Φ(0 2 Mv)exP(ivAo)0> (13.1)
ν = 0
Gj (ω) - 2 a! (v) S (ω ~νΔω)> Ο3·2)
ν =0
где Φ (t) — огибающая отдельного элемента, а 5 (ω) — ее спектр.
Квадрат огибающей частотного сигнала равен квадрату модуля
комплексной огибающей, т. е.
|г/,(01* = Ф»(01'(0|·, (13·3)
250
где w_,w_i
I / (0 l2 = "ft "ft aj (ν) aj (η) ехр ЦШ (ν-η)]. (13.4)
V = 0 η = 0
Из (13.3) следует, что огибающая определяется огибающей
элемента Φ (t) и модулем | / (t) I.
Выбор элемента Φ (t) определяется многими факторами. Во-
первых, огибающая самого сигнала согласно (13.3) определяется
произведением Φ (t)\ I (t) |. Поэтому принципиально
возможно получить ослабление «осцилляции» модуля | / (О I путем
разумного выбора Φ (/), т. е. можно потребовать, чтобы Φ (t) была
согласована с | / (t)\. Во-вторых, огибающая Φ (t) определяет
перекрытие спектров элементов в (13.2). Например, если Φ (t) —
прямоугольный импульс, то спектр S (ω) описывается функцией вида
sin х/Ху которая имеет бесконечную протяженность. Если спектр
S (ω) — прямоуголен и спектры элементов не перекрываются, то
тогда Φ (t) описывается функцией вида sin х/х и сигнал имеет
бесконечную протяженность. В-третьих, перекрытие спектров элементов
в (,13.2) приводит к необходимости сложного суммирования в
определениях корреляционных функций частотных сигналов.
Рассмотрим теперь влияние \Ι (ί)\ на огибающую частотного
сигнала [69]. В двойной сумме (13.4) сгруппируем вместе слагаемые,
номера которых удовлетворяют сравнению (12.111), т. е. положим
ν as η + μ (mod N). (13.5)
Введем ненормированную периодическую АКФ кодовой
последовательности {aj (v)}:
V»= Ε4·(ν + μ)Μν).
ν = 0
Используя (13.5), (13.6), из (13.4) получаем
μ = 0
Если положить, что
v = o
то из (13.7) находим:
| / (/) ρ = м + Л^1 Vj (μ\ ехр (ίΔωίμ).
μ=1
В дискретные моменты времени
(13.6)
(13.7)
(13.8)
(13.9)
t = q 2π/ΝΑω,
(13.10)
251
Где q и Μ — взаимно-Простые числа, имеем
{I^l^N+^V^exp^n^^ (13.11)
μ=1
что полностью совпадает с формулой (12.104). Наименьшее
отклонение от постоянной составляющей (13.8), равной Ν, будет в том
случае, если Vj (μ)= 0 при всех q, т. е. тогда, когда АКФ Vj (μ) имеет
боковые пики, равные нулю. Это возможно для многофазных кодов
Фрэнка [174]. При этом частотные сигналы должны быть и
многофазными.
Если кодовая последовательность {α, (ν)} двоичная, то
наименьший пик-фактор у огибающей частотного сигнала будет в том
случае, когда в качестве кодовых последовательностей используются
последовательности Баркера и М-последовательности. Расчеты*
показывают, что для последовательностей Баркера с N = 7 и N =
— 11 пик-фактор равен 1,3 и 1,1 дБ соответственно, а для других
последовательностей Баркера пик-фактор лежит в пределах 1,8 —
2,8 дБ. Для Λί-последовательностей с N = 15, 31, 63 пик-фактор
равен соответственно 2,8; 3,6; 4,1 дБ, причем выбросы огибающей
будут в промежутках между дискретными моментами времени
(13.10).
Корреляционные функции частотных сигналов. КФ частотных
фазоманипулированных сигналов подробно рассмотрены в работах
[46, 69]. Для таких сигналов символ α,- (ν) записывается в следующем
виде:
fli(v) = exp[i^-6y(v)]f (13.12)
где г и ρ — взаимно-простые числа, bj (ν) — символ кодовой по-
следовательности {bj (ν)}, принимающий значения 0, ρ—1.
В табл. 13.1 приведены окончательные результаты работ [46, 69]
по определению кодовых последовательностей {bj (v)}, объема
систем и оценок максимумов ВКФ.
Система последовательностей первой строки табл. 13.1
образована циклическими перестановками Λί-последовательности с
основанием ρ и памятью я, причем ее длина N = рп — 1.
Во второй строке число а — первообразный корень по модулю
простого числа N + 1. При этом в формуле (13.12) должно быть
положено ρ = N + 1.
Все остальные правила основаны на степенных сравнениях
вида (12.112) для дискретных ФМ сигналов. Поэтому объем систем
и оценки ВКФ аналогичны тем же данным табл. 12.10. Чем больше
объем системы, тем хуже ее корреляционные свойства.
Частотные амплитудно-фазоманипулированные сигналы.
Любой произвольный сигнал можно представить в виде частотного,
* Расчеты проведены В. Н. Власовым.
252
Таблица 13.1
Правила образования
последовательности
Mv) = *(v+/)
bj(v) = c0av+l (modW + 1)
bj (ν) ξξ /ν2 + c-ι v+c0 (modΛ^)
Ьj (ν) = Cj3 V3 + С д V + С0
(mod N)
η
bJ (V) Ξ ^ 0-sVS + C!V +
s=2
+ c0 (modW)
Коэффициенты
{bj (ν)}
—Λί-последовательность
<ч> = 1,#; ν, /=0,7V—1
ci, c0 = 0,W—1;
/ = 1 ,iV— 1
cjs=l,tf-l;
tyi. co, V = 0,N —1
я > 3; cb c0, v = 0,W—1;
cjs = 0,N—\ ифО
одновремен но
η > 3; c/n = l,tf—1;
Cjtn-i = 0', остальные
cjs = 0,N— 1;
сь co = 0,W-l
η > 4 — четное;
ci, Co, v = 0,tf—1;
(Ο,Λ^— 1 при чет-
C/s=< ном S
Ιθ при нечетном S
Объем
системы
N
N
W-1
(Л^—1) Л^
Ν*-1—1
(iV—1) Λ^η-з
Λ/«/2_ι
Максимум
ΒΚΦ
1
1/л/
1
ул
1
У#
2
yw
η—I
Уы
л—1
У57
/г—1
yjv
253
если воспользоваться разложением efo в ряд Фурье. Расширим
пределы суммирования (13.1) до ±оо, ухмножим обе части равенства
(13.1) на ехр (—ΙμΑωί) и проинтегрируем в пределах интервала
(—π/Δω, π/Δω). В результате получим
π/Δω об π/Δω
J 1/,(*)ехр(—ίμΔω/)Λ= 2 αΛν) j" Φ(')Χ
—π/Δω ν=—οο —π/Δω
Χ exp [i (ν—μ) Δω/] Λ. (13.13)
Обозначим постоянную
π/Δω
7φ= Γ Φ{ί)άί (13.14)
—π/Δω
и положим, что 7ф Ф 0. Допустим, что имеет место условие
ортогональности:
*Т Φ0)βχρ[ί(ν-μ)Δωί]Λ = ί ° ПрИ ^^ (13.15)
-π*/Δω I Г*> при V = μ.
При выполнений условия (13Л 5) символы а5 (ν) определяются
из (13ЛЗ) следующим образом:
π/Δω
ty(v) = — f ^WexP(— ίνΔωήΛ. (13.16)
— π/Δω
Для реальных сигналов число слагаемых в суммах вида (13Л)
всегда можно ограничить при допустимой степени точности
воспроизведения сигнала Uj (t). Следовательно, произвольный сигнал с
допустимой степенью точности можно представить в виде частотного.
В общем случае символы α/ν могут содержать и амплитудную, и
фазовую манипуляции, т. е. сигнал будет частотным амплитудно-
фазоманипулированным.
13.2. Системы сигналов со смещением по частоте
Сигналы со смещением по частоте были определены в § 1.7.
Комплексная огибающая таких сигналов и их спектр описываются
формулами (1.99), (1.100), а ВФН —формулой (1ЛЗЗ). ВКФ сигналов
со смещением по частоте в соответствии с (1.133) определяется
следующей формулой
Rjk (τ) = Яф [τ, (/ — Α)Δω] ехр [i(k — 1) Δωτ], (13.17)
где R& (τ, Ω) — ФН исходного сигнала. Из (13.17) следует, что
ВКФ частотных сигналов полностью определяется сечением ФН
исходного сигнала.
254
В работе [198] в системе сигналов со смещением по частоте в
качестве исходного сигнала взята Λί-последовательность, В качестве
исходного можно использовать сигнал с квадратичной частотной
модуляцией [25]. Отметим, что при передаче информации в системе
с подвижными объектами использование сигналов со смещением по
частоте возможно только тогда, когда максимальный доплеровский
сдвиг частоты меньше Δω/2.
Глава 14
СИСТЕМЫ ДИСКРЕТНЫХ ЧАСТОТНЫХ СИГНАЛОВ И
ДИСКРЕТНЫХ СОСТАВНЫХ СИГНАЛОВ
14.1. Корреляционные функции дискретных частотных
сигналов и число совпадений элементов
Определение, свойства и корреляционные функции дискретных
частотных (ДЧ) сигналов были подробно рассмотрены в § 1.6. По-
видимому, первые ДЧ сигналы упоминаются в работе [6], где были
рассмотрены системы ДЧ сигналов небольшого объема. Развитие
методов построения ДЧ сигналов нашло отражение в [46, 65, 68,
75 — 77, 99, 100, 117, 118, 131, 220]. В данном параграфе напомним
основные определения ДЧ сигналов и определим взаимосвязь между
их корреляционными функциями и числом совпадений элементов
на частотно-временной плоскости.
Комплексная огибающая ДЧ сигналов. В § 1.6 была определена
комплексная огибающая ДЧ в общем виде. Конкретизируем это
определение так, чтобы можно было воспользоваться методами
комбинаторики и теории чисел. Положим, что ДЧ сигнал первого
порядка состоит из Μ элементов, а все элементы имеют одинаковую
форму Φ (t). Пусть номера элементов ν изменяются от 0 до Μ — 1,
cij (ν) — комплексная амплитуда v-ro элемента, а положение v-ro
элемента по частоте определяется сдвигом, равным γ7· (ν) Δω, где
γ7· (ν) символ частотной кодовой последовательности (ЧКП)
{уj (v)b причем γ7· (ν) при изменении ν = 0, Μ — 1 меняется в та-
ких же пределах от 0 до Μ — 1, но в определенном порядке.
С учетом сделанных предположений комплексная огибающая
ДЧ сигнала первого порядка в соответствии с (1.60) записывается
следующим образом:
Λί-1
U j (t) = Σ α, (ν) Φ (t — ν At) exp (i γ7· (ν) Δω/), (Η-J)
v=0
рричем здесь и в дальнейшем используется условие
ΔωΔ/ see 0 (mod 2 π), (14.2)
255
где Δω = 2 πΔ/ — ширина спектра элемента, Δ/ — его
длительность. Причем смещение соседних элементов по частоте равно Δω,
а по времени—Δ/. Как видно из (14.1), изменение аргумента у
элемента Φ (ή происходит линейно в соответствии с изменением ν,
а смещение по частоте — в соответствии с изменением γ7· (ν).
Например, для ДЧ сигнала, показанного штриховкой на
частотно-временной плоскости (рис. 14.1), ЧКП {γ7· (ν)} = (085210741963).
В § 1.6 была отмечена частотно-временная дуальность ДЧ
сигналов первого порядка. Использование ее позволяет вдвое
расширять применение тех или
ю
9
в
7
6
δ
δ
2
7
О
И
F
Л
ш
ж
щ
At
О 1
2 3 4 5 6 7 8 9
Г t
10 ι>
иных полученных
результатов. Чтобы воспользоваться
этим, преобразуем
комплексную огибающую ДЧ
сигнала, используя временную
кодовую последовательность
(ВКП) {ν7· (γ)} к
следующему виду:
Λί-1
Uj (t) = Σ aj (γ) Φ U —
— ν7· (γ) Δ Л ехр (ίγΔωί).
(14.3)
В формуле (14.3) 'линейно
меняется смещение по часто-
Рис. 14.1 те в соответствии с
изменением γ = 0, N — 1, а
изменение аргумента у элемента Φ (ή происходит в соответствии
с изменением ВКП {ν7· (γ)}, символы которой изменяются в тех
же пределах от 0 до Μ — 1, но в определенном порядке.
Например, для ДЧ сигнала, изображенного на рис. 14.1, ВКП {ν7· (γ)}=
= (073106295184).
Формулы (14.1), (14.3) и определяют частотно-временную
дуальность ДЧ сигналов: в (14.1) отсчет производится по времени (по
номерам дискретов ν), а в (14.3) — по частоте (по сдвигу частоты,
пропорциональному γ).
Корреляционные функции ДЧ сигналов первого порядка.
Используя определение (1.69) ФН Ro (τ, Ω) элемента Φ (t) и условие
(14.2), из (1.70) можно получить ВФН сигналов (14.1), (14.3).
Полагая Ω = 0 и учитывая предположения, сделанные при определении
комплексных огибающих (14.1), (14.3), из (1.74) найдем, что ВКФ ДЧ
сигнала с ЧКП (14.1)
Λί-ΙΛί-l #
*л W = ТГ Σ Σ as Μ uh 0*) #ф <τ + U* - ν) Δί,
[γ>(ν)—γΛ(μ)]Δω}·
(14.4)
25а
а ВКФ ДЧ сигнала с ВКП (14.3)
М—1М — 1 4
^ft(T)=i Σ Σ м^% ® #*>{*+к©-
-v}(y)]At, (γ-ξ)Δω). (14.5)
Рассмотрим ВКФ (14.4), (14.5) в дискретных точках, полагая
τ = Ш. (14.6)
Подставляя (14.6) в (14.4), (14.5), получаем:
Λί-ΙΛΙ-l #
^(λ)=^Σ Σ αΠν)β*(μ)Λφ{(λ + μ-ν)Δ/,[ϊ,(ν)-ν*^μ)]Δω};
ν=ο μ=ο (14<7)
Λί— 1 Λί— 1
^*(λ)==^ Σ 2^(ν)Α(6)Λφ{[λ + νΛ(6)-νΠν)]Δί.(Τ-ΘΔω}.
Анализ ВКФ (14.7), (14.8) сущестенно упрощается, если
использовать условия ортогональности элементов, которые сводятся к
тому, что различные элементы не перекрываются во времени, а их
спектры не перекрываются по частоте. Отметим, что такие условия
не могут выполняться одновременно, так как спектр функции,
ограниченной по длительности, имеет неограниченную ширину. Но для
простоты анализа будем считать, что условия ортогональности
имеют место. Поэтому положим, что в дискретных точках частотно-
временной плоскости для ФН элемента Φ (ή выполняются условия
ортогональности, а именно:
ό ί А4 А ч Г1 при ρ = 0, q = О, ли оч
Кф(ρΔί, ?Δω) - |0 при остальных значениях р, q. l14-y)
Используя условия ортогональности (14.9) и полагая |α7· (ν) | =
= I ak (μ) Ι = 1» из (14.7), (14.8) получаем оценку модуля ВКФ в
дискретных точках
|Дм(*)| <т/М, (14.10)
где т — число решений следующих систем уравнений:
λ+ μ — ν = 0
νΠν)-Τ*(μ) = 0 J' (14Л1)
^ + vat)-vj(v)-0j (l412)
Система (14.11) соответствует ВКФ (14.7), а система (14.12) —
ВКФ (14.8). В этих системах λ изменяется от — Μ до Λί, а ν, μ,
9 Зак. 2093 257
γ, ξ = Ο, Μ—1. Используя*, одно из уравнений систем (14.11),
(14.12) сведем эти системы к уравнениям:
T/(v)-V* (ν -λ) = 0; (14.13)
ν/ (?) - vft (?) -λ = 0. (14.14)
Число решений целочисленных уравнений (14.13), (14.14)
меньше числа решений соответствующих сравнений по модулю Λί:
?7 (ν) — Тл (ν — λ) = 0 (mod Λί); (14.15)
vy (?) — vft (γ) — λ — 0 (mod Λί). (14.16)
Сравнения (14.15), (14.16) являются частными случаями
сравнения
«у (ν) — OLk (ν — μ) — λ = 0 (mod Λί), (14.17)
где ν = 0, Λί — 1, λ == 0, Λί — 1, μ = — Λί, Λί.
Если сравнение (14.17) имеет /η решений, то оценка (14.10)
преобразуется к следующей
\Rjk(V\<m/M, (14.18)
причем т ^ т. Если m = 0, то формально | Rjk (λ) | = 0, но это
будет в том случае, если всюду выполняется условие
ортогональности (14.9). Но так как строгой ортогональности во всех
дискретных точках добиваться нельзя, то при
т = Q\Rjk (λ)| « ИМ.
Поскольку последовательности {а7·} и {<xk} состоят из символов,
принадлежащих к одному алфавиту (0, 1, ..., Μ — 1), то при
изменении номеров ν, μ, λ рано или поздно возможно совпадение кодовых
последовательностей, т. е. возможно решение сравнения (14.17).
Если при данных ν, μ, λ, /, k имеет место одно решение (одно
совпадение), т. е. т = 1, то | Rjk (λ) | = ИМ. Увеличение числа решений
приводит к следующему. Во-первых, к увеличению максимального
уровня ВКФ согласно (14.18). Во-вторых, ухудшает использование
отведенной полосы частот для сигнала (14.1) с ЧКП, так как спектры
некоторых элементов будут совпадать: ухудшает использование
отведенного времени и пик-фактор сигнала (14.3) с ВКП, так как
будут совпадать некоторые элементы. В-третьих, увеличивает число
сигналов в системе. Именно третье следствие позволяет строить
большие системы сигналов, но при условии /п > 1. Назовем ДЧ
сигналы, обеспечивающие одно совпадение т = 1, оптимальными.
Они будут подробно исследованы в данной главе.
258
14.2. Комбинаторный анализ систем дискретных частотных
сигналов
Дискретные частотные сигналы произвольного порядка. Хотя
основной материал данной главы посвящен ДЧ сигналам первого
порядка, но сначала для общности кратко рассмотрим ДЧ сигналы
порядка К и найдем объем подкласса ДЧ сигналов, частотные
элементы которых расположены на различных частотах. Напомним
(см. § 1.6), что ДЧ сигналы порядка К состоят из N временных
элементов, каждый из которых состоит из К частотных элементов.
Число частот равно М. Необходимым условием того, что совпадений
не будет, является то, что Μ кратно /С, т. е. К делит М. Более того,
должно удовлетворяться равенство
Μ = ΝΚ, (14.19)
так как каждый временной элемент содержит К частотных
элементов, а их общее число ΝΚ не может быть больше Μ. Определим число
способов размещения элементов на частотно-временной плоскости
без совпадения. В первом временном элементе К частотных
элементов на Μ позициях могут быть размещены С*м способами. На долю
частотных элементов второго временного элемента остается Μ — К
позиций. Поэтому К частотных элементов второго временного
элемента могут быть размещены См-к способами и т. д. Поскольку
выбор позиций частотных элементов в различных временных
элементах происходит независимо, то на основании правила
произведения необходимо перемножить все биномиальные коэффициенты
вида См_(/_1)к» где /=1, N. Кроме того необходимо учитывать
амплитудную и фазовую манипуляции элементов, т. е. число
размещений элементов по частоте необходимо умножить на множитель
ρΚΝ _ рМ^ где ро — основание манипуляции (8.1). Окончательно
объем подкласса ДЧ сигналов без совпадения элементов равен
«=Р5Т1 CJS-(/-i,k· (14.20)
Используя определение (8.3), можно непосредственно показать,
что
N
Π Сй_</_!)*= (-^улГ= (Ю)м/к · (14*21)
Подставляя (14.21) в (14.20), получаем
м М\
(ΚΙ)1
259
^ = ^т^да· d4.22)
Найдем отношение объема исследуемого подкласса к объему
класса ДЧ сигналов порядка К- Из (8.5), (14.22) с учетом (14.19)
имеем
L/C _ [(М-К)\]м/К
LK (м\)М1К-1
(14.23)
При К = Μ отношение Lm/Lm = 1, поскольку такие сигналы имеют
всего лишь один временной элемент, т. е. являются частотными.
В случае ДЧ сигналов первого порядка из (14.22) имеем
а отношение (14.23) имеет следующий вид:
Л.
Li
№-\)\
,м
М\
(М\)
М— 1
Μ
м
(1 4.24
(14.25)
В табл. 14.1 приведены значения отношения (14.25) при
различных М.
Таблица 14.1
Μ
LVLi
2
5.10~ι
4
10-1
6
Ι,β.ΙΟ-2
8
2,5-10-3
10
3,6-10-4
Как следует из табл. 14.1, доля ДЧ сигналов без совпадений
элементов резко уменьшается с ростом М. Чтобы выяснить закон
уменьшения ЬУЬк, обратимся к асимптотической формуле Стирлинга
для факториала
(14.26)
п\ ~ У'2пп ппе-п.
Подставляя (14.26) в (14.23) и преобразуя, находим
f.„y2m(V=j£)
(14.27)
Если К СМ» то, используя предел (1 — х'1)* = е"1 при χ
оо, получаем
LK \ Μ )
К ^_Λ1<1_1/2Κ) _Д1
(14.28)
Из (14.28) следует, что уменьшение Vk)L·^ определяется в
основном экспонентой е~м. Из (14.28) для К = 1 имеем
1г
(14.29)
260
Если К соизмеримо с М, то использовать указанный ранее
предел нельзя. Но экспоненциальный характер уменьшения L^/LK
сохраняется до относительно больших /С Например, при К = Λί/2
из (14.27) находим
-£Щ1~УШ2-{м+1\ (14.30)
т. е. отношение (14.30) изменяется в основном как 2гм.
Таким образом, при большом Μ подкласс ДЧ сигналов порядка
К без совпадений элементов составляет малую долю от всего класса.
Если нет регулярного метода, то выбор такого подкласса может быть
сопряжен с большими вычислительными трудностями.
Формулы (14.20), (14.24) позволяют найти объем подкласса ДЧ
сигналов порядка К, не имеющих Ба своей частотно-временной
плоскости совпадений по частоте. Именно такие сигналы будем
рассматривать в данном параграфе. Перейдем к определению числа
совпадений элементов ДЧ сигналов при их взаимодействии, т. е. когда на
полезный сигнал накладывается мешающий. При этом будем
рассматривать ДЧ сигналы первого порядка.
Распределение числа совпадений в периодических
корреляционных функциях. Число совпадений элементов т в ДЧ сигналах
первого порядка согласно (14.10) определяет ВКФ таких сигналов в
дискретных точках. Найдем распределение вероятностей Рм ψι)
появления т совпадений. Сначала рассмотрим случай, когда два
ДЧ сигнала (полезный и мешающий) полностью перекрываются по
времени. При этом число совпадений т может изменяться от 0 до Μ.
Полное перекрытие двух сигналов возможно, когда между полезным
и мешающим сигналом нет временного сдвига или когда каждый из
сигналов излучается непрерывно (периодически). При этом на
выходе согласованного фильтра будем иметь периодическую ВКФ.
Перейдем к распределению числа совпадений.
Число ДЧ сигналов первого порядка без совпадающих частот
определяется формулой (14.24). Поскольку амплитудная и фазовая
манипуляции не влияют на число совпадений т в (14.10), то положим,
что в (14.24) основание манипуляции р0 = 1. При таком
предположении число ДЧ сигналов первого порядка без совпадений элементов
по частоте согласно (14.6) равно
Ц = М1 (14.31)
Соответственно число пар сигналов равно (Λί!)2. Из них М\ пар
сигналов состоят из тождественно одинаковых сигналов и имеют Μ
совпадений, а из оставшихся (М\)2 — М\ пар сигналов половина
не различима, так как каждой паре с номерами / и / соответствует
пара с номерами / и /, т. е. из (Λί!)2 можно исследовать не более
[(Λί!)2 — Λ1Π/2 пар сигналов.
Каждому ДЧ сигналу первого порядка без совпадений
элементов по частоте может быть сопоставлена перестановка цифр 1,2,.., Μ,
261
соответствующая частотной кодовой последовательности. Например,
для Μ = 4 все перестановки приведены в табл. 14.2.
Таблица 14.2
о.
Ном
1
2
3
4
5
6
Перестановка
12 3 4
12 4 3
13 2 4
13 4 2
14 2 3
14 3 2
о.
О)
2
О
7
8
9
10
И
12
Перестановка
2 13 4
2 14 3
2 3 14
2 3 4 1
2 4 13
2 4 3 1
ι α
2
°
13
14
15
16
17
! 18
Перестановка
3 12 4
3 14 2
3 2 14
3 2 4 1
3 4 12
3 4 2 1
1 Л
О)
о
X
19
20
21
22
23
24
Перестановка
4 12 3
4 13 2
4 2 13
4 2 3 1
4 3 12
4 3 2 1
Перестановка № 8 2 1 4 3 соответствует тому, что первый элемент
расположен на второй частотной позиции, второй—на первой,
третий — на четвертой и четвертый — на третьей.
Произвольная пара перестановок может иметь т совпадений,
причем т = 0, М. Определим число пар перестановок, имеющих
заданное число совпадений. Эта задача сводится к комбинаторной
задаче «о встречах» [132]. Решить ее можно следующим образом.
Выберем произвольную перестановку из общего числа, например,
перестановку № 8 из табл. 14.2 или какую-либо другую. Все выборы
равноправны. Обозначим через Dm,™ число перестановок, имеющих
т совпадений с выбранной. Так как число различных выборок
исходной перестановки равно М\, то число пар перестановок,
имеющих т совпадений, будет равноМ\ Dm, m- Относительное число пар
перестановок с т совпадениями или вероятность т совпадений равна
Рм(т)
^DM,m_DM,m
(М!)а
ΛίΙ
(14.32)
Число Dm, m называется субфакториалом[\32], так как доказано,
что оно имеет много свойств аналогичных свойствам факториалов.
Чтобы определить Dai, ™, используем комбинаторный принцип
включения и исключения [132]. Он заключается в следующем. Пусть
имеется N объектов, из них N (а) обладают свойством а. Тогда число
объектов, не обладающих свойством а, равно Ν (α') = N — N (а).
Если рассматриваются два свойства аг и а2> то число объектов, не
обладающих ни одним из этих свойств, равно N (<х\, aQ = N —
-Ν Κ) - JV (α2) + JV К, α2).
Общее правило включения и исключения тех или иных N (...)
дается следующей символической формулой [132]:
Ν (αί, а'2у αί, ...) = N1(1— аг) (1 — а2) (1 — а3) ...]. (14.33)
Смысл символической формулы (14.33) состоит в том, что сначала
вычисляется содержание квадратных скобок, а затем знак функции N
262
применяется к каждому из полученных слагаемых подобно тому,
как это сделано в следующем примере: Ν (αί, ol'2) =
= ЛМ(1 — αχ) (1 — α2)] = Ν (Ι — аг — а2 + αχα2) =
= Ν (1) — N К) — Ν (α2) + Ν (αια2), где Ν (1) = Ν.
Вернемся к перестановкам. Обозначим через αχ то свойство
пары перестановок ( выбранной и произвольной), которые имеют на
одном месте один и тот же элемент а±. Число таких перестановок
обозначим Nfai). Соответственно через N(a2) обозначим число
перестановок, у которых остается на одном и том же месте элемент а2
и т. д. Поскольку элементы (числа) в перестановках равноправны,
то N (аг) = Ν (α2) и т. д. Так как каждый элемент может быть выбран
См = Λί способами в перестановке из Λί элементов, то общее число
перестановок, имеющих на своих местах хотя бы по одной цифре,
равно См N (ax) = CmNv Через аха2 обозначим свойство
перестановок, имеющих на одинаковых местах элементы аг и а2. Общее
число перестановок, имеющих парные совпадения цифр, равно
См N (axa2) = CmN2k т. д. Продолжая подобные рассуждения и
используя формулу (14.33), можно найти [132], что число перестановок,
не имеющих совпадений с выбранной, равно
DM = DM, 0 = N — C1MN1 + C%N2 -
-Cfctf. + ... + (-1)"СЙ#А!, (14.34)
где N = М\. Определим Nj, j = 1, Λί. Если в перестановке
фиксируется один элемент, то остальные Μ — 1 элементы можно выбрать
(Λί — 1)! способами. Поэтому Ν± = (Λί — 1)!. Если фиксируются
два элемента, то остальные можно выбрать (Λί — 2)! способами
и Ν2 = (М — 2)!. В общем случае Nj = (Ν — /)!. Подставляя эти
значения Nj в (14.34) и раскрывая биномиальные коэффициенты,
окончательно получаем выражение для субфакториала
0-_М[,_±. + Л_... + (_,/'Х]. (14.35)
В табл. 14.3 приведены значения для субфакториала DM.
Таблица 14.3
Μ
dm
1
0
2
1
3
2
4
9
5
44
б
265
7
1854
8
14833
9
133496
10
1334961
Например, для Λί = 4, D4 = 9, т. е. имеется 9 перестановок без
совпадений. Для перестановки №8 из табл. 14.2 перестановки с
номерами 1, 3, 6, 15, 17, 18, 22, 23, 24 не имеют совпадений.
263
Перейдем к определению DM, т при т > 0. Число перестановок,
у которых т элементод совпадают, а остальные Μ — т меняют свое
положение, равно
Dm, m = CmDm—ш· (14.36)
Действительно, сначала надо выбрать, какие т элементы остаются
на месте. Это можно сделать См способами. Остальные Μ — т
элементов можно переставлять любыми способами, лишь бы не было
совпадений. Это можно сделать DM-m способами. Используя правило
произведения, получаем (14.36). Соотношения (14.35) и (14.36)
позволяют рассчитать субфакториалы для любых Μ и т. Таблицы DM, m
приведены в [132]. Для субфакториалов известно рекуррентное
соотношение
Dm = MDM-X + (-I)**, (14.37)
которое позволяет найти любое Dm· Формулы (14.32), (14.35) —
(14.37) позволяют найти вероятность т совпадений.
При больших Μ выражение в квадратных скобах (14.35)
стремится к е-"1, что позволяет аппроксимировать распределение
вероятностей (14.32) законом Пуассона со средним значением, равным
единице [132]:
Рм (m) ~-!-. (14.38)
ет\
Формула (14.38) получается при замене субфакториала Dm, m в (14.32)
согласно (14.35), (14.36). Из (14.38) следует, что при Μ > 1
вероятность Рм(т) практически не зависит от Λί. Наиболее вероятны
случаи, когда т = 0 (совпадений нет) и/п= 1 (одно совпадение). Их
вероятности примерно равны е-"1 ^ 0,368. В табл. 14.4 приведены
значения вероятностей Р^ (т) для Μ = 5 и Μ = 9, рассчитанные по
точным формулам (14.32), (14.36) и таблицам, приведенным в [132].
Таблица 14.4
т
Р9 (т)
0
0,366
0,368
1
0,375
0,368
2
0,167
0,184
3
0,083
0,061
4
0
0,015
5
0,0083
0,003
6
510~4
7
Ю-*
8
0
9
З-10-β
Сравнение данных табл. 14.4 с законом (14.38) позволяет
использовать этот закон для приближенных расчетов. Распределение
Р5 (т) при Μ = 5 (табл. 14.4) незначительно отличается от
распределения (14.38), а распределение Р9 (т) при Μ = 9 практически не
отличается от (14.38). Поскольку наиболее вероятными согласно
(14.38) являются или т = 0, или т = 1, то модуль ВКФ (14.10)
наиболее вероятно будет равен или 0 или ИМ. Среднее значение
264
числа совпадений, распределенного по закону Пуассона (14.38),
равно 1. Поэтому среднее значение модуля ВКФ (14.10) будет равно
R = т, { | Rjh (λ) Ι }
1/Λί.
(14.39)
Рис. 14.2
Вероятность появления т = 0 или т = 1 равна 0,736,
вероятность появления т ^ 2 равна 0,92, а вероятность появления т <
<4 равна 0,981. Отметим, что эти вероятности согласно (14.38)
не зависят от М. И поэтому при Μ > 1 уровни ВКФ (14.10) должны
быть малыми.
Распределение числа совпадений в апериодических
корреляционных функциях. Если полезный и мешающий сигналы
перекрываются частично, то в этом случае на
выходе согласованного фильтра будет
иметь место апериодическая ВКФ.
На рис. 14.2 изображено совместное
расположение двух частично
перекрывающихся ДЧ сигналов первого
порядка: сигнал А (левая штриховка)
опережает сигнал В (правая
штриховка) на два элемента. Перекрытие
сигналов возможно только в
прямоугольнике АВ, выделенном толстой
линией. При перекрытии сигналов А
и В, изображенном на рис. 14.2, имеет
место одно совпадение (квадрат с
совпадающими штр иховками).
Распространим задачу «о встречах» на случай смещения во
времени одного сигнала относительно другого. Будем
рассматривать временной сдвиг, кратный длительности элемента Δ/, т. е.
положим τ = ηΔ/, где η — целое число, удовлетворяющее условию
| я | = Ο,Λί, где Μ — число элементов в ДЧ сигнале. При η = 0
имеем случай периодической ВКФ, при | η \ = Μ сигналы не
перекрываются. Так как η полностью характеризует временной сдвиг, то
в дальнейшем будем оперировать только с я.
Задачу «о встречах» при произвольном сдвиге η можно свести к
предыдущей при η = 0. Если сдвиг равен я, то ширина
прямоугольника перекрытия сигналов (прямоугольник АВ на рис. 14.2) равна
Μ — п. Число различных ДЧ сигналов, размещающихся на
прямоугольнике перекрытия без совпадающих частот, будет меньше
определяемого формулой (14.31). Определим это число. На первой
временной позиции элемент может быть выбран Μ способами, на
второй—(Λί — 1) способами , на Μ — η позиции — (η + 1)
способами. В итоге число ДЧ сигналов с числом элементов (М — п)
равно
ΙΐΛ = Λί(Λί-1):..(η+1) = ^. (Η.40)
п\
Число пар тарих сигналов равно (М\/п\)2
265
Выберем произвольный ДЧ. сигнал с числом элементов Μ —η
и числом частотных поеиций Μ и рассмотрим число его совпадений
с другими подобными ДЧ сигналами. Обозначим через Dm, т, n число
сигналов, имеющих т совпадений с выбранным. Отметим, что выбор
исходного сигнала, совпадения которого рассматриваются, не имеет
значения, так как с комбинаторной (вероятностной) точки зрения
все сигналы равноправны. Так как число выборов исходного
сигнала равно L*n (14.40), то число пар сигналов, имеющих т
совпадений, равно DM, т, п L*n. Вероятность т совпадений равна
относительному числу пар с т совпадениями, т. е.
Р /^\ _ L*n DM, m,n_nl DM, m, η (\ΛΛΛ\
Рм,п(т)- — . (14.41)
Формула (14.41) получается непосредственно, если число
сигналов Dm, m,n с т совпадениями с исходным сигналом разделить на
число сигналов L*n (14.40).
Для определения числа Dm, m, n используем принцип включения
и исключения [132], символическая запись которого определяется
формулой (14.33). Обозначим через аг то свойство двух
перекрывающихся сигналов, что элемент аг у них совпадает. Соответственно
через Ν (αχ) обозначим число сигналов, имеющих совпадающий
элемент аг. Точно так же Ν (α2)—число сигналов, имеющих
совпадающий элемент а2 и т. д. Так как элементы в перестановках
равноправны, то Ν (αχ) = N (а2) = ... = Nv Каждый элемент может быть
выбран См-п = Μ — η способами. Поэтому общее число сигналов,
имеющих хотя бы одно совпадение, равно См—п Νν Число Ν±
определяется следующим образом. Так как рассматривается одно
совпадение, то зафиксируем этот элемент. Остальные Μ — η — 1 элементы
можно выбрать (ЛГ — 1) (М — 2) ... (п + 1) = (Λί — 1)!/л!
способами. Следовательно, Ν± = (Λί — 1)! / п\.
Обозначим через αχα2 то свойство двух сигналов, что они имеют
два совпадающих элемента а1э а2. Общее число сигналов, имеющих
двойные совпадения, равно Ch-n Ν (αχα2) =CM-nN2. Фиксируя два
элемента и осуществляя перестановки остальных Μ — η — 2
элементов, получаем Ν2 = (Μ — 2)! In\.
Продолжая рассматривать тройные совпадения и т. д. методом
математической индукции с применением формулы (14.33), находим
число сигналов, не имеющих совпадений с исходным*):
1Jм, of η =—; ; L,M—n-r
+ -fc^-C|i_„-... + (-l)A1-"C^. (14.42)
*) Формула (14.42) была получена О. В. Матвеевой.
266
Преобразуя, получаем
>М% 0, л = ■
М\
1 —
Μ
"М-
М(М — 1)
+ (-!)'
Λί-
(14.43)
При η = 0 правые части формулу (14.42), (14.43) совпадают с
определением субфакториала (14.35). Определим Ом,т,п при числе
совпадений т > 0. Допустим, что два сигнала имеют т совпадений.
Элементы, которые совпадают, можно выбрать С м-η способами.
Остальные Μ — т — η элементов не должны иметь совпадений.
Их число равно Ом-т,0, п* Следовательно, число сигналов,
имеющих т совпадений, равно
Вм,т,п — См —η Dm-
т, 0, п>
(14.44)
где DM-mio,n определяется согласно (14.43).
Расчет вероятностей т совпадений следует производить согласно
формулам (14.41) — (14.44). В табл. 14.5 приведены результаты
расчета этих вероятностей при произвольном сдвиге η для Μ = 5,
а в табл. 14.6 для Μ = 9.
\п |
0
1
2
3
4
Табл ι
а ца 14.5
т
0
0,366
0,442
0,533
0,65
0,8
1
0,375
0,367
0,350
0,30
0,2
I 2
0,167
0,150
0,100
0,05
з 1
0,083
0,033
0,017
4
0
0,0083
5
0,0083
\п\
0
1
2
3
4
5
6
7
8
Τ
а б л и ца 14.6
1 т
1 °
0,368
0,408
0,456
0,505
0,564
0,630
0,708
0,790
0,889
1 | 2
0,368
0,367
0,362
0,356
0,341
0,300
0,256
0,196
0,111
0,184
0,164
0,140
-0,115
0,085
0,062
0,035
0,014
3 | 4 | 5 | 6 | 7 | 8
0,061
0,048
0,035
0,024
0,014
0,007
0,001
0,015
0,010
0,006
0,003
0,001
3-10-4
0,003
0,002
8-10-4
з-ю-4
7.10-5
5.10-4
2-10-4
7,7-10-Ё
1,7-10-5
10-4
2-10-5
5,5-Ю-6
0
З-10-β
•
3-10-6
267
Считая, что сдвиг η может равновероятно принимать любое
значение от — (Λί — 1) до (Λί — 1), определим среднюю по сдвигам
вероятность совпадений следующим образом:
_ Λί—1
Рм(т) = (2М-1)-1 ^ рм,п(т). (14.45)
Л=_(М_1)
Так как совокупность всех сдвигов и совпадений составляет
полную группу событий, имеем
м _
2 РмИ = 1. (Н.46)
В табл. 14.7 приведены средние вероятности совпадений для
Μ = 5 и Μ = 9.
Таблица 14.7
Μ
5
9
т
0 | 1 | 2 | 3 | 4 | 5
0,585
0,604
0,312
0,290
0,085
0,083
0,020
0,019
0,002
0,003
9-10-4
5-Ю-4
6 | 7 | 8
6,8·10-§
.9-10-е
3.10-*
1
9
1,6.10-1
На рис. 14.3 сплошными линиями изображены огибающие,
построенные по значениям вероятностей табл. 14.7. Штриховой линией
показана огибающая закона (14.38).
Если сдвиг η небольшой (п < 0,6 Λί), то для DMt о, п справедлива
следующая приближенная формула:
ОМл0гП~-^-. (14.47)
При этом вероятность совпадений (14.41) с учетом (14.44) будет
приближенно равна
Ст ι Ст
Ραι. η И - ^^ _i_ e J£=« PM (m), (14.48)
Cl mle eg
где Рм(т) определяется согласно (14.38). Более точное приближение
для больших η обеспечивает следующая формула для вероятности
совпадений:
PM,e(«)~-^(l + -JL_W(m). (14.49)
Гт \ М—т
Но формула (14.49) будет справедлива лишь при т < Λί.
Вероятность появления оптимальной пары сигналов.
Оптимальной парой ДЧ сигналов назовем такую, сигналы которой имеют не
268
более одного совпадения при произвольном сдвиге я. Обозначим
вероятность появления такой пары через Рм опт- Для ее определения
обратимся к вероятности совпадения Рм,п (т) и составим таблицу
этих вероятностей при всех пит. Для Μ = 5 эти вероятности
представлены в табл. 14.8.
При η < 0 вероятность PMf-n(m) = Рм, η (tn), что было учтено
при составлении табл. 14.8. Конкретные значения Р5,п(т) приведе-
0,6
0,5
W
цз
0,2
0,1
О 1 2 δ 4 т
Рис. 14.3
ныв табл. 14.5. Пара сигналов будет оптимальной, если при любом η
число совпадений равно 0 или 1. Используя правила сложения и
умножения вероятностей [104], получаем, что при Μ = 5 в
соответствии с табл. 14.8 вероятность появления оптимальной пары
сигналов равна
М— 1
Ρ5οπτ = ίΡ5>ο(0) + Ρ5,ο(1)] Π [Р5,п(0) + Р5>п(1)12. (14.50)
л = 1
Суммы в квадратных скобках равны вероятностям появления
О, 1 при заданном сдвиге т. При выводе (14.50) было допущено, что
совпадения при различных сдвигах независимы друг от друга.
Поэтому Рм опт равна произведению сумм вероятностей при
η = — (Λί — 1), Μ — 1. Так как вероятности совпадений при η < 0
равны вероятностям при η > 0, то под знаком произведения стоят
квадраты сумм вероятностей. Подставляя значения вероятностей из
269
Таблица 14.8
m
0
1
2
3
4
5
η
-4 I -3
Рб.4<0)
РвУ1»
Рв.з0>
Ре.."
Рв.з<2>
-»
Рв,2:°>
Рв,2(1>
Рв>2<2)
Рв,2(3)
-ι
Рвд<0)
Рвл(1)
Рвл"»
Рвл<3)
Рвл<4)
0
Рв,о<0>
Рв.о"
Рв.о(2)
Рв.о(3>
Рв.о<4)
Рв.о<5>
1
Рвл;о>
Рвл2)
Рвл2)
Рвл<3)
Рвл(4)
2 | 3
Рв.2(0>
Ре.·'1»
р...·»
Рв.2<3>
Рв.з<0)
Рв.з(1>
Рв.з(2)
4
Р5.4<0>
Рв.4(1>
табл. 14.5 в (14.50), получаем, что вероятность появления
оптимальной пары сигналов при Μ = 5 равна Р5опТ == 0>34.
При произвольном Μ из формулы (14.50) получаем
Λί—Ι
Рлюпт = [Рм,о(0) + Рл1,о(1)1 Π [ΡΛί,η(0) + ΡΛί,Λ(1)12. (14.51)
л = 1
Вероятность случайного выбора оптимальной ДЧ системы
сигналов. Выберем случайным образом ДЧ систему с объемом У. Найдем
вероятность того, что в выбранной системе все пары сигналов будут
оптимальными, т. е. имеется не более одного совпадения. Такую
систему назовем оптимальной системой.
В системе из J сигналов имеется Ρ пар. Из них J пар
приходится на тождественно одинаковые сигналы, а из оставшихся надо
рассматривать только половину. Поэтому необходимо иметь
Q = о,5 (Р - J)
(14.52)
оптимальных пар. Поскольку вероятность появления случайной
пары равна Рмопт(14.51), то вероятность случайного выбора
оптимальной системы равна
Р</опт = Р&опт> (14.53)
где Q определяется формулой (14.52). В табл. 14.9 приведены
результаты расчета Pjom для Μ = 5 и Р5опТ = 0»34.
С увеличением объема
Таблица 14.9 оптимальной системы
вероятность ее случайного
выбора резко
уменьшается. Согласно (14.52)
показатель степени в (14.53)
J
Pj
•Όπτ
2
0,34
3
3,8-10-2
4
1,4-Ю-з
пропорционален J
обусловливает
уменьшение Pj 0пт
2
что и
сильное
с
ростом J. Следовательно, для нахождения оптимальных ДЧ систем
необходимо иметь регулярные, а не случайные методы.
270
14.3. Полный код дискретных частотных сигналов первого
порядка
Объем оптимальной системы ДЧ сигналов первого порядка.
Структура ДЧ сигнала (рис. 14.1) определяется местоположением
элементов сигнала на частотно-временной плоскости. Взаимное
расположение элементов полностью определяется их задержкой
по времени относительно начала координат. Точно так же
можно описать расположение элементов путем использования из
задержек относительно друг друга, другими словами, интервалов
между ними. Например, интервал между десятым и девятым элементами
(номера указаны по оси частот на рис. 14.1) равен 4Δ/, или просто 4,
а между девятым и восьмым элементами равен — 7. Знак минус
появился из-за изменения направления отсчета. Между двумя
произвольными элементами ДЧ сигнала первого порядка положительные
интервалы могут быть равны 1, 2, ..., Μ — 1, т. е. их число будет
Μ — 1. Точно так же отрицательные интервалы могут быть —1,
—2, ... —(М — 1) и их число равно Μ — 1. Нулевых интервалов
в ДЧ сигнале первого порядка не может быть, так как элементы не
расположены на одном временном интервале. Таким образом, число
различных интервалов между парой элементов равно 2 (Λί — 1).
Возьмем два произвольных ДЧ сигнала первого порядка.
Выберем в каждом из них две произвольные пары элементов на
совпадающих частотах. Если интервал между парой элементов у одного
сигнала не равен интервалу между парой элементов второго сигнала,
то при взаимном сдвиге по времени эти пары дадут не более одного
совпадения. Два совпадения возможны только тогда, когда интервал
между выделенными элементами одного сигнала равен интервалу
между элементами второго сигнала. Таким образом, чтобы две
частотные строки двух сигналов давали не более одного совпадения,
необходимо выбирать интервалы между элементами сигналов
различными.
Так как число различных интервалов между парой элементов
равно 2 (Λί — 1), то можно образовать 2 (М—1) пар частотных строк,
дающих не более одного совпадения при попарном положении этих
строк и любом временном сдвиге. Однако число оптимальных ДЧ
сигналов будет меньше, чем 2 (Λί — 1). Чтобы объяснить этот
результат, будем рассматривать сначала ДЧ сигналы с четным Λί.
Пример такого сигнала приведен на рис. 14.1. Такой сигнал состоит
из Λί/2 пар частотных строк.
Сначала рассмотрим процесс образования пар для
положительных интервалов, число которых, как отмечено ранее, равно Λί—1.
Первую пару частотных строк можно выбрать Λί — 1 способом..
При этом будет использован и максимальный интервал, равный
Λί — 1. Так как элементы в ДЧ сигнале первого порядка не могут
занимать одинаковые временные интервалы, то для последующих
пар частотных строк нельзя использовать интервал, равный Λί — 1.
Поэтому на вторую пару частотных строк приходится Μ — 2 раз-
271
личных интервалов, причем максимальный равен Μ — 2. Точно
так же на третью пару частотных строк будет приходиться Μ — 3
различных интервала, на k-ю пару Μ — k интервалов. Так
как в сигнале всего Μ12 пар, то на последнюю пару приходится
0 0 Ξ 0 0 0 Ξ Ξ Ξ Ξ
11 12 13 14 15 16 17 18 19 20
Ξ Ξ Ξ Ξ Ξ Ξ Ζ3 Ξ Ξ Ξ
21 22 25 24 25 26 27 28 29 30
ΞΊ3ΞΗ0ΞΞΗΞΕ3
31 32 . 33 34 35 36 37 38 39 40
Η й И И S 0 Ξ Ώ Ξ Ξ
41 42 43 44 45 46 47 48 49 50
ΏΞΞΏΞΞΞΞΞΞ
51 52 53 54 55 56 57 58 59 60
Ξ Ξ ЕЭ ЕЭ 0 ЕЭ 0 Ξ И Ξ
07 £2 &J 64 65 66 67 68 69 70
71 72 73 74 75 76 77 76 79 80
ΏΞΞΞΞΞΏΏΞΏ
81 82 83 84 85 86 87 88 89 90
ΗΞΏΞΏΏΗΗΏΞ
91 92 93 94 95 96 97 96 99 100
ΗΗΞΞΗΗΗΞΗΞ
101 102 103 104· 105 106 107 108 109 110
Ξ Ξ 0 0 Ξ Ξ Ξ Ξ Ξ Ξ
111 112 113 114 115 116 117 118 119 120
Ξ Ξ Ξ Ξ ЕЭ S Ξ Ξ Η Κ
Рис. 14.4
Λί—Λί/2=Λί/2 различных интервалов. Из Λί/2 интервалов можно
образовать только Λί/2 частотных строк, которые дадут не более одного
совпадения. Учитывая отрицательные интервалы, получаем, что
максимальное число оптимальных сигналов, которое можно
объединить в систему, равно Μ при четном Λί. При нечетном Λί точно
таким же путем можно показать, что число оптимальных сигналов
•272
в системе будет равно Μ — 1. Объединяя эти результаты, получаем
объем оптимальной системы ДЧ сигналов
/ Μ
= \ Λί —
при четном М,
1 при нечетном М.
(14.54)
Результат (14.54) согласуется со всеми известными
результатами по системам ДЧ сигналов.
Полный код ДЧ сигналов. Число различных сигналов согласно
(14.ЗП равно 5! = 120. Все сигналы с номерами от 1 до 120
приведены на рис. 14.4*). Из них
вторая половина (номера с 61 по ρ (т)г
120) повторяет сигналы первой
половины с точностью до
поворота частотно-временной
плоскости на π/2. По горизонтали
отсчитывается время, по
вертикали — частота.
Были рассчитаны все АКФ и
ВКФ всех пар сигналов.
Корреляционные функции
рассчитывались в дискретных точках,
т. е. при различных временных
сдвигах η определялось число
совпадений. В результате
исследования было установлено: если
выбрать произвольный сигнал,
то он образует 23 оптимальные
пары из 120 возможных.
Например, сигнал номер 1 образует
оптимальные пары с сигналами,
номера которых 11, 14, 24, 30,
37, 45, 51, 56, 68, 70,72,76,83,
84, 87, 90, 107, 108, ПО, 112,
116, 117, 120. Этот факт
справедлив для любых сигналов. Таким образом, вероятность появления
оптимальной пары равна 23/120 = 0,19. В предыдущем параграфе
(см. (14.50) и последующее замечание) было получено, что эта
вероятность равна 0,34. Следовательно, реальная вероятность
появления оптимальной пары меньше. Это обусловлено тем, что между
числом совпадений при различных сдвигах η существуют
корреляционные связи, которые не учитывались при выводе формул (14.50),
(14.51).
Если выбрать пару оптимальных сигналов, например, с
номерами 1 и 11, то для них совместно оптимальными будут десять сиг-
0,5
«4
•0,3
0,2
0,1
V
V
\
\\
\\
NX
2
Рис. 14.5
m
*) Расчеты данного параграфа произведены О. В. Матвеевой.
10 Зак, 2093
273
налов с номерами 14, 24, 30, 45, 51, 56, 84, 87, ПО, 120. Любой из
них образует оптимальную пару как с сигналом номер 1, так и с
сигналом номер 11, и, следовательно, может быть взят в качестве
третьего сигнала системы. Возьмем, например, сигнал номер 14, т. е. имеем
оптимальную систему из сигналов с номерами 1,11, 14. Для этих
трех сигналов оптимальные пары образуют пять сигналов с
номерами 24, 30, 56, 87, 120. Любой из них можно взять в качестве
четвертого сигнала оптимальной системы. Допустим, что выбран сигнал
номер 24. Имеем оптимальную систему с номерами 1, 11, 14, 24.
Дальнейшее увеличение объема оптимальной системы невозможно,
так как ни один из сигналов с номерами 24, 30, 56, 87, 120 не
позволяет увеличить его.
Было установлено, что можно построить оптимальные системы,
число которых существенно больше, чем могут обеспечить известные
алгоритмы. В качестве примера приведем небольшой перечень таких
систем:
1,11,14,24
1,11,14,30
1,11,14,56
1,11,14,87
1,14,37,56
1,14,37,87
1,14,76,87
1,14,76,120,
2,9,18,20
2,9,18,39
2,9,20,55
2,9,20,96
2,9,39,55
2,9,39,96
2,9,53,55
2,9,55,86 и т. д.
Здесь даны 16 оптимальных систем, каждая строка представляет
такую систему. Отметим, что строки первой и второй колонок систем
не имеют совпадающих сигналов в строках третьей и четвертой
колонок.
Случайная система сигналов большого объема. Из 120 сигналов
(рис. 14.4) были случайным образом выбраны 30 сигналов с
номерами: 1,3,8, 11, 16, 19, 24,
Таблица 14.10 27, 32, 35, 40, 43, 48, 51,
56, 59, 64, 67, 72, 75, 80,
83,88,91,96, 99, 104, 107,
112, 115. Эта система
характеризуется
вероятностями совпадений,
приведенными в табл. 14.10 для
В последней строке
табл. 14.10 приведены
средние вероятности
совпадений (14.45). На рис. 14.5
сплошной линией изображены огибающие средних вероятностей
Р5 (т) для случайной системы сигналов (табл. 14.10), а
штриховой линией — огибающие средних вероятностей для полного
кода (табл. 14.7) при Μ = 5. Как видно из рис. 14.5, различие
между кривыми незначительно, т. е. выбранная случайная система
сигналов является типичной, за исключением, что нет совпадений
с /п = 4 и /п = 5,
1 п\
0
1
2
3
4
р5и
т
0 | 1 | 2
0,333
0,366
0,500
0,700
0,766
0,555
0,533
0,434
0,382
0,267
0,234
0,351
0,101
0,167
0,083
0,033
0,075
3
0,033
0,033
0,033
0,019
274
Ί4.4. Регулярные методы построения дискретных частотных
систем
Регулярные методы построения дискретных частотных систем
подробно исследованы в работах [46, 68]. Эти методы были
получены на основе теории чисел. В табл. 14.11 приведены окончательные
результаты работ [46, 68], в которых найдены последовательности
{<Xj (v)}, удовлетворяющие сравнению (14.17). В табл. 14.11
приведены правила образования последовательностей {α7· (ν)};
ограничения, налагаемые на определенные коэффициенты; объем
системы и оценка ВКФ.
В первой строке табл. 14.11 число а — первообразный корень
по модулю простого числа Μ + 1. Все остальные правила основаны
на степенных сравнениях по
модулю простого числа Λί.
В четвертой строке числа г Г
и Μ — 1 взаимно-простые, *■
т. е. (г, Μ — 1) = 1.
Первая строка табл. 14.11
дает алгоритм построения
оптимальной системы с максимальным объемом /, равным числу
элементов в сигнале Λί, а вторая и четвертая строка дают
алгоритмы,! при которых J = Μ — 1, что совпадает с (14.54).
Остальные строки табл. 14.11 дают алгоритмы построения систем,
близких к оптимальным, но большего объема.
Обратимся к примерам. Сначала рассмотрим систему сигналов,
построенную согласно правилу первой строки. Положим Λί + 1=7,
т. е. Μ = 6, а с0 = 1. Символы кодовых последовательностей
определяются сравнением α7· (ν) = α'+ν. В качестве первообразного
корня по модулю 7 возьмем а = 3. После вычислений получаем
следующую систему последовательностей:
13 2 6 4 5
3 2 6 4 5 1
2 6 4 5 13
6 4 5 13 2
4 5 13 2 6
13 2 6 4 . (14.55)
В системе (14.55) кодовыми последовательностями являются
строки, которые представляют циклические перестановки. В
соответствии со значениями цифр необходимо располагать элементы
по времени, т. е. строки (14.55) являются временными кодовыми
последовательностями. Сигналы, построенные в соответствии с
кодовыми последовательностями (14.55), приведены на рис. 14.6.
Номер сигнала соответствует номеру строки. По горизонтали отсчи-
тывается время, по вертикали—частота. Если положить Μ + 1 =
ГЯ F"7I РП SH UJ1
Li La—3 I m й I dCi L. ,mJ
275
Таблица 14.11
Правила образования
последовательностей
(тосШ+1)
a7-(v)^/v+c0 (modA4)
(mod Λί)
aj (ν) ξ /V +c0 (mod Λί)
Γ ι
α;·(ν)=2^ν5 +
s=»l
+ ce (modM)
Коэффициенты
ce=»l,Af; /,ν-Ο,Λί —1
ν, со = 0,М— 1; /= Ι,Λί—1
ν, cl9 Co==0,M —1; / = 1,Λί—1
(r,Μ —1) = 1; /== Ι,ΛΙ—1;
ν, со = 0,М — 1
г > 2; c7-s = 0,M— 1; с0 = 0,Л1—1;
CjS =/= 0 одновременно
г > 2; c^r = 1 ,Λί—1; £7·,Γ_ι = 0;
остальные cjs = 0,M—1;
c0 = 0,Ai— 1 j
1
r>3—нечетное: v,co=0,M—1;
(0,Μ—1 при нечетных s;
I 0 при четных s
Объем
системы
Λί
Λί—1
(Λί—1)Λί
Μ—1
Mr — 1
(Λί-Ι)ΛΡ-2,
M(r+l)/2 I
— 1
Максимум
ВКФ
1/Λί
1/Λί
2/Λί
1/Λί
г/Λί
γ/Μ
г/Λί
276
= И, т. е. Μ = 10, и в качестве первообразного корня по модулю
11 положить а = 2, то имеем следующую систему:
12485 10 9736
2
4
8
5
10
9
7
3
6
4
8
5
10
9
7
3
6
1
8
5
10
9
7
3
6
1
2
5
10
9
7
3
6
1
2
4
10
9
7
3
6
1
2
4
8
9
7
3
6
1
2
4
8
5
7
3
6
1
2
4
8
5
10
3
6
1
2
4
8
5
10
9
6
1
2
4
8
5
10
9
7
1
2
4
8
5.
10
9
7
3
(14.56)
Рассмотрим системы, построенные согласно правилу второй
строки табл. 14.11. Положим Μ = 7, с0 = 0. После вычислений имеем
систему кодовых последовательностей
0 12 3 4 5 6
0 2 4 6 13 5
0 3 6 2 5 14.
0 4 15 2 6 3
0 5 3 16 4 2 (14.57)
0 6 5 4 3 2 1
В отличие от последовательностей (14.55), (14.56), кодовые
последовательности (14.57) могут быть использованы и в качестве
временных, и в качестве частотных. Сигналы, построенные в
соответствии с кодовыми последовательностями (14.57), изображены на
рис. 14.7. При Μ = 11, с0 = 0, имеем следующую систему:
0123456789
02468 10 1357
0369147 10 25
0481 5926 10 3
05 10 4938271
061728394 ΙΟ'
073 10 629518
0852 10 74 1 96
097531 10 864
0 10 98765432
Рассмотрим системы, построенные согласно
строки табл. 14.11. Положим Μ = 7, с0 = 0, г =
ний имеем систему:
0 14 5 2 3 6
0 2 13 4 6 5
0 3 5 16 2 4
0 4 2 6 15 3.
0 5 6 4 3 12
0 6 3 2 5 4 1
10
9
8
7
6
5.
4
3
2
1
(14.58)
правилу четвертой
= 5.
После
вычисле-
(14.59)
27
Соответствующая система сигналов приведена на рис. 14.8. При
Μ «= 11, с0 = 0, г = 3, получим следующую систему кодовых
последовательностей:
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10
8
5
2
10
7
4
1
9
6
3
5
10
4
9
3
8
2
7
1
6
9
7
5
3
1
10
8
6
4
2
4
8
1
5
9
2
6
10
3
7
7
3
10
6
2
9
5
1
8
4
2
4
6
8
10
1
3
5
7
9
6
1
7
2
8
3
9
4
10
5
3
6
9
1
4
7
10
2
5
8
10
9
8
7
6
5.
4
3
2
1
Обратимся к неоптимальным системам. Сначала рассмотрим
систему, правило построения которой приведено в третьей строке
табл. 14.11. Положим, что Μ = 7, с0 = 0, а сг и / меняются в пре-
Рис. 14.7 Рис. 14.8
делах: сг = Ι,Λί — 1, / = 1, Λί — 1. Число сигналов в системе равно
(Λί — 1) Λί = 42. Эти сигналы имеют частотные элементы,
совпадающие по времени, что в свою очередь приводит к появлению
пробелов в сигнале по времени и к ухудшению его пик-фактора.
Максимум ВКФ таких сигналов равен 2/7.
Рассмотрим систему сигналов, построенную согласно правилу
шестой строки табл. 14.11. Положим, что Μ = 7, г = 3, с0 = 0,
cj3 == сз = 1» а сп = £ι изменяется от 0 до 6. Число таких
сигналов равно (Λί — 1) ΛίΓ~2 = 42, а максимум ВКФ равен 3/7.
Сигналы этой системы имеют еще большее число совпадений
элементов по времени, чем предыдущие сигналы, и еще большее число
пробелов по времени. Поэтому система сигналов, полученная с
помощью этого правила, уступает по своим свойствам системе
сигналов, построенной по правилу третьей строки.
14.5. Дискретные составные частотные сигналы
В § 1.2 были определены составные сигналы. В таких сигналах
каждый элемент в свою очередь является сложным сигналом, т. е.
может предствлять набор более простых элементов. Различные
составные сигналы известны давно (см., например, [46, 90, 133, 147, 168,
173, 183, 213]). Иногда их называют каскадными кодами [173].
Составные сигналы являются производными сигналами, так как
278
получаются в результате модуляции одного сложного сигнала
другим, т. е. по сути дела перемножаются два сигнала: исходный и
производящий. Общие свойства таких сигналов и их корреляционные
функции рассмотрены в § 12.2. Они справедливы независимо от
выбора исходных и производящих сигналов.
Обычно составные сигналы применяются для упрощения
аппаратуры формирования и обработки при больших базах производных
сигналов (В > 102—104). В данном параграфе рассмотрим два
примера дискретных составных частотных (ДСЧ) сигналов.
а)
Fo
О
f
Fo¥
δ)
7^?
\
ы
"ν
·;::.
;:■■
til
.
s
Δ
Π
L·»
τ to
Tt
Μ
Tt
Рис. 14.9
Рис. 14.10
Дискретные составные частотные сигналы с частотной
манипуляцией. Принцип построения ДСЧ сигнала с частотной
манипуляцией поясняется рис. 14.9. На рис. 14.9, α изображен исходный ДЧ
сигнал первого порядка с числом элементов Μ = 7. В качестве
производящего сигнала (рис. 14.9, б) взята последовательность из
семи ДЧ сигналов первого порядка также с Μ = 7. После
манипуляции по частоте исходного сигнала производящим сигналом
получим составной (производный) сигнал, изображенный на рис. 14.10.
Он состоит из М2 = 49 элементов.
В общем случае исходный сигнал может содержать Мг элементов,
а одиночный ДЧ сигнал производящего — М2 элементов. В этом
случае составной сигнал будет содержать МгМ2 элементов. Если в
качестве всех ДЧ сигналов, входящих и в исходный сигнал, и в
производящий, взять сигналы, принадлежащие оптимальным ДЧ систе-
279
мам, то максимум ВКФ не будет превышать значения 2/МгМ2. Это
обусловлено тем, что при произвольном временном сдвиге
могут частично перекрываться два элемента исходного сигнала
(рис. 14.9, а)у каждый из которых дает не более одного совпадения.
Объем системы таких сигналов мал и равен объему ДЧ системы
производящего сигнала.
Дискретные составные частотные сигналы с фазовой
манипуляцией. Принцит построения ДСЧ сигнала с фазовой манипуляцией
иллюстрируется рис. 14.11.
Исходный ДЧ сигнал первого
порядка с Μ = 5 изображен на
рис. 14.11, а. В качестве
производящего сигнала (рис. 14.11, б)
взят дискретный ФМ сигнал.
Он представляет
последовательность пяти ФМ сигналов,
каждый из которых состоит из N=8
символов и является в свою
очередь производным сигналом.
Производящий сигнал (рис.
14.11, б) является
последовательностью пяти производных
сигналов, описываемых
первыми пятью кодовыми
последовательностями (14.78),
приведенными в следующем параграфе.
Составной сигнал получается
после перемножения исходного
и производящего сигнала.
Если ФМ сигналы, образующие производящий сигнал, выбраны
так, что их ВКФ имеют максимальные боковые пики, примерно
равные 1/|/1ν7 то максимальные боковые пики ВКФ составных
сигналов будут примерно равны Ι/mVN. Выбор ФМ сигналов может быть
сделан в соответствии с результатами гл. 12.
3)
\[Msmmir t
Рис. 14.11
14.6. Системы дискретных составных
сигналов
фазоманипулированных
Дискретные составные фазоманипулированные (ДСФ) сигналы
рассматривались неоднократно (см., например, [90, 133, 147, 168,
173, 183, 213]). Они образуются при перемножении двух дискретных
ФМ сигналов. Если внимательно изучить структуру ДСФ сигналов,
то окажется, что ДСФ и ДСЧ сигналы обладают некоторыми
общими свойствами, присущими ДЧ сигналам. Эти общие свойства
определяются распределением энергии элементов на частотно-
временной плоскости, что подробно рассмотрено в гл. 1. Поэтому
стало возможным объединить методы исследования, перенеся ряд
результатов из теории ДЧ и ДСЧ сигналов [46, 68] на ДСФ сигналы
[39], что и рассмотрено в данном параграфе.
Взаимная функция неопределенности дискретных составных
фазоманипулированных сигналов. Допустим, что сигнал состоит
из N элементов. Под элементом будем понимать последовательность
элементарных импульсов. На рис. 14.12, а изображен ДСФ сигнал
длительностью Г, состоящий из N0 элементарных прямоугольных
Sj(t)
а)
1-1
N
То
П1Ш1ППШШ11ШТ1М1
ке з»+€ =»*
К—Н<—>т< >■
\т t
в Μ
б)
ι
1L
Ή^Γ^^ *
Рис. 14.12
видеоимпульсов и N элементов. Для ДСФ сигнала рис. 14.12,а Ν0=
= 64, N = 8. Длительность элемента Т0 = T/N. Число импульсов
в элементе равно η = Ν0/Ν. Элементы ДСФ сигнала являются ФМ
сигналами. В предельном случае, когда Ν0=Ν, элемент совпадает
с одиночным импульсом.
Предположим, что для построения ДСФ сигналов используется
множество ffl элементов Uv (t), число которых равно р, т. е, Uv (f)e
ΕΞ S5, ν = 0, ρ — 1. Если энергии всех элементов одинаковы и
равны Е0, то согласно (1.18) (1.20), (1.86) комплексная огибающая
взаимной функции неопределенности (ВФН) v-ro и μ-го элемента
(ν, μ = 0, ρ — 1) равна
оо
#νμ(τ, Ω) = -~- J Uv(t)U*(t-t)eiaidt. (14.61)
281
Отметим, что при |tJ>T0BOH (14.61) тождественно равна
нулю.
Пусть /-й ДСФ сигнал S7· (t) состоит из N элементов, каждый из
которых принадлежит множеству З5. Порядок следования элементов
в /-м сигнале определяется кодовой последовательностью элементов
{Pj (v)} = {Pj (0), ..., Ρι (ν), ..., Pj (Ν — 1)}, а номер ps (v)
элемента на позиции ν принимает одно из возможных ρ значений.
В этом случае комплексная огибающая/-го дискретного сигнала
записывается следующим образом:
Sj(t)= *Σ υρΛν)(ί-νΤ0). (14.62)
v = 0 J
Можно показать, что ВФН ДСФ сигналов с номерами / и k
согласно (1.18) будет равна
Q]k(x, Ω)=^-2 Σ *<νν)Ρ?ί<μ)[τ-(λ-μ)70, Q]e<v<v), (Н.63)
ν = 0 μ = 0
где
γ (ν) = Ω Τ0 ν. (14.64)
Введем переменную суммирования
λ = ν — μ. (14.65)
После этого ВФН (14.63) можно записать в виде
Qjk(x9 Ω) = Ν% Q%(x, Ω), (14.66)
λ=_(Ν-1)
где λ-я компонента ВФН
Q% (τ, QJ-ij RP.(ν) Ph (v-x, (τ-λΤ„, Ω) e»* (ν). (14.67)
ν = λ
Формулы (14.66), (14.67) аналогичны формулам (1.119), (1.120)
для дискретных сигналов.
Отметим, что λ-я компонента ВФН (14.67) тождественно равна
нулю вне интервала ((λ — 1) Т0 < τ < (λ + 1) Т0), что
иллюстрируется рис. 1.19. Поэтому ВФН (14.66) в λ-й полосе
(λΤ0 < τ < (λ + 1) Т0, |Ω| < оо) равна сумме λ-й и λ + 1-й
компонент, т. е.
Qjh (τ, Ω) = Q% (τ, Ω) + Q^1 (τ, Ω) при λΤ0 < τ < (λ + 1) Τ0.
(14.68)
При τ = λΤ0
Qjk(XT0y Ω) = <&(λΓ0, Ω), (14.69)
Q% (λΤ0, Ω) *= -L J RPj (ν) Ph (ν-λ) (0, Ω) e*v (ν). (14.70)
Выясним характер изменения ВФН в зависимости от номера
полосы. Для этого используем ограниченность объема
произвольной ВФН (1.31). Согласно оценке (1.39) средний квадрат ВФН
(14.66) будет равен
σ£ = 1/4 FT. (14.71)
Аналогично, средний квадрат ВФН элементов будет равен
σ£ = l/4fT0 = Νσ%. (14.72)
Из формул (14.67), (14.68) следует, что ВФН ДСФ сигнала в
каждой точке плоскости (τ, Ω), за исключением точек τ=λΤ0, равна
сумме 2Ν — 2λ — 1 слагаемых. При N > 1 эту сумму условно
можно рассматривать как случайную величину с дисперсией
σ}(λ) = JL (2#-2λ-1)σ* = 2^1 -±-±^. (14.73)
Из (14.73) видно, что при малых λ дисперсия σξ> в два раза
превышает средний квадрат (14.71), а по мере роста λ, т. е. с удалением
от центра плоскости, линейно убывает. Таким образом, появление
больших пиков у ВФН более вероятно в полосах с малыми λ.
Полученный результат будет справедлив, если /-й и k-й сигналы
не содержат одинаковых элементов, т. е. в составе ВФН (14.63) или
(14.66), (14.67) нет функций неопределенности, у которых
максимальное значение равно единице. Если же сигналы содержат
некоторое число одинаковых элементов, то в точках (τ = λΤ0, Ω = 0)
при условии выполнения равенства
PjW-Pk (ν-λ) = 0 (14.74)
появляются центральные пики ФН элементов, вклад которых в
(14.67) будет равен 1/Ν.
Если предположить, что сумма (14.68) стремится к нормальной
случайной величине (нормализуется) и возможно совпадение т
элементов, т. е. уравнение (14.74) имеет т решений, то имеем
следующую приближенную оценку максимального пика ВФН:
QMaKC (λ) - 31/2(1 -XI Ν) oQ + ml Ν. (14.75)
Множитель 3 был взят потому, что можно допустить малую
вероятность превышения боковым пиком уровня, равного
утроенному среднеквадратическому значению.
Отметим, что оценки (14.73), (14.75) будут справедливы и для
приближенного определения боковых пиков ФН дискретного сигнала
(/ = k и pj (v) = pk (v)). Центральный пик будет равен сумме
центральных пиков ФН элементов.
Оценки (14.73), (14.75) были получены без конкретизации
структуры элементов, т. е. они справедливы как для ДСФ, так и для
ДСЧ сигналов. Следовательно, полученные результаты имеют
общий характер.
283
Из формул (14.71) (14.73) следует, что средний квадрат ВФН ДСФ
сигналов определяется в основном базой сигналов В = FT и
практически не зависит от взаимокорреляционных свойств элементов.
Однако максимальные значения ВФН (14.75) существенно зависят
от элементов и их расположения в сигналах, что определяется
числом совпадений /п.
В настоящее время в теории ДЧ сигналов известен ряд
регулярных методов (см. § 14.4), позволяющих создавать системы ДЧ
сигналов, обладающих заданным числом совпадений, т.е. с заданными
максимальными пиками корреляционных функций. Распространим
эти методы на ДСФ сигналы.
Автокорреляционная функция ДСФ сигнала. Полагая Ω = О,
/ = k и отбрасывая индексы /, &, из формул (14.66), (14.67) получим
АКФ дискретного составного сигнала
где λ-я компонента АКФ
Если сигнал состоит из различных элементов, то уравнение
(14.74), которое в данном случае записывается как ρ (ν) — ρ (ν —
— λ) = 0, имеет-решения лишь при λ = 0. Следовательно, нулевая
компонента АКФ Q°(t) равна сумме АКФ элементов, а все остальные
компоненты равны сумме ВКФ элементов. Поэтому для уменьшения
боковых пиков АКФ сигнала необходимо составлять его из
элементов, АКФ и ВКФ которых имеют малые боковые пики. Так же как
и в случае ВФН, можно условно считать значение бокового пика АКФ
случайной величиной, дисперсия которой определяется формулой
(14.73). Согласно (9.73) средний квадрат боковых пиков,
усредненный по всем возможным АКФ и ВКФ при данном Л/0, равен σ2 =
= 1/2 Л/0. Следовательно, если положить, что gq = σ2 = 1/2 Ν0,
а т = 0, то приближенное значение максимального бокового пика
АКФ определяется следующим выражением
Qmekc (v) с* ЗУ(1/#о) (1-λ/ΛΟ. (14.77)
Для Ν0 = 64, QManc (0) — 8/8=0,37. Перейдем к построению ДСФ
сигнала.
Возьмем в качестве элементов производные сигналы (см. § 12.2),
построенные на основе сигналов Уолша (12.4). Положим Ν = η = 8,
Ν0 = Ν2 = 64. Если в качестве производящей последовательности
взять нелинейную последовательность в виде 1 1 — 1 — 1 — 1 1
— 1 1, то кодовые последовательности производной системы опреде-
284
ляются посимвольным перемножением
и записываются следующим образом:
—1
—1 -
—1
—1 -
ι -
1
1 -
1
последовательностей (12.4)
(14.78)
Системы элементов (12.4), (14.78) обладают равными средними
квадратами σ# = 5,9 · 10"2. Такое значение σ$ близко к
предельному (9.73) σ2 = 72 N = 6,25 · 10"2. Максимальные боковые
пики у производной системы (14.78) равны #Макс = bU = 0,625,
что не превышает зачения 3 σ = 0,75, в то время как у системы Уол-
uia Rmslkc = 7/s = 0,875. Коэффициент эксцесса, определяющий
максимальные боковые пики, для системы Уолша (12.4) γ = 1,57,
а для производной системы (14.78) γ = 0,23. Чем меньше
коэффициент эксцесса, тем меньше максимальные боковые пики. Именно
по этой причине в качестве элементов были выбраны кодовые
последовательности производной системы (14.78).
Записав последовательно друг за другом строки (14.78), получим
кодовую последовательность, которой соответствует ДСФ сигнал,
изображенный на рис. 14.12, а. Его АКФ представлена на
рис. 14.12, б. Среднеквадратическое значение бокового пика oq =
= 5,6 · Ю-2, что в 1,55 раз меньше предельного значения (9.73):
σ = 1/Υ"2Ν0 = 8,9 · Ю-2. Максимальный боковой пик равен
Q макс=13/в4=0,203, что меньше как 3 σ = 0,27, так и QMaKC (0) =
= 0,37.
Сигнал (рис. 14.12, а) не является единственным. Элементы —
строки (14.78) можно переставить различными способами. Общее
число ДСФ сигналов равно числу перестановок L = N\. Если же
производить изменение знака элементов, то получим V = 2 (N1)
сигналов. Каждый из таких сигналов с большой вероятностью будет
иметь максимальные боковые пики АКФ, приближенно оцениваемые
равенством (14.77). Таким образом, сростом N максимальные
боковые пики АКФ таких сигналов будут уменьшаться в соответствии с
(14.77).
Подчеркнем, что выбор элементов имеет большое значение, так
как при неудачном выборе максимальные боковые пики могут быть
существенно больше значения, определяемого правой частью
(14.77). Это объясняется тем, что если АКФ и ВКФ элементов имеют
большие боковые пики, то сумма в (14.76) слабо нормализуется.
В качестве примера укажем на сигнал, составленный из строк (12.4)
при их последовательной записи. АКФ такого сигнала имеет
максимальный боковой пик, равный QMaKc == 28/64 — 0,44 > QMaKC(0) =
= 0,37.
Конечно, ДСФ сигналы, построенные из элементов,
принадлежащих производной системе, не являются минимаксными. Однако ис-
285
следование их имеет практическое значение по следующим причинам.
Во-первых, ДСФ сигналы с такими АКФ удовлетворяют многим
практическим задачам, особенно в тех случаях, когда N достаточно
велико. Во-вторых, значительно число сигналов. Например, при
N = 8 L ~ 4 · 104. В-третьих, подобные сигналы позволяют
упростить аппаратуру формирования, так как они отличаются только
порядком следования элементов. В-четвертых, такие сигналы могут
служить первым приближением для поиска минимаксных с помощью
ЭВМ.
Взаимокорреляционные функции ДСФ сигналов. Если различные
ДСФ сигналы составляются из одинаковых элементов, то уравнение
(14.74), по крайней мере, будет иметь одно решение, т. е. в состав
ВФН (и конечно, ВКФ) войдет хотя бы одна ФН, дающая значение
l/Ν. Определим класс сигналов, который обеспечивает только одно
решение уравнения (14.74). Такая задача решена в теории ДЧ
сигналов (см. § 14.4). Если уравнение (14.74) заменить сравнением по
простому модулю N, т. е.
Pi (ν) - Ри (ν - λ) - 0 (mod N), (14.79)
то сравнению (14.79) и соответственно уравнению (14.44) будут
удовлетворять кодовые последовательности табл. 14.11. Например, для
последовательностей второй строки табл. 14.11 имеем
Pj (ν), — /ν + с0 (mod N), (14.80)
где с0 = 0, Ν— 1, ν = 0,Ν—1, /-1, Ν— 1. При этом сравнение
(14.80) является сравнением первой степени, которое имеет одно
решение. Например, при N = 5 и с0 = 0 из (14.80) получаем четыре
кодовые последовательности
12 3 4 5
2 4 13 5
3 14 2 5
4 3 2 15 (14.81)
Каждая строка в (14.81) — кодовая последовательность
элементов. Если сигналы построены из элементов с помощью таких
же кодовых последовательностей, то при произвольных временных
сдвигах в точках τ = λΤ0 возможно только одно совпадение
элементов. Если к тому же элементы ортогональны между собой,
то ВКФ в этих точках будет равна UN. В остальных точках будет
справедлива оценка (14.77). Поэтому для ВКФ ДСФ сигналов
имеем:
(Змакс^сЛ1^ "Ρ* τ = λ7^ (14.82)
1 3V(l/N0)(l-X/N) при χφλΤ0.
Рассмотрим пример. Перенумеруем кодовые последовательности
(14.78) сверху вниз и будем использовать первые пять элементов.
При этом {рг (ν)} соответствует первой кодовой последовательности
элементов в (14.81), а {р2 (ν)} — второй кодовой последователь-
286
ности элементов в (14.81). Поэтому кодовая последовательность
первого сигнала равна 1 1 — 1 — 1 — 1 1 — 1 1 1 1 — 1
1—1—1 — 1—11111—111—11—11
— 1 — 111111 — 1—11—11 — 1, а второго — 1 — 1
— 11—1 — 1—1 — 11 — 11 — 1 — 1 — 1 1 111 — 1 — 1
— 11 — 111111 — 111 — 111 — 1—1 1—11 — 1. У обоих
сигналов N0 = 40, η = 8, N = 5. ВКФ таких сигналов имеет сред-
неквадратическое значение oQ ~ 0,11, которое практически
совпадает с предельным значением (9.73). Максимальный боковой пик
Рмакс= 11/40=0,275, что меньше 3 σ = 0,33 и меньше QMaKci0) =
= 0,47.
Приведенный пример показывает, что результаты теории ДЧ
сигналов можно использовать в теории ДСФ сигналов.
В заключение отметим, что при построении систем ДСФ
сигналов можно допускать больше одного совпадения элементов.
Допустим, что сравнение (14.79) имеет т решений. В этом случае в
некоторой точке τ = λΤ0 ВКФ будет равна mIN. Приравнивая
уровни 3/Y~N0 = m/N, получаем, что можно иметь число решений
(совпадений элементов)
т = 3 N/VW0. (14.83)
Если N ^ V~N0, то 1 ^ т ^ 3. В нашем примере т = 2,4, т. е.
можно положить т = 2. При этом число сигналов будет равно
(N—1) N = 20.
Послесловие
Основной проблемой теории систем сигналов является проблема
построения больших систем сигналов с хорошими корреляционными
свойствами. Большой системой является такая, объем которой
(число сигналов /) много больше базы сигналов В, т. е. для
больших систем сигналов должно выполняться неравенство / > В.
При хороших корреляционных свойствах уровни боковых
пиков ВКФ и АКФ сигналов должны быть малыми. Эти уровни можно
оценивать как по максимальному значению модуля /?Макс> так
и по среднеквадратическому значению о%.
Как следует из материала гл. 8 — 10, среднеквадратическое
значение σ% «хороших» систем сигналов должно быть близко к
предельному значению, которое можно определить согласно (9.60) или
(9.63) следующим образом: σ = а/У В, где а — коэффициент,
зависящий от вида корреляционных функций (периодических или
апериодических). Как показывают исследования у большинства
систем сигналов σ# будет близко к этому значению.
Совсем иное положение будет, когда необходимо иметь системы
сигналов с максимальным значением корреляционных функций
Ямакс» МеНЬШИМ некоторого урОВНЯ Ямакс дош т· е· У КОТОрЫХ
А макс ^ А макс доп·
287
Примеры систем сигналов, приведенные в гл. 12 — 14,
показывают, что у большинства систем при / ~ В оценка максимального
бокового пика
Ямакс ^ klYBy
где k > 1 — постоянная, зависит от класса рассматриваемой
системы. Это справедливо для дискретных, частотных и дискретных
частотных сигналов. Увеличение объема системы сигналов,
например для многофазных (табл. 12.1) или для частотных (табл. 13.1),
приводит к увеличению значения /?Макс- Если для системы
многофазных сигналов, характеристики которой приведены на третьей строке
табл. 12.1 и для системы частотных сигналов, характеристики
которой приведены на седьмой строке табл. 13.1, положить параметр
η = 4, то объем таких систем J ^ β2, а #Макс—S/УВ. Чем больше я,
тем больше У, но при этом возрастает и #Макс-
Таким образом, алгоритмы построения систем сигналов, у
которых J > Л2, a Rmslkc < О —3)/УВ, в настоящее время
неизвестны. Следовательно, общая проблема теории систем сигналов еще не
решена. Подчеркнем, что алгоритмы построения таких систем
должны быть детерминированными, так как согласно материалу
гл. 14 (см. табл. 14.9) случайные алгоритмы вряд ли приведут к
построению больших систем сигналов с хорошими корреляционными
свойствами.
Особое внимание необходимо уделить поиску больших систем
дискретных частотных (ДЧ) сигналов, так как такие сигналы
согласно материалам гл. 5 обладают хорошей помехоустойчивостью
относительно комплекса помех. Поскольку системы дискретных
составных частотных и фазоманипулированных сигналов (ДСЧ и
ДСФ) по методу использования частотно-временной плоскости
близки к системам ДЧ сигналов, то использование ДСЧ и ДСФ сигналов
также позволит создавать системы передачи информации с высокой
помехоустойчивостью. Поэтому поиск алгоритмов построения
больших систем ДЧ, ДСЧ и ДСФ сигналов является актуальной задачей
теории систем сигналов.
Постскриптум
За пятилетие, прошедшее с
момента написания данной книги до
выхода ее в свет, было издано
несколько книг, в которых
рассмотрены различные аспекты теории и
техники сигналов.
В классическом учебнике
И. С. Гоноровского [231] даны
современные основы теории и техники
сигналов, в том числе
детерминированные и случайные сигналы,
согласованная фильтрация, обработка
комплексных сигналов, дискретная
обработка, цифровые фильтры,
системы ортогональных сигналов в
виде полиномов и функций Уолша.
В гл. 3 справочника [232]
приведены основы теории
радиолокационных -сигналов и каталог
таких сигналов. Вопросы обработки
радиолокационных сигналов
подробно рассмотрены в книге [233],
среди которых необходимо отметить
селекцию сигналов по различным
параметрам. Ортогональным и
квазиортогональным сигналам посвящена
книга [234], где объединены наиболее
интересные результаты [178, 210].
288
Системы передачи дискретной
информации, в том числе
многостанционные системы со свободным
доступом, рассмотрены в [235].
Среди многостанционных систем со
свободным доступом рассмотрены
системы с частотным, временным и
кодовым разделением каналов.
Отметим также ряд новых
интересных результатов, полученных в
теории систем сигналов.
В [236] приведены результаты
моделирования адаптивного
многоканального приемника,
предназначенного для приема фазоманипули-
рованных сигналов, близкого по
своей структуре к адаптивному
приемнику, рассмотренному в гл. 5.
Базисный прямоугольник сигнала
также разбивается на ряд
неперекрывающихся временных и
частотных полос и анализатор каналов
определяет мощности
частотно-временных элементов, которые затем
суммируются с весом 1 или 0 в
зависимости от уровня мощности. В [237]
получен закон распределения
апериодической КФ фазоманипулиро-
ванных сигналов в виде весовой
суммы биномиальных коэффициентов.
Именно такой же закон содержит
табл. 10.1 (с. 201), но
приведенный в [237] результат позволил
автору в явном виде выразить
интегральную функцию распределения
и произвольные моменты
апериодической КФ. В частности, 2- и 4-й
моменты [237] совпадают со
значениями моментов, приведенных в § 10.2.
Дискретные частотные сигналы
первого и более высоких порядков
рассмотрены в [238], где дано также
доказательство ограниченности
объема системы дискретных частотных
сигналов, аналогичное выражению
(14.54) на с. 273. Статистические
свойства дискретных составных
частотных сигналов с частотной
манипуляцией приведены в [239]. Такие
сигналы кратко описаны в § 14.5.
Доказательство существования
больших систем фазоманипулирован-
ных сигналов с J > В дано в [240].
В ней приведена нижняя граница
объема больших систем фазомани-
пулированных сигналов,
удовлетворяющих условию, при котором КФ
сигналов, образующих систему, не
превышают заданных уровней. В
[240] рассматривались системы
сигналов с заданными
корреляционными свойствами и доказано, что
такие системы фазоманипулирован-
ных сигналов существуют, а объем
их растет экспоненциально с ростом
базы сигналов. С помощью границы
Чернова в [240] найдено, что объем
большой системы фазоманипулиро-
ванных сигналов удовлетворяет
неравенству
*<ФМ Ο/Μ) ΚΙ +
+ R0)l+R°(l-Ro)1-R°]N/2,
где N — число символов в сигнале,
R0 — допустимый уровень КФ,
причем модуль КФ | Rjk (τ) | < R0.
При относительно небольших R0
предыдущая формула
преобразуется в LOM > (1/8Λ0 ехр (ΛΉ«/2),
которая и свидетельствует об
экспоненциальном росте объема большой
системы фазоманипулированных
сигналов. Работа [240] имеет такое же
принципиальное значение для
теории систем сигналов, как теорема
Шеннона о существовании
случайного кода для теории кодирования.
Более того, авторы [240] на основе
разработанного ими метода дали
новое доказательство границы
Гильберта в теории кодирования, тем
самым показав взаимосвязь между
теорией кодирования и теорией
систем сигналов. Вместе с тем ряд
положений [240] вызывают
критические замечания, которые
заключаются в следующем. Во-первых, авторы
сначала рассматривают апериодич-
ские КФ, но при выводе
окончательных формул используют только
центральные значения КФ, что
соответствует периодическим КФ.
Во-вторых, авторы оценивают
биномиальный закон распределения пиков
периодической КФ ФМ сигналов с
помощью границы Чернова,
которая дает лучшее приближение по
сравнению с гауссовым при больших
значениях случайной величины (на
«хвостах» закона распределения).
Это означает, что результаты [240]
более точны для систем с большими
пиками КФ, т. е. для систем с
посредственными корреляционными
свойствами. В-третьих, при
корректном выборе допустимых уровней КФ
и базы ФМ сигналов необходимо
289
учитывать пороговый эффект,
который имеет место в данной, задаче
и который практически не
рассмотрен в 1240]. Как показали
исследования, корректное задание
допустимого уровня КФ должно быть
связано с определенным пороговым
уровнем, что в свою очередь дает только
степенной закон роста объема
системы сигналов, а не
экспоненциальный, как это определено в [240].
В-четвертых, закон распределения
апериодических КФ ФМ сигналов
отличается от биномиального и
нормального законов тем, что
коэффициент эксцесса равен единице (с. 203).
Это приводит к уменьшению объема
системы сигналов.
Проведенные исследования
показали, что среднее значение объема
большой системы фазоманипулиро-
ванных сигналов растет по
степенному закону
^ΦΜ > с («) [In (aJV)]-3/2 N«~l ,
где а = 2*'2л-1'2; с (а) = 3π1/2 Χ
X а~а2-2а3/2, а а определяет
допустимый уровень КФ: Ro =
β уЩШ. Чем больше а, тем
Список литературы
1. Агеев Д. В. Основы теории
линейной селекции. —
Научно-технический сборник ЛЭИС. 1935,
№ 10.
2. Аллен, Уэстерфильд. Цифровые
корреляторы со сжатием во
времени и согласованные фильтры
для активной гидролокации. —
«Зарубежная радиоэлектроника»,
1964, т. 18, №2.
3. Амиантов И. Н. Избранные
вопросы статистической теории
связи. М., «Сов. радио», 1971.
4. Бакулев П. А. Радиолокация
движущихся целей. М., «Сов.
радио», 1964.
5. Банкет В. Л. К расчету
помехоустойчивости реальных
многопозиционных систем связи при флюк-
туационных помехах. —
«Радиотехника», 1968, т. 23, № 12.
6. Бенджамин. Последние
достижения в технике генерирования и об-
Хуже корреляционные свойства
системы сигналов, так как R0
возрастает, но при этом увеличивается
объем системы L. Для дискретных
частотных сигналов первого порядка
было доказано, что среднее
значение объема большой системы таких
сигналов растет по закону
факториала 1дч > 0,25е (п + 1)!, где η —
максимальное допустимое число
совпадений, причем 1дЧ не зависит от
числа элементов Μ ДЧ сигнала.
Приведенные результаты
доказывают, что большие системы
сигналов существуют.
В настоящее время известен только
один регулярный метод построения
больших систем фазоманипулирован-
ных сигналов, предложенный в [242],
основанный на рекуррентном
использовании последовательностей
максимальной вероятности и
сигналов Уолша. Этот метод дает
степенной рост объема системы, но более
медленный, чем следует из
приведенных оценок £ФМ.
Доказательство существования
больших систем сигналов позволяет
надеяться, что регулярные
алгоритмы построения таких систем будут
найдены в ближайшее время.
работки радиолокационных
сигналов. — «Зарубежная радиоэлек·
троника», 1965, т. 19, № 7.
7. Бенжамин Р. Анализ радио- и
гидролокационных сигналов. Пер.
с англ. Под ред. И. Е. Овсиевича.
М., Воениздат, 1969.
8. Берглунд, Болл. Ограничение
рабочих характеристик сдвигового
регистра типа «пожарная
цепочка» на полевых транзисторах
с изолированными затворами. —
«Зарубежная радиоэлектроника»,
1973, т. 27, №8.
9. Блэсбалг. Сравнение
псевдошумовых и обычных методов
модуляции в спутниковых системах
связи с многократным доступом.
«Зарубежная радиоэлектроника»,
1967, т. 21, № 12.
10. Бурру. Цифровые фильтры с
блочной обработкой сигналов. —
290
«Зарубежная радиоэлектроника»,
1972, т. 26, № 10.
11. Бэллард. Новый метод
уплотнения каналов связи. — «Зарубежная
радиоэлектроника», 1963, т. 17,
№ П.
12. Вайнштейн Л. Α., Зубаков В. Д.
Выделение сигналов на фоне
случайных помех. М., «Сов. радио»,
1960.
13. Вакин С. Α., Шустов Л. Н.
Основы радиопротиводействия и
радиотехнической разведки. М.
«Сов. радио», 1968.
14. Вакман Д. Е. Сложные сигналы
и принцип неопределенности в
радиолокации. М., «Сов. радио»,
1965.
15. Вакман Д. Е., Седлецкий P. M.v
Вопросы синтеза
радиолокационных сигналов. М., «Сов. радио»,
1973.
16. Валеев В. Г. Помехоустойчивость
типовых каналов обнаружения
при коррелированных
негауссовых помехах. — «Радиотехника и
электроника», 1974, т. 19, № 8.
17. Ван Блэркэм, Сэре, Фримэн.
Анализ и моделирование приемника
псевдошумовых сигналов с
дискретным согласованным
фильтром. — «Зарубежная
радиоэлектроника», 1968, т. 22, №1.
18. Ван Трис Г. Теория обнаружения,
оценок и модуляции. Т. 1. Пер.
с англ. Под ред. В. И. Тихонова.
М., «Сов. радио», 1972.
19. Варакин Л. Е. Формирование
и обработка сложных сигналов
в радиолокационных и
радиосвязных системах. М., ВЗЭИС,
1967.
20. Варакин Л. Е. О применении
ортогональных сигналов в системах
передачи информации. — «Труды
МЭИС», 1969, вып. 1.
21. Варакин Л. Е. О
целесообразности сложного кодирования. —
«Радиотехника», 1969, т. 24, № 4.
22. Варакин Л. Е. Некоторые
интегральные соотношения между
корреляционными функциями.—
«Радиотехника и электроника», 1969,
т. 14, № 5.
23. Варакин Л. Е. Синтез фазомани-
пулированных сигналов. —
«Радиотехника и электроника», 1969,
т. 14, №5.
24. Варакин Л. Е. Резонанс,
согласованный фильтр и сложные
сигналы. — «Теоретическая
электротехника», 1969, вып. 8.
25. Варакин Л. Е. Теория сложных
сигналов. М., «Сов. радио», 1970.
26. Варакин Л. Е. К вопросу о
критерии синтеза сложных
сигналов. — «Изв. вузов СССР.
Радиоэлектроника», 1970, т. 13, №2.
27. Варакин Л. Е.
Помехоустойчивость приема сложных сигналов.—#
«Радиотехника», 1970, т. 25, № 10.
28. Варакин Л. Е. Вероятность
ошибки при оптимальном
некогерентном приеме. — «Труды учебных
институтов связи», 1970, вып. 49.
29. Варакин Л. Е. Фильтрация
пассивных помех и частичный объем
тела неопределенности. — «Изв.
вузов СССР. Радиоэлектроника»,
1971, т. 14, № Ю.
30. Варакин Л. Е. Оптимальные фа-
зоманипулированные сигналы. —
«Радиотехника», 1971, т. 26, № 11.
31. Варакин Л. Е. Выбор систем
сигналов для ААСС при
когерентном приеме. — «Электросвязь»,
1971, т. 25, № 12.
32. Варакин Л. Е. Корреляционные
свойства производных сигналов.—
«Радиотехника», 1972, т. 27, № 1.
33. Варакин Л. Е. Реальная
помехоустойчивость широкополосных
радиотехнических систем. —
«Радиотехника и электроника», 1973,
т. 18, № 1.
34. Варакин Л. Е. К расчету
систем синхронизации. —
«Радиотехника и электроника», 1973,
т. 18. №4.
35. Варакин Л. Е.
Помехоустойчивость квазиоптимального
некогерентного приема при
ресинхронизации по времени и по
частоте. — «Изв. вузов СССР.
Радиоэлектроника», 1973, т. 16, № 7.
36. Варакин Л. Е. Обнаружение
сложных сигналов и измерение их
параметров. — «Радиотехника и
электроника», 1973, т. 18, № 8.
37. Варакин Л. Е. Свойства полного
кода. ■— «Радиотехника», 1973,
т. 28, №8.
38. Варакин Л. Е. Сельская
радиосвязь и кодовое разделение
каналов. — «Электросвязь», 1973, т.
27, № ю.
39. Варакин Л. Е. Дискретные
сигналы. — «Изв. вузов СССР. Ра-
291
диоэлектроника», 1973, т. 16,
№11.
40. Варакин Л. Е. Число кодовых
последовательностей с заданным
числом блоков. —
«Радиотехника», 1974, т. 29, № 2.
41. Варакин Л. Е. Реальная
помехоустойчивость ААСС с
кварцевыми линиями задержки. Ч. II.
Средняя вероятность ошибки. —
«Радиотехника», 1974, т. 29, № 6.
42. Варакин Л. Е. Экстремумы
корреляционных функций фазомани-
пулированных сигналов. — «Изв.
вузов СССР. Радиоэлектроника»,
1975, т. 18, №11.
43. Варакин Л. Е. Выбор систем
сигналов для ААСС при
некогерентном приеме. — «Труды
учебных институтов связи», 1977,
вып. 81.
44. Варакин Л. Е., Власов В. Н.
Влияние нестабильности частоты
на отношение сигнал/шум при
обработке многомерных
сигналов.— В кн.: Труды
научно-технической конференции «Проблемы
оптимальной фильтрации». М.,
«Сов. радио», 1967.
45. Варакин Л. Е., Власов В. Н.,
Волков Л. Н. К вопросу о
помехоустойчивости дискретного
согласованного фильтра. — «Труды
МЭИС», 1968, вып. 1.
46. Варакин Л. Е., Власов В. Н.
Системы дискретных
многочастотных сигналов. — «Электросвязь»,
1974, т. 28, №7.
47. Варакин Л. Е., Волков Л. Н.
Спектры классических
ортогональных сигналов. — В кн.:
Труды научно-технической
конференции «Проблемы оптимальной
фильтрации». М., «Сов. радио», 1967.
48. Варакин Л. Е., Волков Л. Н.
Корреляционные свойства
сегментов М- последовательностей. —
«Радиотехника», 1973, т. 28, № 2.
49. Варакин Л. Е., Волков Л. Н.
Некоторые корреляционные и
спектральные свойства кодовых
последовательностей Уолша. —
«Труды учебных институтов
связи», 1973, вып. 61.
50. Варакин Л. Е., Житков В. В.
Дисперсия полного
произвольного кода. — «Радиотехника»,
1976, т. 31, № 5.
51. Варакин Л. Е., Житков В. В.
Статистические свойства полного
троичного кода.—«Трудыучебных
институтов связи», 1977, вып. 81.
52. Варакин Л. Е., Левина И. Г.
Реальная помехоустойчивость
ААСС с кварцевыми линиями
задержки. 4.1. Максимальная
вероятность ошибки. —
«Радиотехника», 1972, т. 27, № 7.
53. Варакин Л. Е., Левина И. Г.
Число активных абонентов в ААСС
с учетом рассогласований. —
«Электросвязь», 1972, т. 26, № 10.
54. Варакин Л. Е., Моисеева Г. Г.
Распределение периодических
корреляционных функций фазо-
манипулированных сигналов. —
«Радиотехника», 1976, т. 31, № 12.
55. Варакин Л. Е., Моисеева Г. Г.
Последовательности максимальной
вероятности. — «Труды учебных
институтов связи», 1976, вып. 80.
56. Варакин Л. Е., Пышкин И. М.
К вопросу применения сложных
сигналов в адресных системах
связи. — «Электросвязь», 1967,
т. 21, № 1.
57. Варакин Л. Е., Пышкин И. М.
К вопросу использования
сложных сигналов в адресных
системах с частотно-временным
кодированием адреса. — В кн.:
Труды научно-технической
конференции
профессорско-преподавательского состава МЭИС. Мин-во
связи СССР, 1967.
58. Варакин Л. Е., Пышкин И. М.
О помехоустойчивости
асинхронно-адресной системы связи со
сложными сигналами и частотно-
временным
кодированием.—-«Труды учебных институтов связи»,
1967, вып. 35.
59. Варакин Л. Е., Пышкин И. М.
Анализ помехоустойчивости
асинхронно-адресной системы связи
(ААСС) со сложными сигналами.
В кн.: Труды Второй научно-
технической конференции
«Проблемы оптимальной фильтрации»,
М., МЭИС, 1968, вып. 1.
60. Варакин Л. Е., Пышкин И. М.
Асинхронные адресные системы —
ретроспектива, проблемы,
перспектива. — «Радиотехника»,
1973, т. 28, №11.
61. Варакин Л. Е., Сперанский В. С.
К вопросу статистического
выбора систем фазоманипулирован-
ных сигналов. — «Труды учебных
институтов связи», 1974, вып. 66
292
62. Венедиктов М. Д., Марков В. В.,
Эйдус Г. Г. Асинхронные
адресные системы связи. М., «Связь»,
1968.
63. Виноградов И. М. Основы
теории чисел. М., «Наука», 1965.
64. Витерби Э. Д. Принципы
когерентной связи. Пер. с англ. Под
ред. Б. Р. Левина. М., «Сов.
радио», 1970.
65. Власов В. Н. Система сигналов с
дискретной ЧМ. —«Труды МЭИС»,
1970, вып. 1.
66. Власов В. Н.
Помехоустойчивость нелинейного приемника
многочастотных сигналов. — «Изв.
вузов СССР. Радиоэлектроника»,
1975, т. 18, №4.
67. Власов В. Н., Варакин Л. Е.
Метод синтеза систем дискретных
фазоманипулированных сигналов.
«Изв. вузов СССР.
Радиоэлектроника», 1971, т. 14, № 7.
68. Власов В. Н., Варакин Л. Е.
Системы дискретных частотно-
модулированных сигналов. —
«Радиотехника и электроника»,
1972, т. 17, №5.
69. Власов В. Н., Варакин Л. Е.
Синтез систем дискретных
многочастотных
фазоманипулированных сигналов. — «Труды учебных
институтов связи», 1972, вып. 58.
70. Власов В. Н., Волков Л. Н.,
Варакин Л. Е. Анализ
помехоустойчивости дискретного
согласованного фильтра. — «Труды
учебных институтов связи», 1968,
вып. 41.
71. Власов В. Н., Волков Л. Н.,
Варакин Л. Е. Пассивный прием
двоичной информации,
передаваемой сложными
сигналами.—«Труды МЭИС», 1969, вып. 1.
72. Власов В. Н., Волков Л. Н.
Системы многофазных сигналов
большого объема. — «Изв. вузов
СССР. Радиоэлектроника», 1972,
т. 15, №11.
73. Волков Л. Н., Варакин Л. Е.
Анализ корреляционных свойств
некоторых систем ФМ сигналов.—
«Изв. вузов СССР. Радиоэлектро*
ника», 1973, т. 16, №5.
74. Гарибян М. Л. Определение
целесообразного усложнения
цифровых согласованных фильтров
на интегральных структурах. —
«Радиотехника», 1975, т. 30, № 10.
75. Глазов Б.ВИ. Спектры и
корреляционные функции частотно-
манипулированных шумоподоб-
ных сигналов. — «Радиотехника»,
1970, т. 25, №9.
76. Глазов Б. И. Числовые
периодические последовательности для
формирования шумоподобных
сигналов с частотной модуляцией. —
«Радиотехника», 1972, т. 27, № 3.
77. Глазов Б. И., Котенко Л. П.,
Мерзликин Б. С. Анализ
спектральных и корреляционных
свойств L-ичных дискретных
ЧМ сигналов. — «Радиотехника»,
1975, т. 30, № 12.
78. Гленн. Система связи с кодовым
уплотнением каналов. —
«Зарубежная радиоэлектроника», 1965,
т. 19, №3.
79. Глобус И. А. Двоичное
кодирование в асинхронных системах.
М., «Связь», 1972.
80. Голд Б., Рэйдер Ч. Цифровая
обработка сигналов. Пер. с англ.
Под. ред. А. М. Трахтмана. М.,
«Сов. радио», 1973.
81. Гольденберг Л. М., Левчук Ю. П.,
Поляк Μ. Η. Цифровые фильтры.
М., «Связь», 1974.
82. Горяинов В. Т. Влияние
нестабильности несущей частоты на
помехоустойчивость дискретных
систем связи. — «Электросвязь»,
1966, т. 20, № 12.
83. Горяинов В. Т. Требования к
точности тактовой синхронизации в
системах передачи двоичной
информации. — «Изв. вузов СССР.
Радиоэлектроника», 1970, т. 13,
№7.
84. Гуревич М. С. Спектры
радиосигналов. М., «Связь», 1963.
85. Гутин В. С. Корреляционные
свойства случайных двоичных
последовательностей. —
«Радиотехника и электроника», 1973, т. 18,
№2.
86. Гутин В. С. К расчету
спутниковых радиолиний со структурным
уплотнением. — «Радиотехника»,
1973, т. 28, №6.
87. Гутин В. С, Животовский Л. А.
К оценке потерь при ограничении
группового сигнала ч в линиях
связи со структурным
уплотнением. — «Радиотехника и
электроника», 1973, т. 18, №2.
88. Ди Франко, Рубин. Анализ
искажений при обработке
радиолокационного сигнала. — «Зарубеж-
293
ная радиоэлектроника», 1963, т.
17, №9.
89. Зюко А. Г. Помехоустойчивость
и эффективность систем связи.
М., «Связь», 1972.
90. Истерлинг. Радиолокационное
сопровождение спутника
«Курьер». — «Зарубежная
радиоэлектроника», 1963, т. 17, №8.
91. Кан. Характеристики цифрового
согласованного фильтра при
неизвестной помехе. —
«Зарубежная радиоэлектроника», 1972, т.
26, №11.
92. Каргополов М. И., Мерзляков Ю. И.
Основы теории групп. М.,
«Наука», 1972.
93. Каринский С. С. Устройства
обработки сигналов на
ультразвуковых поверхностных волнах.
М., «Сов. радио», 1975.
94. Каршин В. М. Оценка
эффективности использования
сложных сигналов для борьбы с
внешними помехами в отсутствие
априорных сведений о помехе. —
«Радиотехника и электроника»,
1971, т. 16, №6.
95. К вопросу обработки сложных
сигналов. — «Труды МЭИС»,
1969, вып. 1. Авт.: Л. Е. Вара-
кин, В. Н. Власов, Л. Н.
Волков, В. В. Коричнев, О. А. Ко-
сичкин.
96. Кор, Кручфилд, Мерчиз.
Импульсная УКВ станция,
использующая шумоподобные сигналы.
«Зарубежная радиоэлектроника»,
1966, т. 20, №4.
97. Котельников В. А. Теория
потенциальной
помехоустойчивости. М., Госэнергоиздат, 1956.
98. Кошевой А. А. Телеметрические
комплексы летательных
аппаратов. М., «Машиностроение»,
1975.
99. Кук Ч., Бернфельд М.
Радиолокационные сигналы. Теория и
применение. Пер. с англ. Под
ред. В. С. Кельзона. М., «Сов.
радио», 1971.
100. Кузнецов В. П.
Широкополосные сигналы, основанные на
многозначных кодах. —
«Труды МЭИС», 1968, вып. 1.
101. Кузнецов В. П. Исследование
методов статистического
синтеза систем связи с мешающими
параметрами. Дис. на соиск.
канд. техн. наук.М.,МЭИС, 1967.
102. Кэн. Отношение сигнал/помеха
в полосовых ограничителях. —
«Зарубежная радиоэлектроника»,
1961, т. 15, №8.
103. Левенштейн В. И. Применение
матриц Адамара к одной
задаче кодирования. — «Проблемы
кибернетики», 1961, вып. 5.
104. Левин Б. Р. Теоретические
основы статистической
радиотехники. В 2-х кн. М., «Сов. радио»,
1966, 1968.
105. Лезин Ю. С. Оптимальные
фильтры и накопители импульсных
сигналов. М., «Сов. радио», 1969.
106. Лившиц А. Р., Биленко А. П.
Многоканальные асинхронные
системы передачи информации
(элементы теории). М., «Связь»,
1974.
107. Лихарев В. А. Цифровые методы
и устройства в радиолокации.
М., «Сов. радио», 1973.
108. Логинов В. П. Функции Уолша
и области их применения. —
«Зарубежная радиоэлектроника»
1973, т. 27, №4.
109. Метод статистических
испытаний. (Метод Монте-Карло). Под
ред. Ю. А. Шрейдера. М., Физ-
матгиз, 1962. Авт.: Н. П. Бус-
ленко, Д. И. Голенко, И. М.
Соболь и др.
110. Мешковский К. А.
Оптимальные и близкие к ним двоичные
коды. — «Электросвязь», 1958,
т. 12, №5.
111. Мешковский К. Α.,
Кириллов Η. Ε. Кодирование в
технике связи. М., «Связь», 1966.
112. Многостанционный доступ в
спутниковых системах связи. М.,
«Связь», 1973. Авт.: М. Д.
Венедиктов, С. А. Даниэлян,
В. В. Марков, Г. С. Эйдус.
113. Невдяев Л. М. Исследование
нелинейного преобразования
группового сигнала в системах с
адресным уплотнением и
корреляционным разделением. Дис. на
соиск. канд. техн. наук. М.,
МЭИС, 1972.
114. Нергаард. Сравнительные
характеристики мощных ламповых и
твердотельных генераторов. —
«Зарубежная радиоэлектроника»,
1971, т. 25, №8.
115. Окунев Ю. Б. Системы связи
с инвариантными характеристи-
294
нами помехоустойчивости. Μ.,
«Связь», 1973.
116. Окунев Ю. Б., Яковлев Л. А.
Широкополосные системы
связи с составными сигналами. М.,
«Связь», 1968.
117. Остроухое В. С, Тузов Г. И.
Исследование функции
неопределенности сигнала с частотно-
фазовой манипуляцией. —
«Радиотехника и электроника», 1974,
т. 19, №11.
118. Остроухое В. С, Тузов Г. И.
Функция автокорреляции
сигнала с частотно-фазовой
манипуляцией. — «Радиотехника и
электроника», 1974, т. 19, №11.
119. Пелехатый М. И., Голубев Е. А.
Автокорреляционные свойства
некоторых типов двоичных
последовательностей. —
«Проблемы передачи информации»,
1972, т. 8, № 1.
120. Петрович Н. Т., Размахнин М. К.
Системы связи с шумоподобны-
ми сигналами. М., «Сов. радио»,
1969.
121. Питерсон У. Коды,
исправляющие ошибки. Пер. с англ. М.,
«Мир», 1964.
122. Приборы с поверхностным
переносом заряда (обзор). —
«Зарубежная радиоэлектроника», 1973,
т. 27, № 9. Авт.: А. М. Воробьев,
А. С. Дронов, О. А. Нерусин,
А. П. Ровинский.
123. Пышкин И. М. О
помехоустойчивости дискретных систем
связи при воздействии импульсных
помех. — «Радиотехника», 1970,
т. 25, № 11.
124. Пышкин И. М. Воздействие
негауссовых помех на систему
передачи дискретной информации.
«Радиотехника», 1971, т. 26, № 2.
125. Пышкин И. М. Эффективность
асинхронных адресных систем
связи с кодовым разделением
при передаче дискретной
информации. — «Электросвязь»,
1971, т. 25, №4.
126. Пышкин И. М. Когерентный
прием дискретной информации
при воздействии негауссовых
помех. 4.1. — «Радиотехника»,
1972, т. 27, № 10.
127. Пышкин И. М., Власов В. Н.
К вопросу построения
асинхронно-адресной системы связи
(ААСС) со сложными сигналами
с дискретной частотной
модуляцией (ДЧМ).—«Труды МЭИС»,
1968, вып. 1.
128. Пышкин И. М., Шауро А. В.
Эффективность асинхронных
адресных систем связи при
передаче телефонных сообщений. —
«Электросвязь», 1972, т. 26,
№ 10.
129. Пышкин И. М., Чвилев Г. Д.
Помехоустойчивость и
эффективность асинхронных
адресных систем с
частотно-временным кодированием при
когерентном приеме дискретной
информации. — «Радиотехника и
электроника», 1973, т. 18, № 11.
130. Радиотехнические системы в
ракетной технике. Под ред.
В. И. Галкина, И. И. За-
харченко, Л. В. Михайлова.
М., Воениздат, 1974. Авт.:
В. Д. Великанов, В. И. Галкин,
И. И. Захарченко и др.
131. Рид, Блэсбалг. Эффективные
методы измерения расстояний
и передачи данных в условиях
многолучевого
распространения на линиях самолет—земля
и земля—самолет. — «ТИИЭР»,
1970, т. 58, № з.
132. Риордан Дж. Введение в
комбинаторный анализ. Пер. с англ.
Под ред. Л. Я. Куликова. М.,
ИЛ, 1963.
133. Сагателов В. С. Спектральные
и корреляционные свойства
составных двоичных
последовательностей. — «Радиотехника и
электроника», 1973, т. 18, № 1.
134. Сангстир, Тир. Пожарные
цепочки. — «Зарубежная
радиоэлектроника», 1971, т. 25, № 10.
135. Сандерс. Система связи «Дид-
жилок». — В кн.: Передача
цифровой информации. Пер. с англ.
Под ред. С. И. Самойленко. М.,
ИЛ, 1963.
136. Свердлик М. Б. Оптимальные
дискретные сигналы. ΑΙ., «Сов.
радио», 1975.
137. Семенов А. М., Сикарев А. А.
Широкополосная радиосвязь.
М., Воениздат, 1970.
138. Слепян Д. Класс двоичных
сигнальных алфавитов. — В кн.:
Теория передачи сообщений.
Под ред. В. И. Сифорова. М.,
ИЛ, 1957.
295
139. Слока В. К. Вопросы'обработки
радиолокационных сигналов..
М., «Сов. радио», 1970.
140. Смирнов Н. И. Применение
М-последовательностей в
асинхронных радиотехнических
системах. — «Электросвязь», 1970,
т. 24, № 10.
141. Смирнов Н. И. Построение
больших ансамблей
последовательностей. — «Радиотехника»,
1972, т. 27, № 3.
142. Смирнов Н. И.
Корреляционные свойства
последовательностей с большим ансамблем. —
«Радиотехника», 1972, т. 27,
№6.
143. Смирнов Н. И. О
закономерностях статистических
характеристик корреляционных
функций случайных и
псевдослучайных последовательностей. —
«Радиотехника и
электроника», 1972, т. 17, № 8.
144. Смирнов Н. И.
Характеристики двумерных корреляционных
функций сложных сигналов. —
«Радиотехника», 1974, т. 29,
№ 12.
145. Смирнов Н. И., Могилевский
Л. Ю. О допустимом числе
одновременно действующих адресов
многоадресной системы с
кодовым разделением. —
«Радиотехника», 1971, т. 26, № 10.
146. Смирнов Н. И., Голубков Н. А.
Усеченные авто-и
взаимно-корреляционные функции двоичных
рекуррентных
последовательностей. — «Изв. вузов СССР.
Радиоэлектроника», 1972, т. 15.
№3.
147. Смирнов Н. И., Голубков Н. А.
О свойствах составных
последовательностей. —
«Радиотехника и электроника», 1973, т.
28, No. 1.
148. Смирнов Н. И., Голубков Н. А.
Корреляционные свойства
сегментов Λί-последовательно-
стей. — «Радиотехника», 1973,
т. 28, No. 6.
149. Соммер. Об оптимизации
дискретно-адресных систем
связи с произвольной выборкой. —
«ТИИЭР», 1964, т. 52, № 10.
150. Соммер. Система RADA с
кодированием адресов.—«ТИИЭР»,
1966, т. 54, N° 9.
151. Соммер. Высокоэффективная
система связи с многократным
доступом через ретранслятор
с обработкой сигнала. —
«Зарубежная радиоэлектроника»,
1969, т. 23, No. 7.
152. Современная радиолокация.
Анализ, расчет и проектирование
систем. Пер. с англ. Под ред.
Ю. Б. Кобзарева. М., «Сов.
радио», 1969.
153. Сталдер, Кан. Граничные
значения для пиков
корреляционных функций периодических
последовательностей.— «ТИИЭР»,
1964, т. 52, No. 10.
154. Стиффлер Дж. Дж. Теория
синхронной связи. Пер. с англ.
Под ред. Э. М. Габидулина. М.,
«Связь», 1975.
155. Судовцев В. А. Математические
основы методов
предоставления корреляционных функций
при наличии искажений. —
«Труды учебных институтов свя-
зи», 1972, вып. 59.
156. Теория и применение
псевдослучайных сигналов. М.,
«Наука», 1969. Авт.: А. И.
Алексеев, А. Г. Шереметьев,
Г. И. Тузов, Б. И. Глазов.
157. Теплов Н. Л.
Помехоустойчивость систем передачи
дискретной информации. М., «Связь»,
1964.
158. Теплов Н. Л. К оценке
помехоустойчивости и пропускной
способности систем передачи
дискретной информации
сигналами сложной формы. —
«Радиотехника», 1969, т. 24, № 3.
159. Тепляков И. М. Радиотелеме
трия. М., «Сов. радио», 1966.
160. Титов В. П.
Взаимокорреляционные свойства бинарных
последовательностей. —
«Радиотехника», 1972, т. 27, No 4.
161. Титсворт. Применение булевой
функции для построения
многоканальной телеметрической
системы. — «Зарубежная
радиоэлектроника», 1964, т. 18,
№8.
162. Тихонов В. И. Статистическая
радиотехника. М., «Сов.
радио», 1966.
163. Тихонов В. И., Кульман Н. К.
Нелинейная фильтрация и
квазикогерентный прием сигналов.
М., «Сов. радио», 1975.
164. Тор. Техника сжатия импуль-
296
са с большим произведением
длительности на ширину
спектра. — «Зарубежная
радиоэлектроника», 1963, т. 17, № 12.
165. Тузов Г. И.
Помехоустойчивость условно оптимального
приема псевдослучайных
сигналов. — «Изв. вузов СССР.
Радиоэлектроника», 1972, т. 15,
№ 10.
166. Тузов Г. И. Статистическая
теория приема сложных
сигналов. М., «Сов. радио», 1977.
167. Турин. Согласованные фильтры.
«Зарубежная
радиоэлектроника», 1961, т. 15, № 3.
168. Уздемир А. П.
Корреляционные функции комбинированных
последовательностей. —
«Радиотехника и электроника»,
1972, т. 17, № 3.
169. Уорд. Применение
корреляционного метода радиолокации
к задачам связи и слежения
за объектами в дальнем
космосе. — «Зарубежная
радиоэлектроника», 1964, т. 18, № 12.
170. Фалькович С. Е. Прием
радиолокационных сигналов на фоне
флюктуационных помех. М.,
«Сов. радио», 1961.
171. Финк Л. М. Теория передачи
дискретных сообщений. М.,
«Сов. радио», 1970.
172. Фогельсон Б. А. К теории
линейных искажений при
оценке разрешающей способности
сигнала. — В кн.: Труды
Второй научно-технической
конференции «Проблемы
оптимальной фильтрации», М., МЭИС,
1968, вып. 2.
173. Форни Д. Каскадные коды. Пер.
с англ. Под ред. С. И. Самой-
ленко. М., «Мир», 1970.
174. Фрэнк. Многофазные коды с
хорошими непериодическими
корреляционными свойствами. —
«Зарубежная
радиоэлектроника», 1963, т. 17, № 12.
175. Фрэнке Л. Теория
сигналов. Пер. с англ. М., «Сов.
радио», 1974.
176. Халин Ф. М., Леонов А. Ф.,
Меладзе В. В. Методы
повышения качества электронных
систем коммутации. М., «Связь»,
1971.
177. Харкевич А. А. Спектры и
анализ. Гостехиздат, 1957,
178. Хармут X. Ф. Передача
информации ортогональными
функциями. Пер. с англ. М., «Связь»,
1975.
179. Хаффмен Д. А.
Исследование сигналов, эквивалентных
импульсу. — «Радиотехника»,
1964, т. 19, № 8.
180. Хворостенко Н. П.
Статистическая теория демодуляции
дискретных сигналов. М.,
«Связь», 1968.
181. Цикин И. А. Дискретно-
аналоговые методы оптимальной
обработки сигналов. —
«Радиотехника», 1969, т. 24, № 2.
182. Цикин И. А.
Дискретно-аналоговые согласованные
фильтры. — «Известия вузов СССР.
Радиоэлектроника», 1970, т.
13, № 2.
183. Цифровые методы в
космической связи. Под ред. С. Голом-
ба. Пер. с англ. Под ред.
В. И. Шляпоберского. М.,
«Связь», 1969.
184. Чадвик, Спрингет.
Низкоскоростная система связи с
многократной частотной
манипуляцией. — «Зарубежная
радиоэлектроника», 1971, т. 25,
№ 12.
185. Черняк Ю. Б. О линейных
свойствах системы
широкополосный ограничитель — фильтр. —
«Радиотехника и электроника»,
1962, т. 7, № 7.
186. Черняк Ю. Б.
Чувствительность, точность и разрешающая
способность многоканального
приемника с широкополосным
ограничителем. —
«Радиотехника и электроника», 1962, т. 7,
№8.
187. Чеслер. m-ричная система
RADA. — «ТИИЭР», 1965,
т. 53, № 4.
188. Шахгильдян В. В.,
Лохвицкий М. С. Методы адаптивного
приема сигналов. М., «Связь»,
1974.
189. Шахгильдян В. В., Ляхов-
кин А. А. Системы фазовой
автоподстройки частоты. М.,
«Связь», 1972.
190. Шеннон К. Математическая
теория связи. В кн.: К.
Шеннон. Работы по теории инфор-
297
мации и кибернетике. Пер. с
англ. Под ред. Р. Л. Добру-
шина, О. Б. Лупанова. М.,
ИЛ, 1963.
191. Ширман Я. Д. Разрешение и
сжатие сигналов. М., «Сов.
радио», 1974.
192. Шумоподобные сигналы в
системах передачи информации.
Под ред. В. Б. Пестрякова.
М., «Сов. радио», 1973. Авт.:
В. Б. Пестряков, В. П.
Афанасьев, В. Л. Гурвич и др.
193. Эйнарссон. Импульсные
системы радиосвязи с
частотно-временным кодированием адресов
абонентов. — «Зарубежная
радиоэлектроника», 1967, т. 21,
№3.
194. Экспериментальное
исследование прохождения сложных
сигналов и шумов через
ограничитель. — В кн.: Труды
Второй научно-технической
конференции «Проблемы
оптимальной фильтрации». М., МЭИС,
1968. вып. 1. Авт.: Л. Е. Ва-
ракин, В. Н. Власов, Л. Н.
Волков, И. М. Пышкин.
195. Эпплбаум, Хауэллс. Сигналы
РЛС ближайшего будущего. —
«Зарубежная
радиоэлектроника», 1900, т. 14, № 4.
196. Эсседориан, Якоби. Некоторые
аспекты многократного
доступа в связных спутниках. —
«Зарубежная
радиоэлектроника», 1967, т. 21, № 11.
197. Ярлыков М. С, Черняков М. В.
Квазиоптимальный прием
сигналов в асинхронных адресных
системах связи с
частотно-временной матрицей. — «Изв.
вузов СССР. Радиоэлектроника»,
1973, т. 16, № 5.
198. Blasbalg Η., Freeman D.,
Keeler R. Random-access
communications using frequency
shifted PN (pseudo-noise)
signals. — «IEEE Inter. Conv.
Rec», 1964, pt. 6.
199. Eoehmer A. Binary Pulse
Compression Codes. — «IEEE Trans.
Inf. Th.», 1967, v. IT — 13,
№2.
200. Braasch R. H. The Distribution
of (n - m) terms for Maximal
Length Linear Pseudo-Random
Sequences. — «IEEE Trans.
Inf. Th», 1968, v. IT-14, № 4.
201. Carter D. E. On the
Generation of Pseudo Noise Codes. —
«IEEE Trans. Aerosp. El.
Syst.», 1974, v. AES-10, № 6.
202. Costas I. P. Poisson, Shannon
and Radio amateurs. — «Proc.
IRE», 1959, v. 47, № 12.
203. Dawson С. Н. An Introduction
on to Random-Access
Discrete-Address System. — «IEEE
Inter. Conven. Rec», 1964,
pt. 6.
204. Dawson C. H., Sclar H. False
Addresses in Random-Access
System Employing Discrete
Time-Frequency Addressing. —
«IEEE Inter. Conven. Rec»,
1964, pt. 6.
205. Eisenstadt B. M., Gold B.
Auto Correlation for Boolean
Functions of Noiselive Periodic
Sequences.— «IRE Trans. Electr.
Сотр.», 1961, v. EC—10, № 3.
206. Fredricsson S. A.
Pseudo-Randomness Properties of Binary
Shift Register Sequences. —
«IEEE Trans. Inf. Th.», 1975,
v. IT — 21, № 1.
207. Golay M. J. E. Hybrid Low
Autocorrelation Sequences. —
«IEEE Trans. Inf. Th.», 1975,
v. IT — 21, № 4.
208. Gold R. Optimal Binary
Sequences for Spread Spectrum
Multiplexing. — «IEEE Trans.
Inf. Th», 1967, v. IT-13, № 4.
209. Gold R. Maximal Recursive
Sequences with 3-valued
Recursive Cross-Correlation
Functions. — «IEEE Trans. Inf.
Th.», 1968, v. IT — 14, № 1.
210. Golomb S. W. Shift Register
Sequences. — «Hoi den — Day»,
San-Francisco, 1967.
211. Harwood D. Gagliardi R.
Signal Design for Digital
Multiple Access Communications. —
«IEEE Trans. Commun.», 1975,
v. COM—23, № 3.
212. Helm H. A. Group Codes and
Walsh Functions. — «IEEE
Trans. El. Mag. Comp», 1971,
v. EMC — 13, № 3.
213. Hollis Ε. Ε.
Quasi-Complementary Sequences. — «IEEE
Trans. Aerosp. El. Syst.», 1975,
v. AES — 11, № 1.
214. Kuhn B, G., Morey К. Н.,
298
Smith W. В. The Orthomatch
Date Transmission System. —
«IEEE Trans. Space Electr.
Tel.», 1963, v. SET—9, № 3.
215. Lindhoim I. H. An Analysis
of the Pseudo-Randomness
Properties of Subsequences of Long
m-Sequences. — «IEEE Trans.
Inf. Th.», 1968, v. IT-14, № 4.
216. Mohanty N. С Multiple Frank —
Heimiller Signals For
Multiple Access Systems. — «IEEE
Trans. Aerosp. El. Syst.», 1975,
v. AES—11, № 4.
217. McCalmont. Multiple-Access
Discrete Address
Communication Systems. — «IEEE
Spectrum», 1967, v. 4, № 8.
218. Oswald I. R. CODEST: a New
Pulse-Code Modulation
System for Telegraph and Data
Transmission. — «IEEE Trans.
Com. Tech.», 1970, v. COM —
18, №3.
219. Pierce I. A. An Introduction
to Loran. — «Proc. IRE.»,
1946, v. 34, № 5.
220. Reed I. S. K-th-Order Near-
Orthogonal Codes. — «IEEE
Trans. Inf. Th.», 1971, v. IT —
17, № 1.
221. Savage J. A. Signal Detection
in the Presence of Multiple-
Access Noise. — «IEEE Trans.
Inf. Th.», 1974, v. IT-20, № 1.
222. Sinsky A. I., Wang P. С P.
Error Analysis of a Quadrature
Coherent Detector Processor. —
«IEEE Trans. Aerosp. El.
Syst.», 1974, v. AES — 10,
№6.
Литература к постскриптуму
231. Гоноровский И. С.
Радиотехнические цепи и сигналы. М.,
«Сов. радио», 1977.
232. Справочник по радиолокации.
Пер. с англ. Под ред. Я. С. Иц-
хоки. Т. 1. М., «Сов. радио»,
1976.
233. Свистов В. М.
Радиолокационные сигналы и их обработка.
М., «Сов. радио», 1977.
234. Дялюнов Н. Г., Сенин А. И.
Ортогональные и квазиорто-
I тональные сигналы. М., «Связь»,
Ί977.
223. Sussman S. Μ. Least — Square
^Synthesis of Radar Ambiguity
Functions. — «IRE Trans, on
Inf. Th.», 1962, v. IT — 8,
№ 3.
224. Viterby A. A New Coding
Technique for Asynchronous
Multiple Access Communication. —
«IEEE Trans. Com. Tech.»,
1971, v. COM — 19, № 5.
225. Wainberg S., Wolf I. K.
Subsequences of Pseudo random
Sequences. — «IEEE Trans.
Com. Tech.», 1970, v. COM —
18, №5.
226. Waylan С J., Ohlson J. E.
Optimum Position
Estimation Using Multiple -
Frequency Omega. — «IEEE Trans.
Aerosp. El. Syst.», 1975, v.
AES — 11, № 1.
227. Webb P. R. W. Military
Satellite Communications Using
Small Earth Terminals.—«IEEE
Trans. Aerosp. El. Syst.»,
1974, v. AES — 10, № 3.
228. Weng L. — I.
Decomposition of M-Sequences and Its
Applications. — «IEEE Trans.
Inf. Th.», 1971, v. IT-17, №4.
229. White R. С Experiments with
Digital Computer Simulating
of Pseudo-Random Noise
Generators. — «IEEE Trans.
Electr. Сотр.», 1967, v. EC —
16, № 3.
230. White W. D. Theoretical Aspects
of Asynchronous
Multiplexing.—«Proc. IRE» 1950, v. 38,
№3.
235. Зайдлер. Е. Системы передачи
дискретной информации. Пер.
с польск. Под ред. Б. Р.
Левина. М., «Связь», 1977.
236. Campbell Μ. R., Hoff L. Ε.,
Ziemer R. Ε. A Large Time-
Bathwidth Product Signaling
Technique for Nonwhite Noise
Channels. — «IEEE Trans.»
1976, v. COM-24, № 10.
237. Глобус И. А. О функции
распределения ВКФ полного
кода. — «Радиотехника», 1977,
τ 32, №-1
299
238. Глобус И. А. Регулярный
метод синтеза некоторых классов
ЧВМ сигналов. —
«Радиотехника» , 1977 , т. 32 , № 8.
239. Варакин Л. Е. Статистические
свойства дискретных составных
частотных сигналов с частотной
манипуляцией. —
«Радиотехника» , 1977 , т. 32 , № 9.
240. Shneider К. S. , Orr R. S.
Aperiodic Correlation Constraints on
Large Binary Sequences Sets. —
«IEEE Trans.» , 1975 , v. IT-21 ,
№ 1.
241. Моисеева Г. Г. Построение
больших производных систем
ФМ сигналов. —
«Электросвязь» , 1977 , т. 31 , № 6.
Предметный указатель
Абонент 47 , 51 , 72
— активность 74 , 93
Автокорреляционная функция 25
Адамара матрица 106
Алгоритмы построения сигналов 18 , 19
Алфавит источника 53
— кодера 53
— сигналов 54 , 70
База сигнала 11
— системы 11
— элемента 32 , 114
Блок 176
Блоков , чисто 176 , 206 , 219
Вероятность ложной тревоги , 154
— ошибки 55 , 60 , 67 , 91 , 154 , 162
средняя 164 , 168
— правильного обнаружения 154 , 159
оценка 161
— экстремальных пиков 215 , 219
Вес кодовой последовательности 189 , 217
— сегмента 241
— модуль 190
Взаимная корреляционная функция 25
пики 108 , 241 , 247
— функция неопределенности 23
Гильберта преобразование 9
Группа 178
— двоичная аддитивная 179
мультипликативная 180
— р-ичная аддитивная 180
мультипликативная 180
комплексно-сопряженная 181
— разбиение 184
натуральное 184
— разложение 182
Декодер 54
Дельта-функция 46 , 96
Дисперсия корреляционных функций 195 ,
197
— полного двоичного кода 202
>— системы 105
Интеграл вероятности 55
— корреляционный 132
Канал передачи информации 47
Класс сигналов 19
— смежный 184
Классификация сигналов 13
— систем сигналов 18
Код полный 172
алгебраические свойства 178
двоичный 172 , 198
дискретных частотных сигналов
первого порядка 271 , 273
ортогональность 185
произвольный 172 , 178
р-ичный 182
спектральная плотность мощности 204
300
Кодер 53
Кодирование идеальное 63
Комбинаторика 170
Комплексная огибающая сигнала 20 , 21
дискретного 39
дискретного частотного 29 , 255
частотного 39
Коррелятор 58 , 133
Корреляционная функция 23
апериодическая 192
взаимная 25
групповые свойства 188
дискретного сигнала 43
частотного сигнала первого
порядка 33 , 255
произвольного порядка 37
полного кода 187
производных сигналов 229
распределение 192 , 198 , 200
частотного сигнала 46
Коэффициент асимметрии 101
— корреляций 24
— эксцесса 100 , 106 , 203
Линия задержки многоотводная 137 , 141
— разностная 42
Манипуляция амплитудная 56
— ортогональная 56
— фазовая 56
Множество сигналов 9 , 18
Моменты корреляционных функций 97 , 194 ,
195
Накопление 115
— квазиоптимальное 122
— линейное 116
— оптимальное 118
Обнаружение сложного сигнала 153 , 155
Объем взаимной функции
неопределенности 26
— класса манипулированных сигналов 171
дискретных частотных сигналов 172
— системы сигналов 9
— функции неопределенности 26
Оптимальная пара дискретных частотных
сигналов 268
Отношение сигнал/помеха 91 , 113 , 116 , 119 ,
124
элементное 116
— сигнал/шум 56 , 59
на выходе согласованного фильтра
НО
Плоскость неопределенности 24
— частотно-временная 11 , 12 , 16 , 17
Подгруппа 182
Помеха 54
— взаимная 82 , 89 , 90 , 94 , 108
мощная 109
плотность вероятности 98
— заградительная шумовая 110
— импульсная 111
— сосредоточенная 111
шумовая 113
— структурная 111
Порядок группы 184
— дискретных частотных сигналов 29
— подгруппы 184
Последовательность кодовая 30
амплитудно-фазовая 31
временная 266
прямая 216
произвольная 106 , 218 , 219
обратная 216
фазовая 30
частотная 31 , 265
элементная 31
— позиционная 219
производная 219
Прием квазиоптимальный 133
— когерентный 55
— некогерентный 55
— оптимальный 132
элемента сигнала 112
Приемник адаптивный 120
— оптимальный когерентный 57
некогерентный 58
— нелинейный 123
Пуассона закон 264
Равенства интегральные 26
Радиотехнические системы 130 , 132
инвариантные к комплексу помех 130
Разделение адаптивное кодовое 80
— каналов и абонентов 51
временное 51
кодовое 51 , 87
основы 89
линейное 72
частотное 51
— нелинейное кодовое 83
Разложение по ортогональным функциям
14
Сегменты 229 . 237 , 239
Сигнал 9
— амплитудно-манипулированный 18
— видеочастотный 10
— групповой 73
— дискретный 16 , 38 , 141
частотный 17 , 28 , 135 , 255
первого порядка 29
произвольного порядка 35 , 172 , 259
— манипулированный 13
— модулированный 13
— оптимальный 258
— простой 13
— производный 228
— производящий 229 , 231 , 233
— радиочастотный 9
— свойства структурные 13 , 131
корреляционные 131
энергетические 12
— синхронизации 74
— сложный 13
— со смещением по частоте 39 , 254
— составной 17
частотный 278 , 279 , 280
— структура 15
— фазоманипулированный 10 , 84
оптимальный 206
минимаксный 206
— финитный 9
— частотный 16 , 38 , 139 , 250
— элементарный 15
— энергия 11
Сигналы ортогональные 49
— симплексные 59
Символ 53
— двоичный 53
— ^г-ичный 54
Система адресная асинхронная 50
синхронная 50
— ортогональных функций 14 , 49
— передачи информации 49
двоичная 55
дискретная 53
многоканальная 49
— сигналов 9 , 19
большая 83 , 287
дискретных 223
^_ частотных 270 , 275
исходная 229
многофазных 247 , 249
правило выбора 103 , 105 , 108
производная 228
сегментная 235
циклическая 243
частотных 250
Скорость передачи информации 54
Совпадения 261 , 265
Сообщения 47
Уолша кодовые последовательности 106 ,
225
— системы сигналов 223
Уплотнение каналов и абонентов 51
— кодовое адаптивное 80
нелинейное 83
Устройство поиска 151 , 152
— разделения 73
— уплотнения 73
Фаза 9
— медленноменяющаяся часть 9
Фильтр активный 151
— согласованный 57 , 132
дискретный 144
квазиоптимальный 146 , 149
дискретно-аналоговый 150
— многоканальный 135
постоянная 112
элементный 113
Фильтрация помех 109 , 124 , 127
Форма элемента 30
Фурье преобразование 10
обратное 11
— ряд 15
Частота 9 , 10
Частотно-корреляционная функция 25
Шеннона теорема 63
Шум белый 54
— мощность на выходе фильтра 57
— спектральная плотность мощности 54
Элемент временной 15
— дискретный 15 , 16
частотный 16
— , накопление 115
— нейтральный 179
— обратный 179
— частотный 15
— частотно-временной 15
Эрмита многочлен 100
Эффект пороговый 63
301
Оглавление
Предисловие 3
Основные условные обозначения 6
Основные сокращения 8
РАЗДЕЛ 1 9
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИЕМА СИСТЕМ СИГНАЛОВ ... 9
Глава 1. Сигналы, спектры, корреляционные функции 9
1.1. Сигналы и спектры , 9
1.2. Классификация сигналов 13
1.3. Классификация систем сигналов 18
1.4. Комплексная огибающая сигнала и ее спектр 20
1.5. Корреляционные функции сигналов 23
1.6. Дискретные частотные сигналы 28
1.7. Частотные и дискретные сигналы 38
Глава. 2. Системы сигналов и передача информации 47
2.1. Системы передачи информации 47
2.2. Дискретная система передачи информации 53
2.3. Пороговый эффект в m-ичных системах передачи информации 63
2.4. Сравнение двоичных и m-ичных систем передачи информации 65
2.5. Выбор объема алфавита сигналов 70
Глава 3. Синхронные адресные системы передачи информации .... 72
3.1. Линейное уплотнение и разделение абонентов 72
3.2. Адаптивное частотное уплотнение и разделение абонентов 79
3.3. Адаптивное кодовое уплотнение и разделение абонентов . . 80
3.4. Нелинейное кодовое уплотнение и разделение абонентов . . 83
Глава 4. Асинхронные адресные системы передачи информации ... 87
4.1. Кодовое уплотнение и разделение абонентов в асинхронных
адресных системах 87
4.2. Корреляционные и статистические свойства взаимной помехи 94
4.3. Выбор системы сигналов для асинхронных адресных систем 102
Глава 5. Основы фильтрации мощных помех 109
5.1. Классификация помех 109
5.2. Оптимальный прием элемента сигнала 112
5.3. Накопление элементов 115
5.4. Фильтрация сосредоточенных помех 124
5.5. Фильтрация узкополосных и импульсных помех 127
5.6. Фильтрация структурных помех 128
5.7. Радиотехнические системы, инвариантные к комплексу помех 130
302
Глава 6. Основные методы обработки систем сигналов 131
6.1. Оптимальная и квазиоптимальная линейная обработка
сигналов 131
6.2. Линейные согласованные фильтры 135
6.3. Дискретный согласованный фильтр 144
6.4. Дискретно-аналоговый согласованный фильтр 150
6.5. Активные фильтры 151
Глава 7. Реальная помехоустойчивость радиотехнических систем со
сложными сигналами 153
7.1. Помехоустойчивость приема сложных сигналов с
идеальными корреляционными функциями 153
7.2. Помехоустойчивость приема сложных сигналов с реальными
корреляционными функциями 156
7.3. Помехоустойчивость приема сложных сигналов при
неидеальной синхронизации по времени и частоте 161
7.4. Помехоустойчивость приема сложных сигналов при
рассогласованиях 165
7.5. Определение числа активных абонентов в ААС с учетом
рассогласований , 169
РАЗДЕЛ II 170
ОБЩАЯ ТЕОРИЯ СИСТЕМ СИГНАЛОВ 170
Глава 8. Комбинаторный анализ систем сигналов 170
8.1. Комбинаторика и теория систем сигналов 170
8.2. Дискретные частотные сигналы произвольного порядка . . 172
8.3. Сигналы с двоичной амплитудной манипуляцией 175
8.4. Сигналы с заданным числом блоков 176
Глава 9. Полный произвольный код 178
9.1. Алгебраические свойства полного кода 178
9.2. Ортогональность полного кода . . 185
9.3. Корреляционные функции полного кода 187
9.4. Распределение весов полного кода 189
9.5. Распределение корреляционных функций 192
9.6. Статистические характеристики полного кода 194
Глава 10. Полный двоичный код 198
10.1. Распределение корреляционных функций 198
10.2. Статистические характеристики 202
10.3. Средняя спектральная плотность мощности полного кода 204
10.4. Произвольная система сигналов 205
Глава 11. Оптимальное число блоков и системы сигналов 206
11.1. Гипотеза об оптимальном числе блоков 206
11.2. Вероятность экстремальных пиков и оптимальное число
блоков 215
11.3. Число блоков в кодовой последовательности и ее вес . . . 216
11.4. Число блоков в производной кодовой последовательности
и вероятность экстремальных пиков ... , , , 219
303
РАЗДЕЛ III 223
СИСТЕМЫ СИГНАЛОВ 223
Глава 12. Системы дискретных сигналов 223
12.1. Системы Уолша 223
12.2. Производные системы сигналов 228
12.3. Сегментные системы 235
12.4. Циклические системы 243
12.5. Системы многофазных сигналов 247
Глава 13. Системы частотных сигналов 250
13.1. Системы частотных сигналов 250
13.2. Системы сигналов со смещением по частоте 254
Глава 14. Системы дискретных частотных сигналов и дискретных
составных сигналов 255
14.1. Корреляционные функции дискретных частотных сигналов
и число совпадений элементов 255
14.2. Комбинаторный анализ систем дискретных частотных
сигналов 259
14.3. Полный код дискретных частотных сигналов первого
порядка 271
14.4. Регулярные методы построения дискретных частотных
систем . . . .. 275
14.5. Дискретные составные частотные сигналы 278
14.6. Системы. дискретных составных фазоманипулироваиных
сигналов 280
Послесловие 287
Постскриптум 288
Список литературы 290
Литература к постскриптуму 299
Предметный указатель 300
Л.Е.ВАРАКИН
-■;. \\ Теория
.-.■"..V" систем
-■"■' -"■-"Λ* сигналов
/П^2 I s~ Ъ