C.A. ФРОЛОВ
НЛЧЕРШЕИЬНЛЯ
ГЕО/ИЕТРИЯ
Издание второе, переработанное
и дополненное
Допущено Министерством
высшего и среднего специального
образования СССР в качестве
учебника для студентов
машиностроительных
специальностей вузов
МОСКВА «МАШИНОСТРОЕНИЕ» 1983

ББК 22.151.3Я73
Ф91
УДК 515@75)
РЕЦЕНЗЕНТ:
кафедра начертательной геометрии и черчения
Московского автомеханического института
Фролов С. А.
Ф91 НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ: Учебник для ^ту-
^тузов. — 2-е изд., перераб. и доп. — М.: Машиностроение,
1983.-240 с, ил.
В пер.: 1 р. 20 к.
Учебник полностью соответствует новой программе Министер-
Министерства высшего и среднего специального образования СССР по
начертательной геометрии для втузов (кроме архитектурных и
строительных специальностей). Во втором издании учебника
A-е изд. 1978 г.) подчеркнута роль инвариантных свойств орто-
ортогонального проецирования в создании теоретической базы курса.
Особое внимание уделено способам образования поверхностей
и их заданию на эпюре Монжа. Материал по использованию ЭЦВМ
для решения задач, исходные данные которых представлены в гра-
графической форме, оставлен в прежнем объеме. Иллюстрации вы-
выполнены в многокрасочном исполнении, что способствует лучше-
лучшему восприятию и усвоению матер>цла студентами.
- 1702040000^030 о_ оо ББК 22.151.3я73
Ф 038@1)-83 3°"83 515
ИБ 3961
Сергей Аркадьевич Фролов
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Редактор И. Г. Калашникова Переплет художника А. Г. Антоновой
Художественный редактор , Графики-иллюстраторы:
А С. Вершинкин в л BoraTbipeBi B. п. Новиков,
Макет художника Е. И. Подмарьковои в г цепищев
Технические редакторы Л. П. Гордеева, '
Н. Н. Чистякова Операторы Л. А. Яковлева,
Корректор Н. В. Давыдова Л. В. Данилова
Подписано в печать 14.09.83. Формат 70x108/1/16
Бумага типографская № 1 Гарнитура Сенчури Печать офсетная Усл. печ. л. 21,0
Усл. кр.-отт. 83,^8. Уч.-изд. л. 21,47. Тираж 140 000 экз. Заказ 1957. Цена 1 р. 20 к.
Ордена Трудового Красного Знамени издательство "Машиностроение",
107076 Москва Б-76, Стромынский пер., 4
©Издательство "Машиностроение", 1978 г.
© Издательство "Машиностроение", 1983 г., с изменениями

ОГЛАВЛЕНИЕ
СПИСОК ЛИТЕРАТУРЫ . б
ПРЕДИСЛОВИЕ 6
ВВЕДЕНИЕ . 7
ОБОЗНАЧЕНИЯ И СИМВОЛИКА 8
Глава I. МЕТОД ПРОЕКЦИЙ
§ 1. Некоторые свойства евклидова пространства 13
§ 2. Реконструкция евклидова пространства 14
§ 3. Центральное проецирование 17
§ 4. Параллельное проецирование 18
§ 5. Ортогональное проецирование 19
§ 6. Инвариантные свойства ортогонального проецирования 21
§ 7. Эпюр Монжа 26
§ 8. Неопределяемые понятия геометрии; ортогональные проекции точ-
точки, прямой, плоскости 29
Вопросы для самопроверки 45
Глава II. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 46
I. СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ 48
§ 9. Способ параллельного перемещения 48
§ 10. Способ вращения вокруг оси, перпендикулярной к плоскости
проекции 52
§ 11. Способ вращения вокруг оси, параллельной плоскости проекции
(вращение вокруг линии уровня) 55
§ 12. Способ вращения вокруг оси, принадлежащей плоскости проек-
проекции (совмещение) 57
II. СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 59
§ 13. Замена одной плоскости проекции 59
§ 14. Замена двух плоскостей проекций 61
§ 15. Сочетание способа плоскопараллельного перемещения со спосо-
способом замены плоскостей проекции 62
§ 16. Другие способы преобразования ортогональных проекций 65
Вопросы для самопроверки 68
Глава III. ЛИНИЯ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 6Э
I. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИ
§ 17. Касательные и нормали к пространственной кривой 70
II. ПЛОСКИЕ КРИВЫЕ ЛИНИИ
§ 18. Приближенные способы построения касательной и нормали к
плоской кривой '°
§ 19. Кривизна плоской кривой 74
§ 20. Приближенный способ построения центра кривизны кривой в за-
заданной топке jjjj
§ 21. Эволюта и эвольвента 7jj
§ 22. Классификация точек плоской кривой 'jj
§ 23. Ортогональные проекции линии 78
§ 24. Определение длины пространственной кривой по ее ортогональ-
ортогональным проекциям °1
Вопросы для самопроверки 81

4 Оглавление
Глава IV. ПОВЕРХНОСТЬ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 82
§ 26. Образование поверхности и ее задание на эпюре Монжа 83
§ 26. Определитель поверхности 84
§ 27. Ортогональные проекции поверхности 86
§ 28. Классификация поверхностей 88
КЛАСС I
§ 29. Нелинейчатые поверхности с образующей переменного вида
(группа Aj) 91
§ 30. Нелинейчатые поверхности с образующей постоянного вида
(группа Bi) 93
КЛАСС II
§ 31. Линейчатые поверхности 94
§ 32. Линейчатые поверхности с тремя направляющими (группа Ац) . . 96
§ 33. Линейчатые поверхности с двумя направляющими (группа Бц) . . 101
§ 34. Линейчатые поверхности с двумя направляющими и плоскостью
параллелизма (поверхности Каталана) 102
§ 35. Линейчатые поверхности с одной направляющей — торсы (груп-
(группа Вц) 106
§ 36. Поверхности параллельного переноса (подкласс 1) 109
§ 37. Поверхности вращения (подкласс 2) 111
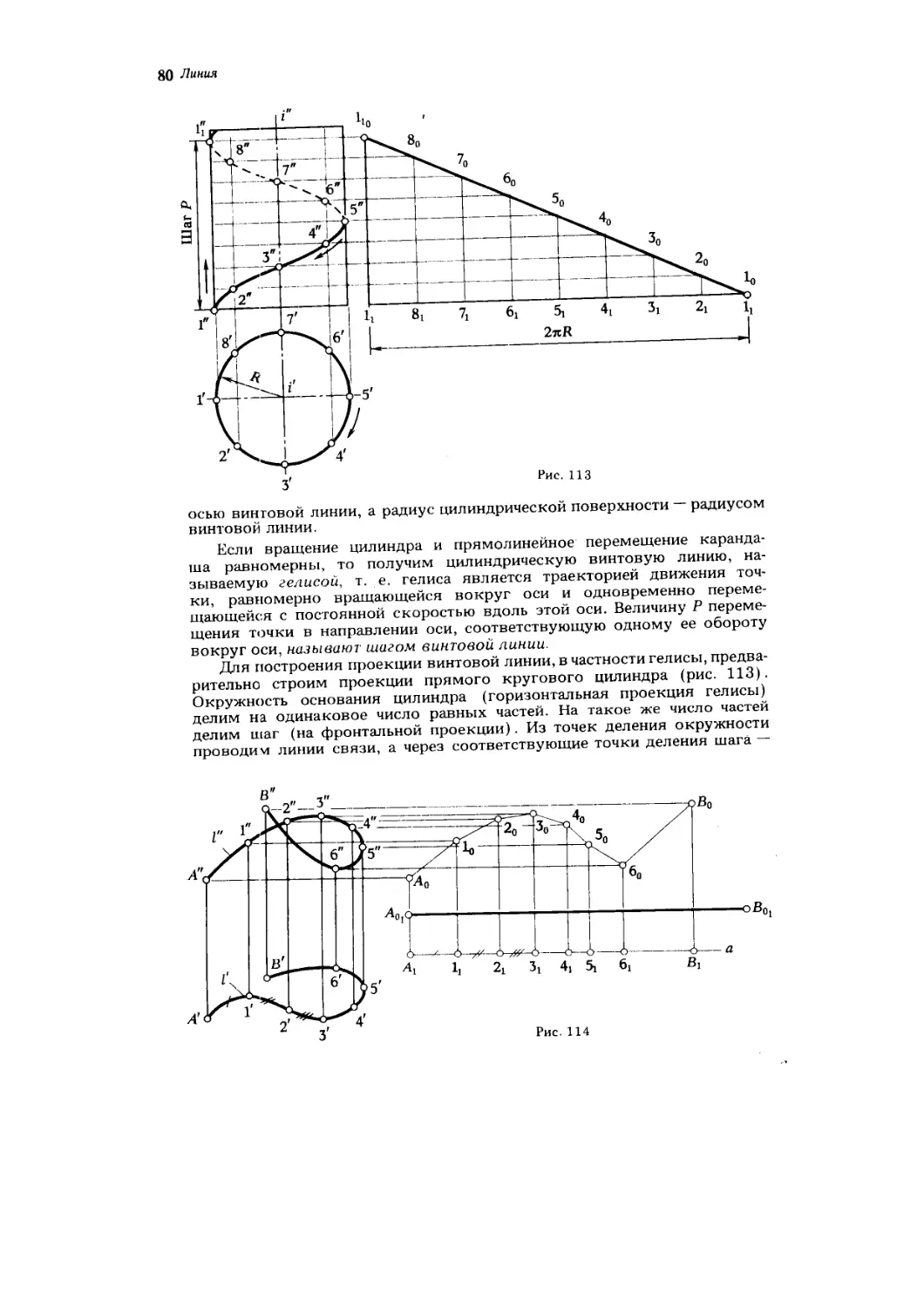
§ 38. Винтовые поверхности (подкласс 3) 114
Вопросы для самопроверки 117
Глава V. ПОЗИЦИОННЫЕ ЗАДАЧИ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 118
§ 39. Принадлежность точки линии (А € /) 119
§ 40. Принадлежность точки поверхности (А & а) 120
§ 41. Принадлежность линии поверхности AС а) 124
§ 42. Пересечение линии с линией (/ П т) 125
§ 43. Пересечение поверхности с поверхностью (аП/3) 126
§ 44. Пересечение плоскостей 128
§ 45. Пересечение поверхности плоскостью (построение сечения) 131
§ 46. Плоскость, касательная к поверхности '. . . 140
§ 47. Построение линии пересечения поверхностей (общий случай) . . . 147
§ 48. Построение линии пересечения поверхностей с помощью вспомо-
вспомогательных секущих плоскостей 148
§ 49. Построение линии пересечения поверхностей с помощью вспомо-
вспомогательных цилиндрических поверхностей 154
§ 50. Построение линии пересечения поверхностей с помощью вспомо-
вспомогательных конических поверхностей
§ 51. Построение линии пересечения поверхностей с помощью семейст-
семейства вспомогательных сферических поверхностей 158
§ 52. Построение линии пересечения поверхностей второго порядка
(частные случаи) 163
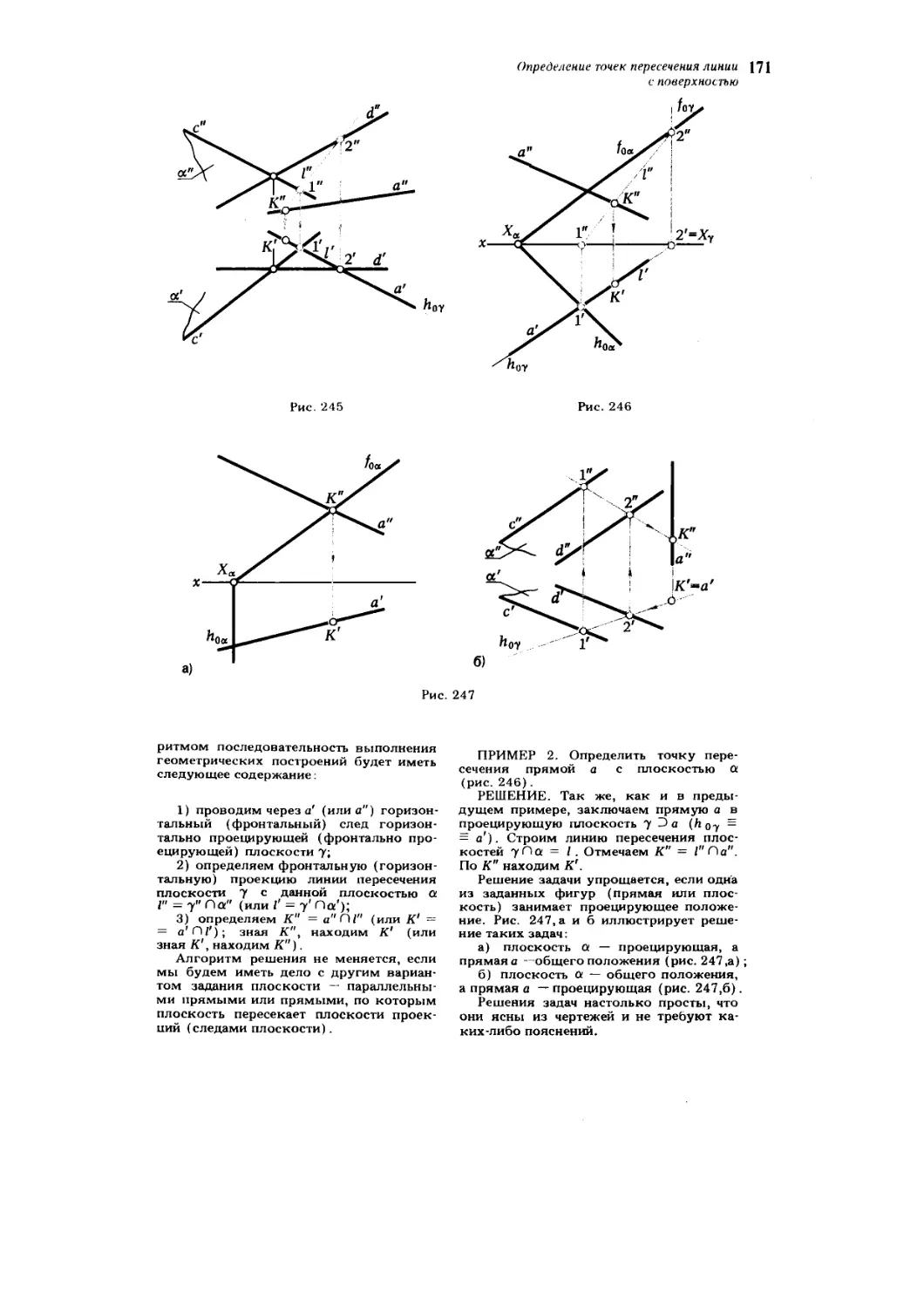
§ 53. Определение точек пересечения линии с поверхностью 165
Вопросы для самопроверки 172
Глава VI. МЕТРИЧЕСКИЕ ЗАДАЧИ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 173
§ 54. Построение взаимно перпендикулярных прямых, прямой и плос-
плоскости, плоскостей
§ 55. Определение расстояния между двумя точками
§ 56. Определение расстояния между точкой и прямой, между парал-
параллельными прямыми ^ *
§ 57. Определение расстояния между точкой и плоскостью, прямой и
плоскостью, между плоскостями и скрещивающимися прямыми 183
§ 58. О проекциях плоских углов ¦*¦"'
§ 59. Определение величины плоского угла по его ортогональным про-
проекциям 189

Список литературы 5
§ 60. Определение угла между прямой и плоскостью 1.90
§ 61. Определение угла между плоскостями 192
§ 62. Определение угла между скрещивающимися прямыми 194
Вопросы для самопроверки , 195
Глава VII. РАЗВЕРТКА ПОВЕРХНОСТЕЙ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 196
§ 63. Основные свойства развертки поверхностей 197
§ 64. Разыертка поверхности многогранников 198
§ 65. Построение приближенных разверток развертывающихся поверх-
поверхностей 201
§ 66. Условная развертка поверхностей 206
Вопросы для самопроверки 209
Глава VIII. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 210
§ 67. Стандартные аксонометрические проекции 212
§ 68. Примеры построения аксонометрических проекций геометричес-
геометрических фигур 215
§ 69. Решение позиционных задач на аксонометрических проекциях . . . 219
§ 70. Решение метрических задач на аксонометрических проекциях . . . 221
Вопросы для самопроверки 222
Глава IX. ИСПОЛЬЗОВАНИЕ ЭЦВМ ДЛЯ ГРАФИЧЕСКОГО РЕШЕНИЯ ЗА-
ЗАДАЧ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 223
§ 71. О возможности использования ЭЦВМ для графического решения
задач 223
§ 72. Основные вопросы проблемы автоматизации процесса графичес-
графического решения задач 226
§ 73. Машинное чтение чертежа 227
§ 74. Метод машинного решения задач 228
§ 75. Составление машинных алгоритмов решения задач 231
§ 76. Определение рационального машинного алгоритма 239
Вопросы для самопроверки 240
СПИСОК ЛИТЕРА IУ РЫ
1. Бубенников А. В., Громов М. Я. 7. Начертательная геометрия/Н. Ф. Чет-
Начертательная геометрия. М.: Высшая верухин, В. С. Левицкий, 3. И. Пряниш-
школа, 1973.416 с. никова и др. М.: Высшая школа, 1963.
2. Добряков А. И. Курс начертатель- 420 с.
ной геометрии. М. — Л.: Госстройиздат, 8 Начертательная геометрия/ С. М. Ко-
1952. 484 с. лотов, М. Ф. Евстифеев, В. Е. Михайлен-
3. Климухин А. Г. Начертательная гео- ко и Киев. Вища школа> 1975. 262 с.
метрия. М.: Стройиздат, 1973. 368 с.
4. Котов И. И. Начертательная геомет- д. Фролов С. А. Автоматизация процес-
рия. М.: Высшая школа, 1970. 382 с. са графического решения задич. Минск:
5. Крылов Н. Н., Лобандиевский П. И., Вышейшая школа, 1980. 255 с.
Мэн С. А. Начертательная геометрия. М.:
Высшая школа, 1977. 231 с. Ю. Фролов С. А. Сборник задач по на-
6. Кузнецов Н. С. Начертательная гео- чертательной геометрии. М.: Машино-
метрия. М.: Высшая школа, 1969. 496 с. строение, 1980. 141 с.

ПРЕДИСЛОВИЕ
Учебник предназначен для сту-
студентов технических вузов (кроме
архитектурных и строительных спе-
специальностей) .
Содержание учебника полностью
соответствует новой A979 г.) про-
программе по начертательной геомет-
геометрии.
Второе издание подверглось зна-
значительной переработке. При подго-
подготовке рукописи к изданию были
учтены отзывы и предложения, по-
полученные автором от читателей и
относящиеся как к содержанию,
так и объему некоторых разделов
учебника, в частности: внесены из-
изменения в систему обозначений
проекций геометрических фигур;
строже изложен вопрос, касающий-
касающийся инвариантных свойств ортого-
ортогонального проецирования, и более
четко подчеркнута их роль в созда-
создании теоретической базы курса на-
начертательной геометрии; подроб-
подробнее изложен материал, связанный с
определителем поверхностей, и
уточнена построенная на его базе
систематизация наиболее распрост-
распространенных видов поверхностей;
внесены уточнения в классифика-
классификацию позиционных и метрических
задач; включен новый материал,
связанный с построением плоскос-
плоскости, касательной к поверхности;
изложение способов преобразова-
преобразования ортогональных проекций дано
в первой главе непосредственно за
методом Монжа. Более раннее зна-
знакомство со способами преобразо-
преобразования ортогональных проекций
позволяет использовать эти спо-
способы на всех этапах изложения
курса.
Во втором издании полностью
сохранен дидактический принцип
изложения материала — от общего
к частному, а не наоборот, как это
имеет место в большинстве курсов
начертательной геометрии.
Для облегчения чтения чертежей
они выполнены линиями разных
цветов. Кроме того, чтобы легче
представить "игру" геометричес-
геометрических образов в пространстве, мно-
многие чертежи, построенные по прави-
правилам ортогонального проецирова-
проецирования, иллюстрируются наглядными
изображениями.
Автор приносит искреннюю бла-
благодарность всем читателям, при-
приславшим пожелания, направленные
на улучшение содержания учебника.

ВВЕДЕНИЕ
Начертательная геометрия явля-
является одним из разделов геометрии,
в котором пространственные фигу-
фигуры, представляющие собой сово-
совокупность точек, линий, поверхнос-
поверхностей, изучаются по их проекцион-
проекционным изображениям на плоскости
(или какой-либо другой поверх-
поверхности) .
Основными задачами начертатель-
начертательной геометрии являются: а) созда-
создание метода изображения геометри-
геометрических фигур на плоскости (по-
(поверхности) , б) разработка спосо-
способов решения позиционных и метри-
метрических задач, связанных с этими
фигурами, при помощи их изобра-
изображений на плоскости (поверхности).
Начертательная геометрия по
своему содержанию занимает осо-
особое положение среди других наук:
она является лучшим средством
развития у человека пространствен-
пространственного воображения, без которого
немыслимо никакое инженерное
творчество.
Начертательная геометрия явля-
является теоретической базой для сос-
составления чертежа — гениального
изобретения человеческой мысли.
Чертеж — :>то своеобразный язык,
с помощью которого, используя-
всего лишь точки, линии и ограни-
ограниченное число геометрических зна-
знаков, букв и цифр, человек имеет
возможность изобразить на поверх-
поверхности, в частности на плоскости,
геометрические фигуры или их со-
сочетания (машины, приборы, инже-
инженерные сооружения и т. д.). При-
Причем этот графический язык являет-
является интернациональным, он понятен
любому технически грамотному че-
человеку независимо от того, на ка-
каком языке он говорит.
Решение ,-задач способами начер-
начертательной геометрии осуществляет-
осуществляется графическим путем. Простейшей
геометрической операцией, кото-
которую приходится выполнять в про-
процессе решения, является определе-
определение точки пересечения двух линий.
Вследствие того, что все геометри-
геометрические построения осуществляются
с помощью только линейки и цир-
циркуля, линиями, точку пересечения
которых следует определять, явля-
являются прямые и окружности. Ины-
Иными словами, путем проведения от-
отрезков прямых и дуг окружностей
(в редких случаях участков лекаль-
лекальных кривых) в определенной по-
последовательности, устанавливаемой
теоремами и правилами начерта-
начертательной геометрии, можно решать
сложные задачи из различных об-
областей науки и техники.
Возможность расчленения про-
процесса решения задач на выполнение
элементарных, однотипных опера-
операций позволяет получить итерацион-
итерационные способы решения задач, кото-
которые легко и естественно могут
быть автоматизированы с помощью
вычислительной техники.
Использование начертательной
геометрии является рациональным
при конструировании сложных по-
поверхностей технических форм с на-
наперед заданными параметрами,
применяемых в авиационной и ав-
автомобильной промышленности,
при создании корпусов судов и су-
судовых движителей и во многих
других областях техники.
Достижения многомерной начер-
начертательной геометрии находят при-
применение при исследовании диаг-
диаграмм состояния многокомпонент-
многокомпонентных систем и сплавов в тех случа-
случаях, когда другие способы исследо-
исследования оказываются чрезвычайно
сложными и не обеспечивают тре-
требуемой точности.
Известна роль начертательной
геометрии в архитектуре, строи-
строительстве, изобразительном искус;
стве. Проекционные способы, раз-
разработанные в начертательной гео-
геометрии, дают возможность полу-
получать наглядные изображения про-
проектируемых объектов и целых
комплексов.
Благодаря начертательной гео-
геометрии появилась возможность
изображать на плоскости рельеф
земной поверхности и решать прос-
простыми графическими способами за-
задачи, связанные с проектированием
дорог, каналов, тоннелей, а также

8 Обозначения и символика
определять объемы выполняемых
при этом земляных работ.
Естественные науки достигают
еще большего расцвета в тех случа-
случаях, когда изучаемые свойства соп-
сопровождаются доступными для че-
человеческого восприятия наглядны-
наглядными геометрическими моделями.
Методы начертательной геомет-
геометрии, позволяюише решать матема-
математические задачи в их графической
интерпретации, находят широкое
применение в физике, химии, меха-
механике, кристаллографии и многих
других науках. Как и другие от-
отрасли математики, начертательная
геометрия развивает логическое
мышление.
Приведенный далеко не полный
перечень вопросов, которые сос-
составляют предмет исследования в
начертательной геометрии, не ос-
оставляет сомнения, что начертатель-
начертательная геометрия входит в число фун-
фундаментальных дисциплин, состав-
составляющих основу инженерного об-
образования.
ОБОЗНАЧЕНИЯ И СИМВОЛИКА
Для обозначения геометрических
фигур и их проекций, для отобра-
отображения отношения между ними, а
также для краткости записей гео-
геометрических предложений, алго-
алгоритмов решения задач и доказа-
доказательства теорем в курсе использу-
используется геометрический язык, состав-
составленный из обозначений и символов,
принятых в курсе математики (в
частности, в новом курсе геомет-
геометрии в средней школе).
Все многообразие обозначений и
символов, а также связи между ни-
ними могут быть подразделены на
две группы:
группа I — обозначения геомет-
геометрических фигур и отношений меж-
между ними;
группа II -¦ обозначения логичес-
логических операций, составляющие син-
синтаксическую основу геометричес-
геометрического языка.
Ниже приводится полный список
математических символов, исполь-
используемых в данном курсе. Особое
внимание уделяется символам, ко-
которые применяются для обозначе-
обозначения проекций геометрических фи-
гур-
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение
геометрических фигур
1. Геометрическая фигура обоз-
обозначается — Ф.
2. Точки обозначаются пропис-
прописными буквами латинского алфави-
алфавита или арабскими цифрами:
А, В, С, D, ... , L, M, N, ...
1, 2, 3, 4, .... 12, 13, 14, ...
3. Линии, произвольно располо-
расположенные по отношению к плоскос-
плоскостям проекций, обозначаются строч-
строчными буквами латинского алфа-
алфавита:
а, Ь, с, d, ... , I, m, п, ...
Линии уровня обозначаются: h —
горизонталь; f— фронталь.
Для прямых используются также
следующие обозначения:
(АВ) — прямая, проходящая
через точки А и В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограни-
ограниченный точками А и В.

Обозначения и символика 9
4. Поверхности обозначаются
строчными буквами греческого ал-
алфавита:
а, 0, 7, 5, ... , f, V, v, ...
Чтобы подчеркнуть способ зада-
задания поверхности, следует указы-
указывать геометрические элементы, ко-
которыми она определяется, напри-
например:
а (а || Ь) — плоскость а определя-
определяется параллельными
прямыми а и Ь;
Р (d, d2ga) — поверхность 0 опреде-
определяется направляющи-
направляющими di и d2, образую-
образующей g и плоскостью па-
параллелизма а.
5. Углы обозначаются:
LABC — угол с вершиной в точ-
точке В, а также La°, Lf3°, ... , Ly°, ...
6. Угловая! величина (градусная
мера) обозначается знаком^, кото-
который ставится над углом:
ABC — величина угла ABC;
ip — величина угла у.
Прямой угол отмечается квадра-
квадратом с точкой внутри tZL •
7. Расстояния между геометри-
геометрическими фигурами обозначаются
двумя вертикальными отрезка-
отрезками — I 1-
Например:
\АВ\ — расстояние между точка-
точками А и В (длина отрезка АВ);
\Аа \ — расстояние от точки А до
линии а;
l^aj —расстояние от точки А до
поверхности a;
\ab\ — расстояние между линия-
линиями а и Ь;
|а/3| расстояние между поверх-
поверхностями а и /3.
8. Для плоскостей проекций при-
приняты обозначения: -пх и я2,
где я, - горизонтальная плоскость
проекций;
я 2 —фронтальная плоскость
проекций.
При замене плоскостей проекций
или введении новых плоскостей по-
последние обозначают тг3, п4 и т. д.
9. Оси проекций обозначаются:
х. у, г, где х — ось абсцисс; у ~
ось ординат; г — ось аппликат.
Постоянную прямую эпюра Мон-
жа обозначают k.
10. Проекции точек, линий, по-
поверхностей, любой геометрической
фигуры обозначаются теми же бук-
буквами (или цифрами), что и ориги-
оригинал, с добавлением верхнего индек-
индекса, соответствующего гшоскости
проекции, на которой они получе-
получены:
А', В\ С, D\ ... , L', М', ЛГ, ... -
горизонтальные проекции точек;
А", В", С", D", ... , L", M", N", ... -
фронтальные проекции точек;
а', Ь\ с', d', ... , Г, т\ ri, ... -
горизонтальные проекции линий;
а", Ь", с", d", ... , I", m", п", ... -
фронтальные проекции линий;
а',0',7\ 5', ...,?', Ц, v',...-
горизонтальные проекции поверх-
поверхностей;
a",p",y",d",...A",v",v",-.-
фронтальные проекции поверхнос-
поверхностей.
11. Следы плоскостей (поверх-
(поверхностей) обозначаются теми же бук-
буквами, что и горизонталь или фрон-
таль, с добавлением подстрочного
индекса Оа, подчеркивающего, что
эти линии лежат в плоскости про-
проекции и принадлежат плоскости
(поверхности) а.
Так: hoa — горизонтальный след
плоскости (поверхности) а;
/о а — фронтальный след
плоскости (поверхности) а.
12. Следы прямых (линий) обоз-
обозначаются заглавными буквами, с
которых начинаются слова, опреде-
определяющие название (в латинской
транскрипции) плоскости проек-
проекции, которую пересекает линия, с
подстрочным индексом, указываю-
указывающим принадлежность к линии.
Например: На — горизонтальный
след прямой (ли-
(линии) а;
Fa — фронтальный
след прямой (ли-
а.

Ю Обозначения и символика
13. Последовательность точек,
линий (любой фигуры) отмечается
подстрочными индексами li2K, n-
Л,, А2, А3, ... , Ап;
«l, аг, аз, ¦¦¦, оп;
*1, *2, <*>3, ¦•• , ФП ИТ. Д.
Вспомогательная проекция точ-
точки, полученная в результате преоб-
преобразования для получения действи-
действительной величины геометрической
фигуры, обозначается той же бук-
буквой с подстрочным индексом 0:
Aq, Bq, Cq, Do, ...
Аксонометрические
проекции
14. Аксонометрические проек-
проекции точек, линий, поверхностей
обозначаются теми же буквами,
что и натура с добавлением верхне-
верхнего индекса °:
A\B\C\D\ ...
1°, 2°, 3°, 4\ ...
a°,b°,c°,d°,...
15. Вторичные проекции обозна-
обозначаются путем добавления верхнего
индекса1 :
л10, в10, с10,
\ з10.
D
10
li0,
a10,
а
1 О
10
di0,
б10,
Для облегчения чтения чертежей
в учебнике при оформлении иллю-
иллюстративного материала использова-
использованы несколько цветов, каждый из
которых имеет определенное смыс-
смысловое значение: линиями (точка-
(точками) черного цвета обозначены ис-
исходные данные; зеленый цвет ис-
использован для линий вспомогатель-
вспомогательных графических построений; крас-
красными линиями (точками) показа-
показаны результаты построений или те
геометрические элементы, на кото-
которые следует обратить особое вни-
внимание.
Б. Символы, обозначающие отношения
между геометрическими фигурами
№
по пор.
1
2
3
4
5
6
7
8
Обозна-
Обозначение
III
ГО
II
i
—
7Т
-»
Содержание
Совпадают
Конгруентны
Подобны
Параллельны
Перпендикулярны
Скрещиваются
Касательные
Отображаются
Пример символической
записи
(АВ) = (CD) — прямая, проходящая
через точки А и В, совпадает с прямой,
проходящей через точки С и D
LABC ^ LMNK — угол ABC конгруеи-
тен углу MNK
Д ABC со Д MNK — треугольники ABC
и MNK подобны
а || Р — плоскость а параллельна плос-
плоскости /3
и 1 Ь- прямые а и Ь перпендикулярны
с — d — прямые end скрещиваются
17T ' ~~ прямая t является касательной
к линии {.
Р 7Т а — плоскость /3 касательная к по-
поверхности 0!
Ф( -* Ф2 — фигура Ф1 отображается на
фигуру Ф2

Обозначения и символика 11
Продолжение табл.
№
по пор.
9
10
11
Обозна
ч<!ние
;?
;;
Р
Содержание
Центр проецирования.
Если центр проецирова-
проецирования несобственная точ-
точка, то его положение
обозначается стрелкой,
указывающей направле-
направление проецирования
Направление проециро-
проецирования
Параллельное проециро-
проецирование
Пример символической
записи
—
рР — параллельное проецирование на
плоскость а в направлении s
В. Оюо
№
по пор
1
2
3
4
5
6
7
8
Обозна-
Обозначение
М, N
А, В, С, ...
(... )
е
с
и
п
значения
Содержание
Множества
Элементы
множества
Состоит из ...
Пустое мно-
множество
Принадлежит,
является эле-
элементом
Включает,
содержит
Объединение
Пересечение
множеств
теоретико-мно
Пример символической
записи
—
—
ф{а, в, с,... |
L — (SJ — множество L
пустое (не содержит эле-
элементов )
2 6: N (где N — множест-
множество натуральных чисел) —
число 2 принадлежит мно-
множеству N
N С М — множество N яв-
является частью (подмно-
(подмножеством) множества М
всех рациональных чисел
С = A U В — множество
С есть объединение мно-
множеств А и В; {1,2 3
4,5} = {1,2,3}LU{4,5}
М ~- К П L — множество
М есть пересечение мно-
множеств К и L (содержит
в себе элементы, принад-
принадлежащие как множеству
К, так и множеству L).
М П N = ^S) ~~ пересечение
множеств М и N есть пус-
пустое множество (множест-
(множества М и N не имеют общих
элементов)
жественные
Пример символической
записи в геометрии
—
—
Ф {а, В, С, ... }—фигура
Ф состоит из точек А, В,
С, ...
А € а — точка А принад-
принадлежит прямой а (точка
А лежит на прямой а )
а С а — прямая а принад-
принадлежит плоскости а (по-
(понимается в смысле: мно-
множество точек прямой а
является подмножест-
подмножеством точек плоскости а)
ABCD = [AB] U [ВС] U $D]
— ломаная линия, ABCD
есть объединение отрез-
ков [АВ], [ВС\, [CD]
а = а П A — прямая а
есть пересечение плоско-
плоскостей аи /3
а П Ь = &) — прямые а и
Ь не пересекаются (не
имеют общих точек)

12 Обозначения и символика
Группа II
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
№
по пор
1
2
3
4
. 5
6
7
8
9
Обозначение
л
V
V
3
31
(Рх)
\
Содержание
Конъюнкция предложений;
соответствует союзу "и".
Предложение (рЛч) истин-
истинно тогда и только тогда,
когда р и q оба истинны
Дизъюнкция предложений;
соответствует союзу "или".
Предложение (pVq) истин-
истинно, когда истинно хотя бы
одно из предложений р или
q (т. е. или р, или q, или
оба).
Импликация — логическое
следствие. Предложение
р=* q означает: "если р, то
не-
неэквивалентность. Предло-
Предложение (р*=* q) понимается
в смысле: "если р, то и q;
если q, то и р"
Квантор общности, читает-
читается: для всякого, для всех,
для любого. Выражение
\f(x) Р(х) означает: "для
всякого jc имеет место
свойство Р(х)"
Квантор существования,
читается: существует. Вы-
Выражение 3 (Х)Р(Х) озна-
означает: "существует jc, обла-
обладающее свойством Р(х)"
Квантор единственности
существования, читается:
существует единственное
(-я,-й)... Выражение (Э1х)
(Рх) означает: "существу-
"существует единственное (только
одно) х, обладающее свой-
свойством Рх"
Отрицание высказывания
(Рх)
Отрицание знака
Пример символической
записи
а П0 = {к : К ЕаЛКе б Пересе-
Пересечение поверхностей аир есть мно-
множество точек (линия), состоящее
из всех тех и только тех точек К,
которые принадлежат как поверх-
поверхности а, так и поверхности /3
—
{а \\с/\Ь || с)=>о ||Ь
Если две прямые параллельны
третьей, то они параллельны меж-
между собой
AGa*»Ae/Ca.
Точка принадлежит плоскости, ес-
если она принадлежит некоторой ли-
линии, принадлежащей этой плоскос-
плоскости. Справедливо также и обратное
утверждение: если точка принад-
принадлежит некоторой линии, принадле-
принадлежащей плоскости, то она принад-
принадлежит и самой плоскости
V(AABC)(A~+ В~+ С~ = 180°).
Для всякого (для любого) треу-
треугольника сумма величин его углов
при вершинах равна 180°
(VaX3a)la?aAa||a].
Для любой плоскости а существу-
существует прямая а, не принадлежащая
плоскости а и параллельная плос-
плоскости a
(V А, В){А ^ В)( 3 lo)(a Э А, В)
Для любых двух различных точек
А и В существует единственная
прямая а, проходящая через эти
точки
а- Ь=*(За)(аЭа, Ь).
Если прямые а и Ь скрещиваются,
то не существует плоскости а, ко-
которая содержит их
[АВ] \ [CD] —отрезок [АВ] не ра-
равен отрезку [CD] .
a X b — линия а не параллельна ли-
линии Ъ

ГЛАВА
I
МЕТОД ПРОЕКЦИЙ
§ 1. НЕКОТОРЫЕ СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВА
С познали теории множеств любую геометрическую фигуру следу-
следует рассматривать как множество всех принадлежащих ей точек. Го-
Говоря иначе, всякая геометрическая фигура есть не пустое множество.
Отображение геометрической фигуры на плоскость (или какую-
либо другую поверхность) можно получить путем проецирования ее
точек на эту плоскость (поверхность).
Прежде чем говорить о сущности метода проецирования, целесо-
целесообразно рассмотреть некоторые свойства евклидова пространства*.
Известно, что эти свойства могут быть выражены при помощи систе-
системы аксиом и предложений, которые устанавливают зависимости и отно-
отношения между элементами пространства. Точки, прямые и плоскости
евклидова пространства находятся в определенном взаимоотношении,
которое может быть обозначено словом принадлежность или инцидент-
инцидентность. Термин инцидентность заменяет такие понятия, как "лежать на",
"проходить через". Вместо выражений "точка А лежит на плоскости а",
"прямая а проходит через точку В" можно употреблять выражения
"точка А инцидентна (принадлежит) плоскости а", "точка В инцидентна
(принадлежит) прямой а". В символической форме эти выражения
можно записать А е а; В € а.
Отношения принадлежности между элементами евклидова про-
пространства могут быть выражены следующими предложениями:
1. Если точка А принадлежит прямой а, а прямая а принадлежит
плоскости «, то точка А принадлежит плоскости а:
ЛеоСа=>Л?а.
2. Две различные точки А и В всегда принадлежат одной и той же
и только одной прямой а или каждой прямой а принадлежат, по крайней
мере, две точки А и В:
(У А, В)(А\ В) => ( 3 1а) (а э А, В).
3. Три различные точки Л, В и С, не принадлежащие одной прямой,
принадлежат одной и той же и только одной плоскости:
(VA,B,C)(A * В*С)Л(А,В,С$а)~ C 1а) (а Э А, В, С).
4. Если две точки Л и В, принадлежащие прямой а, принадлежат
плоскости <*, то прямая а принадлежит плоскости а:
{VA, В)(А \ В)(A, ВЕа)Л (Л, Be а)=> (а С а).
* Основные свойства трехмерного пространства, в котором мы живем, были
изучены до нашей эры греческими геометрами.
Наиболее существенный вклад имели труды по геометрии трехмерного прост-
пространства великого геометра древности Евклида, изложенные им в "Началах" (III в. до
нашей эры). По имени автора "Начал" геометрическому пространству, изучаемому в
элементарной геометрии, присвоено название евклидова пространства.

14 М<:год проекций
Кроме принеденных выше, могут быть сформулированы и другие
предложения принадлежности для элементов евклидова пространства.
К таким предложениям, в частности, относятся:
5. Две прямые, принадлежащие одной плоскости, могут принадле-
принадлежать одной точке, но этого может и не быть.
6. Две плоскости могут принадлежать одной и той же прямой, но
этого можег и не быть.
7. Плоскость и не принадлежащая ей прямая могут принадлежать
одной точке, но этого может и не быть.
Последние три предложения по существу перефразируют аксиому
о параллельности. В самом деле, предложение 5 утверждает, что в евк-
евклидовой плоскости две прямые либо пересекаются (принадлежат одной
точке). либо не имеют общей точки в этом случае они называются
параллельными. Аналогично, предложение 6 говорит о том, что в евк-
евклидовом пространстве две плоскости либо пересекаются (принадлежат
одной прямой). либо они параллельны, а предложение 7 — о том, что
прямая, не принадлежащая плоскости, либо пересекает ее (прямая и
плоскость принадлежат одной точке) , либо они параллельны.
§ 2. РЕКОНСТРУКЦИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
Принятие аксиомы Евклида о параллельности при последующем из-
изложении приводит к определенным трудностям, вызванным тем, что,
рассматривая метод проекций, составляющий основу для изображе-
изображения на плоскости геометрических фигур, расположенных в простран-
пространстве, мы обнаруживаем "неоднородность" евклидова пространства
и погруженных в него геометрических фигур.
Действительно, пусть даны две прямые а и Ь, определяющие плос-
плоскость а (рис. 1). Возьмем в плоскости а произвольную точку S
(S Ц а Л Ь). Через точку S проведем произвольную прямую /, которая
пересечет прямую а в точке Аа, а прямую Ь в точке А*3. Проведем че-
через точку S прямую /[ , пересекающую прямую а в точке Ва, а прямую b в
точке Вь. Аналогично, прямые /2, /3, проведенные через точку S, пересе-
пересекают прямые а и Ь соответственно в точках Са и С*\ Da и D^.
Выполненные построения показывают, что мы каждый раз полу-
получаем две точки — одну на прямой а и одну, однозначно соответствующую
ей точку, на прямой Ь. Так будет продолжаться до тех пор, пока в пучке
Рис. 1

Реконструкция евклидова пространства 15
прямых с центром в точке 6' не появится прямая //, параллельная прямой
Ь. Эта прямая пересекает прямую а в точке Ма. Ввиду параллельности
прямых /,- и Ь они не будут пересекаться, следовательно, не будет и точки
Мь на прямой Ь, однозначно соответствующей точке Ма, т. е. выяв-
выявленная ранее закономерность, состоящая в том, что каждой точке пря-
прямой а соответствует точка прямой Ъ и наоборот, нарушается с появле-
появлением параллельной прямой. Кроме точки Ма появится еще одна точка
N" (N" € Ь), которая также будет отличаться от всех остальных точек
прямой b (так как /^ \\а). Рис. 1 показывает, что мы оказываемся перед
фактом, что прямые аи b (из-за аксиомы о параллельности) не являются
однородными: каждая из них содержит точку (М° и Nb соответственно),
отличную от всех других точек, объединенных в прямые а и Ъ.
Свойства евклидовой плоскости обнаруживают еще одно несоответ-
несоответствие, которое влечет за собой нарушение принципа взаимной непре-
непрерывности.
Действительно, если расстояние Ad между точками Аа и Ва прямой
а — величина бесконечно малая (см. рис. 1), то и расстояние Aid между
соответствующими этим точкам точками Аь и Вь прямой Ь будет также
бесконечно малым.
Приведенные рассуждения будут справедливы и для другой пары со-
соответственных точек (например, CaDa и CbDb).
Но если мы возьмем на прямой а две бесконечно близкие точки
Ка и La, разделенные точкой Ма, то, как видно из чертежа, им будут
соответствовать две бесконечно удаленные точки Кь и L° прямой Ь.
Если мы обратимся к трехмерному евклидову пространству, то в
нем появится множество точек, принадлежащих прямым m и п, по
которым пересекаются плоскости а. и /3 с плоскостями 8 и ), опреде-
определяемыми пучками прямых, параллельных плоскостям а и /3 и принадле-
принадлежащих точке S (рис. 2).
Становится очевидным, что евклидово пространство, свойства ко-
которого определяются, в частности, и аксиомой о параллельности, не
может быть использовано для разработки метода центрального прое-
проецирования. Более того, мы оказываемся перед альтернативой: или
принять на перу существование аксиомы о параллельности и, как след-
следствие, признать неоднородность окружающего нас пространства, или
считать, что пространство однородно, подвергнув сомнению существова-
существование аксиомы о параллельности.

16 Метод проекций
Для того чтобы освободиться от указанных недостатков, необходи-
необходимо трехмерное евклидово пространство подвергнуть реконструкции.
Из рис. 1 видно, что для того чтобы точка Ма не отличалась от осталь-
остальных точек (Аа, Ва, Са, Da) прямой а, достаточно потребовать, чтобы
параллельные прямые /,- и Ь пересекались; при этом точку их пересечения
Ыь будем считать бесконечно удаленной — несобственной точкой (в отли-
отличие от точек евклидова пространства, которые считаются собственными).
Таким образом, дополнение прямой несобственной точкой, в кото-
которой прямая пересекается с параллельной прямой, позволяет устра-
устранить недостаток, являющийся следствием аксиомы о параллельности.
Теперь мы можем утверждать, что любая точка прямой а будет
иметь соответствующую ей точку на прямой Ь. Эта точка может быть
как собственной, так и несобственной.
Наличие на прямой несобственной точки позволяет установить не
только взаимно-однозначное соответствие между точками прямых а
и Ь, но и ликвидирует и второе несоответствие, связанное с наруше-
нарушением непрерывности в расположении точек, принадлежащих прямой.
Точки Кь и Ьь прямой Ь, соответствующие бесконечно близким точ-
точкам Ка и La прямой а, удалены в бесконечность, и расстояние между
ними бесконечно большое.
В то же время расстояние между точками КаМа и LaMa прямой а
бесконечно мало. Для того чтобы избежать разрыва прямой Ь, доста-
достаточно предположить, что расстояние между точками К^М" и L^M^ так же
бесконечно мало, как и между двумя другими бесконечно близкими
точками KbLb. Это может произойти лишь в том случае, если прямая Ь
будет замкнутой. Условная модель такой прямой показана на рис. 3.
На плоскости можно провести бесчисленное множество прямых,
каждая из которых имеет несобственную точку. Что же представляет из
себя множество этих точек плоскости?
Так как каждая прямая плоскости имеет только одну несобствен-
несобственную точку, то она может пересекать множество этих несобственных
точек только в одной точке, поэтому естественно считать множество
несобственных точек плоскости несобственной прямой. Выясним также,
что представляет собой множество несобственных точек пространства.
Представим две параллельные плоскости а и C (рис. 4). Проведем
в каждой из них по одной прямой а и Ь так, чтобы а || Ь. Эти прямые
пересекутся в несобственной точке Ах . Проведем в плоскости а пря-
прямую с, а в плоскости C прямую d, причем с || d. Эти прямые пересекутся
также в несобственной точке В«. Несобст-
Несобственные точки А» и В~ определяют несобс-
несобственную прямую / «.. Так как точки А - и
В _ принадлежат как плоскости а, так и
плоскости /3, то несобственная прямая
также принадлежит этим плоскостям.
Следовательно, в евклидовом простран-
пространстве, дополненном несобственными точ-
точками, две параллельные плоскости пере-
пересекаются по бесконечно удаленной —
несобственной прямой. Ранее было уста-
установлено, что множество несобственных
точек пространства пересекаются прямой
в одной несобственной точке. Теперь мы
показали, что это же множество имеет с
плоскостью одну общую несобственную
Рис. j Прямую.

Центральное проецирование \ 7
а
ел, -;.
Рис. 4
Естественно считать множество несобственных точек пространства
несобственной (бесконечно удаленной) плоскостью*.
Итак, для реконструкции евклидова пространства достаточно: до-
дополнить множество точек прямой несобственной точкой, что приво-
приводит к дополнению евклидовой плоскости несобственной прямой, а трех-
трехмерное пространство — несобственной плоскостью.
Дополненные несобственными элементами евклидовы плоскость
и пространство называют соответственно проективной плоскостью и
проективным пространством.
Отмеченные ранее в пп. 5, 6, 7 (см. § 1, с. 14) свойства евклидова
пространства для проективного пространства могут быть сформулиро-
сформулированы иначе:
п. 5 — две прямые, принадлежащие одной плоскости, всегда при-
принадлежат одной и той же и только одной точке;
п. 6 — две различные плоскости всегда принадлежат одной и той же
и только одной прямой;
п. 7 — плоскость и не принадлежащая ей прямая всегда принадле-
принадлежат одной и той же и только одной точке.
Во всех рассмотренных случаях точка и прямая могут быть как
собственными, так и несобственными.
§ 3. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Сущность центрального проецирования заключается в следующем:
пусть даны плоскость тгх и точка S (S ^ я, рис. 5). Возьмем произ-
произвольную точку А (А \ я,, А Ч S). Через заданную точку S и точку А
проводим прямую (SA) и отмечаем точку А', в которой эта прямая
пересекает плоскость я,. Плоскость я, называют плоскостью проекции,
точку S — центром проекции**, полученную точку А' — центральной
проекцией точки А на плоскость я,, прямую (SA) — проецирующей
прямой. Положения плоскости я, и центра S определяют аппарат цент-
центрального проецирования. Если он задан, то всегда имеется возмож-
возможность определить положение центральной проекции любой точки прост-
пространства на плоскости проекции.
Действительно, пусть дана произвольная точка В (см. рис. 5); про-
проведя проецирующую прямую (SB) и найдя точку ее встречи (пересе-
(пересечения) с плоскостью тг,, определяем центральную проекцию В' точки
* По аналогии с плоскостью евклидова пространства, в котором плоскость мож-
можно рассматривать как множество точек (собственных), которые пересекаются пря-
прямой в одной (собственной) точке и плоскостью по одной (собственной) прямой.
** В некоторых учебниках встречается определение точки S как полюса проекции
или как вершины конической поверхности. В этих случаях проекции называют соот-
соответственно полярными или коническими.

18 Метод проекций
Рис. 5
Рис. 6
В при данном аппарате проецирования (фиксированном положении
я, hS).
В том случае, когда точка С принадлежит плоскости, проходящей
через центр проекции и параллельной плоскости я, , проецирующая
прямая (SC) пересечет плоскость проекции в несобственной точке
С'.. Таким образом, можно сделать вывод, что при заданном аппарате
проецирования каждая точка пространства имеет только одну цент-
центральную проекцию. Это утверждение вытекает из того, что через две
различные точки можно провести только одну прямую. К сожалению,
обратное утверждение — каждой центральной проекции точки одно-
однозначно соответствует точка, не имеет места.
Из рис. 5 видно, что точка А' может быть центральной проекцией
любой точки А,, Аг, А3, ... , Ап, принадлежащей прямой (A'S). Поэ-
Поэтому одна центральная проекция точки не дает возможности судить
о положении самой точки в пространстве.
Для определения положения точки необходимо иметь две ее цент-
центральные проекции, полученные из двух различных центров. Имея две
центральные проекции точки А\ и А'2, полученные из центров S1 и S2
(рис. 6), можно определить положение точки А в пространстве. Для
этого достаточно провести прямые (A\Si) и (A'2S2 ) и отметить точку
их пересечения.
На рис. 6 показано также определение положения точки В по задан-
заданным проекциям В\ и В'г.
§ 4. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
\ Рассмотрим частный случай центрального проецирования, когда
центр проекции помещен в несобственной точке S*. В этом случае про-
проекцией точки А на плоскость я, будет точка А', в которой проецирующая
прямая {Sx А) пересекает плоскость проекции тту (рис. 7).
Для нахождения проекции точки В следует провести прямую
(S^ В) || (Sm А) и определить точку ее пересечения с плоскостью я,.
Очевидно, что при таком положении центра проекции и все остальные
проецирующие прямые будут также параллельны (S А). Множество всех
прямых пространства, имеющих несобственную точку, образуют связ-
* На чертеже несобственная точка указывается направлением s.

Ортогональное проецирование 19
А„ .<
Рис. 7
Рис.8
ку, центр которой — несобственная точка, совпадающая с центром про-
проекции.
В связи с параллельностью проецирующих прямых рассматривае-
рассматриваемый способ проецирования называется параллельным, а полученные
с его помощью проекции — параллельными проекциями.
Аппарат параллельного проецирования полностью определяется
положением плоскости проекции пх и направлением проецирования s.
Отмеченное раньше свойство центрального проецирования сохра-
сохраняется и в данном случае. Применительно к параллельному проециро-
проецированию оно может быть сформулировано:
каждая точка пространства, при заданном аппарате проецирования,
будет иметь только одну параллельную проекцию.
Обратное утверждение, как и в случае центрального проецирова-
проецирования, не имеет места.
Действительно, точка А' (см. рис. 7) может быть параллельной
проекцией любой точки Alt А2, Аъ, ... , Ап, принадлежащей прямой
(A'S^), поэтому одна параллельная проекция точки не позволяет судить
о положении самой точки в пространстве.
Для определения положения точки в пространстве необходимо
иметь две ее параллельные проекции, полученные при двух различ-
различных направлениях проецирования.
В этом случае положение точки А определяется пересечением пря-
прямых, проведенных через А\ и А\ параллельно соответствующим нап-
направлениям s, и s2 (рис.8).
На рис. 8 показано также нахождение положения в пространстве
точки В по известным ее параллельным проекциям В\ и В\.
§ 5. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Частный случай параллельного проецирования, при котором нап-
направление проецирования s перпендикулярно плоскости проекции, на-
называется прямоугольным или ортогональным (от слова orthogonios —
прямоугольный) проецированием.
Ортогональное проецирование находит широкое применение в ин-
инженерной практике для изображения геометрических фигур на плос-
плоскости.
Рис. 9 дает наглядное представление об ортогональном проецирова-
проецировании точки.

20 Метод проекций
Рис. 9
Рис. 10
Раньше отмечалось, что для
решения обратной задачи — опре-
определения положения точки в прос-
пространстве по ее параллельным про-
проекциям — необходимо иметь две параллельные проекции, полученные
при двух направлениях проецирования.
Так как через точку можно провести только одну прямую, перпен-
перпендикулярную к плоскости, то, очевидно, в отличие от центрального и
параллельного (косоугольного) проецирования (см. рис. 5 и 7) при
ортогональном проецировании для получения двух проекций одной
точки необходимо иметь две не параллельные плоскости проекции.
Выделим в пространстве две взаимно перпендикулярные плоскости
я, и тг2. Спроецируем ортогонально точки <[К, ..Л пространства на
плоскость я, , получим множество проекций точек \К', ... "I , образую-
образующих поле проекций точек {X, ..Л , которое условимся называть гори-
горизонтальной плоскостью проекции. При ортогональном проецировании
множества точек пространства {К, ..Л на плоскость я2 получим мно-
множество проекций точек^К",...}, образующих поле проекций точек {К,...} ,
которое будем называть фронтальной плоскостью проекций.
На рис. 10 показаны точки пространства А и В и их ортогональные
проекции А', А" и В', В". Здесь, как и в ранее рассмотренных случаях
центрального проецирования (см. рис. 5) и параллельного проециро-
проецирования (см. рис. 7), одной точке пространства соответствуют две точки —
ее проекции.
Если положение плоскостей тг, и тг2 фиксировано, то каждой точ-
точке пространства будет соответствовать упорядоченная пара точек на
полях проекций.
Справедливым оказывается и обратное утверждение — упорядочен-
упорядоченной паре точек полей проекций соответствует 'единственная точка прост-
пространства.
Отмеченное свойство является фундаментальным — составляю-
составляющим основу построения проекционного чертежа.
'Ортогональное проецирование обладает рядом преимуществ перед
центральным и параллельным (косоугольным) проецированием. К ним
в первую очередь следует отнести:
а) простоту графических построений для определения ортогональ-
ортогональных проекций точек;
б) возможность при определенных условиях сохранить на проек-
проекциях форму и размеры проецируемой фигуры._)
Отмеченные преимущества обеспечили широкое применение орто-
ортогонального проецирования в технике, в частности, для составления
машиностроительных чертежей.

Инвариантные свойства 21
ортогонального проецирования
§ 6. ИНВАРИАНТНЫЕ СВОЙСТВА
ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
Геометрические фигуры проецируются на плоскость проекции в
общем случае с искажением. При этом характер искажений зависит
от аппарата проецирования и положения проецируемой фигуры по от-
отношению к плоскости проекции. В частности, при ортогональном прое-
проецировании, если проецируемая фигура занимает произвольное положение
по отношению к плоскости проекции, ее проекция не сохраняет метри-
метрических характеристик оригинала — происходит искажение линейных и
угловых величин.
Действительно, ^при ортогональном проецировании трапеции ABCD
на плоскость тг, , не параллельную плоскости трапеции (рис. 11), дли-
длины ее сторон, величины углов при вершинах, площадь и другие метри-
метрические характеристики оригинала на проекции A'B'C'D' не сохраняются.\
Наряду с: этим между фигурой-оригиналом и ее ортогональной проек-
проекцией на плоскость существует определенная связь, заключающаяся в том,
что некоторые свойства проецируемой фигуры Ф сохраняются и на ее
проекции Ф'.
Из рис. 11 видно, что точки А, В, С, D — вершины проецируемой
трапеции (фигура Ф) проецируются в точки А', В', С, D' — вершины
трапеции-проекции (фигура Ф'); отрезки [АВ], [ВС], [CD], [DA] —
стороны трапеции проецируются в отрезки [А'В'], [В'С], [C'D ], [D'A'] —
стороны трапеции-проекции.
Параллельным основаниям [АВ] || [DC] проецируемой трапеции со-
соответствуют также параллельные основания- [А'В'] || [D'C] трапеции-
проекции.
Свойства геометрических фигур, которые не изменяются в процес-
процессе проецирования, называются независимыми или инвариантными отно-
относительно выбранного способа проецирования^
Основу любой геометрии составляет система аксиом. Любое гео-
геометрическое; определение и предложение (теорема), равно как и доказа-
доказательства теорем, базируются на принятой системе аксиом.
| При ортогональном проецировании — получении проекций геомет-
геометрической фигуры по ее оригиналу или при решении обратной задачи —
определении формы и размеров оригинала по его ортогональным проек-
проекциям базируются на инвариантных свойствах ортогонального проеци-
проецирования:!
1. Ортогональная проекция точки есть точка:
А-* А'
Рис. 11

22 Метод проекций
2. Если фигура Ф, принадлежит фигуре Ф, го ортогональная проек-
проекция фигуры Ф\ принадлежит ортогональной проекции фигуры Ф'*:
Ф! С Ф => Ф', С Ф'.
Из свойства 1 получаем:
1 а. Ортогональная проекция прямой на плоскость есть прямая,
в частном случае, когда прямая перпендикулярна плоскости проек-
проекции, — точка (рис. 12 и 13) :
Действительно, возьмем на прямой I (рис. 12) ряд точек 1, 2, 3, ...
... , п и проведем через них проецирующие прямые at, аг, а3, ... , ап,
перпендикулярные плоскости тг1 . Каждая из этих прямых пересечет
плоскость Я[ в точках 1', 2', 3', ... , п .
Множество всех прямых {al5 a2, а3, ... ]¦, проходящих через нетож-
нетождественные точки прямой / перпендикулярно к плоскости тг,, образу-
образуют проецирующую плоскость а, которая пересекается с плоскостью
Я[ по прямой, поэтому точки Г, 2', 3', ...,п' (ортогональные проек-
проекции точек 2, 2, 3, ..., п прямой /) принадлежат одной прямой /' — ор-
ортогональной проекции прямой /.
На рис. 13 показан случай, когда прямая / 1 jt i . Из чертежа видно,
что все прямые {а,, а2, а3, ... , ап }. проецирующие точки 1, 2, 3, ... , п
прямой /, совпадают с этой прямой и пересекают плоскость vl в одной
точке 1' = 2' = 3' = ... = п — горизонтальной проекции прямой /'**.
Из свойства 2 следует:
2 а. Если точка А принадлежит линии I, то ортогональная проекция
точки А' принадлежит ортогональной проекции линии I' (рис. 14) :
А е /=* Л'е /'.
2 б. Если линия I принадлежит поверхности а, то ортогональная
проекция линии I' принадлежит ортогональной проекции поверхности
а' (рис. 15) :
/ С а =» /' С а'.
*С позиции теории множеств это свойство можно сформулировать иначе: "ес-
"если множество М принадлежит (является подмножеством) множеству N, то орто-
ортогональная проекция множества М' на плоскость принадлежит ортогональной проек-
проекции N на эту же плоскость.
**На рис. 13 горизонтальная проекция прямой /' обозначена Я;, так как в этом
случае / = Н[.
1-1'
-?•?•...» «Г «'-Н,
Рис. 12
Рис. 13

Инвариантные свойства 23
ортогонального проецирования
Рис. 14
Рис. 15
Рис. 16
Рис. 17
2 в. Если точка А принадлежит поверхности а, то ортогональная
проекция точки А' находится на ортогональной проекции линии /', при-
принадлежащей ортогональной проекции поверхности а' (рис. 16):
А Е а => А' € /' С а'.
В том случае, когда удовлетворяется условие принадлежности А" е /"
и A" G /" с и" на другой плоскости проекции тг2 (л^Ткя, ), справедливы
следующие утверждения:
е /" с а").
Поставленные здесь знаки эквивалентности между левой и правой
частями показывают, что справедливы и обратные утверждения:
— если ортогональные проекции точки А(А' и А") принадлежат со-
соответственно ортогональным проекциям линии /(/' и /"), то точка А
принадлежит линии /;
— если ортогональные проекции точки А (А' и А") принадлежат со-
соответствующим ортогональным проекциям линии /(/' и I'), которые, в
свою очередь, принадлежат одноименным ортогональным проекциям
поверхности а (а' и а"), то точка А принадлежит поверхности а (рис. 17).
2 г. Если фигура Ф принадлежит плоскости а, перпендикулярной
плоскости проекции тг,, то ортогональная проекция этой фигуры при-
принадлежит линии пересечения плоскости а с плоскостью я, —горизонталь-

24 Метод проекций
а
D
Рис. 18
Рис. 19
ному следу hoa плоскости а:
(Ф с а)Л (а 1 тг, ) => Ф' С hoot.
В справедливости этого утвер-
утверждения легко убедиться, рас-
рассматривая рис. 18,а. Пусть а —
плоскость, перпендикулярная
плоскости проекции я i. Плос-
Плоскость а можно рассматривать
как состоящую из множества
прямых |а,, а2, а3, ... , ап } , перпендикулярных тгt , каждая из которых
пересекает плоскость я, в точке, принадлежащей прямой hoa.
Допустим, что в плоскости а задана точка А (А е а). Очевидно, го-
горизонтальная проекция может быть найдена как результат пересечения
прямой а. с плоскостью я, (а, ЭА и а,- С а и а 1 тг, ), но из свойства 1а
(см. рис. 13) следует, что а;- Г\ -л { - А' е hoa.
Если в плоскости а будет задана какая-либо фигура Ф, то, проеци-
проецируя точки В, С, D, ... этой фигуры на плоскость я,, мы каждый раз бу-
будем получать горизонтальные проекции этих точек, принадлежащие сле-
следу hoa плоскости а. Совокупность горизонтальных проекций точек
В', С', D', ... укажет горизонтальную проекцию фигуры Ф', т. е. Ф' с /ioa.
Из рис. 18,6 видно, что отмеченное свойство сохраняется и в том
случае, когда вместо плоскости будет взята произвольная горизонталь-
горизонтально проецирующая поверхность.
2 д. Если фигура Ф принадлежит плоскости /3, параллельной плос-
плоскости проекции я,, го ортогональная проекция этой фигуры на плос-
плоскость 7г j конгруентна самой фигуре (рис. 19) :
(Ф с 0) Л (/3 || я, ) => Ф' ^ Ф.
В справедливости этого свойства ортогонального проецирования лег-
легко убедиться путем следующих рассуждений: представим, что плоскость
0 совпадает с плоскостью проекций я, (частный случай параллельности).
Не вызывает сомнений, что ортогональная проекция фигуры Ф' на плос-
плоскость я, ничем не будет отличаться от самой фигуры Ф.
Если плоскость Р будет перемещаться вдоль проецирующего луча
s, оставаясь при этом параллельной своему первоначальному положе-
положению (плоскости тг i ), то это не повлечет за собой изменения формы и
размеров проецируемой фигуры.
2 е. Следует иметь в виду, что в том случае, когда проецируемой
фигурой является прямой угол, для получения неискаженной орто-
ортогональной проекции этого угла достаточно, чтобы только одна из его

Инвариантные свойства 25
ортогонального проецирования
сторон была параллельна плоскости проекции (при условии, что дру-
другая сторона угла не перпендикулярна плоскости проекции).
Это свойство может быть записано:
(АВС= 90°) Л ([ВС) || я,,[ВА)Ч,я, ) => А' В' С ----- 90°.
Если LABC прямой и сторона ВС этого угла параллельна плоскос-
плоскости проекции я,, а сторона ВА не перпендикулярна плоскости я,, то
ортогональная проекция угла на плоскость я, — А В'С' — 90°.
В большинстве учебников по начертательной геометрии это инва-
инвариантное свойство ортогонального проецирования предлагается в виде
теоремы о частном случае проецирования прямого угла. Ниже при-
приводится одно из возможных доказательств этой теоремы, взятое на-
нами из учебника В. О. Гордона и М. А. Семенцова-Огиевского.
Положим, что сторона ВС прямого угла ABC (рис. 20) параллельна
плоскости проекции я, . В этом случае прямая ВС параллельна В'С'.
Пусть вторая сторона прямого угла, наклонная АВ, пересекает свою
проекцию А'В' в точке К. Проведем в плоскости проекции через точку К
прямую KL параллельно В'С. Прямая KL также параллельна ВС и LB'KL
получается прямым. Согласно теореме о трех перпендикулярах LKBC
также прямой. Следовательно, и LA'B'C' будет прямым.
Отмеченные инвариантные свойства имеют чрезвычайно важное
значение при решении позиционных (свойства 2 а ... 2 г) и метрических
(свойства 2 д и 2 е) задач.
2 ж. Если точка К есть результат пересечения прямых а и Ь, то орто-
ортогональная проекция этой точки К' определяется пересечением ортого-
ортогональных проекций прямых а' и Ь' (рис. 21).
К этому свойству можно прийти путем следующих рассуждений. До-
Допустим нам даны две фигуры Ф,
щуюся в результате их пересечения
и Ф3 С Ф2, на основании аксио-
аксиомы 2 можно записать:
Ф'з С Ф', и Ф'3 С Ф'2 ,
и Ф2. Обозначим фигуру, получаю-
Ф3 • Тогда Ф3 = Ф , п Ф 2, но Ф., с Ф,
т. е.
Ф, = Ф, п ф2 => Ф', = Ф', п Ф'2.
Рис. 20
к (\К .„
Рис. 21
Рпо. :>:>.

26 Метод проекций
,'• В
Рис. 23
Рис. 24
Если в качестве фигуры Ф, будет задана прямая а, а вместо фигу-
фигуры Ф2 — прямая Ь (пересечение прямых а и Ь — точка К), то мы придем
к заключению, которое требовалось доказать:
К = an Ь =» К' = а п Ь'.
В том случае, когда а\\Ь, точкой пересечения прямых а и Ь будет
бесконечно удаленная (несобственная) точка К*,, которая при орто-
ортогональном проецировании на плоскость я, спроецируется также в несоб-
несобственную точку К"„; следовательно, а' \\Ь'. Это свойство можно записать:
(а II Ь)А(а\п1 ) => а' \\ Ь'.
2 з. Если прямые а и Ь параллельны между собой и не перпендикуляр-
перпендикулярны /ыоскости проекции тт{, то параллельны и их ортогональные проекции
на эту плоскость (рис. 22). Приведенный инвариант позволяет сформу-
сформулировать еще два свойства, инвариантные относительно ортогонального
проецирования.
2 и. Если отрезок [АВ] параллелен отрезку [CD], то отношение
длин отрезков равно отношению длин их ортогональных проекций
(рис. 23)*:
[АВ] || [CD]
\АВ\ _ \АВ\
\CD\ ' ~ \C'D'\ ¦
2 к. Если точка С принадлежит отрезку [АВ], то отношение [АС] к
[СВ] равно отношению их проекций. Или иначе, если точка С делит
отрезок а данном отношении, то и проекция С (или С") делит проек-
проекции отрезка в том же отношении (рис. 24) :
Справедливость двух последних утверждений ясна из рис. 23 и 24
и не нуждается в доказательстве.
§ 7. ЭПЮР МОНЖА
В машиностроении для того чтобы иметь возможность по чертежу
судить о форме и размерах изображаемых предметов (деталей, уз-
узлов, машин, агрегатов), при составлении чертежей, как правило, поль-
пользуются не двумя, а несколькими плоскостями проекций.
Наиболее часто используются три плоскости проекции. В связи с тем,
что начертательная геометрия призвана передавать результаты своих
* Имеется в виду, что отрезки не перпендикулярны плоскости проекции.

ЭпюрМонжа 27
теоретических исследований для практического использования, ор-
ортогональное проецирование целесообразно рассматривать также в систе-
системе трех плоскостей проекций.
Положение в пространстве точки, а следовательно, и любой гео-
геометрической фигуры может быть определено, если будет задана ка-
какая-либо координатная система отнесения. Наиболее удобной для фик-
фиксирования положения геометрической фигуры в пространстве и выявле-
выявления ее формы по ортогональным проекциям является декартова система
координат*, состоящая из трех взаимно перпендикулярных плоскостей.
Рис. 25 дает наглядное представление о макете, состоящем из трех
взаимно перпендикулярных плоскостей проекций.
Условимся называть:
плоскость я, — горизонтальной плоскостью проекции;
плоскость 7г2 ~ фронтальной плоскостью проекции;
плоскость я3 — профильной плоскостью проекции.
Линии пересечения плоскостей проекции образуют оси координат.
Ось х называют осью абсцисс, ось у — осью ординат и ось г — осью аппли-
аппликат. Точка пересечения осей принимается за начало координат и обозна-
обозначается буквой О (первая буква латинского слова Origo — начало).
В Советском Союзе, как и в большинстве европейских стран (в от-
отличие от США и некоторых стран Латинской Америки), принята пра-
правая система расположения плоскостей проекций. При этом положи-
положительными направлениями осей считают: для оси х — влево от начала
координат, для оси у -- в сторону зрителя от плоскости тт2, для оси
z — вверх от плоскости ъх ; противоположные направления осей считают
отрицательными.
Плоскости проекции делят пространство на восемь частей — ок-
октантов. Октанты условно принято нумеровать, как это показано рим-
римскими цифрами на рис. 25.
Каждый октант представляет собой прямоугольный трехгранник,
у которого гранями служат части плоскостей проекций (называемые
полами), а ребрами — оси координат.
* Декарт A696—1650) — французский математик и философ, предложивший
систему координат для определения положения системы точек в пространстве.
Рис. 25

28 Метод проекций
Учитывая при отсчете координат точки отмеченные выше направле-
направления осей х, у и г, получим табл. 1 знаков координат.
Т а б л и ц а 1
Октант
I
II
Ш
Знак координаты
л:
У
+
+
2
Октант
V
VI
VII
VIII
Знак координаты
д:
—
У
+
+
2
Пользоваться пространственным макетом, показанным на рис. 25,
для изображения ортогональных проекций геометрических фигур не-
неудобно ввиду его громоздкости, а также из-за того, что на плоскос-
плоскостях я, и я3 (показанных на макете) происходит искажение формы
и размеров проецируемой фигуры.
Поэтому вместо изображения на чертеже пространственного макета
пользуются эпюром — чертежом, составленным из двух или трех свя-
связанных между собой ортогональных проекций геометрической фи-
фигуры*.
Преобразование пространственного макета в эпюр осуществляет-
осуществляется путем совмещения плоскостей Я( и я3 с фронтальной плоскостью
проекции я г. Для совмещения плоскости Я] с я2 поворачиваем ее на 90е
вокруг оси х в направлении движения часовой стрелки (рис. 26).
На рис. 26, для наглядности, плоскость nt повернута на угол, чуть
меньший 90° После совмещения горизонтальной плоскости поворачи-
поворачиваем вокруг оси z также на угол 90° профильную плоскость в направле-
направлении, противоположном движению часовой стрелки. Вместе с полами
* Эпюр — от французского глагола еригег — улучшать, исправлять рисунок.
Рис. 26
Рис.27

к*.
Неопределяемые понятия геометрии; ортогональные проекции 29
точки, прямой, плоскости
плоскостей проекций будет перемещать-
перемещаться и ось у, при этом ось у, принадлежа-
принадлежащая горизонтальной плоскости проек-
проекции, после поворота совпадает с осью z, a
ось у профильной плоскости — с осью х.
После преобразования пространственный
макет примет вид, показанный на рис. 27.
На этом рисунке указана также последо-
последовательность, в которой располагаются
полы плоскостей проекций, так, запись
я 2 [^1 (я3)] указывает, что в этой части
эпюра (ограниченного положительным
направлением осей х и г) ближе к нам
находится верхняя левая пола фронталь-
фронтальной плоскости проекции, за ней распола-
располагается задняя левая пола горизонталь- Рис 2$
ной плоскости проекции, далее — верх-
верхняя задняя пола профильной плоскости
проекции.
Так как плоскости не имеют границ, в совмещенном положении (на
эпюре) границы не показывают; нет необходимости оставлять надписи,
указывающие положение пол плоскостей проекций; излишне также
напоминать, где отрицательное направление осей проекций. Тогда, в
окончательном виде, эпюр, заменяющий чертеж пространственного
макета (см. рис. 25), примет вид, показанный на рис. 28. Плоская мо-
модель (эпюр) пространственного макета несет такую же информацию,
какую содержит пространственный макет.
§ 8. НЕОПРЕДЕЛЯЕМЫЕ ПОНЯТИЯ ГЕОМЕТРИИ;
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ
К основным — неопределяемым — понятиям геометрии относятся:
точка, прямая, плоскость, расстояние и множество; они не могут быть
определены с помощью других, более простых (элементарных) понятий.
В то же аремя с помощью системы аксиом возможно установить
отношения между отмеченными основными понятиями, которые в
дальнейшем служат основанием для формулировки различных гео-
геометрических предложений (теорем), составляющих теоретическую базу
геометрии. Учитывая особую роль, которую играют в геометрии, в том
числе и геометрии начертательной, основные понятия, целесообразно
начать изложение курса начертательной геометрии, связанного с исполь-
использованием метода проецирования, с рассмотрения ортогональных проек-
проекций точки, прямой, плоскости и определения длины отрезка прямой
(являющегося мерой расстояния), заданного ортогональными проек-
проекциями*.
По этой же причине проекции точки, прямой, плоскости и опреде-
определение длины: отрезка прямой рассматриваются вместе, несмотря на
* Рассмотрение проекций множества теряет всякий смысл, так как в геомет-
геометрии имеют дело с множествами, элементами которых являются точки. В общем
случае множество не имеет границ — оно представляет собой пространство, запол-
заполненное точками. Проекция такого множества покроет все поле проекции. Поэтому
речь может идти только о проекциях конечного множества, образующего конкрет-
конкретную геометрическую фигуру. Проекции геометрических фигур будут рассмотрены в
гл. III и IV.

30 Метод проекций -
то, что прямая относится к разделу линия, плоскость является предста-
представителем поверхностей, о которых речь будет идти позже, в гл. III и
IV, а определение расстояния составляет содержание § 55 гл. VI.
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ
To4K?l, как математическое понятие, не имеет размеров. Очевид-
Очевидно, если объект проецирования является нульмерным образом, то го-
говорить о его проецировании бессмысленно.
В геометрии под точкой целесообразно понимать физический объ-
объект, имеющий линейные измерения. Условно за точку можно принять
шарик с бесконечно малым радиусом. При такой трактовке понятия
точки можно говорить о ее проекциях. Более того становится оправдан-
оправданным сделанное ранее (см. с. 13) определение геометрической фигуры
как множества всех принадлежащих ей точек.
При построении ортогональных проекций точки следует руковод-
руководствоваться первым инвариантным свойством ортогонального проеци-
проецирования А -* А'.
Пусть даны в пространстве точка А и три взаимно перпендикуляр-
перпендикулярные плоскости проекции (рис. 29,а). Положение точки в пространстве
определяется тремя координатами (х, у, г), показывающими величи-
величины расстояний, на которые точка удалена от плоскостей проекций.
Чтобы определить эти расстояния, достаточно через точку А провести
прямые, перпендикулярные к плоскостям проекций, определить точ-
точки А', А", А'" встречи этих прямых с плоскостями проекций и изме-
измерить величины отрезков [АЛ], [АА"], [АЛ'"], которые укажут соответ-
соответственно значения аппликаты г, ординаты у и абсциссы х точки А.
Точки А', А", А'" называют ортогональными проекциями точки
А, при этом согласно принятым обозначениям (см. с. 9) : А' — горизон-
горизонтальная проекция точки А; А" — фронтальная проекция точки А; А'" —
профильная проекция точки А. Отрезки: [ЛЛ'"] = [ОЛХ] — абсцисса точки
Л; [АА' ] ^ [ОЛу] — ордината точки Л; [АА'] ^ [OAZ] — аппликата
точки А.*
* Конгруентность отрезков [АА'"} = JCM*], [АА"] = [ОАу], [АА ] = [ОА2] следует
из того, что параллелепипед AA"AZA "А АхОАу прямоугольный.
'Л
¦ч
Г-
h
¦ к
\' '¦"
a)
6)
A'
О
Ay ...
Рис. 29

Неопределяемые понятия геометрии; ортогональные проекции 31
точки, прямой, плоскости
Прямые (АА'), (АА"), (АА'") называются проецирующими пря-
прямыми.
При этом прямую (АА'), проецирующую точку А на горизонтальную
плоскость проекций, называют горизонтально проецирующей прямой.
Аналогично: прямые (АА") и (АА'") называют соответственно:
фронтально (АА") и профильно (АА'") проецирующими прямыми.
Две проецирующие прямые, проходящие через точку А, определя-
определяют плоскость, которую принято называть проецирующей.
Чтобы получить эпюр точки А, преобразуем пространственный макет,
изображенный на рис. 29,а, так, как это было показано в предыдущем
параграфе (см. рис. 26 и 27).
Фронтальная проекция точки А остается на месте, как принадле-
принадлежащая плоскости я 1, которая не меняет своего положения при рас-
рассматриваемом преобразовании.
Горизонтальная проекция А' вместе с горизонтальной плоскостью
проекции повернется по направлению движения часовой стрелки и
расположится на одном перпендикуляре к оси х с фронтальной проек-
проекцией А".
Профильная проекция А'" будет вращаться вместе с профильной
плоскостью проекции и к концу преобразования займет положение,
указанное на рис. 29,6. При этом А'" будет принадлежать перпенди-
перпендикуляру к оси г, проведенному через А", и будет удалена от оси г на
такое же расстояние, на какое горизонтальная проекция А' удалена
от оси х.
Поэтому связь между горизонтальной и профильной проекциями
точки может быть установлена с помощью двух ортогональных от-
отрезков [Л'Лу] и [ЛуЛ'"| и сопрягающей их дуги окружности с цент-
центром в точке пересечения осей х, у, г. Отмеченной связью пользуются для
нахождения недостающей профильной (или горизонтальной) проек-
проекции.
• Положение профильной (горизонтальной) проекции по заданным
горизонтальной (профильной) и фронтальной проекциям может быть
найдено и без проведения дуги окружности. В этом случае связь между
горизонтальной и профильной проекциями может быть установлена с
помощью ломаной линии А'АХА'" с вершиной Ах на биссектрисе угла,
образованного осями у, принадлежащими плоскостям я, и тг3 •
Биссектрису О А х называют постоянной прямой k эпюра Монжа.
Чтобы определить положение точки А в пространстве, необходи-
необходимо знать три ее координаты (х, у, г), равные длинам отрезков [АЛ'"],
[АД"], [АА'} (см. рис. 29,а). Величины этих отрезков могут быть легко
определены на эпюре рис. 29,6:
[AA"']*[A'Ay]?[A"Az];
[АА"]?[А'Ах]?[А'"А2у,
*2
Попутно отметим, что горизонтальная проекция точки А опреде-
определяется абсциссой х и ординатой у; ее фронтальная проекция — абс-
абсциссой х и аппликатой z, а профильная проекция — ординатой у и ап-
аппликатой z, г. е.
А"(х, г);
А'" (у, г).
Из записи A) следует:
1. Точка в пространстве удалена:
A)

32 Метод проекций
а) от плоскости проекции я3 на такую же величину, на какую гори-
горизонтальная проекция этой точки А' удалена от оси у (или же фронталь-
фронтальная проекция А" от оси г);
б) от плоскости проекции я2 на такую же величину, на какую гори-
горизонтальная проекция этой точки А' удалена от оси х (или ее профильная
проекция А'" от оси z);
в) от плоскости проекции л, на такую же величину, на какую ее
фронтальная проекция А" удалена от оси х (или ее профильная проек-
проекция А'" удалена от оси у).
2. Две проекции любой точки принадлежат одному перпендику-
перпендикуляру (одной линии связи):
а) горизонтальная и фронтальная — перпендикуляру к оси х;
б) горизонтальная и профильная — перпендикуляру к оси у;
в) фронтальная и профильная — перпендикуляру к оси г.
3. Для ортогонального проецирования отмеченное ранее свойство
(см. с. 19) может быть сформулировано: положение точки в прост-
пространстве вполне определяется положением ее двух ортогональных проек-
проекций. Как следствие из этого — по двум любым заданным ортогональным
проекциям точки всегда можно построить недостающую ее третью орто-
ортогональную проекцию.
Действительно, сочетание любых двух ортогональных проекций точ-
точки всегда дает нам значения всех трех ее координат.
Пользуясь табл. 1, помещенной в § 7, и зная положительное и от-
отрицательное направление осей, а также принимая во внимание свой-
свойства проекций точки (пп. 1, 2, 3), можно указать на эпюре проекции
точки, если известны ее координаты, или определить, в каком октанте
расположена точка и на какие расстояния она удалена от плоскостей
проекций, если заданы хотя бы две ее ортогональные проекции.
ПРИМЕР. Даны координаты точек А Аналогично находим положение гори-
(-20, -20, +15) и В (+15, +5, -10). зонтальной и фронтальной проекций точ-
Требуется найти положение проекций ки В. пня этого на положительных нап-
этих точек и определить, в каких ок- равлениях осей а: и у откладываем со-
тантах они находятся (рис. 30). ответственно 15 и 5 мм. Эти координа-
Для определения положения гори- ты определяют положение В'. Фронталь-
зонтальной проекции А' точки А откла- ная проекция принадлежит прямой ли-
дываем от начала координат на отрица нии связи, проходящей через В' перпен-
тельном направлении оси х (от точки О дикулярно к оси х, и удалена от этой
вправо) значение х = -20 мм и опреде- оси на заданное значение z = -10.
ляем точку Ах, а на отрицательном на-
направлении оси у откладываем значение Приведенная в § 7 табл. 1 знаков ко-
у = -20 (для плоскости 7ГХ отрицатель- ординат точек, расположенных в разных
ное направление оси у совпадает с поло- октантах, позволяет легко определять,
жительным направлением оси г) и оп- какому октанту принадлежит точка, ес-
ределяем положение точки Ау. ли известны хотя бы две ее проекции.
Пересечение перпендикуляров, вое- Точка д находится в VI октанте про-
проставленных из точек Ах и Ау к со- странств^ так как она располагается за
ответствующим осям хну, укажет по; фронтальной плоскостью проекции (в зо-
ложение горизонтальной проекции А не отрицательнЬ1Х значений ординаты у)
точки Л. выше горизонтальной (аппликата г — по-
Мы знаем, что фронтальная А и го- ложитеЛьна) и правее профильной плос-
ризонтальная А проекции точки при- кости проекцИн (абсцисса х - отрица-
надлежат одному перпендикуляру к тельна), т. е. в части пространства, огра-
оси х (см. п. 2, с. 22) и то, что фрон- ниченной верхней правой полой плос-
тальная проекция удалена от оси х на кости v y задней правой полой плоскос-
величину аппликаты z (в данном слу- ти я и задней верхней полой профиль-
чае z = +15). Поэтому для определе- „ой плоскости проекции я3
ния положения А откладываем от точ-
точки Ах на перпендикуляре к оси х значе- Чтобы найти профильную проекцию
ние аппликаты г = + 15. точки, достаточно из А" провести пря-

Неопределяемые понятия геометрии; ортогональные проекции 33
точки, прямой, плоскости
A'"
о
i
В'
В"
Аг
6 ц
:
Рис.
^гг
0
)Dy
1
30
пЛ'
1.»
-О Л
1
Рис. 31
мую, перпенди!сулярно к оси 2, и отло- Точка В расположена в IV октанте,
жить на ней от этой оси влево (по от- в котором координаты х и у — положи-
рицательному направлению оси у, при- тельны, а координата z — отрицательна,
надлежащей профильной плоскости На рис. 30 указано также положение
проекции) значение у = —20 мм. профильной В'" проекции этой точки.
На рис. 31 показаны горизонтальные и фронтальные проекции точек
А, В, С, D, E, F. Зная положительные и отрицательные направления осей,
можно без труда определить октант, которому принадлежит точка; так,
точка А находится в третьем октанте пространства, а точка В, симмет-
симметричная точке А относительно плоскости я3, принадлежит седьмому
октанту. Точка С находится в восьмом октанте, так как значения абсцис-
абсциссы х и аппликаты z — отрицательны, а значение ординаты у — положи-
положительно.
На рис. 31 показаны проекции D' и D" точки D. Для этой точки
характерно равенство аппликаты z и ординаты у, поэтому точка D уда-
удалена на одинаковое расстояние от плоскостей я, и ттг (\D'DX\ = \D"DX\),
т. е. она принадлежит биссекторной плоскости шестого и восьмого
октантов. На рис. 31 указаны также проекции точек Е и F. Точка Е
принадлежит фронтальной плоскости проекции тг2 (ордината У (-)Е = 0) >
а точка F — горизонтальной плоскости проекции Я) (z(.)f = 0).
В тех случаях, когда нет необходимости в определении положения
точки (или любой геометрической фигуры) относительно системы
плоскостей проекций, можно не указывать на эпюре осей проекций.
Иными словами, для безосного чертежа плоскости проекции принима-
принимаются неопределенными до параллельного переноса (т. е. могут переме-
перемещаться параллельно самим себе) й
В инженерной практике при Составлении чертежей, когда требуется
определить (форму и размеры геометрической фигуры или взаимное
расположение совокупности геометрических фигур, обычно оси проек-
проекций не указывают. Отсутствие на чертеже осей не мешает определять
третью проекцию любой точки по двум ее заданным проекциям, если
указаны три проекции какой-либо другой точки.
ПРИМЕР. Даны три проекции точки
А (А1, А", А'"), а также горизонтальная
и фронтальная проекции точки В (В' и
В"). Требуется найти профильную про-
проекцию В'" (pvc. 32). Через горизонталь-
горизонтальную проекцию точки А проводим пря-
прямую, параллельную линии связи (А"А' '),
а чер«з профильную проекцию А'" про-
проводим прямую, параллельную линии
связи (А'А"), и отмечаем точку их
пересечения A i . Через точку А! прово-
проводим постоянную прямую k. Прямая k
проводится как биссектриса угла
А\А,А'".
Зная положение постоянной прямой,
легко найти недостающую профильную

34 Метод проекций
В"
о
6
В'
А"
о-
6
А'
В'"
9
А"
-о
.¦ЛВ, |
л"
о-
i-
С"
с'
-о
А'"
-О
t С
k
Рис. 32
Рис. 33
проекцию точки В. Для этого через В' дим вертикальную прямую. Точка ее пе-
проводим горизонтальную прямую, от- ресечения с горизонтальной прямой, про-
мечаем точку В, ее пересечения с посто- веденной через В", определяет искомую
янной прямой k. Через точку В[ прово- профильную проекцию В'".
Постоянная прямая позволяет решать задачу по определению третьей
проекции точки по двум заданным независимо от того, в каком октанте
находится точка.
ПРИМЕР. Даны три проекции точки
А(А\ А", А1"), а также горизонтальная
и фронтальная проекции точки С (С' и
С"), расположенной в VI октанте
(рис. 33). Требуется определить С'".
Через данную проекцию А' проводим
горизонтальную прямую и отмечаем точ-
точку Л [ пересечения ее с вертикальной
прямой, проведенной через А1". Через
точку А у проводим постоянную пря-
прямую k.
Для определения третьей проекции
точки С достаточно через точку С' про-
провести горизонтальную прямую, а из точ-
точки Ci пересечения ее с постоянной пря-
прямой k — вертикальную прямую. Точка
пересечения этой вертикали с горизон-
горизонтальной прямой, проведенной через С",
укажет положение искомой проекции
С'". Если на безосном чертеже потребу-
потребуется указать оси, то это всегда можно
сделать (с точностью до параллельного
переноса). Для этого одну из осей, нап-
например х, проводим произвольно, следя
лишь за тем, чтобы она была перпендику-
перпендикулярна линии связи, соединяющей гори-
горизонтальную и фронтальную проекции
точки. Тогда ось z определится как пря-
прямая, перпендикулярная к оси х в точке
пересечения оси х с постоянной прямой k.
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ
При построении проекции прямой следует исходить из инвариант-
инвариантного свойства 1а (см. § 6) ортогонального проецирования:
(V/)A (/**,) :1^ /'*
При „ ортогональном проецировании на плоскость прямая, не пер-
перпендикулярная плоскости проекции, проецируется в прямую.
Поэтому для определения проекции прямой достаточно знать про-
проекции двух не тождественных точек, принадлежащих этой прямой.
[АВ], определяющий прямую I (рис. 34,а), занимает произвольное
(общее) положение по отношению к плоскостям проекций (углы нак-
* Естественно, будут справедливы и следующие утверждения:
) :J->¦/"; 2)

Неопределяемые понятия геометрии; ортогональные проекции 35
точки, прямой, плоскости
В"
Рис. 34
I"
I'
а)
б)
Рис. 35
лона прямой / к плоскостям проекций — произвольные, но отличные
от 0 и 90°). Такая прямая называется прямой общего положения.
На эпюре проекции прямой общего положения составляют с ося-
осями проекций также произвольные углы (рис. 34,6). Прямую на эпю-
эпюре можно задать не только проекциями ее отрезка (см. рис. 34,6),
но и проекциями некоторой произвольной части прямой, не указы-
указывая концевых точек этой части. При этом можно ограничиться обоз-
обозначением проекции только одной буквой, отнеся ее к какой-либо точ-
точке прямой (рис. 35,а) или к прямой (точнее ее проекции) в целом
(рис. 35,6).
Следы прямой
Прямая общего положения пересекает все основные плоскости про-
проекции. Точку пересечения (встречи) прямой с плоскостью проекции
называют следом прямой.
В зависимости от того, с какой плоскостью проекции происходит
встреча прямой /, следы обозначают и называют: Я; — горизонтальный
след прямой /; F\ — фронтальный след прямой I. Я/, Н[', F\, F{' — соот-
соответственно горизонтальная и фронтальная проекции следов Н{ и Ft.
Следует иметь в виду, что Н[ = Н[; Ft = F{'.
Установим правило нахождения следов прямой. Для примера рас-
рассмотрим определение Н1 (см. рис. 34,6). Горизонтальный след — точка,
принадлежащая как прямой I, так и плоскости проекции я, (Я; = /О я, ),
поэтому H'i е /" и Н'( е х, следовательно, Я1/ = Г л х. Горизонтальная
проекция Н\ ? /' (так как Н{ € /). Поэтому для нахождения горизонталь-
горизонтального следа прямой необходимо:

36 Метод проекций
1) отметить точку пересечения фронтальной проекции прямой с
осью* (Г П х = Я'/);
2) через полученную точку провести прямую а, перпендикулярную
оси х (а 1 х);
3) пересечение перпендикуляра а с горизонтальной проекцией пря-
прямой укажет положение горизонтального следа #/(а п /' = #;).
Таким образом, алгоритм определения горизонтального следа пря-
прямой / может быть записан: Я; = (/" г\ х = Я}'); (а 1 х, а э Я1/); а п Г.
Для определения фронтального следа прямой вместо Г Пх выпол-
выполняется операция V О х — F\, а прямая п\ i x проводится через точку
F'i- Последняя операция заключается в нахождении F(" =¦ а1 п I".
Частные случаи расположения прямой
Кроме рассмотренного общего случая (см. рис. 34,а, б), существу-
существуют следующие частные случаи расположения прямой по отношению
к заданной системе плоскостей проекций:
A. Прямая параллельна плоскости проекции.
Б. Прямая перпендикулярна плоскости проекции.
B. Прямая принадлежит плоскости проекции (частный случай па-
параллельности ).
Рассмотрим каждый из этих случаев.
А. Прямая, параллельная плоскости проекции (горизонталь, фрон-
таль)*.
1. Горизонталь — прямая, параллельная горизонтальной плоскости
проекции: h II тг, .
Все точки горизонтали удалены на одинаковые расстояния от плос-
плоскости 7г,. Поэтому фронтальная проекция любой горизонтали параллель-
параллельна оси х. Горизонтальная проекция может занимать^ любое положение
(рис. 36,а иб).УЛеЛ; z( )A ~ const, поэтому h" || х. *
2. Фронталь — прямая, параллельная фронтальной плоскости проек-
проекции: f\\ir2.
Все точки фронтали удалены на одинаковое расстояние от фрон-
фронтальной плоскости я2 • Поэтому горизонтальная проекция любой фронта-
фронтали параллельна оси лс. Фронтальная проекция может занимать любое
положение (рис. 37,а и б). V\B e f; у ( )в ~ const, поэтому f \\ х.
Б. Прямая, перпендикулярная плоскости проекции (проецирую-
(проецирующая прямая).
* Горизонталь и фронталь называют также линиями уровня.
/С h"
а)
A" h"
Рис. 36.

Неопределяемые понятия геометрии; ортого)шльные проекции 37
точки, прямой, плоскости
в:
а)
Рис. 37
б)
6а'-На
Рис. 38
Ь'
Рис. 39
б)
1. Горизонтально проецирующая прямая — прямая, перпендикуляр-
перпендикулярная горизонтальной плоскости проекции: а 1 л, .
Такая прямая проецируется на плоскость я, в точку; ее фронтальная
проекция перпендикулярна оси х (рис. 38,а и 6) : а' — точка, а" — пря-
прямая 1 х.
2. Фронтально проецирующая прямая — прямая, перпендикуляр-
перпендикулярная фронта^хьной плоскости проекции: 6 1я2.
Эта прямая проецируется на плоскость тг2 в точку, а ее горизонталь-
горизонтальная проекция перпендикулярна оси х (рис. 39,а и б): Ь" — точка, Ь' —
прямая 1 х. Прямые а и Ь являются частными случаями соответственно
фронтали и горизонтали.
В. Прямая, принадлежащая плоскости проекции.
Характерным признаком для эпюра, на котором изображена та-
такая прямая, будет принадлежность одной из проекций прямой оси.

38 Метод проекций
/о*/о"
б)
Рис. 40
На рис. 40,а и б показаны проекции прямых hQ и /0. Прямая hQ принад-
принадлежит горизонтальной плоскости проекции: h0 с тг,. Прямая f0 принад-
принадлежит фронтальной плоскости проекции: f0 С тг2 ¦ Прямые п0 и fa явля-
являются нулевыми горизонталью и фронталью.
ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ ПЛОСКОСТИ
Плоскость является простейшей поверхностью. Положение плоско-
плоскости в пространстве однозначно определяется тремя различными точ-
точками А, В, С, не принадлежащими одной прямой. Поэтому для зада-
задания плоскости на эпюре Монжа достаточно указать проекции:
а) трех различных, не принадлежащих одной прямой точек (рис. 41,а);
б) прямой и не принадлежащей ей точки (рис. 41,6);
в) двух прямых, пересекающихся в собственной (рис. 41,в) или
несобственной (рис. 41,г) точке.
Плоскость может быть задана также проекциями отсека плоской
фигуры Ф (рис. 41,d). В некоторых случаях бывает целесообразным
задавать плоскость не произвольными пересекающимися прямыми, а
прямыми, по которым эта плоскость пересекает плоскости проекции.
Такой вариант задания плоскости называют заданием плоскости следами.
На рис. 42;,а показана плоскость а. Эта плоскость пересекает ось проекции
в точке Ха, а плоскости проекции по прямым hoa, foa. Прямую, по ко-
которой плоскость пересекает плоскость проекции, называют следом
плоскости. При этом различают:
hoa = а Г) ¦ni —горизонтальный след плоскости а;
fact = a n п2 —фронтальный след плоскости а.
А"
О
А'
о
В"
о
С"
о
В'
С
о
m
Д)
Рис. 41

a)
Неопределяемые понятия геометрии; ортогональные проекции 39
точки, прямой, плоскости
ha.
б)
Рис. 42
Точку Хс, = х Г\ а пересечения оси jc с плоскостью а называют точкой
схода следов (в этой точке сходятся два следа).
На рис. 42,6 показано задание плоскости следами. Сопоставляя
между собой наглядное изображение (рис. 42,а) и его плоскостную
модель — эпюр Монжа (рис. 42,6), мы видим, что задание плоскости
следами обладает преимуществом перед другими вариантами ее изоб-
изображения на эпюре:
во-первых, сохраняется наглядность изображения, что позволяет
легко представить положение плоскости в пространстве;
во-вторых, при задании плоскости следами требуется указать толь-
только две прямые вместо четырех (см. рис. 41,в, г) или шести (см.
рис. 41,д).
Показанная на рис. 42 плоскость а занимает общее (произвольное)
положение по отношению к плоскостям проекций (углы наклона этой
плоскости к плоскостям проекций — произвольные, но отличные от 0 и
90° ). Такая плоскость называется плоскостью общего положения.
Из рис. 42,6 видно, что на эпюре Монжа следы плоскости общего по-
положения составляют с осью проекции также произвольные углы.
Частные случаи расположения плоскости
Кроме рассмотренного общего случая (см. рис. 42), плоскость по
отношению к плоскостям проекций может занимать следующие частные
положения:
А. Перпендикулярное к плоскости проекции.
Б. Параллельное плоскости проекции.
Рассмотрим эти случаи.
A. Плоскость, перпендикулярная к плоскости проекции. Такие плос-
плоскости называют проецирующими, при этом различают:
1. Горизонтально проецирующую плоскость C 1 тт^ .
2. Фронтально проецирующую плоскость у i n2 ¦
Рис. 43, 44 дают наглядное представление о проецирующих плос-
плоскостях и их задании на эпюре Монжа, причем плоскость C задана сле-
следами, 7 —параллельными прямыми (тип).
B. Плоскость, параллельная плоскости проекции.
Эти плоскости называют плоскостями уровня, причем плоскость 5 II 7т j
называют горизонтальной, а плоскость е II тг2 — фронтальной. Рис. 45,а
дает представление о горизонтальной плоскости 5, а на рис. 46,а показана
фронтальная плоскость е. На рис. 45,6 и 46,6 эти плоскости заданы на
эпюре Монжа.

40 Метод проекций
а)
Рис. 43
а)
_¦**-
Рис. 44
¦ "V
, ^Si
а)
б)
Рис. 45

Неопределяемые понятия геометрии; ортогональные проекции 41
точки, прямой, плоскости
Главные линии плоскости
Главными линиями плоскости называют:
1. Горизонталь —прямую, принадлежащую плоскости и параллельную
горизонтальной плоскости проекции.
2. Фронталь — прямую, принадлежащую плоскости и параллельную
фронтальной плоскости проекции.
3. Линию наибольшего наклона — прямую, принадлежащую плоскос-
плоскости и перпендикулярную к горизонтали или фронтали этой плоскости.
На рис. 47,а показаны горизонталь h и фронталь f плоскости а.
Рис. 47,6 и в иллюстрируют задание этих линий на эпюре Монжа. Из
рис. 47,6, в видно, что горизонталь плоскости параллельна ее горизон-
горизонтальному, а фронталь — фронтальному следу.
Характерные особенности проекций горизонтали и фронтали приве-
приведены ниже:
Проекция:
горизонтальная фронтальная
Горизонталь Параллельна hna Параллельна оси х
Фронталь Параллельна оси х Параллельна f0O
Представление о линии наибольшего наклона плоскости дает рис. 48,
на котором показана прямая с — линия наибольшего наклона плоскости
а к горизонтальной плоскости проекции. В некоторых учебниках ее
называют также линией наибольшего ската.
ГЩ
Рис. 47
с
Нс—Нс
б)
Рис. 48

42 Метод проекций
Отличительной особенностью линии наи-
наибольшего наклона прямой к плоскости -л^
является перпендикулярность ее горизонталь-
горизонтальной проекции горизонтали Н' плоскости а или
ее горизонтальному следу Ноа.
У прямой d — линии наибольшего наклона
плоскости а к плоскости проекции 7г2 —
фронтальная проекция перпендикулярна
фронтальной проекции фронтали плоскости f
или ее фронтальному следу foa. Рис. 48,а
показывает прямую с — линию наибольшего
ската плоскости а; на рис. 48,6 эта линия
задана на эпюре Монжа. На рис. 49 пока-
показана прямая d — линия наибольшего наклона
плоскости р (а || Ь) к плоскости проекции я2.
Так как плоскость C задана параллельными а
прямыми и направление фронтального следа
плоскости fop нам не известно, то для опреде-
определения направления фронтальной проекции
прямой d необходимо построить фронтальный
след плоскости f0 $ или фронтальную проекцию фронтали этой плоскости.
На рис. 49 проведена фронталь f (f, f") плоскости /3 (ее построе-
построение проще, чем определение фронтального следа плоскости C). Затем
через произвольную точку А" (А е /3) проведена фронтальная проек-
проекция d" {d" I /""). Отмечена точка М" = d" П f". По А" и М" найдены
А' и М'. Эти две точки указывают положение горизонтальной проекции
прямой d' — линии наибольшего наклона плоскости C к плоскости про-
проекции я2.
Рис. 49
Г
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ
.Расстояние между двумя точками А и В определяется длиной от-
отрезка прямой, заключенного между этими точками.
Из инвариантных свойств ортогонального проецирования следует,
что ортогональная проекция отрезка будет конгруентна оригиналу
лишь в том случае, когда он параллелен плоскости проекции (см. § 6,
свойство 2д) :
([АВ]|| *,)*» [А'В']--'
Аналогично:
Во всех остальных случаях отрезок проецируется на плоскость про-
проекции с искажением. При этом ортогональная проекция отрезка всегда
будет меньше его длины.
Для установления зависимости между длиной отрезка прямой и
длиной его проекций рассмотрим рис. 50,а. В прямоугольной трапе-
трапеции ABB'А' (углы при вершинах А' и В' — прямые) боковыми сто-
сторонами являются отрезок АВ и его горизонтальная проекция А'В', а
основаниями — отрезки А А' и ВВ', по величине равные удалениям кон-
концов А и В отрезка от горизонтальной плоскости проекции тг х.
Проводим в плоскости трапеции ABB'А' через точку А прямую АВХ,
параллельную горизонтальной проекции отрезка АВ. Получим прямо-
прямоугольный треугольник АВВх, у которого катет АВХ = А'В', а катет
BBi равен разности аппликат концов отрезка (\ВВ'\ - \АА'\). Гипо-

Неопределяемые понятия геометрии; ортогональные проекции 43
точки, прямой, плоскости
Рис.50
тенуза этого треугольника равна длине отрезка АВ.
;АВ\2 = \А'В'\2 + (\ВВ'\- \АА'\J.
Зависимость между длиной отрезка и его фронтальной проекцией
может быть установлена с помощью треугольника АА^В, в котором
гипотенуза ривна длине отрезка, один из катетов — фронтальной проек-
проекции отрезка, а другой — разности удалений концов отрезка от фронталь-
фронтальной плоскости проекции:
\АВ\7 = \А"В"\7 + (\АА"\ - \ВВ"\J.
Приведенные примеры показывают, что для графического опре-
определения на эпюре Монжа длины отрезка достаточно построить пря-
прямоугольный треугольник, взяв за один его катет горизонтальную (фрон-
(фронтальную) проекцию отрезка, а за другой катет — разность удалений
концов отрезка от горизонтальной (фронтальной) проекции.
На рис. 50,6 показано определение действительной величины от-
отрезка АВ с помощью построения треугольника А'В'В0. На этом же чер-
чертеже приведен второй вариант решения задачи — путем построения
треугольника А"В"А0 на базе фронтальной проекции отрезка.
Построение прямоугольного треугольника не единственный гра-
графический способ определения длины отрезка. В дальнейшем будут
показаны различные способы преобразования ортогональных проек-
проекций, с помощью которых можно получить более экономичные решения.
С помощью прямоугольного треугольника можно решать задачу на
построение на эпюре проекции отрезка наперед заданной длины.
ПРИМЕР. На прямой общего положе-
положения а отложить от точки А вправо отре-
отрезок длиной 25 мм (рис. 51).
РЕШЕНИЕ:.
1. Отмечаем на прямой а произволь-
произвольную точку 1 A', 1" );
2. Определяем длину отрезка [А1 ] ;
3. На прямой (A'l0) от точки А
откладываем отрезок А'В0 длиной
25 мм.
4. Из точки Во опускаем перпендику-
перпендикуляр на прямую а'. [АВ*| является гори-
горизонтальной проекцией отрезка заданной
длины.

44 Метод проекций
При последующем изложении материала нам часто придется обра-
обращаться к параллельным прямым и плоскостям. В связи с этим целесо-
целесообразно не только показать задание на эпюре Монжа точки, прямой,
плоскости, но и выяснить условия, которые должны быть выполнены
для изображения параллельных прямых, плоскостей, прямой и плос-
плоскости.
В расширенном евклидовом пространстве (пространстве, допол-
дополненном несобственными точками и прямыми) две прямые, прямая и
плоскость, две плоскости всегда пересекаются. Различие по сравне-
сравнению с обычным евклидовым пространством состоит лишь в том, что
точка пересечения прямых или прямой и плоскости и прямая, являю-
являющаяся результатом пересечения двух плоскостей, могут быть как соб-
собственными, так и несобственными. В последнем случае прямые, прямая и
плоскость, плоскости считаются параллельными.
Изображение на эпюре Монжа параллельных прямых, прямой и пло-
плоскости, плоскостей базируется на инвариантном свойстве 2з (см. § 6)
ортогонального проецирования.
1. Параллельные прямые.
Если а || Ъ, то а п Ь в несобственной точке К„, следовательно, ее
проекции К'ж и KIZ будут также несобственными. Поэтому а' || Ь' тла" \\ Ъ",
т. е. у параллельных прямых параллельны их одноименные проекции.
2. Параллельность прямой и плоскости.
Если а п а = К„ — несобственная точка (иначе а II а), то ее проекции
будут также несобственными точками KL и К„. Поэтому а II а' и а" II а
б) а'
П
Рис. 52

Неопределяемые понятия геометрии; ортогональные проекции 45
точки, прямой, плоскости
Известно, что прямая, параллельная плоскости, должна быть параллельна
какой-либо прямой, принадлежащей этой плоскости. Поэтому, чтобы
задать на эпюре Монжа прямую а, параллельную плоскости а, необходи-
необходимо и достаточно в плоскости а "взять" произвольную прямую Ь и про-
провести а || Ъ по правилу, изложенному в п. 1.
3. Параллельные плоскости.
Две плоскости параллельны, если в одной из них можно провести
две пересекглощиеся прямые, параллельные двум пересекающимся
прямым другой плоскости. Поэтому, чтобы задать на эпюре Монжа
плоскость a (a n b), параллельную плоскости /З(тПп), достаточно
указать проекции пересекающихся прямых а и Ь, соответственно па-
параллельных прямых тип.
В частности, если плоскости заданы следами, то у параллельных
плоскостей будут параллельны их одноименные следы. На рис. 52 по-
показаны эпюры: параллельных прямых а \\ Ь (рис. 52,а); параллель-
параллельных прямой а и плоскости а (рис. 52,6); параллельных плоскостей а
и C (рис. 52,в и г). На рис. 52,в плоскость а (а п Ь), плоскость C (т П п),
на рис. 52,г плоскости заданы следами.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. В чем состоит реконструкция трех-
трехмерного евклидова пространства?
2. Что такое несобственные элементы
пространства?
3. Сформулируйте основные отноше-
отношения принадлежности между элементами
евклидова пространства.
4. Перечислите основные способы ме-
метода проекции.
5. Какие преимущества присущи ор-
ортогональному проецированию по срав-
сравнению с косоугольным проецирова-
проецированием?
6. Укажите основные инвариантные
свойства ортогонального проецирования.
7. Каким образом пространственная
фигура из трех взаимно перпендикуляр-
перпендикулярных плоскостей преобразуется в плос-
плоскую модель?
8. Какой октант имеет отрицательное
направление всех осей?
9. Какими полами плоскостей проек-
проекций ограничены II, III, VI, VII октанты?
10 Как обозначаются проекции точки,
прямой, плоскости на плоскостях про-
проекций?
11. Как по отношению к осям проек-
проекций располагаются проекции точек, на-
находящихся в I, II, III, ... , VIII октантах?
12. Какие знаки имеют координаты
х, у, z точки, находящейся в I, II, III, ...
... , VIII октанте?
13. Какие координаты на эпюре опре-
определяют горизонтальную и фронтальную
проекции точки?
14. В каких октантах значения коор-
координат точки отрицательны, в каких по-
положительны?
15. Как определить положение треть-
третьей проекции точки на безосном чертеже,
если известны две ее проекции и три
проекции другой точки?
16. Дайте определение и способы на-
нахождения следов прямой и плоскости.
17. Какие линии плоскости называют-
называются главными, перечислите характерные
особенности проекций этих линий на эпю-
эпюре Монжа.
18. Какие прямые и плоскости назы-
называются проецирующими, в чем состоит
отличительная особенность их ортого-
ортогональных проекций?

ГЛАВА
II
СПОСОБЫ ПРЕОБРАЗОВАНИЯ
ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Трудоемкость и, как следствие, точность графического решения за-
задач часто зависят не только от сложности задач, но и от того, какое по-
положение занимают геометрические фигуры, входящие в условия зада-
задачи, по отношению к плоскостям проекций.
Проиллюстрируем сказанное примерами.
ПРИМЕР 1. Требуется определить точ- К' на горизонтальном следе плоскости
ку пересечения ("встречи") линии / с hoa: К' ~ '' Q '•оа- Зная положение К,
плоскостью а (рис. 53). определяем К .
Так как и линия /, и плоскость а зани- На рис. 54,6 приведено решение этой
мают произвольное положение как по от- задачи на эпюре Монжа.
ношению друг к другу, так и относитель- ПРИМЕР 2. Определить длины сторон
но плоскостей проекций, то ответить на А ABC и величины углов при его верши-
поставленный вопрос непосредственно нах.
по пространственному изображению или Очевидно, если плоскость А АВС
по ортогональным проекциям (эпюру (плоскость а) занимает произвольное по-
Монжа) без дополнительных графичес- ложение относительно плоскостей проек-
ких построений не представляется воз- иий (рис. 55), или перпендикулярное к
можным. какой-либо плоскости (рис. 56), то для
В то же время ситуация, заданная на решения поставленной задачи необходи-
рис. 54,а, позволяет сразу, без каких- мо выполнить определенные графические
либо дополнительных построений, полу- построения. В то же время ответ на по-
почить ответ ставленные вопросы может быть полу-
Для решения задачи используем инва- чен без каких-либо графических пост-
риантное свойство 2г (см. § 6). роений непосредственно из ортогональ-
Точка К, в которой линия I пересека- ных проекций, если плоскость Д ABC па-
ет плоскость а, как принадлежащая го- раллельна плоскости проекции (рис.
ризонтально проецирующей плоскости, 57,а, б). Это утверждение базируется на
будет иметь горизонтальную проекцию инвариантном свойстве 2д (см. § 6).
Приведенные примеры показывают, что проецируемая фигура мо-
может занимать по отношению к плоскости проекции или произвольное,
или частное положение. В первом случае, как правило, получаются
проекции, неудобные для решения задач. В то же время решение зада-
задачи значительно упрощается, когда мы имеем дело с частным располо-
расположением геометрических фигур относительно плоскости проекции (см.
рис. 54 и 57). Наиболее выгодным частным положением проецируемой
фигуры (в случае ортогонального проецирования), при котором получа-
получаются проекции фигуры, удобные для решения задач, следует считать:
а) положение, перпендикулярное к плоскости проекции, — при
решении позиционных задач (см. рис. 54) *;
* Определения и деление задач на позиционные и метрические см. в гл. V и VI.

Понятия и определения 47
Рис. 53
Ное
Рис. 54
Рис. 55
а
Рис. 57

48 Способы преобразования
ортогональных проекций
б) положение, параллельное плоскости проекции, — для решения
метрических задач (см. рис. 57).
В связи с этим, естественно, возникает вопрос, каким путем мож-
можно получить удобные проекции для решения поставленной задачи по за-
заданным неудобным ортогональным проекциям?
Переход от общего положения геометрической фигуры к частно-
частному можно осуществить изменением взаимного положения проецируе-
проецируемой фигуры и плоскости проекции. При ортогональном проецировании
это может быть достигнуто двумя путями:
во-первых, перемещением в пространстве проецируемой фигуры
так, чтобы она заняла частное положение относительно плоскостей
проекций, которые при этом не меняют своего положения в простран-
пространстве;
во-вторых, выбором новой плоскости проекции, по отношению к
которой проецируемая фигура, не меняющая своего положения в прост-
пространстве, окажется в частном положении.
Первый путь лежит в основе способа плоскопараллельного переме-
перемещения; второй — составляет теоретическую базу способа замены пло-
плоскостей проекций. Рассмотрим каждый из этих способов в отдельности.
I. СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО
ПЕРЕМЕЩЕНИЯ
Изменение взаимного положения проецируемой фигуры и плоскос-
плоскостей проекций способом плоскопараллельного перемещения осущест-
осуществляется •< путем перемещения геометрической фигуры в новое поло-
положение так, чтобы траектории перемещения ее точек находились в па-
параллельных плоскостях.
В зависимости от положения этих плоскостей по отношению к пло-
плоскостям проекций и вида кривой (траектории перемещения точки)
различают несколько способов плоскопараллельного перемещения:
1. Способ параллельного перемещения.
Плоскости — носители траекторий перемещения точек параллель-
параллельны плоскости проекции. Траектория — произвольная плоская линия.
2. Способ вращения вокруг оси, перпендикулярной к плоскости
проекции.
Плоскости — носители траекторий перемещения точек параллель-
параллельны плоскости проекции. Траектории — дуги окружностей, центры кото-
которых находятся на оси, перпендикулярной плоскости проекции.
3. Способ вращения вокруг оси, параллельной плоскости проекции
(вращение вокруг линий уровня).
4. Способ вращения вокруг оси, принадлежащей плоскости проек-
проекции (вращение вокруг следа плоскости).
Рассмотрим каждый из этих способов в отдельности.
§ 9. СПОСОБ ПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
Для параллельного перемещения (переноса) справедливо утвержде-
утверждение, которое может быть выражено в виде следующей теоремы:
при параллельном переносе геометрической фигуры относительно
плоскости проекции проекция фигуры на эту плоскость хотя и ме-

Способ параллельного перемещения 49
/ов
а
Г
Рис. 58
няет свое положение, но остается конгруентной проекции фигуры в
ее исходном положении.
Докажем эту теорему для случая, когда проецируемая фигура плос-
плоская и ее плоскость принадлежит плоскости уровня Ф с а, плоскость а || Hi
(рис. 58). В этом случае на основании инвариантного свойства 2д (см.
§ 6) горизонтальная проекция Ф' будет конгруентна самой фигуре Ф
(Ф'^Ф).
При перемещении фигуры Ф в новое положение Ф ] фигура Ф, бу-
будет конгруентна Ф, так как:
а) расстояние между точками фигуры не меняется;
б) в процессе перемещения фигура Ф все время остается в плос-
плоскости а.
В силу параллельности плоскостей а и -п^ Ф\ = Ф,, но Ф) =Ф,а
Ф = Ф', следовательно, Ф] =* Ф'. Доказанная теорема будет справедли-
справедлива и в случае, когда геометрическая фигура занимает произвольное
положение относительно плоскости проекции.
Отметим еще два свойства параллельного перемещения:
1. При всяком перемещении точки в плоскости, параллельной пло-
плоскости проекции я j, ее фронтальная проекция перемещается по пря-
прямой, параллельной оси х.
2. В случае произвольного перемещения точки в плоскости, парал-
параллельной я2, ее горизонтальная проекция перемещается по прямой, па-
параллельной ОСИ X.
Справедливость отмеченных свойств может быть легко показа-
показана на простом примере.
Возьмем плоскость а, параллельную горизонтальной плоскости
проекции я, (рис. 59). Пусть точка А ? а переместится из положения А в
A t (A ~* Ai ). двигаясь в плоскости а по произвольной траектории (lt, 12
или /3). Очевидно, фронтальная проекция точки А" переместится в Л",
при этом [Л"Л|'] принадлежит следу foa, который параллелен оси х
([А"А[']с foa ||х).
На рис. 59,6 показано перемещение точки Be /3 || я2. Из чертежа видно,
что горизонтальная проекция траектории перемещения точки В из перво-
первоначального положения в новое В, представляет \В'В\ ] с hOfl || x и не
зависит от вида линии — траектории перемещения точки из положения
В в В,.
Пользуясь приведенной теоремой и отмеченными свойствами, легко
построить новые проекции геометрической фигуры по заданным ее
ортогональным проекциям, и, в частности, такие ее проекции, которые

50 Способы преобразования
ортогональных проекций
соответствуют отмеченным выше (см. с. 48) частным положениям
проецируемой фигуры по отношению к плоскости проекции.
Проследим на примерах использование способа параллельного пе-
перемещения для перевода произвольно расположенной геометрической
фигуры в частное положение.
ПРИМЕР 1. [ЛВ\ прямой общего по-
положения а перевести в положение, парал-
параллельное плоскости я2 (рис. 60).
У [АВ], параллельного плоскости 1Г2,
горизонтальная проекция должна быть
параллельна оси х. Поэтому переводим
[Д В'] в новое положение [AiB'i ], парал-
параллельное оси х. Перемещение отрезка в
новое положение осуществляем так, что-
чтобы любые его точки двигались в плос-
плоскостях, параллельных плоскости Я] . При
таком перемещении новая горизонталь-
горизонтальная проекция конгруентна исходной
[AjBi] = I^'B'] (на основании теоремы
с. 49).
Фронтальные проекции точек отрезка
[Л"В"] будут перемещаться в новое по-
положение по прямым, параллельным оси
д: (свойство 1,с.49).
На рис. 60 графические построения
выполнены в указанной ниже последо-
последовательности:
1) через произвольную точку А\ про-
провели прямую а\, параллельную оси^д:;
2) отложили на ней от точки At отре-
3) из точек А\ и В\ восставили пер-
перпендикуляры к оси х и нашли точки пе-
пересечения их с соответствующими гори-
горизонтальными прямыми, проведенными
через точки А" и В".
Полученные точки А т , В{ являются
концами фронтальной проекции отрезка
[А 1 f?i ], параллельного плоскости 7Г2 .
Для перевода отрезка прямой, произвольно расположенной в про-
пространстве, в положение, параллельное плоскости тг2, потребовалось
выполнить только одно перемещение отрезка параллельно плоскос-
плоскости проекции. Для перевода отрезка из общего положения в проецирую-
а)
В" а
А
А'
ho.
Рис.60
Рис. 61

Способ параллельного перемещения 51
Рис. 62
Рис.63
щее необходимо последовательно выполнить два его перемещения па-
параллельно плоскостям проекции: вначале перевести отрезок в поло-
положение, параллельное плоскости я, (или эт2) путем перемещения па-
параллельно плоскости тг2 (или я,), затем перевести отрезок в положе-
положение, перпендикулярное я2 (или тг, ).
ПРИМЕР 2. [CD] прямой общего поло- На рис. 61 [CD] вначале переведен в
жения Ь перевести в положение 1 я2 (рис. положение ||Я[ ([С[ D[ ] ), затем переме-
61). щением параллельно плоскости nt — в
положение 1 я2 ([C2D2 ] ) .
Зная характер геометрических построений, которые необходимо
выполнить для перемещения отрезка из общего положения в проеци-
проецирующее, можно легко перевести плоскость, произвольно расположенную
в пространстве, в частное положение (параллельное или перпендикуляр-
перпендикулярное плоскости проекции).
На рис. 62 показан перевод плоскости общего положения <x{hoa,
foa) в новое а, (Лоа,, /оа, ), при зтома, 1 я2.
Как видно из чертежа, перевод плоскости а в положение aj осу-
осуществлен с помощью горизонтали h, которая переведена в положе-
положение Л, 1 я2, поэтому и а, 1 я2. Следует обратить внимание на то, что
расстояние d остается постоянным:
\hoah'\ = Iftoa^il-
Рис. 63 дает представление о преобразовании ортогональных проек-
проекций Л ABC, определяющего плоскость общего положения /3, в проекции
Л А2В2Сг, задающего плоскость C2 II я, .
Геометрические построения выполнены в последовательности, ука-
указанной индексами, поставленными у проекций точек справа внизу.
Выполненные на эпюре построения соответствуют перемещению плоско-
плоскости в пространстве вначале || тг, во фронтально-проецирующее положение
(Д AlBlCl ), затем перемещением || я2 плоскость треугольника переве-
переведена в положение || т\х (Д АгВ2С2).

52 Способы преобразования
ортогональных проекций
§ 10. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ,
ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ ПРОЕКЦИИ
Вращение вокруг оси, перпендикулярной к плоскости проекции,
является частным случаем параллельного перемещения. Отличие от
общего случая состоит лишь в том, что за траекторию перемещения
точки берется не произвольная линия, а дуга окружности, центр ко-
которой находится на оси вращения, а радиус равен расстоянию между
точкой и осью вращения.
Проследим, как будет изменяться положение точки А при ее вра-
вращении вокруг оси 1, перпендикулярной плоскости я2 (рис. 64). Точ-
Точка А перемещается по дуге окружности в плоскости а (а 1 i и, следо-
следовательно, а || п-2), поэтому эта окружность проецируется на плоскость 7г2
без искажения, а на плоскость -л^ — в отрезок прямой, параллельной оси
х (рис. 64,6).
Таким образом, при вращении точки вокруг оси, перпендикуляр-
перпендикулярной к фронтальной плоскости проекции, фронтальная проекция точ-
точки перемещается по окружности с центром на фронтальной проекции
оси вращ€«ия, а горизонтальная — по прямой, параллельной оси х.
Вращение точки вокруг оси i 1 я, иллюстрирует рис. 65,а. Точка
В перемещается в новое положение Вх по окружности, принадлежащей
л2
б)
Рис. 64
O'ei'
А-О-—О—
в1; о'Щ" в"
б)
Рис. 65

Способ вращения вокруг оси, 53
перпендикулярной к плоскости проекции
плоскости /3 1 i. Так как i 1 я, , то /3 || я, . Поэтому при вращении точ-
точки вокруг оси, перпендикулярной к горизонтальной плоскости проек-
проекции, ее горизонтальная проекция перемещается по окружности, центр
которой принадлежит горизонтальной проекции оси вращения, а фрон-
фронтальная проекция точки — по прямой, параллельной оси х (рис. 65,6).
Выяснив характер проекций траекторий перемещения точки при ее
вращении вокруг оси, перпендикулярной плоскости проекции, легко
осуществить перемещение любой геометрической фигуры из задан-
заданного положения в частное путем ее поворота вокруг оси i 1 я, (или я2).
В качестве примера покажем на эпюре Монжа, как осуществляется
перемещение отрезка произвольной прямой в частное положение путем
вращения вокруг оси, перпендикулярной плоскости проекции.
ПРИМЕР 1. [АВ] прямой общего поло-
положения а перенести в положение, парал-
параллельное я2 (рис. 66).
Чтобы осуществить такое перемеще-
перемещение, достаточно повернуть [АВ] вокруг
оси i 1 Я] на^-i/' • ,\а
Величину угла ц}° выбирают такой,
чтобы после поворота [A'iBj] занял по-
положение II оси х.
Так как точка В принадлежит оси вра-
вращения, то она не будет менять своего поло-
положения в процессе преобразования. Bt = В,
следовательно, В\ = В' и В[' = В". Для на-
нахождения точки А" необходимо из А\
восставить перпендикуляр к оси х и от-
отметить точку его пересечения с горизон-
горизонтальной прямей, проведенной через А".
ПРИМЕР 2. [CD] прямой общего поло-
положения Ь перевести в положение 1 я2
(рис.67).
Чтобы осуществить перемещение от-
отрезка из общего положения в проеци-
проецирующее, необходимо последовательно
выполнить два вращения вокруг осей,
перпендикулярных к плоскостям проек-
проекций.
После первого вращения отрезок пе-
переводится в положение, параллельное
плоскости Я] (или я2 ), и лишь после
этого вращением вокруг оси, перпен-
перпендикулярной плоскости проекции 7Г) (или
Я2) перемещают отрезок в положение,
перпендикулярное плоскости п2 (или
я,).
На рис. 67 [CD] вначале вращением
вокруг ii 1 7Ь переведен в положение
II я, ([Cj D"\ II х), затем вращением вок-
вокруг i2 .17Г! [С 1 ?> 1 ] перемещен во фрон-
фронтально проецирующее положение
* Для упрощения геометрических построений здесь, как и во всех других слу-
случаях использования способа вращения, ось вращения следует выбирать так, что-
чтобы она пересекала вращаемую прямую.
Рис. 66

54 Способы преобразования
ортогональных проекций
В случае перевода плоскости
общего положения в частное
задача решается аналогично толь-
только что рассмотренным приме-
примерам.
Чтобы плоскость, произволь-
произвольно расположенная в пространст-
пространстве, заняла проецирующее поло-
положение, достаточно вращением
перевести прямую, принадлежа-
принадлежащую этой плоскости, в положе-
положение, перпендикулярное плоскос-
ти проекции. Количество графи-
графических построений, которые не-
необходимо выполнить для такого
перемещения, может быть сок-
ращено, если взять не произволь-
НУЮ ПРЯМУЮ> а горизонталь или
фронталь плоскости. Уменьше-
ние графических построений в
этом случае происходит благода-
благодаря тому, что перевод горизон-
горизонтали или фронтали в проецирую-
проецирующее положение можно осущест-
осуществить за один поворот, а не за два,
как это пришлось бы делать,
если поворачивать прямую об-
общего положения.
На рис. 68 плоскость общего
Рис- 68 положения а, заданная параллель-
параллельными прямыми а и Ь, поворотом
вокруг оси i 1 тг i переведена во фронтально проецирующее положение.
Новые проекции прямых aY и й, найдены с помощью горизонтали h.
Геометрические построения, приведенные на рис. 68, выполняем в
следующем порядке:
1. В плоскости а проводим горизонталь h (h', h") .
2. Вращением вокруг оси i, проходящей через горизонталь h и пер-
перпендикулярную плоскости я, , переводим h(h', h") в положение
Л; (h\, h")Lir2.
3. При повороте горизонтали на L у" на такой же угол повернется
все множество точек этой плоскости, поэтому для определения ново-
нового положения проекций прямых с^ и 6, достаточно повернуть вок-
вокруг оси 1 точки 1, 3 и 2, 4 C € а, 4 ? Ь) на тот же/./*.
4. По горизонтальным проекциям 1\, 3\ и 2\, 4\ определяем их
фронтальные проекции.
Если необходимо перевести плоскость в положение || пу, то это
легко сделать, повернув фронтальные проекции прямых а[ и Ь" вокруг
оси ix 17i 2 на угол у° так, чтобы а2' и Ь'^ заняли положение, параллельное
оси х.
¦Новое положение а\ и Ь] можно определить и иначе: через 12 и 2j провести
прямые а\ и Ь\, составляющие с прямой h\ такой же угол, какой а и Ь' составля-
составляют с ti'.

Способ вращения вокруг оси, параллельной плоскости проекции 55
(вращение вокруг линии уровня)
§ 11. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ,
ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИИ
(ВРАЩЕНИЕ ВОКРУГ ЛИНИИ УРОВНЯ)
Эффективным приемом, упрощающим решение задач, связанных
с определением метрических характеристик плоских фигур, является
способ вращения этих фигур вокруг их линий уровня. Путем такого
вращения можно плоскость, которой принадлежит рассматриваемая
фигура, поЕ:ернуть в положение, параллельное плоскости проекции.
В этом случае ортогональная проекция любой принадлежащей плос-
плоскости фигуры будет конгруентна оригиналу и, следовательно, позво-
позволит определить все метрические характеристики проецируемой фигу-
фигуры непосредственно по ее проекции без каких-либо дополнительных
построений.
Очевидно, вращая плоскость вокруг горизонтали, можно перевести
ее в положение, параллельное плоскости я i, и получить неискаженный
вид горизонтальной проекции. Вращение плоскости вокруг фронтали
позволяет перевести ее в положение, параллельное плоскости я2, что
обеспечит получение неискаженного вида фронтальной проекции.
Каждая точка плоскости при ее вращении перемещается по окруж-
окружности, прин.щлежащей плоскости, перпендикулярной к оси вращения.
Центр округкности будет находиться на оси вращения, а величина ра-
радиуса вращения равна расстоянию от точки до оси вращения. Если за
ось вращения взята горизонталь, то окружность, представляющая тра-
траекторию движения точки, будет проецироваться на плоскость тту в отре-
отрезок прямой, перпендикулярной горизонтальной проекции горизонтали.
На плоскость тг2 окружность проецируется в эллипс, построение которо-
которого можно не делать. Точка пересечения горизонтальных проекций гори-
горизонтали и горизонтальной проекции окружности определяет горизонталь-
горизонтальную проекцию центра вращения.
Аналогично, при вращении плоскости вокруг фронтали любая точ-
точка, принадлежащая плоскости, перемещается по окружности, кото-
которая проецируется на плоскость я2 в отрезок прямой, перпендикуляр-
перпендикулярной фронтальной проекции фронтали. Фронтальная проекция. центра
вращения определяется пересечением фронтальных проекций фронта-
фронтали и окружности.
Вращение точки вокруг горизонтали показано на рис. 69. Точка А
при вращении вокруг горизонтали h будет перемещаться по окруж-
окружности с, плоскость которой 0 перпендикулярна оси вращения h. Что-
Чтобы переместить точку в новое положение путем поворота ее вокруг
h, необходимо найти положение центра вращения и определить величину
радиуса вращения. Центр вращения О находится в точке пересечения оси
вращения h с плоскостью 0. Чтобы определить величину радиуса вращения
О А , необходимо построить в плоскости ctj прямоугольный LO'A'A*.
Для этого принимаем горизонтальную проекцию О'А' за катет прямоу-
прямоугольного треугольника; второй катет должен быть равен разности ап-
аппликат концов отрезка ОА: \z(.)a ~ Z()O\ = \A1\- Гипотенуза Д О'А 'А 0
О'А0 = R. Новое, после поворота, положение точки А\ находится в
месте пересечения дуги окружности, проведенной из горизонтальной
¦Величину отрезка [ОА] можно определить и другим путем, например, враще-
вращением его вокруг оси, перпендикулярной плоскости проекции; плоскопараллель-
плоскопараллельным перемещением или, как это будет показано в § 13, с помощью замены плоско-
плоскости проекции.

56 Способы преобразования
ортогональных проекций
Рис. 70
Рис. 71
Рис.69
проекции центра вращения
О' радиусом, равным \О'А0 \,
с горизонтальным следом
hop плоскости C.
На рис. 70 описанные выше построения выполнены на эпюре Мон-
жа. Характер и последовательность геометрических построений, кото-
которые необходимо выполнить для перемещения плоскости, произволь-
произвольно расположенной в пространстве, в положение, параллельное плос-
плоскости проекции я2, вращением вокруг линии уровня, показаны на
рис. 71, на котором плоскость а, заданная пересекающимися прямы-
прямыми а и Ь, переведена вращением вокруг своей фронтали f в положе-
положение, параллельное плоскости я2.
Плоскость а однозначно определяется также тремя точками 1, 2 и
А. Так как точки 1 и 2 принадлежат фронтали f, которая принята за ось
вращения, то они не меняют своего положения в процессе преобразова-
преобразования. Поэтому, чтобы задать новое положение плоскости at II я2, доста-
достаточно осуществить поворот только одной точки А. Ниже приводится
последовательность геометрических построений, которые необходимо
выполнить для поворота точки А:
1) провести горизонтальную проекцию фронтали плоскости а -
-f'(l',2);
2) пользуясь точками Г, 2', найти точки 1", 2", определяющие фрон-
фронтальную проекцию фронтали f"\
3) найти проекции центра вращения (О', О"), для чего через А"
провести прямую, перпендикулярную к f", и отметить точку пересе-
пересечения перпендикуляра с f" — точку О";
4) определить величину радиуса вращения, как гипотенузу прямо-
прямоугольного треугольника О"А"А0, У которого катет А"А0 = 1У(-)а ~
1
5)
из центра О" провести дугу радиусом О"А0, точка пересечения
которой с прямой О"А" укажет положение А['.
Точка Ai совместно с прямой f (точками 1, 2) определяет плос-
плоскость (*i || 7Г2«

Способ вращения вокруг оси, принадлежащей 51
плоскости проекции (совмещение)
§ 12. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ,
ПРИНАДЛЕЖАЩЕЙ ПЛОСКОСТИ ПРОЕКЦИИ (СОВМЕЩЕНИЕ)
Совмещение является частным случаем вращения плоскости вок-
вокруг горизонтали и фронтали. При совмещении за ось вращения при-
принимается не произвольная горизонталь или фронталь плоскости, а ее
горизонтальный или фронтальный след (нулевые горизонталь или фрон-
фронталь) . В этом случае в результате поворота плоскости она совпадает
(совмещается) с плоскостью проекции ттх, если вращение осуществляет-
осуществляется вокруг горизонтального следа плоскости, либо с тг2 при вращении
вокруг ее фронтального следа.
Совмещение так же, как и вращение вокруг горизонтали или фронта-
фронтали, применяется, когда требуется определить истинный вид фигур,
принадлежащих плоскости, или построить в плоскости общего положе-
положения фигуру заданной формы и размеров.
Сущность способа совмещения можно уяснить из рассмотрения
рис. 72,а. Плоскость общего положения а вращается вокруг следа hoa до
совпадения ее с горизонтальной плоскостью проекции. При этом преобра-
преобразовании след hoa, как ось вращения, останется на месте. Поэтому для
нахождения совмещенного положения плоскости достаточно найти
совмещенное положение только одной принадлежащей ей точки (не
лежащей на следе hoct).
В качестве такой точки целесообразно (для упрощения графических
построений) взять точку А, принадлежащую фронтальному следу.
Точка А (А'А") при вращении вокруг оси hoa будет перемещать-
перемещаться по дуге окружности, принадлежащей плоскости C, перпендикулярной
к оси вращения.
Графические построения, которые необходимо выполнить на эпю-
эпюре Монжа для определения положения точки А, приведены на рис. 72,а
(как видно из рисунка, они аналогичны построениям, выполненным
на рис. 70). Совмещенное с плоскостью проекции положение фрон-
фронтального следа f00(l определяется точками Ха и А\.
Следует иметь в виду, что любая геометрическая фигура плоскости
а при ее совмещении с плоскостью проекции тг j проецируется в конг-
руентную фигуру. Поэтому [ХаА"], указывающий расстояние от точки
схода следов Ха до А", принадлежащей фронтальному следу, конг-
б)
Рис. 72

Па.
Рис. 73
58 Способы преобразования
ортогональных проекций
руентен [ХаА',] на совмещенном
положении следа f0 а х. В связи с
этим положение точки А\, а
следовательно, и следа f0 a l мож-
можно определить, не пользуясь
центром и радиусом вращения.
Для этого достаточно из точки
Ха (рис. 72,6) описать дугу
радиусом, равным расстоянию
\ХаА"[, до ее пересечения с
прямой (горизонтальным сле-
следом hop плоскости /3, в кото-
которой будет перемещаться точка
А), проведенной через А' пер-
перпендикулярно к hoa. Через по-
полученную точку пройдет фрон-
фронтальный след плоскости f0 a, при
совмещении его с плоскостью и i.
В § 9 ... 12 мы познакоми-
познакомились с различными способами
перевода геометрической фигу-
фигуры, занимающей общее положе-
положение в пространстве, в частное
положение. Иногда приходится
решать обратную задачу, связан-
связанную с построением проекций плоской фигуры заданной формы и разме-
размеров, принадлежащей плоскости общего положения.
Решение такой задачи можно выполнить, используя способ совме-
совмещения.
План решения задачи следующий:
1) созмещаем плоскость, которой должна принадлежать фигура, с
какой-либо плоскостью проекции;
2) строим (вычерчиваем) на совмещенном положении плоскости
требуемую фигуру;
3) "поднимаем" (поворачиваем) плоскость вместе с изображенной
на ней фигурой в пространство.
Графические построения, которые надо выполнить, чтобы "под-
"поднять" плоскость в пространство, аналогичны построениям, выполняемым
при совмещении плоскости с плоскостью проекции, только выполняются
они в обратной последовательности.
В кг.честве иллюстрации покажем решение задачи на построение
проекций окружности с, принадлежащей плоскости общего положе-
положения а, если известно положение ее центра О и величина радиуса R (рис. 73).
Графические построения осуществляем в последовательности, ука-
указанной в приведенном выше плане решения.
Плоскость а совмещаем с плоскостью i!l так же, как это было сдела-
сделано на рис. 72,6. Затем через точку О (О', О") проводим фронталь f(f, f")
и горизонталь h (h1, h") плоскости а и находим их совмещенное положе-
положение fi (/"[ || fi оа) и h\ (h\ || hOa) ¦ Центр окружности О е /", поэтому для
определения положения центра достаточно через горизонтальную
проекцию О' провести прямую, перпендикулярную оси вращения hoa, и
отметить точку ее пересечения с совмещенной фронталью (горизонталью).
Из центра О\ проводим окружность с\ заданным радиусом R. От-
Отмечаем точки N[, M\, C\, D\, в которых f[ и h\ пересекают окруж-
окружность с\ . По М', находим М' (М 6 f, следовательно, М' € /"'); М\ перехо-

Замена одной плоскости проекции 59
дит в М' по дуге окружности, плоскость которой перпендикулярна к
оси вращения hoa. Дуга этой окружности проецируется на я1 в [М\М'\.
Аналогично находим точки N', С, D' — концы двух диаметров ок-
окружности. На рис. 73 показано также нахождение произвольных то-
точек А', В', Е'.
II. СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ
ПРОЕКЦИЙ
Изменение взаимного положения проецируемой фигуры и плоскостей
проекций способом замены плоскостей проекций достигается путем
перехода от заданных плоскостей проекций к новым. Новая плоскость
проекции выбирается перпендикулярной к одной из старых. Проецируе-
Проецируемые геометрические фигуры при этом не меняют своего положения в
пространстве.
При выборе положения новой плоскости проекции следует руко-
руководствоваться тем, что по отношению к новой плоскости проецируе-
проецируемая фигура должна занимать частное положение, обеспечивающее по-
получение проекций, наиболее удобных для решения поставленной за-
задачи. В некоторых случаях бывает достаточно заменить только одну
плоскость проекции я, на эт3 или Я2 на яз- Если замена одной плос-
плоскости проекции не обеспечивает требуемого вида вспомогательной
проекции, производят замену двух плоскостей. При этом переход от
исходной системы плоскостей проекции х -^*- к новой х2 -^*- может
быть осуществлен по одной из следующих схем:
Я2 Я2 Я4
ХТГ^ Xl я3 ~* *2 л3 ч
или
7Г 2 7Г з 7^3
х ?[ *¦ *i Tj *¦* 7Г4 •
Приведенные схемы показывают, что мы одновременно можем ме-
менять только одну плоскость проекций я, (или л2); другая плоскость
и2 (или irt ) остается неизменной. После того как будут определены
новые фронтальные (или горизонтальные) проекции, можно перехо-
переходить ко второй системе, заменяя плоскость п2 (или я, ) новой пло-
плоскостью. Нгличие одной плоскости проекции, которая не меняет свое-
своего положения, позволяет использовать ее как связующее звено меж-
между старыми (исходными) проекциями и новыми*.
§ 13. ЗАМЕНА ОДНОЙ ПЛОСКОСТИ ПРОЕКЦИИ
Пусть в системе плоскостей х -jp- дана точка А и указаны ее проек-
проекции А' и А" (рис. 74,а). Проследим, как изменится положение проек-
проекций точки А, если плоскость эт2 заменить новой плоскостью я3> пер-
перпендикулярной к я, . Горизонтальная плоскость проекции не меняет
* Следует иметь в виду, что В. Л. Тороховым предложен способ замены плос-
плоскостей я1 и я2 одновременно двумя взаимно перпендикулярными плоскостями
я2 я3
я3 и 7Г4, что позволяет осуществить непосредственный переход от х —— к х2 ,
Я3 7Г2 Я) Я4
минуя промежуточное звено xt ~^— или х1 —— . Подробно с этим способом мож-
можно познакомиться в книге С. А. Фролова "Методы преобразования ортогональных
проекций". М.: Машиностроение, 1970.

60 Способы преобразования
ортогональных проекций
своего положения, т. е. мы осуществляем переход от Системы х г~
к новой системе х^ -^- . Плоскость тг3 пересекается с плоскостью -пх по
прямой х i, которая определяет новую ось проекции. Положение го-
горизонтальной проекции А' точки А остается без изменения, так как
точка А и плоскость я, не меняли своего положения в пространстве.
Для н;исождения новой фронтальной проекции точки А'" достаточно
спроецировать ортогонально точку А на плоскость я3. Из чертежа вид-
видно, что расстояние от новой фронтальной проекции А'" точки А до
новой оси х, равно расстоянию от старой фронтальной проекции Л" до
старой осих (\А'"АХ \<=\А"АХ\)-
Чтобы перейти от пространственного макета к эпюру, необходимо
совместить плоскость я3 с плоскостью чертежа. Метод замены плос-
плоскостей проекций предусматривает совмещение новой плоскости с той
из старых плоскостей, к которой она перпендикулярна. В рассматри-
рассматриваемом случае ввиду перпендикулярности плоскостей я3 и я, плос-
плоскость я3 совмещена с я,. За ось вращения принята новая ось проек-
проекций Xi. Направление поворота не оказывает никакого влияния на ре-
результат преобразования. Поворот следует делать в таком направле-
направлении, при котором новые проекции не накладываются на старые и не
затрудняют чтения чертежа. На рис. 74,а совмещение плоскости я3
с Я1 осуществлено вращением ее по направлению движения часовой
стрелки.
Равенство аппликат новой А'" и старой А" фронтальных проекций
точки А и использование в обоих случаях прямоугольного проециро-
проецирования дешают построение новой фронтальной проекции чрезвычайно
простым Оно состоит в том, что через старую горизонтальную про-
проекцию точки проводят прямую, перпендикулярную к новой оси, и отк-
откладывают на ней от точки пересечения с осью отрезок, равный расстоя-
расстоянию от старой фронтальной проекции до старой оси (рис. 74,6).
Замена горизонтальной плоскости я, новой плоскостью я3 и пост-
построение новых проекций точки А в системе хх -^~ осуществляется анало-
аналогично только что рассмотренному случаю, с той лишь разницей, что
теперь о<ггается без изменения фронтальная проекция точки, а для нахо-
нахождения новой горизонтальной проекции А'" точки А необходимо из
старой фр°нтальной проекции точки опустить перпендикуляр на новую
ось xt и отложить на нем от точки пересечения с осью эс, отрезок, равный
расстоянию от старой горизонтальной проекции до старой оси х.
Построения, выполненные по этому правилу, приведены на рис. 75.
На рис. 76 показан отрезок [АВ], произвольно расположенный в про-
Рис. 74
*"
*.-•
А'"
о

Замена двух плоскостей проекций 61
Л"
О
¦Кг
я,
А'Ь
од'"
Рис. 75
Рис. 76
Рис. 77
странстве, и его новая фронтальная проекция на плоскость я3, которой
он параллелен. Все построения ясны из чертежа и не требуют пояснения.
На рис. 77 приведено решение задачи, при котором плоскость обще-
общего положения а оказалась фронтально проецирующей относительно
плоскости я3. Известно, что горизонтальный след фронтально прое-
проецирующей плоскости перпендикулярен к оси х, следовательно, что-
чтобы плоскость а заняла фронтально проецирующее положение, необхо-
необходимо новую ось хх провести перпендикулярно к hoa. Через точку XUl, в
которой Л о а п jcx , пройдет фронтальный след fQOil. Для определения его
направления достаточно найти одну точку. В качестве такой точки можно
взять произвольную точку 1" € foa и указать ее фронтальную проекцию
1'" на новой плоскости я3. Через XUl и Г" проводим foai .
§ 14. ЗАМЕНА ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Часто при определении действительной величины какой-либо гео-
геометрической фигуры или для получения более полного (наглядного)
ее изображения замены одной плоскости проекций бывает недостаточ-
недостаточно. В таких случаях приходится осуществлять замену двух плоскос-
плоскостей проекций.
Рассмотрим, как определяются новые ортогональные проекции точ-
ки в новой системе плоскостей проекции х2 -=— , если известны ее про-
Ят ^
екции в старой системе плоскостей х -д— . Пусть А' и А" — проекции
точки А на исходных плоскостях проекций х -^- (рис. 78). Для того
чтобы определить положение новых проекций Л'" и А"" в системе х2 ~wj-,
заменяем вначале плоскость ut новой плоскостью п3. Точку, через
которую проводится новая ось, и направление оси можно выбирать
произвольно. Следует следить лишь за тем, чтобы не происходило накла-
накладывания новых проекций на старые и чтобы геометрические фигуры,
расположенные в первой четверти пространства, оставались в нем и после
замены плоскости проекции.
Новая горизонтальная проекция А'" точки А будет принадлежать од-
одной линии связи, проходящей через старую фронтальную проекцию А"

62 Способы преобразования
ортогональных проекций
А\
•^
^."
Рис.78
C
О
Рис.79
и перпендикулярную к новой оси ж,, и будет удалена от новой оси на
такое ж<! расстояние, на какое старая горизонтальная проекция точ-
точки была удалена от старой оси х. Поэтому для определения положе-
положения проекции А'" достаточно от точки Ах на продолжении перпенди-
перпендикуляра А "Ах отложить [Ах А'"], равный отрезку [Л^Л] •
Положение новой фронтальной проекции точки в системе плоскос-
теи проекции х2
7Г4
определяется аналогично только что рассмотрен-
ному случаю с той лишь разницей, что теперь за исходную (старую)
систему будем принимать систему Xi -jf- и от нее переходить к систе-
системе х2 ~^,— ¦ В этом случае плоскость тг3 не меняет своего положения в
пространстве, следовательно, не изменится положение и горизонталь-
горизонтальной проекции А'". Фронтальная проекция А"" будет определена, если из
А'" восставить перпендикуляр к оси х2 и отложить на нем от точки Ах^
[Ах А""], равный расстоянию от точки А" до оси хг — [Ах А"].
Иная правила построения проекций одной точки в новой системе
плоскостей проекций, можно построить новые проекции любого чис-
числа точек, а следовательно, и любой геометрической фигуры.
На рис. 79 показан пример перевода отрезка [CD] прямой общего
положения Ъ в положение [O""D""] отрезка фронтально проецирующей
прямой Ъ(Ь"\ Ь""). Вначале заменой плоскости эт2 плоскостью тг3 пере-
переводим отрезок [CD] в положение II 7г3, затем, заменив 7гj плоскостью я4,
ставим отрезок по отношению к плоскости я4 в проецирующее положе-
положение ([C""D""],[C'"D'"]).
§ 15. СОЧЕТАНИЕ СПОСОБА
ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
СО СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИИ
Пользуясь только одним способом плоскопараллельного переме-
перемещения или только одним способом замены плоскостей проекций, всег-
всегда можно перейти от произвольного расположения геометрической

Сочетание способа плоскопараллельного перемещения 63
со способом замены плоскостей проекции
фигуры к частному, обеспечивающему получение удобного вида проек-
проекций. Однако иногда бывает целесообразно применять не один какой-либо
способ, а использовать сочетание двух способов — плоскопараллельное
перемещение и замену плоскостей проекций.
Существе]яным преимуществом способа замены плоскостей проек-
проекций является построение только одной вспомогательной проекции
(при замене одной плоскости проекции), в то время как способ плоско-
плоскопараллельного перемещения требует построения двух вспомогательных
проекций (при перемещении параллельно одной плоскости) *.
В то же время способ замены плоскостей проекций обладает не-
недостатком, заключающимся в том, что при замене плоскостей проек-
проекций трудно заранее предусмотреть на чертеже место расположения вспо-
вспомогательных проекций. Применяя способ параллельного перемещения,
всегда можно выбрать наиболее удобное положение вспомогательных
проекций на поле чертежа. Решение задач этим способом значительно
облегчается при использовании кальки. В этом случае одну из двух
дополнительных (вспомогательных) проекций не строят, а перечерчива-
перечерчивают на кальку, которую затем прикладывают в наиболее удобном месте
чертежа. Следующую вспомогательную проекцию строят с помощью
проекции, изображенной на кальке, и одной из предшествующих про-
проекций.
Естественно, возникает вопрос, каким путем можно сочетать дос-
достоинства обоих способов: удобное расположение вспомогательных
проекций (характерное для способа плоскопараллельного перемеще-
перемещения) и построение при каждом последовательном преобразовании только
одной проекции (как в способе замены плоскостей проекций).
Возможность совместного применения способов плоскопараллель-
плоскопараллельного перемещения и замены плоскостей проекций была указана еще
В. И. Курдюмовым в 1893 г. Сочетание этих способов известно под
названием способа сложных перемещений, причем сложные перемещения
подразделяют на два вида.
Первый вид сложных перемещений состоит в том, что построение
новых проекций достигается путем последовательного применения сна-
сначала способа замены плоскостей проекций, затем способа вращения
вокруг оси, перпендикулярной к плоскости проекции.
Второй вид сложных перемещений заключается в замене плоскос-
плоскости проекции с последующим совмещением новой плоскости с той из
первоначальных плоскостей, которую она заменила**.
Рассмотрим решение задач с использованием первого (задача 1) и
второго (задача 2) видов сложных перемещений.
ЗАДАЧА 1. Точку А повернуть против кость проекции с искажением, в виде
часовой стрелки вокруг фронтали / на эллипса, с искажением будет проециро-
Ltf)° (рис.80). ватьсяиА^0.
Решение этой задачи способом враще- Решение можно значительно упрос-
ния представлиет определенные трудное- тить, если применить способ сложных
ти, так как при вращении вокруг фрон- перемещений. Ход решения задачи в
тали траектория перемещения точки этом случае состоит в следующем: вна-
проецируется на горизонтальную плос- чале с помощью способа замены плос-
* Исключение составляет только способ вращения вокруг линий уровня, при
котором строится только одна вспомогательная проекция.
¦*Как вариант второго вида сложных перемещений можно рекомендовать на
втором этапе преобразования вместо совмещения с первоначальной плоскостью
выполнить совмещение с плоскостью, параллельной ей.

64 Способы преобразования
ортогональных проекций
Рис.80
кости проекции переводим фронталь в
положение, перпендикулярное плоскос-
плоскости я3, затем, используя способ вращения
вокруг оси, перпендикулярной плоскос-
плоскости 7Гз, поворачиваем точку А'" вокруг
оси f " на заданный L <р° .
Отмеченный ход решения задачи оп-
определяет перечисленную ниже после-
последовательность геометрических построе-
построений:
1) проводим новую ось х 1 If";
2) определяем новые горизонтальные
проекции фронтали /"'и точки А1";
3) поворачиваем точку А'" вокруг
фронтали f" (точки f" = О'"^на <fi и
определяем положение точки А\'\
' 4) построениями, выполненными в об-
обратной последовательности, определяем
новые f ортогональные проекции точки
А'{ и А\.
ЗАДАЧА 2. Определить высоту четы-
четырехгранной пирамиды SABC (рис. 81).
Для решения этой задачи заменяем плос-
плоскость проекции 7Г2 на тг3 с последующим
совмещением ее с плоскостью тг2. Чтобы
определить направление новой оси х i, в
плоскости основания пирамиды ABC про-
проводим горизонталь h (ось xt I h'). Совме-
Совмещаем новую плоскость тг3 с плоскостью
тг2 и строим на ней совмещенную проек-
проекцию пирамиды S'x А'{'В"'С'('. Отрезок пер-
перпендикуляра S'l'K'i , опущенного из вер-
вершины пирамиды S[" на основание
Aj"Bj"c|", определяет высоту пирамиды.
Из приведенных примеров видно, что для получения ответа с помо-
помощью сочетания двух способов потребовалось построить только одну
вспомогательную проекцию вместо двух, необходимых при решении
этих задач способами плоскопараллельного перемещения или замены
плоскостей проекции.
Используя сочетание двух способов, можно существенно упростить
решение целого ряда задач, особенно в тех случаях, когда в ходе решения
необходимо повернуть плоскую фигуру или пространственное тело
вокруг прямой общего положения.
Следует иметь в виду, что количество графических построений будет
уменьшаться только в том случае, когда мы заменяем плоскопараллель-
плоскопараллельное перемещение (в частности, вращение) заменой плоскостей проекций,
а не наоборот.

Другие способы преобразования 65
ортогональных проекций
§ 16. ДРУГИЕ СПОСОБЫ ПРЕОБРАЗОВАНИЯ
ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ
Кроме плоскопараллельного перемещения и замены плоскостей
проекций начертательная геометрия располагает большим количест-
количеством различных способов получения новых, наиболее удобных для ре-
решения задач проекций по заданным неудобным.
В тридцатые годы вышла в свет книга С. М. Колотова "Вспомога-
"Вспомогательное проектирование"*, в которой были изложены основные прин-
принципы получения неискаженного вида прямоугольных проекций на спе-
специально выбранную плоскость, а также построения косоугольных и
центральных: проекций на заданные плоскости проекции.
В последующие годы появилась серия работ, посвященных созда-
созданию новых и усовершенствованию ранее предложенных способов вспо-
вспомогательного проецирования.
Особое место среди этих работ занимают работы, посвященные
криволинейному вспомогательному проецированию. Их авторы ис-
использовали для получения вспомогательных проекций в качестве прое-
проецирующих кривые линии, пространственные или плоские.
В настоящее время имеется много хорошо разработанных и дове-
доведенных до практического использования способов, которые могут
быть объединены под общим названием вспомогательное проецирова-
проецирование.
Рис. 82 ... 85 дают наглядное представление о получении проек-
проекций, удобных для решения задач с помощью вспомогательного прое-
проецирования. Гак, на рис. 82 решена задача по определению расстояния
между скрещивающимися прямыми а и Ь путем ортогонального про-
проецирования этих прямых на вспомогательную плоскость а 1 а. При
этом направление проецирования s \\ а.
Рис. 83 показывает целесообразность использования косоугольно-
косоугольного проецирования на заданную плоскость проекции при решении задачи
по определению точки встречи прямой с плоскостью.
Известно, что точка встречи прямой с плоскостью определяется
элементарно просто, если плоскость занимает проецирующее положение.
В случае, изображенном на рис. 83, плоскость общего положения а
переведена но фронтально проецирующее положение путем проецирова-
проецирования а на плоскость проекции я2 в направлении горизонтали этой плос-
плоскости.
На рис. 84 для определения точек встречи прямой а с произволь-
произвольной конической поверхностью применено центральное проецирование.
За центр проекций принята вершина конической поверхности S. В этом
случае коническая поверхность оказывается проецирующей, что значи-
значительно упрощает решение поставленной задачи.
На рис. 85 приведен пример решения задачи по определению то-
точек встречи прямой с поверхностью кольца. Для упрощения решения
этой задачи использовано криволинейное (в частности, окружностное)
проецирование. При.таком способе проецирования поверхность кольца
оказывается горизонтально проецирующей. Все построения для нахожде-
нахождения положения точек М и N ясны из чертежа и не требуют пояснений.
Использование теорем проективной геометрии и свойств коллине-
арных преобразований дало толчок к созданию различных способов
* Колотое С. М. Вспомогательное проектирование. Киев, 1933.
¦J

66 Способы преобразования
ортогональных проекций
Рис.82
Рис.83
Эллиптический
параболоид
Плоскость родства
Параболоид
вращения
Рис.86
перспективно-аффинных и гомологических преобразований ортого-
ортогональных проекций, составляющих основу проективных преобразований.
На рис. 86 показано перспективно-аффинное преобразование эллип-
эллиптического параболоида в параболоид вращения. Рис. 87 дает нагляд-
наглядное представление о преобразовании поверхности гиперболоида вра-
вращения а в сферу а^ путем гомологических преобразований. Не вызы-

Другие способы преобразования 67
ортогональных проекций
Гиперболоид
вращения
Плоскость гомологии
Рис.87
So-
Рис. 88
вает сомнения целесообразность таких преобразований. Действитель-
Действительно, при решении позиционных задач лучше иметь дело с поверхностью
вращения, чем с эллиптическим параболоидом (рис. 86), и со сферой,
чем с поверхностью гиперболоида вращения (рис. 87). И, наконец,
применение топологических преобразований пространства и погружен-
погруженных в него геометрических фигур привело к созданию чрезвычайно
гибкого спссоба, позволяющего осуществить преобразование сложных
нелинейчатых поверхностей, ограничивающих геометрические тела, в
простые цилиндрические поверхности и даже плоскости.
В основе рассматриваемых преобразований лежат топологические
свойства:
а) взаимная однозначность — каждой точке исходной фигуры Ф
соответствует одна и только одна точка преобразованной фигуры Ф t;
б) взаимная непрерывность — бесконечно близким точкам исход-
исходной фигуры Ф соответствуют также бесконечно близкие точки преобра-
преобразованной фигуры Ф,. На рис. 88 бесконечно близким точкам А и В
фигуры Ф соответствуют две бесконечно близкие точки Ах и В, фи-
фигуры Ф,.
Преобразования, обеспечивающие сохранение топологических свойств
составляют теоретическую базу способа топологических преобразований.

68 Способы преобразования
ортогональных проекций
Рис.89
На рис. 89 показано решение задачи по определению точек встречи
плоской кривой / с произвольной поверхностью вращения а. Тополо-
Топологическим преобразованием фигура Ф, ограниченная произвольной по-
поверхностью вращения а, преобразована в шар at. Указанными преоб-
преобразованиями задача сведена к простейшей — определению точек встре-
встречи плоской кривой с поверхностью сферы. Зная положение точек Мt и
iVj, с помощью линий связи (прямых, параллельных оси х) опреде-
определяем М и N.
Изучение отмеченных выше способов преобразования ортогональ-
ортогональных проекций выходит за рамки учебной программы курса начерта-
начертательной геометрии для втузов. Мы остановились на них лишь для того,
чтобы читатель имел в виду, что кроме классических способов (см..
§ 9 ... 14) в арсенале начертательной геометрии имеются и другие, подчас
более мощные, способы преобразования ортогональных проекций*.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. В чем состоит принцип преобразова-
преобразования ортогональных проекций способом
плоскопараллельного перемещения?
2. В чем: состоит отличие способа вра-
вращения вокруг осей, перпендикулярных к
плоскости проекции, от способа парал-
параллельного перемещения?
3. Как определяется положение центра
вращения и величина радиуса вращения
точки при ее повороте вокруг горизонта-
горизонтали и фронтали?
4. Как можно определить совмещен-
совмещенное с плоскостью Я] (я2) положение фрон-
фронтального (горизонтального) следа плос-
плоскости'без нахождения центра и радиуса
вращения?
5. Как перемещаются проекции точки
при ее вращении вокруг оси, перпенди-
перпендикулярной к плоскости проекции TTj GГ2 ) ?
6. Сколько параллельных перемеще-
перемещений и в какой последовательности необ-
необходимо выполнить, чтобы перевести от-
отрезок прямой общего положения в отре-
отрезок горизонтально (фронтально) проеци-
проецирующей прямой?
7. В чем состоит сущность преобразо-
преобразования ортогональных проекций способом
замены плоскостей проекций?
8. Сколько перемен плоскостей проек-
проекций и в какой последовательности необ-
необходимо выполнить, чтобы перевести от-
отрезок прямой общего положения в отре-
отрезок фронтально (горизонтально) проеци-
проецирующей прямой?
* Более подробные сведения о перечисленных способах преобразования читатель
найдет в книге С. А. Фролова "Методы преобразования ортогональных проекций".
М.: Машиностроение, 1970.

ГЛАВА
III
ЛИНИЯ
Линии занимают особое положение в начертательной геометрии.
Используя линии, можно создать наглядные модели многих процес-
процессов и проследить их течение во времени. Линии позволяют установить
и исследовать функциональную зависимость между различными ве-
величинами. С помощью линий удается решать многие научные и инже-
инженерные задачи, решение которых аналитическим путем часто приво-
приводит к использованию чрезвычайно громоздкого математического ап-
аппарата.
Линии широко используются при конструировании поверхностей
различных технических форм. Умело подбирая линии, дизайнер имеет
возможность придать изящные эстетические формы конструируемым
изделиям.
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В § 8 отмечалось, что при определении геометрических фигур в
геометрии принято исходить из основных (неопределяемых) поня-
понятий — точка, прямая, плоскость и расстояние, а в современном пред-
представлении также понятия множество.
Базируясь на этих элементарных понятиях, линию целесообразно
трактовать как траекторию перемещения точки (рис. 90). Такое пред-
представление линии позволяет получить определение линии, используя такие
основные понятия геометрии, как точка и множество. В этом случае
линию можно рассматривать как непрерывное множество всех принад-
принадлежащих ей точек.
Если учесть, что положение точки при ее движении по заданной
траектории будет зависеть от непрерывно меняющейся величины d
(расстояние до точки от начала координат*), то можно утверждать,
что положение точки, принадлежащей линии, определяется непрерыв-
непрерывно меняющейся величиной d. Тогда, окончательно приняв d за пара-
параметр, приходим к следующему определению — линия есть непрерыв-
непрерывное однопараметрическое множество точек.
В этом определении словом непрерывное подчеркивается, что двум
бесконечно близким значениям параметра соответствуют две также
бесконечно близкие точки.
Следует иметь в виду, что данное определение линии является условным. В дей-
действительности положение точки будет зависеть не только от вектора d (опреде-
(определяющего величину расстояния) , но и от углов его наклона к плоскостям проек-
проекций.
Мы останавливаемся на нем лишь потому, что в дальнейшем, при изложении
гл. IV "Поверхность", оно позволяет получить определение поверхности, основание
также на понятиях точка и множество и, что более важно, подойти к этому определе-
определению с точки зрения кинематического способа получения поверхности.
* В случае окружности начало координат не должно совпадать с ее центром.

70 Линия
Рис. 90
Рассматривая поверхность как
след, который оставляет геометричес-
геометрическая фигура при своем перемещении в
пространстве, можно ввести понятие
определитель, которое играет весьма
важную роль в теории поверхностей.
Линии подразделяются на ал-
алгебраические*, если в декарто-
декартовой системе координат они оп-
определяются алгебраическими
уравнениями, и трансцендент-
трансцендентные**, если они описываются
трансцендентными уравнениями.
Линии могут быть пространственными и плоскими.
Пространственными или линиями двоякой кривизны называют
линии, все точки которых не принадлежат одной плоскости.
Линии, у которых все точки принадлежат одной плоскости, называ-
называют плоскими.
Если 1шгебраическое уравнение, описывающее линию, n-й степени,
то алгебраическая кривая считается n-го порядка. Порядок алгебра-
алгебраической кривой определяется также числом точек ее пересечения с
плоскостью (для пространственной линии) или прямой (для плоской
линии). При этом следует иметь в виду, что в число точек пересече-
пересечения включаются точки с действительными и мнимыми координатами.
Простейшей линией является прямая. Так как свойства прямой
и задание ее на эпюре Монжа уже известны читателю (см. гл. I, § 8),
в настоящей главе речь будет идти о характеристиках и свойствах кри-
кривых линий (пространственных и плоских) и построении их ортогональ-
ортогональных проекций.
!. ПЮСТРЛНСТИШИЫЬ; КРИВЫЕ ЛИНИИ
Было отмечено, что пространственными кривыми называются ли-
линии, все точки которых не принадлежат одной плоскости. Рис. 91 да-
дает наглядное представление о произвольной пространственной кри-
кривой линии.
§ 17. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПРОСТРАНСТВЕННОЙ КРИВОЙ
На рис. 92 показана пространственная кривая /. Возьмем на ней
произвольную точку М и проведем через нее секущие [МЛ) и [MB).
При приближении точки А к точке М [МА) будет поворачиваться
вокруг точки М, и когда точка А совпадет с точкой М, [МА) достиг-
достигнет своего предельного положения (луч ti).
Предельное положение секущей в точке М называется полукаса-
полукасательной к кривой I в точке М.
* К алгебраическим линиям, в частности, относятся окружность, эллипс, пара-
парабола, гипербола, астроида, кардиоида и др.
** К. трансцендентным линиям относятся синусоида, спираль архимеда, циклои-
циклоида и др.

Касательные и нормали к пространственной 71
кривой
[MB) при совпадении точки В с точкой М займет предельное поло-
положение t2. Из чертежа видно, что в точке М к кривой I проведены две
полукасательные, направленные в противоположные стороны. Полу-
Полукасательные ti и t2 образуют прямую, которую называют касатель-
касательной к кривой в данной точке (t\f) ¦
Через касательную к пространственной кривой в данной точке можно
провести пучок плоскостей*. Одна из плоскостей этого пучка, называе-
называемая соприкасающейся плоскостью, играет особую роль при исследовании
свойств пространственных кривых.
Подойти к понятию соприкасающейся плоскости можно путем сле-
следующих рассуждений: пусть дана пространственная кривая I (рис. 93).
Возьмем на ней произвольную точку М и укажем полукасательные
tx и t2 к кривой / в этой точке. Через точку М проведем две секущие
[МА) и [MB). Обозначим полуплоскость, заданную полу касательной
?i и секущей [МА), а( , а плоскость, определяемую полу касательной t2
и [MB), — а2 ¦ При приближении точек А и В к точке М плоскости ах и
а2 будут проворачиваться вокруг полукасательных. Когда секущие
займут положение полу касательных, плоскости at и а2 займут пре-
предельное положение.
Так как полу касательные принадлежат одной прямой, то плоскости
ах и а2 совпадут, образуя одну плоскость а, которую называют соприка-
соприкасающейся плоскостью пространственной кривой в данной точке.
Соприкасающаяся плоскость может быть определена так же, как
предельное положение плоскости, проходящей через три бесконечно
близкие точки пространственной кривой линии.
Соприкасающаяся плоскость неразрывно связана с движущейся по
кривой точкой. Так как каждая точка кривой имеет свою касатель-
касательную (кроме особых точек), то соприкасающаяся плоскость при переме-
перемещении по кривой будет все время менять свое положение. При этом она
будет не только следовать за касательной к кривой, но, одновременно, и
вращаться вокруг нее.
К пространственной кривой линии I в любой ее точке (за исключени-
исключением некоторых особых точек) можно провести пучок перпендикулярных
к ней прямых (рис. 94) **. Множество этих перпендикуляров (норма-
(нормалей) определяют плоскость, которую называют нормальной плоско-
плоскостью 0. Одна из нормалей этого множества, принадлежащая соприкасаю-
соприкасающейся плоскости, называется главной нормалью па.
* Пучком плоскостей называется множество всех плоскостей, проходящих че
рез одну и гу же прямую а; прямая а называется осью этого пучка.
••Пучком прямых называется множество всех прямых плоскости, проходящих
через данную точку М; точка М называется центром пучка.
Рис.91
Рис.92

72 Линия
Рис. 93
Гкс. 94
и -°tK
Другую нормаль этого мно-
множества, перпендикулярную к
соприкасающейся плоскости,
называют бинормалью п@. Би-
Бинормаль п^ и касательная tj^
определяют плоскость у, кото-
которую называют спрямляющей
плоскостью кривой (рис. 95).
Трехгранник Френе. Три
взаимно перпендикулярные
плоскости а, /3 и у (рис. 95),
проходящие через одну точку
пространственной кривой, об-
образуют прямоугольный трех-
трехгранник, называемый основ-
основным или подвижным трехгранником. Его называют также трехгранником
Френе *.
Трехгранник Френе используется в качестве системы плоскостей
проекций, на которые проецируют пространственную кривую для изу-
изучения ее свойств. При этом плоскость а принимают за горизонталь-
горизонтальную, плоскость у за фронтальную и плоскость 0 за профильную плос-
плоскость проекции.
Дифференциальные свойства пространственной кривой исследу-
исследуют по ее паоским проекциям на гранях трехгранника Френе.
Рис. 95
П. ПЛОСКИЕ КРИВЫЕ ЛИНИИ
Кривая линия называется плоской, если все ее точки принадле-
принадлежат одной плоскости.
Основные понятия и определения, приведенные на с. 69 для простран-
пространственных кривых, сохраняются с некоторыми изменениями и для плос-
плоских кривых линий; плоские кривые могут быть также алгебраическими
и трансцендентными.
В первом случае уравнение кривой в декартовых координатах мо-
может быть представлено в форме f(x, у) ~ О, где f{x, у) — целый много-
многочлен от х и у.
Определения полу касательной и касательной в точке плоской кри-
* По имени французского математика Жана Фредерика Френе, предложивше-
предложившего его а 1847 г.

Приближенные способы построения касательной 73
и нормали к плоской кривой
вой также совпадают с аналогичными определениями для пространст-
пространственной кривой.
В отличие от пространственной кривой, для каждой точки которой
может быть проведено множество перпендикулярных к ней прямых,
образующих нормальную плоскость, плоская кривая в каждой ее точке
имеет только одну нормаль — прямую, перпендикулярную к касательной
в данной точке кривой и принадлежащую плоскости кривой.
В инженерной практике часто приходится проводить касательные
и нормали к плоским кривым. Рассмотрим графические способы пост-
построения этих линий.
S 18. ПРИБЛИЖЕННЫЕ СПОСОБЫ ПОСТРОЕНИЯ
КАСАТЕЛЬНОЙ И НОРМАЛИ К ПЛОСКОЙ КРИВОЙ
Графический способ построения касательной и нормали к плоской
кривой базируется на использовании "кривой ошибок'. Для построения
этой кривой из точки, через которую должна проходить искомая каса-
касательная, проводим лучи, пересекающие заданную кривую. Отмечаем
концы хорд, по которым лучи пересекают кривую, и с помощью этих
хорд строим "кривую ошибок".
Сущность способа проследим на конкретных примерах.
ПРИМЕР 1. Построение касательной к
кривой, проходящей через точку, не при-
принадлежащую кривой (рис. 96).
Пусть даны кривая / и точка А
Проведем через точку А ряд секущих
аь а2, аз, а<» • Отметим точки 1, llt 2,
•2Ь 3, 3i, 4, 4i, в которых эти секущие
пересекают кривую I. Через середины
полученных хорд проведем плавную кри-
кривую m (линию m называют "кривой оши-
ошибок").
Пересечение линии тп с заданной кри-
кривой I определит точку касания М. (AM) —
искомая касательная t к кривой /, прове-
проведенная из точки А.
ПРИМЕР 2. Построение касательной к
кривой параллельно заданному направ-
направлению s (рис. 97).
Для определения точки касания М
проведем ряд секущих ах, а2, а$, а$ па-
параллельно заданному направлению s. Че-
Через середины хорд [1 1] ], [2 22 ], [3 33],
[4, 44 ] проведем плавную кривую m и
отметим точку М ее пересечения с задан-
заданной кривой /. Точка М будет точкой ка-
касания, а прямая t, проходящая через эту
точку параллельно s, искомой касатель-
касательной.
ПРИМЕР 3. Построение касательной к
кривой в данной точке касания М (рис.
98).
Проведем произвольную прямую Ь,
примерно перпендикулярную к искомой
касательной, а через точку М ряд секу-
секущих Q|, а;. а3, <i4 так, чтобы они пересе-
пересекали и кривую I и прямую Ь. От точек пе-
пересечения секущих с прямой Ь отложим
(на секущих) отрезки, равные хордам
[Ml] , [М2], [МЗ], [М4\, при этом длины
хорд, расположенных по разные стороны
от точки касания М, отложим с разных
сторон oi прямой Ь. Полученные точки
соединим плавной кривой т.
Пересечение кривой т с прямой Ь ука-
укажет точку \, принадлежащую касатель-
касательной. Соединив А с М прямой линией, по-
получим искомую касательную t.
ПРИМЕР 4. Построение нормали к
кривой, проходящей через точку, не при-
принадлежащую данной кривой (рис.99).
В плоскости даны кривая / и точка А,
не принадлежащая кривой 1. Примем точ-
точку А за центр окружностей разных ра-
радиусов, эти окружности пересекут дан-
данную кривую в точках 1, lt, 2, 2], 3, 3,,
4, 4 j, которые примем за концы хорд. Из
концов хорд восставим перпендикуля-
перпендикуляры. При этом перпендикуляры, восста-
влегшые из точек 1, 2, 3, 4, будут иметь
противоположное направление перпенди-
перпендикулярам, восставленным из точек 11, 2 j,
3], 4,. На »тих перпендикулярах отло-
отложим отрезки, равные длине соответ-
соответствующих хорд.
Полученные точки соединим плавной
кривой т. Пересечение т с ( укажет по-
положение точки М, через которую пройдет
искомая нормаль л(п![1, l^]).Для про-
проведения нормали к кривой линии парал-
параллельно заданному направлению или через
данную на кривой точку предварительно
надо построить касательную к кривой
(см. примеры 1 и 3 на с. 73). Определив
положение точки касания (первый слу-
случай) и направление касательной (второй
случай), легко провести нормаль к
кривой.

74 Линия
Рис. 96
Рис. 97
Рис.98 т—~/  с5 "' Рис.99
§ 19. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
Величина угла а между полукасательными в двух бесконечно близ-
близких точках, отнесенная к длине дуги s, заключенной между этими точка-
точками, характеризует степень искривленности кривой линии. Чем больше
угол а0, тем большую кривизну имеет линия. Обозначив кривизну к,
можно записать k = lim —^ (при As -> 0), т. е. кривизна — предел отноше-
отношения угла между полу касательными к соответствующей дуге.
В общем случае кривизна в каждой точке плоской кривой будет
различней (исключение составляют только окружность и прямая, для
которых кривизна в любой их точке постоянна; для прямой она рав-
равна нулю). Графически определить величину кривизн^ в данной точке
кривой можно с помощью окружности (круга) кривизны.
Окружностью кривизны в данной точке А кривой / называют предель-
предельное положение окружности, проведенной через точку А и две другие
бесконечно близкие ей точки А{ и А2, также принадлежащие кривой /
(рис. 100). Радиус такой окружности г называют радиусом кривизны, а
ее центр О — центром кривизны. Чем меньше величина радиуса кривиз-
кривизны, тем больше искривлена линия. Поэтому количественная характе-
характеристика кривизны определяется величиной, обратной радиусу кривиз-
кривизны k = -у— .

Эволюта и эвольвента 75
Рис. 100
Рис. 101
§ 20. ПРИБЛИЖЕННЫЙ СПОСОБ ПОСТРОЕНИЯ
ЦЕНТРА КРИВИЗНЫ КРИВОЙ В ЗАДАННОЙ ТОЧКЕ
Из рис. 100 видно, что окружность кривизны в точке соприкасания
имеет общую с кривой / касательную tA и нормаль пА. Этим свойством
можно воспользоваться для графического определения центра кривизны
кривой в данной точке.
Пусть даны кривая / и точка М, принадлежащая этой кривой (рис. 101).
Возьмем на кривой / ряд произвольных точек А, В, С. Проведем через
них полукасательные tA, tg, tc и отложим на них равные отрезки произ-
произвольной длины. Через полученные точки Ах, йь С! проведем плавную
кривую /, . Касательная tM к кривой / в точке М пересечет кривую /, в
точке М[ (кривую ^ называют эквитангенциальной относительно /, а
кривую / относительно 1г называют трактрисой). Проведем через М
нормаль пм к кривой /, а через точку Мх — нормаль пм к кривой 1Х и
найдем пересечение нормалей пм и пм ; точка пересечения О укажет
положение центра кривизны для точки lit кривой /. [ОМ] равен радиусу
.1 „ ,
кривизны гм, а отношение к = у— — кривизне кривой / в данной точ-
точке М.
§ 21. ЭВОЛЮТА И ЭВОЛЬВЕНТА
Определение эволюты и эвольвенты неразрывно связано с поня-
понятием кривизны кривой линии. Если определить положение центров
кривизны G>!, О2, ... , Оп ряда, принадлежащих данной кривой / (рис.
102), точек А,, А2, ... , Ап и соединить их плавной кривой, то полу-
получим кривую ш, называемую эволютой кривой /. Итак, эволюта есть
множество точек, являющихся центрами кривизны линии.
Кривая / по отношению к кривой m (своей эволюте) называется
эвольвентой. Образование эвольвенты можно представить из рассмотре-
рассмотрения рис. 103. Отметим на кривой m ряд точек М, Мг, М2, ... , Мп. Примем
их за вершины ломаной линии. Из точки Му как из центра проведем дугу
окружности MLi радиусом г, = \МУМ\ (точка Lx e М2М{). Затем из
точки М2 проведем дугу радиусом r2 = \M2Lt\ и отметим точку ее
пересечения с продолжением звена М3М2 ломаной линии MtM2M3-
L2 ~ LiL2 n (М3М2). Далее проведем дугу радиусом г3 = \M3L2\ и
определим положение точки L3 — L3 = L2L3 п (Л/4М3). Следуя опи-
описанным путем, можно определить точки L{, ... , L^. Множество точек
L,, L2, ... , Ln образуют центровую кривую /. Если число сторон лома-
ломаной линии М, М,, М2, ... , Мп неограниченно возрастает, то в пределе
получим кривую m и соответственно кривую /, состоящую из после-

76 Линия
U
Рис. 102
Рис. 103
довательных дуг окружностей монотонно изменяющихся радиусов.
Кривая I есть эвольвента кривой т.
Эвольвенты находят широкое применение в технике. В частности,
профили зубьев различных зубчатых передач имеют форму эвольвенты
окружности. Ввиду широкого использования эволют и эвольвент в
инженерной практике целесообразно отметить некоторые их свойства,
вытекающие непосредственно из рассмотренных способов построения.
1. Эволюта представляет собой множество точек, являющихся цент-
центрами кривизны всех точек эвольвенты.
2. Касательные эволюты являются нормалями эвольвенты.
3. Всякая плоская кривая линия имеет бесчисленное множество
эвольвент.
4. Через каждую точку касательной к эволюте проходит одна и
только одна эвольвента.
5. Длина дуги эволюты равна абсолютному значению разности ра-
радиусов кривизны эвольвенты в концах ее дуг.
§ 22. КЛАССИФИКАЦИЯ ТОЧЕК ПЛОСКОЙ КРИВОЙ
Вид кривой I вблизи некоторой точки М с единственной касатель-
касательной t зависит от характера движения точки вдоль касательной и нап-
направления: поворота касательной. Поясним это утверждение на примерах.
Пусть по кривой / движется точка М (рис. 104). Перемещение точ-
точки Мо (Мо & I) в положение М, (М, € /) можно рассматривать как
движение точки по дуге кривой / в направлении, указанном зеленой
стрелкой.
Проведем через точки Мо и М, касательные к кривой I. Точку Мо
можно рассматривать не только с позиции ее принадлежности к кри-
кривой I, но и как принадлежащую касательной tQ. В этом случае пере-
перемещение: точки Мо (Мо G t0) в положение М^ (Мх €Е tx ) следует трак-
трактовать как движение точки по касательной в направлении, указанном
зеленой стрелкой. Причем для того чтобы точка Мо б ?0 заняла поло-
положение Mi e ti, необходимо, чтобы касательная t0 при переходе в по-
положение f, поворачивалась в направлении, указанном стрелкой.
При перемещении точки М{ в положение М2 направление ее движе-
движения вдоль кривой (касательной) по сравнению с участком М^МХ не
меняется; не меняется и направление поворота касательной t\.

Классификация точек плоской кривой 77
Из рассмотрения рис. 104 видно, что характер движения точки по
кривой /, выявленный для участков МпМх, М,М2, сохранится и на дру-
других участках М2МЪ, ... , Мп^гМп. Все рассмотренные точки (Мо, М,,
М2, ... , Мп) кривой / и проведенные через них касательные (t0, tx,
t2, ... , tn) обладают общим свойством: направление движения точки
вдоль кривой (и касательной) и направление поворота касательной
не меняются.
Такие точки и проведенные через них касательные к кривой называ-
называют соответственно: обыкновенной (регулярной) точкой и обыкновен-
обыкновенной (регулярной) касательной. Кривую /, состоящую только из ре-
регулярных точек, называют плавной кривой. На рис. 105 изображена
плавная кривая и указаны принадлежащая ей регулярная точка М и
проведенные через нее касательная и нормаль к кривой I.
Если направление движения точки или поворота касательной меня-
меняется, то мы будем иметь дело с особой точкой и особой касательной.
На рис. 106 показана кривая / и указаны принадлежащие ей точки
Мо, Мх, М, М2, Мг с проведенными через них касательными t0, tlt t,
t2, t3. Мы видим, что ни в одной из указанных точек направление их
движения вдоль кривой не меняется. Что касается направления вра-
вращения касательной, то оно меняется на противоположное в точке М.
Такую точку называют точкой перегиба. В точках перегиба касательная
меняет вместе с направлением вращения и сторону кривой. Две ветви
кривой расположены по. разные стороны от общей касательной f и по
разные стороны от нормали п. ' [
На рис. 107 показана кривая / с особой тоЦкой М, которая называ-
называется точкой возврата первого рода или заострённой точкой. В точках
возврата первого рода две ветви кривой располагаются по одну сто-
сторону от нормали и по разные стороны от касательной.
Рис. 108 дает представление о точке возврата второго рода*. Мы
видим, что в точках возврата второго рода две ветви кривой распо-
расположены по одну сторону от общей для обеих ветвей касательной и по
одну сторону от нормали. В точках возврата второго рода изменяется не
только направление движения точки по кривой, но и направление вра-
вращения касательной.
Кроме отмеченных, к особым точкам кривой относятся:
а) угловая точка (рис. 109). В угловой точке (ее называют так-
также точкой излома) направление кривой и касательной к ней изменяется
"скачком", и поэтому кривая имеет в точке М две касательные и, соот-
соответственно, две различные нормали;
* Точку возврата второго рода называют также "клюв".
\*
Рис.
м3
104
t2
Г
-\
\ h
t
>
\
f
1
У
Рис
4/
iJ
пм
105
М-

78 Линия
Рис. 109
Рис. НО
б) узел, иди многократная точка (рис. 110). В узловой точке кривая
пересекает саму себя. В зависимости от числа самопересечений узло-
узловые точки могут быть: двойными, тройными и т. д. На рис. 110,а и б
показаны двойные, на рис. 110,в — тройная точка.
§ 23. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ЛИНИИ
Для построения ортогональных проекций кривой (пространствен-
(пространственной или плоской) необходимо построить проекции ряда точек, при-
принадлежащих этой кривой, и соединить между собой одноименные проек-
проекции в той же последовательности, в "какой они располагались на оригина-
оригинале. При задании кривой ее проекциями необходимо указать по крайней
мере проекции одной точки, принадлежащей кривой. Действительно, если
на проекциях кривой / (рис. 111) не указать проекции точки А (А', А"),
то по одним только проекциям I' и /" нельзя судить о форме кривой.
Следует также иметь в виду, что по двум ортогональным проекци-
проекциям кривой нельзя сразу ответить на вопрос о том, какой кривой (плос-
(плоской или пространственной) соответствуют данные проекции. Чтобы

Ортогональные проекции линии 79
А'
Рис. 111
Рис. 112
установить, какая (плоская или пространственная) кривая линия задана
на эпюре, необходимо выяснить, принадлежат ли все точки кривой одной
плоскости: если принадлежат — кривая плоская, в противном случае —
пространственная. Заданная на рис. 112 кривая I — пространственная, так
как точка М, взятая на кривой, не принадлежит плоскости а, определяе-
определяемой тремя другими точками А, В, С этой кривой.
СВОЙСТВА КРИВЫХ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО
ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
При построении ортогональных проекций кривых необходимо знать
те свойства этих кривых, которые сохраняются (инвариантны) при
проецировании. К таким свойствам относятся:
1. Касательные к кривой проецируются в касательные к ее проек-
проекциям.
2. Несобственным точкам кривой соответствуют несобственные
точки ее проекции.
При проецировании плоских кривых в дополнение к отмеченным
будут справедливы следующие свойства:
3. Порядок проекции алгебраической кривой равен порядку са-
самой кривой.
4. Число узловых точек (точек, в которых кривая пересекает саму
себя) на проекции кривой равно числу узловых точек самой кривой*.
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ВИНТОВОЙ ЛИНИИ
Из пространственных кривых в технике находят широкое приме-
применение винтовые линии. Винтовую линию можно рассматривать как
результат перемещения точки по поверхности вращения.
Если зафиксировать положение точки на поверхности прямого кру-
кругового цилиндра острием хорошо заточенного карандаша, а затем на-
начать вращать цилиндр вокруг его оси и равномерно перемещать ка-
карандаш вдоль оси цилиндра, то острие карандаша опишет на цилинд-
цилиндрической поверхности пространственную кривую, называемую цилинд-
цилиндрической винтовой линией**. Ось цилиндрической поверхности будет
* Случаи, когда касательная проецируется в точку (свойство 1) , а плоская кривая
в прямую (свойства 3 и 4) , не учитываются.
**Если движение точки будет происходить по поверхности вращения другого
вида, например конической или сферической, то получим соответственно кони-
коническую и сферическую винтовые линии.

80 Линия
xio
Рис. 113
осью винтовой линии, а радиус цилиндрической поверхности — радиусом
винтовой линии.
Если вращение цилиндра и прямолинейное перемещение каранда-
карандаша равномерны, то получим цилиндрическую винтовую линию, на-
называемую гелисой, т. е. гелиса является траекторией движения точ-
точки, равномерно вращающейся вокруг оси и одновременно переме-
перемещающейся с постоянной скоростью вдоль этой оси. Величину Р переме-
перемещения точки в направлении оси, соответствующую одному ее обороту
вокруг оси, называют шагом винтовой пинии.
Для построения проекции винтовой линии, в частности гелисы, предва-
предварительно строим проекции прямого кругового цилиндра (рис. 113).
Окружность основания цилиндра (горизонтальная проекция гелисы)
делим на одинаковое число равных частей. На такое же число частей
делим шаг (на фронтальной проекции). Из точек деления окружности
проводим линии связи, а через соответствующие точки деления шага —
Рис. 114

Определение длины пространственной кривой 81
по ее ортогональным проекциям
горизонтальные прямые. Отмечаем точки 1", 2", 3", ... , 8", в которых
пересекаются соответственные прямые. Соединив полученные точки A",
2", 3", ... , 8") плавной кривой, получим фронтальную проекцию вин-
винтовой линии. Цилиндрические винтовые линии подразделяют на пра-
правые и левые (с правым или левым ходом). Основанием для такого де-
деления служит направление движения точки, "спускающейся" по вин-
винтовой линии. Если проекция этого направления на плоскость, перпен-
перпендикулярную к оси винтовой линии, совпадает с направлением дви-
движения часовой стрелки, то винтовая линия — правого хода, в противном
случае винтовую линию считают левой. На рис. 113 показана правая
винтовая линия.
Гипотенуза треугольника l{lll()l0, изображенного на рис. 113
справа, является разверткой гелисы на протяжении ее шага. Цилиндри-
Цилиндрическая винтовая линия вполне определяется радиусом, шагом и ходом.
§ 24. ОПРЕДЕЛЕНИЕ ДЛИНЫ ПРОСТРАНСТВЕННОЙ КРИВОЙ
ПО ЕЕ ОРТОГОНАЛЬНЫМ ПРОЕКЦИЯМ
На рис. 114 даны две проекции пространственной кривой /. Чтобы
определить длину кривой, необходимо осуществить ее спрямление.
Спрямление пространственной кривой, заданной ортогональными про-
проекциями, осуществляется следующим путем:
1. Спрямляем горизонтальную проекцию кривой А'В' в [АХВХ].
Для этого намечаем на I' ряд точек 1', 2', 3', ... так, чтобы дуги, заклю-
заключенные между этими точками, мало отличались по длине от стягиваю-
стягивающих их хорд. Откладываем длины хорд \А'1'\, \1'2'\, \2'3'\, ... , \6'В'\ на
горизонтальной прямой а в последовательности, которую они зани-
занимали на проекции кривой.
2. Из точек At, lx, 2,, 31; ... , В] прямой а восставляем перпендику-
перпендикуляры и отмечаем точки их пересечения с горизонтальными прямыми,
проведенными через соответствующие фронтальные проекции точек
А",1",2",3",...,В".
3. Полученные точки пересечения Ао, 10, 20, 30, ... , Во укажут верши-
вершины ломаной линии, выпрямив которую, получим отрезок [ЛО]Во,]>
равный длине пространственной кривой с точностью аппроксимации
дуг кривой их хордами.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Дайте определение пространствен- а) проходящую через заданную точку,
ной и плоской кривой. не принадлежащую кривой,
2. Что называется порядком алгеб- g) проходящую через точку, заданную
раической кривой и как можно оп- на кривой;
ределить его, если кривая (плоская в) параллельную заданному направле-
или пространственная) задана графи- нию.
чески? 8. Что такое эвольвента и эволюта
3. Перечислите свойства кривой ли- плоской кривой? Дайте определения и
нии, инвариантные относительно парал- укажите основные свойства этих кривых,
лельного проецирования. 9. Что называется кривизной плоской
4. Назовите "особые точки" кривой и кривой в данной точке? Как можно опре-
дайте их определение. делить ее графически?
5. Что такое соприкасающаяся плос- 10. Что такое шаг винтовой линии?
кость? 11. Как построить на чертеже цилиндри-
6. Дайте определение трехгранника ческую винтовую линию?
френе. 12. Как можно определить длину дуги
7. Расскажите, как можно построить пространственной кривой по ее ортого-
касательную к плоской кривой:

ГЛАВА
IV
ПОВЕРХНОСТЬ
Мир поверхностей разнообразен и безграничен. Он простирается от
элементарной, отличающейся простотой и математической строгостью
плоскости, до сложнейших, причудливых форм криволинейных по-
поверхностей, не поддающихся точному математическому описанию.
Без преувеличения можно сказать, что по разнообразию форм и
свойств, по своему значению при формировании различных геомет-
геометрических фигур, по той роли, которую они играют в науке, технике,
архитектуре, изобразительном искусстве, поверхности не имеют себе
равных среди других геометрических фигур.
Естественно, что начертательная геометрия как наука, передающая
результаты своих теоретических исследований в распоряжение инженера
для их практического использования, не может обойти вниманием такие
важные геометрические фигуры, какими являются поверхности.
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В математике nod поверхностью подразумевается непрерывное мно-
множество точек, между координатами которых может быть установлена
зависимость, определяемая в декартовой системе координат уравнением
вида F(x, у, г) = 0, где F(х, у, г) — многочлен п-й степени, или в форме
какой-либо трансцендентной функции. В первом случае поверхности
называют алгебраическими, во втором — трансцендентными.
Если алгебраическая поверхность описывается уравнением n-й степе-
степени, то поверхность считается n-го порядка. Любая произвольно располо-
расположенная секущая плоскость пересекает поверхность по кривой того же
порядка (иногда распадающейся или мнимой), какой имеет сама поверх-
поверхность. Порядок поверхности может быть определен также числом точек
ее пересечения с произвольной прямой, не принадлежащей целиком
поверхности, считая все точки (действительные и мнимые).
В начертательной геометрии геометрические фигуры задаются гра-
графически, поэтому целесообразно рассматривать поверхность как со-
совокупность всех последовательных положений некоторой перемещаю-
перемещающейся в пространстве линии. Образование поверхности с помощью
линии позволяет дать иное определение поверхности, базирующееся
на основных элементарных геометрических понятиях, таких, как точ-
точка и множество. Действительно, если принять, что положение движу-
движущейся в пространстве линии будет непрерывно меняться с течением
времени t, и принять t за параметр, то поверхность можно рассматри-
рассматривать как непрерывное однопараметрическое множество линий. В свою
очередь, линия определяется как непрерывное однопараметрическое мно-
множество точек, поэтому можно дать следующее определение поверхности:
поверхностью называется непрерывное двупараметрическое множество
точек.

Образование поверхности и ее задание 83
на эпюре Монжа
§ 25. ОБРАЗОВАНИЕ ПОВЕРХНОСТИ
И ЕЕ ЗАДАНИЕ НА ЭПЮРЕ МОНЖА
Ранее отмечалось, что поверхность можно рассматривать как со-
совокупность последовательных положений некоторой линии gj, пере-
перемещающейся в пространстве по определенному закону.
Для получения наглядного изображения поверхности на чертеже
(эпюре Монжа) закон перемещения линии gj целесообразно задавать
графически в виде совокупности линий Id, ... |и указаний о характере
перемещения линии gy, при этом указания могут быть заданы также
графически, в частности с помощью направляющей поверхности у.
В процессе образования поверхности линия gj может оставаться
неизменной или менять свою форму. Подвижная линия gj* называ-
называется образующей, неподвижные линии id, ...\ ** и поверхность у —
направляющими.
Процесс образования поверхности может быть легко уяснен на при-
примере, показанном на рис. 115. Здесь в качестве образующей взята плос-
плоская кривая gj. Закон перемещения кривой gj задан двумя направляю-
направляющими d~t и 32 и плоскостью у, при этом имеется в виду, что образую-
образующая gj- скользит по направляющим dx и d2, все время оставаясь парал-
параллельной плоскости 7, а точка А, принадлежащая образующей gj-, переме-
перемещается по кривой d, . Описанный способ образования поверхности
называется кинематическим. Кинематическим способом можно образо-
образовать и с его помощью задать на чертеже разнообразные поверхности.
Каркас поверхности
Другим способом образования поверхности и ее изображения на
чертеже является задание поверхности множеством принадлежащих
ей точек или линий, при этом точки или линии выбираются так, чтобы
они давали возможность с достаточной степенью точности определять
форму поверхности и решать на ней различные задачи.
Упорядоченное множество точек или линий, принадлежащих поверх-
поверхности, называется ее каркасом.
* g —образующая, от латинского слова genero — образую, порождаю.
** d — направляющая, от латинского слова dirigo — направляю.
Рис. 115

84 Поверхность
В зависимости от того, чем
задается каркас поверхности,
точками или линиями, кар-
каркасы подразделяют на точеч-
точечные и линейные. Линейным
каркасом называется множес-
множество линий, имеющих единый
закон образования и связан-
связанных между собой определен-
определенной зависимостью. Условия,
устанавливающие связь между
линиями каркаса, называют
р 11е зависимостью каркаса. Эта за-
зависимость характеризуется
некоторой изменяющейся величиной, называемой параметром каркаса.
Линейный каркас считается непрерывным, если параметр каркаса —
непрерывная функция, в противном случае он называется дискретным.
В качестве линий, образующих каркас, обычно берут семейство
плоских кривых, полученных в результате сечения поверхности пуч-
пучком параллельных плоскостей. В основе теории каркаса лежит поло-
положение о том, что непрерывное однопараметрическое множество ли-
линий в пространстве задает поверхность, и, наоборот, всякая поверх-
поверхность может быть представлена однопараметрическим множеством ли-
линий, свойства которых и закон их распределения в пространстве опреде-
определяют свойства поверхности.
Для того чтобы по каркасу можно бьшо судить о форме поверхнос-
поверхности и иметь возможность осуществлять расширение дискретного кар-
каркаса до непрерывного, поверхности следует задавать каркасом, образо-
образованным двумя семействами плоских сечений.
На рис. 116 показан каркас поверхности, состоящий из двух ортого-
ортогонально расположенных семейств линий а,, а2, аъ, ... , ап и &!, Ь2> &з> ..., Ъп.
При необходимости заданный каркас может быть расширен путем прове-
проведения дополнительных линий а, и Ь, в интервале между соседними линия-
линиями семейства { а ... } и j b.... | соответственно.
§ 26. ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ
Поверхность с позиции кинематического способа ее образования
рассматривают как множество всех положений движущейся линии
(или поверхности). При таком подходе к образованию поверхности
можно утверждать, что поверхность будет задана (определена), если в
любой момент движения образующей будут известны ее положение
и форма, а это, в свою очередь, позволит однозначно ответить на вопрос,
принадлежит ли точка пространства данной поверхности или нет.
Кинематический способ образования поверхности подводит нас к
понятию определителя, под которым мы будем подразумевать необхо-
необходимую и достаточную совокупность геометрических фигур и связей
между ними, которые однозначно определяют поверхность. В число
условий, входящих в состав определителя, должны быть включены:
1. Перечень геометрических фигур, участвующих в образовании
поверхности.
2. Алгоритмическая часть, указывающая на взаимосвязь между
этими фигурами.

Определитель поверхности 85
Итак, определитель поверхности состоит из двух частей: из совокуп-
совокупности геометрических фигур (первая часть) и дополнительных сведе-
сведений о характере изменения формы образующей и законе ее перемеще-
перемещения (вторая часть). Чтобы отличить первую (геометрическую) часть оп-
определителя от второй (алгоритмической) части, условимся заклю-
заключать первую — в круглые, а вторую — в квадратные скобки; тогда в
общем случае определитель поверхности будет иметь следующую струк-
структурную форму:
ф(Л; [А],
где (Г) — геометрическая часть, [А] — алгоритмическая часть.
Для того чтобы определитель относился к конкретному виду по-
поверхности, необходимо в каждую часть определителя вложить конк-
конкретное содержание.
Следует иметь в виду, что при задании поверхности можно в ряде случаев вмес-
вместо геометрических элементов задавать числовые параметры. Например, любая сфера
будет отличаться от всех других сфер только величиной радиуса R, поэтому, задавая
число, указывающее значение R, мы определяем одну единственную сферу. Очевидно,
числовым параметром конической поверхности вращения может служить L кр° —
угол между образующей и осью конической поверхности*.
Параметры поверхности бывают двух видов: параметры формы и параметры
положения.
Параметры, изменение которых вызывает изменение формы поверхности, на-
называют параметрами формы.
Параметры, изменение которых приводит к изменению положения поверхности в
пространстве, называют параметрами положения.
Сумма условий, определяющих совокупность всех независимых параметров
поверхности, называется ее параметрическим числом.
Параметры формы. В только что рассмотренных случаях параметр R для сфе-
сферы и L ф° для конической поверхности относятся к параметрам формы. Число
параметров, изменяющих форму поверхности, может быть любым целым поло-
положительным числом, начиная с нуля. Так, например: число параметров формы для
плоскости равно нулю; для сферы — единице. Если поверхность задана своим урав-
уравнением в канонической форме, все параметры формы входят в это уравнение.
Параметры положения. Число параметров, характеризующих положение поверх-
поверхности в пространстве, не может быть меньше трех и больше шести. Так, например:
для плоскости оно равно трем, для трехосного эллипсоида — шести.
Если уравнение, определяющее поверхность, составлено для произвольного поло-
положения поверхности, то оно содержит не только все параметры формы, но и все
параметры положения, т. е. число независимых параметров уравнения в этом случае
равно параметрическому числу поверхности.
Чтобы найти (установить) определитель поверхности, следует исхо-
исходить из кинематического способа ее образования. Так как поверхность
может быть образована различными путями, очевидно одна и та же по-
поверхность может иметь различные определители, например, поверхность
прямого кругового цилиндра (цилиндрическую поверхность вращения) с
кинематической точки зрения можно представить:
а) как след, оставляемый в пространстве прямой g при ее враще-
вращении вокруг оси i (рис. 117,а); при этом определитель цилиндрической
поверхности вращения будет иметь вид
Ф (#, 0 ; [Sj = Rt (g) ] ;
¦ В обоих случаях положение поверхности в пространстве не учитывалось.

86 Поверхность
1
i
б)
Рис. 117
б) как след от вращения кривой g, принадлежащей поверхности пря-
прямого кругового цилиндра, вокруг оси i (рис. 117,6); в этом случае
определитель поверхности можно записать:
ф(«; 0; lgj = RL(g)f;
в) как результат поступательного перемещения окружности g, при
этом центр окружности О перемещается вдоль оси i, а ее плоскость а все
время остается перпендикулярной к этой оси (рис. 117,в); тогда опре-
определитель поверхности можно записать:
**
Ф (*. 0 ; [ij = Tt (g)A(OG i) Л (? С а 1 i) ] ;
г) как огибающую всех положений сферической поверхности 0,
центр О которой перемещается по оси i (рис. 117,г); определитель в
этом случае примет вид
Ф@, О; [0j= T, ф)Л (О G 0].
Из множества определителей поверхности обычно выбирают наибо-
наиболее простой; в рассматриваемом случае таким определителем будет
ф (?0; [gj= Ri(g)].
§ 27. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПОВЕРХНОСТИ
Вы уже знаете, что две ортогональные проекции на две непарал-
непараллельные плоскости однозначно определяют положение точки и поло-
положение и вид линии. Переходя к рассмотрению ортогональных проек-
* К- — преобразование (рассматривается как вращение вокруг оси i) , переводя-
переводящее любые точки А и В в "такие точки Л, иВ,, что \АВ\ = \А j Bi |.
** Т- — преобразование (рассматривается как параллельное перемещение), пе-
переводящее точки Л и В в такие точки А , и В, , что \АВ\ — \АХ В] \.

Ортогональные проекции поверхности 87
ций поверхностей, мы обнаруживаем, что некоторые поверхности не
могут быть заданы свсими проекциями. В справедливости этого ут-
утверждения можно убедиться на примере проецирования простейшей
поверхности — плоскости. Действительно, если мы будем проецировать
все точки плоскости, занимающей произвольное положение по отноше-
отношению к плоскостям проекций, то проекции множества точек плоскости
покроют полностью все плоскости проекций. Это произойдет потому, что
плоскость является незамкнутой поверхностью — она может быть без-
безгранично продлена в любом направлении.
Не только незамкнутые поверхности невозможно задать проекци-
проекциями всех принадлежащих им точек, но и ряд замкнутых поверхностей
при определенной ориентации их к плоскостям проекций не могут
быть определены (заданы) ортогональными проекциями их точек,
например, если ось поверхности кольца занимает положение, перпендику-
перпендикулярное к плоскости проекции, то кольцевую поверхность можно задать
ее двумя ортогональными проекциями (рис. 118,а), но стоит только
перевести ось кольца в наклонное положение, как задание этой поверх-
поверхности двумя ортогональными проекциями (на те же плоскости проек-
проекций) становится невозможным (рис. 118,6).
Чтобы задать поверхность на чертеже, достаточно указать проекции
не всего множества точек или линий, принадлежащих поверхности,
а только некоторых из них, с помощью которых может быть установлено
взаимно однозначное соответствие между образом (проекцией) и прооб-
прообразом (объектом проецирования). Такими точками или линиями могут
быть точки или линии, входящие либо в состав определителя поверхнос-
поверхности, либо в ее каркас (точечный или линейный). В первом случае поверх-
поверхность задается определителем, во втором — каркасом.
Задание поверхности проекциями ее определителя не всегда обес-
обеспечивает наглядность, а это, в свою очередь, затрудняет чтение чертежа,
поэтому для получения наглядного изображения поверхности на эпюре
а)
б)
or
1-
i
0
a'"
f X
M
Рис. 118

88 Поверхность
Монжа в ряде случаев следует
указывать очерк (очертание)
этой поверхности.
Очерком поверхности (при
ортогональном проецировании)
называют след на плоскости
проекции проецирующей цилинд-
цилиндрической поверхности, которая
огибает заданную поверхность.
Рис. 119 дает наглядное пред-
представление о том, как получается
очерк произвольной замкнутой
поверхности а на горизонталь-
горизонтальную плоскость проекции.
Рис. 119
§ 28. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ*
Многообразие форм поверхностей создает большие трудности при
их изучении. Для того чтобы облегчить процесс изучения поверхнос-
поверхностей, целесообразно осуществить их систематизацию, распределив все
поверхности по классам, подклассам, группам и подгруппам.
При делении поверхностей на классы, подклассы, группы, под-
подгруппы следует к одной классификационной категории относить по-
поверхности, обладающие характерным признаком, который у поверхнос-
поверхностей, входящих в другую категорию, отсутствует. Таким признаком мо-
может служить, в частности, единство способов образования поверхностей,
т. е. тех условий, которые входят в определитель поверхности. Поэтому
в основу систематизации поверхностей может быть положен их опреде-
определитель.
Будем считать, что поверхности принадлежат одному классу, если
они имеют одинаковое содержание геометрической части определите-
определителя. Используя этот критерий, все многообразие поверхностей можно
отнести к двум классам:
класс I составляют поверхности, образующие gj которых — кривые
линии;
класс II объединяет поверхности, образованные прямой линией,
т. е. ?]¦ — прямая.
Поверхности, входящие в класс I, называются нелинейчатыми в от-
отличие от поверхностей класса II, которые считаются линейчатыми.
При отнесении поверхностей к классам I или II во внимание при-
принималась геометрическая часть определителя — вид линии, образую-
образующей поверхность. Условия алгоритмической части определителя, ха-
характеризующие закон движения образующей, позволяют выделить
из классов I и II поверхностей три подкласса (рис. 120).
* Следует иметь в виду, что многообразие поверхностей и способов их полу-
получения не имеет предела, поэтому создать строгую систему для классификации по-
поверхностей не представляется возможным. Более того, с геометрической точки
зрения классификация поверхностей не может иметь научного обоснования. Что
касается методики, используемой в процессе обучения, то здесь, напротив, вся-
всякая попытка систематизации материала, в том числе и рассматриваемого вопро-
вопроса о классификации поверхностей, заслуживает самого серьезного внимания.

Классификация поверхностей 89
Подкласс 1 содержит поверхности, образованные поступательным
перемещением образующей линии. Такие поверхности называют поверх-
поверхностями параллельного переноса. Их определитель — Ф (g, d); [g: =
= Td (g) ] *.
Подкласс 2 составляют поверхности, образованные вращением обра-
образующей линии — поверхности вращения. Их определитель — Ф (g, i);
j i
Подкласс 3 включает поверхности, образованные винтовым пере-
перемещением образующей, — винтовые поверхности. Их определитель —
ф(*,0; [gj= Ti(g)oRi(g)]**.
Поверхности подклассов 1, 2 и 3 имеют одинаковую геометричес-
геометрическую часть определителя. В зависимости от вида образующей (кривая или
прямая) поверхности параллельного переноса, вращения и винтовые
могут быть отнесены как к первому (g — кривая) ***, так и ко второму
(g — прямая) классам (см. рис. 120).
Каждый из классов I и II делится на группы А, Б, ... , которые могут
быть подразделены на подгруппы а, б, ... В свою очередь, подгруппы
состоят из отдельных видов поверхностей а, 0, ... Критерии для деле-
деления на группы, подгруппы и виды также берутся из определителя по-
* Выражения Td(g) и Я,-(?) указывают на характер движения образующей g, так
Td(S) — поступательное перемещение вдоль d, R({g) — вращение вокруг i.
** Здесь Tj(g) о Rj(g) — композиция из двух движений: параллельного пере-
перемещения вдоль оси и вращения вокруг оси i.
***Следует помнить, что образующая кривая |Г не меняет своей формы.
ПОДКЛАСС 1
КЛАСС I
Поверхности <
нелинейчатые
ПОДКЛАСС 2
ПОДКЛАСС 3 i_
КЛАСС II
Поверхности
линейчатые
Рис. 120

90 Поверхность
v т
LJ.JL
«
J
'I |!
S
H I
-H-
«h Э < -V i
Я T? <
0
ч4
af
с та
«
Подкласс 3
t
Подкласс 2
КЛАСС I fgj
Подкласс 1
КЛАСС И да
ПОВЕРХНОСТИ
Вид
(*.p.7)
Под-
Подгруппа
Группа
(А,Б,В)
Подкласс
ОДЗ)
КЛАСС
Рис. 121
верхности. На рис. 121 показана общая структура отнесения поверх-
поверхностей к классам, подклассам, группам, подгруппам и видам. Из рис. 121
видно, что класс II (линейчатые поверхности) содержит три группы Ац,
Бц( Вц- Признаком для такого деления служит число направляющих
линий:
группа Ац — линейчатые поверхности с тремя направляющими
Ф(г"; d,,dj,d3); [gj n {d,,d2,d3} ^ Sj];
группа Бц — линейчатые поверхности с двумя направляющими
(функции третьей направляющей выполняет направляющая плоскость 7)
группа Вц — линейчатые поверхности с одной направляющей (реб-
(ребром возврата); в этом случае все три направляющие "совпадают" с
ребром возврата dx \dt = d2 = d31
; d); [gT\ { d, =d2=d3}

Нелинейчатые поверхности с образующей 91
переменного вида (группа Ajj
В свою очередь, каждая группа подразделяется на подгруппы. Так,
группа Ац содержит четыре подгруппы (см. рис. 121) :
ajj — косой цилиндр с тремя направляющими
Ф(*; 2х,2г,23)\ [*,-л{ dj.dj.da} ^ч 5)],
все три направляющие d,, d2, d3 — кривые;
6jj — дважды косой цилиндроид
Ф(*; d,,^,^); [gj n {dltd2, d3} * §],
две направляющие d[, d2 — кривые, d3 — прямая;
вц — дважды косой коноид
Ф(*; d,,d,,d3); [gj n {d,,d2,d3} * 5)];
одна направляющая d1 — кривая, две d2, d3 - прямые;
rtj — однополостный гиперболоид
Ф (g\ dltd2,d3); [gj n { d,, d2, d3 } Ц S)];
все три направляющие dx, d2, d3 — прямые.
Каждая из подгрупп включает отдельные виды поверхностей, нап-
например, в подгруппу 6jj входят: а — поверхность косого клина, /3 — по-
поверхность дважды косого винтового цилиндроида и у — поверхность
косого перехода.
Рассмотрим более подробно поверхности, входящие в каждый из
отмеченных классов и подклассов.
КЛАСС I
§ 29. НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ОБРАЗУЮЩЕЙ
ПЕРЕМЕННОГО ВИДА (ГРУППА Aj)
Эта группа поверхностей имеет единый по форме определитель
Ф ?,,...,?,; З.Д.Зз);
в котором gj — образующая переменного вида, dj, d2, d3 — направ-
направляющие *.
Примечание. В ряде случаев закон перемещения образующей может быть
задан не тремя, а двумя (d^, d2 ) и даже одной (dj ) направляющей. В двух последних
случаях вместо отсутствующих направляющих указываются дополнительные условия.
В качестве примера можно привести поверхность а, показанную на рис. 115, у
которой закон перемещения образующей gj задан двумя направляющими d{ и d2 и
плоскостью 7. которая выполняет функции третьей направляющей d3. Определитель
этой поверхности имеет вид
') 0
* Здесь, как и в определителе поверхностей групп Б{, Ад, Бд (см. § 28, 30,?2, 33,
34), некоторые из направляющих db d2, d\ могут быть не только кривыми d, но и
прямыми d линиями.

92 Поверхность
Таблица 2. Нелинейчатые поверхности с образующей переменного
вида. Группа Ах; Ф (?", ,...,?„; d, ,d2,d3); [{&,... ,in} n {d,,32, d3}* Ф ]
Рис. 122 Поверхность общего вида
Рис. 123 Каналовая поверхность Fj)
Рис. 124 Циклическая поверхность
Смысловое значение алгоритмической части этого определителя может быть вы-
выражено следующим предложением: криволинейная образующая (g) пересекает
направляющие dy и d2 (пересечение g: с dy и d2 является не пустым множеством
— J/ ^ "^ dt, с/2 \ ^ 5)) и образующая Jy параллельна плоскости у (g.-y = 0° ), а точка А,
принадлежащая образующей gy, скользит по направляющей dx (g: 3 А € d\).
Другим примером может служить трубчатая поверхность /3 (см. рис. 126), у кото-
которой задана только одна направляющая d, . Отсутствие направляющих d2 и d3 компен-

Нелинепчатые поверхности с образующей 93
постоянного вида (группа Ej)
сируется дополнительным условием, входящим в алгоритмическую часть определите-
определителя этой поверхности, которое заключается в том, что центр окружности О перемеща-
перемещается вдоль направляющей dl , а ее плоскость у все время остается перпендикулярной
к dj.
Рассматриваемая группа поверхностей включает в себя три под-
подгруппы.
1. Подгруппа aj — поверхность общего вида а (табл. 2, рис. 122).
Такая поверхность может быть образована перемещением произволъцдй
(плоской или пространственной) кривой ^ по направляющим d,, d2, d3.
В процессе движения образующая g- все время меняет свою форму,
принимая вид gi,g~2,g3, ¦¦¦ , ?„,"
2. Подгруппа бг — каналовая поверхность 0 (табл. 2, рис. 123). Кана-
ловой поверхностью называют поверхность, образованную непрерывным
каркасом замкнутых плоских сечений, определенным образом ориенти-
ориентированных в пространстве. Площади этих сечений могут оставаться посто-
постоянными или монотонно изменяться в процессе перехода от одного сече-
сечения к другому. В инженерной практике наибольшее распространение
получили два способа ориентирования плоскостей образующих:
1) параллельно какой-либо плоскости — каналовые поверхности с
плоскостью параллелизма;
2) перпендикулярно к направляющей линии — прямые канало-
каналовые поверхности.
Каналовая поверхность может быть использована для создания
переходных участков между двумя поверхностями типа трубопрово-
трубопроводов, имеющих:
а) различную форму, но одинаковую площадь нормального сече-
сечения;
б) одинаковую форму, но различные площади сечения;
в) различную форму и различные площади поперечных сечений.
3. Подгруппа Bj — циклическая поверхность у (табл. 2, рис. 124).
Циклическую поверхность можно рассматривать как частный случай
каналовой поверхности. Она образуется с помощью окружности, центр
которой перемещается по криволинейной направляющей. В процессе
движения радиус окружности монотонно меняется.
§ 30. НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
С ОБРАЗУЮЩЕЙ ПОСТОЯННОГО ВИДА (ГРУППА
Определитель таких поверхностей имеет вид
где g1— образующая, 3\ , сГ2, 33 — направляющие.
Нелинейчатые поверхности с образующей постоянного вида (груп-
(группа Bi) содержит две подгруппы.
1. Подгруппа rj — поверхность общего вида (табл. 3, рис. 125) об-
образуется произвольной (плоской или пространственной) кривой g,
характер перемещения которой определяется формой и положением
направляющей dj и дополнительным условием (на рис. 125 оно сос-
состоит в том, что точка А е g скользит по направляющей dt, а бинор-
бинормаль кривой 'g в точке А принадлежит спрямляющей плоскости у кри-
кривой dt).

94 Поверхность
Таблица 3. Нелинейчатые поверхности ^образующей постоянно-
постоянного вида. Группа Б1; Ф {g; dl,d2,d3); [gj n {d,, d2, d3 } * Ф]
Рис. 125 Поверхность общего вида
Рис. 126 Трубчатая поверхность
2. Подгруппа дх — трубчатая поверхность (табл. 3, рис. 126). Трубча-
Трубчатая поверхность является частным случаем циклической и каналовой
поверхностей. Она обладает свойствами, присущими этим видам поверх-
поверхностей. У циклической поверхности она позаимствовала форму образую-
образующей, а у каналовой — закон движения этой образующей.
Итак, трубчатая поверхность может быть получена при движении
окружности постоянного радиуса по криволинейной направляющей;
плоскость окружности все время остается перпендикулярной к нап-
направляющей.
КЛАСС II
§ 31. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
Линейчатая поверхность в общем случае однозначно определяется
тремя направляющими линиями. Действительно, пусть даны три про-
пространственные кривые линии d",, d2 и d3 (рис. 127). Возьмем на кри-
кривой d] произвольную точку М, примем ее за вершину конической по-
поверхности а, а за направляющую этой поверхности примем дугу кривой
d3. Если ЛГ — точка пересечения дуги кривой d2 с поверхностью а, то
(MN) пересечет дугу кривой d3 в точке L. То, что {MN) обязательно
пересечет дугу кривой d3, не вызывает сомнения, так как (MN) и кривая
d3 принадлежит одной и той же поверхности а. Из рис. 127 видно, что
через точку М, взятую на направляющей dx, проходит одна прямолиней-

Линейчатые поверхности 95
ная образующая g, пересекающая две другие направляющие d2 и d3*.
Задавая другое положение точки М -> М, и принимая точку Л/, за верши-
вершину конической поверхности, мы получим при той же направляющей d3
отсек новой конической поверхности с^ , которую дуга кривой d2 пересе-
пересечет в точке Nr . Точки М, и ЛГ, определяют прямую (MjNi ), которая пе-
пересечет третью направляющую d3 в точке Lt . (MiLi) — новая обра-
образующая gi линейчатой поверхности.
Описанным способом можно построить любое число прямолиней-
прямолинейных образующих, которые выделят в пространстве одну единственную
линейчатую поверхность. Следует иметь в виду, что нельзя за направ-
направляющие брать три различные по форме и произвольно расположен-
расположенные линии. Произвольно можно задавать только две направляющие,
форму и положение третьей направляющей выбирают так, чтобы она
находилась внутри конгруенции** прямых, определяемой двумя уже
взятыми направляющими.
Чтобы третья направляющая принадлежала линейчатой поверхности,
она должна входить внутрь конгруенции, определяемой первыми двумя
направляющими. Иными словами, задав дуги двух направляющих линей-
* Несмотря на то, что кривые dit d2 и d3, показанные на рис. 127, будут крат-
кратными (через точку М проходит не одна, а п2 х п3 образующих, где п2 — порядок
кривой d2, пэ — порядок кривой d3 ), мы рассматриваем случай, когда, линия dt
пересекает коническую поверхность а, заданную точкой М и направляющей d~3,
только один раз. Такое допущение возможно в том случае, если рассматривать
не всю поверхность а, а только ее отсек, в формировании которого принимает учас-
участие не вся кривая d3, а только ее дуга 1 2.
**Под конгруенцией прямых подразумевается множество прямых, зависящих от
двух параметров. Например, если взять две произвольные кривые d, и И2 (рис. 128)
и на кривой ofj отметить точку М, приняв ее за вершину конической поверхности с
направляющей d2, то мы получим множество прямых (образующих конической
поверхности), проходящих через точку М S dj, и одну из точек, принадлежащих
множеству, определяющему линию d2. Если принять, что точка М будет перемещать-
перемещаться по кривой di, последовательно занимая положения Mlt M2, М3 Мп, то мы
получим новые конические поверхности а^, а2, аз. •¦• . »п. прямолинейные образую-
образующие которых заполнят некоторый отсек пространства. Множество всех прямых —
образующих конических поверхностей, за вершины которых взяты последовательно
все точки одной линии dj (d2 ), а за направляющую принята вторая линия d2 (dt ), яв-
является двупараметрическим множеством, т. е. конгруенцией.
Рис. 127
Рис. 128

96 Поверхность
чатой поверхности, мы определяем область ее существования. На рис. 128
эта область ограничена линиями красного цвета. Очевидно, дуга кривой
а3, ограниченная точками L и Ьи, будет принимать участие совместно с
дугами кривых d, (MMn) и d2 (NNn) в образовании линейчатой поверх-
поверхности (LLn лежит внутри конгруенции). Кривая d4 может быть исполь-
использована в качестве третьей направляющей только на участке FFn (т. е. в
той части, которая лежит внутри конгруенции).
Кривая е, не погруженная в область конгруенции прямых, не бу-
будет принадлежать линейчатой поверхности и, следовательно, не мо-
может быть принята за третью направляющую*.
Теперь, после того как мы познакомились с требованием к зада-
заданию третьей направляющей линейчатой поверхности, можно перейти
к рассмотрению различных групп этих поверхностей и, в частности,
рассмотреть задание их на чертеже, а также возможности использова-
использования в технике.
§ 32. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
С ТРЕМЯ НАПРАВЛЯЮЩИМИ (ГРУППА Ац)
Классификация линейчатых поверхностей и их распределение по
группам и подгруппам в рамках общей схемы классификации поверх-
поверхностей (см. рис. 121) в зависимости от вида определителя, содержащего
информацию о числе направляющих, показаны на рис. 129.
* Мы рассматриваем случай, когда образующие будут действительными пря-
прямыми.
Однополостный
гиперболоид
1
• Дважды косой
^ коноид
¦
t
Дважды косой
цилиндроид
1
Косой цилиндр
с тремя
направляющими
1
Ац Три направляющие
Дважды косая
плоскость
I
Косой коноид
t
Косой
цилиндроид
t
1—образующая
составляет
постоянный угол
с направляющей
плоскостью
1
Косая
плоскость
1.
Прямой коноид
1
Прямой
цилиндроид
2—образующая
параллельна
плоское™
параллелизма
t
Бц,Две направляющие
O(g^di,dj,7W«)nldr'i-l'»«)A(&vl=<P'>l
]
l
П.Линейчатые
поверхности
Плоскость
|
i
Коническая
поверхность
I
Цилиндрическая
поверхность
•
\
Поверхность
с ребром возврата
t
В,,.Одна направляющая
t
Рис. 129

Линейчатые поверхности с тремя направляющими 97
(группа А И1
Из рис. 129 видно, что все многообразие линейчатых поверхностей
может быть отнесено к трем группам:
группа Аи — линейчатые поверхности с тремя направляющими;
группа Бп — линейчатые поверхности с двумя направляющими;
группа Вц — линейчатые поверхности с одной направляющей. Рас-
Рассмотрение линейчатых поверхностей начнем с группы Аи- Определитель
этой наиболее общей группы линейчатых поверхностей имеет вид
где g — прямая, образующая, d,, d2 и d3 — направляющие.
Таблица 4. Линейчатые поверхности с тремя направляющими.
Группа Аи; Ф (?; d,, d2, d3); [gj n {^ §
Рис. 130 Поверхность общего вида (ко-
(косой цилиндр с тремя направляющими)
Рис. 131 Дважды косой цилиндроид
Рис. l*1 Я Дважды косой коноид
. 1'ис. 133 Однополосгный гиперболоид
d, 

98 Поверхность
В зависимости от формы направляющих и их расположения в про-
пространстве можно получить различные поверхности этой группы, которые
могут быть отнесены к четырем подгруппам (табл. 4, рис. 130 ... 133) .
1. Поверхность косого цилиндра с тремя направляющими (см. табл. 4,
рис. 130). Эта поверхность может быть задана на эпюре Монжа проек-
проекциями трех криволинейных направляющих и пересекающей их прямо-
прямолинейной образующей.
2. Поверхность дважды косого цилиндроида (см. табл. 4, рис. 131).
Она образуется в том случае, когда две из трех направляющих кривые,
а третья — прямая линия. В инженерной практике находят примене-
применение частные случаи поверхностей этого вида.
Поверхность косого клина. Эта поверхность получается в том слу-
случае, когда все три направляющие расположены в параллельных плос-
плоскостях, причем криволинейные направляющие — гладкие кривые. По-
Поверхность косого клина используется при конструировании поверхности,
крыла летательного аппарата (рис. 134). При этом достигаются хорошие
технологические условия изготовления его каркаса.
Поверхность косого перехода. Для образования поверхности ко-
косого перехода в качестве криволинейных направляющих берут дуги
окружностей одинакового радиуса, расположенные в параллельных
плоскостях, а в качестве третьей направляющей — прямую, перпен-
перпендикулярную к плоскостям окружностей и проходящую через середи-
середину отрезка, который соединяет центры окружностей (рис. 135). Поверх-
Поверхности косого перехода применяются в архитектуре и строительной
практике.
3. Поверхность дважды косого коноида (см. табл. 4, рис. 132).
Эта поверхность образуется в том случае, когда одна из трех направ-
направляющих кривая, а две другие — прямые линии.
4. Поверхность однополостного гиперболоида (см. табл. 4, рис. 133).
Поверхность однополостного гиперболоида может быть получена при
движении прямолинейной образующей по трем скрещивающимся пря-
прямым, не параллельным одной плоскости.
На рис. 136 поверхность^ однополостного гиперболоида ^адана пря-
прямыми направляющими d,, d2, d3 и показаны образующие g,, g2 и g3 •
Определение положения образующей рассмотрим на примере пост-
построения прямой gi . На направляющей d, отмечаем произвольную точку
1 (Г, 1"). Эта точка совместно с направляющей d2 (прямая d2 для
упрощения геометрических построений принята горизонтально проеци-
проецирующей) определяет плоскость 0. Находим точку 2 = d3 П hOp. Точки 1 и
2 определяют образующую g, . Аналогично находят проекции прямых
Рис. 134
Рис. 135

Линейчатые поверхности с тремя направляющими 99
(группа,
е"
«2
6'
4'
Рис. 136
Рис. 137
Поверхность однополостного гиперболоида обладает одним замеча-
замечательным свойством: направляющие d,, d2, d3 можно принять за обра-
образующие, а образующие g,, g2, g3 считать направляющими, при этом
получится та же самая поверхность, т. е. определители
; \g~jH {d,, d2,d3
тождественны. Иными словами, в однополостном гиперболоиде име-
имеются два семейства прямолинейных образующих, причем образую-
образующие одного семейства не пересекаются между собой, но каждая из
образующих одного семейства пересекает все образующие другого
семейства.
Можно представить случай, когда три прямолинейные образующие
могут быть совмещены друг с другом путем вращения вокруг неко-
некоторой оси. В этом случае вся поверхность может быть образована враще-
вращением только одной из трех образующих вокруг этой оси. Покажем, что
при этом получается поверхность однополостного гиперболоида.
Пусть прямая g (рис. 137) вращается вокруг оси i (прямая g и ось i
скрещивающиеся). Проведем прямую а, пересекающую ось i в точке А.
Прямые а и i определяют меридиональную плоскость поверхности,
которая образуется вращением прямой g. При вращении прямой а вок-
вокруг оси 1 образуется коническая поверхность вращения, заданная на
чертеже двумя положениями образующей ах, а2 и осью i. Прямая g, не
параллельная этой конической поверхности, пересечет ее в двух точках.
Допустим, что этими точками будут М и N. При вращении прямая g
пересечет прямые а, и а2 в точках М,, N, и М2, N2, т. е. произвольная
прямая меридиональной плоскости пересекает меридиан поверхности в
двух точках. Это говорит о том, что меридиан этой поверхности — кри-
кривая второго порядка.
Ось i меридиана не пересекает, но является для него осью симмет-
симметрии. Это, в свою очередь, говорит о том, что меридиан поверхности —
кривая второго порядка -- гипербола, а прямая i — ее мнимая ось. Мы
показали, что в частном случае линейчатая поверхность с тремя скрещи-
скрещивающимися прямолинейными направляющими пересекается плоскостью,
проходящей через ось поверхности, по гиперболе; отсюда и произошло

100 Поверхность
название чтой поверхности оОиополосгшлй г иппрСюлош) а ращен ил*.
Плоскость, перпендикулярная к оси одиополостпого гиперболоида,
пересекает его по эллипсу, н частном случае по окружности (при
пересечении однополостного гиперболоида вращении) .
Практически для построении проекций однополостного гиперболои-
гиперболоида вращении необходимо: построить проекции двух окружностей, распо-
расположенных в двух параллельных плоскостях; разделить проекции окруж-
окружностей на произвольное ранное число частей (рис. 138) ; затем соединить
прямой линией точку /," нижней окружности с любой (кроме /2') точкой
верхней окружности. Па чертеже 138 точка 1", соединена с точкой 3'2', точ-
точка 2/ с 42 и т. д. Соединив все точки деления нижней окружности с точ-
точками деления верхней окружности, получим проекции каркаса поверх-
поверхности. Второе семейство линий каркаса этой поверхности может быть
образовано, если соединить первую точку верхней окружности с третьей
точкой нижней окружноети (\'г' с ¦!['), точку 2'2 с точкой 4", 3'2 с 5" и т. д.
Поверхность однополостного гиперболоида вращения широко ис-
пользуетсн н технике, в частности, для передачи вращения при скре-
скрещивающихся осях с помощью зубчатых или фрикционных гипербои-
дальных колес. Особенно широкое применение эта поверхность нашла
в строительстве. Одним из примеров может служить башня Шухова,
построенная в Москве для установки антенны радиостанции "Комин-
"Коминтерн" — первой мощной радиостанции в Советском Союзе.
Гиперболический параболоид. В частном случае, когда прямолиней-
прямолинейная образующая скользит по трем скрещивающимся прямым (нап-
(направляющим), параллельным одной плоскости, получается поверхность,
называемая гиперболическим параболоидом. Такому названию эта
поверхность обязана тем, что при пересечении ее плоскостями в сече-
сечениях получаются гипербола и парабола.
Поверхность гиперболического параболоида обладает одним заме-
замечательным свойством, состоящим в том, что не только ее направляю-
направляющие параллельны одной плоскости, но и образующие, скользящие по
этим направляющим, также параллельны некоторой плоскости. Что-
Чтобы убедиться в справедливости этого высказывания, докажем следую-
следующую теорему.
Если прямая перемещается в пространстве по трем прямым, па-
параллельным одной и той же плоскости, то она будет двигаться, все
время оставаясь параллельной некоторой другой плоскости.
Пусть даны три скрещивающиеся направляющие прямые d1, d2n d3,
параллельные горизонтально проецирующей плоскости у (рис. 139).
Чтобы не загромождать чертежа лишними геометрическими построения-
построениями, будем считать, что образующие гиперболического параболоида
принадлежат фронтально проецирующим плоскостям 0,, 02 и 03. При
таких условиях образующие gx, g2, ?з определяются соответственно
точками 1 и. 2, 3 и 4, 5 и 6 пересечения направляющих с плоскостями C,,
02, 0з- Построим [З'7'l, конгруентный и параллельный отрезку [5'6'|, и
проведем прямую 7'4'. Из чертежа видно, что Л 2'3'Т ^ Л 5'6'8', так как
стороны этих треугольников параллельны, а сторона 3'7' Д 3'2'7' конгру-
ентна стороне 5'6' Л 5'6'8'.
Из конгруентности треугольников следует \2'7'\ ^ [5'8'], но [5'8'] ™
^ \1'4'] (как параллельные между параллельными), следовательно,
[2'7'\ ^ \1'4'] . Отсюда вытекает, что отрезки \1'2'] и [4'7'] конгруентны
* Поверхность однополостного гиперболоида вращения можно получить так-
также вращением гиперболы вокруг ее мнимой оси.

Линейчатые поверхности с двумя направляющими 101
(группа Бп)
12',
Нис. 139
Рис. 138
и параллельны. Прямые gl и g3 как
параллельные соответствующим
сторонам Д 3'4'Т параллельны его
плоскости; третья образующая g%
принадлежит плоскости этого тре-
треугольника.
Из изложенного следует, что
произвольно взятые образующие
гиперболического параболоида па-
параллельны некоторой плоскости.
Это, в свою очередь, говорит о том, что на поверхности гиперболического
параболоида имеется два семейства прямых линий, каждое из которых
параллельно своей плоскости, т. е. эта поверхность так же, как и по-
поверхность однополостного гиперболоида, имеет две плоскости парал-
параллелизма. Если плоскости параллелизма взаимно перпендикулярны,
то гиперболический параболоид называют прямым, если не перпенди-
перпендикулярны, то поверхность называют наклонной. Для образования одной
и той же поверхности безразлично, из какого семейства взяты прямые
за направляющие. В рассматриваемом примере можно за направляю-
направляющие принять скрещивающиеся прямые gt, g2, ?з > параллельные плос-
плоскости IS 3'4'Т, тогда образующими поверхности окажутся прямые d,,
d2,d3.
§ 33. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ДВУМЯ НАПРАВЛЯЮЩИМИ
(ГРУППА Бп)
Движение прямой — образующей по трем направляющим, не един-
единственный способ образования линейчатой поверхности. Только что
доказанная теорема убедительно подтверждает справедливость тако-
такого высказывания. Из этой теоремы вытекает важное следствие: линей-

102 Поверхность
читая поверхность может быть однозначно определена двумя направ-
направляющими и плоскостью параллелизма.
В этом случае определитель линейчатой поверхности примет вид
Ф(#; 2,, 5,, 7); [gj
Здесь 7 ~~ направляющая плоскость. В частном случае, если угол между
g:j = 0° (образующая параллельна плоскости 7). то 7 называют плос-
плоскостью параллелизма.
Пусть будут заданы две произвольные кривые d, и d2 и плоскость
7- Можно задать такой закон перемещения прмолинейной образую-
образующей gj, при котором она, скользя по линиям d, и d2, все время сох-
сохраняет постоянный L $° с плоскостью у. Плоскость 7 заменяет ту третью
направляющую, которая образуется множеством точек пересечения
движущейся прямолинейной образующей g: с плоскостью 7-
В рассматриваемую группу поверхностей входят три подгруппы:
а) цилиндроиды, б) коноиды, в) косые плоскости.
Перечисленные подгруппы поверхностей могут быть отнесены к
двум разновидностям:
поверхности, образованные с помощью направляющей плоскости;
поверхности, в создании которых принимала участие плоскость
параллелизма.
К первой разновидности относятся косые линейчатые поверхности
(косой цилиндроид, косой коноид, дважды косая плоскость); ко вто-
второй — прямые линейчатые поверхности (прямой цилиндроид, прямой
коноид, косая плоскость). Поверхности с плоскостью параллелизма
называются поверхностями Каталана*. Из линейчатых поверхностей с
двумя направляющими рассмотрим только поверхности Каталана, так
как именно эти поверхности находят широкое применение в технике.
§ 34. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ДВУМЯ НАПРАВЛЯЮЩИМИ
И ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)
При формировании линейчатой поверхности с помощью плоскости
параллелизма образующие должны быть параллельны. этой плоскости,
поэтому они пересекаются с ней в несобственных точках, множество
которых определяет несобственную прямую; эту прямую следует рас-
рассматривать как третью направляющую линейчатой поверхности, т. е.
плоскость параллелизма является как бы собственным представителем
несобственной прямой. Образование линейчатой поверхности с помощью
плоскости параллелизма является частным случаем общего способа
формирования линейчатой поверхности с двумя направляющими.
Определитель для группы поверхностей Каталана имеет вид
Ф(?; d,,d2,7); \gjC\ {d^d,} 4 §A(gp =.0n)].
Для задания поверхности этой группы на эпюре Монжа достаточно
указать проекции направляющих d, и d2 и положение плоскости па-
параллелизма 7 (табл. 5, рис. 140 ... 142).
* По имени бельгийского математика Каталана (Katalan), исследовавшего свой-
свойства этих поверхностей.

Линейчатые поверхности с двумя направляющими 103
и плоскостью параллелизма (поверхности Каталана)
Таблица 5. Линейчатые поверхности с двумя направляющими и
плоскостью параллелизма. Группа Гщ; Ф (#; d,, d2, у); \g; n jd,, d2 } \
V <V л <#} = o°) i
Рис. 140 Поверхность прямого цилинд-
цилиндроида
Рис. 141 Поверхность прямого коноида
j Рис.142 Косая плоскость

104 Поверхность
1. Поверхность прямого цилиндроида (см. табл. 5, рис. 140). По-
Поверхность прямого цилиндроида образуется в том случае, когда нап-
направляющие d, и d2 гладкие кривые линии, причем одна из них должна
принадлежать плоскости, перпендикулярной плоскости параллелизма.
Для определения проекций прямолинейных образующих поверх-
поверхности прямого цилиндроида достаточно провести прямые, параллель-
параллельные плоскости параллелизма. На рис. 143 показано построение обра-
образующей g
Вначале проводим g'j, определяем точки М' и N', по ним находим М"
и N". (MN) проводим параллельно плоскости параллелизма 7; для это-
этого достаточно, чтобы (M'N') || пОу.
Поверхность прямого цилиндроида находит применение в инженер-
инженерной практике, в частности, она используется при изготовлении воз-
воздухопроводов большого диаметра.
2. Поверхность прямого коноида (см. табл. 5, рис. 141). Отличие по-
поверхности коноида от цилиндроида состоит только в том, что одна из
направляющих линий коноида — прямая. Поэтому для задания поверх-
поверхности коноида на эпюре Монжа необходимо указать проекции: кривой d2
(одна направляющая), прямой d, (вторая направляющая) и плоскости
параллелизма у. Е1сли прямолинейная направляющая перпендикулярна
плоскости параллелизма, то мы будем иметь дело с частным случаем
поверхности, которая называется прямым коноидом.
Для получения проекционного чертежа (эпюра Монжа), обладаю-
обладающего наглядностью, следует указать проекции не одной, а ряда пря-
прямолинейных образующих этой поверхности. Для этого проводим нес-
несколько прямых, параллельных плоскости параллелизма у и пересе-
пересекающих направляющие d, и d2. На рис. 144 показано построение произ-
произвольной образующей gj. Чтобы прямая g- была параллельна плоскости
параллелизма 7, необходимо, чтобы она была параллельна прямой,
принадлежащей плоскости у. Так как плоскость у горизонтально прое-
проецирующая, то горизонтальные проекции всех прямых, принадлежащих
этой плоскости, совпадают с горизонтальным следом плоскости hOy.
Поэтому построение частной образующей поверхности коноида начинаем
Рис. 143
Рис. 144

A ,,
Линейчатые поверхности с двумя направляющими Ю5
и плоскостью параллелизма (поверхности Каталана)
Г
К'
m
I'
m
Рис. 145
с: проведения ее горизонтальной проекции g'j, причем g'j \\ hQy (на основа-
основании инвариантного свойства 2 г (см. § 6) ортогонального проецирова-
проецирования] . Отмечаем точки М' и N', в которых горизонтальная проекция
образующей g'j пересекает горизонтальные проекции направляющих d\ и
d'2, по М' и N' находим точки М" и N", которые определяют фронтальную
проекцию прямой g'j .
Поверхность прямого коноида используется в гидротехническом
строительстве для формирования поверхности устоев мостовых опор.
3. Поверхность гиперболического параболоида — косая плоскость
(см. табл. 5, рис. 142). Гиперболический параболоид может быть по-
получен при скольжении прямой по двум скрещивающимся прямоли-
прямолинейным направляющим, при этом образующая все время остается па-
параллельной, плоскости параллелизма. Гиперболический параболоид
имеет две плоскости параллелизма, соответствующие двум семействам
прямолинейных направляющих. Если плоскости параллелизма перпен-
перпендикулярны друг другу, то гиперболический параболоид называют пря-
прямым. В инженерной практике гиперболический параболоид часто назы-
называют косой плоскостью.
Для задания на чертеже косой плоскости достаточно указать про-'
екции двух скрещивающихся прямых d, и d2 и положение плоскос-
плоскости параллелизма у. Для получения проекционного чертежа, обладаю-
обладающего наглядностью, обычно указывают проекции нескольких прямо-
прямолинейных образующих, для этого:
1) на направляющих d, и d2 выделяют отрезки \АВ\ и \CD\ ;
2) делят проекции отрезков \АВ\ и \CD\ на произвольное число рав-
равных частей (на рис. 145 проекции точек деления обозначены /', ... , б';
1 , ... , о и 1 1, ... , о, ; 11 , ... , о, );
3) одноименные проекции точек деления соединяют прямыми.
Задавая таким путем косую плоскость, мы не пользовались плос-
плоскостями параллелизма. Б!сли требуется определить их положение, то
достаточно через произвольную точку К провести прямые е и /, парал-
параллельные соответственно прямым d2 и с!,. Вторая плоскость паралле-

106 Поверхность
лизма (для семейстпа направляющих #, и ?г ) определяется пересе-
пересекающимися прямыми I и m (I || #,, m || g2 ).
Косая плоскость находит широкое применение в инженерно-строи-
инженерно-строительной практике для формиронапин поверхностей откосов насыпей
железных и автомобильных дорог, набережных гидротехнических соору-
сооружений в местах сопряжения откосов, имеющих различные углы наклона.
4. Плоскость. Ксли направляющие прямые d, и d2 пересекаются или
параллельны, то при движении по ним прямолинейной образующей g по-
получается плоскость. Изображение плоскости па эпюре Монжа и различные
варианты ее расположении по отношению к плоскостям проекций были
подробно рассмотрены и § 8 гл. I.
§ 35. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ОДНОЙ НАПРАВЛЯЮЩЕЙ -
ТОРСЫ (ГРУППА Вп)
Рассматриваемая в этом параграфе группа линейчатых поверхнос-
поверхностей с одной криволинейной направляющей называется торсами, а кри-
криволинейная направляющая таких поверхностей — ребром возврата*.
Поверхностью с ребром возврата (торсом) называют поверхность,
описываемую движением прямой -- образующей g, касающейся некото-
некоторой пространственной кривой — направляющей d.
Торсы обладают замечательным свойством — они могут быть сов-
совмещены с плоскостью без складок и разрывов, путем последователь-
последовательных ее изгибов по прямолинейным образующим. В связи с этим мож-
можно дать и другое определение поверхности торса. Торсом называют
линейчатую поверхность, которую можно совместить всеми ее точка-
точками с плоскостью без складок и разрывов. Такие поверхности называ-
называют также развертывающимися поверхностями.
Если ребро возврата вырождается в точку, то получается частный
вид торса — коническая поверхность (если точка собственная) или ци-
цилиндрическая поверхность в случае вырождения ребра возврата в несоб-
несобственную точку.
Итак, к рассматриваемой группе линейчатых поверхностей относятся:
1) поверхность с ребром возврата (табл. 6, рис. 146);
2) поверхность коническая (табл. 6, рис. 147) ;
3) поверхность цилиндрическая (табл. 6, рис. 148).
В частном случае торсовые поверхности преобразуются в плоскость.
Для этого достаточно, чтобы ребро возврата d, преобразовалось в плос-
плоскую кривую, а направляющая d, конической или цилиндрической по-
поверхности — в прямую линию. Определитель этой группы поверхностей
имеет вид
Ф (g; <Г,, S); [ф тт d, = Sj е d", |.
Рассмотрим более подробно каждую из отмеченных поверхностей.
1. Поверхность с ребром возврата. Образование этой поверхности
можно представить таким образом. Пусть даны плавная кривая d и точка
S, причем S е « э d (рис. 149). Разделим кривую d на п участков, грани-
границы которых отметим точками 1, 2, 3, ... , п. Проведем прямую S1 и
отложим на ней от точки S вниз [SS, ]. Конец отрезка S, соединим
прямой с точкой 2 € d, получим отсек конической поверхности St 1 2.
* Ребро возврата следует рассматривать как кривую, в которой "совпадают'
все три криволинейные направляющие линейчатой поверхности dt = d2 = d3 .

Линейчатые поверхности с одной направляющей 107
(группа Bff)
Таблица 6. Линейчатые поверхности^ одной направляющей —
торсы. Группа Вп; Ф (g; d,, S); [g, п 3, = S, e d, ]
Snlf/
\
V
^^** 1 i.l T^
/ K
III'
/////
Ш 1
\
}
%'•':',
I II
Ik
Рис. 146 Поверхность с ребром возврата
а"
Рис. 147 Коническая поверхность
а
/~
*оо /
/
1 Рис. 148 Цилиндрическая поверхность
а
"-Г
На прямой (Si 2) откладываем [5,52] и конец отрезка S2 соединя-
соединяем с точкой 3 е d — вновь получаем отсек конической поверхности
S223O Повторяя описанные операции п раз, мы получим п следую-
следующих один за другим отсеков конических поверхностей с вершинами
в точках S,, S2, S3, ... , Sn. Если уменьшить длину отрезков [SS, ], [SjS^ ],
[^г^э ],..., [Sn - iSn], то ломаная линия SS, S2S3 ... Sn в пределе превра-
превратится в плавную пространственную кривую d, , называемую ребром
возврата, а прямолинейные звенья этой ломаной линии перейдут в каса-
касательные к кривой d(. Непрерывное множество этих касательных образу-
образует поверхность с ребром возврата (торс).
Из рис. 146 видно, что поверхность с ребром возврата имеет две
полы. Ребро возврата служит границей этих пол. Так как в каждой
точке плавной кривой можно провести только одну касательную, то

108 Поверхность
при задании поверхности с ребром возврата направляющую — кривую
d можно не указывать. Поэтому определитель такой поверхности бу-
будет иметь вид
Ф (g; <Г,, S); [gj U d, - Sj erf,],
где d, пространственная плавная кривая — ребро возврата, g — пря-
прямая образующая, S — точка, принадлежащая кривой d, . Условие,
отражающее закон движения прямолинейной образующей, состоит в
том, что она, двигаясь вдоль ребра возврата, все время остается каса-
касательной к нему.
В машиностроении находит применение частный вид торсовой по-
поверхности, у которой ребром возврата служит цилиндрическая винто-
винтовая линия. Полученную с помощью этой линии поверхность называют
винтовым торсом. На рис. 150 показаны ортогональные проекции отсека
поверхности винтового торса.
2. Коническая поверхность. Все прямолинейные образующие кони-
конической поверхности пересекаются в собственной точке S. Это условие
соблюдается лишь в том случае, когда ребро возврата d, вырожда-
вырождается в собственную точку S (см. рис. 147). Определитель конической
поверхности имеет вид
Ф (g; d,, S); [gj ndt Цдп gj « S].
Приведенная символическая запись определителя конической поверх-
поверхности показывает, что эта поверхность однозначно определяется прямоли-
прямолинейной образующей, кривой направляющей и точкой S, при этом прямоли-
прямолинейная образующая пересекает направляющую (gj п d =^ ^ — пересечение
gj и d не пустое множество) и все образующие пересекаются в одной
точке (n gj =- S).
На рис. 151 показано задание конической поверхности на эпюре
Монжа Проекции образующих gx, g2, gi, ... , gn на рис. 151 указаны
только для наглядности. Коническая поверхность однозначно задает-
задается проекциями ее образующей, направляющей и вершиной (gjd, S).
3. Цилиндрическая поверхность получается в том случае, когда все
прямолинейные образующие пересекаются в несобственной точке SL.
В этом случае определитель поверхности может быть записан:
Ф (g; d, Я„); \gj
n
Л
gj = S.
Рис 149
Отличие определителя ци-
цилиндрической поверхности от
определителя конической по-
поверхности состоит лишь в том,
что образующие цилиндричес-
цилиндрической поверхности параллельны
(пересекаются в несобствен-
несобственной точке), в то время как
для конической поверхности
характерным является пересе-
пересечение всех ее прямолинейных
образующих в собственной
точке.
На рис. 148 (табл. б)
показана произвольная цилинд-
цилиндрическая поверхность. Рис. 152
дает представление о ее задании
на эпюре Монжа.

Рис. 150
а)
Поверхности параллельного переноса 109
{подкласс I)
Рис. 152
Рис. 151
б)
в)
Рис. 153
4. Плоскость. Раньше было отмечено, что частным случаем торсо-
торсовых поверхностей является плоскость, и указаны условия, при ко-
которых поверхность с ребром возврата, коническая и цилиндрическая
преобразуются в плоскость. Рис. 153 дает наглядное представление об
этих преобразованиях.
§ 36. ПОВЕРХНОСТИ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА (ПОДКЛАСС 1)
Поверхностью параллельного переноса называется поверхность, об-
образованная поступательным перемещением плоской линии, при этом
образующие поверхности все время остаются параллельными между
собой.
Рис. 154 дает представление об образовании такой поверхности.
Ввиду того, что поверхности параллельного переноса несут на себе се-
семейства параллельных кривых линий, уместно напомнить, какой смысл
вкладывается в понятие параллельные кривые линии. Под параллельны-
параллельными кривыми линиями подразумеваются линии, получаемые одна из
другой путем параллельного переноса принадлежащих им точек на
некоторое одинаковое расстояние. Например, на рис. 155 кривая # парал-

110 Поверхность
Рис. 154
Рис. 155
л ..л.
лельна кривой g, так как точки A, At, A2, ¦¦¦ , Ап кривой g получены из
точек А, А{,_А2, ¦¦¦ , Ап кривой g путем переноса их по параллельным
прямым (АА), (Л,Л,), (А2А2), ... , (А„Ап) на величину вектора t.
В рассматриваемом примере мы получаем частный случай поверхности
параллельного переноса — цилиндрическую поверхность. Для образова-
образования сложных криволинейных поверхностей параллельный перенос кри-
кривой линии следует осуществлять с помощью мгновенных векторов пе-
переноса, характер изменения ^направления которых может быть задан
графически в виде кривой d (направление мгновенных векторов пе-
переноса определяется хордами кривой d).
В общем случае определитель поверхности параллельного переноса
имеет вид
*(?; d); [gf= TdQ)\.
В геометрическую часть определителя входит образующая кривая
g и направляющая d. Алгоритмическая часть состоит из условия па-
параллельного перемещения точек образующей (gj = Td (g)).

Поверхности вращения (подкласс 2) 111
На рис. 156 поверхность параллельного переноса задана на эпюре
Монжа. Для того чтобы перейти от задания поверхности проекциями
ее определителя (красные^ линии) к заданию поверхности каркасом
достаточно: на кривой d(d', с?') наметить ряд точек А{ (А\А'[),
А2 (А'2А'2'), ... , Ап (А'пА'п); через эти точки провести кривые?), g~2, ...
... , gn, параллельные кривой g. Проведение проекций параллельных
кривых сводится к проведению параллельных линий. Это следует из
свойства параллельного проецирования, состоящего в том, что проекции
равных и параллельных отрезков равны и параллельны. На рис. 156
такими отрезками являются стороны параллелограмма А'А\А'А\, ап-
аппроксимирующего участок криволинейной поверхности отсеком плос-
плоскости. Из чертежа видно, что образующую и направляющую можно
поменять местами. Если за образующую взять кривую d, а за направ-
направляющую кривую ?, то мы получим ту же самую поверхность параллель-
параллельного переноса.
§ 37. ПОВЕРХНОСТИ ВРАЩЕНИЯ (ПОДКЛАСС 2)
А. Поверхности вращения общего вида (рис. 157).
Поверхностью вращения общего вида называют поверхность, кото-
которая образуется произвольной кривой (плоской или пространствен-
пространственной) при ее вращении вокруг неподвижной оси.
В состав определителя поверхности вращения входит образующая g,
ось вращения i и условие о том, что эта образующая вращается вокруг
оси i:
Ф(*.О; l8j = Ri(g)]-
Каждая точка образующей (А, В, С, D, Е) при вращении вокруг
оси i описывает окружность с центром на оси вращения. Эти окруж-
окружности называют параллелями. Наибольшую и наименьшую параллель
называют соответственно экватором и горлом (шейкой).
Плоскости а, проходящие через ось поверхности вращения, назы-
называют меридиональными, а линии, по которым они пересекают поверх-
поверхность, — меридианами.
— Ось (I)
Меридиан
Главный
меридиан
Параллель
Экватор
Рис. 157

112 Поверхность
Меридиональную плоскость alt параллельную плоскости проекции,
принято называть главной меридиональной плоскостью, а линию ее
пересечения с поверхностью вращения — главным меридианом*.
Задание поверхности вращения на эпюре Монжа проекциями гео-
геометрических фигур, входящих в состав его определителя, хотя и од-
однозначно определяет поверхность, но обладает одним недостатком,
заключающимся в том, что при таком задании трудно представить форму
поверхности. Поэтому при задании поверхности вращения обычно ука-
указывают проекции ее оси, главного меридиана и экватора (иногда указы-
указывают окружность, по которой поверхность вращения пересекается с
плоскостью проекции).
При этом указывают только горизонтальную проекцию экватора
(или параллели) и фронтальную проекцию главного меридиана**.
Б. Частные виды поверхностей вращения.
В технике, в частности в машиностроении, поверхности вращения
находят широкое применение. Это объясняется распространенностью
вращательного движения и простотой обработки поверхностей вра-
вращения на станках. Особенно распространены поверхности, имеющие
в меридиональном сечении кривую второго порядка или две прямые,
на которые распадается эта кривая.
Рассмотрим некоторые частные виды поверхностей вращения. Возь-
Возьмем в качестве образующей окружность. В зависимости от взаимного
расположения окружности (или ее дуги) и оси вращения можно полу-
получить различные поверхности.
l.Top.
Тором называется поверхность, которая может быть получена при
вращении окружности g вокруг оси i, не проходящей через ее центр О***.
В зависимости от соотношения величин R — радиуса образующей
окружности и расстояния t от центра окружности до оси вращения
поверхности тора подразделяют на:
открытый тор (или кольцо) при R < t — окружность не пересекает
ось вращения (табл. 7, рис. 158,а);
закрытый тор при R > t — окружность пересекает ось вращения
или касается ее (табл. 7, рис. 158,6).
2. Сфера.
Сфера образуется в том случае, когда центр окружности принадле-
принадлежит оси вращения О G i, т. е. сферу можно рассматривать как частный
случай тора, у которого t = О (табл. 7, рис. 158,в).
3. Глобоид.
Образующей этой поверхности является дуга окружности, плос-
плоскость которой может, в общем случае, не совпадать с осью вращения
(табл. 7, рис. 158,г). Чертежи на рис. 162 дают представление об ор-
* На рис. 157 показаны не меридиональные плоскости а и ot\, а полуплоскости,
расположенные по одну сторону от оси вращения i. Соответственно на рисунке
показаны только половина меридиана и главного меридиана.
** Здесь речь идет о поверхности, ось вращения которой i 1 Ту. Если ось враще-
вращения (' 1 7Г2, то следует указывать фронтальную проекцию экватора и горизонтальную
проекцию главного меридиана.
*** Поверхность тора может быть получена и в том случае, когда плоскость ок-
окружности пересекает ось поверхности. Следует иметь в виду, что в отличие от осталь-
остальных поверхностей вращения, образующая которых — кривая второго порядка (или
прямая), поверхность тора является поверхностью не второго, а четвертого порядка.

Поверхности вращения (подкласс 2) 113
Таблица 7. Поверхности вращения; частные виды.
Подкласс 2. Ф (g; i); [gj = Л, (g) ]
а) б)
Рис. 158: а — открытый тор, б — закрытый тор, в — сфера, г — глобоид
а) б)
Рис. 159 Эллипсоид: а — сжатый, б — вытянутый
Рис. 160 Параболоид вращения
Рис. 161 Гиперболоид вращения: а —
однополостный, б — двухполостный
тогональных проекциях тора (рис. 162,а и б), сферы (рис. 162,в), гло-
глобоида (рис. 162,г). Так как поверхности вращения, изображенные на
рис. 162, симметричны относительно оси (', то при i i Я] их горизонталь-
горизонтальные проекции симметричны относительно горизонтальной оси; поэтому
можно вычерчивать не всю горизонтальную проекцию, а лишь ее полови-
половину, как это сделано на рис. 162 (конечно, если условия задачи не требуют
изображать ее полностью).

114 Поверхность
Рис. 162
4. Эллипсоид вращения.
Этот вид поверхности образуется при вращении эллипса вокруг его
оси, при этом, если за ось вращения принять малую ось [CD] , то полу-
получим сжатый эллипсоид вращения (рис. 159,а); когда вращение осу-
осуществляется вокруг большой оси [АВ] , образуется поверхность вы-
вытянутого эллипсоида вращения (рис. 159,6).
Рассмотренные поверхности вращения: тор, сфера, эллипсоид отно-
относятся к замкнутым поверхностям. Кроме замкнутых поверхностей
вращения существуют незамкнутые поверхности, которые образу-
образуются, в частности, при вращении параболы, гиперболы и прямой (линий,
имеющих несобственные точки).
5. Параболоид вращения.
Для того чтобы получить параболоид вращения, в определителе по-
поверхности вращения за образующую g следует принять параболу, а
за ось вращения i — ее ось (рис. 160). Для задания параболоида вращения
на эпюре Монжа достаточно указать проекции образующей g и оси i.
6. Гиперболоид вращения.
При вращении гиперболы можно получить две различные поверх-
поверхности:
а) однополостный гиперболоид вращения*, образуется при враще-
вращении гиперболы g вокруг ее мнимой оси (, (рис. 161,а);
б) двуполостный гиперболоид вращения, образуется при враще-
вращении гиперболы вокруг ее действительной оси i (рис. 161,6).
7. Коническая и цилиндрическая поверхности вращения.
Эти поверхности можно получить путем вращения прямой g вокруг
оси i. Коническая и цилиндрическая поверхности были подробно рассмот-
рассмотрены в § 35(см.рис. 147, 151 и 148,152).
§ 38. ВИНТОВЫЕ ПОВЕРХНОСТИ (ПОДКЛАСС 3)
Поверхность называется винтовой, ccjiu она получается винтовым
перемещением образующей (рис. 163) **.
* Поверхность однополостного гиперболоида вращения относится также к классу
линейчатых поверхностей. Она может быть получена путем вращении прямой вокруг
оси, скрещивающейся с ней. Подробно однополостный гиперболоид рассматривался
в § 32.
** Винтовое перемещение характеризуется вращением вокруг оси и одновремен-
одновременным поступательным движением, параллельным этой оси

Нинтовые поверхности (поокласс 3) 115
Рис. 1 ал
В зависимости от формы образующей отдельные виды винтовых
поверхностей могут быть отнесены как к классу линейчатых, так и не-
нелинейчатых поверхностей. Выделение этих поверхностей в самостоя-
самостоятельный подкласс связано со стремлением подчеркнуть значение вин-
винтовых поверхностей в технике, архитектурно-строительной практике
и, особенно, в машиностроении. Определитель винтовой поверхнос-
поверхности имеет вид
, 0; \gj
Rl(g)
где g — образующая (кривая или прямая), i — ось винтовой линии,
алгоритмическая часть определителя содержит указание, что образую-
образующая gj совершает винтовое перемещение, которое можно рассматри-
рассматривать как композицию из двух перемещений; а) параллельного пере-
перемещения вдоль оси i и б) вращения вокруг этой оси.
А. Винтовые поверхности с криволинейной образующей.
На рис. 164 показана винтовая поверхность, образованная плос-
плоской кривой g, совершающей винтовое перемещение. Закон этого пе-
перемещения определяется видом винтовой линии d (ее диаметром, шагом
и ходом) и характером расположения образующей g. В случае, показан-
показанном на рис. 164, он определен тем, что в процессе движения плоскость 7,
которой принадлежит образующая, все
время проходит через ось вращения i.
Б. Винтовые поверхности с прямоли-
прямолинейной образующей и направляющей —
винтовой линией постоянного шага.
Все точки образующей при винтовом
движении описывают винтовые линии,
каждая из которых может служить
направляющей поверхности. Такие линии
называют также винтовыми параллеля-
параллелями. Все винтовые параллели имеют
одинаковый шаг Р, называемый шагом
винтовой поверхности. Очевидно и еди-
единичный шаг Ро у этих параллелей будет
общий: Ро = Р/2и.
Характерной особенностью для вин-
винтовых поверхностей с постоянным ша-
шагом является постоянство угла tp° накло-
наклона прямолинейной образующей к направ-
направляющей плоскости, за которую принята
плоскость, перпендикулярная оси винто-
винтовой поверхности. Рис.164
У
Г

116 Поверхность
Рис. 165
Рис. 166
Как уже неоднократно отмечалось, для получения наглядного изоб-
изображения поверхности (в частности, винтовой) ее задание проекциями
геометрической части определителя следует расширить до задания кар-
каркасом, состоящим из двух семейств линий: семейства направляющих
(винтовых параллелей) * и семейства, составленного из последователь-
последовательных положений прямолинейных образующих.
Винтовая линия постоянного шага, построенная на поверхности
прямого кругового цилиндра, называется геписой. Поэтому линей-
линейчатые винтовые поверхности, направляющая которых — гелиса, на-
называются геликоидами. В зависимости от величины угла наклона обра-
образующей к оси геликоиды бывают прямыми, если этот угол равен 90°, и
косыми (наклонными), если угол — произвольный, отличный от 0 и 90° .
Рис. 165 дает представление о прямом геликоиде. Изображенная
на рис. 166 поверхность называется косым геликоидом. На рис. 165
и 166 поверхности указаны только частично, своими отсеками, заклю-
заключенными между направляющей d и осью i.
В свою очередь, прямые и косые геликоиды подразделяются на зак-
закрытые и открытые. Признаком для такого деления служит взаимное
расположение оси геликоида и его образующей. Если образующая и
* На зпюре Монжа, как правило, указывают только одну (или две) винтовые
параллели, принадлежащие семейству направляющих.

Винтовые поверхности (подкласс 3) 117
ось пересекаются, геликоид называют .шкрытым, если скрещивают-
скрещиваются - открытым.
Следует отметить одно важное свойство винтовых поверхностей,
состоящее в том, что эти поверхности, так же как и поверхности враще-
вращения, могут сдвигаться, т. е., совершая винтовое перемещение, поверх-
поверхность скользит вдоль самой себя. Это свойство обеспечивает винтовым
поверхностям широкое применение в технике. Винты, шнеки, сверла,
пружины, поверхности лопаток турбин и вентиляторов, рабочие органы
судовых движителей, конструкции винтовых аппарелей и лестниц — вот
далеко не полный перечень технического использования винтовых по-
поверхностей.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. В чем сущность образования поверх-
поверхностей кинематическим способом?
2. Что называется каркасом поверх-
поверхности?
3. Чем отличается непрерывный кар-
каркас от дискретного?
4. Что такое определитель поверх-
поверхности?
5. Что является содержанием геомет-
геометрической и алгоритмической частей оп-
определителя?
6. Напишите определитель поверхнос-
поверхностей: Каталана, вращения, геликоида,
однополостного гиперболоида, коноида.
7. Как задается поверхность на эпюре
Монжа?
8. Что такое очерк поверхности?
9. Какие поверхности называются по-
поверхностями Каталана?
10. Дайте общую схему классификации
поверхностей.
11. Приведите схему классификации
линейчатых поверхностей.
12. Дайте определение различных видов
линейчатых поверхностей.
13. Как образуются поверхности вра-
вращения?
14. Укажите основные свойства поверх-
поверхности вращения.
15. Как образуются винтовые поверхн-
поверхности?
16. По какому признаку поверхности
геликоида подразделяют на закрытые и
открытые?

ГЛАВА
V
ПОЗИЦИОННЫЕ ЗАДАЧИ
ПОИ Я! IIЯ ПО!
I i !
Круг задач, отпеты на которые могут быть получены графическим
путем, чрезвычайно широк. При лом независимо от степени слож-
сложности их решения и характера нопросов, требующих ответа, нее они
могут быть отнесены нсего лишь к одному из двух классов: 1-й класс —
задачи позиционные; 2-й класс — задачи метрические.
Следует иметь в виду, что деление задач на позиционные и метри-
метрические является условным. Если из нсего многообразия задач позици-
позиционную группу можно выделить, то чисто метрические задачи встреча-
встречаются очень редко; как правило, при решении метрических задач предва-
предварительно приходится выяснять позиционные отношения между геометри-
геометрическими фигурами, входящими в условия задачи или построенными в
процессе решения, т. е. решать позиционную задачу.
Несмотря на это, распределение задач по отмеченным классам в ме-
методическом отношении имеет большой смысл, так как позволяет ус-
установить единые (обобщенные) алгоритмы, пригодные для решения
широкого круга задач, входящих в один класс, и, как следствие, обес-
обеспечить простой и надежный поиск частного алгоритма для решения
поставленной задачи.
В этой главе будут рассмотрены различные виды позиционных задач
и указаны алгоритмы их решения. Под позиционными подразумева-
подразумеваются задачи, решение kotope.ix позволяет получить ответ о принад-
принадлежности элемента (точки) или подмножества (линии) множеству
(поверхности). К позиционным относятся также задачи на определе-
определение общих элементов, принадлежащих различным геометрическим
фигурам.
Первая группа задач может быть объединена под общим названием
задачи на принадлежность (инцидентность). К ним,
в частности, относятся задачи на определение:
1) принадлежности точки линии (А <Е /);
2) принадлежности точки поверхности (А <Е а);
3) принадлежности линии поверхности (/с а).
Ко второй группе относятся задачи на пересечение. Эта
группа содержит также три типа задач:
1) на пересечение линии с линией (/ п т);
2) на пересечение поверхности с поверхностью (а п 0);
3) на пересечение линии с поверхностью (/ п а).
С точки зрения единства принципа, положенного в основу решения
позиционных задач, их можно не делить на две группы. Подходя к пози-
позиционным задачам с таких позиций, можно считать, что все многообразие
позиционных задач может быть сведено к решению задач первой груп-
группы — задач на принадлежность: 1) А ? /, 2) А ? а и 3) / с а. В справедли-

Принадлежность точки линии (A El) 119
вости такого утверждения легко убедиться, перефразировав условия
задач, входящих во вторую группу. Действительно:
1) задачу на определение точки пересечения линии с линией (I П т)
можно заменить задачей 1 (Л е () первой группы: "определить точку,
принадлежащую как линии I, так и линии т";
2) условие "построить линию пересечения поверхностей а иC" (а п Д —
задача 2 второй группы) можно заменить задачей, относящейся к первой
группе: "определить (построить) линию /, принадлежащую как поверх-
поверхности а, так и0" (/ С а — задача 3 первой группы);
3) задачу 3 второй группы "построить точку А пересечения линии /с
поверхностью a (I n а)" можно рассматривать как две задачи первой
группы: А ? / (задача 1) и Л ? а (задача 2).
Если учесть, что линию можно рассматривать как множество при-
принадлежащих ей точек, то задача третьего типа (/ с а) сводится к много-
многократному решению задачи определения А <Е а. Тогда окончательно полу-
получим следующее определение:
к позиционным относятся задачи, решение которых, в конечном
счете, сводится: 1) к построению точки, принадлежащей линии (А ? I), и
2) к построению точки, принадлежащей поверхности (А& а).
Решение таких задач базируется на инвариантном свойстве 2 (см. § 6)
ортогонального проецирования, из которого вытекает:
А ? I <==» (А' е Г)Л(А" Е Г); B)
Лба «== (А'е Г С а')Л(А" е Г С а"). C)
Проследим на примерах, как решаются позиционные задачи.
§ 39. ПРИНАДЛЕЖНОСТЬ ТОЧКИ ЛИНИИ (А ? I)
При выяснении вопроса о принадлежности точки линии или при ре-
решении аналогичной задачи на построение точки, принадлежащей ли-
линии, достаточно использовать только свойство B) из § 38.
Следует иметь в виду, что если линия занимает произвольное поло-
положение по отношению к плоскостям проекций, то решение может быть
получено в системе двух заданных плоскостей проекций. В случае,
когда линия принадлежит плоскости, перпендикулярной оси проек-
проекции, для решения следует пользоваться вспомогательной плоскостью
проекции.
ПРИМЕР 1. На данной кривой / ука- прямую, перпендикулярную оси проек-
зать произвольную точку А, принадлежа- ции, и отмечаем точку ее пересечения с
щую этой кривой (рис. 167). фронтальной проекцией линии /".
РЕШЕНИЕ. Зная, что на основании ПРИМЕР 2. Указать горизонтальную
свойства B) А' ? /' и А" ? /", а также, проекцию точки С по данной ее фрон-
что А' и А" принадлежат одной линии тальной проекции С", если известно, что
связи, перпендикулярной оси проекции точка С ? [ЛВ] (рис.168).
л:, отмечаем на какой-либо проекции ли- РЕШЕНИЕ. Так как отрезок [АВ\ при-
нии / произвольную точку А, обозначаем надлежит плоскости, перпендикулярной
ее тем же индексом, какой имеет проек- оси проекции, то решить эту задачу в сис-
ция линии /. На рис. 167 точка Л' взята на теме заданных плоскостей проекций не
горизонтально^ проекции линии / . Для представляется возможным*. Для ее ре-
определения А через точку А проводим шеНия воспользуемся вспомогательной
* Имеется в виду графическое решение. Ответ на поставленную задачу может быть
получен из условия деления отрезка в данном отношении (см. § 6, инвариант 2 к)

120 Позиционные задачи
В"
о — -
A'n V /
С'
В"
Рис. 167
Рис. 168
плоскостью проекции. В качестве вспо- вспомогательную проекцию С'" точки С.
могательной плоскости возьмем плос- Зная С'", находим С'.
кость Яд, перпендикулярную оси проек- Все необходимые геометрические по-
ции. На плоскости Я, находим проекцию строения ясны из чертежа и не нуждают-
А"'П'" отрезка \ЛВ\ и на ней отмечаем ся в пояснении.
§ 40. ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ (А е а)
При составлении алгоритма решения этой группы задач следует
базироваться на свойстве C) из § 38, т. е. для того чтобы на черте-
чертеже поверхности указать проекции принадлежащей ей точки, необхо-
необходимо вначале построить проекции какой-либо линии, принадлежащей
поверхности, а затем на этой линии отметить точку.
В качестве линии, как правило, выбирается образующая поверх-
поверхности. Если поверхность может быть получена образующей различной
формы, то предпочтение следует отдавать наиболее простым и удобным
для построения линиям: окружностям для поверхностей вращения,
прямым для линейчатых поверхностей (в частности, для плоскости
целесообразно использовать линии уровня*).
ПРИМЕР 1. В плоскости а(а\\Ь) ука-
указать произвольную точку Л (рис. 169).
РЕШЕНИЕ. В плоскости а проводим
произвольную горизонталь h. При пост-
построении ее проекций следует иметь в ви-
виду, что прямая принадлежит плоскости
в том случае, если она содержит две раз-
различные точки, принадлежащие плоскос-
плоскости. В качестве таких точек принимаем
точки 1 и 2, принадлежащие соответст-
соответственно прямым а и Ь, определяющим
плоскость а.
На рис. 1 ()9 построение проекций го-
горизонтали h выполнено в следующей
последовательности:
а) на прямой а взяли произвольную
точку 1, через фронтальную проекцию
этой точки провели фронтальную про-
проекцию горизонтали h";
б) отметили точку 2" - h" П Ь";
в) определили горизонтальные про-
проекции 1' и 2' точек 1 и 2;
г) через точки Г и 2' провели гори-
горизонтальную проекции» горизонтали ti.
Горизонталь h С о, так как h прохо-
проходит через точки 1 и 2, принадлежащие
плоскости а
* Особенно целесообразно пользоваться линиями уровня в случае, когда плос-
плоскость задана следами.

П/чиинЪи'жносгь точки поверхности (Л С t\J 121
к -к
ис. IG9
Рис. 170
На проекциях горизонтали h' и /i"
отмечаем проекции точки Л (Л' <? /Г
п .1" (" h"). Точка .Л С а, так как
л е / с а.
ПРИМЕР 2. В плоскости j3 указать точ-
точку Ч, удаленную от горизонтальной плос-
плоскости проекции на расстояние 15 мм и от
фронтальной плоскости проекции на рас-
расстояние 10 мм (рис. 170) .
РЕШЕНИЕ. Проводим в плоскости [1
фронталь /' и горизонталь /i, удаленные
от плоскостей проекций соответственно
на расстояния 10 и 15 мм. Пересечение
одноименных проекций /и /i укажет про-
проекции искомой точки Н (В' ¦- {' П /i',
И" =-. f'nh").
ПРИМЕР 3. Определить фронтальную
проекцию точки Л, принадлежащей плос-
плоскости Ос, если известна ее горизонтальная
проекция А' (рис. 171 ).
Мы знаем, что Аеа<=>(А'Е1'Са') Л
Л(Д" ? /" С ос"), позтому, чтобы полу-
получить ответ на поставленную задачу, дос-
достаточно через /Г провести горизонталь-
горизонтальную проекцию прямой, принадлежащей
плоскости а, найти ее фронтальную про-
проекции! и на ней отметить точку l". Так
как плоскость а задана следами, то целе-
целесообразно в качестве вспомогательной
прямой использовать одну и) главных
линии плоскости. На рис. 171 проведена
фронталь /'плоскости а.
ПРИМЕР 4. На цилиндрической по-
поверхности а, заданной направляющей d и
образующей g, указать произвольную
точку А (рис. 172).
РЕШЕНИЕ. Проводим произвольную
прямолинейную образующую #. цилинд-
цилиндрической поверхности а. Для зтого на
кривой d отмечаем произвольную точку
1 A' G d' и l" ? d") . Через проекции точ-
точки 1 проводим проекции прямой #. па-
н,-
Рис. 171
Рис. 172

122 Позиционные задачи
d"
раллельно соответствующим проекциям
g' и g". На прямой g: отмечаем произ-
произвольную точку А :
АЕа *=* (A'eg'jCa')A(A"eg'!C а").
ПРИМЕР 5. На конической поверхнос-
поверхности п указать точку А, удаленную от го-
горизонтальной плоскости проекции на рас-
расстояние 20 мм (рис. 17 3).
РЕШЕНИЕ. Проводим плоскость у || Я]
и удаленную от оси х на заданное рас-
расстояние 20 мм. На конической поверх-
поверхности а отмечаем произвольную прямо-
прямолинейную образующую gj (g'.t g".). Точка
пересечения g'j Г) fOy укажет фронталь-
фронтальную проекцию А" искомой точки А. По
А" находим А'.
Следует иметь в виду, что данная зада-
задача имеет бесчисленное множество реше-
решений: любая точка отрезка 3", 4" может
быть принята за фронтальную проекцию
точки, удовлетворяющей условию по-
поставленной задачи.
ПРИМЕР 6. На поверхности наклонно-
наклонного геликоида а указать фронтальную про-
проекцию точки А, если известна ее горизон-
горизонтальная проекция А' (рис. 174).
РЕШЕНИЕ. Через горизонтальную про-
проекцию точки А' проводим горизонталь-
горизонтальную проекцию прямолинейной образую-
образующей g'. Фронтальная проекция g" опреде-
определяется из условия равенства углов нак-
наклона всех прямолинейных образующих
к направляющей плоскости (в нашем
случае за направляющую плоскость при-
принята 77 ] ) .
D\
Рис. 174
Рис. 175

Принадлежность точки поверхности (Л ?ск) 123
Рис. 176
Множество прямых, пересекающих
ось винтовой поверхности ( в точке S, об-
образуют поверхность прямого кругового
конуса /3, прямолинейные образующие
которого составляют заданный угол с
плоскостью Я! . Поэтому для определе-
определения фронтальной проекции g" проводим
прямолинейную образующую g\ коничес-
конической поверхности |3, по которой горизон-
горизонтально проецирующая плоскость 7> про-
проходящая через точку А и ось /, пересекает
поверхность /3. Фронтальная проекция g
должна быть параллельна g". Для ее по-
построении на горизонтальной проекции
d' отмечаем точку 1 , в которой hOy П d ;
по 1' определяем 1". Через 1" проводим
g" \\g'[- Для построения фронтальной про-
проекции А" через А' проводим линию связи
перпендикулярно оси х и отмечаем точку
ее пересечения eg".
ПРИМЕР 7. На поверхности цилинд-
цилиндроида /3 указать фронтальную проекцию
точки А, если известна ее горизонтальная
проекция Л' (рис. 175).
РЕШЕНИЕ. Через горизонтальную про-
проекцию точки А' проводим горизонталь-
горизонтальную проекцию прямолинейной образую-
образующей g' поверхности 0, для этого через
Л проводим прямую g || hOa и отмечаем
точки 1)\ и D2, в которых прямая g' пе-
пересекает направляющие dy и d'2 .
По точкам /.>! и D'2 строим их фрон-
фронтальные проекции D] и D2, которые оп-
определяют фронтальную проекцию обра-
образующей g". На g" находим точку А". Для
ее построения через А' проводим линию
связи перпендикулярно оси д: и отмечаем
точку ее пересечения с g .
ПРИМЕР 8. Построить горизонтальную
проекцию точки, принадлежащей поверх-
поверхности вращения a(g, i), если известна ее
фронтальная проекция А" (рис. 176) .
РЕШЕНИЕ. Через данную фронтальную
проекцию точки А" проводим фронталь-
фронтальную проекцию окружности / , принадле-
принадлежащей поверхности а. Строим горизон-
горизонтальную проекцию этой окружности l'.
Окружность / — параллель поверхности
а, ее следует рассматривать как сечение
поверхности а горизонтальной плоско-
плоскостью у. Длина отрезка О"\" укажет вели-
величину радиуса окружности /'. На /' отмеча-
отмечаем А . Для нахождения А' через А" про-
проводим линию связи перпендикулярно оси
х и отмечаем точку ее пересечения с /'.
В рассмотренных примерах были заданы поверхности линейчатые
или вращения. Это позволило для решения задачи на принадлежность
точки поверхности использовать простые линии — прямые или окруж-
окружности. Для нелинейчатых поверхностей, на которых невозможно провес-

124 Позиционные задачи
ти такие линии, приходится строить кривые, принадлежащие поверх-
поверхности.
Приведенный ниже пример показывает, как следует решать задачу
на принадлежность точки поверхности в случае, когда поверхность
нелинейчатая.
ПРИМЕР 9. Определить недостающую
(фронтальную) проекцию точки А, при-
принадлежащей нелинейчатой поверхности
а, если известна ее горизонтальная про-
проекция Л' (рис. 177).
РЕШЕНИЕ. Определение недостающей
проекции точки А осуществляется анало-
аналогично рассмотренным ранее случаям (см.
примеры 1 ... 8). Вначале через точку А'
проводим прямую ( — горизонтальную
проекцию линии /. Чтобы линия / принад-
принадлежала поверхности tt, необходимо, что-
чтобы любые точки, взятые на этой линии,
принадлежали поверхности а. В качестве
таких точек принимаем точки 1', 2', 3',4',
5', в которых /' пересекает горизонталь-
горизонтальные проекции образующих g\ , g'2, g'j, g'4,
g\ ; зная l', 2', ... , 5',определяем l' ,2' ,...
... , 5". Соединив эти точки плавной кри-
кривой, получим /"; на /"отмечаем А". Точка
Л ? а, так как А' ? ( и А" ? I", а!Са,
Следует иметь в виду, что при реше-
решении подобных задач в качестве линии I
целесообразно пользоваться плоской
кривой, в частности, принадлежащей
проецирующей плоскости (в рассмотрен-
рассмотренном случае кривая / принадлежит гори-
горизонтально проецирующей плоскости 7) ¦
§ 41. ПРИНАДЛЕЖНОСТЬ ЛИНИИ ПОВЕРХНОСТИ (/Со)
Построение линии, принадлежащей поверхности, принципиально
не отличается от построения точки, принадлежащей поверхности (см.
§ 40, примеры 1 ... 9). Различие состоит лишь в том, что определяются
проекции не одной, а п точек, принадлежащих линии.
ПРИМЕР 1. Построить фронтальную
проекцию кривой /, принадлежащей по-
поверхности гиперболического параболои-
параболоида а, заданного направляющими dj, d2 и
плоскостью параллелизма 0, если извест-
известна горизонтальная проекция кривой I'
(рис. 178).
РЕШЕНИЕ. Поверхность а представля-
представляет собой множество точек, а линия /, при-
принадлежащая поверхности а, является
подмножеством этого множества. Поэто-
Поэтому для соблюдения условия / С а необхо-
необходимо, чтобы каждый элемент (точка)
подмножества / принадлежал множеству
Ос. Для обеспечения этого условия необ-
необходимо, чтобы любая точка A: ? I принад-
принадлежала линии g: С а.
Решение сводится к следующему:
1. На горизонтальной проекции поверх-
поверхности а проводим горизонтальные проек-
проекции прямолинейных образующих g,, g'2,
8ъ, ви, 8s параллельно /i0^.
2. Находим фронтальные проекции
этих образующих g'[, g'{, g'3, 84, g's-
3. Отмечаем точки 1', 2', 3', 4', 5', в ко-
которых горизонтальная проекция кривой
/' пересекает горизонтальные проекции
образующих g\, g\, g'3, g'n, g's :
4. Находим фронтальные проекции то-
точек 1", 2", 3", 4", 5" на соответствующих
фронтальных проекциях образующих g",
?2'. 8з'¦ 84, si- Соединив их плавной кри-
кривой, получим искомую фронтальную про-
проекцию /" кривой / С а.
Если необходимо определить проекцию прямой, принадлежащей
плоскости, то решение задачи значительно упрощается.
ПРИМЕР 2. Построить фронтальную
проекцию прямой т, принадлежащей
плоскости а, если известна ее горизон-
горизонтальная проекция т (рис. 179).
РЕШЕНИЕ. Прямая однозначно опре-
определяется двумя не тождественнымиточ-
ками, поэтому для определения т" не-
необходимо и достаточно найти фронталь-
фронтальные проекции двух не тождественных
точек 1 и 2, принадлежащих прямой т,
т. е. дважды решить задачу по определе-
определению проекций точки, принадлежащей
плоскости, если известна одна из ее про-
проекций (см. § 40 пример 3).
' На рис. 179 решение выполнено в сле-
следующем порядке:
1. Отметил^ на горизонтальной про-
проекции прямой т' две различные точки
1' и 2'.
ции
2. Определили их фронтальные проек-
л \" и 2". Положение точек l" и 2"
найдено с помощью фронталей /, Э 1 и
{-1 Э 2.
3. Точки l" и 2" определяют искомую
фронтальную проекцию прямой т".

Пересечение линии с линией (I Пт) 125
Hi,-",.
Рис. 178
Рис. 179
§ 42. ПЕРЕСЕЧЕНИЕ ЛИНИИ С ЛИНИЕЙ (/ п т)
Решение задач на определение общей точки, принадлежащей как ли-
линии /, так и линии т, или иначе, задач по опредатению точки пересече-
пересечения двух линий, вытекает непосредственно из инварианта ортогональ-
ортогонального проецирования
К = an Ь <==> К' = а' п Ь'Л К" = а" о Ь".
ПРИМЕР 1. Показать на эпюре Монжа
две произвольные пересекающиеся линии
тип (рис. 180).
РЕШЕНИЕ. Пусть К ~= т П п, тогда
К Е т и К € п. Из условия принадлежнос-
га n t m вытекает К t m и К fc m .
Так как .f G n, то А." би'и К" ? п". Для
того чтобы т П п, необходимо, чтобы
А'1 и К" принадлежали одному перпенди-
перпендикуляру к оси jc. На рис. 180 показаны пе-
пересекающиеся кривые тип.
ПРИМЕР 2. Данную кривую / пересечь
горизонталью h, проходящей через точку
Л (рис. 181).
РЕШЕНИЕ. Через Л" проводим фрон-
фронтальную проекцию горизонтали h" \\ оси
х. Отмечаем точку К" = h" П /". Находим
К' G /'. Точки К и Л' определяют гори-
горизонтальную проекцию h' горизонтали h.
Рис. 180
Рис. 181

126 Позиционные задачи
§ 43. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПОВЕРХНОСТЬЮ (а П 0)
Две поверхности пересекаются по линии, точки которой принадле-
принадлежат каждой из пересекающихся поверхностей. Поэтому построение
линии пересечения двух поверхностей а и C сводится к нахождению
общих точек, принадлежащих как множеству точек, составляющему
поверхность а, так и другому множеству точек, входящих в состав
поверхности ji.
Способ построения линии пересечения двух поверхностей состоит в
следующем: заданные поверхности пересекают третьей, вспомогатель-
вспомогательной поверхностью (вид и расположение вспомогательной секущей по-
поверхности выбирают с таким расчетом, чтобы можно было легко опреде-
определить линии пересечения этой поверхности с заданными); находят линии,
по которым эта вспомогательная секущая поверхность пересекает каж-
каждую из данных поверхностей. Далее отмечают точку (точки), в которой
пересекаются полученные линии пересечения (рис. 182) .
Построив отмеченные операции п раз, получим множество точек.
Линия /, соединяющая эти точки, является искомой линией пересе-
пересечения поверхностей.
Используя геометрический язык, ход решения задачи можно предс-
представить в виде формализованного алгоритма, записанного в символи-
символической форме.
В табл. 8 дано традиционное для начертательной геометрии словес-
словесное описание алгоритма (слева) и соответствующая ему символичес-
символическая запись на геометрическом языке (справа).
Таблица 8. Описание алгоритма решения задачи по определению
линии пересечения двух поверхностей
Словесное описание на традиционном нзыке
начертательной геометрии
1. Вводим вспомогательную секущую поверх-
поверхность
2. Определяем линии пересечения этой вспо-
вспомогательной поверхности с каждой из заданных
поверхностей
3. Находим точки, в которых пересекаются
полученные линии пересечения. Соединяем эти
точки плавной линией
Символическая запись
на геометрическом языке
Вводим 7/
Определяем m = 7,• П а
nj = т,- Г> 0
Находим Lj - in: П л.
1=- /м U L2 U/,., U... U Л„*
* В некоторых случаях линия пересечения может распадаться на две и более линий,
т. е. множество / может состоять из подмножеств lt , l2, ... , In- Эти линии могут быть
как кривыми (пространственными или плоскими), так и прямыми. При этом линии
могут быть как действительными, так и мнимыми.
Алгоритм нахождения точек, общих для двух заданных множеств
точек — поверхностей а и 0, можно записать в виде
/ = (L, U L2 UL, U ... и L,,); [Ly- = GynQ)n G;П0)]. D)
Повторяя многократно последовательность операций, обозначен-
обозначенных в приведенном алгоритме (каждый раз, естественно, меняя поло-
положение вспомогательной секущей поверхности yj), можно получить любое
число точек, принадлежащих искомой линии пересечения заданных
поверхностей.
Рассматриваемый алгоритм определения точек, принадлежащих ли-
линии пересечения двух поверхностей, является универсальным, так как

Пересечение поверхности с поверхностью \ 27
а
Рис. 182
под а и C могут подразумеваться любые поверхности, в том числе и
плоскости. На выбор вида и расположения вспомогательной секущей
поверхности 7у в приведенном алгоритме также не накладывается ника-
никаких ограничений.
Вдумчивый читатель может задать вполне справедливый вопрос:
"Что это за алгоритм, который предписывает решать задачи по определе-
определению точки (точек), принадлежащей линии пересечения двух поверхнос-
поверхностей, путем решения двух задач, в каждой из которых также приходится
строить линию пересечения поверхностей?".
Такое, на первый взгляд, нелогичное построение алгоритма стано-
становится вполне оправданным, если учесть, что данные поверхности а и
0 могут иметь любую форму и занимать произвольное положение в
пространстве, что не позволяет непосредственно, по эпюру, опреде-
определить линию их пересечения. А в качестве вспомогательной секущей
поверхности jj мы можем выбрать поверхность удобной формы и так
ориентировать ее относительно плоскостей проекций, чтобы получить
простое решение для определения линии ее пересечения с каждой из
заданных поверхностей.
Среди инвариантных свойств ортогонального проецирования нахо-
находим (Ф с 7)А(т ± ^1 ) =* *' с hOy, т. е., если фигура Ф принадлежит
поверхности у 1 плоскости тг,, то ортогональная проекция Ф' на эту
плоскость принадлежит следу поверхности hQy (см. § 6, свойство 2 г).
Поэтому, если принять за вспомогательную секущую поверхность -у ¦ 1 тт,
(или 7г2 ), то линии rrij и rij пересечения этой поверхности с поверхнос-
поверхностями а и /3 будут иметь горизонтальные (или фронтальные) проекции
m'j С h0 у и n'j С hOy . (m'j С f0 y . и п|' с fQ у .), т. е. решение подчас слож-
сложной задачи на построение линии пересечения поверхностей а и j3 мы
заменяем решением двух простейших задач: 1) определить линию пере-
пересечения проецирующей поверхности у: с поверхностью а; 2) определить
линию пересечения той же поверхности т, с поверхностью /3. Очевидно,
что каждая из этих задач сводится к построению второй проекции линии,
принадлежащей поверхности, если известна одна из ее проекций. Решение
последней задачи состоит из многократного определения недостающей
проекции точки, принадлежащей поверхности, т. е. сводится к решению
позиционной задачи второго вида А е а (см. § 40).

128 Позиционные задачи
§ 44. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Использование универсального алгоритма для решения задач по
определению линии пересечения поверхностей проследим вначале на
наиболее простых примерах пересечения двух плоскостей.
Две плоскости пересекаются по прямой линии, для определения
которой достаточно найти две точки, принадлежащие одновременно
каждой из заданных плоскостей.
Чтобы найти такие точки, достаточно ввести две вспомогательные
секущие плоскости у, и у2, т. е. дважды выполнить последователь-
последовательность операций, предусмотренных частью алгоритма D), заключенной
в квадратные скобки (см. § 43):
L, = (т, П а)П G| П C);
L2 = G2 Па)П G2 П0);
1 = {LX,L2).
Рассмотрим общий случай пересечения плоскостей, когда обе плос-
плоскости — общего положения.
ПРИМЕР 1. Определить линию пересе-
пересечения / плоскостей at(a П Ь) и |3(c||d)
{рис. 183).
РЕШЕНИЕ. Проводим вспомогатель-
вспомогательную горичонтально проецирующую плос-
плоскость 7| (''о-у )¦ Определяем проекции
прямых т, - у{ flarni, = У\ ^ /3- Так
как плоскость 7i I тг| , то п\\ и п\ совпа-
совпадут с ^оу, ¦ С помощью точек 1', 2' и 3',
4', принадлежащих прямым т, и Л|, оп-
определяем фронтальные проекции jthx
точек 1 , 2" и .'!' , 4", которые определя-
определяют прямые т\' и л". Отмечаем точку пе-
пересечения фронтальных проекций пря-
прямых /.'/ = т'{ П л". Горизонтальная про-
проекция 1\ принадлежит горизонтальным
проекциям т\ и п\ .
Для нахождения точки h2 вводим
плоскость 72 II У\ ¦ Плоскость 72 пересе-
пересечет заданные плоскости по прямым т2 и
п2, соответственно параллельным пря-
прямым га, иЛ). Поэтому для определения
их проекций достаточно найти проекции
только одной точки, принадлежащей
1-м-кдой из прямых т2 и п2 . На рис. 183
С"
d"
¦«/'

Пересечение плоскостей \ 29
0(Э
—/с
'оу,
Рис. 181
Рис. 185
за такие точки приняты 5 и 6. Пересече-
Пересечение т2 П п2 :г l-iг- Точки L\ и Лj опре-
определяют искомую прямую /.
ПРИМЕР 2. Определить линию пересе-
пересечения плоскостей а и р1, заданных следа-
следами (рис. 184).
РЕШЕНИЕ. В данном случае решение
значительно упрощается в связи с тем,
что отпадает необходимость в выполне-
выполнении построений, предусмотренных пер-
первым и вторым пунктами алгоритма (см.
§ 43, табл. 8) . Это происходит потому,
что роль вспомогательных секущих плос-
плоскостей 7i и 72 ПРИ задании плоскости
следами могут выполнять плоскости
проекций 7Т1 и эт2, а соответствующие
следы йоа. >»о0 и /оa. Л>0 несут функции
проекции прямых m , п ч m , п . Следо-
Следовательно, точки пересечения одноимен-
одноименных следов плоскостей а и A определяют
положение проекций точек Л, и L2 '¦
ПРИМЕР 3. Определить линию пересе-
пересечения плоскостей а и 0 (рис. 185).
РЕШЕНИЕ. Вводим вспомогательные
секущие плоскости 7i II fi и li II л2 •
Эти плоскости пересекают заданные а и
р1 по горизонталям /i| и /г2 (плоскость
7i ) и фронталям Д и / (плоскость 7г ) ¦
Находим точки /м и L2 '¦ L\ — h\ П /i2 ;
/-2 = f\ П /". Зная L'| и //'2', определяем
Л[' и //2. Через одноименные проекции
точек L\L'2 и L'[L'{ проводим проекции
/' и /" искомой прямой пересечения плос-
плоскостей а и р1.
Эту же задачу можно решить иначе.
Вместо двух вспомогательных секущих
плоскостей уровня взять одну плоскость
7 общего положения, параллельную од-
одной из заданных плоскостей а (или /3).
Такой вариант решения основан на том',
что линии пересечении плоскости а дву-
двумя параллельными плоскостями /3 и у па-
параллельны между собой.
L\ = hOa П hoti и L2 = fUa П /¦„
!)¦(,¦
Через одноименные проекции точек
L, и L2 проводим проекции искомой
прямой /' и /".
Если одноименные следы плоскостей
не пересекаются в пределах чертежа, то
не представляется возможным использо-
использовать плоскости проекций в качестве вспо-
вспомогательных секущих плоскостей. В этих
случаях приходится вводить секущие
плоскости, которые целесообразно про-
проводить параллельно плоскостям проек-
проекций. Поясним сказанное на примере ре-
решения задачи по определению линии пе-
пересечения плоскостей аи 0.
ПРИМЕР 4. Определить линию пересе-
пересечения плоскостей а и /3 (рис. 186) .
РЕШЕНИЕ. Проводим вспомогатель-
вспомогательную секущую плоскость у ||0 (hOy || Иоди
А)т II Л>р) • Точку Ху выбираем так, чтобы
одноименные следы плоскостей а и 7 пе-
пересекались в пределах чертежа. Находим
/j — линию пересечения плоскостей а и
у. Проекции 1\ и /'[ указывают направле-
направления проекций линии / пересечения плос-
плоскостей а и /3.
Для определения точек, через которые
пройдут эти проекции, рассмотрим
'J °° AX^L'iXjj. В AXaL'iXy
{L2L1) Д
поэтому

130 Позиционные задачи
Рис. 186
Рис. 187
Рис. 188
\ХаХу\
\XaLs\
. Из этой пропор-
\ХаХр\ ]Ха1А\
ции определяем |XaL'i'l и через точку Три отрезка из четырех заданы на чер-
L" проводим /" || /". теже, это дает возможность определить
Для нахождения горизонтальной про- четвертый [Х„/,г]. Через точку L'2 про-
проекции /' достаточно составить пропор- водим /' ц /'
цию:
Решение задачи по определению линии пересечения плоскостей зна-
значительно упрощается, если одна из плоскостей занимает проецирую-
проецирующее положение. Из рис. 187 и 188 видно, насколько проще решается
задача, когда одна из пересекающихся плоскостей — проецирующая, по
сравнению с задачей (см. пример 1, рис. 183), в которой обе плоскости
занимают общее положение. В этих случаях появляется возможность
воспользоваться инвариантом (Ф с/3)А(рЧя,)=>Ф'с й0C. поэтому одна
из проекций линии пересечения (/' на рис. 187 и /" на рис. 188) нходит в
состав исходных данных задачи (/' = Л0/з на рис. 187 и Г = fop на рис.
188). Решение сводится к определению недостающей проекции прямой,
принадлежащей плоскости (см. § 41, пример 2, рис. 179).

Пересечение поверхности плоскостью 131
(построение сечения)
§ 45. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
(ПОСТРОЕНИЕ СЕЧЕНИЯ)
При пересечении поверхности или какой-либо геометрической фигу-
фигуры плоскостью получается плоская фигура, которую называют сечением.
Сечение поверхности плоскостью в общем случае представляет со-
собой кривую (или прямую, если пересекаются плоскости), принадле-
принадлежащую секущей плоскости.
Определение проекций линий сечения следует начинать с постро-
построения опорных точек — точек, расположенных на очерковых образу-
образующих поверхности (точки, определяющие границы видимости проек-
проекций кривой); точек, удаленных на экстремальные (максимальное и
минимальное) расстояния от плоскостей проекций. После этого опре-
определяют произвольные точки линии сечения.
Если произвольные точки определяются с помощью одного и то-
того же приема, то для нахождения опорных точек, как правило, при-
приходится пользоваться различными способами.
В дальнейшем при построении сечения поверхности и линии пере-
пересечения поверхностей будет показано нахождение как опорных так и
произвольных точек сечения.
А. Построение сечения многогранников.
Многогранником называют пространственную фигуру, ограничен-
ограниченную замкнутой поверхностью, состоящей из отсеков плоскостей, имею-
имеющих форму многоугольников (в частном случае треугольников).
Стороны многоугольников образуют ребра, а плоскости много-
многоугольников — грани многогранника.
Проекциями сечения многогранников, в общем случае, являют-
являются многоугольники, вершины которых принадлежат ребрам, а сто-
стороны — граням многогранника*. Поэтому задачу по определению сечения
многогранника можно свести к многократному решению задачи по
определению точки встречи прямой (ребер многогранника) с плоскостью
или к задаче по нахождению линии пересечения двух плоскостей (грани
многогранника и секущей плоскости).
Первый путь решения называют способом ребер, второй — спо-
способом граней. Какому из способов следует отдать предпочтенение,
надо решать в каждом конкретном случае.
ПРИМЕР 1. Определить сечение четы- Решение задачи значительно упрощает-
рехгранной призмы ABCDEFGH (рис. 189) ся, если секущая плоскость или плоскос-
плоскостью а(а|| Ь). ти граней (если многогранник относит-
РЕШЕНИЕ. Решаем эту задачу спосо- ся к призмам) занимает проецирующее
бом ребер. Для этого заключаем ребра в положение.
горизонтально проецирующие плоскости ПРИМЕР 2. Определить сечение трех-
TV, 1г, 7з, 7ч :7i 3 (А-Е); 72 ^ (BF); гранной пирамиды SABC горизонтально
7з Э (CG); Уц Э (DH). проецирующей плоскостью Of (рис. 190).
Находим проекции линий пересечения Для получения ответа на посталвен-
этих плоскостей с плоскостью а (прямые ную задачу не требуется никаких допол-
1, 2; 3, 4; 5, 6; 7, 8). Отмечаем точки нительных построений. На основании ин-
пересечения полученных прямых с вариантного свойства 2г (§ 6) горизон-
соответствующими ребрами призмы К = тальная проекция сечения пирамиды
= A, 2) П (АЕ); L = C, 4) П (BF); плоскостью а должна принадлежать сле-
М -= E, 6) П (CG); N= G,8) Л (DH). ДУ плоскости Лор. Поэтому достаточно
Четырехугольник KLMN — искомое се- отметить точки М , N1, L1, в которых го-
чение. ризонтальный след h oa секущей плоское-
*В частном случае многоугольник сечения может проецироваться в отрезок пря-
прямой (см. инвариантное свойство 2г, § 6).

132 Почиционные задачи
К
Рис. 189
В'
Е'
Рис. 190
Рис. 191
ти а пересекает горизонтальные проек-
проекции ребер пирамиды.
Фронтальные проекции вершин треу-
треугольника сечения определяются по их го-
горизонтальным проекциям. Для этого до-
достаточно из точек М\ N', L' провести ли-
линии связи — вертикальные прямые и
отметить точки их пересечения с фрон-
фронтальными проекциями ребер пирамиды.
ПРИМЕР 3. Определить сечение пяти-
пятигранной призмы ABCDE, ребра которой
перепендикулярны горизонтальной плос-
плоскости проекции, секущая плоскость а —
общего положения (рис. 191).
Так как ребра призмы перпендикуляр-
перпендикулярны плоскости 7Г|, то горизонтальные про-
проекции точек пересечения этих ребер с
плоскостью а A', 2', 3', 4', 5') совпада-

ют с горизонтальными проекциями ребер,
т. е. точками Л', В', С", D', Е'.
Фронтальные проекции точек встречи
определяем из условия принадлежности
этих точек плоскости Ос Решение сводит-
сводится к нахождению недостающей проек-
Пересечение поверхности плоскостью 133
(построение сечения)
ции точки, принадлежащей плоскости,
если известна хотя бы одна из ее проек-
проекций (см. §40, пример 3, рис. 171). На
рис. 191 фронтальные проекции точек
1", 2", 3", 4", 5" найдены с помощью
фронтальной плоскости а.
Б. Построение сечения поверхности вращения.
Так как для рассматриваемого круга задач в алгоритме / - (L, и
U L2 U L, U ... U Ln); [Lj = (jj П а) П G;- П /3) ] а — поверхность враще-
вращения, а /3 — плоскость, то для нахождения общих точек Lj, ... , принад-
принадлежащих как поверхности а, так и плоскости /3, целесообразно в качест-
качестве вспомогательных секущих поверхностей 7у принять плоскости, пер-
перпендикулярные к оси вращения; в этом случае плоскости у: будут
пересекать поверхность а по окружностям, а плоскость /3 по линиям
уровня*. Определение точек Lj сводится к нахождению точек пересече-
пересечения прямой с окружностью.
ПРИМЕР. Определить сечения поверх-
поверхности сферы а плоскостью общего поло-
положения 0 (рис. 192).
РЕШЕНИЕ. При сечении поверхности
сферы плоскостью получается окруж-
окружность. Если секущая плоскость общего
положения, то эта окружность проеци-
проецируется на плоскости проекций в виде
эллипсов.
Построения начнем с определения
опорных точек. Для нахождения низшей
А и высшей В точки кривой сечения про-
проводим через центр сферы О вспомогатель-
вспомогательную секущую плоскость 7i -L ^ ор- Точки
А и В принадлежат линии пересечения
плоскостей 7i и 0. Эти точки находят в
результате пересечения прямой A, 2) =
= 7i ^ & с поверхностью а. А и В =
= A, 2) Па. Для их определения вос-
воспользуемся способом замены плоскостей
п2
проекций. Перейдем от системы х к
х]—-. Ось Х| проводим перпендикуляр-
но пор. По отношению к я3 плоскость /3
занимает проецирующее положение, поэ-
поэтому точки А" и В", в которых след
/о0, пересекает новую фронтальную
проекцию очерка сферы а", будут вспо-
вспомогательными проекциями искомых то-
точек. Обратными построениями определя-
определяем положение горизонтальных А', В', а
затем и фронтальных А", В" проекций
искомых точек.
[А'В'] является малой осью (диамет-
(диаметром) горизонтальной проекции эллипса.
Для определения большого диаметра это-
этого эллипса [ D' Е' ] достаточно из вспо-
вспомогательной проекции центра сферы
О" провести прямую, перпендикулярную
к отрезку [А'[В'[]. Точка С'[(С\ С"), в
которой перпендикуляр пересекает [А'{,
В'/], является центром эллипса, че-
через который пройдет сопряженный (боль-
(большой) диаметр эллипса DE.
DE принадлежит горизонтали плоскос-
плоскости 0. Для определения точек D и Е вво-
вводим вспомогательную секущую плос-
плоскость 721 проходящую через точку С
и параллельную плоскости проекций Пу.
Эта плоскость пересекает поверхность
сферы по окружности с, которая проеци-
проецируется на плоскость 771 без искажения в
окружность радиуса R = [ 6" 7"], прове-
проведенную из центра О'. Пересечение этой
окружности с горизонтальной проек-
проекцией горизонтали h 2 определяет положе-
положение горизонтальных проекций точек
D' и Е'. Для нахождения точек F и G, яв-
являющихся граничными точками видимос-
видимости для фронтальной проекции эллипса,
воспользуемся плоскостью 7з II ^2 ¦ Эта
плоскость пересечет поверхность сферы
по главному меридиану, который прое-
проецируется на п2 во фронтальную проек-
проекцию очерка сферы, а плоскость /3 по фрон-
тали f3 (/3 /з ) ¦ Пересечение /э с фронталь-
фронтальной проекции очерка сферы укажет по-
положение точек F" и G".
Для нахождения точек М и JV, указы-
указывающих границы видимости на горизон-
горизонтальной проекции сечения, проводим
плоскость 74 II Т\ G4 3 О).
Плоскость 74 П Д = h 4 , а поверхность
сферы — по окружности, которая проеци-
проецируется на плоскость 7Тt в горизонтальную
проекцию очерка сферы.
¦Имеется в виду, что ось поверхности вращения перпендикулярна плоскос-
плоскости проекции.

134 Позиционные задачи
а.
Рис. 192
Пересечение h\ с горизонтальным очер-
очерком сферы ft' определяет положение ис-
искомых горизонтальных проекции точек
ЛГ и ЛГ
Для определения произвольных точек
/. i и L j, принадлежащих линии сечения,
как правило, целесообразно в качестве
вспомогательной секущей плоскости ис-
использовать плоскости уровня
На рие 192 показано построение то-
точек /- | и /- , с помощью горизонтальной
плоскости 7s Проведя плоскости 7/II ~ч ,
мы каждый раз будем получать окруж-
окружность в результате пересечения у. с и
и прямую — горизонталь при пересече-
пересечении 7/ с A. Пересечения окружностей и
прямых укажут положение горизонталь-
горизонтальных проекций точек, принадлежащих го-
горизонтальной проекции линии сечения
Если задана произвольная поверхность вращения, то ход решения
задачи и последовательность выполнения геометрических построений
ничем не отличается от случая, рассмотренного на рис. 192.
Па рис. 198 показано построение сечения пропзиольной поверхности
вращения а плоскостью общего положения /J. Как и в предыдущем
примере, ьначале определены опорные точки: низшая Л и высшая И;
точки С, I) — границы видимости на фронтальной и точки К. F — на
горизонтальной проекциях. На рис. 193 показано также построение
произвольных точек /,, nL.

Пересечение поверхности плоскостью 135
(построение сечения)
Решение задачи но определении) сечения поверхности вращении а
плоскостью значительно упрощается, если секущая плоскость занима-
занимает проецирующее положение. В лом случае одна из проекций сечения —
отрезок прямой, принадлежит следу плоскости.
Задача по определению второй проекции линии сечения сводится к
многократному решению ранее рассмотренной задачи по нахождению
второй проекции точки, принадлежащей плоскости, если известна хо-
хотя бы одна ее проекция (см. § 40, пример 'Л, рис. 171).
Рис. НИ дает представление о таком частном случае решения ча-
чадачи. Из чертежа видно, что оно проще решений, рассмотренных на
рис:. 192 и 1УЗ. Полому целесообразно при решении задач на опре-
определение сечения поверхности плоскостью предварительно перевести
секущую плоскость в проецирующее положение.
U. Построение сечения поверхности прямого кругового конуса.
Поверхность прямого кругового конуса относится к поверхностям
вращения, но мы рассматриваем ее отдельно, так как она занимает
особое место среди других поверхностей вращения. Эта поверхность
и споем роде уникальна, она служит носителем замечательных кри-
кривых второго порядка: окружности, уллипса, параболы и гиперболы. Роль
и области использования лих кривых в науке и, особенно, технике
невозможно переоценить.
Нее перечисленные кривые являются плоскими и, следовательно,
могут быть получены в результате сечения конической поверхности
плоскостью. В связи с этим перечисленные кривые называют также
коническими сечениями. В частных случаях при определенном положе-
положении секущих плоскостей а3, C2, 7i (см. рис. 195, 196, 197) кривые
Рис. 193
Рис. 194

136 Позиционные задачи
второго порядка распадаются на две прямые (действительные или мни-
мнимые *).
Прежде чем говорить о построении ортогональных проекций сече-
сечения поверхности прямого кругового конуса, отметим существование
теоремы, которой будем пользоваться при построении кривых вто-
второго порядка.
Т е о р е м а: ортогональная проекция плоского сечения поверх-
поверхности прямого конуса на плоскость, перпендикулярную к его оси, пред-
представляет собой кривую второго порядка и имеет одним из своих фо-
фокусов ортогональную проекцию на эту плоскость вершины коничес-
конической поверхности.
Условия, которые должны быть выполнены, чтобы получить ту или
иную кривую второго порядка, при сечении конической поверхности
плоскостью могут быть установлены из свойств кривых второго порядка.
Известно, что эллипс представляет кривую второго порядка, не
имеющую бесконечно удаленных (несобственных) точек. Поэтому,
чтобы получить в сечении конической поверхности эллипс, надо выб-
выбрать такую плоскость, которая пересекает все прямолинейные обра-
образующие этой поверхности. В частном случае, когда диаметры эллип-
эллипса равны (секущая плоскость перпендикулярна к оси конической поверх-
поверхности) , в сечении получается окружность.
Из аффинной геометрии известно, что параболой называется кри-
кривая второго порядка, касающаяся несобственной прямой, или, что
то же самое, кривая, имеющая одну несобственную точку. В связи с
этим для получения параболы необходимо, чтобы секущая плоскость
была параллельно одной образующей конической поверхности. В преде-
пределе, когда секущая плоскость переходит в касательную к поверхности,
две симметричные дуги параболы преобразуются в две полупрямые,
принадлежащие одной прямой.
¦Плоскость A, (рис. 195) пересекает коническую поверхность по двум мнимым
прямым, пересекающимся в собственной точке.
Точка
Окружность
Рис. 195
Рис. 196
Рис. 197

Пересечение поверхности плоскостью J37
(построение сечения)
Рис. 198
И, наконец, гипербола с аффинной точки прения представляет со-
собой кривую второго порядка, пересекающую несобственную прямую,
или, иначе, гипербола — кривая второго порядка, имеющая две не-
несобственные точки, т. е. чтобы получить гиперболу, нужно секущую
плоскость взять параллельной двум прямолинейным образующим.
В частном случае, когда секущая плоскость проходит через вершину
конической поверхности, гипербола распадается на две пересекающи-
пересекающиеся прямые.
На рис. 195 показаны положение секущей плоскости для получения
эллипса (плоскость а,) и окружности (плоскость а2) и одна из плос-
плоскостей, принадлежащих связке, проходящей через вершину конической
поверхности, и пересекающих эту поверхность по двум мнимым пря-
прямым, пересекающимся в действительной точке (плоскость а , ) . На рис.
196 показаны положение секущей плоскости для получения параболы
(плоскость /3,) и плоскость /3), имеющая с конической поверхностью
общуи) прямую (точнее две совпавшие прямые). На рис. 197 изображены
плоскость 7i> пересекающая коническую поверхность по гиперболе, и
плоскость 72, и сечении которой образуются две пересекающиеся пря-
прямые.
На рис. 198 приведены фронтальные проекции поверхности прямо-
прямого кругового конуса, следы фронтально проецирующих секущих плос-
плоскостей и указан вид получаемой в сечении кривой. По рис. 198 можно
установить признаки, обеспечивающие получение в сечении той или иной
кривой второго порядка. Так, если обозначить угол наклона образующей
конической поверхности к его оси через /, а угол между секущей
плоскостью и той же осью через ф", то можно утверждать, что при ф" -'
> <р" (рис. 198,а) в сечении получается -.«шипе (в частном случае, если
ф" -- 90°, окружность), при (р" ф" (рис. 198, .3) —парабола и при у" <
< V?" (рис. 198,в) —гипербола.
Проследим па примерах характер графических построений, кото-
которые должны быть выполнены для построения сечения поверхности
прямого кругового конуса.

138 Позиционные шдачи
ПРИМЕР 1 I loci рои гь проекции сече-
сечении поверхности примою кругоного ко
пуса CJ плоскостып о- (рис I'.)')).
РКШЕНИЕ. Плоское it, (V фронтально
проецирующая. Угол между секущей
плоскоссып и ост,id конической поверх
нос I п / ф оолыпе yi ла наклона (образую
ще*' конической поисрхпос ги к его оси,
[юному в сечеппп получим «ллипс,
попинан ось коюпого |/t/i| будет прое
цнропатьсн па iuioi кость Л> без искаже
ппя н |/\"/i"|, a Miiuaii ось >ллипса CD
(¦проецируется па плоскость /ь в ючку
Г" IV
1> , расноложенпу К! в есредние
отрезка |Л"Л"|. Неличина малой оси
| A>\ определяется па условия (С, D) (
'а Проводим через С)" (фронтальную
||роекцию параллели поверхности ос h".
Для построении ее горизонтальной про
екции цз горизонтальной проекции фо-
фокуса >ллипса .S" п|)оводим окружность
радиусом | 1"| и отмечаем точки ее
пересечения (" и I)' с перпендикуляром,
iiocciaiuicHHbiM и середине |/1'Л'|
горизонтальной проекции большой оси
)ллипс<1. (пая большой и малый диамет-
диаметры зллнпса, изнесшым спосоОом строим
зллинс
ПРИМЕР 2. Па рис 2A0 покачаны про-
проекции цоверхносш прямого кругоного
конуса U1 и фрон la.ubiio проецирун>|це>1
плоскости /i. I loci рои it. проекции липни
сечения.
РЕШЕНИЕ. Угол наклона секущей
плоскости (j к оси конической попсрхпос
ти равен углу наклона прямолинейной
образующей к чюй оси ф° уЗ" . Попому
в сечении получится парабола, вершина
KOiopon епроецируется н точку Л {Л1, Л"),
а горичон ыльнан П|)оекцин фокуса в том
ку .S" (по теореме с. 13в). '.{пая положе-
положение вершины Л' и фокуса .S", проводим
директрису параболы. По данным дирек-
директрисе и фокусу строим параболу. Фрон-
Фронтальная проекция дуги параболы прое
цируесси в [Л"Л"|, совпадающий с
ПРИМЕР -i. Поссроитт. проекции сече
ния поверхности ирлмию кругоного ко
нуса СО плоскоесьн) у (рис 201) .
РЕШЕНИЕ. Так как / V наклона секу
щей плоскости 7 к оси конической по-
поверхности меньше угла наклона образу
ющей конической поверхности / ^",
то плоскость 7 пересечет поверхность
CJ по гиперболе. Фокусы и вершины го
ричонтальной проекции ее нетей опре-
определяются непосредственно из чертежа. (¦
помощью фокусов и вершин строим
асимптоты горизонтальной проекции ги
перболы. Зная положение вершин, фоку
сов и асимптот, можно построить любое
число ючек, принадлежащих ветвям ги
перболы
Рис. l'1'.l
Рис. 201)

Пересечение поверхности плоскостью 139
(построение сечения)
рк;
к'"
Рис. 202
В рассмотренных примерах пересекающая коническую поверхность
плоскость занимала проецирующее положение. Если секущая плос-
плоскость общего положения, то целесообразно с помощью способов преоб-
преобразования перевести ее в проецирующее положение. Это позволит свести
задачу к простейшей — одному из рассмотренных случаев (рис. 199 ...
201).
ПРИМЕР 4. Построить проекции сече
ния конической поверхности О) плос-
плоскостью а (рис. 202).
РЕШЕНИЕ. Чтобы упростить решение
задачи, осуществим замену плоскости я2
ноьой плоскостью Я;. Плоскость Яз вь1'
бираем так, чтобы по отношению к ней
секущая плоскость а :>аннла проециру-
проецирующее положение, ('проецируем на плос-
плоскость эт.1 коническую поверхность со.
Выполненные преобразования позволили
свести решение к случаю, рассмотренно-
рассмотренному ранее (см. пример 1, рис. 199) .
Для построения фронтальной проек
ции -эллипса сечения на рис. 202, кроме
точек А, В и С, I), на вспомогательной
проекции взяты точки ?, F и М, /V, го-
горизонтальные и фронтальные проекции
этих точек определены с помощью го-
горизонталей h : и/i]. Кроме опорных то-
точек А и В, являющихся высшей (й) и
низшей (А) точками сечения, на рис. 202
показаны точки Р и L, принадлежащие
фронтальным проекциям очерковых об-
образующих конической поверхности со.
Jth точки служат границей видимости
для фронтальной проекции сечения. Для
нахождения точек I'" и L" пользуемся
фронталью f.

140 Позиционные задачи
§ 46. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ
Касательные плоскости играют большую роль в геометрии. По-
Построение касательных плоскостей в практическом отношении имеет
важное значение, так как наличие их позволяет определить направле-
направление нормали к поверхности в точке касания. Эта задача находит широкое
применение в инженерной практике. К помощи касательных плоскостей
обращаются также для построения очерков геометрических фигур,
ограниченных замкнутыми поверхностями. В теоретическом плане
плоскости, касательные к поверхности, используются в дифференциаль-
дифференциальной геометрии при изучении свойств поверхности в районе точки касания.
Основные понятия и определения
Плоскость, касательную к поверхности, следует рассматривать как
предельное положение секущей плоскости (по аналогии с прямой, каса-
касательной к кривой, которая также определяется как предельное положе-
положение секущей).
Плоскость, касательная к поверхности в заданной на поверхности
точке, есть множество всех прямых — касательных, проведенных к
поверхности через заданную точку.
В дифференциальной геометрии доказывается, что все касательные
к поверхности, проведенные в обыкновенной точке, компланарны
(принадлежат одной плоскости).
Выясним, как проводится прямая, касательная к поверхности. Каса-
Касательная / к поверхности 0 в заданной на поверхности точке М (рис. 203)
представляет предельное положение секущей 1}, пересекающей поверх-
поверхность в двух точках [ММ,, ММ2, ..., ЛШ„), когда точки пересечения
совпадают (М ¦- Мп, ln = tM). Очевидно (м,, М.,, ..., Мп\ с g, так как
g С E. Из сказанного выше вытекает следующее определение:
касательной к поверхности называется прямая, касательная к какой-
либо кривой, принадлежащей поверхности.
Так как плоскость определяется двумя пересекающимися прямыми,
то для задания плоскости, касательной к поверхности в заданной точке,
достаточно провести через эту точку две произвольные линии, принадле-
принадлежащие поверхности (желательно простые по форме), и к каждой из них
построить касательные в точке пересечения этих линий. Построенные
касательные однозначно определяют касательную плоскость. Наглядное
представление о проведении плоскости а, касательной к поверхности 0 в
заданной точке М, дает рис. 204. На
этом рисунке показана также нор-
нормаль п к поверхности /3.
а
Рис. 203
Рис. 204

, касательная к поверхности 141
Рис. 205
Рис. 206
к поверхности в заданной точке наливается прямая, пер-
перпендикулярная к касательной плоскости и проходящая через точку
касания.
Линию пересечении поверхности плоскостью, проходящей через нор-
нормаль, называют нормальным сечением поверхности. В зависимости
от вида понерхности касательная плоскость может иметь с поверх-
ностью как одну, гак и множество точек (линию). Линия касания мо-
может быть в то же время и линией пересечения поверхности с плоскостью.
Возможны также случаи, когда на поверхности имеются точки, в
которых невозможно провести касательную к поверхности; такие
точки называют особыми. В качестве примера особых точек можно
привести точки, принадлежащие ребру возврата торсовой поверхнос-
поверхности, или точку пересечения меридиана поверхности вращения с ее осью,
если меридиан и ось пересекаются не под прямым углом.
Виды касания зависят от характера кривизны поверхности.
Кривизна поверхности
Вопросы кривизны поверхности были исследованы французским
математиком Ф. Дюпеном A784— 1873), который предложил нагляд-
наглядный способ изображения изменения кривизны нормальных сечений
поверхности.
Для зтого в плоскости, касательной к рассматриваемой поверхности
в точке М (рис. 205, 206), на касательных к нормальным сечениям по
обе стороны от данной точки откладываются отрезки, равные корням
квадратным из величин соответствующих радиусов кривизны этих
сечений. Множество точек — концов отрезков задают кривую, называе-
называемую индикатрисой Дюпена. Алгоритм построения индикатрисы Дюпена
(рис. 205) можно записать:
\MN)Cyn;
W", -
1. Af e a, M ? |3 Л a
2. [MiV)ia, [MN) 1 0;
3. [MiV)c 7l, [MN)C 7:, .
4.7, ПД = /,, 72 nj = /j,
6. [ш, ] - \/^t;! [ma2] =;
где Д — радиус кривизны.
(Л, U Л2 и ... и Л„) — индикатриса Дюпена.

142 Позиционные задачи
Рис. 207
Рис. 208
N
Рис. 209
Если индикатриса Дюпена поверхности — эллипс, то точка М на-
называется эллиптической, а поверхность — поверхностью с эллипти-
эллиптическими точками (рис. 206). В этом случае касательная плоскость имеет
с поверхностью только одну общую точку, а все линии, принадлежащие
поверхности и пересекающиеся в рассматриваемой точке, расположены
по одну сторону от касательной плоскости. Примером поверхностей с
эллиптическими точками могут служить: параболоид вращения, эллип-
эллипсоид вращения, сфера (в этом случае индикатриса Дюпена — окружность
и др.).
При проведении касательной плоскости к торсовой поверхности
плоскость будет касаться этой поверхности по прямой образующей.
Точки этой прямой называются параболическими, а поверхность ~
поверхностью с параболическими точками. Индикатриса Дюпена в этом
случае — две параллельные прямые (рис. 207*).
На рис. 208 показана поверхность, состоящая из точек, в кото-
*Кривая второго порядка — парабола — при определенных условиях можот распа-
распадаться на две действительные параллельные прямые, две мнимые параллельные
прямые, две совпадающие прямые. На рис. 207 мы имеем дело с двумя действитель-
действительными параллельными прямыми.

Плоскость, касательная к поверхности 143
рых касательная плоскость пересекает поверхность. Такая поверх-
поверхность называется гиперболической, а принадлежащие ей точки — ги-
гиперболическими точками. Индикатриса Дюпена в данном случае — гипер-
гипербола.
Поверхность, все точки которой являются гиперболическими, имеет
форму седла (косая плоскость, однополостный гиперболоид, вогнутые
поверхности вращения и др.).
Одна поверхность может иметь точки разных видов, например, у
торсовой поверхности (рис. 209) точка М эллиптическая; точка N —
параболическая; точка К — гиперболическая.
В курсе дифференциальной геометрии доказывается, что нормальные сечения,
в которых величины кривизны Kj — l/Rj (где Rj радиус кривизны рассматрива-
рассматриваемого сечения) имеют экстремальные значения, расположены в двух взаимно перпен-
перпендикулярных плоскостях.
Такие кривизны К", - 1/Дтах, К2 = 1/ Wrnin называются главными, а значения
И — (К\ + К2)/2 и К = К^К2 ~ соответственно средней кривизной поверхности и
полной (гауссовой) кривизной поверхности в рассматриваемой точке. Для эллипти-
эллиптических точек К > 0, гиперболических К < 0, параболических К = 0.
Задание плоскости касательной к поверхности
на эпюре Монжа
Ниже на конкретных примерах покажем построение плоскости, ка
сательной к поверхности с эллиптическими (пример 1), параболичес-
параболическими (пример 2) и гиперболическими (пример 3) точками.
ПРИМЕР 1. Построить плоскость а,
касательную к поверхности вращения /3,
с эллиптическими точками. Рассмотрим
два варианта решения этой задачи, а) точ-
каМб^иб) точка M^ji.
Вариант а (рис.210).
Касательная плоскость определяется
двумя касательными (, и t2, проведен-
проведенными в точке М к параллели и меридиа-
меридиану поверхности р\
Проекции касательной 11 к параллели
h поверхности (i будут t\ I (S'M1) и
t" || оси х. Горизонтальная проекция ка-
касательной t'2 к меридиану d поверхности
C, проходящему через точку М, совпадет
с горизонтальной проекцией меридиа-
меридиана. Чтобы найти фронтальную проекцию
касательной t'2\ меридиональную плос-
плоскость 7G "^ М) путем вращения вокруг
оси поверхности |3 переводим в положе-
положение 7i, параллельное плоскости ff2. В
этом случае точка М ~* М| (М\ , М'[).
Проекция касательной
'/"
t'2\ определя-
определяр i 2\ р
ется (M'/S"). Если мы теперь возвратим
плоскость 7i в первоначальное положе-
положение, то точка S" останется на месте (как
принадлежащая оси вращения), а М'[ -*
* М" и фронтальная проекция касатель-
касательной t2 определится (M"S").
Две пересекающиеся в точке М ? C
касательные I, и 12 опре-деляют плос-
плоскость а, касательную к поверхности C.
Вариант б (рис.211)
Для построения плоскости, касатель-
касательной к поверхности проходящей через
точку, не принадлежащую поверхности,
нужно исходить из следующих сообра-
соображений: через точку вне поверхности,
состоящей из эллиптических точек, мож-
можно провести множество плоскостей, каса-
касательных к поверхности. Огибающей этих
поверхностей будет некоторая коничес-
коническая поверхность. Поэтому, если нет до-
дополнительных указаний, то задача имеет
множество решений и в таком случае
сводится к проведению конической по-
поверхности 7> касательной к данной по-
поверхности C.
На рис. 211 показано построение ко-
конической поверхности 7. касательной к
сфере р1. Любая плоскость а, касательная
к конической поверхности 7. будет ка-
касательной к поверхности р\
Для построения проекций поверхнос-
поверхности 7 из точек М' и М" проводим каса-
касательные к окружностям h' и f" — про-
проекциям сферы. Отмечаем точки касания
1 A' и 1"), 2 B' и 2"), 3 C' и 3") и
4 D' и 4 ). Горизонтальная проекция
окружности -линия касания конической
поверхности и сферы спроецируется в
[ l^'l Для нахождения точек эллипса, в
который эта окружность спроецируется
на фронтальную плоскость проекций,
воспользуемся параллелями сферы.
На рис. 211 таким способом опреде-
определены фронтальные проекции точек Е и F
(Е" и F"). Имея коническую поверхность
7, строим к ней касательную плоскость а.
Характер и последовательность графичес-

144 Позиционные задачи
М,
Рис. 210
и"
Рис. 212
Рис. 211
ких построений, которые необходимо
для этого выполнить, приведены в сле-
следующем примере.
ПРИМЕР 2. Построить плоскость а, ка-
касательную к поверхности /3 с параболи-
параболическими точками.
Как в примере 1, рассмотрим два ва-
варианта решении: а) точка N ?= C; б) точ-
точка N^fi.
Вариант а (рис.212).
Коническая поверхность относится к
поверхностям с параболическими точка-
точками (см. рис. 207). Плоскость, касатель-
касательная к конической поверхности, касается
ее по прямолинейной образующей. Для
ее построения необходимо:
1) через данную точку N провести
образующую SN (S'N' и S"N") ;
2) отметить точку пересечения обра-
образующей {SN) с направляющей d.
(SN) C\d = A;
3) провести касательную t к d в точ-
точке А.
Образующая (SA) и пересекающая ее
касательная ( определяют плоскость а,
касательную к конической поверхности /3
в данной точке N*.
Вариант б (рис.213).
Для проведения плоскости а, каса-
касательной к конической поверхности /3 и
проходящей через точку N, не принадле-
*Так как поверхность |3 состоит из параболических точек (кроме вершины S), то
касательная к ней плоскость а будет иметь общую с ней не одну точку N, а прямую
(SN).

Плоскость, касательная к поверхности 145
жащую заданной поверхности, необхо-
необходимо:
1) через данную точку N и вершину S
конической поверхности /3 провести пря-
прямую а (а' и а") ;
2) определить горизонтальный след
этой прямой Иа;
3) через На провести касательные
t\ и t\ к кривой h O0 — горизонтальному
следу конической поверхности;
4) точки касания А (А1 и А") и В (В1
и В") соединить с вершиной конической
поверхности S (S'nS").
Пересекающиеся прямые tlt (AS) и
t2, (BS) определяют искомые касатель-
касательные плоскости tt| и а2
ПРИМЕР 3. Построить плоскость а, ка-
касательную к поверхности /3 с гиперболи-
гиперболическими точками.
Точка К (рис. 214) находится на по-
поверхности глобоида (внутренняя поверх-
поверхность кольца).
Рис. 214

146 Позиционные задачи
Рис. 215
Для определения положения касательной
плоскости а необходимо:
1) провести через точку К параллель
поверхности/3 h(h , h") ;
2) через точку К' провести касатель-
касательную t\ (f» =/,");
3) для определения направлений про-
проекций касательной к меридиональному
сечению необходимо провести через точ-
точку К и ось поверхности плоскость у, го-
горизонтальная проекция t'2 совпадет с
h o7; для построения фронтальной проек-
проекции касательной t'{ предварительно пере-
переведем плоскость 7 путем вращения ее
вокруг оси поверхности вращения в по-
положение у{ II Яг- В этом случае меридио-
меридиональное сечение плоскостью у совместит-
совместится с левой очерковой дугой фронтальной
проекции — полуокружностью g".
Точка К (К1, К"), принадлежащая
кривой меридионального сечения, пере-
переместится в положение К\ (К[, К'{) . Че-
Через К" проводим фронтальную проекцию
касательной B в совмещенном с плос-
плоскостью 7i II ^г положении и отмечаем
точку ее пересечения с фронтальной про-
проекцией оси вращения S". Возвращаем
плоскость 7i B исходное положение, точ-
точка К" -> К" (точка S" = S"). Фронтальная
проекция касательной 1'{ определится
точками К" и S".
Касательные <| и ti определяют иско-
искомую касательную плоскость я, которая
пересекает поверхность /J по кривой / .
ПРИМЕР 4. Построить плоскость а, ка-
касательную к поверхности /5 в точке К.
Точка К находится на поверхности од-
нополостного гиперболоида вращения
(рис. 215).
Эту задачу можно решить, придержи-
придерживаясь алгоритма, использованного в пре-
предыдущем примере, но учитывая, что по-
поверхность однополостного гиперболоида
вращения является линейчатой поверх-
поверхностью, которая имеет два семейства
прямолинейных образующих, причем
каждая из образующих одного семейст-
семейства пересекает все образующие другого
семейства (см. § 32, рис. 138). Через
каждую точку этой поверхности можно
провести две пересекающиеся прямые —
образующие, которые будут одновремен-
одновременно касательными к поверхности одно-
однополостного гиперболоида вращения.

Построение пинии пересечения поверхностей 147
(общий случай)
Эти касательные определяют касатель- тальной проекции окружности A\ — гор-
горную плоскость, т. с. плоскость, касатель- ла поверхности однополостного гипербо-
ная к поверхности одноподостного гипор- лрида вращении; определить точки Г и
Гюлоида нращенин, пересекает >ту понерх- 2 , F) которых l\ и t'2 пересекают одну и-л
ность по двум прямым #, и А'2- Для напраиляютих поверхности с/,. По Г и
построения проекций них прямых моста- 2' находим 1" и 2", которые совместно
точно ич горизонтальной проекции точки е К" определяют фронтальные проекции
К принести касательные 1\ и t\ к i оричон- искомых прямых.
§ 47. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
(ОБЩИЙ СЛУЧАЙ)
В алгоритме для решения задач на построение линии пересечения
двух поверхностей / (L, и /,2 и ЬЛ и ... и Ln); | G; Па) П (т^пр1)]
в качестве вспомогательной поверхности (посредника) jj следует вы-
выбирать поверхности, которые пересекали бы заданные поверхности а
и /3 по наиболее простым для построения линиям — прямым или окруж-
окружностям.
В качестве вспомогательных поверхностей — посредников наиболее
часто используются плоскости и сферы; при решении некоторых задач
бывает целесообразно обращаться за помощью к цилиндрическим и
коническим поверхностям.
Ниже будет показано решение задач на определение линии пересече-
пересечения поверхностей с помощью вспомогательных секущих плоскостей
(§ 48), цилиндрических (§ 49), конических (§ 50), а также сфери-
сферических (§ 51) поверхностей.
Прежде чем решить вопрос, какую вспомогательную секущую по-
поверхность выбрать для построения линии пересечения поверхностей,
следует выяснить, не занимает ли одна из пересекающихся поверхнос-
поверхностей проецирующее положение, так как в данном случае решение по-
поставленной задачи значительно упрощается. Это происходит из-за то-
того, что одна из проекций линии пересечения будет совпадать со сле-
следом проецирующей поверхности, которая входит в условия постав-
поставленной задачи (см. инвариантное свойство 2г, § 6).
Поэтому решение сводится к определению недостающей проекции
линии, принадлежащей поверхности, если известна одна ее проекция
и указаны проекции поверхности (см. § 41, пример 1, рис. 178).
Рис. 216 иллюстрирует решение задачи по определению линии / =
= аПр\ при этом 0 1 я | . Зелеными линиями показано построение фрон-
фронтальной проекции /" — линии пересечения сферической поверхности а с
поверхностью горизонтально проецирующего прямого кругового цилинд-
цилиндра (i. Точка А, принадлежащая линии пересечения поверхностей и являю-
являющаяся ближайшей к вертикальной оси i поверхности сферы, одновремен-
одновременно будет высшей точкой А" на фронтальной проекции кривой /". Точка
Б" — крайняя правая на линии пересечения является также границей
видимости кривой I".
На рис. 217 показано определение горизонтальной проекции /' —
линии пересечения произвольной конической поверхности а с фрон-
фронтально проецирующей цилиндрической поверхностью /3. В этом случае,
как и в предыдущем примере, задача на построение линии пересечения
поверхностей сводится к определению недостающей проекции линии I,
принадлежащей поверхности а. Все построения, необходимые для нахож-
нахождения точек А', В', С', ... кривой I' по заданным точкам А", В", С", ..., вы-
выполнены зелеными линиями и не нуждаются в дополнительных пояс-
пояснениях.

148 Позиционные задачи
¦07,
Рис. 216
Рис. 217
§ 48. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
С ПОМОЩЬЮ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ
При определении линии пересечения поверхностей пользуются не
отдельными плоскостями, а пучками плоскостей, причем ось пучка
может быть как собственной, так несобственной прямой.
Рассмотрим каждый из этих вариантов в отдельности.
1. Определение линии пересечения поверхностей с помощью пучка
плоскостей, ось которого — собственная прямая.
Этот способ применяется для построения линии пересечения:
а) двух конических поверхностей;
б) конической и цилиндрической поверхностей;
в) конической поверхности с поверхностью пирамиды или призмы;
г) двух цилиндрических поверхностей;
д) цилиндрической поверхности с поверхностью пирамиды или приз-
призмы.
Сущность способа легко проследить на примере решения задачи
по определению линии пересечения двух произвольных конических по-
поверхностей а и /3 (рис. 218).
Раньше (см. § 45, рис. 198,в) было установлено, что коническая
поверхность пересекается плоскостью по двум пересекающимся прямым
образующим в том случае, если секущая плоскость проходит через верши-
вершину конической поверхности. Поэтому, если через вершины S, и S2 кони-
конических поверхностей а и /3 провести прямую а и заключить ее в плос-
плоскость 7), то эта плоскость пересечет поверхность а. по прямым (St 1),
(St 2) и поверхность C по прямым (S2 3), (S2 4). Эти прямые пересека-
пересекаются в точках А, В, С, D, принадлежащих искомой линии пересечения.

Построение линии пересечения поверхностей с помощью 149
вспомогательных секущих плоскостей
Повернув вокруг прямой а плоскость 7> на L у° t получим новое по-
положение секущей плоскости 71 • Плоскость у i также пересечет поверх-
поверхности аир по прямым, которые, в свою очередь, пересекаются в точках,
также принадлежащих линии пересечения. Поворачивая плоскость т/
вокруг прямой а , мы будем получать различные положения секущих
плоскостей и соответствующие им прямые линии их пересечения с задан-
заданными поверхностями*.
При построении проекций линий пересечения поверхностей на эпю-
эпюре в первую очередь необходимо определить опорные точки, которые
получаются при сечении поверхностей а и 0 плоскостями, касательными
к одной, в частном случае к двум, пересекающимся поверхностям.
На рис. 218 показаны плоскость у2, проходящая через прямую а и
касательная к поверхности а, и плоскость у3, также проходящая через
прямую а и касательная к поверхности 0.
Горизонтальные следы этих плоскостей hOy2 и h 0Уз определя-
определяют L hOy2 HahQy3, в пределах которого следует проводить горизон-
горизонтальные следы вспомогательных секущих плоскостей. С помощью плос-
плоскостей 7у и 7i можно определить четыре точки, принадлежащие линии
пересечения. На рис. 218 показаны две точки Е и F, полученные с по-
помощью плоскости 7у •
На рис. 219 приведен пример определения положения прямой а , че-
через которую должны проходить вспомогательные секущие плоскос-
плоскости, с помощью которых можно найти точки, принадлежащие линии пе-
пересечения конической и цилиндрической поверхностей.
Решение этой задачи по существу не отличается от только что рас-
рассмотренного примера. Действительно, цилиндрическая поверхность
отличается от конической тем, что точка S (вершина конической поверх-
поверхности) у цилиндрической поверхности оказывается несобственной
точкой Soo. В этом случае прямая а , проходящая через точки S и S»,
"Поэтому описываемый способ
кости.
называют также способом вращающейся плос-
Рис. 218

150 Позиционные задачи
Рис. 219
будет параллельна образующей цилиндрической поверхности. Все осталь-
остальные построения ничем не отличаются от рассмотренных в предыдущем
примере (см. рис. 218).
В качестве примера использования пучка плоскостей для определе-
определения линии пересечения двух поверхностей по заданным их ортогональ-
ортогональным проекциям рассмотрим следующую задачу.
ПРИМЕР. Построить линию пересече-
пересечения двух конических поверхностей а и /3
(рис. 220).
РЕШЕНИЕ.
1. Через вершины конических поверх-
поверхностей Si и S2 проводим прямую а .
2. Определяем горизонтальный след
прямой а — На.
3. Заключаем прямую а во вспомога-
вспомогательную секущую плоскость f\, каса-
касательную к конической поверхности а. От-
Отмечаем прямые (S2 2), (S2 3) и (Sil),
по которым эта плоскость пересекает по-
поверхность 0, и касается поверхности а.
4. Отмечаем точки MY и Мг, принад-
принадлежащие искомой линии пересечения
М, = (S,l)n(S22) и М2 = (S, 1)П
П (S2 3).
5. Через прямую а проводим плос-
плоскость 7г. касательную к конической по-
поверхности /3. Находим прямые (Si 4),
(S! 5) и (S2 6) и отмечаем точки L j и L 2
их взаимного пересечения.
На рис. 220 показано также определе-
определение точек К], K<i и Л/|, N2 с помощью
вспомогательной секущей плоскости Jj.
Соединив в определенной последователь-
последовательности плавными линиями одноименные
проекции точек, получим проекции иско-
искомой кривой пересечения данных поверх-
поверхностей.
2. Определение линии пересечения поверхностей с помощью пучка
плоскостей, ось которого— несобственная прямая.
Этот способ является частным случаем предыдущего. Отличие сос-
состоит лишь в том, что прямая а — несобственная, она проходит через
несобственные точки St „ и S2«, .
Рис. 221 иллюстрирует наглядную геометрическую модель рассмат-
рассматриваемого способа. Чтобы выбрать наиболее рациональное положение
вспомогательной секущей плоскости для определения линии пересечения
двух произвольно расположенных цилиндрических поверхностей, доста-
достаточно представить заданные цилиндрические поверхности как образован-
образованные из конических поверхностей с вершинами в несобственных точках

Построение линии пересечения поверхностей с помощью 151
вспомогательных секущих плоскостей
¦S,,» и S2» . Поэтому семейство секущих плоскостей будет составлять
пучок параллельных плоскостей, проходящих через несобственную
прямую а^ (Sloo S2°° ). Для определения направления горизонтальных
следов плоскостей этого пучка достаточно из произвольной точки прост-
пространства Т провести две прямые: s, , параллельную образующей илиндри-
ческой поверхности а, и s2, параллельную образующей цилиндрической
поверхности /3. Эти пересекающиеся прямые определят направление
вспомогательных секущих плоскостей у, которые пересекают поверх-
поверхности а и /3 по прямым линиям.
Проведя плоскость 7у, параллельную 7, мы получим две прямые, по
которым плоскость 7у пересекает поверхность а, и две прямые при
ее пересечении с поверхностью /3. Взаимное пересечение этих прямых
укажет четыре точки А, В и С, D, принадлежащие линии пересечения.
Для нахождения опорных точек, как и в предыдущем примере,
проводим плоскости 7i и 72 соответственно касательные к поверхнос-
поверхностям а и /3. С помощью этих плоскос-
плоскостей находим точки Мх, Мг и Nx,
N2. Положение горизонтальных сле-
следов h оу 1 и h 0У2 определяют
область (полосу), внутри которой
следует проводить вспомогатель-
вспомогательные секущие плоскости для опре-
определения общих точек, принадле-
принадлежащих линии пересечения.
н'
Рис. 220

152 Позиционные задачи
7, У:
"У,
Рис. 221
Использование семейства вспомогательных секущих плоскостей,
взятых из пучка плоскостей с несобственной осью, для определения
на эпюре Монжа линии пересечения двух поверхностей проследим на
следующем примере.
ПРИМЕР. Определить линию пересече-
пересечения двух произвольно расположенных
эллиптических цилиндрических поверх-
поверхностей а и 0 (рис. 222).
РЕШЕНИЕ.
1. Определяем направление вспомога-
вспомогательных секущих плоскостей. Для этого
через произвольную точку пространства
Т проводим прямые s, и s2, параллель-
параллельные образующим данных цилиндричес-
цилиндрических поверхностей а и (}. Горизонтальные
следы этих прямых HSl и HSi определя-
определяют след вспомогательной секущей плос-
плоскости у.
2. Проводим секущую плоскость 7i ,
параллельную плоскости 7 и касательную
к поверхности |3. Эта плоскость пересе-
пересечет цилиндрическую поверхность а по
прямым (Sloo I), (Si ос 2) и будет касать-
касаться поверхности C по прямой (S2.»3).
Взаимное пересечение этих прямых ука-
укажет точки Af 1 и Мг, принадлежащие ис-
искомой линии пересечения.
3. Проводим плоскость 72 ¦ параллель-
параллельную плоскости 7 и касательную к поверх-
поверхности а. Мы вновь получим две прямые
(S2oo 5) и (S2oo6), по которым плос-
плоскость 72 пересекает поверхность fi. Плос-
Плоскость 7г пересечет (коснется) поверх-
поверхность а по прямой (S|oo4). Получен-
Полученные прямые пересекаются в точках Nt
и N2.
На рис. 222 показано также построе-
построение точек К\, К2 и L|, L2 с помощью
вспомогательной секущей плоскости yj и
точек А 1, А 2, В,, В2 и С,, С2, Dx> D2, най-
найденных при помощи плоскостей 7л и 74 ¦
Способ параллельных секущих плоскостей можно использовать для
определения линии пересечения и в том случае, когда эти плоскости пере-
пересекают заданные поверхности не только по прямым, но и по окруж-
окружностям или комбинации из этих • линий (одну поверхность плоскость
пересекает по прямой, другую — по окружности) *.
Примером может служить пересечение сферической и цилиндри-
цилиндрической поверхностей.
ПРИМЕР. Определить линию пересече-
ния поверхности эллиптического цилинд-
ра а с поверхностью сферы 0 (рис. 223).
РЕШЕНИЕ.
1. Проводим в интервале между точ-
ками 1' и 2' вспомогательные секущие
¦Плоскость можно использовать и в том случае, когда она пересекает поверх-
поверхности по произвольным кривым линиям.

Построение линии пересечения поверхностей с помощью \ S3
ааюмагательных секущих плоскостей
Рис. 222
плоскости 7i, 7г > 7з. 74 > 7s > параллель-
параллельные фронтальной плоскости проекции эт2 •
Каждая из этих плоскостей пересечет ци-
цилиндрическую поверхность по прямоли-
прямолинейным образующим, а поверхность сфе-
сферы по окружностям.
2. Плоскости 7i и 7s > параллельные
я2 и касательные к цилиндрической по-
поверхности, укажут прямые а и 6, кото-
которые будут содержать опорные точки
А, А\ и В, В1— дальние А, А ( и ближ-
ближние В, В\ по отношению к плоскости
Яг точки кривой пересечения.
3. Для определения высшей Mt и низ-
низшей N точек линии пересечения проводим
плоскость 74 > проходящую через центр
поверхности сферы. Эта плоскость пере-
пересечет сферу по главному меридиану.
4. С помощью плоскости 7.1. проведен-
проведенной через ось цилиндрической поверхнос-
поверхности, определяем точки Е, Е\ и F, F, , ука-
указывающие границы видимости линии пе-
пересечения на фронтальной проекции.
На рис. 223 показано построение про
извольных точек, принадлежащих линии
пересечении, с помощью плоскости у2.
проведенной в полосе, ограниченной
плоскостями 71 и 7s ¦

154 Позиционные задачи
Ку.
hoy.
hy.
Рис. 223
§ 49. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
С ПОМОЩЬЮ ВСПОМОГАТЕЛЬНЫХ ЦИЛИНДРИЧЕСКИХ
ПОВЕРХНОСТЕЙ
В тех случаях, когда требуется построить линию пересечения двух
поверхностей, из которых одна — линейчатая цилиндрическая, а дру-
другая — произвольная поверхность вращения, целесообразно в качест-
качестве поверхностей-посредников использовать цилиндрические поверх-
поверхности.
На рис. 224 показано решение задачи по определению линии пере-
пересечения поверхности эллиптического цилиндра а и поверхности коль-

Построение линии пересечения поверхностей с помощью 155
вспомогательных цилиндрических поверхностей
ца C. В данном примере в качестве вспомогательных секущих поверх-
поверхностей целесообразно использовать поверхности эллиптических цилинд-
цилиндров, оси которых параллельны оси заданной цилиндрической поверх-
поверхности а. За направляющие цилиндрических поверхностей следует при-
принять окружности — параллели кольцевой поверхности C.
Определение точек, принадлежащих линии пересечения поверхнос-
поверхностей а и /3, осуществляется следующим путем:
1. Пересекаем поверхность кольца плоскостями е,, е2, е3, ..., па-
параллельными плоскости 7г, . Полученные в сечении окружности сх, с2,
с3, ... принимаем за направляющие цилиндрических поверхностей 7i, 7 2,
7э, •¦•
2. Определяем горизонтальные следы этих поверхностей hoyi, hOy2 ,
Л on > ••• и отмечаем точки пересечения этих следов с горизонтальным
следом заданной цилиндрической поверхности h Oa-
3. Через полученные точки проводим прямолинейные образующие
g\, gi, ?з> #4, gs, gb, по которым поверхности 7i , 7г» 7з> ¦•• пересекают
данную поверхность а.
4. Точку i\ принимаем за центр окружностей — горизонтальных
проекций линий пересечения поверхности кольца плоскостями е,, е2,
5. Отмечаем точки /', 2', 3\ 4', 5', 6' пересечения этих окружностей
с соответствующими прямолинейными образующими цилиндрической
Гис. 224

156 Позиционные задачи
поверхности а. Зная положение точек /', 2' 3', ..., определяем их фрон-
фронтальные проекции 1", 2", 3", ...
Отмеченным путем можно провести любое количество вспомога-
вспомогательных цилиндрических поверхностей и с их помощью определить
достаточное число точек, необходимых для построения линии пересе-
пересечения поверхностей а и /3.
§ 50. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
С ПОМОЩЬЮ ВСПОМОГАТЕЛЬНЫХ КОНИЧЕСКИХ ПОВЕРХНОСТЕЙ
Использование вспомогательных конических поверхностей для упро-
упрощения построения линии пересечения двух поверхностей дает поло-
положительный эффект лишь в том случае, если мы для получения вспо-
вспомогательной проекции воспользуемся центральным проецированием,
приняв за центр проекции вершину конической поверхности S.
В этом случае любая коническая поверхность, принадлежащая связ-
связке конических поверхностей, вершины которых принадлежат точке
S — центру связки, займет проецирующее положение относительно
плоскости проекции, что даст возможность так же, как это было сде-
сделано при использовании плоскостей и цилиндрических поверхностей
(§ 48 и 49), базироваться на инвариантном свойстве 2г*ФС 7 А (у L
1 я, ) => Ф' ch „7 и благодаря этому упростить решение задачи.
Построение линии пересечения поверхностей с помощью коничес-
конических поверхностей целесообразно в тех случаях, когда одна из пере-
пересекающихся поверхностей коническая, а другая поверхность враще-
вращения.
Например, если заданы поверхность вращения и произвольная
коническая поверхность, то для определения линии их пересечения
следует воспользоваться вспомогательными коническими поверхнос-
поверхностями, вершины которых совпадают с вершиной заданной конической
поверхности, а за направляющие этих поверхностей принять окружности,
проведенные на поверхности вращения.
На рис. 225 показано решение задачи на построение линии пере-
пересечения поверхности вращения с конической поверхностью.
Геометрические построения, которые необходимо осуществить
для определения линии пересечения, выполняем в следующем порядке:
1) на поверхности вращения а проводим ряд окружностей с,, с2)
с3, ..., которые можно рассматривать как результат пересечения по-
поверхности а пучком плоскостей [е ...] , параллельных плоскости ttj ;
2) принимаем эти окружности за направляющие конических поверх-
поверхностей 7i, 72. 7з> ••• с вершиной в точке S. Горизонтальными следа-
следами этих поверхностей^ будут окружности h 07l, h 0y2, йо7з> ••¦> ПР°"
веденные из центров 2\ 7', 12'..., радиусами, соответственно равными
фронтальным проекциям отрезков | 2", 3"|, | 7", 8"\ ,\ 12", 13"\ ;
3) определяем прямые (S'4'), (S'5'), (S'9'), (S"lO'), E*14'), (?15'),
по которым вспомогательные секущие поверхности у{, у2, уъ пересека-
пересекают заданную коническую поверхность 0;
"Инвариантное свойство 2г, сформулированное относительно плоскости при
ортогональном проецировании, будет справедливым и для конической поверх-
поверхности, если использовать центральнЮе проецирование.

Построение линии пересечения поверхностей с помощью 157
вспомогательных конических поверхностей
4) отмечаем точки пересечения этих прямых с соответствующими
окружностями. Точки А, В, С, D, E, F принадлежат искомой линии
пересечения.
На рис. 225 показано также определение высшей L и низшей К точек,
принадлежащих линии пересечения. Положение этих точек найдено с
помощью горизонтально проецирующей плоскости f, проходящей через
вершину конической поверхности S и ось i поверхности вращения а.
Плоскость f пересечет коническую поверхность по образующей ST, а по-
поверхность вращения по меридиану g. Для определения точек пересече-
пересечения меридиана g с образующей ST вращаем плоскость f, которой принад-
принадлежат эти точки, вокруг оси, перпендикулярной к я, и проходящей через
вершину конуса S, до положения, параллельного плоскости я2. Находим
фронтальные проекции точек К" и L", а затем К" и L". Зная положение
К' и L", определяем их горизонтальные проекции К' и L'. Соединив одно-
одноименные проекции полученных точек плавной кривой, получим проек-
проекции линии пересечения заданных поверхностей.
S"
Рис. 225

158 Позиционные задачи
§ 51. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
С ПОМОЩЬЮ СЕМЕЙСТВА ВСПОМОГАТЕЛЬНЫХ СФЕРИЧЕСКИХ
ПОВЕРХНОСТЕЙ
Для определения линии пересечения двух произвольных поверх-
поверхностей вращения целесообразно воспользоваться одним свойством,
присущим поверхностям вращения, которое состоит в том, что две лю-
любые соосные поверхности вращения пересекаются по окружностям,
проходящим через точки пересечения меридианов поверхностей
(рис. 226).
В частном случае, если одна из поверхностей вращения — сфера,
приведенное выше предложение может быть сформулировано иначе:
если центр секущей сферы находится на оси поверхности вращения,
то сфера пересечет банную поверхность по окружностям, чисао кото-
которых равно числу точек пересечения главных меридианов поверхностей
(рис.227).
Если ось поверхности вращения перпендикулярна плоскости проек-
проекции 7Г, (ИЛИ 7Г2 ) , ТО ОКРУЖНОСТИ ПрОвЦИруЮТСЯ на ПЛОСКОСТЬ Я[ (ИЛИ 7Г2 )
без искажения, а на плоскость тг2 (или т[1) в отрезки прямых, перпенди-
перпендикулярных фронтальной (горизонтальной) проекции оси вращения (см.
рис. 226).
Поверхность сферы может пересекаться по окружности не толь-
только с соосной поверхностью вращения, но и с любой другой поверхнос-
поверхностью, имеющей семейство окружностей, например, с циклической поверх-
поверхностью, конической поверхностью второго порядка, имеющей в основа-
основании окружность, и др.
Рис. 226
Рис. 227

Построение линии пересечения поверхностей с помощью \ 59
семейства вспомогательных сферических поверхностей
Построить линии пересечения поиерхностеи с помощью вспомога-
вспомогательных секущих сфер можно днумя способами:
J) способом концентрических сфер;
2) способом эксцентрических сфер.
Особенности каждого из этих способов и условия его примене-
применения проследим на конкретных примерах.
1. Способ концентрических сфер.
Этот способ применяется для построения линии пересечения двух
поверхностей вращения, оси которых пересекаются. Для упрощения
графического решения необходимо, чтобы плоскость, определяемая ося-
осями поверхностей вращения, была параллельной какой-либо плоскос-
плоскости проекции.
ПРИМЕР 1. Построить линию пересе-
пересечения двух конических поверхностей
вращения с пересекающимися осями
(рис. 228).
РЕШЕНИЕ.
Сфера, проведенная из точки О" пе-
пересечения фронтальных проекций осей
поверхностей вращения, пересечет повер-
поверхность а по окружности, которая прое-
проецируется на плоскость я2 в отрезок
[ 1"], а поверхность C — по окружнос-
окружности, проецирующейся на ТТ2 в отрезок
[ 3"|. На горизонтальную плоскость
проекции эта окружность спроецируетсн
без искажения в окружность радиуса
JO'/, 3"|, проведенную из центра в точ-
точке О'.
Пересечение отрезков [ 1"| и [3"]
укажет фронтальные проекции двух то-
точек L" и Lj(t" = L2), принадлежащих
линии пересечения поверхностей <Х и р\
Величина радиуса вспомогательных сфер
для определения линии /j изменяется
в пределах от йт;п — \0"М"\ао Ктах —
:= \О"В"\ (точка М" определяется как
точка касания окружности, проведенной
к главному меридиану поверхности C из
центра О"). Для определения точек ли-
линии 12 йтах = \О"С"\, Kmin = \О"М"\.
На рие. 228 показано определение точек
N" и N'2\ принадлежащих линии 12. Г ори-
зонтальная проекция линии пересечения
может быть найдена из условия ее при-
принадлежности поверхности E. Для ее по-
построения необходимо через фронтальные
проекции точек кривых /" и Г2 провести
горизонтальные прямые — фронтальные
проекции параллелей поверхности j3, a
из точки О' — окружности — горизон-
горизонтальные проекции параллелей, на кото-
которых с помощью линий св^зи можно оп-
определить горизонтальные проекции точек,
принадлежащих кривым /, и 1'ъ Особые
точки Л, В, С, D определяются пересе-
пересечением главных меридианов поверхнос-
поверхностей а и /3. Они же являются высшими
(точки А и С) и низшими (точки В и
D) точками линии пересечения поверх-
поверхностей. Границы видимости линии на го-
горизонтальной плоскости проекции опре-
определяются точками, принадлежащими го-
горизонтальному очерку поверхности а
(точки Е\ и Е2 для линии 12 и F\ и У'2р.пя
линии 1\ ) .
ПРИМЕР 2. Построить линию пересе-
пересечения поверхности вращения а произ-
произвольного вида с поверхностью прямого
кругового цилиндра р. Оси поверхнос-
поверхностей пересекаются (рис. 229).
РЕШЕНИЕ.
1. Определяем центр вспомогательных
сфер — точку пересечения осей поверх-
поверхностей вращения О = i\ П i2 .
2. Находим проекции опорных точек,
принадлежащие линии пересечения /
(А", В", С", D"). Так как эти точки
принадлежат плоскости главных мериди-
меридианов поверхностей, которая параллель-
параллельна плоскости 1Т2, то эти точки определя-
определяются пересечением фронтальных проек-
проекций главных меридианов поверхностей.
Рис. 228

160 Позиционные задачи
3. Для определения произвольных
(промежуточных) точек линии пересече-
пересечения из точки О" проводим семейство
концентрических окружностей, являю-
являющихся фронтальными проекциями вспо-
вспомогательных сфер.
Радиус максимальной сферы равен
расстоянию от фронтальной проекции
центра сферы О" до наиболее удаленной
проекции точки, принадлежащей линии
пересечения — точки D". Величина мини-
минимального радиуса вспомогательной се-
секущей сферы равна радиусу окружности,
касающейся цилиндра /3". На рис. 229 по-
показано построение точек К, К | и L, Lj с
помощью вспомогательной сферы Ту-
Горизонтальные проекции точек ли-
линии пересечения строятся при помощи
параллелей поверхности вращения а,
которые проецируются на плоскость 7Г[
без искажения.
ПРИМЕР 3. Построить линию пересе-
пересечения поверхности тора а и сферы /3, оси
которых определяют плоскость, парал-
параллельную фронтальной плоскости проек-
проекции (рис. 230).
РЕШЕНИЕ.
Так как осью сферической поверхнос-
поверхности может быть любая прямая, проходя-
проходящая через центр этой поверхности, то за
центр вспомогательных сферических по-
поверхностей можно принять произволь-
произвольную точку на оси поверхности вращения
(У. Поэтому графическое решение задачи
по определению линии пересечения задан-
заданных поверхностей сводится к выполне-
выполнению следующих геометрических построе-
построений:
1. Принимаем точку О" за центр ок-
окружностей — фронтальных проекций
вспомогательных секущих сфер.
Рис. 229
2. Проводим фронтальную проекцию
вспомогательной сферической поверх-
поверхности 7/.
3. Определяем отрезки [ 1"] и
[ 3" ] — фронтальные проекции окруж-
окружностей, по которым Y; По< и 7/ ^/3.
4. Точки пересечения окружностей
(отрезков [ 1"] и [ 3"] ) Щ и М'{ при-
принадлежат искомой линии пересечения.
5. Фронтальные проекции опорных
точек А" к В" определяются пересечени-
пересечением фронтальных проекций меридианов
поверхностей а и 0.
6. Горизонтальные проекции линии пе-
пересечения определяются с помощью па-
параллелей поверхности /3.
2. Способ эксцентрических сфер.
Способ эксцентрических сфер может быть использован для пост-
построения линии пересечения двух поверхностей, имеющих общую плос-
плоскость симметрии. При этом каждая поверхность должна иметь семейст-
семейство окружностей. Как и в способе концентрических сфер, плоскость
симметрии должна быть параллельна одной из плоскостей проекции.
Сущность способа легко уяснить из следующих примеров.
ПРИМЕР 1. Построить линию пересе-
пересечения поверхности кольца (открытого
тора) а с поверхностью вращения /3,
имеющих общую плоскость симметрии
(рис. 231).
РЕШЕНИЕ.
Хотя мы и имеем дело с поверхнос-
поверхностями вращения, но применить здесь спо-
способ концентрических сфер не представ-
представляется возможным, так как оси поверх-
поверхностей не пересекаются.
Возможность использования способа
эксцентрических сфер обусловливается
тем, что обе поверхности несут на себе
семейства окружностей, по которым они
могут пересекаться эксцентрическими
сферами, причем на кольцевой поверх-
поверхности имеется несколько семейств ок-
окружностей, в том числе и окружностей,
принадлежащих пучку плоскостей, ось
которого совпадает с осью кольца.
Решение задачи сводится к следую-
следующим графическим построениям:
1. Рассечем кольцевую поверхность
фронтально проецирующей плоскостью
6, проходящей через ось кольца; эта плос-

Построение линии пересечения поверхностей с помощью 161
семейства вспомогательных сферических поверхностей
кость пересечет кольцевую поверхность
по окружности, фронтальная проекция
которой — отрезок [1"]. Эта же ок-
окружность может быть получена, если
кольцевую поверхность пересекать се-
семейством эксцентрических сфер, центры
которых расположены на перпендикуля-
перпендикуляре, проведенном через центр окружности
к плоскости 6.
Для того чтобы вспомогательная сфе-
сфера пересекала по окружности и поверх-
поверхность вращения 0, необходимо, чтобы ее
центр принадлежал оси этой поверхности.
Поэтому за центр вспомогательной сфе-
сферы следует брать точку О\ пересечения
упомянутого перпендикуляра с осью по-
поверхности 0. В этом случае сфера, радиус
которой равен расстоянию от точки Ot
до точки 1, пересекает обе поверхности
по окружностям. Окружность с, по ко-
которой сфера пересекает поверхность /3,
является параллелью поверхности /3; эта
параллель проецируется на плоскость я2
в отрезок [3"J. Окружности 1", 2"
и 3", 4" пересекаются в точках L" и L'{
(L" = Lj). Аналогично строятся и другие
произвольные точки, принадлежащие ис-
искомой линии пересечения поверхностей а
и/3.
Фронтальные проекции опорных точек
А" и В" определяются пересечением
фронтальных проекций главных мериди-
меридианов поверхностей а и C. Горизонтальные
проекции (на рис. 231 не показаны) мо-
могут быть построены с помощью паралле-
параллелей поверхности 0 так же, как это было
сделано в примере 2.
Способ эксцентрических сфер можно применять и в тех случаях,
когда одна из пересекающихся поверхностей не является поверхнос-
поверхностью вращения. Необходимым условием является наличие на этой по-
поверхности семейства окружностей, которые можно рассматривать как
результат пересечения поверхности со сферой. В число условий входит
также условие, чтобы перпендикуляры, восставленные из центров кру-
круговых сечений, пересекали ось поверхности вращения.
Задача, помещенная в следующем примере, иллюстрирует возмож-
возможность использования эксцентрических сфер для построения линии пересе-
пересечения двух поверхностей, когда одна из них не являр™>я поверхностью
вращения. f „
ПРИМЕР 2. Построить линию пересе-
пересечения поверхности вращения а с кони-
конической поверхностью второго порядка /3,
имеющей в основании окружность
(рис. 232).
м"~м"
а
Рис. 230
Рис. 231

162 Позиционные задачи
Рис. 232
РЕШЕНИЕ.
1. Выделим на конической поверхнос-
поверхности р1 круговое сечение. Для этого пере-
пересечем поверхность /3 фронтально проеци-
проецирующей плоскостью, параллельной осно-
основанию конуса. Эта плоскость пересечет
коническую поверхность по окружности,
которая проецируется на фронтальную
плоскость проекции в виде отрезка
2. Перпендикуляр, восставленный из
центра этой окружности к ее плос-
плоскости, пересечет ось поверхности враще-
вращения в точке Oi, которую принимаем за
центр вспомогательной секущей сферы
7,-. Центр другой эксцентрической сферы
Jj можно определить аналогично рассмот-
рассмотренному случаю. Построения начинаем с
проведения прямой C"), параллельной
прямой A"); из точки 5" (середины
[ 3"])
отрезка
восставляем перпенди-
перпендикуляр к отрезку [ 3"] и определяем
точку Oi пересечения его с осью поверх-
поверхности вращения а.
3. Сферы, проведенные из центров
О\ и О2 радиусами, соответственно рав-
равными | ОV1"( и | ОгЗ"!, пересекают по ок-
окружностям не только поверхность E, но
и поверхность вращения а. Отрезки
[ 6", 7"] и [ 8", 9"] являются фронталь-
фронтальными проекциями этих окружностей. Пе-
Пересечения отрезков [1", 2"] и [6", 7"],
[3", 4"] и [8", 9"] укажут точки М1',
М" и N ', N'1, принадлежащие линии пе-
пересечения поверхностей а и C.
Фронтальные проекции опорных точек
А" и В" определяются пересечением
фронтальных проекций главных мериди-
меридианов поверхностей а и |3. Горизонтальные
проекции точек, принадлежащих линии
пересечения, определяются известным
способом (см. пример 1, рис. 228).

Построение линии пересечения поверхностей 163
второго порядка (частные случаи)
§ 52. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
ВТОРОГО ПОРЯДКА (ЧАСТНЫЕ СЛУЧАИ)
Рассмотрим некоторые частные случаи пересечения поверхностей
второго порядка.
Известно, что порядок линии пересечения поверхностей равен про-
произведению порядков поверхностей, поэтому две поверхности второго
порядка всегда пересекаются по кривой четвертого порядка. При опре-
определенных условиях эта кривая распадается на несколько линий бо-
более низкого порядка. При этом сумма порядков линий, на. которые
распадается алгебраическая кривая, равна порядку самой линии. В част-
частности, кривая четвертого порядка может распадаться на четыре пря-
прямые или две кривые второго порядка. Следует иметь в виду, что некото-
некоторые линии, на которые распадается кривая, могут быть мнимыми.
Случаи, когда кривая четвертого порядка распадается на четыре пря-
прямые (четыре линии первого порядка), можно проследить на приме-
примерах пересечения поверхностей двух цилиндров второго порядка с парал-
параллельными осями (рис. 233,а), а также двух конических поверхностей
второго порядка, имеющих общую вершину (рис. 233,6).
Условия, при которых кривая четвертого порядка распадается на
две кривые второго порядка, могут быть сформулированы следую-
следующими теоремами:
Теорема 1. Если две поверхности второго порядка пересекают-
пересекаются по одной плоской кривой, то они пересекаются и. еще по одной плос-
плоской кривой.
В качестве иллюстрации этой теоремы на рис. 234 показаны фрон-
фронтальные проекции I" и lj кривых второго порядка (в частности, ок-
окружностей) , полученных при пересечении поверхностей сферы а и эллип-
эллиптического цилиндра /3.
Теорема 2. Если две поверхности второго порядка имеют ка-
касание в двух точках, то линия их пересечения распадается на две кривые
второго порядка, плоскости которых проходят через прямую, соединя-
соединяющую точки касания.
На рис. 235 показано пересечение двух поверхностей второго по-
порядка: конической а и цилиндрической /3. Поверхности а и 0 имеют
две общие касательные плоскости е и б и соответственно две общие
а)

164 Позиционные задачи
точки касания А и В. Поэтому
по теореме 2 они пересекаются
по двум кривым второго по-
порядка, расположенным в плос-
плоскостях f И Г).
Плоскости f и т? проходят
через прямую (АВ). Так как
(АВ) перпендикулярна плос-
плоскости проекции я 2, то плоскос-
плоскости f и г} фронтально проеци-
проецирующие, следовательно, при-
принадлежащие им кривые прое-
проецируются на плоскость 7г2 в
отрезки [C"D"j и [E"F"},
при этом [C"D"] С /of, a
[E"F"]CfOv.
Теорема 2 может быть использована и для решения задачи на опреде-
определение положения плоскостей, пересекающих поверхности второго поряд-
порядка по окружностям.
ПРИМЕР. Определить положение плос- РЕШЕНИЕ. Проведем сферу /3, имею-
костей f и Ц, которые пересекают поверх- щую две общие касательные плоскости с
ность эллиптического цилиндра а по ок- цилиндрической поверхностью (сферами
ружностям (рис. 236). цилиндр а имеют двойное соприкаса-
Рис. 234
L
Рис. 235
Рис. 236

Определение точек пересечения линии 165
с поверхностью
ние) . Для этого центр сферы должен
находиться на оси i цилиндрической по-
поверхности а, а ее радиус И = |i'.4',. Повер-
Поверхности цилиндра и сферы соприкасаются
в точках Л и В. На основании теоремы 2
поверхности сферы и цилиндра пересе-
пересекаются по двум кривым второго поряд-
порядка, принадлежащим фронтально проеци-
проецирующим плоскостям f и Т}. Эти кривые,
проецирующиеся на плоскость Т12 в от-
отрезки [C"D"] и [?"F"] , являются окруж-
окружностями, так как сопряженные диаметры
замкнутой кривой второго порядка рав-
равны между собой \АВ\ = \СП\ и \АВ[ =
= \EF\ .
Рис. 237
Теорема 3. Если две поверхности второго порядка описаны
около третьей поверхности второго порядка или вписаны в нее, то ли-
линия их пересечения распадается на две кривые второго порядка, плос-
плоскости которых проходят через прямую, соединяющую точки пересе-
пересечения линий касания*.
Эта теорема по существу является частным случаем теоремы 2.
Практическое использование теоремы возможно в том случае, когда
две поверхности вращения второго порядка могут быть описаны око-
около сферы или вписаны в нее.
Рис. 237 дает представление о том, как можно определить линии
пересечения двух конических поверхностей а и /3, описанных около
сферы у. Поверхность а соприкасается со сферой у по окружности,
фронтальная проекция которой [ 1"\, а с поверхностью /3 — по окруж-
окружности, проецирующейся в [ 3'4"]. Точки пересечения этих окружностей А
и В являются точками соприкасания поверхностей а и /3.
По теореме 3 плоскости кривых /, и 12 должны проходить через
прямую (АВ). Так как (АВ) 1 я2, то плоскости f Э /, и т? Э 12 фрон-
фронтально проецирующие, а проекции кривых /t и 12 проецируются в отрез-
отрезки [C"D"] k[E"F"\.
Показанные на рис. 237 конические поверхности а и /3 пересекают-
пересекаются по двум кривым, одна из которых lt — эллипс, другая 12 — пара-
парабола (см. § 45, рис. 199, 200).
§ 53. ОПРЕДЕЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ЛИНИИ
С ПОВЕРХНОСТЬЮ
В общем случае для графического решения задачи по опреде-
определению положения точек пересечения (встречи) линии с поверхностью
необходимо выполнить ряд геометрических построений в приведенной
ниже последовательности: заключить данную линию во вспомогательную
поверхность; определить линию пересечения этой вспомогательной
поверхности с заданной поверхностью; отметить точки, в которых
пересекаются полученная линия с заданной (рис. 238).
* Эта теорема известна также как "теорема Монжа", по имени основоположника
начертательной геометрии Гаспара Монжа, доказавшего эту теорему.

166 Позиционные задачи
Запишем указанную последовательность решения в виде табл. 9
(как это сделано в § 43 при составлении алгоритма для решения за-
задачи по определению линии пересечения двух поверхностей). В пра-
правой части таблицы приведена символическая запись, соответствую-
соответствующая смысловому содержанию отмеченных этапов решения.
Таблица 9
Словесное описание на традиционном языке
начертательной геометрии
1. Заключаем данную линию во вспомогательную
поверхность
2. Определяем линию пересечения вспомогатель-
вспомогательной поверхности с заданной поверхностью
3. Отмечаем точки пересечения полученной ли-
линии пересечения с заданной
Символическая запись
на геометрическом языке
Заключаем а с у
Определяем / ~ у n a
Отмечаем {#, ...} - / п a
Алгоритм для решения задачи определения точек пересечения ли-
линии с поверхностью в символической форме можно записать:
[к, ...] = (у.Па)Па.
Здесь, как и у алгоритма определения линии пересечения двух по-
поверхностей, в зависимости от порядка и взаимного расположения задан-
заданных кривой и поверхности множество искомых точек [К, ...} может
состоять из одной, двух и более точек.
Полученный алгоритм является универсальным, пригодным для ре-
решения задачи с любым вариантом задания исходных данных. Рассмот-
Рассмотрим различные варианты решения задачи:
1. Пересечение кривой с поверхностью.
2. Пересечение кривой с плоскостью.
3. Пересечение прямой с поверхностью.
4. Пересечение прямой с плоскостью.
При решении всех этих задач, как правило, целесообразно для умень-
уменьшения графических построений и их упрощения пользоваться в качестве
вспомогательной секущей поверхности у — проецирующей цилиндричес-
Рис. 238

Определение точек пересечения линии 167
с поверхностью
кои поверхностью, в частности,
если определяется точка пересече-
пересечения прямой с поверхностью, —
плоскостью. Упрощение решения
достигается благодаря тому, что
одна из проекций линии пересече-
пересечения I автоматически определяется
положением и формой следа прое-
проецирующей поверхности у. Поэтому
задача по определению точек встре-
встречи линии с поверхностью сводится
к построению второй проекции
линии, принадлежащей поверхнос-
поверхности, если известна одна ее проекция,
т. е. к задаче, которую мы неоднок-
неоднократно решали.
Рис. 239
1. Пересечение кривой с поверхностью.
При определении содержания и последовательности выполнения
геометрических операций, входящих в состав алгоритма для реше-
решения задачи по определению точек пересечения кривой с поверхнос-
поверхностью, мы пользовались наглядным чертежом, изображенным на рис. 238.
Теперь проследим, как решается эта задача на эпюре Монжа.
ПРИМЕР. Определить точки пересече-
пересечения кривой а с произвольной цилинд-
цилиндрической поверхностью а (рис. 239).
РЕШЕНИЕ.
1. Заключаем кривую а во фронталь-
фронтально проецирующую цилиндрическую по-
поверхность у.
2. Определяем линию пересечения по-
поверхностей у и а. Для этого отмечаем на
а" = fQy = I" произвольные точки 1",
2", 3", 4", 5"; зная фронтальные проек-
проекции точек, находим их горизонтальные
проекции 1', 2', 3', 4', 5'. Соединив эти
точки плавной кривой, получим горизон-
горизонтальную проекцию /' кривой /, по кото-
которой вспомогательная цилиндрическая по-
поверхность у пересекает данную поверх-
поверхность а.
3. Отмечаем точки К\ и К\ пересече-
пересечения кривых /' и а'. По горизонтальным
проекциям определяем их фронтальные
проекции К" и К'{.
2. Пересечение кривой с плоскостью.
Решение этой задачи аналогично только что рассмотренной, если и
есть какое-либо отличие, то оно состоит лишь в том, что приходит-
приходится определять вторую проекцию линии, принадлежащую не цилинд-
цилиндрической поверхности, как это было в приведенном выше примере,
а плоскости.
ПРИМЕР. Определить точку встречи
линии а с плоскостью а (рис. 240).
РЕШЕНИЕ.
1. Заключаем линию а в проецирую-
проецирующую цилиндрическую поверхность у, без-
безразлично какую 7-L Я| или у 1 ттг (на
рис. 24 0 у I :г }
2. Обозначим линию пересечения
уПа= I, тогда I" С fOy.
3. Определяем горизонтальную проек-
проекцию /'. Для этого отмечаем на I" ряд то-
точек 1", 2", 3", ..., с помощью горизонта-
горизонталей (Л,, h2, hi, ...) плоскости а нахо-
находим точки 1', 2 , 3',..., принадлежащие I'.
4. Отмечаем точку К' = /' С\а', по К' на-
находим if".
'Л. Пересечение прямой с поверхностью.
В алгоритме решения чадачи для определения точек встречи прямой
с поверхностью в качестве: вспомогательной секущей поверхности следу-
следует брать плоскость.

168 Позиционные задачи
Сложность решения рассматриваемой группы задач зависит от трудо-
трудоемкости нахождения линии пересечения у П а, которая определяется
видом поверхности а и расположением прямой а как относительно
поверхности а, так и по отношению к плоскостям проекций.
Чтобы получить рациональное решение, следует пользоваться наибо-
наиболее простым способом определения линии / (/ = у Г) а). Этого можно
достигнуть двумя путями: 1) соответствующим выбором положения
вспомогательной секущей плоскости у или 2) переводом секущей пря-
прямой а в частное положение. Рассмотрим каждый из этих вариантов
решения.
Вариант 1.
а) Вспомогательная секущая плоскость — проецирующая.
ПРИМЕР. Определить точку пересече-
пересечения прямой а с поверхностью торса
(рис. 241).
РЕШЕНИЕ. Заключаем прямую а во
фронтально проецирующую плоскость
у. Фронтальная проекция линии пересе-
пересечения /" совпадает с /0^ = а". Отмечаем
точку 1", в которой проекция I" пересе-
пересекает проекцию d" ребра возврата d. Зная
положение 1", определяем горизонталь-
горизонтальную проекцию 1'. Проводим ряд прямо-
прямолинейных образующих торсовой поверх-
поверхности (касательных к кривой d) и фик-
фиксируем точки 2", 3", в которых I" пере-
пересекает фронтальные проекции этих обра-
образующих.
На горизонтальных проекциях соот-
соответствующих образующих определяем
горизонтальные проекции 2', 3'. Соеди-
Соединив эти точки плавной кривой, получим
горизонтальную проекцию V. I' О*а' — К'—
горизонтальная проекция искомой точки
встречи. По К' определяем К".
б) Вспомогательная секущая плоскость — общего положения. Исполь-
Использование вспомогательной проецирующей плоскости не всегда упрощает
решение, возможны случаи, когда целесообразно применять плоскость
общего положения.
В качестве иллюстрации, подтверждающей эту мысль, может служить
задача по определению точек пересечения прямой общего положения с
конической поверхностью.
Плоскость пересекает коническую поверхность по кривой. Иск-
Исключение составляет только плоскость, проходящая через вершину кони-
Рис. 240
Рис.2 11

Определение точек пересечения линии 169
с поверхностью
ческой поверхности. В этом случае
кривая второго порядка распада-
распадается на две прямые — образующие
конической поверхности (см.
§ 45) *
ПРИМЕР. Определить точки пересече-
пересечения прямой а с поверхностью прямого
кругового конуса а (рис. 242).
РЕШЕНИЕ. Заключаем прямую а в
плоскость у, проходящую через верши-
вершину конической поверхности S. На
рис. 242 плоскость у задана пересекаю-
пересекающимися прямыми а и h , при этом h —
горизонталь.
Определяем горизонтальный след плос-
плоскости у; для этого находим горизонталь-
горизонтальный след прямой На и через него прово-
проводим h о 7 параллельно горизонтальной
проекции горизонтали h'. Отмечаем точ-
точки 2' и 3', в которых hOynhoa. (S'2;)
и (S'3') — образующие поверхности а,
по которым она пересекается плоскос-
плоскостью у.
Точки К\ и К'2 {К\ = а'П (S'2') и К'2 =
= а' П (S'31)) — горизонтальные проек-
проекции искомых точек пересечения. Зная
положение К\ и К2, определяем К" и К'2'-
Рис. 242
Вариант 2. Перевод секущей прямой в частное положение.
При пересечении поверхности сферы плоскостью в сечении полу-
получается окружность, которая проецируется на плоскости проекции.в об-
общем случае в виде эллипсов или прямой и эллипса (если секущая плос-
плоскость проецирующая). В частном случае, когда секущая плоскость
параллельна плоскости проекции, окружность проецируется на
эту плоскость проекции без искажения. Поэтому, чтобы упростить
решение задачи, следует произвольно расположенную прямую перевес-
перевести в положение, параллельное какой-либо плоскости проекции. Тог-
Тогда представляется возможность заключить прямую в плоскость, па-
параллельную плоскости проекции.
ПРИМЕР 1. Определить точки встре-
встречи прямой а, заданной отрезком [АВ]
с поверхностью сферы а (рис. 243).
РЕШЕНИЕ. Переводим прямую, произ-
произвольно расположенную в пространстве, в
положение, параллельное плоскости про-
проекции. Для этого переходим от системы
1Т2 7Г3
х к системе х\ , в которой тт3 \\ а .
7Г] 7Ti
В этом случае горизонтально прое-
проецирующая плоскость у Э а пересечет по-
поверхность сферы по окружности с ради-
радиуса R (см. рис. 243), которая спроеци-
руется на плоскость 7ГХ в [1'2'], а на
плоскость 7Г3 в окружность сх того же
радиуса R. Точки К"у и К'2\ пересече-
пересечения с" с [ЛУВ"] — вспомогательные про-
проекции искомых точек, по ним определя-
определяем вначале К[ и К^, а затем и К" и К'{.
Если прямая а , пересекающая по-
поверхность вращения, проходит через ось
i этой поверхности, то перевод прямой
а в частное положение целесообразно
осуществить путем вращения прямой
вокруг оси i.
ПРИМЕР 2. Определить точки встре-
встречи прямой а с поверхностью вращения
а (рис. 244).
*Если секущая плоскость проходит через вершину конической поверхности
и составляет с ее осью угол больший, чем угол наклона к этой оси образующей
конической поверхности, то сечение распадается на две мнимые прямые.

170 Позиционные задачи
РЕШЕНИЕ. Горизонтально проециру-
проецирующая плоскость у, в которую заключаем
прямую а , пересечет поверхность вра-
вращения по меридиану g i.
Чтобы не строить искаженной фрон-
фронтальной проекции меридионального сече-
сечения, поворачиваем плоскость у и нахо-
находящуюся в ней прямую а вокруг оси i
до положения, параллельного ТГ2. тогда
g\ совпадает eg' — горизонтальной проек-
проекцией главного меридиана, a h 07 с hOyr
После поворота прямая а займет поло-
положение Q] (а(, а'[). С помощью точек К'[ i
и К 2, , в которых а" П#", определяем по-
положение К" и К J, a затем К\ и К'2.
4. Пересечение прямой с плоскостью.
Определение точки встречи прямой с плоскостью относится к эле-
элементарной задаче, но ее значение для решения самых различных, бо-
более сложных задач, трудно переоценить. Задача по нахождению точ-
точки встречи прямой с плоскостью входит как составная часть (фраг-
(фрагмент) в алгоритм решения широкого круга как позиционных, так и
метрических задач.
Решение этой задачи даже в самом общем случае, когда и плос-
плоскость и прямая занимают произвольное положение в пространстве,
легко сводится к простейшей задаче по определению линии пересе-
пересечения двух плоскостей, из которых одна — проецирующая (см.
§ 44, рис. 187, 188), с последующим определением второй проекции
точки, принадлежащей плоскости, если известна одна из ее проекций (см.
§ 40, примеры 1 ... 3, рис. 169 171). Для этого достаточно пря-
прямую заключить во вспомогательную проецирующую плоскость.
ПРИМЕР 1. Определить точку встречи
прямой а с плоскостью а. (рис. 245).
РЕШЕНИЕ. Так как а — прямая, то
в алгоритме К = GПа) Г\а в качестве
секущей поверхности следует выбирать
плоскость. Эта плоскость пересечет задан-
заданную а по прямой I . Поэтому в рассмат-
рассматриваемом случае предписываемая алго-
a
я2
/
*-_
*<—
ь
0" \
\
'ОТ
07
Рис. 243
Рис. 244

Определение точек пересечения линии 171
с поверхностью
Рис. 245
Рис. 246
К'
Рис. 247
ритмом последовательность выполнения
геометрических построений будет иметь
следующее содержание:
1) проводим через а' (или а") горизон-
горизонтальный (фронтальный) след горизон-
горизонтально проецирующей (фронтально про-
проецирующей) плоскости 7;
2) определяем фронтальную (горизон-
(горизонтальную) проекцию линии пересечения
плоскости у с данной плоскостью а
I" = у" Па" (или I' = у' Па');
3) определяем К" = а"П1" (или К' =
= a'Ol')-t зная К", находим К' (или
зная К', находим К").
Алгоритм решения не меняется, если
мы будем иметь дело с другим вариан-
вариантом задания плоскости — параллельны-
параллельными прямыми или прямыми, по которым
плоскость пересекает плоскости проек-
проекций (следами плоскости).
ПРИМЕР 2. Определить точку пере-
пересечения прямой а с плоскостью а
(рис. 246).
РЕШЕНИЕ. Так же, как и в преды-
предыдущем примере, заключаем прямую а в
проецирующую плоскость у —'а (h оу =
— а'). Строим линию пересечения плос-
плоскостей у Па = / . Отмечаем К" = Г Па".
По К" находим К'.
Решение задачи упрощается, если одна
из заданных фигур (прямая или плос-
плоскость) занимает проецирующее положе-
положение. Рис. 247, а и б иллюстрирует реше-
решение таких задач:
а) плоскость а — проецирующая, а
прямая а —общего положения (рис. 247,а);
б) плоскость а — общего положения,
а прямая а —проецирующая (рис. 247,6).
Решения задач настолько просты, что
они ясны из чертежей и не треЬуют ка-
каких-либо пояснений.

172 Позиционные задачи
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Изложите общий принцип построе-
построения обобщенного алгоритма для решения
задачи по определению линии пересече-
пересечения поверхностей.
2. Сформулируйте возможные вариан-
варианты решения задачи по определению ли-
линии пересечения многогранника плоскос-
плоскостью.
3. В каких случаях для определения
линии пересечения двух поверхностей
можно применять способ:
а) вращающихся плоскостей;
б) пучка плоскостей с несобственной
прямой;
в) концентрических сфер;
г) эксцентрических сфер?
4. Какие точки линии пересечения по-
поверхностей называются опорными?
5. Напишите и дайте пояснение алго-
алгоритма решения задачи по определению
точки встречи прямой с плоскостью.
6. В чем заключается решение задач
по определению сечения поверхности
плоскостью с помощью способа граней
и способа ребер?
7. В каких случаях плоскость пересе-
пересекает поверхность прямого кругового ко-
конуса: по двум пересекающимся прямым,
по окружности, эллипсу, параболе, гипер-
гиперболе?
8. Что представляют собой фронталь-
фронтальные проекции линии пересечения двух
поверхностей вращения второго порядка,
имеющих общую плоскость симметрии,
параллельную плоскости тг2 ?
9. Какая зависимость существует
между порядком пересекающихся по-
поверхностей и порядком линии, получен-
полученной в результате их пересечения?
10. Сформулируйте условия (теоре-
(теоремы) , при которых кривая — линия пере-
пересечения поверхностей — распадается на
две кривые второго порядка?
11. Приведите примеры, когда кри-
кривая — линия пересечения двух цилиндри-
цилиндрических поверхностей — распадается на од-
одну, две, три, четыре прямых.
12. В чем состоит содержание алгорит-
алгоритма решения задачи для определения то-
точек пересечения линии с поверхностью?
13. Чем следует руководствоваться
при выборе вспомогательной секущей
поверхности при определении точек пере-
пересечения линии с поверхностью?
14. В каком случае можно для упро-
упрощения решения задачи по определению
точек встречи прямой с поверхностью
применять способ вращения вокруг оси,
перпендикулярной плоскости проекции?

ГЛАВА
VI
МЕТРИЧЕСКИЕ ЗАДАЧИ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В § 6 гл. I отмечалось, что при параллельном, в частности ортого-
ортогональном, проецировании геометрические фигуры, произвольно распо-
расположенные по отношению к плоскостям проекций, проецируются на эти
плоскости с искажением их метрических характеристик (характеристик,
которые могут быть получены путем измерения линейных и угловых
величин). Для того чтобы иметь возможность по метрически искажен-
искаженным проекциям судить о размерах и форме оригинала, необходимо знать
способы решения задач по определению неискаженных линейных и
угловых величин.
Метрическими называются задачи, решение которых связано с на-
нахождением характеристик геометрических фигур, определяемых (из-
(измеряемых) линейными и угловыми величинами.
Все многообразие метрических задач, в конечном счете, сводит-
сводится к двум видам: А — задачам на определение расстояния между дву-
двумя точками; Б — задачам на нахождение величины угла между двумя
пересекающимися прямыми.
К метрическим относятся также задачи на построение отрезка и уг-
угла с наперед заданным значением соответственно линейной и градус-
градусной (радианной) величины.
Несмотря на то, что чисто метрические задачи встречаются редко,
целесообразно выделить их в самостоятельную группу, включив в нее
и те задачи, в которых на промежуточных этапах решения приходится
выяснять позиционные отношения между геометрическими фигу-
фигурами.
В основе алгоритма решения любой метрической задачи лежит ин-
инвариантное свойство ортогонального проецирования, заключающееся
в том, что любая фигура, принадлежащая плоскости, параллельной
плоскости проекции, проецируется на эту плоскость в конгруентную
фигуру, т.е. (ФС/3) Л @11 я,) => Ф'=Ф.
Рассмотрим возможные пути решения задач на определение метри-
метрических характеристик геометрических фигур.
А. Определение расстояний.
Решение задач на определение расстояния между точкой и прямой,
двумя параллельными прямыми, точкой и плоскостью, прямой и плос-
плоскостью, двумя плоскостями, скрещивающимися прямыми, в конечном
счете, сводится к нахождению расстояния между двумя точками.
Чертежи на рис. 248 подтверждают это утверждение. Из этих черте-
чертежей видно также, что, прежде чем приступить к решению задачи на
определение расстояния между точкой и прямой или двумя параллель-
параллельными прямыми (рис. 248,а и б), необходимо провести плоскость 7,
перпендикулярную к прямой /, или опустить перпендикуляр из точки А
(Лет или Ле/3) на плоскость а (рис. 248,в, г, д, е). Поэтому, прежде чем
решать задачи на определение расстояний, выясним характер и последо-

174 Метрические задачи
а)
в)
\А.аЫ
г)
\m,a\=d
А)
е)
Im./HT. »»--/
Рис. 248
вательность графических построений, которые должны быть выполнены
для построения на эпюре взаимно перпендикулярных прямых, прямой и
плоскости, плоскостей.
§ 54. ПОСТРОЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ,
ПРЯМОЙ И ПЛОСКОСТИ, ПЛОСКОСТЕЙ
Не будет преувеличением утверждать, что построение взаимно пер-
перпендикулярных прямых и плоскостей наряду с определением рассто-
расстояния между двумя точками являются основными графическими опера-
операциями при решении метрических задач.
Теоретической предпосылкой для построения на эпюре Монжа проек-
проекций прямых и плоскостей, перпендикулярных по отношению друг к
другу в пространстве, служит отмеченное раньше (см. § 6) свойство

Построение взаимно перпендикулярных прямых, 175
прямой и плоскости, плоскостей
проекции прямого угла, одна из сторон которого параллельна какой-ли-
какой-либо плоскости проекции:
(АВС=- 90°)ЛA-ВС) || я,,
А'в'с> = 90° •
1. Взаимно перпендикулярные прямые.
Чтобы можно было воспользоваться отмеченным свойством для
построения на эпюре Монжа двух пересекающихся под углом 90° пря-
прямых, необходимо, чтобы одна из них была параллельна какой-либо
плоскости проекции. Поясним сказанное на примерах.
ПРИМЕР 1. Через точку А провести
прямую I , пересекающую горизонталь h
под прямым углом (рис. 249).
Так как одна из сторон h прямого
угла параллельна плоскости 7Г) , то на эту
плоскость прямой угол спроецируется
без искажения. Поэтому через А' прово-
проводим горизонтальную проекцию V Lh'.
Отмечаем точку М' = I'Cih'. Находим
М" (М"&п"). Точки А" и М" определя-
определяют /" (см. рис. 249, а).
Если вместо горизонтали будет задана
фронталь f, то геометрические построе-
построения по проведению прямой / 1 f анало-
аналогичны только что рассмотренным с той
лишь разницей, что построения неиска-
неискаженной проекции прямого угла следует
начинать с фронтальной проекции (см.
рис. 249,6).
ПРИМЕР 2. Через точку А провести
прямую / , пересекающую прямую а , за-
заданную отрезком [ ВС], под углом 90
(рис. 250).
Так как данный отрезок занимает про-
произвольное положение по отношению к
плоскостям проекций, мы не можем, как
в предыдущем примере, воспользоваться
свойством о частном случае проецирова-
проецирования прямого угла, поэтому вначале не-
необходимо [ВС] перевести в положение,
параллельное какой-либо плоскости про-
проекции.
На рис. 250 [ ВС] переведен в поло-
положение, параллельное плоскости Этз• Это
сделано с помощью способа замены плос-
плоскостей проекции путем замены плоскос-
плоскости я, ->7Г3Н [ВС].
В результате такой замены в новой
системе xt —^- [ВС] определяет горизон-
тальную прямую, поэтому все дальней-
дальнейшие простроения выполнены так же, как
это было сделано в предыдущем приме-
примере: после того, как была найдена точка
М J, ее перевели на исходные плоскости
проекции в положение М" и М', эти точ-
точки совместно с А" и А' определяют про-
проекции прямой /.
ПРИМЕР 3. Провести горизонтальную
проекцию стороны [ВС] прямого угла
ABC, если известны его фронтальная про-
проекция LA"B"C" и горизонтальная проек-
проекция стороны [А 'В'] (рис. 251).
РЕШЕНИЕ:
1. Переводим сторону угла [ВА]
в положение || 7Г3 путем перехода от сис-
темы плоскостей проекций х к новой
7Г
а)
Рис. 249
б)

176 Метрические задачи
В''
Рис. 250
Рис. 251
2. Определяем новую фронтальную деляем точку С'{ (С'{ удалена от оси *,
проекцию [ В"А"]. на расстояние | СХ] С'{ | = \СХС"\).
4. Горизонтальная проекция С опреде-
3. Из В" восставляем перпендикуляр к ляется как точка пересечения прямых
[В"д"]. На этом перпендикуляре опре- (C"CXl ) П (С"СХ) = С".
2. Взаимно перпендикулярные прямая и плоскость.
Из курса стереометрии известно, что прямая перпендикулярна плос-
плоскости, если она перпендикулярна хотя бы к двум пересекающимся
прямым, принадлежащим этой плоскости.
Если в плоскости взять не произвольные пересекающиеся прямые, а ее
горизонталь и фронталь, то открывается возможность воспользоваться
свойством проекции прямого угла, как это было сделано в примере 1,
рис. 249.
Рассмотрим следующий пример; пусть из точки А&а требуется вос-
восставить перпендикуляр к плоскости а (рис. 252).
Через точку А проводим горизонталь h и фронталь / плоскости а.
Тогда, по определению (АВ), перпендикулярная jc^tuiocko?th а, должна
быть перпендикулярна к прямым h и f, т. е. ВАМ = ВАК = 90° . Но
сторона AM L ВАМ || тг,, поэтому L ВАМ проецируется на плоскость 7г ] без
искажения, т. е. В'А'М' = 90°. Сторона АК L ВАК \\ тт2 и, следовательно, на
плоскость 7г2 этот угол проецируется также без искажения, т. е. и
В А"К" = 90°. Приведенные рассуждения можно сформулировать в виде
следующей теоремы: для того чтобы прямая в пространстве была перпен-
перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре гори-
горизонтальная проекция прямой была перпендикулярна к горизонтальной
проекции горизонтали плоскости, а фронтальная проекция к фрон-
фронтальной проекции фронтали этой плоскости.
Если плоскость задана следами, то теорема может быть сформули-
сформулирована иначе: для того чтобы прямая в пространстве была перпендику-
перпендикулярна плоскости, необходимо и достаточно, чтобы проекции этой прямой
были перпендикулярны к одноименным следам плоскости.

ОС
Построение взаимно перпендикулярных прямых, 177
прямой и плоскости, плоскостей
Г
Рис. 252
Рис. 253
Установленные теоремой зависимости между прямой в пространст-
пространстве, перпендикулярной к плоскости, и проекциями этой прямой к про-
проекциям линий уровня (следам) плоскости лежат в основе графического
алгоритма решения задачи по проведению прямой, перпендикулярной к
плоскости, а также построения плоскости, перпендикулярной к заданной
прямой.
ПРИМЕР 1. Восставить в вершине А
перпендикуляр AD к плоскости ААВС
(рис. 253).
Для того чтобы определить направле-
направление проекций перпендикуляра, проводим
проекции горизонтали h и фронтали f
плоскости ДАВС. После этого из точки
А' восставляем перпендикуляр к ht, а из
А"-к Л-
ПРИМЕР 2. Из точки А, принадлежа-
принадлежащей плоскости а (т || п), восставить пер-
перпендикуляр к этой плоскости (рис. 254).
РЕШЕНИЕ. Для определения направле-
направления проекций перпендикуляра /' и /",
как и в предыдущем примере, проводим
через точку А (А', А") горизонталь
h (Л', h"), принадлежащую плоскости а.
Зная направление h', строим горизон-
горизонтальную проекцию перпендикуляра
V (I'Lh'). Для определения направления
фронтальной проекции перпендикуляра
через точку А (А', А") проводим фрон-
таль f (/¦', f") плоскости а. В силу парал-
параллельности f фронтальной плоскости про-
проекции прямой угол между / и f проеци-
проецируется на я2 без искажения, поэтому про-
проводим I" If".
На рис. 255 эта же задача решена для
случая, когда плоскость а задана следа-
следами. Для определения направлений проек-
проекций перпендикуляра отпадает необходи-
необходимость в проведении горизонтали и фрон-
Рис. 254.

178 Метрические задачи
Рис. 255
Рис. 256
Рис. 257
тали, так как их функции выполняют
следы плоскости h oq. и f0 а- Как видно
из чертежа, решение сводится к проведе-
проведению через точки А' и А" проекций /' ihoa

W
ПРИМЕР 3. Построить плоскость 7.
перпендикулярную к данной прямой / и
проходящую через заданную точку А
(рис. 256).
РЕШЕНИЕ. Через точку А проводим
горизонталь h и фронталь f. Эти две пе-
пересекающиеся прямые определяют плос-
плоскость; чтобы она была перпендикуляр-
перпендикулярна к прямой / , необходимо, чтобы пря-
прямые h и f составляли с прямой I угол
90°. Для этого проводим Л1!/' и f'i.1".
Фронтальная проекция h" и горизонталь-
горизонтальная проекция f проводятся параллель-
параллельно оси jc.
Рассмотренный случай позволяет по
иному решать задачу, приведенную в при-
примере 3 (с. 175 рис. 251). Сторона [ВС]
L ABC должна принадлежать плоскости
7I [-AB] и проходить через точку В
(рис. 257).
Это условие и определяет ход решения
задачи, который состоит в следующем:
заключаем точку В в плоскость уЦАВ],
для этого через точку В проводим гори-
горизонталь и фронталь плоскости у так,
чтобы h' 1А'ВГиГ'1А"В".
Точка С? (ВС), принадлежащей плос-
плоскости 7, поэтому для нахождения ее го-
горизонтальной проекции проводим через
С" произвольную прямую 1", принад-
принадлежащую плоскости 7; определяем гори-
горизонтальную проекцию этой прямой 1*2' и
на ней отмечаем точку С' (С' определяет-
определяется пересечением линии связи — перпенди-
перпендикуляра, опущенного из С", с горизон-
горизонтальной проекцией прямой 1'2 ). С
совместно с В' определяют горизонталь-
горизонтальную проекцию (ВС) 1 (АВ).
3. Взаимно перпендикулярные плоскости.
Две плоскости перпендикулярны, если одна из них содержит прямую,
перпендикулярную к другой плоскости.
Исходя из определения перпендикулярности плоскостей, задачу
на построение плоскости /3, перпендикулярной к плоскости а, решаем
следующим путем: проводим прямую /, перпендикулярную к плоскости
а; заключаем прямую I в плоскость /3. Плоскость /31а, так как /3 Э / 1 а.
Через прямую I можно провести множество плоскостей, поэтому
задача имеет множество решений. Чтобы конкретизировать ответ, не-
необходимо указать дополнительные условия.
ПРИМЕР 1. Через данную прямую а
провести плоскость 0, перпендикуляр-
перпендикулярную к плоскости а (рис. 258).
РЕШЕНИЕ. Определяем направление
проекций перпендикуляра к плоскости а,
для этого находим горизонтальную про-
проекцию горизонтали (А1) и фронтальную
проекцию фронтали (f") ; из проекций
произвольной точки А ? а проводим про-
проекции перпендикуляра V lh' и I" If".
Плоскость /31 а, так как /3 Э I 1 а.

Построение взаимно перпендикулярных прямых, 179
прямой и плоскости, плоскостей
а"
Рис. 258
ПРИМЕР 2. Через данную точку А про-
провести горизонтально проецирующую плос-
плоскость 7, перпендикулярную к плоскости
а, заданной следами (рис. 259, а).
Искомая плоскость у должна содер-
содержать прямую, перпендикулярную плос-
плоскости а, или быть перпендикулярной
к прямой, принадлежащей плоскости а.
Так как плоскость у должна быть гори-
горизонтально проецирующей, то прямая,
перпендикулярная к ней, должна быть
параллельна плоскости ¦л1, т. е. являться
горизонталью плоскости а или (что то
же самое) горизонтальным следом этой
плоскости—hoa. Поэтому через горизон-
горизонтальную проекцию точки А проводим
горизонтальный след hOyl Л о а. фрон-
фронтальный след foy L оси х.
На рис. 259, б показана фронтально проецирующая плоскость у, про-
проходящая через точку В и перпендикулярная к плоскости я2-
Из чертежа видно, что отличительной особенностью эпюра, на кото-
котором заданы две взаимно перпендикулярные плоскости, из которых од-
одна — фронтально проецирующая, является перпендикулярность их фрон-
фронтальных следов fOy I foa; горизонтальный след фронтально проецирую-
проецирующей плоскости перпендикулярен оси х.
Рис. 259

180 Метрические задачи
§ 55. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ
В § 8 гл. I (см. рис. 50) было показано графическое определение
длины отрезка [ АВ], являющегося мерой расстояния между точками
А и В, путем построения прямоугольного треугольника.
Рассмотрим другие варианты решения этой задачи. Мы знаем, что
ортогональная проекция геометрической фигуры будет конгруент-
на оригиналу в том случае, когда фигура занимает положение, парал-
параллельное плоскости проекции. Поэтому отрезок [ АВ] проецируется
на плоскость 7гг (или я2) без искажения лишь в том случае, когда он
параллелен плоскости irt (или п2). Поэтому решение рассматрива-
рассматриваемой задачи сводится к переводу отрезка в положение, параллельное
какой-либо плоскости проекции.
Перевод отрезка из общего положения в частное (параллельное плос-
плоскости проекции) можно осуществить, применив один из способов преоб-
преобразования ортогональных проекций: или замену плоскости проекции,
или плоскопараллельное перемещение (в частном случае — вращение
вокруг оси, перпендикулярной плоскости проекции).
ПРИМЕР 1. Определить расстояние
между точками А и В (рис. 260). Реше-
Решение задачи сводится к нахождению дли-
длины отрезка, концами которого являют-
являются точки А и В. Переводим отрезок
[АВ] из общего положения в частное —
параллельное плоскости тг3, используя
для этого замену плоскости 7Tj плоскос-
плоскостью Яз. Новую плоскость 7Г3 выбираем
так, чтобы отрезок [АВ] оказался па-
параллелен этой плоскости. Для этого но-
новую ось xi проводим параллельно [ А'В'].
Длина отрезка [Л'/В','] —новой проекции
отрезка [АВ] — укажет искомое рассто-
расстояние.
ПРИМЕР 2. На рис. 261 приведено ре-
решение этой же задачи путем перемещения
отрезка АВ параллельно плоскости 771 в
положение А\В\, параллельное горизон-
горизонтальной плоскости проекции. В этом слу-
случае отрезок будет проецироваться на Т!\
без искажения.
ПРИМЕР 3. На рис. 262 для определе-
определения длины отрезка АВ его перевели в
положение, параллельное плоскости
путем вращения вокруг оси l
Рис. 260
в;
В"-ВГ
Рис. 261
Рис. 262

Определенные расстояния между точкой и прямой, 181
между параллельными прямыми
§ 56. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ,
МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Расстояние от точки до прямой определяется длиной отрезка пер-
перпендикуляра, опущенного из точки на прямую.
Это определение может быть положено в основу составления алго-
алгоритма графического решения задачи определения расстояния от точ-
точки до прямой.
Рис. 263 дает наглядное представление о графическом решении зада-
задачи по определению расстояния от точки А до прямой а . Через точку
А можно провести множество прямых <.1,, 12, 13, ..., ln\ , перпендику-
перпендикулярных к прямой а . Это множество прямых определяет плоскость
•у. Чтобы выделить из \_l\, h, 'з, ••¦, 'л ^единственную прямую lj, пере-
пересекающую прямую а , необходимо найти точку встречи прямой а г.
плоскостью у—М = а п 7; определить длину отрезка [ AM].
Реализация этого алгоритма путем геомет-
геометрических построений значительно упрощается,
если прямая будет параллельна плоскости
проекции.
В этом случае можно без каких-либо
вспомогательных построений провести проек-
проекции прямой, перпендикулярной данной и
проходящей через заданную точку. На рис. 264
показано решение такой задачи. Как видно из
чертежа, решение достигается минимальным
числом геометрических построений. Поэтому
нет смысла решать эту задачу в общем виде,
а следует предварительно с помощью спосо-
способов преобразования ортогональных проекций
перевести прямую в положение, параллельное
плоскости проекции (см. рис. 260, 261,262).
тп\
М
Рис. 264
Рис. 265

182 Метрические задачи
М
m'i
m[
/Мп
Рис. 266
m'
\
Рис. 267
Рис. 268
Решение задачи на определение расстояния между параллельными
прямыми ничем не отличается от только что рассмотренного приме-
примера. Это утверждение базируется на том, что расстояние между парал-
параллельными прямыми определяется величиной перпендикуляра, опу-
опущенного из точки, взятой на одной прямой, на другую прямую.
ПРИМЕР 1. Определить расстояние m и п вокруг оси / (/ ЭЛ, i I и\ ) до по-
между пераллельными прямыми m и п ложения т, || я: и », II тг: ¦ Из точки Л"
(рис. 26В). опускаем перпендикуляр А"М" на пря-
РЕШЕНИЕ. На прямой п отмечаем про- мую нГ|'. Определяем действительную ве
извольную точку Л ?п . Вращаем прямые личину [ AM] .

Определение расстояния между точкой и плоскостью, 183
прямой и плоскостью, между плоскостями и скрещивающимися прямыми
На рис. 266 показан второй вариант
решения этой задачи. С помощью спо-
способа параллельного перемещения прямые
тип переведены в положение, параллель-
параллельное плоскости 7Г2. Дальнейшее решение
сводится к определению расстояния от
точки А, взятой на одной прямой, до дру-
другой прямой m |.
Перевод прямых m и п из общего по-
положения в частное можно осуществить
путем замены плоскости тг2 новой плос-
плоскостью 7Г3, параллельной прямым m и
п. Решение задачи этим способом приве-
приведено на рис. 267.
На рис. 268 рассматриваемая задача
решена путем вращения прямых m и
п вокруг горизонтали h до положения,
параллельного плоскости rti.
§ 57. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ТОЧКОЙ
И ПЛОСКОСТЬЮ, ПРЯМОЙ И ПЛОСКОСТЬЮ,
МЕЖДУ ПЛОСКОСТЯМИ И СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Определение расстояния между: 1 — точкой и плоскостью; 2 — пря-
прямой и плоскостью; 3 — плоскостями; 4 — скрещивающимися прямы-
прямыми рассматривается совместно, так как алгоритм решения для всех
этих задач по существу одинаков и состоит из геометрических построе-
построений, которые нужно выполнить для определения расстояния между за-
заданными точкой А и плоскостью а. Если и есть какое-то различие, то
оно состоит лишь в том, что в случаях 2 и 3 прежде чем приступить
к решению задачи, следует на прямой m (случай 2) или плоскости /3
(случай 3) отметить произвольную точку А. При определении расстоя-
расстояния между скрещивающимися прямыми предварительно заключаем
их в параллельные плоскости а и /3 с последующим определением рас-
расстояния между этими плоскостями.
Рассмотрим каждый из отмеченных случаев решения задач.
1. Определение расстояния между точкой и плоскостью.
Расстояние от точки до плоскости определяется длиной отрезка
перпендикуляра, опущенного из точки на плоскость.
Поэтому решение этой задачи состоит из последовательного вы-
выполнения следующих графических операций:
1) из точки А опускаем перпендикуляра на плоскость а (рис.269);
2) находим точку М пересечения этого перпендикуляра с плоскостью
М =» а П а;
3) определяем длину отрезка [ AM].
Если плоскость а общего положения, то для того чтобы опустить
на эту плоскость перпендикуляр, необходимо предварительно опре-
определить направление проекций горизонтали и фронтали этой плоскос-
плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью
также требует выполнения дополнительных геометрических построений.
Рис. 269

184 Метрические задачи
Рис. 271
Рис. 272
Решение задачи упрощается, если плоскость а занимает частное поло-
положение относительно плоскостей проекций. В этом случае и проведение
проекций перпендикуляра, и нахождение точки его встречи с плоскостью
осуществляется без каких-либо дополнительных вспомогательных по-
построений.
ПРИМЕР 1. Определить расстояние от /' 1 hQCtx a через А" — его фронтальную
точки А до фронтально проецирующей проекцию /" 1 foa- Отмечаем точкуЛГ' =
плоскости а (рис. 270). = Г Г\ foa. Так как АМ\\ттг,то[А М ] =
РЕШЕНИЕ. Через А' проводим гори- = \AM\ = d.
эонтальную проекцию перпендикуляра
Из рассмотренного примера видно, насколько просто решается за-
задача, когда плоскость занимает проецирующее положение. Поэтому, если
в исходных данных будет задана плоскость общего положения, то,
прежде чем приступить к решению, следует перевести плоскость в поло-
положение, перпендикулярное к какой-либо плоскости проекции.
ПРИМЕР 2. Определить расстояние от
точки К до плоскости, заданной Д ABC
(рис. 271).
РЕШЕНИЕ.
1. Переводим плоскость А АВС в про-
проецирующее положение*. Для этого пере-
ходим от системы х к х, ; направ-
7Г, 77,
ление ноной оси jci выбирается перпенди-
перпендикулярным к горизонтальной проекции
горизонтали плоскости треугольника.
2. Проецируем А АВС на новую плос-
плоскость 7Т д (плоскость А А ВС спроециру-
ется на 7Г, в [ С"В"] ).
3. Проецируем на ту же плоскость точ-
точку К (К' ->К",').
4. Через точку К'[ проводим (К"М"I
отрезку [ С"В"] . Искомое расстояние
d = | к';м'!\.
Решение задачи упрощается, если плос-
плоскость задана следами, так как отпадает
необходимость в проведении проекций
линий уровня.
ПРИМЕР 3. Определить расстояние от
точки К до плоскости а, заданной следа-
следами (рис. 272).
*Наиболее рациональным путем перевода плоскости треугольника в проеци-
проецирующее положение является способ замены плоскостей проекций, так как в этом
случае достаточно построить только одну вспомогательную проекцию.

Определение расстояния между точкой и плоскостью, 185
прямой и плоскостью, между плоскостями и скрещивающимися прямыми
РЕШЕНИЕ. Заменяем плоскость тг, = >1оа, n*i) и 1', проводим h oO(l . Опре-
плоскостью тг 1, для этого проводим но- деляем новую горизонтальную проекцию
вую ось х, 1 /оа Ha h oq отмечаем про- точки К -* К\. Из точки К\ опускаем пер-
извольную точку 1' и определяем ее но- пендикуляр на h oq, и отмечаем точку
вую горизонтальную проекцию на плос- его пересечения с h оа, ~ М\. Длина от-
кости тг, A'). Через точки Х(х] (Ac*, - резка К\М\ укажет искомое расстояние.
2. Определение расстояния между прямой и плоскостью.
Расстояние между прямой и плоскостью определяется длиной отрез-
отрезка перпендикуляра, опушенного из произвольной точки прямой на
плоскость (см. рис. 248).
Поэтому решение задачи по определению расстояния между прямой
m и плоскостью а ничем не отличается от рассмотренных в п. 1 примеров
на определение расстояния между точкой и плоскостью (см. рис. 270 ...
272). В качестве точки можно брать любую точку, принадлежащую
прямой т.
3. Определение расстояния между плоскостями.
Расстояние между плоскостями определяется величиной отрезка
перпендикуляра, опущенного из точки, взятой на одной плоскости,
на другую плоскость.
Из этого определения вытекает, что алгоритм решения задачи по на-
нахождению расстояния между плоскостями а и C отличается от анало-
аналогичного алгоритма решения задачи по определению расстояния между
прямой m и плоскостью а лишь тем, что прямая m должна принадлежать
плоскостиа., т. е., чтобы определить расстояние между плоскостями а и C,
следует:
1) взять в плоскости а прямую т;
2) выделить на прямой m произвольную точку А;
3) из точки А опустить перпендикуляр / на плоскость /3;
4) определить точку М — точку встречи перпендикуляра / с плос-
плоскостью C;
5) определить величину отрезка [ AM] .
На практике целесообразно пользоваться другим алгоритмом реше-
решения, который будет отличаться от приведенного лишь тем, что, преж-
прежде чем приступить к выполнению первого пункта, следует перевести
плоскости в проецирующее положение.
Включение в алгоритм этой дополнительной операции упрощает
выполнение всех без исключения остальных пунктов, что, в конеч-
конечном счете, приводит к более простому решению.
ПРИМЕР 1. Определить расстояние плоскости Яд плоскости си и C занимают
между плоскостями а и E (рис. 273). проецирующее положение, поэтому рас-
РЕШЕНИЕ. Переходим от системы стояние между новыми фронтальными
я2 я, следами f,ta, и Aifli является искомым.
х— к х, —. По отношению к новой ' '
я, тг,
В инженерной практике часто приходится решать задачу на построе-
построение плоскости, параллельной данной и удаленной от нее на заданное
расстояние. Приведенный ниже пример 2 иллюстрирует решение такой
задачи.
ПРИМЕР 2. Требуется построить про- 2. Из точки 1 восставляем перпенди-
екции плоскости /3, параллельной данной куляр / к плоскости а (/' 1 h", I" If").
плоскости а (т || п), если известно, что 3. На перпендикуляре / отмечаем про-
расстояние между ними равно d (рис. 274). извольную точку А.
РЕШЕНИЕ. 4. Определяем длину отрезка |1Л] —
1. В плоскости а проводим произволь- [ 1'А(|] (положение [ 1'Л0] указывает на
ные горизонталь h A, 3) и фронталь f эпюре метрически неискаженное направ-
A, 2). ление прямой / ).

186 Метрические задачи
а"
Рис. 273
Рис. 274
))
5. Откладываем на прямой A'Л0)
точки 1' отрезок [ \'В0 ] = d.
6. Отмечаем на проекциях V и /" точки
В' и В", соответствующие точке Во-
7. Через точку В проводим плоскость
Р С*1 ^ Л ) ¦ Чтобы 0 |] а, необходимо со-
соблюдать условие /t, || Л и fi || Л
4. Определение расстояния между скрещивающимися прямыми.
Расстояние между скрещивающимися прямыми определяется длиной
перпендикуляра, заключенного между параллельными плоскостями,
которым принадлежат скрещивающиеся прямые.
Для того чтобы через скрещивающиеся прямые m и f провести вза-
взаимно параллельные плоскости а и 0, достаточно через точку А (А & т)
провести прямую р, параллельную прямой f, а через точку В (В & f) —
прямую k, параллельную прямой т. Пересекающиеся прямые т и р, /и k
определяют взаимно параллельные плоскости а и 0 (см. рис. 248, е).
Расстояние между плоскостями а и 0 равно искомому расстоянию между
скрещивающимися прямыми т и f.
Можно предложить и другой путь для определения расстояния между
скрещивающимися прямыми, который состоит в том, что с помощью
какого-либо способа преобразования ортогональных проекций одна из
скрещивающихся прямых переводится в проецирующее положение. В
этом случае одна проекция прямой вырождается в точку. Расстояние
между новыми проекциями скрещивающихся прямых (точкой А'^ и
отрезком C2D2) является искомым.
На рис. 275 приведено решение задачи на определение расстояния
между скрещивающимися прямыми а и Ь, заданными отрезками [ АВ] и
[ CD]. Решение выполняют в следующей последовательности:
1. Переводят одну из скрещивающихся прямых (а ) в положение,
параллельное плоскости тг3; Для этого переходят от системы плоскостей
проекции х—— к новой х, —Ц ось Xi проводят параллельно горизонталь-
ной проекции прямой а . Определяют а, [А"В"] и b" [C'lD"].
2. Путем замены плоскости я, плоскостью 7Г4 переводят прямую

О проекциях плоских углов 187
Рис. 275
а в положение а[, перпендикулярное плоскости я4 (новую ось х2 прово-
проводят перпендикулярно а',).
3. Строят новую горизонтальную проекцию прямой Ь2 — [ C'2D'2\ .
4. Расстояние от точки А2 до прямой C\D2 ( отрезок [ Л2Л/2] (являет-
(является искомым.
Следует иметь в виду, что перевод одной из скрещивающихся пря-
прямых в проецирующее положение является ничем иным, как переводом
плоскостей параллелизма, в которые можно заключить прямые а и Ь,
также в проецирующее положение.
В самом деле, переведя прямую а в положение, перпендикулярное
плоскости 7г4, мы обеспечиваем перпендикулярность любой плоскости,
содержащей прямую а , плоскости я4, в том числе и плоскости а, опреде-
определяемой прямыми а и т (а п пг, т \\ Ь). Если мы теперь проведем пря-
прямую п, параллельную а и пересекающую прямую Ь, то мы получим
плоскость /3, являющуюся второй плоскостью параллелизма, в которую
заключены скрещивающиеся прямые а и Ъ. Так как 0 || а, то и 0 1 я4.
§ 58. О ПРОЕКЦИЯХ ПЛОСКИХ УГЛОВ
Отметим ряд свойств ортогональных проекций плоских углов, зна-
знание которых поможет в дальнейшем правильно читать эпюр и решать
задачи по определению величины угла, если известны его ортогональные
проекции.
1. Если стороны угла не параллельны плоскости проекции, то угол
проецируется на эту плоскость с искажением.
Следует иметь в виду, что проекции острого или тупого углов могут, при опреде-
определенных условиях, проецироваться на плоскость проекции без искажения, будучи и
не параллельными плоскости проекции.

188 Метрические задачи
Рис. 276
Рис. 277
Рис. 278
Из рис. 276 видно, что все углы с вершиной на прямой (MN), стороны которых
расположены в проецирующих плоскостях Ос и 0, проецируются в LKNL; при этом
проецируемые углы BAD и ВАС могут изменяться в пределах от 0° до 180°. Естест-
Естественно, что среди них будет угол, равный L KNL.
2. Если хотя бы одна сторона тупого, прямого или острого угла
параллельна плоскости проекции, то проекцией угла на эту плоскость
будет угол с тем же названием, что и сам угол (тупой, прямой, ост-
острый).
Убедиться в этом легко на примере, показанном на рис. 277. Пусть
дан отрезок [ АВ] || тт, , строим тупой L ABC и острый L ABD. Сторону BD
угла ABD проводим так, чтобы [ BD] принадлежал плоскости, определя-
определяемой точками Л, В, С. Проводим в плоскости А, В, С отрезок [ BE] 1
1. [ АВ] . Так как L ABE прямой, а сторона угла АВ || тг, , то проекция
этого угла на плоскость тт, также будет равна 90° . Из чертежа видно, что
L. A'B'D < 90°, a L А'В'С > 90°.
3. Если обе стороны любого угла параллельны плоскости проек-
проекции, то на эту плоскость он проецируется без искажения.
Справедливость этого утверждения не вызывает сомнения — оно
вытекает непосредственно из инвариантного свойства ортогонального
проецирования (Ф с /3)Л (/3 II п, ) = Ф' = Ф.
4. Если стороны угла параллельны плоскости проекции или оди-
одинаково наклонены к ней, то деление пополам проекции угла соответст-
соответствует его делению пополам в пространстве (рис. 278).
Стороны /. ABC (рис. 278) наклонены под одинаковым углом к
плоскости проекции я, : АНоаА' = ВНаьВ', L А'В'С' — ортогональ-

Определение величины плоского угла 189
по его ортогональным проекциям
ная проекция L ABC на плоскость тг,, [B'D1] — биссектриса LA'B'C'.
На основании свойства биссектрисы внутреннего угла в треугольни-
Кв iP'C'l ~ IBT'V но п0 СВОИСТВУ 2и (см. гл. I, § 6) .ЛГ>} = | , , следо-
следовательно, \В';А',} = M^rf. Но \В'А'\ = \ВА\ cos<?° и \В'С\ = |ВС| cos </>,
[В С | [DC |
откуда ,—:—т.— », ; „ = -; г. Следовательно, ,——— = ———-, т. е.
\ВС\ \ВС\ cos (^ \BC\ \DC\ \BC\
[BD) — биссектриса L ABC.
В заключение следует еще раз заострить внимание читателя на част-
частном случае проецирования прямого угла. Сформулируем его не в виде
свойства, как это было сделано в гл. I, § 6, а в виде вытекающего из него
следствия: если проекция некоторого угла, у которого одна сторона
параллельна плоскости проекции, равна прямому углу, то и проецируе-
проецируемый угол также прямой.
Это следствие имеет весьма важное значение. Базируясь на нем,
мы можем просто, с минимальным числом геометрических построений
решать на эпюре Монжа задачи по построению:
а) прямых, перпендикулярных друг к другу;
б) прямой, перпендикулярной плоскости;
в) взаимно перпендикулярных плоскостей (см. гл. VI, § 54).
§ 59. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПЛОСКОГО УГЛА ПО ЕГО
ОРТОГОНАЛЬНЫМ ПРОЕКЦИЯМ
В предыдущем параграфе было отмечено, что плоский угол прое-
проецируется на плоскость проекции без искажения в том случае, когда
его стороны параллельны этой плоскости. Это свойство может быть
принято за основу при составлении алгоритма решения задачи на опре-
определение величины угла по его искаженным ортогональным проекциям.
Решение задачи будет сводиться к перемещению плоскости общего
положения, которой принадлежит угол, в положение, параллельное
какой-либо плоскости проекции. Такое перемещение можно осущест-
осуществить с помощью способов преобразования ортогональных проекций.
Наиболее рациональное решение задачи по переводу плоскости угла
в положение, параллельное плоскости проекции, достигается путем
вращения плоскости угла вокруг линии уровня. В этом случае для
получения ответа на поставленную задачу достаточно произвести пово-
поворот только одной точки вокруг горизонтали или фронтали плоскос-
плоскости угла — построить только одну вспомогательную проекцию.
При использовании других способов преобразования нам приш-
пришлось бы дважды менять плоскости проекции, либо дважды осуществ-
осуществлять перемещение (или вращение), параллельное плоскости проекции,
т. е. в обоих случаях потребовалось бы построение двух вспомогатель--
ных проекций.
Приведенные ниже примеры иллюстрируют использование способа
вращения вокруг линии уровня для решения задачи по определению
'величины плоского угла.
ПРИМЕР 1. Определить угол между горизонтали h до нового положения, па-
пересекающимися прямыми а и Ь раллельного плоскости я,. Точки А и В
(рис. 279). принадлежат оси вращения h , поэтому
РЕШЕНИЕ. Вращаем плоскость а, оп- при вращении плоскости а вокруг оси h
ределяемую прямыми а и Ь, вокруг ее они не меняют своего положения. Следо-

190 Метрические задачи
В" h"
1"
Рис. 279
Рис. 280
вательно, для определения нового поло-
положения плоскости а1 достаточно осущест-
осуществить поворот только одной точки К.
Для этого проводим через К' прямую,
перпендикулярную И' (с этой прямой
будет совпадать горизонтальная проек-
проекция окружности, по которой перемещает-
перемещается точка при ее вращении вокруг h ).
Далее определяем положение центра
вращения О и величину радиуса враще-
вращения R для точки К (построения выпол-
выполнены аналогично тому, как это было
сделано на рис. 71, § 11). Положение
точки К\ совместно с Л' и В' определяет
новые проекции прямых а\ и Ь[, задаю-
задающих плоскость и].Поэтому А'К\В' равен
искомому углу <р° .
ПРИМЕР 2. Определить величину уг-
углов Д АВС (рис. 280) .
РЕШЕНИЕ. Вращаем плоскость A ABC
вокруг фронтали f этого треугольника
до положения, параллельного плоскости
ть. Через вершину А А АВС проводим
фронталь / (/¦', /"'). Точки А и D как при-
принадлежащие оси вращения не изменят
своего положения в процессе преобразо-
преобразования. Поэтому, как и в предыдущем
примере, достаточно повернуть только
одну точку. На рис. 280 в качестве такой
точки взята вершина В А ABC-
Вершина треугольника С при враще-
вращении вокруг фронтали будет перемещать-
перемещаться по дуге окружности, плоскость кото-
которой перпендикулярна оси вращения f;
поэтому фронтальная проекция этой
окружности перпендикулярна /" и новое
положение С[ определится в точке
пересечения этого перпендикуляра с
новым положением прямой B"D". После
такого поворота плоскость треугольника
переводится в положение, параллельное
плоскости эт2. Следовательно, на основа-
основании инвариантного свойства 2д (см. § 6)
углы при вершинах А", В" и С" проеци-
проецируются без искажения.
§ 60. ОПРЕДЕЛЕНИЕ УГЛА МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Определение угла между прямой и плоскостью, двумя плоскостями,
скрещивающимися прямыми, сводится к нахождению угла между двумя
прямыми.
Чертежи на рис. 281 подтверждают это высказывание. Известно,
что углом между прямой и плоскостью называется угол между этой
прямой и ее прямоугольной проекцией на данную плоскость*.
*Естественно, речь идет о случае, когда прямая не перпендикулярна плоскости.

Определение угла между прямой и плоскостью 191
a) m a=m ma=ep°
б) a p=w п=Ф
Рис. 281
Геометрическая интерпретация приведенного определения показа-
показана на рис. 281,а. План решения задачи может быть записан в следую-
следующем виде:
1. Из произвольной точки К € т опускаем перпендикуляр на плос-
плоскость а.
2. Определяем точку встречи этого перпендикуляра с плоскостью —
К (точка Ка— ортогональная проекция К на плоскость ft) .
3. Находим точку А — пересечения прямой т с плоскостью а.
4. Проводим (К А) — проекцию прямой т на плоскость а.
5. Угол / КАК01 — искомый.
Решение этой задачи может быть значительно упрощено, если опре-
определять не угол между прямой и плоскостью (L\p°), а дополнитель- '
ный до 90° L ф°. В этом случае отпадает необходимость в определе-
определении точки Ка и проекции та. Зная величину ф°, вычисляем $° = 90° -
~ V ¦
ПРИМЕР 1. Определить угол между
прямой а и плоскостью ft (m ||n|
(рис. 282) .
РЕШЕНИЕ.
1. Определяем направление горичон
тальной проекции горизонтали И' и фрон-
фронтальной проекции фронтали .(" плоскос-
плоскости ft.
2. Из произвольной точки К прямой а
проводим прямую /la; для этого через
К' проводим /' 1 h' и через К" - I" I f".
Л. Определяем величину угла ^° вра-
вращением его вокруг горизонтали до по-
положения, параллельного плоскости я, .
4. Вычисляем значение искомого угла
ф° --- 90 ~ф°
Решение аналогичной задачи упрощается, если плоскость задана
следами, так как в этом случае отпадает необходимость в определении
проекций линий уровня.

192 Метрические задачи
'Оа
0<х
Рис. 282
Рис. 283
ПРИМЕР 2. Определить угол между
прямой а и плоскостью а, заданной сле-
следами (рис. 283).
РЕШЕНИЕ.
1. Из произвольной точки К прямой а
опускаем перпендикуляр / на плоскость
a (l'lhoa,l" Lfoa)-
2. Определяем величину угла ф°.
3. Вычисляем значение искомого угла
а° = 9о° -Ф°.
§ 61. ОПРЕДЕЛЕНИЕ УГЛА МЕЖДУ ПЛОСКОСТЯМИ
Мерой угла между двумя плоскостями служит линейный угол, обра-
образованный двумя прямыми — сечениями граней этого угла плоскостью,
перпендикулярной к их ребру.
Для построения линейного угла, являющегося мерой двугранного
угла, необходимо выполнить следующие геометрические построения:
1. Определить прямую а — линию пересечения данных плоскос-
плоскостей a и /3, а = а п /3 (рис. 284).
2. Провести плоскость у GI а иу i /3).
3. Построить прямые m = у П а ип= -у о /3.
4. Найти величину угла 1р° между прямыми тип. Угол <?° — иско-
искомый.
Рассмотренный план решения задачи предусматривает выполнение
большого числа геометрических построений, связанных с нахождени-
нахождением линии пересечения данных плоскостей (а = аП/3), проведением
плоскости, перпендикулярной к найденной прямой (у 1 a ). Далее
приходится еще дважды решать задачу по определению линии пере-
пересечения плоскостей (пг = уГ\аип= 7П0) и лишь только после это-
этого можно приступить к определению величины искомого углаф°.
Проследим, как можно упростить решение этой задачи. Дополним
чертеж на рис. 284 точкой Ке у и опустим из этой точки перпенди-
перпендикуляры k и / на плоскости а и ^ (рис. 285). Точки М и N пересечения

Определение угла между плоскостями 193
Рис. 284
Рис. 285
Рис. 286
этих перпендикуляров с плоскостями совместно с точками К и
А (Аёд) являются вершинами плоского четырехугольника KNAM,
у которого углы при вершинах М и N прямые. Следовательно, меж-
между углами при вершинах А и К существует зависимость, которую можно
выразить следующим равенством: $° = 180° - ф°. Из рис. 285 видно, что
вместо L ip° гораздо проще определять дополнительный до 180° L ф °. Все
решение сводится к построению угла ф° путем проведения из произволь-
произвольной точки пространства К прямых k и I , перпендикулярных к заданным
плоскостям, и определению угла ф° между этими прямыми; после че-
чего по дсчитывается значение величины $° = 180° - %° (рис.286).
b'-
Рис. 287.

194 Метрические задачи
К
iQa
......:ъ.€ __!„ „
Рис. 288
ПРИМЕР 1. Определить угол между
плоскостями а (а II Ь) и & (с П d)
(рис. 287).
РЕШЕНИЕ.
1. Определяем направление горизон-
горизонтальных проекций горизонталей h[ и h\,
фронтальных проекций фронтален /}' и
f'{ заданных плоскостей а и C.
2. Из произвольной точки К проводим
проекции перпендикуляров k и / (k' I h\,
k" Lf'iuVLh'bl" Lf'i).
3. Определяем величину ф°.
4. Вычисляем значение $>° = 180° - ф°.
Если плоскости, угол между которыми требуется определить, за-
задан следами, то решение упрощается еще больше, так как отпадает
необходимость в выполнении п. 1 только что рассмотренного реше-
решения.
ПРИМЕР 2. Определить угол между плоскостей а и |3 (k' I hOOll k" 1 foa и
плоскостями а и (}, заданными следами /' 1 Л0C. '"-L/ofl)- Затем известным спо-
(рис. 288). собомнаходим величину ф° (на рис. 288
РЕШЕНИЕ. Все геометрические постро- Wwijr определен путем вращения вок-
ения сводятся к проведению через точку руг Фронтали). Зная ф , вычисляем зна-
К прямых, перпендикулярных к следам чение Ф
§ 62. ОПРЕДЕЛЕНИЕ УГЛА МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Углом между скрещивающимися прямыми называется плоский угол,
который образуется между прямыми, проведенными из произволь-
произвольной точки пространства параллельно данным скрещивающимся пря-
прямым.
Поэтому решение задачи по определению величины угла между скре-
скрещивающимися прямыми по существу ничем не отличается от решения
задачи по определению угла между пересекающимися прямыми (см.
Рис. 289

Отделение угла между 195
скрещивающимися прямыми
§ 59). Единственное отличие состоит в том, что на первой стадии ре-
решения необходимо построить плоский угол, являющийся аналогом
искомого угла. Для этого через произвольную точку, которую при-
принимаем за вершину угла, проводим две прямые, параллельные заданным
скрещивающимся прямым. Чтобы не происходило наложения линий
вспомогательных построений на исходные данные задачи, точку, которую
принимают за вершину угла, следует брать в свободном месте чертежа,
как это сделано на рис. 289.
ПРИМЕР 1. Определить угол между
скрещивающимися прямыми а и Ъ
(рис. 289).
РЕШЕНИЕ. Из произвольной точки К
проводим прямые с и d (с \\ а и d \\ Ь).
Определяем величину угла ф° (см. § 59,
пример 1, рис. 279) .
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какие характеристики геометричес-
геометрических фигур называют метрическими?
2. В каких случаях угловые величи-
величины проецируются без искажения?
3. Как решается задача по определе-
определению величины угла между двумя пря-
прямыми, прямой и плоскостью, двумя
плоскостями?
4. Что является мерой угла между
скрещивающимися прямыми?
5. Как построить на эпюре Монжа про-
проекции двух взаимно перпендикулярных
прямых; прямой, перпендикулярной
плоскости; двух взаимно перпендикуляр-
перпендикулярных плоскостей?
6. Как определить величину отрезка
прямой общего положения по его орто-
ортогональным проекциям?
7. Как определить расстояние от точ-
точки до плоскости; между плоскостями;
между параллельными и скрещивающи-
скрещивающимися прямыми?

ГЛАВА
VII
РАЗВЕРТКА ПОВЕРХНОСТЕЙ
Приступая к изучению развертки поверхности, посляднюю целесооб-
целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые
из представленных таким образом поверхностей можно путем изгиба-
изгибания совместить с плоскостью. Если при этом отсек поверхности может
быть совмещен с плоскостью без разрывов и склеивания, то такую
поверхность называют развертывающейся, а полученную плоскую
фигуру — ее разверткой. Поверхности, которые не могут быть
совмещены с плоскостью, относятся к неразвертываемым поверх-
поверхностям.
К группе развертывающихся поверхностей относятся только линей-
линейчатые поверхности и, в частности, те из них, которые имеют пересе-
пересекающиеся смежные образующие. Точка пересечения может быть как
собственной (поверхности с ребром возврата и конические), так и
несобственной (цилиндрические поверхности).
Деформацию поверхности а для получения ее развертки можно
представить как постепенное ее разгибание (совмещение с плоскос-
плоскостью /3, касательной к этой поверхности). На рис. 290 задана коничес-
коническая поверхность а и показана касательная к ней плоскость 0. Обра-
Образующая g — линия касания.
Отметим на направляющей конической поверхности d точку 2; про-
проведем через нее образующую конической поверхности (S2). Если рас-
расстояние между точками 1 и 2 мало, то отсек конической поверхнос-
поверхности, заключенной между образующими S1 и S2, можно с определенной
степенью точности отождествлять с Д IS2. Если теперь мы повернем
A 1S2 вокруг стороны IS до его совмещения с плокостью /3, то по-
получим A1OS2O, представляющий развертку отсека 1S2 поверхности
а на плоскость /3.
При перемещении точки 2 в положение 20 направляющая коничес-
конической поверхности d переместится в положение di, а точка 3 ? d займет
положение 3, &d{. Соединив точку 3] с вершиной S, получим отсек
конической поверхности 20S3{ = 2S3, который, как и в предыдущем
случае, можно с определенной степенью точности рассматривать как
Д 20S3t . Вращая этот треугольник вокруг стороны S20 до совмещения с
плоскостью C, получим Д 20S3a — развертку отсека 2S3 поверхности а на
плоскость /3.
Отметив на направляющей d точки 4, 5, ..., N, принимая их за вер-
вершины треугольников 3S4, 4S5, ..., (N - I)SN и осуществляя их после-
последовательный поворот вокруг предварительно совмещенной стороны
этих треугольников, можно получить приближенную развертку по-
'верхности а на плоскость |3.
Для выполнения показанных на рис. 290 построений необходимо,
чтобы плоскость, касательная к поверхности, касалась ее по прямой

Основные свойства развертки 197
поверхностей
l-lo
Рис. 290
образующей, которую принимаем за первоначальное положение оси
вращения.
Если касательная плоскость касается поверхности в точках, при-
принадлежащих линии, то такие точки называют параболическими (см.
гл. V, § 46). При этом у торсовых поверхностей (конических, цилинд-
цилиндрических, с ребром возврата) линии, образованные параболическими
точками, — прямые, которые можно принять за оси вращения (см.
рис. 290). Поэтому ранее отмеченный признак для развертывающих-
развертывающихся поверхностей может быть заменен следующим: к развертывающим-
развертывающимся поверхностям относятся поверхности, имеющие только параболичес-
параболические точки*.
Построение разверток имеет большое практическое значение, так как
позволяет изготавливать разнообразные изделия из плоского (листово-
(листового) материала путем его изгибания.
§ 63. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
С позиции теории множеств поверхность и ее развертку следует
рассматривать как два точечных множества.
Так как по определению развертка поверхности представляет собой
плоскую фигуру, образованную из поверхности без разрывов и склеива-
склеивания, то между отмеченными двумя множествами устанавливается взаим-
взаимно-однозначное соответствие:
каждой точке (фигуре) на поверхности соответствует точка (фи-
(фигура) на развертке и наоборот.
Фигура 1S2, образованная подмножеством точек, принадлежащих
поверхности а, конгруентна фигуре 1S2O, принадлежащей развертке а0.
Аналогично A 2S3 Са = 2nS30 Ca0 и т. д. Отсюда следует, что рассто-
расстояние между точками 1 и 2 или любыми другими точками, взятыми
на фигуре 1S2, равно расстоянию между точками 10 и 20 фигуры 1OS2O.
На основании этого можно сформулировать следующие свойства:
1. Длины двух соответствующих линий поверхности и ее развертки
равны между собой, следствием чего является:
*К таким поверхностям относятся торсы, при этом особые точки, принадлежа-
принадлежащие ребру возврата или вершине конической поверхности, во внимание не при-
принимаются.

198 Развертка поверхностей
\всы
\ВаС0Ы0
<Р°=<Р°0
Рис. 291
замкнутая линия на поверхности и соответствующая ей линия на раз-
развертке ограничивают одинаковую площадь.
2. Угол между линиями на поверхности равен углу между соот-
соответствующими им линиями на развертке*.
Рис. 291 дает наглядное представление о развертке как взаимно-
взаимнооднозначном преобразовании, сохраняющем равенство:
а) расстояний между точками;
б) углов между линиями;
в) площадей фигур.
Кроме перечисленных свойств, следует отметить также:
3. Прямой на поверхности соответствует также прямая на развертке
(обратное утверждение не имеет смысла).
4. Параллельным прямым на поверхности соответствуют также па-
параллельные прямые на развертке.
5. Если линии, принадлежащей поверхности и соединяющей две
точки поверхности, соответствует прямая на развертке, то эта линия
является геодезической**.
§ 64. РАЗВЕРТКА ПОВЕРХНОСТИ МНОГОГРАННИКОВ
Развертка поверхности многогранников известна читателю из средней
школы. Поэтому на этом вопросе мы останавливаемся кратко, только в
плане повторения известных ранее сведений.
Под разверткой многогранной поверхности подразумевают плос-
плоскую фигуру, составленную из граней этой поверхности, совмещен-
совмещенных с одной плоскостью.
Существуют три способа построения развертки многогранных по-
поверхностей:
1) способ нормального сечения;
* Геометрическое преобразование, при котором сохраняются величины углов, на-
называется конфорным, следовательно, построение разверток является конфорным
преобразованием, а поверхность и ее развертка конфорны.
**Геодезической называется линия, принадлежащая поверхности и соединяю-
соединяющая кратчайшим путем две точки, также принадлежащие поверхности.

Развертка поверхности многогранников 199
2) способ раскатки;
3) способ треугольников (триангуляции).
Первые два применяются для построения развертки призматичес-
призматических поверхностей, третий -- для пирамидальных поверхностей. Рас-
Рассмотрим каждый их этих способов.
1. Способ нормального сечения.
ПРИМЕР. Построить развертку нак-
наклонной трехгранной призмы ABCDEF
(рис. 292).
РЕШЕНИЕ. Пересечем призму ABCDEF
плоскостью 7, перпендикулярной к боко-
боковым ребрам призмы. Построим сечение
заданной призмы этой плоскостью —
Д 123. Определим длины сторон Д 123.
В свободном месте чертежа проведем
прямую а (на рис. 292 прямая а прове-
проведена горизонтально). От произвольной
точки 10, взятой на этой прямой, отло-
отложим отрезки [1020], [2О3О], [3oloL
конгруентные сторонам Д 123. Через точ-
точки 10, 20, 30, 1q проведем прямые,
перпендикулярные к прямой а , и отло-
отложим на них от точек 10, 20, 30, 10 отрез-
отрезки, конгруентные соответствующим дли-
длинам боковых ребер ([1А], [ID], [2B],
[ 2?], ...). Полученные точки A0BqC0Aq
и Do Ео Fo Do соединяем прямыми*
Плоская фигура A0BQC0A0D0F0E0D0
представляет собой развертку боковой
поверхности призмы.
Чтобы получить полную развертку
призмы, необходимо к развертке боко-
боковой поверхности пристроить основания
призмы — &А0В0С0 иД DqE0F0 , предва-
предварительно определив их неискаженные
размеры.
¦На рис. 292 ребра AD, BE и CF параллельны плоскости TTi, поэтому они проеци-
проецируются на эту плоскость без искажения. Если ребра призмы занимают произвольное
положение, то прежде чем приступить к построению развертки, следует с помощью
способов преобразования перевести их в положение, параллельное какой-либо плос-
плоскости проекции.
Рис. 292

200 Развертка поверхностей
2. Способ раскатки.
Этот способ целесообразно использовать для построения разверт-
развертки поверхности призмы в том случае, когда основание призмы парал-
параллельно какой-либо одной плоскости проекции, а ее ребра параллель-
параллельны другой плоскости проекции.
ПРИМЕР. Построить развертку боко-
боковой поверхности наклонной трехгранной
призмы ABCDEF (рис. 293).
РЕШЕНИЕ. Примем за плоскость раз-
развертки плоскость 7> проходящую через
ребро AD, параллельную фронтальной
плоскости проекции. Совместим грань
ADEB с плоскостью 7- Для этого мыслен-
мысленно разрежем боковую поверхность приз-
призмы по ребру AD, а затем осуществим по-
поворот грани ADEB вокруг ребра AD
(A"D").
Для нахождения совмещенного с плос-
плоскостью 7 положения ребра B0EQ из точ-
точки В" проводим луч, перпендикулярный
к A"D" и засекаем на нем дугой радиуса
I А'В'\ , проведенной из центра А , точку
Во. Через Во проводим прямую В0Е0,
параллельную (А"П").
Принимаем совмещенное положение
ребра В0Е0 за новую ось вращения и по-
поворачиваем вокруг нее грань BEFC до
совмещения с плоскостью у. Для этого
из точки С" проводим луч, перпендику-
перпендикулярный к совмещенному ребру B0Eq,
а из точки В о — дугу окружности радиу-
радиусом, равным |В'С'|; пересечение дуги
с лучом определит положение точки Со.
Через Со проводим C0F0 параллельно
B0EQ. Аналогично находим положение
ребра А0П0. Соединив точки А"В0С0А0
и D'EqF0D0 прямыми, получим фигуру
A"BQC0A0DQF0E0D" — развертку боко-
боковой поверхности призмы. Для получения
полной развертки призмы достаточно к
какому-либо из звеньев ломаной линии
A"BqC0Aq и D"E0F0Do пристроить треу-
треугольники основания Л0В0С()И DqE0F0.
3. Способ треугольников (триангуляции).
ПРИМЕР. Построить развертку боко-
боковой поверхности пирамиды SABC
(рис. 294).
Развертка боковой поверхности пира-
пирамиды представляет собой плоскую фигу-
фигуру, состоящую из треугольников —граней
пирамиды.
На рис. 294 определение длин ребер
пирамиды выполнено с помощью враще-
вращения их вокруг оси i Э Я и < 1 тг,. Путем
вращения ребра пирамиды совмещаются
с плоскостью 7 плоскость 7 II 7Г2 и 7 -^ '
Посде того как определены длины ребер
\S"A2\, |S"B2|, \S"C2\, приступаем к пост-
д
Е'

Построение приближенных разверток 201
развертывающихся поверхностей
г3=1С/Г|
Рис. 294
роению развертки. Для этого через про-
произвольную точку So проводим прямую а.
Откладываем на ней от точки S 0 [ S 0А 0 ] —
= [S"A 2 ]¦ Из точки Л о проводим дугу ра-
радиусом г , = | Л'В'!, а из точки So —ду-
—дугу радиусом fi| = \S"B2\- Пересечение
дуг укажет положение вершины Во
AS0A0B0 (AS0A0B0 ^ A SAB - грани
пирамиды). Аналогично находятся точки
Со и Ао. Соединив точки А0В0С0А0,
получим развертку боковой поверхности
пирамиды SABC.
§ 65. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ РАЗВЕРТОК
РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
Мы уже указывали, что к развертывающимся поверхностям отно-
относятся только торсы (поверхности с ребром возврата, коническая и ци-
цилиндрическая поверхности).
Развертка любой развертывающейся поверхности (кроме гран-
ных) является приближенной. Это объясняется тем, что при развертке
поверхности последнюю аппроксимируют поверхностями вписанных
или описанных многогранников, имеющих грани в форме прямоуголь-
прямоугольников или треугольников. Поэтому при графическом выполнении раз-
развертки поверхности всегда приходится производить разгибание или
спрямление кривых линий, принадлежащих поверхности, что неизбежно
приводит к потере точности.
Рассмотрим способы построения приближенных разверток поверх-
поверхностей: цилиндрической, конической и с ребром возврата.
А. Построение развертки цилиндрической поверхности.
Для построения развертки цилиндрической поверхности исполь-
используются те же способы нормального сечения и раскатки, которые при-
применяются при развертывании боковой поверхности призмы.
В обоих случаях цилиндрическую поверхность заменяют призматичес-
призматической поверхностью, вписанной (или описанной) в данную цилиндричес-
цилиндрическую. Затем задачу решают так же, как это было показано в примерах
1 и 2 предыдущего параграфа. На рис. 295 и 296 показано построение бо-
боковой поверхности цилиндра способом нормального сечения (рис. 295) и
способом раскатки (рис. 296).

202 Развертка поверхностей
Рис. 296

Построение приближенных разверток 203
развертывающихся поверхностей
При построении развертки поверхности цилиндра вращения пред-
предпочтение следует отдать способу нормального сечения, так как в этом
случае можно не прибегать к замене цилиндрической поверхности приз-
призматической.
Для того чтобы построить развертку поверхности прямого кру-
кругового цилиндра, выполняем следующие геометрические построения:
1. Рассекаем цилиндрическую поверхность а плоскостью у, перпен-
перпендикулярной к прямолинейной образующей цилиндрической поверх-
поверхности.
2. Делим окружность с — линию сечения а п у на одинаковое число
частей п.
3. Проводим в свободном месте чертежа прямую а и отмечаем на
ней отрезок 1010, равный длине окружности сечения с.
4. Делим [1010] на такое же число одинаковых частей п, на кото-
которое была разделена окружность с.
5. Через точки деления 10, 20, 30, ..., 120, 10 проводим прямые,
перпендикулярные к прямой а , и откладываем на них от точек 10, 20,
30, ..., 120, 10 отрезки, равные длине соответствующих образующих
нижней и верхней частей цилиндрической поверхности.
6. Соединив концы образующих плавной кривой, получим разверт-
развертку цилиндрической поверхности.
На рис. 296 приведен пример построения развертки боковой по-
поверхности эллиптического цилиндра способом раскатки. Необходи-
Необходимые геометрические построения выполняем в следующем порядке:
1. Делим окружность основания цилиндра на и равных частей (на
рис. 296 п = 12).
2. Через точки деления проводим прямолинейные образующие ци-
цилиндрической поверхности — ребра призмы, которой мы заменяем
цилиндрическую поверхность а.
3. Принимаем за плоскость развертки горизонтальную плоскость
0, проходящую через ребро 1 призмы, тождественное 1-й образующей
цилиндрической поверхности
Дальнейшие построения аналогичны выполненным на рис. 293 при
построении развертки боковой поверхности призмы ABCDEF.
Б. Построение развертки конической поверхности.
Задача на построение развертки конической поверхности решается
так же, как в случае построения развертки боковой поверхности пира-
пирамиды — способом треугольников (см. рис. 294). Для этого коническая
поверхность аппроксимируется вписанной в нее пирамидальной по-
поверхностью.
На рис. 297 показана развертка поверхности пирамиды SABCDEF...,впи-
SABCDEF...,вписанной в заданную коническую поверхность а. Фигуру S0A0B0C0DoE0Fo ¦¦¦
... Л о принимаем за приближенную развертку конической поверхности.
Чем больше число граней у вписанной пирамиды, тем меньше будет
разница между действительной и приближенной развертками конической
поверхности.
Если задана поверхность прямого кругового конуса (рис. 298), то
развертка его боковой поверхности представляет круговой сектор,
радиус которого равен длине образующей конической поверхности
/ = \SA\, а центральный угол <р° = 2яг//, где г — радиус окружности осно-
основания конуса. Величина угла у получается в радианах. На практике
бывает целесообразно иметь его градусную величину. Это легко сделать,
подставив в приведенное равенство значение величины /, выраженное че-
через радиус основания конуса г и угол наклона образующей коничес-

204 Развертка поверхностей
кой поверхности к плоскости я, (/. ф '). В лом случае / r/cos ф'\ тог-
тогда^' -- 2лгсоаф' /г 360' cos^J.
На рис. 299 показано построение развертки поверхности прямого
кругового усеченного конуса, вершина которого находится за преде-
пределами поля чертежа.
Решение этой задачи осуществляется следующим путем:
1) строим вспомогательный конус A, подобный данному конусу а,
диаметр d основания конуса /3 следует выбирать так, чтобы отноше-
отношение D/d (где I) - диаметр окружности основания конуса а) выражалось
целым числом (на рис. 299 оно равно 2);
2) строим развертку боковой поверхности нспомогательного ко-
конуса/3 -Я0Л0Л,20 ... 50А„;
ех
E"F"D" С" В" А"
Рис. 297
Рис. 298

Построение приближенных разверток 205
развертывающихся поверхностей
Рис. 299
3) из произвольной точки О0, принадлежащей биссектрисе угла
A0S0A0, проводим лучи {О0А0), [О010), [О020), ..., [О0А0) и на них
откладываем отрезки [О0 Л, 0 ] = k[O0A0], [O0llo] = k[O0l0], [0Q2lo] =
= k[O020],..., [O0AlQ) = k[O0A0\,raek = D/d= 2.
Для построения развертки поверхности а достаточно определить
положение точки Л,о и через нее провести дугу окружности радиу-
радиусом, равным длине отрезка [O0AiQ] из центра в точке О0. Эта окруж-
окружность пересечет лучи [О010), [О020), ... в точках ll(), 2lQ, ... Из точек
Л10' ii0' 2io' - проводим прямые (Ах В1д), (llQl2 ), B,о.22о), па-
параллельные соответствующим1 прямым (A0S0), AOSO), B0S0), ..., и на
них откладываем отрезки [Л,о В,о], [J,o 12q], [21о 22q], ..., равные / -
длине образующей АВ усеченного конуса а.
В. Построение развертки поверхности с ребром возврата.
Построение развертки поверхности с ребром возврата осуществля-
осуществляется путем аппроксимации ее отсеками конической поверхности с по-
последующей заменой их плоскими треугольниками. В качестве иллюст-
иллюстрации решения такой задачи обратимся к следующему примеру:
пусть на эпюре Монжа заданы проекции поверхности с ребром воз-
возврата а; построить ее развертку (рис.300).
На ребре возврата d отмечаем ряд точек 1, 2, 3, 4, 5 и через их проек-
проекции проводим касательные к проекциям d' и d" — [ 11 х ], [ 221 J , [ 331 ],
[ 441 ], [ 551 ]. В отсеках поверхностей, ограниченных этими касательны-
касательными, проводим диагонали 21 у, 32, , ..., которые делят каждый из криво-
криволинейных четырехугольников на два "треугольника".
Если расстояния между точками 1 и 2, 2 и 3, 3 и4, 4 и 5 будут доста-
достаточно малыми, то стороны "треугольников", противолежащие вер-
вершинам 7,, 2,, 3t, 4] (и 11q, 2j0, <3,0> 4,0), можно считать прямо-
прямолинейными.
Для построения развертки многогранной поверхности, аппроксими-
аппроксимирующей заданную поверхность а, определяем длины сторон этих треуголь-
треугольников. По трем сторонам строим треугольники, начиная с А 1о2о11о, к
которому пристраиваем остальные в последовательности, указанной
на рис. 300 римскими цифрами. Фигура 1020304050 5,041() 3,0 21о ilo —
приближенная развертка поверхности а.

206 Развертка поверхностей
Рис. 300
§ 66. УСЛОВНАЯ РАЗВЕРТКА ПОВЕРХНОСТЕЙ
В двух предыдущих параграфах было показано построение развер-
разверток гранных и торсовых поверхностей. Все остальные поверхности
относятся к неразвертываемым — они не могут быть совмещены с плос-
плоскостью без разрывов и склеивания, т. е. теоретически неразвертываемые
поверхности не имеют своей развертки. Поэтому в дальнейшем мы
будем говорить лишь об условном решении задачи по построению раз-
разверток неразвертываемых поверхностей.
При необходимости изготовить из листового материала неразвер-
тываемую поверхность приходится кроме изгибания осуществлять так-
также сжатие и растяжение определенных участков листа.
Общий прием решения задачи на построение условной развертки не-
развертываемой поверхности состоит в том, что отсеки заданной поверх-
поверхности аппроксимируются отсеками развертывающихся поверхностей —
гранными, цилиндрическими или коническими.
Рассмотрим наиболее часто встречающиеся способы построения ус-
условных разверток.
Допустим, что требуется изготовить из листового материала по-
поверхность цилиндроида а, сопрягающего две трубы одинакового диамет-
диаметра (рис. 301). Решение сводится к следующему: заданную неразвер-
тываемую поверхность цилиндроида аппроксимируем вписанными в
нее отсеками конической поверхности, которые, в свою очередь, заме-
заменяем треугольниками.
Чтобы заменить поверхность цилиндроида отсеками конических
поверхностей, проводим на поверхности цилиндроида семейство пря-
прямолинейных образующих, параллельных плоскости параллелизма. В рас-
рассматриваемом случае плоскостью параллелизма служит фронтальная
плоскость проекции. На участке поверхности, заключенной между двумя
смежными образующими /Ли 2В, проводим "диагональ" 2 А, получен-
полученные отсеки поверхности 1А2 и А2В принимаем за плоские треугольники^
Также поступаем и со всеми остальными отсеками поверхности цилинд-
цилиндроида, заключенными между образующими. После этого осуществляем
построение развертки многогранной поверхности, составленной из
треугольников так же, как это было сделано на рис. 297.

Условная развертка поверхностей 207
Точки /„, 2„, ... и Л„, /i0, ... соединяем плавными кривыми. На
рис. 301 показана только половина развертки — вторая половина сим-
симметрична ей относительно прямой N(tn(t.
При построении условных разверток поверхностей вращения можно
в качестве вспомогательных (аппроксимирующих) поверхностей исполь-
использовать развертывающиеся цилиндрические и конические поверхности.
Рис. 302 и 303 дают наглядное представление о графическом спо-
способе построения условной развертки с помощью этих поверхностей.
На рис. 302 показана произвольная поверхность вращения а, состоя-
состоящая из кусков а,, а2, а3, ..., границами между которыми служат ме-
меридианы поверхности а.
Куски а,, а2, a.i, ••• неразвертывающейся поверхности а заменяем
кусками цилиндрических поверхностей /3| , /32, Рз, ¦¦¦ (н<* рис. 302 указан
только один кусок - отсек /3, ). После этого осуществляем развертку
составной цилиндрической поверхности /3 — 0, и /J2 и /J3 •••
Ао Во Со Da
1о2о
rD'
Рис. 301
Pi—отсек цилиндрической
поверхности
i-отсек конической
поверхности
Рис. 302
Рис. 303

208 Развертка поверхностей
hOy.
i
\А0А0\=2пг
Рис. 304
На рис. 303 показан пример перехода от произвольной поверхнос-
поверхности вращения а к поверхности C, составленной из отсеков конических
поверхностей /3, , 02, C3, ..., которыми заменяются куски а,, а2, а3, ... по-
поверхности а; границами между этими кусками являются параллели
поверхности а (на рис. 303 показан только один отсек $х ).
Развертка отсеков конических поверхностей ру осуществляется по
способу, изложенному на с. 204, рис. 299.
В качестве примера использования цилиндрической поверхности
для построения условной развертки построим развертку поверхнос-
поверхности сферы (рис. 304).
Для ее построения пересекаем поверхность сферы горизонтально
проецирующими плоскостями 7i , 1г, 7з, •¦•> проходящими через центр
сферы. Куски сферической поверхности а,, а2, а3, ..., заключенные
между меридиональными сечениями hOy — hOy , hOy — hOy , hOy —
hOy , заменяем кусками цилиндрических поверхностей 0,, 02. @з > прямо-
прямолинейные образующие которых перпендикулярны к плоскости средних
меридиональных сечений hOy ,hOy ,hOy^ , ...
Длина образующих, в которые преобразуются дуги параллелей по-
поверхности вращения, определяется отрезками прямых, заключенных
между соседними меридиональными плоскостями А~В -> [А0В0 ].
Чтобы построить развертку куска цилиндрической поверхности /3, ,
аппроксимирующего участок сферы аг, проводим горизонтальную
прямую а. На ней откладываем [А0В0]. Через середину этого отрез-
отрезка проводим вертикальную прямую, на которой откладываем спрям-
спрямленное меридиональное сечение (на рис. 304 показана только его поло-
половина) и отмечаем на нем точки пересечения с параллелями сферы (Мо,
^о, 20, 30 ). Через точки Мо, 10, 20, 30 проводим горизонтальные прямые
и откладываем на них по обе стороны от вертикали M0S0 отрезки,

Условная развертка поверхностей 209,
равные половине длин касательных, проведенных в точках М\ 1', 2', 3'
и заключенных между следами плоскостей hOy и hOy .
Полученные точки Ао, А,о, А2о, АЛо и Во, В,о, В2о, BSoсоединяем
плавными кривыми. Фигура A0S0B0 — условная развертка половины
участка сферической поверхности ctj . Пристроив к ней другую половину,
расположенную симметрично относительно прямой а , получим разверг-
КУ 0io участка а, . Для получения развертки всей сферической поверх-
поверхности необходимо к участку /3 i0 пристроить п (в нашем случае пять)
фигур 02(), 0зо, 04О, /35о, 06о, конгруентных фигуре/3,0.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что называется разверткой поверх-
поверхности?
2. Какие поверхности относятся к раз-
развертывающимся?
3. Перечислите свойства поверхности,
которые сохраняются на ее развертке.
4. Назовите способы построения раз-
разверток и сформулируйте содержание
каждого из них.
5. В каких случаях для построения
развертки используются способы: нор-
нормального сечения, раскатки, треугольни-
треугольников?
6. В чем состоит общий прием реше-
решения задачи на построение условной раз-
развертки неразвертываемых поверхнос-
поверхностей?
7. Сформулируйте и дайте подробное
объяснение способов построения услов-
условной развертки.
8. Как можно построить развертку
усеченной конической поверхности с не-
недоступной вершиной?
9. Какой способ целесообразно исполь-
использовать для построения условной разверт-
развертки поверхности сферы?

ГЛАВА
VIII
АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
понятия и опРЕДкл
РассмотреьшЕ.ш в предыдущих главах ортогональные проекции на-
находят широкое распространение в технике при составлении чертежей.
Это объясняется тем, что выполнение чертежей с помощью ортого-
ортогональных проекций достаточно просто, при этом можно получить про-
проекции, сохраняющие метрические характеристики оригинала. С помо-
помощью чертежей, построенных в ортогональных проекциях, если их до-
дополнить вспомогательными изображениями — видами, разрезами и
сечениями, можно получить представление о форме изображаемого
предмета (как о внешнем виде, так и о внутреннем строении) и его
размерах.
Наряду с отмеченными достоинствами метод ортогонального про-
проецирования имеет существенный недостаток. Для того чтобы полу-
получить представление о пространственном геометрическом образе, задан-
заданном его ортогональными проекциями, приходится одновременно рас-
рассматривать две, три, а иногда и больше проекций, что значительно за-
затрудняет мысленное воспроизведение геометрической фигуры по ее
проекциям.
В ряде случаев бывает необходимо наряду с чертежом геометри-
геометрической фигуры, выполненным в ортогональных проекциях, иметь ее
наглядное изображение. Такое изображение может быть получено пу-
путем проецирования оригинала на специально выбранную плоскость.
Мы знаем, что одна центральная или параллельная проекция на одну
плоскость проекции не определяет положения фигуры в пространстве и
не позволяет установить ее форму. Чтобы устранить эту неопределен-
неопределенность и получить обратимый чертеж (чертеж, обеспечивающий взаимную
однозначность между точками, принадлежащими проецируемой фигуре и
ее проекции), необходимо иметь не одну, а две ее проекции.
Получить две взаимосвязанные проекции одной фигуры на одну
плоскость можно следующим путем: пусть в пространстве задан от-
отрезок [АВ\ (рис. 305); чтобы получить параллельные проекции это-
этого отрезка на произвольную плоскость а*, по которым можно определить
расположение заданной фигуры в пространстве, следует взять какую-
либо плоскость 7 и найти на ней ортогональную проекцию заданной
фигуры (отрезка). Затем надо спроецировать отрезок \АВ] и его орто-
ортогональную проекцию [Л'В'] на плоскость а в направлении s. При таком
способе проецирования каждой точке пространства соответствуют две ее
проекции на плоскости а.
* Плоскость а называют картинной плоскостью.

Понятия и определения 211
В качестве плоскости у можно взять не произвольную плоскость,
а одну из координатных плоскостей, например хОу. Если теперь спрое-
спроецировать координатные оси Oxyz и горизонтальную проекцию А' точки А
совместно с самой точкой А на плоскость а, то мы получим в плоскости
а чертеж, который называют аксонометрическим, при этом проекцию
точки А - А0 называют аксонометрической (иногда главной) проекцией
точки А, а точку Ai0 — вторичной проекцией точки А (рис. 306).
Таким образом, в аксонометрии имеются два поля проекций: поле
главных и поле вторичных проекций. В этом отношении аксономет-
аксонометрические проекции не имеют принципиального отличия от ортогональ-
ортогональных проекций.
Для того чтобы на аксонометрических проекциях можно было ре-
решать метрические задачи относительно изображенных геометричес-
геометрических фигур, на аксонометрическом чертеже указывают проекции коор-
координатных осей с изображенными на них отрезками е° о, е°о, е°о — проек-
проекциями натурального масштаба е. Проекции е°о, е°о, е^о натурального
масштаба ех, еу, е2 называют аксонометрическим масштабом по осям
x\y°,z°.
Положение точки А в пространстве относительно натуральной сис-
системы координат Oxyz определяется пространственной координатной
ломаной ОАХА'А (рис. 306). Аксонометрическая проекция А0 точки А
определяется плоской координатной ломаной О0 А°хчАХ0А°, у которой
звено О0 А°хо совпадает по направлению с осью х° , а А°хо А10 иЛ'°Л° па-
параллельны соответственно осям у0 и г° .
В общем случае отрезки О0 А0 о. А0 о А10,
А А не равны между
собой и ни один из них не равен натуральному масштабу е. Отноше-
ОтношеA°oA10
ния
называют показателя-
OAX ' "У" АХА' ' '^- A'A
ми (коэффициентами) искажений по аксонометрическим осям.
Очевидно, принимая различное взаимное расположение натураль-
натуральной системы координат и картинной плоскости и задавая разные направ-
направления проецирования, можно получить множество аксонометрических
проекций, отличающихся друг от друга как направлением аксонометри-
ОС
Рис. 306

212 Аксонометрические
проекции
ческих осей, так и величиной коэффициентов искажения вдоль этих осей.
Справедливость этого утверждения была доказана немецким геометром
Карлом Польке. Теорема Польке утверждает, что три отрезка произ-
произвольной длины, лежащих в одной плоскости и выходящих из одной
точки под произвольными углами друг к другу, представляют парал-
параллельную проекцию трех равных отрезков, отложенных на прямоуголь-
прямоугольных осях координат от начала.
На основании этой теоремы аксонометрические оси и коэффициенты
искажения по ним могут выбираться произвольно. При этом коэффи-
коэффициенты искажения по аксонометрическим осям можно принять: раз-
различными для всех аксонометрических осей (k о Ф k о Ф kzn); оди-
одинаковыми для каких-либо двух осей (например, /г^о = k о); равными
для всех аксонометрических осей (fe^o = k о = kzo ). В первом случае
аксонометрическую проекцию называют триметрической, во втором —
диметрической и в третьем — изометрической.
В зависимости от угла между направлением проецирования и кар-
картинной плоскостью аксонометрия может быть прямоугольной (орто-
(ортогональной) , если этот угол прямой; в противном случае ее считают ко-
косоугольной.
§ 67. СТАНДАРТНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
В инженерной практике, в частности в машиностроении, наиболь-
наибольшее распространение получили прямоугольные диметрические и изо-
изометрические проекции. Отметим некоторые свойства этих проекций.
1. Зависимость коэффициентов искажения по аксонометрическим
осям от направления проецирования.
Установление зависимости между коэффициентами искажения и
направлением проецирования представляет определенный практичес-
практический интерес.
Картинная плоскость пересекает координатные оси в точках Ха =
= Х°а, Ya = Y°a, Za = Z°a, а. плоскости проекций по прямым XaYa,
XaZa, YaZa. Точки XQ, YQ, Zq определяют треугольник, называемый
треугольником следов (рис. 307). Очевидно, Л XaYaZa = Л X^Y^Z^,.
Опустим из начала координат О перпендикуляр на плоскость а. Точ-
Точка О0, в которой этот перпендикуляр пересекает плоскость а, является
прямоугольной проекцией точки О. Отрезки О0Х°а, О0 Y°a и О0Z°a —
прямоугольные аксонометрические проекции отрезков координатных
осей ОХа, OYa, OZa. Треугольники ОО°Х?, 00° Y°, 00°Z° - пря-
прямоугольные, отрезки О0 X^, О0 У„, О0 Z? ~ их катеты, а отрезки ?
OY%,, OZq — гипотенузы этих треугольников. Отсюда
где а° , j3 *, 7 ° — углы наклона осей х, у, z к картинной плоскости.
Так как ох„а = fe^o, —ovo° = kya , QZ* = kza , то fe^o = coso°
k о — cosE°, k о = cos 70.
В прямоугольной аксонометрии коэффициенты искажения связаны
зависимостью k\ + k2« + k\ - 2.
Изометрическая проекция. В прямоугольной изометрической проек-
проекции коэффициенты искажения по всем осям одинаковы:

Стандартные аксонометрические 21
проекции
а.
k „ = -±-k о ). Поэтому 2/г2 + ~ = 2, /г2 = -§-, k = sM- - 0,94, т. е. ко-
Рис. 307
/го = k2y0 = k\o = 2, т. е. 3/г2 = 2, fe = У|" ,
следовательно, коэффициенты искажения но осям х", у0, z" равны 0,82.
Изометрическую проекцию, как правило, выполняют без искажения
(т. е. коэффициент искажения k - 1), что соответствует увеличению ли-
линейных размеров изображения по сравнению с действительными в 1,22
раза A/0,82 * 1,22).
Диметрическая проекция. Для прямоугольной диметрической проек-
проекции характерно равенство коэффициентов искажения по двум осям
fc^.0 = /г,о; коэффициент искажения по третьей оси k о - ~2~^х" (или
„ = -±-k о )Поэтому 2/г2 + M
У
эффициент искажения по осям х" и z" равен 0,94, а по оси у" - 0,47.
Диметрическую проекцию, как и изометрию, выполняют, как правило,
без искажения по осям х" и у" и с искажением k <> - 0, 5 по осиу"„ В
этом случае увеличение линейных размеров изображения по сравнению с
действительными происходит в 1/0,94 = 1,06 раза.
2. Определение углов между осями стандартных аксонометричес-
аксонометрических проекций.
Изометрическая проекция. Для прямоугольной (ортогональной)
аксонометрии справедливо следующее утверждение: коэффициенты
искажения по аксонометрическим осям равны косинусам углов наклона
координатных осей к картинной плоскости (доказательство см. п. 1).
Так как для изометрии fe^o = k о = kzo = 1, то отрезки О" Х^ = О" Y^ =
= О"Z?. Это, в свою очередь, означает, что в прямоугольной аксономет-
аксонометрии треугольник следов равносторонний.
В теории ортогональных аксонометрических проекций доказывает-
доказывается, что аксонометрические оси являются высотами треугольника следов.
Из элементарной геометрии известно, что в равностороннем треугольни-
треугольнике высоты попарно пересекаются между собой под углом в 120°. Поэто-
Поэтому совпадающие с ними аксонометрические оси в ортогональной изомет-
изометрии образуют между собой углы в 120°. Обычно ось г" принимают
вертикальной (рис. 308).

214 Аксонометрические
проекции
Рис. 308
Рис. 309
Рис. 310
Диметрическая проекция. Для диметрической проекции характер-
характерно равенство двух коэффициентов искажения по осям х° и z°, коэф-
коэффициент искажения по третьей оси равен их половине:
fc о = k о = 2k о .
АЛ у
Равенство fe^o = kzo обеспечивает конгруентность отрезков O°X^ =
= О° Z?, т. е. треугольник следов —равнобедренный (рис. 309). В этом
треугольнике высота Y?Ao , совпадающая с направлением аксонометри-
аксонометрической оси у0, делит пополам сторону X^Z^; \Х^А° | = \А°Z^\ = ^ .
Приняво|О°Х°\ = -\O°Z?\ = 1, имеем X^Z^ = V21. Из А О0 А°Z% определя-
определяем sin б °:
Z°A° sf? 2Ч/27
sto6e = -5?^ = -5-: -з-=0,75,
что соответствует равенству угла б° = 48е 35'. Тогда
LX°aO°Z°a= 2L8° = 97° 10'.

Примеры построения аксонометрических проекций 215
геометрических фигур
Обычно при построении диметрических проекций ось z° распо-
располагают вертикально. Тогда треугольник следов и его высоты (аксоно-
(аксонометрические оси) займут положение, показанное на рис. 309. В этом
случае
ДО°Зг° = B5° - 90° ) = (97° 10' - 90° ) = 7° 10';
#б°Л° = CO°Y°a = (8° - 7° 10') = D8° 35' - 7° 10') = 41° 25'.
Приближенно аксонометрические оси стандартной диметрии мож-
можно построить, если принять tg7°10' ^ 1/8, a tg41°25' = 7/8. Тогда аксоно-
аксонометрические оси х° и у0 проводят так, как это показано на рис. 310. Ось
у0 может быть проведена так же, как продолжение биссектрисы L х° О0 z° .
§ 68. ПРИМЕРЫ ПОСТРОЕНИЯ
АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ ГЕОМЕТРИЧЕСКИХ ФИГУР
При построении аксонометрических проекций пользоваться коэф-
коэффициентами искажения неудобно. Поэтому обычно строят рекомен-
рекомендованные ГОСТ 2.317—69 (СТ СЭВ 1979—79) стандартные прямоуголь-
прямоугольные изометрию и диметрию, принимая соответствующие масштабы
увеличения в 1,22 раза для изометрии и в 1,06 раза для диметрии. Введе-
Введение этих масштабов позволяет строить аксонометрические проекции без
сокращения размеров, откладываемых по аксонометрическим осям. Для
диметрической проекции размеры по оси у0 сокращают вдвое.
А. Построение аксонометрических проекций геометрических фи-
фигур, ограниченных отрезками прямых и отсеками плоскостей.
При параллельном проецировании на плоскость прямые проеци-
проецируются в прямые (см. § 6, 1а), следовательно, для построения ак-
аксонометрического изображения прямой а достаточно определить аксо-
аксонометрические проекции двух принадлежащих ей точек, которые одно-
однозначно определяют прямую а ° — аксонометрическую проекцию пря-
прямой а .
Построение аксонометрических проекций многогранников, в част-
частном случае многоугольников, сводится к определению аксонометри-
аксонометрических проекций их вершин, которые затем соединяют между собой
отрезками прямых линий.
На рис. 311,6 показано построение стандартной изометрической
проекции шестигранной пирамиды, ортогональные проекции которой
заданы на рис. 311, а. Построение выполняем в следующей последо-
последовательности: проводим прямые х, у, z, которые принимаем за оси на-
натуральной системы координат; за начало координат принимаем точку
О (О\ О"). Затем проводим аксонометрические оси х°, у0, z°. Измерив
на ортогональном чертеже натуральные координаты вершин основания
пирамиды (точки 1, 2, 3, 4, 5, 6) и ее вершины (точка S), строим их
аксонометрические проекции (точки 1°, 2°, 3°, 4°, 5°, 6°, S0). Чтобы
получить изометрическую проекцию пирамиды, соединяем полученные
точки отрезками прямых линий в той же последовательности, в какой
они соединены на ортогональных проекциях.
Б. Построение аксонометрических проекций геометрических фи-
фигур, ограниченных кривыми линиями и поверхностями.
В общем случае аксонометрической проекцией кривой линии (или
поверхности) будет также кривая линия (поверхность).
Пример построения стандартной изометрии произвольной простран-
пространственной кривой / показан на рис. 312. Построение аксонометрических

216 Аксонометрические
проекции
б)
Рис. 311
а)
Рис. 312
проекций точек, принадлежащих кривой Z, осуществляется в последова-
последовательности, указанной ниже.
1. Относим данную линию к некоторой натуральной системе коор-
координат Oxyz.
2. Отмечаем на кривой I точки 1, 2, 3, ... и определяем их орто-
ортогональные координаты (рис. 312,а).

Примеры построения аксонометрических проекций 217
геометрических фигур
3. По координатам точек 1, 2, 3, ... строим их вторичные проек-
проекции I10, 210, 3i0 , ... (рис. 312,6).
4. Через вторичные проекции точек проводим прямые, параллель-
параллельные аксонометрической оси 2°, и откладываем на них отрезки, рав-
равные значению соответствующих аппликат точек A, 2, 3, ...); находим
точки;0, 2°, 3°, ...
5. Соединив найденные аксонометрические проекции точек 1°, 2°,
3°, ... плавной линией, получим аксонометрическую проекцию кри-
кривой I °.
В практике построения аксонометрических проекций машиностро-
машиностроительных деталей часто приходится строить аксонометрические проек-
проекции окружностей. В большинстве случаев плоскости окружностей быва-
бывают параллельны какой-либо из координатных плоскостей. Рассмот-
Рассмотрим возможные варианты построения окружности в изометрической
и диметрической проекциях.
Чтобы иметь более наглядное представление о расположении и вели-
величине осей эллипсов, в которые проецируются окружности, последние
вписаны в грани куба. На рис. 313,а показана проекция куба в изомет-
рии, а на рис. 313,6 — в диметрии. Окружность, вписанная в грань куба,
касается его ребер в их середине. Так как касание является инвариантом
параллельного проецирования, то в аксонометрических проекциях точки
касания эллипсов, в которые преобразуются окружности, будут нахо
диться так же в серединах ребер куба. Кроме |Этих четырех точек можно
указать еще четыре точки, принадлежащие концам большого и малого
диаметров эллипса. В прямоугольных изометрических и диметрических
проекциях направления больших осей эллипсов перпендикулярны сво-
свободным аксонометрическим осям, а малые оси эллипсов совпадают по
направлению со свободными аксонометрическими осями.
Для прямоугольной (практической) изометрии величина большого
диаметра эллипса равна l,22d окружности, малого диаметра — .0,71d
(см. рис. 313,а). В прямоугольной диметрии большой диаметр эллип-
эллипса равен l,06d, малый диаметр для эллипсов, расположенных в гранях
куба, параллельных координатным плоскостям Оху и Oyz, равен 0,35d.
Для эллипса, принадлежащего грани куба, параллельной плоскости Oxz,
малый диаметр равен 0,95d (см. рис. 313,6).
¦ с.
Рис. 313

218 Аксонометрические
проекции
Чтобы исключить арифметические подсчеты при определении длин
отрезков, умноженных на величину масштаба искажения, следует поль-
пользоваться пропорциональным масштабом. Для его построения достаточно
провести две взаимно перпендикулярные прямые а и Ь (рис. 314) и на
одной из них от точки пересечения К отложить [ КО], равный 100 едини-
единицам, а на другой - отрезки [ KI], [КЩ, [К1Щ, [KIV], [KV], [KVI], соответ-
соответственно равные 35, 50, 71, 95, 106, 122 единицам измерения. Точки
/, //, ... VI соединяем с точкой О. Если теперь от точки О на прямой ОК от-
отложить [ОВ] заданной длины / и из конца В отрезка [ОВ] восставить
перпендикуляр к [ОК], то он пересечет прямые @1), (ОН), (ОШ),
(OIV), (OV), (OVI) в точках 1, 2, 3, 4, 5, 6. Полученные отрезки [В1],
[В2], [ВЗ], [В4], [В5], [В6] будут равны соответственно 0,35/-, 0,5/, 0,71/,
0,95/, 1,06/, 1,22/.
Если плоскость окружности занимает произвольное положение по
отношению к координатным плоскостям, то построение аксономет-
аксонометрической проекции окружности осуществляется так же, как это делается
при построении аксонометрической проекции кривой (см. с. 215 п. Б,
рис. 312). Построение аксонометрических проекций поверхностей,
ограничивающих геометрические фигуры, можно осуществить двумя
способами:
1. Способ сечений. Этот способ заключается в следующем:
1) поверхность геометрической фигуры, аксонометрическую проек-
проекцию которой требуется построить, рассекаем плоскостями 7i > 72, 7з> ••¦>
уп (рис. 315);
2) определяем линии пересечения заданной фигуры Ф плоскос-
плоскостями 7у (/i, /2, /з, ¦¦¦, 1п)\
3) строим аксонометрические проекции линий- /,, 12, /з, ¦¦-, In ~*
-*¦ '?, Z". 'з, ¦¦-, $; для упрощения определения, линий lj и построения их
аксонометрических проекций секущие плоскости следует принимать
параллельными какой-либо плоскости проекции;
4) кривая d°, огибающая линии /,°, /2°, /3°, ¦¦•, In, является очерковой
линией — линией видимого контура фигуры Ф° .
2. Способ вписывания сферических поверхностей. Целесообраз-
Целесообразность применения этого способа основывается на том, что в прямо-
К
б)
Рис. 314
Рис. 315

Решение позиционных задач 219
на аксонометрических проекциях
г°=1,22г
Рис. 316
угольной аксонометрии поверхность сферы проецируется на картинную
плоскость в виде круга. Этот способ следует использовать в тех случаях,
когда фигура ограничена поверхностью вращения. Так как в любую по-
поверхность вращения могут быть вписаны сферические поверхности, то
аксонометрическую проекцию поверхности вращения можно рассматри-
рассматривать как огибающую этих сфер.
Сущность способа покажем на конкретном примере. Пусть требу-
требуется построить аксонометрическую проекцию (прямоугольную изомет-
рию) кольца (рис. 316,а). Построения выполняем в следующей пос-
последовательности :
1) строим эллипс с0 — аксонометрическую проекцию окружнос-
окружности с (ACBD);
2) из произвольных точек эллипса с0, О{\ 0°, 0°, •••, On, ("W Of;
Oj G c°) проводим окружности bj радиусом г — аксонометрические
проекции вписанных сферических поверхностей /3;
3) огибающие d? и d° окружностей bj являются видимым очерком
аксонометрической проекции кольца (рис. 316,6).
§ 69. РЕШЕНИЕ ПОЗИЦИОННЫХ ЗАДАЧ
НА АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ
Решение позиционных задач на аксонометрическом чертеже не от-
отличается от решения этих задач в ортогональных проекциях на эпюре
Монжа.
Алгоритмы решения задач для определения линии пересечения двух
поверхностей (см. § 43, табл. 8) и нахождения точек встречи линии 6
поверхностью (см. § 53, табл. 9), составленные для ортогональных
проекций, остаются без изменения при решении аналогичных задач в
аксонометрических проекциях. Рассмотрим решение основных пози-
позиционных задач: определение точки встречи прямой с плоскостью и по-
построение линии пересечения двух поверхностей.
ЗАДАЧА 1. Определить точку К = m П 0 (рис. 317).

220 Аксонометрические
проекции
f
Рис. 317
Рис. 318
РЕШЕНИЕ.
1. Заключаем данную прямую тп во вспомогательную плоскость у,
перпендикулярную какой-либо координатной плоскости (на рис. 317
у i плоскости О°х°у°). Горизонтальный след hOy плоскости 7 совпада-
совпадает со вторичной проекцией т10 прямой пг.
2. Отмечаем A°2°), по которой пересекаются плоскости у и /3:
(/°2°) = 7П0.
3. Находим К0 = т°Л A° 2° ).
4. Зная К° , определяем вторичную проекцию К10 .
ЗАДАЧА 2. Построить линию /° пересечения конической 0 и цилинд-
цилиндрической 6 поверхностей /° = 0 п 5 (рис. 318).
Эта задача может быть решена двумя способами.
Способ 1. Решают эту задачу в ортогональных проекциях, а затем
строят аксонометрическую проекцию полученной линии пересечения.
Способ 2. Состоит в построении искомой линии пересечения непо-
непосредственно на аксонометрической проекции. При этом решение осу-
осуществляется по алгоритму, составленному для решения аналогичной
задачи в ортогональных проекциях.
Решение приведено на рис. 318. Как видно из чертежа, для опреде-
определения точек (Lj и Lj ) е 1° (Iij - rrij n nj) используются плоскости,
принадлежащие пучку плоскостей, проходящих через прямую SA. Лю-
Любая плоскость этого пучка пересекает поверхности р и 5 по прямым т°
ип°.
Точки Lj и Ly принадлежат искомой линии пересечения поверхнос-
поверхностей C и S.

Решение метрических задач 221
на аксонометрических проекциях
§ 70. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ
НА АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ
Между ортогональными и аксонометрическими проекциями су-
существует зависимость, которая позволяет по ортогональным проекци-
проекциям геометрической фигуры и заданному направлению аксонометричес-
аксонометрического проецирования построить треугольник следов и, наоборот, по
заданной проекции треугольника следов определить направление аксоно-
аксонометрического проецирования. Связь между ортогональными и аксоно-
аксонометрическими проекциями позволяет преобразовать последние в проек-
проекции ортогональные и решать на них метрические задачи.
В тех случаях, когда геометрическая фигура Ф расположена в од-
одной из координатных плоскостей или в плоскостях, параллельных коор-
координатным, для определения метрических характеристик фигуры Ф доста-
достаточно выполнить построения, переводящие плоскость фигуры в положе-
положение, совмещенное с плоскостью чертежа (или параллельное ей).
Геометрические построения, которые необходимо осуществить
для совмещения координатной плоскости с плоскостью аксономет-
аксонометрической проекции, можно проследить на рис. 319. Пусть заданы ак-
аксонометрические оси х°, у0 и г0 . Строим треугольник следов, для чего на
оси х° отмечаем произвольную точку Х^. Через Х? проводим стороны
треугольника X%Y?lг°, X°aZ?lу0 и Z°Y^ ix° . Прямые (X°aY°a), (X°Z%),
(Z^Y°) являются следами картинной плоскости а на координатных
плоскостях (Х° У°) = /i°oa, (X°aZ°) = fSa и B°7?) = шо°а. Для совмеще-
совмещения плоскости хОу с плоскостью а необходимо повернуть ее вокруг го-
горизонтального следа h°oa. При этом точки Х^ и Y^ плоскости хОу, как
принадлежащие оси вращения h°oa, не меняют своего положения во
время вращения. Поэтому для определения совмещенного положе-
положения плоскости хОу достаточно повернуть точку О до ее совмещения
с плоскостью а. Точка О0 при вращении вокруг оси /io« будет переме-
перемещаться по окружности с центром в точке С0. Эта окружность принад-
принадлежит плоскости у 1 а.
Уо
Рис. 319
Рис. 320

222 Аксонометрические
проекции
Совмещенное положение точки О0 находится в точке пересечении
перпендикуляра к оси вращении h"oa, проведенного через О", и дуги
окружности с центром в точке С", радиусом С0Х%. Справедливость
этого утверждении вытекает из того, что в натуре X^OjYq = 90°. Выпол-
Выполненные построения обеспечивают равенство Х^О^У^ 90е, так как он
образован хордами, опирающимисн на диаметр. Дли определении совме-
совмещенного с плоскостью а положении точки А, принадлежащей плоскости
хОу, достаточно провести прнмую а" ~г> (О"Л°), найти ее совмещенное
положение а 0 и на а 0 определить точку Ао .
Совмещенное положение плоскостей xOz и yOz с аксонометри-
аксонометрической плоскостью а находитсн аналогично рассмотренному случаю
с той лишь разницей, что вращение плоскостей осуществляетсн соот-
соответственно вокруг осей f^a и ш^а.
Проведение примой, перпендикулнрной к плоскости, нвлнется одной
из основных метрических задач. Проследим, как может быть решена эта
задача с помощью совмещения координатной плоскости с аксонометри-
аксонометрической. Пусть требуется провести прямую / , перпендикулнрную плос-
плоскости 0 и проходящую через точку О (рис. 320).
РЕШЕНИЕ.
1. Строим треугольник следов X^Y^Z'^, для чего на оси х° отме-
отмечаем точку Х?. При выборе положения точки Х? необходимо следить за
тем, чтобы две стороны треугольника следов пересекали следы заданной
плоскости 0.
2. Определяем (А" В") — линию пересечения плоскости C с плос-
плоскостью аксонометрии а [ (АпВ" ) - /3 П а] .
3. (Ап В0 ) — след плоскости /3 на плоскости а, поэтому аксонометри-
аксонометрическая проекция перпендикуляра /° будет перпендикулярна к {А0В0 ).
Проводим 1° так, чтобы /° i (А0 В0 ) А A° ЭО°).
4* Чтобы построить вторичную проекцию перпендикуляра, совме-
совмещаем координатную плоскость хОу с плоскостью а (построения выпол-
выполнены аналогично показанным на рис. 319). Совмещенное положение
следа йоо0о определяется точками Х^оВ0. Из точки О0 опускаем пер-
перпендикуляр O0Cq на прямую h°Opo. Зная положение Со°, находим Ср.
Определяем вторичную аксонометрическую проекцию перпендикуля-
ра/10.
Следует иметь в виду, что решение метрических задач на аксоно-
аксонометрических проекциях сопряжено с определенными трудностями. По-
Поэтому целесообразно при выявлении метрических характеристик ге-
геометрической фигуры, заданной в аксонометрических проекциях, пе-
перейти к заданию этой фигуры в ортогональных проекциях и решать
задачу так, как это было рекомендовано в гл. VI.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какие проекции называются аксо- рических и диметрических) проекций?
нометрическими? 6. Что такое аксонометрический масш-
2. Как производится переход от ор- таб?
тогональных координат к аксонометри- 7. Укажите коэффициенты искажения
ческим? для большой и малой оси эллипса — ак-
3. Что такое треугольник следов? сонометрической проекции окружности,
4. Чему равны показатели искажения принадлежащей координатной плоскости
по аксонометрическим осям в прямо- (или параллельной ей) для изометрии
угольных изометрических и диметричес- и диметрии.
ких проекциях? 8. Сформулируйте теорему Польке.
5. Как определить аксонометрические 9. В чем различие между прямоуголь-
оси, если задан треугольник следов ор- ными и косоугольными аксонометричес-
тогональных аксонометрических (изомет- кими проекциями?

ГЛАВА
IX
ИСПОЛЬЗОВАНИЕ ЭЦВМ
ДЛЯ ГРАФИЧЕСКОГО
РЕШЕНИЯ ЗАДАЧ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Всего лишь три десятилетия отделяют нас от того дня, когда пер-
первая ЭЦВМ решила первую задачу. Сейчас трудно найти область науч-
научной, инженерной и административно-хозяйственной деятельности, где бы
ни использовались быстродействующие вычислительные машины и
комплексы.
Начиная с 1963 г., в Советском Союзе ведутся работы по созданию
машинных языков для описания графической информации и исполь-
использованию ЭЦВМ для автоматизации процесса конструирования, в част-
частности автоматизации процесса составления и чтения чертежей.
Несколько позже появились работы, посвященные решению пробле-
проблемы комплексной автоматизации графического решения задач с использо-
использованием для этой цели электроники и вычислительной техники.
Приведенный ниже матриал познакомит вас с основными вопро-
вопросами проблемы автоматизации процесса решения задач, исходные дан-
данные которых представлены в графической форме, и возможными путями
их практической реализации. Вы освоите также технику программирова-
программирования, точнее — составления управляющих программ (схем счета) и спосо-
способы выбора наиболее рационального машинного алгоритма.
§ 71. О ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ЭЦВМ
ДЛЯ ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ
Отметим сразу, что использование современной электронно-вычис-
электронно-вычислительной машины является не только возможным, но, как это бу-
будет показано, вполне логичным путем для решения задач, исходные
данные которых представлены в графической форме.
Возможность применения ЭЦВМ для аналитического решения задач
сейчас ни у кого не вызывает сомнения.
Если мы обратимся к графическому решению задач, то легко убе-
убедиться, что между графическим и аналитическим способами решения
имеется много общего. Эта общность вытекает из изоморфизма между
алгеброй и геометрией.
Действительно, основными неопределяемыми понятиями математи-
математики являются точка и число. Многообразие (множество) точек опре-
определяют различные геометрические фигуры, которые являются предме-
предметом изучения в геометрии. Изучением многообразия (множества) чисел,

224 Использование ЭЦВМ
для графического решения задач
выраженных в символической форме, занимается алгебра. Любое теоре-
теоретическое исследование в области точных наук осуществляется путем
использования различных математических операций. Простейшей опера-
операцией в геометрии является движение, с помощью которого можно каж-
каждую точку (множество точек) перевести в некоторую другую точку
(другое множество), установив взаимное соответствие между старым
(исходным) и новым (преобразованным) положениями. Аналогичной
операцией в алгебре служит преобразование, устанавливающее соответ-
соответствие между числами и их многообразиями. Изоморфизм между алгеб-
алгеброй и геометрией позволяет алгебре приобретать геометрическую форму
и наоборот.
Достаточно ввести понятие гипоточка (элемент пространства, то-
чечность которого на единицу меньше точечности точки — пустое мно-
множество) , чтобы записать элементы многомерного пространства в сим-
символике арабских цифр в виде конечного множества 0, 1, 2, 3, ..., N,
полностью сходного с конечным множеством чисел 0, 1, 2, 3, ..., N.
Между операциями над элементами пространства и действиями над
числами много общего. Так, например, пересечение элементов прост-
пространства, выраженное в аддитивной записи, напоминает сложение це-
целых чисел. Аналитическое решение задач, выраженное в форме уравне-
уравнений, сводится к операции исключения неизвестных.
Аналогичные приемы применяют и при графических решениях. Бо-
Более того, в самой идее проецирования трехмерных объектов на плос-
плоскость проекции (основного метода начертательной геометрии) исполь-
используется прием исключения одной из трех координат.
Соответствие между алгеброй и геометрией позволяет при решении
математических задач не делать (с чисто формальной точки зрения)
различия, каким способом оно осуществляется: аналитическим или
графическим.
Различие между графическими построениями и алгебраическими
преобразованиями, являющимися промежуточными операциями, ко-
которые приходится выполнять в процессе решения задачи, есть лишь
формальная сторона вопроса. Она не может служить поводом для утвер-
утверждения, что имеется принципиальное отличие между графическим и
аналитическим методами решения. Более существенным оказывается не
отличие двух методов решения, а то общее, что объединяет эти методы.
Основанием для такого объединения является:
1) выполнение в определенной последовательности различных ло-
логических и арифметических (или графических) операций;
2) использование промежуточных результатов в ходе последую-
последующих операций;
3) необходимость изменять направление процесса решения в зави-
зависимости от результатов промежуточных операций.
Таким образом, для осуществления автоматизации процесса реше-
решения задач нужно иметь машину, которая должна:
— производить в определенной последовательности различные ло-
логические и арифметические операции, необходимые для решения за-
задачи;
— иметь устройство для хранения исходных величин и промежуточ-
промежуточных результатов;
— быть способной автоматически выбирать нужное продолжение даль-
дальнейшего процесса решения в зависимости от результатов промежуточных
операций.

О возможности использования ЭЦВМ 225
для графического решения задач
Всем этим требованиям отвечают электронные цифровые вычисли-
вычислительные машины. Что касается выполнения геометрических построе-
построений, то они необходимы, если решение задачи осуществляется вруч-
вручную. При переходе к машинному решению оказывается возможным
избежать таких построений (см. § 74). Последнее утверждение осно-
основано на богатом опыте, накопленном в результате механизации про-
процесса ручного труда.
Известно, что машина выполняет какие-либо операции, взятые из
сферы физической деятельности человека, не так, как это делает че-
человек. В этом легко убедиться на простом примере: швейная машина,
предназначенная для облегчения труда швеи, сшивает ткани лучше
и быстрее, но не так, как это делает швея. Очевидно, машинизируя про-
процессы, взятые из области умственной деятельности человека, мы встре-
встретимся с таким же явлением.
Можно показать, что использование ЭЦВМ для автоматизации про-
процесса решения задачи графическим методом является не только воз-
возможным, но в1 ряде случаев и более логичным, чем применение таких
машин для автоматизации процесса решения задач аналитическим спо-
способом.
В защиту такой постановки вопроса можно привести высказыва-
высказывание крупнейшего философа и математика Г. Лейбница A646—1716),
который впервые обратил внимание на перспективность использования
двоичной системы счисления. Он писал, в частности, что "... вычисление
с помощью двоек, т. е. О и 1, в вознаграждение его длиннот является для
науки основным и порождает новые открытия, которые оказываются
полезными впоследствии даже в практике чисел, а особенно в геометрии,
причиной чего служит то обстоятельство, что при сведении чисел к прос-
простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок".
Г. Лейбниц не имел в виду использование двоичной системы счисле-
счисления в ЭЦВМ, но его прогноз был поистине гениальным. В ЭЦВМ при-
применяется, как правило, двоичная система счисления.
И еще одно обстоятельство, на которое мы хотим обратить внима-
внимание читателя. Чертеж, являющийся формой задания исходных данных
задачи, решение которой целесообразно осуществлять графическими
методами, может быть расчленен на черные (принадлежащие линиям) и
белые (определяющие свободное поле чертежа) элементарные пло-
площадки, т. е. любой чертеж может быть представлен в виде двоичных
сигналов (черное — да, 1; белое — нет, 0), передаваемых в машину.
Причем информацию о чертеже, выраженную в форме только двух
резко отличающихся сигналов, можно получить и ввести в машину без
участия человека. Это удобнее, чем трансформирование в такие же
сигналы величин, входящих, в качестве исходных данных в аналитические
вьфажения.
Получив информацию об исходных данных Задачи, ЭЦВМ может,
по указанию человека, приступить к обработке этой информации по
программе, составленной, в частности, и по алгоритму графического
решения задач.
Все сказанное не оставляет сомнения в том, что имеется принци-
принципиальная возможность использовать ЭЦВМ для графического реше-
решения задач.

226 Использование ЭЦВМ
для графического решения задач
§ 72. ОСНОВНЫЕ ВОПРОСЫ ПРОБЛЕМЫ
АВТОМАТИЗАЦИИ ПРОЦЕССА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ
Для выяснения вопросов, которые должны быть решены, чтобы пол-
полностью автоматизировать процесс решения задач, проследим за деятель-
деятельностью человека, решающего задачу графическим путем. При решении
задачи человек последовательно выполняет следующие операции:
1) выясняет требования поставленной задачи — какой вопрос сле-
следует решить;
2) знакомится с условиями задачи — видом и характером располо-
расположения геометрических фигур, входящих в исходные данные;
3) составляет и сохраняет в памяти (или записывает на бумаге)
алгоритм решения;
4) на основании теорем и правил, хранящихся в памяти, осуществля-
осуществляет реализацию этого алгоритма путем выполнения необходимых гео-
геометрических построений;
5) убеждается в правильности полученного решения.
В выполнении всех перечисленных выше операций принимает учас-
участие головной мозг человека. При этом выполнение первой и второй
операции немыслимо без связи головного мозга с внешним миром
посредством органов чувств (зрения или слуха для выполнения пер-
первой операции и зрения — для второй операции). Третья операция, если не
производится запись алгоритма, выполняется только головным мозгом.
Четвертая операция выполняется рабочими органами (руками) под
действием команд, поступающих от головного мозга и под его контро-
контролем. Пятая операция выполняется либо головным мозгом и органами
зрения, либо головным мозгом, органами зрения и рабочими органами.
Проследим, в какой степени использование ЭЦВМ позволяет вы-
выполнить эти операции. Условия задачи, решаемой графическими ме-
методами, задаются в виде чертежа. Такая форма задания непосредст-
непосредственно не может быть использована машиной. Поэтому необходимо
чертеж преобразовать в цифровой код и представить последний в "по-
"понятной" для машины форме. Для этого машина должна быть обору-
оборудована дополнительным устройством, которое могло бы самостоятельно,
без участия человека, преобразовать чертеж в цифровой код.
Наиболее трудоемким является составление алгоритма решения за-
задачи и его реализации на машине. Для автоматизации этого процесса
необходимо разработать новый метод решения задач, учитывающий воз-
возможности ЭЦВМ, и на его основе составить программу работы машины.
Результаты решения на ЭЦВМ выдаются в цифровой форме. В связи
с этим, чтобы получить ответ в виде чертежа, следует предусмотреть на
выходе машины преобразователь цифровых величин в аналоговые
(линии чертежа).
Таким образом, чтобы осуществить автоматизацию процесса гра-
графического решения задач, необходимо решить следующие вопросы:
1) создать конструкцию "читающего" устройства (преобразовате-
(преобразователя аналог — код);
2) разработать теорию обработки информации, полученной в ре-
результате преобразования чертежа в цифровой код;
3) разработать метод решения задач, учитывающий возможность
его реализации на ЭЦВМ;
4) создать теоретическую базу для программирования графическо-
графического решения задач, установив критерии, выполнение которых гаранти-
гарантирует получение правильного ответа;

Машинное чтение чертежа 227
5) создать конструкцию пишущего устройства (преобразователя
код — аналог).
Если будут решены перечисленные выше вопросы, то три основ-
основные операции из пяти, которые выполняет человек при решении задачи
графическими методами, могут быть выполнены техническими средства-
средствами без его участия. Несмотря на многообразие задач, решаемых графи-
графическими методами, каждое из таких решений состоит из комбинации не-
небольшого числа однотипных операций, которые можно представить в ви-
виде стандартных подпрограмм (операторов); с помощью последних легко
может быть составлена программа для решения любой задачи. Когда
будут составлены программы, роль человека при решении задач сведется
только:
1) к определению типа задачи;
2) к выбору необходимой программы или, в крайнем случае, состав-
составлению компилирующей программы из имеющегося набора операторов;
3) к установке чертежа, который содержит исходные данные задачи,
в "читающее" устройство и чистого листа бумаги в преобразователь
код — аналог ("пишущее" устройство).
Все остальные операции, связанные с чтением чертежа, решением
задачи, проверкой правильности решения и графического изображе-
изображении ответа, будут выполнены машиной без участия человека.
§ 73. МАШИННОЕ ЧТЕНИЕ ЧЕРТЕЖА
Независимо от того, решает ли задачу человек или ее решение бу-
будет поручено машине, первая операция процесса решения должна вклю-
включать в себя ознакомление с исходными данными, т. е. чтение чертежа. Под
выражением "прочесть чертеж" мы подразумеваем совершающийся в ко-
коре головного мозга процесс обработки информации о чертеже, получен-
полученной посредством органов зрения. В результате его выполнения мы
получаем возможность представить, какие геометрические фигуры изоб-
изображены на чертеже и каково их взаимное расположение.
Говоря о чтении чертежа машиной, мы вкладываем в это понятие
иной смысл, а именно: машина должна определить координаты полно-
полностью или частично черных растрэлементов и установить их принадлеж-
принадлежность к каждой из заданных на чертеже линий или точке*. Такое опреде-
определение основано на машинном методе графического решения задач,
который будет изложен в следующем параграфе.
Так как ЭЦВМ может оперировать только с числами, представлен-
представленными в виде электрических сигналов, то первым шагом на пути ма-
машинизации процесса чтения чертежа является:
1) выявление на поле чертежа элементарных площадок (растрэле-
(растрэлементов) , принадлежащих линии;
2) определение их координат;
3) преобразование последних из цифровой формы в электрическую.
Отмеченные выше преобразования могут быть реализованы аппа-
аппаратурными средствами с помощью преобразователя аналог — код и
счетчика координат. Выявление растрэлементов, принадлежащих линиям
чертежа, может быть выполнено посредством развертки с помощью
светового (или электронного) анализирующего луча, который, переме-
перемещаясь по определенному закону, последовательно, строка за строкой,
"просматривает" (анализирует) все поле чертежа.
Имеется в виду, что чертеж выполнен черными линиями.

228 Использование ЭЦВМ
для графического решения задач
Мы не будем останавливаться в рамках учебника по курсу начерта-
начертательной геометрии на изложении теоретических основ и созданной на их
базе программы "чтения" чертежа*
§ 74. МЕТОД МАШИННОГО РЕШЕНИЯ ЗАДАЧ
Решение задач, исходные данные которых представлены в графичес-
графической форме, целесообразно осуществлять графическими методами.
Для реализации процесса решения задач предполагается исполь-
использовать цифровую электронно-вычислительную машину, принцип дейст-
действия которой позволяет оперировать только с числами. Поэтому в про-
процессе подготовки задачи для машинного решения необходимо осущест-
осуществить ее арифметизацию, выбрать численный метод решения и составить
расчетные формулы.
Таким образом, мы приходим к двум взаимно исключающим выво-
выводам: с одной стороны, форма задания исходных данных требует графи-
графического метода решения; с другой — реализация процесса решения на
ЭЦВМ допускает применять только аналитический метод.
Использовать каждый из этих методов в том виде, в котором они
обычно применяются, невозможно. Принцип действия и конструктив-
конструктивные особенности существующих ЭЦВМ не позволяют использовать
их в качестве чертежной машины для выполнения всех тех геомет-
геометрических построений, которые свойственны графическому методу
решения. Трудности в использовании аналитического метода состоят
в том, что для него необходимо иметь уравнения всех геометричес-
геометрических фигур, представленных на чертеже.
Для того чтобы составить (описать) уравнение геометрической
фигуры, машина должна опознать ее. В настоящее время наука не распо-
располагает данными, которые необходимы для опознавания широкого круга
материальных образов. Поэтому не представляется возможным соста-
составить алгоритм опознавания, а следовательно, и моделировать его на
машине.
Из сказанного следует, что решение задачи, исходные данные которой
представлены в графической форме, невозможно осуществить на ЭЦВМ,
используя только аналитический или графический методы в их "чистом"
виде. Необходимо разработать новый метод решения задач, учитываю-
учитывающий характер задания исходных данных и возможности вычислительной
машины.
Этот метод должен отвечать двум основным требованиям: во-первых,
решение должно осуществляться без каких-либо геометрических пост-
построений; во-вторых, обходиться без определения уравнений геометричес-
геометрических образов, заданных на чертеже (за исключением прямых и окруж-
окружностей) .
Для решения графическим методом не требуется знание уравнений
геометрических образов; при аналитическом решении нет необходи-
необходимости в геометрических построениях. Поэтому, если воспользоваться
этими свойствами графического и аналитического методов, то можно
с их помощью создать новый метод, удовлетворяющий отмеченным
требованиям. Для этого достаточно, чтобы логика нового метода строи-
строилась на базе графического метода решения, а необходимые геометри-
"Подробно аспекты машинного "чтения" чертежа, а также другие вопросы
автоматизации процесса графического решения задач изложены в книге С. А. Фро-
Фролова "Кибернетика и инженерная графика". М.: Машиностроение, 1974.

Метод машинного решения задач 229
чес кие построения заменялись алгебраическими решениями, харак-
характерными для аналитического метода.
В новом методе фигурирует алгебра, но эта алгебра качественно
отличается от той, с которой приходится иметь дело в аналитическом
методе. Она заменяет собой геометрические построения, которые выпол-
выполняются с помощью линейки и циркуля, т. е. в этом случае она ограничи-
ограничивается только операциями с уравнениями прямых и окружностей. Из-
Известно, что основу графического метода решения задач составляют раз-
различные геометрические построения, которые выполняются только для
того, чтобы найти точки пересечения прямых и окружностей, проведен-
проведенных в процессе решения задачи, как между собой, так и с линиями,
заданными на чертеже. Иначе говоря, основной, наиболее существенной
отличительной особенностью графического метода является выполнение
в определенной логической последовательности операций по определе-
определению точки (точек) пересечения двух линий.
Решение задач на ЭЦВМ новым методом не противоречит принци-
принципам ее работы, так как этот метод позволяет использовать ее не в ка-
качестве чертежного агрегата, а как машину для определения коорди-
координат точек пересечения двух линий, в общем случае заданных значени-
значением координат некоторой последовательности принадлежащих им то-
точек (растрэлементов), выявленных в процессе автоматического "чте-
"чтения" исходных данных.
Если при решении задачи по определению точки пересечения двух
линий "вручную" не имеет значения, какие линии пересекаются, то для
машинного решения мы должны четко различать следующие случаи:
1) пересечение двух прямых;
2) пересечение прямой с кривой (в частном случае с окружностью);
3) пересечение двух кривых (в частности, двух окружностей).
Иногда операция по нахождению координат точки пересечения двух
прямых или прямой и кривой, если прямая занимает горизонтальное или
вертикальное положение, может быть заменена определением на линии
точки с заданным значением абсциссы (ординаты), если известна величи-
величина ее ординаты (абсциссы).
Итак, для автоматизации процесса графического решения задач с
помощью ЭЦВМ ее функции могут быть сведены к выполнению ариф-
арифметических операций по определению координат точки пересечения
двух линий и решению логических задач, связанных с нахождением
последовательности, в которой определяются координаты точек.
Если логическая схема решения (алгоритм) всецело зависит от ус-
условий поставленной задачи и вида исходных данных, то определение
координат точек пересечения линий для всех задач одинаково. Отличие
может состоять лишь в том, с каким из отмеченных выше случаев пере-
пересечения приходится иметь дело.
В отличие от человека для машины определение точки пересечения
двух линий является не элементарной операцией, а задачей. Число и
характер команд, которые должна выполнить машина для ее решения,
во всех перечисленных выше случаях будут различными. Если для оп-
определения координат точки пересечения двух прямых (случай 1), или
пересечения прямой и окружности, или двух окружностей (частные ва-
варианты случаев 2 и 3) машине достаточно решить систему уравнений,
которыми описываются эти линии, то в общем варианте случая 2 (рис.
321) машина должна сначала на кривой выделить точки 2 и 2, располо-
расположенные ближе к прямой (множество Мх {... }), чем любые другие точки
множества М2 {—~}\ составить уравнение прямой, проходящей через эти
точки, и лишь после этого приступить к определению координат точки

230 Использование ЭЦВМ
для графического решения задач
Рис. 321
Рис. 322
Рис. 323
пересечения К. В случае 3 (рис. 322) машина предварительно должна
выделить две пары таких точек (по одной паре из каждого множества
Мх{ ...} и М2 {•••}) 1 чтобы расстояние между ними было наименьшим из
всех возможных в данной ситуации, и только после этого приступить к
составлению уравнений прямых, проходящих через эти точки 1, 2 и 3, 4,
и совместному решению этих уравнений.
Если одна из координат искомой точки известна, то в зависимости
от того, на какой линии — прямой или кривой — определяется недоста-
недостающая координата точки, возможны два варианта решения. В первом ва-
варианте (прямая линия) задача решается подстановкой значения х (или у)
в уравнение прямой и решения этого уравнения относительно у (или д:).
Во втором варианте (кривая линия) отыскания в множестве М, {.•¦}¦
точки (растрэлемента) с абсциссой х является случайностью (рис. 323).
Как правило, такой точки в Мх { ... }не будет, поэтому можно говорить
только о нахождении в М, -Г ... \ точек 1 и 2, у которых абсолютное
значение разности \xR - х, | и |*2 - хк\ меньше наперед заданной величи-
величины Ad. Затем машина составляет уравнение прямой, проходящей через
выявленные точки 1 и 2, и на ней определяет искомую точку (так, как
это делается в первом варианте).
Геометрические построения при графическом способе решения за-
задач выполняются с помощью линейки и циркуля, т. е. приведением
простейших линий — прямых и окружностей.
Для ЭЦВМ "провести" прямую или окружность означает составить
ее уравнение. Проведение прямых нужно для того, чтобы в дальней-
дальнейшем выделить на них какие-либо точки (в частности, точки пересе-
пересечения с другими линиями); проведение окружностей необходимо для
решения таких задач, как:
1) определение на заданной линии точек, удаленных от данной точки
на расстояние d;
2) определение на плоскости точек, удаленных от данной точки А
на расстояние d, и от точки В на расстояние d2 ¦
При решении метрических задач машина должна уметь определять
расстояние между двумя точками, делить отрезок в данном отношении.
Для того чтобы ЭЦВМ можно было поручить решать задачу, необ-
необходимо, чтобы она умела выполнять элементарные графические опера-
операции, входящие составной частью в решение этих задач.
В табл. 10 приведен перечень операций, которые должна "уметь"
выполнять ЭЦВМ.
Запрограммировав перечисленные в табл. 10 операции, мы получим
подпрограммы (операторы), с помощью которых можно составить
компилирующую программу, пригодную для решения любой задачи,
исходные данные которой представлены в графической форме.

Составление машинных алгоритмов 231
решения задач
Таблица 10
Содержание операции
Обозначение
Число
команд
Определить уравнение прямой, проходящей через две
данные точки
Определить уравнение прямой, параллельной данной,
проходящей через заданную точку
Определить уравнение прямой, перпендикулярной дан-
данной, проходящей через заданную точку
Определить уравнение горизонтальной прямой, прохо-
проходящей через заданную точку
Найти точку пересечения двух заданных прямых
На данной прямой найти точку с заданным значением
абсциссы
На данной прямой найти точку с заданным значением
ординаты
Найти расстояние между двумя заданными точками . . .
Разделить заданный отрезок в данном отношении
На данной прямой найти точки, удаленные от данной
точки, на заданное расстояние
Определить уравнение прямой, проходящей через две
точки, удаленные от двух данных точек на заданное
расстояние
Найти на заданной кривой две точки, ближайшие к дан-
данной прямой
Найти на двух заданных кривых по паре точек, чтобы
две точки, выделенные на одной кривой, являлись бли-
ближайшими к двум выделенным точкам другой кривой . .
Найти на заданной кривой точки, расстояние от кото-
которых до данной точки ближе всего к заданному расстоя-
расстоянию
Найти точки пересечения кривой с окружностью, прове-
проведенной из заданного центра данным радиусом
Определить уравнение прямой по совокупности ее
точек
I
II
III
IV
V
Via
VI6
VII
VIII
IXa
1Хб
X
XI
XIIa
хпб
XIII
10
7
9
5
17
11
10
8
5
40
11
23
26
25
19
57
§ 75. СОСТАВЛЕНИЕ МАШИННЫХ АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧ
Простейший пример алгоритма — математическая формула, она ука-
указывает, над какими величинами и в какой последовательности необ-
необходимо выполнять арифметические операции для решения более слож-
сложных задач. Если при графическом методе процесс решения нельзя за-
записать в виде формулы, то это можно сделать с помощью схемы счета,
указывающей последовательность выполнения различных геометричес-
геометрических операций, реализуемых с помощью операторов, приведенных в
табл. 10.
Установим алгоритм и запишем его в виде схемы счета, составлен-
составленной из стандартных операторов для решения задачи по определению
точки встречи прямой с плоскостью (рис. 324). Пусть заданы плос-
плоскость а (а || Ь) и пересекающая ее прямая т. Требуется найти точку
К - т Л а.
Мы знаем, что для решения этой задачи необходимо прямую т зак-
заключить в плоскость у; найти прямую пересечения плоскостей у Л а =
= п; отметить проекцию точки К, в которой пересекаются одноимен-
одноименные проекции заданной прямой m и полученной линии пересечения п.
Все необходимые построения приведены на рис. 324. Индексация араб-
арабскими цифрами указывает на последовательность определения точек.

232 Использование ЭЦВМ
для графического решения задач
т
Рис. 324
Рис. 325
В рассматриваемом случае схема счета, представляющая алгоритм
решения задачи, записанный в символах стандартных операторов (табл.
10), примет вид
VJIIjVsV^IIsVe^V.IIIsV,,,.
Выполнение двух операторов IIInVn+1 можно заменить одним опера-
оператором VIa*. Окончательно схема счета машинного алгоритма запишется
V, VIa, V3 VIa4 I5 V6 VI.,.
A) B) C) D) (K')(K") E)
Арабские цифры и буквы в скобках указывают точку, обозначен-
обозначенную на чертеже, которая получается в результате выполнения опера-
оператора, под которым она поставлена.
Проследим, как будет изменяться схема счета, а следовательно, и
алгоритм решения задачи в зависимости от взаимного расположения
геометрических фигур как между собой, так и по отношению к плос-
плоскостям проекций.
Внесем изменение в эпюр, задающий исходные данные предыду-
предыдущей задачи (см. рис. 324) так, чтобы горизонтальная проекция т' пря-
прямой т заняла положение, параллельное горизонтальным проекциям а' и
Ь' прямых а и Ъ (рис. 325).
В данном случае решить задачу так, как в предыдущем случае, не
представляется возможным. Действительно, если мы заключим прямую
т в горизонтально проецирующую плоскость 7, а затем будем опреде-
определять с помощью оператора V точку 1, то сделать это нам не удастся, так
как пересечение а" и Ь" произойдет в несобственной точке (а" п Ь" =
= 1Ж) ¦ По той же причине нельзя определить и точку 3. Не имея точек 1 и
3, мы не получим точек 2 и 4, а следовательно, нам не удастся найти
проекцию п" прямой п. Но эта задача может быть решена по схеме счета
E), если решение начать с фронтальных проекций (см. рис. 325).
* Такая замена целесообразна, так как она уменьшает затраты машинного време-
времени. На выполнение двух операторов III, V требуется 26 команд, оператор VIa реализу-
реализуется с помощью только 11 команд.

Составление машинных алгоритмов 233
решения задач
Как следует из рис. 325, схема счета по формальным признакам
ничем не отличается от предыдущей:
F)
V VIa V VIa I V VIa-
E) F) G) (8) (K')(K")
Условимся считать этот путь вторым вариантом решения в отличие
от первого варианта, описанного схемой счета E).
Когда одна из заданных геометрических фигур (прямая или плос-
плоскость) занимает проецирующее положение, решение задачи представ-
представляется следующими схемами счета:
а) прямая — проецирующая, плоскость общего положения зада-
задана параллельными прямыми (рис. 326,а) :
VI6 Via VI6 VIa I V VIa;
G)
(9) A0) A1) A2) (K')(K")
б) прямая — проецирующая, плоскость общего положения зада-
задана следами (рис. 326,6) :
vie via и v;
A3) A4) (К1) 1 '
в) плоскость — проецирующая, прямая общего положения (рис. 326,в) :
V VIa.
(К1) (К11)
Все многообразие случаев задания исходных данных задачи по оп-
определению точки встречи прямой с плоскостью может быть отнесено к
семи альтернативным вариантам. Кроме схем счета E), F), G), (8),
(9) отметим еще:
V VIa И V Via
^"WL-Ч (Ю)
(9)
(рис. 327,а)
(рис. 327,6)
VI6 VIa VI6 VI.
A7) A8) (К") (К1)
(И)
в)
Рис. 326

234 Использование ЭЦВМ
для графического решения задач
К"
15
К'
т"
Рис. 327
Приведенные примеры иллюстрируют изменение алгоритма реше-
решения одной и той же задачи в зависимости от характера расположения
геометрических фигур.
Программирование решения многих задач является трудоемким
процессом. Поэтому, чтобы каждый раз, когда машина приступает
к решению задачи с другими исходными данными, не составлять новую
программу (схему счета, которая является управляющей программой),
следует создать единый (обобщенный) алгоритм, запрограммировав
который получим программу, пригодную для решения всех вариантов
данной задачи. Чтобы выяснить логическую схему построения обобщен-
обобщенного алгоритма, выпишем составленные ранее схемы счета частных
алгоритмов в виде табл. 11.
Из табл. 11 (строка 1) видно, что если после выполнения опера-
оператора V, точка пересечения найдена, то следует переходить к выполне-
выполнению оператора VIfl2, если и в этом случае точка определяется, то ма-
машина должна приступить к выполнению следующего оператора V3 и т. д.,
пока не будет выполнен оператор VIa7 , завершающий решение задачи.
Это решение соответствует исходным данным, показанным на рис. 324.
Если при решении задачи по варианту I после выполнения оператора V6
точку не получили (случай, изображенный на рис. 326,а), то следует пере-
переходить к выполнению группы операторов Vl6]5 VIaj6 vie VIa I19 ^2о
(табл. 11, строка 2). Если в результате выполнения оператора VIg,7
новой точки не будет, то следует переходить к выполнению операто-
операторов П21 V22 (табл. 11, строка 3, рис. 326,6).
Таблица 11
Схема счета общего случая
Вариант I
Вариант II
Необходимое добавление
в основную схему
для решения частных случаев
v,via2v3via4i5v6
v,via2v3via4isv6
v,via2v3via4
v,via2v3
V,
v,
VI6isVIa16Vl617VIai8I19V20
v23via24
v25via26n27v28via29
v8via9vioviani12v13viai4

Составление машинных алгоритмов 235
решения задач
Отсутствие новой точки после выполнения оператора VIa4 может
служить указанием для перехода к выполнению операторов V23 VIaj4
(табл. 11, строка 4, рис. 326,в). В том случае, когда не найдена новая
точка после выполнения оператора V3, переходят к выполнению груп-
группы операторов V25 VIa26 II27V28 VIa29 (табл. 11, строка 5, рис. 327,а).
Если при выполнении оператора V, точку не получили, переходят к
выполнению варианта II решения (табл. 11, строка 6, рис. 325). И, нако-
наконец, если точку не получают при выполнении операторов V, и V8, то не-
необходимо переходить к выполнению участка подпрограммы, состоящего
из операторов Vl630 VIa3] Vl632 VIa33 (табл. 11, строка 7, рис. 327,6).
Схемы счета для решения частных вариантов задачи, сведенные в
табл. 11, могут быть объединены в одну схему счета, представляю-
представляющую обобщенный алгоритм:
Г'
V1VIfl2V3VIfl4I,V6VIa7-.VgVIe4VloVIauI12Vl3VIfl14iVI6lsVIflieVI617VIeMIwV2o=
2V2
12)
Для наглядности и выявления структуры построения обобщенно-
обобщенного алгоритма для решения задачи по определению точки встречи прямой
с плоскостью полученную схему счета целесообразно представить гра-
графически в виде "дерева", устанавливающего связь между исходны-
исходными данными задачи и алгоритмом ее решения (рис. 328).
VI
Рис. 328

236 Использование ЭЦВМ
для графического решения задач
Из приведенной схемы видно, что машина сможет самостоятельно
выбрать правильный путь решения, если программа будет составлена
так, чтобы она начала работать по "жесткой" подпрограмме E) ос-
основного (вариант I) алгоритма. После выполнения оператора Vj выпол-
выполняется проба а, позволяющая выяснить, определяется ли точка в резуль-
результате его выполнения*. Если да, то машина приступает к выполнению
оператора VIa2, если нет, то ей следует выполнять оператор V8. Анало-
Аналогичные пробы выполняются и после операторов V3, VIa4 , V6. По резуль-
результатам этих проб машина либо продолжает решение по основной програм-
программе, если точка определена, либо приступает к выполнению другого участ-
участка программы, когда точка не получена. Выбор нового участка зави-
зависит от того, при выполнении какого оператора не получена новая точ-
точка пересечения.
Пользуясь схемой счета A2) обобщенного алгоритма, машина само-
самостоятельно решает любую задачу по нахождению точки встречи прямой с
плоскостью, независимо от характера расположения исходных данных и
варианта задания плоскости **.
Нахождение точки встречи прямой с плоскостью является элементар-
элементарной, но часто встречающейся задачей, входящей в состав алгоритма для
решения более сложных задач, например, задач по определению линии
сечения линейчатой поверхности плоскостью.
Обозначим через R схему счета (алгоритм) для решения задачи по
нахождению точки встречи прямой с плоскостью. Тогда в общем слу-
случае алгоритм для решения задачи по определению линии сечения ли-
линейчатой поверхности плоскостью в символической форме может быть
записан:
где 20 (<*() — различные пробы, позволяющие выбрать правильный
путь решения в зависимости от вида и характера расположения ис-
исходных данных; 2, (Р,) — логическая последовательность элементарных
операций для нахождения точки, через которую проходит прямолинейная
образующая линейчатой поверхности; 22 (S,-) — последовательность
выполнения операторов I или II для нахождения проекций прямолиней-
прямолинейных образующих; 23 (-RP,) —вспомогательные операции.
Выполнение R для всех задач рассматриваемого типа одинаково,
оно может меняться только в пределах вариантов задания и распо-
расположения секущей плоскости. При определении сечения линейчатой
поверхности плоскостью задача сводится к многократному выпол-
выполнению подпрограммы R — определению точки встречи прямой с плос-
плоскостью. Содержание B,, 22, 23) продиктовано задачей определения
частных положений последовательности прямолинейных образующих
линейчатой поверхности; очевидно, для различных поверхностей оно
будет различным.
Проследим изменение 2,, ? г, 2 3 в зависимости от вида линейчатой
поверхности.
* На схеме (рис. 328) указаны также проба а0 и оператор Vo, а0 — проба на число
геометрических образов, заданных на чертеже. Если N = 4, то прежде чем приступить
к выполнению основной программы, необходимо определить координаты точки
схода следов (оператор Vo).
¦¦Исключение составляют два случая: если плоскость, проходящая через ось jc,
задана следами; если пересекающая плоскость прямая — профильная.

Составление машинных алгоритмов 237
решения задач
мл...:
Рис. 329
Рис. 330
ПРИМЕР 1. Определить сечение цилин-
цилиндрической поверхности плоскостью
(рис. 329).
Для определения линии сечения произ-
произвольной цилиндрической поверхности
плоскостью может быть рекомендован
следующий план машинного решения за-
задачи:
1) из массива ячеек памяти, где хра-
хранятся координаты растрэлементов, при-
принадлежащих горизонтальной проекции
криволинейной направляющей (множест-
(множества М1 { ... } ), выбрать точку 1\, имею-
имеющую минимальное значение х;
2) найти на фронтальной проекции
криволинейной направляющей Л/2|\.Дточ-
кУ1'1 cjc=*(.)li; J
3) определить уравнение прямой лЭ 11
и || прямой, определяемой множеством
растрэлементов Л/8 { ...} ;
4) определить уравнение прямой п1 Э11
и || прямой Mi {"••¦};
5) найти точку встречи прямой пх с
плоскостью а, заданной пересекающими-
пересекающимися прямыми, представленными множест-
множествами М3 Г ... 1 , М4 { ... Л и Ms ( ...\,
М6 {.Л. Х -" J Х J
Чтобы найти вторую точку, принадле-
принадлежащую искомой линии сечения, нужно
определить уравнения проекции следую-
следующей прямолинейной образующей поверх-
поверхности. Для этого повторяем операции,
предусмотренные пп. 1...4. Для опреде-
определения положения второй (п1-,) ч всех по-
последующих (п'з, п'4, .... пп) проекций
прямых берем на кривой М7 \---j следу-
следующую из записанных точку (растрэле-
мент). После того, как будут определе-
определены уравнения проекций п'2 и п^' (n'2\\n'i
и n^'lln"), машина приступает к выпол-
выполнению п. 5. Цикл из операций, предусмот-
предусмотренных в пп. 1... 5, выполняется до тех
пор, пока на кривой Af7 {•••} не останет-
останется ни одной точки. Тогда в символике
машинных операторов операции 2(, 22,
?з можно записать:
2i(P,) -ПШХ1 V;* A4)
HII; A5)
-Я. A6)
Схема счета программы для решения
поставленной задачи примет вид
n^IIjXaUVsIIelbRg. A7)
Цикл П ... Rs выполняется до тех пор,
пока в М7 /...% не останется ни одной
точки.
ПРИМЕР 2. Определить сечение кони-
конической поверхности плоскостью (рис. 330)
Отличие решения этой задачи от пре-
предыдущей будет состоять лишь в том, что
выражение A5) может быть записано
Е — I I и схема счета примет вид
A8)
ПРИМЕР 3. Определить сечение одно-
полостного гиперболоида плоскостью
(рис. 331).
Для определения характера и после-
последовательности выполнения операторов,
входящих в ?,, 22 и 23, воспользуем-
воспользуемся свойством направляющих рассматри-
рассматриваемой поверхности, состоящим в том,
что если спроецировать точку, взятую на
одной из трех направляющих (принад-
* П — операция обращения к первой
записанной в М7 ¦{"•••} массиве точке.

238 Использование ЭЦВМ
для графического решения задач
МЛ...)
М101. .
М,о[. . .\
Рис. 331
Рис. 332
лежащих одному семейству), на плос- II1III2V3I4V5IIeiII7II8II9R10R11R12fi13I|4I15V,6III17
кость а в направлении двух других нап-
направляющих и полученные точки соеди- VlsnlgIII20V2,II22n23II24II25R26R27I28I29V30III3]V32
нить с соответствующими проекциями | 'f
(следами) двух других направляющих, *
то полученные прямые будут принадле- A9)
жать второму семейству образующих.
Точки пересечения соответственных ПРИМЕР 4. Определить сечение коно-
прямых, принадлежащих разным семейст- ида плоскостью (рис. 332).
вам, определяют кривую второго поряд- Решение этой задачи аналогично преды-
ка — сечение однополосного гиперболой- дущей с той лишь разницей, что точки
да плоскостью а. В этом случае выраже- следует брать на криволинейной направ-
ния A4), A5) и A6) примут вид ляющей и проецировать их на секущую
о . П III V T V- плоскость в направлении прямолинейной
''¦' ' направляющей коноида.
5,) — П II IIII; Схема счета в этом случае примет вид
Е3(ДР,) - R R R R I I V III V
для первого цикла, а для всех последую- nlIII2X3I4V5II6II7II8IIgR10RuR12R13I14I15Vjf)III17Vi8
щих циклов
— R R I I V III V. П1д1112ОХ21122У2з112411251126П2^2^291зо1зЛ'з21НззУз4 •
Схема счета программы запишется в
виде
3,
B0)
Чтобы машина самостоятельно (без участия человека) могла выб-
выбрать правильный путь решения задачи, ей должна быть известна по-
поверхность, линию пересечения с которой требуется определить. Приз-
Признаками, с помощью которых машина сможет "распознать" по эпюру
Монжа, с какой поверхностью она имеет дело при решении задачи,
служат:
1) присутствие точечного образа;
2) отсутствие криволинейных образов;
3) число криволинейных образов.
Эти признаки положены в основу проб, составляющих содержание
20 (о,-) [из выражения A3)], которые должна выполнить машина для
выбора нужного варианта решения.
Обозначим:
а) схемы счета A7)-Q,; A8)-Q2; A9) - Q3; B0) -Q4;

Определение рационального машинного 239
алгоритма
б) пробы: си — проба на наличие точечного образа, если точечный
образ есть (о^ = 1), то выполняется массив Q2, если нет (а, = 0), то
следует переходить к пробе а 2; а2 — проба на наличие криволинейного
образа, если такой образ есть (а2 = 1), то необходимо выполнять пробу
а3, если нет (а2 = 0), то машина должна приступить к выполнению
массива Q3; а3 — проба на число криволинейных образов, если образ
один (а3 = 1), то выполняется массив <Э.,,если два (а3 = 2), то машина
приступает к выполнению массива Q4 ¦
Вариант задания секущей плоскости не влияет на характер поиска,
так как при составлении признаков прямолинейные образы не учиты-
учитывались. В общем виде схема счета программы для решения рассмот-
рассмотренных задач примет вид
а,-0
«1=1
«v
л
Q2; Q-ъ
«2=1
а,=2
§ 76. ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНОГО МАШИННОГО' АЛГОРИТМА
Решение одной и той же задачи может быть осуществлено различны-
различными графическими способами, каждому из которых соответствует свой
машинный алгоритм. Возникает вопрос, какому из них отдать предпо-
предпочтение? Чтобы ответить на этот вопрос, достаточно сопоставить между
собой "схемы счета" сравниваемых алгоритмов.
Сравнение осуществляется путем подсчета суммарного числа машин-
машинных операций (команд), которые необходимо выполнить для реали-
реализации алгоритма на ЭЦВМ. С этой целью в графе 3 табл. 10 указано
число команд, которые должна выполнить машина для реализации пе-
перечисленных в таблице стандартных операторов.
Поясним сказанное на примере: пусть требуется определить рассто-
расстояние от точки А до плоскости а (рис. 333).
Эта задача может быть решена различными способами, в том чис-
числе и теми, что представлены на рис. 334 и 335. В первом случае решение
осуществляется без применения способов преобразования (рис. 334).
Во втором плоскость общего положения а переведена во фронталь-
фронтально проецирующее положение с помощью перемещения || vx (рис. 335).
Выясним, какое решение требует меньшей затраты машинного вре-
времени. Для этого составим схемы счета для каждого варианта решения.
Схема счета, отражающая логику графического решения задачи, без
применения способов преобразования будет иметь вид
III, V2 VIa3 V4 VIas I6 III, V8 VIfl9 II10 VI6n VII12III13 IX, 14 VII1S.
A)B)C)D) E) F) G) (8)
Схема счета решения этой же задачи с применением способа парал-
параллельного перемещения может быть записана:
viaiiiiJV3Vii4ixasiii6ii7v8i,iiilov11vii1Jix.13iii,4iiisV16m17v18vii1,.
A) B) C) D) E) F) G) (8)

240 Использование ЭЦВМ
для графического решения задач
оА
Рис. 333
Рис. 334
Рис. 335
Подсганпв число команд, которые необходимо выполнить для каждо-
каждого оператора, и суммировав их, мы получим: для первого варианта —
195 команд, для второго варианта — 278. Если условно принять, что
время выполнения одной команды одинаково для различных команд, то
можно сделать вывод, что первый вариант решения лучше. Машина
затратит на ЗО'с меньше времени, чем решая эту же задачу по второму
варианту. Что касается точности решения, то в обоих случаях она будет
одинаковой (определяется точностью задания исходных данных).
Уместно отметить, что, переходя на машинный метод решения задач,
мы обнаруживаем, что не все те способы решения, которым следо-
следовало отдать предпочтение при решении задачи "вручную", оказывают-
оказываются удобными для машины. И наоборот, громоздкий, нерациональный
способ, если он выполняется с помощью линейки и циркуля, может
дать весьма рациональное машинное решение, т. е., переходя на ма-
машинный способ решения, образно говоря, необходимо произвести "пере-
"переоценку ценностей".
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Перечислите основные вопросы, ко-
которые должны быть решены для осущест-
осуществления автоматизации процесса графичес-
графического решения задач.
2. Нарисуйте структурную схему уста-
установки, включающую ЭЦВМ, которая обе-
обеспечивает комплексную автоматизацию
процесса графического решения задач, и
дайте объяснение назначения всех элемен-
элементов, входящих в схему.
3. Что подразумевается под терми-
термином" машинное чтение чертежа"?
4. Каким образом осуществляется вы-
выявление растрэлементов, принадлежащих
линии чертежа, и как определяется зна-
значение координат этих растрэлементов?
5. Каким требованиям должен отве-
отвечать машинный метод решения задач,
исходные данные которых представлены
в графической форме?
6. В чем сущность машинного метода
решения задач?
7. Что такое стандартный оператор?
8. Что такое схема счета и что служит
основанием для ее составления?
9. Составьте схему счета для машин-
машинного решения задач:
а) определить расстояние между дву-
двумя плоскостями;
б) определить точки встречи прямой
с поверхностью прямого конуса, цилинд-
цилиндра, сферы;
в) найти линию пересечения поверх-
поверхностей сферы и кругового цилиндра, ось
которого не проходит через центр сферы.
10. Как определяется рациональный
машинный алгоритм?
11. Определите, какой способ решения
задачи по нахождению расстояния между
скрещивающимися прямыми будет наи-
наиболее целесообразным для машины:
а) без способов преобразования;
б) с использованием способа замены
плоскостей проекций;
в) способом параллельного перемеще-
перемещения.