Author: Яглом И.М. Шклярский Д.О. Ченцов Н.Н.
Text
ПРЕДИСЛОВИЕ
Первое издание настоящей книги вышло в свет
в 1950 г.; эта книга открывала серию «Библиотека ма-
математического кружка». Около 15 задач в первоначаль-
первоначальном варианте книги было заимствованно из рукописи
одного из основателей кружка при МГУ Давида Оска-
Оскаровича Шклярского A918—1942), в возрасте 23 лет
погибшего в партизанском отряде в Белоруссии. При
этом влияние Додика Шклярского на всю работу, про-
проводимую в Москве с интересующимися математикой
школьниками, и, в частности, на книги серии «Библио-
«Библиотека математического кружка» было настолько значи-
значительным, что постановка его фамилии на первое место
в списке авторов этих сборников является вполне уме-
уместной1). В 1954 г. эта книга была переиздана в значи-
значительно переработанном и дополненном виде; в 1959
и в 1965 гг. книга снова переиздавалась, но уже без
существенных изменений.
Сборники «Избранных задач и теорем элементарной
математики» построены на материалах школьных ма-
математических кружков и математических олимпиад. Они
содержат задачи «олимпиадского» типа, т. е. такие, для
понимания условий и для решения которых вполне
достаточно знания курса математики средней школы,
однако методы решения этих задач, зачастую, являются
непривычными для школьной практики, приближаясь
к приемам, с которыми сталкиваются математики в сво-
своей исследовательской работе. В отличие от большин-
') Относительно истории школьного математического кружка при
МГУ и московских математических олимпиад и роли, которую сыг-
сыграл здесь Д. О. Шклярский, см. вводную статью В. Г. Болтянского и
И. М. Яглома к книге [I] (числа в квадратных скобках отсылают чи-
читателя к списку литературы — см. ниже стр. 381—384).
ства задачников, предназначенных для учащихся сред-
средней школы, эти сборники ставят своей целью не столько
закрепить и углубить знания читателя, полученные им
в школе, сколько ознакомить его с рядом новых для
него методов и идей и привить вкус к самостоятельным
изысканиям. В связи с этим здесь почти полностью
отсутствуют задачи, для решения которых достаточно
только формального усвоения школьного курса матема-
математики. Очень слабо представлены в сборниках наиболее
привычные для школьников типы задач «на сообрази-
сообразительность», скажем, задачи на искусственные методы рг-
шения уравнений и систем уравнений высших
степеней; зато сборники содержат много задач с нестан-
нестандартными формулировками, требующих для своего ре-
решения новых подходов.
При подборе задач больше внимания уделялось тем
разделам элементарной математики, которые находят
продолжение в современных исследованиях (для приме-
примера назовем темы: «Матрицы, последовательности, функ-
функции» или «Алгебра многочленов»). Некоторые циклы
задач излагают в переработанном и приспособленном
для школьников виде отдельные вопросы, которые обыч-
обычно относят к «высшей» математике (скажем, элементы
теории чисел). Отдельные задачи заимствованы из со-
сочинений классиков математики и из статей, напечатан-
напечатанных в научных математических журналах.
Книга предназначена для интересующихся матема-
математикой учащихся старших G—10) классов средней шко-
школы. Она может быть также положена в основу работы
школьного математического кружка; при этом руково-
руководителю (и участникам) кружка может оказаться полез-
полезной и дополнительная литература, указанная в списке
на стр. 381—384. Перед решением задач полезно про-
прочесть «Указания к пользованию книгой» (стр. 7—8).
В связи с некоторой необычностью содержания сбор-
сборники «Избранных задач и теорем» могут показаться
трудными читателю, привыкшему к «стандартным» за-
задачникам, предназначенным для учащихся средней
школы. Тем не менее опыт математических кружков и
олимпиад показывает, что собранные здесь задачи для
достаточно настойчивого школьника вполне доступны.
При переработке книги для нового издания мы ста-
старались ее, по возможности, упростить—для этого из
нее были исключены все без исключения задачи, номера
5
которых помечались во 2-м —4-м изданиях двумя звез-
звездочками (в «Указаниях к пользованию книгой» эти за-
задачи рекомендовалось рассматривать как «теорию», чи-
читая их решения сразу после условий), а также наиболее
трудные из задач, номера которых были помечены одной
звездочкой: хотя таким образом из книги выпало не-
несколько интересных задач, но зато она стала доступнее
в качестве пособия для самостоятельной работы учащих-
учащихся. Некоторые задачи были опущены потому, что они
показались нам менее интересными, чем другие; два
последних цикла задач исключены как «слишком тео-
теоретические» (так, например, задачи этих циклов было
невозможно решать «в разбивку»). Взамен исключенных
книга дополнена рядом новых задач, в основном заим-
заимствованных из материалов последних московских, все-
всесоюзных и международных олимпиад. Из-за резкого
увеличения числа предлагавшихся на олимпиадах задач
мы исключили из книги список номеров таких задач
(который ныне должен был бы содержать больше поло-
половины всех номеров).
Использование три работе над книгой материалов
математических олимпиад превращает когорту нынеш-
нынешних «олимпиадчиков»: И. Бернштейна, Н. Васильева,
Г. Гальперина, Ю. Ионина, А. Лемана, А. Савина,
А. Толпыго, А. Тоома и многих других, в соавторов этого
сборника; особо хочется отметить помогавших автору
своими советами В. Гутенмахера и Л. Макара-Лиманова.
Значительное содействие оказала мне в моей работе
также и Л. И. Головина. При всем том я не знаю, уме-
уместно ли специально выражать здесь всем перечисленным
'лицам свою признательность: заботу об интересующих-
интересующихся математикой школьниках я воспринимаю как наше
общее дело, в котором все мы участвуем, отдавая тем
самым свой долг людям, которые некогда учили нас (и
в этой связи мне снова хочется помянуть моего учите-
учителя Д. Шклярского).
И. М, Яглом
УКАЗАНИЯ К ПОЛЬЗОВАНИЮ КНИГОЙ
Настоящая книга состоит из условий задач, ответов и указаний
К ним и решений. Ради удобства читателей «Ответы и указания>
помещены в конце книги; так же как и «Решения», они напечатаны
мелким шрифтом.
Номера задач, решение которых не требует знаний, выходящих
за пределы программы 8-го класса средней школы, набраны курси-
курсивом; решение большинства из этих задач доступно даже семиклас-
семиклассникам. Звездочкой отмечены задачи, которые кажутся автору более
трудными. При этом не исключено, разумеется, что читателю пока-
покажется относительно легкой какая-нибудь из отмеченных нами задач,
или, наоборот, его серьезно затруднит задача, не отмеченная звез-
звездочкой,— ведь точных критериев, определяющих трудность задачи,
не существует.
Читателю рекомендуется попытаться самостоятельно решить
заинтересовавшую его задачу, не заглядывая в указание или в реше-
решение. Если эта попытка не увенчается успехом, то следует посмотреть
указание или ответ, знание которого тоже может облегчить решение
задачи. Если же и после этого задача не будет решена, то следует
прочитать решение задачи. Если задачу удалось решить, не загляды-
заглядывая в указание, то рекомендуется сравнить ответ с приведенным
в «Ответах и указаниях» (если таковой там имеется) и при расхо-
расхождении попытаться обнаружить свою ошибку. Если же ответы
совпадут, то полезно сравнить свое решение с приведенными в книге.
Если в книге дано несколько решений задачи, интересно сравнить
их между собой. Этот порядок может быть нарушен по отношению
к задачам, отмеченным звездочкой,— здесь можно рекомендовать
иногда с самого начала ознакомиться с указанием и только после
этого приступить к решению задачи.
Как правило, задачи сборника независимы одна от другой; лишь
изредка решение задачи использует предложение одной из соседних
. с ней задачи. Исключением в этом отношении являются лишь два по-
последние цикла задач: «Комплексные числа» и «Несколько задач из
теории чисел» — в этих циклах задачи более тесно связаны друг
с другом.
Причины, по которым те или иные задачи объединены в один
цикл, могут быть различными: иногда это общность методов и поста-
постановок вопросов (таков, например, цикл «Алгебра многочленов»),
иногда — внешнее сходство условий задач; иногда специальный цикл
составляют задачи смешанного содержания, почти не связанные
между собой. Некоторые циклы состоят из задач, связанных между
собой настолько тесно, что их естественно решать подряд (такова,
например, значительная часть цикла «Задачи на делимость чисел»
и весь цикл «Перестановки цифр в числе»); эти циклы задач могут
служить темой специальных занятий математических кружков (при-
(причем здесь может оказаться полезной и указанная в конце книги до-
дополнительная литература). Иногда циклы задач можно естественно
разбить на части, различающиеся по методам решения и условиям; эти
части циклов отделяются одна от другой черточками. Следует от-
отметить, что названия циклов часто являются условными и передают
только их общее содержание: для многих задач невозможно точно
определить, к какому циклу их следует отнести.
Задачи сборника рекомендуется решать не «в разбивку», а выбрать
сначала определенный цикл и потратить некоторое время на решение
задач этого цикла; лишь после ознакомления с одним циклом (кото-
(которое, конечно, вовсе не должно состоять в решении всех илн большин-
большинства его задач) следует перейти к другому циклу, и т. д. При этом,
разумеется, переходить от одного цикла к другому вовсе не необхо-
необходимо именно в том порядке, в котором циклы расположены в книге.
В конце некоторых из решений задач указаны возможные обоб-
обобщения условий задачи; в других случаях читатель сам увидит воз-
возможность расширительного толкования стоящего перед ним вопроса
или придумает другие задачи, родственные собранным в этой кни-
книге — и этими возможностями никак не следует пренебрегать. В од-
одном случае в книге сохранена (идущая от И. М. Гельфанда) наро-
нарочито неопределенная формулировка условия задачи, оставляющая
широкий простор инициативе читателя (см. задачу 194 на Стр. 43);
в иных случаях родственную постановку вопроса учащийся сможет
предложить сам.
В известном смысле продолжением этой книги являются после-
последующие сборники задач, входящие в «Библиотеку математического
кружка» и объединенные с этой книгой общим списком авторов,
а также другие .книги серии «Библиотека математического кружка»
(см. список литературы ь конце книги).
ЗАДАЧИ
1. ВВОДНЫЕ ЗАДАЧИ
Собранные здесь задачи, как правило, являются просто упражне-
упражнениями для развития логического мышления и не связаны ни с каким
определенным разделом математики; впрочем, в этот цикл входят и
несколько задач, которые можно отнести к арифметике (см., напри-
например, задачи 25—29). Часть задач этого цикла можно связать с тео-
теорией графов (о ней см., например, названную на стр. 383 книгу
[43]), изучающей системы точек (вершин графа; рис. 1, а), некото-
некоторые из которых связаны между собой линиями (ребрами графа);
иногда на этих линиях стрелками указано направление движения по
ребру — и тогда граф называется ориентированным (рис. 1, б'). На
а)
Рис. 1.
языке теории графов можно, скажем, сформулировать те из ниже-
нижеприведенных задач, которые касаются транспортных сетей (причем сеть
дорог с односторонним движением по ним естественно изображать
ориентированным графом) или отношений знакомства между людьми:
группу лиц можно изобразить системой точек, соединяя между собой
те пары точек, которые соответствуют знакомым ').
') В задачах этого цикла отношение знакомства всегда считается
симметричным, т. е. полагается, что если А знаком с В, го В знаком
с А; если отказаться от этого условия, то систему знакомств придется
изображать ориентированным графом.
9
Большинство задач этого цикла не требуют почти никаких знаний
по математике; с этой точки зрения они доступны учащимся 5-х—6-х
классов средней школы. Впрочем, при решении некоторых задач ис-
используется метод математической индукции (см. о нем
[42]), который изучается лишь в старших классах школы. В реше-
решении других задач может оказаться полезным так называемый
«принцип клеток» Дирихле1), в образной форме часто фор-
формулируемый следующим образом: пусть мы имеем 7 кроликов и
5 клеток (или, вообще, m кроликов и п<т клеток); тогда, если рас-
рассадить этих кроликов по клеткам, то хотя бы в одной клетке обяза-
обязательно окажутся два (или более) кролика.
1. 200 учеников выстроены прямоугольником по
10 человек в каждом поперечном ряду и по 20 человек
в каждом продольном ряду. В каждом поперечном ряду
выбран самый низкий ученик, а затем среди отобранных
20 выбран самый высокий; с другой стороны, из тех же
200 учеников в каждом продольном ряду выбран сасиый
высокий ученик, а затем среди отобранных 10 выбран
самый низкий. Кто из двоих окажется выше (если это
разные лица) —самый низкий из самых высоких учени-
учеников, или самый высокий из самых низких?
2. Каждый из людей, когда-либо живших на земле,
обменялся с другими определенным числом рукопожа-
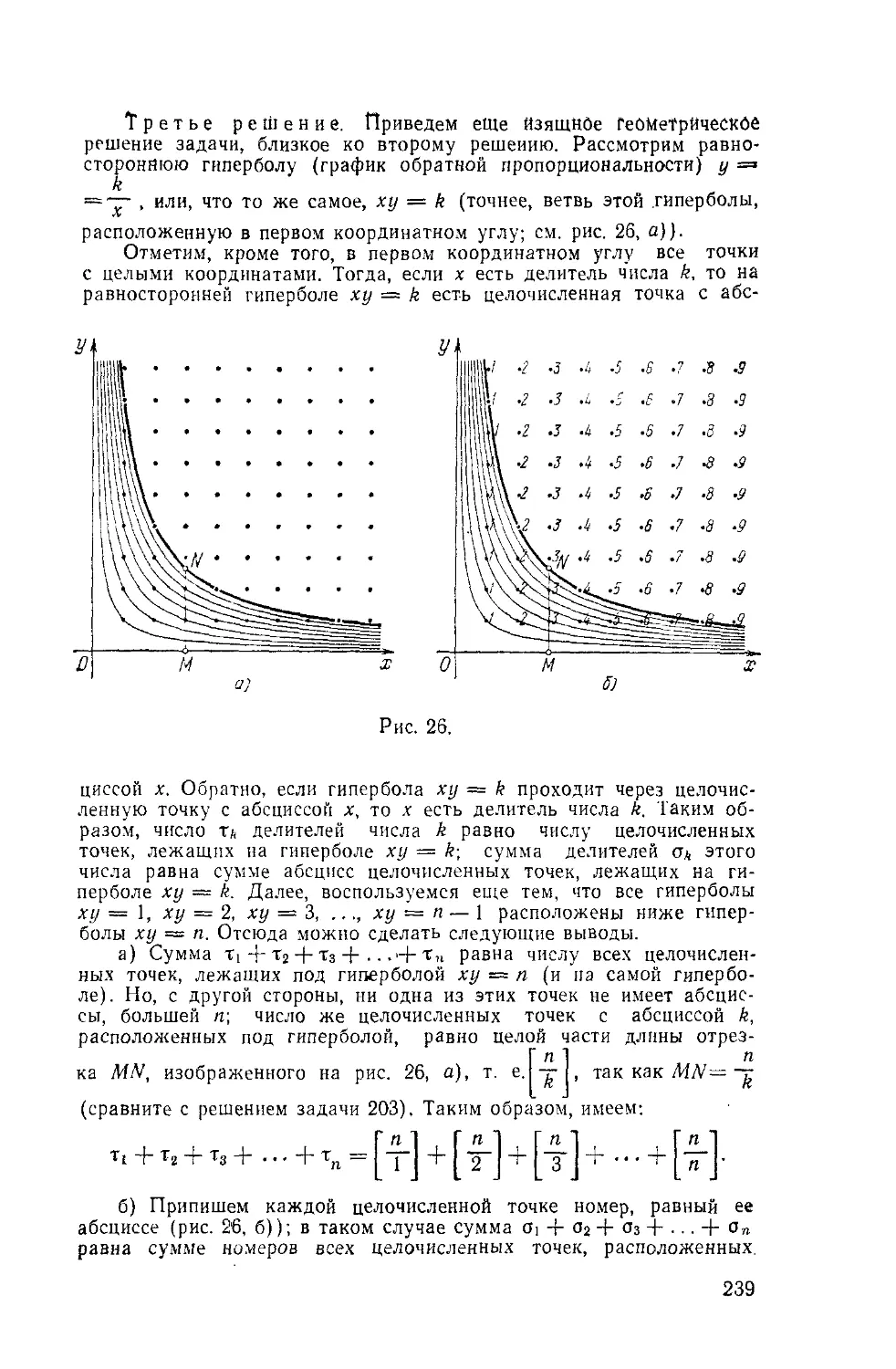
рукопожатий. Доказать, что число людей, обменявшихся нечет-
нечетным числом рукопожатий, четно.
3. Доказать, что среди любых шести человек най-
найдутся либо трое попарно знакомых, либо трое попарно
незнакомых.
4. На заседании присутствуют несколько человек
(разумеется, больше одного человека — иначе какое
же это было бы «заседание»?).
а) Может ли быть, что никакие двое из присутствую-
присутствующих не имеют одинакового числа знакомых?
б) Доказать, что при любом числе участников засе-
заседания может случиться так, что никакие трое из при-
присутствующих не имеют одинакового числа знакомых.
5. На некотором собрании присутствовало 2п чело-
человек, каждый из которых был знаком не менее чем с п
присутствующими. Доказать, что за круглый стол на
4_лица мож.но посадить четырех из присутствующих так,
чтобы каждый сидел между своими знакомыми.
6. На конгресс приехало большое число ученых; од-
одни из них были раньше знакомы друг с другом, другие —
') Поль Лежен Дирихле A806—1859) — выдающийся не-
немецкий математик.
10
нет. При этом оказалось, что никакие два ученых, имею»
щих одно и то же число знакомых, не имеют общих зна-
знакомых. Доказать, что среди присутствующих на кон-
конгрессе ученых найдется ученый, знакомый ровно с одним
участником конгресса.
7. На конгресс приехало 1000 делегатов из разных
стран. Известно, что каждые трое из них могут говорить
друг с другом без помощи остальных (однако при этом
возможно, что одному из трех лиц придется служить
переводчиком для двух других). Доказать, что всех
делегатов конгресса можно так разместить в гостинице
с двуместными номерами, что в каждом номере будут
помещены делегаты, которые могут говорить друг
с другом.
8. На международной конференции присутствуют
17 ученых. Каждые два из них беседуют друг с другом
на определенном языке; при этом всего все 17 человек
знают три языка. Доказать, что среди участников кон-
конференции найдутся трое, которые говорят друг с другом
на одном и том же языке.
9. На некотором собрании присутствовало п человек.
Известно, что каждые два знакомых из них не имеют
никаких общих знакомых, а каждые два незнакомых
между собой лица имеют ровно двух общих знакомых.
а) Доказать, что все присутствующие имеют одно и
то же число знакомых.
б) При каких п возможно условие задачи?
10. В городе «Многообразие» живут 10 000 жителей,
каждые два из которых либо враждуют, либо дружат
между собой. Каждый день не более чем один житель
города может «начать новую жизнь», т.е. перессорить-
перессориться со всеми своими друзьями и подружиться со всеми
врагами; при этом любые три жителя могут подру-
подружиться между собой. Доказать, что все без исключения
жители могут подружиться между собой. Какого на-
наименьшего числа дней наверное достаточно для этого?
//*. В стране Оз имеется несколько замков, из 'каж-
'каждого из которых ведут три пути. Странствующий ры-
рыцарь выехал из своего родового замка и пустился в
путешествие по стране. Рыцарь любит разнообразие;
поэтому, доезжая до очередного замка, он каждый раз
поворачивает налево, если в предшествующий раз
повернул направо, и поворачивает направо, если до
этого он повернул налево. (Проезжая первый на своего
11
пути замок, рыцарь может повернуть в любую сторону.)
Докажите, что когда-нибудь рыцарь вернется в свой
замок.
12*. При дворе короля Артура собрались 2п рыцарей,
причем каждый из них имеет среди присутствующих
не более п—1 врагов. Доказать, что Мерлин — совет-
советник Артура — может так рассадить рыцарей за круг-
круглым столом, что ни один из них не будет сидеть рядом
со своим врагом.
13. а) Известно, что среди 80 монет имеется одна
фальшивая, более легкая, чем остальные, имеющие
все одинаковый вес. При помощи четырех взвешиваний
на чашечных весах без гирь найти фальшивую монету.
б) Известно, что среди п монет есть одна фальши-
фальшивая, более легкая, чем остальные, имеющие все оди-
одинаковый вес. Каково наименьшее число k такое, что к
взвешиваниями на чашечных весах без гирь всегда
можно выделить фальшивую монету?
14. Некоторые из 20 металлических кубиков, оди-
одинаковых по размеру и внешнему виду, алюминиевые,
остальные — дюралевые (более тяжелые). Как при по-
помощи не более 11 взвешиваний на чашечных весах без
гирь определить число дюралевых кубиков?
Примечание. В задаче предполагается, что все кубики мо-
могут быть алюминиевые, но дюрэлевыми все они быть не могут (ведь,
если бы все кубики оказались одного веса, то без этого условия мы
никак не смогли бы определить, алюминиевые они или дюралевые).
15*. Среди 12 монет имеется одна фальшивая. Из-
Известно, что фальшивая монета отличается по весу от
настоящих, но не известно, легче она настоящих или
тяжелее. Настоящие монеты все одного веса. С помощью
трех взвешиваний на чашечных весах без гирь выделить
фальшивую монету и одновременно установить, легче
она или тяжелее остальных.
Примечание. В условиях задачи 15 тремя взвешиваниями
можно выделить фальшивую монету не только из 12, но и из 13 мо-
монет; в последнем случае нельзя, однако, определить, легче или тяже-
тяжелее фальшивая монета, чем настоящая. Для случая 14 монет необхо-
необходимы уже четыре взвешивания.
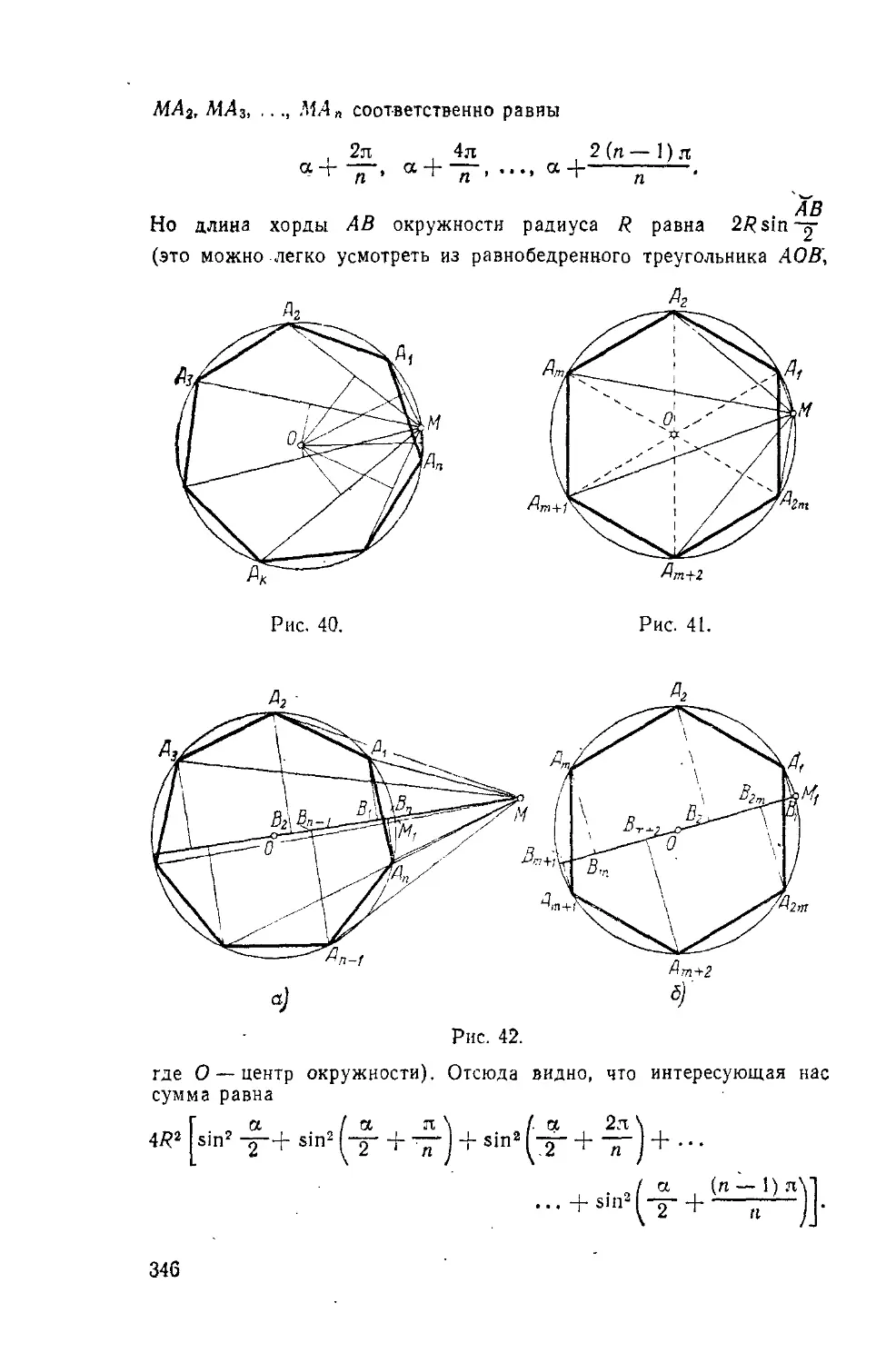
Можно также доказать (однако это доказательство является до-
довольно сложным!), что если у нас имеется произвольное число N мо-
монет, одна из которых является фальшивой и имеет иной вес, чем ос-
остальные, то наименьшее число k взвешиваний на чашечных весах без
гирь, обеспечивающее возможность найти эту монету и одновременно
указать, легче ли она или тяжелее остальных, равно log3BiV-f 3), если
12
2N+3 является целой степенью тройки, и равно [1og3BN+3)]-H,
если 2iV+3 степенью тройки не является (т. е. если число log3Btt+3)
— не целое; квадратные скобки здесь обозначают целую часть
числа — см. стр. 37); при N = 12 это и дает нам k = 3. Было бы инте-
интересно также указать, чему равно наименьшее число kx взвешиваний,
позволяющих в этих общих условиях лишь найти фальшивую мо-
монету, не определяя, легче ли она или тяжелее остальных (при N «=
= 12 или 13 число k\ = 3, а при N = 14 уже k[ = 4; общее значе-
значение величины kt = k)(M) цока, кажется, никем не определено).
По поводу решения общей «задачи об N монетах» (опирающе-
(опирающегося, впрочем, на далекие от содержания настоящей книги идеи) см.
книгу [44], где также подробно обсуждаются причины; с которыми
связан возникший в последние десятилетия большой интерес матема-
математиков и связистов к задачам типа задач 13—15.
16. а) К хозяину гостиницы однажды пришел по-
постоялец, не имевший денег, но обладавший серебряной
цепочкой, состоящей из семи звеньев. Хозяин согласился
держать этого постояльца неделю, при условии, что тот
будет ему ежедневно отдавать в виде платы одно из
звеньев цепочки. Какое наименьшее число звеньев надо
распилить для того, чтобы владелец цепочки смог ежед-
ежедневно в течение семи дней расплачиваться с хозяином
(быть может, забирая у него при этом отданные ранее
звенья и выдавая взамен их другие)?
б) Цепь состоит из 2000 звеньев. Какое наименьшее
число звеньев надо распилить для того, чтобы любое
число звеньев от 1 до 2000 можно было набрать, взяв
некоторое число из образовавшихся частей?
17. В городе Лиссе все станции метро связаны
между собой, т. е. с любой станции можно проехать
(возможно с пересадками) на любую другую. Доказать,
что при этом можно закрыть одну станцию метро (без
права проезда через нее) так, чтобы с любой из остав-
оставшихся станций можно было проехать на любую другую
станцию.
18*. На всех улицах города Зурбагана существова-
существовало двустороннее движение. Когда, однако, городским
властям потребовалось произвести ремонт всех доро,г,
они вынуждены были временно ввести на части улиц
одностороннее движение, оставив движение на осталь-
остальных улицах двусторонним; после этого, напротив, одно-
односторонним было сделано движение по тем улицам, кото-
которые ранее не ремонтировались, а по улицам, где движе-
движение ранее было односторонним, снова было разрешено
ехать в обоих направлениях. При этом в период ремон-
ремонта дорог в обоих случаях можно было проехать
13
из любого пункта Зурбаганэ в любой другой. Дока-
Доказать, что в Зурбагане можно ввести одностороннее дви-
движение по всем улицамч так, чтобы проезд из любого
пункта города в любой другой оставался возможным.
19*. В стране Дельфиний имеется п городов, каждые
два из которых соединены шоссе, причем движение по
всем шоссе является односторонним. Доказать,- что
если пф2 или 4, го направления движения по шоссе
можно выбрать так, чтобы из каждого города в любой
другой можно было попасть с заездом не более чем еще
в один город; если же п—2 или 4, то так движение
организовать нельзя.
20*. В Швамбрании имеется 100 городов; при этом
если два города А и В не соединены прямой телефон-
телефонной связью, то имеются регулярные авиарейсы из А
в В и наоборот, а если между А и В прямая телефон-
телефонная связь есть, то таких рейсов нет. Известно, что
в Швамбрании каждые два города могут быть (может
быть — через- посредство нескольких промежуточных
пунктов) соединены между собой телефоном и что из
каждого города в каждый другой можно долететь
самолетом,— возможно, с несколькими посадками
в пути. Докажите, что в Швамбрании имеются такие
4 города, что из каждого из них можно и дозвониться
и долететь в любой другой, используя, в случае необ-
необходимости, в качестве промежуточных пунктов лишь
два других города этой четверки.
21. Можно ли ходом шахматного коня попасть из
левого нижнего угла доски в правый верхний, побывав
на каждом поле ровно один раз?
22. Задача о короле-самоубийце. На шах-
шахматной доске размером 1000ХЮ00 клеток стоит белый
король и 499 черных ладей. Доказать, что при произ-
произвольном положении фигур (и при произвольной игре
черных) король может «сыграть в поддавки», т. е. за
ряд ходов стать на находящееся под боем одной из
ладей поле, вынудив тем самым себя побить. (Фигуры
на нашей доске ходят по обычным правилам.)
23. 12 полей расположены по кругу и на четырех
соседних полях стоят четыре разноцветные фишки:
красная, желтая, зеленая и синяя.
Одним ходом можно передвинуть любую фишку
с поля, на котором она стоит, через четыре любых поля
на пятое (если оно свободно) в любом из двух воз-
14
можных направлений. После нескольких ходов фишки
могут стать снова на те же четыре поля. Как они мо-
могут при этом переставиться?
24. Среди принятых в университет студентов имеет-
имеется ровно 50 знающих английский язык, ровно 50 знаю-
знающих французский язык и ровно 50 знающих немецкий
язык (при этом, разумеется, среди студентов могут
быть та>кие, которые знают сразу два или даже все
три языка, так что общее число знающих хоть один
язык студентов, вообще говоря, меньше 3-50 =150).
Докажите, что всех студентов можно разбить на 5 та-
таких (вообще говоря — не совпадающих по численности)
групп, что в каждой группе ровно 10 человек будут
знать английский язык, ровно 10 человек — француз-
французский и ровно 10 человек — немецкий
25. а) На спортивных соревнованиях выступают
20 спортсменов; судят соревнования 9 судей. Каждый
судья расставляет в своем списке соревнующихся в по-
порядке от 1-го до 20-го в соответствии с тем, как он рас-
расценил их выступления, причем впоследствии оказалось,
что оценки всех судей разнятся не слишком значитель-
значительно: ни один спортсмен не получил у двух судей места,
отличающиеся более чем на три. В основу окончатель-
окончательного распределения мест положено «среднее место»
спортсмена по оценкам 9 судей, т. е. сумма всех при-
приписанных ему мест, деленная на число судей (на 9).
Каково наибольшее возможное значение «среднего
места» лучшего из 20 спортсменов?
б) Теннисная федерация присвоила квалификацион-
квалификационные номера всем теннисистам страны: 1-й номер — силь-
сильнейшему из них, 2-й — следующему по силе, и т.д.; при
этом известно, что в состязании теннисистов, номера
которых в квалификационном списке разнятся более
чем на две единицы, всегда побеждает теннисист с мень-
меньшим номером. 1024 теннисиста страны устраивают
соревнования по олимпийской системе, т. е. так, что
после каждого этапа соревнований все проигравшие
выбывают из игры, а оставшиеся разбиваются на пары
соперников в следующем туре случайным образам.
Спрашивается, какой наибольший номер может иметь
победитель таких соревнований?
26*. Спартакиада продолжалась п дней; на ней бы-
были разыграны N комплектов медалей; при этом в 1-й
День был вручен 1 комплект медалей и 1/7 часть от
16
оставшегося их количества; во 2-й день — 2 комплекта
медалей и 1/7 часть от оставшегося их количества; ...;
в предпоследний, (п—1)-й день— (п—1) комплект меда-
медалей и 1/7 часть всех оставшихся медалей; наконец, в по-
последний день были вручены п последних комплектов
медалей. Сколько дней продолжалась спартакиада и
сколько комплектов медалей на ней разыгрывалось?
27. Пять приятелей, один из которых имел обезья-
обезьяну, купили однажды мешок орехов, которые они пред-
предполагали утром следующего дня поделить между собой.
Однако ночью один из приятелей проснулся и захотел
орехов; о« разделил все орехи в мешке на пять равных
частей, причем у него остался один лишний орех, кото-
который он отдал обезьяне, и взял себе пятую часть. Вслгд
за ним проснулся другой из хозяев орехов; не зная, что
орехи уже кто-то брал, он разделил все оставшееся со-
содержимое мешка снова на пять частей, причем остав-
оставшийся лишний орех отдал обезьяне, и взял себе пятую
часть. Затем последовательно проделали ту же опера-
операцию оставшиеся трое приятелей; при этом каждый из
них, не зная о поступке остальных, делил все орехи
на пять частей, брал себе пятую часть и каждый раз
оставался один лишний орех, который отдавали обезья-
обезьяне. Наконец, утром все пятеро вместе достали мешок,
разделили оставшиеся орехи на пять частей, а один
орех, оказавшийся лишним, снова отдали обезьяне.
Требуется определить наименьшее число орехов в меш-
мешке, гари котором возможен подобный раздел их.
28. Два брата продали принадлежащее им обоим
стадо овец, взяв за каждую овцу столько рублей, сколь-
сколько было овец в стаде. Полученные деньги братья по-
поделили следующим образам: сначала старший браг
взял себе десять рублей из вырученной сум.мы, затем
взял десять рублей второй брат, после этого первый
брат взял еще десять рублей, и т. д. При этом младше-
младшему брату не хватило десяти рублей; поэтому он взял
все оставшиеся после дележа мелкие деньги, а кроме
того, чтобы дележ был справедливым, старший брат
отдал младшему свой перочинный нож. Во что был
оценен перочинный нож?
29. а) С какого дня чаще начинается новый год:
с субботы или с воскресенья?
б) На какой день недели чаще всего приходится
30-е число месяца?
1в
2. ПЕРЕСТАНОВКИ ЦИФР В ЧИСЛЕ
30. Какие целые числа от зачеркивания последней
цифры уменьшаются в целое число раз?.
31. а) Найти все целые числа, начинающиеся с циф-
цифры 6 и от зачеркивания этой цифры уменьшающиеся
в 25 раз.
б) Доказать, что не существует целых чисел, кото-
которые при зачеркивании первой цифры уменьшаются
в 35 раз.
32*. Целое число уменьшается в 9 раз при зачер-
зачеркивании некоторой его цифры; при этом полученное
число тоже делится на 9.
а) Доказать, что для того, чтобы разделить получен-
полученное число на 9, тоже достаточно вычеркнуть в нем
одну цифру.
б) Найти все целые числа, удовлетворяющие усло-
условию задачи.
33. а) Найти все числа, которые при зачеркивании
третьей цифры уменьшаются в целое число раз.
б)* Найти все числа, которые при зачеркивании
второй цифры уменьшаются в целое число раз.
34. а) Найти наименьшее целое число, начинающее-
начинающееся с цифры 1 и такое, что если переставить эту цифру
в конец, то число увеличится втрое. Найти все такие
числа.
б) Какими цифрами могут начинаться отличные от
нуля целые числа, увеличивающиеся втрое от переста-
перестановки первой цифры в конец? Найти все такие числа.
35. Найти наименьшее натуральное число, оканчи-
оканчивающееся цифрой 6, которое увеличивается в 4 раза
при перенесении его последней цифры в начало числа.
36. Доказать, что нет целых чисел (отличных от
нуля), которые от перестановки начальной цифры в ко-
нец увеличиваются в 5 раз, в 6 раз или в 8 раз.
37. Доказать, что нет целых чисел (отличных от
нуля), которые увеличиваются вдвое от перестановки
начальной цифры в конец.
38. а) Доказать, что нет отличных от нуля целых
чисел, которые от перестановки начальной цифры в ко-
конец увеличиваются в 7 или в 9 раз.
б) Доказать, что нет отличных от нуля целых чисел,
которые увеличиваются в 4 раза от перестановки на-
начальной цифры в конец.
2 Д. О., Шклирский и др. 17
39. Найти наименьшее целое число, начинающееся
цифрой 7 и уменьшающееся втрое от перестановки
этой цифры в конец Найти все такие числа.
40. а) Доказать, что отличное от нуля целое число
не может быть меньше в 2, 3, б, 6, 7 или 8 раз своего
обращенного (т. е. числа, состоящего из тех же цифр,
записанных в обратном порядке).
б)* Найти все целые числа, которые в 4 раза или
в 9 раз меньше своего обращенного.
41 а) Найти шестизначное число, которое увеличи-
увеличивается в 6 раз, если три последние цифры числа, не
меняя их порядка, переставить в начало числа.
б) Доказать, что не существует восьмизначного чис-
числа, увеличивающегося в 6 раз при перестановке четырех
последних цифр на первые четыре места с сохранением
их порядка.
42. Найти шестизначное число, произведения кото-
которого на 2, на 3, на 4, на 5 и на 6 записываются теми
же цифрами, что и оно само, но в другом порядке.
43. Найти все трехзначные числа, равные среднему
арифметическому всех чисел,- получающихся из задан-
заданного числа всевозможными перестановками его цифр
(включая, разумеется, и «тождественную перестановку»,
оставляющую все цифры числа на месте).
44. Пусть А — некоторое целое положительное чис-
число, А' — число, составленное из тех же цифр, но пере-
переставленных в каком-то другом порядке. Доказать, что
если /4+/Г=1010, то А делится на 10.
45. Пусть М — некоторое 17-значное число, N — чис-
число, полученное «переворачиванием» М, т. е. записывае-
записываемое теми же цифрами, следующими, однако, в обратном
порядке. Доказать, что хотя бы одна цифра десятичной
записи числа M-\-N — четная.
3. ЗАДАЧ И НА ДЕЛ ИМОСТЬ Ч ИСЕЛ
Начатые задачами этого цикла темы, в основной своей части от-
относящиеся к «высшей арифметике» — к теории чисел,— находят не-
некоторое продолжение в дальнейших разделах книги, в первую оче-
очередь—в циклах 4, 5 и 11. По поводу общих идей, лежащих в основе
решения многих из приведенных ниже задач, читателя можно отослать
к статье [45], брошюр» [46] или к изложениям начал теории чисел
(см., например, связанные с так называемой «теорией сравнений»
разделы учебников [64] — [67] или статьи [68]). Особо хочется по-
порекомендовать читателю в связи с материалом настоящего цикла за-
задач раздел 2 книги [5], по характеру изложения наиболее подходя-
подходящий для учащихся старших и средних классов школы.
18 ¦
46. Доказать, что при всяком целом п
а) п3 — п делится на 3;
б) п5 — п делится на 5;
в) п7 — п делится на 7;
г) пп — п делится на 11;
д) /г13 — п делится на 13.
Примечание. Отметим, что п9— л уже не обязатель-
обязательно делится на 9 (например, 29 — 2 = 510 не делится на 9).
Задачи а) — д) составляют частные случаи одной более общей
теоремы: см. ниже задачу 340 (стр. 71).
47. Доказать, что при всяком целом п
а) З6" —26" делится на 35 (здесь п ^г 0);
б) п5 — 5п3 + 4« делится на 120;
в) /г2 + Зп + 5 не делится на 121.
48. Доказать, что при всех целых тип
¦а)* тп{т60—пе0) делится на 56 786 730;
б) ш5-\-Зт4п — 5m3n2—15/n2n3 + 4mn4 + 12я5 нерав-
неравно 33.
49. При каких целых положительных п число 20" +
+ 16" —3"—1 делится на 323?
50. Существует ли такое натуральное число п, что
п2 + п + 1 делится на 1955?
51. Какие остатки может давать сотая степень це-
целого числа при делении на 125?
52. Доказать, что если целое число N взаимно просто
с 10, то 101-я степень числа N оканчивается теми, же
тремя цифрами, что и N (так, например, 1233101 окан-
оканчивается цифрами 233, а 37101 — цифрами 037).
53. Найти трехзначное число, всякая целая степень
которого оканчивается тремя цифрами, составляющими
первоначальное число.
54*. Пусть W — четное число, не делящееся на 10.
Какова будет цифра десятков числа JV20? Какова будет
цифра сотен числа Л200?
55. Доказать, что сумма
где п есть произвольное целое положительное число, а
k нечетно, делится на 1+2+3+ ... +п.
56. Вывести признак делимости чисел на 11.
57. Число 123456789A0)A1)A2)(!3)A4) написано
по 15-ричной системе счисления, т. е. это число равно
2* 19
153+ ... +2-1512+1513.
Какой остаток дает оно при делении на 7?
58. Доказать, что единственными числами К такими,
что если N делится на К, то и любое число, полученное
из N перестановкой цифр, делится на К, являются 1,
3 и 9. (Для К = 1 это свойство очевидно, для К = 3 и
К, = 9 следует из известных признаков делимости на
3 и на 9.)
59. Найти наименьшее целое число, записываемое
одними единицами, которое делится без остатка на
число 333...33.
100 троек
60. Пусть а — последняя цифра целого числа N = 2\
А — число, в которое обращается N, если зачеркнуть
в нем эту последнюю цифру. Доказать, что при всех
6>3 число аА делится на 6.
61. Доказать, что 27 1958— 10887s-f-10 1528 делится
без остатка на 26 460.
62. Доказать, что И10—1 делится на 100.
63. Доказать, что 22225555+55552222 делится на 7.
64. Доказать, что число, составленное из Зп одина-
одинаковых цифр, делится на 3" (так, число 222 делится на
3, число 777 777 777 делится на 9, и т.д.).
65. Найти остаток от деления на 7 чисда
1Ою+ Ю(H3)+ ... + ЮA01\
66. а) Найти последнюю цифру чисел 9f9 ', 2а1).
б) Найти две последние цифры чисел 2999, З999.
в) * Найти две последние цифры числа 14<44"'.
67. Доказать, что
а) две последние цифры десятичных записей чисел
„99 пч"9 , г>ч9 /-.(q9}\
9 и 9 (где, например, 9 означает 9 ') одинаковы;
б)* шесть последних цифр десятичных записей чи-
чисел 77 и 77 одинаковы.
68. а) Какова последняя цифра числа
(...
(возведение в степень 7 повторяется 1000 раз)? Каковы
две последние цифры этого числа?
20 •
б) Какова последняя цифра числа
7W
записанного с помощью 1001 семерки, аналогично числу
задачи а), однако с иным порядком возведения в сте-
степень? Каковы две последние цифры этого числа?
69*. Определить пять последних цифр числа
N =
записанного с помощью 1001 девятки аналогично числу
задачи 686).
70. При каких натуральных п сумма 5n-f- n5 делит-
делится на 13? Каково наименьшее п, удовлетворяющее это-
этому условию?
71. Каковы две последние цифры числа
где п — произвольное целое неотрицательное число и
а) а = 4; б) а = 8?
72*. Найти последние 1000 цифр числа
N = 1 + 50 + 502+ 503+.. .+50999.
73. Натуральное число М делится на 7; доказать,
что если число цифр числа делится на 6, то при пере-
переносе последней цифры в начало мы получим число N,
также делящееся на 7.
74. Сколькими нулями оканчивается произведение
всех целых чисел от 1 до 100 включительно?
В дальшейшем мы будем пользоваться следующим обозначением:
1ФЗ-4... (л — 1)-« = я1
(читается: п факториал). Так предыдущую задачу можно короче
сформулировать так: сколькими нулями оканчивается число 100! ?
75. а) Доказать, что произведение п последователь-
последовательных целых чисел делится на п\.
б) Доказать, что дробь -^-~—^ есть число целое,
если только a-\-b-\-...-\-k*gZn.
в) Доказать, что (я!)! делится на л!(п)!.
21
г) * Доказать, что произведение п последовательных
целых чисел, образующих арифметическую прогрессию,
разность которой взаимно проста с п!, делится на nl.
Примечание. Задача 75г) является обобщением задачи 75а).
76. Делится ли на 7 число сочетаний из 1000 эле-
элементов по 500?
77. а) Найти все числа п между 1 и 100, такие, что
(п—1)! не делится на п.
б) Найти все числа п между 1 и 100, такие, что
(п—1)! не делится на га2.
78*. Найти все целые числа п,_делящиеся на все
целые числа, не превосходящие ^п.
79. а) Доказать, что сумма квадратов пяти последо-
последовательных целых чисел не может быть полным квадра-
квадратом целого числа.
б) Доказать, что сумма одинаковых четных степеней
трех последовательных целых чисел не может равняться
четной степени целого числа.
в) Доказать, что сумма одинаковых четных степеней
девяти последовательных целых чисел не может рав-
равняться никакой степени целого числа (разумеется,
с показателем, большим 1).
80. а) Пусть А и В— два различных семизначных
числа, каждое из которых составлено из всех цифр от
1 до 7. Доказать, что А не делится на В.
б) Из всех цифр от 1 до 9 составить три трехзнач-
трехзначных числа, относящихся друг к другу как 1:2:3.
81. Квадрат целого числа оканчивается четырьмя
одинаковыми цифрами. Какими?
82. Доказать, что если обе стороны прямоугольника
и его диагональ выражаются целыми числами, то пло-
площадь прямоугольника делится на 12.
83. Доказать, что если все коэффициенты квадратно-
квадратного уравнения
ах2 + Ъх + с = 0
— целые нечетные числа, то корни уравнения не могут
быть рациональными.
84. Доказать, что если сумму простых дробей
1.1,1
п "•" л+1 ^ п + 2
(п — целое число) обратить в десятичную, то получен-
полученная дробь будет смешанной периодической.
22
85. Доказать, что числа
(я, m — целые положительные) не могут быть целыми.
86. а) Доказать, что дробь а ° ^а " t несократима
ни при каком целом значении а.
б) Указать все (натуральные) числа, на которые
, 5л + 6
может оказаться сократимой дробь 8~ 1 7 при целом п.
87. 1953 цифры выписаны по кругу. Доказать, что
если при чтении этих цифр в направлении вращения
часовой стрелки, начиная с какой-то цифры, получится
1953-значное число, делящееся на 27, то и при чтении
этих цифр в том же направлении, начиная с любого
другого места, тоже получится 1953-значное число, де-
делящееся на 27.
88. Доказать, что существует делящееся на 51000 чис-
число, Десятичная запись которого не содержит нулей.
89. Доказать, что все числа вида 10 001, 100010001,
1000 100 010 001,...— составные.
90. Доказать, что каждые два числа последователь-
последовательности
2+1, 22+1, 2^+1, 28+1, 216+1, ..., 22"+1, ...
являются взаимно -простыми.
Примечание. Из результата настоящей задачи, в частности,
следует, что существует бесконечно много простых чисел (см. также
по этому поводу задачи 234 и 349) В самом деле, если бы число про-
простых чисел было конечным, то не могло бы существовать бесконечно
много чисел, каждые два из которых взаимно просты.
91. Доказать, что если одно из чисел 2"—1 и 2"+ 1,
где п > 2, простое, то второе является составным (при
п = 2 оба числа 2"— 1=3 и 2"+ 1=5 — простые).
92. а) Доказать, что если р и 8р— 1 —простые числа,
то 8р + 1 — составное число.
б) Доказать, что. если р и 8р2 + I — простые числа,
то 8р2 — 1 — простое число,
23
93. Доказать, что квадрат любого простого числа,
кроме чисел 2 и 3, при делении на 12 дает в остатке 1.
94. Доказать, что если три простых числа, больших
числа 3, образуют арифметическую прогрессию, то раз-
разность прогрессии делится на 6.
95*. а) Десять простых чисел, меньших 3000, состав-
составляют арифметическую прогрессию. Найти эти числа.
б) Доказать, что не существует 11 простых чисел,
меньших 20 000, которые составляли бы арифметическую
прогрессию.
96. а) Доказать, что из пяти последовательных целых
чисел всегда можно выбрать одно, взаимно простое со
всеми остальными.
б) Доказать, что из 16 последовательных целых чи-
чисел всегда можно выбрать одно число, взаимно простое
со всеми остальными.
4. РАЗНЫЕ ЗАДАЧИ ИЗ АРИФМЕТИКИ
97. Число А записывается в десятичной системе счис-
счисления при помощи 666 троек, а число В—.при помощи
666 шестерок. Из каких цифр состоит произведение А-В?
98. Найти частное и остаток от деления числа А, за-
записываемого с помощью 1001 семерки, на число 1001.
99. Найти наименьший квадрат, начинающийся с
шести двоек.
100. Существуют ли такие целые числа тип, что
т2=я2+1954?
101. Дописать к 523 ... три цифры так, чтобы полу-
полученное шестизначное число делилось на 7, на 8 и на 9.
102. Найти четырехзначное число, которое при деле-
делении на 131 дает в остатке 112, а при делении на 132
дает в остатке 98.
103. а) Доказать, что сумма всех я-значных чисел
(п>2) равна 494 99 ... 9 55 00 ... 0 (так, сумма всех
(п—Я)раз (п—2)раз
трехзначных чисел равна 494 550, а сумма всех шести-
шестизначных чисел 494 999 550 000).
б) Найти сумму всех четырехзначных четных чисел,
которые можно записать цифрами 0, 1, 2, 3, 4, 5 (одна и
та же цифра в числе может повторяться).
104. Сколько и каких цифр понадобится для того,
чтобы записать все целые числа от 1 до 100 000 000 вклю-
включительно?
24
105. Все целые числа выписаны подряд, начиная от
единицы. Определить, какая цифра стоит на 206 788-м
месте.
106. Будет ли дробь 0,1234567891011121314..., ко-
которая получится, если вьгаисать после нуля подряд все
целые числа, периодической?
107. Каждое из целых чисел от единицы до мил-
миллиарда включительно заменяется суммой цифр числа;
однозначные числа при этом, разумеется, не меняются,
а остальные уменьшаются. Затем каждое из вновь по-
полученных чисел снова заменяется суммой его цифр —
и так до тех пор, пока не получится миллиард одно-
однозначных чисел. Каких чисел будет больше среди полу-
полученных чисел — единиц или двоек?
108. Может ли являться полным квадратом целое
число, запись которого в десятичной системе счисления
содержит
а) некоторое количество шестерок и некоторое ко-
количество нулей;
б) цифры 1, 2, 3, 4, 5, 6, 7, 8, и 9 (каждую — по од-
одному разу), причем цифра 5 стоит на последнем месте?
109. На карточках написаны все пятизначные числа
от 11111 до 99 999 включительно (число таких чисел,
очевидно, равно 88 889). Затем эти карточки произволь-
произвольным образом выложили в одну цепочку. Доказать, что
полученное таким путем 444 445-значное число D44 445 =
= 88 889-5) не является степенью двойки.
110. Найти все десятизначные числа такие, что 1-я
цифра числа равна числу нулей в его десятичной запи-
записи, 2-я цифра —числу единиц, и т. д. вплоть До десятой
цифры, равной числу девяток в записи числа.
111. На какое целое число надо умножить 999 999 999,
чтобы получить число, состоящее из одних единиц?
112. Пусть А — некоторое натуральное число. До-
Доказать, что существует бесконечно много таких (нату-
(натуральных) чисел N, записываемых цифрами 1, 2, ..., 9
(без нулей!), что числа N и AN имеют одинаковые сум-
суммы цифр ').
') Оговорка об отсутствии нулей в десятичной записи чисел N
связана с тем, что если приписать к записи N любое число нулей в
конце, то суммы цифр чисел N и AN, разумеется, не изменятся; по-
поэтому без этой оговорки из существования одного удовлетворяю-
удовлетворяющего условию задачи числа N сразу же следовало бы существование
бесконечного множества таких чисел.
25
113. Пусть п ^ 2 и щ, яг, ...'—все не более, чем
n-значные неотрицательные целые числа, сумма цифр ко-
которых четна, а Ь\, Ь2, ...— те не более чем п-значные
числа, сумма цифр которых нечетна. Доказать, что
ai -f a2 -f ... = &i -f 62 + • • •
при всех (натуральных) /n<n. Будет ли верно утверж-
утверждение задачи также и при пг^п?
114. В числовом треугольнике
1
1 1 1
12321
1367631
каждое число равно сумме трех чисел, расположенных
в предыдущей строке над этим числом и его соседя-
соседями справа и слева; в случае отсутствия в предыдущей
строке одного из двух таких чисел они заменяются
нулями.
Доказать, что в каждой строке, начиная с третьей,
найдется четное число.
115. Дана треугольная таблица чисел:
0123 1956 1957 1958
13 5 3913 3915
4 8 7828
в которой каждое число (кроме чисел верхней строки]
равна сумме двух стоящих над ним чисел предшествую-
предшествующей строки. Доказать, что последнее число, стоящее в
самой нижней строке этой таблицы, делится на 1958.
116. Расстояние от пункта А до пункта В равно
999 км. Вдоль соединяющей А и В дороги стоят кило-
километровые столбы, на которых указаны расстояния до А
и до В — надписи на них выглядят так:
0 | 999, 1 |998, 2 1 997 999 | 0.
Сколько из этих столбов таких, на которых имеются
лишь две различные цифры?
417. Мальчик, проезжая в автобусе мимо кинотеатра,
успел заметить только часы (но не минуты!) начала
26
четырех сеансов:
1-й сеанс — 12 час. ... мин.;
2-й сеанс—13 час. ... мин.;
7-й сеанс — 23 час. ... мин.;
8-й сеанс — 24 час. ... мин.
Как по этим данным восстановить начала всех сеан-
сеансов (предполагается, что продолжительность всех вось-
восьми сеансов одинакова)?
118. Шоссе, по которому круглосуточно ходит авто-
автобус, пересекает железную дорогу. По дороге каждый
час проходят два поезда, которые достигают шоссе
ровно в п час. и в п час. 38 мин., где п принимает все
значения от 0 до 23; каждый раз, когда проходит поезд,
опускается на 5 мин. шлагбаум, преграждающий путь
по шоссе. Требуется так составить расписание автобу-
автобусов, чтобы они ходили с одним и тем же интервалом
Т мин. между машинами и чтобы ни одна машина не
задерживалась на переезде. При каких интервалах
между автобусами, меньших получаса, так спланировать
движение возможно?
119. Чему равно наибольшее возможное значение
отношения трехзначного числа к сумме его цифр?
120. Вычеркнуть 100 цифр из числа
12345678910111213 ... 979899100
так, чтобы полученное после этого число было
а) возможно большим; б) возможно меньшим.
121. Из всех цифр от 1 до 9 составить три трехзнач-
трехзначных числа, произведение которых было бы
а) наименьшим; б) наибольшим.
122. Сумма нескольких последовательных целых по-
положительных чисел равна 1000. Найти эти числа.
123. а) Доказать, что всякое число, не являющееся
степенью двойки, может быть представлено в виде сум-
суммы по меньшей мере двух последовательных Целых по-
положительных чисел, а для степеней двойки такое пред-
представление невозможно.
б) Доказать, что всякое составное нечетное число
может быть представлено в виде суммы по меньшей
мере двух последовательных нечетных чисел, а ни одно
простое число нельзя представить в таком виде. Какие
27
четные числа можно представить в виде суммы несколь-
нескольких последовательных нечетных чисел?
в) Доказать, что каждую степень целого полржи-
тельного числа п (разумеется, с показателем, большим 1)
можно представить в виде суммы п последователь-
последовательных нечетных чисел.
124. Доказать, что произведение четырех последо-
последовательных чисел в сумме с единицей дает полный
квадрат.
125. Имеется 4п положительных чисел, таких, что
из любых четырех попарно различных можно составить
геометрическую пропорцию. Доказать, что среди этих
чисел найдется п одинаковых.
126. Даны 27 гирь, веса которых равны соответствен-
соответственно I2, 22, З2, ..., 272. Разложить эти гири на три группы
равного веса.
127. Имеется 13 гирь, каждая из которых весит це-
целое число граммов. Известно, что любые 12 из них
можно разложить на чашках весов, по шесть на каж-
каждой чашке, так, что наступит равновесие. Доказать, что
все гири имеют один и тот же вес.
128*. Четыре (произвольные) числа а, Ь, с, d выпи-
выписаны рядом друг с другом. Под этими числами выписы-
выписывается новая четверка чисел a\—ab, bi — Ьс, ct = cd,
d\ — da; под ними выписываются числа а.2 = а\Ь\, Ь2—Ь)Си
C2=C\dx, d2=dlau и т. д. Доказать, что либо все полу-
полученные таким образом четверки чисел различны, либо
все они, начиная с некоторой, совпадают между собой.
129. Дан произвольный набор из N (где А/—полная
степень двух: N=2h) чисел щ, а2, ..., а*-, каждое из ко-
которых равно -f-1 или —1. Исходя из этих чисел, следую-
следующим образом составляется новый набор чисел, каждое
из которых также равно +1 или —1: а\ — fljG,, а'2 =
= a2a3, ..., a'N_t — aN_iaN, a'N = aNax; затем по числам
а\, а'2, .... a'N точно так же находятся числаа'г а'^, ...
..., a"N, и т. д. Доказать, что в конце концов мы полу-
получим набор, состоящий из одних лишь чисел +1.
130*. Пусть ai, п2, . ¦., ап, где я>2,— целые числа;
по этим числам составляется новая система чисел
, _ а} + аг . Q2 + а3 ' _ дп-1 + °п _- _
"l — 2 ' 2 ~ 2 ' " ' ' "—1 ~ 2 ' п —
— -^-g—;по числам at, az, .. .,апточно так же находят-
28
„ / а, + о'2\
ся числа а, I = —^— I» а2> • • •< а«> и т- п- Доказать, что
если все получаемые таким путем числа — целые, то
al = a2=... = an.
131. Пусть х=\, у, z — произвольные три числа; хи
ух, г\ — абсолютные величины \х—у\, \у—г|, |г—х\
попарных разностей этих чисел; х2, у2, z% — абсолютные
величины попарных разностей чисел Х\, уи Z\ (т. е.
числа |xi—j/i|, \yt—2]|, |2i—*i|); x3, y3, z% — абсолют-
ные величины разностей чисел х2, у2, z2, и т. д. Извест-
Известно, что для какого-то п тройка чисел хп, уп, zn не отли-
отличается от тройки чисел х, у, z. Чему равны числа у и г?
132*. а) Даны четыре произвольных целых положи-
положительных числа А, В, С, D. Доказать, что если образо-
образовать из них четыре числа Аи Ви Си D\, равных соот-
соответственно разностям между А и В, между В и С, между
С и D и между D и А (мы каждый раз вычитаем мень-
меньшее число из большего), затем из чисел Au Blt Cu ?>i
образовать точно так же новую четверку чисел А2, В2,
С2, D2, и т. д., то через несколько шагов мы обязательно
придем к четверке нулей.
Так, например, начиная с четверки чисел 32, 1, 110, 7,
мы последовательно получим
32, 1, ПО, 7;
31, 109, 103, 25;
78, 6, 78, 6;
72, 72, 72, 72;
0, 0, 0, 0.
б) Сохраняет ли силу утверждение задачи а); если
(положительные) числа А, В, С, D являются рациональ-
рациональными, но не обязательно целыми? А если эти числа
иррациональны?
133*. а) Расположить числа от 1 до 100 таким об-
образом, чтобы никакие 11 (не обязательно последователь-
последовательных!) из этих чисел не следовали одно за другим в
порядке возрастания или убывания.
б) Доказать, что в каком бы порядке ни располо-
расположить числа от 1 до 101, всегда из этих чисел можно
выбрать 11 (не обязательно последовательных!) чисел,
29
которые следуют одно за другим в порядке возрастания
или убывания.
134. а) Из первых 200 целых чисел от 1 до 200 вы?
брано 101 число. Доказать, что среди выбранных чисел
найдется пара таких, что одно из них делится на
другое.
б) Выбрать из первых 200 целых чисел 100 чисел так,
чтобы ни одно из них не делилось на другое.
в) Доказать, что если хотя бы одно из 100 целых
чисел, не превосходящих 200, меньше 16, то одно из
8тих чисел обязательно делится на другое.
135. Доказать, что
а) из любых 52 целых чисел всегда можно выбрать
два, сумма или разность которых делится на 100;
б) из любых 100 целых чисел всегда можно выбрать
несколько чисел (быть может —одно), сумма которых
делится на 100;
в) если числа задачи б) положительны и не превы-
превышают 100, а их сумма равна 200, то можно отобрать
несколько чисел так, чтобы их сумма равнялась 100;
г)* из любых 200 целых чисел можно выбрать 100
чисел, сумма которых делится на 100.
136. Дана невозрастающая последовательность аи
Ог, ..., а„ положительных чисел, сумма которых равна 1,
а самое большее из них равно т^, где k—целое:
'-??- = аг > а2 > а3 > ... > ап > 0, аг + а2 + ... + ап = 1.
Доказать, что из этих чисел можно выбрать k таких
чисел, что самое маленькое из них больше половины
самого большого.
137. По кругу выписаны р крестиков и q нуликов;
число пар стоящих рядом крестиков обозначим через а,
а число пар стоящих рядом нуликов — через Ь. Дока-
Доказать, что а—b—p—q.
138. Пусть /i, /г, ..., /»— это числа 1, 2, ..., п, но
только расставленные в каком-то, воообще говоря, новом
порядке. Доказать, что при п четном произведение
A—ii) B—/г) C—1з)...(п—/„) может быть как четным,
так и нечетным; однако при п нечетном оно обязательно
четно.
SO
х 139. Дано п чисел Х\, Хг, *з> •.., х„, каждое и» кото-
которых равно +1 или —1. Доказать, что если XiX2+xzx3+...
.. .+xn_iJtn+*n*i=0, то п делится на 4.
140. Доказать, что совокупность всех десятизначных
чисел, записываемых исключительно цифрами 1 и 2, мож-
можно разбить на такие две группы, что запись суммы лю-
любых двух чисел из одной группы будет содержать не
менее двух цифр 3.
141. Из цифр 1 и 2 составлено пять 100-значных чи-
чисел; при этом известно, что у каждых двух чисел ровно
в г разрядах совпадают цифры, однако ни в одном раз-
разряде не совпадают все пять цифр. Доказать, что это
возможно лишь в том случае, если г заключено в пре-
пределах: 40<rs^60.
142. Имеютвя два набора з»в<ков «+» и «—» по
1958 знаков в каждом наборе. Доказать, что за некоторое
число «шагов», на каждом из которых позволяется
менять произвольно выбранные 11 знаков 1-го набора,
можно 1-й набор превратить во 2-й. (Наборы считаются
одинаковыми, если у них на одинаковых местах стоят
одинаковые знаки.)
143*. Шахматист для тренировки играет не менее од-
одной партии в день; при этом, чтобы не переутомить-
переутомиться, он играет не более, чем 12 партий в неделю. Дока-
Доказать, что можно найти несколько таких последователь-
последовательных дней, в течение которых он сыграет ровно 20
партий.
, 144. Пусть N—произвольное целое положительное
число. Доказать, что существует целое число, кратное
N, которое в десятичной системе счисления записывает-
записывается одними лишь цифрами 0 и 1. При этом, если N
взаимно просто с 10 (т.е. не делится ни на 2, ни иа 5),
то существует делящееся на N число, составленное из
одних только единиц (если N не взаимно просто с 10,
то, разумеется, никакое число вида 11 ... 1 не может
п раз
делиться на N).
145. Расположить на числовой оси систему непере-
.крывающихся (не имеющих общих внутренних точек или
общих концов) отрезков длины 1 так, чтобы для любой
(бесконечной) арифметической прогрессии (с произволь-
произвольным первым членом прогрессии и какой-угодно раз-
разностью!) хоть один ее член попал внутрь одного из от-
отрезков нашей системы.
81
146. Пусть m и n-т-два взаимно простых целых по-
положительных числа. Доказать, что если дроби:
т-\-п 2 (т -f n) 3(« -f я) (т— 1) (w -f n).
т ' т ' т ' ' ' '' т '
m + n 2 (т + я) 3 (т -f я) (я— I) (т + я)
я ' п я ' * ' "' я
изобразить точками на числовой оси, то в каждый из
интервалов A, 2), B, 3), C, 4), ..., (т+п—2, т+п— 1)
оси попадает ровно одна из дробей (см. рис. 2, где по-
положено т = 3, п=4).
7 7 « 14 &
-Ч 1 >-+-. ! • 1 *-4-^ 1 (—
^ 1 2 3 4 5 6 7
Рис. 2.
/47*. Пусть а\, п2, пз, ..., Дп — какие-то целые поло-
положительные числа, такие, что каждое из этих чисел мень-
меньше 1000, а общее наименьшее кратное любых двух чи-
чисел больше 1000. Доказать, что сумма обратных величин
чисел аи а2, а3, ..., а„ меньше двух.
148*. Дробь — с нечетным простым знаменателем
рфЪ разложена в бесконечную периодическую десятич-
десятичную дробь. Доказать, что если число цифр в периоде
дроби четно, то среднее арифметическое всех цифр пе-
периода равно 4,5 (т. е. совпадает со средним арифмети-
арифметическим всех цифр 0, 1,2,..., 9; это означает, что «боль-
«большие» и «маленькие» цифры встречаются в периоде дро-
дроби одинаково часто). Если же число цифр в периоде
дроби нечетно, то среднее арифметическое всех цифр
обязательно отлично от 4,5.
149*. Доказать, что если разложить дроби
(р — простое, отличное от 2 и 5, а\, а2, ..., а„ ...— ка-
какие угодно целые числа, взаимно простые с р) в беско-
бесконечные периодические десятичные дроби, то несколько
первых дробей (может быть, одна) будут иметь одина-
32
ковое число цифр в периоде, а каждая из последую-
последующих — в р раз больше цифр в периоде, чем предыдущая.
Так, например, ~ = 0,C), -|" = °.D). 17 = °'C70>'
¦^-=0,(987654320), ^ имеет27цифр в периоде, ^име-
^имеет 81 цифру в периоде, и т. д.
5. РЕШЕНИЕ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ
150. а) Найти четырехзначное число, являющееся
точным квадратом и такое, что его первые две цифры
равны между собой и последние две цифры также равны
между собой.
б) Двузначное число в сумме с числом, записанным
теми же цифрами, но в обратном порядке, дает полный
квадрат. Найти все такие числа.
151. Найти четырехзначное число, равное квадрату
суммы двух двузначных чисел, образованных двумя
первыми и двумя последними цифрами числа.
152. Найти все четырехзначные числа, являющиеся
полными квадратами и записываемые
а) четырьмя четными цифрами;
б) четырьмя нечетными цифрами.
153. а) Найти все трехзначные числа, равные сум-
сумме факториалов своих цифр.
б) Найти все целые числа, равные сумме квадратов
своих цифр.
154. Найти все целые числа, равные -
а) квадрату суммы цифр числа;
б) сумме цифр куба числа.
155. Решить в целых числах уравнения:
а) 1! + 2! + 3! + ...+*! = #2;
б) И+ 2!+31+ ...+*!«= jf;
156. Сколькими способами можно разложить 2П на
сумму четырех квадратов целых положительных чисел?
157. а) Доказать, что равенство
Для целых х, у, г верно только при x=»j/=«z=0.
8 Д. О. Шклярсквй м др, . 33
б) Найти целые числа х, у, z, v, такие, что
158*. а) При каких целых значениях k возможно
равенство
*+*+2
где х, у, г — целые положительные числа?
б) Найти в пределах первой тысячи всевозможные
тройки целых чисел, сумма квадратов которых делится
на их произведение,
159. Решить в целых числах уравнение
х3—2у3—4z3 = 0.
160. Решить в целых числах уравнение
161. Решить в целых положительных числах урав-
уравнение
162. Решить в целых числах х, у, г уравнение
у корней
163*. Доказать, что уравнение х2-\-х-\-\ = ру имеет
решения в целых числах х, у для бесконечно многих
простых значений коэффициента р.
164*. Найти четыре целых (положительных) числа
таких, что квадрат каждого из них, сложенный с сум-
суммой трех остальных, тоже является полным квадратом.
165. Найти все пары целых чисел, сумма которых рав-
равна их произведению.
166. Сумма обратных величин трех целых положи-
положительных чисел равна единице. Каковы эти числа?
167. а) Доказать, что уравнение — + — =• —, где
п>1 — натуральное число, имеет при п простом ровно
три решения в натуральных числах х, у (где решения
х=а, у***Ь и *=&, у=*а при афЪ считаются различны-
различными), а при составном п — более трех решений.
б) Найти все решения в целых числах уравнения
задачи а) при я=14.
34
в)* Решить в целых числах х, у, z уравнение
'— ^—V =Т (Указать формулы, дающие все решения).
168. а) Найти все целые положительные, не равные
между собой числа х, у, удовлетворяющие уравнению
ху=у*.
б) Найти все рациональные положительные, не рав-
равные между собой числа х, у, удовлетворяющие уравнению
'(указать формулу, дающую все решения).
169. В шахматном турнире участвовали два учени-
ученика 7-го класса и некоторое число учеников 8-го класса.
Каждый участник играл с каждым другим один раз. Два
семиклассника набрали вместе 8 очков, а все восьми-
восьмиклассники набрали одинаковое число очков (в турнире
каждому участнику sa выигранную партию засчитывает-
ся 1 очко, а за партию, окончившуюся вничью, 1/2 очка).
Сколько восьмиклассников участвовало в турнире?
170. В шахматном турнире участвовали ученики 9-го
и 10-го классов. Каждый участник, играл с каждым дру-
другим один раз. Десятиклассников было в 10 раз больше,
чем девятиклассников, а они набрали вместе в 4,5 раза
больше очков, чем все девятиклассники. Сколько уче-
учеников 9-го класса участвовало в турнире и сколько они
набрали очков?
171*. Целочисленным треугольником на-
называется треугольник, длины сторон которого выража-
выражаются целыми числами. Найти все целочисленные треу-
треугольники, периметр каждого из которых равен его пло-
площади.
Задача 171 открывает большую тему в учении о решении уравне-
уравнений в целых числах; мы здесь не затрагиваем ее глубже именно в
связи с ее необъятностью (эта проблематика частично освещена в
указанной в списке литературы книге [53]). Так, например, пред-
представляет интерес вопрос о целочисленных треугольниках с углами,
соизмеримыми с «полным» углом в 360°,— можно доказать, что ника-
никаких углов, соизмеримых с полным углом и отличных от Ь(Г, 90° и
120°, целочисленный треугольник иметь не может, причем нетрудно
получить формулы, дающие длины сторон всех целочисленных тре-
треугольников с данным углом а. где а=60°, или 90°, или 120° (цело-
(целочисленные прямоугольные треугольники часто называют пифаго-
пифагоровыми треугольниками). Можно также искать целочисленные
3* 35
треугольники, величины двух углов которых имеют Заданное отноше-
отношение, скажем, один угол вдвое, втрое, впятеро или вшестеро больше
другого,— например, несложно доказать, что наименьший целочис-
целочисленный треугольник, один угол которого вдвое больше другого, име-
имеет стороны 4, 5, 6, в то время как наименьшие возможные длины
сторон целочисленного треугольника, один угол которого вшестеро
больше другого, таковы: 30 421, 46 656, 72 930. Дальнейшие задачи
возникают, если, скажем, накладывать определенные условия н на
углы и на стороны целочисленного треугольника: так, нетрудно
указать сколь угодно много пифагоровых треугольников,
у которых гипотенуза или один катет являются полными квадратами,
но не существует ни одного пифагорова треугольника, сразу
две стороны которого являлись бы полными квадратами. При этом
среди целочисленных прямоугольных треугольников (пифагоровых
треугольников), гипотенуза каждого из которых является полным
квадратом, существует бесконечно много таких, сумма катетов ко-
которых тоже дает полный квадрат, однако стороны всех таких тре-
треугольников весьма велики: как показал еще в 1643 г. П. Ферма !),
наименьший из пифагоровых треугольников, стороны которых удов-
удовлетворяют этим условияц, имеет стороны:
а—\ 061 652 293 520
6 = 4 565 486 027 76 У,
с=4 687 298 610 289.
6. МАТРИЦЫ, ПОСЛЕДОВАТЕЛЬНОСТИ,
ФУНКЦИИ
Матрицей размера тХ" (или (тХ")-матрицей) называется
просто таблица чисел, имеющая m строк и п столбцов; так, например,
ниже выписаны BX4)-матрица, CX3)-матрица (квадратная матри-
матрица 3-го порядка), (ЗХ1)-матрица и AХ5)-матрица [AХ«)-матрицы
и (mXl)-матрицы называются также векторами—соответствен-
векторами—соответственно векторами-строками и векторами-столбцами];
Г 3 2 01 Г УГ
П/2 -1/2 1/3 1/71 l.j | _УЗ
1.2/7 —4/3 3/4 0 J: I 12 1 __ij; ~
L г.
[10 —9 8 —7 6].
Матрица, все элементы которой представляют собой целые числа,
называется целочисленной — так, из выписанных выше матриц
целочисленными являются вторая и четвертая (но не первая и не
третья). Термин «матрица» пока не вошел в школьную программу по
математике и не ислользуется в нижеследующих задачах; однако
большая важность этого понятия (см., например, [55] или [56]) за.
ставляет нас упомянуть этот термин в названии настоящего цикла.
') Пьер Ферма A602—1665)—великий французский матема-
математик, один из основоположников теории чисел.
36
Числовой последовательностью называется упорядочен-
упорядоченный набор чисел
вь иг, аз ап, ...
(чаще всего — бесконечный). Для задания последовательности надо
указать правило образования ее членов at, а%, ...; »то правило может
иметь вид формулы, позволяющей по произвольно заданному номе-
номеру п вычислить число ап, или"алгоритма, указывающего, как тем
или иным путем найти ап для любого конкретного значения п. Так,
например, для фигурирующей в нескольких из задач этого цикла так
называемой последовательности Фибоначчи1)
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... (*)
(числа Фибоначчи; о них см. [57] или [58]) этот алгоритм
задается правилами2):
а,=.я2=1; а„ ¦« а„_, + а„_, ¦ при л > 2. (**)
Впрочем, в математике приходится иногда иметь дело и с так назы-
называемыми «случайными последовательностями:», образование членов
которых не регулируется жесткими правилами (ср. с задачей 192).
Под функцией y = f(x) понимается закон /: х (-*• у отобра-
отображения множества X «допустимых» значений аргумента х в множество
У значений функции у; при этом каждому значению х@Х должно
соответствовать единственное значение #"¦/(*). В «высшей арифме-
арифметике» (в теории чисел) главный интерес представляют функции, свя-
связанные с целыми числами — такие, для которых область определения
X или область У значений функции состоит из целых чисел. Если
область определения Х- = {1, 2, 3, ...} есть множество всех натураль-
натуральных чисел, то аргумент х функции чаще обозначается буквой п; при
этом сама функция п>-*¦ у(п) или n-i->-an есть просто числовая после-
последовательность {ai, Й2, аз, ...}. Типичным (и часто встречающимся)
примером функции, у которой область значений У состоит из целых
чисел, является так называемая целая часть [х] числа х, т.е.
наибольшее не превосходящее х целое число (так что, например,
[2,5] =2, [4]-= 4, [—3,2] <=—4); близкой к [х] является и функция
(х) — ближайшее к х целое число (если таких чисел два, то (х)
принимается равным большему из них, так что B,5) =3, D) =4,
(—3,2) «щ—3; ср. графики функций [х] и (х) на рис. 3, а, б). В не-
некоторых вопросах математики встречается также функция {х} =
¦=*—[х]—дробная часть числа х (рис 3, в; для сравнения на
рис. 3, г изображен график функции |* — (х)\, указывающей отклоне-
отклонение х от ближайшего целого числа). Но наибольшую роль в теории
чисел играют «чисто арифметические» функции, для которых и об-
область определения X и область значений У состоят из целых чисел;
') Леонардо Пизанский по прозвищу Фибоначчи
A180—1240)—крупнейший математик европейского средневековья.
2) Существуют и другие описания чисел Фибоначчи (*)—так,
например, из правил (**) можно вывести явную формулу
" Т/Б»
•ависимости л-го числа Фибоначчи и„ от его номера я.
37
в качестве примеров таких функций можно назвать фигурирующие
в некоторых из собранных ниже задач число делителей т(я)=»т„
(натурального) числа п, сумму его делителей а(п)=а„ или (.неявно
участвующую в задаче 197) так называемую функцию Мёбиуса')
[i{n), равную 1 при и=1, равную 0 при п, кратном хоть одному
A)*
[{) ру р ру р
квадрату натурального числа, -и равную (—1)* при pPР
где Р\, Pi рн — попарно различные простые числа. [Заметим,
1
- -+
]
—¦¦
*•
г/
Si
н
Рис. 3.
кстати, что все три функции т(я), о (п.) и ц(и) обладают так назы-
называемым «мультипликативным свойством»: если <р(га) любая из этих
функций,, то ф(«!«2) —<p(«i) -ф(и2) для любых двух взаимно про-
простых натуральных чисел П\ и п^.]
Собранные в этом цикле задачи являются довольно разнообраз-
разнообразными по содержанию и по методам их решения; в частности, в не-
некоторых 8адачах используется так называемая «целочисленная ре-
решетка» — множество всех точек плоскости с целочисленными коорди-
!) Август Фердинанд Мёбиус C790—1868) —выдающийся не-
немецкий математик, специализировавшийся, в первую очередь, в об-
области геометрии.
натами, плодотворность применения которой в теоретико-числовых
исследованиях была установлена еще Г. Минковским ') и Г. Ф. Во-
Вороным 2).
172. Числа 1, 2, 3 п2 расположены в виде квад-
квадратной таблицы:
1 2 3 . . . п -
п + 1 п + 2 п + 3 . . . 2;i
2/г +1 2/1-1-2 2/1+3 ... Зд
л — 1)я+1 (ft—1)л + 2 (я—1)п + 3. . . яЕ_
Из этой таблицы выбирается произвольное число, а
строка и столбец, содержащие это число, вычеркивают-
вычеркиваются. Затем из оставшихся чисел снова выбирается одно
число, и снова вычеркиваютсяхтрока и столбец, содержа-
содержащие это число,— и так до тех пор, пока в таблице не
останется единственное число,которое автоматически по-
попадает в число отобранных. Чему равна сумма всех вы-
выбранных таким путем чисел?
173. Квадратная таблица из п2 клеток заполнена
целыми числами от 1 до п так, что в каждой строке и в
каждом столбце таблицы встречаются все числа от 1
до п. Доказать, что если таблица симметрична относи-
относительно диагонали, ведущей из ее левого верхнего уг-
угла в правый нижний угол, и п нечетно, то на этой диа-
диагонали встретятся все числа от 1 да п. Будет ли вер-
верно это утверждение также и в том случае, когда п четно?
174. п2 целых чисел от 1 до п2 выписаны в квадрат-
ную таблицу размером пУ(п: при этом число 1 стоит на
любом месте в таблице; 2 принадлежит строке, порядко-
порядковый номер которой равен номеру столбца, которому при-
принадлежит 1; число 3 принадлежит строке, номер которой
совпадает с номером столбца, содержащего число 2,
и т. д. На сколько отличается сумма чисел строки, со-
содержащей число 1, от суммы чисел столбца, содержа-
содержащего число п2?
1) Герман Мннковский A864—1906) — выдающийся немец-
немецкий ученый, внесший большой вклад в геометрию, в физику (теория
относительности) и в теорию чисел; один из основоположников «гео-
«геометрической» теории чисел.
2) Георгий Федосьевич Вороной (IS6S—1&08)—выдающийся
русский математик, один из основоположников «геометрической» тео
рии чисел.
99
175. Дана прямоугольная таблица размером
во все клетки которой вписаны некоторые числа. Разре-
Разрешается одновременно менять знаки у всех чисел одной
строки или у всех чисел одного столбца. Доказать, что,
применяя эту операцию несколько раз, мы всегда можем
прийти к таблице, у которой суммы чисел каждой стро-
строки и каждого столбца неотрицательны.
176. 800 чисел выписаны в виде прямоугольной таб-
таблицы, имеющей 100 строк и 80 столбцов; при этом про-
произведение суммы всех чисел любого столбца на сумму
всех чисел любой строки равно числу, стоящему в пере-
пересечении этого столбца и этой строки. Известно, что чис-
число, стоящее в правом верхнем углу таблицы, положи-
положительно. Чему равна сумма всех составляющих таблицу
чисел? .
177. 64 неотрицательных числа с общей суммой 1956
записаны на 64 клетках шахматной доски; при этом из-
известно, что сумма чисел, выписанных на каждой из двух
диагоналей доски, равна 112, и что числа, занимающие
клетки, симметричные относительно одной или симмет-
симметричные относительно другой диагонали, равны между со-
собой. Доказать, что сумма чисел, выписанных в любом
ряду (т. е. в любой строке или в любом столбце) доски,
меньше 518.
178. В клетках шахматной доски размером «Х« рас-
расставлены некоторые числа так, что при любой расста-
расстановке на доске п ладей, никакие две из которых не бьют
-друг друга, сумма закрытых этими ладьями чисел будет
одной и той же. Обозначим число, стоящее на пересече-
пересечении /-й строки доски и /-го ее столбца, через atj. Дока-
Доказать, что существуют два таких набора чисел хи х2, ...
...,>*„ и ух, у2, ..., ijn, что ац—Xi+ys.
179. В клетках шахматной доски размером яХ« рас-
расставлены числа; число, стоящее на пересечении р-й
строки и #-го столбца, обозначено через xpq. Доказать,
что если для любых /, / и k (где 1=0', /, k^n) имеет
место тождество xls-\-Xjh+xM=Q, то существуют п таких
чисел tu h, ..., tn, что xtj=ti—tj.
180. В некоторых клетках шахматной доски размером
пУ(п стоят звездочки; известно, что если вычеркнуть лю-
любой набор строк доски (только, разумеется, не все!), то
найдется столбец, в котором имеется ровно одна неза-
черкнугая звездочка. (В частности, если вовсе никакие
строки не вычеркивать, то тоже найдется столбец,, в ко-
40
тором имеется ровно одна звездочка.) Доказать, что если
вычеркнуть любой набор столбцов (но не все), то най-
найдется строка, в которой имеется ровно одна незачеркну-
тая звездочка.
181*. Во всех, кроме одной, клетках шахматной до-
доски размером п~Х_п стоят знаки «+», а в одной клетке
стоит знак «—»; при этом
а) /1=4 я знак «—» стоит с краю доски, но не в
ее углу;
б) п = 8 и знак «—» стоит не в углу доски.
Разрешается одновременно менять все знаки в одном
(произвольно взятом) столбце, или в одной (произволь-
(произвольной) строке, или в одном (произвольно выбранном)
«наклонном» ряду, параллельном диагонали доски.
(В частности, можно изменить знак в любом угловом
поле, которое образует самостоятельный «наклонный
ряд».) Доказать, что любым числом «допустимых» изме-
изменений знаков нельзя избавиться от знака «—», т.е.прий-
т.е.прийти к доске, во всех клетках которой стоит знак «+».
182. а) Во всех клетках шахматной доски размером
8X8 стоят знаки «+» или «—». Разрешается, выделив
на доске любой квадрат размером 3X3 или 4X4, поме-
поменять знаки во всех клетках этого квадрата. Мы хотим
при помощи подобных операций добиться того, чтобы все
стоящие на доске знаки стали знаками «+»; всегда ли
это возможно?
б) Во всех клетках (обыкновенной) шахматной до-
доски стоят натуральные числа; разрешается увеличивать
на единицу все числа, стоящие в клетках любого «мало-
«малого» квадрата из четырех соседних клеток доски, или все
числа, стоящие в (любых) двух соседних строках доски,
или, наконец, все числа, стоящие в двух (любых) сосед-
соседних столбцах доски. Всегда ли подобными операциями
можно добиться того, чтобы все числа доски делились
на 10?
183. а) Имеются три кучки камней; играющему с
ними мальчику разрешается брать по одному камню од-
одновременно из всех трех кучек или удваивать число кам-
камней в одной (произвольной) кучке. Сможет ли мальчик
за несколько подобных «ходов» выбрать из кучек все
камни?
б) Во всех клетках прямоугольной таблицы, имею-
имеющей 8 строк и 5 столбцов, расставлены натуральные чис-
числа. Разрешается удвоить число одного столбца (любогс)
или вычесть единицу из всех чисел одной строки. Дока-
Доказать, что несколькими «допустимыми» преобразования-
преобразованиями таблицы чисел можно добиться того, что во всех ее
клетках окажутся одни нули.
184. Таблица из двух столбцов целых положительных
чисел и какого-то числа строк выписывается по следую-
следующему правилу. В верхней строке мы пишем произволь-
произвольные числа а и Ь\ далее под а выписываем (целое поло-
положительное) число а\, равное -у, если а четно, и равное
——, если а нечетно, а под b выписываем число Ъ\ = 2Ъ.
Далее мы поступаем с числами а,\ и Ь\ точно так же, как
раньше поступили с числами а и Ь: под at мы пишем
число а2, равное —-, если ai четно, и равное ^Ц— если
п\ -нечетно; под Ъ\ же мы пишем число b2 = 2bi. Под а2
и Ь2 мы располагаем числа а3 и Ь3, образованные из а2
и Ь2 точно так же, как числа а2 и Ь2 образуются из чисел
а\ и Ь\, и т.д.; этот процесс мы кончаем в тот момент,
когда доходим до некоторого числа ап=\ (которому от-
отвечает число Ьп = 2Ьп-\). Доказать, что сумма всех стоя-
стоящих в правом столбце чисел Ьи которым отвечают не-
нечетные числа at (здесь г'=0, 1, ..., п\ под#0 и bo мы
понимаем числа а и Ь), равна произведению ab.
185. Доказать, что каждое натуральное число либо
является числом Фибоначчи (членом последовательно-
?ти Фибоначчи (*), см. стр. 37), либо может быть пред-
представлено в виде суммы нескольких (различных), чисел
Фибоначчи.
186. Доказать, что сумма никаких восьми последова-
последовательных чисел Фибоначчи (см. задачу 185) не является
числом Фибоначчи.
187. Доказать, что если натуральное число п делится
на 5, ,то и n-е число Фибоначчи ип (см. задачу 185) так-
также делится на 5.
188. Найдется ли среди 100 000 001 первых чисел Фи-
Фибоначчи (см. вадачу 185) число, оканчивающееся че-
четырьмя нулями?
/89. Последовательность чисел а,\, а2, а3,... образо-
образована по следующему правилу: п\ = 1; ап = ап~\ Н
И— 1
при «>1. Доказать, что 14<flioo<;18.
12
190. Последовательность чисел пи аг, аз. •••> а» тако-
такова, что
а, = 0, |aa| = |ai+l|, |аз| = IM-1I..... |а„| — |ап_, + 11.
Доказать, что среднее арифметическое а "
п
1
всех чисел не меньше —к-.
191*. Последовательность натуральных чисел ао> #ь
а2, аз. ¦ • • составляется по следующему правилу:
а0, аи а2=\а0—а{\, аг= \ах—а3\, ...
(и вообще an=\an-2—an-i\ при всех п^-2); продолжа-
продолжается последовательность до первого нуля. Известно, что
каждое входящее в последовательность число не превос-
ходит 1967. Какое наибольшее количество чисел может
содержать такая последовательность?
192. Подряд выписывается бесконечная последова-
последовательность цифр aia2a3«4- • • •. где под аь а.2, «з, a,i,... по-
понимается любая из цифр, кроме девятки. Доказать, что
среди чисел ai, ai<X2, aia2«3, aiazoisa^... (где под aia2
понимается число арЮ+ссг, и т.д.) имеется бесконечно
много составных.
193. В последовательности 1975... каждая цифра,
начиная с пятой, равна последней цифре суммы пред-
предшествующих четырех цифр; Встретятся ли в этой после-
последовательности
а) подряд цифры 1234; б) вторично четверка цифр
1975?
194. Выписываются подряд все числа, кратные
девяти:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117,... (*)
и для каждого из этих чисел находится сумма его цифр:
9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 18, 9, 9,... (**)
На каком месте последовательности (**) впервые
появится число 81 и каково будет следующее за ним
число? Что раньше встретится в этой последовательно-
последовательности: 4 раза подряд число 27 или 3 раза подряд число
36? Что еще можно сказать о чередовании чисел в по-
последовательности (**)?
195. Рассмотрим следующую последовательность на-
наборов (натуральных) чисел. Первый набор /о образуют
43
две единицы 1,1. Затем между этими числами вставим
их сумму 1 + 1 =¦ 2; мы получим набор /ill, 2, 1. Потом
между каждыми двумя из чисел набора 1\ вставим сум-
сумму этих чисел; мы получим набор /г.'Ь 3, 2, 3, 1; затем,
поступая таким же образом и с набором 1%, мы придем
к набору /3:1, 4, 3, 5, 2, 5, 3, 4, 1, и т. д. Сколько раз в
миллионном наборе /юооооо встретится число 1973?
196. Имеется (конечная) последовательность нулей
и единиц такая, что различны все пятерки последова-
последовательных цифр, которые можно из нее выделить (причем
эти пятерки могут, разумеется, и перекрываться по-
подобно пятеркам 01011 и 01101, расположенным так:
...0101101...). Доказать, что если последовательность
нельзя продолжить с сохранением сформулированного
ее свойства, то первые четыре цифры последовательно-
последовательности совпадают с ее последними четырьмя цифрами.
197. В одну строку выписаны . все делители числа
N=2-3-5-7¦ II-13-17-19-23-29-31-37. Под числом 1 и те-
теми числами, которые представляют собой произведение
четного числа простых множителей, подписано число
+ 1, а под числами, представляющими собой произведе-
произведение нечетного числа простых множителей, подписано чис-'
ло —1. Доказать, что сумма всех выписанных в нижней
строке чисел равна нулю.
198. Пусть р и q — два взаимно простых натураль-
натуральных числа. Натуральное число п условимся называть
«хорошим», если его можно представить в виде px-\-qy,
где х и у — целые неотрицательные числа, и «плохим»
в противном случае.
а) Доказать, что существует такое число А, что если
сумма двух целых чисел равна А, то обязательно одно
из них «хорошее», а второе — «плохое».
б) Если числа р и q заданы, то как найти число все-
всевозможных «плохих» натуральных чисел?
199. Доказать, что если число п неотрицательно, то
его можно (и притом единственным образом!) предста-
(х + уJ + Зх + у
вить в виде п = -— 2 —, где х и у — целые не-
неотрицательные числа.
200. Пусть t — произвольное положительное число;
число несократимых дробей —, числитель р и знамена-
знаменатель q которых не превосходят t, обозначим через d{t\s
44
Чему равна сумма
201. Доказать следующие свойства целой части чис-
числа (см. стр. 37):
2) \Щ = \-j], « — целое число»
3) [х + 4-] = 12х]-М;
4) [х] +[* +4"] + [х +4
202. Упростить сумму
+П , Гя + 21 , Гп+4
где л — целое положительное число.
203*. Доказать, что если р и q — взаимно простые
целые числа, то
204. Доказать, что
а) Т1+т2+т3+...+т„
где тп — число делителей натурального числа п\
б) 01+02+03+...+аЛ=«
где а„ — сумма делителей натурального числа п.
46
205. Существует ли такое целое положительное чис-
число п, что «дробная часть» числа B+|^2)п,т. е. разность
(B + V2)n} = B + V2)n - [B + /2 )"],
(см. стр. 37) больше 0,999999?
206*. а) Доказать, что при любом целом положитель-
положительном п число [B + ]/3 )п] нечетно.
б) Найти наивысшую степень 2, на которую делится
число [A +УЗ)"].
207. Доказать, что если р — простое число, большее 2,
то разность
[B+V5)*] — 2p+I
делится на р.
208*. Доказать, что если р — простое число, то раз-
разность
-р Г « 1
делится на р (С? — число сочетаний из п элементов
по р; п — произвольное целое положительное число, не
меньшее р).
Так, например, С*ц = "".^чУ
= 462 — 2 делится на 5.
209. Указать все такие числа а, что числа [а], [2а],
[За], ..., [Na], где Л^ — фиксированное натуральное
число, все различны и числа — , \ — \, — ¦¦••! —
тоже все различны.
В задаче 209 требуется найти такое число а, чтобы были различны
числа [а], [2а], [За] [Na] и [р], [20], [Зр] [Лф], где
Р="а~> Более содержательной является задача об определении та-
таких аир (гд» уже не обязательно{5 =» —),чтобы бесконечные
последовательности [а], [2а], [За],...; [р], [2р], [Зр],... состояли
из попарно различных чисел; так, например, можно доказать, что
выписанные последовательности содержат все без исключения нату-
натуральные числа, причем каждое число — ровно по одному разу, в том
и только в том случае, когда а иррационально и ~ + ~о" ¦» 1.
46
210*.Доказать, что в равенстве
'(N — произвольное целое положительное число) можно
заменить все дроби ближайшими к ним целыми чис-
числами:
'(относительно обозначений см. стр. 37).
7. ОЦЕНКИ СУММ И ПРОИЗВЕДЕНИЙ
211. Сколько цифр имеет число 2100?
212. а) Доказать, что
'5 10 >Л2~ 2 " 4 ' 6 '"¦ 100^ 10"
б) * Доказать, что
J 3_ _5_ 99 1
2 ' 4 ' 6 ' " ' 00^ 12 '
Примечание Результат задачи б), очевидно, представляет
собой усиление результата задачи а).
213. Какое из чисел больше: 31й или 17й?
214. Какое из чисел больше:
.2 ..3
а) Л=22 или В = З3 , где в записи числа А фи-
фигурируют 1001 двойка, а в записи числа В—1000 троек;
.•4
б) В или С = 44 , где в записи числа С фигурир^-
ют 999 четверок? (В этой задаче под а^% ' всюду
понимается с_
215. Доказать, что в десятичной системе счисления
записи чисел 1974" и 1974" +2" при любом натураль-
натуральном п содержат одинаковое количество цифр.
2.16. Среди всех чисел вида 36т—5", где т и п — на-
натуральные числа, найти наименьшее по абсолютной ве-
величине.
47
217. Доказать, что
(Cioo — число сочетаний из 100 элементов по 50).
218. Что больше 99" + 100" или 101" (и —целое по-
положительное число)?
219. Что больше I00300 или 300!?
220. Доказать, что для любого целого положитель-
положительного п
221". Что больше A,000001I00000° или 2?
222. Что больше 10001000 или 1001999?
223. Доказать, что для любого целого «>6
2"
224*. Доказать, что при т>п (га, п — целые поло-
положительные числа)
1 \ъ 9 п 1 ' '\'
Так, например, ^ + -jj = ~f — 2Y' a (] + "я"
64 0 10 ^ 9 I
\7П+1
/ 1 V 27 3 ' ( \\4
Так, например, \l + -jj =-g-=3-g-,a II + у) =
256 „13 ^ о 3
"if ~ °8l ^^Т*
Из аадачи в) еледует, что в последовательности чисел 1 + -у I ,
/ 1 \2 / 1 \3 / 1 \"
[1 Ф*5") . I 1 +-§~ 1 . - ••. I 1 Н--^" 1 .... каждое последующее чис-
число больше предыдущего. А так как, с другой стороны, ни одно из
чисел не превосходит 3 (см. задачу 220), то при п-*-<х> величина
/ 1 \п
1 4- —- стремится к некоторому определенному пределу (заклю-
13
ченному, очевидно, между 2 и 3)'. ©тот предел обозначается бук-
буквой е; приближенно он равен 2,71-8281828459045...
Аналогично, задача" б) утверждает, что в последовательности
/ 1 \3 / 1 г / ¦ 1 \6 / 1 V+1
чисел[1_+Т], («+yj. A+т)"—A + т) •••' каж'
дое последующее меньше предыдущего. А так как все эти числа
¦ / 1 \п+1
больше 1, то величина 1 -) I при п, неограниченно возрастаю-
возрастающем, стремится к какому-то пределу. При этом числа второй пос-
последовательности все более приближаются к числам первой последо-
/ 1 \"+1 / 1 \п 1
вательности (отношение м + — I :'"Ь — I == 1 —f— — все меньше
отличается от 1); следовательно, этот предел должен равняться тому
же самому числу е. Число е играет в математике очень большую
роль и встречается в самых разнообразных вопросах (см., например,
задачу 225 или примечания к задачам 231 и 234).
225. Доказать, что при любом целом п, большем шес-
шести, справедливы неравенства
<п1<п[Т) ,
I 1 \п
где е = 2,71828 ... есть предел выражения A-f —I
при п-*- оо.
Этот результат является усилением результата задачи 223. Из
него, в частности, следует, что для любых двух чисел а.\ и а2,
таких, что ai<e<a2 (т. е., например, для ^ = 2,7, а2 = 2,8 или
ai = 2,71, а2=2,72, или ai = 2,718, а2 = 2,719. и т. д.) при всех п,
больших некоторого определенного числа (различ-
(различного для различных а,) имеют м е ctxlh еравенства
Таким образом, число е является той «границей», которая отделяет
числа а такие, что1-~") растет «быстрее» п\, от чисел а таких, что
I n \п
I — I растет «медленнее» п\ (существование такой границы следу-
следует из задачи 223).
I п\п
Действительно,! — ] < «1 при любом п, большем шести (ибо
In \п\
аг > е, а при я>6, в силу задачи 226, я!> 1—1 I. Далее, из резуль-
результатов задач 220 и 224 вытекает, что при /г^З выполняются
4 Д. О. Шклярский и др. 49
неравенства
п,—
следовательно, при п^З величина уп убывает, если л растет.
Легко видеть, что при п достаточно большом, -yfn ^становится сколь
угодно близким к единице: это следует, например, из того, что
Ig у 10 =—й при достаточно большом k будет сколь угодно малым.
w e
Выберем теперь N так, чтобы выполнялось неравенство у N <С ~z~\
¦а г- , е
тогда при n~>N тем более будет у' п<^—, откуда, в силу результа-
(п \п [ п\п
~е— 1 "^l") '
V
у п
Неравенство задачи 225 допускает значительное уточнение.
А именно, можно показать, что при больших п число п\ приближен-
приближенYn\~) >
но равно cYn\~) > где С есть постоянное число, равное
(точнее, можно доказать, что при п, стремящемся к бесконечности,
отношение
стремится к единице — см. задачу 161 книги [6]).
226. Доказать, что
(п и k — произвольные целые числа).
Примечание. Из результата задачи 226 следует, в частно-
частности, что
lim
227. Доказать, что при всяком целом
а) ~^«+1+п + 2+ ' * * + 2« ^ 4 '
б) 1 ^ п~+~1 + Г+2 + • • • + ШГ+1 < 2
50
228*. а) Определить целую часть числа
/1 /1/4 /1000 000*
б) Определить сумму
+ ... +
VlOOOO 1/10 001 1/10 002 Vl 000 000
1
с точностью до 50"
229*. Найти целую часть числа
1,1,1, , 1
+ + +
у 4 у 5 |/6 i/ 1 000 000
230. а) Определить сумму
Ю2" Ц2 "Г 122Т '•• "Г ш002
с точностью до 0,006.
б) Определить сумму
_1 ! 1 1 , ¦ 1
10! ' 11! + 12! + ••• + 1000!
с точностью до 0,000000015.
231. Доказать, что сумма
превзойдет любое наперед заданное число N, если толь-
только п достаточно велико.
Примечание. Результат настоящей задачи может быть зна-
значительно уточнен. А именно, можно показать, что рассматриваемая
сумма 1+"о" + "з" + ~4"+ • • • ~Ь — ПРИ больших п мало отличает-
отличается от log n (логарифм берется при основании е == 2,718 •..}. Точнее
говоря, можно доказать, что при любом п разность
не превосходит единицы (см., например, [6]).
232. Доказать, что если в сумме
! + + + + +
61
вычеркнуть все члены, у которых в знаменателе встре-
встречается цифра 9, то сумма оставшихся членов при лю-
любом п будет меньше 80.
233. а) Доказать, что при любом п
1+Т + Т + Тб + 25+-" + ^<2'
б) Доказать, что при любом п
1+ + i + L++i<1
Очевидно, что неравенство задачи б) является усилением нера-
неравенства задачи а). Еще более сильный результат содержится в за-
задаче 332. Именно из этой.задачи вытекает, что при любом п сумма
1 + Т + "9" + • •' + Г2
зх2
меньше чем "g- =1,6449340668... (но для любого числа N, меньшего
ла
чем -g-, например для JV=!,64 или N= 1,644934, можно найти такое
п, что сумма 1 + -j- + "д~ + • • • ~Ь ^2 будет больше N).
234*. Рассмотрим сумму
JL1L1l1J1L1JIL1lIJ I1
где в знаменателях дробей стоят все простыв числа от 2
до некоторого простого числа р. Доказать, что эта сум-
сумма может быть сделана больше любого наперед задан-
заданного числа N (для этого следует только выбрать чис-
число р достаточно большим).
Примечание. Результат настоящей задачи может быть зна-
значительно уточнен. А именно, можно показать, что при больших р
сумма 1+~2~ + у + -+у + ]]т'"'+ —сравнительно мало от-
отличается от log log р (логарифм берется при основании е = 2,718...).
Точнее говоря, можно доказать (см., например, [6] или [69]), что
при любом р разность
1+ + + + ++ + 1
не превосходит числа 15.
Отметим еще, что сравнение результата настоящей задачи с ре-
результатами задач 232 и 233 позволяет утверждать, что простых чи-
чисел имеется в ряду всех целых чисел «довольно много» (в частности,
52
из этой задачи следует, что их бесконечно много). Можно,
например, сказать, что простые числа встречаются в ряду натураль-
натуральных чисел «чаще», чем квадраты или чем числа, в записи которых
нет цифры 9, поскольку сумма обратных величин всех квадратов или
сумма обратных величин всех целых чисел, в записи которых не фи-
фигурирует девятка, ограничены, а сумма обратных величин всех про-
простых чисел может быть сделана сколь угодно большой.
8. РАЗНЫЕ ЗАДАЧИ ИЗ АЛГЕБРЫ
В то время как большая часть содержания настоящей книги от-
относится к арифметике (и к «высшей арифметике» — к теории чисел),
циклы задач 8—10 посвящены алгебре. При этом при решении от-
отдельных задач этих циклов могут оказаться полезными, например,
представление о так называемой основной теореме ал-
алгебры, утверждающей, что каждое алгебраическое уравнение сте-
степени п (с вещественными или с произвольными комплексными
коэффициентами) имеет-ровно я (вещественных или комплексных)
корней (которые, однако, не обязаны быть все различны); форму-
формулы Виета'), указывающие связь корней уравнения с его коэффи-
коэффициентами; знание правил деления «углом» произвольных многочле-
многочленов; тригонометрическая форма или геометрическое представление
комплексных чисел (см. в конце книги литературу к циклам 8—10).
235. Доказать, что
(а + Ь + сK33 — а333 — б333 — с333
делится на
(а + Ь-\- сK —а3 —б3 —с3.
236. Разложить на множители выражение •.
237. Доказать, что многочлен
X9999 I Х8888 I Х7777 I хш6 4- X5555 -f- XiiU 4- X3333 -4- X2222 4-
делится на х9 -f- хв -f- х7 -\- Xе + х5 + х4 + х3 + х2 + 1.
238. а) Разложить на множители выражение
аз + 53 + с3 — ЗаЬс.
б) Воспользовавшись результатом задачи а), найти
общую формулу для решения кубического уравнения
х3 -f- рх + q = 0.
') Франсуа Виета A540—1603)—видный французский ма-
математик, один из создателей современной алгебраической символики
L(a тем самым ¦» и алгебры).
53
Примечание. Отметим, что результат настоящей задачи поз-
позволяет решить всякое уравнение третьей степени. Действительно,
пусть
х3+Ах2+Вх+С=0
есть какое-то кубическое уравнение (коэффициент при х3 всегда
можно считать равным 1, так как в противном случае мы можем
разделить все уравнение на этот коэффициент). Сделаем в этом
уравнении подстановку: х~у+с. Тогда получим:
у3 + За/2 + ЗА/ + с3 + А(у* + 2су + с2) + В(у + с) + С » О,
или
уз + (Зс + А)уг + (Зс2 + 2Лс + В)(/ + (с3 + Ас2 + Вс+С) = 0.
А А
Отсюда видно, что положив с =—"о"(т- е. х =у — ~3~)> мы ПРН"
дем к уравнению
[ЗА2 2Л2 А [А3 Ла АВ
которое имеет такой же вид, как и уравнение данной задачи:
г/3 + Р# + <7 = 0, где р =
239. Решить уравнение
• Л2 . 2Л3 ЛВ
= 0, где р = — у + В, 9 = -27" — -g-
— |^а + л: = х.
240*. Найти действительные корни уравнения
^л 16
. Найти действительные корни уравнения
У х + 2~У х + 2Ух + ... + 2V х + 2У"Зх = х
, и радикалов
(все квадратные корни считаются положительными).
242. Решить уравнение
1Н г = X
(в выражении слева знак дроби повторяется п раз).
243. Найти действительные корни уравнения
(все квадратные корни считаются положительными),
54
244. Решить уравнение
245. Решить уравнение
U—I) *(*—!)(* —2)
1-2-3
1 _ JL 4
1 1 "¦
1-2
"*"
246. Решить уравнение х3—[х]=3, где, как обычно,
[х]—целая часть числах (см. стр. 37).
247. Система двух уравнений второй степени
л-2 — г/2- =, о,
имеет, вообще говоря, четыре решения. При каких зна-
значениях а число решений этой суммы уменьшается до
трех или до двух?
248. а) Решить систему уравнений
ах + у = а2,
х + ау = 1.
При каких значениях а эта система вовсе не имеет ре-
решений и при каких имеет бесконечно много решений?
б) Тот же вопрос относительно системы
ах+у = а3,
х + ау=\.
в) Тот же вопрос относительно системы
+ г/ + г = 1,
х +ау + z = а,
249. Найти условия, которым должны удовлетворять
данные числа а\, аг, сз, аи для того, чтобы система б
уравнений с 4 неизвестными
4- *4 =
4" хз =
4- -^4 =
з 4" Xi =
55
имела решения. Найти значения неизвестных Х\, х2,
Хз, х4.
250. Сколько действительных решений имеет система
х + у = 2,
251. Найти все вещественные решения системы
** + /=-1.
252. Найти всевозможные решения х, х\, х2, х3, х4, х3
системы уравнений:
253. Найти всевозможные системы таких четырех ве-
вещественных чисел, что сумма каждого из них с произ-
произведением остальных равна 2.
254. Решить систему четырех уравнений с четырьмя
неизвестными
\a—b\y+\a—c\z+\a—d\r=\,
\b-a\x . -\-\b- c\z-\-\b— d\t=\,
\с-а\х+\с-Ь\у +|c_d|/=«l,
\d—a\x+\d—b\y+\d—c\z «=1;
здесь а, Ь, с, d— какие-то четыре попарно различных
вещественных числа.
255. Дана система п уравнений с л неизвестными
ах\ + Ъхх-+• с = ха, ах\ + Ьх% + с =» х„ ...
..., axl-i + bxn-i + с = хп, ах\ + Ьхп + с = atx
(здесь а=7^=0). Доказать, что эта система не имеет ни
одного решения, если (Ь—IJ — 4ос<0, имеет единст-
единственное решение при (Ь— IJ — Аас «= 0 и более одного
решения при (Ъ — IJ — 4ас>0.
256. Пусть все числа аи ait .... а» (где л>2) поло-
положительны; сколько вещественных решений имеет систе-
система уравнений:
бв
257. а) Сколько корней имеет уравнение
б) Сколько корней имеет уравнение
sin х •- lg х?
258. Известно, что
й1 —
а2 —
ат — 4ai + З
Пусть ai = 1; чему равны тогда числа Яг, из, • •.,
259. Пусть я, Ь, с, d — какие угодно четыре положи
тельных числа. Доказать, что три неравенства
(a+b) (c+d) <ab+cd,
(я + b)cd<(c
не могут иметь место одновременно.
260. Доказать, что дробь
V2+... +/2
где в числителе стоят п радикалов, а в знаменателе —
(п — 1) радикалов, при любом п~^.\ будет больше-г-.
261. Произведение трех положительных чисел равно
1; их сумма больше суммы обратных величин этих чи-
чисел. Доказать, что из трех рассматриваемых чисел одно
больше единицы, а два остальных — меньше единицы.
262. Сумма 1959 положительных чисел ab a$, a3, ...
• •-, «1959 .равна 1; доказать, что сумма всевозможных
произведений по 1000 разных сомножителей из числа
наших чисел меньше 1. [В число рассматриваемых про-
произведений включаются все, отличающиеся друг от друга
хоть одним сомножителем, ио не произведения,
57
отличающиеся только порядком сомножителей —: такие
произведения считаются одинаковыми и засчитывается
из них лишь одно.]
263. Пусть N^2 — некоторое натуральное число. Че-
Чему равна сумма всех дробей вида —> где т и п —
взаимно простые натуральные числа такие, что 1^т<С
<m^.N и т + n>N}
264. 1973 положительных числа аи «2, аз, . . ., <2i973
таковы, что
0-i- — a-i = а3 — ...= (aL9l2) = (ашз) .
Доказать, что ах = ai973.
265*. Доказать, что если Х\ и х2 — корни уравнения
х2 — 6х + 1 = 0, то хп\ -\- х\ при любом целом п являет-
является целым числом, не делящимся на 5.
266. Может ли выражение
• • • 4-20999^100,
где некоторые из чисел аи а2, ..., a999, ато положитель-
положительны, а другие отрицательны, содержать одинаковое чис-
число положительных и отрицательных попарных произве-
произведений?
Рассмотрите аналогичную задачу для выражения
(Я1+Й2+ • • • +Й9999 + Й10000J.
267. Доказать, что любую целую степень числа
1 можно представить в виде У N — VN— 1 , где N —
целое число_ (так, ^например, (У2 — 1)- = 3— 2 ]/ =•
", а A/2"-1K=51/2"-7=)/5б-)/49").
268. Доказать, что выражение 99999+111111 К
зя представить в виде (Л + 51^3 J, где А а В — це-
целые числа. 3 _
269. Доказать, чтоУ 2 нельзя представить в виде
p+q.Vr, где р, q, г—рациональные числа.
270. Известно, что А имеет вид А — Г 2" ~ ) *"
где т, п~^2 — натуральные числа. Доказать, что А
я k + Т/А2 —4
можно также представить в виде А = ——^ , где
k — натуральное число.
53
271. Существуют ли такие рациональные числа х, у,
г и t, что при некотором натуральном п
272. Даны две бочки бесконечно большой емкости.
Можно ли, пользуясь двумя ковшами емкости |/2лит-
|/2литров и 2—1^2 литров, перелить из одной из них в другую
ровно 1 литр воды?
273. При каких рациональных х выражение Зх2 —
— 5л; + 9 будет представлять собой квадрат рациональ-
рационального числа?
274. Дискриминант A = p2—iq квадратного уравне-
уравнения x2-\-px-\-q — 0 имеет величину порядка 10; доказать,
что если при округлении свободного члена q уравнения
мы изменили его на величину порядка 0,01, то значения
корней уравнения изменятся на величину порядка
0,001.
275. Округлением числа мы назовем целое число,
отличающееся от исходного менее чем на 1. Доказать,
что любые п положительных чисел можно округлить так,
что сумма любого количества этих чисел будет отличать-
ся от суммы их округлении не более чем на •——.
276. В десятичной записи положительного числа а
отброшены все десятичные знаки, начиная с четвертого
знака после запятой, т. е. взято округление с недостатком
а0 числа а с точностью до 0,001. Полученное число а0 де-
лится на само число а и частное снова округляется с не-
недостатком с той же точностью. Указать все числа, кото-
которые при этом могут получиться.
277*. Пусть а — произвольное иррациональное число.
Очевидно, что каково бы ни было целое число п, та из
л - 0 п 1 2 3 й
дробей ряда — = 0,—, —, —,..., которая ближе всего
к а, отличается от а не больше чем на половину—.Дока-
половину—.Доказать, что существуют такие п, для которых дробь со зна-
знаменателем п, наиболее близкая к а, отличается от а
меньше чем на 0,001 • —
278. а) Доказать, что если а записывается десятичной
дробью 0,999..., начинающейся со 100 девяток, то и
59
\/а = 0,999... записывается десятичной дробью, начинаю-
начинающейся со 100 девяток. '
б)* Вычислить значение корня |/0,1111... 111 с точ-
100 единиц
ностыодо!) 100; 2) 101; 3) 200; 4) 300 знаков после
запятой.
279. а) Что больше
2,00000000004
l,OJJJJJ00JJ4J -j- 2,00000000004 ИЛИ
2,00000000002 ,
A,00000000002J + .2,00000000002'
б) Пусть а>6>-0. Что больше
1 + Ь + б2 + . ¦ ¦ + б" ?
280. Даны п чисел аи аг, а3, ..., ап. Найти число к,
такое, чтобы сумма
имела наименьшее возможное значение.
281. а) Даны четыре действительных попарно нерав-
неравных числа ai<a2<a3-<a4- Расположить эти числа в та-
таком порядке й1„ cti,, й;3, ait (iu i2, i3, t4—те же номера 1,
2, 3, 4, только как-то переставленные), чтобы сумма
- Ф = (о,, - auf + (аи - atf -f- (a;, - ai( J + (au - aij2
имела наименьшее возможное значение.
б)* Даны п действительных попарно неравных чисел
#ь #2, й3, , ап. Расположить эти числа в таком поряд-
порядке uilt ait, а1з,.... ain, чтобы сумма
Ф = (ah - о,2J + (щ. - altJ + ... + (aln_t - ainf +
имела наименьшее возможное значение.
282. а) Доказать, что каковы бы ни были действи-
действительные числа дь а2, :.., ап; Ьи Ь2 Ьа, всегда
При каких условиях имеет место равенство?
60
б) Пирамида называется прямой, если в основание
пирамиды можно вписать окружность и центр этой
окружности совпадает с основанием высоты пирамиды.
Доказать, что прямая пирамида имеет меньшую боковую
поверхность, чем всякая другая пирамида той же высо-
высоты, основание которой имеет ту же площадь и тот же
периметр.
Примечание. Неравенство задачи а) составляет частный
случай так называемого неравенства Минковского, сог-
согласно которому
К *?
283*. Доказать, что при любых - значениях действи-
действительных чисел п\, а2,..., ап имеет место неравенство
У at + A - а2Г + У 4 + A - я3J + ...
... + VaU + A - al) + У& + A -
При каких значениях этих чисел левая часть нера-
неравенства точно равна правой части?
284. Доказать, что если числа хх и х2 по абсолютной
величине не превосходят единицу, то
При каких значениях х\ и х2 левая часть этого неравен-
неравенства точно равна правой части?
285. Что больше cos sin x или sin cos x? ----
286. Доказать, не пользуясь логарифмическими таб>
лицами, что
287. Доказать, что если а и р — острые углы и а<[5,
то , .
a) a—sina<p—sin 0, б) tga—a<tgp—p.
288*. Доказать, что если a и р — острые углыиа<Р,
то i?2<**JP .
61
289. Найти соотношение между arcsin cos arcsin x и
arccos sin arccos x.
290. Доказать, что каковы бы ни были коэффициенты
Язь а30, • • •> а2, аи сумма
cos32х-{-йз1 cos31x+a3ocos30x+ ... +a2cos 2х -}- а.\ cosx
не может принимать при всех х только положительные
значения.
• 291. Пусть некоторые из чисел аи а2, ..., ап равны
+ 1, а остальные равны —1. Доказать, что
= ах У 2 + аг Уч. + а3 V2+... + anVT.
Так, например, при а{ — а2— ... =ап=1 получаем:
У 2 + У~2 +¦••'+ У2~.
п корней
9. АЛГЕБРА МНОГОЧЛЕНОВ
292. Найти сумму коэффициентов многочлена, полу-
получающегося после раскрытия скобок и приведения подоб-
подобных членов в выражении
A —Зх+Зл:2O43 A +3х—Зх2) п\
293. В каком из выражений
A+х2—х3I000 и A— х2+х3)то
будет стоять после раскрытия скобок и приведения по-
подобных членов больший коэффициент при х20?
294. Доказать, что в произведении
A— Х-\-Х2—Х3+ . . . —Х99+Х'00) X
х
после раскрытия скобок и приведения подобных чле-
членов не останется членов, содержащих х в нечетной
степени.
&2
295. Найти коэффициент при х50 после раскрытия ско-
скобок и приведения подобных членов в выражениях:
а) A+хI000 + *A +х)"9 + х2A +x)m + ... + xi0W>;
б)
296 *. Определить коэффициент при х2 после раскры-
раскрытия скобок и приведения подобных членов в выражении
h раз
297. Найти остаток от деления многочлена
а) на х—1; б) на х2— 1.
298. Неизвестный многочлен дает при делении на
х—1 остаток 2, а при делении на х—2 — остаток 1. Ка-
Какой остаток дает этот многочлен при делении на
)()
299. При делении многочлена х1951 — 1 на
+2+я+1 получаются частное и остаток. Найти в
частном коэффициент при хи.
300. Найти все многочлены Р(х), для которых спра-
справедливо тождество
xP(x—l)=s(x—26)P(x).
301. Дан многочлен Р{х)=айхп-\-аххп~х-\-.. .+а11_1л;+
Я-а- с . ¦ •
а) натуральными; б) целыми
коэффициентами Ooi а\ ап\ сумму цифр числа Р(п)
обозначим через s(n) (ясно, что величина s(n) имеет
смысл лишь в том случае, если число Р(п) —натураль-
—натуральное; в противном случае s(n) просто не существует).
Доказать, что если последовательность s(\), sB),
sC),... содержит бесконечно много чисел, то она содер-
содержит бесконечно много одинаковых чисел,
302. Доказать, что многочлен лг2Оог/2оо-г-1 нельзя пред-
представить как произведение f(x)-g(y) двух многочленов:
от одного переменного х и от одного переменного у.
303. Квадратный трехчлен р(х) —ах2+Ьх-}-с таков,
что уравнение р(х)=х не имеет (вещественных) корней.
Доказать, что тогда и уравнение р(р(х))=х также не
Имеет вещественных корней.
03
304. Квадратный трехчлен р(х)=ах2+Ьх-}-с таков,
что если |д;|^1, то и \р(х) | ^1. Доказать, что в таком
случае из |х| ^1 следует также |pi(x)|^2, где р\(х) ==
= сх2-{-Ьх-\-а.
305. Доказать, что если х^ — корень уравнения
ax2+bx+c=0, A)
а х2 — корень уравнения
—ax2+bx+c=0, B)
то найдется промежуточный между ними корень х3 урав-
уравнения
~x2 + bx+c = 0, C)
т. е. такой, что либо Х1^х3^.хг, либо
306. Пусть а и р — корни уравнения
a f и б — корни уравнения
x2+P
Выразить произведение
—б)
через коэффициенты данных уравнений.
307. Даны два уравнения:
Определить все значения коэффициента а, при которых
эти уравнения имеют хотя бы один общий корень.
308. а) Найти целое число а такое, что
(х—а)(х—10)+1
разлагается в произведение (х-\-Ь) (х-\-с) двух множи-
множителей с целыми b и с.
б) Найти такие отличные от нуля не равные между
собой целые числа а, Ь, с, чтобы многочлен четвертой сте-
степени с целыми коэффициентами
х(х-а)(х-Ь)(х—с)
можно было представить в виде ¦ произведения двух
других многочленов с целыми коэффициентами.
64
309. При каких отличных друг от друга целых числах
аи а2, ..., ап многочлены с целыми коэффициентами
а) (x—al)(x—a2)(x—a3)...(x—an) — l,
б) (х—а1)(х—а2)(х—аз)...(х—ап) + 1
разлагаются в произведения других многочленов?
310*. Доказать, что при любых отличных друг от
друга целых числах аи а2, ..., ап многочлен
(х-а,J(х-а2J.. .(х~апJ+\
не разлагается в произведение двух других многочленов
с целыми коэффициентами.
311. Доказать, что если многочлен
Р(х) =аохп+а1хп-1+.. .+ап-хх+ап
с целыми коэффициентами принимает при четырех целых
значениях х значение 7, то он не может принимать зна-
значение 14 ни при каком целом значении х.
312. Доказать, что если многочлен 7-й степени с це-
целыми коэффициентами
при 7 целых значениях х принимает значения + 1 и —1,
то его нельзя представить в виде произведения двух мно-
многочленов с целыми коэффициентами.
313. Доказать, что если многочлен с целыми коэффи-
коэффициентами
Р(х) =аохп+а1хп-1+.. .+ап-гх+ап
принимает при х—0 и х=\ нечетные значения, то урав-
уравнение Р(х)—0 не имеет целых корней.
314*. Доказать, что если многочлен
Р(х) =а0хп+а1Х"-]+а2хп-2+.. .+ап-Хх+ап
с целыми коэффициентами при двух целых значениях
х—р и x=q (p>q) равен по абсолютной величине 1 и
уравнение Р(х)==0 имеет рациональный корень а, то
р—q равно 1 или 2 и а = ^-j^-
315*. Доказать, что многочлены
а) х2222+2х222О+4х22^+6х2Ш+8х22Ы+...
.. .+2218x4+2220jk2+2222;
б) л;25О+л;2494-*248+A'244-*243+.. .+х2+х+1
б Д. О, Шклярский it др. 65
не могут быть разложены в произведения многочле-
многочленов с целыми коэффициентами.
316. Доказать, что если два многочлена с целыми, ко-
коэффициентами в произведении дают многочлен с четны-
четными коэффициентами, не все из которых делятся на 4, то
в одном из перемножаемых многочленов все коэффици-
коэффициенты — четные, а в другом—не все четные.
317. Доказать, что все рациональные корни много-
многочлена
Р(х) ==:Х«+а1л;1г-!+а2л:'г-2+.. .+an-ix+an
с целыми коэффициентами и с коэффициентом при стар-
старшей степени х равным 1, являются целыми.
318*. Доказать, что не существует такого многочлена
Р(х) =aQxn+alxn-l+.. ,+an-lx-\-an,
что все числа Р@), РA), РB), ,,, являются простыми.
Примечание. Предложение, сформулированное в задаче,
было впервые доказано Л. Эйлером1). Ему же принадлежат при-
примеры многочленов, значения которых'при многих последовательных
целых значениях х являются простыми (так, например, в случае
многочлена Р(х) ~#2 — Щ+1601 80 чисел Р@)=1601, РA)=1523,
РB), РC), ..., РG9) являются простыми).
, 319. Доказать, что если многочлен
Р(Х) *=xn+Alxn-*+A2x-t+.. .+Ап-!Х+Ап
при всех целых значениях х принимает целые значения,
то его можно представить в виде суммы многочленов
Ро (х) = 1, Л(х) = х, Р,(х) = ^ТТ1,...
•• •> rn\A) — 1 . 2 • З...л '
обладающих тем же свойством (в силу задачи 75 а)),
взятых с целыми коэффициентами.
320. а) Доказать, что если многочлен п-Ъ. степени
Р(х) принимает целые значения при х=0, 1, 2, ..., п,то
он принимает целые значения и при всех целых значе-
значениях х.
') Работавший, главным образом, в России и в Германии швей-
швейцарец Леонард Эйлер A707—1783) был, бесспорно, крупнейшим
математиком XVIII в., внесшим значительный вклад во все разделы
математической науки.
66
б) Доказать, что всякий многочлен степени п, прини-
принимающий при каких-то п-f-l последовательных целых зна-
значениях х целые значения, принимает целое значение при
всяком целом х.
в) Доказать, что если многочлен Р(х) степени «при-
«принимает целые значения при х—0, 1, 4, 9, 16,..., п2, то он
принимает целое значение и при любом целом значении
х, являющемся полным квадратом (но не обязательно
принимает целые значения при всех целых х).
Привести пример многочлена, принимающего целые
значения при каждом целом значении х, являющемся
полным квадратом, но при некоторых других целых х
принимающего дробные значения.
10. КОМПЛЕКСНЫЕ ЧИСЛА
321. а) Доказать, что
cos 5a=cos5 a—10 cos3 a sin2 a+5 cos a sin4 a,
sin 5a=sin5 a—10 sin3 a cos2 a+5 sin a cos4 a.
б) Доказать, что при каждом целом п
,сог па = cosn a — Cn cos"" a sin2 a + Cn cosn~4 a sin4 a —
sin na. = C\i cos" a sin a — Cn cosn~3 a sin3 a +
+ C\ cos"" a sin6 a — ....
где обозначенные точками члены, закон образования ко-
которых легко подметить, выписываются до тех пор, пока
сохраняют смысл биномиальные коэффициенты.
Примечание. Задача б), очевидно, является обобщением
задачи а).
322. Выразить tg6a через tga.
323. Доказать, что если х ^ =2 cos a, то хп -)—— =
Х X
¦=2 cos па.
324. Доказать, что
sin ф + sin (ф + a) + sin (ф + 2a) + ... + sin (cp + па) =
. (п + 1) a . / па
sin g sin IФ + X
a
sin-о"
б* 67
cos ф + cos (ф -f- a) -f- cos (ф + 2a) + ... + cos (ф -f- na) =
sin „— cos
а
sin ¦
2
325. Упростить
cos2 а+cos2 2а+- • .+cos2 па
и
sin2 а+sin2 2a-j-.. .-j-sin2 na.
326. Упростить
cos a -f Cn cos 2a + Cn cos 3a + ...+ C^1 cos na+
+ cos (и + l)a
и
sin a + Ci sin 2a + Cn sin 3a + ... + Cf1 sin na +
-f sin (и + l)a.
327. Доказать, что если m, n, p — произвольные це-
целые числа, то
j-, если m + n делится на 2p, am — пне делится
на 2p;
-|-, если т — п делится на 2/7, а т + п не делится
на 2/7;
О, если т-\- п и т — п одновременно делятся или
одновременно не делятся на 2р.
328. Доказать, что
68
329. Составить уравнение, корнями которого явля-
являлись бы числа:
sin»
б) ctg-gj^., ctg^, ctgg^,..., ctg^
330. Упростить суммы:
я\ сы2 п + cte3 2л 4- cte2 Зл 4- 4- cts?2
a) cxg 2n + ; + cig 2n + j -t- ctg 2„ + i + • • • + Cl§
4- cte 4- 4- cts?
2n + j -t- ctg 2„ + i + • • • + Cl§ 2n + 1'
6) cosec2 5~4л + cosec3 ~—^ + cosec2
... + cosec2 „ ..
331. Упростить произведения:
2n + 1 2л + 1 2л + 1 2л + 1
и
я . 2я . Зя . (п — 1) я
sin -5- sin -к— sin г— ... sin v—ttj—\
2л 2л 2л 2л '
-. я 2я Зл ля
б) cos cos 2 cos 2 . ... cos _^-
я 2л Зл (л — 1) я
COS r— COS д— COS 5— ... COS —»——.
2л 2л 2л 2л
332. Вывести из результатов задач 330 а) и б), что
при любом целом положительном п сумма
i + _L + J_+ +_L
заключается между (l - 2Tqri)(l -2TTl) "Г и
L_Vi + _!_)isl
2/1+ lj\l 2л+ l/ 6
Примечание. Из результата з.адачи 332, в частности, сле-
следует, что
_1_ J_ _1_ яа_
1 + 22 + З2 + 42 "*" *' • = 6 '
гДе под суммой бесконечного ряда 1 + -^ + -jpr + "ТГ + • • •
69
понимается предел, к которому стремится величина 1-]-— +—+••¦
-j 22 3-
...-f — при п->оо (ср. также раздел «Четыре формулы для чис-
числа я» книги [6], в котором дается существенное развитие этого
результата).
333. а) На окружности, описанной около правильно-
правильного га-уголышка А\А2.. .Ап, взята точка М. Доказать, что
сумма квадратов расстояний от этой точки до всех вер-
вершин га-уголышка не зависит от положения точки на ок-
окружности и равна 2nR2, где R есть радиус окружности.
б) Доказать, что сумма квадратов расстояний от про-
произвольной точки М, взятой в плоскости правильного
я-уголышка А1А2.: .А„, до всех вершин га-угольника зави-
зависит только от расстояния / точки М от центра О много-
многоугольника и равна n(R2jrl2), где R есть радиус окружно-
окружности, описанной около я-угольника. ^
в) Доказать, что утверждение предыдущей задачи
остается в силе и в том случае, когда точка М не лежит
в плоскости «-угольника А\А2 ... Ап.
334. На дуге А\Ап окружности, описанной около пра-
правильного га-угольника АХА2 ... Ап, взята точка М. Дока-
Доказать, что:
а) если га четно, то сумма квадратов расстояний от
точки М до вершин га-угольника с четными номерами
равна сумме квадратов расстояний от этой же точки до
нечетных вершин;
б) если га нечетно, то сумма расстояний от точки М
до вершин га-угольника с четными номерами равна сум-
сумме расстояний от этой же точки до нечетных
вершин.
Примечание. Геометрическое доказательство теоремы зада-
задачи 334 б) см. в решении задачи 137 книги [8].
335. Радиус окружности, описанной около правильно-
правильного «-угольника А\Аъ ... А„, равен R. Доказать, что:
а) сумма квадратов всех сторон и всех диагоналей
га-угольника равна n2R2;
б) сумма всех сторон и всех диагоналей га-угольника
равна и ctg-^- R;
в) произведение всех сторон и всех диагоналей
п п(п—1)
«-угольника равно п1 р i ,
70
336*. Найти сумму 50-х степеней всех сторон и всех
диагоналей правильного 100-угольника, вписанного в ок-
окружность радиуса R.
337. Известно, что
1
= а; какое наибольшее и
z
какое наименьшее значения может иметь модуль \г\
комплексного числа z?
338. Пусть сумма п комплексных чисел равна нулю,
доказать, что среди них найдутся два числа, аргументы
которых разнятся не менее чем на 120°.
Можно ли заменить здесь величину 120° меньшей?
339. Пусть С\, с2, ..., сп, z —такие комплексные чис-
числа, что
z — а г — с2 ' z~cn
Доказать, что если числа с\, с2, .. ., сп представляются
на комплексной плоскости вершинами выпуклого
п-угольника, то число г представляется точкой, лежащей
внутри этого п-угольника.
11. НЕСКОЛЬКО ЗАДАЧ ИЗ ТЕОРИИ ЧИСЕЛ
3'40. Теорема Ферма. Доказать, что если р есть
простое число, то разность ар—а при любом целом а де-
делится на р.
Примечание. Частными случаями этой теоремы являются
предложения задач 46 а)—д).
341. Теорема Эйлера. Пусть N есть какое-то
целое число и г — число чисел ряда 1, 2, 3, ..., jV—1,
взаимно простых с N. Доказать, что если а есть произ-
произвольное целое число, взаимно простое с N, то разность
йг— 1 делится на N.
Примечание. Если число Л' — простое, то все выписанные
числа взаимно просты с Л', т. е. r = N— 1, и теорема Эйл°ра сводит-
сводится к следующей: разность ал'-'—1, где Л' — простое, делится на N.
Отсюда видно, что теорему Ферма (см. задачу 340) можно рас-
рассматривать как частный случай теоремы Эйлера.
Если N—pn, где р — простое, то из N—l=pn — 1 чисел 1, 2,
3,..., Л'—1 не будут взаимно простыми с N=pn только числа р,
2р, Зр,..., N — р=(рп~1 — 1)р. Таким образом, в этом случае
г в= (рп — 1) — (рп~1 — 1) = рп — рп~1, и теорема Эйлера сводится
71
к следующей: разность аР р —1,где р — простое, а а не делится
на р, обязательно делится на рп.
Если N = р"'р ... p"ft, где Ри рг, •••. Р*— различные между
собой простые числа, то число г простых чисел, меньших N и взаим-
взаимно простых с N, дается формулой
(см., например, [64] — [68]). Если N = pn-—степень простого числа
р, то эта формула дает
' р
т. е. результат, полученный выше.
342*. Согласно теореме Эйлера разность 2к— 1, где
k—on—5", делится на 5" (см. задачу 341, в частности,
примечание к этой задаче). Доказать, что ни при каком
k, меньшем чем 5"—5n~', разность 2к—1 не делится на 5".
343. Выпишем подряд последовательные степени чис-
числа 2:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096,...
Легко заметить, что в этом ряду чисел последние цифры
периодически повторяются с периодом 4:
2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6, ...
Доказать, что и последние 10 цифр в этом ряду чисел,
начиная с некоторого числа, также будут периодически
повторяться. Найти длину периода и номер числа в ря-
ряду, начиная с которого наблюдается периодичность.
344*. Доказать, что существует такая степень числа 2,
последние 1000 цифр которой все будут единицами и
двойками.
345. Пара (различных) натуральных чисел т и «на-
«называется «хорошей», если эти числа состоят из одинако-
одинаковых простых делителей, взятых, однако, в (вообще гово-
говоря) несовпадающих степенях (пример: 90 = 2-32-5 и
150=2 • 3 • 52), и «очень хорошей», если «хорошими» явля-
являются и пара т, п и пара т-\-\, п+1 (пример: 6=2-3 и
48=24-3 —ведь 6+1 = 7, а 48+1 = 49=72). Конечно или
бесконечно число «очень хороших» пар натуральных
чисел?
72
3'46. Пусть a, a-\-d, a-\-2d, a-\-3d, ...^произвольная
'(бесконечная) арифметическая прогрессия, начальный
член а и разность d которой являются натуральными
числами. Доказать, что прогрессия содержит бесконечно
много членов, разложение которых на простые множите-
множители содержит одни и те же множители (но взятые, разу-
разумеется, в разных степенях).
347. Теорема Вильсона1)- Доказать, что если
целое число р— простое, то число (р—1)! + 1 делится на
р; если же р — составное, то (р—1I + 1 не делится на р.
348. Доказать, что
а) для каждого простого числа р можно найти такие
целые числа х и у, что х2+г/2+1 делится на р;
б)* если простое число р дает при делении на 4 оста-
остаток 1 (и для нечетных простых чисел — только в этом
случае), существует такое целое число х, что х2+1 де-
делится на р.
Задача 348 связана с проблематикой, касающейся представления
натуральных чисел в виде сумм степеней (с показателями степени
«>!) других натуральных чисел (эта проблематика отражена в
большинстве книг и статей, отнесенных в списке литературы к этому
диклу задач). Так, из результата задачи 3486) можно вывести, что
натуральное число N в том и только в том случае может быть пред-
представлено в виде суммы квадратов двух натуральных чисел, когда в
разложение N на простые множители все простые множители вида
4я+3 (множители, дающие при делении на 4 остаток 3) входят в
четных степенях. Из результата задачи 348а) можно вывести кра-
красивую теорему о том, что все без исключения натуральные числа мо-
могут быть представлены в виде суммы квадратов четырех (или мень-
меньшего количества) натуральных чисел; последний результат, в свою
очередь, позволяет установить, что все натуральные числа могут
также быть представлены в виде суммы ограниченного числа четвер-
четвертых степеней натуральных чисел,— скажем, в виде суммы 53 (или
меньшего количества) полных четвертых степеней натуральных чисел.
(Более тонкие средства позволяют заменить здесь оценку 53 на 21,
однако и этот результат, видимо, не является окончательным: скорее
всего каждое натуральное число может быть представлено в виде
суммы не более чем 19 полных четвертых степеней целых чисел.)
Доказано также, что всякое целое число представимо в виде суммы
кубов не более чем девяти целых чисел (вот здесь число 9 не может
быть заменено меньшим!).
Все эти предложения охватываются следующей замечательной
теоремой: для любого целого положительного числа k существует
такое целое число N (разумеется, зависящее от k), что каждое це-
целое положительное число представимо в виде суммы не более чем
N слагаемых, являющихся k-ми степенями целых чисел. Эта послед-
') Александр Вильсон A714*—1786)—шотландский астроном
и математик-любитель, профессор астрономии в Глазго.
73
няя теорема имеет несколько различных доказательств, но до самого
последнего времени были известны лишь такие ее доказательства, ко-
которые используют очень сложный математический аппарат (отно-
(относящийся к высшей математике). Лишь в 1942 г. ленинградский
математик Ю. В. Линник дал чисто арифметическое ее доказа-
доказательство (см. [72]), которое, однако, является исключительно
сложным. Установлено также, например, что каждое рациональное
число может быть представлено в виде суммы не более чем трех
кубов рациональных чисел, хотя, например, число 1 не может быть
представлено в виде сумуы кубов двух рациональных чисел (дока-
(доказательство этого последнего факта имеется, например, Ё книгах
153] и [541).
349. Доказать, что существует бесконечно много про-
простых чисел.
350. а) Доказать, что среди членов арифметических
прогрессий 3, 7, 11, 15, 19, 23, ... и 5, 11, 17, 23, 29, 35,...
имеется бесконечно много простых чисел.
б) * Доказать, что среди членов арифметической про-
прогрессии
11, 21, 31, 41, 51, 61, ...
имеется бесконечно много простых чисел.
Аналогично решению задач 350а)—б), но несколько сложнее,
можно также доказать, что и среди членов арифметической прогрес-
прогрессии 5, 9, 13, 17, 21, 25,... имеется бесконечно много простых чисел.
Имеет место и общее предложение о существовании бесконечного
числа простых чисел в каждой арифметической прогрессии, пер-
первый член которой взаимно прост с ее разностью, однако доказатель-
доказательство этого предложения является чрезвычайно сложным (интересно
отметить, что не использующее высшей математики, хотя и очень
сложное, доказательство этой классической теоремы теории чисел
было найдено впервые лишь в 1950 г. датским математиком
А. Сельбергом; до этого были известны лишь доказательства,
относящиеся к высшей математике}.
РЕШЕНИЯ
1. Пусть А— первый из двух выбранных учеников, а В — вто-
второй. Если А и В стоят п одном поперечном ряду, то В выше Л, ибо
А — самый низкий ученик в своем поперечном ряду; если А и В сто-
стоят в одном продольном ряду, то В также выше А, ибо В самый вы-
высокий ученик в своем продольном ряду; наконец, если А и В стоят
в разных поперечных и разных продольных рядах и С стоит в том же
поперечном ряду, что и А, и в том же продольном ряду, что и В, то
В выше Л, так как В выше С, а А ниже С.
2. Составим общую сумму чисел всех рукопожатий, сделанных
когда-либо каждым из людей. Эта сумма обязательно четна, потому
что каждое рукопожатие, которым обменялись два лица А и В, уве-
увеличивает на 1 число рукопожатий^ сделанных Л, и на 1 число рука-
пожатий, сделанных В, и, следовательно, дает слагаемое 2 в общей
сумме. Но, с другой стороны, эта сумма составляется из чисел руко-
рукопожатий, сделанных каждым отдельным человеком. Из четности
суммы вытекает, что число нечетных слагаемых в ней четно, что
и требовалось доказать.
3. Пусть Л — одно из данных лиц; ясно, что либо Г А имеет
среди присутствующих трех знакомых Вь В2 и Вз; либо 2° имеются
трое лиц С[, С2 и С3, ни с одним из которых Л не знаком (среди 5
отличных от Л лиц у него есть либо трое знакомых, либо трое не-
• знакомых). В случае 1° если Ви В2 и Въ попарно незнакомы, то они
образуют требуемую тройку; если же, например, Bt и В2 знакомы, то
имеем тройку попарно знакомых лиц Л, В\ и В2. Аналогично, если
в случае 2° Си С2 и Сз попарно знакомы, то- они образуют нужную
нам тройку; если же, скажем, С], не знаком с С2, то мы приходим
к тройке А, С\ и С2.
4. а) Каждое из N присутствующих лиц может иметь 0, 1, 2,...
..., N—1 знакомых. Здесь мы имеем N возможных значений числа
знакомых; однако если некто имеет 0 знакомых, то никто не имеет
N — 1 знакомых (и наоборот — если некто имеет N—1 знакомого,
то никто не имеет 0 знакомых). Отсюда уже следует, что двое лиц с
одним и тем же числом знакомых обязательно существуют (ср. со
сказанным о принципе Дирихле па стр. 10).
б) Занумеруем присутствующих на заседании Л' лиц номерами
1, 2,..., N и рассмотрим такое «распределение знакомств»: пусть
N
для всех значений 1 = 0, 1, 2,..., где К. -к~, лицо с номером N — I
знакомо со всеми лицами, кроме первых i лиц (т. е. Af-e лицо знакомо
со всеми без исключения; (N — 1)-е — со всеми, кроме 1-го лица;
(N — 2)-е — со всеми, кроме 1-го и 2-го;...); все же лица с номерами
Л' -1-1
I, где 1^!=^—я—между собой незнакомы. В таком случае, при
75
jV=3, очевидно, 1-е и 2-е лнна знакомы лишь с 3-м, а 3-е лицо имеет
двух знакомых; аналогично, при N=4 1-е лицо знакомо лишь с 4-м;
2-е — с 4-м и с 3-м; 3-е — с 4-м и со 2-м; 4-е имеет трех знакомых.
Точно так же можно убедиться, что при N=2k+l нечетном чис-
числа я,- знакомых у l-то лица имеют значения: «1 = 1, «2 = 2, ...
... t пк = к, пк+1 = к, nh+i — к + 1 nN = N— 1, а при Л' =
= 2*+ 2 четном Щ = 1, п2 = 2 яЛ+1 = к + 1, иА+2 = ft + 1,
яА+3 = & + 2, ..., nN = N—\. Таким образом, здесь во всех слу-
случаях никакие трое лиц не имеют одинакового числа знакомых.
5. Если все присутствующие знакомы друг с другом, то возмож-
возможность рассадить таким образом 4-х человек сомнения не вызывает.
Пусть теперь А и В незнакомы между собой. Каждый из них имеет
среди остальных 2я — 2 присутствующих не менее п знакомых; так
как п-\-п = 2п={2п— 2)+2, то у А и В имеется, минимум, два об-
общих знакомых Ci и Сг— и мы можем посадить А и В напротив друг
друга, а между ними посадить Cj и С2.
6. Рассмотрим ученого А, имеющего среди присутствующих паи-
большее число п знакомых (или одного из таких ученых, если их не-
несколько); при этом п>0, поскольку мы предположили, что некото-
некоторые из участников конгресса знакомы друг с другом. Все знакомые
А имеют разное число знакомых (ибо любые два из них имеют
общего знакомого Л); при этом ни один из них не имеет больше чем
п знакомых. Поэтому один из знакомых А (некто В) обязательно
имеет одного знакомого, второй —двух, третий—трех наконец,
последний (пн) знакомый А, так же как и А, имеет п знакомых.
Существование лица'В и доказывает утверждение задачи.
7. Выберем каких-то трех делегатов конгресса; среди них най-
найдутся двое, знающие один язык — их-то мы и поместим в одном
номере гостиницы. Из оставшихся 998 делегатов снова отберем троих,
среди которых снова найдутся двое, которых можно будет разме-
разместить в одном номере —_и т. д.„ пока у нас не останутся всего 4 де-
делегата А, В, С к D. Если каждые два из них могут говорить между
собой, то с размещением этих делегатов не будет никаких трудностей;
если же Л и В между собой не говорят, то и С, и D могут служить
для них переводчиками (что и делает возможным общение в трой-
тройках Л, В, С и А, В, D делегатов); это позволяет поместить, скажем
С в один номер с Л, a D — в один номер с В.
8. Пусть Л—какой-то один из присутствующих на конференции
ученых; с каждым из 16 остальных он говорит на одном из трех
(или на меньшем числе, если он не владеет, всеми тремя) языков.
Нетрудно" видеть, что имеется такой язык (назовем его «тарабар-
«тарабарским»), на котором А разговаривает не менее чем с 6 учеными: в са-
самом деле, в противном случае собеседников у Л будет не больше чем
5-3 = 15, а по условию задачи любые два ученых могут говорить
между собой. Если двое из этих 6 ученых говорят между собой на
тарабарском языке, то утверждение задачи доказано; если же это не
так, то между собой 6 ученых говорят лишь на двух языках.
Пусть теперь В — произвольный из выделенных 6 ученых. Ясно,
что найдутся такие 3 из 5 остальных ученых, с которыми он говорит
па одном н том же («таратарабарском») языке; ведь если бы это
было не так, то среди 5 ученых В мог бы иметь не более чем 2-2=4
собеседников. Если хоть какие-то два — скажем С и D — из этих
трех участников конференции говорят между собой на таратарабар-
таратарабарском языке, то мы уже гюлучаем тройку ученых В, С и D, разговари-
разговаривающих между собой на одном языке; если же эти трое ученых
7.G
между собой говорят на третьем («таратаратарабарском») языке, то
они и составляют искомую тройку.
9. а) Выберем одного из собравшихся А; всех знакомых с ним
лиц мы обозначим через Аи А2,..., Ак- Ясно, что никакие два из
этих двух лиц не знакомы друг с другом и каждые два лица — ска-
скажем, Ai и Aj — имеют двух общих знакомых: А и некоторое лицо
k(k-l)
Ац\ здесь i, / =• 1, 2, ..., k и i ф /. При этом никакие два из g
лиц Ац, очевидно, не совпадают, ибо в противном случае это лицо
имело бы с Л не менее трех общих знакомых. С другой стороны, так
как каждое не знакомое с А лицо имеет с А двух общих знакомых
(очевидно, из числа лиц А\, А2, ..., Ак), то Ам, А\%, ..., Ak-uk —
это в с е не знакомые с А лица, и, значит, общее число я присутству-
присутствующих на собрании людей" равно
A —это A; k — это лица At; ^ —это лица Ац).
Заметим теперь, что в силу равенства (*), которое можно пере-
переписать еще и так:
— Bл — 2)= 0, (**)
имеем
(второй корень квадратного уравнения (**) k' — — у— у -г +2п—2
не подходит, ибо он отрицателен). Таким образом, число k знакомых
с некоторым лицом А лиц однозначно определяется по общему числу
п присутствующих на собрании лиц, т. е. оно является одним
и тем же для всех лиц А.
б) В силу (*) имеем
k(k-\-\)
п*= 9+1. (***)
т. е. п должно быть на единицу больше так называемого треуголь-
k{k-\-\)
ного числа1) —tj—¦ ^Ри 9ТОМ Для записываемого по формуле (***)
числа п количество знакомых у каждого из присутствующих лиц
равно k; здесь k *» 1, 2, 3,... — произвольное натуральное число.
10. Пусть А, В и С — какие-то три жителя города. Ясно, что
возможен случай, когда все они дружат между собой; возмож-
возможно также, что один из них (скажем, А) не дружит ни с В, ни с С,
а В и С дружат между собой: тогда для того, чтобы А, В я С все
подружились, достаточно, чтобы А «начал новую жизнь». Нетрудно
'} По этому поводу см., например, [64J, стр. 122—123.
77
также видеть, что два других случая: когда все три жителя А, В и
С между собой враждуют и когда один житель,— например, тот же
Л,— дружит с В и с С, а те враждуют между собой, уже невоз-
невозможны: в этих случаях среди трех пар А, В; А, С к В, С жителей
Многообразия имеется нечетное C или 1) число в пар врагов и чет-
четное @ или 2) число д пар друзей; при любых изменениях отноше-
отношений в этой тройке лиц (во всех случаях, когда А, В или С «начина-
«начинают новую жизнь») четность чисел в и д не меняется (нечетное число
в может замениться лишь нечетным же числом в', а четное число
д — четным же числом д'), в силу чего все лица А, В и С никогда
не смогут подружиться между собой (число в не сможет стать
равным 0).
Описанное строение «отношения дружбы» между любыми тремя
лицами А, В и С доказывает, что в пределах всего города это от-
отношение можно описать весьма просто: в городе имеются две группы
жителей (две партии Л и Л), такие, что все жители принадлежат
либо к одной, либо к другой партии (но никогда — к обеим сразу),
причем каокдые два члена одной партии между собой дружат, а жи-
жители, принадлежащие к разным партиям, обязательно враждуют.
В самом деле, присоединим к нашим трем жителям А, В и С города
Многообразие еще одного жителя D; в таком случае, если Л и В
дружат между собой и D дружит хоть с одним из них, то он дружит
и со вторым — и, значит, принадлежит к партии, в которую входят
и Л, и В; если же Л и В между собой враждуют, то D дружит
лишь с одним из них (но с одним дружит непременно!). Это рассуж-
рассуждение обеспечивает возможность разбиения четверки жителей А, В,
С и D на две партии М и Л (впрочем, одна из этих партий может
быть и «пустой»: так будет, если все жители А, В, С и D дружат
между собой). Поступая так же и дальше, т.е. последовательно
присоединяя к уже рассмотренным жителям города по одному чело-
человеку, мы докажем возможность разбиения на две партии всех
Ю 000 жителей города.
Теперь доказательство утверждения задачи не представляет уже
никакого труда. Если все жители города дружат между собой, то
нам и доказывать нечего; если же ни одна из партий М и Л не
«пуста», то мы предложим каждый день одному из участников пар-
партии Л «начинать новую жизнь», т. е„ попросту, переходить в партию
Л'. Если в партии Л имеется k человек, то все жители города смо-
смогут подружиться за k дней; отсюда ясно, что 5000 дней (да 14 лет)
заведомо будет достаточно для того, чтобы все жители города
смогли подружиться (ибо хоть одна из партий Ж и Л" содержит не
более 50О0 членов).
11. Естественно называть «дорогой» отрезок пути между двумя
замками; все замки страны Оз связаны каким-то конечным числом
п дорог. Если рыцарь странствует по стране достаточно долго, то он
проедет достаточно много дорог; если это число ^4/г+1, то хоть по
одной дороге АВ (где А и В —замки) он проедет не менее 5 раз.
При этом не менее 3 раз он проедет по этой дороге в одном и том
же направлении (скажем, от Л к В); поэтому, если из замка В, кро-
кроме ВА, ведут еще две дороги ВС и BD, то рыцарь минимум дваж-
дважды,— скажем, после t-ro и после /-го посещения замка В, где />t,—
сворачивал, выезжая из В (куда он оба раза приезжал из Л) в одну
и ту же сторону, скажем, в сторону замка С. Но из условий зада-
задачи тогда следует, что не только в г-е и в /-е посещение
В рыцарь приехал в В из одного замка —из замка А,— но и в Л он
78
оба раза приезжал из одного и того же замка (из замка Р в обозна-
обозначениях рис. 4: ведь если рыцарь после В свернул на дорогу ВС,
т. е. налево, то в Л он должен был свернуть направо, т. е. приехать
в Л он должен был из Р). Аналогично этому устанавливается, что
полностью совпадают пути рыцаря, предшествующие двум рассматри-
рассматриваемым посещениям замка В; так, в замок Р он оба раза попал из
Рис. 4.
одного и того же замка (из замка U рис. 4), и т.д. Но тогда, если
рыцарь до 1-го посещения В миновал, начиная с выезда из своего
замка X, какое-то число k замков, то и за k замков до /-го посещения
В он снова был в X, что и доказывает утверждение задачи.
12. Условимся называть «друзьями» любых двух рыцарей, не яв-
являющихся врагами; далее, начнем с того, что рассадим всех ры-
рыцарей за круглым столом произвольно. Пусть где-то за столом
5)
Рис. 5.
сидят рядом рыцарь А и его враг В; для определенности будем счи-
считать, что В сидит справа от А. Мы утверждаем, что за столом най-
найдется такое место, где рядом сидят рыцари Л'— друг А и В' — друг
В, причем В' сидит справа от А' (см. рис. 5, а). В самом деле, ры-
рыцарь А имеет не менее п друзей; мест справа от них также имеется
п, а врагов у В не более п— 1 —значит, хоть одно из мест справа
от друга А' рыцаря А занимает друг В' рыцаря В. Пересадим теперь
в обратном порядке всех рыцарей, сидящих справа от А, начиная
с рыцаря В и вплоть до рыцаря А' (рис. 5, б). Ясно, что при этом
изменятся лишь пары А, В л А', В' соседей — они заменятся на пары
друзей А, А' и В, В'. Таким образом, число пар сидящих рядом вра-
врагов уменьшится минимум на 1 (оно уменьшится даже на 2, если ры-
рыцари Л''и В' — враги). Продолжая пересаживать рыцарей таким же
образом и далее, Мерлин может окончательно разъединить за сто-
столом все пары сидящих рядом врагов.
13. а) Разделим наши монеты на три группы: две группы по 27
монет и одну в 26 монет. При первом взвешивании поместим на
чашки весов группы по 27 монет. Если весы не уравновесятся, то
фальшивая монета находится на более «легкой» чашке. Если же ве-
весы окажутся в равновесии, то фальшивая монета содержится в груп-
группе из 26 монет. Таким образом, нам достаточно научиться решать
задачу: тремя взвешиваниями выделить фальшивую монету из группы
в 27 монет (задача выделить фальшивую монету из группы в 26 мо-
монет может быть сведена к этой задаче, например, добавлением к
группе из 26 монет еще одной произвольной монеты из числа ос-
остальных 54).
При втором взвешивании разделим группу в 27 монет на три
группы по 9 монет в каждой. Поместив на обе-чашки весов по груп-
группе из 9 монет, найдем группу из 9 монет, в которой содержится
фальшивая монета.
Разделив группу из 9 монет, одна из которых фальшивая, на
три группы по 3 монеты, мы третьим взвешиванием выделим тройку
монет, в которой содержится фальшивая.
Наконец, тем же путем при четвертом взвешивании найдем фаль-
фальшивую монету.
б) Пусть k—натуральное число, удовлетворяющее неравенствам
3k~l<.n^i3k. Покажем, что это число k удовлетворяет условиям
задачи.
Прежде всего покажем, что при помощи k взвешиваний всегда
можно определить фальшивую монету. Разделим наши монеты на
три группы так, чтобы в двух равных группах было по 3й (или
меньше) монет, а число монет в третьей группе было бы не больше
3*-i (это возможно, ибо n^'3h). Положив на чашки весов две группы
из равного числа монет, мы определим, в какой из трех групп содер-
содержится фальшивая монета (ср. с решением задачи а)). Таким образом,
после первого взвешивания мы выделим группу из Зк~1 монет, среди
которых содержится фальшивая- (если окажется, что фальшивая
монета находится в группе, содержащей меньше З* монет, то мы
можем дополнить эту группу монет произвольными монетами до
З*). При каждом последующем взвешивании будем делить наши
монеты на три равные группы и определять, в какой из них находится
монета. Таким образом, после k взвешиваний мы придем к группе из
одной монеты, т. е. выделим фальшивую монету.
Теперь остается показать, что k есть минимальное число
взвешиваний, с помощью которых всегда можно выделить фальши-
фальшивую монету, т. е. что при любых способах взвешивания результаты
взвешиваний могут сложиться таким неблагоприятным для нас обра-
образом, что после k — 1 взвешиваний фальшивая монета не будет вы-
выделена.
При каждом взвешивании монеты распадаются на три группы:
монеты, попавшие на одну чашку, попавшие на другую чашку и не
80
"попавшие ни на одну из чашек. Если на чашки весов было положено
одинаковое число монет и весы уравновесились, то фальшивая моне-
монета заведомо находится в группе монет, не попавших при взвешивании
ни на одну чашку. Если одна из чашек перетянет (при равном числе
монет на чашках), то фальшивая монета находится на второй чашке.
Наконец, если на чашки весов было положено разное число монет,
то в случае, когда перетянула чашка, где монет больше, фальшивая
монета может оказаться в любой из трех групп и такое взвешивание
вообще не даст нам никаких сведений о местонахождении фальши-
фальшивой монеты. Пусть теперь при произвольно производимых взвешива-
взвешиваниях результат взвешивания каждый раз оказывается наиболее не-
неблагоприятным, т. е. фальшивая монета каждый раз оказывается
в той из трех групп, которая содержит наибольшее число монет.
Тогда при каждом взвешивании число монет группы, содержащей
фальшивую монету, убывает не более чем в 3 раза (ибо при делении
некоторого числа монет на три группы всегда по крайней мере одна
из трех групп содержит не менее чем треть от общего числа монет);
поэтому после k — 1 взвешиваний число монет группы, содержащей
п
фальшивую монету, остается не меньшим чем k—i> и так как п->
>3Й~, то после k—1 взвешиваний фальшивая монета не будет
выделена.
Примечание. Можно коротко записать ответ задачи в такой
форме: минимальное число взвешиваний, необходимое для выделения
Г ( ' 1
. фальшивой монеты из группы в п монет, есть log3l n —-п~ +1, где
прямые скобки обозначают целую часть числа (см. стр. 37).
14. Положим на чашки весов по одному кубику (первое взве-
взвешивание). При этом могут иметь место два различных случая.
1°. При первом взвешивании одна чашка весов
перетянула. В таком случае из двух взвешиваемых кубиков
один обязательно является алюминиевым, а второй — дюралевым.
Далее кладем эти два кубика на одну чашку весов, а на вторую —
последовательно по паре оставшихся кубиков (разбиение 18 остав-
оставшихся кубиков на 9 пар производим произвольно). Если какая-ни-
какая-нибудь пара кубиков перетягивает нашу пару, то это значит, что оба
кубика во второй паре дюралевые; если перетягивает первая пара,
то оба кубика второй пары — алюминиевые; если обе пары имеют
один вес, то, значит, вторая пара тоже содержит один алюминиевый
и один дюралевый кубики. Таким образом, в случае 1° мы можем
определить число дюралевых кубиков при помощи 10 взвешиваний
(одно взвешивание и еще 9).
2°. При первом взвешивании чашки весов оста-
остались в равновесии. В таком случае кубики первой пары
или оба алюминиевые, или оба дюралевые. Кладем, далее, эти два
кубика на одну чашку весов, а на вторую — последовательно кладем
по паре кубиков из числа оставшихся 18. Пусть первые k из этих
пар оказываются одного веса с первоначальной, а F+1)-я пара —
Другого веса. (Если А«=9, то все кубики оказываются одного веса
и, следовательно, дюралевых кубиков нет вовсе; случай k=Q ничем
Не отличается от общего случая). Предположим для определенности,
что (к+1)-я пара оказалась более тяжелой, чем первоначальная
&'- Д. О. Щклярский и др, в!
(рассуждение мало изменилось бы, если F+1)-я пара оказалась
бы более легкой). В таком случае первые два кубика, а следователь-
следовательно, и кубики тех k пар, которые оказались с ними одного веса, обя-
обязательно алюминиевые. Итак, мы произвели пока 1 + (&+1) =k-\-2
взвешиваний и выделили при этом k-\-l пар алюминиевых кубиков.
Теперь положим на чашки весов по кубику из последней взвешен-
взвешенной пары ((&+3)-е взвешивание). Если оба кубика окажутся оди-
одинакового веса, то оба они должны быть дюралевыми; в противном
случае — один из них алюминиевый, а второй дюралевый. В обоих
случаях мы можем после k+З взвешиваний указать пару из двух
кубиков, один из которых алюминиевый, а второй дюралевый. С по-
помощью этой пары мы 8 — k взвешиваниями определим число дюра-
дюралевых кубиков среди ортавшихся 20—2 (?+2)¦= 16—2k кубиков
аналогично тому, как мы поступали в случае 1°. Общее число взве-
взвешиваний в случае 2° будет равно k + 3 + (8 — k) = 11.
15. Разделим наши монеты на три группы по четыре монеты
в каждой. При первом взвешивании поместим на каждую чашку
весов по группе из четырех монет. Возможны два варианта:
1°. Чашки весов уравновесились.
2°. Одна из чашек перевесила.
Рассмотрим оба варианта в отдельности.
1°. При первом взвешивании чашки весов урав-
уравновесились. Следовательно, фальшивая монета находится в
оставшейся группе, а 8 монет на весах — настоящие. Перенумеруем
монеты из оставшейся группы: 1, 2, 3, 4. Положим при втором взве-
взвешивании монеты 1, 2 и 3 на одну чашку, а на другую — три монеты
из числа восьми заведомо настоящих. Возможны два случая:
А) Чашки весов уравновесились. Тогда монета 4 — фальшивая.
Сравнивая третьим взвешиванием ее с настоящей, мы находим,
легче она или тяжелее, чем настоящая.
Б) Одна из чашек перетянула. В этом случая фальшивой явля-
является одна из монет 1, 2 или 3. При этом, если перетянула чашка
с настоящими монетами, то фальшивая монета легче настоящих;
одним взвешиванием мы без труда выделяем более легкую из трех
монет: 1, 2 и 3 (ср. с решением задачи 13а)). Если же перетянула
чашка с монетами 1, 2, 3, то фальшивая монета тяжелее настоящих;
и в этом случае ее легко определить одним взвешиванием.
2°. При первом взвешивании одна из чашек ве-
весов перетянула. Тогда все монеты в оставшейся группе —
настоящие. Обозначим монеты, лежавшие на перетянувшей чашке,
через 1, 2-, 3, 4 (если одна из этих монет фальшивая, то она тяже-
тяжелее настоящих), а монеты на другой чашке — через 1', 2', 3', 4' (если
одна из этих монет фальшивая, то она легче настоящих). При
втором взвешивании поместим на одну чашку монеты 1, 2 и 1', .а на
другую — монеты 3, 4 и 2'. Возможны опять-таки различные случаи:
А) Чашки уравновесились. Тогда фальшивая одна из монет 3'
или 4 (и при этом она легче настоящих). При третьем взвешивании
поместим на одну чашку весов монету 3', а на вторую — монету 4';
та из этих монет, которая окажется легче другой, и будет фаль-
фальшивой.
Б) Перетянула чашка с монетами 1, 2, 1'. В этом случае монеты
3. 4 и 1' — настоящие; в самом деле, если бы одна из монет 3, 4
была бы тяжелее остальных или монета 1' была бы легче остальных,
то при втором взвешивании чашка, на которой лежат монеты 3, 4
и 2', должна была бы перетянуть, чего на самом деле не случилось,
Итак, фальшивой является одна из монет I, 2 (в этом случае фаль-
фальшивая монета тяжелее настоящих) или 2' (в этом случае фальшивая
монета легче настоящих). Положим при третьем взвешивании на
одну чашку монету 1, а на другую — монету 2. Если чашки уравно-
уравновесились, то фальшивая монета 2', а если одна из чашек перетянула,
то на перетянувшей чашке лежит фальшивая монета.
В) Перетянула чашка с монетами 3. 4, 2'. Рассуждая аналогич-
аналогично предыдущему, мы заключаем, что монеты 1, 2 и 2' — настоящие
и что либо одна из монет 3, 4 фальшивая и тяжелее настоящих, либо
монета 1' фальшивая и легче настоящих. При третьем взвешивании
положим на одну чашку монету 3, а на другую — монету 4. Если
весы уравновесились, то фальшивая монета 1 . Если же одна из ча-
чашек перетянула, то па ней и находится фальшивая монета.
16. а) Достаточно распилить одно третье звено; при этом цепоч-
цепочка распадется на две части, содержащие соответственно 2 и 4 зве-
звена, и на одно отдельное (распиленное) звено. В первый день постоя-
постоялец отдаст это звено; i:o второй — заберет его обратно и отдаст
взамен часть цепочки, состоящую из двух звеньев; в третий — добавит
снова распиленное звено; в четвертый — заберет все, что дал раньше,
и передаст часть цепочки из четырех звеньев; в пятый—добавит еще
раз распиленное звено; в шестой — возьмет обратно это звено
и даст взамен часть цепочки из двух звеньев; в седьмой — отдаст
последнее звено.
б) Удобно сначала разобрать следующую задачу: при каком
наибольшем п достаточно распилить k звеньев /г-звенной цепи для
того, чтобы любое число звеньев от 1 до п можно было получить,
взяв некоторые из образовавшихся частей цепи? Для решения этой
задачи рассмотрим, каково наиболее выгодное расположение k рас-
распиленных звеньев. Так как после перепиливання k звеньев у нас бу-
будет k отдельных (распиленных) звеньев, то любое число звеньев от
1 до k мы сможем набрать уже только из них. Но k-\-\ звеньев мы
уже не сможем получить, если у нас не будет части, состоящей из
«+1 или менее звеньев. Ясно, что наиболее выгодно будет иметь
часть точно из /г+1 звеньев; тогда из этой части и k отдельных
звеньев мы сможем набрать лю.бое число от 1 до 2/г+1. Для того
чтобы можно было получить также 2k-\-2 = 2(k-\-\) звеньев, нам
надо будет иметь еще часть, содержащую 2(k-\-\) или менее звень-
звеньев; наиболее выгодно для пас будет, если эта часть будет содер-
содержать ровно 2(/<+1) звеньев. Теперь мы можем уже составить все
числа от 1 до 2к-\-\ + 2 (?4-1) =4A-j-3; следующая по величине часть,
которая нам необходима,—это часть, содержащая 4(й4-1) звеньев.
Продолжая рассуждать таким же образом, убедимся, что наиболее
выгодным будет, если k-\-\ частей, получающихся после того, как мы
распилили k звеньев (отдельные k звеньев, получающихся при этом, мы
здесь не засчитываем в число частей), будут иметь соответственно сле-
следующие числа звеньев:
A+I, 2(k + \), 4(/г+1), 8(й+ 1),...,
В этом случае любое число звеньев от 1 и до
n = k+ {A+ 1 +2F+ 1) + 4(А+ 1) +...
= А+BА + ' — 1) (k+\) =
можно будет составить из частей цепи.
6* 83
Итак, если 2*?^я^2*+1(* + П — I, то можно обойтись k раз-
разрывами цепи, но нельзя обойтись k — 1 разрывами. В частности,
при- 2<nsg7 k=\, при 160<n«S383 6=5,
при 8<ns?23 6=2, при 384<n<895 6=6,
при 24<яг?63 6=3, при 896«Srt«S2047 6 = 7.
при 64<n<159 6 = 4,
Итак, мы видим, что при я=2000 наименьшее число распиленных
звеньев равно 7. Условия задачи будут выполнены, если выбрать
эти звенья так, чтобы получающиеся 8 частей цепи G отдельных
звеньев мы здесь не считаем) имели соответственно 8, 16, 32, 64, 128,
256, 512 и 977 звеньев.
17. Пусть S — какая-то станция метро, Т — самая далекая от S
станция, т. е. такая, что кратчайший путь из S в Г ведет через
большее (или, по крайней мере, не меньшее) число станций, чем
кратчайший путь от S до любой другой станции. Закроем теперь стан-
станцию Т. При этом из S мы по-прежнему сможем проехать в любую
другую (не закрытую) станцию U, ибо кратчайший путь из S
в U никак не может вести через Т — ведь иначе станция U была бы
расположена дальше от S, чем станция Т. Поэтому, если U и V —
две какие угодно отличные от Т станции метро, то из одной из них мы
заведомо смол-сем проехать в другую, минуя Г: для этого достаточно,
например, если U и V отличны от S, проехать из U в 6', а отту-
оттуда — в V.
18. Будем доказывать утверждение задачи методом мате-
математической индукции по числу городских перекрестков (из
которых исходят более двух дорог). Если в Зурбагане имеются
всего два перекрестка А и В, то утверждение задачи очевидно: из
Л в В ведут не менее двух дорог (если бы такая дорога была одна,
то при введении по ней одностороннего движения — скажем, в на-
направлении от Л к В — мы не смогли бы проехать из В в Л); поэтому
установив по одной из этих дорог движение от Л к В, а по вто-
второй — от В к А, мы сможем проехать от любого перекрестка до
любого, отличного от него. Это простое рассуждение неожиданно
«работает» и в общей ситуации. Предположим, что для всех городов,
число перекрестков в которых не превосходит п, утверждение зада-
задачи уже доказано; рассмотрим теперь новый город (пусть это и бу-
будет Зурбаган), имеющий п+1 перекресток. Рассмотрим два сосед-
соседних из этих-перекрестков— перекрестки Л и В, соединенные улицей
АВ. Ясно, что поскольку после введения на улице АВ (при ее ре-
ремонте) одностороннего движения — скажем, от Л к В — проехать
от В к Л было возможно, то из перекрестка В в перекресток Л ве-
ведет некоторая не включающая улицы АВ «цепочка» улиц. (Разуме-
(Разумеется, эту «цепочку» можно считать не имеющей самопересечений —
ведь если -бы она дважды проходила через один и тот же перекре-
перекресток С, то «цикл» между первым вхождением в С и последующим
вхождением в ту же точку мы могли бы просто отбросить.) Таким
образом, мы приходим к существованию в Зурбагане «кольца»
s — замкнутой сети улиц, ведущей из Л в В, а затем (через ряд
«промежуточных» перекрестков)—снова в Л. Рассмотрим теперь
условный город, план которого получается из плана Зурбагана
«склеиванием» всех перекрестков нашего кольца s в один перекре-
перекресток S, из которого исходят все улицы, реально «упирающиеся» в
84
кольцо s'). Число перекрестков такого условного города меньше
га+ 1; поэтому, по предположению индукции, в нем можно ввести по
всем улицам одностороннее движение с соблюдением требований
задачи. Если мы затем оставим движение по всем не входящим в
кольцо 5 улицам таким же, каким оно было в этом условном «го-
«городе», а по кольцу s пустим движение в одном (безразлично каком!)
направлении, то на всех улицах Зурбагана будет установлено одно-
одностороннее движение — и притом с любого перекрестка можно будет
проехать в любой другой.
19. Ясно, что если в стране имеются 2 города, соединенные
одним шоссе с односторонним движением по нему, то из одного
города вообще не удастся попасть во второй. Если городов 4, то
мы можем считать их вершинами четырехугольника ЛИ2Л3Л4; при
этом либо движение по контуру четырехугольника является «цик-
«циклическим» (рис. .6, а), либо хоть одна из вершин — например, вер-
вершина А]—такова, что две проходящие через нее стороны четырех-
четырехугольника изображают ведущие из города шоссе (рис. 6, б). Но в
ю
5)
Рис. 6.
первом случае вершины четырехугольника равноправны и любой
выбор направлений по диагоналям четырехугольника по существу
не отличается от любого другого, а меж тем, на рис. 6, а мы не
можем с заездом в один лишь город проехать из Л3 в Л2. Если же
шоссе А{А2 и ЛИ4 ведут из Ль то для того, чтобы мы могли с
соблюдением требований задачи проехать из Л2 и из Л) в Ль на-
направления движения на шоссе Л2Л3, Л4Л3 и АзА, надо выбрать
такими, как указано стрелками на рис. 6, б; но при этом мы снова
приходим к «симметричной» ситуации, позволяющей ограничиться
рассмотрением варианта, отвечающего какому-то (какому угодно!)
') «План» города здесь можно понимать просто как таблицу,
в которой перечислены все улицы города и все перекрестки, причем
указано, какие улицы упираются в какие перекрестки — реально мо-
может случиться, что полученный описанным 'образом план «условно-
«условного" города» нарисовать на листе бумаги будет нельзя (а только лишь
на глобусе или более сложной поверхности — нам это совершенно
неважно).
85
выбору направления движения по шоссе А2АА,— а в случае рис. 6, б
из Ai в А2 нельзя проехать с заездом в один лишь город. При п =»
= 3 или 6 выбор направлений движения с соблюдением всех^ по-
поставленных требований возможен (см. рис. 7, а и б; на рис. 7, б мы
даже ограничились изображением не всех шоссе).
Рис. 7.
Далее воспользуемся методом математической ин-
индукции. А именно, пусть для некоторого числа п городов утвер-
утверждение задачи уже доказано; покажем, что тогда оно будет спра-
справедливо и для на 2 большего
числа городов п + 2. Для этого
направления движения на всех
шоссе, соединяющих любые
два из первых п городов
Аи А2 Ап, мы устано-
установим такими, чтобы из любого
из этих городов в любой дру-
другой можно было проехать с
заездом не более чем в один
«промежуточный» город (это
возможно в силу предположе-
предположения индукции). Далее, повеем
шоссе, ведущим из (я+1)-го
города /4,i + i в один из го-
городов Аи Аг, ..., А„, направим
движение в сторону городов
Ai, /42, .. ., А„, а из каждо-
каждого из этих городов направим
движение в сторону (« + 2)-го
города Ап+2 (рис. 8); тогда из
An + i в каждый из городов
Рис. 8. Аи А2 Ап и из каждого из
этих городов в Ап+2 можно
будет попасть без заездов
в какой-либо другой город. Наконец, направим движение по сое-
соединяющему Ап+1 и -4„+2 шоссе от Ан+2 к Ап+} — тогда из Ап+2 в
Л„+1 мы попадем «за один шаг», а из Л„+2 в любой из городов Ль
86
'А2 А„ и из любого из этих городов в An + i — за два «шага»
(с заездом, соответственно, в An+i или в Лп+2).
Так как утверждение задачи справедливо для я = 3 и для
п = 6, то из' доказанного следует, что оно также справедливо для
всех нечетных п ^ 3 и для всех чётных п ^б.
20. Вот более «математическая» формулировка той же задачи.
На плоскости (на карте Швамбрании) имеется 100 точек (городов);
каждые две точки соединены либо сплошной линией (это означает,
что между соответствующими городами имеется прямая телефон-
телефонная связь), либо пунктирной линией (означающей наличие авиа-
авиарейсов из одного города в другой); при этом известно, что из лю-
любой из заданных точек, (из любого города) в любую другую мож-
можно пройти как по цепочке сплошных линий, соединяющих наши
точки, так и по цепочке пунктирных линий. Нам требуется дока-
доказать, что в таком случае среди имеющихся 100 точек можно вы-
выбрать такие 4, что здесь тоже из каждой точки можно пройти в
любую из трех других как по цепочке сплошных, так и по цепоч-
цепочке пунктирных линий, используя при этом лишь линии, соединяю-
соединяющие наши 4 точки.
Доказывать это утверждение мы будем от противного:
предположим, что такой четверки не существует, и, пользуясь этим,
выделим из наших 100 точек-городов бесконечную их последова-
последовательность, что, разумеется, невозможно.
Мы начнем с некоторых (каких угодно!) точек А\ и А2, соеди-
соединенных сплошной линией. По условию Ai и А2 можно также со-
соединить цепочкой пунктирных линий; пусть А^АЪА'3Л'3 .. .А2 — крат-
кратчайшая из таких цепочек, т. е. цепочка, проходящая через наи-
наименьшее число промежуточных точек (городов). В таком случае
любые две не соседние точки этой цепочки соединены сплошной
линией — ведь иначе мы могли бы сократить нашу цепочку, просто
в.)
Рис. 9.
отбросив все города, промежуточные между этими двумя. Но от-
отсюда следует, что если бы наша цепочка содержала более одного
промежуточного города — скажем, содержала, бы города Л3) А3
иА'3 (где А'3 может и совпадать с А2),— то города А\, А3, А3 и А3
(см. рис. 9, а) уже образовывали бы требуемую четверку городов
(по нашему предположению отсутствующую!), поэтому А\ и А2 со-
соединены «ПуНКТИрНЫМ ДВуСТОрОННИКОМ» /4i/l3<4ji.
87
_ Рассмотрим теперь (соединенные пунктирной линией.!)' города
Ац и Аз\ в точности, как и ранее, устанавливается, что существует
состоящий всего из двух звеньев сплошной путь /42<44i43 из А2 в
<43. Докажем, что точка Л4 соединена с А{ сплошной линией. В са-
самом деле, если бы Л4 и А\ были соединены пунктирной линией, то
А\, А2, Аг и At образовывали бы запрещенную по нашему предпо-
предположению четверку городов с требуемыми свойствами (ср. рис. 9, б).
Итак, мы нашли такие 4 точки А\, А2, Аз и /Ц, что А2 соедине-
соединена cAi сплошной линией; Аз соединена с Ау и с А2 пунктирными
линиями; А4 соединена с Аи А2 и А3 сплошными линиями. Далее
воспользуемся методом математической индукции.
Предположим, что мы уже нашли такие точки Аи А2, As,..., A,,
что каждая из точек А3, As,... (точек с нечетными номера-
номерами) соединена со всеми предшествующими точками пунктирными
линиями, а каждая из точек А2, А*,... (точек с четными номе-
номерами) соединена с каждой из предшествующих ей точек сплошны-
сплошными линиями, и покажем, что этот ряд точек можно продолжить.
Пусть, для определенности, линия A\-\Ai является сплошной; рас-
рассмотрим кратчайшую пунктирную ломаную Ai-iAi+iAt, соединяю-
соединяющую Л,_1 и А\. Ясно, что точка At+\ не совпадает ни с одной из
точек А\, А2, . .., At-2 (и, конечно, .4;_i, A{)—ведь все предшест-
предшествующие Ai-\ точки соединены с одной из точек At-\, Л,- сплошной
линией, а со второй — пунктирной, в то время как At+1 соединена
пунктирными линиями с ними обеими. С другой стороны, со всеми
точками Ль А2,..., Лг_2 (а также и с Л;_ь At) точка Л1+1 соеди-
соединена пунктирными линиями, ибо если линия AjAi+; (где/<1—1) —
сплошная, то точки Aj, Л;_ь Ai, Ai+i образуют «запрещен-
«запрещенную» по нашему предположению четверку точек (рис. 9, б).
Тем самым мы «продолжили на один шаг» конструируемую
цепочку Аи А2,..., 4<_i, At, Л<+],... точек-городов, которую, та-
таким образом, можно сделать сколь угодно длинной.
21, Для того чтобы обойти все 64 клетки шахматной доски,
побывав на каждом поле один раз, конь должен сделать 63 хода.
Так как при каждом ходе конь переходит с белого поля на черное
или с черного на белое, то после ходов с четными номерами конь
будет попадать на поля того же цвета, что и исходное, а посла ¦
ходов с нечетными номерами — на поля другого цвета. Поэтому
конь не может 63-м ходом попасть на поле, находящееся на одной
диагонали с исходным, так как эти поля окрашены в один цвет.
22. Король может избрать следующую «самоубийственную» (но
ведь самоубийство и является его целью!) стратегию: сначала он
перейдет в нижний левый угол доски, а оттуда двинется по диаго-
диагонали слева вверх направо. После того, как король сделает 1-й ход
по диагонали, он окажется на помеченном звездочкой на рис. 10, а
поле; при этом если хоть одна ладья (после ответа черных на пос-
последний ход короля) окажется вне заштрихованного на этом рисун-
рисунке квадрата размера 997X997, то король сможет стать под удар
следующим своим ходом. Аналогично устанавливается, что после
998 ходов по диагонали, когда король окажется на поле, помечен-
помеченном звездочкой на рис. 10, б, все черные ладьи должны будут на-
находиться в заштрихованном на этом рисунке квадрате. При этом
если в процессе движения короля хоть одна ладья осталась на той
же горизонтальной строке или на том же вертикальном столбце
шахматной доски, где она стояла ранее, то король "в процессе своего
движения пересечет эту строку или этот столбец — и тем самым
88
окажется под боем. Поэтому, если «черные» стремятся не брать
короля, то за время движения короля от положения рис. 10, а до
положения рис. 10, б (король за это время сделал 997 ходов)
каждая из 499 ладей должна сделать минимум 2 хода (ибо каждым
ходом она меняет либо строку, на которой стоит, либо столбец, но
никогда — строку и столбец одновременно); но на 2-499 = 998
ш
у/у
УУ}
у^у
0
1
щ
уу/
'4
у/
///
Уу
У/,
щ
у/
УУ/
щ
//,
ж
т
УУ,
щ
щ
т
Уу
ш
\/у
У*.
щ.
¦УУ/
т
f//
'УУ<
ш
т
'ё
уА
УУУ/,
уУу/
У/'
р.
%
У/у.
т
т
i
УУ//
Уу
У/
Ш
уу
А
ш
//г
У/
У//у
/у
%
Ш
щ
У/
f/y
У^
У'у
/УА
У/,
Г/у
щ
/У,
'УУ
Ж
Уу
к.
ш
//
У/
У/,
Уу
Уа
т
У/у
У/а
щ%
0.
У/
%
УУ/
щ
уу
У/а
ш\
Уу
'Уу
Уу
Уу\
т
ш
щ
{/у
Уу
ш
Щ
щ
У/
Уу,
ш
*
ю
SJ
Рис. 10.
ходов у ладей не хватит времени (королю ведь достаточно сделать
лишь 997 ходов!).
23. Изменим порядок расположения полей по кругу, а именно,
расположим их в порядке, при котором можно было бы перехо-
переходить с одного поля на соседнее. Иными словами, после поля / по-
поместим 6 (ибо по условию задачи с поля 1 можно перейти на 6),
после 6 поместим поле // (с поля б можно перейти на //), затем
4 (ибо с поля // можно перейти на 4), и т.д. При этом мы полу-
получим порядок полей, изображенный на следующей схеме:
Мы можем считать, что имеем 12 полей, расположенных имен-
именно таким образом (ведь фактически занимаемое полем место зна-
значения не имеет) и занумерованных так, как это указано на нашей
схеме. При этом фишки первоначально стояли так, как это обозна-
обозначено на схеме буквами сверху и снизу полей (буква К обозначает
красную фишку, буква Ж ^- желтую,' буква 3 — зеленую и буква
С — синюю). Правило движения фишек при этом новом располо-
расположении полей оказывается чрезвычайно простым — каждая фишка
89
может сдвинуться на одно поле влево или вправо, если только это
соседнее поле не занято.
Теперь совершенно ясно, что единственный способ, каким фиш-
фишки могут поменяться местами, — это двигаться по кругу в одном
или другом направлении: ведь ни одна фишка не может «пере-
«перегнать» другую, ибо другая преграждает ей путь. Таким образом,
если фишка К займет поле 4, то фишка С должна будет занять
поле 2, фишка Ж — поле 3 и фишка 3 — поле /. Если фишка К
займет поле 2, то фишка С должна будет занять поле 3, фишка
Ж — поле /, фишка 3 — поле 4. Если фишка К займет поле 3, то
фишка С должна будет занять поле /, фишка Ж — поле 4 и фиш-
фишка 3 — поле 2.
Никакие другие новые расположения фишек невозможны.
24. Докажем, прежде всего, что если в некотором коллективе
студентов каждый из трех языков —а (английский), ф (француз-
(французский) и н (немецкий) знают ровно п человек, где л>2, то можно
составить такую группу студентов, в которой каждый язык будут
знать ровно 2 человека. Ясно, что из сформулированного предло-
предложения утверждение задачи уже вытекает: выбрав (и исключив из
рассмотрения) указанную группу студентов, мы цридем к совокуп-
совокупности студентов, в которой каждый из трех языков знают ровно
50 — 2 = 48 студентов; из этой совокупности студентов мы снова
можем выбрать группу, в которой каждый язык знают ровно 2 сту-
студента, после чего у нас останется коллектив, в котором каждый
язык знают ровно 48 — 2 = 46 студентов, и т. д. Объединив затем
пять отобранных таким образом небольших групп, в которых каж-
каждый язык знают по 2 человека, мы получим первую из интересую-
интересующих нас групп, в которой каждый язык знают ровно 10 человек;
далее так же (т. е. исходя из «маленьких» групп, в которых каж-
каждый язык знают ровно 2 студента) мы станем составлять вторую и
третью группы студентов (каждая из них будет состоять из 5 «ма-
«маленьких» групп).
Для доказательства напечатанного выше курсивом утвержде-
утверждения можно использовать метод математической индук*
ц и и. В самом деле, ясно, что если я = 2, то наше утверждение
выполняется (рассматриваемая группа здесь — это совокупность
всех студентов); предположим теперь, что оно верно для всех
значений п, меньших некоторого, и докажем, что в таком случае
оно справедливо и для этого значения п. Условимся обозначать
число студентов, знающих только английский язык, через Na; знаю-
знающих английский и французский языки, но не немецкий, через Na<p,
и т. д.; соответственно символ а (или а', или а") будет обозна-
обозначать студента, знающего только английский язык; символ аф (или
(аф)')—студента, знающего языки а и ф, но не я, и Т.д. Если
при этом Na Ф 0, Nф ф 0, Nп ф О, то мы просто исключим из наше-
нашего коллектива трех студентов а, ф и н и придем к новой совокупно-
совокупности студентов, для которой наше утверждение выполняется в силу
предположения индукции; аналогично этому, если МафНф0, то мы
откинем студента афн и снова придем к новому коллективу, для
которого наше утверждение верно. Далее, если МафФ0, Na-цфц и
Л'^к^О, то сформулированное предложение выполняется тривиаль-
тривиально — требуемую группу составляют три студента аф, ан и фн.
Наконец, если два из чисел Na$, Nan и N$H отличны от нуля,
а третье,— скажем, последнее из них — равно нулю, то отличны от
нуля числа Л^^ и NH (ибо в объединении всех студентов аф, (фу
90
и т.д. и всех студентов ан, (аи)', и т.д. больше студентов знают
язык а, чем язык ф и чем язык к); поэтому мы можем исключить
из числа студентов двух студентов аф и н и снова прийти к кол-
коллективу студентов, в котором каждый язык знают я — 1 человек и
в котором, по предположению индукции, требуемую «малую» группу
студентов составить можно. Аналогично, если скажем, лишь ЫафФ
?= 0, а Л'ок = Мфн = 0, то, очевидно, NH ?= 0 — и мы можем сно-
снова использовать предположение индукции, удалив студентов аф и
я. [Заметим, что равенства Ыпф = Nan = Ыфн = 0 (и Ы„фН = 0)
противоречат предположению, что хоть одно из чисел Nа, Мф и
Л'к равно нулю.]
Примечание. Ясно, что числа 50 и 10 в условии этой за-
задачи являются случайными: в точности так же можно доказать, что
если в нашем коллективе студентов каждый из трех языков (где,
впрочем, и число 3 можно пытаться заменять другими) знают ровно
п студентов, то из описанных «малых» групп можно конструировать
группы, в которых каждый из языков знают любое не большее п
заданное четное число m студентов; однако предположение о четно-
четности m здесь является существенным (попытайтесь доказать это!)
25. а) Ясно, что наименьшее значение «среднего места»
равно 1—это значение достигается, если все судьи приписали 1-е
место одному и тому оке спортсмену. С другой стороны, 5 или бо-
более спортсменов получить (у разных судей) первое место не могут:
в самом деле, эти п "^ 5 спортсменов получили бы тогда в совокуп-
совокупности у девяти судей 9 первых мест и 9п— 9^9-5 — 9 = 36 иных
мест (ибо всего 9 судей приписывают им 9я мест); по условию за-
задачи ни одно из этих мест не может быть ниже 4-го, что невозмож-
невозможно, так как мест с 3-го по 4е судьи указывают лишь 3-9 = 27.
Таким образом, остается лишь рассмотреть случаи, когда 1-е место
(у разных судей) получили 2, 3 или 4 спортсмена.
1 ° Если 1-е место судьями приписано лишь двум спортсменам,
то один из них назван 1-м не менее чем пятью судьями — и так
как остальными судьями он поставлен не ниже чем на 4-е место,
1
то «среднее место» этого спортсмена не ниже -jr- E-1 + 4-4) =
21 / 1
2° Если 1-е место приписано трем спортсменам, то в совокуп-
совокупности эти спортсмены получили 9 первых мест и еще 3-9 — 9= 18
иных мест, ни одно из которых не может быть ниже четвертого; но
так как 9 судей могут указать лишь 9 четвертых мест, то в «худ-
«худшем» случае наши спортсмены получили 9 четвертых и 9 третьих
мест. Таким образом, общая сумма приписанных этим трем спорт-
спортсменам мест не больше 9-11+ 9-4 + 9-3 = 72, в силу чего хоть
72
один из них имеет не большую -jt- —¦ 24 сумму мест и «среднее ме-
24 / 2
сто», не худшее -д- = 2-д-
3° Наконец, если 1-е место приписано четырем спортсменам, то
эти 4 лица получили в совокупности 9 первых мест и еще 4-9 —
— 9 = 27 иных мест, не низших 4-го; из них 9 могут быть 4-ми
91
местами, 9— 3-ми и последние 9 — 2-ми. Таким образом, общая
сумма мест четырех спортсменов здесь равна 9-1 <+ 9-2 + 9-3 +
-(-9-4 = 90 (<4-23); а значит, лучший из этих четырех спортсме-
спортсменов имеет сумму мест, не большую 22, и «среднее место», не худ-
22 / 4 2 \
Итак, «среднее место» лучшего спортсмена никак не может
2 2
быть ниже 2~о~; при этом равняться 2— оно может лишь в том слу-
случае, когда каждый из трех лучших спортсменов получил у трех
судей 1-е место, у трех других — 3-е и у. трех последних — 4-е (так
что в этом случае победителями соревнований явятся сразу три
спортсмена).
Примечание. Разумеется, те же рассуждения, где лишь
вместо k-то места фигурирует B1—k)-e, показывает что «среднее
место» последнего спортсмена никак не может быть выше 18~о~(но
может равняться 18—g—).
б) Ясно, что после каждого тура соревнований номер сильней-
сильнейшего из оставшихся участников соревнований не уменьшается; при.
этом увеличиться он может не более чем на 2 (если сильнейшего
теннисиста случайно победил теннисист, номер которого на две
единицы выше, чем у него). Так как 1024 = 210 и после каждого
тура число участников соревнований уменьшается вдвое, то всего
мы будем иметь 10 туров соревнования, после которых останется
лишь 2°= 1 теннисист — победитель соревнования. Поскольку пос-
после каждого тура номер лучшего из оставшихся теннисистов может
возрасти на 2, то отсюда, как будто, вытекает, что победителем
соревнований может оказаться 21-й по списку теннисист.
На самом деле, однако, и 21-й теннисист не имеет шансов ока-
оказаться победителем. В самом деле, для этого необходимо, чтобы
на каждом этапе соревнований выбывали два сильнейших игрока;
другими словами, надо, чтобы в первом туре выбыли 1-й и 2-й иг-
игроки, проигравшие, соответственно, 3-му и 4-му; во втором туре
выбыли 3-й и 4-й игроки, проигравшие, соответственно, 5-му и 6-му,
и т.д. Но в таком случае в полуфинальных соревнованиях должны
были выбыть. 17-й и 18-й игроки, проигравшие 19-му и 20-му; по-
поэтому 19-й и 20-й игроки выходят в финал — и победителем
соревнований становится один из них, а не игрок с номером 21.
Покажем, наконец, что 20-й игрок победителем соревнований
оказаться может. В самом деле, при наличии всего 21 = 2 игроков,
разумеется, победителем может оказаться игрок с номером 2 = 2-1;
если же теннисистов 22 = 4, то победителем может стать теннисист
с номером 2-2 = 4: в паре первых двух игроков может победить
2-й, в паре двух других — 4-й, а 4-й, в принципе, может и выиграть
финал у 2-го. Аналогично, если игроков 23 = 8, то победителем
может оказаться 6-й теннисист: в самом деле, если четверо сильней-
сильнейших игроков попадут в одну подгруппу, то в ней сильнейшим
может оказаться 4-й; во второй подгруппе 6-й теннисист может и
выиграть у 5-го; при этом в финале он встретится с 4-м, кото-
которого может и победить. Точно так же с помощью метода м а-
92
тематической индукции легко доказать, что победителем
в соревнованиях 2™ теннисистов может оказаться Bга)-й по силе
теннисист: для этого лишь надо, чтобы первые 2п — 2 игрока попа-
попали в одну подгруппу из 2"-1 игроков, где (в силу предположения
индукции) победителем может стать Bга — 2)-й теннисист; во вто-
второй же подгруппе победителем вполне может стать Bга)-й игрок,
которому после этого надо лишь в финале выиграть у Bл — 2)-го
игрока,— может быть, и трудная, по возможная задача.
26. Обозначим число комплектов медалей, оставшихся не вру-
врученными к началу 1-го дня соревнования, через Nt, где i= 1,2,...
..., п; можно, впрочем, считать, что величина Л'; имеет смысл и
при i > п, обращаясь в этих случаях в 0. Из условий задачи
(и нашего соглашения) вытекает, что Ni^N, N„ = п, Nn+;==_Q;
кроме того, значения Nt и Л^+i связаны соотношением:
или #4 =
Из (*) последовательно находим
n~2 - D")* я + "Г (я - О + (я - 2)i
7 \я / 7 \2
7 \п — I I J \n—i — i I 7 \п—i—2
J +{ A) + () (Л-2Н-...-Н
(общая формула, разумеется, без всякого труда доказывается ме-
методом математической индукции).
Таким образом, мы получаем:
J +() ^1)+(J ("-2)+....
К 7 \п~1 / 7
¦г) +(-
г/ 7 \«—2 / 7 \п—3
-If—j +2()
+()
где через Si и S2 обозначены две заключенные в квадратные
скобки суммы. Но по формуле суммы членов геометрической
93
прогрессии, очевидно,
7 \ /7 \«—1 / 7 \п—2*
б"-1
С другой стороны, как легко видеть,
_7
6
= Si — я = 6
так что
S2 = 36|[ —
и, следовательно,
N = 6 [("б") — 1 |я — Зб|(-д-)П— ll + 6/i =6 (я —6) f-gj +36.
(**)
т л, 7"(я-6)
Так как N — целое число, то и число Rn—\—> а значит и
я —6
. i должны быть целыми; поэтому я кратно 6. С другой
стороны, очевидно, что при всех k ^ 2 имеет место неравенство
6/г — 6 < б6*, или А—1 < б6*1 (почему?)—и, значит, дробь
я —6
„_! при я > 6 не может быть целым числом. Таким образом, мы
и
приходим к единственчому возможному решению задачи: я = 6 и,
значит (в силу (**)) N = 36.
27. Первое решение. Пусть я — число орехов, которое
досталось утром каждому из приятелей; в таком случае 5я + 1
есть число орехов, которое было утром в мешке. Последний из
, 5я + 1
проснувшихся ночью, очевидно, взял себе—-—,а до этого в меш-
5я + 1 25я + 9
ке было 5—т +1 = —¦: орехов. Предпоследний проснувшийся
1 25п + 9 1 25я + 9
взял себе -?¦¦—т. . а до этого в мешке было 5--|--—^ +
125я + 61 „ 1 125я + 61
.+1 = Tg орехов; третий взял себе-т/-. rg ', а до этого
1 125я + 61 625я + 369
в мешке было 5-~- fg" + ' == Ш орехов; второй взял
1 625я + 369 ' 1 625я + 369
себе -г-- ft , а до этого в мешке было 5-~j~- g7 + 1 =•
94
3125л+ 2101 „ 1 3125л+ 2101
«=¦ 25g орехов; наконец, первый взял себе -г-- 256 »
а первоначально в мешке было
1 3125п +¦ 2101 15625Л+11529
" ~5' 4 ' 256 + 1 = 1024 =
265л + 265
15л+11+•
1024
орехов. Так как это число должно быть целым, то 265 (я>+ 1) долж-
должно делиться на 1024. Наименьшее значение п, удовлетворяющее
этому условию, равно, очевидно, 1023 и в этом случае
N = 15- 1023 + 11+265= 15 621.
Второе решение. Эту задачу можно решить значительно
быстрее и почти без всяких подсчетов, если внимательно рассмот-
рассмотреть те условия, которые накладывает ее содержание на общее
число N орехов. Первое условие задачи заключается в том, что при
первом разделе на пять частей в остатке остается один орех. Это
условие означает, что N при делении на 5 должно дать в остатке
¦1, т. е. Л7 = 5/+1; числа, удовлетворяющие этому условию, встре-
встречаются в натуральном ряду чисел с интервалом в пять чисел, и,
зная одно такое число, мы можем найти неограниченно много дру-
других, прибавляя к нему (или вычитая из него) числа , кратные 5.
4
Второе условие задачи утверждает, что A«=-z-(Ar—1)=4^дает
при делении на 5 остаток 1, т. е. k — 5l{ + 1. Это требование равно-
равносильно тому, что / дает при делении на 5 остаток 4 или что N =
= 5/ + 1 дает при делении на 25 остаток 21; числа, удовлетворяю-
удовлетворяющие этому условию, встречаются в числовом ряду с интервалом в
25 чисел, и, зная одно такое число, мы можем получить сколько
угодно других, прибавляя к "нему (или вычитая из него) числа, крат-
кратные 25. Точно так же третье условие задачи утверждает, что ki =
4
= ~r~ (k — 1) = Hi дает при делении на 5 остаток 1; это условие
определяет остаток от деления числа 1{ на 5 или остатки от деления
чисел k и / на 25, или остаток от деления N на 125. Все условия
задачи определяют остаток от деления числа N на 56 = 15 625;
числа, удовлетворяющие этим условиям, встречаются в натуральном
ряду чисел с интервалом в 15 625.
Мы могли бы подсчитать остаток, который дает при делении на
5е число ./V, но в этом нет нужды. Дело в том, что одно число, удов-
удовлетворяющее всем условиям задачи, является очевидным. Этим чис-
числом является —4. Действительно, при делении на 5 число —4 дает
в частном —1 и в остатке +1| поэтому, если вычесть из —4 число
4
1 и взять -г от полученной разности, уже делящейся на 5, то мы
получим то же число —4. Также и при всех последующих делениях
на 5 мы будем иметь тот же остаток + 1. Правда, число —4 не
может служить ответом нашей задачи, так как, по условию, число N
должно быть положительным; но, зная одно число, удовлетворяющее
условиям задачи, мы можем получить сколько угодно других, при-
прибавляя к нашему числу кратные 5е, Наименьшее положительное
93
число, удовлетворяющее условиям, есть, очевидно, —4 + 5' =*
= 15625 —4= 15 621.
28. Обозначим число овец в стаде через п\ в таком случае
братья взяли за каждую овцу п рублей и, следовательно, всего
выручили N = п • п = п2 рублей. Пусть d есть число целых десят-
десятков числа п, а е — число единиц; тогда п = IQd + e и
N => A0d + еJ = 100<i2 + 2Qde + el
Из условий дележа следует, что старшему брату досталось од-
одной десяткой больше, чем младшему, т. е. что общая сумма ./V со-
содержит нечетное число десятков (и какой-то остаток). Но
100d2 + 20de = 2OdEd + е) делится на 20 (содержит четное число
десятков); следовательно, число е2 должно содержать нечетное число
десятков. Так как е меньше 10 (е есть остаток от деления числа п
на 10), то е2 может иметь только одно из следующих значений:
1, 4, 9, 16, 25, 36, 49, 64, 81.
Но из этих чисел только 16 и 36 содержат нечетное число десят-
десятков; следовательно, е2 равно 16 или 36. Оба эти числа оканчиваются
на 6; значит, тот остаток, который получил младший брат взамен
нехвативших ему 10 рублей, равен 6 рублям, и старший получил на
4 рубля больше младшего. Поэтому, для того чтобы раздел был
справедливым, старший должен еще доплатить младшему 2 рубля.
Следовательно, перочинный нож был оценен в 2 рубля.
29. а) Наш календарь устроен следующим образом. Каждый год
имеет 365 дней. Исключением являются годы, номера которых де-
делятся на 4: эти годы (високосные годы) имеют лишний 366-й день
B9 февраля). Однако и это правило имеет исключения: годы, номе-
номера которых делятся на 100, по не делятся на 400, имеют не 366 дней,
а 365, т. е. не являются високосными; так, 1900 и 1800 гг. не были
високосными, не будет високосным и 2100 г., в то время как 2000 г.
будет високосным B000 делится на 400). Задача заключается ,в том,
чтобы выяснить, каким днем чаще бывает по нашему календарю
1 января: субботой или воскресеньем.
Промежутки, через которые следуют друг за другом числа 1 ян-
января, не всегда постоянны, но эти промежутки изменяются периоди-
периодически, с периодом в 400 лет. При этом 400 лет содержат целое число
недель: действительно, невисокосный год содержит 52 недели и еще
1 день, а високосный — 52' недели и 2 дня; в течение четырех лег
(из которых- один високосный) набегает, таким образом, сверх
4 • 52 недель еще 5 дней; в течение 400 лет должно было бы набе-
набежать еще 500 дней, но так как три года, делящиеся на 100, но не
делящиеся на 400, не являются високосными, то за 40О лет сверх
400 ¦ 52 недель набегает всего 500 — 3 = 497 дней, т. е. ровно 71 не-
неделя. Поэтому нам достаточно выяснить, каким днем чаще бывает
1 января за какие-либо 400 лет; этим днем будет чаще 1 января и
за любые другие 400 лет.
Рассмотрим теперь промежуток в 400 лет с 1901 по 2301 г.
Отметим, что если в течение 28 лет каждый четвертый год является
високосным (т. е. эти 28 лет не содержат года, номер которого де-
делится на 100, но не делится на 4О0), то эти 28 лет содержат целое
число недель: в течение каждых четырех лет набегает сверх целого
числа недель еще 5 дней, а за 28 лет набегает 5 • 7 = 35 дней, т. е.
5 недель. Теперь отметим, что 1 января 1952 г. было вторником. Так
95
как каждый невисокосный год содержит целое число недель и один
день-, а високосный — целое число недель и 2 дня, то I января
1953 г.—четверг A952 г.—високосный), 1 января 1954 г.—пятница,
1 января 1955 г.—суббота, и т.д.; точно так ж_е 1 января 1951 г.
было понедельником, 1 января 1950 г. было воскресеньем, и т. д.
Таким образом, подсчитываем, что за 28 лет с 1929 по 1956 г. 1 ян-
января является каждым из семи дней недели ровно по 4 раза. Точно
такое же распределение дней, с которых начинается новый, год,
было и в течение 28 лет с 1901 по 1928 г. (напоминаем, что 28 лет,
среди которых каждый четвертый является високосным, содержит
целое число недель, и, следовательно, через каждые 28 лет будет
повторяться точно такое же распределение первых дней года, как
и в предыдущие 28 лет); такое же распределение первых дней года
будет и в периоды 1957—1984, 1985—2012 B000 г., как делящийся
на 403, будет високосным), 2013—2040, 2041—2068 и 2069—2096 гг.
Итак, в промежутке 1901—2096 гг. 1 января будет одинаковое число
раз каждым днем недели.
Далее, 1 января 2097 г. будет тем же самым днем, что 1 января
1901 г. или 1 января 1929 г., т. е. вторником, 1 января 2098 г. будет
средой, 1 января 2099 г.— четвергом, 1 января 2100 г.— пятниц», i,
1 января 2101 г.— субботой B100 год не будет високосным). После-
Последующие 28 лет будут отличаться от промежутка 1901—1928 гг. тем,
что они начались не со вторника, а с субботы; это вызовет соответ-
соответствующую перестановку дней, которыми будут являться 1 января;
однако, так как в течение 28 лет с 1901 по 1928 г. 1 января'было
ровно по 4 раза каждым днем недели, то и в промежутке с 2101 по
2128 г. 1 января будет каждым днем недели по 4 раза. Это сообра-
соображение относится и к промежуткам 2129—2156 гг. и 2157—2184 гг.;
2185 г. начнется с того же самого дня, что и 2101, т. е. с субботы.
Это позволяет определить, с каких дней будут начинаться годы
с 2185 по 2201. Простой подсчет показывает, что в промежутке
между 2185 и 2200 гг. 1 января будет по 2 раза понедельником, сре-
средой, четвергом, пятницей и субботой и по 3 раза — воскресеньем
и вторником. 1 января 2201 г. будет четвергом. В течение 3 • 28 ==
— 84 лет с 2201 по 2284 г. 1 января будет каждым днем недели
одинаковое число раз. 1 января 2285 г. будет тем же днем, что и
1 января 2201 г., т. е. четвергом. Это позволяет определить распре-
распределение дней, с которых начинается год в интервале с 2285 по
2300 г.; оказывается, в течение этого интервала 1 января будет по
2 раза понедельником, вторником, средой, четвергом и субботой и по
3 раза — воскресеньем и пятницей. Таким образом, сверх тех перио-
периодов, в течение которых 1 января бывает одинаковое число раз каж-
каждым днем недели, мы получили еще 2 + 2 = 4 понедельника, 1 +
+3 + 2=6 вторников, 1+2 + 2 = 5 сред, 1 + 2 + 2 = 5 четвер-
четвергов, 1+2 + 3 = 6 пятниц, 2 + 2 = 4 субботы и 3 + 3 = 6 воскре-
воскресений. Отсюда следует, что 1 января чаще бывает воскресеньем,
чем субботой.
б) Аналогично решению задачи 29а) можно показать, что в ин-
интервале 400 лет 30-е число бывает воскресеньем 687 раз, понедель-
понедельником 685 раз, вторником 685 раз, средой 687 раз, четвергом 684 ра-
раза, пятницей 688 раз, субботой 684 раза. Итак, Чаще всего 30-е число
приходится на пятницу.
30. Легко видеть, что при зачеркивании последней цифры це-
целое число уменьшается не меньше чем в 10 раз. Ровно в 10 раз
уменьшаются при зачеркивании последней цифры числа, оканчива-
7 Д. О. Шклярский и др. ' °?
ющиеся нулем; следовательно, все эти числа удовлетворяют условию
задачи.
Допустим теперь, что целое число х при зачеркивании последней
цифры уменьшается в целое число раз, большее чем 10, а именно
в 104- а раз (а ^ 1); пусть у — число целых десятков числа х (не
цифр,а, а число!); г— цифра единиц': х= 10(/ + г. После отбрасыва- '
нйя последней цифры число х переходит в число у; поэтому наши
условия дают
х~(\0 + а)'У,
или
Wy + z = A0 + а) ¦ у,
откуда
г = ау.
Так как г < 10, то и у < 10, а < 10; следовательно, числа, обла-
обладающие нужным свойством, двузначны и при отбрасывании послед-
последней цифры могут уменьшиться не более чем в 19 раз. Теперь легко
видеть, что при зачеркивании последней цифры в 11 раз уменьшают-
уменьшаются только числа 11, 22, 33, 44, 55, 66, 77, 88 и 99; в самом деле, если
10 + а = 11, то а = 1; следовательно, г = ау = г/, х = \Ьу + г =
= Ну, где у = 1, 2, 3,..., 9. Аналогично найдем, что в 12 раз
уменьшаются лишь числа 12, 24, 36, 48; в 13 раз— 13, 26, 39; в 14
раз—14, 28; в 15, 16, 17, 18 и 19 раз — только соответственно числа
15, 16, 17, 18 и 19.
31. а) Пусть искомое число имеет k + 1 цифр; в таком случае
оно имеет вид 6 ¦ \Qh-\-y, где у есть &-значное число (которое мс
жет начинаться с одного или нескольких нулей). По условию зада-
задачи имеем:
6. Ю* + у = 25- у,
откуда
6-10*
Отсюда вытекает, что k не может быть меньше 2 (иначе 6 • \0h
не делилось бы на 24). При k ^ 2 число у оказывается равным
25- 10ft~2, т. е. имеет вид 250 ... 0. Поэтому все искомые числа имеют
(ft—2)нулей
вид 6250 . .. 0 (и = 0, 1, 2,...).'
пнулей
б) Решая задачу: найти число, начинающееся с данной цифры
а и уменьшающееся при зачеркивании этой цифры в 35 раз, анало-
аналогично задаче а), мы придем к следующему равенству:
a-\0h
где у — целое число (см. решение задачи а)). Но это равенство,
очевидно, не можег иметь места ни при каких целых а ^ 9 и k.
Примечание. Совершенно аналогично решениям задач 31а)
и б) можно показать, что число, начинающееся с известной цифры а,
может уменьшаться при зачеркивании этой цифры в целое число 6
раз только в том случае, если Ь—1 есть большее а число,
такое, что все простые делители 6 — 1, отличные от
2 и 5, в-х о д я т (и притомв не меньшей степени) также
а
и в состав числа а (т. е. что t ¦' есть правильная дробь,
93
которую можно превратить в конечную десятичную дробь). Так, на-
например, никакое число не может при зачеркивании первой цифры
уменьшаться в 85 раз (85—1 «= 84 делится на 3 • 7, а никакая цифра
не может одновременно делиться на 3 и на 7), а число, уменьшающееся
при зачеркивании первой цифры в 15 раз, должно начинаться с
цифры 7 A5—1 = 14 делится на 7). Общий вид чисел, которые при
зачеркивании известной первой цифры а уменьшаются в данное
.число Ь раз, легко найги.
32. а) Покажем прежде всего, что никакое число N не может
уменьшиться в 9 раз при зачеркивании цифры, стоящей дальше чем
на втором месте. Действительно, если это1 не так, то обозначая
цифры числа N через а0, fli..., an, т.е. полагая
Со • 10" + ах • 10—¦ + ... + а„ = N,
N
мы заключим, что число -jr имеет п цифр, первые две из которых
аа и п\, т. е.
Умножая последнее равенство на 10 и вычитая первое, получим:
9 ^" *
что невозможно, так как
-^• = ао-1Оп-1+ ... > Юп-!.
С другой стороны, из признака делимости на 9 вытекает, что
если число N делится на 9 одновременно с числом, получаемым из
N вычеркиванием одной цифры, то эта цифра есть 0 или 9. Таким
образом, в нашем случае возможно только, что первая или вторая
цифра числа Л' равна 0 или 9 и вычеркивание этой цифры равно-
равносильно делению N на 9. Но первая цифра N не может равняться О,
N
а если бы она была равна 9, то число -д- имело бы столько же
цифр, сколько Л', и не могло получаться из N вычеркиванием одной
цифры. Далее, если вторая цифра N равна 9 и число, получаемое
N
из N зачеркиванием этой цифры, равно -д-, то мы имеем:
N = а0 ¦ 10» + 9 • 10—' + а2 ¦ 10"-! + ... + аа.
откуда опять, умножая второе равенство на L0 и вычитая из него
первое, получим:
т < 1<)П~"
(ибо а2^9). Таким образом, мы убеждаемся, чтодлятого, чтобы
7* ¦ " 99
уменьшить число N в 9 раз, в нем надо зачеркнуть
¦ цифру 0, стоящую на втором месте.
Теперь мы имеем:
N = о0 • 10" + а2 • 10"-2 + ... + а„,
-у = ао-10"-1 +а2-10"-2+ ... + ап.
Отсюда следует
Y = iV- я,-10" + я,- Ю"-1 = N- Со-10"—*-9
и, наконец,
Т'Т =Т~а°'10" '
N
последнее означает, что, для того чтобы разделить число -g- на 9,
в нем достаточно зачеркнуть первую цифру,
б) Имеем (см. решение задачи а)):
откуда сразу следует
п. . 1ПП—1.Я1
8
Теперь, считая а0 равным соответственно 1, 2, 3, и т. д.,
получим, что N может быть равно одному из чисел 10 125,
2025, 30 375, 405,-50 625, 6075, 70 875 или отличаться от одного из
этих чисел каким-то количеством нулей в конце (а0 не может быть
равно 8 или 9, так как в этом случае вторая цифра N уже не бу-
будет нулем).
33. а) Аналогично решению задачи 32 а) в предположении, что
целое число N уменьшается в т раз при зачеркивании третьей циф-
цифры, имеем:
N 10101+l0n-2+ ... +а„.
При т<10 получаем N<C.l0n~l, что невозможно, так как
—т—-"ТО' а [оЛ'=а:ао'10"~1 + -1->10П~1- ПР("К>11 получаем
—— Л'<10п^1, что невозможно по аналогичной причине |ибо
т— 10 М 1
2~т—> Jo)-HaKOHeUl если /п==11> т0 Должно быть—jy < Ю",
N N
т. е. — = -y-f имеет на две цифры меньше, чем N, что тоже невоз-
невозможно,
100
Таким образом, единственным возможным случаем является
т=Ю; следовательно, условию задачи удовлетворяют числа, все
цифры которых кроме первых двух — нули, и только эти числа.
Примечание. Совершенно аналогично можно показать, что
единственные целые числа, уменьшающиеся в целое число раз при
вычеркивании k-н цифры, где k > 3, суть числа, все цифры которых
кроме первых k — 1 — нули.
б) Аналогично решению задачи 32 имеем, принимая, что целое
число N уменьшается при вычеркивании второй цифры в т раз:
- 10"-»+,,. +ап,
Отсюда следует
вли после несложных преобразований
Последнее выражение можно еще представить в следующей
виде:
Но, с другой стороны, мы знаем, что N есть (п+1)-значное число,
начинающееся с цифр а0 и аг.
JV = а0- 10" + aj ¦ 10"-' + а2 • Ю11 + ... + о»,
где можно считать, что не все цифры Д2, .... ап равны нулю (про-
(противоположный случай сводится к рассмотрению двузначных чи-
чисел Л'; см. решение задачи 30). Таким образом, должно иметь место
неравенство
или, что равносильно,
«о<^<*о+1. Г)
Итак, окончательно мы имеем следующие результаты. Искомые
числа N выражаются формулой (*), где 0г?а0г?9, 0^aisg9; так
как Л' целое, а т и т — 1 взаимно просты, то отсюда следует, что
9а0 + ai
простую дробь т ^ можно обратить в десятичную. При этом воз-
возможные значения аа, а.\ и т должны удовлетворять неравенству (**)
(кроме того, отдельно следует присоединить к возможным значе-
значениям N двузначные числа, полученные в решении задачи 30).
101
Теперь остается только последовательно рассмотреть все возможные
значения а0.
1°. а0 = 1. В этом случае неравенство (**) дает
1< i<1« <2
придавая т—1 последовательно значения 5, 6, 7,..., 17 и
рая каждый раз подходящие значения аь мы получаем следукшые
значения N:
N=108; 105; 10 125, 1125, 12 375, 135, 14 625, 1575,
16 875; 121, 132, " 143, 154, 165, 176, 187, 198; 1625,
195; 192, 180 625, 19 125,
к каждому из которых еще можно приписать в конце" произвольное
число нулей.
Аналогично далее получаем; .ь
2°. ао=2:
N=2025, 21375, 225, 23 625, 2475, 25 875; 231, 242,
253, 264, 275, 286, 297; 2925.
3°. ао=3:
N=30 725, 315, 32 625, 3375, 34 875; 341, 352, 363,
374, 385, 396.
4°. ао = 4:
N = 405, 41625, 4275, 43875; 451, 462, 473, 484, 495.
г о г.
N=50 625 5175, 52 875; 561, 572, 583, 594.
N=6075; 61875; 671, 682, 693.
N=781, 792.
N=891.
Значению ао=9 не отвечает ни одно значение N.
Всего, включая результаты задачи 30, мы получаем для числа N
104 значения, к каждому из которых еще можно приписать в кон-
конце произвольное количество нулей.
34. а) Первое решение. Обозначим (m-значное) число,
которое получается, если отбросить у искомого числа первую циф-
цифру 1, через X. В таком случае мы по условию задачи имеем:
откуда
3 107" — 1
Из последнего равенства уже нетрудно определить число X. Для
этого надо число 3-10"'= 30 000... делить на 7, пока в остатке не
102
получится 1. В результате имеем:
3000...О
л.
60
56
40
35
50
49
1
Таким образом, наименьшее возможное значение числа X равно
42 857, а наименьшее значение искомого числа 142 857.
В процессе деления можно было бы не останавливаться на пер-
первой единице, а продолжать деление до следующей, и т. д.; при этом
мы получили бы числа
И2857 142 857 ... 142 857,
h раз
тоже удовлетворяющие условию задачи.
Второе решение. Обозначим вторую цифру искомого чис-
числа через х, третью — через у, и т. д., т. е. предположим, что иско-
искомое число имеет вид \xy...zt (черта наверху означает, что здесь
мы имеем не произведение 1 -х-у ... z-t, а число, составленное из
цифр 1, х, (/,..., 2, /). В таком случае по условию задачи имеем:
\ху .. .zt-3 = xy .. ,zt\.
Отсюда следует, что t = 7 (ни в каком ином случае произведение
слева не оканчивалось бы на 1). Следовательно, цифра десятков
числа, которое стоит справа, равна 7. Но это возможно только, ес-
если произведение z ¦ 3 оканчивается на 7—2 = 5 (два десятка справа
получаются за счет произведения последней цифры искомого числа 7
на 3), т. е. 2 = 5. Теперь мы знаем уже цифру сотен числа справа:
5; поэтому цифра сотен искомого числа должна давать при умно-
умножении на 3 число, оканчивающееся на 5—1=4 A есть цифра де-
десятков произведения 5-3). Вычисления закончатся ,тогда, когда мы
придем к первой цифре 1. Их удобно расположить следующим об-
образом:
1 4 2 8 5 7 42857
. . Х3= 1
4—1=3, 2—0=2, 8-2=6, 5—1=4, 7—2=5 '
(вычисления проводятся справа налево). Таким образом, наи-
наименьшим числом, удовлетворяющим условиям задачи, будет
142857.
Если в наших вычислениях не останавливаться иа первой полу-
полученной единице, а продолжать дальше, то мы получим другие числа,
103
удовлетворяющие условию задачи:
142 857 142857 ... ^42857.
А раз
б) Так как при увеличении такого числа втрое количество
цифр его не увеличилось, то первая цифра числа может быть равна
только 1, 2 или 3.
Как мы видели в решении задачи а), она может быть равна 1.
Покажем теперь, что она не может быть равна 3.
Действительно, если первая цифра искомого числа равна 3, то
вторая цифра, равная первой цифре утроенного данного числа, рав-
равна 9. Но результат умножения на 3 числа, начинающегося с цифр 39,
имеет больше цифр, чем само исходное число; поэтому оно не мо-
может получаться из первоначального числа перенесением первой циф-
цифры в конец.
Предоставляем читателям самостоятельно доказать, что искомые
числа могут начинаться с цифры 2. Наименьшее подобное число
есть 285 714; все такие числа, начинающиеся с цифры 2, имеют вид
285 714 285 714 ... 285 714
h ргз
(доказательство аналогично решению задачи а)).
35. Первое решение. Пусть число X удовлетворяет условиям
задачи: /
^а^ац.. .an-fi и АХ = Ы\п2.. .ап-и
где а\, п2, ..., ап-и 6 — цифры числа X. Так как последняя цифра X
есть 6, то последняя цифра ап_, числа 4Х есть 4; таким образом,
Х = а1а2 ... а„_2 46, что позволяет найти предпоследнюю цифру
а„_2=8 числа 4Х. Записав теперь X в виде ... 846, мы сможем
найти, что ап-з = 3, и т. д. Этот процесс мы будем продолжать до
тех пор, пока не получим в числе 4Х цифры 6, которую можно счи-
считать перенесенной из конца числа X. Так мы находим, что н а и-
меньшее возможное число, удовлетворяющее условию задачи,
есть А"= 153 846; при этом 4А'=615 384.
Второе решение. Так как искомое число X оканчивается
цифрой 6, то его можно записать в виде Х—\0х-{-6, где х— чис-
число, получающееся из X зачеркиванием последней цифры 6. Если
число х является д-значным, то из условия задачи вытекает, что
4-A0х+6)=6-10п+*,
т. е.
2 (юп 4)
39*=6-A0п — 4), или х = - 13 '. (*)
Число 10" —4, очевидно, равно 6, или 96, или 996, или 9996, ...
Наименьшее из таких чисел, кратное 13,— это число 99 996=13-7692;
ему отвечает значение п = Ь. Но в таком случае равенство (*) дает
*=15 384, и, значит, Х= 153846.
36. Если при увеличении числа в 5 раз количество его цифр
не меняется, то искомое число должно, начинаться с цифры 1. При
104
перенесении этой цифры в конец мы получим число, оканчивающее-
оканчивающееся цифрой 1. Но такое число не может делиться на 5.
Так же доказывается, что не существует чисел, увеличивающих-
увеличивающихся в били 8 раз от перестановки начальной цифры в конец.
37. Первое решение. Так как произведение искомого чис-
числа на 2 имеет то же самое число цифр, то первая цифра числа не
может быть больше 4. Так как при перенесении первой цифры в
конец мы должны получить четное число (удвоенное исходное чис-
число), то первая цифра должна быть четной. Поэтому она может быть
равна только 2 или 4.
Теперь, предполагая, что первая цифра искомого числа равна 2
или 4, и обозначая число, получаемое из искомого отбрасыванием
первой цифры, через X, мы получим аналогично первому решению
задачи 34а):
B-10"l + X)-2=10-X+2> откуда X = ^ = =-^ -,
или
Л. mm , v\ о m v , , v 810m —4 210m—l
D-10 -j- л)-2 = 10-Л -|- 4, откуда Л= g = „ •
Но обе полученные формулы для числа X невозможны (целое
число не может быть равно дроби, числитель которой нечетен, а
знаменатель четен).
Второе решение. Как и в первом решении, убеждаемся,
что первая цифра числа может быть равна только 2 или 4. Далее
получаем в принятых ранее обозначениях (см. второе решение за-
задачи 34а)):
2ху ... zt ¦ 2 — ху ... zt2 или 4ху ... zt ¦ 2 = ху ... zti.
В первом случае / может быть равно только 1 или 6 (в про-
противном случае произведение слева не может оканчиваться цифрой
2). Но если t = 1, то мы получаем слева число, не делящееся на 4,
а справа — число, делящееся на 4 (оканчивающееся на 12). Если
t = 6, то, наоборот, слева будет стоять число, делящееся на 4,
а справа —не делящееся на 4 (оканчивающееся на 62).
Во втором случае t может быть равно 2 или 7. Но если / = 2,
то аналогично второму решению задачи 34а) находим, что z = 1
или 6; при г = 1 произведение слева делится на 8 (произведение
на 2 числа, оканчивающегося на 12), а число справа — не делится
на 8 (оканчивается на 124); при 2 = 6 число справа делится на 8,
а произведение слева — только на 4. Аналогично показывается,
что t не может равняться 7.
38. а) Первое решение. Число, увеличивающееся при пе-
перенесении первой цифры в "конец в 7 раз, должно начинаться
с цифры 1 (иначе число, большее первоначального в 7 раз, будет
иметь больше цифр, чем первоначальное). Обозначая далее
m-значное число, полученное из исходного отбрасыванием пер-
первой цифры, через X, мы будем иметь (ср. с решением задачи 34а))
A • 10m + X) .7= \0-Х+ 1,
откуда получаем:
7-10ш—1
Л
105
Но очевидно, что подобное число X ни при каком т не будет
[l' ¦ 10m 1 \
m-значным I ъ > Ют )¦
Аналогично можно доказать, что не существует чисел, увели-
увеличивающихся в 9 раз от перестановки . начальной цифры в конец.
Второе решение. Как в первом решении, показываем,
что искомое число может начинаться только с цифры 1. Далее,
имеем в принятых обозначениях:
\ху ... zt • 7 = ху ... 2/1.
Отсюда следует, что произведение / • 7 оканчивается цифрой I.
Следовательно, t = 3. Подставим это значение /: имеем
\ху ... гЗ • 7 = ху_... г31. Ввиду того что 3-7 = 21, а произве-
произведение числа z3 на 7 оканчивается на 31, произве-
произведение z • 7 должно оканчиваться на 1. Следовательно, z также
равно 3. Таким же образом доказывается, что каждая следующая
(если рассматривать с конца) цифра нашего числа равна 3.
Но начальная цифра должна быть 1. Этого мы никогда достичь
не можем. Поэтому чисел, увеличивающихся в 7 раз от переста-
перестановки начальной цифры в конец, не существует.
Аналогично можно доказать, что не существует чисел, увели-
увеличивающихся от перестановки начальной цифры в конец в 9 раэ.
б) Первое решение. Так как произведение искомого чис-
числа на 4 имеет не больше цифр, чем само число, то первая цифра
числа должна быть не больше 2. Так как при перенесении первой
цифры в конец мы получаем четное число, то первая цифра должна
быть равна 2. Далее, обозначая через X m-значное число, которое
получается из искомого при отбрасывании первой цифры, имеем:
. B-10т + ХL = 10Х + 2, откуда X = —g ,
что невозможно, так как g > 10m (ср. с.первым решением
задачи а)).
Второе решение. Как в первом решении, получаем, что
первая цифра искомого числа может быть только 2. Далее имеем:
2ху ... zt-A=xy ... zt2,
откуда следует, что < = 3 или 8 (t-A оканчивается на 2).
Если бы t равнялось 8, то число справа оканчивалось бы на
82 и не могло бы делиться на 4. Если же t = 3, то
2xy...z3-4=xy...z32,
откуда
2ху ...zO-4
2ху . ..z-A=xy.. .z2.
Таким образом, мы видим, что число 2ху... г обладает тем же
свойством, что и 2ху...zt. Поэтому, применив те же рассуждения,
№
получим г = 3. Продолжая дальше эти вычисления и двигаясь по-
последовательно справа налево, мы получим, что в десятичной записи
нашего числа стоят только цифры 3. В то же время оно начинается
с 2. Значит, такого числа не существует.
39. Первое решение. Обозначим неизвестные пока циф-
цифры искомого числа через х, у, ..., z, t. В таком случае в обозначе-
обозначениях второго решения задачи 34 а) имеем:
7ху ... it ¦ -5- = ху ... ztl,
ху... zt7-3 — 7xy . ..zt.
Теперь сразу ясно, что t=\; после этого мы можем опреде-
определить цифру г A7-3 оканчивается на 51; значит, г=5) и так после-
последовательно с конца находить новые и новые цифры искомого чис-
числа. Вычисление следует прекратить тогда, когда мы придем к циф-
цифре 7. Его удобно расположить следующим образом:
241379310344827586206896551 7241379310344827586206896551
. . 7-3= ;
(вычисления проводятся справа налев.о). Таким образом,'наи-
образом,'наименьшим числом, удовлетворяющим условиям задачи, будет
7 241 379 310 344 827 586 206 896 551.
Если в наших вычислениях не останавливаться на первой се-
семерке, а продолжать дальше, то мы получим другие числа, удов-
удовлетворяющие условию задачи. Все такие числа будут иметь виг
7241379310344S275862C6896551 ... 7241379310344827586206896551.
— -
h раз
Второе решение. Пусть 7xyz ... t — искомое число. Тог-
Тогда при делении его на 3 получится число хуг... П. Запишем это в
виде
7хуг ... t I 3
хуг ... а
Отсюда ясно, что х = 2. Если мы запишем в делимом и част-
частном это значение, то можно будет найти вторую цифру частного;
воспользовавшись ею, можно будет найти третью цифру делимого;
отсюда можно найти третью цифру частного, и т. д. Процесс за-
закончится тогда, когда последняя полученная цифра частного бу-
будет 7, а выписанное делимое разделится на 3 без остатка.
Легко видеть, что это число является искомым, так как если
мы в нем переставим 7 из начала в конец, то получится число,
записанное нами в качестве частного, т. е. втрое меньшее.
Так как до этого места мы по написанным уже цифрам с необ-
необходимостью получали следующую, то указанное число будет наи-
наименьшим, обладающим требуемым свойством. Вычисления можно
расположить так: в верхней строке будем выписывать цифры де-
делимого, во второй - строке — число, при делении которого иа 3
107
получается очередная цифра частного, а в нижней «• эту цифру}
7
7
2
2
12
4
4
4
1
1
11
3
3
23
7
7
27
9
9
9
3
3
3
1
1
1
0
0
10
3
3
13
4
4
14
4
4
24
8
8
8
2
2
22
7
7
17
5
5
25
8
0
20
6
8
18
6
6
26
8
6
6
2
2
2
0
8
28
9
9
19
6
6
16
5
5
15
5
5
5
1
I
21
7
Итак, наименьшее число, обладающее требуемым свойством:
7 241 379 310 344 827 586 206896 551. *
Третье решение. Аналогично первому решению задачи
34 а), используя похожие обозначения, будем иметь:
j
откуда
., 710™-21
Л- 29
Таким образом, задача сводится к определению такого числа
вида 70 000..., которое при делении на 29 дает в остатке 21. Пре-
Предоставляем читателю самому проверить, что при этом мы прихо-
приходим к тому же результату, что и в первых двух решениях.
Примечание. Аналогично можно решить следующую за-
задачу:
Найти наименьшее число, начинающееся с известной цифры,
которое уменьшается в 3 раза от перестановки первой цифры в ко-
конец. Для того чтобы можно было искать и решения, начинающиеся
с цифр 1 и 2, будем считать, что 0 может стоять в начале числа.
Если в начале числа стоит цифра 0. то легко убедиться, что
требуемым свойством обладает лишь число 0. Выпишем остальные
числа, обладающие этим свойством:
1 034 482 7.58 620 689 655 172 413 793
2 068 965 517 241 379 310 344 827 586
3 103 448 275 862 068 965 517 241 379
4 137 931 034 482 758 620 689 655 172
5 172-413 793 103 448 275 862 068 965
6 206 896 551 724 137 931 034 482 758
8 275 862 068 965 517 241 379 310 344
9 310 344 827 586 206 896 551 724 137
Таким же способом можно решить задачу:
Найти наименьшее целое число, начинающееся заданной циф-
цифрой а и уменьшающееся от перестановки этой цифры в конец
в / раз. Найти все такие числа.
40. а) По условию задачи имеем!
ху ...zt • а = tz... ух,
где а есть одно из чисел 2, 3, 5, 6, 7 или 8.
Если а = 5, то х должно равняться 1, так как иначе число
ху ... zt ¦ Ъ будет иметь больше цифр, чем ху ...zt (случай х = О
108
исключаем, так Как в этом случае у.. .zt = 2 • tz... у, т. е. мы
приходим к той же задаче с а=»2). Но число tz...y\ не может
делиться на 5. Аналогично доказываем, что а не может быть рав-
равно 6 или 8.
Если а = 7, то х тоже должно равняться 1. Но в таком слу-
случае t должно равняться трем,— иначе \у ...zt • 7 не будет оканчи-
оканчиваться цифрой 1. А равенство \у ... гЗ • 7 =3г ... г/1,, очевидно, яв-
является абсурдным (левая часть равенства явно больше правой).
Если а = 2, то х не может быть больше 4. А так как число
tz...yx в этом случае четно, то х должно быть разно 2 или 4.
Но при х = 4 цифра / (первая цифра числа 4г/... zt ¦ 2) может
быть равна только 8 или 9, а ни 4</... г8 ¦ 2, ни 4г/... г9 • 2 не
могут оканчиваться на 4. Если х = 2, то t (первая цифра числа
2у ... zt ¦ 2) может быть равна только 4 или 5; но ни 2у ... z4 ¦ 2,
ни 2г/... г5 • 2 не могут оканчиваться на 2.
Наконец, если а = 3, то х не может быть больше 3. Если х —
= 1, то f должно быть равно 7 (<-3 оканчивается на 1); если х —
= 2, то / должно быть равно 4; если х = 3, то / должно быть рав-
равно 1. Но в первом случае tz...yx больше, чем xy...zt-З, а во
втором и в третьем — меньше.
б) Пусть ху ... zt — такое число! тогда
ху ... zt • 4 = tz ... ух.
Так, как xy...zt-4 имеет то же число цифр, что и xy...zt, то х
может быть равен лишь 0, 1 или 2; так как tz... ух делится на 4,
то х должен быть четным. Следовательно, х может быть равен О
или 2.
Пусть х = 0. Очевидно, что число 0 обладает требуемым свой-
свойством. Будем допускать десятичные записи, в начале которых мо-
жет стоять один или несколько нулей. Тогда мы имеем у... zt-4 =
= tz ... уО, откуда / = 0 (нбо t < 4) н у ... г-4 = z... у: если
число обладает требуемым свойством и начинается нулем, то оно
оканчивается также нулем, и число, которое получится, если мы за-
зачеркнем первый и последний нули, также будет обладать требуе-
требуемым свойством.
Поэтому достаточно рассмотреть случай х = 2. Тогда имеем
2у ... zt-4 = tz ... у2. Ввиду того что 2-4 = 8, / может быть рав-
равно лишь 8 или 9. Но произведение t-4 оканчивается на 2; следова-
следовательно, /= 8, т. е. можно написать 2у ... z8-4 = 8z ... у2. Так как
23 • 4 > 90, у может быть равно лишь 0, 1 или 2; но при любом г
в произведении г8-4 цифра десятков нечетная. Следовательно, у =
=• 1. Так как нам известны две последние цифры произведения
2(/... г8 • 4, то для предпоследней цифры z этого числа остаются
лишь две возможности: г может быть равно лишь 2 или 7. Но 21Х
X 4 > 82, значит, г =. 7. _____
Итак, наше число, имеет вид 21 ... 78. Если оно четырехзначно,
то мы получаем число 2178, удовлетворяющее условию задачи. Рас-
Рассмотрим теперь случай, когда число цифр рассматриваемого числа
109
больше 4~ В этом случае имеем:
2luv ...rs78'-4 = &7sr... vu\2,
или после очевидных преобразований
84 • 10"+* + 312 + uv ... rsOO ¦ 4 = 87- 10"+г + 12 + sr... vuOO,
uv ... rs ¦ 4 + 3 = 3sr ... vu.
Так как число uv...rs при умножении на 4 дает число, имею-
имеющее больше цифр, чем оно само, и при этом начинающееся с циф-
цифры 3 (или, в крайнем случае, с комбинации цифр 29), то и может
быть равно только 9, 8 или 7. Так как 3sr... vu нечетно, то и мо-
может быть равно только 9 или 7. Рассмотрим эти случаи последова-
последовательно.
1°. и = 9. В таком случае, очевидно, получаем:
9у .../-5-4 + 3 = 3sr...v9,
'откуда следует, что s = 9 (s • 4 оканчивается на 6; если s = 4, то
34г ... v9 меньше, чем 9v ... г АЛ + 3) и
9о...г9-4 + 3 = 39/-...У9, v .. .г-А + 3 = Зг ... v,
т. е. число, получаемое из uv...rs отбрасыванием цифры 9 в нача-
начале и в конце, обладает тем же свойством, что и само число uv... rs.
В частности, uv...rs может равняться 9, 99, 999, и т. д.; при этом
мы получаем числа
21978, 219 978, 2 199 978, ...,
удовлетворяющие условию задачи.
2°. и = 7. В этом случае имеем:
7у ...rs-4 + З = 3sr...jj7,
откуда аналогично тому, как мы рассуждали в начале решения зада-
задачи, легко получить, что s = 1; v = 8; г «=¦ 2, т. е. что число uv .. .rs
имеет вид 78 ... 21 и что число, которое получается из uv ... rs отбра-
отбрасыванием 78 в начале и 21 в конце, в 4 раза меньше своего обра-
обращенного.
Отсюда видно, что если число, в 4 раза меньшее своего обра-
обращенного, отлично от чисел ряда
О, 2178, 21 978, 219 978 2199... 978, 2199 ... 9978 (*)
k цифр №+1) цифр
то в начале и в конце его стоит одна и та же последовательность
цифр, составляющих одно из чисел этого ряда, и если зачеркнуть
эти цифры (и в начале и в конце), то получится также число, в
4 раза меньшее своего, обращенного, или, как в случае числа
21 782 178, при этом будут зачеркнуты все цифры нашего числа.
Поэтому десятичная запись любого числа, в 4 раза меньшего
своего обращенного, имеет вид
Р1Рг,..Рп-1РпРп-1...Р3Р1
¦110
или же
PiPl...Pn-tPnPnPn-l.-..РгРи
где Ри />2, • •., Рп — последовательности цифр, составляющие какие-
либо числа из написанного выше ряда (*)-.Таковы, например, числа:
2 197 821 978, 2 199 782 178 219 978,
21 978 021 997 800 219 978 021 978, 02 199 999 780
(последнее число следует считать решением задачи, если условиться,
что можно в начале десятичной записи числа ставить 0).
. Аналогично доказывается, что все числа, в 9 раз меньшие свое-
своего обращенного, получаются из чисел ряда
0, 1089, 10 989, 109 989 1099... 989, 1099 ... 9989, ...
h раз (&+1) раз
таким же образом, как и числа, в 4 раза меньшие своего обращен-
обращенного, получаются из чисел ряда (*).
41. а) Обозначим число, составленное первыми тремя цифрами
искомого числа N, через р, а число, образуемое тремя последними
цифрами числа N, — через q. В таком случае условие задачи даст
6A000p+?) («=6iV),
откуда
A000? + р) — A000/? + ?) =999 (q — р) — 5jV,
т. е. N делится на 999.
Далее, р + q = A000/? + q) — 999/> = N — 999/7, откуда следу-
следует, что р + q тоже делится на 999. Но р и q — трехзначные числа,
которые, очевидно, не могут оба равняться 999; следовательно,
р + q = 999.
Теперь без труда находим:
(\QOOq + p) + (lOOQp + q) = 1001 (р + q) =1N
и, значит,
7jV = 999 999, N = 142 857.
б) Совершенно аналогично решению задачи а), обозначая че-
через р число, образуемое первыми четырьмя цифрами искомого чис-
числа N, а через q — число, образуемое последними четырьмя цифрами,
находим:
IN — 10 001 (p + q) = 99 999 999,
что невозможно при целом N (ибо 9Э 999 999 не делится на 7).
42. Пусть х — число, удовлетворяющее этому условию. Так ка-к
6х, так же как и х, — шестизначное число, то первая цифра деся-
десятичной записи числа х равна 1. Поэтому:
1) первые цифры десятичной записи чисел х, 2xt Зх, Ах, Ьх и блг
все различны, следовательно, составляют полный набор цифр, участ-
участвующих в десятичной записи числа х\.
2) все цифры в десятичной записи числа х различны между
собой.
111
Среди *тих цифр нет 0, поэтому последняя цифра числа х не-
нечетна (иначе Бх оканчивается нулем) и отлична от 5 (иначе 2х
оканчивается нулем). Вследствие этого последние цифры десятич-
десятичной записи чисел х, 2х, Зх, 4х, Ьх и 6х все различны, а значит, так-
также составляют полный набор цифр, участвующих в десятичной за-
записи числа х. Поэтому среди них есть 1. Оканчиваться на 1 мо-
может лишь число Зх, так как 2х, 4х и Ьх оканчиваются на четные
цифры, 5х оканчивается на 5, а в десятичной записи х уже есть 1
(первая цифра). Следовательно, х оканчивается цифрой 7, 2х —
цифрой 4, Зх — цифрой 1, 4х — цифрой 8, 5а; — цифрой 5 и Ьх — циф-
цифрой 2. Так как первые цифры этих чисел — цифры того же набора,
расположенные в возрастающем порядке, то можно написать:
х -1 = 1****7,
*.2 = 2****4,
х- 3 = 4**** 1,
л>4 = 5****8,
х-5 = 7****5,
х- 6=. 8****2
(звездочки стоят на месте неизвестных нам пока цифр).
Отметим теперь, что в выписанной таблице не только в каж-
каждой строке стоят в каком-то порядке шесть разных цифр 1, 2, 4, 5,
7 и 8, но и в каждом столбце стоят в каком-то порядке те же са-
самые шесть разных цифр. Действительно, предположим, например,
что в числах х-2 и х-5 на третьем месте стоит одна и та же циф-
цифра а (а может иметь одно из двух значений, не занятых первыми и
последними цифрами рассматриваемых двух чисел). В таком случае
разность х-5—х-2 ¦= х-3 будет представлять собой шестизначное
число, в десятичной записи которого на третьем месте стоит циф-
цифра 0 илн.цифра 9 (это следует из правила вычитания многознач-
многозначных чисел «столбиком»). Но это невозможно, так как мы знаем,
что число х-3 записывается цифрами 1, 2, 4, 5, 7 и 8.
Сложим теперь числа
х, 1 = 1 * * * * 7,
х-2 = 2****4,
х-3 = 4****1,
х-4 = 5****8,
д>5 = 7****5,
х-6= 8****2
«столбиком», учитывая, что сумма цифр каждого столбца равна 1 +
+ 2 + 4 + 5 + 7 + 8 = 27. Мы получим:
х-21 =«2 999 997,
или х = 142 857. Это и есть искомое число; действительно,
х = 142857,
2х = 285714,
Зх = 428571,
4х = 571428,
5х = 714285,
6* = 857142.
112
43. Пусть N = xyz = 100* + 10(/ + z — искомое число, х, у,
г — цифры числа. Перестановкам» цифр из N получаются числа
N\ = yxz = IOOi/ + 10* + z, ..., N5 = Тух = lOOz+Юг/ + *. Сумма
N + Nt+ ... +jV5 всех этих чисел должна равняться ушестеренному
числу N, откуда без труда получаем:
B-100+ 2-10+ 2) (х + у + г) = 6A00* + Юу + г)
(ибо в шестерке чисел Л', Nu N2, iV3, Nt, N5 каждая из цифр, на-
например, х, 2 раза встречается на первом месте, 2 раза — на втором
и 2 раза — на третьем), или
37 (* + у + z) = 100а; + \0у + z,
т. е.
63* = 27 у + 36г.
Сокращая обе части на 9, находим:
7х = Зу + 4г, или 7(х — у) = 4(г — у).
Но разности х — у и z — у по абсолютной величине не превос-
превосходят 9, откуда вытекает, что последнее равенство возможно
лишь, если
х — у = 0, z — у = 0, или * — у = 4, г —г/=7, или
х — у = —4, г — у = —7.
При этом если г — у = 7, то г = 9, 8 или 7; если г — у = — 7, то
у = 9, 8 или 7; поэтому (отбрасывая сомнительное «решение» jV =»
= 000) получаем 15 возможных значений числа N:
N = 111, 222, 333, 444, 555, 666, 777, 888, 999, 407,
518, 629, 370, 481 или 592.
44. Ясно, что числа А к А' должны быть 10-значными; пусть
А = aiCa9a8... fli и А' = fl10aga8... ai (a10, «9, a8, ..., а\ — последова-
последовательные цифры числаЛ, а a'i0, а9 а,— цифры числа А'), Пред-
Представим себе процесс сложения «столбиком» чисел А и А'. Ясно,
что в сумме может получиться число L010 = 10 000 000 000 лишь в
том случае, если существует такой номер i (где 0 ^ i ^ 9), что
aa + а\ = 0, аг + а'2 = 0 а{ + а\ = 0,
(если i = 9, то равных девяти сумм о^2~^ ai+z> ai+3 + fli+3' •••
просто нет, а если i = 0, то отсутствуют равные нулю суммы
Oi + Op ..., Oj + a,'). Сложим теперь все суммы (*); мы получим
(а1 + а'1) + (аг+а'2)+ ...+ [а10 + а[0) = 10 + 9(9-»).
А так как а\, аг, .. ., а,0 и а(; а'2 о4 0 — это одниите же циф-
цифры (только взятые в разном порядке), то в правой части последнего
8 Д. О. Шклярский и др, ИЗ
равенства стоит четное число 2(а\ + а2 4- • • • 4- ою); поэтому, чис-
число 10 4-9(9 — /) тоже чегло. Отсюда следует, что число / — обяза-
обязательно нечетно, т. е. i не может быть нулем {i = 1, или 3, или
5, ...); поэтому ai + aj = 0, т. е. а^= а, = 0. Но это и означает,
что числа А и А' делятся на 10.
45. Представим себе выписанные друг под другом числа М и
N и процесс сложения «столбиком» этих чисел; при этом пусть все
цифры полученной суммы М + N — нечетные. Отеюда следует, что
сумма цифр последнего столбика нечетна; а тогда и сумма цифр
первого столбика, отличающегося от последнего столбца лишь по-
порядком цифр, также нечетна. Но это возможно лишь в том случае,
если при сложении цифр 2-го столбца из этого столбца в первый не
переносится единица, т. е. если сумма цифр 2-го (а значит — и пред-
предпоследнего) столбца меньше 10. Поэтому из предпоследнего столбца
также не переносится в 3-й от конца столбец единица: ведь случай,
когда сумма цифр предпоследнего столбца равна 9 (т. е. < 10), но
единица из этого столбца в следующий все же переносится за счет
заимствованной из последнего столбца единицы, явно невозможен,
ибо в этом случае предпоследняя цифра суммы М + N будет рав-
равна 0, т. е. окажется четной. Таким образом, два последних (и
два первых) столбца пашей суммы никак не влияют на остальные
цифры суммы М 4- N\ поэтому мы можем отбросить в числах М
и iV по две первые и две последние цифры — и продолжать наши
рассмотрения, исходя уже из «усеченных» A3-значных) чисел
М, и /V,.
Составим теперь сумму Mi 4- N[ чисел Mi и Ny\ при этом,
как и выше, можно показать, что если все цифры числа Mi + iVi
нечетные, то при сложении столбиком 13-значных чисел М\ и Ni
два последних и два первых столбца не влияют на «средние» циф-
цифры суммы М, + N, (на все цифры, кроме двух первых и двух
последних). Поэтому мы можем «усечь» также и числа Mi и Nu
отбросив в каждом из них по две последние и по две первые
цифры и перейдя, таким образом, к 9-значным числам М2 и N2-
С числами М2 и N2 мы затем производим ту же операцию, пере-
переходя к 5-значным числам Мг и /V3; наконец, мы таким же образом
«усекаем» числа М3 и N%, переходя к (однозначным!) числам М«
и М,, записываемым одной («средней») цифрой чисел М nN, Но ясно,
что цифры (точнее — цифра!) числа Af4 + iV4 = 2М4 не могут быть
нечетными (ибо число 2М4 четно!); этим и устанавливается, что
также и все цифры суммы М -\- N не могут быть нечетными.
Примечание. Ясно, что проведенное рассуждение имеет
общий характер, сохраняя силу для любых двух «перевернутых»
чисел М и N, число цифр в каждом из которых имеет вид- Аи -\- 1,
т. е. дает при делении на 4 остаток 1. Если же число цифр числа
М (и «перевернутого» числа N) не имеет вида 4п + 1, то сумма
М -{¦ N может записываться одними лишь нечетными цифрами
(докажите это!).
46. а) л3 — п = (п~ \)п{п -f 1)> а из трех последовательных
целых чисел одно обязательно делится на 3.
б) пъ — п = п(п—1) (п + 1) (rfi + 1). Если целое число окан-
оканчивается одной из цифр 0, 1, 4, 5, 6 или 9, то один из первых
трех множителей делится на 5. Если п оканчивается одной из
114
цифр 2, 3, 7 или 8, то л2 оканчивается на 4 или 9 и л2 + 1 делится
на 5.
в) л7 — л = п(п - I) (п + I) (п> — п + \)(п2+п+ 1). Если п
делится на 7 или дает при делении на 7 остаток 1 или 6, то один из
первых трех множителей делится на 7. Если п дает при делении на 7
остаток 2 (« = 7? + 2), то п2 дает при делении на 7 остаток 4
(л2 = 49?2 + 286 + 4) и, следовательно, /г2 + п + 1 делится иа 7.
Точно так же показывается, что если п дает при делении на 7
остаток 4, то п2 + /г + 1 делится на 7, а если л дает при делении
на 7 остаток 3 или 5, то п2 — п + 1 делится на 7.
г) пи — п = п(п— 1)(п + 1)(л8 + л6 + /г4 + /г2 + 1). Если /г
делится на 11 или дает при делении на 11 остаток 1 или 10,
то один из первых трех множителей делится на 11. Если л дает
при делении на 11 остаток 2 или9(л = 116 ±2), то п2 дает при де-
делении на 11 остаток 4 (пг = \2\k2 ± 446 + 4, л4— остаток
5= 16—11, л6 —остаток 9 = 20— 11 (л6 = л4 • л2 = A1*, + 5)Х
XA1 *2 + 4) = \2\kxk2+ llD*i +5*2) +20) и л8 —остаток 3 =
= 25 — 22; отсюда следует, что л8 + л6 + л4 + п2 + 1 делится на 11.
Точно так же показывается, что л8 + л6 + л4 + и2 + 1 делится
.на 11, если л дает при делении на 11 остаток ±3, ±4 или ±5.
Д) пп-п = п(п-\)(п+ 1)(п2+1)(п4-п2 + 1)(п< + п2+1).
Аналогично решению предыдущих задач замечаем, что если и де-
делится на 13 или дает при делении на 13 остаток ±1, то один
из первых трех-множителей делится на 13; если л дает при делении
на 13 остаток ±5, то п2 + 1 делится на 13; если п дает при деле-
делении на 13 остаток ±2 или ±6, то п4 — п2 + 1 делится на 13; если
п дает при делении на 13 остаток ±3 и^и ±4, то п* + п2 + 1
делится на 13.
47. а) Разность одинаковых четных степеней делится на сумму
оснований; поэтому З6" — 26" = 272п — 82" делится на 27 + 8 = 35.
б) Нетрудно проверить, что
„s_5/if+ 4« = п(п2-1)(п2-4) = (л_2)(л—1)л(л+1)(л + 2).
Но из пяти последовательных целых чисел одно наверное делится
на 5, по крайней мере одно на 3 и по крайней мере два на 2,
причем из этих двух последних чисел одно наверное делится на 4.
Таким образом, произведение пяти последова-тельных целых чисел
всегда делится на 5 • 3 • 2 • 4 = 120 (ср. с решением задачи 46а)).
в) Воспользуемся тождеством
п2 + 2,п + 5 = (п + 7) (п - 4) + 33.
Для того чтобы это выражение делилось на 11, необходимо,
чтобы (п + 7)(п —4) делилось на 11. Но так как (п + 7) — (п —
— 4) = 11, то оба сомножителя делятся или не делятся на 11 одно-
одновременно. Поэтому если (и + 7) (п — 4) делится на 11, то оно делит-
делится и на 121 и, следовательно, (и+ 7) (л —4) +33 не может делить-
делиться на 121.
48. а) Нетрудно проверить, что
56 786 730 = 2 ¦ 3- 5 • 7 ¦ 11 • 13- 31 -61;
таким образом, остается доказать, что наше выражение делится
на каждый из этих простых делителей. Если тип оба нечетны,
то тт — пт — четио; следовательно, mn(mw — л60) обязательно
• четно (делится на 2). Далее из результата задачи 46 следует, что
8* . 115
если k равно 3, 5, 7, 11 или 13 и л ие делится на k, то разность
nh~l — 1 обязательно будет делиться на k. Отсюда, в частности,
вытекает, что если т и п не делятся на 3, то тт— 1 = (т30J— 1
и я60— 1 = (я30J—1 делятся на 3, т. е. т60 и га60 дают при деле-
делении иа 3 один и тот же остаток 1; следовательно, если тп не де-
. лится на 3, то тт — пв0 .делится на 3 и, значит, произведение
mn(mso — л60) делится на 3 во всех- случаях. Точно так же дока-
доказывается, что разность
тт — лм = (mi3)< — (л15L = (т|0)«— (л'0)« =
= (т6I0 — (л«)|0 = (т5I2— (л5I2
делится на 5, если ни т., ни п не делятся на 5; делится иа 7,
если ни т, ни /г не делятся на 7; делится на 11, если ни т, ни л
не делятся на 11; делится на 13, если ни т, ни л не делятся на 13.
Таким образом, мы доказали, что тп(тт — л60) всегда делится
на 2 -3 - 5-7- И • 13.
Аналогично показывается, что выражение тп(тьи — «60) де-
делится на 31 и на 61 (так как л31 — л при всяком целом л делится
на 31 и я61— п при всяком целом п делится на 61: см. ниже зада-
задачу 340).
б) Представим данное выражение в виде
(т — 2л) (т — п)(т + п) (т + 2л) (т + Зл).
При л Ф 0 все пять сомножителей этого произведения попарно
различны. Между тем число 33 нельзя разложить более чем на че-
четыре различных целых множителя (разложение на четыре множи-
множителя возможно несколькими способами, например, 33= (—11) X
ХЗ • 1 • (— 1) или 33= 11 • (-3) • 1 ¦ (—1)).
При /7 = 0 наше выражение есть ть и не равно 33 ни при
каком целом т.
49. Заметим, прежде всего, что 323 = 17 ¦ 19; таким образом,
нам надо выяснить, когда выписанное в условии задачи число N
делится и на 17, и иа 19. Пусть сначала число л = 26— четное.
Ясно, что 20" — 3" при всех л делится на 20—3= 17; с другой
стороны, 16"— 1" = 162ft~ l2ft'делится на 162 — I2 = A6 — 1) X
X A6 + 1) = 15 • 17, а значит, при четном п также и число 16" — 1
делится на 17, т. е. в этом случае N = B0"—3") + A6П — I)
делится на 17. С другой стороны, число 20ll — 1 при всех л делит-
делится на 20—1 = 19, а число 16" — 3" = 162* — 32к делится на 162—
_32= A6 —3)A6 + 3) = 19- 13, т. е. также делится на 19; поэ-
поэтому и число jV == B0" — 1) + A6" — 3") делится на 19. Таким
образом, при всех четных л число N на 323 делится. С другой
стороны, если iV = 2?-fl нечетно, то число 20"—3" по-преж-
по-прежнему делится на 17; поскольку же 162/l — 1 делится на .17, то 162Й
при делении на 17 дает остаток 1, а значит, число 162*+ ' =
=> 162* • 16 при делении на 17 дает остаток 1 ¦ 16 = 16; поэтому
число 16П — 1 = 162* + ' — 1 на 17 не делится (оно дает при
делении на 17 остаток 15). Таким образом, при п нечетном число
jV ие делится уже на, 17—и тем более оно не делится на 323.
Итак, число jV делится на 323 в том и только в том случае,
когда л — четное:
50. Если число п оканчивается, соотвественно, цифрой 0, 1, 2,
3, 4, 5, 6, 7, 8, 9, то л2 оканчивается цифрой 0, 1, 4, 9, 6, 5, 6, 9, 4,
116
1 и, значит, га2 + п оканчивается на 0, 2, 6, 2, О, О, 2, 6, 2, 0, а чис-
число п2 + п + 1 оканчивается цифрой 1, 3, 7, 3, 1, 1, 3, 7, 3, 1. Таким
образом, число п2 + /г + 1 никогда не кончается цифрой 0 или 5,
т. е. никогда ие делится на 5 (а значит,' не делится и на 1955).
51. Всякое целое число или делится на 5 или может быть пред-
представлено в одном из следующих четырех видов 5k + 1, 5k + 2, 5k — 2
или 5* — 1. Если число делится на 5, то его сотая степень, очевид-
очевидно, делится на 53 «= 125. Далее, по формуле бинома Ньютона по-
получим:
100 99
Ek ± 1)юо E*I00± +
где все невыписанные члены содержат множитель 5k в степени,
не меньшей 3, и, следовательно, делятся на 125. Аналогично
100-99
E* + 2I00 = E6I00± ... + ь2 E6J-298 ± 100-56-2"+ 2100.
100-99
Но ¦ j.-g- EkJ = 125-990&2 и 100-56 = 125-46 делятся на 125. Что
касается числа 2100, то его можно представить в виде
50-49
E— IM0 = 550— ... +-J7J--5-50-5 + 1,
откуда видно, что оно дает при делении на 125 остаток 1.
Итак, сотая степень числа, делящегося на 5, делится на 125; со-
сотая степень числа, не делящегося на 5, дает при делении на 125
остаток 1.
52. Нам надо доказать, что если N взаимно просто с 10, то
Л1— N = N(Nm— 1) делится на 1000, т. е. что Л"™—1 делится
на 1С00. Прежде всего совершенно ясно, что если N нечетно, "то
Nm—l — (iV50 +l)(iV25+ 1) (N25 — 1) делится на 8. Далее, из ре-
результата предыдущей задачи следует, что если N не делится на 5, то
Л0— 1 делится на 125. Таким образом, мы видим, что действитель-
действительно Л0—1 при N, взаимно простом с 10, делится на 8-125= 1000.
53. Пусть N — искомое число; тогда, в частности, N1 — N окан-
оканчивается тремя нулями, т. е. делится на 1000. Так как jV2— N =
= N(N— 1), a iV и N —\ —взаимно простые числа, то это возмож-
возможно лишь в том случае, когда одно из этих чисел делится на 8, а вто-
второе— на 125 (на 1000 ни одно из этих чисел само делиться не мо-
может, так как N трехзначно).
Если N есть трехзначное число, делящееся на 125, то jV—1, как
легко проверить, будет делиться на 8, лишь если N = 625, N — 1 =
= 624. Так же легко проверяется, что если N—1 есть трехзначное
число, делящееся на 125, то N будет делиться на 8 лишь при jV —
— 1 = 375, N = 376.
Заметим теперь, что так как Л-' — 1 при любом целом k гэ= 2
делится без остатка на N — 1, то Nh — N = N(NK~{ — 1) при любом
целом k будет делиться без остатка на N(N— 1) = iV2 — jV; поэтому
если jV2 — jV оканчивается тремя нулями, то и Nh—N при любом
целом 6^2 будет оканчиваться тремя нулями, т. е. jV* будет окан-
оканчиваться теми же тремя цифрами, что и N. Отсюда вытекает,
что числа 625 и 376 (и только они) удовлетворяют условиям
задачи.
117
54. Найдем две последние цифры числа jV20. Число Л'20 делится
на 4 (ибо N четно). Далее, число N не делится на 5 (иначе оно де-
делилось бы на 10) и, значит, представимо в виде 5k ± 1 или в виде
5k ±2 (ср. с решением задачи 51). Но число
20-19
EЛ± 1J0= E6J0±20Efc)ls+ ... + ~yifEk)* ± 20-5t + 1
дает при делении на 25 остаток 1, а число
E6±2J0 = E6J0±20 E6I9-2+ ...
20-19
дает при делении на 25 тот же остаток, что и число 220 = B10J =
= A024J = A025—IJ, т. е. тоже остаток 1. Из того, что число
дг20 дает ПрИ делении на 25 остаток 1, следует, что последними дву-
двумя цифрами этого числа могут быть лишь цифры 01, 26, 51 или 76.
Учитывая еще, что iV2Q должно делиться на 4, получим, что двумя
последними цифрами этого числа могут быть лишь цифры 76. Итак,
цифрой десятков числа iV20 будет цифра 7.
Найдем теперь три последние цифры числа jV200. Число Л™> де-
делится на 8. Далее, так как jV взаимно просто с 5, то Л0 дает при
делении на 125 остаток 1 (см. решение задачи 51): Л0 = 1256+ 1.
Но тогда и .V200 = A256 + IJ = 125262 + 2506 + 1 дает при делении
на 125 остаток 1. Следовательно, jV200 может оканчиваться цифрами
126, 251, 376, 501, 626, 751 или 876; но так как jV200 делится на 8, то
оно должно оканчиваться цифрами 376. Итак, цифра сотен числа
iV200 равна 3.
Примечание. Нетрудно видеть, что уже число Л-0 обяза-
обязательно оканчивается тремя цифрами 376.
п (п -\- 1)
55. Сумма 1 + 2 + 3 + ... +п равна g •' следовательно,
нам надо доказать, 'что если к нечетно, то Sj, = \h + 2h + 3k + ... +
, ь n(n+\)
+ nh делится на —g •
Отметим прежде всего, что при k нечетном ак + й* делится на
а + Ь. Рассмотрим теперь отдельно два случая:
А. Чргсло п четно. В таком случае сумма S/, делится на я + I,
так как каждая из сумм
i*j-»h Ф j_ си пк ih,(n *\Ь (jL\ki(n , Ah
I -f- n , l -{- (n— i) , 6 -f- (и — <2) , ..., -д- I + "o" + 1 I
V l 1 \z I
делится на
сумма Sh делится также на -тр, ибо 1* + (п—1)*-, 2*+ (я —2)\
In \& In \k I п \k п
3" + (n —3)*, .. ->l <p—1 1 + \~2 + ' 1 • 1~) >л* все делятся на^".
118
Б. Число « нечетно. В этом случае сумма S* делится на —~—,
так как 1* + я\ 2*+(я—1)\ 3* + (п — 2)\ ..., (^Г^ )" +
/я+1
' 1*~2—
л + 1 о
все делятся на ~~2—> ^* делится также на п,
так как 1* * (л- 1)\ 2й + (п-2)*, 3* + (я_з)\ • ¦-
—2—1 ,nh все делятся на л.
58. Пусть
N = а„ ¦ 10" + ап-\ ¦ 10"-' + а„_2 • 10" + ... + а, • 10 + а0
— данное число (ап, ап-\, ап-2 а,, а0 — цифры числа, которые
могут принимать значения 0, 1, 2, ..., 9).
Вычтем из N число
М=аа — а\ +а2 — аг-\-,., ±а„,
представляющее собой алгебраическую сумму цифр чис-
числа jV, взятых с чередующимися знаками. Группируя
подходящим образом члены, мы получим число
N — M = й,A0+ 1) +а2A02- 1) +о3A03+ 1) +
+ а4(!04— 1) +... + апA0" ± 1),
делящееся на 11, ибо каждое его слагаемое делится на II. (Из то-
того, что при перемножении чисел остатки, даваемые ими при деле-
делении на некоторое число, перемножаются, легко вывести, что
Ю* =A1 — 1)"
дает при делении на 11 остаток — 1 при k нечетном и остаток + 1
при k четном.) Таким образом, разность N — M делится на 11, т. е.
число N делится или не делится на 11 одновремен-
одновременно с ч и с л о м М.
57. Число 15 дает при делении на 7 остаток 1. Отсюда следует,
что и
152= G-2+1). G-2+1) = 7л,+ 1
дает при делении на 7 остаток 1,
153= 152-15=Gл1 + 1) • G-2 + 1) = 7п2+ 1
дает при делении на 7 остаток 1, и вообще любая степень числа 15
при делении на 7 дает остаток 1. Если мы теперь вычтем из задан-
заданного нам числа сумму 1+2 + 3 + 4 + ... + 14 = 105, то, сгруппи-
сгруппировав соответствующим образом члены, мы получим:
13A5— 1) + 12A52—1) +
-1) + 1A5"—1)_,
т. е. число, делящееся на 7. Но из того,- что разность заданного
числа и числа 105 = 7 • 15 -делится на 7, следует, что исходное
число тоже делится на 7.
119
58. Пусть К есть я-значное число. Среди (п + 2)-значных
чисел, начинающихся цифрами 1, 0 (т. е. среди чисел вида
JOciOj... а„, где 1, 0, щ, ..., а„—цифры числа), всегда найдется,
по крайней мере, одно, делящееся на К. Пусть это число есть
104>162 ... Ьп- Тогда, по условию, числа й)Й2 ... Ь„\0иЬФ2 ... Ьп01
оба делятся на К. Их разность равна 9 и также делится на К.
Но у 9 делителями служат лишь 1, 3 и 9, откуда и следует наше
утверждение.
59. Ясно, что d = 333 ... 33 = 3111 ... 11 = Ъп\ поэтому ис-
100 троек 100 единиц
комое число N = 1111 ... 11 должно делиться без остатка на чис-
h единиц
ла п и 3 (я не делится на 3, ибо сумма цифр числа п, равная
100, не делится на 3). Но если число k= \00q + г, где г < 100
(но г Js 0), то, очевидно, N = 11 ... 1100 ... 00 + И ... 11 = Af + У?,
100<7 единиц г нулей г единиц
где /?= 11.. .11 , а М = 11. ..1100.. .00 делится на п (для
г единиц ' 1 OOqr единиц г нулей
того чтобы убедиться в этом, достаточно представить себе про-
' цесс деления «углом» М на п). Таким образом, N делится на п
в том и только в том случае, когда R = 0, т. е. когда г — 0,
и, значит, k делится на 100.
Теперь, если 6=1009, то сумма цифр числа jV равна 100<?; она
делится на 3 (а значит — и N делится на 3) в том и только в том
случае, если q делится на 3. Поэтому, наименьшее число N = 111 ... И,
к единиц
делящееся на d, будет состоять из 300 единиц.
60. Поскольку а, очевидно, число четное, то нам надо только
доказать, что произведение аА делится на 3. Так как последняя циф-
цифра числа 2*+' = 2iV та же, что и у числа 2а (где а — последняя
цифра iV), то, последовательно умножая степени двойки еще на 2
(т. е. последовательно увеличивая показатель степени), мы найдем,
что последние цифры чисел ряда 2' — 2, 22 = 4, 23 = 8, 2* =16,
25 = 32, ... образуют следующую периодически повторяющуюся
последовательность:
2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6, ...
С другой-стороны, если 2* = N дает при делении на 3 остаток 1,
то число 2h+1 = 2N дает при делении на 3 остаток 2, а если jV =
- = 3/ + 2, то число 2"+1 = 2iV имеет вид 3-B/)+4 = 3- B/ + 1)+ I,
т. е. дает при делении на 3 остаток 1; поэтому та же последова-
последовательность степеней двойки дает при делении на 3 следующие чере-
чередующиеся остатки:
2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, ...
Таким образом, если число N кончается цифрой 2 или 8 (если
а — 2 или а = 8), то N при делении на 3 дает остаток 2, а если
а = 4, то N при делении на 3 дает остаток 1 (случай же, когда
о = 6, нам вообще не интересен, ибо здесь произведение аА = 6Л
наверняка будет делиться на 6). Отсюда следует, что во всех этих
трех случаях число N — а — ЮА делится на 3, а значит, и А бу-
будет делиться на 3. Таким образом, произведение аА делится на 6
120
при всех k~^\\ однако при k = 1, 2 или 3 это заключение неинте-
неинтересно, ибо здесь А = 0 (и аА = 0 делится на любое число).
61. Нам надо показать, что число
N = 27 1958 — 10 8878 + 10 1528
делится без остатка на 26 460 = 22-33-5-73. Доказательство прово-
проводится в два приема.
1°. jV = 27 1958 — A0 8878 — 10 1528).
Но 27 195 = 3-5-72-37; следовательно, это число делится на
5-72. С другой стороны, разность, заключенная в круглые скобки,
делится на
10 887— 10 152 = 735 = 3-5-72
(ибо разность восьмых степеней двух чисел делится на разность ос-
оснований). Отсюда следует, что iV делится на 5-72.
2°. N = B7 1958 — 10 8878) + 10 1528.
Но 10 152 = 23 ¦ 3' • 47 делится на 22 • З3. С другой стороны, разность,
заключенная в круглые скобки, делится на
27 195—10 887= 16 308 = 22-33-151.
Таким образом, jV делится на 22-33.
Так как jV делится на 5-72 и 22-33, то N делится и на произве-
произведение этих чисел, равное 26 460.
62. Нетрудно проверить, что
Легко видеть, что второй сомножитель в правой части делится на 10,
так как он представляет собой сумму 10 слагаемых, каждое из ко-
которых оканчивается на 1.
Итак, И10—I есть произведение Юна число, делящееся на 10,
и, значит, делится на 100.
63. 22225555
= B2225555 + 45555) + E5552222 _ 42^2) _ D5555 — 42) _
Из трех выражений, стоящих в круглых скобках, первое делит-
делится на 2222 + 4 = 2226 = 7-318 (сумма нечетных степеней делится
на сумму оснований) и, следовательно, делится на 7; второе тоже
делится на 7, так как оно делится на 5555 — 4 = 5551 =7-793
(разность любых целых степеней делится на разность основании).
Что касается третьего выражения, то его можно переписать в виде
42222D:>333 _ 1) „. 42222F4111! — 1),
откуда видно, что оно делится на разность 64—1 =63 и, следова-
следовательно, делится на 7 (разность одинаковых целых степеней делится
на разность оснований).
64. Воспользуемся методом математической индукции. Число
ааа, составленное из трех одинаковых цифр а (черта наверху постав-
поставлена, чтобы не путать с произведением а-а а), делится на 3 (так
121
как сумма цифр этого числа, равная За, делится на 3). Далее, пред-
предположим, что наше утверждение уже доказано для каждого числа,
составленного из 3" одинаковых цифр. Число, составленное из 3"+1
одинаковых цифр, можно представить в следующем виде:
аа ... а аа ... а аа ... а — аа ... а-100 ... 0100 ... 01.
Зп раз 3" раз 3™ раз Зп раз Зп цифр Зп цифр
Но из двух сомножителей первый в силу предположения индукции
делится на 3", а второй делится на 3 (сумма цифр этого числа рав-
равна 3); следовательно, все произведение делится на 3"+>
65. Заметим прежде всего, что 106—1 =999 999 делится на 7
(так как 999 999 = 7-142 857). Отсюда легко следует, что 1О'\ где,
jV — какое угодно целое число, дает при делении на 7 такой же
остаток, как и №, где г есть остаток от деления N на 6. Действи-
Действительно, если N = 6к + г, то
10* _ 10г = 106*+г — 10г = 10* (l0eft — 1) =
= 10г • A06 - 1) A06*-6 + 106*-12... + Ю6 -1- 1)
делится на 7.
Но любая целая степень 10 дает при делении на 6 остаток 4;
в самом деле, 10" — 4 =999 ... 96 всегда делится на 2 3 = 6 (в си-
(п—1) раз
лу признаков делимости на 2 и на 3). Таким образом, все сложные
показатели степени у слагаемых нашей суммы дают при делении на
6 остаток 4. Следовательно, каждое из этих 10 слагаемых дает при
делении на 7 такой Же остаток, как и число 104, а вся сумма — та-
такой же остаток, как и число
Ю« + КL + 10' + 104 + 104 + 104 + Ю4 + 104 + 104 + 104 =
= Ю5 = 100 000 = 7-14 285 + 5.
Итак, искомый остаток равен 5.
66. а) Каждая четная степень 9 представила в виде
92n _ gin = 81-81 ... 81
п раз
и, следовательно, оканчивается цифрой 1. Каждая нечетная степень
9 представима в виде 92|1+| = 9-81" и, следовательно, оканчивается
цифрой 9 (как произведение числа, оканчивающегося единицей,
на 9). В частности, 9(9>) есть нечетная степень 9; значит, 9(ь8) окан-
оканчивается цифрой 9.
Заметим теперь, что любая целая степень 6 оканчивается циф-
цифрой 6; действительно, б1 = 6, и если 6П оканчивается на 6, то и
6"+' = 6"-6 оканчивается на 6. Но 16" оканчивается на ту же циф-
цифру, что и 6"; следовательно, любая целая степень 16 оканчивается
цифрой 6. Таким образом, любая степень двойки, кратная четы-
четырем, оканчивается шестеркой (ибо 24п — 16П). Но З4—1 делится
на 3+1=4; значит, 2<34~1} оканчивается цифрой 6, а 2C4) =
= 2 • 2C ^''оканчивается цифрой 2 (как произведение 2 на число,
оканчивающееся шестеркой).
122
б) Нам надо найти остаток от деления 2999 на 100 (это и есть
две последние цифры числа 2999). Покажем прежде всего, что при
делении на 25 число 21000 дает остаток 1. Действительно, 2'° + 1 =
= 1024 + 1 = 1025 делится на 25; следовательно, и 22° — 1 = B10 +
+ 1)B10—1) делится на 25, а 21000— 1 = B2°NU- 1 делится на
220—1. Отсюда вытекает, что последние две цифры числа 21000 мо-
могут образовать число 01, или 01 + 25 = 26, или 01 + 50 = 51, или
01 + 75 = 76; но так как 21000, конечно, делится на 4, то этими циф-
цифрами могут быть только 76. Таким образом, 2999 равно частному от
деления числа, оканчивающегося на 76, на 2, т. е. оно может окан-
оканчиваться только цифрами 38 или 88 (так как 76:2 = 38, 176:2 =
= 88). Но так как это число делится на 4, то оно оканчивается
цифрами 88.
Найдем теперь остаток от деления числа З999 на 100. Напомним,
что каждая четная степень 9 оканчивается цифрой 1, а каждая не-
нечетная степень 9 — цифрой 9 (см. решение задачи а)). Воспользо-
Воспользовавшись этим, найдем остаток от деления числа 95 + 1 на 100:
95+1 =(9+ 1).(94-93 + 92 — 9+ 1)= 10-(94-93 + 92-9+1),
а в алгебраической сумме, стоящей в скобках, каждое из трех по-
положительных слагаемых оканчивается на i и каждое из двух от-
отрицательных слагаемых — на 9; таким образом, число 94 + 92 + 1
оканчивается на 3, а число 93 + 9 — на 8 и, значит, все выражение,
стоящее в скобках, оканчивается на 5. Итак, число 95+1 при делении
на 1СО дает остаток 10 • 5 = 50. Отсюда вытекает, что число 9!0— 1 =
= (95 + 1) ¦ (95 — 1) делится на 1 СО, а так как З'мо — 1 = 950° _ i =
_ (910M0— 1 делится на 910— 1 (разность целых степеней делится на
разность оснований), то и З1000 — 1 делится на 100. Таким образом,
число З'000 оканчивается цифрами 01. Но это число делится на з';
следовательно, его число сотен при делении на 3 должно давать
в остатке 2 (если бы при делении сотен на 3 в остатке оставалась
одна сотня или ни одной, то это число сотен плюс 01 не могло
бы делиться на 3). Итак, мы нашли, что число З999 = З'000:3
должно оканчиваться теми же двумя цифрами, что и число
201 : 3 = 67.
в) Нам надо найти остаток от деления числа 14<14'4) = G-2)A4'4)
на 100,— это и есть две последние цифры числа 14'14'4^. Найдем в от-
отдельности остаток от деления на 100 чисел 7' ^ и 2*14'4*.
Число 74 — 1 =2 401 — 1 =2 400 делится на 100. Отсюда сле-
следует, что если п = 4& делится на 4, то 7" — 1 делится на 100 (ибо
74» — 1 = G4)* — A)" делится на 74 —1). Но 1414 = 214 • 714 делит-
делится на 4; следовательно, 7^14'4)— 1 делится.на 100 и, значит, число 7^14'*
оканчивается цифрами 01.
Далее, в решении задачи б) было показано, что 220—1 делится
на 25; следовательно, если п = 20й делится на 20, то 2" — 1 делит-
делится на 25. Найдем теперь остаток от деления числа 1414 на 20. Оче-
Очевидно, 1414 = 214-714. Но 214 = 4-212; так как 212—1 =B4K—1 де-
делится на 24—1 = 16—1 = 15, то 4B12—1) делится на 20, а слет
довательно, 214 = 4-212 дает при делении на 20 остаток 4. Далее,
714 = 49-712; так как 712 дает при делении на 20 остаток 1 (так как
12 делится на 4, то 712— 1 делится на 10Э), то 49-712 дает при де-
делении на 20 такой же остаток, как и число 49, т.е. 9. Таким обра-
образом, 1414 = 214-714 дает при делении на 20 такой же остаток, как
123
и произведение 4 • 9 = 36, т. е. остаток 16: I414 = 20/( + 16. А отсю-
отсюда следует, что 2A4'4) =216 • 220к дает при делении на 25 такой же
остаток, как и число 21в = 65 536, т. е. 2A4'4) может оканчиваться
только цифрами 11,36,61 или 86. Но так как 2A4"' делится на 4,
то 2A4'4) оканчивается цифрами 36.
Итак, число 7*|4'4) оканчивается цифрами 01, а число 2(!414)—циф-
2(!414)—цифрами 36. Следовательно, их произведение 7<14'^ • 2A4'4) = 14A4"'
оканчивается цифрами 36.
67. а) Ясно, что оба числа 9 и 9J оканчиваются цифрой 9
(ср. с решением задачи 66а))—таким образом, последние цифры
у них совпадают. Далее, по формуле бинома Ньютона,
Л = 9э9 = A0— 1)99 =
a—2- ... + с\• ю-
и
„q9
= iob-c*-iob-i + cf-ioh-2 —... _j-с*¦ ю — 1,
где а = 99 и 6 = 99 ; таким образом, две последние цифры рассмат-
рассматриваемых чисел совпадают с двумя последними цифрами чисел
Сд-10— 1 = 10а — 1 и С*-10 — 1 = 106— 1.
Но (см. снова решение задачи 66а)) числа а = 9s и 6 = 99 оба
оканчиваются цифрой 9; поэтому числа Юа и 106 оканчиваются
цифрами 90—и числа Л и В оканчиваются цифрами 89.
б) Аналогично решению задачи а) здесь можно найти шесть
последних цифр двух рассматриваемых чисел (причем роль лежаще-
лежащего в основе решения задачи а) равенства 9= 10—1 здесь будет
играть соотношение 72 = 50—1) и убедиться, что эти цифры оди-
одинаковы. Однако в виду некоторой громоздкости такого решения
(ведь речь здесь идет не о двух, а о шести последних цифрах!) мы
предпочтем пойти по другому пути.
Нам надо убедиться, что совпадают 6 последних цифр чисел
А = 7" и В = 7й, где теперь а = 7 и 6 = 7 , т. е. что разность
А — В = 7" — 7Ь = 7Ь G<-ь — 1)
(а значит, и число
где d = а — 6) делится на 1 000 000 = 26 • 5s; таким образом, за-
задача сводится к выяснению того, на какие степени двойки и пя-
пятерки делится число D, имеющее вид 7d — 1, где d — некоторое
натуральное число. Рассмотрим отдельно вопросы о делимости числа
D на 2а (где нам надо доказать, что a J2= 6) и о делимости D на 5^.
Г. Пусть О=7С—1, где с = 2*<? (здесь q нечетно); мы ут-
утверждаем, что при этом С «= 2аРР, где Р нечетно, а (зависящий
лишь от р, но не от q\) показатель степени ар при р > 1 удовлет-
124
воряет («рекуррентному») соотношению:
osj, «= a,-i + 1. (*)
Но поскольку число 7*2''— 1 = 72—1 = 48 делится на 2* = 16
(но не на 25) и, значит, ai = 4, то из (*) с очевидностью вытекает:
ар в р -f- 3 при всех р ^ 1
— если наибольшая степень двойки, на которую делится число с,
равна р J2= 1, то наибольшая степень аР двойки, на которую делит-
делится число С = 7е — 1, равна р + 3 (при р = 0 имеем <х0 = 1, по-
поскольку число 72° —1 =7— 1 =6 делится лишь на 2).
Покажем сперва, что число аР не зависит от q; это вытекает
из следующей формулы:
где стоящая в фигурной скобке сумма нечетного числа q нечетных
слагаемых, очевидно, нечетна — и, значит, число 7 — 1 делится
на ту же степень двойки, что и число 72 — 1. Поэтому далее можно
считать, что q = 1, т. е. заменить число С = 7 — 1 числом Ср =
*=72Р-1.
Теперь нам остается лишь воспользоваться формулой
-L?-" -1] IT' * + 1J=Cp-i-C.
Поскольку 7 дает при делении на 4 остаток —1, то 7™ дает при
делении на 4 остаток ¦—1 при т нечетном и остаток +1 при т
четном, а значит, 72 + 1 (и даже 72п + 1) при любом (натураль-
(натуральном) п дает при делении на 4, остаток 2, т. е. делится на2, но не де-
делится уже на 22. Таким образом, в равенстве Ср = Cp~i • С
левая часть Ср делится на 2 р, число Ср_, делится на 2 р—1,аС'
делится лишь на 2, откуда и вытекает формула (*).
[Ясно, что случай р = 1 является особым, ибо здесь С = 72° + 1 =
= 7+1 =8 делится не только на 21, но на 23 — отличие возникает
вследствие того, что в этом единственном случае показатель степе-
на 2° в выражении для С — число нечетное.]
Итак, для определения показателя степени а в формуле D =»
= 7d — 1 — 2а • Q (где Q нечетно) надо лишь выяснить, на какую
степень двойки делится число d = а — 6=7"'—7Ь' = 7Ь' Gdl—l)
(т. е. число 7d' — \), где а, = 71 , Ь, = 77, а^1 = а1 —6,.
А для этого, как мы ,знаем, необходимо (и достаточно) установить,
на какую степень двойки делится показатель степени di = ах —
" 7
— Ь\ ™ 7 2 — 7 * = 7 * G 2 —- 1), где #2 == 7 , ?>2 ==s 7 и d% =*
=a, — 62 ==7aj — 7bl = 7Ьз Gdl — 1), где теперь Ьг ==1, а3 = 7?
125
и d3 = а3 —6з = 77—1. Но поскольку число 7 — нечетно, ТО из =¦
= V—1 делится лишь на 2а° = 21 = 2. Отсюда, в свою очередь,
вытекает, что число 7ds — 1 делится на 2а' = 24; таким образом,
число d.z — 7Ьэ ( 7d'—l) делится на 24—и, значит, число 7d'—1
делится на 2а* = 27. Но если cfx = 7ba Gd:l — l) делится на 27,
то 7dl— 1 делится на 2а' = 21»; поэтому и d = 7Ь» Gd-> — l)
делится на 210, и, следовательно, D = 2d — 1 делится на2а"> = 21.3.
2°. Совершенно аналогично рассматривается и вопрос о дели-
делимости чисел С = 7е—1, где теперь только уместно считать с =
= 5rs, на степени пятерки; однако здесь целесообразно оговорить,
что (не делящееся на 5) число s делится, по крайней мере, на 22,
ибо случай, когда s нечетно или делится лишь на 2, но не на 4,
приводит к несколько иным выводам. При s = 4si, или с = 5Г ¦ 4si,
где s, — целое, наибольшая степень $г пятерки, на которую делится
число С, как и выше, зависит лишь от показателя степени г в фор-
формуле для с, т. е. число EГ не зависит от sf, при этом по-прежнему
имеет место аналогичное (*) («рекуррентное») соотношение
р\ = р\._, + 1. (**)
А так как число У — 1 = G2J — 1 = G2 + 1) G2 — 1) = 50 • 48
делится' на 52 = 25, т. е. р0 = 2, то из (**) следует, что при всех
r^z О
р\ = г + 2
— если показатель степени с в выражении С = 7е — 1 делится
на 4 и наибольшая степень пятерки, на которую делится с, равна
г, то наибольшая степень pV пятерки, на которую делится С, равна
г + 2.
Для доказательства независимости рг от Si достаточно вос-
воспользоваться формулой:
С = 7е— 1 =75Г-48'-! =G5Г'4M'-18' =
Но так как 74 = G2J = E0— IJ = 502—2 -50 + 1 дает при де-
делении на 5 остаток 1, то и число G4)" при любом п дает при де-
делении на 5 остаток 1; поэтому в фигурной скобке в правой части
последней формулы стоит сумма st чисел, каждое из которых дает
при делении на 5 остаток 1, откуда, поскольку s{ не делится на 5,
вытекает, что эта сумма не делится на 5. Поэтому число С =*
— 7°r'4s' — 1 делится на ту же степень пятерки, что и число Ег =»
= 75 4 — 1, что позволяет в дальнейшем считать S[ = 1, т.е. заме-
заменить число С числом Ег.
Далее,
+ 7+1}=?г-1-?.
Отсюда, прежде всего, следует, что Ет делится на ?r-i, т. е. Ет
126 , ~
делится на не меньшую степень пятерки, чем Ег-т, другими словами
pr ^ pr_i, или, так как р0 = 2,
2 = Ро < Pi < h < • •.
Таким образом, при всех г J2= 1 число ZTr—i = 7е '*—1 делится
на 25, а значит число ег— 1 = е = 7 дает при делении на 25
остаток I, — и любая степень е* числа е также дает при делении
на 25 остаток 1. А так как стоящее в фигурных скобках в правой
части формулы для Ет выражение Е' равно сумме е4 + е3 + е2 +
+ е + 1, то оно дает при делении на 25 остаток 5, т. е. Е' делится
на 5', но не делится на 52. Отсюда и из формулы Er = ?V-1 • Е'
и вытекает соотношение (**).
Обратимся теперь снова к интересующему нас числу А—В =
= 7Ь ¦ D, где D = 7d— 1. Поскольку, как мы видели выше, число
d на 4 делится (оно делится даже на 210 = 1024), то нам остается
только выяснить, на какую степень пятерки делится число d —
= 7°' — 7b' =7b'Gdl — l),где d, = at — b{ (см. конец п. 1° реше-
решения настоящей задачи). Но так как d\ также делится на 4 (и даже
на 27), то наша задача сводится к определению того, на какую
степень 5 делится число d, = 7"г — 7Ьг = 7Ьг {ldz — l), где d2 =
= а2 — 62 = 7аз —7Ьэ = 7Ь' Gf'3— l) делится на 4 (даже на 24)
и d3 = 77— 1. Но, как мы знаем, число d3 делится на 2 и не де-
делится на 4, т. е. d3 = 2/, где f—нечетно; поэтому 7d' — 1 ч= 49' —
— 1 = E0—1)' — 1 на 5 не делится (дает при делении на 5 оста-
остаток — 2, т. е. остаток 3); с другой стороны, число 7 3 — 1 (как и число
di = 7Ъз G ' — 1)) уже делится на 4. Но отсюда следует, что число
7 — 1 делится на б*30 = 52 (и не делится на более высокую
степень пятерки); поэтому d\ = jb'Gd2— l) делится на 52 и d =
_7biGdl— l) делится на Ф = 54, a D = 7d — 1 (и рассматри-
рассматриваемое в этой задаче число А — В = 7Ь ¦ D) делится на б''1' = 5е.
Это рассуждение и завершает решение задачи.
Примечание. Ясно, что совершенно аналогично решению
этой задачи можно установить, что числа А„+2 и А„, составленные
наподобие фигурирующих в настоящей задаче чисел А к В
из (п + 2)-х, соответственно из п семерок, имеют 2/г — 2 одинако-
одинаковые последние цифры; рекомендуем читателю самостоятельно по-
постараться оценить число одинаковых последних цифр у чисел Ап
и А,„, составленных из п, соответственно из m семерок (здесь естест-
естественно начинать со случая небольших разностей п — пг).
68. а) Если перемножить два числа, одно из которых оканчи-
оканчивается на цифру а, а второе на цифру Ь, то их произведение будет
оканчиваться на ту же цифру, что и произведение ab. Это замечание
позволяет просто решить поставленную задачу. Будем последователь-
последовательно производить возвышения в степень, следя только за последней циф-
цифрой числа: 72 оканчивается цифрой 9, 73 = 72 • 7 оканчивается циф-
цифрой 3, 7* = 73 • 7 оканчивается цифрой 1 и 77 = 74 • 73 оканчивается
цифрой 3.
Далее, точно таким же образом найдем, что G7O оканчивается .
снова цифрой 7 (действительно, G7J оканчивается цифрой 9, G7K
оканчивается цифрой 7, G7L оканчивается цифрой 1 и(G7O окан-
127
чивается цифрой 7). Отсюда следует, что число (G7OO оканчива-
оканчивается той же цифрой, что и число 77, Т. е. Цифрой 3, число ((G"OO)
оканчивается снова цифрой 7, и т. д. Продолжая таким же образом,
мы после нечетного числа возведений в степень 7 будем каждый
раз приходить к числу, оканчивающемуся цифрой 3, а после чет-
четного числа возведений в степень 7 — к числу, оканчивающемуся
цифрой 7. Так как 1000 есть число четное, то интересующее нас
число оканчивается цифрой 7.
Если одно число оканчивается двузначным числом А, а вто-
второе— двузначным числом В, то их произведение оканчивается
на те же самые две цифры, что и произведение А ¦ В. Это
позволяет найти и две последние цифры интересующего нас числа.
Как прежде, проверяем, что 77 оканчивается двумя цифрами 43,
а G7)' оканчивается теми же цифрами, что и 437, а именно цифра-
цифрами 07. Отсюда следует, что, возводя последовательно числа 7, 77,
G7O,... в степень 7, мы после нечетного числа возведений в степень
будем приходить к числу, оканчивающемуся цифрами 43, а после
четного числа возведений — к числу, оканчивающемуся цифрами
07. Следовательно, искомое число оканчивается цифрами 07.
б) В решении задачи а) мы виделн, что 7* оканчивается циф-
цифрой 1. Отсюда следует, что 7ih = G4) тоже оканчивается цифрой
1 и 7ih^~l, где / есть одно из чисел 0, 1, 2 или 3, оканчивается
той же цифрой, что и 7 17 ' —7 к-7 ). Таким образом, задача сво-
сводится к тому, чтобы определить, какой остаток дает при делении
на 4 число, являющееся степенью, в которую надо возвести 7,
чтобы получить число задачи.
Степень, в которую в задаче возводится число 7, сама
представляет собой 7 в некоторой очень большой степени;
'нам надо выяснить, какой остаток дает эта степень семи при деле-
делении на 4. Но 7 = 8—1; отсюда следует, что 72 = (8—1) • (8—1)
дает при делении на 4 остаток 1, 73 = 72 • (S— 1) дает при делении
на 4 остаток — 1 (или, что то же самое, остаток 3) и вообще каж-
каждая четная степень 7 дает при делении на 4 остаток 1, а нечетная — ос-
остаток — 1 (т. е. +3). Но интересующая нас в настоящем случае сте-
степень 7 заведомо является числом нечетным (так как она сама есть
степень 7), а следовательно, фигурирующее в условии задачи число
имеет вид 7 ' и, следовательно, оканчивается той же цифрой,
что и 73, т. е. цифрой 3.
Так как 74 оканчивается цифрами 01, то 7 ' оканчивается да-
даже теми же двумя цифрами, что и 7'. Следовательно, интересую-
интересующее нас число оканчивается теми же двумя цифрами, что и число 73,
т. е. цифрами 43.
69. Рассмотрим последовательно числа:
1°. Zi = 9,
2°. 2a = 9Zl = A0— l)Zl —
=» 10Zl— ClZi-lQz'-l+ ...4-C^-IO—1,
где опущенные члены разложения все делятся на 100. Но CZi = 9;
следовательно, две последние цифры числа Za будут теми же самыми,
128
что и две последние цифры числа 9 • 10— 1 = 89.
3'. Z3 = 9z' = A0 — if1 =
^ 10z* - cl • КJ*-1 + ... - C'i ¦ 102 + Ci • 10 - 1.
Ho Z2 оканчивается на 89; следовательно, С\ — Z., оканчивается на
, Z, (Z.,— 1) ...89-... 88
89, a (-^ — j—9 — j—?; (точками обозначены неиз-
неизвестные цифры) оканчивается цифрой 6. Следовательно, три послед-
последние цифры числа Z3 будут теми же самыми чго и три последние циф-
цифры числа — 600 + 890—1 = 289.
= 10Zj — Ci ¦Ю23"-1^ ... — Cl -103 — Cl • 103 -f- Ci -10—1.
Так как Z3 оканчивается на 289, тег и С^з — Z3 оканчивается на 289;
2 Z3(Z3 — 1) ...289-...288
Cz, = Ь2 "= Ь2
оканчивается на 16;
-1 Z3 (Z:< — 1) (Z3 — 2) .. ,289-.. .288'.. .287
Cz,= 1-2-3 = 1-2-3
оканчивается цифрой 4. Следовательно, четыре последние цифры чис-
числа Z4 будут теми же самыми, что и последние четыре цифры числа
4000 — 1600 + 2890 — 1 = 5289.
5°. Z5 = 9Z' ^A0 — \)Zi = \QZi — CiZi-lQZi~ijr ...
... -Ci -Wj-Cl -№ — Cl -102 + C' -10—1.
Так как Z4 оканчивается на 5289, го С\ — Z4 оканчивается на 5289;
7.^{Z%~ 1) ...5289-...5288
'Cz,."= 1-2 = 1-2
оканчивается на 116;
з Z4(Z4—l)(Z4-2) ...5289-, ..5288-...5287
CZi-= 1-2-3 ~ 1-2-3
оканчивается на 64; наконец,
4 /4(Z4— 1)(Z4 — 2)(Z4— 3) .. .5289-...5288-.. .5287-...5286
CZ4 = 1-2-3-4 = 1-2-3-4
оканчивается цифрой 6. Следовательно, Z5 оканчивается на те же
9 Д. О. Шклярский и др. 129
самые пять цифр, что и число
— 60 000 + 64 000 — 11 600 + 52 890 — 1 =45 289.' "
Далее из того, что последние четыре цифры числа Z5 совпадают
с последними четырьмя цифрами числа Z*, следует, что последние
пять цифр числа Z6 = 9'Z' = A0—\)z' совпадают с последними
пятью цифрами числа Z6(=9Z'}. Точно так же показывается, что
все числа ряда
Zh, Ze - 9ZS Z, = 9Z", ..., Z1000 = 9Z»» , Zlooi = 9г" ••
оканчиваются на одни и те же пять цифр, а именно на 45289. Но
Ziooi это и есть число N условия задачи.
70. Найдем, прежде всего, остатки от деления на 13 чисел 5"
и п5 для ряда первых значений га = 0, 1, 2, ... При этом удобнее
начать с чисел 5":
п
Число 5
Остаток
п.
от
деления 5"
на
13
0
1
1
1
5
о
2
25
— 1
3
125
—5
1
625
1
[Здесь мы пишем «остаток — 1» вместо «остаток 12» и «остаток —3»
вместо «остаток 8», что позволяет очень просто находить все следую-
следующие остатки: если 5" дает при делении на 13 остаток — 1, т. е. 5" =
= 13ft— 1, где А—целое, то 5n+1 = 5П • 5 = A3ft — 1M =
=г 13Eft) —5 дает при делении на 13 остаток —5; аналогично, если
5" дает при делении на 13 остаток —5, т. е. 5т = Ш — 5, то
5m4i = 5»i . 5 «= A3/ — 5M= 13E/) —25 = 13E/ —2) + 1 дает при
делении на 13 остаток 1.] Продолжать таблицу далее нам нет нужды:
поскольку 5* ¦= 13G + '. т0 5s = 54 • 5 = A3<7 + 1M дает при деле-
делении на 13 тот же остаток, что и число 5 (остаток 5); число 5е =
= 5* • 52 — A3<7 + 1M2 дает при делении на 13 тот же остаток, что
и число 52 (остаток — 1), и т. д.; таким образом, в нашем «ряду ос-
остатков» последовательно чередуются числа 1, 5, -—1, —5.
Аналогично можно составить и таблицу остатков от деления на
13 чисел я5, где п «= 0, 1, 2, ..., и т. д. Но число A3/J + rM =
«=¦ A3/? + /-) (\3р + г) . ..A3р + г) дает при делении на 13 тот же
5 множителей
остаток, что и число гь; поэтому нам достаточно ограничиться значе-
значениями п «= 0, 1, 2, 3, ..., 12. Далее, если число п равно (или дает
при делении на 13 остаток)^, а число п1 дает при делении на 13
остаток /, то число н5 = п2 ¦ пг ¦ л дает при делении на 13 тот же
остаток, что и прои?ведение t • t "•' s -? это обстоятельство может
облегчить составление требуемой таблицы для значений п •= 4, 5, 6.
Наконец, заметим еще, что если число л5 дает при делении на 13
остаток и, то число A3 — n)s = A3 — п) A3 — га) ... A3 — га) дает*
5 множителей
при делении на 13 тот же остаток, что и число (—гаM, т. е. остаток
— и, или 13 — и. *
130 )
Теперь мы можем
л
п>
п'
Остаток от деления
п2 на 13
Остаток от деления
га5 на 13
п
„5
Д2
Остаток от деления
л2 на 13
Остаток от деления
п5 на 13
составить
0
0
0
1
1
1
2
32
6
6
36
—3
—3—3-6,
нашу
3
243
—4
3-
или 2
таблицу.
4
16
3
3-4, или
¦7
-2
8
-5
— 3
9
3
5
25
—1
-I (-1M-5
10
4
11
-6
12
—1
...
(отвечающие значениям п = 7, 8, .... 12 остатки выписываются исхо-
исходя из того, что числа пь и A3 —яM дают при делении на 13 «допол-
«дополнительные» остатки и и — и). После же значения га = 12 в нашей
таблице будут «периодически» повторяться те же остатки 0, 1, 6, —4,
-3,5, 2, -2,-5,3,4,-6,-1.
Так как первая таблица имеет «период» 4, а вторая — «период»
13, то значение 4- 13 = 52 является «периодом» объединения обеих
таблиц: при увеличении п на число 52 (или па любое число, крат-
кратное 52) остатки от деления на 13 обоих числя 5" и я5 не меняются.
Далее, нас могут интересовать лишь те столбцы второй таблицы, ко-
которые отвечают остаткам ± 1 и ± 5 (ибо в первой таблице чередуются
лишь остатки 1, 5, — 1, — 5). Но в пределах от га = 0 до п = 51
остаток 1 во второй таблице отвечает значениям га = 1, 1 + 13 = 14,
1 + 2- 13 — 27 и 1 + 3 ¦ 13 = 40; из Э1их четырех чисел лишь 14
имеет вид Ах + 2, которому в первой таблице соответствует остаток
—1; таким образом, число л = 14 удовлетворяет требуемому условию
EI4+ 145 делится на 13). Аналогично, остаток — 1 во второй таб-
таблице в тех же пределах отвечает значениям п = 12, 12 + 13 = 25,
12 + 2 • 13 = 38 и 12 + 3 • 13 = 51; из этих чисел лишь 12 имеет
вид 4г/, который в первой таблице приводит к остатку 1. Точно так
же остаток 5 во второй таблице отвечает значениям п = 5, 5 + 13 =
•" 18, 5 + 2 • 13 = 31 и 5 + 3 • 13 = 44, а остаток — 5 — значениям
л — 8, 8 + 13 — 21, 8 + 2 • 13 = 34 и 8 + 3 • 13 == 47; но из первых
четырех чисел лишь 31 имеет вид 4г + 3, обеспечивающий остаток
— 5 от деления 531 на 13, а из последних четырех чисел только 21
имеет вид 4ш + 1, обеспечивающий остаток 5 от деления 521 на 13.
Таким образом, в пределах 0 ^ п ^ 52 требуемому условию удовлет-
удовлетворяют следующие четыре натуральных числа: п = 12, 14, 21 и 31;
»с ж« множество удовлетворяющих условию задачи натуральных
131
чисел состоит из следующих четырех «серий» чисел:
я = 52т + 12, я — 52т + 14 (т. е. л = 26B/и) + 12 и
n = 26Bm+l)—12);
п =» 52т + 21 и л = 52т+ 31 (т. е. п = 52т ±21);
здесь т •= 0, 1, 2, ... (и лишь в формуле п = 52т — 21 надо счи-
считать т>0).
Ясно, что наименьшее п., удовлетворяющее условиям зада-
задачи — это п = 12.
71. Ясно, что две последние цифры чисел п, я2, п3,..., где я —
целое неотрицательное число, зависят лишь от двух последних цифр
числа п — это следует из правила умножения многозначных
чисел «столбиком». С другой стороны, последние цифры 100 последо-
последовательных целых неотрицательных чисел обязательно пробегают ряд
значений 00, 01, 02, ..., 99-(хотя, вообще говоря, и не в этом поряд-
порядке) ; поэтому наша задача сводится к нахождению двух последних
цифр суммы (при а = 4 и а = 8)
A^a = 0" + Iя Н- 2° + ... + 99".
а) Если п = Юх + у — двузначное число, то
п* =-A0* + уУ = 10V + 4 ¦ 103*'</ + 6 • 10W + 4 • IQxtf + у\
причем на две последние цифры числа п* влияют лишь два последних
слагаемых, ибо все остальные слагаемые оканчиваются двумя нуля-
нулями. Следовательно, нам надо найти лишь две последние цифры
сумм
и 2 2
к у х у
(=10 2 У4
\ V
где х и у независимо друг от друга пробегают значения от 0 до 9
и положено 0° = 1 (так что ? х° = 0° + 1° + ... + 9° = 10).
X
Заметим теперь, что при фиксированном у
24-10л-?/3 = 410@+ 1 -!- 2 + 3 + 4 + 5 + 6+7+8+9)-у3=1800г/3
х
оканчивается двумя нулями; поэтому n22j4-lCbri/3 оканчивается
х у
двумя нулями — и не 'вносит никакого вклада в две последние циф-
цифры числа Ni. Итак, нам осталось лишь найти две последние цифры
числа
10 2 {/4=Ю@4+1< + 24 + 34 + 44 + 54 + 64 + 74 + 84 + 94) = 1054>
у
или последнюю цифру суммы S4.
Но эту задачу решить легко: в нижеследующей таблице после-
последовательно выписаны последние цифры чисел у, у2 и у4:
у 0 123456789
у1 0149656941
у4 0 16 16 5 6 16 1
132
Поэтому последняя цифра суммы St совпадает с последней цифрой
суммы
О + 1 + 6 + 1 + ... + 1 = 4A + 6) + 5 = 33,
а значит, две последние цифры суммы Nt (а также и фигурирующего
в условии задачи числа)—это 30.
б) В точности аналогично решению задачи а) находим, что и
при а=8 две последние цифры суммы Ns (a значит, и интересующе-
интересующего нас числа) совпадают с двумя последними цифрами числа lOSs,
где S8 = 08+ Is + ... + 98. Но из выписанной таблицы последних
цифр чисел у*, а также из равенства yih = (г/4)* следует, что чис-
число у1к (где у — цифра) оканчивается той же цифрой, что и у*. Поэ-
Поэтому и при а = 8 две последние цифры рассматриваемого числа бу-
будут теми же, что и при а — 4, т. е. это будут цифры 30.
Примечание. Нетрудно видеть, что тот же результат мы
получим и при всех кратных 4 значениях а, т.е.приа =,4,8, 12, 16,...
72. Согласно формуле для суммы членов геометрической про-
прогрессии
501000 — 1 Б01000 — I
N =
50—1 - 49 *
1
Но -jg" обращается в чистую периодическую десятичную дробь, пе-
период которой, состоящий из 42 знаков, нетрудно найти простым де-
делением:
-49"= 0, @20408163265306122448979591836734693877551),
или сокращенно
0(Р)
где Р изображает выписанную выше последовательность из 42 цифр.
Ближайшее к показателю степени 1000 целое кратное числа 42
есть 1008 •= 24 • 42. Следовательно,
1Q100J 1
-^- = Ю-»»' • -^ =РР ... Р, Р...
24 раза
Таким образом, дробь
1П1008 _
М
11
М _ —«= 10Ю08. — —
Л1 « 49 ¦= Ш 49 49
есть целое число, состоящее и? 1008 цифр, которые можно разбить
на 24 группы из повторяющихся 42 цифр (фактически число М
содержит не 1008 цифр, а 1007, так как наше число Р начинается
нулем).
Составим теперь разность между интересующим нас числом N
и числом М:
51000. ](IО0О 1 j(I008 ] 51000 Ю8
N-M- 49 49 = 49 ' 10100О; '
133
Так как разность N — M двух Целых чисел — Целое чиело и 10100Й
взаимно просто с 49, то 5W0°— 108 должно делиться на 49. Следова-
51000 ю»
тельно, число х = тн является целым и разность N — М =
= 10!00° • х оканчивается на 1000 нулей. Таким образом, последние
1000 цифр числа N — те же самые, что и последние 1000 цифр чис-
числа М, а именно:
рРР ... Р
23 раза
где р — группа из 34 цифр, являющихся последними 34 цифрами
числа Р.
73. Обозначим исходное число М = 10.4 + а, где а — последняя
цифра М; тогда, полученное из М указанным способом число N бу-
будет, очевидно, равно а ¦ 106"-' + Л, где 6я— число цифр числа М.
Образуем теперь выражение
Л/ — 3W = A04 +о) — C ¦ 106»-1а + ЗЛ)=^7Л—C • 106"-1 — \)а.
Уменьшаемое М в левой части делится на 7 по условию; число 7.4,
очевидно, делится на 7; если мы докажем, что на 7 делится и чиело
3-Ю6" —1 (а значит, и выражение C • 106" — 1)а), то на 7
должно будет делиться и число 3N, а значит и число N.
Число 10 дает при делении на 7 остаток 3, число 102 — тот же
остаток, что и число 3 • 3 = 9, т. е. остаток 2, а значит, число 103 =
«= 102 • 10 —остаток 2-3 = 6; число 106 = 103 • 103 дает при деле-
делении на 7 тот же остаток, что и 6 • 6 = 36, т. е. остаток 1, и, значит,
это число имеет вид 7k + 1; число 105 = I03 • 102 дает при делении
на 7 тот же остаток, что и 6 • 2 =¦ 12, т. в. остаток 5, другими сло-
словами, оно имеет вид 7/ + 5; поэтому
]0«п-1 = ю6"—в • 105 = (Ю0)"^1 • 10* =»
- G? + 1)GН- 1) ¦¦¦ GМ-1)G/ + 5) = IK + 5,
п—1 раз
т. е. это число дает при делении на 7 остаток 5. Наконец, число
3 ¦ 10е"-1 при делении на 7 дает тот же остаток, что и 3 • 5 = 15,
т. е. остаток 1, а зяачит, число 3 • Ю6" — 1 делится на 7.
Это и дока?ывает утверждение задачи.
74. Число пулей в конце числа показывает, сколько раз 10 встре-
встречается сомножителем в этом числе. Число 10 равно произведению
2 ¦ 5; в произведении всех целых чисел от 1 до 100 множитель 2 вхо-
входит в большей степени, чем множитель 5. Следовательно, произведе-
произведение 1 ¦ 2 • 3. ..100 делится на такую степень 10 (т. е. оканчивается
на такое число нулей), сколько это произведение содержит множите-
множителей 5. Но до 100 имеется 20 чисел, кратных пяти, причем четыре из
них B5, 50, 75 и 100) кратны также 25, т. е. содержат по два мно-
множителя 5. Следовательно, всего в произведении 1 • 2-3. ..100 число
5 встретится сомножителем 24 раза; поэтому и нулей в конце этого
произведения будет 24.
75. Первое решение задач а) и б). Решим сначала за-
задачу а). Пусть t + 1, t + 2, ..., t + п будут п произвольных, после-
последовательных целых чисел. Подсчитаем для каждого простого числа р
наивысшую степень т, с которой оно входит в произведение и!,
134
и наивысшую степень s, с которой оно входит в произведение (/ + I) • ¦ ¦
...(/ +я). Для этого обозначим черег п\\ число чисел ряда 1, 2, ...
..., л, в которые р входит по крайней мере в первой степени, через
тг — число чисел того же ряда, в которые р входит по крайней мерс
во второй степени, н т. д. Тогда показатель, с которым р входит в
п\, будет равен т = mt + т^ +...
Если теперь s( — число чисел ряда t-\-\, ..., ( + п, делящихся
на р, S2 — число чисел этого же ряда, делящихся на р2, и т. д., то
показатель s, с которым р входит в произведение (t + 1)...(/+ я),
равен s = si + Sj +...
Но число чисел ряда t-\-l, ..., t + «* делящихся на р, не мень-
меньше чем т\. Действительно, среди чисел t-\-\, ..., t-\-n находятся
также числа t + р, ( + 2р, ..., t -\- тф, а в каждом промежутке меж-
между t + ftp и t + (k+])p (& = О, 1, 2, ..., тх — 1) есть хотя бы
одно число, делящееся на р. Таюш образом, S\ J2= т.)-, аналогично
S2 S5 /иг, и т. д., а потому 5'^ т. Но это означает, что каждый про-
простой сомножитель числа /г\ входит в состав числа (/-f 1)...(/+ я),
причем в степени, не меньшей чем он входит в я!, т. е. число (/+1)...
,..(t-\-n) делится на я!.
б) Произведение первых а сомножителей в га! совпадает с а!;
произведение следующих b сомножителей в силу задачи а) делится
на 6!; произведение следующих с сомножителей — на с!, и т. д. Так
как а + 6 + с + ... + й^я, то отсюда следует, что я! разделится
на а\Ы.М
Другое решение задач а) и б). Решим сначала задачу
0). Показатель т, с которым некоторое простое число р входит з
о!, как мы "видели, равен т = п%\ + т2 + ..., где тх — число чисел
ряда 1, 2, ..., а, кратных р, т^ — кратных р2, и т. д. Но число чисел.
р, равно — , кратных р2 — равно -^г- и т. д., где \ — I
LPJ LP2J IP 1
п а
— целые части дробей-.—j",.. .(см. стр. 37). Таким образом,
кратных
И-
т -— — I -J- —- I -j- ... Пусть теперь р — любое простое
Тогда показатель, с которым р войдет в числитель, равен I — I -\-
-Ч—- I т" ••¦ . Показатель, с которым р войдет в знаменатель, равен
число.
Но так как га ^ а + 6 + ... + /г, то, используя результат задачи 201,
1), мы получим отсюда, что
т. в. р войдет в числитель в большей степени, чем в знаменатель.
Значит, наша дробь есть целое число.
133
Решим теперь задачу а). Дополним для этого произведение
(I + 1)...(< + я) до (t + n)l. По только что доказанному дробь
(t + n)...(t + l)t(t-l)...l (я+ Q1 (t+l).*(t + n)
n\t(t—l)...l ~ n\t\ ~ п\
есть число целое.
в) (га!)! есть произведение п\ первых целых чисел. Но эти л!
чисел можно разбить на (п—1)! групп по га последовательных це-
целых чисел, а произведение чисел каждой из этих групп в силу ре-
результата задачи а) делится на л!.
г) Пусть рассматриваемые числа будут а, а + d, a + 2rf, ...
..., а + (п — l)rf. Докажем сначала, что существует такое целое
число k, что произведение kd дает при делении на я! в остатке 1.
Действительно, рассмотрим п! — 1 чисел d, 2d, 3d, ..., («! —l)d.
Ни одно и? этих чисел не делится на /;!, так как d взаимно просто
с я!. С другой стороны, никакие два произведения pd и qd, где р,
q— целые числа, меньшие л!, не могут давать при делении па «!
одинаковые остатки, так как иначе разность pd — qd = (p—g)d де-
делилась бы на п\. Таким образом, рассматриваемые га! — 1 чисел дол-
должны при делении на п\ давать га! — 1 разных остатков, откуда вы-
вытекает существование числа к, такого, что произведение kd дает при
делении на я! остаток 1: kd = г • п\ + 1.
Обозначим теперь ka через Л. Тогда мы имеем:
ka = A,
k(a + d) = А + kd = (Л + 1) +г ¦ п\,
k(a +2d) «= Л = 2Ы =» (А + 2) + 2г • га!,
Л + (я— 1)М= [Л + (га — 1)] + (я —1)г •«!.
Отсюда следует, что произведение
ft"a(a + d)(a+2rf)...[a +(«—l)d]
дает при делении на п\ такой же остаток, как и произведешь
А (А + \){А + 2)...[А + (я— 1)]. Но последнее из этих двух произ-
произведений делится на га! в силу задачи a), a kn взаимно просто с п\,
так как, если бы k не было взаимно просто с га!, kd тоже не могло
бы быть взаимно просто с л!.
1000!
76. Число сочетаний из 1000 элементов по 500 равно
Так как 7 — простое число, то наивысшая степень, с которой 7 вой-
войдет в 1000! (см. второе решение задачи 756), равна ___ + L__ U-
-j- L21iz =¦ 142 + 20 + 2 «= 164. Наивысшая степень, с которой 7 вой-
дет в 500!, равиа^] + J5MJ+ jjOjJ =yJ + ,„ + { _ g2
вательно, наивысшая степень, с которой 7 войдет в знаменатель, рав-
равна 82 • 2 = 164. Таким образом, и числитель и знаменатель содержат
7 в 164-й степени. После сокращения числитель не будет уже содер-
136
, 1606!
жать множителем 7, и следовательно, целое число ,нщгг~ не дели1'-
ся на 7.
77. а) Число (я— 1)! не делится на п только в том случае,
если п — простое число или если я = 4. Действительно, если п —
составное число, которое можно представить в виде произведения
двух неравных множител'ей а и 6, то и а и Ь меньше я — 1 и, следо-
следовательно, входят в состав (я— 1)!; значит, (я—1)! делится на
ab = п. Если п есть квадрат простого числа р, большего двух, то
я—1 = р2—1 > 2р. Поэтому и р и 2р входят в состав (га— 1)!;
значит, (я— 1)! делится на р ¦ 2р = 2р2 = 2га. Итак, условию зада-
задачи удовлетворяют только числа 2, 3, 4, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, т. е. число 4 и все
простые числа меньшие 100.
б) (я—1)! не делится на я2 только в следующих случаях: я
есть простое число, я есть удвоенное простое число, я = 8, я = 9.
Действительно, если я не является ни простым числом, ни удвоенным
простым числом, ни квадратом простого числа и не равно ни 8, ни
16, то я можно представить в виде я = ab, где а и 6 —различные
числа, не меньшие 3. Мы будем считать, что 6 > а, а ^= 3. В таком
случае числа а, 6, 2а, 26, За все меньше я — 1 и при этом а, 6 и 2й
заведомо различны, а из чисел 2а и За хотя бы одно отлично о г
чисел а, 6 и 26. Таким образом, в (я— 1)! входят множители а, 6,
26, 2а или а, 6, 26, За (а может быть, входят и все множители а, 6,
26, 2а, За); во всех случаях (га — 1)! делится на а262 = п2.
Далее, если га = рг, где р есть простое число большее 4, то
я — 1 > Ар и (я —1)! содержит множители р, 2р, Зр, 4р и. следо-
следовательно, делится на р4 = я2. Если п = 2р, то (га— 1)! не делится
на р2, а, следовательно, и па я2; когда я = 8 или 9, то (я— 1)! не
делится на я2 G! не делится на 82 и 8! не делится на 92); когда га =
= 16, то (я—1)! делится на я2 A5! содержит множители 2, 4 =
= 22, 6 = 3 • 2, 8 = 23, 10 = 2-5, 12 = 22 • 3, 14 = 2-7 и, следо-
следовательно, делится на ?'+г+'+з+1+а+1 = 211 = 162 • 23).
Таким обра?ом, условию задачи б) удовлетворяют все числа,
удовлетворяющие условию задачи а), и, кроме того, числа 6, 8, 9,
10/ 14, 22, 26, 34, 38, 46, 58, 62, 74, 82, 86, 94, т.е. все простые числа,
все удвоенные простые числа и числа 8 и 9.
78. Предположим, что число я делится на все числа т, меньшие
пли равные У п. Составим общее наименьшее кратное К всех таких
чисел т. В него, очевидно, будут входить все простые числа, мень-
меньшие Vn_i.nPH4eM каждое простое число р в такой степени k, что
Pfe< "jAn, но pft+1> Vя. Предположим, что число простых чисел,
меньших У^я, равно /; эти простые числа мы обозначим через
Рь Рг. .••, Pi- Наименьшее общее кратное К всех чисел, меньших
У~п,представляет собой произведениер11р22<" Pi '• гДе ^i таково, что
Р*1 < /п<Р?'+1. *2 таково, что р^ ^ Уп < р^+' , и т. д.
Перемножив теперь / неравенств
получим;
13?
Ho p\^p\'+i ... pfi+i = p\'P%> .. . pf< . P,P, ...Pt <KK ибо
Pi'P^2 •. • P*' = К, а следовательно, р,р2 ...pi^K. Таким образом,
имеем:
(VnI < /С».
Но так как согласно нашему предположению я должно делиться
на К, то К ^ п; следовательно, (Кл) <! л2. Отсюда / < 4; так как
р\, ..., /J/ — все простые числа, меньшие У п, то р< = 7> Уп (чет-
(четвертое простое число есть 7) и я < 49.
Перебирая все числа, меньшие 49, мы без труда убеждаемся, что
из них требуемым свойством обладают только числа 24, 12, 8, б,
4 и 2.
79. а) Обозначим пять последовательных целых чисел через
л —2, л—1, л, rt-fl, n + 2.
Тогда
(я-2J + (,г-1)* + п2+ («+ l
= 5я2+ 10 = 5(л2 + 2).
Если бы число 5(п2 + 2) было полным квадратом, то оно де-
делилось бы на ?5, следовательно, п2 -(- 2 делилось бы на 5. Но это
возможно лишь в том случае, если последняя цифра числа п1 есть
либо 8, либо 3, а никакой квадрат целого чидла не оканчивается на
зти цифры.
б) Из трех последовательных целых чисел одно наверное де-
делится на 3, второе дает при делении на 3 остаток 1 и третье —
остаток 2 или же, что равносильно, остаток—1. При перемножении
чисел остатки от деления их на какое-либо число тоже перемножа-
перемножаются; в самом деле,
(pk + г) (qk + s) «= pqk2 + pks + qkr -\- rs = k(pqk + ps-\-qr) + rs.
Поэтому, если число при делении иа 3 дает остаток 1, то любая его
степень при делении иа 3 тоже дает остаток 1; если же число при
делении на 3 дает остаток—1, то любая его нечетная степень при
делении на 3 дает остаток— 1, а любая четная — остаток 1.
Таким образом, из трех четных степеней последовательных целых
чисел одна делится на 3, а две другие дают при делении на 3 оста-
остаток 1. Следовательно, сумма четных степеней трех последовательных
целых чисел дает при делении на 3 остаток 2, или, что то же самое,
остаток — 1. А мы уже видели, что такой остаток не может дать
при делении на 3 четная степень никакого целого числа.
Примечание. Интересно отметить, что в приведенном дока-
доказательстве.нигде не используется тот факт, что четные степени, в кото-
которые возводятся три числа, одинаковы. Таким образом, имеет место
следующее предложение — более общее, чем утверждение задачи:
сумма четных степеней (может быть различных!) трех последова-
последовательных целых чисел не может выть четной степенью никакого
целого числа.
в) Как мы видели в решении задачи б), сумма четных степеней
трех последовательных целых чисел дает при делении на 3 остаток 2.
Отсюда вытекает, что сумма четных степеней девяти последов а тель-
138
ных чисел дает лри делении на 3 остаток 2 -f- 2 + 2 = 6, т. е. де-
делится на 3. Докажем теперь, что сумма одинаковых четных степеней
девяти последовательных целых чисел не делится на З2 = 9; отсюда
будет сразу следовать утверждение задачи .
И? девяти последовательных целых чисел одно обязательно де-
делится на 9, одно дает при делении на 9 остаток 1, одно —остаток 2,
и т. д. Отсюда следует, что если 2k есть общая степень в которую
возводятся девять чисел, то наша сумма дает при делении на 9 тот
же самый остаток, что и сумма
О + 1»" + 2г* + 32* + 4" + S2" + 62ft + Tik + 82\
или сумма
2A" + 4*+ 7'')
(так как З2 и б2 делятся на 9; I2 и 8* = 64 дают при делении на 9
остаток 1; 22 = 4 и 72 = 49 дают при делении на 9 остаток 4;
42 — 16 и 52 = 26 дают при делении на 9 остаток 7).
Отметим теперь, что I3 = 1, 43 = 64 и 73 = 343 все дают при
делении на 9 остаток 1. Отсюда следует, что если k — 31, то
1* + 4й + 7й = I1 + 64' + 343' дает при делении на 9 тот же оста-
остаток, что и сумма 1' + 1' + 1' = 3, т. е. не делится на 9; если к =
¦= 3/ + 1, то Iй + 4А + 7* = 1г • 1 + 64' • 4 + 343! • 7 дает при деле-
делении на 9 тот же остаток, что и сумма 1 • 1 + 1 • 4 + 1 • 7 = 12, т, е.
не делится на 9; если k = 3/ + 2, то 1* + 4h + 7* = 1' • 1 + 64' ¦ 42 +
4- 343! • 72 дает при делении на 9 тот же остаток, что и сумма 1 • 1 +
-f- 1 • 16 + 1 • 49 == 66, т. е. не делится на 9.
80. а) Сумма цифр каждого из чисел А и В равна
1+2 + 3 + 4 + 5 + 6 + 7 = 28?
отсюда следует, что оба числа дают при делении на 9 остаток 1
(каждое число дает при делении на 9 такой же остаток, как и сумма
А
его цифр). Но если бы было ~g~ =* п, или, что то же самое, А = пВ,
где п — целое число, отличное от 1, то из того, что В =¦ 9/V + 1,
следовало бы, что А — пВ = 9М + п; таким образом, п должно да-
давать при делении на 9 остаток 1. Наименьшее такое число п
есть 10; но ~g~<C Ю.так как оба числа Л и В состоят из 7 цифр.
б) Обозначим искомые числа через N, 2N, 3N. Каждо» целое
число дает при делении на 9 такой же остаток, нвк и его сумма цифр;
поэтому сумма N -\-2N + 3/V дает при делении на 9 такой же оста-
остаток, как и сумма 1 + 2 + 3 + ... + 9 =45, т. е. 6iV (а следователь-
следовательно, и 3N) делится на 9.
Так как 3N трехзначно, то первая цифра числа N не может быть
больше 3; поэтому последняя цифра N не может равняться 1 (тек
как в этом случае 2N оканчивается цифрой 2, a 3N — цифрой 3
и вс« три цифры 1, 2., 3 оказываются занятыми). Число N не может
также оканчиваться цифрой 5 (в этом случае 2N оканчивалось бы
нулем). Предположим теперь, что последняя цифра N есть 2; в та-
таком случае последние цифры 2N и ЗА/ равны соответственно 4 и 6.
Для двух первых цифр 3N остаются возможными значения 1, 3, 5,
7, 8 и 9; так как сумма всех цифр 3N кратна 9, то первые две цифры
3JV есть 3 и 9 или 5 и 7. Проверяя все представляющиеся случаи,
находим одну тройку чисел, удовлетворяющих условию ладачи! 192,
139
384, 576. Аналогично исследуются случаи, когда N оканчивается на 3,
4, 6, 7, 8 или 9; при этом обнаруживаются еще три решения задачи:
273, 546, 819; 327, 654, 981 и 219, 438, 657.
81. Полный квадрат может оканчиваться только цифрами 0, 1, 4,
9, 6 и 5. Далее, квадрат каждого четного числа, очевидно, делится
на 4, а квадрат нечетного числа дает при делении на 4 остаток 1
(BkJ = Ak2, Bk + IJ = A(k2 + k) + 1); поэтому квадрат никакого
числа не может оканчиваться цифрами 11, 99, 66 и 55 (числа, окан-
оканчивающиеся двумя цифрами 11, 99, 66 или 55, дают при делении на 4
соответственно остатки 3, 3, 2 и 3). Рассмотрим, наконец, какие
остатки может давать квадрат целого числа при делении на 16. Каж-
Каждое целое число можно представить в одном из следующих видов:
%k, %k±\, 8* ±2, 8?±3 или 8? + 4;
квадраты этих чисел имеют вид
16- D6*), 16Dй2±?) + 1, 16Dfe2±2k) +4,
или 16D?s + 4?+ 1).
Таким образом, мы видим, что квадрат целого числа или делится на
16 или дает при делении на 16 один и? остатков 1, 4 и 9. Число же,
оканчивающееся цифрами 4444, дает при делении на 16 остаток 12 и,
следовательно, не может быть полным квадратом.
Итак, если полный квадрат оканчивается четырьмя одинаковыми
цифрами, то эти цифры — четыре нуля (например, 1002 = 10 000).
82. Обозначим стороны прямоугольника через х и у, а диаго-
диагональ— через г; тогда по теореме Пифагора будем иметь:
х* + у2 = г5.
Нам надо доказать, что произведение ху делится на 12. Покажем
сначала, что это произведение делится иа 3, а затем — что оно де-
делится на 4. Так как
Ak + 1) +1,
то квадрат каждого числа, не кратного 3, дает при делении на 3
остаток 1. Поэтому, если бы ни х ни у не делились на 3, то сумма
х2 + у'2 давала бы при делении на 3 остаток 2 и поэтому не могла бы
быть равна квадрату никакого целого числа. Следовательно, если
х2 + у2 равно квадрату целого числа г, то хотя бы одно из чисел
хну делится на 3, а значит, и ху делится на 3.
Далее ясно, что оба числа хну одновременно нечетными быть
не могут; если х =. 2т + 1, у = 2п + 1, то
х3 + у1 = 4т2 + Ш + 1 + 4п! + An + 1 == 4(т2 + т + л2 + п) + 2
не может равняться квадрату никакого целого числа (квадрат нечет-
нечетного числа нечетен, а квадрат четного числа делится на 4). Если
и х, и у — четные числа, то их произведение делится на 4. Предполо-
Предположим теперь, что х четно, а (/ — нечетно: х = 2т, у = 2л + 1. Чис-
Число г при этом будет нечетным (ибо г2 = хг + у2 нечетно): г = 2р +
+ 1. В этом случае имеем:
BтJ = Bр+ IJ — B« +¦ IJ = 4р2 + 4р + I — 4«2 — 4н — 1,
и ,
т~ р(р+\)~п(п+1).
140
Отсюда вытекает, что т* четно (произведения последовательных целых
чисел р(р-{-\) и л(я+1) оба четные); следовательно, т четно
и х =¦= 2/п делится на 4. Значит, и в этом случае произведение ху
делится на 4.
83. По формуле решения квадратного уравнения имеем:
следовательно, для того чтобы корни уравнения были рациональны,
надо, чтобы выражение Ь2 — Аас являлось полным квадратом. Поло-
Положим b = 2л + 1. о. = 2р + 1, с ¦= 2ц + 1; в таком случае будем
иметь:
Bп+ I)8 — 4Bр+ 1) B?+ 1) = 4/i* + An —
8р — 8? — 3 = 8
•(-
Так как это число нечетно Iя'—i-есть целое число, ибо произве-
произведение двух последовательных целых чисел всегда четно); то оно мо-
может быть квадратом только нечетного числа. Но каждое нечетно?
число можно представить в виде \k ± Г, квадрат этого числа равен
Dk ± 1)» =. 16ft2 ± 8k + 1 = 8B?2 ± k) + 1
и, следовательно, всегда дает при делении на 8 остаток 1. Посколь-
Поскольку число Ь2 — 4ас дает при делении на 8 остаток 5, оно не может
являться полным квадратом.
84. Имеем:
п T/i-|-lT'i + 2"" п (п -[- 1) (п + 2) '
Числитель нашей дроби не делится-на 3, а знаменатель делится,
так как он является произведением трех последовательных целых
чисел. Следовательно, в знаменателе есть множители, отличные от
2 и 5, а потому в ра?ложении получится бесконечная перио-
периодическая десятичная дробь.
Из двух целых чисел п и п + 1 одно должно быть четным. Если
четно п+ 1, то п нечетно, следовательно, нечетно Зп2, а потому и весь
числитель. Если же п четно, то и п + 2' делится на 2 и, следовательно,
янаменатель наверняка делится на 22; числитель же делится только
на 2, так как если п = 2k, то
Поэтому знаменатель полученной после сокращения дроби не будет
взаимно прост с 10, и десятичная дробь будет смешанной перио-
периодической.
И!
85. а), б). Приведем все слагаемые в сумме
п ' п + \ ' л + 2 ' ' n+mj
к общему знаменателю. Из всех дробей, входящих в нашу сумму,
рассмотрим ту, в знаменателе которой стоит самая высокая степень
двух (такая дробь может быть только одна). Тогда во все осталь-
остальные дроби число 2 войдет дополнительным множителем, в то время
как в этой дроби дополнительным множителем обязательно будет
число нечетное. У всей дроби Л1 (или N) знаменатель есть, конечно,
число четное, а числитель, как мы видим, состоит из суммы некото-
некоторого числа четных чисел и одного нечетного. Следовательно, числи-
числитель есть число нечетное, а потому вся дробь не может быть целой,
в) Рассмотрим дробь в сумме Л, в знаменателе которой стоит
самая высокая (k-я) степень числа 3. Так как у нас знаменателями
являются только нечетные числа, то дробь -—-т в сумме К отсут.
ствует. Поэтому при приведении суммы дробей к общему знаменате-
знаменателю дополнительные множители всех дробей, кроме рассмотренной,
будет делиться на 3. а дополнительный множитель этой дроби не бу-
будет делиться на 3. Следовательно, в сумме получим дробь, знамена-
знаменатель которой делится на 3, а числитель не делится.
a» J- 2а
86. Дробьа4 , заз j. 1 сократима или несократима одновремен-
а* + За2 -i- 1 , а2 + 1
но с дробью —fl3 _|_ 2а— "" а "¦ а3 + 2а' нли ~~ °ДновРемснио С
дробью аз _i_ 2а' -^Р°°ь а3 ' 2а сокРатима или несократима одно-
a3Jr2a a
временно с дробью а2 i ) =a+ aa _l ]¦ 11ЛН —одновременно с дробью
а _ , а
2 11 -Дробь 2 i 1 сократима или несократима одновременно с
дробью —— ""» "Г —. или — одновременно с дробью —, которая
при целом а, очевидно, несократима.
б) Если как число ч = 5л + 6, так и число з = 8га + 7 делятся
на целое число rf, то на d делится также их разность р = з — ч =
= 3«+1 и разность pi = ч — р = 2п + 5, а также разности ^2 =
— Р — Р\ = п —4; рз = Pi — Рг = л + 9; р4 = Рз — рг *= 13. Таким
образом, на с! обязательно должно делиться (простое!) число 13, от-
откуда видно, что d может иметь лишь одно только значение 13. То,
что значение d = 13 возможно, легко показать на примере; так, если
5л + 6 26
п •= 4, то дробь оп i ^ = "до" сократима на 13.
87. Ясно, что достаточно доказать утверждение задачи в пред-
предположении, что во второй раз мы начали чтение со второй циф-
цифры первоначального числа: ведь, сдвигаясь подобным обратом на
одну цифру, мы можем последовательно перейти от заданной
начальной цифры числа к любой другой, принимаемой в новом чтении
142-
За начальную; если же t(a каждом Шаге мы будем йолучать делящее-
делящееся на 27 число, то оно будет делиться на втот множитель и после
любого количества подобных «шагов». Итак, пусть первая цифра
прочитанного первоначально 1953-значного числа а\ ¦» а; образуемое
остальными цифрами 1952-значиое число обозначим через В. В таком
случае наше «первое» число равно а • 10'952 + В, а прочитанное, на-
начиная со 2-й цифры (с начала числа В), число будет равно В • 10 + а.
Нам дано, что число а ¦ 10!952 + В делится на 27. Но число
101952 — 1 состоит из 1952 девяток; разделив это число на 9, мы полу-
получим число из 1952 выписанных подряд единиц, дающее при делении
на 3 такой же остаток, как и сумма его цифр 1952, т. е. остаток 2;
следовательно, число 101952 — 1 дает при делении на 27 остаток
2 • 9 = 18, а число 101Э52 —остаток .19. Поэтому, обозначив остаток
от деления числа В на 27 через 6, мы получим, что а • 101952 + В
дает при делении на 27 такой же остаток, как и число \%а-\-Ь\ та-
таким образом, условие задачи утверждает, что число М = 19а + b
делится на 27.
Перейдем теперь к «новому» числу В • 10 +а. Это число даёт
при делении па 27 тот же остаток, что и число N = 106 + а; таким
образом, наша задача сводится к доказательству того, что если М =
= 19а + 6 делится на 27, то и N = 106 + а делится на 27. Но пос-
последнее утверждение очевидно, ибо ЮМ — TV =» 189а делится на 27
(так как 189 = 27 • 7), а N = ЮМ — 189а.
88. Очевидно, что десятичная запись всех чисел 5", где п — на-
натуральное, оканчивается цифрой 5; поэтому н запись числа а = 51000
оканчивается цифрой 5 (не нулем!). Предположим теперь, что в за-
записи числа а встречаются и нули; пусть первый из них (считая с
конца!) стоит на i-м месте. Ясно, что число 51000 • 10' оканчивается
цифра ми 5000 ... 0; поэтому /—1 последних цифр десятичной запи-
i—'1 нулей
си суммы а\ = 51000 + 51000 • 1О'~' не отличаются от I— 1 последних
цифр числа а (т. е. все они отличны от нуля), a i-я с конца цифра
числа ах есть 5 (т. е. тоже не нуль!). Исправив таким- образом ;'-ю циф-
цифру (для чего нам пришлось заменить число а числом аи десятичная
запись которого содержит больше цифр), мы перейдем к следующей
от конца цифре (разумеется, цифре числа fli), которая равна нулю
(если только такая цифра есть), и точно таким же путем исправим
и ее: если равна иулю /-я от конца цифра числа at (где, конечно, / >
> i), то это число мы заменим числом а2 = а\ + 51000 • Ю-*, которое
также делится на 51000и у которого уже / последних цифр отличны
от нуля (на ;'-м от конца месте стоит цифра 5).
Если продолжая этот процесс, мы придем к какому-то числу ah
(где k — 0, 1, 2, ...; под по мы понимаем само число а = 51000), де-
десятичная запись которого не содержит нулей, то утверждение задачи
доказано; но так как число цифр чисел а0 = а, аи а2,... все время
возрастает, то наш процесс может и никогда не кончиться. Однако
если мы дошли в наших построениях до какого-то числа а/, 1000 пос-
последних цифр которого отличны от нуля, то далее мы можем и не про-
продолжать. В самом деле, число щ = Ю1000 ¦ А + В, где десятичную
запись числа В составляют 1000 последних цифр числа а{ (и, значлт,
•се цифры числа В отличны от нуля), а десятичная запись числа А
состоит из всех предшествующих 1000-й цифр числа а;. Отсюда сл#-
А что
fi-.a(--ig'0l)e A,
" 141
и, значит, число В делится на 51000 (поскольку на 51000 делятся и Cti
и 101000 -А =21000 • 51000 • А).
89. Числа нашего ряда имеют вид 1 + 104 + 108 + ... + 104*.
Рассмотрим наряду с этими числами числа 1 + 10* + 104 + 106 +..,
...+ Ю2*. Непосредственной проверкой нетрудно убедится в том,
что
Ю«"+4_
Ю2*+2 —
1
1
= A04 —
= (Ю2-
1) •
1) •
A
A
+
+
104
102
+
+
108 + .,
Ю4 + .,
..+ Ю4").
,.+ 10").
Кроме того, очевидно,
]0«+4— 1 = (H2ft+2— 1) A02*+2 + 1).
Сопоставляя все эти равенства, получаем:
Ю4"+4— 1 = (Ю4—1)A + 104+ 108 + ..,+ 10*) =¦
= (Ю2— 1) A + 102 + 104 + ... + 102*)A02*+2 + 1),
104 — 1
или, так как jg2 , = 102 —f— 1 = 101,
A + iO'> + 108 + ...+104ft) • 101 =
= A + 102 + Ю4 + ...+ 102й)A02й+2+ О*
Так как 101 есть простое число, то или 1 + 102+ 104 + ... + 102А,
или 102ft+2 + 1 делится на 101; при этом, если k>\, то частное боль-
больше 1. Сократив на 101, мы получим, что число 1 + 104 + 108 + • •.
.. . + 104* при к > 1 разлагается по крайней мере на два множи-
множителя, что и требовалось доказать. При k = 1 мы имеем число 104 +
4- 1 = 10001, которое тоже является составным A0001 = 73 • 137).
Примечание. Точно так же можно доказать, что и все
числа ряда
100... о ЮО ... 01, 100 ... 0 100 ... 0 100 ... 01, ...
Bfc+I) раз B*+1)~раз B~к+\) раз Bfc+l> раз B* + 1) раз
являются составными.
90. Заметим, что
(в силу формулы а2 — б2 ¦= (а-\-Ь)(а — 6); последний множитель
2 — 1 •= 1 можно отбросить). Таким образом, число 22"—1 =B2П+
+ 1)—2 делится на все предыдущие числа нашего ряда. Отсюда
следует, что если 22"+ 1 и 22Й+ 1, где к < п, имеют общий делитель,
то на этот общий делитель должно делиться и число 2. Но 2 не мо-
может быть общим делителем двух чисел последовательности, так как
все эти числа нечетные; следовательно, каждые два числа последо-
последовательности являются взаимно простыми.
91. 2П, разумеется, не может делиться на 3. Если 2" дает при
делении на 3 остаток 1, то 2П — 1 делится иа 3; если 2" дает при
144
делении на 3 остаток 2, то 2" + 1 делится на 8. Поэтому во
случаях одно из двух чисел 2" — 1 и 2" + 1 делится иа 3, и следо-
следовательно, если оба эти числа больше 3, то они не могут быть одно-
одновременно простыми.
92. а) Если бы простое число р > 3 давало при делении на 3
остаток 2, то 8р — 1 делилось бы на 3. Поэтому число р должно да-
давать при делении на 3 остаток 1; но в этом случае &р + 1 делится
на 3. Если же р = 3, то 8^+1 = 25 — тоже составное число.
б) Если р не делится на 3, то р2 дает при делении на 3 остаток
1 (см. решение задачи 796)) и, следовательно, &р2 + 1 делится на 3.
Таким образом, должно быть р = 3, 8р2 + 1 = 73. Но в атом слу-
случае и число &р2 — 1 =71 — простое число.
93. Простые числа кроме 2 и 3 дают при делении на 6 остаток
1 или 5, ибо если бы число давало при делении иа Ц остаток 2 или
4, то оно было бы четным, а если бы оно давало остаток 3, то де-
делилось бы на 3. Таким образом, любое простое число, большее 3,
можно записать в виде 6га + 1 или 6га + 5. Квадраты этих выраже-
выражений имеют вид 36га2 + 12га + 1 и 36га2 + 60га + 25. В обоих случаях
при делении на 12 получается в остатке 1.
94. Из трех чисел, имеющих вид бге + 1 или 6га + 5 (см. преды-
предыдущую задачу), по крайней мере два имеют одинаковый вид. Сле-
Следовательно, их разность, равная d или Id, где d — разность прогрес-
прогрессии, делится на 6; поэтому d делится на 3. Кроме того, d как раз-
разность двух нечетных чисел делится на 2, поэтому d делится на 6.
(См. также решение задачи 95а).)
95. а) Так как простые числа (кроме 2) —числа нечетные, то
разность прогрессии — число четное. Далее, если бы разность прог-
прогрессии не делилась на 3, то три члена прогрессии аи п[ + d, a\ + 2d
все давали бы разные остатки при делении на 3 (разность никаких
двух из них не делится на 3) и, следовательно, хотя бы одно из них
делилось бы на 3, что невозможно, так как все члены прогрессии по
условию — простые числа (если at = 3, то а, + 3d тоже делится на
3). Точно так же, если бы d не делилось на 5, то все числа аь ai + d,
Ci + 2d, C| + 3d и а\ + Ad давали бы при делении на 5 разнке остат-
остатки и, следовательно, одно из них делилось бы на 5. Аналогично по-
показывается, что если все члены арифметической прогрессии — прос-
простые, то разность прогрессии должна делиться на 7. Итак, разность
d искомой прогрессии должна быть кратна 2 • 3 • 5 • 7 = 210; d =»
«= 210*.
По условию задачи
я10 = ai + Ы — а{ + 1890Й < 3000.
Но это неравенство невозможно при k Js 2; значит, k = 1, Отсюда"
следует, что а, < 3000 — Ы = 1110.
Далее 210=11-19+1; следовательно, (т+1)-й член прог-
прогрессии можно представить в виде
flm+i = а,.+ A1 • 19+1) -ш= 11 • 19т+ (щ + т).
Отсюда следует, что если п\ дает при делении на 11 остаток 2, то
«ю делится на 11; если а,- дает при делении на 11 остаток 3, то а»
делится на 11, и т. д. Таким образом, доказываем, что ai не может
давать при делении на 11 остаток 2, 3, 4, ... или 10. Если ai отлич-
отлично от 11, то а\ не может делиться иа 11 (ибо ai — простое); значит,
°i или равно 11, или дает при делении на 11 остаток 1. Далее,
Ю Д. О. Шклярский я Xf. 1*5
используя то, что 2l6 = 13 • 16 + 2 и; следоватеЛЫМ,
om+1 = а, + A3 • 16 + Ч)т = 13 • 16m + (а, + 2т),
можно показать, что fli при делении на 13 может давать только
остатки 2, 4, 6, 8, 10 или 12. Учитывая, что at нечетно (ибо все чле-
члены прогрессии нечетны), мы заключаем, что а\ или равно 11 или име-
имеет один из следующих видов:
2 • 11 • 13/ + 23 = 286/ + 23, 286/ + 45, 286/ + 67,
286/+155, 286/+177 или 286/+ 199.
Поскольку «1 < 1 110, нам остается только проверить следую-
следующие возможные значения at:
И; 23, 309, 595, 881; 45, 331, 615, 903; 67, 353, 637, 925; 155, 441, 727,
1 013; 177, 463, 749, 1 035; 199, 485, 771, 1 057.
Простыми из этих чисел являются только:
11, 23, 881, 331, 67, 353, 727, 1 013, 463 и 199.
Проверив соответствующие 10 прогрессий, мы найдем единствен-
единственную прогрессию, удовлетворяющую условиям задачи:
199, 409, 619, 829, 1 039, 1 249, 1 459, 1 669, 1 879, 2 089.
б) Задача решается аналогично задаче а). Прежде всего, если
Oi отлично от 11, то совершенно аналогично решению задачи а) по-
показывается, что знаменатель d прогрессии должен быть пропорцио-
пропорционален 2 - 3 • 5 - 7 - 1 ] =2 310 (d = 2310k); отсюда вытекает, что
ал = а, + 23 100ft > 20 000.
Остается исследовать случай ai = 11; здесь можно толь-
только утверждать, что d = 210/f. Воспользовавшись тем, что 210 =•
= 13-16 + 2, мы сможем записать следующее выражение дйя об-
общего члена прогрессии:
а„+1 = И + A3 • 16 + 2)Ы= 13A6?я + 1) + 2(Ы — 1).
Но при k = 1, 2, 3, 4, 5, 7, 8, 9, 10 удается подобрать такой
номер п < 10, что kn — 1 делится на 13 и, следовательно, ап+1
делится на 13 и не является простым; это значение п будет соответ-
соответственно равно 1, 7, 9, 10, 8, 2, 5, 3, 4. Если же k = 6, d = 210 ¦ 6 =,
= 1 260, то
я4=М+3-1260 = 3791
делится на 17. Таким образом, если а,-= 11, то k > 10, а следова-
следовательно, d ^ 2 100 и опять а10 > 20 000.
Примечание. В задачах а) и б), в соответствии с обычным
употреблением термина «простое число», мы считали все члены прог-
прогрессии положительными. Если же не требовать этого (т. е. называть
«простым> такое целое число п, которое не имеет делителей, отлич-
отличных от ±1 и ±л), то удовлетворяющие условиям задачи б) прогрес-
прогрессии существуют (вот пример такой прогрессии—И, 199, 409, 619,
829, 1039, 1249, 1459, 1669, 1879, 2039).
96. а) Если два неравных числа отличаются одно от другого яв
больше чем на 4, то они не могут иметь общих делителей, больших 4,
Ив
Таким образом, два числа из наших пяти последовательных чисел
могут иметь или общин делитель 2, или общий делитель 3, или об-
общий делитель 4, или быть взаимно простыми. Из пяти последователь-
последовательных чисел по крайней мере два будут нечетны; из двух последователь-
последовательных нечетных чисел по крайней мере одно не будет делиться на 3.
Следовательно, среди наших чисел имеется хотя бы одно нечетное
число, не делящееся иа 3; это число заведомо будет взаимно просто
с остальными четырьмя числами.
б) Решение этой задачи близко к решению задачи а), но значи-
значительно сложнее. Если два неравных числа отличаются друг от дру-
друга не больше чем на 15, то они не могут иметь общих делителей
больших 15. Так как два числа заведомо взаимно просты, если они
не имеют общих простых делителей, го, для того, чтобы доказать
пашу теорему, достаточно показать, что среди 16 последовательных
целых чисел можно найти число, не имеющее с остальными 15 чис-
числами — общих делителей 2, 3, 5, 7, и 13: это число и будет взаимно
просто со всеми остальными.
Прежде всего из 16 чисел вычеркнем как не удовлетворяющие
нашим требованиям восемь четных чисел; после этого у нас останется
восемь последовательных нечетных чисел. Из восьми последователь-
последовательных нечетных чисел, очевидно, на 3 делятся или 1-е, 4-е, 7-е, или 2-е,
5-е, 8-е, или 3-е, 6-е; на 5 делятся или 1-е и 6-е, или 2-е и 7-е, или
3-е и 8-е, или же только одно число; на 7 делятся или 1-е и 8-е, или
же только одно число; на 11 и 13 делится не больше одного чис-
числа. Если среди наших восьми последовательных нечетных чисел име-
имеется не больше пяти чисел, делящихся па 3, или па 5, или на 7, го
среди этих восьми чисел найдется число, не делящееся ни на 3, ни
на 5, ни на 7, ни иа 11, ни на 13; это число заведомо будет взаимно
просто со всеми остальными. Рассмотрим теперь все те случаи, копа
чисел, делящихся или на 3, или на 5, или на 7, будет не меньше 6.
Пусть среди наших восьми нечетных последовательных чисел на
3 делятся три числа; тогда на 5 могут делиться два из оставшихся
чисел только в том случае, если одно из крайних чисел делится на 3,
а второе — на 5. Вычеркнув эти пять чисел, мы оставим 2-е, 5-е и
6-е числа, или же 7-е, 4-е, и 3-е числа. Рассмотрим сначала первый
случаи. 2-е, 5-е н 6-е нечетные числа являются в ряду всех 16 после-
последовательных чисел 4-м, 10-м и 12-м или 3-м, 9-м и 11-м числами.
Ни одно из этих чисел не может иметь ни с одним из остальных 15
чисел общий делитель 13, так как каждое из остальных чисел от-
отличается от него меньше чем на 13. Следовательно, если эти три чис-
числа не делятся ни на 3, ни на 5, то одно из них (а именно, то, которое
не делится ни на 7, ни на 11) будет взаимно просто со всеми осталь-
остальными числами. Точно так же проводится доказательство и в том
случае, когда после вычеркивания чисел, делящихся на 3 и на 5,
остаются 3-е, 4-е и 7-е числа.
Если из наших восьми чисел на 3 делятся три числа, то на 7 не
могут делиться никакие два из оставшихся. Если же на 3 делттся
только два числа, 3-е и 6-е, то возможно, что из оставшихся на 7 де-
делятся два, а именно 1-е и 8-е, и на 5 делятся два: 2-е и 7-е. Вычерк-
Вычеркнув эти шесть чисел, мы оставим из наших восьми нечетных чисел
4-е и 5-е, которые не будут уже делиться ни на 3, ни на 5, ни на 7.
Оба эти числа будут взаимно простыми с каждым из остальных 15
чисел нашей последовательности, так как каждое из остальных чисел
отличается от них меньше чем на 11 и поэтому не может иметь с
ними общий делитель 11 или 13.
Ю* 147
Итак, мы полностью доказали, что из J6 последовательных
целых чисел всегда можно выбрать одно, взаимно простое с ос-
остальными.
Примечание. Аналогично, но более просто доказывается,
что из 8 или из 10, или из любого другого числа, меньшего 16,
последовательных целых чисел всегда можно выбрать одно, взаимно
простое с остальными. Для 17 чисел это предложение уже неверно:
например, среди 17 последовательных чисел от 1 184 до I 220 нет
ни одного взаимно простого со всеми остальными. По-видимому, и
для любого другого числа к, большего 16, можно найти k последо-
последовательных целых чисел, среди которых нет ни одного взаимно прос-
простого со всеми остальными; однако доказательство этого общего пред-
предложения, как будто, неизвестно.
97. Искомое число будет равно произведению А\ • В\, где Л\
состоит из 666 цифр 9, а В\— иэ 666 цифр 2. Но А\ на 1 меньше
числа 10656, выражаемого единицей с 666 нулями. Поэтому умножить
число В[ на это число — то же самое, что умножить В[ на 1066S (при
этом получится число, состоящее из 666 двоек и 666 нулей) и из ре-
результата вычесть число В\. Нетрудно видеть, что получаемая раз-
разность будет иметь вид 22 ... 2177 ... 78.
865 раз 665 раз
98. Число 777 777 делится без остатка на 1001 и дает в частном
777. Поэтому число 777... 700000 дает при делении на 1001 в
996 раз
частном
777000777000 ... 77700000.
rfyaua 777OSO повторяется 16С раз
Так как, кроме того, число 77 777 дает при делении на 1001 в
частном Пив остатке 700, vo частное от деления А иа 1 001 имеет
вид
777000777000 ... 77700077,
группа 777000 повторяется 166 раз
а остаток равен 700.
99. Так как число 222 222 не является полным квадратом, то
десятичная запись искомого числа имеет вид 222222а?а8 . • ¦ an,' где
aj, о8, ..., ап — какие-то неизвестные нам цифры.
Предположим сначала, что число п цифр искомого числа четно-
п = 2k. Будем теперь извлекать корень из этого числа по обычным
правилам:
У22 22 22 a7as ... a2k_la2h *= 471 405
16
87
6 22
6 09
941
1
9424
4
13 22
941
3 81 a,at
3 76 9 6
942805
5
4 7 1 4 0 2 Б
148
'(пятая цифра результата есть 0, так как Х\, очевидно, может быть
равно только 4 или 5 и, следовательно, меньше 9; по аналогичной
причине шестая цифра, если она последняя, есть 5).
Остаток равен нулю, если аа = 4, а\0 =•= 0, ац = 2, а^ = 5;
Х\ = 4, ль = 7, яз = 1, откуда легко выводим as = § + 1 = 7, а7 =
= G + 9)—10 = 6. Таким образом, наименьшее число, имеющее
четное число цифр и удовлетворяющее условию задачи, есть,
222 222 674 025 = 471 4052.
Аналогично рассматривается случай, когда п = 2k + 1 нечетно:
24
4
У2 22 22 2a7asa» ... a2fta.>ft+1 = 149071 ...
-L
122
289
9
_96
26 22
26 01
29807
7
21 2a7asae
20 86 4 9
Так как число, образованное цифрами Л'ь л'г, не меньше 33 =
(= 119—86) и не больше 43 (= 129—86), то шестая цифра корня
равна 1, причем на этом процесс извлечения корня не обрывается,
а продолжается дальше. Следовательно, наименьшее число, имеющее
нечетное число цифр и удовлетворяющее условию задачи, не менее
чем тринадцатизначно, т. е. превосходит число 222 222 674 025. Итак,
искомым числом будет 222 222 674 025.
100. Из равенства т2 = пг + 1954 вытекает, что числа т2 и
п2 — одинаковой четности (т. е. оба четные или оба нечетные); сле-
следовательно, то же можно сказать и о числах m и п. Но в таком слу-
случае число 1954 = in2 — я2 = (т + я) (т — п) обязательно должно
делиться на 4 (ибо числа m + п и m — п — оба четные), в то время
как 1954 на 4 не делится. Следовательно, требуемых чисел m и и
не существует.
101. Искомое шестизначное число, начинающееся с цифр 523 и
делящееся без остатка на .7 • 8 • 9 = 504, можно представить в виде
523 000 + X, где X — трехзначное число. Но непосредственное деле-
деление дает 523 000 = 504 • 1037 + 352, т. е. 523 000 дает при делении
иа 504 остаток 352. Так как сумма числа 523 000 и трехзначного чис-
числа X должна делиться на 504, то отсюда следует, что X может быть
равно либо
504 — 352 = 152,
либо
2-504 — 352 = 656
(ибо число 3 • 504 — 352 уже четырехзнанно). Итак, условию задачи
удовлетворяют два числа: 523 152 и 523 656.
102. Пусть N — искомое число. По условию задачи мы имеем:
N *= 131А+ И2= 132/ + 98,
где k н / — целые положительные числа. При этом так как iV
149
четырехзначно, то, очевидно,
_ N — 98^ 10 000 — 98
' = 132 132 *= 75#
Далее, имеем:
131/г + 112= 132/ + 98; 131D — /) =/—14.
Отсюда видно, что если k — / отлично от нуля, то I — 14 по абсолют-
абсолютной величине превосходит 130, что невозможно, если / =д; 75. Таким
образом, должно быть k — / = 0, k = /, откуда сразу получаем:
/— 14 = 0, k — I = 14,
N = 131 • 14 + 112 = A32 • 14+98) =* 1946.
103. а) Выписанное в условии задачи 2л-?начнов число можно n^.i»
образовать так:
4. Ю-11-1 + 9-102"-2 + 4-102'1-3 + 9 AО2'г~4 + 102'1-5 + ...
... + 10") + 5-10"-1 + 5.10"-2 = 4-102"-1 + 9- iO2'1-2 +
1—3
I
+ 4-102"-3 + 9- 10n ^—g + 5-Ш"-1 + 5-10'1-2 =»
= 4- Ю-'1 + 9- Ю-"-2 + 5- Ю2"-3 — 1О'г + 5-10"—' +
+ 5-1011-2 = 4" (8-102'1-1 + 18- I02rt-2 + 10-10-"—3 -
— 2-10" -f 10п + 10"-1) = -j- (9- Ю271-1 + 9- 102n~2 — 9.10"-')
Но этому же равна н сумма арифметической прогрессии с раз-
разностью 1, первым членом 10" и последним членом 10" —" 1 (число
членов прогрессии равно 10" — 10"-' = 9 • 10"~1)—сумма всех
я-значных чисел.
б) Число тех из рассматриваемых чисел, у которых на первом
место стоит данная цифра а (а может быть равно 1, 2, 3, 4 или 5),
есть 6 • 6 • 3 «=¦ 108 (ибо на втором и третьем месте может стоять
любая из шести цифр 0, 1, 2, 3, 4, 5, а иа третьем месте — любая
из трех цифр 0, 2, 4, так как рассматриваются только четные чис-
числа). Отсюда общая сумма всех целых тысяч, содержащихся во всех
наших числах, равна A + 2 + 3 + 4 + 5) • 108 • 1000 => 1 620 000.
Аналогично, число чисел, у которых на втором месте стоит дан-
данная цифра, равно 5 • 6 • 3 •=¦ 90, так как на первом месте может
стоять одна из пяти цифр 1, 2, 3, 4 или 5. Отсюда общая сумма
всех целых сотен (после вычета всех целых тысяч), содержащихся
во всех наших числах, равна A + 2 + 3 + 4 + 5) • 90 ¦ 100 = 135 000.
Таким же образом получаем, что общая сумма всех целых де-
десятков равна A + 2 + 3 + 4 + 5)- 90 • 10 -= 13500 и, наконец, сум.
ма единиц равна B + 4) • 5 • 6 • 6 • 1 = 1080.
Искомая сумма равна
1 620 000 + 135 000 + 13 500 + 1080 =¦ 1 769 580.
150
. * 164. Рассмотрим сначала йсе Целые числа от б до 99 99999$; npil
этом те из этих чисел, которые имеют меньше восьми цифр, допол-
дополним слева нулями так, чтобы они стали восьмизначными. Мы будем
иметь 100 000 000 восьмизначных чисел, для записи которых нам по-
потребуется, очевидно, 800 000 000 цифр. При этом здесь каждая из
10 цифр будет использована равное число раз, поскольку все они
совершенно равноправны (нуль может стоять ;ia первом месте точно
так же, как и всякая другая цифра). Следовательно, каждая цифра
будет у нас использована 80 000 000 раз.
Теперь подсчитаем, сколько здесь будет лишних нулей (т. е. ну-
нулей, приписанных спереди чисел, имеющих меньше восьми цифр).
Однозначных чисел (не считая нуля) имеется в:его' девять, двузнач-
двузначных чисел 99—9 = 90, трехзначных чисел 999—99 = 900, и т. д.
Так как к однозначной цифре мы приписали слева семь нулей, к
двузначной — шесть, и т. д., то общее число лишних нулей (не счи-
считая цифр первого числа, которое у нас записывалось так: 00 000 000)
будет равно
7 • 9 + 6 • 90 + 5 ¦ 900 + 4 • 9 000 + 3 ¦ 90 000 + 2 • 900 000 +
+ 1 ¦ 9000 000= 11 111 103,
Припишем теперь 1 слева первого числа 00 000 000; при этом мы
получим все целые числа от 1 до 100 000 000. Мы видим, что для
записи этих чисел требуется 80 000 000 двоек, троек, и т. д. до девя-
девяток, 80 000 001 единица (одну лишнюю единицу мы приписали слева
числа 00 000 000) и 80 000 000 — 11 111 103 = 68 888 897 нулей.
105. Однозначных чисел всего имеется девять, двузначных всего
имеется 99 — 9 — 90, трехзначных 999 — 99 = 900 и вообще я-знач-
ных 9 • 10"-1.
Однозначные числа гаймут в выписанном нами ряду девять мест,
двузначные 90 • 2 = 180 мест, трехзначных 900 • 3 = 2700 мест,
четырехзначные 9000-4 = 36 000 мест, пятизначные 90 000-5 =
i= 450 000 мест. Отсюда видно, что интересующая нас цифра будет
принадлежать пятизначному числу.
Цифры, принадлежащие не более чем четырехзначным числам,
будут иметь номера от 1 и до 9 + 180 + 2700 + 36 000 = 38 889. Для
того чтобы узнать, сколько пятизначных чисел уложится в промежут-
промежутке от 38 889-го места до - 206 788-го, надо разделить разность
206 788 — 38 889 = 167 899 на 5 (деление с остатком):
206 788 — 38 889 = 5 • 33 579 + 4.
Таким образом, искомая цифра будет принадлежать 33 580-му
пятизначному числу, т. е. числу 43 579 (так как первое пятизначное
число есть 10000). В этом числе интересующая нас цифра стоит па
4-м месте. Следовательно, искомая цифра есть 7.
106. Допустим, что дробь 0,1234... — периодическая, я —число
цифр периода, k — число цифр до периода. Рассмотрим число N =
¦= 10'", где т — какое-нибудь целое число, не меньшее чем п + к;
это есть единица с т нулями на конце. При составлении нашей дро-
дроби мы выписываем подряд все целые числа; следовательно, где-то
будет расположено и число N. Но из того, что в ряду цифр «ашей
бесконечной десятичной дроби где-то стоят подряд т ^ п + k нулей,
следует, что период дроби состоит из одних нулей. Так как »то,
очевидно, невозможно, то дробь 0,1234 ... — непериодическая.
Ш
107. Хорошо известпб, что КажАбе Целое положительное число
N дает при делении на 9 тот же остаток, что и сумма его цифр. (Это
следует иэ того, что стоящая на (k + 1)-м от конца месте цифра ак
десятичной записи N символизирует слагаемое а* • 10* в разложении
N по степеням десяти; но а* • 10* = а* • (99 ... 9 + 1) = 99... 9а* +
+ а* дает при делении на 9 тот же остаток, что и а/,.) Отсюда выте-
вытекает, что если число N дает при делении на 9 остаток гФО, то при
многократной замене 4исла суммой его цифр мы в конце концов
придем к однозначному числу г, а если N делится на 9 —к числу 9.
Таким образом, единицы-среди нашего миллиарда однозначных чисел
будут соответствовать числам 1, 10, 19. 28, ..., 1000 000 000, даю-
дающим при делении на 9 остаток 1, а двойки—числам 2, 11, 20,
29, ..., 999 999 992, дающим при делении на 9 остаток 2. Но первых
чисел, очевидно, на одно больше, чем вторых; поэтому единиц мы
получим на одну больше, чем двоек.
108. а) Не может. Если десятичная запись числа N — п2 оканчи-
оканчивается нулем, то она обязательно оканчивается четным числом нулей
и число Nu получаемое из N вычеркиванием этих нулей в конце, так-
также является полным квадратом; поэтому достаточно доказать, что
не может являться полным квадратом число, записываемое лишь
цифрами 6 и 0 н кончающееся цифрой 6. Но такое число кончается
либо цифрами 06, либо цифрами 66, т. е. оно делится на 2 я не делит-
делится на 4; а значит, и е может быть полным квадратом.
б) Не может. Если десятичная запись числа N = п2 оканчивает-
оканчивается цифрой 5, то и п должно оканчиваться той же цифрой, т. е. л =
= Юга, +5,л2= A0я1 + 5J= lOO/if+lOOmf 25 = ЮОя^п, + 1) +
+25; таким образом, число N = l00N\ + 25 оканчивается цифрами 25
и Mi = п.\(п\ + О- Но ясно, что последняя цифра произведения
"i('li + 1) совпадает с последней цифрой произведения последних
цифр чисел П\ и п\ + 1, которая может представлять собой лишь циф-
цифру 0, 2 или 6, ибо произведения 0-1, 4-5, 5-6и9-0 кончаются
цифрой 0, произведения 1 • 2, 3 • 4, 6 • 7 и 8 • 9 — цифрой 2 и произ-
произведения 2-3 и 7 • 8 — цифрой 6. Таким образом, последней цифрой
числа N\ — и третьей от конца цифрой числа N — обязательно являет-
является цифра 6, ибо ни комбинацией цифр 025, ни цифрами 225 число N
кончаться не может (запись N вообще ие содержит цифры 0, а циф-
цифру 2 содержит лишь один раз). Но если N = 1000<V2 + 625, то N
делится на 53 — 125 (ибо и \060N2, и 625 делятся на 125); а тогда,
поскольку N есть полный квадрат, N делится даже на 54 = 625.
Но если N делится на 54, то и число IOOO1V2 = W — 625 делится
на 54, а значит, Л^ делится на 5. Если же Л^ делится на 5, то оканчи-
оканчиваться запись этого числа может лишь цифрами 0 или 5; а это зна-
значит, что запись числа N оканчивается четырьмя цифрами 0625 или
5625, что, однако, невозможно (ибо запись N содержит лишь одну
цифру 5 и вовсе не содержит цифры 0).
109. Для того, чтобы доказать требуемое утверждение, достаточ-
достаточно проверить, что 444 445-значное число А, полученное выписыванием
друг за другом 88 889 пятизначных чисел аи а2, а3,..., авв 889, делит-
делится на какое-либо отличное от 2 число. Но А делится на 11 111. В са-
самом деле, наше число А = aia2a3...a88a887a8e 888^88 889, очевидно, равно
А = а88 889 + амт • Ю5 +а 88 887 • 1010 + ... + а, ¦ 10« "° =
= (dl + 02 + • • • + O8?!g88 + 088 889) + O88 888( 105 — 1) +
152
А гак как аи а2, ..., а8г ввэ—это все целые числа от 11 111 до
99 999, то их сумма равна
11 111 + 11 112+П 113 + ... + 99 999 =»
11 111 + 99 999
¦88889 = 11 111-5-88 889
т. е. она делится на 11111. Все остальные слагаемые правой части
формулы (*) тоже делятся на 11111 (ибо при всех натуральных ft
разность 105* — 1 = A05)* — 1* делится на разность оснований
Ю5— 1 = 99999 = 9 • 11 111, а значит и на 11 111); поэтому А де-
делится на 11111.
110. Пусть искомое число X — aQaia2 . .. о9 (где ае, а , а9 —
цифры числа); при этом а0 есть количество нулей среди цифр X, а\ —
количество единиц, а2— количество двоек, и т. д. Поэтому сумма
всех цифр X равна
я0 + fli + а2 + ... + а9 = а0 ¦ 0 + а{ • 1 + а2 ¦ 2 + ... + я9 • 9,
откуда получаем
а0 = а2 + 2а3 + За4 + 4а6 + 5й6 + 6а7 + 7о8 + 8а9. (*)
Равенство До = 0 исключается условиями задачи (иначе число
X не было бы 10-значным; впрочем, условие а0 Ф 0 сразу следует
и из (*)); равенство по = 1 приводит к невозможным значениям
До = 02 = 1, Oi = 8 (ибо всего мы должны иметь 10 цифр), все ос-
остальные цифры — нули; равенство а0 = 2 совместимо лишь с (также
невозможными!) значениями а0 = а2 = 2, ct\ = 6, все остальные циф-
цифры— нули, или ао = 2, а3 = 1, Q| = 7, остальные цифры —нули.
Пусть теперь а0 = ?>2; равенство (*) мы перепишем так:'
аа = i = аг + 2а3 + ... +((— 1)а< + ... + 8а9 (**)
(если i — 3, то слагаемые 2а3 и (i— \)at совпадают; если I = 9, то
совпадают (i— i)at и 8аэ). При этом а,- —число равных i цифр чис-
числа X —отлично от нуля (ибо а0 = <); с другой стороны, (**) невоз-
невозможно при а> > 1, так что а* = 1. Поэтому (**) можно переписать
так:
1 =а2 + 2о3 + ...+ (? —2)а,-_1 + ю(+1 + ... + 8о9, (***)
откуда сразу следует, что 02= I, а все отличные от ао, Яь Яг и а>
цифры числа X равны нулю. Но если а2 = 1, то среди цифр числа X
есть двойка, которой, очевидно, может быть лишь цифра О|. Таким
образом, в десятичной записи X отличны от нуля лишь цифры
а0 ( = i), cii — 2, а2 = 1 и с,- = 1, т. е. среди цифр X есть I нулей,
2 единицы, 1 двойка и 1 цифра (, откуда (поскольку X 10-гпачно) i =
= Ю — 2- 1 — 1 =6.
И гак, X = 6 210 001 000 (легко проверить, что это число действи-
действительно удовлетворяет всем условиям задачи).
Ш. Так как А — 999 999 999 = 1 000 000 000 — 1,то произведение
АХ = 109ЛГ — X = х,х2. .. *t000 000 000 — Х\Хг .. . хк, где X =
== х{х2 ... X/, — произвольное натуральное число (записываемое циф-
цифрами Xi,-Vj X),). Нам требуется, чтобы число АХ записывалось
153
одними единицами, т. е. чтобы было
A",.v2 ... .VftOOO 000 000 — xlx2...xk = 11 ... 1111,
или ..
.ViA-2 ... jcfc000 000 000 — 11 ... 1111 = a-'i-Vj ... хк.
А так как все цифры вычитаемого нам известны, то мы можем про-
производить вычитание «столбиком», последовательно определяя все
цифры числа X, начиная с последней:
8 цифр
G) (8)... (8) (8) (9)
000 000 000
... 1 1 ... 1 1 1111111 111
... 6 7' ... 7 77 888 888 889
9 цифр
где сверху в скобках выписываются последовательно определяемые
цифры числа X. Этот процесс придется продолжать до тех пор, пока
мы не придем к группе единиц, которые при образовании разности
сократятся: ведь только за счет того, что полученное в разности чис-
число X будет в нашей записи начинаться с группы (разумеется, не
учитываемых) нулей, можно будет добиться совпадения записей К
в уменьшаемом и в разности!
Окончательно мы приходим к следующему значению числа X =.
= Л'о:
Хо ^ 11 ... 1 22 ... 2 33 ... 3 ... 77 ... 7 88 .^_8 9;
9 цифр 9 цифр 9 цифр 9 цифр 8 цифр
запись этого числа состоит из 9 + 9 -f- • .9 +8+1= 72 цифр.
7 слагаемых
Полученное число Ха является, очевидно, н а и м е и ь ш н м из
всех обладающих требуемым свойством, но оно не является единст-
единственным таким числом. У нас процесс вычитания завершился, когда
в начале образующего разность числа X появились 9 цифр 0, кото-
которые мы просто отбросили, считая, что их можно не засчитывать,
ибо ими запись X начинается. Можно, однако, счесть все эти циф-
цифры 0 «существенными», выписать их вслед за цифрами 1 в уменьшае-
уменьшаемом и продолжать вычитание. Ясно, что после этих девяти нулей
у нас снова начнут появляться цифры числа Ао — и запись X
приобретет вид:
А', = Хо 00 ... 0 Ха,
9 цифр
где Хо — десятичная запись числа Хо. Вообще, как следует из нашего
рассуждения, все удовлетворяющие условлю задачи числа X имеют
вид:
х- хп-То оо... оТ„ осц^л) Хо оо ... о То... х„ «хк^оИо,
9 цифр 9 цифр 9 цифр 9 цифр
где число п наборов из девяти последовательных нулей может быть
любым: п — 0, 1, 2, ...; число Хп состоит из 72(л + 1) + 9я = 81л +
+ Z2 цифр.
112. Пусть число А •= апап_\. ..а^ я-эначно. Мы можем, разу-
разумеется, считать, что а\фО, ибо нули в конце записи А можно просто
отбросить — это нв^игменит суммы цифр числа AN для любого N.
Рассмотрим теперь число N = 10™ — 1 = 999 ... 9, где т ^ п. Оче-
т девяток
видно, что число
AN = ЮтЛ — A ш anan__{ ... ai 000_.^_0 — anan_i ... о, =
m нулей
=- aHan_i ... a, (a,—1)999 ... 9(9 -a,») (9— an_,).. .(9-a4) A0—a,)
m—n девяток
имеет ту же сумму 9т цифр, что и число Л'.
113. Заметим, прежде всего, что утверждение задачи можно счи-
считать верным и при т «= 0 (в таком случае оговорка «^2 становится
необязательной—мы можем допускать и п -= 1), если только поло-
положить 0° = 1 (поскольку а0 = 1 для всех а). Пусть, например, п = 1;
обозначая все четные цифры (включая и цифру 0) через аь aj, ...,
а нечетные цифры — через р\, рг, ..., получим:
а° + а?, -Ь ... = 0° + 2° -г 4° + 6° + 8° - 1 -j- 1 + 1 + 1 -}- 1 = 5
и
Р° -f р.1? + . .. - 1° + 3° + 5° -f 7° + 9° = 1 + 1 + 1 + 1 + I - 5.
Перейдем теперь к следующему значению п: пусть п = 2; через
cti, а2, ... и р*ь ^2, ¦ •. мы по-прежнему обозначим все четные и все
нечетные цифры, а через Л|, Л2,.. и В\, В^... — все не более чем
двузначные числа с четной, соответственно с нечетной суммами цифр.
Так как, очевидно, каждое число Л,- имеет либо вид aj,ai(= 10a* •+-
-fa;), либо вид p*»fy(" ЮрЧ + $i), а числа Sj, напротив, имеют вид
aIpT== IQctk + & и j5Aa; = !0р* + а/, то, обозначая через 2Л,- и через
2Bj сумму всевозможных не более чем двузначных неотрицательных
чисел с четной, соответственно с нечетной суммами цифр, а через 2аА
и Spi —сумму всех четных и всех нечетных цифр, получим:
Pi) =
и, аналогично,
эти два равенства и доказывают, что 2Л,- = SSj.
В точности то же рассуждение лежит в основе общего доказа-
доказательства требуемого утверждения методом математиче-
математической индукции. Пусть мы уже установили справедливость
его для некоторого п (и всех m<n); рассмотрим следую-
следующее натуральное число п-\- 1 (и какую-то степень т < я + 1). Усло-
Условимся обозначать все не более чем я-значные неотрицательные числа
155
с четной, соответственно с нечетной суммами цифр, через пи о% ¦ ¦.
и через bi, b2, ..., далее, как и раньше, все не более чем (п-\- 1)-
значные числа с четной, соответственно с нечетной суммами цифр обо-
обозначим через Л|, А2, ... и через Ви В2, ...; наконец, сохраним обо-
обозначения <Х], Яг.... и Рь Рг,... для четных и для нечетных цифр. По
предположению индукции имеем
1Х 2? (»р)
к к
кроме того, условимся обозначать через
S*,P = 2 «? + !>? <**>
ft к
сумму р-х степеней всех не более чем л-значных чисел.
Заметим далее, что каждое число А\ имеет либо вид а*а/ =
=• Шом, + а;, либо вид bh$i — 106ft + Pi; аналогично, числа Bj могут
иметь форму ah$i = Юа* + Р; или bka.i = 106* + К;. Используя ана-
аналогичные употребленным выше обозначейия, найдем
*/i + Pi)m; здесь
Но, по формуле бинома Ньютона, например,
A0aft + a;)m = 10m-a^ + C^-10m-1fl^-iaJ +
+ С2т- 10m-2a™-2af + ... + С™-1 • К
Поэтому, используя обозначения ('*), получим:
,. 10
«f + ¦ • •
И, аналогично,
2
¦ • • + сш~1 ¦10 2 *ft I] P™
Таким образом,
С*,-lO^'s^^tS^j + С»,-
156
Используя те же обозначения (*) и (**), формулу бинома Нью-
Ньютона и производя аналогичные преобразования, мы придем к точно
такому же выражению для суммы
2 дг = 2 («Ч + h)n + 2 № + «i)"
что и доказывает требуемое утверждение.
Несправедливость выписанного в условии задачи тождества для
степеней т^п следует уже из того, что при п = т = 1 имеем:
2«!=2аг =0+2+4 + 6+8=20,3
114. Выпишем в каждой строке, начиная с третьей, четыре пер-
первых числа и поставим на месте четного числа букву ч, а на месте
нечетного числа — букву н. Получится полоса:
н ч н ч
н н ч н
н ч ч ч
н н н ч
н ч н ч
Мы _видим, что пятая строка полосы совпала с первой.
С другой" стороны, четность или нечетность первых четырех чисел
каждой строки нашего числового треугольника зависит только от
четности или нечетности первых четырех чисел предыдущей строки;
следовательно, в нашей полосе строки будут периодически повто-
повторяться через каждые четыре строки. Так как в каждой из четырех
первых строк полосы имеется четное число, то отсюда вытекает,
что оно будет и во всех последующих строках.
115. Докажем, что сумма чисел каждой строки нашей таблицы
делится на 1958:2 = 979, причем сумма чисел каждой строки, начи-
начиная со 2-й, делится даже на 1958; отсюда уже следует утверждение
задачи, поскольку в последней (нижней) строке имеется единственное
число и «сумма чисел» этой строки совпадает с этим числом. Ясно,
что сумма Si чисел верхней строки (сумма первых 1958 чисел нату-
натурального ряда, образующих арифметическую прогрессию) равна
'/2A958 • 1959), т. е. S, делится на 1958: 2. Далее сумма S2 чисел 2-й
строки, очевидно, равна: S2 = @ + 1) + A + 2) + B + 3) + ...
...+A956+ 1957)+ A957+ 1958)= 2S, — @+ 1958), поскольку
почти все слагаемые суммы S) входят в выписанное выражение S2
дважды — исключение составляют лишь «крайние» члены 0 и 1958,
которые входят в S2 по одному разу. Но поскольку и 2Sj и 0 +
+ 1958 = 1958 делятся на 1958, то и сумма S2 на 1958 делится.
Перейдем теперь к 3-й строке нашей таблицы. Ясно, что сумма
S3 всех чисел этой строки равна
S3= (l+3) + C + 5)+...+C913 + 3915) = 2S2-A +3915);
в самом деле, в выражении для S3 фигурируют дважды все числа
из 2-й строки, кроме одних лишь «крайних» чисел 1 н 3915, которые
157
входят в сумму Ss по одному разу. Но числа второго ряда I и 3915
имеют следующее происхождение: 1 = 0+1 и 3915 = 1957 + 1958;
поэтому
1 + 3915 = @ + 1) + A957+ 1958) =
= @ + 1958) + A + 1957) = 2 ¦ 1958
делится на 1958, откуда н вытекает, что также и сумма Ss делится
на 1958.
Это рассуждение может быть продолжено. Так, сумма S4 всех
чисел 4-й строки равна
S4 = 2S3-D+7828)(
где 4 (= 1 + 3) н 7828 (= 3913 + 3915) — «крайние» числа 3-й стрп-
ки. Но из правила образования нашей таблицы сразу следует, что
4 + 7828 = A + 3) + C913 + 3915) =
= @+ 1) + A +2) + A956+ 1957)+ A957+ 1958) =
¦= @ + 1958) + A + 1957) + A + 1957) + B + 1956) = 4-1958
делится на 1958, откуда и вытекает делимость на 1958 суммы St. Точ-
Точно так же устанавливается делимость на 1958 суммы чисел всех
последующих строк (формальное доказательство можно провести
методом математической индукции), что и завершает доказательство
требуемого утверждения.
116. Ясно, что если на столбе указаны числа xyz\xitjizt (где х,
у, ... — цифры), то XiyiZi = 999 — xyz и, значит, г, = 9 — г, ij\ =
«= 9 — у, Xi = 9 — х. (Если х = 9 или х = у = 9, то цифры xt =
= 0, или Х\ = у\ = 0 па столбе не проставляются.) Отсюда сразу
следует, что если х = у = г (и, значит, Х) = у\ = Z\ = 9 — х), то
наши условия будут выполнены; это дает 10 удовлетворяющих усло-
условию задачи столбов (отвечающих расстояниям 0=000, 111,
222, ..., 999 км от пункта А). Если же число xyz записывается двумя
разными цифрами, то эти цифры должны быть таковы, что каждая
из них дополняет вторуу до числа 9 — в этом случае и число
Xiyi^i «= 9 — jc, 9 — у. Ч — г будет зтписываться теми же цифрами.
Подобных пар цифр существует, очевидно, пять: @, 9), A, 8), B,7),
C, 6) и D, 5); я трехзначных чисел, лаписывающихся двумя данны-
данными ц-ифрами а и Ь, имеется всего шесть: три иэ них записываются
двумя цифрами а и одной цифрой b (которая может занимать любо*
из 3-х имеющихся мест) и, аналогично, три числа записываются од-
одной цифрой а и двумя цифрами Ь. Таким образом, мы получаем еще
Б • 6 •= 30 удовлетворяющих условию задачи расстояний искомого
столба от пункта А; поэтому общее чи;ло удовлетворяющих сформу-
сформулированным требованиям столбов: 10+30 = 40
117. Первое решение. Семь сеансов (считая от начала сеан-
сеанса до начала следующего) заняли меньше 13 часов A-й сеанс на-
начался не раньше 12 час, а 7-й кончился до 1 часа ночи), а 5 сеансов
заняли больше 9 часов B-й сеанс начался до 14 час, а 6-й кон-
кончился не раньше 23 час). Следовательно, длительность сеанса мень-
меньше чем 1 час. 52 мин. и больше чем 1 час 4? мин. Отсюда длитель-
длительность сеанса равна 1 час. 50 мин , ибо она выражается всегда числом
иияут, кратным 5.
158
Так как первый сеанс кончится до 14 час, то он мог начаться
либо в 12 час. 00 мин., либо в 12 час. 05 мин.; соответственно этому
второй сеанс начинается в 13 час. 50 мин. нли в 13 час. 55 мин.,
и т. д.
Если не требовать, чтобы длительность сеанса была кратной пяти
минутам, то мы получим не два, а большее число возможных реше-
решений задачи.
Второе решение. Пусть 12 + у — начало 1-го сеанса, ах —
продолжительность сеанса (х и у выражаются в часах). Тогда сеан-
сеансы начинаются в следующие часы:
1-й в 12 + у
2-й в \2 + у
7-й в 12 + У
8-й в 12 + 0
(от 12 час.до 13 час);
х (от 13 час. до 14 час);
6* (от 23 час. до 24 час);
7* (от 24 час. до 1 час.);
отсюда
12 < 12 + 0 < 13, нли 0 s? У < 1,
13 s? 12+ х + у < 14, или 1 <* + «/< 2,
23 s? 12 + 6х + у < 24, или 11 < 6* + у < 12,
24 < 12 + 7* + У < 25, или 12 s? 7* + у < 13.
Отбрасывая неравенства, вытекающие из других, получим сис-
систему:
О < у < 1; 1 < * + у < 2; 11 < 6* + г/; 7* + у < 13,
которую нетрудно решить графически (рис. II). Решение (*, у) дает-
любая точка из заштрихованного четырехугольника PQQP
\
1
D
У-1
<*\
\
4
\
'\
\l
МП
Рис.
118. Будем считать, что каждый час шлагбаум закрыт от 0 мин. до
5 мни. и от 38 мин. до 43 мин. Если указанные 5-минутные интервалы
начинаются, скажем, за 1 мии. до подхода поезда к шлагбауму,
то мы просто «переведем часы назад на 1 мин.» (а после решения
задачи, чтобы исправить составленное с использованием неверных
159
часов расписание движения автобусов, снова переведем на 1 мии.
стрелки часов). Отметим иа циферблате часов все положения минут-
минутной стрелки, отвечающие моментам, когда автобус проходит шлаг-
шлагбаум — для эгого пометим черточкой время to мин. прохождения пер-
первого (с начала суток) автобуса, а затем, двигаясь в направлении вра-
вращения часовой стрелки, станем отмечать последующие моменты
/о + Т, ta -f- 2Г, и т. д., откладывая каждый раз по циферблату дугу,
отвечающему интервалу в Т мин. Нам надо так выбрать t0 и to,
Рис. 12.
чтобы ни одна из полученных отметок не попала в «запрещенные»
(заштрихованные на рис. 12) интервалы времени от 0 до 5 мин. и от
38 до 43 мин.
Заметим, прежде всего, что среди полученных таким образом от-
отметок на циферблате могут иметься на более 12 различных1). В са-
самом деле, пусть R и /?i — две ближайшие друг к другу отметка иа
циферблате, которым отвечает угол RORt = а" (где О —центр
циферблата), соответствующий временному интервалу в т мин.; от-
отметки R и Ri указывают моменты времени t0 + iT и ta + jT, где i
') Ясно, что общее число отметок на циферблате, в принципе,
может быть даже бесконечно большим. [Можно доказать,
что бесконечно большим это число отметок будет в том случае, если
интервал Т несоизмерим с интервалом в 1 час, отвечающим «полно-
«полному» повороту минутной стрелки (повороту на угол в 360°), причем
если это последнее обстоятельство имеет место, то отметки на цифер-
циферблате будут расположены «плотно», т. е. среди них найдутся отмет-
отметки, удаленные от произвольно выбранной "точки М циферблата на
, (дуговое) расстояние, меньшее любого наперед заданного (сколь
угодно малого!) числа в.]
160
и / — какие-то целые числа. В таком случае два автобуса —i-й и /-и
(где мы считаем у > /) —следуют один за другим через целое число
к часов ±т минут; для определенности условимся считать, что вре-
временной интервал между автобусами равен 'к час. +т мйн., так что
<uRR\ имеет на циферблате направление вращения часовой стрелки
(рис. 12; в рассуждениях почти ничего не изменилось бы, если бы
kjRRi имела обратное направление). В таком случае [у + (у — /)]-й
(т. е. B/ — ;')-й) автобус будет следовать за у-м через k час. т мин.,
и моменту его проезда через железнодорожный путь отвечает на ци-
циферблате отметка R2 такая, что ^RiR2 = ^RRi = a°; fBy — i) + l
+ (/ — 0]'мУ (т. е." C/ — 2г)-му) автобусу отвечает такая отметка
Ri, что wi?2^3 = «°, и т. д. С другой стороны, [i— (у—/)]-й (т. е.
B/ — /)"й) автобус следует за к час. и т мин. до /-то, т. е. ему отве-
отвечает отметка R-\ такая, что R-i и R^ расположены по разные сто-
стороны от R и \^R-iR= ^jRRi = а°, и т. д. Таким путем мы получим
на циферблате «сетку» отметок, расположенных друг от .друга на
«дуговом» растоянии в а°, или на «временном» расстоянии в т мин.;
ясно, что если т < 5 (или а < 30°, поскольку 5 мин. на циферблате
отвечает центральный угол в 30°), то хоть одна из этих отметок по-
попадет в «запрещенный» интервал времени и соответствующему авто-
автобусу путь через переезд будет закрыт. Но если на циферблате име-
имеется система отметок, причем наименьшее из (дуговых) расстояний
360°
между отметками ^ 30°, то общее число отметок < ¦oqo" = 12.
Итак, расписание движения автобусов указывается на цифер-
циферблате к ^ 12 отметками R, Rt, R2,...; из сказанного выше вытека-
вытекает, что w RRi = w R1R2 = w ^2^3 = .. -I т. е. что RRiR2...Rk^!
(= Ми) — это вписанный в окружность циферблата правильны й
А-угольник. Нам надо найти все к, отвечающие правильным мно-
многоугольникам Mh, которые можно так повернуть вокруг центра
О циферблата, чтобы ни одна вершина Мк не попала на зашт-
заштрихованные на рис. 12 дуги АВ и CD. Ясно, что при к = 1 (один
автобус в час) или к = 2 (два автобуса; здесь надо указать на
циферблате две диаметрально противоположные отмет-
отметки R и R\, не попадающие на дуги АВ и CD) это возможно; условие
Т < 30 мин. требует указать решения задачи, отвечающие значени-
значениям к > 2. С другой стороны, очевидно, что значение к = 12 (т. е.
а° «= 30° ит = 5 мин.) нам не подходит: свободной от отметок дуга
АВ может быть лишь в том случае, если ее концы А а В совпадают
с какими-то отметками R и Ri; но в таком случае 9-я отметка отве-
отвечает моменту времени 0 + 8-5 мин. = 40 мин.— и она попадает на
Дугу CD. Аналогично, не подходят нам также значения k = 10, 9 и
/ 60 60 2 . 60 4
7[т. е. значеният •= Jq-^6 мин., -д— = 6-д-мин. и —= 8у мин.
так, если т = 6 мин., то ближайшая за А отметка R, если только
она не попадает на дугу АВ, должна разместиться где-то внутри
(временного) интервала [5 мин., 6 мин.]; но тогда 7-му автобусу
ответит отметка, приходящаяся на временной интервал [5 + 6-6 =
¦=41 мин., 6+6-6 = 42 мин.], целиком принадлежащий «запре-
«запрещенной» Дуге CD. (Проверьте сами, что если отметка R попадает
Г 2
на интервал 5 мин. , 6-jt мин.
6й 5й
соответственно 5 мин.
го 6-й, соответственно 5-й автобус неизбежно попадут в интервал
Д. О. Шк-пфский и др. 161
CD.) Напротив, значения k— 11, 8, 6, 5, 4 и 3, отвечающие значе-
60 5 60 ,„ 60 , 60 п
ниям т= -ту = б-урмин., -g- = 12 мин., -т- = 15 мин. и-з-=20мин.,
являются допустимыми: так, например, если ?=11, то автобусы
могут проезжать шлагбаум, скажем, в моменты времени 5 мин.,
10-рг мин. , 15 -ту мин. , 21гу мин. , 26гумин. , 32угмин., 37ут
2 7 16
мин., 43гг мин., 48гт мин., 54тт мин. и 59гт мин., а если k = 5, то воз-
возможно следующее расписание движения, автобусов: автобусы про-
проходят шлагбаум в 8 мин., 8 + 12 = 20 мин., 32 мин., 44 мин. и 56 мин.
Таким образом, при Т < 30 мин. требуемым образом движение
автобуса можно организовать при Т = 20 мин., 15 мин., 12 мин.,
1 5
7 ~2 мин. и 5 ту мин.-— и только при этих значениях 1.
119. Пусть jV = abc, где a,b,c — цифры числа; ясно, что для «круг-
N
лых» чисел N = 100, 200 900 имеемfl^ ^ , =100. Далее, если
число N — не «круглое», то 6 + с > 0 и a + 6 + c^a+l, а так
как старшая цифра N равна а, то N < (а + 1) 100 и
N (а+1)-100
< 100
Таким образом, наибольшее значение рассматриваемого отноше-
отношения равно 100; достигается это значение лишь для «.круглых-» чисел.
Примечание. Точно так же доказывается, что наибольшее
значение отношения &-значного числа N = ahah-\.. .а\ к сумме а*, +
т°*-1-г...+в| его цифр равно Ю*; достигается оио лишь для
«круглых» чисел, k — 1 последних цифр которых — нули.
120. В данном числе 192 цифры; в числе, полученном из него вычер-
вычеркиванием 100 цифр — 92 цифры.
а) Первые цифры интересующего нас числа должны быть воз-
возможно большими. Мы можем сделать так, чтобы это число начи-
начиналось с 5 девяток, заимствовав эти девятки иэ чисел 9, 19, 29, 39
и 4S; при этом нам придется вычеркнуть 8 -f- 19 + 19 + 19 + 19 = 84
цифры. После этого следующая цифра уже не может быть сделана
девяткой, так как для этого нам пришлось бы вычеркнуть еще 19
цифр (чтобы «добраться» до ближайшей девятки — цифры числа 59);
при этом вычеркнуто будет 84 + 19 = 103 цифры., т. е. больше чем
нужно.
Ближайшая к оставшимся цифрам восьм:рка относится к числу
58; для того чтобы она следовала непосредственно за девятками,
пришлось бы вычеркнуть еще 17 цифр, что тоже невозможно (ибо
84 + 17= 101 > 100). Поэтому лучшее, что мы можем сделать,—
это вычеркнуть еще 15 цифр, предшествующих семерке в числе 57.
Итак, всего мы вычеркнули пока 84+ 15 = 99 цифр; нам позволено
вычеркнуть еще одну цифру. Ясно, что целесообразно вычеркнуть
пятерку в числе 58; итак, требуемое число:
'9999978096061... 100.
162
б) Мы можем добиться, чтобы оставшееся число начиналось с
5 нулей (эти нули фигурируют в записи чисел 10, 20, 30, 40 и 50); при
этом вычеркнуты будут 10 + 19 + 19 + 19 + 19 = 86 цифр. До сле-
следующего нуля (в числе 60) мы добраться не можем; однако, вычерк-
вычеркнув всего одну пятерку, мы сделаем так, чтобы за 5 нулями в полу-
полученном числе следовала единица. Следующую за этим цифру мы не
можем сделать также единицей; однако, вычеркнув еще одну пя-
пятерку, мы сделаем следующую цифру двойкой. Это рассуждение
можно продолжить; так мы убедимся, что, вычеркнув всего 86 +
+ 1 + 1 + 1 + 1 = 90 цифр, мы придем к числу, начинающемуся с
комбинации цифр: 000001234, вслед за которыми следуют цифры
55565758596061... Ясно, что цифра, следующая за выписанными вы-
выше первыми девятью цифрами искомого числа, может быть пятеркой,
но не может быть меньше 5; для того же, чтобы она оказалась пя-
пятеркой, нам вообще не потребуется никаких вычеркиваний цифр. Пос-
После этого мы,— наконец-то!— получаем возможность добраться до
нуля вычеркнув 10 предшествующих ему цифр (что еще допустимо);
поэтому интересующее нас число таково:
00000123450616263. ..100
(это число начинается с пяти нулей, так что реально оно содер-
содержит 87 значащих цифр).
121. а) Первые цифры трех искомых чисел должны быть наимень-
наименьшими; следовательно, эти числа в десятичной записи имеют вид:
Ша, Mb, ЗСс,
где символ хуг обозначает число, записываемое цифрами х, у, г
Докажем, что: 1) А < В <С; 2) а <Ь < с; 3) каждая и?
цифр а, Ь, с больше каждой из цифр А, В, С.
Действительно: _
1) Если бы, например, было А> В, то мы и_м?ли бы Аа > ВЬ
и Т/Га -Wb -~'2AajjB~b_^ A00 + Аа) • B00 + ВЬ)~ B00 + Аи)Х
Х(Ю0 + ВЬ)= \00 (Аи —Щ > 0 и, следовательно, \ВЬ ¦ 2Аи Х
X ЗСс < \Аа ¦ 2ВЬ • ЗСс.
2) Если бы, например, было а > Ь, то мы имели бы
\Аа ¦ 2ВЬ—ТА~Ь • Ша = A0 • М~+ а) A0 • 2В~+Ь) —
— A0 • 1Л~+й)A0- 2~В~+а) = A0 -W— 10 • U) (а — Ь) > 0
и, следовательно, 1Л6 • 2Ва ¦ ЗСс < \Аа ¦ 2ВЬ ¦ ЗСс.
3) Если бы было С > а, С = а + х, где х > 0 (в силу 1) и
2) С — самая большая из цифр А, В, С, а а — самая маленькая и?
цифр а, Ь, с), то мы имйди бы i
Ша ¦ We — Ш • Зое = \Аа ¦ (Зас+ 10*) — (Ыа + х) (Зое) =
= *A0 • Ыа — Зас) >0
и, следовательно, 1АС ¦ 2ВЬ ¦ Зас < ТТа ¦ 2ВЬ ¦ ЗСс.
Из 1), 2) и 3) следует
А<В<С<а<Ь<с,
U* 163
и искомое произведение имеет вид
147 • 258 • 369.
б) Искомое произведение должно иметь вид
1Ш" Ш> ¦ 7Сс.
Аналогично решению задачи а) можно доказать, что 1) А <
< В <; С, 2) а < b < с, 3) каждая из цифр а, Ь, с меньше каждой
из цифр А, В, С.
Из 1), 2) и 3) следует, что
а<Ь<с<А<В<С
и, следовательно, искомое произведение имеет вид
941 • 852 • 763.
122. Нам дано, что т + (т + 1)+ ,,. + (т + k) = 1000. По
формуле суммы членов арифметической прогрессии имеем:
или
Bm + k)(k + l) =»2000.
Так как
{2т + k) — (k+l)~*Zm— 1
нечетно, то из двух последних множителей один четен, а второй
нечетен. Кроме того, очевидно, 2т + k > k + [. Отсюда вытекает,
что наша задача имеет следующие решения:
2т + k
2m + k
2m + k
2m + k
= 2000,
— 400,
— 80,
— 125,
k-
кЦ
&H
*H
h 1
-1
h 1
h 1
= 1,
= 5,
= 25,
= 16,
m
m
m
m
= 1000,
[= 19S,
•ш 28,
= 55,
k
k
k
S3-
= 0;
- 4;
= 24;
= 15.
123. а) Пусть наше число N отлично от любой степени 2. Тогда
имеет место равенство
где 2я — наибольшая' степень 2, на которую делится Л' (k может
быть равно нулю), а 2/+ 1 — наибольший нечетный делитель числа
N. Далее, имеем:
Bk —l) + Bh— l+ 1)+ ... +B?! — 1 + 21— l) + Bft — I+ 21) ~
При этом, если несколько первых из этих 21 + 1 последователь-
последовательных целых чисел будут отрицательными (т. е. / > 2й), то их можно
будет сократить с первыми положительными числами и Л' опять
представится в виде суммы некоторого числа (меньшего 2/+1)
положите ль и ы х целых чисел.
Предположим теперь, 4to какое-нибудь число вида йк можно
представить в виде суммы т последовательных целых положитель-
положительных чисел я, я + 1,..., я + т — 2, п + т — !. Тогда
2*+' = 2[я + (я+1) + ...+(я + т — 2) + (п + т— 1)J =
= т(п-\- п-\- т — 1) —тBп + т — I).
Но разность Bя + т—1)—т = 2я — 1 нечетна, следовательно,
одно из чисел, т или 2я + m—1, нечетно (причем оба они отличны
от 1, ибо tn> \ ия>0). Значит, последнее равенство невозможно
(ибо 2h + i не имеет нечетных делителей, отличных от 1).
б) Имеем:
Bв + 1) + Bл + 3) + Bя + 5) + ... + Bт - 1) =
Bн+1) + Bм-1)
= 2 ' (т ~~ п) — \т + п)' ('" — п) ¦
Поэтому если число N прсдставимо в виле суммы последовательных
нечетных чисел, то оно составное (разлагается па множители т -f- n
и т — я). С другой стороны, каждое нечетное составное число /V
можно представить в виде произведения двух нечетных множи-
множителей а и Ь (а :э= Ь) и, следовательно, N = аЬ = (т + я) (т — я),
о -!- Ь а — Ь
где m = —п—> /г = —о—' есть сУмма нечетных чисел от а — о -\- \
до а + b — 1.
Далее, в формуле N = (/n -f- я) ('" — 'г) множители т + я и
/п — я оба четны или оба нечетны; если N четно, то эти множители,
очевидно, должны быть четными. По в таком случае N делится на 4
(и т + п и т — п делятся па 2); следовательно, если четное число
Л' не делится на 4, то его нельзя представить в виде суммы после-
последовательных нечетных чисел. Если же N = 4/г делится на 4, то /V
можно представить в виде суммы двух последовательных нечетных
чисел 2'п — 1 и 2я + 1.
в) Легко видеть, что
я*1-1 - п + О + (я*1 - л + 3) + ... + («''-1 - 1) +
+ (л* + 0 -f .. . + (л* + п - 3) + (п*-1 -1- л - \) =
(nfc-i _я+ 1)+ (»"-' + >.- 0 _ ft
(все слагаемые этой суммы нечетны, ибо я'' и я одновременно
четны или нечетны).
124. Обозначим эти числа через п, я+1, я + 2, я + 3. Сумма
их произведения и единицы имеет вид
= (п2 + Зя) (я2 + Зя + 2) + I =
= (я2 + 3яJ + 2(я2 + 3я) + 1 = (я2 + 3л + IJ;
следовательно, эта сумма является квадратом целого числа (п2 +
+ Зл+1).
125. Докажем, что эти числа принимают не более четырех раз-
различных значений. Допустим, что это неверно и среди наших 4я
105
Чисел существует пять чисел п\, а2, й3, а4, я5, попарно различных меж-
между собой. Будем считать, что <Х\ < а2 < а3 < а4 < аь.
Рассмотрим числа О[, а2, Яз и а4. Согласно нашему условию из
них можно составить геометрическую пропорцию; следовательно,
произведение двух из этих чисел (крайних членов пропорции) рав-
равно произведенрш двух других. Но это возможно только, если
(равенство п\п^ = а2а^ невозможно, так как fli <a2, а3 < а4; еще
очевиднее, что не может иметь места равенство ata2 = аъа^.
Рассмотрим теперь числа аь а2, а$, а$. Таким же оОразом, как
п выше, можно доказать, что aia5 = а2а^. Следовательно, ахац =
= а^з, ai = as, что противоречит нашему предположению.
Итак, мы доказали, что каждое из 4я чисел принимает одно нэ
не более чем четырех различных значений. Поэтому какое-нибудь,
из этих значений принимается не менее "чем п числами.
126. Разложим сначала девять гирь, веса которых равны соот-
соответственно n2, ('i+lJ, ('1 + 2J,..., (п + 8J, на три группы сле-
следующим образом:
I группа п\ (я + 5)*, (яЧ-7J:
II группа (л-(-IJ, (« + 3J, (п + 8J:
(п+ 1J+(п + 3J+(я + 8J = 3«2
III группа (я + 2J, (« + 4J, (п + вI:
(п+2J+(д+4J+ (я+6J = 3
Таким образом, мы видим, что вес первой и второй групп-один
и тот же, а третья — легче их на 18. Затем следующие за ними де-
девять гирь разложим аналогично, однако так, чтобы первая и третья
группы имели одинаковый вес, а вторая была легче их на 18; нако-
наконец, последующие девять гирь разложим так, чтобы вторая и третья
группы имели одинаковый вес, а первая была легче их на 18. Сгруп-
Сгруппировав затем все первые, все вторые и все третьи группы этих
трех разбиений, мы получим разложение любых 27 последователь-
последовательных гирь на три группы равного веса.
127. Из условия задачи, прежде всего, следует, что все гири
одновременно имеют или четный, или нечетный вес. Действи-
Действительно, из того, что каждые 12 гирь можно разбить на две группы
равного веса, следует, что общий вес каждых 12 гирь четен. При
этом общий вес 12 гирь останется четным и в том случае, если про-
. извольную из них заменить отложенной 13-й гирей. А это возможно
только в том случае, если вес каждой из 12 гирь четен или нечетен
одновременно с весом отложенной 13-й гири, что и приводит к на-
нашему заключению.
Вычтем теперь из весов всех гирь вес самой легкой гири (или
самых легких, если их несколько). При этом мы, очевидно, получим
чсвую систему гирь, которая тоже удовлетворяет условиям задачи;
следовательно, веса всех новых гирь тоже имеют одинаковую чет-
четкость. А так как среди новых гирь имеются «гири» нулевого веса,
го вес всех новых гирь должен быть четным. Разделим, веса всех
гирь на два; при этом мы получим новую систему гирь, тоже удов-
удовлетворяющую условиям задачи,
F3
Предположим теперь, что не все исходные гири имеют одинако-
одинаковый вес. В таком случае не все гири второй системы, веса которых
получаются-из весов первоначальных гирь вычитанием веса наилег-
наилегчайших гирь, будут «нулевыми». В этом случае путем последова-
последовательного деления весов всех гирь на два мы в конце концов придем
к системе гирь, часть из которых имеет четный вес (например, вес
«нуль»), а часть — нечетный вес. Но мы уже показали, что такая
система гирь не может существовать. Полученное противоречие и
доказывает утверждение задачи.
Примечание. В условии задачи требовалось, чтобы веса
всех гирь были целыми числами.- Однако нетрудно видеть, что если
считать веса гирь числами рациональными, а не целыми, результа г
задачи не изменится. Действительно, в этом случае, умножив веса
всех гирь на некоторый множитель (приведя все веса к общему зна-
знаменателю и отбросив знаменатель), можно свести задачу к случаю
целых весов. Более того, если позволить весам гирь быть произволь-
произвольными иррациональными числами, мы все равно сможем утверждать,
что все они равны между собой: это следует из того, что можно
найти рациональные числа, сколь угодно близкие к данным иррацио-
иррациональным числам (рекомендуем читателю попытаться самостоятельно
провести полное доказательство; следует, впрочем, предупредить,
что сделать это аккуратно не так уж просто).
128. Заметим, прежде всего, что если для каких-то натуральных
k и /#? полученные описанным образом четверки ah, bh, ch, dh и
аи bi, C[, di одинаковы, то либо все числа ац = аи b\ = Ь/, си =
= a, dh = di равны нулю, либо все они положительны. В самом
деле, если хоть одно из чисел а, Ь, с, d, равно нулю, то не позже
чем на четвертом «шагу» мы приходим к строчке из одних лишь ну-
нулей, которая затем неограниченно повторяется; при этом ранее
никакие две из выписанных четверок чисел не совпадают. Действи-
Действительно, если равно нулю ровно одно из наших чисел, скажем а =
= 0, то первые 4 четверки выглядят так:
О, Ь, с, d; О, be, cd, 0; 0, ЪсЧ, 0, 0; 0, 0, 0, 0
— здесь никакие две из первых трех четверок не могут совпасть,
поскольку нули в них стоят на разных местах. Ясно также, что ес-
если более чем одно из чисел а, Ь, с, d равно нулю, то к чет-
четверке нулей мы также придем не позже чем на 4-м шагу, причем и
здесь легко проверить, что не состоящие из одних нулей четверки
обязательно будут все различны.
Сказанным исчерпывается разбор случая, когда abed = 0;
пусть теперь abed ф 0. Ясно, что здесь все числа всех четверок бу-
будут отличны от нуля. Далее, если среди чисел а, Ь, с, d отрицатель-
отрицательным является только одно — скажем, первое, — то обозначая по-
положительное число символом «+», а отрицательное — символом
«—», мы придем к следующему чередованию знаков в первых пяти
последовательностях:
таким образом, здесь 5-я четверка состоит из одних лишь положи-
положительных чисел, причем ранее никакие две четверки не могут сов-
совпасть, ибо чередование знаков в них различно. Из выписанной схе-
схемы видно также, что если среди чисел а, Ь, с, d имеются два со-
соседних отрицательных (как во 2-Й из выписанных четверок: ведь
167
упорядочение чисел в четверках здесь надо считать «циклическим»,
так что 1-е и 4-е числа являются «соседними»), или два не сосед-
соседних отрицательных (как в 3-й четверке), или четыре отрицательных
(как в 4-й четверке), то также не позже чем на 4-м шагу мы при-
придем к одним лишь положительным числам (и ранее этого четверки
будут различными). Аналогично рассматривается случай "четверки из
трех отрицательных и одного положительного числа, на первом же ша-
шагу переходящей во 2-ю из выписанных выше четверок:
Итак, далее мы можем считать все числа а, й, с, d положитель-
положительными; положим еще abed = р. При этом, очевидно,
uib^idi = (ab) (be) (cd) (da) = (abedJ, = p2;
аналогично, a2b2c2d2 = (a^iCtd,J = p4; a3b3c3d3 = p8 и вообще
akbhChdh >= (pJ (где k = 0, 1, 2,...; иод flj, 60, Co, d0 мы понима-
понимаем исходные числа а, Ь, с, d). Поэтому, если четверки ан, bk, сн, dk
н ai, bi, Си di (где I > к) совпадут, то
ok , , , о[ о! 9& . .
р = ahhchh = alJicri — Р и, значит, pJ Л = 1, т. е. р = 1.
Пусть теперь abed = 1 (ясно, что нам надо разобрать лишь
этот случай). В таком случае, поскольку cd = —г-, то из двух чисел
ab и cd одно ^ 1, а второе ^1; для определенности положим, что
аЬ = а ^ 1, a erf = -^г < 1 • Аналогично, из пар чисел be и
da~-?- одно не меньше, а второе не больше единицы; для опре-
определенности будем считать, что be «= ji ^ 1, a da = ~тр < 1 и что
а ^ р (все иные варианты, по существу, не отличаются от рассматри-
рассматриваемого). В таком случае мы последовательно получаем следующие
!;ст.,„рКИ чисел:
11 Р 1 « 1 1
а, Ь, с. d; a, 0, —, -р aP, —, ^р, у, Р2, -^, ра, <х-.
При этом во 2-й четверке наибольшее число равно а; в 3-й оно
равно сф ^ а; в 4-й четверке оно равно а2 ^ ар, и т. д. (заметим,
что 4-я четверка отличается от 2-й только тем, что роль а и р в
ней играют числа о2 и р2).
Итак, мы видим, что наибольшее из чисел четверки все время
не убывает. Если a > 1, Р > 1, то наибольшее число даже все вре-
время растет; поэтому здесь никакие две четверки, каждая из кото-
которых отлична от 1-й, не могут совпадать между собой. Более того,
если отлично от 1 хоть одно из двух чисел о и р, то н тогда ника-
никакие две четверки чисел, отличные от 1-й четверки, никогда не сов-
совпадут. В самом деле, если а > 1, а р = 1, то 2-я и следующие за
ней четверки имеют вид:
1 1 Г 1
Таким образом, здеСь через Два шага наибольшее число Чет-
Четверки увеличивается (что не позволяет четверке совпасть с какой-
либо из предшествующих), а в двух первых четверках числа тоже
различны. Поэтому, если совпадают между собой k-я и 1-я четвер-
четверки, где t > k р> \, то а = р = 1;' но в таком случае все четверки
чисел, начиная со 2-й, совпадают между собой (это — четверки из
одних единиц).
^_Мы до сих пор игнорировали в наших рассуждениях 1-ю чет-
четверку а, й, с, d; следовало бы еще выяснить, не может ли она
совпасть с одной из последующих. Но это исключено из-за того,
что, как мы видели, во всех четверках чисел, начиная со 2-й, име-
имеются две пары чисел, произведение которых равно 1; поэтому, если
четверка й, й, с, d совпадает с одной из последующих и,' скажем,
йс = [3 > 1 и ой = а ;зг [3 > 1, то (поскольку cd -— — < 1 и
da = "ТГ^ О придется считать, что ас = bd = 1. Это предположе-
предположение приводит к следующим значениям чисел 1-й четверки:
~ТГ 1
(почему?), что снова позволяет воспользоваться сравнением наи-
наибольших чисел а и У afi 1-й и 2-й четверок, совпадающих лишь
при р = «х, т.е. тогда, когда наша 1-я четверка совпадает со 2-й
четверкой, отвечающей случаю [3 = 1, и «эволюционирует» далее,
как эта 2-я четверка. Аналогично рассматривается и случай ? = 1.
Это рассуждение и завершает доказательство теоремы.
Примечание. Решение задачи позволяет также оценить
количество «шагов», необходимых для того, чтобы все получаемые
четверки чисел стали совпадать друг с другом (в том случае, когда
эти четверки не все различны): для случая abed = 0, как мы ви-
видели, совпадают все четверки, начиная с 4-й; для случая иоложи-
.тельпых чисел а, й, с, rf, таких, что ab = be = cd = da = 1, сов-
совпадают все четверки, начиная со 2-й (а если эти равенства не вы-
выполняются, го никакие две четверки не совпадают между собой);
для случая не обязательно положительных чисел могут понадо-
понадобиться еще 4 шага для того, чтобы сделать все числа положитель-
положительными.
129. Поскольку квадрат каждого из чисел а,- (где (= 1, 2,
..., N = 2й) равен единице, то первые три последовательности чи-
чисел имеют следующий вид:
йь . а2, ... a,v-i, ац\
а\й2, #2#з, '** йу_ 1#дг, а^а\\
- fljy jfli, a^a^a2 = й^а2;
таким образом, в 3-й последовательности все числа получаются ум-
умножением каждого из чисел последовательности на следующее за
ним через одно (последовательность мы считаем «циклической», т. е.
169
Полагаем, что за числом aN следует аи затем й2, и т. д.). Анало-
Аналогично, еще через два шага мы будем иметь набор, получающийся
из 3-го в точности так же, как 3-й получается из 1-го, т.е. набор
(а2аА) {сца&) — a2as, .,,, (aNa2) (а2а4) = aNa4,
числа которого получаются из первого (циклического) набора пе-
перемножением чисел, Следующих один за другим через 3. Еще че-
через <f шага мы получим набор, получающийся из 5-го в точности
так же, 5-й набор получается из 1-го, т. е, набор
(o^i) (а5в9) = а^а, (а2а6) (о6аш) = а2а10,..., (йка4) (а4аа) = аЛйс,
числа которого получаются из первоначального набора перемноже-
перемножением чисел, следующих один за другим через 7.
Вообще через 2р шагов мы придем к набору
ata , пф , .... a a ,
2^+1 2Т+2 N 21
получаемому из первоначального перемножением чисел, следующих
один за другим через 2A> — 1 чисел. Но отсюда следует, что через
2k шагов мы придем к последовательности, получающейся из нашей
(циклической!) последовательности перемножением чисел, следую-
следующих друг за другом через 2*— 1 «= N—1 номеров, т. е. к последо-
последовательности
tfifli = ai = l, ага2 = а\ = 1, .. ., aNaN — а^ = 1,
состоящей из одних единиц.
130. Покажем, прежде всего, что при переходе от исходного
набора чисел аь а2 , а„ к «производному» набору а4, й2, ..., ап
наши числа «выравниваются», т. е. разность между наибольшим и
наименьшим из чисел не увеличивается. В самом деле, поскольку
полусумма (среднее арифметическое) двух чисел всегда не больше
наибольшего из них (и равна наибольшему лишь, если числа рав-
равны), то наибольшее из чисел а\, а'2> .... а'„, равное полусумме ка-
каких-то двух чисел первоначального набора, не превосходит наиболь-
. шего из этих двух чисел, а тем самым — и наибольшего из всех я
чисел а(; таким образом, при переходе от набора at к набору а^
наибольшее число может лишь уменьшиться. Более того, из этого
рассуждения видно, что наибольшее из чисел а{ может рав-
равняться наибольшему из чисел оц лишь в том случае, когда в на-
наборе ui наибольшее число А встречается несколько раз, причем в
этом наборе (считающемся упорядоченным циклически, т. е. так,
что за ап следует снова аО стоят подряд два равных А числа.
Далее, легко видеть, что если в наборе чисел at наибольшая по
длине цепочка из следующих друг за другом равных А чисел имеет
длину k (где k<n), то в наборе чисел ai будет иметься цепочка
из следующих друг за другом k — 1 равных А чисел: так, если
ai+l = ai+i =.....= ai+y = A (a at < А и ai+k+i<A), тоа{+1=
a
i+2
ai+h—i = ^ (a a\ <C А и ci-fn < Л). Поэтому пос
af~i')
ле k—1 шагов мы придем к числамaf~i), ..., а?~1\ среди кото-
170
рых не будет двух следующих подряд равных А чисел, а на следую-
следующем, k-м шагу максимальное среди рассматриваемых чисел умень-
уменьшите я; следовательно, если не все числа af равны друг другу, мы
можем быть уверены, что при (п— 1)-кратном повторении описанной
в условии задачи процедуры наибольшее из рассматриваемых чисел
уменьшится. Точно так же доказывается, что наименьшее из рас-
сматриваемых чисел никогда не уменьшается, а если не все числа
равны друг другу, то после (п — 1)-кратного повторения нашей
процедуры оно наверняка увеличится.
Но если числа аь а% . • ¦, ап и все последовательно получаемые
из них числа — целые, то «выравнивание» их, т.е. уменьшение раз-
разности между наибольшим и наименьшим, неизбежно приведет в
конце концов к тому, что эта разность станет равной нулю, т. е. что
все числа сравняются между собой. В самом деле, первоначально
эта разность А—а = max a; — min at равнялась какому-то целому
г г
положительному числу р; при уменьшении А = max а,- или при уве-
i
личении а = min а; эта разность уменьшается не меньше чем на
г
единицу — и, следовательно, не более чем через р таких шагов она
станет равной нулю. Поэтому, если мы покажем, что не все равные
между собой числа аь а2,..., а„ никогда не приведут нас к системе
одинаковых чисел, то угверждение задачи будет доказано.
Рассмотрим теперь, как одинаковые числа Ьх = а '™' ,
Ь2 = а!™\ ..., Ь = а%")могут получиться из неодинаковых чисел
- __ „(m —I) r _ Am—1) . „ п(т—1)
Ci — flj , с2 — а2 , .. •, сп — ап
Ясно, что для этого иобходимо, чтобы числа С\, с2, с3, ... «сов-
«совпадали через одно», т. е. чтобы выполнялись равенства
С\ = С3 = С5 =...(= С) И С2 = С4 = f6 = ...(= С). (*)
Но так как числа С\, с% Сз, ¦ ¦ ¦ упорядочены циклически, т.е. число,
сп + \ надо считать совпадающим с си то равенства (*) (где С ф с)
вовсе невозможны при п = 2/ + 1 нечетном (когда числа
п -f 1 = 2/ + 2 и 1 имеют разную четность); поэтому остается
предположить, что п = 21 четно. Сделаем теперь еще один «шаг
назад», вернувшись от чисел си с2,..., с„ к предшествующим им
числам dt = a[m-2), d2 =-- 4™-2) dn = а^~2). Мы, очевид-
очевидно, имеем
сэ — о • • ¦ • > C2l—l —
d2 + rf, di + db d2l
d2l +
но из равенств (**) и (*) следует, что dt + d2 + d3 -\- ... + d^i =
¦= 2/c, а из равенств (***) и (*) — что rf, -f rf2 + ^з + • • • +d2i —
¦= 2/C =5^= 2/c. Полученное противоречие и завершает доказательство.
171
131. Выясним, прежде всего, при каких числах х, у, г возможно
совпадение троек (х„, уп, zn) и (х, у, г). Так как все тройки чи-
чисел, начиная с хи уи Z\, заведомо неотрицательны, то и числа х,
У, г должны быть неотрицательными. Условимся, далее, считать,
что х :э= у ^ z и xt ^ yf ^ Zi при всех г = 1, 2, 3,... Поскольку,
очевидно, Xi = Xt_\ — Zi_\ при всех (^ 1 (где под ха и го понима-
понимаются числа х и г), то х ^ Х[ ^ х2 5Э= х3 ^ ..., причем, если хоть
одно число Zi (/= 0, 1, 2,...) больше нуля, то Xt+i < xt < x (и
все Xj, где / > i, также меньше х); поэтому, если хп = х, то Z{ = О
при (' = 0, 1, ..., я — 1. Таким образом, должно быть г = 0 и
Z\ = 0, откуда уже вытекает, что либо у — х (и г, = д; — у = 0),
либо г/ = г = 0 (и Z\ = у — г = 0). Итак, мы видим, что для
совпадения тройки чисел (х, у, г) с какой-либо тройкой (хп, уп, г„)
необходимо, чтобы исходная тройка имела (при х = 1)
либо вид A, 1, 0), либо вид A, 0, 0). При этом второй случаи
можно сразу же откинуть, ибо от тройки A, 0, 0) мы переходим к
(отличной от исходной) тройке A, 1, 0); поэтому, если X = 1 и
тропка (х, у, г) совпадает с (хп, уп, гп), то (х, у, г) —это тройка
чисел A, 1, 0) (и тройки (хп, уп, zn) при всех п имеют такое же
строение);
132. а) Отметим, что четность или нечетность разности двух
чисел зависит только от четности и нечетности уменьшаемого и вы-
вычитаемого. Условимся обозначать четные числа буквой ч, а нечет-
нечетные— буквой н. Всего возможны следующие шесть существенно
различных комбинаций начальных чисел А, В, С, D: 1° ч, ч, ч, ч\
2° ч, ч, ч, н; 3° ч, ч, н, н; 4° ч, я, ч, н; 5° ч, н, к, я и 6° н, я, я, к;
все остальные комбинации могут быть получены из этих шести
циклической перестановкой чисел (перестановкой без изменения по-
порядка; при этом 1-е число считается следующим за 4-м). Прове-
Проверил!, что во всех случаях не позднее чем через четыре шага мы
придем к четверке четных чисел. Действительно, комбинация 1°
сразу состоит из четных чисел; в случае комбинации 6° мы в один
таг приходим к комбинации 1°; в случае комбинации 4° мы в один
шаг приходим к комбинации 6° и, следовательно, в два шага —
к комбинации 1"; в случае комбинации 3°мы в один шаг приходим
к комбинации 4° и, следовательно, в три шага — к комбинации 1°;-
иаконец, в случае комбинаций 2° и 5° мы в один шаг приходим
к комбинации 3° (в случае комбинации 5° — к комбинации, получа-
получающейся из 3° циклической перестановкой) и, следовательно, в че-
четыре шага — к комбинации 1°. Таким образом, мы во всех слу-
случаях через четыре шага придем к четверке четных чисел.
Продолжим теперь процесс образования новых четверок чисел;
так же, как выше, мы убедимся, что еще через четыре шага мы
придем к числам, делящимся на 4, еще через четыре шага — к чис-
числам, делящимся на 8, и т. д. Таким образом, продолжая процесс
достаточно долго, мы сможем прийти к четверке чисел, делящихся
па любую (сколь угодно высокую!) степень двух. Так как чис-
числа по абсолютной величина не увеличиваются, то это означает, что
мы, в конце концов, придем к четверке чисел, состоящей из одних
нулей (если все числа А, В, С, D меньше 2", то мы заведомо при-
придем к четверке нулей через An шагов, но можем прийти к ней и
значительно раньше).
Примечание. Аналогично можно показать, что если взять
не 4, а 8, 16, ...или любое другое число п = 2к целых положитель-
172
ных чисел, то, поступая аналогично вышеизложенному, мы через
колечное число шагов придем к системе п чисел, являющихся ну-
нулями. Если число п не является степенью двух, то дело обстоит
по-другому; так, например, исходя из тройки чисел 1, 1, 0, мы ни-
никогда не придем к тройке 0, 0, 0:
1, 1, 0,
0, 1, 1,
1, 0, 1,
1, 1, 0,
(ср. с решением задачи 131).
б) Ясно, что если числа А = —, В = —г-, С = —-, D = —т~
, °о °о со "о
суть рациональные ироои, то, умножая их все на определенным мно-
множитель k (па общий знаменатель всех дробей, например, па aJ)aCid-),
мы придем к целым числам А' = kA, В' = кВ, С = кС и W = кЬ,
а из того, что утверждение задачи а) верно для чисел Л', В', С"
и D', следует, что оно верно также и для чисел А, В, С » О.
Если числа А, В, С, D иррациональны, то утверждение задачи
а) может уже и не выполняться. Для доказательства этого до-
достаточно указать хотя бы одну четверку чисел А, В, С, D, для
которых это будет так. Положим Л = 1, В = л, С = х2, D — x3, где
х — какое-то положительное число, которое мы можем выбрать по
своему усмотрению. При этом, оче-
очевидно,
у] ==\х [I g =|л;2 х\=х\х II ^
С, = \х? — хЧ =х*\х — \\.
пропорци-
пропорци1П
т. е. числа Аи Вь Сь D рр
ональны 1, х, х2 и х2 + х -\- 1. Поэто-
Поэтому, если мы- сумеем подобрать х
так, чтобы выполнялось равенство
х2+х + 1 = х3, (*)
то числа Аи Ви С,, D, окажутся про-
пропорциональными А, В, С, D — и наш
процесс получения последовательных
четверок чисел никогда не кончится.
Но из рис. 13, на котором совмест-
совместно изображены графики функций
[ j + JL {эт0
есть парабола) и у = хъ {кубическая
парабола), видно, что соответствую-
щие линии пересекаются в некото-
некоторой точке М(х0, (/о), так что х =
= х0 — это есть (положительный) корень уравнения (*). Тем са-
самым мы установили существование таких (очевидно — иррациональ-
иррациональных!) чисел А = 1, В = х0, С = х\ и D = х\ (= х\ + х0 -fl), для
которых утверждение задачи а) неверно.
рис [3.
173
133. а) Нетрудно видеть, что следующее расположение 100 пер-'
вых целых чисел удовлетворяет условию задачи:
10 9 8 7 б 5 4 3 2 1 20 19 18 17 16 15 14 13 12 11
30 29 28 27 26.25 24 23 22 21 40 39 38 37 36 35 34 33 32 31
50 49 48 47 46 45 44 43 42 41 60 59 58 57 56 55 54 53 52 51
70 69 68 67 66 65 64 63 62 61 80 79 78 77 76 75 74 73 72 71
90 89 88 87 86 85 84 83 82 81 100 99 98 97 96 95 94 93 92 91.
б) Пусть <2j" есть первое (самое левое) из выписанных чисел;
0*2'—первое из оставшихся, большее чем а\'; а^ — первое из сле-
следующих за оB1', большее чем а^\ и т.д. Таким образом мы соста-
составим последовательность возрастающих чисел а\1\ а^\ а^,..., а^К
Если в этой последовательности имеется больше 10 чисел
(т. е. если i\ > 10), то задача уже решена Если же i\ ==C 10,
то мы вычеркнем все эти числа и из оставшихся 101 — i\ чисел
составим точно таким же образом новую последователь-
последовательность e^, ai,2), а1Р,..., а({^ возрастающих чисел. Продолжая этот
процесс, мы выделим из наших 101 чисел ряд возрастающих
последовательностей. Если хотя бы одна из этих последовательно-
последовательностей содержит больше 10 чисел, то наша задача уже решена; таким
образом, нам остается только рассмотреть случай, когда в каждой
и:з выделенных последовательностей имеется не больше 10 чисел.
Так как у нас имеется всего 101 число, то в рассматриваемом
случае общее число k выделенных последовательностей возраста-
возрастающих чисел не может быть меньше 11. В таком случае мы утвержда-
утверждаем, что в ряду из 101 числа можно выбрать 11 чисел, следующих
один за другим в убывающем порядке. Эти числа мы будем
выбирать с конца следующим образом. Последним из них будет
последнее число а^ последней из наших возрастающих последо-
последовательностей. Затем выберем число из предпоследней последова-
последовательности, расположенное слева от <цу ближе всего к нему. Это
число больше а<^\ ибо в противном случае в процессе построения
предпоследней последовательности мы бы выписали вслед за ним
число a(,k\ в то время как на самом деле число а^ попало в
другую последовательность. Точно так же вслед за этим выписы-
выписываем число из третьей от конца последовательности, расположенное
слева от выбранного числа предпоследней последовательности, бли-
ближе всего к нему, и т.д. Таким образом мы построим последова-
последовательность чисел, которые идут возрастая, если их рассматривать
в порядке справа налево, т. е. убывающую последовательность;
число членов этой последовательности равно числу k выбранных
вырастающих последовательностей, т. е. не меньше 11.
Примечание. Совершенно аналогично можно доказать, что
(л—1J целых положительных чисел можно расположить так, что
никакие и из них не будут следовать одно за другим в порядке
возрастания или убывания, но при любом расположении к > (п — IJ
целых положительных чисел какие-то л из этих чисел обя-
174
зательно будут Следовать одно за другим в порядке возрастания:
или убывания.
134. а) Первое решение. Рассмотрим наибольшие нечет-
нечетные делители выбранных 101 чисел, т. е. числа, которые получают-
получаются, если разделить каждое число на наибольшую степень двойки,
которую оно содержит множителем. Так как различных нечетных
чисел, не превосходящих 20О, имеется всего 100, то среди этих
наибольших нечетных делителей чисел будут два одинаковых. Но
это означает, что среди наших 101 чисел имеются два, отличаю-
отличающихся одно от другого только тем, что множитель 2 входит в эти
числа в разных степенях. Очевидно, что большее из этих чисел бу-
будет делиться на второе.
Второе решение. Можно также доказать это предложе-
предложение методом математической индукции. Проверим, что
если из четырех чисел 1, 2, 3 и 4 выбраны три числа, то одно из них
делится на другое (еще легче видеть, что если из чисел 1,2 выбраны
два числа, то одно из них делится на второе). Докажем теперь, что
если из 2га чисел от 1 до 2я нельзя выбрать га + 1 чисел так, чтобы
никакое из них не делилось на другое, то из первых 2(га + 1) целых
положительных чисел нельзя будет выбрать га + 2 чисел так, чтобы
ни одно из них не делилось на другое.
Действительно, рассмотрим какие-либо я + 2 чисел, выбранных
из первых 2(я+1) целых положительных чисел. Если среди них
нет иисел 2га + 1 и 2я + 2 или есть только одно из этих чисел, то
среди них есть я + 1 ¦ чисел, не превосходящих 2га, и по сделанному
предположению одно из этих чисел обязательно делится на другое.
Если среди них есть оба числа 2га -f- 1 и 2д -f- 2 и есть также число
п+1, то мы уже имеем пару чисел, делящихся одно на другое,
а именно, га + 1 и 2га + 2. Наконец, если среди наших чисел есть
числа 2га + 1 и 2га + 2, но нет числа п + 1, то исключим из рассмот-
рассмотрения числа 2га + 1 и 2га + 2 и добавим я+1. Мы получим я+1
чисел, не превосходящих 2га; по сделанному предположению Одно
из этих чисел делится на другое. Если это число не есть я+1,
то мы уже получаем пару чисел из выбранных нами Л+ 2 чисел,
одно из которых делится на другое. Если же число, 'делящееся на
другое, есть п + 1, то и 2га + 2 делится на одно из выбранных
чисел.
б) Выберем наши числа следующим образом: нечетные числа
от 101 до 199 E0 чисел), нечетные числа от 51 до 99, умноженные
каждое на 2 B5 чисел), нечетные числа от 27 до 49, умноженные
каждое на 4 A2 чисел), нечетные числа от 13 до 25, умноженные
каждое на 8 G чисел), нечетные числа от 7 до 11, умноженные
каждое на 16 C числа), числа 3-32, 5-32, 1-64.
в) Предположим, что мы выбрали 100 целых чисел, не пре-
превосходящих 200, ни одно из которых не делится на другое; дока-
докажем, что среди этих чисел не может быть ни одного из чисел 1—15.
Как в первом решении задачи а), рассмотрим все наибольшие
нечетные делители выбранных чисел; очевидно, это будут все не-
нечетные числа, не превосходящие 200 (см. решение задачи а)).
В частности, среди этих нечетных делителей есть числа 1, 3, 9, 27
и 81. Так как никакие два из чисел, отвечающих этим нечетным
делителям, не делятся одно на другое, то число, содержащее не-
нечетный делитель 27, должно делиться на 2 в степени не ниже
первой; число, содержащее нечетный делитель 9,— на 2 в степени
175
не ниже второй; число, содержащее делитель 3,— на 2 в степени,
не ниже третьей и число, содержащее делитель 1,— на 2 в степени
нз ниже четвертой. Но это значит, что числа 1, 21 = Ь2, 3, 4 = 1-22,
6 = 3 • 2, 8 = 1 • 23, 9 и 12 = 3 • 22 не входят в число 200 чисел.
Точно так же, рассматривая числа, имеющие наибольшими не-
нечетными делителями 5, 15' и 45, убеждаемся, что среди наших чи-
чисел нет чисел 5, 10 = 5-2, 15; рассматривая числа, имеющие
наибольшими нечетными делителями 7 и 21, убеждаемся, что среди
200 чисел нет числа 7; рассматривая числа, имеющие наибольшими
нечетными делителями 11 и 33, убеждаемся, что среди наших чисел
нет 11, и, рассматривая числа, имеющие наибольшими нечетными
делителями 13 и 39, убеждаемся, что среди них нет числа 13.
Примечание. Аналогично решениям задач а)—в) можно
показать, что из In (или меньше) первых целых положительных
чисел нельзя выбрать я+1 чисел так, чтобы никакие два не дели-
делились одно па другое, но можно выбрать п (или меньше) таких
чисел. При этом, если 3й < In < Зк + \ то из 2п первых целых чи-
чисел нельзя выбрать п чисел, хотя бы одно из которых
меньше 2к и таких, что никакое из этих чисел не делится на
другое, ио можно выбрать п таких чисел, наименьшее из которых
равно 2к (так, из 200 чисел можно выбрать 100, наименьшее
из которых равно 16 и ни одно из которых не делится на другое).
135. а) Рассмотрим наименьшие по абсолютной величине остат-
остатки, которые дают наши числа при делении на 100 (т.е. если какое-
либо число а дает при делении на 100 остаток, больший 50, то мы
будем производить деление с избытком' и рассмотрим отрицатель-
отрицательный остаток —г; а= 100 а —г, где 0<г<50). Так, как поло-
положительных чисел, не превосходящих 50, существует всего 51 (а
именно, 0, 1, 2,..., 50), а остатков мы имеем 52, то два из этих
остатков равны по абсолютной величине. Если эти остатки равны
и но знаку, то разность соответствующих чисел делится на 100;
если они противоположны, то сумма чисел делится на 100.
б) Пусть а,, а2, а3 ..., «юо — данные числа (расположенные
в произвольном порядке). Рассмотрим суммы
s, = аь s2 = fli + a2, s3 = a, + а2 + а3, ...
. • •, $юо = О| + а2 + из + ... + ат.
Так как этих сумм имеется 100, то в том случае, когда ни одна из
них не делится на 100, по крайней мере две из сумм дают при
делении на 100 одинаковые остатки (ибо различных не равных ну-
нулю остатков от деления на 100 существует только 99). Вычтя из
большей из двух сумм, дающих одинаковые остатки, меньшую,
мы получим некоторую сумму вида Oa + i + flk+г + . •. + яш, кото-
которая будет делиться на 100.
Примечание. Разумеется, в точности аналогично решению
этой задачи можно показать, что из любых п целых чисел (где
п — произвольное натуральное число) всегда можно отобрать не-
несколько, сумма которых делится на п.
в) Если все рассматриваемые числа равны между собой (и,
значит равны 2), то утверждение задачи очевидно: сумма любых 50
чисел равна 100. Если, скажем, а, ф а% то рассмотрим следующие
17G
суммы (ср. с решением задачи б)):
Si = аь s2 = а2, s3 =-a\ + а2,
s4 = а, _|- а2 + аг,..., sm = a{i+ a2+ ...+ ат.
Как и выше, заключаем, что либо одна из этих сумм делится на
100, либо две из них дают при делении на 100 одинаковые остат-
остатки, а тогда разность st—sj этих двух сумм определяет набор на-
наших чисел, сумма которых делится на 100. (Заметим, что посколь-
поскольку ахФ а2 и а и а2 ^ 100, «суммы» s, =ai и s2 = a2 не могут да-
давать при делении на 100 одинаковые остатки.) Но если сумма
некоторых из наших чисел (не всех — в нее наверное не входит
число аюо) делится на 100, то, поскольку эта сумма положительна
и меньше 200, она обязательно равна 100.
г) Заметим, прежде всего, что из любых четырех целых чисел
можно выбрать два, сумма которых делится на 2, и что из любых
десяти целых чисел можно выбрать пять, сумма которых делится
на 5; эти утверждения, родственные тому, которое нам требуется
доказать, разумеется, проще него (и, кроме того, используются в
его доказательстве). Впрочем, все перечисленные оценки (включая
и результат настоящей задачи) можно еще и.несколько улучшить:
два числа, сумма которых делится на 2, можно отобрать из любой
совокупности трех чисел; точно так же пять чисел, сумма кото-
которых делится па 5, можно отобрать из любой совокупности девя-
девяти чисел, а 100 чисег, сумма которых делится на 100, можно
отобрать из любой совокупности 199 чисел (см. Примечание в кон-
конце решения задачи).
Итак, мы последовательно будем доказывать три факта.
1°. Пусть даны 3 числа alt a2 и а3; из них молено выбрать
2 числа так, чтобы сумма этих чисел делилась на 2. Это предло-
предложение является совершенно очевидным: достаточно выбрать два
числа' одинаковой четности (оба четные или оба нечет-
нечетные), а такие числа среди наших трех конечно есть.
Ясно, что основным в этом простом рассуждении является воз-
возможность замены самих чисел аи а2 и а3 их остатками ги г2 и г3
от деления на 2: ведь если сумма остатков делится на 2, то и сум-
сумма самих чисел делится на 2. Но числа ги г2 и гг могут иметь
лишь значения 0 или 1 — и здесь совсем легко 'видеть, что среди
них всегда есть 2, сумма которых делится на 2.
2°. Рассмотрим теперь 9 чисел а\, а2, ..., а9; мы утверждаем,
что из них можно выбрать 5 чисел так, чтобы сумма этих чисег
делилась на 5. Заменим опять сами числа ai (где t= 1, 2,..., 9)
их остатками Л; от деления на 5. Все числа г; имеют одно из пяти
значений 0, 1, 2, 3 или 4; с этими маленькими числами удобнее ра-
работать, чем с самими числами at. Но, кроме того, ко всем 9 числам
г{ можно прибавить одно и то же (или отнять от них одно и то
же) произвольно выбранное число с — ведь при этом остаток от
деления с*уммы произвольных 5 наших чисел на 5 не изменится.
[Разумеется, после этой операции «сдвига» остатков мы снова за-
заменим полученные числа г^ «гч ± с их остатками от деления па 5;
эти новые остатки мы по-прежнему будем обозначать через г,-.]
Это замечание позволяет считать, что среди 9 чисел г, (каждое из
которых равно 0, 1, 2, 3 или 4) число 0 встречается реже, чем
остальные остатки: ведь если бы среди наших чисел было больше
всего чисел k > 0, то мы просто отняли бы от всех чисел по k.
12 Д. О. Шклпрский и др. • 177
При этом ясно, что число t нулей Может заключаться 6 пределах
2 ^ 15g:9 ,{/ > 1, так как среди 9 чисел хоть один остаток повто-
повторяется дважды!); при этом, если /^5, то доказывать нечего: в
этом случае мы имеем 5 делящихся на 5 чисел, сумма которых то-
тоже, конечно, делится на 5.
Дальнейшие рассуждения несложны, но несколько кропотливы.
Если t = 2, то в нашей совокупности девяти остатков п ни одно
число не повторяется более чем 2 раза; другими словами, 4 остат-
остатка повторяются в этой совокупности дважды, и лишь один встреча-
встречается однократно. Но тогда с помощью того же приема «сдвига»
всех остатков на одно и то же число с мы можем добиться равен-
равенства этого «непарного» остатка числу 4. Но если совокупность чи-
чисел представляет собой набор чисел 0, 0, 1, 1, 2, 2, 3, 3, 4 (мы счи-
считаем, что здесь последовательно выписаны числа rh r2, п га),
то, например, сумма Г\ + г2 + гъ + ^1+ г7 делится на 5 (равна 5).
Если же t ¦= 3 или 4, то условимся считать, что г\ = г2 = ^з = О
и что все числа г$, Ге,..., г9 отличны от нуля; при этом число г4
может равняться 0 или быть больше 0—это нам безразлично.
Далее, из совокупности 5 (отличных от 0) чисел rs, re, г7, /¦« и г9
всегда можно отобрать несколько (больше одного!) чисел так, что-
чтобы их сумма делилась на 5 — доказать это можно аналогично ре-
решению задачи б) (ср. с Примечанием в конце решения задачи б)).
Дополнив же затем полученную совокупность чисел нужным чис-
числом нулей из числа чисел rlf r% и г% до пяти чисел (возможно, впро-
впрочем, что нам не придется sth числа дополнять), мы и придем к со-
совокупности пяти чисел, сумма которых делится на 5.
3°. Теперь мы можем установить, что из совокупности произ-
произвольных 199 чисел alt a2..., ада всегда можно выбрать 1О0 чисел,
сумма которых делится на 100. Ясно, что из этих 199 чисел можно
выбрать 99 пар чисел одинаковой четности: будем выде-
выделять такие пары последовательно; после того как мы отберем 98
пар, у нас останутся 3 числа, из которых, в силу п. 1°, последние
2 требуемых числа выбрать можно. Перенумеруем наши числа, счи-
считая, что а{ и п2, а3 и с<,..., 0197 и aigs — числа одинаковой четно-
четности; затем заменим каждые два числа aal-i и ац (где t ¦= 1, 2,...,
99) их полусуммой bt *» 2l~< Si . Ясно, что если среди 99 (це-
(целых) чисел b 1 мы сможем выбрать 50, сумма которых делится на 50, то
(в два раза большая) сумма всех чисел а(, отвечающих 50 ото-
отобранным числам bt, будет делиться на 100. Таким образом, нам
достаточно установить, что из каждых 99 целых чисел можно вы-
выбрать 50, сумма которых делится на 50. Далее, в точности, как и.
выше, отберем из 99 чисел bt 49 пар чисел одинаковой чет-
четности. Считая, что Ь, и Ь2, 6з и bt,..., 697 и 6S8 — числа одинако-
одинаковой четности, заменим каждые два числа 62ft—i и Ьгн (где. k <= 1,
2,..., 49) одним числом — их полусуммой cft= —-—— ;при stom,
если сумма каких-то 25 чисел с» будет делиться на 25, то сумма 50
отвечающих ям чисел bt будет делиться на 50. Однако далее этот
прием уже отказывается работать, так как 25 — число нечетное;
поэтому теперь нам придется объединять числа ск не в пары, а в
пятерки чисел.
Из каждых 9 чисел, как мы знаем, можно выбрать 5 чисел,
сумма которых делится на 5; тем более из числа наших 49 чисел
178
С;, можно выбрать 5 таких чисел — назовем их си с2, е3, с^ с$.
После этого у нас останется 49 — 5 = 44 числа, из которых можно
выбрать еще 5 чисел, сумма которых делится на 5,— и затем продол-
продолжать этот процесс далее. Выделив таким образом 8 пятерок чисел,
таких, что сумма чисел в каждой пятерке делится на 5, мы придем
к оставшейся совокупности 49 — 8-5 = 9 чисел, из которых, в силу
п. 2°, нам удастся выбрать последнюю, девятую пятерку. Теперь
заменим каждую пятерку чисел cSi-t, с5г-з, Csi-2. C5i-i, сы их сред-
средним арифметическим d{ = ~л1 • —. Ясно, что если
о
мы найдем 5 чисел d\, сумма которых делится на 5, то (в 5 раз боль-
большая этой суммы!) сумма отвечающих им чисел С;, будет делиться
на 25, — а возможность выбора таких чисел ch нам как раз и тре-
требуется доказать. Но (здесь мы снова апеллируем к п. 2°!) из 9
чисел rfi, d2, ds, dh d5, de, d7, ds и d9, пять чисел, сумма которых
белится на 5, выбрать можно, чем и завершается доказательство.
Примечание. В обобщение пп. Г, 2° и 3° решения и задачи г)
можно также установить, что из каждых In — 1 целых чисел (где
п — произвольное натуральное число) можно выбрать п чисел так,
чтобы сумма их делилась на п; однако доказательство этого обще-
общего факта значительно сложнее вывода его частных случаев, отве-
отвечающих значениям п = 2, п = 5 или даже п = 100.
136. Так как сумма всех наших чисел равна 1, а наибольшее
из них равно гГ?~, то общее количество чисел не меньше 2k. Будем
доказывать наше утверждение от противного, т.е. предполо-
предположим, что в любой группе из k чисел нашей последовательности
наименьшее не превосходит половины наибольшего, и пока-
покажем, что это предположение приводит к противоречию. При сде-
сделанном предположении для группы из k чисел аи а2,.... ак (где
а' = ~2k —наибольшее число, а а^—наименьшее) будем иметь
1
ah <~2~ai; аналогично, из рассмотрения группы а^, а*+1,..., a2k-i
1 1
чисел получаем fl^ft— 1 ^~9~ ah ^ ~2?' °х'' из Рассмотрения чисел а2к-и
a2k а3л-2 (эта группа чисел существует лишь при 3? — 2 ^ л)
имеем fl3ft—2 ^ ~2~а2А—1 ^ ~~9з аъ и т- Д- Суммируя все получен-
полученные неравенства, заключаем, что
1 1 \
" + ~& ••• I
2а,
(первые две суммы слева содержат лишь конечное число членов, а
1 + ~2~ + 2" + • • • понимается бесконечная геометрическая
прогрессия). А так как наша последовательность аи а2, а3, ...
12* 179
'является невозрастающеи, то
Ч + a*+i + a2k + аз/.-1 + .,. < S < 2а,,
а3 + а*ь2 + в2* + ! + аЗА + ...< 5 < 2а,, (**
Оа-1 + а2й-2 + а3й-з + ... < S < 2а,.
Сложив, наконец, неравенство (*) и все неравенства (**), по-
получим:
«1 + а.г + а3 -f ... + ап < 2ах + 2at + ¦. ¦ + 2ах = 2Aa, =
Л слагаемых
в то время .как по условию задачи О] -f- а2 + • • • ~т~ ал == '• Полу-
Полученное противоречие и доказывает требуемое утверждение.
137. Будем обходчть наш круг, например, по часовой стрелке,
начиная с нулика, пока снова не придем к этому же нулику. При
этом всех переходов от нулика (к нулику или крестику) будет
столько, сколько нуликов, т. е. а. В числе этих переходов будут
переходы к нулику — их столько, сколько пар рядом стоящих нули-
нуликов, т. е. Ь. Тогда переходов от нулика к крестику будет q — b.
Аналогично, при таком же обходе можно подсчитать число пе-
переходов от крестика к нулику — их будет р — а.
Но число переходов от нулика к крестику равно числу перехо-
переходов от крестика к нулику, так как по завершении обхода мы долж-
должны остановиться опять па исходном нулике. Значит, q — b = р — а,
откуда
а — Ь = р — о.
138. Ясно, что если какое-либо число it, = k, то рассматривае-
рассматриваемое произведение равно нулю (четно), а если мы переставим в ряду
чисел 1, 2, 3, 4,..., 1ш — 1, 2т каждые два соседних числа, придя
к последовательности jj = 2, i2 = 1, h = 4, i4 = 3,..., <2m-i = 2m,
i2m = 2m — 1, то произведение
A—f,)B-i2) ...Bm-i2m) =
= (-1) • 1 • (-1) • 1 •...• (-1) • 1 = (-1)™ • 1'» = (-1)"'
будет нечетным; поэтому нам остается лишь показать, что при и =
= 2/п +1 нечетном рассматриваемое произведение будет чет-
четным всегда.
Первое доказательство. Среди чисел 1, 2 п =
«= 2т + 1 будет всего т ( <С —к~= ——:—[четных (это будут числа
2, 4,..., 2т); поэтому среди чисел ii, i2 in четных чисел с не-
нечетными номерами будет не больше чем m (ибо мы имеем всего :п
четных чисел) и нечетных чисел с четными номерами будет тоже
не больше m (ибо всего-то мы имеем m четных номеров). Таким
образом, объединение всех номеров первого и второго классов не
может охватывать все п = 2т + 1 номеров; поэтому найдется такой
номер /, что либо ни' четны, либо и ц и I нечетны. Но в обоих
случаях разность, ['г — / будет четной; поэтому произведение всех
множителей k — ih, где k = 1, 2,..., 2т + 1, заведомо будет
четным.
180
Второе доказательство. Так как сумма вс* просмат-
просматриваемых множителей
A-/,) + B-у + C-fc) +...+ (я-*.) -
= A+2 + 3 + ... + П)- A+2 + 3 + ...тп) -0.
то при я нечетном все эти множители не могут быть нечетными
(ибо сумма нечетного числа нечетных чисел нечетна). Поэтому сре-
среди этих множителей имеется хоть один четный — а значит, их
произведение четно.
139. Ясно, что поскольку каждое из произведений Х\Х% х%х%,..,
хпХ\ равно +1 или —1, то сумма всех этих произведений может
равняться нулю лишь в том случае, если число слагаемых в ней
п = 2ш— четно и m из этих слагаемых равны +1, a m других
равны —1. Но если —1 равны ровно m произведений из числа Х\ХЪ
х2Хз,. х3х4,..., *„_,*„, хпхь то в цепочке хи х2, *з,..., хп-\, хп, *i
происходит от перемен знаков. Отсюда уже следует, что число m
должно быть четным (« = 2/г), а значит, я делится на 4 (п = 4k),
ибо первое и последнее числа этой цепочки совпадают, и, значит,
число перемен знаков между ними не может быть нечетным.
140. Отнесем к одной группе все те числа, десятичная запись
которых содержит четное число единиц; все же числа, в записи ко-
которых фигурирует нечетное число единиц, составят вторую группу.
Пусть Л и В — два различных десятизначных числа из одной груп-
группы. Если записи Л и В содержат одно и то же число п единиц
(где 1 =?J п г^ 9, ведь если я = 0 или я = 10, то числа Л и В не
могут быть различными), то, предположив, что на каком-то опре-
определенном (i-м) месте в записи А стоит цифра 1, а в записи В —
цифра 2, мы вынуждены будем считать, что на другом (/-м) месте,
-напротив, в записи А стоит 2, а в записи В—цифра 1: ведь записи
обоих чисел содержат поровну единиц. Но в таком случае в записи
суммы А + В и на г'-м и на у-м местах будет стоять цифра 3, т. е.
эта запись будет содержать не меньше двух троек. Если же запись
числа А включает п единиц, а запись В содержит m ф п единиц,
где, скажем, п. > т, то поскольку числа п и т — одинаковой
четности (т.е. оба четные или оба нечетные: ведь А и В — чис-
числа из одной группы), то п — т ^ 2, и, значит, найдутся, по край-
крайней мере, два такие места, скажем k-e и 1-е, что в записи А на этих
местах стоит цифра 1, а в записи В — цифра 2. Отсюда следует, что
в записи суммы А + В и на k-м, и на 1-й местах (снова — не менее
чем на двух местах) будет стоять цифра 3.
141. Выпишем наши пять 100-значных чисел одно под другим;
в каждом разряде (т. е. в каждом столбце) рассмотрим всевозмож-
всевозможные пары цифр. Из 5 нифр можно, очевидно, составить 10 пар
цифр; поэтому всего мы будем иметь 10-100 = 1000 пар цифр. При
этом в каждом столбе будут встречаться обе разные цифры 1 и
2; если среди них имеется одна цифра 1 и четыре цифры 2 (или
наоборот), то пар одинаковых цифр будет 6, а если в столбце имеют-
имеются две цифры 1 и три цифры 2 (или наоборот), то число пар
одинаковых цифр будет равно 4. Таким образом, общее число пар
одинаковых цифр (по всем 100 разрядам) может- колебаться в
пределах от 4-100 =¦ 400 до 6-100 = 600.
С другой стороны, если А = а^ .. ¦ аюо и В = btbi... blao —
Два из наших чисел, то, как мы знаем, среди пар цифр а\ и Ьи
С2 и 62, .,., аюо и Ьюо будет равно г пар одинаковых чисел. А так
181
как из 5 чисел можно образовать 10 пар чисел, то таким путем мы
насчитаем Юг пар одинаковых чисел. Так мы приходим к двойно-
двойному неравенству
400 <1О s? 600,
откуда и следует, что 40 < г < 60.
Примечание. Разумеется, то же рассуждение показывает,
что если считать наши пять чисел я-значными, то определенное та-
2 3
ким же путем число г должно заключаться в пределах: -^ns^r^-rn;
рекомендуем читателю самостоятельно рассмотреть вопрос об ана-
аналогичных оценках числа г при замене количества 5 наших чисел
другим их количеством.
142. Ясно, что достаточно убедиться в возможности с помощью
наших «шагов» изменить любой знак 1-го набора, не меняя ни од-
одного из других знаков: ведь тогда, меняя последовательно все те
знаки 1-го набора, которые отличны от стоящих па тех же местах
знаков 2-го набора, мы переведем 1-й набор во 2-й. Но изменить
одновременно два произвольных знака — скажем, i-й знак af и у-й
знак Oj—1-го набора мы, очевидно, можем: для этого достаточно
дополнить паши два знака еще какими-то 10 (разумеется, одними
И теми же!) знаками (Jft , оАг,..., о"А 1-го набора до двух групп а\,
ahl> %••••• aft10 и aj' ^г ah2 %„ из И знаков, а затем по-
последовательно изменить сначала знаки aj,afti, aAj>.. .,aftio,a затем—
8наки о,, ah , oft ,..., ад. Теперь пусть ар — произвольно выбран-
выбранный знак 1-го набора; дополним его еще 10 знаками aqi, a^,..., aq^
до группы ар, aqi aq^ из 11 знаков, а затем сначала поменяем
все эти знаки, а потом —с помощью описанного выше приема —
знаки а и а , затем — знакио" , а .., наконец,— знаки а и о
При этом мы сохраним прежними все знаки 1-го набора, кроме од-
одного лишь знака Ор,—«откуда и следует утверждение задачи.
143. Предположим, что за какой-то понедельник шахматист
сыграл О] партий, за понедельник и вторник — а2 партий, за три
дня — а3 партий, и т. д., наконец, за 77 дней — я77 партий. Рассмот-
Рассмотрим теперь следующую совокупность чисел: аи а2, а3 а77; ах + 20,
а21+ 20, а3 + 20 а77 + 20.
Всего мы имеем здесь 2-77 = 154 числа, каждое из которых не
больше чем 132 + 20= 152 (число а77 не больше чем 11-12= 132,
так как 77 дней — это ровно 11 недель); следовательно, по крайней
мере, два из этих 154 чисел равны между собой (ср. со сказанным
на стр. 10). Но никакие два числа из ряда аи а% а3,..., а77 не могут
быть равны между собой (ибо шахматист каждый день играет не
меньше одной партии); точно так же не могут быть равны между
собой никакие два числа из ряда а{ + 20, a24-20, a3 + 20
077 + 20. Таким образом, для каких-то k и / должно иметь место
равенство
ak = а, + 20;
8то равенство означает, что аи— at = 20, т.е. что за k—l дней,
с (/+1)-го по k-й включительно, шахматист сыграл ровно 20
партий,
182 *
144. Первое решение. Рассмотрим остатки от Деления чисел
1,11,111 ПИ •¦• 1
N единиц
ва N. Так как этих чисел N, а различных не равных нулю остат-
остатков при делении на N может получиться только N — 1, то если ни
одно из этих чисел не делится на N (противное доказывало бы
предложение задачи), то какие-то два из них, например
а: = 11... 1 и l = пи ... 1 {1>щ,
k единиц I единиц
дают при делении на Л? один и тот же остаток. В таком слу-
случае разность
L — K= И ... 100...О
I—к единиц к нулей
делится на N.
Если N взаимно просто с 10, то из делимости числа L — К =
= 11 .. Л- 10* на N следует, что число 11 ... 1 делится на N.
I — к единиц !—к единиц
Второе решение. Рассмотрим разложение числа -^- в пе-
периодическую десятичную дробь:
—=0, ftjft.2 ... bk (а^г •¦ ¦ а{) (где ауаг ... аг — период ).
По правилу обращения периодических десятичных дробей в обыкно-
обыкновенные, мы будем иметь:
к
N ~ 999 ... 9 00 ... 0
I девяток k нулей
Отсюда вытекает, что число А = 999 ... 900 ... 0 делится на N. Но
! девяток к нулей
А = 9Аи где А1 = 11 ... 100 ... 0. Рассмотрим теперь число
I единиц к нулей
В = 11 ... 100 .^JMl ... 100... 0 ... 1! .„J00 ...0,
I цифр к цифр 1 цифр к цифр i цифр к цифр
получающееся, если число А\ выписать 9 раз подряд. Очевидно, что
В равно произведению числа А\ на число
100... 0 100... 0 ... 100 ... 01,
п+й)"цифрA+&)цифр ('; f ft) цифр
8 раз
делящееся на 9 (по признаку делимости на 9). Следовательно, чис-
число В, состоящее из одних единиц и нулей, делится на 9Ai = А, а
значит, и на N.
Если N взаимно просто с 10, то -jj- при обращении в десятич-
десятичную дробь дает дробь чисто периодическую, так что В в
этом случае будет состоять из одних единиц.
183
Примечание. Ясно, что если запись числа А состоит из р
единиц, а запись В— из pq единиц, то В делится на Л; поэтому
(в предположении, что N взаимно просто с 10; впрочем, это верно
и в общем случае) существует даже бесконечно много чисел,
удовлетворяющих условию задачи.
145. Пусть aN и aN+i = aN-\-d— два последователь-
последовательных члена нашей прогрессии; тогда расстояние между соответст-
соответствующими точками Аи и An+i числовой оси равно разности d прог-
прогрессии.. Пусть d > 0; если число d — нецелое, то обозначим через
а = {d} = d— [d] > 0 дробную часть числа d (ср. стр. 3"), а ес-
если d—-целое, то примем а равным 1 (во всех случаях а равно
разности между d и наибольшим из меньших d целых чисел). Мы
хотим так-расположить наши отрезки длины 1, чтобы можно было
утверждать, что хоть одна из точек Л v попадет на один из отрез-
отрезков системы, иными словами, чтобы можно было исключить случаи,
когда все точки AN попадают в промежутки между отрезками.
Но если имеет место именно этот последний случай, то каждый из
отрезков ANAn+i длины d будет состоять из целого числа отрезков
системы (общая длина которых, разумеется, выражается целым
числом) и некоторого числа промежутков между отрезками (вклю-
(включая сюда и два нецелых промежутка); ясно, что общая длина всех
этих промежутков (и двух частей промежутков) никак не может
быть меньше а. Поэтому, если нам удгелся указать систему отрез-
отрезков, в которой для достаточно больших номеров N число а нельзя
«набрать» из длин (и частей длин) промежутков между отрезками,
то для этой системы и будет выполняться стоящее в условии задачи
требование.
Сказанное делает ясной следующую конструкцию. Расположим
на положительной полуоси единичные отрезки, начиная с отрезка
A, 2), так, чтобы промежутки между соседними отрезками образо-
образовывали, скажем, геометрическую прогрессию со знаменателем ~n~j
т. е вслед за A, 2) расположим отрезок C, 4), затем — отрезок
И ' 5 —-), затем — отрезок 15—, 6 —), затем — отрезок (б _,7 _ |,
и т. д. (см. рис. 14); при этом каждый следующий промежуток будет
—Е—i—i—Е Э о Е 3—Е—*—3-Н Э-& * •
-J -2 -1 0 1 Z 3 k 5 Б
Рис. 14.
вдвое меньше предыдущего). Тогда сумма длин всех промежутков
1 + ~2" + -4~+'д' + ... = 2| а сумма Rt длин всех промежутков, начи-
начиная с ([ + 1) -го, -?т- -f ^щ + ^щ +•••¦= Tp^i будет при достаточ-
достаточно большом ( сколь угодно мала. Поэтому, каково бы ни было
(отвечающее выбранной нами арифметической прогрессии с положи-'
тельной разностью d) число а = {d} (или а = 1), всегда найдется
184
такой номер t0, что а > ¦ io_t, т. е. а > #i(|. Следовательно, если
Л1 настолько велико, что все промежутки вплоть до io-то располо-
расположены слева от точки An (а этого всегда можно достигнуть, ибо
при d > 0 последовательность Л[, Лг, Л3, •• •, Л„, ¦ ¦¦ уходит неогра-
неограниченно далеко вправо), то на отрезок ANAN+\ длины d могут
попасть лишь начинающиеся с (го + 1) -го промежутки длин
-т^> oi0+i' io_j_2 > ¦ •• Но так как сумма Ri0 длин всех этих проме-
промежутков меньше а, то обе точки Аи и Д,у-н не могут одновременно
принадлежать этим промежуткам — и хоть одна из них непремен-
непременно попадет на отрезок нашей системы.
Мы до сих пор считали, что d > 0; для того чтобы доказать
утверждение задачи и для арифметических прогрессий с отрица-
отрицательной разностью d, достаточно продолжить нашу систему от-
отрезков на отрицательную полуось числовой оси, скажем, отразив ее
симметрично от нулевой точки О.
146. Прежде всего очевидно, что ии одна из рассматриваемых
дробей не 'равна целому числу: действительно, если бы, например,
k(m + n)
какая-то дробь — (k — одно из чисел 1, 2, 3, .., т—1)
была целым числом, то т + и должно было бы иметь общие делите-
делители с числом т (ибо k < т и не может делиться на т); но тогда
и число п = (ш -)- п) — ш не было бы взаимно просто с т. Далее ни-
никакие две из этих дробей не равны друг другу: если бы было
k(rn-\-ri) I (m -1- п)
tn ~~ n
(k — одно из чисел 1, 2, ..., т — 1; I — одно из чисел 1, 2 л — 1),
то мы имели бы
k I k
— = —; т- L п,
и снова т и п не были бы взаимно простыми (так как / < л и не
может делиться на п)_.
Рассмотрим теперь некоторое целое положительное число А,
меньшое т + п- Дроби
т + я 2 (in + п) k (m + п)
т ' га т.
остаются меньшими А, пока k(tn-\-ri) < Л/л, или ?< - 'д; число
Г Am Л Ат °
таких дробей, очевидно, равно целой части числа ¦ i ¦„- .
\_т -\- /ij '" т п
Точно так же дроби
т-\-п 2 (т + п) 1(т-\-п)
п ' п п
' An
остаются меньшими А, пока / < -т . п; число таких дробей разно
Ч Отиодительнд обозначений см. стр. 37.
целой части Ап числа Ап . Числа Ат и _^1_ оба
-» l_m +nj /n+n m-f-я m-f-я
не целые, ибо т, п и /л + га попарно взаимно просты; сумма этих
двух чисел равна А:
Am An
т -\- п ' т-{- п~~
Но если сумма двух чисел а и (J, не являющихся целыми, равна
целому числу Л, то
доказательство этого предложения сразу следует из рис. 15. Таким
образом,
откуда следует, что в интервале (О, А) числовой оси имеется ровно
А — 1 наших дробей.
м й
_л_
±_Х 4
-у
Рис. 15.
Из доказанного Сразу вытекает утверждение задачи. Действи-
Действительно, положим сначала А = 1; мы получим, что в интервале @, 1)
вовсе нет наших дробей. Далее, пусть А = 2; из того, что в интер-
интервале @, 2) имеется одна дробь, вытекает, что одна дробь есть в
интервале A, 2). Затем положим А == 3; из того, что в интервале
(О, 3) содержатся две дроби, т. е. на одну больше, чем в интервале
(О, 2), вытекает, что в интервале B, 3) имеется одна из наших дро-
дробей. Продолжая рассуждать таким же образом, мы полностью до-
докажем требуемое предложение.
147. Первое решение. Если число а заключено в интерва-
1000 1000
ле —^- > а > т , р то всего имеется, очевидно, т целых чисел,
не превосходящих 10СО, кратных а (а именно а, 2а, За, ..., та).
Поэтому если мы обозначим через k\ число тех из наших чисел,
1000
которые заключены между 10СО и' 9 > через k% — число чисел, за-
1000 1000
ключенных между ¦ о и ~Т~! через k% — число чисел, заключеп-
1000 1000
ных между ~о~ и ~~^~, и т. д., то мы будем иметь всего
k, + 2k2 + 3k, + ..,
чисел, не превосходящих ЮОО и кратных хотя бы одному из нащих
186
чисел. Но по условию задачи все эти кратные различны; следова-
следовательно,
6i+2&2 + 3&3 + . • • < 1000.
Теперь остается заметить, что сумма обратных величин всех
наших чисел меньше чем
! . ь ! 2^ + 3^ + 4^+¦¦•
ъ
2
1000 ~ к'л 1000 + •¦• — Ю00
10С0
(здесь мы заменили к\ наибольших из наших чисел на g ; сле-
юоо юоо
дующие к2 чисел— на ""д~; следующие к3 чисел — на ——,
и т. д.). Но
= (*i + 2/г2 + 3?3+ ...) + (ki + k2 + h + ...) =
= (ki + 2k2 + 3k31+ ...) + n < 1C00 + « < 2000;
следовательно, сумма обратных величин всех наших чисел меньше 2.
Второе решение. Приведем здесь еще один изящный ва-
вариант того же рассуждения. Число членов ряда 1, 2, ..., 1000, деля-
Г 10001
щихся на целое число п/,, очевидно, равно целой части —— дроби
L я J
юоо
. Так как наименьшее общее кратное любых двух из чисел аи
"h
«2, ¦••, ап больше 1000, то среди чисел 1, 2, 3 1000 не найдется
ни одного, делящегося одновременно на два из чисел fli, а?, ,.., ап.
Отсюда вытекает, что число членов ряда 1, 2, 3 1000, делящих-
делящихся хотя бы на одно из чисел а.\, а2, аг,..., а„, равно сумме
ПОООП Г10001 Г10С01 Г10001
l^rj+l—1+И + + И-
г Так как в ряду 1, 2, 3,..., ЮОО всего имеется 1000 чисел, то
должно быть
Г1000] Г10001 Г10001 Г10001
L fli J Lfl» J Lв» J L an J
Но целая часть дроби отличается от самой дроби меньше чем на
единицу, т. е.
П000] 1000 Г1000] 1000 ГГ0001 1000
Следовательно,
/1000 \ /1000 \ /1000
187
т.
ф
е.
1000
ах ~>
1000
аа "•
1000
1000
п
и, таким образом,
Примечание. Оценку настоящей задачи можно значительно
уточнить. Рассмотрим все кратные наших чисел, не превосходящие
500. Очевидно, k\ из наших чисел будут сами больше 500; k2 + k$
500
чисел будут не большем 5СО, но больше -?г; к± + къ чисел будут
500 500
не больше -q", но больше -tj-, и т. д. Отсюда, в точности как
в первом решении задачи, заключаем, что общее число чисел, не
превосходящих 500 и кратных хотя бы одному из заданных п чисел,
равно
(k2 + h) +2(kt + h)
следовательно,
(h + h) + 2{ki + ks) + 3(k6 + k7) +... <500.
Отметим теперь, что разность 500—[(k2 + h) i+ 2(Ь* + ^5) +
+ 3(^6+^7) + ...] выражает число чисел, не превосходящих 500 и
не кратных ни одному из наших чисел, а разность 1000 —
— (ki + 2&2i+ ЗАз +•• •)—число чисел, не превосходящих 1000 и
не кратных ни одному из наших чисел. Следовательно,
500 -l(kt + kt) +2(k 4+ ks) i+З(ft, + h) +...]<
< 1CO0— (ki + 2k2 + 3/г3
откуда получаем:
(*i + *a) + 2(^з + *<) + 3(^5 + h) + ... <500.
. Теперь остается только заметить, что
+ [(ki + k2) + 2 (A3 + kt) + 3(^5 + йв) +...]<
< 1000 + 500 = 1500
и, следовательно, сумма обратных величин всех наших чисел, мень-
2А43? + 4?+ 1
14г + 3+
шая JQQQ , наверняка меньше '~2~-
Аналогично, рассматривая кратные наших чисел, не превосходя-
превосходящие 333, можно доказать, что сумма обратных величин всех наажч
чисел даже меньше l~g~»
Отметим еще, что число 1000 в условии этой задачи можно за-
заменить любым другим целым числом,
183
148. Рассмотрим, как образуется разложение простой дроби —
в периодическую десятичную дробь
— = А, ахаг ... ahaia.2 ... акахаг ...
(здесь А—целое число, а а\, а2, ..., #/, — цифры периода дроби).
Очевидно, что Л есть частное от деления q на р:
q = Ар + qu
где остаток q{ меньший р. Далее Aat есть частное от деления 1 Oq
на р (Аа1 составлено из цифр числа А и цифры п[):
Щ = Аах -р + q2, где q2 < р.
Точно так же
; 102 ¦ q — Aaia2 ¦ p + q, Ю* q = Aaxa2 ... ak ¦ p + <
Период дроби начнется снова в тот момент, когда при делении
какого-либо числа lQhq на р мы получим тот же остаток <7ft + i = Я и
что и при делении числа q на р. Таким образом, число k цифр в
периоде дроби определится как наименьшая степень 10, такая, что
№hq дает при делении на р тот же самый остаток, что и q. Послед-
Последнее означает, что разность 10'*<7 — <? = A0й — \)q делится на р
или что разность 10й — 1 делится на р (ибо q, разумеется, вза-
взаимно просто С р).
Предположим теперь, что k четно: k = 21; из того, что разность
10й —1 =• A0'—1)A0' +1) делится на р, следует, что либо 10' —1
делится на р, либо 10'+ 1 делится па р. Но W—1 не может де-
делиться на р, так как в противном случае 10' давало бы при делении
q
на р тот же самый остаток, что и q, и период дроби -г-равнялся
бы /, а не k = 21. Тачим образом, мы заключаем, что 10' -f- 1 де-
делится на р.
10l?7 , q
Из последнего результата следует, что сумма —- + —!~ есть
целое число. Но
Ю'о , а -л 1
• + -2- •= Ащпь .. .йг, Я;_}.1Й1_|_2 • ¦ • a2la\ai • • • Я; • • • +
таким образом, сумма дробей
A, aia2 ... alal+l ... а.г1 ...;
О, a;+ia,+2... i72(a,a4 ... a,... + 0,
есть целое число. Так как каждая из этих дробей меньше 1 и боль-
больше нуля, то эта сумма должна равняться 1 = 0,999..., что возмож-
возможно только в том случае, если
.9 а,
Из последних соотношений сразу следует, что
+ аг1 _ g
2/ 1Г
189
<7i -|- fl2 -f- • • • -f Яь О
Если же k нечетно, то равенство — —^,
k 2
очевидно, невозможно, так как знаменатель дроби, стоящей в левой
части этого равенства, не делится на 2.
149. Число цифр в периодах дробей —- и ¦ n^_i равно наи-
наименьшим целым положительным числам к и /, таким, что IC — 1
делится на рп, соответственно 10'— 1 делится на pn + i (см. решение
предыдущей задачи). Составим теперь разность
A'(У —1) — A0" —1) = 10" A0'-" — 1).
Из того, что эта разность делится на рп, следует, что 10'~* — 1 де-
делится на рп. Покажем теперь, что из того, что 1О'~"—1 делится
на рп и 10ft—1 делится на рп, следует, что и 10'' — 1, где d есть
общий наибольший делитель чисел l — k и к, делится на рп.
Действительно, пусть /—-k = qk-\-r. В таком случае имеем:
10'-" — 1 = Ю9"+г—1 = ЮфО"*— .1) + A0г—1).
Но 10«А — 1 .= A0ft)« —И делится на 10й — 1, т. е. делится на рп\
следовательно, и 10г—1 делится на р". Точно так же показывается,
что и 10г'— 1, где Г\ есть остаток от деления k на г, делится на
рп; что 10г<—1, где г2 есть остаток от деления г на г,; делится
нар"; что ЮГз— 1, где rs есть остаток от деления гх на п, делится
на рп, и т. д.1). Но нетрудно показать, что ряд чисел г, п, Г2. • ¦ •
должен закончиться числом d. Действительно, так как / — k и k
делятся на d, то и r= (l — k)—qk делится на d\ так как k и г
делятся на d, то и г{ делится на d\ так как г п г\ делятся на d,
то и г2 делится на d, и т. д.; следовательно, все числа нашего ряда
делятся на d. С другой стороны, если последнее число в этом ряду
есть гк (т. е. /¦(,_! делится на г&, так что следующий за г/, остаток
уже равен нулю)., то гй_! делится на rk; />_2 делится на г^ (ибо
Гк~\ и гк делятся на Гк)\ г*_з делится на rh (ибо гА_2 и гк-{ делятся
на rk), и т. д; наконец, к и / — к делятся на г&. Но в таком случае
неравенство г* > d противоречило бы тому, что d есть общий
наибольший делитель / — k и k.
По условию к есть наименьшее целое число, такое, что
10* — 1 делится на рп. Поэтому из того, что 10d — 1 тоже делится
на рп, следует что d = k, I — к кратно к и, значит, / кратно к:
I = km.
Разложим теперь 10'—1 на множители: ч
10'—1 = 10Ьт —1 =
«= A0* — l)A0<m-'>* + 10<™-2)ft + ... + 10й1+ 1).
Так как 10* — 1 делится на рп, то 10* дает при делении на рп
остаток 1, откуда следует, что и 102* = ЮМС дает при делении
на рп остаток 1 и 103fe = 102ft- 10fe дает при делении на рп остаток
1, и т. д. Следовательно, каждый член суммы, стоящей в скобках,
дает при делении на р" остаток 1 и, таким образом, вся сумма дает
остаток т. Отсюда следует, что если 10* — 1 не делилось на рп+х,
') Этот процесс получения ряда последовательных остатков ru
т%, rs, ... носит название алгоритма Евклида.
190
то наименьшее значение /, такое, что 10'—1 делится на pn+1, равно
рк; при этом1 \Qvk— 1 делится на pn+i, но не делится на рп~2 (ибо
выражение в скобках не делится на р2).
Отсюда и вытекает утверждение задачи.
150. а) Пусть а — первая, а 6— последняя цифра искомого
числа N. Тогда это число равно 1000 а + 100 а + 10 Ь + b = 1100 а +
+ 116= 11A00а + 6). Так как число N является точным квадра-
квадратом, то из того, что оно делится на 11, вытекает, что оно делится и
N
на 121, т. е. уу- = 100а + 6 делится на 11. Но
100а + 6 = 99а + (а + 6) = 11 ¦ 9а + (а + 6).
Следовательно, а + b делится на 11. Так как и а, п b не больше
9 и а не равно 0, то 1 ^ а + Ь ^ 18, а потому а + Ь = 11.
Отсюда
100а+ 6 = 11-9а+ 11 = 11(9а+ 1),
N 100а + Ь
т = —iT- =9а + >•
N
Так как N — точный квадрат, то у^у — также точный квадрат. Но
из чисел вида 9а + 1, где а меняется от 1 до 9, только 9-7 + 1 =
= 64 является точным квадратом. Следовательно, Af=121-64 =
= 7744 = 882.
б) Пусть а — цифра десятков этого числа, а & — цифра единиц.
Тогда число равно 10а + b, a число, записанное этими же цифрами
в обратном порядке, равно 106 + а. В силу условия задачи, 10а +
+ 6 + 106 + а = 11 (а + 6) = k\
Отсюда Следует, что к% делится на 11, поэтому а + b также де-
делится на 11. Так как а + 6 =SC 18, то это возможно лишь в случае,
если а + & = 11, /г2 = 121. Таким образом, искомыми числами яв-
являются
29, 38, 47, 56, 65, 74, 83, 92.
151. Обозначим двузначное число, образованное первыми двумя
цифрами искомого числа N, через а, а число, образованное его дву-
двумя последними цифрами, — через Ь. В таком случае N = 100а -\- Ь,
так что условие задачи дает
100а+ 6 = (а + 6J,
или
99а = (а + 6J— (а + 6) = (а + b) (a + 6 — 1). (*)
Итак, произведение (а + Ь) (а + 6—1) должно делиться на 99.
Рассмотрим теперь отдельные возможные случаи.
1°. а + 6 = 99?, а+ b — 1 = -г. Так как а и b — двузначные
числа, то k sg; 2, причел случай k = 2 сразу приводит к не удовлет-
удовлетворяющим основному равенству (*) значениям а = 99, b = 99.
Таким образом, приходится считать, что
k=l, a + b = 99, а = а + 6 — 1=98, N -= 9801 = (98 + \)\
2°. а + 6 = 11ш, а + 6 — 1 — 9п, тп = а. В этом случае имеем
9п = \\т—1. Из того, что 11 т — 1 делится иа 9, следует, что чис-
191
ло т дает при делении на 9 остаток 5 (непосредственной проверкой
убеждаемся, что если бы m давало при делении на 9 какой-либо
другой остаток, то llm — 1 не делилось бы на 9). Итак, т = 9/i-f- 5,
откуда следует, что 9п = 99* + 54, п = 1 Н + 6. Теперь имеем:
с = mn= (9/ + 5)(Ш + 6) = 99^+ 109^ + 30.
Так как а число двузначное, то отсюда сразу вытекает, что
t — 0. Следовательно, а = 30, а + 6 = llm = 55, Ь =25, N =
= 3025 = (ЭО + 25J.
3°. а + Ь = 9т, а + Ь — 1 = 11л, тп = а. Исследование, анало-
аналогичное тому, которое мы провели в случае 2°, дает единственный
ответ Л' = 2025 = B0 + 25J.
4°. а + b = 33m, a -f Ъ — 1 = Зл или а + & = Зт, а + Ь — 1 =
= 33л, что невозможно, так как а-\-Ъ и а-\-b — 1— числа взаимно
простые.
5°. а + Ъ — 1 = 99?, а -\- Ъ »» -г-. В этом случае имеем
{а-\-Ь) (а + b — \)
а + Ь — 1= 99, а + Ь= 100, а = !—'—^ ' = 100, что не-
невозможно. Итак, условию задачи удовлетворяют лишь числа 9801,
3025 и 2025.
152. а) Четырехзначное число, записываемое четырьмя четными
цифрами, может начинаться с цифр 2; 4, 6 или 8; другими Словами,
оно заключено между 1999 и 3000, или между 3999 и 5000, или меж-
между 5999 и 70С0, или между 7999 и 9000. Поэтому корень квадратный
из этого числа заключается между 44 и 55, или между 63 и 71, или
между 77 и 84, нли между 89 и 95. Заметим еще, что так как
(№ + УУ =• 100x2 + 2to/ + i/2, то при 0 < </s?9 цифра десятков
числа (IOx+i/J четна или нечетна одновременно с цифрой десятков
числа у2. Поэтому корень квадратный из искомого числа не может
оканчиваться цифрами 4 и 6.
Так как корень квадратный из искомого числа четен, то он мо-
может равняться лишь одному из следующих 10 чисел:
48, 50, 52, 68, 70, 78, 80, 82, 90 и 92.
Непосредственная проверка показывает, что условию задачи удов-
удовлетворяют числа:
682 •= 4624; 782 =» 6084; S32 «= 6400; 92J «= 8464.
б) Рассуждения, аналогичные тем, которые привели нас к ре-
решению задачи а), показывают, что вовсе не существует четырех-
четырехзначных чисел, являющихся полными квадратами и записывающихся
четырьмя не,четны-ми цифрами.
153. а) Обозначим цифры сотен, десятков и единиц искомого
числа N соответственно через х, у, и г, так что N = 100х + 10j/ + г,
В таком случае условие задачи дает "
100* + 10(/ + г = х\ +yl + г\.
Отметим, что 7! = 5040 есть число четырехзначное; поэтому ни
одна цифра числа N не может превосходить 6. Следовательно, само
число N не превосходит 700, откуда вытекает, что ни одна его циф-
цифра не может превосходить 5 (ибо 6! = 720 > 700). Хотя бы одна
цифра числа N равна 5, так как даже 3-4! = 72 < 100, а N трех-
192
значно. При этом х не может быть равно 5, так как даже 3-5! =
= 360 < 500. Отсюда следует также, что * не превосходит 3. Да-
Далее можно утверждать, что х не превосходит 2, так как даже 3! +
-f- 2 • 5! = 246 < 300. Но число 255 не удовлетворяет условию зада-
задачи, а если лишь одна цифра искомого числа равна 5, то х не может
быть больше 1, ибо даже 2! + 5! + 4! = 146 < 200. Более того, так
как 1! + 5! + 4! =• 145 •< 150, то мы заключ-аем, что у не может
превосходить 4; следовательно, г «= 5, так как хо_тя бы одна цифра
числа N должна равняться 5. Таким образом, мы имеем х = 1,
4=^i/=^0 и ? *= 5; это позволяет легко обнаружить единственное
решение задачи: N »* 145.
б) Искомое число N не может иметь больше чем три цифры,
так как даже 4-Э2 «= 324 — число трехзначное. Поэтому мы можем
написать jV = 103x + Юу + г, где *, у, г — цифры числа; при этом
х или даже х и у одновременно могут быть равны нулю.
Из условия задачи имеем ЮОх + 10</ + г => х1 + у2 + г2, откуда
A00 — *)*+ A0 — у)ужг(г— 1). (*)
Из последнего равенства прежде всего следует, что х = 0 —
в противном случае число, стоящее в левой части равенства, не
меньше чем 90(х 5= 1, 100 —х Зг 90, A0 — у)у 3= 0), а число, стоя-
стоящее справа, не больше чем 9-8 = 72 (ибо г =?1 9). Следовательно,
уравнение (*) имеет вид A0 — у)у = z(z — 1). Легко проверить,
что это последнее равенство не удовлетворяется ни при каких целых
положительных х и у, не превосходящих 9, если только у Ф 0.
Если (/ = 0, то мы имеем единственное очевидное решение г= 1.
Таким образом, условию задачи удовлетворяет единственное
число jV = 1.
154. а) Очевидно, что искомое число N не может иметь более
четырех цифр, так как сумма цифр пятизначного числа не превос-
превосходит 5-9 = 45, а 452 = 2025 — число четырехзначное. Далее, так
как 4-9 = 36, а 362 == 1?96, то при N четырехзначном первая цифра
Л' не превосходит 1. Но 1 + 3 ¦ 9 = 28, а 282 = 784 трехзначно; зна-
значит, N вообще не может быть четырехзначным числом. Итак, мы
можем предположить, что N = 100х+ Юг/ + г, где х, у, г — цифры
искомого числа; при этом возможно, что * = 0 или даже х = у = 0.
Теперь условие задачи можно записать в виде
100* + Юу + z = (* + y + z)\
или
99*+ fy = (х + у + гУ- (х + у + z) = (х + у + z) (x+y+z- 1).
Таким образом, мы видим, что либо x + y + z, либо * + # +
+ z—1 делится на 9 (каждое из этих двух чисел делиться на 3 не
может, так как они взаимно простые). Но 1 =sc х + у + г ^ 27.
Рассмотрим теперь отдельно все представляющиеся случаи.
1'. х + у + z — 1 = 0; 99х + 9(/ = 0, * = у = 0, г = 1; N = 1.
2°. х + у + г = 9; 99* + 9у = 9 ¦ 8 = 72, * «= 0, 9</ = 72, у = 8,
г= 1; Л/ = 81( = (8+ IJ).
3°. х + у + г — 1 = 9; 99* + 9у = 9 ¦ 10 = 90, * = 0, 9у — 90,
что невозможно.
4°. х + у + г = 18; 99х + 9у = 18 • 17 = 306, * = 3, у == 1, г =
«= 18— C + 1) = 14, что невозможно.
13 д. о. Шклярский и др. 193
5°. х + у + г — 1 ,= 18; 99* + 9# = 19 • 18 = 342, х = 3, у = 5,
г = 19 — C + 5) = 11, что невозможно.
6°. х + у + г = 27; 99х + 9г/ = 27 • 26 = 702, х = 7, г/ = 1,
г = 27— G + 1) = 19, что невозможно.
Итак, условию задачи удовлетворяют только числа 1 и 81.
б) Куб трехзначного числа может содержать не более девяти
цифр; поэтому сумма цифр куба этого числа не превосходит 9-9 =
= 81 < 10О. Отсюда следует, что искомое число не может быть
трехзначным; аналогично показывается, что оно не может содержать
и больше трех цифр. Итак, искомое число обязательно будет одно-
однозначным или двузначным.
Куб двузначного числа не может иметь более шести цифр; по-
поэтому сумма цифр куба не превосходит 6-9 = 54. Итак, искомое
число не может превосходить 54. Но если куб числа, не превосходя-
превосходящего 54, даже"~и имеет шесть цифр, то первая цифра его равна 1;
поэтому сумма цифр куба не превосходит 5-9+ 1 = 46. Итак, иско-
искомое число не превосходит 46.
Если число не превосходит 46, то куб его содержит не более
пяти цифр, и так как он меньше 99 999, то сумма цифр куба не
превосходит 4-9 + 8 = 44; так как куб числа 44 есть пятизначное
число, оканчивающееся на 4, то и 44 больше суммы цифр своего
куба. Итак, искомое число не превосходит 43.
Далее, так как сумма цифр каждого числа дает при делении
на 9 такой же остаток, как и само число, то искомое число и его
куб должны давать при делении на 9 одинаковые остатки. Но это
возможно только в том случае, если искомое число дает при деле-
делении на 9 остаток —1, 0 или 1.
Итак, искомое число не превосходит 43 и дает при делении на
9 остаток —1, 0 или 1. Этим условиям удовлетворяют лишь следую-
следующие 13 чисел:
1, 8, 9, 10, 17, 18,-19, 26, 27, 28, 35, 36, 37.
Проверка показывает, что условию задачи удовлетворяют числа:
1 A3 = 1), 8(83 = 512), 17A73 = 4193),
18A83 = 5832), 26B63 = 17 576), 27B73 = 19683).
155. а) Непосредственной проверкой убеждаемся, что при х < 5
единственными решениями нашего уравнения будут числа х = 1,
f/ = ±l и х,= 3, у = ±3. Докажем теперь, что при х ;з= 5 реше-
решений нет. Для этого заметим, что 1! + 2! + 3! + 4! = 33 оканчива-
оканчивается цифрой 3, а 5!, 6!, 7!,... все оканчиваются нулем. Таким обра-
образом, при х ;з= 5 сумма 1! + 2! + ... + *! оканчивается цифрой 3, а
поэтому не может равняться квадрату целого числа у (никакой
квадрат целого числа не оканчивается на 3).
б) Рассмотрим два случая:
1°. г = 2п — четное число. Этот случай легко сводится к пре-
предыдущей задаче, ибо у2п = (упJ. Таким образом, при четном г
решения таковы:
х = 1; у — ± 1; г — любое четное;
х = 3; у — ± 3; г = 2.
2°. г — нечетное число. При г = 1 годится любое значение х,
причем у = И + 21 + ... + xl. • Пусть г ^ 3. Заметим, что 11 + 2! +
194
+ 3! + 4! + 5! + 6! + 7!,+ 8! = 46 233. Число 46 233 делится на .9,
но не делится на 27, а при п ^ 9 число п\ делится на 27. Сумма
9! + 10! + • ¦ • +xl делится на 27; поскольку, однако, 1! + 2! + ... +
+ 8! делится на 9, но не делится на 27, вся сумма 11 + 21 + ...+
+ xl при х 5г 8 делится на 9, но не делится на 27. Для того чтобы
уг делилось на 9, необходимо, чтобы у делилось на 3. Но тогда
у' делится на 27 (ибо z ^ 3) и, следовательно, при х ^ 8, г Зг 3
решений в целых числах нет. Остается рассмотреть случай х < 8.
Имеем 1! = 1 = 1г, где г — любое натуральное число; 11 + 2! = 3,
т. е. не равно никакой целой, отличной от 1 степени никакого нату-
ральЕюго числа; II + 2! + 3! = З2, и далее:
1! + 2! + 3! + 4! = 33,
1! + 2! + ... + 5! = 153,
1! + 2! + ... + 6! = 873.
1! + 2! + ... + 7! = 5913.
Ни одно из чисел 33, 153, 873 и 5913 не является целой, отлич-
отличной от единицы степенью никакого натурального числа. Таким обра-
образом, при нечетном г окончательно имеем лишь следующие решения:
х = 1, у = 1, г = любое нечетное;
х — любое натуральное, у = 1! + 2! + ... + *!, г = !.
158. Пусть
а* + Ь2 + с2 + d2 — 2".
Обозначим наибольшую степень двойки, на которую делятся все
четыре числа а, Ь, с и d, через р. Сократив обе части нашего равен-
равенства на 22?, мы получим:
л2 | /,2 | ,2 I j2 <)П—2р
Й1 + bi i С1 "г = ¦* i
где из четырех чисел ах, Ьх, Сх, dx, хотя бы одно является нечетным.
Если из четырех чисел аь 6,, сх, dx только одно или три явля-
являются нечетными, то ci\ + b\-\-c\-\-d^ нечетно и наше равенство не-
невозможно. Если из чисел alt bx, с,, dx два, например ах =26+ I и
Ьх = 2J + 1, являются нечетными, а остальные два, Сх = 2т и dx =
= 2п, четны, то мы имеем:
о\ + Ь\ + с\ + d] = Ш + 4? + 1 + 4Р + 4/ + 1 + 4т2 + 4«2 =
= 2[2(&2 + ? + /2 + / + m2 + n;i) + 1],
что противоречит тому, что а\-\-b\ + с\-\-d\ = 2n~2p не имеет нечет-
нечетных делителей (выражение в квадратных скобках не может рав-
равняться единице, так кач в противном случае мы имели бы k — I =
,= т = я =0, ci = di = 0 и с = d = 0). Если же все четыре чис-
числа ах = 2k+ 1, 6, = /!/ +1, Сх = 2т + 1, d, = 2я + 1 нечетны, то
мы имеем:
= 4Й2 + 4й + 1 + 4/2 + 4/+ 1 + 4т2 + 4п2 =
+ 4т + 1 + 4п2 + 4/г + 1 =
Но произведение двух последовательных целых чисел всегда
четно (один из сомножителей обязательно четен). Следовательно,
13* 195
выражение в квадратных скобках нечетно, и, значит, оно равно 1.
Таким образом, п — 2р = 2, л = 2р + 2 и fe = / = m = n = 0,
ах = bi = С! = dx = 1, а = b ¦=» с = d = 2*1.
Итак, если л есть число нечетное, "то 2" вовсе не разлагается
на Сумму четырех квадратов; если п = 2р четно, то 2" допускает
единственное разложение
157. а) Первое решение. Уравнение
х2 + У3 + г2 = 2хуг
удовлетворяется значениями х = О, г/ = 0, г = 0. При этом если
одно из чисел х, </, г равно 0, то и остальные должны быть равны
0, ибо сумма их квадратов в этом случае равна 0.
Пусть теперь все числа х, у, г, удовлетворяющие нашему урав-
уравнению, отличны от 0. Каждое из них можно представить в виде
х = 2ах, у = 2fyi, г = 2Уги
где X], у\, Z\ нечетны (если какое-нибудь из чисел х, у или г нечет-
нечетно, то соответствующий показатель степени 2 равен 0).
Так как х, у, г входят в наше уравнение симметрично, то мож-
можно считать, что х делится на наименьшую степень 2, а 2 — на наи-
наибольшую, т. е что
а < К Г
Выясним, на какую степень 2 делится левая часть нашего ра-
равенства.
1°. Если а < р" sg; ч или же а = $ = ч, то после вынесения за
скобки 2га в скобках будет стоять сумма нечетного и двух четных
чисел или же сумма трех нечетных чисел, т. е. нечетное число.
2°. Если же а =.{1 < "(, то можно написать:
х = 2«B?+1), г/ = 2*B/+ 1), ' г = 2* ¦ 1т.
В этом случае
= 22а D/г2 + 4* + 1 + 4/2 + 41 + 1 + 4.г,2) =
= 22а"н [2(/г2 + ? + /2+/+т2)+ I],
т.е. после вынесения за скобки 22а+'в скобках остается нечетное
число.
С другой стороны, правая часть равенства делится на
2"*+P+v+i_ й0 правая часть равенства должна делиться на такую же
степень 2, что и левая.
В случае 1° отсюда следует, что 2а = а + р + ч+1. Так как
а ^ Р =? "i, то из этого равенства следует абсурдное неравенство
2а ^ За+ 1.
В случае 2° отсюда следует, что 2а + 1 = а + {1 + ч + 1. Так
как а = р < ч, то отсюда следует неравенство 2а + 1 > За + 1,
которое также не может иметь места.
Следовательно, не существует -решений в целых числах уравне-
уравнения х2 + у2 + г2 = 2хг/г, отличных от решения х = 0, J/ = 0, г «= 0.
196
Второе решение. Так как сумма квадратов чисел х, у й
г четна, то либо все эти числа четиы, либо одно из них четно, а два
нечетны. Но в последнем случае сумма х2 + у2 + г2 делилась бы
только на 2, а произведение 2хуг — на 4 (сравните с первым реше-
решением задачи). Итак, мы можем считать, что х, у и z четны: х = 2хи
у = 2</ь'г = 2zi. Подставляя эти значения з наше исходное урав-
уравнение и сокращая на 4, получаем:
А + у\ + г\
Отсюда, в точности как выше, выводим, что числа Х\, у\, Z\ —
все четные. Но в таком случае, обозначив хх = 2х% у, = 2уг, Z\ =
о xi х у г
•ж 2zj, мы для чисел х2= ~7Г ^ ~~Т~> Уч~ ~Т~< г2 *= ~ получим урав-
уравнение
откуда, как прежде, выводится, что эти числа тоже четные.
Продолжая тот же процесс, мы заключаем, что все числа
х у г х у г
х. У, г; Xi ¦= -j-, i/, =» -у, гх =• -у; х., = —, </2 = —, г2 = —
х у z
х3 = -g~, Уз = "§" . гз = "g"'. ¦ • •
__L _JL __i-
• • •' XA ~ 2h ' Vh ~ 2h ' *k ~ 2h ' "
— четные (числа Хь, Ук, zh должны удовлетворять уравнению х^
+ у\ + zh = ^h^ixh^hzh)' ^° это возможно только в том случае,
если х = у = г = 0.
б) Так же, как и выше, доказывается, что единственным реше-
решением уравнения х2 -\- у2 + г2 + v2 = 2xyzv в целых числах является
решение х = 0, {/ = 0, z = 0, у = 0.
Здесь специального рассмотрения заслуживает случай, когда
наивысшие степени 2, на которые делятся х, у, z и у, олинаковы,
т. е. когда
х = 2аB& + 1), I/ = 2С1B/+ 1),
2 = 2аBш +1), v == 2аBл + 1),
где а —целое неотрицательное число, a k, I, m и п — целые числа.
Тогда
х2 + у2 + г2 + у2 = 22*[D?2 + 4* + 1) + (АР + 4/ + 1) +
-f Dm2 + 4m+ 1) + Dл2 + 4л + 1I =
= 22*+2{k2 + k + I2 + I + m2 + m + n2 + n+ 1) =
+/(/+ 1) +m(m+ 1) +п(п+ 1) + 1].
Но выражение в квадратных скобках обязательно нечетно
(см. выше, стр. 195). Поэтому наивысшая степень 2, на кото-
которую делится левая часть равенства, равна 2а + 2. Правая же часть
делится на 24а+1. Поэтому должно выполняться равенство 2а+2 —
= 4а + 1, что невозможно при целых а.
197
Второе решение задачи б) аналогично второму решению
задачи а) и предоставляется читателю.
158. а) Пусть х, у, г —какие-то три целых положительных чис-
числа, удовлетворяющих уравнению
х2 + у1 + г2 = kxyz. (*)
Покажем прежде всего, что всегда можно считать справедли-
справедливыми неравенства
kyz kxz kxy
*<-§-. и < х- г<Т~ ( ^
(т. е., другими словами, что ни одно из слагаемых, стоящих в левой
части уравнения (*), не превосходит половины правой части),
kxy
Действительно, если бы было, например, г>—гр.то мы рассмотрели
бы не числа х, у, г, а меньшие числа х, у и Z\ = kxy — г, которые,
как нетрудно видеть, тоже удовлетворяют уравнению (*):
х2 + У2 + (kxy— zJ = kxy(kxy-z).
Если из этих новых чисел какое-нибудь опять будет больше произ-
k
ведения двух других, ууноженного m-j-.to мы проведем снова
аналогичную замену и так будем поступать до тех пор, пока не
станут выполняться условия (**) (после этого наш процесс уже
не приведет к уменьшению чисел х, у, г).
Б^дем считать, что х =sc у =sc г. Прежде всего из того, что
kxy
У ^ г sg; —j- , следует
kx
1 > -j-; kx > 2.
Уравнение (*), очевидно, можно переписать в виде
Так как г ^ —о~' . то ПРИ замене в левой части последнего равенства
числа 2 на у sj г эта левая часть возрастает (или — в случае у = г
— не меняется); следовательно,
Отсюда, раскрывая скобки, получаем:
х2 + 2у2 5г kxy2.
Так как по условию х ^ у, то тем более
т. е.
198
Таким образом, мы имеем 2 < kx ^ 3, т. е. kx равно 2 или 3.
Но если kx = 2, то уравнение (*) принимает вид
*2 + F2 + г2 = 2</г, или х2 + ((/ — гJ = О,
откуда х = 0 и kx =» 0, а не 2. Следовательно, ?х = 3 и, значит,
& может равняться только 1 или 3. Нетрудно убедиться на простых
примерах, что эти значения k являются возможными (см. решение
задачи б)).
б) Продолжим рассуждения, которые привели к решению задачи
а). Выше мы имели х2 + 2</2 ^ kxy2; так как kx = 3, то это нера-
неравенство можно переписать в виде
хг + 2</2 5г Зг/2, или х2 > </2.
Но мы предполагали, что х ^у; следовательно, х = у. Пола-
Полагая теперь з основном уравнении (*) х = у, kx = 3, мы получим:
2х2 + г2 = Зхг, или (г — х) (г — 2х) = 0.
6«/ Зг/ Зх
Таким образом, 2 = х или г = 2х. Но так какг<~2~ = ~~2~ = "о"'
то г не может равняться 2х; следовательно, г = х.
Итак, мы видим, что если только выполняются условия (**), то
должно быть х = у = г. Но так как kx = 3, то х может быть рав*
но только 1 или 3. Соответственно этому получаем два решения
уравнения (*):
х=г/ = г=1 (fe = 3)
В решении задачи а) мы видели, что всякую тройку чисел х,
у, г, удовлетворяющих уравнению (*), можно последовательными
подстановками вида Z\ = kxy — z привести к тройке чисел, удов-
удовлетворяющих неравенствам (**). Но если zx = kxy — г, то г =
= kxy —1\\ поэтому каждое решение уравнения (*) можно полу-
получить из выписанных выше наименьших решений последовательными
подстановками вида 2i = kxy — г. В частности, таким образом, по-
получаем следующие решения уравнения (*), не превосходящие 1000:
Г. Случай k = 3.
х=111111 1 12 2 2 5 5
у = 1 1 2 5 13 34 89 233 5 29 169 13 29
2 = 1 2 5 13 34 89 233 610 29 169 985 194 433
2°. Случай k=\.
х = 3333 3 3 36 б 15
у = 3 3 6 15 39 102 267 15' 87 39
г = 3 6 15 39 102 267 699 87 507 582
(то, что решения, отвечающие значению k = 1, получаются из ре-
решений, отвечающие значению k = 3, простым умножением чисел х,
У и 2 на 3, сразу следует из того, что так связаны между собой
наименьшие решения уравнений х2 + У2 + г2 = xyz и х2 + у2 +
+ г2 = Ъхуг).
199
i 159. Из равенства *3 =¦ 2(</3 + 2Z3) (где х, у, г — целые) сле-
следует, что х = 2*1 — четное, что позволяет переписать наше уравне-
уравнение так:
8.^— 2у3 — 4г3 = 0, или Ах\ —г/3 — 2г3 = 0.
^Так как у3 = 2 B;q— г3), то у = 2у\— четное; поэтому имеем
4*i — 8(/j — 2г3 = 0, или 1х\ — 4f/f —г3=0.
Наконец, поскольку г3 = 2 (*i — 2</j), то и г »» 2zt — четное, и мы
получаем
2.vf -г- 4t/f — 8z^ = 0, или х\ — 2у\ — 4г\ — 0.
Таким образом, если х, у, г — решение исходного уравнения, то
х у
вс« эти три числа — четные, причем их половины*! = -гр, У\ = ~,
Zi = -к удовлетворяют точно такому же уравнению:
х\ ~ 2у\ - Аг\ = 0.
Отсюда следует, что и числа Xi = 2х2, У\ = 2(/г. 2j = 2г2 — четные,
причем и числа х2, г/г, г2 удовлетворяют исходному уравнению, т. е.
и они являются четными, и т.д. Окончательно мы заключаем, что
целые числа х, у, г делятся на любую степень двойки, что, разу-
разумеется, возможно лишь в том случае, когда все они равны нулю.
Итак, единственное решение исходного уравнения в целых числах
имеет вид
х = у = г = 0.
160. Дополним левую часть уравнения до полного квадрата,
для чего достаточно умножить обе части уравнения на 4 и приба-
прибавить к ним по 1:
Bх + IJ = V + 4?» + 4i/2 + 4у + 1.
Но
4г/3 + 4у2 + 4у+\ = Dу< + 4</3 + у2) + C#2
у+1) (=
а так как квадратный трехчлен Q(y) = 3t/2 -f- 4t/ -J- 1 имеет (вещест-
(вещественные) корни У\ = — 1 и г/г = — ~з"| то при всех целых у, отличных
от у = —1, этот трехчлен положителен (см. график функции t =
=3y2+4y+l на рис. 16, а), и, значит, Bх + IJ > (Р(у)J =
= Bi/2 + i/J.
, С другой стороны, мы имеем
4У* + № + 4</2 + 4у + 1 =
«= Bу2 + у+\J+Bу-у*)(-= {Pi{y)J + Q, (у)).
Но график функции Qi(iy) = 2</ — I/2 имеет изображенный на
рис. 16, б вид (корни квадратного двучлена Q\(y) равны 0 и 2), и,
200
значит, при всех целых у, отличных от 0, 1 и 2, имеем Q\(y) < О,
откуда Bх+1J< (Рх(у)J = Bуг + у+ 1J.
Таким образом, при всех целых у Ф —1, 0, 1 и 2 имеет место
двойное неравенство
т.е. при таких у величина Bх+1J заключена между квадратами
V
В)
Рис. 16.
двух песледовательных целых чисел Q(y) и Qt(y), и поэтому число
2х + 1 не может быть целым.
Итак, если у — целое число, то х может быть целым лишь при
у = —1, 0, 1 и 2, т.е. когда правая часть исходного уравнения рав-
равна 0, 0, 4 и 30. Нам осталось только решить 3 квадратных уравнения
х2 + х = с, где с = 0, 4 или 30. (*)
Целые корни этих уравнений таковы:
х = 0 или — 1 (при с »= 0); х = 5 или — 6 (при с = 30;
при с = 4 уравнение (*) целых корней не имеет).
Таким образом, окончательно получаем следующий набор решений
заданного уравнения в целых числах (здесь запись {а, Ь) означает,
что х = а, у = Ь):
@, -1), (-1, -1); @, 0), (-1, 0); E, 2), (-6, 2)
(всего 6 решений).
161. При у — 1 мы приходим к квадратному уравнению
х2 + (х+ 1J= (х + 2J, или х2 — 2х — 3 = 0,
имеющему единственный целый положительный корень х = 3 (вто-
(второй корень уравнения х = —1 отрицателен). Пусть теперь у > 1.
Заметим, что поскольку х2у и (х + 2J" — числа одинаковой четно-
четности, то число .(•*+ IJ" [ = (x-f-2J" — Xs*] будет четным; поэтому
~" 201
и число х 4- 1 = 2^i — четное. Далее мы имеем
= Bх1+1J>'-Bх1-\)гУ. (*)
Раскрыв скобки в стоящих справа выражениях с помощью формулы
бинома Ньютона, получаем:
BXlfv - 2 [с\у {2х^у-1 + ClyBXlfy-3 + ... + с\у B*,)].
что, уединяя в левую часть последний член правой части равенства,
можно переписать еще и так:
2 • 2</ • 2хх =
«= (adJ» - 2 • 2(/ B*!J"-1 - 2 • CJjy (гххJ^-3 - ... - 2-С\у Bх^
(заметьте, что поскольку у Г5= 2, то 2i/ ^ 4). Но все стоящие справа
члены, очевидно, делятся на Bх1K, откуда вытекает, что у должно
делиться на х\.
Далее, разделив обе части равенства (*) на Bx1Ji', получим:
( 1 \2у ! 1 \2у
откуда следует, что 1 + — =1+ 1 — _— < 2. Но, с другой
стороны в силу той же формулы бинома Ньютона
и, значит,
-l+f+
1 + -J- < 2, или -j- < 1, откуда у < Xll
что, однако, противоречит делимости у на х\. Поэтому наше урав-
уравнение не имеет таких решений, что у > 1 и все решения уравнения
исчерпываются одним найденным выше: у = 1, х = 3.
162. Обозначим^ д: + V *+¦¦ .+Ух через Лу (л;); в таком случае,
у корней
очевидно,
х+ Ay_i {х) = х + Ух + ¦ • ¦ + У"х~. = г2, или Лу-1 (ж) =г2— х
у—1 корней
Таким образом, если число Ау(х) =¦ г — целое, то и число Ау-\{х)
(=22 — х)—целое; но тогда и число Ау-2(х) ( ==_ (г2 — хJ — х)
— тоже целое, и Ау~3(х) —целое и At(x) = Ух — целое. А из
того, что.1^* *=t — целое, следует, что х = t2 (где t — целое).
202
Ясно, что для любого целого t значения * = t2, у — 1, 2 = t
являются решениями нашего уравнения. Пусть теперь (/> 1. При
этом числа
Ax(x)=Vx =t и Аг(х) = Ух + Ух =yt* + t=Vt(t + \)
должны быть целыми; но числа t и / + 1 — взаимно простые, отку-
да следует, что произведение ^4-1) может быть полным квад-
квадратом, лишь если и t, и 14- 1—полные квадраты, т. е. если
t = 0. А если t = 0, то, очевидно, х = 0 и Ау(х) =0 при л ю-
б о м х.
Таким образом, все решения рассматриваемого уравнения та-
таковы: х = t2, у = 1 и г — t (где t — любое целое число; если корни
понимаются в арифметическом смысле, то t следует считать нату-
натуральным числом), и х = 0, у = t — произвольное натуральное
число, z = 0.
163. Воспользуемся методом доказательства от противно-
г о: предположим, что выписанное в условии задачи уравнение име-
имеет решения в целых хну лишь для конечного числа простых
значений р и что наибольшим из них является n-е простое число
рп. Составим теперь число 2-3• 5-7-1 i • \3-...-рп = х и рассмотрим
выражение X = х*-{- х + 1. Так как число X—1 = jc2 -f- дг ==
= х(х 4- 1) делится на все простые числа 2, 3, 5,..., рп, то число X
не может делиться ни на одно из них; поэтому число X имеет боль-
больший Рп простой делитель Р, т. е. X = Ру, где у — некоторое нату-
натуральное число. (Здесь не исключен, разумеется, случай Р = X,
у = 1.) Таким образом, для р = Р наше уравнение имеет решение
х, у в целых числах, что противоречит предположению о том, что
рп — наибольшее простое значение коэффициента р, при кото-
котором такое решение существует. Полученное предположение и дока-
доказывает утверждение задачи.
Примечание. Очевидна близость этого рассуждения к из-
известному доказательству теоремы о существовании бесконечного
числа простых чисел (сч. решение задачи 349).
164. Задача состоит в том, чтобы решить в целых положитель-
положительных числах следующую систему уравнений (х, у, z и и — искомые
числа):
xi-\-y + z + u= (х 4- vI,
z' + x + y + u= (z + tJ,
или
у + z + и — 2vx + v2,
х 4- г 4- и = 2wy 4- ш2,
х 4- у 4- и = 2tz + Л
х 4- # 4" г = 2s" + s2-
203
Сложив все уравнения (*), получим:
Bv — 3)x+ Bw — 3)y + Bt — 3J+ Bs —3)u
+ w2 + t2 + s2 = 0. (**)
Отметим прежде всего, что из равенства (**) следует, что хотя
бы одно из чисел 2v — 3, 2w — 3, 2t — 3, 2s — 3 отрицательно, —
иначе мы имели бы в левой части этого равенства сумму положи-
положительных чисел. Предположим, например, что 2v — 3 ¦< 0. Это воз--
можно только в том случае, если v -= 0 или v =» 1. В первом слу-
случае первое уравнение системы (*) сразу дает у + z + и «= 0, что
невозможно, если у, г, и положительны. Поэтому надо считать, что
все числа v, w, t, s положительны и v = 1. В таком случае равен-
равенство (**) перепишется в виде
хш. Bw — 3)y+ {2t — 3)z+ B* —3)и + w3 + t2 + s2+\. (***)
Рассмотрим теперь разные возможные случаи.
1°. Числа х, у, z, и все попарно различны. В этом
случае и числа у, w, t, s все попарно различны; действительно, счи-
считая, например, что v = w, мы получим, вычитая друг из друга пер-
первые два равенства (*), у — х = 2v(x — у), что невозможно при v
положительном и х ф у. Далее, первое из равенств (*) в предполо-
предположении v «« 1 дает 2* = у + г + и — 1, х— —^ У + ~2~г "^ ~2~и ~~2~<
что несовместимо с равенством (***), где коэффициенты при у, г я
и в правой части — целые положительные (ибо w, t, s не могут быть
равны 1, так как они не равны у, a v = 1). Итак, этот случай яв-
является невозможным.
2°. Д"в а из чисел х, у, г, и равны между собой;
остальные различны. Здесь надо отдельно рассмотреть два
подслучая.
А) г — и. В этом случае t = s. Равенство (***) и первое урав-
уравнение (*) здесь принимают вид
2х — у + 2г— 1;
эти равенства по-прежнему несовместимы.
Б) х = у. Здесь w = v = 1. Равенство (**) и первое из ра-
равенств (*) в этом случае соответственно имеют вид
1х = B* — 3)г + Bs — 3)и + t2 + s2 + 2
и
X ¦•= * + U — 1.
Подставляя второе из этих равенств в первое, получим:
Bt — 5J+ Bs — 5)u+*2 + sz + 4 = 0, (*¦*)
откуда следует, что хотя бы одно из двух чисел 2t — 5, 2s — 5
должно быть отрицательным. Пусть 2t — 5 < 0; так как (>0 и
t Ф 1 (ибо t»==l; t Ф v, так как г Ф х), то, следовательно, t = 2.
204
Теперь, прибавляя к третьему уравнению (*) удвоенное первое
3
уравнение, находим 4г + 4* + 6 = 4х + 2г + За, т. е. г =¦ — и — 3.
о
Полагая в уравнении ( ) i = 2, г = -g- и — 3, получим:
Ds— 13)и + 2s2 + 22 = 0.
Отсюда ясно, что 4s — 13 < 0. Так как s > 0, s Ф 1, s # 2,
то, очевидно, s = 3. Подставляя-все эти значения в уравнения (*),
получаем систему трех уравнений первой степени с тремя неизвест-
неизвестными:
х + г + и = 2х + 1,
2х + и = 4г + 4,
2х + г = 6« + 9,
из которой без труда находим х(= у) =96, г = 57, ы = 40.
3°. С р е д и чисел х, </, г, и имеются две п а р ы п о-
парно равных. Пусть, например, х = у, г = и. В таком слу-
случае первое уравнение (*) дает х = 1г— 1; подставляя этот резуль-
результат в уравнение (**):
х = Bt — 3)г + *2+ 1,
находим:
B/ — 5) г-И2+ 2 = 0.
Отсюда след\ет, что 2/ — 5 < 0, или так как/ > 0, / ф 1, то / = 2.
Теперь уравнения (*) принимают вид
х + 2г = 2х + 1,
2х + г = 4г + 4,
откуда х{ — у) = 11, г( = и) = 6.
4°. Т р и из чисел х, у, г, и равны между собой.
Зде^ь тоже приходится отдельно рассматривать два подслучая.
А) у = г = и. В этом случае уравнение (***) и первое урав-
уравнение {*} принимают вид
х = 3Bш — 3).(/ + 3ш2+ 1; 2х = Зу—\
и, очевидно, являются несовместимыми.
Б) х — у = г. Первое уравнение (*) дает в рассматриваемом
случае
2х + и = 2х + 1,
откуда и = 1; последнее уравнение (*) дает
s (s + 2)
Зх = 2s« + s2 = 2s + s2; л: «= -L-^—-.
Но х — целое число; следовательно, нли s или S + 2 должно де-
делиться на 3, т. е. s = 3*, х = kCk + 2), или s = 3k — 2, х =
= Ck — 2)k\ здесь k — произвольное целое число.
5°.. Все числа х, у, г, и равны между еобой.
В этом случае первое уравнение (*) сразу дает Зх = 2х + 1, х = 1.
Я05
Итак, мы получаем следующие решения задачи:
х = у = 96, z = 57, и = 40; х = у — 11, г = и = 6;
д: = у = z = ?C6 ±2), ы= 1;лг = (/ = г = И= 1
(случай * = 1 и знака «—» в предшествующих формулах),
165. Обозначая искомые числа через х а у, имеем:
х + У = ху,
или
ху — х — у+1 = 1,
(х-1)(у-1) = 1.
Но так как единицу можно только двумя способами разложить
в произведение целых множителей, то сразу получаем:
х—1 = \,у—1 = 1;х = 2,у=2,
или
х— 1 = —1, у— 1 = — 1; х =. 0, у = 0.
166. Прежде всего устанавливаем, что хотя бы одно из трех
чисел х, у, и z, таких, что
111
должно быть меньше 4: если бы все эти числа были ^ 4, то сумма
111 1113
— + — + — была бы <~+~ + 1~ = ~- Таким обра-
образом, если считать, что х г? у г? г, то для х остаются возможными
только два значения: х = 2 и х = 3 (ибо х > 1). Рассмотрим эти
две возможности в отдельности.
1) х = 2; тогда ~ + ~Г = 1 — ~==Г- Приведя дроби к об-
общему знаменателю и отбросив знаменатель, получим:
уг — 2у — 2г = 0, г/г — 1у — 2z + 4 = 4,
или
(</-2)(г-2) =4.
Так как у я z больше 1, то у — 2 и г — 2 не могут быть отри-
отрицательными и возможны только следующие случаи:
А) у — 2 = 2, г — 2 = 2; у = 4, г = 4.
Б) г/ - 2 = 1, г - 2 = 4; у = 3, г = 6.
11 12
2) * = 3; тогда —- + — = 1 — — = —, или
2уг — 3(/ — 3z = 0, 4г/г — 6г/ — 6г + 9 = 9, Bг/ — 3) Bг — 3) =9.
Так как у ^ х = 3, 2(/ — 3 > 3, 2г — 3 ^ 3, то возможен только
один случай:
Чу — 3 = 3, 2z — 3 = 3; (/ = 3, z = 3.
Таким образом, все решения задачи даются следующими равен-
равенствами:
1 L . !. L ¦ L4JiL , L . L,
206
167. а) Из уравнения, очевидно, следует, что х, у > п\ поло-
положим х = п -f хи у = п + у\. В таком случае наше уравнение пре-
преобразуется так:
= —, или (п2 + пхх) + (п2 + пУ1) =
¦=» п2 -J- nxi + ru/i + Х1У1, т. е. a^j^ = п2. (*)
Но ясно, что при п простом равенство (*) допускает лишь три ре-
решения в натуральных числах хи Уъ а именно, (х\, у{) = (п, п), или
A, и2), или (п2, 1), что приводит к трем решениям исходного урав-
уравнения:
Если же п = аЬ — составное, то возможно также, скажем, решение
(хи Hi) — (а2, б2), что дает отличные от (**) значения х и у.
б) Если —- 4- —— = — , то, избавляясь от знаменателя дроби,
X у II
мы получим:
пх + пу = ху,
что равносильно
(х-п)(у-п) =п2
(ср. с решением задачи а)). Последнее уравнение имеет 2v—1 ре-
решений в целых числах, где v есть число делителей числа п2 (включая
1 и само число п2): для того чтобы получить все эти решения, надо
выписать 2v возможных систем вида х — п = d, у — п = ~^~и
х — п = —d, у — п = ——г (где d есть делитель числа п2), кроме
системы х~ п.= — п, у — п = — п, которая приводит к абсурдно-
абсурдному в условиях данной задачи результату: х = 0, у = 0.
Если п = 14, то п1 = 196 и делители числа п2 = 196 имеют
вид:
1, 2, 4, 7, 14, 28, 49, 98, 196.
Соответственно этому мы получаем следующие 17 решений на-
нашего уравнения:
х 15 16 18 21 28 42 63 112 210 13 12
у 210 112 63 42 28 2! 18 16 15 —182 —84
х 10 7—14—35—84 —182
у — 35 —14 7 10 12 13'
в) Заданное уравнение можно привести к виду
(x — z)(y — z) =z2 (*)
(см. решение задачи а)). Пусть теперь t есть общий наибольший
делитель трех чисел х, у и г, т. е. х = xtt, у = ytt, z = Z\t, где хи
У\ и Z\ взаимно просты. Далее обозначим через m общий наиболь-
наибольший делитель чисел Ху и Z\ и через п — общий наибольший делитель
чисел У\ и zh т. е, положим хх *= mx% zx «и mz2; У\ = пу2, zx = zn2,
207
где х2 н z2, у2 и г2 взаимно просты. Числа тип взаимно просты,
ибо хи у, и Zi взаимно просты. Так как zx делится и на т, и на п, то
можем положить гх = тпр.
Подставим теперь в основное уравнение (*) х = mx2t, у = ny2t,
z = mnpt. По сокращении на mnt2 будем иметь:
(*2 — «р) ((/а — mp) = mnp2. (**)
Но х2 взаимно просто с р, ибо m есть общий наибольший
делитель чисел Х\ = тх2 н Zi = тяр; аналогично у? взаимно про-
просто с р. По раскрытии-же скобок в уравнении (**) мы получаем,
что х2у2 = х2тр + у2пр делится на р. Отсюда следует, что р = 1,
и наше уравнение принимает вид
(х2 — п) (у2 — т) «=• mft.
х2 взаимно просто с п, ибо три числа Х\ •=• тх%, у\ = пу2 и Zi =¦
= mn взаимно просты. Следовательно, х2 — п взаимно просто с я,
а следовательно, у2 — т делится на п. Аналогично х2 — п делится
яа т. Таким образом, х2 — п = ±/л, у2 — т =» ± п; х2 = ± у2 =
= ± я + я и, следовательно,
х = m(ra + n)t, у = ±п(т + n)t, г = тя/,
где т, я, ^ — произвольные целые числа.
168. а) Из равенства ху = ух видно, что простые делители чисел
х и у — одни и те же:
х = р?'Р22 • • • />?"¦ У = рМ' • •' Р»".
где pi, р2,..., рп — простые числа. Тогда, ввиду нашего равенства,
а,г/ = р\х, сед = 32.r, ..., апу — Р«х.
Будем считать, что у >• х\ тогда из написанных равенств следует,
что
а, < р,, а2< J32 <хп <Рп.
Следовательно, у делится на х, у *= kx, где k — целое. Подставим
это значение у в наше равенство:
Отсюда, извлекая корень *-й степени, получим:
х* = kx, или хк~1 = k.
Так как (/ > х, то А > 1, откуда х > 1. Но легко видеть, что
22 = 2, а при х > 2 или ft > 2 всегда д;* > й. Действительно,
при k > 2, х ^ 2
ж*-1 > 2" > ?,
так как уже 23 > 3, а при к = 2, д; > 2
х6-1 = х > 2 = к.
Поэтому единственным решением нашего уравнения в целых поло-
положительных числах будет х = 2, k = 2, г/ = kx = 4.
б) Обозначим отношение -j через ?, тогда у = ?х. Подставляя
это выражение для у в наше уравнение, получим:
xh* =(kx)*,
208
или, извлекая из обеих частей корень Степени х и затем деля на х,
' ж*-1 = k,
откуда
1 1 к
1 p
Пусть рациональное число ^ д равно несократимой дроби—-.
Подставляя это выражение для . . в наши формулы, получим:
_Lift = 1 + x= t±it -L. = \
Так как /г и 9 взаимно просты, то, для того чтобы хну были
рациональными числами, нобходимо, очевидно, чтобы из целых чи-
чисел р и р + q можно было извлечь корень степени q. Но так как
при q :> 2 и р = пя будет иметь место неравенство
<Р
то это возможно только при g=I.
Итак, все положительные рациональные числа, удовлетворяющие
нашему уравнению, даются формулой
, у-
где р — произвольное целое число (кроме 0 и — 1).
169. Пусть п —число восьмиклассников, т — число очков, на-
набранных каждым из иих. В таком случае число очков, набранных
всеми участниками турнира, равно тп + 8. Это число равно числу
сыгранных партий. Так как участников турнира п + 2 и каждый
играл по одному разу с каждым из п + 1 остальных, то ими всего
(л-т-2)(п+ 1)
было сыграно 2 партий (в произведении (п + 2) (п + 1)
каждая партия учитывается 2 раза). Таким образом, мы получаем:
, 0 (п + 2)(п+\)
| 8
или, после несложных преобразований,
14.
Здесь п — целое число; число в скобках — также целое (ибо т —
либо целое, либо дробь с знаменателем 2).
Так как п — делитель 14, то п может быть равнсь одному из
чисел 1, 2, 7, 14. Значения п — 1 и п =» 2 мы должны отбросить,
так как в этом случае общее число участников не превышает 4 и
Два семиклассника не могли бы набрать вдвоем 8 очков.
'•* Д. О. Шклярскнй я др. 209
Остается п = 7 и п = 14.
Если п = 7, то 7G + 3 — 2т) = 14; т — 4.
Если п = 14, то 14A4 + 3 — 1т) = 14; т = 8.
170. Пусть девятиклассников было п и набрали они т очкоэ.
Тогда десятиклассников было 10п и набрали они 4,5т очков. Всех
же участников турнира было \\п и набрали они 5,5т очков.
Общее число набранных всеми очков равно числу сыгранных
1 In A In —• 1)
партий. Партий сыграно было т> .Отсюда
Пя(Пя-1)
5,5/л = 2
и, следовательно,
т = п(\\п — 1).
Каждый девятиклассник сыграл 11л — 1 партий (ибо число
участников турнира равно 11п), а потому п девятиклассников могли
набрать пA1п—1) очков только в случае, если каждый из них
выиграл все партии. Это возможно лишь при п = 1 (так как два
девятиклассника не могут одновременно выиграть друг у друга).
Итак, получаем единственное решение п = 1, т = 10.
171. По условию задачи имеем:
а + Ь + с
где о, Ь, с — целые числа а р ~ ^ • Обозначим р — а == х,
р —Ь = у, р —с = г; тогда будем иметь:
+ г) хуг =2(х + у-\-г),
к
или, возведя обе части равенства в квадрат,
хуг = 4(х + у + г).
Здесь х, у и г — или целые положительные числа, или же полови-
половины нечетных целых чисел. Но второй случай невозможен, так как
тогда слева у нас стояло бы дробное число, а справа — целое. Итак,
х, у и z — целые.
Пусть теперь х :> у :> г. Из нашего уравнения найдем, что
4(/ + 4г
* ~ г/г — 4 '
следовательно, мы будем иметь:
Последнее неравенство можно умножить на yz — 4 (ясно, что
уг — 4 > 0, ибо иначе х было бы отрицательным) и рассматривать
как квадратное неравенство относительно у:
y*z-8y - 4z <0, т. е. (у - ух) {у - уг) ^ 0, (*)
где У\ и у2 — корни уравнения zy2 — By — 4z = 0, зависящие,
210
разумеется, от 2:
ffi =-
Но г/2 отрицательно и, значит, всегда у—(/г >0 (ибо у поло-
положительно); следовательно, для того чтобы выполнялось неравенство
(*), надо чтобы было
Итак, имеем уг ^ 4+ ]/"l6 -f- 4г2 откуда и подавно г2 — 4^
/ 4г2 (ибо z^y). Возведя обе части в квадрат, получим:
16 + 4г2; z4< 12z2,
что, очевидно, выполняется только при z ^3.
Рассмотрим теперь ряд возможных случаев.
уг —
у —
будет
J
целым положительным только, если у = 5 (в этом случае х = 24),
г/ = 6 (в этом случае je == 14), (/ == 8 (в этом случае д; = 9).
.4
2
<5, х =
у г — 4 2</ — 4
2(/ + 4
е= 2 будет целым и не меньшим у только, если у =3 (в этом
случае ж = 10) и г/ = 4 (в этом случае д; = 6).
з,,< i?| р ,
3 i/г
не будет целым.
Итак, мы получили следующие пять решений задачи:
X
24
14
9
10
6
У
5
6
8
3
4
г
1
1
1
2
2
30
21
18
15
12
а
6
7
9
5
6
25
15
10
12
8
с
29
20
17
13
10
172. Первую строку таблицы можно переписать так: 0+1,
0 + 2,..., 0 + п; последний столбец запишем в виде: 0 + п, л + я,
2л + п,..., (п — I)п.-\-п. Каждое число таблицы представлено те-
теперь в виде суммы двух чисел, причем первое слагаемое одинаково
У всех чисел, стоящих в одной строке, а второе — у всех чисел од-
одного столбца. Так как среди выбранных чисел будет по одному
14»
211
слагаемому ия каждого столбца и по одному слагаемому из каж-
каждой строки, то сумма всех первых слагаемых выбранных чисел
равна
а сумма вторых слагаемых —
I + I + ... -\- п
Таким образом, общая сумма S всех отобранных чисел равна
п (п° — п) i п (и ~\- 1) п (п2 + 1)
173. Пусть п нечетно. Если наша таблица симметрична от-
относительно указанной в условии диагонали (эту диагональ мы будем
называть «главной» и обозначать буквой d), то каждому числу,
расположенному сверху от d, будет отвечать равное ему число,
расположенное снизу от d: это число занимает место, симметричное
относительно d месту, на котором стоит первое число. Отсюда сле-
следует, что совокупность всех расположенных сверху от d чисел сов-
совпадает с совокупностью чисел, расположенных снизу от d\ поэтому,
в совокупности всех не принадлежащих диагонали d чисел нашей
таблицы любое число k встречается четное число я*, раз (воз-
(возможно, что о* = 0). А так как в каждой из п строк таблицы каж-
каждое число k встречается точно один раз (ибо п мест этой строки
занимают п чисел 1, 2,..., п), то всего число k встречается в нашей
таблице нечетное число п раз; поэтому на диагонали d число к
встретится нечетное число п — а>, раз. Отсюда следует, что
каждое число k (где 1 ^ k ^ п) хотя бы раз встретится на диаго-
диагонали d (ибо нуль —число четное), а так как эта диагональ содер-
содержит всего п чисел, то каждое из чисел 1, 2,..., п встретится на ней
ровно один раз. [Отсюда, в частности, вытекает, что а\ = аг =
= ... — ап = п— \.]
Пример таблицы показывает, что при п четном сфор-
сформулированное утверждение может не выполняться; близкие к при-
приведенным выше рассуждения показывают, что при п четном оно
даже не йожет выполняться (ибо в этом случае каждое число k
встретится на главной диагонали d четное число п — aft раз).
174. Условимся обозначать число, стоящее на пересечении i'-й
строки и /-го столбца таблицы, через a(j; в таком случае a,j =
= 1 п3, где 1, /= 1,..., п. Пусть теперь l=Oj {j;тогда по условию
задачи 2 «= at ¦„ , 3=-a,- j , и т. д. — вплоть до п2 = a t ,i .. ,. При
JSJi Jilt Jn2JTt«_j_l r
этом числа /i, /2, /3,..., /„'+1 разумеется, не все различны: ведь они могут
иметь лишь п различных значений 1, 2,..., п. Заметим, что каждое
конкретное значение k встречается в ряду чисел /i, /2, /г, /з, /з, . • •
• ••>!пг' in'' /n'+iP0BH0 2n раз, поскольку наша таблица содержит
п чисел в k-w .строке и п чисел в k-м столбце. А так как «внутри» це-
цепочки /i, /г, /г. /з. ••-. /'„«. /V-H (т-е- не на первом и не на послед-
последнем месте) каждое число повторяется дважды, то из того, что значе-
значение /i должно входить .в цепочку четное число 2п раз, следует, что
212
7n._|_j=»=/i — наша цепочка обязательно завершается тем же числом
}и которым она начиналась. ,_
Таким образом, задача требует оценить разность между сум-
суммой чисел /i-й строки таблицы и суммой чисел /i-го ее столбца —
столбца, номер которого совпадает с номером рассматриваемой
строки. Но, в силу правила образования таблицы, если а^ ^s
(где / Ф jnz и, следовательно, пара (/, /,) не является в нашей це-
цепочке последней, т. е. s Ф я2), то s + 1 = ctjjj другими словами,
каждому отличному от п2 числу s из \\-го столбца отвечает в ]\-й
строке число s + 1. При этом полученные таким путем числа s+ 1 =
= ujj^ —это все числа /гй строки, кроме одного лишь числа 1
(которое, очевидно, не может следовать ни за каким из чисел /i-ro
столбца, поскольку является самым малым в таблице); поэтому
если обозначить отличные от п2 числа /i-ro столбца через «i, S2,..
..., Sn-i, то отличные от 1 числа /гй строки будут равны st + 1
S2 + 1,---, *n-i + 1- А отсюда уже следует, что разность меж
ду суммой чисел /-го столбца и суммой чисел /-й строки будет равна:
175. Ясно, что если o,j— элемент таблицы, стоящий в ней на
пересечении (-и строки и /-го столбца (где i, / = 1, 2,... или
от, соответственно п), то во всех таблицах, получаемых из исходной
«допустимыми» преобразованиями, на этом месте стоит либо число
ац, либо число —ui) (ибо наши преобразования таблиц сводятся
к переменам знаков некоторых из входящих в таблицу чисел). По-
Поэтому общее число «допустимых» таблиц заведомо не превосходит
?"'", т.е. конечно. (Число 2mn равно количеству всевозможных
наборов шп чисел ац, каждое из которых может иметь два значе-
значения.) Из конечности числа рассматриваемых таблиц следует, что
среди них можно указать такую, для которой сумма всех входящих
в нее чисел максимальна (или несколько таблиц с одной и
той же суммой чисел, большей суммы чисел всех других допустимых
таблиц). Но если в такой «максимальной» таблице сумма элементов
какой-либо строки или какого-либо столбца отрицательна, то, по-
поменяв знаки всех чисел этой строки или этого столбца, мы придем
к новой «допустимой» таблице с большей суммой входящих в нее
чисел; поэтому в «максимальной» таблице суммы всех элементов
любой строки и любого столбца заведомо неотрицательны.
176. Обозначим сумму всех чисел таблицы буквой S; сумму
всех чисел i-й строки (где 1= 1, 2,..., 10Э) —через sr, сумму всех
чисел /-го столбца (где / =1, 2,..., 80) —через о,-; наконец, число,
стоящее в пересечении г'-й строки и /-го столбца, обозначим через
a,j. По условию задачи
ац = SiO-j, (*)
откуда
Si = Я,1 + ai2 + . • • + Я(, 80 =
= SiOi + SiO + . . . 4" SiOeo = Si(O\ + Oi + . . . + Ojjo) =
= SiS (?=1,..., 100),
и, значит, либо S = 1, либо все Si = 0. Но если s; = 0 при всех
213
8
7
щ
5
Ч
г
1
7
1k
щ
11
11
ш
9
2
ш
ш
ш
щ
щ
ш
ш
т
5
12
ш
20
19
т
11
//
ш
19
20
Щ
12
5
ш
т
ш
щ
щ
щ
щ
ж
г
9
ш
11
12
щ.
14
/
Z
т
5
В,
7
8
Рис. 17.
?= 1,..., 100, то, в силу (*), все элементы пц нашей таблицы
равны нулю. А так как, по условию задачи, «угловой» элемент
аи >0, то S = 1.
177. Из равенства чисел, выписанных в симметричных относи-
относительно диагонали клетках, следует, что среди наших 64 чисел не бо-
более 20 различных (см. рис. 17, на котором числами 1, 2,..., 20 обо-
обозначены какие-то числа а,, а2 а30,
не обязательно все различные между
собой); при этом числа, скажем, i-й
строки (где/=» 1, 2 8) совпада-
совпадают с числами (9 — t) -й строки и 1-го
и (9 — f)-ro столбцов. Если найдет-
найдется такое i, то сумма чисел *-й стро-
строки больше 518, то то же справедливо
и для (9 — I) -й строки и для t-ro и
(9 — 0'Го столбцов (см. тот же рис.
17, где принято i = 3 и соответствую-
соответствующие строки и столбцы заштрихова-
заштрихованы); сложив эти четыре (одинаковые)
суммы чисел, мы получим результат,
заведомо не меньший 4 ¦ 518 = 2072.
При этом в соответствующей сум-
сумме четыре числа, стоящие на клетках,
отмеченных на рис. 17 двойной штри-
штриховкой, будут учитываться дважды,
а числа, стоящие в остальных за-
заштрихованных клетках — один раз; поэтому общая сумма всех вы-
выписанных в заштрихованных клетках чисел будет не меньше чем
2072 — о, где а — сумма чисел, выписанных в дважды заштрихо-
заштрихованных клетках. А так как, по условию задачи, а ^ 112 (ибо 112
это сумма чисел, выписанных во всех диагональных клетках),
то сумма «заштрихованных» чисел не меньше чем 2072—112 =
= I960 — в то время как сумма всех вообще выписанных чисел
равна 1956. Полученное противоречие и доказывает утверждение
задачи.
178. Заметим, что наше условие равносильно следующему: для
любых четырех номеров i, j, k и I, где i ф k и i ф I, имеет место
равенство: at} + а,а = aki + asu другими словами, для любого взя-
взятого на доске прямоугольника ABCD (рис. 18, а) сумма чисел, стоя-
стоящих в двух его противоположных вершинах Л и С, равна сумме
чисел, стоящих в двух других вершинах В и D. В самом деле, пред-
предположим, что в вершинах А я С находятся две из наших п ладей;
разумеется, эти ладьи можно будет переставить в клетки В и D
с тем, чтобы они по-прежнему держали под боем i-ю и /г-ю строку и
/-й и /-и столбцы. Таким образом, при указанной перестановке сум-
сумма всех покрытых ладьями чисел не может измениться; поэтому-то
сумма стоящих в клетках А и С чисел обязательно равна сумме чи-
чисел, стоящих в клетках В и D.
Далее уже все просто: обозначим числа, стоящие в нижней стро-
строке доски, через у\, уг Уп, а числа, стоящие в ее первом столб-
столбце,—через ух, У\-\-х2, yi + х3,..., У\-\-хп (рис. 18, б); кроме того,
положим Х\ = 0. Ясно, что при этом для чисел нижней A-й) строки
и левого A-го) столбца имеем ац = I/,- = Х\ + г/i (ибо xt = 0);
Яд = Xj -\- I/,. С другой стороны, если t > 1, / > 1, то стоящее в
клетке М число at; можно вычислить, исходя из выделенного на
214
рис. 18, б прямоугольника MPOQ: в силу доказанного ранее имеем
ai} + yi= (xt i+ yi) + У), откуда а„ = xt + ys.
Нетрудно видеть, что если существуют такие числа хи х% ..., хп;
уи у2 уп> что ац = Xi + Уь то в указанное в формулировке за-
задачи условие, связанное с расстановкой на доске ладей (таких «до-
«допустимых» расстановок ладей будет п\ — почему?), обязательно вы-
выполняется.
179. Ясно, что при / = k = (' связывающее хц, xih и Хы урав-
уравнение принимает вид 3xit = 0; таким образом, хц == 0 при всех
к
X
w
Щ
Щ
т.
ж
Щ
ш
р
ш
ж
'Ш
Wa
т
щ
Ж
ш
ш
Ш
щ
ж
п
ё
'0
к
h
К
1
—
—
На
й)
Рис. 18.
i = 1, 2 п. Пусть теперь k = / ф i; тогда то же равенство при-
принимает вид;
хц + хц + хц = О,
откуда, в силу того, что хи = 0, имеем xjt = —xi}. Наконец, про-
просуммируем все равенства, отвечающие номерам i, ;', 1; i, /, 2; ..., i,
j, n, где i и / какие-то фиксированные номера; мы получим:
ПХц + (Xj[ + Xji^r . . . -f" ^jn) — (Xi\ — Xii — ... Xin) = 0
(здесь использована то, что xhi = —хц,). Поэтому, обозначив
п,
получим:
Хц = tt — t].
180. Ясно, что для «доски» размером 1 X 1 (состоящей из одной
единственной клетки) утверждение задачи выполняется (здесь оно
бессодержательно: ведь наша «доска» состоит из единственной клет-
клетки, в которой стоит звездочка); это делает возможным использова-
использование метода математической индукции. При п — 2,
очевидно, доска будет содержать столбец (а следовательно, и стро-
строку), в котором имеется точно одна звездочка; переставив, если это
215
понадобится, Строки и столбцы так, чтобы свободное место оказа-
оказалось правым верхним, мы придем к таблице, им'еющей «треуголь-
«треугольное» строение (см. рис. 19, а, где знак «+» означает, что в соответст-
соответствующей клетке звездочка может как стоять, так и не стоять). До-
Докажем, что и при произвольном п строки и столбцы таблицы можно
переставить так, чтобы таблица приняла «.треугольный» вид, т. е.
чтобы все звездочки в таблице стояли на идущей сверху вниз на-
направо диагонали и, быть может, под ней, — однако все клетки над
диагональю обязательно были пустыми. В самом деле предположим,
*
+
+
+
+
+
*
+
+
+
*
+
*
+
Рис. 19.
что это уже доказано для удовлетворяющих нашим условиям таб-
таблиц размером (п — 1) X (п—'). и рассмотрим таблицу размером
п\п. Эта таблица содержит столбец, в котором имеется ровно од-
одна звездочка; переставим этот столбец на последнее место, а затем
переставим строки так, чтобы звездочка в нем оказалась внизу
(рис. 19, б), и вычеркнем содержащую эту звездочку строку и по-
последний столбец. При этом мы придем к таблице размером (п— 1) X
X A — 1), также удовлетворяющей условиям задачи; по предполо-
предположению индукции строки и столбцы этой таблицы можно переста-
переставить так, чтобы она имела «треугольный» вид, после чего примет
«треугольный» вид и исходная таблица.
«Треугольное» строение рассматриваемых таблиц (его можно
считать «треугольным», ибо с точки зрения интересующих нас свойств
таблиц допустимы любые перестановки строк и столбцов) доказы-
доказывает равноправность строк и столбцов таблицы, а значит и справед-
справедливость утверждения задачи (наглядно очевидного для «треуголь-
«треугольных» таблиц).
181. а) На доске размером 4X4 имеются 4 столбца, 4 строки и
2-7 = 14 параллельных диагонали рядов (из которых 4 «ряда», со-
содержат лишь по одной угловой клетке); нетрудно убедиться, что
каждый из этих 4 + 4+ 14 = 22 вертикальных, горизонтальных или
наклонных рядов содержит четное число (а именно — либо 0, либо2|
заштрихованных на рис. 20, а клеток. Но первоначально лишь
одна из этих клеток содержала знак «—»; поэтому при всех наших
переменах знаков число заштрихованных клеток, помеченных знаком
«—», останется нечетным — и, значит, никогда не станет рав-
равным 0.
б) Где бы ни был расположенный на доске знак «—», мы всег-
всегда можем «вырезать» из нашей доски размером 8 Х8 «малую» доску
размером 4X4 так, чтобы на ней расположение знаков было таким,
216
чек в условии задачи а) (см. рис. 20, б — в, где изображены два
возможных варианта расположения знака «—» на большей доске).
А так как наши изменения знаков на большой доске порождают на
«малой» доске описанные в условии задачи а) перемены знаков, то
требуемый результат следует из результата задачи а).
182. а) Подсчитаем, прежде всего, число всевозможных квадра-
квадратов размером 3X3 и размером 4X4, которые можно разместить на
Ш
////
'ft;
¦'///
й)
В)
Рис. 20.
4,
ш
ш
V//'
У.'/,
—
1 .
ш
т
%
Щ
'4
S)
шахматной доске. Ясно, что левый нижний угол квадрата размером
3X3 может совпасть с любой клеткой квадрата размером 6X6, за-
заштрихованного на рис. 21 горизонтальной штриховкой, а левый ниж-
нижний угол квадрата размером 4X4 — с любой клеткой (меньшего)
квадрата размером 5X5, заштрихованного на том же рис. 21 вер-
вертикальной штриховкой; таким образом, все-
всего мы имеем на доске 6-6+ 5-5 = 36 +
+ 25 = 61 квадрат размером 3X3, или
4X4. Поэтому, исходя из доски, на всех
клетках которой стоят знаки «+», мы мо-
можем описанными операциями получить
не более 261 возможных распределений
знаков во всех клетках доски, ибо в каж-
каждом из 61 рассматриваемых квадратов мы
можем, независимо от остальных квадра-
квадратов, изменить все знаки или не менять их.
А так как всего возможных распределений
знаков «+» и «—» в 64 клетках шахмат-
шахматной доски существует 2а4 > 2Ы, то, исходя
из доски с одними лишь знаками «+•», лю-
любое распределение знаков на доске полу-
получить нельзя. Но если рассмотреть теперь
какое-либо распределение знаков, которое нельзя получить описан-
описанным образом из распределения, содержащего только знаки «+»,
то, и обратно, исходя из этого распределения знаков, мы никогда
не сможем прийти к одним лишь знакам «+», откуда и следует
отрицательный ответ на вопрос задачи.
. б) Эта задача очень близка к задаче а). Общее число «BX2)-
квадратов», которые можно выделить из шахматной доски, равно
7-7 = 49, а число пар соседних строк или соседних столбцов доски
I i =
Рис. ?1.
217
рабно 7 + 7 = 14; таким образом, мы имеем 1049+м «= 1063 способов
менять последние цифры чисел, стоящих в клетках доски. (К числу
этих 1063 способов относится и тот, когда ни одна цифра не меня-
меняется). Отсюда следует, что, исходя из расположения чисел, такого,
что все числа оканчиваются на 0, мы не можем получить все вооб-
вообще возможные распределения последних цифр чисел, стоящих в 64
клетках доски, ибо число таких распределений равно Ю64 > 1063;
поэтому найдутся такие распределения последних цифр, от которых
нельзя перейти к «нулевому».
Примечание. Разумеется, решение (и отрицательный ре-
результат) задачи сохраняет силу и в том случае, если требуется.до-
требуется.добиться делимости всех чисел таблицы не на 10, а на любое другое
натуральное число п, скажем на число 1976.
183. а) Сможет. Ясно, что, выбирая по одному камню из всех
кучек, мальчик может добиться того, чтобы хоть в одной кучке ос-
остался единственный камень. Затем, удваивая число камней в
той кучке (или в тех кучках), в которой имеется 1 камень, и снова
вычитая по камню из всех кучек, мальчик уменьшит на единицу
число камней в кучках, где оно отлично от 1, сохранив 1 камень в
кучках, где этот камень был единственным. Продолжая поступать
так же, мальчик может добиться того, чтобы во всех кучках оста-
осталось по одному камню; после этого он может забрать их все.
б) Эта задача во всем подобна задаче а) (заметим, что фигу-
фигурирующие в задаче а) числа камней можно расположить в виде
«таблицы» из одной строки и трех столбцов — по одному числу в
столбце). В самом деле, если мы сначала будем рассматривать чис-
числа лишь одной,— скажем, 1-й — строки, то наши операции позволят
удвоить любое из чисел этой строки или вычесть единицу из всех
этих чисел; поэтому, в точности как в решении задачи а), можно об-
обратить все числа этой строки в 0. После этого мы точно так же об-
обратим в 0 все числа 2-й строки — и так поступим со всеми строками
таблицы.
184. Запишем число а в «двоичной системе счисления»1), т. е.
в виде
а = а„-2" + СС-Г2"-1 + ап-2-2п-2 + ... + а,-2 + а0-1,
где все «цифры» а0, <Xi, ..., а„_2, an_i, ап равны 0 или 1 (стар-
(старшую «цифру» ап числа а, разумеется, можно считать равной 1). Яс-
Ясно, что если число а четно, то а0 = 0 и ах = JL = а„-2"~' +
+ а„_1-2п~2 + an_2-2n + ... + ai• 1; если же а нечетно, то
а —1
а0 = 1 — и число а\ = —9—имеет точно такое же строение. Таким
образом, если а записывается в двоичной системе счисления после-
последовательностью «цифр» а = anan-ian-2 • • • aiao, то п\ записывается
в той же системе счисления как п\ = anan_1an-2. ¦ ¦ кг, соответ-
ственно этому аг записывается как аг = anan_!... a2, а3 — как аз =
= апа.п-\ ...аг, и т. д.— вплоть до числа' ап = <х„ = 1. С другой
стороны, очевидно, fc| = 2b, b2 = 2b\ = 22b, b3 = 23&, и т. д.—
вплоть до числа Ьп = 2П&.
') См., например, [47].
218
• ' Ясно, что cti = anan-i... ai = а„ ¦ 2п~* + an-i • 2п~<~1 + ..,
... +a,+i • 2 +¦ a,- • 1 (где » = О, 1, 2,.... п) будет нечетным, если
«цифра» <Xi равна 1 (напомним, что а; может равняться лишь О
или 1). Таким образом, в этом случае bt = 2* b — (at • 2')Ь. По-
Поэтому интересующую нас сумму всех &,-, отвечающих нечетным
аи можно записать так:
• b = ab,
где в сумме ап-2" + а„_1-2"-1 + ... + аг2 + щЛ (=я) реаль-
реально участвуют лишь слагаемые, отвечающие равным 1 значениям
«цифр» On, an-i, • •.. а».
185. Самое короткое решение этой задачи доставляет метод
математической индукции. Условимся обозначать &-е
число Фибоначчи, где k = 1, 2, 3 через и*. Предположим, что
наше утверждение уже доказано для всех натуральных чисел п,
меньших k-то числа Фибоначчи ик\ справедливость его для всех чи-
чисел, например, меньших ы5 = 5, легко проверить непосредственно.
Ясно, что то же утверждение будет выполняться и для числа Uh.
Далее, поскольку все числа между ик и uh+l = uk + ый_] предста-
вимы в виде Uk + т, где 0</n<«*_i, и поскольку, по предположе-
предположению индукции, все меньшие uh-i числа т могут быть представлены
в виде суммы каких-то различных чисел Фибоначчи, номера которых
меньше к — 1, то число п = ик + т также представляется в виде
суммы чисел Фибоначчи («старшее» из которых есть и&, а номера
остальных меньше k—1). Таким образом, мы установили, что наше
предположение верно и для всех натуральных чисел, меньших Uk-i,
откуда и вытекает его справедливость для всех натуральных чисел.
Примечание. Из доказанного следует, что в рассматривае-
рассматриваемых суммах чисел Фибоначчи (где мы, разумеется, считаем, скажем,
2 = и3, но не 2 = 1 + 1 = и\ + и2, или 4 = 3+ 1 = и4 + , а не 4 =|
= 2 + 1 + 1 = и3 + и2 + Ц|) не могут фигурировать два «соседних»
числа Фибоначчи (почему?); нетрудно показать, что всевозможные
суммы чисел Фибоначчи, удовлетворяющие последнему условию —
это и есть все натуральные числа, причем каждое число встречается
в последовательности всех таких сумм единственный раз (ср.
с решением задачи 129 из книги [6]).
186. Нас интересуют суммы sh = ыЛ+1 + ик+2-\-... + uk+i вось-
восьми последовательных чисел Фибоначчи. Поскольку числа Фибоначчи,
очевидно, монотонно возрастают: «i = щ < и3 < щ < ... < ип <
<и„+\ < ..., то ясно, что утверждение задачи будет доказано,
если мы покажем, что сумма sk заключена между иА+9 и
т. е. что Uh+9 < sh < ик + 10. Но ясно, что
+ «Л+7 < «*+8 + "А+7 + "а+6 + • ¦ • + «*+! = sk',
таким образом, остается лишь доказать неравенство sk < ик+\о. Не-
Нетрудно, однако, видеть, что сумма Sn = «i + «2 + Из + ... + и„
первых п чисел Фибоначчи на единицу меньше (я+ 2)-го числа
"и+г; установить это можно, например методом математи-
математической индукции. В самом деле, очевидно, Si = 1 + 1 =
•= 3 — 1 = ы4 — 1; с другой стороны, если требуемое утверждение
справедливо для какого-то номера п, то, заменяя я на п + I и
219
используя предположение индукции, получим:
Sn + 1 = Ui + Ui + ... + «„ i+ Un + 1 = Sn + «n + l =
¦= («n+2— 1) + "n + l = («n + l + Ип+2) — 1 =" Ип+3— 1»
— что и требовалось доказать. А теперь сразу получаем:
Sf, = Uk+1 + Uk+2 + . . . + И*+8 = Sfc + s — Sft =
= (М/, + 10— 1 ) — («ft + 2 — 1) = "ft + 10 — Uk+2 < «й+10,
чем и завершается решение задачи.
Примечания. 1. Ясно, что так же можно доказать,, что
сумма любых т последовательных чисел Фибоначчи, гд$ m > 3,
нг может быть числом Фибоначчи.
2. Неравенство sh •< и* + ю можно также доказать, последова-
последовательно преобразуя выражение для
= Uh+a + Uk+7 + («А+7 + «*+б) = «J.+8 + Ий+7 + «fc+6
+ ("ft+в + "*+б) = "А+8 + »*+7 +«*+в + «fi+5 + (Ма+5 +
("ft + 2 + «k + l) = Sft
187. Условимся обозначать остатки >от деления чисел Фибоначчи
«1, «2, «з,... на 5 через <хь а.% а3>... Ясно, что из равенства и* =
= и*_1 + uft_2, где fe •= 3, 4, 5,..., следует, что
_ \ak-i + ak-2' если aA_rfaA_2<5;
a* ~ l«ft_1 + aft_2 - 5, если aft_j + aA_2 > 5.
Формулы (*) позволяют выписать сколь угодно много членов пос-
последовательности а&:
1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4, 3, 2, 0, 2, 2, 4, 1, 0, 1, 1, ...
При этом для того, чтобы выписать любое число следующих далее
членов последовательности ад, нам уже нет нужды прибегать к фор-
формулам (*): ведь <x2i = аи а22 •=¦ а2, и, значит, (в силу (*)), агз =
= а3, а24 = а4) и т. д., т. е. «последовательность остатков» ai, a2,
a3,... является периодической с периодом 20. А так как в пер-
первой серии из 20 остатков а* на 5-м, 10-м, 15-м и 20-м местах стоят
нули, но также и впоследствии на всех кратных 5 местах в этой пос-
последовательности будут стоять нули.
188. Оставим в каждом члене ряда Фибоначчи, записывающем-
записывающемся пятью и более цифрами, только последние четыре цифры. У нас
получится последовательность чисел, каждое из которых меньше
чем 104. Обозначим через я*, член этой последовательности, стоящий
на k-m месте. Заметим, что если нам известно ah + i и аи, то мы мо-
можем вычислить aft_i, ибо (k— 1)-й член ряда Фибоначчи равен раз-
разности (k + 1)-го и k-то членов, а последние четыре цифры разности
можно определить по последним четырем цифрам уменьшаемого и
вычитаемого. Отсюда следует, что если для некоторых номеров k
и п окажется, что ак = an+h, a*+i «= an+» + i, то тогда ua-i =
= an+ft_i, ак-2 = an+h-2 а, = ап + \. Но так как а, -= 0, то это
будет означать, что ап + \ = 0, т. е. что в ряде Фибоначчи на
(п -\- 1)-м месте стоит число, оканчивающееся четырьмя нулями.
220
Остается показать, что среди 108 + 1 пар
аи а2,
. аз,
аюа аю»+р
а108+1' °108+2
найдутся хотя бы две одинаковые. Но это непременно будет так,
ибо все числа ai, а% аъ °jo"+2 не превышают 104, а из 104 чи-
сел 0, 1, 2, 3, 4, ..., 9999 можно составить только 104-104 = 10s
различных пар (ибо первое число может принимать Ю4 различных
значений и второе число может принимать J04 различных значений).
Примечание. Можно даже точно указать первое из чисел
ряда Фибоначчи, оканчивающееся четырьмя нулями; номер этого
числа 7501 (см. задачу 174 книги [5] и следствия из нее).
189. Поскольку при п > 1 имеем
= ""-1 +2 + 417 > а«->+ 2>
417
то из а\ = 1 получаем
а|> 1 -f- 2 = 3, flf>l + 2.2 = 5, a\ > 1 + 3-2 =- 7, ...
•¦•> a?no> 1+99-2- 199,
откуда и следует, что. а1Оо > У 199 > 14. Аналогично, используя
неравенство
а\ Цап_, + ^f=-~ 4-1 + 2 + -4— < 4-1 + 3,
также верное при всех п>1 (причем в равенство оно обращается
лишь при п = 2), получаем:
02=1+3^4, af<l + 2-3--7, а\ < 1 + 3-3 = 10, .. .
.... а2ш< 1+99-3 = 298,
откуда вытекает, что аюо < 1/298< 18.
190. Первое решение. Дополним нашу последовательность
чисел еще одним числом ап + 1, таким, что |on + i| = \а„ + 1|, возве-
возведем в квадрат все данные в условии задачи равенства (включая
сюда и «дополнительное» равенство, связывающее числа а„ и ап+\):
4 = 0, af
f =
IJ = а\ + 2яг+ 1, .. ., а\ . оп2_)
221
и затем сложим их:
Л2 i 2 1 _2 _| i 2 i 2 -
•а* + аа+ ...+ап) + п-\.
Из последнего равенства следует, что
2 (ах -j- а2 + я3 + ... +ап) = — л + a^.j ^ — л,
а значит,
й\ + а» + Оз + • • • +сп 1
- >— -if-
Второе решение. Заметим, что при п = 1 рассматривае-
рассматриваемое среднее арифметическое равно "Г"— 0; при п = 2 (где, очевидно,
at = I и, значит, а2 = + 1 или — 1) оно равно -Цч—- = —^—- =
а2 11
~2~, т. е. равно к или —~о~> таким образом, в этих двух случаях требу-
требуемое неравенство выполняется. Воспользуемся теперь методом
математической индукции: предположим, что в случае,
когда количество рассматриваемых чисел меньше п, утверждение
задачи справедливо, и покажем, что в хаком случае оно будет вы-
выполняться также и для п чисел. Пусть аи а2, ..., я„ — удовлетво-
удовлетворяющая условиям задачи последовательность п чисел, и пусть ат
(где т — один из номеров 1, 2, 3, ..., или п)—наименьшее из
них. В таком случае, разумеется, можно считать, что ат<0 (ибо
если все наши числа неотрицательны, то нам и доказывать нечего:
конечно, тут их среднее арифметическое больше—^Jи что ат =
= — ат-\—1 (ибо лишь в этом случае \ат\ ¦= |am_i-f-l| и
От < flm-i), т. е. среднее арифметическое чисел am_] и ап
Заметим теперь, что если исключить из нашей последовательно-
последовательности числа am_i и ат, то оставшиеся m — 2 числа также будут
удовлетворять требуемым условиям. В самом деле, ясно, что m Ф 1
(ибо О[ = 0, а ат < 0)—именно поэтому мы и можем говорить о
числе ат-\- Далее, если т = 2, то ат = aj = — 1. аз = 0 (ибо
|о3| = |а2+ 1|), и мы, разумеется, можем отбросить числа ai и а2
и начинать последовательность сразу с я3( = 0); аналогично, если
т = п, то мы можем отбросить два последних числа я„_, и а„ и
оставшиеся числа по-прежнему будут удовлетворять требуемым ра-
равенствам. Наконец, если З^т^л— 1, то
]am-s+ l| = |am_,| = |— ат — 1| и \ат+1\ = \ат + 11 ==\— ат — 11,
так что |am-j+l| = |flm+i|—и, значит, в самом деле числа п\,
а2 ат-2, йш+1, ..., ап будут удовлетворять требуемым в фор-
формулировке задачи условиям,
222
Теперь, по предположению индукции, выполняющемуся для
п — 2 чисел,
... +ат_2 + ат+1 + ... + ап j
п — 2 >~ 2 '
те. at + a2 + ... + ат_2+ат+1 + ... + ап>— -у (л— 2).
С другой стороны, как мы уже знаем,
2 = ~~2~1 т'е' am-i + am = —1;
поэтому
ах + й2 + • • • + ат_2 + «т-1 + ат + ат+1 + • • • + <*„. >
— что нам и требовалось доказать.
191. Нетрудно понять, что наибольшим числом нашей последо-
последовательности может быть лишь одно из первых двух чисел а0 и а,\
(ибо каждое ak при k ^ 2 обязательно < тах[д*_1, aft_2]>). Легко
даже видеть, что в наибольшей по длине последовательности самым
большим является именно число аи ибо если последовательность
начинается с чисел а,, аг, а3,..., где а, > а2, то ее можно,
не меняя, «продолжить назад», условившись начинать так:
До = fli — а2, аи а2 = \at — ао|, из,... (здесь, очевидно, ах >
> а0 = а! — я2)- Поэтому в дальнейшем мы ограничимся лишь рас-
рассмотрением последовательностей, начинающихся с наибольшего
числа й2 (нам только при этом придется в окончательном ответе уве-
увеличить длину последовательности на 1 за счет «нулевого» по номеру
числа по = п\ — а2).
Ясно, что если наибольший член последовательности а, = 1, то
последовательность состоит не более чем из двух чисел (продол-
(продолжить ее можно лишь одним числом а2 = 1); если наибольший член
последовательности а\ = 2, то количество входящих в последова-
последовательность чисел sg 3 (если а2 = 2, то последовательность имеет вид:
2, 2, а если а2 = 1, то она такова: 2, 1, 1); если а1 = 3, то число
входящих в последовательность чисел ^ 5 (полагая, что а2 = 3, 2
или 1, мы приходим к последовательностям: 3, 3; или 3, 2, 1;
или, наконец, 3, 1, 2, 1, 1). Эти примеры подсказывают заключение
о том, что «оптимальная» последовательность, по-видимому, должна
начинаться с чисел ах = га, а2 = 1. При этом начало ее выглядит так:
п, 1, я-1, га-2, 1, .... (*)
откуда вытекает, что, обозначив количество чисел, составляющих
последовательность (*), через kn, мы получим;
/г„=3 + /г„_3 (**)
(ведь, начиная с 4-го члена at = n — 2, мы приходим к подоб-
подобной же последовательности, где п заменено на п — 2).
') Ср. сноску на стр. 228.
223
Из соотношения (**) находим:
k, = 2, ki = 3, ks = 3 + 2 = 5, kt = 3 + 3 = 6,
ks «= 3 + 5 = 8, kt «= 3 + 6 = 9, ...;
все эти числа kn задаются следующей формулой:
где квадратные скобки, как всегда (ср. стр. 37),' обозначают целую
часть числа. (Формулу (***), разумеется, совсем просто вывести
из (**) с помощью метода математической индукции:
для п = I и п = 2 она, как мы видели, справедлива; если (••*) верно
для значения п — 2, то для значения п это соотношение тоже верно:
у и . , ГЗ(я-2)+М ГЗя+1]
kn = kn~2 + 3 = [ 2 J + 3 = [~2J-
Итак, мы уже построили (начинающуюся с наибольшего чис-
числа!) последовательность (*), длина kn которой связана с величи-
величиной п наибольшего числа соотношением (***); покажем теперь,
что если описанная в условии задачи последовательность, начина-
начинается с наибольшего числа а\ •= п, то длина ее не может
превзойти указываемого формулой (***) кисла kn. Доказывать
это мы будем, естественно, по индукции: предположим, что на-
напечатанное курсивом утверждение уже доказано для всех значений
п, меньших- некоторого (а справедливость его для значений п = 1, 2
и 3 мы уже проверили), и покажем, что тогда оно будет справед-
справедливо и для значения п. В самом деле, пусть задана удовлетворяю-
удовлетворяющая условиям задачи последовательность, начинающаяся числами:
п, 'ш, ...,
где m ^ п. Далее рассмотрим ряд вариантов, отвечающих разным
значениям т.
1°. Если т = п, то последовательность обрывается на 2-м чле-
члене; для нее наше утверждение, конечно, выполнено.
2°. Если « — четное число и т= —~-, то последовательность
п п
обрывается на 3-м члене: п, -у, — , и здесь тоже, разумеется,
длина последовательности меньше kn.
п
3°. Если п > т>-2~, то, отбросив в нашей последовательности
первое число п, мы получим «в остатке» последовательность т,
п — т,..., тоже начинающуюся с большего числа т; по предполо-
[Зт+П
жению индукции, этот «остаток» содержит не более « = I—п—
чисел. Но так как одно число мы при этом отбросили и так
как пг ^ п — 1, то вся последовательность содержит не более чем
3(ч—1)+ 1
чисел.
224
4°. Если, наконец, т < ~>то наша последовательность начи-
начинается так: п, т, п— т., п — 2т, т, ... При этом если п — 1т ~$> т
п
¦ (т. е. m ^ g), то «остаток» последовательности, получающийся
после отбрасывания первых трех чисел (остаток, начинающийся
с числа п — 2т), таков, что наибольшим в этой последовательности
чисел является первое ее число; поэтому, по предположению индук-
индукции, количество содержащихся в остатке чисел не превосходит
в последовательность чисел <ftm-
Тем самым мы полностью доказали утверждение, относящееся
к последовательностям, начинающимся с наибольшего числа. А от-
отсюда следует, что заданная в условии задачи последовательность
[31967 + 1]
Г З(га-2т)+4 [3(га-2)+П Г3»+Ч „
кп-2т - [ 2 J ^ [ 2 J = [~2~J~3
(ибо т^ 1), и, значит, общее число чисел не превосходит —g— — ? •
Если же п — 2т < m (т. е. т. >-^ ), то поскольку здесь шестое число
о
последовательности т — (п — 2т) < т, то начинающийся с пято-
пятого числа т «остаток» будет таков, что в нем наибольшее число т
стоит на первом месте; поэтому число чисел «остатка» sg km —
ГЗи+Ч ГЭп+21'
= —j—\ \—5— —и снова общее количество входящих
ГЗп + 2"? ГЗп+П
—^— + 4 < —х— = kn
ли утверждение, относящее
я с наибольшего числа. А о
у уии задачи последовательнос
. . . , , [3-1967 + 1]
не может содержать больше чем 1 + kml = 1 + I s ~
= 2952 числа; количество входящих в последовательность чисел
равно 2952 в том и только в том случае, если она начинается с чи-
чисел: 1966, 1967, 1, 1966, 1965, 1, 1964, 1963, 1, ...
192. Будем доказывать наше утверждение от противного.
Предположим, что в последовательности чисел ось а^г, а^газ, ...
имеется лишь конечное число составных. Ясно, что в этом
случае в последовательности цифр аь а2, а3,... имеется лишь ко-
конечное число четных цифр (ибо каждое число, десятичная
запись которого кончается четной цифрой, является составным),
и, значит, все цифры а„, а„+ь ап+2 начиная с какой-то п-й
цифры, будут нечетными. Точно так же устанавливается, что в на-
нашей последовательности аь аг, аз, ... цифр будет лишь конечное
число пятерок (ибо каждое число^ оканчивающееся на 5, де-
делится на 5); таким образом, начиная с какого-то места в последо-
последовательности будут встречаться лишь единицы, тройки и семерки
(ибо девяток в ней нет по условию задачи). Но приписывание
к числу тройки в конце не меняет остатка от деления »того числа
на 3, а приписывание. единицы или семерки увеличивает остаток
от деления на 3 на единицу (ибо 7 = 2-3+1); поэтому если
число единиц и семерок в нашем ряду цифр бесконечно, то каждое
третье из оканчивающихся на 1 или на 7 чисел будут делиться на 3,
т. в. будет составным. Таким образом, если, стремиться к тому,
чтобы лишь конечное число чисел ряда «i, aiaj, ai»^,... были
: 15 Д,. О. Шклярскай и др. ч ?2§
составными, мы должны, начиная с какого-то /V-ro места в ряду
цифр аи <х2, <Хз приписывать в конце ранее имеющегося числа
тройку; при этом мы приходим к последовательности чисел вида
М = c^ajj ... aN_x 333 ... 3 = lOhA + 35,
ft раз
Пусть теперь р—простой делитель числа А (возможно, сов-
совпадающий с Л); можно считать р отличным от 2 и от 5, ибо если
Л' достаточно велико, то a;v-i = 1, 7 или 3 (значение a.v-i = 3
здесь ие исключается!). Но существует бесконечно много
таких значений k, что записываемое с помощью k единиц число В
делится на р (см. Примечание в конце решения задачи 144); всем
этим значениям k отвечают составные (делящиеся на А) числа М =
= ЮМ + 36, т. е. вопреки сделанному предположению среди чи-
чисел М имеется бесконечно много составных. Полученное противоре-
противоречие и доказывает утверждение задачи.
193. а) Четность или нечетность последней цифры суммы че-
четырех цифр (другими словами — самой этой суммы) зависит лишь
от четности или нечетности рассматриваемых цифр. Если буквой и
обозначить нечетное, а буквой ч — четное число, то легко видеть,
что наша последовательность начинается так:
ннннчннннчннннч ...,
причем далее она, очевидно, продолжается периодически:
после каждых четырех нечетных чисел (н) следует одно четное чис-
число (ч). Но отсюда уже следует, что последовательность 1234, имею-
имеющая характер нчнч, нигде не может встретиться в нашем ряду цифр,
б) Различных четверок цифр, каждая из которых может иметь
10 значений: 0, 1, ..., 9, существует 104; поэтому в последователь-
последовательности из 10 004 цифр обязательно два раза встретится» одна
и та же четверка (образованная соседними цифрами). Но если
1-я, (»'+ 1)-я, (i' + 2)-я и ((' + 3)-я цифры совпадают с /-й, (у + 1)-й,
(/ + 2)-й и (/ + 3)-й цифрами (где мы считаем j<i), то, в силу
самого закона образования последовательности, (/—1)-я цифра
совпадает с (/—1)-й, (i — 2)-я — с (/ —2)-й, и т. д. Поэтому
(' —/—1)-я, (( — /)-я (i —/+1)-я и ((' —/ + 2)-я цифры нашей
последовательности обязательно совпадут с 1-й, 2-й, 3-й и 4-й циф-
цифрами, т. е. они образуют четверку 1975.
194. Ответ на первый водрос задачи является совсем простым:
ясно, что среди 8-значных и еще меньших чисел мы ие можем
встретить такого, сумма цифр которого равна 9 • 9 = 81, а среди
9-значных чисел таким является одно лишь число 999 999 999;
соответственно этому в ряду (**) число 81 впервые встретится
на 111111 111-м месте; следующее за ним число ряда (**) будет 9
(сумма цифр числа 1000 000 008).
Несложен и ответ на второй вопрос. Так как среди тех чисел
ряда (**), которые отвечают не более чем трехзначным числам ря-
ряда (*), число 27 встретится единственный раз (на 111-м месте
в этом ряду —в ряду (*) на этом месте стоит число 999), то здесь
не приходится рассчитывать на четырехкратное повторение числа
27. Среди же четырехзначных чисел ряда (*) можно отыскать
226
4 последовательных числа, сумма цифр которых равна 27 — это
будут числа 3969, 3978, 3987 и 3996; ясно, что соответствующие
числа 27, 27, 27, 27 ряда (**) предшествуют первой тройке чисел
36 в этом ряду (и даже вообще первому числу 36, отвечающему
числу 9999 ряда (*)).
Менее определенно сформулирован последний вопрос,— а между
тем именно с ним и связаны пути подбора указанной выше чет-
четверки чисел 3969, ... Не останавливаясь на подробном обсуждении
этого вопроса, укажем лишь, что строение чисел ряда (**) связано
с монотонностью ряда цифр в числах, получаемых делением чисел
ряда (*) на 9; в частности, числа 441 (=3969:9), 442, 443, 444,
отвечающие рассмотренной четверке чисел ряда (*), таковы, что их
цифры не возрастают. Выпишем, например, в таблицу все числа
от 1 до ПО, где жирным набраны двузначные числа, для которых
цифры числа (отличные от цифры 0) не возрастают, и трех-
трехзначные числа, цифры которых (снова отличные от 0) н е у б ы в а ю т.
123456789 10 11
12
23
34
45
56
67
78
89
13
24
35
46
57
68
79
90
14
25
36
47
58
69
80
91
15
26
37
48
59
70
81
92
16
27
38
49
60
71
82
93
17
28
39
50
61
72
83
94
18
29
40
51
62
73
84
95
19
30
41
52
63
74
85
96
20
31
42
53
64
75
86
97
21
32
*43
54
65
76
87
98
22
33
44
55
66
77
88
99
100 101 102 103 104 105 106 107 108 109 ПО
Умножив все эти числа на 9 и образовав для каждого из них сум-
сумму цифр, мы придем к такой красивой таблице:
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
18
9
9
9
9
9
9
9
18
18
9
9
9
9
9
9
18
18
18
9
9
9
9
9
18
18
18
18
9
9
9
9
18
18
18
18
18
9
9
9
18
18
18
18
18
18
9
9
18
18
18
18
18
18
18
9
18
18
18
18
18
18
18
18
18
18
18
18
18
18
18
18
18
9 18 18 18 18 18
¦ Существуют и другие изящные конфигурации чисел последова-
последовательности (**).
195. Заметим, прежде всего, что каждый из наборов /0, Л,
1ъ ... получается из предшествующего добавлением к нему некото-
некоторого количества новых чисел; при этом все ранее имевшиеся числа
в новом наборе сохраняются. Легко видеть, далее, что все вновь
15* 227
появляющиеся в наборе /„ числа будут больше п; поэтому число
1973 в наборах "с номерами, большими 1973, уже не возникает —
и все такие наборы содержат одно и то же количество чисел
1973. Докажем теиерь, что фиксированная пара чисел а, Ь (где а
стоит, скажем, слева от Ь; таким образом, а, Ь и Ь, а мы счи-
считаем разными парами!) встретится в последовательности /о, Л.
/2, • ¦ •, In, ¦ ¦. наборов ровно один раз, если числа а и b взаимно
просты, и не встретится ни разу в противном случае. Это утвержде-
утверждение очевидно для пар чисел а, Ь, наибольшее из которых не пре-
превосходит 2 (таких пар имеется всего две: 1, 2 и 2, 1 — и встречает-
встречается каждая из этих пар один лишь раз, а именно, в последователь-
последовательности li\ 1, 2, 1); докажем его методом математической
индукции. Предположим, что наше утверждение уже доказано
для всех таких пар чисел a, b что max [a, b] <^п[), и покажем
что оно будет справедливо и для пар а, Ь, где max [а, Ь] = п.
В самом деле, пусть a, b — пара целых положительных чисел, где,
скажем, max[a, b] = b = п. Ясно, что пара а, Ъ может появиться
в каком-то наборе h лишь в том случае, если в предыдущем набо-
наборе Ik-i мы имели пару стоящих рядом чисел а, Ь — а. Но поскольку
max [a, b—a] <max[e, Ь](= Ъ = л), то в силу предположения
индукции пара чисел а, 6—а встречалась в наших наборах U,...
..., /(,_] один раз, если а и Ь — а взаимно просты, и ни разу,
если а и b—а имеют общий делитель d > l.'Ho отсюда сразу сле-
следует что и пара чисел a, b встречается в наших наборах один раз,
если а и b взаимно просты, и не встречается вовсе в противном
случае: ведь числа а и b взаимно просты в том и только в том
случае, если взаимно простыми являются числа а и b — а.
Теперь уже ясно, что, поскольку число 1973 — простое (про-
(проверьте это!), в наших наборах по одному разу встретится каждая
из пар чисел 1,1972; 2,1971; 3,1970; ...; 1971,2; 1972,1—ведь всеэто
суть пары взаимно простых чисел. А отсюда следует, что число 1973
встречается в наборах /„ с номерами л > 1973 (в частности, в на-
наборе Лоооооо) ровно 1972 раза (это число равно количаству пар
1,1972; 2,1971; ...; 1972,1).
Примечание. Из решения задачи также следует, что про-
произвольное натуральное число N встречается в наборах /„ (где п >
> N) ровно <p(jV) раз, где <${N) —число чисел, меньших N и вза-
взаимно простых с N; относительно вычисления (по числу Л') величи-
величины ф(Л') см. Примечание,и условию задачи 341 (стр. 71—72).
186. Пусть а,а2аз«4 (где sceaj, 1=1, 2, 3, 4,—цифры 0 или 1)
последние четыре цифры последовательности. Если бы в по-
последовательности нигде не стояли подряд цифры о^агОСзаА то ее
можно было бы продолжить, приписав в конце 0; аналогично, ес-
если бы из последовательности цифр нельзя было бы выделить пятер-
пятерки цифр a1a2a3a4l, то мы могли бы приписать в конце цифру 1.
Поэтому в нашей последовательности три раза встречаются после-
последовательные четверки цифр о^агосзо^ (за одной из' них следует
цифра 0; за второй — цифра U третья стоит в конце). Двум из этих
четверок предшествуют цифры 0 и 1, а третьей уже не может пред-
предшествовать никакая цифра Оо (ибо иначе в последовательности
дважды встретилась бы пятерка цифр a0aia2a3a4); поэтому третий
') Символ max[a, b] означает большее (точнее — не меньшее)
из чисел а, Ь; так, max[2, 7] = 7 и max [4, 4] = 4.
228
раз четверка цифр а^азй^ должна стоять в начале последо-
последовательности.
197. Число N представляет собой произведение всех простых
чисел от 2 до 37 включительно; каждый делитель числа N пред-
представляет собой произведение некоторых из этих чисел. Покажем,
что утверждение задачи справедливо для любого числа /Vft =
=¦= 2-3-5-7- ... -Ph — произведения k первых простых чисел1).
Докажем наше утверждение методом математической
индукции (по числу k). Ясно, что при k ¦= 1 мы приходим к
числу N\ = 2, имеющему лишь два делителя 1 и 2, под которыми бу-
будут подписаны, соответственно, числа +1 и — 1; здесь + 1 -г
+ (— 1) «= 0. Далее, пусть наше утверждение уже доказано для чис-
числа Nk, равного произведению k первых простых чисел; другими сло-
словами, мы считаем доказанным, что число Nh имеет четное число 2и
делителей (включая сюда числа 1 и Nh), n из которых представля-
представляют собой произведение четного числа простых сомножителей (эти
делители мы условимся называть «четными»; к их числу относится,,
в частности, число 1, которое имеет четное число нуль простых
множителей, поскольку ] не причисляют ни к простым, ни к со-
составным натуральным числам), а п остальных — произведение не-
нечетного числа простых множителей (их мы назовем «нечетными» де-
делителями Nk). Докажем, что утверждение задачи будет верно и
для числа Nk+l = Nk • Ps+i, где Ps+i — (k + l)-e простое число. Яс-
Ясно, что все делители числа Nk являются также и делителями числа
Nk+u это дает In делителей Nk+u из которых п являются «четны-
«четными», а п остальных — «нечетными». Но наряду с этим число Nk+l
имеет н делители, не являющиеся делителями числа JV*,— те, кото-
которые делятся на Ph+i- Их можно получить умножением всех дели-
делителей числа Nk на Ph+ъ при этом п «четных» делителей Nk дадут п
делителей Nk+i, каждый из которых состоит из нечетного числа про-
простых множителей, а п «нечетных» делителей N/, дадут п «четных» де-
делителей iVft+1. Таким,образом, мы видим, что число Nk+i имеет все-
всего 4га делителей, 2л(=л + я) из которых «четны» и 2я(=л +
+ л) — «нечетны». Поэтому для него выписанные в нижнем ря-
ряду числа — это 2я чисел +1 и In чисел —1; в сумме они также
дадут 0.
Примечание. Приведенное рассуждение позволяет даже не-
несколько уточнить высказанное в условии утверждение: из него сле-
следует, что число Nk имеет 2k~l «четных» и 2к~1 «нечетных» делите-
делителей (в частности, фигурирующее в условии задачи число Л' = Nu
имеет 2й = 2048 «четных» и 2048 «нечетных» делителей), и, значит,
в случае числа Nk выписанный в нижней строке ряд чисел состоит
из 2й B048 в случае числа Л') чисел -f 1 и 2к~* чисел —1.
198. Из того, что р и q — взаимно просты, с помощью алгорит-
алгоритма Евклида устанавливается, что любое цело* число п можно
представить в виде:
п = рх -f qy, где х и у — целые числа. (*)
В самом деле, пусть р> Ц\ тогда р =• qd + г, где 0 < г < q, т. в.
г ¦= р ¦ 1 + q{— d) (— pxi + qyx)
. ') Оно справедливо даже для всех «свободных от квадратов»
натуральных чисел, т. е. таких, которые разлагаются в произведение
попарно различных простых множителей.
229
(здесь d — частное, а г — остаток от деления р на q). Далее, имеем
q = rdi + ru где 0 < Г\ < г (число гх — остаток от деления q на г);
объединяя эти два равенства, получаем представление г, в виде (*):
П = Я — rdi = q—(pXi + qy{]dx =
где *2(= —X\d[ = —d\) и y2{ = 1 —г/idi = 1 + drfi) —целые числа.
Затем, полагая г = rxd2-\- r2, где 0<г2<ги и пользуясь предше-
предшествующим равенством, мы точно так же можем представить г2 в
виде комбинации рх% -f qy% чисел р и q, и т. д.— вплоть до обще-
общего наибольшего делителя 1 чисел р и q. (Легко видеть,
что последний отличный от нуля остаток будет общим наибольшим
делителем чисел р и q — в рассматриваемом случае он равен 1.) Но
если единицу можно записать в виде 1 = рхк + qy>,, где **, yi, —
целые числа, то и любое число п = п-1 = п(рхк + qyk) =
= p(nxh)-\- q(nyk) можно записать в виде (*).
Далее, из того, что р и q взаимно просты, вытекает, что
если п представляется в виде (*) двумя разными способами:
п — рх + qy — рх' + qy', где х, у; х', у' — целые, (**)
то х — х' кратно q и у — у' кратно р: в самом деле, из (**), напри-
У — У'
мер, следует что р (х — х') = — q(у — у'), или х — х' = — q —-— ,
и так как р и q не имеют общих простых делителей, то х — х' делит-
делится на q. Последнее утверждение можно сформулировать как утверж-
утверждение об «единственности» представления (*): каждое целое чис-
число п можно — и притом единственным образом — записать в
виде (*), где 0 ^ х < q: в самом деле, число х в формуле (*) всегда
можно представить в виде х = kq + *о, где О =SJ xa < q (xo есть
остаток от деления х на q); при этом
п = рх + qy = p(kq + xo)+qy = pV+ <7(/>* + У) = Р*а + Wo,
где 0 =^#о < q и ха, уа — целые (***),
С другой стороны, два разных представления (***) (т. е. равен-
равенство (**), где 0 ^ х < q и 0 ^ х' < q) невозможны, ибо при этом
\х — х'\ < q и разность х — х' не делится на q. Число л, очевидно,
будет «хорошим», если у0 в формуле (***) неотрицательно, и «пло-
«плохим», если уа отрицательно: ведь если п = рх0 + qyo, где О ==S Xo < q
и Уй < 0, то, заменив #0 на * = х0 — Xq и г/о на </ = х0 + Кр,
где Я — целое, мы никогда не придем к представлению (*) числа п,
в котором х и у оба неотрицательны.
Эти замечания позволяют без труда решить задачу.
а) Очевидно, наименьшим «хорошим» числом является число
О = О-р + О-д; наибольшим «плохим» числом, в силу сказанного
выше, является число вида (***), где х0 — наибольшее из «допусти-
«допустимых» (положительных) чисел, т. е. х0 = q—¦ 1, а Уа — наименьшее
из отрицательных чисел, т. е. уа — — 1; таким образом, наибольшее
«плохое» число Р = p(q — l)-f q(— 1) =¦ pq — P — q- При этом есте-
естественно считать, что эти два числа 0 и Я как раз и «дополняют»
друг друга до фигурирующего в условии задачи числа Л, т. е. что
за число А следует принять Р = pq — р — q. И действительно, если
число п имеет вид (***), то число
п' = А — п — (pq — p — q) — {pxa + qya) =»
= p(q — 1 — *o)+ <?(— 1 — Уй)
230
имеет тот же вид (***), где только роль х0 играет число х '0 =
= <?—1— х0, а роль г/о— число уо= — 1—Уо- Но если О^дго<
^<?—1, то и O^xo^.q — 1 и из чисел уо и у0 одно положительно,
а другое отрицательно; это и доказывает утверждение задачи.
б) Первое решение. Из результата задачи а) непосред-
непосредственно следует, что среди чисел п., где О^яг^Я = pq — р — q
(Я— это наибольшее «плохое» число), ровно половина будет «пло-
«плохими», а остальные — «хорошими»; так как при этом мы учтем все
натуральные «плохие» числа, то интересующее нас количество t та-
таких чисел
Я+1 pq — р — <?-+ 1 (р—1) (<?—1)
' - 2 ~ 2
Второе решение. «Плохими»
числа п, которые представимы в виде
и рх0 + <?г/о> 0 (ибо число п положи-
положительно). На плоскости с координата-
координатами Хо, Уо линии х0 = q, Уо = 0, рх0 +
+ ЯУо — 0 выделяют заштрихован-
заштрихованный на рис. 22 треугольник; нам надо
найти число «целых точек» в этом
треугольнике. Но ясно, что это число
ровно вдвое меньше числа «целых
точек» в прямоугольнике ОАВС (на
диагонали прямоугольника «целых
•точек» нет, ибо р и q взаимно про-
просты) . Так как число «целых точек»
внутри прямоугольника, очевидно,
равно (р—l)-(q-l), то мы при- '
ходим к тому же значению искомо-
искомого числа t, что и выше.
199. Первое решение. Нам
надо доказать, что каждое целое
неотрицательное число п единственным
в виде:
являются такие натуральные
(***), где Osgxo<<7, Уо<О
Рис. 22.
образом представляется
п =
(х
(х + уJ
2х
2
(х + УJ + (* + у)
где X — х + у и, значит, X ^ 0 и О^х^Х (напомним, что чис-'
ла х и у неотрицательны). Но ясно, что при фиксированном Х^О
и х, меняющемся в «допустимых» пределах от 0 до X, число п =
= п Ь •* будет принимать все целые значения в пределах
(случай х = 0) и
X(случай
х — Х), причем каждое из этих значений встретится по одному разу. Сле-
Следующее целое число N х +1 = 2 + X + 1 k
отвечает на единицу большему значению X (значению Х+ 1) и ве-
величине х = 0; при изменении х от 0 до X + 1 мы точно так же
231
получим все целые числа
2
до ,
та.ми х, у получит номер п =
следовать утверждение задачи
Л'а+2— 1, и т. д. Это рассуждение доказывает утверждение задачи.
Второе решение. Перенумеруем все точки плоскости с не-
неотрицательными координатами (х, у) в таком порядке, как это по-
показано на рис. 23. Мы утверждаем, что при этом точка с координа-
(* + г/J + Зх + г/
„ —отсюда и будет
ибо в такой бесконечной цепочке
точек х, у точка с (целым неотри-
неотрицательным) номером п встретится
ровно один раз.
Доказательство можно провес-
ти индукцией по п. Ясно, что
номер п = 0 будет иметь точка
с координатами @,0) а номер 1 —
точка с координатами @,1); при
этом
0 =
с координатами
(О + ОJ+ 3-0 +О
1 =
@+1J + 3-0
Предположим теперь, что для всех
точек нашей цепочки, вплоть до
Рис. 23. точки с номером п, требуемое ут-
утверждение уже доказано; при этом
««-я» точка пусть имеет координаты х, у. Если здесь уфО, то
«(п+1)-я» точка будет иметь координаты х+1, у—1— и дей-
действительно
К*+1L- (У—1)J + 3 (*+!) +(у—1) (* + уJ + Зх+г/ , .
, -т-1 -ч
если же у
и также
«=«+ I;
0, то «(« + 1)-я» точка имеет координаты @, х + 1) —
*-fli< +3-0+ (*+!)
(х + ОJ + 3* + О
2
1.
200. Каждой несократимой дроби---, гда
0 < р < 100, 0 < q < 100,
(*)
сопоставим точку Л! с координатами р, q; при этом неравенства (*)
указывают, что точка М расположена внутри заштрихованного на
рйс. 24 квадрата Ж = ОАСВ, ограниченного осями координат и
прямыми х ¦¦ 100 и у ¦» 100 (или, в крайнем случае, М принадле-
принадлежит стороне АС ил» стороне ВС квадрата Ж), а несократимость
дроби ? означает, что на отрезке ОМ нет никаких отличных от М
Я
«целых» точек (точек с целыми координатами: в самом деле, равен-
232
ства р = kpu q = kqu указывающие, что дробь — можно сокра-
сократить на k, означают, что отрезку ОМ принадлежит также целая точ-
точка. М\(ру q{). При этом если высекаемый квадратом Ж на прохо-
проходящей через О прямой / отрезок ОР содержит п целых точек (р0, q0),
Bро, 2q0), (Зр0, Здл), .. ., (пр0, nq0) (где Мо(ро, <?о) —¦ самая близкая
к О из этих точек), то (поскольку пр0 «^ 100, nq0 ^ 100) имевмро«*^-
/ 100
I <c I
100
, Pn /100'
и, значит несократимая дробь — учитывается в слагаемых d |-г
/Г
Рис. 24.
100'
100
суммы 5, т. е. всего участвует в этой сумме
л раз (а сократимые дроби
оро пр0
, s—» •••, zrr, разумеется, вообще
-то ^40 пЧо
Рч
не учитываются в сумме S). Таким образом, вклад дроби — в сум-
сумму S равен п, т. е. равен числу целых точек на отрезке UP.
Из доказанного следует, что общее число учитываемых в сум-
сумме S дробен — т. е. численное значение суммы S — равно полному
числу всех целых точек в квадрате Ж, т. е. S = 100-100= 10 000.
201. 1) Пусть х — любое действительное число. Тогда его мож-
можно представить в виде суммы х =[х]-\- а, где а — неотрицательное
число меньшее единицы. Представим теперь у в виде у— [«/] +
+ р1 @ =gji < 1). Тогда х -f- У = [*] + [#]+<* + Р- Так как а +
+ Р ^ 0, то из этого равенства видно, что [я] + [у] есть целое чис-
число, не превосходящее х + у. А так как [х + у] есть наибольшее
из таких целых чисел, то [х + у] ^ [х] + [у].
2) Первое решение. Представим х в виде [х] +<х, где
0=^а<1. Пусть целое число [х] при делении на я дает в част-
частном q и в остатке г, т. е. [х] = qn + г @ ^ г ^ /г— 1). В таком
случае имеем:
233
х /-1 г*1 ГМ1
где /¦] =г + а<п,— =<?+—. — =<?= — ¦ чт0 и требовалось
доказать. -
Второе решение. Рассмотрим все целые числа, делящие-
делящиеся на п и не большие х. Их число, очевидно равно — .Рассмотрим
также все целые числа, делящиеся на п и не большие [х]. Их число
равно — . Но так как это — одни и те же числа, то их количества
ГМ1 Г*!
равны; следовательно, — = — .
3) Если (х) = [х](т. е. х- [х] < -yj, то ]х + у!= М;
[2х] = 2[х] и [2х] - [х] = 2[х] - [х] = [х] = \х+ \\ если
же (х) = М + 1 (т. е.х-[х] >-А< ™\х + \]=[х\ + \,[1х} =
= 2[х] + 1 — и опять [2х] — [х] = 2[дг] + 1 — [х] = [х] + 1 =
-[,+4-].
4) Первое решение. Представим дг в виде *=[*]+ а.
Так как 0 ^ а < 1, то а содержится между некоторыми двумя
0 1 п— 1 п
соседними из дробей -, —, ..., п , —.Пусть эти дроби будут
k k+I k k+\
~ и —— , т. е. пусть— ^ а<——; тогда имеем:
n—k—\ n—k—\
А+1 n—k—
п — й п — k k п — k
+ -1Г = И + а + — > [дг] + — + -^ = [х] +
— 1 « — 1 k А- \ п — 1
4
Отсюда следует, что
Г 1 1 Г 21 Г n — k—I I
i < Iх + т\ < [* + т| < • • • < ]_*+ —«—J
234
\=--=[х +—п—
п — k+l
——
Так как первых чисел п — k, а вторых k, то
Но тому же равна и целая часть числа пх. Действительно,
так как ft < па < ft + 1, то па = & + р, где 0 < {$ < 1. Следова-
Следовательно,
[пх] = [я[лг] + па] = [и[д;] + ft + W = и W + k. ¦
Таким образом, доказано, что
Второе решение. Рассмотрим левую часть равенства.
1 1 п— 1
Если 0 ^ х <—, то все числа х, х + —, ..., х -f- —-—меньше 1,
а целая часть от них равна 0; [пх] тоже равно 0. Поэтому для
таких х равенство верно.
Пусть теперь х — произвольное. Если увеличить х на-т , то все
слагаемые в левой части сдвинутся на одно место вправо, а послед-
Г п-\Л
нее слагаемое х +—-— перейдет в [х + 1], которое на 1 больше,
чем [х]. Значит, с увеличением х на —левая часть увеличивается
1
на 1. Правая часть с увеличением х на —тоже увеличивается на 1.
Для любого х можно найти такое число а, заключенное между 0
1 / 1 \ т
и "Г" I 0 ^ tx <[ — ), что х отличается от а на —, где т — целое
число. Отсюда следует, что равенство сохраняется при любом х.
202. Первое решение. В силу результата задачи 201 3)
интересующая нас сумма (которая, очевидно, содержит лишь ко-
конечное число отличных от нуля членов) равна
1
235
Г« ' 1 Г« П Г"
[2 +Tj + [4 +Tj + [8
Второе решение. При п — 1 рассматриваемая сумма,
очевидно, равна 1. Далее, при замене п на п+\ каждый, член
суммы либо не меняется, либо возрастает на 1; при этом реально
возрастает на 1 единственный член этой суммы — отвечаю-
отвечающий такому значению k, что 2й есть наивысшая степень двойки,
на которую делится п+ 1. В самом деле, если я+ 1 = 2*B/и+ 1),
то
п
l+2ft
2*+'
2ft Bm
2h+i
U + 2ft1 Г II
в то время как при i Ф k имеем
п+1
(почему?).
2ш j ^
Отсюда, в силу принципа математической индукции,
вытекает, что интересующая нас сумма при всех п равна п.
203. Отметим все точки плоскости с обеими целыми координа-
координатами («целые» точки), для которых 1 ^ х ^ <? — 1, 1 ^ г/ ^ р— 1
(х и у — координаты точек). Эти точки лежат внутри прямоуголь-
прямоугольника ОАВС, длины сторон которого равны ОА — q и ОС = р
с
1
р
1
\
0
у(ы
'^~-~— ц '——
/
-^
В
X
Рис. 25.
(рис. 25); число всех точек равно {q — \)(р— 1). Проведем диаго-
диагональ ОВ прямоугольника. Ясно, что на этой диагонали не будет
расположена ни одна «целая» точка (координаты х и у всех точек
v х ОА q
диагонали ОВ связаны соотношением—= ^ = —; но так как q
и р—взаимно простые, то не существует целых положительных
чисел х < р и у < q, таких, чтоу = у J. Заметим теперь, что чис-
число «целых» точек, имеющих абсциссу, равную k (k — какое-то целое
236
положительное число, меньшее </)', и расположенных под диаго-
диагональю ОВ, равно целой части длины отрезка MN, изображен-
ОМ kp
ного на рис. 25. Так как MN = ^д~ • АВ = —, то это число рав-
\ЬрЛ
I— .
Следовательно, сумма
равна общему числу всех «целых» точек, расположенных под диа-
диагональю ОВ. Но всего внутри прямоугольника имеется (q—1) X
X (р—1) «целых» точек; из симметрии расположения этих точек
относительно центра прямоугольника ОАВС следует, что ровно
половина из них расположена под диагональю ОВ (здесь сущест-
существенно, что на самой диагонали не лежит ни одна из точек). Таким
образом,
Точно так же доказывается, что
(Р-1)
204. Первое решение. При п = 1 мы в левой и правой
частях равенств имеем по одному члену, равному 1; следовательно,
в этом случае равенства справедливы. Докажем теперь, что если
наше равенство справедливо для какого-то значения л, то оно
будет справедливо и для значения п>-\- !; в силу принципа мате,
м этической индукции, отсюда будет следовать, что равен-
равенство справедливо при всех значениях п.
Отметим, что если п + 1 не делится на ki
где остаток г заключен между 1 и k— 1, то п =*> qk + г', где г' =
«=¦ г—1, т. е. О ^ г' < k — 2; отсюда следует, что в этом случае
Гл -г П \ п"[
величины —^—I и НН совпадают (обе они равны q). Если же
Гл+ П Гя]
я + 1 делится на к: л+ 1 •= д?, то, очевидно, —^— = g, -j- =
[я + П Г я 1
*= q — 1, т. е. —jjj— »= -^- + 1 • Таким образом,
—т— = \~k\' если не есть Делитель числа п+ 1;
Гя-Ь П Г я 1
—?— = "F М" ' если * есть Делитель числа я -f 1.
237
А отсюда вытекает, что:
а
т. е. если
то
Гп+11 . Гя+1
J+ ¦•• + [«+!
т. е. если
то.
Второе решение. Число чисел ряда 1, 2, 3 и, деля-
делящихся на какое-то выбранное число fe, рав,но I-?- (это будут числа
й, 2^, ЗА, ..., -г- й); сумма делителей k всех таких чисел равна
Отсюда следует, что:
¦ft
а) Сумма I— + -у + ... + гН + ••• + Т равна ЧИСЛУ
чисел ряда 1, 2, 3, ..., л, делящихся на 1, плюс число чисел это-
этого ряда, делящихся на 2, .. ., плюс число чисел этого ряда,
делящихся на п. Но этому же равна сумма 1\ + т2 + т3 + ... + т„.
б) Сумма 1 ~ + 2 ~2~ + ••• "^ И Х М~ ¦¦'~^га|гГ Равна
сумме делителей 1 всех- чисел ряда 1, 2, 3, . .., п, плюс сумма дели-
делителей 2 всех чисел этого ряда, плюс сумма делителей 3 всех чисел
этого ряда, ..., плюс сумма делителей п всех чисел этого ряда. Но
этому же равна и сумма оч + аг + аз + ... + оп.
238
Третье решение. Приведем еще йзящНбе Геометрические
решение задачи, близкое ко второму решению. Рассмотрим равно-
равностороннюю гиперболу (график обратной пропорциональности) у =•
k
= ~ , или, что то же самое, ху = k (точнее, ветвь этой гиперболы,
расположенную в первом координатном углу; см. рис. 26, а)).
Отметим, кроме того, в первом координатном углу все точки
с целыми координатами. Тогда, если х есть делитель числа k, то на
равносторонней гиперболе ху = k есть целочисленная точка с абс-
5)
циссой х. Обратно, если гипербола ху — k проходит через целочис-
целочисленную точку с абсциссой х, то х есть делитель числа к. Таким об-
образом, число т* делителей числа k равно числу целочисленных
точек, лежащих на гиперболе ху = k; сумма делителей а* этого
числа равна сумме абсцисс целочисленных точек, лежащих на ги-
гиперболе ху = к. Далее, воспользуемся еще тем, что все гиперболы
ху = 1, ху = 2, ху = 3, ..., ху = п — 1 расположены ниже гипер-
гиперболы ху = п. Отсюда можно сделать следующие выводы.
а) Сумма х{ + т2 + т3 + ...'+ т„ равна числу всех целочислен-
целочисленных точек, лежащих под гиперболой ху = п (и па самой гипербо-
гиперболе). Но, с другой стороны, ни одна из этих точек не имеет абсцис-
абсциссы, большей л; число же целочисленных точек с абсциссой k,
расположенных под гиперболой, равно целой части длины отрез-
[п ] п
-j , так как MN= -g
(сравните с решением задачи 203), Таким образом, имеем:
б) Припишем каждой целочисленной точке номер, равный ее
абсциссе (рис. 26, б)); в таком случае сумма Oi + о2 + о3 + ... + ап
равна сумме номеров всех целочисленных точек, расположенных.
239
под гиперболой ху = п. С другой стороны, сумма номеров всех
таких точек, имеющих абсциссу k, равна k I-pi.Таким образом,
имеем:
205. Очевидно, что B + ~[/2)п -\- B— ~\/2)п есть целое число;
действительно, если B + У2)п = an + Ьп 1/2, где ав и Ь„ —целые
числа, то B — ~l/2)n = an — Ьп "|/2(это вытекает из формулы бинома
Ньютона, а также может быть доказано методом математической
индукции). Так как B— "|/2)п< 1, то отсюда следует, что
[B + /2М «= B + /2> + B - У2)п - 1
и, следовательно,
B + /2)п - [B + /2)п] = 1 - B
Но так как B — У 2) < 1, то, взяв степень и достаточно боль-
большой, можно сделать выражение B — Y~2)n сколь угодно малым.
А если B — У 2)" < 0,000001, то
B + }/2)п — [B + У1)п] = 1 — B — yl)" > 0,99Э999.
206. а) Первое решение. Так как B + yl)" -f B — УЪ)п
есть целое число и B — Уъ)п < 1, то
[B + УЪ)П] = B + /З)п + B - Уз)п - 1
(сравните с решением задачи 205). Но, раскрыв скобки по формуле
бинома Ньютона, получим, что
B + yli)n + B - /З)п = 2 BП + ф"-2-
делится на 2 и, следовательно, [B + ^З)"] = B + У5)п +
+B - Уз)п - 1 нечетно.
Второе решение. Число B + Уз)" можно представить
в виде "п^^/З, где а„ и Ьп — целые числа. Докажем, что
Доказательство проведем методом математической индукции.
Прежде всего для п = 1 имеем fli = 2, 4» 1 = 1 и 27 — 3 • 1 = 1.
Далее предположим, что для некоторого п
240
где а\ — Ъь\*т If в таком случае имеем:
B + /з)п+1 = (ап + Ьп VI) B +
Отсюда an+i = 1ап -f 36„;
- ЗЬ?|+1 = Bап
ым доказано, чт
юда следует, что
h + К уЩ = °п + [&п
л + 1 = ап + 26„. Следовательно,
bnf -Цап + 2bJ- = а2 - 36*
Тем самым доказано, что а\ — 36^ = 1 при любом п.
Отсюда следует, что
т. е. [B + /3)"] = [an
б) Заметим, что
нечетно.
~1 при я четном-
при «нечетном.
Действительно, стоящая в нашей формуле справа сумма является
целым числом (см. первое решение задачи а)). При п четном О <С
< A — у"з)" < 1, а при п нечетном — 1 < A — yl)* < 0.
Рассмотрим теперь отдельно случаи четного и нечетного, п.
1) п четно, п — 2т; тогда
[A + УЪJт\ = A + /зJт + A - YWm - 1 =
= D + 2 УЪ)т + D - 2 V~Z)m ~ 1 =
= 2m [B + ]A3)m + B - Vl)m\ - 1.
Но стоящее в фигурных скобках число является, очевидно, целым,
и следовательно, число [(l + У 3)"m] = 2rajV — 1 всегда нечетно. Та-
Таким образом, при четном п наивысшая степень 2, на которую делится
[A + УЪ)п\, равна нулю.
2) п нечетно, п = 2т + 1; тогда
[A + ylJm+1] = A + уЪJт+' + A - У'зУ-т+{ =.
= D + 2/3)m(l + УЗ) + D - 2 У3)тA - /3) =
16 Д. о. Шклярскнй и др,
241
Пусть B -f T^3)m = ат + Ът Уз, где ат и Ьт — целые числа; тогда
B — УЪ)т = ат — Ьт У%. Подставив эти значения, получим:
[A + /зJ»+'] = 2™ \ат + Ьт УЗ + ат - Ьп /3 +
Но ат + 36т нечетно. Действительно,
К + 3fcm) («m - 3"m) = «m - 9&m = («m " ^m) - 66^ = 1 - <
(см. второе решение задачи а)). Так как 1 —66^ нечетно, то оба
множителя (ат + ЗЬт) и (ат—ЗЪт) нечетны. Следовательно, наи-
наивысшая степень 2, на которую делится [(l + }^3)п] при нечетном
л = 2т + 1, равна
207. Из того, что B + УЪ)Р + B — /5)р— целое число и — I <
—1^б)р <С 0 (ибо р нечетно), следует, что
[B + УЪП = B + /5)Р + B - }/5)Р
(сравните с решениями задач 205 и 206). По формуле бинома Нью-
Ньютона имеем:
р~1\
)
р-1
2
так что
Но все биномиальные коэффициенты
2 р(р-1) 4 _ р(р-1)(р-
_ __
ьр- b2 • S~ 1-2-3-4 •••1'СР ~ р
делятся на простое число р (ибо числитель выражения для С* де-
делится на р, а знаменатель не делится). Значит, и разность
[B + У^5)р] — 2Р~^ делится на р, что и требовалось доказать.
опа гр я(я-1)(я-2) ...(я-Р+1)
208. С{| = -^] • Из р последователь-
последовательных целых чисел п, п — \, п — 2, ..., п — р+1 одно и только одно чис-
число делится на р; обозначим это число буквой N. В таком случае
242
— I = "р~и разность, стоящая в условии задачи, принимает вид
р! Р '
Заметим теперь, что числа п, :п — 1, ..., JV+1, N—1. ...
..., п — />+1 дают при делении на р всевозможные остатки 1, 2, 3,...
..., р — 1 (р последовательных целых чисел от п — р + 1 до п да-
дают при делении на р все остатки 0, 1, 2, .... р—1, причем каждый
из них по одному разу). Отсюда следует, что разность
делится на р (для доказательства достаточно перемножить почленно
все равенства п — k\p + аи п — 1 = k2p + а2, ..., ЛЛ -+- 1 == ktp +
+ at, N — 1 = ki+lp + ai+i n — p + 1 = kp-ip + ap_,, где k{,
k2,..., kp-i — целые числа, а аи а2,..., Qp_i равны числам 1,
2, ..., p—1, взятым в каком-то неизвестном нам порядке). Умно-
N
жая эту разность на целое число —, получим:
п(п—\) ... (п — р+ 1) N(p—\)\
Р ~ р '•
новая разность, разумеется, будет по-прежнему делиться на р. Раз-
Разделив, наконец, оба члена последней разности на (р—1)!, мы при-
придем к требуемому результату (частное от деления на (р — 1)! также
будет делиться на р, ибо (р— 1)! взаимно просто с р).
209. Пусть a > 0. Ясно, что значение a = 1 удовлетворяет усло-
условию задачи; если же a > 1 и, соответственно,— = [J < 1, то [а],
[2а], [За], ..., [Л'а] все различны между собой — и нам лишь надо,
чтобы были все различны числа №], [2[5], [Зр], ..., [Лф]. Но по-
поскольку [Лф] ^ Лф < N, то [Лф] ^ N— 1 —и единственная воз-
возможность для N неотрицательных чисел [р], [2р], ..., [Лф] прини-
принимать N различных значений доставляется равенствами
[И =0, [2E] = 1, [ЗИ =2,..., [Лф] =N-1. " (*)
А так как равенство [k$] = k —1 равносильно неравенствам
k — 1 «S *ф < к, т. е.
1-4-<Р<1 (* = 1.2 N), (**)
то система равенств (*) равносильна неравенствам (**), т. е. двой-
двойному неравенству
N-1 „ 1
Итак, если a > 1, то —jj— «S р = "^~<'» и. значит, 1 < а ^
Л' N — 1
г j, а если a < 1,то —jj— «S a < 1 (мы это, по существу, уже
16* 243
выше доказали). Присоединяя сюда значение а = 1, заключаем, что
N— 1 N
при а > 0 должно быть—тт— < а < WZZ~['< аналогично этому уста-
N— 1 N
навливается, что при а < 0 должно быть — —^— > а > — дг j •
210. Первое решение. Очевидно, что (а) = а + -у ; та-
таким образом, равенство, которое нам требуется доказать, принимает вид
N
Пусть теперь
(ап, ап~\, ..., п\, а0 равны 0 или 1}—разложение числа N по степе-
степеням двойки (запись N в двоичной системе счисления). В таком слу-
случае, очевидно:
ап
on—2
?. > 1Л„ .,п-2
ЛГ . 1 , , ^ , , _^ , _
—1>
ЛГ 11 ГЯп + 1 en_,
" 2 ]-[*•+* "•¦ !!
(напоминаем, что оп,..., а0 равны 0 или 1). Таким образом, имеем:
[Т + TJ + [Т + TJ + • • • + \p+i + Т\ + ¦ ¦ ¦ =
+ а„_, B"-2 + 2"-3 + ... + 1 + 1) + ... + аг A + 1) + а„ -
"= au2n + «n_j-2n~1-f ... -f ах-2 -f а0 = Л',
что и требовалось доказать,
244
Второе решение. Очевидно, что число нечетных чисел,
/V /V+ 1 f N] , ,
не превосходящих N, равно-^, если N четно, и равно—g—= ~jf '
(N\
если N нечетно, т. е. равно l-g- . Точно так же число не превосходя-
превосходящих Л? четных чисел, не делящихся на 4, равно |-7|t если ^ Делится
[т]-
ГЛП
I -т-\ + 1, есл
ГЛП
на 4 или дает при делении на 4 остаток 1, и равно I -т-\ + 1, если N да-
дает при делении на 4 остаток 2 или 3; другими словами, это число всег-
( Л' \
да равно! -т"|. Точно гак же число не превосходящих N чисел, дел'я-
ГЛП
щихся на 4, но не делящихся на 8, равно " , если N делится на 8
ГЛП
или дает при делании на 8 остатки 1, 2 или 3, и равно " "г ' в против-
(N\
ном случае, т. е. это число всегда равно\~o~\-Аналогичнодоказывает-
/iV\
ся, что Гц I равно числу не превосходящих N чисел, делящихся на
/iV\
8 и не делящихся на 16; I ^ I равно числу не превосходящих N чи-
чисел, делящихся на 16, но не делящихся на 32, и т. д. Таким образом
мы переберем все целые числа от 1 до Л'; следовательно,
что и требовалось доказать.
211. Легко проверить, что 210 = 1024; таким образом, 2100 =
= 102410. Так как 100010 = 1030 представляет собой число, состав-
составленное из единицы с 30 нулями, а 102410 > 100010, то число 2100 =
= 102410 не может иметь меньше 31 цифры. С Другой стороны,
1024'° /1025 у /41\Ю
100010 ^ ( 1000) ~
4_1_ 4_1 4J_ <И 4j_ 41 41 41 41 41
==40'40'40'400'40'40'40'40'40'^
41403938373635343332 41
< 40'39'38'37'36'35'34'33'32'3l = ЗТ
так как
41 40 39
4~0<39<38 •¦•' ИТ' Д-
41 1 40 1 \
Г0-=1 + 40; 39=1+39'ит- Д-J"
245
Таким образом,
2100= 102410< 10-100010,
откуда следует, что 2100 содержит меньше 32 цифр. Итак, число 2100
состоит из 31 цифры.
Примечание. Эту задачу очень легко решить, если пользо-
пользоваться логарифмами: так как log 2 = 0,30103, то log 2100 =
= 100 log 2 = 30,103 и, следовательно, число 2100 имеет 31 цифру.
Смысл задачи состоит в том, чтобы получить этот результат, ие
пользуясь логарифмами.
212. а) Первое решение. Обозначим произведение
13 5 99
¦s-j ' -g- ... Jqq через А и рассмотрим еще произведение
2 4 6 98
5==Т'Т-Т-"99- Так как
Т^Т' 5 > 4 ' 7 > 6 99>93' 1 ^ЮО'
то В > А. Но
А-В ="' 3 ' 4 ¦ 5 ¦ 6 ¦ 7 ¦¦• 99'100 ~ 100*
Отсюда следует, что
Л2<Д? = щ, а значит, А < у^.
г, „, 3 5 7 99
Далее, В < 2Л = —.-g---g-... щ, ибо
_2__3__4__5__6__7_ 98 99
3^4' 5 < 6 • 7 < 8 ' - #' • 99 < 100"
Следовательно,
А-2А>АВ = Ш и, значит, А > ^тр=.
Второе решение. Обозначим, как выше,
_ 3 5 99
2 '
Тогда
2 ' 4 ' 6 •'• 100 ~ А-
1! ё! 5! -??1
22'Р'62 ••¦ 1002
откуда
— ' 52—1 992— 1
42 ' б2 •¦• ЮО2 <Л2<
I2 32 52 992
<22— Г42ГГб2"^ГТ ¦¦• ЮО2 —1"
24G
Разлагая теперь числители дробей слева и знаменатели дробей спра-
справа по формуле разности квадратов, получим:
J_ 2-4 4_^> 98-I00 J_ 3_3 5J5 99 99
2-2'4.4'6-6 •'• 100 100 < <1-3'3-5'5-7-" 99-101'
или после сбкращения
200 <Л2<Ш; 7о~У
что и требовалось доказать.
Примечание. Совершенно так же можно доказать и более
общее соотношение
1 _1_ _3_ _5_ 2п — 1 1
о п/-< 2 ' 4 ' 6 ¦• • 2я <п/о;•
б) Докажем, что при л>1
J 3 5_ 2п—1
2 ' 4 ' 6 ¦ • • 2я
<
Доказательство проще всего провести методом математической
индукции. При п = 1 имеем:
Предположим теперь, что для какого-то значения п
1 3 5 2п— 1 1
2 ' ' 6 •' • 2я *= у^-.
Умножим обе части последнего неравенства на
\_ _3_ _5_ 2я— 1 2я+ 1
2 ' 4 ' 6 • •• 2я '2
Но
2я + 1 у Bя+ IJ
2) /3F+7/ 12 + 28я» + 20п + 4
-я ~ B/г + 1J
откуда следует, что
2я + 1 ^ 1
B/г + 2) /3/1 + 1 УЪп + 4'
Таким образом, получаем:
_1_ _3_ _5_ 2п— 1 2/г + 1 1
247
Отсюда, в силу принципа индукции, Заключаем, что при всяком Л
J_ _3_ 5 2я —
2-4'Т
причем равенство достигается только при я = 1.
Подставим теперь в последнее неравенство п = 50. Мы получим:
2 ' 4 ' 6 ••• 100<]/3.50+ 1 "~/Т51= 12,288...'
что даже сильнее того, что нам требовалось доказать.
213. Решение задачи вытекает из следующих двух очевидных не-
неравенств:
3111 < 32й — B5I1 = 25"п=255
==24- Н=256 (>255),
откуда 31й < 1714. (Заметим, что десятичная запись чисел 31й и
1714 содержит несколько десятков цифр; вычислить эти числа точ-
точно— нелегкая задача.)
214. а) Так как 228= 24 «•= 16 < 27 = З3, то, очевидно, при лю-
любом п > 1 (и, в частности, при п = 1000)
22'' (я-f 1 число) <22' (я чисел) < З3' (п чисел).
(При п = 2 последнее неравенство обращается в равенство, но пер-
первое неравенство остается строгим; в единственном случае п = 1 на-
наше неравенство вообще меняет знак: ясно, что 4 = 22 > 3.)
б) Докажем, что при любом п > 1 (в частности, и при п =
= 1000) имеет место неравенство
_..4 ..-3 ..3
444 (я—1 цифр) < 223 (п цифр)<Зз3 (л цифр);
здесь последнее неравенство очевидно, так что доказать надо лишь
первое неравенство. Но его можно установить с помощью метода
математич8вкой индукции. Ясно, что при п = 2, я —
— 2 = 0 слева и справа стоит одно и то же число 4 = 22; предполо-
предположим, что соответствующее неравенство уже доказано для некоторого
значения п, и рассмотрим «следующее» значение п + 1 5s 3. Мы
имеем:
.4 ..4 .-3
— 44 (я четверок) = B2L (я—1 четверка) < B')"~
(я — 2 тройки; здесь используется предположение индукции) =
¦=222 (я —2 тройки) =22^2 ~ (я — 2 тройки)<
' '3
о.З3 ''
< 2' (л — 1 тройка),
3
.•з
<
-3
ибо, очевидно, З3 (л—1 тройка) > 2 + 1 (в последней
«сверхстепени» участвуют я— 1 цифр).
248
Это рассуждение и завершает доказательство требуемого нера-
неравенства.
215. Пусть запись числа 1974" содержит k цифр; это означает, что
10*-1 < 1974" < 10*. (Так как 1974" > 1000" ¦= 103", то ясно, что
k ^ Зп.) Если запись числа 1974" + 2" содержит больше чем k цифр,
то 1974" + 2" > 10*. Но поскольку 1974" = 2"-987", а 1974" +
+ 2" = 2"(987П + 1), то мы имеем, сокращая соответствуйте нера-
неравенства на 2",
987" < 2"-"-5\ а 987" + 1 > 2*-"-5\
что возможно только, если 987" + 1 = 2к~" • 5* (а 987" =
= 2"-" • 5" — 1).
Так как k — л ^ Зл — л = 2л, то при л>2 число 2h~n • 5"
кратно 8 (и даже 16). С другой стороны, 987 дает при делении на 8
остаток 3; поэтому 987" дает при делении на 8 тот же остаток, что
и 3". Но возводя последовательно 3 в степени 1, 2, 3, ... и заменяя
каждый раз само число остатком от его деления на 8, мы получим,
что,степени тройки дают при делении на 8 чередующийся ряд остат-
остатков: 3, 1, 3, 1; 3, 1; ...; поэтому число 987" + 1 может при делении
на 8 давать лишь остатки 4 и 2— и никогда не разделится на 8
без остатка. Полученное противоречие и доказывает утверждение
задачи.
216. Так как 36™ при любом натуральном т кончается циф-
цифрой 6, а 5" при любом натуральном п кончается цифрой 5, то при
36т > 5" разность 36'" — 5" оканчивается цифрой 1, а при 36т •<
< 5" разность 5П—36™ оканчивается цифрой 9; поэтому десятич-
десятичная запись числа Л' «= |36™ — 5"| может кончаться лишь цифрами
1 и 9, и наименьшие возможные значения его — это 1, 9 и П. Но
при т = 1, п = 2, очевидно, N = 11; покажем, что равенства N = 9
и Л' = 1 невозможны, т. с, что значение N «= 11 и является наи-
наименьшим. В самом деле, из равенства 5" — 36т »= 9 вытекало
бы, что 5" «= 36т + 9 кратно 9, что невозможно; из равенства же
36'" — б" •= 1 вытекало бы, что 5" •=¦ 36™ — 1 =» 62т — 1 —
•=F + 1) Fт— 1), т. е. что 6"' — 1 == 5\ а 6т + 1 -*¦ 5"**. Но
число 6т + 1 оканчивается цифрой 7 — и никак не может быть сте-
степенью 5, что и требовалось доказать.
217. Имеем;
J_ .50 '-2'3---Ю0
'100- 250 A-2-3 ... 5О)-2ао A -2-3 ...50) "
1-2-3... 100 1-3-5../99
B-4-6 ... 100)-B-4-б ... 100) -2-4-6... 100-
Далее остается только применить результат задачи 212а).
218. Требуется определить, что больше: 101"—99" или 100".
Составим отношение
100™ 100п 100"
я(я —1)(п —2)
0+ 31-ЮО3 +-
249
Отсюда сразу ясно, что это отношение больше 1 при п ^ 50.
Покажем, что при п = 49 оно тоже больше 1:
/49 4Э-48-47 \ / 4§ 18 424\
* \Ш + ЗЫ003 + — / ^* \100 ~т
/49 1002\
>2 Тоо + ТоР =ь
Покажем теперь, что при п = 48 наше отношение будет уже
меньше 1. Действительно,
48 48-47-46 48-47-4S-45-44
100+ 3M003 + 51-1006 +-
483
/_48_
<-2^100+
100+A-2-3)-1003 +
4« , 48^
A-2-3) B-3) 1006 + A-2-3) B-3) B-3) 100'+ •'•
/48 1 / 48 \3 1 /48\5 \
~^Too + l"^Tooj + ~6*{w6) +¦¦¦)<
48
100 9600
~9616'
'~ 6 \100
Тем более, при п < 48 отношение будет меньше 1.
Итак, окончательно получаем: 99" + 100" больше чем 101" при
ft ^ 48 и меньше чем 101" при п > 48.
219. Докажем предварительно, что произведение п последова-
последовательных целых чисел больше чем квадратный корень из произведения
крайних чисел в степени п. Обозначим эти числа через а, а + 1, ...
..., а + п—1. Тогда k-e число от начала будет а-\-k — 1, k-e от
конца а + п — k. Их произведение
&za2 + an — a = а(а + п—1),
где равенство может достигаться только при k = 1 или k = п. Дру-
Другими словами, произведение двух чисел, равноотстоящих от концов
(в случае нечетного п эти два числа могут, в частности, оба равняться
среднему числу), всегда больше чем произведение крайних. Но тог-
тогда произведение всех чисел
п
а(а+\)...(а + п—\)>[а(а + п-\)}2 = \У а (а + п— 1)]",
где знак равенства имеет место только при п = 1 или п — 2."
Докажем теперь, что 3001 > 100300. Имеем:
1-2 ... 25 >/25^= 5";
26... 50>(/26~50J5>352&;
250
51 ... 100 > (/51 • 100Г > 7050;
101 ... 200>/lO010O-/200lo° = 10200-250;
201 ... 300 > /200100 • /300100 = 10a00-250-350.
Перемножая левые и правые части неравенств, получим:
300! > 525 • 3525 • 7050 • Ют • 2ШО • Зьо =
= 550 • 725 • 550 • 1450 • 1О4С0 • 2100 ¦ З50 = 10500 • 725 • 1450 • З50 =
= Ю500 . 2J25 . 4225 . 1425 > 1 Q500 . 2(J5 . 4(J5 . 1425 =
_ 10550 . 225 . 42й . 1425 = JQ550 . ] ^25 =
= 10600 • 1,1225 > 10600 = 100300.
Примечание. Более общий результат сформулирован в ус-
условии задачи 223.
220. Докажем, что для любого целого положительного к ^ п
k k"-
Доказательство проведем методом индукции. Для к = 1 оно очевид-
очевидно. Пусть теперь оно справедливо для некоторого к; докажем его
для к + 1. Имеем:
заметим, что здесь мы не пользовались тем, что k^n. Следователь-
Следовательно, это неравенство справедливо для любого целого положительно-
положительного к. Полагая теперь k^n, получим:
1 \ь+1
fe + l k* -f 2k + 1 k -f 1
n + «2 7F
n(k+\)~k>-
< 1 + ~ +
ибо n{k+ 1)> ft2 при n^k.
Подставив в выведенные неравенства значение к = п, получим:
251
221. В силу результата предыдущей задачи
(J \1000oOO
+ 1 000 0001 •>
222. Очевидно, имеем:
A001)88" у _]_ _j j^ ^
= (TJ ТТ*^1 +TOOOJ '1001 <3'1001
(см. задачу 220) и, следовательно,
1ОООюоо > Ю019".
223. Пусть неравенства задачи справедливы для некоторого п.
Чтобы показать справедливость их для п -f- 1, достаточно прове-
проверить справедливость следующих неравенств:
n +
Г
После сокращения на п + 1 эти неравенства приводятся к неравеп-
\ ( \
|1+ —I >1^~з~М+~) .которые следуют из нера-
I 1 \
венств 2 < 1 +— <3.
Остается только заметить, что для п, равного 6, утверждение
?адачи справедливо, ибо
6 \в /6 \в
-s- = 3е =-729, 6! =720, Нг =2в=64.
z у V d /
224. а) По формуле бинома Ньютона имеем:
"("-') J_ , n(n—l)(n — 2) J_
2! я2 + 3! «з + •¦•
n (n— 1) ... 2 1 n (n— 1) ... 1 . 1
(n — 1I „»-i + я! ^
¦4г)..М-я-
" ' ~ п\ у п ] \ п 1 \ п
и аналогично
71+1
3!
252
• • ¦ (' -
- rh) •
/ 1 \n+l
Из сравнения этих выражений сразу следует, что 1 + " .
п . , откуда и вытекает утверждение задачи,
б) Составим отношение
Но при
J , я(я~1) J
J
"¦„-' -г 2! л^ "" 31 п«
п(я— 1)(я — 2) (я— 3) 1
4!
<! J_,_LJ_ _L_L
С другой стороны,
1 1\/ 1\ 1 ! 11
Ц1+ I~~Т1?~~~<
Следовательно, 1 — -^ I 11+ — I < 1, и значит,
1 \n+l I \ \п / 1 \n-f-i / j \п
: '+„=, <1. .1+
откуда и следует, утверждение задачи.
225. Доказательство проведем методом математической
индукции.
1°. Докажем, что
253
при любом целом положительном п. Действительно, при п = 1 это
неравенство очевидно выполняется: 1! = 1 >—. Предположим те-
теперь, что неравенство (*) уже доказано, и покажем, что в таком слу-
случае будет выполняться неравенство
п+1
¦В силу результата задачи 224а)
e
Используя неравенство (*), получаем:
\п+1
В силу принципа математической индукции, отсюда вытекает, что
неравенство (*) верно при любом целом положительном п.
2 с. Перейдем к неразенству
Нам надо доказать, что это неравенство выполняется для всех це-
целых п, больших 6. С помощью логарифмических таблиц (особенно
удобны здесь таблицы натуральных логарифмов) нетрудно проверить,
что при п = 7 неравенство (**) справедливо;
7 \7
т. е. 6! <( —) , ибо In 6! = In 720 « 6,58, а
lnf—) =7 (In 7— 1) ж 6,62.
Предположим теперь, что неравенство (**) уже доказано. В си-
силу результата задачи 224 б)
\n+i e
) >'• т-е- <b
2G4
А теперь из неравенства (**) выводим:
(я+1)! =(й + 1)„1<(„+1)„/-^П
n+i e
т. е. будет верно аналогичное неравенство, в котором п заменено
на п+1. Так как при л = 7 неравенство (**) верно, то отсюда, в
силу принципа математической индукции, вытекает, что оно будет
верно при любом целом п, большем 6, что и требовалось доказать.
226. Воспользуемся тем, что в сумме S = х* -f- xk~l -f- xk~2 + ...
... + *+ 1 при х > 1 наибольшим является первый член и наи-
наименьшим — последний, а при х < 1 — наоборот. Отсюда следует, что
{k+ \)xk >S > k + 1, если х>1;
< 5 < k+\, если х<1.
Умножив теперь обе части полученных неравенств на х— 1, получим'
при хФ\
(k + 1)хь(х— 1) > хь+>— 1 > (k+ \){х— 1).
р
Положим теперь в этом неравенстве х—т^\ тогда найдем:
(*¦
шалогично,
{k
Отсюда
(р-
+ \) р\ р"-1
ПОЛОЖИВ X =
+ 1)(р + 1)\
ph+1
имеем:
И)*+»_р*+1;
-(Р- l)fe+1
—г—, получим
(p+\f+i_l
Ph+i
>(*+1)р*>
или, положив здесь последовательно р =
з"+'-2"+':
>(k + 1I* >
> (?+ 1J* >
>(fe+ 1K* >
^ (А + 1) (р — 1)"
,fe + i _^ (ft+l)pft
/ p*+i •
p»+._(p_l)»+i
1,2, 3 я,
1*+' — 0
2* + i jft+i
3»i+i 2*+1,
—(я— 1)
Сложив все эти неравенства, получим:
(п+ 1)*+' —1 >(fe+ l)(l* + 2* + 3* + ...l+«'l)
255
или, разделив все члены неравенства на k + 1,
Но отсюда и следует неравенство, которое требовалось доказать.
227. а) Прежде всего очевидно
2 *
п раз
С другой стороны, имеем:
1 . 1 \ . / 1 . 1 \ , /1,1
71 + 1 ^ 2п — 1/ т \п + 2 "!" 27i - 2j т • • • т ^2/г т тг
+ +
2)
¦ • ¦ + 2tT2J
(п+1) раз
1 3 3 3 3
= 2 (п+1O Т ^<Т
откуда и вытекает второе утверждение задачи,
б) Отметим прежде-всего, что
_L ' _L J_ J_
3/i +3n+l< 2« + 2тг = /г •
Теперь получаем:
т+т + --- + ~+~к = т = 2-
2л— 1 раз
С другой стороны, имеем:
1 1 . . 1 1 Г/ 1 1
+
1 Г 4я + 2 4п + 2
[д+1J —7J2 +Bтг+1J—(п-
256
An + 2 ' 4я + 2
+ Bn+ lJ—(я — 2J+ ••• + Bя+ IJ — ri
1 Г 4n+2 4я + 2 4n + 2 ]
> T I Bя+!)»+( n+iy- +--' + Bn+l)al
Bn+l) раз
228. а) Прежде всего докажем, что
2 Уя~+1 — 2Уя<^=-<2Ул-2 У^=1.
Уп
Действительно,
Уп+1+-
2
if аналогично доказывается вторая часть неравенства.
Теперь имеем:
1 + + + + >1 +
+ (У4 —Уз)+ ... +(У1 oooooi — y^i оооооо)] =
= 1 + 2(У1С00 001 — УЗ) > 2-1001 — У§+1>
> 2000 — 3 + 1 = 1998.
Аналогично
1 + + + + <1 +
(УЗ —У2)+ ... +(У1 000 000—У 999 999)
= 1 +2(У1 000000— 1) = 1 +2-999 = 1999.
Следовательно, целая часть суммы 1 + у= + у= + ... + у===
равна 1998.
б) Совершенно аналогично решению задачи а) получаем:
УПГооо -V кГооГ "^ ''' "*" у 1 ооо ооо
¦ • • + (УГоШюТ — уГоооооо)] =
= 2 (УГООТОШ — У lTOOO) > 2 A000 — 100) = 1800
17 А Т Щктярский и др, 257
1
1
1
ooo ^ уШюТ ^"'
< 2 [(У HHJOO — V9999)
000 000 ^
— У Toooo + ...
... + У1 000 000 — У999 999)] =
2 (У 1000 000 — У9999) =
= 2000 — У39996 <2000 — 199,98= 1800,02.
1
Следовательно, сумма
:+¦
У1 000 000
УЮОио"' У10 001
с точностью до 0,02 будет равна 1800.
229. Прежде всего отметим, что из сравнения двух выражений
/ 1 \2 11
V й п I п 6 п II п
следует, что при каждом целом положительном п
'21
Отсюда имеем: 1+-о" ~>1 1 + "Г") " . Умножая последнее нера-
о it \ п /
1 - 2 -— —
венство нал 3 , получаем: л3+-д-п 3 >(л+IK и окончательно
Аналогично
3 п
п + 3 п2~27п3
' ~ 2 п + л2 -
11 8 1
так как T;?-27^
3 п
1 1 1
откуда следует
1 2
258
Теперь можем написать:
1 i 1
++ +
/4 /5 |Л 000 000
... + (y"l 000 0012 - \r\ 000 0002)] =
= -j (t'1 000 002 000 001 — уТб) > -|-- ЮООО — vr54 >
> 15 000 —4 = 14 996.
С другой стороны,
1.1 1
у^5 ' '"
уТОООООО
... + (v^l 000 0002 — ^999 9992)] =
= Y(Vl 000 000 000 000 — у"9).< y A0 000 — 2) = 14997.
1 1 1
Таким образом, целая часть суммы t~z. +Г1: + • •• + .. —
У 4 /Ь У\ 000 000
равна 14 996.
230. а) Очевидно, имеем:
J_ _L 1 1 1 1
102 + Ц2 + ••• + Ю002> 10-11 + 11-12+ ••• + 1000-1001 ~
Н) ~Tl j~{ 11 ~ 12 J+ ¦•• + 1^1000 ~ 1001J =
jo - Tool
и аналогично
= "jo" - Tool > 0,1-0,001 =0,099
Ю002<;9-10" 10-11 "г • • • "г 999-1000
--1 "Г" ^999 ~ 1000)
<01
Следовательно, сумма ygj + ур + ¦ • • + Joon* с точностью Д°
0,006 равна 0,105.
17* 259
б) Отметим прежде всего, что
J_ J_ J_ 1 1 1
10! "^ ГП + 12! ~t~ •*- ¦*" 1000! -> 10! = В 628 800 * °.000000275<
С другой стороны,
1,1
,1,1, ,
"*~ 111 "+¦ 12! "т" ••• '
1,1,1, ,
10! "*~ 111 "+¦ 12! "т" ••• ' 1000! <-
_2_ Г_9_ _Ш , _П_ 999 }
< 9 (l0!+ 11!"^ 12! + ••• + 1000!/=
10 — 1 11 — 1 12—1 1000 —
9 I 10! ! 11! r 12! т ••• -r 10001
1_M_ J_ J_ J__,_l_ J_ , J_ 1
" 9 [9! ~ 101 + 10! ~ П! '" 11!~ 1-2! ~ •••+999!~ 1000!
= "T ("§T - Тш] <"§= 3 265 920 * 0-000000305.
\ ' J
1 1 1
Таким образом, сумма удТ + -j"T] + -т. -f- 'moo! c точностью
до 0,000000015 равна 0,00000029.
231. Докажем, что сумму
л__!_ J__L 1 1_
можно сделать больше любого числа N. Будем считать N целым и
возьмем п = 22Л*; тогда
j_ j_ j_ l j JL /_L J.
i i l l \ /i l
ЛГ~1 + 1 + 22N~l + 2
j > 1 + + + ++>
22JV _
Г
(каждая сумма в скобках больше-g" в силу результата задачи 227а)).
Примечание. Можно было бы так же доказать утверждение
задачи, исходя из результата задачи 227 б).
232. Обозначим через л* число незачеркнутых слагаемых между
11 1 1 1
¦^ и loft+i - включая —h, но не у^-р.Если слагаемое—, распо-
1 1
ложенное между . k—l и Тф< не был0 зачеркнуто, то из слагаемых
1 1 1 1 1
Г0^ 109 + 1' Ю?+ 2 10?+ 8' 10?+ 9' Расположенных между
260
1 1
—ft и fe_j_j, будет зачеркнуто только последнее; если же слагаемой
1 111
-— было зачеркнуто, то все слагаемые щ, j q , j, ..., jq , g
'l0g -l 9 также будут зачеркнуты. Отсюда следует, что
nk = 9nk~i.
I - 11 11
Так как па — 8 из слагаемых 1, —~~, —z- -5-, -тт зачерк-
\ Z о о У г -
1
нуто только -д-
щ = 8 • 9 •= 72, п2 = 8 • 92, ..., л* = 8 • 9\
Пусть теперь в сумме 1 -f- -к- -f- "о~+ •• • + "Т" число п <С
< 10™+'. Дополним ее до суммы 1 + -g- + — + ••. + ](.m+i _ '
вычеркнем члены, знаменатели которых содержат девятку, и сгруп-
сгруппируем оставшиеся члены:
/11 1
TO + IT + 12 + • • • + 18 + 20
1 , ,_LW ,/_L
-t- 101 -t- ¦•¦ t- 888) ' ¦• ' ^[\от
, (m+l) раз
1 1 1
+ + +
10^
так как вместо каждой скобки поставлено произведение наибольше-
наибольшего слагаемого этой скобки на число членов в скобке. Продолжим эту
оценку дальше:
1 1 1 1
+ + +
о 02 Qm — 1
+ TO" + TO7- +¦'•• + lom-l +
9m+1 .
'— lom+l j
-8- 9~~<8 g-=8-10 = 80.
1 ~l0 1~T0
Таким образом, утверждение задачи доказано.
261
233. а) Предположим, что в сумме 1 -f- ~т + -к + .. • + "JT5"
I 1
число п меньше чем 2fe+1. Рассмотрим сумму l-f-'or + Г + ¦••
• • • + 7717+1 р и аналогично решению задачи 231 сгруппируем
члены следующим образом:
22 "I
1
42 г ga "r ga 1 72 I "г • • •
что и требовалось доказать.
Примечание. Совершенно так же можно показать, что если
число а больше 1, то при любом п
L J _L 2а-'
] + + + + па< 2*-l _ j •
+ да + • • • + п
Таким образом, при любом а > 1 сумма
остается ограниченной, сколь бы большое значение п мы ни брали
(из задачи 231 следует, что при а ^ 1 сумма 1-J- —^ -f- —^ + ... +—-
может быть сделана сколь угодно большой, если только выбрать
достаточно большое значение п).
б) Очевидно, имеем;
-1-4- — + — + — JL _l-L^
22 Т 3! Т j! Т J'! I ¦ • • ~Г Я2 *^
Г2~"Т" +2^ + 3^4 + П+ ¦•• +(л-1)л='
= (—+ — + — •
V1 23 3'4
4 •
262
и, следовательно,
11 1 / 1 \ 3
что и требовалось доказать.
234. Докажем, прежде всего, что
111 11
'+— + — + - + ••• + — + —
где k — такое целое число, что 2к ^ п < 2fc+1, a pj — наибольшее
простое число, не превосходящее п. Действительно, раскроем скобки
в правой части неравенства. Так как каждое целое число т от
1 до п представимо в виде произведения степеней простых чисел
1, 3, 5, ..., pv.
где все показатели а,, а2, а3 а; —целые неотрицательные числа,
не превосходящие, разумеется, к, то в этой сумме встретится член,
равный — , который получится, если взять из первой скобки г^,
1 1
из второй-^, из третьей— , п т. д. Поэтому в правой части неравен-
о о
1 1
ства после раскрытия скобок будут стоять в с е слагаемые 1, ~о~>~з~.
— —и еще какие-то другие положительные слагаемые.
4 п — 1' п
Значит, правая часть нашего неравенства в самом деле больше левой.
Логарифмируя это неравенство, мы получим;
263
А
Но для всякого целого k и целого р ^ 2
ig(i + T + 7*- + 7^ + -v
Действительно, имеем:
_1
, , 1 1 . 1 '"р^1
Но из результата задачи 220 следует
и, очевидно,
21g3^ Ig3
>
P—
Таким образом, мы заключаем, что
,2!g3 2lg3 , 2lg3 , 21g3
' + Т+ •••+~j<^l^^~3~^~5~"i- ••• "t-~
Если бы существовало такое число N, что для всякого целого поло-
! 1 1 1
жительного / сумма 1 -j- -5- + ~~о~ + ~г~ + • • • + "^~ была бы мень-
ше iV, то для всякого целого положительного числа п выполнялось
бы неравенство
/111 11
'е h + т + т + т + •••+,—+ v
отскзДа после потенцирования следовало бы, чтб
1 1 I II
111 1 1 т 9/ТУ i\
где N\ не гависит от п. Но в задаче 231 было доказано, что такого
числа /Vi не существует; следовательно, не существует и такого чис-
числа /V, что для всякого целого положительного /
111 1
где pi — 1-е простое число в ряду натуральных чисел.
235. Нетрудно видеть, что (a -f- b -f- сK — а3 — б3 — с3 =
= 3(а-J-Ь) F + с) (c-f-а) (проверьте это!); поэтому достаточно до-
доказать, что
Р(а, Ь, с) = (а + Ь + с)зм — а333 — Ь333 — с333
делится на а -\- Ь, на Ь -)- с и 'на а 4- с. Но, очевидно, многочлен (с
буквенными коэффициентами) Я(х, Ь, с) = (х-)-1) + с)щ-гм-
— й333.— с333 от переменной х при подстановке в него вместо х зна-
значения —Ъ обращается в нуль; поэтому Р(х, Ь, с) делится на х —
— (— Ъ) = х + 6, а значит, Я (а, Ь, с) делится на а + b. Аналогич-
Аналогично доказывается и то, что Я (о, 6, с) делится на b-\-с и на с-\-а
(это также следует из того, что буквы а, 6, с входят в выражение
для Р(а, Ь, с) симметрично).
(а6K— 1 а1»—1
(а3M— 1 (а3—1 )(а12 + а9 4- о" + a3 -f 1)
(а— 1) (а4 + я3 + а2 + а 4- 1)= (я — 1)(а* + я8 + а2 + a + 1)
(aa+ a 4- I)(fl124-ae4-ae4-a3 4- 1)
~ а4 4-a3 4-а2 + a + 1 -
Но непосредственное деление дэет
= « — о' 4- а6 — а4 + а3 — a 4- 1
—3——5~i—T~i ГТ
а4 + а3 + а2 + а -\- 1
и, следовательно,
аю + а5+ 1 = (а* + а+ 1)(а8 —а7 +а5 —а4 + йЛ —о+ 1).
237. Первое решение. Обо?начим наши многочлены соот-
соответственно через В и А. В таком случае имеем:
В— А = (х9999 — х9) + (х8888 — Xs) 4- (х7777 — х7) 4- (хвь6В — х6) +
-f (х5555 — х5) 4- (*4444 — хА) + (х3333 — х3) +
4- (х2222 —х2) + (х1111— х) =
= х9[(х10)999— 1] +х8[(х10)888— 1] +x7[(xlg)'"— IJ +
+ х6[(х10N65— 1] +х5[(х10M55— 1] 4-х4[(х10L44— I] 4-
+ х3[(х10K33— 1] + х2[(х10J22— 1] +х[(л:!0)!11—1].
Но каждое выражение в скобках делится на х10—1, а следова-
х10— 1
тельно, и на А = х_\ • Таким образом, мы видим, что В— А де-
делится на А, а значит, и В делится на А. »
265
Второе решение.
Xе + X8 + *' + X6 -f X5 + X4 + X3 + X2 -f X + 1 = •
x10 — 1 (x— 1) (x— at) (x— g2) (x— a3) ... (x — g9)
= x—\ °= F^l =
= (x— aj.) (x —a2) ... (x —a8),
2k n 2k л
где a* = cos-jTj- + i sin -Jq- (k = 1, 2, ..., 9), ибо корни уравнения
x10—1 = 0 — корни, десятой степени из единицы — имеют именно
такой вид. Следовательно, для того чтобы доказать наше утвержде-
утверждение, достаточно проверить, что
Х9999 _|_ XSSSS _|_ д.7777 _|_ Х6в66_|_ Х5555 _|_ д-4444 _(. д.3333 _|_ д-2222 _f_ jg-1 J11 _J_ J
делится на каждый из множителей (х—а,), (х — а2), ..., (х — а9).
Но последнее равносильно тому, что уравнение
д-9999 I д-8888 ;_|_ д;7777 i д-бввб I д;5555 _| д;4444_|_
+ X3333+X2222 + X1U1 + 1 = 0 (*)
имеет корни ai, a2, аз «э- Проверим, что эти значения дейст-
действительно удовлетворя ?
{k = 1, 2, 3 9), то
вительно удовлетворяют уравнению (*): так как а? = 1
„9999 9990+9 ( 10Л999 9 9
ak — ah - \.ak ) ak — ak<
y8S8S _ „8880+8 _ / 10\888 „8 _ „8 HT „
9999 + «8888 + „7777 + „бввв + ^5555 + „4444
U = 1, 2 9).
238. а) Первое решение. Имеем:
а3 + Ь3 + с3 — ЗаЬс =
= а3 + ЗаЬ (а + Ь) + Ь3 + с3 — ЗаЬс — 3ab{a + b) =
= а3 + За26 + ЗаЬ2 + Ь3 + с3 — ЗаЬ (с + а + Ь) =
= (а + ЬK + с3 — ЗаЬ (a -f b + с) =
= [(а + 6) +с] [(а + ЬJ— (a.+ b)c + caj — Зой(а + & + с) =
= (а+6 + с) [(а-+&J— (а+ *)<: +с2— 3obj =
= (a + b+c) (о2 -f 2ab + й2 — ас — Ьс + с2 — Зай) =
= (a+b + c)
Второе решение. Заменим в обозначениях задачи букву а
на х и положим х + Ь + с = 0; преобразовав (х + b + сK,
266
получим, что х3 + b3 4- с3 — ЗхЬс = 0, если х -f- b -f- c = 0. Поэтому
уравнение х3 — ЗЬсх + Ь3 + с3 = 0 имеет корень х = — Ь — с, и
многочлен х3 — ЗЬсх + Ь3 •+• с3 делится на х — (— b — с) .= х -f 6 +
Af с, а значит a3 -f b3 + с3—ЗаЬс делится на а + b + с. Выполнив
непосредственно деление (для чего удобно рассматривать многочле;
ны а3 — ЪаЬс + Ь3 + с3 и а + й + с расположенными по степеням
буквы а), мы придем к прежнему результату:
а* + Ь*¦+с* — ЗаЬс = (а + b + с) (а2 + Ь2 + с2 — ab — ас —be).
б) Подберем такие два числа а и Ь, чтобы иметь равенство
х3 + рх + q = х3 + а3 + Ь3 — ЗаЬх,
р
Для этого достаточно, чтобы было а3 + b3 = q, ab =—-s~;
из этой системы двух уравнений с двумя неизвестными нетрудно оп-
Р3
ределить а и Ь. Имеем а3 + й3 = <?. а>Ь3 — —"оу";отсюда следует, что
Р3
а3 и Ь3 — корни квадратного уравнения z2 — qz — -wf =0 и, следова-
следовательно ').
Теперь, в силу результата задачи а), имеем'
х3 + рх + q = х3 + а3 + Ь3 — ЗаЬх =
= (а _|_ ь + х) (а2 + Ь2 + х2 — ab — ах — Ьх).
Следовательно, решение нашего кубического уравнения сводится
к решению уравнения первой степени:
а + Ь + х = О,
откуда имеем:
или
и квадратного уравнения
х2 — (а + Ъ) х + а2 + Ь2 — ab = 0;
')
Числа а и Ь, определяемые по формулам (*). являются дей-
qi рз q-i рз
ствительными, если — +7 > 0. Если же— +у<0, то под
знаком корня третьей степени в формулах (*) будут комплексные
числа. В этом случае числа а и b тоже являются комплексными; их мож-
можно отыскать, например, с помощью формулы для корня п-й степе-
степени из комплексного числа. При этом за а можно с равным основа-
основанием принять любое из трех значений корня кубического из комплекс-
q -. Г д2 i „з
ного числа —к~ -f- I/ -!— -!—', тогда о определим из соотноше-
z Г 4 27
ния а& = — -д-.
267
->тсюда следует
х -a + b ' (а — Ь) УЗ{ х _а + Ь_(а — Ь)УЬ~ .
г 2 . т- 2 .з 2 2
где а и Ь определяются формулами (*).
239. Первое решение. Обозначим~]/а + хчерез у, получим
систему из двух уравнений.
Уа + х = г/, /а — у = х.
Возведем эти уравнения в квадрат:
а + х г= у2, а — у = х2.
Вычтем из первого второе:
х + у = у2 — х2,
г1ЛИ
х2-(/2 + х+г/= (х + у)(х-у+\) =0.
Отсюда имеются две возможности:
1) х + у = 0; у = —х и х2 — х — а = 0, откуда
2) х — г/ + 1 = 0; тогда у = х+ \ и хг + х + 1 — а = 0,
откуда
Можно убедиться проверкой, что при соответствующем выборе
знака у каждого из радикалов, встречающихся в исходном уравне-
уравнении, корни Х\, Хч, х3 и А'4 удовлетворяют этому уравнению1).
Второе решение. Освободимся от радикалов в нашем урав-
уравнении:
а—уа + х = х1,
(а — х2J = а + х,
х* — 2ахг — х + о2 — о = 0.
Таким образом, мы приходим к уравнению четвертой степени.
Однако это последнее уравнение является квадратным по отношению
к а. Решим это уравнение относительно а, т. е. примем на время,
') Если же, как это иногда делается, считать все корни положи-
положительными, то уравнение будет иметь единственный корень х3 =
2~ + |/ а —. если а ^ 1, и вовсе не будет иметь корней, если
268
что х нам известно, а наоборот, а требуется определить:
а* — Bх2.+ 1)а + х* — х = 0,
± У4х* + 4х2 + 1 — 4л:4 + 4л: _
2х2 + I + У" 4х2 + Ах + 1 2х'2 + 1 + Bл: + П
2 = 2
а2 = л:^— л:.
Таким образом, мы видим, что уравнение
а2_ Bх2+ \)а + х* — х = 0
имеет корни
. Qi = Xs -\- х + 1, а2 =х2 — л:,
откуда согласно общим свойствам квадратных уравнений
а2_ Bх2 + 1) а + х* — х = (а —а,) (о — о2) =
= (а — х2 — л:— 1)(о — х2 + *).
Таким обратом, наше уравнение принимает вид
(х2 — х — а)(х2 + х~ а+ 1) =0
и без труда решается:
240. Первое решение. Обозначим
* + 2ах + ±. у, a + }/a + x-Lyl.
В таком случае наше уравнение принимает вид
У = </i-
Выразим теперь х через уь Простое вычисление дает
ж = У\ + 2a(/j + -jg .
• Таким образом, мы видим, что х выражается через у\ точно та-
таким же образом, как у через х. Отсюда следует, что если мы начер-
начертим графики функций
22
Ух=~а+ Y^ + x-JL,
269
то эти графики (параболы) будут симметричны относительно бис-
сек1рисы первого координатного угла (рис. 27; каждой точке х =
= х0, у = (/о первого графика отвечает симметричная относительна
биссектрисы координатного угла точка х = г/о, У = хй второго гра-
графика). Точки пересечения этих
двух графиков отвечают таким
г п 1 / / значениям х, что у = ylt т. е.
? +iB+-7 = </ч / / корням нашего уравнения; эти
точки обязательно лежат на оси
симметрии обеих кривых, т. е.
удовлетворяют условию
У — х = г/i.
Решая уравнение у — х,
1
т. е.
2ах -
Г/+^+!«я
Рис. 27.
16
мы получаем:
Тб"
1
Можно убедиться проверкой, что при 0 <Са <С~^~ оба эти корня
являются действительными и удовлетворяют исходному уравнению.
Второе решение. Эту задачу можно решить и более обыч-
обычным путем. Избавляясь от радикала в уравнении, получим:
или после раскрытия скобок и приведения подобных членов
2а+ ' W-
х* + 4а*3 + Dа2
а 1
Т~ + "Та"
16 "Г Тб5
= 0.
Левую часть получившегося уравнения можно разложить на множи-
множители:
j
+ [Bа + 1) х* + Dа* - 1) х* + JJL
16
][¦
д«+Bа+1)* + [2a+lL
270
Отсюда сразу получаем решений!
1— 2а Г~
16'
17
2
1
При 0 < а < -т- первые два. корня являются действительными и
удовлетворяют исходному уравнению; последние два корня —комп-
—комплексные.
241. Для того чтобы при действительном х левая часть уравнения
была действительна, необходимо, чтобы все подкоренные выражения
были положительны. Обозначая эти положительные подкоренные вы-
выражения, начиная с последнего (т. е. с Зх) и до первого, через
у\, У%, у\ y'n-v yl, будем иметь:
3* =
х +
* +
х + 2х
к 4- 2^]
с + 2у2
2уп—2
2уп,
= уЬ
= у%
-уЬ
= у1
= у1
где все числа yit уг,..., уп действительны и положительны. Само
исходное уравнение в новых обозначениях примет вид
Уп = X.
Докажем теперь, что у\ = х. Действительно, предположим, на-
например, что х > г/i. В таком случае из сравнения первого и второго
из наших равенств будет следовать, что у\ ~> у$. Точно так же из
сравнения второго и третьего равенств находим, что j/г > Уг, далее,
аналогично получаем, что
Уз > 1/4 > ¦•• > Уп-1 > Уп.
Таким образом, при х > у} будем иметь х > уп, что противоречит
уравнению. Аналогично доказывается, что и при х < yt не может
быть уп = х (в этом случае обязательно х <. (/„).
Так как у\ = Зх, то, следовательно, должно быть
Зх = х\
откуда сразу получаем два единственно возможных значения х:
хх = 3, х2 = 0.
271
Проверка показывает, что оба эти значения удовлетворяют наше-
нашему уравнению.
Примечание. Наметим здесь еще один метод решения урав-
уравнения
... +2
п радикалов
Подставим в левую часть этого уравнения вместо последнего чис-
числа х его выражение, даваемое равенством (*); получим:
•= V X+2V х + 2У
-f 2 V х -f 2 V х + .-.. + 2 у х + 2х .
2п радикалов
Далее, снова заменяя последнее х подобным же образом, будем
иметь:
¦ = V х + 2 V х + 2Y
2х =
Зп радикалов
.V,
... + 2 Ух -f 2x = ...
in радикалов
На основании этого мы можем записать:
х+2Ух +2Ух+ ...=
im У д
= lim ? x + 2V x + 2y x + ... + 2 у х + 2х .(**)
/V радикалов
Отсюда получаем:
2]/x+2/a:+ ...J = Ух + 2х, (***)
откуда имеем х = У3х,х2 = Зх и, следовательно, х, = 0, х2 = 3.
В частности, это решение срагу показывает, что корни уравнения (*)
не зависят от п (ибо уравнение (**) не зависит от п).
Приведенное рассуждение в таком виде нельзя, разумеется, счи-
считать решением задачи, поскольку не доказано существование предела
(**) и не обоснованы преобразования (**¦*). Однако это рассуждение
можно сделать совсем строгим.
272
242. Будем последовательно упрощать дробь, стоящую слева:
х+ 1 __ Зх_
' 2х + 1 = 2х -
Окончательно мы получим какое-то уравнение вида
где о, Ь, с и d — неизвестные нам целые числа. Это уравнение равно-
равносильно квадратному уравнению х(сх -f d) = ax -f ft; отсю-
отсюда следует, что наше исходное уравнение может иметь не больше
двух различных корней (тождеством это уравнение быть не может,
так как иначе ему удовлетворяли бы любые значения х, а х = О,
очевидно, уравнению не удовлетворяет).
Но дв.а корня нашего уравнения нетрудно найти. Действительно,
предположим, что х таково, что
В таком случае, последовательно упрощая нашу дробь «с конца» мы
будем получать
1 1 1
1 + — = *; 1+ — = *; 1 + —= *;...
и окончательно придем к тождеству
х = х.
1
Таким образом, мы видим, что корни уравнения 1 + — = х,
пли х2 — х — 1 = 0, т. е.
1 + VI у _ 1-V5
х1 —, х2 —,
удовлетворяют заданному уравнению. Никаких других корней это
уравнение иметь не может.
Примечание. Наметим здесь еще один метод решения рас-
рассматриваемого уравнения (сравните с примечанием к решению за-
задачи 241). Подставим в левую часть уравнения вместо х его выраже-
выражение в виде многоэтажной дроби, даваемое самим уравнением. При
этом мы получим точно такое же уравнение, где, однако, в много-
многоэтажной дроби слева знак дроби будет повторяться 2л раг. Продол-
Продолжая далее тот же процесс, мы будем приходить к таким же уравне-
уравнениям, где слева будет стоять дробь, имеющая все больше и больше.
18 Д. о. Шклярский и др. 273
«Этажей». На этом основании Мы можем написать:
1
l-flim
+-Г
Знак дроби повторяется N раз
где слева стоит бесконечное выражение. Отсюда получаем:
+
т. е. то же квадратное уравнение для х, которое фигурировало и в
приведенном выше решении задачи. Такое решение исходного урав-
уравнения сразу показывает, что корни его не могут зависеть от п.
Приведенное рассуждение в таком виде нельзя считать решением
задачи, так как не доказано существование предела (*) и равенство
х этому пределу и не обоснованы преобразования (**). Однако, это
рассуждение можно сделать вполне строгим.
243. Имеем:
х + 3 — 4 Ух— 1 = х — 1 — 4 Ух^Х + 4 =
= (КГ^П"J - 4 Ух~=Л + 4 = (/^Л - 2J
и аналогично
х + 8 — 6 /лГ^Т — лг — 1 — 6 УТ^Л + 9 = (У~х^~1 — ЗJ.
Таким образом, наше уравнение можно записать в виде
или, так как мы считаем все корни положительными,
где \у\ обозначает абсолютную величину числа у.
Рассмотрим теперь несколько случаев.
1°. Если yj^Tx— 2>0, УТ^~\— 3»0, т. е. если
Ух—1 > 3, х — 1 > 9, лг > 10, то . | Ух~^П — 2 | =
= Ух— 1 — 2, | |/"х— 1 — 3 | = Ух— 1 — 3 и уравнение
274
принимает вид
УТ^Л — 2 + УТ^Л — 3 = 1,
откуда
2 Ух—1 =6, jc — 1 =9, х = 10.
2". Если Ух— 1 —2 > 0, У*— 1 — 3 s? 0, т. е. если
х— 1 > 2, * > 5, но Ух— 1 < 3, х ^ 10, то
|>/х — 1 — 2| = У^=Л — 2, |УГ=Т — 3| =— /Г=Т + 3
и уравнение превращается в тождество
Ух~=7 — 2 — У х^П + 3 = 1.
Таким образом, нашему уравнению удовлетворяют все значе-
значения х между х — 5 и х = 10.
3°. Если У* — 1 — 2 < 0, Ух — 1 — 3 < 0, т.
е. если
5, то |УГ^Т-2|= — У*^Л + 2, lyl^l—3| =
=—Ух— 1 +3 и уравнение принимает вид
— Ух—1 + 2 — УТ^Л + 3 = 1,
откуда
2 Ух — 1 = 4, х — 1 = 4, х = 5.
4°. Случай ]^ х — 1 — 2^0, Ух — 1 — 3^0, очевидно, не-
невозможен.
Таким образом, решением этого уравнения служат все значе-
значения х между х = 5 и х = 10, т. е. 5 ^ х^ 10.
244. Для того чтобы решить это уравнение, мы будем искать
сначала его корни, лежащие на отрезке от 2 до оо, затем на отрез-
отрезках от 1 до 2, от 0 до 1, от — 1 до 0 и от — оо до — 1.
1°. Пусть х Зг 2. Тогда х+1>0, х>0, х— 1 > 0, х — 2^0;
поэтому |х+1|=х+1, |х]=х, \ х— 11 = х— 1; ] х — 2 | =
== х — 2, и мы получаем уравнение
х+ 1— х + 3(х— 1)— 2(х-2) =х + 2,
которое удовлетворяется тождественно.
Таким образом, любое число, большее либо равное 2, является
кор-нем нашего уравнения.
2°. Пусть 1 < х < 2. Тогда х + 1 > 0, х > 0, х — 1 >0 и
х —2 < 0 и, значит, |х+1|=х+1, |х|=х, \х— 1] = х— 1,
|*-2| =-(х-2).
Таким образом, мы получаем уравнение
х + 1 — х + 3(х — 1) + 2(х — 2) =- х + 2.
Отсюда 4х = 8, х = 2, т. е. лежит вне отрезка 1 ^ х < 2. Сле-
Следовательно, наше уравнение не имеет корней, больших либо равных 1,
но меньших 2.
18* 275
3°. Пусть, далее, 0 ^ х < 1. Тогда имеем:
|х— 1| = — (х— 1), |х— 2| = _ (х —2).
" х + 1 _ х — 3 (х — 1) + 2 (х — 2) •«= jc + 2, х = —1,
т. е. лежит вне отрезка 0 ^ х < 1.
Значит,
. леж р
Получаем, что корней, больших либо равных 0, но меньших
нет.
4°. Пусть теперь — 1 < х < 0. Тогда \х + 11 = х + 1,
|л-| =—х, | jc — 11 = — (х— 1) и \х — 2\ = — (х —2);
х+1+х — 3(х— 1) +2(х — 2) =х + 2,
что невозможно, т. е. на этом участке также нег корней.
5°. Наконец, пусть х < — 1. При этом | х + 1 | = — (х + 1),
\х\ = _х, | х— 1 | = — (х— 1) и |х — 2 | = — (х — 2);
— _(х+ 1) +л; — 3(х— 1) +2(х — 2) =х + 2, х = —2.
Получаем еще один корень х = — 2.
Окончательно уравнению удовлетворяют: число — 2 и любое чис-
число, большее либо равное 2.
Рис. 28.
Примечание. Результаты настоящей задачи становятся со-
совершенно ясными, если изобразить график функции
г/=|х+Ч — М+3|х— 1|— 2|х — 2| — {х + 2).
На рис. 28 изображены тонкими линиями графики функций
У\ — |х + 1|, г/2 = — |х|, (уз =¦ 3|х— 1|, г/4 = — 2|х —2| и (/5 ==
276
= — (x -f- 2) и жирной линией—график функции у = у{ -f- у2 +
+ #s + </4 + </5 («сложение графиков»). Из этого чертежа сразу вид-
видно, что у обращается в нуль на луче х ^ 2 и еще в одной точке
х = —2.
245. Обозначим правую часть рассматриваемого уравнения п-й
степени через fn{x). Легко видеть, что уравнение fi{x) = О, т. е.
1 —х = 0, имеет корень Xi = 1; уравнение h(x) — 0, т. е.
х (х — 1) — 2х + 2 = 0, или х2 — Зх + 2 = 0, имеет корни xt = 1 и
,<2 = 2. Докажем теперь, что уравнение /„ (х) = 0 tuieer следующие
корни:
хх = 1, х2 = 2, х3 = 3, ..., х„_1 = я— 1, х„ = л. (*)
Воспользуемся методом математической индукции,
т. е. предположим, что наше утверждение уже доказано для уравне-
уравнения /я (х) = 0, и проверим, что и таком случае уравнение f,l + l(x) = 0
имеет корни (*) и дополнительный корень х„ + 1 = л+ 1. Прежде все-
всего, ясно, что поскольку
f (x^-f Ы-Cf *(x-l)(x-2)...U-tt+1)(x-/i)
tn+l (x) - fn (x) + (-1) GГ+7)!
то если уравнение fn(x) ^0 имеет корни (*), то те же корни имеет
и уравнение fn+i(x). Наконец, равенство /n + i(i+l) =0, т. е.
п+ 1 (га+ \)п (п+ \)п(п-\) t
1 1+1-2 1-2-3 ~ •••
можно, очевидно, записать так:
1 - cln+i + с2п+1 - с3п+1 + ... + (- i)n+1 сппХ\ = о, («)
ft (я-|-1)я(д-1) ...(ft-fe+2;
где C^i ¦= ^] — так называемые
биномиальные коэффициенты; но по формуле бинома Ньютона пра-
правая часть (**) равна A — 1)" + 1 = 0, откуда и следует, что число
хп + 1 = п + 1 также является корнем уравнения /n + iW = 0-
246. Обозначим через {л-} = х—[х] так называемую дробную
часть числа х (см. стр. 37); ясно, что 0 ^ {х} < 1 и что [х] —
= х—{х}. Таким образом, наше уравнение можно переписать так:
х3— (х— {х}) = 3, или х3 — х = 3— {х},
откуда следует, что 2 < х:< — х ^ 3. Но, очевидно, при х^2 мы
имеем х3 — х = х (х2— 1) ^ 2 D— 1) = 6 > 3; при х <С — 1 имеем
х2 1 > 0 и хъ — х = х(.v2 — 1) < 0 < 2; при х = — 1 имеем х3 —
— х = 0 < 2; при — 1 < .1- < 0 имеем х3 — х sg — х < 1; при 0 <
1 s 3 ^ 1 П б 1 < < 2
< ^ им < ^ у
и, значит, [х] = 1. А тогда исходное уравнение принимает вид:
х3 — 1 =3, откуда х3 = 4
— это и есть (единственное) решение задачи.
277
247. Из первого уравнения системы немедленно получаем:
у2 — х'2, у = ± х.
Подставляя это значение у2 во второе уравнение, находим:
(х — аJ + х2 = 1 (¦)
— квадратное уравнение, которое, вообще говоря, дает два гначе-
ния х. Так как каждому значению х отвечают два значения у, то всего
система имеет четыре решения.
Число решений системы уменьшается до трех, если одно из зна-
значений х равно нулю; нулевому значению х (и только нулевому зна-
значению) соответствует единственное значение у = 0, а не два разных
значения у = ± х. Подставляя х = О в уравнение (*), получаем:
о2 = 1, а = ±1;
только при этих значениях а система имеет три решения.
Число решений системы уменьшается до двух, если уравнение
для х имеет одно-единственное значение. Для того чтобы квадратное
уравнение (х — оJ-J-х2 = 1, пли 2х2 — 2ах + а1 — 1 = 0, имело
единственный корень (два совпадающих значения корня), надо,
чтобы было _
а2 — 2 (а2— 1) = 0, о2 = 2, а= + У 2;
при этих значениях а система имеет два решения.
248. а) Решая систему, получаем:
рз — 1 — о2 + а
х = ~&=Л' у = а2 - 1 •
Отсюда видно, что если п-\-\ ^=0иа — 1 ^=0, то система имеет
а2 + а + 1 — а
единственное решение х — —а , j—, У = а i ;. Если а — — 1
или а = -f- 1, то наши формулы теряют смысл; в первом случае
мы приходим к системе
(-х+у = 1,
I х-у=\,
которая противоречива (не имеет решений), во втором случае —
к системе
(*+</ = !, ' ¦
которая имеет бесконечно много решений (х произвольно, у = 1 х).
б) Решая систему, получаем:
а* —1 —а3 + а
х ~~ а2 — 1' у = а2 — 1 "
Таким образом, и ?десь, если а2— 1 Ф 0, го система имеет единст
венное решение х = а2 + 1, г/ = — о. В. случаях же а = — 1 и а =
= 1 мы приходим к системам
и р
х — у = 1 И \х-\-у =
которые имеют бесконечно много решений.
в) Из первого и второго уравнений получаема
(у + 2=1 — ах и ay + z = а — х\
рассматривая эти два равенства как систему двух уравнений с двумя
неизвестными (/иг, имеем:
а—х—\+ах (а—\)(\+х)
У ~ а-1 ~ а-1
а(\—ах) — а-\-х — х(а2—1)
2
'~ а —1 ~ а-1
Таким образом, если а Ф 1, то у = 1 + х, г = —A + а)х; подстав-
подставляя эти значения у и г в третье уравнение, находим:
х+A + х) — оA +а)х = а2, хB — a — a2) = а2— 1,
— *(а + 2)(а—1)= а2—1.
Поэтому при a — 1=7^0, а + 2=5^0 система имеет единственное
решение
В случаях а = 1 и а = — 2 мы приходим соответственно к системам
х+г/-Ьг = 1, и дг— 2(у + г = — 2,
г = 1 х+(у — 2г = 4,
первая из которых имеет бесконечно много решений, а вторая не
имеет ни одного решения (складывая первые два уравнения второй
системы, мы получаем —х — у -\-2z = — 1, что противоречит треть-
третьему уравнению).
249. Вычитая второе уравнение из первого и шестое из пятого
и приравнивая два полученных выражения для х2—х%, получим:
а](а2 — а3) = а4(«2 — «з), или (а, — а4) (а2 — а3) = 0.
Точно так же, составляя по два различных выражения для раз-
разностей х\— х2 и Х\—хз, получим еще два соотношения:
(си — а2) (а3 — а„) = 0, (а, — а3) (а2 — а4) =» 0.
Из первого из полученных трех соотношений следует, что at =
= а4 или а2 = а3. Предположим для определенности, что а2 ='
= а3 = а. Из второго соотношения следует, что cti = а или сц = а.
Каждое из этих равенств обращает третье соотношение в тождество.
Таким образом, для того чтобы наша система была сов-
совместной, необходимо, чтобы три из четырех вели-
величин cti, <Х2, а3, а4 б ы л и равны м е ж д у с о б о й.
Предположим теперь, что а\ = а2 = а3 = а, а4 = р. Вспоминая
те выражения для разностей хх — хг. Х\ — х$, х2 — ха, при помощи
279
которых мы получили соотношения между ось й2, из и &4, Немедлен-
Немедленно получаем:
Xl = Х2 = Х3.
Обозначим теперь Х\ = х2 = х3 просто через х, а Х4 — через (у.
В таком случае наши шесть уравнений с четырьмя неизвестными
перейдут в два уравнения с двумя неизвестными:
2х = а2, х + </ = ар,
откуда
2 f ' а
—
Примечание. Аналогичными рассуждениями можно пока-
показать, что более общая система
= a1aa... am_,am+1,
—2+ • • -+xn—
lan+m2" • >an—lan
-un+m_l"n+m_2-""n-l"'n>
состоящая из С™ уравнений с п неизвестными (n>m-f-l), будет
разрешима только в следующих двух случаях:
1° ai = а2 =...== an-i = а; а„ = [3
, п—\
п—1
в этом случае х\ — х2 —...— хп_х=—, хп=а ip— -^— a
2° п — m + 1 или больше из величин аь а2 а„ равны нулю
(в этом случае xi = х2 =...•= х„ =0).
250. Из первого уравнения получаем х = 2 — у; подставляем во
второе:
2у — уг—г2 = 1,
или
г2 + t/ — 2у -М = 0, т.е. г2 + (г/— IJ = 0.
Каждое из слагаемых последнего равенства неотрицательно и,
следовательно, равно нулю. Отсюда
2 = 0,. у = 1
и, значит,
х= 1.»
Таким образом, система имеет единственное действительное ре-
решение
251. Если х" + г/4=1, то либо х4 = 1, у4 = 0, либо х4 = 0,
г/4 = 1, либо, наконец, 0 < х4, у4 < 1 (ибо числа х4 и г/4 неотрица-
неотрицательны). Но при х4 < 1, г/4 < 1 мы имеем также |х| < 1 и \у\ <1,
а в таком случае
откуда следует, что два числа х, у одного знака, такие, что \х\ < 1,
\у\ < 1 не могут служить решением нашей системы. Еще яснее, что
280
и два числа х, у разных знаков, где |х| < 1, \у\ < 1, тоже не мо-
могут служить решением, ибо в этом случае
х3+1/а< \х*,+ у*\ < тах(|х3|, \УЦ) <1.
Таким образом, решения системы приходится искать среди таких
значений х, у, что х4 = 1, г/4 = 0, или наоборот, т. е. среди пар
х = ±\, у = Q и .V = 0, г/ = ±1; ясно, что из этих четырех пар чи-
чисел решениями являются только две; х = 1, у = 0 и х = 0, г/ = 1.
252. Одно решение (точнее система решений) очевидно: Х\ =
= х2~= х3 = х4 = хд = 0, х —¦ произвольно; поэтому далее мы бу-
будем считать, что хоть одно из х, (i = 1, 2, 3, 4, 5) отлично от ну-
нуля. Далее, из первого и последнего уравнений системы имеем
jc3 = xx2 — хх и х5 = хх1 — х2; (*)
аналогично, второе и предпоследнее ее уравнения дают
Х4 = ХХ3 — Х2 И Х4 = XXS — ДС[. (**)
Подставив в (**) х3 и х5 из (*), находим
Х4 = (х2 — 1)х2 — XXi И Х4 = (х2 — 1)^! — ХХ2. .(***)
Приравняем теперь правые части (***):
(Х2 — 1)*2 — XXi = (Х2 — l)xj — ХХ2,
Далее естественно различать два случая. Если х1 -j- х — 1 =^0,
то, очевидно, xt — x2. Но все неизвестные хь х2, *г, х4, х5 входят
в наши уравнения симметрично (одинаково); поэтому точно так же
можно установить, что в этом случае х2 = х3, х3 = х^, а;4 = х5.
Таким образом, здесь мы имеем хх = х2 = х3 = х4 = х5; подставив
эти значения в исходные уравнения, находим, что х = 2. Наконец, ес-
если а-2 +х — 1 = 0( т. е. х2— 1 = — х и х = ni-i-Kl), то
(***) —это одно уравнение
xi = —x(x2 + xl). ' (****)
Непосредственной подстановкой легко убедиться, что в этом случае
значения х3 = хх2 — х,, х4 = — х(Х[ + х2) и х5 = ххх — х2 удовлет-
удовлетворяют нашей системе при произвольных х\ и х2.
Ответ: Х\ — х2 = х3 = xt = х5 = 0, х произвольно; х{ =
= х2 = Хз = х4 = Xg произвольны, х == 2; Xi и Xj произвольны,
, , , -1 ±/5
х3 = хх2 — Хь х4 = — х(х! + х2), Xi = xxt — х2, х «= 2 •
253. Пусть х, у, г, t — искомые числа и xyzt = А; заметим, что
А =т^= 0, поскольку если, например, х = 0, то условий задачи приводят
к противоречивым равенствам y = z = t = 2w yzt = 2. Далее, урав-
уравнение х + Уг^ = 2 можно переписать так;
х + —=2, или х2 —2х + А = 0.
Аналогично получаем
1,2 _ 2у + А = 0, г2 — 2г + А = 0, ^ — 2t + А = 0.
28)
Но уравнение х2— 2х + А = 0 может иметь (при данном А) лишь
два разных корня; поэтому среди чисел х, у, г, t имеется не более
двух различных. Далее мы рассмотрим отдельно несколько возмож-
возможных случаев.
1°. Если х = у = z = t, то наши уравнения дают
х -f х3 = 2, или х3 + х — 2 = 0,
или, наконец, (х — 1) {хг + х + 2) =0,
— 1 + V~
откуда х\ = 1, лгг, s == 2 • Таким образом, здесь мы
имеем единственное решение системы в вещественных числах:
х — y = z = t — 1.
2е. Если х — у = г, а / может быть и иным, то условия задачи
дают
х + хЧ = 2 и t + х3 = 2. (*)
Вычитая равенства (*) одно из другого, получаем:
х3 — хЧ — х + t = 0, или (x — t) (х2— 1) = 0;
поэтому либо х = t (этот случай мы уже разобрали выше), либо
х = ±1. Но при х = 1 первое из уравнений (*) сразу дает t =
= 1 — и мы снова приходим к полученному выше решению; если же
х = — 1, то то же уравнение дает t = 3.
3°. Если х = у и г = /, то система сводится- к следующей:
х + xz2 = 2, г + х2г = 2. (**)
Вычитая почленно эти уравнения, получаем:
х — г+ хг2 — x2z = 0, или (х —г) A — л-г) = 0.
Но равенство х = г сразу приводит нас к случаю 1°, а если хг = 1
и (в силу первого из уравнений (**)) а + г = 2, то мы снова нахо-
находим уже известное решение х = z = 1.
Ответ: либо все 4 числа равны 1, либо три иг них равны — 1
и одно равно 3.
254. Для того чтобы подчеркнуть полную симметрию уравнений
нашей системы относительно входящих в систему неизвестных и коэф-
коэффициентов при этих неизвестных, обозначим х = хи у = х2, г = хг
и t = хА; а — аи b = а2, с = а3, d = a4; при этом наши уравнения
можно будет записать так:
4
2К-а;К = 1 (« = 1,2,3,4). (*)
j=l
Далее, пусть, например, at > а2> а3 > о4; тогда имеем
(aii — аг)х2 + (я:— оз)х3 -f (ai — a4)x4 = 1,
(Oi — Я2)*1 + («2 — О3)Хз + (а2 — «4)X4 = 1, (**)
(ai — о3)х, + (а2 — а3)х2 + (о3 — а4)х4 = 1,
(ai — о4)х! + («2 — а4)х2 + (а4 — а3)х3 = 1.
Вычтем из первого уравнения системы (**) второе, из второго —
третье и из третьего — четвертое; мы получим:
(а, — а2) (— хх + хг + х3 + xt) = О,
(а2 — а3) (— *i — х2 + хъ + xt) = О,
(а3 — а4,)(—Х1—'х2 — х3 + хА)=0.
Так как числа аь а2, а3, а4 попарно различны, то
Х\ = Хг + х3 + *4, хх + х2 — х3 + х4, хх + х2 + хъ = xt,
откуда следует, что
х2 = х3 = О, л"] = х4,
а тогда (например, из последнего из уравнений (**)) находим:
1
Проверка показывает, что значения х2 = х3 ~ 0, хх = дг4 =
1
= действительно удовлетворяют всем уравнениям системы.
Ответ: если a>6>c>rf, то х — t = ,, у = г = 0.
255. Обозначим х2 — ^i = Xi, л3 — х2 = Х2, ..., *„—ж„_1 =
= Х„_ь х,—х„ = Х„. Тогда Л, + Х2+...+ Хп_1 + Хп =0, а
заданную систему уравнений можно переписать так:
Но ясно, что если дискриминант А = F — IJ — \ас стоящих в левой
части (*) квадратных двучленов отрицателен, то все эти двучлены
сохраняют знак (а именно, их знак совпадает со знаком а); поэто-
поэтому все неизвестные Xh Х2, ..., Хп должны иметь тот же знак, что и
коэффициент а уравнений — и сумма их не может равняться нулю,
т. е, наша система не имеет вещественных решений. Если Д = 0,
1—6
то правые части уравнений (*) лишь при хх = —„—(соответствен-
1— Ь\
но при х2 = хъ = ... *= хп = -п— I принимают значение 0 (а при
других значениях хх, х2, ..., хп они имеют тот же знак, что и чис-
число а); поэтому равенство X, + Х2 -\-... + Хп = 0 возможно лишь
1 — Ъ
при Хх = Х2 = ... = Хп = 0 и Х\ = х2 = ... = хп = 2а ¦ Нако-
Наконец при Д > 0 наша система имеет, по крайней мере, два разных
решения
* *
И "X ""~~~ " ™" • • • ¦"' "«, »— Лп j
1— Ь ± У A— бJ — Аас
где ^1,2 = Та •
256. Рассмотрим отдельно два случая.
1°. п четно. Перемножив «нечетные» (т. е. 1-е, 3-е, ...
..., (п— 1)-е) и «четные» уравнения нашей системы, получим:
...х„ = аха3а5... ап-х и xtx2x3 ...xn =
283
откуда ясно, что при аха3аъ... а„_, Фа2а4ав...ап система вовсе не
имеет решений. Если же a,a3as • •. O-n-i = а2а4ав ¦ ¦ ¦ я», то, приняв
значение х1 каким угодно (конечно, отличным от 0), мы затем
из 1-го, 2-го, . ., (п — 1)-го уравнений системы последовательно на-
находим:
Х2 ==
Подстановка всех этих значений в последнее уравнение показывает,
что оно тоже удовлетворяется.
2°. п нечетно. -Разделив произведение «нечетных» A-го,
3-го, ..., я-ro) уравнений на произведение «четных» уравнений, по-
получим:
fi2o4
п_1
f aia3o:, ...an
(напомним, что все at положительны). Далее из 1-го, 2-го, ...
..., {п— 1)-го уравнений последовательно находим:
1
„ > Х3
Л1
Проверка показывает, что при этом в силу (*) удовлетворяется так-
также и последнее уравнение системы.
Ответ: 0, если п четно и а{а3... ап-Х Ф а2а4... ап; бесконечно
много, если я четно и ata3... an-i = Й2Й4 • • • о„\ 2, если п нечетно,
257. а) Заметим, прежде всего, что если х0 является корнем
уравнения, то — х0 есть также корень. Следовательно, отрицатель-
отрицательных корней столько же, сколько и положительных. Далее, число О
есть корень уравнения. Таким образом, нам достаточно найти число
х
положительных корней. Отметим теперь, что если щ >=sinA:,
то
|х| = 100|sinx| sg 100- 1 = 100.
Мы получаем, что корень уравнения по абсолютной величине
больше 100 быть не может.
Разделим участок оси Ох от х = 0 до х = 100 на отрезки
длиной 2я (последний отрезок может иметь меньшую длину) и под-
подсчитаем число корней нашего уравнения на каждом из этих отрез-
отрезков. Обратимся к рис. 29.
На первом отрезке' (от 0 до 2я) имеется один положительный
корень (и один корень нуль), на каждом следующем, исключая
последний, — по два корня. Для того чтобы определить число кор-
100
ней на последнем отрезке, оценим его размеры: -^ заключается,
/100 100
очевидно, между 15 и 16 l-jg- =* 6,66 .... > 2л; -jg- = 6,25 < 2л
следовательно, всего мы имеем 15 отрезков длиной по 2я и одни
неполный отрезок. Длина этого последнего отрезка равна 100 —
— 15 • 2я > 5 > я; следовательно, на этом отрезке целиком пом;-
284
шается положительная полуволна синусоиды и, значит, на нем
тоже имеются два корня.
Итак, всего мы имеем 1 + 14 ¦ 2 + 2 = 31 положительный ко-
корень нашего уравнения. Столько же имеется отрицательных корней,
и еще один корень равен нулю.
Окончательно общее число корней равно 31 -2+1 =63.
Рис. 29.
б) Решение этой задачи аналогично решению задачи а).
Прежде всего очевидно, что если sin х = lg х, то х sg 10 (в про-
противном случае левая часть нашего равенства не больше 1, а пра-
правая— больше). Так как 2 • 2я > 10, то на участке оси Ох от х =
= 0 до х = 10 помещаются одна полная волна синусоиды у =
= sin х и часть следующей волны (рис. 30). График y — \gx,
Рис. 30.
очевидно, пересекает первую волну синусоиды в одной точке. Далее,
л ' 5л
так как 2л +~?р < 10, то в точке х = -у- имеем sin х = 1 > \g x
и, значит, график у = lg .v пересекает первую половину второй по-
положительной полуволны: так как lg х = 1 > sin х в точке х = 10,
то он должен пересечь и вторую половину этой полуволны. Таким'
образом, мы заключаем, что уравнение sin x = lg x имеет всего
три корня.
258. Сложив левые части всех, наших неравенств, мы получим
сумму чисел а.\, а2, ..., а99, Ото, каждое из которых берется с коэф-
коэффициентом 1 + (—4)+3 = 0, т. е. число 0. Но если сумма 100
неотрицательных чисел равна нулю, то все эти числа равны нулю;
таким образом, наша система неравенств реально обращается
в систему равенств:
а, — 4а2 4- За3 = 0, а2 — 1а3 4" Зй4 = D,
аюо — 4ai 4-
о,
285.
которую можно также переписать следующим образом:
а, —а2 = 3(а2— а3), а2— а3 = 3(а3 — а4), а3 — а4 =
= 3(а4 — as). ..., Оэ9 — аюо = 3(аюо — а,), аюо — 01 = 3@, — а2).
Теперь последовательно получаем:
а, — а2 = 3(а2 — о3) = 32(а3 — с4) = 33(а4 — а5) = ...
... = 3"(aloo-a,) ==31ии(О!-а2).
Но из равенства а\— о2 = 3100(ai — a2) следует, что а\—а2 = 0;
1 1
поэтому и а2— аз=~з~(а1 — as)= 0, и аз — а4 =~о-(Я2— из) =
1
= 0, ..., и аюо — о.\=- ~ (аээ — аюо) = 0.
Таким образом, все наши числа аи а^ ..., авэ, aioo равны между
собой; поэтому, если a{ = 1, то и а2 = й3 = ... = аюо = Ь
259. Первое решение. Перепишем наши неравенства сле-
следующим образом:
А =— a — b + с + d >0,
В = ab — ac — ad — bc — bd + cd>0, (*)
С = abc + аМ — аса1 — bed > О,
и рассмотрим уравнение
Р(х) = (x-a)(*-6)(x + c)(*+d) =
= х4 + Лх3 + Вх* + Сх + abed = 0.
Поскольку все коэффициенты этого уравнения в силу неравенств (*)
и положительности чисел а, Ь, с, d положительны, то оно не имеет
положительных корней (при х > 0 и Р(х) — х4 + Ах* -j- Bx2 -\-
+ Сх + abed > 0); но, с другой стороны, уравнение Я(л) ==0 име-
имеет даже два положительных корня х = а и х = Ь. Полученное про-
противоречие и доказывает требуемое утверждение.
Второе решение. Из первых двух неравенств задачи сле-
следует, что
(a + by(c + d)<(c + d){ab + cd), или (а + Ь)*< ab + cd (••)
(ведь с + ^ > 0); аналогично, из двух последних неравенств полу-
получаем:
(а + bJ{c + d)cd < (ab + cd) (e 4- d)ab, или
(a4-6J«f <(ab + cd)ab. (***)
Но так как (а + b)'*—\ab = (a — 6)*3s 0 и, значит, (а + bJ^ 4ab,
то из неравенств (**) и (***) следует:
4ab < ab 4- cd и 4abcd < (a& + cd)ab,
т. e. ed > 3ab и 4cd < ab -\- cd, или ab > 3cd,
— но невозможно, чтобы одновременно было cd > ЗаЬ и cd < -g ai.
286
260. Так как, очевидно,
B - у 2 + j/~2 + Vi + ... +К2) X
п радикалов
X B + у 2 + jA + V2 + ... + У 2) = 2= —
н радикалов
B+1^2 +/2+...+ >^2) =2-1^2 4-/2+ ••• + V 2 ,
. п—1 радикалов п—1 радикалов
то фигурирующая в условии задача дробь равна числу, обратному
выражению
#n = 2 + |/ 2 + ]/ 2 + . . . + У 2 ;
n—1 радикалов
таким образом, остается лишь показать, что Rn < 4. Докажем это
методом математической индукции. Ясно, что R\ =
¦= 2 < 4 и что
если ^n_t<4, то и Rn=2
Примечание. Нетрудно видеть, что lim Rn — 4; в самом
деле последовательность Rn имеет предел, так как она ограничена
(#„ < 4 при всех п) и монотонно возрастает (Rn+\ > Лп, ибо Rn + \
получается из Rn, если под знаком последнего радикала заменить 2
большим числом 2 + ]^2); положив lim Rn = R = г2 и устремляя
п в соотношении #n + i = 2+VRn к бесконечности, получим в преде-
пределе: гг = 2 + г, или B — г) A + г) =0, т. е. г = 2 (ведь л > 0) и
R — 4. Отсюда следует, что при п-*¦ <х> предел выписанной в условии
задачи дроби равен -г-; поэтому улучшить данную в условии задачи
оценку нельзя.
261. Пусть а, 6, с — данные числа; так как abc =1, то с = -т.
Второе условие задачи утверждает, что
а + 6 + с>Т + Т + Т- или a + b + ^> + +b О
но неравенство (*) можно преобразовать так:
или
287
Талим образом, неравенство (*) равносильно следующему:
Поэтому из трех чисел а— 1; ft—1 и— — 1( = с— 1) имеется чет>
ное число отрицательных; другими словами, две из этих разностей
отрицательны, а третья положительна, что нам и требовалось дока-
доказать, fЯсно, что все три разности положительными быть не могут,
ибо если а >• 1 и Ь > 1, то заведомо с = —. <1 и, значит, разность
262. Ясно, что числа 1959 и 1000 в формулировке этой задачи
являются случайными — факт, который нам требуется доказать,
состоит в том, что если все а% > 0 и ^а^ = aj + о.2 + ... + ап = 1,
п
то сумма Sn ч= ^ aiai а., всевозможных произведений
4Uift=i ' '"' li
no k из п наших чисел (где 1<6<л) всегда ^1, причем, если
k > 1, то эта сумма строго < 1. Доказать это можно, например, м е-
тодом математической индукции по числам п и k. Ясно,
что при я = 1 и при я = 2 утверждение задачи справедливо; далее
предположим его уже доказанным для всех п, меньших данного,
а для этого п — справедливым для всех k, меньших фиксирован-
фиксированного k ^ 2 (при любом я и k = 1 утверждение задачи тривиально).
п
Рассмотрим теперь сумму Snh = _ 2 . _ att ас, ... aik.
Выделяя в этой сумме все произведения, содержащие множитель а",
получим:
п—1
•Vfc=. . Zi .ачач •¦¦ aik-ian +
n—i
где Sn-\,k-\ и Sn_1? s — суммы всевозможных произведений по
k — 1 и k сомножителей из чисел а,, а2,..., ак-\. Но сумма этих
последних п— 1 чисел равна
<*i + "а + • • • + ап-\ = (fli -f- a2 + ... -f а„_, -f а„) —я„ = 1 — а„.
Заменим теперь числа аи а2, г.., a,,_i числамиа'4 =,—-^—, а'2 =
а2 . »-1
= 1 _а . ¦••. en_i = 1 _а , сумма которых уже равна 1; суммы
п п
же всевозможных произведений по k—1 и по k из этих новых
п— 1 чисел мы обозначим через Sn__l k ^ и Sn i k По предполо-
предположению индукции, Sn_lift_j < 1 и Sj,_i h <1; с другой стороны,
в силу пропорциональности чисел а'{ и а,- (где 1 = 1 п— 1),
очевидно, имеем:
Sn_iih_i = S;_1>ft_, -A - aj"-1 < A - ап)к~1
и 5n_1>ft=S;i_1,ft-(l-an)ft<(l-Onf.
Теперь окончательно получаем:
¦— что и требовалось доказать.
263. При N == 2 мы имеем лишь одну пару удовлетворяющих
условию задачи чисел т и я, а именно, m = 1, /г = 2; здесь «сумма»
11
52 рассматриваемых дробей—^ — -у. При N — 3 таких пар чисел бу-
будет уже две (пары т = 1, /г = 3 и m = 2, п = 3); сумма s3 рас-
рассматриваемых дробей здесь«3 =^у7з + 2~3=Т' Д°кажем теперь, что
для любого натурального N > 1 интересующая нас сумма sN рав-
равна о'
Так как для N = 2 и iV = 3 сформулированное утверждение
верно, то мы можем воспользоваться методом математиче-
математической индукции. Предположим, что некоторая суммаsN_i= -к-;
1
докажем, что тогда и s<\ = ~п~. Ясно, что суммы sN-j и slV связаны
^следующим образом: для получения из суммы Sw-i суммы Sn надо,
с одной стороны, исключить все слагаемые суммы s,v-i, имеющие
1 1 N
вид —, где m + п = N, т. е. имеющие вид . ,., -,1' (здесь 1< i •< -к-
mn l \" li z
и числа i и N—(' взаимно просты). С другой стороны, к сумме
Sa---i надо прибавить всевозможные дроби вида -jjj, где 1 ^ / < N
и числа ] и N взаимно просты. Но так как для каждого I
1 J_ 1
i (N — i) = iN + (N — i) N
и числа ;', N — i взаимно просты тогда и только тогда, когда взаимно
просты i и N, а значит и N — I и N, то сумма sx получается из сум-
суммы Sn-i исключением ряда дробей вида • /д, •> и добавлением
вместо каждой такой дроби «компенсирующей» ее суммы дробей
11 / 1
Ш + (N — О N' ПОЭТОМУ sjv = siv-i [^ Т
264. Мы утверждаем, что все наши 1973 числа одинаковы. В са-
самом деле, пусть, это не так и, скажем, at = аг = аз =.. . = а;=^=аг+1.
Для простоты перенумеруем наши числа циклически, присвоив номер
1 числу ui, номер 2 — числу aj+i, и т. д.— вплоть до числа flU-i
19 Д. О. Шклярский и др. 289
которое теперь получит номер 1973. Итак, далее мы будем считать,
что наши числа не все равны, причем at Ф а2, например а\ > а2
(случай а\ <а2 рассматривается аналогично).
Ясно, что из выписанных в условии задачи равенств следует,
что либо все рассматриваемые числа больше 1, либо все Они меньше
1, либо, наконец, все эти числа равны 1. Но в последнем случае все
числа ah (где k= 1, 2,..., 1973) равны между собой, поэтому нам
остается рассмотреть два других случая.
1°. Все числа a.k больше 1. В таком случае
из а"* = а?' и aL > а.г следует, что
из а^—а^' и а2<а3 следует, чтэ a:t> ai;
из а?,4 = а"' и о3>о4 следует, что
Таким образом, мы имеем:
а{ > а2 < аъ > а4 < а5 • • •
Полученное противоречие а\ > а2 и at <. а2 и доказывает, что в слу-
случае Г обязательно at = а2 = а3 = ... =0,973.
2°. Все чирла а меньше 1. В этом случае
из аахг = а^3 и ai>a2 следует, что а-г'У а3\
из а1?;'= а%' и аг> an следует, что
Таким образом, здесь мы имеем:
а\ > аг > аъ > а4 > • • • > «1973 > сц.
Полученное противоречие а{ > at показывает, что и в этом случае
все ak обязательно равны между собой.
265. Предложение задачи является справедливым при п = 1 и
п = 2, ибо
*? + *§ = 1 + 1 =2, x1 + %=6,
*2 + х\ = (*! + *2J - 2^!Л:2 = (бJ — 2-1 = 34.
Далее мы имеем:
или
290
"'
Из этой формулы прежде всего следует, что если я" -\- х1^
и х™ + я™— целые числа, то и х™ -|- х7^ — целое число, откуда, в
силу принципа математической индукции, вытекает
первое утверждение задачи.
Пусть теперь п есть первое натуральное число, такое,
что х^ -[- ^делится на 5. Из формулы (*) следует, что в этом слу-
случае разность [х™~1 4" х\ ) ~~\хл Н~ Х2~ )также должна делить-
делиться на 5. Но, заменив в" формуле (*) п на п— 1, мы получим:
(*Г2
откуда следует, что
„п—з _| „те—з
"—2 , ,.п—2\ [¦/,« —1 , „п —1\ / п—2
2\]
тоже должно делиться на 5, что противоречит предположению о том,
что для всех чисел т, меньших п, х™ + х™ не делится на 5. От-
Отсюда следует, что такого целого положительного п, для которого
х? "Ь х\ делится на б, вовсе не может существовать. Легко видеть,
что утверждение задачи верно и для целых отрицательных п: если
п < 0, то
vn _| „и | ' г „—п |^ —п
Л1 "г-*2 ~ v—» "г v—п ~ ~xl "Л2
* *2
— целое число, не делящееся на 5, так как —п > 0.
266. Предположим, что сумма а, 4- а2 4- • • • + аюоо содержит п
положительных и 1000 — п отрицательных членов. В таком случае
все попарные произведения п положительных членов (их, очевидно,
будет о ) и все попарные произведения 1000 — п отрицатель-
г I
I A000 — п) A000 — п— 1)\
ных членов (их число равно 9 будут по-
положительными, а произведения положительных членов на отрица-
отрицательные (их будет пA000 — п))—отрицательны. Условие задачи
требует, #чтобы было
п{п-\) A000-я) A000-я-1)
2 4- 2 = " A00° —")>
или
п2 — п 4- (Ю00 — «J — С 000 — я)
2
999 000
2л2-2000я 4-—2— =0-
1000 + У\ 000 000 — 999 000 1000 ± /ГООО
п = 2 ' = о •
а это, очевидно, невозможно.
19* 291
В случае второго выражения мы, рассуждая аналогично, при-
придем к условию
1QOQO + V10 000 10 000 + 100
n= : 2 = 2
Отсюда следует, что это выражение может содержать равное число
положительных и отрицательных удвоенных произведений; для этого
10 000+ 100
достаточно, чтобы исходный многочлен содержал jj = 5050
10 000— 100
положительных членов и s = 4950 отрицательных (или
5050 отрицательных членов и 4050 положительных).
267. Прежде всего имеем:
(/2 — 1 J - 3 - 2 У 2 = /9 - /8.
Докажем теперь, что если только
(У 2 — IJ* =ВУ2 — А = УШ —
можно представить в виде^Л' —У N — 1, т.е. если 2В2— А2 = 1,
то и число
(/2-1Р+1 = В'/2-Л'
можно представить в гаком виде, т.е. 2В'2— А'2 = 1. Для этого
достаточно заметить, чтл
(У2- lJ^1 = (У2- IJ* (/2- IJ =
^= (В У 2 - Л) C - 2 /2) = (ЗВ + 2Л) /2 - DВ + ЗЛ);
следовательно,
В' = ЗВ + 2/4, А' = 4В + ЗЛ
2Л)?— DS + ЗЛJ =
*= 18 S2 + 24 ЛВ + 8 Л2— 16 В2 — 24 АВ — 9 Л2 =
что и требовалось доказать.
Точно так же показывается, что если число()/Л2 — \)~h= С — D \ 2
можно представить в виде^Л1 — Уы — 1, то и число()/' 2— lJfc+2=
= С — Dy2 можно представить в таком виде.
Отсюда, в силу принципа математической индукции, вытекает
утверждение задачи.
268. Если (Л + В УзТ = С + D /3~, то С = Л2_+ ЗВ2, D = 2ЛВ
и (А — В узJ = Л2 + ЗВ2 — 2ЛВ Уз = С — ?> ~|/3. Следовательно,
если бы было (Л + В "J/3 J = 99 999 +_ 111 111 "l/З, то было 'бы так-
также (Л—В 1/§J= 99 999—111 111 "]/з, что невозможно, так как
99^99 — 111 111~1/з меньше нуля, а квадрат каждого действительного
числа больше нуля.
292
269. Предположим, что -/ = р + q У г, и возведем обе части
этого равенства в куб. В таком случае получим:
2 = рз -f- 3p2q У~г + 3pq2r -f q*r У~г,
или
2 = p (p2 -|- 2,q2r) + q Cp2 + q2r) У7.
Покажем теперь, что если у = р + ^Т/г, то У2еоть рацио-
о _
н а л ь н о е число. Действительно, если q = 0, то \/~2 = р есть
рациональное число. Если q ф 0 и Зр2 -)- ^ ?= 0, то из последнего
равенства следует
v q (Зр2 + 92r) '
откуда
3r- , 2 - р (р2 + 3<?V)
^ - ^ -г v ? Cр2 + 92Л) ,
т. е. опять рационально. Если же Зр2 + q2r = 0, то
и опять у 2 = — 2р есть число рациональное.
Таким образом, нам остается только показать, что у' 2 не явля-
является рациональным числом. Это доказательство хорошо известно.
3 — m m3
В самом деле, если у 2 равен несократимой дроби — , то 2 —-j-,
in3 = 2п3. Таким образом, число т3 (а также и т) есть четное число,
следовательно, оно делится на 8. В таком случае п3~ -^-тоже должно
быть четным, а следовательно, и п четно, что противоречит предпо-
т
ложенню о несократимости дроби —. Итак, предположение, что
у 2 = р -\- q У г, привело нас к абсурду.
п+ -\/пг _ 4
270. Обозначим „ = х\ в таком случае
J_
~ = п + yW^i = 4 = 2
так что х удовлетворяет квадратному уравнению х-\- — =п. Но
1 1
если число х + — —целое (= п), то числох"» + ^ —тоже це-
целое, что легко доказывается методом математической ин-
индукции: если считать уже известным, что все числа ai =
=х1 +—— при всех ( ^ N —целые, то и число aN+l =
293
__xw+i_[____—тоже целое, как это вытекает из следующей
X
выкладки:
откуда
Таким образом, обозначив хт = у, мы имеем у -f — = #,
где?(=йт)—натуральное число; решая это квадратное уравнение
k±~\/k- — 4
относительно «, получаем (/= , . Но так как число х =
I, то и jcm = у > 1, откуда и следует, что г/
1 k
271. Заметим, прежде всего, что вещественное число а не может
двумя разными способами быть представлено в виде суммы а =
х -f- у У 2, где х и у рациональны, ибо если а = а 4-йУ2=О]+
-\-Ь ЛУ2 (где а, Ь, аи Ь\ рациональны), то У2 = , , , что (в силу
рациональности разностей а — а{ и Ь, — 6 и иррациональности чис-
числа У2) возможно лишь при а = at и 6 = Ь^ Таким образом, из вы-
выписанного в условии задачи равенства, которое можно «развернуть»
по формулам бинома Ньютона:
(X + У У2) + {Z+T У1) =5 + 4 У2,
где
X =x2n + cllx2n-2-2y*+...;
Y = С\пх^i V3
и т. д., вытекает
Вычтя теперь почленно из первого из равенств (*) второе равен-
равенство, умноженное на }2, получим:
(X — Y У2) + (Z—T У2) =5 — 4 У2,
или {х-уУ2Jп + (г-1У2Jп = 5-4У2, (**)
которое, таким образом, обязательно должно выполняться, если
только имеет место выписанное в условии задачи равенство. Однако
294
из второй формы равенства (**) сразу следует его невозможность,
ибо здесь левая часть равенства положительна, а его правая часть —
отрицательна. Отсюда и вытекает, что и выписанное в условии за-
задачи равенство не может иметь-места.
272. Нельзя. В самом деле, пусть мы k\ раз переливали воду
из 1-й бочки во 2-ю первым ковшом и k% раз переливали тем же
ковшом воду из 2-й бочки в 1-ю; окончательно мы при этом перели-
перелили из 1-й бочки во 2-ю (k\—&2Я/2 = & ¦ /2 литров воды, где целое
число k = kx — k2 может быть и неположительным. Аналогично, пе-
переливая воду 1\ раз из 1-й бочки во 2-ю вторым ковшом и h раз
тем же ковшом переливая воду из 2-й бочки в 1-ю, мы всего пе-
перельем из 1-й бочки во 2-ю A\ — h) B -~1/2) = 1-\2— "[/2) литров
воды, где число / — целое; поэтому условие задачи требует выполне-
выполнения равенства k~|/2 + / B — "|/2)= 1, или (/ — К) "J/2 = 2/ — 1, т. е.
_ 21 1 _
~|/2 — , у . Но так как число у 2—иррациональное, то последнее
равенство может иметь место (при целых k и /), лишь если /— k ~
= О (т. е. I = К) и 21— 1 = 0, откуда/ = -^ , что, однако, невоз-
невозможно, ибо I—целое число.
273. Первое решение. В задаче требуется найти все ра-
рациональные решения (х, у) (где у ^ 0) уравнения Зх2— 5* + 9 =
= у2 с двумя неизвестными х и у (ср. с циклом задач 5). Очевидно,
что одно решение имеет вид х = 0, у = 3. Положим х = хи у =
= У\ + 3; тогда получим:
Ъх\ — у\ — 5*! — 6yt = 0.
Для всякого решения (хи yi), отличного от @, 0), — = —, где
m и п—взаимно простые целые числа, у\ = Xi- (mjn); следователь-
следовательно, имеем:
,, т2 .) ш
Щ — -^ х\ — 5*i — 6 Г xi = °.
5п2 + бтп 5п2 -р б'»"
или, поскольку х ф 0, хх = Эд3_от2 '¦ Формула х = Зд2 _ т2
и дает полный ответ на вопрос задачи (ответ х = 0 получается
при п = 0).
Второе решение. Если (х, у)—рациональная точка кри-
кривой второго порядка (гиперболы) у2 = 3х2—5л+9, то отношение
k ="~^—р ационально (может быть, бесконечно). С другой сто
роны, если k рационально, то прямая у = kx + 3 пересекает кривую
,п о, f6k + 5 3/г2 + 5? + Э\
в двух рациональных точках: @, 3) и I g ^2\ —g ^2— I. Отсю-
Отсюда следует, что все рааиональные точки кривой отвечают таким х,
6k + 5
¦"•o* = 3ZTp-
274. Пусть х2 + рх + д=0 и у2 + ру + q\ = 0 — исходное и
«округленное» уравнения, где \qi — q\ = |e| «0,01., Вычитая
295
нгорое уравнение из первого, найдем; (х2 — уг) + р(х — у) = q\ —
— g = е, или (л — у) (х + У + р) =в, откуда, обозначив через х{
и (/] близкие друг другу корни двух наших уравнений, а через х2—
второй корень первого из этих уравнений, так что — (xi + х2) = р,
получим:
1 У1 *' ~ I *i + </i + /»I ~ I 2х, - (х, + х,) | — | дсж — дс„ | - Д •
— что нам и требовалось доказать.
275. Ясно, что если среди наших чисел имеется несколько целых,
то их можно просто отбросить — ведь разность между суммой округ-
округлений любого количества чисел и суммой самих этих чисел не изме-
изменится от дополнения множества чисел еще какими-то целыми числа-
числами, а сумма чисел при этом увеличится; поэтому если утверждение
задачи верно для любых нецелых чисел, то оно верно и для
любых чисел. Обозначим теперь сами числа через оь а2,..., о»; их
целые части — через [а,], [о2],..., [ап]\ их дробные части {at} =
= fli — [ai] (где i = 1, 2,..., п) — через аь а2,. •., ап (ср. выше,
стр. 37); при этом условимся располагать числа так, чтобы их дроб-
дробные части не убывали:
О < й! sg a2 sg ... <а„<1.
Округлим теперь k первых чисел а, (здесь 1 ^ t ^ k\ выбор числа
k, где 0 ^ k :=С п, мы еще уточним в дальнейшем) до (меньших их)
чисел [а,]; оставшиеся же л — k чисел а,- (где А < / :=С /г) округ-
округлим до больших чисел [а,] + 1. Ясно, что ошибка при замене сум-
суммы чисел суммой их округлений будет наибольшей для сумм
а\ + в-2 + .. . +ah и a,J + 1 + O/.+2 + • ¦ •-f-On—в первом случае она
будет равна
а, + а2 + ¦ ¦ ¦ +ah < kak,
а во втором —
A—aft+1) + (I -ctft+2) +..•+(! — а„) «S (п — А) A
Таким образом, условие задачи будет выполнено, если к тако-
таково, что
я+1 я+1
/г«„<-1— и {n-k){\- a.h+i)^-^-.
Пусть теперь к — наибольшее из таких целых чисел, что^а^^
я+1 я+1
<—7—, или ah <^ д^ (это А может равняться и 0); оговорка о
том что число к — наибольшее возможное, ознаачет, что,
я+ 1
заменив номер k на й + 1, мы уже получаем aft+1 > J7^~X~n- Но
из последнего неравенства следует, что
/ п +1\ я + 1
Проверим, что (я — к)\ 1 — ^ (ft + П / ^ 4 ' Действительно, это
29Q
Неравенство равносильно неравенству
(п _ k) Dk — п + 3) ^ (n+l)(k+\);
последнее же равносильно очевидному, справедливому при всех п и
k, неравенству
[я — Bk + 1)]2> 0.
Примечание. Из решения задачи нетрудно усмотреть, что
при п = 11 -f- 1 нечетном улучшить оценку задачи нельзя (соответст-
(соответствующий пример мы получим, положив п[ = ai = ... ап =~о~, где-
очевидно, оптимальным будет вариант, когда мы I чисел заменим
нулями, а /+1 остальных — единицами или наоборот); если же
п = 21 четно, то величину (я-)-1)/4 в условии задачи можно умень-
уменьшить (почему- на сколько?).
276. Ясно, что при а < 0,001 округление а0 числа а равно 0,
а значит, и частное — (и любое округление этого частного) равно
0; поэтому далее мы будем считать, что а ^ 0,001. Но при этом,
разумеется, и а0 ;== 0,001, в то время как «погрешность приближе-
приближения» а = а — а0 < 0,001; поэтому интересующая нас дробь
,__«0_а — а j а
заключена между 0 и 1: ясно, что 0 < d ST 1. Далее из того, что
а < 0,001, а йо > 0,001, следует, что а < а0 и, значит, а + а = 2а <
а 1
< а0 + а = й, откуда — <С~гГ и поэтому
— вот эта оценка дроби d является уже окончательной, ибо отноше-
отношение б = — может принимать любое значение в пределах 0 sj 5 <
1 1
< ~(а значит, d —любое значение в пределах —^ < d < 1). В c:i-
мом деле, приняв й0 равным 0,001, мы получим, что дробь б =
= оТТ^ = О,ОоГ+ а • ОткУда
а = 0,001ГГгё; (**)
такое а при любом б I где 0 ^ б <^ -^-\ удовлетворяет неравенству
0 ==: а <С 0,001, а соответствующее а = 0,001 + а отвечает значению
d = 1—б. Ясно, что если б пробегает все значения между 0 и —,
то d принимает все значения от тр, цо 1, т.е. d может иметь любое
из следующих значений 0; 0,5; 0,501; 0,502; ...; 0,999; 1.
277. Рассмотрим 1001 число
0 • а = 0, а, 2а, За, ..., 1000а
297
й возьмем дробную часть каждого из ?тйх чисел (разность Между
данным числом и наибольшим целым числом, не превосходящим
данного). Эти дробные части будут представлять собой 1001 число,
не превосходящее 1. Разделим теперь отрезок числовой оси от 0 до 1
на 1000 равных отрезков длины щ^ (к каждому отрезку мы бу-
будем причислять его левый конец, но не причислять правый) и рас-
рассмотрим распределение точек, изображающих наши дробные части,
по этим отрезкам. Так как число отрезков равно 1000, а число то-
точек 1001, то, по крайней мере, в одном отрезке будут находиться
две точки. Но это означает, что существуют два таких неравных
числа р и q (оба не превосходящих 1000), что разность дробных до-
1
лей чисел ра и qa меньше
Пусть, например, p>q. Рассмотрим число (р — q)a = pa — qa.
Так как pa = P + d\, qa = Q + d% где Р и Q — целые числа, d\ и
^2 — дробные доли pa л qa, то (р.— q)a = (Р—Q) -f-^i— dt отли-
отличается от целого числа Р — Q меньше чем" на tKqq- Но это означа-
Р — Q 1
ет, что дробь отличается от а меньше чем на 0,001- .
278. а) Если число а меньше 1, то и "j/аменьше 1. Предполо-
Предположим теперь, что десятичная дробь, равная Т/а, начинается с мень-
шего числа девяток, чел 100; это означает, что~1/а < 1—I-j-q)
Возводя обе части последнего неравенства в квадрат, получим:
юо / 1 \200
но a<'-2Goj + (То
/ 1 N100 / I \200 / 1 N100 / 1 \ 100
1 - 2 (то) + (то) <' - (то) ; поэтому а <' ~ (Го)
и, значит, десятичная дробь, равная а, не может начинаться со 100
девяток.
б) Заметим, прежде всего что0,1Ш... 111 =-g- 0,9999.. .999=-§Х
100 единиц 100 девяток
/ / 1 \100N 1 1 /" /1 N100
Xll—(jqI |!таким образом, нам требуется оценить—у 1—\Тп) .
Далее мы ограничимся рассмотрением одной лишь задачи 4), из
результата которой вытекают и результаты остальных задач.
Известно, что при любом а<1 имеет место неравенство "]/l—а<
< 1 —- ~2~ а, поскольку 1 т? а\ = 1 — а + -j- а2 > 1 — а; поэтому
Too
jq) 1= 0,9999 ... 9995^..
\ 100 девяток /
Й98
Уточним эту оценку — найдем два таких положительных числа
и с2, что
1 / 1 уоо / 1 \200
Т [То) ~ Cl [Щ >
yob 1/,\юо
-To >i-t(to/ -'
Возведя в квадрат все члены двойного неравенства
1
200
1 —~2 а — 1
—а>1—-й-а —
получим:
l+-^a- + qa4— a — 2Cla2+c,a3> 1 — а>
> 1 + -j- а2 + с|а4 — а — 2с,а2 + с2а3,
или, вычитая из всех частей неравенства 1 — а и сокращая затем
- 2сЛ + сга
0> [т -
/ 1 N100
Нас интересует случай a=(m) ; покажем, что здесь можно,
11 /1 \ Ю2 1 ,
+ 0125 + I i
11 /1
например, принять су =-g- + Jqq a = 0,125 + Jq
и с3 =-
1 / 1 N101
a ~ 0,125+ \jq\ . Дсйсгвитслыю, при любом a>0
KJ
1 1
T+Too
1 1
T+Too
_1_ 1
IF + HX
I 1
с другой стороны, при а = I щ I
}__ ./ 1 . 1 \ . / 1 . 1
10'
/1 1\ 3/iyoo
поскольку I-?-—-g-1 a = Tg I Jq I явно больше последнего члена
/I I \ 37 37/1 \200
неравенства, близкого к \т0 + Щ а'^ Ш ф ^320 (loj *
299
Таким образом, мы имеем
1 /IV00 /' / 1 \102\ / 1 \200
1~Т ТО - °>125 + ГО ГО
2 То - °>125 + 1То Го
V У ^ К 1 l\ I Г 1Q0 цифр
1 / I \1ОО / / 1 \101\ / 1 \200
>'-t(ToJ ~[°'125 + [То) )[п) ¦
Последнее двойное неравенство можно переписать так:
I / Т\ loo
0,9999 ... 99949999... 9998749999...999 > J/ 1 —(То) >
100 девяток 99 девяток 99 девяток
> 0,9999 ... 99949999 .. . 9998749999 .'.. 999,
100 девяток 99 девяток 98 девяток
откуда, деля на 3, получаем, что с точностью до 301 знака после
запятой
0,1111 . .,111^0,3333.., 33316666 ..". 66624999... 999.
100 единиц 100 троек 100 шестерок 98 девяток
279. а) Обозначим 1,00000000004 через a, a 1,00000000002 —
через [3. В таком случае фигурирующие в условии задачи выражения
примут вид i + a"a2 и TTJ~FW
1+а 1 1 1
1 + а - • { а?
» + и
¦
Так
1
Р
\
Р
как
1
+ Р
Р2
а
+
>
Р
- 1
1 +
Р,
+
Р
то,
Р'
+
очевидно,
Р2
1 + а -1Т1+а/1Т1>[|- 1+Р
и, наконец,
1 + a + а» - ' • ^ 1 + а /^1-\ 1 + Р
Таким образом, второе из двух выражений больше первого.
б) Обозначим фигурирующие в условии задачи выражения со-
соответственно через Л и В. Тогда, очевидно, имеем:
А 1 + 1+й + а2+ ... + ап~1
= • + l + a + «2+...+Q«-1 = l + I f
a"
1 - 1
T = i + —-j- у-
ъп + ьп-1 + ¦¦¦+ Ь
300
an ^ „n—i I" ¦ • • г а
Отсюда сразу следует, что ~г > ~к н, следовательно, В > А.
280. Будем исходить из формулы
Следовательно,
[(X - а,J + (X - а2J + ...+ (*_ а,,J]
... +а„) A-х
+ о2 + . .. + ап
х + 2 +
Если положить в последнем выражении х =
то оно будет положительным; действительно, мы будем иметь:
[(X - а,J + (X ~ о2J + ... + (X - а,,J] -
Отсюда вытекает, что искомым значением х является
281, а) Мы имеем всего три существенно различных располо-
расположения:
Г. а,„ а2, аь, а4:
Ф, = (а, —а2)*+ (а2-й3J+ (а3-а4J+ (Qi-a,J.
2°. ai, о3, 02, 04:
Ф2= (Ol-a3J-f (a3-a2J+ (а2-а4J+ (а4-й,J,
3°. di, u2, Q4, a3:
Ф3= (ai-a2j2+ (й2-й4J+ (а4-а3)г+(а3-й,J.
Но легко видеть, что
Фз — Ф| = — 2a2«4 — 2а,а3 + 2а2а3 +
= 2(о2-а,)(й3-о4) <0;
ф3 — ф2 = — ?а,а2 — 2а3й4 + 2а2а3 +
й1) (а2 — а4) < 0.
Следовательно, требуемое расположение имеет вид: аь а2> а4, аз.
б) Первое решение. Рассмотрим выражение
Ф = (aU ~ аЧ
К - <Ч)Ч • • • + hn_i - ain
где О; , ai2..., ai —наши п чисел, расположенные в требуемом
30J
порядке. Пусть аг , а. , (а < E) — какие-то два из этих чисел. Мы
утверждаем, что если aia б о л ь ш е (или наоборот меньше)
а., то а% больше (соответственно меньше) ej» , (')'
Действительно, если бы это было не так, т. е. если бы было
/а. —а. \ fa. —а1ал.Л<--^' то перестановка, изменяющая поря-
порядок чисел аг , ах , аг ,2 ащ на обратный, уменьшила бы
величину суммы Ф, так как разность новой суммы Ф' и первоначаль--
ной суммы Ф будет, очевидно, равна
Ф' — Ф = — 2а.
Uir,-i
Это замечание позволяет получить полное решение задачи.
Прежде всего, так как циклическая перестановка всех чисел (т. е.
перестановка, при которой сохраняется порядок чисел, выписанных
одно за другим по кругу) не меняет величины суммы Ф, то мы
можем считать, что а{ есть наименьшее из наших чисел а;, т. е. ii = 1.
Отсюда можно вывести, что а ( и a/^есть два следующих по величине
числа. Действительно, если тбы было, например а^ <Са<г{р ф п), то
мы имели бы 1а^—ai«)(ai,—aia i) < 0, а если бы было а{ <
а( ($ Ф 2), то мы имели 6u[ai1~aio_l)(ain —aia\<^ ¦ Так как
можно изменить порядок следования в цепочке а^, a^, ai , ..., at
ai, на обратный без того, чтобы изменить сумму Ф, то мы можем
считать, что а^ < at , /2 = 2, '„ = 3.
Далее мы утверждаем, что числа a;3, «in_i следуют по величи-
величине за уже использованными числамиа^, aJ2, ai действительно, если бы
было, например, aif^> а{ ($ ф 1, 2; п — 1, п), то мы имели бы
[аг3 aip) [aU a«p+iJ<0. А так как, кроме того, должно быть
()()>0<
()()
Точно так же показывается, что числа а; и а, —следующие
по величине за уже использованными и ai < ai (т. е. D = 6,
in-2 = 7), что числа aif и аг —следующие по величине заранее
использованными и-a; < fl| (it =8,in— з = 9J, и т.д. Окончатель-
но приходим к следующему расположению чисел:
при п = 2k четном at{ >on
Чйз — о5 — а7— ... — ап_{
,аг — а4 — ав — ... — ап_1
при п — 2k -f- I нечетном аУ j
хй3 —а6- в,— ...—ап
') Здесь мы условно считаем. а{ = а{ .
302
(черточки указывают порядок Следования чисел; так, например,
для п четного имеем расположение а\, аг, о4, а6.. , а„_2, а„, an-i, ¦ ¦.
..., а7, о5, и3) •
Второе решение. Если каким-либо образом догадаться,
что искомое расположение имеет такой вид, как указано в конце
первого решения, то доказательство этого факта можно получить
при помощи метода математической индукции. Действительно, при
я = 4 доказательство получается весьма просто (см. решение зада-
задачи а)). Предположим теперь, что для какого-то четного п мы уже
доказали, что сумма Ф„, соответствующая выписанному в конце
первого решения расположению чисел О| < Ог < о3 < ... < ап,
меньше суммы Ф'п, соответствующей любому другому расположе-
расположению. Покажем теперь, что сумма Ф„ + ь соответствующая выписан-
выписанному выше расположению п + 1 чисел п\ < йг < Оз < ... < ап <
< яя + |, меньше суммы Ф'п+ь соответствующей какому-либо друго-
другому расположению п + I чисел. Имеем:
Ф„ + , — Ф„ = (а„- оп+,J+ (ап + 1 — а„_,J — (ап - а»_,J =
= 2о2п + 1 — 2а„ап + 1 — 2й„_1оГ1 + 1 + 2а„_1а„ =
== 2(on + 1 — an)(an+i — an_i).
С другой стороны, если в расположении, отвечающем сумме
Ф„_)-1, число а„+! стояло между какими-то числами аа и ар и Ф„
отвечает расположению га чисел, которое получается из расположе-
расположения л+1 чисел, приводящего к сумме Фп ^_() вычеркиванием числа
fln+l, TO
Ф;+1 - Ф; = (аа- an+lf + {an+i - a&f - (аа - atf -
= 2on+l - 2aaan+i ~ 2%an^ + iaaat ==
= 2 (an+1 - fla) (an+1 - а3) > Ф„+1 - Фп.
Таким образом, мы видим, что
(первая скобка неположительна в силу предположения индукции,
вторая — по доказанному). При этом, если сумма O?i_j_j, отличается
от Фи + i, то либо Фп — Фп < 0 (и, следовательно, Фп+1 — Ф^.1<
< 0), либо (Фп+1 —ФП)— (ф'п+i — ф'„) <° (и. следовательяо,
опять Фп+1 < Ф„_|_1]-Аналогично осуществляется переход от л к
л+1, если п нечетно.
Третье решение. Задача имеет также несложное геомет-
геометрическое решение. Изобразим числа at < а% < о3 < ... <.а„ точка-
точками Аи Аг, А3,..., А„ на числовой оси; отрезки ЛИг, А2А3, A^At
. .. Ап~\Ап обозначим соответственно через di, d2, d3 dn-i- В таком
случае сумма Ф = {аи-аи)*+(аи-аи)*+... + [а^^ - a.J2 +
+ {ain-*bJ=A\A\+AiAl + ... + Ain_lA\n+AinAlv*m»
сумме квадратов длин звеньев «ломаной» AiAifAi ... Ai Ai Л^
(все звенья которой л«жат на одной прямой; рис. 31, а)).
' 303
Так как наша замкнутая ломаная покрывает весь отрезок /4]/4п,
то каждый из отрезков AhAk+i = dk минимум два раза входит в
нашу ломаную (один раз в направлении от Ан к Аь+\, второй раз —
в обратном направлении). Поэтому, в каком бы порядке мы ни рас-
располагали точки, сумма Ф, если выразить ее через отрезки d\, d2 . ¦ ¦
..., dn-i и раскрыть скобки, обязательно содержит член2с(?, а следо-
следовательно, и все члены 2rfj, 2d2 2d^ j. Далее, пусть Ak-\Ah —
= dk-i и AkAh+i = dk — два соседних из рассматриваемых отрезков.
Очевидно, что если звено ломаной, покрывающее отрезок АиАь+\ в на-
направлении от А к к Ad+i, начинается в точке Ah, то звено, покрывающее
этот отрезок в обратном направлении, не может кончаться в точке
Ah', поэтому во всех случаях должно существовать звено, которое
покрывает одновременно отрезки Ak-\Ak и АкАь+\. А отсюда выте-
вытекает, что сумма Ф во всех случаях должна содержать член 2*4-А,
а следовательно, и все члены 2did2, 2d2d3 2dn_2dn_i.
Теперь остается только заметить, что в случае, если расположе-
расположение точек таково, как указано в конце первого решения задачи, то
Ф = 2d\ + 2d\ + ... + 2dl_i + 2dxdi + 2<Мз + ¦¦¦+ 2dn_2dn_l
(рис. 31, б)). Отсюда и из сказанного выше вытекает, что в этом
случае сумма Ф будет наименьшей.
282. а) Отметим, прежде всего, что мы с самого начала можем
считать все оь аъ ¦ ¦ •, а«; b\, b2,..., bn положительными; в против-
противном случае мы изменили бы знаки отрицательных чисел на противо-
противоположные: левая часть неравенства при этом не изменится, а правая
может только увеличиться. Рассмотрим теперь ломаную А0А\А2. . .
...Ап, такую, что проекции отрезков ЛОЛЬ Л[Л2, ..., Ап-\Ап на ось
Ох равны соответственно а1у а2 ап, а проекции этих же отрез-
отрезков на ось Оу — &ь Ь2,. ¦., Ьп; при этом пусть каждая вершина ло-
ломаной расположена правее и выше предшествующей (рис. 32). В та-
таком случае из теоремы Пифагора следует, что
--- A,_iAn
AQAn = У(п1 + аг+... + anf + (й0 + b, + ... + bnf,
откуда и получается неравенство задачи.
Ломаная Л0А1Л2...Л„ будет равна отрезку А0Ап только в
том случае, если все звенья этой ломаной являются продолжениями
одно другого (ломаная является отрезком прямой). Нетрудно ви-
видеть, что это обстоятельство будет иметь место в том случае, если
ЗС4
-г
<Ц п
= т~ = ... =т~; лишь в этом случае имеет место равенство
б). Обозначим через h высоту пирамиды, через оь а2,
стороны основания (а{ -\- п2 + ¦.. -\- ал = Р) и через Ь\, й2,
.., ап
У,
т
&
/
К ап И х
Рис. 32.
длины перпендикуляров, опущенных из основания высоты на сторо-
стороны основания I -g- aib1 + -у «'А + • • • + ~2" ап*п = S I. В таком слу-
случае боковая поверхность 2 пирамиды будет равна
Т а, ]Л? + А* + "г" о* |Л| + Л2 + • •. + у *„ ]/ ^
Но согласно неравенству задачи а)
2 2 = У(^ЛРТТ^Г2 + У(а2й,J + (a.J,f + ...
причем равенство достигается только, если а,Ь{ : аф2: ... : anbn =
= a\h : a2h : . . . : anh, т. е. Ъ\ — Ь2 = .. . = Ьп.
Отсюда и вытекает утверждение задачи.
283. Рассмотрим отдельно случаи п четного и п нечетного.
1°. Число п четно. Построим ступенчатую ломаную
'АхАъАъ ¦ • ¦ АпАп + 1Ап+2 так, чтобы длины всех отрезков AtA2, Л2Л3,
Л3Л4, ..., An+iAn+2 равнялись единице и отрезки А\А% А3А4,
AsAe An-iAn, An+lAn+2 были бы параллельны между собой и
20 Д. О. Шклярский и др.
305
перпендикулярны к отрезкам А2А3, AtAs Л„/4„+! (рис. 33; на
нем п = 4). На каждом из отрезкив Л.Л.-и ('= 1, 2, ...,'л+1)
или на его продолжении возьмем точку Bj так, чтобы длина отрезка
BiAi+i равнялась ai(an+\ мы полагаем здесь равным а\, т. е. Bn+i
выберем так, чтобы было Bn+iAn+2 = at); при этом точку В,
мы будем располагать левее или ниже точки Л"-м> если а> > 0> и
Рис. аз.
правее или выше точки Л(+ь если о,- < 0 (нэ рис. 33 0 < а < 1,
О < аз < 1; Яз >1; о* < 0). Проведем теперь ломаную BiB2 ... Bn+i.
По теореме Пифагора
Но В,Л,ч-1
вательно,
а, и, как легко видеть, Bi+iAi+1 = |1 — о,-+1|; следо-
следоТаким образом, интересующая нас сумма
... + 1/"вп-1+A-вп)г +
равна длине ломаной В,В2Вз... Вп+1.
Очевидно, что длина ломаной BtB2B3... В„+1 всегда не меньше,
чем длина отрезка BiBn+i. Вычислим теперь длину этого отрезка.
С этой целью построим прямоугольный треугольник BfiBn+i
306
'{рис. 33). Тогда
= АА + АА + + AnAn+i
Bfi = АгАа + А,АЪ + ...+ AnAn+i = -j-
и
п
CBn_|_j = AtAz + AaAi + ... + An—jAn = 2
(ибо AiBt = Л„+1Вп+1 == 11 — a,\). Отсюда
Я \2 . / Я \2 «1/2
что и доказывает требуемое неравенство.
Теперь уже легко выяснить, в каком случае в этом неравенстве
знак ^ можно заменить знаком равенства. Для этого необходимо,
чтобы все точки Въ В3л.., Вп лежали на прямой BiBn+1 (т.е. В(
должно совпадать с точкой пересечения прямых BiBn + i и Л,Л, +1).
Так как прямая BtBu+i образует угол 45° с прямой Bfi (ибо В{С =
= CBn+i), то это будет при
Bi*42 = А2В2 = В3Л4 z== A$Bi = ... = Вп—\Ап => А пВп,
т. е. при о, «= A — а2) = а3 = (I — а4) = ... = an-i = A —яп).
Итак, при п четном равенство достигается при
где о может быть любым.
2°. Число я нечетно1). Положим an+i = Оь о„+2 =
= а2,..., о2п = ап и рассмотрим сумму
которая, очевидно, будет равна удвоенной сумме:
(каждое слагаемое этой последней суммы в первой сумме встреча-
2я у'2
ется дважды). Но по уже доказанному первая сумма< —к—>
отсюда вытекает, что
т. е. мы получили требуемое неравенство.
') Мы предоставляем читателю выяснить на примере п = 3,
почему доказательство, проведенное для четного я, не проходит для
я нечетного.
20» 307
Знак равенства в последнем неравенстве имеет место только,
если
= а3 = ... = а2п-! = 1 — а2 == 1 —
Л —а2п
(см. выше случай 1°). Но так как у нас а{ = оп+1 и п нечетно, то
последнее равенство возможно только, если
1
a1=u2 = ... =fln = -2-.
284. Первое решение. Обе части равенства положительны,
поэтому, возводя их в квадрат, получим:
1 - х\ + 1 - х\ + 2 ]/ (I - xf) A - xf) < 4 - {х\ + 2хЛ + 4)
2]/ A-х?) A-
/О
Возведем опять обе части в квадрат:
перенося все члены направо, получим:
Последнее неравенство очевидно; равенство здесь имеет место
лишь при х\ = х2. Отсюда вытекает, что исходное неравенство
всегда имеет место и обра-
У
N,
щается в равенство лишь при
A'l = Х2.
Второе решение. Эта
задача имеет и геометрическое
решение; аналогичные решения
можно найти и для многих зна-
значительно более сложных задач.
Введем на плоскости прямо-
прямоугольную декартову систему
координат и рассмотрим окруж-
окружность с центром в начале коор-
координат и радиусом, равным еди-
единице (рис. 34'). Координаты х,
у точек этой окружности будут
связаны соотношением
Рис. 34. Отмегим теперь на оси Ох
две точки М\ и М2, имеющие
абсциссы Х\ и х2; так как |х,| ^ 1 и |*2| ^ 1, то обе точки будут
расположены внутри (или на границе) единичной окружности. Вос-
Восставим в этих точках перпендикуляры к оси абсцисс до пересечения
их с верхней полуокружностью в точках N; и N2; тогда, очевидно,
308
M\Nx = У 1 — x\ и МгЫг =]/ 1 —x\. Заметим теперь, что абсциссу
Хх + X,
'—2—' будет иметь середина М отрезка MiM2'). Отсюда вытекает,
что величина
будет равна длине отрезка MN,
где N есть точка пересечения с окружностью перпендикуляра к оси
абсцисс, восставленного в точке М. Но сумма MiNr-}- M2N2 равна
удвоенной длине средней линии N'M трапеции M\N\NzMi, т. е. мень-
меньше, чем удвоенная длина отрезка MN. Тем самым нужное нам нера-
неравенство доказано; из доказательства видно, что это неравенство
обращается в равенство, лишь если точки Mi и М2 совпадают, т. е.
если Х\ =х2.
Рис. 35.
Рис. 36.
Примечание. Прием, примененный во втором решении за-
задачи 284, позволяет вывести много интересных неравенств. Так, на-
например, рассмотрим сферу с центром в начале координат и радиу-
радиусом 1 (рис. 35); и пусть Mt и М2 — две произвольные точки плоско-
плоскости Оху, расположенные внутри или на границе сферы, Nx и N2 —
') Это утверждение очевидно, если х,- и х2 положительны; легко
проверить, что оно остается справедливым и при любых знаках
Х\ и х2. (Заметим, впрочем, что приведенное в условии задачи нера-
неравенство достаточно доказать для положительных X] и х2: действи-
действительно, если Х\ и х2 неположительны, то, заменив эти числа их
абсолютными значениями, мы не изменим левой части неравенства,
а правую уменьшим.)
309
Точки пересечения со сферой перпендикуляров к плоскости Оху, вос-
восставленных в точках М\ и М% N и N'—точки пересечения перпен-
перпендикуляра, восставленного к плоскости Оху в середине М отрезка
М\Мг, со сферой и с отрезком NtN2. Если (хи yt) и (х2, у2) — коор-
координаты точек М, и М2, то -
MxNi = у • — x: — y\
MN =
- -к (MxNi JrMtNt)i
и из того, что AW ^ MN, вытекает, что
(*)
если только все подкоренные выражения положительны; равенство
2 ¦
Рис. 37.
здесь имеет место только в том случае, когда Х\ = х2, yt — у2, т. е.
когда точки М, и М2 совпадают.
Точно так же, восставив к плоскости Оху перпендикуляры, в
трех точках Ми М2 и М3 и в точке М пересечения медиан треуголь-
треугольника М\М2М$ (рис. 36), придем к неравенству
х 1 -t- х-, ¦
Уу-ТУгЛ- Уз
3
{**)
310
выражающему, что отрезок MN' не превосходит отрезка MN. Нера
венство (**) тоже имеет место во всех случаях, когда все подкорен-
подкоренные выражения положительны; равенство здесь имеет место, лишь
когда Xi = хг = Хз и У\ = у2 = уз, т. е. когда точки Ми М2 и Л43
все совпадают между собой.
Заменяя сферу конусом, вершина которого совпадает с началом
координат, осью служит ось Ог и угол при вершине равен 90°
(рис. 37), получим неравенство
справедливое при любых хи х2, х3; у\, у2, уз, равенство здесь будет
Хх Хч Х3
иметь место только в том случае, когда— = —— = —iT_ e. когда
Hi У% Уз
точки N\, N2 и N3 лежат на одной образующей конуса. Ал-
Алгебраическое доказательство неравенств (*), (**) и (***) пред-
представляет очень большие трудности.
285. Так как sin cos x = —cos I-у + eos x\, то
/я N
cos sin x —sin cos x = cos sin x -\- cos I -q- + cos x 1 ==
я л
~2~ + cos x + sin x — + cosx — sin x
2 —
— 2 cos 5 cos
Ho
cos д: -f- sin л: | = "^cos2 x -j- 2 cos x sin x -f- sin-* =
= /l +sin2x ^ УТ
(|cos лг + sin x\ =\ 2 , только если sin 2x — 1) и точно так же
| cos x — sin x | = J^cos3 x — 2 cos x sin x -j- sin2 x =
= /1 — sin 2x < /2"
(|cos x — sin *| =У% , только если sin 2x = — 1). А так как
я 3,14 r—
~2~ « ~2~ = 1,57 больше чем у 2 я 1,41, то отсюда следует, что
~2~ + cos л: -f- sin л: -р-+ cos л: — sin л:
Х> 2 i >0 и ~> 2 " >0>
-g-+ cos де-f sin * —+ cos* — sin*
значит, как cos <j • так и cos 2
311
всегда Положительны. Таким образом, разность cos sin x — sin cos x
всегда положительна, т. е. cos sin x при любом х больше чем
sin cos x.
286. а) Обозначим \og2n = a, logs я = 6. Из равенства
2" = я, 56 = я получаем л1"/" = 2, я1/ь = 5, я1/а-я1/ь = 2-5 = 10,
я1/а+1/ь = 10. Но я2 яг 3,142 < 10, откуда следует справедливость
неравенства -—¦ -f- —^~ > 2, что и требовалось доказать.
б) Обозначим Iog2 л = a, logn 2 = Ъ. В таком случае имеем
2° = л, яь = 2; из второго равенства вытекает 21/ь = л, или Ь =
= . Теперь наше неравенство принимает вид
1 1
-2а
М>2а,
Последнее неравенство является
очевидным.
287. Первое решение.
Требуется доказать, что если {1 >
> а, то
a) sin C — sin a < fl — а.
Но, очевидно,
sin р — sin а =
1-а В + а ^
—¦ 2 sin ¦
¦ cos •
¦' =
Рис. 38.
(ибо для каждого отличного от
нуля угла х первой четверти
sin х < х, cos л: < 1')).
б) tgp-tga>p-a.
Но, очевидно,
P-a< tg(P-a)=.
tgp-tga
l+tgptga
" < tg P — tg a
(ибо для каждого отличного от нуля угла х первой четверти
tgx> х1)).
Второе решение. Рассмотрим здесь только задачу а), так
как решение задачи б) совершенно аналогично.
Проведем единичную окружность с центром в точке О, и пусть
дуга АЕ равна а и дуга AF равна р. Если ЕМ и FP — перпендику-
См., например, ниже стр. 345.
312
ляры, опущенные из точек Е и F на радиус ОА (рис. 38), то
= Т sin а<
SAOFA = — «in 3
и
с _ _» о __!_в
°еект ОЕА — 2 ' ^сект OF А ~ ? lJ-
где буква S, как обычно, означает, площадь.
Отсюда следует, что
а — sin а = 2ScerMAmE
Р — Sin P = 2ScerM-4?F
и, следовательно,
a — sin а < р — sin р.
288. Пусть АЕ и Л/7 —дуги единичной окружности с центром
в точке О, равные соответственно а и Р, В и С — точки пересечения
перпендикуляра, восставленного в точке Л к диаметру ОА, с пря-
прямыми ОЕ и О/7, М и N — точки пересечения перпендикуляра, опу-
опущенного из точки Е на диаметр ОА с прямыми ОА и OF (см.
рис. 38). Тогда имеем;
Sb0AB = — tg «. 5ДОАС = ~2~ 'S Р.
„ L <; ___LR
^сект ОАЕ ~~ 2 а' сект OAF ~ 2 Р
и, следовательно,
tg a s\oab tg Р 5до.4С
а ^сект ОАя'
Но, как нетрудно видеть,
Действительно,
сект ОАЕ ^сект OEF
АОАВ АОВС .
^сскт ОАЕ ^АОЕМ ' ^сект OEF
SAOEM SAOEN
SAOBC . SAOAB
Из того, что "? >•? , следует, что
^cchtOEF ^сект ОАЕ
SAOAB + SAOBC ?ДОАВ
•-"сект ОАЕ " ^сект OEF^
Т. е. ЧТО
с
°сектОАК
что и требовалось доказать,
289. Пусть
arcsin cos arsin x = a.
Угол а заключен в пределах О^а^-гр.ибо 0 ^ cos arcsjn x sj I
так как — -JL < arcsin х ^ — |. Далее, sin a = cos arcsin x; следо-
следовательно,
arcsin л; = + [ — — а) и х = sin ± (— — а) = + cos а-
я
я
Точно так же, если arccos sin arccos x = j$, то О^р^т; (ибо
О ^ sin arccos х ^ 1, так как 0 ^ arccos x sg; я) и cos р = sin arccos x\
следовательно,
arccos jc=JL+Phx = cos (— + Р] = + sin p.
Из того, что cos a = sin fS ( = ± х), заключаем:
а + Р = arcsin cos arcsin л; + arccos sin arccos x = -к-.
290. Предположим, что сумма
cos 32л: + аЪ\ cos 31л: + агй cos 30л; + a2S cos 29л; +...
... + а2 cos 2л: + a, cos x (*)
при всех значениях х принимает только положительные значения.
Заменим в этой сумме х на * + я; мы придем к выражению
cos 32(л: + я) + Оз1 cos 31 (х + я) + а30 cos 30(л; + я) +
+ а29 cos 29(л: + я) + ... +о2 cos 2(л: + я) + oi соз(л; + я) =
= cos 32х — Оз1 cos 31% + O30COS 30* — U29COS 29л; + ...
... + а2 cos 2х — О[ cos x, (**)
которое тоже должно принимать при всех значениях х положитель-
положительные значения. А в таком случае и полусумма выражений (*) и (**),
равная
cos 32л" + изо cos 30л; + ... + at cos Ах + aj cos 2л",
тоже будет принимать при всех х только положительные значения.
я
Теперь заменим в последнем выражении х на х +~<Г> получим:
os 32(л; +-?-) + °зо cos 30 (х + -?-j +
+ о2В cos 28 [х + Jl) + ... + a, cos 4 [х + JLJ +
+ я2 cos 2 ( л- + _?L j = cos 32л: — азп cos 30л; +
+ а2я cos 28л — ,., + 04 cos 4х — пч cos 2л,
314-
Составив полусумму двух последних выражений, найдем, что сумма
cos 32л: + Яге cos 28л: + аи cos 24л: + ... + о8 cos 8л: + а4 cos 4л:
тоже должна принимать при всех х только положительные зна-
значения.
Заменяя в последнем выражении х иах-\--г~и составляя полу-
полусумму полученного выражения и первоначального, мы придем к
сумме
cos 32 х + д24 cos 24л: + ate cos 16л: -f as cos 8л:;
заменяя в ней х нах-\--тг и складывая полученное выражение с
первоначальным, мы придем к сумме
Cos 32л: + aI6cos 16x;
наконец, точно так же убеждаемся, что выражение
cos 32л:
тоже должно принимать при всех значениях х только положитель-
п
ные значения. Но при * ¦= "оо" последнее выражение равно —1.
Полученное противоречие и доказывает утверждение задачи.
291. Будем исходить из формулы для синуса половинного
угла:
2 sin -7j- = + 1^2 — 2 cos a,
где знак корня берется в соответствии с известным правилом знаков
для синуса. Пользуясь этой формулой, мы будем последовательно
определять синусы углов
M5°;(al + iiy4-450;la1 + -2
Предположим, что мы уже определили синус угла
М 45",
где <хх, о2, а3 а» принимают какие-то значения, равные 1 или
315
— 1. Так как
yai -т 2 + 4 +.-.-t- ^h—i + 2й
Г / аа а а \ Л
= ± 90° + а2 + ??3 + ... + —3"'.fe .ft+< • 45° ,
L \ 2 2s-1 / J
где знак плюс соответствует п\ = + 1, а знак минус ах = — 1, и
то мы можем после этого определить синус следующего угла:
- ±
При этом следует иметь в виду, что так как все рассматривае-
рассматриваемые углы по абсолютной величине меньше 90° (ибо даже I ' ~Ь ~к~ ~^~
1 1 \ 1
+¦4"+ ...+-Г^|-45° = 90° —— 90° меньше 90°), а знак этих уг-
углов определяется знаком аь то корень квадратный в последних фор-
формулах следует брать со знаком плюс или минус в зависимости от
знака а\. Другими словами, можно написать:
_„, yA+2.inL+Mi+. ..+"•* ;¦:;»+') .45-.
Теперь, прежде всего, очевидно, что
2 sin аг 45° = ахУ~2.
Отсюда последовательно получаем:
2 sin L + 5^2. j • 45° = аУг + а.2 /2,
316
2 sin L + flgi + ?lg?2 + а1а2Й3аЛ , 45° =
V 2 4 8 /
== я, К2
а3
2 sin
= в1
2 -f a, К 2 + o3 Y2 +...+any2,
что и требовалось доказать.
292. Предположим, что разложение заданного выражения по
степеням х имеет вид
¦ A — Зх + 3х2O43A + 3х — 3х2O44 = Л0 + Л1х + А2х2 + ... + Алх'\
где Ло, А,, Л2 Ап — неизвестные нам коэффициенты, сумму ко-
которых требуется определить, а п — степень этого выражения (кото-
(которая, как легко видеть, равна 743-2 + 744^2 = 2974). Положим в
этом равенстве х = 1; тогда получим:
Таким образом, искомая сумма равна единице.
293. Раскрыв скобки и сделав приведение подобных членов в
двух рассматриваемых выражениях, мы получим два многочлена
относительно х. Заменим теперь в наших выражениях л: на —х. При
этом нам придется заменить х на —х также и в полученных мно-
многочленах, т. е. в каждом из них оставить прежние коэффициенты
при х в четных степенях и заменить знаки коэффициентов на обрат-
обратные при х в нечетных степенях. В частности, коэффициенты при хга
при этой операции не изменяется. Таким образом, мы видим, что
наши два многочлена имеют те же коэффициенты при л;20, что и
многочлены, получаемые при раскрытии скобок и приведении подоб-
подобных членов в выражениях A + х2 + х3) 100° и A—х2 — л;3I000.
Но ясно, что первый из этих новых многочленов имеет больший
коэффициент при х20. Действительно, при раскрытии скобок в пер-
первом выражении мы по 1учим исключительно положительные коэф-
коэффициенты при различных степенях х, и при приведении подобных
членов все эти коэффициенты будут складываться. Во втором вы-
выражении при раскрытии скобок мы получим при различных степенях
х коэффициенты, имеющие те же абсолютные величины, что и коэф-
коэффициенты первого многочлена, но знаки их могут быть различны —
и при приведении подобных членов у нас произойдет умень-
уменьшение коэффициентов.
Итак, после раскрытия скобок и приведения подобных членов
в выражениях A -f- х2 — х3I000 и A — х2 + х3)то мы получим в
первом из них больший коэффициент при х20, чем во втором.
317
294. Утверждение задачи непосредственно "вытекает из следую-
следующих преобразований:
1 — х + х* — *3 + ... — хм + хт) A + х + х3 + х3 + ...
. . .1+ *" + *100) = [A + X2 + X* + . . . +Хт) —
— *A + X* + *< + ...+ Xs8)] [(\\+х* + Х* + ... + Хт) +
295. а) Согласно формуле суммы геометрической прогрессии и
формуле бинома Ньютона имеем:
„1001
X— 1 — X
¦ — 1
— (\ \ y\iooi *,юо1
\ 1 ^^ А] Л '
= 1 + 1001* + Cf001 х2 + Cf001 хг + ... + 1001л:1000.
ча 1001!
Таким образом, искомый коэффициент равен C,q01 = 5OL 951! *
б) Обозначим наше выражение через Р(х). Тогда имеем:
A +х)Р(х) —Р(х)= [A +хJ + 2A + *)»+...
... + 999A +л:I000+ 1000A + л:)'001] — [A +*)+2A + хJ+
+ 3A1+л:K + ...+ 1000A +л:I000] = 1000A +л:I001 —
=1000A+,I0о1_
j
Отсюда
1000 A+л:I»01 (\ + хIШ — A + х)
Р{х)~ ; Т
— 1000 [1001
- [Ciooi + C\ooix+C\oolx^ + ... + 1001*«» + *•••].
Таким образом, искомый коэффициент равен
51 Л52 1000 ¦ Ю0П 1001!
юоос1001 — с1001 — 51! 950! — 52! 949, =»
1001! 51050 • 1001!
" 52!—950Г I52 • 100° - 95°1 = -52Т-950Г-
296. Найдем, прежде всего, свободный член, который получится,
если в выражении
h раз
318
раскрыть скобки и привести подобные члены. Он равен значению
этого выражения при х = 0, т. е.
(,..(((-2J-2)*-2J-...-2J =
А раз
= (¦.¦(D-2J-2J-...-2)' =
А—1 раз
= (... (D-2J — 2J— ,..— 2)" = ...
А—2~раза
.... = (D — 2J — 2J = D — 2J = 4.
Обозначим теперь через Ак — коэффициент при х, через Вk —
коэффициент при хг и через Pftx3-—сумму членов, которые содержат
х в более высоких степенях. Тогда имеем: ^
Ahx + 4.
А раз
С другой стороны,
А раз
= ((... ((*—2J-2J 2J—2J
А—1 раз
\(Pk-ix3 + Bk-ix* + Ak-i* + 4) -
+ DPft_, + 2В„_Иа-.) хз + DВ,_4 +
+ 4^fe_tx + 4 = [Pi.!*» + 2P4_lBh
+ BРЛ_,Л4_, + S2A_,) x + DРЛ_, + 2Bh_tAk_i)] x» +
+ DBA_, + Л|_() х-2 + 4ЛЙ_^ + 4.
Отсюда
Так как (х— 2J = х2 — 4х + 4, то Л, =—4. Следовательно,
Л2 = — 4- 4 = —42, Л3 = —43,. .., и вообще Лй = —4*.
Вычислим теперь Вк:
Вк = А\_{ + 4Bk_{ = Л|_, + 4 (Л|_2 + 45ft_2) =
4» (Л|_3 + 4SA-3)
Д,.
319
Подставляя сюда
В, = 1, Л, = — 4, А2 = — 42,
Л3 = -43 ЛА_, = -4й-1>
получим:
Ва = 42А-2 + 4 . 42ft-4 + 42 . 42ft-6 + . . . + 4А-2 . 4» + 4*-1
= 42"-2 + 42ft~3 + 42ft~4 + ... + 4ft+1 + 4h + 4ft~f =
= 4ft-l4*.
4 — 1
297. а/ Первое решение. Так как при любом целом поло-
положительном k двучлен хк — 1 делится на х— 1, то
х + х3 + ха + х37 + х81 + х243 = (х — 1) + (х3 — 1) i+
+ (х9— 1) + (х27— 1) + (л;81—1) + (*2«— 1) +6
дает при делении на i — 1 остаток 6.
Второе решение. Обозначим частное от деления х + хъ -f-
+ х9 + х17 + xsi-\-х2*3 на х—1 через <?(*) и остаток через г. Тогда
х + хъ + Xя + л27 + х81 + X243 = д(х) (х—\) + г.
Полагая в этом равенстве х = 1, получим 6 = г.
б) Аналогично второму решению предыдущей задачи предпо-
предположим, что q(x) есть частное от деления нашего многочлена на
х2—1, а гхх~\-гъ есть искомый остаток (остаток от деления много-
многочлена на квадратный трехчлен является двучленом первой степени):
х + х3 + х9 + х27 + я81 + хиз = q(x)(x2—\) +r,x + г2.
Полагая в последнем равенстве х = 1 и х = — 1, мы получаем:
6 = г\ + г2 — 6 = — п + г2, откуда гх = 6, г2 = 0.
Таким образом, искомый остаток равен их.
298. Пусть р(л:) есть наш неизвестный многочлен, q(x) — част-
частное от деления этого многочлена на (х — 1) (х — 2),'г(х) = ах -\- Ь —
искомый остаток:
= (x-l)(x-2)q(x)+ax+b. (*)
По условию задачи имеем:
р(х) = (*—1 )<?,(*) Ч-2, откуда рA) =2;
р(х) = (х — 2)qz(x) + 1, откуда рB) = 1.
Подставляя теперь в равенство (*) х = 1 и * = 2, получаем:
2 =
откуда
о = —1, 6 = 3.
Таким образом, искомый остаток есть —х -f- 3.
320
299. Многочлен х* + х* + 2хг + х + 1 можно разложить на мно-
множители; он равен (хг >+ 1) (х3 + х + 1). Отсюда легко усмотреть,
что этот многочлен является делителем многочлена
х»—\ = (*6
а именно:
х12 — 1
~ л:8 — х7 — х6 + 2х5 + +
Разделить х1951 — 1 на х4 + х3 + ?х2 + х 4- 1 — это то же самое,
что разделить я1 — 1 на х12—1, а затем результат помножить на
Xs — х7 — Xs + 2хь — 2х3 + хг-|-х—1. Но легко видеть, что
1
1989 + 192' + 1918 + >9°з + + х1
(в этом легко убедиться, если произвести деление «углом» по пра-
правилам деления расположенных многочленов или если заметить, что
д-1951 _ [ _ хт[(х12Iбг— 1] + х7 — 1 и воспользоваться известной
формулой деления разности четных степеней двух одночленов на
разность оснований). Отсюда следует, что искомый коэффициент
совпадает с коэффициентом при хи в произведении
Lm» 4- х1в" + .. + f + + з
X (х8 — х7 — Xе + 2х5 — 2х3 + х2 + * — 1)
который равен —1.
300. Из выписанного в условии задачи тождества следует,
что искомый многочлен Р(х) = Рп{х) (где п — степень многочле-
многочлена) делится на х, т. е. Р„(х) — xPn-t(x), где Рп-\(х) — какой-то
новый многочлен степени п — 1. Поэтому
Р(х-\) = (х-\)Рп-1(х-\),
и, значит,
х{х— 1)Р„_,(л;— 1) =хР(х— !) = (х — 26)/>(x),
в силу чего Р(х) делится я на х— 1, т. е. Рп(х) — х(х— 1)Яп_2(х)
(на х—1 делится многочлен Pn_i(jc) = (x—l)Pn_2(.v)). Новта-
ком случае Р(х—\) = (х — 1) (х — 2)Рп~г{х — 1), и мы получаем:
х(л.--1)(х-2)Л,-2(*-1) =
= (х —26) Р„(х) = (х-26)х(х-1)Я„_2(д;),
— откуда следует, что Р„(х) делится и на х — 2 (т.е. Pn-i(x) де-
делится на х — 2), и, значит, />„(х) = х(х—1) (х — 2)Р„_3(х). Под-
Подставляя это значение Р{х) в исходное соотношение, мы аналогично
убеждаемся в том, что Р(х) делится и на х—3, т. е. Рп(х) =
= х(х —\)(х — 2)(х~Ъ)Рп-А(х), и т. д.
21 Д. О. ШклярскиЛ и др. 321
Продолжая поступать таким же образом, мы в конце концов
приходим к следующей форме многочлена Р(х):
Р(х) =Рп(х) = х(х- 1) (х-2) (х-3) ... (х -25)/>„_26(х).
Подставляя в заданное тождество это выражение многочлена
Р(х), мы получим:
= (x-26)x(x-l) ...(x-25)Pn-x(x),
откуда вытекает, что для многочлена Рп-2&{х) = Q(x) степени
п — 26'
Q(x-\)^Q(x). (•)
Ясно, что если Q(x) = Q0(x) = с — многочлен нулевой степени
(число!), то соотношение (*) имеет место; покажем, что оно
имеет место только в этом случае. В самом деле, если Q(x) =
= Qt,(x) = айхк + a,**-1 + .., + ak_lx + ак, где ft > 1 и а0 Ф О,
то, приравнивая с обеих сторон тождества (*)
коэффициенты при хк~1, в силу формулы бинома Ньютона, полу-
получаем:
kaa + a! = аь или а0 = О,
что, однако, противоречит предположению ап Ф 0. Таким образом,
k = 0, Q(x)= с и
Р(х) = сх(х - 1) (х — 2) ... (х — 25)'
— многочлен 26-й степени.
301. а) Если все коэффициенты Р(х) неотрицательны, то все
числа s(l), sB), sC), ... имеют смысл. Рассмотрим такую
степень десяти N = 10й, что Л' больше всех коэффициентов
по, ах, а2, ... многочлена Р(х). Тогда число Р(Л^) = Р( 10й), оче-
очевидно, начинается с тех цифр, которыми записывается коэффициент
аз многочлена; затем (после, быть может, некоторого числа нулей)
идут цифры числа п\\ затем (возможно, опять после нулей) —
цифры числа о2, и т. д. —вплоть до цифр числа ап; поэтому число
sA0'i)=S равно сумме всех цифр всех чисел а0, о,, ..., а„. Но
этому же самому числу 5 равны и величины sA0'i+I), sA0'l+2),...
откуда и следует, что в последовательности s(l), sB), ... число
S встречается бесконечно много раз.
б) Ясно,- что если старший коэффициент о0 многочлена Р(х)
отрицателен, то среди чисел s A), s B), s C), ... будет вообще
лишь конечное число имеющих смысл (ибо при всех достаточно
больших х многочлен Р(х) имеет тот же знак, что и его старший
Р (х)
коэффициент о0 — это следует, например, из того, что hm = 1) •
х-»оо OffX
Таким "образом, остается лишь рассмотреть случай по > 0. Но
в этом случае, как мы покажем,_ существует таков число М > О,
что у «сдвинутого», многочлена Р(х) = Р(х-\-М) все коэффициен-
коэффициенты положительны. Отсюда будет следовать,_что последовательность
F(l), 7B),~sC), ... сумм цифр чисел Р{1), РB), РC), ... содержит
322
1'- -
бесконечно много одинаковых чисел, а так. как, очевидно, s(l) =
= s(M4- \),JB)=s{M + 2), sC) = s(M+ 3), .... то и последо-
последовательность s(l), sB), sC), ... также содержит бесконечно много
одинаковых чисел.
Итак, нам остается лишь доказать напечатанное выше курсивом
утверждение. Но если
Р(х) = Р(х + М) =
= ао(х + М) "+ at(x + М) «-' + а2(х + М) »-« + ...
... + Qn_i(x+AJ)+an = aoJC"+a1JC"-1+a2*"~2+ .. ¦ +ап-\Х+ап,
то, в силу формулы бинома Ньютона,
а{ = а0 ¦ С\Мп~х + а, ¦ C^Af"-* + ... + а,,
где i = 0, 1, 2, ..., п. Таким образом, а,- имеет вид многочлена
(степени п — i) от М со старшим коэффициентом ао-Сгп>О; поэтому
все а,- (где i = I, 2, ...; заметим, что а0 = а0 > 0) при достаточно
большом М будут положительны, что и требовалось доказать.
302. Пусть многочлены }(х) и g(y) имеют свободные члены а0
(т. е. f(x) н= а0 + а{х + ... + а„хп) и Ьо. Положим в равенстве
х200ут + 1 = f(x)g(y) переменное х равным 0; тогда получим
aog(y) = 1, т. e.g(y)=—; таким образом, g(y) равно— при всех у,
т. е. это есть постоянная — (многочлен нулевой степени). Анало-
Аналоге
гично доказывается, что f {х) = -г—, т. е. f (x) g {у) = , Ф
Ф хШу2т _). 1 Полученное противоречие и доказывает утвержде-
утверждение задачи.
303. Так как- (квадратное) уравнение р(х) = ах'2 + Ьх -f с = х
не имеет вещественных корней, то квадратный трехчлен р(х)—х =
= йх2+(Ь — \)х-\-с при всех х принимает значения одного знака,
скажем, р(х)—х > 0 при всех х Но в таком случае для любого
х = хй имеем р(р(ха)) — р(ха) > 0, т. е. р(р{хо))> р(ха), и так как,
по предположению, р(хо)—хо > 0, т. е. р(хо)> х0, то р(р(х0)) >*о
и, значит, *оне может служить корнем уравнения D-й степени)
р(р(х)) = х.
304. Будем считать, что a Js 0—в противном случае мы заме-
заменим многочлен р(х) на (удовлетворяющий тем же условиям) много-
многочлен— р(х) = —ах2—Ьх — с. Аналогично будем считать и что
b ^ 0—в противном случае мы заменим р(х) на р(— х)—ахг —
— Ьх + с. Подставив теперь значения х = I, х = 0их = — 1 в не-
неравенство | р (лг) | = | ах2 + Ьх + с | ^ 1, получим
|а + Ь + с|<1, |с|^1 и \а — Ь + с|<1, т. е. |с|^1
и |а + 6| <2, \а — Ь\ ^2
Далее, если с>0 и, значит, (при |х|^1) 0 ^ схг ^ с, а
— Ъ ^ Ьх ^ Ь, имеем
Pix = ex2 + Ьх + а < с + Ь + а ^ 1
и pi (л) = сх2 + Ьл: + а ^ 0 + (— Ь) + а = а — Ъ ^ — 2,
21* 323
откуда следует, что |p,(x)|<2. Аналогично, при с < 0, когда
с ^ сх2 ^ 0 (и по-прежнему — Ь sg; Ьх ^ Ь),
и р,(х) — сх2 + Ьх + а 5г с + (—Ь) + а = а — Ь + с ^ —1,
откуда вытекает, что и здесь |p,(x)|^ 2.
305. Исключим из рассмотрения мало интересный случай а = О,
когда три уравнения A), B) и C) являются уравнениями 1-й степе-
степени, т. е. имеют единственный корень каждое, и все совпадают меж-
между собой (здесь х\ = Х2 — х3), а также случай, когда, скажем,
с = 0 и наши три уравнения имеют корни) — —, 01, (-, 0 |и( — —, О I
\ а I \а J \ а /
— здесь корень х3 — 0 уравнения C) заключен между любым корнем
уравнения A) и любым из корней уравнения B)).
Далее, если ах\ -f- bxx + с = 0, то
-J- х\ + Ьхх + с = {ах\ + Ьх, + с) - -J- х\ = - \ х\;
аналогично, если — ах\ + Ьхг + с = 0, то
Go о 2 2
Следовательно, величины -^- дс^ + to; + с I = — — в*^ I и — х\ +
= —а*||имеют разные знаки. Но это означает, что
й
точки (х,, /(Х|)) и (х2, f(x2)) парабоЛы у — f(x)=~2~x2 + Ьх + с
лежат по разные стороны от оси х, откуда и следует, что существу-
существует промежуточная между этими точками точка (дгз, 0) параболы,
в которой эта кривая пересекает ось х; х3 и есть искомый корень
уравнения C).
306. Если а и р — корни уравнения
х2 + рх + q = О,
то
(X-a)(x-4,)=x2 + px + q.
Следовательно,
(а-тг)(р-тг)(а-6)(р-6) =
= [<ЧГ-аHг--р)][(в-а)(8-р)] = (f + и + <?) (С» + рб + q).
Но
¦у + 6 = — Я, yS = Q
и, значит,
(а - т) (Р - Т) (« — 6) (Р — в) = (f + p-i + q) F2 + рб.+ <?) =
qf + РТЙ2 + P2ffi + Р< '
= Q2 - pFQ + q(P2- 2Q) + p'-Q - pjP + q2 =
= Q2 + q2 - pP(Q + q)+qP2 + p2Q _ 2,Q.
324
307. Первое решение. Вычислим из второго уравнения
коэффициент а и подставим его в первое уравнение. Тогда получим:
Х3 — (Х2 + х)Х + 1 = 0,
хг — 1 = 0,
(х-])(х* + х+ 1)=0.
Отсюда имеем:
и, следовательно, так как а = —(.v2 + x), то Oi = —2, а2> з = 1.
Второе решение. Используя результат задачи 306, мы мо-
можем утверждать, что, для того чтобы наши уравнения имели хотя
бы один общий корень, необходимо и достаточно, чтобы обращалось
в нуль выражение
а2 + 1— а ¦ \(а + 1) + 1 + а3 — 2а = аг — За+ 2 =
= (а - 1) (а2 + а - 2) = (а - \)Ца + 2).
Отсюда получаем:
а, = —2, а2, з = 1.
308. а) Пусть (.V — а) (* — 10)+ 1 = (х + Ь){х + с). Полагая
в обеих частях равенства х = — Ь, получим:
' (_ ъ - а) (-6 - 10) + 1 = (- Ъ + Ъ) (— Ь + с) = 0.
Отсюда
Так как а и Ь — целые, то Ь+а и Ь+iO —также целые. Но
— 1 может быть представлена в виде произведения двух целых чи-
чисел только одним способом: — 1 = 1 ¦ (— 1). Поэтому имеются
только две возможности:
1) ь + 10 = 1, Ь = — 9; тогда b +а = — 9 + я = — 1,
т. е. а = 8:
(х — 8)(.v— 10)+ 1 =(х — 9J.
2) б + Ю = —1, Ь == — 11; тогда 6+а = —П+а=1,
т. е. а = 12:
(*— 12) (х— 10)+ 1 =(х— ИJ.
б) Так как многочлен четвертой степени можно разложить или
в произведение многочлена первой степени и многочлена третьей
степени или в произведение двух многочленов второй степени, то
нам следует рассмотреть отдельна два случая:
А) х(х-а){х-Ь)(х-с)+1 =(x + p)(x* + qx* + rx + s) (*)
(коэффициенты в правой части равенства при х в первом множите-
множителе и при х3 во втором множителе оба равны 1 или оба равны — 1,
325
так как в произведении этих множителей коэффициент при х* должен
быть равен коэффициенту при х* в выражении х(х — а) (х — Ь)Х
Х(* — с)+ 1, т. е. 1; равенство же х(х — а) (х — Ъ) (х — с) + 1 ==
= (—x+pi)(—х3 + qxx2 + r\X + sx) можно привести к виду (*),
умножив оба сомножителя правой части' на — 1).
Положив в равенстве (*) последовательно * = О, * = я, х = Ь
и х =' с и учитывая, что 1 разлагается на множители только двумя
способами 1 = Ы =(—1)-(—1), мы получим, что четыре раз-
различных числа 0 + р = р, ai-f Р> b + р и с -\- р (напоминаем, что
числа 0, а, Ь„ с все различны) могут иметь только два значения + 1
и — 1, что невозможно.
Б) х(х-а)(х-Ь)(х-с)+1 = (x2 + px + q)(x2 + rx+s).
Отсюда, как и выше, получаем, что при х = 0, х = а, х = Ь и
х = с оба многочлена, как х2 + px-\-q, так и x2-\-rx.-\- s, принимают
.значения 1 или —1. Но квадратный трехчлен х2 + рх + q не может
принимать одно и то же значение а при трех различных значениях
х (в противном случае квадратное уравнение х2 + рх + q — a = 1
имело бы три различных корня), откуда следует, что при двух из
четырех значений х = 0, х = а, х = 6, х =с этот трехчлен прини-
принимает значение 1, а при двух других — значение — 1. Предположим,
что 02 + p-0-\-q = q=\, и пусть х = а есть то из значений х=а,
х = Ь и х — с, при котором этот трехчлен принимает то же самое
значение 1; в таком случае при х=Ьих = сон принимает значе-
значение — 1. Итак, мы имеем:
а2 + ра + 1 = 1, Ь2 +рЬ + 1 = — 1, с2 + рс + 1 = — 1.
Из а2 + pa = a (a -f р) = 0 следует, что я + р = 0, р = — a
(ибо, по предположению, афО). Таким образом, два последних ра-
равенства принимают вид
Ь2 — аЬ = Ь(Ь — а)=—2, с2 — ас = с (с — а)= —2.
Вычитая из первого равенства второе, получим:
Ь*—аЬ — с2 + ас= (Ь — с) (Ь + с) — а{Ь —с) =
= (Ь— с)(Ь + с — а) =0,
откуда, так как b ф с, имеем: Ь + с — a = 0, a = 6 + c, Ь — а =
= — с, с — a=i — Ь. Теперь из равенства
Ь(Ь — а)= —Ьс = —2
получаем следующие значения для 6, с и а:
6=1, с == 2, а = Ь + с = 3,
*(* —а)(х —6)(х —с)+1 =*(* —3)(*—1)(* — 2)+1 =
«=(х2 — Зх+ IJ
и
Ь = — 1, с = — 2, а = Ь+с = — 3,
*(дс —0)(дс-6)(дс-с)+1 =х(х + 3)(х+1)(х+2)+1 =
„ - (х» + Эх + Ц*.
326
Аналогично, если хг + рх + q принимает при х = 0, и х = а
значение — 1, при х = b и х = с значение + 1, то мы имеем:
q = _ 1, а? + ра - 1 = — 1, б2 + рЬ — 1 = 1, с2 + рс - 1 = 1,
откуда
р = — a, b(b —а)= с(с — а) = 2, б2 — аЬ — с2 + ас = О,
(Ь — с) (Ь + с — а) — О, а = Ь + с, Ь — а = — с, —be = 2.
Мы получаем, таким образом, еще две возможные системы значений
для a, b и с:
6 = 2, с = — \, а = Ь+с=\,
х(х — а) (х — Ъ) (х — с) = х(х — 1) (х — 2) (л; +1) + 1 =
.6 = 1, с=— 2, а = Ь + с = — 1,
*(*— а)(х — Ь)(х — с) = х(х+ 1)(«— 1)(х + 2) + 1 =
= (Х2+Х- 1J.
Примечание. Другое решение этой задачи приведено в заклю-
заключительной части решения задачи 309 б).
309. а) Предположим, что
(х — а,)(х — а2)(х — а3)...(х— ап)— 1 = p(x)q(x),
где р(х) и q(x) —многочлены с целыми коэффициентами, сумма сте-
степеней которых равна л; можно считать, что в обоих этих многочле-
многочленах старший коэффициент равен I (сравните с решением предыду-
предыдущей задачи). Подставляя в это равенство значения х = аи х = а2,
х = а3>. . • •, х = а„ и учитывая, что — 1 разлагается на два целых
множителя единственным образом: — 1 = !•(— 1), мы получим, что
р(х) = 1, q(x) = — 1, или наоборот, при каждом из рассматривае-
рассматриваемых значений х. Таким образом, мы видим, что сумма р(х) -\-q(x)
равна нулю при х = аи а2, а3, ¦ ¦ ¦, ап. Итак, уравнение р(х) +
-f-<7(x)=0 имеет своими корнями Х\ === ct\, х2 = а2, ..., хп = ап\
отсюда следует, что многочлен p(x)-\-q(x) делится- на х — а\,
х—а2, .. •, х — а„, а следовательно, и на произведение
(х — ai) (х — а2) ... (х — а„). Но степень уравнения р(х) + q(x) = 0,
равная наибольшей степени многочленов р{х), q(x), меньше п (п есть
степень выражения (х — а,) (х — а2).. .(х — а„)— 1). Отсюда сле-
следует, что р(х) + q(x) не может делиться на произведение
(х — а{) (х — а2)...(х — ап), а следовательно, разложение, существо-
существование которого мы предположили, невозможно,
б) Предположим, что
(х — aj)(x — а2)(х — а3)...(х — ап)+ 1 = p(x)q(x),
где р(х) и q(x)— многочлены с целыми коэффициентами, старшие
коэффициенты которых равны 1. Подставив в это равенство значе-
значения х — аи х = а2, х — <23, ..., х = ап, мы получим, что при каж-
каждом из рассматриваемых значений х
р(х)=\, q(x)=\ или р(х) = — 1, q(x)= — \.
Таким образом, р(х)—q(x) обращается в нуль при п различных
значениях х, и, следовательно, во-первых, р(х)—q(x) = 0, р(х) ^
327
es<7(x) (сравните с решением задачи а)) и, во-вторых, число п чет-
четно: п = 2k, где k есть степень каждого из многочленов р(х)= q(x).
Перепишем теперь наше равенство в виде
или (х — а{] (х — а2) (х — аъ).. .{х — айк) =[p(x)Y — \,
(*-а,) (*-*,)(*-а,)...(*-а,0 = [рМ+1][р(*)-1].
Итак, произведение двух многочленов р(х)-\- 1 и р(х)—1 об-
обращается в нуль при х = аь х — а2, х = а3 л: = а2ь. Следова-
Следовательно, при каждом из этих значений х обращается в нуль хотя бы
один из сомножителей, а это значит, что или р(х) + 1, или р(х) — 1
делится на х — аи или р(х) + 1, или р(х) — 1 делится на х — аг, и
т. д. Так как многочлен степени k не может делиться на произведе-
произведение больше чем k различных выражений вида х — at и так как из
^того, что многочлен степени k со старшим коэффициентом 1 делится
на произведение k выражений вида х — сц, следует, что он равен
этому произведению, то мы можем утверждать, что р(х)+\ равно
произведению k из 2k сомножителей левой части последнего равен-
равенства, а р(х)— 1 равно произведению остальных k сомножителей.
Предположим, например, что
р(х)+ 1 =(x — al)(x —
Вычитая из первого равенства второе, получим:
2 = (х — а,) (х — а3) ... {x — a2h-i) — (х — а2) (х — а4) .. (х — а«).
Подставив сюда, например, х = а2, мы получим разложение
числа 2 в произведение k целых множителей:
2= (а2 — ai)(a2 — a3). ..(аг — a2h-i).
, Так как число 2 нельзя разложить в произведение больше чем
трех различных множителей, то отсюда сразу следует, что k sg 3.
Но случай k = 3 тоже является невозможным по следующей при-
причине. Число 2 может быть разложено в произведение трех различных
сомножителей только одним единственным способом: 2 = 1 ¦ (— 1)Х
Х(—2). Предположим, что k = 3, а1 < а3 < аь. Тогда 2=(а2--
— а,)(о2 — аг)(а2 — а5), где а2— а{> а2 —а3*> а2 — аъ, и, следова-
следовательно, а2 — ai = 1, а2 — а3 = — 1, а2 — а5 = —2. Подставив в
формулу
2 = (х — а,) (х — а3) (х — а5) — (х — а2) (х — at) (x — а6)
х = at, мы придем к другому разложению 2 на три различных мно-
множителя: 2 = (а4 — Я]) (а4 — а3) (а4 — о5), где тоже а4 — ai > а4 —
— аз > а4 — а5- Отсюда следует, что а4 — at = 1, a4 — a3 = — 1,
a4 — a5 = —2 и, значит, о4 = a2, что противоречит условию задачи.
Итак, возможными являются только два случая: k = 2 и k = 1.
1°. Если & = 1, то мы имеем:
2=(х — а,) — (х —а2),
откуда a2 = a, + 2, "и, обозначая а\ просто через а, получим:
(сравните с решением задачи Э08 а)).
328
2°. Если k = 2, то имеем:
2 = (дс — а,)(х — а3) — (х — а2) (дс — а4),
где будем считать а! < а3, Q-г < 04- Подставляя в последнее равен-
равенство х = а2 и * = «4, получим:
2 = (а2 —
2 = (а4 —а,)(а4 —а3), а4 —ai>a4 —а3.
Но 2 можно разложить на два множителя, следующих в убы-
убывающем порядке, только двумя способами: 2 = 2 • 1- и 2 = (— 1)Х
Х(—2). Так как, кроме того, а2— a{ < a4 — а{, то мы имеем:
а2 — а.\ = — 1, а2 — аз = — 2,
а4 — а, = 2, аА — аъ — 1,
откуда, обозначая а,\ через а, получим:
а2 = а— 1, a3 = a + I, a4 = a + 2
и
(х — а,)(х — а2)(х — а3)(х — а4) + 1 =
= (х — а) (х — а + \) (х — а ~ \) (х — а — 2) +1 =
= [х2- Bа -1)х + а2 + а —ip
(ср. с решением задачи 3086)).
310. Аналогично решению предыдущей задачи из предполагае-
предполагаемого равенства
(х-а1)Цх-а2)Цх — а3у...(х-апу+\ = p(x)q(x), (*)
где р(х), q(x)—какие-то многочлены с целыми коэффициентами
(и с коэффициентами при старших членах, равными 1), следует,
что либо р{х) = 1, q(x) = 1, либо р(х) = — 1, q(x) = — 1
при каждом из значений х = а.\, х = а2, х = а3, ..., х = ап. По-
Покажем, что многочлен р(х) (и, разумеется, также и q{x)) мо-
может быть либо при всех значениях х = аь х = аг, ..., х = а„
равен 1, либо при всех этих значениях х равен — 1.
В самом деле, если бы, например, многочлен р(х) при х — а,-
принимал значение 1, а при х = а, — значение — 1, то при некото-
некотором промежуточном значении х, заключенном между а,- и ajy он
обращался бы в нуль (если график функции у = р(х) при х = а,-
находится сверху от оси Ох, а при х = а, оказывается снизу
от этой оси, то непрерывная кривая у = р(х) где-то между х = а{
и х = а,- пересекает ось Ох), что невозможно, ибо левая часть
равенства (*) всегда ^ 1 и потому в нуль обратиться не может.
Предположим, что как р{х), так и q(x) при х—а\, х=а2, ..., х =
= ап принимают значения 1. В таком случае как р(х)— 1, так и
q(x) — 1 обращаются в нуль при х = at, х = а2, ..., х = ап и, сле-
следовательно р(х) — 1 и q(x) — 1 делятся на произведение (дс — ах) X
Х(* — а2)...(х — а„). Так как сумма степеней многочленов р(х)
и q(x) равна степени (х — аО2(дс — а2J... (х — а„J + 1, т. е. 2л,
то р(х) ~l = (x — ai) ... (х — ап) и q(x) — 1 = (дс — аО ...
... (х — ап) (ср. с.решением предыдущей задачи),
' 329
Таким образом, мы прлходим к равенству
— а1)Чх~а2)г...(х-апу+\ = p(x)q(x) =
= [(х ~ щ) ... (х - ап) + \][(х -щ) ... (х - ап) + I]
откуда
(х~щ)(х — а2) ... {х — а„) ег О,
что неверно. Точно так же доказывается, что р(х) и q(x) не могут
принимать в точках х = а,\, х — а^, ..., х = ап значения — 1
(в этом случае мы получили бы р{х) — q(x) = (х— fli)X
Х( — а2) ...(* —а„) — 1).
Итак, мы видим, что разложение выражения
(х-а1)*(х-ая)*...1х-ап)>+\
в произведение двух многочленов с целыми коэффициентами
невозможно.
311. Пусть многочлен Р(х) равен 7 при х = а, х = Ь, х = с
и х = d. В таком случае уравнение Р(х)—7 = 0 имеет четыре
целых корня а, Ь, с и й. Это значит, что многочлен Р(х) — 7 делит-
делится на х — а, х — Ь, х — с, х — d •), т. е.
Р(х) — 7 = (х — а) (х— Ъ) (х - с) (х - d)p{x),
где р(х) может равняться 1.
Предположим теперь, что многочлен Р(х) принимает при целом
значении х = А значение 14. Подставив х = А в последнее равен-
равенство, мы получим:
7= (A—a)(A — b)(A — c)(A—d)p(A),
что невозможно, так как целые числа А — а, А — Ь, А — с и А — й
все различны, а 7 нельзя разложить в произведение пяти множи-
множителей, из которых по крайней мере четыре отличны друг от друга.'
312. Если многочлен седьмой степени Р(х). разлагается в про-
произведение двух многочленов р(х) и q(x) с целыми коэффициента-
коэффициентами, то степень хотя бы одного из сомножителей не больше 3;
будем считать, что этим сомножителем является р(х). Если Р(х)
при семи целых значениях х принимает значение ± I, то р(х) при
тех же значениях х тоже принимает значения ± 1 (так как
p(x)q{x) = Р(х)). Среди семи целых значений х, при которых ?(х)
принимает значения ± 1, найдутся четыре таких, при которых
р(х) принимает значение 1, или четыре таких, при которых р(х) прини-
принимает значение — 1. В первом случае уравнение третьей степени
р{х) — 1=0 имеет четыре корня, во втором случае уравнение
р(х) + 1=0 имеет четыре корня. Ни то, ни другое не может
иметь места, так как, например, в первом случае р(х) — \ должно
') Пусть Р(х)—7 дает при делении на х — а остаток г:
/>(*)-7= (x — a)Q(x)+r.
Подставляя в это равенство х = а, получаем 7—7 = 0 + /", т. е,
г = 0, и, значит, Р(х) — 7= (x-a)Q(x) делится на х — а.
330
было бы делиться на многочлен четвертой степени (сравните с ре-
решением задачи ЗО9а)).
313. Пусть р и q— два целых числа, одновременно четных
или нечетных. Тогда разность Р(р)—P(q) четна. Действительно,
выражение
P(p)—P(q) =
делится на четное число р — q.
В частности, при р четном разность Р(р)—Я@) четна. Но
по условию Я@) нечетно: следовательно, Р(р) также нечетно, а по-
потому Р(р) ф 0. Аналогично при р нечетном разность Р(р)—ЯA)
четна; так как по условию Р{\) нечетно, то отсюда, как и выше,
следует, что Р(р) ф 0.
Следовательно, Р(х) не может обращаться в нуль ни при
каком целом значении х (как четном, так и нечетном), т. е. много-
многочлен Р(х) не имеет целых корней.
314. Предположим, что уравнение Р(х) = 0 имеет рациональ-
рациональный корень х= ——, т.е. W—т- 1= 0. Разложим многочлен Р(х)
по степеням х — р, т. е. запишем его в виде
Р(х) =со(х — р)»+с1(х — р)п-> +
+ С2(Х — р)п~2+ ...+ Сп-^Х— р) +С„,
где со, С\, С2. • • ¦> сп — некоторые целые числа, которые нетрудно
найти, если известны On, а.\, ..., ан (с0 равно старшему коэффици-
коэффициенту аэ многочлена Р{х), с, —старшему коэффициенту многочлена
Р(х)—со(х — р)п степени п—1, с2 — старшему коэффициенту
многочлена Р(х) — С(,{х — р) " — сх(х — р) "-• степени п — 2, и т. д.).
Подставив х = р в последнее выражение для Р(х), мы получим
сп = Р(р) = ± I.
k
Подставив в это же выражение х = -j- и умножив результат
на Iй, мы получим:
• + c,P [k - plf-2 + ... +сп_{1п~1 (ft - pi) + cnln = 0,
I k \
откуда следует, что если Р (—-— I = 0, то
С»П _ ±!п _— г... (к— п/лп-1 _
k—pl k — pl
-Cll{k-Pl)n-2-.,.-cn_2ln~2(k-pl)~ cn_,/n-J
есть целое число. Но так как pi делится, на /, a k взаимно-просто
с /1 иначе дробь—можно было бы сократить ,то к — pi взаимно
331
просто с !, а следовательно, k — pi взаимно просто и с 1п. Отсюда,
+ Г
следует, что -7-=—: может быть целым числом только, если
k — pl
k — pl = ±i.
Точно так же докажем, что и k — ql = ± 1. >
Вычтя теперь равенство k — pi = ± 1 из равенства k — ql =
= ± 1, мы получим:
{p — q)l = 0, или ( р — q)l = ±2.
Но (р— q)l > 0, так как p>q и /> 0, а следовательно,
(р —<7)/ = 2, k — pl = — \, k~ql = 1.
Итак, если р— q > 2, то уравнение Р(х) =0 вовсе не может
иметь рациональных корней. Если же р — q = 2 или р— 9=1.
то рациональный корень —г- может существовать. При этом, скла-
складывая равенства
k — pl = — \, k — ql=l,
мы получаем:
что и требовалось доказать.
315. а) Предположим, что наш многочлен можно разложить
на множители с целыми коэффициентами:
д.2222 + 2х2220 + 4*2218 + ... + 2220л;2 + 2222 =
= (апх« + ап-{х"-> + а„_2л-»-2 + ... + а0) X
X (Ьш*™ + ftm-l*-1 + bm-2^m-2 + • • • + 60),
где т + п = 2222. В таком случае aobo = 2222 и, следовательно,
из двух целых чисел а0, Ьо одно является четным, а другое — не-
нечетным. Предположим, что а0 есть четное число, а Ьо — нечетное.
Мы утверждаем, что в таком случае все коэффициенты многочлена
а„хп ,+ ап-ххп-1 + . .. + а0 должны быть четными. Действитель-
Действительно, предположим, что а* есть первый с конца нечетный коэффици-
коэффициент этого многочлена. Коэффициент при xh в произведении
(апхп + an-ixn~l + ... + а0) (Ьтхт + Ът-Ххт-^ + ... + Ьо)
будет равен
(в случае, если k > m, эта сумма окончится членом пи-тЬт). Этот
коэффициент равен соответствующему коэффициенту при хк в ис-
исходном многочлене, т. е. равен нулю, если k нечетно, и представля-
представляет собой четное число, если k четно (ибо все коэффициенты много-
многочлена, заданного в условии задачи, кроме первого, четны, a i<
^ п < 2222). Но так как, по предположению, все числа ан-\, пь-г,
uk-з по четны, то в сумме (*) все члены, кроме первого, четны
и, следовательно, четным должно быть и произведение akb0, что
невозможно, так как ah и Ьо нечетны.
Таким образом, мы видим, что все коэффициенты многочлена
а„хп + ап-ххп-1 + ... + п0 должны быть четны, что противоречит
332
тому, что апЪт должно равняться единице. Следовательно, неверно
и наше предположение о возможности разложения данного много-
многочлена в произведение двух многочленов с целыми коэффициентами.
б) Положим * = (/+1- В таком случае мы получим:
*260 + л:219 + *2« + \-х+\ =
= (У + IJ60 + (У+ О249 +•••+ (</+!) + ! =
•= у™° + 251</2« + Cl51y««" + С32ъху™ + ... + С|м</ + 251.
Дальше, используя то, что все, кроме первого, коэффициен-
коэффициенты полученного многочлена делятся на простое- число 251
/„Л rk 251 • 250 • 249 ... B51 — k+ 1)\ ,
I ибо C25i = 5 —I —I и что свободный член
\ 1 J
25i 5 —I
многочлена, равный 251, не делится на 2512, мы можем почти дослов-
дословно повторить рассуждения решения задачи а), заменив лишь чет-
четность и нечетность коэффициентов делимостью на 251. Таким обра-
образом, мы докажем, что если бы наш многочлен разлагался в произ-
произведение двух множителей, то все коэффициенты одного из сомно-
сомножителей должны были бы делиться на 251, что невозможно, ибо
первый коэффициент нашего многочлена равен 1.
316. Запишем многочлены в виде
А = а0 + ахх + агх'х -+-... + апхп
и
< В = bo + b,x + b2x2 + ... + Ьтхт.
Так как по условию в произведении не все коэффициенты делятся
на 4, то у обоих многочленов все коэффициенты не могут быть
четными. Следовательно, у одного из них, например у многочлена
В, не все коэффициенты четные. Допустим, что в многочлене А тоже
есть нечетные коэффициенты. Рассмотрим первый из них (имеющий
наименьший номер); пусть это будет коэффициент а,. Пусть, далее,
первый нечетный коэффициент многочлена В будет Ьк. Рассмотрим
коэффициент при xk+s в произведении многочленов А и В. Степень
xk+s в произведении могла получиться только из таких степеней х,
сумма показателей которых равна k + s; следовательно, этот коэф-
коэффициент равен
a0bi,+3 + афь+s-! + ... + a3-ibh + i + asbh +
+ a,+1bft_i + ... + a,+hba.
В этой сумме все произведения, стоящие до члена а,Ьк, четны,
так как четны все числа а0, аи ..., а,-\. Также четны все произве-
произведения, стоящие после asbh, так как bk-\, Ь*-2, ..., Ьо — четные
числа. Произведение же а,Ьк — число нечетное, так как и а,, и bk —
числа нечетные. Следовательно, и наша сумма нечетна, что противо-
противоречит тому, что в произведении все коэффициенты четны. Таким об-
образом, предположение, что у многочлена А есть нечетные коэффи-
коэффициенты, неверно, и, следовательно, все коэффициенты А — четные
числа. А это и требовалось доказать.
317. Докажем, что при любом рациональном, но не целом зна-
значении х многочлен Р(х) не может быть целым числом, а значит,
не равен нулю, ибо нуль — целое число.
333
р
Пусть х=--—т-, где р и q взаимно просты. Тогда
Р (х) = хп+ aixn-1 + a.zxn~2+ ... + an_iX + ап =
^=2 + • • • 4- an_i
n~2q 2+ ¦, ¦ + fln-
p" + 9 (otp"-1 + flap"? + ... + an_iP^n-2 + a,
Число p", как h p, взаимно просто с q; следовательно, р™ +
Ч- q(a\pn~x + ... + anqn~l) также взаимно просто с q, а значит,
и с I/™. Поэтому у нас получилась несократимая дробь, которая
не может быть равна целому числу.
318. Пусть N — некоторое целое число и P(N) = М. При лю-
любом целом k
P{N + Ш) —P(N) =
+ a{[(N + kM) "-' —N"-1] +... + an_][{N + Ш) —
делится на kM (ибо (А^ + /гУИ)г — Л" делится на (N¦+kM) — N =*
= kM), а значит, и на М; поэтому P(N + kM) делится на М при
любом целом k.
Таким образом, если доказать, что среди значений P{NA-kM)
(k = 0, 1, 2, ...) встречаются числа, отличные от ± М, то тем ¦
самым будет доказано, что не все они являются простыми. Но мно-
многочлен Р(х) я-й степени принимает любое значение А, самое боль-
большее для п различных значений х (ибо иначе уравнение л-й степени
Р(х)—А =0 имело бы больше п корней). Таким образом, среди
первых 2п + 1 значений P(N + kM) (k = 0, 1, 2, ..., 2п) имеется
по крайней мере одно, отличное от + М и — М.
319. Заметим прежде всего, что каждый многочлен я-й степени
Р(х) можно представить в виде суммы многочленов
Р0(х) = 1, Р,(х) =х,
P=W= 1-2 РтЛх)- 1 -2-З...Я
взятых с некоторыми коэффициентами:
ь
Для доказательства этого заметим, что если —у равно старшему
коэффициенту многочлена Р(х), то Р(х) и ЬпЯ„(л:) имеют одинако-
bn_t
вые коэффициенты при хп; если, кроме того,- ~- равно старше-4
му коэффициенту Р(х) — ЬпРп(х), то Я(х) и Ь„Р„(х) +bn-iPn-,{x)
имеют одинаковые коэффициенты при хп и хп~и, если, кроме того,
334
^-равно старшему коэффициенту многочлена Р(х)—ЬпРп{х)—
< )
— bn-iPn-i(x), то Р(х) и ЪпРп(х) +Ьл_,Я„_,(л:).+ 6п_2Яп_2(*)
имеют одинаковые коэффициенты при хп, л:"-1 и х"~2, и т. д.; таким
образом, можно определить bn, Ьп-\ Ь\, Ьа так, чтобы много-
многочлены Р(х) и ЬпРп(х) +bn-1Pn-i(x) +... + b,Pl(x) +Ь0Р0(х) пол-
полностью совпадали.
Пусть теперь многочлен n-й степени Р(х) таков, что Р@),
Р(\), ..., Р(п)—целые числа. Как и всякий многочлен, его можно
представить в виде
Р(х)=Ь0Р0(х)+Ь1Р1(х)+Ь2Р2(х)+... + ЬпРп(х).
Заметим, что
... ¦= />„_,(/!-2) = Рп(п- 2) = Рп(п~\) = 0,
Яо(О) = Р,A) = Р2B) = ... = Я„_,(я— I) = Ря(я) = 1.
Поэтому
Р@)= Ь0Яо@), откуда Ьо = Я @);
РA) = 60Р0A) +6,Р,A), откуда Ь, = РA) -Ь0РоA);
РB)= 60РоB)+Ь,Р,B)+62Р2B),
откуда . Ь2 = РB)-ЬоРоB)-Ь1Р,B);
Я(л) =Ь0Р„(п) +Ь1Р1(п) +... + Ь?1_1Рп_,(п) +Ь„Рп(п),
откуда Ь„= Р(п)— ЬаРа(п)— biP^n)— ...— 6п_,Яп_,(я).
Таким образом, все коэффициенты Ьо, Ьь 62 Ьп являются
целыми числами.
320. а) Из решения задачи 319 следует, что подобный многочлен
можно представить в виде суммы многочленов Ра(х), Рх(х),„ ...
..., Рп(х) сцелыми коэффициентами Отсюда и из того, что много-
многочлены Po(-v), P\(x), ..., Рп(х) принимают целые значения при каж-
каждом целом х (см. задачу.75а)), следует утверждение задачи.
б) Если многочлен Р(х) = апхп + а,-!*'" + ап~2хП~2 + ...
... + п\Х + а0 принимает целые значения при х = k, k + 1, k +2, ...
...,-k+n, то многочлен Q(x) =P(x + k) — а„ (х + k) n+ aK_i(x +
+ k)n~l + ... + a,(x + к) + a0 принимает целые значения при* == 0,
1, 2, 3, ..., п. В силу задачи а) отсюда следует, что Q{x) принимает
целые значения при всех целых х. А отсюда мы заключаем, что и
многочлен Р(х) = Q{x — k) принимает целые значения при всех це-
целых х.
в) Пусть многочлен Р(х) = апхп + an-ixn~* + ... + ад + аа
принимает целые значения при х = 0, 1, 4, 9, .... л2. Тогда много-
многочлен Q{x)=P(x2) =а„(х2)« +an_,(x2)'>-1 + ...+aiX-z + ao сте-
степени 2л принимает'целые значения при 2п+ 1 последовательных зна-
значениях х = — п, —(л—1), — (л — 2), ..., —1, 0, 1, ..., 1—1, я.
«35
В самом деле, очевидно, <?@)=Я@), Q(\) = Q(— 1) = ЯA)\
QB)=Q(-2)=PD), QC)=Q(-3)=/>(9), .... Q(«)=Q(-«) =
<= P(n2), а все эти числа по условию являются целыми. Следова-
Следовательно, В' силу задачи б) многочлен Q(x) принимает целые значения
при каждом целом значении х. А это и означает, что Р{№)= Q(k)
при любом целом k есть число целое.
х(х-1)
Примером может служить многочлен Р(х) = —j^j—Для которого
х*(х2—\) х*{х— \)(х+ 1)
Q(x) = P (х*) = 12 = — /2 =
„ (х+2) (*+!)*(*-I) (х+1)х(х-\)
~2 1-2-3-4 1-2-3
321. а) Используя формулу Муавра и формулу бинома Ньюто-
Ньютона, будем иметь:
cos 5а + ( sin 5а = (cos а + t sin аM =
= cos5 а + 5 cos4 а i sin а + 10 cos3 а (i sin аJ +
+ 10 cos2 а(» sin аK + 5 cos а(( sin аL + (i sin аM =
= (cos5 а — 10 cos3 а sin8 а + 5 cos а sin4 а) -f-
+ iE cos4oe sin а — 10 cos2 a sins a -J- sin5 a).
Приравнивая действительные и мнимые части слева и справа, полу-
получаем требуемые формулы.
б) Аналогично решению задачи а) имеем:
cos na + I sin na = (cos a + i sin a)" =
== cosn a + С^ cos™ ai sin a + С\ cosn~2 a (i sin aJ +
+ С% cos"" a (j sin о)» + С* cosn~4 a (i sin aL + ... =.
= (cosn a — Cl cos" a sin2 a + С* cos" a sin4 a —...) +
+ 1 (C^cos"-1 a sin a — Съп cos"" a sin3 a +...).
Отсюда и вытекают нужные форм-улы.
322. Согласно формулам задачи 321 б) имеем:
sin 6a 6cos6 a sin a — 20 cos3 a sin3 a -f- 6 cos a, sin5a
^ cos 6a ~~ cose a — 15 cos4 a sin2 a + 15 cos2 a sin4 a — sinn a'
Разделав числитель и знаменатель последней дроби на cos8 a,
получаем искомую формулу:
6 tg a — 20 tg» a + 6 tg5 a
tg6a - i _ is tg2о + 15 tg4.a — tg« a '
323. Уравнение ¦lc + ~ = 2 cos a перепишем в виде
x2 + 1 = 2x cos a, или x2 — 2x cos a + 1 = 0.
Значит,
x = cos a J; y'cos2a — 1 = cos«f /sin a.
336
Отсюда вытекает, что
хп = cos n a ± i sin n а;
+ lsinna-
После сложения получим:
х" + — =2cos n а.
S24. Рассмотрим сумму
[cos ф + 1 sin ф] + [cos (ф + a) + i sin (ф + a) ] +
+ [соз(ф + 2a)+'sin((p'+ 2a)]+ ... +[cos((p + na)-fi sin(q> + na)].
Наша задача сводится к вычислению коэффициентов при мнимой и
действительной частях этой суммы. Обозначая cos ф + i sin ф через
а и cos a + i sin a через x и применяя формулу для произведения
комплексных чисел и формулу Муавра, найдем, что рассматриваемая
сумма равна
a + ах + ахг + ... + ахп =
__ axnJri — a cos (п + 1) a + i sin (n + 1) a — 1
~ x_x = (со5ф + 1 sin Ф) cosa + tslna-1 =
-^fT'81"*' [(cos a-1) +isin a]
o . ,"+• . .. . я+l n+\
— 2 sin2 —2— a + 2i sin —g— a c°s —о— a
: (COS ф + ( Sin ф) =
— 2 sin2 -g— -f- 2» sin у cos -g—
• n+\ Г я+l , . . n+1 I
2i sin —g— a cos ~~2— a + « sin —— a
= (cos ф + I sin ф) 1 . . J =
a Г a a 1
2i sin -g- cos ~2 + i sm -j-
. я-f-l
sin
2 w
—— (cos ф + i sin ф) X
sin —
/ я+l , . л+1 V a a
cos —5— a + 1 sin —5— a cos -5- — i sin -5-
\. z z / \ й ^_
x a a
cos2 — + sin2 -y
sin 2 аГ / л N / л N1
¦ — cos I ф + -у I a + ( sin (ф + -у a 11
sin -яг- L \ / \ / J
sin -y
22 д. о, Шклярский и др. 337
(здесь снова используется формула умножения комплексных чисел,
а . . а / а \ . / а \\
а также то, что cos— — ism — = cos I g- I 4- < sin I — -y I).
Отсюда сразу следуют требуемые формулы.
1 4- cos 2x
325. Воспользуемся тем, что cos2* = g • Отсюда, исполь-
используя результат предыдущей задачи, получим:
cos2 а 4- cos2 2а 4- • ¦ • + cos2 па =
= -у [cos 2а 4- cos 4а 4- ... 4- cos 2па -\-п\ =
1 Гзш (п 4~ 1) а cos па 1 _п_ sin (п -\- 1) а cos па п — 1
= ~[ sin а 'J ' Т = 2 sin а +~2~'
А так как sin2* = 1 — cos*x, то
sin2a 4- sin2 2a 4- • • ¦ + sin2 no. =
sin (n-f l)a cos no. n — 1 n 4- ' sin (л 4~ 1) a cos n0L
= n~ 2 sin a ~ ~ = 2 ~ 2 sin a "
326. Требуется вычислить действительную часть и коэффициент
при мнимой части суммы
(cos a 4-' sin a) 4" С„ (cos 2a 4-1 sin 2a) 4-
4- C\ (cos 3a 4- i sin 3a) 4- .. • + (cos (n 4- 1) a 4-! sin (n + l)a).
Обозначая cos a 4- « sin a через х и используя формулу Муавра
и формулу бинома Ньютона, преобразуем эту сумму следующим
образом:
= (cos a 4" 1 sin a) (cos a 4- ' + < sin a)" =
/ a a a \"
= (cos a 4"' sin a) 12 cos2 -y 4- 2/ cos -y sin -y I =
= 2™ cos" — (cos a 4- 1 sin a) I cos -y 4- » sin -y =>
„ a / n4-2 . . П4-2
= 2 cos -5- cos —5— a 4-' sin —5— a
Отсюда следует,'что
cos a 4~ C1^ cos 2a 4" Cn cos 3a + ... 4" cos (« 4" ') a =
„„ „a «4-2
= 2" cos" -y cos —y- a,
sin a 4- Cj, sin 2a 4- C2n sin 3a'+...+ sin (л + 1) a =s
¦= 2" cos" -y sin ^-y- a.
S33
327. Воспользуемся формулой
sin A sin В — — [cos (A — В) — cos {A + В)].
Отсюда следует, что нашу сумму можно предоставить в виде
Г
(т — я) я 2(т — л) л 3(т — я) я
+ cos + cos
-j-Jcos + cos + cos -г...
(р — \)(т — я) л! 1 Г (т + п) я
... + cos j - — l^cos +
2 (m + я) л 3 (т + п) л (р—1)(т + я)я'
I +COS +...+COS
1-
Но сумма
21гл , 36л (р — 1) fax
+ co + f s
kn 21гл , 36л
cos — + cos — + cos — + ... -f cos
+ cos + cos + ... -f cos
равна p— 1, если k делится на 2р (в этом случае каждое слагаемое
суммы равно 1); в случае же, когда к не делится на 2р, эта сумма,
в силу результата задачи 324, равна
pkn (p-\)kn
-g- cos Т
l = sm^—
. p
sin -g- cos Тр л
l sm^
О, если k нечетно,
¦ 1, если k четно.
Отметим еще, что оба числа т + п и т—п будут четны или нечетны
одновременно; в частности, если m + п или m — п делится на 2р,
то и т + п и т — п — четные числа. Отсюда вытекает равенство,
требуемое условием задачи.
328. Рассмотрим уравнение х2п+1— 1 = 0, корни которого:
, 2л . . 2л 4л . . 4л
*¦ C0S 2л~ТТ + ' sln 2^П' C0S2^TT+'SIn27rTT' '••
4ял Ann
Так как коэффициент при х2п в уравнении равен нулю, то сумма
всех этих корней равна нулю: .
1
2я 4л , 4ля
+ + +
я ,
cos 2я~+1 + cos 27ГТТ + • • • + cos
[2я 4л 4лл
sin 21Г+1 + Sln 2Т+1 + • • • + sin 2JT
Следовательно, выражение в каждой скобке равно нулю, откуда,
в частности,
2л , 4я 4ял
cos 2Т+Т + cos 27ГТТ + • * • + C0S 2лТ7 = ~ 1 •
22* 339
Но
2я inn An Dn — 2) я
cos 2^ТрТ " cos 5Г+7' cos 2Т+Т = C0S 2n+l '
и т. д., значит,
Г 2я 4я 2пл
2 [cos 2к~П + C0S 2п~+\ + ¦ ¦ ¦ + cos 21ГП
т. е.
2л 4я . 2яя
1
^ 2п + 1 I" си!> 2п + 1 "Г • • • т LUJ 2n + 1 - 2 '
Примечание. Можно также решить эту задачу, исходя из
формул задачи 324.
329. а) В силу результата задачи 3216) имеем:
sinB«+ I) a = CJ,n+i (I — sin2 а)" sin а—
— C|n+1 (I— sin2 a)n-1 sin3 а + ... + (—l)nsin2n+f а.
л 2л . «л
Отсюда вытекает, что числа 0, sin я—;—г. sin z—j—г, ..., sin «„ i i,
2л \ 2л
/ nn \
•¦ • - sin — 5—r-r =— sin;
являются корнями такого уравнения Bп 4- [)-й степени: '
C2n+i(l-^)n^-C32n+1(l-*2)n-1^+...+(-l)n*2n+1 =0.
Следовательно, числа sin8^ , ^, sin2 2п+ V •'•• sin2 2—П"
являются корнями уравнения п-степени:
Cl2n+1 (\-x)n-C\n+i (l-xI1-1 х+...+(-1)пхп = 0.
б) Заменим в формуле задачи 32i6) п на 2п + 1 и запишем
ее в следующем виде:
sin Bn+ 1) а = sin2^1 а (c'n+1 ctg2" а - C32n+1 ctg2"-2 а +
т ^2п+1 С1§ «— •• )¦
_ ¦ л 2я Зл пл
Отсюда следует, что при а =2^Г]. г^ТТ1 2Т+7'"- 2^1
имеет место равенство
C\n+i ctg2» « - С32„+1 ctg2»-2 « + C\n+i ctg2"-* «-...= 0,
, n ¦ 2л яп
т. е. что числа ctg ^rp-j ctg2 2n ; j ctg2 2^y являются корнями
340
следующего уравнения га-й степени:
330. а) Сумма корней уравнения га-й степени
хп _ ?|2±1 хп-1 + ?*!+! хп-2 _ _ _ _ = 0
(см. решение задачи 229 6)) равна коэффициенту при хп~\ взятому
с обратным знаком, т. е.
t2+t2 + t2^ + +^^
пBп —
б) Так как cosec2a = ctg2a + 1, то из формулы задачи а)
следует
л , 2л Зя .
cosec2 о„ | | -f- cosec2On , ^ + cosec*
- cosec2
2л+1^игс" 2л+1^ •••
пл п Bп— 1) 2га (/г + 1)
п 2л
331. а) Первое решение. Числа sin22/ , ^, sin22^ _, ^ ¦¦•
• •¦< sin2» | , являются корнями уравнения л-и степени, полу-
полученного в решении задачи 329а). Коэффициент при старшем члене
хп этого уравнения равен (— 1)"[с1,„+1 + c\n+i + ... + C2?+l + l] ¦
Но сумма в квадратных скобках составляет половину от общей сум-
суммы биномиальных коэффициентов l-f-C^n+r^iJn+r^1 • •"T"^2n+i "Ь '¦
й A + lJ+1 22+1 фф
равной, как известно, A + lJn+1 = 22n+1; следовательно, коэффи-
коэффициент при хп в нашем уравнении равен (—1)2'\ Далее, свобод-
свободный член этого уравнения есть С\п+1 = 2п + 1. Но произведение
корней уравнения n-й степени равно свободному члену приведенно-
приведенного уравнения (уравнения с коэффициентом при старшем члене,
равным единице), умноженному на (—1)", т. е. равно свободному
члену, умноженному на (—I)" и деленному на коэффициент при
старшем члене. Отсюда имеем:
я 2л пл 2п + 1
( '} SIn 2п + 1 sln 2n + 1 ¦ • • Sln 2n + t - <- 1) ^Г
и, следовательно,
. я . 2л . ля У2я+ 1
¦••31П2я+1
341
Аналогично можно доказать, что
л 2л (я — 1) я Уп
sin ~2п Sln 2п~ ¦ • • SIn 2я = '^=~v
Второе решение. Корни уравнения х2п— 1=0 равны
ля 2л . . 2л
1, —1, cos —+ <sin—, cos—+i sin—,
Зл Зл Bл—1) я B.1—1) я
cos — + tsin—, ...,cos -И sin -— .
Поэтому имеем:
х2п — 1 = (ж — 1) (Х + 1) (х — соз -^- — i sin -y j X
2л . . 2л\ / (п - 1) л . . (л — 1) л\
X \х — cos — — tsm— ... дс —cos — isin |х
X { х - cos i sin | X ...
Bя— 1)л . Bл —1)я\
...X^-cos -«sin j.
Bя — k) л ?л . Bя — k) л fen
Но cos = cos -^-*, s'n Z = — s'n ~Z~'i отсюда сле-
следует, что
л л W Bя— I) л Bл— 1) л
х — cos —— — i sin — х — cos — i sin ^
xcosisin
= х2 — 2х cos -7- + 1,
/ 2л .. 2лW
^x-cos— -ism— j[x-
Bп — 2) л Bк — 2) л
cos — i sin
2л
= хг — 2х cos — + 1,
(л— 1) л (я— !) л\
: — cos — i sin X
X U'-cos^—^—fsin' ln ' I =.x^-2xcosv „ +1.
Поэтому разложение многочлена х2п — I на множители можно
переписать так:
х2п — 1 =(х2— 1)U2 — 2хcos-^-+ l)(x2 — 2xcos —- + l) ...
>-1)я
' п '
342
Отсюда
х2"- 1
х2 — 1
Положив здесь х = 1 и воспользовавшись тем, что 2 —2 cos a =
а
4 sin2 -5-, получим :
п = ч sin- 2^ 5Ш 2л '''
откуда вытекает, что
я 2я (я — !) я
sin 2«"sin2T'--sin 2n :
Аналогично можно доказать, что
я 2л . ля
2л
2—1
У2я
+ 1
аш 2п + 1 al" 2п + 1 •••S1|12n+ I - 2"
б) Требуемый результат может быть получен совершенно ана-
аналогично первому или второму решению задачи а); однако мы здесь
не будем повторять этих решений, а сразу выведем нужные форму-
формулы из формул задачи а).
Так как
. л 2/гл . Зл Bя—2)я
sln2T+l==sln2T+l' Sln ЪГЛ~\ = sln 2п + 1 '
5я Bп — 4) л
то
bill
(см
¦ • •
2 л . 4 л
2л -4- 1 мп 2л +
. а))» Разделив
ял }^
Sln2n + 1 ~
2л
, sin
я
эту
2/г +
2П
я
6л
2я + 1 • • • ;
. 2я .
2ля
>ш 2л + 1
Зл
формулу почленно на s
¦ 1
— и воспользовавшись
я . 4я
ля V2/1-+1
о|" 2/г + 1 2"
я 2л
2л+15Ш2/!+1 ¦'¦
. тем, что
2л „
sin о„ , , =2 sin
2я 2я 2лл „ . пп ля
i2m
343
получаем:
я 2я Зя «я
cos 2^+icos srqncos г^тт • ¦ •cos 2^т
Аналогично имеем:
JL ... 2я „„ (я-1)^ /.,_ " .,_ 2я _:_ (я - 1) л\
я . 2я ¦ . (л — 1)я
. (я —1)л . 2л (л —2) л
п
поэтому
л 2я (я—1)п
при я = 2А + 1 нечетном sin— sin —^- ... sin - =
= I sin п. , , sin „. :, , ... sin
2А -j- I 2& + 1 '' * 2k 4- 1 / I о* I ifi—V
-г -г -г ] у г i г
. я . 2л . (я—1)я
при я = 2А четном sln~ sm — • • • sln ^ =
я . 2л . (k — \)n\2 ( V"k
(см. задачу а)). Отсюда получаем:
я 2л (я — 1)я 1 2
cos 2TCOS 27T'--COS In ^4^~
"-1
»—1
Примечание. Разделив формулы задач 331а) и б) одну на
другую, получим:
я . 2л , ля _ ,-
tt*V2 + l'
я 2л (я — 1) л
^Г{§-27Г--л§ 2Д =
Впрочем, второе из этих равенств совершенно очевидно, так как
kn (п — к) л kn kn
^2Т1§ Тп ^^г^^Кгя = ' ПРИ *"'¦ 2> ¦•- "~] и
л
tg т"= 1. Из этого равенства и второй формулы задачи 331а) мож-
* _,_ я 2л (я— 1)л
но было бы просто вывести формулу cosy cos jjJJ- •• • cos g^ ^
~ 2"—1
Можно также получить эти формулы аналогично первому ре-
решению задачи 331а).
344
Т
332. Покажем, что для любого положительного угла, меньшего
sin а < а < tg а.
Имеем (рис. 39):
с 1ч •
ь\аов = "г" sin а,
5сект АОВ~
с- зэ-
(радиус круга принимаем равным еди-
единице, углы измеряются в радианах).
Но так как S&aob < ScemAOB <
<Saaoc, to sin a < а < tg a.
Из того, что sin а < а < tg а,
следует, что ctga < —< coseca. Поэтому из формул задач 330а)
и б) вытекает:
пBя—I)
< cosec^
3л
¦ + cosec 2T+1
г + ... + cosec2
пп 2я(п+1)
I ^
2I+T
Разделив все члены последнего двойного неравенства на
+1J л
5 , будем иметь:
2п
— \ я2
Г 6
2м
22 + З2
<2я + 1'2/г + Г 6
что и требовалось доказать.
333. а) Предположим, что точка М взята на дуге АхАп окруж-
окружности (рис. 40). Обозначим дугу МА{ через а; в таком случае дуги
345
MAir МАз МА„ соответственно равны
2л
—,
4л
—
2 (п — 1) я
АВ
Но длина хорды ЛВ окружности радиуса R равна 2^sin -g-
(это можно легко усмотреть из равнобедренного треугольника АОВ\
Рис. 40.
Рис. 42.
где О — центр окружности). Отсюда видно, что интересующая нас
сумма равна
4S° [sin' -f + sin* (-f- + -Д) + sin* (-f + -^) + ...
34G
1 — cos 2x
известной формулой sin2A;= g > получим, что это выражение
равно
п Г / ¦2л\ I 4я\
S = ~2~ — cos a + cos I а + — 1 + cos I а + — I + ...
... + cos I a 4
Но по формуле задачи 324 имеем:
cos +
(л-1)я
sin n cos a
я
sin —
n
n
следовательно, S = —n~. Отсюда и вытекает утверждение задачи.
Примечание. При п = 2т четном (рис. 41) утверждение за-
задачи является очевидным, так как, в силу теоремы Пифагора,
MA2 + MA^+i = MA\ + МА^+2 — ... = MA2m + MA\m = 4R*.
'б) Пусть A\BX, A2B2, ..., A „ Bn — перпендикуляры, опущенные
из точек Аь /4 2, ..., Л„ на прямую ОМ (рис. 42, а). В таком случае
по известной теореме имеем:
МА\~ MO2 + OAl~2MO-OBk~ /2-l R2r~2l-OBh
(k == 1, 2 n), где отрезки OBh берутся со знаками + или —
в зависимости от того, расположена ли точка Bk на луче ОМ или
вне его. Следовательно,
МА\ + МА\ + ... + МА\ =
= л(/2 + Я2) - 2/@5,+ ОВ2 + ... + ОВ,,).
Но если Z. А/ОЛ i = а, то
0Bt = О A j cos Z AjOM = ? cos а, 0В2 = R cos (а + — ),
0В3 = /? cos [а+Х) 0Bn = fl cos fа + " ~ } "
А так как в решении задачи а) было показано, что
/ . 2я\ / 2{п~\)л\ п
cos a 4- cos f а 4" ~ + • • • + с°з I а 4 Г =0,
\ / \ /
то ОВ, 4- 0В2 4- • • • 4- ОВ„ = 0; отсюда и вытекает утверждение
задачи.
347
Примечание. При п = 1т четном (рис. 42, б), утверждение
задачи доказывается геометрически: в этом случае OB, + 0Bm+1 =
= ОВ2 + 0Вт+2= 0Вт + 0В1т = 0.
в) Пусть М] — проекция точки М на плоскость «-угольника
(рис. 43). В таком случае имеемМА\ = MVA^ + ММ\ (к = 1, 2, ...
..., п) и, следовательно,
Но
/2 = ОМ2 ^О/И^
.. + MiA* + n-MMf.
{ Mf) (см. задачу б)) и
2. Отсюда и вытекает утверждение задачи.
334. а) Утверждение задачи сразу следует из теоремы задачи
333а), если учесть, что при п четном четные (и нечетные) вершины
л-угольника сами служат вершинами вписанных в окружность пра-
п
вильных -7)--угольников.
б) Пусть я = 2т + 1. Из решения задачи 333а) выводим, что
достаточно доказать равенство между собой следующих сумм;
348
2тп
Но, согласно задаче 324, имеем:
(т + I) я
Sln
2m
sin2^"+T
mn (а я
. sin 2т~П Sln [T + 2m~T~\
S, = z = Si
sin
2т + 1
что и доказывает теорему.
335. а) В силу задачи 333 а) сумма квадратов расстояний от
точки окружности, описанной около правильного я-угольника, до
всех его вершин равна 2nR2. Предполагая, что М совпадает с At,
получаем, что сумма всех сторон и диагоналей я-угольника, выходя-
выходящих из одной вершины, равна 2nR2. Если умножить эту сумму на п
(число вершин л-угольника), то мы получим удвоенную сумму всех
сторон и диагоналей я-угольника (так как каждая сторона или диа-
диагональ имеет два конца, то она будет фигурировать в такой сумме
дважды). Отсюда искомая сумма равна -K~-2nR} = л2#2.
б) Сумма всех сторон и диагоналей правильного многоугольни-
многоугольника, выходящих из одной вершины Аи равна
ППГ • я , • 2л , , • (" — ')"
2R sin j- sin — -j- ... + sin
я (я — 1) я
Sin -§- Sin —g;
(ср. задачу 3346)). Умножая эту сумму на я и деля пополам, полу-
получаем требуемый результат: #nctg^.
в) Произведение всех сторон и всех диагоналей я-угольника,
выходящих из одной вершины, очевидно, равно
..п ^- .ш ^ :.. .ш
-2-
(см. задачу 331а)). Возводя это произведение в я-ю степень и из-
извлекая затем квадратный корень, получаем требуемый результат.
336.. Вычислим сумму 50-х степеней всех сторон и всех диагона-
диагоналей 100-угольника, выходящих из одной вершины Аи Задача сводится
349
к нахождению суммы
я
(сравните с решением задачи 333а)). Таким образом, нам надо сум-
суммировать 50-е степени синусов некоторых углов. Но
(cos а + ( sin а) — (cos а — I sin а)\60
_ j =
где обозначено cos a + I sin а = х; в таком случае cos а — i sin а
= —-. Следовательно,
а =
~
' • • + С50
- 2С\й cos 48а + 2С\й cos 46а - ... + 2C^.cos 2а + СЦ)
[здесь использовано то, что xk +-r=(cos ka + i sin Aa) + (cos ka.—
x"
— i sin ka) = 2 cos ?a].
Итак, сумма 2 может быть переписана следующим образом:
- 2С\0 (cos 48 щ + cos 48щ + ... + cos 4&Щ
л 2я 99я\
^ + cos 46 ^ + ... + cos 46WJ -
2л 99л\
-50 !'-"='•' Too т "-"" Тбо+ •• • + cos ТОО") ~~99С50
25l_
50 —
2^50s" • • • + 2C5qS25 99C60j,
35C
где через sb s2, ,.., s25 обозначены суммы, стоящие в круглых скоб-
скобках. Но из формулы задачи 324 сразу следует, что Si = sj = ... =
= s25 = —1. Следовательно, имеем:
2 = R>° B - 2С';) + 2С1 - ... + 2СЦ + 99Cf0) =
= /?»« [A - IM00 +
Отсюда сразу получаем, что сумма 50-х степеней всех сторон
и всех диагоналей 100-угольника равна
5000 • 50!
1002
337. Так как \г\ = |г| = |— г| = |— г[ и
1
_1_
г '
— г — ¦
г+т
то достаточно рассмотреть лишь то из
чисел г, г,—г н —г, которое лежит в первой четверти. Если ]г| дости
гает наибольшего возможного значения, то ~р[—Т7Т~~ наименьшего.
Поэтому достаточно найти те г, модуль которых является наи-
наибольшим возможным; при этом
— . Пусть аргумент ф чис-
числа г нам задан; 0 ^ ф ^ ^• Т°г'
да из рис. 44 имеем (напомним,
= а', ниже обозна-
обозначено |г| = г):
а1 = г* + ji — 2 cos 2ф =
1 Рис. 44.
= '2 + 7г~2 + 4 со&г Ф =
/ ) \2
=(/-— —] +4cos29.
Так как, согласно нашему предположению, г ^ —• , то с ростом t
1 / 1 \2
растет и разность г——, и наоборот. Но I г — — I = о2 — 4со&гф ^
0
)-р
¦ /
2
г
; при ф=~ имеем\г—— I = а2. При этом г——=а, г =
35)
Соответственно этому наибольшее значение |г| =^,а-}- ~\/аг -f- 4)
достигается при г = g"(a + V°2 + 4)> а наименьшее
— (Уа2 + 4 - а). — при г = —
— (Уа2 + 4 - а). — при г = —^(/а^+Т—а).
338. Ясно, что три комплексных числа 1 (= l + (-0 = cosO +
+ isinO), ~ 2 (=cos 120°+ ( sin 120°) и ~ ~~2
(= cos(— 120°) + isin(— 120°)) таковы, что аргументы каждых
двух из них разнятся в точности на 120°, а сумма всех чисел равна
нулю — поэтому заменить в усло-
условии задачи величину 120° боль-
большей заведомо невозможно. Пусть
теперь |6( —0,| < 120°, где I,
i = 1, 2 п и 1ф\ (здесь
6ь 62 6„ — аргументы наших
комплексных чисел; ясно, что если
одно из этих чисел равно нулю
и, следовательно, не имеет одно-
однозначно определенного аргумента,
то это число можно просто отки-
откинуть); докажем, что в этом случае
равенство Zi+z2+.. .+zn=0 иметь
места не может. В самом де-
деле, из сделанного предположения
вытекает, что отвечающие комп-
комплексным числам zu г% ..., г„ точ-
точки Аи Л2, ..., Ап комплексной пло-
плоскости с полярными координатами
(ги в,), (г2, е2) (г„, е„)
D ., принадлежат некоторому меньшему
рис 4Э- 120° углу POQ, ограниченному
лучами 6 = Qk и 6 = 6/, где Ак
и Л, —«крайние» из наших точек,
т. е. отвечающие числам zh и zt с «крайними» значениями аргумен-
аргументов (рис. 45). Пусть луч OR, отвечающий значению 6 = 0О поляр-
полярного угла,— это биссектриса <POQ, ,a_ z0 = cos 9n-f i sin 90—
комплексное число единичного модуля, изображаемое точкой Ао это-
этого луча. Так как числа г\ — -р- [rx cos(9 — 60)+ IsinF — Во)],
¦г, , Zn
г, = , ..., г„—— имеют те же модули ги г2, ..., гп, что и числа
Z\, г2, .. ., г„ , но аргументы 6| — 90, 62--6о, . .Г0П — 60 вместо
аргументов 9ь 62 6„ чисел гь г2/..,, гп. то отвечающие числам
2j, г2, ..., гпточки/4р /42, ..., Апкомплексной плоскости полу-
получаются из точек А\, Л2 Л„ поворотом вокруг О на угол Go по
часовой стрелке. Но отсюда следует, что все эти точки принад-
принадлежат полученному из POQ указанным поворотом углу P'OQ' <
< 120°, биссектриса OR' которого совпадает с осью Ох веществен-
вещественных чисел. А отсюда, в свою очередь, вытекает, что вещественные
части с',, а'2 а'п чисел z\ =ai-jrib'i, г'2 = а'2+ ib'p ...
352
... , zn•= an -\-ibn вес положительны; поэтому сумма
г\+г'2+...+ г'п = (а\ + ib\) -|- (а'2 + »;)+...+ (а,'г + ib'n)
а'п^> 0)- Но из
никак не может равняться нулю (ибо aj -f- a2 ~~Ь • • •
того, что
следует, что также и 2i + r2 + ... + г„ =5^= 0.
339. Предположим, что отвечающая комплексному числу г точка
А комплексной плоскости не принадлежит выпуклому многоугольни-
многоугольнику С[С2 ... С„, вершины которого отвечают числам си сг, ..., с„
Рис.
(рис. 46). В этом случае все лучи АС,, АС2 АС„ «направлены
в одну сторону» в том смысле, что все эти лучи лежат по одну
сторону от некоторой прямой I, проходящей через А. Заметим теперь,
23 д. о. Шклярский и др,
383
что, 9 силу правила вычитания комплексных чисел, числам zt =»'
в г — сь 22 = г — Сг, ..., г„ = г — с„ отвечают на комплексной
плоскости такие точки Ль_Л2. :J_1 An, что векторы ОАи ОЛг, ...
..., ОА-п равны векторам СХА, СгА, ..., С„Л; поэтому все лучи ОА\,
ОАг, ..., ОАа лежат по одну сторону от проходящей через О пря-
прямой 1Ц\1. С другой стороны, если w'=-tt,to при oi = r(cos8+-
-f isin 8) имеем w' =.—[cos (— 6) + ' sin (—6)], т. е, числа шиш'
изображаются такими точками В и В' комплексной плоскости, что
лучи ОВ и ОВ' симметричны относительно оси Ох вещественных чи-
- 1 1 , i .1
сел. Отсюда следует, что числам г{~~— г с ¦ Z2~ J" гп ^Y
отвечают такие точки/4j, Л2,..., Ап, что лучи QA±, 0А0, ..., 0Ап сим-
симметричны лучам OAU ОAt ОАп относительно оси Ох,
откуда следует, что все эти лучи лежат по одну сторону от пря-
прямой I", симметричной /'• относительно оси Ох (см. тот же рис. 46).
Дальнейшая часть доказательства близка к решению задачи
338. Если 2о = cos 6o + i sin Go — комплексное число модуля 1, изоб-
г1 •• г2 » гп
ражаемое точкой прямой/", то числаг. =-т~, г^ = —, .... г„ =—
., „ ° го '1 г„,
изображаются точками Л,', А, ..., Ап, получаемыми из точек А\
А<? А п поворотом вокруг О на угол 80; поэтому все оии
лежат по одну сторону от оси Ох, получаемой тем же поворотом из пря-
прямой /". Но отсюда следует, что коэффициенты b[, Ь2 Ьп при
мнимых частях чисел г'[ = а\ -f it"it г., — о" + ib, ..., г'п — а"п + ib"a
все одного знака — и, значит,
ибо by -f *2+ •'• *Ь b'n ф 0. А из того, что
вытекает, что также и
340. Первое решение. Пусть а не делится на р. В таком
случае числа а, 2а, За, ..., (р—\)а тоже не будут делиться на р
и все будут давать при делении на р разные остатки: действительно,
если бы ka и la (где р— 1 ^ k > I) давали бы при делении на р
одинаковые остатки, то разность ka — la = (k — 1)а делилась бы на
р, что невозможно, так как р простое, а не делится на р и k — l
меньше р. Но все возможные остатки при делении на р исчерпы-
354
ваются р—1 числами 1, 2, 3, .-.., р—1. Таким образом, должно
быть:
о = QiP + аи 2а = qtp + а2, За = цър + а3, .... (р — 1)а =
= qP-\P + пр-и
где ai, а2, ..., av-\ — числа 1, 2 р—I, взятые в каком-то по-
порядке. Перемножая все эти равенства, получим:
.[1-2- ...-{р— \)]ат-* = Np + ам...ар-и
или
[1-2. ....(p-\)](ar-'-\)=Np.
Отсюда следует, что о?— 1 делится на р, а значит, и а? — а де-
делится на р.
Если а делится на р, то утверждение теоремы Ферма является
очевидным.
Второе решение. Теорема является очевидной при а = 7,
так как в этом случае а? — а = 1 — 1 =0 делится на любое число
Будем теперь доказывать ее методом математической ин-
индукции, т. е. предположим, что нам уже известно, что а* — а
делится на р, и докажем, что в этом случае (а-f- 1)р— (а+ 1) де-
делится на р.
По формуле бинома Ньютона . .
- (ар - а) + рар-' + С^" + ... + С?-V + ра.
Но все биномиальные коэффициенты
rh P(p-l)(p-2)..,(p-fe+l)
Cp=i 1-2-3 ... А
делятся на простое число р, так как числитель выписанного выраже-
выражения содержит множитель р, а знаменатель не содержит этого мно-
множителя. А так как, по предположению, и а^—а делится на р, то
(а + 1)р—(а + 1) делится на р.
Примечание. Приведем еще один ^изящный вариант того
же самого доказательства. В силу того, что все биноминальные коэф-
коэффициенты С * делятся на р, разность
{A + Bf — Ар — Вр =
- рАр~*В + С2рАр~2В* + ... + CP-2/l2fiP-2 +рАВр~2,
где А, В — какие угодно целые числа, всегда делится на р. Последо-
Последовательным применением этого результата получаем, что
(A + B + Qp— Ар— Вр — О =
= {[(Л +В)+С]р— (A + B)p — Cp} + (A + B)p — Ap — Bv
всегда делится на р,
{А + В + С + D)p—Ap— Вр— С'— D" ={[(А +B + C)+DJp —
~(А+В + C)p—Dp) + (A+B + C)p~Ap—Bp — Cp
23* ¦ 355
всегда делится на р и вообще
всегда делится на р.
Г1оложив теперь в последнем соотношении А = В = С = ...
... = /(= 1 н взяв число этих чисел равным а, мы придем к теоре-
теореме Ферма: ар — а делится на р.
341. Доказательство теоремы Эйлера совершенно» аналогично
первому доказательству теоремы Ферма; г чисел, меньших N и взаим-
взаимно простых с N, мы обозначим через k\, k2, &з, •.., kr. Рассмотрим
г чисел k,a, k2a kTa, Все они взаимно просты с N (ибо а вза-
взаимно просто с N по условию задачи), и все они дают при делении
на N различные остатки (это доказывается в точности так же, как
в решении задачи 340). Отсюда следует, что
кха = qxN + аи k2a = q2N + а2, . . ., kra = qr~N + ar,
где Я], а2, ..., аг — это те же числа k\, k2t ..., kr, только располо-
расположенные в другом порядке. Перемножив все наши равенства, по-
получим:
kikz ... krar = MN + а, а2 ...ar, kxk% ... k,(ar — \)— MN,
откуда и следует, что число аг — 1 делится на N.
342. Доказательство проведем методом математической индук-
индукции. Прежде всего очевидно, что при и = 1 предложение задачи
справедливо: 21 — 1 = 1, 22— 1=3 и 23— 1=7 не делятся на 5.
Докажем еще это предложение для п = 2. Пусть 2к есть наимень-
наименьшая степень числа 2, дающая при делении на ба = 25 остаток 1
(т. е. такая, что 2h— 1 делится на 25); предположим, что k < 52 —
— 5 = 25 — 5 = 20. Если 20 не делится на k, так что 20 = 9* +
+ г, где г < к, то мы будем иметь:
2м— 1 = 2«fc+r— 1 = 2гBв* — 1) + BГ— 1).
Но 220 —I делится на 25, в силу теоремы Эйлера, а 2*к—1 =
= Bft)'— 1« делится на 2* — 1, т. е., в силу нашего предположения,
тоже делится на 25; следовательно, и 2Г— 1, делится на 25, что про-
противоречит тому, что k есть наименьшее число, для которого
2й — 1 делится на 25. Итак, k должно быть делителем числа 20, т. е.
может равняться только 2, 4, 5 или 10. Но 22— 1 =3, 25— 1 =31
и 210— 1 = 1023 не делятся даже на 5, а 24— 1 = 15 делится на 5,
но не делится на 25. Значит, действительно и для п »= 2 предложе-
предложение задачи справедливо.
Предположим теперь, что для какого-то л предложение задачи
справедливо, а для значения л+1 оно неверно: наименьшее к, та-
такое, что 2к — 1 делится на 5n+1, меньше чем 5Я+1—5" =4-5".
В точности, как выше (для п = 2), доказывается, что k должно яв-
являться делителем числа 4-5". С другой стороны, аналогично доказы-
доказывается, что число 5" — 5"~' = 4-5" должно являться делителем
числа k: если бы было k = q-4-in~> + г, где г < 4-5:1"\ то чис-
число 5Г — 1 делилось бы на 5", что противоречит предположению о
справедливости утверждения задачи для числа п. Таким образом,-
для k остается единственное возможное значение, а именно: k =
=4-5"~1. ¦
Так как число 2ъП~1—Ъп~2— 1 = 24-5"—2_ ] делится на 5П~1
(в силу теоремы Эйлера) и не делится на 5" (иначе предложение
356
задачи не было бы справедливо для числа п), то 24-5" -q -5n -
+ 1, где q не делится на 5. Воспользовавшись теперь формулой
(а + 6M «, аь + 5а4й + 10а3й2 + Юа'Ь* + 5а61 + Ь\
получим:
= 5"+1 (qb • 54"-6 + q* ¦ 53n~4 + V • б2" + 2?* • 5n~2) + <?-5n,
откуда видно,что 2*'° — 1 не делится на 5"+1. Итак, действитель-
действительно, из справедливости предложения задачи для какого-то и следует
справедливость его и для п + 1.
343. По теореме Эйлера (см. задачу 341) число ?5'° б"—| ¦=
— 24-5' —1 = 27 812 50°—1 делится на 5'°; следовательно, при л5*
> 10 разность 27812500+" — 2П = 2ПB7812500—1) делится на 1010,
т. е. последние 10 шярр чисел 27812500+'1 и 2" совпадают. Это озна-
означает, что последние 10 цифр чисел ряда 21, 22, 23, ..., 2", ... повто-
повторяются через каждые 7 812 500 чисел, причем эта периодичность на-
начинается с десятого числа этого ряда —с числа 210.
То, что период на самом деле не меньше чем 7 812 500, сле-
следует из результата задачи 342.
Примечание. Аналогично доказывается, что последние п
цифр чисел рассматриваемого ряда повторяются через каждые
4-5"-' чисел, начиная с л-го числа этого ряда (так, например,
последние две цифры повторяются, начиная со второго числа,
через каждые 20 чисел).
344. Докажем даже более общее предложение, а именно, что
каково бы ни было целое число N, всегда найдется такая степень
числа 2, последние N цифр которой все будут единицами и двойками.
Так как 25 = 32 и 29 = 512, то при N = \ и N = 2 это утверждение
справедливо. Далее доказательство мы проведем при помощи
метода математической индукции. Предположим, что
последние N цифр числа 2" являются единицами и двойками, и до-
докажем, что в таком случае найдется степень числа 2, последние
JV+1 цифр которой являются единицами и двойками. Согласно
сделанному предположению 2" ¦= \0Na + й, где b есть iV-значное
число, записываемое с помощью двух цифр: 1 и 2. Обозначим чис-
число 5я — 5W~' = 4 • 5Я~' буквой г; тогда согласно теореме Эйлера
(задача 341) разность 2Г—1 будет делиться на 5'v. Отсюда выте-
вытекает, что если целое число k делится на 2Я+1, то разность 2rk — k =
= kBT—1) будет делиться на 2- 10-v, т. е. jV последних цифр
чисел 2rk и k будут совпадать, a (N + 1)-е с конца цифры этих чи-
чисел будут одинаковой четности.
Рассмотрим теперь следующие пять степеней числа 2:
2п 2Л+Г г= 2Г • 2п 2'1"''2'' = 2Г • 2"~*"r 2n~*~ir = 2r • 2п+'^г
Согласно доказанному последние N цифр всех этих чисел совпа-
совпадают между собой (т. е. все они оканчиваются тем же числом Ь,
составленным из двоек и единиц, что и число 2"), a (N+i)-e
с конца цифры у всех у них одновременно четны или нечетны.
Докажем теперь, что ни у каких двух из этих пяти чисел (N + 1)-е
с конца цифры не могут быть одинаковыми Действительно, разность
357
любых двух из наших чисел представима в виде 2n+m'r Bт'т—1)
где m-i = 0, 1,2 или 3, а ш2 = 1, 2, 3 или 4. Если бы эта разность
делилась на 10^', то число 2"hr —1 должно было бы делиться
на 5-v+1; но так как
m2r = m2 • EЛ- — 5Л'-') < 5 • EЛ' — 5Л'~') = 5*+' — 5Л',
то это противоречит результату задачи 342.
Итак, (N + 1)-е с конца цифры выписанных пяти чисел — это
или 1, 3, 5, 7 и 9 (в каком-то неизвестном нам порядке) или же
О, 2, 4, 6 и 8. В обоих случаях хотя бы для одного из этих чисел
(N + 1)-я с конца цифра равна 1 или 2. Значит, во всех случаях
существует степень числа 2, последние N + 1 цифр которой все
являются единицами и двойками; в силу принципа математической
индукции отсюда следует требуемое предложение.
345. Ясно, что пара натуральных чисел я и п2 является «хо-
«хорошей» при любом я > 1. С другой стороны, пара чисел п—1
и л2—I = (п—1)(л+1) наверное будет «хорошей», если число
п -f- 1 представляет собой целую степень двойки, т. е. л + 1 = 2k,
где k J^ 1 — целое число: в самом деле, в таком случае числа
п— 1 и л2 — 1 =2"(я— 1)
отличаются лишь тем, что во второе из них простой делитель 2
входит в степени, на k большей, чем в первое (число п — 1 содер-
содержит простой делитель 2, ибо при п + 1 = 2\ т. е. при я = 2k — 1,
также и число л—1 = 2й — 2 является четным). Отсюда уже вы-
вытекает бесконечность числа «очень хороших» пар: ведь такими яв-
являются, например, все пары «чисел
л—1 =2*—2 и л2—1 = (я—1)(я+ 1) = 2* B*— 2),
где ft «= 1, 2, 3, ...
346. Ясно, что начальный член а и разность d прогрессии мож-
можно считать числами взаимно простыми: ведь если бы и а, и d де-
делились на какое-то число k > 1, то мы просто сократили бы все
члены-прогрессии на k. Если же а и d взаимно просты, то в силу
теоремы Эйлера (задача 341) найдется такое целое число г, что
ат—I, а следовательно, и ar+1 — а делятся на d. Но в таком слу-
случае ar+l—а = Nd, т. е. ar+1 = а + Nd, где N—натуральное чис-.
ло, т. е. число ar+1 принадлежит нашей арифметической прогрес-
прогрессии. Более того, в таком случае также и все числа аТЛ+1, где k =
= 1, 2, 3, ..., принадлежат прогрессии, поскольку arh—1 =
= (аг — 1)(аг(*-') -f a'd-2» + ... + 1) делится на ат—\, т. е. де-
делится на d; следовательно, и а'*"* — а = Md делится на d
и arh+i = а + Md есть (М + 1)-й член прогрессии. Ясно, что числа
a, ar+l, а2г+1, а3г+1, ... разлагаются на одинаковые простые мно-
множители (в разных степенях), что и завершает доказательство
утверждения задачи.
347. Пусть а — какое-нибудь из чисел ряда 2, 3, ..., р — 2.
Рассмотрим числа
а, 2а, ..., (р— 1)а. ;
Никакие два из этих чисел не могут давать одинаковых остатков
при делении на р; следовательно, эти числа дают при делении
на р остатки 1, 2, ...,/>— 1 и притом каждый из этих остатков по-
получается только один раз (ср. с решением задачи 340). В частности,
найдется такое целое число Ь из ряда 1, 2, .... р — 1, что Ьа при
делении на р дает остаток !. При этом b ф \ и Ъ Ф р—\, ибо 2 ^
^ а ^ р— 2; следовательно, при 6= 1 число Ьа = а при деле-
делении на р дает остаток а Ф'\, а при b = р— 1 число Ьа =
= (Р—1)а = ра — а при делении на р дает остаток р — а ^ 1.
Кроме того, b Ф а, так как если бы а2 при делении на р давало
остаток 1, то а2—\ — (а + I) (а—1) делилось бы на р, что воз-
возможно только при а = 1 и а = р— 1. Следовательно, 2 ^ b ^
^р — 2 и b ф а, т. е. все числа 2, 3 р — 2 распада-
распадаются на пары чисел, произведение которых при делении на р дает
остаток 1.
Произведение 2-3-...- (р — 2), содержащее —g— таких пар
чисел, тоже дает при делении на р остаток 1. Число р—1 при де-
делении на р дает остаток —1. Следовательно, (р—1)! =
= 1 -2-3-...- (р-2)-(р-1)= [2.3 • ... .(р_2)]-(р-1) при
делении на р дает остаток — I, т. е. (р — 1)! = &р — 1; (р —1)! +
+ Г = /гр. Таким образом, (р — 1)! + 1 делится на р.
Если р — непростое, то оно имеет простой делитель q < р.
Тогда (р—1)! делится на <?; поэтому (р— 1)! + 1 не делится на <?
и, значит, не может делиться также и на р.
348. а) Если р = 2, то р = 12 + 02+ I. Пусть теперь простое
число р нечетно; покажем, что можно найти два числа х и у,
р
оба меньших чем -g", удовлетворяющих условию задачи.
Рассмотрим —к— чисел 0, 1, 2, ..., —ц—. Квадраты любых
двух из этих чисел будут давать при делении на р различные
остатки; действительно, если было бы
х\ = V -г г и х\ = ?.2р + г,
то имело бы место равенство
х\ — х\ = (*! — х2)(*1 + «г) = (*i — *г) Р.
т е (v, — .y2) (x'i + х2) делилось бы на р, что невозможно, так как
Л'1 < -4-, х.г < ~и -vi + х2 < р, | -Vi — л-3| < р (напоминаем,
р+1
р — простое). Итак, —j— чисел
что
Р+ 1
при делении на р дают —„— различных остатков. Отсюда вытека-
ет, что и следующие —о— (отрицательных!) чисел: —1, —V2—1,
— 22—1 —I ?——| —1 также при делении на р дают Т
различных остатков (если бы —Xj — 1 и —х| — 1давали одинако-
359
вые остатки, то и х\ и х\ давали бы одинаковые остатки) '). Но
так как при делении на р могут встречаться лишь р различных
остатков (а именно, 0, 1, 2, ..., р—1), то ясно, что из р + 1 чи-
чисел О2, I2, 22, ...,Г~'| , — !, — I2—1, — 22-1,.,., —Itill-i) -1
по крайней мере два дают при делении на р одинаковые остат-
остатки. В силу доказанного выше из такой пары чисел одно обязатель-
обязательно должно быть вида х2, а второе — вида — if—1. Но если
х2 ¦= kp + г и —у2 — 1 >•=* 1р -\- г, то
х2 + у2 = (k — l)p—\ •= mp — i,
т. в. х2 -(- у2 + 1 = тр делится на р.
Примечание. В условии задачи можно требовать даже, =
чтобы оба искомых числа х к у не. превосходили -»-, т. е. чтобы
сумма х2 + У2 + I была меньше р1, и, значит, частное т от деления
суммы х2-\-у2-{¦ 1 на /I было меньше р.
б) Пусть /7 «= 4л -)- 1 — простое число. В силу теоремы Виль-
Вильсона (задача 347) число
(/7—1)! + 1 = 1 -2 -3- .... D«) + 1
делится на р. Заменим теперь в последнем выражении все множи-
Р— 1
гели большие —s—— 2л, через разности числа р и чисел меньших
2 :
(/)— 1)! + 1 = 1 • 2-3 • ...¦2п(р-2п)(р-2п + \) • ...X
Х(Р-У) -Ы = A • 2- 3 • ... • 2/г)[Л/7+ (-1JпХ
ХB»-1)-...- 1] + 1 «Л,/7+ A -2-3-... • 2/гJ+1.
Так как это число делится на р, то и сумма (Bл)!J-)- 1 делит-
делится на р. Итак, условию задачи удовлетворяет число х= Bл)! =.
Примечание. Заметил!, что если число х дает при делении
на р остаток Х\, то из того, что х2 + 1 = {kp + x-i);!+ I = (Кгр +
+ 2kxi)p -\-x-\- 1 делится на /7, следует, что и Xj+1 делится на р.
Поэтому в условии задачи можно всегда считать, что число х
меньше р, х2 + 1 меньше р" и частное т от деления х2 + I на р
меньше р.
') Частное k и остаток г от деления целого числа а на число р
определяются формулой а = kp ~\- г, где 0 =sS г < р (если а отри-
отрицательно, то и частное k отрицательно).
360
349. Существование бесконечного числа простых чисел следует
из результата задачи 234 (из этой задачи вытекает даже, что прос-
простые числа встречаются в ряду всех целых чисел достаточно «часто»,
например, «чаще», чем квадраты; см. примечание к этой задаче). Из
результата задачи 90 также можно усмотреть, что простых чисел
существует .бесконечно много: если бы всего существовало только п
простых чисел, то не могло бы быть больше чем п взаимно простых
друг с другом чисел. Но наиболее простым доказательством теоре-
теоремы о бесконечности числа простых чисел является следующее до-
доказательство, принадлежавшее Евклиду.
Предположим, что имеется всего и простых чисел 2, 3, 5, 7,
11,..., р„. Образуем число N = 2 • 3 ¦ 5 • 7 • 11 • ... • р„ -\- I. Число .V
больше всех простых чисел 2, 3, 5, . . ., р„ и поэтому должно быть
составным. Но так как N—1 делится на 2, 3, 5, 7, ..., рп, то Л/
взаимно просто со всеми простыми числами. Полученное противоре-
противоречие и доказывает теорем)'.
350. а) Доказательство этой теоремы очень близко к доказа-
доказательству Евклида бесконечное!и числа простых чисел. Предположим,
что среди чисел вида Ак — 1 имеется только конечное число прос-
простых чисел, а именно 3, 7, 11, 19, 23, ..., рп- Составим число N =
= 4C-7-11 • 19-23-.. .-рп)— 1. Оно больше всех принадлежащих
прогрессии простых чисел и, следовательно, должно быть составным.
Разложим число N па простые множители. Среди них не может быть
чисел вида Ак—1, так как число N -j- 1 = 4C-7-11 • 19-23... рп) де-
делится на все простые числа вида Ак— 1, а следовательно, N взаим-
взаимно просто со всеми этими числами. Так как N нечетно, то оно долж-
должно представлять собой произведение нескольких простых чисел вида
Ак + 1. Но это невозможно, так как произведение двух чисел вида
4/е + 1 имеет тог же вид-:
а следовательно, и произведение нескольких чисел вида Ак + 1 имеет
тот же вид, в то время как число N имеет вид Ак — 1. Полученное
противоречие и доказывает теорему.
Аналогично доказывается, что существует бесконечно много
простых чисел, принадлежащих прогрессии 5, 11, 17, 23, ... (простых
чисел вида 6к — 1).
б) Доказательство настоящей теоремы несколько сложнее дока-
доказательств теорем задачи а), хотя построено на той же идее.
Предположим, что в ряду чисел 11, 21, 31, 41, 51, 61, ... имеет-
имеется только конечное число простых: 11, 3l, 41, 61, ..., рп. Составим
число N ==> A1-31-41-61.. .р„M— 1. Оно взаимно просто со всеми
простыми числами 11, 31, 41, ..., рп, так как число N + 1 делится
на все эти числа. Обозначим произведение II - 31 • 41 ... р„ через
а, тогда N = а5 — 1 = (а — )) (о4 + а3 + а' + а + 1).
Рассмотрим, какие простые делители может иметь второй мно-
множитель а* + а3 + а2 + а + 1 последнего произведения. Очевидно, что
а* + а3 + а2 + а + 1 не делится на 2 (сумма пяти нечетных чисел
нечетна). Далее, а4 + а3 + а2 + а + 1 делится на 5, поскольку а
оканчивается на 1 (как произведение ряда чисел, каждое из которых
оканчивается на 1), а2, а3 и а4 все оканчиваются на 1 и, следователь-
следовательно, сумма а4 + о3 + а2 + а + 1 оканчивается на 5. Пусть теперь р
361
есть простой деЛитель числа а* + а3 + os -f a + 1, отличный от 5.
В таком случае а — 1 не может делиться, на р, так как иначе а
имело бы вид kp-\- 1, следовательно, а2, а3 и а* (равные соответст-
соответственно (ftp + IJ, (kp-\- IK и (kp -f- lL) имели бы такой же вид и
число
давало бы при делении на р остаток 5. Отсюда следует, что р — 1
должно делиться на 5. Действительно, предположим, например, что
р— 1 дает при делении на 5 остаток 4: р—1 = 5ft + 4. Отметим,
что в силу теоремы Ферма (задача 240) a*1 — 1 делится на р. Но
в этом случае
а*"-' — 1 = а5"+4— 1 = аЦа™ — 1) + (о4— 1),
а так как а5*— 1 =(а5)к— 1А делится на а5— 1, а значит и на р,
то и а*—1 делится на р. Но а5—1 — а(а*—\)-\-(а—1); следо-
следовательно, если а5—1 и а4—1 делятся на р, то и а—1 .должно
было бы делиться на р, что, как мы уже показали выше, невозмож-
невозможно. Аналогично показывается, что число р—Г не может давать при
делении на 5 остатки 1, 2 или 3.
Итак, р— 1 делится на 5 и четно (р— 1 четно, ибо р нечетно);
следовательно, р—1 делится на 10 и, значит, р имеет вид 10ft + 1,
т. е. принадлежит нашей прогрессии. Итак, нами установлено, что
простыми делителями числа a4 + fl3 + fl2 + a + 1 могут быть только
число 5 и простые числа вида 10/г+ 1-
Но число а4 + а3 + а2 + а + 1, очевидно, больше 5 и не делится
на 52 = 25. Действительно, число а оканчивается на 1 и, следова-
следовательно, имеет вид 5^+1. "Далее, по формуле бинома Ньютона
a4 + o3-f a2 + a+ 1 = Eft + 1L+ Eft + 1)э+ Eft + 1J +
+ 5ft+ 1 + 1 = 625ft4 + 4- 125ft3 + 6-25ft2 + 4-5ft +
+ 1 + 125ft3 + 3-25ft2 + 3-5ft+l+25ft2 + 2-5ft+ 1 +
l+.5ft+ 1 + 1 = 625ft4 + 5- 125ft3 + 10-25*2 + 10-56 + 5 =
=5-[5B5ft4 + 25ft3+ 10ft2.+ 2ft)+1].
Отсюда следует, что это число, а значит, и число N — а5—1
должно иметь хотя бы один простой делитель вида 10ft + 1. Но,
по нашему предположению, N взаимно просто со всеми просты-
простыми числами вида 10ft + 1. Полученное противоречие и доказывает
теорему.
Примечание. Отметим, что проведенное доказательство поч-
почти без всяких изменений позволяет доказать, что во всякой арифме-
арифметической прогрессии, составленной из чисел вида 2pk-\-\, где р —
какое-то нечетное простое число, имеется бесконечно много простых
чисел.
ОТВЕТЫ И УКАЗАНИЯ
1. Самый высокий из самых низких.
2. Составьте сумму всех сделанных каждым из людей рукопо-
рукопожатий.
3. Пусть А — произвольное лицо; оно имеет либо трех знако-
знакомых, либо существуют трое лиц, с которыми А незнаком.
4. а) Не может, б) Постройте пример удовлетворяющего ус-
условиям задачи «распределения знакомств».
5. Докажите, что если А и В незнакомы, то они имеют двух
общих знакомых.
в. Рассмотрите ученого, имеющего среди присутствующих
наибольшее число знакомых.
7. Последовательно исключайте из числа делегатов пары гово-
говорящих на одном языке.
8. Пусть А — произвольный участник конференции; найдется
такой язык, на котором он может говорить не менее чем с 6 дру-
другими участниками.
k (*+•!)
9. п = 2 ~ ~Ь 1. гДе ^ — целое.
10. 5000 дней (в городе существуют две такие 'партии, что два
жителя дружат в том и только в том случае, когда они принадле-
принадлежат к одной партии).
11. Если странствия рыцаря длятся достаточно долго, то най-
найдется такой участок АВ пути (где А и В —замки), по которому
(в направлении от А к В) рыцарь проедет не менее трех раз.
,12. Пусть А и В — два рядом сидящих врага; докажите, что
Мерлин может пересадить часть рыцарей так, чтобы пара сидящих
рядом врагов заменилась парой А, А' сидящих рядом друзей, а ни
одна пара соседей-друзей не заменилась парой врагов.
13. а) При первом взвешивании поместите на каждую чашку
по 27 монет, б) Число k определяется неравенствами 3ft~' < п ^
«?3*.
14. Сначала положите на чашку весов по одному кубику;
затем, положив на одну чашку оба эти кубика, на вторую кладите
поочередно по паре из оставшихся кубиков.
15. При первом взвешивании поместите на каждую чашку ве-
весов по четыре монеты.
16. а) Одно звено, б) 7 звеньев.
17. Пусть S — какая-то станция метро; рассмотрите самую да-
далекую от нее станцию Т.
18—19. Воспользуйтесь методом математической индукции.
20. Воспользуйтесь методом доказательства от противного:
предположите, что утверждение задачи неверно, и, пользуясь этим,
постройте бесконечную цепочку городов Швамбрании (при кон-
363
струировании этой цепочки удобно воспользоваться методом мате-1
матической индукции).
21. Нельзя.
22. Королю достаточно пройти в один из углов доски и далее
идти по диагонали доски.
23. Измените порядок следования полей так, чтобы с каждого
поля можно было перейти на соседнее.
24. Докажите (скажем, методом математической индукции),
что если в некотором коллективе студентов каждый из трех языков
знает ровно п человек (где п^2), то можно составить такую
группу студентов, в которой каждый язык знают ровно 2 человека.
25. a) 2-jp б) 20.
26. 6 дней; 36 комплектов медалей.
27. 15 621.
28. Два рубля.
29. а) Закон чередования дней в году по нашему календарю
таков: через каждые четыре года один год, номер которого делит-
делится па 4, является високосным; исключение составляют годы, номера
которых делятся на 100, но не делятся на 400. Отсюда легко ус-
усмотреть, что 400 лет содержат целое число недель; следовательно,
остается проверить, начинается ли в течение каких-либо 400 лет
новый год чаще с субботы или е воскресенья. Ответ: с воскре-
воскресенья, б) На пятницу.
30. Все числа, оканчивающиеся на 0, и двузначные числа:
11, 23, 33, 44, 55, 66, 77, 88, 99; 12, 24, 36, 48; 13, 26, 39; 14,
28; 15; 16; 17; 18; 19.
31. а) 6250... 0, п — 0, 1, 2, ... б) Попытайтесь решить эа-
и раз
дачу: найти целое число, начинающееся с известной цифры а и при
зачеркивании этой цифры уменьшающееся в 35 раз.
32. а) Докажите предварительно, что число уменьшается в 9 раз
при зачеркивании цифры 0, стоящей на втором месте, б) 10 125 2025,
30 375, 405, 50 625, 6075, 70 875 (к каждому из этих чисел можно
еще приписать в конце произвольное число нулей).
33. а) Числа, у которых все цифры, кроме первых двух, нули,
б) Рассмотрите отдельно случаи, когда первая цифра искомого
числа есть 1, 2, 3, .... 9. Всего имеется 104 различных числа, удов-
удовлетворяющих условию задачи, к каждому из которых можно в кон-
конце приписать произвольное число нулей.
34. а) Наименьшее возможное число 142 857. б) Цифрами 1 или
2. Наименьшее число, начинающееся цифрой 2, есть 285 714.
35. 153 846.
36. Используйте то, что числа, которые делятся на 5, должны
оканчиваться цифрами 0 или 5; числа, которые делятся на 6 или
на 8, оканчиваются четной цифрой.
37. Попытайтесь решить задачу: найти число, увеличивающееся
вдвое от перенесения начальной цифры в конец.
38. Решается аналогично предыдущей задаче.
39. Наименьшее число, удовлетворяющее условию задачи,
7 241 379 310 344 827 586 206 896 551.
40. а) Число, меньшее своего обращенного в б, 6, 8 или 7 раз,
должно начинаться с цифры 1; число, меньшее своего обращенного
в 2 и 3 раза, может начинаться с цифр 1, 2, 3, 4, соответственно
364
I, 2, 3. б) Числа, в 4 раза меньшие своего обращенного,—это числа
О, 2 178, 21978, 219 978, 2199 978 (*)
и числа, десятичная запись которых Р\Рц.. .Pn-iPnPn-\- ¦ -РгРи где
Л, Рг,.--;Ря — какие-то числа ряда (*).
41. йг) 142 857. б) Попытайтесь найти восьмизначное число, уве-
увеличивающееся в 6 раз при перестановке четырех последних цифр на
первые четыре места с сохранением их порядка.
42. 142 857.
43. 111, 222, 333, ..., 999, 407, 518, 629, 370, 481, 592.
44—45. Рассмотрите процесс сложения «столбиком» рассмат-
рассматриваемых чисел.
46. Разложите на множители многочлены, выписанные в усло-
условии задачи; рассмотрите, какие остатки может давать число п при
делении на 3 (соответственно на 5, на 7, и т. д.).
47. а) Воспользуйтесь тем, что разность одинаковых четных сте-
степеней делится на сумму оснований, б) См. указание к задаче 46.
48. а) 56 786 730 =- 2 ¦ 3 • 5 • 7 ¦ 11 • 13 • 31 ¦ 61. Далее восполь-
воспользуйтесь предложениями задач 46 а) — д) и аналогичными предло-
предложениями, вытекающими из теоремы Ферма (см. задачу 340). б) Раз-
Разложите заданное выражение на множители и сравните число мно-
множителей с числом множителей числа 33.
в) Воспользуйтесь тем, что га2 + 3/г + 5 = (п + 7) (п — 4) + 33.
49. При четных п,
50. Не существует.
51. Воспользуйтесь тем, что всякое целое число, не делящееся
на 5, можно представить в виде bk ± 1 или 6ft rfc 2. Ответ: 0 или 1.
52. Воспользуйтесь результатом предыдущей задачи.
53. 625 и 376.
54. Найдите две последние цифры числа /V20, три последние
цифры числа Nm. Ответ: 7; 3.
п (п ~'г 1)
55. 1 -J~2 -J- 3 -'-... + я = g • Группируя отдельные члены
суммы 1* + 2к + 3й + ... + /Is, докажите, что эта сумма делится
п п + 1
на ~о~ и на (« + !), или на п и на —^—.
56. Разность суммы цифр числа, стоящих на четных местах,
и суммы цифр, стоящих на нечетных местах, должна делиться
на И.
57. Число делится на 7.
58. Всегда можно найти число, начинаю.щееся с цифр 1, 0
и делящееся на К. Переставляя подходящим образом цифры этого
числа и вычитая одно из другого два делящихся на К числа, можно
доказать, что 9 делится на К.
59. Искомое число состоит из 300 единиц.
60. Рассмотрите последние цифры чисел N =>=¦ 2* (где к = 1,
2, 3, ...), а также остатки от деления чисел N на 3. •
61. 26 460 = 22 • З3 • б • 72. Докажите в отдельности, что задан-
заданное выражение делится на 5 • 72 и что оно делится на 22 ¦ З3.
62. Воспользуйтесь тождеством
1110 — 110 =
,_ (П — 1)A19 + И8,+ 11'+ 116 + 115+114.-т- 113+112+11 + 1).
365
63. Запишите данное число в виде
B2225555 + 4s555) + E555м22 — 42222) — D5SS5 — 2222).
64. Воспользуйтесь методом математической индукции.
65. Воспользуйтесь тем, что 10е—1 =999 999 делится на 7
и что любая степень десяти дает при делении на 6 остаток 4. От-
Ответ: 5.
66. а) 9; 2. б) 88; 67. в) Найдите, какими двумя цифрами окан-
оканчиваются числа 7(ии)и 2 <14'Ч Ответ: 36.
67. а) Оба числа оканчиваются цифрами 89. б) Докажите, что
разность рассматриваемых чисел делится на 1 000 000 = 2е • 56.
68. а) 7; 07. б) 3; 43.
69. Рассмотрите числа
?.х — У, ?г — У ', Z3 = У ,..•, ^1001 — а — '*
и определите последовательно одну последнюю цифру числа Z\,
две последние цифры числа Z%, три последние цифры числа Z%, че-
четыре последние цифры числа Z4, пять последних цифр числа Zs,
пять последних цифр чисел Z6, Z7, ..., Ziooi — N. Ответ: 45 289.
70. Составьте таблицы остатков от деления на 13 чисел 5" и
пъ. Наименьшее п, удовлетворяющее условию задачи,— это я == 12.
71. При всех а, кратных 4, последние цифры рассматриваемого
числа — это 30.
72. Искомые 1000 цифр будут рРР ... Р, где
23 раза
Р = 020408163265306122448979591836734693877551
— период чистой периодической дроби, в которую обращается -|д-,
ар — группа последних 34 цифр числа Р. Для доказательства вос-
воспользуйтесь тем, что
50100° — 1 501000 —1
N ¦¦
50—1 ~ 49
73. Рассмотрите разность М — 3jV.
74. 24.
75. а) Сравните степени, в которых входит какое-нибудь прос-
простое число р в произведение о! и в произведение (t¦+ 1) (t + 2)...
...(< +о), б), в) Воспользуйтесь результатом задачи а), г) Дока-
Докажите сначала существование такого числа к, что kd, где d — раз-
разность прогрессии, дает при делении на п! остаток 1.
76. Не делится.
77. а) (п— 1)! не делится иа п, если п простое число или п ='
= 4. б) (п—1)! не делится на п2, если п есть простое число,
удвоенное простое число, или если п =¦= 8, п = 9.
78. Докажите, что все такие числа меньше 72 = 49. Ответ:
24, 12, 8, 6, 4 и 2.
79. а) Докажите, что сумма квадратов пяти последовательных
целых чисел делится на 5, ио не делится на 25.
б) Определите остаток, который дает сумма четных степеней
трех последовательных целых чисел при делении на 3.
в) Определите остаток, который дает сумма одинаковых четных
степеней девяти последовательных целых чисел при делении на 9.
366
SO. а). Найдите остатки деления чисел А и В на 9. б) 192, 384,
576, или 273, 546, 819, или 327, 654, 981 или 219, 438, 657.
81. Четырьмя нулями.
82. Воспользуйтесь теоремой Пифагора. *¦
83. Рассмотрите остаток от деления Ь'г — Аас иа 8.
84. Докажите, что при сложении дробей и возможном сокраще-
сокращении суммы получится дробь, знаменатель которой делится на 3 и на 2.
85. Для доказательства того, что числа М и N не являются це-
целыми, надо показать, что после сложения мы получим дробь, знаме-
знаменатель которой делится на более высокую степень 2, чем числитель,
Доказывая, что число К не является целым, надо в предше-
предшествующих рассуждениях заменить степень двойки степенью тройки.
86. а) Воспользуйтесь тем, что дробь pjq сократима или несок-
несократима одновременно с дробью qlp. б) На 13.
87. Пусть N = а • 10'952 -+- А — одно из читаемых указанным в ус-
условии задачи образом чисел (где а — первая цифра N); докажите,
что если N делится на 27, то и число jVi == ЮЛ + а делится на 27.'
88. Докажите, что если в записи числа а = 51000 есть нули, то
можно указать делящееся на а число, первый нуль в записи которого
(если он имеется) располЪжен дальше от конца числа, чем у а.
89. Докажите сначала тождество
A + 10<+ Ю8+ ...+ 10й) • 101
90. Покажите, что B2" +0 — 2 делится на все предшествующие
числа заданной последовательности; отсюда будет следовать, что
23" + 1не может иметь с предыдущим числом последовательности
общий делитель, отличный от 2.
91. Рассмотрите, какие остатки могут давать числа 2" — 1 и
2" + 1 при делении на 3.
92. а) Рассмотрите, какие остатки могут давать числа р, 8р — 1
и 8/3+1 при делении на 3. б) Рассмотрите, какие остатки могут да-
давать числа р, вр2 + 1 и 8/т2 — 1 при делении на 3.
93. Рассмотрите, какие остатки может давать простое число при
делении на 6.
94. См. указание к предыдущей задаче.
95. а) Докажите, что разность прогрессии должна делиться на
2 . 3 • 5 • 7 = 210. Ответ: 199, 409, 619, ..., 2089. б) Докажите,
что если первый член прогрессии отличен от 11, то разность должна
делиться на 2 • 3 • 5 • 7 • 11 = 2310; если первый член равен. 11, то
разность должна делиться на 210. [При решении задач а) и б) удоб-
удобно пользоваться таблицами простых чисел,]
96. а) Таким будет нечетное число, не делящееся на 3.
б) Достаточно найти число, ие имеющее с остальными 15 из
рассматриваемых 16 чисел общих множителей 2, 3, 5, 7, 11 и 13.
22... 2177... 78.
97. Произведение равно —• •——-—•
г ** г 665 раз 665раз
98. Частное равно777 000 777 000 ... 777 000 77,
^_ ^- остаток 700.
группа 777000 повторяется 186 рез
99. 222 222 674 025 = 471 4052.
100. Не существуют.
101. 523 152 и 523 656.
102. 1946.
367
103. а) Преобразуйте выписанное число и сравните его с выра-
выражением для суммы членов арифметической прогрегсии с разностью 1,
первым членом 10™ ~ ' и последним членом 10" ' 1- б) 1 769 580.
104. Рассмотрите сначала все целые числа от 0 до 99 999 999,
приписав к тем из них, которые имеют меньше восьми^ цифр, нули
слева так, чтобы эти числа стали восьмизначными.
105. 7.
106. Нет.
107. Единиц будет на одну больше, чем двоек.
... 108. Не может.
109. Это число делится на 11 111.
ПО. 6 210 001000.
111. Так как заданное число А = 109— 1, то для любого числа
А' = ххх2 ... хк имеем АХ =.v,.v2... л^ООООООООО — xLx2 ... xh = M —
— iV; рассмотрите процесс вычитания «столбиком» Л' из М.
112. Условию задачи удовлетворяют все такие N ^ А, что N =
= 10"' — 1.
113. Воспользуйтесь методом математической индукции (по чис-
числу п); при т ^ я утверждение задачи неверно,
114. Уже на одном из первых четырех мест каждой строки
встретится четное число.
115. Докажите, что сумма всех чисел каждой строки таблицы
(начиная со 2-й) делится на 1958.
116. 40.
117. Если начало 1-го сеанса 12 + х, а продолжительность сеан-
сеанса (/, то х и у удовлетворяют системе линейных неравенств.
1 5
118. Возможны значения Т = 20, 15, 12, 7 ~п~ и 5 -ту мнн-
119. 100.
120. Искомое число должно начинаться с наибольшего возмож-
возможного количества девяток, соотвественно нулей.
121. а) 147, 258, 369; б) 94l, &32, 763."
122—123. Воспользуйтесь формулой для суммы членов арифме-
арифметической прогрессии.
124. Представьте выражение п(п + 1) (п -\- 2) (п -f- 3) + 1 в виде
квадрата многочлена.
125. Докажите, что среди рассматриваемых чисел не может быть
больше четырех попарно различных.
126. Разбейте 9 гирь последовательно возрастающих весов на
три группы, две из которых имеют одинаковый вес, а третья легче их.
127. Докажите, что веса всех гирь четны или все "они нечетны.
128. Достаточно рассмотреть случай, когда все рассматриваемые
числа положительны, а их произведение равно 1.
129. К такому набору мы наверняка придем через 2к шагов.
130. Докажите, что в процессе описанного преобразования си-
систем чисел эти числа постепенно выравниваются.
131. (х, у, z) = (l, 1, 0).
132. а) Докажите, прежде всего, что каковы бы ни были перво-
первоначальные числа, мы вскере получим четверку чётных чисел, б) Для
рациональных чисел утверждение задачи а) сохраняет силу, а для
иррациональных — нет (здесь можно подобрать числа так, чтобы
все четверки были пропорциональны исходной).
133. б) Постройте возрастающую последовательность, начиная
с первого из выписанных 101 числа. Если в этой последовательности
368 '
будет- меньше 11 чисел, to вычеркните эти числа и построите, новую1
возрастающую последовательность, начинающуюся с первого остав-
. шегося числа; если и в этой последовательности будет меньше 11 чи-
чисел, то вычеркните и ее и постройте новую возрастающую последо-
последовательность, и т. д. Если все построенные последовательности со-
содержат меньше 11 чисел, то у нас будет не меньше II последова-
последовательностей; используя это обстоятельство, можно построить убываю-
убывающую последовательность из 11 чисел.
134. Рассмотрите наибольшие нечетные делители этих чисел.
135. а) Рассмотрите наименьшие по абсолютной величине остат-
остатки, которые дают числа при делении на 100.
б) Пусть п], иг, ..., at00 — данные числа. Рассмотрите остатки
от деления на 101 чисел а,, а\ -\- а2, at -f- a2 -f fi3,
в) Если сумма нескольких чисел <2ОЗ и делится па 1 СО, то она
равна 100.
г) Докажите последовательно, что из любых 3 целых чисел мож-
можно отобрать 2, гумма которых делится на 2; из любых 9 целых чи-
чисел можно отобрать 5, сумма которых делится на 5; из.любых 199
целых чисел можно отобрать 100, сумма которых делится на 100
(в доказательстве 3-го факта используются первые два).
136. Воспользуйтесь методом доказательства от противного.
137. Рассмотрите число переходов (при движении по кругу в
одном направлении) от крестика к нулику и от нулика к крестику.
138. Рассмотрите сумму всех множителей этого произведения.
139. Половина слагаемых рассматриваемой суммы должна рав-
равняться + 1, а вторая половина — равняться —1.
140. Отнесите к 1-й группе все числа, запись которых содержит
четное число единиц.
141. Выпишите 5 чисел одно под другим; тогда в каждом стол-
столбике число пар одинаковых цифр лежит в пределах от 400 до 600,
14,2. Докажите, что за несколько «шагов» можно изменить лю-
любой знак, сохраняя все остальные.
143. Используйте-принцип Дирихле (см, стр. 10).
144. Разложите число ~гг в (периодическую) десятичную дробь.
145. Пусть d — разность прогрессии и с. = {d} (см. стр. 37) при
нецелом d и а «= 1 при целом d; достаточно расположить отрезки
так, чтобы отрезок длины а нельзя был® «набрать» из (расположен-
(расположенных «далеко» от точки, отвечающей начальному члену прогрессии)
промежутков между рассматриваемыми отрезками (и их частей).
146. Докажите, что в интервале @, А) числовой оси (где А ^
^ m 4- п) содержится ровно А — I из наших дробей.
147. Обозначьте через ?,(/= 1, 2, 3, ...) число тех из наших
1000 1000
чисел, которые заключаются между —;— и -г—;—т- и подсчитайте
i i — - 1
число меньших 1000 чисел, кратных хотя бы одному из чисел а\,
с2, . .., ап,
р
148. Длина k периода —— может быть определена как наимень-
наименьшая степень k, для которой 10* —1 делится на q. Если k =*¦ 21, то
отсюда следует, что 10' + 1 делится на q, т. е. —it— есть це-
q
лое число. Из" последнего можно вывести, что в периоде
24 д. о. Шклярский и др, 369
—^ , р
. а* дроби —
Q-1 -\- Л/ц-i = U2 -4- О(+2 =: ¦ • • === fll "Ь ^2 ^ 9.
149. Воспользуйтесь тем, что число цифр в периодах дробей
q a I *
п п+1
~п"" n+i Равно наименьшим положительным числам к и / таким, что
10* — 1 делится на />", соответственно 10'—1 делится на рп + К
150. а) 7744. б) 29, 38, 47, 56, 65, 74, 83 и 92.
151. Если а — число, образованное первыми двумя цифрами ис-
искомого числа, а Ь — число, образованное двумя последними цифрами,
то 99а =(а + ЬJ— (а + Ь) = (а + Ь)(а + b — 1). Ответ: 9801,
3025, 2025.
152. а) 4624, 6084, 6400, 8464. б) Таких чисел вовсе нет.
153. а) 145. б) Только число 1.
154. а) 1, 81. б) 1, 8, 17, 18, 26, 27.
155. а) х не может быть больше 4. О т в е т: дс = 1, _/ ¦=» ± 1;
х = 3, у = ± 3. 6) дг = 1, у = dbl, z — любое четное; х = 3,
i/ = ±3, z = 2; * = 1, 1/ = 1, z — любое нечетное; х — любое поло-
положительно, у = 11 -4- 2! + ... -j- x\, z = 1.
156. Рассмотрите, на какую степень двойки могут делиться ис-
искомые четыре числа. Ответ: при п нечетном разложение невоз-
невозможно, при п четном существует единственное разложение:
157. См. указание к задаче 156. В задаче б) аналогично задаче
а) единственный ответ: x = y = z = v = 0.
158. а) Можно показать, что если х, у и z удовлетворяют вы-
^ Ьху
писанному равенству, и, например, г>-к", то эти числа можно
уменьшить, с тем чтобы они продолжали удовлетворять тому же
kyz kxz kxy
равенству. Если же *^ -у, у^~, г < -j- и х ^ у < z, то дЪлж-
но быть 2 ^ kx ^ 3. Ответ: k = 1 и ft = 3. б) Каждую такую
тройку целых чисел можно получить при помощи последовательных
подстановок вида хх = х, ух = у, z( = ?*(/ — г из одной из троек 1,
1, 1 и 3, 3, 3. Всего в пределах первой тысячи 23 тройки целых чисел,
удовлетворяющих условиям задачи.
159. Докажите, что х, у, z — четные. Ответ: x=(/ = z = 0.
160. (х,у) = @, -1), (-1,-1), @,0), (—1, 0), E, 2), (-6,2).
161. х = 3, у = 1.
162. х = п2,'у = I, г = п или х = 0, у = т, z — 0.
163. Предположите, что утверждение задач» неверно, и рассмот-
рассмотрите наибольшее простое число, для которого имеется решения.
164. Последовательно рассмотрите случаи, когда все четыре чис-
числа различны; два числа равны, остальные различны; две пары чи-
чисел попарно равны, и т. д. Ответы: 96, 96, 57, 40; ll, 11, 6, 6;
*Cfc±2), k(Sk±2), kCk±'2) I (k — произвольное целое число,
такое, что &C&±2) положительно); 1, 1, 1, 1.
165. 2, 2 и 0, 0.
1 1 1 111 1 1 1
Ш| ^_-_— t ! I I _____ . | _______ | ______
¦1~2 + 4'4 = 2+3 +ТГ= 3 ' 3 ~ ~3~-
Ч7П
167. а) Положите х = х\ + п, у = у\ + п. б) Ср. с указанием
к задаче а), в) х = т(т + n)t, у = п(т + n)t, г = mnt, где т, п,
t — произвольные целые числа.
168. а) Пусть у > х; покажите, что в этом случае у делится на х.
Ответ: ,-2, «, = 4. б) x = {!L±l)P. * = ('-±!)*+\ где ,-
произвольное целое число, отличное от 0 и — I.
169. 7 или 14.
170. Из соотношения количества очков, набранных девятиклас-
девятиклассниками, и числа сыгранных ими партий можно получить, что все
девятиклассники выиграли все сыгранные ими партии. Отсюда сле-
следует, что в турнире участвовал единственный девятиклассник.'
171. Обозначьте р— а = х, р — Ь = у, р — с — г, где а, Ь,
с—стороны треугольника, а р — его полупериметр. В таком случае
задача сведется к решению в целых числах уравнения хуг =» 4(х -\-
4у-\-4г
+ у + г), или х = цг_4 ¦ Условие х ^ у можно рассматривать как
квадратное неравенство относительно у (с коэффициентами, зави-
зависящими от г); отсюда можно найти границы, в которых должны
заключаться г и у (всего задача имеет 5 решений). -
„(„» + »)
173. Докажите, что каждое число встретится на диагонали не-
нечетное число раз. При п четном утверждение задачи неверно.
174. На iv1 —п.
175. Рассмотрите ту из таблиц, получаемых описанным образом,
у которой сумма всех чисел таблицы максимальна.
176. 1.
177. Воспользуйтесь тем, что в t-й строке, (9 — ()-й строке,
t'-м столбце и (9 — i)-M столбце выписаны одни и те же числа.
178. Воспользуйтесь тем, что Gjj + аи = ani + аи для любых
i, /, к, I.
179. Воспользуйтесь тем, что при всех t u ] имеем аи = 0,
а ц = —flij.
180. Воспользуйтесь методом математической индукции.
181. а) Рассмотрите, как меняются знаки, стоящие в 8 клетках,
примыкающих к краям доски, но не угловых, б) Сведите задачу к
задаче а).
182. а) Не всегда (докажите, что не любое распределение знаков
можно получить описанным образом из доски, на всех клетках ко-
которой стоят знаки «+»). б) Не всегда (ср. с указанием к задаче а)).
183. а) Сможет, б) Можно последовательно обратить в 0 все
числа 1-й, затем 2-й, и т. д. строк.
184. Запишите число а в двоичной системе счисления.
;| 185. Воспользуйтесь методом математической индукции.
186. Пусть un+lun+i + ... + un+8 = Sn (где uk—k-e число
Фибоначчи); докажите, что ип+я <sn < un+w.
187. Рассмотрите последовательность остатков от деления чи-
чисел Фибоначчи на 5.
188. Последние четыре цифры разности вполне определяются
последними четырьмя цифрами уменьшаемого и вычитаемого. Дока-
Докажите, что существуют п и k такие, что последние четыре цифры
(n + k)-ro и (n + k+l)-ro чисел Фибоначчи соответственно рав-
равны последним цифрам fc-ro и (к + 1) -го чисел; в таком случае пос-
24* 371
ледние четыре цифры (я + й — 1)-го числа будут равны последним
четырем цифрам (k — 1)-го числа Фибоначчи, и т. д. Так можно
найти число Фибоначчи, последние четыре цифры которого совпа-
совпадают с последними четырьмя цифрами первого числа, равного нулю.
189. Воспользуйтесь тем, что "„_i + 2<й^<а^_4 + 3.
190. Первое решение. Дополните последовательность чис-
числом ап+1. Второе решение. Воспользуйтесь методом матема-
математической индукции.
191. 2952 (докажите, что наибольшее число чисел в удовлетво-
удовлетворяющей условиям задачи последовательности, начинающейся с наи-
наибольшего числа ai — я, равно
?LD— I.
192. Воспользуйтесь методом доказательства от противного; рас-
рассмотрите, какими могут быть цифры а„, ап + 1, .... при приписыва-
приписывании которых ранее имеющееся число все время остается простым.
193. а) не встретятся; б) встретятся.
184. Число 81 впервые встретится на 111 111 111-м месте; 4 раза
подряд 27 встретится раньше, чем впервые встретится число 36.
195. 1972 раза (воспользуйтесь тем, что если числа а и Ь взаим-
взаимно просты, то пара а, Ь единственный раз встретится в нашем ряду
/о, /[, ... наборов, а если а и Ь не взаимно просты — не встретятся
ни разу).
196. Пусть а4, аз, и2, «i — 4 последние цифры последовательно-
последовательности; выясните, сколько раз встречается в нашей последовательности
группа цифр а.\а-р.^а^
197. Пусть N'u — произведение к первых простых чисел; докажите
(методом математической индукции), что наше утверждение верно
для чисел Nh при любом к.
198. Докажите, что любое натуральное число п можно един-
единственным образом представить в виде п = рх + qy, где х и у—
целые и 0 ^ х < q.
199. Представьте фигурирующее в условии задачи число в виде
'—' ^ + х, где X 3= 0, и 0 < х s? X.
200. Рассмотрите все точки с целочисленными координатами
(л-, у), расположенные внутри квадрата, ограниченного осями коор-
координат и прямыми х'= 100 и у = 100.
201. Представьте х в виде х = [х] + а, где а •— {х}.
202. Воспользуйтесь результатом задачи 201 3).
203. Рассмотрите все точки с целочисленными координатами
У Р
х, у, где 0 < х < q, 0 < у < р И~<-"Т~-
204. Воспользуйтесь методом математической индукции. (Можно
также решить задачу, исходя из геометрических соображений; для
этого надо рассмотреть все точки с целыми координатами, располо-
расположенные в первом координатном углу под гиперболой ху »= п.)
205—207. В решении задачи 205 следует использовать то, что
[B + УТ)п] = B + /Г)" + B - УТ)П ~ 1.
Аналогично решаются и задачи 206а), б), 207.
208. Из р последовательных чисел п, п—1, п — 2, ..., я — р Л- 1
одно (и только одно) делится на р; если это число равно N, то
372
I— = —. Таким образом, разностьCj| —I -^-1
можно записать так:
п(п— 1) ... (N + I) N (N — 1) ... (п — р-'г \) _ N
~ Р
N ¦
209. Если а>0, то —д|— < а < JfZZ~\-
210. Докажите, что 1~) Равно числу не превосходящих N це-
целых чисел, делящихся на 2к~', но не делящихся на 2*.
211. 31.
2 4
212. а) Сравните данное произведение со следующим: -g- • ~г~ ¦
6 98
' ~~7~ ' '' "Ш ил" возвед11те доказываемое неравенство в квадрат,
б) Докажите, пользуясь методом математической индукции, что
1 3 5 2п — 1 ^ 1
Т ' Т ' Т • • • ~ЪГ < /з^ГГГ"
213. Второе.
214. а) Первое из чисел меньше., б) Первое из чисел больше
(воспользуйтесь методом математической индукции).
215. Докажите, что если Ю^1 < 1974" < 10'', то невозможно
неравенство 1974" + 2" Э= 10*.
216. ±11.
217. Воспользуйтесь неравенством задачи 212а).
218. 99" + 1С'О" больше, чем 101" при п < 48, и меньше, чем
101" при и > 48.
219. 300!
220. Докажите предварительно, что для любого целого положи-
положительного k ^ п
\
221 —222. Воспользуйтесь результатом задачи 220.
223. Воспользуйтесь методом математической индукции.
224. Используйте формулу бинома Ньютона.
225. Воспользуйтесь методом математической индукции.
226. Воспользуйтесь неравенством
из которого можно получить, что для каждого целого положи-
положительного р
(Р+ 1)* + 1 _р* + »> (ft+ ЦрК >pft + l_ (р _!)*+!.
227. Эти неравенства можно получить, заменив члены сумм
большими (соответственно меньшими) числами, может быть, предва-
предварительно сгруппировав подходящим образом эти члены (т. е. преоб-
преобразовав суммы в новые, состоящие из меньшего числа членов).
228. Докажите предварительно, что 2 ~]/п + 1 — Т\/п < —— <
V п
<2/л —2//1—1. Ответы: а) 1998.6.) 1800.
373
229. Докажите предварительно, что
Ответ: 14 996.
230. а) 0,105. б) Воспользуйтесь тем, что
1 1 i 1 | ( 9 10 П 999
Т51+11! +12!+'--+ТОООТ <-g-ll0! +1J!+12!+•••+ Tl
Ответ: 0,00000029.
231. Воспользуйтесь результатом задачи 227.
232. Найдите предварительно число незачеркнутых слагаемых
^ и
г.
233. а) Решается аналогично задаче 231. б) Воспользуйтесь, тем,
чт0 ТТ + 1~3" +••••+ (п-\)п = ' ~ ~п~-
234. Докажите, что для всякого целого k и целого р 5= 2
Воспользовавшись этим, выведите, что
где pi — наибольшее простое число среди чисел от 1 до п.
235. Воспользуйтесь тождеством (a -f- b + сK — а3 — Ь3—с3
3( Ь)(Ь + )( + )
236. Воспользуйтесь тем, что а10 + а5 + 1 = t 1 , а а15 —
— 1 = (в3)'—1.
237. Докажите, что разность (*"" + *8Ш + ... + хпи + 1) —
— (х9 + Xs + ... + х + 1) делится на л:9 + Xй + ... +х + 1.
238. а) а3 + Ь3 + с3.— ЪаЬс делится на a -j- b + с. б) jfj =— а—й,
239. Избавьтесь от радикалов и решите полученное уравнение
относительно а.
240. Воспользуйтесь тем, что если х2 + 2а* + fg" = 1/, то * =
= — 6 + 1/ а2 + У — —'. рассмотрите графики функций у = хг +¦
г 16
+ 2ах +-L и У1 « - а + |/а2 + х - -1..
.474
241. Докажите, что должно быть 3* = xi.
242. а) Докажите, что должно быть . , = х.
243. Корни уравнения — все числа, заключенные между 5 и 10.
244. Корни уравнения: число — 2 и любое число не меньшее 2.
245. .v, = 1, х% =«2, ..., .*„ = п.
246. х = \ГА.
247. При о = ± 1 система имеет три решения; прн а = + }^2
система имеет два решения.
248. а) При а = —1 система не имеет решений, при а = !
система имеет бесконечно много решений, б) При а = ± 1 система
имеет бесконечно много решений, в) При а = 1 система имеет
бесконечно много решений, при а = — 2 — не имеет ни одного ре-
решения.
249. Для того чтобы система имела решения, необходимо, что-
чтобы три из четырех чисел cti, <Xi, с.з, а.< были равны между собой.
Если
Kl = а2 = а3 = а, а4 = р\ то хг=х„ =-- х3 = i^L, *4 = а/р — -Я.
250. Единственное вещественное решение х = 1, у — I, z = 0.
251. х=1, (/=0 и к=О, (/=1.
252. дг1=х2=д;з = ^4 = -«5=О, х произвольно; Xi = X2=x3—Xi = X5
произвольны, дг = ?; х= . ^_L_?, xt и х2 произвольны, х3^Л'.г2 — А'ь
(),
253. Все числа равны 1, или три из них равны —1, а последнег
равно 3.
254. При а > Ь > с > d имеем х ~ t — Q ^, ,у = г = 0.
255. Заметьте, что в зависимости от знака Д= (Ь—IJ — Аас
квадратный двучлен а\2 + (Ь—1I +с либо сохраняет знак при
всех |, либо обращается в 0 при единственном значении |, либо
имеет два разных корня ! = ?i и I = |г-
256. 0, если п четно и а{аз... ап-\ ?= а2а4... а„; бесконечно мно-
много, если п четно и а,\а3... ап-\ = а2а4... ап; 2, если п нечетно.
* 257. а) Число действительных корней уравнения равно числу
точек пересечения прямой у = Tqq х и синусоиды ^ = sin x. б) Чис-
Число корней равно числу точек пересечения синусоиды у = sin x и ло-
логарифмической кривой у = log х.
258. Все числа а,, а2,..., ат равны между собой.
259. Рассмотрите коэффициенты уравнения- Р(х) = (х — а) X
X (х — Ь) (х + с) (х + d) =0.
280. Рассмотрите число, обратное фигурирующей в условии за-
задачи дроби; избавьтесь от радикалов в знаменателе полученной
дроби.
261. Если а, Ь и —г-— данные числа, то условие задачи утвер-
утверждает, что а + Ь + —? > — + — + аЬ.
375
262. Докажите (методом математической индукции), что для лю-
любых (натуральных) п и к из равенства 1 суммы п положительных
чисел вытекает, что сумма всевозможных произведений по k (где
1 < k ^ п) из наших чисел меньше 1.
263. -р
264. Все числа Я| (где i = 1, 2,..., 1973) равны между собой
(рассмотрите отдельно случаи а\ > 1 и ai < 1).
265. Воспользуйтесь методом математической индукции.
266. Не может (дчя второго многочлена ответ положителен).
267. Воспользуйтесь методом математической индукции.
268. Если 99 999+11ПИ Уз - (А + В VW, то 99 999 —
— Ill 111 > '3 = (А —В УзK.
269. Докажите, что если') 2 =* р -\- qYri т0 \ 2 есть рациональ-
рациональное число.
270. Пусть А = *"'; тогда х + — = л.
А
271. Не существуют,
272. Нельзя.
6/;-)-5
273. При х — п ^ ¦ гДе & — рационально.
274. Оцените разность ух — х{ близких корней уравнений
х2 + рх + q = 0 и у2 + ру + ?, = 0, где \q{ — q] « 0,01.
275. Обозначим через 0 < Я] <С Яг < ... < ап дробные части
наших чисел alt а2,..., а„; округлите числа at, а2, ... ак по недо-
недостатку, а числа а^.и, ak+2t..., an—no избытку; подберите ¦*.
276. 0; 0,5; 0,501; 0,502;...; 0,999; 1.
277. Рассмотрите дробные части чисел 0, а, 2а, За,..., 1030а;
воспользуйтесь принципом Дирихле (стр. 10). _
278. а) Докажите, что если а < 1 —@,1)'™, той /а < 1 — @,1I0|>.
б) Воспользуйтесь тем, что рассматриваемое число х равно
/ / 1 \liiu
1— То" -Ответ: с точностью до 300 цифр пссле
запятой:
х = 0,3333 ... 333 166 666 ... 6666 250000 ... 000
100 троек .100 шестерок 07 нулей
279. Второе из двух выражений больше первого.
а, + а., 4- .. .+ а
280. х =-!-!—_ —ii.
п
281. а) аь а2, аА, а3. б) Докажите, что если а{ 'и а( —какие-
то два из заданных чисел (а <В ) и а. , а, — числа, стоящие
*ct—1 р+1
в искомом расположении перед аг и после а. то
-1 /
У
376
282. а) Рассмотрите ломаную ADA,A2...An, такую, что проекции
отрезков А0Аи АхАг Ап-\Ап на ось Ох равны соответственно
а.;, аг ап, а на ось Оу — bu b% ..., Ьп. Равенство имеет место,
если
at a.
а
~п~ =«• ~и~ = ... = -г- . б) Воспользуйтесь неравенством за-
12 71
дачи а).
283. При п четном задача может быть "решена геометрически
аналогично решению задачи 282а); случай нечетного п может быть
сведен к случаю четного п. Равенство имеет место при п четном,
если а, «= 1 — а3 = <з3 = 1 — а* = ... = а„_] — а„, а при п нечет-
1
пом — только если а, = д2 = ... = д„ = -^-.
284. Возведите обе части неравенства в квадрат.
285. cos sin x больше, чем sin cos x при любом х.
286. а) Если \»g2n = a, logs л = Ь, то я° ^ й — 10. б) Если
log 2л = о, log.T.2 — b, то b — —.
287. а) Воспользуйтесь тем, что для каждого угла х первой
четверти sin х < х. б) Воспользуйтесь тем, что для каждого угла х
первой четверти tg x > х.
288. Воспользуйтесь геометрическим определением тангенсов как
длин отрезков в тригонометрическом круге или как удвоенных пло-
площадей некоторых треугольников.
я
289. aresin cos arcsin x + arccos sin arccos x = —.
290. Замените в сумме cos 32* + аи cos 31 лг + ... + п\ cos x
угол х на х + я и сложите полученное выражение с первона-
первоначальным.
291. Исходя из формулы 2 sin ~о~= + 1^2—2cosa, вы-
вычислите
последовательно при л = 1, 2, ...
292. 1.
293. Воспользуйтесь тем, что данные многочлены имеют те же
самые коэффициенты при к2а, что и A + х2 + а-3I000, соответственно
A _ Д.-2 __ д;3) 1000_
294. Воспользуйтесь формулой (a-i-b)fa — b) = a2 — b2.
5fl 1001! 5, у, 51050. 1001!
295. а) С1001 *=50! . 951,- б) 1000-С10(И —Cft;01—- 52! • 950! '
296. Обозначим данное выражение через ГЦ; в таком случае
П* = (П4_,—2J. Ответ: D2"-' — 4й-1) : 3.
297. а) 6. б) 6.V.
298. —х + 3.
299. Воспользуйтесь тем, что многочлен х4 -f х3 + 2х2 + х + 1
есть делитель двучлена xxi—1. Ответ: —1.
300. Р(х) = сх(х — 1) (* — 2) ... (х — 26), где с — постоянное.
301. а) Рассмотрите числа ЯA0;'), где N достаточно велико,
б) Воспользуйтесь результатом задачи а).
- . 377
302. Положите в равенстве хтуго° -4- 1. = f(x)g(y) сначала
у — О, а затем х = 0.
303. Воспользуйтесь тем, что квадратный трехчлен -р(х)—х
сохраняет знак при всех х.
304. Воспользуйтесь неравенствами |рA)| ^ 1, |р@)| ^1 и
305. Рассмотрите два числа р(х{) и р(х2), где р(х) —многочлен,
стоящий в левой части уравнения C).
306. Q2 + q2 — pP(Q + q) + qP2 + Qp2 — 2Qq.
307. a = l и a = —2.
308. a) a = 8 и a = 12. 6) b — 1, с = 2, a = 3; b — — 1,
с = —2, a = —3; b = 2, с = — 1, a = 1 и b = 1, с = —2, a = —1.
309. а) Никогда, б). Только если п = 2, <з2 = а, + 2 и я = 4;
а2 = ai — 1, а3 = «I + 1, а4 = a, -f- 2.
310. Воспользуйтесь тем, что если
(х — а\J(х — а2J... (х — а„J + 1 = р(х)q(x),
то р(л-) и q(x), так же как и (х — a,J(x— a2J... (х — anJ-f I, ни
при каком л: не обращаются в нуль и поэтому не могут менять знака.
В остальном решение аналогично решению задачи 309а).
311. Используйте то, что 14—7 = 7 нельзя разложить в произ-
произведение нескольких целых множителей, из который четыре являются
различными.
312. Воспользуйтесь тем, что если многочлен разлагается па
множители с целыми коэффициентами, то при тех х, при которых
многочлен равен ±1, сомножители его тоже равны ±1, а также тем,
что многочлен третьей степени не может принимать одно и то же
значение более трех раз.
313. Воспользуйтесь тем, что если р и q — два целых числа, то
Р(р) —P(q) делится на p — q.
314. Докажите, что если Pl-_j =0, то *-р( = ±1 и*-
315. а) Приравняйте коэффициенты при одинаковых степенях х
в обеих частях равенства
(а0 + ахх -f- а2х2 + ... +апхп) (b0 + bxx -f- b2x2 + ... +Ьпх") =
= С0 + С\Х -f C2X2 -f . . . + Сп + тХп + т
и, воспользовавшись полученной формулой, покажите, что если бы
рассматриваемый многочлен разлагался на два множителя, то все
коэффициенты одного из сомножителей должны были бы быть чет-
четными (что невозможно, так как в исходном многочлене старший
коэффициент равен 1).
б) Положите в рассматриваемом многочлене х — у -\- 1 и затем
аналогично решению задачи а) покажите, что если бы полученный
многочлен разлагался на два множителя, то все коэффициенты од-
одного из сомножителей делились бы на простое число 251.
316. Воспользуйтесь той же формулой, что и при решении зада-
задачи 315а) (см. указание к этой задаче).
317. Докажите, что Pi JLJ, где -?-—несократимая дробь, не
может быть целым числом.
318. Пусть P(N) = М; докажите, что P(N + kM) — P(N) при
всяком k делится на Л4.
319. Представьте многочлен Р(х), принимающий при целых х
целые значения, в виде суммы Р(хI = ЬоРо(х) +Ь\Р[(х) -+-..,
... + Ь„Р„(х) с неопределенными коэффициентами bo, Ьл •.., Ь„,
где (при целом х ^ k) Рк {х) = С*> и определите эти коэффициенты,
подставляя в последнее равенство последовательно х =
= 0, 1, 2,3 , п.
320. а) См. указание к предыдущей задаче, б) Сделайте в мно-
многочлене замену переменных: у = х + к, в) Рассмотрите многочлен
Q(x) = Р(х*).
321. Воспользуйтесь формулой Муавра.
322. Воспользуйтесь результатом задачи 3216).
323. Если х + ~— 2 cos а, то х = cos а ± i sin а.
324. Воспользуйтесь формулой Муавра.
325. Воспользуйтесь результатом предыдущей задачи. Ответ:
п — 1 sin (/; + 1) a cos па
cos2 а + cos2 2а + ... + cos2 п а = 2 + 2 sin а "
326. Воспользуйтесь формулами Муавра и бинома Ньютона.
327. Воспользуйтесь формулой
sin A sin В = -у [cos (Л — В) — cos (Л + В)]
и результатами задачи 324.
328. Рассмотрите корни уравнения х'2и+1 — 1=0.
329. Воспользуйтесь формулами задачи 3216).
330. Воспользуйтесь результатом задачи 3296).
, п Bп-1) 2п(п+\)
Ответ: а) о • о) g .
331. Воспользуйтесь результатом задачи 329а).
. ^27+1 Vn 1 ул
Ответ: а) и -—i. б) — и ^rj.
332. Воспользуйтесь тем, что если а есть угол первой четверти,
то sin а < а < tga.
333. а), б). Воспользуйтесь формулой задачи 324. в) Воспользуй-
Воспользуйтесь результатом задачи 6).
334. а) Воспользуйтесь предложением задачи 333а). б) Вос-
Воспользуйтесь формулой задачи 324.
335. а) Воспользуйтесь предложением задачи 333а). б) См.
указание к задаче 3346). в) Воспользуйтесь результатом задачи 331а).
336. Воспользовавшись формулой Муавра, представьте sin50 a в
виде суммы косинусов углов, кратных а, взятых с некоторыми ко-
коэффициентами. Ответ: 5000 С^/?50 = E000 ¦ 50! /?50) : B5!J.
337. Наибольшее значение: |г| = — (а -j- Yср —- 4); наименьшее
338. Докажите, что если наибольшая из разностей аргументов
наших чисел меньше 120°, то их можно умножить на число единич-
единичного модуля так, чтобы вещественная часть суммы полученных про-
произведений была положительна. Заменить в условии задачи величину
120° большей нельзя.
379
839. Воспользуйтесь тем, что если изображающая г точка Л ком-
комплексной плоскости лежит вне отвечающего числам С\, Сг,..., с„
многоугольника М = CiC2...Cn, то она лежит «по одну сторону» от
М в том смысле, что все векторы AM, где М е М, направлены в одну
сторону от некоторой проходящей через А прямой /.
340. Воспользуйтесь тем, что если а не делится на р, то числа
а, 2а, За,..., (р—1)а лают при делении на р различные остатки.
341. Воспользуйтесь тем, что если k\, kz,..., kT — все целые
числа меньшие N и взаимно простые с N, то числа k^a, k2a, ,.., kra
дают при делении на N разные остатки.
342. Воспользуйтесь методом математической индукции.
343. Воспользуйтесь теоремой Эйлера (задача 341).
344. Докажите, пользуясь методом математической индукции,
что, каково бы ни было целое число N, всегда найдется такая сте-
степень числа 2, N последних цифр которой все будут единицами и
двойками; при доказательстве воспользуйтесь теоремой Эйлера (за-
(задача 341) и предложением задачи 342.
345. Ясно, что пара чисел пап2 является «хорошей»; сравните
разложения на множители чисел п— 1 и п2— 1.
346. Пусть and взаимно просты; с помощью теоремы Эйлера
(задача 341) докажите, что прогрессия содержит бесконечно много
натуральных степеней числа а.
347. См. указание к задаче 340.
348. а) Докажите, что для каждого нечетного простого числа
р существуют • два таких целых положительных числа х, у (где
х, у-^-Е- \, что х2 и у2—• 1 дают при делении на р одинаковые остат-
остатки, б) Воспользуйтесь теоремой Вильсона (задача 347).
349. Пусть Р\, рг,..., рп—п простых чисел. Найдите число,
которое не делится ни на одно из этих чисел и больше каждого
из них.
350. а) Пусть ри р2,..., рп — я простых чисел вида 4k — 1
(или 6k—1). Найдите число вида 4N — 1 (или 6N—1), которое не
делится ни на одно из чисел pi, p%..., рп и больше каждого из них.
б) Идея решения близка к использованной в решении задачи а).
ЛИТЕРАТУРА
А. Сборники «олимп иадских» задач
На русском языке имеется много книг, из которых можно черпать допол-
дополнительные- задач» повышенной трудности (задачи «олимпиадного» типа).
Из их числа, в первую очередь, хочется указать следующие:
1. А. А. Л е м а н (сост.), Сборник задач московских математических
олимпиад, М., «Просвещение», 1965.
2. Н. Б. Васильев, А. А. Егоров, Сборник подготовительных
задач к Всероссийской олимпиаде юных математиков, М., Учпед-
Учпедгиз, 1963.
3. Е. А. М о р о з о в а, И. С. П е т р а к о в, Международные матема-
математические олимпиады, М., «Просвещение», 1971.
4. И. Л. Бабин ска я, Задачи математических олимпиад, М., «На-
«Наука», 1975.
Книги серии «Библиотека математического кружка»
5. Е. Б. Д ы н к и н, В. А. Успенски й, Математические беседы,
М.— Л., Гостехиздаг, 1952.
6. А. М. Яглом, И. М. Я г л о м, Неэлементарные задачи в эле-
элементарном изложении, М., Гостехиздат, 1954.
7. И. М. Яглом, В. Г. Б о л т я н с к и й, Выпуклые фигуры, М.— Л.,
Гостехиздат, 1951.
8. Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в, И. М. Я г л о м, Избран-
Избранные задачи и теоремы планиметрии, М., «Наука», 1967.
9. Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в, И. М. Я г л о м, Избран-
Избранные задачи и теоремы элементарной математики; геометрия (сте-
(стереометрия), М., Гостехиздат, 1954.
10. Д. О. Ш к л я р с к и й, Н, Н. Ч е н ц о в, И. М. Яглом, Геомет-
Геометрические неравенства и задачи на максимум и минимум, М.,
«Наука», 1970.
11. Д. О. Шклярский, Н. Н. Ч е н ц о в, И. М. Яглом, Гео-
Геометрические оценки и задачи из комбинаторной геометрии, М.,
«Наука», 1974.
Книги серии «Библиотечка физико-математической школы»
12. Е. Б. Дынкин, С. А. Молчанов, А. Л. Розенталь,
А. К. Толпы го, Математические задачи, М., «Наука», 1971,
13. Е. Б. Дынкин, С. А. М о л ч а н о в, А. Л. Р о з е п т а л ь, Ма-
Математические соревнования (арифметика и алгебра), М., «На-
«Наука», 1970.
14. Н. Б. В а си л ье в, С. A. Me л ч а и о в, А. Л. Розенталь,
А. П. С а в и н, Математические соревнования (геометрия), М.,
«Наука», 1974, .
381
15. С. И. Гельфанд, М. Л. Гер вер, А. А. Кириллов,
Н. Н. Константинов, А. Г. Кушнеренко, Задачи по
элементарной математике (последовательности, комбинаторика,
пределы), М., «Наука», 1965 (см. также А. А. Кириллов, Пре-
Пределы, М., «Наука», 1973),
а также другие книги той же серии, хоть и не имеющие характера задачни-
задачников, но содержащие много удачных задач н упражнений:
16. Н. Б. Васильев, В. Л. Гутенмахер, Прямые и кривые,
М., «Наука», 1970.
17. М. И. Б а ш м а к о в Уравнения и неравенства, М., «Наука», 1Q71.
18. И. М. Гельфанд, Е. Г. Глаголева, А» А. Кириллов,
Метод координат, М., «Наука», 1973.
19. И. М. Г е л ь ф а н д, Е. Г. Г л а г о л е в а, Э. Э. Ш н о л ь, Функ-
Функции и графики (основные приемы), М., «Наука», 1973.
Наконец, следует еще назвать книги:
20. Г. Штейн га уз, Сто задач, М., «Наука», 1976.
21. В. А. К р е ч м а р, Задачник по алгебре, М., «Наука», 1972.
22. Б. Н. Делоне, О. К- Житомирский, Задачник по геомет-
геометрии, М., Физматгиз, 1959.
Журналы и непериодические сборники
23. Журнал «Квант».
24. Журнал «Математика в школе».
25. Сборники «Математическое просвещение» (новая серия; 1957—
1961).
Здесь имеются в виду раздел «Задачник „Кванта"» (и примыкающие
к этому разделу заметки и статьи, также содержащие, как правило, много
задач); раздел задач сборников «Математическое просвещение»; регулярна
помещаемые в журнале «Математика в школе», отчеты о московских, всесо-
всесоюзных и международных олимпиадах, содержащие перечень всех предложен-
предложенных задач, и тщательно составленный обзор их решений.
Б. Общая литература о том, как решать задачи
26. Д. Пой а, Математическое открытие, М., «Наука», 1976.
27. Д. П о й а, Математика и правдоподобные рассуждения, М.,
«¦Наука», 1975.
28. Д. По й а, Как решать задачу, М., Учпедгиз, 1959.
В книгах [26]—[28] обсуждается сам процесс решения задачи и даются
прямые рекомендации решающим; особый интерес представляют первые две из
них, в которых общие положения автора иллюстрируются многочисленными
примерами и задачами для самостоятельного решения.
В. Литература к отдельным циклам задач
1. Вводные задачи
«Логические» задачи типа многих, собранных в этом цикле задач, широ-
широко представлены в книгах о «математических развлечениях», рассчитанных
на учащихся средних классов школы:
29. Б. А. К о р д е м с к и й, Математическая смекалка, М., «Наука»,
1965.
30. А. П. Д о м (Тр я д, Математические игры и развлечения, М., Физ-
Физматгиз, 1961. •
382
31. М. Гарднер, Математические чудеса и тайны, М., «Наука»
1964.
32. В. Л и т ц м а н, Веселое и занимательное о числах и фигурах,
М., Фнзматгиэ, 1963.
33. Еленьский, По следам Пифагора, М., Детгиз, 1961.
См. также рассчитанные на несколько более опытного читателя книги се-
серии переводных сочинений на ту же тему, выпускаемые издательством «Мир»:
34. М. Гарднер, Математические головоломки и развлечения, М.,
«Мир», 1971.
35. М. Гарднер, Математические досуги, М., «Мир», 1972.
36. М. Г а р д и е р, Математические новеллы, М., «Мир», 1974.
37. Л. К э р р о л, История с узелками, М., «Мир», 1973.
38. Г. Штейн ray з, Мысли и размышления, М, «Мир», 1974.
39. Г. Э. Д ь ю д е н и, 520 головоломок, М., «Мир», 1975.
40. С. Го лом б, Полимино, М., «Мир», 1975.
41. Д. Б и з а м, Я. Г е р ц е г, Игры и логика, М., «Мир», 1975.
Допо тигельная литература к циклу 1
42. И. С. С о м и н с к и й, Л. И. Г о л о в и н а, И. М. Я г л о м, О ма-
математической индукции, М., «Наука», 1967 (см. также И. С. С о-
минский, Метод математической индукции, М., «Наука», 1975;
Л. И. Головина, И. М. Я г лом, Индукция в геометрии, М.,
Физматгиз, 1961).
43. О. О р е, Графы и их приложения, М., «Мир», 1965.
44. А. М. Я г л о м, И. М. Я г л о м, Вероятность и информация, М.,
«Наука», 1973.
3, Задачи на делимость чисел
45. В. Г. Бо л т я н с к и й, Г. Г. Л е в и т а с, Делимость чисел и про-
простые числа, сборник «Дополнительные главы но курсу матема-
математики в 7—8 кл. для факультативных занятий» (сост. К. П. Сикор-
ский), М., «Просвещение», 1974, стр. 5—69.
46. Н. Н. Воробьев, Признаки делимости, М., «Наука», 1974.
47. СВ. Ф о м и н, Системы счисления, М., «Наука», 1975.
4. Разные задачи по арифметике
Из числа сборников арифметических задач, а которых можно найти допол-
дополнительные задачи, в первую очередь, хочется упомянуть (весьма, впрочем,
непростую) книгу
48. В. С ер пине кий, 10О простых, но одновременно и трудных
вопросов арифметики, М., Учпедгиз, 1961
(ср. [52]—[53] и [701—171!), а также гораздо более доступные для начинающих
сборники:
49. А. И. О с т р о в с к и й, 75 задач по элементарной математике —
простых, но..., М., «Просвещение», 1966.
50. А. И. Островский, Б. А. К о р д е м с к и й, Геометрия помо-
помогает арифметике, М, Физматгиз, 1960.
5. Решение уравнений в целых числах
51. А. О. Гельфонд, Решение уравнений в целых числах, М.— Л.,
Гостехиздат, 1952.
52. В. С е р п и н с к и и, О решении уравнений в целых числах, М.,
Физматгиз, 1961,
383
53. В. Серпинский, Пифагоровы треугольники, М, Учпедгиз,
1959.
54. А. Я. Хипчин. Великая теорема Ферма, М.—Л„ ОНТИ, 1934.
6. Матрицы, последовательности, функции
55. А. К о ф м а н, Р. Ф о р, Займемся исследованием операций, М.,
«Мнр», 1966.
56. Дж. К е м е и и, Дж. Спел л, Дж. Томпсон, Введение в ко-
конечную математику, гл. V—VII, М., «Мир», 1964.
57. Н. Н. В о р о б ь е в, Числа Фибоначчи, М., «Наука», 1969.
58. А. И. Маркушевич, Возвратные последовательности, М,,
«Наука», 1975.
8—10. Дополнительная литература по алгебре
59. Д. К. Фаддеев, И. С. С о м и н с к и и, Алгебра, М., «Наука»,
1966.
60. И. С. С о м и п с к и й, Элементарная алгебра, М., Физматгиз,
1963.
61. В. Г. Болтянский, Ю. В. Сидоров, М. И. Ш а б у н и н,
Лекции н задачи по элементарной математике, М., «Наука», 1974.
62. А. И. М а р к у ш е з и ч, Деление с остатком в арифметике и в
алгебре, М.— Л., Изд. Акад. пед. наук РСФСР, 1949.
63. Р. О. Кузьмин, Д. К. Фа.ддеев, Алгебра и арифметика
комплексных чисел, Л., Учпедгиз, 1939.
11. Несколько задач из теории чисел
64. И. В. Арнольд, Теория чисел, М., Учпедгиз, 1939.
65. А. А. Б у х ш т а б, Теория чисел, М., «Просвещение», 1966.
66. И. М. Виноградов, Основы теории чисел, М., «Наука», 1972.
67. Г. Д э в е н п о р т, Высшая арифметика, М., «Наука», 1965.
68. А. Я- X и н ч и и, Элементы теории чисел, Энциклопедия элемен-
элементарной математики кн. 1 (математика), М.— Л., Гостехиздат,
1951, стр. 251—353.
69. Л. Г. Шнирельмзн, Простые числа, М.— Л., Гостехиздат,
1940.
70. В. Серп и н с к и ft, 230 задач по элементарной теории чисел, М.,
«Просвещение», 1968.
71. В. Серпинский, Что мы знаем и чего не знаем о простых
числах, М.— Л., Физматгиз, 1963.
72. А. Я- X и п ч и и, Три жемчужины теории чисел, М.— Л., Гостех-
Гостехиздат, 1948.