Author: Савин А.Н. Андреев А.А. Люлев А.И.
Tags: математика задачи по математике школьная математика
Year: 1997
Text
САМАРСКИЙ МУНИЦИПАЛЬНЫЙ КОМПЛЕКС
НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
«Университет Наяновой»
САМАРА
1997
САМАРСКИЙ МУНИЦИПАЛЬНЫЙ КОМПЛЕКС
НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
«Университет Наяновой»
ЛА. Андреев, А.И. Люлев, А.Н. Савин
Антье
Серия А: Математика
Выпуск 2
Издательство «Пифагор»
Самара
1997
Серия А:
Математика
Андреев А. А., Люлев А. И., Савин А. Н.
Антье. Учебное издание. Серия А: Математика. Вып. 2. — Самара:
Пифагор, 1997. — 23 с.
Цель этой брошюры — познакомить читателя с некоторыми свойствами функ-
ции целой и дробной части действительного числа.
Книга снабжена многочисленными примерами и задачами и предназначена для
учащихся старших классов, но может также быть использована в работе школьно-
го математического кружка.
Учебное издание
Редактор серии канд. физ.-мат. наук, доцент Андреев А, А.
Рецензент докт. физ.-мат. наук., профессор Кислов Н. В., кафедра
математического моделирования, Московский Государ-
ственный Технический Университет (МЭИ)
© Андреев А. А., Люлев А. И., Савин А. Н., 1997
Введение
Антье — это известный французский
математик 18 века.
(Из студенческого фольклора)
В различных математических олимпиадах последних лет
(Соросовская олимпиада, олимпиады Физико-Технического Ин-
ститута, Всероссийская олимпиада) присутствуют задачи, осно-
ванные на применении целой и дробной части действительного
числа. В курсе математики средней школы эти понятия, как пра-
вило, не изучаются, и, поэтому, многие школьники вообще не при-
ступают к решению подобных задач.
Настоящая брошюра преследует цель ознакомить читателя с
понятиями антье и дробной части. В ней подробно рассмотрены
приемы решения различных уравнений, содержащих выражения
под знаком антье, а также примеры построения графиков функ-
ций. Особое внимание уделено задачам на делимость натуральных
чисел и популярному разделу «антье в геометрии».
В конце сборника приведены задачи для самостоятельного ре-
шения.
з
1. Антье и её свойства.
Целой частью действительного числа х называется наибольшее
целое число, не превосходящее х. Обозначается целая часть х сим-
волом “[х]”. Ясно, что [х] - такое целое число, что [х]<х<[х]+1.
Далее целую часть х будем также называть “антье” (от франц.
Entier - целый). Например: [3,5]=3, [“3,5]=~4,[3]=3,[-5]=-5.
Наряду с целой частью числа существует понятие дробной час-
ти числа, которая обозначается {х} и определяется следующим
образом: {х}=х-[х]. Очевидно, что для любого действительного
числа х выполняется двойное неравенство: 0<{х}<1. В самом деле,
0<{х}=х~[х]<1. Так {3,5}=0,5, {-3,2}=0,8, {5}=0, {-5}=0.
Антье обладает различными свойствами. Перечислим некото-
рые из них.
1°. Если х>0, то [х]>0. Если х<0 , то [х]<0.
2°. Если р - целое число, то [х+р]=[х]+р.
Так как дробная часть числа х равна дробной части числа х+р,
то из равенства {х+р}={х} следует х+р~[х+р]=х~[х], откуда получаем
[х+р]=[х]+р.
3°. Для любых двух действительных чисел х и у справедливо
[x+y]S:[x]+|>]-
Действительно, а=[а]+{а}, Р=[Р]+{Р}. Следовательно,
а+р=[а]+ +[р]+{а}+{Р}. Так как [а] и [р]-целые числа, то по свой-
ству 2° [а+р]=[[а]+[Р]+{а}+{Р}>[а]+[Р]+[{а}+{Р}]5:[а]+[р], потому
что {а},{Р}>0 и по свойству 1° [{а}+{Р}]>0.
Свойство 3° распространяется также на любое конечное число
действительных чисел: [а+р+...+ш]>[а]+[Р]+...+[ш].
4°. Если [х]=[у], то I х-у | <1.
Так как х=[х]+{х}, у=[у]+{Я. то |х-у| = |[х]+{х}-|>]-{у} | =
= I {х}_{.У} I <1- Последнее неравенство следует из того, что дробная
часть числа больше или равна нулю и меньше единицы. Следова-
тельно, разность дробных частей двух чисел больше -1 и меньше 1,
а модуль этой разности меньше 1. Отсюда | х-у | <1.
5°. Если п - натуральное число, то для любого действительного х
выполняется
Так как x=[x]+a=n^+r+a, 0<r<n, a={x}, то
nq + г + a
Пример 1. Доказать, что для всех, вещественных аир вы-
полняется неравенство [a]+[a+P]+[P]^[2a]+[2p];
Пусть [а+р]=[а]+[Р]+Ез; [2a]=2[a]+sj; [2Р]=2[Р]+е2; где число Si-
целое. Покажем, что ез равно 0 или 1;. Имеет место неравенство
-Ha+p-l-a-p<[a+p]-[a]-[p]<a+p-a+l-p+l=2. Отсюда получаем,
что -1<ез<2, откуда Ез=0 или ез=1, то же верно для Si, е2. Рассмотрим
разность .< [2a]+[2p]-[a]-[p]-[a+p]=[a+a]+[p+p]-[a]-[a+p]-[p]=[a]+
+[а]+Е1+[р]+[р]+Е2-[а]-[а]-[Р]-Ез^[р]=^Е1,+Е2-бз: Осталось показать,
что Е1+е2-ез>0, Si=0 или 1. Это неравенство может быть нарушено
только при Ei=e2=0 и Ез=1. Покажем, что это невозможно. Если
£1.2=0, то [2a]=2[a], т.е. a=N+8, где N - целое, а 6<8<0,5, аналогично,
р=К+1, где К - целое, а 0<1<0,5, но тогда [a+P]=N+K=[a]+[P], т.е.
Ез=0. Мы пришли к противоречию, следовательно, [a]+[a+P]+
+[p]^[2a]+[2p], что и требовалось доказать.
2. Графики антье
Наверно вы уже где-нибудь встречали графики функции р=[х],
так называемые “ступени”, и ,у={х} - “забор”; оба графика приве-
дены на рисунках 1 и 2 соответственно.
5
Рассмотрим общий метод построения графиков функций
у=ш\, ^=ЛИ), У=Ш},
Итак, пусть график функции y=flx) задан (рис.З). Построение
графика функции у=[/(х)] выполняют в следующем порядке:
1) проводят прямые у=п (neZ) и рассматривают одну из полос,
образованных прямыми у=п и у=и+1;
2) точки пересечения прямых у=л, у=л+1 с графиком функции
y=f(x) будут принадлежать графику функции у=[Дх)], поскольку их
ординаты - целые числа; другие точки графика у=[/(х)] в рассмат-
риваемой полосе получим как проекцию части графика у=/(х) на
прямую у=п, поскольку любая точка этой части графика функции
y=ftx) имеет такую ординатур, что п<у\<п+\, т.е. [yi]=n;
3) в каждой другой полосе, где есть точки графика функции
y=f(x), построение проводится аналогично (рис. 3).
Пусть график функции y=f(x) задан (рис. 5). Построение графи-
ка функции _у=/([х]) выполняют в следующем порядке:
1) проводят прямые х-п (neZ) и рассматривают одну из полос,
образованную линиями х=и, х=п+\;
2) точки пересечения графика функции y=f(x) с прямыми у=п
принадлежат графику функции р=з/([х]), поскольку их абсциссы -
целые числа; другие точки графика функции _у=ЛМ) в рассматри-
ваемой полосе получим как проекцию части графика функции
у=/(х), которая находится в этой полосе, на прямую у=/(п), посколь-
6
ку любая точка этой части графика имеет такую абсциссу xi, что
Теперь рассмотрим метод построения графика функции
3^={Дх)}. Так как {Дх)}=Лх)-[Дх)], то вместо графика функции
{/(х)} строят разность графиков функций у=/(х) и j/=[/(x)].
Практически это построение выполняют так:
1) строят график функции у=Дх) и проводят прямые у-п (neZ);
2) в точках пересечения этих прямых с графиком функции
y=f(x) проводят прямые, параллельные оси ординат. Значения
функции р={Дх)} попадают в образованные прямоугольники. Час-
ти графика функции y=flx), которые попали в эти прямоугольники
и располагаются в верхней полуплоскости, опускают вниз на рас-
стояние п. Части графика функции, попавшие в нижнюю полуплос-
кость переносят вверх на расстояние |л|+1.
Проще всего строятся графики функции у=Д{х}). Легко заме-
тить, что такие функции периодичны с периодом Т=1, и на отрезке
[0;1] Л{х}>/(х). Отсюда следует способ построения графика функ-
ции у=Д{х}):
1) строят график функции у=/(х) на [0; 1); .
2) продолжают этот график, учитывая свойство периодичности
функции у=Л{х}) (рис. 9, 10).
7
С х
рис. ю y=i#f
3. Антье в уравнениях
3.1. Аналитический метод решения уравнений
Часто приходится решать задачи в которых параметры в раз-
личных областях изменяются по различным законам, при этом
необходимо рассматривать уравнения с антье. Существует несколь-
ко способов решения таких уравнений, но самыми известными и
простыми являются аналитический и графический.
В основе аналитического способа лежит использование свойств
антье и дробной части. Обычно, применяя различные подстановки,
8
уравнения с антье сводят к двойному неравенству, которое уже не
содержит антье, таким образом получают диапазон изменения
переменной и, производя обратную подстановку, получают ответ.
Вот несколько примеров.
_ _ Г7 + 8х1 10х-1.
Пример 2. Решить уравнение —-— =—-—.
„ 10х-1 Зу + 1
Обозначим —-— = у. Тогда х= —• Подставим х в урав-
нение, получим
(1)
L 25 J
или
39 + 12,. [39 +12у|
25 1 25 )
Правая часть уравнения (2) больше или равна нулю и меньше еди-
ницы, тогда
Л 39 + 12у
0<---------у<1,
25
25
0<39ИЗу<25,
14
13
как
<14
Таким образом у содержится в интервале , но из уравнения
(1) видно, что у - целое число, следовательно, либо у = 2, либо
о l-т г 3 у +1
у = 3. Производя обратную замену х = и подставляя значе-
ние у для каждого случая, получим х^= ;и х = 1, которые,
убеждаемся проверкой, являются единственными решениями
ходного уравнения.
{15х — 41 5х — 3
-------1 =-----.
6 J 5
Преобразуем уравнение так, чтобы оно содержало антье:
ис-
9
15х-4 15х-4
'15х-4~| 45х-2
6 J 30
„ „ 45х-2
Теперь произведем замену у =-------и выразим х через у:
х = ^,
45
подставим х в последнее уравнение:
= Ь
У-
Проведя рассуждения, аналогичные тем, которые были в предыду-
щем примере, получим:
ЗОу-Ю
9
0 < бу - 5 < 9,
0< %££y<ty£<3.
/и ' /о
Так как у - целое число, то у может быть равно только 1 или 2.
Следовательно, х будет равно или соответственно.
Рассмотрим более сложный пример.
Пример 4. Доказать тождество: + 4п + 1] = p477 + 2j5fl eN.
Так как
4и2 + 4п < 4л2 + 4п +1,
4и(л + 1) <(2и + 1)2,
то, извлекая корень из обеих частей неравенства, получим
2л/лл/л+1 < 2п +1
или
2п +1 + 24п4п +1 < 2(2и +1),
значит,
{4п + Vw + l)2 <4п + 2.
Тогда
ю
4п + л/л+ 1 < л/4л+ 2
и, следовательно,
[4п + л/л + lj < р4и + 2 .
Предположим, что + л/л + 1J < |л/4л + 2J. Тогда существует
такое натуральное число т, что
л/л + л/л ч-1 <т< л14п + 2.
или
2у1п(п..+ 1) <т2- (2л +1) < 2л +1,
4л(л +1) < (т2 - (2л +1))2 < (2л +1)2,
(2л +1)2 -1 < (т2 - (2л +1))2 < (2л +1)2.
Так как (т2 -(2л+1))2 - целое число, содержащееся между двумя
последовательными числами (2л +1)2 -1 и (2л +1)2, то из последне-
го неравенства следует (т2 - (2п +1))2 = (2л +1)2, то есть
т2 = 2(2л +1). Получилось, что т2 делится на 2, но не делится на 4,
что невозможно, следовательно, мы пришли к противоречию, и,
значит,
[д/л + л/л+ 1| = |л/4л + 2
что и требовалось доказать.
Пример 5. Найти все числа х на отрезке [-10;2], которые
удовлетворяют уравнению [х2]=[х]2.
Если х - целое число, то [х]=х и [х2]=х=[х]2, т.е. всякое целое
число из отрезка [-10; 2] будет решением уравнения. Пусть х -
нецелое число. Если [х]<х<0, то 0<[х2]<х2<[х]2=[х2]; следовательно,
[х2]<х2<[х]2, т.е. уравнение не имеет нецелых решений в этом случае.
Осталось проверить два случая: [х]=0 и [х]=1. Если [х]=0, то
х={х} и [х2]=[<{х}2]=0, т.е. любое число из интервала (0;1) удовлетво-
ряет уравнению.
Если [х]=1, то х=1+{х} и х2=1+2{х}+{х}2. По условию
[х^ЭДМ, а это возможно только при 2{х}+{х}2<1, т.е.;0<{х}<
<л/2-1, следовательно, уравнению удовлетворяют все числа из
промежутка [1; л/2).
Ответ: все целые числа из отрезка [-10;2] и интервал (0; л/2).
п
чётно?
Пример 6. При каких п число
Положим а = (з + ->/17^2, b = (з-л/17)/2, хп=ап+Ьп. Тогда а и
b - корни уравнения х^Зх-Т^О и
х^^^^сГЧЬ^а+Ьу-аЬ^+^Зх^+гх,.
Так как xi=3 и Х2=13- нечетны, то все числа хп- нечётны, и по-
скольку -1 <Ь<0, то при чётном п и поэтому
т.е. [а”]- чётное число, а при нечётном п 0<№<1, и
т.е. [а"] -нечётноечисло.
Таким образом, заданное число чётно при чётных п.
Пример 7. Решить уравнение [х]+[х2]=[х3].
Если -1<х<0, то -1<х3<0, 0<х2<1 и, следовательно, [х]=[х3]=-1,
[х2]=0. Если 0<х<1, то [х]=[х2]=[х3]=0. Если |х|>1, то [х2]>1, тогда
х<1+[х]<[х3]<х2 и, значит, х3>х. Отсюда х>1, но тогда [х3]=[х-х2]>
S[[x] [x2]]=[x]-[x2]. Теперь из уравнения следует, что W+fx^^xJ-fx2],
или ([x^J-lXM-l)^!. Таким образом, [х2]<2, т.е. [х2]=1 или [х2]=2.
Если [х2]=1, то l<x<V2. Тогда [х]=1, [х3]=2, 2|/,3<х<31/3, т.е.
21/3<x<V2. Если [х2]=2, то 72<х<Л. Тогда [х]=1, [х3]=3,
31/3 <,х< 41/3, т.е. 31/3 х < 41/3.
Таким образом, мы получили ответ: -1<х<1, 2l,Z3<x<V2,
З1/3 < х < 4^3
Пример 8. Решить уравнение
Очевидно, что уравнению не могут удовлетворять как те зна-
х3 -2
чения х, при которых —-— > х +1, так и те значения х, при кото-
х3 -2
рых —-— < х -1. Среди решений первого из этих неравенств будут
х3 — 2
значения х>3. Действительно, если —-— > х +1, то х3 > Зх + 5, или
х2(х-3)>-3х2 +Зх + 5. При х>3 левая часть последнего неравен-
ства будет неотрицательной, тогда как трёхчлен, стоящий в правой
12
части, будет отрицателен, т.е. все х>3 входят в число решений
рассматриваемого неравенства,
х3 -2
Покажем теперь, что среди решений неравенства------<х-1
будут значения х < -2. В самом деле, в этом случае х3 < Зх -1 или
х2(х + 2)<2х2 + Зх-1. При х<-2 левая часть последнего неравен-
ства будет не больше нуля, тогда как трёхчлен, стоящий в правой
части, будет положителен.
Таким образом, решения данного уравнения следует искать
лишь на промежутке -2 < х < 3. Для этого достаточно решить сле-
дующие системы неравенств:
-2<х<-1;
2<х<3.
Система 3) не имеет решений. Остальные системы соответственно
дадут:
-V4 <х <-1, -1<х<0, V5<x<2, 2^x<Vll
и окончательно
-у/4 <х<0 и у[5<х< V1T.
Пример 9. Решить уравнение
х = [х / 2] + [х / 3] + [х / 4]+.. .+[х /1993].
Так как [х]^х<[х] + 1 и х = х/2 + х/3 + х/6, то
[х/2] + [х/3] + [х/6]<х<[х/2] + [х/3] + [х/6] + 3.
Отсюда следует, что
0<[х/4] + [х/5] + [х/7]+...+[х/1993]<3,
и поэтому, во-первых, х>0, а во-вторых, в сумме, стоящей в середи-
не полученного двойного неравенства, все слагаемые, начиная с
третьего, равны нулю, так что х<7.
Поскольку х - целое число, то остаётся проверить значения от
О до 6. Решениями уравнения оказываются числа 0,4 и 5.
13
3.2. Графический метод решения уравнений
В основе графического метода лежит нахождение точек пересе-
чения графиков функций левой и правой частей уравнения. Обычно
данный метод применяется, когда графики обеих частей уравнения
достаточно просто строятся и легко находятся точки пересечения
этих графиков.
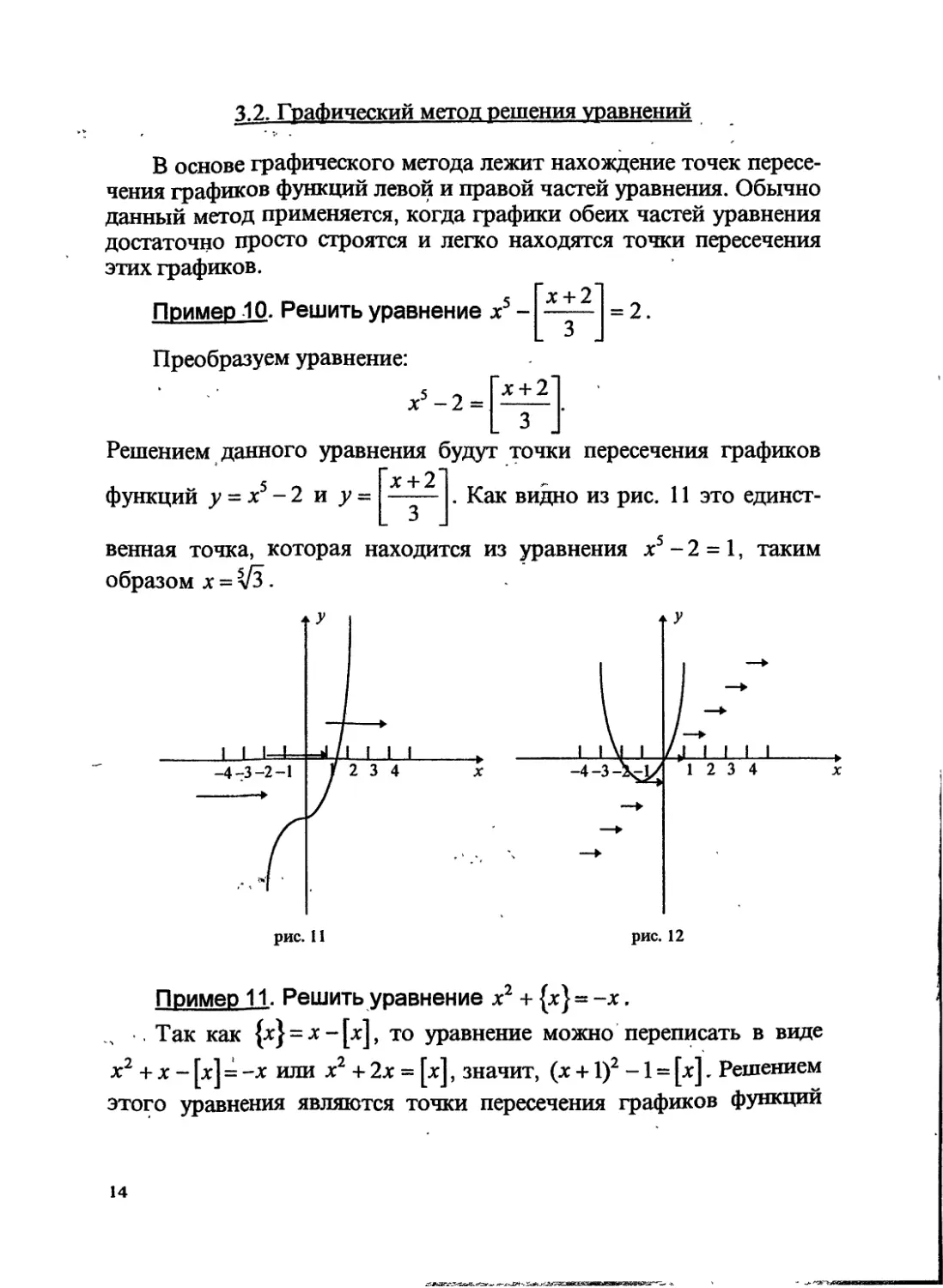
Пример 10. Решить уравнение х5 -
х + 2
3
= 2.
Преобразуем уравнение:
5 _ Гх + 2
х - 2 = ----.
3
Решением данного уравнения будут точки пересечения графиков
функций у = х5-2иу = Х +
. Как видно из рис. 11 это единст-
3
венная точка, которая находится из уравнения х5 - 2 = 1, таким
образом х = V3 .
рис. 12
Пример 11. Решить уравнение х2 + {х}= -х.
. Так как {х} = х-[х], то уравнение можно переписать в виде
х2 + х - [х] = -х или х2 + 2х = [х], значит, (х +1)2 -1 = [х]. Решением
этого уравнения являются точки пересечения графиков функции
14
у - (х +1)2 -1 и у = [х]. Как видно (рис. 12), это две точки х = 0 и
X = -1.
Итак, мы убедились на примерах 10 и 11 , графический способ
намного легче и эффективнее аналитического, однако,, в более
сложных примерах, линейных и нелинейных системах уравнений,
содержащих большое количество переменных, рекомендуется
использовать аналитический метод решения уравнений, так как в
этом случае он будет более лёгок в применении, нежели графиче-
ский.
4. Делимость.
Всякое натуральное число т можно разложить на простые
множители и притом единственным способом. Очевидно, показа-
тель степени а, с которым простое число р ьхсяуп в разложение
числа т на простые множители: ..р^к, равен макси-
мальной степени числа р, на которую делится т.
Возьмём число N!=l-2-... N. Пусть р- некоторое простое чис-
ло. Как узнать: на какую максимальную степень числа р делится
N!?
Посчитаем, сколько в последовательности 1, 2, ..., N чисел,
кратных р. Если таких чисел к, то число кр среди них - наиболь-
N
шее, и поэтому kp<N <(к + 1)р, т.е. к <— <к +1. Значит,
Р
N
Р
Итак, среди чисел 1,2,..., N кратными р будут числа
и мы можем записать N! так:
= р-2р-3р-..
— р-М^/М-1-1-2-3-.
15
N
где число MY на р уже не делится. Если — < р, то максимальная
. L/\
степень числа р, на которую делится 7V!, равна
N с
— . Если же
,Р.
N
— >p, то выделим числа, кратные числу р, среди чисел
_pj
п
_Р_
образом,
— . Их будет [[N/p]/p], или ( свойство 5°) - . Таким
где число
' N'
Гал.
у]! = р-2р.
уже не делится на р. если при этом мы
N и
— Р-^2 =
L/> J
N
N
4 !-^2>
— < р, то задача решена, и а = — + — . Если
же
получили
' N~
Lp J
то, повторив предыдущие рассуждения, найдём
' N~
4+... (*)
|_Р J
Через конечное число шагов мы получим степень
Г к~\
— = 0. Следовательно, в сумме (♦) число
LXJ
конечное, и мы можем дать окончательный ответ: простое число р
входит в разложение числа N! с показателем
“ N '
т.е.
a =
LPJ
\_Р J
[_Р J
jVl
-P-+ -P1.
N
ps, большую
слагаемых
a= —
LpJ \.p‘
где s - таково, что p3 ~l<N<ps.
Применим полученную формулу к решению задач.
Пример 12 . Сколькими нулями оканчивается число 1996!?
Задача будет решена, если мы найдём, чему равна максималь-
ная степень числа 10, на которую делится 1996!. Но поскольку
10=5-2, нам достаточно подсчитать, в какой степени число 5 входит
в разложение на простые множители числа 1996! (ясно, что 2 войдёт
в 1996! сомножителем большее число раз, нежели 5). Так как
,2
У J’
54<1996<5s, то мы получаем следующий ответ: число 1996! оканчи-
вается
1996
5
[19961 [19961
+
52
+
53
1996'
. S4 .
= 399 + 79 + 15 + 3 = 496 нуля-
ми.
Пример 13. Доказать, что число С^6 делится на 762.
Поскольку 76=22-19, то для делимости на 762 необходимо и дос-
таточно, чтобы делилось на 24 и 192. .
гт ^976 1976! тт ~ “
Имеем С1976 = Найдем, чему равны показатели сте-
пеней аь а2, аз и рь р2, рз, с которыми числа 2 и 19 входят в разло-
жения на простые множители чисел 1976!, 976! й 1000!. Имеем
Г19761 Г19761 Г19761
• ,+
а.
2
210
’976'
L29 /
'1000'
L 29 .
и (Xj - а2 - а3 = 4, т.е. С™6 делится на 24.
Аналогично,
а2 =
. 22 .
[9761 [9761
а3 =
2
'10001 [1000'
2
22
[19761 . [1976'
Pi _
19
= 1969,
= 971,
=994
= 109,
. 192 .
[9761 [9761
Ы+М=5'
_ [10001 . [1000'
Рз -
₽2 =
= 54
19
и Р1-Р2~Рз=2, т.е. С9^б делится и на 192. Следовательно, де-
лится на 762.
19
5, Антье в геометрии
Под целыми точками мы будем понимать точки (х, у) коорди-
натной плоскости с целочисленными координатами х и у. Спраши-
17
вается, как подсчитать число целых точек, лежащих внутри данной
плоской области?
Пример 14. Сколько целых точек расположено на сторонах и
2 1 ” 1П
внутри треугольника, образованного прямыми у=—х- —, х=® и
осью абсцисс?
2 1
Найдём значения функции У=^х~2 ПРИ целых х=^< 2, •••> Ю
(заметим, что у=0 при х=3/4); получим ординаты 1/6, 5/6, 3/2, 13/6,
17/6, 7/2, 25/6, 29/6, 11/2, 37/6. Легко подсчитать, что общее число
целых точек, лежащих в данном треугольнике (учитывая точки на
границе), равно, сумме целых частей этих ординат плюс десять
точек, лежащих на оси абсцисс:
[1/6]+[5/6]+[3/2]+[13/6]+[17/6]+[7/2]+[25/6]+[29/6]+[11/2]+[37/6]+
+10=1+2+2+3+4+4+5+6+10=37.
Таким образом, внутри данного треугольника лежат 37 целых
точек.
Пример 15. Доказать тождество
V
Р.
2?1 Г3?'
Р
2
Р
(р и q-взаимно простые натуральные числа).
Рассмотрим прямоугольник с вершинами 0(0; 0), А(р; 0),
В(р; q), С(0; q). Отметим внутри прямоугольника все целые точки
(х, у): 1<х</?-1, \<y<q-\. Число этих точек равно произведению
(p-l)to-l).
Проведём диагональ ОВ нашего прямоугольника; её
уравнение - у = —х. Так какр и q взаимно просты, а х=1, 2,..., р -1,
Р
то числа —х - не целые, т.е. на диагонали ОВ нет целых точек, и
Р
таким образом в треугольнике, лежащем под диагональю ОВ, будет
~
----------L целых точек. С другой стороны, способом , описанным
в предыдущем примере, получаем, что число этих точек равно
_ р _
Р
сумме
L р .
доказано. ,
Р
, и, значит, нужное тождество
18
Пример 16. Пусть в интервале Q<x<R функция /(х) непре-
рывна и неотрицательна. Доказать, что ^[/(х)] выражает число
Q<x^R
целых точек плоской области: Q<x<R, 0<у</(х).
На любой ординате у0 кривой y = f(x) с абсциссой х лежит
[/(х)] целых точек данной области. Тогда во всей области содер-
жится £ \f (х)] целых точек.
Задачи для самостоятельного решения
1. Решить уравнение: х2-10[х]+9=0.
2. Решить систему уравнений:
х2 + [у] = 10,
у1 + х =13.
3. Решить уравнение [2 sin х] = 2 cos^3x + .
4. Определить число целых неотрицательных решений уравнения:
где а, целое число, большее 1.
Сколько различных чисел встречается среди чисел
I2
1980
22 1 Г З2
1980 ’ 1980
19792! Г19802
1980 ’ 1980
Сколько решений имеет уравнение
х-10-1000={х10}?
Найдите все простые числа, представимые в виде
натуральное число.
8. Найдите все решения уравнения
9. Решить уравнение
х2-8[х]+7=0.
где п -
10. Доказать, что уравнение
19
[х]+[2х]+[4х]+[8х]+[16х]+[32х]=12345
не имеет решений.
11. Для каждого значения heN определить, сколько решений имеет
уравнение х2-[х2]={х2} на отрезке*[1; л].
12. Доказать, что среди членов последовательности {а*}, заданной
соотношениями
(Х1=2, a„+I=[(3/2)a„] при weN,
имеется бесконечно много чётных и бесконечно много нечётных
чисел.
13. Доказать, что для любых неотрицательных чисел х, у справед-
ливо неравенство
[5x]+[5^]>[3x+j/]+[3.y+x].
14. Доказать, что если числа а, Ь, с при каждом значении weN
удовлетворяют равенству [ла]+[лй]=[пс], то хотя бы одно из чисел а,
b является целым.
15. Решить уравнение
[Vi]+[V2]+- • -+[Vx3 -1] = 400
в натуральных числах.
16. Доказать, что
2х-1 1 + Г 2х-1 г п
—--------arctg tg—— п =[х].
2 п к 2 J L J
17. Найти максимум и минимум дроби
2
X
9
18. Доказать равенство Эрмита
г 1 Г 11
2
л-1
п
19. Доказать, что
arcsin(sinx) = (-1)”тг^— + - (-1)” у.
20. Найти [х], если х = 1 + -U+--+ ,
72, л/1000000
21. Исследовать функцию на экстремум
’ ~'У = [х]+№}-
20
22. Какие натуральные числа нельзя представить в виде
+ 4п 4- 1/2], где wgN?
23. Для каждого значения wgN найти наибольшее значение к gZ+,
Г/ .
делится на 2.
при котором число
24. Доказать, что для любого значения п gN имеет место оценка
причём для любого s>0 найдётся число weN, удовлетворяющее
неравенству
{ил/2}<(1 + £)Д2п>/2).
25. Доказать, что число
(5ти)!(5и)!
т[п\(3т + и)!(3л + т)\
является целым при всех значениях т, п е N
26. Доказать, что для любых чисел х>0 и п gN справедливо нера-
венство
L J 1 2 п
27. Доказать, что существует бесконечно много чисел В, для кото-
рых уравнение
х^2
= В
имеет по крайней мере 1980 решений в натуральных числах х, у.
28. Будут ли периодическими последовательности (а„) и (р„), со-
стоящие соответственно из последних целых чисел [(л/10)"] и
[(V2)”]?
29. Решить уравнение 2х24-[х]=х4.
Гтш1
30. Найти lim -—
Л->00 П
31. Решить уравнение х3-[х]=3.
32. Построить множество точек (х;у), задающееся следующими
соотношениями:
а) [х]=Ы;
б) х4хНН>];
в) х- [х]>^-[у].
21
33. Построить графики функций а) у = [х2-5х + 6] 6) у=2[х]2-3[х] + 1
в) y={tgx} г) у = X + [х]
д) у = х + {х} е) y = {cos[x]}
ж) y=[cos{x}] з) У = {2{х}2}
ч 1 и) У~ pi LMJ 34. Решить графически уравнения: а) [х]2-[х] б) cos{x} = в) 2м =1,5. = 2, £ 4’
35. Решить уравнение:
Г8х+191 16(х+1)
7 J 11
36. Доказать тождество:
п ~и+Г 1. .. 1 п+к-\ — W
к т к т* к
б) (п+1Х«+2).. .(2я - 1)2п = 2" • (2п+1)!!
(Через S!! обозначается произведение натуральных чисел от 1 до S
одинаковой чётности с S. Например, 8!!=2-4-6-8; 9!!=1-3-5-7-9).
22
Содержание
Введение 3
1. Антье и ее свойства 4
2. Графики антье 5
3. Антье в уравнениях 8
3.1. Аналитический метод решения уравнений 8
3.2. Графический метод решения уравнений 14
4. Делимость 15
5. Антье в геометрии 17
Задачи для самостоятельного решения 19
23
Авторы будут благодарны за все замечания и пожелания,
которые просим направлять по адресу:
443001, Самара, ул. Молодогвардейская 196.
Издательство СМКНО «Университет Наяновой»
«Пифагор».
Компьютерная верстка:
Зайнуллин И, X, Илюшкин А. В,, Саушкин М. Н.
Формат 60x84 1/16. Бумага писчая, белая. Печать офсетная. Объём 1,2
усл. печ. л.; 1,3 уч.-изд. л. Тираж 300 экз.
Издательство «Пифагор». 443001, Самара, ул. Молодогвардейская 196.