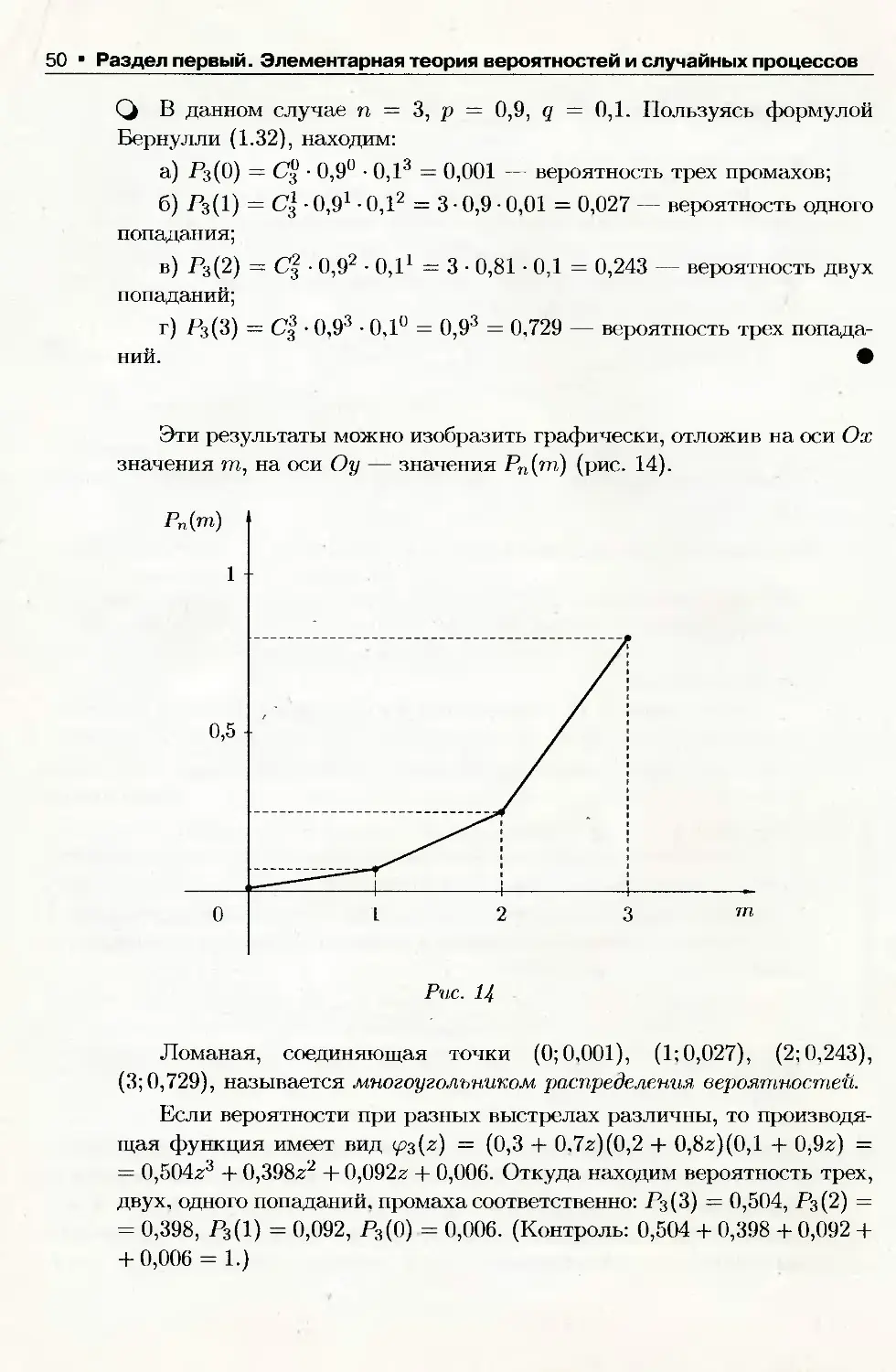
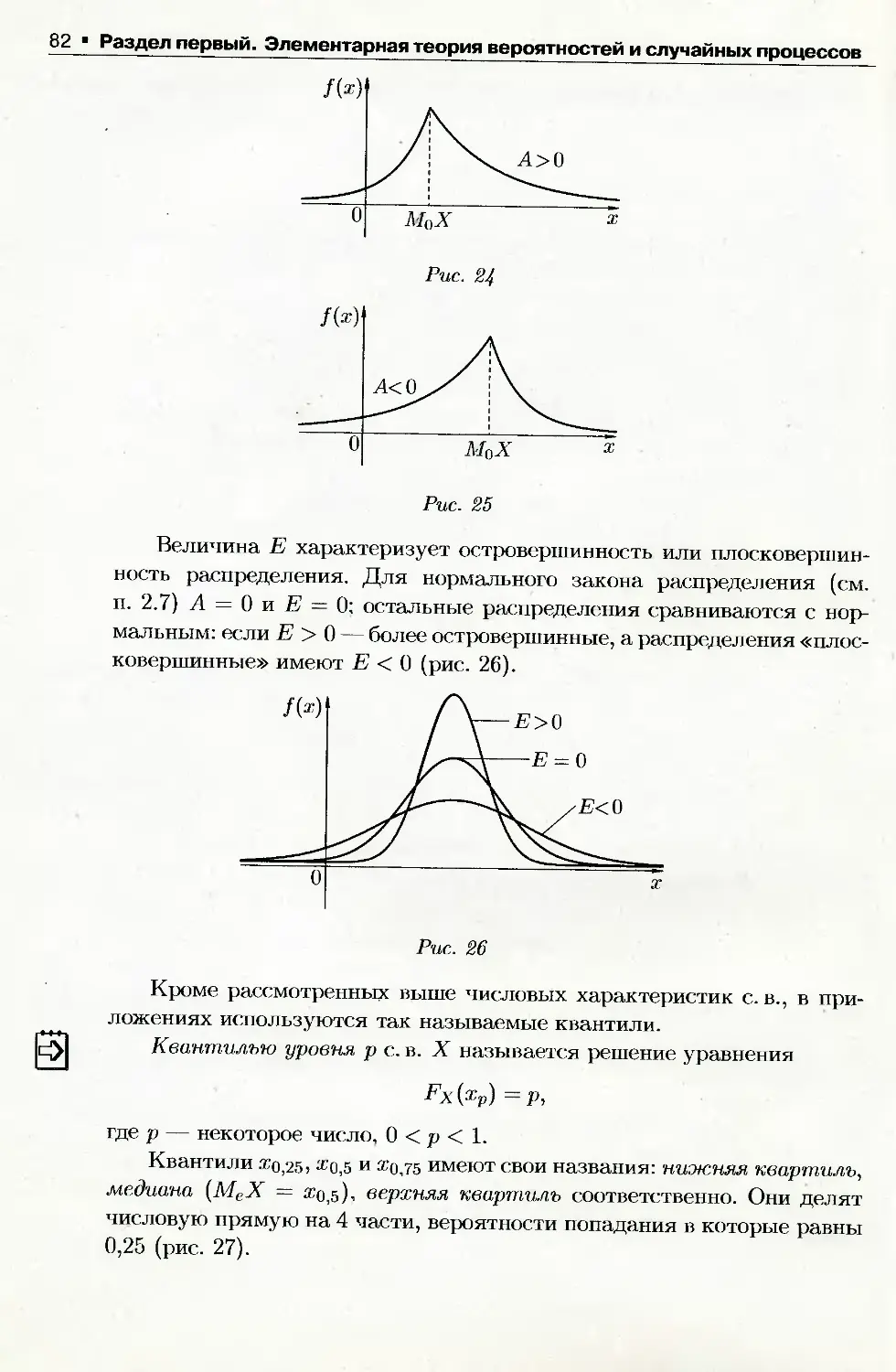
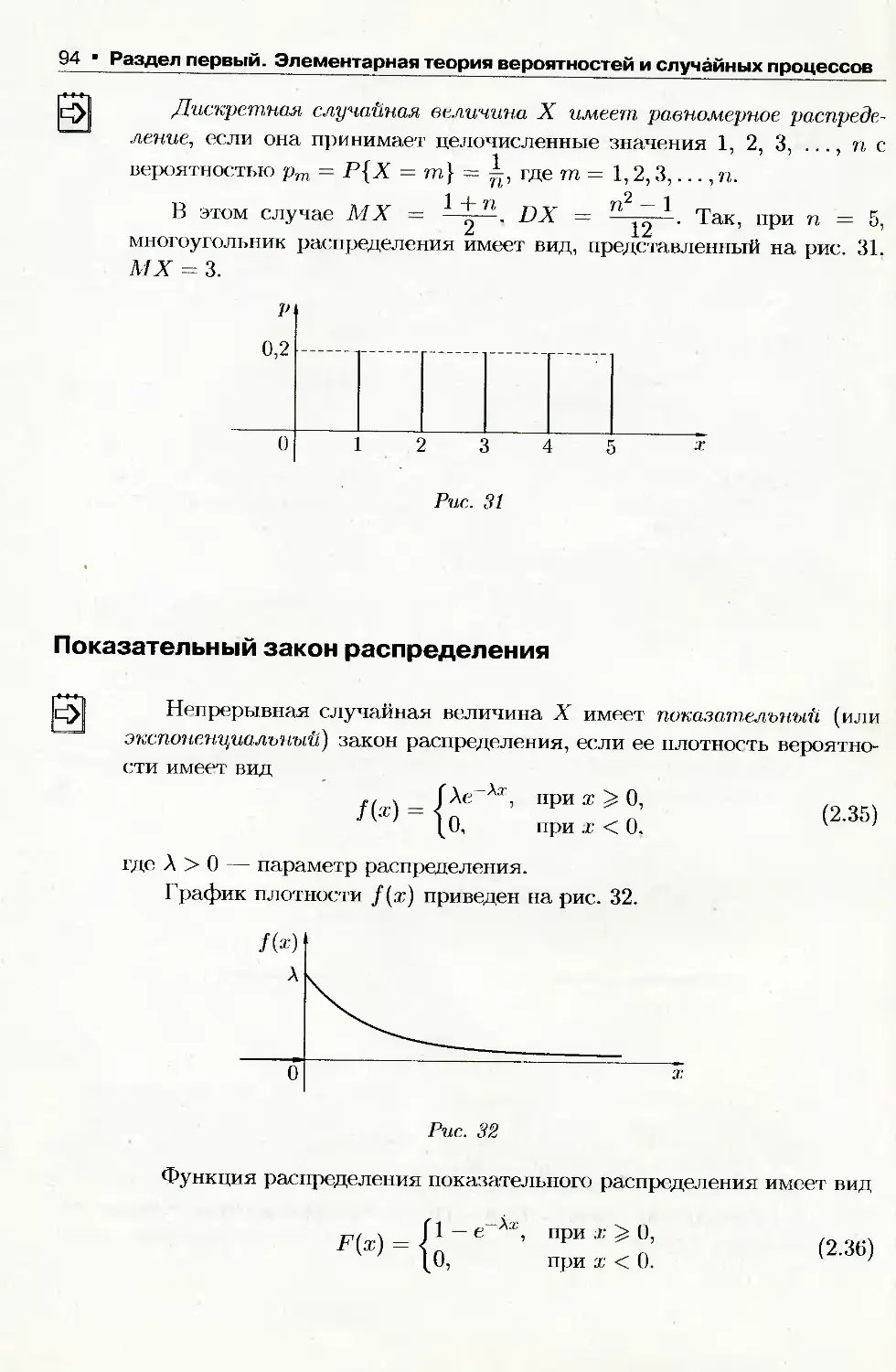
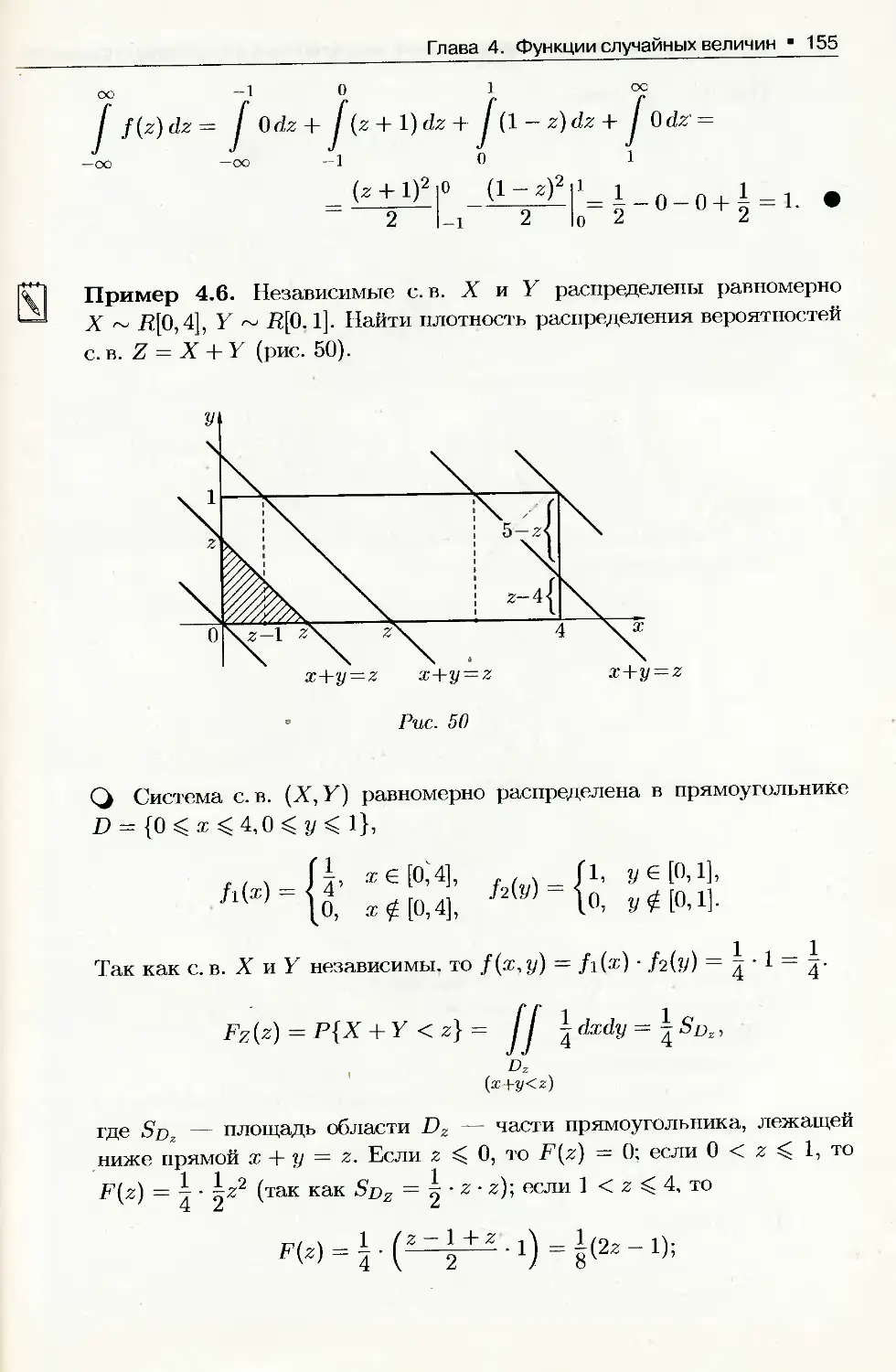
Author: Письменный Д.
Tags: теория вероятностей и математическая статистика здравоохранение медицинские науки теория вероятностей высшая математика математическая статистика
ISBN: 978-5-8112-2966-6
Year: 2008
Text
Дмитрий Письменный
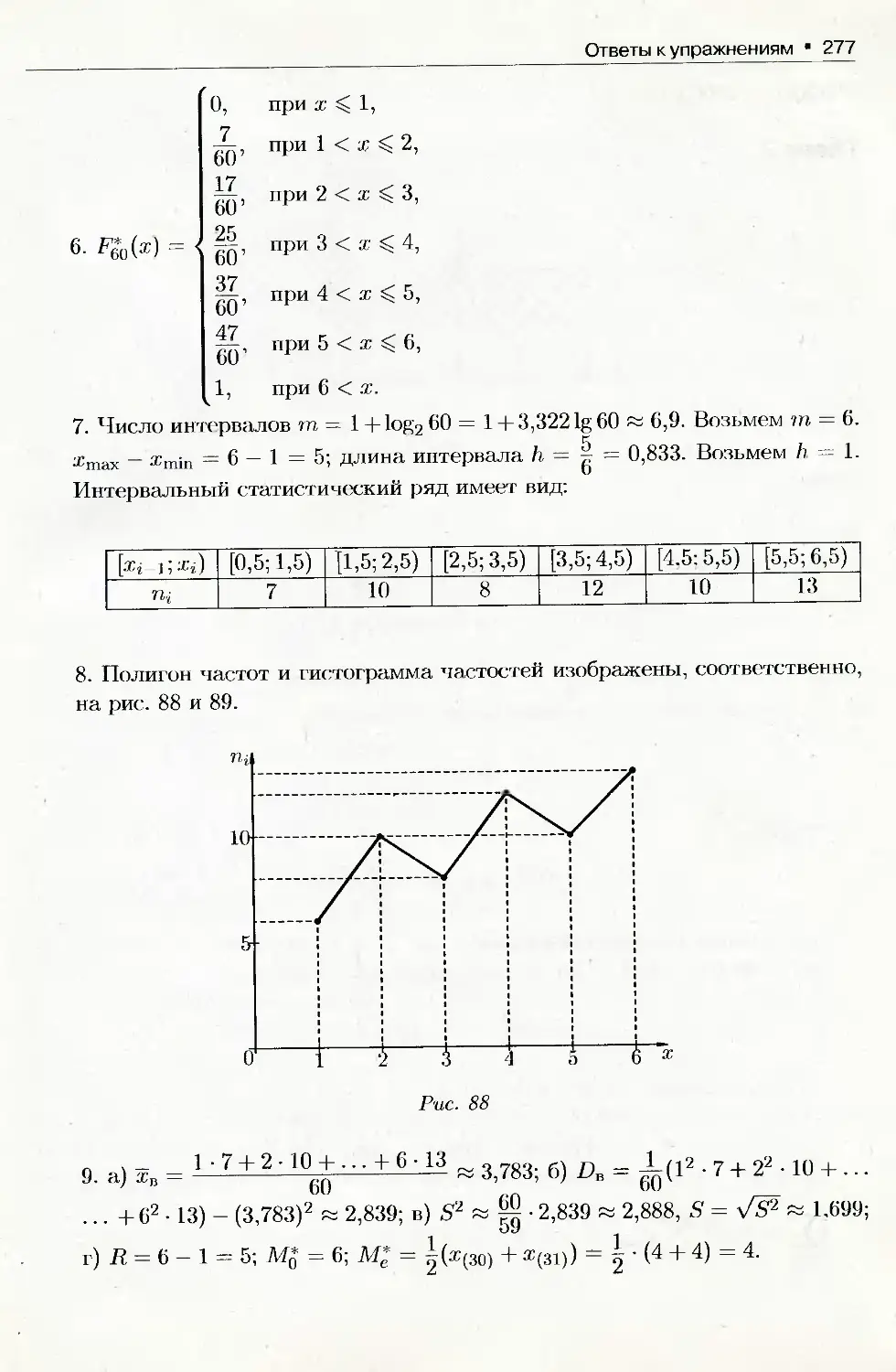
Конспект лекций
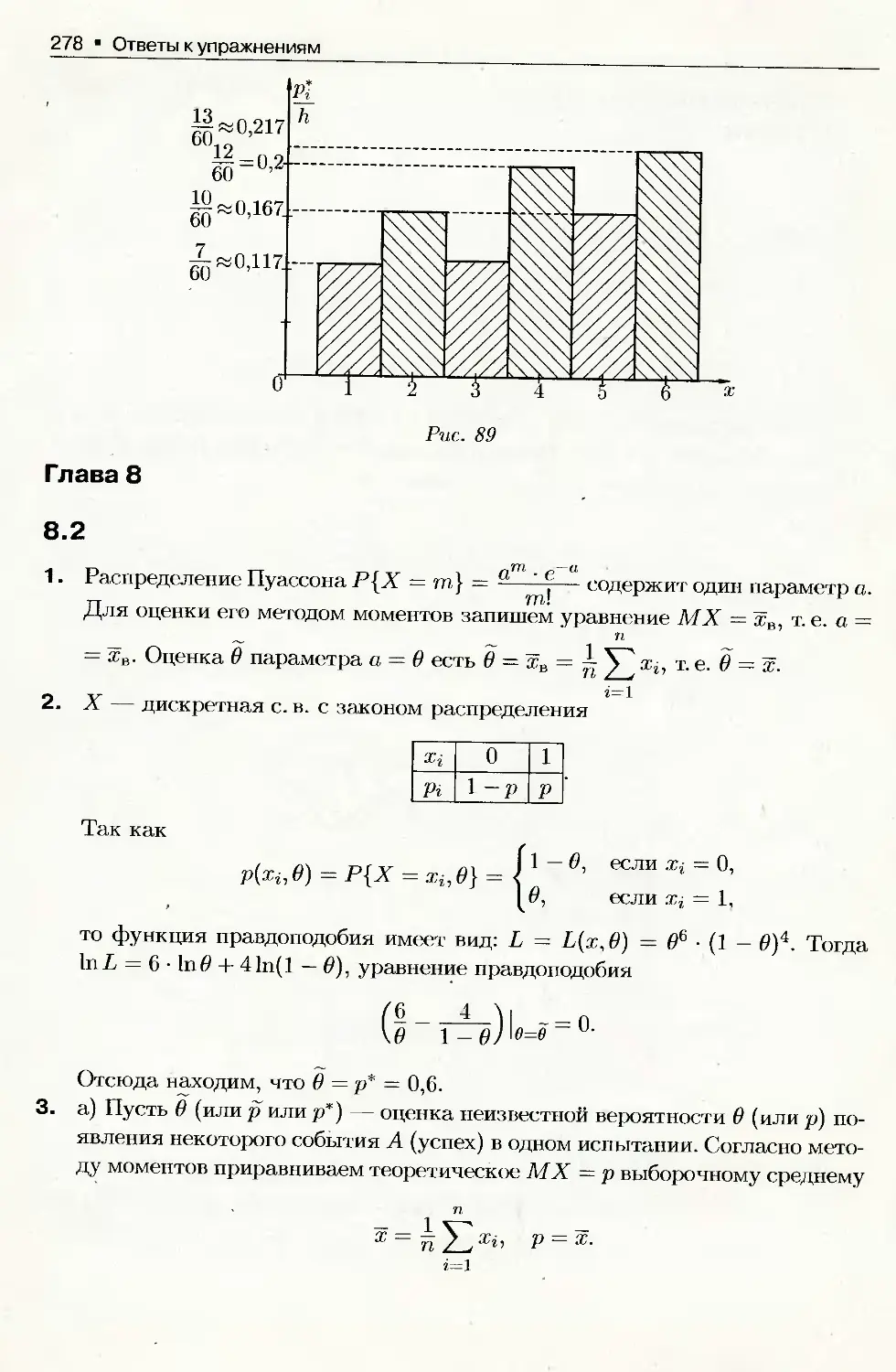
по теории________
вероятностей,
математической
статистике_______
и случайным
процессам
Высшее образование
3-е издание
МОСКВА
АЙРИС ПРЕСС
2008
УДК
ББК
519.2(075.8)
22.17я73-2
П35
Все права защищены.
Никакая часть данной книги не может переиздаваться
или распространяться в любой форме и любыми средствами,
электронными или механическими, включая фотокопирование,
звукозапись, любые запоминающие устройства
и системы поиска информации,
без письменного разрешения правообладателя.
Серийное оформление А. М. Драгового
Письменный, Д. Т.
П35 Конспект лекций по теории вероятностей, математической ста-
тистике и случайным процессам / Дмитрий Письменный. — 3-е
изд. — М.: Айрис-пресс, 2008. — 288 с. — (Высшее образование).
ISBN 978-5-8112-2966-6
Настоящая книга представляет собой курс лекций по теории вероятностей,
случайным процессам и математической статистике.
Первая часть книги содержит основные понятия и теоремы теории вероятно-
стей, такие как случайные события, вероятность, случайные функции, корреля-
ция, условная вероятность, закон больших чисел и предельные теоремы. В от-
дельной главе приведены основные понятия теории случайных процессов (ста-
ционарный процесс, марковский процесс, теорема Винера-Хинчина).
Вторая часть книги посвящена математической статистике, в ней излагают-
ся основы выборочного метода, теории оценок и проверки гипотез. Изложение
теоретического материала сопровождается рассмотрением большого количества
примеров и задач, ведется на доступном, по возможности строгом языке.
Предназначена для студентов экономических и технических вузов.
ББК 22.17я73-2
УДК 519.2(075.8)
ISBN 978-5-8112-2966-6
© ООО «Издательство
«АЙРИС-пресс», 2004
Содержание
Введение ....................................................... 6
J
Раздел первый
Элементарная теория вероятностей и случайных процессов
Глава 1. Случайные события
1.1. Предмет теории вероятностей.................................... 8
1.2. Случайные события, их классификация ........................... 9
1.3. Действия над событиями........................................ 11
1.4. Случайные события. Алгебра событий. (Теоретико-множественная
трактовка) ...................................................... 13
1.5. Свойство статистической устойчивости относительной частоты
события............................................................ 16
1.6. Статистическое определение вероятности........................ 17
1.7. Классическое определение вероятности.......................... 18
1.8. Элементы комбинаторики ....................................... 20
1.9. Примеры вычисления вероятностей .. /.......................... 28
1.10. Геометрическое определение вероятности....................... 31
1.11. Аксиоматическое определение вероятности...................... 34
1.12. Свойства вероятностей...................................... 35
1 13. Конечное вероятностное пространство........................ 36
1.14. Условные вероятности......................................... 37
1.15. Вероятность произведения событий. Независимость событий...... 38
1.16. Вероятность суммы событий.................................. 42
1.17. Формула полной вероятности................................... 14
1.18. Формула Байеса (теорема гипотез)............................. 45
1.19. Независимые испытания. Схема Бернулли........................ 47
1.20. Формула Бернулли............................................. 48
1.21. Предельные теоремы в схеме Бернулли.......................... 51
Глава 2. Случайные величины
2.1. Понятие случайной величины. Закон распределения случайной
величины .......................................................... 60
2.2. Закон распределения декретной случайной величины. Многоугольник
распределения...................................................... 61
2.3. Функция распределения и ее свойства. Функция распределения
дискретной случайной величины...................................... 64
2.4. Плотность распределения и ее свойства......................... 69
2.5. Числовые характеристики случайных величин..................... 73
2.6. Производящая функция.......................................... 84
2.7. Основные законы распределения случайных величин............... 85
4 Содержание
Глава 3. Системы случайных величин
3.1. Понятие о системе случайных величин и законе ее распределения.104
3.2. Функция распределения двумерной случайной 'величины и ее свойства .. 107
3.3. Плотность распределения вероятностей двумерной случайной величины
и ее свойства.....................................................110
3.4. Зависимость и независимость двух случайных величин..........116
3.5. Условные законы распределения............................... 118
3.6. Числовые характеристики двумерной случайной величины.
Математическое ожидание и дисперсия.............................. 122
3.7. Корреляционный момент, коэффициент корреляции................124
3.8. Двумерное нормальное распределение.......................... 131
3.9. Регрессия. Теорема о нормальной корреляции.................. . 135
3.10. Многомерная (n-мерная) случайная величина (общие сведения)....139
3.11. Характеристическая функция и ее свойства.................... 140
3.12. Характеристическая функция нормальной случайной величины......143
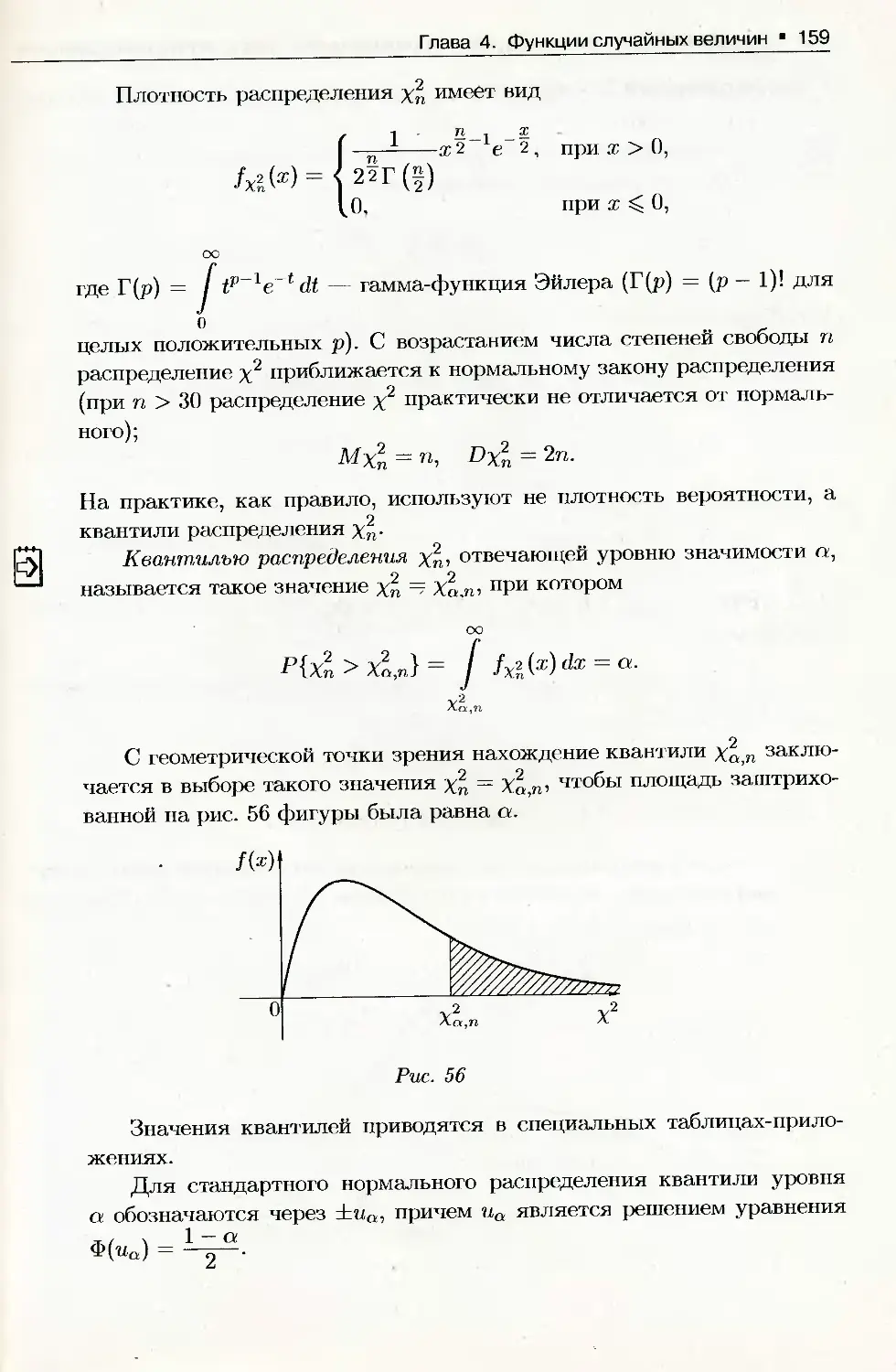
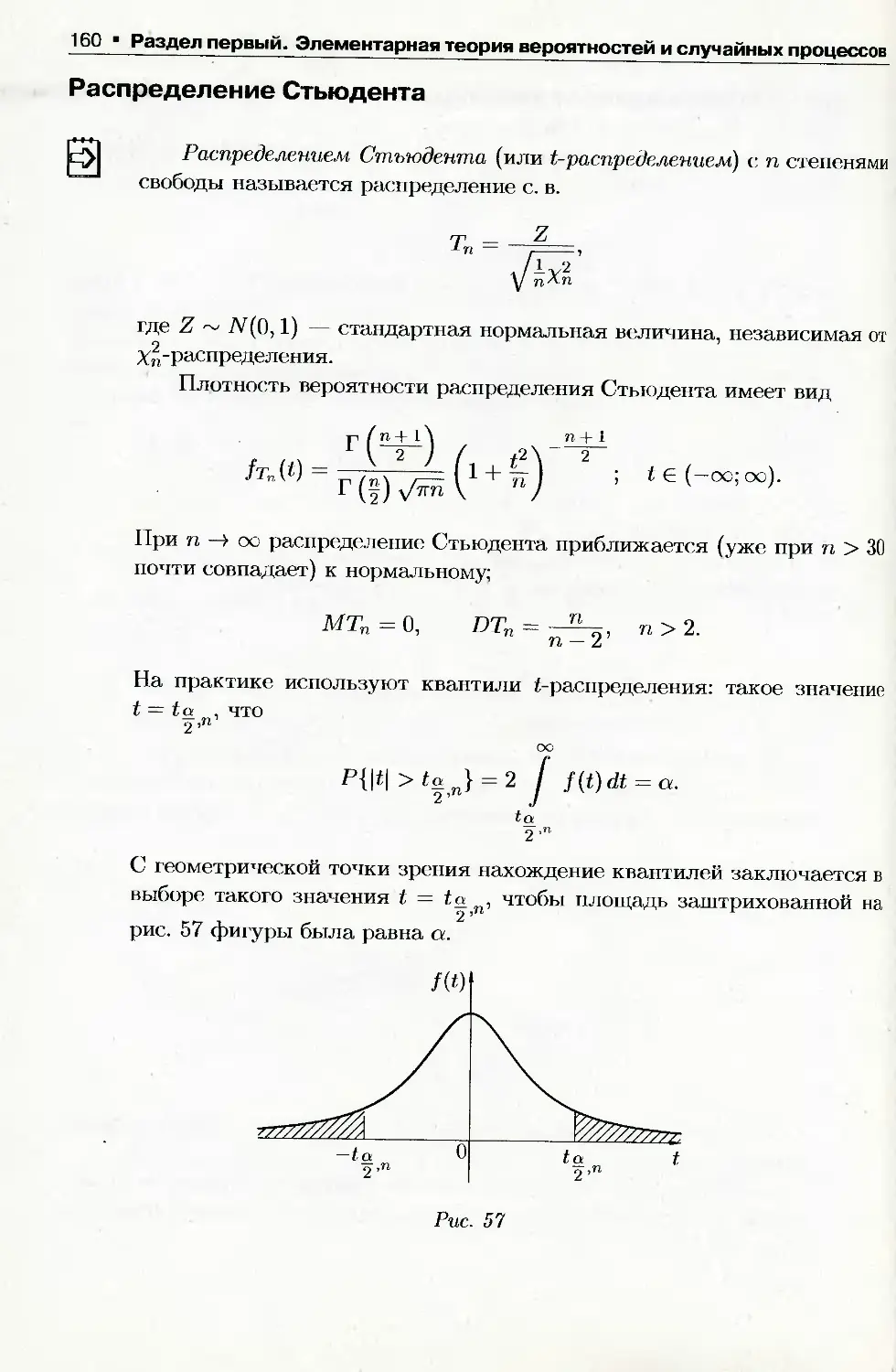
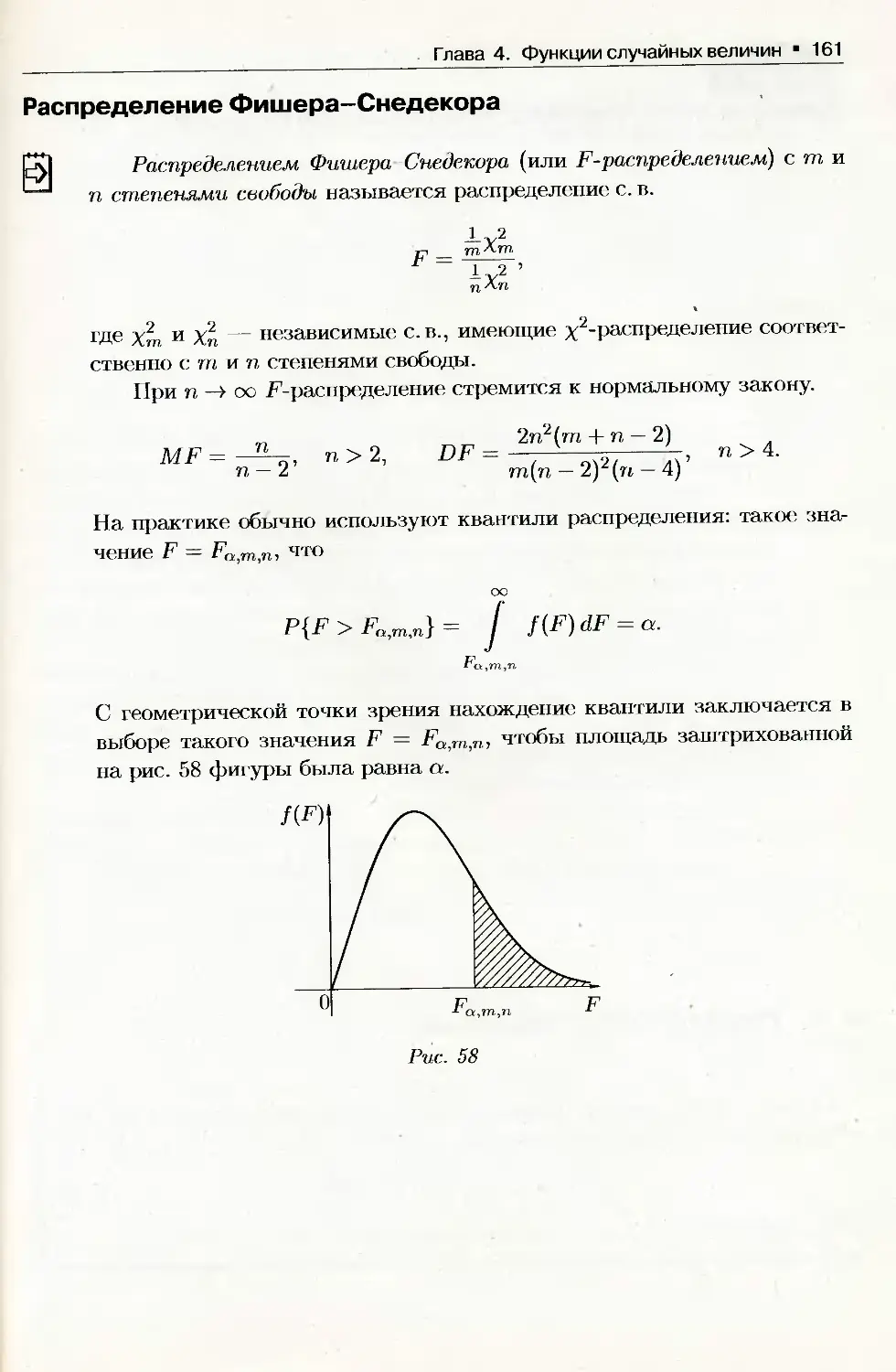
Глава 4. Функции случайных величин
4.1. Функция одного случайного аргумента......................... 145
4.2. Функции двух случайных аргументов........................... 150
4.3. Распределение функций нормальных случайных величин.......... 158
Глава 5. Предельные теоремы теории вероятностей
5.1. Неравенство Чебышева.........................................162
5.2. Теорема Чебышева............................................ 165
5.3. Теорема Бернулли.............................................168
5.4. Центральная предельная теорема...............................170
5.5. Интегральная теорема Муавра-Лапласа......................... 172
Глава 6. Основы теории случайных процессов
6.1. Понятие случайной функции (процесса).........................176
6.2. Классификация случайных процессов.....:......................178
6.3. Основные характеристики случайного процесса ................ 179
6.4. Стационарный случайный процесс в узком и широком смысле......187
6.5. Линейные и нелинейные преобразования случайных процессов.... 190
_6.6. Дифференцирование и интегрирование случайных процессов.......191
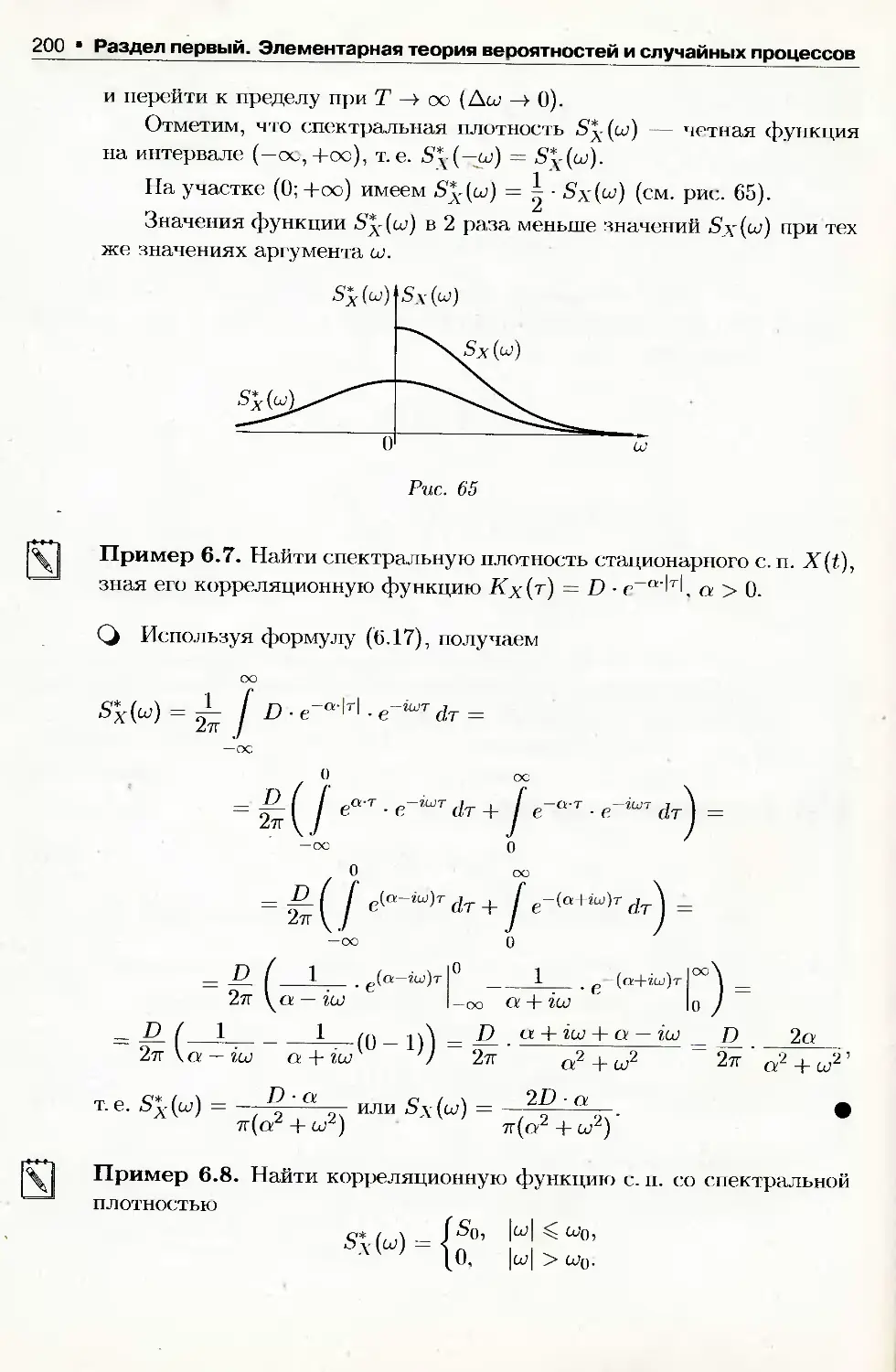
6.7. Спектральное разложение стационарного случайного процесса....194
6.8. Спектральная плотность случайного процесса. Теорема
Винера Хинчина................................................... 197
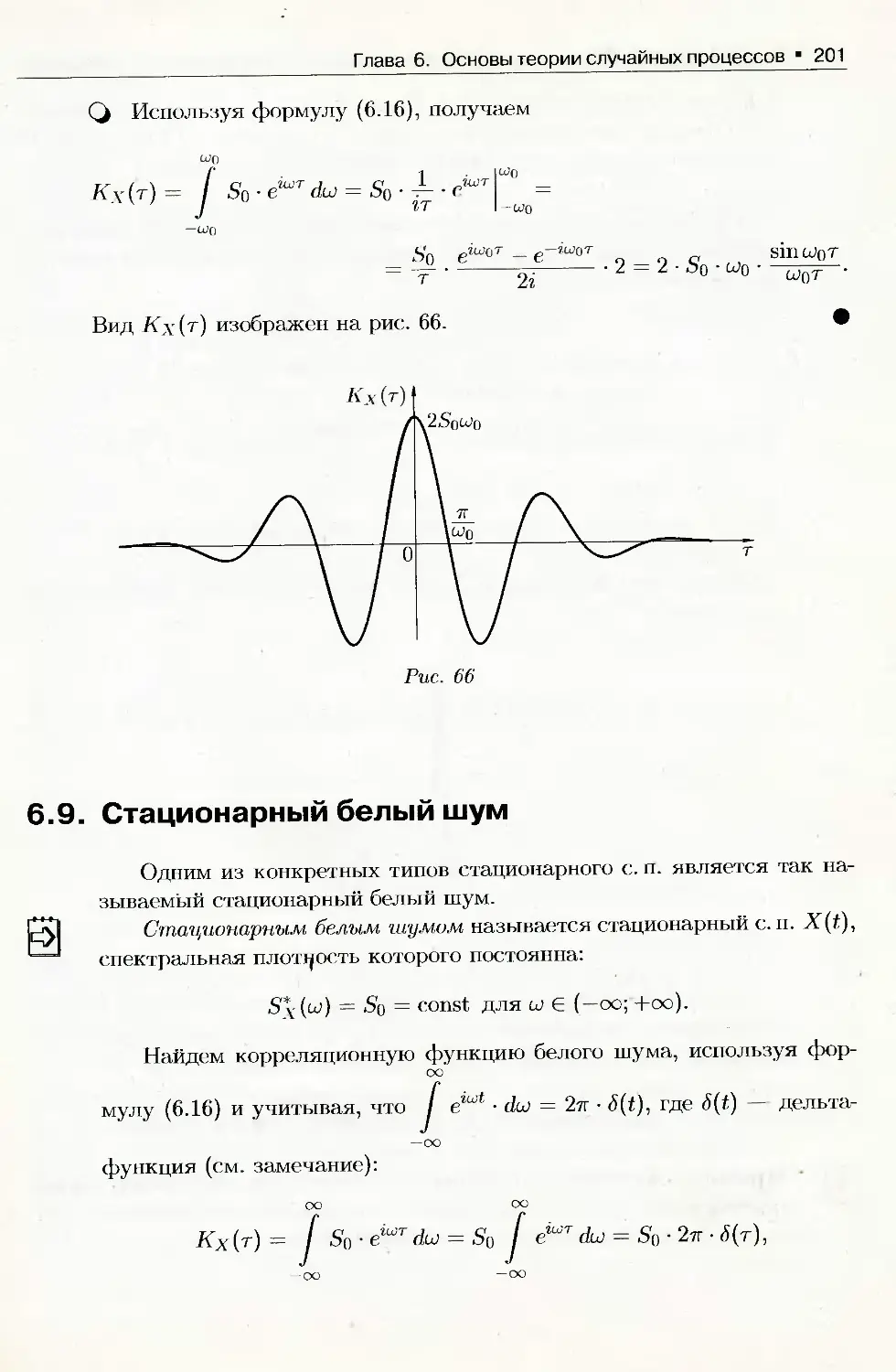
6.9. Стационарный белый шум.......................................201
6.10. Понятие марковского случайного процесса..................... 203
6.11. Дискретный марковский процесс. Цепь Маркова .................205
6.12. Понятие о непрерывном марковском процессе. Уравнения
Колмогорова......................•.................................207
Содержание 5
Раздел второй
Основы математической статистики
Глава 7. Выборки и их характеристики
7.1. Предмет математической статистики............................212
7.2. Генеральная и выборочная совокупности .......................213
7.3. Статистическое распределение выборки. Эмпирическая функция
_ распределения....................................................215
7.4. Графическое изображение статистического распределения........219
7.5. Числовые характеристики статистического распределения........221
Глава 8. Элементы теории оценок и проверки гипотез
8.1. Оценка неизвестных параметров................................225
8.2. Методы нахождения точечных оценок............................231
8.3. Понятие интервального оценивания параметров..................236
8.4. Доверительные интервалы для параметров норйального
распределения.....................................................238
8.5. Проверка статистических гипотез............................ 244
8.6. Проверка гипотез о законе распределения .................... 248
Ответы к упражнениям................................................255
Приложения..........................................................284
Введение
Теория вероятностей, как и другие науки, возникла из потребностей прак-
тики. Ее элементы были «знакомы» еще первобытным людям: шансы убить
зверя у двух охотников, конечно, больше, чем у одного.
Возникновение «математики случайного» относится к середине XVII века
и связано с попыткой создания теории азартных игр, особенно в кости.
Пример одной из ситуаций: два игрока договорились играть в кости до мо-
мента, когда одному из них удастся выиграть три партии; игра была прервана,
когда первый игрок выиграл две партии, а второй — одну; как справедливо
разделить ставку? 3:1 — как показали французские математики Б. Паскаль
(1623-1662) и П. Ферма (1601 1665). И в настоящее время примеры из области
азартных игр широко применяются в теории вероятностей, так как для них
легко строить математические модели.
Первую книгу по теории вероятностей «О расчетах в азартной игре» опу-
бликовал голландский математик X. Гюйгенс (162!) 1695).
Становление теории вероятностей как математической науки связано с
именем Я. Бернулли (1654 1705), который ввел классическое определение со-
бытия и доказал простейший случай закона больших чисел.
В XVIII XIX веках центральное место в развитии теории вероятностей
занимали предельные теоремы. К этому периоду относятся работы А. Муавра
(1667-1754), П. Лапласа (1749-1827), К. Гаусса (1777 1855), С. Пуассона (1781-
1840).
В конце XIX — начале XX века благодаря усилиям П. Л. Чебышева (1821
1894), А. А. Маркова (1856 1922), А. М. Ляпунова (1857 -1918) созданы методы
доказательства предельных теорем для сумм независимых произвольно рас-
пределенных случайных величин.
Дальнейшее развитие теории вероятностей связано с именами русских
математиков Е. Е. Слуцкого (1880 1948), А. Я. Хинчина (1894 1959), А. Н. Кол-
могорова (1903-1987), Б. В. Гнеденко (1912 1995), а также зарубежных уче-
ных Н. Винера (1894 1964), Э. Бореля (1871-1956), В. Феллера (1906 1970),
Р. Фишера (1890 1962) и др. Теория вероятностей получила строгое формаль-
но-логическое основание на базе теории множеств. Следует особо отметить
академика А. Н. Колмогорова, установившего аксиоматику теории вероятно-
стей. Огромное развитие получили «отпочковавшиеся» от теории вероятно-
стей такие отрасли науки, как математическая статистика, теория случайных
процессов, теория массового обслуживания, теория информации и др.
Современная теория вероятностей — строго обоснованная .математиче-
ская наука. Она широко использует достижения других математических наук
(по этому поводу современный вероятностик Дж. Дуб в шутку как-то сказал:
«Всем специалистам по теории вероятностей хорошо известно, что математи-
ка представляет собой часть теории вероятностей»); имеет, в свою очередь,
многочисленные приложения в естественных и гуманитарных науках.
Элементарная
теория_________
вероятностей
и случайных
процессов
Раздел первый
Глава 1
Случайные события
1.1. Предмет теории вероятностей
Любая точная наука изучает не сами явления, протекающие в при-
роде, в обществе, а их математические модели, т. е. описание явлений
при помощи набора строго определенных символов и операций над ни-
ми, При этом для построения математической модели реального явле-
ния во многих случаях достаточно учитывать только основные фак-
торы, закономерности, которые позволяют предвидеть результат опы-
та (наблюдения, эксперимента) по его заданным начальным условиям.
Этим и занимаются большинство математических (и других) дисцип-
лин. Обнаруженные закономерности явления называются детермини-
стическими (определенными). Так, например, формула
S=^gt2
позволяет найти путь, пройденный свободно падающим телом за t се-
кунд от начала движения.
Однако есть множество задач, для решения которых приходится
(надо!) учитывать и случайные факторы, придающие исходу опыта
элемент неопределенности. Например, в вопросах стрельбы по цели не-
возможно без учета случайных факторов ответить на вопрос: сколько
ракет нужно потратить для поражения цели? Невозможно предсказать,
какая сторона выпадет при бросании монеты. Сколько лет проживет
родившийся сегодня ребенок? Сколько времени проработает куплен-
ный нами телевизор? Сколько студентов опоздают на лекцию по тео-
рии вероятностей? И т. д. Такие задачи, исход которых нельзя пред-
сказать с полной уверенностью, требуют изучения не только основ-
ных, главных закономерностей, определяющих явление в общих чер-
тах, по и случайных, второстепенных факторов. Выявленные в таких
задачах (опытах) закономерности называются статистическими (или
Глава 1. Случайные события * 9
вероятностными). Статистические закономерности исследуются мето-
дами специальных математических дисциплин — теории вероятностей
и математической статистики.
Теория вероятностей — математическая наука, изучающая зако-
номерности, присущие массовым случайным явлениям. При этом из-
учаемые явления рассматриваются в абстрактной форме, независимо
от их конкретной природы. То есть теория вероятностей рассматрива-
ет не сами реальные явления, а их упрощенные схемы — математиче-
ские модели. Предметом теории вероятностей являются математи-
ческие модели случайных явлений. При этом под случайным явлением
понимают явление, предсказать исход которого невозможно (при не-
однократном воспроизведении одного и того же опыта оно протекает
каждый раз несколько по-иному). Примеры случайных явлений: вы-
падение герба при подбрасывании монеты, выигрыш по купленному
лотерейному билету, результат измерения какой-либо величины, дли-
тельность работы телевизора и т. п.
Цель теории вероятностей — осуществление прогноза в области
случайных явлений, влияние на ход этих явлений, контроль их, огра-
ничение сферы действия случайности. В настоящее время нет практи-
чески ни одной области науки, в которой в той или иной степени не
применялись бы вероятностные методы.
1.2. Случайные события, их классификация
Сначала определим понятие «случайное событие» исходя из его ин-
туитивного, наглядного понимания. Пусть проводится некоторый опыт
(эксперимент, наблюдение, испытание), исход которого предсказать за-
ранее нельзя. Такие эксперименты в теории вероятностей называют
случайными. При этом рассматриваются только такие эксперименты,
которые можно повторять, хотя бы теоретически, при неизменном ком-
плексе условий произвольное число раз.
Случайным событием (или просто: событием) называется любой
исход опыта, который может произойти или не произойти.
События обозначаются, как правило, заглавными буквами латин-
ского алфавита: А, В, С, ... .
Пример 1.1. Опыт: бросание игральной кости; событие А — выпа-
дение 5 очков, событие В выпадение четного числа очков, событие
С — выпадение 7 очков, событие D — выпадение целого числа очков,
событие Е — выпадение не менее 3-х очков, ....
10 Раздел первый. Элементарная теория вероятностей и случайных процессов
О
Непосредственные исходы опыта называются элементарными со-
бытиями и обозначаются через w. Элементарные события (их назы-
вают также «элементами», «точками», «случаями») рассматриваются
как неразложимые и взаимоисключающие исходы гщ, W2, • • - этого
опыта.
Множество всех элементарных событий называется пространст-
вом элементарных событий или пространством, исходов, обозначает-
ся через Q.
Рассмотрим пример 1.1. Здесь б элементарных событий wj, w?, W3,
W4, W5, we- Событие Wi означает, что в результате бросания кости вы-
пало i очков, i — 1,2.3,4,5.6. Пространство элементарных событий
таково: Q = {wi, W2, w%, W4,w&,wg } или Q = {1,2,3,4,5,6}.
Событие называется достоверным, если они обязательно наступит
в результате данного опыта, обозначается через Q.
Событие называется невозможным, если оно заведомо не произой-
дет в результате проведения опыта, обозначается через 0.
В примере 1.1 события Аи В — случайные, событие С — невоз-
можное, событие D — достоверное.
Два события называются несовместными, если появление одного
из них исключает появление другого события в одном и том же опыте,
т. е. не смогут произойти вместе в одном опыте. В противном случае
события называются совместными.
Так, в примере 1.1 события А и В - несовместные, .1 и Е со-
вместные.
События Ai, А2, , А„ называются попарно-несовместными, если
любые два из них несовместны.
Несколько событий образуют полную группу, гели они попарно не-
совместны и в результате каждого опыта происходит одно и только
одно из них.
В примере 1.1 события гщ wg образуют полную группу, Wj w5
нет.
Несколько событий в данном опыте называются равновозможны-
ми, если ни одно из них не является объективно более возможным, чем
другие, т. е. все события имеют равные «шансы».
В примере 1.1 элементарные события , и’2, W3, mi, w§, wg равно-
возможны. Выпадение герба (Л) или решки (В) при бросании монеты -
равновозможные события, если, конечно, монета имеет симметричную
форму, не погнута, ....
Глава 1. Случайные события "11
1.3. Действия над событиями
Ф
Введем основные операции над событиями; они полностью соответ-
ствуют основным операциям над множествами.
Суммой событий А и В называется событие С = А + В. состоящее
в наступлении хотя бы одного из них (т. е. или А, или В, или А и В
вместе).
Произведением, событий А и В называется событие С = А • В,
состоящее в совместном наступлении этих событий (т. е. и А и В одно-
временно) .
Разностью событий А и В называется событие С = А — В, про-
исходящее тогда и только тогда, когда происходит событие А, ио не
происходит событие В.
Противоположным событию А называется событие А, которое
происходит тогда и только тогда, когда не происходит событие А (т. е.
А означает, что событие А не наступило).
Событие А влечет событие В (или А является частным случаем
В), если из того, что происходит событие А, следует, что происходит
событие В; записывают АС В.
Если А С В и В С А, то события А и В называются равными-,
записывают А = В.
Так, в примере 1.1 (п. 1.2) В = {2,4,6}, Е = {3,4,5.6}. А = {5},
D = {1,2,3,4,5,6}. Тогда: В + Е = {2,3,4,5,6}, B E = {4,6},
В-Е = {2}, А = {1,2,3,4,6}, В С D, D = Q = {1,2,3,4,5.6}.
События и действия над ними можно наглядно иллюстрировать с
помощью диаграмм Эйлера-Венна: достоверное событие Q изобража-
ется прямоугольником; элементарные случайные события — точками
црямоугольника; случайное событие — областью внутри него.
Действия над событиями можно изобразить так, как показано на
рис. 15.
Операции над событиями обладают следующими свойствами:
А + В — В + А, А - В = В А (переместительное);
(А + В) С = А • С + В • С, А В + С = (А -Г С) (В + С) (распреде-
лительное);
• (А + В) + С = А + (В + С), (А В) С = А • (В • С) (сочетательное);
. А + А = А, А-А = А:
А + О = Q, А • J2 = А;
. А + А = Q, А • А = 0;
0 = Q, Q - 0, А = А;
• А —В = А В; _____
• А + В = А- ВиА-В = А + В — законы де Моргана.
12 Раздел первый. Элементарная теория вероятностей и случайных процессов
Рис. 4
Рис. 5
В их справедливости можно убедиться с помощью диаграмм Эйле-
ра Венна.
Пример 1.2. Доказать формулу А + В = А + АВ.
Q Используя некоторые из выше приведенных правил, получаем:
А+В = (А+В)-П = А-П+В-П = A-Q + B(A+A) = A-Q + (A + A)-B =
= А-П + А-В + А-В = (Q + B)- А + А-В = П-А + А- В = А + А-В.
Таким образом, сумму любых двух событий .можно представить в
виде суммы двух несовместных событий.
Геометрическое доказательство представлено на рис. 6. •
А + В
Рис. 6
А+АВ
Глава 1. Случайные события • 13
Упражнения
1. Доказать формулы: 1) В = А-В+А-В; 2) (А+С')-(В+С) = А-В+С;
3) А + В = А В.
2. Пусть А, В и С — три произвольных события. Выразить через них
следующие события: а) произошли все три события; б) произошло
только С; в) произошло хотя бы одно из событий; г) ни одного
события не произошло; д) произошли А и В. но С не произошло;
е) произошло одно из этих событий; ж) произошло не более двух
событий.
3. Релейная схема (рис. 7) состоит из 6 элементов. Пусть события Аг
(г = 1,6) состоят в том, что соответствующие элементы работают
безотказно в течение времени Т. Выразить через At событие, состо-
ящее в том, что схема за время Т работает безотказно.
Рис. 7
1.4. Случайные события. Алгебра событий.
(Теоретико-множественная трактовка)
Определим теперь основные понятия теории вероятностей, следуя
теоретико-множественному подходу, разработанному академиком Кол-
могоровым А. Н. в 1933 году.
Пусть производится некоторый опыт со случайным исходом.
|Дм Множество Q = {сД всех возможных взаимоисключающих исхо-
дов данного опыта называется пространством элементарных событий
(коротко: ПЭС), а сами исходы щ — элементарными событиями (или
«элементами», «точками»).
14 Раздел первый. Элементарная теория вероятностей и случайных процессов
Случайным событием, А (или просто событием Л) называется лю-
бое подмножество множества И, если Q конечно или счетно (т. е. эле-
менты этого множества можно пронумеровать с помощью множества
натуральных чисел): А С Q.
Элементарные события, входящие в подмножество А пространства
Q, называются благоприятствующими событию А.
Множество Q называется достоверным событием. Ему благопри-
ятствует любое элементарное событие: в результате опыта оно обяза-
тельно произойдет.
Пустое множество 0 называется невозможным событием; в {резуль-
тате опыта оно произойти не может.
Пример 1.3. Опыт: один раз бросают игральную кость. В этом случае
ПЭС таково: Q = {1,2,3,4, 5.6} или Q = {?щ. w?, • • - н?б }, где 'иу г-=1эле-
ментарное событие, состоящее в выпадении грани с 'сочками (i = 1,6).
В данном случае Q конечно. Примером события А является, например,
выпадение нечетного числа очков; очевидно, что А = фщ, W3, W5}; со-
бытию А благоприятствуют элементарные события wj, W3, W5. Однако
если нас интересует только факт выпадения четного числа очков, то
ПЭС можно построить иначе: Q = {сс|, где сщ — выпадение четного
числа очков, ш-2 — нечетного.
Пример 1.4. Опыт: стрельба по цели до первого попадания. Тогда
о Г П НП ННП НННП 1 гт
= iw?1 w3 ’—W4—•••{’ где 11 означает попадание в цель,
Н — непопадание. Исходов у этого опыта бесконечно (теоретически);
Q счетно.
Пример 1.5. Опыт: наблюдение за временем безотказной работы не-
которого агрегата. В этом случае в качестве результата может появить-
ся любое число 1^0; время t меняется непрерывно; ПЭС таково:
О, — {t, 0^£<ос}. Исходов у этого опыта бесконечно, Q несчетно
(континуально).
Над событиями можно проводить все операции, выполнимые для
множеств.
Сумма, (или объединение) двух событий A G И и В Е И (обознача-
ется А + В или ЛиВ) это множество, которое содержит элементы,
принадлежащие хотя бы одному из событий Л и В.
Произведение двух событий Л G И и В Е S2 (обозначается АВ или
Л Г) В) — это множество, которое содержит элементы, общие для собы-
тий Л и В.
Глава 1. Случайные события *15
>
Разность событий A Е Q и В Е Q (обозначается А —В или А\В) -
это множество, которое содержит элементы события А. не принадле-
жащие событию В.
Противоположное событию А Е Q событие А = Q\A. ( А называют
также дополнением множества А.)
Событие А влечет событие В (обозначается А С В), если каждый
элемент события А содержится в В.
По определению: 0 С А для любого А.
События А и В называются несовместными, если их произведение
есть невозможное событие, т. е. А • В = 0.
Несколько событий Ai, А2,..., Ап образуют полную группу несов-
местных событий, если их сумма представляет все ПЭС, а сами события
п
несовместны, т. е. ^2 А , = Q и А, • Aj = 0 (г j).
г=1
Полную группу образуют, например, события А и А (А + А = Q,
А • А = 0),
В случае несчетного пространства Q в качестве событий рассмат-
риваются не все подмножества П. а лишь некоторые классы этих под-
множеств, называемые алгебрами и п-алгебрами множеств.
Класс S подмножеств пространства Q называется алгеброй мно-
жеств (событий), если:
1. 0 Е S, Q Е S:
2. из А Е S' вытекает, что А Е S;
3. из А Е S. В Е S вытекает, что А + В Е S, А • В Е S'.
Заметим, что в условии 3 достаточно требовать либо А + В Е S,
либо АВ Е S, так как А + В = А В, А В = А + В.
Алгебру событий образует, например, система подмножеств S =
= {0. Q}. Действительно, в результате применения любой из вышепри-
веденных операций к любым двум элементам класса S снова получа-
ется элемент данного класса: 0 + Q = Q, 0 • Q = 0, 0 = П, Q = 0.
При расширении операций сложения и умножения на случай счет-
ного множества алгебра множеств S называется сг-алгеброй,
оо оо
если из Ап Е S, п = 1,2,3,..., следует ^2 At G S, П А. Е S (доста-
71=1 П=1
ОО оо
точно требовать либо J2 A„ Е S, либо [ J Ап Е S').
п~1 п=1
Множество всех подмножеств множества Q, если оно конечно или
счетно, образует алгебру.
16 Раздел первый. Элементарная теория вероятностей и случайных процессов
1.5. Свойство статистической устойчивости
относительной частоты события
Пусть в п повторяющихся опытах некоторое событие А наступило
пд раз.
Число пд называется частотой события А, а отношение
= (1.1)
называется относительной частотой (или частостью) события А в
рассматриваемой серии опытов.
Относительная частота события обладает следующими свойствами:
1. Частость любого события заключена между нулем и единицей, т. е.
О Р*(А) 1.
2. Частость невозможного события равна нулю, т. е.
Р*(0) = 0.
3. Частость достоверного события равна 1, т. е.
P*(ty = 1.
4. Частость суммы двух несовместных событий равна сумме часто-
стей этих событий, т. е. если АВ = 0, то
Р*(А + В) = Р*(А) + Р*(В).
□ Свойства очевидны, так как 0 пд п для любого события А; для
невозможного события пд = 0; для достоверного события пд = п; если
события А и В несовместны (АВ = 0), то пд+в = пд + пв, следова-
тельно, Р*(А + В) = = ПА-+ ПВ = ^ + ?£ = Р*(А)+Р*(В).
Частость обладает еще одним фундаментальным свойством, назы-
ваемым свойством статистической устойчивости: с увеличением чи-
сла опытов (т. е. п) она принимает значения, близкие к некоторому по-
стоянному числу (говорят: «частость стабилизируется, приближаясь
к некоторому числу», «частость колеблется около некоторого числа»,
или «ее значения группируются около некоторого числа»).
Так, например, в опыте — бросание монеты (однородной, симмет-
ричной, ...) — относительная частота появления герба при 4040 броса-
ниях (Ж. Бюффон) оказалась равной 0,5069 = а в опыте с 12000
Глава 1. Случайные события • 17
и 24000 бросаниями (К. Пирсон) она оказалась равной соответствен-
но 0,5015 = и 0-5005 = , т е частность приближается к
числу = 0,500.... А частость рождения мальчика, как показывают
наблюдения, колеблется около числа 0,515.
Отметим, что теория вероятностей изучает только те массовые слу-
чайные явления с неопределенным исходом, для которых предполага-
ется наличие устойчивости относительной частоты.
1.6. Статистическое определение вероятности
Для математического изучения случайного события необходимо
ввести какую-либо количественную оценку события. Понятно, что одни
события имеют больше шансов («более вероятны») наступить, чем дру-
гие. Такой оценкой является вероятность события, т. е. число, выра-
жающее степень возможности его появления в рассматриваемом опыте.
Математических определений вероятности существует несколько, все
они дополняют и обобщают друг друга.
Рассмотрим опыт, который можно повторять любое число раз (го-
ворят: «проводятся повторные испытания»), в котором наблюдается
некоторое событие А.
рм Статистической вероятностью события А называется число,
около которого колеблется относительная частота события А при до-
статочно большом числе испытаний (опытов).
Вероятность события А обозначается символом Р(А). Согласно
данному определению
Р(А) « Р*(А) = (1.2)
Математическим обоснованием близости относительной частоты Р* (А)
и вероятности Р(А) некоторого события А служит теорема Я. Бернулли
(см. и. 5.3).
Вероятности Р(А) приписываются свойства 1^4 относительной ча-
стоты:
1. Статистическая вероятность любого события заключена между ну-
лем и единицей, т. е.
0 Р(А) С 1.
2. Статистическая вероятность невозможного события равна нулю,
т. е.
Р(0) = 0.
18 Раздел первый. Элементарная теория вероятностей и случайных процессов
3. Статистическая вероятность достоверного события равна единице,
т. е.
P(Q) = 1.
4. Статистическая вероятность суммы несовместных событий равна
сумме вероятностей этих событий, т. е. если А • В = 0, то
Р(Л + В) = Р(Л)+Р(В).
Статистический способ определения вероятности, опирающийся на
реальный опыт, достаточно полно выявляет содержание этого поня-
тия. Некоторые ученые (Р. Мизес и другие) считают, что эмпирическое
определение вероятности (т. е. р — пт —) следует считать основным
п—>оо
определением вероятности.
Недостатком статистического определения является неоднознач-
ность статистической вероятности; так в примере с бросанием монеты
(п. 1.5) в качестве вероятности можно принять не только число 0,5, но
и 0,49 или 0,51 и т. д. Для надежного определения вероятности нуж-
но проделать большое число испытаний (опытов), что не всегда просто
(или дешево).
1.7. Классическое определение вероятности
Существует простой способ определения вероятности события,
основанный на равновозможности любого из конечного числа исходов
опыта. Пусть проводится опыт с п исходами, которые можно предста-
вить в виде полной группы несовместных равновозможных событий.
Такие исходы называются случаям,и, шансами, элементарными собы-
тиями, опыт — классическим. Про такой опыт говорят, что он сводится
к схеме случаев или схеме урн (ибо вероятностную задачу для такого
опыта можно заменить эквивалентной ей задачей с урнами, содержа-
щими шары разных цветов).
Случай ш, который приводит к наступлению события А, называет-
ся благоприятным (или — благоприятствующим) ему, т. е. случай w
влечет событие A: w С А.
Вероятностью события А называется отношение числа т случаев,
благоприятствующих этому событию, к общему числу п случаев, т. е.
Р(А) = (1.3)
Наряду с обозначением Р(А) для вероятности события А используется
обозначение р, т. е. р = Р(А).
Глава 1. Случайные события *19
Из классического определения вероятности (1.3) вытекают следу-
ющие свойства:
1. Вероятность любого события заключена между нулем и единицей,
т. е.
О Р(А) 1.
2. Вероятность невозможного события равна нулю. т. е.
Р(0) = О.
3. Вероятность достоверного с< >бытия равна единице, т. е.
Р(И) = 1.
4. Вероятность суммы несовместных событий равна сумме вероятно-
стей этих событий, т. е. если А В = 0, то
Р(Л + В) = Р(А) + Р(В).
Они проверяются так же, как и для относительной частоты (п. 1.5).
В настоящее время свойства вероятности определяются в виде аксиом
(см. п. 1.11).
Пример 1.6. В урне (емкости) находятся 12 белых и 8 черных шаров.
Какова вероятность того, что наудачу вынутый шар будет белым?
О Пусть А — событие, состоящее в том, что вынут белый шар. Яс-
но, что п = 12 + 8 = 20 — число всех равповозможных случаев (исхо-
дов опыта). Число случаев, благоприятствующих событию А, равно 12,
12
т. е. т = 12. Следовательно, по формуле (1.3) имеем: Р(Л) = т. е.
Р(А) = 0,6. “ •
Упражнения
1. Найти вероятность того, что в наудачу написанном двузначном чи-
сле цифры разные.
2. Набирая номер телефона, абонент забыл 2 последние цифры и на-
брал их наугад. Найти вероятность того, что набраны нужные ци-
фры.
20 Раздел первый. Элементарная теория вероятностей и случайных процессов
1.8. Элементы комбинаторики
Согласно классическому определению подсчет вероятности собы-
тия А сводится к подсчету числа благоприятствующих ему исходов.
Делают это обычно комбинаторными методами.
Комбинаторика — раздел математики, в котором изучаются за-
дачи выбора элементов из заданного множества и расположения их в
группы по заданным правилам, в частности задачи о подсчете числа
комбинаций (выборок), получаемых из элементов заданного конечно-
го множества. В каждой из них требуется подсчитать число возмож-
ных вариантов осуществления некоторого действия, ответить на вопрос
«сколькими способами?».
Многие комбинаторные задачи могут быть решены с помощью сле-
дующих двух важных правил, называемых соответственно правилами
умножения и сложения.
Правило умножения (основной принцип): если из некоторого ко-
нечного множества первый объект (элемент х) можно выбрать щ спо-
собами и после каждого такого выбора второй объект (элемент у) мож-
но выбрать «2 способами, то оба объекта (х и у) в указанном порядке
можно выбрать п\ п? способами.
Этот принцип, очевидно, распространяется на случай трех и более
объектов.
Пример 1.7. Сколько трехзначных чисел можно составить из цифр 1.
2, 3. 4, 5, если: а) цифры не повторяются? б) цифры могут повторяться?
О Имеется 5 различных способов выбора цифры для первого места
(слева в трехзначном числе). После того как первое место занято, на-
пример, цифрой 2, осталось четыре цифры для заполнения второго
места. Для заполнения третьего места остается выбор из трех цифр.
Следовательно, согласно правилу умножения имеется 5 • 4 3 = 60 спо-
собов расстановки цифр. т. е. искомое число трехзначных чисел есть
60. (Вот некоторые из этих чисел: 243, 541, 514, 132, ....) Понятно, что
если цифры могут повторяться, то трехзначных чисел 5-5-5 = 125.
(Вот некоторые из них: 255, 333, 414, 111, ...) •
Правило суммы. Если некоторый объект х можно выбрать П| спосо-
бами, а объект у можно выбрать ?г2 способами, причем первые и вторые
способы не пересекаются, то любой из указанных объектов (ж или у),
можно выбрать щ + п? способами.
Это правило распространяется на любое конечное число объектов.
Глава 1. Случайные события 21
Пример 1.8. В студенческой группе 14 девушек и 6 юношей. Сколь-
кими способами можно выбрать, для выполнения различных заданий,
двух студентов одного пола?
Q По правилу умножения двух девушек можно выбрать 14 13 = 182
способами, а двух юношей — 6 • 5 = 30 способами. Следует выбрать
двух студентов одного пола: двух студенток или двух юношей. Соглас-
но правилу сложения таких способов выбора будет 182 + 30 = 212. •
Решение вероятностных (и не только их) задач часто облегчается,
если использовать комбинаторные формулы. Каждая из них опреде-
ляет число всевозможных исходов в некотором опыте (эксперименте),
состоящем в выборе наудачу т элементов из п различных элементов
рассматриваемого множества.
Существуют две схемы выбора т элементов (0 < т С п) из исход-
ного множества: беи возвращения (без повторений) и с возвращением (с
повторением). В первом случае выбранные элементы не возвращаются
обратно; можно отобрать сразу все т элементов или последовательно
отбирать их по одному. Во второй схеме выбор осуществляется поэле-
ментно с обязательным возвращением отобранного элемента на каждом
шаге.
Схема выбора без возвращений
О
Пусть дано множество, состоящее из п различных элементов.
Размещением из п элементов по т элементов (0 < т п) назы-
вается любое упорядоченное подмножество данного множества, содер-
жащее т элементов.
Из определения вытекает, что размещения — это выборки (комби-
нации), состоящие из т элементов, которые отличаются друг от друга
либо составом элементов, либо порядком их расположения.
Число размещений из п элементов по т элементов обозначается
символом А™ («А из эн по эм») и вычисляется по формуле
А™ = п(п — 1)(п — 2) ... • (п — т + 1) (1.4)
или
А™ = , п' Ч|, где n! = 1 • 2 - 3 •... • n, 1! = 1, 0! = 1. (1.5)
(п-т)!
22 Раздел первый. Элементарная теория вероятностей и случайных процессов
□ Для составления размещения А™ надо выбрать т элементов из
множества с п элементами и упорядочить их, т. е. заполнить т мест
элементами множества. Первый элемент можно выбрать п способами,
т. е. на первое место можно поместить любой из п элементов. После
этого второй элемент можно выбрать из оставшихся п — 1 элементов
п — 1 способами. Для выбора третьего элемента имеется п — 2 способа,
четвертого — п — 3 способа, и, наконец, для последнего m-го элемен-
та — (п — (т — 1)) способов. Таким образом, по правилу умножения,
существует п(п — 1)(п — 2)... (n — (т — 1)) способов выбора т элементов
из данных п элементов, т. е. А™ = п(п — 1)(п — 2)... (п — т + 1).
Пример 1.9. Составить различные размещения по 2 из элементов мно-
жества D — {а, Ь, с}; подсчитать их число.
Q Из трех элементов можно образовать следующие размещения по
два элемента: (а, Ь), (Ь,а), (а, с), (с, а), (Ь,с), (с,Ь). Согласно форму-
ле (1.4) их число: А| = 3 • 2 = 6. •
О
Перестановкой из п элементов называется размещение из п эле-
ментов по п элементов.
Из определения вытекает, что перестановки — это выборки (ком-
бинации), состоящие из п элементов и отличающиеся друг от друга
только порядком следования элементов. Число перестановок из п эле-
ментов обозначается символом Рп («пэ из эн») и вычисляется по фор-
муле
Рп = п!. (1.6)
Формула (1.6) следует из определения перестановки:
Р — Ап
Гп — ПТ1
___= п! = п!
(п — п)! О!
Пример 1.10. Составить различные перестановки из элементов мно-
жества Е = {2, 7,8}; подсчитать их число.
Q Из элементов данного множества можно составить следующие пе-
рестановки: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). По фор-
муле (1.6) имеем: Pj = 3! = 1 2 3 = 6. •
Пример 1.11. Сколькими способами можно расставить на полке 5
различных книг?
Глава 1. Случайные события * 23
О Искомое число способов равно числу перестановок из 5 элементов
(книг), т. е. F5 = 5! = 1 • 2 • 3 • 4 • 5 = 120. •
Сочетанием из п элементов по т (0 < т п) элементов назы-
вается любое подмножество, которое содержит т элементов данного
множества.
Из определения вытекает, что сочетания — это выборки (комбина-
ции), каждая из которых состоит из m элементов, взятых из данных
п элементов, и которые отличаются друг от друга хотя бы одним эле-
ментом, т. е. отличаются только составом элементов.
Число сочетаний из п элементов по т элементов обозначается сим-
волом С™ («цэ из эн по эм») и вычисляется по формуле
п(п — 1)(п — 2)... (п — т + 1)
1 • 2 3... т
или
f~rm _ _____п!_____
п m!(n —т)!'
(1.8)
Q Число А"' размещений из п элементов по т элементов можно най-
ти следующим образом: выбрать т элементов из множества, содержа-
щего п элементов (это можно сделать С™ способами); затем в каж-
дом из полученных сочетаний (подмножеств) сделать все перестанов-
ки для упорядочения подмножеств (это можно сделать Рт способа-
ми). Следовательно, согласно правилу умножения, можно записать:
А"1 п(п — 1)(п — 2)... (п — т + 1)
W = С™ - Рт. Отсюда С™ = ^- = ------------ 1.2.3...т------------ ИЛИ
(jm _ n! _
п т\(п — т)1
Можно показать, что имеют место формулы:
С- = СГт, (m < n), (1.9)
-Г ... + С” = 2”, (1.10)
^ = C-1 + C--11, (1 < m < n). (1.11)
Формулу (1.9) удобно использовать при вычислении сочетаний, когда
т > Так, = 105. Формула (1.10) выражает число
всех подмножеств множества из п элементов (оно равно 2")- Числа
бф, С^, С%, ..., С™ являются коэффициентами в разложении бинома
Ньютона: (а + b)n = C°anb° + С\ип~1Ь + ... + С£а°Ьп.
24 Раздел первый. Элементарная теория вероятностей и случайных процессов
pQ Пример 1.12. Составить различные сочетания по 2 из элементов мно-
жества D = {о, Ь, с}; подсчитать их число.
О Из трех элементов можно образовать следующие сочетания по два
элемента: (а, Ь); (а, с); (Ь,с). Их число: к = 3 (формула (1.7)).
•
|^| Пример 1.13. Сколькими способами можно выбрать 3 цветка из вазы,
в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1
красную гвоздику и 2 розовых?
О Так как порядок выбора цветов не имеет значения, то выбрать 3
цветка из вазы, в которой стоят 14 гвоздик, можно С44 способами. По
формуле (1.7) находим: С44 = =7.13.4 = 364. Далее: крас-
ную гвоздику можно выбрать С(о = 10 способами. Выбрать две розовые
гвоздики из имеющихся четырех можно С4 = = 6 способами. По-
этому букет из одной красной и двух розовых гвоздик можно составить,
по правилу умножения, CJo • С4 = 10 • 6 = 60 способами. •
Схема выбора с возвращением
Если при выборке т элементов из п элементы возвращаются обрат-
но и упорядочиваются, то говорят, что это размещения с повторе-
ниями.
Размещения с повторениями могут отличаться друг от друга эле-
ментами, их порядком и количеством повторений элементов. Числе»
всех размещений из п элементов по т с повторениями обозначается
символом А™ и вычисляется по формуле
А™ = пт
(1.12)
Пример 1.14. Из 3 элементов а, Ь, с составить все размещения по два
элемента с повторениями.
Q По формуле (1-12) число размещений по два с повторениями равно
А2 = З2 = 9. Это: (а,а), (а, 6), (а, с), (6, 6), (Ь, а), (Ь, с), (с,с), (с.а), (с.Ь).
Глава 1. Случайные события 25
Пример 1.15. Сколько пятизначных чисел можно составить, исполь-
зуя цифры: а) 2, 5, 7, 8; б) 0, 1, 9?
О а) Все пятизначные числа, составленные из цифр 2, 5, 7, 8, отли-
чаются друг от друга либо порядком их следования (например, 25558
и 52855), либо самими цифрами (например, 52788 и 78888). Следова-
тельно, они являются размещениями из 4 элементов по 5 с повторени-
ями, т. е. Л'\. Таким образом, искомое число пятизначных чисел равно
= 45 = 1024. Этот же результат можно получить, используя правило
умножения: первую цифру слева в пятизначном числе можно выбрать
четырьмя способами, вторую — тоже четырьмя способами, третью
четырьмя, четвертую — четырьмя, пятую — четырьмя. Всего получа-
ется 4 4 • 4 • 4 4 = 1024 пятизначных чисел.
б) Если пятизначные числа состоят из цифр 0, 1,9, то первую ци-
фру слева можно выбрать двумяспособами (0 не может занимать пер-
вую позицию), каждую из оставшихся четырех цифр можно выбрать
тремя способами. Согласно правилу умножения, таких чисел будет
2 • 3 • 3 3 • 3 = 162. (Иначе: = 243 - 81 = 162.) •
Если при выборке т элементов из п элементы возвращаются обрат-
но без последующего упорядочивания, то говорят, что это сочетанья с
повторениями.
Число всех сочетаний из п элементов по т с повторениями обозна-
чается символом 6'™ и вычисляется по формуле
С™ = С“т1. (1.13)
Пример 1.16. Из трех элементов а, Ь, с составить все сочетания по
два элемента с повторениями.
Q По формуле (1.13) число сочетаний по два с повторениями равно
Cf = C'f_|_2_ 1=6'4 = = 6. Составляем эти сочетания с повторени-
ями: (а, а), (а, Ь), (а, с), (Ь, Ь), (Ь,с), (с, с). •
Пример 1.17. Сколькими способами можно составить букет из 5 цве-
тов, если в наличии есть цветы трех сортов?
О Рассматриваемое множество состоит из трех различных элементов,
а выборки имеют объем, равный 5. Поскольку порядок расположения
цветов в букете не играет роли, то искомое число букетов равно чи-
слу сочетаний с повторениями из трех элементов по 5 в каждом. По
формуле (1-13) имеем С'| = Су = С'?-5 = С? = |= 21. •
1 * 2-’
26 Раздел первый. Элементарная теория вероятностей и случайных процессов
ф Пусть в множестве с п элементами есть к различных элементов,
при этом 1-й элемент повторяется nj раз, 2-й элемент — пг-раз .... к- й
элемент — гц. раз, причем гц + пЛ + ... + пк = п.
Перестановки из п элементов данного множества называют пере-
становками с повторениями из п элементов.
Число перестановок с повторениями из п элементов обозначается
символом Pn(ni, п?,..., /ц.) и вычисляется по формуле
ПИ(П1, п2,...,пк) = —:—--------г.
(1-14)
Пример 1.18. Сколько различных пятизначных чисел можно соста-
вить из цифр 3, 3, 5, 5, 8?
Q Применим формулу (1.14). Здесь п = 5, nj — 2, = 2, = 1. Чи-
сло различных пятизначных чисел, содержащих цифры 3. 5 и 8, равно
Упражнения
1. Сколько различных «слов», состоящих из трех букв, можно обра-
зовать из букв слова БУРАН? А если «слова» содержат не менее
трех букв?
2. Сколькими способами можно выбрать один цветок из корзины, в
которой имеется 12 гвоздик, 15 роз и 7 хризантем?
3. Группа студентов изучает 10 различных дисциплин. Сколькими
способами можно составить расписание занятий в понедельник,
если в этот день должно быть 4 разных занятия?
4. Из 10 мальчиков и 10 девочек спортивного класса для участия в
эстафете надо составить три команды, каждая из которых состоит
из мальчика и девочки. Сколькими способами это можно сделать?
5. Сколько можно составить четырехзначных чисел так, чтобы любые
две соседние цифры были различны?
Глава 1. Случайные события * 27
6. В электричке 12 вагонов. Сколько существует способов размещения
4 пассажиров, если в одном вагоне должно быть не более одного
пассажира?
7. Сколькими способами 3 награды могут быть распределены между
10 участниками соревнования?
8. Из 4 первокурсников, 5 второкурсников и 6 третьекурсников надо
выбрать 3 студента на конференцию. Сколькими способами мож-
но осуществить этот выбор, если среди выбранных должны быть
студенты разных курсов?
9. Сколькими способами можно расставить на полке 7 различных
книг, чтобы определенные три книги стояли рядом? Не радом?
10. Сколькими способами можно рассадить 5 человек за круглым сто-
лом? (Рассматривается только расположение сидящих относитель-
но друг друга.)
11. 10 студентов, среди которых С. Федин и А. Шилов, случайным обра-
зом занимают очередь в библиотеку. Сколько имеется вариантов
расстановки студентов, когда между Фединым и Шиловым окажут-
ся 6 студентов?
12. У одного школьника имеется 7 различных книг для обмена, а у
другого — 16. Сколькими способами они могут осуществить обмен:
книга на книгу? Две книги на две книги?
13. В урне 12 белых и 8 черных шаров. Сколькими способами можно
выбрать 5 шаров, чтобы среди них было: а) 5 черных; б) 3 белых и
2 черных?
14. Сколькими способами можно распределить 15 выпускников по трем
районам, если в одном из них имеется 8, в другом - 5 и в третьем —
2 вакантных места?
15. Известно, что 7 студентов сдали экзамен по теории вероятностей на
хорошо и отлично. Сколькими способами могли быть поставлены
им оценки?
16. Игральная кость (на ее 6 гранях нанесены цифры от 1 до 6) бро-
сается 3 раза. Сколько существует вариантов выпадения очков в
данном опыте? Напишите некоторые из них.
28 Раздел первый. Элементарная теория вероятностей и случайных процессов
17. Сколькими способами можно распределить 6 различных подарков
между четырьмя ребятишками?
18. Сколькими способами можно составить набор из 6 пирожных, если
имеется 4 сорта пирожных?
19. Группа учащихся из 8 человек отправляется в путешествие по Кры-
му. Сколькими способами можно составить группу из учащихся 5 7
классов?
20. Сколькими способами можно распределить 4 книги на трех пол-
ках книжного шкафа? Найти число способов расстановки книг на
полках, если порядок их расположения на полке имеет значение.
21. Сколько «слов» можно получить, переставляя буквы в слове:
а) ГОРА: б) ИНСТИТУТ?
22. Сколько существует способов размещения 9 человек в двухмест-
ный, трехместный и четырехместный номера гостиницы?
23. Сколькими способами можно распределить 16 видов товаров по
трем магазинам, если в 1-й магазин надо доставить 9, во 2-й -
4, а в третий — 3 вида товаров?
1.9. Примеры вычисления вероятностей
Пример 1.19. В урне находятся 12 белых и 8 черных шаров. Найти
вероятность того, что среди наугад вынутых 5 шаров 3 будут черными?
Q Выбрать 5 шаров из 20 можно С20 различными способами (все вы-
борки — неупорядоченные подмножества, состоящие из 5 элементов),
т. е. п — С-2(Г Определим число случаев, благоприятствующих событию
В — «среди 5 вынутых шаров 3 будут черными». Число способов вы-
брать 3 черных шара из 8, находящихся в урне, равно С|. Каждому
такому выбору соответствует С\2 способов выбора 2-х белых шаров из
12 белых в урне. Следовательно, по основному правилу комбинаторики
(правилу умножения), имеем: т = С^2- По формуле (1.3) находим,
что Р(В) = 8 12 Rs 0,24. •
Глава 1. Случайные события • 29
Пример 1.20. В коробке 5 синих, 4 красных и 3 зеленых карандаша.
Наудачу вынимают 3 карандаша. Какова вероятность того, что: а) все
они одного цвета; б) все они разных цветов; в) среди них 2 синих и 1
зеленый карандаш.
Q Сначала заметим, что число способов выбрать 3 карандаша из 12
имеющихся в наличии равно п = С^2 = 220.
а) Выбрать 3 синих карандаша из 5 можно Cf способами; 3 крас-
ных из имеющихся 4 можно выбрать С% способами; 3 зеленых из 3
зеленых — С| способами.
По правилу сложения общее число т случаев, благоприятствую-
щих событию А = {три карандаша, вынутых из коробки, одного цвета},
равно т — Cf + С% + С% = 15. Отсюда Р(А) = ~ J — = Д.
б) Пусть событие В = {три вынутых карандаша разных цветов}.
Число т исходов, благоприятствующих наступлению события В, по
правилу умножения равно т = Cg • С'( • = 5 • 4 • 3 = 60. Поэтому
pi ла — HL = 60 _ JL
у ’ п 220 11’
в) Пусть событие С = {из трех выбранных карандашей 2 синих и
1 зеленый}. Выбрать 2 синих карандаша из имеющихся 5 синих можно
Cl способами, а 1 зеленый из имеющихся 3 зеленых — С\ способами.
Отсюда по правилу умножения имеем: т, = С'{ = 30. Поэтому
p/z-n _тгь _ 30 _ 3 а
- п - 220 ~ 22’
Пример 1.21. Дано шесть карточек с буквами Н, М, И, Я, Л, О. Найти
вероятность того, что: а) получится слово ЛОМ, если наугад одна за
другой выбираются три карточки; б) получится слово МОЛНИЯ, если
наугад одна за другой выбираются шесть карточек и располагаются в
ряд в порядке появления.
Q а) Из шести данных букв можно составить п, = А| — 120 трехбук-
венных «слов» (НИЛ, ОЛЯ, ОНИ, ЛЯМ, МИЛ и т.д.). Слово ЛОМ
при этом появится лишь один раз, т. е. т = 1. Поэтому вероятность
появления слова ЛОМ (событие А) равна Р(А) = ~
б) Шестибуквенные «слова» отличаются друг от друга лишь по-
рядком расположения букв (НОЛМИЯ, ЯНОЛИМ. ОЛНИЯМ и т. д.).
Их число равно числу перестановок из 6 букв, т. е. п — Р$ = 6!. Очевид-
но, что т = 1. Тогда вероятность появления слова МОЛНИЯ (событие
В) равна Р(В) = ™ •
30 Раздел первый. Элементарная теория вероятностей и случайных процессов
|^| Пример 1.22. В почтовом отделении имеются открытки 6 видов. Ка-
кова вероятность того, что среди 1 проданных открыток все открытки:
а) одинаковы, б) различны?
Q Выбрать 4 открытки 6 видов можно = 126 способами, т. е.
п = 126.
а) Пусть событие А = {продано 4 одинаковые открытки}. Число
т исходов, благоприятствующих наступлению события А, равно числу
видов открыток, т. е. т = 6. Поэтому
= 126 = 21'
б) Пусть событие В = {проданы 4 различные открытки}. Выбрать
4 открытки из 6 можно = 15 способами, т. е. m = 15. Следовательно,
Упражнения
1. В лифт 9-этажного дома вошли 4 человека. Каждый из них неза-
висимо друг от друга может выйти на любом (начиная со второго)
этаже. Какова вероятность того, что все вышли: а) на разных эта-
жах; б) на одном этаже: в) на 5 этаже?
2. Из колоды карт (их 36) вытаскивают наудачу 5 карт. Какова веро-
ятность того, что будут вытащены 2 туза и 3 шестерки?
3. Семь человек рассаживаются наудачу на скамейке. Какова веро-
ятность того, что два определенных человека будут сидеть рядом?
4. На 5 карточках разрезной азбуки изображены буквы Е, Е, Л, П, П.
Ребенок случайным образом выкладывает их в ряд. Какова веро-
ятность того, что у него получится слово ПЕПЕЛ?
5. Из 60 вопросов, входящих в экзаменационные билеты, студент зна-
ет 50. Найти вероятность того, что среди 3-х наугад выбранных
вопросов студент знает: а) все вопросы; б) два вопроса.
6. В барабане револьвера 7 гнезд, из них в 5 заложены патроны. Бара-
бан приводится во вращение, потом нажимается спусковой курок.
Какова вероятность того, что, повторив такой опыт 2 раза подряд:
а) оба раза не выстрелит; б) оба раза револьвер выстрелит?
Глава 1. Случайные события * 31
7. Для проведения соревнования 10 команд, среди которых 3 лиде-
ра, путем жеребьевки распределяются на 2 группы по 5 команд
в каждой. Какова вероятность того, что 2 лидера попадут в одну
группу, 1 лидер — в другую?
8. Из колоды карт (их 36) наугад вынимают 2 карты. Найти вероят-
ность, что среди них окажется хотя бы одна «дама».
1.10. Геометрическое определение вероятности
Геометрическое определение вероятности применяется в случае,
когда, исходы опыта равновозможны, а ПЭС (или И) есть бесконечное
несчетное множество. Рассмотрим на плоскости некоторую область И,
имеющую площадь Sq, и внутри области П область D с площадью Sp
(см. рис. 8).
Рис. 8
В области Q случайно выбирается точка X. Этот выбор можно ин-
терпретировать как бросание точки X в область Q. При этом попа-
дание точки в область Q — достоверное событие, в D — случайное.
Предполагается, что все точки области П равноправны (все элементар-
ные события равновозможны), т. е. что брошенная точка может попасть
в любую точку области Q и вероятность попасть в область D пропор-
циональна площади этой области и не зависит от ее расположения и
формы. Пусть событие А = {X Е £>}, т. е. брошенная точка попадет в
область D.
Геометрической вероятностью события А называется отношение
площади области D к площади области Q, т. е.
Р(Л) =
Sp
So
(1.15)
32 Раздел первый. Элементарная теория вероятностей и случайных процессов
Геометрическое определение вероятности события применимо и в
случае, когда области Q и D обе линейные или объемные. В первом
случае
Р(А) = ^, (1.16)
во втором —
Р(А) = ^, (1.17)
где I — длина, а V — объем соответствующей области.
Все три формулы ((1.15)), ((1.16)), ((1.17)) можно записать в виде
Р(А) = (1.18)
tries Q
где через mes обозначена мера (S, I, Г) области.
Геометрическая вероятность обладает всеми свойствами, присущи-
ми классическому (и другим) определению:
1. Геометрическая вероятность любого события заключена между ну-
лем и единицей, т. е.
О Р(Л) «С 1.
2. Геометрическая вероятность невозможного события равна нулю,
т. е.
Р(0) = 0.
3. Геометрическая вероятность достоверного события равна единице,
т. е.
P(Q) = 1.
4. Геометрическая вероятность суммы несовместимых событий равна
сумме вероятностей этих событий, т. е. если А В = 0, то
Р(А + В) = Р(А)+Р(Р).
Проверим, например, свойство 4: пусть А = {х G /Л}, В =
— {х 6 Иг}, где = 0, т. е. Di и £>2 непересекающиеся области.
Тогда Р(А +В) = = + = Р(А) + Р(В).
|%1 Пример 1.23. (Задача о встрече.) Два человека договорились о встре-
че между 9 и 10 часами утра. Пришедший первым ждет второго в те-
чение 15 мин, после чего уходит (если не встретились). Найти веро-
ятность того, что встреча состоится, если каждый наудачу выбирает
момент своего прихода.
Г лава 1. Случайные события 33
Q Пусть х — время прихода первого, а у второго. Возможные зна-
чения х и у. О С х 60, 0 С у С 60 (в качестве единиц масштаба
возьмем минуты), которые на плоскости Оху определяют квадрат со
стороной, равной 60. Точки этого квадрата изображают время встреча-
ющихся (см. рис. 9).
Рис. 9
Тогда П = {(ж, у) : 0 х С 60,0 у 60}; все исходы Q равновоз-
можны, так как лица приходят наудачу. Событие А — лица встретят-
ся — произойдет, если разность между моментами их прихода будет не
более 15 мин (по модулю), т. е. А = {(ж,у) \у — х\ < 15}. Неравенство
\у — ж| 15, т. е. х — 15 С у х + 15 определяет область, заштри-
хованную на рис. 9, т. е. точки полосы есть исходы, благоприятству-
ющие встрече. Искомая вероятность определяется по формуле (1.15):
602 - 2 • | • 45 • 45
Р(Л) =
602
— « 0 44
16 ’
Упражнения
1. В круг радиуса R вписан правильный треугольник. Найти вероят-
ность того, что точка, брошенная в этот круг, попадет в данный
треугольник.
2. На отрезке [0,5] случайно выбирается точка. Найти вероятность то-
го, что расстояние от нее до правого конца отрезка не превосходит
1,6 единиц.
3. Стержень длины I разломан в двух наугад выбранных точках. Най-
ти вероятность того, что из полученных отрезков можно составить
треугольник.
34 Раздел первый. Элементарная теория вероятностей и случайных процессов
1.11. Аксиоматическое определение вероятности
Аксиоматическое построение теории вероятностей создано в начале
30-х годов академиком А. Н. Колмогоровым. Аксиомы теории вероят-
ностей вводятся таким образом, чтобы вероятность события обладала
основными свойствами статистической вероятности, характеризующей
ее практический смысл. В этом случае теория хорошо согласуется с
практикой.
Пусть Q — множество всех возможных исходов некоторого опы-
та (эксперимента), S — алгебра событий. Напомним (см. п. 1.4), что
совокупность S подмножеств множества П называется алгеброй (<т-
алгеброй). если выполнены следующие условия:
1. S содержит невозможное и достоверное события.
2. Если события Ai, Аг, Аз, ... (конечное или счетное множество)
принадлежат S, то S принадлежит сумма, произведение и дополнение
(т. е. противоположное для А,) этих событий.
Вероятностью называется функция Р(А), определенная на алгеб-
ре событий S, принимающая действительные значения и удовлетворя-
ющая следующим аксиомам:
А1. Аксиома неотрицательности: вероятность любого события A G S
неотрицательна, т. е.
Р(А) 0.
А2. Аксиома нормированности: вероятность достоверного события
равна единице, т. е.
P(Q) = 1.
АЗ. Аксиома аддитивности: вероятность суммы несовместных собы-
тий равна сумме вероятностей этих событий, т. е. если Аг • Aj = 0
(i ± j), то
Р(ЕЛ*) = £р<л*)-
k ' к
Совокупность объектов (П, S, Р), где Q — пространство элементар-
ных событий, S — алгебра событий, Р — числовая функция, удовлетво-
ряющая аксиомам А1 АЗ, называется вероятностным пространством
случайного эксперимента.
Вероятностное пространство служит математической моделью лю-
бого случайного явления; заданием этого пространства завершается ак-
сиоматика теории вероятностей.
Глава 1. Случайные события 35
1.12. Свойства вероятностей
Приведем ряд свойств вероятности, являющихся следствием акси-
ом Колмогорова.
С1. Вероятность невозможного события равна нулю, т. е.
Р(0) = 0.
С2. Сумма вероятностей противоположных событий равна единице,
т. е.
Р(А) + Р(А) = 1.
СЗ. Вероятность любого события не превосходит единицы, т. е.
Р(А) 1.
С4. Если А С В, т. е. событие А влечет за собой событие В, то
Р(Л) Р(В).
С5. Если события Ai, А?, -.., Ап образуют полную группу несовмест-
ных событий, т. е. Ai — и Аг ‘ Aj = 0, то
г=1
£m) = i-
Q С1. Так как А + 0 = А и А • 0 = 0, то согласно аксиоме АЗ имеем
Р(А) + Р(0) = Р(А), следовательно, Р(0) = 0.
С2. Поскольку А + А = Q, то Р(А + А) = P(Q), а так как А • А = 0,
то в силу аксиом А2 и АЗ получаем Р(А) + Р(А) = 1.
СЗ. Из свойства С2 вытекает, что Р(А) = 1 — Р(А). С учетом ак-
сиомы А1 получаем Р(А) 1.
С4. Так как В = (В — А) + А при А С В и (В — А) • А = 0, то
согласно аксиоме АЗ получаем Р(В) = Р(В—А)+Р(А). Но Р(В—А) 0
(аксиома А1), поэтому Р(В) Р(А).
С5. Так как А] + А2 + • • • + An = Q, то, согласно аксиомам А2 и АЗ.
имеем Р(Аг + Аг + ... + А„) = P(Ai) + Р(А2) + ... + Р(АП) — 1.
Заметим, что из Р(А) = 0 не следует А = 0.
2*
36 Раздел первый. Элементарная теория вероятностей и случайных процессов
Пример 1.24. Из колоды, содержащей 36 карт, наудачу вынимают три
карты. Найти вероятность того, что среди них окажется хотя бы одна
«дама».
Q Пусть А — интересующее нас событие, Ai — появление одной «да-
мы», А2 — двух «дам», Аз — трех «дам». Тогда А = Ах + А2 + Аз,
причем события Ах, А2, Аз несовместные. Поэтому Р(А) = Р(АХ) +
+ Р(А2) + Р(А3). Число всевозможных случаев выбора трех карт из 36
равно Сз6; число случаев, благоприятных событиям Ах, А2, А3, соот-
ветственно равно mi = C’l • Сз2, т2 = С% Сд2, тз = Cf С®2. Таким
образом, P(A) = C.4-42 + 4 •G32+C4-G32 o,3i
Qus
Задача решается проще, если воспользоваться свойством С2. Нахо-
дим Р(А), где А - среди вынутых карт нет ни одной «дамы»! Р(А) =
С3
= —к, 0,69. Значит, Р(А) = 1 — 0,69 = 0,31. *
1.13. Конечное вероятностное пространство
Пусть производится некоторый опыт (эксперимент), который имеет
конечное число возможных исходов гщ. w2, ш3, ..., wn. В этом случае
Q = {wi,w2, • • •, wn} (или коротко П = {'«’}) — конечное пространство,
S — алгебра событий, состоящая из всех (их 2") подмножеств множе-
ства Q.
Каждому элементарному событию Wi Е П, i = 1,2,..., п поставим в
соответствие числор(у/;,), которое назовем «вероятностью элементарно-
го события», т. е. зададим на П числовую функцию, удовлетворяющую
двум условиям:
1) условие неотрицательности: р ('»:,) 0 для любого W} Е Q;
П
2) условие нормированности 52 р ('"’, ) = 1.
г=1
Вероятность Р(А) для любого подмножества А Е П определим как
сумму
Р(А) = £ РМ, (1-19)
т. е. вероятностью Р(А) события А назовем сумму вероятностей элемен-
тарных событий, составляющих событие А. Введенная таким образом
Глава 1. Случайные события 37
вероятность удовлетворяет аксиомам Колмогорова (А1-ЛЗ):
п
Р(А) О, P(Q) = 22
шгеП г=1
р(а + в) = = 52+ 52= + р(в^'
ицЕА+В WiEA w,EB
если АВ = 0. т. е. А и В два несовместных события. Так опре-
деленная тройка {Q, S, Р} есть конечное вероятностное пространство,
называемое «дискретным вероятностным пространством».
Частным случаем определения вероятности (1.19) является клас-
сическое определение вероятности, когда все исходы опыта равновоз-
можны: p(wi) — p(wz) = ... = p(wn) = (следует из условия нормиро-
п
ванности: ]Р p(wi) = 1)- Формула (1.19) приобретает вид:
г=1
— 52 P^W^ п п + п п '
WiEA v
т. е. Р(А) = —, где т — число элементарных событий, образующих
событие А (т. е. т — число случаев, благоприятствующих появлению
события А).
1.14. Условные вероятности
Пусть Ли В — два события, рассматриваемые в данном опыте. На-
ступление одного события (скажем, А) может влиять на возможность
наступления другого (В). Для характеристики зависимости одних со-
бытий от других вводится понятие условной вероятности.
Условной вероятностью события В при условии, что произошло
событие А. называется отношение вероятности произведения этих со-
бытий к вероятности события А, причем Р(А) А 0. обозначается сим-
волом Р(В|А).
Таким образом, по определению
Р(В|А) = Р(^^, Р(А)^0. (1.20)
Вероятность Р(В), в отличие от условной, называется безусловной ве-
роятностью.
38 Раздел первый. Элементарная теория вероятностей и случайных процессов
Аналогично определяется условная вероятность события" А при
условии В, т. е. Р(А\В):
(1-21)
Р(А|В) = Р{А-^ ; Р(В)^0.
Отметим, что условная вероятность, скажем Р(В|А), удовлетворя-
ет аксиомам Колмогорова (и. 1.11): Р(В|А) 0. очевидно: Р(П|А) =
= = = 1; Р((Р + С) 1 л) = р(в| Л) + р(с| л)’если в ’с =
= 0. Поэтому для условной вероятности справедливы все следствия
(свойства) из аксиом, полученные в п. 1.12. Формула (1-20) принимает-
ся по определению при аксиоматическом определении вероятности; в
случае классического (геометрического, статистического) определения
она может быть доказана.
Пример 1.25. В урне 2 белых и 7 черных шаров. Из нее последователь-
но вынимают два шара. Какова вероятность того, что 2-й шар окажется
белым при условии, что 1-й шар был черным?
Q Решим задачу двумя способами.
1. Пусть А — 1-й шар черный, В — 2-й шар белый. Так как событие
А произошло, то в урне осталось 8 шаров, из которых 2 белых. Поэтому
Р(В|Л) = 1 = 1.
2. Найдем Р(В|А) по формуле (1.20). Очевидно, что В (А) =
Находим Р(АВ\. п = 9 • 8 — 72 — общее число исходов (появление двух
шаров). Событию АВ благоприятствуют т — С\ • С] = 14 исходов.
14 7 7 7 1
Поэтому Р(АВ) — = «г • Следовательно, Р(В\А) = = -г . •
f Zi оо оО У ~г
1.15. Вероятность произведения событий.
Независимость событий
Из определения условной вероятности (п. 1.14) следует, что
Р(А • В) = Р(А) • Р(В|А) = Р(В) • Р(А|В), (1.22)
т. е. вероятность произведения двух событий равна произведению ве-
роятности одного из них на условную вероятность другого при условии,
что первое событие произошло.
Глава 1. Случайные события 39
Равенство (1-22) называют правилом или теоремой (для схемы слу-
чаев оно доказывается) умножения вероятностей. Это правило обоб-
щается на случай п событий:
Р(А1-А2-...-А„) =
= Р(А^ Р(А2\А!) PiA^Ai • А2) •... • Р(Ап\Аг • А2 •... An_i).
(1-23)
Так для 3-х событий Ai, А2, Аз получаем
P(Ai • А2 • Аз) = F((Ai • А2) • Аз) = Р(А] • А2) • P(A3|Aj • А2) —
= Р(А1)-Р(А2|А1)-Р(А3|А1-А2).
Пример 1.26. В коробке находится 4 белых. 3 синих и 2 черных шара.
Наудачу последовательно вынимают 3 шара. Какова, вероятность того,
что 1-й шар будет белым, 2-й — синим, 3-й — черным?
Cj Введем следующие события: Ai — первым вытащили белый шар,
А2 — вторым — синий, А3 — третьим — черный. Тогда интересую-
щее нас событие А представится в виде А = А3 • А2 А3. По прави-
лу умножения вероятностей Р(А) = P(Ai) • P(A2|Ai) • P(A3|Ai • А2).
4 3
Но P(Ai) = ; P(A2|Ai) = о , так как шаров осталось 8, а число
2
благоприятных случаев для события А2 равно 3; Р(А3|Ах • А2) = = ,
так как уже два шара (белый и синий) вытащены. Следовательно,
Р^А') = 9 ’ 8 ‘ 7 = 21 ~ °’05’ *
О
Правило умножения вероятностей имеет особо простой вид, если
события, образующие произведение, независимы.
Событие А называется независимым от события В, если его услов-
ная вероятность равна безусловной, т. е. если выполняется равенство
Р(А|Р) = Р(А). (1.24)
Лемма 1.1 (о взаимной независимости событий). Если событие А
не зависит от события В, то и событие В не зависит от события А.
□ Из равенства (1.22), с учетом равенства (1.24), следует Р(В\А) =
Р(А\В) Р(В) _ Р(А) • Р(В) _
Р(А) Р(А) V б • •
Р(Р|А) = Р(В), (1.25)
40 Раздел первый. Элементарная теория вероятностей и случайных процессов
а это означает, что событие В не зависит от события А.
Можно дать следующее (новое) определение независимости собы-
тий.
Два события называются независимыми, если появление одного из
них не меняет вероятность появления другого.
Для независимых событий правило умножения вероятностей (1.22)
принимает вид:
Р(А В) = Р(А) • Р(В), (1.26)
т. е. вероятность произведения двух независимых событий равна про-
изведению вероятностей этих событий.
Равенство (1.26) часто используют в качестве определения (еще од-
ного!) независимости событий: события Аи В называются независимы-
ми, если Р(А В) = Р(А) Р(В).
Можно показать, что если события А и В независимы, то незави-
симы события А и В, Л и В, Л и В.
На практике о независимости тех или иных событий часто судят
исходя из интуитивных соображений и анализа условий опыта, считая
независимыми события, «между которыми нет причинно-следственных
связей».
Понятие независимости может быть распространено на случай п
событий.
События Ai, А2,..., А„ называются независимыми (или независи-
мыми в совокупности), если каждое из них не зависит от произведения
любого числа остальных событий и от каждого в отдельности. В про-
тивном случае события А±, А2,..., Ап называются зависимыми.
Для независимых событий их условные вероятности равны без-
условным. и формула (1-23) упрощается
P(Ai • А2 •... Ап) - Р(Д) Р(Л2) •... - Р(Л„). (1.27)
Из попарной независимости событий А\, А2, -., Ап (любые два из
них независимы) не следует их независимость в совокупности (обратное
верно).
Убедимся в этом, рассмотрев следующий пример.
Пример 1.27. Производится выбор (наудачу) флага из 4-х. имеющих-
ся в наличии: красного, голубого, белого и трехцветного (красно-бело-
голубого). Исследовать на независимость события: К — выбранный
флаг имеет красный цвет; Г — имеет голубой цвет; Б — имеет белый
цвет.
Глава 1. Случайные события *41
C_j Возможных исходов выбора 4; событию К благоприятствуют 2 исхо-
2 1
да (красный цвет имеется у двух флагов). Поэтому F(K) = - = - . Ана-
логично находим, что Р(Г) = Р(Б) = ~ . Событию КГ — выбран флаг,
имеющий 2 цвета (красный и голубой), — благоприятствует один исход.
Поэтому, П(К Г) = |. И так как Р(К - Г) = | | | = Р(К) - Р(Г), то
события К и Г независимы. Аналогично убеждаемся в независимости
событий К и Б, Б и Г. Стало быть, события К, Б, Г попарно независи-
мы. А так как Р(К • Г • Б) = i / F(K) • Р(Г) • Р(Б) = i , то события К,
Г и Б не являются независимыми в совокупности. •
Упражнения
1. Бросается игральная кость. Пусть событие А — появление четного
числа очков, событие В — появление более трех очков. Зависимы
или нет события А и В1
2. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Како-
ва вероятность того. что. перемешав буквы и укладывая их в ряд по
одной (наудачу), получим слово : а) ТИСКИ; б) КИСКА; в) КИТ:
г) СТАТИСТИКА?
3. Найти вероятность отказа схемы (рис. 10), предполагая, что отказы
отдельных элементов независимы, а вероятность отказа элемента
, с номером i равна 0,2.
Рис. 10
42 * Раздел первый. Элементарная теория вероятностей и случайных процессов
1.16. Вероятность суммы событий
Как известно (п. 1.11), вероятность суммы двух несовместных со-
бытий определяется аксиомой АЗ: Р(А + В) = Р(А) + Р(В). А • В = 0.
Выведем формулу вероятности суммы двух совместных событий.
Теорема 1.1. Вероятность суммы двух совместных событий равна сумме
их вероятностей без вероятности их произведения,
Р(А + В) = Р(А) + Р(В) -Р(А В). (1.28)
Ц Представим события А + В и В в виде суммы двух несовместных
событий: А+В = А+В-А, В = АВ+ВА (см. п. 1.3, пример 1.2 и упраж-
нение 1). В справедливости этих формул можно наглядно убедиться на
рис. 11.
Рис. 11
Тогда, согласно аксиоме АЗ, имеем Р(А + В) = Р(А) + Р(В • А) и
Р(В) = Р(А В) + Р(В А). Отсюда следует Р(А + В) = Р(А) + Р(В) —
- Р(А В).
Формула (1.28) справедлива для любых событий А и В.
Можно получить формулу вероятности суммы трех и большего чи-
сла совместных событий; для трех событий она имеет вид
Р(А + В + С) = Р(А) + Р(В) + Р(С)-
- Р(А • В) - Р(А С) - Р(В С) + Р(А В • С). (1.29)
Справедливость равенства поясняет рис. 12.
Проще, однако, найти вероятность суммы нескольких совместных
событий Р(В) = Р(А] +А2+.. .-ЬАП), используя равенство P(S)+P(S) =
= 1, где S = Ai • А4 • ... • Ап — противоположно событию S. Тогда
Р(5) = 1 — P(.S'). Мы уже использовали этот прием в п. 1.12.
Глава 1. Случайные события 43
Рис. 12
Пример 1.28. Бросаются две игральные кости. Какова вероятность
появления хотя бы одной шестерки?
Q Введем события: А — появление шестерки на первой кости. В —
на второй кости. Тогда А+В — появление хотя бы одной шестерки при
бросании костей. События А и В совместные. По формуле (1.28) нахо-
димР(Л+В) = 1 + = 11. (Иначе: P(S) = Р(А-В) = j-j = || .
6 6 6 6 36 6 6 36
Упражнения
1. В урне 2 белых и 7 черных шаров. Из нее наудачу вынимают (без
возврата) 2 шара. Какова вероятность того, что они оба будут раз-
ных цветов?
2. Три орудия стреляют в цель независимо друг от друга. Вероятность
попадания в цель каждого равна 0,7. Найти вероятность попадания
в цель: а) только одного из орудий; б) хотя бы одного.
3. Надежность (т. е. вероятность безотказной работы) прибора равна
0,7. Для повышения надежности данного прибора он дублируется
п — 1 другими такими же приборами (рис. 13). Сколько приборов
надо взять, чтобы повысить его надежность до 0,95?
44 Раздел первый. Элементарная теория вероятностей и случайных процессов
Рис. 13
1.17. Формула полной вероятности
Одним из следствий совместного применения теорем сложения и
умножения вероятностей являются формулы полной вероятности и
Байеса. Напомним, что события Аг, А2, ..., Ап образуют полную груп-
п
пу, если A, -Aj = 0,j jh £ А, =й. Систему таких событий называют
г=1
также разбиением.
Теорема 1.2. Пусть события Hi, Ip, ..., Нп образуют полную группу.
Тогда для любого, наблюдаемого в опыте, события А имеет место фор-
мула полной вероятности или средней вероятности.
P(A) = ^P(Hi)-P(A\Hi),
i=L
(1.30)
□ Так как Н\ 4- Н% + ... 4- Нп = Q, то в силу свойств операций
над событиями (п. 1.3), А = А - Q = А • (Hi + Н? + ... + Нп) =
= А Hi + А Н? 4- ... 4- А • Нп. Из того, что Hi Hj = 0, следу-
ет, что (А • Hi) (А • Hj) = 0, i J, т. е. события А • Н, и А - Н3
также несовместны. Тогда по теореме сложения вероятностей Р(А) —
п
= Р(А • Hl) + Р(А • Н2) + ... + Р(А Нп) т. е. Р(А) = Hi)- По
i 1
теореме умножения вероятностей Р(А Hi) = P(Hi) Р(Л\Н,), откуда и
следует формула (1.30).
Отметим, что в формуле (1.30) события Hi, Ip, ..., Нп обычно на-
зывают гипотезами1, они исчерпывают все возможные предположения
(гипотезы) относительно исходов как бы первого этапа опыта, событие
А — один из возможных исходов второго этапа.
Глава 1. Случайные события 45
Пример 1.29. В сборочный цех завода поступает 40% деталей из I цеха
и 60% — из II цеха. В I цехе производится 90% стандартных деталей,
а во II — 95%. Найти вероятность того, что наудачу взятая сборщиком
деталь окажется стандартной.
Cj Взятие детали можно разбить на два этапа. Первый — это выбор
цеха. Имеется две гипотезы: Н\ — деталь изготовлена I цехом, Н-/ -
II цехом. Второй этап — взятие детали. Событие А взятая наудачу
деталь стандартна. Очевидно, события Hi и Н? образуют полную груп-
пу, P(Hi) = 0,4, Р(Н?) = 0,6. Числа 0,90 и 0.95 являются условными
вероятностями события А при условии гипотез Hi и Н? соответствен-
но, т.е. P(A\Hi) = 0,90 и P(A\Hz) = 0.95. По формуле (1.30) находим
Р(А) = £ Р(Нг) Р(А\Нг) = 0,4 • 0,90 + 0,6 0,95 = 0,93.
г=1
1.18. Формула Байеса (теорема гипотез)
i
Следствием формулы (1.30) является формула Байеса или теоре-
ма гипотез. Она позволяет переоценить вероятности гипотез Н? , приня-
тых до опыта и называемых априорными («а priori», доопытные, лат.)
по результатам уже проведенного опыта, т. е. найти условные веро-
ятности P(Hj\A), которые называют апостериорными («а posteriori»,
послеопытные).
Теорема 1.3. Пусть события Ну, Н^,..., Нп образуют полную группу
событий. Тогда условная вероятность события Н) (к = 1, п) при условии,
что событие А произошло, задается формулой
P№|A) =
(1-31)
где Р(А) — P(Hi) Р(А\Нф) + ... + Р(Нп) Р(А\Нп) — формула полной
вероятности. Формула (1.31) называется формулой Байеса1.
11702 1761, английский священник, математик
46 Раздел первый. Элементарная теория вероятностей и случайных процессов
Q Применив формулы условной вероятности (п. 1.14) и умножения
вероятностей (п. 1.15), имеем
P(Ht) P(A\Ht)
= Р(А) =---------FW-------
где Р(А) — формула полной вероятности (п. 1.17)
Пример 1.30. В примере 1.29 (п. 1.17) найти вероятность того, что эта
стандартная деталь изготовлена II цехом.
Q Определим вероятность гипотезы Н? при условии, что событие А
(взятая деталь стандартна) уже произошло, т. е. Р(Я2|Л):
Р(Я2|Л) =
Р(Я2) Р(А|Я2)
Р(Л) -
0,6 • 0,95 _ 19
0,93 ~ 31
0,613.
Упражнения
1. Прибор содержит две микросхемы. Вероятность выхода из строя в
течение 10 лет первой микросхемы равна 0,07, а второй — 0,10. Из-
вестно, что из строя вышла одна микросхема. Какова вероятность
того, что вышла из строя первая микросхема?
2. Из 40 экзаменационных билетов студент П выучил только 30. Ка-
ким выгоднее ему зайти на экзамен, первым или вторым?
3. Известно, что 90% изделий, выпускаемых данным предприятием,
отвечает стандарту. Упрощенная схема проверки качества продук-
ции признает пригодной стандартную деталь с вероятностью 0,96 и
нестандартную с вероятностью 0.06. Определить вероятность того,
что:
а) взятое наудачу изделие пройдет контроль;
б) изделие, прошедшее контроль качества, отвечает стандарту.
Глава 1. Случайные события 47
1.19. Независимые испытания. Схема Бернулли
а
С понятием «независимых событий» связано понятие «независи-
мых испытаний (опытов)».
Несколько опытов называются независимыми, если их исходы
представляют собой независимые события (независимые в совокупно-
сти).
Другими словами, если проводится несколько испытаний, т. е. опыт
выполняется при данном комплексе условий многократно (такое явле-
ние называется «последовательностью испытаний»), причем вероят-
ность наступления некоторого события А в каждом испытании не за-
висит от исходов других испытаний, то такие испытания называются
независимыми.
Примерами независимых испытаний могут служить: несколько (п
раз) подбрасываний монеты; стрельба (п раз) по мишени без поправок
на ранее допущенную ошибку при новом выстреле; несколько (п раз)
выниманий из урны одинаковых на ощупь занумерованных шаров, если
шары каждый раз (после просмотра) возвращаются назад в урну, и т. д.
При практическом применении теории вероятностей часто исполь-
зуется стандартная схема, называемая схемой Бернулли или схемой
независимых испытаний.
Последовательность п независимых испытаний, в каждом из кото-
рых может произойти некоторое событие А (его называют успехом) с
вероятностью Р(А) = р или противоположное ему событие А (его на-
зывают неудачеИ) с вероятностью Р(А) = q = 1 — р, называется схемой
Бернулли.
Например, при стрельбе по мишени: событие А — попадание
(успех), событие А — промах (неудача); при обследовании п изделий
на предмет годности: событие А — деталь годная (успех), событие А —
деталь бракованная (неудача) и т. д.
В каждом таком опыте ПЭС состоит только из двух элементар-
ных событий, т. е. Q = {wq,wi}, где шо — неудача, wi — успех, при
этом А = {ш|}, А = {'«’о}- Вероятности этих событий обозначают че-
рез р и q соответственно (р + q = 1). Множество элементарных исхо-
дов для п опытов состоит из 2п элементов. Например, при 7/ = 3, т. е.
((А, А, А) (А, А, А) (А, А, А) (А, А, А)
опыт повторяется 3 раза, И = <------;---—----;---;--------йр,--’
(АДА) (А, А, А) (А, А, А) (А,А,АП „
---Вероятность каждого элемен-
тарного события определяется однозначно. По теореме умножения ве-
48 * Раздел первый. Элементарная теория вероятностей и случайных процессов
роятность события, скажем wq = (А, А, А), равна q-q-p = pq2, события
W7 — р • р • р = родч = р и т. д.
Часто успеху сопоставляют число 1, неудаче — число 0. Элемен-
тарным событием для п опытов будет последовательность из п нулей
и единиц. Тройка чисел (0,0,0) означает, что во всех трех опытах со-
бытие А не наступило; тройка чисел (0,1,0) означает, что событие А
наступило во 2-м опыте, а в 1-м и 3-м — не наступило.
1.20. Формула Бернулли
Простейшая задача, относящаяся к схеме Бернулли, состоит в
определении вероятности того, что в п независимых испытаниях собы-
тие А наступит т раз (0 С т С п). Обозначается искомая вероятность
так: Рп(т) или Рп,т или Р(рп = т), где //,, — число появления события
А в серии из п опытов.
Например, при бросании игральной кости 3 раза Рз(2) означает
вероятность того, что в 3-х опытах событие А — выпадение цифры
4 — произойдет 2 раза. Очевидно,
рз(2) = p2q + p2q + p2q =
= [{(А. А. А); (А, А, А); (А, А, А)}]
= 3p2Q = 3- = =0,069.
Теорема 1.4. Если производится п независимых испытаний, в каждом
из которых вероятность появления события А равна р, а вероятность
его непоявления равна q = 1 — р, то вероятность того, что событие А
произойдет т раз определяется формулой Бернулли
Рп(т) = С™pm-qll1'\ m = 0,1,2,... ,п. (1.32)
Ц Вероятность одного сложного события, состоящего в том, что со-
бытие А в п независимых опытах появится т раз в первых т опы-
тах и не появится (п — т) раз в остальных опытах (это событие
А • А А • ... А • А - А ... А) по теореме умножения вероятностей рав-
раз (п-т) раз
na.pmqn~m. Вероятность появления события А снова т раз, но в другом
Глава 1. Случайные события * 49
порядке (например, А А - А... А А • А •... А или АААА •... • АА и т. д.)
т раз
будет той же самой, т. е. pmqn~m.
Число таких сложных событий — в п опытах т раз встречается со-
бытие А в различном порядке — равно числу сочетаний из п по т, т. е.
С™. Так как все эти сложные события несовместны, то по теореме сло-
жения вероятностей искомая вероятность равна сумме вероятностей
всех возможных сложных событий, т. е.
Pn(m) = + ... + pmqn~m = C™pmqn~m, m = 0,1.......n.
С™ слагаемых
Можно заметить, что вероятности Р„(тп), т — 0.1.?г являются
коэффициентами при хт в разложении (г/ + рх)п по формуле бинома
Ньютона:
(q + =qn + Pr\qnlpx + C2qn~2p2x2 +... + С™уп~тртхт +... +рпхп.
Поэтому совокупность вероятностей Рп(т) называют биномиальным
законом распределения вероятностей (см. п. 2.7), а функцию у>(ж) =
= (q + рх)п — производящей функцией, для последовательности неза-
висимых опытов.
Если в каждом из независимых испытаний вероятности наступле-
ния события А разные, то вероятность того, что событие А наступит
т раз в 7?, опытах, равна коэффициенту при rn-й степени многочлена
Т’п(^) = (<Л +Р1^)(92 + P‘2z) ... • (qn + pnz), где <pn(z) — производящая
функция.
Если в серии из п независимых опытов, в каждом из которых может
произойти одно и только одно из к событий А[, /1-2, .... Ак с соответ-
ствующими вероятностями р\. р?. ..., рк. то вероятность того, что в
этих опытах событие Ai появится mi раз, событие А^ — т? раз, ...,
событие Ак - тк раз, равна
Рп(тът^....тк) = (133)
где + 7/12 + - - - + тк — п. Вероятности (1.33) называются полиноми-
альным распределением.
\
Пример 1.31. Производится 3 независимых выстрела по цели. Веро-
ятности попадания при разных выстрелах одинаковы и равны р = 0,9.
Какова вероятность: а) промаха; б) одного попадания; в) двух попа-
даний; г) трех попаданий? Решить задачу в случае, если вщюятности
попадания при разных выстрелах различны: pi — 0,7, р% = 0,8, рз = 0,9.
50
Раздел первый. Элементарная теория вероятностей и случайных процессов
Q В данном случае п = 3, р = 0,9, q = 0,1. Пользуясь формулой
Бернулли (1.32), находим:
а) -Рз(О) = 0,9° • 0,13 = 0,001 — вероятность трех промахов;
б) Р3(1) = Cl • Оф1 • 0,12 = 3 • 0,9 • 0,01 = 0,027 — вероятность одного
попадания;
в) Р3(2) = С2 • 0,92 • 0,1х = 3 • 0,81 • 0,1 = 0,243 — вероятность двух
попаданий;
г) Рз(3) — С% 0,93 -0,1° = 0,93 = 0,729 — вероятность трех попада-
ний. •
Эти результаты можно изобразить графически, отложив на оси Ох
значения т, на оси Оу — значения Рп(гп) (рис. 14).
Ломаная, соединяющая точки (0; 0,001), (1; 0,027), (2; 0,243),
(3; 0,729), называется многоугольником распределения вероятностен.
Если вероятности при разных выстрелах различны, то производя-
щая функция имеет вид <^з(г) = (0,3 + 0,7г)(0,2 + 0,8г) (0,1 + 0,9г) =
= 0,504г3 + 0,398г2 + 0,092г + 0,006. Откуда находим вероятность трех,
двух, одного попаданий, промаха соответственно: Рз(3) = 0,504, Рз(2) =
= 0,398, Р3(1) = 0,092, Р3(0) = 0,006. (Контроль: 0,504 + 0,398 + 0,092 +
+ 0,006 = 1.)
Глава 1. Случайные события 51
Упражнения
1. Монету подбрасывают 10 раз. Какова вероятность того, что герб
выпадет (появится): а) 4 раза; б) ни разу; в) хотя бы один раз.
2. Что вероятнее выиграть у равносильного противника-шахматиста:
две партии из четырех или три из шести? Ничьи во внимание не
принимаются.
3. В семье трое детей. Какова вероятность того, что: а) все они маль-
чики; б) один мальчик и две девочки. Считать вероятность рожде-
ния мальчика 0,51, а девочки — 0,49.
4. В каждом из карманов (их 2) лежит по коробку спичек (по 10 спи-
чек в коробке). При каждом закуривании карман выбирается нау-
дачу. При очередном закуривании коробок оказался пустым. Найти
вероятность того, что во втором коробке 6 спичек.
1.21. Предельные теоремы в схеме Бернулли
Использование формулы Бернулли (1.32) при больших значениях п
и m вызывает большие трудности, так как это связано с громоздкими
вычислениями. Так, при п — 200, т = 116, р = 0.72 формула Бер-
нулли принимает вид Р2оо(116) = С*200 ' (0,72)1|(> • (0,28)84. Подсчитать
результат практически невозможно. Вычисление Р/г(т) вызывает за-
труднения также при малых значениях р (q). Возникает необходимость
в отыскании приближенных формул для вычисления Рп(?7г), обеспечи-
вающих необходимую точность. Такие формулы дают нам предельные
теоремы; они содержат так называемые асимптотические формулы, ко-
торые при больших значениях испытаний дают сколь угодно малую
относительную погрешность. Рассмотрим три предельные теоремы, со-
держащие асимптотические формулы для вычисления биномиальной
вероятности Рп(т) при п —> оо.
52 Раздел первый. Элементарная теория вероятностей и случайных процессов
Теорема Пуассона
Теорема 1.5. Если число испытаний неограничено увеличивается
(п —> оо) и вероятность р наступления события А в каждом испыта-
нии неограничено уменьшается (р -» 0), но так, что их произведение пр
является постоянной величиной (пр = а = const), то вероятность Рп(т)
удовлетворяет предельному равенству
lim Рп(т) =
п—>оо
ате~а
т!
(1-34)
Выражение (1-34) называется асимптотической формулой Пуас-
сона.
□ Преобразуем формулу Бернулли (1.32) с учетом того, что р = :
Переходя к пределу при п —» оо, получим lim Рп(т) =------
п->ос ml
(lim (1-£)" =с- ° согласно второму замечательному пределу).
Из предельного равенства (1.34) при больших п и малых р вытекает
приближенная формула Пуассона,
а
Рп(т) »-----;—, а = пр, т. = 0,1,2,.... (1.35)
ml
Формулу (1.35) применяют, когда вероятность р = const успеха крайне
мала, т. е. сам по себе успех (появление события Л) является редким
событием (например, выигрыш автомобиля по лотерейному билету),
но количество испытаний п велико, среднее число успехов пр = а, не-
значительно. Приближенную формулу (1.35) обычно используют, когда
п 50, а пр 10.
Формула Пуассона находит применение в теории массового обслу-
живания.
Глава 1. Случайные события 53
Пример 1.32. Завод «Золотая балка» (Крым) отправил в Москву 1500
бутылок вина «Каберне». Вероятность того, что в пути бутылка может
разбиться, равна 0,002. Найти вероятность того, что в пути будет раз-
бито не более 4-х бутылок (событие А).
О Искомая вероятность равна
Р1500(0) + Дг,00 (1) + Абоо(2) + Абоо(З) + Pi5oo(4).
Так как п ~ 1500, р = 0,002, то а = |пр] = 3. Вероятность события А
найдем, используя формулу Пуассона (1.35):
/ , 3° 3 Ч1 - <=~3 Ч2 • е~3 Ч3 • с 3 Ч4 3
Р(А) = « 0,815.
Формулу Пуассона можно считать математической моделью про-
стейшего потока событий.
Потоком событий называют последовательность событий, насту-
пающих в случайные моменты времени (например, поток посетителей в
парикмахерской, поток вызовов на телефонной станции, поток отказов
элементов, поток обслуженных абонентов и т.п.).
Поток событий, обладающий свойствами стационарности, ординар-
ности и отсутствия последствия называется простейшим (пуассонов-
ским) потоком.
Свойство стационарности означает, что вероятность появления к
событий на участке времени длины т зависит только от его длины
(т. е. не зависит от начала его отсчета). Следовательно, среднее 'число
событий, появляющихся в единицу времени, так называемая интен-
сивность А потока, есть величина постоянная: X(t) = X.
Свойство ординарности означает, что событие появляется не груп-
пами, а поодиночке. Другими словами, вероятность появления более
одного события на малый участок времени Af пренебрежительно мала
по сравнению с вероятностью появления только одного события (на-
пример, поток катеров, подходящих к причалу, ординарен).
Свойство отсутствия последствия означает, что вероятность по-
явления к событий на любом участке времени длины г не зависит от
того, сколько событий появилось на любом другом не пересекающимся
с ним участком (говорят: «будущее» потока не зависит от «прошлого»,
например, поток людей, входящих в супермаркет).
Можно доказать, что вероятность появления т событий простей-
шего потока за время продолжительностью t определяется формулой
54 Раздел первый. Элементарная теория вероятностей и случайных процессов
Пуассона
Pt(rn) =рт =
(Xt)m • e-Af
m!
|К | Пример 1.33. Телефонная станция обслуживает 2000 абонентов. Веро-
ятность позвонить любому абоненту в течение часа равна 0,003. Какова
вероятность того, что в течение часа позвонят 5 абонентов?
Q Среднее число позвонивших в течение часа абонентов равно
2000 • 0.003 — 6 (а = пр = At). Стало быть, р?, = —=— ~ 0,13. •
Локальная и интегральная теоремы Муавра-Лапласа
В тех случаях, когда число испытаний п велико, а вероятность
р не близка к нулю (р 0, р 1), для вычисления биномиальных
вероятностей используют теоремы Муавра-Лапласа. Приведем только
их формулировки в силу сложности доказательства.
Теорема 1.6 (Локальная теорема Муавра-Лапласа). Если вероят-
ность р наступления события А в каждом испытании постоянна и отлична
от нуля и единицы, а число независимых испытаний достаточно велико,
то вероятность Pn(m) может быть вычислена по приближенной формуле
‘2
где х = ^. (1.36)
VWQ д/2тг \/npQ
Равенство (1.36) тем точнее, чем больше п.
Выражение
1 х
= ^(ж)
VZ7T
(1-37)
называется функцией Гаусса, а ее график — кривой вероятностей (см.
рис. 15).
Равенство (1.36) можно переписать в виде
Pn(m) « Д— <р(х), где х = т . (1.38)
y/npq y/npq
Г лава 1. Случайные события • 55
Для функции р(х) составлены таблицы значений (они находятся, как
правило, в так называемых «Приложениях» книг по теории вероятно-
стей см. приложение 1 на с. 284). Пользуясь таблицей, следует учиты-
вать, что:
а) функция четная, т. е. <Д—я) = <Дя);
б) при х 4 можно считать, что <Дж) = 0.
Функция Гаусса (1.37) будет подробнее рассмотрена в п. 2.7.
Пример 1.34. Вероятность попадания в мишень при одном выстреле
для данного стрелка равна 0,7. Найти вероятность того, что при 200
выстрелах мишень будет поражена 160 раз.
Q Здесь п = 200, р = 0,7, q = 0,3, т = 160. Применим форму-
лу (1.38). Имеем: y/npq = Д200 • 0,7 • 0,3 — >/42 ~ 6,48, следователь-
160-200-0,7 20 Ог.п ЛГ /о мНЧ полол
но, х = -------—------ = 7ГЛЦ ~ 3,09. Учитывая, что <ДЗ,09) « 0,0034,
л/42 6,48
получаем Р2ос(16О) ~ дта • 0,0034 « 0,0005. •
о,4о
В тех случаях, когда требуется вычислить вероятность того, что
в п независимых испытаниях событие А появится не менее к\ раз, но
не более раз, т. е. Рп(к\ тп кА) или Pn(-fci; fo), используют инте-
гральную теорему Муавра Лапласа (является частным случаем более
общей теоремы — центральной предельной теоремы).
56 Раздел первый. Элементарная теория вероятностей и случайных процессов
Теорема 1.7 (Интегральная теорема Муавра-Лапласа). Если ве-
роятность р наступления события А в каждом испытании постоянна и
отлична от нуля и единицы, то вероятность Рп(к\ т к%) может быть
найдена по приближенной формуле
Pn(ki < fc2) ~ 4^ [ е 2 dx, где х± = — —Пр , х^ = . Пр .
хГРх J \pvpq у/прд
(1.39)
Равенство (1.39) тем точнее, чем больше п.
Используя функцию Гаусса (1.37), равенство (1.39) можно записать
в виде
P„(A:i,A;2)
<г(ж)
dx.
Однако для упрощения вычислений, при использовании форму-
лы (1.39), вводят специальную функцию
Фо (т) = -J= jf е dt, (!-40)
о
называемую нормированной функцией Лапласа.
I -''_Г
Функция (1.40) нечетна (Фо(—ж) — J в 2 dt = [t = — z] =
у2тг о
Я? ^2
=-----= ] е 2 dz ~ — Фо(ж)); при х 5 можно считать, что Фо(^) =
v2tf о
= 0,5; график функции Фо(т) приведен на рис. 16.
Рис. 16
Глава 1. Случайные события 57
Выразим правую часть равенства (1.39) через функцию Лапла-
са (1.40):
о
j е 2 dt = Ф0(ж2) - Фо(жх).
о
Равенство (1.39) принимает вид
Рп(к! < т А2) = Фо(ж2) - Фо(^г),
А1 — пр к2 — пр
где Я] = —- , ж2 = — - . щ.ы;
y/npq y/npq
t
Эту формулу обычно используют на практике.
Наряду с нормированной функцией Лапласа (1.40) используют
функцию
X 2
ф(ж) = _1_ [ e~i: dt, (1.42)
уДл ./
—оо
называемую также функцией Лапласа. Для нее справедливо равенство
Ф(—х) + Ф(л) = 1; она связана с функцией Фо(®) формулой
Ф(т) = 0.5 + Фо(ж).
(1-43)
Имеются таблицы приближенных значений функций Фо(ж) и Ф(т) (ин-
теграл нс берется в элементарных функциях), которые приводятся в
большинстве учебников по теории вероятностей (см. также приложе-
ние 2 на с. 285).
Приближенную формулу для вычисления вероятности Pn(ki <
т А2) (1.39) можно записать в виде
Л„(А:1 hi. к2) = Ф(х2) - Ф(.Т1) = Фо(ж?) ~ Фо(жх),
где
к] — пр
y/npq
к2 — пр
Х2 = —
y/npq
(1.4 1)
Пример 1.35. Проверкой установлено, что цех в среднем выпускает
96% продукции высшего сорта. На базе приемщик проверяет 200 изде-
лий этого цеха. Если среди них окажется более 10 изделий не высшего
сорта, то вся партия изделий бракуется, т. е. возвращается в цех. Ка-
кова вероятность того, что партия будет принята?
58 Раздел первый. Элементарная теория вероятностей и случайных процессов
Q Здесь п = 200, р = 0,04 (вероятность негодного изделия), q =
= 0,96. Вероятность принятия всей партии, т. е. РгооСО тп10),
можно найти по формуле (1.44); здесь к\ = 0. = 10. Находим,
0 - 200 • 0,04 о оп 10 - 200 - 0,04
что х\ = — га —2,89, а?2 = , га 0,72,
у/200 • 0,04 • 0,96 ^/200 • 0,04 • 0,96
Р2оо(О < m < 10) = Фо(О,72) - Ф0(-2,89) = 0,26424 + 0,49807 =
= 0,7623. Заметим, что Ф(0,72) - Ф(-2,89) = 0,7642 - (1 - Ф(2,89)) =
= 0,7642 - (1 - 0,998074) = 0,7623. •
Замечание. С помощью функции Лапласа можно найти вероят-
ность отклонения относительной частоты — от вероятности рви не-
зависимых испытаниях. Имеет место формула
р{|^-р|«4=2ф«(е-\/1)'
где Е > 0 — некоторое число.
Q Из |^- — р е следует: —е
По формуле (1.39) получаем:
па
—----Р Е, пр — ПЕ Па пр + ПЕ.
Пример 1.36. Вероятность попадания в цель при одном выстреле рав-
на 0,6. Найти вероятность того, что при п = 1200 независимых выстре-
лах отклонение «частости» от вероятности по модулю не превышает
е = 0,05.
О Р1200
= 0,9996.
= 2Ф0(3,54) =
{|^
Глава 1. Случайные события 59
Упражнения
1. На лекции по теории вероятностей присутствуют 84 студента. Ка-
кова вероятность того, что среди них есть 2 студента, у которых
сегодня день рождения?
2. Вероятность брака при изготовлении некоторого изделия равна
0,02. Найти вероятность того, что среди 200 произведенных изде-
лий не более одного бракованного.
3. Найти вероятность того, что при подбрасывании монеты 100 раз
событие А — появление герба — наступит ровно 60 раз.
4. Найти такое число т, чтобы с вероятностью 0,95 можно было бы
утверждать, что среди 800 новорожденных более т девочек. Счи-
тать, что вероятность рождения девочки равна 0,485.
Глава 2
Случайные величины
2.1. Понятие случайной величины. Закон
распределения случайной величины
Одним из важнейших понятий теории вероятностей (наряду со слу-
чайным событием и вероятностью) является понятие случайной вели-
чины.
|^| Под случайной величиной понимают величину, которая в результа-
те опыта принимает то или иное значение, причем неизвестно заранее,
какое именно.
Случайные величины (сокращенно: с. в.) обозначаются прописны-
ми латинскими буквами X. Y, Z.... (или строчными греческими буква-
ми £ (кси), г] (эта), в (тэта), гр (пси) и т. д.), а принимаемые ими значения
соответственно малыми буквами х±, Х2, - • -, yi, у?, уз, • • • •
Примерами с. в. могут служить: 1) X число очков, появляющих-
ся при бросании игральной кости; 2) Y — число выстрелов до первого
попадания в цель; 3) Z — время безотказной работы прибора и т. п.
(рост человека, курс доллара, количество бракованных деталей в пар-
тии, температура воздуха, выигрыш игрока, координата точки при слу-
чайном выборе ее на [0; 1], прибыль фирмы, ...).
|н\| Случайная величина, принимающая конечное или счетное множе-
ство значений, называется дискретной (сокращенно: д. с. в.).
Если же множество возможных значений с. в. несчетно, то такая
величина называется непрерывной (сокращенно: и. с. в.).
То есть д. с. в. принимает отдельные изолированные друг от дру-
га значения, а н. с. в. может принимать любые значения из некоторого
промежутка (например, значения на отрезке, на всей числовой прямой
и т. д.). Случайные величины X и Y (примеры 1) и 2)) являются дис-
кретными. С. в. Z (пример 3)) является непрерывной: ее возможные
значения принадлежат промежутку [0, t), где t 0, правая граница
не определена (теоретически I = +оо). Отметим, что рассматриваются
также с. в. смешанного типа.
Дадим теперь строгое определение с. в., исходя из теоретико-мно-
жественной трактовки основных понятий теории вероятностей.
Глава 2. Случайные величины • 61
Случайной величиной X называется числовая функция, опреде-
ленная на пространстве элементарных событий Q, которая каждому
элементарному событию w ставит в соответствие число X(w), т. е.
X = X(w), w G Q (или X = f(w)).
Пример. Опыт состоит в бросании монеты 2 раза. На ПЭС О =
= w-21 W3, W4}, где = ГГ. ы? = ГР. w:< — РГ. w4 = РР, можно
рассмотреть с. в. X — число появлений герба. С. в. X является функ-
цией от элементарного события wp. Х(гщ) = 2, Х(и>2) = 1, Х(ггз) = 1.
X(w4) = 0; X — д. с. в. со значениями х4 = 0, Х2 = 1, хз = 2.
Отметим, что если множество Л койечно или счетно, то случай-
ной величиной является любая функция, определенная на Л. В общем
случае функция Х(ш) должна быть такова, чтобы для любых х G Ж
событие А = {w : X(w) < х} принадлежало ст-алгебре множеств S
и, значит, для любого такого события была определена вероятность
Р(А) = Р{Х < х).
Для полного описания с. в. недостаточно лишь знания ее возмож-
ных значений; необходимо еще знать вероятности этих значений.
Любое правило (таблица, функция, график), позволяющее нахо-
дить вероятности произвольных событий А С S (S — о-апгебра собы-
тий пространства О), в частности, указывающее вероятности отдель-
ных значений случайной величины или множества этих значений, на-
зывается законом распределения случайной величины (или просто: рас-
пределением) . Про с. в. говорят, что «она подчиняется данному закону
распределения»:
2.2. Закон распределения дискретной случайной
величины. Многоугольник оаспределения
Пусть X — д. с. в., которая принимает значения х4, Х2, х-з,..., хп,...
(множество этих значений конечно или счетно) с некоторой вероят-
ностью р^, где i = 1.2.3....п..... Закон распределения д. с. в. удобно
задавать с помощью формулы р, = Р{Х = хД, г = 1,2,3,... , п,...,
определяющей вероятность того, что в результате опыта с. в. X примет
значение Xi. Для д. с. в. X закон распределения может быть задан в
виде таблицы распределения,:
х Х1 «2
р Р1 Р2 Рп
62 Раздел первый. Элементарная теория вероятностей и случайных процессов
где первая строка содержит все возможные значения (обычно в порядке
возрастания) с. в., а вторая — их вероятности. Такую таблицу называ-
ют рядом распределения.
Так как события {X = жД, {X = х%} ... несовместны и образуют
полную группу, то сумма их вероятностей равна единице (см. п. 1.12),
т.е. = !
г
Закон распределения д. с. в. можно задать графически, если на оси
абсцисс отложить возможные значения с. в., а на оси ординат — вероят-
ности этих значений. Ломаную, соединяющую последовательно точки
(ai,pi), (ж2,Рг)х ••• называют многоугольником (или полигоном) рас-
пределения (см. рис. 17).
Теперь можно дать более точное определение д. с. в.
Случайная величина X дискретна, если существует конечное или
счетное множество чисел Ж1, х%, ...таких, что Р{Х = Х{} = pi > О
(г = 1,2,...) и pi +р2 + Рз + ••• = 1-
Определим математические операции над дискретными с. в.
Суммой (разностью, произведением) д. с. в. X, принимающей зна-
чения Xi с вероятностями pi = Р{Х = Xi},i = 1,2,..., п и д. с. в. Y. при-
нимающей значения у3 с вероятностями pj — P{Y = y:i}, j = 1,2,... ,т,
называется д. с. в. Z = X + Y (Z = X — У, Z = X • У), принимающая
значения zij = Xi + у3 (z-tj = Xi — yj, Zij = Xi уj) с вероятностями
Pij = P{X — Xi, Y = уj} для всех указанных значений г и j. В случае
совпадения некоторых сумм ж, + у3 (разностей Xi — yj, произведений
Xiyj) соответствующие вероятности складываются.
Произведение д. с. в. на число с называется д. с. в. сХ, принимающая
значения cxj с вероятностями pi = Р{Х = жД.
Две д. с. в. X и У называются независимыми, если события
{X = Xi} = Ai и {У = yj} = Bj независимы для любых i = 1,2,... ,п;
Глава 2. Случайные величины * 63
j — 1,2,... ,т, т. е.
Р{Х = Xi-Y = У]} = Р{Х = Xi} • P{Y = Vj}.
В противном случае с. в. называются зависимыми. Несколько с. в. на-
зываются взаимно независимыми, если закон распределения любой из
них не зависит от того, какие возможные значения приняли остальные
величины.
Пример 2.1. В урне 8 шаров, из которых 5 белых, остальные — чер-
ные. Из нее вынимают наудачу 3 шара. Найти закон распределения
числа белых шаров в выборке.
О Возможные значения с. в. X — числа белых шаров в выборке есть
xi = О, Х‘2 = 1, хз = 2, х$ = 3. Вероятности их соответственно будут
- Р(Х = (В = ' С% = 1 „ - PfX = 11 = ELJZi = И
и 6} 5g, Р2 "М 1} 5g,
8 8
рз = , Pi = . Закон распределения запишем в виде таблицы.
Ом Ом
х 0 1 2 3
р 1 56 15 56 30 56 10 56
/тг __ 1 . 15 । 30 . 10 ___1 \
(Контроль: - 56 + 56 + 56 + 56 - !•)
Упражнения
1. Монета бросается 4 раза. Построить многоугольник распределения
с. в. X — числа выпадений герба.
2. Вероятность сдачи экзамена первым студентом равна 0,6, а вто-
рым — 0,9. Составить ряд распределения с. в. X — числа студен-
тов, успешно сдавших экзамен в случае, когда: а) экзамены пере-
сдавать нельзя; б) экзамен можно один раз пересдать.
64 Раздел первый. Элементарная теория вероятностей и случайных процессов
2.3. Функция распределения и ее свойства. Функция
распределения дискретной случайной величины
Очевидно, ряд распределения с. в, может быть построен только для
д. с. в.; для н. с. в. нельзя даже перечислить все ее возможные значения.
Кроме того, как увидим позже (п. 2.3, 2.4), вероятность каждого отдель-
но взятого значения н. с. в. равна нулю! Представим себе вероятность
того, что рост мужчины — н. с. в. — точно равен а/З = 1,7320508 ... ме-
тров; купленная нами лампа проработает — н. с. в. — ровно 900 часов;
.... Удивительно интересный факт: событие возможное, но имеет ну-
левую вероятность.
Для характеристики поведения н. с. в. целесообразно использовать
вероятность события {А' < х} (а не {X = ж}), где х — некоторое дей-
ствительное число. С точки зрения практики нас мало интересует собы-
тие, состоящее, например, в том, что лампочка проработает ровно 900
часов, т. е. X = 900. Более важным является событие вида {X < 900}
(или (X > 900}). Такое событие имеет ненулевую вероятность; при из-
менении х вероятность события {X < х} в общем случае будет менять-
ся. Следовательно, вероятность Р{Х < ж} является функцией от х.
Универсальным способом задания закона распределения вероятно-
стей, пригодным как для дискретных, так и для непрерывных случай-
ных величин, является ее функция распределения, обозначаемая Fx(ar)
(или просто F(®), без индекса, если ясно, о какой с. в. идет речь).
Функцией распределения с. в. X называется функция F(x), которая
для любого числа х € R равна вероятности события {X < х}.
Таким образом, по определению
F(x) = Р{Х < х} т. е. F(s) = P{w : X(w) < х}.
(2-1)
Функцию F(t) называют также интегральной функцией распределения.
Геометрически равенство (2.1) можно истолковать так: F(t) есть
вероятность того, что с. в. X примет значение, которое изображается
на числовой оси точкой, лежащей левее точки х, т. е. случайная точка
X попадет в интервал (—оо,ж), см. рис. 18.
г/////>
Рис. 18
Функция распределения обладает следующими свойствами:
Глава 2. Случайные величины 65
1. F(x) ограничена, т. е.
О F(x) 1.
2. F(x) — неубывающая функция на R, т. е. если х2 > ,7j, то
F(x2) > Г(ж1).
3. F(x) обращает в ноль на минус бесконечности и равна единице в
плюс бесконечности, т. е.
F(—оо) = 0, F(Too) = 1.
4. Вероятность попадания с. в. X в промежуток [а, Ь) равна прираще-
нию ее функции распределения на этом промежутке, т. е.
Р{а^Х <b} = F(b) — F(a). (2.2)
5. F(x) непрерывна слева, т. е.
lim F(x) = F(xo).
х—>XQ — О
Q 1. Первое свойство следует из определения (2.1) и свойств вероят-
ности (п. 1.11, 1.12).
2. Пусть А = {X < Ж1}, В = {X < Х2}. Если xi < :г.2- то собы-
тие А влечет событие В (п. 1.4), т. е. А С В. Но тогда согласно свой-
ству 4 (п. 1.12), имеем Р(А) Р(В), т. е. Р{Х < xi} С Р{Х < х2} или
F(X1) F(x2).
Геометрически свойство 2 очевидно: при перемещении точки х
вправо по числовой оси вероятность попадания случайной точки X в
интервал (—оо, х) не может уменьшаться.
3. Третье свойство вытекает непосредственно из того, что
{X < —оо} — 0, а {X < Too} = Q; согласно свойствам вероятности
(п. 1.11, 1.12), имеем: F(—00) = Р{Х < —оо} = Р{&} = 0, F(Too) =
= F{X < Too} = F{Q} = 1.
4. Так как а < Ъ, то очевидно, что {X < 6} = {X < а}т{а X < Ь}
(это хорошо видно на рис. 19).
Так как слагаемые в правой части — несовместные события, то
по теореме сложения вероятностей (п. 1.11) получаем Р{Х < Ь} =
= Р{Х < а} Т Р{а X < Ь}. Отсюда следует Р{п, X < Ь} =
= Р{Х < Ь} - Р{Х < а} = F(b) - F(a).
5. Свойство 5 проиллюстрируем далее на примере 2.2.
66 Раздел первый. Элементарная теория вероятностей и случайных процессов
___________{£<4______________
///////////////Д<ХХХХХ«ХХХХХХ)|---—
Ж yb X
{.¥ < а} {а X < 6}
Рис. 19
Всякая функция Е(т), обладающая свойствами 1 3, 5, может быть
функцией распределения некоторой случайной величины.
Заметим, что формула (2.2) (свойство 4) справедлива и для н.с. в.,
и для д. с. в.
С помощью функции распределения можно вычислить вероятность
события {X х}:
Р{Х х} = 1 - F(x). (2.3)
Можно дать более точное определение н. с. в.
Случайную величину X называют непрерывной, если ее функция
распределения непрерывна в любой точке и дифференцируема всюду,
кроме, может быть, отдельных точек.
Используя свойство 4 можно показать, что «вероятность того, что
н. с. в. X примет заранее указанное определенное значение а, равна ну-
лю».
Действительно, применим формулу (2.2) к промежутку [а, х):
Р{а X < х} — F(x)—F(a). Будем неограниченно приближать точку ж
к а. Так как функция F(x) непрерывна в точке а, то lim F(x) = F(a). В
х-^а
пределе получим Р{Х = а} = lim F(x) — F(a) = F(a) — F(a) = 0. Если
. x—
функция Е(ж) везде непрерывна, то вероятность каждого отдельного
значения с. в. равна нулю.
Следовательно, для н. с. в. справедливы равенства
Р{а х < Ь} = Р{а < х < b} = Р{а х Ъ} = Р{Х G (а, Ь]}.
Действительно,
Р{а х < Ь} — Р{Х = а} + Р{а < х < Ь} — Р{а < х < Ь}
и т. д.
Функция распределения д. с. в. имеет вид
F(®) = Ц Рд
(2-4)
Здесь суммирование ведется по всем i, для которых xi < х. Равен-
ство (2.4) непосредственно вытекает из определения (2.1).
Глава 2. Случайные величины * 67
Пример 2.2. По условию примера 2.1 (п. 2.2) найти функцию распре-
деления F(s) и построить ее график.
Q Будем задавать различные значения х и находить для них F(x) =
= Р{Х < х}:
1. Если х 0, то, очевидно, F(x) = F{X < 0} = 0;
2. Если 0 < х 1, то F(x) = Р{Х < т} = Р{Х = 0} =
3. Если 1 < х < 2, то Fix) = Р{Х = 0} + Р{Х = 1} = ;
' ' 1 J 1 ' 56 56 56
4. Если 2 < х < 3, то F(x) = Р{Х = 0} + Р{Х = 1} + Р{Х = 2} =
1 15 , 30 46
56 56 56 56’
5. Если 3 < х, то F(x) = Р{Х = 0} + Р{Х = 1} + F{X = 2} + F{X =
= 3} = g + || = l.
J 56 56
Итак,
если х 0;
если 0 < х 1;
если 1 < х С 2; (2-5)
если 2 < х С 3;
если 3 < х.
0,
1
56 ’
16 '
56 ’
46
56 ’
1,
F(a?) = <
Строим график F(t), рис. 20.
з*
скачками рг в точках arj, функция, «непрерывная слева» (при подходе
к точке разрыва слева функция F(x) сохраняет значение). Ее график
имеет ступенчатый вид.
68 Раздел первый. Элементарная теория вероятностей и случайных процессов
Отметим, что, пользуясь равенством (2.4), функцию распределения
можно сразу записать в виде (2.5)
'0, 1 56 ’ х ; 0 < $ 0,
С х 1,
Д(т) = < 1 , 15 56 56 ’ 1 < С х $ 2,
1 , 15 , 30 56 56 56 ’ 1 , 15 , 30 , 10 156 56 56 56 ’ 2 < 3 < С х С х. 3,
Упражнения
1. Два стрелка делают по одному выстрелу в одну мишень. Вероят-
ность попадания для первого стрелка равна 0.6. а для второго —
0,8. Найти и построить функцию распределения с. в. X — числа
попаданий в мишень.
2. Убедиться, что функция
Г(ж) =
Г°,
(1 -е
если х 0,
если х > 0
является функцией распределения некоторой случайной величины.
Найти Р{0 х < 1} и построить график F(x).
3. Дана функция распределения
Ду (ж) = <
0,
ж2
2
при х 0,
при 0 < х л/2,
при х > д/2.
Найти вероятность того, что в результате четырех испытаний с. в.
X трижды примет значение, принадлежащее интервалу (0; 1).
Глава 2. Случайные величины 69
2.4. Плотность распределения и ее свойства
Важнейшей характеристикой непрерывной случайной величины
(помимо функции распределения) является плотность распределения
вероятностей. Напомним (см. п. 2.3), что: с. в. X называется непрерыв-
ной, если ее функция распределения непрерывна и дифференцируема
всюду, кроме, быть может, отдельных точек.
Плотностью распределения вероятностей (плотностью распреде-
ления, плотностью вероятностей или просто плотностью) непрерыв-
ной случайной величины X называется производная ее функции рас-
пределения.
Обозначается плотность распределения н.с. в. X через /%(ж) (или
рх(х)) или просто f(x) (или р(х)), если ясно о какой с. в. идет речь.
Таким образом, по определению
f(x) = F'(x).
(2-6)
Функцию f(x) называют также дифференциальной функцией распреде-
ления-, она является одной из форм закона распределения случайной
величины, существует только для непрерывных случайных величин.
Установим вероятностный смысл плотности распределения. Из
определения производной следует
/и) =
lim
Дх—>0
XF(x)
lim
Дх—>0
F(x + Дж) — Р(ж)
Дж
Но согласно формуле (2.2), F(x + Дж) - /?(ж) = Р{х X < ж + Дж}.
Р | х X <С х Ч- Хх Т
Отношение -----——т----------- представляет собой среднюю вероят-
Дж
ность, которая приходится на единицу длины участка [ж, ж + Дж), т. е.
среднюю плотность распределения вероятности. Тогда
/(«)
lim
Дх>0
Р{х X < ж + Дж}
Дж
(2-7)
т. е. плотность распределения есть предел отношения вероятности по-
падания с. в. в промежуток [ж; ж + Дж) к длине Дж этого промежутка,
когда Дж стремится к нулю. Из равенства (2.7) следует, что
Р{х X < ж + Дж} « /(ж)Дж.
То есть плотность вероятности определяется как функция f(x), удо-
влетворяющая условию Р{х eZ X < х + dx] ~ f(x)dx; выражение
/(ж) dx называется элементом вероятности.
70 Раздел первый. Элементарная теория вероятностей и случайных процессов
Отметим, что плотность /(ж) аналогична таким понятиям, как
плотность распределения масс на оси абсцисс или плотность тока в
теории электричества.
Плотность распределения обладает следующими свойствами:
1. f(x) неотрицательная, т. е.
/(т) 0.
2. Вероятность попадания н. с. в. в промежуток [а; 6] равна определен-
ному интегралу от ее плотности в пределах от а до 6, т. е.
ь
Р{а^Х ^b} = J f(x) dx. (2.8)
а
3. Функция распределения н. с. в. может быть выражена через ее
плотность вероятности по формуле
X
F(x) = У f(t)dt.
—ОО
4. Условие нормировки: несобственный интеграл от плотности веро-
ятности н.с. в. в бесконечных пределах равен единице, т. е.
ОО
У f(x)dx = l.
—ОО
□ 1. Плотность распределения /(ж) — неотрицательная функция:
F(x) — неубывающая функция (п. 2.3), следовательно, F'(x) 0, т. е.
/(а) 0. Это означает, что график плотности /(ж), называемый кривой
распределения, не ниже оси абсцисс; плотность может принимать сколь
угодно большие значения.
2. Так как F(x) есть первообразная для плотности /(ж), то по фор-
муле Ньютона- Лейбница имеем
ь
У f(x)dx = F(b)-F(a).
а
Отсюда в силу свойства 4 функции распределения (формула (2.2)), по-
лучаем
ь
У f(x)dx = Р{а^Х ^Ь}.
а
Глава 2. Случайные величины • 71
Геометрически эта вероятность равна площади S фигуры, ограничен-
ной сверху кривой распределения /(ж) и опирающейся на отрезок [о; 6]
(рис. 21).
3. Используя свойство 2, получаем:
F(x) = Р{Х < ж} = Р{—ое
(буква t для ясности).
4. Полагая в формуле (2.8) а = —оо и b = +оо, получаем достовер-
ное событие X С (—оо;+оо). Следовательно,
+оо
f(x) dx = Р{—оо < X < +оо} = Р{П} = 1.
—сю
Геометрически свойство нормировки означает, что площадь фигуры,
ограниченной кривой распределения f(x) и осью абсцисс, равна еди-
нице. И
Можно дать такое определение непрерывной случайной величины:
случайная величина X называется непрерывной, если существует не-
отрицательная функция / (ж) такая, что' при любом ж функцию распре-
деления Р(ж) можно представить в виде
/(t)dt.
А затем получить, что /(ж) = F'(x). Отсюда следует, что Р(ж) и /(ж)
являются эквивалентными обобщающими характеристиками с. в. X.
72 Раздел первый. Элементарная теория вероятностей и случайных процессов
Как отмечалось ранее (п. 2.3) для н. с. в. X, вероятность события
{X = с}, где с — число, равна нулю. Действительно.
Р{Х = с} = Р{с X
f(x) dx = 0.
Отсюда также следует, что
Р{Х G [«; Ь)} = Р{Х G [а;Ь]} = Р{Х G (а; 6)}.
Пример 2.3. Плотность распределения с. в. X задана функцией/(ж) —
— —z-. Найти значение параметра п.
1 + ж2
О Согласно свойству 4 плотности, имеем
+оо
[ TT^dx = 1'
J 1 + xz
—оо
d
т. е. a lim [ —dx = 1,
<!^+оо J ] _|_
т.е. a- lim arctg.T|d= 1
d—>+оо 'С
с—> —оо
или а = 1 и, наконец, получаем атг = 1, т. е. а = ~ .
Упражнения
1. Случайная величина X задана функцией распределения:
{О, при х С — 1,
а(х + I)2, при — 1 < х 2,
1, при х > 2.
Найти значение а, построить графики F(x) и /(ж).
2. Кривая распределения н. с. в. X имеет вид, указанный на рис. 22.
Найти выражение для j'x(x'), функцию распределения F% (х), веро-
ятность события {х 6 i 1)
Глава 2. Случайные величины 73
3.
Является ли плотностью распределения некоторой с. в. каждая из
следующих функций:
а) /(ж) = ,л Х ?ч ПРИ е (—оо;+оо);
7Г(1 + ж)
'1
б) /(«) = 2 ’
О,
аж2,
в) /(ж) =
при ж G (—1; 1],
при ж (—1; 1];
при ж < 0 и ж > 2,
при 0 ж 2.
2.5. Числовые характеристики случайных величин
Закон распределения полностью характеризует случайную величи-
ну. Однако при решении многих практических задач достаточно знать
лишь некоторые числовые параметры, характеризующие отдельные
существенные свойства (черты) закона распределения с. в. Такие чи-
сла принято называть числовыми характеристиками с. в.
Важнейшими среди них являются характеристики положения: ма-
тематическое ожидание (центр распределения с. в.), мода, медиана; ха-
рактеристики рассеяния: дисперсия (отклонение значений с. в. от ее
центра), среднее квадратическое отклонение.
Математическое ожидание случайной величины
Математическим ожиданием (или средним значением) д. с. в. X,
имеющей закон распределения pi = Р{Х — жД, i = 1,2,3,..., п, назы-
вается число, равное сумме произведений всех ее значений на соответ-
ствующие им вероятности.
74 « Раздел первый. Элементарная теория вероятностей и случайных процессов
Математическое ожидание (сокращенно: м. о.) обозначается через
MX (или: М[А'], М(Х), ЕХ. тх. ах).
Таким образом, по определению
п
MX = У^ж, -рг.
i=l
(2-9)
Если число возможных значений с. в. X бесконечно (счетно), то
оо
MX = ‘Pi,
i= 1
(2.10)
причем ряд в правой части предполагается сходящимся (в противном
случае с. в. X не имеет м. о.).
Формулы (2.9) и (2.10) можно записать в виде MX = E'riP«-
Вероятностный смысл математического ожидания состоит в том,
п
что оно является средним значением с. в. Действительно, т. к. Е Pi —
г=1
ТО
п Е хгРг
MX — XiPi — — — -- ^среднее’
i=1 Е Pi
i=l
Математическим ожиданием н. с. в. X с плотностью вероятности
/'(ж), называется число
MX =
ОО
f х f(x) dx.
(2.П)
Интеграл в правой части равенства (2.11) предполагается абсолютно
сходящимся, т. е-
[ |ж| /(ж) dx < сю
—ОО
(в противном случае н.с. в. X не имеет м. о.).
Формула (2.11) является интегральным аналогом формулы (2.9).
Заменяя в ней «прыгающий» аргумент жг на непрерывно меняющий-
ся ж, вероятность р^ — элементом вероятности f(x)dx (f(x)dx =
= F'(x)dx = dF(x) « XF(x) = Р(ж + Дж) — F(x) = P{x < X < ж + Дж}),
получим равенство (2.11).
Глава 2. Случайные величины 75
Отметим, что MX имеет ту же размерность, что и с. в. X.
Свойства математического ожидания.
1. Математическое ожидание постоянной равно самой этой постоян-
ной, т. е.
Мс = с.
2. Постоянный множитель выносится за знак м.о., т. е.
М(сХ) = сМХ.
3. М. о. суммы с. в. равно сумме их м. о., т. е.
М (X + У) = MX + MY.
4. М. о. отклонения с. в. от ее м. о. равно нулю, т. е.
М(Х - MX) == 0.
5. М.о. произведения независимых с.в. равно произведению их м.о.,
т. е. если X и У независимы, то
М(Х У) = MX MY.
Q 1. Постоянную с можно рассматривать как д. с. в. X, принимающую
лишь одно значение с вероятностью 1. Поэтому Мс = с Р{Х — с} =
= с • 1 — с.
2. Так как д. с. в. сХ принимает значения ex, (i — 1,п) с вероятно-
стями Pi, то
п п
МсХ = У cxi • pi = с У XiPi = сМХ.
г—1 г=1
3. Так как д. с. в. X + У принимает значения х.[ + yj с вероятностями
Pij = P{Xi =Xi,Y = yj}, то
n т пт пт
м (х+у) = у 52 +yj)pij = 52 52 xipii + 52 52узр^ =
г=1 j= I £=1 .7=1 ?=1 j=l
пт т п п т
=52ж* 52pi>+52 Уз Ylpi3 = YlXi'pi+^2y3'p3 = мх+MY-
г=1 j=l j=l i=l i=l j=l
При доказательстве воспользовались, в частности, тем, что
т п
'^pij=pi И ^2pij=pj-
г=1
76 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Действительно: так как
5?Х - Xi-Y = yj} = {X = .тД £{У = уД = {X = хД • Q = {X = ЖД.
J=1 J—1
то
Pi = Р{Х = хг} = Р(Е{Х = Y = %}) =
т т
= ^2р{х = Хг,У = уД = 52^';
j=i j=i
аналогично получаем
п
Рз = У^РЦ-
i=l
Свойство 3 распространяется на произвольное конечное число слагае-
мых.
4. Согласно свойствам 1 и 3, имеем: М(Х—MX) — МХ-М(МХ) =
= MX — MX = 0. Отметим, что разность X — MX (или X — тх) назы-
вается отклонением с. в. X от ее м. о. MX и обозначается символом X:
Х = Х-МХ.
Эта с. в. X называется также центрированной с. в.
5. Так как с. в. X и У независимы, то pij — Р{Х — xp,Y = уД =
= Р{Х = Xi) Р{У = уД = pi • pj. Следовательно,
п т
MXY = 5252 х*уз р{х = Xj;Y = yj} =
1=1 7 = 1 ' * Z
J Pij
n m n m
52 52 Xiy3 = Xj) P{Y = yj], = £ Xipt ^PjPj = MX MY.
i= 1 ’=1 ' p. '' p3 ' i=1 J=1
Свойства м. о., доказанные для д. с. в., остаются справедливы и для
непрерывных с. в. Так, например,
cxf (ж)dx =
= сМХ.
Глава 2. Случайные величины 77
Пример 2.4. В лотерее имеется 1000 билетов, из них выигрышных: 10
по 500 руб. 50 по 50 руб, 100.no 10 руб, 150 по 1 руб. Найти математи-
ческое ожидание выигрыша на один билет.
О Ряд распределения с. в. X — суммы выигрыша на один билет таков:
X 500 50 10 1 0
p 0,01 0,05 0,1 0,15. 0,69
5
(Контроль: 52 ft = 1.) Находим MX:
MX = 500 • 0Д1 + 50 • 0,05 + 10 0.1 + 1 • 0,15 + 0 • 0,69 = 8,65 руб.
Дисперсия
а
Дисперсией (рассеянием) с. в. X называется математическое ожи-
дание квадрата ее отклонения от своего математического ожидания.
Обозначается дисперсия через DX (или Л[А'], D\, D(X)). Таким
образом, по определению
DX = М(Х - MX)2,
(2.12)
или DX = MX2, или DX = М(Х — т.\)2. Дисперсия характеризует
разброс значений с. в. X относительно ее м. о. Из определения диспер-
сии следуют формулы для ее вычисления:
£>Х = У~^(^ — MX)2 -р^—дляд. с. в. X, (2.13)
i
|-оо
DX = (х — MX)2 f(x) dx—длян.с. в. X. (2-14)
—оо
На практике дисперсию с. в. удобно находить по формуле
DX = MX2 - (MX)2. (2.15)
Она получается из формулы (2.12): DX = М(Х2 —2Х-МХ + (МХ)2) =
= MX2 - М(2Х • MX) + М(МХ)2 = MX2 - 2МХ • MX + (MX)2 =
= MX2 - (MX)2.
78 Раздел первый. Элементарная теория вероятностей и случайных процессов
Это позволяет записать формулы для ее вычисления ((2.13) и
(2.14)) в другом виде:
DX = £ ж2 • - (MX)2, (2.16)
г
-Ьоо
DX = J х2 /(ж) dx - (MX)2. (2.17)
—ОО
Свойства дисперсии.
1. Дисперсия постоянной равна нулю. т. е.
De — 0.
2. Постоянный множитель можно выносить за знак дисперсии, возве-
дя его в квадрат, т. е.
DcX = с2 DX.
3. Дисперсия суммы независимых с. в. равна сумме их дисперсий, т. е.
если X и У независимы, то
О(Х + У) = DX + DY.
4. Дисперсия с. в. не изменится, если к этой с. в. прибавить постоян-
ную, т. е.
D(X + с) = DX.
5. Если с. в. X и У независимы, то
О(ХУ) = MX2 МУ2 - (MX)2 (МУ)2.
□ 1. De = М(с - Мс)2 = М(с - с)2 = M0 = U.
2. DcX = М(сХ -М(сХ))2 = М(сХ-сМХ)2 = М(с2(Х-МХ)2) =
= с2М(Х - MX)2 = e?DX.
3. Используя формулу (2.15), получаем D(X + У) = М(Х + У)2 —
-(М(Х + У))2 = МХ2 + 2МХУ + МУ2-(МХ)2-2МХ-МУ-(,МУ)2 =
= MX2 - (MX)2 + МУ2 - (MY)2 + 2(МХУ - MX • МУ) = DX + DY +
+ 2(МХ • МУ - MX • МУ) = DX + DY.
Отметим, что если с. в. X и У зависимы, то
D(X + У) = DX + DY + 2М((Х - MX) (У - МУ)).
4. D(c + X) = М((с + X) - М(с + X))2 = М(Х - MX)2 = DX.
Доказательство свойства 5 не приводим.
Свойства дисперсии, доказанные выше для дискретных случайных
величин, остаются справедливыми и для непрерывных с. в.
Глава 2. Случайные величины • 79
Среднее квадратическое отклонение
Дисперсия DX имеет размерность квадрата с. в. X, что в сравни-
тельных целях неудобно. Когда желательно, чтобы оценка разброса
(рассеяния) имела размерность с. в., используют еще одну числовую
характеристику — среднее квадратическое отклонение (сокращенно:
с. к. о.).
Средним квадратическим, отклонением или стандартным откло-
нением с. в. X называется квадратный корень из ее дисперсии, обозна-
чают через ах (или аХ, а). Таким образом, по определению
ах = у/DX.
(2-18)
Из свойств дисперсии вытекают соответствующие свойства с. к. о.:
ас = 0, асх = |c|ct.y, а (с + X) = ах-
Для изучения свойств случайного явления, независящих от выбо-
ра масштаба измерения и положения центра группирования, исходную
случайную величину X приводят к некоторому стандартному виду: ее
центрируют, т. е. записывают разность X — MX (геометрически озна-
чает, что начало координат переносится в точку с абсциссой, равной
м. о.), затем делят на с. к. о. сгд-.
„ X - MX Я
Случайную величину Z — ----—---- называют стандартной слу-
чайной величиной. Ее м. о. равно 0, а дисперсия равна 1. Действительно,
MZ = М ах1*) = Ъ^М(Х ~ МХ>> = °’
DZ = -^Г(Х - MX) = = =
4- <т2- DX
То есть Z — центрированная (MZ — 0) и нормированная (DZ = 1)
случайная величина.
Пример 2.5. Д. с. в. X задана рядом распределения.
х -1 0 1 2
р 0,2 0,1 0,3 0,4
Найти MX. DX, ах-
Q Используем формулы (2.9), (2.13), (2.18): MX = —1 0,2 + 0 0,1 +
+ 1-0,3+2-0,4 = 0,9; DX = (-1-0,9)2-0,2+(0-0,9)2-0,1 + (1-0,9)2-0,3 +
+ (2—0,9)2-0,4 — 1,29 (или, используя формулу (2.16). DX = (—I)2-0,2+
+ О2 0,1 + I2 • 0,3 + 22 • 0,4 - (0.9)2 = 1,29); ах = \/Ё29 и 1,14. •
80 Раздел первый. Элементарная теория вероятностей и случайных процессов
Мода и медиана. Моменты случайных величин. Асимметрия
и эксцесс. Квантили
Модой д. с. в. X называется ее значение, принимаемое с наибольшей
вероятностью по сравнению с двумя соседними значениями, обознача-
ется через MqX. Для н. с. в. М$Х — точка максимума (локального)
плотности /а (ж).
Если мода единственна, то распределение с. в. называется унимо-
дальным, в противном случае — полимодальным (рис. 23).
/(*)
Рис. 23
х
Медианой МеХ н. с. в. X называется такое ее значение хр, для ко-
торого
Р{Х < хр} = Р{Х > хр} = 1, (2.19)
£
т. е. одинаково вероятно, окажется ли с. в. X меньше хр или больше хр
(рис. 23).
С помощью функции распределения F(x) равенство (2.19) можно
записать в виде F(MeX) = 1 — F(MeX). Отсюда F(M(X) — | .
Для д. с. в. медиана обычно не определяется.
Математическое ожидание и дисперсия являются частными случа-
ями следующих более общих понятий — моментов с. в.
Начальным моментом порядка к с. в. X называется м. о. fc-й сте-
пени этой величины, обозначается через а^.
Таким образом, по определению
ak = М(Хк).
Для д. с. в. начальный момент выражается суммой:
а к = 52 ’рг’
i
Глава 2. Случайные величины 81
а для н. с. в. интегралом:
«fc =
оо
j хк f(x) dx.
В частности, оц = MX, т.е. начальный момент 1-го порядка есть м.о.
Центральным моментом порядка к с. в. X называется м. о. вели-
чины (X — МХ)к, обозначается через рк.
Таким образом, по определению
Рк = М(Х - МХ)к.
В частности, р2 = DX, т. е. центральный момент 2-го порядка есть
дисперсия; щ = М(X — MX) = 0 (см. свойство 4 м.о.).
Для д. с. в.:
Рк = 52 (^ ~ МХ)к - pi,
i
а для и. с. в.:
ос
рк = j (х ~ МХ)к f(x) dx.
—оо
Центральные моменты могут быть выражены через начальные
моменты. Так, р^ = DX = се? — си2 (действительно: р2 = DX =
= MX2 — (MX)2 — oi2 — «1); Р'а = «з — 3ai«2 + 2а3, д4 = а4 — 4aioi3 +
+ — Зо4 и т. д.
Среди моментов высших порядков особое значение имеют цен-
тральные моменты 3-го и 4-го порядков, называемых соответственно
коэффициентами асимметрии и эксцесса.
Коэффициентом, асимметрии («скошенности») А с. в. X называ-
ется величина
. РЗ _ М(Х - MX)3
А — — „
(ПХ)2
Если А > 0, то кривая распределения более полога справа от МдХ
(рис. 24).
Если А < 0, то кривая распределения более полога слева от MqX
(рис. 25).
Коэффициентом эксцесса («островершинности») Е с. в. X назы-
вается величина
Д4 М(Х - MX)4
П/ — —---о = --------------о.
4 (DXf
82 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Величина Е характеризует островершинность или плосковершин-
ность распределения. Для нормального закона распределения (см.
п. 2.7) А = 0 и Е = 0; остальные распределения сравниваются с нор-
мальным: если Е > 0 — более островершинные, а распределения «плос-
ковершинные» имеют Е < 0 (рис. 26).
Рис. 26
Кроме рассмотренных выше числовых характеристик с. в., в при-
ложениях используются так называемые квантили.
Квантилью уровня р с. в. X называется решение уравнения
Fx{xp) = р,
где р — некоторое число, 0 < р < 1.
Квантили so,25> ^0,5 и ®о,75 имеют свои названия: нижняя квартиль,
медиана (МеХ = жод)- верхняя квартиль соответственно. Они делят
числовую прямую на 4 части, вероятности попадания в которые равны
0,25 (рис. 27).
Глава 2. Случайные величины 83
Упражнения
1. Производится 3 независимых выстрела по цели. Вероятности по-
падания при разных выстрелах одинаковы и равны р = 0,9. Найти
м.о. числа попаданий. Решить задачу в случае, если вероятности
попадания при разных выстрелах различны: a) pi = 0,7, б) р? = 0,8,
в) рз = 0,9.
2. Непрерывная случайная величина задана плотностью распределе-
ния
0.
= Ь h
при X 0 И X > 7Г,
при 0 < X 7Г.
Найти математическое ожидание случайной величины X.
3. Пусть А’ и У — независимые д.с. в., причем MX = 2, MY = —3,
DX = 2, DY = 9. Найти MZ и DZ, если Z = 5A — ЗУ + 2.
4. По условию упражнения 2 найти DX и <7д-.
5. С. в. X задана функцией распределения
(0,
Н(ж) = 0,25х2,
при х А,
при А < х В,
при В < х.
Найти значения А и В, MX и сх-
6. Пусть А']. X?.....Хп — последовательность независимых с. в.
с MXi = а и DXt - ст2, i = 1,2, ...,п. Найти м.о. и дисперсию
среднего арифметического п независимых с. в. Аф
84 Раздел первый. Элементарная теория вероятностей и случайных процессов
2.6. Производящая функция
Нахождение важнейших числовых характеристик д. с. в. с целыми
неотрицательными значениями удобно производить с помощью произ-
водящих функций.
Пусть д. с. в. X принимает значения 0,1, 2,..., к,... с вероятностя-
ми ро,Р1,Р2, ,Рк = Р{Х = к},....
Производящей функцией для д. с. в. X называется функция вида
</?(z) = 52Pfe ‘ z* = Ро + PlZ + Р^2 + • • ’ (2-2°)
fc=0
где z — произвольный параметр, 0 < z 1.
Отметим, что коэффициентами степенного ряда (2.20) являются
вероятности закона распределения д. с. в. X.
Дифференцируя по z производящую функцию, получим
СЮ
</(z) = ^2^ рк zk~l.
fc=q
Тогда
30
<Д(1) = 57 к ' Рк = MX = «1,
к=0
т. е.
аг = MX = <р(1). (2.21)
Взяв вторую производную функции </?(г) и положив в ней z = 1, полу-
чим:
СЮ' сю сю
</'(*) = J2 ^(^ - 1) • Рк zk~2, </(1) = - 52 А: • Pfc = а2 - «1,
k=0 k-0
где «2 и «1 _ ~ начальные моменты соответственно 2-го и 1-го порядков
(«2 = MX2, «1 = MX). Тогда DX = MX2 - (MX)2 = «2 - а2 =
= («2 - сц) + «1 - a2 = </'(1) + ~ (^(l))2, T-e-
DX = /'(l) + ^(l)-(/(l))2. (2.22)
Полученные формулы (2.21) и (2.22) используются для нахождения
м. о. и дисперсии рассматриваемого распределения.
Ч
Пример 2.6. Найти дисперсию с. в. X — числа попаданий в упражне-
нии 1 (п. 2.5).
Глава 2. Случайные величины 85
Q Ряд распределения с. в. X:
X 0 1 2 3
р 0,01 0,027 0,243 0,729
Найдем DX. используя формулу (2.22). Производящая функция <Дг) =
= 0,01 + 0,027г + 0,243г2 + 0,729г3. Тогда <Д(г) = 0,027 + 0,486г + 2,187г2.
Полагая z = 1, находим Д(1) = 2,7 = MX (упражнение 1 из п. 2.5).
Д'(г) = 0,486 + 4,374г. Поэтому Д'(1) = 4,46 и DX = 4,86 + 2,7-(2,7)2 =
= 0,27 (формула (2.22)).
Аналогично решаем во втором случае, когда вероятности при раз-
ных выстрелах различны (п. 1.20, пример 1.31). у?(г) = 0,006 + 0,092г +
+ 0,398г2 + 0,504г3. <Д(г) = 0,092 + 0,796г + 1,512г2, <Д(1) = 2.4 = MX.
<p"(z) = 0,796 + 3,024г, <Д'(1) = 3,82. Поэтому DX = 3,82 + 2,4 - (2,4)2 =
= 0,46. •
2.7. Основные законы распределения случайных
величин
Биномиальный закон распределения
О
Среди законов распределения д. с. в. наиболее распространенным
является биномиальное распределение, с которым мы уже встречались
(п. 1.20).
Дискретная с. в. X имеет биномиальное распределение (или рас-
пределена по биномиальному закону), если она принимает значения
0,1,2,3,..., п, с вероятностями:
pm = P{X=m}=C™pmqn~m,
(2.23)
где 0 < р < 1, q = 1 — р, т = 0,1,..., п.
Случайная величина X, распределенная по биномиальному закону,
является числом успехов с вероятностью р в схеме Бернулли проведе-
ния п независимых опытов.
Если требуется вычислить вероятность «не менее т успехов в п
независимых опытах», т. е. Р{Х т}, то имеем : Рт = Р{Х т} =
= Р{Х — т} + Р{Х = т +1} +... + Р{Х = п}. Вероятность Рт бывает
86 * Раздел первый. Элементарная теория вероятностей и случайных процессов
удобно находить через вероятность противоположного события: Рт =
= Р{Х т} = 1 — Р{Х < т}; та из двух формул лучше, где меньше
слагаемых.
Ряд распределения д. с. в. X, имеющей биномиальное распределе-
ние, имеет вид:
X — т 0 1 2 . . . т п
рт = Р{Х = т} qn C^qn~} Clp2qn-2 тпп~т рп
Контроль: £ рт = (р + q)n = 1.
m=0
Функция распределения с. в. X, распределенной по биномиальному
закону, имеет вид:
'О,
< £ C^qn-m
т<х
д,
при х О
при 0 < х п
при п < х.
Найдем числовые характеристики этого распределения. Производящей
функцией биномиального распределения является
п п
¥>(г) = Е C^pmqn~mzm = Е C^(pz)mqn~m = (q + pz)n,
m=0 m=0
т. e. <p(z) = (g + pz)n. Тогда
ip'(z) = n(g + pz)n~1p, p"(z) = n(n — l)p2(g + pz)n~2.
Следовательно (см. п. 2.6), MX = <p'(l) = пр, т. к. р + q = 1, DX =
= g/'(l) + g/(l) — (<pz(l))2 = n(n — l)p2 + np — n2p2 = npq. Итак,
MX — np, DX = npq.
(2.24)
Эти формулы полезно знать.
Пример 2.7. По условию упражнения 1 из п. 2.5 найти MX и DX, где
X — число попаданий в цель.
О С. в. X имеет биномиальное распределение. Здесь п = 3, р = 0,9,
q = 0,1. По формулам (2.24) находим MX и DX: MX = 3 • 0,9 = 2,7,
DX = 3-0,9- 0,1 = 0,27. •
Глава 2. Случайные величины 87
Распределение Пуассона
Дискретная случайная величина X имеет распределение Пуассона,
если ее возможные значения: 0,1,2,..., т,... (счетное множество зна-
чений), а соответствующие вероятности выражаются формулой Пуас-
сона
,.т
Рт = Р{Х = т} = а , (2.25)
где т — 0,1,2,..., а — параметр.
Распределение Пуассона является предельным для биномиального,
когда п —> ос и р —> 0 так, что пр — а — постоянно. Примерами слу-
чайных величин, имеющих распределение Пуассона, являются: число
вызовов на телефонной станции за время /; число опечаток в большом
тексте; число бракованных деталей в большой партии; число а-частиц,
испускаемых радиоактивным источником, и т. д. При этом считается,
что события появляются независимо друг от друга с постоянной сред-
ней интенсивностью, характеризующейся параметром а = пр.
Случайная величина X, распределенная по закону Пуассона, имеет
следующий ряд распределения
X = т 0 1 2 т
Рт а е~а 1! а2 еа 2! ат е~а т!
оо оо
Контроль: V рт = е~а V = е а е“ = 1.
Найдем м.о. и дисперсию с.в. X, распределенной по закону Пуас-
сона. Производящей функцией распределения Пуассона будет
\p{z) = £ = е~а £ = е~а е- = е^,
' m! t—' т\
т=0 гп=0
т. е. p(z) = ea(z~l\ Тогда у?,(-г) = ° ’ еа^2-1\ <p"(z} = а2 е“(2-1). Стало
быть, MX = <Д(1) = a, DX = ^"(l) + ^(l) — (<//(1))2 = а2 + а — а2 = а.
Итак,
MX = DX = а, (2.26)
т. е. параметр а пуассоновского распределения равен одновременно м. о.
и дисперсии с. в. X, имеющей это распределение. В этом состоит отли-
чительная особенность изучаемого распределения, которая использу-
ется на практике (на основании опытных данных находят оценки для
м. о. и дисперсии; если они близки между собой, то есть основание счи-
тать, что с. в. распределена по закону Пуассона).
88 Раздел первый. Элементарная теория вероятностей и случайных процессов
Пример 2.8. Вероятность попадания в цель при одном выстреле равна.
0,01. Какова вероятность того, что число попаданий при 200 выстрелах
составит не менее 5 и не более 10?
О Вероятность р = 0,01 очень мала, а число выстрелов (опытов)
достаточно велико. Поэтому искомую вероятность будем находить,
используя формулу Пуассона. С. в. X — число попаданий. Требу-
ется найти Р{5 С X 10}. По теореме сложения вероятностей
Р{5 X 10} = Р{Х = 5} + Р{Х = 6} + ... + Р{Х = 10}. Име-
ем: а = пр = 200 • 0.01 = 2. еа = е~2 и 0,135,
(о5 96 п7 98 99 9IO \
tl + 6! + 7! + 8! + 9! + Wi) ” °'°53' *
Геометрическое распределение
Дискретная с. в. X имеет геометрическое распределение, если ее
возможные значения: 1,2,3,4,..., а вероятности этих значений:
Рт = Р{Х =т} = q^p, (2.27)
где т = 1,2,3,....
Геометрическое распределение имеет с. в. X, равная числу опы-
тов в схеме Бернулли, проведенных до первого успеха, с вероятностью
успеха р в единичном опыте. Примерами реальных случайных величин,
распределенных по геометрическому закону, являются: число выстре-
лов до первого попадания, число испытаний прибора до первого отказа,
число бросаний монеты до первого выпадения решки и т. д.
Ряд распределения случайной величины X, имеющей геометриче-
ское распределение, имеет вид
X = т 1 2 з
Рт Р qp q2p . ..
Контроль: 52 PQm 1 = Р 12 Ят 1 — Р' । 3 = ? = 1-
m=i m=i 1— 9 Р
Вероятности рт образуют геометрическую прогрессию р, qp, q2p,
qsp, .... По этой причине распределение (2.27) называют геометриче-
ским.
Глава 2. Случайные величины 89
Найдем математическое ожидание и дисперсию геометрического
распределения. Производящей функцией для с. в. X является функ-
ция
ОО оо
-р-Х
т—] т=1
т.е. <Дг) = PZ . Для нее <p'(z) = Р <p"(z) = 2рЧ . Стало
i — qz (1 — qzy (1 — qz)
быть,
DX = Z(l) + v'W - (v'(l))2 = ^+|-A = 4
p 1 p p
(2.28)
1 Q м
t. e. MX = -, DX = — и, значит, ax =
P P
Пример 2.9. Вероятность попадания в цель при отдельном выстре-
ле для данного стрелка равна 0,1. Найти математическое ожидание и
дисперсию с. в. X — числа выстрелов по цели до первого попадания.
Q С. в. X имеет геометрическое распределение с параметром р = 0,1.
По формулам (2.28): MX = = 10, DX = = 90 (ах = =
= Зх/10). •
Замечание. Геометрическое распределение является частным слу-
чаем так называемого распределения Паскаля- Р{Х = тп} =
= Crr+Am__Yprqm- l, т = 1,2,3,..., г > 0 — целое; MX = £, DX =
При г = 1 распределение Паскаля совпадает с геометрическим; при
г > 1 — совпадает с распределением суммы независимых с. в., имею-
щих геометрическое распределение; при натуральном г оно описывает
число опытов в схеме Бернулли, необходимых для того, чтобы полу-
чить значение 1 ровно г раз. Распределение Паскаля имеет приложение
к статистике несчастных случаев и заболеваний и т. д.
90 Раздел первый. Элементарная теория вероятностей и случайных процессов
Гипергеометрический закон распределения
Дискретная с. в. X имеет гипергеометрическое распределение, если
она принимает значения 0.1.2... .,m,... ,min(n, М) с вероятностями
/^т /-т—т
Рт = Р{Х = т} =------, (2.29)
где т = 0,1,..., min(n, Л/), XI < N, т < п, п < TV; п. М. N — нату-
ральные числа.
Гипергеометрическое распределение возникает в случаях, подоб-
ных следующему: в урне N шаров, из них М белых, а остальные чер-
ные; из нее вынимается п шаров. Требуется найти вероятность того,
что среди извлеченных шаров будет ровно т белых (остальные чер-
ные) . Случайная величина X — число белых шаров среди извлеченных
из урны.
В п. 1.7 разобран пример 1.6 подобного типа.
Математические ожидания д. с. в. X, имеющей гипергеометриче-
ское распределение, есть
XIX (2.30)
а ее дисперсия
г л,г (N — M)(N — n)
м=«-угт----------------------- <2-31)
Гипергеометрическое распределение определяется тремя параметрами
N, М, п. Если п мало по сравнению с N (практически при п < i.ZV),
он приближается к биномиальному распределению с параметрами п и
(~т—тп \
М N—M т п—тп |
Сп Р Ч I •
Гипергеометрическое распределение используется при решении задач,
связанных с контролем качества продукции (и других).
Пример 2.10. В группе из 21 студентов 5 девушек. Из этой группы
наудачу отбирается 3 студента. Составить закон распределения д. с. в.
X числа девушек из отобранных студентов. Найти XIX.
Q С. в. X принимает значения 0.1.2,3. Вероятности этих значений
00.03
находим по формуле (2.29): ро = Р{Х = 0} = 5 3 16 ~ 0,4211,
Qi
Глава 2. Случайные величины 91
г'»! /-<2 Л'2 (ji
Pi = Р{Х = 1} =......16 » 0,4511, р2 = Р{Х = 2} = 5 16 « 0.1203.
С21 с2]
рз = Р{Х = 3} = 5 3 16 « 0,0075. Ряд распределения:
^21
X =_т 0 1 2 3
Рт 0,4211 0.4511 0,1203 0,0075
Значение MX найдем двумя способами: а)по ряду распределения:
MX = 0 • 0,4211 + 1 • 0,4511 + 2 0.1203 + 3 • 0,0075 = 0,7142; б)по форму-
ле (2.30) MX = 3 • | и 0,7142. •
I
Равномерный закон распределения
а
Непрерывная с. в. X имеет равномерное распределение на отрезке
[а, 6], если ее плотность вероятности f(x) постоянна на этом отрезке, а
вне его равна нулю:
/(®) =
' 1
< Ъ — а'
0,
при х G [а, 6],
при х 0 [а, 5],
(2.32)
(т. е. /(ж) = с при х € [а, 6], но
I6
отсюда следует, что сх = 1, с =
1а
----; вместо отрезка [а, Ь]
о — а
можно
писать (а,6) или (а,Ь], [а, 5), так как с. в. X — непрерывна.)
График плотности /(ж) для равномерного распределения н. с. в. X
изображен на рис. 28.
Равномерное распределение с. в. X на участке [а, Ь] (или (а, Ь)) бу-
дем обозначать: X ~ R[a, 5]. ч
Найдем функцию распределения F(x) для X ~ R[a. Ь]. Согласно
формуле (см. п. 2.4)
X
F{x}= I
—ОО
92 ‘ Раздел первый. Элементарная теория вероятностей и случайных процессов
/(ж)
х
Рис. 28
t l^— х — а
b — a la b — а
X
+ I Odt =
J Ъ — а
ь
при х > Ь. Таким образом,
при
при
при
(2.33)
График F(x) изображен на рис. 29.
Определим MX и DX с. в. X ~ R[a, Ь].
Согласно формуле (2.11),
х • 0 dx +
а + b
2 '
(Ожидаемый результат: математическое ожидание с. в. X ~ Д[а, Ь]
равно абсциссе середины отрезка; MX совпадает с медианой, т. е.
MX = МеХ.)
Глава 2. Случайные величины 93
Согласно формуле (2.14),
DX =
ь
Г(.-^)2
а
а + Ъ
1Г
dx
b — а
а
— а)3 (а — Ь)3
8
3(6 — а)
Таким образом, для н. с. в. X ~ Я[а, Ь] имеем
мх = ца, dxDDXL
(Ь-а)2
12
(2.34)
1
8
1%*1 Пример 2.11. Пусть с. в. X ~ Я(а,Ь). Найти вероятность попадания
1—1 с. в. X в интервал (а, /3), принадлежащий целиком интервалу (а, Ь).
Q Согласно формуле (2.8), имеем
/3 /?
Р{Хб(«,/?)} = I f(x)dx = I ^-dx =^,
а о
т.е. F{Xg(q,^)} = |^.
Геометрически эта вероятность представляет собой площадь пря-
моугольника, заштрихованного на рис. 30. •
К случайным величинам, имеющим равномерное распределение,
относятся: время ожидания пассажиром транспорта, курсирующего с
определенным интервалом; ошибка округления числа до целого (она
равномерно распределена на отрезке [—0,5; 0,5]). И вообще случайные
величины, о которых известно, что все ее значения лежат внутри не-
которого интервала и все они имеют одинаковую вероятность (плот-
ность).
94 Раздел первый. Элементарная теория вероятностей и случайных процессов
а
Дискретная случайная величина X имеет равномерное распреде-
ление, если она принимает целочисленные значения 1, 2, 3, ..., п с
вероятностью рт = Р{Х = т} = где т = 1,2,3,, п.
В этом случае MX = n. DX = П • ^ак’ ПРИ п = 5,
многоугольник распределения имеет вид, представленный на рис. 31.
MX = 3.
Р
0,2
0 1 2 3 4 5 *
Рис. 31
Показательный закон распределения
а
Непрерывная случайная величина X имеет показательный (или
экспоненциальный) закон распределения, если ее плотность вероятно-
сти имеет вид
ГАе-Ла\
при х 0,
при х < 0.
(2.35)
где Л > 0 — параметр распределения.
График плотности Дх) приведен на рис. 32.
Функция распределения показательного распределения имеет вид
Г(ж) =
Г1 - е“Аж,
10,
при х U,
при х < 0.
(2.36)
Глава 2. Случайные величины ° 95
Найдем математическое ожидание и дисперсию показательного
распределения:
оо b
MX = / х • Хе~Хх dx = lim / х • Хе~Хх dx = [интегрируем по частям] =
J Ь-чоо J
О О
= lim (-х е-Ла=|Ь-| е~Аа;|Ь^ = 0 - |(0 - 1) =
Ь—>ос у 10 А I о / А А
оо оо
DX = I х2 f (х) dx — (МX)2 — [формула (2.17)] = Л [ х2е'Хх dx—=
./ J Хг
—оо 0
= [дважды интегрируем по частям] =
=а (& Н' "'+х (~fai - 0 - £=
= а(о + |(о + о-А(о-1)))-± = ^-± = А
Таким образом,
МХ = \, DX=± стх = |. (2.37)
A Az А
Найдем вероятность попадания случайной величины X, распределен-
ной по показательному закону, в интервал (а, Ь). Используя форму-
лу (2.2) и формулу (2.36), получаем
Р{а<Х <b} = F(b) - F(a) = (1 - e'Afc) - (1 - е“Аа) = е^Ха - е'Х\
т. е. Р{а < X < Ь} = е~Ха - е~хь.
96 Раздел первый. Элементарная теория вероятностей и случайных процессов
Пример 2.12. Случайная величина Т — время работы радиолампы
имеет показательное распределение. Найти вероятность того, что лам-
па проработает не менее 800 часов, если среднее время работы радио-
лампы 400 часов.
О МТ = 400, значит (формула (2.37)), А = . Искомая вероятность
800
Р{Т 800} = 1-Р{Т< 800} = 1—F(800) = 1-(1-е“400) = e-2ss0,135.
Показательное распределение используется в приложениях теории
вероятностей, особенно в теории массового обслуживания (ТМО), в фи-
зике, в теории надежности. Оно используется для описания распреде-
ления случайной величины вида: длительность работы прибора до пер-
вого отказа, длительность времени обслуживания в системе массового
обслуживания и т. д.
Рассмотрим, например, н.с. в. Т — длительность безотказной ра-
боты прибора. Функция распределения с. в. У, т. е. F(£) = Р{Т < t},
определяет вероятность отказа за время длительностью t. И, значит,
вероятность безотказной работы за время t равна R(t) — Р{Т > t} =
= 1 — F(t). Функция R(t) называется функцией надежности.
Случайная величина Т часто имеет показательное распределение.
Ее функция распределения имеет вид F(t) = 1 — e~xt (формула (2.36)).
В этом случае функция надежности имеет вид R(t) = 1 — F(t) =
= 1 —(1—е~Л() = e~At, т. е. R(t) = ext, где А— интенсивность отказов,
т. е. среднее число отказов в единицу времени.
Показательный закон — единственный из законов распределения,
который обладает свойством «отсутствия последствия» (т. е. если про-
межуток времени Т уже длился некоторое время т, то показатель-
ный закон распределения остается таким же и для оставшейся части
Ti = Т — т промежутка).
Нормальный закон распределения
Нормальный закон («закон Гаусса») играет исключительную роль
в теории вероятностей. Главная особенность закона Гаусса состоит в
том, что он является предельным законом, к которому приближаются,
при определенных условиях, другие законы распределения. Нормаль-
ный закон наиболее часто встречается на практике.
Глава 2. Случайные величины 97
Непрерывная с. в. X распределена по нормальному закону с пара-
метрами а и ст > 0, если ее плотность распределения имеет вид
(х — а)2
f(x) =----X е R. (2.38)
а • х/2тг
Тот факт, что с. в. X имеет нормальное (или гауссовское) распреде-
ление с параметрами а и ст, сокращенно записывается так: X ~ N(a, ст).
Убедимся, что f(x) -v это функция плотности. Очевидно, /(ж) > 0.
ОО
Проверим выполнение условия нормировки J f(x)dx = 1. Имеем:
— ОО
Здесь применили подстановку и использовали «интеграл Пуассона»
ОО
j е~* dt = у/тт. (2.39)
—оо
Из равенства (2.39) следует:
X
Функция распределения F(x) = J f(t) dt н. с. в. X ~ N(a, ст) имеет
—ОО
ВИД
Е(ж) =-----±— / е 2а2 dt. (2.41)
ст • у2тг J
—ОО
Если а = 0 и ст = 1, то нормальное распределение с такими параме-
трами называется стандартным. Плотность стандартной случайной
величины имеет вид
1
>р(х) = —ze 2 •
•у2тг
98 Раздел первый. Элементарная теория вероятностей и случайных процессов
С ней мы уже встречались в п. 1.21, формула (1.37).
Функция распределения с. в. X ~ Л?(0.1) имеет вид
Ф(.г) =
и называется, как мы уже знаем (и. 1.21, формула (1.42)), функци-
ей Лапласа. Она связана с нормированной функцией Лапласа Фо (ж)
(п. 1.21, формула (1.40)), как мы уже знаем (формула (1.43) ц. 1.21),
равенством
Ф(ж) = 0,5 + Ф0(ж). (2.42)
Действительно,
(см. (2.40)).
Установим смысл параметров а и о нормального распределения.
Для этого найдем математическое ожидание и дисперсию с. в. X ~
~N(a,a).
т. е. MX = а. Первый интеграл равен нулю, так как подинтегральная
функция нечетная, а пределы интегрирования симметричны относи-
тельно нуля, а второй интеграл равен уД (см. равенство (2.39)). Таким
образом, параметр а — математическое ожидание.
При нахождении дисперсии с. в. X ~ N(a,cr) снова сделаем подста-
новку 1/--' = t и применим метод интегрирования по частям:
у2<7
Глава 2. Случайные величины 99
Таким образом, DX = ст2, а <т — среднее квадратичное отклонение.
Можно показать, что для с. в. X ~ N(a, <j): MqX = МеХ = а.
= £?=^|-3 = 0.
<т3 о4
Исследуем дифференциальную функцию (2.38) нормального за-
кона:
1. /(ж) > 0 при любом х G (—сю, оо); график функции расположен
выше оси Ох.
2. Ось Ох служит асимптотой графика функции /(ж), так как
Пш /(ж) = U.
х—>±оо
3. Функция f(x) имеет один максимум при х = равный /(п) =
= —1=. Действительно,
Отсюда f'(x) = 0 при х = а, при этом: если х < а, то f'(x) > 0, а
если х > а, то f'(x) < 0. Это и означает, что х = а точка максимума
и /max = f(a) — у=-
try 2tv
4. График функции /(ж) симметричен относительно прямой х = а,
так как аналитическое выражение /(ж) содержит разность х — а в
квадрате.
5. Можно убедиться, что точки
/ i _ А
Mi ( а — а.--е 2
V о\/2х
/ 1 _ А
и М-2 I а + <т, ——= е 2
\ <т у2тг
являются точками перегиба графика функции /(ж).
Пользуясь результатами исследования, строим график плотности
распределения вероятности нормального закона - кривую распреде-
ления, называемую нормальной кривой, или кривой Гаусса (рис. 34).
100* Раздел первый. Элементарная теория вероятностей и случайных процессов
Как влияет изменение параметров а и су на форму кривой Гаус-
са? Очевидно, что изменение а не изменяет форму нормальной кривой
(графики функции /(ж) и f(x — а) имеют одинаковую форму; график
f(x — а) получается из графика функции f(x) путем сдвига последнего
на а единиц вправо, если а > 0, и влево, если а < 0). С изменением ст
максимальная ордината точки кривой изменяется. Так как площадь,
ограниченная кривой распределения, равна единице при любом значе-
нии ст, то с возрастанием о кривая Гаусса становится более пологой,
растягивается вдоль оси Ох ....
На рис. 35 изображены нормальные кривые при различных значе-
ниях ст (cTi < ст < ст2) и некотором значении а (одинаковом для всех
трех кривых).
Нормальному закону подчиняются ошибки измерений, величины
износа деталей в механизмах, рост человека, ошибки стрельбы, вес
клубней картофеля, величина шума в радиоприемном устройстве, ко-
лебания курса акций и т. д.
Глава 2. Случайные величины 101
Найдем вероятность попадания с. в. X ~ N(a,cr) на заданный уча-
сток (а,/3). Как было показано,
ь
Р{а < X < 6} = J f(x) dx.
а
(п. 2.4, формула (2.8)). В случае нормального распределения
Используя функцию Лапласа (см. и. 1.21, формула (1.40))
получаем
Р{а < X < /3} = Фо - ф« (^)
(2-43)
Через функцию Лапласа Фо (я ) выражается и функция распределения
F(.r) нормально распределенной с. в. X.
г ,
F(a?) = / —-= е 2<т2 dt = Р{—оо < X < х,} =
.1
—ОО
ЯЛ = 5 + Фо(Ч-ф ,-'м>
Здесь воспользуемся формулой (2.43), нечетностью функции Фо(.т) и
тем, что Фо(оо) = i, действительно
102 • Раздел первый. Элементарная теория вероятностей и случайных процессов
X!
Если функция Лапласа (или «интеграл вероятностей») есть
X
Ф(ж) = - / е 2 dt,
72^ J
—ОО
ТО
F(s) = Ф (^) (2.45)
(непосредственно вытекает из равенств (2.42)) и (2.44)).
Равенство (2.43) можно переписать и так:
Р{а < X < /3} = Ф - Ф (^) • (2-46)
На практике часто приходиться вычислять вероятность попада-
ния нормально распределенной случайной величины в интервал, сим-
метричный относительно центра рассеяния а. Пусть таким интер-
валом будет (а — l,a + I) длины 21. Тогда Р{а — I < X < а + 1} =
= Р{\Х - а| < 1} = Фо - Фо (g~4~Q) = 2фо (|), т.е.
Р{|Х - О| < 1} = 2Ф0 (|) = 2Ф (|) - 1. (2.47)
Полагая в равенстве (2.47) I = За. получим Р{|Х — а| < Зет} = 2Фо(3).
По таблице значений для Фо(.т) находим: Фо(3) = 0.49865. Следова-
тельно, Р{|Х — а| < Зег} « 0.9973, т.е. отклонение с. в. X от своего
математического ожидания меньше, чем Зег — почти достоверное собы-
тие.
Важный вывод: практически достоверно, что с. в. X N(a,a) при-
нимает свои значения в промежутке (а — За, а + Зет). Это утверждение
называется «правилом трех сигм».
Пример 2.13. При измерении детали получаются случайные ошибки,
подчиненные нормальному закону с параметром а = 10 мм. Произво-
дится 3 независимых измерения детали. Найти вероятность того, что
ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
О По формуле (2.47) находим:
Р{ |X - а| < 2} = 2Ф0 « 2 • 0,07926 = 0,15852.
Вероятность того, что эта ошибка (погрешность) превышает 2 мм в
одном опыте (измерении), равна
Р{\Х -а\>2} = 1- F{|X - а| < 2} = 0,84148.
Глава 2. Случайные величины • 103
По теореме умножения вероятность того, что во всех трех опытах ошиб-
ка измерения превышает 2 мм. равна 0.841483 ~ 0,5958. Следовательно,
искомая вероятность равна 1 — 0,5958 = 0,4042. •
Упражнения
1. Известно, что с. в. X ~ 7V(3,2). Найти
Р{—3 < X < 5}, Р{Х<4}, Р{|Х - 3| < 6}.
2. Нормально распределенная с. в. X задана плотностью вероятно-
стей
1
/ (ж) = а 2
\ Z7T
Найти: а) вероятность попадания с. в. в интервал (1,3); б) симмет-
ричный относительно математического ожидания интервал, в ко-
торый с вероятностью 0,8926 попадет с. в. X в результате опыта;
в) МоХ и МеХ. Построить нормальную кривую /(х).
3. Найти коэффициенты асимметрии и эксцесса нормального распре-
деления с параметром а = 0.
Глава 3
Системы случайных величин
3.1. Понятие о системе случайных величин и законе
ее распределения
При изучении случайных явлений часто приходится иметь дело с
двумя, тремя и большим числом случайных величин. Совместное рас-
смотрение нескольких случайных величин приводит к системам слу-
чайных величин. Так, точка попадания снаряда характеризуется си-
стемой (X, У) двух случайных величин: абсциссой X и ординатой У;
успеваемость наудачу взятого абитуриента характеризуется системой
п случайных величин (Xi, Х2, • , Хп) — оценками, проставленными в
его аттестате зрелости.
Упорядоченный набор (Xi,Х2,.. -, Хп) случайных величин Xi (i —
= 1,п), заданных на одном и том же ПЭС Q. называется п-мерной
случайной величиной или системой п случайных величин.
Одномерные с. в. Xi, Х2,..., Хп называются компонентами или
составляющими п-мерной с. в. (Х|, Х2,..., Х„). Их удобно рассма-
тривать как координаты случайной точки или случайного вектора
X = (Х|. Х-2,..., Хп) в пространстве п измерений.
На многомерные случайные величины распространяются почти без
изменений основные понятия и определения, относящиеся к одномер-
ным случайным величинам. Ограничимся для простоты рассмотрени-
ем системы двух случайных величин; основные понятия обобщаются
на случай большего числа компонент.
Упорядоченная пара (X, У) двух случайных величин X и У назы-
вается двумерной случайной величиной или системой двух одномерных
случайных величин X и У.
Систему (X, У) можно изобразить случайной точкой M(X,Y) или
случайным вектором ОМ (рис. 36 и 37).
Система (X, У) есть функция элементарного события: (X, У) =
— у’(н’). Каждому элементарному событию w ставится в соответствие
два действительных числа х и у (или xi и ж2) — значения X и У (или
Xi и Х2) в данном опыте. В этом случае вектор х = (xj, ж2) называется
реализацией случайного вектора X = (Xi,X2).
Глава 3. Системы случайных величин 105
Пример 3.1. Бросаются две игральные кости. Пусть с. в. X — число
выпавших очков на первой кости, с. в. Y — на второй; ПЭС состоит
из 36 элементов: Q = {(1,1), (1,2),... , (1.6), (2,1), (2,2),... , (6,4), (6,5),
(6,6)}. Элементарному событию, например, (6,5) = '«у,5 соответствует
пара чисел х = 6 и у = 5. Совокупность этих значений — функция
элементарного события w.
Системы случайных величин могут быть дискретными, непрерыв-
ными и смешанными в зависимости от типа случайных величин, обра-
зующих систему. В первом случае компоненты этих случайных систем
дискретны, во втором — непрерывны, в третьем — разных типов.
Полной характеристикой системы (X, Y) является ее закон рас-
пределения вероятностей, указывающий область возможных значе-
ний системы случайных величин и вероятности этих значений. Как
и для отдельных случайных величин закон распределения системы
может иметь разные формы (таблица, функция распределения, плот-
ность, ...).
Так, закон распределения дискретной двумерной с. в. (X. У) можно
задать формулой
Pij = Р{Х = Xi,Y = yj}, i = l,n, j = l,m (3.1)
или в форме таблицы с двойным входом:
Х\У У} У2 УЗ Ут
Ж1 Рп Р12 Р13 Р1т
Ж2 Р21 Р22 Р23 Р2т
Рт Рп2 РпЗ Рпт
Причем, сумма всех вероятностей p,v как сумма вероятностей полной
группы несовместных событий {X = Xj, У ~ уj}, равна единице:
тг т
5212^ = L
г=1 j=l
106 Раздел первый. Элементарная теория вероятностей и случайных процессов
На рис. 38 приведен примерный график распределения двумерной
дискретной случайной величины (X, У).
Рис. 38
Зная закон распределения двумерной дискретной случайной ве-
личины, можно найти законы распределения каждой из компонент.
(обратное, вообще говоря, неверно). Так. рЖ) = Р(Х = .7j| = рп +
+ Р12 + . • • + Pim-. что следует из теоремы сложения несовместных со-
бытий {X = а'1,У = yi}, {X = xt.Y = у2}- {X = хг,У = ут}.
Аналогично можно найти
772 П.
Pxi = Р{Х = Xi} = ^Pij, Pyj = P{Y = у7} =^Рц.
j = l 2=1
Пример 3.2. В урне 4 шара: 2 белых, I черный, 1 синий. Из нее наудачу
извлекают два шара. Пусть с. в. X — число черных шаров в выборке,
с. в. У — число синих шаров в выборке. Составить закон распределения
для системы (X, У). Найти законы распределения X и У.
О С. в. X может принимать значения 0, 1; с. в. У — значения 0, 1.
Вычислим соответствующие вероятности: р, । = Р{Х = 0, У = 0} =
zt2 ft 1
= ё| = I ,и"и: 1 ™ = °’г = *> = с| = 5;
Р21 = Т{Х = 1,У = 0} = |; РИ = P(.V = 1,У = 1) = 1. Таблица
распределения системы (X, У) имеет вид:
Глава 3. Системы случайных величин "107
Отсюда следует: Р{Х = 0} = | | Р{Х = 1} = | 4- | = i;
P{Y т 0} = | + | = |, P{Y — 1} = | 4 | Законы распределения
составляющих X и Y имеют вид:
X 0 1
Р 1 2 1 2
У 0 1
р 1 2 1 2
3.2. Функция распределения двумерной случайной
величины и ее свойства
Универсальной формой задания распределения двумерной случай-
ной величины является функция распределения (или «интегральная
функция»), пригодная как для дискретной, так и для непрерывной слу-
чайной величины, обозначаемая Fxty(x,y) или просто F(x,y).
Р\| Функцией распределения двумерной случайной величины (X. Y) на-
—1 зывается функция F(x, у), которая для любых действительных чисел х
и у равна вероятности совместного выполнения двух событий {X < х}
и {Y < у}.
Таким образом, по определению
F(x,y) = P{X<x,Y <у} (3.2)
(событие {X < ж. Y < у} означает произведение событий {X < х} и
{>' < ?;})
Геометрически функция F(x, у) интерпретируется как вероятность
попадания случайной точки (X, У) в бесконечный квадрант с вершиной
в точке (ж, у), лежащий левее и ниже ее (рис. 39).
Функция распределения двумерной дискретной случайной величи-
ны (X, У) находится суммированием всех вероятностей pij, для кото-
рых Xi < х, yj < у, т. е.
Г(ж, у) = 52 52 PiF (3-3)
Геометрическая интерпретация функции распределения позволяет
наглядно иллюстрировать ее свойства.
108 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Рис. 39
Свойства функции распределения двумерной случайной
величины:
1. Функция распределения F(x, у) ограничена, т. е.
0^F(®, у) < 1.
2. F(x, у) не убывает по каждому из своих аргументов при фиксиро-
ванном другом, т. е.
F(x2,y) F(xi,y) при Х2 > тц;
F(x,y2) F(x,yi) при У2 > У!-
3. Если хотя бы один из аргументов обращается в —оо, то функция
распределения F(x, у) равна нулю. т. е.
F(x, —оо) = F(—оо,у) = F(—оо, —оо) = 0.
4. Если оба аргумента обращаются в +оо, то F(ir, у) равна 1, т. е.
F(+oo, +оо) = 1.
5. Если один из аргументов обращается в +оо, то функция распреде-
ления системы случайных величин становится функцией распре-
деления с. в., соответствующей другому элементу, т. е.
F(t,+oo) = Fi (ж) = Fx(x), F(+oo,y) = F2(y) = Fy(y). (3.4)
6. F(x.,y) непрерывна слева по каждому из своих аргументов, т. е.
lim F(T,y) = F(a,’o,y), lim F(x,y) = F(x,yo).
x—>xo~ 0 y->yo—0
Глава 3. Системы случайных величин 109
Q 1. F(x, у) есть вероятность, следовательно, 0 F{x.,y) 1.
2. При увеличении какого-либо из аргументов (ж, у) заштрихован-
ная на рис. 39 область увеличивается; значит, вероятность попадания
в нее случайной точки (X, У) не может уменьшаться.
3. События {X < —оо}, {У < —оо} и их произведение невозмож-
ны: попадание в квадрант с отодвинутой в —оо границей невозможно.
Вероятность такого события равна нулю.
4. Событие {X < +оо} • {У < +оо} достоверно, следовательно, его
вероятность равна единице.
5. {X < +оо) — достоверное событие, следовательно {X < +оо}х
х{У < у] = {У < у} и F(+oo,у) = Р{Х < +оо;У < у} = P{Y < у} =
= Fy(y).
Аналогично, F(x, +оо) = Р\(ж).
Подчеркнем: зная совместное распределение двух случайных вели-
чин X и У, можно найти одномерные распределения этих случайных
величин, но обратное, вообще говоря, неверно.
Отметим, что с геометрической точки зрения F(x, у) есть некото-
рая поверхность {ступенчатая для двумерной дискретной случайной
величины), обладающая указанными свойствами.
С помощью функции F(x, у) легко можно найти вероятность по-
падания случайной точки (X, У) в прямоугольник D со сторонами, па-
раллельными координатным осям:
П{ж1 X X X ж2,У1 X У X Уг} =
= У(ж>, у2) - F(ti, у2) - Г(ж2, У1) + Г(Ж1, У1). (3.5)
Приведем «геометрическое доказательство», см. рис. 40.
Рис. 40
110 Раздел первый. Элементарная теория вероятностей и случайных процессов
Здесь F(x-2,y2) — вероятность попадания случайной точки в
область, заштрихованную косыми линиями, F(a?i,y2) — вертикальны-
ми, F(s2,yi) -горизонтальными, F(x.i,yi) — косыми, вертикальными,
горизонтальными (эту область дважды вычли, следует один раз при-
бавить) .
Пример 3.3. По таблицам распределения системы (X, У) компонент
X и У примера 3.2 п. 3.1 найти Ft(x), F2(y), F(x,у).
Q Используя формулу (2.4), находим функции распределения Fi(x)
и F2(y):
Fl (ж) = 0,5,
1,
при х 0,
при 0 < х 1,
при X > 1,
(°’
F2(y) = < 0,5,
11.
при у 0,
при 0 < у 1.
при у > 1.
Используя формулу (3.3), находим функцию распределения F(x, у):
А\У у < 0 0 < у 1 1 < У
х 0 0 0 0
0 < х < 1 0 1 6 1 (= 1 + 2) 2 \ 6 6/
1 < X 0 Ы>| — ЛГ' + OiltO + + СЧЮ +
3.3. Плотность распределения вероятностей
двумерной случайной величины и ее свойства
Исчерпывающей характеристикой непрерывной двумерной случай-
ной величины является плотность вероятности. Вводится это понятие
аналогично тому, как это делалось при рассмотрении плотности рас-
пределения вероятностей одной случайной величины (п. 2.4).
Двумерная случайная величина называется непрерывной, если ее
функция распределения F(x.y) есть непрерывная функция, диффе-
ренцируемая по каждому из аргументов, у которой сушествует вторая
смешанная производная F''(x, у).
Плотностью распределения вероятностей (или совместной, плот-
ностью) непрерывной двумерной случайной величины (А”, У) называ-
ется вторая смешанная производная ее функции распределения.
Глава 3. Системы случайных величин • 111
Обозначается совместная плотность системы двух непрерывных
случайных величин (X, У) через f(x,y) (или р(х,у\).
Таким образом, по определению
d2F(x,y) „
У> = дхду = Fxy(x’ уУ <3-6)
Плотность распределения вероятностей непрерывной двумерной слу-
чайной величины (X, У) есть предел отношения вероятности попадания
случайной точки (X, У) в элементарный прямоугольник со сторонами
Дж и Ду, примыкающий к точке (ж, у), к площади этого прямоуголь-
ника. когда его размеры Дж и Ду стремятся к нулю (рис. 41).
Рис. 41
Действительно, используя формулу (3.5), получаем: средняя плот-
ность вероятности в данном прямоугольнике равна
Р{х < X < х + Дж, у С У < у + Ду}
Дж Ду
1 / И(ж + Дж, у + Ду) - Н(ж, у + Ду) F(x + Дж, у) - У(ж, у)
Ду I Дж Дж
Переходя к пределу при Дж -» 0 и Ду G, получаем
lim fcv — lim
Дгг-Ш
Aj/—>0
Г'(ж,у +Ду) - Р'(ж.у)
Ду
т.е. /(ж, у) = (ИДж,у))^ = Д^(ж,у).
По аналогии с плотностью вероятности одномерной непрерывной
случайной величины, для двумерной случайной величины (X, У) плот-
ность вероятности определяется как функция /(ж, у), удовлетворяю-
щая условию
Р{х < X < х + dx, у У < у + dy} к f(x, у) dxdy: (3.7)
выражение f(x,y) dxdy называется элементом вероятности двумер-
ной случайной величины (X, У).
112 Раздел первый. Элементарная теория вероятностей и случайных процессов
Геометрически плотность распределения вероятностей f(x,y) си-
стемы двух случайных величин (X, У) представляет собой некоторую
поверхность, называемую поверхностью распределения (рис. 42).
Плотность распределения f(x,y) обладает следующими
свойствами:
1. Плотность распределения двумерной случайной величины неотри-
цательна. т. е.
/(ж, у) 0.
2. Вероятность попадания случайной точки (X, У) в область D равна
двойному интегралу от плотности по области D. т. е.
Р{(Х,У) е D} =
УУ f(x,y)dxdy.
D
(з.«)
3. Функция распределения двумерной случайной величины может
быть выражена через ее плотность распределения по формуле:
X у
F(x, у) = j .fx.Y («,v)dudv. (3.9)
—оо —oe
4. Условие нормировки: двойной несобственный интеграл в бесконеч-
ных пределах от плотности вероятности двумерной с. в. равен еди-
нице, т. е.
ос оо
У У f(x,y)dxdy = 1.
—оо —оо
Глава 3. Системы случайных величин * 113
5. Плотности распределения одномерных составляющих X и У могут
быть найдены по формулам:
+оо
У /(«,?/) dy = fl&) =
—ос
4-оо
У /(ж, у) dx = f2(y) = fx(y)-
—ОО
(3.10)
□ 1. Следует из того, что F(x,y) есть неубывающая функция по каж-
дому из аргументов.
2. Элемент вероятности f(x,y) dxdy (см. (3.7)) представляет собой
вероятность попадания случайной точки (X, У) в прямоугольник со
сторонами dx и dy (с точностью до бесконечно малых более высокого
порядка по сравнению с произведением dxdy). Разбив область D на пря-
моугольники и применив к каждому из них равенство (3.7), получаем,
по теореме сложения вероятностей, при стремлении к нулю площадей
прямоугольников (т. е. dx —> 0 и dy —> 0), формулу (3.8). Геометрически
эта вероятность изображается объемом цилиндрического тела, ограни-
ченного сверху поверхностью распределения / (ж, у) и опирающегося на
область D.
3. Выражение функции распределения F(x,y) системы случайных
величин (X, У) через плотность /(ж, у) получим, используя форму-
лу (3.8) (область D есть прямоугольник, ограниченный абсциссами
—оо, х и ординатами —ос, у):
F(x, у) = Р{Х < ж, У < у] = Р{—оа < X < ж, -оо < У < у} =
X у
= f f f(u,v)dudv.
—оо —оо
4. Положив в формуле (3.9) ж = у = +оо и учитывая, что
F(+oo,+оо) = 1, получим
ОО X)
У(+оо, +оо) = У J f(x, у) dxdy — 1.
—оо —оо
Геометрически свойство 4 означает, что объем тела, ограниченного по-
верхностью распределения и плоскостью Оху, равен единице.
5. Найдем сначала функции распределения (зная совместную плот-
ность двумерной случайной величины (X, У)), составляющих X и У:
г +ос
Г1(ж) = Г(ж,+оо) = У У f{u,y)dudy,
—оо —оо
114 Раздел первый. Элементарная теория вероятностей и случайных процессов
+оо у
Fi{y) = Г(+оо,т/) = У У /(.т,г>) dxdv,
—ОО —оо
т. е.
(3.11)
Дифференцируя первое равенство по х, а второе по у, получим плот-
ности распределения случайных величин X и Y:
ос
/1(ж) = ^(ж) = У f(x,y)dy
-ос
И
оо
h(y) = F^y) = У /(ж, у) dx.
—ОО
Отметим, что решение обратной задачи (восстановить закон распреде-
ления системы (X, У) по известным законам распределения составля-
ющих системы) в общем случае невозможно.
Пример 3.4. Двумерная случайная величина (X, У) задана плотно-
стью распределения вероятностей f(x,y} = -------------—. Найти:
(1+ж2)(1 + у2)
1) А: 2) F(x,y\, 3) Р{Х < 1,У < 1}; 4) ,/Дт) и /2(у).
Q 1) Постоянную А найдем, используя условие нормировки:
ос ос
/ / (1+т2Д1+у2)(Му = 1,
-оо —оо
оо оо
л / [ -A- = i,
J 1 + х2 J 1 + у2
—оо —оо
|+оо |+оо
A-arctgrr -arctgy = 1,
l—oo l—oo
А • я2 = 1.
Следовательно, Л = Д-.
7Г2
Глава 3. Системы случайных величин 115
2) Используя формулу (3.9), находим:
F(x,y)
= arctgj: + у,) (JarctgУ + |) •
3) P{X < 1,Г < 1} = F(l.l) = (1. | + 1) (1 + |) = A
(использовали формулу (3.2), можно воспользоваться формулой (3.8)).
4) По формуле (3.10) получаем:
_____1 ___
я2(1 + ж2)
arctgу
1
7Г(1 + Ж2) ’
1
я(1 +у2)
Упражнения
1. Двумерная случайная величина (X, Y) задана совместной плотно-
стью распределения
. • (Ae~x~y, при ж is 0,у 0,
г (ж, у) = <
' (0, в противном случае.
Найти: 1) коэффициент Л; 2) Fy.y (-Н у); 3) Дх (ж) и Ну (у); 4) /а (;г)
и/у(у); 5) Р{Х>0,У<1}.
2. Непрерывная двумерная случайная величина (X,Y) равномерно
распределена (т. е. f(x,y) — с) внутри треугольника с вершина-
ми 0(0,0), Л(0,4), В(4,0). Найти: 1) совместную плотность /(ж,у);
2) /х(ж) и /у(у); 3) вероятность события
Л = {0 < X < 1,1 < Y < 3}.
116 * Раздел первый. Элементарная теория вероятностей и случайных процессов
3. Вероятность попадания в цель при одном выстреле для I стрел-
ка равна 0,4, для II — 0,6. Оба стрелка, независимо друг от дру-
га, делают по два выстрела в цель. Найти: 1) закон распределе-
ния случайных величин X и У; 2) совместный закон распределе-
ния системы случайных величин (X, Y); 3) функцию распределе-
ния F\-j-(2;,y), если случайная величина X — число попаданий!
стрелка, случайная величина Y — II стрелка.
3.4. Зависимость и независимость двух случайных
величин
Зная законы распределения случайных величин X и У, входящих
в систему (X, У), можно найти закон распределения системы только в
случае, когда случайные величины X и У — независимы. С понятием
независимости случайных величин мы уже встречались в п. 2.2: две
случайные величины называются независимыми, если закон распреде-
ления каждой из них не зависит от того, какие значения принимает
другая. В противном случае случайные величины называются зависи-
мыми.
Теперь дадим общее определение независимости случайных вели-
чин.
Случайные величины X и У называются независимыми, если не-
зависимыми являются события {X < ж} и {У < у} для любых действи-
тельных х и у. В противном случае случайные величины называются
зависимыми.
Сформулируем условие независимости случайных величин.
Теорема 3.1. Для того, чтобы случайные величины X и У были незави-
симы, необходимо и достаточно, чтобы функция распределения системы
(X, У) была равна произведению функций распределения составляющих:
F(x,y) = ЕДж) • F2(y). (3.12)
□ Если случайные величины X и У независимы, то события {X < ж}
и {У < у} независимы. Следовательно, Р{Х < х, У < у} = Р{Х < ж}х
хР{У < у}, т. е. F(x,y) = Fi(ж) • F2(y). Если же имеет место равен-
Глава 3. Системы случайных величин *117
ство (3.12), то Р{Х < x,Y < у} = Р{Х < ж} • Р{У < у}. Значит,
случайные величины А’ и У независимы. И
Заметим, что условие (3.12) есть иначе записанное условие неза-
висимости двух событий: Р(А В) = Р(А) Р(В) (и. 1.15) для случая
событий А = {X < ж}. В = {У < у}.
Теорема 3.2. Необходимым и достаточным условием независимости
двух непрерывных случайных величин, образующих систему (А, У), яв-
ляется равенство
/(ж,у) = /1(ж) • fo(y)- (3.13)
Q| Если А и У независимые непрерывные случайные величины, то
имеет место равенство (3.12). Дифференцируя это равенство по х, а
затем по у, получим f(x, у) = ~^Р^ХУ^Р^У) или/(ж,у) = Л С7’Л (у) •
И обратно. Интегрируя равенство (3.13) по ж и по у, получим
х у
J I
— сю -сю
fo(v)dv,
т. е. F(x,y) = Hi (ж) • FA'y)- На основании теоремы 3.1 заключаем, что
случайные величины А и У независимы.
Теорема 3.3. Необходимым и достаточным условием независимости
двух дискретных случайных величин А и У, образующих систему (А, У),
является равенство
Р{Х = xiyY = у3} = Р{Х = Xi} • P{Y = у3} (3.14)
для любых г = 1,2, j =
(или, что то же самое: р13 = pXi pyj, i = 1, n, j = 1, m).
Пример 3.5. Зависимы или независимы случайные величины А и У,
рассмотренные в примерах а) 3.2 п. 3.1; б) 3.4 п. 3.3?
118 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Q а) рп = Р{Х = О,У = 0} = |, а Р{Х = 0} - P{Y = 0} = | ±
т. е. рц рХ1 • рУ1. Случайные величины X и Y зависимы.
6) »*.!/) = 2,|2. 2\/, 2,.а/1Ы = ГГзЦ.ЬЫ = l'7-Ц'
7TZ(1 + ЯГ)(1 + У) } + 1+уЛ
Так как f(x,y) = fi(x) faiy), то, согласно условию (3.13), заключаем:
случайные величины X и Y независимы. •
3.5. Условные законы распределения
Если случайные величины X и У, образующие систему (X, У), за-
висимы между собой, то для характеристики их зависимости вводится
понятие условных законов распределения случайных величин.
Условным законом распределения одной из случайных величин, вхо-
дящей в систему (X, У), называется ее закон распределения, найден-
ный при условии, что другая случайная величина приняла определен-
ное значение (или попала в какой-то интервал).
Пусть (X, У) — дискретная двумерная случайная величина и рц =
— Р{Х = Xi, У = y-j}, i = 1,п, j = l,m. В соответствии с определени-
ем условных вероятностей событий (напоминание: Р(В|Л) =
п. 1.14), условная вероятность того, что случайная величина У при-
мет значение yj при условии, что X = хг определяется равенством
Р(АВ)
Р(А) ’
P{Y = yj\X = Xi} =
P{X = Xi,Y = y3}
Р{Х =
i = 1,2,..., n;
j = (3.15)
(или коротко: p(yj\xi) - ~).
Совокупность вероятностей (3.15), т.е. p(yi\xi),p^y^Xi), ..
• • iP{.yrn\xi)-, представляет собой условный закон распределения случай-
ной величины У при условии X = Xi- Сумма условных вероятностей
равна 1, действительно:
т т т
£,Р»<) = = IF1 = 1
z—J J Pxi PX} J PXi
J=1
771
(см. n. 3.1: pXi = ^Pij)-
Глава 3. Системы случайных величин 119
Аналогично определяются условная вероятность, условный закон
распределения случайной величины X при условии Y = ур.
r , , Р{Х = Xi,Y = уЛ
г = 1,2,...,п; j = l,2,...,m (3.16)
(или коротко: р(а?,|ад) = где pyj = ^Pij)-
i=l
Пример 3.6. Задана таблица распределения двумерной случайной ве-
личины (X, У):
Х\У 1 2 3
0,1 0,12 0,08 0,40
0,2 0,16 0,10 0.14
Найти: а) безусловные законы распределения случайных величин X и
У; б) условный закон распределения случайной величины X при У = 2.
Ш
О а) Так как pxi - ^Pij и pyj
.7=1
п
^2 'Pij, то
г=1
х 0,1 0,2
р 0,60 0,40
У 1 2 3
р 0,28 0,18 0,54
б) С учетом формулы (3.16) имеем: Р{Х — 0,1|У = 2} =
Р{Х — 0,2|У = 2} = Таким образом, условный закон распре-
деления случайной величины X при У = 2 таков
х 0,1 0,2
Py=2 4 9 5 9
2
(У~^Р1 = !)• Очевидно несовпадение условного и безусловного законов
i=l
распределения случайной величины X. Следовательно, случайные ве-
личины X и У зависимы. •
Пусть теперь (X, У) — непрерывная двумерная случайная вели-
чина с плотностью f(x,y)-, /1(ж) и /2 (у) — плотности распределения
соответственно случайной величины X и случайной величины У
120 Раздел первый. Элементарная теория вероятностей и случайных процессов
Плотность вероятности условного распределения (или условная
плотность) случайной величины Y при условии X = х определяется
равенством
| X Ж У) /(Х,у) /ох-
f (Ук) = = ’ Ч1С А(ж) 0. (3.17)
f(x,y)dy
—сю
Условная плотность обладает свойствами плотности распределения,
оо
так: f(y\x) 0, / f(y\x)dy = 1.
—ОО
Аналогично определяется условная плотность распределения слу-
чайной величины X при условии Y — у:
f, , х f(x,y) f(x,y)
f™ = ~ЫуТ = h y °’ 3’18
I f(x,y)dx
—co
Используя соотношения (3.17) и (3.18), можно записать
f(x,y) = /Дж) - f(y|s) = f2(y) • f(x\y), (3.19)
т. e. совместная плотность распределения системы случайных величин
равна произведению плотности одной составляющей на условную плот-
ность другой составляющей при заданном значении первой.
Равенство (3.19) называют теоремой (правилом) умножения
плотностей распределений (она аналогична теореме умножения ве-
роятностей для событий, П. 1:15).
ч
Пример 3.7. Двумерная случайная величина (X, Y) задана плотно-
стью совместного распределения
ft \ (Сху,
j{x,y) =
при (ж, у) G D,
при (х,у) £ D,
где D — область на плоскости
У > -х,
У <2,
х < 0.
Найти безусловное и условное распределение составляющей X. Убе-
диться, что случайные величины X и Y зависимы.
Глава 3. Системы случайных величин 121
Q Область D изображена на рис. 43.
Сначала найдем коэффициент С из условия нормировки:
I У f(x,y)dxdy = 1.
—оо —оо
= -2С.
Поэтому С = — у Теперь находим
оо
—оо
3 — 4х
= -1Ж(4-ж2) = 4
2
X
2 2
т.е. /х(ж) = ^(.т3 — 4т), х Е (—2,0) (контроль:
оо О
У /х(т) dx = 11(т3 - 4.Т) dx = | (^ - 2хЛ
—оо —2
Для нахождения f(x\y) воспользуемся формулой (3.18), предваритель-
но найдя
° - 1
-2 4
1 т2 |0
dx = у
—оо
-у
4
4
О
У
-у 4 ’
122 Раздел первый. Элементарная теория вероятностей и случайных процессов
f(x,y)'
. Ш .
у е (0,2). Тогда /(т|у) =
(контроль:
1 УА 2х 7 1 г- п
~2ху т := (ж’у) е D
оо
J f(x\y)dx =
—ОО
Их =
j_£i°
у2 2 I-?/
-4(о - х/2) = 1).
yz
Как видно, безусловный закон распределения случайной величины А'
(/1(ж)) не совпадает с условным законом распределения случайной ве-
личины X (/(т|у)); случайные величины X и Y — зависимы. •
В случае произвольного типа случайных величин функция распре-
деления F(x,y) системы зависимых случайных величин (X, У) может
быть записана в виде:
F(.r,y) = ^(ж) F2(y|X < х) = F2(y) Fi(z|Y < у),
где F2(y|X < х) — P{Y < у\Х < ./} — условная функция распреде-
ления случайной величины Y при условии {X < ж}; Fi(®|y < у) =
= Р{Х < ж|У < у} — условная функция распределения случайной
величины X при условии {У < у}.
3.6. Числовые характеристики двумерной случайной
величины. Математическое ожидание и дисперсия
Для системы случайных величин также вводятся числовые харак-
теристики, подобные тем, какие были для одной случайной величины.
В качестве числовых характеристик системы (X, У) обычно рассмат-
ривают моменты различных порядков (см. п. 2.5). На практике чаше
всего используются моменты 1 и II порядков: математическое ожидание
(м. о.), дисперсия и корреляционный момент. Математическое ожида-
ние и дисперсия двумерной случайной величины служат соответствен-
но средним значением и мерой рассеяния. Корреляционный момент вы-
ражает меру взаимного влияния случайньгх величин, входящих в си-
стему (X, У).
Математическим ожиданием двумерной с. в. (X, У) называется
совокупность двух м. о. MX и MY, определяемых равенствами:
п т п т
мх=т3. = ^2 52 XipiF MY = ту = 5252 yjpiF
1=1 7-1 i=l j=l
(3.20)
Глава 3. Системы случайных величин 123
если (X, У) — дискретная система с. в. (здесь = Р{Х = Y = у?});
и
оо
MX = ./ / х f(x,y) dxdy, MY = У У У f(x,y) dxdy, (3.21)
—оо —оо —оо —оо
если (X, У) — непрерывная система с. в. (здесь f(x,y) — плотность
распределения системы).
Дисперсией системы с. в. (X, У) называется совокупность двух
дисперсий DX и DY, определяемых равенствами:
п т пт
DX = ^2 У (жг - W'x'fpij, DY = ^2 У (ад - my)2Pij-> (3-22)
1—1 J = 1 Z=1 J = 1
если (X, У) — дискретная система с. в. и
оо
DX = I I (х - mx)2f(x,y)dxdy, DY = J j (у - ту)2 f(x,y) dxdy,
—оо — ос —оо—ОС
(3.23)
если (X, У) — непрерывная система с. в.
Дисперсии DX и DY характеризуют рассеяние (разброс) случай-
ной точки (X, У) в направлении осей Ох и Оу вокруг точки (тх,ту)
на плоскости Оху — центра рассеяния.
Математические ожидания тх и ту являются частными случаями
начального момента ak,s порядка k + s системы (X, У), определяемого
равенством
= M(XkYs)-
тх = М(Х’У°) = сид и ту = M^Y1) = а0,1-
Дисперсии DX и DY являются частными случаями центрального
момента p.k,s порядка k + s системы (X, У), определяемого равенством
Pk,s = М((Х - mx)k(Y - туП,
DX = М(Х — тх)2 = Д2,о и DY = M(Y — ту)2 = цо,2-
Математическое ожидание с. в. <р{Х, У), являющейся функцией
компонент X и У двумерной с. в. (X, У) находится, аналогично, по фор-
мулам:
ОО ОС
Дх, y)f(x, у) dxdy (3.24)
— ос —ОО
W(x,y))= I I
124 Раздел первый. Элементарная теория вероятностей и случайных процессов
для непрерывного случая и
п тп
м (^(х у)) = 52 52 ’ y^pi3 (3-25)
i=i J=i
для дискретного случая.
Начальный момент II порядка сцд = MXY часто встречается в
приложениях. Вычисляется по формуле
п т
mxy = 52 52^^
г=1 7=1
(3.26)
для дискретных с. в.
MXY =
У J xyf(x,y)dxdy
(3.27)
для непрерывных с. в.
3.7. Корреляционный момент, коэффициент
корреляции
Особую роль играет центральный смешанный момент второго по-
рядка Д]д = М(Х—mx)(Y—ту) — MXY, называемый корреляционным
моментом или моментом связи.
|ф| Корреляционным моментом (или ковариацией) двух случайных ве-
личин X и У называется м. о. произведения отклонений этих с. в. от их
м.о. и обозначается через Kxy или <:ov(A', У).
Таким образом, по определению
KXY = cov(X. У) = М[(Х - mx)(Y - ту)] = MXY. (3.28)
При этом: если (X, У) — дискретная двумерная с. в., то ковариация
вычисляется по формуле
71 т
Kxy = 52 52^ “ т^)(у3 - my)pij; (3.29)
i=l j=l
если (X, У) — непрерывная двумерная с. в., то
ОО ОС
Kxy = j У (® - тх)(у - my)f (x, у) dxdy (3.30)
—оо —оо
Глава 3. Системы случайных величин ‘125
(формулы (3.29) и (3.30) получены на основании формул (3.24) и
(3.25)).
Ковариацию часто удобно вычислять по формуле
KXY = cov(X, У) = MXY - MX MY, (3.31)
которая получается из определения (3.28) на основании свойств мате-
матического ожидания:
Kxy = М[(Х — mx)(Y — m^)] = M(XY — Хту — Ymx + тхту) =
= MXY — туMX — mxMY + mxmy = MXY — mxmy — mxmy 4- mxmy =
= MXY - MX MY.
Формулу (3.30) можно записать в виде
ОО оо
Kxy = У j ху f(x,y)dxdy — тхту. (3.32)
—оо —оо
Свойства ковариации:
1. Ковариация симметрична, т. е.
Kxy = Kyx-
2. Дисперсия с. в. есть ковариация ее с самой собой, т. е.
Кхх — DX, Kyy ~ DY.
3. Если случайные величины X и У независимы, то
Kxy - 0.
4. Дисперсия суммы (разности) двух случайных величин равна сумме
их дисперсий плюс (мищ у удвоенная ковариация этих случайных
величин, т. е.
D(X ± У) = DX + DY ± 2КХУ.
5. Постоянный множитель можно вынести за знак ковариаций, т. е.
Kcx,y = с-Kxy = или соу(сХ, У) = c-cov(X, У) = cov(X, сУ).
6. Ковариация не изменится, если к одной из с. в. (или к обоим сразу)
прибавить постоянную, т. е.
Ка+с,у = Kxy = Kx,y+c = Kx+c,y+c
126* Раздел первый. Элементарная теория вероятностей и случайных процессов
или
cov(X + с. Y) = cov(X, У) = cov(X, У + с) = cov(X + с, У + с).
7. Ковариация двух случайных величин по абсолютной величине не
превосходит их с. к. о., т. е.
|^Ху| • (Ту.
Q 1. Следует из определения (3.28) ковариации.
2. Кхх = М[(Х - тх)(Х - тпД] = М(Х - mJ2 = DX.
3. Из независимости с. в. X и У следует независимость их откло-
нений X — тх и У — ту. Пользуясь свойствами м.о. (п. 2.5), получаем
Kxy = М(Х — тх) М(У — ту) = 0.
4. D(X 4- У) = М((Х + У) - М(Х + У))2 =
= М((Х-МХ)+(У-МУ))2 = M(X-MX)2+2M(X-MX)(Y-MY)+
+ М(У - МУ)2 = DX +DY + 2Лд-у,
D(X - У) = DX + Р(-У) + 2М(Х - MX)(-Y - М(-У)) =
= DX + DY - 2КХу-
5. КсХ,у = М(сХ - McX)(Y - MY) = М[с(Х - MX)(У - МУ)] =
= сКху •
6. Доказывается аналогично.
-т кг , X - тх Y ~ ту
Л 11рименяя свойство 4 к двум стандартным с. в. ——-и —
С'Х <Jy
(см. п. 2.5), получаем:
Любая дисперсия неотрицательна, поэтому
2 ( 1 ± 0- (3-33)
\ °.сиу J
Отсюда следует, что — сгх(Ту Ку у п-лСГу, т. е. |Х'аг|
Глава 3. Системы случайных величин 127
Из свойства 3 следует, что если Kxy 0, то с. в. X и Y зависимы.
Случайные величины X и Y в этом случае {К у у 0) называют корре-
лированными. Однако из того, что Кху = 0. не следует независимость
с. в. X и Y. В этом случае {Kxy = 0) с. в. X и К называют некоррелиро-
ванными. Из независимости вытекает некоррелированность; обратное,
вообще говоря, неверно.
Как следует из свойств ковариации, она {Кху) характеризует и
степень зависимости случайных величин, и их рассеяние вокруг точки
(тж, Шу). Размерность ковариации равна произведению размерностей
с. в. X и У. В качестве числовой характеристики зависимости (а не
рассеяния) с. в. X и У берут безразмерную величину — коэффициент
корреляции. Он является лучшей оценкой степени влияния одной с. в.
на другую.
Коэффициентом корреляции гху двух с. в. X и У называется от-
ношение их ковариации (корреляционного момента) к произведению их
с. к. о.:
_ КХу _ соу(Х,У)
rAi ~ ~ s/DXVdy'
(3.34)
Очевидно, коэффициент корреляции равен ковариации стандартных
CZ К ---- ?ПХ „ ) “ Шу
с. в. Z( = - и Z2 = ——, т.е. гХу = cov(Zi,Z2).
Свойства коэффициента корреляции:
1. Коэффициент корреляции по абсолютной величине не превосходит
1, т.е.
1гхг I 1 или ~ 1 rXY 1-
2. Если X и У независимы, то
rxY = 0.
3. Если с. в. X и У связаны линейной зависимостью, т. е. У = аХ + Ь,
а 0, то
кх-у| = 1,
причем гху = 1 при а > 0,
гху = — 1 при а < 0.
4. Если |г.х-у| = 1, то с. в. X и У связаны линейной функциональной
зависимостью.
□ 1. Так как |Ка'У'| <?х <гу (свойство 7 ковариации), то
I Kxy | <
^х<Уу Оу^х
= 1.
128 * Раздел первый. Элементарная теория вероятностей и случайных процессов
2. Кху = 0 в случае независимости X и Y. Следовательно,
Kxy
°Х°У
3. Согласно свойствам ковариации, имеем
cov(X, Y) — cov(X, аХ + b) — cov(aX + b, X) = «cov Х^ =
= acov(X, X) =aDX
и DY = D(aX + b) = a2DX. Поэтому
rxY = ~COV(X>F) = aDX = a = fl, при a > 0,
Y^DXVDY \[DX • |a| • \[PX |«| f-1, a < 0.
4. Пусть txy = 1- Тогда из равенства
P / X - mx _ У — my\ _ 2 I ] _ Kxy A
\ &X Oy I I ^x^y I
(см. свойство 7 ковариации) получаем
_ ( X - mx Y -my\
D --------------= °’
\ ux {Jy 1
X -mx Y - my
t. e. —~------------= c — постоянная. Ho
vff Uy
„,/Х-Шх У-ШуХ (Х-тЛ
у . ^У J \ J \ ^у j
= 0-0 = 0,
„ о X - тг г - ту (Jy
т. е. с = 0. Значит, — ---= -——--------, т. е. Y = — (X - тх) + mv. При
СГЖ (Ту ’ сгж' у г
rxY — —1 получаем
У = -^(Х-тг)+т?/.
Таким образом, при txy = ±1 с. в. X и У связаны линейной функцио-
нальной зависимостью.
Итак, для независимых случайных величин r\-y = 0, для линейно
связанных |г'а’у| = 1, а в остальных случаях —1 < txy < 1; гово-
рят, что с. в. связаны поламсителъной корреляцией, если r\Y > 0; если
Глава 3. Системы случайных величин 129
rxY < 0 — отрицательной корреляцией. Чем ближе |гху-| к единице,
тем больше оснований считать, что А' и Y связаны линейной зависи-
мостью. Отметим, что корреляционные моменты и дисперсии системы
с. в. обычно задаются корреляционной матрицей-.
Кхх
Кух
Kxy\
Kyy)
или
DX Kxy]
DY )'
Пример 3.8. Закон распределения дискретной двумерной с. в. задан
таблицей:
X\Y -1 0 1
0 0,15 0,40 0,05
1 1 0,20 0,10 0,10
Найти коэффициент корреляции txy-
Q Находим законы распределения составляющих X и Y:
х 0 1
р 0,6 0,4
У -1 0 1
р 0,35 0,50 0,15
Находим математическое ожидание составляющих: тх = 0:0,6+1-0.4 =
= 0,4. ту = — 1 • 0,35 + 0 0,50 + 1 • 0,15 = —0.20 (их можно было бы
найти, используя формулу (3.20); так
2 з
тх = ИУ£2Хг'1>гз = о-о,15+0-0,40+0-0,05+1-0,20+1-0,10+1-0,10 = 0,4).
г=1 j -1
Находим дисперсии составляющих:
DX = [MX2 - (MX)2] = (О2 • 0,6 + I2 • 0,4) - (0,4)2 = 0.24,
DY = ((-I)2 - 0,35 + О2 0,50 + I2 • 0,15) - (-0.20)2 = 0,46.
Стало быть: сгх = -^/0,24 ~ 0,49, сту = \/0,46 ~ 0,68. Находим MXY,
используя формулу (3.26): МXY — 0- (—1) -0,15 + 0-0-0,40 + 0-1 -0,05 +
+1 - (—1) • 0,20 + 1 • 0 • 0,10 + 1 • 1 - 0,10 = —0.10 (можно было бы составить
закон распределения Z = АГУ, а затем найти MZ = MXY:
Z = XY -1 0 1
Р 0,20 0,70 0,10
130 Раздел первый. Элементарная теория вероятностей и случайных процессов
MZ = MXY — —1-0.20+0-0,70+1-0,10 = —0,10). Находим корреляци-
онный момент, используя формулу (3.31): Кху = [MXY — MX -MY\ -
= —0,10—0,4-(—0.20) = —0,10+0,08 = —0,02 0. Находим коэффициент
корреляции (формула (3.34)):
-0,02
0,49 • 0,68
-0,06,
отрицательная корреляция.
Упражнения
1. Двумерная с. в. (X, У) задана законом распределения.
Х\У 1 2 3 4
1 0,07 0,04 0.11 0,11
2 0,08 0,11 0,06 0,08
3 0,09 0,13 0,10 0,02
Проверить, зависимы ли с. в. X и У. Найти cov(X, У).
2. Плотность совместного распределения с. в. X и У задана формулой
Га(1 - ®у3), при |ж| + 1, |у| 1,
(0, в остальных случаях.
Найти постоянную и и коэффициент корреляции.
3. Непрерывная двумерная с. в. (X, У) задана плотностью распреде-
ления вероятностей
с(т +у),
0,
/Ы =
при 0 х 1, 0 у 1,
в противном случае.
Зависимы ли с. в. X и У? Найти м. о. и дисперсию с. в. X и У.
Глава 3. Системы случайных величин • 131
3.8. Двумерное нормальное распределение
Среди законов распределения двумерной с. в. (А”, У) на практике
чаще всего встречается нормальное (гауссовское) распределение веро-
ятностей. Оно применяется, в частности, для описания 2-х результатов
измерения, абсциссы и ординаты точки попадания (А", У) при стрельбе
И т. д.
К| Двумерная с. в. (А", У) называется распределенной по нормальному
закону, если ее совместная плотность f(x,y) имеет вид
2тгсгТОу \/1 — г'2
1 /(я - тх)2 2г(х - тх)(у - mv) (у-тпу)2\
х^ 2(1—г2)^ а2 ” + а2 (3 35)
где тх, ту, ах, cry, г = txy — параметры этого распределения.
Распределение (3.35) называется также нормальным законом, рас-
пределения, на плоскости или двумерным нормальным (гауссовским)
распределением.
Можно доказать, что f(x,y) — это функция плотности, т. е. спра-
ведливо равенство
оо оо
У У /(ж, у) dxdV = 1:
- оо —ос
тх = MX, ту = MY; ох и сту — средние квадратические отклонения
(с. к. о.); г — коэффициент корреляции с. в. X и У.
Это означает, что двумерное нормальное распределение полностью
определяется заданием его числовых характеристик, что удобно на
практике (опытным путем находят эти параметры-характеристики и
получают совместную плотность f(x,y) двух нормально распределен-
ных с. в. X и У).
Выясним смысл, например, параметров тх и ах, найдя распреде-
ление вероятностей составляющей X (т. е. плотность вероятностей од-
номерной с. в. А). Согласно формуле (3.10) (п. 3.3) имеем:
ОС' (х-тх)2
Ш = [ f{x,y)dy=--------------i—-’2)х
J 2тгстхсгу\/1 — rz
—оо
ОО 1 / (у - ту)2 2г(х-тх)(у ту)\
- - U
—ос
5*
132 * Раздел первый. Элементарная теория вероятностей и случайных процессов
X — тз , У ~ ту
подстановки ——----= t, —— = z
/— «2 ОО
--------2 [ --2 (г2-2г4-г) .
= —------------- — -е i-г2 / е 1 r2V dz =
2я<Та.<Тг.\/] — г2 ./
—оо
1
——-------- е
\/2'Kcrxyj\ — г2
dz
t2 r2t2
g 1 — r2 1 — r2
л/2я<тж у/] — r2
(z — rt)2
1 - r2 dz =
z — rt
подстановка — —
\/l — r2
e f2 y/1 — r2 f
x/^TTCTxx/l — r2 J
—00
e^du =
СЮ
так как fe~u du = — интеграл Пуассона, формула (2.39) -
-ОО
(х - тх)2
= —2^
V2?Г (7Х
т. е.
(х - тх)2
fi(x) = —L-e“ 2^ . (3.36)
Случайная величина X имеет нормальное распределение с м. о. тх и
дисперсией а^.. Аналогично получаем
/2 (у) =
(у-ту)2
—А-—е 2а2
(3.37)
т. е. Y ~ N{my^(yy).
График плотности f(x,y) нормального распределения двумерной
с. в. (X, У) представляет собой холмообразную поверхность, верши-
1
2ттхстг/\/1 — г2
мум функции f(x,y) достигается в точке (гпх, Шу), рис. 42. Сечения
на которой находится в точке I
, т. е. макси-
поверхности распределения плоскостями, проходящими через точку
Глава 3. Системы случайных величин • 133
I тх, ту,---------- I перпендикулярно плоскости Оху, предста-
\ 27rcrJ.o'.(/ \/1 — г2 /
вляют собой кривые Гаусса вида z = be~a^x т*)2. Пересекая поверх-
ность распределения z = f(x,y) плоскостью z = zg, где 0 < zg < zmax,
параллельной плоскости Оху, получим в сечении эллипс, уравнение
проекции которого на плоскость Оху, имеет вид
(х-тх)2 (х - тх)(у - ту) (у - ту)2
---------2г------ + -
У-----------------------------------ау
(3.38)
где h2 = —2(1 — г2) ln(27rzo<Ta.o'2/x/l — г2). (В силу ограничения на zg ар-
гумент логарифма меньше 1, следовательно, значение логарифма отри-
цательно.) Если осуществить преобразование параллельного переноса
и поворота осей по формулам
(х = тх + хд cos <У- ~ уо sin а,
(г/ = ту + sin а + уо cos а,
2гахсгу
где угол а подобран так, что tg2a = —----то уравнение (3.38) пре-
- ° у
образуется в каноническое уравнение эллипса. Эллипс (3.38) называют
эллипсом рассеяния; оси симметрии эллипса (они образуют с осью Ох
углы а и + а) — главными осям,и рассеяния, а центр эллипса (точка
(гпх, тпу)) — - центром рассеяния.
Если компоненты двумерной нормально распределенной с. в. (X, У)
некоррелированы (г = гху = 0), то функция плотности (3.35) прини-
мает вид
/(ж, у} =
l( (х - тх)2 , (у -ту)2
1 с ч
2к<Ух<Уу
= /1(ж) • Л(?/),
т. е. /(ж, у) = /Дж) • /?(?/), где /1(ж) — плотность распределения с. в. X.
/2 (у) — с. в. Y. Отсюда следует- вывод: некоррелированные нормально
распределенные случайные величины являются также и независимы-
ми. Справедливо и обратное утверждение. Таким образом, для нор-
мально распределенных с. в. термины «независимость» и «некоррели-
рованность» эквивалентны.
134 Раздел первый. Элементарная теория вероятностей и случайных процессов
Уравнение эллипса рассеяния для некоррелированных с. в. запи-
сывается в виде
(х - тхУ (у - ту)2 = 1
(hcrx)2 (hay)2
(следует из равенства (3.38) при г = 0). На рис. 44 изображен один
такой эллипс (при h = 1).
Рис. 44
У тверждение. Если с. в. X и Y независимы, то вероятность попа-
дания случайной точки (X, У), распределенной по нормальному закону,
в прямоугольник R = {а х Ь. с у d}, находится по формуле:
1 х
где Фо(Ж) = -^=/в“ 2 dz — функция Лапласа.
Q Используя формулу (3.8),находим:
Произвольную область D можно приближенно заменить областью,
составленной из прямоугольников. На этом основано применение так
называемых «сеток рассеивания».
Глава 3. Системы случайных величин * 135
Можно показать, что вероятность попадания такой же точки (А', У)
в один из эллипсов рассеяния равна
.2
I2 (у - ГПу)2
' 2
Л2 = 1 -e“2h2
Пример 3.9. Найти вероятность попадания точки (А\ У) в прямо-
угольник {|ж| С 1, |у| 2}, если плотность совместного распределения
1 х2 +4у2
с. в. X и У равна /(х, у) = -^-е 6
(j Функцию f(x,y) можно переписать в виде
/(ж, у) =
(у-О)2
. (*~о)2 , -А/зА2
—1—е 2(\/з)2 . —1—е \ 2 /
х/Зу/2^
= Л (®) Л (у).
Значит, с. в. X и У независимы и А ~ \/3), У ~ N I 0, -у- I - Поэто-
му Р{|s| 1, |у| 2} = 2Ф0 ( -М 2Ф0 ( -^ ) = 4Фо(О,58) Фо(2,31) =
= 0,428. •
3.9. Регрессия. Теорема о нормальной корреляции
При изучении двумерной случайной величины рассматриваются не
только числовые характеристики одномерных компонент А и У (см.
п. 3.6), но и числовые характеристики условных распределений: услов-
ные м.о., условные дисперсии.
К| Условным математическим ожиданием одной из с. в., входящих
1—1 в систему (А”,У) называется ее м.о., вычисляемое при условии, что
другая с. в. приняла определенное значение (или попала в данный ин-
тервал). Обозначается: М(У|АГ = х) или М(У|ж) и 7И(А|у).
Вычисляются эти характеристики по обычным формулам м.о., в
которых вместо плотности распределения и вероятностей событий ис-
пользуются условные плотности распределения или условные вероят-
ности (п. 3.5).
136 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Для непрерывных с. в.
ОО оо
М(У|ж) = j yf(y\x)dy, М(Х\у)= I xf(x\y)dx, (3.39)
—ОО —оо
где /(у|ж) и f(x\y) — условные плотности распределения с. в. X и У,
определяемые равенствами (3.17) и (3.18) п. 3.5.
Для дискретных с.в. X и У условные м.о. вычисляются по фор-
мулам
т п
M(Y\xi) = ^2yjp(yj\xi) M(X\yj) = '^xip(xi\yj)1 (3.40)
j=i i=l
где p(yj\xi) = P{Y = yj\X = х{}, р(х}уд) = P{X = аДУ = t/Д, форму-
лы (3.15) и (3.16).
ф Условное математическое ожидание с. в. У при заданном X = х, т. е.
ЛДУ|.т) = (р(х), называется функцией регрессии или просто регрессией
У на ж (или У по х). Аналогично, М(Х\у) = — регрессия X на у
(или X по у).
Графики этих функций называются соответственно линиями (или
«кривыми») регрессии У на х и X на у.
ф Если обе функции регрессии У на х и X на у линейны, то говорят,
что с. в. X и У связаны линейной корреляционной зависимостью.
Теорема 3.4 (Теорема о нормальной корреляции). Если двумерная
с. в. (X, У) распределена по нормальному закону, то с. в. X и У связаны
линейной корреляционной зависимостью.
□ Условное м.о. Л/(У|,т) (т.е. функцию регрессии У на х) найдем,
используя условный закон распределения с. в. У при X = х, кото-
рый определяется условной плотностью распределения f(y\x). Соглас-
У (ж, y'j
но формуле (3.17) /(Дж) = — А- . Совместная плотность f(x,y) зада-
J 1 \Х )
на формулой (3.35), а плотность распределения составляющей X есть
(х — тх)2
= J- е
у/2тгох
(см. формулу (3.36)). Имеем
Глава 3. Системы случайных величин 137
,f{y\x) =
2тгстх<Ту\/1 - г2
1 /(х- - тпх)2
2(1 -г2Д а2
2т(х - тпх)(у - тпи) (у - ту)2
а2
(л: - та-,)2
Произведем упрощение показателя экспоненты в последней формуле.
Так как
1
2(1 - г2)
(ж - тх)2 2г(х - тх)(у - ту) (у- ту)2
(х-тх)2 1-г2 = _ 1
2сг2 1 —г2 2(1 —г2)
(х-тх)2 2г(х - тх)(у - ту) (х-тх)2(1-г2) (у-ту)2
О /Т ZT О ' О
1 ((у - ту)2
2(1 - г2) V а2
2г{х — тх){у — ту)
ТО
Как видно, условный закон распределения является тоже нормальным
с условным м. о. и условной дисперсией, определяемыми формулами
M(Y\x) = ту + г —- и D(Y\x) = <т2(1 - г2). (3.41)
Аналогично можно получить функцию регрессии X на у:
^у) = М(Х\у) = тх+г-С^^ и П(Х|?;)=п2(1-г2). (3.42)
Так как обе функции регрессии (3.41) и (3.42) линейны, то корреляция
между с. в. А' и У линейная. И
138 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Пример 3.10. Построить линию регрессии Y на х для двумерной с. в.
(Х,У), закон распределения которой задан таблицей:
X\Y -1 0 1 Е
0 0,10 0,15 0,20 0,45
1 0,15 0,25 0,15 0,55
Е 0.25 0,40 0,35 1
Q Находим условные ряды распределения с. в. Y при х.\ = 0, х? = 1,
используя формулы (3.15).
Р(У1Ы = P{Y = -1|Х = 0} = = ||,
рЫ*1) = P{Y = 0|Х = 0} = £|| = ||,
P&M = P{Y = 1|Х = 0} = ® = §.
Согласно (3.40) имеем Af(y|xi) = —1-|р+0-|р + 1- ?р = Ш.
45 45 45 45
Далее:
НшЫ = P{Y = -1|Х = д = £|| = ||,
рЫх2) = P{Y = 0|Х = 1} = £|| = ,
и,ио оо
НузЫ = P{Y = 1|Х = 1} = = ||.
Следовательно, M(Y\x2) = — 1-М + 0- р^ + 1- |^ = 0.
55 55 55
Линия регрессии У на х изображена на рис. 45.
Рис. 45
Глава 3. Системы случайных величин 139
Упражнения
1. Построить линию регрессии X на у по условию примера 3.10.
2. Пусть (АГ, Y) — двумерная нормальная с. в. с параметрами тх =
= ту = 0, ах = <Ту = 1. Найти условную плотность распределения
с. в. X при условии, что Y — у и с. в. Y при условии, что X = х
(воспользоваться формулами (3.36) и (3.37)).
ЗЛО. Многомерная (n-мерная) случайная величина
(общие сведения)
Систему п случайных величин называют п-мерной (многомерной)
с. в. или случайным вектором X — (Ai, Аг, • • , Хп).
Многомерная с. в. есть функция элементарного события w:
(Ai, Аг,..., Хп) = p(w); каждому элементарному событию w ста-
вится в соответствие п действительных чисел х\, х2-, .... хп —
значения, принятые с.в. Ai, А2, ..., Хп в результате опыта. Век-
тор х — (х]_,Х2, •. • ,хп) называется реализацией случайного вектора
(А\, Аг, -.., Хп) = X.
Закон распределения вероятностей n-мерной с. в. задается ее функ-
цией распределения
^А'ьА'г.-.Лп^!,^,. - . ,Хп) = P{Xi < XI, Х2 < Х2,-.-,Хп < Хп}.
Функция распределения F(xi, х2,. , тп) обладает такими же свойства-
ми, как и функция распределения двух с. в. F(x,y). В частности: она
принимает значения на отрезке [0,1], F(+oo, +00,..., 00) = 1, F^(x^) =
= F(+oo, +00, хз, +оо,..., +оо).
Плотность распределения системы п непрерывных с. в. (Aj, А2....
... , Хп) определяется равенством
, , dnF(xl,x2,...,xn)
/АьА^.лДЖ!,^,...,^) - дХ1дХ2...дхп ’
При этом: f(x\,x2,-
Хп) 0 и
,Ж2,
хп) dxidx2 ..., dxn = 1.
140 Раздел первый. Элементарная теория вероятностей и случайных процессов
Вероятность попадания случайной точки (Xj, Х2,.. , Хп) в область
D из '//-мерного пространства выражается n-кратным интегралом
^{(^1,^2, • • • ,Хп) е D} = У ... 1^ f(xl,x2,...,xn)dxidx2...,dxri.
(Ь)
Функция распределения Х2, • -, хп) выражается через плотность
/(xi,я?2, - , хп) n-кратным интегралом
п
Необходимым и достаточным условием взаимной независимости
п с. в. является равенство:
Fxi,X2,...,xAx1,x2, ,Хп) = FV1(ti) Fx.2(x2) ... FXn(xn)-
для п непрерывных с. в.:
fXi.X2,...,X„(x1,X2, .. .,хп) = fxdxi) fx2(x2) - fxn(xn).
Основными числовыми характеристиками многомерной с. в. (Xi,
Х2,.. -, Хп) являются:
1. п м.о. составляющих Xi, т.е. mi = МХг, m2 = МХ2, , тп =
= МХп-,
2. п дисперсий составляющих Хр т.е. Di = DX\, D2 = DX%, ....
Dn — DXn, при этом Di = M(Xi — пч)2, i = l,n;
3. n(n—1) ковариаций, т. e. K,3 = M{Xi-Xj), i j, при этом Ki3 — Kji,
Кц = Di.
Ковариации Kl3 образуют ковариационную матрицу
[Кп К12 К1п\ /Вх К12 • к1п\
К21 К22 - К2п или D2 К2п
\Кп1 КП2 • Кпп/ 1 Dn)
3.11. Характеристическая функция и ее свойства
Наряду с функцией распределения, содержащей все сведения о с. в.,
для ее описания можно использовать так называемую характеристи-
ческую функцию. С ее помощью, в частности, упрощается задача на-
хождения распределения суммы независимых с. в., нахождения число-
вых характеристик с. в.
Глава 3. Системы случайных величин 141
Характеристической функцией с. в. X называется м. о. с. в. е’7Л,
обозначается через y>x(t) или просто </?(£).
Таким образом, по определению
Ы*) = Meitx,
где t — параметр, i = 1 — мнимая единица.
Для д. с. в. X. принимающей значения Xi, х?, ...с вероятностями
pk = Р{Х = Xk}, k = 1, 2,3,..., характеристическая функция опреде-
ляется формулой
ОО
^х(/) = £ег^рА.. (3.43)
к=1
для н. с. в. с плотностью /(ж) — формулой
оо
¥>х(0 = [ eitxf(x)dx. (3.44)
—ОО
Заметим, что:
1. Характеристическая функция н. с. в. есть преобразование Фурье от
плотности ее распределения: плотность /(ж) выражается через tp(t)
обратным преобразованием Фурье:
ОО
= I ^e-^dt.
—ОО
2. Если с. в. принимает целочисленные значения 0,1,2,..., то </?(/) =
= где z = ел. Тогда
ОО
ф(х) = т zk?k
к=0
(см. п. 2.6).
Свойства характеристической функции:
1. Для всех t G R имеет место неравенство
И*)1 «С <Д0) = 1.
2. Если У = аХ + Ь, где а и b постоянные, то
</?y(f) = eltb<px(at).
142 Раздел первый. Элементарная теория вероятностей и случайных процессов
3. Характеристическая функция суммы двух независимых с. в. X и У
равна произведению их характеристистических функций, т. е.
Vx+r(t) = y>A-(t)
4. Если для некоторого к существует начальный момент к-т порядка
с. в. X, т. е. а*, = М(Хк), то существует к-я призводная характери-
стической функции и ее значение при t — 0 равно пк, умноженному
к
на г , т. е.
^}(0) = ikM(Xk) = ikak.
□ 1. |^o(t)| = |Me*tA| < M\eltx\ = Ml = 1. (Действительно. |ег/Л | -
= | cosfX + isinfX| = у/cos2 tX + sin2 tX = 1); <Д0) = Me0 = Ml = 1.
2. ^r(f) = MeifV = Meit(-aX+b} = M(eitbeiaXt) = eabMeiatx =
= eltb^x(ai).
3. <^A-1+X2(t) = Мей(Х1+А'2) = M(e’tA1e?'fA2) = MeitX1 Meitx* =
= tpxi (t) ’ 9?л'2 (0- Свойство справедливо для суммы п независимых с. в.
4. ^k\t) = = ikM(XkeitX). Поэтому при t = 0 имеем
^(0) = ikM(Xk) = ikak.
Из свойства 4 следует ак = i~Kq>x дО). Отсюда, как частный случай,
можно получить:
«I = MX = (Г1 = I = = -С- =
а2 = MX2 = -<^"(0),
DX = a2 - a2 = -</(0) + (</(0))2.
(3.45)
Пример 3.11. Найти характеристическую функцию с. в. X, распреде-
ленной по биномиальному закону. Найти MX и DX.
Q С. в. А' принимает значения 0,1,2,.... п с вероятностями
рк = Р{Х = к} = Ckpkqn~k
Поэтому, используя формулу (3.43) и формулу бинома Ньютона, нахо-
дим, что
п п
= £ смСкркд^к = £ Ск(еи - p)kqn~k = (е'ф + q)n,
kQ k=Q
Глава 3. Системы случайных величин 143
т. е. (p(t) = (eltp + q)n. Используя формулы (3.45), находим:
MX = -г(п^р + q)n~l -ре'1 - г)|
= пр, DX = npq.
t=o
Упражнения
1. Найти характеристическую функцию с. в. X, равномерно распре-
деленной на отрезке [а, 6].
2. Найти MX с. в. X, распределенной по закону Пуассона с параме-
тром а, используя характеристическую функцию <рх (t)
_ „ , , . f — 2ж, при х G [-1,0], v
3. Дано fx(x) = < _ 1 — плотность с. в. X.
[0, в противном случае
Найти tpx (f).
3.12. Характеристическая функция нормальной
случайной величины
Согласно формуле (3.44), характеристическая функция с. в. X ~
~ N(a. ст) равна
?? (х — а)2 х2 — 2(а + iter2 )х + а2
udt) = -1 - / eitxe 2<z2 dx = Дг / e 2a2 dx =
\/2яст J J
—co — co
?? x2 — 2x(a + ita2) + (g 4- ita2)2 -b a2 — (a + ita2)2
= —i— / e 2<z2 dx —
\[2тго J
—co
?? (x — (a + iter2))2 2aita2 + (iter2)2
= —i— e 2<r2 e 2a2 dx =
J
—co
2aita2 - t2<r4 'r' _ (a - (o + ita2))2
= ------e. 2a2 / e 2(z2 dx =
V27FCT J
—co
144 Раздел первый. Элементарная теория вероятностей и случайных процессов
оо ( х — (а + На2) 2
хГХко J \ \/2ст /
-ос
1 л - t2a2
= ~^—e ta 2 дД = elta 2
х/тг
(оо '
У е" du = д/я — интеграл Пуассона
-ос /
.. 12°2
Таким образом. (£) = с 2 , если X ~ N(a, ст).
Пример 3.12. Найти с помощью характеристической функции м.о. и
дисперсию с. в. X ~ N(a, ст).
О Применим формулы (3.45):
, t2a2 ।
MX = [—^(0)1 = —ieia 2 (ia — /ст2) = — i • 1 • ia — a,
lt=o
t. e. MX — a;
DX = [—y/'(0) + (<//(0))2] =
(t2a2 t2a2 \ i
7^iat-. 2\2 iat— „ \ , t \'2
—ст e 2 + [га — /ст ) e 2 +(га) =
J lt=o
= ст2-г2а2 + г2ст2 = ст2,
т.е. DX — ст2. Получили известные нам результаты: а — м.о., ст —
с. к. о.; эти параметры полностью определяют с. в., распределенную по
нормальному закону. •
Глава 4
Функции случайных величин
Часто возникают задачи, в которых по известному закону распре-
деления (или числовым характеристикам) одной (или нескольких) слу-
чайной величины требуется определить распределение другой (или не-
скольких) случайной величины, функционально связанной с первой.
Построение законов распределения функций некоторых д. с. в. (с А",
X + У, X Y) уже было рассмотрено в п. 2.5 (свойства 2, 3, 5 мате-
матического ожидания).
4.1. Функция одного случайного аргумента
pt| Если каждому возможному значению с. в. X по определенному пра-
— вилу соответствует одно возможное значение с. в. У, то У называют
функцией случайного аргумента А’, записывают У = <р(Х).
Пусть X — д. с. в. с возможными значениями xi, х%, хз,..., хп, ве-
роятности которых равны соответственно • • ,Рт т.е. pi =
= Р{Х = xj, i — 1,2,3,... ,п. Очевидно, что с. в. У = </2(Х) так'
же д.с. в. с возможными значениями yi = <p(xi), у2 = т?(хг), Уз =
= </?(хз),..., уп = ip(xn), вероятности которых равны соответственно
Р1,Р2,Рз, • ,Рп, т. е. если у, = то = P{Y = yj = Р{Х = xj,
i = 1, п.
Отметим, что различным значениям с. в. X могут соответствовать
одинаковые значения с. в. У. В этом случае вероятности повторяющих-
ся значений следует складывать.
Математическое ожидание и дисперсия функции У = <р(Х) опреде-
ляются соответственно равенствами
MY = У 9з(х,;)рг, DY = У(у(хг) - ту?Рг-
г=1 1=1
146 Раздел первый. Элементарная теория вероятностей и случайных процессов
Пример 4.1. Задан закон распределения д. с. в. X:
X -1 1 2
р 0,1 0,3 0,6
Найти МУ, если: а) У = X2, б) У — 2Х + 10.
О а) С. в. У принимает значения у, = <p(xi) — (—I)2 = 1, у2 = I2 =
= 1, уз = 22 = 4. т. е. она принимает два значения: 1 и 4, причем
Pi = P{Y = 1} = Р{Х = -1} + Р{Х = 1} = 0,1 + 0,3 = 0,4, р2 =
= Р{У = 4} = Р{Х = 2} = 0,6. Следовательно, MY = 1 • 0,4 + 4 • 0,6 =
= 2,8.
б) Закон распределения У имеет вид
У 8 12 14
р 0,1 0,3 0,6
Значит, MY = 8 0,1 + 12 • 0,3 + 14 • 0,6 = 12,8.
Пусть X — непрерывная с.в. с плотностью распределения /(ж), а
с. в. У есть функция от X, т. е. У — <р(Х). Найдем закон распределе-
ния с. в. У. Будем считать функцию У = <р(Х”) непрерывной, строго
возрастающей и дифференцируемой в интервале (а. Ь) (он может быть
бесконечным: (—оо, оо)) всех возможных значений с. в. X. Тогда суще-
ствует функция х — ^(у), обратная функции у = <р(.т) (случайная точка
(X, У) лежит на кривой у = <р(х)). Функция распределения Су(у) (ее
можно обозначить и так: G(y), Fy(y) или Ру(х)) с. в. У определяется по
формуле G(y) = P{Y < у}. И так как событие {У < у} эквивалентно
событию {X < ^(у)} (рис. 46), то
Рис. Jf6
Глава 4. Функции случайных величин 147
V’t’/)
С(у) = Р{У<у} = Р{Х<№)}=ГА-(№))= I f^dx.
а
Дг/)
G(y) = / f(x)dx.
Дифференцируя полученное равенство по у, найдем плотность распре
деления с. в. Y:
д(у) = = fWy)) 4~(№)) = Ш1.уУ) Ф'(у),
ау ау
т. е.
<Яу) = fWyW(y)-
(4.1)
Если функция у = Дж) в интервале (а, Ь) строго убывает, то событие
{У < у} эквивалентно событию {А > 'ф(у)}. Поэтому
ь
G(y) = У f(x) dx -
•Ку)
dx.
Отсюда следует, что
д(у) = ^МуУ)Ф'(у)-
(4-2)
Учитывая, что плотность распределения не может быть отрицательной,
формулы (4.1) и (4.2) можно объединить в одну
д(у) = /(Ф(у))1Ф'(у)1-
(4-3)
И, наконец, если функция у — <р(х) немонотонна в интервале (а, 6), то
для нахождения д(у) следует разбить интервал на п участков монотон-
ности, найти обратную функцию на каждом из них и воспользоваться
формулой
п
д(у) = $2/№(?/)) |^(?/)1- (4-4)
г=1
Если с. в. X является непрерывной и /(ж) — плотность ее распреде-
ления, то для нахождения числовых характеристик с. в. У — <р(Х)
необязательно находить закон ее распределения, можно пользоваться
148 • Раздел первый. Элементарная теория вероятностей и случайных процессов
формулами
оо
МУ = М(<^(Х)) = У <p(x)f(x)dx,
—ОО
ОС'
DY = D(<^(X)) = J — my)2 * * 5f(x)dx.
—ОО
(4.5)
Пример 4.2. Найти плотность распределения функции У = — 5Х + 2,
считая X н. с. в. с плотностью /(ж).
Q Функция у = —5а? + 2 монотонно убывает в интервале (—оо, оо).
Обратная функция есть х = ~(2 — у) = 'Ф'('У) — — к- По форму-
О и
Проиллюстрируем на примере 4.2 вывод формул для функции и
плотности распределения:
2-у
5
2-у
5
2~^\ +
5 J
ьг 2-у
5
= 1 - Fx
Mb
2-У
5
так как Р ^Х = } = 0, т. е. G(y) = 1 — Fx
распределения с. в. У. Тогда
2-у
5
— функция
</(у) = G'(y) =
2-у\
5 /
' у
2~у\ / П
5 J к 5/
т. е. <у(у) = |.f
, у Е (—оо, оо).
2-У
5
Отметим, что линейное преобразование У = аХ + b не меняет ха-
рактера распределения: из нормальной с. в. получается нормальная; из
равномерной — равномерная.
Глава 4. Функции случайных величин 149
Пример 4.3. Пусть с. в. X имеет равномерное распределение в интер-
вале
математическое ожидание с. в. У = cos X: а) най-
дя плотность д(у); б) не находя у(у).
Q а) Имеем:
/(ж) = <
1
5-, х ) функция у = cos х не монотонна: в 1—^.0] функ-
(о, — убывает. На первом участке обратная функ-
В интервале
ция возрастает, в
ция жх = — arccosy — ^i(y), на втором — = arccosy = гМу). По
формуле (4.4) имеем
= f(V4(y))IV4(y)l + /Шу)Ж(у)1 =
7Г
____1
- у2
1
\/1 - у2
2
7Гу/1 - У2
т. е.
у(у) = *
0,
2
- у2’
при 0 < у < 1,
при у 0 или у 1.
Тогда
MY =
1
т.е. MY= %.
б) Используем формулу (4.5):
7Г
2
т.е. MY = |.
150 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Упражнения
1. Дискретная с. в. X задана законом распределения
х -2 -1 0 1 2 3
р 0,10 0,20 0,30 0,25 0,10 0,05
Найти закон распределения случайных величин: a) Y — 2Х2 — 3:
б) Y = л/Х + 2; в) У = sin ?-Х.
О
2. Дискретная с. в. X задана своим рядом распределения
х 0 1 2 3
р 0,3 0,4 0,2 0,1
Построить многоугольник распределения с. в. X и У = cos2 ^Х.
Найти MY и ст У.
3.
Найти плотность распределения и дисперсию с. в. У = X + 1, если
4. Случайная величина X ~ N(0,1). Найти плотность распределения
с. в.: а) У = ЗХ3; б) У = |Х|.
5. Пусть X — и. с. в. с плотностью
,, . _ J е х, при ж 0,
ДЖ)~(0, при ж < 0.
Найти функцию распределения и плотность распределения с. в. У,
если а) У = 2Х — 1; б) У = X2.
4.2. Функции двух случайных аргументов
Для решения ряда практических задач необходимо знать закон рас-
пределения (или числовые характеристики) случайных величин вида
Z = X ± У, Z = X • У, Z = у/Х2 + У2, Z = тах(Х, У) и других.
Если каждой паре возможных значений с. в. X и Y по определен-
ному правилу соответствует одно возможное значение с. в. Z, то Z
называют функцией двух случайных аргументов X и У, записывают
Z = ДХ,У).
Глава 4 Функции случайных величин • 151
Найдем закон распределения суммы двух случайных величин (наи-
более важный на практике), т. е. закон распределения с. в. Z = X + Y.
Пусть система двух непрерывных с. в. (X, Y) имеет совместную
плотность распределения /(ж, у). Найдем по формуле (3.8) функцию
распределения с. в. Z — X + Y.
Fz(z) = P{Z
z} = Р{Х -Г Y
f(x,y)dxdy.
Здесь Dz — множество точек плоскости Оху, координаты которых удо-
влетворяют неравенству х + у < z, см. рис. 47.
Имеем
Рис. 47
ОО Z—X
Fz(z) = У (У f(x,y)dy^
dx.
--ос —ос
Дифференцируя полученное равенство по переменной z, входящей в
верхний предел внутреннего интеграла, получаем выражение для плот-
ности распределения с. в. Z = X + У:
(4.6)
Если с. в. X и У независимы, то, как известно (п. 3.4), f(x,y) =
— /1(ж)/2(у)- Формула (4.6) примет вид
ОО
fz(z) = fx+Y(z) = У /1(ж)/2(г-ж)с?ж. (4.7)
—со
Закон распределения суммы независимых с. в. называется компо-
зицией или сверткой законов распределения слагаемых.
152 Раздел первый. Элементарная теория вероятностей и случайных процессов
Плотность распределения с. в. Z можно записать в виде fx+Y =
= fx * Jy-, где * — знак свертки, а формулу (4.7) называют формулой
свертки или формулой композиции двух распределений.
Записав Z в виде Z = Y+X, можно получить другое представление
для а именно
ОО
fz(z) = У f(z-y,y)dy
— ос
И
ос
/г(г) = У fi(г - y)f2(y) dy
—оо
в случае независимости с. в. X и Y.
Задача нахождения закона распределения с. в. вида Z — X — У,
Z = X • Y и других решаются аналогично.
Пример 4.4. Пусть с. в. X ~ 7V(0,1), с. в. Y ~ 7V(0,1). Найти закон
распределения с. в. Z = X + У, считая X и У независимыми с. в.
О Используя формулу (4.7), получаем
z
Сумма независимых нормальных с. в. (с т = 0, о = 1) имеет нормаль-
ное распределение (с т = 0, о = у/2). •
Глава 4. Функции случайных величин 153
Пример 4.5. Совместное распределение с. в. X и Y задано плотностью
распределения вероятностей
, . (х + у,
f(x,y) = |0
при 0 ж 1, 0 у С 1,
в противном случае.
Найти плотность распределения вероятностей с. в. Z = X — Y.
Q Найдем сначала функцию распределения F(z) с. в. Z, а затем — ее
производную F'z(z) =
Fz(z) = P{Z < z} = P{X -Y < z} = / / (x + y) dxdy,
где Dz — множество точек, координаты которых удовлетворяют нера-
венству х — у < z, т. е. у > х — z (они находятся выше прямой у = х — z),
где z — произвольное число. Очевидно, если z —1, то F(z) = 0; так
как f(x,y) = 0 вне квадрата 0^ж^1,0^у^1. Область интегриро-
вания Dz при — 1 < z 0 изображена на рис. 48, при 0 < z 1 — на
рис. 49).
154 * Раздел первый. Элементарная теория вероятностей и случайных процессов
При 0 < z 1 имеем
При z > 1 имеем
Таким образом,
Fz(z) =
О,
(г + 1)2
2 ’
-г2 + 2г + 1
при г — 1,
при — 1 < г О,
при 0 < г 1,
при г > 1.
Следовательно.
'О,
F'z(z) = fz{z) = г + 1,
! - г,
при z < —1, г > 1,
при — 1 < г О,
при 0 < г 1.
Контроль:
Глава 4. функции случайных величин 155
Пример 4.6. Независимые с. в. X и Y распределены равномерно
X ~ 7?[0,4], Y ~ _R[0.1]. Найти плотность распределения вероятностей
с. в. Z = X + Y (рис. 50).
Q Система с. в. (X, У) равномерно распределена в прямоугольнике
D = {0 < х < 4,0 у 1},
* / \ же [0,4], . fl, у G [0,1],
,-|о, ж£[0,4], ЫУ) (0, У £[0,1].
Так как с. в. X и У независимы, то /(ж, у) = Д(ж) • /г(у) = ^ • 1 = |-
Fz(z) =P{X + Y <z} = Ц ±dxdy = ±SDz,
(x+y<z)
где Sdz — площадь области Dz — части прямоугольника, лежащей
ниже прямой ж + у = z. Если z 0, то F(z) — 0; если 0 < z 1, то
F(z) — | (так как Sdz = z z); если 1 < z 4, то
| ’ C~2±Z '1)=Z8(2Z~ 1)5
156 * Раздел первый. Элементарная теория вероятностей и случайных процессов
если 4 < z 5, то
F(z) = l-(1.4-|(5-z)(J
если 5 < z, то F(z) = i • 4 = 1. Итак,
/(*) = F'z(z) =
О,
0,25z,
0,25,
0.25(5 - г),
z 0, z > 5,
0 < z < 1,
1 < z 4,
4 < z С 5.
Контроль:
1
О
4
/ldz+*J
1 4
5
= 1.
Полученную плотность распределения fz(z) можно найти другим
способом, используя формулу
оо
/(z) = У Л (ж) • - х) dx.
—ОО
Имеем 4 4
f(z) = I ~ х) dx = | J ~ dx-
о о
Функция под знаком интеграла отлична от нуля лишь в случае
(0 С х 4,
[0 < z — х 1,
т. е.
Решение системы зависит от значения z.
1. Если z 0, система несовместна; отрезки [0.4] и [z — l,z] не
пересекаются, (см. рис. 51).
Следовательно, f^(z — х) = 0 и /\-+y(z) = 0.
2. Если 0 < z С 1, система (4.8) эквивалентна неравенству 0 х < z
(см. рис. 52).
Поэтому
Z
0
Глава 4. Функции случайных величин 157
—HZZZZZI--------------------------—
z—1 z х
-----------HZZZZZZZZZZZZZZZZZZ1 -
О 4-X
Рис. 51
Рис. 52
3. Если 1 < z С 4, система (4.8) эквивалентна неравенству z — 1
х < z (см. рис. 53).
------------HZZZZZJ--------------—
2—1 z----------------------------х
----t/ZZZZZZZZZZZZZZZZZH —
0 1 4 X
Рис. 53
Поэтому
Z
fx+Y(z) = | J ldz= |(г-г +1) =
z-l
4. Если 4<z^5, тог — 1^®<4 (см. рис. 54).
—HZZZZZJ 1-------—
2-1 2 5 X
Рис. 54
Поэтому
4
/г(г) = | I idx = y\4z_=^-z + l) = ^
Z-l
Ч---ZZZZZ^-1----
5 z-l 2 X
Рис. 55
158 Раздел первый. Элементарная теория вероятностей и случайных процессов
5. Если 5 < г, то система (4.8) несовместна (см. рис. 55), а, значит,
fz(z) — 0- Итак.
/U) =
0,25г,
0,25,
k0,25(5 - г),
z 0, z > 5,
0 < z 1,
1 < z 4,
4 < z < 5.
Упражнения
1. По условию примера 4.5 найти функцию и плотность распределе-
ния вероятностей с. в. Z = X + Y.
2. По условию примера 4.5 найти плотность распределения вероятно-
у
стей с. в. Z — —.
4.3. Распределение функций нормальных случайных
величин
Рассмотрим распределение некоторых с. в., представляющих функ-
ции нормальных величин, используемые в математической статистике.
Распределение у2 (хи-квадрат или Пирсона)
Распределением х^ сп степенями свободы называется распределе-
ние суммы квадратов п независимых стандартных случайных величин,
т. е.
п
у2 = ВДе Xi~N(0,1), i = 1,2.......п.
г—1
Плотность вероятности с. в. у2 зависит только от числа п, т.е. чи-
сла слагаемых. Если п = 1, то у2 = X2, где X ~ Х(0,1),
/а (ж) =
2 .
Плотность распределения с. в. У = X2 равна (согласно (4.4))
1
s(y) = 2,
у2тгу
0.
Глава 4. Функции случайных величин 159
Плотность распределения Хп имеет вид
{1 — -1 — —
-----— ж 2 е 2, при х > О,
22Г(а)
О, при х С О,
ОО
где Г(р) = dt — гамма-функция Эйлера (Г(р) = (р — 1)! для
о
целых положительных р). С возрастанием числа степеней свободы п
распределение у2 приближается к нормальному закону распределения
(при п > 30 распределение х2 практически не отличается от нормаль-
ного);
МХп = п, DXn = 2п-
На практике, как правило, используют не плотность вероятности, а
9
квантили распределения Хп-
Квантилью распределения у2, отвечающей уровню значимости а,
2 2
называется такое значение Хп Хы» ПРИ котором
ос
Р{Хп > Х2а,п} = У /Х2 (ж) dx = а.
С геометрической точки зрения нахождение квантили Хп п заклю-
чается в выборе такого значения Хп ~ Хап, чтобы площадь заштрихо-
ванной на рис. 56 фигуры была равна а.
Значения квантилей приводятся в специальных таблицах-прило-
жениях.
Для стандартного нормального распределения квантили уровня
а обозначаются через ±uQ, причем иа является решением уравнения
160 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Распределение Стьюдента
Распределением Стьюдента (или t-распределением) с п степенями
свободы называется распределение с. в.
Тп
Z
где Z ~ W((), 1) — стандартная нормальная величина, независимая от
2
Х^-распределения.
Плотность вероятности распределения Стьюдента имеет вид
тч f п -J- 1 \ и 1
1 / /2\ “ 2
/тД*) = г (^) v + ;
При п оо распределение Стьюдента приближается (уже при п > 30
почти совпадает) к нормальному;
МТп = 0, DTn = п>2.
На практике используют квантили ^-распределения: такое значение
t — ta . ЧТО
ос
Р{|4| ><«.„} = 2 У
/(t) dt = а.
С геометрической точки зрения нахождение квантилей заключается в
выборе такого значения t = ta
2
рис. 57 фигуры была равна а.
, чтобы площадь заштрихованной на
Рис. 57
Глава 4. Функции случайных величин 161
Распределение Фишера-Снедекора
Распределением Фишера Снедекора (или F-распределением) с т и
п степенями свободы называется распределение с. в.
щХ-т
9 9 9
где Хт и Хп — независимые с. в., имеющие х -распределение соответ-
ственно сшил степенями свободы.
При /г —> оо F-распределение стремится к нормальному закону.
MF =
п > 2,
2п2(т + г?, — 2)
DF =------------ъ
т(п — 2)2(7t — 4)
п > 4.
На практике обычно используют квантили распределения: такое зна-
чение F = FQ,m>n, что
Р{^ > Fa,т.п}
f(F) dF = а.
С геометрической точки зрения нахождение квантили заключается в
выборе такого значения F = Fa^mjn, чтобы площадь заштрихованной
на рис. 58 фигуры была равна а.
Рис. 58
Глава 5
Предельные теоремы теории вероятностей
Рассмотрим ряд утверждений и теорем из большой группы так на-
зываемых предельных теорем теории вероятностей, устанавливающих
связь между теоретическими и экспериментальными характеристика-
ми случайных величин при большом числе испытаний над ними. Они
составляют основу математической статистики. Предельные теоремы
условно делят на две группы. Первая группа теорем, называемая зако-
ном больших чисел (коротко: ЗБЧ), устанавливает устойчивость сред-
них значений: при большом числе испытаний их средний результат пе-
рестает быть случайным и может быть предсказан с достаточной точ-
ностью. Вторая группа теорем, называемая центральной предельной
теоремой (коротко: ЦПТ), устанавливает условия, при которых закон
распределения суммы большого числа случайных величин неограни-
ченно приближается к нормальному.
В начале рассмотрим неравенство Чебышева, которое можно ис-
пользовать: а) для грубой оценки вероятностей событий, связанных со
с. в., распределение которых неизвестно: б) доказательства ряда теорем
ЗБЧ.
5.1. Неравенство Чебышева
Теорема 5.1. Если с. в. X имеет м. о. МX — а и дисперсию DX, то для
любого е > 0 справедливо неравенство Чебышева
Р{\Х - МХ\ > е} (5.1)
Глава 5. Предельные теоремы теории вероятностей *163
Q Докажем неравенство (5.1) для непрерывной с. в. X с плотностью
/(л). Вероятность Р{|А" — а| с} есть вероятность попадания с. в. X в
область, лежащую вне промежутка [а — е, а + е]. Можно записать
а—е +оо
Р{|А' —g|>e} = I f(x)clx+ j f(x)dx = J f(x)dx =
—ос а+е |ж—
= I Lf(x)dx^ У ~f(x)dx,
|х-с|^е |х—а|^е
так как область интегрирования |а? — «| > е можно записать в виде
. \9 9 -I Т/Г
(х — а) е , откуда следует 1 5---. Имеем
так как интеграл от неотрицательной функции при расширении обла-
сти интегрирования может только возрасти. Таким образом,
ОС
Р{|X - о| > е} s: X j (х- a)2f(x) dx = ±DX,
т.е. P{|X-a| >e}
E
Аналогично доказывается неравенство Чебышева и для дискрет-
ной с. в. X, принимающей значения яд, я:2. ®з,... с вероятностями pi, р2,
Рз,...; только интегралы (вида / ) заменяются соответствующими
|z—а|^е
суммами (вида ).
а|^е
Отметим, что неравенство Чебышева можно записать в другой
форме:
Р{\Х-МХ\ <е} (5.2)
Е^
В форме (5.2) оно устанавливает нижнюю границу вероятности собы-
тия, а в форме (5.1) — верхнюю.
164 Раздел первый. Элементарная теория вероятностей и случайных процессов
Неравенство Чебышева справедливо для любых с. в. В частности,
для с. в. X = т, имеющей биномиальное распределение с математиче-
ским ожиданием MX = а — пр и дисперсией DX — npq (п. 2.7), оно
принимает вид
Р{\т - np| < е} 1 - (5.3)
е
для частости ™ (или п. 1.5) события в п независимых испы-
таниях, в каждом из которых оно может произойти с вероятностью
р = М = а, дисперсия которых D (ДО = неравенство Чебыше-
ва имеет вид
(5.4)
Оценку вероятности попадания с. в. X в промежуток [е, оо) дает
неравенство Маркова.
Теорема 5.2 (Неравенство Маркова). Для любой неотрицательной
с. в. X, имеющей м. о. MX и е > 0, справедливо неравенство:
Р{Х
ОО ОС
□ Р{Х^е} = I f(x)dx^ I %f(x)dx =
е е
о
Неравенство (5.5) можно записать в форме
Р{Х < е} > 1 -
(5-6)
Пример 5.1. Оценить с помощью неравенства Чебышева вероятность
того, что отклонение с. в. X от своего м. о. будет меньше трех с. к. о.,
т. е. меньше 3<тх.
О Полагая е = Зщ, в формуле (5.2), получаем
2
Г{|Х - МХ\ < ЗпД > 1 - = 1 _ 1 | « 0,8889.
(ЗстД2 9 9
Эта оценка, как известно (п. 2.7), называется правилом трех сигм- для
с. в. X ~ 7V(a, ст) эта вероятность равна 0,9973. •
Глава 5. Предельные теоремы теории вероятностей * 165
5.2. Теорема Чебышева
Основное утверждение ЗБЧ содержится в теореме Чебышева. В ней
и других теоремах ЗБЧ используется понятие «сходимости случайных
величин по вероятности».
Случайные величины Xi, А'з,..., Хп,... сходятся по вероятности
к величине А (случайной или неслучайной), если для любого е > О
вероятность события {JA^ — А| < е} при п —> оо стремится к единице,
т. е.
lim F{|Xn - А| < е} = 1
(или Р{|ХП — А| < е} —> 1). Сходимость по вероятности символически
записывают так:
Хп —Р—^ А.
П—>ОО
Следует отметить, что сходи~м.остъ по вероятности требует, чтобы
неравенство |Хп — Л| < е выполнялось для подавляющего числа членов
последовательности (в математическом анализе — для всех п > N, где
N — некоторое число), а при п —> оо практически все члены последо-
вательности должны попасть в Е-окрестность А.
Теорема 5.3 (ЗБЧ в форме П. Л. Чебышева, 1886 г.). Если случай-
ные величины Аф Х2, ..., Хп, ... независимы и существует такое число
С > 0, что РХг С, i = 1,2,.... то для любого е > О
lim Р
п—>оо
п п
PLX*-PLMX‘
г=1 г—1
(5-7)
т. е. среднее арифметическое этих случайных величин сходится по веро-
ятности к среднему арифметическому их м.о.:
п—юс
р
□ Так как DXj С, i = 1,2,..., то
166 * Раздел первый. Элементарная теория вероятностей и случайных процессов
= -~(DX\ + DX2 + ... + DXn) J-(C + С + ... + С) = ±Сп =
п п п
Тогда, применяя к с. в.
г=1
неравенство Чебышева (5.2), имеем
Переходя к пределу при п —> оо и учитывая, что вероятность любого
события не превышает 1, получаем
Следствие. Если с. в. Xi, Х2, .... Хп, ... независимы и одинаково
распределены, МХг = a, DXt = ст2, то для любого е > О
(5-9)
т. е. среднее арифметическое с. в. сходится по вероятности к математи-
ческому ожиданию а:
Q Так как
п
\ MXj — ~ (XIA j +Л/ .А'2 Т- • + Л/Ап) = (g+g+. ..+а) = -па = и,
I и е -J lb' ' I L ' lb
i=l
а дисперсии с. в. А) равны числу ст2, т. е. ограничены, то, применив ЗБЧ
в форме Чебышева (5.7), получим утверждение (5.9).
Следствие (5.9) теоремы Чебышева обосновывает «принцип сред-
него арифметического с. в. А"г», постоянно используемый на практике.
Так, пусть произведено п независимых измерений некоторой величи-
ны, истинное значение которой а (оно неизвестно). Результат каждого
Глава 5. Предельные теоремы теории вероятностей 167
измерения есть с. в. Хг. Согласно следствию (5.9), в качестве прибли-
женного значения величины а можно взять среднее арифметическое
результатов измерений:
Равенство тем точнее, чем больше п.
На тесьме Чебышева основан также широко применяемый в ста-
тистике выборочный метод, суть которого в том, что о качестве боль-
шого количества однородного материала можно судить по небольшой -
его пробе.
Теорема Чебышева подтверждает связь между случайностью и не-
обходимостью: среднее значение случайной величины
г=1
практически не отличается от неслучайной величины,
п
г=1
Пример 5.2. Глубина моря измеряется прибором, не имеющим систе-
матической ошибки. Среднее квадратическое отклонение измерений не
превосходит 15 м. Сколько нужно сделать независимых измерений, что-
бы с вероятностью, не меньшей 0,9, можно было утверждать, что сред-
нее арифметическое этих измерений отличается от а (глубины моря)
по модулю меньше, чем на 5 м?
Q Обозначим через X., результаты п независимых измерений глубины
моря. Нужно найти число п, которое удовлетворяет неравенству (5.8):
где М Xi = а, что означает отсутствие при измерениях системати-
ческой ошибки (т. е. измерения производятся с одинаковой точностью).
По условию г = 5, С = 225, так как а = y/DX = 15м; Отсюда
т. е. 0,1 п 90. Измерение нужно проводить не менее 90 раз.
168 * Раздел первый. Элементарная теория вероятностей и случайных процессов
5.3. Теорема Бернулли
Теорема Бернулли исторически является первой и наиболее про-
стой формой закона больших чисел. Она теоретически обосновывает
свойство устойчивости относительной частоты (см. п. 1.5).
Теорема 5.4 (ЗБЧ в форме Я. Бернулли, 1713 г.). Если вероятность
появления события А в одном испытании равна р, число наступления
этого события при п независимых испытаниях равно пд, то для любого
числа е > 0 имеет место равенство
^-р<е| = 1, (5.10)
т. е. относительная частота Р*(А) события А сходится по вероятности к
р
вероятности р события Л: Р*(А) -> Р(А)-
п—>оо
lim Р
Q Введем с. в. Аф Аф..., Хп следующим образом: Xi — 1, если в г-м
испытании появилось событие А, а если не появилось, то Xi = 0. Тогда
число пд (число успехов) можно представить в виде
п
ПА = 52 А
г=1
М. о. и дисперсия с. в. А", равны: MXi = 1 • р + 0 • (1 — р) — р,
DXi = (0 — р)2(1 — р) + (1 — рУр = р(1 — р) = pq. Закон распределения
с. в. Xi имеет вид
Xi 0 1
р 1 -р р,
при любом г. Таким образом, с. в. Aj независимы, их дисперсии огра-
ничены одним и тем же числом так как
р(1-р) =р-р2 = | - (р-
Поэтому к этим с. в. можно применить теорему Чебышева (5.7):
Глава 5. Предельные теоремы теории вероятностей • 169
Но
йЕа'. = тг- йЕл«. = й-"р=р-
i=l г=1
Следовательно, lim Р < — р
71—>ОО
< Е | = 1.
Теорема Бернулли теоретически обосновывает возможность при-
ближенного вычисления вероятности события с помощью его относи-
тельной частоты. Так, например, за вероятность рождения девочки
можно взять относительную частоту этого события, которая, соглас-
но статистическим данным, приближенно равна 0,485.
Неравенство Чебышева (5.2) для случайных величин
п
ПА = У^Хг
г=1
принимает вид
(5.П)
Обобщением теоремы Бернулли на случай, когда вероятности pi
появления события А в каждом из п испытаний различны, является
теорема Пуассона-.
п
Р*(А) i
/г-чоо "
г—1
(5-12)
где pi — вероятность события А в г-м испытании.
Пример 5.3. Вероятность наличия опечатки на одной странице руко-
писи равна 0,2. Оценить вероятность того, что в рукописи, содержащей
400 страниц, частость появления опечатки отличается от соответству-
ющей вероятности по модулю меньше, чем 0,05.
Q Воспользуемся формулой (5.11). В данном случае р = 0,2, q — 0,8,
п = 400, е — 0,05. Имеем
1--^- = 1-
ПЕ2
°'2-°'8-, = 0,84,
400 • 0,052
т. е. р 0,84.
170 * Раздел первый. Элементарная теория вероятностей и случайных процессов
5.4. Центральная предельная теорема
Центральная предельная теорема (ЦПТ) представляет собой вто-
рую группу предельных теорем, которые устанавливают связь между
законом распределения суммы с. в. и его предельной формой — нор-
мальным законом распределения.
Сформулируем ЦПТ для случая, когда члены суммы имеют одина-
ковое распределение (именно.эта теорема чаще других используется на
практике, так в математической статистике выборочные случайные ве-
личины имеют одинаковые распределения, так как получены из одной
и той же генеральной совокупности).
Теорема 5.5. Пусть с.в. Х±, Х%, .... Хп независимы, одинаково распре-
делены, имеют конечные математическое ожидание МА', — а и диспер-
сию DX, — ст2, i = 1,п. Тогда функция распределения центрированной и
нормированной суммы этих случайных величин стремится при п —> ос к
функции распределения стандартной нормальной случайной величины:
(5.13)
Ж
/^2
еГХ di.
—ОО
Из соотношения (5.13) следует, что при достаточно большом п сумма Zn
приближенно распределена по нормальному закону: Zn ~ 7V(0,1). Это
означает, что сумма Sn = A'i + А'2 + ... + Хп приближенно распределена
по нормальному закону: Sn ~ N(na, у/па). Говорят, что при п —> оо с. в.
п
асимптотически нормальна.
i=i
Напомним, что:
1. С. в. X называется центрированной и нормированной (т. е. стан-
дартной), если МА' = 0, a DX = 1.
2. Если с. в. A,, i — 1,п независимы, MX-i = a, DXj = сг2, то
= o + a + ... + ci = па,
Глава 5. Предельные теоремы теории вероятностей • 171
(п ч п
Xi j = У2 = <Т2 + <т2 + . . . + О'2 = пет2.
г=1 ' i— 1
X
1 г X 1
3. Ф(ж) = —-— е 2 dt — функция Лапласа; ФЦ) = й + Фо(ж), где
\/2я J ' 2
— ОО
X
1 [
Фо(#) = е 2 dt — нормированная функция Лапласа.
/2я J
о
Формула (5.13) позволяет при больших п вычислять вероятности
различных событий, связанных с суммами случайных величин. Так,
перейдя от с. в.
п
к стандартной с. в., получим:
формула для определения вероятности того, что сумма нескольких с. в.
окажется в заданных пределах (см. (2.43) и (2.46)). Часто ЦПТ исполь-
зуют, если п > 10.
Пример 5.4. Независимые с. в. У, распределены равномерно на отрез-
ке [0,1]. Найти закон распределения с. в.
100
г=1
а также вероятность того, что 55 < У < 70.
(J Условия ЦПТ соблюдаются, поэтому с. в. У имеет приближенно
плотность распределения
(</ - ту}2
172 Раздел первый. Элементарная теория вероятностей и случайных процессов
По известным формулам для м.о. и дисперсии в случае равномерного
распределения находим: MXi =
crX, =
1 = _J_
>/12 2х/з’
Тогда
Оу = „ . Поэтому
о
0 + 1 _ 1 Пу _ (1 ~~ о)2 _ х
2 2’ г 12 12’
(100 X 100
52 ) = 52 MXi ~ 100 • 1 = 50,
г=1 г=1
(100 ч 100
= £r>xi = iooi = f,
' iz о
г=1 ' г=1
/у (у)
3(у - 50)2
~е 50
Используя формулу (5.14), находим
Р{55 < У < 70} = Ф I ZQ^O ] _ ф [ 55 50 j = ф(4Хз) - Ф(^) =
I 5 у 3 J I 5уЗ I
X “Г" / X “3~ /
= Ф(6,9282) - Ф(1,73) « 0,04.
т. е. Р{55 < У < 70} ss 0,04. •
5.5. Интегральная теорема Муавра-Лапласа
Следствиями ЦПТ являются рассмотренные ранее (п. 1.21) локаль-
ная и интегральная теоремы Муавра Лапласа. Приведем вывод инте-
гральной теоремы Муавра Лапласа.
Рассмотрим схему Бернулли. Пусть пд — число появления собы-
тия А (число успехов) в п независимых испытаниях, в каждом из кото-
рых оно может появиться с вероятностью р (не появиться — с вероят-
ностью q = 1 — р). Случайную величину пд можно представить в виде
суммы п независимых с. в. Ад, Хг,..., Хп таких, что Х{ = 1, если в г-м
испытании событие А наступило, и Ад = 0 в противном случае, т. е.
Глава 5. Предельные теоремы теории вероятностей • 173
Так как MXi = р, DXi = pq (п. 5.3), то
Мпа = М
- пр.
Рид ~ D
= npq
(да это уже давно известно, см. (2.24), ведь с. в. пд имеет биномиальный
закон распределения). Тогда с. в.
па — пр
представляет также сумму п независимых, одинаково распределенных
случайных величин. При этом Zn ~ N(0.1), действительно:
и
пд — пр
y/npq
пр - пр =()
•/npq
MZn = м
1 n = ?w = 1
npqunA npq L'
Следовательно, на основании ЦПТ (5.13) с. в. Zn при большом чи-
сле п имеет приближенно нормальное распределение. Согласно свой-
ству (2.46) нормального закона, записываем
P{zy Zn г2} « Ф (^у^) - Ф (^у^) = ф(*2) - Ф01)
(Ф(г) — функция Лапласа). Полагая
kY — пр
zi = —
/npq
к2 — пр
~2 = --7==-
npq
двойное неравенство в скобках
ку - пр < п.4 - пр < к2 — пр
y/npq y/npq y/npq
можно переписать в эквивалентном виде кд пд А:2. Таким образом,
получаем
Р{кд пд к2} = Ф(г2) - ФЦ1),
т. е. интегральную формулу Муавра-Лапласа.
174 Раздел первый. Элементарная теория вероятностей и случайных процессов
Заметим, что: 1. Интегральная предельная теорема Муавра Ла-
пласа
( s/ripq J
для схемы Бернулли непосредствнно вытекает из ЦПТ (5.13) с учетом
п
результатов, полученных в п. 5.3 (дд = 52 Х{, MXt = р, DX, = pq:
1
тогда па = пр, ау/п = у/рср/п = y/npq).
2. Для подсчета сумм биномиальных вероятностей можно восполь-
зоваться приближенной формулой
(5.16)
Действительно,
т
52 Рп^ = Р{ПА т} = р{-°° < пА т} =
к=0
т-, f К'А ~ tip tn — tip ] / т — пр \
= Р < -оо < - _____ < - • > = ф -------- - Ф(-оо) =
( x/npq y/tipq J \ x/npq J
\ y/npq
где Ф(.г) - функция Лапласа.
Пример 5.5. Машинистке требуется напечатать текст, содержащий
8000 слов, состоящих из четырех и более букв. Вероятность сделать
ошибку в любом из этих слов равна 0,01. Какова вероятность, что при
печатании будет сделано не более 90 ошибок?
Q Применим формулу (5.16). Так как п — 8000, р = 0,01, q = 0,99,
т = 90, то
~= = — — - _ . = -L= « 0.112.
Pqpq ^8000 • 0,01 0,99 у/79.2
« 1.12.
Jnpq 8,9
90
Ф(1,12) = 0,8686. Следовательно, Р{пд 90} = 52 рп,к ~ 0,869.
fc-0
Глава 5. Предельные теоремы теории вероятностей 175
Упражнения
1. Оценить с помощью неравенства Чебьппева вероятность того, что:
а) при бросании монеты 500 раз число выпадений герба будет за-
ключено между 200 и 300; б) при бросании 10 игральных костей
сумма очков отклонится от м. о. меньше, чем на 8,
2. Дисперсия каждой из данных независимых случайных величин не
превышает 5. Найти число этих величин, при котором вероятность
отклонения их средней арифметической от средней арифметиче-
ской их м. о. менее чем на 0,1 превысит 0,9.
3. Оценить вероятность того, что при бросании монеты 500 раз ча-
стость появления герба отклонится от вероятности появления гер-
ба при одном бросании по модулю менее чем на 0,1.
4. Стрелок попадает при выстреле в мишень в десятку с вероятностью
0,5, в девятку — 0,3, в восьмерку — 0,1, в семерку — 0,1. Стрелок
сделал 100 выстрелов. Какова вероятность того, что он набрал не
менее 940 очков?
5. Приживаются в среднем 70% числа посаженных саженцев. Сколь-
ко нужно посадить саженцев, чтобы с вероятностью не меньшей 0,9
ожидать, что отклонение числа прижившихся саженцев от их м. о.
не превышало по модулю 40? Решить задачу с помощью неравен-
ства Чебышева.
Глава 6
Основы теории случайных процессов
6.1. Понятие случайной функции (процесса)
При изучении ряда явлений часто приходится иметь дело со слу-
чайными величинами, изменяющимися в процессе наблюдения (опыта,
испытания) с течением времени. Примерами таких случайных величин
могут служить: сигнал на выходе радиоприемника под воздействием
помех, загруженность студентов в семестре, длина очереди за билетом
в «Ленком», колебания напряжения в сети, рейтинг политической пар-
тии, траектория частиц в броуновском движении и т. д.
Такие случайные величины, изменяющиеся в процессе опыта, на-
зывают случайными функциями.
Раздел математики, изучающий случайные явления в динамике их
развития, называется теорией случайных функций (случайных процес-
сов). Ее методы используются, в частности, в теории автоматическо-
го управления, при анализе и планировании финансовой деятельности
предприятий (и отдельной семьи), при обработке и передаче сигналов
радиотехнических устройств, в экономике, в теории массового обслу-
живания.
Рассмотрим основные понятия теории случайных процессов (с. п.).
Если каждому значению tET, где Т — некоторое множество дей-
ствительных чисел, поставлена в соответствие с. в. X(t), то говорят,
что на множестве Т задана случайная функция (с. ф.) X(t). Другими
словами, случайной функцией X(t) называют с. в., зависящую от не-
случайного аргумента t.
Если параметр I интерпретируется как время, то с. ф. называется
случайным процессом. Другими словами, случайным процессом назы-
вается семейство случайных величин X(t, w), заданных на одном и том
же пространстве элементарных событий Q, зависящих от параметра
t ЕТ. Обозначается через X(t,w) или X(t), Xt.
Случайный процесс можно задать формулой, если вид случайной
функции известен, а случайные величины, определяющие параметры
с. ф., можно задать аналитически. Так, с. ф. X(t) = Y • sint, где t О,
Глава 6. Основы теории случайных процессов 177
Y ~ /?[(); 1] с. в., имеющая равномерное распределение, является слу-
чайным процессом.
При фиксированном значении т. е. при t = to Е Т, случайный
процесс обращается в с. в. X(to,cv), называемую сечением слу-
чайного процесса.
Реализацией или траекторией случайного процесса X(t, ю) назы-
вается неслучайная функция времени x(t) = X(i, u?o) при фиксирован-
ном щ = т- е. конкретный вид, принимаемый случайным процессом
в результате испытания.
Реализации с. п. обозначают через Xj (t), ^(t), . • -, где индекс ука-
зывает номер опыта.
На рис. 59 показаны три реализации ад(£), x2(t), x-s(t) случайного
процесса при со = од, ио = из = Щв (они напоминают траектории
трех приходов домой подвыпившего после работы грузчика). Каждая
такая реализация (траектория) является обычной функцией x(t). В ви-
де жирных точек на рисунке изображены значения с. в. Х(/.(),<л) в трех
опытах.
Рис. 59
Так, если в рассмотренном выше примере с. в. У в первом опыте
приняла значение 1, во втором — 2, в третьем — то получим три
реализации с. п.: Ti(i) = sin/., x2(t) = 2sini, x^(t) = ^sint — неслучай-
ные функции. Если же в этом примере зафиксировать момент времени,
например t = то получим сечение: X т-е- X — слу-
чайная величина.
В заключение параграфа отметим, что функция Ft(x) =
= P{X(t) < х] — так называемый одномерный закон распределения
случайного процесса X(t) — не является исчерпывающей характери-
стикой случайного процесса. Случайный процесс X (t) представляет со-
бой совокупность всех сечений при различных значениях t Е Т, поэто-
му для его полного описания надо рассматривать совместную функцию
распределения сечений процесса:
...,тп) = P{X(ti) < xi,X(t2) < x.2,...,X(tn) < xn} -
178 • Раздел первый. Элементарная теория вероятностей и случайных процессов
так называемый конечномерный закон распределения с. п. в моменты
ti, tn, т.е. рассматривать многомерную с.в. (А'(Н), А(^), •••
X(t„j).
Таким образом, понятие случайного процесса является обобщением
понятия системы случайных величин, когда этих величин — бесконеч-
ное множество.
6.2. Классификация случайных процессов
Случайный процесс, протекающий в любой физической системе 5,
представляет собой случайные переходы системы из одного состояния в
другое. В зависимости от множества этих состояний Иг, от множества?
значений аргумента t все случайные процессы делят на классы:
1. Дискретный процесс (дискретное состояние) с дискретным време-
нем.
2. Дискретный процесс с непрерывным временем.
3. Непрерывный процесс (непрерывное состояние) с дискретным вре-
менем.
4. Непрерывный процесс с непрерывным временем.
В 1-м и 3-м случаях множество Т дискретно, т. е. аргумент t при-
нимает дискретные значения t0, <1Д2, • • - (обычно t = 0,1.2.3,...); в 1-м
случае множество значений случайной функции X(t), т.е. А(ф) — -То,
А"(/у) — — дискретное множество (множество W конечно или
сч етно), а в 3-м случае — множество W несчетно, т. е. сечение случай-
ного процесса в любой момент времени t представляет собой непрерыв-
ную случайную величину.
Во 2-м и J-м случаях множество Т непрерывно, во 2-м случае
множество состояний системы W конечно или счетно, а в 4-м случае -
W несчетное.
Примерами случайных процессов 1 1 классов являются соответ-
ственно:
1. Футболист может забить или не забить один или несколько голов
в ворота соперника во время матчей, проводимых в определенные
моменты (согласно расписанию игр) времени НДг, • • • Случайный
процесс X (/) — число забитых голов до момента t.
2. X(t) — число просмотренных телепрограмм на первом канале от
начала работы телевизора до момента t.
Глава 6. Основы теории случайных процессов 179
3. В определенные моменты времени t0, ti,<2. -.. измеряется темпера-
тура K(t) заболевшего человека. У(<) случайный процесс непре-
рывного типа с дискретным временем.
4. Давление воздуха P(t) в шине колеса автомобиля.
Отметим, что рассматриваются и другие, более сложные классы
случайных процессов. Для различных классов случайных процессов
разработаны различные методы их изучения.
6.3. Основные характеристики случайного процесса
Для случайного процесса также вводятся простейшие характери-
стики, аналогичные основным характеристикам случайных величин.
Знание их оказывается также достаточно для решения многих задач
(напомним, полная характеристика случайного процесса дается ее мно-
гомерным (конечномерным) законом распределения). В отличие от чи-
словых характеристик с. в., представляющих собой определенные чи-
сла, характеристики с. п. представляют собой в общем случае не числа,
а функции.
.
Математическое ожидание случайного процесса
...
Р\| Математическим, ожиданием. с.п. X(t) называется неслучайная
“ функция которая при любом фиксированном значении аргу-
мента 1 равна математическому ожиданию соответствующего сечения
случайного процесса:
тх{Т) = MX(t). (6.1)
Математическое ожидание с. и. обозначают кратко и так: m(t), a(i).
Функция т х (t) характеризует поведение с. п. в среднем. Геомет-
рически математическое ожидание ?n(t) истолковывается как «сред-
няя кривая», около которой расположены кривые реализации (см.
рис. 60).
Опираясь на свойства математического ожидания случайной вели-
чины и учитывая, что X (t) случайный процесс, a f(t) неслучайная
функция, получаем свойства математического ожидания случайного
процесса-.
180 * Раздел первый. Элементарная теория вероятностей и случайных процессов
1. Математическое ожидание неслучайной функции равно самой
функций, т. е.
м (Ж)
2. Неслучайный множитель можно выносить за знак математического
ожидания случайного процесса, т. е.
M(/(t)-X(t))=/(t)-mA(t).
3. Математическое ожидание суммы (разности) двух случайных про-
цессов равно сумме (разности) математических ожиданий слагае-
мых, т. е.
М (X(t) ±F(t)) = mA-(t) zbmy(t).
Отметим, что, зафиксировав аргумент t и переходя от случайного
процесса к случайной величине (т. е. к сечению случайного процесса),
можно найти математическое ожидание этого процесса.
Так, если сечение с. п. X(t) при данном t есть непрерывная с. в. с
плотностью /(t,®), то его математическое ожидание можно найти по
формуле
ОС
MX(t) = [ x f(t.x)dx. (6.2)
—ос
Пример 6.1. Случайный процесс определяется формулой
¥Ц) = Хе~*, t > О, X~7V(3;1),
т. е. X — с. в., распределена по нормальному закону с а = 3, ст = 1.
Найти математическое ожидание случайного процесса F(t).
Глава 6. Основы теории случайных процессов 181
(ж-з)2
Q Так как /(х) = ---------— • е 2 -12 , то, используя формулу (6.2),
1 • v2tt
находим:
т. е. my(t) = 3 • е z.
Приведем другое решение: согласно свойству 2
my(t) = М (X е1) = е~1 MX,
но X ~ 7V(3; 1), следовательно, MX = 3 и т\ (t) = 3e-t.
Дисперсия случайного процесса
Дисперсией случайного процесса A'(t) называется неслучайная
функция Dzy(t), которая при каждом значении t равна дисперсии соот-
ветствующего сечения:
Л Y(t) = DX(t) = MX\t) - (6.3)
182 Раздел первый. Элементарная теория вероятностей и случайных процессов
Дисперсия Д\ (4) с. п. характеризует разброс (рассеяние) возмож-
ных значений с. п. относительно его математического ожидания.
Наряду с дисперсией с. п. рассматривается также среднее квадра-
тическое отклонение (коротко с.к.о.), определяемое равенством:
O'x(t) = (О- (6.4)
Размерность функции ах (О равна размерности с. п. X(t).
Значения реализаций с. п. при каждом t отклоняются от математи-
ческого ожидания m%(t) на величину порядка <7у(<) (см. рис. 60).
Очевидны следующие свойства дисперсии с. п.
1. Дисперсия неслучайной функции равна нулю, т.е.
Z?(/(i))=0.
2. Дисперсия с. п. неотрицательна, т. е.
Лг(/) = 4(<)-
3. Дисперсия произведения неслучайной функции на случайную
функцию равна произведению квадрата неслучайной функции на
дисперсию случайной функции, т. е.
DX (f(t)-X(t)) = f\t)DxX(t).
4. Дисперсия суммы с. п. и неслучайной функции равна дисперсии
с. п., т. е.
Dx(X(t)±f(t))=Dx(t).
Пример 6.2. Используя условие примера 6.1, найти дисперсию и сред-
нее квадратическое отклонение с. п.
Q Находим дисперсию, используя ее свойство 3: Dy(t) = D(X e-f) =
= (e-t)2 • DX = DX. Но X ~ Af(3,1), следовательно, [DX — a2,
cm. c. 99] DX = I2 = 1.
Поэтому Dy(t) = e~2t 1 = e-2t, т.е. Dy(t) = e~2t.
ay(t) — ve 2t = e l, t. e. cry(t) = e *
Глава 6 Основы теории случайных процессов • 183
Корреляционная функция случайного процесса
Математическое ожидание и дисперсия не являются исчерпываю-
щими характеристиками случайного процесса.
В частности, зная математическое ожидание и дисперсию, ничего
нельзя сказать о зависимости двух (и более) сечений с. п.
Для определения связи между различными сечениями с. п. исполь-
зуется корреляционная функция — аналог ковариации
Kxy — М ((X — тх) (У — my)) = MXY — ту ту,
характеризующей степень связи между двумя с. в. X и Y.
К| Корреляционной (ковариационной, автоковариационной, автокор-
реляционной) функцией с. п. Х(1) называется неслучайная функция
двух аргументов Кх(1рЛ2), которая при каждой паре значений tj и
/2 равна корреляционному моменту (ковариации) соответствующих се-
чений X'(ti) и Х(<2):
Kx(ti;t2) = М((Х(Д) - m(ti)) • (X(t2) - m(t2)))
или
Kx(tYt2) = М(Х(Д) Ж)) = Af (X(ti) X(t2)) - mx(h) mx(t2),
где X(t) — X(t) — m(t) — центрированная случайная функция.
Приведем основные свойства корреляционной (автоковариацион-
ной) функции K\(i,\',t2) случайного процесса X(t).
1. Корреляционная функция при одинаковых значениях аргументов
равна дисперсии с. п., т. е.
Kx(t-t) = Dx(t).
□ Действительно,
Kx(t-,t) = cov(X(t),X(f)) = м((Х(<) - m(t)) (X(i) - m(t))} =
= M(X(t)-m(t))2 = Dx(t).
Это свойство позволяет считать математическое ожидание и корре-
ляционную функцию главными характеристиками с. п.; необходимость
в дисперсии отпадает.
184 • Раздел первый. Элементарная теория вероятностей и случайных процессов
2. Корреляционная функция не меняется при перестановке аргумен-
тов местами, т. е.
(ti; <2) = К\ (^2; Н) •
Это свойство непосредственно вытекает из определения корреля-
ционной функции.
3. Если к с. п. прибавить неслучайную функцию, то корреляционная
функция не изменится, т. е. если Y(t) = X(t) + /(t), то
#у(й;<г) = Ку(Н;йО-
□ Так как my(t) = mx(J) + /(t), то
Y(t) - my(t) = X(t) + /(t) - mx(t) - f(t),
t. e. Y(t) — my(t) = X(t) — my-(t). Отсюда следует, что Ky(ti;/2) =
= KA-(ti;t2).
4. Модуль корреляционной функции не превосходит произведения
среднеквадратических отклонений, т. е.
|Ку(й;<2)| VDx(ti) Dx(t2) = <7л (й) ax(t2).
Свойство 4 непосредственно вытекает из соответствующего свой-
ства корреляционного момента двух с. в. (см. п. 3.7) с учетом пер-
вого свойства корреляционной функции с.п. X(t).
5. При умножении с.п. X(t) на. неслучайный множитель f(t) ее кор-
реляционная функция умножится на произведение /(ti) f(t2), т. е.
если Y(t) = X(t) f(t), то
^y(ti;fe) = /(<i) /(<2) • Kx(ti',t2).
Наряду с корреляционной функцией с. п. рассматривается также
нормированная корреляционная функция (или нормированная авто-
ковариационная функция) rx(t,p,t2), определяемая равенством
/4 j. \ ^а(Н;<2)
rx(ti-,t2) =--.-------7—.
СТаЧН) -<7а (<2)
С учетом свойства 1 можно записать так:
y/Kx(ti',ti) у/Кх^Г-Лъ)
Глава 6. Основы теории случайных процессов * 185
По своему смыслу r\ (й; t2) аналогична коэффициенту корреляции для
с. в., но не является постоянной величиной, зависит от аргументов й
и t2-
Свойства нормированной корреляционной функции аналогичны
свойствам коэффициента корреляции (см. и. 3.7):
1. Ый;й)| < 1;
2. rY(t;t) = l;
3. rx(tr,t2) = гу(й;й)-
S
Пример 6.3. Используя условие примера 6.1, найти корреляционную
и нормированную корреляционную функции с. п. Y(t).
Q Действительно,
АГу(Й;й) = М((Х • e“fl - 3 • e-tl) • (X • e~t2 - 3 • е^2)) =
= М(Х2 е“41 • e~t2 - 6Х • e“t] • е~1'2 + 9е-й с'2) =
= М(с~1' e~t2 (X - З)2) = e"h • е~*2 • DX = e-tl • е“‘2 I2 =
т.е. Ху(й;й) =e ^1+t2).
Тогда гу(й;й) = e_? ' 6 ? = 1, т.е. гу(йДг) = 1-
e 1 • e 2
При решении примера использовались определения корреляцион-
ной и нормированной корреляционной функций, а также результат ре-
шения примера 6.2. •
Взаимная корреляционная функция случайного процесса
Для определения степени зависимости сечений двух случайных
процессов используют корреляционную функцию связи или взаимную
корреляционную функцию.
Взаимной корреляционной функцией двух с. п. X(t) и Y(t) называ-
ется неслучайная функция Rxy(й 5 А) Двух независимых аргументов 11
и t2, которая при каждой паре значений й и t2 равна корреляционному
моменту двух сечений Х(й) и K(t2):
Дуу(Й;Й) = м((Х(й)-тл(й))-(У(й)-ту(Й))) = М(Х(й) Y(t2)).
186 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Два с. п. X(t) и У(<) называются некоррелированными, если их
взаимная корреляционная функция тождественно равна нулю, т.е.
Rxy (И; h) = О для любых ti и t2. Если 0, то с. п. X[t) и
У(<) называются коррелированными (или связанными).
Свойства взаимной корреляционной функции непосредственно вы-
текают из ее определения и свойств корреляционного момента (см.
н. 3.7):
1. При одновременной перестановке индексов и аргументов взаимная
корреляционная функция не меняется, т. е.
7?ау(НИ2) = Яух^Н).
2. Модуль взаимной корреляционной функции двух с. п. не превыша-
ет произведения их средних квадратических отклонений, т. е.
|#Х1 (*i;*2)1 <7.\ (П) • ffy(t2).
3. Корреляционная функция не изменится, если к с. п. X(t) и У (4)
прибавить неслучайные функции /(/) и ip(t) соответственно, т.е.
RxiYi (* 1; h) = Rxy (<i ; t‘2),
где Xx(t) = X(t) + /(t), Y^t) = Y(t) + <p(t).
4. Неслучайные множители можно вынести за знак корреляции, т.е.
если Xi(4) = /(4) • X(t), У, (4) = <p(t) Y(t), то
T?Aiii(ti; 42) — /(Н) • <Д^2)-Кау(Н; ^)-
5. Если X(t) — X[(t) + Х2(4), то
Kx^ch) = (Н;i2) 1 -fCv2(4i; 42) + Ла1А2(НП2) + Rx2Xj (4i;42).
6. Если с. н. Xi (/.) и X2(4) некоррелированы. то корреляционная функ-
ция их суммы равна сумме их корреляционных функций:
Kx(ti;t2) = Kxi(tp,t2) + Ka2(4i;42).
Для оценки степени зависимости сечений двух с. н. используют
также нормированную взаимную корреляционную функцию гху -'(4i;42),
определяемую равенством:
Д\у(Н; h) =
7?ау (^i; t‘j) _Д\у(Н;Ь)
\/Dx{O Dy(12) y/Kx(tp,ti) • УKy(t2; t-2)
Глава 6. Основы теории случайных процессов 187
Функция гд-у(Д;<2) обладает теми же свойствами, что и функция
^2), но свойство 2 заменяется на следующее: |гд-у (Д; £2)! !•
т. е. модуль нормированной взаимной корреляционной функции не пре-
вышает единицы.
RT1 Пример 6.4. Найти взаимную корреляционную функцию двух с. п.
Х(£) — t V тл Y(t) = (£ + 2) V, где V — с. в., причем DV — 3.
Q Так как тд(£) = = t-MV = t-my. amy(t) = M((£+2)-V) —
— (£ + 2) • ту. to
Rxy= M faV - timv) ((£2 + 2)V - (£2 + 2)my) =
= M(ti(V - my)) ((t2 + 2)(V - my)) = tx (t2 + 2) • M(V - my)2 =
= £i • (£2 + 2)ПУ = ЗД • (£2 + 2),
t.e. /?xy(£i;£2) = 3ti • [t2 + 2). •
Упражнения
1. Случайный процесс определяется формулой X(t) = V sint, где
t О, V ~ 7?[2; 4J — случайная величина, имеющая равномерное
распределение. Найти: а) сечение с. п. X(t) в момент времени t =
б) реализацию с. п. при одном испытании, в котором с. в. V приняла
значение 2.
2. Для случайного процесса из упражнения 1 найти: а) математи-
ческое ожидание с.п.; б) дисперсию и среднее квадратическое от-
клонение: в) корреляционную (автоковариационную) функцию; г)
нормированную корреляционную функцию с. п. X (£).
6.4. Стационарный случайный процесс в узком
и широком смысле
Важным классом с. п. являются стационарные случайные процес-
сы, т. е. процессы, не изменяющие свои характеристики с течением вре-
мени. Они имеют вид непрерывных случайных колебаний вокруг неко-
торого среднего значения. Таковыми являются: давление газа в газо-
проводе, колебания самолета при «автополете», колебания напряжения
в электрической сети и т. д.
188 Раздел первый. Элементарная теория вероятностей и случайных процессов
|ф| Случайный процесс Х{1) называется стационарным в широком
смысле, если его математическое ожидание mx(t) постоянно, а корре-
ляционная функция зависит только от разности аргументов,
т. е.
mx(t) = т = const, Kx(tr, t2) = ^х(Д - h)-
Из этого определения следует, что корреляционная функция ста-
ционарного процесса есть функция одного аргумента:
Kx(h', h) = Кх(т), где т = t2 - И-
Это обстоятельство зачастую упрощает операции над стационарными
случайными процессами.
Случайный процесс называют стационарным, в узком смысле, если
все его характеристики зависят не от значений аргументов, а лишь
от их взаимного расположения. То есть для функций распределения
сечений процесса должно выполняться равенство:
^1+М2+С....и+А(жЬж2, • • • ,Хп) = Ftut^tn{X].,X2, • • .Хп),
при любых h > 0, п 1, t\, t2,- • - ,tn Е Т.
Отметим, что из стационарности с. п. в узком смысле следует ста-
ционарность его в широком смысле; обратное утверждение неверно.
В дальнейшем будем рассматривать только стационарные с. п. в
широком смысле.
Приведем основные свойства корреляционной функции стационар-
ного случайного процесса (с. с. п.).
1. Дисперсия с.с. п. постоянна и равна значению корреляционной
функции в нуле, т. е.
Dy (t) = К\ (0) = const
(т.е. в начале координат Ра(0 = Ку(t’t) — Ky(t — t) = Кд (0)).
2. Корреляционная функция с. с. п. является четной, т. е.
Кх(т) = Кх{-т).
3. Модуль корреляционной функции с. с. п. не превышает ее значения
при т = 0, т. е.
|Кх (т)| ^Кх-(О).
Нормированная корреляционная функция с. с. п. есть неслучайная
функция аргумента г:
, . Кх(т) Кх{т)
ТХ\Т) = к <а\ = --2~’ ПРИ ЭТОМ 1ГЛ (T)l L
лх(0) а*
Глава 6. Основы теории случайных процессов • 189
Большинство с. с. п. обладают важным для практики эргодическим
свойством, сущность которого состоит в том, что по одной, достаточно
длинной, отдельной реализации можно судить о всех свойствах процес-
са также как по любому количеству реализаций, т. е., другими словами,
отдельные характеристики с. с. п. {т/, Кх(т)} могут быть определены
как соответствующие средние по времени для одной реализации доста-
точно большой продолжительности. Связь между классами стационар-
ных и эргодических с. п. приведена на рисунке 61.
Достаточным условием эргодического с. п. X(t) относительно мате-
матического ожидания и корреляционной функции является стремле-
ние к нулю его корреляционной функции при т —> оо, т. е. lim Кх (т) — 0.
В качестве оценок характеристик эргодических с. с. п. принимают
усредненное по времени значение:
т
mx{t) = ? f x^dt'
о
Т-т
&А'(т) = (®(<) - mA-(t)) • (x(t + т) - mA-(t)) dt.
о
Интегралы, в правых частях равенств, вычисляют на практике при-
ближенно.
Случайные процессы X(t) и Y(t) называются стационарно связан-
ными, если их взаимно корреляционная функция Kxy(ti;,t2) зависит
только от т — ti —1.2- В качестве примера стационарного процесса мож-
но взять с. п. X(t) = А • cos(wt + — гармоническое колебание. Можно
показать, что mx(t) = 0, а
Kx(ti'i h) = 2^(А2) • cosw(ti — 1-2) = &х ‘
190 Раздел первый. Элементарная теория вероятностей и случайных процессов
6.5. Линейные и нелинейные преобразования
случайных процессов
При проектировании различных систем (систем автоматического
управления или регулирования и т. д.) и других практических задач
возникает следующая задача: на вход системы S подается «входной
сигнал» с. п. А'(/ ) с известными характеристиками; система преобра-
зует этот сигнал, в результате чего на выходе системы S получается
с. и. У(£). называемый «выходным сигналом»; требуется определить ха-
рактеристики с. п. Y(t) на выходе системы S (см. рис. 62).
Х(*)
И*)
Рис. 62
Преобразование с. п. X(t) в с. п. У(/), осуществляемое системой
(прибором) S', символически записывается в виде У(4) = А{X(t)}. где
А преобразование или оператор системы S.
Оператор А может иметь любой вид: оператор сложения или умно-
жения, оператор дифференцирования или интегрирования и т. д.
Так, например, если j,(t) = sin2t, оператор А есть оператор инте-
t
грировапия А = х(т) dr, то
о t
y(t) = .4 {sin 2/} = j sin2V dV — — i cos2v| = i(l — cos2t).
о
Все виды подобных преобразований (операторов) можно разделить на
две различные группы: линейные L и нелинейные N. В свою очередь
линейные преобразования делятся на линейные однородные Lq и ли-
нейные неоднородные L//.
Преобразование (оператор) Lq называется линейным, однородным,
если оно (он) обладает свойствами:
1. Оператор суммы функций (с. п.) равен сумме операторов от каждой
функции, входящих в с.умму, т. е.
To{A'i(f) + Хг(0} = То{Х] (/)} + L0{X2(t)}.
2. Постоянную величину можно выносить за знак оператора, т. е.
L0{c-X(t)}=cL0{X(t)}.
Глава 6. Основы теории случайных процессов • 191
Преобразование Lp называется линейным неоднородным, если оно
состоит из линейного однородного преобразования Lq с прибавлением
заданной неслучайной функции f(t), т.е. £н{А”(£)} = L0{X(t)} + f(t).
Все преобразования, не являющиеся линейными, называются не-
линейными.
Примерами линейных однородных операторов являются оператор
дифференцирования K(t) — опеРатОР интегрирования Y(t) =
t
= j Х(т)дт, оператор умножения на заданную функцию У(£) =
о
= /(t) - X(f). Примерами линейных неоднородных —
И*) = +/(«),
У(4) = У Х(т)*- + /(«),
О
y(i) = f(t)-A(i)+^(t).
Примерами нелинейных — Y(t) = А’2(/.), У(/) =
dX (t)
6.6. Дифференцирование и интегрирование
случайных процессов
Пусть с.n. X(t), характеристики которого mx(t) и Kx(t\-,t2) зада-
ны, подвергается дифференцированию Y(t) = —Требуется найти
характеристики my(t) и А'у-(Н;^2) «выходного сигнала» — с. п. Y(t).
Предполагая, что с. п. X(t) является непрерывным, производная от
него существует, а м. о. предела равно пределу математического ожи-
дания, от равенства
X(i + Ai)-A(i)
I (t) — hm
At->0
д/
перейдем к следующему
, mx(t + Xt) — mx(t) . . dmx(t)
МГ(|) = mA-(i) = jim ---------, T.e. = _k2
Д/
Итак, математическое ожидание производной с. п. равно производной
от ее м. о. (коротко: m^(t) = или XI (Ar'(i)) = (ЛГА'(/))/).
192 * Раздел первый. Элементарная теория вероятностей и случайных процессов
Можно показать, что корреляционная функция производной от
с. п. X (/,) равна второй смешанной частной производной от корреля-
ционной функции с. п. X (t):
dKx{tr,t2)
dti dt2
Пример 6.5. Используя результаты решений примеров 6.1 и 6.3, найти
м. о. и корреляционную функцию с. п. Y(t) =
dX(t}
dt
Q Искомое м.о. есть ЛГ(У(/.)) = M(A'(t)) = ^M(A(t))^ = (Зе 4)' =
= —Зе-4.
Находим корреляционную функцию с. п. У(£):
^y(fi;i2) —
акЛ-(н;^2)
dh dt2
де 41 t2
dti dt2
= JL (e-ti
dt2 и
<2 V
Itl
= (-e-41-f2) = (-e-41-42)' = e-41-42 = e ^41+t2)
СД2 V 742
Пусть известны характеристики mx(t) и Kx(tp,t2) с. n. Ar(t), а ли-
нейное преобразование с. п. состоит в его гштегрироеаншп
t
K(t) =
X (т) dr.
Требуется найти характеристики с. п. Y (/,).
Можно доказать, что математическое ожидание интеграла от
с. п. равно интегралу от м. о. этого с. п., т. е.
о
чих (т) д,т.
Иными словами, операции нахождения м. о. и интегрирования можно
менять местами:
У МХ(т)дт.
о
Глава 6. Основы теории случайных процессов "193
Корреляционная функция интеграла от с. п. равна двойному интегралу
от корреляционной функции с. и., т. е.
<1 ?2
KY(ti;t2)= [ [ Кх(т1;т2)(1т1(1т2.
о о
Пример 6.6. Зная м.о. mx(t) = 3 • e"f и корреляционную функцию
КлЧИДг) = e-tl~f2, найти м.о. и корреляционную функцию с. п.
K(t) = / X(r)dr.
Q Искомое м. о. есть = / 3-е т dr = —3 • е т = 3 — Зе 1
Далее:
= I е T1 т'2 dTy_dT2 = е T1 di\
е Т2 dr2 =
d.Tl = (1-е"*2)-(-е-Т1)Г‘= (1-с'2)(1-е”м). •
Упражнения
1. Какие из приведенные ниже случайных процессов являются ста-
ционарными (в широком смысле):
a) X(t) = V sin/, t О, V ~ 7V[2; 4] — случайная величина;
б) X(t) = sin(t + <р), / 0, ~ /?[(); 2тг] — случайная величина;
в) X(t) = A-cos(t-r</>0), t 0, (ро = const /,, А — случайная величина;
г) X (t) — Y • cos 3t, Y — случайная величина.
2. Известны характеристики двух некоррелированных случайных
процессов X(t) и Y(t): mx(t) = t + 2, Kx{t\\t2} = ti • /2, W (i) =
= — t + 3, Ki (ti;/2) = 2e t1-*2. Найти математическое ожидание и
корреляционную функцию с. п. Z(t) = X(t) -Г Y(t).
194 Раздел первый. Элементарная теория вероятностей и случайных процессов
3.
Зная математическое ожидание и корреляционную функцию с. и.
X = V sint, t О, V ~ R[2; 4], m\(t) = 3 - sinf. Kx^tijt^) =
= sintj sint2, найти: а) математическое ожидание и корреляцион-
, . dX(t)
ную функцию с.и. У (t) = ———; б) м.о. и корреляционную функ-
цию с. п.
о
4. Задан с.п. X(t) = Y cost, где t О, Y ~ 7V(2; 1) — нормально
распределенная с. в. Является ли с. и. X(t) стационарным? Найти
mz(t) и Kz{ti',t.2) случайного процесса Z(f) = X(t) — 2 •
6.7. Спектральное разложение стационарного
случайного процесса
Как известно, неслучайную функцию x(t), удовлетворяющую опре-
деленным условиям (условиям Дирихле), можно разложить в проме-
жутке [-Т;+Т] в ряд Фурье.
Оказывается, что любой с. п. Х(1) также можно разложить (т. е.
представить в виде суммы так называемых элементарных случайных
процессов) в ряд вида
ОС
X(t) = </?o(i) + Vk <Pk(t)-
к=1
где V/. — случайные величины, ipk (t) — неслучайные функции времени.
Метод разложения с. п. упрощает различные преобразования с. и.
(линейных и нелинейных), в частности, упрощает определение харак-
теристик выходного процесса стационарной линейной системы по из-
вестным характеристикам входного сигнала.
Рассмотрим с. и.
X(t) = U coscvt + V sinwt, (6-5)
где U и V — некоррелированные случайные величины с м.о., рав-
ными нулю и одинаковыми дисперсиями, ш — действительное число
Глава 6. Основы теории случайных процессов 195
(или коротко: ш - константа, ту = ту = (J, Dy — Dy — D, Куу =
= M(U- V) = 0).
Покажем, что этот процесс является стационарным.
□ Находим м.о. с. п. X(t):
М (X(t)) = mx{t) — MU coscut + MV • sin cut = 0.
Следует, что X(t) = X{t) (напомним, что X(t) = X(t) — т.е.
X (/) — центрированный случайный процесс.
Находим теперь корреляционную функцию:
#а-(Ж) = w(i(H) • Ж)) = м (Х(Н) • Ж)) =
= М (U • coscuti + V • sincuti) (U coscuts + V • sincut2) =
= M(U2) cos cuti • cos wt? + At(H2) sin cuti • sin cuts + 0 =
= D(U) coscuti • coscuta + D(V) sincuti • sincut2 = D • coscu(tj — ts)-
Следовательно, X(t) c. c. n. (cm. h. 6.4). В
Рассмотрим теперь с. п.
ОС
X(t) = тх + Uk • cos сид ! + Vk sin сид!, (6.6)
k=o
где MUk = 0 = MVk, DUk = DVk = Dk, M(Uk HJ = 0, M(Vk Vi) =
= M(JUk U/) = 0 при k I, wk — константы.
Этот с. п. также является стационарным.
Действительно,
(ОС \
У2 Uк (-osivkt + Vk sincufct j = тх + 0 = тх-
к=о '
Следовательно, X (t) = X(t).
Так как слагаемые в с. п. (6.6) некоррелированны, то с учетом фор-
мулы для корреляционной функции с. п. (6.5) и свойства 6 (см. с. 186)
корреляционной функции получаем
ОС
^а(Н;!2) = y^PfcCQScufeT, где г = tx —12. (6.7)
fc=o
Итак, с. п. (6.6) является стационарным с. п.
7*
196 Раздел первый. Элементарная теория вероятностей и случайных процессов
Отметим, что равенство (6.7) можно рассматривать как разложе-
ние корреляционной функции К\(Д; на промежутке [—Т; 4-Т] в ряд
Фурье по косинусам: Кх(ДД2) = Кд(т) = 52 cos wkTi где
к=0
Т
wk = kwx D° = 2Т / Кх(т) dr,
- т
т т
Dk = т / Кх COS ШкТ (,Т = Т / Кх COS ШкТ (,т'
-т о
(6.8)
Можно доказать, что Dk 0 для любой корреляционной функции
с. с. п. X(t).
Каноническое разложение (6.6) называется спектральным разло-
жением стационарного случайного процесса.
Разложение (6.7) называется спектральным разложением корре-
ляционной функции с. н. X(t).
Отметим, что спектральное разложение с. с. п. (6.6) можно предста-
вить в виде суммы гармонических колебаний со случайными амплиту-
дами Ак, фазами ipk и частотами шк:
ОС
X(t) = тх + А • sin(wfct + ipk),
k=0
где Ak = Jul + Vfc2, <pk = arctg
Дисперсия с. c. ii., представленного в виде (6.6), равна сумме дис-
персий всех гармоник его спектрального разложения:
ОС
Dx = У2 Dk-
k=0
Действительно,
Dx = [Кх (Д t)] = Кх (0) = Dk co^k • 0) = Dk.
k=0 k=0
Совокупность дисперсий Dk называют спектром с. с. п., а ординаты
Dk — спектральными линиями, соответствующими частотами шк.
Глава 6. Основы теории случайных процессов 197
Спектр можно изобразить графически (рис. 63).
Сумма всех ординат спектра равна дисперсии с. п. X(t). Спектр
с. п. (6.6) называется линейчатым дискретным с бесконечным числом
равноотстоящих спектральных линий. Расстояние между соседними
линиями по частоте равно ац = = Aw.
6.8. Спектральная плотность случайного процесса.
Теорема Винера-Хинчина
Спектральное разложение с. п. на промежутке [—Т;Т] дает при-
ближенное его описание. Более полное представление о с. п. при его
спектральном разложении может быть получено при увеличении вели-
чины Т.
При неограниченном увеличении промежутка разложения (Т —> оо)
ОО
число слагаемых в сумме Dx = 52 Dk неограниченно увеличивается
fc=o
(Dfe — коэффициент разложения корреляционной функции, см. (6.7)),
каждое слагаемое неограниченно уменьшается, но сумма остается
постоянной. Интервал между соседними частотами W| = — = Aw будет
стремиться к нулю. т. е. Aw —> 0.
Обозначим среднюю плотность дисперсии -г-^- через S'x(w/,.), т. е.
ZXcu
(6-9)
О
Спектральной плотностью Sy-fw) стационарного случайного про-
цесса X(t) называется предел отношения дисперсии, приходящийся на
интервал частот Aw к длине этого интервала, когда последняя стре-
мится к нулю:
S'y-(w) = lim
Лш->о Aw
(6.10)
198 * Раздел первый. Элементарная теория вероятностей и случайных процессов
т. е. спектральная плотность с. с. п. есть предел средней плотности дис-
персии (6.9), когда Aw —> 0.
Получим формулы, связывающие спектральную плотность Sx(cv)
и корреляционную функцию К\-(т) в случае, когда Т —> оо (Aw —> 0).
Выразим дисперсию Г)к из равенства (6.9) и подставим ее в равен-
ства (6.7) и (6.8). Получаем: Dk — Sx
Kx(ti\t2) = Kx(t) = Sx(uk) costdfc7 • Aw, (6.11)
fc=0
т
Dk = Sx (wfc) У (T) cos dr,
0
t. e.
т
Sx(^i. ) = | У Кх(т) cos шкт dr. (6.12)
о
Переходя к пределу при Т -> ос (Aw —> 0), из равенств (6.11) и (6.12)
получаем следующее утверждение.
Теорема 6.1 (Теорема Винера—Хинчина). Корреляционная функция
и спектральная плотность с. с. п. связаны между собой взаимно обратны-
ми косинус-преобразованиями Фурье:
ОС
Кх(т) = У S'x(w) coswrdw, (6.13)
о
оо
S\(w) = / Кх (т) cos шт dr. (6.14)
о
Дискретный линейчатый спектр разложения переходит, при Т —>
—> оо, в непрерывный спектр, в котором каждой частоте w 0 соответ-
ствует неотрицательная ордината ,S'x(w).
Кривая Sx (w) изображает плотность распределения дисперсий по
частотам непрерывного спектра (см. рис. 64).
Спектральная плотность S'y(w) стационарного с.п. обладает сле-
дующими свойствами:
1. Спектральная плотность — неотрицательная функция, т.е.
S’x(w) ^0.
I
Глава 6. Основы теории случайных процессов 199
Это свойство вытекает из определения (6.10), где D/. 0, Аш > 0.
2. Интеграл от спектральной плотности в пределах от 0 до оо равен
дисперсии с. с. п., т. е.
У Sx(w)dw = DX-
о
Это свойство вытекает из равенства (6.13):
cos
о
Отметим, что для упрощения математических выкладок удобно ис-
пользовать спектральное разложение с. с. п. в комплексной форме, счи-
тая, что частоты изменяются в интервале (—оо, +оо) (частоты ш < 0
физического смысла не имеют).
Спектральной плотностью стационарного с. п. в комплексной
форме называется функция
5И^) = |-МИ- (6-15)
Формулы Винера-Хинчина в комплексной форме имеют вид
/
оо
Кх(г) = У" Sl(w) • eiuJT du, (6.16)
—ОО
X)
= 1 / Кх(т)-е~™-dr. (6.17)
— ОО
Они получаются, если в спектральном разложении (6.7) заменить три-
гонометрические функции, используя формулы Эйлера
coscvfcr =------~, sincjfcT =-----------—-------?
200 Раздел первый. Элементарная теория вероятностей и случайных процессов
и перейти к пределу при Т —> оо (Aw —> 0).
Отметим, что спектральная плотность S^(w) — четная функция
на интервале (—ос,+оо), т.е. 5у(—w) = S'y(w).
На участке (0:+оо) имеем Sx(w) = | - .S'x(w) (см. рис. 65).
Значения функции Sx(w) в 2 раза меньше значений б’д-(ш) при тех
же значениях аргумента w.
Пример 6.7. Найти спектральную плотность стационарного с. п. X(t),
зная его корреляционную функцию К\(т) — D а > 0.
О Используя формулу (6.17), получаем
ОО
S'^(w) = У D • • e~iuT dr =
—ос
е^а~^т dr +
_ [ 1 . е(а-й^)т|° 1 . е (а+гш)т|°° | _
2тг уо — ш I-оо а + ш Io )
D ( 1_______________1 zf) _ 1А _ D и + ш + а — ш _ D 2о
2я — iuj а + ш ) 2-тг а2 4. w2 2-тг а2 _|_ ш2 ’
т.е. S*x(w) =
D а
я(а2 + w2)
или S'x(w) =
2D а
я(а2 + w2)
Пример 6.8. Найти корреляционную функцию с. п. со спектральной
плотностью
SvM = {f°’
|w| U>0,
|w| > w0.
Глава 6. Основы теории случайных процессов 201
Q Используя формулу (6.16), получаем
S0 e»W0T _ е-го;от 8Н1Ш0Т
~ т ' 2i • 2 — 2 So М) • Ш()Т
Вид Кх(т) изображен на рис. 66.
6.9. Стационарный белый шум
Одним из конкретных типов стационарного с. п. является так на-
зываемый стационарный белый шум.
Стационарным белым шумом называется стационарный с. п. 2C(t),
спектральная плотность которого постоянна:
Sy(w) = So = const для w 6 (—оо; +оо).
Найдем корреляционную функцию белого шума, используя фор-
ОО
мулу (6.16) и учитывая, что J eiu}t • da) = 2я • 5(f), где 5(f) — дельта-
--ОС
функция (см. замечание):
оо
Кх(г) = j
—ОО
So eiL0T dw = Sb
e™T dw = So • 2я • <5(т),
202 Раздел первый. Элементарная теория вероятностей и случайных процессов
т. е.
Кх(т) = 2тг50 • <5(т).
Как видно, корреляционная функция стационарного белого шума про-
порциональна дельта-функции; коэффициент 2тг,5'о называется интен-
сивностью белого шума.
Замечание 1. Дельта-функция Дирака 6(х) есть предел последова-
—~— 1Д < £
тельности функций ф(т): 8(х) = 1пп<5е(ж), где 6£(х) = 2 • е’
£->° [0, |ж| > Е.
30
Условно записывают так: 5(х) = s ’ 2’, причем / fi(x)dx = 1.
[ оо, х = 0; J
—ОО
оо
Дельта-функция представима интегралом Фурье: 6(х) = ^~ dx.
2я J
- оо
Наглядно график функции Дирака похож на график, изображенный
на рисунке 67.
Дельта-функция может быть представлена как плотность распре-
деления масс, при которой в точке х = 0 сосредоточена единичная
масса, а масса в остальных точках равна нулю.
Замечание 2. Равенство Кх(т) = У()-2тг-А(т) означает некоррелиро-
ванность любых двух различных сечений Х(Н) и X(tz) (ведь 8(х) = О
при всех значениях х 0). В силу этого осуществить белый шум невоз-
можно, т. е. белый шум — полезная математическая абстракция. Белый
шум используется в случаях, когда спектральная плотность с. п. при-
мерно постоянна в определенном диапазоне (интересующем нас) час-
тот.
Глава 6. Основы теории случайных процессов 203
Упражнения
1. Задана корреляционная функция некоторого случайного процес-
Г2 It~I < Т
са X(t): KyM = s ’ । ’ Выяснить, является ли заданный
(U. |т| > 1.
с. п. X(t) стационарным в широком смысле?
2. Показать, что функция Кх(т) = Зе может быть корреляционной
функцией стационарного с. и. X (/).
3. Найти корреляционную функцию стационарного с. п. X(f), зная,
что mx(t) = 1, а спектральная плотность SC(w) = ——-—х-.
7г( 1 + а/)
4. Известно, что спектральная плотность стационарного с. п. X(t)
Q
имеет вид S'x(w) = ——---
7г(1 + иг)
Найти дисперсию случайного процесса X(f).
6.10. Понятие марковского случайного процесса
Среди случайных процессов особое место занимают марковские
случайные процессы.
Рассмотрим некоторую физическую систему S, в которой происхо-
дит случайный процесс. С течением времени она может под влиянием
случайных факторов переходить из одного состояния в другое состоя-
ние.
Случайный процесс называется процессом с дискретными состо-
яниями, если множество его возможных состояний sj, s%, S3,..., Sj,...
конечно или счетно (можно заранее перечислить), а переход из одно-
го состояния в другое осуществляется скачком, переходы возможны
только в определенные моменты времени И, t?, t%,....
Если переходы возможны в любой момент времени, т. е. моменты
пе}юходов из одного состояния в другое случайны, то процесс называ-
ется процессом с непрерывным временем.
Случайный процесс с дискретными состояниями называется мар-
ковским, если для любого момента времени to условная вероятность
каждого из состояний системы S в будущем (т.е. при t > to) зависит
только от ее состояния в настоящем (т.е. при t = to) и не зависит от
204 Раздел первый. Элементарная теория вероятностей и случайных процессов
того, когда и как система пришла в это состояние (т. е. каковы были
состояния системы S в прошлом, при t < to).
Марковский процесс называют также процессом без последствия:
будущее в нем зависит от прошлого только через настоящее, т. е. ве-
роятность системы S попасть в состояние Sj в момент времени tk
(S(tk) = Sj) зависит лишь от состояния Sj, в котором система нахо-
дилась в предыдущий момент времени tk_\ (S(tk-i) = S{):
F (S(tfc) = I S(ti) = Ж1, S(t2) = x2,..., S(tk_i) = Si) ==
= P(S(tk) = sj\S(tk^) = sl),
где rci, X2 •. — есть возможные состояния системы {si, s2,..., Sj,...
• • • 5 ф’5 • • 1 }•
Марковский процесс служит моделью для многих процессов в био-
логии (распределение эпидемий, рост популяции), в физике (распад
радиоактивного вещества), в теории массового обслуживания. Отме-
тим, что в СМО множество состояний системы определяется числом
каналов, т.е. линий связи, вычислительные машины, продавцы и т.д.;
переходы между состояниями системы S происходят под воздействием
потока событий (т.е. потока заявок, требований, отказов и т. д.), кото-
рые являются простейшими, пуассоновскими.
Случайные процессы с дискретными состояниями удобно иллю-
стрировать с помощью так называемого графа состояний. В нем со-
стояния si,s2,... системы S изображаются прямоугольниками (или
кружками), а возможные непосредственные переходы из состояния в
состояние — стрелками (или ориентированными дугами), соединяю-
щими состояния.
Пример 6.9. Построить граф состояний следующего с. и.: устройство S
в случайный момент времени может выйти из строя, оно осматривается
в определенные моменты времени, например через каждые 3 часа, и в
случае необходимости — ремонтируется.
Q Возможные состояния системы (устройства) S: Si — устройство
исправно; s% - - устройство неисправно, требуется ремонт; S3 — устрой-
ство неисправно, ремонту не подлежит, списано.
Графсистемы имеет вид, изображенный на рис. 68.
Процесс представляет собой случайное блуждение системы S по
состояниям, время (3 часа) — шаг процесса.
Реализация с. п. блуждения системы может иметь, в частности, та-
кой вид:
„(1) „(2) „(3) (4) (5) (6) (7)
*1 5*1 5*1 5*2 5*1 5*1 5*3 5
Глава 6. Основы теории случайных процессов 205
Рис. 68
что означает: при 1-м, 2-м, 3-м осмотрах устройство исправно; при
4-м осмотре — неисправно, ремонтируется; при 5-м, 6-м — исправ-
но; при 7-м — устройство признано негодным, списано. Процесс закон-
чился. •
Для описания с. и. с дискретными состояниями пользуются веро-
ятностями состояний системы S, то есть значениями pi(f),P2(t), ..
... ,pn(.t), где Pi(t) = P{S(t) = Sj} — вероятность того, что в момент
времени t система находится в состоянии sp S(t) — случайное состоя-
ние системы S в момент t.
Очевидно, что для любого момента t сумма вероятностей всех со-
стояний равна единице (как сумма вероятностей полной группы нссов-
местных событий):
п
'Epiw = !•
1=1
6.11. Дискретный марковский процесс. Цепь
Маркова
Пусть в некоторой системе S происходит с. и. с дискретными состо-
яниями si, s%,..., sn и дискретным временем, т. е. переход системы из
одного состояния в другое происходит только в определенные моменты
времени to, ti, t^,.... Эти моменты называют шагами процесса (обычно
разности смежных моментов наблюдения ti — ti-i равны постоянному
числу - длине шага, принимаемого в качестве единицы времени); to —
начало процесса.
Этот с. п. можно рассматривать как последовательность (цепь) со-
бытий 5(0), 5(1), 5(2),... (5(0) — начальное состояние системы, т.е.
перед 1-м шагом; 5(1) состояние системы после 1-го шага. 5(2) по-
сле 2-го шага и т. д.), т. е. событий вида {5(fc) = Sj}, где i = 1,2,3,..., n;
к = 0,1,2,....
206
a
Раздел первый. Элементарная теория вероятностей и случайных процессов
Марковский случайный процесс с дискретными состояниями и дис-
кретным временем называют марковской цепью (цепь Маркова).
Отметим, что цепь, в которой условные вероятности состояний
в будущем зависят только от состояния на данном, последнем ша-
ге (и не зависят от предыдущих), называют простой цепью Маркова.
(А. А. Марков (1856 1922) —русский математик).
Будем рассматривать только простые цепи Маркова,- вычислять ве-
роятности состояний системы
Pi(k) = P{S(k) = Sj}, i = 1,2,3,..., n: k = 0.1.2,..
Здесь P{S(k) = Sj} — безусловная вероятность того, что на k-м шаге
система будет находиться в состоянии sz.
Для нахождения безусловной вероятности нужно знать начальное
распределение вероятностей pi(0),(0),... ,рп(0), т. е. вероятности со-
стояний рг(0) в момент времени tg = 0 (начало процесса) и так называ-
емые переходные вероятности Pij(k) марковской цепи на fc-м шаге.
Переходной вероятностью Pij(k) называют условную вероятность
перехода системы S на fc-м шаге в состояние Sj, если известно, что на
предыдущем (fc — 1)-м шаге она была в состоянии sz, т. е.
Pij(fc) = P{S(fc) = Sj | S(fc — 1) = Si}, i, j = 1,2,3,... ,n
(первый индекс указывает номер предшествующего, а второй — номер
последующего состояния).
Цепь Маркова называется однородной, если Pij(fc) ~ Pij, т.е. услов-
ные вероятности Pij(fc) не зависят от номера испытаний.
Далее будем рассматривать только однородные цепи, которые мо-
гут быть заданы с помощью вектора (pi(0),p2(0),...,р„(0)) — вероят-
ности состояний в момент времени tg = 0 и матрицы
/рп Р12 Р1п\
р _ Р21 Р22 • • Р'2/i
\Рп1 Рп2 Рпп/
называемой матрицей перехода системы.
Элементы матрицы Р обладают следующими свойствами:
a) Pij 0.
п
б) Pij = 1 (« = 1,2,3,...,п), т.е. сумма вероятностей каждой
1=1
строки матрицы перехода равна единице (как вероятности событий —
Глава 6. Основы теории случайных процессов • 207
перехода из одного состояния .чг в любое возможное состояние s:) —
-образующих полную группу).
Справедлива формула Р(п) = Рп, т. е. матрица переходов за п ша-
гов есть n-я степень матрицы переходов за один шаг.
Пример 6.10. Задана матрица перехода Р =
матрицу вероятностей переходов за два шага.
0,2
0,3
0,5
0,3
0,2
0,3
0,5\
0,5
0,2/
. Найти
Q По формуле Р(2) = Р2 находим
/0,2 0,3 0,5\ /0,2 0.3 0,5\ /0,38 0,27 0,35\
Р(2) = 1 0,3 0,2 0,5 I 1 о,3 0,2 0,5 I = I 0,37 0,28 0,35 I . •
\0,5 0,3 0,2/ \0,5 0,3 0.2/ \0,29 0,27 0,44/
Заметим, что цепь Маркова представляет собой дальнейшее обоб-
щение схемы Бернулли уже на случай зависимых испытаний; незави-
симые испытания являются частным случаем марковской цепи. Под
«событием» понимается состояние системы, а под «испытанием» — из-
менение ее состояния.
Если «испытания» (опыты) независимы, то появление определен-
ного события в любом опыте не зависит от результатов ранее произве-
денных испытаний.
6.12. Понятие о непрерывном марковском процессе.
Уравнения Колмогорова
Пусть в некоторой системе S происходит марковский с. п. с дис-
кретными СОСТОЯНИЯМИ 6’1, S2, • • •, sn.
Если переходы системы из состояния в состояние происходят не в
фиксированные моменты ф, Н, ^2, • , а в случайные моменты времени
(что чаще встречается на практике), то такой процесс называют мар-
ковским процессом с дискретными состояниями и непрерывным вре-
менем.
Марковские с. п. указанного типа используются, в частности, для
исследования реальных систем массового обслуживания (СМО); про-
цессы в них протекают в непрерывном времени. Под состоянием систе-
мы понимается число требований (заявок) на обслуживание, находя-
щихся в системе.
208 Раздел первый. Элементарная теория вероятностей и случайных процессов
Будем считать, что переходы системы из состояния Sj в состояние
Sj осуществляются под воздействием пуассоновского потока событий
(см. п. 1.21) с интенсивностью Л;; = const.
Граф состояний системы с проставленными у стрелок интенсивно-
стями называют размеченным (см. рис. 69).
Рис. 69
Переход системы из состояния sj в s? происходит в момент, когда
наступает первое событие потока.
Вероятность события, состоящего в том, что в момент времени t си-
стема S будет находиться в состоянии sj, как уже знаем, обозначается
через pj(t):
п
Pi(t) = P{S(t) = sj, причем J^p^t) = 1.
i=i
Для нахождения этих вероятностей, т.е. pi(t) — вероятностей состоя-
ний системы si, S2, •. •, sn. нужно решить систему дифференциальных
уравнений — уравнений Колмогорова, имеющих вид
, п п
~ ’ Pj(ty ~ Pitt) ’ (^ = 1, 2, 3, . . . , п)
1=1 1=1
с начальными условиями pi(0),p2(0),... .рп(0); рфО) > 0, 52 рДО) = 1 и
i=i
условием нормировки 52 Pi(t) = 1-
г=1
При составлении системы уравнений Колмогорова удобно пользо-
ваться размеченным графом состояний системы.
Правило составления уравнений Колмогорова таково: в левой ча-
сти каждого из уравнений стоит производная вероятности Si состояния,
dpi(t)
т.е. ———; в правой части — сумма произведений вероятностей p,;(t)
всех состояний (когда стрелка ведет в данное состояние) на интенсив-
ности соответствующих потоков минус суммарная интенсивность всех
потоков (когда стрелка ведет из данного состояния), умноженная на
вероятность данного s, состояния.
Глава 6. Основы теории случайных процессов • 209
Рис. 70
Например, для системы S, размеченный граф состояний которой
показан на рис. 70, система дифференциальных уравнений будет:
p'i(t) = А21 • P2(t) — (А12 + А13) • Р1(£)>
p'2(t) = A12 • pi(t) - (A21 + А2з)
p'3(Z) = A13 -Pl(t) + A23
Нормировочное условие pi(t) + Pztt) + рз(£) = 1-
При интегрировании такой системы следует учесть состояние си-
стемы в начальный момент, т. е. при t = 0. Так, если в этот момент она
была в состоянии .s/c, то полагают р; (0) = 1, р-,(0) = 0 при i к.
Замечание. Случайный процесс, устанавливающийся в системе при
t ос (т. и. предельный стационарный режим), характеризуют так
называемые предельные вероятности состояний, т. е. вероятности р,- (t)
при t —> 00.
Предельные вероятности существуют, если число состояний конеч-
но, «состояний без выхода» (из них невозможен переход ни в какое
другое состояние) нет, потоки событий стационарны (А,7 = const).
Предельная вероятность состояния Sj показывает среднее относи-
тельное время пребывания системы в этом, состоянии.
Для нахождения предельных вероятностей в уравнениях Колмо-
dpi(t) п
горова полагают все производные ——— равными U и решают систему
п
алгебраических уравнений (с учетом нормировки Pi(t) = !)•
i=l
Пример 6.11. Найти предельные вероятности для системы S. граф
которой изображен на рис. 71.
Рис.. 71
210 • Раздел первый. Элементарная теория вероятностей и случайных процессов
Q Составляем дифференциальные уравнения Колмогорова:
>1 = ф?2 - Р1,
* РГ2 = Pi + 3Рз - (2 + 4) Р2-
фз = 2 • Р‘2 - 3 • р3.
Тогда система алгебраических уравнений, описывающих стационарный
режим системы S, принимает вид
'4р2 - Pi = 0,
< Р1 + Зрз - 6р2 = 0,
2р2 - Зрз = 0,
,Р1 +Р2 +РЗ = 1-
12 3 2
Решая эту систему, находим рг = —. р2 = рз = т. е. система S в
среднем 70,6 % будет находиться в состоянии Si; 17,6 % — в состоянии
s2; 11,8 % — в состоянии S3. •
Упражнения
1. Цепь Маркова управляется матрицей перехода
/1 1\
-р — j 2 2 1
I 1 2 I ’
\3 3/
Определить матрицу вероятностей переходов за три шага.
2. Цепь Маркова с двумя состояниями si и s2 задана матрицей веро-
ятностей переходов
/2 1\
р = | 3 3 |
(1 1г
\2 2/
В качестве начального состояния процесса некоторое устройство
выбирает Si с вероятностью 1 и s2 — с вероятностью |. Постро-
ить граф, соответствующий матрице. Найти вероятность того, что
после первого шага процесс перейдет в состояние зц
3. Матрица вероятностей переходов за один шаг цепи Маркова имеет
' вид
/0,2 0,3 0,5\
V = 0,4 0,2 0.4 .
\0,5 0,2 0,3/
Найти предельные вероятности.
Основы_________
математической
статистики
Раздел второй
Глава 7
Выборки и их характеристики
7.1. Предмет математической статистики
Математическая статистика, — раздел математики, в котором
изучаются методы сбора, систематизации и обработки результатов на-
блюдений массовых случайных явлений для выявления существующих
закономерностей.
Математическая статистика тесно связана с теорией вероятностей.
Обе эти математические дисциплины изучают массовые случайные
явления. Связующим звеном между ними являются предельные теоре-
мы теории вероятностей. При этом теория вероятностей выводит из ма-
тематической модели свойства реального процесса, а математическая
статистика устанавливает свойства математической модели, исходя из
данных наблюдений (говорят «из статистических данных»).
Предметом математической статистики является изучение случай-
ных величин (или случайных событий, процессов) по результатам на-
блюдений. Полученные в результате наблюдения (опыта, эксперимен-
та) данные сначала надо каким-либо образом обработать: упорядочить,
представить в удобном для обозрения и анализа виде. Это первая зада-
ча. Затем, это уже вторая задача, оценить, хотя бы приблизительно,
интересующие нас характеристики наблюдаемой случайной величи-
ны. Например, дать оценку неизвестной вероятности события, оценку
неизвестной функции распределения, оценку математического ожида-
ния, оценку дисперсии случайной величины, оценку параметров рас-
пределения, вид которого неизвестен, и т. д.
Следующей, назовем ее условно третьей, задачей является провер-
ка, статистических гипотез, т. е. решение вопроса согласования ре-
зультатов оценивания с опытными данными. Например, выдвигается
гипотеза, что: а) наблюдаемая с. в. подчиняется нормальному закону;
б) м. о. наблюдаемой с. в. равно нулю; в) случайное событие обладает
данной вероятностью и т. д.
Одной из важнейших задач математической статистики является
разработка методов, позволяющих по результатам обследования вы-
Глава 7. Выборки и их характеристики 213
борки (т. е. части исследуемой совокупности объектов) делать обосно-
ванные выводы о распределении признака (с. в. X) изучаемых объектов
по всей совокупности.
Для обработки статистических данных созданы специальные про-
граммные пакеты (STADIA, СтатЭксперт, Эвриста, SYSTAT, STAT-
GRAPHICS и др.), которые выполняют трудоемкую работу по расче-
ту различных статистик, построению таблиц и графиков. Простейшие
статистические функции имеются в программируемых калькуляторах
и популярных офисных программах (EXCEL).
Результаты исследования статистических данных методами мате-
матической статистики используются для принятия решения (в зада-
чах планирования, управления, прогнозирования и организации произ-
водства, при контроле качества продукции, при выборе оптимального
времени настройки или замены действующей аппаратуры и т. д.), т. е.
для научных и практических выводов.
Говорят, что «математическая статистика — это теория принятия
решений в условиях неопределенности».
Математическая статистика возникла в XVIII веке в работах
Я. Бернулли, П. Лапласа, К. Пирсона. В ее современном развитии опре-
деляющую роль сыграли труды Г. Крамера, Р. Фишера, Ю. Неймана
и др. Большой вклад в математическую статистику внесли русские уче-
ные П. Л. Чебышев, А. М. Ляпунов, А. Н. Колмогоров, Б. В. Гнеденко
и другие.
7.2. Генеральная и выборочная совокупности
Пусть требуется изучить данную совокупность объектов относи-
тельно некоторого признака. Например, рассматривая работу диспет-
чера (продавца, парикмахера,...), можно исследовать: его загружен-
ность, тип клиентов, скорость обслуживания, моменты поступления
заявок и т. д. Каждый такой признак (и их комбинации) образует слу-
чайную величину, наблюдения над которой мы и производим.
Совокупность всех подлежащих изучению объектов или возможных
результатов всех мыслимых наблюдений, производимых в неизменных
условиях над одним объектом, называется генеральной совокупностью.
Более строго: генеральная совокупность — это с. в. X(ш), заданная
на пространстве элементарных событий Q с выделенным в нем классом
S подмножеств событий, для которых указаны их вероятности.
214 Раздел второй. Основы математической статистики
Зачастую проводить сплошное обследование, когда изучаются все
объекты (например - перепись населения), трудно или дорого, эконо-
мически нецелесообразно (например — не вскрывать же каждую кон-
сервную банку для проверки качества продукции), а иногда невозмож-
но. В этих случаях наилучшим способом обследования является вы-
борочное наблюдение: выбирают из генеральной совокупности часть ее
объектов («выборку») и подвергают их изучению.
Выборочной совокупностью {выборкой) называется совокупность
объектов, отобранных случайным образом из генеральной совокупно-
сти.
Более строго: выборка — это последовательность Х^, Х%,..., Хп
независимых одинаково распределенных с. в., распределение каждой
из которых совпадает с распределением генеральной случайной вели-
чины.
Число объектов (наблюдений) в совокупности, генеральной или вы-
борочной, называется ее объемом; обозначается соответственно через N
и п.
Конкретные значения выборки, полученные в результате наблюде-
ний (испытаний), называют реализацией выборки и обозначают строч-
ными буквами .Ti,Х2,... ,хп.
Метод статистического исследования, состоящий в том. что на осно-
ве изучения выборочной совокупности делается заключение о всей ге-
неральной совокупности, называется выборочным.
Для получения хороших оценок характеристик генеральной сово-
купности необходимо, чтобы выборка была репрезентативной (или
представительной), т. е. достаточно полно представлять изучаемые
признаки генеральной совокупности. Условием обеспечения репрезен-
тативности выборки является, согласно закону больших чисел, соблю-
дение случайности отбора, т. е. все объекты генеральной совокупности
должны иметь равные вероятности попасть в выборку.
Различают выборки с возвращением {повторные) и без возвраще-
ния {бесповторные). В первом случае отобранный объект возвращается
в генеральную совокупность перед извлечением следующего; во вто-
ром не возвращается. На практике чаще используется бесповторная
выборка.
Заметим, если объем выборки значительно меньше объеме! гене-
ральной совокупности, различие между повторной и бесповторной вы-
борками очень мало, его можно не учитывать.
В зависимости от конкретных условий для обеспечения репрезента-
тивности применяют различные способы отбора: простой, при котором
из генеральной совокупности извлекают по одному объекту; типиче-
Глава 7. Выборки и их характеристики • 215
ский, при котором генеральную совокупность делят на «типические»
части и отбор осуществляется из каждой части (например, мнение о
референдуме спросить у случайно отобранных людей, разделенных по
признаку пола, возраста,...); механический. при котором отбор произ-
водится через определенный интервал (например, мнение спросить у
каждого шестидесятого...серийный, при котором объекты из гене-
ральной совокупности отбираются «сериями», которые должны иссле-
доваться при помощи сплошного обследования.
На практике пользуются сочетанием вышеупомянутых способов от-
бора.
Пример 7.1. Десять абитуриентов проходят тестирование по матема-
тике. Каждый из них может набрать от 0 до 5 баллов включительно.
Пусть — количество баллов, набранных k-м (к = 1,2,..., 10) аби-
туриентом.
Тогда значения 0, 1, 2, 3, 4, 5 — все возможные количества бал-
лов, набранных одним абитуриентом, — образуют генеральную сово-
купность.
Выборка АД, АД, Х3,..., Ащ - - результат тестирования 10 абитури-
ентов.
Реализациями выборки могут быть следующие наборы чисел: {5,
3, 0, 1, 4, 2. 5. 4. 1, 5} или {4, 4, 5, 3, 3, 1, 5, 5, 2, 5} или {3, 4, 5. 0. 1. 2.
3, 4, 5, 4} и т. д.
7.3. Статистическое распределение выборки.
Эмпирическая функция распределения
Пусть изучается некоторая с. в. X. С этой целью над с. в. X про-
изводится ряд независимых опытов (наблюдений). В каждом из этих
опытов величина X принимает то или иное значение.
Пусть она приняла п\ раз значение Xi, п? раз — значение «2, ...,
Пк раз — значение х^. При этом 'щ +П2 + •. + п& = п — объем выборки.
Значения «1, .тг,..., х^ называются вариантам.и с. в. X.
Вся совокупность значений с. в. X представляет собой первичный
статистический материал, который подлежит дальнейшей обработке,
прежде всего — упорядочению.
Операция расположения значений случайной величины (призна-
ка) по неубыванию называется ранжированием статистических дан-
ных. Полученная таким образом последовательность j), a?(2), • • , жщ)
216 Раздел второй. Основы математической статистики
О
значений с. в. X (где хщ Ж(2) ^ ... ^ Х(п) и ж^) = х™™ • • • > х(п) =
= max Хг) называется вариационным рядом.
l^i^n
Числа щ, показывающие, сколько раз встречаются варианты ж« в
ряде наблюдений, называются частотами, а отношение их к объему
выборки — частостями или относительными частотами (р*), т.е.
* П;
Pi — Pl
(7.1)
к
где п = щ.
i=i
Перечень вариантов и соответствующих им частот или частостей
называется статистическим распределением выборки или статисти-
ческим рядом.
Записывается статистическое распределение в виде таблицы. Пер-
вая строка содержит варианты, а вторая — их частоты п, (или часто-
сти р*).
Пример 7.2. В результате тестирования (см. пример 7.1) группа аби-
туриентов набрала баллы: 5. 3. О, 1, 4, 2, 5, 4, 1, 5. Записать полученную
выборку в виде: а) вариационного ряда; б) статистического ряда.
Q а) Проранжировав статистические данные (т. е. исходный ряд), по-
лучим вариационный ряд (ж^, жр), • • • • ^(io)):
(О, 1, 1, 2. 3, 4, 4, 5, 5, 5).
б) Подсчитав частоту и частость вариантов ,tj = 0, ж 2 = 1, жз = 2,
Ж4 = 3, жз = 4, же = 5, получим статистическое распределение выборки
(так называемый дискретный статистический ряд)
или
Хг 0 1 2 3 4 5
Щ 1 2 1 1 2 3
Жг 0 1 2 3 4 5
Pi 1 10 2 10 1 10 1 10 2 10 3 10
Статистическое распределение выборки является оценкой неиз-
вестного распределения. В соответствии с теоремой Бернулли (и. 5.3)
относительные частоты р* сходятся при п —> оо к соответствующим
Глава 7. Выборки и их характеристики 217
р
вероятностям рд т.е. р”:-----> '/>г. Поэтому при больших значениях ?г
го—>оо
статистическое распределение мало отличается от истинного распре-
деления.
В случае, когда число значений признака (с. в. X) велико или при-
знак является непрерывным (т. е. когда с. в. X может принять любое
значение в некотором интервале), составляют интервальный стати-
стический ряд. В первую строку таблицы статистического распределе-
ния вписывают частичные промежутки (.го,Ж|), [ад, т2),. - -, [ад д, х^).
которые берут обычно одинаковыми по длине: h = xi — а?о = ж2 — ад =
= .... Для определения величины интервала (Л) можно использовать
формулу Стерджеса:
__ ^‘max ^min
1 -I- log2 п
где жтах — жтт — разность между наибольшим и наименьшим значени-
ями признака, т = 1 + log2 п — число интервалов (log2 п » 3,3221g п).
За начало первого интервала рекомендуется брать величину жнач =
Г
— Жщш — £ • Во второй строчке статистического ряда вписывают коли-
чество наблюдений щ (г = 1,/с), попавших в каждый интервал.
Пример 7.3. Измерили рост (с точностью до см) 30 наудачу отобран-
ных студентов. Результаты измерений таковы:
178, 160, 154, 183, 155, 153, 167. 186. 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
179, 165, 156, 179, 158, 171, 175. 173, 164. 172.
Построить интервальный статистический ряд.
Q Для удобства проранжируем полученные данные:
153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167. 169,
170, 171, 171, 172, 173, 173, 175, 175. 178. 179, 179, 182, 183, 186.
Отметим, что X — рост студента — непрерывная с. в. При более
точном измерении роста значения с. в. X обычно не повторяются (веро-
ятность наличия на Земле двух человек, рост которых равен, скажем
д/З = 1,732050808... метров, равна, нулю!).
Как видим. rcmjn = 153, .ттах = 186; по формуле Стерджеса, при
п = 30, находим длину частичного интервала
. = 186 - 153 ~ 33 ~ 33 ~ г rq
1 + log2 30 ~ 1 + 3,3221g 30 ~ 5.907 ~ ’
Примем h = 6. Тогда жнач = 153 — | = 150. Исходные данные
разбиваем на 6 (т = 1 + log2 30 = 5,907 ~ 6) интервалов: [150.156),
[156,162), [162,168), [168,174), [174, 180), [180, 186).
218 • Раздел второй. Основы математической статистики
Подсчитав число студентов (гц), попавших в каждый из получен-
ных промежутков, получим интервальный статистический ряд:
Рост [150 156) [156-162) [162 168) [168-174) [174 180) [180- 186)
Частота 4 5 6 7 5 ' 3
Частость 0,13 0,17 0.20 0,23 0,17 0,10
Одним из способов обработки вариационного ряда является постро-
ение эмпирической функции распределения.
Эмпирической (статистической) функцией распределения называ-
ется функция F*(x), определяющая для каждого значения х частость
события {X < х}:
F*(x)=p*{X<x}. (7.2)
Для нахождения значений эмпирической функции удобно F* (а;) за-
писать в виде
W
где п. — объем выборки, пх — число наблюдений, меныпих х (х G Ж).
Очевидно, что F* (х) удовлетворяет тем же условиям, что и истин-
ная функция распределения F(.r) (см. п. 2.3).
При увеличении числа п наблюдений (опытов) относительная ча-
стота события {X < .г} приближается к вероятности этого события
(теорема Бернулли, п. 5.3). Эмпирическая функция распределения
F*(x) является оценкой вероятности события {.Y < т}, т.е. оценкой
теоретической функции распределения F(x) с. в. X. Имеет место
Теорема 7.1. Пусть F(.r) — теоретическая функция распределения с. в.
X, a F*(x) — эмпирическая. Тогда для любого е > О
lim P{\F*(x)-F(x)\ <Д = 1.
Пример 7.4. Построить функцию F*(x). используя условие и резуль-
таты примера 7.2.
Q Здесь п = 10. Имеем F(0(x) = = 0 при х 0 (наблюдений мень-
ше 0 нет); F1*0(t) = — при 0 < х eZ 1 (здесь пТ = 1) и т. д. Окончательно
Глава 7. Выборки и их характеристики • 219
получаем
'о, при Ж 5 С о.
0,1, при 0 < С ж 1.
0,3, при 1 < С х 2,
FioH = < 0,4, при 2 < ; ж 3,
0.5, при 3 < С ж 4,
0,7, при 4 < ' х 5,
1, при 5 < ' X.
График эмпирической функции распределения приведен на рис. 72. •
7.4. Графическое изображение статистического
распределения
Статистическое распределение изображается графически (для на-
глядности) в виде так называёмых полигона и гистограммы. Полигон,
как правило, служит для изображения дискретного (т. е. варианты от-
личаются на постоянную величину) статистического ряда.
РО Полигоном частот называют ломаную, отрезки которой соединя-
— ют точки с координатами (ж1, nj), (ж2, п^), , (жд,,щ,); полигоном ча-
стостей — с координатами (жцр*), (ж2,Р2)> • • • (жл-,р^.).
Варианты (ж^) откладываются на оси абсцисс, а частоты и, соот-
ветственно, частости — на оси ординат.
220 • Раздел второй. Основы математической статистики
Пример 7.5. Для примера 7.2 (п. 7.3) полигон частостей имеет вид,
изображенный на рис. 73.
Заметим, что р^ + р^ + ... + р% = 1.
Как видно, полигон частостей является статистическим аналогом
многоугольника распределения (см. п. 2.2).
Для непрерывно распределенного признака (т. е. варианты могут
отличаться один от другого на сколь угодно малую величину) можно
построить полигон частот, взяв середины интервалов в качестве значе-
ний .Г1,а?2, - • •,Xfc. Более употребительна так называемая гистограмма.
Гистограммой частот (частостей) называют ступенчатую фигу-
ру, состоящую из прямоугольников, основаниями которых служат ча-
стичные интервалы длины h. а высоты равны отношению — — плот-
* ™
/ Pi fl'i к ,
ность частоты (-г- или ------плотности частости).
h п h
Очевидно, площадь гистограммы частот равна объему выборки, а
площадь гистограммы частостей равна единице.
Пример 7.6. Используя условие и результаты примера 7.3 из п. 7.3
построить гистограмму частостей.
О В данном случае длина интервала равна h = 6. Находим высоты
hi прямоугольников: ф = -~Д га 0,022, h-2 — —~ 0.028, /гз = га
0 23 0 17 0 1
га 0,033, /г4 = ~ 0,038, h5 га = 0,028, /г6 га = 0,017.
ООО
Гистограмма частостей изображена на рис. 74.
Гистограмма частот является статистическим аналогом дифферен-
циала функции распределения (плотности) /(.т) с. в. X. Сумма площа-
Глава 7. Выборки и их характеристики • 221
дей прямоугольников равна единице
(, Pi . । > Рб _ * , . * _ 1
I h ——Н ... + h — — Pi + ... + pg — 1
что соответствует условию
оо
У f(x)dx = 1
—оо
для плотности вероятностей /(ж) (см. п. 2.4). На рис. 74 показана и
плотность вероятностей f(x).
Если соединить середины верхних оснований прямоугольников от-
резками прямой, то получим полигон того же распределения. •
7.5. Числовые характеристики статистического
распределения
Для выборки можно определить ряд числовых характеристик, ана-
логичным тем, что в теории вероятностей определялись для случайных
величин (см. п. 2.5).
Пусть статистическое распределение выборки объема п имеет вид:
Xi Xi Ж2 Хк
Щ П1 п2 тг3 ™к
Выборочным средним хв называется среднее арифметическое всех
значений выборки:
к
Хв — X} ' 14- 1 / .4)
г=1
222 • Раздел второй. Основы математической статистики
Выборочное среднее можно записать и так:
к
xe = ^xi-p*i, (7-5)
4=1
где р* = — частость. Для обозначения выборочного среднего ис-
пользуют следующие символы: ж, М*(Х), т*.
Отмстим, что в случае интервального статистического ряда в ра-
венстве (7.4) в качестве Xj берут середины его интервалов, а щ со-
ответствующие им частоты.
Выборочной дисперсией DB называется среднее арифметическое
квадратов отклонений значений выборки от выборочной средней жв,
т. е.
к
DB = i 52(®i - Жв)2 • Hi (7.6)
i=l
или, что то же самое.
к
Рв = £(х;-хв)2-р*. (7.7)
i=i
Можно показать, что DB может быть подсчитана также по формуле:
к
&в = Xi ‘ П1 ~ T- e‘
4=1
DB=^2-(x)2, (7.8)
здесь x = xB.
Выборочное среднее квадратическое отклонение выборки опреде-
ляется формулой
св = у/В~в. (7.9)
Особенность выборочного с. к. о. (сгв) состоит в том, что оно изме-
ряется в тех же единицах, что и изучаемый признак.
При решении практических задач используется и величина
к
S2 = ' (^ - ЖВ)2 • Щ, (7.10)
4=1
т. е.
S2 = (7.11)
п — 1
Г лава 7. Выборки и их характеристики 223
а
а
которая называется исправленной выборочной дисперсией (см. далее
п. 8.1).
Величина
S=yf& (7.12)
называется исправленным выборочным средним квадратическим от-
клонением.
Для непрерывно распределенного признака формулы для выбо-
рочных средних будут такими же, но за значения xi,X2, ,Хк на-
до брать не концы промежутков [жо,Ж1), [Ж1,Ж2),.. .а а их середины
хо + Xi Xi + а?2
2 ’ 2
В качестве описательных характеристик вариационного ряда ж^п,
ж(2) 5 • • •, ®(и) (или полученного из него статистического распределения
выборки (7.3)) используется медиана, мода, размах вариации (выбор-
ки) и т. д.
Размахом вариации называется число R = — х^, где хщ =
= min XiХ(„\ = max xi или R — жтах—жтн1- где ®тах — наибольший,
•A-min — наименьший вариант ряда.
Модой М* вариационного ряда называется вариант, имеющий наи-
большую частоту.
Медианой М* вариационного ряда называется значение признака
(с. в. X), приходящееся на середину ряда.
Если п = 2k (т.е. ряд ж^рЖр),... ,x^),x^+ip ... ,х^к) имеет четное
число членов), то М* —------! если п = 2k + 1, то М* = x^+i)-
Пример 7.7. По условию примера 7.2 из п. 7.3 найти характеристики
выборки — результаты тестирования 10 абитуриентов.
Q Используя формулы (7.4) (7.12) и определения из п. 7.5, находим:
жв = j— • (0 • 1 + 1 • 2 + ... + 5 3) = 3,
рв - X ((0 - З)2 • 1 4- (1 - З)2 2 + ... + (5 - З)2 3) = 3,2,
сгв = ч/3.2 ~ 1.79.
S2 = у • 3,2 и 3,56,
5* = Дф56 « 1,87,
R = 5 - 0 = 5,
М* = 5,
М* = Х+Х = з15. •
224 Раздел второй. Основы математической статистики
Упражнения
1. Найти и построить эмпирическую функцию распределения для вы-
борки, представленной статистическим рядом.
Xi 1 3 6
Tli 10 8 12
2. На телефонной станции производились наблюдения за числом не-
правильных соединений в минуту. Результаты наблюдений в тече-
ние часа представлены в виде статистического распределения.
Xi 0 1 2 3 4 5 6
8 17 16 10 6 2 1
Найти выборочные среднее и дисперсию. Сравнить распределение
X ., а в
частостей с распределением Пуассона In.,, т «-;—
\ ’ т!
3. Изучается с. в. X — число выпавших очков при бросании игральной
кости. Кость подбросили 60 раз. Получены следующие результаты:
3, 2, 5, 6, 6, 1, 4, 6, 4, 6, 3, 6, 4, 2, 1, 5, 3, 1, 6, 4,
5, 4, 2, 2, 4, 2, 6, 3. 1, 5, 6, 1, 6, 6, 4, 2, 5, 4, 3, 6,
4, 1, 5, 6, 3, 2, 4, 4, 5, 2, 5, 6, 2, 3, 5, 4, 1, 2, 5, 3.
1. Что в данном опыте-наблюдении представляет генеральную со-
вокупность? 2. Перечислите элементы этой совокупности. 3. Что
представляет собой выборка? 4. Приведите 1-2 реализации выбор-
ки. 5. Оформите ее в виде: а) вариационного ряда; б) статистическо-
го ряда. 6. Найдите эмпирическую функцию распределения выбор-
ки. 7. Постройте интервальный статистический ряд. 8. Постройте
полигон частот и гистограмму частостей. 9. Найдите: а) выбороч-
ную среднюю; б) выборочную дисперсию: в) исправленную выбо-
рочную дисперсию и исправленное среднее квадратическое откло-
нение; г) размах вариации, моду и медиану.
Глава 8
Элементы теории оценок и проверки гипотез
8.1. Оценка неизвестных параметров
Понятие оценки параметров
Пусть изучается случайная величина X с законом распределения,
зависящим от одного или нескольких параметров. Например, это пара-
метр <1 в распределении Пуассона I Р{Х = т} =
или пара-
метры а и а для нормального закона распределения.
Требуется по выборке Xi, Х%,..., Хп, полученной в результате п
наблюдений (опытов), оценить неизвестный параметр в.
Напомним, что Xi, Х2, , Х„ — случайные величины: X] — ре-
зультат первого наблюдения, Х2 — второго и т. д., причем с. в. Xj,
г = 1,2,..., п, имеют такое же распределение, что и с. в. X; конкретная
выборка Xi, х2, - , хп — это значения (реализация) независимых с. в.
Хх,Х2,...,Хп.
Статистической оценкой 0п (далее просто оценкой 3) параме-
тра 3 теоретического распределения называют его приближенное зна-
чение, зависящее от данных выбора.
Очевидно, что оценка в есть значение некоторой функции резуль-
татов наблюдений над случайной величиной, т. е.
з = з(х1,х2,...,хп).
(8.1)
Функцию результатов наблюдений (т. е. функцию выборки) назы-
вают статистикой.
Можно сказать, что оценка, 3 параметра 3 есть статистика, которая
в определенном смысле близка к истинному значению 3.
Так, F*(x) есть оценка Т\(ж), гистограмма — плотности /(ж). (
226 * Раздел второй. Основы математической статистики
Оценка 0 является случайной величиной, так как является функ-
цией независимых с. в. , Х%,..., Хп; если произвести другую выборку,
то функция примет, вообще говоря, другое значение.
Если число опытов (наблюдений) невелико, то замена неизвестного
параметра 0 его оценкой 0, например математического ожидания сред-
ним арифметическим, приводит к ошибке. Это ошибка в среднем тем
больше, чем меньше число опытов.
К оценке любого параметра предъявляется ряд требований, кото-
рым она должна удовлетворять, чтобы быть «близкой» к истинному
значению параметра, т. е. быть в каком-то смысле «доброкачественной»
оценкой.
Свойства статистических оценок
Качество оценки определяют, проверяя, обладает ли она свойства-
ми несмещенности, состоятельности, эффективности.
Оценка 0 параметра 0 называется несмещенной, если М0 = 0.
Если М0 0, то оценка 0 называется смещенной.
Чтобы оценка 0 не давала систематической ошибки (ошибки одного
знака) в сторону завышения (М0 > 0) или занижения (М0 < 0), на-
до потребовать, чтобы «математическое ожидание оценки было равно
оцениваемому параметру».
Если М0п —> 0, то оценка 0п называется асимптотически несме-
щенной.
Требование несмещенности особенно важно при малом числе на-
блюдений (опытов).
Оценка 0п параметра 0 называется состоятельной, если она схо-
дится по вероятности к оцениваемому параметру:
0п ~JL^ 0,
т. е. для любого е > 0 выполнено
lim Р /|0.„ — 01 < = 1.
п—>оо I )
Это означает, что с увеличением объема выборки мы все ближе
приближаемся к истинному значению параметра 0, т. е. практически
достоверно 0п ~ 0.
Свойство состоятельности обязательно для любого правила оцени-
вания (несостоятельные оценки не используются).
Глава 8. Элементы теории оценок и проверки гипотез * 227
Состоятельность оценки 0п часто может быть установлена с помо-
щью следующей теоремы.
Теорема 8.1. Если оценка 0п параметра 0 является несмещенной и
D0.„ —> 0 при п —> оо, то 0п — состоятельная оценка.
□ Запишем неравенство Чебышева для с. в. 0п для любого е > 0:
Р(\0п - 0\ < е) > 1 -
Так как по условию lim D0n = 0, то lim Р(\0п — 0\ < е) 1. Но
71~~>ОО 72—>00
вероятность любого события не превышает 1 и, следовательно,
lim Р(|0П — 01 < е) — 1,
т. е. 0п — состоятельная оценка параметра 0.
Несмещенная оценка 0п параметра 0 называется эффективной,
если она имеет наименьшую дисперсию среди всех возможных несме-
щенных оценок параметра 0, т. е. оценка 0п эффективна, если ее дис-
персия минимальна.
Эффективную оценку в ряде случаев можно найти, используя не-
равенство Рао-Крамера-.
D0n > -±~Т,
п 1
где I = 1(0) — информация Фингера, определяемая в дискретном слу-
чае формулой
г я 12 [р'п(х,,0)12
I = =g[^J ₽(^),
где p(x, 0) = p{X = ж}, а в непрерывном — формулой
оо 2
Г=М[|111/(Х,в)]2=У ./(x.^dc,
—оо
где f(x,0) — плотность распределения н. с. в. X.
Эффективность оценки определяется отношением
D0-
D0n
8*
228 • Раздел второй. Основы математической статистики
где — эффективная оценка (dO^ = . Чем ближе eff 0п к 1,
тем эффективнее оценка 0п. Если eff вп —> 1 при п ос. то оценка
называется асимптотически эффективной.
Отметим, что на практике не всегда удается удовлетворить всем
перечисленным выше требованиям (несмещенность, состоятельность,
эффективность), и поэтому приходится довольствоваться оценками, не
обладающими сразу всеми тремя свойствами. Все же три свойства, как
правило, выделяют оценку однозначно.
Точечные оценки математического ожидания и дисперсии
Пусть изучается с. в. X с математическим ожиданием а = MX и
дисперсией DX-. оба параметра неизвестны.
Статистика, используемая в качестве приближенного значения не-
известного параметра генеральной совокупности, называется ее точеч-
ной оценкой. То есть точечная оценка характеристики генеральной со-
вокупности — это число, определяемое по выборке.
Пусть ад, а?2,.. -, хп — выборка, полученная в результате проведе-
ния п независимых наблюдений за с. в. X. Чтобы подчеркнуть случай-
ный характер величин ад, Ж2, • • •, перепишем их в виде Xi,X2,...
... , Хп, т. е. под Xi будем понимать значение с. в. X в г-м опыте.
Случайные величины А|, АД.. , Хп можно рассматривать как п не-
зависимых «экземпляров» величины А. Поэтому МХ\ = МХ2 = ...
... = МХп = MX = a, DXi = DX2 = ... = DXn = DX.
Теорема 8.2. Пусть Ai, АД..., Хп — выборка из генеральной совокуп-
ности и MXi = MX = a, DXi = DX (г = 1,п). Тогда выборочное среднее
п
АГВ — - Xi — несмещенная и состоятельная оценка математического
г=1
ожидания MX.
□ Найдем м. о. оценки Хв:
Отсюда по определению получаем, что А”в несмещенная оценка MX.
Далее, согласно теореме Чебышева (п. 5.2), для любого £ > 0 имеет
Глава 8. Элементы теории оценок и проверки гипотез 229
место равенство
= 1,
которое, согласно условию теоремы, можно переписать так:
lim Р{\ХВ-МХ\ < Д = 1
п—>оо v J
или, что то же самое, lim Р {|0 — #1 < г} =1. Согласно определению,
получаем, что Хв — состоятельная оценка MX.
Можно показать, что при нормальном распределении с. в. X эта
оценка, т. е. Хв, будет и эффективной. На практике во всех случа-
ях в качестве оценки математического ожидания используется среднее
арифметическое, т. е. Хв.
В статистике оценку математического ожидания принято обозна-
чать через X или Хв, а не X.
Покажем, что
MDB = ~1)Х. (8.2)
Действительно.
- ± - м(х} +х2 + ... + хп)2 = ±(мх2 + MX2 + ...+ MX2) —
п.
-±--м(х2+Х2+.. .+Х2+2(Х^2 + ХгХ3 + Х2Хз + • • • + хп =
7Г ' '------------v------------' '
cl
= (МХ2х + МХ'1 + ... + МХ2)-
п2
- - (МХг МХ2 + МХУМХ3 + мх2мх3 + ... + МХп^МХп) =
п2
= ?-xL-(mx2 + мх2 + ... + мх2)-
п2 '------------'
п
- ^{МХ - MX + MX MX + ... + MX MX) =
n2
= . n. MX2 - 4 • n(n9~ X- • (MX)2 = 11^-MX2-1^-(MX)2 =
n2 n2
230 Раздел второй. Основы математической статистики
= ^-(ЛН'2 - (MX)2) = DX.
Из равенства (8.2) следует, что MDB DX, т.е. выборочная дис-
персия является смещенной оценкой дисперсии DX. Поэтому выбороч-
ную дисперсию исправляют, умножив ее на
S2 = (см. (7.11)).
получая формулу
Теорема 8.3. Пусть Xi, Х2,..., Хп — выборка из генеральной совокуп-
ности и MXi — MX = a, DXi = DX (i — l,n). Тогда исправленная
п
выборочная дисперсия S2 = У^(Хг- ~-%)2 = rJl \ ' — несмещен-
i=i
ная состоятельная оценка дисперсии DX.
□ Примем без доказательства состоятельность оценки S'2. Докажем
ее несмещенность.
Имеем
MS2 = м
\п — 1 /
1 MD‘ = Дт " = Dx-
т.е. MS2 — DX. Отсюда по определению получаем, что S2 — несме-
щенная оценка DX.
Отметим, что при больших значениях п разница между DB и S2
очень мала и они практически равны, поэтому оценку S2 используют
для оценки дисперсии при малых выборках, обычно при п 30.
Имеют место следующие теоремы.
Теорема 8.4. Относительная частота появления события А в п не-
зависимых испытаниях является несмещенной состоятельной и эффек-
тивной оценкой неизвестной вероятности р = Р(А) этого события (р —
вероятность наступления события А в каждом испытании).
Отметим, что состоятельность оценки в = непосредственно вы-
текает из теоремы Бернулли (см. п. 5.3).
Теорема 8.5. Эмпирическая функция распределения выборки F*(rr)
является несмещенной состоятельной оценкой функции распределения
F(x) случайной величины X.
Глава 8. Элементы теории оценок и проверки гипотез *231
Пример 8.1. Монету подбрасывают п раз. Вероятность выпадения гер-
ба при каждом подбрасывания равна р. В ходе опыта монета выпала
гербом па раз. Показать несмещенность оценки в = вероятности
в = р выпадения герба в каждом опыте.
Q Число успехов (пд) имеет распределение Бернулли. Тогда М(па) =
= пр, D(tia) = npq = пр(1 — р). Следовательно, Мв = М ~
= i М(па) = п • р — р - в, т. е. оценка 6 = — несмещенная. •
8.2. Методы нахождения точечных оценок
Рассмотрим наиболее распространенные методы получения точеч-
ных оценок параметров распределения: метод моментов и метод макси-
мального правдоподобия (кратко: ММП) и метод наименьших квадра-
тов (кратко МНК).
Метод моментов
Метод моментов для нахождения точечных оценок неизвестных
параметров заданного распределения состоит в приравнивании теоре-
тических моментов распределения соответствующим эмпирическим
моментам, найденных по выборке.
Так. если распределение зависит от одного параметра в (например,
задан вид плотности распределения f(x, в)), то для нахождения его
оценки надо решить относительно в одно уравнение:
MX = ХВ
ОО
(MX = Jx' f(x, в) dx = tp(0) есть функция от в).
—ос
Если распределение зависит от двух параметров (например, вид
плотности распределения f(x,6i,0z)) — надо решить относительно
и 6*2 систему уравнений:
' MX = хв,
' DX = DB.
<
232 Раздел второй. Основы математической статистики
И, наконец, если надо оценить п параметров . ,вп надо
решить одну из систем вида:
= хг,
г=1
м2 = '> Ё
г=1
= i Е X*;
. г=1
ИЛИ
' MX = X,
DX = DB,
<
М(Х - MX)k = (*г - Хв)к.
i=l
Метод моментов является наиболее простым методом оценки пара-
метров. Он был предложен в 1894 г. Пирсоном. Оценки метода момен-
тов обычно состоятельны, однако их эффективность часто значительно
меньше единицы.
Пример 8.2. Найти оценки параметров нормального распределения
с. в. X методом моментов.
О Требуется по выборке X), х2, , найти точечные оценки неиз-
вестных параметров а — MX = в\ и <т — у/DX = 02.
По методу моментов приравниваем их. соответственно, к выбороч-
ному среднему и выборочной дисперсии (»i = MX — начальный мо-
мент I порядка, /12 = DX — центральный момент П порядка). Полу-
чаем
'МХ = 1В,
' DX = D„.
т. е.
а = жв,
’ о2 = DB.
Итак, искомые оценки параметров нормального распределения:
0| = хв и в2 = у/Db- •
Метод максимального правдоподобия
Пусть T’i.;T2,... — выборка, полученная в результате проведе-
ния п независимых наблюдений за с. в. X. И пусть вид закона рас-
пределения величины X, например, вид плотности /(ж,0), известен, но
Глава 8. Элементы теории оценок и проверки гипотез • 233
!>
неизвестен параметр в, которым определяется этот закон. Требуется
по выборке оценить параметр 0.
В основе метода максимального правдоподобия (ММП), предло-
женного Р. Фишером, лежит понятие функции правдоподобия.
Функцией правдоподобия, построенной по выборке Xi, х%,..., жп, на-
зывается функция аргумента 0 вида
£(./?!, .г2,..., хп-, S') = /(a"i,0) /(т2,6») •... • ф(хп. 0)
ИЛИ
п
ц*.0) = Пж,0),
г=1
где /(х, 6) — плотность распределения с. в. X в случае, если X — не-
прерывная. Если X — дискретная с. в., то функция правдоподобия име-
ет вид
Цх,0) = -р(ж2,0) • • -р(хп,0) = JJpM),
г=1
где р(хг,0) = Р{Х =
Из определения следует, что чем больше значение функции L(x, 0),
тем более вероятно (правдоподобнее) появление (при фиксированном
0) в результате наблюдений чисел ari,»2,.. , хп.
За точечную оценку параметра 0, согласно ММП, берут такое
его значение 0, при котором функция правдоподобия достигает мак-
симума.
Эта оценка, называемая оценкой максимального правдоподобия,
является решением уравнения
dL(x,0) I
д0 \е=ё
Так как функции L(x,0) и 1пЦх,0) достигают максимума при од-
ном и том же значении 0, то вместо отыскания максимума функции
Т(а;,6) ищут (что проще) максимум функции In Цх,&).
Таким образом, для нахождения оценки максимального правдопо-
добия надо:
1. решить уравнение правдоподобия
d(lnL(M))|
d0 ’
234 Раздел второй. Основы математической статистики
2. отобрать то решение, которое обращает функцию 1п£(ж, в) в мак-
симум (удобно использовать вторую производную: если
d2 In/Дж, в) I
d62 1е=0 < °’
то в = 0 — точка максимума).
Если оценке подлежат несколько параметров 61,62, ,6п распре-
деления. то оценки 61,... ,6п определяются решением системы уравне-
ний правдоподобия:
a(inL) =
д61
д(1п£)
д6п
Пример 8.3. Найти оценку параметра а распределения Пуассона ме-
тодом максимального правдоподобия.
,.т . „—а
О В данном случае Р{Х = т} =--------—. Поэтому
д.т, - в
p(Xi, 6) = Р{Х = хг, 0} =
х^.
при ж2- € N. Составляем функцию правдоподобия (для дискретной
с. в. X):
цх,в) - е-". ..... = е* . eS,n . 1_____т.
Ж1’ ж2! хп\ Х1'.-...-хп\
Тогда
п
In L(x, 6) — —п 6 + Xi In 6 — ln(®i! • Ж2! •... • жп!)
г=1
сНп£(ж, 6)
М
Уравнение правдоподобия имеет вид:
= °.
Глава 8. Элементы теории оценок и проверки гипотез * 235
Отсюда находим
п
~ n'YLXi = Хв'
1=1
А так как
d2ln£(®,6')| 1 А
de2 I о=о (р
i=i
то оценка 0 = хв является оценкой максимального правдоподобия.
Итак. 6 = а = хв. •
Метод наименьших квадратов
Метод, нахождения оценки в неизвестного параметра 6, основанный
на минимизации суммы квадратов отклонений выборочных данных от
определяемой (искомой) оценки 0, называется методом наименьших
квадратов (коротко:-МНК).
Другими словами, в МНК требуется найти такое значение 6, кото-
рое минимизировало бы сумму
F(6) = ^(Xi ~0)2 -> min.
i=i
Отметим, что МНК является наиболее простым методом нахождения
оценок параметра 6.
Пример 8.4. Найти оценку параметра а, распределения Пуассона ме-
тодом наименьших квадратов.
п
Q Найдем точку минимума функции F(0) = У~^(Х; — 6)2:
г=1
(71 \ Г 71
Г = ^(Х^-6)2) =^2(Х^- 6) •(-!);
i=l 'е г=1
71
из уравнения F'(0) = 0 находим критическую точку: —2 У^(Хг — 6) = О,
г=1
71 71 71 71
т. е. Xi - 0 = О, т. е. У^ Хг = п0. 6кр = У^ Хр А так как
г=1 г=1 1=1 i~l
Х"(М = (-2£(Хг-бЛ =-2УУ-1) = 2п>0
' г=1 'в г=1
236 Раздел второй. Основы математической статистики
п
при любом значении 0, то $кр = — точка минимума функ-
i=i
ции Таким образом, оценкой параметра а в распределении Пуас-
сона Pirn; а) — ----Ц—, ш = 0,1,2.... согласно МНК, является
т!
п
1=1
Можно доказать, что:
М(в)=в = а, D(0) = ^ •
Упражнения
1. Найти оценку параметра распределения Пуассона методом момен-
тов.
2. Пользуясь ММП, оценить вероятность появления герба, если при
10 бросаниях монеты герб появился 6 раз.
3. Найти оценку неизвестной вероятности успеха в схеме Бернулли
методом моментов и ММП.
4. Дано: с.в. X ~ /?[rz,/>]. По выборке я?],Ж2,.-. ,хп оценить величины
а и b методом моментов.
5. Найти оценки параметров нормального распределения с. в. X ме-
тодом максимального правдоподобия.
8.3. Понятие интервального оценивания параметров
Точечные оценки неизвестного параметра в хороши в качестве пер-
воначальных результатов обработки наблюдений. Их недостаток в том,
что неизвестно, с какой точностью они дают оцениваемый параметр.
Глава 8. Элементы теории оценок и проверки гипотез 237
Для выборок небольшого объема вопрос о точности оценок очень су-
щественен, так как между в и в может быть большое расхождение в
этом случае. Кроме того, при решении практических задач часто тре-
буется определи! ь и надежность этих оценок. Тогда и возникает зада-
ча о приближении параметра в не одним числом, а целым интервалом
(01,02)-
Оценка неизвестного параметра называется интервальной, если
она определяется двумя числами — концами интервала.
Задачу интервального оценивания можно сформулировать так: по
данным выборки построить числовой интервал (01,02), относительно
которого с заранее выбранной вероятностью 7 можно сказать, что вну-
три этого интервала находится точное значение оцениваемого парамет-
ра (см. рис. 75).
О
02 3
Рис. 75
Интервал (0 ц 02), накрывающий с вероятностью 7 истинное зна-
чение параметра 0. называется доверительным интервалом, а вероят-
ность 7 — надежностью оценки или доверительной вероятностью.
Очень часто (но не всегда) доверительный интервал выбирается
симметричным относительно несмещенной точечной оценки 0, т. е. вы-
бирается интервал вида (0 — е.в + е) такой, что
f{0G (0-е,0 + е)} = Р{|0 - 0| <£} =7-
Число е > 0 характеризует точность оценки: чем меньше разность
|0 — 0|, тем точнее оценка.
Величина 7 выбирается заранее, ее выбор зависит от конкретно
решаемой задачи. Так, степень доверия авиапассажира к надежности
самолета, очевидно, должна быть выше степени доверия покупателя к
надежности телевизора, лампочки, игрушки... Надежность 7 принято
выбирать равной 0,9; 0,95; 0,99 или 0,999. Тогда практически достоверно
нахождение параметра 0 в доверительном интервале (0 — е, 0 + е).
238 Раздел второй. Основы математической статистики
8.4. Доверительные интервалы для параметров
нормального распределения
Построим доверительные интервалы для параметров нормального
распределения, т. е. когда выборка производится из генеральной сово-
купности, имеющей нормальное распределение с параметрами а и ст.
Доверительный интервал для математического ожидания при
известной дисперсии
Пусть с. в. X ~ о — известна, доверительная вероятность
(надежность) 7 — задана.
Пусть Ж1,Ж2,..., хп — выборка, полученная в результате проведе-
ния п независимых наблюдений за с. в. X. Чтобы подчеркнуть случай-
ный характер величин sj, х2,..., перепишем их в виде АфХа,...
... ,Хп, т.е. под Xi будем понимать значение с. в. X в г-м опыте.
Случайные величины Ху,Х2,... ,Хп — независимы, закон распреде-
ления любой из них совпадает е законом распределения с. в. X (т. е.
Xi ~ N(a, ст)). А это значит, что MXi = МХ2 = ... = МХп — MX = а,
БХг = DX2 = ... = DXn = DX.
Выборочное среднее
также будет распределено по нормальному закону (примем без дока-
зательства). Параметры распределения X таковы: М(Х) = a. D(X) =
0-2
— —. Действительно.
(п \ п п
= Уумх1 = уумх = уп-мх = а,
! v f -4 ] IV I V f -7 I V
i=l z i=l i=l
(n \ n 71 2
-t 7 IV... / V , / V
2=1 ' 2=1 2=1
N (а, -%).
у хПЧ
Таким образом, X
Следовательно, пользуясь формулой
р{|Х-а|<Д=2Ф0(^)=2ф(1)-1
Глава 8. Элементы теории оценок и проверки гипотез 239
(формула (2.47)), можно записать
__ / g . х/ТЪ \
7 = Р{|А" - а| < е} = 2Ф0 I —— I - 2Ф0(£),
Е • УП тт
где t = —-—. Из последнего равенства находим
t <j
(8-3)
поэтому 7 = Р < |А — а| < > = 2Фр(£) или
I у™ J
Р / X - t < а < X + t • I = 2Ф0(<) = 7-
I V'11 vn J
(8.4)
В соответствии с определением доверительного интервала получа-
ем, что доверительный интервал для а = MX есть
(Х-t- -?-,X + t- ) , (8.5)
\ у/n \/П J
где I определяется из равенства (8.4), т.е. из уравнения
Фо(О = J (8.6)
1 4” 'У
(или Ф(Д = ——); ПРИ заданном 7 по таблице функции Лапласа на-
ходим аргумент t.
Заметим, что из равенства (8.3) следует: с возрастанием объема
выборки п число е убывает и. значит, точность оценки увеличивается;
увеличение надежности 7 влечет уменьшение точности оценки.
Пример 8.5. Произведено 5 независимых наблюдений над с. в. X
~ 7V(o,20). Результаты наблюдений таковы: xj = —25, ж 2 = 34. S3 =
= —20, а,'4 = 10, ж'5 = 21. Найти оценку для а = MX, а также построить
для него 95%-й доверительный интервал.
Q Находим сначала хк: х = р (—25 + 34 — 20 + 10 + 21) = 4. т. е.
Т
х = 4. Учитывая, что 7 = 0,95 и Фо(1) — получаем Фо(1) = 0,475.
По таблице (см. Приложение) выясняем, что t = t7 = 1.96. Тогда е =
1 96 • 20
= —------ rs 17,5 (формула (8.3)). Доверительный интервал для а. =
Уо
= MX (согласно (8.5)) таков: (4 — 17,5;4 + 17,5), т. е. (—13,5;21,5). •
240 Раздел второй. Основы математической статистики
Доверительный интервал для математического ожидания при
неизвестной дисперсии
Пусть с. в. X ~ 7V(a. <т), а неизвестна, 7 - задана. Найдем такое
число е, чтобы выполнялось соотношение Р{Х — е < а < X + е} = 7
или
Г{|Х-а|<£} = 7-
(8-7)
Введем случайную величину
где S — исправленное среднее квадратическое отклонение с. в. X, вы-
численное по выборке:
1
п — 1
п
>> - ху.
1=1
Доказывается, что с. в. Т имеет распределение Стьюдента (см.
и. 4.3) с п — 1 степенью свободы. Плотность этого распределения имеет
вид:
fr(t,n
2
СЮ
где Г(р) = [ ир~* e~udu — гамма-функция; п — 1) — четная
о
функция.
Перейдем в левой части равенства (8.7) от с. в. X к с. в. Т:
= 'у или Р{|Т| < Д} = 7, где
(8-8)
Глава 8. Элементы теории оценок и проверки гипотез 241
Величина t7 находится из условия
Р{\т\<ц} = J
fr(t. п — 1) dt = 2 - J /т(Х n — 1) dt = 7,
о
т. е. из равенства
fr(t, п — l)dt = 7.
Пользуясь таблицей квантилей распределения Стьюдента (см. прило-
жение 4 на с. 287), находим значение ty в зависимости от доверительной
вероятности 7 и числа степеней свободы п — 1 (/7 — квантиль уров-
ня 1 — 7).
Определив значение t7, из равенства (8.8), находим значение е:
е=*7-4
л/п
(8-9)
Следовательно, равенство (8.7) принимает вид
А это значит, что интервал
покрывает а = MX с вероятностью 7, т.е. является доверительным
интервалом для неизвестного математического ожидания с. в. X.
Пример 8.6. По условию примера 8.5. считая, что с. в. X ~ N(a.,a),
построить для неизвестного MX = а доверительный интервал. Считать
у.= 0,95.
О Оценку х для MX уже знаем: х = 4. Находим значение S:
S2 = 1 ((-25 - 4)2 • 1 + (34 - 4)2 + (-20 - 4)2 + (10 - 4)2 + (21 - 4)2) =
= 660,5; S « 25,7. По таблице для 7 = 0,95 и п— 1 =4 находим t7 — 2,78.
25,7
Следовательно, е = 2,78 • «31,9. Доверительный интервал таков:
(-27,9; 35,9). ’ •
242 Раздел второй. Основы математической статистики
Доверительный интервал для среднего квадратического
отклонения нормального распределения
Пусть с. в. X ~ N(a, с), а — неизвестно, 7 — задано. Можно по-
казать. что если MX = а известно, то доверительный интервал для
среднего квадратического отклонения о имеет вид:
1 п
где п — объем выборки, -Sq = д 52 ~ а)2, а
2 2 2 2
Xi X1 + 7 , Л*2 X1 — 7
~2~’п
являются квантилями ^-распределения с п степенями свободы (см.
п. 4.3), определяемые по таблице квантилей х2 п распределения у2 (см.
приложение 3 на с. 286).
Если а = MX неизвестно, то доверительный интервал для неиз-
вестного гг имеет вид:
где п — объем выборки, S =
1
п — 1
исправленное
среднее квадратическое отклонение, квантили
2 2 2 2
Х1 — Х1 + 7 » %2 — Х1-7
—2—;л—1 —2—;л-1
л 2 j 1 1 + 7 1 — 7
определяются по таблице ха к при к = п — 1 и а = —— и а = ——
соответственно.
Пример 8.7. Для оценки параметра нормально распределенной слу-
чайной величины была сделана выборка объема в 30 единиц и вычи-
слено S = 1,5. Найти доверительный интервал, покрывающий с ве-
роятностью 7 = 0,90.
Q Имеем п = 30, 7 = 0,9. По таблице Ха к нах°дим
Х? = Х21 + о,9 — №(0,95; 29) = 17,7,
--5-2—,30-1
Глава 8. Элементы теории оценок и проверки гипотез 243
Х1 = хко,9 = X2 (0,05; 29) = 42,6.
—тг— .30 -1
Доверительный интервал имеет вид:
у/3(ЬП 1,5 у/ЗСГ=~Т -1,5\
у/42,6 ’ ДТТД )
или 1.238 < СТ < 1,920.
Скажем несколько слов о доверительном интервале для оценки ве-
роятности успеха при большом числе испытаний Бернулли.
Доверительный интервал, который с надежностью 7 покрывает
оцениваемый параметр р при больших значениях п (порядка сотен),
имеет вид (pi,P2), где
* J.
Pl=p -t-
и Р2=Р* + t-
(8.10)
рД1-рД
п
где р* = — относительная частота события A; t определяется из
равенства 2Фд(1) = 7.
Для оценки приближенного равенства р » р* можно использовать
равенство Р{|р* — р\ < е} = 2Фо (—7==“^ (см- п- 1-21, замечание).
Упражнения
1. Глубина моря измеряется прибором, систематическая ошибка ко-
торого равна нулю, а случайные ошибки распределены нормально
с о = 15 м. Сколько надо сделать независимых измерений, чтобы
определить глубину моря с ошибкой не более 5 м при надежности
7 = 0,9?
2. По условию примера 7.3 найти точечную оценку и доверительный
интервал для среднего роста студентов, считать 7 = 0,95.
3. Производятся независимые испытания с одинаковой, но с неизвест-
ной вероятностью р появления события А в каждом испытании.
Найти доверительный интервал для оценки р с надежностью 0,95,
если в 400 испытаниях события А появилось 80 раз.
244 Раздел второй. Основы математической статистики
8.5. Проверка статистических гипотез
Задачи статистической проверки гипотез
Одна из часто встречающихся на практике задач, связанных с при-
менением статистических методов, состоит в решении вопроса о том,
должно ли на основании данной выборки быть принято или, напро-
тив, отвергнуто некоторое предположение (гипотеза) относительно ге-
неральной совокупности (случайной величины).
Например, новое лекарство испытано на определенном числе лю-
дей. Можно ли сделать по данным результатам лечения обоснованный
вывод о том, что новое лекарство более эффективно, чем применявшие-
ся ранее методы лечения? Аналогичный вопрос логично задать, говоря
о новом правиле поступления в вуз, о новом методе обучения, о пользе
быстрой ходьбы, о преимуществах новой модели автомобиля или тех-
нологического процесса и т. д.
Процедура сопоставления высказанного предположения (гипотезы)
с выборочными данными называется проверкой гипотез.
Задачи статистической проверки гипотез ставятся в следующем
виде: относительно некоторой генеральной совокупности высказыва-
ется та или иная гипотеза Н. Из этой генеральной совокупности из-
влекается выборка. Требуется указать правило, при помощи которого
можно было бы по выборке решить вопрос о том, следует ли отклонить
гипотезу Н или принять ее.
Следует отметить, что статистическими методами гипотезу можно
только опровергнуть или не опровергнуть, но не доказать. Например,
для проверки утверждения (гипотеза Н) автора, что «в рукописи нет
ошибок», рецензент прочел (изучил) несколько страниц рукописи.
Если он обнаружил хотя бы одну ошибку, то гипотеза Н отверга-
ется, в противном случае - не отвергается, говорят, что «результат
проверки с гипотезой согласуется».
Выдвинутая гипотеза может быть правильной или неправильной,
поэтому возникает необходимость ее проверки.
Статистическая гипотеза. Статистический критерий
Под статистической гипотезой (или просто гипотезой) понима-
ют всякое высказывание (предположение) о генеральной совокупности,
проверяемое по выборке.
Глава 8, Элементы теории оценок и проверки гипотез 245
Статистические гипотезы делятся на гипотезы о параметрах рас-
пределения известного вида (это так называемые параметрические ги-
потезы) и гипотезы о виде неизвестного распределения {непараметри-
ческие гипотезы).
Одну из гипотез выделяют в качестве основной (или нулевой) и
обозначают Но, а другую, являющуюся логическим отрицанием Но,
т. е. противоположную Но — в качестве конкурирующей (или альтер-
нативной) гипотезы и обозначают Ну.
Гипотезу, однозначно фиксирующую распределение наблюдений,
называют простой (в ней идет речь об одном значении параметра), в
противном случае сложной.
Например, гипотеза Но, состоящая в том что математическое ожи-
дание с.в. X равно «о т.е. MX = ао, является простой. В качестве
альтернативной гипотезы можно рассматривать одну из следующих ги-
потез: Ну: MX > ао (сложная гипотеза), Ну. MX < oq (сложная), Ну:
MX ао (сложная) или Ну. MX = ay (простая гипотеза).
Имея две гипотезы Но и Ну, надо на основе выборки Лц,...,.¥п
принять либо основную гипотезу Но, либо конкурирующую Ну.
Правило, по которому принимается решение принять или откло-
нить гипотезу Но (соответственно, отклонить или принять Ну), назы-
вается статистическим критерием (или просто критерием) проверки
гипотезы Но-
Проверку гипотез осуществляют на основании результатов выбор-
ки Л1, Аф • - •, Хп, из которых формируют функцию выборки Тп =
= Т{Ху, Ху..., Хп), называемой статистикой критерия.
Основной принцип проверки гипотез состоит в следующем. Мно-
жество возможных значений статистики критерия Тп разбивается на
два непересекающихся подмножества: критическую области S, т. е.
область отклонения гипотезы Hq и области S принятия этой гипоте-
зы. Если фактически наблюдаемое значение статистики критерия (т. е.
значение критерия, вычисленное по выборке: ТНабл = Т{ху,х2, ,хп))
попадает в критическую область S, то основная гипотеза Но отклоняет-
ся и принимается альтернативная гипотеза Ну, если же 'Тнабл попадает
в S, то принимается Но, а Ну отклоняется.
При проверке гипотезы может быть принято неправильное реше-
ние, т. е. могут быть допущены ошибки двух родов:
Ошибка первого рода состоит в том, что отвергается нулевая гипо-
теза Но, когда на самом деле она верна.
Ошибка второго рода состоит в том, что отвергается альтернатив-
ная гипотеза Ну, когда она на самом деле верна.
246 Раздел второй. Основы математической статистики
Рассматриваемые случаи наглядно иллюстрирует следующая таб-
лица.
Гипотеза Нц Отвергается Принимается
верна неверна ошибка 1-го рода правильное решение правильное решение ошибка 2-го рода
Вероятность ошибки 1-го рода (обозначается через а) называется
уровнем значимости критерия.
Очевидно, а = P(Hi\Hq). Чем меньше а, тем меньше вероятность
отклонить верную гипотезу. Допустимую ошибку 1-го рода обычно за-
дают заранее.
В одних случаях считается возможным пренебречь событиями, ве-
роятность которых меньше 0,05 (а = 0,05 означает, что в среднем в 5
случаях из 100 испытаний верная гипотеза будет отвергнута), в других
случаях, когда речь идет, например, о разрушении сооружений, гибе-
ли судна и т. п., нельзя пренебречь обстоятельствами, которые могут
появиться с вероятностью, равной 0,001.
Обычно для а используются стандартные значения: а — 0,05;
а = 0,01; 0,005; 0,001.
Вероятность ошибки 2-го рода обозначается через /3, т. е. /3 =
= Р(Н0|Я1).
Величину 1 — /3, т. е. вероятность недопущения ошибки 2-го рода
(отвергнуть неверную гипотезу Но, принять верную Hi), называется
мощностью критерия.
Очевидно, 1 - /3 = P)Hi\Hi) = P((®i,X’2, • • ,хп) G S\Hi).
Чем больше мощность критерия, тем вероятность ошибки 2-го рода
меньше, что, конечно, желательно (как и уменьшение а).
Последствия ошибок 1-го, 2-го рода могут быть совершенно раз-
личными: в одних случаях надо минимизировать а, в другом — (3.
Так, применительно к радиолокации говорят, что а — вероятность
пропуска сигнала, (3 — вероятность ложной тревоги; применительно
к производству, к торговле можно сказать, что а — риск поставщика
(т. е. забраковка по выборке всей партии изделий, удовлетворяющих
стандарту), /3 — риск потребителя (т. е. прием по выборке всей партии
изделий, не удовлетворяющей стандарту); применительно к судебной
системе, ошибка 1-го рода приводит к оправданию виновного, ошибка
2-го рода — осуждению невиновного.
Отметим, что одновременное уменьшение ошибок 1-го и 2-го рода
возможно лишь при увеличении объема выборок. Поэтому обычно при
заданном уровне значимости а отыскивается критерий с наибольшей
мощностью.
Глава 8. Элементы теории оценок и проверки гипотез 247
Методика проверки гипотез сводится к следующему:
1. Располагая выборкой , Хп, формируют нулевую гипотезу
Но и альтернативную Н±.
2. В каждом конкретном случае подбирают статистику критерия Тп =
= T(A"i, Х‘2,.... Хп), обычно из перечисленных ниже: U — нормаль-
ное распределение, х2 — распределение хи-квадрат (Пирсона), t —
распределение Стьюдента, F — распределение Фишера Снедекора.
3. По статистике критерия Тп и уровню значимости о определяют
критическую область S (и S). Для ее отыскания достаточно найти
критическую точку £кр, т.е. границу (или квантиль), отделяющую
область S от S.
Границы областей определяются, соответственно, из соотношений:
Р(Тп > /кр) = о, для правосторонней критической области S
(рис. 76); Р(Тп < tKp) = а, для левосторонней критической обла-
сти S (рис. 77); Р(Тп < t£p) = Р(Тп > t™p) = для двусторонней
критической области S (рис. 78).
Для каждого критерия имеются соответствующие таблицы, по ко-
торым и находят критическую точку, удовлетворяющую приведен-
ным выше соотношениям.
4. Для полученной реализации выборки х = (.r-j, гс-^,подсчи-
тывают значение критерия, т. е. ТНабл = T(xi, •, хп) = t.
5. Если t G S (например, t > tKp для правосторонней области S'), то
нулевую гипотезу Но отвергают; если же t G S (t < tKp), то нет
оснований, чтобы отвергнуть гипотезу Hq.
248 Раздел второй. Основы математической статистики
8.6. Проверка гипотез о законе распределения
Во многих случаях закон распределения изучаемой случайно вели-
чины неизвестен, но есть основания предположить, что он имеет вполне
определенный вид: нормальный, биномиальный или какой-либо дру-
гой.
Пусть необходимо проверить гипотезу Но о том, что с. в. X под-
чиняется определенному закону распределения, заданному функцией
распределения Fq(x), т. е. Hq: F\-(х) = Fq(x). Под альтернативной гипо-
тезой Hi будем понимать в данном случае то, что просто не выполнена
основная (т.е. Н^. Fx(x) Fo(x)).
Глава 8. Элементы теории оценок и проверки гипотез • 249
Для проверки гипотезы о распределении случайной величины X
проведем выборку, которую оформим в виде статистического ряда:
Xi «2 Хщ
ni П1 П2 . . . Пщ
(8-11)
m
где щ = п — объем выборки.
2=1
Требуется сделать заключение: согласуются ли результаты наблю-
дений с высказанным предположением. Для этого используем специ-
ально подобранную величину — критерий согласия.
Критерием согласия называют статистический критерий проверки
гипотезы о предполагаемом законе неизвестного распределения. (Он
используется для проверки согласия предполагаемого вида распреде-
ления с опытными данными на основании выборки.)
Существуют различные критерии согласия: Пирсона. Колмогорова,
Фишера, Смирнова и др.
Критерий согласия Пирсона — наиболее часто употребляемый кри-
терий для проверки простой гипотезы о законе распределения.
Критерий х2 Пирсона
Для проверки гипотезы Но поступают следующим образом.
Разбивают всю область значений с. в. X на ш интервалов Д [,
Д 2,. ., Д-„(. и подсчитывают вероятности р-, ('/' = 1,2,...,тп) попа-
дания с.в. X (т.е. наблюдения) в интервал Д,, используя формулу
Р{а С X /3} = Fq(/3) — Fo(«). Тогда теоретическое число значений
с. в. X, попавших в интервал Д^, можно рассчитать по формуле п щ.
Таким образом, имеем статистический ряд распределения с. в. X (8.11)
и теоретический ряд распределения:
Д1 Аг
Ц = пру «2 — ПР2 п'т = прт
(8.12)
Если эмпирические частоты (пг) сильно отличаются от теоретиче-
ских (npj = п'), то проверяемую гипотезу Но следует отвергнуть; в
противном случае — принять.
Каким критерием, характеризующим степень расхождения между
эмпирическими и теоретическими частотами, следует воспользовать-
ся? В качестве меры расхождения между щ и пр-, для г = 1,2, ...pin
250 Раздел второй. Основы математической статистики
К. Пирсон (1857-1936; англ, математик, статик, биолог, философ) пред-
ложил величину («критерий Пирсона»):
т / W 9
= = (S-13)
1=1 1=1
Согласно теореме Пирсона, при п —> ос статистика (8.13) имеет у2-
распределение с k = т — г — 1 степенями свободы, где т — число групп
(интервалов) выборки, г — число параметров предполагаемого распре-
деления. В частности, если предполагаемое распределение нормально,
то оценивают два параметра (а и ст), поэтому число степеней свободы
к — т — 3.
Правило применения критерия у2 сводится к следующему:
1. По формуле (8.13) вычисляют у2абл — выборочное значение стати-
стики критерия.
2. Выбрав уровень значимости о/ критерия, по таблице у ^распреде-
ления находим критическую точку (квантиль) у2 к.
3. Если у2абл У)щ., то гипотеза Н(| не противоречит опытным дан-
ным; если у2абл > Ха к-> то гипотеза Но отвергается.
Необходимым условием применения критерия Пирсона является
наличие в каждом из интервалов не менее 5 наблюдений (т.е. гц 5).
Если в отдельных интервалах их меньше, то число интервалов надо
уменьшить путем объединения (укрупнения) соседних интервалов.
Пример 8.8. Измерены 100 обработанных деталей; отклонения от за-
данного размера приведены в таблице:
[я-г, ) [-3,-2) [-2,-1) [-1,0) [ОД) [1,2) [2-3) [3,4) [4,5)
пг- 3 10 15 24 25 13 7 3
Проверить при уровне значимости а = 0,01 гипотезу Но о том. что
отклонения от проектного размера подчиняются нормальному закону
распределения.
Q Число наблюдений в крайних интервалах меньше 5, поэтому объ-
единим их с соседними. Получим следующий ряд распределения (п =
= 100):
[®j,Ti+l) [-3,-1) [-1,0) [0,1) [1,2) [2,3) [3,5)
13 15 24 25 13 10
Случайную величину — отклонение — обозначим через X. Для вычи-
сления вероятностей pi необходимо вычислить параметры, определя-
ющие нормальный закон распределения (а и а). Их оценки вычислим
Глава 8. Элементы теории оценок и проверки гипотез 251
по выборке: х = • (—2 13 + (—0,5) • 15 + ... + 4 • 10) = 0,885 » 0,9,
DB = yjL (4.13 + 0,25-15 + ...-+16-10) - (0,885)2 « 2,809, о « 1,676 « 1,7.
Находим pi (i = 1,6). Так как с. в. X ~ N(a. ст) определена на
(—оо, оо), то крайние интервалы в ряде распределения заменяем, соот-
ветственно, на (—оо,—1) и (3, +оо). Тогда — Р{—оо < X < — 1} =
= Фо 7~'^ ~ Ф°(~Q°) = ~ Фо(1Д2) = 0,1314. Аналогично по-
лучаем: р2 — 0,1667, рз = 0,2258, р4 — 0.2183, р§ = 0,1503, р<, =
= р{3 X < оо} = Ф0(оо) - Фо (3 ~в’9) = 0,5 - Фо(1,24) = 0,1075.
Полученные результаты приведем в следующей таблице:
[®г,Жг+1) (-00,-1) [-1,0) [0,1) [1,2) [2,3) [3, оо)
13 15 24 25 13 10
п' = npi 13,14 16.67 22,58 21,83 15,03 10,75
Вычисляем у2абл:
6 2
2 \ Пг
Хнабл — / npi ~ п ~
i =1
132 , 152 , , 102 А
13,14 + 16,67 10,75/
- 100 = 101,(145 - 100,
т-е- Хнабл ~ 1,045.
Находим число степеней свободы; по выборке рассчитаны два па-
раметра, значит, г — 2. Количество интервалов 6, т.е. т = 6. Следо-
вательно, к = 6 — 2 — 1 = 3. Зная, что а = 0,01 и к = 3, по таблице
^-распределения находим х^ к = 11.3. Итак, у2абл < следова-
тельно, нет оснований отвергнуть проверяемую гипотезу. •
Критерий Колмогорова
Критерий Колмогорова для простой гипотезы является наиболее
простым критерием проверки гипотезы о виде закона распределения.
Он связывает эмпирическую функцию распределения F* (т) с функци-
ей распределения F(x) непрерывной случайной величины X.
252 • Раздел второй. Основы математической статистики
Пусть Т], х-2, • • • - — конкретная выборка из распределения с не-
известной непрерывной функцией распределения F(x) и F*(x) — эмпи-
рическая функция распределения. Выдвигается простая гипотеза Но:
F(x) = Fq(x) (альтернативная Н\: F(x) Fo(x), х е R).
Сущность критерия Колмогорова состоит в том, что вводят в рас-
смотрение функцию
Dn = max |F*(x) - F0(a?)|, (8.14)
—oo<x<oo
называемой статистикой Колмогорова, представляющей собой мак-
симальное отклонение эмпирической функции распределения F* (ж) от
гипотетической (т. е. соответствующей теоретической) функции распре-
деления Fo(«).
Колмогоров доказал, что при п —> оо закон распределения слу-
чайной величины у/п • Dn независимо от вида распределения с. в. X
стремится к закону распределения Колмогорова:
P{y/n-Dn<x} К(х),
где К(х) — функция распределения Колмогорова, для которой соста-
влена таблица, ее можно использовать для расчетов уже при п 20:
(У 0,1 0,05 0,02 0,01 0,001
ж0 1,224 1.358 1,520 1,627 1,950
Найдем Dq такое, что P(Dn > Do) = а.
Рассмотрим уравнение К{х) = 1 —а. С помощью функции Колмого-
рова найдем корень жо этого уравнения. Тогда по теореме Колмогорова,
Р{у/п • Dn < ж0} = 1 - а, Р{\/п • Dn > х*о} — а, откуда Do =
х/п
Если Dn < Do, то гипотезу Но нет оснований отвергать; в против-
ном случае — ее отвергают.
Пример 8.9. Монету бросали 4040 раз (Бюффон). Получили п\ = 2048
выпадений герба и n-z = 1992 выпадений решки. Проверить, используя
а) критерий Колмогорова; б) критерий Пирсона, согласуются ли эти
данные с гипотезой Но о симметричности монеты (а = 0.05).
О Случайная величина X принимает два значения: ад = — 1 (решка)
и а?2 = 1 (герб). Гипотеза Hq: Р{Х — —1} = Р{Х = 1} = i.
а) По таблице распределения Колмогорова находим корень урав-
нения К(х) = 1 — а при а = 0,05. Следует Xq = 1,358. Тогда Do — ~~ =
= 0,021.
/4040
Глава 8. Элементы теории оценок и проверки гипотез 253
Для нахождения по выборке Dn строим функции Fo(x) и F*(x) и
вычисляем величину Dn = max|F*(.r) — Fo(x)|.
Xi решка Si = —1 герб ®2 = 1 —> F0(x) = < 0, 0,5, при х —1, при — 1 < X 5 г в
Pi 0,5 0,5 1, при 1 < X.
Xi решка X] = —1 герб Х-2 = 1 0, при х —1, —> F*(x) = < 0,493, при — 1 < х 1, 1, при 1 < X.
Пг 1992 2048
Pi ~ 0,493 ~ 0,507
Максимальное отклонение Fo(rc) от F*(x) равно 0,007, т.е. Dn =
= 0,007. Поскольку Dn < Do, то нет оснований отвергать гипотезу
Но] опытные данные согласуются с гипотезой Но о симметричности
монеты.
б) Вычисляем статистику у2:
2 2
2 _ 5—' ni
Хиабл — / у npi
i=l
1992£_ + 20482 __ 404Q = 0 77б
| • 4040 | 4040
По таблице х2_РаспРеДеления находим критическую точку %2 к =
= X2 О5.х = 3,8. Так как у2абл < Xo,O5;is то опытные данные согласуются
с гипотезой о симметричности монеты. •
Упражнения
1. Распределение признака X (случайной величины А") в выборке за-
дано следующей таблице.*..
«г-1 - Xi 0-0,1 0,1 - 0,2 0,2 - 0,3 0,3-0,4 0,4 - 0.5
Щ 105 95 100 100 102
1 0,5 - 0,6 0,6 - 0,7 0,7-0,8 0,8 - 0,9 0,9 - 1,0
Tli 98 104 96 105 95
При уровне значимости а = 0,01 проверить гипотезу Но, состоящую
в том, что с. в. X имеет равномерное распределение на отрезке [0,1]
(вероятности р, определяются формулами рт = h, (г = 1,2,...,/г),
/ к \
где hi — длина г’-го отрезка [а^_г:;жг] I ^2 /гг = 1 I).
\г=1 /
254 Раздел второй. Основы математической статистики
2. Результаты наблюдений над с. в. X (рост мужчины) представлены
в виде статистического ряда:
X(рост) [150 - 155) [155 - 160) [160 - 165) [165 - 170)
iii (частота) 6 22 36 46
А" (рост) [170 - 175) [175 - 180) [180 - 185) [185 - 190)
Пг (частота) 56 24 8 2
Проверить при уровне значимости а — 0,05 гипотезу Но о том, что
с. в. X подчиняется нормальному закону распределения, используя
критерий согласия Пирсона.
3. По данным упражнения 2 проверить гипотезу о нормальном рас-
пределении с. в. X, используя критерий Колмогорова.
Ответы к упражнениям
Раздел первый
Глава 1
1.3
1. 1) В = В • = В(А + А) = А • В + А • В; 2) (А + С) (В + С) =
= АВ+АС+ВС+С = АВ+АС+С = А-В+С; 3)_Пусть w еА + В
А + В => w A, w В => w 6 A, w Е В => w 6 А В, т. е. А + В С А • В.
Аналогично убеждаемся, что А-ВСА + В + А+ В = А-В.
2. а) АВС; б) А-В-С; в) А+В+С; г) А-В-С; д) АВС; е) АВ-С+АВС+А-ВС;
ж) АВС А + В + С.
3. А1А2(А,з + А4 + Аб)Аб.
1.7
1. Из 90 двузначных чисел 9 имеют одинаковые цифры, т. е. п = 90, т =
О]
= 90 — 9 = 81'. Следовательно, р = = 0.9.
2. р = 0,01, так как т = 1, п = 10 - 10 = 100.
1.8
1. 5-4-3 = 60; 5-4-3 + 5- 4- 3- 2 + 5- 4- 3- 2-1 = 300.
2. 12 + 15 + 7 = 34.
3. 10 • 9 • 8 7 = 5040.
4. (10 - 9 • 8)2 = 7202 = 518400 или А?о • Af0.
5. 94 = 6561.
6. Af2 = 12 11 • 10-9 = 11880.
7. А?о = 720.
8. А| • А4 - AJ = 120.
9. Р5 • Рз = 720; Р7 - 720 = 4320.
256 Ответы к упражнениям
10. Р4 = 4! = 24 (один сел где угодно).
11. 3-2-8! = 241920 (см. рис. 79).
Рис. 79
12. 112 = 7 • 16; 2520 = С% • С\26.
13. a) Cf = 56; б) С?2 • Cj = 6160.
14. Cf5 • С* • Cl или = 135135.
15. = 27 = 128 или2 • 2 • 2 • 2 • 2 • 2 • 2.
16. 63 = 216. Это 234. 666. 165, ....
17. = 46 = 4096.
18. Cf = С$ = С% = = 21 - 4 = 84.
19. Cf = Cfo = Cfo = 45.
20. C% = C$ = Cl = 15, 15 • P4 = 360.
21. a) 4! = 24; 6) ^1.3!. „ . = 3360.
22- = 12“-
23‘ erf - з! = 400400 = c«'c’' c>-
1.9
1.
2.
3.
4.
5.
6.
7.
n = A% = 84 = 4096 a) m = 8 - 7 - 6 5 = 1680, Pl = « 0.41: 6) m = 8,
P2 = ~ 0,00195; в) m = 1, p3 = 0,00024.
n = C%6, m = Cl-Cl,p= -- и 0.000064.
6*36
n = 7!, m = 6! 2, p = ? =s 0,29.
n — 5! = 120, m = 2 2 1 • 1; p = = 0,033....
J-
p3 (^2 A<1
a) p = » 0,573; 6) p = ' 10 » 0,36.
°60 °60
a) p = « 0,08; 6) p = « 0,408.
Группа из 5 команд может быть выбрана С^о способами (вторая группа
образуется автоматически), т.е. п = В первую группу попадет ли-
бо один лидер, либо два. Стало быть, тп
Л*1 । г^2 /^3
О7 ~Г С/о * С/7
Р = —--------~ 0,833.
= С3 - С4 + Cl • С?. Поэтому
С.»
Ответы к упражнениям 257
8. Р =
Cl • С3г2
С36
z<2 А'(1
°4 ' °32
Г2
°36
0,21. Воспользовались свойством: Р(А + В) =
= Р(А) + Р(В), АВ = 0. Здесь А = {одна дама}, В = {две дамы}.
1.10
1.
2.
3.
о /о о ЗВ? \/3 3\/3
Сторона треугольника равна /т-уЗ. Значит, р = — = «
«0,41.
р=^=0,32.
Обозначим длину I отрезка через х, II — через у, тогда III отрезок имеет
длину I — х — у. Q = {(х,у) : 0 < х + у < /}, т. е. О < х + у < I — все
возможные комбинации длин частей отрезка. Чтобы из них можно было
составить треугольник, необходимо выполнение условий: х + у > I — х — у,
х + I — х — у > у, у + I — х — у > х, т. е. х < у < х + у > Эти
неравенства определяют область, заштрихованную на рис. 80.
Рис. 80
к . к . к
Имеем: Р = —— = 0,25.
±1-1
1.15
Да. И = {1,2,3,4,5,6}, А = {2,4,6}, В = {4,5,6}. Ясно, чтоР(А) = |
Р(В) = |, а Р(АВ) = | = 1, т.е. Р(АВ) = | / Р(А) • F(B) = | | = |.
а) А] — первая буква Т, А^ — вторая буква И, ..., А5 — пятая буква
1.
2.
И. Вероятность события А — получится слово ТИСКИ, равна Р(А) =
= Р(А1ДМзЛА>) = ^•|•|||= —L- « 0,0004; б) 0, так как второй
J.U У о i U
буквы К в слове СТАТИСТИКА нет; в) р =
ч _ 2 3 2 2 2 1 1 1 1 п _ п поит то
1 ю’э'в’т’б'бЧ’з'г1^ °’0000132-
Qi = 0,2 — вероятность отказа А го элемента, pi = 0,8 — вероятность его
I I = Т5б и 0Л’и8;
исправной работы. Цепь последовательно соединенных элементов 1 2 3
258 Ответы к упражнениям
будет работать, если исправны все три элемента: pi23 = Pi -Р2 'Рз — 0,83 =
— 0,512. Цепь параллельно соединенных элементов 5 6 откажет, только в
случае отказа обоих элементов: q^ = 95% = 0,22 = 0,04, а вероятность ее
исправной работы равна p56 = 1 - 956 = 0,96: /м,г>е = pi Рзв — 0,8 • 0,96 =
= 0,768; Р123456 = 1 - 9123 9456 = 1 - (1 - 0,512) • (1 - 0,768) « 0,887;
Ротк = 1 - Р123456 • Р7 - 1 - 0,887 • 0,8 И 0,291.
1.16
1.
2.
3.
А — первый шар белый, В — второй шар черный. Тогда АВ + АВ — оба
шара разных цветов. Р(АВ + АВ) =
2 7,7 2 = 28 =
9 8 9’8 72 18
« 0,39.
а) А1 — попадание первого орудия, А2 — второго, Аз — третьего. Значит,
АВС + АВС + АВС = D — попадание только одного из них. P(D) =
= 0,7-0,3-0,3-3 = 0,189; б) S = А] А2А3 — три промаха. P(S) = 0,3-0,3-0,3 =
= 0,027. Значит, P(S) = P(Ai + А2 + А3) = 1 - P(S) = 1 - 0,027 = 0,973.
Вероятность выхода из строя всех п приборов равна
(1 - 0,7) • (1 - 0,7) •... • (1 - 0,7) = 0,Зп.
п
Следовательно, вероятность безотказной работы равна 1 — 0,3". По усло-
вию 1 — 0,3" > 0,95. Отсюда 0,3” С 0,05, п In 0,3 In 0,05,
п > In 0.05 : In 0,3 к 2,488,
т.е. п> 3.
1.18
1. А — вышла из строя одна микросхема, Яо — отказали обе, Hi — отка-
зала первая микросхема, Н2 — отказала вторая, Н3 — обе не отказали.
Тогда Р(Н0) = 0,07 • 0,1 = 0,007, Р(Нг) = 0,063, Р(Н2) = 0,093, Р(Я3) =
з
= 0,837 (Контроль: £ Р(Я^) = 1). Р(А\Н0) = 0, Р(А|ЯХ) = 1, Р(А\Н2) =
г=0
= 1, Р(А\Н3) = 0. Значит, Р(А) = 0,156 и Р(ЯХ|А) ~ 0,404.
30 3
2. Ах — студент П сдаст экзамен, если зайдет первым, P(Ai) = 4g = 4-
А2 — студент П сдаст экзамен, если зайдет вторым, Р(А2) = ? Введем
гипотезы: Hi — первый студент вытащил билет, который знает студент
П, Н2 — первый студент вытащил билет, который не знает студент П.
р<н‘) = ® = 3- = 36 = з (з+3 = ') Далее: = I’
Р(Л2|Я2) = Значит, Р(А2) = ’.| + 1.а = |. Все равно.
ОУ ть ОУ а ОУ т:
Ответь, к упражнениям 259
3. Пусть А --- изделие пройдет контроль, Hi — взятое изделие стандарт-
но, Н-2, — не стандартно. = 0,9; P{Hz) = 0,1; P(A\Hi) = 0,96;
P(A\Hz) — 0,06. Следовательно, а) Р(А} = 0,9 0,96 + 0.1 • 0.06 = 0.87;
0 9 • 0 96
б) Р(Я1|А) = ^^^ 0.993.
1.20
.1. а) Р10(4) = С40 • (1) « 0,21; б) Р10(0) = « 0.00098; в) р =
= Р10(1) + Рю(2) + • • • + Рю(10) = 1 - Pio(0) « 0,999.
2. р = 9 = 1. Р4(2) = Cl • (|)2 (I)2 = |; Р6(3) = Cl • (I)3 • (I)3 =
Следует, что P4(2) > Pg(3), т.е. 2 из 4.
3. a) P3(3) = Cl 0.513 • 0.49° « 0.133, б) P3(l) = O[ • 0,51 • 0,492 w 0,368.
4. Спички брались 2 10 — 6 = 14 раз, из них 10 раз из коробки, которая
оказалась пустой. Имеем 10 «успехов» в 14 «испытаниях», т.е. Р44(10) =
= с™ • « о,об1.
1.21
1. р = 1 : 365 ~ 0,0027, п = 84, а ~ 0,23. По формуле Пуассона Pg4(2) «
« °’232 ^-7915 « 0,021. (е-0-23 « 0,7945).
2. п = 200, р = 0,02. Значит, а = [пр] = 4. Искомая вероятность;
Р2оо(0) + Р200(1) = + ^Г~ 0,09.
3. Здесь п = 100. т = 60, р = q = i. Используем локальную теорему Муав-
ра Лапласа: х = 9,3 — 2. Тогда Рюо(6О) = i<p(2) = 0,2-0,054 «
V100 0,5 • 0,5 5^v
» 0,0108.
4. P8oo(m,800) = 0,95. Используем интегральную теорему Муавра-Лапласа:
т — 388 оп о
Xi = 14—, x-z = 29. Значит,
Фо(ж2) = 0.5; 0.5 - Фо 143--) = 0,95.
ж (388 т
Откуда Фо —у4—
) = 0,45,
388 — т
14
= 1,65. Значит, т = 365.
9*
260 Ответы к упражнениям
Глава 2
2.2
1. Возможные значения с. в. X есть 0, 1, 2, 3, 4. Их вероятности равны со-
/ -| \ 0 / -j \ 4 -]
ответственно: р\ = Р{Х = 0} = С4 • ( =) • (к) = А, р2 = Р{Х = 1} =
\ £ J \ zj / L L)
= ' (2) (2) = 16’Рз = Тб’ Р4 = 16’р5 = р^х = = пг
2. Пусть Ai — первый студент сдает экзамен, А^ — второй сдает экзамен.
С. в. X принимает три значения: 0.1.2. а) р\ = Р{Х = 0} = F(AiA2) =
= 0,4 • 0,1 = 0,04; р2 = Р{Х = 1} = F(AXA2 + ЙМ2) = 0,6 0,1 + 0,4 0,9 =
= 0,42; рз = Р{Х = 2} = F(AM2) = 0,6 • 0,9 = 0,54 = 1); б) Р1 =
= Р{Х = 0} = F(AMXЛ2Л2) = 0,4 • 0,4 0,1 0,1 = 0,0016; р2 = Р{Х = 1} =
= П(ЛХЛ2Л2 + А1Л1А2 + А] А2А1А2 + А1А1А2А2) = ... = 0,1668;
Рз — F{ X — 2} — F(AiA2 + А1А2А2 + j4xAiA2 + А1А2АхА2) —
= 0,6 • 0,9 + 0.6 • 0,1 • 0,9 + 0,4 • 0,6 • 0,9 + 0,4 • 0,1 • 0,6 - 0,9 = 0,8316
(Eft = 1)-
i=i
2.3
1. Ai — попадание I стрелка, A2 — II. Тогда P{X = xi) = P{X = 0} =
= P(A1A2) = 0,08, P{X = x2} = P{X = 1} = P(AiA2 + ЙМ2) = 0.44,
P{X = 2} = 0,48.
'0, x 0;
1, 2<ж.
2. F(x) удовлетворяет свойствам функции распределения;
F{0 х < 1} = F(l) - F(0) = 1 - e"1 = 1 - | w 0.632.
3. P{X 6 (0,1)} = F(l) - F(0) = 1. Значит, F4(3) = C43 • Q)3 • (|/ = 0,25.
2.4
1. F(2) = 1. Значит,
l = a(2 + l)2, a = |
(2(ж + 1)
/(т) = F'(x) = <Г“
.0,
x e (-1;2],
ж^(-1;2].
Ответы к упражнениям 261
11 V — 4
2. 5д = ~ = 1. Значит, ОМ = h = 4. Уравнение MN:
у = —8х + 4. Стало быть,
х — О
5-0’
т. е.
если х 0, то
Odi = 0;
3.
если 0 < х <
таким образом
0,
= 1:
а) нет, так как /(ж) 0 при х
О
а = §, то /(ж) — плотность распределения; а - — нет.
О о
а = Если
О
262 Ответы к упражнениям
2.5
1.
2.
Учитывать результаты примера примера 1.31 (п. 1.20) в первом случае
имеем: MX = 0 • 0,001 + 1 0,027 + 2 • 0,243 + 3 • 0,729 = 2,7; во втором
случае: MX = 0 • 0,006 + 1 • 0,092 + 2 0,398 + 3 • 0,504 = 2.4.
ОС 0 7Г ОО
/l.rsin^.r+
о
MX =
—ОО
2 j
о
х sin х dx =
3.
= А
- 2’
Согласно свойствам м. о. и дисперсии, имеем MZ = М (5Х — ЗУ + 2) —
= М5Х - МЗУ + М2 = 5МХ - 3MY + 2 = 5 - 2 - 3 (-3) + 2 = 21 и
DZ = D(5X - ЗУ + 2) = D5X + В(-ЗУ) + D2 = 25DX + 9DY + 0 =
= 25-2 + 9-9 = 131.
ОО
О
4.
DX =
—оо —оо
7Г
! 1 / 2 7Г2 1
= „ х sin xdx---------------т- =
2 / 4 2
о
—X2 COS X
5.
х2 i sin х
х2 Qdx —
+ COS X
о
„2 2 _2 г_____
У_2-^ = У- 2й 0,467; ах = « 0,68.
-> А, то F(.t) -4- 0, lim 0,25.т2 = 0, т.е. 0,25А2 = 0. А = 0;
п2
4
Если х
lim 0,25ж2 = 1, т. е. 0,25В2 = 1, В = 2. Поэтому
х—>В
{0,
0,25®2,
1,
при х 0,
при 0 < х 2,
при 2 < х.
Тогда
0,
0,5ж,
при х 0 и х > 2,
при 0 < х 2.
Поэтому
Ответы к упражнениям 263
2.7
1. Р{—3 < X < 5} - Фо - Фо (^2^) = фо(1) + Фо(3) = 0,8413;
Р{Х 4} = Р{-оо < X 4} = Фо (^) - Фо 3) = фо(О,5) +
+ ф0(оо) = 0,19146 + 0,5 = 0,69146; Р{|Х - 3| < 6} = Р{|Х - 3| < 3 2} =
= 2Ф0(3) = 0,9973.
2. По условию а = 0, ст = 1 а) Р{Х G (1,3)} = Фо — Фо f~~j —
= Фо(3) - Фо(1) = 0,49865 - 0,34134 = 0,1573; б) 2Ф0 = 0,8926, отсюда
Фо(/) = 0,4463. По таблицам находим, I ~ 1,62, и интервал имеет вид
(-1,62; 1,62); в) М0Х = 0; Ме = 0.
3. Коэффициент асимметрии А нормального распределения равен 0 (А = 0),
так как кривая Гаусса симметрична относительно прямой х = а. исходя-
щей через центр распределения а. Найдем (аналитически) коэффициент
эксцесса, т. е. Е = — 3. Сначала найдем /ц:
Стало быть: Е — — 3 = 3 — 3 = 0.
<74
264 Ответы к упражнениям
Глава 3
3.3
f(x,y)dxdy
Поэтому А
о о
о
е~х~у dxdy = А
dxx
при х 0, у О,
(1 - с '' )(1 -е У),
О,
в противном случае.
3) Fx(x) =
—сю -сю () ()
-Iх -
= — е и| = 1 — е х. при х 0, т. е.
1 • е “ du =
Fx =
1 - е~х,
О,
при х О,
при х < 0.
Аналогично
при у 0,
при у < 0.
Аналогично, /у (у) =
5) Р{Х > О,У < 1}
СЮ 1
= 1 - I к 0,63.
л с
4) /Дж) = /Х(Ж) = F'x(x)
при у 0,
при у < 0.
СЮ 1
при х О,
при х < О,
при х О,
при х < 0.
е у dy = — (е 1
Ответы к упражнениям • 265
оо эо
1) У У f(x,y)dxdy = 1
' 1
Следовательно, f(x,y) = 8’
О,
4
4
= 1, С У (4 -а
0 0 о
при х 0, у 0, х 4- у С 4;
в противном случае.
1
8’
оо
//1 1 р
f(x,y)dy = / 8^=8^
—оо 0
0 < у < 4: 3) F{0 < X < 1,1 <
О
х Е (0,4), fY(y) =
о
П1
1 з
О 1
Рис. 81
3. 1) С. в. X принимает значения 0, 1, 2. Очевидно, р\ = Р{Х = 0} = 0,6-0,6 =
= 0,36, Р2 = 0,4 • 0,6 4- 0,6 0,4 = 0.48. р3 = 0,4 0.4 = 0,16. Стало быть:
X 0 1 2
р 0,36 0,48 0,16
з
pj = 1). Аналогично находим, что
г=1
Y 0 1 2
р 0,16 0,48 0,36
есть ряд распределения с. в. У. 2) Возможные значения системы (А", У):
(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2). Совместная таблица
266 Ответы к упражнениям
распределения имеет вид:
X\Y 0 1 2
0 0,0576 0,1728 0,1296
1 0,0768 0,2304 0,1728
2 0.0256 0,0768 0,0576
так как рп = Р{Х = О, У = 0} = 0,4 • 0,4 • 0,6 0,6 = 0,16 • 0,36 = 0,0576,
Р12 = Р{Х = 0, У = 1} = 0,36 • 0,48 = 0,1728, р13 = Р{Х = О, У = 2} =
= 0,36 • 0,36 = 0,1296, Р21 = Р{Х = 1,У = 0} = 0,48 • 0,16 = 0,0768,
р-22 = Р{Х = 1,У = 1} = 0,48 • 0,48 = 0,2304, р2з = Р{Х = 1.У = 2} =
= 0,48 • 0,36 = 0,1728, р3| = Р{Х = 2, У = 0} = 0,16 • 0,16 = 0,0256,
Р32 = Р{Х = 2, У = 1} = 0,16 • 0,48 = 0,0768, р33 = Р{Х = 2,У = 2} =
= 0,16-0,36 = 0,0576. 3) По таблице распределения, пользуясь равенством
F(.v;, у) = ЕЕ Pij, находим значения функции распределения F(x,y):
Xi<xyj<y
Х\У У о 0<у^1 7 |/Л к у >2
х < 0 0 0 0 0
0 < х 1 0 0,0576 0,2304 0,3600
1 < х + 2 0 0,1344 0,5376 0,8400
х > 2 0 0,1600 0,6400 1,0000
3.7
1. Имеем
X 1 2 3 И Y 1 2 3 4
Р 0,33 0,33 0,34 р 0,24 0,28 0,27 0,21
Тогда тх = 1 • 0.33 + 2 • 0.33 + 3 • 0,34 = 2,01, ту = 1 0,24 + 2 • 0,28 + 3 • 0,27 +
+ 4 • 0,21 = 2,45. Так как
Р{Х = 1, У = 1} = 0,07 Р{Х = 1} • P{Y = 1} = 0,33 • 0,24 = 0,0792,
то с. в. X и У — зависимы. Находим MXY: MXY — 1 • 0,07 + 2 • 0,04 +
+ 3-0,11 + 4-0,11 4-2-0,08 + 4-0,11+6-0,06 + 8-0,08 + 3-0,09 + 6-0,13 + 9-0,10 +
+ 12 - 0,02 = 4,71. Поэтому cov(X, У) = 4,71 - 2,01 • 2,45 = -0,2145.
2. f(x,y)dxdy = 1, поэтому
D
Ответы к упражнениям ° 267
y2(l-xy3)dy
j J (y~my)2f(x,y)dxdy
—оо —оо
1
3’
значит, <7у =
1 1
KxY = ху^ ~ ху3>> dxdy ~ ° = ‘ ’ = ~1Ь’
-1 -1
3.
_ 1
Следовательно, гху = —;—= — н-
. _4-._ о
Сз >/з
1 1
с У dx j (х + у) dy = 1. Отсюда с = 1. Находим плотность вероятности:
о о
268 Ответы к упражнениям
MY = П’
или
DY =
11
144'
3.9
1. Найдем условное распределение X: р(хi |yi) = Р{Х = 0|У = —]} = =
= 25, р(ж2|?/1) = 0 25 = 25- Значит, М(Х\у}) = ° j| + 1j| = || = °-6-
Р(^1Ы - = Ц, р(ж2|Р2) = ||- Значит, М(Х|у2) = 0 || + 1 • || =
= Ц ~ 0,63. рЫуз) = Ц, р(ж2Ы = Ц- Значит, М(Х|у3) = || ~ 0,43.
Кривая регрессии X на у имеет вид, изображенный на рис. 82.
2. Как известно, для нормально распределенной с. в. (X, У) ее составляющая
У также распределена по нормальному закону (формула (3.37)):
Му) =
у v 2 я
2<т2 *
Имеем
fW) =
f(x,y)
fa(y)
1 ^^rb)(a:2-2rw2). 1 c-y4
2я\/1 — г2 д/2я
Ответы к упражнениям 269
(х - уг)2
________1 р2(уЛг2)2 ,
\Z2tt • \/1 — г2
т. е. условная плотность распределения f(x\y) есть плотность нормального
распределения с параметрами т = уг и о — \/1 — г2. Аналогично находим,
что
У (у|ж) =
У (ж,?/)
У1(ж)
(у - дт)2
1 ___Р 2(>/1 - г2)2 .
у/2тг\/Т — г2
3.11
1. Так как
У(ж) =
< b — а'
О,
х G [а, Ь],
х [а, 6],
то
ь
<p(t) = -3— / eitx dx = -У— •
b — a J b — a it'
a
^ita^ _ 1
(а — b)t
2. Так как pi- = а~^\— А; = 0,1,2,..то
°0 k -г, °°
^v(t) = £ = е~° £ = е"° • еа= е а^.
к—0 к=0
3.
Тогда </>'(£) = е е!^-(—н)-(—ег,)-У значит, MX = [—г<р'(О)] = —г-(1-ог) =
Глава 4
4.1
Y -3 -1 5 15
Р 0,30 0,45 0,20 0,05
270 Ответы к упражнениям
у 0 1 \/2 л/3 2 л/5
р 0,10 0,20 0,30 0,25 0,10 0,05
Y _у/3 2 0 т/З 2
р 0,3 0,35 0,35
у 0 1
р 0,5 0,5
Многоугольники распределения с. в. X и У изображены, соответственно,
на рис. 83, 84.
МУ = 0-0,5+ 1-0,5 = 0,5; DY = [МУ2 - (МУ)2] = О2 -0.5 +12 -0.5- (0,5)2 =
= 0,5 - 0,25 = 0,25. Отсюда аУ = \ГВУ = ^(),25 = 0,5.
3. С. в. X имеет равномерное распределение, значит.
fl
fx(x) = j4’
х G [-2,2],
x i [-2,2].
Функция у = x + 1 строго возрастает в (—оо,оо), обратная функция
х = у - 1 = tp(y), у е [-1,3]. По формуле д(у) = f(ip(y)) - |^'(у)| нахо-
дим:
Ji t
д(у) = । Q
у е [-1,3],
у [-1,3],
з
т.е. У ~ В[—1,3]. Находим МУ: МУ = J ~ dy = 1 (или МУ = М(Х + 1) =
-1
2 3 2
(х +1) • | dx = 1). DY = МУ2 - (МУ)2 = I dy - I2 = |, аУ = -^=.
J у 3
-2 -1
Ответы к упражнениям * 271
4.
х
1 ——
По условию fx(x) = -1 е 2 . а) Функция у = Зх3 имеет обратную
\2т\
, ж' = Т(у) = ПоэтомУ
дУу) ~ “4
К=е
У 0.
Х 0’ На (—оо,0) обратная функция для у = |ж| есть
Xf х (J.
6) у — |®| =
Xi = —у = ipi(y)- На [0.оо) обратная функция есть х% = у = ^{уУ Стало
быть,
2
„ 1 .J? 1 9
у(у) = 52 №i(y)M(y)l = ~т=е 2 • 1 + е 2.1 = е 2 ,
2—' - х2я V 2тг V 2тг
г=1
у 6 [0, оо).
5. а) По условию f(x) = е~х, х 0 и Р(ж) = 1 — е~х, х 0. G(y) =
= P{Y < у} = Р{2Х -1 < у} = р[х< = F =
у+ 1
= 1 — е 2 , у —1 (так как условие х 0 переходит для у = 2х — 1
в условие у —1). Следовательно, у(у) = G'(y) = —е 2 ( — -) =
— 2 при у > —1 (у(у) = 0 при у < —1). б) Если у 0, то G(y) =
= P{Y < 0} = 0 и у(у) = G'(y) = 0. При у > 0 имеем G(y) = P{Y < у} =
= F{X2 <у}= F{|X| <^} = Р{-^у < X < Jy} = Р{0 < X < ^у} =
= Р{Х < ^/у}-Р{Х < 0} = Р(7у)-Р(0) = (l-e-v^)-(l-e0) = 1 -е~^,
у > 0. Тогда у(у) •= G'(y) = (1 - e_v^)^ = -J— • e-v^, т. e.
2^/y
y(y) =
у > 0,
у < 0.
yr-lOO
= = —(0 — 1) = 1. (Иначе: при x € (0, оо) имеем x — Gy = ^(У)-
’° r- 1
Поэтому y(y) = /(^/y) • (Ty)y = e • ^=, У > 0.)
272 Ответы к упражнениям
1. Находим Fx+y(z). F(z) = Р{Х + Y < z} = J J (x + у) dxdy. F(z) = 0 при
Dz
(x+y<z)
z 0; при 0 < z 1 (на рис. 85 область Dz заштрихована вертикальными
линиями) имеем
при 1 < z 2 (область Dz заштрихована горизонтальными линиями)
имеем
Отсюда
/(г) = Г(г) =
г2,
2г — г2,
z 0, или z > 2,
0 < z 1.
1 < г < 2.
Ответы к упражнениям 273
2.
имеем
Следовательно,
1
Зг2
При 1 < z < оо имеем
2г2 2г Зг 6г2’
1,
'О,
1
Г'(г) = /(г) = 3 1 3’
^2 +
Зг2 Зг3
Зг2 ™
Глава 5
5.5
1. а) С. в. X — число выпавших гербов. MX = 500 ~ — 250. Неравенство
200 < X < 300 можно переписать в виде —50 < X—250 < 50 или |Х—250| <
274 Ответы к упражнениям
50. А так как DX = [пр^] = 500 • | | = 125, то Р{200 < X < 300} =
zS Li
= 1 - = 1 - 0.05 = 0,95; б) с. в.
502
1 _ DX
Е2
= Р{\Х - 250| < 50}
X — сумма очков, X, — число очков на Той кости (г = 1,2,..., 6). X =
= Хг + Х2 + ... + Х10. МХг = |(1+2 + 3 + 4 + 5 + 6) = 3,5, DXi = ||-
ю
Значит, MX = = 35, DX = Поэтому Р{|Х - 35| < 8} is
г=1
1 ~ (ГН4 = 1 “ 0,4557 = °’5443’
С п п X
2.
3.
4.
i=i
= , при 6 = 0.1 и С = 5 получаем:
г=1 7
1------—-= > 0.9. Отсюда п > 5000.
п-(0.1)2
ч "5 > п£-
р — q = Получаем Р {I - 0,51
LIOvU ।
Пусть Xi — число набранных очков при г-м выстреле, а Р100 — суммарное
число очков при 100 выстрелах. Тогда МХг = 10-0,5+9-0,3+8-0,1+7-0,1 =
= 9,2,
pq
—-. Из условия следует, что п = 500, е = 0.1,
ПЕ1
, 0,5 • 0,5
1--------------х = 0,95.
500 • (0,1)2
zioo
м( V
= 9,2 • 100 = 920;
Р
4=1 '
DXi = 100 • 0,5 + 81 • 0,3 + 64 • 0,1 + 49 • 0,1 - (9.2)2 = 0,96,
/ЮО \
D\^2Xi) = 0,96-100 = 96.
По формуле (5.14) Р{940 5юо < оо} « Ф(оо) - Ф ( ---------—— ) =
\ v/96 /
= 1 - Ф(2.04) = 1 - 0,9793 = 0,0207.
5. Пусть X — число прижившихся из п посаженных саженцев. По усло-
вию р = 0.7, q = 0,3. Тогда MX = 0,7n, DX = 0,3 • 0,7п = 0,21п.
Р{|Х - 0,7п| 40} 1 - 9^. Имеем 1 - 0,9, п < 761.
Глава 6
6.3
1. a) Xi = б) j?i = 2sin4.
Ответы к упражнениям • 275
2. a) m%(i) = 3sini; б) D\(t) = | - sin2 i, <rA-(i) = • |sint|; в) Kx{h;t2) =
6 V3
1 - - x / x fl, sin ti • sin to > 0, , . „
=-smti smt2; r) rx(ti;t2) = S , • . • , . n t тгп, n G Z.
о I — 1, sintj -sint2 < u,
6.6
1. а) нестационарный; б) стационарный: в),г) нестационарные с. и.
2. MZ(t) =5; Kz(ti;t2) = й«2 +
3. a) niy-(i) — 3cost; jFfy(<i;t2) = |cosi] • cost2; 6) niy(i) = 3(1 — cost);
Ky(«i;i2) = |(1 -costi)(l — cost2).
4. с. n. X(t) не является стационарным процессом, mz(i) = 2(cost 4- 2sint);
Kz(t) = (cost] 4- 2sint])(cost2 4- 2sint2).
6.9
1. X(t) — нестационарный c. n.
3. K'xH =4е-М.
4. £»a=4.
6.12
43
72
65
108
1.
2.
/ 29
I 72
I 43
\108
Граф, соответствующий матрице P изображен на рис. 87. Обозначим че-
рез А событие, состоящие в переходе процесса после первого хода в со-
стояние Sy; событие Н] — устройство выбирает состояние si; событие
— устройство выбирает состояние s2. Тогда P(Hi) = Т’(Т/2) =
2 1
и F(A|Hi) = Р(Л|Я2) = По формуле полной вероятности находим
Р(А) = | • | 4
3 1 = 13
4’2 24’
1
2
Рис. 87
з Л- JL. _52_
131’ 131’ 13Г
276 Ответы к упражнениям
Раздел второй
Глава 7
7.5
1.
o, при х ; $ 1,
n = 30, Pl = 1g, Pl = — V* = 30’ Pi F^x) = < 1 3’ 3 5’ при при 1 < 3 < С х $ : х $ 3. ^6,
1, при 6 < ; х.
хв = 1,983 и 2; _ОВ = 1,949 ~ 1,95. Частость р* такова: р, — ~ ~ 0,133,
Р2 = ~ 0,283, р*3 = 0,267. р\ = 0.167, р*ъ = 0,100, р*& = 0,033, ру = 0,017
2.
7
= 1)- Находим вероятности рг по формуле Пуассона, считая а =
г=1
п 0,135 • 22
0,270, рз = ~----------
7
с 2 2° м , чг , е-2-21
= —pj— ~ 0,135, р2 =
°-3g,~ 2 ~ 0,180, р5 ~ 0,090, р6 « 0.036. р7 « 0,017 (^Pi =
г=1
= 1). Как видим, с. в. X — число неправильных соединений имеет прак-
= хв = 2. pi
0,270. р4 =
тическое пуассоновское распределение.
3. 1. Все возможные значения с. в. X — числа очков, выпавших на верхней
грани кости при одном подбрасывании ее.
2. Это числа 1, 2, 3, 4, 5, 6.
3. Это результат 60-ти подбрасываний игральной кости, описывается с. в.
Xi,Х%, _¥3,..., Х59,Х60.
4. Первая реализация выборки приведена в условии, вторая — может быть
такая: 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2. 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4,
4, 4, 4. 4, 4, 4. 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6. 6. 6, 6. 6. 6, 6, 6,
6, 6. Здесь ж(1) = 1,..., ж(30) = 4. ж(31) = 4,..., х(60) = 6.
5. а) Вторая реализация и представляет собой вариационный ряд.
б) Статистический ряд таков:
Xi 1 2 3 4 5 6
ni 7 10 8 12 10 13
Pi 7 60 10 60 8 60 12 60 10 60 13 60
6 6
(52 й’ = 60. 52 Pi = !)•
2=1 2 = 1
Ответы к упражнениям 277
0, при х 1, 7 7777, при 1 < X 2, 60 17 7777, при 2 < х 3, 60
6- ^(т) = < |jij, при 3 < х 4, 37 7777, при 4 < X 5, 60 47 г / « gg, при 5 < X 6, 1, при 6 < X.
7. Число интервалов т = 1 + log2 60 = 1 + 3,3221g 60 rs 6,9. Возьмем т = 6.
xmax — Жппп = 6 — 1 =5; длина интервала h — = 0,833. Возьмем h — 1.
Интервальный статистический ряд имеет вид:
[0,5; 1,5) [1,5; 2,5) [2,5; 3,5) [3,5; 4,5) [4.5: 5,5) [5,5; 6,5)
ni 7 10 8 12 10 13
8. Полигон частот и гистограмма частостей изображены, соответственно,
на рис. 88 и 89.
9. а) хв = 1'7 + 2'9 10б+ • • • ±-6 .Ail ~ 3,783; б) DB = ^(12 • 7 + 22 • 10 + ...
... + 62 • 13) - (3,783)2 « 2,839; в) S2 и || • 2,839 « 2,888, S = VS2 « 1.699;
г) R = 6 - 1 = 5; М* = 6; М* = |(Ж(30) + Ж(31)) = 1 - (4 + 4) = 4.
278 Ответы к упражнениям
Глава 8
8.2
1. Распределение Пуассона Р{Х = ш} = -—~— содержит один параметр а.
Для оценки его методом моментов запишем уравнение MX = хв, т. е. а =
п
= хв. Оценка 0 параметра а = 0 есть 0 = хв = 1 т. е. 0 = х.
2. X — дискретная с. в. с законом распределения
Xi 0 1
Рг 1 -р р
Так как
p(xi,0) = Р{Х = xi,0} = 1
если X} — О,
если Xi = 1,
то функция правдоподобия имеет вид: L = L(x,0) =
1п£ = 6 • In# + 41п(1 — #), уравнение правдоподобия
#6 • (1 - #)4. Тогда
... ~ = О
1 _ е) \о=о и-
Отсюда находим, что 0 = р* = 0,6.
3. а) Пусть 0 (или р или р*) — оценка неизвестной вероятности 0 (или р) по-
явления некоторого события А (успех) в одном испытании. Согласно мето-
ду моментов приравниваем теоретическое MX = р выборочному среднему
п
X=^^Xi, р = Х.
г=1
Ответы к упражнениям 279
Искомая оценка есть в = х.
б) Так как
= Р{Х = xi,0} = <
1-6,
е.
если xi = О,
если Xi = 1,
то функция правдоподобия имеет вид:
L = L(»i, х2, - • , хп\ 6) = Р{Х = Xi, 6} =
= р{х1,6}р{х2,6}-...р{хп,6} = 6^-(1-6)п-п\
п
где пд = Xi — число успехов (наступления события А) в п независи-
г=1
мых испытаниях. In L = пд • In# + (п — пд)1п(1 — 6). Решаем уравнение
, Пд П~Пд „ п пд д п.4
правдоподобия ----у—= 0. Отсюда Р = т.е. оценка и =
((1п£)",<0).
4. Требуется оценить две величины 6\ и 62, т. е. а и Ъ, методом моментов. Так
как для с. в. X ~ R[a. b], то MX = Q DX = • Решаем систему
уравнений
{( Q Т" Ъ —
MX = хв, —£~ =
т.е. \ (h
DX = DB, I lb~a> = а2
< 12
b = 2жв — а, (2®в — 2а)I 2 3 = 12ст2, т.е. (хв — а)2 = За2, хв — а = ±-у/3<7в,
хв = а+у/3ав и. значит, а = хв—х/3<тв, Ь — хв+у/Зсгв (вариант хв = а—\/Зав,
т. е. а = хв + х/3<тв, b = хв — \/Зсгв исключаем, так как а < Ь).
Таким образом, оценки величин а и b таковы: 6i = а = хв — \/3<тв,
02 = Ъ — хв + л/3сгв.
Отметим, что, решая систему
( MX = 1 £ Xi = х,
J г=1
I MX2 = 1 £ X2 = X2,
V г=1
получим те же оценки для а и Ь. В этом случае
ь. ь
MX = [ MX2 = [ = a2±ab + ^.
J Ь — а 2 J Ъ — а 3
а а
Система принимает вид:
{а. + Ь _
-у- = х,
а2 + аЬ Т Ь2 _ 2
3 ~х ’
280 Ответы к упражнениям
Отсюда следует, а = х - д/З • у/ж2 - (ж)2 = ж - л/З • = х - л/3ств,
Ъ = х + \/Зств.
5. В данном случае
(х — а)2
fx (ж) = —т=е 2ст2 = fx(ж, а, ст).
СТу2тТ
Так как
(ж» - 01)2
f(xi,0) =-----2е-2 ,
02 •
то функция правдоподобия имеет вид:
п
Ё (ж, - 01 )2 L = L(x, 0) = i—- • е 202 0% (2я) 2
Тогда 1п£ = -п1П02 - 511127Г - . У(ж^ - 0Х)2. 2 2(ъ
Система уравнений максимального правдоподобия имеет вид:
fdln£_l А , z> \ _ л 1 д0г -02’Ё(Жг 1)-0, | dln£ = _ п_ , X . У(х- _ 6», )2 - 0 [ 90-2 0-2 + 03 ^(Хг 3l) -U-
Отсюда п п ^Xi- П01 =0, т. е. = - ^2 Жг = ж,
32 = п ~ ($2 — оценка неизвестного параметра ст = 02). Можно
г=1 ~
убедиться, что (0i,02) — точка максимума функции 1п£(ж,0). Найдем
Д = АС — В2, где
_ д2 In £ 1 1 _ 90^ 1(01,02) ~ п 02’
о _ д2 In L I 90x902 1(01,02) п - 01) = -^--0 = 0, дЗ 7 дЗ ’ и2 г=1 и2
Ответы к упражнениям
281
c=#4ilZ| _ _ А.у( 0Х)2 = ^_ А.п.02 = _А.
del ^1’02) 02 в4 ()2 в4 д‘2
„2 ~ ~
Следовательно, Д = ~ > О, А < 0, поэтому точка (0ц 02) есть точка
^2
максимума функции L(rc, 0).
8.4
J 'У
Воспользуемся‘формулой (8.3): е — —— и (8.6) Фо(£) = к- Имеем е — 5,
\/п &
а = 15, 7 = 0,9, Фо(£) = 0.45. По таблице находим, что t = 1,65. Тогда
с 1,65-15 _
5 =----——. Отсюда п =
\/п
менее 25 измерений.
1 652 • 152
—--------= 24,5025, т. е. необходимо сделать не
П2
2.
6
хв = х = ^У"хгщ = i-(153-4+159-5 + 165-6 + 171-7 + 177-5 +183-3) =
i= 1
= 167,6; S = 9,28; при 7 = 0.95 и п — 1 = 29 по таблице распределения
2 05 • 9 28
Стьюдента находим С = 2,05. Следовательно, е = ——« 3.47. Дове-
у/ЗО
рительный интервал таков: (164,13; 171,07).
По условию п = 400, п,\ = 80, 7 = 0,95. Относительная частота события А
есть р* = — 0,2. Из соотношения Фо(<) = Z = 0,475 находим /, пользу-
ясь таблицей значений функции Лапласа: t = 1,96. Находим и р? (фор-
/о ? • OR /л О Q
мула (8.10)): Pl = 0.2-1,96-J ~ 0,161, р2 = 0,2+ 1,96 - J «
~ 0,239. Итак, доверительный интервал есть (0,161; 0,239).
8.6
1. п = 1000, X ~ [0,1], т.е. а = 0, 0 = 1, pi = 0,1 = р2 = - - • = Рю; Хнабл =
, = таг + тё + - + таг ' гё - 1000 = 1:4- = 21-7' Так
9 ^2
А^набл < Xooi-9-> то гипотеза не отвергается.
2. Находим хв. и хъ = (152,5 • 6 + 157.5 • 22 + 162,5 • 36 +... +187,5 • 2) • =
1 /'о и г о 1 го г 150 + 155 . ГГ7 г 155 + 160 р,
= 168,45. Здесь 152,5 = --------2----, 157,5 = ---------- и т-д- '-'в =
= i(152,52 • 6 + 157,52 22 + ... + 187,52 • 2) - (168.45)2 = 53,348. Тогда
<т = 7,3. Так как ng = 2 — мало, то последние два интервала объединяем.
Составляем таблицу:
(—оо, 155) [155,160) [160,165) [165,170) [170,175) [175,180) [180, +ос)
6 22 36 46 56 24 10
282 * Ответы к упражнениям
Для расчета вероятностей попадания случайной величины X в г-й ин-
тервал используем функцию Лапласа:
Pi = Фо
Р2 = Фо
155 - 168,45
7,3
160 - 168,45
“^3
- Фо(-оо) = 0.5 - Фо(1,84) = 0,5 - 0,4671 = 0,0329,
— Фо
/155 - 168.45
\ 7,3
= Фо(—1,15) - Фо(—1,84) = 0,0922,
Рз = Фо
165 - 168,45
7,3
— Фо
/160 — 168,45
V 7,3
= Фо(—0,47) - Фо(—1,15) = 0,1941,
Р4 = Фо
170 - 168,45
7,3
— Фо
/155 - 168,45
V 7,3
= Фо(-0.21) - Фо(—0.47) = 0.264.
р5 = 0,2327, р6 = 0,127, р7 = 0,5 - Фо(1,58) = 0,0571.
Тогда
7
2
п/
Гфг П
Хнабл
. 1 f 62 . 222 , , 1Q2 \
200 у0,0329 0,0922 ’ ‘ ‘ 0,0571)
- 200 « 4.
По таблице %2А. = х205;4 = 9,5- Так как %1абл < Хо,О5;4, то гипотеза По не
отвергается.
X [150.155) [155,160) [160,165) [165,170)
6 22 36 46
5k Pi 200 = °’°3 0,11 0,18 0,23
X [170,175) [175,180) [180,185) [185,190)
rii 56 24 8 2
Pi 0,28 0,12 0,04 0,01
^р* = 1, хв = 168,45, о- = 7,3.
i=l
Составим таблицу:
X 150 155 160 165 170
0 0,03 0,14 ' 0,32 0,55
^o(-r) 0,0057 0,0329 0,123 0,3192 0,5832
0,0057 0,0029 0,017 0,0008 0,0332
Ответы к упражнениям 283
X 175 180 185 190
F*(x) 0,83 0,95 0,99 1
F0(x) 0,8159 0,9429 0,9884 0,9984
Л = К* - ^о| 0,0141 0,0071 0,0016 0,0016
Проверяемая гипотеза состоит в том, что с. в. X имеет нормальное рас-
пределение, т. е. Fq(x) = 0,5 + $о(Ж о- °):
Fo(15O) = 0,5 + Фо ( <150 - 168,45\ 7,3 ) = 0,5 - Фо(2,53) = 0,0057;
F0(155) = 0,5 + Фо ( <155 - 168,45 \ 7,3 ) = 0,5 - Ф0(1,84) = 0.0329;
Fq(160) = 0,5 + Фо /160 - 168,45 \ 7,3 , ) = 0.5 — Ф0(1.16) = 0,123;
F0(165) = 0,5 + Фо ( <165- 168,45 А 7,3 ) = 0.5 - Фо(О,47) = 0,3192;
F0(170) = 0,5 + Фо ( <170 - 168,45 \ У 7’3 ) = 0,5 + Фп(0,21) = 0,5832;
F0(175) =0,5 +Фо ( <175 - 168,45^ 7,3 ) = 0,5 + Фо(О,9О) = 0,8159;
Fo(18O) = 0,5 + Фо ( <180- 168,45 \ 7,3 ) = 0,5 + Фо(1,58) = 0,9429;
F0(185) = 0,5 + Фо | <185 - 168,45 \ < 7,3 J = 0,5 + Фо(2,27) = 0,9884:
Fo(19O) = 0,5 + Фо ( <190 — 168,45 А к 7.3 ) = 0,5 + Фо(2,95) = 0.9984.
Максимальное отклонение эмпирической функции распределения от тео-
ретической есть Dn = |F^(170) — Fq(170)| = 0,0332. Следовательно,
Dn у/п = V200 • 0,0332 » 0,47. Критическое значение критерия Кол-
могорова равно Ло,о5 — = 1,36. Так как Dn\/n < Ао, то гипотеза Но
согласуется с опытными данными.
Приложения
i
Приложение 1. Значение; функции ip(x) = -е 2
у/Ъп
X Сотые доли ,т
0 1 2 3 4 5 6 7 8 9
0,0 0,3989 3989 3989 3988 3986 3984 3982 3980 3977 3973
0,1 3970 3965 3961 3956 3951 3945 3939 3932 3925 3918
0,2 3910 3902 3894 3885 3876 3867 3857 3847 3836 3825
0,3 3814 3802 3790 3778 3765 3752 3739 3726 3712 3697
0,4 3683 3668 3653 3637 3721 3605 3588 3572 3555 3538
0,5 3521 3503 3485 3467 3448 3429 3411 3391 3372 3352
0,6 3332 3312 3292 3271 3251 3230 3209 3187 3166 3144
0,7 3123 3101 3079 3056 3034 ЗОН 2989 2966 2943 2920
0,8 2897 2874 2850 2827 2803 2780 2756 2732 2709 2685
0,9 2661 2637 2613 2589 2565 2541 2516 2492 2468 2444
1,0 2420 2396 2371 2347 2323 2299 2275 2251 2227 2203
1,1 2179 2155 2131 2107 2083 2059 2036 2012 1989 1965
1,2 1942 1919 1895 1872 1849 1827 1804 1781 1759 1736
1,3 1714 1692 1669 1647 1626 1604 1582 1561 1540 1518
1,4 1497 1476 1456 1435 1415 1394 1374 1354 1334 1315
1,5 1295 1276 1257 1238 1219 1200 1181 1163 1145 1127
1.6 1109 1092 1074 1057 1040 1023 1006 0989 0973 0957
1,7 0941 0925 0909 0893 0878 0863 0848 0833 0818 0804
1,8 0790 0775 0761 0718 0734 0721 0707 0694 0681 0669
1,9 0656 0644 0632 0620 0608 0596 0584 0573 0562 0551
Десятые доли х
X 0 1 2 3 4 5 6 7 8 9
2. 0540 0440 0355 0283 0224 0175 0136 0104 0079 0060
з, 0044 0033 0024 0017 0012 0009 0006 0004 0030 0020
L, 0001
Приложения 285
1 / — —
Приложение 2. Значение функции Фо (ж) = — I е 2 dt
x/'Z'K J
о
X Сотые доли х
0 1 2 3 4 5 6 7 8 9
0,0 0,0000 0040 0080 0112 0160 0199 0239 0279 0319 0359
0,1 0398 0438 0478 0517 0557 0596 0636 0675 0714 0754
0,2 0793 0832 0871 0910 0948 0987 1026 1064 1103 1141
0,3 1179 1217 1255 1293 1331 1368 1406 1443 1480 1517
0,4 1554 1591 1628 1664 1700 1736 1772 1808 1844 1879
0,5 1915 1950 1985 2019 2054 2088 2123 2157 2190 2224
0,6 2258 2291 2324 2357 2389 2422 2454 2486 2518 2549
0,7 2580 2612 2642 2673 2704 2734 2764 2794 2823 2852
0,8 2881 2910 2939 2967 2996 3023 3051 3079 3106 3133
0,9 3159 3186 3212 3238 3264 3289 3315 3340 3365 3389
1,0 3413 3438 3461 3485 3508 3531 3553 3577 3599 3621
1Д 3643 3665 3686 3708 3729 3749 3770 3790 3810 3830
1,2 3849 3869 3888 3907 3925 3944 3962 3980 3997 4015
1,3 4032 1049 4066 4082 1099 4115 4131 4147 4162 4177
1,4 4192 4207 4222 4236 4251 4265 4279 4292 4306 4319
1,5 4332 4345 4357 4370 4382 4394 4406 1418 4430 4441
1.6 4452 4463 4474 4485 4495 4505 4515 4525 4535 4545
1,7 4554 4564 4573 4582 1591 4599 4608 4616 4625 4633
1,8 4641 4649 4656 4664 4671 4678 4686 1693 4700 4706
1,9 4713 4719 4726 4732 4738 4744 4750 4756 4762 4767
Десятые доли х
X 0 1 2 3 4 5 6 7 8 9
2, 4773 4821 4861 4893 4918 4938 4953 4965 4974 4981
з, 4987 4990 4993 4995 4997 4998 4998 4999 4999 50001
1Точное значение отличается меньше, чем на 5 • 10 5
286 Приложения
Приложение 3. Квантили у& к распределения ук
(к — число степеней свободы)
к Уровень значимости а
0,01 0,025 0,05 0,95 0,975 0,99
1 6,6 5.0 3,8 0,0039 0,00098 0,00016
2 9,2 7,4 6,0 0,103 0,051 0,020
3 11.3 9,4 7,8 0,352 0,216 0,115
4 13,3 11,1 9,5 0,711 0,484 0,297
5 15,1 12,8 ИД 1,15 0,831 0,554
6 16,8 14,4 12,6 1,64 1,24 0,872
7 18,5 16,0 14,1 2.17 1,69 1,24
8 20,1 17,5 15.5 2.73 2,18 1,65
9 21,7 19.0 16,9 3,33 2,70 2,09
10 23,2 20,5 18,3 3,94 3,25 2,56
11 24.7 21,9 19,7 4,57 3,82 3,05
12 26.2 23,3 21,0 5,23 4,40 3,57
13 27,7 24,7 22,4 5,89 5,01 4,11
14 29,1 26,1 23,7 6,57 5,63 4.66
15 30,6 27,5 25,0 7,26 6,26 5,23
16 32,0 28,8 26,3 7,96 6.91 5,81
17 33,4 30,2 27,6 8,67 7,56 6,41
18 34,8 31,5 28,9 9,39 8,23 7,01
19 36,2 32.9 30,1 10,1 8,91 7,63
20 37,6 34,2 31,4 10,9 9,59 8,26
21 38,9 35,5 32,7 11,6 10,3 8,26
22 40,3 36,8 33,9 12,3 11,0 9,54
23 41,6 38,1 35,2 13,1 11,7 10.2
24 43,0 39,4 36,4 13,8 12.4 10,9
25 44,3 40,6 37,7 14,6 13,1 11,5
26 45,6 41,9 38,9 15.4 13,8 12,2
27 47,0 43,3 40,1 16,2 14,6 12,9
28 48,3 44.5 41,3 16,9 15,3 13,6
29 49.6 45,7 42,6 17,7 16,0 ' 14,3
30 50,9 47,0 43,8 18,5 16,8 15,0
Приложения • 287
Приложение 4. Квантили /-распределения Стьюдента
(А: — число степеней свободы)
к Уровень значимости а (двусторонняя критическая область)
0,10 0,05 0,02 0,01 0,002 0,001
1 6,31 12,7 31,82 63,7 318,3 637,0
2 2,92 4,30 6,97 9,92 22,33 31.6
3 2,35 3,18 4,54 5,84 10,22 12,9
1 2,13 2.78 3,75 4,60 7,17 8,61
5 2,01 2,57 3.37 4,03 5,89 6,86
6 1,94 2,45 3,14 3,71 5,21 5,96
7 1,89 2,36 3,00 3,50 4,79 . 5,40
8 1,86 2,31 2,90 3,36 4,50 5,04
9 1,83 2,26 2,82 3,25 4.30 3,78
10 1,81 2,23 2,76 3,17 4,14 4.59
11 1,80 2,20 2,72 3,11 4,03 4.44
12 1.78 2,18 2,68 3,05 3,93 4,32
13 1,77 2.16 2,65 3,01 3,85 4,22
14 1,76 2,14 2,62 2,98 3,79 4,14
15 1,75 2,13 2.60 2,95 3,73 4,07
16 1,75 2,12 2,58 2,92 3,69 4,01
17 1,74 2,11 2,57 2,90 3,65 3,96
18 1,73 2,10 2,55 2,88 3,61 3,92
19 1,73 2,09 2,54 2,86 3,58 3,88
20 1,73 2,09 2,53 2,85 3,55 3,85
21 1,72 2,08 2,52 2,83 3,53 3,82
22 1,72 2.07 2,51 2,82 3,51 3,79
23 1,71 2,07 2,50 2,81 3,49 3,77
24 1,71 2,06 2,49 2,80 3,47 3,74
25 1,71 2,06 2,49 2.79 3,45 3,72
26 1,71 2,05 2,48 2,78 3,44 3,71
27 1,71 2,05 2,47 2,77 3,42 3,69
28 1,70 2,05 2,46 2,76 3,40 3.66
29 1.70 2,05 2,46 2,76 3,40 3,66
30 1,70 2,04 2,46 2,75 3,39 3,65
40 1,68 2.02 2,42 2,70 3,31 3,55
60 1,67 2,00 2,39 2,66 3,23 3,46
120 1,66 1,98 2,36 2,62 3,17 3,37
00 1,64 1,96 2,33 2,58 3,09 3,29
По вопросам оптовых закупок обращаться:
тел./факс: (495) 785-15-30, e-mail: trade@airis.ru
Адрес: Москва, пр. Мира, 104
Наш сайт: www.airis.ru
Вы можете приобрести наши книги
с II00 до 1730, кроме субботы, воскресенья,
в киоске по адресу: нр. Мира, д. 106, тел.: (495) 785-15-30
Адрес редакции: 129626, Москва, а/я 66
Издательство «АЙРИС-пресс» приглашает к сотрудничеству
авторов образовательной и развивающей литературы.
По всем вопросам обращаться
по тел.: (495) 785-15-33, e-mail: editor@airis.ru
Учебное издание
Письменный Дмитрий Трофимович
КОНСПЕКТ ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ,
МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
И СЛУЧАЙНЫМ ПРОЦЕССАМ
Ведущий редактор В. В. Черноруцкий
Редактор Н. Г. Рысьева
Художественный редактор, оформление А.М.Драговой
Технический редактор С. С. Коломеец
Компьютерная верстка Е. Г. Иванов
Корректор З.А. Тихонова
Подписано в печать 19.10.07. Формат 70x100/16.
Печать офсетная. Печ. л. 18. Усл.-печ. л. 23,4.
Тираж 5000 экз. Заказ № 2257.
ООО «Издательство «АЙРИС-пресс»
113184, Москва, ул. Б. Полянка, д. 50, стр. 3.
Отпечатано в ОАО «Можайский полиграфический комбинат»
143200, г. Можайск, ул. Мира, 93
Дмитрий Письменный
КОНСПЕКТ^
по теории вероятностей,
математической статистике
ПрЖти^Ки все современные отрасли естествознания
используют статистические методы,
которые, в свою очередь,
базируются на теории вероятностей.
Знания основ теории вероятностей, случайных процессов
и математической статистики необходимы в настоящее
время как инженеру практически любого профиля,
так и менеджеру и маркетологу,
поскольку серьезный анализ рынка немыслим
без владения статистическими методами.
Курс лекций Д. Т. Письменного - это находка для студента,
который при наличии дефицита времени
сможет получить достаточный объем знаний
и приобрести начальные практические навыки,
необходимые, чтобы уверенно себя чувствовать
на зачете и экзамене по этим непростым дисциплинам.