А. В. ЛЫКОВ
ТЕПЛОМАССООБМЕН
СПРАВОЧНИК
ВТОРОЕ ИЗДАНИЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
МОСКВА
ЭНЕРГИЯ
1978
А. В. ЛЫКОВ
ТЕПЛОМАССООБМЕН
СПРАВОЧНИК
ВТОРОЕ ИЗДАНИЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
МОСКВА
ЭНЕРГИЯ
1978
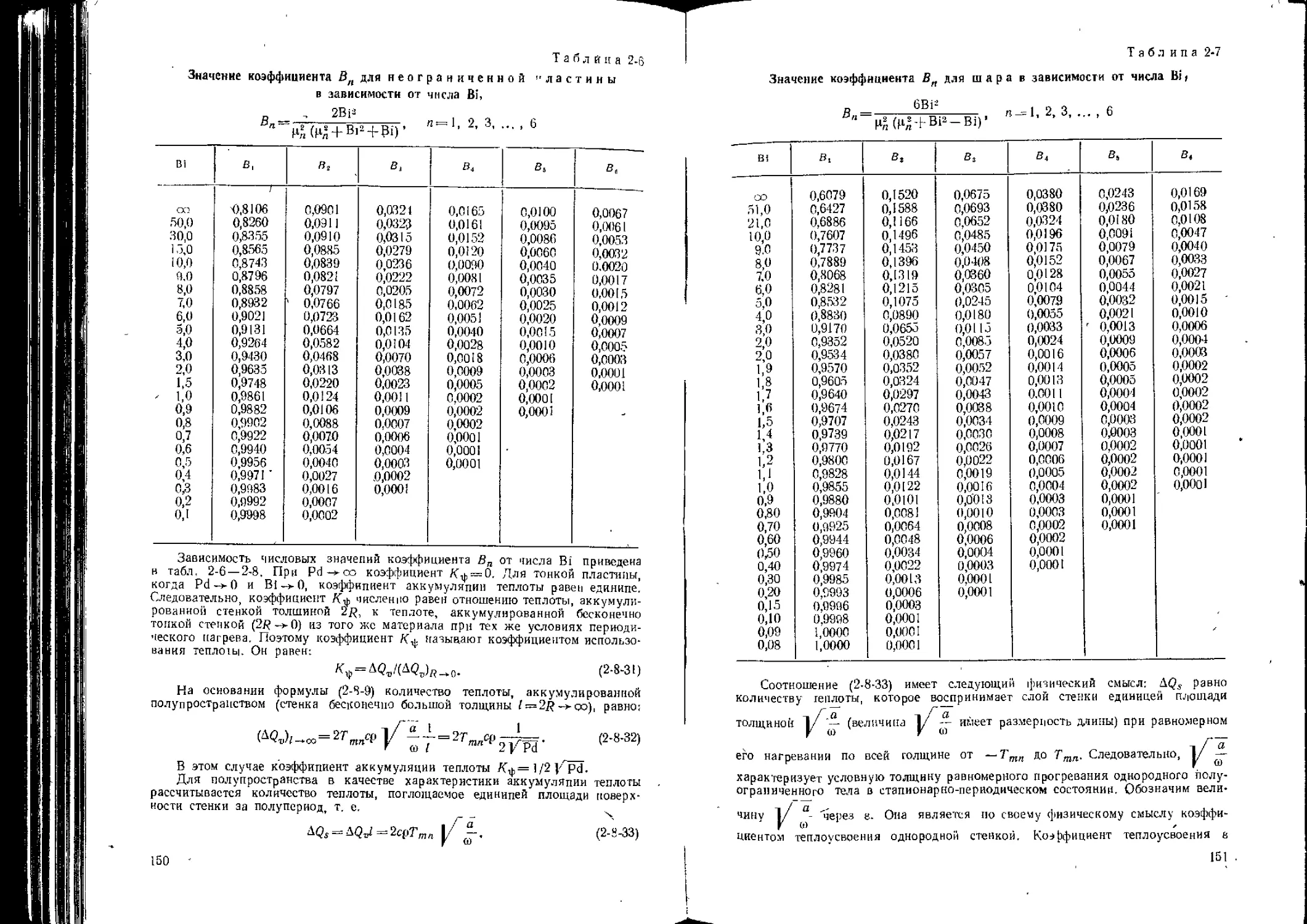
31.31
Л 88
УДК 621.1.016.4 (03)
iiWi 6-K.J Л!1 БССР f
при институте тепло- и j
массобмена *
Лыков А. В.
Л88 Тепломассообмен: (Справочник). 2-е изд., пере-
раб. и доп. — М.: Энергия, 1978. — 480 с., ил.
Предлагаемая вниманию читателей книга является систематизиро-
ванным обзором современного состояния науки о взаимосвязанном
тепломассообмене, который состоит из критического анализа новейших
работ в этой области и аналитических решений в разнообразных фор-
мах с расчетными формулами, таблицами и другими справочными
материалами, Большое внимание уделяется нестационарным задачам
переноса, сопряженным задачам конвективного тепломассообмена, а
также явлениям тенломассопереноса в капиллярно-пористых телах.
Книга является справочником нового типа по теории тепломассо-
обмена.
Справочник рассчитан на научных сотрудников, инженеров, зани-
мающихся теплофизнческими проблемами, и аспирантов.
30302-219
051(01)-78 * 8’78
31.31
6П2.2
© Издательство «Энергия», 1978.
ПРЕДИСЛОВИЕ РЕДАКТОРА
Настоящая книга была подготовлена выдающимся советским ученым ака-
демиком АН БССР, профессором Алексеем Васильевичем Лыковым незадолго
до его кончины в 1974 г.
Опа представляет собой переработанное и дополненное второе издание
известного справочника А. В. Лыкова «Тепломассообмен», вышедшего в 1972 г.
Тепломассообмен объединяет в единую теорию переноса энергии (теплоты),
количества движения (импульса) и массы некоторые разделы молекулярной
физики, гидроаэродинамики, термодинамики обратимых и необратимых процес-
сов, физико-химии поверхностных явлений и химической технологии,
Явления конвективно-диффузионного переноса рассматриваются в книге
с позиций термодинамики необратимых процессов и нелинейной тсрмомсханики
сплошных сред. Во втором издании автор значительное место уделил асим-
метричной гидродинамике, имея в виду, что ряд химических материалов пред-
ставляет собой типичные реологические среды, для которых классические
уравнения переноса неприменимы. Закономерности, основанные па нелинейных
законах переноса с учетом памяти (системы с наследственностью), более точно
описывают явления переноса в таких средах.
Переработаны и дополнены разделы «Теплопроводность» и «Конвективный
перенос». При решении задач конвективного теплообмена автор вместо гранич-
ных условий третьего рода применяет граничные условия четвертого рода.
Теплоперенос в жидкости во всех' случаях рассматривается во взаимосвязи
с переносом теплоты в стенке твердого тела.
Раздел «Явления переноса в капиллярно-пористых телах» дополнен теоре-
тическим исследованием процессов переноса массы в этих телах при наличии
фазовых превращений (испарение жидкости). Последнее имеет большое прак-
тическое значение для разработки инженерных методов расчета пористого испа-
рительного охлаждения и длительности процессов сушки влажных материалов.
Шестой раздел «Аналитическая теория диффузии тепла и массы» включает
в себя анализ систем дифференциальных уравнений тепловлагопереноса в капил-
лярно-пористых коллоидных телах при предельных переходах применитель-
но к процессам сушки и экспериментальным методам определения теплофизи-
ческих характеристик.
Редактор считает своим долгом донести4 до читателя в наибольшей мере
оригинальный, современный и интересный материал рукописи, ограничиваясь
только небольшими .примечаниями. Редактор благодарит профессоров Н. И.
Гамаюнова, А, И. Леонтьева, А. Г1. Прудникова, доцентов В. А. Бубнова и
А. А. Алексашенко за ценные замечания по отдельным разделам рукописи.
Профессор В. В. Красников
ПРЕДИСЛОВИЕ АВТОРА К ПЕРВОМУ ИЗДАНИЮ 
Наука о переносе энергии (тепла) и массы вещества является одной
современных областей знаний; она имеет большое практическое значение для
интенсификации теплоэнергетических, энерготехпологических и химико-техно-
логических процессов в разных отраслях промышленности и сельского хозяй-
ства. Особенно большое значение проблема тепломассообмена приобретает для
новой техники, в частности для атомной энергетики и космической техники,
на базе бурного развития которых и возникла наука о взаимосвязанном пере-
носе энергии и массы. Она объединяет ряд разделов таких научных дисциплин,
как классическая и неравновесная термодинамика, физическая газодинамика,
уравнения математической физики, физико-химических поверхностных явлений
и дисперсных систем.
За последние 10 —15 лет эта область научных знаний значительно расши-
рилась и продвинулась вперед. Появились многочисленные приложения теории
в станционной и промышленной энергетике, в технологических процессах, '
в химической технологии, в строительной индустрии и сельском хозяйстве.
При этом в разных отраслях техники уровень научных исследований, инже-
нерно-технических разработок весьма различен. Если в новой технике уровень
исследований достаточно высок, то в ряде отраслей техники он сильно отстает
от современного развития общей теории тепломассопереноса.
Отсюда возникла весьма актуальная задача сделать обзор современного
состояния теории тепломассопереноса и наметить пути дальнейшего ее раз-
вития, особо выделив новейшие направления в данной проблеме. Такой позор
будет представлять собой систематизированный справочный материал, который
позволит быстро ориентироваться читателю в любом разделе тепломассообмена.
Таким образом, предлагаемая читателю книга является справочником
нового типа, который состоит не из набора формул, таблиц и номограмм,
а представляет собой, как было указано выше, систематизированный, направлен-
ный обзор современных знаний по тепломассообмену и содержит критический
анализ; в нем приводится аналитическое описание процессов в разнообразных
формах и видах..и намечаются новые пути их развития.
Данная книга ни в коей мере не заменяет и не дублирует существующий
справочник по теплотехнике и теплопередаче, так как, во-первых, методически
она построена по иному принципу и, во-вторых, в основном рассматривает
взаимосвязанные процессы тепломассопереноса и математическую теорию пере-
носа, которая в одинаковой мере применима к переносу как тепла, так и
массы вещества. Вследствие этого вопросы передачи тепла излучением, задачи
чистого теплообмена и ряд других разделов теплопередачи в книге не рас-
сматриваются. Большое внимание уделяется аналитической теории пере-
носа тепла и массы, в частности нестационарным задачам теплопроводности
(разд. 2), где путем введения обобщенных функций удалось одновременно опи-
сать одномерные температурные поля в телах классической формы, по-новому,
в более простом виде, описать распространение температурных волн, дать
обобщение регулярным режимам теплового пагрева тел и ряд других обоб-
щений. На основе дальнейшего развития аналитической теории теплопроводно-
сти приведены последние работы по решениям системы дифференциальных урав-
4
нений тепломассопереноса (разд. 6), подробно рассмотрены гиперболические
уравнения диффузии тепла и массы с учетом конечной скорости распростра-
нения. Установлена связь этого нового направления в описании явлений тепло-
массоперсноса с работами американской школы по диффузии массы в пористых
средах.
Одним из основных разделов обзорного справочника является тепломассо-
перенос в капиллярно-пористых телах (разд. 5). Это обусловлено тем обстоя-
тельством, что закономерности технологических и химико-технологических про-
цессов в разных отраслях промышленности определяются тепломассоперсносом
в капиллярно-пористых телах. Кроме того, значимость проблемы тепломассо-
переноса в капиллярно-пористых телах значительно возросла в связи с широ-
ким применением капиллярно-пористых тел в космической технике, в частности
в устройствах по транспорту жидкостей и энергии (тепловые трубки, тепло-
обменники и т. п.).
Новым направлением в исследовании задач конвективного теплообмена
является решение так называемых сопряженных задач, когда в отличие от
традиционного подхода теплообмен твердого тела с потоком жидкости рассмат-
ривается как взаимосвязанная задача переноса тепла в жидкостях и твердых
телах. В разд. 4 приведен обзор последних работ по решению задач внешнего
и внутреннего теплообмена. Данное направление весьма'актуально особенно
при решении нестационарных задач конвективного тепло- и массообмена, При-
ведено также описание новых явлений: свободная конвекция при нагреве
сверху (векторы потока тепла н силы гравитации совпадают), термоконвектив-
ные волны, а также рассматривается ряд других вопросов в последних рабо-
тах по тепломассообмену (разд 3).
Написание справочника нового типа по сложной проблеме современной
науки — весьма трудная задача, и, совершенно естественно, полностью отра-
вить все работы в этой области знаний не представляется возможным. Автор
заранее благодарен всем, кто сообщит о своих замечаниях в адрес данной
книги. Автор надеется, что такая первая попытка в создании справочника-об-
зора будет способствовать написанию аналогичных книг по другим разделам
современной науки и техники что послужит дальнейшему развитию техничес-
кого прогресса в нашей стране.
Автор приносит благодарность редактору международного журнала «Теп-
ло- и мйссоперенос» Э. А. Богачевой за помощь в подготовке рукописи.
РАЗДЕЛ ПЕРВЫЙ
ЯВЛЕНИЯ КОНВЕКТИВНО-ДИФФУЗИОННОГО ПЕРЕНОСА
Перенос любой субстанции (массы, импульса, энергии и т. д.) в подвиж-
ных средах может происходить как молекулярным (хаотическим тепловым дви-
жением), так и конвективным (гидродинамическим макроскопическим движе-
нием) путем. По своей физической природе молекулярный перенос обусловлен
диффузией (молекулярным перемешиванием) и поэтому его можно назв'ать диф-
фузионным переносом. В этом случае перенос теплоты (теплопроводностью
в однородной жидкости является переносом теплоты при помощи самодиффу-
зли*. конвективный перенос субстанции обусловлен видимым (организован-
ным) движением самой среды, которое происходит за счет внешних сил и пере-
пада давления.
В первую очередь остановимся на основных аналитических соотношениях,
лежащих в основе математических преобразований и выводов уравнений пере-
носа.
1-1. НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ СООТНОШЕНИЯ
При выводе уравнений переноса будут использованы аналитические соот-
ношения, которые мало освещены в литературе. Поэтому мы Приводим основ-
ные из них.
а)	Производная по времени
Производная по времени т некоторой скалярной функции <р определяется
соотношением
л м-ol а.т J	'
Если величина <р зависит только от Времени, то соотношение (1-1-1) пол-
ностью определяет значение производной по времени. Если же <р—функция
координат, то это определение нуждается в уточнении.
Рассмотрим среду, состоящую из движущихся частиц. Пусть хр—коорди-
ната частицы р (рис. 1-1). Тогда производная dxp!dx есть скорость движения ut
частипы р в х направлении:
dx
* Не надо смешивать
Дюфо) в газовых смесях.
(М-2)
с явлением диффузионной теплопроводности (эффект
6
Эту производную обычно называют материальной или субстанциональной
производной
dx \ dx .//?
(1-1-3)
где индекс /? указывает, что система координат среды неподвижна. При опре-
делении производной температуры по времени могут быть два случая: в одном
из них температура в данной точке изменяется независимо от движения (дат-
чик температуры движется вместе с частицей)—это локальная производная
температуры дТ/дх:
dT\ __ дТ .
dx dx '
(1-1-4)
Затем температура частицы изменяется за счет движения самой частицы.
При неподвижных координатах полная
производная температуры является
субстанциональной производной
f dT \ = dT = dT (dxj_\ ,
\ dx Ir	dx	dxt dx
dT ! dx2 \ dT ( dx3 \
dx Ук 1 дх3 \ dx Ji?
дТ у дТ , дТ ,
ТТ + 01&г+',3'®г +
ат
+°3&Г'
(М-5)
где Of, оа, vs—компоненты скорости
движения среды в направлении декарто-
вых координат.
Соотношение (1-1-5) можно написать
так;
di dx ~
(1-1-0}
Во втором случае система координат изменяется по времени х(т), у (х),
z (т), тогда полная производная будет равна;
ДТ __ дТ_ дТ_ I dx \	дТ_ !dy_\	0Т_ fdz_\
Dx dx^dx^dx)1 dy [dx )^"дг \dx j' * 'I'7’
где dx/dx, dyltx, dzldx— компоненты вектора скорости w, который характе-
ризует движение датчика температуры:
= ^+s.w.
Dx dx
(1-1-8)
Это наиболее общее выражение производной по времени [Л.1-1]. Соотно-
шение (1-1-6) является частным случаем (1-1-8), когда w = v-
б)	Метод скользящих индексов
Метод скользящих индексов наряду с символикой тензорного анализа
весьма удобен для записи математических формул. Он сокращает запись и
облегчает уяснение физического смысла. Независимые переменные обозначаются
разными индексами, а не различными наименованиями. Например, декартовые
координаты х, у, г обозначаются xL, х2, xs (xi==x; х2 = у, x3 = z). Для сла-
гаемых суммы находится общий член суммы, из которого отдельные слагаемые
'	7
получаются при соответствующих частных значениях индексов. Поясним это
на примере.
Квадрат элсмеша длины ds2 в ортогональных криволинейных координатах
?2> *з) выражается формулой Гаусса
=	. (t-1-9)
i
где
i=i'2’3'	о-'-10»
k~ J
Знак суммы опускается, а слагаемые суммы должны представляться мно-
жителями, в которых индексы повторяются, тогда вместо соотношений (1-1-9)
и (1-1-10) будем иметь:
= = (1-1-11)
Повторяющиеся индексы приобретают особое значение при интерпретации
формул, они получили название скользящих индексов. Например,
+	Т=^-+.,Т,6 /=1,2,1	(1-1-12)
=	'./=1,2,3. (1-1-13)
Индекс, обозначенный малой буквой латинского алфавита с запятой после
него, обозначает дифференцирование в частных производных по пространствен-
ной координате х^, а точка обозначает материальную производную. Если из
суммы необходимо выделить одно слагаемое, в котором не долх<но происхо-
дить суммирование, то один из повторяющихся индексов заключается в скобки.
Например, если из соотношения (1-1-11) следует выделить составляющую ds^
элемента ~ds в направлении координатной линии то пишут:
ds» = A,4,	(1-1-14)
Заключение в скобки индекса k означает, что суммирование по этому
индексу производиться не должно, хотя этот индекс в формуле повторяется.
в)	Преобразование координат
Рассмотрим преобразование прямоугольной системы координат (%/) в орто-
гональную криволинейную систему координат
(Ех, Ы. *= 1,2.3.
Используя соотношения (1-1-9) и (1-1-10), получаем (JI.1-2J:
gradT-VTfo, Е„ Ь)= 2 V'i?’	(1’И5>
i~ 1
где	— единичный вектор в направлении системы координат (£х, |2, с8).
Дивергенция от вектора плотности потока тепла ~q (|1( Ед)
(М.,6)
«
где qi — компоненты вектора q вдоль направления Оператор Лапласа V2T
равен:
.	(1-1-17)
В качестве примера рассмотрим цилиндрическую систему координат
(г, 0, г), где 6 — полярный угол (угол между радиус-вектором г и осью xL):
Xi = x = rcos6; х2 = у = г sin 0; х3 = г = г;
А’= Ш+О)3+(^У=ras’ “+sW ’+0’1;
Ae= (^г)3 +	+ (^У = <-'sin ®)2+('“s»)=+о=л
ИёУ+(^У+(ёУ=о+о+1=1-
Следовательно, Az=l, hq = r, й3=1;
1 д ! дТ \	1 д2Т &Т
^Т(Г, », х1)=7__(г~) + __^ + —.	(1-1-18)
Для сферической системы координат (г, О, Ф), где 0—угол между проек-
цией радиус-вектора г на плоскость х0х2 и осью х1( Ф — угол между векто-
ром г и осью х3,
х = г sin Ф cos 0; ха = г sin ф sin 0; х3 = г cos Ф.
Аналогичным путем находим:
hr=\, /гв=/-81пФ, йф = г;
v ’ г2 dr \ dr J r3 sui Ф дф \ дФ ) 1
1 сРТ
-	+ гг sin2 Ф два 	(1-1-19)
г) Теоремы переноса
1 6!
Выделим некоторый объем Ио(т), который движется со скоростью
(рис. 1-2). Тогда ^производная скалярной функции <р в данном объеме буд
d
dr
(pdV— lim
Ат-» о
f ср (т-|-Дт) dV — j <p(T)rfl/-
Va (T + At)___________________VO(T)___________
Дт
(1-1-20)
Выразив элементарные объемы dV через элементарные поверхности dS,
можно получить следующее выражение для общей теоремы переноса:
" ~^х	<р^И=	dV ершл1^. (1-1-2!)
va(T)	sa%
Если щ==0> то 1/д(т) = 17' и
<р dV = dV.	(1-1-22)
9
Если скорость w равна скорости движения текущей среды у (щ = -у), то
из соотношения (1-1-22) получаем теорему переноса Рейнольдса:
f ф1/И= (	f tpo-n'dS, (1-1-23)
*	ПТ J	J ОТ	1
vm(T)	smm
где Vm (т) и Sff, (т) — соответственно объем и поверхность движущейся жидко-
сти. Если переносимая величина — векторная, например Т, то в общем случае
теорема переноса имеет вид:
( vdV = j J^dV+ j v(w-n^dS. (1-1-24)
v»«	sa<'t>
В работе [Л. 1-3] дано обобщение теоремы переноса для любой скалярной
величины ф при дифференцировании ее по направлению Г.
J 'И- J	о-1-26)
U’(0	/ V (Z)	S(Z)
Если в движущейся субстанции имеется сингулярная поверхность, напри-
мер двухфазный поток, то уравнение теоремы переноса примет иной вид [Л.1-4].
Рис. 1-2. Движущийся объем среды
Va W-
S+
Рис. 1-3. Сингуляр-
ная поверхность в
движущейся среде.
Обозначим площадь сингулярной поверхности через Ssin (т). Она делит объем И
на две области ]/+ и V~, а поверхность S —на S+ и S" (рис 1-3).
Обозначим скорость движения сингулярной поверхности внутри текущей
среды через и, тогда будем иметь (рис. 1-3):
_	( р на поверхности S+;
| iia поверхности Ssin>
_	( v на поверхности S“;
u" = J----
I на поверхности Ssin>
где V — единичный вектор по нормали к поверхности Ss[n,
Воспользуемся соотношением
~ t VdV^~- СфЛ- + -± f (f dV;	(1-1-26)
rfT А ’ rfx J v dT J r	v '
Vm^>	f-
10
тогда для уравнения (1-1-23) получим:
jL С (ndV' = С	( cp»-n1rfS— ( (p+U£  ^gS; (1-1-27)
rfx	J	J	dT	J	J
5sinW
—-	f	m	dV =	f	-~-d]Z4-	(	roV-nMSH"	i*	(p_Us-VrfS- (1-1-28)
dr	J	1	J	dT -	J	J
И^(Т)	S,nw	Ssinfr)
Используя соотношение (1-1-2G), получаем:
—	С	rn dV = (	^-dV 4-	\	cp-n^dS— f	lq:]«^dS, (1-1-29)
dr	j	»)	dT	J	v
V„m	vm^K-	Sm<‘e>	Ssi“(”
где
|ф]ЕЕ<р+ — ф-	(1-1-30)
При выводе уравнений переноса используют следующие теоремы:
теорема Стокса
фЛ- dL=J[LV X А] • dS =J curl А • nldS,	(1-1-31)
l S \	S
Где %____векторная величина, изменяющаяся-вдоль направления L;
теорема Гаусса —Остроградского
Jdiv A dK=| A-dS=§ А - n^dS;	(1-1-32)
теорема Грина получается из формулы Гаусса, если воспользоваться под-
'становкой
A— a Vb = agrad b	(1-1-33)
Тогда
div X=v . A = aV2^ + (Vfl • V&)=a div grad H-grad a - grad b, (1-1-34)
откуда получим:
J |oV!b + (Va- V6)j ilV=^ aVb-dS.	(1-1-35)
Если поменять местами скалярные величины а и Ь, то получим соотноше-
ние, аналогичное (1-1-35). Из этих двух соотношений получаем второй вид
формулы Грина:
J (а?2» —67ги) <1У=^(а?Ь —5Va)ni<lS.	(1-1-36)
д) Операция дифференцирования
Обобщенная операция дифференцирования обозначается символом набла V,
называемым оператором Гамильтона. Оператор V определяется соотношением
V== «} -^-+ л! 7Д-+ ni =grad,	(1-1-37)
1 dxi т ’ dxa 1 дх3 ь
где nj,	nJ—ортогональные между собой векторы единичной длины, направ-
ленные по осям декартовых координат хъ х2> хз, или (сокращенно) орты.
11
Градиент от скалярной величины ср является вектором (тензор первого
ранга):
grad <рVcp=n!	—Ь "э'^Г“== У п\^~-	(1-1-38)
6 Y *	1 дх} ‘ * дх3 1 3 дх3 Zj 1 dxj '	’
z=l
Скалярное произведение двух векторов V и А ^является дивергенцией от
вектора X:
з
div^V.l=. 24^-.	(1.1.39)
Векторное произведение х Л) называется операцией rot X или curl Л и
является величиной векторной;
п{ п\ п\
Л] Л3 Ла
где ej/fc—функция, равная:
О, если все индексы равны;
+1, если Ijk = 123,231 или 312;	(1-1-41/
—1, если 1/4=132,213 или 321,
Дивергенция от градиента скалярной величины есть величина скалярная:
з
div (grad <р) = V  (V<p) = У	(1-1-42)
Z=1	1
где V2—оператор Лапласа,
V1 й2 д2
divgrad^J^.-gj-^i _	(1-1-43)
Оператор (Л • V) равен:
3
(T-V)T = y ?(Д- Я)-(Zx (V х .41).	(1-1-45)
Полезны следующие соотношения’
V  аЛ= (Л-Va) +а (V  Л);	(1-1-46)
(V-{Tb)) = (T.V)B + 8 (V-X);	(1-1-47У
(V X аЛ) = а (V X X) + (Va X 3)1	(1-1-48)
[V-(VxT)l = 0;	(1-1-49)
(VX (Xx^]=(3-ivX)j-[Z.(vS)j+l(V.3)-ff(V.4	(1-1-50)
12
где (4 В) и (ГЙ) являются диадами, они имеют девять ^компонент; их не надо
смешивать со скалярными произведениями А-В и (V • 4):
	4^1 4А 4ХВЭ	
1в =	A^Bj A%BS 4гВд	(1-1-51)
	4зВх 4ЭВ3 43В3	
Можно показать, что		
div (grad о)7 =grad (dive),		
Г. = V (V-и),	(1-1-52)
где (grad v)T = (Vo)r = vV —транспонированная диада.
1-2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРЕНОСА
а)	Уравнение переноса субстанции
В выделенном произвольном объеме V, ограниченном поверхностью S,
в котором действует источник или сток субстанции С .объемной мощностью IVt
уравнение переноса имеет вид:
5-^417 + ^) С = — ^(7^)^+ j !vdV, (1-2-1)
s	.sv
где ws — скорость движения поверхности S; n1 — единичный вектор вдоль нор-
мали п к поверхности S; /с—диффузионный (молекулярный) поток субстан-
ции С.	_
Если воспользоваться теоремой Гаусса —Остроградского и положить ws =
=ц, будем иметь:
j (-|£+divCo+div/c-/1/)dV=0,	(1-2-2)
V '
откуда получаем дифференциальное уравнение переноса:
-Ц-+ div (ЙГ) = - div7c + /l,.	(1-2-3)
Левая часть уравнения (1-2-3) состоит из локального изменения концен-
трации переносимой субстанции (дС/дт) и ее конвективного переноса (div Су).
Правая часть характеризует диффузионный перенос (div ;с) и действие источ-
ников или стоков субстанции lv.
б)	Уравнение переноса массы
Из уравнения (1-2-3) можно получить дифференциальное уравнение пере-
носа массы, импульса и энергии.
Если сжимаемая жидкость содержит k компонент, то диффузионный поток
равен:	-	_	_
7*=Р*Й& — »)	О*2’4)
13
где вая	Vh—скорость движения молекул среды компоненты; Г—среднемассо- скорость, определяемая по соотношению v = ^yp„;j';i,	(1-2-5)
здесь р* —концентрация или плотность £-й группы молекул, связанная с плот-
ностью смеси р соотношением
Р = Ц₽4.	(1-2-6)
k
Полагая рЛ=С из уравнения (1-2-3) получаем:
^-+ div (р4Г)=- div7*+/rft.	(1-2-7)
Суммируя по всем k компонентам, получаем:
-^ + div рЙ=О, .	(1-2-8)
так как
-	(1-2-9)
k	ft	'	'
Используя соотношение
div po=cTgrad p-J-p div v,	(1-2-10)
уравнение переноса (1-2-8) можно написать
-^- + °  grad р=— pdiv	(1-2-11)
Обозначив субстанциональную производную через
d д	—
di ~ дт	v ’
можно уравнение (1-2-11) переписать в виде
dp , —
-^-«-divti.	(1-2-12)
Если жидкость несжимаема (р = const,
А^
-г~ = 0 , то
dr У ’
div'o=Q.
(1-2-13)
Воспользуемся соотношением
dbp ,	db
^L + dlv(bpIJ) = P1?.
Тогда уравнение переноса массы k-'й компоненты (1-2-7) можно переписать
так:
p~dT“”div^+^>	(1-2-14)
где рйо—относительная концентрация (р?го — р^/р)-
Молекулярный поток вещества fe-й компоненты определяется законом диф-
фузии, При наличии градиента относительной концентрации Vp^.o, темпера-
14
туры ГТ, давления Гр диффузионный поток массы А-ft компоненты равен
[Л.1-2]:
7»=-oe(vpto+Mln7'+MinP),	(1-2-15)
где первый член характеризует перенос массы за счет концентрационной диф-
фузии или обычной диффузии, второй член — величину термодиффузии и пос-
ледний член учитывает эффект бародиффузии.
Относительные коэффициенты термодиффузии kT и бародиффузии kp выра-
жаются через производные химического потенциала соответственно по темпера-
туре и давлению.
Если в-уравнение (1-2-14) подставить (1-2-15), то получим дифференциаль-
ное уравнение переноса массы:
p-^2- = div[Op(Vpto + JrV!nT+^Vlnp)]+/M. (1-2-16)
Если коэффициент диффузии и плотность не зависят от координат, то из
(1-2-16) получим;
^-=o(v’P1„+4f-V=7+iv»p) + -^-.	(1-2-17)
При этом было сделано допущение, что kT/T и kp/p также не зависят от
координат.
в)	Уравнение переноса количества движения (переноса импульса)
Уравнение количества движения или импульса выводится па основе урав-
нения баланса количества движения, рассчитанного па единицу массы жидкости:
~ С (mav= ( pFav+ ( 'Sas’, (1-2-18)
Т
где а —плотность поверхностных сил (поверхностные силы, рассчитанные на
единицу площади поверхности). Первый член (1-2-18) дает^полную скорость
изменения количества движения, она равна сумме внешних F и поверхностных
а сил, действующих в объеме Vm (т).
Вектор поверхностных сил а определяется через единичный вектор л1,
направленный по нормали п к поверхности S, и тензор внутренних напря-
жений П по соотношению
a = nin.	,	(1-2-19)
Используя теорему Гаусса—Остроградского, из уравнения (1-2-18) полу-
чаем уравнение движения Коши:
₽4r==p?+'iivri-	11-2’2о>
Введем тензор давления Р как отрицательный тензор напряжений
Р = -П.	. (1-2-21)
Тогда вместо уравнения (1-2-20) получим:
р-^- =- div Р-ЬрА	(1-2-22)
15
или
+ div (Р+ро») = ₽?,	(1-2-23)
где р7=2р»?».
Уравнение (1-2-23) можно было получить непосредственно из уравнения
(1-2-3), полагая, что переносимой субстанцией является количество движения
(С=ргГ)- Тогда Диффузионным (молекулярным) потоком субстанции является
тензор давления Р, а источником движения —действие внешних сил (/K=pF).
Тензор давления Р мЛкно разделить па две составляющие тензора.1 тензор
механического давления Р₽ (равновесная часть) и тензор вязкого давления Р”
(неравновесная часть Р):
Р = Р' + Р”.	(1-2-24)
Если жидкость изотропна, то в состоянии равновесия Рг' = 0, т. е.
I Р 0 0 I
Р = Ре=рб = 0 р 0 .	(1-2-25)
I о о р | 
где 6—единичный тензор, р — гидродинамическое давление.
Соотношение (1-2-25) можно написать так;
Рц = реа = Р = U 2- 3).	(1-2-26)
Для этого частного случая невязкой жидкости (pv = 0) из уравнения (1-2-22)
'получаем уравнение движения Эйлера:
p5 4-Vp=p?,	(1-2-27)
где
*=-^- + (o-V)o.	(1-2-28)
Воспользуемся соотношением (1-1-50), тогда уравнение (1-2-28) примет форму
уравнения Лэмба—Громеки:
5 =-|^- + у Vu2 + [» X curl o'] = F—у Vp.	(1-2-29)
Для гомогенных изотропных вязких сред тензор давления равен:
P = p6-|-Pz',	(1-2-30)
где Р’ является функцией градиента скорости Vy, для ньютоновских жидко-
стей Р71 является линейной функцией Vy. Тензор Рг может быть представлен
как сумма двух тензоров:
‘ p’ + p^+f>\	(1-2-31)
где р° — одна треть следа тензора Р’, т. е.
<	'’’==тр’:е“1<гр’,=4р£;	(1-2-32>
тензор вязкого давления с нулевым следом (Рт:	В общем ।
случае тензор Р^ может быть и несимметричным, т. е.
Р’ = р’Ь + P’s +Р’“ = у 1г Р’б +Р™+^,	(1-2-33)
так как след антисимметричной части тензора Р1*0 равен нулю.
16
Соотношение (1-2-33) можно написать в виде матрицы
pv pf Р«
r lir 21‘ 31
pv pv pv
r li~ 22' 32
no pv pv
Г18Г23‘ 33
1 U
зК-Л+Я ° i O H-
IO о i |
1 (2P?,	1 (₽’, +Я) | (P” +Я)
| (PS. + p?x) | « - PS. ~ PS.) ~ (P?, + PS.) +
4 (РГа + РЮ 4 И + Я) 4 W.-Pn
4(я-я)
4 (PS. -PS.)
±(ps.-p?,) 4(p--p'=i
о j-(PS.-PS.)
I (PS.-PS.) '	0
(1-2-34)
так как
p"=^(pv+pfl). р?,а=ъ(р</-р/1)’ ^Ц(р</+р»)+
+ 4м«: i, 4=1. 2, 3.	(I-2-35)
Принимая во внимание соотношение (1-2-30), тензор давлений в общем
случае равен;
Р^Ср + р^бЧ-Р^+Р^.’	(1-2-36)
Величина pv характеризует вязкий тензор давления при всестороннем
сжатии, характеризуемом величиной div и!
pz’ = — T)Kdivo,	(1-2^7)
где rip-— коэффициент объемной вязкости.
г 5 — характеризует вязкое давление, возникающее от сдвиговой деформа-
ции *:
₽” = - 2г, (V . о)’ = - 2Ч (vI)• + | n div «в, (I-2-38)
где т)—коэффициент сдвиговой вязкости;
(vj)s = (vr)s + 4div	(1-2-39)
Антисимметричная часть тензора вязкого давления равна аксиальному
вектору, который зависит от rot у и Q, т. е. является линейной функцией
градиента скорости:
₽то=-«), (?хГ—2П),	(1-2-40)
где Q—собственная угловая скорость вращения частиц, гр.—коэффициент вра-
щательной вязкости.
* Согласно закону виутреинедо-тренйя иафбй&е^ие трения является линей-
ной функцией градиепта--с-ко'рЗсти. t А ‘ u u \
Ш1-'11"-;'	.1С	\	17
В работе [Л.1-7] показано, что антисимметричная часть тензора вязких
давлений обусловлена внутренними микромоментами поверхностных сил,
Если в уравнение (1-2-22) подставить следующее выражение для тензора
давления
Р = р6-(г|1,-ул) divv6-2r|(vS)s-r>(vxo-26),	(1-2-41)
то получим дифференциальное уравнение движения:
р-^= pf-Vp + rjV2»+(уГ)+т|р) V div о+Пг curl (2Q-Curl'S). (1-2-42)
При этом используем следующие соотношения:
div рб = V (рб) = 2 (pfy) = 2”^	= ^р; *• / = !« 2« 3« (1-2-43)
i, i !	i 1
где
б/у = 0; /=/=/; 6у=1; i=/; 2(?7i)s = [Vv+(^)q; (1-2-44)
div (vu)r = V (div u).	(1-2-45)
Справедливость последнего равенства легко проверить, В самом деле, ком-
понента тензора третьего ранга Q/у* равна:
= <Ь2-46>
Следовательно, Qy/e = 0 для любой криволинейной системы координат.
Поэтому результат неоднократного ковариантного дифференцирования не зависит
от порядка дифференцирования для эвклидова пространства. Уравнение (1-2-42)
впервые было выведено де Гроотом [Л.1-5].
Если тензор вязких напряжений^ симметричен Рг'=(Рх’)г, то уравнение
(1-2-42) отличается от обычного уравнения Навье—Стокса
р	pF - Vp + riV2” +(4“ T|+,|l') grad div ”	(1-2-47)
членом т]г curl (2Q —curl v), характеризующим перенос импульса вращательной
диффузией. Для несжимаемой жидкости (р = 0), последний член уравнения
(1-2-47) равен нулю (div о=0), тогда уравнение (1-2-27) получается из урав-
нения (1-2-47).
г)	Уравнение переноса моментов количества движения
Система дифференциальных уравнений движения сплошной среды не замк-
нута. Можно получить другие универсальные уравнения, не зависящие от
свойств движущейся среды. Если в классическом уравнении механики
m-^- = F	(1-2-48)
ах
умножим на радиус-вектор г обе его части, то получйм уравнение моментов
количества движения для материальной точки:
^-=7х?,	(1-2-49)
ах
где
fe=[7xw^]«	(1-2-50)
18
Следовательно, уравнение (1-2-49) — следствие второго закона механики
Ньютона.
Момент количества движения объема V сплошной среды равен:
^=5 Fx?]pdV.	(1-2-51)
V
Для некоторых модельных жидкостей, особенно при наличии действия
внешних полей, необходимо учитывать плотность собственных или внутренних
моментов количества движения К1. Тогда в общем случае будем иметь:
j [7х v] pdV 4- J KlpdV.	(1-2-52)
V	V
Все атомы и молекулы обладают собственными моментами количества дви-
жения К1, ио в силу хаотичности движения сумма этих моментов равна нулю.
Однако при некоторых условиях (наличие электромагнитного поля, реологи-
ческих свойств жидкости) сумма внутренних моментов будет отлична от нуля.
В классической механике сплошной среды внутренние моменты X' не учиты-
ваются.
При наличии К1 необходимо допустить существование распределенных мас-
совых и поверхностных пар сил, действующих на частицу сплошной среды.
Обозначим через F' и о' моменты массовых сил, рассчитанных на единицу
массы, и поверхностных пар, рассчитанных на единицу поверхности, Тогда
уравнение моментов количества движения для конечного объема сплошной
среды будет иметь вид:
(7х Л pdv+ ( 7'pdl/l-[(7 х ?)+F] р dv + [(7xa)+a‘]dS.
V J V	s
(1-2-53)
Полная производная по времени от момента количества движения объема V
сплошной среды с учетом собственных моментов равна сумме моментов внешних
массовых и поверхностных сил, действующих на этот объем, и сумме собствен-
ных моментов, распределенных массовых и поверхностных сил. Переходя от
поверхностных сил к тензору внутренних напряжений П по соотношению
(1-2-19) и затем заменяя тензор напряжений П па тензор давления Р (Р —— П),
уравнение (1-2-50) в отсутствие внешних сил (f=0) и внутренних сил и
моментов (F1 = Л? = 0) получаем в виде
^4-[rXdivP] = 0,	(1-2-54)
где К*—внешний угловой момент или внешний момент количества движения,
точка означает производную по времени (_Ke = dKe/dx)’
Воспользуемся соотношением
[7xdivP] = div(7xP)+Pr — Р,	(1-2-55)
а также
Р-Р7'=2Р”“,	(1-2-56)
где Pva—аксиальный вектор, равный антисимметричной части тензора давле-
ния Pv. Тогда из уравнения (1-2-54) получим:
p^e + div[7xP] = 2P“.	(1-2-57)
Уравнение (1-2-57) можно переписать в виде
Д^ + div [7 xP+pKev] = 2?’‘>.	(1-2-58)
Уравнение (1-2-58) аналогично уравнению переноса любой субстанции
(1-2-3). Роль источника угловых моментов движения играет аксиальный вектор
Pva, величина (гхР) является молекулярной составляющей частью переноса
угловых моментов, a pKev— конвективной составляющей переноса.
Если тензор вязких напряжений симметричен (Р = Р7'), то аксиальный
вектор Рта равен нулю.
Если учесть внутренние угловые моменты К1, то можно положить
+	(1-2-59)
где ^=^/й; Q—«собственная» угловая скорость вращения частиц среды*,
/ — момент инерции частиц среды.
Тогда, если обозначим тензор внутреннего углового момента через 5й, то
получим для консервативной системы [Л.1-6]:
рК -I- div ([7 X Р] + IT5) = О,	(1 -2-60)
где — полярный тензор третьего ранга.
Если воспользоваться уравнением (1-2-57), то из уравнения (1-2-60) получим:
pi?'+<tiv ^ = — 2Р’“.	(1-2-61)
Следовательно, несимметричность тензора напряжений обусловлена микро-
моментами. При наличии объемно-распределенных моментов в результате внут-
ренних сил F1 они также являются причиной несимметричности тензора напря-
жений П. При наличии внешней силы F уравнение (1-2-60) примет вид:
рЛЧ-div ([7xP]+^)=p(7xf).	(1-2-62)
д)	Уравнение переноса энергии
Вначале рассмотрим уравнение переноса кинетической энергии движения,
для чего воспользуемся уравнением (1-2-22), которое написано в виде
ро =—div Р-Ьр/7-	(1-2-63)
Умножим обе части равенства (1-2-63) на в и используем соотношение
v div P = div (Р • y)4-(Pr:Vo)-	(1-2-64)
Тогда получим уравнение переноса кинетической энергии, которое в вектор-
ной форме будет иметь вид:
рй£ = —div (Р ."о) +(Рг: Vp)-}-pF • о >	(1-2-65)
1 -
где ek = ~2 V2—кинетическая энергия единицы массы жидкости.
Это уравнение можно переписать так:
+ div (Р • u4-pf>ftv) = tr (PVu) +p(F  v)>	(1-2-66)
Следовательно, диффузионный перенос кинетической энергии характери-
зуется величиной (P-v), а источником является работа внешних сил (р. и)
и внутренних сил tr(PVu). На последнем остановимся несколько подробнее.
* Под угловой скоростью следует понимать величину, усредненную по
физически малому объему, характеризующую некоторое внутреннее вращение
в нем, отличное от движения его как целого.
20
Градиент скорости Vo является диадой (тензор второго ранга), он может
быть представлен в виде
tr(Va)6 + (vo)s4-(Vo)a.	(1-2-67)
где
tr (Vo) = (V’L':6) = diV v	*	(1-2-68)
— след тензора V7. Последующие члены равны:
(vv)‘ = -i(Vo + (Vo)r)-y div о8;	(1-2-69)
(V»)s=4(V”+(rtr):	(1-2-70)
(V? + (?Г)Г)-	(1-2-71)
Кроме того, Рв’рбН-Р®, а величина Р® определяется из соотношения
(1-2-36), поэтому можно написать:
(Pr:vL) = (p + pt')divo+[f)t'5 : (vT)5]-[Р7"1: (Vo)°].	(1-2-72)
При выводе были учтены соотношения Pv'r = (PB,y)r, Pw,3 =—(Рм)г. В гидро-
динамике вводится вращательный вектор Q по соотношению
y[VX»] = (V0»=/Q-	(1-2-73)
Тогда можно написать:
(Р”° : Й“) = - ?“ (VXv)= - 2ЯР”“.	(1 -2-74)
Таким образом, источниками переноса кинетической энергии являются
вращение жидкости, ее сжимаемость и температурное изменение за счет
диссипации механической энергии, При наличии вращения жидкости кинети-
ческая энергия состоит из энергии поступательного движения g-t»2 и враща-
тельного движения JQ*:
«Л—^+4 да	'	(1-2-75)
где J—момент инерции единицы массы.
Тогда уравнение (1-2-65) примет вид:
р l(t> i) +/ (S5)J +<tiv (PSj-pF.S+fp + p’) divo-Hf’” : (Vo)SJ +
+ [P“(VXD~2Q)].	(1-2-76)
При этом было использовано уравнение
£21Р’“— 2й.Рм.	.	(1-2-77)
При наличии поля консервативных внешних сил вводится скалярный
потенциал фд с компонентами k согласно соотношениям
^-=0.	(1-2-78)
21
Тогда потенциал жидкости <р равен:
п	п
<Р = ~	₽**₽*= 2 РлоФй-	(1-2-79)
4 = 1	4=]
Следовательно
п
?=~ 2 РЛ = — Тф-	(1-2-80)
4=1
Тогда полная механическая энергия единицы массы жидкости равна:
ет =~2 у2 +у ^2+ф>	(1-2-81)
а уравнение переноса механической энергии будет иметь вид:
p;n[H-div7fm=/em,	(1-2-82)
где —диффузионный поток механической энергии,
7гя = (₽ ”)+.£ ыТь;	(1-2-83)
Й=]
'Гет - источник механической энергии,
/c„=(p+p’)‘Hv” + P”I'(',?)1s+p’“(Vx';-2Q)+ 2
k — ] у = 1
- S 7i?«. (1-2-84)
k= 1
здесь v^Y—стехиометрический коэффициент химической реакции у (у= 1, 2,
3,	, Г); /у — поток массы при химической реакции у.
Все члены выражения источника lefn являются внутренними источниками,
за исключением последнего, который отображает работу внешних сил,
Уравнение переноса механической энергии может быть написано в виде
+	(7ет+рея”)”=Лт-	(1-2-85)
В заключение рассмотрим перенос внутренней энергии и.
Энергия единицы массы жидкости е равна:
(1-2-86)
По закону сохранения энергии
e-f-div /с=0,	(1-2-87)
где уе—диффузионный поток энергии.
Воспользуемся соотношением
Р (е —em) + <liv (Ze — £.„,) = - lem.	(1-2-88)
Тогда будем иметь;
p«+div7a=/a,	(1-2-89)
22
где
=	+ div piw;	(1-2-90)
^=-!em=-(P^pv)^^-ipvs--m]s-^a (vxli-2fi)4-s 7Л-
4== 1
(1-2-91)
Если обозначить удельную энтальпию через h, то при отсутствии хими-
ческих реакций и при симметричном тензоре внутренних напряжений диф-
ференциальное уравнение переноса энтальпии примет вид:
P^- + divS, = ^-(P’:V'S) + 27A.	(1-2-92)
k
где /л — поток энтальпии.
Используя уравнение переноса (1-2-16) и полагая удельный поток энталь-
пии /д равным потоку тепла /д(/\=/?), из уравнения (1-2-87) получаем диф-
ференциальное уравнение Фурье —Кирхгофа [Л. 1-2]:
V = div (МТ + Q’DpVpt„) + 2 V+ rff + Л®, +
k
+ ScJ>"/»v7’+S	(1-2-93)
где Ср—удельная изобарная теплоемкость,
dh V	V dhk	п .
Ср — dT ~ Aj — Zj ~ат Pft0’	(1-2-94)
k	k
здесь Ср^—удельная изобарная теплоемкость Л-го компонента; Zt& — удельная
энтальпия А-го компонента; X—коэффициент теплопроводности;
‘ /
где Ф„ —диссипативная функция Рэлея.
При выводе уравнения (1-2-88) эффектом бародиффузии пренебрегаем и
принимаем 1^=0 (объемная вязкость равна нулю).
Согласно исследованиям Трусделла [Л.1-8] предел применения уравнений
Навье—Стокса для разреженного газа определяется соотношением Тг < 1,
где Тг—число Трусделла, равное:
Тг=^.	(1-2-96)
Если принять максвелловский закон распределения молекул, то число
Трусделла пропорционально произведению числа Кнудсена (Кп) на число
Маха (М);
Тг = -|- Кп М.	(1-2-97)
Таким образом, для разреженного газа, движущегося с большой скоростью
(М> 1), число Трусделла может быть больше единицы (Ti > 1). В этом слу-
чае уравнение Навье—Стокса не будет применимо для описания движения
сжимаемой жидкости.
Однако в случае движения несжимаемой, но очень вязкой жидкости при
больших скоростях деформации сдвига число Трусделла также может быть
23
больше единицы. Поэтому и в этом случае уравнение Навье—Стокса также
не будет иметь места.
Ьторая особенность уравнения движения состоит в том, чтв на основе его
решения нельзя объяснить процесс возникновения вихрей. Решения уравнения
Навье—Сгокса объясняют процесс исчезновения вихрей, а не их образование.
Можно показать, что движение жидкости дискретной структуры описы- -
вается обобщенным уравнением Навье—Стокса [Л.1-8]. Дискретность струк-
туры для разреженного газа определяется тем обстоятельством, что в пределах
физически малого объема переносные скорости молекул различны. Другими
словами, в пределах малого объема, по которому происходило усреднение
микроскопических величин, изменяется скорость видимого движения. Поэтому
приходится переопределять среднюю скорость движения. Такая же физическая
картина имеет место при вихревой структуре жидкости (жидкость состоит
из отдельных вихревых трубок). В этом случае распределение скорости движе-
ния жидкости описывается разрывной функцией.
Для вывода уравнения движения приходится также использовать правило
усреднения или методику нахождения производных от разрывных функций.
1-3. ТЕРМОДИНАМИКА ЯВЛЕНИЙ ПЕРЕНОСА
Перенос импульса, энергии и массы сопровождается ростом энтропии
текучей среды. Возникновение энтропии в явлениях конвективно-диффузион-
ного переноса может служить характеристикой термодинамических движущихся
сил X и соответствующих потоков f. Источник энтропии по основному соот-
ношению термодинамики необратимых процессов пропорционален сумме произ-
ведений потоков па термодинамические силы [ЛЛ-&]:
=	=	С’3'1»
где потоки Ji и силы Xj могут быть тензорными величинами любого ранга.
Величина disldx является мощностью источника энтропии ls (/5 = d^s/dT).
Для того чтобы определить ls, необходимо иметь уравнение переноса
энтропии, которое выводится из уравнения переноса внутренней энергии
с использованием уравнения Гиббса:
+	(1-3-2)
где й —производная удельного объема (ti«l/p); щ —химический потенциал
А-го компонента.
Это уравнение будет иметь вид:
Tpi+div7«-2> divT»=S 2 mWv+S /Л-tr (PV ») + 25?“.
k	k V	k
(1-3-3)
Используя соотношения
div7? = T div (Tj/n-rivV (1);	(1-3-4)
wdlv7*=Tdivi^—.('-3-5)
уравнение (1-3-3) перепишем так:
где js—диффузионный поток энтропии,
/.-£ Vv+Гл+Е /л+р’^+£'“ :х;+р”х;, о-з-8>
V	№
здесь /Ц—химическое сродство реакции у, ,
^=-“21^4^: Y=l. 2, 3,	, Г.	(1-3-9)
На основе соотношения (1-3-1) находим, что термодинамической силой
химической реакции у является химическое сродство Ау (скалярная величина),
а потоком массы при химической реакции является скорость химической
реакции (скаляр):
Ху =3 А у: J у = /у*
(1-3-10)
Полярный вектор (тензор первого ранга) Xq является термодинамической
силой теплопроводности, поток которой равен jq.
X,=-2„- = -VlnT; Г, = г,-	(1-3-11)
Термодинамической силой диффузии является вектор Хд:
7*=Д.	(1-3-12)
Скалярная величина ХФ является термодинамической силой переноса
импульса при всестороннем сжатии жидкости с потоком, равным
XB==-div£ Jv~pv.	(1-3-13)
Тензорная сила вязкости соответствующая симметричной части тен-
зора вязкого давления с нулевым следом Р®, вызывает перенос импульса при
сдвиговой деформации:
X» =-(?;)“; W”	(1-3-14)
Аксиальный вектор Х& является термодинамической силой переноса им-
пульса при вращательной вязкости:
X“ = -(VXO-2SJ); 7О=?’“.	(1-3-15)
В соответствии с основным положением термодинамики необратимых про-
цессов потоки определяются соотношением Опзагера
7(=£Ь(Л,	(1-3-16)
k
где Lot—кинетические коэффициенты.
Для изотропной среды согласно принципу Кюри сочетание У] Ь^Х^
k
возможно лишь в том случае, если термодинамические силы Х% являются
тензорами одинакового ранга или разница в рангах четная [Л. 1-5].
Следовательно, тензорные силы второго ранга могут сочетаться между
собой или со скалярными силами (скаляр-тензор нулевого ранга), а вектор-
ные силы сочетаются между собой и тензорными силами третьего ранга, так
как вектор —эго тензор первого ранга.
25
Следовательно, для изотропной Среды можно написать:
^у/~У1	/=1» %, 3.....Г; (1-3-17)
v
p’=24^v+t('%;	(ьз-|8)
V
jq = LqqXg -р У] Lq^Xk',	(1-3-19)
k
Ti^^ia^q-V'S^ikXk; 1=1, 2, 3.........й-1;	(1-3-20)
k
pva = [(aa)%(a),	(1-3-21)
£*™ = L(MXs0.	(1-3-22)
Индексы в скобках у кинетических коэффициентов («), (аа), (tf) обозна-
чают характер потока и силы: скаляр—скаляр, аксиальный вектор — аксиаль-
ный вектор и тензор—тензор.
Сравнивая полученные соотношения (1-3-17)—(1-3-22) с известными соот-
ношениями диффузии, теплопроводности и вязкости, получаем:
ЬЯЯ=ХТ-, =	1\“'=2Л- Z.(‘“’ = ^,	(1-3-23)
где т)г—коэффициенты вращательной вязкости.
Для анизотропной среды нелинейная система уравнений примет вид
(SS) (SS)	(SD)	k — 1 (SV)	(sa)	(st)
Ji =2 ЧеЛ+ ^4+ Л+ 2 rT 	: *V:
7	(1-3-24)
(SS) (SS)	(so)	k — 1 (SV)	(sa)	(st)
P” = 2 ЦСАУ+ Li,vxv+ £v“-xq+ 2 L''“.X’k+ Lvv -Xy +LVV Xsv;
V	k
(1-3-25)
(vs) (vs)	(vv)	(vv)	(va)	(vt)
/>2Ф\ +	L^X?4-S	UvX° + Uv (1-3-26)
-v	k
(vs) (vs)	(vv) _ (vv)	(va)	(vt)
Л=2 Г?Я+ Lfxv+ .^+3 L".x^+ E" .X“v + Cf”: XV;
V	V
(1-3-27)
(as) (as)	(at>)	(av)	(aa)	(at)
РИ“ = 2 r^+ L‘'l,Xv+El'’.X,+ SLy''.XJ+ L^.XJ + L^XV;
V	V
(1-3-28)
(Is) (IS)	(tv)	(IC)	(ta)	(it) _
Pl's = 2 L^v+ Ll'l%+ L<V«>.X? + SL".XJ + LV'V -XV+ Lv'v:XV.
V	*	>
(1-3-29)
Индексы обозначают: (sa) есть скаляр—аксиальный вектор; (/о) — симмет-
ричный тензор с нулевым следом — аксиальным вектором и т. д. В табл. 1-1
прйведены кинетические коэффициенты с пояснением их тензорных величин.
Из соотношений (1-3-24)—(1-3-29) следует, что для сложной текучей среды
все явления переноса импульса, массы и энергии, а также химические и фазо-
вые превращения взаимосвязаны и влияют друг па друга.
26
Таблица 1-1
Кинетические коэффициенты (Л.1-6]
Порядок тензора		Полярный тензор	Аксиальный тензор		
0	(скаляр)	(SS) (SS)	(S?)	(ss) Lf, Z-4'c,			
1	(вектор)	(sv) (sv)	(SV) (vs; (vs) L^, LV(i, L™, L*d, Lf, (VS) (vs) (vs) c t’1', if	(sa)	(sa) (as) Lvv. LVC.	(as) Lvv
2	(тензор)	(vv)	(VV)	(VV)	(vv)	(Si) L™, Lf, Ldt>, Ldd, L9V' (Sf)	(is)	(is)	(aa) Lvv, L^c, Lvr,	va L"v,	(va) (av) LfVt 1У\	(av) tVd Lk
3	(тензор)	(V/)	(V«	(/V)	tfV) j_q\/	^dV	[У Q	[У d		(a()	(ta) Lvv, Lvv	
4	(тензор)				
Отсюда вытекает, что уравнения переноса существенно зависят от свойств
самой среды,
Дальнейшим развитием термодинамики необратимых процессов является
нелинейная термодинамика сплошных сред, созданная работами К. Трусделла
и его последователей [Л.1-8—1-10|. В ней рассматриваются явления пере-
носа для любых материальных сред с нелинейными законами. J
1-4. МНОГОКОМПОНЕНТНЫЕ СМЕСИ
Дифференциальные уравнения переноса массы, импульса и энергии для
многокомпонентной системы остаются прежними:
fe = -div(z\ + pt?) + /ra; li=l,2,3......п- (М-1)
^H-=-div (^+рв7)+2рЛ:	О-4-2)
k
'	= div ру -|-	У + (о • <^)j+ Д Ffr (pbV-Vjk)'
(1-4-3)
Условно обозначим:
^“/'и + Р! (и +	+	(М-4)
л = ^ + рЕГ^	(1.4.5)
-т - _	--
"iA“PAV4-/ft«ppAoU4-/A,	(1-4-6)
27
где —полный поток энергии жидкости (текучей среды), состоящий из диф-
фузионного потока внутренней энергии конвективного потока кинетиче-
ской энергии видимого движения и внутренней энергии и конвективного пере-
носа энергии давления и сил внутреннего трения. Тензор л состоит из тензора
давления и диады ру ц, поток массы равен сумме диффузионного и
конвективного р*у потоков массы,
Тогда уравнения (1-4-1)—(1-4-3) можно написать так:
^ = -<04	+	4=1,2...;	(1-4-7)
,	п
fc-=_<Hvn+2^P»:	(1-4-8J
k
J^pU + -i-p^) = -div/,, + 2;s'"»'	О'4'9)
k
Если внешние силы являются консервативными и не изменяются с тече-
нием времени, то их можно заменить соответствующими потенциалами, а ра-
боту внешних сил —потенциальной энергией:
Л = — gradi|>s = — V-ф*; ^/94=0.	(1-4-10)
Обозначим потенциальную энергию единицы массы смесн через
^=';УрЛ- ’	(1-4-11)
Тогда дифференциальное уравнение переноса потенциальной энергии
можно будет написать в виде
® = - div +	—2	О'4'12)
\ k /	/г	ч
Частная производная по времени от объемной плотности потенциальной
энергии равна сумме дивергенции потока энергии и стоков потенциальной
энергии. Поток потенциальной энергии состоит из конвективной рфц и кон-
дуктивной 2 составляющих. Сток потенциальной энергии обусловлен
работой внешних сил при движении жидкости у - р^Гд и работой внешних
k
СИЛ При диффузии У] /fe  В этом случае полная удельная энергия равна:
k
е = у +	(1-4-13)
плотность потока энергии
Л = ре»+7(/ + 27Л + (”’-'35).	(1-4-14)
k
Полный поток энергии Те состоит из:
1)	конвективного потока энергии, вызванного движением жидкости, pev;
2)	диффузионного (молекулярного) потока энергии /у, передаваемого хао-
тическим движением молекул;
3)	молекулярного потока потенциальной энергии 2 вызванного диф-
к
фузией вещества в поле внешних сил;
28
4)	конвективного потока энергии молекулярного давления и сил внутрен-
него трения v 
Дифференциальное уравнение переноса энергии приобретает простой вид;
= — div 4	(1-4-15)
В табл. 1-2 приведены разные формы записи уравнения переноса энергии.
Такие записи уравнения переноса энергии вытекают из физической сущ-
ности энергии. По закону сохранения энергии энергия не создается и не исче-
зает, а лишь переходит из одной формы в другую. Поэтому если уравнение
переноса записано для полной энергии е, то источников или сгоков в урав-
нении переноса быть не может. Тогда уравнение переноса энергии формули-
руется гак: локальное изменение по времени объемной концентрации энергии
равно дивергенции от-плотности потока энергии. Уравнение (1-4-15) является
уравнением Умова, а вектор переноса полной энергии ]е называют вектором
Умова. Дифференциальный поток массы jdll А-го компонента определяется
соотношением
=	*=!. 2.......".	(1-4-16)
где /^-диффузионный поток при системе отсчета а скорости движения
жидкости va, т. е. индекс а характеризует систему отсчета. Все системы от-
счета должны удовлетворять соотношению
(1-4-17)
А = 1
где — нормированные веса, удовлетворяющие равенству
2 "4=1.	(1-4-18)
k=l
В табл. 1-3 приведены наиболее употребительные весовые множители,
системы отсчета и диффузионные потоки.
Массовая скорость движения жидкости
-----= Vfw‘: (>	(1-4-19)
k	4
Весом при отсчете является относительная концентрация pft0.
Мольная скорость движения жидкости
с	с=2с4- 	(1-4-20)
k	1г
Весом при отсчете является относительная мольная концентрация.
Для бинарной смеси, состоящей из компонентов Л и В, основные соотно-
шения приведены в табл. 1-4, а массовые и мольные потоки —в табл. 1-5 [Л. 1-11].
Из основного соотношения	Для бинарной смеси имеем;
Л=-----/в.	(1-4-21)
Различные формы записи закона концентрационной диффузии для бинарной
смеси приведены в табл. 1-6. В общем случае многокомпонентной смеси диф-
29
Таблица 1-2
Уравнение переноса энергии многокомпонентной системы
£ = /7+^+'Ф при условии ^Y==oj;
P^ = -(V;«)-(vb95-t’l)+ 2
i — 1
t/+K = t/+y»2:
1 = 1
к=Г-
p^-=-(»[v^j+ 2
1 = 1
1/1 ' „ •
P^ = -(V-/«)-(^:Vp)+2 (W<);
H:
P^- = - (*'•/«)+27-'(°:V”>+ 2
CP:
pcp^ = — (?-/«) — (a:V0)+ 2 (il-gl) +
i—i
Cvt
^^ = -(v-/«)-(^-M+2 </г'«>+(р“7‘(5т)р. CJ v'“+
I — I
+ 2[t/‘-+(p-7'w;)y'][(v"/,>”/iI;
Hl-.
2 w^=(vwr>+3r-(o:V[,’+2(w,)-
30
Таблица 1-3
Весовые множители а/г в разных системах отсчета
Веса	Скорость системы отсчета иа	Диффузионный поток
Массовая концентрация Рао	Массовая скорость 7=2 Р*""»	Й = Р4&— v)
Мольная концентрация Cko	Средняя мольная скорость h	7Г=р,<С*-Л .
PfcVA	Средняя объемная скорость °°=2 р*0*’* *	74=Р4С,-"0)
^ki	Средняя скорость t-ro ком- понента й=2л'“'3'	7;,=pt(?;-”,-)
Примечание.
szCjjC — относительная
pfe0 —относительная массовая
мольная концентрация.
концентрация, Pfe0 = P^/P; Скй=-
Таблица 1-4
Основные соотношения для бинарной смеси (Л -|- В)
СЛ(| + СО0~ ''
<7Л + Л Л(Г'^Л=,г!;
, Рло/Мл
л° ₽л«/мл+₽до/мв'
аРм
Рло + Рао = 1;
Рл«/'ил + Рв«/'ив=м:
0 С^мл .
₽ло Сл<,Мл + С80Мя’
,	^д'^в^Ло
Рло (Са<^а + СМ*-
Примечания; 1. р = Р/|-|-Рз —плотность смеси, г/см’. 2, Р_д = СдAiд — концент-
рация компонента Д, с/см’, смеси, 3. Рдо= р^/Р—относительная концентрация. 4. С =
= + —мольная плотность смеси, гмоль/см*. 5. Сд =р^/М—мольная концентрация
компонента А, гмоль/см*, смеси 6. Сдо = Сд/С —относительная мольная концентрация.
7. Af =р/С —молекулярная масса смеси.
фуэиоиный поток концентрационной диффузии
(1-4-22)
где Voj есть (п— 1)-мерный вектор с компонентами Vco/, Va>2, ...,	а «а —
некоторая величина, характеризующая состав смеси, например pfe, Ck, и т. д.
Величина Daa является тензором из I)2 коэффициентов диффузии,
соответствующим скорости системы отсчета иа и параметров состава w. Для
Другой скорости системы отсчета ~vb получим;
р = —D^Voj.	(1-4-23)
31
Плотность мольного потока компо-
нента А, гмоль/(см2«с)
Суммарный поток массы, г/(см2 • с)
32
Таблица 1-6
5?
ч
.a.
II
• 5
s
«t? «з
5 I?
II
£
*•<
II
+
II
• =L
Эквивалентные формы формулы закона диффузии Фика для бинарной смеси
Поток	Градиент	Форма для закона диффузии
		-Рло (^л + “в) =-
	vc,!o	Рл“ САо (Ил + Рл) = — СОАВ,САС
г ‘л		/л = -рО1ВТрЛ0
1		J^—CDab^Ao
1 /л	vcao -	1А = -С* МлМвОав^аь
J1	'р.40	JA=^Ci/^)D*B'^
С(“л~“а)		CD a jj
Тензор Dba связан с тензором Da<a соотношением

где ВаЬ—тензор, не зависящий от выбора w и определяемый соотношением
(1-4-25)
здесь k, j = l, 2, л—1.
Поэтому для определения коэффициентов диффузии Da<a выбирают систему
отсчета и параметр состава смеси со; тогда соотношение (1-4-22) является исход-
ной расчетной формулой. Если состав смеси характеризуется другим парамет-
ром ф, то между ними существует соотношение
ГШ=~Тф,
дф т
(1-4-26)
где dw/дф есть (л—1)-мерная матрица с элементами Ло^/дфу.
Таким образом, в общем случае
it'= — BbaDaw~W.
1	дф Y
(1-4-27)


Более подробно методика расчета диффузионных потоков в многокомпо-
нентной смеси изложена в [Л. 1-5].
Молекулярный (диффузионный) перенос происходит под действием несколь-
ких термодинамических сил. Обычно различают концентрационную диффузию
(термодинамическая сила является градиентом концентрации), термодиффузию
VT, бародиффузию Vp и силовую диффузию (диффузию под действием внешних
сил Fh)
2 Лыков А. В.
33
Обозначим относительную мольную свободную энтальпию через G, а моль-
ный обьем через И, тогда
2	2 (1^,),. с Ч»|; <м-28>
1=1	L ;=1 S^I, / J
=w 2 MkM,Du [С'Л (й ~	т₽]:	(1-4-29>
’^=~^г 2 МкМ‘°» [ с‘°м< [о - 2 ?'У1; (м'зо)
/=1 L \ y=i р yj
/(Л=-Л{Г1ПГ,	(1-4-31)
где Dkl — коэффициент диффузии газовой смеси; — коэффицнеш термической
диффузии'. Они удовлетворяют соотношениям
Du=°; S DTt=0-,	(1-4-32)
А = 1
J	(1-4-33)
fe=J
Для п>2 величина Dy не равна Djf.
В частном случае для бипарной смеси имеем:
С2	Г/ дб, \
-7(?л-?В) + (^-7)^]-^1п^	(1-4-34)
Используя равенство (dGr — RTd (In а)т, где а—химическое сродство,
а также введя термодиффузионнос отношение
= аСА0СВ0 ~сСАоСВоТ’	(! '4*35)
где а —постоянная термодиффузии; а—коэффициент Соре, уравнение (1-4-34)
перепишем так;
.	maMi]daiiт ?САа-
 (М-36>
В заключение остановимся на молекулярном (диффузионном) потоке энер-
гии /у. Он состоит из потока теплоты теплопроводностью, определенной зако-
ном Фурье, диффузионной теплопроводностью (эффект Дюфи) fa и переноса
энергии за счет диффузии
=	(1-1-37)
34
' В общем случае коэффициент теплопроводности К является тензором
В отсутствие магнитного поля тензор теплопроводности симметричен:
k=L	(1-4-38)
Диффузионная теплопроводность для многокомпонентной системы иссле-
дована мало; кроме того, ее величина незначительна (;rf = 0), Общий поток
энергии равен:
	=	+ i	(1-4-39?.
k	k
Если поле внешних сил отсутствует (ф = 0), то, пренебрегая переносом
кинетической энергии видимого движения, диффузионной теплопроводностью
и работой сил внутреннего трения, получаем;
je - МТ + S Ад?* + pUv + pi - MT + 2 hift + phi=
k	k
= -7ST +2 (Л/Л + рЛТ) = — иг + 2 ОрЛ + рЛ?) =
k	k	~
=— WT+2*»™»,	(1-4-40)
k
где h — ^pkffhk.
k
Выражение (1-4-40) для потока энергии встречается в ряде статей и мо-
нографий.
1-5. ВЫВОД УРАВНЕНИЙ ПЕРЕНОСА НА ОСНОВЕ КИНЕТИЧЕСКОЙ
ТЕОРИИ ГАЗОВ
Уравнения, описывающие явления переноса массы, импульса и энергии,
можно получить из решений интегрально-дифференциального уравнения
Больцмана
о-5-1’
где ft (i, Г»т) dr dWt — число молекул сорта k, находящихся в момент вре-
мени т в интервале (7, 7-f-Jr) и обладающих скоростями (Wk, Wk-[-dWk)
в многокомпонентной смеси нереагирующих газов.
Второй член в левой части искомого уравнения представляет собой изме-
нение функции распределения вследствие молекулярного движения, третий
член — ускорение под действием внешней силы F/t (на единицу массы) и, на-
конец, член правой части определяет скорость изменения за счет бинарных
столкновений с частицами того же сорта k и других сортов I. При этом пред-
полагается, что молекулы не обладают внутренними степенями свободы, а силы
взаимодействия между ними являются короткодействующими центральными
силами.
Массовая плотность
=	=	' (1-5-2)
где т/t и пь — масса и плотность молекул сорта k соответственно. При этом
полная плотность смеси
P =	=	(1-5-3)
2*
35
Продифференцировав по времени (1-5-2) с учетом основного уравне-
ния (1-5-1) и используя известное свойство интегралов столкновения, получим
уравнение сохранения массы ^-компоненты:
dr J дх	J	dr	dWk
J (1-5-4)
Так как fk быстро стремится к нулю при больших значениях то вто-
рой член правой части уравнения (1-5-4) равен нулю. Аналогично и последний
член равен нулю'в силу известных свойств интегралов столкновений.
Следовательно;
^ = -divp4rt,	(1-5-5)
Где =	dWk — средняя скорость компонентов.
Если ввести массовую скорость по соотношению
5 ^kfkdWk, k	.k		(1-5-6)
то уравнение сохранения массы примет вид:	«	
= —divpj» —(Iiv7s,		(1-5-7)
причем величина		
/4 = ™» J (л7» — dw»		(1-5-8)
является диффузионным потоком массы.
Уравнение движения или уравнение переноса импульса получим, продиф-
ференцировав (1-5-6) по времени;
^ = —<tiv (ркТ+^+^РЛ-	(1-5-9)
k
Здесь тензор давления
X1-5-I0)
Плотность внутренней энергии р(/ определяется соотношением
f (Ws-7)3/4 dWk.	(1-S-ll)
k
Для температуры T (кинетической температуры) справедливо соотношение
-|/^а=р(,'=-‘-У m, j (Ui-'i-o)3,-,.. ,1114,	(1-5-12)
где п — плотность частиц смеси /я = ^дА\.
\ k )
Продифференцировав (1-5-11) по времени и используя уравнение Больц-
мана, получим;
^ = ^dlv(pt/u4-79)-(^jVi;)-V7ftFfe.	(1-5-13)
36
Здесь тепловой поток (поток энергии) равен:
 (1-5-14)
k
Таким образом, классические уравнения переноса описывают физически
механизм переноса в системах, подчиняющихся уравнению Больцмана.
Однако уравнения (1-5-13) и (1-5-9) являются незамкнутыми, так как
входящие сюда тензор давления и тепловой поток fa не определены; для их
определения необходимо знать функцию распределения fa, которую мы можем
отыскивать из решений уравнения Больцмана, Поэтому точность замыкания
указанных выше уравнении связана с точностью решений уравнения Больц-
мана.
Известно, что решение уравнения Больцмана в первом приближении при-
водит уравнение (1-5-9) к форме уравнения Павье—Стокса. Второе прибли-
жение, найденное Барнеттом по методу Чепмена — Энскога, вводит в систему
уравнений движения новые члены, которые уже в какой-то степени учитывают
изменения градиентов скоростей н температур на средней длине свободного
пути молекул. Существует решение уравнения Больцмана и в третьем прибли-
жении. Оно известно под названием супербарнеттовского решения.
В течение нескольких десятилетий результаты этих приближений счита-
лись бесспорными. Однако в период с 1949 по 1954 г. были проведены опыты
по определению толщины ударной волны и измерению скорости ультраакусти-
ческих волн в разреженном гелии. Основным результатом этих тщательных
опытов являются неожиданные факты:
I. Уравнения Навье—Стокса справедливы в более широких пределах, чем
последующие приближения.
2. Для ©писания явлений в очень разреженных средах ни та, ни другая
теория недостаточна.
Анализируя описанное столкновение молекулярно-кинетической теории
с опытными фактами, А. С. Предводителев в работе [Л.1-12] писал: «Если
допустить, что разработанные математиками методы решения уравнения Больц-
мана совершенно правильны, то мы обязаны искать объяснение описанных
противоречий в неполноте этого уравнения».
Действительно, в уравнении Больцмана приравниваются две операции над
функцией распределения молекул по тепловым скоростям. С помощью первой "
операции подсчгггывается за единицу времени изменение функции по времени,
координатам и скоростям. Если принять массы всех молекул равными, то это
изменение можно записать так;
д! J-Г ^4-11? д! 4-F af J-F d! 4-F Sf (1 R 1R,
С помощью второй операции подсчитывается изменение за единицу вре-
мени той же функции, обусловленное столкновением молекул.
Если через	обозначить компоненты скорогти молекул пер-
вого типа, а через W2y, W22—-молекул второго типа до столкновения
их, то меру вероятности их сближения можно будет положить равной Д/3.
Индексы указывают, от каких компонент тепловых скоростей следует брать
функцию распределения.
После столкновения компоненты скоростей молекул первого и второго
типов примут значения
Wjy, и IV'ax, W%у IV'azi	(1-5-16)
а мерой вероятности их расхождения будет .служить произведение/^. '
Таким образом, каждое столкновение одной группы молекул с другой
будет характеризоваться разностью
/^-/1/3 = 6/^.	(1-5-17)
37
Если просуммировать эти разности по всему фйзовому объему, то ми по-
лучим за единицу времени изменение функции /, обусловленное столкнове-
ниями молекул. Итак, имеем:
--=*	... bf^gb db d(ihd®s de.	(1-5-18)
Здесь gb db don dw2 de— элемент фазового объема. В нем g —относитель-
ная скорость сталкивающихся молекул; Ь —кратчайшее расстояние между
прямолинейными траекториями молекул; в—угол между плоскостью траекто-
рии относительного движения молекулы первого типа и некоторой постоянной
плоскостью, проходящей через g; doh—произведение dWlx d№\y dWlz,. Возни-
кает вопрос: всегда ли равноценны обе указанные операции? Первая операция
по своему характеру может давать непрерывные значения координа-Гфазового
пространства. Вторая операция может приводить к прерывным значениям, так
как вариация бД/2 может и не быть бесконечно малой величиной, А это озна-
чает, чти мы принципиально не можем считать указанные операции равно-
ценными .
Отмеченные замечания заставляют возвратиться к кинетической теории
Максвелла.
Уравнение переноса для любой величины Q согласно теории Максвелла
имеет вид ]Л.1-9, 1-13]:
+	.	(1-5-19)
где декартовы координаты (Xj = x, хг = у, xs^z) и Q — осредненное зна-
чение	—
4-00
^ = 7f	J J Q (»/) dtOi dm2 dKig,	(1-5-20)
где /—функция распределения скоростей молекул и и?;—скорость молекул.
Обозначим скорость видимого (гидродинамического) движения жидкости
через vt, тогда скорость любой молекулы относительно неподвижной системы
координат можно представить в виде суммы видимого и теплового движений уг-
и щ соответственно;
(1-5-21)
Таким образом, газ представлен как движение модельной непрерывной
среды, в которой точки массы движутся хаотически. В этом случае, очевидно,
справедливы равенства
=	r7z=0,	(1-5-22)
т. е. средняя скорость теплового движения равна нулю. Если умножить все
члены уравнения (1-5-19) на массу молекулы, то при условии, что р(р=/пгс)
есть плотность, для Q=1 получим уравнение непрерывности:
др д
й +	=	(1-3-23)
Из уравнений (1-5-19) и (1-5-23) получим:
" И? ra'F‘fS + л<?’	‘Г5’24'
где 1=1, 2, 3,
Величина AQ определяется е помощью интеграла столкновений;
AQ = j (Qr — Q") tizgb db dtf'f" doij dw2,	(1-5-25)
t> 0
за
где d<£>t=dWu dlF21 dW^; g=^(Wn~Wl2)z; b~расстояние между соударя-
ющимися молекулами в направлении относительной скорости; е—двугранный
угол между плоскостью, проходящей через линию, соединяющую сблизившиеся
молекулы и вектор относительной скорости, и плоскостью, проходящей через
ось x1(x1szx) и вектор относительной скорости.
Следовательно, линия направления относительной скорости будет секущей
для указанных выше плоскостей. Индексы ' и " соответствуют значениям до
и после столкновений.
Чтобы рассчитать интеграл столкновений (1-5-25), необходимо знать функ-
ции распределений f и f. Однако если ввести среднее значений переносимой
величины Q по соотношению	.
naQ = J ... ( typf'f dtoj,	(1 -5-26)
о
тогда нет необходимости находить эти функции. В этом и состоит преимущество
метода Максвелла по сравнению с методом, основанным на уравпении’Больц-
мана.
Величина b db характеризует эффективное сечение соударений молекул.
Если потенциал взаимодействия обратно пропорционален расстоянию между
молекулами в пятой степени, то получим равенство
Тогда [Л.1-13],
Д<2 (ПЭ = У [(№) - (“I’)]+р24	+
+ 4₽,лл(^-”;)2+(“;—(i-s-ssj
где
2-3);
Hi — 4л j acos’J6da; Л3=л a sin2 29 da.	(1-5-29)
о	О
Если
<г = тш; = тр,+и,),	(1-5-30)
то из уравнения (1-5-24) получим;
р^ + £^)=рЛ; 1=1.2.3; ;-=|2з. (15з1)
Из уравнения (1-5-31) можно получить уравнение переноса для идеальной
и вязкой жидкостей.
Если видимое движение не влияет на тепловое, тогда
иг-нг=0 при =	(1-5-32)
Давление в такой среде является одинаковым по всем направлениям и
равным;
Р^~ J-	= pu| = p«|; i = l, 2, 3.	(1-5-33)
зу
n \ St dvt St J дХ1 (nu,w +
+	("“«) +A<2: / = 1,2,3; i = l, 2,3.
Предположим, что существует соотношение
тогда из уравнения (1-5-35) следует:
AQ (W^) = AQ (t^)= AQ (SS).
Считая Q = w^ и учитывая, что
Q=w‘f -J-uj; ut-Qs=2o1u]u/4-u(Up i=l, 2, 3,
получаем:
m A« =p + ss;	) 
Если предположить, что
:=0 при	u2Ui = 0 при г = 1, 2, 3
С помощью соотношения (1-5-33) из уравнения (1-5-31) получаем уравнение
Эйлера для идеальной жидкости;
р-^тУР = Р?-	(1-5-34)
Из уравнения (1-5-24) можно вычислить величину AQ. Предполагая Q=^,
умножая уравнение (1-5-24) на dQ/dvt и вычитая уравнение, полученное из
уравнения переноса (1-5-33), получаем;
(1-5-35)
(7-5-36)
(1-5-37)
(1-5-38)
(1-5-39)
(1-5-40)
и формула (1-5-33) справедлива, т, е. р = 1/Зрс2, тогда из уравнения (1-5-39)
получаем:
»!AQ(WD=₽-^- + 2pg.	(1-5-4))
Сравнение уравнений (1-5-41) и (1-5-28) дает:
P^V+2P^=,]/r'(^2-»;’)+Зр.42 (р-|1й|)].	(1-5-42)
Сделаем несколько допущений для скоростей переноса у- и и* соударяющихся
молекул;
(o[)2~(«i)2> (у/— v/)2; ; = 1, 2, 3; (и^ —uft) >(с( — с[) (v!,—v*). (1-5-43)
Учитывая, что
+р div Й= + ~р +Р divV« р ,	0-5-44)
из уравнения (1-5-42) получаем:
%+р div V+2pil =	1(М; (ч;1— р^ + ЗрЛ, (р —	(l-S-45)
40
Если течение газа адиабатическое, тогда
1“ = —ydivl7,	(1-5-46)
где у ггСр/Ср —отношение теплоемкостей при постоянном давлении и постоянном
объеме.
Затем из уравнения (1-5-45) получаем:
pSf=Р + Р fcr2 -»:2) -2ч <Иу v),	(1 -5-«)
где ^ — коэффициент вязкости, равный:
”=3^/Т-	(1-5-48)
Аналогично получаем соотношение для р«|, puj, т. е.
('-5-49)
Если в физически малом объеме имеют месго те же скорости переноса,
т. е. v’ = тогда для одноатомного газа (у = 5/3) из уравнения (1-5-49)
можно найти уравнения Навье—Стокса.
Аналогично можно определить компоненты тензора напряжений;
___ (dv> dvf\ д,
+	+	«,/—Ь 2. з. (i-5-so)
Учитывая уравнение (1-5-31), получаем [Л.1-13];
dut А<, ( д , „ „	, , )
= -’Р1 + ч[’Ч + (2-?)^-<11ур] + рГ,; 1, /=1,2,3. (1-5-51)
Система уравнений (1-5-51) является незамкнутой и для ее замыкания
необходимо определить v'( и и" через v(. Профессор А. С. Предводителев пред-
положил, что справедливы следующие соотношения;
dV/	(1-5-52)
р*=0,-Л[(^-хй)]^-;	ё=1, 2, 3; / = 1,2,3,	7
где Х[0—координаты центра силы тяжести физически малого объема, по кото-
рому осуществляется усреднение.	7
Поскольку неизвестно отношение величин v'j и vj, то знак градиента
скорости dvjldxi в формулах (1-5-52) определяется по характеру взаимодействия
потока с твердой поверхностью. Если используются соотношения (1-5-52), тогда
из уравнения (1-5-51) получаем обобщенное уравнение Навье — Стокса, которое
впервые было предложено А- С. Предводителевым [Л.1-14];
р — р£ (nV) V— рро div у = р?—Vp + i]Vao-]-(2— у) grad div v,	(1-5-53)
где р —параметр псидеальной сплошности, который мы называем числом Пред-
водителева Pd,
2 дд
Pds^i= 3 П5Г-	(1-5-54)
41
На основе простых соотношений можно показать, что число Предводителева
пропорционально числу Маха (М) и числу Кнудсена (Кп):
Pd = |-КпМ.	(1-5-55)
Если число Pd = 0 (Кп<1 и М<1) и. у = 5/3, тогда уравнение (1-5-53)
сводится к уравнению Навье—Стокса.
Таким образом, обобщенное уравнение (1-5-53) справедливо при Pd > 0;
такой случай имеет место при КпМ^-0, т. е. в потоке разреженного газа
(Кп 0) при больших скоростях (Мз>1).
С помощью функции распределения Максвелла можно показать, что число
Прсдводителева прямо пропорционально числу Трусделла:
Pd = ₽=-|~KnM=2,2S22 Тг,	(4-5-56)
где Тг —число Трусделла.
Число Трусделла характеризует нелинейную зависимость тензора вязкого
напряжения от тензора скорости деформации. Соотношение (1-5-54) обнаружи-
вает, что влияние нелинейности в такой зависимости аналогично влиянию
параметра неидеальной дискретности, Число Предводителева характеризует
дискретную структуру газа. В одной из наших работ [Л.1-17] было показано,
что уравнение движения жидкости, состоящей из системы вихревых трубок’
описывается аналогичным уравнением вида (1-5-52), если в последнем предпо-
лагается, что у = 5/3 (одноатомный газ). В этом случае коэффициент 0 или число
Предводителева характеризует асимметрию тензора вязкого напряжения появ-
ляющуюся за счет весьма выраженной дискретной структуры жидкости.' Физи-
ческая картина такой дискретности следующая: жидкость состоит из отдельных
вихревых трубок, на границе контакта вихревых трубок происходит разрыв
гидродинамической скорости движения.
Уравнение движения выводится с помощью понятия производной от раз-
рывных функций. В этом случае коэффициент 0 характеризует вязкость, возни-
кающую в результате вращения элементарного объема жидкости, т. е. ен ха-
рактеризует ротационную вязкость.
Ротационная или вращательная вязкость, которая возникает при наличии
асимметрии тензора вязкого напряжения, вносит свой дополнительный вклад
в величину переноса импульса, аналогично тому вкладу, который вносится
нелинейными членами в законе вязкого течения.
Таким образом, число Предводителева Pd характеризует дискретную
структуру жидкости и усиливает тот дополнительный вид переноса импульса,
который происходит в таких системах.
О равновесном давлении жидкости в состоянии движения
Возвратимся к формулам (1-5-47) и (1-5-48) и рассмотрим эйлеровский газ,
т. е. газ, вязкость которого равна нулю. В этом случае составляющие тензора
нормальных давлений равны:
p,r‘=p+^f’(l’‘Z~v‘S)-	(1-5-57)
Формула (1-5-57) показывает, что видимые движения вносят поправку
в тензор нормальных давлении.
Отсюда возникает проблема: действуют ли эти поправки только через
уравнения гидродинамики в форме А. С. Предводителева или, кроме того
видимые движения еще и разрушают тепловое движение атомов или молекул?
Последнее утверждение требует уточнения уравнения состояния в форме
Клапейрона.
Представим, что газ, определяемый (1-5-57) —равновесный, но его статисти-
ческое состояние неизогропно, т. е. тепловые, скорости атомов или молекул
42
коррелируют. Определим давление в таком газе:
(|'5’58)
•	i	i
или с учетом гипотезы Л. С. Предводителева (1-5-52)
<=1.2.3.	(1-S-S9)
У/Ц	ОХ(
i
Помножим обе части формулы (1-5-59) на объем одного моля Ут:
pvm=pvm{t- 7 [<*'_ *м)	•	(| ‘6’60)
Здесь введено очевидное обозначение =
Если через У обозначить число Авогадро, то количество молекул в еди-
нице объема
У
п = ^.	(1-5-61)
► т
Кинетическая энергия молекул в тепловом движении К выражается через
давление р:
~~	р~^-пК.	(1-5-62)
Теперь нетрудно сообразить, что кинетическая энергия молекул в пере-
носном движении определяется равенством
2пК1=р(х;-хи)^1.	(1-6-63)
Так как в состоянии равновесия К = Кь то уравнение (1-5-60) в состоянии
равновесия примет вид:
pVm = pVm(l-P).	(1-5-64)
Но из опыта известно, что при pVm = RT, тогда последнюю формулу
перепишем так:
PVm=RT(l-$),	(1-5-65)
или, выразив объем одного моля через удельный объем и молекулярный вес,
получим окончательно:
pv=<' "Р’К’	(1’3'66)
Максвелловская функция распределения молекул по скоростям приводит
к следующей формуле для средней скорости атомов или молекул, находя-
щихся в тепловом движении:
а=2/1уХ-	с-6-67)
Уравнение (1-5-66) позволяет последнюю формулу переписать так;
<1-5'68>
т. е. коррелирование осуществляется через величину RT.
Формула для коэффициента вязкости в такой статистической системе при-
мет вид;
(1-3-69)
43
Следовательно, основная характеристика переноса ичпульса—динамичес-
кая вязкость т].для жидкости дискретной структуры— зависит от числа
Предводйтелева Pd.
Отсюда можно получить и другое физическое обоснование числа Прел-
водителей, как величины, характеризующей эффективную вязкость или вяз-
кость жидкости дискретной структуры:
PdU-1-l).	(1-5-70)
\ По !
 Поэтому коэффициент неидеальной сплошности (число Предводителева) можно
' трактовать как поправку на вязкость системы дискретной структуры.
Взаимодействие газа с твердой стенкой
Рассмотрим задачу о переносе количества движения через слой газа, огра-
ниченный двумя плоскими параллельными стенками. Течение слоя газа вызы-
вается движением одной из стенок по направлению, лежащему в плоскости
самой стенки. Предположим, что в этом случае гидродинамическое течение —
одномерное, о1 = о1 (у). В таком движении составляющие скорости молекулы
раскладываются на тепловую и гидродинамическую так:
Однако в нашем случае Pi = t’i(y), y2 = v3 = 0. Следовательно, ^ — ско-
рость движения слоев газа параллельно твердым стенкам.
Условия, возникающие на границе газа и стенки, впервые сформулировал
Максвелл. Все молекулы, падающие на стенку, делятся на две группы. Моле-
кулы первой, группы доля которых (1—v), прилипают к стенке, т. е. их пере-
носная скорость равна скорости твердой стенки и*. Молекулы второй группы,
доля которых есть v, диффузно отталкиваются от стенки, т, е. их переносная
скорость равна скорости прилегающего к стенке слоя газа ох.
В этой задаче надо различать два вида движения: видимое—в направле-
нии оси х, определяемое средней скоростью и>х, и тепловое движение в направ-
лении оси у. определяемое средней скоростью теплового движения и>2—й2.
При этом в-соответствии с формулой (1-5-68)
,	й>==2 V" л р(1-₽) У"
Подсчитаем теперь количество движения газа через единицу плоскости ху,
определяемое величиной ри1хю2- С одной стороны, эта величина определяется
через видимое и тепловое движение так? доля молекул, прилипших к стенке
(1 — v) р, теряет скорость в направлении оси х на величину (v* — v). Эта же
доля молекул в направлении оси у участвует только в тепловом движении и
имеет скорость
°а = У"ТГр (1 — ₽)	*	(1’6'72)
Следовательно,
PJX=(i-v)p (о*-»,)
С другой стороны, эту величину можно выразить через видимое движение;
p5S=-(l+v)i1~i.	(1-6-74)
Здесь учтено, что в видимом движении доля молекул пополнится за счет
отраженных молекул на величину v. Учитывая формулу (1-5-69) для коэф-
44
фициента вязкости, получаем окончательно:
рйл>=-0+v)	(1-5-75)
Знак минус в последней'формуле взят потому, что количество движения
передается в сторону убывающей скорости.
Приравнивая скорости (1-5-75) и (1-5-73), получаем:
-(1+V)(1-W ^^(l-v) («>-«)
или	_____
(1.6.78)
2р К Мо (1 —v) dy	'	'
Введем коэффициент скольжения:	4
2p(i-v) V ^ЙГ-	( Б77)
Теперь формулу (1-5-76) перепишем так;
=	,	(1-5-78)
1-6. УРАВНЕНИЯ ПЕРЕНОСА ДЛЯ АСИММЕТРИЧНОЙ ЖИДКОСТИ
Двухфазная среда является типичной моделью асимметричной жидкости.
К. таким средам можно отнести некоторые реологические жидкости. Иногда
такие среды называют микрожидкостями, для которых каждый элемент жид-
кости имеет две степени свободы;
I)	поступательные степени свободы, вызывающие среднее движение (клас-
сическая скорость движения):
2)	вращение и растяжение, благодаря которым частицы жидкости подвер-
гаются независимым собственным внутренним вращениям и однородным дефор-
мациям. Иногда считают, что последние степени свободы возникают в резуль-
тате независимых движений и деформации «трех направлений», связанных
с каждой материальной точкой.
Наиболее общей теорией явлений переноса является теория А. С. Эрингена
[Л.1-15], в которой на основе нелинейной термомеханики сплошных сред
получены уравнения переноса импульса и теплоты в их взаимосвязи. В част-
ности, были показаны наличие термодинамического тензора напряжений, связь
температурного градиента с основными уравнениями моментов напряжения и
наличие микровращений в уравнении теплопроводности.
Обозначим:	= тензор микроинерции; л*/ —тензор напряжения;
— первый тензор момента напряжения; s—удельная энтропия; — ско-
рость поверхности разрыва; v*/—тензор вращения. Тогда можно написать
уравнения Эрингена в виде" [Л. 1-15]:
I)	уравнения сохранения массы
^ + (poj).s = °; [р (Г-и)]-« = 0;	(1-6-1)
< 2) уравнения сохранения микроинерции
^+‘ы.	[pffei (о-и)Ь л=О; (1-6-2)
3)	уравнения баланса количества движения
^ki, H-ptfz— ^)=0;	л*=°;	0-6-3)
45
4)	уравнения баланса моментов количества движения
пНт.	—P^m(vlk + vlrvrk)	—P^rntvlr (Pii — ufc)] nlt ~
(1-6-4)
5)	уравнения сохранения энергии
— рё +.nMO/.fe + .nft/mvZm, fc + (nw —лЛ/) v;ft4-7A, А+р(?= 0; [ ?а + ла/с/ +
Rfcitnyim p +"2" y2Ч-ду	(yfe" wfc)| nk—О» (Ь6-5)
6)	неравенства энтропии
ps-(^/( + yQ=sO; (f>s (vj-uj) — у]п4=гО. (1-6-6)
Здесь лА/ — средний тензор напряжения (л/?/ = Л/А); Q— источник теплоты.
Остальные обозначения общепринятые. Суммирование производится по повто-
ряющимся индексам. Индекс, следующий за запятой, указывает на частную
производную относительно пространственных прямоугольных координат хА,
а верхняя точка обозначает вещественную (материальную) производную, т. е.
dvi,	• dvi>
Vk'l=^dxi' Ufe = W+Vfe-£l>p	О’6’?)
В работе (Л. 1-16] рассматривается асимметричная жидкость с жесткой
структурой. Частицы жидкости имеют собственные угловые скорости со, отлич-
ные от скорости поворота участка среды как целого, Таким образом, наряду
с обычной сдвиговой вязкостью т| и объемной вязкостью существует вра-
щательная вязкость (вязкость от внутреннего вращения частиц), характери-
зуемая тремя коэффициентами вязкости: т|г, и т|’. В этом случае диф-
ференциальные уравнения движения для асимметричной жидкости имеют вид
[Л. Ы6]:
pi = р? — w + n(l — Т/Ч) V2“ +(’lv+-§-4+vj V >ll¥ о —2-fturl й;
(1-6-8)
(rlr + rk) V div &j~’1rv2«4-2yw—у curl v 4-рПг=0,	(1-6-9)
где nv—плотность обпемио-распределенных моментов сил.
Система уравнений (1-6-8) —(1-6-9) имеет три компонента скорости ~v,
три компонента угловой скорости о, давление р (р, Г) и плотность р. Коэф-
фициент у характеризует меру сцепления частицы с окружающей средой. Если
у—0, то частица свободно вращается относительно окружающей среды (сцеп-
ления нет), если у.—со, то частица вращается вместе с прилегающим к ней
участком среды. Уравнение неразрывности не связано с уравнением напря-
женного состояния и имеет обычный вид.
Для решения уравнений (1-6-8) —(1-6-9) необходимо задать граничные
условия для конкретной задачи. Обычно в классической гидродинамике при-
нимаются условия прилипания, т. с. считаете я, что скорость жидкости на стенке
равна нулю. Эти условия можно сохранить для скорости поступательного
движения. Однако надо задать условия па стенке для угловых скоростей вз.
Если частица не вращается па стенке (предельный случай сильного взаимо-
действия жидкости и стенки), то (со)5= 0. Если же частица свободно враща-
ется на стенке (предельный случай слабого взаимодействия), то
(П°-	(1-6-10)
В реальном случае, очевидно, имеет место трение между вращающейся
частицей и стенкой, которое можно считать пропорциональным разности угло-
46
вых скоростей Aw, характеризующих вышеупомянутые два предельных случая.
В работе {Л. 1-16] граничные условия на стенке принимаются в виде
м=[2ч; divmM2^+2^“!]s.	(i-6-n)
где р —коэффициент вращательно-поверхностного трения.
а) Течение жидкости в цилиндрической трубе
Для данных граничных условий была решена простейшая задача течения
жидкости из цилиндрического капилляра. Полагая поле скоростей симметрич-
ным и считая F =0;	получим решение н виде [Л. 1-16]:
± Fi _ Л . 1 lQ(kr/R)~I0 Ш
4^ дг L R2 + Л* *-i/x (k) 4- BI3 (fe)J ’
(1-6-12)
где
1/2Л;
V n,
k=R
flRl-'
П/ I
(1-6-13)
A = R
Здесь /0, /i, /а — модифицированные функции Бесселя первого рода и
соответственно нулевого, первого и второго порядков.
Рис. 1-4. Зависимость V/Vo от кри-
терия асимметричности А для Двух
предельных значений р (1,3 — р = 0
и 2,4 — р = оо) и для значений
у/т] > 1 (кривые 1 и 2) и для значе-
ний уп\ = 1 (кривые 3 и 4).
Количество жидкости V, вытекающей из капилляра в единицу времени.
будет равно:	Л=1-±Гв+-^а-Г,	(1-в-и) v»	L ы, tk) J
где Vn —количество мулой Пуазейля:	жидкости, вытекающе’й^из капилляра, определяемое фор- (1-6-16) „	8т| дг	1	'
Как видно из формулы (1-6-14), количество вытекающей Р жидкости будет
меньше по сравнению с Ул. Эта разница будет тем больше, чем меньше радиус
капилляра. Если	то k~A.
Тогда
У о	лч Л4(Л)]
(1-6-16)
47
Значение В в основном определяется коэффициентом трения который
изменяется от 0 до со (0 < |3 <си). На рис 1-4 приведены кривые K/Vo —-f(A)
для двух предельных значений р и для некоторых значений у. Из рисунка
видно, что во всех случаях при Л <8 пользоваться классической формулой
ПуазеЙля нельзя.
' б) Теплообмен в цилиндрической трубе
Уравнение переноса теплоты Фурье — Кирхгофа будет отличаться от обыч-
ного уравнения наличием дополнительного члена в выражении для работы сил
трения (диссипативная функция). В общем виде уравнение будет иметь вид
(Л.1-15]:
'S“ = ,'V2T’ + ^ + (a‘7n</+nW)’	(1-6-17)
где Dy—тензор скорости деформации; vy—тензор скорости микрокручений и
микроизгибов.
В качестве конкретного примера рассмотрим теплообмен при ламинарном
движении жидкости в цилиндрической трубе.
Распределение скорости v(r) в цилиндрической трубе при постоянном гра-
диенте давления (dp/dz== const) дается соотношением (1-6-12).
Для симметричной задачи уравнение теплопереноса имеет вид
Ж	гЭ . 2	1 ,IfURs
дг* + г dr X L > + Я2 k-'I^ + BUlk) Г (	}
где vm—максимальная скорость на оси трубы диаметром 2R,
=	С-6-19)
При этом предполагается, что физические характеристики постоянны. Рас-
пределение температуры по длине цилиндра г при постоянном потоке теплоты
принимаем:
i=Cz^T(r).	(1-6-20)
Уравнение для функции т (г) получается из решения дифференциального
уравнения
 if rdT\-Г, r* a.2
7~лДг~^}--------)Г[1->++	f1'6-21’
Решение этого уравнения для граничных условий первого рода имеет вид:
TfrV- 1 [1	2/"^1 Г" 1 rt 3	] 4+*2	Н.6 22!
1 V>~' 4 [* М J У?2	16	4 k*M ф 2™ ’	( Ь }
где
Число Нуссельта определено по формуле
Nu=^S_	(1-6-23)
Т„„ \ Sr )г-ц'	'	'
где Ттп—средняя температура, определяемая по формуле
R
‘	j rT(r)udrt	(1-6-24)
48
Для малых значений k	и 7—мало) можно получить приближенно
значения для скорости и, температуры Т к числа Нуссельта Nij. Если пре-
небречь величиной выше (kr//?)2 в разложении функций Бесселя /0, /х и /2, то
Nu=« 4,36(1-^,
(1-6-25)
(1-6-26)
(1-6-27)
где
n=.. 4-w:1-
1 +ТЧ’1
87T?^(1-.2S)];
Y>0.
(1-6-28)
Из формул (1-6-27), (1-6-28) следует, что для асимметричной жидкости
число Нуссельта является функцией параметров Д, (v^-1), В:
№j==f(Z, В, у т]-1).	(1-6-29)
Это новый результат в теории теплообмена, Из анализа формулы (1-6-28)
следует, что при В > 0,5 число Нуссельта меньше по сравнению с числом
Нуссельта для симметричной жидкости
при прочих равных условиях. 
В зависимости от величины В, а
следовательно, в зависимости от А число
Нуссельта для асимметричной жидкости
можег быть и больше по сравнению с
числом Нуссельта для симметричной жид-
кости.
На рис. 1-5 дана зависимость числа
Нуссельта от параметра А при значе-
ниях Bt равных нулю и единице. Из
формулы (1-6-22) следует, что темпера-
тура жидкости в данном точке (гь 27)
будет отличаться от температуры в этой
точке для симметричной жидкости.
При условии В > 0,5 температура
жидкости будет больше, чем В обычных
условиях.
24
20
16
12
8
4
О 4	8	12	16	20
Таким образом, в теории конвек-
тивного теплообмена для асимметричной
жидкости появляется новый критерий,
SaBiibjft R (Srj/r],-)0,5, или параметр А.
,ля обычной (симметричной) жидкости
Рис. 1-5. Зависимость числа Нус-
сельта от критерия А для тех же
условий, что и па рис. 1-4.
этот критерий стремится к бесконечности (Л-»-со), так как коэффициент
вращательной вязкости стремится к нулю (т]г-»-0).
1-7. ГИДРОДИНАМИКА ЖИДКОСТИ ВИХРЕВОЙ СТРУКТУРЫ
Представим себе текучую среду в виде жидкости вихревой структуры, т. е.
совокупность вихревых шнуров, движущихся поступательно. Известно, что
решение уравнения Эйлера для вихревых течений приводит к теореме Гельм-
грльца о сохранении ннхревых линий. Однако этот вывод находится в проти-
воречии с опытом. На основе уравнения Эйлера нельзя объяснить процесс
возникновения и исчезновения вихрей. Решения Навье—Стокса объясняют
процесс затухания вихрей, а не процесс их образования. Поэтому возникает
проблема обобщения уравнения Навье—Стокса. Впервые на это обратил вни-
мание Н. П. Кастории [Л.1-18]. Он предложил вихревую модель жидкости-
49
Представим себе, что жидкость состоит из отдельных вихревых трубок.
Если выделить две рядом расположенные вихревые трубки, то векторы их
угловых скоростей имеют одинаковое направление. Тогда в точке их сопри-
'косновспия линейная скорость жидкости не имеет единственного значения. От
первой вихревой трубки линейная скорость будет иметь одно направление,
а от второй —прямо противоположное.
Такая схема физически нереальна. Поэтому предполагаем, что вблизи вих- .
ревых трубок, в области их соприкосновения, имеется тонкий слой жидкости,
в пределах которого линейная скорость меняется разрывом от одной вихревой
трубки к другой. Идея разрыва линейкой скорости потока жидкости легла
в основу вывода уравнений гидродинамики Кастйрина.
Таким образом, полагаем, что поле скоростей жидкости описывается раз-
рывной функцией f(x). Для вывода уравнения гидродинамики в работе {Л.1-19]
использован метод теории
конечных разностей. Суть
этого метода состоит в том,
что отрезок изменения аргу-
мента х разбивается на k
частей: x*==x0-j-/’/i.
При этом функция f (хй)
постоянна в пределах каж-
дой сеточной ячейки и изме-
няется скачком в узлах сет-
ки (рис. 1-6). Обозначим
координаты центров каждой -
сеточной ячейки через
xok = xk + -g- (Х®+) —Xh),
Рис. 1-6. К выводу уравнения вращения элемен-
тарного объема.
тогда внутри отрезка (x0®_lt
*ak) разрывную функцию
можно аппроксимировать си-
стемой гладких функций
фл(х). При этом функции фп(х) должны прикасаться к отрезкам прямой в
точках Xq®.!, хоа ..., при этом поведение функции внутри отрезка (x0®_b xftfe)
может быть любым, так как конечно-разностные отрезки не стягиваются в
точки. Очевидно, функции грп (х) имеют перегиб внутри отрезка (xoft_i, xok).
Согласно теории обобщенных функций <рл (х) образует пространство (п =
= 1, 2, 3 .,.) основных функций для функции	бтрезок (xft_1( xk+1) —
интервал функции f (хк), a (xq®.!, xofe) —носитель функции <р„(х).
Эти условия удовлетворяются, если положить
Эти условия удовлетворяются, если
при х®.
M ' I f6 = const
, , ( h-t= const при
(x)== <
t fh = const при x^xo®;
если
если
xk+i‘,
(’-7-2)
М =
Условия примыкания к отрезкам прямой
производных в точках х0®, xot-i ..., т. е.
сводятся к равенству нулю всех
^1г”фа(А-) п
----.=о при XofeSgXsSXo®-!-
(1-7-3)
50
Обобщением разрывной функции [(X/j) будем называть линейный непре-
рывный функционал
X0k	Xk	X0k
(f. ф) = $ ?(^)ф»И^=/б-1 $ ф«(х)Л+/4 $ ф„(х)<1х. (17-4)
Х0*-1	*0Й-1	Xk
Производная обобщенной функции f(x$) равна функционалу
</', ф«)= $ /'(**) Фи (*)*=№» I “ — $ /ф,; (х)*=W-
'»-!	1 “-1	«0S-!
(1-7-6)
Таким же способом с использованием соотношений (1-7-3) вычисляются и
последующие производные:
	0-7-6)
Если обозначить абсолютную величину первой конечно-разностной произ-
водной
^x0k-l (x0k — x0k-l) *
(1-7-7)
то формула (1-7-6) будет иметь вид:
(/ фп) ffife-i __а fk — fk—i
dx"	rfxo*_r “-1 (x0(e—Хоц,,) ’
(1-7-8У
где
=(- О"’1 ф!Г - ° (Ч).	О-?-9)
Из формулы (1-7-9) видно, что коэффициент ал_х определяет направление
скачка разрывной функции, поэтому an<.i > 0 или an_: < 0.
Полученные соотношения позволяют вывести уравнение движения жидко-
сти вихревой структуры.
Предположим, что вектор гидродинамической скорости o(r(i<) описывается
разрывной функцией f (х*). В потоке жидкости элементарная ячейка (/> —/>-1)
изолирована (г-радиус-вектор с координатами х, у, г) (рис. 1-7), Скорость
сеточной ячейки (/&, 7fe+l) разложим в ряд Тейлора с использованием фор-
мулы (1-7-8):
vk —	(rok — гo*-i)	“	(1-7-10)
О^ОЙ-1
Обозначим отношение размеров двух сеточных ячеек через
1 г	Г k— Г k-1	(1-7-11)
тогда	Т* =	+ Р ( Х04-, — 74_!)	,	(1-7-12)
где	О ГOk-1 Р = (1 +^й)	(1-7-13)
На основе	формулы (1-7-9) коэффициент р может быть положительным или	
отрицательным	в зависимости от величины ал_х. Изменение скорости	ОТ Ofe-1
		51
до v/i вызовет дополнительное вращение всех точек сеточной ячейки вокруг
центра тяжести ячейки с угловой скоростью (рис. 1-8)
curlv^.j.	(1-7-14)
Соотношение (1-7-14) представляет самостоятельный интерес.
Обычно угловая скорость определяется через линейную скорость соотно-
шением о>—1/2 curl у. В нашем случае это соотношение имеет более общий
характер. Коэффициент <хд^ аналогичен коэффициенту сцепления частицы жид-
кости с окружающей средой в теории асимметричной гидродинамики, но в от-
личие от последней коэффициент а,^ может быть больше или меньше нуля,
Рис. 1-7. Элементарная сеточная ячей-
ка в движущейся жидкости.
Рис. 1-8. К расчету враще-
ния элементарного объема.
Это дополнительное вращение вызовет изменение средней линейной скорости
всех точек соседней ячейки на величину т. е.
= ««-i[curl Vix (7о/1-'-»л-1)] = Нгаг1ой-1х	Ч^-u)]- О-'-15)
Учтем еще скорость объемного расширения при деформации ячейки;
=₽	dlv “t-v	(1-7-16)
Таким образом, полная скорость сеточной ячейки k будет равна:
г=+7;+тг	(1-7-17)
Кинетическая энергия сеточной ячейки массой т равна:
„ ти2
Е>=—~
1 +*'	СигГ”*-1 х -1 +""-l diV ”4-1]}-
(1-7-18)
Потенциальная энергия сеточной ячейки при наличии однородного поля
поверхностных сил F равна:
£ll=-?7«s.	.	(1-7-19)
52
Тогда проекции вектора будут равны:
/=1,2,3,	(1-7-20)
р SV
где р —плотность сеточной ячейки; Р — напряжение сеточной ячейки.
Тогда формула (1-7-19) примет вид:
‘=>.2. з- С'7’21»
Воспользуемся уравнением Лагранжа, в котором за обобщенные коорди-
наты возьмем 70^! и (v^^d/ok-i/dx):
______d- уи_.=о,	(i-7-аз)
dT duk-i
где Н = E^—Ek— кинетический потенциал.
Найдем необходимые соотношения;
dfi— = — m / 1 	+в | й4 -1	+ (curl ОX u + 4-1 <1 iv f *-x F<;
Orot-i ip <«; L sr^-i	J)
(1-7-23)
d dH dvk-i Г di'k_i ./*«-»“ 1 нт
— -=-----=>»------т^-=т -^- + (04-14^-1 .	(1-7-24)
dx dvft-i dx	dx	J
Тогда
+(' - Ю (4-^)4-i - ₽4-1 <i r v 4-i = 4-		( 7’25>
О I	P *-A;
Полученное уравнение справедливо для любых соседних ячеек, поэтому
значок (k— I) можно опустить. Затем воспользуемся формулой Стокса для
тензора вязких напряжений Тогда получим;
= — Vp4-T]V2y	— y pj V divy-bP (y7) с +P div v . (1-7-26)
Это уравнение тождественно уравнению Предводителева, только физиче-
ский смысл коэффициента р иной
В уравнении Предводителева для разреженного газа коэффициент 0 имел
смысл параметра неидеальной сплошности, он характеризовал изменение гид-
родинамической скорости в пределах физически малого объема, по которому
происходит усреднение всех микровеличин на основе газодинамических пред-
ставлений.
В нашем случае коэффициент р определяет выбор основной функции,
аппроксимирующей разрывную функцию, а согласно формуле (1-7-13) он харак-
теризует дискретность структуры жидкости (г. е. переход от одной вихревой
трубки к другой по закону усреднения разрывных функций), а также взаи-
модействие вихревой трубки с окружающей средой, разделяющей эти вихре-
вые трубки.
Общим являются дискретная структура жидкости и метод усреднения
путем разложения неизвестной функции в ряд Тэйлора. Однако последний
вывед носит более общий характер.
В частности, уравнение (1-7-26) справедливо для несжимаемой (divo#=0)
и невязкой жидкости (ц=0),
Коэффициент р в нашем случае зависит от самой вихревой структуры
жидкости. Если положить 0 — 2» то из уравнения (1-7-26) получим уравнение
Кастерипа. При t| = 0 и div о = 0 из уравнения (1-7-26) получаем решение вида
53
формулы Бернулли
(1 -Р)ру2+р =Ро+ 2 ри*.
(1-7-27)
где ро и ^0 — соответственно давление и скорость в набегающем потоке при
обтекании тела.
Обозначим давление и скорость позади обтекаемого тела через р№ и
югда
(Роо—Ро)= 4о—0)аМ-	(Ь7-28> •
Если (3 = 0, то получаем классическую формулу1 Эйлера:
Pc»-Po=YP(v5^“«).	(1-7-29)
Для невязкой жидкости'(^ = 0), v0==осо, это приводит к парадоксу Далам- >
бера (Ры=Рц).
Если положить [3 = 2, то получим:
Рс«-Р0 = ^Р(^ + ^)	(1-7-30)
— соотношение Кястерина, которое подтвердил экспериментально Милович
[Л.1-20]. Соотношения (1-7-28) и (1-7-29) показывают, что сила лобового сопро-
тивления пропорциональна скоростному напору, что согласуется с формулами
Жуковского о силе давления потока, создаваемого вихревыми шнурами. Непол-
нота уравнений Эйлера приводит к тому факту, что при наличии резких изме-
нений градиентов гидродинамических величин в потоке жидкостей уравнения
в форме Эйлера не имеют единственных решений [Л.1-21]. Эти же трудности
возникают при расчете течений смежными скачками уплотнений. Течение диск-
ретной жидкости в виде совокупности вихревых трубок, описываемое уравне-
нием (1-7-26), представляет интерес и для приближенных решений асимметрии- '
пой гидродинамики.
Обобщенное уравнение Навье —Стокса для асимметричной гидродинамики
приведено в § 6 [см. уравнение (1-6-8)].
Последний член уравнения (1-6-8) определяется из дополнительного урав-
нения, описывающего перенос момента микроимпульсов, т. е. у curl о =
= f(f, v. К, Л).
Выше отмечалась некоторая аналогия между коэффициентами у и Урав-
нения (L-6-8) и (1-7-26) отличаются от уравнения Навье —Стокса наличием
дополнительных членов. В отличие от уравнения (1-6-8) уравнение (1-7-26)
содержит единственный дополнительный коэффициент тогда как для реше-
ния уравнения (1-6-8) надо знать три коэффициента вращательной вязкости,
коэффициент у и поле угловых скоростей частиц жидкости.
Такая разница вполне понятна, поскольку в асимметричной гидродина-
мике описывается детально механизм переноса импульса поступательной и
вращательной диффузий. Общим является то обстоятельство, что текучая среда
(жидкость) имеет дискретную структуру, а следовательно, при корректном
описании такой среды, как гомогенной текучей среды, мы должны использо-
вать математический аппарат теории разрывных функций. Представляет инте-
рес вопрос о взаимодействии такой среды с поверхностью твердого тела. Обычно
принимают закон прилипания жидкости к поверхности твердого тела, т. с.
скорость поступательного движения жидкости на поверхности твердого тела
равна нулю; u = yfl, где vq — скорость движения поверхности твердого тела
(скорость границы).
Вопрос о взаимодействии вихревой трубки с поверхностью твердого тела
неясен. В предельном случае, когда поверхность тела и жидкость сильно взаи-
54
модействуют, угловая скорость вихревой трубки равна скорости самой поверх-
ности:
(й)5 = -^- curl	(1-7-31)
В другом предельном случае (предельно слабое взаимодействие) вихревая
трубка свободно вращается относительно поверхности твердого тела:
(M;)s = 0,	(1-7-32)
где М£ —плотность моментов трубки.
В общем случае можно считать, что перепад угловых скоростей Д(0/
------------curl с'о^ прямо пропорционален (МД$- Коэффициент пропорцио-
нальности будет характеризовать поверхностное трение. В нашей модели вих-
ревая трубка является частью жидкости дискретной структуры. Поэтому
исходя из соотношения (1-7-14), приходим к заключению, что на поверхности
твердого тела скорость жидкости не равна нулю, г. е. условие прилипания
не имеет места:
=	(’-7’33’
где 6 — коэффициент скольжения, который прямо пропорционален (1— Р)а, т. е.
6^(1-р)3.	(1-7-34)
Соотношение (1-7-34) аналогично формуле (1-5-77), полученной методом
молекулярно-кинетической теории. Качественные соотношения для границы
твердого тела с текучей средой вихревой структуры также аналогичны выво-
дам из решений уравнений асимметричной гидродинамики. Эти результаты
сводятся к следующему. Отклонение от результатов классической'(симметрич-
ной) гидродинамики тем больше, чем меньше линейные размеры системы.
Неклассические результаты можно получить, если в формулах обычной гид-
родинамики (количество вытекающей жидкости из труб, силы сопротивления,
вязкость) заменить истинный размер на эффективный ^эф^эф —+ Д), где Д
определяется свойством жидкости. Последнее равнозначно тому, что, сохраняя
размеры системы (/ = const), мы принимаем условия скольжения жидкости
у поверхности твердого тела.
1-8. ПРОЦЕССЫ ПЕРЕНОСА ПРИ НЕОДНОРОДНОЙ ТУРБУЛЕНТНОСТИ
Известно, что существуют ламинарное и турбулентное течения. Всем
хорошо известка фотография’движения дыма от зажженной папиросы [Л. 1-22].
Дым вначале поднимается в виде прямой струйки, потом она делается волни-
стой и кудреватой и, наконец, дым совершенно исчезает, перемешиваясь с воз-
духом. Первая часть струйки дыма представляет собой ламинарную форму
потока, вторая—турбулентную. Особенностью турбулентного потока является
гидродинамическое перемешивание движущемся среды, что обусловливает более
интенсивный перенос импульса, теплоты и массы по сравнению с переносом
в ламинарном потоке.
Если измерить скорости турбулентного потока в определенных местах
в разные моменты времени, то получим зависимость v=f(r) в виде графика,
приведенного на рис. 1-9.
Под неоднородной турбулентностью понимают турбулентность при наличии
градиента скорости основного потока.
Согласно основному положению Рейнольдса (1895 г.) скорость может быть
представлена в виде суммы среднего ее значения v я флуктуации скорости v':
c>=v_)_7'; vt = Ui-\-Vi.	(1-8-1)
. '	55
Турбулентный поток называется стационарным, когда f?/ не изменяется
во времени.
Для полей векторной и скалярной субстанций концепция Рейнольдса
распространяется на асе характеристики, т. е. любое значение может быть
представлено в виде осредненного и его пульсаций.
Время т
Рис. 1-9. Флуктуации скорости в турбулентном потоке.
В соответствии с правилами осреднения имеем:
v^^v.v/^v'vj,	(1-8-2)
___	2	У
т. е. v^v'i Ф 0, а также v’{ Ф 0.
Используя эти правила осреднения, можно получить уравнения переноса )
при турбулентном потоке.	j
Уравнения переноса импульса
* Уравнение сплошности для турбулентного потока можно написать так:
Ap,+djVpir=|p__|_t|iv(p-[;)+(j|V (р'о<)=о,	(1-8-3)
так как р'= 0.
Таким образом, в случае турбулентного потока уравнение непрерывности
дополняется членом div (р'о?).
Если плотность —величина постоянная (p = const; р' = 0), то из (1-8-3) слй-
. • дует: ’	__
diva=0.	(1-8-4)
Тогда
div сГ = div v + div v' — 0,
откуда
divy'=0.	(1-8-5)
Прежде чем перейти к выводу уравнений Рейнольдса для турбулентного
движения, напишем уравнение Навье—Стокса. Для компоненты это урав-
нение имеет вид: •*
При этом считаем, что жидкость несжимаема и внешние силы отсутствуют.
Выражение для полной производной можно написать в виде
dux	дих	dvx dvx dvx
dr	дх	dx	'3rVy dy	'J"1'3 дг	~~
56
что легко проверить путем дифференцирования и использования уравнения
сплошности:
dvx dvu dv,
~^+~дТ+~дГ=й-
Если теперь вместо vXt vy, vz подставить соответствующие выражения по
соотношению (1-8-1), то получим:
р[ di н дх +
а (р+р-) . „ Г д2 , а2 (л., +0^) а2 +
дх т- [ дх2	ду2	дг2
откуда после осреднения будем иметь:
dvx Г ддх _ dvx , _ dvx , dfb'l
р л'=-р1"аГ+г’'ТГх- + в»^_+02^г]
=_	р	++
дх 1 1	' [ дх 1 ду 1 дг
(1-8-8)
Уравнение (1-8-8) отличается от уравнения (1-8-G) тем, что актуальные
значения vx, р заменены осредненными значениями vXl р и, кроме того, появ-
ляется добавочный член, связанный с пульсационными характеристиками
(выражение в квадратных скобках правой части уравнения).
Указанные соотношения можно получить более общим методом. Среднее
по времени значение любой величины В (т) определяется формулой
S (т)
т + Д1
Л? j «МЛ-,
(1-8-9)
где величина В (т) может быть скалярной, векторной или тензорной.
Применим формулу (1-8-9) к уравнению непрерывности:
т 4- Дт
д? j (^-+<1«рГ)л' = 0.	(1-8-10)
Тогда получим:
-^T-H-div (рГ) = О.	(1-8-11)
Это усредненное по времени уравнение непрерывности, оно тождественно
уравнению (1-8-3), если учесть формулу (1-8-2). Произведем усреднение урав-
нения движения;
1
Дт
4-div (ру y)4-Vp— diva—p/j
du'==O.
(1-8-12)
Тогда получим:
4- div (р у о) 4- W 4- div (а + nJ 4- pF =* 0,	(1 -8-13)
где турбулентный 1ензор рейнольдсовых напряжений равен;
о;=руу —руу.	(1-8-14)
57
Если жидкость несжимаемая, то
р (dv/дт -|-Vv 	V/34-div (04-07)-J-pF,	(1-8-15)
где	___________
<т^ = p — v c')^p (у — у) (у — p).	(1-8-16)
Турбулентное трение
Величины pv^v'- являются характеристиками турбулентного потока, назы-
ваемыми рейнольдсовыми турбулентными напряжениями. В декартовой системе
координат тензор турбулентных напряжений
имеет вид:
Рис. 1-10. Распределение
осредненной продольной ско-
рости при обтекании поверх-
ности тела турбулентным
потоком.
р p'v'
(1-8-17)
V1.
Для иллюстрации рассмотрим возникнове-
ние трения в турбулентном плоскопараллель-
ном поюке (уг = 0). Пусть распределение про- *
Дольной осредненной компоненты скорости vx (д),
вблизи поверхности стенки будет отображаться
кривой, приведенной на рис. 1-10. Тогда ко-
личество движения' пульсирующего потока ру'
индивидуального моля жидкости будет пере-
мещаться вверх и вниз с пульсационной попе-
речной скоростью Uy. Этот пульсационный про-
цесс будет создавать добавочное к молекуляр-
ному внутреннему трению турбулентное трение, величина которого будет рав-
на t>v'xv'y. Таким образом, турбулентное напряжение трения будет равно:
В любой плоскости турбулентное.потока полное напряжение трения будет
являться суммой молекулярного внутреннего трения $т и турбулентного тре-
ния fy;
I дщ dvf \	___
<4, =	- vp	+	+‘К';°Ь	19)
Уравнения переноса энергии и массы
Если пренебречь диффузией эптальпии, то уравнение Фурье—Кирхгофа
в отсутствие источников массы можно написать так:
4г=и'2Г+4?+’’ф”-	t1-®’20)
Воспользуемся формулой осреднения (1-8-9)
-WpP div (o7,) = div (^V?)4-Tpy,	(1-8-21)
Фч> = (Фг|)гя4~ (Фи)/-
Предполагается, что удельная теплоемкость срр и коэффициент теплопро-
водности X. постоянны (p = const; div i» = 0).
58
Поскольку
vT — vT — 'vT-^-vt^vT— (vT—vT), ’	(1-8-22)
то уравнение (1-8-21) может быть записано иначе.-
Срр + Ы) =dlv (W7) + <iiv Й<) + П®»- 	(1-8-23)
где вектор турбулентного переноса
ft=cpP (vT—vT-).	(1-8-24)
Диссипативная функция турбулентного переноса равна:
(ФЛ = т2[2^+(”1',(-”/1 i)2].	(1-8-25)
Аналогично перенос массы в турбулентном потоке происходит за счет
молекулярной и турбулентной диффузии:
Гь = hm +Tkt= — СрГри + ppio ?.	(1 -8-26)
где pto —относительная концентрация (p*o = Pfto4-p^o)-
Если полученное соотношение (1-8-26) подставить в уравнение переноса
массы, то после осреднения получим;
=DpV2pft0 —о div рлоу'*	(1-8-27)
Так как число входящих в нелинейные уравнения неизвестных функций
преобладает над числом описывающих их уравнений, то проблема турбулент-
ного переноса состоит в замыкании уравнений переноса.
Ранние феноменологические теории переноса
На ранних этапах развития исследований турбулентного переноса фено-
менологические теории имели своей целью описание лишь осредненных полей.
В первую очередь остановимся на теории Буссинеска [Л.1-23].
Теория Буссинеска. Существо этой теории сводится к следующему. Турбу-
лентные потоки субстанции (векторной или скалярной) структурно аналогичны
соответствующим молекулярным потокам, т. е. прямо пропорциональны градиен-
там соответствующей субстанции. Проиллюстрируем это на конкретном примере
переноса импульса и теплоты.
Рассмотрим перенос импульса и теплоты в пограничном слое при обтека-
нии бесконечно длинной плоской пластины. Молекулярный перенос импульса
и теплоты описывается соответствующими уравнениями:
== ~ Л =	(1-8-28)
откуда получаем:
. ч /. dt	a di	. А_
Ят~— (?ху) т -----------<9ху)т ~ Ср .	(1 -8-29)
Рассмотрим перенос импульса и теплоты через контрольную поверхность
в пограничном слое (рис. 1-11). Через единицу площади этой поверхности
в единицу времени пройдет масса жидкости которая до переноса имела
скорость vxl и температуру Т*. Эго количество жидкости и соответствующая
энтальпия Cppvyl\ будут перенесены к поверхности 2t В стационарном состоя-
69
ним эти же количества жидкости и энтальпии при помощи турбулентного
обмена будут перенесены от плоскости 2 к плоскости 1. Разность энтальпий
(Cppv'yT^—Cp^VyTi) будет равна турбулентному потоку теплоты;
<7/=	(^2 —	(1-8-30)
Если vxS > Uxi, то при переходе частиц (молей) из слоя 1 в слой 2
скорость их будет увеличиваться, и наоборот. Следовательно, при турбулент*
ном обмене происходит изменение количества движения, что вызывает турбу-
лентное трение;
	(1-8-31)
Отсюда получим:
Qt~cp (axy)f ср	(1-8-32)
Это соотношение было впервые получено Рейнольдсом [Л.1-22] и называется
аналогией Рейнольдса.
Рис. 1-11.' Приближенная схема турбулентного обмена.
Сравнивая (1-8-32) и (1-8-29), можно прийти к формальному выводу о том,
что молекулярный и турбулентный переносы могут быть описаны в анало-
гичном виде, если число Прандтля равно единице (Pr = v/a=l), т. е.
(1-8-33)
W = —СрРО/^-,	(1-8-34)
где V/ и а(—соответственно коэффициенты турбулентной вязкости и турбулент-
ной температуропроводности.
Обозначим коэффициент турбулентной кинематической вязкости через ve,
а коэффициент турбулентной температуропроводности через ^(де^а^). Вслед-
ствие этого индекс турбулентности t заменим е, а индекс ламинарного переноса
опустим-
Перенос массы путем турбулентного движения обычно называют турбулент-
ной диффузией.
По аналогии с молекулярной диффузией можно написать:
(/^ = -pDeVpft0,	(1-8-35)
где'£>е—коэффициент турбулентной диффузии,
60
Таким образом, по теории Буссинеска [Л.1-23] турбулентный перенос
является аналогом молекулярного переноса. Конечно, эта аналогия является
"	*	- в качестве расчетной схемы, при
По аналогии можно рассматривать в
грубым приближением; ее можно принять
которой коэффициенты турбулентного
переноса ve, а&, Da определяются экс-
периментально.
В общем случае уравнения переноса
запишутся так;	'
о = р (v + ve)e; а//=р (v + vg) в/у;
(1-8-36)
<7 = pc₽(a + ae)V7;	jk = p (D4-Dg) Vpfc0,
' (1-8-37)
где e—тензор скоростей деформаций.
Теория Прандтля. Прандтль [Л.1-24]
сделал попытку связать величины vE и аъ
с характеристиками турбулентности. Со-
гласно кинетической теории газов коэф-
фициент кинематической вязкости про-
порционален произведению среднеквад-
ратичной скорости теплового движения
на среднюю длину свободного пробега. Г'	. .... . г_____г_____ _
качестве переносимой (сохраняющей свои свойства на определенном расстоянии)
субстанции турбулентный импульс моля жидкости.
Рассмотрим конкретный пример, аналогичный приведенному выше (обтека-
ние плоской пластины турбулентным потоком).
Распределение •	 *
приведено* на рис.
рс'И'Р.
В соответствии с рис. 1-12 имеем:
осрсдненной продольной скорости в пограничном слое
1-12. Турбулентное трение (стжр)е определяется величиной
^2 — vxi^=lv = lv
(1-8-38)
На основании уравнения сплошности для плоского потока
dvx	dvy
дх ~ ду
можно считать:
Тогда будем иметь:
.	.	д | <53х I dvx
(1-8-39)
(1-8-40)
(1-8-41)
Если сравнить это выражение для (стхр)8 с формулой (1-8-26), то получим:
(1-8-42)
Величина lv является параметром длины, пропорциональным среднеквадра-
тичному значению расстояния, на котором турбулентные моли жидкости
сохраняют свою индивидуальность. Обычно lv называют длиной пути смещения
при переносе импульса. Подобная аналогия может быть использована при
рассмотрении турбулентного потока скалярной субстанции (концентрации или
температуры) как транспортабельной субстанции. При этом выражение коэф-
61
фициента турбулентной диффузии имеет вид:
Ое_Ге_/Д|^|,
(1-8-43)
где 1т—параметр длины, характеризующий расстояние, на котором турбулент-
ный поток скалярной субстанции сохраняет свою индивидуальность.
Отметим, что параметры lv и 1т не имеют определенного физического
смысла: они используются для «стыковки» теоретических и экспериментальных
результатов по распределению осредненных величин 5, Т, р^0.
Теория Тэйлора. Теория переноса Тэйлора [Л.1-25] основана па предполо-
жении о том, что в турбулентном потоке свойствами транспортабельной суб-
станции обладает завихренность. При этом в полном соответствии с теорией
, ди3 ди[
переноса импульса поток завихренности ш' = ~ представляется про-
С'ьТ	н
порциональцым градиенту осредненной завихренности с использованием в каче-
стве коэффициента пропорциональности так называемого коэффициента турбу-
лентной завихренности
,s
— la)
I dvx I
|“dTr
(1-8-44)

где w = — dvx!dy—осредненная завихренность.
Двум рассмотренным вкратце феноменологическим теориям переноса,
основанным на понятии «пути смешения», присущи очевидные недостатки^
главными из которых являются, по-видимому, следующие:
1	Невозможность описать с их помощью процессы переноса в точках, где
dvxldy=$ и dTldy=Q. Действительно, в этих точках ve=ae=8w = 0,’в то
время как в действительности коэффициенты турбулентного переноса должны
иметь конечную величину, определяемую турбулентным переносом потоков
и ojT”' со скоростью пульсационного движения.
2.	Невозможность учета в рамках этих теорий влияния пульсаций давле-
ния на процессы переноса. Между тем это влияние является принципиальным,
так как перенос импульса может осуществиться под действием перепада давле-
'ния, даже когда «индивидуальный» жидкий моль сам по себе не перемещается.
3.	Концепция «вихревой» вязкости и теплопроводности является чисто
формальной.
4.	Понятие «пути смешения» является весьма неопределенным, так же как и
породившее его понятие «индивидуальности» турбулентных молей.
Перечисление недостатков феноменологических теорий турбулентности,
основанных на гипотезе о «пути смешения», может быть продолжено. Следует,
однако, иметь в виду, что все они органически присущи рассматриваемым
теориям, которые не предусматривают сколько-нибудь правильного описания
механизма процессов переноса. Плодотворность же этих теорий объясняется
тем, что они позволили получить практически полезные полуэмпирические
соотношения, которые используются в инженерной практике.
Кратко рассмотренные теории турбулентности являются дедуктивными:
принимается определенная гипотеза о пульсационных потоках импульса,
скалярной субстанции или завихренности, на основе которой с помощью
осредненных уравнений переноса выводятся (дедуцируются) профиль осреднен-
ней скорости и профиль скалярной субстанции. Очевидно, что при этом
осредненные характеристики (профиль скорости или скалярной субстанции)
выводятся на основе физически сомнительных гипотез.
Рейхард [Л. 1-26], отметив это обстоятельство и подвергнув критике
дедуктивные теории переноса, предложил индуктивную теорию.
62
Теория Рейхарда Эта теория была разработана для турбулентных свобод-
ных струй- Суть се сводится к следующему. Отметив, что распределение полной
продольной скорости в поперечных сечениях эоны смешения струи следует
кривой Гаусса, Рейхард предположил, что процесс турбулентного переноса
является статистическим и в точности аналогичен процессу молекулярного
переноса. Следовательно, дифференциальное уравнение, описывающее измене-
ние должно быть идентично уравнению молекулярной диффузии. Значит,
надо преобразовать уравнение движения так, чтобы получить уравнение
диффузии. Так, при условии пренебрежения членами, содержащими давление,
и членами, содержащими вязкость^ проекцию уравнения движения на направле-
ние движения струи напишем в виде уравнения
-т-----Р о). —г-и	—— = 0,	(1-8-46)
От ‘ 1 дх ~ 3 ду	к ’
которое с помощью уравнения несжимаемости может быть приведено к виду
+	0.	(1-8-47)
От ‘ дх 1 ду	к '
Осреднив это уравнение в предположении стационарности турбулентного
движения, получим:
fe? Ц^=о	(1.8.48)
дх ‘ ду	'	’
С другой стороны, если величина со(2 следует гауссовому закону, то она
должна удовлетворять уравнению
0о)[2	. д2(в[2
дх = ду2
(1-8-49)
Здесь величина L, имеющая размерность длины, математически представ-
ляет собой коэффициент диффузии; какого-либо определенного физического
смысла опа лишена. Таким образом, чтобы преобразовать (1-8-47) в (1-8-48),
надо постулировать:
(1-8-50)
Это соотношение Рейхард назвал законом переноса импульса: «интенсив-
ность переноса импульса, соответствующего компоненте ои, в поперечном
направлении со скоростью пропорциональна изменению потока импульса
(и'2 в этом направлении» (аналогичный «закон» может быть получен и для
переноса скалярном субстанции). Этот закон является неудовлетворительным,
так как уравнение (1-8-49) «отдает предпочтение» оси х по сравнению с осью у,
что совершенно неоправданно.
Теория Рейхарда, как и предыдущие теории, не описывает действительной
картины механизма турбулентного переноса и даже не делает попытки каким-
либо способом углубить представления об этом механизме.
В заключение надо отметить, что из всех описанных полуэмпирических
теорий турбулентности невозможно получить представление о взаимосвязи
осредненных и пульсационных характеристик переноса. Между тем эти вопросы
имеют глубокое принципиальное значение, определяемое необходимостью
углубления современных представлений о механизме турбулентного переноса,
и представляют чисто прикладной интерес. Действительно, мы зачастую сталки-
ваемся с такими задачами турбулентного переноса, в которых определение
компонента тензора реннольдсоных напряжении в пульсационных потоков ска-
лярной субстанции не только вызывался необходимостью замыкания осреднеп-
63
них уравнений переноса, но и является самоцелью исследования. К таким
задачам можно отнести, в частности, задачи, связанные с проблемами переноса
теплоты и массы внутрь пограничного слоя из внешнего турбулентного потока,
распространения электромагнитных волн в средах с систематическими и слу-
чайными неоднородностями диэлектрической проницаемости и т. и. При этом
полуэмпирические соотношения (1-8-33) для касательных турбулентных напря-
жений и поперечных турбулентных потоков скалярной субстанции (1-8-34),
полученные на основе феноменологической теории «Пути смешения», оказываются
недостаточными.
В связи с этим оказывается целесообразным обратиться к статистическим
методам описания турбулентности. Прежде всего обратимся к тем феномено-
логическим теориям турбулентности, которые используют статистические методы
математического описания случайных процессов.
Теория автора. В первую очередь остановимся на турбулентном переносе
тепла как наиболее простом случае турбулентного переноса. Для упрощения
анализа положим жидкость несжимаемой (р== const). Обычно осредиеяную
величину CpDvT заменяют соотношением
сррй’ = с,'ро7—срр(сТ—«П^СрРоТ— Cpfiv’T'. 	(1-8-51)
Однако возможен и другой способ. Величина ut является векторной
величиной, она может быть заменена векторной величиной иТ при помощи
тензора второго ранга А:
vT^b-vT.	(1-8-52)
Тогда уравнение Фурье —Кирхгофа для турбулентного переноса теплоты
будет иметь вид:
+ (cppVT)  (v- Ь) + сррТЬ (^)-{-сррТёdiv A=div [МТ). (1-8-53)
Для несжимаемой жидкости divv = 0. Предположим, что тензор А равен;
А=а|,	(1-8-54)
где а —скалярная величина.
Тогда имеем:
div (a- vT) = v grad (аТ)-\-аТ div у.	(1-8-55)
Тогда уравнение (1-8-53) примет вид:
о V(a?lj-div(ZV7).	(1-8-56)
Аналогично диаду v v заменим диадой v и по соотношению
pF у — В • рц у.	(1-8-57)
Тогда будем иметь:
div pFF = В • div (ру F)-|-pv F • div В.	(1-8-58)
Тогда уравнение турбулентного переноса импульса будет иметь вид:
-4-В • div (pFF) = — V£H-div о —poF • div Вф-pF. (1-8-59)
Уравнение (1-8-59) отличается от уравнения Навье—Стокса, оно может
быть написано в другой форме, если использовать соотношение
div (pFF • в) =Vp (F о ; в)-}-р [(vF/ у): в)] -l-po(Vy) ; B-j-ati • div В. (1-8-60)
64
Статистико-феноменологическая теория переноса
в неоднородной турбулентности
Особенность статистико-феноменологической теории турбулентного переноса
состоит в том, что турбулентные поля рассматриваемых субстанций трактуются
как случайные функции пространственных координат и времени. Описание
процессов турбулентного переноса при этом производится через статистические
характеристики полей—распределение вероятностей для значений этих полей.
Для замыкания же уравнений, описывающих распределение в пространстве и
времени этих статистических характеристик, используются феноменологические
гипотезы.
При таком подходе к проблеме турбулентности задача турбулентного пере-
носа ставится следующим образом: выразить характеристики переноса какой-
либо субстанции полностью через статистические функции поля скорости, а также
начальные и граничные условия с привлечением феноменологических гипотез
для некоторых характеристик тонкой структуры турбулентности. Этот подход
к проблеме переноса при неоднородной турбулентности является сравнительно
новым и буквально до последних лет использовался лишь для рассмотрения
переноса импульса. Основа статистико-феноменологического подхода к проблеме
неоднородной турбулентности заложена работой Колмогорова ]Л,1-27|, в кото-
рой турбулентность характеризовалась двумя параметрами —интенсивностью и
масштабом (близкая идея немного позже была выдвинута Прандтлем [Л.1-28]).
Наиболее полное отражение идеи Колмогорова—Прандтля получили в теории
Ротта [Л. 1*29].
Теория Ротта турбулентного переноса импульса. Уравнения Рейнольдса,
содержащие составляющие тензора турбулентных напряжений	допол-
няются системой уравнений, описывающих изменение этих напряжений; Для
вывода уравнений движения можно воспользоваться общим методом составления
уравнений для моментов, предложенным Келлером и Фридманом. [Л. 1-30].
Уравнения имеют следующий вид;
, V - д — , v I— *7 , —7 sii \ ,
-л- +2+ 2+ ad +
1г	k
Vi dv't &v'r 1	{до', ди', \	___
dlk P \dfy dli J 1 I r
^6«+5?p7M=o- .
k
Входящие в уравнения (1-8-61) члены соответственно характеризуют полное
изменение в единицу времени рейнольдсовых напряжений, их генерацию за
счет осреднеиного поля скорости, вязкую диссипацию, обмен энергией пуль-
саций по различным направлениям за счет пульсаций давления (без изменения
полной кинетической энергии пульсаций), вязкую и турбулентную диффузию.
Уравнения (1-8-61) можно дополнить членами для корреляций моментов
более высокого порядка, Для конкретных задач необходимо ограничиться не-
большим членом уравнений для моментов —уравнениями для низких моментов
и постараться замкнуть систему уравнений первых и более высоких моментов
путем введения некоторых феноменологических гипотез, которые позволили бы
выразить моменты, остающиеся неопределенными, через основные, количество
которых соответствует числу рассматриваемых дифференциальных уравнений
для моментов.
В качестве основных функций, описывающих турбулентное течение в точке,
можно 'выбрать осреднениую скорость, осреднекное давление, одноточечные вто-
рые моменты пульсаций скорости и масштаб турбулентности. Все остальные
-моменты, входящие в уравнения для указанных основных функций, могут быть
приближенно выражены через основные.
-3 Лыков А. в.	55
Если систему уравнений ограничить уравнениями для вторых моментов
(1-8-61), то для замыкания полной системы уравнений, состоящей из уравнений
Рейнольдса и уравнений для рейнольдсовых напряжений (1-8-61), необходимы
феноменологические гипотезы для следующих сгатистических характеристик,
которые не могут быть определены из указанной системы уравнений:
корреляции пульсации давления с градиентами пульсационной скорости
1 f dui dv'i \
р^7р'\^+а^)‘	(1'8'62)
диссипативной функции
Vi Зо. dv';
ф’=2^« <1-8-63*
Й
и турбулентной диффузии рейнольдсовых напряжений
lv‘°'i0't + ¥ ₽’	+°‘М •	(1'8И)
Используемые здесь гипотезы таковы:
1.	Процесс перераспределения энергии пульсаций по различным направле- л
ниям аналогичен эффекту упругого столкновения молекул идеального газа,
учитывающемуся в кинетическом уравнении Больцмана. Из этой аналогии полу-
чается следующая аппроксимация корреляции (1-8-62):
р 1/2 /_______ о '
(1-8-64а)
где Е = -g- 2	— полная кинетическая энергия пульсаций; Lv = -~-x
it
F (k, т) ,,	„	,	,
•——- dfe — интегральный масштаб турбулентности;’ kv — эмпирическая
константа; F (k, т)—энергетический спектр турбулентности; k— волновое число.
2.	Диссипация кинетической энергии пульсаций в теплоту является резуль-
татом суперпозиции диссипации при большкх и малых числах Рейнольдса
2
Ф® = v Av —— fy
(1-8-65)
где Av, эмпирические константы.
3.	Диффузия энергии пульсаций (кинетическая энергия плюс энергия
давления) предполагается транспортабельной субстанцией, для которой вводится
градиентное представление Прандтля
Vi d ( ди'-и, \
a’=L'S\D‘'d*r)’	(1'8'56)
k
где DB—коэффициент турбулентной диффузии.
С учетом аппроксимаций (1-8-64а)—(1-8-66) система уравнений движения
становится замкнутой относительно основных характеристик турбулентности —
осреднеипой скорости и рейнольдсовых напряжений (масштаб турбулентности
входит параметрически). Для масштаба турбулентности либо выписывается
соответствующее дифференциальное уравнение (как это сделано Ротта), по
66
rTnVKTvpe аналогичное уравнению (1-8-61), либо эмпирически задается зависи-
мость масштаба от координат.
В рассматриваемой теории турбулентности содержится ряд эмпирических
констант. Значения некоторых из них определяются по экспериментальным
-езультатам топкой структуры турбулентности^ а для остальных могут быть
определены оценочные значения.
н Таким образом, рассматриваемая теория турбулентности хотя и оперирует
со статистическими характеристиками, по своей сути является полуэмпирической,
причем включающей большее по сравнению с теорией Прандтля—Буссинсска
число эмпирических констант. Однако, несмотря на сравнительную сложность
и необходимость привлечения обширных опытных данных по статистическим
характеристикам, она лишена весьма принципиальных недостатков теории пути
смешения, перечисленных выше. Что же касается эмпирических коэффициентов,
то при современном уровне развития аэродинамического эксперимента их опре-
деление не составляет большого труда. При этом их достоинством является
универсальность для различных пристенных течений. Наконец, следует отметить,
что рассматриваемую теорию не следует противопоставлять феноменологической
теории Прандтля. Л1ожио легко показать, в частности, что из уравнений для
вторых моментов получается выражение для касательных рейнольдсовых напря-
жений с точностью до константы, совпадающее с соотношением Прандтля (1-8-41).
Для этого достаточно в уравнениях (1-8-61) для стационарного полностью раз-
витого течения типа пограничного слоя отбросить диффузионные члены и поло-
жить —------> 1 -
Таким образом, феноменологическая теория пути смешения может клас-
сифицироваться как частный случай более общей теории, 'использующей
уравнения для моментов пульсаций скорости, справедливый лишь в области
турбулентного ядра течения. Поэтому для не претендующих на большую
точность инженерных расчетов, в которых важно знать профиль осред-
ненной скорости хотя бы во внутренней части пристенного течения, предпоч-
тение следует отдать теории Прандтля. Однако для более точных расчетов
турбулентного пограничного слоя, особенно когда речь идет о необходимости
более или менее детального рассмотрения различных факторов, определяющих
картину турбулентного переноса во всей области турбулентного пограничного
слоя, использование рассматриваемой теории является, несомненно, оправданным
[Л.1-51].
Теория турбулентного переноса скалярной субстанции. Знание по возмож-
ности более точной картины турбулентного переноса импульса является осо-
бенно актуальным при исследовании вопросов переноса тепла и массы в турбу-
лентных пристенных течениях, При этом желательно использовать преимущества
динамической теории, использующей уравнения одноточечных моментов пульса-
ций скорости, для усовершенствования полуэмпирической теории переноса ска-
лярной субстанции (теплоты и массы) в турбулентных потоках со сдвигом,
основанной лишь на предположении о некоторой аналогии между переносом
скалярной субстанции и переносом импульса. Осредненное-уравнение переноса
скалярной субстанции, содержащее компоненты пульсационных тепловых пото-
ков о[Т’, дополняется системой уравнений, описывающих изменения этих потоков
в пространстве. Эти уравнения выводятся из уравнения переноса (1-8-6) и осред-
иенных уравнений переноса и имеют вид:
k	k
____	____ 1 дТ <1 ди', дТ'
+2^(’йг'+-р'777)=о	ч-8-67)
3*
67
(для простоты здесь рассматривается случай молекулярного числа Прандтля,
равного единице) [Л. 1-24].
В этих уравнениях два первых члена характеризуют полное изменение
в единицу времени пульсационного потока скалярной субстанции (с точностью
до константы), третий член — непосредственное порождение v'-T' из осредиен-
ного поля Г, четвертый •—производство пульсационных потоков скалярной
субстанции за счет взаимодействия пульсационного движения и среднего тече-
ния; последующие члены определяют молекулярную диффузию, изменение
за счет связи пульсаций давления с градиентом пульсаций Т', вязкую «дисси-
пацию;? и диффузию за счет турбулентного переноса энергии пульсационного
движения.
Для замыкания системы уравнений (1-8-67) необходимы феноменологические
гипотезы для следующих статистических характеристик:
1)	корреляции пульсаций давления с градиентами пульсаций скалярной
субстанции	______
<‘-8-68>
2)	корреляции, характеризующей «размывание» пульсационных тепловых
потоков за счет термического сопротивления среды,
2dv'- дТ'
3)	турбулентной диффузии пульсационных тепловых потоков
°’'=24г(5Г^+7'М.	t1-8-70)
Используемые здесь гипотезы таковы:
1.	Процесс выравнивания пульсационных тепловых потерь по различным
направлениям аналогичен процессу выравнивания кинетической энергии по этим
направлениям. Принимая во внимание соотношение (1-8-64а), следует исполь-
зовать следующую аппроксимацию корреляции (1-8-68):
₽1/а __
Pvf=— fy—,—ЦТ',	(1-8-71)
где Lv{ — интегральный масштаб, определяемый пространственной корреляцией,
скорость—скалярная субстанция.
2.	Эффект «размывания» пульсационных тепловых потоков есть результат
суперпозиции этих эффектов при Re£—>0 и Re^-^-co, т. е.
(1-8-72)
L©/
/здесь принято во внимание то, что Ит Ф?>/=0\.
(	Ре£-оэ	J
3.	Турбулентный перенос пульсационных потоков скаляпной субстанции
происходит под действием вихревой диффузии, т. о. для (1-8-70) может быть
введено градиентное представление вида
. (1-8-73)
С учетом аппроксимаций (1-8-71)—(1-8-73) уравнения Фурье —Кирхгофа
замыкаются относительно основных характеристик турбулентного переноса —
осреднеяиогр значения скалярной субстанции Т и пульсационных потоков о<Т'.
68
Рассматриваемая теория переноса скалярной субстанции, как и теория
переноса импульса, содержит ряд эмпирических констант Можно показать
P1.1-3I], что для ky и A1Vf могут быть даны оценочные значения, которые
впоследствии могут быть уточнены на otHOBe соответствующих эксперименталь-
ных данных, касающихся статистических характеристик турбулентного тепло-
обмена.
Предлагаемая теория переноса скалярной субстанции в турбулентных
неоднородных потоках предусматривает использование уравнений для стати-
стических моментов пульсационных величин, причем чем большее количество
уравнений (для моментов все более высокого порядка) привлекается, тем более
полное описание процессов переноса может быть достигнуто. Замыкание си-
стемы уравнений, описывающей процесс турбулентного переноса скалярной
субстанции, осуществляется путем введения некоторых феноменологических
аппроксимаций, позволяющих избавиться от «новых», т. е, нс определяемых
выбранной системой уравнений, моментов. В конце концов оправданием вве-
денных аппроксимаций является опыт. Поэтому предлагаемая теория по су-
ществу является полуэмпирической.
Однако используемые в теории гипотетические связи между «неизвестными»
и «известными» величинами касаются пульсационных характеристик в отличие
от чисто эвристических связей между осредненными и пульсационными вели-
чинами, используемыми в теории Прандтля —Буссинеска; между прочим, эти
последние основаны на предположении о том, что турбулентный перенос импульса
и скалярной субстанции осуществляется одинаковым образом. Однако анало-
гия между процессами переноса импульса и теплоты существует только в том
случае, если vt = aT, где а—коэффициент пропорциональности; тогда осред-
ненные уравнения переноса импульса и скалярной субстанции, в которых
в общем случае присутствует еще «движущая сила» Ft, становятся идентич-
ными. Это возможно, если выполняются условия
--^•+4=оГ(; Рг=1; Рг'=1’
р
где Ft— плотность внешних сил.
В общем случае этим условиям удовлетворить невозможно. Очевидным
преимуществом теории переноса, использующей уравнения для статистических
моментов пульсаций, является ее независимость от подобных ограничений.
Важным преимуществом рассматриваемой теории является также возможность
учета с ее помощью влияния внешнего турбулентного течения на процессы
переноса внутри пограничного слоя. Действительно, благодаря наличию в урав-
нениях для вторых моментов членов, характеризующих турбулентную диффу-
зию, является возможным расчет характеристик переноса вплоть до внешней
границы пограничного слоя и, следовательно, учет (через посредство гранич-
ных условий) турбулентности внешнего потока. Следующим принципиальным
преимуществом рассматриваемой теории является возможность учета влияния
пульсаций давления на изменение пульсационных потоков скалярной субстан-
ции, что невозможно при использовании феноменологической теории, основан-
ной на понятии «пути смешения».
Рассматриваемая теория в приложении к конкретным задачам пристенных
течений по предусматривает введения многослойных моделей течения, присущих
феноменологическим теориям переноса. Действительно, с помощью уравнений
для вторых моментов характеристики осредненных и пульсационных полей
могут быть рассчитаны во всей области течения. При этом возможность расчета
характеристик пульсационных полей несомненно является достоинством метода
в тех случаях, когда знание этих характеристик является целью задачи.
Следует отметить, что рассматриваемую теорию переноса скалярной суб-
станции не следует противопоставлять теории Прандтля —Буссинеска. Так же
как и в рассмотренной выше теории переноса импульса, можно показать
[Л.1-31), что введенное в феноменологической теории переноса соотношение для
турбулентных потоков скалярной субстанции может быть получено из урав-
69
нений для соответствующих вторых моментов при 1 и пренебрежении
турбулентной диффузией.
Таким образом, феноменологическая теория переноса Прандтля —Бусси-
неска может в этом смысле рассматриваться как частный случай более общей
теории, использующей уравнения для пульсационных потоков скалярной суб-
станции, пригодной лишь в области турбулентного ядра. Поэтому для инже-
нерных расчетов, которые не претендуют на более или менее детальную кар-
тину процессов турбулентного переноса скалярной субстанции, а предполагают
знание лишь осредненного поля скалярной субстанции хотя бы в централь-
ной части пристенного течения (профиль в непосредственной близости от стенки
может быть определен путем введения двухслойной модели), по-видимому, це-
лесообразно использовать теорию Прандтля— Буссинеска. Однако в тех слу-
чаях, когда необходимо более детальное рассмотрение различных факторов,
определяющих картину турбулентного переноса скалярной субстанции в области
пристеночных турбулентных течений (в том числе и в тех случаях, когда опре-
деление характеристик пульсационного поля скалярной субстанции является
целью задачи), использование рассмотренной в работе теории переноса является
оправданным.
На основе предложенной теории переноса были выполнены численные ре-
шения ряда задач турбулентного переноса: турбулентный теплообмен в плоском
канале при постоянном тепловом потоке на стенке [Л.1-31], теплообмен в круг-
лой вращающейся трубе [Л.1-32], турбулентный теплообмен при естественной
конвекции в узкой вертикальной ячейке. В этих задачах впервые были вычис-
лены распределения пульсационных тепловых потоков во всем пространстве
пристеночной турбулентной области.
Несмотря на явные преимущества статистико-феноменологической теории
переноса по сравнению с чисто феноменологической теорией Прандтля —Бусси-
неска, нетрудно видеть, что эта новая теория все-таки не свободна от эмпири-
ческих соотношений, связанных с введением феноменологических аппроксима-
ций некоторых статистических характеристик.
Возникает вопрос: нельзя ли попытаться обойтись без указанных феноме-
нологических аппроксимаций, но постараться, оставаясь в рамках статистиче-
ского описания турбулентности, дать математическое описание «неизвестных»
статистических характеристик, делающих уравнения для высших моментов
незамкнутыми, т. с. в конце концов избавиться от обилия эмпирических кон-
стант? Естественным путем достижения этой цели кажется попытка вывести
дифференциальные уравнения для этих «лишних» статистических характеристик,
т. е. придать теории переноса в неоднородной турбулентности чисто статисти-
ческий смыслх. Ниже мы кратко изложим основные положения этой теории.
Корреляционная модель неоднородной турбулентности
Сформулируем корреляционные модели неполного статистического описа-
ния процессов переноса импульса и скалярной субстанции при неоднородной
турбулентности, не прибегая к введению полуэмпирических замыкающих соот-
ношений (которые содержали бы при таком количестве уравнений огромное
количество эмпирических констант). Предложенные модели в отличие от боль-
шинства полуэмпирических моделей обладают необходимыми условиями гали-
леевой и тензорной инвариантности уравнений, являются универсальными
с точки зрения их использования для любых геометрических конфигураций
в общем случае нестационарных турбулентных потоков при любых числах
Прандтля (в пределах концепции несжимаемости).
Основу теоретических исследований составляет статистический подход
к проблеме турбулентного переноса импульса и скалярной субстанции в тер-
минах одноточечных и двухточечных моментов гидродинамических полей (ско-
рость, давление я температура, концентрация примеси), рассматриваемых как
1 Такая попытка была сделана в работе [Л. 1-33],
70
случайные функции пространства—времени. Исходными являются уравнения
Навье — Стокса движения вязкой несжимаемой жидкости и уравнение переноса
скалярной субстанции:
ди-i dui __________1_ др д2и. 5Г дГ _
~дт;^ик дх/г~ р дх^^ дх^' dx^Ukdxk~ дхк'
Корреляционная модель неполного статистического описания неоднородной
турбулентности сформулирована [Л. 1-33] в видесистемы конечного числа «за-
цепляющихся уравнений» для моментов
+	(1-8-74)
ОХ ОХк “Хк	Р
^^t + Ol~u^rt + -^ului<ul+... = 0;	(1-8-75)
g, UjUtUi	+ - -=°.	(l«-76)
где черта обозначает теоретико-вероятностное осреднение (математическое ожи-
дание), Обрывание цепочки уравнений для моментов производится с помощью
гипотезы квазинормальности Миллнонщикова для моментов четвертого порядка.
Идея замыкания этих уравнений относительно неизвестных моментов сводится
к их кинематической трансформации с помощью переменных Бюргерса с по-
следующим использованием предложенной гипотезы квазиоднородности [Л.1-33].
Окончательная система- уравнений неоднородной турбулентности содержит
дифференциальные уравнения для следующих характеристик: первых, вторых
и третьих центральных моментов поля скорости (yi\ ищиь), вторых и
третьих смешанных моментов скорости и давления («/р, ищр), тензора вто-
рого ранга микромасштабов турбулентности 1ц. Эта.система замкнута с точ-
ностью до двух «однородных» статистических коэффициентов, которые .при
изотропии переходят в известные статистические коэффициенты.
Корреляционная модель неполного статистического описания переноса
скалярной субстанции при неоднородной турбулентности сформулирована
[Л. 1-33] в виде системы конечного числа зацепляющихся уравнений для пер-
вого момента поля скалярной субстанции и смешанных моментов более высо-
кого порядка:
'	+A“S-x?7 = 0;	(1-8-77)
дх г дх/ дх^ dxj	'	'
й“Гт+',61г + ^‘^+-=0;	(1-8-78)
д_____ duiU/f д ____________
3?	+v” + аЦ +•  =0 •	-8-79)
Как и прежде, обрывание цепочки уравнений производится с помощью
гипотезы квазинормальности Миллионщикова [Л. 1-34]
ukf 4-и{ак
а замыкание относительно неизвестньТх моментов —с помощью гипотезы квази-
однородности. Окончательная система уравнений, определяющая следующие
характерстики переноса скалярной субстанции:
Г, tiff, щщу, ур, utyp,
замкнута также с точностью до двух статистических коэффициентов, ранее
Не вводившихся.
71
По аналогии с предыдущими моделями формируется корреляционная мо-
дель поля пульсаций скалярной субстанции при неоднородной турбулентности
<?va д —
^+< + ^+=0;	0-8-зо>
^+0*т^ + ^“^+---=°>	t1-8'81»
где также используются гипотеза Миллионщикова [Л. 1-35]
“ад2=“.-ад2+2«ir ад
и гипотеза квазиодпородности. Окончательная система уравнений описывает
следующие характеристики поля скалярной субстанции; вторые и третьи мо-
менты у2, Ujy2, ру2, а также микромасштаб пульсаций скалярной субстанции X,.
Система уравнении содержит два «однородных» статистических коэффициента,
которые при изотропии переходят в известные статистические коэффициенты
изотропного скалярного ноля.
На основе предложенных моделей неполного статистического описания
процессов переноса при неоднородной турбулентности производится численное
решение класса «модельных» краевых задач пристенной и свободной турбулент-
ности.
1-9. ОСНОВЫ НЕЛИНЕЙНОЙ ТЕРМОМЕХАНИКИ СПЛОШНЫХ СРЕД
В настоящее время существуют три феноменологические теории явлений
переноса в сплошной среде: 1) термодинамика необратимых процессов (ТИП);
2) термодинамика переноса, основанная на понятии свободной энтропии (ТПСЭ),
и 3) нелинейная термомеханика (НТМ).
Первая была создана Онзагером и де Гроотом и является обобщением
классической термодинамики. ТПСЭ основана на работах'Ж. Мейкснера [Л. 1-35],
в которых используется классическое определение энтропии, данное Клаузиу-
сом. НТМ создана С. Трусделлом и его учениками и описывает нелинейные
законы переноса в самой общей форме для сред различной материальной струк-
туры. В этом параграфе и будут изложены основы НТ.М.
Все три теории основаны на законах сохранения: массы, количества дви-
жения (импульса), момента количества движения и энергии. Предполагается
наличие трех видов механического взаимодействия; 1) контактных сил, дей-
ствующих между частями тела, 2) контактных сил, возникающих па поверх-
ности тела, и 3) массовых сил, действующих на тело на расстоянии со сто-
роны внешней среды. Для описания тепловых эффектов используются поня-
тия температуры Т (z, т), которая в каждой точке г пространства и в любое
время т имеет положительное значение, и удельной энтропия $ (г, т). Здесь
уместно остановиться на понятии тела и описании его движения. Тело опре-
деляется как некоторая контрольная или отсчетная конфигурация, в которой
находятся частицы тела г. Движение тела известно в том случае, если мы
знаем положение / (Z, т), 'занятое частицей Z в любое время т. Предпола-
гается, что /—функция, дифференцируемая такое количество раз, какое нам
необходимо. Надо отметить, чсо две различные частицы Z и Y не могут зани-
мать одно и то же положение / (Z, т)#=/(К, т), если	Можно вместо
материальных координат (Z, т) в качестве независимых переменных взять обыч-
ные координаты (z, т). Тогда уравнение z=/(Z, т) будет обратным, чтобы
выразить Z через г и т и использовать его для описания скалярного, вектор-
ного и тензорного полей как функцию пространственных координат (г, т). Для
того чтобы отличать градиенты, взятые по переменной г и 'Z, введем обозна-
чения:
grad<p(z, =	grad^(2,	Т).; ( = 1, 2, 3. (1-9-1)
72
Тогда производные по времени будут равны:
ф(7,	(г^ x)grad<p (z7 т);
(1-9'2)
(1-9-3)
При сделанных предположениях относительно функции f(Z> т) детерми-
нант тензора деформации G(-) всегда больше нуля:
G = grad/(Z, т).	(1-9-4)
Если контрольная конфигурация является конфигурацией тела в какой-то
момент времени, то у тензора G должен быть положительный детерминант.
Движение тела является однопараметрической сменой конфигураций
с положительным временем;
!=/(?’): 2=/-1.(7, т).	(1-9-5)
Важным понятием является локализация. Кривые	и деформируются
по соотношению (1-9-5) в кривые и . Если dZ есть элемент дуги вдоль
то при помощи замены переменных получим:
J [...] dZK=J [...]ZK,t	(1-9-6)
Пространственное поле dz определяется через материальное поле dZ
dZK= Z.f dj4,	(1-9-7)
решение которого для dz
dz = z, ^dZ*.	(1-9-8)
В формуле (1-9-8) dz есть поле, описывающее деформируемый материал, опре-
деление которого требует знания деформации вблизи z. Величина z,£- является
компонентом градиента деформации G. Тензор G можно разложить на тензор
вращения R и чистую деформацию в виде симметричного тензора натяже-
нкя U (правый положительно определенный тензор натяжения):
G = RU=VR,	(1-9-9)
где V —левый положительно определенный тензор натяжения.
Часто более удобно использовать правый С и’левый В тензоры натяжения
Коши —Грина
C = GTG=U2; B = GGT=Va.	(1-9-10)
Компоненты тензора Коши —Грина являются рациональными функциями
компонентов G, в то время как компоненты U и V не являются такими функ-
циями.
Если Ь — исходная конфигурация в момент времени т0 и 0 (т) и 0 (0) —
конфигурации в моменты т и 0, тогда с помощью обычных преобразований
определяется относительный градиент деформации [Л. 1-36]:
G (9) = G1T) (fl) G (т),		(1-9-11)
где ;
G (0): 60 (0); G (т): b -+ 0 (т); Glt) (6): 0 (?) -> 0 (6).
73
Таким образом, относительный градиент скорости деформации и момент т
можно представить как
L (т) ~ Glt) W = -^- Gltl (в) |в.т = GItIG (T)-i,	(1-9-12)
что полностью совпадает с пространственным градиентом скорости gradi-
Аналогично пространственный градиент n-го ускорения равен:
I-™«^-=Gf‘>(T)=gradzl'>>; л=|, 2...	(1-9-13)
При
L0=I; f,f=L.	(1-9-14)
Используя полярное разложение Градиента относительной деформации и
дифференцируя по времени, определяем скорость натяжения D н спин W:
D = ultl(T) = l(L + LT);	О'9'15)
W = Rlt,(T)=l (L —LT),	(1-9-16)
где D, очевидно, симметричная часть L, называемая иногда тензором скорости
деформации.
Легко вывести соотношение:
tr D = tr L= div i-	(1-9-17)
Если p—плотность массы тела, ро — плотность массы тела в контрольной
конфигурации н 4^—область, занятая частью тела, то по закону сохранения
массы имеем:
J р»(2) Л- (Z)= $ р (Z, т) dV (г),	(1.9.18)
где ($о—область, занятая контрольной конфигурацией. Сделав замену перемен-
ной z—f (Z, т) под знаком интеграла в правой части, находим, что ро и р
связаны уравнением
н	p0=pdetG.	(1-9-19)
Если мы возьмем производную по времени от равенства (1-9-19) и восполь-
зуемся тождеством
gra d и = GG'1,	(1 -9-20)
а также формулой (1-9-2), то получим уравнение непрерывности:
(ри)=О - или -~£--l-tr grad рГ=О.
Если имеется поле контактных сил л (г, т), рассчитанное на единицу
площади, затем поле массовых объемных сил F (г, т), то па основе уравнения
баланса импульса можно написать:
П - п dA -J- j pf dV = p5 dV,	(1 9 21\
(A)	(V}	(P)	1	'
где И—тензор напряжений, связанный с вектором напряжений л соотношением
л (г, п, 1) = П(г, т)л,	(1-9-22)
где л —нормаль к поверхности (А), ограничивающей объем (V). Из уравнения
(1-9-21) получим уравнение движения Коши
p7i = div П-|~-р54	.(1'9-23)
где р —плотность тела отсчетной конфигурации,.
74
Обозначим вектор теплового потока через q, т. е.
q(z, ~п, т) = —<f(z, т)-п,	(1-9-24)
внутреннюю энергию через и и источник тепла через Q, тогда можно написать:
A- С р (u-f- у dlZ == (сЛ Пп — q  п) dA -ф \ р (р  f-j-Q) dP". /1-9-25)
(V) '	(3)	(П
Используя теорему Остроградского —Гаусса, получаем уравнение переноса
энергии в дифференциальной форме;
piz==-— div q 4- tr (Пт grad o) + pQ.	(1-9-26)
Второй задачей нелинейной термомеханики является представление мно-
гообразия материалов в виде определяющих уравнений, Теория определяющих
уравнений основана на следующих принципах:
1)	детерминизма (напряжение тела определяется историей движения тела);
2)	локального действия (напряжение в частице определяется только дви-
жением вблизи этой частицы);
3)	независимости свойств материалов от системы отсчета;
4)	равпоприсутствия (величина, присутствующая в качестве независимой
переменной в одном определяющем уравнении, присутствует но всех остальных
уравнениях, если только ее появление не запрещено общими законами физики
или условиями инвариантности).' Применение этих принципов к решению конк-
ретных задач нелинейной термомеханики сплошных сред описано в трудах
К. Трусделла и его учеников,
Остановимся несколько подробнее на принципе равноприсутствия. Из
принципа равноприсутствия как частный случай получается основной принцип
термодинамики необратимых процессов —принцип Кюри для изотропных ма-
териалов. Согласно принципу равноприсутствия основные характеристики тер-
момеханического процесса (тензор напряжений П, поток тепла q, внутренняя
энергия и и энтропия $) должны быть функциями одного н того же набора
независимых переменных (г, z, G, G, Т, t. VT, VT), т, е.
П
’ >=Фм(г, G, G, Т, t, 4),	(1-9-27)
5
где g = grad Т =VT —градиент температуры; Ф(1) — функционал соответствую-
щей величины П, q, и, $.
Если материал изотропный, то независимые переменные z и z выпадают
из определяющих уравнений (1-9-27). Определяющие уравнения (1-9-27) должны
удовлетворить основным принципам термомеханики, изложенным вадще, Кроме
того, для термомеханических процессов определяющие уравнения должны
удовлетворять основному неравенству' термомеханики — неравенству Клау-
диуса — Дюгема
div-Aj^O.	(1-9-28)
В это неравенство входит величина pQ, зависящая от источника теплоты Q,
ее можно исключить, еелк воспользоваться уравнением переноса энергии. Обо-
значим несимметричный тензор Пиола — Кирхгофа через ег:
(1-9-29)
тогда уравнение (1-9-29) напишем так:
ри— — div q	: G.	(1-9-30)
75
Исключив из уравнения (1-9-30) величину pQ и выполнив операцию div
получим неравенство Клаузиуса—Дюгема в форме
(1-9-31)
Колеман показал, что
S5-0 ппи G = u="o—0; 1
Р . J }	(1-9-32)
и^О при G=$=(/^0. J
Таким образом, можно заметить, что в типичном случае релаксации напря-
жений в условиях постоянства температуры удельная внутренняя энергия
уменьшается, а энтропия увеличивается, Принцип равноприсутствия имеет
большое значение, так как он отражает взаимосвязь явлений переноса. Однако
этот принцип ве противоречит классической форме описания этих явлений.
Для некоторых модельных материалов при малых отклонениях от равновесия
количество независимых, переменных сокращается, и в частном случае перенос
импульса, теплоты и массы описывается раздельными переменными. Проил-
люстрируем это положение на примере.
Пусть для некоторого материала система определяющих уравнений имеет
вид:
П I
’ f=a>,.,(7, 7. о. о).	(i-9-зз)’
s 1
Если удовлетворить определяющие уравнения неравенству Клаузиуса —
Дюгема, то переменные q и G в уравнениях для и и s выпадают. Однако
в определяющие уравнения для П и q будут входить переменные G и ~q. Если
затем удовлетворить определяющие уравнения для Пи? принципу незави-
симости свойств материала от системы отсчета, то статическая часть тензора
напряжения будет определяться только термодинамическими переменными
(переменные G, G, ~q выпадают). Если материал является простой жидкостью
(группа изотропии всех четырех определяющих уравнений есть унимодулярная
группа), то, как показано в работе [J1.1-37J, определяющие уравнения примут
вид:
7. V„, D);	(1-9-34)
7=Фг0, 7 v«. D):	(1-9-35)
и = ф„(5, V„); r =	1	(1-9-36)
где Фа и Фд — изотропные функции; Ус —удельный объем (V0=l/p).
Из определяющих уравнений (1-9-34) — (1-9-36) видно, что получено только
частичное разделение эффектов. Если определяющие функции фо и ф? разло-
жить в окрестности D==0 и т'—О, то с погрешностью
О (KtrD»+72)
определяющие уравнения (1-9-34) и (1-9-35) примут вид:
П = --Й7	О + 2ПО;	(1-9-37)
q = — XgradT,	(1-9-38)
76
т. е. получаем классические, полностью разделенные уравнения переноса
импульса и теплоты для жидкости с линейной вязкостью и линейной тепло-
лоо водностью.
' Для ориентированных сред и микрожидкости неравенство Клаузиуса —
Дюгема должно быть обобщено, оно имеет вид [Л.1-15]:
рй = —(ФЧ-Ts) л-kiVz> й-ф-лут nki)
+ '-р-л111тУ1т. k “ЬфТ	(1-9-39)
. где ф —свободная энергия Гиббса, остальные обозначения см. § 1-6.
Используя неравенство (1-9-39), Эринген показал существование термоди-
намического тензора напряжений и влияние микровращения на перенос теп-
лоты теплопроводностью [Л,1-15]. В частности, для термомикрополярной жид-
кости при линейных определяющих уравнениях поток теплоты q равен:
9 = —	+	(1-9-40)
где В-постоянный коэффициент.
Плодбтворность применения методов нелинейной термомеханики к явле-
ниям переноса проиллюстрируем несколькими примерами. Рассмотрим неизо-
термическую диффузию в газовой смеси.
Введем следующие обозначения:
p*»=V: Sp«“1;	“/=Spto“s:
г k	k	k
k	k	k
Индекс k обозначает, что данная величина относится к £-й компоненте
смеси газов.
Тогда уравнения переноса можно написать относительно Л-й компоненты.
Они будут'иметь вид [Л.1-8]:
+ div	= р4 + р4 div ik - р/„ = 0;	(1-9-41)
,	Pt?»— divll* — pJn+piA — pm* = 0;	(1-9-42)
PMt=.n4-nJ;	(1-9-43)
Ph (“4—ф 4?) +	+ pmtzk - tr (IT gra d 4,) - div	- pQb — p4(;), = 0,
(1-9-44)
где !kt ilk) mii> /Й&—соответственно источники массы, энергии, линейного мо-
мента и вращательного момента.
Для смеси газов сумма всех источников равна нулю:
24=0; ^/»=0; 24=0; 2л<„ = °.	(1-9-45)
k	k	к	k
Диффузионная* скорость определяется по соотношению
(1-9-46)
77
Тогда, используя обычные представления о смеси газов, можно написать
[Л. 1-38]:
П = 11,—2р*шА:	(1-9-47)
“=“,+-j-2P4om’l	O'948)
k
’ + +	(1’М9)
<?=<?,+2р„<Л а-	а-9-50)
k
Используя соотношения -(1’9-47) — (1-9-50), можно из уравнений переноса
(1-9-41)—(1-9-44) получить обычные уравнения переноса импульса, теплоты
и массы.
Этот метод был использован в работе |Л.1-38] для определения термоди-
намических движущих сил в бинарной газовой смеси.
В результате, были получены следующие уравнения переноса:
7i=P14S = -^7'(Y-^gradlnT-gx1;	(1.9-51)
? = - (iT +	grad In Г + Xi, (1-9-52)
где
Xr = grad (ir -?‘r + -J- div Пг + ^-^^-Ч- i div (рлй), (1-9-53)
Pl	Pl (K Pl
Q* —изотермическая теплоте переноса; рг и у — постоянные коэффициенты;
щ — химический потенциал. Из этих уравнений видно, что перенос массы и
теплоты определяется не только действием термодинамических сил gradm и
grad Т, но и зависит от тензора П и скорости «р Если положить у = 0, то
получим известное равенство кинетических коэффициентов Онгазера или прин-
цип взаимности в термодинамике необратимых процессов.
В качестве второго примера Приведем результаты из работы [Л.1-39],
в которой рассматривалась задача конвективного теплообмена при полностью
развитом ламинарном течении в цилиндрической трубе при граничных усло-
виях второго рода (поток теплоты на поверхности трубы постоянный). Клас-
сическое решение этой задачи дает для числа Нуссельта Nu постоянное зна-
чение:
. Nu = 4,36 = const.	(1-9-54)
При определении потока теплоты формулой
?"*=—Agradr+PiDgrad?	(1-9-55)
решение задачи привело к формуле
Nu=4,36-Kd,	(1-9-56)
где KD —безразмерная величина, учитывающая влияние гидродинамического
движения на молекулярный перенос теплоты (теплопроводность) и равная:
<1-9-57>
где Я —радиус трубы; 0г — постоянный коэффициент.
78
Формула (1-9-56) является новым результатом в теплотехнике. Таким
образом, методы нелинейной механики сплошных сред не только представляют
общий научный интерес, но и дают важные практические результаты.
1-10. НЕКОТОРЫЕ ОСОБЕННОСТИ ГИДРОДИНАМИКИ
РЕОЛОГИЧЕСКИХ ЖИДКОСТЕЙ
Нелинейная механика сплошных сред дает такое определение простой
жидкости. Простая жидкость есть материал, механическое поведение которого
определяется из опыта однородной деформацией.
Обычно считают, что жидкость, для которой справедлив закон вязкого
течения, является ньютоновской жидкостью.
Согласно закону Стокса, состоящему в том, что вязкие напряжения, воз-
никающие в любой точке сплошной среды, зависят только от относительного
движения жидкости вблизи этой точки, связь между тензором вязких напря-
жений и тензором скорости сдвига в простейшем случае имеет вид:
Vij=Pij — (—(1-10-1)
где ^—коэффициент сдвиговой вязкости, а объемная вязкость исключена со-
гласно гипотезе Стокса.
Уравнение (1-10-1) является исходным для замыкания уравнений гидроди-
намики в форме Навье —Стокса.
Коэффициент вязкости можно подсчитать по формулам кинетической тео-
рии газов, которые зависят от потенциала взаимодействия сталкивающихся
молекул. Однако вязкость можно определить и экспериментально. Для этого
перепишем уравнение (1-10-1) для одномерного сдвигового течения:
°» = —’IJ-T (*г = И>-	(1-10-2)
Если процесс идет при постоянной температуре, то r| = const. Тогда, от-
кладывая на оси абсцисс значения напряжений ai2, а на оси ординат скорости
сдвига dvi/dx2, получим прямую линию, тангенс угла наклона которой равен
коэффициенту вязкости. Следовательно, если на опыте реализовать условия
чистого сдвига и измерить скорости сдвига и соответствующие им напряже-
ния, то по отмеченной выше методике можно определить коэффициент вязко-
сти. Приборы такого типа называются вискозиметрами, а уравнения типа
(1-10-2) в реологии называются кривыми течения.
Если в уравнении (1-10-2) перейтн от напряжения к силам, то оно в точ-
ности будет соответствовать уравнению Ньютона для материальной точки. При
этом элементарный объем жидкости надо отождествлять с материальной точ-
кой, масса которой скрыта в коэффициенте вязкости, В этом смысле жидко-
сти, подчиняющиеся уравнениям (1-10-1) и (1-10-2), называются ньютоновскими.
Обратный переход от уравнения (1-10-2) к (1-10-1) возможен только при
дополнительном постулировании изотропности пространства. Поэтому уравне-
ние (1-10-2) мы должны трактовать как эмпирическую формулу, в то время
как соотношение (1-10-1) можно возвести в ранг закона.
Однако многочисленные вискозиметрические измерения показали, что очень
узкий класс жидкостей подчиняется реологической формуле (1-10-2), и для
многих жидкостей кривые течения имеют нелинейный характер. В этом случае
эмпирическую формулу (1-10-2) можно подправить так, чтобы опа с какой-то
степенью точности аппроксимировала нелинейные кривые течения. Например,
вместо (1-10-2) можно записать:
fdv<\n
(1-10-3)
Теперь, выбирая г] и п, можно в определенном интервале скоростей сдвига
аппроксимировать нелинейную кривую течения достаточно точно. Однако,
основываясь на эмпирической формуле (1-10-3), обобщить закон (1-10-1) мы не
79
можем. Во-первых, коэффициент t] при I уже не есть вязкость, хотя бы
потому, что его размерность зависит от числа п. Во-вторых, даже введя гипо-
тезу об изотропности пространства, мы не можем величину dVijdx^ в формуле
(1-10-3) заменить тензором 6ц, так как операция возведения матрицы в сте-
пень неэквивалентна возведению в степень каждого элемента этой матрицы.
Таким образом, налицо противоречие с основными положениями кинетической
теории.
Правда, противоречие с правилами тензорного анализа в реологии устра-
нили, введя понятие эффективной вязкости
п — 1
(1-10-4)
где 12 — второй инвариант тензора скорости деформации.
Теперь вместо-закона (1-10-1) имеем так называемый степенной закон:
п — I
2 й/=п,фй|/-	,	(ыо-5)
Но сразу возникает вопрос: что такое эффективная вязкость с точки зре-
ния кинетической теории газов или жидкостей? На него можно получить
ответ, что степенной закон справедлив для жидкостей, а кинетическая теория
жидкостей еще не создана. Однако при этом полезло заметить, что уравнения
Навье —Стокса выведены Навье и Максвеллом для газов, но они оказываются
справедливыми и для жидкостей, а все различие сводится только к различным
видам потенциала взаимодействия сталкивающихся атомов или молекул.
Таким образом, пытаясь на основе эмпирических формул (1-10-2) и (1-10-3)
обобщить законы типа (1-10-1), мы неизбежно приходим в противоречие
с основными положениями существующих теорий.
Эту проблему правильно понял Трусделл- Он первым ввел разумное
обобщение указанной гипотезы Стокса.
Следуя Трусделлу, дадим определение обобщенной стоксовской жидкости
(Л. 1-40).
Стоксовская жидкость—непрерывная среда, в которой существуют мате-
риальные константы и Т^, называемые естественной вязкостью и характер-
ном температурой, размерности которых
1Ти]=е,	(МО-6)
а тензор визких напряжений зависит от тензора скорости деформации Dy и
величин т)о, То, Pm, р, Т
^/=/(тю, Ль Рт, Р, Т, Dif);	(1-10-7)
ау=0, если D/y=0-
Дли изотропной среды, пользуясь известным тождеством Кэли — Гамиль-
тона, уравнению (1-10-7) можно придать вид:
□/у = Eifiij -^EjDij-^-E^DifrDfy-,	(1-10-8)
причем
£0,	&2~f 01<ь Л’ Л», Р, Г U’ ^«5* ^з),
где h. ^2. 18—-инварианты тензора скорости деформации.
С точностью до квадратичных членов уравнению (1-10-8) Трусделл при-
дал вид:
4~~~ [4-^uooli^O'4-^qiHoMey4"(1-10-9)
Введем тензор скорости сдвига ко формулам
D = £,у-11^; Я$)к/ = DlkDkj~ 1 (1? - 21а) 8г/	(1-10-10)
80
и, если
3/?oioo4"/?iooo = 0; 3Fo20a4'^'iioo4_^,2000=0^ З/^оо^о—2F20W=0, (1-10-11)
то вместо (1-10-9) будем иметь:
aZ/ = ilo^,iooo^//4’’~ l^iiooU^b'+^sow^fePjyb (1-10-12)
Ро
Формула (1-10-12) является исходной для замыкания уравнений гидроди-
намики по Трусделлу.
Тензор полных напряжений имеет вид:
Pif=-P^+uij.	(1-10-13)
Здесь Р — гидростатическое или равновесное давление, определяемое через
тепловое движение атомов или молекул.
Тензор дает добавку к равновесному давлению, вызванному видимым
движением.
В пределах справедливости уравнений Навье—Стокса видимые и тепло-
вые движения сосуществуют. Трусделл неявно предположил, что даже в пре-
делах справедливости формулы (1-16-9) условия сосуществования этих движе-
ний не нарушены. Поэтому величину гидростатического давления он определил
так же, как и в классическом случае, что в свою очередь привело к условиям
(1-10-11).
В одной из последних своих работ Трусделл, пользуясь критерием
ввел понятие предела применимости уравнений Навье—Стокса.
Действительно, в пределах гипотезы Стокса формула для тензора полных
напряжений будет такой:
Рц=-Р^ч + ^Ц-	(1-10-14)
В движущейся жидкости выделим элементарный объем и будем определять
напряженное состояние в нем по формуле (1-10-14). Если (т^£>у/р) < 1, то
характер напряженного состояния будет таким же, как и в равновесном со-
стоянии. Если же указанный комплекс будет больше единицы, то в рассматри-
ваемом объеме изменится характер напряженного состояния, т. е. всестороннее
сжатие может превратиться во всестороннее напряжение. Этот факт Трусделл
назвал верхним пределом применимости уравнений Навье—Сгокса.
Мы же склонны считать, что этот критерий в первую очередь указывает
на нарушение условий сосуществования видимого и теплового движений. Это
приводит к переопределению давления в потоке.
Для этого перепишем формулу (1-10-9) так;
17г/ — Но иим Ч- Р loooj Ч-
4" ИИМ^/Ч"	^2000^/fc^fe/] .	(1-10-15)
(1-10-16)
Давление в потоке определим по формуле
р ——3 (Р11^_Р2г‘^33)	—з" (а11‘4'а22'Ч'сзз)-
Добавку в формуле (1-10-16) определим из (1-10-15):
(°пЧ"с22Ч‘сзз) —'Пц Г01О0 4- -g Fю00\ 1г4-
(1-10-17)
я I
Чтобы формула (1-10-17) была одинаковой для сжимаемых и несжимаемых
материалов, предположим, что
3/?Moo4-f'iooo==0; 3F^00-pf-,11()0-!--f’2Wt)=0.	(1-10-18)
Теперь формула (1-10-16) примет вид:
р = р— ^Ffjtno	у £а<юо^~ ^2’	(1-Ю-19)
причем коэффициенты Fooio» £2000 есть произвольные функции от температуры
в соответствии с представлениями Трусделла.
Формула (1-10-19) приводит к следующему обобщению уравнения для
равновесного давления:
£ = ^1—^ooio + y^ooo ।	(1-10-20)
Сравнивая данную формулу с формулой (1-5-66), видим, что они анало-
гичны. Это объясняется тем, что реологическую жидкость можно рассматри-
ват>, как дискретную систему, состоящую из ньютоновской жидкости с добав-
лением небольшого количества полимера. Молекулы полимерной жидкости
играют роль структурных частиц. Конечно, эта модель является очень гру-
бым приближением к действительной структуре, однако из опыта известно,
что добавление небольшого количества полимера к ньютоновским жидкостям
вызывает асимметричность тензора вязких напряжений.
Теперь в соответствии с гипотезой (1-10-18) формулу для вязких напря-
жений надо переписать так:
» и2 Г/ 2	\	о	=^= I
оу = T]oFioi)i)Dy -j—- Ц^ооТо — "g" F2000 J ^г^у + F)(мДх^у4-FiwoDikDkjj. (1-10-21)
Разбирая задачу о передаче количества движения через слой жидкости,
ограниченной двумя плоскими твердыми параллельными стенками, и пользу-
ясь формулами (1-10-20) и (1-10-21), можно показать, что граничные условия
вблизи стенки примут вид:
(' + '’) F„ (1 -Fim, + I F,»oo)	Лп дв
V °	2(1—v)	У Л!о рду-
В последней формуле можно ввести коэффициент скольжения,
сделал Максвелл:
(1-10-22)
как это
(1-10-23)
(1 4-м) F1000
6 =	-------------
Р
уИ0 ‘
Если Fiooq=1, fooio=F2mjo = °. то формула (1-10-13) переходит в формулу
Максвелла.
Анализ условий скольжений или прилипания удобно проводить по фор-
муле (1-10-22). Действительно, если (т]о/Р) (dv/dy) много меньше единицы, то
всегда скорости прилегающего слоя жидкости и стенки совпадают, т. е. имеет
место прилипание жидкости.
Прилипание может быть и в случае, если (г^/р) (ди/ду) =« 1 и
1 — F0010 4- g Г2ооо — О-
(1-10-24)
Скольжение жидкости вблизи твердой стенки наступает, если (x\o/p)(dv/dy')=s
я» 1 и правая часть формулы (1-10-22) —существенно’отрицательная величина.
Последнее утверждение равносильно требованию
Fюов — £ooio + -д- £2000) >	(1-10-25)
82
Нами не разобран случай, когда (г]0/р)
и
2	'
I — Fоою 4" у Fгооо
(1-10-26)
Изложенные выше рассуждения приводят к уточнению тензора нормаль-
ных давлений и тензора вязких напряжений. Поэтому при написании урав-
нений гидродинамики возникает вопрос —через какой из отмеченных тензоров
необходимо ввести уточнение в указанные выше уравнения? Ответ надо искать
а сопоставлении наших рассуждений с опытом.
Явление скольжения жидкости вдоль твердой стенки экспериментально
было открыто еще в 1860 г. Гельмгольцем и Пиотровским. Интерес к этому
делу может снова возникнуть в связи с изучением реологических свойств
неньютоновских жидкостей. Таким образом, при движении жидкости дискрет-
ной структуры необходимо учитывать явление скольжения вдоль твердой стенки
при условии, что число Трусделла близко к единице.
Па основе анализа многочисленных реологических кривых u = f(&) была
получена следующая эмпирическая формула [Л. 1-41]:
--	1 j
(1-10-27)
где п, т—постоянные, определяемые яз опыта; а0—постоянная предела теку-
чести; е —скорость деформации (&=Ле,'Лт:). Если n =	а а0 = 0, то полу-
чаем соотношение для ньютоновской жидкости. Если положить n=m~l, то
получим соотношение для жидкости Шведова —Бингама. При значении п = 1
формула (1-10-27) превращается в формулу Бакли —Гершеля.
В случае чисто вязкой жидкости (ст0 = 0) формула (1-10-27) переходит
в степенное реологическое уравнение с показателем степени, равным n/m.
Формулу (1-10-27) в безразмерных переменных можно переписать так:
= +	’	-	(1-10-28)
где
а‘ = а/а0; в* = ^-8; Л = а/"Г.	(1-10-29)
Оо
Если (dao*/de*2) < 0, то формула (1-10-28) отображает поведение псевдо-
пластических жидкостей при (d2a*/de*2) > 0 жидкости называются дилантант-
НЫМИ.
Если жидкость несжимаемая, то при помощи метода Прагера —Гогенемсра
[Л. 1-42] формулу (1-10-28) можно обобщить на случай пространственной дефор-
мации нелинейно-вязкопластичной среды и написать ее в виде
„	Л~'	(МО-ЗО)
CTf/=2Lau -f-т] J/l Vi/,
где 7(7 = -^-(о;,уф-р/, J — тензор скоростей деформации при перемещении среды;
А = (2у/ду|-)1''2 — интенсивность скоростей деформации.
Насколько известно автору, в литературе отсутствует замкнутая система
уравнений, описывающая движение нелинейно-вязкопластичных сред. Обычно
уравнения переноса импульса и энергии решаются на основе уравнений погра-
ничного слоя. Для некоторых чисто вязких реологических жидкосгей были
выведены и решены такие уравнения пограничного слоя для простейших слу-
чаев обтекания твердых тел [Л. 1-43].
83
Впервые уравнения динамического пограничного слоя линейно-вязкоплас-
тичной жидкости получил Олдройд [Л. 1-44). Анализ уравнений пограничного
слоя вязкопластичной.жидкости Шведова — Бингама при обтекании произволь-
ной поверхности приведен в работе [Л. 1-45).
Уравнение движения несжимаемой жидкости в декартовой системе коор-
динат имеет вид:
dvi/dx + vjv^^Fi-jp^+a^i-,	(1-10-31)
Vi,i=0; i, i=4, 2, 3,
где ст/у определяется соотношениями
оу=2Ви/;О// = В (и/./Н-О/,/) при 1 #/;	(1-10-32)
B=[a"D- '" + г|"]л”-1 ’	(1-Ю-ЗЗ)
Лг = 2(0;г^+(ог1/ + 1>Уг()2.		(1-10-34)
Рассмотрим плоский пограничный слой. Будем считать гидродинамические
характеристики постоянными. Тензор вязких напряжений определяется соот-
ношением (1-10-30).
Введем безразмерные величины согласно соотношениям
4=т; Х?=Ь °*=^’ '”=Ъг- (М0-36>
Тогда уравнения (1-10-31) —(1-10-34) примут вид:
dvf
5^=0. 1=1.2;	(1-10-36)
{dv¥ Дфл
х +*2а#' '/='• Ле-'0®)
где
'[“(ЗНЙ+'Э’]. ->•* !“•>
— обобщенное число Рейнольдса;
(1-10-40)
— безразмерный параметр нелинейной вязкопластичности.
Для случая т = п комплекс S равен критерию Ильюшина и выражает
соотношение между пластичной и вязкой диссипациями.
84
В зависимости от соотношения величин Л, Re и S могут возникать потрав
ничные слои разного типа. Рассмотрим наиболее характерные.
1 +1 11
1. Если и"1 Rc««l, Srl	то можно пренебречь членами, учиты-
_ т
вающими влияние пластичности. В этом случае u=Re п + т, и если р* поло-
жить равным (р*=ру^^ то получим уравнение пограничного слоя для
степенной чисто вязкой жидкости;
t.'iOiri + 0A,1=-p,i+^	(1-10-41)
t>£ 1 + fg, 2 —	р.2 = 0,	(1-10-42)
где индекс * опущен.
В теории асимптотического пограничного слоя важную роль играют авто-
модельные решения, зависящие от одного аргумента. Возможны два типа
автомодельных краевых условий:
а) Закон скорости Фолкнера —Скэна
г,со = *а>	(1-10-43)
что соответствует обтеканию клина.
Тогда автомодельные переменные будут*.-
В случае а= 1/3 (прямоугольный клин, обтекаемый симметрично грани)
преобразование (1-10-44) не зависит от реологических параметров^
б) Закон скорости Гольдштика
(1-10-45)
тогда автомодельными переменными будут:
/	2-—	\	-	/	1-2-1	\
£=уехр(— ———fex j; /=4>ехр(---- kx I . (1-10-46)
\	щ 1	/	\	1 +	/
Постоянная k может принимать любые вещественные значения, отличные
от нуля.
Для данных краевых задач уравнения пограничного сдоя будут иметь вид-.
V?- /„ Т < = 1 +	t1’1047)
“!+-) 5
1—2-1	п
,а^——(/•)”.	(1-Ю-4»)
( +т]
* Обыкновенные автомодельные переменные обозначаются г|, тр, Д мы при-
держиваемся обозначений, принятых в [Л. 1-2].
85
2, Предположим, что х mRe=l и	Тогда, полагая
-(ч3")
— Re s т‘ и р0==ру^, получаем следующие уравнения пограничного слоя:
»Ь1 + У2, в==°; Р.а=°;	(1-10-49)
Wi. 1+»».,= -p.i+Ь" Re"	,)s]>2-	(1'10'50)
Уравнение (1-10-50) учитывает пластичность и вязкость. Наибольшая труд-
.носгь, возникающая при решении уравнения (1-10-50), состоит в определении
величины 5. Дело в том, что для вязкопластичных тел нельзя использовать
равенство классической гидродинамики — ptl	j. В упомянутой рабо-
те [Л. 1-45) принимается р—const для всех тел, отличных ог пластины, при
обтекании их жидкостью Шведова —Бингама.
Один из путей преодоления этих трудностей —переход на методы расчета
пограничного слоя конечной толщины. В работе [Л. 1-41] получены интег-
ральные уравнения пограничного слоя и даны их решения методом Кармака—
Польгаузепа. В частности, решалась задача при граничных условиях:
.	при ха=0; Vj = 0; оа=0;	(1-10-51)
при ха = 6(х1); Ojs=l; оЬ2—0; о = а0.	(1-10-52)
В этом случае интегральное уравнение имеет вид;
(МО-58).
\ о	/	g-n
где N —критерий нелинейной вязкопластичности, равный:
В случае т=п интегрирование уравнения (1-10-53) доводится до конца.
Для частного случая п*=2 (жидкость Кэссона) получается следующее
соотношение:
(‘ + ФС 2	(ЫО-55)
л=4
где
С~ 16-280№’ g / •	(1-Ю-56)
Если ограничиться первым членом в разложении (1-10-55), то получим:
(1-10-57)
Соотношение (1-10-57) является формулой Скелланда (Л.1-46] для пла-
стины, продольно обтекаемой жидкостью Шведова —Бингама. Следовательно,
первый член разложения (1-10-55) учитывает линейную часть реологических
свойств жидкости, а последующие —нелинейную вязкопластичность
В работе [Л. 1-4IJ рассмотрен случай v.m Re < 1 и	. Тогда
можно пренебречь инерционными членами, а величину и можно принять рав-
ной:
m
Ях=5-п(1 + 2»>\	(1-10.58)
За характерное давление принимается р0 = ко0, Этот случай соответствует
медленному пристенному течению, где силы пластического происхождения
доминируют над вязкими силами, Подробный анализ данного случая движения
дан в работе [Л. 1-41 ].
Все вышеприведенные решения уравнений гидродинамики реологических
жидкостей были получены в предположении, что тензор вязких напряжений
является симметричным (и/7=иуг-).
Однако многие реологические жидкости не удовлетворяют условию сим-
метрии, так как они являются ориентированными средами, Поэтому их надо
рассматривать как асимметричные жидкости,
1-11. О ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЯХ ТЕПЛОМАССОПЕРЕНОСА
Перепое массы и энергии (теплоты) описывается дифференциальными урав- 1
нениями параболического типа. Они выводятся па основе законов сохранения I
массы и энергии, а также путем введения гипотез Фика и Фурье о связи ;
между потоками массы и теплоты и градиентами температуры и концентрации. \
Гиперболическими уравнениями, в которые в качестве основного параметра
входит скорость распространения волны (скорость звука или скорость света),
описывается распространение звуковых и электромагнитных воли. Эти уравне-
ния выводятся на основе законов сохранения без каких-либо дополнительных
гипотез, что объясняется следующим, Параболические уравнения неинвариантны
относительно знака у переменной т, т. е. замена времени т на —т изменяет
само уравнение, что видно из уравнения теплопроводности
"	дТ
-g^=a^T,	(1-11-1)
поэтому параболические уравнения теплопроводности описывают необратимый
процесс распространения теплоты.
Гиперболическое уравнение, описывающее распространение волн,
(1-11-2)
где с—скорость распространения волны, инвариантно по отношению к знаку
(алгебраическому) у переменной т, поэтому оно описывает обратимый процесс
распространения волн. Следовательно, если дифференциальное уравнение инва-
риантно по отношению к преобразованию инверсии относительно времени, то
процесс, описываемый этим уравнением, является обратимым процессом. Про-
цесс теплопереноса является необратимым процессом распространения теплоты.
Физическое различие между распространением теплоты и света имеет свое
математическое обоснование. Любой физический процесс протекает в простран-
стве и времени. Поэтому исследуемый процесс переноса характеризуется какой-
либо физической величиной, являющейся функцией пространства и времени.
Например, процесс теплопереноса характеризуется распространением темпера-
туры в пространстве и времени,
Если изучаемая физическая величина является скалярной {температура,
концентрация массы, энергия), то для описания распространения этой вели-
чины вводятся дифференциальные инварианты первого и второго порядков.
Дифференциальным инвариантом первого порядка функций ср3 и ф2 является
87
$21 определимое соотношением
_2jpl2si I б(й ^фз । дф,- дф
ф8~ дх дх ду ду ф дг dz '
Если функции <рх и фз равны (ф1 = фп = ф)> то
М(Ж£НЭТ2=;^ ’
(1-11-3)
(ММ)
Так,
4^- = 4^ cos (tt, х);	= 4®-cos (л, у); 4^-= 4^-cos(n, z);	(1-11-5)
дх дп	ду дп ' dz дп ' ' >’	'	>
'cos2 (/t, x)H-cos2(n, y)-j-cos2(n, г)==1;	(1-11-6)
о-"-7)
Между дифференциальными инвариантами первого порядка имеется сле-
дующая связь:
Нф,, фа = Нф^,cos (нф!, Лф2).	(1-11-8)
Этим соотношением определяется угол в многообразии трех измерений.
Дифференциальным инвариантом второго порядка от функции является
величина
0-^)
Дифференциальные инварианты первого и второго порядка взаимосвязаны
при помощи теоремы Грина
^н’ф,<йЛ’=	(1-11-10)
(V)	(*S)	(V)
которая превращается в формулу Гаусса, если фа постоянно или нормаль его
ортогональна к нормали функции фх:
С dS = 72фйИ.	(1-11-11)
s	(И
Интегрирование в формулах (1-11-10) и (1-11-11) происходит по замкнутой
поверхности S, ограничивающей объем V.
Рассмотрим' перенос теплоты. Изотермическая поверхность, или поверх-
ность одинаковых температур, в эвклидовом пространство описывается урав-
нением
Т(к, у, г, т) =const.	(1-11-12)
Для вывода дифференциальных уравнений выбирают основные физические
величины, которые не должны зависеть от выбора системы координат, и при
помощи их замыкают дифференциальные инварианты. Первый дифференциаль-
ный инвариант изотермической поверхности Нт равен абсолютной величине
градиента температуры:
При помощи этого дифференциального инварианта можно установить связь
между скоростью распространения изотермы uiy и локальной производной тем-
88
пературы по времени дТ;дх. Продифференцировав (1-11-12), будем иметь:
-4Дл1+4^йт = О.	(1-11-14)
дп 1 дт	'	'
Обозначим
dn
dT
(1-11-15)

и назовем ее скоростью распространения изотерической поверхности. Тогда
_ __ JT (dLV1 __L 2L
WT~ дх { дп J Нт дх ‘
(1-11-16)
Для того ч,тобы замкнуть дифференциальные инварианты, необходимо вос-
пользоваться законом сохранения энергии. Температура, вернее градиент тем-
пературы, определяет поток 'энергии. Между ними должна быть связь. Эта
связь устанавливается при помощи гипотезы Фурье:
f = —(1-11-17)
При этом поток энергии (теплоты/-нйй 3k	должен быть связан с выбором
системы координат.
На основе уравнения сохранения получаем уравнение переноса теплоты:
-	^-=яу2Г + 1,/Срр,	(1-11-18)
где а—коэффициент температуропроводности иля коэффициент диффузии теп-
лоты (а = А/срр),
Коэффициент температуропроводности прямо пропорционален скорости
распространения изотермы:
=	(1-11-19)
Однако это не единственный путь описания процесса переноса теплоты.
Для некоторых частных случаев можно замкнуть дифференциальные инва-
рианты без введения гипотезы Фурье. Остановимся на этом подробнее [Л.1-47].
Изотермическая поверхность Т (х, у, г, т) является одной из класса
поверхностей состояния среды. Существует второй класс поверхностей состоя-
ния среды, характеризуемый уравнением
<	р (х, у, г, т, p) = const,	(1-11-20)
где р — свободный параметр.
При непрерывном изменении параметра получим множество пересекаю-
щихся поверхностей, образующих новую огибающую поверхность; чтобы найти
ее уравнение, надо исключить параметр р из уравнения
4^ = 0.	(1-11-21)
др	’
Эта огибающая поверхность будет геометрическим местом характеристик
и называется поверхностью Монжа. Характеристики —эго кривые касания
огибающей поверхности к каждой из огибаемых. Поверхность Монжа по своей
физической сущности характеризует совмещенные процессы. Примером может
служить фронт световой волны, который является огибающей поверхностью
вторичных волн (принцип Гюйгенса — Френеля). Согласно принципу Гюйгенса—
Френеля для нахождения нового фронта световой волны необходимо каждую
точку фронта волны считать источником, самостоятельно испускающим сфери-
ческие волны. Огибающая всех этих вторичных волн и дает новый фронт све-
товой волны.
89
А, С. Предводителей расширил область физических характеристик поверх-
ности Монжа, которая должна отображать такие совмещенные процессы, в ко-
торых выполняются законы сохранения. Такой поверхностью может быть
поверхность фазового перехода или поверхность химических превращений,
т. с, в любой точке процессы должны быть совмещенными, Это обстоятельство
резко отличает поверхность второго класса р(х, у, г, т, р) от поверхности
первого класса Т (х, у, z, т).
В самом деле, изотермическая поверхность Т(х, у, z, т) делит среду па
две области —возмущенную и невозмущенную. Переход из одной области
в другую сопровождается непрерывным изменением Т (х, у, г, т) и ее произ-
водных.
Поверхность второго класса тоже разделяет среду на две области, но пере-
ход из одной области в другую сопровождается разрывом непрерывности,
т. е, на поверхности раздела среда приобретает особые свойства,
х Условия совместимости состоянии среды, разделенной поверхностью Монжа,
были получены Гюгонио и Адамаром.
Возьмем некоторую функцию состояния среды второго класса Ф (х, у, г, т).
Тогда при переходе через поверхность Монжа будут иметь место’' соотношения
=_^	«Л.	(,.,1.22,
дх Hf дх дх ду Haf дх ду дх3	дх /
Я	8Т	Я ^Ф Ч /	\2	2	,1 1, Г»
о  ----------—=—е<Щ/; б — —4-	=z2Wf (1-1-23)
дх Hf dr 1 /f дт3 Hj \дх) 2 r> 1	1
где /—функция Монжа; в* и е2 — соответственно параметры разрыва первого
и второго порядков, величины постоянные; Шу—скорость распространения
поверхности Монжа; 6 —символ Аппеля, обозначающий операцию перехода
через поверхности Л1онжа.
Из соотношений (1-11-22) и (1-11-23) получим:
6Г!Ф = в2; 6-5£- = в„ш",.	(1-11-24)
ОТ3 1 I	'
Отсюда
(1-11-25)
Для символа Аппеля б справедливы следующие перестановочные формулы:
d6 = 6d;	(1-11-26)
дп дп	'	'
Величина есть непрерывная функция координат и времени во всех
точках пространства, поэтому операция 6 обратима. В результате получим
следующее дифференциальное уравнение:
-	^=w^+f(x, у, z, т),	(1-11-27)
где f (х, yt z, т)—любая непрерывная функция.
При выводе гиперболического уравнения (1-11-27) законы сохранения были
использованы для определения поверхности Монжа. При этом должны быть
вторичные процессы, компенсирующие диссипацию энергии.
Однако наибольший интерес представляют дифференциальные уравнения
теплопроводности материалов с переменной памятью.
. В работе [Л.1-49] удельный поток теплоты определяется соотношением
q (Т) - р (9) g (Т -9) rf6,	(1-11-28)
и
- 90
где grad T — градиент температуры, Таким образом, удельный ,поток теп-
лоты6 не зависит от температурного градиента в данный момент времени. Кроме
того, соотношение (1-11-28) справедливо для изотропных материалов.
Если градиент температуры g не зависит от времени 9, тогда, обозначив
через X величину
X=^fe(B)tiB,	(1-11-29)
получим классическую формулу закона теплопроводности фурье#=—Xgrad Г,
где X — коэффициент теплопроводности в равновесном состоянии.
Если положить
i(8) = A-eXp(-J-j,	(1-11-30)
где тг—время релаксации по Максвеллу —Каттапео, то получим выражение
для потока теплоты с учетом конечной скорости распространения теплоты
в виде
~q~ — Xgrad Т — тгд.	(1-11-31)
Время релаксации тг обратно пропорционально квадрату конечной ско-
рости распространения теплоты Wq и прямо пропорционально коэффициенту
температуропроводности a (rr=a/w^.
Используем линеаризованное определяющее уравнение для потока теплоты q
и внутренней энергии в в виде [Л.1-49]
Ч = — f k (9) g (г - 8) М=к’ (в) g' (8) t№;	(1-11-32)
о	b
e = (?0-J-CT-j (p'0) 7T(9)d0;	(1-11-33)
4-F(»)=^(9) = S(t-9);	(1-11-34)
С—объемная теплоемкость твердого тела; р (0)—функция релаксации внут-
ренней энергии. Тогда получим следующие соотношения для производных по
' времени от потока теплоты q и внутренней энергии ё:
f_,-^(0)S-J^(8)S(T-e)rfe;	(1-11-35)
о
₽	+3 (0) ТO)dO.	(1-11-36)
о
Если воспользоваться уравнением сохранения энергии, то получим следую-
щее обобщенное линейное уравнение теплопроводности;
g—j Р' (0) атт) +
СО	•
+ J k' (8) V2T (х, 1.-0) dO + Q (х, г),	(1-11-37)
О
где Q (х; т) — внешний источник деплоты, Уравнение (1-11-37) отличается
от гиперболического дифференциального уравнения теплопроводности наличием
91
дополнительных интегральных членов, учитывающих релаксационные функции
теплопроводности и внутренней энергии. Соотношения (1-11-35)— (1-11-36)
показывают, что время релаксации теплового напряжения и внутренней энер-
гии различно.
В [Л.1-48] для изотропной среды используется линеаризированное опре-
деляющее уравнение для теплового потока в виде
~q (т) = — X (0)	(т) - j X' (9)	(т - 6) dd,
которое учитывает зависимость потока теплоты от градиента температуры
в данный момент времени. Если положить V (9) = 0, то получим классическое
уравнение теплопроводности Фурье. При 1(0) = 0 получаем соотношение, ана-
логичное (1-11-28). Величина Х(б) называется мгновенным коэффициентом тепло-
проводности. В этом случае дифференциальное уравнение теплопроводности
будет иметь вид:
со	.
С(о)^кыГ+(а,(9)^(^)^ .
О
= Ь(0)	т)4- | V (0)^Г (х, т-9)	(х, т).	(1-11-38)
При выводе уравнения (1-11-38) было использовано линеаризированное
определяющее уравнение для внутренней энергии
е^ео + С(О)Т+j a'(9)T(t-9)rf0,	(1-11-39)
где а (9) — релаксационная функция внутренней энергии; С (0) — мгновенная
объемная теплоемкость.
Дифференциальное уравнение (1-11-38) было решено для полупространства,
когда ядра интегральных соотношений а (0) и X (0) являются степенными или
экспоненциальными функциями времени 0. Наличие интегральных соотноше-
ний в уравнении теплопроводности (1-11-38) не вносит больших трудностей
при его решении методом интегрального преобразования Лапласа, поскольку
интегрирование в этих соотношениях производится по времени в пределах
от 0 до со [Л.1-50]. Особый интерес представляют температурные волны
в материалах с памятью, они имеют свою особенность, скорости их распро-
странения и коэффициенты затухания отличны от аналогичных соотношений
в классической теории теплопроводности.
Из вышеуказанного уравнения получается как частный случай гипербо-
лическое уравнение теплопроводности. Если предположить, что 0' (9) = 0
и k'(B) = O, то
—J^1- + V, т) = а (0) ГУ (7, г),	(1-11-40)
где
а(0) = £ (0)0(0); xrq=clk(0).
Уравнение (1-11-40) отличается от уравнения теплопроводности Фурье
наличием дополнительного члена, который характеризует волновой процесс
распространения теплоты.
Учет конечной скорости распространения теплоты в теле зависит от без-
размерной величины, называемой числом Верона Ve:_
‘ . (1-1М1>
где / — характерный размер; а — коэффициент температуропроводности.
92
Для процессов теплопереноса, характеризующихся перемещением фронта
фазовых или химических превращений со скоростью w/, число Верона равно:
Ve = ^r.	(1-11-42)
Так как соотношение (1-1141) для случая конечной скорости распростра-
нения тепла	число Верона равно: Ve = a/w(jl.
'РАЗДЕЛ ВТОРОЙ
ТЕПЛОПРОВОДНОСТЬ
2-1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Дифференциальное уравнение Фурье — Кирхгофа описывает перенос тепла
в движущейся среде. Если пренебречь диффузионной теплопроводностью и пере-
носом теплоты за счет диффузии, то в отсутствие поля внешних сил уравне-
ние примет вид:
с),р^-= divp.graiiT) + ^+n®4.	С2’!’1)
где Jq—источник теплоты; Фо — диссипативная функция Рэлея. Для твердого
тела материальная производная dTidt равна частной производной, поскольку
отсутствует давление тела (t?=0), а удельная изобарная теплоемкость ср равна
изохорной теплоемкости cv (cp^cv=c). Тогда уравнение (2-1-1) примет вид:
ср-^-= div (XgradT) + /?.	(2-1-2)
В общем случае коэффициент теплопроводности X и удельная теплоемкость с,
а также источник теплоты Iq зависят от температуры. Обычно X и ср считают
постоянными, и тогда уравнение теплопроводности (2-1-2) принимает вид клас-
сического уравнения, теплопроводности Фурье
АТ-	I
-^-=0Т2Г+-’,	(2-1-3)
дт	'ср	к '
где я — коэффициент температуропроводности (а = Х/ср). Для твердого тела
закон теплопроводности Фурье можно написать так:
дТ	/ дТ \ duv	,	/е> . ..
где Uy—объемная концентрация внутренней энергии; av —коэффициент темпе-
ратуропроводности при постоянном объеме, Sy=X/Cyp, так как
/duv \
Verjv=CvP'
Следовательно, плотность потока теплоты согласно формуле (2-14) прямо,
пропорциональна градиенту концентрации внутренней энергии тела. Коэффи-
циент пропорциональности av является коэффициентом диффузии внутренней
энергии.
При постоянном давлении коэффициент температуропроводности опреде-
ляется соотношением
Ор='к!Ср^),	(2-1-6)
.где Ср—удельная изобарная теплоемкость, равная:
1
'’“7 аг •	<2’’’7)
Здесь Ну — объемная концентрация энтальпии.
93
В этом случае закон теплопроводности Фурье можно написать в виде
/ дТ \
где коэффициент пропорциональности ар между тепловым потоком и градиентом
объемной концентрации энтальпии является коэффициентом диффузии энтальпии.
Таким образом, коэффициент температуропроводности является коэффициен-
том диффузии внутренней энергии av или энтальпии ар в зависимости от усло-
вий сопряжения тела с окружающей средой (V = const или р—const).
Для анизотропных тел коэффициент теплопроводности является тензором
второго ранга Ау.
Тогда закон теплопроводности Фурье примет вид:
дТ
=	'7=1, 2,3.	(2-1-9)
В этом случае дифференциальное уравнение теплопроводности имеет вид:
Ср₽ ~дт ^~д^	(2’М0>
Если перейти от прямоугольных координат 0, хг- (/=1, 2, 3) к прямоуголь-
ным координатам 0,	(г’ = 1, 2, 3), направленным по главным осям кристалла
(анизотропного тела), то уравнение (2-J-10) можно написать так:
дТ д*Т
=	+	<=1,2,3,	(2-1-11)
где ta — теплопроводность в направлении главных осей.
Введем новые координаты т]/ по соотношению
Ч1 = (^)2^. (=1, 2, 3,	(2-1-12)
где Л — постоянная величина, тогда уравнение (2-1-10) примет вид:
дТ д*Т
срР = Л , 1=1, 2, 3.	(2-1-13)
Коэффициент теплопроводности жидких (текучих) сред может зависеть
от градиента деформации G (см. § 1-9), в этом случае уравнение для потока
тепла будет;
7=-Х(Т, G) grad Г.	(2-1-14)
Тогда уравнение теплопроводности будет иметь вид;
₽Р-^~- = div (A grad r) = tr (Asgrad2 Г)-(-div (Agrad T),	(2-1-15)
где A5 — симметричная часть тензора,
,>-s = j-(> + >)	(2-1-16)
Если плотность р и градиент деформации' G есть величины постоянные,
а теплоемкость с(Т) и коэффициент теплопроводности А (7) зависят только
от температуры, то уравнение (2-1-15) можно переписать так:
=1г (^grada T)+grad Т --^gradT’.	(2-1-17)
94
2-2. КРАЕВЫЕ УСЛОВИЯ
Дифференциальное уравнение теплопроводности устанавливает связь между
временными и пространственными изменениями температуры тела; оно матема-
тически описывает перенос теплоты внутри тела, Для того чтобы найти темпе-
ратурное поле внутри тела в любой момент времени, т. е. решить дифферен-
циальное уравнение, надо знать распределение температуры внутри тела
в начальный момент времени (начальное условие), геометрическую форму тела
и закон взаимодействия между окружающей средой и поверхностью тела (гра-
ничное условие).
Совокупность начального и граничного условий называется краевыми усло-
виями; начальное условие называется временным краевым условием, а гранич-
ное условие—пространственным краевым условием.
Начальное условие определяется заданием закона распределения темпера-
туры внутри тела в начальный момент времени, т. е. при
т=0; 7’o = /ij(^ii	=fo (xi)i	(2-2-1)
где fo(х^ — известная функция координат хь х2, хп. В декартовых коор-
динатах f0(xl) = f(x, у, г), так как *i = x; х2 = у; x9=z.
Во многих задачах принимают равномерное распределение температуры
в начальный момент времени, тогда
То = const.	(2-2-2)
Граничное условие может быть задано различными способами.
1,	Граничное условие первого рода состоит в задании распределения тем-
пературы по поверхности тела в любой момент времени:
Л = <Р»(т, Xis),	(2-2-3)
где индекс s обозначает поверхность тела.
В частном случае Т5 = ТС = const, т. с. температура на поверхности
постоянна на протяжении всего процесса теплообмена (однородное граничное
условие первого рода). Это может быть осуществлено при искусственном под-
держании постоянной температуры или при особых условиях теплообмена между
окружающей средой и поверхностью тела (см. граничное условие третьего рода).
2.	Граничное условие второго рода состоит в задании плотности теплового
потока для каждой точки поверхности тела как функции времени, т. е.
xls),	(2-2-4)
где /= 1, 2, 3 ...; k — число сплошных пограничных поверхностей тела; напри-
мер, для параллелепипеда й=6.
Простейший случай граничного условия второго рода (однородное гранич-
ное условие второго рода) состоит в постоянстве плотности теплового потока:
~^5(js;)s=’c=const-	(2-2-5)
Такой случай теплообмена имеет место при нагревании тел в высокотем-
пературных печах, где передача теплоты в основном происходит излучением
(по закону Стефана — Больцмана), когда температура тела значительно меньше
температуры излучающих поверхностей.
3.	Граничное условие третьего рода обычно характеризует закон конвек-
тивного теплообмена между поверхностью тела и окружающей средой при
постоянном потоке теплоты (стационарное температурное поле). В этом случае
количество теплоты, передаваемой в единицу времени с единицы площади
поверхности тела в окружающую среду с температурой Тс в процессе охлаж-
дения (ts > Тс), прямо пропорционально разности температур между поверх-
ностью тела и окружающей средой, т. е.
—к_/ (Тjs—Тс) (/ = 1, 2, ,k)t	(2-2-6)
95
где а/ — коэффициент пропорциональности, называемый коэффициентом тепло-
обмена, Вт/(м2 • °C).
Для процесса нагревания тела можно написать аналогичное соотношение,
поменяв местами TjS и Тс Коэффициент теплообмена численно равен коли-
честву теплоты, отдаваемой (или получаемой) единицей площади поверхности
тела в единицу времени при разности температур между поверхностью и окру-
жающей средой 1°С.	•	*
Соотношение (2-2-6) можно получить из закона теплопроводности Фурье,
полагая, что при обтекании поверхности тела жидкостью или газом-передача
теплоты от жидкости к телу вблизи его поверхности происходит по закону
Фурье:
!дТт\^	—ЛНм
=а' (r's~~Tc> (~ (2'2'7)
где Лу—коэффициент теплопроводности жидкости; бу—условная толщина
пограничного слоя; 1Л/—единичный вектор по нормали к изотермической
поверхности; а/ = Ху/бу.
Следовательно, вектор теплового потока q^s направлен по нормали
к изотермической поверхности и его скалярная величина равна q}-s.
Условная толщина пограничного слоя бу зависит от скорости движения
жидкости и ее физических свойств. Поэтому коэффициент теплообмена зависит
от скорости движения жидкости и ее температуры и изменяется вдоль поверх-
ности тела в направлении движения. В качестве приближения можно считать
коэффициент теплообмена постоянным, не зависящим от температуры, и
одинаковым для всей поверхности тела.
Строго говоря, соотношение (2-2-6) справедливо только при постоянной
температуре T,s. Однако в большинстве случаев ТjS изменяется вдоль поверх-
ности тела Это изменение зависит от свойств обтекаемого тела. Поэтому в слу-
чае конвективного теплообмена соотношение (2-2-6) можно принять в качестве
граничного условия как расчетную схему первого приближения.
Граничные условия третьего рода могут быть использованы при рассмотре-
нии нагревания или охлаждения тел лучеиспусканием. По закону Стефана —
Больцмана лучистый поток теплоты между двумя поверхностями равен:
(2-2-8)
где о* — приведенный коэффициент лучеиспускания; Та — абсолютная темпера-
тура поверхности тепловоспринимающего тела.
При малой разности температур TjS — Ta соотношение (2-2-8) можно
приближенно написать так:
=	‘ (2-2-9)
где а, (Г)— коэффициент лучистого теплообмена, имеющий ту же размерность,
что и коэффициент конвективного теплообмена:
«/ (Г) “	+ Та) (Tl, + Та) 4 =	(Г).	(2-2-10)
Изменения /((Г) я зависимости от температур TfS и Та приведены на
рис. 2-1 (К=10*ая).
Соотношение (2-2-9) является выражением закона Ньютона охлаждения
или нагревания тела; при этом Та обозначает температуру поверхности тела,
воспринимающего теплоту. Хотя соотношение (2-2-9) аналогично выражению
(2-2-6) для закона конвективного теплообмена при постоянном потоке теплоты,
его физический смысл совсем иной. Коэффициент лучистого теплообмена «у(Т)
зависит от температуры (рис. 2-1), а также от свойств поверхности тел,
участвующих в лучистом теплообмене. Если температура TjS изменяется
незначительно, то коэффициент (Т) приближенно можно принять постоянным.
Если температура окружающей среды (воздуха) Тс и температура тепло-
воспринимающего тела Та одинаковы, а коэффициент лучепоглощения среды
96
Рис. 2-1. Зависимость коэффициента К (Т) от температур 7\ и Тц.
97
очень мал, то в соотношении (2-2-9) вместо Та можно написать Тс. При этом
небольшая доля потока теплоты, отдаваемой телом путем конвекции, может
быть положена равной СС;*ЛТ, где а,* —коэффициент конвективного теплообмена,
В этом случае в соотношении
«/, = «, (T/S-Tc)	(2-2-11)
коэффициент а.^ будет суммарным коэффициентом теплообмена,
«/=^+«/(7).	(2-2-12)
В дальнейшем теплообмен тела, механизм которого описывается соотноше-
нием (2-2-11), будем называть теплообменом по закону Ньютона,
По закону сохранения энергии количество теплоты qjSt отданной поверх-
ностью тела, равно количеству теплоты, которое подводится изнутри к поверх-
ности тела в единицу времени к единице площади поверхности путем тепло-
проводности, т, е.	'
= Usb	(2-2-13)
где для общности постановки задачи температура Тс считается переменной,
а коэффициент теплообмена a, (Г) приближенно принят постоянным (с4/(Т) =
=.а7-= const).
В случае однородного граничного условия имеем;
М,1Ц+а/ITs-TJ»0-	(2-2-14)
। Из граничного условия третьего рода как частный случай можно получить
( граничное условие первого рода. Если соотношение аД стремится к беско-
нечности (коэффициент теплообмена имеет большое значение (а-*-се) или
, коэффициент теплопроводности мал Д/->0), го
ШЦН <2-2-is)
откуда
Tls-=rc,
т. е. температура поверхности теплоотдающего тела равна температуре
окружающей среды. Аналогично при а7->0 из (2-2-14) получаем частный слу-
 чаи граничного условия второго рода—равенство нулю потока теплоты через
поверхность тела.
4.	Граничное условие четвертого рода с ответствует теплообмену поверх-
ности тела с окружающей средой (конвективный теплообмен тела с жидкостью)
или теплообмену соприкасающихся твердых тел, когда температура сопри-
касающихся тел одинакова. При обтекании твердого тела потоком жидкости
(или газа) передача теплоты от жидкости (газа) к поверхности тела в непосред-
ственной близости к поверхности тела (ламинарный пограничный слой или
ламинарный подслой) происходит по закону теплопроводности (молекулярный
перенос теплоты), т. е. имеет место теплообмен, соответствующий граничному
условию четвертого рода:
Т!$ (x;s, т) = [7"с (Х[, т)]у5.	(2-2-16)
Помимо равенства температур имеет место также равенство потоков
।оплоты;
.	(2-2-17)
J \dtif Jn xdnJs
98
Пои изменении агрегатного состояния тела (в задачах промерзания,
ппавлепия и т. п.) условие (2-2-17) заменяется следующим:
(2-2-18)
\'п1 /а	\ин) /а
где ф-(т)—функция, характеризующая поток теплоты фазового превращения,
Дифференциальное уравнение совместно с начальным и граничным усло-
виями полностью определяет задачу, т. е., зная геометрическую форму тела,
начальные и граничные условия, можно дифференциальное уравнение решить
по конца и, следовательно, найти функцию распределения температуры в любой
момент времени. Таким образом, в результате решения должна быть найдена
функция
Г(хАТ) = <р(хг, т).	(2-2-19)
функция Ф (х/, т) должка удовлетворять дифференциальному уравнению
(при подстановке ее вместо Т в дифференциальное уравнение теплопроводности
оно должно обращаться в тождество), а также начальному и граничному
условиям.
По теореме единственности решения, если некоторая функция Г (X/, т)
удовлетворяет дифференциальному уравнению теплопроводности, начальным и
граничным условиям, то она является единственным решением данной задачи.
2-3. МЕТОДЫ РАСЧЕТА РАСХОДА ТЕПЛОТЫ
В процессе нагревания или охлаждения тело воспринимает или отдает
определенное количество теплоты. Существует три способа определения расхода
теплоты в процессе теплообмена.
1.	К элементу поверхности ds за время dx подводится теплота, равная;
(2'8-1)
Для нахождения количества теплоты AQ воспринимаемой телом за промежу-
ток времени Дт = т3 —нужно соотношение (2-3-1) проинтегрировать по всей
поверхности S/ и интервалу времени;
Хг k
Д<3 = -J J	dS dx; / = 1,2,3.....k. (2-3-2)
Обычно температура и температурный градиент одинаковы вдоль поверх-
ности; тогда расчетная формула (2-3-2) упрощается:
т»
AQ = a-Qi = -VS/j	(2-3-3)
2.	Элемент объема dV за время Дт = т2 — Tf нагревается от до Та;
он Воспринимает количество теплоты, равное;
со (Г2—7\) dV.	(2-3-4)
Общее количество теплоты AQ, которое пошдо-па нагревание за время Ат
найдем, если проинтегрируем по всему объему, т. е.
Л<2=а-<?1=Ф J (Tt-TJdV^cpV ~ j (Ti-TtjdV. (2-3-5)
(V)	IV)
4*
99
Обозначим среднюю (интегральную) температуру по всему объему тела
через Т, т. е.
f TdV,
(V)
тогда можно написать:
AQ = <?3 - <21 - фИ (Л - Л),	(2-3-6)
так как в процессе нагревания 7а > Д.
Расход теплоты (?—<?0 ла нагревание за время т от начала (Ti —0)
процесса равен:
Q-Qu=CpH (Г-70),	' (2-3-7)
где ТГ)— средняя (интегральная) начальная температура.
Если начальная температура одинакова во всех точках тела, т. е. То =
= TQ = const, то удельный расход теплоты равен:
Л<2у=ф(7'-Г0)	(2-3-8)
Следовательно, основная задача в этом методе расчета сводится к опреде-
лению 7'(т).
3.	Элемент поверхности dS за время йт воспринимает из окружающей
среды количество теплоты равное:
aj(Tc-T}s}dSdx.	(2-3-9)
Для нахождения общего количества теплоты AQ, воспринимаемой всей
поверхностью тела, нужно проинтегрировать (2-3-9) по всей поверхности и
промежутку времени. Ат.
Если температура поверхности тела одинакова во всех точках и коэффи-" -
циент а/ нс зависит от температуры то
т*
[Тс-Tls (т)] Л.	(2-3-10)
В дальнейшем одновременно с нахождением температуры Т тела в задачах
будет определяться и Т. Зная Г, можно определить теплосодержание Q тела
и расход теплоты на нагревание (Q—<2о) или потерю теплоты (Qo —Q) при
охлаждении тела,
В гех случаях, когда определить Т трудно, расход теплоты может быть
подсчитан по формуле (2-3-3).
Для одномерных задач, когда температура является функцией времени и
одной координаты Т (т), средняя по объему температура равна:
/?
?'W= 1	( zfr (хь т)Л,	(2-3-11)
R «
где Г—постоянная; для пластины Г = 0 (а^ — х); для цилиндра Г=! fosr);
для шара Г = 2 (хх s г).
2-4. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ
Перенос теплоты теплопроводностью или перенос массы при помощи диф-
фузии описывается уравнением параболического типа
дТ
Ф^- = 7(Л7Г)+/?;
для стационарного режим? == 0.
1и0
Аналитическая теория решения этих уравнений при переменных характе-
пистиках, зависящих от температуры, пространственных координат и времени,
io сих пор не разработана. Имеющиеся в литературе решения посвящены
лишь некоторым частным задачам. В данном параграфе мы рассмотрим методы
пешекия -задач теплопроводности, когда теплофизическне характеристики
постоянны или зависят от координат и времени.
Метод разделения переменных (метод Фурье) однородных задач
теплопроводности
Этот метод, применимый лишь для тел конечных размеров, состоит в том,
что решение отыскивается в виде частных решений, удовлетворяющих однород-
ным граничным условиям. Рассмотрим например, уравнение
дТ
= (т)р(т)	= v [М*г) V74	(2-4-1)
при однородных граничных условиях, Частное решение представим в виде
произведения функций, одна из которых зависит только от времени, а другая —
от координат, т. с.
Т-ММ^).	(2-4-2)
Подстановка (2-4-2) в (2-4-1) приводит к уравнениям
с(т) р (т) 6’ (т) = — ц20 (т);	(2-4-3)
V [/. (х,_) Го (Х() 1 = — ц2о (х;),	(2-4'4)
решение первого из которых находится без труда:
в (г) = exp — ц2 J tr 1 (тх) р-2 (т,)	;	(2-4-5)
решение второго в общем виде не получено (есть решения лишь для некоторых
частных случаев).
При постоянных теплофизических характеристиках (c = const; р—-const;
const) уравнение (2-4-4) превращается в уравнение Гельмгольца, Система
уравнений (2-4-4) имеет нетривиальные решения для определенных значений
называемых собственными значениями; ее решение имеет вид:
оэ	__ 2
Т'я=2 •UW' ОТ" ,	(2-4-6)
1
где vn(Xi)~ о (vn, Л/)—собственные .функции; постоянные Ап определяются
из начального условия: при т=0 T=f(xi), т. е.
)' <Xi) Пх<)dXb
(Л)
где индекс R обозначает конечную область; /V —норма характеристической
функции оа(х/), равная:
^(*0^	(2-4-71
(Л)	v '
интеграл берется по всем характерным координатам.
Таким образом, решение будет иметь вид:
Т(х;,-г)=^ ^б„(х<)е_,ЭТ'!Т ? <МЧ)Н*1)1(Ч-	(2-4-8)
,	«-1	(Я)
101
Показано, что существует 11 ортогональных системв которых уравнение
Гельмгольца разделяется па обычные дифференциальные уравнения (табл. 2-1),
Суммирование в (2-4-8) ведется по всему дискретному спектру собственных
значений vn. Для трехмерных задач в конечной области суммирования (2-4-8)
является тройной суммой.
4	Т а б л и ц а 2-1
Ортогональные системы координат,
позволяющие произвести разделение переменных в уравнении Гельмгольца
Система координат
Прямоугольная
Круговая цилиндрическая
Эллиптико-цилиндричсская
Параболо-цилиндрическая
Сферическая
Вытянутый сфероид
Сплющенный сфероид
Параболическая
Коническая
Эллипсоидальная
Параболоидальная
Функции, входящие в решение
уравнения Гельмгольца
Экспоненциальные, тригонометрические, ги-
перболические
Экспоненциальные, Бесселя, тригонометри-
ческие
Матье, тригонометрические
Вебера, тригонометрические
Лежандра, степенная, тригонометрическая
Лежандра, тригонометрическая
Бесселя, тригонометрическая
Ляме, степенная
Ляме
Бэра
Иногда собственные функции можно получить такими, чтобы нормы были
равны единице. Тогда, определив нормализованные собственные функции в виде
К (ft, Ч)=	о» ft),	(2-4-7')
решение (2-4-8) запишем в виде
т ft, *) = У, к (ft, х,) J ц (Xni	f	(2-4.9)
n = l	(R)
Вопросы обоснования метода Фурье рассмотрены, например, в ]Л.2-1—2-3,
2-18, 2-19).
К недостаткам метода разделения переменных следует отнести: 1) невоз-
можность его применения для нолуограпиченных и неограниченных тел1 2;
2) невозможность его непосредственного применения в случае неоднородных
граничных условий, которые вначале должны быть приведены к однородным
(что не всегда легко сделать); 3) значительные трудности, связанные с реше-
нием краевых задач при граничных условиях четвертого рода.
Метод функций источников (функций Грина)
Метод функций источников (функция Грина) позволяет решать краевые
задачи при неоднородных краевых условиях как для конечных, так и для
бесконечных тел. При этой функция Грина определяется как потенциал пере-
1 Ортогональность функций v„ определяется свойством собственных функ-
ций задачи Штурма—Лиувилля (см. ниже).
2 За исключением тех случаев, когда спектр собственных значений на
бесконечных или полубесконечкых интервалах является дискретным.
102
пса в точке Р (х, у, z) в момент времени х, обусловленный действием мгно-
Н иного точечного источника единичной мощности, помещенного в точке
Р (х У1» zi) ПРИ т = т>’ ,1Ричем значения потенциала переноса в начальный
момент времени и условия на поверхности тела однородны. Пусть требуется
найти решение уравнения
H7-1e^c(t)p(t)^--V[>. (х, у, z)VT] = ir (х, у, г, т) (2-4-10)
при неоднородных граничных и начальных условиях, В этом случае функция
Грина определяется из решения уравнения
L [й] = в(х—у—уг, г-гъ т — т,),	. (2-4-11)
где 6 —дельта-функция (при однородных краевых условиях).
Если функция Грина найдена, то решение уравнения (24-10) с неодно-
родными краевыми условиями может быть выписано в явном виде. Например,
в случае граничных условий первого рода решение уравнения (2-4-10) с усло-
виями (2-2-1) —(2-2-3) имеет вид [Л.2-4, 2-26]:
т= j G (Р,	T-t1)]Ti,0HP1)dl'1+U (л,	+
(V)	£>	(3)
р	С W
-фа I dT1 I — G(p, Ръ	x—T^dV-i,.	(2-4-12)
Cl	(V)
Аналогичные формулы	имеются	для	граничных	условий (2-2-4) и (2-2-6),
а также для смешанных условий на границах.
Существует несколько методов построения функции Грина для уравнения
вида (2-4-10). Рассмотрим один из них, с нашей точки зрения, наиболее удобный
и простой, в котором для построения функции Грина используется свойство
6-функции [Л.2-5, 2-6, 2-21, 2-22].
1.	Если / (х, у, г, т) —непрерывная функция в области D(cl<x<d1,
с2 < У < bit с3 < г < Ь3, 0 < т < со), то
со bt bt bt
1 S 1 /ft. гь т1)в(х“хь У—Уь г~*1, f-TJrfx,. dy^dz^f.
о Cl Cs Cs
(2-4-13)
В частности,
со	by bt ь3
j J J’ fi (x—xb y—yi, z — Zj, t—Tj) • rfxx dyL dzi=l.	(2-4-14)
о	ci ct Ci
2.	Используем свойство расщепления:
fi (X — ХЬ У — У1, 2— Zj, х —т3) =
«Й (х—Xi) 6 (у — Уг) 6 (z — Z1) 6 (х —Х().	(2-4-15)
3.	Используем разложение 6-функции в ряды и представление ее в виде
интецэалов.
Если (v/i (х))—замкнутая ортонормируемая система в конечном интервале
(cii ^i), а {йл(х))—комплексно сопряженная ей система, то
6(х—x1) = 2oft(x)vfc(x1); cL<zx,xl<bl.	(2-4-16)
b
103
В случае бесконечных и полубескояечных интервалов формула -(2-4-16)
обобщается-так:
6 (х —	J ехр [(£ (х—хх)] da; — со<х;х1<со; (2-4-17)
6 (х — Xj) = ~ (exp [fa (х—xJl — exp [га (x + xi)]} da; О^х; Хх<со. (2-4-18)
О
Изложим на конкретном примере метод построения функции Грина. Рас-
смотрим краевую задачу:
дТ д^Т
(*>	(2-4-19)
Т {с, т) = ф! (г); Г (&, т) = гр2 (т);	(2-4-20)
Г (х, 0) = f (х).	(2-4-21)
Если известна функция Грина, то решение краевой задачи (2-4-19)—(2-4-21)
может быть записано в следующем виде:
ь
Т[х, т)=$С(х, х,, T-T,)^=Df ft)ft +
 +а J h -T2 ‘Ti) -kL.=o] dT1+
т b
Г	f w
-I-a I dTi I —G (x, xb t—Tj) dXi.	(2-4-22)
о	о
Функцию Грина определим нз уравнения
L[G] = 6 (х —хь т—Tj),	(2-4-23)
откуда с учетом (2-4-15) следует:
L[G]«5(x—Xj)6(t —Ti).	(2-4-24)
Принимая во внимание (2-4-16) и (2-4-17), получаем;
6(х—х1) = 2фй(х)фА(х1);	(2-4-25)
6(т — тх)=-^- у ехр [га (т — тх)] da,	(2-4-26)
ГДе Фгг (х) — решение соответствующей задачи Штурма —Лнувилля (собственные
функции).
Подставив (2-4-25) и (2-4-26) в (2-4-24), получим:
G (х, хъ т, t1) = L-1 [б (х— хх) б (т —тх)] =
=	) ехр(—	(2-4-27)
k	— эо
При этом нетрудно показать, что
Lri 1Ф* ft exp (tax)! =	[.тТ| .	(2-4-28)
га -” а
104
Подставив (2-4-28) в (2-4-27) и проинтегрировав последнее, получим окон-
чательное выражение для функции Грина:
в(г, Л'1, т, т,)-Vex-f [— т‘к (г-т,)|	(х)ф,, (х,).	(2-4-29)
К достоинствам метода функции Грина следует отнести его универсаль-
ность, позволяющую применять его для решения задач в общей постановке:
на конечном и бесконечных интервалах, при неоднородных граничных и началь-
ных условиях и для неоднородных уравнений. К недостатку следует отнести
то что построение функции Грина требует определенной изобретательности и
в некоторых случаях трудновыполнимо.
Метод тепловых потенциалов
Тепловыми потенциалами простого и двойного слоя называются соответ-
ственно интегралы [Л,2-4, 2-7, 2-8, 2-20]
Ut (Р., т) = J dTL {... J Xi (Pi, т2) Ф, .(Р, Plt т - Т1) dSi; (2-4-30)
Ь * Т
U-ЛР, П = ( <1Ь ( 	Ь)--^Ф1(Л Л, т—г,)^.	(2-4-31)
o' J s' -
В одномерном и двумерном случаях для декартовых координат соответ-
ственно получим:	*
(/, (х, T)=s Г exp I - - 7 X)\-l “V.	(2-4-32)
2Vn J /т-r, I 4«(t-tj)J
U2lx, T) = —(x-f)exp Г-1 dr,; 12-4-33)
1 4F«J	[	4a(r-T,)J
U, (x, V, t)= 4“- j Л1 С	exp [-	4St- (2-4-34)
0 s
b'a (x, y, t)=--L C c/Tj i X2_^£z_E1L . exp Г-----------IdS^
’ 31 ! 2n ,) J t — Tj dn p |_ 4а(т—Tt)J
0 S
--г— C dTi C	exp Г—j—7~----r] r cos p°, n) dSv (2-4-35)
4ал J 1 J (t — Tj)2 HL 4й(т —Tj)]	1	'	1 '	'
Тепловые потенциалы вне точек поверхности S, по которой происходит
интегрирование, являются решениями однородного уравнения теплопроводности
н удовлетворяют однородным начальным условиям; что следует из того, что
они строятся на основе'фундаментальных решений уравнения теплопроводности
(источника и диполя). При подходе к точкам поверхности S тепловой потен-
циал двойного слоя и производная по нормали от теплового потенциала про-
105
стого слоя терпят разрыв; аналитически это записывается так:
Uj(P*.	(?*-	т);	(2-4-36)
(/-(р*, т) = -0,5х2 (Р*, т) + (/2 (Р*, т);	(2-4-37)
«црл = _ o,5Z1 (₽., г) +	(2.4.38)
дп	дп	'	1
dUT{Pr, т) =	j Jiff*. т)	(2-4-39)
дп	' '	' дп	'	1
где иГ, Ifi (j —1,2) —предельные значения тепловых потенциалов при подходе
вдоль нормали к точке Р* боковой поверхности S соответственно изнутри
и извне.
Пусть рассматривается однородное уравнение (2-4-6) при нулевом начальном
условии; его решение при граничных условиях первого рода (2-2-3) отыски-
вается в виде потенциала двойного слоя;
X f !л exp Г-----------------------| г cos (г, п) dSLl (2-4-40)
•’ Кт-т^ Ц 4«(т-Т1)]	'	'
при граничных условиях второго и третьего рода —в виде потенциала простого
слоя;
Т (х, у, г, т)= —7—т Г dTr f Л* exp Г-------------------------1 dS,, (2-4-41)
8 J' ал3 J J Kfr-T,)3 L	4а(т —Ti)J
где
rs = (x - Xt)2 (y - ytf (г - 2i)2.
Отметим, что плотности тепловых потенциалов %t-, ул являются неизвест-
ными функциями, определяемыми из решения интегральных уравнений, полу-
ченных подстановкой соответственно (2-4-40) и (2-4-41) в граничные усло-
вия (2-2-3) и (2-2-4) с учетом (2-4-36)—(2-4-39). Отметим, что имеется ряд за-
дач, для которых метод тепловых потенциалов незаменим; задачи с подвижными
границами, с переменным коэффициентом обмена и т. п.
Одним из достоинств метода тепловых потенциалов является то, что он
позволяет сводить решение дифференциального уравнения параболического
типа к интегральному уравнению, которое более удобно для проведения число-
вых расчетов.
К недостаткам метода тепловых потенциалов следует отнести его некото-
рую сложность и громоздкость, а также невозможность его непосредственного
применения в случае неоднородных начальных условий (которые вначале должны
быть сведены к однородным); в последнем случае нетрудно обойти указанное
затруднение с помощью использования интеграла Пуассона.
Интегральные преобразования
Классические методы решения краевых задач, изложенные выше, обладают
рядом недостатков; они требуют определенной изобретательности, дают реше-
ния, малопригодные для числовых расчетов, и т. п. Методы интегральных пре-
образований обладают рядом преимуществ перед классическими методами: они
стандартны, позволяют получать решения в удобном для расчета виде (напри-
мер. для малых и больших значений независимой, переменной); использование
таблиц изображения функций ускоряет и упрощает процесс нахождения реше-
106
я и т. д. Наряду с очевидными достоинствами интегральные преобразования
имеют общий существенный недостаток: они применимы лишь к линейным
уравнениям-
Выражение
h(J>, х2, .... х„) = (к(Р, х,)/(х,. х>, ....	(2-4-42)
а
называется интегральным преобразованием функции / (хъ xg, ..., хл) по пере-
менной Xi- При этом ft {Р,	, хп) называется изображением (образом)
оригинала f(xlt ха, ..., хл), а К. (Р, Xj) —ядром интегрального преобразования.
Отметим, что наряду с преобразованиями вида (2-4-42) рассматриваются так
называемые кратные интегральные преобразования, т. е. преобразования по
нескольким переменным. Мы рассмотрим интегральные преобразования как
с конечными, так и с бесконечными пределами. Применение интегрального
преобразования (2-4-42) уменьшает число независимых переменных на единицу,
причем полученные для изображений уравнения, как правило, являются более
простыми, чем исходные- Переход от изображений к оригиналам производится
по формуле обращения
d
f[x„ хг,	х„) = ^'й(Р, х,)/,!/. х2, .... x„)dP. (2-4-43)
Интегральные преобразования в бесконечных пределах
Рассмотрим некоторые наиболее применяемые интегральные преобразова-
ния. Интегральное преобразование Лапласа задается соотношением
Д (Р) — / (т) ехр [— Рт] rfT = / (т) ехр )— от] ехр [— /ест] dx
О	о
(Р-=а ± «а),	(2-4-44)
причем оригинал f (т), являющийся функцией действительного переменного т,
удовлетворяет следующим условиям:
1) /(т) —кусочно-непрерывная функция вместе со своими производными
достаточно высокого порядка;
2) i (т) возрастает не быстрее экспоненциальной функции, т. е. существуют
такие постоянные М > 0 и о0^0, что
/ (т) < М ехр (о0т);	(2-4-45)
f(T) = 0 т<0.	(2-4-40)
После решения задачи в изображениях переход к оригиналам осущест-
вляется по формуле	•
о 4- /со
Ш = j Л(₽)ехр[Рт]ЙР.	(2-4-47)
ст — ix>
Интегрирование в (2-4-47) происходит в комплексной плоскости вдоль пря-
мой Re Р = о > о2 > о0.
Нахождение оригинала функции по ее изображению может быть выпол-
нено особенно просто, если изображение совпадает с одним из изображений,
содержащихся в таблицах изображений функций. Вместо формулы (2-4-47) Для
определения / (т) можно воспользоваться следующей формулой обращения:
107
J
Эта формула дает возможность получить оригинал функции лишь при
помощи операций дифференцирования и перехода к пределу. Наряду, с пре-
образованием (2-4-43) в некоторых случаях рассматривают так называемое
двустороннее преобразование Лапласа [Л.2-9, 2-23, 2-24];
/(₽) = 5 / (Г)-ехр [—Рт! Л.
Положив P = o-f-za и введя обозначения
получим;
f (т) exp [- ar] = F (т); I, (а~Н'а) = f, (а),
I 2л
f(T) = —1— С р (а) ехр [гат] da;
1 2л .)
F, (а) = -tL f F (т) ехр [— iar] dr.
И 2л «)
(2-4-44')
(2-4-48)
(2-4-49)
(2-4-50)
Выражения (2-4-49) и (2-4-50) называются соответственно прямым и обрат,
ным преобразованием Фурье- Отмстим, что интеграл в (2-4-49) существует,
если функция р (а) абсолютно интегрируема на числовой прямой, т. е.
j j F (а) ] da <oo,	(2-4-51)
Условие (2-4-51) значительно ограничивает область применимости инте-
грального преобразования Фурье (2-4-50). Так, ело неприменимо даже для
г (т) —const, sin т, cos тит. и., т. е. для функций, часто встречающихся
в практике теплофизического расчета. В то же время преобразование Лапласа
свободно от этого недостатка, поскольку наличие дополнительного множества
ехр (—ат) в (2-4-44) расширяет класс оригиналов до функций, удовлетворяю-
щих условию (2-4-45), т. е. для большинства практически важных случаев.
Если функция г (т) задана на полубесконечном ин гервале (0, со) или (— со, 0),
то ее можно продолжить четным или нечетным образом соответственно на
интервал (—оо, 0) или (0, оэ). В нервом случае (2-4-50) и (2-4-49) запишутся
так;
Гс (а)= |/" j Р (т)cos £?T’‘	(2-4-52)
о
F(T) = уЛFc (a) cos ат da.	(2-4-53)
о
Во втором случае получим:
=	(т) ест dr !	(2-“4-54)
‘о
/~"2 F
F(r)=J/ — I Fs(a) sin-ат da.	(2«4-55)
о
Выражения (2-4-52) и (2-4-54) называются соответственно косинус- и си-
нус-преобразованиями Фурье [Л,2-10—2-121. Отметим, в частности, что для
108
них должно выполняться ограничительное соотношение, аналогичное (2-4-51)
и значительно сужающее область их применения;
Ffr) [Л<оо.	(2-4-56)
{)
Чтобы расширить область применения этих преобразований, удобно вместо
/2-4-52)__(2-4-55) использовать так называемые обобщенные косинус- и синус-
преобразовапия Фурье;
	exp [—от] F (t) cos ат dr; 0	(2-4-57)
fs m=]/	j GXP [— ТТ1Л (T) sin CCT rfl; 0	(2-4-58)
f(4 = l/"v lim 1 r n <7 — 0 i 0	exp [от] Fc (a) соз ат da;	(2-4-59)
	exp (or] Fs (a) sin ax da.	(2-4-GO)
Использование (2-4-57) и (2-4-58) позволяет переходить к изображению
для более широкого класса функций, например при F (т)—const, cost, shit, т
и т. п., т. с. в тех случаях, когда обычные преобразования неприменимы.
Замена переменных Р ла — Р, т на t = e* и функций / (In t)—g (/),
(b(~p)--=Si (Р) Д^т:
г/(Р)=Гг(Щ₽“'*:	(2-4-61)
О
1 Si (р)
г(0=^ j	(2-’'62)
о — 1<х>
Выражения (2-4-G1) и (2-4-G2) определяют интегральное преобразование
Меллина. которое является некоторым видоизменением интегрального преобра-
зования Лапласа; свойства преобразования Меллина могут быть получены из
соответствующих свойств преобразования Лапласа [Л.2-9, 2-13, 2-14].
Интегральным преобразованием Ханкеля называется выражение
Z/ («) = ^ rf (r) 7v (m) dr (v>—0,5),	(2-4-63)
b
Формула обращения в этом случае имеет виц:
f(r)=^	(a) /у1(га) a da.	(2-4-G4)
и
Формулы (2-4-G3) и (2-4-64) могут быть получены из кратного (двойного)
интегрального преобразования Фурье переходом к полярным, координатам.
Имеется еще ряд интегральных преобразований, которые, как и преобра-
зование Ханкеля, относятся к так называемым преобразованиям Бесселя,
ЮР
в ядро которых входят функции Бесселя. К последним относятся преобразо-
вания Канторовича- Лебедева, Мейера и т. п. В отличие от рассмотренных
выше интегральных преобразований область применимости последних при ре-
шении задач теплопроводности значительно уже и они имеют скорее теорети-
ческое, чем практическое значение, так как задачи, которые могут быть ре-
шены с их помощью, гораздо проще решаются другими методами.
Интегральные преобразования в конечных пределах
Метод конечных интегральных преобразований является, с нашей точки
зрения, наиболее удобным для решения неоднородных уравнений параболиче-
ского типа с неоднородными краевыми условиями. Впервые идея метода ко-
нечных интегральных преобразований была предложена Н. С. Кошляко-
вым [Л.2-15]. Однако наиболее полно теория таких интегральных преобразова-
ний разработана была Г. А. Гринбергом [Л.2-16], который дал обобщение на
случай скачкообразного изменения свойств средЕД в направлении той коорди-
наты, по которой производится преобразование.
Общее решение параболического уравнения теплопроводности дано
М. Д. Михайловым [Л.2-17].
Рассмотрим нестационарную задачу теплопроводности в конечной
области с переменным источником теплоты Q(r, т) и излучением тела
в окружающую среду с нулевой температурой по закону Ньютона. Дифферен-
циальное уравнение можно написать в области (У^)
с (Т) г (7)ЭГ^ A^div [I (7) grad Т (7, т)] + [а (т) Г (7) -а (7)] Т (7, т) +
+ <?Г,т),	(2-4-66)
где С(т)=-ср—объемная теплоемкость, которая зависит от времени.
Начальное условие имеет вид:
ори т = 0 Т (7, 0)=Щ7).	(2-4-66)
Граничное условие напишем в общем виде на поверхности S:
Л Т)- + В (7> Т (7’ TW <7' т>-	(2-4-67)
Здесь А (г), В (г) и f (г, т) —заданные кусочно-регулярные функции.
Из условия (2-4-67) получаются три рода граничных условий. Условия пер-
вого рода: А(7) = 0, В(г)=1; второго рода: А(г)=К(7); В(7)==0 и
/(7, т) = д(7, т) и третьего рода: А (7) = Х (7)/а (7), В (г) == 1, / (7, т) —
= Ту(т), где Tf (т) — температура жидкости (окружающей твердое тело среды).
Собственные функции ф (7) находятся из решения системы уравнений
Штурма —Ли увилля:
в области
div [х(7) gradi) (7)]--|-(v'| (7)-а (7)]ф (7) _ 0;	(2-4-68)
на поверхности S
М'г)^+»ШЙ = 0,	(2-4-69)
где Vj —собственные значения.
Собственные значения неограниченно возрастают с возрастанием но-
мера i. Так как <j(r)>0, то v,->0. Все собственные функции, соответствую-
щие одному и тому же собственному числу, отличаются лишь постоянным мно-
110
жителем. Пусть ф/(г) я фу (/•) —дое собственные функции, соответствующие
различным собственным значениям ту и v(
v’r (7) 4ч (7) = а(7) 1р| (7)-div [А (7) grad -ф; (7)];	(2-4-70)
v/Г (7) if, (r) = ff(7) ф, (7) — div [х (7) grad ф/ (7)]	(2-4-71)
При условии, ЧТО
Л(7я)+^!^ + й(7!,)ф1(75) = 0;	(2-4-72)
Л(7,)+^ + В(75)ф/(7г)=0.	(2-4-73)
Умножим уравнение (2-4-70) на фу (г) и, вычитая из него уравнение
(2-4-71), предварительно умноженное на фг(г), а затем, интегрируя с учетом
формулы Остроградского —Гаусса, получаем:
№,Ф/)=)	(2'4'74’
$	'	! 3 I % И) Ф/. п (г) I
где запятая после индекса означает производную по нормали, т. е. Ф,. ч =
= d4V/drc, фу. п zs-dtyidn. На основе граничных условий (2-4-72), (2-4-73) при
i j величина (ipf, ф) = 0, т. о. собственные функции, соответствующие раз-
ным собственным значениям, ортогональны между собой с весом Г (г). Если
в сот ношении (2-4-74) положить v/ = vf-, то получим неопределенность. Рас-
крываем се цо правилу Лопиталя. Тогда норма будет равна Vs^-, ф/];
'МЧ*.	(2-4-75).
{)	2v'J 1'1>.-(г)	Ч’г-.Ж) I
где ф^. п, v = 5гф//5п dv; фу, v = дф<Idv-
Примем собственную функцию в качестве ядра интегрального преобра-
зоваЕщя
Т (Vf, т)=^фг(т)Т (г> т)сЛ/.	(2-4-76)
Тогда, умножая уравнение (2-4-65) на ф, (г) и вычитая из него уравнение
(2-4-72), предварительно умноженное па Т (г, т), и затем интегрируя по
объему, получаем:
C(T)-r-g'-T)-+ [V? — е(т)] T(Vi, Т) = м (г),	(2-4-77)
где
Ai(r)JX(7s)|'fi(?)	Ls-J. рм?)<?(7. T)dl/. (2-4-78)
S \Ttr,. т) T,„(/S,4l v
Из уравнений (2-4-69) и (2-4-72) определим A (rs) и В (rs). В результате
суммирования результатов получим:
I Ф« (rs) Фг. ft (rs) I __ с (-р* Ti Ф' ({д) ~Ф/._ге (rs)	/9.4.79,
IT-(7S. Ч T,„(7s,r)|	111 Л(Л) + В(7У) 
После подстановки уравнения (2-4-79) в уравнение (2-4-78) будем иметь
линейное уравнение первого порядка, решение которого легко можно по-
лучить.
Ill
Затем воспользуемся формулой обращения
т (Л '0= 2 Чнб’Г (vi> т)
(2-4-80)
и получим решение задачи:
Vi i	I С е (Н—V1 \
т (' 4= 2, N ’h WexP I } —ср) dTl x
( C -	fl /' vi — 8 (0	1
г (r)И dV + J c^j~e*plv Cp)—dTl Л1(т)ЛД. (2-4-81)
Если и (г) —О и B(rs)_ О (граничные условия второго рода), jxo = O и
4o = const также являются собственными значениями и собственной функцией
задачи Штурма —Лиувилля. Тогда решение примет вид:
Для упрощения анализа принимаем С(т)^--1, е(т) = 0. Тогда для улучше-
ния сходимости рядов (2-4-81} и (2-4-82) проинтегрируем по частям содержа-
щиеся в них интегралы по времени. Тогда будем иметь;
. Т(7, = т) + 2 Л' Ч’1ЙХ
<=!
{№, М М (0) - Л. J 3’ ^2-Л ,	(2-4.83)
(	1 ‘о	J
Та Й т) = У (Г) М (т);
№, fo! = } Г (г) ф,- (г) + (о Й Й1Л
V
(2-4-84)
Решение (2-4-83) названо Олгером [Л.2-24] квазистационариым решением
нулевого порядка.
112
Аналогичное квазистационарное решение нулевого порядка для граничных
условий второго рода имеет вид:

+ У(М-да’
I	*7	*1 9)	Ми I
где
И Й Т)» 2 -фГ Й) м (Т).	(2-4-86)
Edie более значительное улучшение сходимости рядов, входящих в реше-
ния, дает m-кратное интегрирование по частям содержащихся в них интегра-
лов’по времени. Тогда получим:
т [Г, т) =- 2 т„ (Г, Г) + S »~Чч Й X
п ~ О	i =- 1
-v7x(rl г, V /	1	d"M(0) ,	J VM^LM(T) , ]
Шь А)]	’) 2OI+-1) g-n + 20П + 1) )е <Этт+1
I *0 ч	'< о ат I
(2-4-87)
где
г„ <г, т) = 2	(г)	(2-4-88)
я по терминологии Олгера [2-24] называется квазистациоиарпым решением
п-го порядка.
Для удобства вычисления целесообразно ввести нормализованные собст-
венные функции в формулы преобразования и обращения по соотношению
П=^Ч’«(Г).	(2-4-89)
Тогда формулы интегрального преобразования и обращения будут иметь
вид:
П (₽„. Т) =	([)„, rj Т Й г) <№;	(2-4-90)
Г Г._т) = S к- №». 7> т> №»• т>-	(2-4-91)
В. ьтом случае решение уравнения теплопроводности
ЭГ^ Т) -^Г(7;	 (2-4-92)
113
при граничных и начальных условиях
дТ (гул) —	1
Х« dn/s +aiT ('ts’ т);	(2-4-93)
Т (Z 0) =/„(/) J
имеет вид:	«
т (', Ч = S r"’”V (Р„, 7) К, (Р„) + ( е“₽"’с (Р„, г) л|, (2-4-94)
п = I	(	О	J
где
, £(?/!> Ч-) — Qi т)'Ьа^ К (?«> r/s) fj (rjs) $£{',	(2-4-95)
где
/oi (Рл)= $ К (ря, г) /о (г) dV.
v
При переходе к граничным условиям первого рода К (₽л, г) заменяется
па	• Ллп улучшения сходимости воспользуемся квазистационар-
ным решением нулевого порядка:
т(~, т)= S П: (7. Т)+ 2 e“"teTK(D„, (j L (Р„)-£ |ТМ (D„, 0)]Д —
1=0	П=}	(	i=0	J
о	J
(«[ (Р„) -
р
;рл, 0)], = Jк(рл, r)T0/(Z o^dv.
(2-4-96)
Точка сверху обозначает производную по времени. В случае, когда проще
вычислить интегралы по поверхности, чем интегралы по объему, решение
(2-4-97) можно написать в виде
* 03 D?
Т Сг. Ч = s П/ (7. т) + S c-s"Tx
/=0	Я = 1
хК (Р«, ч|(о, (W - j21 о) + 2 У к(Р- ;'4> 1‘	т)^dS‘-
_ e«s;t I <?№». ч + J _д к (|5л1 -s) -fi (-si ТЛ dS 1 (2.4.9в)
На основе принципа суперпозиции температурных полей можно расчле-
нив» неоднородную задачу на ряд более простых задач. Общее решение нахо-
дится путем суммирования вспомогательных задач. Особенно удачным такой
прием решения оказывается для задач с источниками теплоты.
Для одномерных задач М. Д. Михайлов дал обобщенное интегральное
преобразование Фурье —Ханкеля; которое объединяет конечные преобразова-
114
ния Фурье и преобразование Хапкеля для сплошного цилиндра. Это преобра-
зование имеет вид:
s)f(M	(2-4-99)
О
где /(£)—функция, удовлетворяющая условиям Дирихле при £ = 0+1; р—
корень характеристических уравнений1;
Fplp.)-0; Vr(n) = 0;	(2-4-100)
IFr(u) Н
г = —,	(2-4-101)
|7Г (|А) В,
где IFr и Vr —следующие обобщенные функции:
г _____________ва ... у__________________
2(Г + 0+2-4(Г + 1)(Г + 3)
_______________ ...... .	. л, = У _(—l)fe	. /2_4.102)
2-4-6(ГЦ-1)(Г4-3)(ГЦ-5)	^(2Л)!!(Г + 2/г-1)!!’	'	1
JZ (Е) = _1__________З3________L
ИГ'=/ г+1	2(Г4-1) (Г + 3)
, ________________________________ у (-i)^*11	,2.4_103)
ф 2-4(Г + 1)(Г + 3)(Г + 5) ••• Zjo(2A)!! (Г+2^+1)!!‘ 1	’
Функции (£) и Иг(£) равномерно сходятся в интервале | от 0 до 1.
Если положить Г = 0, то получим:
F0(|) = cos£; 1% (В) =sin t	(2-4-104)
т, е. косинус-преобразование Фурье. Это преобразование применимо при ре-
шении задач теплопроводности для пластины.
При Г=1,
FH^/оф, И1(|)--Л^)	(2-4-105)
получаем конечное преобразование Ханкеля, которое применимо при решении
задач для неограниченного сплошного цилиндра.
Если Г = 2,
Га(Е) = +1, ^(6)=^++°^	- (2-4-106)
получаем обобщенное синус-преобразование Фурье, которое применяем при
решении задач теплопроводности для шара.
Характеристические уравнения (2-4-100) соответствуют граничным усло-
виям первого и второго родов, а уравнение (2-4-101)—граничным условиям
третьего рода.
Конечное интегральное преобразование имеет свое физическое обоснова-
ние. Дело в том, что любое интегральное преобразование, взятое по простран-
ственным координатам, является с физической точки зрения некоторым усред-
нением исследуемой физической величины. Вполне естественно, что это усред-
нение должно* быть сделано >не только в соответствии с характером процесса
и формой тела (видом дифференциального уравнения), по и в соответствии
с граничными условиями. В этом случае решение для изображения функции
х) Зависимость между характеристическими числами vn и имеет вид:
Н = где ^- — характерные размеры тела. Для одномерных задач li = l£-
115
будет представлять самостоятельный интерес, поскольку такое преобразование
в физическом отношении яплястс$е переходом от анализа актуальных значений
исследуемых функций (дифференциальное уравнение, условия однозначности)
к усредненным значениям, сделанным в соответствии с конкретной постановкой
той или иной физической задачи.
Таким образом, методы интегрального преобразования приобретают весьма
существенное преимущество перед классическими методами, так как они дают
возможность получить ряд закономерностей протекания физических процессов
на основе анализа решения для усредненных значений исследуемой физиче-
ской величины (анализ решения для изображения). Это обстоятельство сбли-
жает данные аналитические методы с методами теории подобия.
Особые преимущества интегральных преобразований обнаруживаются при
решении систем дифференциальных уравнений в частных производных. Мето-
дика решения систем уравнений при этом принципиально не отличается от
методики решения отдельных уравнений и заключается в осуществлении ряда
последовательных операций. Например, для одномерных задач теплопроводно-
сти, зависящих от координат и времени, необходимо;
I)	на основе анализа дифференциального уравнения и краевых условий
выбрать подходящее интегральное преобразование или группу интегральных
преобразований;
2)	умножить дифференциальное уравнение и граничные условия на выбран-
ное ядро преобразования и проинтегрировать полученные выражения в соот-
ветствующих пределах по переменной, подлежащей' исключению; в результате
вместо системы дифференциальных уравнений в частных производных относи-
тельно оригинала функций получим систему обыкновенных дифференциальных
уравнений для изображений функций, которые учитывают начальные (при
использовании преобразования Лапласа) или граничные (при использовании
преобразования Фурье) условия;
3)	решить обыкновенное дифференциальное уравнение относительно преоб-
разованных функций. Если решение полученного уравнения вызывает извест-
ные трудности, то к нему следует еще раз применить подходящее интегральное
преобразование относительно второй независимой переменной. В результате
преобразования получим алгебраическое уравнение, решение которого более
элементарно. После нахождения выражений для дважды преобразованных
функций к ним применяют обратное преобразование. Получаемое решение и
будет являться решением искомого дифференциального уравнения;
4)	уточнить выражения произвольных постоянных, содержащихся в реше-
нии уравнения, для чего используются краевые условия рассматриваемой
задачи;
5)	используя известные соотношения между изображением функции и ее
оригиналом или формулы обратного преобразования, найти оригиналы преоб-
разованных функций, а следовательно, и окончательное решение задачи.
2-5. СТАЦИОНАРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
Для стационарного состояния (дТ/дт:=0) при отсутствии внутренних
источников теплоты (Л; = 0) дифференциальное уравнение теплопроводности
(2-1-3) примет вид:
div (XVT) = 0.	(2-5-1)*
Следовательно, в стационарном состоянии перенос теплоты теплопровод-
ностью определяется градиентом температуры и коэффициентом теплопровод- ’
ногти X- Коэффициент теплопроводности разных веществ изменяется в широ-
ких пределах: от 0,0074 ккал/(м • ч • СС) (четыреххлористый углерод при Ю0гС)
до 358 ккал/(м • ч • °C) (серебро при 0dC). Коэффициент теплопроводности зави-
сит от химического состава, физического строения и состояния вещества.
Теплопроводность в газах и парах в значительной мере обусловлена моле- '•
кулярным переносом кинетической энергии движения молекул, поэтому вполне
естественно, что коэффициенты X для газов и паров малы.
116
В жидкостях перенос теплоты теплопроводностей происходит по типу
распространения продольных колебаний аналогично распространению звука.
Поэтому коэффициенты теплопроводности жидкостей больше коэффициентов
теплопроводности газов. Молекулярная структура кристаллических тел спо-
собствует переносу теплоты.
В металлах перенос теплоты теплопроводностью в значительной мере опре-
деляется переносом энергии свободными электронами. Различая в коэффи-
циенте теплопроводности разнообразных неоднородных материалов объясняются
эффектом пористости. Для зернистых материалов типичным нарушением одно-
родности является анизотропия, проявляющаяся в неодинаковой теплопровод-
ности в различных направлениях. Коэффициент теплопроводности зависит рт
температуры, для многих металлов он уменьшается с повышением температуры
по линейному закону.
Коэффициент зеплопроводности газов увеличивается с повышением темпе-
ратуры, а от давления практически не зависит, за исключением очень высоких
(больше 2000 кгс/см8) и очень низких (меньше 10 мм рт. ст.) давлении. Для
смеси газов коэффициент теплопроводности может быть определен только
опытным путем, закон аддитивности для X непригоден. Коэффициент теплопро-
водности жидкости лежит в пределах ог 0,08 до 0,6 ккал/(м  ч • rC). С повы-
шением температуры у большинства жидкостей коэффициент теплопроводности
уменьшается, исключение составляют вода и глицерин. Коэффициент тепло-
проводности неметаллических материалов изменяется в пределах от 0,02 до 2,5
ккал/(м- Ч’-'С), с повышением температуры он увеличивается примерно во
линейному закону. Материалы с низким значением коэффициента теплопровод-
ности [?v sg 0,2 ккал/(м > ч • СС)] обычно называют теплоизоляционными мате-
риалами.
Для практических расчетов можно принять линейный закон изменения
коэффициента теплопроводности газов от температуры
const,	(2-5-2)
Для определенного интервала температуры ДТ=Т2 —можно считать
коэффициент теплопроводности постоянным, равным среднему арифметическому
значению коэффициента /. при температурах Ts и Т\.
Решению задач стационарной теплопроводности посвящено много работ.
Эти задачи систематизированы в (Д.2-27 и 2-28]. Ниже будут рассмотрены
методики решения и некоторые частные задачи (в качестве иллюстрации).
Одномерные задачи
Для одномерного юмпературпого поля, когда температура зависит только
от одной координаты, решение дифференциального уравнения (2-5-1) при
постоянном коэффициенте теплопроводности (А,= const) имеет вид:
1)	для плоской стенки (неограниченной пластины)
7’=б1Х + 52;	(2-5-3)
2)	для полого неограниченного цилиндра (I’&R)
(2-5-4)
3)	для полого шара
Т^В,~+В2.	(2-5-5)
Постоянные Вл и В2 определяются из граничных условий.
Рассмотрим более подробно елхчай неограниченной пластины. При гра-
ничных условиях первого рода (при х = 0 Т = 7\, при x = L Т=Т2) решение
117
(2-5-3) напишется в виде
Т^Т,—(2-5-6)
Где /. — толщина стенки (рис. 2-2). Поток тепла q согласно закону Фурье
=	(2-5-7)
Соотношение (2-5-7) аналогично закону Ома для электрического тока (сила
тока равна отношению разности потенциалов к сопротивлению данного участка
проводника), поэтому по аналогии с электрическим сопротивлением величину
Рис. 2-2, Распределение температуры в не-
ограниченной пластине в стационарном со-
стоянии при обтекании ее потоком газа.
а — граничное условие первого рода (а'— рпи
dk/dT >0; а" — при cfrjdt < 0); в — граничное
условие третьего рода,
L/Х называют тепловым или термическим сопротивлением пластины, а обрат-
ную величину Х//- —тепловой проводимостью пластины.
В случае граничного условия третьего рода (рис. 2-2)
при %-—О
X^4-ai(Tci-7\.u)=0,'	(2-5-8)
при х — L
->--^ + «!(Г^1-Тег) = 0,	(2-5-9)
- где Tci и Тса — соответственно температуры газа с левой и правой сторон пла-
стины; а3 и а2—коэффициенты теплообмена поверхностей пластины.
Постоянные и В2 определяютс ,:
В1 =----/ .	; Вг = Ге1 + Ай11 (2.5.10)
х—+ 4+—
\ а, 1 к 1 а2/
а распределение температуры принимает вид:
Г^Гс?-т^-^;[± + Л].	(2-5-11)
1 X- а2 -
Из формулы (2-5-11) находим поток тепла:
‘'=‘-х4г=7 1 -L-Л (Та~Та}- (2-5-12)
В этом случае тепловое сопротивление
= т+	(2-5-13)
Л, СС2
118
Если коэффициенты теплообмена ау и а2 велики (ау-^со а2-*-со), то
тепловое сопротивление
(2-5-14)
Для многослойной стоики, состоящей из отдельных однородных пластин
толщиной L} (г=1, 2, 3, п) с соответствующими коэффициентами тепло-
проводности Xt- тепловое сопротивление
п
s’=i+2v+^;	<2-s-ls>
i — 1
при этом предполагается, что между отдельными пластинами, составляющими
стейку, существует соверЩенный тепловой контакт (7\=Тг)1). Если коэффи-
циент теплопроводности является величиной переменной (dk/dT Ф 0), то рас-
пределение температуры по толщине пластины нс будет линейным. При уве-
личении коэффициента теплопроводности с температурой (dk/dT >0) распре-
деление температуры Т (х) представляет собой кривую, обращенную выпукло-
стью вверх (см. рис. 2-2), и, наоборот, при dk/dT < 0 выпуклость кривой
Т (х) обращена к оси абсцисс.
Аналогичным методом можно получить расчетные формулы для цилиндри-
ческих и сферических оболочек. Распределение температуры в оболочках
в форме параллелепипеда, например стены обычной комнаты или печи, не
описывается одномерным температурным полем. Аналитически эти задачи реша-
ются с большим трудом. Ленгмюр, используя метод электроаналогип, получил
простые эмпирические формулы для определения часового расхода тепла Q,
ккал/ч, через оболочки в форме параллелепипеда [Л.2-29],
При наличии источника теплоты постоянной мощности /д, ккал/(м3-ч),
решение задач одномерного стационарного температурного поля сводится к ре-
шению дифференциального уравнения
где Г — постоянное число (для неограниченной пластины Г=0, для цилиндра
Г=1, для шара Г = 2); координата, выбираемая в соответствии с формой
тела. При этом предполагается, что коэффициент теплопроводности является
постоянным,
Для неограниченной пластины, когда теплообмен противоположных ее
поверхностей с окружающим газом (Tf = const) происходит одинаково (аг -
^a2 = a=const), решение уравнения (2-5-16) в критериальной форме имеет
вид:
-Г^=ТРо(1->+вТг	(2-5-17)
Где R — половина толщины пластины (L=2R); Bi—критерий Био (Bi — aR/ky
критерий Померанцева
Po=IgR2,:kTc	(2-5-18)
показывает отношение количества теплоты IqR2, выделяемой источником в еди-
ницу времени в объеме R *, к количеству теплоты, передаваемой теплопровод-
ностью	через слой толщиной R при перепаде температуры в нем, рзв-
\ R /
ном Тс, Следовательно, распределение температуры по толщине пластины
будет описываться параболическим законом.
* Объем параллелепипеда, площадь основания которого равна единице,
а высота равна м.
119
Для сплошных неограниченного цилиндра и шаря решение можно напи-
сать так:
Т — Т 1	/ г2 2 \
^=уН'-^+в4	(2-5-is)
где V—постоянное число (для цилиндра У = 4, для шара 2V = 6).
Рассмотрим охлаждение пористой пластины при помощи продувания через
нее холодной жидкости или газа.
Если объемная пористость П (отношение объема пор к объему тела) равна
поверхностной пористости (отношению площади дырок к площади поверхности
тела), то единичная площадь для потока жидкости внутри пластины Af равна
пористости (Af—П). Единичная площадь скелета пластины (площадь скелета,
приходящаяся на единицу площади поверхности пластины) Ат равна (1—Л/)>
т. е.	Z7. Расход жидкости /у, кг/(м2-ч), равен произведению плотно-
сти жидкости на скорость ее движения у (/у=руУ). Внутри пластины скорость
движения жидкости будет в П раз больше, т. е. расход жидкости внутри
пластин равен (i-i/П). При малых значениях /у, определяемых неравенством
j-;di
Re -	< 1, температура жидкости равна температуре скелета тела.
Задача формулируется так; одна поверхность пластины нагрета до темпе-
ратуры T^const, противоположная поверхность пластины соприкасается
с жидкостью, теплообмен с которой происходит при помощи теплопроводности
(граничное условие четвертого рода). Решение этой задачи было дано Вейн-
баумом и Веллером [Л.2-34]. Дифференциальные уравнения переноса теплоты-
в жидкости и пластине имеют вид:
<^Т dT
= 0 (-СОС.КО);	(2.5.20)
<1“Т	dT
(2-5-21)
где Ср>—изобарная удельная теплоемкость жидкости.
Отсутствие множителя, зависящего от IT, во втором члене уравнения
объясняется тем, что скорость движения жидкости внутри пластины равна
v/П и единичная поверхность для движения жидкости составляет Л^=П. При
этом предполагается, что передача теплоты внутри пластины происходит
только через скелет тела. Поэтому в первом члене уравнения (2-5-21) имеется
множитель (1 — П), равный единичной площади скелета тела. Такое предполо-'
женнс оправдывается при продувании газа, теплопроводность которого мала
по сравнению с теплопроводностью тела. Однако для пористых теплоизоля-
ционных материалов при продувании через них жидкости это упрощение не
будет соответствовать действительности, так как передачей теплоты теплопро-
водностью через поры, заполненные жидкостью, пренебречь нельзя. В этом
случае вместо Хг(1—И) надо написать эквивалентный коэффициент теплопро-
водности равный Х7--]-П —Хг).
Граничные условия для системы уравнений (2-5-20) —(2-5-21) запишутся
так (рис. 2-3);
при х-L Т—Т* — const; \
I	(2-5-22)
при х = 0 (7’)+«_о = (7')-»-о; J
(М-2з>
при х =— со	Г-»- Тс = const.	(2-5-24)
Решение для распределения температуры в пластине имеет вид:
^_^_=ехр	(1- Кп],	(2-5-23)
120
где Kn— число охлаждения пористых тел,
Кп =
jfcpfL
Хт (1 — П)
(2-5-26)
Физический смысл числа Кп состоит в том, что он характеризует меру
отношения количества теплоты, переносимой конвективным движением жидко-
сти внутри пористой пластины, к
количеству теплоты, передаваемой
теплопроводностью при одинаковом
температурном напоре.
Рис. 2-4. Распределение температуры и
Рис. 2-3. Пористое охлаждение
плоской пластины (I == L).
средняя температура в пористой пластине
в зависимости от числа Кп.
Число Кп может быть выражено через число Пекле Ре:
с nfpiuL vL	Xf
Kn = (i -ny= at: x,. (i -uy “ Pe УГ-:тт; >7. 	(2’5’2 >
На рис. 2-4 приведены кривые распределения-температуры по толщине
пластины для разных значений числа Кп от 0 до 10. Из рис. 2-4 видно, что
с уменьшением числа К11 распределение температуры приближается к линей-
ному. Пунктирной линией отмечено изменение средней температуры Т в зави-
симости от Кп. Эта линия построена на основании следующей формулы:
(Т^ут	(2.5.28)
Способ пористого охлаждения в настоящее время широко применяется
в новой технике. Одно из главных преимуществ этого метода заключается в том,
что можно достигнуть эффективного отвода теплоты при малых градиентах
температуры внутри тела.
Двумерная задача
В заключение рассмотрим задачу по нахождению температурного поля
в клиновидном теле, для которого уравнение теплопроводимости имеет вид
(0 < г < со, 0 < ф < а):
д2Т дТ д*Т
+ ₽-5-29)
1Z1
при граничных условиях
Т (г, 0) = ф! (Г); Т (г, а) = ф3 (г).	(2-5-30)
Полагаем, что функции <рх (г) и ф3 (г) таковы, чго интеграл
f (г) гр - 1 dr (i, = 1,2)	(2-5-31)
существует. Решение уравнения (2-5-29) при граничных условиях (2-5-30) полу-
чим с помощью преобразования Меллина:
Т^Цр) =$ Trp~} dr.
(2-5-32)
Считаем, что Т, гдТ{дг равномерно ограничены при г->0 и ведут себя
на бесконечности как г**6(б>0).
Тогда, применяя уравнение (2-5-32) к (2-5-29), (2-5-30), получаем:
d2T - —
—+ p27'^W'(P,(f) = 0;	(2-5-33)
Т(г, 0) = ф1(Р); T(r, a)=<fc(P).	(2-5-34)
Интегрируя (2-5-33) с учетом (2-5-34), получаем:
Т,п X ,п\ sin Р (а~ Ф) I - ГП-. sm Р<₽
Т (Р, Ф) = Ф1 (Р)--—— — фа (Р) -—~ __
 т>	/	Sin ра	-I-	)	S10 ра
— j G (Р, ф, Ф1) И7 (Р, Ф1) ^ф1 (2-5-35)
где _	t
{sin Р<р sin Р (а —ср,)
----Р sin Ра >
_	(2-5-36)
sin Рф1 sin Р (а - ф)	1
----ршп*—'
Переход к оригиналам осуществляется по формуле обращения
O-f-zco
Т('. <Й=2Л ) TIP. <f)r-p dP.	(2-5-37)
При переходе к оригиналам прямая ReP = o дополняется до замкнутого
контура, и в предположении, что Т является мероморфной функцией, а при
достаточно больших R интеграл по дуге круга аге _ Р | = Р стремится к нулю,
можно воспользоваться теоремой вычетов.
Рассмотрим подробнее обратный переход для конкретного случая 1^=0 и
Т(г, 0) = р+В”Г-
Г (г
r>h,
0<г^й;
г >Ь-
(2-5-38)
(2-5-39)

Тогда формула (2-5-35) будет иметь вид:
_ _	/ . bp D tp_^bisinP(a—ф)
TIP	р +S»P+T? sin Ра ’
Ц 1 Р + 1 P+1/sinPa*
(2-5-40)
122
Нетрудно видеть, что Т—мсроморфная функция, а интеграл (2-5-37)
по дуге агс|Р| = Я стремится к пулю при достаточно больших R. Тогда,
подставляя (2-5-40) в (2-5-37) и используя теорему вычетов (причем контур
интегрирования дополняется дугой круга бесконечно большого радиуса, рас-
положенной слева от прямой ReP = o при условии г<Ь и справа от пря-
мой при условии г>Ь, получим окончательное решение краевой задачи
(2-5-29) —(2-5-30), (2-5-38) — (2-5’-39):
Т(г,	Л(а-ф) , Аф , 1 V (- 1)” у а ~ а л	п
X	/мпл/аг . пят	. лл(ф—а)1	Г г» sm (а — ф) , _ sm ф! , r	A sin—£ +sin—“	' +п Вп—1	ii + B,	+ \ b /	| 1	а	а J L	sm а	, sm <хJ . 1 V (— В"*1 ! ''\ПЛ/аГО •	s.D • '««Pl	- -М П = 1 (2-5-41)
Т(г,	1 V ( — l)n+1 / b\wa Г . . пл,ф , . . пл(ф— а)1 , я 2 п \г) И‘5,П а +-4”51" а ] + гь= [ + ± У (- l)^1 [АГ-'^В. sin "Jtfc^) + B1Sin	(2.5.42) ft Aj а4-лл	а	a J '	’
(ПР"	b<r<co).
2-6. РЕШЕНИЕ СТАЦИОНАРНЫХ ЗАДАЧ
МЕТОДОМ КОНФОРМНЫХ ОТОБРАЖЕНИЙ
Этот метод применим для решения уравнения Лапласа на плоскости
с помощью которого описываются стационарные процессы переноса теплоты
вещества и т. д. Основным преимуществом метода конформных отображений
перед другими классическими методами является возможность получения реше-
ния уравнения (2-6-1) не только для простейших областей (пластина, цилиндр
и т. д.) на плоскости, но и для практически любой фигуры. Это преимущество
весьма существенно, так как на практике как раз часто встречаются области
сложной формы, которые не могут быть представлены в виде простейших
областей.
Как известно, любая аналитическая функция комплексного переменного
удовлетворяет уравнению Лапласа (2-6-1), поэтому в основе метода конформ-
ных отображений лежит сведение заданной сложной области с помощью
некоторой аналитической функции к простейшей области (например, полуплос-
кости), для которой решение получить нетрудно. При этом уравнение Лапласа
(2-6-1) и граничные условия сохраняют свой вид. Поэтому, если в полученной
простейшей области мы подберем аналитическую функцию, удовлетворяющую
рассматриваемым граничным условиям, задача считается решенной.
1. Введем понятие комплексного потенциала переноса аналогично тому,
как это делается в гидромеханике. Если обозначить
q=— Xgradu,	(2-6-2)
то из уравнения теплопроводности следует, что
=	-	(2-6-3)
4 дх ду		1
123
Кроме того, так как
(2-6-4)
(2-6-5)
rat grad и — О,
то из (2-6-2) при X = const получим:
*Zs._^ = 0
дх ду
Комплексным потенциалом теплового потока назовем функцию комплекс-
ного переменного
(2-6-7)
ф(г) = У (х, у)+ш(х, у),	(2-6-6)
где V (х, у) — некоторая функция, называемая по аналогии с гидромеханикой
функцией тока и связанная с и (х, у) условиями Коши—Римана
дУ _ ди _ __ _]_	дУ _ _ ди __ j_
дх ~ ду~ X	ду ~ дх ~ Т ’*
Таким образом искомая функция и (х, у) определяется так:
н(х, y) = Im [ф(г)].
Отметим, что метод конформных отображений применим лишь
нарным задачам переноса и не может быть применен к решению
парных задач.
2. Наибольшей трудностью метода конформных отображений
(2-6-8)
к стацио-
нестацио-
..	. ...гг .	.....Р----- является
нахождение функции, преобразующей заданную область S3 на полуплоскость
(в дальнейшем в качестве простейшей области мы будем рассматривать верх-
нюю полуплоскость) Мы оудем рассматривать области, имеющие вид много-
угольника, которые отображаются на верхнюю полуплоскость с помощью интег-
рала Кристоффеля—Шварца [Л. 2-14, 2-30];
w = с 5 (г -	1 (г -а2)“° -1... (г’ дг +cit (3-6-9)
где ai — точки действительной оси полуплоскости j, в которые переходят точки
многоугольника при конформном отображении; cq —углы многоугольника,
выраженные в долях л; С, С, —постоянные. Отметим, что в (2-6-9) множители,
соответствующие бесконечно удаленным точкам, выпадают. По теореме сущест-
вования конформных отображений |Л. 2-30] три точки на действительной оси
могут задаваться произвольно, а остальные ее точки, а также постоянные С
и Сг находятся из условий задачи.
Рис. 2-5. Схема расчета температурного поля.
а — угла здания; и — пятиугольной стенки.
Пример 1. Найти стационарное распределение температуры в стене
вблизи угла здания при постоянных различных температурах на наружной и
внутренней поверхностях (рис. 2-5, а) [Л. 2-14, 2-31]. С помощью интеграла
Кристоффеля — Шварца отобразим фигуру AiA2A3AtAi, представляющую „четы-.
рехугольник11 с вершинами Л1 = 0, Ла = со, А3~Н Л4=со, углы при кото-
' 124
рых соответственно равны ах = 1/2, а2 —О, а8—3/2, а4 = 0. Для наглядности
сведем эти данные в таблицу, причем три точки из четырех на действительной
оси зададим произвольно:
k	л„		ak
1	0	0,5	0
2 	оо	0	1
3	Н -4-471	1.5	а
4	- со	0	со -
Тогда в нашем случае интеграл (2-6-9) принимает вид:
B?=ci ;^г~п Ф+е,.	(2-6-10)
J (г- 1)	1	.
Для определения трех постоянных С, С\ и а необходимо иметь три урав-
нения, два из которых получаются из условий соответствия	а3-*А8;
так как
Г = 2С arclg У	+ arcth рСС] +С„	(2-6-11)
то
Ci = 0;
+	(2-6-12)
Для нахождения третьего уравнения воспользуемся следующим соображе- •
ннем: при переходе с луча на луч Л2Л3 в плоскости 50 функция W полу-
чает приращение
ЛГ = гЛ4-0(р),	(2-6-13)
где 0 (р) означает комплексную функцию, бесконечно малую при р->0. Это
соответствует в 'плоскости ] обходу по полуокружности бесконечно малого
радиуса с центром в точке 0. Подставляя г—l-J-pe^ в (2-6-10) и вычисляя
интеграл при р->0, получаем:
ЛГ = —Сл /а-1.	(2-6-14)
Сравнивая (2-6-13) с (2-6-14), получаем соотношение
с =-------
(2-6-15)
После нахождения постоянных из системы уравнений (2-6-12), (2-6-15) полу-
чим окончательное выражение для функции, отображающей полуплоскость
на „четырехугольник"
Г = 22[Аагс18А У^+Н^у^]-	(2-6-16)
Из формулы (2-6-16) легко видеть, что внутренняя граница "четырехуголь-
ника” ЛаЛ^44 переходит в отрицательную часть действительной оси, а внеш-
няя Л4Л1Ла—в положительную. Подберем теперь аналитическую в верхней
полуплоскости функцию, мнимая часть которой на интервале (—оо, 0) прини-
мает значение и3, на интервале (0, 1)—значение Uj, на интервале (1, оо) —
значение на. Такую функцию естественно искать в виде [Л. 2-30]
««Ciar^i— z) + C2arg(2-l)4-C8>	(2-6-17)
125
где
(О и	О:
аго={	•	п	(2-6-18)
1_л, у < О.
Постоянные в (2-6-17) находятся из граничных условий с учетом (2-6-18):
C1 = U1^3.	С,=в,_В1+и,.
Тогда
“ = ~‘й“' агв <— г) + "1~Ц2 агй (г — 1) + “з — “1 + “г,	(2-6-19)
после чего нетрудно подобрать аналитическую функцию с мнимой частью вида
(2-5-19); в качестве такой функции можно выбрать
4’ И =111 In (— z) + In (г—1) + и,-а, + и,.
Тогда окончательное решение задачи примет вид:
д “3 ln(—z)-h 1,1 л ln(z— l)j + «3 — ui+na, (2-6-20)
где г выражается через W с помощью формулы (2-6-16).
Так как z не выражается в явном виде через W, то при расчетах по фор-
муле (2-6-20) следует задавать вначале г, находить из (2-6-16) соответствующее
значение W и таким образом получать соответствующее значение потенциала
переноса в заданной плоскости.
Пример 2. Найти стационарное температурное поле в части плоскости,
ограниченной «пятиугольником» 4i484344464i при следующих граничных усло-
виях: u = uL па ломаной	и = п2 на ломаной 4243; и=и3 на ломаной
434.145 (Рис- 2-5, б).
Аналогично предыдущему примеру отобразим конформно, верхнюю полу-
плоскость на фигуру	с помощью интеграла Кристоффеля —
Шварца. Для наглядности сведем данные в таблицу
к		ч	ak
1	0	1,5	0
2	со	0	1
3	СО	0	а
4	— лг)-( (Лг-М	1,5	со
5	СО •	0	— Ь
В таблице укажем также и точки а^, причем три из них flj=0, a2=l,
а4 = со зададим произвольно; две остальные точки а,а = а, °з = —b на действи-
тельной оси являются неизвестными, подлежащими в дальнейшем определению.
Интеграл (2-6-9) в этом случае имеет вид:
Г==С
_______Kg] dzj________
(zi-1) (Z! - а) (г24-б) ’
(2-6-21)
При нахождении трех неизвестных постоянных С, а и b воспользуемся
следующими соображениями: при переходе с луча Л1Д2 на ЛУЧ Аг4а в пло-
скости 2В функция № получает приращение
Д1У «tfiH-O (р),	(2-6-22)
126
где 0 (р) означает комплексную функцию, бесконечно малую при р->0. Это
соответствует в плоскости } обходу по полуокружности бесконечно малого
радиуса с центром в точке 1. Подставляя z =- 1 4-ре'Ф в (2-6-21) и вычисляя
интеграл по полуокружности при р-*0, получаем:
__________
(1-а)(14*)‘
(2-6-23)
Сравнивая (2-6-22) и (2-6-23), находим:
Сл
111 (1-а) (!+*)
(2-6-24)
Аналогичным образом, рассматривая в плоскости 39 переход с лучей
и А^А6 соогветствепно па лучиМ8^4 и АйА1 (что соответствует в плоскости
обходу по полуокружностям бесконечно малого радиуса соответственно вокруг
точек а и — Ь), получаем соотношения:
А Сл
3 (афй) (а— 1) ’
Сл №
3 (а + &) (6 4 1) ’
(2-6-25)
(2-6-26)
Решая уравнения (2-6-24) — (2-6-26), находим постоянные. Вычисляя ин-
теграл (2-6-21), получаем:
2С
* и In
2 (а— 1)
/г — У а	b , j/г	а А-b	,
Цп---------------arctg -F- 4--------!------ In
1'г+кЬ 1+4 )<ft т 2(l-a)(l+ft)
(2-6-27)
где постоянные С, а и б определяются по (2-6-24) — (2-6-26).
При отображении (2-6-27) ломаные линии A5AlA2i А2А3> А3А4А5,
чинаюшие «пятиугольник» 241242А5714245/11, переходят соответственно в
действительной оси плоскости: [— б, 1], [1, А [-со. -ft), [а, ос).
Таким образом, рассматриваемая задача сводится к нахождению ;
ческой в верхней полуплоскости функции, мнимая часть которой на т
действительной оси принимает соответственно
значения «j, иг и и3. Такая функция находит-
ся аналогично тому, как это сделано в преды-
дущем примере, в виде
«•= ~ tm [(и3 —u,) In (г + ft) +
+ to (г— l)+(»2 — “a) I" (z— a)J + n3.
Пример 3. Найти распределение темпе-
ратуры в плоской области, ограниченной ром-
бом ^124а^аЛ4 (рис. 2-6),' па смежных сторо-
нах которого A4Ai, А1А2 и Л2^3, /1д^4 заданы
соответственно температуры и и2 [Л.2-31 ].
С помощью интеграла Кристоффеля— Шварца отобразим фигуру
на верхнюю полуплоскость, Соответствие точек зададим так:
Й9[Л1=О, A2 = d, <4a=rf(14e^a), <44 = dc‘n:a]-> j (0, 1, со, й).
Интеграл Кристоффеля — Шварца в рассматриваемом случае имеет вид:
ограни-
отрезки
аналити-
отрезках
Рис. 2-6, Схема расчета тем-
пературного поля ромбо-
идальной плоской сгонки.
/?г и, Яь

№ -Ср“‘~ 1 (ax-lr^ (zi-^J-^^ + Cb
о
(2-6-28)
127
Три точки па плоскости } мы, как обычно, зададим произвольно: aj = 0,
а2 = 1, »э = :х>; для определения четвертой точки	воспользуемся прин-
ципом симметрии. Так как фигура AiA2A3At симметрична относительно диаго-
нали а точка As переходит в i со на плоскости то по принципу сим-
метрии треугольник Л]-?12Л8 переходит в правую часть верхней полуплоскости,
а треугольник —в левую ее часть. Отсюда сразу заключаем, что Ь =—1.
Постоянные С и Cj находятся из условий соответствия точек 0 и A2 = d
на плоскости 2В точкам ах==0, а2=1 на плоскости j:
С1 = 0;	(2-6-29)
С=2^(1-г1)“/!~ 'гГ “dr, j	--,•	(2-6-30)
«	1	В^-<1	•
Тогда аналитическая функция, отображающая верхнюю полуплоскость на
ромб	с учетом (2-6-29) и (2-6-30) запишется так;
Граничные условия после отображения на плоскость $ запишутся так:
=	(— со<х< — 1); u — uIt (—1<х<1); и-= и2 (1 < х < со).
Найдем теперь аналитическую в верхней полуплоскости функцию удов-
летворяющую этим условиям. Такую функцию естественно искать в виде
u = C, arg (г +1) +Cj arg (г — 1)+CS.	(2-6-32)
Для нахождения постоянных воспользуемся условиями
С"1Л —р-	*4— С'з WjJ ^-* 2“^ —1~ ^3	, £'3 = ^2,
откуда
или окончательно
u = ~ Im [(uB —Ui) 1п (г 4-1) + («1 — н2) 1п (г — !)] -ф н2.	(2-6-33)
Используя методы решения, описанные в предыдущем параграфе, можно
решить некоторые задачи стационарной теплопроводности,
2-7. ОДНОМЕРНОЕ НЕСТАЦИОНАРНОЕ ПОЛЕ
<	(ПЛАСТИНА, ШАР, ЦИЛИНДР)
Решению задач на нестационарное температурное поле посвящены фунда-
ментальные монографии [Л.2-18 и 2-22]. Здесь мы приведем некоторые обобще-
ния известных решений. В первую очередь рассмотрим одномерные задачи для
простейших тел: неограниченная пластина (R-^l), неограниченный цилиндр
(R<^1) и шар, где R — радиус или половина толщины пластины, / — длина
тела.
Различают два вида нестационарных состояний — апериодические и перио-
дические. В апериодическом состоянии температура в любой точке тела изме-
няется как некоторая функция времени. В периодическом нестационарном
состоянии температура тела в любой точке является периодической функцией
времени. Эго периодическое изменение может быть регулярным или нерегу-
лярный, но обязательно циклическим. Регулярное циклическое изменение ха-
128
рактеризуется гармонической синусоидальной или косинусоидальной функцией,
з нерегулярные периодические изменения—любой циклической функцией.
Дифференциальное уравнение теплопроводности в нашем случае можно
написать так;
т)' п /д2Т (х, т) Г дТ (х, т)\	/я(х,	т)
дх	\ дх2 ' х дх	ср	’	'
здесь	Г —постоянное число; для пластины Г = 0	(х = х),	для	цилиндра
Г== 1 (х = г) и для шара Г —2 (х= г),
Источник теплоты в общем случае является функцией температуры. Для
некоторых частных случаев можно написать уравнение в виде
lq(x, t)=Q(x, т)4-й[Т(х, т)-Щ,	(2-7-2)
где Ь —некоторый коэффициент, зависящий от времени; То~температура тела
в начальный момент времени, т. с.
Т(х, 0)=7V
Решения будут приведены для симметричных задач, т. е.
ОТ (0, т) _0	(2-7-3)
с)х	’
Средняя объемная температура Т (т), необходимая для расчета, расхода
теплоты, определяется формулой
Я
ГМ” 'rt1, i хтТ(х, т)0х.	,	(2-7-4)
К 1 J
о
(2-7-5)
Введем следующие обозначения:
E = J; «('. Ро)=Ц^Ь^-; 1
ШГО)^; ₽O(E,Fo).M, |
где Fo — число Фурье; Ро —число Померанцева.
Тогда дифференциальное уравнение примет вид:
Я	+138 % F<>) + A (F°)8IX F°) + P° (S. Fo). (2-7-6)
О 1 о	g og
Это уравнение будет решено для граничных условий первого, второго и
третьего родов и при произвольном распределении температуры в начальный
момент времени.
С этой целью введем следующие критерии подобия:
Ki(Fo)“W“=^);
MFO)^^.
(2-7-7)
где qn (т) — удельный поток теплоты на поверхности тела; Тс (г) —темпера-
тура окружающей среды; Ki (Fo) и Bj — cooibctctbciiho числа Кирпичева и
Био.
Начальное условие запишем так;
0) = f (5).	(2-7-8)
129
5 Лыков А. В.
Граничные условия:
первого рода
9(1 Fo^—ff(Fo);	(2-7-9)
второго рода
^£a=Ki(Fo);	(2-7-10)
третьего рода
+	P°)=MFo);	(2-7-11)
условия симметрии
,S(0, Fo)^.co. '	(2-7-12)
Последнее неравенство отмечает тог физический факт, что в центре тела
температура не может быть равной бесконечности. Средняя безразмерная тем-
пература
0(Fo) = (r+l)hr8(g, Fo)^.	(2-7-13'
&
Для обобщения решений пластины, цилиндра и шара воспользуемся обоб-
щенным конечным интегральным преобразованием М. Д. Михайлова. Введем
функции Й7Г(|) и Vr(£), определяемые соотношениями (2-4-102) и (2-4-103).
Используя преобразование (2-4-99), решим уравнение (2-7-6) при граничных
условиях (2-7-9). Среднюю температуру определяем по формуле (2-7-13).
Для граничного условия первого рода решения имеют вид [Л.2-32]:
Fo) = У 1Щ^-Иехр[ f A(Fo)dFo-^Fo| х
Vr (Н„)	| о	J
{1	Fo
( ЕГ*Т (И„. 5) I ©	+ (t„Vr (ц,) lj <р (Fo*) exp х
о	о
[Fo*	Л	1 Fo
pJFo-~ j ^(Fo)d Fo* dFo-4-J J	s)Po(g, Fo*)expX
o	Job
X^fiJFo*- j A (Fold FoJdgdFo'j-.	(2-7-14)
Средняя безразмерная температура будет равна:
сс	I Fo	-]
S(Fo) = 1 esp	X
“ "лгГ("п/ L(I	I
/1	Fo
+	5 4=(Fo*)expX
(о	о
[Fo*	П	I Ь о
p^Fo* — A (Fo) d Fo d Fo*-M‘ £rlFr (ил, *) Po (£, Fo*) exp x
b	J	о о
X^ Fo— A (Fo) d Fo^ d£ d Fo*^,	(2-7-15)
где ]1л — корпи характеристического уравнения ЙХг(р.)=ж0.
130
Если в решения (2-7-14) и (2-7-15) подставить соответствующие выражения
для 1Гг (£) и Уг(£) из (2-4-94)—(2-4-96), то получим решения для пластины,
цилиндра и шара.
Рассмотрим ряд частных случаев;
Ро (g, Fo) = 0; <p(Fo) = 0; А = const.
Решения (2-7-14) и (2-7-15) примут вид:
5(5. №)= У	S) exp [(Л - р,]) Fo] ( F 'V/,- (И,, g) f 6) dg; (2-7.16)
СО	I
“(Fo)= 2 ЛГ7Г)ехР[(Л-^)РО]	5)/(5)<Ч.	(2-7-’П
_ п“ 1 г	о
Если /1 = 0, а /(£)=! (равномерное начальное распределение темпера-
туры), то из (2-7-16) и (2-7-17) получим:
5(g, Fo) = У	р°;	(2-7-18)
5 (Fo) = У ехР (- Hi Fo).	(2-7-19)
п = 1	"
Для малых значений времени, точнее числа Фурье, решения (2-7-18) и
(2-7-19) можно написать в форме Лапласа для пластины:
5= У (—l)”-i Гег1с(—+erfc Р-Я~1№Л-	(2-7-20)
’ L 2l' Fo	2)/Fo J’ '	'
a=4-l-2 1/'5’4-4/F0 У (-!)»’ eric	(2-7-21)
r 71	у Fo
Для шара	5
5=1--'- У Г eric	'2_~ 5 - eric(2" ~ 'j+Я.	(2-7-22)
5 “ L 2 v Fo	2 Y Fo ]	’
Для цилиндра можно получить только приближенное решение:
8*
131
Для параболического начального распределения температуры f (£)=(! —12)
решения будут иметь вид:
V 4(Г + Г|№г(11я, £)
8 (5' го’=J схр (“ F°); 42-6 7'24’
»(F°)= У 4<ruf 1)2ехр (—цД Fo).	(2-7-24')
Представляет интерес рассмотреть частный случай, когда /(Е) = 1₽'г	£).
Как было показано в [Л.2-32],
i	(	(Pm Hi);
(Н»Л) IFf (Иг ЕИ=	,	(2-7-25)
о	[ —; (h«=Hi).
Тогда решения (2-7-16) и (2-7-17) будут иметь вид (при Ро (£, Fo) = 0,
tp(Fo) = 0 и Л = 0):
5(£, Fo) = l^r (цр Н)ехр(—p|Fo);	(2-7-26)
8 <Fo,=v г (|Ji)схр (- niFo)- с2-7-27)
Решения (2-7-26) и (2-7-27) интересны в том отношении, что нестационарны;!
процесс нагревания или охлаждения описывается простой экспонентой. Данный
режим нагревания обычно называют регулярным режимом. Из решений (2-7-26)
и (2-7-27) следует, что при некотором заданном начальном распределении тем-
пературы регулярный режим теплообмена тела будет наблюдаться с самого
начала процесса. Этот вывод был впервые сделан автором книги в 1941 г.
в его монографии (Л.2-33].
Для случая нагревания тела при Ро (£, fo) = 0, 5(t, 0)=/(|)==0, ,4=0
решения имеют вид:
8Fo) = 2 S) exp(-F?.F°)X
Fo
xj <p (Fo*)exp Fo*) d Fo*;	(2-7-28)
о
S(5, Ро) = 2(Г4-1) У exp(—ц=, Fo) J ф(Ро*)ехр (pj Fo«) d Fo*. (2-7-29)
n - t	0
Рассмотрим случаи, когда температура поверхности тела является линей-
ной функцией времени 9(1, Fo) = ф (Fo) = Pd Fo, где Pd —число Предводите-
лева, Pd==W?2/a (Тс — Т0). Решения для этого случая имеют вид:
9(£, Fo)	1-а2 2Гг(ця,
-M~=Fo -2ДГДТ + ъ руг(цд~ех11 <“ Fo)> (2-7-30>
6	— Fo__________1 I У LiLi-Uexn/_ Lia Fox (9 7 3I\
Pd “h0 (Г 4-1) (Г 4-3)+ 2 6XP( ^F°)’	(2’7‘31>
n — 1
132
Если температура поверхности тела изменяется по закону экспоненты
9(1, Ео) = ф(Fo)= 1 — ехр (— Pd Fo), то решения примут вид:
гг g /и)
-	8 g, Fo) = 1------Ц__ ехр (- Pd Fo) -
W'pf/Pd)
2	(ti
--------- -V1ехр *- F°):	(2’7‘з2)
рЗ-]
(Г +1) Vr (/Pd)
5 (Fo) = 1--ехр (- Pd Fo)—
'	/Pdrr(}'Pd)	'
~ 2 2,(Г+1- ,	(2-7-33)
Для случая 9 (g, 0) = 0, (p(Fo) = 0, Л=0 и Po (£, Fo) = po — const решения
будут иметь вид:
B(g, Fo) l-p
po 2(r+i) (2 р/мк))еХГ,( F"F°);
5(Fo)	1	V 2(Г4-1)	v
Po (Г+1) (Г + 3) 2j ех₽( P»F0)-
n = ]
(2-7-34)
(2-7-35)
Если источник теплоты является параболической функцией времени, то
решения имеют вид:
9(*, Fo) I-**	.
Ро 2(Г + 1)	2(Г+3)
2 2Гг (u„, £)
п =-. 1
Источник теплоты Po (g, Fo) = Po Wr	£), Для этого частного случая
решения получаем в виде
=	[I—ехр (-	Fo)J;	(2-7-38)
Ц^'ТГ ‘'«.(Н1И1-ехр(— niFo)]. .	(2-7-39)
133
Если источник теплоты —экспоненциальная функция времени P®(g, Fo) =
= Роехр (—Pd Fo), то решения имеют вид:
po Lw'rO'Pd) Jpd
(2-7-40)
Po LkPdWr(k'Pd) J Pd
л— I '	'
Приведем решения дифференциального уравнения (2-7-6) для
условия (2-7-10) второго рода [Л.2-32]:
FFo	1 Р
В(Е, Ро) = (ГЧ- 1) ехр ( A (Fo*)dFo* К Ег/(Е) rfg +
Fo	Г Fo*	I	i Fo
+ J Ki (Fo*) exp — Л (Fo**) d Fo**) d Fo*J gr Po g,
0	L о	Joo
Г Fo*	1	1
X exp — ( A (Fo**) dFo** Ш Fo*| +
wi 2и?р(ц , 7) I (*	J
+ 2	. “P M <Fo*) d F°’ -rt Fo X
XpF^rfli,,, д)/(Е)а5 + Гг(р„) j Ki (Fo*)exp^> Fo*~
Fo*	p Fo
— J A (Fo**)d (Fo**) dFo*+J j J ггшг
b	J lb о
(	Fo*
x|j4Fo*— f 4(Fo**)dFo**
(2-7-41)
граничного
Fo*)
*)Ро(Е» Fo*)expx
(2-7-42)
6 (Fo) = (Г-(. 1) exp
Fo
4- $ Ki(Fo*)ex.
a
] Fo	г Fo*
+ J J f Po& Fo*)exp — J
J A (Fo**) dFo**J|$	(M +
Fo’	“I
dFo*4-
(2-7-43)
Рассмотрим частный случай:
4==0; po(t Fo) = 0; в & 0) = /(£)=0; Ki (Fo)« Ki-const.
134
Для этого частного случая имеем:
6Й- н°)	, i)Fo , 1	, г+±\ У	. ро,
К1 -(1+>)Ю+2 +г + 3/) £	₽(
(2-7-44)
Для малых чисел Fo решения можно написать в форме Лапласа:
для пластины
В2 Кi I'f5 У [ierfc	+ ierfc g"~D±i1.	(2-745)
2.	2 lr Fo	2 V Fo ’	'
n= 1 I	J
для шара при £ > О
6 = 5-1 Гехр ' Fo —L + l\rfcf Fo I-erfc ‘tLI; (2-7-46)
g I. '	6	'	'.2^Fo	/	2 1- FoJ '	'
для цилиндра при £>0 (приближенное решение)
В К1 ^_Е° Г ierfc 1 ~1_ + -Я+3ЦР9 Р erfc '"А 4-...1. (2-7-47)
|/g [	2 [- Fo 2g/g	2 )‘ Fo J
Средняя температура равна:
Ё (Fo)
Ki
= (r+l)Fo.
Число Кирпичева иаменгется во времени по закону экспоненты Kt (Fo) —
— Kiexp(—Pd Fo) при условии 4 = 0; Po (£, Fo)=0:
- 6(g, Fo)	Г + 1	ГГЙГЙ)
--------------------r=_________ exp (—PdFo) —
Ki Pd I- PdVr(|/Pd)
S 2ГГ (|i„, g)
“ 2 (Fj-Pd»)rrti„ ex₽ (-Р-Й Fo);
n = l
(2-7-48)
(2-7-49)
Решения для граничного условия третьего рода можно написать так
[Л,2-32]:
v 21МЬр £)	В(3
йй’ F0) n2	ri + Bis + (l-Г)В1Х
X ехр rj A (Fo*) d Fo* - Fo] {£ГГГ (ц,,, g) f © <ig +
I 0	J lo
Fo	Г	Fo*	T
+lft(l‘.)S 'tW^P Йро’- S TUFo-JdFo* dF0* +
o	L о	J
1 Fo	Г	To*	1	1
bJJ БГв7Г (нл. ъ) Po (t Fo*) exp )i*Fo*- J A (Fo*) d Fo* pg dFo*l;
oo	1. о	J - J
(2-7-50)
135
to	|-Po	-i
B(Fo’=2	$ ;(Fo.).Fo.-^Fo X
x h Er^"r (P„, 6) / (E) © + 1‘J'r (И„) $ 6C (F°') X
to -	0
Xexp p.«Fo*— J Л (Fo*)tf Fo*pFo*4-
+ J Jgrll?r(H„, E)Pog, Fo»)cxp|^Fo«- J A (Fo*) d Fo-] dg d Fo-l,
oo	L о	J J
(2-7.51)
где Fn— корни характеристического уравнения
^r(M) z M
Vr(ji) Bi*
(2-7-52)
Из решений (2-7-50) и (2-7-51) можно получить решения (2-7-14) и (2-7-15),
если положить Bi = co.
Рассмотрим некоторые частные случаи.
1. Л(Го) = 0; Ро(£, Fo)=0; /(£)=0 ec(Fo) = l;
ХЧ 2lFr (]1я, &)
8© Fo)= 1 - 2 А С» “Р F°):	<2-7-53»
“л' Г (r',nl
п = 1	'	'
B(Fo)==l-2-^^са<х<Р(-1*Е Fo),	(2-7-54)
n = 1	”
где
С =________ша
”	Й+В.-у1-Г)В,-
— постоянные коэффициенты, зависящие’от критерия Bi (см. табл. 2-2_2-4).
Для пластины (Г = 0) можно привести приближенное решение, справедли-
вое при малых числах Фурье;
ц^°-
1 _6	'	/1 ____t	_
S=sserfc—-~=—ехр [Bi (1 —£)-}- Bia Fol erfc (—-[-Bi ИF
2 V Fo	\ 2 V Fo
4-erJc— ехр [Bi (1 -[-£)-[-Bi2 Fol erfc	Bi Fo 1
2J/Fo	\2/Fo	I
2. Температура среды является линейной функцией времени:
2
+ 13Г~^ Vi 2lFr/u, £)
2(Г + 1) + 2	(F„) С* СХР F°) ’
(2-7-55)
(2-7-56)
£Ea.=F„_____________
Pd	(Г + 1)(Г + 3)
2 У* с«ехР (“ ЙРо).
(2-7-57)
Анализ решения (2-7-56) показывает, что начиная с определенного значе-
ния чисел ro^Fot суммой можно пренебречь. Тогда температура в любой
точке тела будет линейной функцией времени, а распределение температуры
описывается параболой.
136
Таблица 2-2
Значение коэффициентов Сп (п = 1, 2, .... 6) для пластины
при разных значениях Bi
Bi	Ct	Cs	Са			С*	С,	С*	
0,01	0,0050	0,0000				
0,02	0,0099	0,0000				
0,04	0,0197	0.0002	0,0000			
0,06	0,0294	0,0004	0,0001	0,0000		
0,08	0,0390	0,0006	0,0002	0,0001	0,0000	
0,10	0,0481	0,0010	0,0002	0,0001	0,0001	0,0000
0,15	0,0714	0,0022	0,0006	0,0002	0,0001	0,0001
0,20	0,0936	0,0038	0,0010	0,0004	0,0002	0,0002
0,30	0,1359	0,0083	0,0022	0,0010	0,0006	0,0004
0,40	0,1754	0,0143	0,0039	0,0018	0,0010	0,0006
0,50	0,2124	0,0216	0,0061	0,0028	0,0016	0,0010
0,60	0,2471	0,0300	0,0086	0,0040	0,0022	0,0014
0,70	0,2795	0,0395	0,0116	0,0054	0,0030	0,0020
0,80	0,3098	0,0499	0,0151	0,0070	0,0040	0,0026
0,90	0,3383	0,0610	0,0188	0,0088	0.0030	0,0032
1,0	0,3649	0,0728	0,0280	0,0108	0,0062	0,0010
1.5	0,4760	0,1381	0,0488	0,0236	0,0137	0,0089
2,0	0,5587	0,2075	0,0812	0,0405	0,0238	0,0156
3,0	0,6705	0,3395	0,1580	0,0845	0,0512	0,0340
4,0	0,7408	0,4509	0,2408	0,1376	0,0862	0,0583
5,0	0,7880	0,5403	0,3216	0,1955	0,1267	0,0873
6,0	0,8215	0,6111	0,3960	0,2547	0,1706	0,1200
7,0	0,8484	0,6673	0,4627	0,3127	0,2163	0,1552
8,0	0,8654	0,7122	0,5212	0,3680	0,2623	0,1920
9,0	0,8804	0,7484	0,5722	0,4196	0,3076	0,2295
10,0	0,8925	0,7780	0,6163	0,4672	0,3514	0,2671
15,0	0,9291	0,8668	0,7635	0,6466	0,5360	0,4407
20,0	0,9478	0,9087	0,8400	0,7540	0,6629	0,5754
30,0	0,9653	0,9466	0,91И	0,8625	0,8051	0,7431
40,0	0,9742	0,9632	0,9419	0,9116	0,8740	0,8312
50,0	0,9795	0,9722	0,9581	0,9376	0,9116	0,88 Н
60,0	0,9830	0,9779	0,9678	0,9531	0,9342	0,9116
80,0	0,9873	0,9844	0,9786	0,9700	0,9588	0,9454
юо.о	0,9899	0,9880	0,9842	0,9786	0,9712	0,9622
137
Таблица 2-3
Таблица 2-4
Значение коэффициентов С„ (п-1, 2, .... 6)	Значение коэффициентов Сп(п=\, 2, ...,6)
для шара при разных значениях Bi	для цилиндра при разных значениях Bi
Bi	Ci	сг	с»	с4	С,	Bi			С.	Сг	с3	с4	сБ	сй
0,01	0,0050	0,0000					К	0,01	0,0050	0,0000				
0,02	0,0100	0,0000						0,02	0,0100	0,0000				
0,04	0,0193	0,0001	0,0000					0,04	0,0198	0,0001	0,0000			
0,06	0,0296	0,0002	0,0001	0,0000				0,06	0,0296	0,0002	0,0001	0,0000		
0,08	0,0394	0,0003	0,0001	0,0000				0,08	0,0392	0,0004	0,0001	0,0001	0,0000	
0,10	0,0490	0,0005	0,0002	0,0001	0,0000			0,10	0,0488	0 0007	0,0002	0,0001	0,0000	
0,15	0,0728	0,0011	0,0004	0,0002	0,0001	0,0001		0,15	0,0722	00015	0,0004 ’	’0,0002	0,0001	0,0001
0,20	0,0960	0,0020	0,0007	о,о()0з	0,0002	0,0001 ‘		0,20	0,0951	0,0026	0,0008	0,0001	0,0002	0,0001
0,30	0,1411	0,0044	0,0015	0,0008	0,0001	0,0003		0,30	0,1390	0 0058	0,0018	. 0,0009	0,0005	0,0003
0,40	0,1842	0,0077	0,0026	0,0013	0,0008	0,0005		0,40	0,1808	0,0102	0,0032	0,0015	0,0009	0,0006
0,50	0,2255	0,0119	0,0041	0,0021	0,0012	0,0008		0,50	0,2202	0,0157	0,0050	0,0024	0,0014	0?0009
0,60	0,2650	0,0170	0,0059	0,0030	• 0,0018	0,0012		0,60	0,2576	0,0222	0,0071	0,0034	0,0020	0,0013
0,70	0.3026	0,0229	0,0080	0,0041	0,0025	0,0016		0,70	0,2930	0,0296	0,0096	0,0046	0,0027	0,0018
0,80	0,3385	0,0296	0,0105	0,0053	0,0082	0,0021		0,80	0,3265	0,0379	0,0124	0,0060	0,0036	0,0023
0,90	0,3727	0,0370	0,0132	0,0067	0,0040	0,0027		0,90	0,3581	0,0469	0,0155	0,0076	0,0045	 0,0030
1,0	0,4053	0,0450	0,0162	0,008.3	0,0050	0,0033		1,0	0,3880	0,0567	0,0192	0,0094	0,0055	0,0036
1,5	0,5457	0,0940	0,0355	0,0183	0,0112	0,0075		1.5	0,5146	0,1136	0,0413	0,0207	0,0123	0,0081
2,0	0,6540	0,1530	0,0609	0,0320	0,0196	0,0132		2,0	0,6099	0,1785	0,0700	00359	0,0216	0,0143
3,0	0,8008	0,2823	0,1258	0,0688	0,0429	0,0292		3,0	0,7377	0,3112	0,1408	0,0760	0,0468	0,0314
4,0	0,8874	0,4063	0,2017	0,1154	0,0735	0,0506		4,0	0,8146	0,4304	0,2205	0,1258	0,0795	0,0512
5,0	0,9396	0,5137	0,2811	0,1684	0,1098	0,0766		5,0	0,8633	0,5295	0,3011	0,1814	0,117#	0,0817
6,0	0,9719	0,6025	0,3585	0,2248	0,1504	0,1064	V	6,0	0,8956	0 6094	0,3776	0,2393	0,1601	0,1129
7,0	0,9923	0,6743	0,4308	0,2820	0,1936	0,1392		7,0	0,9179	0,6732	0,4474	0,2972	0,2046	0,1469
8,0	1,0055	0,7319	0,4903	0,3383	0,2382	0,1740		8,0	0,9339	0,7241	0,5097	0,3532’	0,2500	0,1827
9,0	1,0142	0,7780	0,5547	0,3922	0,2830	0,2102		9,0	0,9457	0,7649	0,5645	0,4061	0,2951	0,2196
ю,о	1,0199	0,8151	0,6062	0,4429	0,3271	0,2469		10,0	0,9546	0,7979	0,6123	0,4544	0,3392	0,2568
15,0	1,0292	0,9197	0,7799	0,6415	0,5211	0,4230		15,0	0,9780	0,8936	0,7724	0,6446	0,5289	0,4320
20,0	1,0285	0,9621	0,8682	0,7682	0,6599	0,5656		20,0	0,9871	0,9354	0,8545	0,7591	0,6618	0,5708
30,0	1,0236 .	0,9924	0,9442	0,8840	0,8168	0,7472		30,0	0,9940	0,9693	0,9277	0,8734	0,8112	0,7454
40,0	1,0195	1,0015	0,9729	0,9355	0,8913 -	0,8426		40,0	0,9966	0,9822	0,9573	0,9236	0,8828	0,8370
50,0	1,0165	1,0048	0,9860	0,9609	0,9803	0,8955		50,0	0,9978	0,9884	0,9720	0,9492	0,9210	0,8883
60,0	1,0142	1,0061	0,9928	0,9749	0,9527	0,9269		60,0	0,9984	0,9919	0,9803	0,9640	0,9434	0,9193
80,0	1,0111	1,0065	0,9990	0,9886	0,9755	0,9600		80,0	0,9991	' 0,9954	0,9887	0,9792	0,9671	0,9526
100,0	1,0091	1,0062	1,0013	0,9946	0,9860	0,9758		100,0	0,9994	0,9970	0,9927	0,9866	0,9786	0,9690
1.38
139
Ядра конечного интегрального преобразования и характеристическое
уравнение для неограниченной пластины
Таблица 2-5
Граничные условия		Ядро Л’(ПЛ. х,‘)	Характеристические уравнения для
при х = 0	при X—-I						
/Л = со	Н, = сп	1 /' 2 • 1/ — sinprtx/Z	sin ц = 0
	Я2=0	т/2  '	1/ sinp^x/Z	созц = 0
н^-о		л 2 у --cosp^x/Z	sin ц — 0
н1=0	я2=о	|/ -|-COS	sin ц=0
	Н2 = const	i/2l	]1/2 У /L+.чАм cos“"	iitgp=W2Z
J7J=const	/У2=ло	F z L^+^z2+//1/J	p.ctg р, = —
H1l = const		2 Г	11/2	jxtgjx = tfiZ
		+//;/=-; hj |	Л/о	
		1/”2	p„cosu„x/Z4-WxZ sinp,„x/Z	. , «(/лг + ад.
Нг= const	Я2 = const		
		|j>n । лг) i,1 1	4j	
• Первый корень ц равеп кулю. //.-«-.граничные условия перво™ рода; ПЕ —0— граничные условна второго рода я ЯЕ - const-rpa.
личные условия третьего рода; Ц =
.где
А т>=v q> <₽«'т)+/1«]. „+[ л (т);
«;(₽„. H = U(₽„. X)Q(*- ^dx<
О
здесь Q(x, т)- источники теплоты.
Решение для оригинала:
Т (х, т)= 2 е““Й^(Р,„ х) {/»(₽„)(Р„, т)л1. <2-7-64)
п-=1	I б	J
Положим fa (т) = /2 (т)— 0; /о(л-) = О. Тогда ядро интегрального преобразо-
вания в соответствии с табл. 2-5 (см. случай — const, n2 = const)
(P»™Pnx + WiSlnP»x)< 2
х,“ ((₽:,+№) [/+//Ж+^)]+^}''2'	‘	’
Решение задачи
Т (х.т) = 2	(₽,.. X) J	т)Л. (2-7-66)
/1=1	о
Предположим, что
Q(*, t)=Q06(x—*)б(т-0),	(2-7-67)
где Qo—мгновенный источник теплоты, расположенный в плоскости х=Ь.
Тогда
Г(х, т) =
=2Q» V (|i»cosH„*/<+Bi1 sin цех,7) cosp^fr/f-[-Bl,sinр„&/2)___
Vl	[(^ + Bi;)l +Bi.2/(n= +Bi|) + BiJ exp(
(2-7-68)
Если ax = 0, to dT (0, T)/ck = 0, Bix = 0, Bia = Bi, тогда из уравнения
(2-7-68) получим;
Т (*, т) = У -----' . -------cos ц„х,'/ cos р.л Ь;1е~~^пРо ,	(2-7-69)
' Ср/	|Дгг ЗШ COS fl,;	' глг
п = 1
так как 1 -J-Bj (ц* Вi2)-1 = р"5 (fi* 4- sin цл cos ия). Остальные случаи с постоян-
ными источниками или при равномерном начальном распределении температуры
решаются аналогичным способом.
В заключение рассмотрим обобщение простейших одномерных задач (пла-
стина, цилиндр и шар) с помощью бесселевых уравнений полуцелого порядка.
Уравнение теплопроводности (2-7-6) для случая H(Fo) = Po(|, Fo)=0 и
при равномерном начальном распределении температуры можно решить методом
преобразования Лапласа:
LV (Fo)l = /z (s)^ 5 / (Fo) ехр (—sFo) dFo.	(2-7-70)
о
Применив это Преобразование (2-7-70) к уравнению (2-7-6), получим;
5)+^±0£й, s)-sBtg, s) = 0,	(2-7-71)
где v = (r—1)/2, т. е. для пластины Г = 0, v==—1/2, для цилиндра Г = 1,
v=0 и шара Г = 2, v— 1/2.
142
Сделаем замену переменных:
е =	(2-7-72)
Тогда из уравнения (2-7-71) получим модифицированное уравнение Бесселя
v-ro порядка:
+^'-(v24-s^2) и=0.	'	(2-7-73)
Его решение имеет вид:
« = Лх/у(Г^)+Л2^(И^).
(2-7-74)
где !у и Kv — соответственно модифицированные функции Бесселя v-ro порядка
первого и второго родо». Для симметричных задач Л2=0, а так как при
*->0 /(v-»-oo, решение для изображения имеет вид:
®д (5, 1)=Л (1-7?) (PTg).	(2-7-75)
Для граничных условий первого рода (температура поверхности тела
постоянна)
e, (l. s) = -^.	(2-7-76)
Решение уравнения (2-7-75) будет иметь вид:
В	Ф(«)
'  E'sZv(Cs) *(')
Воспользуемся теоремой разложения
(2-7-77)
(2-7-78)
где sn — корни характеристического уравнения
/г.(Г«) = 0.	(2-7-79)
Тогда решение будет иметь вид;
i<r^,)op(’i'"Fo)'	(2-7'80)
n " I
где-рп = г V's„, Jy —функция Бесселя первого рода v-ro порядка,
i4v(.x) = Jv(i, X).
Характеристическое уравнение можно написать так:
Jv(p)-:^0.	(2-7-81)
Решение уравнения (2-7-80) является обобщенным решением для пластины,
цилиндра и шэра.
Для пластины у — — 1/2ч	______
Р-7-82)
следовательно, согласно уравнению (2-7-81) созрл = 0; р,л= (2п— 1) Тогда
из уравнения (2-7-80) получим:
^-^='-1 (-1Г14~с“^‘Г"“,'“-	(2-7-83)
гг — 1
143
Для цилиндра v = 0
По) , у 2 4 0^ -K=FO
ес Z' м. Jy ОМ •	(	}
71 — )
Решение для шара (v=!/2) ролучаем, используя соотношения
)
I 2 \2
Л/, (Вл Й =	smii„s;	(2-7-85)
h/f (I1») =	" “s Вл) 	(2-7-86)
\	/	\ P/l	/
Из уравнения (2-7-82) находим- sin рл = 0, р„ = л.*т, следовательно,
Bfe Fo),.) V ( |)Л+. 2 sing„g eyl4l’»>
C	n I	n
Для граничных условий третьего рода
50, (I, s) I 0, Л 1 _
Решение уравнения (2-7-77) имеет вид:
е.= j________________'у(Н^)__________
Решение для оригинала будет:
(2-7-87)
(2-7-88)
(2-7-89)
° (6. Ч = 1 _ У 2Bi^ t.v Л ()i„g)	Fo)
"	(B^ + pj-2vBi) /v41 (ц„) Р
(2-7-90)
где — sn определяются из характеристического уравнения, которое
можно написать так:
М/1-) ==--Tjpw-1 (l/s):	(2-7-91)
Jv W =
Jv+i (Ц) Bi
(2-7-92)
Подставляя соответствующие значения v, получаем решения для плас1ины,
цилиндра и шара ц соответствующие характеристические уравнения,
Для граничных условий второго рода с постоянным тепловым потоком
изображения имеют вид;
50l(I, s)
Ki0c Л
-----==0.
(2-7-93)
Решения для изображения имеют вид:
Bz-(S. s>—
М‘МЧ)
si Кs JV ri (t Ks)
(2-7-94)
144
Для того чтобы выяснить кратность корня ,$ = 0 перепишем решение для
изображения в виде
el(s, q Ki Jv (4-7 6) фи
ес	(s) s2ip (s) ’	(
где
'	co	244-v
у У	-T-
. Ms)- г (* + v + 2) k! \2)
k-Q
Имеем следующие корни: s = 0 (двукратный корень) и бесчисленное множе-
ство корней i yrs„ =Цп, которые определяются из характеристического урав-
нения
д,+1 (ц) = 0.	(2-7-96)
Применяя теорему разложения и используя соотношение
,4% U fS F” |} = Ki [F°  2(V+ ') + Т	(V 2) ' 4 ] •
получаем решение для оригинала:
=Ki [2<v+ ') F° + ^ + tV* (v-2)-|] - .
(2'7’98)
6 ГЛ JV-1 1ГЛ/
n=l
2-8. ТЕМПЕРАТУРНЫЕ ВОЛНЫ
Среди нестационарных температурных полей большой интерес представляют
поля с периодическим изменением температуры тела.
Рассмотрим наиболее простой случай, когда температура поверхности полу-
ограниченного тела изменяется по закону простого гармонического колебания:
в« = 7’,-7’„ = 7'„„соз<»т,	(2-8-1)
где Гп~среднее значение температуры поверхности; Тт„~амплитуда изменения
температуры на поверхности (общий интервал изменения температуры); со—цик-
лическая частота колебания температуры (o>”2nv, v —количество колебаний
в единицу времени).
В начале процесса на температурное поле гела будет оказывать влияние
начальное распределение температуры. Затем спустя определенный промежуток
времени наступает стационарное периодическое состояние, характеризующееся
тем, что температура в любой точке тела совершает гармоническое колебание
с постепенно уменьшающейся-амплитмдой по мере удаления от поверхности тела
(устанавливается периодический поток теплоты стационарного типа).
Решение для полуограниченного тела имеет вид:
В~ Т~ Тп =е 30 \os (шт—1/"~х).	(2-8-2)
> mn	\	'	1
Уменьшение амплитуды с глубиной показано на рис. 2-8, где представлены
кривые изменения температуры с течением времени на равных глубинах, Макси-
мумы и минимумы колебаний не только уменьшаются с глубиной, по по мере
удаления от поверхности появление их наблюдается все позже и позже. На
поверхности тела температура достигает своего среднего значения Тп, когда
145
cos®T = 0, т. e. ври (Tj),. 0—.t/2w“1. Па гтубиио а- температура принимает
значение T, когда cos (гот- J/ х \ =л 0, или в момент времени
(Чл = |»-1+’/^7*.	(2-8-3)
Этот момент наступает позднее, чем на поверхности тела, па промежуток
времени
Ат = т/"-J— х = -11/'х,	(2-8-4)
Г 2ао> 2 г ла ,	'	'
где Р —период колебаний (о) = 2л/Р).
Величина Дт называется временем запаздывания температурной волны,
Для заданной глубины время запаздывания прямо пропорционально корню
квадратному из периода колебания температуры.
Рис, 2-8. Зависимость температуры 9 от времени orc в полуограниченном теле
па различных глубинах х (л/аР)'^'2 при изменении температуры поверхности
по закону гармонического колебания.
Обозначим скорость распространения температурной волны через и, тогда
“ = Д “ V 2«о = 2|/ Д •	(2-8-5)
Длина волны I периодической температуры равна расстоянию, пройденному
волной за одно полное колебание, т. е. за время, равное периоду колебания:
I = иР = л	=2УлаР.	(2-8-6)
Поток теплоты через единицу площади на поверхности тела, ккал/(м*-ч),
= —	o =	j/"-^-sni(wT-C05a)T).	(2-8-7)
146	i
Воспользуемся известным равенством cos (сдт4*гг/4) — (cos art — sin
Тогда для величины мгновенного потока теплоты на поверхности тела получим
выражение:
?л = Тот„КХс(ХйСО5(™т 1-Л/4).	(2-8-8)
Интегрирование этого уравнения дает общий расход теплоты на поверх-
ности тела площадью Л (м2). В этом случае Q;1 будет положительной величиной,
когда cos (©T-J-n/4) > 0, т. е. когда изменяется аргумент косинуса от — л/2, до
_ л/2, что соответствует интервалу от т^Зл/Чго до т2 = л/4со. Учитывая это.
получаем:
т,	_____
а„=А у ?„ rfr = 2Arln„]/	(2-8.9)
Tt
Расход теплоты является положительной величиной для первой поло-
вины никла, в течение остальной половины цикла от поверхности тела отводится
таксе же количество теплоты.
Если температура среды изменяется по закону простого гармонического
колебания, то между поверхностью полуограничешгого тела я средой происходит
теплообмен по закону Ньютона (граничное условие третьего рода), т. о.
- \ аТ Т). + и [Г^е cos шт - Г (0, т)|_0.	(2-8-10)
В этом случае решение имеет вид:
(2-8-11)
где

. , п-1/’ я 2
а У аР ' а2аР !
является максимальной безразмерной амплитудой колебания температуры на
поверхности тела; Ттс — средняя температура среды; Л4 —смещение по фазе
колебания температуры поверхности геля по отношению к колебанию темпера-
туры окружающей среды,
Если число Bi —со (а,1 = сс), то амплитуда колебания относительной тем-
пературы на поверхности равна единице. Сдвиг по фазе между косинусоидами
бс(т) и 5л (т) равен Л4, при этот сдвиг будет равен л/2.
Напишем решение (2-8-11) в обобщенных переменных. Обозначим локальное
число Фурье Fox-ат/х2, локальное число Предводителева Pdx = ojx2/a, число
Фурье (критерий периодичности) Рохр~аР'2т1х'!‘ и обобщенное число Био (Bi*)
B,'=w?	(2-8-|3>
тогда будем иметь:
Т	= h exp [-J/^ Pd« ] X
xcos\^'-|/ATpd^-Ml'	(2'8'14’
147
где
м=агс‘4ттй^)
(2-8-15)
(2-8-16)
Выясним физический'смысл числа Bi*. Мгновенный поток теплоты на
поверхности тела равен;
7(0, т) = — ъС^х-jx о= ~ t-Tln„yr (sin шт-cos шт). (2-8-17)
Воспользуемся соотношением
/	. л \
cos сот - - —
\	4!
= (cos (от — sin (от) (К2) \
тогда получим, что величина мгновенного потока теплоты на поверхности тела
равна:
<7 (°, T)=K>-C',®rm„cos (шт+ = ?mcos(fflT +	(2-8-18)
где qm — максимальный удельный поток теплоты (или амплитуда колебаний
удельного потока теплоты), равный:
Qm = Ттп l^XfpCO.	(2-8-19)
Отношение амплитуды колебаний потока теплоты и температуры равно:
(2-8-20)
 тп
Следовательно, значение	равно максимальному мгновенному потоку
теплоты, подведенному к поверхности тела при амплитуде колебания темпера-
туры на поверхности стенки, равной единице (ЬаТтс=Ттп— \ К).
Таким образом, число Bi* равно отношению стационарного потока
теплоты аДТ при единичном температурном напоре (ДТ=1) к максимальному
потоку теплоты ]• Херы в стационарно-периодическом состоянии при единичной
амплитуде колебания температуры (7mzf = l).
Другими словами, число Bi* является модифицированным числом Био дл^
стационарно-периодического состояния.
Решения для неограниченной пластины, шара и неограниченного цилиндра
можно написать так:
О = -J- pd Fo + N_f‘ Ptl F°) -
-1
n — 1
rt + Pd* ("ЛМ
c„ exP(-4F°).
(2-8-21)
где Pd — число Предводителева, равное:
_ 2луД3 _ (dj?3
(2-8-22)
jVf и ALj —некоторые функции Bi и Pd и t [Л.2-18].
Анализ коэффициентов .V, и N_i показывает, что они удовлетворяют усло-
виям Дирихле, Поэтому их можно разложить в ряд в интервале (—R-s-x^R)
по фундаментальным функциям W (рП, £).
148
После небольших преобразований решение (2-8-21) можно написать так:
6(5, Fo, Pd)== У
„ё++№
XCM(cosPd Fo-arctg-Ы.-ехр (-р;, Fo)l = ?~(S’ F°’ М) . (2-8-23)
I	rn	')	1 me
Таким образом, при достаточно большом времени величина е F° будет
малой, тогда наступит стационарно-периодическое состояние.
Средняя температура будет равна;
2 (Г 4-1) / pi \	/	Pd \
О (Fo, Pd)=2 "-4F2- _LPda ' Сп cos Pd Fo-arctg-U . (2-8-24)
Ни ' P/i г1 u /	\	Pn /
n = [
Следовательно, средняя температура тела будет периодической функцией
времени.
, Удельный расход теплоты за промежуток времени Дт = т2 —тх будет равен:
ЛС,=ф[ё(та)---в(т1)]7’,„с,	(2-8-25)
т. е.
X? 2 (Г 4-1) и’
= Ттсср >	С„	[cos Pd Fo, - cos Pd FoJ. (2-8-26)
Hu	Н<1Т‘У
n — i
Отсюда получим:
Z 2 (Г 4-1)	uj, л	л
1—	_i_pd2 S1'n ~p (T1 —	sin p (’T1 + Тг)' (2‘®‘2^
n = l
Примем 14 = 0 (начало отсчета времени), т3 = -^-Р, т, е, рассмотрим расход
теплоты за полупериод. В этом случае sin (tj4-t2) и sinp-(ra—тг) будут
равны единице.
Введем обозначение
V 14	2 (Г-}-1)
^(в‘’м’=2	<2-8-28>
п — 1
Тогда расход теплоты за полупериод будет равен:
bQv = ‘2ci>TmrK^i, Pd).	(2-«-29)
Величина называется коэффициентом аккумуляции теплоты и являемся
функцией чисел Pd и Bi; при Pd -> 0 (переход периодического изменения
температуры в апериодическое) коэффициент /<^.->1, так как
у 2 (Г+1) с, _t
л=i
Обозначим коэффициент тепловой амплитуды апериодического изменения
средней температуры
а,=ШД£»,	(2-8-зо)
М'Л
149
Таблица 2-6
Значение коэффициента Вп для неограниченной "ластины
в зависимости от числа Bi,
2Bjs
ВПЖ + В'!+Й' "=1.2.3.........6
Bi	В,	Вг	8,	84	Вь	в.
ол	0,8106	0,0901	0,0321	0,0165	0,0100	0,0067
50,0	0,8260	0,0911	0,0323	0,0161	0,0095	0,0061
30,0	0,8355	0,0910	0,0315	0,0152	0,0086	0,0053
15,0	0,8565	0,0885	0,0279	0,0120	0,0060	0,0032
10,0	0,8743	0,0839	0 0236	0,0090	0,0040	0.0020
0.0	0,8796	0,0821	0,0222	0,0081	0,0035	0,0017
8,0	0,8858	0,0797	0,0205	0,0072	0,0030	0,0015
7,0	0,8932	1 0,0766	0,0185	0,0062	0,0025	0,0012
6,0	0,9021	0,0723	0,0162	0,0051	0,0020	0,0009
5,0	0,9131	0,0664	0,0135	0,0040	0,0015	0,0007
4,0	0,9264	0,0582	0,0104	0,0028	0,0010	0,0005
3,0	0,9430	0,0468	0,0070	0,0018	0,0006	0,0003
2,0	0,9635	0,0313	00038	0,0009	0,0003	0,0001
1,5	0,9748	0,0220	0,0023	0,0005	0,0002	0,0001
' 1,0	0,9861	0,0124	0,0011	0,0002	0,0001	
0,9	0,9882	0,0106	0,0009	0,0002	0,0001	
0,8	0,9902	0,0088	0,0007	00002		
0,7	0,9922	0,0070	0,0006	0,0001		
0,6	0,9940	0,0054	0,0004	0,0001		
0,5	0,9956	0,0040	0,0003	0,0001		
0,4	0,9971 ’	0,0027	0,0002			
ОД	0,9983	0,0016	0,0001			
0,2	0,0992	0,0007				
0,1	0,9998	0,0002				
Зависимость числовых значений коэффициента Вп от числа Bi приведена
в табл, 2-6 —2-8. При Pd-*-oo коэффициент /(^ = 0. Для тонкой пластины,
когда Pd->0 и В1 -> 0, коэффициент аккумуляпин теплоты равен единипе.
Следовательно, коэффициент численно равен отношению теплоты, аккумули-
рованной стенкой толщиной 2д, к теплоте, аккумулированной бесконечно
тонкой стенкой (2/? -> 0) из того же материала при тех же условиях периоди-
ческого нагрева. Поэтому коэффициент называют коэффициентом использо-
вания теплоты. Он равен:
S = AM'4,)«-.o-	(2-8-31)
На основании формулы (2-8-9) количество теплоты, аккумулированной
полупространством (стенка бесконечно большой толщины / = 22?->оо)| равно:
W(-a.= 27'm^p)Cil = 2Wp^=.	(2-8-32)
В этом случае коэффициент аккумуляции теплоты Яф= ]/2 V^Pd.
Для полупространства в качестве характеристики аккумуляции теплоты
рассчитывается количество теплоты, поглощаемое единицей площади поверх-
ности стенки за полупериод, т. е.	х
- bQJ. - 2сеТт„ .	(2-8-33)
150
Т а б л и п a 2-7
Значение коэффициента Вп для шара в зависимости от числа Bi,
д	бвр
п ц* (p.®-|-Bi2 —Bi)’
п—-1, 2, 3,
6
Bi	в.	в,	Вз	в4	Bs	В,
	0,6079	0,1520	0,0675	0,0380	0,0243	0,0169
51,0	0,6427	0,1588	0,0693	0,0380	0,0236	0,0158
21,0	0,6886	0,1166	0,0652	0,0324	0,0180	0,0108
10,0 9.0	0,7607	0,1496	0,0485	0,0196	0,0091	0,0047
	0,7737	0,1453	0,0450	0,0175	0,0079	0,0040
8,0	0,7889	0,1396	0,0408	0,0152	0,0067	0,0033
7.0	0,8068	0,1319	0,0360	0 0128	0,0055	0,0027
6,0	0,8281	0,1215	0,0305	00104	0,0044	0,0021
5,0	0,8532	0,1075	0,0245	0,0075	0,0032	0,0015
4,0	0,8830	0,0890	0,0180	0,0055	0,0021	0,0010
з,о	0,9170	0,0655	0,0115	0,0033	' 0,0013	0,0006
2,0	0,9352	0,0520	0.0085	0,0024	0,0009	0,0004
20	0,9534	0,0380	0,0057	0,0016	0,0006	0,0003
1,9	0,9570	0,0352	0,0052	0,0014	0,0005	0,0002
1,8	0,9605	0,0324	0,0047	0,0013	0,0005	0,0002
1,7	0,9640	0,0297	0,0043	0.0011	0,0004	00002
1,6	0,9674	0,0270	0,0088	0,0010	0,0004	0,0002
1,5	0,9707	0,0243	0,0034	0,0009	0,0003	0,0002
1,4	0,9739	0,0217	0,0030	0,0008	одэооз	0,0001
1,3	0,9770	0,0192	0,0026	0,0007	0,0002	0,0001
L2	0,9800	0,0167	0,0022	0,0006	0,0002	0,0001
1,1 1,0	0,9828	0,0144	0,0019	0,0005	0,0002	0,0001
	0,9855	0,0122	0,0016	0,0004	0,0002	0,0001
0,9	0,9880	0,0101	0,0013	0,0003	0,0001	
0,80	0,9904	0,0081	0,0010	0,0003	0,0001	
0,70 0,60 0,50 0,40 0,30 0,20 0,15 0,10 0,09 0,08	0,9925 0,9944 0,9960 0,9974 0,9985 0,9993 0,9996 0,9998 1,0000 1,0000	0,0064 0,0048 0,0034 0,0022 0,0013 0,0006 0,0003 0,0001 0,0001 0,0001	0,0008 0,0006 0,0004 0,0003 0,0001 0,0001	0,0002 0,0002 0,0001 0,0001	0,0001	
Соотношение (2-8-33) имеет следующий физический смысл: &QS равно
количеству теплоты, которое воспринимает слой стенки единицей площади
толщиной (величина ~ имеет размерность милы) при равномерном
его нагревании по всей толщине от —Ттп до Ттп. Следовательно,
характеризует условную толщину равномерного прогревания однородного полу-
ограниченного тела в стапионарко-периодическом состоянии. Обозначим вели-
чину а- "через в. Она является по своему физическому смыслу коэффи-
циентом теплоусвоения однородной стенкой. Коэффициент теплоусвоения в
151 .
примерно в 9 раз меньше длины температурной волны Л (р, = 0,11Л), так как
Л=К8л"|/ J=Jz8«8-	(2-8-34)
Коэффициент теплоусвоения обратно пропорционален и прямо про-
_ порциопален а. Поэтому с увеличением частоты колебаний температуры
коэффициент теплоусвоения уменьшается. При больших частотах теллоусиоеиие
мало. При постоянной частоте (<0 = 00051) коэффициент теплоусвоения зависит
только от коэффициента температуропроводности. Например, при периоде
колебания 24 Гц (co = n/12) коэффициент теплоусвоения пробковых плит (е —
= 0,039 м) примерно в 3,5 раза меньше коэффициента теплоусвоения мрамор-
ных плит (е = 0,137 м).
Таблица 2-8
Значение коэффициента Вп для цилиндра в зависимости от числа Bi.
»=1, 2, 3, ... , 6
Bi	В,	в2	в3	В,	Вл	Я,
со	0,6917	0,1313	0,0534	0,0288	0,0179	0,0122
50,0	0,7183	0,1350	0,0540	0,0284	0,0172	0,0113
30,0	0,7348	0,1359	0,0529	0,0268	0,0155	0,0097
10,0	о.воаэ	0,1260	0,0387	0,0152	0,0070	0.0Q36
9,0	0,8133	0,1229	0,0361	0,0137	0,0061	0,0030
8,0	0,8244	0,1188	0,0331	0,0120	0,0052	0,0006
7,0	0,8375	0,1132	0,0296	00102	0,0043 '	0,0021
6,0	0,8532	0,1056	0,0254	0,0084	0,0034	0,0016
5,0	0,8721	0,0953	0/1207	0,0064	0,0025	0,0012
40	0,8950	0,0813	0,0156	0,0045	0,0017	0,0008
8,0	0,9224	0,0625	0,0102	0,0028	0,0010	0,0004
2,0	0,9536	0,0388	0,0053	0,0013	0,0005	0,0002
1,5	0,9696	0,0259	0,0032	0,0008	0,0003	0,0001
1,0	0,9843	0,0136	0,0015	0,0004	0,0001	
6,90	0,9869	0,0114	0,0012	0,0003	0,0001	
0,80	0,9893	0,0093	0,0010	0,0002	0,0001	
. 0,70 0,60	0,9916 0,9936	0,0074 0,0056	0,0008 0,0006	0,0002 0,0001	0,0001	
0,50 0,40 0,30 0,20 0,15 0,10 0,08	0,9954 0,9970 0,9983 0,9992 0,9995 0,9998 0,9999 ।	0,0040 0,0026 0,0015 0,0007 0,0004 0,0002 0,0001	0,0004 0,0002 0,0001 0,0001	0,0001		
Если передача теплоты через воздушную прослойку происходит посред-
ством теплопроводности, то коэффициент теплоусвоения ее очень большой
(е —0,543, <о = л/12, Т = 293 К).
Коэффициент теплоусвоения определяет интенсивность затуханий темпера-
турных колебаний в толще стены.
Глубина на которой температурные колебания уменьшаются в п раз
по сравнению с колебаниями на поверхности, составляет;
Хл=]^2 е Ш п = ЛДп).	(2-8-35)
Значения функции f(n) приведены в табл. 2-9, из которой видно, что
при п=2 /(п) = 0,И0- Следовательно, при п=2 Хв = 0,110 Л = е, т. е. коэф-
152
фициент а Численно равен глубине слоя Хл, в котором колебания температуры
уменьшились в 2 раза по сравнению с колебаниями температуры на поверх-
ности.
Таблица 2-9
Значение функции затухания f(n) температурных колебаний
л	2	4	10	20	50	100	1000
И")	0,110	0,221	0,367	0,477	0,623	0,733	1,100'
Количество теплоты, аккумулированное единицей поверхности полуограни-
чснной стенки за полупериод при В|* #= О, будет равно:
У ^ = Ы>Тт„	' (2-8.36)
т. е. получаем соотношение, аналогичное (2-8-33), поскольку температура
колебания на поверхности стенки равна Tmffi v Остановимся на температурных
волнах в материалах с памятью. Линейная теория для таких материалов дает
дифференциальное уравнение теплопроводности в виде интегрально-дифферен-
циального уравнения [Л. 2-25]. Рассмотрим плоские бегущие волны:
с (0) Т (г, т) + j а' (В) t (г,	= Х (0) WT (г, т) + X' (В) V!T X
о	о
х(лт —e)de. .	(2-8-37)
Пусть температурное поле описывается соотношением
Т (г, т) — Т$ = A Re ^ехр (—V- л1) ехр —~ г 	(2-8-38)
где г=х— Хо; £ —коэффициент затухания; п1 — единичная нормаль к поверх-
ности; А — амплитуда.
Решение (2-8-38) удовлетворяет уравнению (2-8-37), если внешний источник
теплоты равен нулю и имеет место соотношение [Л. 2-25]
™[c(0)+^-]=(5+g-){X(0)+x;(o)}, '	(2-8.39)
где Ср (со) и X-f (со) — изображения по Фурье величин d (со), ?/(«). Любые
значения w = (со) 0 и £=£(«) 3^0 удовлетворяют соотношению (2-8-39)
в случае, если они соответственно равны:
~	(scc 1 v (“) ~ t (“W <lv (“)~ f (ш)14-sec [vm + <p (ш))};
[C(0)4-Cf (ш)1
(2-8-40)
E= tg [v (ш) — <p (m)] + sec [v (co) + <p (ш)]},	(2-8-41)
где tgv (ш) =;m	+	: tg v (Ю)=^О)+С: (“)l .
Re[?.(0) + XF (m)]	Re[C (0) + Cg(tD)]
Для классической теории С (0) == С (со) «const; X (6) —X, (со) «const. Тогда
из уравнения (2-4-40) получим;
<2-м2>
153
Из формул преобразования по Фурье следует:
lim Ср (о) = С (оо) — С (0); lim hjCf (и) = 0	(2-8-43)
Ш-кО
и
lim Cf (cd) = O;	lim Cf(o)) = —iC'(0).	(2-4-44)
СЙ -» CO	Ш —* CO	'
Аналогичные формулы имеют место и для Х'р (©). Используя формулы
(2-8-43) —(2-8-44) из формул (2-8-39)—(2-8-40), получаем;
при ©->0 ад(©) = адс/; g(w) = ^f/;	(2-8-45)
2: '(“Над1]2’ (2'М6)
где cl обозначает классическое значение этих величин. Следовательно, при
низких частотах (©->0) скорость ад (и) и коэффициент затухания £(©) стре-
мятся к их классическим значениям, для высоких частот (©->сс) скорость
распространения температурных волн и коэффициент затухания положительны
и отличны от их классических значений.
Величина а (0) (а (0) = X (0)/с(0)] может быть больше или меньше класси-
ческого значения коэффициента температуропроводности [а (0)	а], следова-
тельно, и скорости распространения волн ад^адс/.
В работе [Л.2-36] решается дифференциальное уравнение для полупро-
странства (0 < х < со, т > 0)
о
= k(0)W(x, t) + J й'(В)Т2Г(х, T-SJdS,
о
где k' (т) и р' (т) — соответственно функции релаксации теплового потока и
внутренней энергии.
Краевые условия имеют вид:
Т (0,т) = / (т) Н (т); Г (х, 0) = Г (х, 0) = 0,	(2-8 47)
где Н (т) —единичная функция Хевисайда.
Общее решение имеет вид:
T = j К ! (fl) /;(т—е, ?) Job sin xg 4.	(2-8-48)
о	J
Предположим, что	'
^(т) = Л-}-*1т^, В(х) = В-гВ^''-	vjsl. (2-8-49)
Тогда для достаточно малых значений времени будем иметь [Л.2-36]:
Т(х, t) ~ Н (г-х>) f (г-х/И)	|;2ехр [-	, (2-8-50)
где А«х©лад —скорость распространения теплоты,
ад = |/'^(6)/С.	(2-8-51)
154 .
Для больших значений времени k (т) k (t)v; р (т) Biv (О> v >— 1)
получим:	______
'	(2-8-32)
где символ © обозначает свертку функции.
Предположим, что
К (Т) = ке-оп и р (т) = Ве~а*.	(2-8-53)
Тогда для больших т получим:
т (х'т) ~ ехр V-
Если /(т) = 70 = const, тогда из уравнения (2-8-54) будем иметь:
Т (х, т) яв То erf с .	(2-8-55)
Для случая / (т) = То = const и о) = о получено точное решение [Л.2-38]:
7 (I’ Т)	i е"ае	(т-m),	(2-8-56)
'«	[	J	(в — m3)1'-	)
где rrt=x/w; 2C6=S —Со.
Критерием применимости дифференциального уравнения теплопроводности
с учетом конечной скорости распространения теплоты является число Верона,
равное:
Ve —(2-8-57)
wl ’	'	'
где / — характерный размер тела.
Для металлических оболочек (/== 1 мм) число Верона имеет порядок
Ю-4-ь Ю-6 (10-* < Ve < Ю-5).
2-9. ГРАНИЧНЫЕ УСЛОВИЯ ЧЕТВЕРТОГО РОДА
Граничные условия четвертого рода отображают нагревание или охлажде-
ние системы тел, находящихся в соприкосновении (идеальный тепловой кон-
такт), Кроме того, строгая формулировка задач конвективного теплообмена
тела сводится к решению сопряженной задачи с граничными условиями чет-
вертого рода.
Рассмотрим несколько характерных задач:
а) Система двух полуограниченных цилиндрических тел, находящихся
в соприкосновении.
Имеем:
ЗГ|(Х, Т) _ oVi(x, т) Ч
дт:	‘ дх’* '
т > 0, / = 1, 2, при i=l х>0, при i — 2 х<0.	(2-9-1)
Краевые условия следующие:
Л (х, 0) = Г„,; Га(х, 0) = Тга;
Л(+0, т)-Л(-0, т);
дГ1 (0, т) = _ 1; дТа (0, г) .
дх	X, дх 1
ЭТ,(+ со, т) _ dra(-co, 1) _
дх	дх
(2-9-2)
(2-9-3)
(2-9-4)
(2-9-5,
155
Решение имеет вид:
Q = 1	/14- I
7" 01 — Т 02	’1-+*Ле; Кв
Qa = Га <х’ т)~~Т™ =__erfc
T’oi — Т’ог 1 + Кв
где Кв~критерий, характеризующий тепловую активность первого е} гела по
отношению ко второму е2,
2 fliT У
(2-9-6)
(2-9-7)
(2-9-8)
(2-9-9)
(2-9-10)
К = — — 1/ 1 mi =
6 V
Из анализа решений следует, что при т->со (в стационарном состоянии)
относительная температура обоих стержней будет одинакова и равна:
в(*'
Если тепловые активности стержней одинаковы (7Се=1), то относительная
температура в стационарном состоянии будет равна 0 = -^,
На границе соприкосновения эта температура устанавливается сразу после
соприкосновения тел и остается постоянной на протяжении всего процесса
теплообмена, так как
б<0, т) = 0(х, со) = т-р^- = const-
I ~г Кг
Если тепловая активность одного тела значительно больше другого (вх еа),
то Ks > 1- В этом случае б (0. т) будет максимальна и равна 0 (б, т)= 1. Если
же относительная тепловая активность тела мала (/(е->0), то б (0, т)=0. Сле-
довательно, значение 0 (0, т) изменяется от нуля (минимальная тепловая
активность тела) до единицы (максимальная тепловая активность).
Таким образом, величина 0 (0, т) характеризует понижение относительной
температуры тюлуограниченного тела при его соприкосновении с другим полу-
ограниченным телом. Поэтому величина
1-0 (0, т) =
(2-9-11)
может быть названа холодящим эффектом. Если 0(0, т) = 1 (Х^=0), то холо-
дящий эффект равен нулю; наоборот, если 0(0, т) = 0 (Х= I), то холодящий
эффект максимален.
Если на границе соприкосновения действует источник теплоты мощностью
то решения будут иметь вид:
81 =	~ Г ierfc —7=;
1 +Кв	2 К Foj
е2=-г^Й- /Foa ierfc- 1
1 + ке	2 V Fo2
где введены следующие обозначения:
Fo1 = a1T/x2; Foa = ayv/x8; Kli = go*/Wo;
(2-9-12)
(2-9-13)
Kis = <?o*/Vo; ierfczехр (— г8)— г erfcг.
б) Ограниченный стержень длиной R приведен в .соприкосновение с полу-
ограниченяым, имеющим другие теплофизические характеристики Боковые
поверхности стержней имеют тепловую изоляцию,
156
Краевые условия следующие:
Л (х, 0) = То; Т2(х, 0)=0: A (R, т) = Т3 (/?, т);
Xi т) = дТв(7?, т), т ,0 тх = г =const; Т3(оо, т) = 0.	(2-9-14)
\2 дх	дх ’	4	'	’
Решения имеют вид:
е1=11£^=ег1с
' С ~ 1 0
Л У Л»« erfc
2/Я1г
Л»-1 erfc
2/<hT
(2-9-15)
_ Тг (х, г) _ 2Ке У A„-1(!rfcp-R + <?n- 1) К„ ,)2R
2 Тс-Та 1+Кв Li
2 I/ ййт
а+кет-п)
__________________erfc X~!L +
(Тс —To) (1-h Ke)_2 ) o2r
'x-R + 2nK~,,2R
2 ^a2x
(2-9-16)
где — К8)/(1 + Ке): iCT—г'1'-',: Ка =Кйа/а1*
Здесь введено условное обозначение ±Ф(+г) = -Ф(-г) 4-Ф (4- г).
в) Имеются две неограниченные пластины R-, и R2, находящиеся в сопри-
косновении. Начальная температура их одинакова. Одна из свободных поверх-
ностей поддерживается при температуре Тс', другая —при То.
Решение этой задачи приведено в монографии автора [2-18]. Если тепло-
обмен между поверхностью пластины (х = — R,) происходит по закону Ньютона
qs = ct [Тс — Т (— R, т)], то температура на границе соприкосновения пластин
(х—0) и на поверхности (Xi = —7?i) определится из графиков рис. 2-9, 2-10.
Графики получены для случая, когда Х2->со и для разных значений р,:
.. п + (^ + Р
р - Bi,
(2-9-17)
где
„ = ^Рф, = Fo,—
ciPiPi	Ъ ’ Rl
по оси ординат (рис. 2-9) отложена величина
7с-7о
(2-9-18)
а на рис, 2-10— величина
[T(-R, т)-Т0|
(Тс-Т„)
(2-9-19)

г) Дана неограниченная пластина толщиной 2R при температуре То. В на-
чальный момент времени она помещается в среду с температурой Tc<zT0.
Охлаждение происходит путем теплопроводности Начальные условия:
7’1 (х, 0) = 7'fl; Та (х, 0) = Т&.	(2-9-20)
157
Рис. 2-9. Зависимость между обобщенной переменной 0 * и числом Fox на границе соприкосновения пластин (х = 0) для разных
значений p (n —	Bix = a^t//Xx; л2 —► °о).
Рис. 2-10. Зависимость между обобщенной переменной 0п и числом Fox для поверхности пластины (х— —при разных зна-
чениях р в случае двухслойной пластины (и — c2y2P?/ci	— aPj/Xf, оо).
Если начало координат поместить в середине пластины, го граничные
условия можно написать так:
T1(±R. t)-T.(±R, Т); 0Т1^ 4=0; —- =°-	(2-9-22)
Решения имеют вид:
Л(*, ^~тс)
Т„-Тс
‘ 1+К8
Т2(х, т)—Тс
Т9-Тс
= *» erfe-^_
14-Ке 2У а2х
I 2 У ait	2 V aiT J
(2-9-23)
-^1
x-R+^R l/j-
________Г 01
2 Уа2т
(2-9-24)
Предположим, что Кг-»-0 (тепловая активность пластины бесконечно мала
по сравнению с тепловой активностью среды); это означает мгновенное вос-
приятие теплоты от нагретой пластины, сопровождающееся быстрым понижением
температуры поверхности пластины до температуры среды. Действительно, если
положить Ке.~О (ft=l), то	а первое решение превратится
в следующее;
81=1- 2
п = 1
ет!с(221-1)Л^ + ег(е<2"-1>Л+И (2-9-25)
2 V ахт	2 у aLi J'
Уравнение (2-9-25) представляет собой решение задачи охлаждения неогра-
ниченной пластины, когда температура на поверхности се мгновенно понижа-
ется до температуры среды, а затем остается постоянной на протяжении всего
процесса охлаждения (граничное условие первого рода).
Температура па границе соприкосновения равна:
#е 2#g
1+Ке 0 + *е)2
2 <-л>
п ~1 erfc
V Q1T *
(2-9-26)
Таким образом, 6 (Я, т) непрерывно уменьшается, ее максимальное значе-
,	л ±	п&
ние соответствует начальному моменту - времени (при т-»-и функция —
V
стремится к нулю), тогда
' 1+Кг
(2-9-27)
— та относительная температура, которая становится на границе соприкосно-
вения двух полуограничеппых тел. Величина
1-t4V=1-8(R, 0)=Х	(2-9-28)
i -f-лг
называется холодящим эффектом. Интенсивность изменения б5,0 зависит от
коэффициента температуропроводности и толщины пластины. При малых
значениях Fox= величина 0а11 мало изменяется.
160
Анализ решения (2-9-23), (2-9-24) показывает, что температура в любой
тачке среды вначале увеличивается, достигает максимума, а потом уменьша-
ется. Максимум температуры на границе соприкосновения x = R устанавлива-
ется мгновенно, а по мере увеличения x(x>R) время, необходимое для
установления максимума, увеличивается.
При малых значениях Foa— можно из всего ряда в решении (2-9-24)
ограничиться одним первым членом, н тогда можно написать приближенное
равенство:
K£_erfc _R_!__________erfc * + K“ .	(2.9.29)
+*. ’ 2/F57 (1+K,)a 2ГР5 •	(
Если взять производную и приравнять ее нулю, то получим урав-
нение, из которого можно определить (Foa)OT — число Фурье, соответствующее
максимальному значению температуры;
(FoJm ------
К„1п
(2-9-30)
Из соотношения (2-9-30) видно, что относительное время достижения
максимума увеличивается с увеличением относительной координаты: (FOj)ffl =
= 0 для x = R.
д) Задачи на охлаждение сферы и неограниченного цилиндра в неогра-
ниченной среде приведены в монографии автора [Л. 2-18].
2-10. ДВУХ- И ТРЕХМЕРНЫЕ ЗАДАЧИ
Решение задач в декартовой системе координат
Большинство задач нестационарной теплопроводности можно решить мето-
дом конечных интегральных преобрааований. Иллюстрируем это примером
на двумерной задаче.
Имеем:
, д*Т <?(ж, у, т) 1 дТ
+ ду* + Ji в а 5т ;
— Х,^ + а1Г=/1(»1. Т) при Х = 0; |
?5+“‘Г=^(У1’ П₽И Х=>1’ )
дТ	>,
~ ^8	(^. т) при у=0,
т) при у = /а;
Г-ф-(х, у) при т^О; Т~Т(х, у, т).
(2-10-1)
(2-10-2)
(2-10-3)
(2-10-4)
161
6 Лыков A. S.
Воспользуемся интегральным преобразованием
Л Ф». Ут. т) = Й К ф„, х) к (Ут. У) Т (х, у, т) dx dy. (2-10-5)
о а
Тогда дифференциальное уравнение примет вид:
-1№"'тТ"'Т-)-+а (й+?у Л (£„, ут, т) = Л (р„. Тт, г), (2-10-6)
где
А (0л, Тт, т) = у j j К (Рл, *) К (?«. У) Q (*> У> т) dx dy+
о о
+ (К *)]*=о V К (уЩ’ у) fi (у> т) dy-J- (К (Рл, x)]x=l Г X
М	J	л2	1 j
О	О
Z,
X К (?т> У) fi(y< dy -J- 7— [К (Ут, У)! у = о f К (Р«« *) /з (•*> т) dX-[~
Л3	J
' Л
+ £-K(Vm,	j КФ«, x)f,(x, T)dx, (2-10-7)
Решение уравнения (2-Ю-6) переводится в оригинал по формуле обращения
Т(х, у, т)= 2 3 к®„, х)ЩУт. У)Т,((,п.	т);	(2-Ю-8)
п= I т^= (
Т(х, у, т)=3 3 ехр[-а(И+тУт]К#«. *) К (Vm. У) <ф, Ут) +
Iт=J
+ $ехр[а(^+тут]Л	т) Л4 (2-I0-9)
о	I ’
где
Тт) = ГЛ#»> V"' т)]г-о=П VKtim. у) <F (х. y)dxdy.
б о
(2-10-10)
Из решений для граничного условия третьего рода можно получит!,
решения для граничного условия первого рода, для чего надо величину
^k
1 dK
заменить на —при Х^ = 0 (k=l, 2, 3, 4; i=l, 2; хг=х; х2 = у).
Интегральное преобразование (2-10-5) с формулой обращения можно при-
менить для полуограниченных и неограниченных тел [Л. 2-211. Соответствую-
щие формулы преобразования и обращения приведены в табл. 2-10, 2-11.
При решении стационарных задач можно использовать принцип супер-
позиции температурных полей, например при решении уравнения Лапласа
при граничных условиях третьего рода
0;	= на границе Sj.
(2-10-11)
162
системе- координат [Л.2-21]
	4	"t?	•5^
			
		t £ к	Цг *
		4 % «	
i4l			•	л к • п —
S я 2	-ОЧИ * + * —	е в	‘“Ч и U (У a + "U +	2Г к -S? + S
S	II	«в _ -_- са	S. II
	+	-J	।	+ К	4-
		II	
	1	-J	7
	X	X	
			
			
X		st n '	X -ч
V g	К (₽ »)Т	.	J£ к	₽> «) ”] d₽
я	8MJ £?	8JXJII -	!se "S 8«-оо	.
2 & е	- к 8{ХЦ х	8IXU 3 .	8«-оо — II *
	II	врф *	s> х
		Г х	
		•8	
R		х $	а
Ж ж S	X 'н'	я- 4	"S
	« -Й	«г ~	к
<о 1	к ь- Е	5'тк 0 К (еА	
			
2			- - g
О	II х	II J	
е		ь7	8^о
		X	11_
		м	е«	«9	8 8
	V/ V/	\fl VI V/	V V/
5 о	V V/	Н	5h	*» V/	VI	VI	н &> V/ v?
		ООО	О о
6«
163
Продолжение табл. 2-10
Область	Формула преобразования	Формула обращения	Преобразование V’T
ООО /А	Л	/Л n	«:	н /А	/А	/Л 8	8	8	7',=?f f Ж(р, х)Х ООО X К (у, у) К (8. г) dx dy dz	T=I Ик<р’1)К у,х ХК (в, г) Т| dp dy ds	-(P!+V’+=S)7'I + + 2 z=i ft) L=K®, x)K(T, SO K(e. г)
8 8 8 V V V Н	N V V V 8 8 8 1 1 1	л=5+5 $ехр[/(а*+ -rW-rK)l Tdxdydz	1 C+f°C 7'=WJ J 4-yy+ ez)l T] dp dy de	_(р+т2+8!)Г|
О о Л Л и «: Л Л 8 ~	Т,= Н'тК(₽, х)х § 0 ХК (Ут, y}dxdy	T= SjK®- *)x XK(Vm. y)T,df	-(₽’+^)Л+2 $4, L=-K (₽. x) К (ym. у)
— оо^х^ со	rI = +J J г‘^К(у, у)х X T dx dy	Г=тИ J 0 —co X Tj dpdy	-^г+Г)Т1+ § L=^ К (у, у)
Продолжение табл. 2-Ю
Область	Формула преобразования	Формула обращения	Преобразование р’Т
ООО /Л	(А	/А N	h /А	/А	/Л 8	?1“Т J1гк<₽’ <*х X К (ут, у) К (»». г) dx dy dz	оо	со со 7=SJ S jK®- Х>Х X'ffV»-. У)К^„,	-(р'+-й+<=гН1+ ft) L = K№, x)K(Ym, у)К(ч,, г)
8 8 . i? 1 * W V V	СО 00 It Ti=j'	J K(e*. z) X X exp (ipx 4- iyy) Tdxdydz	СО	СО	СО f=w21 j/(“’')x X ехр [— 1 (fx+те)] т, df,dy	-(S’+№+4)Tl + + 2 L = K(ei,, г) ехр [i фх +
Osgx co O^zyco 0^z^la П p имена _ лемме нормали к ш Ch сл 		Г1=НИа x,K(v’y,x’ XK(8t, z^Tdxdydz и e. Ядро К берется из табл. 2-5, для зверхностн S -.	т= S,	Х)К^’ 0* хК(ги, г) Т( dpdy раквчных условий первого рода заменить	-^+У‘+Ч)Т,+ + 2 И /— 1 (Sy) L=K(p, х)К(у, y)K(E*. г) Kf	i <i*j -s- иа величину —- -т— , где в. — наврав* Ay	Cty ап.	/
Таблица 2-11
Ядра интегрального преобразования для полупространственной задачи
(О х < со)
Граничные условия лрн х = 0	Ядро К Ф, х)
Третьего рода ,,	а1	L Н!—— — const Второго рода //1 = 0 (oi = 0) Первого рода Н1=оо (^==0)	/ 2 у/г Р COS px-j- Нх sin fix \л/	Кра + ^ / 2	д — ; COS fix (ATsinpj:
Примечание. Формула преобразования; ?'[(₽)— К (f>, х} Т (х) dx; формула
обращения; Т (х) = К ф, х) Т[ ф) d|3; граничные условия: —Х)-~4-а1Т=0
6	*
Таблица 2-12
Ядра К (!-’ч, r/R) интегрального преобразования Ханкеля для конечной
области (0 =£~ г /?) в цилиндрической системе координат
Граничные усло- вия Лрн г — R	Ядро Kv (ця, r/R)	Характеристические уравнения
Первого рода		
и “ П =®у= <2°		A(l*)-o
(Х=0) Второго рода		
Н = 0 (а = 0)	j/T г, jy-1'1" J* imfi) R L «J 7vW	
Третьего рода		
// =const	«Lk) Л kj x	pl'v<.V-)+HRJv(ii.) = 0
	v / v /.w	
Примечание, р.п = ^: Ц = Н
166
Решение можно представить как сумму решений вспомогательных задач
Т = 2 Tk>	(2-10-12)
fc=i
где т*—решения вспомогательных задач:
V2J,‘=0’ ^ж-+“А=ад>	<2-1о-1з>
/=1, 2, k\ £=1, 2, k\ bjh—дельта-функция.
Рис. 2-11. Суперпозиция температурных двумерных полей.
На рис. 2-11 дана иллюстрация принципа суперпозиции двумерного темпе-
ратурного поля для граничных условий первого рода.
Решение задач в цилиндрической системе координат
Конечные интегральные преобразования для цилиндрических тел обычно
называют преобразованием Ханкеля.
Формулы обращения имеют вид:
2 Kv(₽„, У)Г,(Щ);	(2-10-14)
п = 1
f,(P„)=^Kv(P„, r)F<r)dr,	(2-10-15)
Rt
где Kv(Pn* г) —нормализованная собственная функция,
Xv(P„, =	(2-10-16)
где Uv (Ря, г) является собственной функцией уравнения
^(г + Я1<г<г?2’ (2’1(М7>
с однородными граничными условиями
— М + cqi/= 0 при г = Я15	(2-10-18)
Аа-^-+«аС/=О при г = Яа.	(2-10-19)
Уравнение (2-10-17) является уравнением Бесселя v-ro порядка, пред-
ставляющее собой частный случай системы Штурма—Лиувиллй; собственные
функции Uv (рд, /) ортогональны в интервале [	| г R2 с весом функции
г (х) —rt т- е.
(/<МРл-	r) dr—0 при m Ф п. (2-10-20)
167
Таблица 2-13
Ядра интегрального преобразования Ханкеля для голого цилиндра [Л.2-21]
(RiS=r==R,)RHl*», r/R,) = p=W,(l*., r/R,), 4=R^R„
Граничные условия		Ут (Мд, </Я,) Н JV	Me	харамтерястжчееквго уравнения)
при г = J?j	при г = Я,		
Третьего рода 4 е® const; dj я= const	Третьего рода 4= const; сц= const	t4(Fn. >7Я1) = 	Jv (Нв r/^i) Ri		 	Yi^r/R^Rt	-fA,/; о»)+«лли_ их,;; (pij+a,/?,/,»!*) — tAJ' (р) + a1R1>'v (Н) hv;	w
Третьего рода 4 = const; СЦ = const*,	Второго рода сц=0; *,= 1; ^(и.. ч-«	,,ад -АО1/'**)** /') ,лм ^.у;м  ‘>-	—J'r <rt +	(f) y;w
Продолжение табл. 2-13
Граннч при г = Л,	ные условия при г = я.	v- (•*», '«1) " «	Ла (корни характеристического уравнения!
-Третьего рода 4 ex const; ,at=const	Первого рода а,= 1; Х,=0; У>(Н». к) = »	Vv(F..	ГУ": + (1-^(|X., »	— И»./; w +	(ц) _ Jv Oik) r; (I**)
Второго
рода
04=0;
4=1;
1)=о
Третьего рода
ctj= const;
4=const
у» 0*л, r/Ri) =
A ly-,slRi)Ri
W,M+WrM
rT0*»r/Ri)R* .
/;w
_______ytw	.
(jxA> + ctjRjKv (|*4)
Продолжение табл. 2-13
Граничные условия		"v ((*„, '«l) “ "	ця (корни характеристического уравнения)
при г = Ri	при г = К,		
Второго рода «1=0; 1)=0	Второго рода а2=0; Ч=й и у (р, t)=o	И i'll ,/D \ —	#1	V (Pnr/#1) ,	1 j ; w г; <н> j; и) y; _
Второго рода «1=0; М=1; i)=o	Первого рода а2= 1; Х2 = 0; Uv (ц, А)=0	и <„ -- '«Mil)	Y^wlR,) . Uy^n.rR.) Jv(M)	Kv(M) . D2	02 /	v2 \ (p„, ft) -	^1 - j Ul (ц„, 1)	Jy (P) Yy (Ю jу (i**) г; и)
Продолжение табл. 2-13
Граничные условия		'/«о и Л /	(корни характеристического уравнения)
tipa r — Ri	при r= Rt		
Первого рода «1=1; М=о; U,(p. 1) = 0	Третьего рода a2 = const; Х2 = Const	и Л. Г1(п	hMKdKi	 v ,ц” ,К1>	М +«A'v (0„4	Ми)
		(м+алмм) ’ /?? 1)	|лХз;^ Ойц-а^д, (М) 	Щк>	=о л/; (1*Ч1-''.,л15/г И)
Первого рода at= 1; Xi=O; t/v(p, |)=Q	Второго рода а2= 0; b2=h ч=о	„ ,	Jy(lvlRi)Ri Yv(iw/R1)R1. Uy(^, r/R.) ^Jy^	ц„Л,(М)  N “-ф- —яяc%’	u"(|Л”!)	AW Гу(р) }’у И) У у W
Первого рода «1=1; 2и = 0; у„(р. 1)=0	Первого рода а2 = 1; ^2=0; (Jv (fl,	1,1,. -,n '	rv 1.^'IRJ . Uy^n, UR,)- Л (ряА)	Kv(Mi) , U’y-^,	1)	Мр) А,(и) д Jv(|i*) Гу(ц)г)
Таблица 2-14
Интегральные преобразования Ханкеля для двумерных задач теплопроводности в цилиндрической системе координат |Л.2-21|
Область	Формула преобразования	Формула обращения	Изображение v*T
Сплошной цилиндр O^r^Ri	Rs Г/- J гК0(ря, r)Tdr 0	T= n— 1	хГ'Ч-лЛ
0^г<со	Ty=fr/«(₽r)T<i' b	т=рЛ,(МГ;«Ц	-рт,
o=sr=sfla; 0^0^ 2л	Rt 2л T,= ^ JrKV(fl”r) x X cosv (fl—0‘) Td6' dr	r=^2	(?,.') л V=Dn=1	-W+ *2 [—(^,Г)1,л. «
r^Rs; O^z^l	R, I Ti= J JrK.».. 'lx , X К (Ут, z) Tdz dr	r=2 2 *o(P„. ')К(у„. г)Т, m=l n= 1	-ВД7, + tf2 [*"№• ')]r=R. f2, (Тж)+ + [*VL'«W + + [^гЧ-.Л'<р»)
O^r^R*; 0s£ raS co	Ri co r,= J J ZK«(P», г) x 0 0 X К (у. z) Tdz dr	г=Г 2 Mb.' /)«(?. ^T,dy b Я— 1	-x;r,+ r2 №;> ] B f,i m+ L л» _И = К»
	Rt °° t,= j j гк,да..ох b —co X e*v*Tdz dr	T=S $ У Ka	e^T.dy —co n = l	-Х.Г/+Й2[«^).]г_яу„(т)

Продолжение табл. 2-14
Область	Формула преобразования	Формула обращения	Изображение
0	г < со; 0	fl 2л	со 2л Т,= f J л/уфх) X 0 0 X 7 cos v (6 — 6‘) dtf dr	«3 co v=0 6	-₽!r,
о о л/л /А Л ~8	Tt^\rJ,»r)x 0 0 XK(Ym. z) Tdz dr	T= S (fWo (₽<)* (Tm. m= 1 0	-ВД+[-^^Ц0Ь7«» + + [K(^)]2=/4/(₽)
0 < Г < со; 0^2<СО	co co T,=J J r-MMx X К (у, z) Tdz dr	Т = И0А)(МК(1Г. г) T,dyd» 0 0	w'+[/C(r,U'’'(W
О^гссо; —со<г<оэ	t/=T T г/офг)^Х б Лз X Tdz dr	Г = ^Д J 0 —co	—№Tt
Полый цилиндр R^r^R2	Rt Ty = ^ гКофд. r)Tdr	T=2	r'!T‘ n=)	-₽-r, + «1 [^^]Г_Я Л,+ «2Х
R^r^R^, Os^fl s^2n	Rt 2л Ti= f zKv(0n, г) X Ai о X cos v (0 — 0’) Td0r dr	r4~2 2м₽- ')т< 1	V= 0 n - l	-K^+ R>	А/ M +
продолжение табл. 2-14
Для сплошного цилиндра О-^r^R надо положить: ^ = ^ = 0; R2 = R-,
Я]==0. В этом случае
. смв., г) = ЛЛМ.	(2-10-21)
Из граничного условия (2-10-19) получим характеристическое уравнение:
X!p/v(p/?) + «g/v(p/?> = 0.	(2-10-22)
Норма W равна:
л== J	(М)+;‘-	=
= (2-10-23>
где
[в равенстве (2-10-23) было использовано характеристическое
Ха
уравнение (2-10-22)].
Тогда ядро интегрального преобразования равно:
Kvtfn, г) =
/2 Г	1/2 Л-(М _
R [ [Зл \ |W?/J JvtynR)
(2-10-24)
1Щ,
Vn
Л
Ядра интегрального преобразования для сплошного цилиндра приведены
в табл. 2-12.
Аналогичным путем находятся решения для полого цилиндра.
В табл. 2-13 приведены собственные функции Uv (|3n, г), нормы N и харак-
теристические уравнения для полого цилиндра. Если температура цилиндра
зависит от двух координат Т [г, г) или Т (г, в), то для таких двумерных задач
формула преобразования содержит функции от двух переменных (табл. 2-14).
Техника решения остается прежней. Однако если коэффициент теплообмена
является функцией времени, то задача не может быть решена методом конеч-
ного интегрального преобразования, она решается с использованием метода
тепловых потенциалов [Л.2-35].
Решение задач в сферической системе координат
Дифференциальное уравнение теплопроводности в сферических координа-
тах можно написать так:
д*Т , 2	дТ 1 д Г ,	2> £7] ,	1	дЧ 1 дТ	,9]п0,.
+	!‘)“a7J+	г’(1-ц»)	<иг	“a’W	* 0 5)
где [_1 = со8Ф.
Уравнение (2-10-25) можно решить методом разделения переменных:
7 (Л М- А. т) = $(т)Щг)М(ц)©(6).
. Тогда уравнение (2-10-25) распадается на следующие четыре уравнения:
ла	/ЛА
4-	-^-+^© = 0;	(2-10-26)
(2-10-27)
ф I1 -^Н"	- Т^г]м = 0'	<2-,0-28>
175
Решением уравнений (2-10-26) —(2-10-28) будет:
бein /п9; cos/nD;	(2-10-29)
и ~ (М~ Т /„ + ,д (Рг); (₽г)-	+ |/2 (рг);	(2-10-30)
(2-10-31)
где Р” (ц) и	(ц) — соответственно функция Лежандра степени п, порядка т —
первого рода и степени п, порядка т — второго рода.
Если ввести новую переменную lF = (pr)"~ ]'2U, то уравнение (2-10-27)
примет вид,-	5
«PIT 1 dlT Г 1 /	1 \8i
*Г' + 7ТГ+[?’-7,('- + у)]^=0-	(2-10-32)
Уравнение (2-10-32) является уравнением Бесселя 4--^-j-ro порядка.
Решением этого уравнения являются функции Бесселя.
Очевидно, решение уравнения (2-10-32) будет связано со сферическими
функциями Бесселя первого и второго рода (д = 0, 1, 2, 3):
/л(х)3|/Г" 2Х Jn -j- 1/2 (х); Ул(х)—j/” 2х^я+'/2^'	(2-10-33)
В частности, можно отметить, что при rt = O,l
. . . sinx . х cosх . , v	sinx—хсовх
/0(х)« —; y0(x) =----------—; Л(х)=---------------------
. .	COSX —X Sin X
J6 W =----------------.
(2-10-34)
Значение р, изменяется от —1 доц. 1, так хак угол Ф изменяется от 0 до л.
При разложении функции F (ц) по функциям Р” (ц) в интервале — 1 <ц < 1
формулы преобразования имеют вид:
У К" (ц) F, (л, т):
п = 0
4-1
F, (д, m)= J /С”(|1)Р (U)dji>
(2-10-35)
(2-10-36)
где

(2-10-37)
Так как функции Лежандра Р™ (ц) ортогональны в интервале (— 1 < ц < I)
с весовой функцией, равной единице, то
4-1	|	0	при п Ф h\
$	2	(л^/л)!	пил .	(2-10-36)
I 7S+T7 (л-лг)1	пр»"-*-
В табл. 2-15 приведены формулы преобразования и обращения для пере-
менной ц для разных интервалов.
176
Интегральное преобразование Лежандра и соответствующие формулы обращения
для различных интервалов изменения переменной р
Ядро преобразования	а.' 1+ см II 3 к'	й ft. li %. JI е « ас-	К!я(|1)“К4п+1 1	Бе s4 1 + +L Ге гс-
Формула обращений	з е * epq» «'	4~ £ ьГ 3 й кГ 8 >17 II "		i	S =2	1 
Интегральное преобразование	I -^т 1)	’ipj, W)т+"'>/ ?=(।+«г) '1	Г;(2„)=]^Я(М)Т^ 0	V “^7 11 s' е
' Интервал взмеяенмя и	V/ л. V/ 7	V/ V/ <э	1 о	V/ 'V/ 7
177
Таблица 2-IG
Примечание. В настоящей таблице ядра преобразований следующие:
178
I
Дифференциальный оператор от переменной ц
входящий в уравнение (2-10-28) превращается в дифференциальное уравнение
Лежандра
^[(1“ц2)]^+',('!+1)к"=0’	(2-10-39)
где (и) — нормализованная функция Лежандра.
Это' уравнение решается при помощи интегрального преобразования
Лежандра
т=^кпыт,.	(2-10-40)
4=0
Вид ядра преобразования Кп (ц) определяем интервалом изменения ц
(см. табл. 2-15).
Если же оператор D имеет вид:
+	-1 <н<1, 0<»<2«.	(2.1041)
то для решения применяются формулы
2л
Т, (Р, т, 0) = j cosm(0' —0) Т(ц, О') £20';	(2-10-42)
Г(ц, 0) = ^	Т1<^,	«).	(2-10-43)
41—0
где m = 0, 1, 2, 3 ...
Формула преобразования, а также интегральное преобразование V2/1 при-
ведены в табч. 2-16. Используя табл. 2-15 и 2-16, можно решать конкретные
задачи.
В данной главе мы не рассматриваем задач с граничными условиями чет-
вертого рода. Решение задач па систему соприкасающихся тел, находящихся
в тепловом контакте, можно решать методом конечных интегральных преобра-
зований [Л.2-21] или совместно методами преобразования Лапласа и Фурье —
Ханкеля [Л,2-18], Что же касается задач конвективного теплообмена, которые
решаются при граничных условиях четвертого рода, то они будут рассмот-
рены в гл. 4.
РАЗДЕЛ ТРЕТИЙ
КОНВЕКТИВНЫЙ ПЕРЕНОС
3-1. ТЕПЛОМАССООБМЕН ПРИ ОБТЕКАНИИ ПЛОСКОЙ ПЛАСТИНЫ
Тепломассообмен между поверхностью тела и окружающей средой (жид-
костью) 1 может происходить под действием внешних сил и благодаря разности
плотностей, вызванной местным нагревом в поле действия сил тяжести. В пер-
вом случае мы имеем тепломассообмен в условиях вынужденной конвекции;
во втором случае имеет место свободная конвекция.
1 Обычно в гидродинамике под жидкостью понимают газ и газовые смеси;
если необходимо отметить специфику жидкообразного состояния вещества,
то говорят о капельной жидкости
179
Рассмотрим простейший случай стационарного обтекания плоской пластины
достаточно большой длины I. Если направить пластину вдоль потока так,
чтобы ось х совпадала с направлением потока, ось у —с направлением перпен-
дикуляра к пластине, а ось г—с направлением ширины пластины, то в нашем
случае ог»= 0; d!dz=Q и д/дтвО, т. е. рассматривается плоскопараллельный
поток жидкости.
Гидродинамика потока при обтекании плоской пластины
Турдулентный
\ Ламинарный
х
Ламинарный
подслой
Рис. З-t. Упрощенная модель перехода
в пограничном слое из ламинарного
в туобулентное течение на плоской
Если измерять продольную скорость движения жидкости vx в направле-
нии оси у при обтекании плоской пластины, то получим кривую распределе-
ния продольной скорости vx (у) или профиль скорости vx (у), показанный
на рис. 3-1.
В направлении у скорость движения увеличивается, а затем, начиная
с некоторого расстояния 6 от поверхности, почти не изменяется. Следовательно,
основной перепад скорости движения от значения, равного нулю, до величины
foe = ус, соответствующей скорости вдали от стенки (основной поток жидкости),
происходит в слое толщиной б, кото-
рый называется пограничным слоем.
Причиной постепенного уменьшения
скорости от v>c до 0 является вязкость,
т. е. способность жидкости оказывать
сопротивление относительному переме-
щению ее частиц благодаря молеку-
лярному хаотическому движению.
Следовательно, весь поток жид-
кости можно разделить на две об- -
ласти: пограничный слой, где прояв-
ляется действие сил вязкости, и основ-
ной поток, где вязкостью можно пре-
небречь, а движущуюся жидкость рас-
сматривать как идеальную.
—• Известно, что по характеру дви-
жения жидкости различают ламинар-
ное и турбулентное движение. Тепло-
обмен в турбулентном потоке происходит более интенсивно, чем в ламинарном,
благодаря хаотическому движению частиц (макрообъемов) жидкости. Турбу-
лентный режим может иметь место и в области пограничного слоя.
Развитие пограничного слоя вдоль поверхности тела в направлении дви-
жения показано на рис. 3-1. Толщина пограничного слоя непрерывно увели-
чивается вдоль поверхности пластины, начиная от нуля у переднего края.
На некотором расстоянии х^ от переднего края режим движения в погранич-
ном слое меняется, переходя от ламинарного к турбулентному. При увеличе-
нии скорости vc значение критического расстояния х# уменьшается, но произ-
ведение VfXk при этом остается постоянным,
Если произвести опыты с жидкостями различной вязкости, то можно
установить, что переход от ламинарного движения к турбулентному происхо-
дит при определенном значения	т. е. характеризуется критическим
значением числа Рейнольдса Re = -LJ£-.
Значение Re = 3.10° является верхним пределом для пограничного лами-
нарного слоя плоской пластины, значение Rea«8- 104 —нижним пределом, При
создании более сильных возмущений в потоке нижний предел перехода от
одного режима к другому можно несколько снизить. Для практических усло-
вий можно считать, что при Re > 5 • Ю6 движение в пограничном слое проис-
ходит при турбулентном режиме. При течении жидкости внутри трубы крити-
ческое число Рейнольдса примерно постоянно и равно 2300 [Л.3-1].
Для несжимаемой жидкости (р = const; др/с>т = О; div сГ-«О) в отсутствие поля
внешних сил (^ = 0) и для стационарного (д/с>т = 0) обтекания пластины плос-
180
непараллельным потоком жидкости уравнение Навье—Стокса можно напи-
сать так:
в направлении х
J dvx , dvx\ др . fdzvx ,
17}= “ di++ Vr
в направлении у
/ dov dvu\ др [д*Си d2vy \
=	+1FJ-
Уравнение непрерывности будет:
, &У_п
дх т ду и'
Граничные условия: прилипание жидкости к стенке
ux=Vi/ — O при у = 0;
(3-1-2)
(3-1-3)
(3-1-4)
совпадение скорости vx вдали от пограничного слоя со скоростью основного
ядра потока
^• = ^00	при у СО.	(3-1-5)
Можно показать, что в топком пограничном слое наибольшее изменение
их происходит в направлении у и лишь незначительное — в направлении х.
В направлении потока величина х изменяется от нуля до I, где / — характер-
ный размер тела, в нашем случае —длина пластины. В направлении у пара-
метры потока изменяются в пределах пограничного слоя. Толщина погранич-
ного слоя 6 значительно меньше длины пластины (6<</).
Согласно общеизвестным оценкам теории пограничного слоя в уравнениях
(3-1-1)—(3-1-3) можно отбросить члены порядка 6”=у (6* < 1). Тогда из
двух уравнений Навье —Стокса остается одно и указанную систему уравнений
можно записать так:
dvj
(3-1-6)
(3-1-7)
(3-1-1)

, dvx	1 др , dfyx
ду ~	р дх ду3 ‘
, диУ _ п
'дх ду
Система уравнений (3-1-6) и (3-1-7) называется уравнениями Прандтля для
пограничного слоя. Граничными условиями будут;
при у = 0	vx = Vy — Q;	(3-1-8)
при у «со	ря.= 1>ю(х, т).	(3-1-9)
Решение задачи (3-1-6)—(3-1-9) представляет большие трудности даже для
стационарного течения. Для частного случая очень тонкой пластинки беско-
нечной длины (/->ос) решение уравнения (3-1-9) дано Блазиусом [Л.3-2].
В рассматриваемом случае скорость потенциального течения постоянна
(oc = const), следовательно, из уравнения Бернулли вытекает др/дх = О.
Приведем ход этого решения. Введем величину ф, называемую функцией
тока жидкости, по соотношениям
дф	дф
= ду ’ Vy=z~ дх‘
Тогда ф будет функцией безразмерной величины «, определяемой соот-
ношением
У
(ХТ/РЮ) 1/2 У 'rv /
(3-1-10)
у_______
~ V R®*»
(3-1-11)
181
где Re^ = %x/v;
* = f	| % I™',1,2 “i (ot«) 1,2 j;“ I &
V	V ', CO.’ л ЯО,'	V \vm/
(3-1-12)
При этом были использованы соотношения
Тогда
Кроме того, имеем:
dip
^ = *~dT
df с,
' V‘x '
гГ4Т
Подстановка соотношений (3-1-15) и (3-1-16) в уравнение
дает:
откуда
dox , dvx d-vx
v”^ + ^-dy=''SF
О?	Op	Op
-2?yr+2^"(V'-fi = v-r.
/Т+2Г=0.
Граничные условия (3-1-8) и (3-1-9) запишутся так:
при £ = 0	f=f'=^
при £ = СО /'= 1.
(3-1-13)
(3-1-14)
(3-1-15)
(3-1-16)
(3-1-17)
(3-1-18)
Блазиусом были получены решение уравнения (3-1-17) в виде сходящихся
рядов для малых значений £ и асимптотическое приближение для больших
значений £, Хоуартом (Л.3-3] было дацо численное решение уравнений (3-1-17).
Результаты приведены в табл. 3-1, На рис. 3-2 приведен график ол./осо=/:' (£).
Из табл. 3-1 и рис. 3-2 видно; что начиная с скорость их практически
равна скорости потока vc (при 5f =0,99),
На рис. 3-3 приведен график изменения поперечной скорости vy вдоль
оси у, из которого видно, что при £->со величина Rex стремится к опре-
деленному пределу 0,8604. Следовательно, на внешнем крае пограничного слоя
поперечная скорость равна;
Ж'	(3-1-19’
Если сложный профиль Vy (у), приведенный на рис. 3-2, заменить прямо-
линейным, т. е. прямой, соединяющей начало координат с точкой £ = 5,2, то
182
приближенное соотношение будет иметь вид:
и
-£ = 0,165—;	0<?<5,2.
(3-1-20)
Следовательно, на внешнем крае пограничного слоя имеется составляющая
скорость, направленная перпендикулярно пластине. Это происходит потому,
О 1	2 3 4	5 6 7
Рис. 3-2. Распределение про-
дольной скорости vx по направ-
лению у в пограничном слое
при обтекании пластины.
Рис. 3-3. Распределение попе-
речной СКОрОСТИ Vy вдоль оси у
в пограничном слое при обтека-
нии пластины.
что жидкость па своем пути вдоль пластины несколько оттесняется от поверх-
ности вследствие нарастания толщины пограничного слоя 6 (х) вдоль по те-
чению.
Таблица 3-1
Функция f (S) Блазиуса для плоской пластины
/vco\l/2	f	V	Г		f	,,=	г
0	0	0	0,33206	4,6	2,88826	0,98269	0,02948
0.2	0,00664	0,06641	0,33199	4,8	8,08534	0,98779	0 02187
0,4	0,02656	0,13277	0.33147	5,0	3,28329	0,99155	0,01591
0,6	0,05974	0,19894	0,33008	5,2	3,48189	0,99425	0,01134
0,8	0,10611	0,26471	0,32739	5,4	8,68094	0,99616	0,00793
1,0	0,16557	0,32979	0,32301	5,6	3,88031	0,99748	0 00543
1,2	0,23795	0,39378	0,31659	5,8	4.07990	0,99838	0,00365
1,4	0,32298	0,45627	0,30787	6,0	4,27964	0,99898	0.00240
1,6	0,42032	0,51676	0,29667	6,2	<47948	0,99937	0,00155
1,8	0,52952	0,57477	0,28293	6,4	4,87938	0,99961	0,00098
2,0	0,65003	0,62977	0,26675	6,6	4,87931	0,99977	0,00061
2,2	0,78120	0,68132	0.24835	6,8	5,07928	0,99987	0,00037
2,4	0,92230	0,72899	0,22800	7,0	5,27926	0,99992	0,00022
2,6	1,07252	0,77246	0,20646	7,2	5,47025	0,99996	0,00013
2,8	1,23099	0,81152	0,18401	7,4	5,67924	0,99998	0,00007
8,0	1,39682	0,84605	0,16136	7,6	5,87924	0,99999	0,00004
3,2	1,56911	0,87609	0,13913	7,8 8,0	6,07923	1,00000	0,00002
3,4	1,74696	0,90177	0,11788		6,27923	1,00000	0,00001
3,6	1,92954	0,92333	0,09809	8,2	6,47923	1,00000	0.00001
3,8	2J1605	0,94112	0^8013	8.4	6,67923	1,00000	0,00000
4,0	2,30576	0,95552	0^16424	8.6	6,87923	1,00000	0,00000
4,2 4,4	2,49806 2,692138	0,96696 0,97587	0,05052 0,03897	8,8	7,07923	1,00000	0,00000
183
Напряжение трения на поверхности будет равно:
г<0>~
- -0,33206Фм	Д = -1>.33206р[^ ре; * .
Обычно вводится безразмерная величина, называемая локальным
цаентом треиня,
С - ~q° _ 0>664L
(3-1-21)
КОЭффи.
(3-1-22)
Средний коэффициент трения С будет равен:
(3-1-23)
Из дифференциальных уравнений (3-1-6) и (3-1-7) можно получить интег-
ральное уравнение пограничного слоя.
Проинтегрируем уравнение (3-1-6) по у от 0 до 6. Тогда для стационар-
ноге/потока (д/дт = 0) будем иметь:
б	в	б	б
Jdvx . , Г dvx j С <&>x j 1 С др . т , __
ООО
Воспользуемся соотношениями х 	1
б	б	б
д С , f дуу , . Г dvx
^WydV-y^dy+^-^dy-,
0	0	о
б	б б	б
д С j I С dux л do* dvy	С dvv
°« = ~J
ООО	о
Тогда будем '«меть:
тх У dy~l У У °-- v(^L -I6- <3-1-25’
ооо
При этом были использованы следующие граничные условия: при р=*0
vx = ti^=®0, при у = 6 оЛ. = псо; кроме того, предполагалось, что давление вдоль
“си у не изменяется.
Уравнение (3-1-24) можно переписать так;
д и	dv
J ^dy-j-0,+ ^6.	(3-1-261.
Уравнение (3-1-26) известно как интегральное уравнение пограничного
слоя при ламинарном обтекании плоской пластины. Иногда его записывают
в иной форме. С этой целью вводятся, два линейных параметр!': толщина вы*
V84
теснения скорости бв. с и толщина вытеснения импульса бв.и

по соотношениям
СО	ОС
ОО V	О \	‘''со/ voo
(3-1-27)
(3-1.28)
На рис. 3-4 дана геометрическая интерпретация толщины вытеснения ско-
рости 6Bi с. Положим, что пограничный слой
простирается до бесконечности (б->сс), и
заменим его условным конечным слоем тол-
щиной бв.с так, чтобы площадь над кривой
была равна площади прямоугольника
Гео-
физически это означает, что в потоке
жидкости без трения и без пограничного
слоя поле скорости осталось таким же, как
в потоке реальной жидкости с пограничным
слоем, только при смещении стенки на ве-
личину бв. с.
Если бы распределение скорости их (у)
было линейным, то бв. с = у б, 6В.И= д-6
при условии, что при y = &vx — vc, т. е. при
замене предела со на б.
Из уравнения Бернулли находим:
их.
о
Рис. 3-4. К определению тол-
щины вытеснения скорости бв,с.
Е др dvc f
б з- = — р \ vc dy.
дх н дх J с а
(3-1-29)
• Тогда интегральное уравнение пограничного слоя будет иметь вид:
д	о0
й(в,.»’У+М,.е-^-?. -	(3-1-30)
Из уравнения движения (3-1-6) можно получить уравнение энергии путем
умножения первого уравнения на vx. Затем аналогичным путем получим ин-
тегральное уравнение энергии:
б	й
й	у (^“у-	(3-1-31)
Введя безразмерные величины —толщину вытеснения энергии бв.а и без-
размерную диссипативную функцию Ф* по соотношениям
(э-1-32)
СО V
(3-1-33)
Ух _.1
получим интегральное уравнение энергии для пограничного слоя в виде
ф.
dx ~ &	1
(3-1-34)
185
Интегральное уравнение пограничного слоя применяется для приближен-
ных решений, в основе которых лежит заданный профиль скорости. Напри-
мер, положим, что профиль скорости vx (у) описывается многочленом
^ = Л + Вц + Суг+О1г>,	(3-1-35)
где Л, В, С, D—постоянные, которые определяются из следующих гранич-
ных условий:
при »=0 Vi = 0; ^ = °;	(3-1-36)
(3-1-38)
(3-1-39)
Эти граничные условия отображают условия прилипания жидкости на
стенке (уд. = 0), постоянство трения на стенке (dvx/dy~ const) и неизменность
продольной скорости их по направлению у на расстояниях, больших 6 (ох —
= const при у 6).
Удовлетворяя этим условиям, получаем значения постоянных:
Л=0; В=-^; С = 0; D=-±£.
Тогда кривая распределения скорости будет иметь вид:
Vx __ 3_ у _ _1_ !у_' з
2 6	2 \ 6 J ’
т. е. профиль поперечной скорости будет описываться полукубической пара-
болой,
Найдем толщины вытеснения импульса:
б
1 С	чч
б».и = ^ J	(3-1-40)
Напряжение трения на стенке равно:
/dvx\	3
(3-М1)
Тогда, полагая в интегральном уравнении (3-1-29) дусо/дх = 0, получаем,-
39	d6 3
2SO	rfx = — 2 V Т'
После интегрирования (3-1-42) получим:
(3-1-42)
(3-1-43)
так как при х = 0 6=0.
Следовательно, толщина пограничного слоя прямо пропорциональна
Соотношение (3-1-42) можно переписать так:
6	4,64
х ~ l"'R~
Если это соотношение подставить в формулу (3-1-41), то получим:
0,323р^
а0 =----------------------------,
I- Re*
(3-1-44)
(3-1-45)
186
Формула (3-1-45) отличается от (3-1-21), полученной па основе решения
Блазиуса, только числовым коэффициентом. Вместо коэффициента 0,33206
в формуле (3-1-45) числовой коэффициент равен 0,323, т. е, меньше примерно
на 3%- Кстати, можно отмстить, что если профиль скорости vx (у) описы-
вается формулой (3-1-39), то толщина вытеснения скорости 6в>с==0,3756, а
3Q 1
6в.» = ^5б~ТМЛ.З-4].	(3-1-46)
Числовые коэффициенты, входящие в формулы толщины пограничного
слоя и трения, зависят от распределения скорости в пограничном слое
(табл. 3-2).
Таблица 3-2
Влияние профиля скорости в пограничном слое
на толщину пограничного слоя и коэффициент трения
Профиль скорости	Граничные условия г/ = 0	(	у = б			С/Re
Ух = У 6			3,46	1,156
6 И/	dX)x;C	у==0	5,47	1,462
G 1 II' ьо| СО 1 “1- Оэ|^	ох = 0 ^ = 0	рл = со ^ = 0 dy	4,64	1,292
Решение Блазиуса	-	—	5,0	1,328
Теплообмен при обтекании плоской пластины
При обтекании плоской пластины жадностью ее температура изменяется
от Tw (температура на поверхности пластины) до температуры Тм жидкости
вдали от поверхности. Это изменение температуры Т^— Tw происходит в не-
большом слое 6г, характеризующем толщину теплового пограничного слоя.
Последняя отличается от толщины гидродинамического пограничного слоя.
Она может быть больше или меньше 6 (6/^6) в зависимости от числа
Прандгля;
_ 1_
6 ~ Г Рг '
(3-1-47).
Следовательно, если Рг 1, то 6,^)6, если же Procl, то 6, 5г 6.
На рис. 3-5 приведены кривые распределения продольной скорости ох и
температуры Т в пограничном слое для предельных значений критерия
Прандтля.
Оценив функцию Ф*, можно показать, что все члены этой функции при-
мерно равны §*2, за исключением первого, который составляет 1. Если сде-
лать оценку всех членов, входящих в уравнение Фурье — КнрхгОфа для погра-
ничного слоя, то будем иметь при обтекании плоской пластины в стационарном
187
режиме (dT/dt<=Q)
! дТ , дТ \ „ д*Г , (дих \2
• (3-'-48’
Для потока с малой скоростью уравнение количества движения (3-1-Ц)
при постоянном давлении др/дх = 0 и уравнение переноса теплоты (3-1-48)
без чисто диссипативной функции аналогичны. Если коэффициент кинемати-
ческой вязкости равен коэффициенту температуропроводности (a=v, Рг=1),
то решения уравнений будут одинаковыми (профили поля скорости и поля
температур в пограничном слое совпадают), а толщины гидродинамического и
теплового пограничных слоев будут равными (6 = 6/)
«) 1)
Рис. 3-5. Профили скоростей vx (у) и температуры Т (у) в ламинарном погранич-
ном слое для предельных значений числа Рг.
Представляет интерес сделать оценку величины диссипативного члена
г) (дих/ду)*. Расчеты показывают, что если р*/с ДТ < 1, то этим членом можно
пренебречь. Например, для воздуха при разности температур Д7' = 5,6вС
можно пренебречь вязкой диссипацией, если vc < 152 м/с На практике ско-
рости движения жидкости значительно меньше, поэтому величиной (^х/ду)9
можно пренебрегать.
Продольная скорость vx и поперечная скорость vy изменяются в зависи-
мости от у. Интегральное уравнение теплового пограничного слоя выводится
из уравнения (3-1-48) путем интегрирования по у в пределах от 0 до 6/, при
этом используются соотношения
б/
VXT dy--' Т dy-%- vx~^-d.y ;
О	О	0
в,
М Т J С дТ . с ~ dvK .
и граничные условия:
при у«0 vx—Vy^Q; при у->со Г = Тз,;
В результате получаем:
о
(3-1-49)
(3-1-50)
(3-1-51)
(3-1-52)
188
Локальный коэффициент теплообмена, определяемый по соотношению
“-(А)’	' <3153>
будет равен;
б,
‘к(дТ/ду)и-о	1	(*
^=- ; _7 = F77f--rT	(3-'-54>
' СО 1 в1	р" ' СО ®' J
Уравнение (3-1-48) можно решить аналитическими или численными мето-
дами. Если ввести функции 5 и f согласно (3-1-11) и (3-1-14), то уравнение
(3-1-48) можно переписать так:
^-+-Lpr/-^- = -PrEc7„tfT.	(3-1-55)
где Ес —число Эккерта; Ec — v^/c^T^.
Граничные условия следующие:
при £ = 0 T = TW, при £ =	Г = ГМ.	(3-1-56)
Уравнение (3-1-55) является обычным дифференциальным уравнением и
решается стандартным методом.
Если диссипативной функцией пренебречь (ф = 0), то уравнение упро-
щается и принимает вид:
Г + уРг/в' = 0,	(3-1-57)
где в—безразмерная температура, равная:
а граничные условия примут вид:
при ; = 0 8=1, при | = оо 6 = 0.	(3-1-58)
Решение уравнения (3-1-57) при граничных условиях (3-1-58) было дано
впервые Шлихтингом [Л. 3-1], оно имеет вид:
Г (ПРг
«-4---------•	(з-1-59)
j (/')рг<«
о
Если Pr = 1, то профиль температуры 6(£) и профиль скоростей и* (у)
будул совпадать, 1ак как 6 = 1 — /’»1 —
На рис. 3-6 дано распределение безразмерной температуры по обобщен-
ной координате £ для разных значений Рг от 0,5 до 1000.
Введем переменную О по соотношению
тогда уравнение (3-1-55) будет иметь вид:
®’+-|-Рг/е'=-2Рг(Н!.	(з-1-бо>
Решение уравнения (3-1-60) может быть получено методом квадратур.
18.
Если
при | = 0 А' = 0; при £ =	£ = 0,	(3-1-61)
то решение имеет вид:
°р ГЕ	J
fl = 2Prj (nPrK(/')2-PrdH^.	(3-1-62)
Для адиабатических условий, когда Tw — Ta,
(з-‘-бз)
Величина fl (0) для разных значений критерия Рг приведена в табл. 3-3
и на рис. 3-7.
Таблица 3-3
Влияние числа Прандтля на распределение температуры
при адиабатическом обтекании плоской пластины
Рг	0,6	0,7	о.з	0,9	1,0	1.1	7.0	10,0	15.0
fl (0)	0,770	0,835	0,895	0,950	1,000	1,050	2,515	2,965	3,535
На рис, 3-8 даны профили температуры в пограничном слое для адиаба-
тически нагреваемой пластины при различных значениях критерия Прандтля.
Решение уравнения 3-1-55) будет иметь вид:
'	7’oo-'r’J,('r’0-7’„)9+	(3-1-64)
Поток теплоты будет равен:
?=	~ (Т’д Тц.,)]' Rex 0'(0),	(3-1-65)
Уравнение переноса теплоты (3-1-57) было численно решено Эвансом
(Л. 3-5]. Мерк (Л, 3-6] дал решение в следующем виде:
2Ё*==0,33875Рг'‘'3| I—— +----------------, ...1, Рг=»0,5, (3-1-67)
L «Рг 675Рга J	’ (	•
где Nux=avx/X—локальное число Нуссельта.
Для числа 0,5«£Рг«£50 формула для числа Нуссельта имеет следующий
аид;
-^4= = 0,332Рг1/3 .	(3-1-68)
TRe.r
Решение уравнения переноса теплоты в ламинарном пограничном слог
можно получить следующим образом, Для малых чисел Рг толщина гидроди-
намического пограничного слоя мала (см. рис. 3-5) В силу этого поперечная
скорость Vy значительно меньше продольной, так как из приближенного соот-
ношения
У
— ^0,165 —	(3-1-59)
ссо	*
следует, что при у = б -> 0	0.
190
Рис. 3-6. Распределение температуры 6 в ламинарном пограничном слое при раз-
ных значениях числа Рг.
Рис. 3-7. Зависимость -fr (0) от числа Рг.
Рис. 3-8. Зависимость (0) [(Тм — Т)/{Т-а — 7^]) от обобщенной перемен-
ной £^=^-J/’Re^ длй‘Рг = 0,6-к- 1000.
191
Поэтому уравнения переноса теплоты можно написать так:
дТ
v^~a-a? “р"
Граничные условия имеют вид:
при у = 0	Рж = 0,
при	0^.*=^,
Рг->0.
(3-1-70)
(3-1-71)
при у—4-СО VX=V^,
Можно в качестве приближения считать также, что = const. Тогда
решение уравнения (3-1-70) будет иметь вид:
Т-Т„
erf
уУу*
2Уах
(3-1-72)
где erf z — интегральная функция ошибок Гаусса,
Локальное число Нуссельта будет равно:
Nuv-2^=-----------*------Ж _ ‘	(э.1-73)
Ь (т=»-7'а,) \	/»=0
С X
где Re^s=—--------локальное число Рейнольдса.
Решение (3-1-76) будет совпадать с решением (3-1-66), если в последнем
ограничиться первым членом разложения.
Рис. 3-9. Гидродинамический и тепло-	Рис. 3-10. К Определению числа
вой пограничный слой при ламннар-	Нуссельта по условной толщине
ном обтекании плоской пластины. теплового пограничного слоя.
Зависимость между Nux и числами Re.v и Рг можно получить на основе
интегрального уравнения переноса теплоты в пограничном слое (3-1-52).
Рассмотрим общий случай, когда кривые распределения (у) и Т (у) не
совпадают между собой, при этом начальный участок пластины х0 не нагре-
вается, а поддерживается при постоянной температуре Тс = ТсО= const. Гидро-
динамический слой начинается у переднего края пластины, а тепловой —у
границы нагреваемой части пластины (рис. 3-9).
При стационарном режиме	= const, следовательно, ™ 0» так как
-|^- = const. :> этом случае профиль температуры будет также описываться
кубической параболой [Л, 3-4[:
о 3
2 вг 2 (ет) •
(3-1-74)
где «=Т-Т„.
192
Интегральное уравнение переноса теплоты можно написать так:
Ор
д	/ ла \
Ъ j	(34-75)
Тогда интеграл левой части уравнения (3-1-52) будет равен:
бу
j (*«,-«') “х	А4).	(3-1-76)
где Д1=6г/6. При этом было использовано соотношение (3-1-39). ЕслихД^!,
то величиной Д4 можно пренебречь. Тогда будем иметь:
3 d 3 ft,
=	.		(3-1-77)
з
так как (dft/dy)0— -^a-&gs/6r.
Величину 6 определяем из соотношения (3-1-44):
, Для вязких масел Pr==el000, тогда при хо = О (пластина нагревается по
всей длине) Д = 0,1, Для газов (Рг < 1) формула, строго говоря, непригодна.
Локальное число Нуссельта будет равно:
№л = 0,331Рг1/3КеУ2 (1 -	1/3-	(3-1-79)
При нагревании пластины по всей длине (хо = О) формула (3-1-79) почти
совпадает с формулой (3-1-68),
Среднее число Нуссельта (Nu) будет равно:
Nu = -^- = 2NUj.,	-	(3-1-80)
и для случая хо = О
NU = 0,662Pr1/3/RT	(3-1-81)
Для капельных жидкостей зависимость между Nu и Re Рг, полученная
на основе обработки большого количества экспериментов, имеет вид:
/ Рг \О 25
Nu =0,76 /КГ Рг’-43 -н^-) ' .	(3-1-82)
При обработке экспериментальных данных по профилю температуры в по-
граничном слое локальное число Нуссельта удобно определять по величине
условной толщины теплового пограничного слоя 6'г, численно равной отрезку
отсекаемой на прямой ft = const касательной к кривой распределения темпе-
ратуры ft(y), проведенной в точку t/ = 0 (рис. 3-10).
тогда
ахх х / дЬ\ х
Nu«=—== (М-83)
Этот графический метод определения числа Nux применим только ри
малых скоростях потока жидкости, когда величина 6^ соизмерима с х.
7 Лыков А. В, '	|93
Обтекание клинообразных тел
Выше были рассмотрены явления теплообмена при обтекании плоской
пластины, пли так называемое безградиентное обтекание (др/дх~ 0).
При обтекании клинообразных тел с углом раствора л0 (рис. 3-11) тра-
диепт давления вдоль оси х (направление движения потока) не равен нулю.
В этом случае принимается зависимость между vc и координатой х в виде
vc = Axrn,	(3-1-84)
где zn —показатель степени,
2-р •
(3-1-85)
Для плоской пластины р — 0, тогда /н = 0 и vc=vM=const; для пластины,
расположенной перпендикулярно потоку, 0 = 1,0; т=1. Для клинообразных
°)
Ъ)
Рис. 3-11. Обтекание клинообразного тела.
а — схема обтекания: б — пределы скорости (зависимость от £*); в — профили - тем-
пературы (зависимость 0 or при разных числах Рг и р.
тел 0 < 0 < 1 и	В этом случае дифференциальное уравнение
пограничного слоя
, dvx 1 др , dzvt
дх JrVy ду р ~дх V ду‘
dvx	dvu
>—* =0
дх	ду
(3-1-86)
при подстановке формул
(3-1-87)
превращается в уравнение
2/'"+Л+0(1 -№)-а
(3-1-88)
194
Уравнение (3-1-88) отличается от уравнения (3-1-17) наличием третьего
дополнительного члена. Решение этого уравнения численными методами полу-
чено Д. Хартри [Л. 3-7]. Результаты решения для некоторых клинообразных
тел приведены па рис. 3-11.
В этом случае локальное число массообмена будет равно:
NU - 0 56 (Р+0‘2)0,1 д^0.5 pj.0.333 -г-0.067В — 0,02в6г.
(2 р)0,5 х
/ J' ______у \
Распределение безразмерной температуры 8-10==-^—=—1 по
\ w *
'	2	\
%i = — В J приведено на рис. 3-11, в для разных углов
i V 2 р /
(3-1-89)
координате
раствора р.
Массообмен при обтекании плоской пластины
Дифференциальное уравнение переноса массы в пограничном слое при
обтекании плоской пластины аналогично уравнению переноса теплоты. Для
плоского стационарного потока (д/дт = 0, <5/dz = 0, vz = 0) дифференциальное
уравнение переноса массы А-й компоненты имеет вид:
+	+	(3-1-90)
где /у—объемный источник массы вещества, обусловленный фазовыми или
химическими превращениями. При этом предполагается, что эффектами термо-
диффузии и бародиффузии можно пренебречь. При выводе уравнения’(3-1-90)
был использован метод оценки порядка членов в дифференциальном уравнении
переноса.
Если источник массы отсутствует (Jv=Gj, то из дифференциального урав-
нения (3-1-90) аналогичным способом находим интегральное уравнение погра-
ничного СЛОЯ:
bD
(3-1-51)
Полученные решения для профиля температуры можно распространить на
профиль концентраций, поскольку они совпадают между собой при равенстве
критериев (Pr=Sc). Число Шмидта Sc или диффузионное число Прандтля
РГд (pr^ = Sc) может быть выражено через тепловое число Прандтля Рг при
помощи числа Льюиса Le(Le = D/a);
Sc — Рг^ = Рг/Le.
Коэффициент массообмена <хт обычно определяется по соотношению
tx_____________________	(dpko/dy)w
т' (P*w“Paco) (Paw“Paco)
где f/tw—плотность потока массы А-го компонента.
Тогда локальное массообменное число Нуссельта (Мпд.)д будет равно:
(NuI)o=^ = 0,33)Sc1'3 кж;.
(3-1-92)
(3-1-93)
Если число Рг и Sc равны (Le— 1), то Nux= (Nux)0, откуда
О-1-”)
7*	’ IW
т. с. отношение коэффициента теплообмена к коэффициенту массообмена равего
объемной изобарной теплоемкости жидкости. Это соотношение известно под
названием формулы Льюиса, оно справедливо при указанных выше допуще-
ниях. В ряде работ коэффициент массообмена относится к разности парциаль-
вых давлений Лр (Лр=р„ —р„):
В этом случае
Жадкость
Рис. 3-12. Распределение концент-
рации пара pi0 и сухого воздуха
р2о по высоте у сосуда в процессе
испарения жидкости.
/kw &p(Pvr Рсо)‘
“'""Mfrp’
(3-1-95)
(3-1-96)
где М и — соответственно молекулярные массы смеси и А-го компонента. Строго
говоря, формулы (3-1-93)—(3-1-96) справедливы для бинарной смеси, когда
диффузия обоих компонентов происходит с одинаковой скоростью. Если ско-
ростя диффузии компонентов разные, то
помимо диффузионного движения возйн-
кает видимое движение всей смеси, вы-
званное градиентом общего давления.
В качестве простейшего примера рас-
смотрим случай диффузии при испаре-
нии жидкости из сосуда. В первом при-
ближении будем считать, что темпера-
тура поверхности жидкости одинакова
и равна температуре адиабатического
насыщения воздуха или температуре
мокрого термометра tn. Температура
окружающей среды (влажного воздуха)
постоянна (tc = const). Влажный воздух
условно принимаем за бинарную смесь,
состоящую из водяного пара (Мх=18)
и сухого воздуха (М2 = 29).
При испарении жидкости из сосуда
имеет место не только взаимная диф-
фузия пара и сухого воздуха во влажный воздух, но и конвективный поток
влажного воздуха от поверхности жидкости. Дело в том, что поверхность жид-
кости является непроницаемой преградой для воздуха, в результате чего диф-
фузия воздуха стремится создать избыточное давление, но избыток давления
релаксируется и вызывает в смеси движение, направленное от поверхности
жидкости. Предположим, что общее давление постоянно (р== const), так как
избыток давления релаксируется со скоростью звука:
p = pi4-p2 = const.
Пар диффундирует от поверхности жидкости в воздух под влиянием гра-
диента относительной концентрации дри/ду (рис. 3-12), одновременно воздух
диффундирует к поверхности жидкости в обратном направлении под влия-
нием градиента относительной концентрации воздуха dpgo/dy.
Поскольку
Pi + p2 = P; Pio + Рго = 1»	(3-1-97)
ТО Зри/й^ — дрш'ду.
Если пар свободно диффундирует в воздух, то для последнего поверхность
жидкости является преградой, в результате количество воздуха у поверхности
жидкости должно было бы непрерывно увеличиваться, вызывая повышение
общего давления. Поскольку давление постоянно (p = const), то для выполне-
ния этого условия необходимо движение всей смеси в виде молярного (кон-
вективного) переноса с некоторой скоростью о* (рис. 3-12).
Суммарный поток пара равен сумме диффузионного и конвективного по-
токов пара:
+	(3-1-98)
196
Суммарный поток воздуха у поверхности жидкости равен нулю:
;! = -D21p^+pjC* = 0.	(3-1-99)
Из последней формулы находим:
так как О21 = О12, др^/ду^—др^/ду. Подставив полученное выражение для
vk в формулу (3-1-98), получим:
h = _-^_pD1!^«.	(3-1-101)
1 — Pio оу
Таким образом, конвективный перенос пара учитывается множителем
1д)_рхо). Если диффузионный перенос пара принять за 1, то доля конвек-
тивного переноса составляет p10/(l — pw).
Из формул (3-1-100) и (3-1-101) следует:
t4=/i/p,	(3-1-102)
т. .е. скорость конвективного переноса равна плотности потока пара, поделен-
ной на плотность парогазовой смеси. Иногда величину называют скоростью
стефановского потока. Эту скорость видимого движения не надо смешивать
с линейной скоростью диффузионного (молекулярного) переноса пара И1ДИф =
= /i/Pi- Можно перейти от относительных концентраций к парциальным дав-
лениям, используя формулы
Р1»=Р1»^,	(3-1-103)
где Pio—Pi/P—относительное парциальное давление пара,
Тогда получим;
1	/J__ 1 \i 1
1 dpi
RT (1 -p10) dy ’
(3-1-104)
(3-1-105)
где g— универсальная газовая постоянная.
Если в формуле (3-1-105) произвести интегрирование по у от 0 (поверх-
ность жидкости) до | (расстояние до края сосуда от поверхности жидкости),
то получим известную формулу Стефана;
Г (1—рю),
Л’“—й7^1п|г=ы;
(3-1-106)
где индекс ш обозначает поверхность, а с —окружающую среду.
При выводе формул (3-1-98) и (3-1-106) мы пренебрегли явлением термо-
диффузии, а также конвективным переносом пара в виде теплового скольже-
ния и диффузионного скольжения.
Известно, что при наличии градиента давления на поверхности стенки
сосуда возникает конвективный перенос у самой поверхности в сторону высо-
ких температур (против потока теплоты). Линейная скорость такого видимого
движения
(3-1'107’
Аналогичный эффект (диффузионное скольжение) имеет место у поверх-
ности сосуда, если по высоте его вблизи стенок существует градиент одного
-197
из компонентов бинарной смеси. Эта скорость vgr в первом приближении равна:
Для парогазовой смеси (М2 = 29, Мх=18) получим:
vsc = 0,270 -ф,	'	(3-1-109)
4	рз ду	у >
что близко совпадает с данными, приведенными в статье [Л.3-8].
Легко показать, что скорости конвективного переноса-у^, v^c, Vgc имеют
один и тот же порядок. По отношению к линейной скорости диффузионного
переноса оДИф они составляют около 5% для обычных условий испарения
жидкости в атмосферу (природные условия испарения). Таким образом, если
необходимо ввести поправку на стефановский поток, но надо учитывать потоки
теплового и диффузионного скольжения.
Формула Стефана (3-1-106) неоднократно проверялась экспериментами по
испарению жидкости из капиллярных трубок. Если теплота, необходимая для
испарения, берется из окружающего воздуха (стеклянные трубки с жидкостью
расположены в потоке нагретого воздуха), то в формулу Стефана надо внести
поправку. Вместо £ надо ввести величину (g —go)» где ^ — постоянный коэф-
фициент, зависящий от скорости и температуры потока воздуха [Л.3-9].
Турбулентный обмен
Кратко остановимся па тепломассообмене между поверхностью стенки и
турбулентным потоком. Для получения обобщенного соотношения, характери-
зующего профиль скоростей в турбулентном пограничном слое, вводятся без-
размерная скорость v*, безразмерное расстояние от стенки у* или от поверх-
ности трубы г* по формулам
где f(j—так называемая скорость трения, равная:
В случае молекулярного переноса импульса, определяемого	законом
Ньютона, зависимость между v* и у* может быть получена из решения диф- ференциального уравнения о	dvx a‘=V~d»'	<34'112)	
отсюда у*=у*.	(3-1-113)
При обтекании плоской пластины уравнение переноса импульса яичном слое определяется формулой Прандтля	В ПОГра-
On , ,л I dv и I dvv
Из соотношения (3-1-112) после интегрирования и использования соотно*
шений (3-J-110) получим:
1'*-=^ 1п	ч	(3-1-115)
где k{ и ^ — постоянные, определяемые из опыта.
Таким образом, распределение скорости у* в пограничном слое в направле»
нии, перпендикулярном поверхности, описывается логарифмическим законов
isa
По данным Никурадзе [Л.3-10], постоянные и соответственно равны
2,5 и 5,5, г. е.
и* = 2,5 In у* 4 5,5.	(3-1-116)
Между линейным законом изменения скорости (3-1-113) и логарифмическим
законом (3-1-116) существует переходная зона, для которой Рихарт [Л.3-11]
на основе обработки экспериментальных данных получил формулу
н* = 5,01пу*—3,05.	(3-1-117)
Результаты, полученные по разным эмпирическим формулам, представлены
в виде графика на рис. 3-13, из которого видно, что экспериментальные дан-
ные расположены вблизи кривых, начерченных по приведенным выше форму-
лам. При обтекании пластины,
а также при течении в трубах
профиль скорости часто аппрок-
симируется формулой
В частном случае, когда
Су = 0,0791Re"<)’85, из соотноше-
ния (3-1-118) получим:
о*_ 8,74 fa')1'7. (3-1-119)
Эта зависимость также на-
несена на график на рис. 3-13,
из которого видно, что в интер-
вале 100 < у* < 1200 график,
построенный по данной форму-
ле, близок к графику, пост-
роенному по формуле Никурад-
зе (3-1-И6).
Приведенные выше форму-
лы для профиля скорости в
пограничном слое непригодны
для слоя вблизи стенки, так
Рис. 3-13. Универсальный профиль скорости
о* (у*) при турбулентном обтекании пласти-
ны.
Числа показывают номер формулы: t — у* =у*-
v* = 5,01пу* — 3,05; J — о* 8,74(//*) V?; 4 —
v* = 2,5 1п у*-|- 5,5. Заштрихованная часть — раз-
брос экспериментальных точек.
как напряжение трения, про-
порциональное dvx/dy, при
р~>0 получается бесконечно
большим. Это обьясняется тем,
что у самой поверхности тур-
булентность исчезает, Поэтому
для тонкого слоя вблизи стенки „ ____ ,-г- -- - г—--, -	- --- -г—
ложил гипотезу о существовании ламинарного подслоя 6$, в котором ско-
рость распределяется по линейному закону. В пределах изменения у от 0 до
б?, имеет место линейное распределение %х{у), т. е, ъх*=ку, где А—постоян-
пая. Затем на участке (6й < у < 6) профиль скорости описывается формулой
(3-1-118) или (3-1-115).
Используя интегральное уравнение пограничного слоя с учетом профиля
скорости и закона трения (3-1-127), определяемого формулой (3-1-118), для тол-
щины турбулентного пограничного слоя получим формулу
даннью формулы непригодны. Прандтль пред-
l==0,376Re/'\
(3-1-120)
При этом предполагается, что величина х условно отсчитывается от самого
края пластины (известно, что турбулентный пограничный слой начинается на
некотором расстоянии Ху от края пластины). Толщина вытеснения скорости
ба.с в нашем случае будет равна 6/8. Если для критического расстояния ху
199
рассчитывать толщину 5 по формулам для ламинарного и турбулентного погра-
ничных слоев, то в последнем случае она окажется больше. Скачкообразно
толщина пограничного слоя увеличиваться не может, Переход ламинарного
Рис. 3-14. Распределение темпе-
ратуры Т (с/) и скорости vx (у) в
турбулентном пограничном слое
с ламинарным подслоем (6$),
пограничного слоя в турбулентный происхо-
дит не сразу, а постепенно с наличием пе-
реходной области, В этой области вначале
возникают колебания со сравнительно длин-
ной волной, движение в пограничном слое
, становится неустойчивым. Затем волны при-
обретают неправильную форму, превращаясь
в завихрения, и, наконец, совсем размы-
ваются, приобретая характер умеренного
турбулентного движения Переходная зона
трудно поддается изучению, поскольку в
ней имеют место неправильные флуктуации,
Карман [Л.3-12] разделил весь поток
жидкости, обтекающий твердое тело, на три
области: 1) ламинарный подслой; 2) переход-
ный слой; 3) турбулентное ядро потока. По-
ток в ламинарном подслое полностью лами-
нарный, а перенос происходит молекулярным
путем. В турбулентном ядре турбулентная
много раз больше, чем молекулярная вязкость
вязкость и теплопроводность во ,	,	u
и теплопроводность. В буферном подслое поток постепенно меняется от ла-
минарного к турбулентному. Помимо того, Карман принимает Ргв=1.
В нашем случае толщина ламинарного подслоя 6$ будет равна:
О
(3-1-121)
Напряжение трения на поверхности
—Т—==0,0296Re^o,E.
(3-1-122)
Для локального коэффициента трения Cf Прапдтлем и Шлихтипгом [Л.3-1]
предложена формула	
При больших числах Rex влиянием ламинарного пограничного слоя можно
пренеоречь.
Используя схему ламинарного подслоя с линейным распределением темпе-
ратуры (рис. 3-14) и аналогию между переносом теплоты и импульса в виде
wco vb

(3-1-125)
из формул (3-1-124) и (3-1-125) можно исключить неизвестную величину Ть-
Тогда-для коэффициента теплообмена а при условии Рге = 1 получим:
<?0	_ Р0СрЛсо
т^~то 1+2*{рг_])
200
Напряжение трения* у поверхности пластины можно определить по фор-
муле Блазиуса, справедливой для жидких поверхностей при Re < 107:
£>,,= 0,0228(114 Ref”’25.	(3-1-127)
Из профиля скоростей в ламинарном подслое и турбулентном пограничном
слое получаем:
иь 2,12
Re”’1
(3-1-128)
В результате будем иметь:
0,0296 Re”,8Pr
Nur==-------—--------------------.---.
1 + 1,305 (Pr-1) ReJ1 Рг~,/6 '
Для газов число Рг близко к единице и формула (3-1-129) ..............
упрощается. Если предположить, что пограничный сдой является турбулент-
ным по всей длине, то среднее число Нуссельта для пластины длиной / равно:
Nu = Niv_,=0,037Re°'8Prl’'J.	(3-1-130)
Опыты подтверждают пригодность формулы (3-1-130), полученной расчет-
ным путем.
При обработке экспериментальных данных разных авторов по теплообмену
при ибгекании пластины воздухом
получаем следующую формулу:
Nu = 0,032 Re”’8.	(3-1-131)
' Для капельных жидкостей фор-
мула имеет вид:
Nu=0,037 Rc°’8PrJ’43
(3-1-129)
значительно
____Турбулентный
—ра.жим
Переходи Ь^~Т^-Д~~
 режим
Ламинарный
режим
(3-1-132)
В расчетах по данной схеме обыч-
но предполагается полная- аналогия
между теплообменом и массообменом.
Тогда Nn^=(NuJC)/n, где массообмец-^
ное число Нуссельта равно теплооб-
менному числу Нуссельта. Коэффи-
циент сопротивления С при обтекании
пластины зависит от степени турбу-
лентности е или от критического значения числа (Rej)Kp, так как между ни-
ми существует однозначная зависимость (рис. 3-15).
Зависимость между коэффициентом С и числом Re; может быть представ-
лена в виде [Л.3-131
0,074_____А
Rc°'2 Re; ’
где постоянная А определяется из табл. 3-4.
е*Юг
0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 '
Рис. 3-15. Зависимость критического
числа Рейнольдса Re от степени тур-
булентности е.
3
2
(3-1-133)
Зависимость постоянной А от (Re#)K
(Rez)KP	) • 10»	3-10’	5-10S	' ЫО»
А	360	1050	1700	3300
201
3*2. ВЗАИМОСВЯЗАННЫЙ ТЕПЛОМАССООБМЕН
ПРИ ЛАМИНАРНОМ ОБТЕКАНИИ ПЛОСКОЙ ПЛАСТИНЫ
Вдув в пограничный слой
Тепломассообмен пористой пластины со вдувом в пограничный сдой, газо-
образного хладоагента является одной из важнейших задач современной тех-
ники. Задача формулируется так; пори-
стая пластина обтекается потоком нагре-
того газа. Для охлаждения поверхности
пластины через се поры подается инерт-
ный газ с некоторой постоянной скоро-
стью вдува v-щ. Требуется рассчитать
профили скорости vx(y), температуры
Т (0 и концентрации W (£/) в погранич-
ном слое (рис. 3-16). Систему дифферен-
циальных уравнений переноса импуль-
са, теплоты и массы для стационар-
Рис. 3-16. К расчету тепломассообмена при
обтекании пористой пластины со вдувом
газа в пограничный слой.
ного плоскопараллельного потока (фУт)=0; (пг==0) можно написать так;
. dvx д / dvx\
рнл--7 - -г ру» ~3— = -г- п ;	(3-2-1)
Зх у ду ду\* ду}'	4	’
^(р"Л+^ (₽”»)=°:	<3'2'2>
дТ , дТ д I, 9Т\ , fdvx\* ,	, ,дТдК „ о Оч
+	(3'2'3)
dW , dW д ! „ dW\	о 4
v дх у ду ду\ ду'	>
где W — относительная концентрация (№ s р10).
Предполагается, что обтекающая жидкость является двухкомпонентпой
газовой смесью при постоянном давлении p=const. Индекс 1 обозначает обте-
кающий пластину -газ, индекс 2—-вдуваемый газ. Эффектами Соре и Дюфо
пренебрегаем. Граничные условия имеют вид (см. рис. 3-15):
при у^Ъ; v^ = 0 vy = ow = const; Г = 7^ = const
или
!дТ \
Ы^0; ir=^®=const;	(3-2-5)
при у^ со =	Т^Т^; Й7 = 1?7ОО.
Для решения системы уравнений (3-2-1) —(3-2-4) можно ввести дальнейшие
упрощения- 1) пренебречь переносом теплоты путем диффузии; 2) считать жид-
кость несжимаемой; 3) считать переносные свойства жидкости постоянными
(4 = consf, A=const, DIS —const). Тогда система уравнений (3-2-1) —(3-2-4)
примет вид;
х . дих cPvx dvx . dVy _
—— + рП(/ — = г) —-; _ -)--------------£ = 0;
дх ду ду2 дх ду
дТ ,	дТ	д2Т
vx^~ + utis- =
х дх ‘ и ду	ду2 ’
дУ7 , dW „d2W
V х т- + V у -V- = и -Z-Z- .
дх у ду ду2
(3-2-6)
(3-2-7)
(3-2-8)
20?
Из системы дифференциальных уравнений переноса можно получить инте-
гральные уравнения переноса пограничного слоя для граничных условий (3-2-5).
Дифференциальное уравнение переноса импульса для случая градиентного
обтекания (rJp/dx =£ 0) плоской пластины стационарным потоком жидкости
можно записать так:
ди-„ d(vrv„\ dvrc. d2v
d(PW*) ,	dv^
dx	dy ~ Vjc dx '
При этом было использовано уравнение Бернулли
dv^ dp
dx ~ dx '
(3-2-9)
(3-2-10)
(3-2-11)
Вычитая почленно из уравнения (3-2-9) уравнение (3-2-10), получаем:
аах [Р“.	- М]+^ [р°9	р	. (3-2-12)
Интегрируем уравнение (3-2-12) по у в пределах от 0 до 6, при этом
используем условия (3-2-5):
б	б
о	о
(3-2-13)
Уравнение (3-2-13) отличается от соответствующего уравнения без вдува
дополнительным членом	характеризующим виртуальное трение за счет
вдува, Интегральное уравнение пограничного слоя для переноса теплоты по-
лучаем из дифференциального уравнения для случая, когда dpfdx^O.
Проинтегрируем уравнение переноса теплоты по у в пределах от 0 до 6:
бу	бу 1	бу	бу
Р ЛТ С dT (• dvca с Л I лт\
( aT^+J	(3-2-U)
о	о	о	о
Вторые члены левой и правой частей уравнения (3-2-13) можно проинте-
грировать с использованием граничных условий (3-2-5):
бу	бу бу
(*	(?Г	11’ ^(Ррх)
j epPVx ~^Лу+Ср(ЯуТ I + срТ———d'y —
Приняв во внимание, что
и переставив операции интегрирования и дифференцирования, получим:
бу
J (cfK»T<»—срт) Pvxdy = ^[^w + P^ 1СРЛ~ cp&Twy (3-2-16)
203
Уравийвиъ (3-246) отличается от интегрального уравнения пограничного
слоя без вдува дополнительным членом, характеризующим молярный перенос
теплоты вдуваемым газом. Аналогичным путем получим интегральное уравне-
ние переноса массы:
(^»-ИрМ» = рЛ2(^-₽„М₽«-’М- (3-2-17)
о
Интегральные уравнения переноса (3-2-13)—(3-2-15) и (3-2-16) используются
для приближенных расчетов взаимосвязанного переноса теплоты н массы в по-
граничном слое.
Вернемся к системе дифференциальных уравнений (3-2-6)—(3-2-8). Эккерт
и Хартнетт [Л-3-14] решили эту систему, введя следующие упрощения: I) жид-
кость несжимаема; 2) свойства компонентов не зависят от давления и темпе-
ратуры и мало отличаются друг от друга.
При граничных условиях (3-2-5) эти уравнения можно привести к обык-
новенным дифференциальным уравнениям, вводя функцию тока
vy —— дф/дх) и используя следующие обозначения:
5= | lA>ex/v;
1У», —1У
•
" 1Й w со	•
Полагая, что oc = const, др{дк=<Ь, f, в и ф зависят
т. е. температура поверхности Тк. и концентрация подаваемого
постоянны по поверхности пластины и не зависят от х, получаем:
Ф (vx — dtydy.
(3-2-18)
ТОЛЬКО от
вещества W„,
уравнение	переноса	импульса d’f 4	-Lf^=0. 2'dfi	(3-2-19)
уравнение	переноса	массы		(3-2-20)
уравнение	переноса	теплоты d«0 <й +	ТР<=°	(3-2-21)
при следующих граничных условиях:
пр» £=о i-t\ -0; /„ = -2^VrG; 6=0; Ф=0; j
(3-2-22)
при 5-УСО ЗЕ3’'1 ° = 1; ф”ь	-	J
Из граничных условий (3-2-22) непосредственно следует, что удовлетворе-
ние условия зависимости [ только от £ означает, что vw изменяется обратно
пропорционально ^х.
Отметим здесь, что уравнения (3-2-19)—(3-2-21) можно обобщить на обте-
кание бесконечного клина с углом (ki, где ^ = 2m/(m-^-\), если принять, что
скорость на внешней границе пограничного слоя изменяется по закону
усо = Лхот,
Для потока с постоянными свойствами компонентов уравнение движения
решается независимо от уравнений энергии и диффузии для широкого интер-
204
вала значений fw (величина или ’/a fw называется параметром вдува), а ре-
шения динамической задачи используются для расчета уравнений энергии и
диффузии.
При решении уравнения диффузии существенно следующее обстоятельство:
если стенка не полностью проницаема для обоих компонентов, то вследствие
постоянства полного давления смеси поперек пограничного слоя (др/ду=О)
Рис. 3-17. Развитие безразмерного
профиля скорости в ламинарном
пограничном слое в зависимости
от параметра вдува.
Рис. 3-18. Безразмерные профили тем-
пературы 6 и концентрации ф в лами-
нарном пограничном слое плоской пла-
стины при разных параметрах вдува
r^J^Re^ Для критерия Прандтля 1,0
и 0,7 (сплошная линия — Рг = 0,7,
Sc==0,7; пунктирная — Рг= 1, Sc= I).
возникает молярное движение смеси, которым частично отводятся от стенки
одновременно оба компонента. Для полностью непроницаемой для газа основ-
ного потока стенки величина vw составляет;
_______012 __	\
w~ l-Ww\dy)w‘
(3-2-23)
Путем несложных преобразований можно получить:
1-Гк,
'	)а>
(3-2-24)
Условие (3-2-24) означает, что существует определенная связь между па-
раметром вдува и концентрациями подаваемого газа на обоих границах
пограничного слоя, т. е. величины / , Ww, нельзя выбирать произвольно.
Этим и объясняется, что число граничных условий на стенке и на внешней
границе пограничного слоя не совпадает.
Результаты расчетов решений уравнений (3-2-19)—(3-2-21) представлены
ла рис. ,3-17 — 3-19,
На рис. 3-17 приведены графики ех/есо = /(^) для параметров вд^ва от
0,6 до 0,0 н для отсоса (параметр вдува отрицателен). Из рис. 3-17 видно, что
при параметре вдува 0,619 продольная скорость vx равна нулю, т. е. погра-
ничный слой оттеснен вдувом.
На рис. 3-18 даны графики 0=/(S) и гр (£) для вдуаа и отсоса при изме-
нении параметра KRe# от 0,6 до 2,5 при условии, что концентрация
равна нулю.
205
Графики qj=f(g) для случая 1^ф = 0 приведены на рис. 3-19.
Обращают па себя внимание некоторые существенные и важные в смысле
практического применения закономерности:
1, Вдув дестабилизирует пограничный слой, с ростом /а, происходит утол-
щение, урезание и искривление профилей, они принимают S-образную форму.
Эммонс и Лей ГЛ.3-151 показали, что
Рис. 3-19. Профили концентрации
ф в ламинарном пограничном слое
при разных значениях параметра
вдува	1Р«.= О, т = 0
(сплошная линия —Sc = 0,7; пунк-
тирная — Sc = 1).
слоя заставляет искать ценой потер
при f—>-0,619 решение уравнений по-
граничного слоя содержит условия
(6vx/6y)w=O и ох=0 при любом конеч-
ном у. При этом происходит оттесне-
ние пограничного слоя от поверхности
пластины и, следовательно, система урав-
нений пограничного слоя при сильных
вдувах не отражает истинной картины
переноса в ламинарном потоке.
2. С ростом параметра вдува сни-
жаются поверхностное ’трение и интен-
сивность теплообмена, т. е. вдув может
служить средством защиты поверхностей
от нагрева.
3. При равенстве чисел Рг и Sc по-
перечный поток оказывает одинаковое
воздействие на развитие и деформацию
профилей температуры и концентрации, а
при соблюдении условия Pr=Sc = l на-
блюдается тройная аналогия—это прямо
следует из уравнений (3-2-19)—(3-2-21).
Сложность непосредственных реше-
ний системы уравнений пограничного
и точности более простые пути получения
результатов.
Одним из способов упрощения системы уравнений пограничного слоя
является переход от локального их удовлетворения в каждой точке рассмат-
риваемого пространства к осреднению
по толщине пограничного слоя, т. е. к
использованию интегральных уравнений
пограничного слоя.
Састри и Хартнетт [Л.3-16] иссле-
довали влияние начального участка
пластины Xq, па котором вдув отсутствует
(рис. 3-20).
Результаты решений системы урав-
нений переноса представлены ца рис,
3-21—3-24. Из рис. 3-20 видно, что влияние
начального участка особенно сильно ска-
зывается при параметре вдува, большем
0,2, Рядом показан график, взятый из
работы Спэрроу и Стара [Л.3-17], когда
начальный участок был равен нулю. На
рис. 3-22 показано влияние начального
участка х0 на число Стантона при вдуве St
при параметрах вдува 0,25 и 0,5. Число
Стантона в отсутствие вдува обозначено ч<
Рис. 3-20. Схема вдува в-погранич-
ный слой при обтекании пластины.
St0. На рис. 3-23 дана зависимость
относительного коэффициента трения Су/Су0 от параметра вдува ~
для разных значений параметра х/х0 от 1,2 до со, На рис. 3-24 сравниваются
расчетные данные авторов с известными литературными данными [Л-3-17, 3-18].
Приведенные графики показывают значительное влияние начального участка х0
на все интегральные характеристики переноса импульса и энергии,
20U
Для случая безградиентпого обтекания плоской пластины с пористым под-
ВОдом* вещества установившимся потоком газа интегральные уравнения (3-2-13),
Рис. 3-21. Влияние начального участ-
ка х0 на теплообмен при разных пара-
метрах вдува [Л, 3-161-Пунктиром по-
казано решение, приведенное в вабоге
[Л. 3-17].
Рис. 3-22. Зависимость St/Sf®
от x!xq для параметров вдува
0,25 и 0,5 [Л. 3-16].
Рис. 3-23. Зависимость относительно-
го коэффициента трения С;/Су0 от па-
раметра вдува при разных значениях
х/х0 (сплошная линия — расчет, пунк-
тирная — данные Спэрроу).
Рис. 3-24. Сравнеггие расчетных дан-
ных {Л. 3-16] (сплошная линия) сдан-
ными, приведенными в работе [Л.3-17]
для случаи х0 = 0 (пунктир) н
с данными '[Л. 3-18] при х!хй = 2
{Л. 3-18] (штрих-пунктир).
(3-2-16) и (3-2-17) можно представить в упрощенном виде [пренебрегая вторым
членом в левой части уравнения (3-2-13)]:
уравнение переноса импульсов
уравнение энтальпии
А. И	Су
dx	~ 2 ’
CpwPw^w
(3-2-25)
(3-2-26)
207
уравнение диффузии
dx
РЭД/В&1___Pw
P^“ m POT ’
(3-2-27)
где 6B.1|t 6В,Э и бв.м — соответственно толщины вытеснения импульса, энергии
и массы, равные;
S„.„= (
Для решения обыкновенных дифференциальных уравнении (3-2-25)—(3-2-27)
необходимо знать связь между характеристиками пограничного слоя и пото-
ками импульса, энергии и массы па стейке.
Базируясь на теории динамического слоя конечной толщины, Карман и
Польгаузен предложили заменить неизвестный профиль продольной скорости
в пограничном слое некоторой интерполяцией (в частности, полиномиальной),
удовлетворяющей определенным, наперед заданным краевым условиям па
стенке и па внешней границе пограничного слоя. Уравнение профиля запи-
сывается в безразмерных координатах у/б, так что после подстановки его
в-интегральное соотношение импульсов оно превращается в обыкновенное диф-
ференциальное нелинейное уравнение относительно одного неизвестного б (х).
Решив это уравнение любым приближенным способом, определяют б (х), а за-
тем и все искомые характеристики.
Таким образом, результаты расчета будут зависеть от" того, насколько
удачно выбран вид интерполяционной формулы для профиля скорости и Гра-
ничных условий, определяющих коэффициенты в этой формуле. Такого рода
подход к решению задачи весьма удобен при анализе экспериментальных дан-
ных, когда имеются непосредственные измерения в пограничном слое, а также
известные условия на стенке Tw (х), qw (х) и /да (х).
Систематизация всех имеющихся экспериментальных данных по вдуву
различных газов в ламинарный пограничный слой плоской пористой пластины,
омываемой воздушным потоком, позволила получить обобщенные соотношения
для расчета локального теплообмена и поверхностного трения [Л.З-19|;
~= I - 2,08	~— Г Res:	(3-2-28)
-3-=1-1,82 (4^У/3-₽Л	(3-2-29)
где М—молекулярная масса.
Величины р и Rex вычисляются по определяющей температуре Г*;
7* =^ + 0,5 (Тт-Тю)+0,22	Тю),	(3-2-30)
где Тго — температура восстановления на поверхности твердого тела без подвода
массы, но с идентичными граничными условиями. Из (3-2-28) и (3-2-29) следует
физически достоверный и подтвержденный на практике вывод о том, что
легкие газы являются более эффективными охладителями.
Интенсивное развитие в последнее время быстродействующей вычислитель-
ной техники открыло почти неограниченные возможности для весьма надежных
208
и точных численных расчетов совместно протекающих процессов тепломассооб-
мена при минимальных по количеству и силе допущениях. Правда, недостатком
численных решений является их некоторая узость и ограниченность; для полу-
чения общих количественных связей требуется дополнительная обработка боль-
шого числа таких частных решений. Однако конкретную задачу численно
можно решить сколь угодно точно. Вероятно, этим и обьясняется сравнительно
ограниченное количество экспериментальных работ по вдуву в ламинарный
пограничный слой.
Тепломассообмен при испарении.
Теоретические результаты по вдуву инертных неконденсируемых газов
принято обобщать и на случай испарения с поверхности тела в вынужденный
лоток газа. При этом предполагается, что реализация условия независимости
величин Tw и Ww от х выполняется автоматически: испарение относится к
числу фазовых переходов первого рода, протекающих при постоянной темпера-
туре, а концентрация генерируемого пара связана однозначно с температурой
испарения по уравнению кривой насыщения. При этом отпадает необходи-
мость создания пористых материалов, закон изменения пористости которых
обеспечивал бы условие подачи инжектапта пропорционально х~°-5.
Имеющиеся экспериментальные исследования такого предположения не
подтверждают. Так, например, при
3. П. Шульманом [Л.3-20], с данны-
ми [Л.3-21] по теплообмену кругового
цилиндра обнаруживается, что в лами-
нарном пограничном слое при одина-
ковых параметрах fw испарение су-
щественно эффективнее вдува в смысле
защиты поверхности. Аналогичная
картина получается, если сопоставить
результаты теоретических расчетов
|Л.'3-14] с этими же экспериментами.
Оказалось, что в одном и том же ин-
тервале значений параметра вдува
теплообмен при испарении в 1,5—1,9
раза меньше, чем при вдуве.
Такое разногласие может быть вы-
звано объективными причинами, отра-
жающими как существенное различие
процессов вдува и испарения, так и
специфические моменты, присущие толь-
ко испарению. Линейная скорость испа-
рения /i/pt’ хотя и имеет размерность
сравнении зависимостей, полученных
Рис, 3-25. Изменение относительных
коэффициентов тепло- и массообмепа
в зависимости от параметра вдува
Уда-------------------
скорости, но не является скоростью
в обычном понимании этого слова, как величина, характеризующая макроско-.
пическое перемещение тела в единицу времени (скорость молярного движения).
Испарение представляет собой диффузионный процесс, вызываемый наличием
.перепада концентраций в пограничном слое. При отсутствии перепада концент-
раций испарение невозможно, тогда как можно осуществить механический пдув
газа, однородного с основным, даже в изотермический поток газа, поскольку
собственно вдув представляет собой молярный процесс по типу гидродинами-
ческого истечения вследствие наличия перепада полных давлений между источни-
ком инжектанта и газовым потоком.
Процесс диффузии представляет собой перемешивание вещества при помощи
молекулярного (хаотического) движения. В направлении диффузионного потока
вещества проходит большее количество молекул, чем возвращается обратно.
Это и обусловливает молекулярный поток вещества, характеризуемый условной
линейной скоростью диффузии.
На долю конвективного переноса приходится лишь ^1/(1—IFf) молекуляр-
ного (скорость стефановского потока	где р—плотность смеси). Именно
209
этот поток при испарении и оказывает свое воздействие ла гидродинамику
в пограничном слое. Таким образом, в результате неодинакового механизма
переноса вдува и испарения поперечный массовый поток оказывает разное
действие па теплообмен.
Кроме того, испарение имеет и другие характерные отличия.
Для анализа влияния переноса пара при испарении на тепломассообмен
вернемся к решению Эккерта и Хартнетта [Л.3-14]. Если рассчитать коэффици-
енты тепло- и массообмена по формулам
pD(dW/dy)w
(3-2-31)
(3-2-32)
и обозначить их значение при отсутствии вдува через” а0 и ат0, то результаты
расчетов можно представить в виде графиков, приведенных на рис. 3-25.
Из рис. 3-25 видно, что с увеличением vw коэффициенты тепло- и массообмена
уменьшаются и при значении (ит/иСХ)/['гЦех=0,64 становятся равными нулю.
Наоборот, при обратном направлении конвективного потока коэффициенты тепло-
и массообмена увеличиваются; так, при значениях j/Rex = 4 и Рг —Sc= 1
они возрастают в 12 раз.
Можно показать, что в процессах испарения жидкости фактор поперечного
потока массы fw = (y^/v^ j/ Rex мал и не может влиять на коэффициенты
тепло- и массообмена.
Поперечная скорость vw в процессе испарения жидкости со свободной
поверхности равна;
Пр { д\У \ /w_________
I — Ww ду /w (1 —№да)р ’
(3-2-33)
где jw— интенсивность испарения.
Для упрощения положим	— Рю=О, vw = -~-, Тогда будем иметь;
Прй стационарном режиме интенсивность испарения
. _ аА- СО ~~ Tw)
/и>—	r	—	-------- г=
“^М/Ж(Г»-Лв)Рг1''3.
Если подставить (3-2-35) в формулу (3-2-34), то получим:
гр,.2/3
(3-2-34)
(3-2-35)
(3-2-36)
Следовательно, fu. зависит не от скорости движения, а от температурного
напора Т	и теплофцзических свойств потока.
Для того чтобы коэффициенты а и агп уменьшились по сравнению с коэф-
фициентами ссп и ага0 на 10%, значение [w должно быть не меньше 0,05
(см. рис. 3-25). Если положить /да = 0,05, г=579 ккал/кг, ЛА-==0,3, Рг —0,7,
то температурный напор \Т = Т1Х}—Tw должен быть выше 26072. Дакие тем-
пературные напоры при конвективной сушке встречаются очень редко. Поэ-
210
тому решение, представленное на графиках на рис, 3-25, справедливо для
случая обтекания пористой пластины при вдуве в пограничный слой инерт-
ного газа со значительной скоростью.
Один из существенных эффектов молекулярного взаимодействия жидкости
со своим паром и со скелетом стенки —связь жидкости с материалом стенки,
характеризуемая величиной энергии связи. Поэтому при термическом способе
удаления жидкости из смоченного ею капиллярно-пористого тела необходимо
учитывать кроме теплоты фазового перехода еще и энергию связи, величина
которой зависит от вида связи жидкости с материалом капиллярно-пористого
тела. По классификации акад- П. А. Ребиндера [Л,3-22] все формы связи
делятся на три большие группы: химическую, физико-химическую и физико-
механическую.
При испарении происходит изменение проточной системы пор. Часть кана-
лов может стать непроходимой для пара из-за закупорки их зависающими
столбиками —«пробками»' жидкости. Структура естественного пористого мате-
риала в обшем неоднородна. Большинство открытых наружу пор пересекается
между собой, и уровень жидкости в них определяется не только выбором
величины гидростатического подпора при ее подаче, но и геометрическими
характеристиками структуры. Некоторое количество жидкости растекается по
внешней поверхности пористого тела, заполняя впадины между отверстиями
пор и бугорками шероховатостей. Поверхности менисков и открытых наружу
поровых каналов искривлены, поэтому эффективная поверхность массообмена
оказывается существенно большей, чем суммарная площадь поперечных сече-
ний открытых пор.
Особенностями, присущими только процессу испарения, являются моляр-
ное диспергирование и испарение субмикроскоцических капель жидкости
в пограничном слое. Гипотеза объемного испарения, связанная с динамиче-
ским характером процессов сорбции и десорбции, выдвинута в работе [Л.3-23]
и состоит в следующем: в результате воздействия потока (механическое увели-
чение и конденсация по стенке) с поверхности в пограничный слой попадают
мельчайшие частицы жидкости. По теории адсорбции Де Бура [Л.3-24] про-
цесс испарения есть динамический процесс десорбции и сорбции. Молекулы
жидкости не только покидают поверхность (испарение), но и непрерывно воз-
вращаются (конденсация). Интенсивность испарения пропорциональна разности
потоков молекул. Так как конденсация происходит неравномерно [Л.3-25] и
на некоторых участках поверхности имеет место неполное смачивание адсор-
бированным слоем ожиженного пара, то образуются капли, менее прочно свя-
занные с жидкостью, которые выносятся потоком газа в пограничный слой и
испаряются в его объеме. Объемное испарение представляет собой источник
пара и отрицательный источник теплоты в уравнениях пограничного слоя,
В подтверждение этой гипотезы можно-привести непосредственные наблюдения
Мальмквиста и Мейснера [Л.3-26], которые в опытах по сушке древесины
в перегретом паре с помощью теплера обнаружили вынос полимеризованных
молекул пара в пограничный слой и их испарение в его объеме. Г1рч испаре-
нии жидкости из капиллярно-пористого тела могут иметь место три различных
случая расположения поверхности испарения.
I.	Поверхность тела все время покрыта слоем жидкости постоянной тол-
щины. В этом случае процесс аналогичен испарению со свободной поверхности.
2.	Очаговое испарение, когда процесс происходит из концов капилляров
тела. Уровень жидкости в капиллярах совпадает с видимой геометрической
поверхностью тела, таким образом, не вся внешняя стенка является зеркалом
испарения. При очаговом характере испарения па омываемой средой поверх-
ности происходит быстрое изменение объема вещества, которое даже может
изменить характер движения в пограничном слое.
3.	Поверхность испарения может смещаться в глубину материала. Заглуб-
ление зоны испарения происходит неравномерно по отношению к поверхности
стенки и зависит от размеров капилляров. .Благодаря сухой прослойке обра-
зуется дополнительное термическое сопротивление переносу теплоты и веше-
ства от жидкости во внешнюю среду. При таком испарении происходят цир-
куляция теплоносителя в освободившихся капиллярах и повышение полного
211
(3-2-38)
(3-2-39)
(3-2-40)
(3-2-41)
давления, способствующее выносу капелек жидкости в пограничный слой, На
интенсивность протекания процесса большое влияние оказывает структура
материала, следовательно, между внутренней и внешней задачами тепломассо-
обмена должна существовать глубокая связь.
Таким образом, для правильного суждения об интенсивности испарения
нужно в каждом конкретном случае выявить все эти эффекты и дать им коли-
чественную оценку. Перечисленные факторы весьма усложняют аналитические
решения краевых задач для совместно протекающих процессов конвективного
переноса при испарении жидкости в пограничный слой.
Аналитическое решение задачи о -Тепломассообмене при испарении жидко-
сти из глубины пористой пластины в ламинарный пограничный слой изложено
в работе [Л.3-27]. где рассматривалось дифференциальное уравнение переноса
теплоты в виде
ат^.у) ат (х, у) _ »т (х, у) с„-с1а ат(х,у)
°' дх • ду ~а а^	—Гу—•	(3'2’37)
Для качественного анализа влияния углубления поверхности испарения
па теплообмен можно воспользоваться решением уравнения (3-2-37)\при еле-
дующих упрощениях. Если Рг«^1, то можно положить;
vx=!&x — const; vy= vy = consi; /7р = соп$
Тогда (3-2-37) можно записать так:
я дТ (* У> । дТ л У)
Vx дх у ду ~ dtp
где
Ср1~Ср$
V* = V„ -|--------V. = const-
y У Ср I
Температура поверхности испарения считается постоянной:
Г (х, —!)^Te=const.
Таким образом, граничные условия можно написать так;
при х=0	Г (0, у) = Т^-
при у=—В Т (—В, х) = Те = const;
л , дТ (х, 0)	, дТ (х, 0)
„Р„	, = 0
при у=со Т (х, со) = Та~.
Индекс а обозначает твердое, тело, а индекс/— жидкость. При этом предпо-
лагается, что энтальпия потока, пара в пограничном слое тела (—0) одина-
кова с энтальпией пара в пограничном слое воздуха (0, б). Энтальпия воды
переходит в пар без затраты теплоты.
Для малых значений £ (£//	1) можно принять линейный закон распре-
деления температуры в сухом слое £. Тогда при у = 0
~--"ду Х’гН\ГЛ, *>-Г,]=0,	(3-2-42)
где
При больших значениях заглубления зоны парообразования £ профиль
температур внутри сухой прослойки можно аппроксимировать экспоненциаль-
ным законом [Л,3-28]:
Т(~у, х)=Тв+/(х)[1-е-л^,],	(3-2-43)
212
k—постоянная; f (х) —функция, отображающая изменение температуры
 --------------  направлении потока жидкости. При этом'сохраняется
где
поверхности пластины в
условие (3-2-42), но

11 J./(cxpAi—1)
(3-2-44)
Решение уравнения (3-2-39) при данных граничных условиях имеет вид:
Из решения (3-2-45) можно получить частные случаи; а) теплообмен, не
осложненный массообменом; б) теплообмен при испарении жидкости с поверх-
ности капиллярно-пористого тела (£ = 0, Я->-сс).
Определим локальное число Нуссельта:
Nu -	____ат^.л
"	Т„-Т(0, х) ду
и введем функцию ЛЛ (/(, В):	х
Nu,  -------------- аг (0, Х> = kite^Pr ЩК, В),	(3-2-46)
7'СО-Т(0,х) ду Гл
где
Ф (К, В) — у /л В erfc у В
N(K,B)=------у----------------------j---------j--; (3-2.47)
( 1 - }- (К К^)-1 Ф (К, й) + у	erfc g В
здесь
<р (К, В) = (1 - -2- А) |/л к ехр (№ - В К) erfc (к—в) 
На рис. 3-26 приведены графики V (/<>	для разных значений В
(от 0 до 2). Если положить V*=6 (малые значения критерия Прандтля Рг —> 0),
то В = 0. В этом случае /V (К,	1 [кривая N (К, 0) асимптотически при-
ближается к единице]. Следовательно, число Нуссельта при углублении поверх-
ности испарения будет больше числа Нуссельта при испарении на поверхности
тела (^ = 0, /( = со). Этот вывод непосредственно следует из решения (3-2-45),
так как температура поверхности пластины увеличивается вдоль потока жид-
кости (вдоль оси х). Из общей теории теплообмена известно, что в этом слу-
чае коэффициент теплообмена будет увеличиваться.
213
Покажем, что коэффициент В зависит от числа Рг и скорости стефанов-
ского потока (i>i— jw/p). Если принять распределение скорости по формуле
(3-1-39), то ^ = 5/80^, если же взять функцию распределения Блазиуса Л
(табл. 3-1), то vx — 0,66‘у^;
В = В1+В2- fl1 = 1.23/Re.tPrB,Ao;
В,- 1,23 I Cfl~c'a j\.
\ Pcnfro /
(3-2-49)
Если воспользоваться приближенной формулой (3-1-20), то из рис. 3-3
находим v
х Тогда коэффициент Bj будет зависеть только от числа Рг:
Bi = 0,53 КРг*
(3-2-50)
Например, для воздуха (Рг = 0,7) Bi = 0,44. Коэффициент В2 является
величиной, пропорциональной парамет-
ру вдува fw [см. формулу (3-2-34)]. На-
пример, для влажного воздуха с,р1 = О,47,
Ср2 = 0,24, тогда
В2=0,427 i-I RSI - (3-2-51)
К для разных значений В.
Если в качестве параметра вдува
воздуха принять формулу (3-2-34), то по-
лучим:
В2 = 0,427/'а,.	(3-2-52)
В процессах конвективной сушки
большинства материалов параметр вдува
значительно меньше 0,05. Следователь-
но, коэффициент В2 меньше коэффици-
ента Bi (отношение В^/В^ < 0,05), т. е.
Вг Bi- Сделаем оценку метода реше-
ния уравнения (3-2-37) путем усредне-
ния скоростей vx и Vy по пограничному
слою. Положим, что испарение отсутствует, т. е. В2 = 0, £ = 0, а коэффициент
К-- со.
В этом случае
ф (со, В)=ехр(-------— Ь	(3-2-53)
/	02 '	1	I
N (оз, В)_ехр(---—В erfcВ,
(3-2-54)
где В = Вг [для воздуха В = 0,44; V (со; 0,44) = 0,659].
Тогда в соответствии с формулой (3-2-46)
Nu^= Re^PrN (со,
У л
В) = 0,252/Re* ,
(3-2-55)
так как (Rex)1'’2 = 0,81 Re]/2,
Согласно формуле (3-1-73) коэффициент пропорциональности между Nu^
и Re.* равен:
NUj; = 0,332	=0 294,	(3-2-56)
214
что отличается от коэффициента в формуле (3-2-55) примерно па 10%. Следо-
вательно, метод усреднения скоростей &х и vy дает удовлетворительные
результаты.
Из формулы (3-2-54) видно, что с увеличением В величина Л' (со, В) умень-
шается, т. е. увеличение интенсивности испарения (увеличение коэффициента В,)
вызывает уменьшение числа Nuv.
Однако углубление поверхности испарения (уменьшение коэффициента /<)
вызывает увеличение Л' (/(, В), а следовательно, и числа Nux (см. рис. 3-25).
Поэтому в зависимости от конкрет-
ных значений коэффициентов и В
число Нуссельта при испарении жид-
кости из пористых тел может быть
больше или меньше числа Нуссельта
Nux0 в отсутствие испарения /V (/(, В)=
= ДА (со, Bi)
Рис. 3-27. Зависимость безраз-
мерного числа Нуссельта от
относительной скорости сушки
для различных материалов в
процессе конвективной сушки.
Рис. 3-28. Зависимость между величи-
ной ДА'	» S^V(co, B)j и
величиной.
а — пористость П = 42%; б — П = 38%; в —
Л = 36%; .г —/7 = 35%.
Например, при конвективной сушке различных материалов среднее число
Нуссельта Nu увеличивается с увеличением интенсивности сушки jw. На
рис. 3-27 показана зависимость NuKp/Nu от относительной интенсивности
сушки (/да = /а,//дакр), где индекс «кр» обозначает значение величин при
критическом влагосодержании материала. На основании рис. 3-27 можно
написать:
N“ = Nu«p/l0'E7-	(3-2-57)
Отсюда можно сделать вывод, что в Процессе сушки испарение жидкости
происходит па некоторой глубине от поверхности тела ($ ^ 0, /<^со).
Экспериментальная проверка предложенной физической модели показала
ее достоверность [Л.3-30]. Были поставлены опыты по испарению воды в лами-
нарный пограничный слой пористой пластины | при различных заглублениях
поверхности испарения и разной пористости П. На рис. 3-28 построен график
= по данным формулы (3-2-47) для В — 0,2 и нанесены эксперимен-
тальные точки. Из рис. 3-28 видно, что опытные точки близки к расчетной
кривой.
Для удобства пользования формулой (3-2-46) в практических расчетах
можно получить ряд приближенных формул для величины N (К, В),
215
Обозначим:
(3-2-58)
/У(К, В) Ы1К
М (со, В)	(Nux)|_0 ’
Число (V* равно отношению числа Нуссельта при углублении поверхности
испарения к числу Нуссельта при отсутствии углубления (испарение проис-
ходит па поверхности тела).
Тогда будем иметь следующие приближенные формулы:
Л'* — 1=#* — аК при 0,1 <^<1,0;	(3-2-59)
при 1 < К < со.	(3-2-60)
Постоянные коэффициенты N%, а, р зависят от коэффициента В (см. табл. 3-5).
Таблица 3-5
Зависимость коэффициентов Af?, а и £ от коэффициента В
Коэффи- циент В	0	0,1	0,2	0.3	0,4	0,5	0,6
	0,56	0,61	0,7	0,79	0,90 д	1,0	1,6 <
а	0,21	0,25	0,29	0,33	0,37	0,41	0,44
	—	0,46	0,54	0,62	0,74	0,83	0,92
Расчеты показывают [Л. 3-27], что при углублении даже на 0,5 мм
интенсивность теплообмена возрастает примерно на 25 % по сравнению
с теплообменом при испарении с поверхности.
Вместе с тем при' столь малых заглублениях очень трудно измерить
действительную температуру поверхности и температуру испарения и в расчеты
Nux вводят перепад температур Тм—Те- Поэтому более правильно говорить
о коэффициенте теплопередачи от нагретого газа к поверхности испарения
через пограничный слой среды и обезвоженный пористый слой;
- (3-2-64
Если коэффициент теплообмена определять к разности температур (Г^ —
— Те), тогда формула для числа Нуссельта примет иной вид;
Nu„_---------------- (0-	= ‘ Vr1?p7jV (7<, В),	(3-2-62)
ду Ул	‘	1	1
где
Ne(K, В)=(1-^Р|ф(К( В) — -^/^Вег[с1в’|.	(3-2-63)
Из формул (3-2-62) следует, что с увеличением К Ne(K, В) увеличивается,
т. е. с углублением поверхности испарения (с, возрастает, коэффициент К
уменьшается) число Нуссельта Nuv<? будет уменьшаться, В этом случае углуб-
ление поверхности испарения действует аналогично вдуву газа в пограничный
слой. Физически это объясняется так; поскольку температурный напор (Т—
— Те) является постоянным, то с углублением поверхности испарения коэф-
фициент теплопередачи уменьшается за счет увеличения термического -сопро-
тивления пограничного слоя твердого тела. В этом случае в число Нуссельта
Nu.ve вместо коэффициента теплообмена ос входиг коэффициент теплопередачи k.
Ддя приближенных расчетов можно использовать формулу
д/s Ne {К, В) Nuxr Ck'mi	/з 9 64)
N- (3- 541
где С и m—постоянные.
216
В работе ]Л. 3-37] приведены экспериментальные данные по испарению
воды из пористой бронзовой пластины (20x8,7x1,4 см) пористостью/7 = 40%.
Скорость потока воздуха изменялась от 1 до 10 м/с, а температура —от 50
120^С. Результаты экспериментов представлены на'рис. 3-29, из которого сле-
дует:
Nue = 0,05 Re°’6K0-22 при 104 < Re < Ю5.	(3-2-65)
В ряде работ [Л. 3-13 — 3-20] показатель степени т в формуле (3-2-65)
был 0,3 или 0,28.
Рис. 3-29. Зависимость Nu//Re016 от К-
Заглубление g = 0.Z мм; О — 1,8 мм; 0 — 3,2 мм; 0 — 4,5 мм.
Аналогично решается дифференциальное уравнение диффузии:
яД— =	(3-2-66)
х дх у ду ду1	к '
Однако изменение массообменного (диффузионного) числа Нуссельта (Nux)m
не совпадает с изменением теплообменного числа Нуссельта Nux от коэффи-
циентов К и В, так как имеет место неравенство
Ь/ Of ‘
(3-2-67)
Во всех экспериментальных исследованиях было установлено, что с увели-
чением интенсивности испарения диффузионное число Нуссельта увеличивается.
Так, в работе [Л. 3-37] приведена эмпирическая формула по испарению воды
в поток воздуха, полученная на основе обработки экспериментальных данных
ряда исследователей:
Num = Sh== 0,078 Re°-6№0>6 при 1,5.101 < Re <2.10’, (3-2-68)
где Sh —число Шервуда.
Д. Сполдинг [Л. 3-31] .предложил .упрощенный метод расчета конвектив-
ного потока теплоты для условий стационарного неадиабатического испарения
с поверхности обтекаемого тела, В основе метода лежит допущение о пропор-
циональности удельного конвективного потока теплоты qa при неадиабати-
ческом испарении величине отклонения действительной температуры поверх-
ности Tw от равновесной Те, которую приняла бы поверхность в адиабати-
ческом процессе, т. е.
(3-2-69)
сРт
здесь «о — коэффициент чистого теплообмена непроницаемой стенки, помещен-
ной в одинаковые тепловые и гидродинамические условия с влажной пористой
217
поверхностью; СрЭфф — эффективная теплоемкость парогазовой смеси, равная:
срзФФ:==у >	(3-2-70)
‘ е , Т w
где Л —энтальпия.
Если ввести коэффициент теплообмена обычным способом, то получим:
® -- ZfZLt Срэфф - —ZZZZ—	П 9 7Ь
а	7 _т с	~~с Т —с Т '	V5-4-/1)
О ‘ со it> pea рю со рсо w
При вынужденном обтекании тела концентрацию паров жидкости в ядре
потока можно принять равной нулю, следовательно, Cp^T^ — h.^. Если
пренебречь изменением теплоемкости в интервале температур от Т.^ до
(как показали расчеты, для воздуха при изменении температуры на
не превышает 3%), то cp^Tw равно энтальпии воздуха у поверхности
без испарения,
Тогда можно написать:
I ОО'С оно
пластины
(3-2- 72)
процессе,
на стенке
парогазо-

Следовательно, коэффициенты теплообмена при испарении и в
не осложненном массообменом, при одинаковых условиях в потоке и
относятся как перепады энтальпии в пограничном слое. Энтальпия
вой смеси вычисляется по аддитивному правилу для газовых смесей в зависи-
мости от теплоемкостей и концентраций компонентов. Из формулы (3-2-72) сле-
дует, что (а„/а0)<1, если cpf>Cp2 (теплоемкость пара жидкости больше
теплоемкости газа основного потока) и (а„/а0) > 1 при сР1<Ср2-
Опытами подтверждается возможность снижения теплообмена при испаре-
нии воды, этилового спирта и ряда других жидкостей, теплоемкость паров
которых выше теплоемкости воздуха по сравнению с «сухим» теплообменом.
Однако второе неравенство нуждается в дополнительной проверке, так как
нам неизвестны экспериментальные работы, где бы изучалось испарение
жидкостей с	В заключение остановимся на работах А. В. Нестеренко
[Л. 3-32], в которых было показано, что экспериментальные данные многих
исследователей располагаются на одной кривой, если ввести число Gu (число
Гухмана).
В результате обработки многочисленных данных по тепломассообмену при
вынужденном движении влажного газа А. В. Нестеренко было установлено
следующее соотношение;
NU = 2 + ЛРг0'33 Re" Gu"1.	(3-2-73)
Аналогичное соотношение для массообмена таково;
Sh = Num =2+A' (Sc)0'33 Re"' Gu	(3-2-74)
Постоянные А, п и т, А', п' и т' приведены в табл- 3-6.
Таблица 3-6
Значения постоянных в формуле Нестеренко
Число Re -	A	n	m	A’	n’	m'
1—2-102 3,15- 103-2,2- IO4 2,2- 1СН —3,15 - (Оз 		L .			1,07 0,51 0,027	0.-18 0.61 0,90	0,175 0,175 0,175	0,83 0,49 0,0218	0,53 0,61 0,90	0,135 0,13-5 0,130
218
При более строгом анализе тепломассообмена как единого процесса
необходимо было физические свойства среды характеризовать одновременно
числами Рг и Sc или их произведением. Однако обработка экспериментальных
данных показывает, что влияние числа Sc на теплообмен мало (показатель
степени при Sc в соотношении да Nu очень мал). Так же несущественно
влияние критерия Рг на массообмен.
Строгого физического обоснования введения числа Gu в формулы для
расчета Nu и Nuw до сих пор нет, Одна из гипотез состоит в том, что при
обтекании поверхности жидкости потоком воздуха в пограничный слой попадают
мельчайшие частицы жидкости1.
Объемное испарение частиц жидкости происходит в адиабатических усло-
виях, температура их близка к температуре адиабатического насыщения
воздуха /др Поэтому уравнение переноса теплоты надо дополнить отрицатель-
ным источником теплоты, равным произведению удельной теплоты испарения г
на источник пара /у{г!у). В дифференциальное уравнение диффузии надо
ввести источник массы
Рис. 3-30, Профили относительной скорости (а) и температуры (б) в пограничном
слое у тающей плоской поверхности для различных значений температурного
напора.
Приближенный распет показывает, что величина источника массы !v
прямо пропорциональна числу Gu:
lv~Gu=.T-±Tp' .	(3-2-75)
При наличии радиационного теплообмена объемное испарение будет интен-
сифицироваться за счет поглощения инфракрасных лучей частицами жидкости.
Тогда в критериальное соотношение Nu = f (Re, Рг, Gu) вводится дополни-
тельно параметрическое число Лебедева Lb (Lb — ТГ!ТС), где Тг—температура
излучающего тела. Таким образом, число Gu по данной гипотезе характеризует
объемное испарение в пограничном слое мельчайших частиц жидкости,
Нужно отметить то обстоятельство, что с увеличением числа Gu (уменьше- -
ние относительной влажности) число Нуссельта возрастает. Следовательно,
интенсивность теплообмена, осложненного массообменом, больше, чем интенсив-
ность чистого теплообмена («сухой» теплообмен). Это будет справедливо не
только при ламинарном, но и при турбулентном обтекании поверхности
жидкости.
I Механизм выноса частиц в пограничный слой был обсужден выше,
219
Таким образом, в процессах сушки, и испарения жидкости со свободной
поверхностью влияние поперечного потока парогазовой смеси (стефановского
z	потока) на теплообмен мало. В
Рис. 3-31. Зависимость относительного
числа Нуссельта от числа Кутателадзе
(сплошная линия — расчет, пунктир-
ная — данные).
I — для поды; ? — для этиленгликоля,
репциальных уравнений (3-2-6), (3-2-7),
следующие:
отличие от вдува газа в погранич-
ный слой увеличение скорости ис-
парения вызывает не уменьшение
а увеличение числа Нуссельта, Од’
нако эти выводы нельзя распро-
странить на испарение льда (суб-
лимацию льда). Если при конвек-
тивной сушке параметр вдува
согласно формуле (3-2-36) меньше
0,05, то при сублимации он будет
значительно больше, поскольку теп-
лота плавления льда г значитель-
но меньше теплоты парообразова-
ния.
В работе [Л. 3-32] решалась
задача тепломассообмена при об-
текании затвердевшей жидкости
нагретым потоком газа. Для этой
задачи исходная система диффе-
граничные условия принимались
при у=0 ох = 0;	= WT/ду^грОц..;
при у-*- со 4=0^; 7=7%.
(3-2-76)
(3-2-77)
Решение было получено методом итераций, На рис. 3-30 приведены профили
скорости и температуры для различных значений температурного напора.
На рис. 3-31 приведено изменение-относительного локального числа Нуссельта
от параметра Параметр /Cj- обратно пропорционален параметру вдува:
кт=г л*Рг-2/3 '	(з-2-тв)
•'ргсо
Из рис. 3-31 видно, что с уменьшением параметра К?, т. е. с увеличением
параметра вдува fu., число Нуссельта уменьшается.
При конвективной сушке (г =«580, АТ 200X2, ср = 0,25) параметр Кг^±
=«12*. Тогда согласно рис. 3-31 уменьшение числа Нуссельта не больше-2%.
При сублимации льда (/ = 80, ДТ = 50°С, <?р = 0,25) параметр Кг=6,4. Тогда
уменьшение числа Нуссельта будет около 10%.
Таблица 3-7
Значение постоянных а, Ь н ш в формуле (3-3-2)
Условия на стейке	Профиль скорости	Рт	Nux	N"co-	а	ь	иг
7\, = const	Параболи- ческий	Любой	Усред- ненный	3,66	0,0668	0,040	2/3
Тщ, = const	Развитый	0,7	У сред- ценный	3,66	0,1040	0,016	0,8
qw~ const	Параболи- ческий	Любой	Локаль- ный	4,36	0,023	0,0012	1,0
gw=const	Развитый	0,7	Локаль- ный	4,36	0,036	0,0011	1,0
* Удельная теплоемкость влажного воздуха равна (0,24—0,47) d, где d —
влагосодержание воздуха.
220
3*3. ТЕПЛОМАССООБМЕН ПРИ ТЕЧЕНИИ В ТРУБАХ
И ПРИ ОБТЕКАНИИ СЛОЖНЫХ ТЕЛ
Течение в трубах
При ламинарном течении несжимаемой жидкости в цилиндрической трубе
устанавливается параболический закон распределения скорости и температуры
(рис. 3-32). Длина участка гидро-
динамической стабилизации Xv и
термической стабилизации Хт со-
ответственно равны:
*^ = 0,05 Re^D;
Хг = 0,05 Rc^Pr,	(3-3-1)
где в формуле для числа Рей-
нольдса в качестве характерного
размера взят диаметр трубы D.
Локальное число Нуссельта
Nha.—наибольшее в начале дли-
ны трубы (у входа жидкости),
затем уменьшается, постепенно
приближаясь к постоянному зна-
чению Nu^ (см. рис. 3-32). При
Рис. 3-32. Распределение температур и
скоростей во входном участке трубы ох-
лаждающейся жидкости.
граничных условиях первого рода:
температура стенки трубы постоянна 7^ = const; число Nu^—3,66, а при
граничных условиях второго рода: поток тепла на стейке трубы постоянный
q = const; число NuM = 4,36.
Если в выражении для числа Нуссельта взять в качестве характерного
размера диаметр трубы: Nu==aD/Ay, то можно написать следующую формулу
для локального числа Нуссельта [Л. 3-13]:
№,=«".+« [(|) R'd Рг] {[' "И [у Rt'o РгГ}'
(3-3-2)
постоянные at Ъ и tn приведены в табл. 3-7.
Вместо формулы (3-3-2) можно воспользоваться формулой, предложенной
автором работы (Л. 3-34] в виде
Nu^= 1,86 Rei/3₽rI/3 173 (tf-)0'14.	‘	(3-3-3)
где Ыил>3,66 при ReoPr>100; —коэффициент вязкости при средней
температуре.
Для неиилипдрических труб числа Нуссельта на стабилизированном
участке можно получить из табл. 3-8, которая была составлена В. К. Шахом
и А. Л. Лондоном [Л. 3-33] на основе обработки большого количества
экспериментальных данных. Если направление течения жидкости принять за х
(направление длины трубы), то площадь сечения трубы лежит в плоскости ху.
'Различают три случая граничных условий: первый случай классический:
1)	7"^:= const независимо от х, у, г, (Nu^^Nuj);
2)	7w = const независимо от у, г (Nu^ — Nun);
dT
?'(x) = cP°Ai-j7L = const	(3-3-4)
независимо от х, где Тт — средняя температура; — массовая скорость
жидкости;
221
Таблица 3-8
Значение Nura для труб различного сечения
для трех граничных условий
Геометрия L/'C^ > 100	Nuj	КПП	М»ш	/Ре
	2,39	3,014	1,474	12,630
2а za А гьЦ	2,47	з,ш	1,8Й2	13,383
гь л| | й”’	2,976	3,608	3,091	14,227
2а,	3,33	4,002	3,862	15,054
2bl	1^=1 гь1	12а 2	3,391	4,123	3,017	15,548
2а	3,657	4,364	4,364	16,000
zTf ") -Й = 0,9	3,66	5,099		18,700
7.1	 гь1—-JzT'T	4,439	5,331	2,930	18,233
2а 9М-	i2b1 г^га *	5,597	6,490	2,904	20,585
=й-0	7,541	8,235	8,235	24,000
Применение: °Л —	4,861 гидравлически!	5,385 диаметр.		24,000
№
3)	q=. const независимо от (у, г) (Nu^, s Nuni);
«'(*)= C„VM = const	(3-3-5)
независимо от x.
При турбулентном течении в цилиндрической трубе можно использовать
для расчета числа Нуссельта следующую формулу:
NilD=~ =0,023 Рг,/3 ReJ8.	(3-3-6)
Л/
При 101 < Rep < 105 в интервале изменения числа (0,5 Рг < 100) LjD > GO.
Некоторые исследователи считают, что показатель степени при числе Пран-
дтля должен быть различен: При охлаждении надо вместо 1/3 брать 0,3, а при
нагревании 0,4.
При больших числах Рг часто применяют эмпирическую формулу
Nu£,= 0,023Pr1''3Rejyf— I0’'4	(3-3-7)
\ 'Ow 7
в следующих интервалах изменения чисел Re^ и Рг: 101<Re£)<105; 0,7 <
< Рг < 10 700; при £/£>>60.
Обтекание тел
Обработка экспериментальных данных разных авторов по обтеканию шара
и цилиндра дала возможность автору [JL3-34J предложить следующие прибли»
женныо расчетные формулы:
для шара
Nu-2 = (0,4 Re0’6 +0,06 Re2-'3) Рг0’4 /Л+б’25	(3-3-8)
\ Чад /	>
при 3,5 < Re <7,6. 104; 0,7<Рг<380;
для цилиндра
№ = (0,4Ре°-5+0,06реад) pRM	(3-3-9)
\ ‘П® /
при 1 < Re < !05; 0,7<Рг<300.
Как видно, формула (3-3-9) отличается от формулы (3-3-8) только коэф-
фициентом 2, так как для цилиндра-Nu -> 0 при Re->0.
Одна из первых попыток иолучцть приближенную формулу для расчета
числа Нуссельта при обсекании тел сложной формы была сделана О. Крише-
ром и Г. Лоосом |Л.З-54]- Вместо обычных определяющих размеров вводится
универсальный определяющий размер I' —длина обтекания тела. Для шара и
цилиндра (поперечное обтекание) /' = 1 /2л; D, для ромба Г — а-\,Ь, где а и b —
стороны ромба; для треугольной призмы I' = 3/21, где I—длина стороны призмы
и т. д. Тогда можно воспользоваться обычной формулой
Kur =0,662 PrV3Re$;5.
(3-3-10)
Диффузионное число Нуссельта или число Шервуда вычисляется по теп-
ловому числу Нуссельта по формуле
Shi-^Nu,,/^,	(3-3-11)
где Лгр — поправочный коэффициент, равный;
A’p=(Rwlf-pi0£»)-'1nT1^ls2-,	(3-3-12)
где и р1(|Со~соответственно относительное парциальное давление пара
на поверхности тела и в потоке воздуха
223
При продувании нагретого газа через слой частиц числа Рейнольдса и
Нуссельта определяются по формулам
V\1Dn .	а£>о I П \
Ке = ^7(Т^лГ’	(3-3-13)
где /7 —пористость; т|/— коэффициент вязкости жидкости; Ху —коэффициент
теплопроводности жидкости; —массовая скорость (кгм/с); D1 2—приведенный
диаметр частицы, равный шестикратному объему частицы, поделенному на
поверхность частицы Ss (A)p=6Vs/Ss).
Тогда формула для числа Нуссельта при продувании воздухом (Рг=0,7)
имеет вид:
Nu = (6,5 Re°'6+0,2 Re2'3) Рг1/3	14	(3-3-14)
\ T|w /
при 22 < Re < 8 • 10э.
3*4. ВЗАИМОСВЯЗАННЫЙ ТУРБУЛЕНТНЫЙ ТЕПЛОМАССООБМЕН
До настоящего времени не существует строгого математического решения
проблемы переноса в турбулентном пограничном слое, хотя литература по
этому вопросу весьма обширна1. Природа пристенной пеизотронной турбулент-
ности не выяснена, и это не дает* возможности составить замкнутое аналити-
ческое описание процесса молярного переноса импульса, энергии и массы.
Методы расчета либо основаны на весьма приближенных и упрощенных моде-
лях явления, представляющих трактовку идей Прандтля и Кармана о длине
пути смешения, ламинарном идурбулентпом подслоях и т. п., либо базируются
на интегральных соотношениях импульса энергии и диффузии с привлечением
недостающих зависимостей из эксперимента. Такие теории называются полу-
эмпирическими, так как эксперименту в них отводится очень важная роль.
Интерес к задачам турбулентного переноса отнюдь не случаен, так как
большинство пограничных слоев, встречающихся в инженерией практике й
в природе (геофизические приложения), являются турбулентными, а кроме
того, поперечный массовый поток, направленный от поверхности, дестабили-
зирует пограничный слой и даже может изменить режим течения в нем.
Патанкар и Сполдинг |Л.З-35] приводят следующую классификационную
схему теорий пограничного слоя.
Физические предпосылки	. Математические особенности
1. Полные
Основанные на эмпирических дан-
ных выражения для локальных свойств,
таких, как эффективная вязкость, эф-
фективное число Рг, эффективное чис-
ло Sc
2. Я в п о
теории
Вычислительные методы для реше-
ния дифференциальных уравнений в
частных производных переноса массы,
импульса, энергии, химических и дру-
гих субстанций
интегральные теории
Эмпирические соотношения, свя-
зывающие интегральные характеристи-
ки, такие как коэффициент поверх-
ности трения, толщина потери импуль-
са и толщина вытеснения
Вычислительный метод для реше-
ния обыкновенных дифференциальных
уравнений, описывающих интеграль-
ные свойства пограничного слоя
1 Краткий обзор теории турбулентности дан в разд. 1.
224
По сравнению с подходами, рассматриваемыми в группе 1, интегральные
теории строятся на менее общих уравнениях и требуют большой эмпирической
информации.
Дифференциальные уравнения
Рассмотрим обтекание закругленных тел при наличии тепломассообмена.
В общем случае в пограничном слое могут происходить химические или фазо-
вые превращения (источник массы и
теплоты). Будем считать, что в погра-
ничном слое имеет место термодинами-
ческое равновесие. Тогда термодинами-
ческие характеристики можно предста-
вить так.
Удельная энтальпия смеси газов (по-
тока жидкости)
(3-4-1)
где hi—удельная энтальпия ьго компо-
нента, равная:
ОД;ЗД<<8
т
cpl dT
b
Рис, 3-33. Координатная система
(3-4-2) пограничного слоя для закруглен-
ного тела.
ho — удельная теплота химических или фазовых превращений: р^ —относитель-
ная концентрация г-го компонента (Р;о = р,/р); р —плотность смеси,
р=1> £р,«=1.	(3-4-3)
Если h0 не зависит от температуры, то удельная изобарная теплоемкость
i-ro компонента равна:
_ din
pi dT '
(3-4-4)
В соответствии с принятой системой координат (рис. 3-33) уравнение нераз-
рывности будет иметь вид:
dpvxr!i дрПуГЛ
ds "и ду
(3-4-5)
где г (s)—радиус загруженного тела; при тело вырождается в плоскую
пластину.
Уравнение переноса импульса пограничного слоя в случае сжимаемой жид-
кости будет иметь вид:
dVs
f”s
Др , д {	\
ds ду 1 ду )'
(3-4-6)
1
М,
при этом предполагается, что др/ду = О; p=pc = const.
Удельный поток теплоты равен:
q = — Mt + J] htii = — W — J] hfDpVpio,	(3-4-7)
где /i —поток массы ^-го компонента.
8 Лыков А. В.
225
Используя соотношения
Л =2рл^< + 2а' d₽‘«: cp = Xp^i>’’	(3-4-8)
i	i	i
а также формулу (3-4-4), получаем;
?=—apWi+Dp	- 1	Л , Три,	(3-4 -9)
еде Le —число Льюиса (Le==D/a).
. Если обозначить через И энтальпию торможения
/7=/г + уУа,	(3-4-10)
то уравнение переноса энергии будет иметь вид:
дН , дН
Р“«-аг+Рв«-57- =
д Г дН /	1 \ 1 ди‘1 д Г/ 1	\	v,, др.л
=^-|а',ТЛГА''|'|-р7-'2 W.I"	Р-4'")
Преобразуем уравнение (3*4-11), Используя (3-4-6) и (3-4-10) будем иметь:
dH дН dh , dh ,	/	ди< \
*-+₽*»17+р°.7Г+₽“» "эг)
dff dH dh , д/г д / ди»\ дп
v=(Wsх+|я’ w+“s ~Sy Ь'sir^ si'•
d / dv \ d / 1 di>*\	/ dv.\2
”s 'fl? (’’"ST) ~~ ~dy C'T	/ •
Из формулы (3-4-10) получим:
______П VI dp/o ОТ
Рг dy ~ Рг Л/ ду Pr” ~dy~ *
(3-4-12)
"(3-4-13)
(3-4-14)
Следовательно, уравнение (3-4-11) примет вид:
dh , dh dp д /. dT , „ \1, dp/e \	! dv^ \®
^i7+Pa»i7=“*ir + lj(’-V+pD2Ai4^H’i(<)  <3-4-15)
\	‘ i
Дифференциальное уравнение переноса массы будет иметь вид:
+	J3’4-13)
Обычно принимают следующие граничные условия:
при у=0 р = р£р, Тh^h^y 11 НPg = Oj p/o = (pn>)ii>> 1
При у->со р->рс; т~^те; h-+hc; Н-rHc; vs-+vff, и^-^О; ? (3-4-17)
р/о“*(р/о)с'	1	'
Переносные свойства [г)(р^, Т), Х(рд>, Т), D (TjJ и давление р (s) являются
в общем случае переменными. Система уравнении (3-4-6), (3-4-15) и (3-4-16)
решается численно на ЭВМ
226
Если эффектами Соре и Дюфо пренебречь нельзя, то уравнения переноса
энергии и массы будут иметь вид:
Oh dh др д \,дТ Sf, пдр№1 (dvs'f
P^as +р^-^=^-&+~яу ’•аг+(’о2(',|+<г‘,~лг +п\-ЭГУ 
(3-4-18)
(9р, dpj д Г / др^ Кт дТ 1
+	= pD+ -J л Ч-г/г, (3-4-19)
s ds у ду ду L ду 1 Т ду ,Д v’	’
Где Q* —изотермическая теплота переноса; АГг — относительный коэффициент
термодиффузии.
Коэффициент зависит от следующих факторов: а) отношения масс и
диаметров двух видов молекул возрастает с увеличением этих отношений);
б) природы межмолекулярных сил; в) относительного содержания компонен-
тов pji). Для бинарной смеси коэффициент Ку зависит от термодиффузионной
постоянной а* и концентрации pi0 и рг():
К г=	(3-4-20)
величины а* и определяются экспериментально.
Тогда плотность диффузионного потока массы будет равна:
/1=- рР»	(3-4-21)
Первый член в уравнении (3-4-21) определяет поток массы под воздействием
концентрационной диффузии, второй —поток вследствие влияния температур-
ного градиента. Знак второго члена зависит от знака дТ‘ду и а*.
Если компонент 1 является более легким, то а* <_ 0, если более тяжелым,
то а* > 0. Величина а* уменьшается с содержанием более тяжелого компо-
нента.
Если пограничный слой турбулентный, то надо считать коэффициенты диф-
фузии D, вязкости г] и теплопроводности суммарными коэффициентами, состоя-
щими из суммы коэффициентов молекулярного переноса и коэффициентов тур-
булентного переноса.
В интегральных теориях турбулентного пограничного слоя используются
уравнения (Л.3-41, 3-42]
= Re, (1 +А) /= Re, (ф Ч +/S) !	(3-4-22)
d Reh	,	*4
-s-i+Re4/»-Re»(St+/S).	(3-4-23)
d ReC,
-2-£ + Re/i) = Re1(StD + /*),	(3-4-24)
где Re', Re£, Re^ —числа Рейнольдса, рассчитанные по толщине вытеснения
импульса, вытеснеЕ[ИЯ энергии и вытеснения массы; cf — коэффициент трения; /, /д,
/о-форпараметры, равные:
-	6' dv^	d (л^)	(APfe)
—	ДЯ dx ’ '° “ Лрй dx ’
(3-4-25)
й^сЛгйаРамег? вдУва‘
8*
227
Вдув неконденсирующихся газов
В. П. Мотулевич |Л.З-З6] рассмотрел задачу теплообмена и трения пла-
стины в потоке газа при образовании турбулентного пограничного слоя с по-
ристой подачей инородного вещества. Решается система уравнений бинарного
турбулентного пограничного слоя (см. разд. 1); т|, Z, D считались суммар.
пыми (молеКулярные-4-молярные). Уравнение состояния было записано в виде
_р /М Рм> ('—WcPi) 1
р» и L >-?!(, (>“тЛ) J
(3-4-26)
где // — энтальпия торможения, пг—молекулярная масса.
Были приняты следующие граничные условия;
при у=0 с., = 0;	= T^const; p10s, = const; 1
при „=6 п, = р„; Т = Та, р„„ = 0.	j (З-4-27)
Кроме того, были приняты некоторые упрощающие допущения:
1)	пограничный слой турбулентен с самого начала пластины;
2)	теплоемкость каждого компонента не зависит от температуры;
3)	парциальная плотность каждого компонента определяется уравнением
Клапейрона;
4)	суммарные (молекулярные и- молярные) числа Рг и Sc равны 1. Из
последнего упрощения следует подобие полей скорости, энтальпии торможения
и концентрации подаваемого вещества:
Ох ____ //о— //ра.
Pio1—рю o’
Р’Пда
(3-4-28)
Из соотношения (3-4-28) непосредственно вытекает связь между распреде-
лением температур и скоростей в пограничном слое:
Г’= _₽м”(1 Т1 +
+ [1 - [1 -рю® (1 -4)] Л + ^- Mi.] vi - МЫ’); (3-4-29)
здесь	- (
* v* * cpi
=	; vx =------; Cn=--------: M— число Маха.
Аналогично можно получить зависимость между распределением плотно-
сти и скорости в пограничном слое.
Если (3-4-29) продифференцировать по у и положить (ОТ/dy)w = 0, полу-
чим выражение, определяющее равновесную температуру стенки:
(3-4-30)
Уравнение (3-4-30) показывает, что на равновесную температуру не вли-
яют ни род подаваемого вещества, ни факт его подачи. Из соотношений (3-4-29)
и (3-4-30) следует, что
Nu=-|-QRe1	(3-4-31)
т. е. подача инородного вещества влияет одинаково на теплообмен и трение.
Следовательно, для решения задачи в такой постановке необходимо и доста-
точно исследовать динамические характеристики пограничного слоя.
Вблизи стенки приближенно справедливо равенство
g w=а —	^0 х.	(3-4-32)
22В
Дальнейший анализ строится на гипотезе Прандтля о длине пути смеше-
ния I и ее связи с пульсационными скоростями и на закономерности Ван-
Дрзпста [Л. 3-38] для напряжения трения в турбулентном потоке сжимаемой
жидкости.
Уравнение (3-4-32) можно преобразовать к виду
f ди “	ди
а®=	+ Л	•	(3-4-33)
Обычно молекулярным трением пренебрегают. Исходя из связи температуры
и концентрации со скоростью (3-4-28)— (3-4-33), можно получить аналогичную
зависимость для плотности, которая используется для интегрирования уравне-
ния (3-4-33) Распределение скоростей в пограничном слое описывается сле-
дующей зависимостью:
= j {п & [1 -ри„ (1 - с*)] (l +20«	(1 +2»; X
Г1'”
X ! _Р1№ (, _„>)	Лх+const. (3-4.34)
Постоянная в формуле (3-4-34) определяется из условия получения лога-ч
рифмического профиля скоростей Кармана при p^yw = p10u, = М,^ —0 и
Дорранс и Дор [Л. 3-39] показали, что при умеренных массовых потоках
_ 1	SL — Dxl=consf,	(3-4-35)
х L Я® “ Р® 2 J
где Dj — постоянная.
Подставляя (3-4-35) в (3-4-34), получаем окончательное выражение для
профиля скорости в пограничном слое:
где
t>? г	।	„ л	ma\	п—1/2
л I .	* \ Pio® (• “	( 1 —)	I
д (0*)= \ Е (n-2u*^- l-i---------л-----„Д,	1+Зо*-4Мг do*-
Маг) J |Д Cfi	Х Х] *’
(3-4-36)
гё-1) М2
Для определения постоянных Df и х привлекается уравнение
=		(3-4-37)
которое решается для внешней границы пограничного слоя. Численные зна-
чения х и D] оказались равными: x«s0,4; D1=«6(38. К окончательным соот-
ношениям, позволяющим рассчитать поверхностное трение и толщину погра-
ничного слоя, относятся:
уравнение для расчета поверхностного трения
(С, 4- 2ш*) ReM = 0,388 3^ Za;	. (3-4-38)
229
уравнение для определения толщины пограничного слоя
•	/I Л \
n F	_ / 1 “ PiOtt' I 1 “ хг
- =0,194 [1 -рм„ (1 - $)) Т1 > ехр Л (1) 1/ г- - 2^
Чоо кссо	L ‘ РМа, (< С \
V&
V* П “ Ох) ехР Л
X ~7 - -п^- -	- (3-4-39)
]/ (1 +2oJI (1 J-Bvj - А2»*’)3
Поскольку было принято, что Рг — Sc= 1, то полученные результаты могут
быть использованы для расчета интенсивности тепломассообмена.
Ю. В. Лапин [Л. 3-40] решал систему уравнений переноса при тех же
допущениях, что и в [Л- 3-36], однако для расчета характеристик турбулент-
ного пограничного слоя используется гипотеза Кармана,-
(3-4-40)
Кроме того, принимается, что х постоянно и при подводе вещества оста-
ется универсальным и равным 0,40.
Для расчета коэффициента трения С? плоской пористой пластины, через
поверхность которой подаегся в поток вещество, получена зависимость ,
где С/о —коэффициент трения пластины при обтекании ее несжимаемой изо-
термической жидкостью, когда отсутствует поперечный вынос массы,
С/о = 0,0263 Re”1'7; /•'= 0,25 C)J1''2 = 1,55 Re1'14;	(3-4-42)
(3-4-43)
В=]~	=	(3-4-44)
<3-4-451
Hcovco
Величина в формуле (3-4-4[) определяется решением трансцендентного
уравнения
Л + 1g N = 1g Ф +	,	(3-4-46)
где
G = lg—.
230
Выражение (3-4-41) для расчета коэффициента трения является общим
в том смысле, чтэ не зависит от конкретного вида функции плотности от ско-
рости в пограничном слое и формулы вязкости и поэтому может быть исполь-
зовано при самых различных предположениях о характере этих зависимостей,
Из (3-4-4!) следует, что имеется некоторое предельное значение коэффициента
расхода Cq, при котором трение на стенке становится равным 0. Если Re -+•
-♦-се Или, что то же, F->co, то
£t=№,	(3-4-47)
с-уо
или
Полагая Су/Су0 —0, получаем значение предельного коэффициента рас-
хода *;
.	Р-4-49)
Если подавать газ, плотность которого такая же, как и газа омывающего
потока (р =	--- const), то в этом случае Cq 1Jni = 46^.
Необходимая для расчета связь плотности и скорости в пограничном слое
p.'poo^f (t'J) в зависимости от принимаемых допущений может быть различной.
Если
Prc = Scc = l; Cpf — coiibt; Tw (х) = const,
то
р_ в
Роа
(1 + в['1-(|	(1	(1 -М-7)
(3-4-50)
где
Рассчитав Су, можно определить интенсивность теплообмена, пользуясь
аналогией Рейнольдса по соотношению St=Cy/2,
В действительности г.ри течении газовых смесей в пограЕшчпом слое числа
Рг и Sc не только отличаются от I, но и не будут постоянными по сечению
пограничного слоя, Особенно существенные отклонения от 1 чисел Рг и Sc
наблюдаются при подаче наиболее эффективных охладителей —Н2 и Не. Напри-
мер, для газовой смеси Н2 — воздух при условиях 7"— 273 К и р = 1 кге/см2
величина Sc меняется от 0,2 до 1,7 в зависимости от интенсивности вдува;
примерно аналогичные изменения претерпевает Sc и при гдуве Не в воздух,
Непостоянство и отличие от 1 чисел Рг и Se по сечению ламинарного
подслоя приводят к нарушению аналогии Рейнольдса и к значительному усло-
жнению анализа. Для Pr^Sc=#l в [Л. 3-40] приводится расчетное соотно-
шение, позволяющее рассчитать связь между плотностью и скоростью в погра-
* Формулы (3-4-47)—(3-4.49) были впервые получены С. С, Кутателадзе и
Л, И. Леонтьевым в 1962 г.
23)
ничном слое:
{> 4- В [1 - (1 ->)(1 -^)]} (I-а - V)
{‘+в [*-(' -Э1 -“9JH1 +fi(1
(3-4-51)
(3-4-52)
здесь /// — равновесная энтальпия газа у .стенки при отсутствии теплообмена
между газом и стенкой, равная:	‘
Н, _______________l-(l-Pr)'-(pfK,_____________
\Ср2 /	C02ZP
(v*)v/— безразмерная скорость на границе ламинарного подслоя,
_________________________________LE'+.LW1
( i-^pF л + 2 Рг (, h ) ’
(3-4-53)
где ₽ = 1 4“Р1ва, (с*—1); Не — число Рейнольдса, построенное по толщине лами-
нарного подслоя 8V и динамической скорости,
Re = 6',°« =	= 6v(W.»)1/2.	(3-4-541
Va» Тщ,	7ц,
Величина Re принимается равной се значению для несжимаемого газа без
подвода вещества Re0=ll,5, значение динамической вязкости в ламинарном
подслое принимается постоянным и равным i]w. Остальные величины равны:
,	Pi^=l-<H-Br‘[l4-e(«;)o|(i’‘Sa.	(3-4-55)
В последней формуле величина (о*)^ —безразмерная скорость на границе
диффузионного ламинарного подслоя.
Кроме того, получено соотношение для расчета связи между трением и
теплообменом (параметр аналогии Рейнольдса);
St	- 
9/2
1 -Sc В' (Sc- Рг) (CJH-1) (1 - Р1Ш)
1 _(1 _pr) p}) _ в Pr [fl (1 - Pr) + (Sc- Pr) (^ -1 bl - p1№)
V	L	\cpl /	2P J
(3-4-56)
Расчеты выполняются методом последовательных приближений. Анализ их
обнаруживает следующее:
]. Отличие чисел Рг и Sc от 1 в ламинарном подслое мало влияет на коэф-
фициент трения. Поэтому расчет Су может быть выполнен но методикам,
построенным на допущении равенства Pr*«Sc«=»l.
232
2.	При расчете теплообмена между газом и стенкой и коэффициента вос-
становления
<3-4-57)
Г1эО ср<х>1 со п аэ
необходимо учитывать отличие Рг и Sc от 1.
3.	Подача вещества в пограничный слой приводит к уменьшению величины
St (С//2).
4.	Коэффициент восстановления энтальпии	с увеличением
интенсивности вдува возрастает и может быть больше 1 *.
Интегральные уравнения импульсов и энергии пограничного слоя могут
быть решены, если известны законы сопротивления и теплообмена турбулент-
ного пограничного слоя.
В общем случае и зависят от температурных факторов и от безраз-
мерных параметров, учитывающих влияние продольного градиента давления,
поперечного потока вещества па поверхности теплообмена, степени диссоциа-
ции набегающего потока и др,
С. С. Кутателадзе и А. И. Леонтьев [Л. 3-41, 3-42] построили теорию
расчета характеристик турбулентного пограничного слоя па так называемых
предельных законах сопротивления и теплообмена турбулентного пограничного
слоя, которые имеют место в процессах с исчезающе малой динамической вяз-
костью, т. е. при Re->co. Для случая продольного обтекания проницаемой
пластины неизотермическим потоком предельный закон сопротивления имеет
вид:
« iZw + My-
а критическое значение параметра вдува, соответствующее отрыву погранич-
ного слоя (ф = 0), равно:
d(i)
V (Кс/Р)”^
(3-4-59)
Принимается, что ф^ф^.. В соот[юшениях (3-4-58) и (3-4-59) использованы
обозначения авторов работы [Д.3-41]:
о) = -2--безразмерная скорость:
_2ртоОд,----фактор проницаемости стенки;
С/0Рсо°оз
/ с( \
ф=  ) —относительное изменение коэффициентов трения при
\ Ц /Re**
Re**s=idem;
/ St \
ф_= тг—!	— относительное изменение числа Стантона при Re£* = idem.
Т \s*o/r4*	1
Функцию ф в формуле (3-4-58) можно подсчитать по уравнению
ф = К	;	(3-4-60)
* Этот вывод противоречит опытным данным. (Прим, ред.)
233
а критический параметр вдува

т/
1______________
1/№ + (1 - W wjm
Ri '
(3-4-61;
В формулах (3-4-60) и (3-4.61) введены следующие обозначения:	—
температурный фактор; R — газовая постоянная; —2р^ощ}/С^р.гоо0.— фактор
проницаемости стенки, отнесенный к действительному значению коэффициента
трения
4>l = PWPe.-
При выводе соотношения (3-4-61) учитывалось, что в точке отрыва
P®=--Pi© и ЧчМ’-д1 *-.
Формулу (3-4-61) можно аппроксимировать простыми зависимостями;
а) при вдуве газов тяжелее основного потока (тг > т$)
('в,37 + 0,67-^' );	(3-4-62)
б)	при ггц <.т%
6«р«>6кр1(о,25+0,75-^-';,	(3-4-62а)
•	\	т2 J
где Лкр1 соответствует критическому параметру вдува для однородного неизо-
термического пограничного слоя и может быть вычислено по следующим фор-
мулам:
1) при ф < 1
1+И-фГ.
2) при ф > 1
Для очень легких
,	1	/	2-ф\2
"«Р=ф37г(агс“5	
газов
^2	V Ф + 1 /
(3-4-63)
(3-4-64)
(3-4-65)
Уравнение (3-4-60) решается численными методами. Зная ф, можно решать
уравнение импульсов, а зная фг—уравнение энергии.
Патанкар .и Сполдинг [Л.3-35] предложили метод расчета турбулентного
пограничного слоя, основанный на интегрировании уравнений одномерного
пограничного слоя в непосредственной близости от стенки1. В результате для
широкого спектра задач получены соотношения, связывающие потоки коли-
чества движения, массы или энтальпии вблизи стенки с величинами скорости,
концентрации и температуры на соответствующих внешних границах одномерного
слоя.
Рассмотренными подходами далеко не исчерпываются способы решения задач
турбулентного переноса. Расхождение между расчетными величинами Nu и Cj
по различным теориям составляет 100% и более.
На рис. 3-34 представлена рассчитанная разными способами зависимость
St;St0=:/(h) для различного вида охладителей. Очевидно, что при умеренных
'»р'=ТТ^'
1 Этот метод по существу является методом Кутателадзе —Леонтьева
|Л.З-42]. (Прим, ред,)
Вдувах совпадение между расчетом и экспериментом значительно лучше, чем
при больших; кроме того, имеются заметные отклонения от расчетов при подаче
легких газов и испарении жидкости (как правило, все решения уравнений,
когда приняты граничные условия Гда = const и p10a)=const, распространяются
и на случай фазовых превращений на твердой границе пограничного слоя).
Несовпадение результатов расчета с экспериментами при подаче легких
газов можно объяснить влиянием вторичных эффектов (термодифф^зией и диф-
фузионной теплопроводностью). Болес детально влияние этих эффектов будет
рассмотрено в следующем параграфе.
Расхождение расчетных и измеренных значений коэффициентов поверх-
ностного трения и теплообмена в области больших вдувов прежде всего может
быть объяснено тем, что в одну теорию закладывается предположение о	О
Рис. 3-34. Зависимость между St/St0 и параметром
вдува Ь (Ь= P^/p^St^) лрх вдуве через пори-
стую пластину по данным разных авторов.
1 —фреон-12 [Л.3-611; 2 — СО4 ГЛ.З-бЦ; 3—гелий [Л,3-431;
4 — гелий [Л.3-611; 5 —гелий [Л.3-44]: 6—фреон-12 [Л.3-36];
7 — гелий [Л.3-45]; 8 — гелий [Л.3-36]; 9 — гелий [Л.3-46];
10 — гелий [Л.3-47]; // — бензол [Л.3-48];	/2 — ацетон
[Л.3-48]; 13 — этиловый спирт [Л.3-48].
Вопрос о том, существуют ли критические режимы вдува при умеренных
расходах инжектанта, в настоящее время является спорным, так как появляются
существенные погрешности при измерении малых сил трения и малых тепловых
потоков.
Вместе с тем интерес к таким задачам возникает из-за необходимости создать
вблизи поверхностного слоя вещества /00%-ную концентрацию инжектанта,
при необходимости оградить стенку от химической или механической эрозии
со стороны газа набегающего потока, при создании защитной лучепоглощающей
завесы и т. п.
Имеющиеся немногочисленные пока данные показывают, что в принципе
возможны режимы, при которых имеет место концентрация инжектанта, близ-
кая к 100%.
В [Л.3-49] излагаются результаты опытов по исследованию турбулентного
пограничного слоя па проницаемой поверхности в области сильных вдувов и
конечных чисел Рейнольдса. Опыты основаны на химическом взаимодействии
основного потока (кислотная среда) с вдуваемой жидкостью (щелочная среда).
При определенных вдовах на поверхности пористой пластины образовывался
слой только вдуваемой жидкости, что четко фиксировалось находящимся в ней
индикатором (фенолфталеином), причем пленка с p10w~ 100% появлялась при
одних и тех же критических значениях параметра вдува, даже если концент-
рация инжектанта уменьшалась до 0,0015% NaOH (резко разбавленный раствор),
235
а концентрация соляной кислоты в основном потоке достигала 30%. Из уело
вия нейтрализации растворов можно было оценить р1ида'. расчеты показали,
что она превысила 99,994%.
В [Л.3-50] также обсуждается вопрос о взаимодействии потока газа с телами
при интенсивной пористой подаче вещества. В работе отмечается, что если для
ламинарного движения в принципе можно получить точные численные решения
Рис. 3-35. Интерферограммы пограничного слоя при подаче углекисло-
го газа через пористую пластину.
Рис. 3-36. Схема потока газа в пограничном
слое при вдуве.
на базе совместного рассмотрения уравнений Навье—Стокса, энергии и диф-
фузии, то для турбулентного переноса нет точного решения даже для значи-
тельно более простых случаев. Правильно выбрать модель явления и дать базу
для ее расчета позволяет эксперимент с использованием интерферометрических
и термоанемометрических изме-
рительных схем, минимально ис-
кажающих общую картину те-
чения. Были проведены измере-
ния при ламинарном и турбу-
лентном обтекании пористых
проницаемых тел.
На рис. 3-35 показаны ин-
терферограммы пограничного
слоя при вдуве углекислого
газа через пористую пластину
с разной плотностью попереч-
ного потока вещества,- ясно вид-
но оттеснение пограничного
слоя от поверхности пластины.
Этот процесс схематически изо-
бражен на рис. 3-36. В эоне от-
теснения продольная скорость мала, а концентрация почти не изменяется, что
подтверждается экспериментами (рис. 3-37). Аналогичные экспериментальные
данные для турбулентного пограничного слоя приведены на рис. 3-38, 3-39.
На рис. 3-37 видно, что профили скорости имеют S-образную форму с точ-
кой перегиба в середине зоны смешения; профили концентрации также имеют
S-образную форму; с ростом интенсивности вдува концентрация вблизи стенки
растет и начиная с некоторых значений поперечного массового потока стано-
вится равной 100%. Анализ полученных данных показывает, что при этом
пограничный слой состоит из двух характерных областей оттесненного слоя,
где градиенты всех параметров малы, а концентрация инжектанта стремится
к Ю0%/ и относительно узкой зоны вязкого взаимодействия, в которой все
вначелия быстро .меняются от значений в оттесненной зоне до параметров
невозмущенного потока.
236
Расстояние, мм
Рис. 3-37. Профили скорости и концентрации при аду-
ве СО2 через пористую пластину.
Сад “ М и/с>'	79,6 мы; I — pz'y = 0,00?; 2 — 0,014; 3 — 0,016;
4 — 0,027.
Рис. 3-38. Интерферограммы турбулентного погранично-
го слоя при подаче Не при ^со = 28 м/с.
Вверху — ро,ида/роо0со = 0,002; посередине -10,004; внизу - 0,0(16.
23/
Пластина перестает быть телом с р ==const, появляется отрицательный гра-
диент давления, который необходимо учитывать при создании метода расчета.
Возможно, условием dp/dx<.0 и объясняется, что при ламинарном обтекании
оттеснение наступало при параметре вдува fw— 1,534- 1,84 (при Re=4-103-u
20-10’), тогда как теорией Эккерта и Хартнетта [Л.3-14] предсказывается
значение (fw)Kp = 0,619.
При взаимодействиях пористой проницаемой пластины с турбулентным
потоком газа общая картина получилась аналогичной ламинарному течению;
также наблюдается зона оттеснения с малыми градиентами параметров, огра-
ниченная с наружной стороны зоной интенсивного взаимодействия. При вдуве
легких газов оттеснение наступает при значительно меньших расходах инжек-
танта.
Рис, 3-39, Профили молярной концентрации См
углекислого газа при вдуве через пористую пла-
стину.
= 28 м/с; х — 60 мм, / — puJr= 0,031; 2 —	= 0,042; 3 — pvy = 0,053.
Основным результатом всех известных нам теоретических исследований по
влиянию поперечной подачи массы на теплообмен в пограничном слое является
монотонное снижение интенсивности переноса с ростом относительного расхода
иижектанта. Вместе с тем имеются данные, которые обнаруживают эффект
интенсификации теплообмена при малых расходах охладителя [Л.3-51, 3-52].
Возможно, что при малых расходах это явление вызвано отсутствием сплошной
пелены вдуваемого газа сразу же на выходе из пористой стенки. Газ в этом
случае вытекает из пористой стенки в виде отдельных струек (сказывается
неоднородность материала), которые разрушают вязкий подслой, усиливают
перемешивание молей газа и тем самым интенсифицируют теплообмен.
Для расчета локального тепломассообмена при умеренных вДувах (&0=0,1-4-4)
в работе [Л.3-53] были получены эмпирические соотношения:
Nux = 0,0289 Re£8 Рг0,4 ехр (— 0,36&я)-(	(3-4-66)
^Nux^ = 0,0195 Re^Sc-o^x-’,	(3-4-67)
где bf}=—---------------относительный энтальпийный параметр массообмена;
СрсоРсо°со ‘’Ч
Ьо=—-----------относительный динамический параметр массообмена;
Р«>иго“о
х —мольная или объемная концентрация охладителя.
Формулы (3-4-66) и (3-4-67) свидетельствуют о том, что поперечный поток
массы неодинаково влияет на тепломассообмен: в этом интервале параметров
вдува теплообмен снижается, а массообмен интенсифицируется.
238
3-Г. СВОБОДНАЯ КОНВЕКЦИЯ
Движение жидкостей, вызванное разностью плотности в поле внешних сил,
обычно называют свободной конвекцией. Такими внешними силами являются
силы тяжести, а разность плотностей в простейшем случае вызывается пере-
падом температур между поверхностью твердого тела и жидкостью. Толщина
пограничного слоя в условиях свободной конвекции значительно больше, чем
при вынужденном движении, поскольку скорости свободного движения малы.
Свободная конвекция в неограниченном объеме
Рассмотрим теплообмен между вертикальной пластиной и жидкостью.
Направим ось х вдоль пластины (вертикальное направление), а ось у —перпен-
дикулярно (горизонтальное направление).
Уравнения переноса импульса и энергии для\нашего случая можно папи-
сать так:	> +		(з-з-» дТ , дТ &Т	.	„ _ 0. Wa--5	Г а —а~ГТ1	(3-5-2) А дх J ду «=— ду* '	' dvx	dvu + ~^ = 0,	,	(3-5-3) . дх	ду	'	’ '
где р — коэффициент объемног	расширения. Граничные условия	имеют вид:
при у = (	vx— 0; «# = 0; Т — Tw;	(3-5-4)
ври у=с	а ол = 0; Г=ТМ,	(3-5-5)
Введем следующие обозначения: . .	' “	V-	: 5 х \ 4 Gr*l :		(3-5-6)
здесь Gr*. —локальное число Грастофа. Тогда функция тока ф будет равна:	* ф=^('5ь.';,/,ф©; 		(3-5-7)
	г 4vx,%„ 4\,2	]	Ф •	(3-5-8)
yy = VX-l/4	4v.	] (sf Зф) .	(3-5-9)
Уравнения (3-5-1) и (3-5-2) примут вид: <р'" -f-Зфср' — 2ср'8 -(-8= 0;		(3-5-10)
б’ + ЗРг ф6'==0, т~т где 6=^—		безразмерная температура. Граничные условия следующие: при ^ = 0 ф«ф' = 0; 8=lj		(3-5-11) (3-5-12)
при § = со ф'— 0;.6=0,		(3-5-13)
239
Уравнения (.3-5-10) и (3-5-11) решены Острахом с помощью численного
метода. Распределение относительной скорости с/ [<р' = v^x/2v (Gr*-)1 2J в зави-
симости от безразмерной координаты Ь, дано на рис. 3-40, а [<р (£)], а распре-
деление температуры 0(£)—на рис- 3-40,6 (для разных значений числа Рг).
Рис. 3-40. Зависимость относительной скорости tp' (я) и температуры
размерного комплекса £ = Grx|.
в (6) от без-
Локальное число Нуссельта будет равно:
,	(3-5-14)
Значения 0' (0) и (0) приведены в табл. 3-9.
Таблица 3-9
Значения — 9'(0) и ср" (0)
Значения 0 и ф"	Числа Рг						
	0,01	0,733	|	1		s	10	100	1D00
-9(0)	0,0812	0,5080	0,5671'	0,7165	1,1694	2.191	3,966
ф’(0)	0,9862	0,6741	0,6421	0,5713	0,4192	0,2317	0,1450
Данную задачу можно решить приближенно. Принимаем параболический
закон распределения температуры по нормали к поверхности:
о =	(1 — Tg-)5,	(3-5-15}
где —fc== const —значение разности температур при t/ = 0, Распреде-
ление скорости цv (у) задается в ниде
-у)2.	(3-S-16)
240
где Vi~ некоторый коэффициент, не зависящий от у и имеющий размерность
скорости.
Из уравнения (3-5-16) следует, что скорость движения жидкости вдоль
пластины максимальна на расстоянии у = 1 /3 6 от поверхности. Тогда вели-
чина С’1 будет равна’27/4 (& v)MdKC. '
Используя метод Кармана, получаем зависимость для толщины погранич-
ного слоя 6 в виде
6 = 3,93 Рг-»-' + (0,952-|-Pr)»'!s (GrJ",s>.	(3-5-17)
где Gr,v —локальное число Грасгофа,
Gr,= -^|’-;	(3-5-18)
здесь р - коэффициент объемного расширения жидкости; g—ускорение силы
тяжести,
Поток теплоты от поверхности пластины
/ 5ft \ 2Xft„	.« _ 10
Следовательно, локальное число Нуссельта
№, = — =2 4,	'	(3-5-20)
Л О
а локальный коэффициент теплообмена обратно пропорционален корню четвер-
той степени из х. Подставляя вместо 6 соответствующие выражения, получаем-
№, =0,508 Рг0-5 (0,952 + Pr)-°-25 (Gr,)0-25.	(3-5-21)
Среднее значение коэффициента теплообмена а = 4/3а.
Для идеальных газов коэффициент объемного расширения р равен 1 ,'Т;
при небольшой разности температур можно принять р=1;7с Для воздуха
число Рг = 0,714, тогда будем иметь:
Nux = 0,378(Grj°-25.	‘	(3-5-22)
Точные вычисления приводят к тому же соотношению между Nu,c и Grx,
только вместо коэффициента 0,378 получается 0,360. Следовательно, прибли-
женные расчеты дают результаты, близкие к точным, весьма трудоемким
вычислениям.
Опытные данные подтверждают расчетные формулы (3-5-20) —(3-5-22) и ис-
ходные уравнения (3-5-15) и (3-5-16) о профиле температуры и скорости в по-
граничном слое. Точность совпадения расчетных и опытных данных около 10%
в пределах чисел Прандтля от 0,01 до 1000.
Решение (3-5-21) дает лучшие результаты, чем распространенная формула
№ , = В (Gr, Рг)° 25,	(3-5-23)
которая была получена па основании обобщения опытных данных для воздуха.
Пограничный слой при свободной конвекции вдали от края становится
турбулентным, когда его толщина достигает определенного значения. Для
воздуха этот переход происходит при критическом значении (Grx)fr= 10% что
соответствует (Re^ 550, где Re(5 = t'MaKc^/v-
Движение жидкости около нагретых горизонтальных плит носит иной
характер и зависит от размера пластины. Пластины, обращенные нагретой
поверхностью вверх, образуют восходящие потоки по схеме, показанной па
рис. 3-41, а (малые размеры плаепш), в по схеме, показанной па рис. 3-41, б
(большие размеры). В последнем случае центральная часть пластины как бы
изолирована потоками жидкости, восходящими с краев пластины. Охлаждение
241
центральной части пластины происходит за счет притока (провала) холодной
жидкости сверху.
Когда нагретая поверхность обращена вниз, движение жидкости происхо-
дит в пограничном слое по схеме, показанной на рис. 3-41, в, ниже этого слоя
жидкость остается неподвижной.
Для тонких проволочек {d — 0,2 4- 1,0 мм) ламинарный режим движения
сохраняется и при больших температурных напорах. При малых температур,
пых напорах около проволочки образуется неподвижная пленка нагретой
жидкости, что соответствует теплопереносу при пленочном режиме.
а.)	в)
Рис. 3-41, Схема свободного движения жидкости около
нагретых горизонтальных пластин.
Свободная конвекция в условиях турбулентного движения жидкости вдо;:ь
вертикальной нагретой пластины описывается уравнениями распределения тем-
пературы и скорости в пограничном слое в виде следующих формул:
(3-5-24’
В формуле распределения скорости множитель (у/б)1// был специально
введен для вычисления напряжения трения аналогично турбулентному трению
при вынужденном движении.
В результате расчета, аналогичного рассмотренному ранее, получаем сле-
дующее критериальное уравнение:
N’uv = 0,0295 (GrJ2/5 Рг7-'5 [1 +0,494Рг2/3]~2''5.	(3-5-25)
Наибольшее распространение получила эмпирическая формула, полученная
на основании обобщения экспериментальных данных по теплоотдаче тел раз-
личной формы (плиты, проволоки, трубы, шара) при свободной конвекции
[Л,3-62]. В качестве определяющего размера для труб и тара принимался
диаметр, для пластины —ее высота. Коэффициенты и термодинамические пара-
метры вычислялись для средней температуры пограничного слоя.
Критериальное соотношение имеет вид:
Ku — В (Gr Prf;	(3-5-26)
значения постоянных Вил приведены в табл, 3-10.
'	Таблица 3-10
Значения постоянных В и п
GrPr	в	п
1 . Ю-ft _ 5.1Q2	1,18	1/8
1 . 102 -2. 107	0,54	1/4
2- I07—1 • I013	0,135	1/3
242
Рис. 3-42. Схема раз-
в ити я	пограни иного
слоя и распределение
температуры между
вертикальными пла-
стинами.
При значении (Gr Рг) < 1 число Нуссельта Практически остается неизмбН
ным я равным 0,5. Следовательно, теплообмен происходит при помощи тепло-
проводности (а = 0,5Л//). Из анализа значений В и п можно сделать следую-
щий важный для практики вывод: в области значений (GrPr) = l • 10:= 1 • 1013
; показатель степени л=1Д Следовательно, в этой области теплообмен не зависит
' от геометрических размеров, так как определяющий размер входит в число Nu
в первой степени, а в число Gr—в третьей степени. Таким образом, в этой
области процесс теплообмена автомоделей, что дает возможность исследовать
теплообмен на малых моделях; это имеет большое практическое значение для
строительной теплотехники.
Обзор работ по свободной конвекции дан в работе [Л.3-55]. В работе
[Л.3-56] была решена задача при условиях, когда поверхность пластины была
наклонена под углом к горизонту. Температура пластины поддерживалась
постоянной.
 Свободная конвекция в ограниченном объеме
Вначале рассмотрим теплообмен между двумя параллельными пластинами
с различными температурами	Если пластины расположены горизон-
тально и верхняя пластина имеет более высокую температуру по сравнению
с нижней > ?2), то передача теплоты от одной пластины к другой через слой
жидкости будет происходить путем теплопроводности;
нарушение этого будет иметь место только около
краев пластины.
Если верхняя пластина имеет более низкую тем-
пературу, чем нижняя, то нагретые частицы будут
собираться у верхней пластины- Это приводит к не-
устойчивому состоянию, которое при (GrPr)>=1700
превращается в состояние замкнутых конвективных
потоков жидкости в пространстве между пластинами.
В случае вертикальных стенок характер движе-
ния зависит от соотношения высоты плиты I и рас-
стояния между плитами L. Исследования показывают,
что при значении числа
Gtl < 124 Pr-2 (f + Pr) 1	(3-5-27)
распределение температуры в слое жидкости по нор-
мали к пластинам следует линейному закону. Только
возле нижних и верхних краев пластин происходит
отклонение от линейного закона; это отклонение рас-
пространяется внутрь слоя на расстояние L. Перенос
теплоты происходит при помощи теплопроводности.
На основании исследования интерференционных
фотографий установлена картина расположения по-
граничных слоев в пространстве между пластинами,
приведенная па рис. 3-42. Толщина пограничного слоя
правлении снизу вверх на более нагретой пластине; на г,
нагретой пластине толщина б2 растет в обратном направлении.
В центральной части объема жидкости температура постоянна. Распреде-
ление температуры в пограничном слое аналогично распределению температуры
в пограничном слое одиночной пластины. Коэффициенты теплообмена в случае
двух пластин отличаются не более чем на 20%, если провести расчет по фор-
мулам для единичной пластины, при этом температура неподвижной жидкости
принимается равной температуре vq ядра жидкости между двумя пластинами.
Это состояние сохраняется до тех пор, пока два пограничных слоя не сольются
в один, что происходит при уменьшении GrPr. Однако, как показали опыты,
температура ядра жидкости не постоянна, а увеличивается в направлении
снизу вверх.
увеличивается в на-
(потивоположной. менее
243
L
7г
U
'л2
Рис. 3-43. Схема циркуляции жид-
кости в вертикальных и горизон-
тальных щелях.
Э. Шмидтом [Л-3-О71 было установлено, что перенос теплоты от горячей
ч холодной поверхностей через вертикальный слой жидкости увеличивается
если пространство между пластинами
разделено тонкими горизонтальными
стенками. Это объясняется развитием
пограничных слоев при больших значе-
ниях Gr^-Pr. Пограничные слои у нагре-
той и холодной пластин начинаются у
каждой горизонтальной перегородки,
они становятся тоньше, чем в отсутст-
вие перегородок, это приводит к интен-
сификации теплообмена.
На рис. 3-43 приведены схемы цир-
куляции жидкости в щелях в зависи-
мости от их ширины. Если ширина ще-
ли L достаточно велика, то восходящий
и нисходящий потоки протекают без
взаимных помех (рис, 3-43, а). Если ве-
личина L мала, то вследствие взаимных
помех может возникнуть внутренняя
циркуляция, как при наличии перего-
родок (рис. 3-43, б). В случае горизон-
тальных пластин, как уже было отме-
чено выше, конвекция может отсутство-
вать, если нагретая поверхность распо-
ложена сверху (рис. 3-43, в). При об-
ратном расположении возникают ячеистые
циркуляционные токи (рис. 3-43, ?).
В большинстве случаев двумерные
задачи свободной конвекции решались
численно или были даны приближен-
но. Читателей, интересующихся этими
решениями, отсылаем к оригинальным
работам [Л.3-57].
При наличии такой сложной гидро-
динамической картины расчет коэффи-
циентов теплообмена для жидкости в ог-
раниченном пространстве очень сложен.
Поэтому в инженерных расчетах перенос
теплоты между пластинами через слой жидкости в щели рассматривают как
перенос теплоты теплопроводностью, вводя эквивалентный коэффициент теп-
лопроводности
(3-5-28)
к ч
Отношение эквивалентного коэффициента теплопроводности к истинному
коэффициенту теплопроводности жидкости называется коэффициентом конвекции
8fti = циркуляция жидкости внутри щели зависит от Gr Рг, поэтому
84=ЦОгРг).
На рис. 3-44 приведен график вй=/(СгРг), заимствованный из [Д.3-58].
При вычислении Qr Рг за определяющий размер щели принята ее ширина L
(независимо от формы щели); параметры вычислены для средней температуры,
равной 0,5 (7\i + ГП2)• Ия графика видно, что при Gr Рг < 1000 р£= 1. Следо-
вательно, при Gr Рг < 1000 перенос теплоты через слон жидкости в щели про-
исходит теплопроводностью. В первом приближении отдельные участки графика
lgefe=/[lg(Gr Рг)] допустимо принять за прямые. Тогда можно написать:
e6 = 0,105(GrPr)°-3 при 108<СгРг< 10»;	(3-5-29)
e# = 0,40(Gr Рг)0-' при 10“ <6г f>r < Ю1.0.	(3-5-30)
244
Уменьшение интенсивности теплообмена при больших значениях (Gr Рг)
можно объяснить взаимной помехой пагрегых и охлажденных потоков жидкости
внутри щели.
Рис. 3-44. Зависимость коэффициента естественной конвекции
от критерия (Gr Рг) при теплообмене в замкнутом простран-
стве.
1 — плоская газоная прослойка горизонтальная; 2 — то же верти-
кальная; 3 — цилиндрическая газовая прослойка; 4 — цилиндриче-
ская прослойка жидкости; 5—шаровая газовая прослойка
В приближенных расчетах вместо формул (3-5-29) и (3-5-30) при Gr Рг > 1О3
можно пользоваться соотношением
efe = 0,18 (pg Рг)1/4 УГРЫ,	(3-5-31)
где Д7’ = 7’п1—7’я2—разность температур между стенками щели.
Свободная конвекция при нагревании сверху
Среди новых задач свободной конвекции представляет интерес Проблема
возбуждения конвекции нагревом сверху. Детальное экспериментальное и теоре-
тическое исследование этого явления в строго горизонтальной полости было
проведено в Институте тепло- и массообмена АН БССР.
Численное изучение свободной конвекции, возбуждаемой неравномерным
нагревом сверху, проводилось в полостях прямоугольной формы.
Матемашческая формулировка задачи имела следующий вид [JL3-59J:
+	(3-5.32)
dr Y дх ду дудх дх ’	'	’
ат ' ,гт+^^т
,	дт Рг дх ду ду дх ’	'	’
ф = —(3-5-34)
где Г—температура; ф и ср — соответственно безразмерная функция тока и
вихрь скорости. В безразмерные соотношения для функции гока, температуры,
координат х, у и времени входят кинематическая вязкость v, характерная
разность температур на границе области 5, длина стороны квадрата I и отно-
шение №{у.
Числа Gr и Рг определяются, как обычно, по формулам
Gr*=(v; Рг = v /а,
На границе области составляющие скорости и функция тока считались
равными пулю.
245
Для температуры рассматривалось несколько типов граничных условий.
1.	Нагрев сверху в „чистом" виде. При	1, у=0 температура равна
нулю. Граничные условия на верхней стенке приведены ниже.
Расчетный
вариант
' 1
2
3
4
5
Г раничные условия
Т = sin лх
т i sin 2лх
1	О
г | sin 4лх
Т~\	О
Т = 1- (2х —1)я
Т= [1 — (2х—1)2]|/2
OsSx-s I
0^х^0,5;
0,5^х< J
О х 0,5;
0,5 =<х < 1
О^х-с I
OsSx^ 1.
2.	Совместный нагрев сверху и сбоку, Одна боковая и нижняя стороны
квадрата поддерживались при постоянной температуре, равной нулю, а на
верхней и боковой границе задавалось линейное распределение безразмерных
температур:
у= 1, Т=х; х= 1, Т — у.
3.	Подогрев сверху, сбоку и снизу реализовался следующим распределением
температур, Нижняя и обе боковые стороны поддерживались при постоянной
температуре, равной нулю, а на верхней задавалось синусоидальное распреде-
ление вида
T = sin/mx, п = 2, 3, 4.
Для данных граничных условий дифференциальные уравнения решались
численно на ЭВМ. Полученные решения были изучены, и построены соответст-
вующие графики зависимости. С целью проверки полученных закономерностей
были проведены прямые эксперименты. Изучение проводилось и полости, обра-
зованной двумя горизонтальными латунными пластинами, боковыми стенками
из оптического стекла и торцовыми вкладышами из оргстекла. Через боковые
стенки проводились визуальные наблюдения и фотографирование картины течения.
В горизонтальных и торцовых стенках зачеканивались 30 медьконстантановых
термопар для исследования распределения температуры по стенкам.
Различные законы температурного распределения на верхней стенке соз-
давались прокачиванием воды через секционированную рубашку на внешней
стороне пластины от трех термостатов.
Изотермичность нижней холодной пластины поддерживалась интенсивной
циркуляцией термостатированной воды при температуре окружающего воздуха
через мвогосекционированпую рубашку, Во всех опытах отклонение от средней
температуры стенки не превышало 0,15°С.
Визуальные наблюдения картины сечения и измерение температуры с помощью
передвижной константановой термопары показали, что в центральной области,
составляющей около 11% ширины полости, существует двумерное течение
с идентичными скоростями движения и размерами ячеек. При приближении
к передней и задней стенкам размеры ячеек уменьшаются, а скорость движе-
жения падает до нуля.
В дальнейшем все замеры проводились в центральной плоскости z/2. Были
проведены гидродинамические и тепловые опыты. В качестве рабочей среды
использовались воздух и дистиллированная вода.
Скорость конвекции измерялась следующим образом. Полость, заполненная
воздухом со взвешенными частицами стеарата цинка или водой с частицами
алюминиевой пудры, освещалась с торца. Источником света служил оптический
квантовый генератор ЛГ-55. Картина течения фотографировалась при преры-
вистом освещении. Таким образом, по величине треков можно было подсчитать
скорость течения в данной точке. Фотографирование проводилось в отраженном
свете. Обтюратор представлял-собой алюминиевый диск толщиной 1,1 мм с 60
радиальными прорезями, который вращался синхронным электродвигателем.
246
При тепловых экспериментах для точных, температурных измерении вся
установка дополнительно изолировалась стекловатой, Поле температур в каждой
ячейке было получено с помощью передвижной медьконстэнуановой термопары
(диаметр проводов 0,05 мм) с компенсационным нагревателем. Перемещение
термопары по высоте полости осуществлялось координатпиком с точностью
0,02 мм.
Данные теплообмена были получены с помощью найденных из опыта
вертикальных градиентов температуры на поверхности горячей стенки.
Среди различных законов распределения температуры были выделены перио-
дическое, дельтообразное и приближеннолинейное.
! ' li^Ssggg’
Рис, 3-45. Конвективное движение воздуха при дельтообразном подогреве сверху.
Для изучения конвекции при периодическом законе нагрева удалось экс-
периментально получить распределение, которое можно с точностью до 10%
считать косинусоидальным.
В случае дельтообразного распределения было экспериментально осущест-
влено распределение температуры, которое с точностью до 7% аппроксимируется
функцией
Т As - с и - М7|! + В (0.07 - я)2,
где х — координата по длине полости: О^х^О, 14; Л, В, С —коэффициенты:
30 А 50; 2700 В й 3700; 300 С fS 400.
Конвективное движение воздуха при дельтообразном подогреве сверху
изображено на рис. 3-45. Для визуализации был использован табачный дым.
Конвекция при приближепнолинейном изменении температуры исследо-
валась на распределении, которое с точностью до 3,6% описывается функцией
где 2 < А ^20; 21,4 В 42,4; 0,03 с < 0,05.
Рассмотренные случаи позволяют сделать следующие выводы о структуре
конвекции при нагреве сверху:
а)	течение имеет ярко выраженный ячеистый характер;
б)	каждый экстремум в распределении температур на верхней стенке об-
разует границу раздела ячеек;
в)	форма границы, разделяющей ячейки, зависит от формы профиля тем-
ператур вблизи экстремума; проводился специальный опыт с изменением
крутизны температурного профиля в случае дельтообразного нагрева сверху;
незначительное увеличение градиента температуры приводило к отклонению
границы в сторону большего градиента (рис. 3-46);
г)	форма неоднородности температуры на верхней стенке при одинаковых
величинах неоднородности ЬТL = *макс~7’МИ|| влияет на структуру течения
(рис. 3-47); при изменении характера приближеннолинейного нагрева меняется
форма конвекционной ячейки;
д)	направление движения жидкости в каждой ячейке возле верхней стенки
противоположно градиенту температуры в ней;
е)	ячейка заполняет всю полость по высоте, а по 'Длине сосредоточена на
расстоянии, равном характерному размеру неоднородности температуры.
247
Рис. 3-47- Структура течения для
приближеннолинейного распределения
температуры на верхней стенке-поло-
сти.
Рис. 3-46. Структура течения
в полости для дельтообразного
распределения температуры на
верхней стенке полости.
Температура няжней стенки по-
стоянная
Рис, 3-48. Безразмерный профиль тем-
иератур в — (Т — Т„) ! (Тh — Т„) в
опускных в подъемных потоках ячеек
при периодическом нагреве верхней
стенки.
i —температура в стенке на расстоянии
б мм; 2 — 35 мм; 3—75 мм; 4 — 110мм;
5—135 мм; б — совпадение размеров в
подъемных слоях; 7 — совпадение размеров
в опускных слоях,
Рис. 3-49. Скорость течения в ячей-
ке при неравномерном нагреве свер-
ху.
Показан профиль скоростей в централь-
ных сечениях всех четырех ячеек при пе-
риодическом нагреве сверху; точки на
кривой — совпадение замеров; заштрихо-
ванные участки — область эксперименталь-
ных точек,
248
10s	1(Г	1Q3
Рис. 3-50. Зависимость числа
Нуссельта от числа Рэлея (Ra)
при ЬТ*акс/ЬТ“а“с^1.
На рис. 3-48 приводится график относительной температуры 0 =
(Т— Т0)/(Т/1 — Т0) где Го—температура холодной стенки; ГЛ—температура
верхней горячей стенки и изучаемом сече-
нии в опускных п подъемных потоках кон-
векционных ячеек для одного и того же
режима периодического нагрева сверху. Из
рис. 3-48 видно, что передача теплоты через
полость для данного режима происходит в
основном теплопроводностью с незначитель-
ными конвективными добавками в опускном
и подъемном течениях.
Профили горизонтальной скорости в
середине каждой ячейки для этого же ре-
жима представлены на рис. 3-49. Профили
скоростей в разных ячейках практически
совпадают и имеют ярко выраженную асим-
метрию.
Зависимость числа Nu от числа Ra =
= Gr Рг, где Gr—- число Грасгофа, построен-
ное по высоте полости h и максимальному перепаду температуры на
верхней стенке	ТМИ[1, изображена на рис. 3-50 Для этого гра-
фика Рг = 0,707, а температурный критерий Д7’£ахс/'Д7’£ИН«« 1.
Очевидно, что влияние конвекции на теплообмен начинает сказываться
с чисел Рэлея Ra^slO4.
3-6. ТЕРМОКОНВЕКТИВНЫЕ ВОЛНЫ
Колебательные движения с малыми амплитудами в сжимаемой жидкости
называют звуковыми волнами.
В силу малости колебаний в звуковой волне скорость в ней мала. Поэтому
в уравнении Эйлера
^ + Rv)3=-vp/p	(з-6-i)
членом (vV) у можно прспебреяь.
Пусть
Р = рц-Ьр'>	(3-6-2)
P=po_l“p,>	(3-G-3)
где Ри и Ро — постоянные равновесные значения давления и плотности, а р' и р' —
их изменения (р' <<ро; р' <Сро).
Уравнение непрерывности
& + div pv =0	(3-6-4)
после подстановки (3-6-3) примет вид:
div v=0.	(3-6-5)
Так как р'. р', v—величины первого порядка малости, а их произведе-
ния— величины второго порядка малости, то ими можно пренебречь, тогда
уравнение (3-6-1) примет вид:
(3-6-6)
дт, г ри
249
Предполагается, что скорость движения частиц у значительно меньше
скорости звука с(о<с). Это выполняется исходя из условия (3-6-3): так как
p7p*CL то с/с^1. В идеальной жидкости звуковая волпа при адиабатиче-
ских условиях и при малом изменении р' и р{ описывается соотношением
Определим р' из (3-6-7) и подставим в (3-6-5):
Уравнения (3-6-8) и (3-6-6) полностью описывают движение звуковой вол-
ны. количество переменных и и р' можно свести к одной, введя потенциал
скорости
v =?ф.	(3-6-9)
Из уравнения Эйлера (3-6-6) получим:
(индекс у р0 и ро опускаем). Теперь уравнение (3-6-8) примет вид:
t№<p = O,		(3-6-11)
где с— некоторая величина, равная:
-/«к
(3-6-12)
Уравнение (3-6-1!) является гиперболическим или волновым уравнением.
В колебательных движениях в жидкости величину с называют скоростью звука.
Если взять операцию grad в уравнении ср, то видно, что каждая из ком-
понент скорости v удовлетворяет волновому уравнению. Взяв производную
по времени от (3-6-11), также получим гиперболическое уравнение для р',
а следовательно, и для р'. Для одномерной задачи можно написать так;
Ар_______1_ 02<р _ -
"дх? ~	дт*"^и'
(3-6-13)
 Введем новые переменные по соотношениям
тогда уравнение (3-6-11) примет вид:
^L=0.
Интегрируя по *, находим:
ОТ]	' 1
где F (ц)— некоторая функция только переменного г].
Интегрируя (3-6-16) при фиксированном получаем:
Ф Й, Ч) = S F (П) *l+ft © = ft © +ft (Ч).
Следовательно,
(3-6-14)
(3-6-15)
(3-6-16)
(3-6-17)
(3-6-18)
250
Функциями такого же вида описывается распределение р', р' и & в плоской
волне.
Пусть для плотности р' функция /i равна нулю, тогда
р' = /2 (х — ст).	(3-6-19)
В каждой плоскости x==const плотность меняется со временем. В каждый
момент времени плотность различна для разных х. Плотность одинакова при
условии
х—cr = const.
Если в некоторый момент времени т = 0 в некоторой точке плотность
имеет определенное значение, то через определенное время т то же значение
плотность будет иметь при х=ст.
Следовательно, f2(x—ст) представляв! бегущую плоскую волну, распро-
страняющуюся в положительном направлении оси х. Очевидно, /д (х-|-ст) пред-
ставляет волну, распространяющуюся в противоположном (отрицательном)
направлении оси х. Скорость в звуковой волне
<>х =
dtp
~дх
(3-6-20)
направлена вдоль оси .г, т. е. в направлении распространения волны. Поэтому
звуковые волны в жидкое ж являются продольными. Можно получить связь
между v и с. Имеем:
ф=/’(х — ст); у, = -^-=и=/' (х — ст);	‘	(3-6-21)
Р'“ -Р-^- = (*7' (х~ст).
Отсюда получим:
Так как согласно (3-6-7) и (3-6-12) p'==t2p'r то
Ф'
Р
Колебание температуры Т определяем гак:
Г = (дТ \
Р' \ др )s*
Известно, что
(дТ\	Т {дУ\
\ др Л	с0 дТ }р
(3-6-22)
(3-6-23)
(3-6-24)
(3-6-25)
(3-6-26)
где у —объем; ср — изобарная теплоемкость среды. Если обозначить коэффи-
циент ’теплового расширения через |i:
f} =
Т'

(3-6-27)
(3-6-28)
Здесь уместно определить скорость звука в идеальном газе. Из термоди-
намики известно что
(3-6-29)
25)
Тогда, используя уравнение идеального газа
Р =
pRT
М
находим:

(3-6-30)
где уcp/cv — отношение изобарной и изохорной теплоемкостей; М —молеку-
лярная масса и — универсальная газовая постоянная.
Скорость звука в газах имеет примерно тот же порядок, что и средняя
тепловая скорость молекул,
Покажем, что в вязкой теплопроводной жидкости, находящейся в постоянном
гравитационном поле, могут распространяться слабозатухающие тепловые кон-
вективные волны.
В изотермической жидкости, в которой не учитываются силы тяжести,
как известно [Л. 3-59], поперечные и температурные волны являются сильно-
затухающими. На расстоянии, равном длине волны, амплитуда этих волн
уменьшается в ехр (2л) =«540 раз. По существу это апериодическое движение,
которое было бы правильней назвать не волновым, а просто колебательным’
Ипаве обстоит дело с неизотермической жидкостью. Пусть существует
градиент температур вдоль направления гравитационного поля, В условиях
механического равновесия градиент должен быть постоянным. Если уТ совпадает
по направлению с гравитационным полем, то существует критическая абсолютная
величина градиента, выше которой возникает конвекция [Л. 3-60]. Будем
предполагать, что условия, необходимые для механического равновесия, вы-
полнены.
Изучим, как на фоне этого механически равновесного состояния с посто-
янным градиентом температуры распространяются малые возмущения темпера-
туры, скорости, давления и плотности, Для выяснения принципиальных
особенностей достаточно рассмотреть простой типичный пример.
Предположим, что жидкость занимает правое полупространство х^О
и ограничена плоской поверхностью х==0. Гравитационное поле g выделяет
направление, которое янтипараллельно оси у. Будем считать, что оси х, у
взаимно перпендикулярны, Вдоль направления оси у во всем полупространстве
х 0 имеется постоянный градиент температур дТ^ду-^у- Пусть ограничи-
вающая жидкость поверхность может колебаться в собственной плоскости
вдоль оси у с частотой со, а температура поверхности меняется во времени по
гармоническому закону. Требуется определить возникающее при этом устано-
вившееся движение и распределение температур в жидкости. Сформулированная
задача является типичной двумерной задачей совместной свободной и вынуж-
денной конвекции и описывается следующей системой уравнений,-
Гдр . -1
p[-^ + (cv) о ]= —vp+nv3" :
P=p[af + PVT'J-Xv’T’+n®; + div (pv) = 0;	0 6 31)
?(р. р, п-0.
При граничных условиях
f 7"==6CO8Ci)^ tk0 cos ©ft
х=0<	zo ’	(3-6-32)
1. p = m°0 cos (of, р — Па cos cof;
lim (Г, vt, p, p) = 0.	(3-6-33)
X—»co
В граничных условиях (3-6-32) учтены возможные периодические колебания
плотности, давления и всех составляющих скоростей. Если амплитуда колебаний
252
температуры Т и скорости v невелика, то решение систем (3-6-31) —(3-6-33)
естественно искать в виде
?	(3-6-34)
Р = Ро+Р' (х, 0; р^ро~[-р' (х, f). ’
Индексом нуль отмечены равновесные распределения температуры, плотности
и давления; Т’, р', р'— малые возмущения этих параметров, Малой того же
порядка будем считать и скорость v'r Подставляя разложения (3-6-34) в систему
(3-6-31) — (3-6-33) и пренебрегая малыми величинами порядка выше первого,
а также опуская индекс (штрих), получаем следующую линейную систему:
дТ ,	д2т	дТ0	X дт + ^Vy а дх2 ’	~ ду ' а~ p-fip ’	(3-6-35)
&vy	(д?\ =	^Р^.дт)т^Та = const;	(3-6-36)
• р 1\дТ}Т=та'	(3-6-37)
др	dvK , -s-H-po -4^=0; <?т г дх	(3-6-38)
dvx _ 1 др d2Ux . дт ~ po dx V dx? ’	(3-6-391
f T = 60exp (/сот); yy = pyOexp (/cot); 1	—улоехР (йот); р = Поехр (tarry,	(3-6-40)
lim (T, vx, vy, p)=0,	_	(3-6-41)
где vx, Vy — компоненты скорости вдоль осей х и у.
При выводе уравнений (3-6-37) —(3-6-41) изменением плотности вследствие
изменения давления мы пренебрегли. Предполагалось также, что равновесное
распределение плотности р0 можно считать постоянным. По-видимому, при
отрицательном градиенте температур у<0 это ограничение несущественно.
Изменение плотности за счет температуры компенсируется в этом случае из-
менением плотности за счет давления. В противоположном случае, когда оба
поля действуют в одном направлении, уравнения (3-6-35) —(3-6-39) справедливы
для нс слишком больших областей вдоль оси у.
Будем искать периодическое установившееся решение уравнений (3-6-35) —
(3-6-39) в виде плоских волн:
Т = вехр/(шт-Л»; op=t>exp I (шт-ЛГх);-1	42
Vx — ^exp i (сот —Л»; р — П expt (сот — Кх). f
Первые три уравнения могут быть проинтегрированы независимо и приводят
к следующему дисперсионному уравнению, определяющему связь между волновым
вектором /С и частотой со:
(v-/-<2)—<а2—ру=О.	{3-6-43)
Для того чтобы волны затухали на бесконечности, необходимо потребовать,
чтобы волновом вектор был комплексным, т. с. /< = /<, 4-i/<3, а мнимая часть
волнового вектора —отрицательной (Ks<0). Частоту будем ^читать дсйсгви-
253
тельной. Тогда из (3-6-43) нетрудно получить:
I. г—ш2 (V — a)2 — 4ov0y 0; )
/ (3'6'44)
Ла=—M±(4avf1r1''2}1''2; 0V > 0; 1
Ki—— {±	1 г1/2}1/2;	Ру<0; 1	(3-6-45)
1Мэ=а>!: J
, to(v4-a)
2. г < 0;	^/Са=—А‘>	(3 6-47)
Л(»--{±В+(Л2+В!)|/2!1/2;	(3-6-48)
В-Т (4av)"1 (-г)|/2.	(3-6-49)
Из выражений (3-6-44) —(3-6-48) видно, что в зависимости от абсолютного
значения и знака величины русо-6 в жидкости могут распространяться принци-
пиально разные типы температурных волн. Для всех частот со при условии
ру <2 0 и для частот	— в слУчае	как и в изотермиче-
ской жидкости без учета действия гравитации, распространяются лишь сильно-
затухающие волны [(3-6-45) —(3-6-47)]. Действительно, глубина проникновения
(или затухания) Е = одного порядка с длиной волны / = |^лКД i. Этот
случай малоинтересен.
Большой интерес представляет распространение воли с частотами ©<
<	— в среде, которая приготовлена так, чтобы ру > 0. В жидкости,
у которой плотность уменьшается с ростом температуры, р < 0, это означает,
что градиент температур в выбранной нами системе координат должен быть
отрицательным, и наоборот. Для газов коэффицисн! термического расширения
меньше нуля, значит, гравитационное ноле и градиент температур должны
быть параллельны.-В этом случае, как видно из (3-6-47) и (3-6-48), с задан-
ной частотой со распространяются две волны. Одна, соответствующая выбору
знака плюс перед В в выражении (3-6-48), является сильнозатухающей. Дру-
гая, компоненты волнового вектора которой
К, = Л[а(ИГ+1^-1)]- V2; )
K,=-VB (^i+A‘B-> -I)'/2, )
при некоторых условиях может быть слабозатухающей.
Выясним эти условия. Во-первых, необходимо потребовать, чтобы абсо-
лютное значение глубины затухания L — ' ЛГг’ । было велико. Это возможно,
когда 42В-2	1 Во-вторых, глубина проникновения в масштабах длин волн
должна быть велика. Для ответа на вопрос, когда это выполняется, нужно
проанализировать выражение L/-1:’
-----------— — - -- —  '
I 2кКа 2лВ(/1+Л28-! -1)
Учитывая условие А2В~2 <: ], упро.тим выражение (3-6-51):
£	[4avgT-»>3fr-°)''T/2	,3.6.52)
I	nw(V-|-fl)	'	'	'
Теперь нетрудно видеть, что отношение L/I будет тем больше, чем больше
коэффициент термического расширения и градиент температур, чем меньше
частота и чем ближе численные значения коэффициентов кинематической вяз-
254
кости и температуропроводности Абсолютная величина градиента температур,
как мы уже отмечали, ограничена сверху, поэтому существует конечный верх-
ний предел частот, которые распространяются с малым затуханием, со <; У fly •
Слабозатухающими, как показывают расчеты, являются низкочастотные коле-
бания. Приведем численные оценки. Лучшими в смысле пропускания высоких
частот являются среды с cv«sa. Такой средой является, например, воздух:.
v= 13 • 10"в м2/с; а=19-10-® м2/с.
При градиенте температур 102 град/м на частоте Ю*3 Гц глубина проник-
новения 10 .м,' или 103 длин волн.
Таким образом, в иеизотермических жидкостях с градиентом температур,
параллельным гравитационному по.тю (или антипараллельным, если fl >0),
в направлении, перпендикулярном g и vT, могуг распространяться слабоза-
тухающие температурные волны.
Амплитуды и фазы этих воли зависят от условий на ограничивающей
жидкость поверхности. Чтобы удовлетворить граничным условиям (3-6-40),
будем искать решение в виде суммы обеих волн — слабозатухающей и сильно-
затухающей— с частотой со и волновыми векторами	k=kt-yikz-
T=Re {о ехр t (шт —/Сх)-|-ёехр i" (сот — Кх)};	1	(3-6-53)
fycRe {vj;expi (ют —/(x)-|-yv expt (сот — Кх)}, j
где	ла
6 = в1~|—6 = 6i4-t62; I'y = у yi 4~ ^vyz< vy = Vyi -}~
Не останавливаясь на деталях довольно громоздкого расчета, выпишем
действительные выражения для температуры и поперечной составляющей
скорости:
Т=6Х cos'1 g exp K^x cos (сот — Kjx 4-£) -(- -t- 6X cos-1£ exp K2xcos (сот — Kix -f-g );	(3-6-54)
Vy = (/n6x — n02) cos-1 x exp /C2x cos (сот —/C1x-|-x)-|-	
4- (тбх -|-n62) cos*1/ exp /C2x cos (сот —	(3-6-55)
где	
?и6(|-|-Огл) cos e	y„0 sin 8 — л60	
61	2m	 ®a ‘	2m	(3-6-56)
л mfyj — Сщ) cos 8	
6i=		•	62 = — 62; 1	2m	’	2	2	(3-6-57)
. g = arctg 92ei| = arctg 92б(	(3-6-58)
, тбаЧ-яб, »	, m02 — яб* X=arctg~y-:—S-.	x_arclg_^	_L_.	(3-6-59)
zn6x — пОз	m6j -j-n02 /	
а У — r	a — v	
=	6	• n = co—5. *	2avr ’	2yv	(3-6-60)
Проанализируем полученные выражения. В первую очередь ответим на
вопрос, может ли распространяться только одна слабозатухающая волна, и
если может, то при каких граничных условиях? Оказывается, это возможно.
Пусть амплитуда поперечных колебаний стенки (х==0) равна v1/0 = m60cos"1 е,
а сдвиг фаз между колебаниями температур и поперечной скорости па стенке
равен e = arctg пт~1. Тогда, как следует из (3-6-56) и (3-6-57), 6j = 62=0 и
в среде распространяются только слабозатухающие тепловые волны:
Г = 6уехр/Сахсоз((от — Kix);	)
ехр KiX ерз (сот — Kix -|- arctg ntnrl). }
255
Максимальная амплитуда тепловых и скоростных колебаний совпадает
с амплитудой колебаний на ограничивающей поверхности, а сдвис фаз между
тепловой и скоростной волнами в любой точке волны совпадает со сдвигом
фаз на стенке.
Можно подобрать такие краевые условия, когда, наоборот, слабозатухаю-
щая волна будет подавлена н вся энергия на границе будет использована на
генерирование только сильнозатухающей волям. Это происходит, когда
иуО — пво sin-1 е; е = - arctg пт'1.
Еще два вопроса представляют, па наш взгляд, большой интерес. Какие
волны генерируются только за счет температурных колебаний на стенке и
только за счет колебаний ограничивающей поверхности? Нетрудно показать,
что в обоих случаях генерируются как колебания скорости, так и колебания
температуры, т. е. можно говорить о возбуждении в неизотермической жидко-
сти, находящейся в гравитационном поле, поперечных колебаний тепловыми
и возбуждении температурных колебаний поперечными колебаниями ограни-
чивающего поверхности.
Пусть амплитуда температурных колебаний на стенке равна нулю,
тогда из уравнений (3-6-54) — (3-6-60) следует;
Т = 1ехР Кг-хсоз (ют — Kjx) —ехр /<2xcos (ют —Л1*)];	(3-6-62)
ciZ = y^(2cosx)-1 X
X [ехрcos (ют— KiX— — ехр/<2лгcos (ют— Кгх — %)],	(3-6-63)
где у = arctg пит1
Пусть теперь стенка покоится, т. е. yyU = 0. Тогда выражения (3-6-62) и
(3-6-63) остаются справедливыми, если амплитуду волн заменить соответственно
на (fo (2 cos %)-’ и 0О (т2 + п2) (2m)-*. В обоих случаях генерируются оба типа
волн—сильно- и слабозйтухающие.
До сих пор мы говорили лишь о колебаниях температуры и поперечной
составляющей скорости. Подставляя полученные для Т и иу выражения
в уравнения состояния (3-6-37), неразрывности (3-6-38) и движения (3-5-59),
нетрудно найти слабо- и силыюзатухающие волны плотности, продольной'
составляющей скорости и давления. Всю совокупность температурных, ско-
ростных, звуковых и плотностных волн, распространяющихся в неизотерми-
чеикой жидкости, находящейся в гравитационном поле, только за счет терми-
ческой сжимаемости, будем называть термоконвективными. Среди термокон-
вективных волн наибольший интерес представляют, конечно, предсказанные и
исследованные выше слабозатухающие тепловые волны.
РАЗДЕЛ ЧЕТВЕРТЫЙ
СОПРЯЖЕННЫЕ ЗАДАЧИ ТЕПЛООБМЕНА
Id. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ СОПРЯЖЕННЫХ ЗАДАЧ
ТЕПЛООБМЕНА
Явления конвективного теплообмена имеют большое значение во многих
областях современной техники. Существенную роль играют процессы теплооб-
мена в теплотехнике, в атомной энергетике и других отраслях новой техники.
Особое значение приобретают проблемы теплообмена для современных лета-
тельных аппаратов, движущихся с большими скоростями, которые обусловли-
вают значительный аэродинамический нагрев конструкций.
При аналитических исследованиях теплопередачи в твердых телах, обте-
каемых потоками жидкости или газа, на границе между телом и жидкостью,
как правило, рассматриваются так называемые граничные условия третьего
256
рода, т. с. условия пропорциональности теплового потока у стенки q (х, т)
разности температур стенки и некоторой характерной температуре набегаю-
щего потока (TfSj—-Tca), причем вводится коэффициент пропорциональности
а (х, т), называемый коэффициентом теплообмена;
Ч(х, т) = «(х,	= №<(*. г) Л (7^-7^),	(4.Ы)
"где / — характерный размер; X— коэффициент теплопроводности жидкости.
Это соотношение обычно называют законом Ньютона. Коэффициент тепло-
обмена определяют как теоретически (из решения уравнений пограничного
слоя), так и экспериментально. (При теоретическом расчете предполагают обычно,
что условия на стенке заданы и постоянны (это позволяет считать задачу автомо- ]
дельной, что облегчает ее решение). Отметим, что температура стенки, например, /
может считаться постоянной (не зависящей от пространственных координат) (
лишь в исключительном случае бесконечно большой теплопроводности твердого О
тела. Однако на практике часто встречаются случаи, когда температура на /
поверхности обтекаемого тела не может считаться постоянной. Это относится / .
в первую очередь к высокоинтенсивным процессам теплообмена (например, I
при обтекании потоком, имеющим температуру, значительно отличающуюся !
от температуры тела).
В . то время как задача при постоянных условиях па стенке при тепло-
обмене между телом и жидкостью достаточно хороню изучена как теоретически,
так и экспериментально, для случая переменной температуры поверхности она
изучена гораздо меньше Одна из первых попыток в этом направлении была
сделана в работе [JJ. 4-1), где исследовался теплообмен при продольном обтека-
нии пластины ламинарным сверхзвуковым потоком сжимаемого газа, причем
температура стенки задавалась переменной в виде степенного ряда. В качестве
примера была рассмотрена параболическая зависимость температуры стенки
от продольной координаты;
Tw Те И- Те (0,25- О.ЗЗх + 0,33x2).	(4-1-2
При такой температуре обтекаемой поверхности были получены локаль
иые значения теплового потока, коэффициента теплообмена и числа Нуссельта.
При этом оказалось, что имеются точки, в которых коэффициент теплооб-
мена отрицателен или даже терпит бесконечный разрыв, что, конечно, физи-
чески неприемлемо. Подобным противоречивым результатам было дано объ-
яснение в работе {Л. 4-2], где рассматривалось обтекание пластины потоком
несжимаемой жидкости. Там же был дан качественный анализ распределения
температур в пограничном слое при условии, что температура поверхности
изменяется по некоторому заданному закону (рис. 4-1). Можно заключить, что
вблизи передней кромки температурный профиль в пограничном слое близок
к типу А (рис. 4-1), который подобен обычному профилю для постоянной тем-
пературы стенки (рис. 4-1). Уменьшение температуры стенки вниз по потоку
(dTw[dx с О) оказывает влияние прежде всего в той части пограничного слоя,
которая близка к обтекаемой поверхности. К внешним слоям охлаждение про-
никает только значительно ниже по потоку. Вследствие этого оказывается, что
в точке 8, где температура стенки совпадает с температурой внешнего потока,
(дТ1'ду)ш > 0, т. е. имеет знак, противоположный знаку градиента в точке А
Тепловой поток у стенки запишем двояко;
по закону Фурье
. \
г=-х!л71 :
\ оу ) ®
по закону Ньютона
(4-1-3)
(4-1-4)
В точке 8 при использовании закона (4-1-3) получается, что теплота пере-
дастся от жидкости к стенке, хотя температура стенки равна внешней темпе
ратуре и, следовательно, по закону (4-1-4) тепловой поток равен пулю.
9 Ликов А, В.
257
Вниз по потоку от точки В оказывается, что жидкость имеет температуру
вблизи стенки меньше, а при удалении от поверхности больше, чем у стенки.
Далее между точками А и В должна существовать точка Б, для которой
(dT/d§)w = 0, т. е по уравнению (4-1-3) тепловой поток равен кулю, в то время
как по уравнению (4-1-4) он в нуль не обращается. На всем отрезке между
типами Б и В теплота передается от жидкости к стенке, хотя повсюду Т >Т
При формальном рассмотрении, если бы мы использовали уравнение (4-1-4),
то были бы вынуждены принять в этой области Nu <0, а в точке В Nu-»-co.
На основании вышесказанного можно утверждать, что для переменной темпе-
ратуры обтекаемой поверхности ньютоновский закон охлаждения не пригоден
и поэтому определение числа Нуссельта по закону (4 14) теряет физический
смысл. В работе [Л. 4-3] дан обзор исследований теплообмена при перемен-
ных условиях на стенке, причем приведены результаты, сходные с рассмотрен-
ными выше; в частности, получено, что числа Нуссельта при переменных и по-
стоянных условиях на границе могут сильно различаться.
Рис. 4-1. Профиль температуры в пограничном слое (а) и рас-
пределение температуры вдоль поверхности тела (б).
Во всех вышеупомянутых работах было показано, что при заданных зара-
нее переменных условиях на поверхности тела (близких к реальным) исполь-
зование закона Ньютона, а следовательно, и коэффициента теплообмена непри-
емлемо. Однако закон зависимости температуры стенки от координат и от вре-
мени не может быть задав «apriori», а должен быть получен путем совместного
решения уравнений распространения теплоты в жидкости и твердом теле вместе
с уравнениями движения, причем на границе твердое тело — жидкость темпе-
ратуры и тепловые потоки равны, т. е. должна решаться так называемая соп-
ряженная задача теплообмена [Л. 4-4, 4-5]. При такой постановке учитывается
взаимное тепловое влияние тела и жидкости, которое при прежней постановке
не учитывалось, в результате чего теплообмен оказывался не зависящим от
свойств тела, его теплофизических характеристик, размеров, распределения
источников в теле и т. д., что, очевидно, противоречит физическому смыслу.
Особенно важно рассматривать задачи теплообмена как сопряженные для слу-
чая нестационарного теплообмена. Действительна, даже в предельном случае,
когда коэффициент теплопроводности Твердого тела очень большой (Х5->-со)'
температуру поверхности нельзя считать постоянной, так как хотя она и не
зависит от координат точек поверхности, но изменяется во времени. Однако
в отличие от стационарного теплообмена даже и в этом предельном случае
258
закон изменения температуры поверхности во времени не может быть напе-
ред задан, а следовательно, практически все задачи нестационарного конвек-
тивного теплообмена должны формулироваться как сопряженные.
В настоящее время известно небольшое количество работ, в которых при-
нята подобная постановка.
Граничные условия четвертого рода для внутренней задачи теплообмена
ставились довольно давно. Отметим работы Г. А. Остроумова и его учеников
[Л. 4-6] по свободной конвекции; следует подчеркнуть, что рассмотренные
ими методы решения являются приближенными: это линеаризация задач путем
разложения решения в ряд по параметру Gr Рг, который в некоторых реаль-
ных случаях бывает велик, поэтому получаемые ряды могут оказаться расхо-
дящимися.
В работе |Л. 4-4] рассмотрена задача нестационарного теплообмена при
обтекании полуограпиченного тела потоком несжимаемой жидкости в трубе
прямоугольного сечения. Несмотря на упрощающие предположения (скорость
потока считалась постоянной, уравнение энергии осредиялось вдоль потока),
полученное решение дает качественную картину явления. В работе [Л. 4-21]
были рассмотрены сопряженные задачи теплообмена в круглом и плоском
каналах как аналитически, так и численно.
Внешняя сопряженная задача теплообмена впервые была поставлена
в работе ]Л. 4-4], показавшей целесообразность такой постановки. А. А. Поме-
ранцев [Л. 4-7] рассматривал обтекание стенки газовым потоком; темпера-
тура стенки задавалась по степенному закону. Задача рассматривалась при
упрощающих предположениях: усреднение температуры по поперечной коорди-
нате и пренебрежение теплопроводностью по продольной координате. Т. Л.
Перельман [Л. 4-5] рассмотрел стационарную задачу при обтекании пла-
стины с источниками теплоты потоком несжимаемой жидкости. Задача реша-
лась при ограничительном предположении относительно числа Прандтля
(Рг<1). В работе [Л. 4-8] была решена стационарная задача при обтекании
газовым потоком бесконечно тонкой пластины (что является всьма ограничи-
тельным условием).
Для решения сопряженных задач конвективного теплообмена при течении
в трубах А. Заргари [Л. 4-11] была выведена обобщенная теорема преобра-
зования Лапласа. Разработке численных методов решения сопряженных задач
посвящены работы [Л. 4-10, 4-31]. В статьях [Л. 4-13 4-14] приведены реше-
ния сопряженных задач по свободной конвекции. В последнее время был
опубликован ряд работ по решению сопряженных задач 1Л. 4-15, 4-16].
Решение сопряженных задач теплообмена связано с преодолением прин-
ципиальных математических трудностей. Основная трудность состоит в том,
что приходится решать систему уравнений в частных производных, имеющих
различный вид на разных интервалах, в случае стационарных задач мы
сталкиваемся даже с дифференциальными уравнениями разных типов: для
жидкости получается уравнение в частных производных параболического
типа, а для твердого тела — эллиптическою типа. Наиболее рациональным под-
ходом к решению сопряженных задач является введение на границе сопряже-
ния неизвестной функции, равной температуре или тепловому потоку на этой
границе, которое позволяет свести систему уравнений в частных производных
к двум «несвязанным» краевым задачам. Неизвестная функция определяется
в дальнейшем из оставшихся условий сопряжения.
Для внешних сопряженных задач, как стационарных, так и нестационар-
ных, были получены асимптотические решения при обтекании пластины сверх-
звуковым газовым потоком (отметим, что рассматриваемые внешние задачи не
могут быть решены точно, так как уравнения пограничного слоя в области
передней кромки обтекаемого тела несправедливы, поэтому все решения, полу-
ченные с использованием теории пограничного слоя, являются асимптотически-
ми).
Несмотря па большое количество аналитических решений по сопряженным
задачам, экспериментальных работ очень мало. В упомянутой выше работе
[Л. 4-14] убедительно показано влияние температурного поля пластины па тем.
пературное поле и профиль скоростей в пограничном слое жидкости (рис. 4-2,
259
<-/
О 0,02 0,04 0,06 0,08 0,10
Рис. 4-2. Температурное поле п пластине
(керамика) и пограничном слое жидко-
сти с нижним нагревателем.
Гу — температура жидкости; — темпера-
туры пластины;----колсчпо-разностное ре-
шение; -----------интегральное решение.
Рис. 4-3. Температурное • поле в стек-
лянной пластине (нижний нагреватель)
и в пограничном слое жидкости. Обозна-
чения те же, что и на рис. 4-2.
Х< 1,0 0,8 0,6 0,4 0,2 О
О 0,02 0,04 0,06 0,08 0,10
Рис. 4-4	Рис 4-5.
Рис. 4-4, Влияние теплопроводности пластины на распределение температуры
поверхности вертикальной пластины в отсутствие излучения.
Рис. 4-5, Локальное число Нуссельта (керамическая и стеклянная пластинки
с включенным нижним нагревателем) в зависимости от координаты х.
260
4-3). Здесь приняты обозначения: X и V— безразмерные координаты (Х—хЦ,
у^у/Гу, е —безразмерная температура, равная:
gp/^T-T^)
6=	\,2	,	(4-1-5)
где коэффициент объемного расширения газа.
Рисунки 4-2 и 4-3 показывают, что конечно-разностное и интегральное
пешепия совпадают и близки к экспериментальным значениям.
Р На рис. 4-4 показано распределение температуры вдоль пластины при
разных отяошевих Х^Д/. Из рис. 4-4 видно, что при Х5/Х/ = 2500 изменение
температуры составляет около 5сС на 65°С. В случае больших Х5/Х/ ведущую
роль играет теплопроводность пластины, и тепловое взаимодействие происхо-
дит в основном через пластину. При Х5/Х/=1 (теплопроводность пластины
очень мала) тепловое взаимодействие происходит в основном через погранич-
ный слой, и большая часть теплоты от источников остается вблизи них.
На рис. 4-5 показана зависимость локального числа Нуссельта Nu^ от
координаты X для керамической и стеклянной пластины. Из рис. 4-5 видно,
что число NUjc существенно зависит'от теплопроводности пластины, Для неко-
торых значений X число Нуссельта становится отрицательным, что экспери-
ментально подтверждает вышеприведенный анализ (см. рис, 4-1), Таким обра-
зом, теоретически и экспериментально показано, что для задач конвективного
теплообмена сопряженная постановка является правильной, Возникает вопрос,
при каких условиях можно решать задачи конвективного теплообмена тради-
ционным путем без учета теплопроводности тел, оббкаемых потоком жидкости.
На этот вопрос в ряде случаев отвечает число сопряженности Брюна (Вг).
4-2. КРИТЕРИЙ СОПРЯЖЕННОСТИ
При решении задач конвективного теплообмена вместо граничных условий
третьего рода принимаются граничные условия четертого рода, т.е.
/dTf\	[dTs\
-М.	(4-2-‘>
(Тj)w = (J's)w>	(4-2-2)
где — источник теплоты на поверхности тела; индекс / и з —соответственно
обозначают жидкость и твердое тело, а индекс ш — ловерхность^тела.
РГз граничного условия (4-2-1) в отсутствие источника теплоты (Qw = 0)
приближенно получаем:
(ДГДг, _ Л/ й
(ДТ1f)6*,	*
(4-2-3)
где Ь — толщина стенки; &'т —условная толщина термического пограничного
слоя (см. рис. 3-10). Следовательно, отношение перепада температуры по тол-
щине стенки (&Ts)b к перепаду температуры в пограничном слое жидкости
(ДГ/)^ зависит не только от отношения коэффициентов теплопроводности
жидкости и стенки kffks, по и от отношения толщины стенки к условной
толщине термического пограничного слоя b/fy. При этом необходимо отме-
тить, что замена потока теплоты па поверхности твердого *тела, т. е.
fdTs \ _ ХИАГД)Й
\ ду	1
(4-2-4)
справедлива только при линейном законе распределения температуры по толщине
стенки. Это будет иметь ме^то при малых толщинах или при больших коэф-
фициентах теплопроводности тела при отсутствии источников теплоты в теле.
261
Если распределение температуры по толщине стенки нелинейное, то в соот-
ветствии с правилами теории подобия (теория обобщенных переменных) можно
написать:
_ (ЛЛ)а
[ ду	Ь ’
где е —поправочный множитель на искажение профиля температуры по толщине
стенки, который является однозначной функцией (&Ts)b/b:
Следовательно, имеем:
(А8’4=^)к=е i!- т (г)’	(4'2-6)
х \°Т /
где- (Д6)ь— относительный перепад температуры по толщине стенки. Условия
постоянства температуры на поверхности пластины соответствуют бесконечно
большой теплопроводности стенки (ks^> Ху), что приводит к бесконечно малому
перепаду температуры (ATS)O-> 0.
Если относительный перепад (M)t, <0,01, то с точностью до 1% перепа-
дом температуры в стенке можно пренебречь и считать температуру ее постоян-
ной (7’J)a, = const,
Из формулы (4-2-6) видно, что относительный перепад в стенке зависит
не только от отношения коэффициентов теплопроводности, толщины стенки,
по и от толщины условного теплового пограничного слоя б?, который зави-
сит от скорости движения жидкости, ее вязкости и изменяется вдоль направ-
ления движения (вдоль оси х).
Согласно формуле (3-1-86) величина х/Ъ'т равна локальному числу Нус-
сельта (Nux = x/6'r). Локальное число Нуссельта Nux определяется приближен-
ным соотношением вида
Nnx=^Pr« Re*,
где Ах, т и п — постоянные.
Тогда
(4!)),, = ^ -^P^Re".	.	(4-2-7)
Таким образом, относительный перепад температуры (Д6)& является одно-
значной функцией безразмерной величины [AfA«) Рг'” Re*], называемой чис-
лом Брюна *:
(AQ)6 = f (Вг)х,	(4-2-8)
где Вгх —локальное число Брюна,
ЬЬ
Qrx=~Prm Re*.	(4-2-9)
Число Вгх является критерием сопряженности.
Если число Вгх малое (Вгх < Вгхмии), то задачу конвективного теплооб-
мена можно решать традиционным путем, без учета сопряжения с температур-
ным полем в толще стенки. Величина Вгхмин определяется па основе оценки
точных аналитических решений или экспериментальным путем. В соответст-
вии с формулой (4-2-7) она будет зависеть от характера движения жидкости
(ламинарное или турбулентное). При турбулентном движении жидкости при
одинаковом отношении ‘kjbfksX число Вгх будет больше по сравнению с лами-
нарным движением. Поэтому BrXMtlH должно определяться в зависимости от
характера движения жидкости.
* Э. Брюн —выдающийся французский ученый.
262
Среднее число Брюпа будет равно:
2lfb
Вг = ^-Д- Pr'"Rc*,	(4-2-10)
Можно сделать приближенную оценку Вгмин. Предположим, что (Д0)$	0,05
(точность 5%), тогда при линейном распределении температуры по толщине
стеики (е=1) и ламинарном обтекании пластины (4 = 0,662) число ВгМ0Н <0,08
или приближенно Вгиин<0,1. В работе [Л.4-15] расчетами по аналитическому
пешению было установлено, что задачи конвективного теплообмена при обте-
кании плоской пластины ламинарным потоком "воздуха должны решаться как
'сопряженные задачи, если безразмерный параметр х больше единицы (х2^ !)•
Между параметром х и числом ВгЛ-существует такая связь:
ВгЛ=2Рг|/3Е“ V2x= 2Рг'/3(уУ',ги.	(4-2-11)
Для воздуха (Рг = 0,7) при 6/х = 0,01; x$s 1 число Вгх будет больше 0,18
(ВгЛ 0,18).
Представляет интерес вычисление числа Вг при ламинарном обтекании
пластины из разных материалов воздухом и водой. Положим 6/х = 0,05, тогда
при обтекании стальной пластины [Xs = 46 Вт/(м • °C)] водой {Х/=О,68 Вт/(м • °C)]
при Re = 108 Вг=1,8. При обтекании этой пластины воздухом [Ху—
— 0,028 Вт/(м-°С)] число Вг = 0,0?4, т. е. значительно меньше 0,1.
При обтекании пластины из стекла [Xs = 0,96 Вт/(м • *£)] водой при
Re=106 Вг = 8,7, а при Re=104 Вг = 8,7. При обтекании стеклянной пла-
стины воздухом при Re=106 Вг = 4,8, а при Re=104 Вг = 0,48. Следова-
тельно, при обтекании стеклянной пластины водой и воздухом задачу надо
решать как сопряженную.
4-1 ПРИБЛИЖЕННЫЕ РЕШЕНИЯ ЗАДАЧИ ЛАМИНАРНОГО
ОБТЕКАНИЯ ПЛАСТИНЫ
В качестве приближенного решения сопряженной задачи ламинарного
обтекания бесконечно длинной пластины можно воспользоваться решением
задачи обтекания пористой пластины при углублении поверхности испарения.
В этом случае расстояние поверхности испарения от поверхности пластины 5
принимаем за толщину пластины (£ = 6 = const). Температура па поверхности
испарения Те буиът равна температуре одной из поверхностей пластины
T’&=(7’e = 7’6 = const). Кроме того, отсутствует испарение (Jj — O, В2 = 0, B—B^,
Остальные обозначения сохраняются. Таким образом, задача является несим-
метричной, т. е. одна из поверхностей пластины (у = 0) обтекается ламинар-
ным потоком нагретой жидкости, противоположная поверхность пластины
(у= —&) поддерживается при постоянной температуре Ть (граничные условия
первого рода). Решение такой задачи представлено в виде формул (3-2-46) —
(3-2-48).	_
Коэффициент /^зависит только от числа Рг (В = 0,53 У Рг), акоэффнциеш
К будет обратно пропорционален числу Вгх:
1=0,81 PfSBr,.	(4-3-1)
К
Для воздуха (Рг = 0,7) Вгл=1,32 (1//Q.
Тогда можно воспользоваться формулами (3-2-59) и (3-2-60). В этом слу-
чае величина №* будет равна отношению локального числа Нуссельта Nu*
сопряженной задачи к локальному числу Нуссельта Nuxll обычной задачи,
т. е. когда число Вгх = 0 (температура по толщине пластины одинакова и_по-
стоянна; 7'e = Tw=const),
263
Следовательно, при малых значениях числа Вг*(Вг^< 1) можно написать:
«• — 1 = 0,81 Рг1/3 р Вгх,	(4-3-2)
где постоянная 0 берется из табл. 3-5, Для воздуха (0 = 0,78, В = 0,44)
будем иметь:
tf*-l=0,63 Bt>.	(4-3-3)
Представляет интерес сравнить это выражение с аналогичным соотноше-
нием, полученным из точного решения Если воспользоваться графиками
приведенными в работе [Л. 4-15], и формулой (4-3-1), то получим;
№* — 1 = 0,48 Вгх,	(4-3-4)
что близко к формуле (4-2-14). С учетом того, что в работе решалась более
общая задача, но условию которой температура Те изменяется по длине пла-
стины; Г(—/>, х)—Те{х).
При больших значениях числа Вгл(Вгх> 1) можно воспользоваться фор-
мулой (3-2-60) тогда величина (Л7* —1) будет линейной функцией Вг7‘«
Можно решить поставленную задачу, используя интегральные уравнения
(3-1-75).
Примем профиль температуры и скорости в пограничном слое в виде
полукубической параболы, т. е.
в-Э«-+2 6г ' у— 2	а». У' <4'3’5)
где 0 = 7/ — Tb-, ’b-Sl = Tw—ТTw— температура на поверхности пластины,
которая обтекается жидкостью (7® = Т(0х); Т/—температура жидкости.
Распределение температуры по толщине пластины принимаем за линейное
«'“М'+гУ	(4-3'7>
где ^' = TS — ГTs—температура пластины.
Подставив формулы (4-3-5), (4-3-6) в интегральное уравнение пограничного
слоя
/ d’O'1
— v)t>x (y)dy^a{^-
(4-3-8)
получим
дифференциальное уравнение:
6т
20
3. а
2	(1 -J- z) ’
(4-3-9)
где
При
вертого рода
_ зу>
2 2Xs6r •
выводе уравнения (4-3-9) было использовано граничное условие чет-
А — А А
исо ии>  w
х	>.
(4-3-10)
(4-3-11)
из которого было получено выражение для неизвестной температуры Оо,;
ft г
ОЗ-12)
1^2
264
Если положить г = О (пренебрегаем влиянием температурного поля пла-
стины на температурное поле пограничного слоя), то получим формулу (3-1-77)
Таким образом, наше уравнение пограничного слоя (4-3-9) отличается от обыч-
ного уравнения пограничного слоя наличием дополнительной величины г.
Прямо пропорциональной числу ВгЛ [формула (4-3-9)],
Если пренебречь вторым членом в скобках в формуле (4-3-9) по сравне-
нию с первым, получим:
d Г 1	] Юаг
dx[z2(l^z)6]~ у3(1^г)нм’	(4-3-13)
ЗХ/
где
Легко найти два асимптотических решения:
1)	при г 0 и х—* со
^«уПТРгЛЗ	(4-3-14)
ог
— это классическое решение [формула (3-1-78)];
2)	при z со и соответственно х -* О
v=Alpr-	<4-3-15)
Получим более точные решения вблизи г ->-0 и г->оо, полагая
А = Рг1/3[^+Ф (х)],	(4-3-16)
где <р(х) —малая функция, так что <р3(х) —0; .4 — постоянная,
Тогда
гЛуРгУ1р+|ф(х)].	(4-3-17)
Подставив (4-3-17) в (4-3-13), получим дифференциальное уравнение пер-
вого порядка относительно г.
Воспользуемся асимптотическими решениями этого уравнения для опреде-
ления локальных чисел Нуссельта:
3 х 3/14
N“-«=TT V 13РГ-	(4’3’18)
где Мил-о—число Нуссельта для классической задачи;
(4-3-19)
где Nu,.—число Нуссельта для сопряженной задачи.
Тогда
Тогда для малых значений z, а следовательно, и чисел Вгх получаем:
/У*-1 = 0,ЗЗВг^ Вг/< 1.	(4-3-21)
Для больших значений чисел Вгх
N* — 1 = 0,26 — 0,07Вт'1; Вг^> 1,	(4-3-22)
т. е, в качественном отношении получаем аналогичные зависимости между N*
и Вг^, разница только в значении коэффициентов Последнее объясняется пре-
265
делами изменения Вгх. Для практических расчетов формул, когда число ВгЛ
изменяется от 0 до некоторого конечного числа N (0 < Brx < 2V), можно поль-
зоваться формулой
(4-3-23)
где С и т—постоянные, определяемые из точного решения задачи или экспе-
риментально.
4-4. ТОЧНЫЕ РЕШЕНИЯ ЗАДАЧИ ТЕПЛООБМЕНА ПЛАСТИНЫ
В ПОТОКЕ СЖИМАЕМОГО ГАЗА С ИСТОЧНИКОМ ТЕППОТЫ
В первую очередь рассмотрим обтекани--1 пластины. Введем следующую
систему обозначений; продольную скорость vx обозначим через u(ox = u),
поперечную скорость vy —через v(vy = v), динамическую вязкость —через ц,
Рис. 4-6. Профили скорости vx (у) и тем-
пературы 0 (у) в' пограничном слое при
обтекании пластины.
па рис. 4-6, система уравнений переноса
(4-4-1)
(4-4-2)
(4-4-3)
тогда согласно схеме, изображенной
имеет вид1;
ди ,
а(ри) ,
дх ди
as as i д /
f,u dx + IK’dy~ PFdy ul
Полагаем Pr = const и = const. Принимаем следующие граничные условия:
при у=£) и- н=0 е = еда(х);
при у —со н и = чоз 9 = 7^
При этом -принимается следующая зависимость коэффициента вязкости
от температуры [Л.4-1]:
(4-4-4)
(4-4-5)
где В — постоянная;-0№ — средняя температура поверхности. Приведем резуль-
таты, которые опубликованы в [Л.4-15]. Температура пластины определяется
решением дифференциального уравнения
&Т . д21 = _ (*> У)
ch? + ду*
(4-4-6)
1 Изменение обозначения вязкости (вместо г| вводится ц) обусловлено тем,
что в решениях задач во внешнему теплообмену буквой т| обозначают обобщен-
ную координату.
266
где Q (х, у} —источник теплоты (непрерывная функция х, у) при условиях
Для симметрично обтекаемой пластины толщиной 26
На границе раздела имеют место обычные граничные условия
Г-^(S)^l	=-ls(d^\	;	(4-4-9)
L ’ А/Ь-О (ДД,_0’
S (х, 0) = 8„ (х) = 0е + Э (х) = (Т-),.,.	(4-4-10)
где —температура теплоизолированной поверхности,
Задача может состоять или в определении температуры поверхности и теп-
лового потока через нее, или в определении вида источника теплоты 0 (х, у),
необходимого для того, чтобы температура поверхности или тепловой поток
через нее принимали заданное значение.
Для тонкой пластины уравнение (4-4-6) с использованием (4-4-8)—(4-4-10)
может быть записано в виде
где ^(х) —тепловой поток через поверхность пластина —поток; 1Г (х) —осред-
ненный источник,
v (X) = 2 И?„х“.
п=0
Условие (4-4-7) приме* вид:
/d0TO (х)\	__ 7d0w (х)\ =q	(4-4-12)
\ dx	\ dx Jx-l '	k 1
Уравнение энергии можего написать так:
+ Рг I ~ - 2Рг /'»• ~ = - ^ (V - 1) М (/')’,	(4-4-13)
Зг|2 <5т|	' дх* 4 ‘	' v ’	\	!
где x*=sx/L; 6* =0/7^,—безразмерные переменные, а т| определяется соотно-
шением
Г(г))=--^=;	(4-4-14)
У х*
здесь ф*— безразмерная функция тока,
Функция f (1]) является решением уравнения Блазиуса:
f'" + ff = Q-	-j
)(0)=0; f'(0)-=0; Г(оэ) = 2. }	(4'4'1в)
Граничные условия для уравнения (4-4-13) напишутся так: -
6*(х*, 0) = 0* (х*) = б* + й* (х*);	6*(х*, со) = 1.	(4.4.|7)
267
Решение уравнения энергии имеет вид:
S’ (»«, !)) = «(,])+ 2	+	(4-4-18)
п = 0
Функция Ур (т)) определяется из уравнения
К; + Рг/У'-2РгГрУр = 0	(4-4-19)
с граничными условиями
М°)=1;	1/р(со) = 0;	(4-4-20)
Л'(Ч) = 1+:^ЛЙ>г(11);	(4-4-21)
СО	?
'М-4 Рг )' [ГЙ)1Рг j	(4-4-22)
П	(J
здесь р = а.п\ апф-Р; ал-f-y (n = 0, 1, 2 а, 0, у>0 (положительные
числа). Коэффициенты Ап, Рп и Q„ определяются по соответствующим фор-
мулам [J1.4-25],
Коэффициент теплообмена а определяется из равенства
4(х*) = аТю[е*(х*)-0*]-
2	v	S №/1ГЗ/2п (0) Н-РдХ 1,2Уз/2п-Ь 1/2 (0) +
*	“ п = 0
+ <?л^*Кз/2п+I (0)]х 2 .	(4-4-23)
Учитывая, что 4о=6*(0, 0)— в*, Pos=Q(J==0, получаем:
а С^(х*)[б* (0, 0)—б*]
®	C[S£(X‘)-SJ]	2[S* (%•)-6J] Х
xj/^EPc 2 M«^/-(0)+^-'-=rt/2„ + 1/2(0)+
+QZF3/2/4-1 (0)№/2п.	(4-4-24)
где а—коэффициент теплообмена при 6ТО = const;
Собственные функции Ур (т)) вычисляются по формулам, приведенным
в [Л.4-16],
Из решения сопряженной задачи следует, что нельзя задать температуры
на поверхности пластины в виде ряда Тэйлора по степеням х. За исключением
тривиальных случаев, температура поверхности не будет аналитической функ-
цией х, а будет иметь особую точку при х = 0. Следовательно, заранее задать
температуру поверхности, если она переменна, нельзя.
268
4-5. НЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ ИСТОЧНИКА ТЕПЛОТЫ
Граничные условия первого рода
В данном разделе мы ограничимся рассмотрением стационарной сопряжен-
ной задачи теплообмена при обтекания пластины (длиной L, толщиной &,
с теплопроводностью fy), продольным газовым потоком, имеющим на бесконеч-
ности постоянные скорость и температуру Т^; температуру па внутренней
поверхности принимаем постоянной (аналогичное решение получается в случае
задания потока на внутренней поверхности) [/1.4-16].
Предполагается, что скорость газа зависит от температуры и меняется по
линейному закону; число Прандтля считается постоянным.
1.	Математически задача сводится к решению в безразмерных переменных '
уравнения для газа
Р + Ргф- 2Рг ф- ® < = - Pr(V'-' 1’1' ®)! (4-5-1)
<7u.'	О'-,	og	t	«
с граничными условиями
	(4-5-2)
и уравнения для твердого тела	
	(4-5-3)
с граничными условиями m5^o = eM: (^1^ = °'	(4-5-4)
где О00 —температура торможения:	
(8)„л=Э« + Х©: (8)9.-i=«6.	(4-5 5)
где ^ — температура восстановления. На границе раздела твердое тело — жидкость условия сопряжения в виде	даются (4-5-6)
где О — безразмерная температура жидкости; 0—безразмерная температура
твердой стопки.
Здесь используются следующие обозначения: Х = 1Х1/’Хх С02)] — безразмер-
ная температура на границе тело —газ: %т — температура на границе тело —
жидкость (газ); у~х2,'Ь — безразмерные пространственные координаты; £ =
= лу/й — ордината;
г____
; = 0,5|'0'sJ pdy; ух = уИКесс-
о
Величина -л равна:
*=0,5 J/rTT= 0,5 у ,	(4-5-7)
где индекс со относится к потоку жидкости вдали от стенки.
Неизвестная функция (%(£)) определяется в дальнейшем из второго усло-
вия сопряженности (4-5-6) для потоков,
При линейной зависимости вязкости от температуры, как известно, гидро-
динамическая задача автономна, т. е. функции (%>(£)), (ср' (£)), (ср" (С)) известны,
это обычный блазиусовский профиль,
269
Решение уравнений (4-5-1), (4-5-2) для газа ищем в виде
«к,	(э+ое, 5).
где
t (С) ~ 2 Рг J [ф" &)]Рг dti f [ф" с2)]2’ Pr dt2,
£	' о
з О — удовлетворяет краевой задаче
<Э20- , _	50 _ n ,t д$ п
aF+Pl'P<-2Pr'P^=°:
(»V«,= o.
Применяя обобщенное синуопреобразование Фурье
и, (а.) = lim ( и © sin пЕ ехр (—
И-»0. О
перепишем (4-5-9) и (4-5-10) в изображениях в виде
<*+рг^+2ргфМ^+я^]=о;
Решение (4-5-12)—(4-5-13) ищем в виде ряда
а)=Д]С,г,га’‘.
Решение (4-5-14) и соотношения
v , (v,H-1) sin Г-|-(v, -f-1) л1
а ‘---------------!------J
л	^l+v<
будет записано так:
8 (Е, Е) =4 25(V|+')C,/'(v,+ *>	[т(Vl + ’)"]z'i ©=
= l2r(v'+l)D‘Mo,
(4-5-8)
(4-5-9)
(4-5-10)
(4-5-11)
(4-5-12)
(4-5-13)
(4-5 14)
(4-5-15)
(4-5-16)
где (Z (£)) удовлетворяет краевой задаче
2ЧО+Ртф2^ + 2РгФ'(1 + *)2ф = 0;	(4-5-17)
ZU=1- zlt-~=°:	(4‘5-18)
D,, V/ —постоянные, подлежащие в дальнейшем определению, причем
О<=С,Г (v,+ t) sin (v, 4- 1)л].	(4-5-19)
Решение в изображениях (4-5-3), (4-5-5) с учетом (4-5-11) можно запи-
сать так.-
„ ею , sh (к) (1 + «)	(9„-9e)sh (a)(l+« + (9j— O»)sha</
- 7Г+ sh«	ashes
(4-5-20)
270
Дифференцируя (4-5-14) и (4-5-20) и подставляя полученные результаты
во второе условие сопряжения (4-5-G) для потоков, записанное для изображе-
ний, получаем уравнение, из' которого находятся постоянные и D/t
Z-J, (0) и”' ch я
= (®е —Mch® +
+(Оо» —	(v, + 1) sin
(4-5-21)
Разлагая в степенные ряды функции, входящие в (4-5-21), и приравнивая
коэффициенты при одинаковых степенях а, получаем значения м,=0,5(г —2),
после чего с учетом (4-5-15) получаем окончательно распределение температуры
в пограничном слое:
о (С. 5)=1+[(Л-1)/81Мь,'Р(С)+ '
+ (О» - м [<р* (?i) 1Рг <111^ 1<р" К1)1Рг ) +
6	\6	/
+ xZL, (0) (Э„-Э£) {[Ф" ©/ср’ (0)]PT"'5+0,25Z,,5(J) V2-’ +
+ o,25kz;.5 (0) z, © r3+o,25z»z; (0) z;.s © z,.s ©
+ (7,5 К2/16 / л) X»z;,, (0) z; (0) z;,s (0) z, © r*+-  •) •	(4-5-22)
Из уравнения (4-5-22) при £ = 0 получим температуру поверхности, обте-
каемой потоком газа:
= (Ф)£-о - (ОVo =	4~ xZL1 (0) (fy, - Of) X
X{l-n-'4-0,25g-s-’ + 0,25xZtJ0)g-84-0,25y?2' (0) ZJ.5 (0)	-J-..(4-5-23)
Отметим, что функции ZVj. в уравнениях (4-5-22) и (4-5-23) при найден-
ных Vj определяются как решение краевой задачи'
2*i+PrTZ^(l+vi)^ = 0;	-	(4'5-24)
(Zv;k-o=I:	(4-5-25)
точные решения которой получены лишь в двух случаях —при v0 = —1 и
vx =—0,5;	t	i
Z_! [фя (S1>]Pr ri£i {j [<p"(W]Pr	;	(4-5-2G)
2-».5(г) = [^Г	<4’5.‘27)
При остальных значениях v/ функции ZVj могут быть получены только
численно; для этого необходимо вначале найти асимптотическое решение
уравнений (4-5-24) и (4-5-25). Входящие в них функции Блазиуса ср (£) и
ср' (с) не выражаются аналитически, но для больших значений ^(^2=3,5)
могут быть представлены гак:
cpQ^2(£-0.86); О)=2; ^3,5.	(4-5-28)
Подставляя (4-5-28) в (4-5-24) и (4-5-25), получаем для больших £ урав-
нение
(0 -f- 2 Рг (С - 0,86) Z'; (?) 4- 4 РГ (1 + v,) Z (С) = 0
(2^оэ=0.	(4-5-29)
271
решение которого представим в виде
Ч- Ьз.з = С W [-°-5 C-W2]}.	(4-5-30)
Численный расчет производится с учетом (4-5-30), при этом постоянная С
определяется в конце при £ = 0. Результаты расчета, произведенного методам
конечных разностей, приведены в {Л. 4-9]. Отметим, что функции ZV/ при
V|-5=0 немонотонны.
Подчеркнем, что в решения (4-5-22), (4-5-23), входит новый критерий х
[см. (4-5-7)], который включает в себя характеристики как набегающего по-
Рис. 4-7. Зависимость Nu (£) /Nu* от Рис. 4-8. Зависимость (относи-
параметров £ и х.	тельная разность температур) от па-
раметров X И
тока, так и обтекаемого тела. При х->0 (что соответствует бесконечной тепло-
проводности твердого тела или бесконечно малой толщине пластины b -* 0)
получаем известное распределение температуры газа при постоянной темпера-
туре обтекаемого тела:
«-с, э= пт «(с, «=
х-»0
= 1 +КК- 1)/81 ю + («<.-«К1)1Рг db [Т (<Р" &)1Рг	'. (4-5-31)
_ Критерий х, вообще говоря, может принимать значения от 0 до со (для
..большинства реальных случаев х«»1); отмстим, что предельный случай х->со
соответствует тепловой изоляции обтекаемого тела, а х->0 характеризует тот
случай, когда возможно использовать закон Ньютона с погрешностью, кото-
рую можно определить.
Во всех остальных случаях (0<х<со) можно лишь формально ввести
коэффициент теплоотдачи, а следовательно, и число Нуссельта, которое с уче-
том (4-5-26) определится следующим образом [Л. 4-16]:
Nu (|) = 0,5	0,664 ’/pT-xZl, (0) [0,25Z;,s (0)g-’.’ +
+ 0,25xZ( (0) z;„ (O)|-= + o,25^z;,,(O) zj (0) z;,:, И ra-5+...)} x '
X (1 + xZS, (0)	+ 0,25g-<'" + 0,25xZ(„ (0) Г8 + . -Г1}.	(4-5-32)
Легко видеть, что при х->0 из (4-5-32) получается широко известное вы-
ражение для числа Нуссельта:
Nu* — lim Nu = 0,332 p'Rel ,z'Pr,	(4-5-33)
x-»0
где Re^=Pobx/va3.
272
2. Рассмотрим два примера расчета по выведенным формулам {Л. 4-9].
б) Плохо проводящий материал [fy = 2,52 Вт/(м • г • СС)|.
Пластина имеет толщину Ь — 0,01 м. Характеристики набегающего потока
следующие: М=3; 7% = 280' К; 7^ = 223 -К;
vOT = 9,54xlO-8 ма/с; ^ = 2,04x10^ (Вт/(м.°С);	= 900 м/с; t/£> = 400 м/с.
В этом случае: х(1'=3,95; х12) = 2,64. По формулам (4-5-23) и (4-5-32)
были подсчитаны температура поверхности обтекания и значения числа Нус-
сельта. Результаты расчетов представлены на рис. 4-7 и 4-8.
б) Хорошо проводящий материал [Х/= 15,6 Вт/(м-°С)]. В этом случае
х'11 =0,639. Результаты расчетов, аналогичных случаю «а», представлены на
рис. 4-7 и 4-3.
Из полученных графиков видно, что значения и Nu могут сильно
отличаться от обычно используемых (при х->0). Так, например, в случае «а»
значения Nu в несколько раз отличаются в отдельных точках от общеприня-
того Nu* то же самое относится и к температуре обтекаемой поверхности
(поскольку при х —* 0, 0j1=.ftz>). В то же время для хорошо проводящего ма-
териала в случае «б» величины •0,Е) и Nu сравнительно ненамного (нс более чем
на 25%) отличаются от соответствующих значений 0» и Nu* (для случая
х->о/
Граничные условия второго рода
Вышеприведенное решение было получено при заданной температуре на
внутренней поверхности твердого тела в потоке. Ниже будет дано решение
при заданном тепловом потоке па внутренней поверхности:
<4-5-з4>
Можно следующим образом преобразовать решение краевой задачи
(4-5-1)—(4-5-2):
(«. Q =	+	. (4-5-35)
Решение краевой задачи (4-5-3)—(4-5-4) для твердого тела (условие на
внутренней поверхности) заменяется на (4-5-34) и может быть сведено к урав-
нению
о, + L [а) + ch	,4.5.36)
s а । (ли ) 1 а j с[] а c^cha 1	'
Дифференцирование выражений (4-5-35) и (4-5-36) и подстановка в усло-
вие сопряжения (4-5-6) в преобразованном виде дают;
х2сНго?*+ 1,5 ch а = (^Дю)« sh а — g ф-2	2 sh а. (4-5-37)
i	I
Из указанного выше уравнения, приравнивая коэффициенты с одинако-
выми степенями а, находим:
V! = 4 ("'- 1): С< = -ф''+1 П .	(4-5-38)
где
f 17 TI’1
Л < = Zv, (0) Г (vf 4-1) Sin Л ] |Г + т) Sin L----------2~^~ |/ *	(4'5'39)
273
Используя найденные значения v,- и С/ и преобразуя (4-5-35) с учетом
уравнения (4-5-14) и формулы обращения
ccH+i	г	л I«	vt-u-wj
Г (p-f-1) sin [Jp-f-1)-g-J
получаем распределение температуры в пограничном слое:
9	=1+V -MZOTT X
X {Z-i.s ® £"' + 4°J;(0) - 2^z; р) Z77(O5 +}•	(4-5-41)
Из уравнения (4-5-41) при £ = 0 получаем температуру поверхности
в потоке:
= ^-0 = <>1М = &«? "т „5 С,—TrZ X
b *	1 eoXAyZ'-l.g (0)
vzL., I Е"1___________Г3,5	,	35g-« --	]	,4t.
•	+4zZ'(0) 2x2Zo'(0)ZJ.5(0)+ 8x3ZJZ!.J0)Z3'(0) +,,’J’ (4’b’42)
Рассмотрим предельные случаи формул (4-5-41), (4-5-42). ‘
а)	х~>со, случай термически изолированной поверхности. Выражения
(4-5*41), (4-5-42) дают известные соотношения:
Ош= lim i>te, = i>;	(4-5-43)
«-*°(\-0)
#*(£. =	(4-5-44)
Лу-0
б)	6Д5->0, случай тонкого тела. Выражсния'(4-5-41) и (4-5-42) имеют вид:
*	’	2?1 Кх
]>№= lim	—;	(4-5-45)
b/ks^o	Ml 1.5 (°) Л»	1
»* = lim = 1 +-^- Mi-v К) - Г 1т* 	(4-5-46)
6/A.s-0	°	Лоэг‘-115(и) 'со
Следует отметить, что уравнение (4-5-45) имеет такой же вид, как и фор-
' мула, Представленная в ]Л.4-3), при постоянном тепловыделении в тонкой стенке.
Это еще раз подтверждает универсальность решений (4-5-41) и (4-5-42),
которые являются обобщением имеющихся результатов некоторых частных слу-
чаев (хорошие или плохие проводники теплоты и т. д.) и могут быть исполь-
зованы во всех практических случаях.
С помощью уравнений (4-5-41) и (4-5-42), используя формально закон
Ньютона', можно найти выражения для локального числа Нуссельта;
Nu(x)=—(0)! L1_______________________L.2_—।	. д_______г 1у
2	+4х	2x®z;(0)+8x’z;(0)Z[.s (0) + ---f х
х {б"‘+ 4xz;(0) _2^ (0)Z;,5(0) '|-(О) z;„ (0)Z;(0) + '4 ’ (4'6'47)
Что касается внешних задач, то в случае «а» (х->оо из уравнений (4-5-43),
(4-5-44) следует, что число Нуссельта равно пулю; в случае «б» (d/Xs~>0) из
, 274
1
уравнений (4-5-36), (4-5-37) получаем выражение для числа Нуссельта:
lim Kus=0,5Z' .«(0) V Rex.
b/ь ->o	'°
(4-5-48)
Сравнение этого уравнения с формулой, полученной в работе [Л,4-3] для
аналогичной задачи,
Мцл = 0,455 Рг|/3 KRe,
(4-5-49)
указывает па их соответствие (при Рг = 0,72, ZL,.S = O,82).
В заключение следует отметить, что более подробно распределение темпе-
ратуры в твердом теле для рассмотренных задач приводится в [Л.4-9].
4-6. ВНУТРЕННИЕ СОПРЯЖЕННЫЕ ЗАДАЧИ
В основе разработанного общего метода решения внутренних сопряженных
задач теплообмена лежит сведение задачи к решению сингулярного интеграль-
ного уравнения для неизвестной температуры обтекаемой поверхности ]Л.4-9|.
Он позволяет получать точные решения в случаз как стационарного, так и
нестационарного теплообмена при ламинарном и турбулентном режимах те-
чения.
В данной работе мы ограничимся (за неимением места) рассмотрением ста-
ционарной задачи теплообмена при ламинарной вынужденной конвекции в круг-
лой и плоской трубах при установившемся пуазейлевском распределении ско-
ростей с учетом диссипации механической энергии.
I.	Математически задача сводится к решению в безразмерных переменных
уравнений для жидкости
Pe(l—qa)	0MSl, 0-g^co (4-6-1
с граничными условиями
=	=	+	.	(4-6-2)
wL=°' s"-®	(«-3)
и уравнений для твердого тела
дЧ<т 1 д ! ^tm\
—г——1----йг~г~а^~ T)r,n~I) —\	=0; l^n<6, O^g<co (4-6-4)
др 1 Y^rn-i dq \ 1 dq /	’	1	’	®	’
с граничными условиями
^fm | £-0	(Tl)*	(4-6-5)
fym 1ц-1= Xm (E)>	fym Iti—6 = 4’m (£)	(4-6-6)
На границе тело—жидкость имеем следующие условия сопряжения:
От 'п-1 — ^fm 'n-i — Xm (Е)>
I SOfm 1
15 Sr, = St, h., 
(4-6-7)
(4-6-3)
Отметим что условия при £-*оо в (4-6-2) и (4-6-3) получены из решения
поставленной задачи при £->оз.
275
2.	Решения*(4-6-1) — (4-6-3) нетрудно получить, используя принцип супер-
позиции в виде
а>	I
=	S A„mR„ (ч) J х (51) «р [——5;)] d5t +
n= |	О
+ 2 ^пЛт (г|) ехР [	'	(4-6-9)
я=1
где
5«„»(ч1)4?“‘(1-чЙ‘,ч1
л о	2
Rnm Ы 4?~ ' (' - Ч?) Ч	Р™ (йСЪ
2 S (Чх) чГ' (! -ч!) [%--4т (1-41)1 Ч
п	О_________________________________________.
пт	[(dRnrn/dRnirtf (dR пт /Л))1Ч.1
Rnm (4) ~ ехР । H>'il3nm42ll [ят- Pm- ^\тЧ31-
Si= '"Z"1 1 а8= 2 f”8 1 Р1 = °Д Ps=l; Ртг = Ьл„\ Р„„-корни на-
рактеристического уравнения
Jx&m, Pm- Рт) = ^	(4-6-Ю)
имеющиеся, например, в 1Л.4-20].
3.	Решение краевой задачи для твердого тела по уравнениям (4-6-4) —
(4-6-6) находится с помощью обобщенного синус-преобразования Фурье в виде
efi = l>fio+ Нт 7, \ ( {[?.(“)-—1 slice (Р — Г|) +
ц -»о д \ J ч а J
[6/ю 1	1 ехр [—на]	\
'h W ~	sh а (Ч ~ 1V sh а (6 - 1) -sln а£ rfa /; t4’6’11)
в/а=1-0,25р«1п>1+ Нт-/С /б И -1~|к°<а8)	(аЧ)_
'	п-ои \J (Ll «1 /»(а) Ка (яв)— /о рб) Ко (я)
— j G (4, 41; «) )0,25рЯ ]п ч,(оэ)51/11,1 ехр [—ца| sin /4-6-12)
я IK (ач,) /„ (аб) (яб) /„ (ссгц)]	.	„
GI а) =	'»(a8)	'
Т|' 111 я|К«(ач) /0(а8) — К„ (а8) /0 («ч)1 ,
------------------------------------------'»<«4i)- 41-S 4 -S «
Подставив уравнения (4-6-9), (4-6-11) и (4-6-12) в условие сопряжения
(4-6-8), записанное для изображений, получим уравнение для определения
изображения неизвестной функции (а);
фт (0 “т (0 - бт И "Xzy- rfT “/m (0.
О
276
гле фи (=); 1=аг;
01W= У	/Й(б-О;
»=i	+ '
М;)=О,5Ц У	'
,^Т1 bhi+l
со	л_
/lW==”H77+fl 2 в"1/?"'(1)FT7"'
3 V i	bni +1
n= I
r-
-°«“с',,|/(/я6-1’+1гЖет:
CO	,	2
„ /Л V (Ч ь”г
Zl= I
/fk» (а (П)/,(/?) + /„ (а О к, (П)].
фоУТШ/иаЗ-иИаНД/ ()]
,, ... i V	.
(4-6-13)
= у в^(1)П+‘ И С о- (1, р„ /
Ьпч + t	Р V
X [ Р1----4’2 (СО)"| rfpj +
к» (а И) л (/ -) + л, (а (/?) к, (И)
/»(/О к„ (а//)-/0(а И) к„ (//) ’
4.	Уравнение (4-6-13) является сингулярным интегральным уравнением
с ядром Коши (4-6-14). Для его решения воспользуемся идеей аналитического
продолжения в комплексную область. Сведем уравнение (4-6-13) к краевой
задаче Римана с разрывными коэффициентами. Введем кусочно-аналитическую
функцию
L
Где контур L является положительной частью действительной оси, Используя
формулы Сохотского—Племеля, получаем:
ф(/)=ф+(0-Ф-(0‘,	(4-6-15)
X	+ ф.	(4-6-16)
Подставляя (4-6-15), (4-6-16) в (4-6-13). получаем:
ф+(?)=(?(/)©-и(I),
(4-6-17)
277
G it) == Q (0 + &	=fjt)-------
Неаднеродная краевая задача Римана (4-6-15) может быть решена в общем
виде, если индекс задачи не отрицателен. Нетрудно показать, что в нашем
случае индекс равен нулю [Л.4-9] и решение (4-6-13) имеет вид:
X (a)=0,5g(«*) (1 +G-1 (a»)j + |/[G («2)1 exp (7 (a*)| |1 -G'l (и»)| x
X ‘ С _________1(У’)У“У---------,	(4-6-18)
где	-	•
r(/)-=5L f JUS-dT,
( ’ 2ju J x — t
Искомые температуры и получаются из (4-6-9), (4-6-11), (4-6-12)
учетом (4-6-18) и соотношения
Х/п	Um ( хт («)ехр |— ца] sin da.
1^0 о
4-7, НЕСТАЦИОНАРНЫЙ ТЕПЛООБМЕН ПРИ ЛАМИНАРНОМ ДВИЖЕНИИ
НЕСЖИМАЕМОЙ ЖИДКОСТИ В ПЛОСКОЙ И КРУГЛОЙ ТРУБАХ
В этом разделе приведем точные аналитические решения нестационарной
сопряженной задачи теплообмена при ламинарной вынужденной конвекции
в круглой и плоской трубах при пуазейлевском распределении скоростей.
Система уравнений (4-5-3)s (4-5-4) в данном случае примет вид (в безразмерных
переменных):
дв,-	di); 1 д / dfy \
—+ Ре(1-Ч=)-= — —	+	(4-7-1)
о Fo	г/ 1 1т) \ ch)!
e/|Fo-0=°. 0<ч<1, 0<г<ОО;
S/V»=1;	F°);
dii I 0	X/(?, Fo)-T„ .
STL- -------------^-T, ’
SFo 1^-' M ‘MJ
ss/|fo-0 = °: 1<4<6; 0<g.<(co;
(4-7-2)
(4-7-3)
(4-7-4)
(4-7-5)
(4-7-6)
®S,|E-O=1; 6s/|,-a> = ()s„(I1, Fo);
7.1(1. Fo) — T№ ,	1V(E, Fo) — Ts„ _
n—1 —	t t »	ti—fle	т- т «
.; si— 1 so	1 si —1 so
1(^1 — o) 6-F TqI «= |(TS!— T’so) 5$ -|- sol In-il
I _ I
1 L-i вч L-i’
(4-7-7)
(4-7-8)
(4-7-9)
(4-7-10)
где %(£, Fo) —известная функция, задаваемая в общем виде: х, (^, Fo)—неиз-
вестная функция, подлежащая определению в дальнейшем, а 5^ и 0siXj опре-
278
делаются как решение системы (4-7-1) —(4-7-10) при |-*оэ и имеют соответ-
ственно вид:
0ад СП. Ро) = Я (Fo + .Fo2) +
Fo
а С
+ (?!—То)'1 -^-1 [Z1 (со, FoiJ-T-o] ^[0,51], Fo-Fojl rfFof
Fo
*Ч27ЙГ ОИ; (4-741>
8^(4. F«) =4 <’-’!•)+
+ 2 У J444<7’1-7’«)"1 ([7.2(“.FOi)-7'„]exp[-^(F<>--F°i)]1/FOi-
" I 1,Ця)	V
п= ।	a	i
“4” 2t^'xp(-^f°)
Fo
®S<X>2:
Zi, (Tal-Tsc) №)	J Usl ’ ’
X exp [— a-„ (Fo - FoJ] d Ро,-л (Г^-Т^х
•a® FoJ dFoi,
(4-7-12)
причем an, p,n—соответственно корни уравнений:
J0(a) Fu (a6) — 70(aS) Уо (я) = 0;	Jo (pi) = 0,
«о (ayj) = Jo (ат)) M) — h (afy Y (aij).
(4-7-13)
(4-7-14)
Решение краевой задачи (4-7-1) —(4-7-10) получается с помощью преобра-
зования Лапласа по времеЕЕИ. При этом задача в изображениях по виду похожа
на соответствующую стационарную задачу (решается аналогично тому, как это
было сделано выше). Опуская промежуточные выкладки [Л.’4-9], приведем тем-
пературные поля в жидкости и твердом теле соответственно для плоской и
круглой труб:
n. Fo) = Sa,;(T), Fo) —1+2 У P„,exp
|2ф1/(’1> Ш- Fo)~
Fo	)
-e»)(nr °)Фу(Ч. ’ll. Fo)- $ Ф+^.Чг Fo,)eot,,(i1,Fo-Fo1)dFo1!<ftll+
2
t- -p^	— Г ) Zj Р'" ) ‘И \ VArl— рп/ (TU — FU1JJ А
1	°	0 и»
Fo	\
х 5 ф1/(п> П1’ Fo,)[X/gj Fo — FOj)— X/ (со, Fo — FOi)] d FoJ(4-7-15)
279
,я g’п'Fo)~((б-i)" П(со‘F°’’ л,|!4’ ом’!"
п
-1X1 (со. F01) —7\0| Д.[ДД , тДДД]р Fo,+ ДД’1’) X
х/| Fsta а2 Ц А „8 [ДД, кДД-)г] е Д- 2ДД (а, Го- Fo,) -
loo
д Г т~1 1 Fo, 1	/ № For \	1
., (Гл-ЛлГ [Д ДУ) j а , Г 1-1 fo, 1
ХоКп(6- 1) WFo.Mdn 3 [2(6-1)’ ка (8-1)! J
ХЬ(И. Fo —Fo,) —-Дз[ДД-, тДДгДоэ, FO - Fo,)} d Fo, +
— f dni I (5, l '1^ -1-, —I-
4|ЛП(3—1) J 1 .1 v [2(6-1) Ka(b-i)d
~ ЧДб- I) ' K„(S-l)s' ]} x
М»
x ---Д. ' (m Fo- Fo,) - 1 ] d Fo, + 0ral (T), Fo); (4-7.16)
0 (t „ Fo) = 0	(„ Fo)+ - f f ?0(а6)2С9(аг1)-?„(а11)К„(аа)
ra(” Л’ ' 3=02 № +пД (.М'<.(»)-/.ИК.И
X sin a|Xso (a- F°i) F°i 4-
2 у anJi> (%)!«(8”g) К (a»4)Y»(%) - <> (an)y0 (%4)]
л	(T si—7\o) [ Ai (a/?) ^'i (^ал)1
;i= 1
co	Fo
xlj sina'da ex [- Ka Fo, (а24-х = )]^-ДД~р01) d F01-
0	0	n
co	Fo
——Tso)—sina^d-x P2 (1, fi, i], a) y2 (оз, Fo —FoJdFoj —
о	0
2(7\i-^oF у
J0 (^-n) ~ J n (&&n)
H = l
хДп^Д-Р[~*<Ж±^1х
J J “+“i
X [i|>s3 (a. Fo — Fo,) —	(::CJ.' }--—E£1Lj d F01 _|_
L	J
280
4 п ,)	' К,(а) )„(aS)-/0(o.)K„(aS) Х
xj J [М«П1) Ко(аб) — /о(а8) Ko (aiii)] $«2 fol, Fo — Foj) — a] d Fot 'ir|i +
Jad J о (ССЛ) J 0 (OCc^)
п— I
б Fo
X ( j У,	Ко (а„б) - Y„ (а„щ) (a„S)j X
1 о
ехр[— К,, Fo. (а24~а2)1 а, ,	,
iFo-Fo,)- 1] Л) Fob
где
Ф1/(п
R„i(4	^^(‘-'^expjp,, Го) '
J a I dR,tl dR„i h
laP, [dp,, di]
, /-Toi'i f.Lp.._ A , 1+L 1+.L в„Л.
(4-7.17)
(4-7-18)

Р^ и ря/ определяются из системы трансцендентных уравнений:
.F. I—______________________Ё. _t_ 7 + j_ i±_L й| = Л
(4-7-19)
ап—корни уравнения
J„ (<х8) У'и (а) —(а) 1,, (а8) = 0;
р и к „ ?о(М>Ки (ц)-?»(н)к»(ич) .
|Х”(Р + “!«ОГ^”'5.
(4-7-20)
(4-7-21)
(4-7-22)
Неизвестную функцию % (|, Fo) найдем, применяя к уравнениям (4-7-15)—
(4-7-17) двойное интегральное преобразование: преобразование Лапласа по
времени и обобщенное синус-преобразование Фурье по Тогда для изобра-
жения неизвестной функции
Xs/ (а, p) = lijn | j x (s, Fo) exp (— P Fo) exp (— o£) sin a fyi ^d Fo
получим сингулярное интегральное уравнение g ядром. Kouih:
С q/(T- Р)
nV.	t'. F) ) T_t	P),	(4-7-23)
u
281
где
Zs/(a, P) = 44.V. РУ
“<'	АЛ,(1)^-
Кк k;/+^^~cth ИГр/г; <а—1),
ь. н р\= clsZ у bni	.
11 ’ П 2^-70) Z 1?=(М21 ’
П=1
hit. p)=rVt у —^«0) _
П = i	1 +t
______г____ V ^niRni (l)5n I (со> Р) -
(Л-Г0)Ре	t+fti
п— 1	*
ф(/, Р) —^(со, P)-yL-
j, у	У PKa~{-t cs^ к PKa-j-t х
1 S1 — ‘so
1)-^‘ x(C°/)>rWa + < cth и PKZ+t (8-1)-
G'i . 4. 41,
G1 (Л. 41.	f") =
._______2
$«1р
Sil	(8—TU)Jsh [/wa + ^ (4-1)]
KPlG+^shiyPKa + a> (6-1)]	’
1 <4! <4 <6;
sh[/PKa+a‘(6-4)]»h[V'PKl,+a»(r|i-l)] .
KP^ + «ash[)'p/<-a + ai(6_l)]	’
1 < tij < t| < 6;
j Rnl (41) d4i
арм /п-1
'nj
— Р
Л-1 .
2B"I J U"’< fl’ P)]R"/dr Р)41(>-4])«4]
fi«='
<>Ral dR,, \
<Vni л, A-,
r v Ч-» f;o. 6. >. p)
и2(1. Р)-(Г1_Го) 2	r„-T№ ~
a~ 1
282
1,3 (/’ ₽) 2(Л-Г„) 1	;
П = 1
fl (t, Р)=rVi £ вм^2 (') 7^j7 -
Л=1
~ (Г,-То) 2|	/ + 5“2 Х(“' Р)_
п—1
Фо (“. Р)-/=-
--. г,-т/ *^(1' 8' ” р>-
ЛТХ(“. Р)	, ' ««„(1. Р)
a(TSI —тм) ‘	 Р) а Л|
_ 6
—Vt Jg;(K<, n. ni. p) [&»2 (л. пь КО—
1 к кг (i, Р)
С?Т)
I?о(И) Ко (rt~Ко (rtl) Io (rtl 1?о(ЦП1) Ко(|18)~7„ (|х8) Ко (|1П1)1
Ко(|1) !о(|18)-/о(Н)Ко(116)
сг(п, ш. pH	1<п<ш<8;
1ММ1)К1>(ц)—Коdnii) '.(rtl t?o(nn)Kii(ii8)—?д(ца)К1|(|11|)|
Ко (И) /о (118) — /0 fill Ко (цб)	’
1	<4! <п <S;
с ,, я „	/о(ц8)Ко(цг|)-;„(|лд)Ко(ца) .
Л(1, о, П, W ;„(iiS)Ko(n)-;odi)K„M ’
F ,1 s „ Mf6)Ko(nWo(|i)Ko(Rl)
2	(w ?o (fS) Ко (rt - /о (rt Ко (1*8) •
Решение интегрального уравнения (4-7-23) получается аналогично тому,
как это изложено выше (см. гл. 2-2). Поэтому, опуская промежуточные вы-
кладки. выпишем сразу изображение неизвестной функции х/(ъ> F°)- Как и
ранее, легко показать, что индекс краевой задачи Римана, соответствующей
интегральному уравнению (4-7-23), равен нулю:
Zj/ (а Р)-0,5г/ (а’, Р) [I +GF- (а’, Р)] +
- + ЙС/(“2. Р) “Р Ю («’. Р)1 [1 -G? (“2. Р)] X
1 ?____________g/(У2. P)g^____________
Х ТГ J /Су(у2, Р) ехр (Г, (9’, Р)| (9г -а=)-	(4’7'24)
ГДе г ,, р, rtd- P)+8jd. P)m	f/C. Р)
‘	a/(i, P)-bt(t, Р)т	> ai(ft P) — bf(t, Р)т ’
Л((' Р>- 2SZ ) -^=1--------Л’
283
По формуле обращения находим величину неизвестной функции;
со	с 4- I со
Х/(Е. Ро)-^^ j sina'da j exP (—та) exp (P Fo) Xs (a. P)M\ (4-7-25)
Q	C—(CO
Распределение температур в ^жидкости и в твердом теле окончательно
находим, подставляя (4-7-25) в уравнения (4-7-15) и (4-7-16). Таким образом
задача решается до конца.	j
Данная задача решается в [Л. 4-11] по иному методу. Скорость движения
в трубе V/ принимается постоянной и одинаковой в сечении. Однако темпера-
тура жидкости на границе соприкосновения со стенкой трубы [0 (/?, х, т) =
= ф (х, т)] принимается отличной от температуры самой стенки трубы [Г (/?, х,
т) = ф(х, т)|, где /? —внутренний радиус трубы. Таким образом, на границе
соприкосновения жидкости и стенки трубЬ[ имеет место скачок температуры.
В то же время потоки тепла одинаковы. Эти допущения, хотя и несколько
необычны, но позволяют решить задачу до конца. Обозначим температуру
жидкости через в (х, г, т), а стенки трубы Т (х, г, т), где х—направление вдоль
трубы, совпадающее с направлением течения жидкости.
Введем операторы и по соотношениям:
1 д	1 $
г дг	дг'1 О] дх а, дх
= 1	_____la
’ г дг дг- а2 дх ’
(4-7-26)
(4-7-27)
где и я2—соответственно коэффициенты температуропроводности жидкости
и стенки трубы.
Система дифференциальных уравнений имеет вид:
^х(0) = О; 0<г</?; х^О; т^О;
%ъ(Т)=0- R<r<Re-, х^О; т>0,
(4-7-28)
(4-7-29)
где Re — внешний радиус трубы; (Re—R)—толщина стенки трубы.
Начальные условия
6=0;
7 = 0;
Q<r<R;
R<r cRj
х^О; т^О.
(4-7-30)
Граничные условия
•^- = ° ПР" г = 0:	ПР»
e = l о <г <R
R,
7=1 R
(4-7-31)
О
Условия сопряжения
=	Ха(4/^)г^я=сс(1!:~ф>: х>0- т^0’
(4-7-32)
где Ф и ф —заданные температуры жидкости и стенки трубы на границе их
соприкосновения,
Ф (к, т)=0 (R, х, т); ф(х, т) = 7(/?, х, т).	(4-7-33)
В частном случае, ’ когда коэффициент теплообмена а -* со, ф = ф, тогда
получаем сопряжение в виде граничного условия четвертого рода
/ 00 \	/ дТ '
=	• x^sO; т^О.	(4-7-34)
1 \ дг Д = д 2 дг Д =	*	1
284
Функции Фиф связаны между собой соотношением
ф =	.	(4-7-35)
а \ дг }г = r	'	’
Для решения поставленной задачи используется метод интегрального Пре-
образования Лапласа. С этой целью была введена теорема интегрального пре-
образования от обобщенной функции. Пусть функция от оператора Лапласа
имеет вид:
/(“) = -^exp[-Km(sj],	(4-7-36)
где /и (s) —мероморфная функция, нули которой $ = —а^, а полюсы $ = —4^
удовлетворяют неравенству
О < С а2 <	.. < aN < bN со.	(4-7-37)
Тогда для т>0 обратное преобразование Лапласа дает оригинал функ-
ции f(s):	»
F = If (s)) = exp [- ц (0)] -
» ‘1 4
— У ( у exp (— XT) sin (x)] dx,	(4-7-38)
4-i a4
где	__________
- Ц (*) = /[« (-*)!•	'	'	(4-7-39)
Если имеется конечное число (N—1) пар a^cb/г и добавочный пуль
№ —av (ajV>7»jV_1), тогда необходимо добавить JV-й полюс $ = --^=8—со,
чтобы получить количество пар X. При наличии бесконечного числа пар
ak < b принимают X = со.
В результате было получено следующее решение:
В(г, х, т)= У [<i,„	(х, т) +
п = 1
+ <?а.л (0 5Ф(Е. т ~ Ч) Ki. „ (х, 5, т, ч) A)dgl; (4-7-40)
О l>	J -
Г (/, X, Т) = У] ^з,7г(г)^21/г(х>т)4-
г-т1)Ка,д(х, т, t])di]^1	(4-7-41)
ио	,	J
где коэффициенты Q, X, К, входящие в решение (4-7-40), (4-7-41), равны:
XIira(x, T) = exp/-^i\ e-v^crfc/±z2^1L\_j_
\ 2«i )	\ 2 у Ojt /
+ ?nJ; erfe ' £±_£^L\ >	(4-7-42)
i v > «И J
где
VH — pn-j-fl'y/Soi)3,	(4-7-43)
285
i ргг —корни характеристического уравнения
Ja(f>R) = O-,	(4-7-44)
Х2.„(х,	+ eVerfcp±to,	(4-7-45)
\ 2 У агт I	2Уа,т )	1
где —корни характеристического уравнения
<#i (ft ft, Т) = 0;	(4-7-46У
здесь —функция, определяемая соотношением
Л (г, Re, у) = J„ (yr) Yn (yRt) _ YR (vr) Jn (yRj:	(4-7-47)
где J, Y — функции Бесселя первого и второго рода;
О (r\ 1	@п> г) •
V1,n() м J1M ’
о гн 1 J°(M.
ft iff1! (R. Re', УпУ,^1 (r, Re; yn)
y„R’^l (R.R'iU-Rl^lR’R; T„);
I r	0^1 (r, Re, V»)___
vA «Mft ft; 'lriJr~19\(R, Re. y„)
(4-7-48)
(4-7-49)
(4-7-50)
(4-7-51)
E, T, Л)=]/'-Д- P> exp [^-Ё-ч (^+«Л)]х
Н-^]-ы4-“]};	(4-7-54
- ft.H*. T, П) = Т»]Л~-«1>(-ЗДЙ)х
х{ехр[“-^]-ех!,Ь'егёг]Ь	(4-7-S3>
Для того • чтобы задача была решена до конца, необходимо определить
функции Фиф, Между ними существует связь
‘ а \дг /< = /?*
/ дв \ /дТ\
Производные	и	соответственно равны:
(>U=4
। L
СО X
4-^ \'ф(£, Т — Т])/<1,,,(х, g, Т, T])dT]dg
и 0
(“57'),.—д ~ 2 ^3’п ^2’п (х’ т^
+ «4,	I, т.
(4-7-54)
(4-7-55)
(4*7-56)
286
Если использовать граничное условие (4-7-31) и формулу (4-7-54), то
получим интегральное уравнение:
Л (х. ч+j j-B (х, ё, Т, 1|) Ф g, т-ч) =
г	Т СОТ —Т]	-1
— - С(х, т)4-J J D (х, т, т], 8, р) Ф (е, т —т|—р) dp de е/т| ,	(4-7-57)
Looo	J
где
Л (X, Т) =	^I,n	п (R) ^2. п (х> T)^j J
п = 1
в (х, g, т, п) = У *£. п (*. I. т- n) +М4, «(R) Ка. л (X, t Т, T])J;
п= I
с(х, ч=х,х2 2 ИД)И 2 Xi.,» g, ’-чКиСЛь
п— 1	0 0 т — 1
D(x, т, ч, в, ₽)=МХ2 2 *«-4(Я) 2 Г Ki.mfs. t т-п. ₽)Х 
n= I	т=1 О
хК2.„ (х, J, t. ч)^-
Таким образом, даже при значительных упрощениях задача решается
примерно так же, как и при точном решении.
4-8. СОПРЯЖЕННАЯ ЗАДАЧА ТЕПЛООБМЕНА
ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ ЖИДКОСТИ И ГАЗА
В этом разделе будет показано, что методы решения сопряженных задач,
развитые в предыдущих пунктах для ламинарного режима течения, могут
быть с успехом перенесены на турбулентный режим. Отметим, что во избе-
жание повторений (и за недостатком места) решение задачи будет дано схе-
матически.
Несжимаемая жидкость
В этом случае система уравнений переноса в безразмерном виде запишется
так:
дО, 1 д Г	дО, ’	
	; 0 < т] < 1; 0 < £ < со; (4-8-1)
дО,-	
0/ 'v-°= 1;	= 0;	(4-8-2)
56/ I в0; о/ т 5т| |п=^0	'	-1==^;	(<-8-3)
&6sf 0Wsf	
	<б; 0<£<со;	(4-8-4)
	1
ew Н”1'	“5;	<4-8-5>
287
X/©
Ч>/ (И
Лв/	In-i—х/ ©;
dfy I df)sj 1
ч- |л=| ’
(4-8-6)
(4-8-7)
'	(4-8-8)
гДе ф/(?) ~ заданная функция; у (£) —неизвестная функция, в дальнейшем
подлежащая определению. Значения распределения скорости Л (т]) и турбулент-
ной геплопроводности gf (т;) можно найти, например в [Л.4-18].
Температурное поле в жидкости для плоской и круглой труб может быть
найдено подобно тому, как это делалось в § 4-7. Тогда решение краевой
задачи (4-8-1) —(4-8-3) можно записать сразу:
»/(Ч. 6) = всо+ S й«Л/('1)Мр[-6„|]-
п =» I
СО	|
-ТГ S Л'«К"/(’1))ехР1-Ь'"Й~©)ИХ/©)-7'11‘1Ь,	(4-8-9)
rj = 1	о
где Rnj удовлетворяет краевой задаче Штурма —Лиувилля
1 d Г
"77 h'S(4)-7~ -VW®/”0’
ту dx\ L ebl J
Rj |г| = 0 = 0; Ry |n  | = 0.
Так как /у(т[) и £/(п) определяются экспериментально, а в аналитической
записи имеют сложный вид, то Rnj (г\) находятся численно (см., например,
[Л.4-18]). Учитывая ортогональность Rn/(q) на интервале (0,1), получаем выра-
жение для постоянных Ап; и Влу:
с	dR„/(l)
= — = = ;
J 4'7, (Ч;) Rni (Tli) Ч, J ЧЛ (41)	('ll) *h
о	о
“со (4!)] 4ЛЧ) Ral (Ч,)*),.
в„/=---------!--------------------------.
1 ч,7, (4,) Rs„: (ч,) 'Ч
Распределение температур в твердом теле получается по формулам обра-
щения, описанным выше, если в них положить Л/=0.
Сжимаемая жидкость
При не очень высоких числах Маха М для турбулентного газового потока
в круглой трубе основная система уравнений запишется в виде [Л-4-19]:
DR^(l-ri^	(4-8-10)
0 <Т] < 1;
0<£<со;
288
Ч-о=‘;	5-1 Is -* 00	(4-8-11)
=с *1 |г|_о	Ь 8 1п-! = ^-,	(4-8-12)
f-t, d^s _ dt? + a,,» “	о; 1<п<8; ,0<Е,<со;	(4-8-13)
|&_о=1;	41 =“	(4-8-14)
8, In-! = 4^ 1 Si	 в 1	Ч1 © . ‘ $1	(4-8-15)
ТЛ |„-1 =	|п.1 = Х©1	(4-8^16)
о. 8в I ri л лг L 	=А| ’ = 1 п Г| In = Г	(4-8-17)
' Легко видеть,-что если а системе (4-8-1) — (4-8-8) принять Ре -+• D (Re)9,2®,
f (Т|) _> (1 _ т])1^7, g (q) -*• (1 —1]2)6/7, то эта система совпадаете системой (4-8-10) —
(4-8-17). Поэтому решение последней совпадает с формулой (4-8-9), если в ней
сделать указанную замену.
В § 4-6 —4-8 применяются следующие обозначения: Т/, TSj—соответствен-
но телшература жидкости и тела; Оу и bSf — соответственно безразмерные темпе-
ратуры жидкости и тела:
б/ = Т//Х (со);	=	(со);	(4-8-18)
X (х, т) —температура на границе сопряжения; ф/(х, т)—температура на внеш-
ней границе трубы.
Для стационарной задачи эти температуры обозначены через X (х) и сру (х).
В нестационарных задачах 0/ (х) и 65/(х) определяются как
в.= ДДк. в, =	(4-8-19)
‘	‘ 0	‘si — ‘so
То и Tso~соответственно начальные температуры жидкости и тела; 7\ и Tsl—
соответственно температуры жидкости и тела при х=0; х, у—продольная
и поперечная координаты; £ и т] — безразмерные продольная и поперечная
координаты; Ui— средняя скорость; X и — коэффициенты теплопроводности
жидкости и тела; а —параметр преобразования Фурье; Р~ параметр преобра-
зования Лапласа в интегральесых соотношениях; а = Рг;
8=4г;	«« = !-;	(4-8-20)
«	f-S	as
п	И°/^		(4-8-22)
а	О'; (от)	
3	л	^(п)=1+^.4 (‘-п):	(4-8-23)
иоа=2мг;	Fs(n)=1~Кх4 1ПХ|;	(4-8-24)
289
10 Лыков А. В,
ug(u, z)=l-f-2 У] exp (—Ji2£3z) cos
k = 1
иа(и, z) =
-тМ2“'Ь^Ь2“-1~-ЕН-
' Ц = 0	Л=—1	J
Wi (u, z) = 2	(—l)fe exp Г—л3 6?-|-2^ x"| sin (2fe-f-l) u.
(4-8-25)
(4-8-26)
(4-8-27)
Индексы: /=0 (или /= 1 в§ 4-7) — плоская труба; /= 1 (или / = 2 в § 4-7) —
круглая труба; 0 относится к начальным условиям; 1 —к условиям на поверх-
ности; s —к изображениям по синус-преобразовапию Фурье; С —к косипус-
преобразованию Фурье; s— к твердому телу; со —к параметрам набегающего
потока; зу —к условиям на стенке; Ь — к условиям на внутренней поверхности.
Сопряженные задачи конвективного теплообмена имеют большое значение
для исследования химико-технологических процессов. Работами И. АС Жаво-
ронкова и его учеников [Л-4-22, 4-23] показано, что внешний тепломассообмен
в ряде аппаратов химической промышленности определяется не только гидро-
динамикой движения жидкости, но и взаимосвязанным (с поверхностями твер-
дого тела) тепломассообменом. Сопряженные задачи со вдувом вещества
в пограничный слой рассмотрены в [Л.4-24], там же приведены и некоторые
другие задачи.
РАЗДЕЛ ПЯТЫЙ
ЯВЛЕНИЯ ПЕРЕНОСА В КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛАХ
5-1. СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ
Пористые характеристики
Под пористой средой обычно понимают твердое тело, содержащее поры.
Дать точное геометрическое определение понятия „поры” достаточно трудно.
Обычно под порами понимают пустые промежутки, распределенные в твердом
теле. Поры в пористом теле могут быть сообщающимися друг с другом и не
сообщающимися. Иногда взаимосообщающуюся часть порового пространства
называют эффективным поровым пространством. Этот термин широко приме-
няется в теории фильтрации. Многие тела имеют большую общую пористость,
но малую эффективную пористость.
Пористость nv обычно определяется как отношение объема пор Vn0[J
к объему тела VTej] (Пу = Vno /1/те1), Наряду с объемной пористостью вводится
понятие поверхностной пористости, или просветности, П3, представляющей
отношение эффективной площади пор Ипор к общей площади поверхности тела
^тел	Поверхность пористости П3 иногда называется просве-
том. В первом приближении можно считать Пу—П3 = П,
Простейшей моделью пористого тела является система из сферических
частиц достаточно малого радиуса и одинакового размера.
Сферические частички могут быть уложены разным образом (рис. 5-1).
Различают наименее плотную (кубическую, и«=90а) и наиболее плотную (гекса-
гональную и = 60*) укладки. Пористость такой среды зависит от угла и
(укладки), а не от радиуса частиц. При кубической укладке /7^=47,64%,
а при гексагональной—25,95%. В первом случае радиус наиболее узких про-
ходов, соединяющих соседние поры между собой (радиус окружности, вписан-
290
ный между четырьмя соседними частицами), равен 0,41/? (/? —радиус сфери-
ческой частицы). Радиус поры в наиболее широкой части равен 0,73/?-
При гексагональной укладке каждая частица соприкасается с 12 сосед-
ними частицами- Поры имеют двоякую форму: тетраэдрическую и ромбоэдри-
ческую, причем число последних в 2 раза больше первых. Радиус наиболее
узких проходов (рис. 5-1, б) равен 0,155/?, Радиус наиболее широких прохо-
дов составляет 0,288/? —для тетраэдрической поры и 0,414/? —для ромбоэдри-
ческой. На долю тетраэдрических пор приходится 7.37% объема, а па поры
ромбоэдрические— 18,58%.
Пористость системы, составленной из одинаковых шаров, не должна зави-
сеть от радиуса шаров. Однако для природных сыпучих материалов, напри-
мер, песка, пористость увеличивается при уменьшении размера зерен.
 Такая пористая система представляет собой тело, пронизанное капилляр-
ными трубками с кривой осью, которая совпадает с ходом поверхности сфе-
рических частиц, Поры представляются в сечении треугольными, площадь их
поперечного сечения испытывает правильные чередования от некоторого мак-
симума до минимума
Рис. 5-1. Укладка сферических частиц при образовании ячейки.
а —общий случай укладки; б — кубическая укладка (tf = 90°); а—гексагональная укладка
Наряду с пористостью можно ввести и другие геометрические характе-
ристики пористого тела, Часто используются кривые распределения пор по
радиусам Л (г), а для зернистых сред—кривые распределения частиц по раз-
мерам (кривая гранулометрического состава), Иногда принимают распределе-
ние частиц по размерам логарифмически нормальным и характеризуют его
двумя параметрами: средним размером (диаметром частиц) d и дисперсий D.
В большинстве исследований ограничиваются указанием одеюго характерного
размера: пор d или зерен I.
В химической технологии в качестве характерного размера пористой среды
принимают величину 1/Sy, где Sv — полная поверхность частиц в единице
объема пористой среды (удельная поверхность пористого материала). Эта вели-
чина хорошо определяется экспериментально.
Удельная'поверхность Sy (размерность обратной единицы длины) опреде-
ляется адсорбционным методом, статистическим методом или по проницаемости.
Проницаемость — это свойство пористого материала пропускать через себя
жидкость под действием приложенного градиента давления. Проницаемость
есть проводимость материала по отношению к жидкости:
Проницаемость (или коэффициент проницаемости) К/ определяется из урав-
нения закона Дарси. Если обозначить перепад давления по толщине образца I
через Др, а объемный расход жидкости — через jw, то проницаемость К/ равна:
где т}—вязкость жидкости} А — площадь поперечного сечения образца.
10*	291
Коэффициент Kf имеет размерность Квадрата длины и может служить гру-
бой мерой среднеквадратичного порового диаметра. Проницаемость является
макроскопической характеристикой пористого материала и определяется гео-
метрией поровой структуры. Полный оозор соответствующих теорий Приведен
в работе [Л-5-5]. Рассмотрим некоторые из них.
В теории Козени пористая среда представляется в виде связки тонких
трубок равной длины. Проницаемость такой системы равна:
где о —безразмерная постоянная, зависящая только от геометрической формы
поперечного сечения трубок. Для кругового сечения а = 0,5 для квадратного
сечения 0,5619, для сечения в виде равностороннего треугольника а = 0,5974.
Величина а называется постоянной Козени.
Усовершенствованием теории Козени является введение извилистости
определяемой как отношение средней длины траектории жидкой частицы
в образце материала к длине образца. С введением этой поправки формула
Козени-примет вид:
=		(5-1.3)
Формулу Козени трудно проверить, так как трудно определить незави-
симо Sv и
Другой подход к проницаемости состоит в том, что вводится минималь-
ное число параметров распределения, например распределение частиц пористой
среды по размерам, которого достаточно для определения проницаемости.
Наиболее естественное предположение состоит в том, что проницаемость
пропорциональна квадрату характерного среднего размера dsm и зависит
от неоднородности состава частиц и плотности их упаковок;
К] == dsm^D (D, 77),	(5-1-4)
где D — дисперсия распределения размеров зерен.
Очевидно, что при весьма неоднородном распределении частиц возможна
плотная укладка, при которой мелкие частицы заполняют промежутки между
крупными, так что величина должна убывать с ростом D. Корреляции типа
(5-1'4) могут быть построены для отдельных модельных систем пористых
сред.
Скорость фильтрации через пористые среды (закон Дарси) равна:
К/	— X-
-=> =----— (Vp-i-pVA),	(5-1-5)
где р — внешнее давление; h — гравитационное-давление.
Если ввести потенциал движения жидкости Ф по соотношению
Ф=н+ j -i dp,	(5-1-6)
Ра
то формула закона Дарси примет вид-.
Для некоторых жидкостей необходимо ввести поправку в формулу (5-1-7)
на клинкерберговский эффект [Л. 5-1]:
_ рК/ / а \
ТГ V + 7;7Ф== Т <vp+pvft>*
292
где
а —постоянная.
На основе анализа размерностей и свойств инвариантности можно считать:

(5-1-9)
Разлагая функцию / по степеням аргумента и ограничиваясь первыми
двумя членами, получаем
„	Т) - Ври -
Гр =----
р	k Vk
(5-1-10)
__так называемый двучленный закон фильтрации. Постоянная 0 является
дополнительной характеристикой пористой среды М. Д. Миллионщиков пред-
ложил принимать за характерный размер	а за характерную скорость
а /ре= —), при этом совмещаются все данные, относящиеся к безынер-
ционной области.
С ростом Re квадратичный член в формуле (5-I-I0) оказывает все более
существенное влияние; это наблюдается в средах, состоящих из крупных
частиц. По аналогии с течением в трубах с ростом Re наступает режим
турбулентной автомодельности, причем роль шероховатости стенок играет
извилистость. Иногда турбулентной фильтрацией называют такое течение, для
которого существенна квадратичная поправка. Однако это не так, потому что
инерционная составляющая сопротивления	'
при неравномерном движении становится су-
щественной задолго до того, как поток переход
дит в турбулентный.
При малых скоростях фильтрации также
наблюдаются отклонения от закона Дарси, В
ряде работ [Л. 5-3 —5-5] обнаруживалось уве-
личение скорости фильтрации с ростом гра-
диента давления более- быстрое, чем при ли-
нейной зависимости. Это отклонение наблюдает-
ся в коллоидных капиллярно-пористых телах.
В этом случае можно написать:
k
о =-----Vp
Т]
где Q—некоторая постоянная, имеющая раз-
мерность градиента давления,
Аналогичное явление наблюдается при филь-
трации реологических жидкостей через пористые
среды, например через кварцевый песок. 
В [Л. 5-,8] исследовалась фильтрация воды
и растворов электролитов в глинизированном
песчанике с малым содержанием глинистых ча-
стиц, Результаты представлены на рис. 5-2,
из которого видно, что зависимость между
градиентом давления и скоростью фильтрации
нелинейна. Одной из причин такого отклоне-
ния от закона Дарси является более прочная связь воды со скелетом
тела. В частности, в коллоидных капиллярно-пористых телах наблюдаются
осмотическое поглощение’ воды и капиллярное связывание жидкости. По-
этому необходимо более детально рассмотреть связь жидкости в пористых
телах.
(5-1-11)
Рис. 5-2. Фильтрация элект-
ролитов через глинизирован-
ный песчаник.
/ — вода; 2—10%-ныЙ раствор
NaCl; 3 — 5%-вый раствор NaCl.
293
В ряде работ извилистость £ определяется из экспериментов по диффузии
пара через слой пористого тела. Суть метода состоит в следующем. Опреде-
ляется коэффициент диффузии D парообразной влаги при испарении жидкости
из пористого тела. Зная коэффициент диффузии пара в воздух О12, определяют
коэффициент сопротивления диффузии
Dj2
Извилистость определяется по формуле
(5-1-12)
(5-1-13)
приближенно полагают П5=Пу=П.
Рис. 5-3. Ромбическая четырехугольная укладкаюферических
частиц.
Для • системы, состоящей из сферических частиц правильной укладки,
можно вычислить коэффициент [Л. 5-2]. Схема расчета приведена на
рис. 5-3- Коэффициент сопротивления диффузии будет равен [Л. 5-2]:
г /3
3.4 0 rii f dz
^~~Г^ } Д’
(5-1-14)
где Ао — полная поверхность сечения; гц—число частиц в слое материала;
пр—число проходов через слой; А — поверхность сечения прохода, сущест-
вующего между соприкасающимися сферами; г—пространственная координата.
Для системы правильной геометрии
‘НН-'	(5‘‘'15)
Тогда интегрирование уравнения (5-1-14) дает:
Ио=34^2/п,[21/з/я_1],/2агс((,2 ДА-1)1''2).	(5-М6)
Так как l —	' А0 = 4г3Пр, то ро = 3,52. Пористость нашей системы
/7 = 0,3955, тогда £ = 0,3955.3,52=1,39. В табл. 5-1 приведены эксперименталь-
ные и расчетные данные для коэффициента извилистости £. Эксперименты
проводились по диффузии водяного пара при 8°С сквозь слой толщиной 30 мм,
состоящий из сферических частиц диаметром 2 мм.
Таблица 5-1 показывает удовлетворительное совпадение расчетных и
экспериментальных данных.
Кришером [Л. 5-76] было экспериментально установлено, что для строи-
тельных материалов ~ ЗП~ тогда извилистость
%~П-Ч2,	(5-1-17)
294
Таблица 5-1
Сравнение теоретических и экспериментальных параметров
диффузионного сопротивления для двухмнллиметровых сфер
Структура	Пористость П		Коэффициент диф- фузионного сопро- тивления		Извилистость I	
	расчет	экспери- мент	расчет	экспери- мент	расчет	экспери- мент
Кубическая	0,4764	0,485	2,65	2,95	1,26	• 1,43
ромбическая четырех-	0,3955	0,4285	3,52	3,72	1,39	1,59 '
угольная Ромбическая трех-	0,3955	0,409	4,34	4,66	1,72	1,90
угольная Октаэдрическая	0,2595.	0,330	5,00	5,05	1,53	1,67
Тетраэдрическая	0,2595	0,302	6,43	6,00	1,67	1,81
Неупорядоченная	—	0,37	—	4,25	—	1,57
Таблица 5-2
Диффузионные параметры для движения влаги через пористые материалы
Материал	Объемная плотность р^,, кг/м1	Пористость П, м*/м*	Извилистость м/м	Коэффициент Диффузион- ного сопро- тивления Ц,£
Стеклянные сферы, 1,9мм		0,365	1,13	3,1 3,8
Стеклянные сферы, 0,5 мм	—	0,37	1,4	
Морской песок, 0,2 мм	—	0,36	1,7	4,7
Строительные материалы Фибровый картон	300-380	0,81-0,76	2,0-2,6 3,0 —3,9	2,5 —3,2 4,0-5,1
Пемзобетон	650 — 840	0,71-0,62	4,1-5,3	5,8—7,5
			4,3 —5,5 <	6,9-8 9
Шлакобетон Известковая штукатурка,	1140	0,50	4,3 —5,0	8,5-10
1/3 гравия Цементная штукатурка,	1800	0,28 0,21	2,4-2,7 10,5- 17,5	8,6 —9,8 5,0-83,5
1/3 гравия	2140			
Пищевые продукты Сушеные овощи	135	0,907	1,6	1,7
Яичный порошок	805	0,79	1,9	2.4
Кофейная гуща	400	0,725	1,16	6,8
Шоколадный пудинг в	725	0,5	3,4	6,8
порошке Молоко, высушенное рас-		0,482		3,3
пылением	750		1,6	
Другие материалы Хромовая кожа			0,280 — 0,405	1,4—2,6 1,8- 7,7	3,2—7,5
Полухромовая кожа	—	—		7,3-33
295
В табл. 5-2 приведены, экспериментальные данные для извилистости g и
коэффициента для ряда материалов, из которой видно, что извилистость
изменяется в широких пределах:
1,13 <£<17,5.	.	'(5’1-18)
Этот метод определения извилистости по коэффициенту сопротивления диф-
фузии можно критиковать в том отношении, что во влажном материале при
испарении жидкости может происходить не только диффузия влаги, но и диф-
фузия жидкости в виде капиллярного и пленочного движения (см. § 5-7),
Поэтому в работе («Л. 5-10] были приведены расчеты по определению коэффи-
циента эффузионного сопротивления (сопротивление пористого тела эффузии
пара внутри тела). Экспериментальные данные приведены в табл. 5-3. Они
показывают удовлетворительное совпадение расчетных и экспериментальных
данных.
Таблица 5-3
Сравнение теоретических и экспериментальных эффузионных параметров
для двухмиллиметровых сфер
Структура	Пористость П		Коэффициент эффузионного сопротивления		Извилистость 1	
	расчет	экспе- римент	расчет	экспе- римент	расчет	экспе- римент
Кубическая	0,4764	0,480	3,76	4,40	1,79	2,11
Ромбическая четырехугольная	0,3955	0,405	4,32	4,29	1,71	1,74
Ромбическая трехугольная	0,3955	0,404	10,92	10,64	4,32	4,30
Октаэдрическая	0,2595	0,321	9,13	8,54	2,37	2,74
Тетраэдрическая	0,2595	0,294	9,39	9,38	2,44	2,76
Неупорядоченная	—	0,38	—	5 52	—	2,1
Обычно структуры пористых сред характеризуют однородностью, анизо-
тропностью и гетерогенностью. Структурные характеристики являются макро-
скопическими. Осреднение производится по элементу объема радиуса R, при
этом R должно быть достаточно большим, чтобы можно было применить
закон Дарси,
Определения гетерогенности, неоднородности и анизотропии основаны
на распределении вероятности проницаемости элементарных объемов, взятых
из пористой среды.
Коэффициент проницаемости, или просто проницаемость, описывается диф-
ференциальной поверхностной кривой распределения f (k) аналог чно дифферен-
циальной кривой распределения пор по поверхности fs (г).
Под однородной средой понимают такую среду, в которой функция
является либо дельта-функцией (3), либо их линейной комбинацией, т. е.
N
(Б-1-19)
i = l
где —постоянная, удовлетворяющая условию
до
2^=1;	(5-1-20)
здесь А1—конечная величина,
296
Примеры однородных сред приведены на рис. 5-4, а неоднородных —на
пис. о-5.
р Таким образом, под неоднородной средой понимается такая среда, в кото-
ой f (k) нельзя описать конечным числом весовых дельта-функций. Гетероген-
ная среда описывается минимум двумя кривыми распределения проницаемости
Грис. 5-4, б, в и рис. 5-5, б, в). При этом подразумевается, что среда гомо-
скедастична'. Однако если f (ft) зависит от положения в пространстве или
е)
Рис. 5-4. Проницаемость
однородных сред: гомоген-
ной (а) и гетерогенной
(б, в).
Л я,
>)
Рис. 5-5. Проницаемость
неоднородных сред: гомо-
генной (о) и гетерогенной
(в. в).

от ориентации в пористой среде, то мы имеем неидеальность второго рода.
Если проницаемость в элементарном объеме зависит от направления, то среда
называется анизотропной. В общем случае функция / (k) зависит от положения
и фиксации, сс можно описать пятью независимыми переменными: прямоуголь-
ными координатами Х( (1=1, 2, 3) для характеристики положения и двумя
угловыми координатами в и t для ориентации:
р (fti ft ft2) = $ f (Xi, б,	(5-1-21)
ft.
Если f (k)— функция распределения проницаемости — не зависит от б и гр,
то пористая среда изотропна. Если f (ft) выражается конечной линейной ком-
бинацией 5-функций, то среда однородна; если / (ft) моцомодельна, то среда
гомогенная; если f (ft) непостоянна, то имеет место неидеальность второго рода:
var2
р (va?! sS var k йс var2) = J f (Xi, б, ф) dxi d6 dip. (5-1-22)
vaFj
Пористое тело считается капиллярно-пористым в том случае, если действием
силы тяжестица'жйдкость в капилляре можно пренебречь. Поры тела делятся
на каверны (макропоры), макрокапилляры и микрокапилляры. Простейшей
моделью капиллярно-пористого тела является система цилиндрических капил-
лярных трубок, связанных между собой. Часто пористое тело сводится к экви-
валентному капилляру конической или щелеобразной формы.
297
Основной структурной характеристикой капиллярно-пористых тел являете,
кривая распределения пор по радиусу поры. Интегральная кривая распред<
ления пор характеризует изменение относительного объема пор V* (отношенг.,;
объема пор к объему тела) по радиусу капилляра г. Кривая р'*=/(г) начя
нается с некоторого значения гм1|Н (минимальный радиус капиллярной поры*
и пересекает ось объема V* при значении г-=гмакс. Таким образом, в пределе
^мин ~Т. г-';гмлкс относительный объем V* непрерывно увеличивается с увели-
чением г. Если на некотором участке rj.<r<r2 пор такого радиуса нет, то
кривая У* = /(г) превращается в прямую, параллельную Оси г. Зависимость
dV*jdr — fv(r) называется дифференциальной кривой распределения пор или
дифференциальным уравнением объемной характеристики пор. Эта кривая может
быть получена из интегральной кривой V* = f(r) методом графического диф-
ференцирования.
На участке отсутствия пор (f\<r<zr^) дифференциальная кривая рас-
пределения пор fv (г) обрывается и совпадает с осью г, так как на этом участке
dV*/dr — 0. Площадь под кривой fv(r) на любом участке г численно равна
объему пор, радиусы которых изменяются в пределах этого участка.
Суммарный объем пор в единице объема тела, равный пористости тела,
определяется соотношением
’макс	гмзкс
С	dV*	С
J	'dT‘Ir=	J	(5-1-23.,
fMHH	Лмив
Максимальное содержание жидкости «макс будет равно:
“макс" 1/максР/ = Л1/Р/.	(5-1-24)
Удельное содержание жидкости, или относительная ее концентрация (масса
жидкости в пористом теле, отнесенная к единице массы абсолютно сухого
тела), равно:
=	( М')*.	(5-1-25J
Ps Ps J
гчив
где р5~плотность абсолютно сухого пористого тела.
хДля расчета плотности потока жидкости, проходящей через пористое тело,
вводится понятие дифференциальной кривой поверхностной пористости тела.
Пусть площадь сечения тела равна 1 см3, часть этой площади занимают
капилляры (дырки), остальную часть — вещество самого тела. Если все капил-
ляры заполнены жидкостью, то удельное ее содержание равно:
$ ptAtdL
“=-1^-ттто	<5-‘-26>
где Ai — площадь, занимаемая жидкостью, т. е. площадь всех дырок, запол-
ненных жидкостью и находящихся на 1 см2 сечения тела; L —глубина (толщина)
слоя.
Обозначим количество цилиндрических капилляров в данном сечении,
имеющих радиус от г до r-\~dr, через dns, тогда поверхностная пористость
(просвет) равна:
,м?‘кс dn„
ns=A,~ j nrs-^-dr,	(5-1-27)
гмин
* '’мин-это экспериментально определенный размер минимальных пор;
в действительности размеры пор изменяются от 0 до гмакс.
298
где ^ — количество капилляров, приходящихся .па единицу площади сечения
тела.
Если А{ не зависит от L. т. е. поверхностная пористость одинакова в любом
сечении тела, что равнозначно равенству поверхностной и объемной пори*
стостй тела (Пу=П5), то можно написать:
гиакс	,
а=?'Л,--р' Г пг» —— dr'	(5-1-28)
Р5 ' PS J	dr -
Для многих тол поверхностная пористость тела изменяется в направлении
координат тела, поэтому наряду с дифференциальной объемной характеристикой
пор fv(r) вводится дифференциальная поверхностная характеристика nop fs(r),
равная:
d А.	dtz о	.г- 1 лп(
f(r]=_inrb S	(5-1-29)
5-2. ТЕРМОДИНАМИКА ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ
Две соприкасающиеся фазы, например две нерастворимые и несмачиваЮ-
щие жидкости (а и £), имеют неоднородную пограничную зону раздела
(рис. 5-6, а). Свойства этой зоны раздела изменяются вдоль нормали п к поверх-
ности раздела. Гиббс предложил зону раздела фаз заменить геометрической
зона
— Нормаль __гЦраз5елсг
Поверхность раздела Гиб5с^но^ная
поверхно-
стная
зона
^свойствами 6по-
граничной зоне
Рис. 5-6. Модель Гиббса для соприкасающихся фаз (v = N).
поверхностью раздела (рис, 5-6, б). Такое модельное представление системы
двух соприкасающихся фаз дает возможность использовать аппарат термодина-
мики. При этом предполагается, что свойства фазы а не изменяются вплоть
до геометрической поверхности раздела. Это же предположение справедливо и
для фазы р.
Для такой модели соприкасающихся фаз объем системы V равен сумме
объемов соприкасающихся фаз (Г=Уа-ТУ^). Обозначим обьемную кон-
центрацию растворимого вещества k — компонента Сд, а число молей —через
N*(NA = CftV). Тогда можно написать:
+	(5-2-1)
где (jVft)s —число молей на поверхности раздела.
Аналогичное соотношение имеет место для свободной энергии Гиббса F;
F^ + ffi + fs-	(S’2'2)
Воспользуемся уравнением Гиббса'—Гельмгольца
dF = —S' dT^ У	dVa-PpdVp + odAap,	(5-2-3)
A-J
299
где с, р, S' —соответственно поверхностное натяжение, химический потенциал
и энтропия.
Используя соотношение (5-2-2), а также равенства
<if„= 2 V-kdtNIlk-PadVa. №$= 2 |Л4</ (Ns)s-Pg, dVf,;
6=1	6=1
для изотермических условий (dT-О) будем иметь;
= 5 V-kdNk— У М(М“ У Ил d(W*)p + o (5-2-4)
6 = 1	6 = 1	Ы
Затем, используя соотношение (5-2-1), получаем:
dFs= У Н* d (Nfe)s + ст (Ы,	(5-2-5)
6=1
где А — суммарная площадь поверхности 5.
Если обозначим поверхностную концентрацию компонента k через Г& ((#б)$ ==
= Г&Л), то из уравнения (5-2-5) будем иметь:
dFS= У	у A dFk-\-vdA,	(5-2-6)
6=1	6 = 1
так как d (N k)s^rkdAA‘ A dF^ Из уравнения (5-2-6) получим:
df	п	п
й.и,«=2>г‘+2	(М-7)
k — I	k = 1
В общем случае поверхностная концентрация Г/г изменяется вдоль поверх-
ности; для частного случая Г* может не зависеть от-А, т. е.
Тогда
'	р	п
' ;s=-f-= 2'1»г‘+а'	<5'2-8»
Для системы с единичным компонентом, образуемой чистой жидкостью и
ее паром, разделяющую поверхность можно расположить так, что Г = 0, тогда
Zs = a-	(5-2-9)
Однако в общем случае поверхностное натяжение, численно равное обра-
тимой работе образования единицы поверхности жидкости при растяжении,
нс равно свободной поверхности энергии fs.
Из уравнения (5-2-7) следует, что при Г~0
fdF\
= <Т-
\(ЗЛ /т, V, w
Если гт не зависит от А, то
/ AF\
-гт ==о.
\ДД Д, и, N
(5-2-10)
(5-2-11)
300
Если же ст зависит от А, как это имеет место при наличии поверхностно-
активных веществ, то получим:
(ЛГ)г v N= \a(A)dA.	(5-2-12)
л.
При рассмотрении капиллярных явлений мы должны учитывать влияние
кривизны поверхности жидкости на поверхностное натяжение и расположение
поверхности Гиббса. Однако этот эффект необходимо учитывать лишь тогда,
когда радиус кривизны сравним с молекулярными размерами.
Пусть имеется система, состоящая из двух фаз аир, соприкасающихся
с поверхностью S твердого тела. Используем ту же модель Гиббса. Тогда
концентрация k-ro компонента на линии трехфазного контакта будет
определяться из соотношения
Aft == (,Vft)a + (,Vft)f) + (,Va)s + ft)s (a, p) + <^)s (5a) + (^ft)s(Sp) + (,Vft)z-
(5-2-13)
Для рассматриваемых систем долей свободной энергии, обусловленной
изменением длины трехфазной линии контакта в результате изменения площа-
дей поверхности, можно пренебречь.
Если твердое тело гладкое, педеформируемое и угол смачивания является
постоянным, то условие термодинамического равновесия по Гиббсу определяется
соотношением
з
2 CTft(dL)dx3--°,		(5-2-14)
где di, — элемент длины вдоль трехфазной линии контакта; dx—смещение по
поверхности твердого тела, перпендикулярное к элементу dL.
Используя соотношения
dASa = dLdx-t dAs^ = —dLdx; dAa$ = dL dxcosfl,
из (5-2-14) получаем уравнение Юнга:
an5cose+aSa-aSU = 0'	(S'2'15)
Это уравнение часто выводят из уравнения баланса сил. Однако силы,
действующие вдоль поверхности раздела фаз. не равны CT^Q и о^р,
Кроме того, если твердое тело частично растворимо в одной из фаз, то
адсорбция приводит к значительному снижению оар. Гиббс в качестве модель-
ного тела принимает неизменное твердое тело, которое нерастворимо в жидких
фазах и поверхностное натяжение которого не изменяется от наличия находя-
щейся сверху жидкости. Тогда поверхностное натяжение жидкости a'Sa опре-
деляется соотношением
aS« = aSa-aS.	<5-2'16)
Следовательно, поверхностное натяжение на поверхности раздела твердое
тело—жидкость ст$а равно сумме двух составляющих: сг'$а и ст5. Наличие
твердого вещества влияет на силы сжатия внутри жидкости, в результате
получаем составляющую о$а, которую Гиббс назвал поверхностным натяже-
нием жидкости, находящейся в соприкосновении с твердым телом.
В состоянии равновесия имеем:
°S0 + aS = ffSa + cos	(5'2' 17)
откуда
asp-"sI1=<Tc.s<:ose.	(5-2-18)
Угол смачивания 0 зависит от направления движения трехфазной линии
контактов (гистерезис угла смачивания), от поверхностно-активных веществ,
от шероховатости поверхности и других причин.
301
Если система состоит’из капельной жидкости (а = 0, насыщенного пара
(р = с) и твердого тела S, то согласно модели Мельроуза плоская поверхность
жидкость —пар сосуществует с поверхностью твердого тела, йо которой
жидкость растекается. Растекание можно предотвратить инертным механическим
Лар
Сила	|ч.
Лдсордированная пленка	
	=-^Жадкость—-
Твердое тело
3 I
-с ft?7
Рис. 5-7. Модель Мельроуза для
равновесия системы жидкость —
пар — твердое тело.
I — барьер, свободно перемещающий-
ся без трения вдоль поверхности в го-
ризонтальном направлении под дейст-
вием силы.
g га’
2 ft?2
I
§ 10
	Капиллярная ч		
-к	трудна		—
X			Пар
				
	Лдсорвированная		
	^пленка		
X			
	-Поверхность		
X	твердого тела		f£u
—			
			
	Пар		Стыковая
-			жидкость _
X			поверхность
			воды
0,00
0,07
93,99 |
99,939
93,00*
to
99, г?°2
I
99,92 |
Рис. 5-8. Равновесная адсорбиро-
ванная пленка воды на поверхно-
сти твердого тела и впитывание
воды капилляром (а) и анизотро-
пия поверхностного натяжения (б)
в зависимости от высоты h и отно-
сительного давления (относительной
влажности) о = J (л, — пл) dn;
п — расстояние вдоль нормали к
поверхности.
'к
I?
Относи-
тельная
Влаж-
ность
°)
I)
барьером, который двигается вдоль . поверхности тела без трения (рис. 5-7).
Если жидкость не растекается, то к барьеру должна быть приложена сила,
равная на единицу длины:
4, = ^ + 'Is;- "s.-	<5-2-19)
Согласно уравнению (5-2-15)-величина этой силы равна:
(I — cos б).	(3-2 -20)
Для растекания необходимо поглощение пара, которое продолжается до
тех пор, пока сила не исчезнет. В равновесном состоянии положение барьера
не меняет свободной энергии системы, так как он перемещается без трения.
Следовательно, если адсорбированная пленка заменяется тонким слоем жидкости,
то свободная энергия системы не изменяется.
Условия равновесия определяют толщину пленки. При равновесии внешние
молекулы пленки должны иметь тот же химический потенциал, что и молекулы
пара и поверхностные молекулы жидкости. Адсорбированный слой утолщается
до тех пор, пока на внешние молекулы не перестанут действовать силы притя-
жения твердого тела. Следовательно, натяжение внешней части пленки должно
быть равно натяжению поверхности раздела жидкость — пар, а натяжение
302
s М3
нижней части пленки — натяжению поверхности раздела твердое тело.— жидкость-
Такие пленки Харкинс называет двойными пленками.
На рис. 5-8, а показано растекание пленки жидкости вдоль вертикальной
поверхности твердого тела. Если обозначить давление пара на расстоянии h от
свободной поверхности жидкости через ph, а давление на поверхности жидкости —
через р0, то будем иметь:
ф=100-^ехР(--^“),	(5-2-2!)
где Др=^(р2 — р..) —разность плотностей жидкости и пара; g—ускорение силы
тяжести; Л4—молекулярная масса; ср — относительная влажность или относи-
тельное давление пара; Я —универсальная газовая постоянная.
На бесконечно большой высоте (Л=оо) давление пара равно нулю (рЛ = 0),
а поверхностное натяжение твердого тела относительно вакуума равно ст$.
На рис. 5-8,а схематически показано изменение толщины пленки с высотой,
а следовательно, согласно формуле (5-2-21), изменение относительной влажно-
сти ф от высоты (ф=f (/))).
Действительная толщина пленки неизвестна. При больших значениях гр
толщина пленки может достигать 10 — 30 А '(4—12 молекулярных слоев воды),
в некоторых работах приводится значение около 100 А. Поверхностное натя-
жение можно определить по величине тензора напряжения л:
а = ^(Л[—лп)с1п,	(5-2-22)
где Л/ и пл —соответственно тангенциальная и нормальная составляющие
тензора напряжения.
На рис. 5-8-, б показано влияние анизотропии натяжения в зависимости
от относительной влажности, т, с. от изменения высоты. По мере увеличения
толщины пленки (область больших ф) появляются два максимума в анизотро-
пии натяжения.
На поверхности воды (р= 100%. и адсорбированная пленка будет являться
двойной пленкой в соответствии с моделью, показанной на рис. 5-7.
Гиббсом получено соотношение для величины адсорбированной массы m
жидкости на твердой поверхности- в поле силы тяжести в виде соотношения
dtj' — mgdh,	(5-2-23)
откуда избыточная масса т' адсорбированной пленки между высотами ДЛ = /г2—
т'£=(а')м —(а'Ьг.	(5-2-24)
Более точный расчет производится по соотношению (5-2-22), т. е.
(П<”'М ЦЛ Ли’	(5-2-25)
где
а*= [S - "'>> dn]» -[S <л' -М	(5-2-26)
Капилляры правильной геометрической формы (цилиндрические и коничес-
кие трубки, щели) иногда называют элементарными капиллярами. Капиллярное
давление рс в таких капиллярах определяется формулой Лапласа:
Pc~$iv (~~г" “Г ст-1 = 2п;Ф	(5-2-27)
где /[ и г' — главные радиусы кривизны мениска в любой его точке; ( —I —
средняя кривизна мениска, равная:
Ш=И?г+-И-	(5-2-28)
V 1	* VI Г2 !
303
В состоянии равновесия капиллярное давление уравновешивается грави-
тационным давлением (pc = Ap/?g), т. е.
h —	= —— f —
gip g&p'/' j‘
(5-2-29)
Для цилиндрического капилляра (г[ — г'й = г') высота поднятия будет
равна:
(5-2-30)
ft— 2с?г, _ 2c^ti СОЗ 6
- ~gAV' ~~ gW
так как Др — pj — pv «= р/.
Между радиусом капилляра г и радиусом мениска г' существует простая
зависимость (г = г'созб). В случае полного смачивания (созб==1) на стенках
капилляра образуется пленка толщиной б. Зависимость между радиусом ка-
пилляра и радиусом мениска будет такова:
-6-6
(5-2-31)
где а—постоянная, зависящая от свойств жидкости и поверхности стенки.
На рис. 5-8, а показана высота поднятия воды в цилиндрическом капил-
ляре диаметром 10ц, Рядом показана пленка жидкости двух соприкасающихся
шаров диаметром 10ц на высоте 100 и 1000 см от свободной поверхности
воды. Адсорбированные пленки имеют несколько меньшую толщину на выпук-
лых твердых поверхностях и несколько большую — на вогнутых по сравнению
с пленкой на соответствующей плоской поверхности. При растекании жидко-
сти увеличение свободной энергии ДЛ равно:
Air = MA. + 'W	(5-2-32)
По аналогии с гравитационным потенциалом 4g (4g = gA) вводится поня-
тие капиллярного потенциала фс по соотношению
(5-2-33)
Для смачивающей жидкости капиллярный потенциал фс < 0, так как
для вогнутой поверхности отрицательно, а для несмачивающей жидкости
(cos б •< 0) 4с > 0. Смачивающая жидкость перемещается от низшего потен-
циала 4с к высшему (узкий капилляр высасывает жидкость из широкого ка-
пилляра), а несмачивающая—от высшего к низшему.
Соотношение (5-2-33) справедливо для капилляра, один конец которого
находится в соприкосновении е жидкостью. Для конического капилляра,
средние кривизны менисков которого соответственно равны —для узкого
конца и f-ipi —для широкого конца, капиллярный потенциал 4с равен:
♦-WKU (5-2-34>
В таком капилляре смачивающая жидкость перемещается в сторону более
узкого конца до тех пор, пока мениск нс займет крайнее положение- Если
капилляр цилиндрический (r{ — rt-=r'), то 4с равно нулю. Столбик жидкости
в таком капилляре может быть ра:чоложен в любом месте, и перемещение
жидкости в нем отсутствует. Капиллярный потенциал 4с определяется по ве-
личине капиллярного давления рс или по величине гравитационного потенци-
ала 4g’ В состоянии равновесия гравитационный потенциал равен капилляр-
ному (4c=^g). физически это реализуется так. Капиллярно-пористое тело
304
приводится в соприкосновение с жидкостью. В состоянии равновесия строят '
крииую распределения содержания жидкости по высоте h\ это распределение
будет характеризовать зависи-
мость капиллярного потенпиада
tj, = от влагосодержа-
ВИЯ-
Наиболее распространен
метод определения капиллярно-
го давления пористого тела по
вытеснению воды из пористого
тела другой жидкостью, несме- ’
шиваюшейся с первой, напри-
мер, маслом.Схема такого при-
бора приведена на рис. 5-9. По-
ристое тело сначала насыщается
смачивающей фазой (водой) и
приводится в соприкосновение
с мелкопористой мембраной,
которая остается все время
насыщенной водой. Давление на
Капиллярное давление
О ш 100
Рис. 5-9. Схема прибора для определения
капиллярного давления.
газ
Pi
Влажное
пористое
тело
водяной фазе равно давлению
газа pi в левой камере (рис. 5-9). Несмэчивающая фаза (масло) находится
в контакте с пористым телом, ее давление равно давлению газа в правой
камере, действующему на соответствующий поршень. При этом гидростатиче-
ским давлением пренебрегаем и считаем, что поршни перемещаются без тре-
ния. Разность давлений p0—pi равна капиллярному давлению рс (ре= р<> — pi).
Насыщенность еу( измеряется как отношение объема пор в теле, занятого во-
дой, ко всему объему пор. Количество вытесненной воды Ь
(5-2-35)

где Vs — объем пористого тела; Пу—объемная пористость.
Внешняя работа вытеснения,- проделанная над замкнутой системой при
вытеснении элементарного объема воды dV i из тела, (р0— pijdl’i. Эта вели-
чина по абсолютному значению равна изменению свободной энергии dF
в системе
‘tV', + al«iAl0Jr0SlldASl, + <!SlrlAsp (5-2-36)
но обратна ему по знаку. Общее изменение свободной энергии dFQ$ системы
и окружающей среды равно пулю:
= 0== (Ро~Pi) i~P's s -PidVi ~~Pe о +
+°jo +	+ ^sr	(5-2-37)
Если пренебречь работой сжатия (dV’s = dVj'=dVJ==O) и считать общую
поверхность тела постоянной (сМ5о = —tMs/), то на основании уравнения
(5-2-15) получим:
= — jpc rfV;=aZ() d(4Z|>-|-45oCQs 6),	(5-2-38)
Выведенные соотношения дают возможность ие только получить экспери-
ментальные кривые pc=^f(<B)t но и вычислить изменение свободной энергии при
вытеснении или обводнении.
Прежде чем перейти к анализу кривых капиллярного давления pc=f((B),
рассмотрим бесконечно медленное вытеснение на капиллярной, модели (рис.
О'Ю, а). Жидкость удаляется обратимо до тех пор, пока мениск не достигнет
расширения в трубке Л. Затем жидкость быстро снижается цо устойчивого
положения В.
Схема предусматривает наличие идеально работающего клапана. Если
0 нем создается давление из-за перераспределения жидкости, он мгновенно
305
закрывается. Клапан открывается снова, когда конфигурация жидкости ста?
вится устойчивой и давление жидкости на внешней стороне клапана становит
равным давлению системы.
Приведенный график давление —объем жидкости показывает, что проце
состоит из плавных обратимых изменений, связанных с самопроизвольш.
изменением давления при постоянном насыщении; обратимые изменения чер
дуются с необратимыми изменениями объема, а весь процесс удаления жидк
сти является квантовым.
Давление медленно повышается по мере осушения, пока неустойчив,
конфигурация не вызовет скачок давления при постоянном насыщении. Э
скачки давления Мелъроуз называет реонами. В этот момент система не мож
совершать работу. Отрезки кривой рс==/((о) между реонами, соответстве-югщ
обратимым вытеснениям, называются изонами. Таким образом, рсон характ
Рис. 5-10. Механизм осушения.
Изолированная жидкоск
й Насыщение воды, °/а
0
а — R капиллярной модели; / — обратимое вытеснение; 2 — перераспределение при постоян-
ней! объеме; 3 — обратимое вытеснение; б—осушение в дисперсной среде или засыпке.
ризует самопроизвольное перераспределение жидкости внутри пористой системы.
Объем жидкости, самопроизвольно вытесненный из какой-либо области, может
изменяться от части одной поры до целой группы. Например, при наличии
шероховатости поверхности вытеснение из одной области поры аналогично
действию часового механизма с храповиком. Совместное влияние может вызвать
вытеснение из нескольких пор на участке одн<ло реопа. Число реоиов па
кривой	обратно пропорционально среднему диаметру поры в третьей
степени и зависит от размера образца.
Согласно второму закону термодинамики свободная энергия системы умень-
шается в результате самопроизвольного изменения. Поскольку изменение проиС’
ходит при постоянном насыщении, то потеря свободной энергии равна:
Af=aW<A/1oz + A‘4Si>“se)'	(5-2-39)
при этом величина в скобках должна быть отрицательной. Изоны можно
характеризовать как вытеснение одной фазы другой из пористой среды в усло-
виях равновесия. Эти вытеснения происходят плавно и обратимо. Следова-
тельно, имеет место соотношение
nvvS 5 Pcdw' = Httd<'4«) + '4SuC0seb	(5-2-40)
306
При осушении совершается работа над пористой системой и свободная
энергия поверхности увеличивается. Изменения происходят изотермически, и
теплота при совершении работы отдается окружающей среде. В мелкодисперс-
ных системах и капиллярно-пористых телах кривые капиллярного давления,
будучи необратимыми, являются плавными и сплошными, так как разрывы
непрерывности (сочетание рсонов и изонов) незначительны и практически не
наблюдаемы (рис. 5-11), Это происходит потому, что емкость системы (порис-
тое те?ю) велика по сравнению с объемом жидкости, перераспределенной на
участке реопа.
На кривых капиллярного давления различают:
1)	минимальное насыщение (Лц (объем смачивающей фазы, соответствую-
щий высоким капиллярным давлениям), которое не зависит от дальнейшего
повышения давления;
Рис. 5-11. Гистерезис капиллярного давления для микрошариков диаметром
48 мкм (а) и 60 мкм (б).
2)	остаточное насыщение ®/0, соответствующее нулевому давлению;
3)	кривую начального осушения Ro (вытеснение смачивающей фазы от
100% насыщения до
4)	кривую впитывания А (увеличение насыщения от щго до (&ц);
5)	вторичную кривую осушения R.
Экспериментальные данные для многих материалов показывают, что (£>ц
одинаково для начальном и вторичной кривых осушения.
.Кривые вторичного осушения и впитывания образуют петлю гистерезиса
RA со всеми последующими опорными точками, лежащими внутри этой петли.
Кривые развертки первичного осушения, которые начинаются на кривой впи-
тывания А, либо встречаются на пересечении кривой (рис. 5-11, б), либо схо-
дятся на кривой вторичного осушения в области, близкой к пересечению.
Поведение кривых развертки впитывания аналогично. Любая точка внутри
петли гистерезиса может быть получена многими путями.
Приведенные выше закономерности кривых капиллярного давления согла-
суются с термодинамическими соотношениями процесса вытеснения смачиваю-
307
шей фазы. Хорошее совпадение экспериментальных данных с расчетными имеет
место для дисперсных сред, частицы которых не набухают (отсутствие кол-
лоидных частиц) к поверхность которых нешероховата.
Для многих материалов кривые Pc=f (2) сходны между собой, поэтому
Леверетт [Л. 5-7] ввел безразмерную функцию / (Q), называемую функцией
Леверетта, она равна:
Рс iffy
'(Q» = o- V П--	<5-2'4‘)
где Kf—проницаемость.
На рис. 5-12 приведена функция Леверетта для рыхлых песков.
На рис. 5-12 видно, что при	капиллярное давление Рс->со. Это
Рис. 5-12, / —функция Леверетта для
рыхлых песков.
предельное насыщение, иногда назы-
ваемое остаточным, характеризует
связанную жидкость. Предельное на-
сыщение (связанная жидкость) для
многих тел зависит от проницаемости.
Например, для песчаника существует
такая эмпирическая зависимость'.
Q„ = 0,7-0,3-10-ал7,	(5-2-42)
где л/ — проницаемость в миллидарси.
Необходимо отметить, что прове-
дение экспериментов по нахождению
кривых pc = f(ffl) представляет боль-
шие трудности. Необходимо очень точ-
но поддерживать температуру, так
как малейшие колебания сказываются
на величине капиллярного давления
(табл. 5-4). Необходимо также следить
за чистотой смачивающей жидкости,
незначительные примеси соли в воде
резко влияют на капиллярное давле-
ние. На основании кривых pc = /(w)
можно рассчитать поверхность сопри-
косновения частиц, работу вытеснения
и ряд других показателей процесса
вытеснения. Эти исследования пред-
ставляют большой интерес для теории
фильтрации.
Если считать, что наибольшая
высота капиллярного подъема жид-
кости определяется поперечниками узких проходов, то максимальный капил-
лярный потенциал равен:
____	_ 2о cos 6
vc-/w-cg--pzS/? ,
(5-2-43)
где (j = g[v; В — постоянная, зависящая от вида укладки и способа подвода
жидкости (влияние капиллярного гистерезиса). Если поглощение жидкости
происходит снизу и сухим телом, то надо брать радиус наиболее широкой поры;
если поглощение происходит сверху или тело было предварительно смочено,
то надо брать радиус наиболее узкой части поры.
Максимальная высота поднятия воды в сухом теле (в высокой колонне,
состоящей из сферических частиц) при температуре 20 °C будет равна: при куби-
ческой укладке й = 0,205/?-1, при гексагональной укладке /^0,52/?-1. В смо-
ченном теле максимальная высота поднятия воды будет соответственно равна
/i = 0.366R-i (и=90°) и /?==0,968/?-1 (и = бО{).
В точке контакта сферических частиц по мере поступления жидкости обра-
зуется скопление жидкости в форме двояковогнутой линзы (рис, 5-13, а). Ьо*
308
ковая поверхность этой линзы является выпукло-вогнутой (rj—радиус выпук-
лой поверхности, а г2 —вогнутой поверхности).
Таблица 5-4
Сравнительное уменьшение капиллярного давления в зависимости
от относительной влажности, кривизны поверхности мениска воды,
колебания температуры и раствора соли
Капиллярное давление pc!S ДР. СМ вод- ст	Кривизна поверхности »Л»	Радиус ци- линдрического капидвярэ при 0 = 0 С“	Относительная влажность Ф = р7р»- <00. %	Эквивалентная разность температуры ДТ при 20е С	Эквивалентная концентрация NaCl. гмоль/л
0	0	100	100	0	0
10	1,36- J О2	1,47 • IO"2	99,999	1,6- Кг1	3-10-<
103	1,36- ю3	1,47 • IO"3	99,99	1,6- 10-3	3 • 10-3
103	1,36-10*	1,47 - 10-“	99,92	1,3- 10-2	2,4- IO"2
104	I 36• 105	1,47-10-5	99,27	1,2 • J0-1	0,22
)03	1,36- 106	0,47 • 10'8	93,00	1,16	2,1
Средняя кривизна такой поверхности равна;
(5-2-44)
что соответствует вогнутой поверхности, так как	Такое скопление жид-
кости называется жидкостной манжеткой, а жидкость стыковой (пендулярной), ,
Рис, 5-13. Структура капиллярной и пленочной жидкости в по-
,	рах тела,
a — жидкостная манжетка-, б— переход от стоксового состояния (защем-
ленная вода) к канатному состоянию; в — канатное состояние (защемленный
воздух).
Капиллярное давление стыковой жидкости при полном смачивании (costal)
равно:
ре = 2а (±^ = £к,	(5-2-45)
\ г / К
где Д'—постоянная, зависящая от угла о.
Если жидкости мало, то она распределена дискретными разобщенными
кольцами в точках соприкосновения частиц (капиллярно-разобщенное состоя-
ние или состояние защемленной жидкости). По мере поступления жидкости
манжеты постепенно увеличиваются и сливаются между собой. Такое слияние
происходят при угле и = 30° (рис. 5-13, б, в). В этот момент капиллярное дав-
ление рс1 при наиболее плотной укладке равно 4,1а(рс1 = 4,1а//?), а содержа-
ние жидкости составляет 22,6% объема пор (18,3% при кубической укладке).
Клинья жидкости теперь находятся в контакте между собой, н имеется
возможность непрерывного перехода от одной точки жидкой пленки к другой.
309
По мере увеличения жидкости пленка утолщается в перехвате, и, наконец,
ячейка полностью заполняется жидкостью. Наступает капиллярное Состояние’
при котором Рс2~6,9 u/R. Это значение рс2 соответствует переходу канатного
состояния в капиллярное в процессе поглощения жидкости.
В обратном процессе (обезвоживание), при переходе от капиллярного состоя-
ния в канатное, сначала, образуется мениск в поверхностных порах, который
продвигается внутрь. Капиллярное давление увеличивается, и при вступлении
Испарение
Время г
мениска в наиболее узкую часть поры
становится равным рс3= 12,9cj/R. в
процессе обводнения в этом переход-
ном состоянии капиллярное давление
было равно 4,1<т//?. Следовательно,
процессы поглощения и удаления ка-
пиллярной жидкости необратимы. За-
тем, по мере уменьшения жидкости,
мениск продвигается в следующую
ячейку и расширяется. Это расшире-
ние. 5-14. Схема прибора для изме-
рения пульсаций давления.
3 — засыпка из стеклянных шаров (/?==
= 1,5 мм); 2 — высокопроницаемая перего-
родка из обожженного стекла; 3 — датчик;
4 — регистратор давления
пне мениска происходит внезапно (не-
устойчивое состояние), и жидкость
перераспределяется с небольшим
уменьшением рс. Такой квантовый
процесс изменения капиллярного дав-
ления при обезвоживании можно на-
блюдать экспериментально.
Простейшая установка приведена
на рис. 5-14. Стеклянные шарики насы-.
пались на проницаемую мембрану, предварительно шарики насыщались лету-
чей жидкостью. Мембрана соединялась с измерителем давления. По мере испа-
рения жидкости давление уменьшалось, но не плавно, а скачкообразно. Сле-
довательно, вытеснение жидкости из таких дисперсных систем не может быть
обратимым и плавным из-за произвольных изменений конфигурации жидкости.
Вернемся к состоянию равновесия стыковой и пленочной жидкости. Пред-
положим, что мениски, ограничивающие элементы стыковой жидкости, не сомк-
нулись, и кривизна соединяющей их пленки равна кривизне поверхности
частиц (шариков). При этом участки пленки малы по сравнению с размерами
частиц и менисков. Обозначим толщину шейки элемента стыковой жидкости
через б а радиус свободных от жидкости просветов пор через Ro (см. рис. 5-13, в),
тогда будем иметь:
«=«-%;
R» =
R КЗ
(5-2-46)
В этом случае равновесие между пленочной и стыковой жидкостью будет
существовать при условии, если рс = аР — бо/R, т. е. когда пленка может
развивать положительное расклинивающее давление aft.
При увеличении количества жидкости участки пленки исчезают' и мениски
смыкаются. Для сохранения равновесия между пленкой и мениском должно
соблюдаться условие =	(1 — т. е. наличие отрицательного раскли-
К
кивающего давления; изменение злака обычно не наблюдается, т. е. рав-
новесие между пленочной и стыковой жидкостью невозможно. Предельное
значение капиллярного потенциала, когда возможно существование' пленочной
й стыковой жидкости, называют критическим капиллярным потенциалом. При
достижении критического капиллярного потенциала происходит скачкообраз-
ное заполнение лор жидкостью.
Если в уравнение закона Дарси (5-1-5), вместо перепада гидростатиче-
ского давления подставить капиллярное давление
о cos 5
Ркап — п
(5-2-47)
310
То для коэффициента проницаемости получим следующую формулу [Л.5-9]:
о cos б $ r*f (г) dr
Klc‘ 4rV(r)s2(“)
(5-248)
где £ (со) —извилистость, зависящая от удельного содержания жидкости. Функ-
ция / (г) определяется соотношением
f (г) = 4-',К,°.	'	(5-2-49)
1 v ’ 2o cos 0 \ dio /	*•	’
Если воспользоваться соотношениями между рЛа„ и ©, то получим:
ДМЛ	(5.2.50,
а коэффициент проницаемости
' (5-2-51)
Го
Величина Sv обозначает смоченную поверхность, приходящуюся на еди-
ницу объема. Если обозначить величину | (w) Sv через fs {г), то формула (5-2-51)
становится тождественной формуле автора [Л.5-10], которая была получена
из Модели пористого тела, как системы, состоящей из капилляров. В этом
случае fs(r) обозначает дифференциальную кривую распределения пор по ра-
диусу, она является функцией влагосодержания и извилистости.
Свойства тонких слоев жидкости
В капиллярно-пористых’ телах или дисперсных системах при некотором
влагосодержапии стенки капилляров имеют слои сорбированной жидкости. Эти
тонкие слои жидкости па поверхности твердого тела обладают специфическими
свойствами. Остановимся на этом несколько подробнее.
Условием термодинамического равновесия любой системы является ра-
венство химических потенциалов и температур. Пусть имеется топкий слой
жидкости на поверхности твердого тела. Химический потенциал в граничном
слое жидкости иг не равен химическому потенциалу в большом объеме жид*,
кости И о (.ис Ра-,)- Тогда при изотермических условиях (ТС==ТОЯ) в гранич-
ном слое жидкости возникает добавочное давление названное Б. В. Деря-
гиным расклинивающим давлением:
'	<5-2-52)
' т
где Vm — молярный объем.
Расклинивающее давление определяется перепадом давления между фазами
жидкость — твердое тело при переходе через плоскую межфазовую поверхность
От жидкости, находящейся в тонком слое Н, к объемной жидкости, гранича-
щей с тонким слоем. Обозначим этот перепад давления через Дрн, тогда
— Лрн~а^с,	(5-2-53)
т. е. перепад давления &р[{ численно равен расклинивающему давлению, но
имеет обратный знак.
Все эти рассуждения были справедливы для плоской междуфазовой по-
верхности. В общем случае перепад давления на границе фаз жидкость —пар
311
будет равен:
лР = АР0 + ^Ри,	(5-2-54)
где &ра — перепад давления, обусловленный кривизной поверхности жидкости
определяемый по формуле	Лапласа:	’
дР»=а(^ + ^“).	(5-2-55)
а перепад давления определяется величиной расклинивающего давления.
Когда жидкость течет с большой скоростью через пористое тело, то по-
мимо капиллярных и гравитационных сил существенную роль играют силы
инерции. Их можно определить с помощью чисел Рейнольдса.
Поведение пористого тела, через которое течет жидкость, может быть
также определено с помощью чисел Бонда и Вебера:
Re=e^; Bo.esL2; We=e^.
Т] ’ ст ’	ст
(5-2-56)
где о —скорость жидкости; А —характерный размер.
Число Рейнольдса характеризует отношение между силами инерции и
вязкости. Число Бонда есть отпоше-
We Инерция 10	В
во 0,01 0,2 1 0,1 Капиллярность 0,01 We	<^70
ние гравитационной силы к капил-
лярным, и число Вебера есть отно-
шение сил инерции к капиллярным
силам.
Определенная комбинация чисел
Вебера и Бонда дает известное чис-
ло Фруда
Fr = _	(5.2.57)
Рис. 5-15. Схематическое соотношение
инерционных, гравитационных и ка-
пиллярных сил при течении жидкости
которое представляет собой отноше-
ние силы инерции к гравитационной.
Необходимо разграничить обла-
сти по доминирующим силам: ^инер-
ции; 2) капиллярным; 3) гравитацион-
ным. В случае течения жидкости при
малых значениях We и Во капилляр-
через пористое тело.	вые силы являются доминирующими
(рис. 5-15), а эффектами гравитации
можно пренебречь. При малых значениях числа Бонда число Вебера определяет
решающую роль капиллярных и гравитационных сил. При больших числах
Фруда эффектами гравитации пренебрегают.
5-3. ЗАКОНОМЕРНОСТИ УСРЕДНЕНИЯ
Реальные пористые среды являются сложными, неупорядоченными струк-
турами. Для структурной характеристики таких сред применяются статисти-
ческий метод и метод геометрического моделирования. Обычно рассматриваются
две модели: пространственно-периодическая модель Бренера (рис. 5-16, а) и
модель со скошенными капиллярами (рис. 5-16, б).
Модель Бренера представляет собой неограниченную решетку, содержащую
одну твердую частицу или более. Границей элементарной ячейки является
жидкость. Поэтому допускается существование жесткой опоры пренебрежи-
тельно малого гидравлического сопротивления, которая удерживает элемен-
тарные частицы в пространстве.
Модель со скошенными капиллярами не может быть получена из модели
с прямыми капиллярами путем преобразования коо,динат, так как граничные
условия изменяются с преобразованием координат.
312
Третий метод исследования сочетает статистическое и геометрическое мо-
делирование; он основан на правильном усреднении уравнений переноса. Эти
уравнения должны быть справедливы для любой геометрии, и им должна
удовлетворять статистическая модель.
Будем рассматривать движение несжимаемой жидкости (divos=0) с по-
стоянной вязкостью (т] = const) в пористой среде.
°)
Рис. 5-16. Модель пористой среды.
a — пространственно-периодическая; б — скощенные капилляры.
Вектор скорости движения жидкости v и вектор положения г связаны
с пористой средой. Для стационарного давления уравнение Навье—Стокса
в пашем случае упрощается, так как	^Функция распределения
пор / {г) характеризуется соотношениями
( I, если г находится в жидкой области;
I 0, если г находится в твердой области.
При этом принимается, что все поры заполнены жидкостью, так что
объемная пористость
Vf
nv=y.	(5-3-1)
где Vf—объем жидкости в порах среды;
Jf(r)dK.	(5-3-2)
(V)
Полагаем, что объем усреднения V постоянный, a Vf меняется с положе-
нием.
Если бы функция / (г) была известна, то задачу движения жидкости можно
было бы решить до конца, однако f(r) неизвестно, поэтому приходится иметь
дело с усредненными значениями. Правильное усреднение имеет большое зна-
чение.
Для пористой среды характерны следующие величины:
I) величина d (размер пор или диаметр зерна), в пределах которой имеет
место значительное изменение скорости v\
2) величина 1~некоторый линейный размер пористой среды, в пределах
которой происходит усреднение по объему скорости движения (у).
Среднее по объему значение (некоторой функции ф((ф)), характеризую-
щее жидкость в пористой среде, определяется соотношением
31.
Функция ф может быть тензором любого ранга, оно является непрерыв-
ной для любого значения V.
Если I — характерная длина объема усреднения, то существует ограниче-
ние на соотношение (5-3-3):
-	(5-3-4)
Затем вводится дополнительное ограничение: среднее от среднего должно
быть равно среднему;
((Ф»=да-	(5-3.5)
Это справедливо при
/<£,	(5-3-G)
где 1.—характерная длина пористой среды, через которую происходит фильт-
рация и в пределах которой происходит значительное изменение усредненной
по объему скорости.
'Остановимся на усреднении по площади. Выберем объем усреднения та...
чтобы он включал площадь усреднения .плоскости которая должна бьц
постоянной. Например, если V—объем куба Is, то А^ь,— площадь, равная /
и параллельная плоскости (Jk). Если начало координат в центре куба, к-
среднее по поверхности в начале координат tyj- будет равно:
^',4’=-Г— f 1|> ЛА,	(5-3-7)
A<f. k) J
0/)
где Af — часть площади Л^|Л)( занимаемой жидкостью.
- Среднее по объему (ф}0 равно:
Ш>=У J	(5-3-8)
*(<>=-т!
Применяя метод, изложенный в [Л.5-6], получаем:
да0=,|,!,л(5-3-9,
Таким образом, при условии (5-3-6) усреднения по площади и по объему
одинаковы.
Этот вывод справедлив и для функции распределения пор. Полагая ф =
= f (г), получаем:
(?)«/<' й при l< L.	(5-3-10)
Так как	то из соотношения (5-3-10) следует;-
Пи=о/(1' 2>те/<2- 3>=»/<3’ О.	-	(5-3-11)
Соотношение (5-3-10) справедливо и для анизотропных пористых сред.
В уравнение переноса входят градиенты от характерных функций. Отсюда
возникает необходимость установить связь между усредненным градиентом
функции ф ((уф)) и градиентом от усредненной функции (V (ФУ)*
Такое соотношение было установлено С. Вайтекером [Л. 5-6] оно имеет вид:
J уф dV — v J ф dV + j ф '6а dA,	(5-3-12)
где —объем, занимаемый жидкостью, ограниченный поверхностью Af. Если
обозначить через Ai поверХЕЮСть жидкости на границе раздела объема пор. а
314
площадь входа и выхода жидкости через Аг, то
А; = Л + Аг.	(5-3-13)
Тогда получаем важное соотношение:
М) = V <Ч>> + V ( ф 5» <М.	(5-3-14)
В качестве примера приведем уравнение непрерывности:
j -V • “ <iV=v •	“-6„ЙЛ = О. (5-3-15)
17	А1
Если пористая среда неподвижна, то о = 0 на поверхности (отсутствие
скольжения), тогда
v <о)=0.	(5-3-16)
Остановимся теперь на уравнении движения жидкости. Для нашего слу-
чая его можно написать так:
'	— 7р+ПУ®о=0.	(5-3-17)
где р_общее давление, включающее и гравитационное давление. В [Л. 5-6]
показано, что между "у и (у^> существует взаимосвязь в виде соотношения
с =	(5-3-18)
где vlt —тензорное преобразование, которое устанавливает связь между локаль-
ной скоростью^ и усредненной по объему (о). Это преобразование является
единственным, но не обязательно линейным. Матрица преобразования опре-
деляется из уравнения
при этом йа поверхности Aj^f=O, а при r0(^/f)~u	(5-3-19)
(5-3-20)
s (р
j ’6„ J X-(?«/) <1S<M,	(5-3-21)
А? 0
где X—вектор касательный -к произвольной кривой, лежащей в жидкой
области.
Предположим, что при = 0	^) = 0, тогда можно показать, что
имеет обращение, и написать:
(v) = -1Ж (у <р)1 - -1 Ж {у |(р) + р (Ф»}.	(5-3-22)
Усредненная гравитационная постоянная
(7-5)dV = -H7g.	(5-3-23)
VJ
так как является постоянной величиной; /— вектор положения, характери-
зующий центр тяжести объема жидкости.
Среднее давление в уравнении (5-3-22) определяется по соотношению
' <Р>=Я‘Ш	(5-3-24)
315
Используя закономерности усреднения градиентных величин, окончательно
получаем:
<«>=у ж (П1л (р>/-р«] + [<р>/—p'g] ?я}	(5-3.25)
Если пористость не изменяется с координатами, то второй член в правой
части формулы (5-3-25) равен нулю (^/7==0). Оценка тензора & дает такой
порядок:
<у£ = 0(^2).	(5-3-26)
Тогда, обозначив безразмерный тензор через (а%Г* = а%^/£р), получим:
<»>=—(5-3-27)
Тензор зависит от структуры пористой среды. Скалярные компоненты
тензора должны определяться экспериментально. В соответствии с геомет-
рической капиллярной моделью Козени <%** пропорционально /72/(1— 77)2.
Для пространственно-периодической модели <2%?* является симметричным, даже
в случае анизотропных пористых сред, а именно:
(5'3'28)
где X/ —скалярные компоненты единичного вектора, направленные вдоль
капилляров.
Для анизотропной пористой среды $£ есть функция где £—единичный
вектор ориентации, отображающий преимущественное направление. Для изо-
тропной среды ;~0, для модели со скошенными капиллярами | параллельно
капиллярам. Если бы частицы в модели Бренера были эллипсоидами, то вектор
£ был бы параллелен главной оси. Если пористая среда симметрична отно-
сительно одной плоскости, то
/Кп	0	0	\
<з^= 0	К22	К23|	(5-3-29)
\ о	Kgg	К33/ ’
так как Ki2 = K2]I=jf',3i = K13==0. Если пористая среда симметричная отно-
сительно двух ортогональных плоскостей, то дополнительно у<23 =s/f32 = О, т. е.
/Хп	0	0 X
= 0	К22	О I	(5-3-30)
\о о kJ-
Очевидно, что если пористая среда симметрична относительно двух орто-
гональных плоскостей, то она должна быть симметричной относительно порис-
той ортогональной плоскости. Материалы, для которых тензор опреде-
ляется главными значениями Kii, Kss, называются ортотропными. Если
Ка2 = /<зз, то такие среды называют поперечно изотропными.
В [Л. 5-6] показано, что тензор может быть представлен в виде
Ki/= Bti 4- Bj/.'.Kfe +'Bl)mn\m'kn,	(5-3-31)
где тензоры В являются полиномами от X—единичный вектор ориентации
В этом случае закон Дарси будет имееть вид:
<">==- 4г 1~В^+В^'> Ь <₽>r-№L (5-3-32)
где индекс * обозначает безразмерную величину, а 6 — единичный тензор.
Для модели со скошенными капиллярами	Таким образом, для
точного описания фильтрации жидкости через пористые среды необходимо
316
спериментально определить четыре скалярные величины: В?р> B?2l, Xj, Х8.
Сравнивая (формулы (5-3-32) и (5-3-27), находим;
+	(5-3-33)
откуда получаем:
S<2> = (8« Kli ~ SS(‘>) •	(5-3-34)
Соотношения (5-3-33), (5-3-34) справедливы для поперечно-изотропного
тела; анизотропный характер определяется однозначно единичным вектором
ориентаций | при справедливости принципа безразличия пористой структуры
к закону Дарси.
Существуют две теоремы усреднения по объему для градиента величины 8
и для дивергенции этой величины (Л. 5-11] (величина В может быть вектором
иля тензором):
(Vs) = V (В) + F ) Вп1	(5-3-35)
(div B>=div (B>+i ( впЧА.	(5-3-36)
Соотношение (5-3-35) называется теоремой усреднения градиента, а соот-
ношение (5-3-36)—теоремой усреднения дивергенции.
Применяя эти теоремы усреднения к уравнению Навье—Стокса, полу-
чаем [Л. 5-11J:
? div (ри о) = div (&>) 4- р (F ) + у J • n1 dA[t (5-3-37)
Aj
где — тензор напряжений; F — внешняя сила; At— часть произвольной
поверхности, охватывающая объем V и совпадающая с поверхностью пор. Это
уравнение движения в пористой среде отличается от аналогичного уравнения
сплошной среды наличием дополнительного члена (третий член справа).
Для частного случая стационарного движения (<?р0/дт=»О) и несжимаемой
жидкости (divv=0) уравнение (5-3-37) можно упростить, если ввести сле-
дующие соотношения:
? = -?©, (р> = (р»> + р(Ф),	(5-3-38)
где Ф— потенциал внешней силы; (р) — локально усредненное по объему дав-
ление с учетом действия внешней силы. Тогда получим:
V «р — Ра» — div (е^ — рб> —у J	— (р0—рФ) 6] n1 =	(5-3-39)
где р0—постоянное исходное давление.
Последний член уравнения (5-3-39) является выражением силы, с которой
действует жидкость на стенки пор (сверх гидростатической силы или силы
взаимодействия), рассчитанной на единицу объема. Эта сила возникает в
результате движения:
g= —J-)'1.9s —(р„ —рФ) 51 n1 <iS.	(5-3-40)
ь/
В этом случае уравнение движения примет вид:
— div«^— pd))+g=X (и),	(5-3-41)
где д'—сопротивление движению жидкости в пористой среде.
317
Если коэффициент вязкости ц—величина постоянная, то
div ((5s —p6>) = T]div (о>,	(5-3-42 ।
откуда получим уравнение, которое является выражением модифицировав I
ного уравнения Дарси
V ((p-p»»-ndiv (V (»))+R (о)=0, 	(5-3-43)
где R — коэффициент сопротивления для неориентированной пористой струн,
туры, определяемый из соотношения
g = R ]<» — <«>],	(5-3-44)
здесь (и) —локальная усредненная по объему скорость движения пористого
тела.
Уравнение (5-3-43) впервые было получено Д. С. Слеттери; на основе этого
уравнения был решен ряд частных задач. Применяя раздельно уравнение
Фурье —Кирхгофа к жидкости в пористом теле и к скелету пористого тела
Слеттери получил следующее уравнение теплопереноса [Л. 5-1 []:
д (Т\т
[ПрЛ + (1 +П) рА]	div [П (туи („>,] =
=Х; div [у {П (Туп + ’к, div {v [(I-П) (7’>'"]}+div q*, (5-3-45)
где П— пористость; (Т)т—средняя температура, определяемая по соотношению
(7’>”=Г~77<7’>1=(Г<7’>'Л’	(М-«)
здесь индекс / обозначает жидкость, з—твердое тело.
Вектор теплового потока д* равен;
7* = рЛ {(Г><л (о)Ф-(То>сЛ}+ (>.;_>.,) 2. ( (ту Й1 dA. (5-3-47)
Если пористость не зависит От координат, то уравнение (5-3-45) упро-
щается:
д (Т\т
—Я) pscsJ -ft—НПр/Cydiv [(7’>“ (oyj= — div q, (5-3-48)
где вектор q равен:
7=-[OT./+(l-n)VIgrad (T>™'+5*.	(5-3-49)
Уравнение (5-3-48) отличается от обычного уравнения Фурье—Кирхгофа
для пористой среды Егаличием дополнительного вектора потока тепла ~q*-
Согласно формуле (5-3-47) первый член, стоящий в фигурных скобках,
является аналогом турбулентного потока теплоты, так как определяется соот-
ношением
(Tv — Tv).	(5-3-50)
Таким образом, в пористой среде существует дополнительный перенос теп-
лоты, обусловленный сложным механизмом движения жидкости.
Однако, этот дополнительный вид переноса теплоты имеет место при доста-
точно интенсивном движении жидкости в пористой среде, например в процес-
сах фильтрации.
318
I. ТЕРМОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВЛАГОПЕРЕНОСА
Влажные материалы являются коллоидными капиллярно-пористыми телами.
Влага в таких материалах связана различными силами.
В монографии авгора [Л.5-12] подробно разбираются термодинамические
свойства коллоидных, капиллярно-пористых и коллоидных капиллярно-пористых
В состоянии термодинамического и молекулярного равновесия влажный
материал имеет определенную влажность, его влагосодержание называется
„авновссным или гигроскопическим влагосодержанием. В этом случае давле-
ние паров жидкости в материале ри равно парциальному давлению пара влаж-
ного воздуха. Тогда относительная влажность воздуха ф (ф==ря/р5) будет
равна относительному давлению пара в материале ((f>~pu/ps). где ps—давле-
ние насыщенного пара при данной температуре.
Равновесное влагосодержание тела ие зависит от относительной влажности
воздуха и его температуры: ие (ф, Т).
Графическая зависимость между ие и ф при постоянной температуре назы-
вается изотермой сорбции или десорбции в зависимости от того, как было
достигнуто равновесие—путем сорбции или десорбции. Изотермы сорбции
и десорбции имеют S-образный характер и не совпадают между собой на про-
тяжении всего интервала ф за исключением двух точек: ф = 0 и ф=1.
До настоящего времени пет достаточно строгой теории, объясняющей
гистерезис сорбции и десорбции. Форма изотермы десорбции или сорбции опре-
деляется формой связи влаги с влажным материалом. Анализ изотерм сорбции
и десорбции позволяет сделать следующее заключение:
() первоначальный участок изотермы <р«0ч-0,J имеет характерную для
мопомолеку^ярной адсорбции выпуклость кривой ф^Н^е/^т) к оси влаго-
содержания; поглощение жидкости сопровождается значительным выделением
теплоты;
2) на участке ф = 0,1-4-0,9 изотерма обращена выпуклостью к осн влаж-
ности воздуха, чсо характерно для полимолекулярцон адсорбции; поглощение
жидкости также сопровождается выделением теплоты, но в значительно мень-
шем количестве, чем в первом случае;	'
3) на участке ф = 0,9-4- 1,0 жидкость поглощается без выделения теплоты
и в основном является капиллярной,
Дальнейшее поглощение жидкости сверх максимального гигроскопического
влагосодержания происходит путем непосредственного соприкосновения мате-
риала с жидкостью, В этом процессе поглощения жидкости имеет место запол-
нение Микрокапилляров и пор, а также осмотическое поглощение жидкости
через полупроницаемые клетки замкнутых стенок, Свойства этой поглощенной
жидкости ле отличаются от свойств свободной жидкости, и, в частности, дав-
ление пара жидкости тела практически равно давлению насыщенного пара
свободной ЖИДКОСТИ (фе=1).
Данная схема не претендует на полноту, но анализ большого эксперимен-
тального материала по исследованию коэффициентов переноса теплоты и массы
вещества в зависимости от массосодержания поглощенного теплей. Веществвги1^'
подтверждает ее. По энергии связи различают три вида свЯЗй': "химическая
связь, физико-химическая связь и физико-механическая связь (схема класси-
фикации академика П. А. Ребиндера). Обычно рассматривают последние два
вида связи, так как химическая связь наиболее прочная и не разрушается
пги нагревании до 120— 150=С.
Для кристаллогидратов сульфата меди при температуре 25ЭС энергия
связи составляет (8—3) • 10’° эрг/моль.
К физико-химической связи относят адсорбционную связь вещества с пори-
стым телом, а также осмотическое поглощение жидкости. К этой же форме
связи надо отнести и иммобилизацию жидкости (жидкость, находящаяся внутри
клетки, захваченная при образовании коллоидного тела).
К. физико-механически связанной жидкости относится жидкость, находя-
щаяся в капиллярах, и жидкость смачивания. Величина работы А по отрыву
одного моля воды при изотермически обратимом процессе прямо пропорцио-
319
нальпа логарифму относительного давления (In ф);
А = -/?Г1пф.	(54]j
Используя уравнение Гиббса —Гельмгольца, для теплоты испарения п
связанной воды получим выражение;	х
Q ~ RT2 1пр„ in (и) Qo,	(5-4-2)
где QL(u) = RT2d/dT (Inри) — теплота испарения воды из влажного тела- О
= RTW/dT (in ps) — теплота испарения свободной воды, Из условия' бч
> 0 (Qi (u)>Qo) следует, что давление пара жидкости'в теле рп меньше дав
ления'пара свободной жидкости Ps (ри < ps), а темп роста кривой 1п р, = / (т'\
выше темпа роста кривой 1пр5 = /(Г).	'v >
Рис, 5-17. Схематические изотермы
сорбции водяного пара для по-
верхностей: гидрофильной (/), гид-
рофобной (7/7) и промежуточной
(//).
Точки /, 2t S соответствуют моментам
образования насыщенного мономолеку-
лярного слоя,
Рис. 5-18. Термограмма сушки (7) и
кривая кинетики сушки (//) капил-
лярно-пористых материалов различной
природы.
Виды связи влаги; а — осмотическая влага
коллоидного тела иди влага капиллярного
состояния в порах (г > J0-5 см): б —сты-
ковая влага (г > 10-а см); в — капилляр-
ная влага микропор {г < 10-* см); г — вла-
га полимолекулярной адсорбции; д—влага
мономолекулярной адсорбции
В небольшом интервале температур можно счигать <?== const,’ тогда полу-
чим;
p„=psexp(--5,-),	(5-4-3)
Адсорбционная связь зависит от удельного массосодержания (влагосодер-
жания) и может быть определена из изотерм сорбции иди десорбции ие==/(<р)
(рис. 5-17), Например, при ср=я0,25 энергия адсорбционной связи около
4 • IO® Дж/моль.
Жидкость, заключенная в капиллярах и ограниченная менисками, является
свободной жидкостью, за исключением тончайшего слоя жидкости, адсорбционно-
связанной у стенок капилляра. Понижение давления пара над поверхностью
мениска^формально характеризует энергию связи капиллярной жидкости, опре-
деляемой не взаимодействием твердой поверхности с жидкостью, а действием
320
искривленного мениска. Поэтому энергия капиллярной связи не зависит от
природы стенок в условиях полного смачивания и от количества жидкости
в капиллярах.	u
Энергия капиллярной связи А (г) равна:
4(г) = ^- Го,
(5-4-4)
(5-4-5)
где Vo —полный объем.
Представление об энергии капиллярной связи воды дают следующие дан-
ные: при 2г—Ю-зсм А (г) = 5,3-Дж/моль, при 2г==10"6 см А (г) =
= 5 3 - 102 Дж/моль.
Обычно давление пара жидкости ри капиллярно-пористого тела определяют
по формуле Томсона
.	2opncosS
in ф == — ——------,
9fPsrm
г е Гт_средний радиус капилляра. При этом надо учесть поправку на тол-
щину адсорбционного слоя пара на стенках капилляров.
Формула может быть применена для капилляров, радиус которых лежит
в пределах 0,5 • 10-7r < I0-6 см. Нижний предел обусловлен размерами моле-
кул тела, радиус которых примерно 10~8 см, Для капилляров с радиусом
больше 10"5 см давление пара над мениском практически равно давлению
насыщенного пара над плоской поверхностью.
Работами М. Ф. Казанского и его учеников было установлено, что сущест-
вует три вида капиллярной влаги: капиллярная и стыковая вода в грубых
порах и капиллярная вода в микрокапиллярах (рис. 5-18).
На основании анализа изотерм десорбции и термограмм, сушки принята
классификация капилляров на макро- (г > 10"® см) и микрокапилляры (г <
< 10"б"см). В некоторых работах микрокапиллярами считаются капилляры
с радиусом меньше Ю"6 см. В табл. 5-5 приводятся характеристики макро-
и микрокапилляров некоторых материалов [Л. 5-2].
Таблица 5-5
Свойства некоторых капиллярно-пористых материалов
Материал	Плотность, кг/м5	Объем пор. ма/ м3	Микропоры (z<0.01 мкм)	
			Объем, м’/м5	Объемная часть
Фосфор	2530	0,031	0,0034	0,109
Каолинит	2370	0,369	0,126	0,341
Древесный уголь из сосны	1720	0,883	0,354	0,412.
Древесный уголь из березы	1720	0,936	0,656	0,700
Активный уголь	1780	0 870	0,856	0,986
Давление пара жидкости над тонкой пленкой определяется форму-
лой (5-2-21). Из приведенных формул видно, что зависимость между величи-
ной, обратной влагосодсржанию, и |п ф имеет линейный характер. Эта зависи-
мость, как показал Б. А. Поснов [Л. 5-13), хорошо подтверждав гея экспери-
ментальными данными. Формула Поснова имеет вид;
<5-4-6»
где Wm — максимальное гигроскопическое влагосодержание материала; В —
некоторый коэффициент, зависящий от температуры В (Г). Формула (5-3-38)
справедлива при <р = 0,1 4-1,0. Максимальное гигроскопическое влагосодержа-
ние обратно пропорционально абсолютной температуре (№т~Т-1).
В табл, 5-6 приведены значения Wm и В для некоторых материалов при
разной температуре
321
11 Лыков А. В,
Таблица 5-8
Максимальное приведенное гигроскопическое влагосодержание и коэффициент £
Материал	t, °C	Wm	
Асбестовое волокно	‘24	1.00	021
Бумага: асбестовая	24	4,54	0,58
газетная	24	13.0	0,16
лакированная	24	8,33	0,46
оберточная (хвойная)	—	17.2	0,10
писчая	24	17,5 17,2	0,12
упаковочная (крафт)	24		0,98
Вата гигроскопическая	—	28,6	0,03
Вата стеклянная	—.	0,62	4,92
	40	3,31	0,83 ’
	20	3,50	0,75
Войлок шерстяной	।	0	3,50	0,71
	-20	3,70	0,59
	-40	4 00	0,58
Гипсошлакобетом	20	11,5	о,11
Глина часовъярская	—	11,1 23,8	0,21
Дерево	20		009 '
Дерево восле предварительного просушивания	20	22,2	0,15
	40	13,15	0,23
	20	14,28	0,20
Сосна	I	0	14,28	0,17
	-20	14,28	0,15
	-40	14,70	0,13
Джут	24	25,00	0,08
Древесная мука (сосна)	—	13,7	0,08
Каолин	24	1,43	0,65
Каучук	24	1.61	1,15
Керамика из блоков	20	1,56	4,07
Кизельгур	24	400	0,71
Кирпич глиняный	20	0,59	13,0
	400	1,00	10,90
	20	1,11	7,70
Кирпич красный 	0	1,25	4,28
	-20	1,33	4,28
	— 40 .	1,54	3,54
	40	5,55	0,41
	20	5,71	0,33
Кирпич саманный	0	6,09	0,29
	— 20	6,28	0,24
	-40	6,57	0,20
	40	1,82	1,93
	20	1,88	1,55
Кирпич силикатный	0	2,00	1,30
	-20	2,15	1,07
	—40	2,38	0,95
Клей			14,7	0,09
Кокс				1,02
Ден (полотно)	24	11,75	0,15
Льняная пряжа		13,9	0,07
Мыло	—	40,0	0,12
322
Продолжение табл. 5-6
Материал	t, °C		в.Ь%
			40	2,90	1,08
	20	2,94	0,88
Пенобетон	_	j	0 — 20	3,07 3,33	0,70 0,63
	-40	3,64	0,52
Пеногипс	60	25,2	0,003
	40	1,88	1,85
	20	2,00	1,46
Пеносиликат	।	0	2,08	1,21
	—20	2,22	1,02
	-40	2,38	0,83
Пеностекло после предварительного просушивания	20	1,33	10,0
Шелк нитроцеллюлозный	—	17,8	0,07
Шелк-сырец	24	19,2	0,08
Шерсть	—	31,2	0,67
Шерсть стеклянная	24	4,34	3,18
	40	2,90	1.08
	20	2,94	0,88
Шлакобетон	।	0	3,07	0,07
	-20	3,33	0,63
	—40	3,64	0,52
Потенциал влагопереноса
Кинетика переноса теплоты н массы вещества в капиллярно-пористых телах
определяется разностью потенциалов переноса. Понятие потенциала переноса
теплоты (температуры) было введено очень давно и получило в термодинамике
строгое обоснование. Понятие потенциала переноса влаги во влажных телах
было введено только в последнее время па основе термодинамической аналогии
тепломассообмена.
Термодинамика в отличие от молекулярной физики изучает макроскопи-
ческие свойства тела или системы тел и процессы их взаимодействия, не
интересуясь микроскопической картиной. Эго обстоятельство имеет особо важ-
ное значение при исследовании переноса влаги в капиллярно-пористых телах,
где молекулярная картина необычайно сложна. В то же время применение
термодинамических методов не означает отказ от молекулярно-кинетического
метода. Термодинамика и молекулярно-кинетическая теория должны взаимно
Дополнять друг друга, один и тот же опытный материал должен служить
предметом комплексного анализа. Перенос влаги неотделим от переноса теплоты,
и явления тепломассопереноса необходимо рассматривать в их неразрывной
связи. Поэтому вполне естественным является применение к массопереносу тех
методов и той системы понятий, которые с успехом применяются в явлениях
переноса теплоты.
Известно, что потенциалом переноса парообразной влаги во влажном
воздухе является химический потенциал, который зависит от температуры и1
парциального давления пара. Следовательно, в области гигроскопического
состояния химический потенциал парообразной влаги может быть выражен
через влагосодержание и температуру тела. Р области нлзжного состояния
тела химический потенциал, рассчитанный на единицу массы поглощенной
воды, равен химическому потенциалу свободной воды, т. е. является величиной
постоянной (изменение давления пара над поверхностью мениска макрокапил-
ляров с изменением радиуса капилляров практически равно нулю),
11*	323
Представляют интерес экспериментальные методы определения единого
потенциала переноса влаги для любого влагосодержания материала как для'
гигроскопического, так и для влажного состояния.
По аналогии с тепловым потенциалом (температурой) введем понятие по
тенциала переноса влаги. С этой целью используем следующие опытные факты
В состоянии термодинамического равновесия, например при гигрометрическом
равновесии, существует определенное распределение влаги в теле или системе
тел. При увеличении общей массы влаги растет и содержание. Потенциал
влагопереноса есть некоторая функция влагосодержания и внешних парамег-
Песок й^10°/о	Торф й^ЗООУо
8f=600	82= 350
	
‘У
				1 \й=2,1 кг/кг				
фильтровало-} Торф Тая Тимага"^'^ м								-
Ц=0,5кг/кг				—। 	|				
1 IX				_1_				
Расстояние от плоскости сопри-
Свинеи, П=8 ккал/кг ^=200 °C	Алюми- нии. h=20 ккал/кг Ьг=100°С ^Тепло
косновения, см

5)
У
Рис. 5-19. Распределение тепло- и влагосодержания и потенциалов
тепло- и влагопереноса в системе двух соприкасающихся тел (а, б).
Переход тепла и массы от тела с меньшим содержанием к телу с
большим содержанием (в. г).
ров, которые в состоянии термодинамического равновесия должны быть одина-
ковы во всех частях тела или системы тел.
На рис. 5-19 приведены распределения теплового потенциала и энтальпии
двух тел (свинца и железа) и распределения аналогичных равновесных пара-
метров вещества для пластины из торфа и листов фильтровальной бумаги,
Из рис. 5-19 видно, что температура свинца и железа одинакова и равна 50гС-
Энтальпия на границе соприкосновения этих тел испытывает скачок: энталь-
пия железа равна 5,5 ккал/кг, а свинца—1,5 ккал/кг. Рисунок 5-19 показы-
вает, что распределение влагосодержания в торфе и бумаге равномерное:
в бумажной пластине оно равно 0,5, а в торфе —2,1 кг/кг. На границе сопри-
косновения торфа и бумаги имеет место скачок влагосодержания, аналогичный
324
качку энтальпии. Как будет показано ниже, потенциал переноса вещества
Спя обоих тел одинаков и равен 180 влагообмеппым градусам. Из роста влаго-
олеожания для всех частей системы следует, что функция потенциала является
либо монотонно возрастающей, либо монотонно убывающей.
Мы всегда можем выбрать потенциал 0 (и, Т) так, чтобы 0 росло с увели-
58 л
чением и, и Для всех шкал потенциала принять -^->0.
Влагоемкость влажного тела
По аналогии с удельной теплоемкостью с введем понятие "удельной изотер-
мической влагосмкости по соотношению

(5-4-7)
где (du/50)r—частная производная от удельного влагосодержания по потенци-
алу влагопереноса при постоянной температуре.
Если удельная влагоемкость ст постоянна, то из соотношения (5-4-7) сле-
дует:
и=Я-ств,	(5-4-8)
где —некоторая постоянная.
Следовательно, потенциал влагопереноса при постоянной температуре и
влагосмкости является линейной функцией влагосодержания. Единица измере-
ния удельной влагоемкости —кг/(кг-°М), где °М обозначает массообменный
(влагообмеиный) градус.
Напомним, что в случае молярного переноса капиллярной жидкости потен-
циалом влагопереноса является капиллярный потенциал ф. Капиллярный по-
тенциал по определению является отрицательной величиной, и влагоперенос
происходит от низшего капиллярного потенциала к высшему аналогично тепло-
переносу в области отрицательных температур, определяемых по шкале Цель-
сия (/<0°С), При влагосодержании w = 0 капиллярный потенциал максимален
(фмакс), а при некотором максимальном влагосодержании (влажность намока-
ния)— равен нулю. Следовательно, для капиллярного потенциала постоянная
в соотношении (5-4-8) равна произведению максимального капиллярного потен-
циала иа удельную влагоемкость. Если влагоперенос происходит молекуляр-
ным путем (избирательная диффузия), то потенциалом переноса является осмо-
тическое давление р, для которого производная др/ди отрицательна.
Потенциал влагопереноса 0 будем считать положительным > oj,
а постоянную b в области малых значений влагосодержания —равной нулю,
полагая, что потенциал влагопереноса абсолютно сухого тела равен нулю.
В этом случае потенциал переноса капиллярной жидкости будет равен разности
между максимальным капиллярным потенциалом фыакс и капиллярным потен-
циалом при данном влагосодержании ф (6=фМакс-*ф)- Градиент потенциала
влагопереноса будет равен градиенту капиллярного потенциала с обратным
знаком (V0 = —Уф). Аналогичная зависимость будет иметь место и для диф-
фузионного переноса жидкости.
К данному механизму переноса жидкости можно отнести перенос влаги
внутри капиллярной поры, закрытой жидкостными менисками, когда испарение
жидкости происходит па одном мениске поры, а конденсация пара — на про-
тивоположном. При этом необходимо, чтобы перепад температуры вдоль капил-
лярной поры в направлении переноса был бесконечно мал, т. е. испарение и
конденсация происходили бы при одинаковой температуре. Само собой разу-
меется, что количество жидкости, испарившейся с одного мениска, должно
быть равно количеству сконденсировавшегося пара на противоположном
S2&
равны друг
(5-4-10)
их влагоем-
мениске. Такой процесс переноса пара внутри закрытой капиллярной парц '
термодинамически равнозначен переносу жидкости. 1
При постоянной удельной влагоемкости в области малых значений влаго-
содержания из формулы (5-4-8) получим:
и = гт6,	(5-4.9)
т. е. шкала потенциала 6 влагопереноса аналогична шкале Цельсия в области
положительных температур.
Согласно принятой шкале влагоперенос направлен от тела с большим
потенциалом к телу с меньшим потенциалом. В состоянии термодинамического
равновесия потенциалы тел, находящихся в соприкосновении,
другу (0£ —0а), а удельные их влагосодержания неодинаковы.
Из формулы (5-4-9) следует, что при 0j = 08
ui __ cmi
и% спа
т. е. отношение удельных влагосодсржаний пропорционально
костям. Для одного и того же тела = и ий, т. е. распределение
влагосодержания в теле .в состоянии равновесия будет равномерным (см.
рис. 5-19). Количество влаги ДМВ, перешедшей от одного тела к другому при
соприкосновении тел с разными потенциалами,
=	=	(5-4-11)
где 01 и 08—потенциалы влагопереноса соответственно до начала влаГообмсна
и в конце его; Л10—масса абсолютно сухого тела.
Формула (5-4-Ц) аналогична элементарной формуле теплообмена
Д<2=с,Л1«	(5-4-12;
где Со — удельная теплоемкость тела.
Произведение удельной влагоемкости ст на массу абсолютно сухого тела /И4-
назовем влагосмкостыо тела:
=ст^о ==CfflPolzo-	(5-4-13)
Произведение стр0, равное отношению Cm/VOt является объемной влаго-
емкостью тела.
Соотношения (5-4-9) -(5-4-13) справедливы для тел с постоянной влагоем-
костью. Если влагоемкость изменяется в зависимости от потенциала влаго-
переноса 0, а следовательно, и от влагосодержания и, то в этих соотношениях
под величиной ст надо понимать среднюю удельную влагоемкость в интервале
потенциала влагопереноса Д0 = О3 —0Х.
Экспериментальная шкала потенциала влагопереноса
Для того чтобы воспользоваться выведенными соотношениями, необходимо
иметь экспериментальную шкалу потенциала влагопереноса 0. В отличие от
экспериментальной термодинамики, где потенциал теплопереноса (температура)
измеряется непосредственно, в нашем случае непосредственно определяется
влагосодержание путем сушки тела до абсолютно сухого состояния. ДдЯ
лучшего уяснении принципа построения шкалы потенциала 0 обратимся к ана-
логии.
1 В теории фильтрации такие „закрытые1* поры ие входят в эффективную
пористость тела, и при расчете движения жидкости они исключаются. В этом
принципиальная разница теории фильтрации и влагопереноса в процессе
сушки [Л-5-12],
326
Напомним элементарный калориметрический опыт по определению тепло-
емкости тела- Нагретое до определенной температуры исследуемое тело при-
бочят в соприкосновение с калориметрической жидкостью (водой). В результате
тепюобмена между телом и жидкостью устанавливается тепловое равновесие.
Определив повышение температуры'жидкости, находят теплоемкость тела. При
этом удельную теплоемкость калориметрической жидкости (воды) принимают
за единину- В этом случае удельное теплосодержание (энтальпия) эталонной
(калориметрической) жидкости будет равно температуре тела и жидкости,
а удельная -теплоемкость исследуемого тела будет равна отношению удельных
энтальпий тела и эталонной жидкости. В этом элементарном опыте теплоем-
кости тела и жидкости считают постоянными.
.Таким образом, наиболее простой метод построения шкалы потенциала 9
состоит в определении удельных влагосодержапий системы двух тел (исследуе-
мого и эталонного), приведенных в непосредственное соприкосновение друг
с другом и находящихся в состоянии термодинамического равновесия. При
этом важно, чтобы непосредственный контакт обеспечивал свободный влагооб-
мен между телами. Если влагосодсржание тела больше максимального сорбци-
онного ытагосодержапия (м>ит), то влагообмен происходит при непосред-
ственном соприкосновении капиллярно-пористых тел. При влагосодержании,
меньшем максимального сорбционного (u < необходимым условием термо-
динамического равновесия является не только постоянство температур, но и
постоянство нлажносги окружающего воздуха (7= const, <p = coust). В этом
случае имеет место влагообмен путем сорбции и десорбции для паровоздушной
смеси, а также непосредственный массообмен жидкости через соприкасающиеся
поверхности тел.
В качестве эталонного тела аналогично калориметрической жидкости слу-
жит целлюлоза, так как она имеет большую гигроскопичность (максимальное
сорбционное влагосодержание при 7 = 25°С около 0,28 кг/кг) и обладает
хорошим намоканием.
Простейший опыт состоит в следующем. В полый цилиндр, открытый
с двух концов и наполовину заполненный листами фильтровальной бумаги
определенного влагосодержания, помещается исследуемое тело (например, на-
сыпается кварцевый песок). Затем цилиндр закрывается с концов, взвеши-
вается для определения плотности исследуемого тела и помещается в термо-
стат к. По истечении определенного промежутка времени обычными способами
исследуется распределение влагосодержания в эталонном и исследуемом телах.
Из приведенных на рис. 5-19 грг;фиков легко определить влагосодержание
исследуемого и эталонного тел на границе соприкосновения (для торфа —
= 2,1 кг/кг, а для эталонного тела — фильтровальной бумаги —= 0,5 кг,'кг).
Чтобы найти потенциал влагопереноса 0 по удельному влагосодержанию
эталонного тела, необходимо задать его удельную влагоемкость. В отличие от
удельной теплоемкости эталонной калориметрической жидкости удельную изо-
термическую влагоемкость эталонного тела (стэ)т принимаем равной не еди-
нице, а 1/100 максимального сорбционного влагосодержания:
f3-4'14)
т. е. удельному влагосодержанию эталонного тела ист соответствует потенциал О
а Ю0"М. Такой выбор удельной влагоемкости обусловлен следующими обсто-
ятельствами: во-первых, максимальное сорбционное влагосодержание при опре-
деленной температуре является константой, не зависящей от способа его до-
стижения (изотермы сорбции и десорбции при ср—1 совпадают); во-вторых,
при применении разных эталонных тел в точке максимальной гигроскопичности
(ф— 1) получим один и тот же потенциал 0, равный 10О°М. Благодаря этому
1 Если влагосодержание тела меньше максимального сорбционного влаго-
содержания, то цилиндр с открытыми концами помещают в эксикатор с опре-
деленной влажностью воздуха (Г—const, (p = const).
327
вводится единая экспериментальная шкала потенциала 9, корректирующая
некоторое различие в эталонных образцах-
Следовательно, потенциал влагопереноса 6 определяем по влагосодержание
эталонного тела иэ, для которого удельную влагоемкость принимаем постоя^,
ной и равной 0,01 ист> где ист — максимальное сорбционное влагосодержание
эталонного тела при /=25°С, т. е.
е
и9
(стэ)т
 100.
tttcm / Т
(5-4-15)
Для фильтровальной бумаги при температуре 25"С um®«0,277. Тогда
потенциал массопереноса 0 для системы соприкасающихся тел, приведенных
иа рис. 5*19 (снизу),
’“оТ^100”180™-
Этому потенциалу соответствует влагосодержание торфа, равное 2,1 кг/кг.
Влагоемкость тела может служить качественной характеристикой связи
Рис. 5-20. Зависимость между относи-
тельным равновесным влагосодержапием
фильтровальной бумаги ир'ис с потен-
циалом влагопереноса 0 от относитель-
ной влажности воздуха ф.
влаги с влажными телами. Влаго-
емкостъ зависит от эталонного
тела. В качестве эталонного тела
была выбрана целлюлоза в форме
листов фильтровальной бумаги.
Это было обусловлено следующи-
ми обстоятельствами,- 1) целлюло-
за содержит влагу всех видов свя-
зи (адсорбционную, капиллярную
и осмотическую); 2) изменение
равновесного влагосодержания с
повышением температуры при раз-
ных значениях влажности воздуха
<р происходит примерно одинаково.
Так, на рис. 5-20 приведены изо-
термы сорбции фильтровальной бу-
маги при температурах от 22до 80сС,
построенные ио данным Н. В. Арци-
ховской. Видно, что относительное
равновесное влагосодержание прак-
тически не зависит от температу-
ры и является однозначной функ-
цией влажности воздуха (неболь-
шие колебания в величине ир!ис в зависимости от температуры носят случай-
ный характер, связанный с постановкой эксперимента). Этот результат является
очень важным, так как позволяет сделать вывод, что потенциал влагопереноса
в гигроскопической области зависит только от ср. Эта зависимость 0=f((p)
представлена на том же рисунке в виде графика, полученного путем осредне-
ния изотерм сорбции для разных температур. Отсюда следуег, что потенциал
массопереноса 0, измеряемый эталонным телом (целлюлозой), в гигроскопи-
ческой области характеризует изотермический массоперенос пара и жидкости
в капиллярно-пористых телах.
Из простого термодинамического анализа, подтвержденного прямыми экс-
периментами Г. А. Максимова, следует, что равновесное влагосодержание тела
при определенных tc и ср не зависит от того, находилось ли тело в соприкос-
новении с другими телами или равновесие достигалось одним телом. При этом
предполагается, что соприкосновение не вызывает каких-либо химических
взаимодействий или изменения структуры тел.
Следовательно, максимальному сорбционному влагосодержанию любого
тела соответствует потенциал влагопереноса 100°М., а область гигроскопического
состояния соответствует интервалу потенциала от 0 до 100аМ Таким образом,
потенциал влагопереноса 0 (0 < 0 < 100) определяется по значению влажности
328
oaivxa, с которым тело находится в равновесии, т. е. исходным эталоном
экспериментальной шкалы влагопереноса является влажный воздух.
** Логарифм влажности воздуха, равный логарифму отношения давления
пара воды над телом к давлению насыщенного пара над поверхностью свобод-
ной воды, прямо пропорционален изотермической свободной энергии связи
энного количества влаги ир в теле. Следовательно, потенциал влагопереноса 0
является функцией изотермической свободной энергии связи влаги с капил-
лярно-пористым телом.
Представляет интерес сравнение потенциала 0 с потенциалом переноса
влаги, применяемым в агрофизике. В работах американских исследователей
в качестве потенциала переноса влаги в грунтах и почвах принимается значе-
ние pF, равное логарифму от сосущей силы F. В области влажного состояния
тела ее величина пропорциональна капиллярному давлению, экспериментально
определяемому тензометром. В гигроскопической области сосущая сила F опре-
деляется по относительной влажности воздуха, соответствующей равновесному
влагосодержанию тела:
F = ^ln<p,
М] т’
(5-4-17)
где Mi—молекулярная масса; R — универсальная газовая постоянная.
Сосущая сила F в обоих случаях измеряется в единицах давления (см
вод. ст.).
Специальными опытами был определен потенциал pF для нашего эталон-
ного тела (фильтровальная бумага) в области влажного состояния, а в гигро-
скопической области он был подсчитан по формуле (5-4-12). Оказалось, что
в области влажного состояния pF является линейной функцией влагосодержа-
ния. Следовательно, в этой области между потенциалом О и pF существует
простая зависимость
pF=3,66—1,5 -10-30	(5-4-18)
при 0> 100°М.
В гигроскопической области соотношение между pF и 0 имеет сложный
вид’, однако важно отметить то обстоятельство, что потенциал 0 однозначно
определяется влажностью воздуха ср. Имея однозначную зависимость 0 = f (ср),
можно из экспериментальных данных по равновесному влагосодержанию
(изотермы сорбции и десорбции) различных материалов определить потенциал
влагопереноса 0, а из кривых up^f(8)—удельную изотермическую влагоем-
кость.
Таким образом, в гигроскопической области (0<в<100®М) потенциал
влагопереноса и удельная влагоемкость определяются из изотерм сорбции или
десорбции. В области влажного состояния (0> 10(РМ) эти параметры опреде-
ляются по влагосодержанию эталонного тела, находящегося в соприкоснове-
нии с исследуемым материалом в состоянии термодинамического равновесия.
Как показали. опыты с разными материалами, в большинстве случаев
зависимость u=f(0) имеет вид ломаной для коллоидных капиллярно-пористых
тел (пис. 5-21), и только для грубодксперсных материалов зависимость
u=f(v) представляет собой кривую, обращенную выпуклостью к оси 6.
наличие излома в точке а в гигроскопической области (0 < 0 < 10(УМ)
объясняет переход от одной формы связи к другой, например от полимоле-
кулярной адсорбционно-связанной воды к капиллярной влаге. Влагоемкость
тела увеличивается при переходе от свободной влаги к связанной.
1 Применив формулу Поснова в качестве первого приближения для фильтч
ровальной бумаги н положив при этом, что произведение Вир не зависит от
температуры, получим 0= 100 — Вир • 1Q0 1п ф. Следовательно, величина (100 — 0)
пропорциональна 1п ф, а потенциал pF пропорционален In In <pj, поэтому
между pF и 0 нет линейной зависимости.
329
По влагоемкости можно подсчитать влагосодержапие по следующим d’op
мулам:	1 ’
w==c',9; 0 < 6 < 9й;	(5-4-ipj
" = ^(Э~Шс;Лг 9a<e<WM;	(5-4-20)
“ = <п" (9-100) + ^ (100—	при 9 > 1WM, _ (5-4-21)
где с^, с^, с''' —удельные изотермические влагоемкости в соотнегствующцх
интервалах потенциала 9; их значения для некоторых материалов приведены
в табл. 5-7.
Таблица 5-7
Изотермические удельные влагоемкости некоторых влажных тел при 25°С
Материалы	">а	^‘,0!	4"-^	Материалы		с'п-	4г’01	4Г-Ю»
Пенобетон, ро^’00 Торфоплита	0,140 0,674	0,040 0,052	—	1 Кирпич 1 красный 1 Кварцевый 1 песок:		0,004	0,009	
Древесина (сосна)	0,380	0,270	0,21	100 <	9 < 300	—	—	0,007
Фибролит	0,130	0,090	—	300 <	9 <550	—			0,025
Красная глина Торф низинный	0,180	0,180 1,200	0,03 0,51	! 550 < 5 < 700		—	—	0,90
В большинстве случаев потенциал 9 мало изменяется с температуре i
Однако для ряда капиллярно-пористых тел зависимость между 6 и Т близ,
Рис. 5-21. Типичная зависимость между
влагосодержанием й и потенциалом вла-
гоперснося 6, °Л1, для коллоидных ка-
пиллярно-пористых тел (7) и грубодис-
персных материалов (//).
к линейной. Например, для кварцевого песка, по данным Ф. М. Полонской
[Л. 5-14}, температурный коэффициент потенциала влагопереноса д$]дТи
= 0,6°М/°С при 200<9<30(ГМ; 105</<8п3С).
Термограднентный коэффициент
К числу термодинамических параметров относится, и термоградиентный
коэффициент др, ок определяется как отношение перепада влагосодержания Дп
к перепаду температуры в Стационарном состоянии при отсутствии влагопе-
реноса.-
33Q
формула закона'влагопроводности будет:
J = ->vmve- —	(5-4.23)
ст
где Л71—коэффициент влагопроводности.
J Из этой формулы получаем выражение термоградиептного коэффициента 6е,
отнесенного к разности масссюбменных потенциалов,
Чтобы размерность 6Р и 69 была одинакова (град-1), вводим в формулу
(5-4-23) величину ст. Тогда
(S'4'24)
Поскольку потенциал массопереноса зависит от влагосодержания и тем-
пературы, то имеем:
<м-25’
Где О'гт=:(д0/дТ)ц—температурный коэффициент потенциала влагопереноса.
Используя соотношения (5-4-24), получаем выражение закона диффузии влаги;
- ) = — o_«o»VU-omP»6pV?’,	(5-4-26)
где 6р—термограднентный коэффициент, равный:
lV=lVl'Mr-	(5-4-2?)
Если 60==О,' т. е. неизотермический перенос влаги описывается только
градиентом потенциала влагопереноса (69 = 0), то
=	.	(5-4-28)
Если же перенос влаги обусловлен не только \?0, но и уТ, что наблю-
дается в области влажного состояния, то надо использовать выражение (3-4-2?).
Для ряда капиллярно-пористых материалов
с^0'г<6е, тогда будем иметь:
6р = б0 = 6.	(5-4-29)
Термоградиентный коэффициент капилляр-
но-пористых тел увеличивается с повышением
влагосодержания, достигая некоторого макси-
мального значения, а затем уменьшается. Ха-
рактер изменения коэффициента 6р зависит от
капиллярно-пористой структуры тела и рас-
пределения в нем капиллярной влаги. Не ис-
ключена возможность влияния защемленного
О Злашодержиние  n/.rjxr
Рис. 5-22. Схематический
ход кривых Cmjl = Д (и),
кряои.х Чг (и) Я
кривых 8р — /з (и) для кол-
лоидных капиллярно-пори-
стых тел.
воздуха на распределение жидкости при пере-
паде температуры. В нагретых мостах пористо-
го тела защемленный воздух расширяется и
проталкивает жидкость в более холодные места.
Аналогичный расчет, выполненный по дан-
ной схеме, показывает, что при достижении
максимального влагосодержания коэффициент
6р равен пулю, так как в этом состоянии все
Поры заполнены жидкостью н защемленный
воздух отсутствует.
Для типичных коллоидных тел кривая 6р—f(u) имеет максимум, при
некоторых влагосодержаниях кривая 5Р (и) пересекает ось влагосодержания
(коэффициент 6р = 0).
В области больших влагосодержании значение и0, соответствующее 6Р —О,
отмечает границу между осмотической и адсорбционной влагой. В области
331
малых значений влагосодержаний величина и0 характеризует термодиффузион
ный и эффузионный переносы пара в макрокапиллярах тела.
Термоградиентный коэффициент коллоидных капиллярно-пористых ?ел
показан на рис. 5-22, на котором видно, что кривая 6р=/(н) имеетмаксимум
который смещается с повышением температуры в сторону меньших влагосо-
держаний.
Как и для коллоидного тела, у сосны при больших влагосодержаниях
коэффициент 6Р равен нулю, а максимумы кривых = f (и) с уменьшением
температуры смещаются вправо. Коэффициент с повышением температуры
уменьшается, что тоже характерно для осмотической влаги, за исключением
малых влагосодержавий, при которых, наоборот, коэффициент с повыше-
нием температуры увеличивается [Л. 5-10].
Применение химического потенциала к расчету влагоемкости
и термоградиентного коэффициента
Выше было показано, что химический потенциал pf является потенциалом
переноса парообразной влаги. Если считать, что парообразная влага в каче-
стве первого приближения подчиняется закону идеальных газов, то химиче-
ский потенциал будет функцией парциального давления рг и температуры Г
т. е. |Xi=f(Pi, Т). В области гигроскопического состояния парциальное дав-
ление пара является функцией температуры и влагосодержания pi = f(u, Г).
Поэтому химический потенциал щ будет также функцией влагосодержания и
температуры pi = f(u, Т}.
В области гигроскопического состояния материала жидкообразпая влага
связана адсорбционными силами (влага моно- и полимолекулярпои адсорбции),
капиллярными силами (влага микрокапилляров) и диффузионно-осмотическими
силами (осмотическая связь влаги).
В этих случаях можно в первом приближении принять в качестве потен-
циала влагопереноса жидкообраэной влаги химический потенциал ji2, который
будет также функцией влагосодержания и температуры тела jt2 = f(u, Г).
Таким образом, в гигроскопической области в качестве потенциала влаго-
переноса можно принять химический потенциал р., являющийся функцией
температуры и влагосодержания тела. В области влажного состояния хими-
ческий потенциал не может служить в качестве потенциала влагопереноса!.
В [Л. 5-15] показано, что величина v(p.fT), являющаяся движущей силой Хт
переноса массы в термодинамике необратимых процессов, приблизительно про-
порциональна логарифму относительной влажности воздуха
(-^)=ЯГу1пф.	(5-4-30)
Учитывая, что энергия связи £ влаги с материалом равна:
Е = (~\ ^-STtnm,	(М-31)
\ dm )т	Y
можно прийти к выводу, что потенциалом влагопереноса является Е. Необ-
ходимо отметить, что впервые этот вывод был сделан в [Л. 5-16] на основании
анализа экспериментальных кривых распределения относительной влажности
воздуха в пограничном слое при сушке гипсовых пластин. Принимая за по-
тенциал влагопереноса химический потенциал ц и используя соотношение
р>= RT 1п ф,	(5-4-32)
подсчитали значения ц, Дж^моль, для разных $ и Г [Л. 5-13]. Затем с по-
мощью изотерм сорбции и десорбции u = Г) подсчитывали значения хими-
1 Химический потенциал в принципе может быть применен ко всем об-
ластям влажного состояния, но практическое его использование затруднено
в области влажного состояния, (Прим, ред.)
332
ского потенциала для разных материалов как функции влагосодержания и
температуры ц—,f(u, Т). На основе графиков	Т) методом графиче-
ского дифференцирования были рассчитаны изотермические удельные влаго-
емкости с'т по соотношению
и температурный коэффициент химического потенциала (фх/дГ)м. Результаты
таких расчётов опубликованы в (Л. 5-15].
В этом случае термоградиектный коэффициент будет равен:
= <.(>)„•	(5-«4)
Значения удельной влагоемкости, температурного коэффициента, химиче-
ского потенциала (дц/дТ)а и термоградиентного коэффициента для некоторых
материалов приведены в [Л. 5-16]*.
Анализ экспериментальных материалов показывает, что удельная массо-
емкость с,Иц» моль/Дж, мало зависит от температуры, гак что в первом при-
ближении можно считать, что изотермическая влагоемкость есть однозначная
функция влагосодержания. Схематический ход кривой cmp — f (и) показан на
рис. 5-22.
Температурный коэффициент химического потенциала	с увеличе-
нием влагосодержания и значительно уменьшается Экспериментальные данные
показывают, что (с?р./(77')а практически ие зависит от температуры. Термогра-
диеитный коэффициент в большинстве случаев с увеличением влагосодер-
жання увеличивается. Для древесины на кривых 6p=f(u) имеет место мак-
симум, аналогичный вил имеют кривые и для других материалов.
Если сравнить данные о коэффициенте 6Р, полученные расчетным путем
по формуле (5-4-22), с экспериментальными значениями 6р, когда опреде-
лялась непосредственно по перепаду влагосодержания, то получаем хорошее
совпадение [Л. 5-12[.
Это лишний раз подтверждает, что термоградиентпый коэффициент явля-
ется термодинамической характеристикой и может быть рассчитан по изотер-
мам сорбции и десорбции.
5-5. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД
Ниже приводится детальное описание механизма переноса пара при сво-
бодномалек'улярном течении в тонком капилляре (микрокапилляре) с учетом
испарения не только с мсциска жидкости, но и с боковой поверхности капил-
ляра при наличии градиента температуры вдоль стенки капилляра [Л. 5-99].
В результате анализа такого механизма было установлено, что внутри капил-
лярно-пористого тела, частично заполненного жидкостью, могут происходить
процессы испарения и конденсации. Основными определяющими величинами
являются безразмерные параметры s и 1. Первая представляет собой произве-
дение безразмерной теплоты фазового перехода жидкость — пар и относитель-
ного температурного перепада вдоль капилляра, вторая —отношение длины
капилляра к его радиусу (безразмерная длина капилляра).
Грубая оценка величины s цля испарения жидкости в вакуум (T=220sC,
ДГ = 1б°С) дает значение в~1,3. Тогда для величин l~s прн /> 1 (т. е.
когда длина капилляра больше его радиуса) может иметь место у мениска
капилляра конденсация пара, а вблизи выхода —испарение. Однако если I <_ 1
(длина капилляра меньше его радиуса), то при тех же условиях (l=s) на
обоих концах капилляра имеет место испарение. Таким образом, структура
* Эти коэффициенты применимы для равновесных условий, поэтому они
справедливы лишь при очень малой скорости сушки. (Прим, ред.)
333
пор (Z) существенно влияет на механизм миграции пара. Значение I всегда
положительно, значение же s может быть и отрицательным в зависимости от
знака перепада температуры АТ вдоль капилляра (ч5Й 0). Если s<0, то при
соотношении 1~—s механизм миграции пара будет отличен от механизма
миграции при l = s. Следовательно, направление' температурного градиента
влияет на процессы испарения и конденсации в капилляре. Эго явление
наблюдается только в яеизотермических условиях и может быть названо гер-
мичсским эффектом миграции парообразной влаги.
Последовательная конденсация и испарение в поре или капилляре на
менисках жидкости рассматривались и ранее, но считалось, что эти процессы
происходят при изотермических условиях. В нашем случае испарение и кон-
денсация влаги в капилляре определяются перепадом температуры вдоль его
длины и геометрической структурой пор и капилляров тела. В этом принци-
пиальная сторона рассматриваемого нами механизма переноса влаги в капилляре.
Рядом исследований было установлено, что существенную роль в процессе
переноса играет поверхностная диффузия пара или газа. Поэтому скорость
миграции пара по длине капилляра зависит не только от линейной скорости
диффузии, ио и от времени адсорбции молекул на поверхности стенки капил-
ляра, т. е. скорости поверхностной диффузии. Полученные соотношения могут
быть использованы для анализа механизма процесса сушки влажных материа-
лов и пористого испарительного охлаждения теплозащитных материалов.
В заключение показано, как можно использовать приближенную теорию
средней длины свободного пробега для исследования кинетики переноса пара
через высокодисперсное пористое тело, когда капиллярная модель является
неточной.
Течение пара в микрокапнлляре при наличии фазовых превращений
Рассмотрим цилиндрический капилляр, ограниченный г одной сторон'
(Х=0) плоским дном, причем как на боковой поверхности, так и на дне пр<-
исходит испарение (сублимация) По длине капилляра задан постоянный гра-
диент температуры. Число молекул, испаряющихся с единицы поверхности
в единицу времени,
равно:
i(a, Т)=а -.-МП
(2пт4Т) 1/2
(5-5-1)
где т — масса молекулы: k —постоянная Больцмана; ре—давление насыщен-
ных паров; а—коэффициент испарения (конденсации).
Предполагаем, что поток молекул, вылетающих с единицы поверхности,
содержит часть а испаряющихся молекул и часть 1—а отраженных. В работе
рассмотрены две схемы отражения — диффузная [Л. 5-17J и зеркальная.
1. При диффузном отражении для потока молекул, вылетающих с единицы
боковой поверхности капилляра, получим следующее уравнение (поток отнесен
к величине j (1, 7'0)==/0):
'	+	(6-5-2)
ре (* 0) \ 1 г	L J
здесь первое слагаемое описывает испаряющиеся молекулы, второе — попада-
ющие на единицу боковой поверхности в окрестности точки х = с осталь-
ной части боковой поверхности (интегральное слагаемое) и дна (/0К(х)) и затем
отражающиеся,
/„ = «„+21 (1 -«„) р © К © 01,1=	(6-5-3)
о
334
£ —длина капилляра; £ —радиус капилляра. Выражения для функций
X (х), A’lW приведены в [Л.5-18];
=	1I: K1(X)=«W.	(3-5-4)
2(Л^ + 4)1/2	2	d*	{	'
При неизотермической поверхности капилляра, если температура поверх-
ности изменяется по закону	’	»
r(x) = T0(l+/U)	(3-3-5)
и j А 1 ‘С I. давление ре может быть выражено так:
Ре (х) = В ехр {—= В ехр (- (I - Л.е)|.	(5-5-6)
В ряде работ (например, [Л.5-19]) показано, что функции К (х) и
'для сравнительно коротких капилляров с достаточной степенью точности могут
быть заменены экспонентами. Так,
-V	{-ft).
Подставляем (5-5-6) в (5-5-2), используя Приближенные выражения для
X и Кг- Дифференцируя (5-5-2) дважды и комбинируя найденное отношение
с исходным, получаем следующее дифференциальное уравнение:
d2/
dxi--Л = )м₽М	(5-5-7)
где
s = с’ = аР; Ь=.а^-Р),
(здесь Q — теплота, необходимая для испарения одной молекулы).
Решение уравнения (5-5-7) для + c имеет вид.-
/ — ^ехр (и) J-о, ехр (-сх)	ехР (“)	(5-5-S)
Коэффициенты aL и <?2 находим, подставляя (5-5-8) в (5-5-2) (полагаем при
этом а,п==о.) и приравнивая коэффициенты при ехр {1х} и ехр { — lx}:
exp(cj ехр (— с} Ь ехр (х)
01 ~^=1-----а'-~Т+1------;
Ol(_-2-7- + -Lz2-(exp(c-/)-t)) +
+а’ - 4тг(м₽ < -(1+с>} - *>]=-^^4 (s-й) -т~
(8-5-9)
Если з — ±с (что для а=1 можно записать в виде	—— =±: 1),
«Уд Тgl ’
решение уравнения (5-5-7) выражается следующим образом:
/ = а(ехр {(.x')-f-a2exp{—ст) +'^''resP 15Л:Ь	(5-5-10)
где а' и а*, также как ах и в (5-5-8), определяются из системы алгебраиче^
ских уравнений, получаемых при подстановке (5-5-10) в (5-5-2).
335
где
Для потока молекул на выходе из капилляра находим:
Л' = /»пД’ /„K2(l) + 2l J I (х) К (1-х)*
(5-5-11)
В частном случае (при а = 1 и $=#£) ддя приближенных
из (5-5-2) и (5-5-11) получаем:
« К2(х)
Л/=/„яд’ехр {-(} [l+yiy (ехр {s + l)-1)].	' (5-5-12)
Из (5-5-12) следует, что при I > $ поток выражается следующей формулой: -
Л’=/олЯ2^1— ехр {s},
(5-5-13)

Рис. 5-23. Зависимость потока
М па выходе из капилляра от Г
при диффузной схеме отражения
(Тй = 213 К; /= Ю-1 см).
Пунктирная линия: ДТ = 0, сплош-
ная линия: ДГ — — 10.
т. е. N стремится к значению /ол/?2ехр {s}, не зависящему от I.
При а--1 и s —0 (изотермический слу-
чай) из (5-5-2) и (5-5-11) получаем значение
потока, не зависящее от Г,
(5-5-14)
причем к такому же соотношению приходим
и при точных вьтажениях для функций
К (х) и К2 (х). Подобный результат качествен-
но объясняется в [Л. 5-2о]. ”
В случае a=j£ 1 выражения для / (х) и
W становятся довольно громоздкими. Числен-
ные расчеты были проведены для льда при
То = 213 К, причем использовались прибли-
женные функции К(х), Ki(x) и Кг(х}.
Расчеты показали, что для а=£ 1 и ДТ=0
поток на выходе из капилляра при малых I
увеличивается с ростом I, а затем практиче-
ски перестает зависеть от I (рис. 5-23). В
случае ДТ^0 поведение кривых,
характеризующих зависимость потока от /,
становится более сложным.
Результирующий безразмерный поток
молекул на боковой поверхности опреде-
ляется следующим выражением:
/ (х)=— [Г (х) —/ (х)]=^а[/’(х)—ехр {sx}].
(5-5-15)
где Г — поток молекул, падающих на еди-
ницу боковой поверхности, определяемый из
уравнения
)^ + ^(х).
(5-5-16)
Определив / из (5-5-2), вычисляем из (5-5-16) Г и затем из (5-5-15) —
результирующий поток молекул.
336
Не приводя довольно громоздкой общей формулы, записываем поток J (я)
для частного случая а==1. При $¥= + 1
/(*)=4'ехр1~1x1 ["р?Т “PW + Ok}—
--p^Texp(I(2x + p-l)f—руу].	(6-5-17)
Где pes//, а положительное значение J соответствует испарению.
Из (5-5-17) следует, что поведение функции J (я) определяется значениями I
и R. Так, для 1 < 0 < ехр {/ (0 — 1)} при я = 0 J < 0, при х= 1 J > 0. Что же
касается случая 0 = 0, т. е. изотермического капилляра, то для него по всей
длине происходит испарение, причем поток J достигает максимального значе-
ния при х= 1:
для s = Z
/(Ч = -уех₽ I—	-•*)) ехр (2/*) --у];	- (5-5-1S)
ДЛЯ Д =—I
./(.ij-JpEXp (—/х)[^(1+ехр (2/(х — 1)})(5-5-19)
Из (5-5-18) видно, что для l<l J(0)>0 и J (I) > 0, т, е. на обоих кон-
цах капилляра имеет место испарение, а при I > 1 J (0) < 0, J (I) > 0, т. е.
при возрастании я происходит переход от конденсации к испарению.
Выражение (5-5-19) свидетельствует о том, что для всех I при я = 0 про-
исходит испарение, а для х=1 при I <1 имеет место испарение, при Z> 1—
конденсация.
Когда испарение происходит только на дне при диффузном отражении
молекул от боковой поверхности, поток / можно получить из (5-5-2). полагая
а= 0.
2. Выясним влияние зеркального отражения молекул на результирующий
поток на выходе из капилляра.
Число молекул, испарившихся с боковой поверхности и после многократных
зеркальных отражений вышедших из капилляра, записывается следующим
образом [Л. 5-21]:
2я/?а/ р (а, Т) Sj (1 -я) dx,	(5-5-20)
где
СЙ
Н=1
Для числа молекул, испарившихся со дна, а затем многократно отразив--
шихся от стенок и вылетевших из капилляра, получаем (полагая cto=a):
/V& = ^/(a, Т0)5а(1),	(5-5-21)
где
Сй
(*)«*,«+2
п= 1
Кроме того, следует принять Во внимание молекулы, вышедшие из капил-
ляра после испарения с боковой поверхности, попадания на дно и зеркального
отражения от него. Учитываем их приближенно, заменив молекулами, отра-
женными диффузио:
Л^ = 2лДз/52(1)(1-а)р(а, Т) Зх (я) dx.	(5-5-22)
837
I
Поток па выходе из капилляра определяем суммированием (5-5-20) — (5-5-22)
Из результатов расчетов для схем диффузного и зеркального отражений
следует, что при малых I значения потоков на выходе близки. С ростом^
в случае зеркального отражения поток увеличивается быстрее, чем для схемы
диффузного отражения.
Случай испарения со дна при зеркальном отражении от него п диффузном
от боковой поверхности рассмотрен ниже.
Влияние поверхностной диффузии на свободномолекулярное течение пара
через капилляр
Экспериментальные исследования течения газов в капиллярах в условиях
свободномолекулярного режима обнаружили отличие измеренной проводимости
от рассчитанной по формуле Кнудсена. Одной из причин этого различия явля-
ется поверхностная диффузия {Л. 5-22]. Она объясняется тем, что при малых
значениях плотности адсорбированных на поверхности молекул последние могуг
рассматриваться как двумерный газ, так что при наличии градиента плотности
имеет место двумерный диффузионный поток, описываемый выражением
.	_ dn.	_ '
s — Ds ,	(5-0-23)
где Ds— коэффициент поверхностной диффузии.
Известно несколько работ, в которых учтено явление поверхностной диф-
фузии. Так, в [Л, 5-23] рассмотрена задача о кнудсеновском течении в длинной
трубе при наличии поверхностного диффузионного потока, причем влияние
поверхностной диффузии вследствие линейной зависимости поверхностной плот-
ности от координаты сводится только к добавлению этого потока к кнудсенов-
скому.
В других работах решается интегрально-дифференциальное уравнение для
поверхностной плотности молекул, которое в предельном случае отсутствия
поверхностной диффузии переходит в интегральное уравнение Клаузингй.
В частности, в [Л. 5-24] методом итераций найдено решение этого уравнения
в случае короткого капилляра ~	1^, а в [Л. 5-18 — 5-25] аналогичная
задача решена численно для любых 1. Однако в указанных работах не иссле-
дуется влияние различных членов интегрально-дифференциального уравнения
на проводимость капилляра.
Нижс*'рассматривается метод приближенного аналитического исследования
свободномолекулярного течения пара с учетом поверхностной диффузии в ци-
линдрическом капилляре, ограниченном с одной стороны (Х = 0) плоской поверх-
ностью испаряющейся жидкости, а с другой (Х==Д)—соединенном с резервуаром,
заполненным парами этой жидкости. Поверхность жидкости характеризуется
коэффициентом зеркального отражения о.
Интегрально-дифференциальное уравнение для поверхностной плотности
молекул имеет следующий вид:
X W, (’ х-$ I l+oK! (x+E)J dg—К (X) -
~-~1К (1-х)+аК (1+х)1,
пп
(5-5-24)
где п — безразмерная поверхностная плотность молекул по отношению к плот-
ности ло = п(О); т—-время адсорбции; и Д/j—соответственно потоки моле-
33&
куЛ, диффузно испущенных единицей поверхности дна, и молекул, прошедших
через единицу площади открытого конца из резервуара,
В уравнении (5-5-24) член в. левой части обусловлен поверхностной диф-
фузией молекул, интегральный член в правой-части соответствует потоку
молекул, падающих на единицу боковой поверхности капилляра в результате
десорбции по закону косинуса с остальной части поверхности (первое слагаемое)
н зеркального отражения от дна (второе слагаемое)'. Первый внеинтегральный
член характеризует поток молекул, диффузно испущенных дном и падающих
на единицу поверхности капилляра, второй и третий члены — потоки молекул,
вошедших в капилляр через открытый конец и соответственно падающих на
стенку непосредстзенно и после зеркального отражения от дна.
Сформулируем граничные условия для интегрально-дифференциального
уравнения (5-5-24). Заметим, что явление поверхностной диффузии имеет место
не только в капилляре, по и на внутренней поверхности резервуара. При этом
считаем, что па расстоянии около Х=1/угЁ1 на поверхности резервуара
достигается адсорбционное равновесие, т. е. плотность молекул (размерная)
определяется выражением
=	(5-5-25)
Тогда для открытого конца капилляра при учете условий сопряжения
(равенства плотностей и потоков) на стыке поверхностей капилляра и резер-
вуара может быть записано следующее условие третьего рода:
~ = LfE[(ne-n),	(5-5-26)
где
е	1
^(1)^(0 '
Для правильной формулировки граничного условия при х = 0 следует
задать величины, характеризующие'кинетику двумерного испарения [Л. 5-26].
Поскольку таких данных в литературе нет, в работе использовалось условие вида
п(0)«1.	(5-5-27)
Потоки /Vo и Л'1 вычислялись по формулам
Л/„=(1-о)-----р‘ ,; ,V,=--------Pi- ,-s-.
(2.чт«Г,)6'2 (2nmfrl)v2
1, Изотермический случай. Полагая T=const, Ds = const и заменяя К (х)
экспонентой, из (5-5-24) получаем:
i
е/.-^г = п W-4 J " © >ех₽г Iх—51}+оехР {—г ('+?)) dl— -
(J
-	{—1х} —	|ехр (—/(1 -х))+оехр {— 1 (1+х))|.	(5-5-28)
где
Из уравнения (5-5-28) следует, что чем больше безразмерный параметр GZ1
гем значительнее роль поверхностной диффузии в распределении п по поверх-
ности капилляра. В частности, при GL 1 плотность п фактически опреде-
ляется решением уравнения
= °	•	(5-5-29)
339
с граничными условиями (5-5-26) и (5-5-27), т. е. изменяется линейно:
П=1+Вх;
С другой стороны, в случае GL I уравнение (5-5-28) имеет малый пара-
метр при старшей производной. Поэтому при сколь угодно малых значениях G
на концах капилляра, вообще говоря, существуют области (пограничные слои)
где необходимо учитывать дифференциальный член в уравнении (5-5-28), т. е'
при использовании метода малого параметра возмущенное решение не будет
равномерно пригодно во всей области изменения х. Как известно [Л.5-27]
неоднородность может проявиться только тогда, когда параметр возмущения
представляет собой отношение двух длин. В дайной задаче G^2 является отно-
шением среднеквадратичного смещения частицы по поверхности 1/|/Е к длине
капилляра L.
Для решения уравнения (5-5-28) следует продифференцировать его дважды
по х. Комбинируя полученное выражение с исходным уравнением (5-5-28), по-
лучаем следующее соотношение;
=	4=^ + ®’-	(5-5-31)
Решение уравнения (5-5-31) записывается следующим образом:
/1=^ ехр {— <г1х}Ч-а2 ехр {— а (I — х)} +	+ о4.	(5-5-32)
Подставляя (5-5-32) в (5-5-31) и приравнивая коэффициенты при ехр {—1х)
и ехр {/х}, получаем два уравнения для определения аа, а31 о4. Два дру-
гнх" уравнения находим из граничных условий (5-5-26) и (5-5-27). Следова-
тельно, для вычисления четырех неизвестных коэффициентов следует решить
систему четырех линейных уравнений:
<м₽ <” +'» - ’>] + а‘‘[(нт£ + х
Хехр {— с} - ехр {—(}] +	[—1-а+аехр {-()(( + 1)1+
+а, (1-а+аехр {— ()) = Т (Wo+a.V, ехр {— 1});	_
llQ	IO-W-OOJ
/а.	,	, , ta2 ,	1-4-1 , WiT
_X_exp{_C1}+_-+,Js_r. + „, =_1_.
Ъ exp {- cx} (1	+ (1 +c1G}/2)+aa (1 + &F)+ + ™+;
ai+ojexp {—cI} + a4= 1.	j
Для исследования полученного решения были проведены численные расчеты.
Особый интерес представляет случай GL < I (заметим, что для С£ = 0 решение
уравнения (5-5-28) является линейной функцией). Как и следовало ожидать,
при таких значениях G^ отчетливо проявляется наличие пограничных слоев
на концах капилляра, а в его средней части кривая п (х) переходит в линей-
ную функцию (рис. 5-24), наклон которой совпадает с наклоном прямой,
являющейся решением уравнения (5-5-24) при б£ = 0. Это объясняется тем,
что основной вклад в решение уравнения (5-5-28) в этой области вносит его
правая часть. Указанная особенность зависимости п от х при GL < 1 видиа
на рисунке, где приведены результаты численных расчетов для воды при сле-
дующих значениях параметров: GL^4 • 10“2; («0,1; о = 0 и 0,8; Т=300 К;
ре = 3430 Н/м2,- р!=490 Н/м3.
340
Что же касается течений в случае, если G^ примерно равен единице, то
есЬ нельзя произвести явного разделения кривой п (х) на три зоны.
Д резмльтирующий ноток молекул на выходе из капилляра равен сумме по-
верхностного диффузионного потока Ns (l)=-^2nRJs (I) и потока молекул/V (1),
вылетающих через открытый конец капилляра. При этом следует иметь в виду,
,топри.бк>1 JV^JV, а при OR<1 NS<N ^так как 0ff=^ характе-
оизует отношение проводимостей, обусловленных поверхностной и кнудсенов-
СКОЙ диффузией).
Выражение для N имеет вид-.
(Ij-.Vi [1-о^а (2)]} +
+ 2я/^п°.- f rt(x)[K(I-x) + aK(I+x)]'dx-	(5-5-34)
Здесь первое слагаемое характеризует поток молекул, диффузно испущен-
ных дном и прошедших расстояние L без столкновений, второе —поток моле-
кул. вошедших в капилляр через открытый ко-
нец, третье —лоток молекул, которые без столкно-
вений достигли дна, зеркально отразились от него
и затем вышли через открытый конец, интеграль-
ный член — потоки молекул, десорбированных внут-
ренней поверхностью капилляра н вышедших из
него соответственно без столкновений со стенкой
и после зеркального отражения от дна. Сравне-
ние приближенного аналитического решения урав-
нения (5-5-24) и его численного решения для точ-
ной функции К (х) показало, что значения п (х),
соответствующие точному и приближенному вы-
ражениям /С (х), различаются весьма незначитель-
но, причем разность увеличивается с уменьше-
нием 0^ и ростом I. Что же касается соответст-
вующих значений N, то они отличаются одно от
другого в больше?) степени, чем п (х).
В (5-5-34) с целью уменьшения погрешностей
вычисления следует использовать не приближенное,
а точное выражение для функции К (х). Однако для
I в результате интегрирования членов с и /?2 получаем малый вклад
в значение N. Поэтому для упрощения интегрирования в (5-5-34) можно
частично использовать приближенное экспоненциальное выражение для Д’(х)
(в слагаемых, содержащих Oj и а^.
В случае отсутствия поверхностной диффузии имеем для # соотноше-
ние (5-5-34), в котором п (х) является решением интегрального уравнения (5-5-28)
при G;=0 с экспоненциальным ядром, т. е. линейной функцией. Это позво-
ляет легко вычислить интегральный член в (5-5-34) с точным ядром К (х).
В частности, в случае L>R и Л\«=0 с точностью до Rz/L3 получаем:
„ 7 R	(, 6a R \
v 7 J-
Это выражение является обобщением известной формулы Кнудсена [Л.5-28]
на случай испарения из капилляра конечной длины. Для сравнения следует
указать, что в точной формуле Кнудсена	1, о=0^ стоит коэффи-
циент 8/3, а при использовании в (5-5-34) экспоненциального ядра — коэффи-
циент 2.
0
0,5
п L__	
V-	сс=О
	«=0,8
	Is
0,5	1,0
Рис. 5-24. Зависимость
поверхностной плотности
молекул от продольной
координаты.
(5-5-35)
341
2. Неизотермический случай. Величины т и Ds связаны с температуру
поверхности следующим образом [Л.5-22]-.	н
'“'•“’{гйЬ Ds=DsOexp{--^}. (5'5’ЗГ|)
Пусть Т == То (I-J-Лх) и [ А | << I, тогда линеаризация
пой {х)==п (х) ехр	приводят уравнение для ггт
и замена перемен.
к виду, аналогия.
ному уравнению в случае изотермического капилляра, за исключением юго
что в левой части появляется член, содержащий первую производную
т-.	'	dx '
При этом отношение коэффициентов при первой и второй производных равно-
ЛГ Ё —21/
То ЬТ0
(5-5.37)
где U и е — соответственно энергия адсорбции и энергия активации, приходя,
шиеся на одну молекулу.
Поскольку из приближенного анализа [Л.5-22] следует, что
„ 2 U ,	ДТ U _
*= — , а т=- > I, у по порядку величины равно -г=~. Если у «= I, то при
О KI g	Z Q RI у
Сг(0)<1, т. е, при наличии коротких пограничных слоев, член, содержащий
вторую производную, в пограничных слоях гораздо больше слагаемого, содер-
жащего первую производную. Следовательно, решение уравнения для /ц всюду,
кроме ближайшей окрестности открытого конца (где из-за граничного условия
на выходе (5-5-26) проявляется влияние температуры Tj), может быть пред-
ставлено в виде
/ ч Щ (*) то
(х)	,
т. е.
п (*) =* П1 М ex Р	(5-3-38)
(индекс i относится к изотермическому случаю).
Поток N на выходе из капилляра выражается формулой, отличающейся
от (5-5-34) лишь тем, что 1/т(х) вносится в подынтегральное выражение.
Вследствие соотношения (5-5-38) на величину интеграла для I А | I почти
не влияет наличие неизотсрмичности. Первое слагаемое в (й-5-34) зависит
только от То. Два других слагаемых, содержащих поток N зависят от Т]~!/2,
но поскольку Т1 = Тд (I Н-Д) и I А |	1, эта зависимость не является значи-
тельной. Следовательно, поток N при малом перепаде температуры не зависит
от наличия неизотермичпости, в то время как поверхностные плотности п(х)
для ,4=0 и А б существенно различны. Следовательно, результирующий
поток молекул на выходе из капилляра	в неизотермическом случае
отличается от соответствующего потока в изотермическом капилляре ^так как
2л£\ (I) пд dn\
I dx)'
Численное решение уравнения (5-5-24) для случая испарения льда пока-
зало справедливость вышеупомянутых рассуждений, в частности выраже-
ния (5-5-38). Что же касается случаев, когда О;(0)г==1, т. е. отсутствия
пограничных слоев, и | А | ==« 4, т. е_ больших перепадов температуры, то здесь
для определения п(х) н N уравнение (5-0-24) решалось численно.
342
О кинетике переноса пара через пористое тело
рассмотрим плоскопараллельный слой высокодисперского пористого тела,
гРэВиченнын снизу испаряющейся жидкостью, а сверху —парами этой же
ипкоети. Система находится в изотермических условиях.
Самым сложным с точки зрения теоретического описания является пере-
ходный режим течения пара, часто встречающийся в технологических процес-
сах Рассмотрим течение пара через сухой слой пористого тела, представив
систему пористое тело —газ как бинарную смесь, причем молекулы одной из
компонент неподвижны и имеют размеры и массу, намного превышающие раз-
меры и массу второй компоненты (реальный газ) [Л.5-29—5-31].
Учтем, что вероятность прохождения молекулой без столкновения рас-
стояния X равна [Л.5-32] ехр {—(Х/Х)}. В дальнейшем будем предполагать,
что длина свободного пробега постоянна. В рассматриваемой здесь модели X
имеет вид (Л.5-32, 5-33]:
(5-5-39)
X Хц
где Хц —длина свободного пробега реальных молекул относительно самих же
молекул; Х12—длина свободного пробега реальных молекул относительно не-
подвижных молекул. При определении Х12 нужно учитывать собственный объем
неподвижных молекул и возможность их взаимного перекрытия.
Рассмотрим поверхность раздела испаряющаяся жидкость—пористое тело.
Испаряющаяся жидкость занимает часть П всей площади поверхности. Часть
поверхности I— П занята твердыми частицами пористого тела и диффузно
отражает все падающие на вее молекулы.
Суммарный поток молекул, проходящих через слой пористого тела в на-
правлении оси X, состоит из разности числа молекул, летящих вверх, и мо-
лекмл, летящих вниз. В стационарном состоянии этот поток не зависит от
координаты и с учетом вышесказанного имеет вид:
г—2Л«Р,	Д Г £
UawrfT-)1'2 '	[ J 4Z Т
+ —?(-	Дз'll!-Ез-М+1	(*-Е)'и5- -
+ (2лт47)'/2 3U/Jf \ jJ J 2Х U /
- L f Е2 (— (£ -хЙ dt,---------''©^—А	(5-5-40)
J 2Х Ь 1 (2птЮ)Ч^ X )’	1
где и' —объемная плотность молекул; п—средняя тепловая скорость молекул;
£»«= ( хр у---;}
о
здесь р, —косинус угла между вектором скорости и нормалью к плоскости KZ;
В уравнении (5-5-40) первые четыре члена представляют число молекул,
проходящих вверх через плоскость YZ, расположенную на расстоянии X от
поверхности жидкости. В их число входят испарившиеся молекулы, молекулы,
рассеявшиеся в слое между испарившейся поверхностью и плоскостью YZ,
молекулы, рассеявшиеся в слое толщиной L, попавшие на граничную поверх-
ность и отразившиеся от нее диффузио, молекулы, попавшие из объема, нахо-
дящегося лад пористым телом, и отраженные диффузио от граничной поверх-
ности. Два последних члена представляют собой молекулы, пришедшие из га-
зовой среды над пористым телом, и молекулы, столкнувшиеся в слое пористор
тела толщиной L— X.
343
В общем виде уравнение (5-5-40) решению не поддается. Поэтому пройд,
водим замену функций £3, £3 экспоненциальными функциями по аналоги,,
с [Л.5-34].	’	!
Дифференцируя уравнение (5-5-4СА дважды и комбинируя полученное вы.
ражение с исходным, приходим к дифференциальному уравнению для плотно-
сти молекул. Из полученного уравнения и (5-5-40) получаем выражение для
потока молекул1.
дг 41Па	Ре~М1)
1	(2лт/гТ)1'2 4А+3£аП
X
При —-*-со из (5-5-41) находим выражение для испарения со свободной
поверхности:
(5-5-41)
(5-5-42)
(2xmkT)1'2
X
При -£--* О получаем обычное выражение для диффузионного потока
[если принять в данном диффузионном приближении ne^n(Q)]i
ял I , «“ (1)— л'(0)
А1! — —- иХ ——U
(5-543)
где п'—объемная плотность молекул; w—тепловая скорость молекул.
В нестационарном случае поток частиц зависит от координаты и времени.
Рассмотрим случай, когда аП = 1. При пулевых начальных условиях с помощью
преобразования Лапласа и предположений, сделанных при решении уравне-
ния (5-5-40), легко показать, что уравнение для потока молекул в безразмер-
ных координатах ^1==s^-, t* — характерное время задачи^ имеет вид:
4 / X \2^V	V52.V	X 5W
9\£/ d^^\ct*) dt{ + + ct*
1 X дп'
3ЙТ1?'
X X
Так как обычно величины -j-, малы, оставляем в уравнении члены
первого порядка малости. Тогда уравнение (5-5-44) принимает вид:
.. о к aw 1 х аП'
(5-5-45)
где первый член справа учитывает конечную скорость распространения массы с.
S-6. ТЕПЛОПРОВОДНОСТЬ КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛ
И ДИСПЕРСНЫХ СРЕД
Исследование теплопроводности капиллярно-пористых тел и дисперсных
сред проводится двумя путями.
Первый путь — экспериментальное исследование теплофнзичрских харак-
теристик материалов при помощи известных методов, базирующихся па решении
задач теплопроводности для тел различной формы. Хотя теоретические предпо-
сылки при этом в большинстве случаев соблюдаются с некоторым приближением,
этот путь дает возможность определить эффективные значения теплофизических
характеристик с достаточно высокой точностью.
Надежные измерения теплопроводности капиллярно-пористых тел и дисперс-
ных материалов необходимы не только для получения количественных данных,
но и для понимания основных явлений переноса теплоты в таких системах, так
как хорошо поставленный эксперимент дает возможность изучить зависимость
тепловых свойств материалов от температуры, давления н рода газа в порах,
пористости, зерен твердой фазы и другик факторов.
344
Однако чисто эмпирический подход к проблеме переноса теплоты в капил-
пярно-пористых и дисперсных системах, как и при рассмотрении других явлений,
явно недостаточен. Акцентирование внимания на чисто количественных величи-
нах н2 многочисленных эмпирических и полуэмпирических соотношениях без
теоретического анализа, без рассмотрения взаимного влияния различных факто-
ров уводит от понимания фундаментальных процессов переноса теплоты, имеющих
место в ге1срогенных системах.
Поэтому весьма распространенным является второй путь, основанный на
рассмотрении реальной структуры капиллярно-пористого или дисперсного мате-
пиала, моделировании такой системы и последующем расчете ее эффективной теп-
лопроводности для реальных условий работы материала.
Несмотря на большое разнообразие реальных гетерогенных пористых систем
по их химическому составу, пористости, размерам частиц и пор, их различную
ориентацию по отношению к тепловому потоку и сложность теоретического ана-
лиза и матема гического описания тепловых процессов, происходящих в таких
материалах, в настоящее время уже существуют теоретические зависимости, по-
зволяющие с большей или меньшей точностью рассчитать эффективную теплопро-
водность пористых гетерогенных систем. Однако наряду с этим необходимо под-
черкнуть, что все еще отсутствуют достаточно надежные соотношения, которые
были бы общепринятыми для расчета эффективной теплопроводности капиллярно-
пористых и дисперсных систем определенных классов материалов. Развитие работ
в этой области может привести к нахождению таких соотношений, что позволит
сократить необходимость, проведения сложных, зачастую длительных, трудоем-
ких и дорогостоящих экспериментальных исследований.
Широко распространенным и достаточно эффективным методом теоретиче-
ского исследования теплопроводности капиллярно-пористых тел и дисперсных
сред является использование для этой цели принципа обобщенной проводимости
[Л. 5-35, 5-36], базирующегося на аналогии между дифференциальными уравне-
ниями стационарного потока теплоты, электрического тока, электрической и маг-
нитной индукции, потока массы. Такая аналогия дает возможность использовать
для расчета тепловой проводимости системы основные соотношения электроста-
тики и электродинамики.
Необходимо отметить, что использование принципа обобщенной проводи-
мости оказывается наиболее эффективным, если оно сопровождается рассмотре-
нием структуры материала, оценкой пористости системы, размеров частиц и пор,
способов контактирования частиц между собой, оценкой влияния кондуктивной,
конвективной и радиационной составляющих на эффективную теплопроводность
системы.
Передача теплоты в Дисперсных материалах осуществляется посредством:
I)	теплопроводности самих частиц материала;
2)	теплопроводности газа, заполняющего поры материала;
3)	теплопроводности газового микрозазора между частицами;
4)	передачи теплоты теплопроводностью от одной частицы к другой в местах
их соприкосновения (контактной теплопроводностью);
5)	конвекции газа, в среде которого находится засыпка;
6)	излучения от частицы к частице.
Даже простое перечисление всех видов переноса в дисперсных системах
Делает очевидным тот факт, что эффективная теплопроводность такой системы
является сложнейшей функцией температуры, давления газа, Химического со-
става материала и газа, пористости, размеров и формы частиц и пор, степени чер-
ноты и температуры граничных поверхностей, коэффициента аккомодации по-
верхности частиц по отношению к газу-наполнителю и многих других факторов.
Составление, анализ и решение уравнений, учитывающих все виды переноса
теплоты и все указанные выше факторы, встречает очень большие трудности.
Поэтому все полученные к настоящему времени расчетные соотношения выведены
на основе некоторых принципиальных и частных допущений, на основе упроще-
ния физической картины рассматриваемого процесса и идеализированного пред-
ставления о структуре материала.
Одним из основных допущений, общепринятых при рассмотрении процессов
переноса теплоты в дисперсных средах при определенных условиях, является
345
предположение об аддитивности различных механизмов переноса теплоты в заки..
средах и в связи с этим о возможности пренебрежения тем или иным видом лер^
носа зеплоты в определенных условиях. Анализ, с одной стороны, многочислен-
ных теоретических исследований, а с другой стороны, большого числа экспорт
ментальных данных позволяет в общем случае выявить следующие чисто даче,
ствениые закономерности переноса теплоты в капиллярно-пористых телах в дИс.
перспых средах:
1.	Теплопроводность материала частиц не оказывает решающего влияния
на эффективную теплопроводность дисперсного материала, и ее роль, особенно
для неметаллических материалов, достаточно мала [Л. 5-37, 5-38J.
2.	Эффективная теплопроводность капиллярно-пористых и дисперсных ма-
териалов очень сильно зависит от теплопроводности газа-наполнителя (рис. 5-25),
3.	Значительное влияние на эффективную теплопроводность материала ока-
зывает теплопроводность газового микрозазора между частицами дисперсного
материала.
4.	Контактная теплопроводность между частицами играет большую роль
и является определяющей при невысоких температурах и низком давлении газа;
при нормальном давлении ею можно пренебречь.
5.	Эффективная теплопроводность капиллярно-пористых и дисперсных мате-
риалов начинает зависеть от давления газа-наполнителя при определенных зна-
чениях числа Кнудсена (рис. 5-26 — 5-29).
6.	При глубоком вакууме эффективная теплопроводность дисперсного'мате-
риала при повышенных температурах почти полностью обусловлена лучистым
теплообменом; в условиях высоких температур лучистая составляющая теплопро-
водности является определяющей при любых давлениях газа-наполнителя
(рис. 5-30 — 5-32).
7.	Конвективным переносом теплоты в дисперсной или капиллярно-пористой
системе в подавляющем большинстве случаев можно пренебречь, так как очень
малые размеры пор.и микрозазоров ца стыке частиц препятствуют возникновению
конвективных токов под действием температурного градиента. Известно, что кон-
вективным теплообменом в порах можно пренебречь при величинах GrPr < 10s
[Л. 5-10], что справедливо для частиц диаметром не более 4—6 мм, Большинство
реальных дисперсных систем имеет размер частиц меньше указанного.
8.	Большое влияние на эффективную теплопроводность дисперсной системы
при повышенных температурах оказывает диаметр частиц, так как ои определяет
«число экранов». При прочих равных условиях системы с большим диаметром
частиц имеют большую теплопроводность, гак как «число экранов» при этом
меньше (рис. 5-33 — 5-35).
Огромное количество расчетных соотношений, выведенных для определения
эффективной теплопроводности дисперсных систем, можно чисто условно разде-
лить на три группы: соотношения, позволяющие оценить эффективную тепло-
проводность дисперсных материалов при давлении, близком к атмосферному, при
низких и умеренных температурах; соотношения, учитывающие зависимость теп-
лопроводности газа от давления и поэтому используемые для расчета эффективной
теплопроводности материалов в разреженной среде; соотношения, учитывающие
лучистую теплопередачу и используемые при расчете эффективной теплопровод-
ности при повышенных температурах.
В качестве простейшей дисперсной системы рассматривается система, состоя-
щая из чередующихся друг с другом плоских слоев твердого скелета системы и
газа, где слои могут быть расположены как перпендикулярно направлению теп-
лового потока,, так и параллельно ему 1Л. 5-39], В первом случае эффективная
теплопроводность системы будет минимальной и определяется выражением
-.МИН ______^д^-н______
/7Хд+(1-2/)Хн'
(5-6-1)
Во втором случае эффективная теплопроводность системы будет максималь*
ной:
^фГ=7П»+<|-'и)\
346

Рис. 5-25. Зависимость коэффициентов
теплопроводности^ зернистого слоя от ко-
эффициентов теплопроводности материала
зерен и заполняющего газа.
п по данным 1Л.5-Й0]; х — по данным
[JI 5-911; Л —по данным [Л.5-82]1. ф —по дан-
ным [Л-5-Т6]; 5 — по формуле [Л.5-501; 6 — ло
формуле [Л.5-52]; 7 — по формуле [Л.5-67].
-W’KJ’IO1 102 10* 10s 106
Рис. 5-26.
Рис. 5-26. Зависимость теплопро-
водности дисперсных материалов
от давления [Л. 5-77J.
/ — магнезия (опъп), 7=185 К, d =
= 35 мкм; 2 3 — то же, расчет по фор-
муле [Л.5-57], a=i >i a = 0,7, у =
= 3,04-104 Н/м», Я = 0,95; 4 — крем-
ве.гель, опыт, d — 1,5 мкм, V = 10® Н/м®;
5, б—то же расчет, a = I и а = 0,7»
7 = 2,4-10® Н/м», Л =0,95; 7, S — пер-
лит, опыт, d —0,015 мм, у = 3,7-10» Н/м9
и 4 = 0,3 мм, у — 1,7 • 10® Н/м3- 9, i0 —
то же расчет, 4=0,015, 1,0 мм и а —
0,7» у = 3,7. 10» Н/м», П = 0,84; Я —
воздух» опыт. 7 = 330 К {Л-5-79].
Рис. 5-27, Корреляция расчетных
к опытных значений эффективного
коэффициента теплопроводности за-
сыпок 1Л. 5-55J.
В гелии: ?, 2 — соответстренио плано-
вые чугунные шарики фракций 2,0—
3,0 мм (формула },Н.5-65]у 3—8 —соот-
ветственно шлаковые и чугунные шари-
ки Фракций 2,9—3,9 мм (соответственно
Формулы [Л.5-67], [Л.5-52], [Л,5-401 с
Учетом Хо); в дауокнен углерода: 9, 10,
12, 15, 16 — соответетаенпо шлако-
вые и чугунные шарики фракций 2,0—
3,0 мм (соответственно формулам
1Л.6-55], {Л.Ь-67], 1Я.5-741 с учетом
13 — шлаковые шарики фракций
2,0—3,0 мм (формула JJJ.S-40] с учс-
*ои Лр); 14 — чугунные шарики фрак»
Цнй 2to—3tQ мм (фопМулу [л,5-59] С
учетом
6Л
5,6
9,0
3?2
2,9
1,6
0,8
0	0,8 1,6 2,9 3,2 9,0
PkU. 0-27.
347
где Ал и Хв — теплопроводность соответственно диспергированной и непрерывной
фазы; П — пористость. Эти соотношения ввиду исключительности описываемы*
ВтЦм-Ъ)
Рис. 5-28. Зависимость коэффи
циента теплопроводности волок^
нистых материалов от давления
воздуха [Л, 5-67J.
Рис. 5-29. Кажущийся коэффи-
циент теплопроводности мипоры
(а), кремнегсля (б) и минераль-
ной ваты (е), Вт/ (м-°С) по
|Л. 5-83] при температуре гра-
нитных стенок 290 и 90 К в за-
висимости от давления газа,
Н/ма, заполняющего поры мате-
риала (сплошные кривые—опыт-
ные данные, штриховые — по
формуле (Л. 5-83]).
1 — гелий; 2 — воздух; У— криптон.
ими предельных случаев и игнорирования характера контактов и структуры
могут служить лишь для обозначения того диапазона, в котором лежат значения
аффективной теплопроводности реальных дисперсных систем,
34$
рис. 5-30. Коэффициент теплопровод-
ности порошков при атмосферном дав-
лении [Л. 5-64].
/—ламповая сажа, у = 210 кг/м*, d =
= 0,1 мкм; 2—аэрогель, у = 93кг/м’; 4 =
«s.0,025 мкм; 3 — аэрогель, у = 50 кг/м»,
4 = 0,025 мкм; 4 — перлит арагацкий,у=
= 118 кг/м», 5 — перлит арагацкий, у =
= 70 кг/м‘; 5—окись магния, ? = 400 кг/м»,
4 = 30 мкм; 7—кварцевый песок, у =
= 1770 кг/м», 4 = 120 мкм, ?.^=0,3
Вт/(м.°С); штриховые линии — результаты
расчетов по формуле (Л,5-64].
Рис. 5-31. Зависимость Х.э4)ф от тем-
пературы [Л. 5-55] 1—3 MgO (d ~
= 0,20з мм; П = 0,42) соответственно в
гелии, воздухе и аргоне [Л. 5-76];
штриховая линия — расчет по форму-
ле [Л. 5-55].
Н0’2 34 68)0' г St 8‘8ffl4 2 StH/lt1
Рис. 5-33. Зависимость безразмерного
коэффициента теплопроводности гелия
от числа Кнудсена и коэффициента
аккомодации [Л. 5-77].
С — экспериментальные данные [Л .5-78]
при / = 40°(Э, 6 = 37,5 мм, Д/= 13бС’С,
поверхности хромированы; 2, 3, 4 — расчет
пр формуле [Л.5-77], at = as^=l\ 0,4 и 0,1.
Рис, 5-32. Зависимость коэффициен-
та теплопроводности порошков кар-
бида кремния от давлеииягаза [Л. 5-67].
J — d = 0,194 мм (заполняющий газ — воз-
дух); 2 — 4 = 0,194 мм (гелий); 3 — 4 =
®=0.27 мм (воздух); 4 — 4 =0,027 мм (ВОЗ-
ДУХ); точки — по опытным данным, линии —
по формуле £Л-б-57].
Рис. 5-34. Зависимость Авф,ъ от дав-
ления газа—наполнителя ]Л. 5-55].
/, 2 — стеклянные шарики диаметром со-
ответственно 470 к 29 мкм (Л.6-75]; штри-
ховые лицин—расчет по формуле [Л.5-55].
349
В отечественной литературе широко распространена формула В. 3. Богомл
лова [Л. 5-40]:	°'
, л 0.434-0,31/7
л9фф—ЗЛАдШ д — 0,26 '	(5-6-2)
Она выведена для плотном гексагональной укладки частиц с пористостью
равной или. близкой 26%, и не учитывает теплопроводности материала частиц'
Кроме того, как показано в (Л. 5-4], содержащийся в ней численный коэффициент
ошибочно завышен в 2 раза. Однако в приведенном выше виде она- лучше согла-
суется с экспериментальными данными.
Рис. 5-35. Отношение характерного
газового зазора к радиусу частицы
1Л. 5-64].
О—обработка экспериментальных данных
{Л.5-811: © —тоже [Л.5-67, 5-80, 5-83Г
<Э — тоже {Л.5-82]; «—тоже [Л.5-89]:
ф — то же {Л.5-82]; линия — результаты
расчета по формуле [Л.5-65].
Одно из первых направлений применения принципа обобщенной проводи-
мости указал Максвелл [Л. 5-35]. Он рассчитал электрическое поле системы,
состоящей из изотропной среды, в которую вкраплены посторонние частицы сфе-
рической формы. Полученное Максвеллом соотношение
^+2Хи + (1-Л)(Х,-W J
(5-6-3)
применительно в тех случаях, когда пористость системы велика, так как Максвелл
принимал, что расстояние между частицами велико по сравнению с размерами
частиц.
Позднее Бургер ]Л. 5-42] и Фрик [Л. 5-43] распространили теорию Максвелла
на эллипсоидальные частицы, а Эйкен (Л. 5-44] рассмотрел случай, когда в дис-
персной среде имеется несколько видов частиц различной формы.
Бруггеман (Л. 5-451 вывел соотношение, которое применимо для расчета про-
водимости смесей, состоящих из плоских частиц, эллипсоидов и сферических
частиц. Для последних это соотношение имеет вид:
.	.. ^д ^Эфф
л" *д-К
(5-6-4)
Оценивая теорию Максвелла—Эйкена—Бургера и сопоставляя расчетные
данные, полученные па основании этой теории, с результатами многочисленных
экспериментов, де Вриз ]Л. 5-46] пришел к выводу, что эта теория дает хорошие
результаты, если проводимость частиц меньше проводимости среды. Если же имеет
место обратное явление, то чем больше отношение этих проводимостей, тем больше
экспериментальные данные совпадают с теорией Бруггмана. Уравнения типа урав-
нений Максвелла дают результаты, которые обычно хорошо согласуются с экспе-
риментальными данными для ячеистых материалов и эмульсий,
350
Во многих работах игнорируются реальные системы дисперсных структур,
первую очередь такие важные структурно-механические свойства, как тип
структуры в целом, размеры и форма частиц и пор и характер контактирования
1	.... ..zi'izTr, zr.l'Jnu Рг'Т'ОГТПГиГСГГ, ггтЛ Ъттг r'rnvir.
Рис. 5-36. Обработка расчет-
ных соотношений, предло-
женных различными авто-
рами в виде зависимости
(п) Для случая,
когда \ВДГ = 100.
! — соотношение, прнаедениое в
[Л.5-52, 5-&41; 2 — в ГЛ.5-57—
5-591; 3-в	[Л.5-10]; 4 — в
[Л.5-841: 5 —в [Л.5-67].
кастиц между собой. Естественно, что эти струк-
турно-механические свойства определяют кар-
thhv теплообмена в дисперсной системе. На ос-
нове анализа структуры реальных 1 дисперсных
материалов был получен ряд расчетных фор-
мул в [Л. 5-46-5-5Ц (рис: 5-36).
Однако необходимо' отметить, что многие
расчетные зависимости дают заметное расхожде-
ние с экспериментом, что объясняется многими
причинами, в том числе следующими:
]) требуется резко различный подход к рас-
четам эффективной теплопроводности дисперс-
ных систем в зависимости от взаимного располо-
жения и количества составляющих систему фаз;
2)	ни одна теория не может учесть влияния
па контактную теплопроводность реального рас-
пределения частиц и пор по размерам, их форм
и контактов между соседними частицами;
3)	ни одна теория не может пока правиль-
но количественно оценить наличие температур-
ного скачка на границе частицы с газом;
4)	наличие лучистой составляющей тепло-
проводности либо вовсе не учитывается, либо
учитывается недостаючно правильно.
В связи с этим важно отметить то обстоя-
тельство, что в последнее время наблюдается
тенденция к более детальному анализу всех ме-
ханизмов переноса теплоты в капиллярно-пори-
стых и дисперсных системах, к получению рас-
четных соотношений, в которых наряду с теп-
лопроводностью материала частиц и газа учи-
тывалась бы контактная и радиационная тепло-
проводность, а также зависимость теплопровод-
ности газа от давления.
Так, М. Г. Каганер [Л. 5-67], рассмотрев
с двумя контактными площадками, получил формулу для определения контакт-
ной теплопроводности зернистых материалов в виде
1,1 Р1/3
Хл = 3,12(1-/7)4/3^-,
тепловое сопротивление шара
(5-6-5)
где Е — модуль Юнга.
В |Л. 5-52] контактная теплопроводность дисперсных систем рассматри
вается как сумма контактной теплопроводности свободно насыпанного мате-
риала ^св, зависящей от геометрии частиц, их взаимного расположения, веса и
пористости, и величины Х(Р), определяемой внешней механической нагрузкой Р:
k/l = A-Cg ~i~ & (Е),	(5-6-6)
где ЦР) = ^уР2,3Кс для Р<3. 10> Н/м» и X (Р) = Р^Кц для
75
Е>3-10?Н/м2; Q=J/ iqq_ д > й Кь — эмпирические коэффициенты. При
изменении механической нагрузки от 106 до 3-I05 Н/мг величина изменяется
от 0,35 до 0,45, а при изменении нагрузки от 4-I06 до 12 I05 Н/ц8 величина Ki,
изменяется почти линейно от 2,2 до 2,9.
В (Л. 5-53] приведены величины Асв: для частиц минерального происхожде-
ния; < (1	2) Вт/(м SC), Хя = (2* 15)-10-3 Вт/(м-°С), для засыпок ме-
351
таллических частиц Хсв = (3 -г- 10)-10_> Вт/(м-°С). Эти данные подтверждаются
эмпирическими величинами, приведенными в |Л. 5-54, 5-55]: для чугунной дпплн
Xfe = 0,06 4- 0,07 Вт/(м-°С), для шлаковых шариков — 0,015 Вт/(М‘°С).
Для определения контактной теплопроводности может быть использована
формула Римана — Вебера, выведенная для кубической кладки сферических
частиц диаметром L и радиусом контактного пятна гп;	*
Х'‘=М^;+^1П^) 	<5’6-7)
Радиус контактного пятна для двух сферических частиц может быть опре-
делен по формуле Герца [Л, 5-56].
Л. Л. Васильев [Л. 5-57] представляет контактное сопротивление зернистых
систем как сумму трех составляющих:
=	+	(5-6-8)
где RL — тепловое сопротивление, обусловленное сужением проходного сечения
для теплового потока через две контактирующие друг с другом частицы; —
термическое сопротивление микрошероховатостей на стыке двух частиц; Ro —
сопротивление окисной пленки.
Контактная теплопроводность определяется выражением
(М.9)
Сравнение расчетных и экспериментальных данных, приведенное в. [Л. 5-58,
5-59], показало, что методика Л. Л, Васильева находится в хорошем согласии
с экспериментом.
Вопрос о роли излучения в-процессе передачи теплоты в капиллярно-пори-
стых и дисперсных системах чрезвычайно сложен и наименее изучен,
Трудности при расчете теплообмена излучением в дисперсных и капиллярно-
пористых телах заключаются в гетерогенной структуре этих материалов, Излу-
чение в дисперсных системах зависит от коэффициентов излучения, поглощенря
и рассеяния частиц, от их формы, размеров и взаимного расположения. Для тбго
чтобы получить возможность производить технические расчеты, необходимы
определенные допущения,
Широко распространен метод, отождествляющий процесс лучистого тепло-
обмена между двумя бесконечными параллельными пластинами. Вполне очевидно,
что такой подход весьма ориентировочен.
В большинстве работ, посвященных изучению лучистого теплообмена в дис-
персных и капиллярно-пористых телах, обзор которых дан в [Л. 5-39], выражение
для радиационной составляющей эффективной теплопроводности дается в виде
Х,р = 4/оТЧ	(5-6-Ю)
где d — размер частицы.
Значение параметра / приведено в табл, 5-8. В. С. Никитин [Л, 5-55] получил
следующую формулу:
377£ -{-(i — 77) 8u
(5-6-11)
Расчеты по (5-6-10) с использованием указанных коэффициентов в ряде слу-
чаев дают хорошее совпадение с экспериментальными данными, однако рекомен-
довать какую-либо из формул как наилучшую пока не представляегся возможным.
Существенное влияние на эффективную теплопроводность дисперсных и
капиллярно-пористых систем оказывает давление iaaa в порах. Из кинетической
теории газов известно, что теплопроводность газа при нормальных условиях от
давления газа не зависит, однако эта зависимость начинает проявляться с пони-
жением давления, когда средняя длина свободного пробега молекул газа одного
порядка с расстоянием д между обменивающимися теплотой поверхностями или
больше него* т, е, число Кнудсена (Кп = V6) близко к единице или больше нее.
352
Таблица 5-8
Параметр ? по данным различных авторов
f	Исследователи
1/3	Босворт [Л. 5-62]
eA-l/(2"”E.-Vl)	Арго и Смит [Л. 5-60}
ЕМ	Шотте [Л. 5-61]
2/(b^2c-jd	Чен и Черчилль [Л. 5-63]
Нsm /2d	Чудновский [Л. 5-36]
/1 , 5 • i°~5\ °>i6 v^- r	Серебряный, Зарудпый и Шорин [Л. 5-64]
	Лоеб [Л. 5-48]
Примечание, Н — размер поры; Г — геометрический фактор; /" = 2/3 4-1,
Существуют различные оценки значения числа Кнудсена, при которой теп-
лопроводность газов начинает зависеть от давления. Например, Р. С. Прасолов
[Л. 5-65] и некоторые другие авторы рассматривают три области: область конти-
нуума (Кп <С I), область свободпомолекулярного потока (Кп I), где тепло-
проводность газа от давления не зависит, и так называемую переходную область
(1Сг2 < Кп < I0+2), 1 де теплопроводность 1аза зависит от давления.
В капиллярно-пористых телах и дисперсных системах предельные длины
свободного пробега молекул, при которых эффективная теплопроводность мате-
риала начинает зависеть от давления газа, определяются размерами пор. В связи
с этим интересной особенностью мелкодисперсных пористых материалов с малыми
порами является то обстоятельство, что для них достаточно большое значение
числа Кнудсена характерно даже при атмосферном давлении, А это означает,
что в таких системах уже при атмосферном давлении имеют место явления, при-
сущие вакуумированным системам. Это имеет большое практическое значение.
Средний размер поры дисперсного материала можно определить по одной
из формул, предлагаемых в [Л. 5-53], а средняя дайна свободного пробега молекул
газа связана с давлением р и температурой газа4!1 соотношением [Л. 5-66]:
=	V-.	(б-6-!2)
'	Р 1 -4- Л
Т
где с* и Ту — постоянные, зависящие от рода газа. Для воздуха с’ = 8,42 X
X 10-» Н/м и Ту= ИЗ К-
Рядом авторов (Л. 5-67, 5-68] было обнаружено, что эффективная теплопро-
водность дисперсных систем начинает зависеть от давления газа-наполнителя не
при значениях числа Кнудсена, близких к единице, а при гораздо меньших зна-
чениях этой величины, примерно при Кп = 10~3. Это явление объясняют тем
обстоятельством, что выбор среднего размера поры в качестве определяющего при
вычислениях величины Кп физически является некорректным, так как значи-
тельная часть теплоты в дисперсных и капиллярно-пористых телах передается
через газовый слой возле контактной площадки, где расстояние между поверхно-
стями, обменивающимися теплотой, значительно меньше среднего размера поры,
В литературе опубликовано большое количество полученных теоретическим
Путем зависимостей теплопроводности газа от давления. Наиболее известны из
них формулы Смолуховского ]Л. 5-69], исходившего из наличия "температурного
скачка на поверхности частиц, а также формулы Максвелла и КпуДсела, Ь па-
12 Лыкин А. В.	353
стоящее время получило распространение предложенное в [Л. 5-65] обобщен^,
уравнение теплопроводности газа
'  1
г~ , , 2К /2-aj , 2-а^ Кп ’	(°-S-13)
+К + Ц + яа J Рг
где X' — теплопроводность газа при нормальном давлении; К — cp!cv\ at и аг —
коэффициенты аккомодации; Кп и Рг — соответственно числа Кнудсена и Пран-
дтля. Примеры использования этого уравнения приведены в [Л. 5-59, 5-65|.
Необходимо отметить, что имеющиеся в литературе данные о коэффициен-
тах аккомодации весьма скудны, что ограничивает использование приведенного
выше соотношения. В связи с этим заслуживает внимание методика, изложенная
в [Л. 5-76|, где эффект неполноты обмена энергией учитывается с помощью коэф-
фициента, определяющего эффективную удельную поверхность материала.
Несмотря на многочисленные попытки получить расчетную формулу для
определения эффективной теплопроводности дисперсных и капиллярно-пористых
систем в широком диапазоне изменения температур и давления газа-наполнителя,
эта задача полностью еще не решена. Сравнительно подробно теоретически изу-
чены процессы молекулярного переноса теплоты в дисперсных системах как при
нормальном, так и при пониженном давлении. Контактный теплообмен можно
пока оценивать ориентировочно и в ряде случаев — на основании эксперимен-
тальных данных, Недостаточно изучены процессы лучистого теплообмена в дис-
персных системах, в большинстве работ не учитываются такие важные факторы,
как зависимость степени черноты слоя дисперсного материала от свойств мате-
риала, гранулометрического состава, температуры и другие. Хотя общие физиче-
ские соображения приводят во всех расчетах к качественно правильному соот-
ношению между Хр, с одной стороны, и диаметром частиц и температурой — с дру-
гой, численные множители оказываются пока разными, что создает неудобство
при расчетах.
Несмотря на это многочисленные литературные данные и широкое сравнение
теоретических расчетов с экспериментальными результатами говорят о том, что
задача расчета теплофизических свойств дисперсных и капиллярно-пористых
систем является вполне реальной. Необходимое условие для этого—надежные
данные по пористости системы, теплопроводности твердой фазы материала, раз-
меру частиц, температуре, давлению и другим исходным свойствам системы,
Наряду с приведенными выше зависимостями существует еще целый ряд
теоретических соотношений, расчеты по которым показали удовлетворительное,
а во многих случаях хорошее совпадение с экспериментальными данными в широ-
ком диапазоне температур, давлений, пористости и химического состава материала.
Хорошие результаты при расчетах эффективных теплофизических свойств
неметаллических и металлических систем дает использование соотношения, пред-
ложенного Л. Л. Васильевым [Л. 5-57 — 5-59]:
(5-6-14)
где hll и h/L — функции пористости системы;
л___________1
~Xft , Хг (h\*
10»
(5-6-15)
здесь Kk и Кт— эмпирические коэффициенты.
Эта зависимость была получена на основе принципа обобщенной проводи-
мости путем выделения из рассматриваемой дисперсной системы элементарной
ячейки, обладающей всеми свойствами системы, рассмотрения на основе метода
электротепловой аналогии геиловых сопротивлений этой ячейки и вычисления ее
354
те[[Лов°й проводимости. С учетом поправки на зависимость теплопроводности
газа от' давления и температуры это соотношение широко использовалось для
расчета эффективной теплопроводности неметаллических и Металлических зер-
нистых и порошкообразных материалов. Результаты расчетов в большинстве
случаев удовлетворительно совпадали с экспериментальными данными.
Соотношение, предложенное в [Л. 5-67], имеет вид:
Г5,8 (i -II)* И Ьм К\ I
^эфф=Хг|------%-----(я	2 Н1]-	(5-6-16)
где /С= I —дает неплохое соответствие с экспериментальными данными
для порошкообразных материалов.
Зависимость, приведенная в [Л. 5-71], дает удовлетворительное совпадение
расчетных данных с экспериментальными для зернистой структуры со сравни-
тельно большой теплопроводностью твердой фазы, так как авторы при ее выводе
пренебрегли термическим сопротивлением частиц.
В [Л. 5-55] получена полуэмпирическая зависимость для расчета эффектив-
ной теплопроводности дисперсных систем в виде
Л-йфф—И 4-3>9I (I —17) А*'?1 1п 11	/ А \0.&5
3,46а<»дЗД6„ + (1-Д)6д] т л
(5-6-17)
где у и ут — соответственно объемный вес дисперсного материала и удельный вес
вещества твердой фазы; е^ и ел — соответственно степень черноты материала и
поры.
Использование этого уравнения дало удовлетворительные результаты’ при
расчете ЛЭфф дисперсных материалов с пористостью 30—60% при повышенных
температурах.
Необходимо остановиться подробнее на методике расчета эффективной теп-
лопроводности твердых капиллярно-пористых'тел. Здесь оказалось эффективным
использование метода обобщенной проводимости [Л. 5-59, 5-72]. Для двухфазной
системы, твердая фаза которой состоит из двух или более компонентов, может
быть рекомендована следующая методика расчета.
Теплопроводность двухкомпоцентной твердой фазы рассматриваемой системы
может быть определена путем использования соотношения В. И. Оделевского
!Л. 5-47], полученного для расчета проводимости матричной двухфазной гетеро-
генной системы:
У”1- 1 V-у
.Аз з
Ai-
где Xj и ^2 — соответственно теплопроводность непрерывного и диспергирован-
ного компонентов твердой фазы; — объемная доля диспергированного компо-
нента. При этом принимается, что непрерывным компонентом является больший
по объему компонент твердой фазы.
Наряду с формулой (5-6-18) для расчета теплопроводности твердой фазы
можно пользоваться соотношением Максвелла — Эйкена
Атв_ а2А1/А2 +
Ai j у % t Ai/Aa
4^+1
12*
(5-6-19)
355
Второй этап расчета состоит в определении эффективной теплопроводности
капиллярно-пористой системы л целом. Если исследуемый материал имеет только
сообщающиеся поры или процент закрытых пор невелик, можно воспользоваться
формулой, приведенной в (Л. 5-73(, полученной для двухкомпоиентной диспер;.
ной системы с сообщающимися порами:
(5-6-20)
при этом твердая фаза рассматривается уже как гомогенный материал.
Из анализа формулы (5-6-20) следует, что если экспериментально определить
значение Х9фф материала, например, в воздухе, ю, зная пористость этого мате-
риала, можно найти теплопроводность его твердой фазы..Зная же теплопровод,
ность какого-либо другого газа, можно, использовав это же соотношение, рассчи-
тать ХЭфф в атмосфере этого газа, что в ряде случаев исключает необходимость
постановки сложных экспериментов,
В [Л. 5-59| приведены расчетные и экспериментальные данные, подтверждаю-
щие правомерность использования приведенных выше соотношений.	.»
Во влажном капиллярно-пористом теле вместе с переносом энергии в виде
теплоты происходит перенос энергии за счет массопереноса, т, е. поток энергии
4
Ге = -ЮТ+ 2 Ml,	(5-6-21)
поэтому, чтобы определить истинный коэффициент теплопроводности влажного
тела, необходимо свести массоперепос к минимуму. С этой точки зрения стацио-
нарные методы определения коэффициента теплопроводности Непригодны, так
как они определяют условный коэффициент теплопроводности Х!э, равный.’
Ъ =	(5-6-22)
В результате зависимость между коэффициентом теплопроводности Хэ и
влагосодержаиисм имеет такой вид: при увеличении влагосодержания коэффи-
циент теплопроводности увеличивается, а затем достигает максимального значе-
ния, Дальнейшее увеличение влагосодержания тела мало влияет на теплопровод-
ность, а для некоторых влажных тел даже дает снижение Х9 [кривая Хэ (1Г) имеет
максимум].
Для теплоизоляционных материалов В, И. Дубницккм [Л. 5-74] было полу-
чено опытным путем такое соотношение для коэффициента теплопроводности:
Х = Хо4- Atu exp (— Bu),	(5-6-23)
где Хо—коэффициент теплопроводности абсолютно сухого тела при темпера-
туре /= 0°С; Л и В — постоянные, определяемые из опыта. Для диатомовой
крошки А = 0,037; В = 2.
Различают удельную теплоемкость влажного тела, рассчитанную на единицу
массы абсолютно сухого тела (с) и на единицу массы влажного тела (с0). Если
усадкой тела пренебречь, то между ними существует следующая зависимость:
с.Р = ср» = (Си + С1И1 + c,us) р = (Со + сги2) Ро,	(5-6-24)
где индекс I обозначает пар, 2—воду, 0 — абсолютно сухое состояние.
Следовательно,
J5-6-2S)
356
С учетом усадки тела будем иметь:	а
свР—сР|>(|+Р?‘Т1'	(5-6-26)
где — коэффициент объемной усадки.
Удельные теплоемкости абсолютно сухих капиллярно-пористых тел мало
отличаются друг от друга и лежат в пределах от 0,2 до 0,4 кал/(г-°С). Темпера-
тура мало влияет на удельную теплоемкость сп. Удельная теплоемкость боль-
шинства влажных тел с является линейной функцией влагосодержания и, однако
для некоторых тел, например древесины, теплоемкость с изменяется в зависимости
от влагосодержания по более сложному закону.
Коэффициент температуропроводности или диффузии теплоты (а:=Х/ср)
с увеличением влагосодержания увеличивается, а затем уменьшается, так что
Кривая а (и) имеет максимум. Этот максимум соответствует переходу от одной
формы связи влаги к другой.
Исследованиями М. Ф, Казанского [Л, 5-75] и его учеников было установлено
существование ряда особых точек на кривых А. (и), а (и), отражающих состояние
капиллярной влаги стыкового и канатного состояний, а также максимальное
гигроскопическое влагосодержание.
Таким образом, исследование по зависимости переносных коэффициентов
(А, а) влажных капиллярно-пористых тел от влагосодержания дает возможность
установить формы связи влаги с влажными телами, что является новым методом
физико-химического анализа влажных материалов.
5>7. ПЕРЕНОС ВЛАГИ В ПОРИСТЫХ ТЕЛАХ
В качестве изучаемой системы берется капиллярно-пористое тело, скелет
которого является лиофильным веществом, т. с. стенки капилляров и пор сорби-
руют газы, пары и жидкости; при этом может иметь место диффузионно-осмотиче-
ская связь сорбируемого вещества со скелетом тела.
Такая система существенно отличается от модельных дисперсных сред, рас-
сматриваемых классической теорией фильтрации.
Связываемое скелетом капиллярно-пористого тела вещество может быть
в виде жидкости, пара, инертного газа, твердого вещества, переохлажденной
жидкости в зависимости от условий тепломассообмена, В зависимости от вида
связи вещества с телом температура замерзания жидкости изменяется в широких
пределах. Поэтому в капиллярно-пористых телах при температуре ниже 0°С
всегда имеется некоторое количество переохлажденной жидкости (воды).
Необходимо также отметить, что в большинстве случаев поры и капилляры
тела заполнены жидкостью или льдом, а частично и парогазовой смесью. Для
упрощения анализа нашей системы в качестве жидкости принимается вода без
каких-либо растворимых веществ. Наличие растворимых веществ и жидкости
изменяет процесс массопереноса и вызывает ряд дополнительных эффектов.
Будем отмечать парообразную влагу (пар) индексом I, жидкость — 2, влагу
в твердом состоянии (лед) — 3, инертный газ (сухой воздух) — 4 и скелет — 0.
Объемная концентрация связанного вещества ш
ы =	=	(5-7-1)
где т,- — масса связанного вещества в состоянии i (i = 1, 2, 3, 4); tty — объем-
ная концентрация f-ro связанного вещества, равная;
Масса всего связанного вещества т равна сумме масс сухого воздуха, пара,
Жидкости и льда, т. е,
/п = JS]
357
Обычно объем тела V изменяется в зависимости от концентрации со по линей
ному закону, Поэтому вместо объемной концентрации <у вводится относительная
концентрация или влагосодержание тела и:
пг V ©
— = ? ui = —
т0	р
(5-7-3)
где р — объемная концентрация скелета тела, определяемая соотношением
т0
р = -^; Hi — относительная концентрация i-ro связанного вещества:
И,
mt
тд'
(5-7-4)
Если объем тела мало зависит от влагосодержания, т. е.если усадкой можно
пренебречь (V — Ко = const), то объемная концентрация скелета тела будет
равна плотности абсолютно сухого тела
то т0 .	~
Ра =	= у = const,	(о-7-5)
где Vo — обьем тела в абсолютно сухом состоянии.
Следовательно, относительная концентрация щ и объемная концентрация*
прямо пропорциональны;
to^UiPo; a> = upo.	(5-7-6)
Если стенки скелета тела мало гидрофильны, а изменением плотности жид-
кости мономолекулярпого адсорбированного слоя можно пренебречь, то количе-
ство влаги физико-механической связи (капиллярная влага, лед, пар и воздух)
можно определить по соотношению
<ill=IIvbfil = Po‘ll-	(5-7-7)
В случае монокапиллярно-пористого тела пористость Пv пропорциональна г3,
для поликапиллярно-пористого
nv= 5 fvl-r'>dr'	(5-7-8)
rn
где fv(r) —дифференциальная кривая распределения пор; ru и гмакс — предель-
ные значения изменения радиусов пор тела. Для насыщенности пор Ь( имеет место
соотношение
26' = 1-	 (5-7-9)
Необходимо отметить, что соотношение .(5-7-7) не будет справедливым для
физико-химически связанной влаги, т. е. 'to£ т. и и< и,,. Однако формально
можно принять за основу расчета концентрации влаги в любой форме связи фор-
мулу (5-7-7), но тогда величина bi не будет определять степени насыщенности свя-
занным веществом (влагой) пор тела и соотношение (5-7-9) утрачивает свою силу.
Только для типичных капиллярно-пористых тел с малой гигроскопической влаж-
ностью можно принять равенства щс = to^, = ufl сохранив при этом соотно-
шснис (5-7-9).
При молярном (гидродинамическом) движении влаги (жидкости, газа, пара)
по порам тела в процессе '	
к;,'(ма• с), будет равна:
фильтрации плотность потока j-го вещества iimoi* '
(5-7-10)
где Vi — средняя линейная скорость молярного движения 7-го вещества, м/с;
ns — поверхностная пористость тела, равная отношению площади всех пор
358
(дырок) к площади сечения тела н направлении, 'перпендикулярном направлению
вектора iimoi-	'
Эта величина для поликапиллярно-порисгого тела равна:
гмакс
ns“ J М1’)*.
(5-7-11)
r%efs(r) —дифференциальная кривая распределения поверхностной пористости
тела по радиусу пор. Для однородных тел поверхностная пористость тела (про-
свет тела) Пs приближенно равна объемной пористости тела.
Строго говоря, величина 6, в соотношении (5-7-10) отлична ог величины
в формуле (5-7-7), однако при условии Пу = П$~ П она будет характеризовать
степень заполнения пор i-м связанным веществом.
Следовательно, можно написать;
/l™< = npitw	(5-7-12)
Соотношением (5-7-12) можно воспользоваться для определения плотности
потока капиллярной влаги в монокапиллярно-пористом теле. В этом случае
у — ^аклп» где ^2кап — линейная скорость движения жидкости в монокапиллярно-
пористом теле под действием капиллярных сил.
Кроме того, важно отметить следующее обстоятельство. При обычных усло-
виях, когда давление влажного воздуха в порах тела мало отличается от баромет-
рического, масса воздуха и пара в порах тела ничтожно мала но сравнению с мас-
сой жидкости или массой льда. Конечно, при этом предполагается, что тело нахо-
дится в равновесии с окружающим влажным воздухом, т. е. что его влагосодер-
жаиие отлично or нуля. По расчетам Б. А. Поснова [Л. 5-13] при нормальных
условиях для тел с максимальной пористостью (керамика, древесина и т. д.)
масса влажного воздуха в порах тела составляет около 10-а% массы жидкости,
соответствующей равновесному влагосодержанию тела. Поэтому общее влагосо-
держание тела и можно считать равным суммарному влагосодержанию жидко-
сти uj и льда и9:
и=^и{=ил-^и3.	(5-7-13)
Соотношением (5-7-13) мы воспользуемся при расчете источников связанного
вещества, обусловленных фазовыми переходами.
Уравнение переноса
В первую очередь необходимо остановиться на вопросе о влиянии пористой
структуры тела на уравнения переноса. Большинство законов переноса описы-
ваются соотношением вида (5-6-21) — плотность потока массы пропорциональна
градиенту соответствующего потенциала переноса. Для пористого тела это соот-
ношение можно написать так:
/ =	=	(5-7-14)
Г
где в — коэффициент, характеризующий сопротивление переносу. Величину,
обратную 8, О. Кришер (Л, 5-76] называет коэффициентом сопротивления
Если поверхностная пористость тела равна объемной пористости (Пр =
=® ns— П), то 8= — —U. Однако пористость П влажных тел зависит от влаго-
содержания, поэтому величина е или t-p также будет зависеть от влагосодержа-
ния; например, при изменении влагосодержания древесины от 10 до 20% е воз-
359
растает в 10 раз [Л. 5-10], а’при изменении влагосодержания картофеля от 6 до
16% р. увеличивается в 250 раз [Л. 5-10|. Кроме того, коэффициент а зависит от
температуры. Поэтому вряд ли целесообразно определять величину е или ц как
структурные факторы для влажного материала. С нашей точки зрения, лучше цря.
мой путь определения коэффициента переноса km для данного тела (km =
Остановимся на этом более подробно. Известно, что формула (5-7-14) анало-
гична формуле Пуазейля, которая выводится следующим об'разом. Уравнение
Навье — Стокса при течении жидкости по цилиндрической трубе с постоянной
!dvx л dvx л\
скоростью 1-^=0; -у^ = 01 имеет вид:
[д-8х , I	др .
”(a7r + 7^ = -s = c0nst’	(5-7'15>
где х— направление вдоль погока*(по длине трубки); при этом считаем др!дх
величиной постоянной: после интегрирования в пределах от г = 0 (ось трубки)
до г = R (радиус трубки) получим:
/-2 др
Vjc_4t] дх
Постоянная А равна нулю (Аг=0), так как при r = 0 их^=ос>. Постоян-
ная В находится из условия сх=0 при r = R (скорость на стенке - '
равна нулю — так называемое условие прилипания).
Отсюда
(5-7-16)
трубки
_	R2~r2 др
Vx ~	41) дх '
Средняя скорость течения жидкости vx=vt
R2 др
’ V	8т] дх’
Однако при течении жидкости в макрокалилляре надо учитывать все виды
скольжения (гидродинамическое и тепловое), а в случае течения смеси газов—*’
и диффузионное скольжение. Все виды скольжения вносят вклад в величину
скорости v видимого движения (молярного переноса). Все виды скольжения
надо учитывать, если число Кнудсена.лежит в пределах
0,01 < Кп <0,1.	(5-7-19)
При гидродинамическом скольжении скорость движения на стенке не равна
нулю (условие прилипания жидкости становится несправедливым).
Скорость гидродинамического скольжения рг.с определится соотношением
(5-7-17)
(5-7-18)
=-к,
= ~ Кг.
'г—я’
(5-7-20)
где д- —градиент скорости у стенки, в нашем случае он равен
Из формулы (5-7-17) следует:
ЖЛ =А^.
\ дг 2т) дх ’
'г-Я
(5-7-21)
Тогда будем иметь:
n _R2-r2dp R_d±- (^-Л+2КГЛД!) др '
*	4г( дх г,с2т) дх 4	4т| дх ’
Средняя скорость будет равна:
(5-7-22)
к ах
(5-7-23)
>60
ГА	£>2	R
Предположим, что вдоль стенок капиллярной трубки имеют место темпе-
_аТуриый градиент и градиент концентрации пара (рассматривается движение
парогазовой смеси). Если пренебречь радиальными потоками и считать давле-
ние р, плотность р и концентрацию p^0 (fe=l,2) постоянными по сечению,
тогда'средняя скорость v будет равна:
B=-K^ + v,.l + v,.c.	(5-7-25)
Тепловое и диффузионное скольжение является молярным (конвективным)
переносом, который происходит без наличия градиента общего давления.
Линейные скорости диффузионного оД1С и теплового от. с скольжения
равны соответственно:
»д.е = ^. = ^;	(5-7-26)
(5-7-27)
где Кц.с,’ Кт.с—соответственно коэффициенты диффузионного и теплового
скольжения.
Предположим, что градиент общего давления др/дх мал и выражается
через сумму градиентов парциального давления пара (дрцдх) и неконденси-
рующегося газа (др^дх):
д£=д^’
Градиент парциального давления пара прямо пропорционален градиенту
относительной концентрации рю (рю=р1/р):
. Mi
aPi _ ф1° м _ м, аР1„ д(>ш
дх dx М dx М2 дх	'
при условии, что молекулярная масса смеси не зависит от концентрации
р2С< 1,
При наличии испарения с мениска жидкости, через который не протекает
неконденснрующийся газ (воздух), градиент парциального давления воз-
духа определяем исходя из условия, что суммарный (молекулярный и модер-
ный) поток воздуха ;2 через поперечное сечение капилляра равен нулю; это
означает приближенное -постоянство общего давления, или для индивидуаль-
ных потоков принимаем р —const:
h =	,	(5-7-3°)
Отсюда получим:
=	(5-7-31)
дх Г12 Mi
так как для бинарной смеси Dl2 = D2!.
Тогда формулу (5-7-25) можно написать так1 *:
г,___	-	Г ifдрю । ff dpio , д, <571	_ „п,
ГКрМ?+ 1с аг + к'-‘аГ] (5-7'32’
1 Строго говоря, необходимо было учесть эффект бародиффузии, однако
он значительно меньше концентрационной диффузии.
361
При выводе этой формулы учитываем скорость стефановского движения
Если пренебречь скольжением (/Сд, с~ Кт,с = 0) и принять p = const (отсутст-
вие пуазейлевского течения), что означает [ftp (I — Рю)/013]	> I, то ив фор.
мулы (5-7-32) получим формулу для стефановского потока:
Рц dpio
1 —Рю дх
(5-7-33)
Соотношение (5-7-33) для стефановского потока можно получить из фор.
мулы (5-7-32), положив 7?-»-оо (/<->-со). Это означает замену капиллярной
трубки с мениском жидкости свободной поверхностью жидкости, для. которой
конвективный перенос массы состоит только из стефановского потока (отсут-
ствие стенок капилляра, а следовательно, и скольжения).
Кроме того, формула (5-7-32) дает возможность ввести поправку на гидро-
динамическое, тепловое и диффузионное скольжение при безградиентном кон-
вективном переносе с некоторой линейной скоростью. Такая поправка необ-
ходима для конвективного переноса в капиллярно-пористых телах.
В этом случае будем иметь:
р„ др„ вд, г agjj ari
дх + к₽(1-р10)м2 [*'с а* +к’-сах г (5'7'34'
Первый член в формуле дает скорость стефановского потока, второй —
скорость диффузионного скольжения с поправкой на гидродинамическое сколь-
жение и третий член—скорость теплового скольжения с той же поправкой.
Хотя формула (5-7-32) выведена в предположении -> 0, однако из нее
можно получить формулу Пуазейля, если положить
Кд.е = Кт.е = 0; \Кр (1 -₽1»)/Р121^- < 1-
Перенос в коллоидных телах
В коллоидных телах влага связана в основном адсорбционными и диффу-
зионно-осмотическими силами. Перенос жидкообразной влаги происходит диф-
фузионным путем по типу избирательной диффузии, вызванной разностью
осмотических давлений. Следовательно, плотность потока жидкообразной вла-
ги /2 прямо пропорциональна градиенту осмотического давления Vpn. При
обычных влагосодержапиях ограниченно набухающего тела осмотическое дав-
ление, или давление набухания, является функцией влагосодержания, т. е.
градиент давления набухания будет прямо пропорционален, градиенту влаго-
содержапия. Следовательно, имеем:
/а = — £}рз^Рн= —	— a2£PoV^.	(5-7-35)
где Ор2—коэффициент диффузии жидкообразной влаги в коллоидном теле,
отнесенный к разности давления набухания; —коэффициент диффузии жид-
кости в коллоидном теле, отнесенный к разности влагосодержаняй.
Влажное коллоидное тело состоит из однородных мицелл, расстояние
между которыми сравнимо с молекулярным. Моделью коллоидного тела может
служить тело с многочисленными микрокапиллярами молекулярного порядка.
Следовательно, в таком модельном теле будет иметь место типичный перенос
жидкости, обусловленный градиентом расклинивающего давления или гра-
362
диемтом толщины пленки И, так как ffl^f(ft)*. Толщина пленки жидкости
ппямо пропорциональна влагосодержанию тела (ft и), поэтому в общем слу-
чае неизотермического переноса пленкообразной жидкости будем иметь:
4„л=-	“+kLp»VT •	(5'7-3S)
Где и — коэффициенты соответственно изотермического и неизотерми-
иеского пленочного движения жидкости.
Таким образом, общий поток жидкообразной влаги будет равен;
'2=-(“4S+Ao,)₽o7“+Cp»'77'-	<5-7-37)
Перенос пара в первом приближении будет определяться процессом моле-
кулярного течения (эффузией). Плотность молекулярного потока будет про-
порциональна градиенту от величины pftVT'
h = -1,064r, ]/V ,	(6-7-38)
1
Где Гз — эквивалентный радиус молекулярного течения пара; гэ —----- х
Gmkc — г о
гэ- «акс
X //(r)tfr, здесь г0 —минимальный радиус капилляров тела; лэ,маКс —
То
максимальный радиус капилляров, по которым происходит эффузия. Вели-
чина г3 имеет размерность длины и зависит от кривой распределения пор по
радиусу / (I-).
Если микрокапилляры, по которым проходит пар, частично заполнены
жидкостью, то с увеличением влагосодержания г3 будет увеличиваться. Бла-
годаря наличию под интегралом множителя г зависимость между лэ и и не
будет линейной.
Парциальное давление пара рг согласно изотерме сорбции есть функция
влаюсодержапия и температуры pi (и, Т). Следовательно, pft\fT (и, Т).
Тогда будем иметь:
) = —1,064г,	(5-7-39)
где а1э и а^—соответственно коэффициенты эффузии и термической эффузии
пара в пористом теле,
Так как поток парообразной и жидкообразной влаги определяется вели-
чинами и 7Т, то общий поток влаги в коллоидном теле будет равен:
/ = 11+/г == - “m4₽oV11 - “Lp»’7'.	(5-7-41)
где коэффициенты диффузии и термодиффузии влаги в коллоидном теле равны:
am k = а1 э+aafe	л>
с£/? = ав+^пл-
* Пленочное движение жидкости имеет место и в капиллярно-пористом
теле. Однако пленочное движение в макрокапиллярах незначительно по срав-
нению с капиллярным движением жидкости.
363
' Перенос жидкообразной влаги в капиллярно-пористом теле
Предположим, что капиллярно-пористое тело имеет влагу макрокапилтя
ров, связанную физико-механическим путем (осмотически связанной и адсоп
бированной влагой пренебрегаем). Для тела монокапиллярной структур^
Поток массы жидкообразной влаги будет прямо пропорционален скорости дви.
жения жидкости в одиночном капилляре у2кап, т- $
,	/2кап =^Р2^2у2Кап-	(5-7-43)
Скорость капиллярного движения является линейной функцией 1/х;
где В — постоянная величина, зависящая от структуры тела; ф —суммарный
потенциал (ф>— фя),
В отличие от тела поликапиллярной структуры тело монокапиллярной
структуры имеет постоянный капиллярный потенциал фг, определяемый из
опыта.
Для пористого тела с поликапиллярной структурой поток жидкости прямо
пропорционален градиенту капиллярного потенциала Гф:
/капв^1^Ф’	(5-7-4$)
где коэффициент капиллярной проводимости,
Градиент капиллярного потенциала равен:
р™,8 Гг-	(5-7-46)
Для монокапиллярного тела fs(r)~co, а следовательно, Аф —со, Гф=0, •’
так как Vr = 0, поэтому формула (5-7-46) для этого тела неприменима.
Капиллярный потенциал ф есть функция температуры и влагосодержания
тела. Для изотермических условий Гф прямо пропорционально Vu:
Тогда будем иметь:
/2кап = ^экапРоГи,	(5-7*48)
где
о cos 6	(*
°2 «dr- <5-M9>
Соотношение (5-7-48) аналогично закону концентрационной диффузии,
поэтому капиллярное перемещение жидкости в поликапиллярном теле назы-
вают капиллярной диффузией, а коэффициент я2кап—коэффициентом капил-
лярной диффузии жидкости.
Для меизотермических условий поток капиллярной влаги равен:
/2«ап =Ч’’1’=_г'2ка.,Ро',“-«2капРо'77',	(5-7-50)
где Д2кап— коэффициент капиллярной термодиффузии жидкости,
J ?4S И dr-
у Рз cos 0 rfo
а2кац- 4р0Т1аГ4/Т
(5-7-51)
364
Капиллярное движение жидкости при испарении
и конденсации влаги
Если влажность тела превышает максимальную гигроскопическую, то мак-
рокапилляры пористого тела частично заполнены водой. В-этих условиях дви-
жение капиллярной жидкости происходит при -перепаде капиллярного потен-
циала. В отличие от случая капиллярного впитывания жидкости, происходящего
при непосредственном соприкосновении тел с жидкостью, капиллярный потен-
циал определяется здесь неоднозначно. Например, если в пористое тело с одно-
родным составом капилляров (песок) ввести ограниченное количество жидкости,
то она заполняет не все тело, а только часть его, при этом влажный участок гра-
ничит с сухим. Поведение жидкости в песке очень похоже на се поведение в эле-
ментарном капилляре с ограниченным содержанием жидкости. В обоих случаях
капиллярный потенциал равен нулю, так как Кривизна менисков по периметру
влажного участка одинакова. Для элементарного капилляра имеем:
t 2о / §
ф = — ।
Р2
(5-7-52)
Отсюда следует, что при = г'2 потенциал ф равен нулю. Прибавление
жидкости только увеличивает зону влажного участка, не изменяя его потен-
циала.
Этим объясняется отсутствие переноса влаги, которое наблюдается между
двумя образцами некоторых влажных тел с монодисперсной структурой при раз-
личной их влажности. Вода, сосредоточенная отдельно, ограниченными скопле-
ниями, не перемещается пи внутри образца, ни от одного образца к другому.
Все различие между образцами состоит только в количестве скопления жидкости
(.макрокапилляры этих образцов влажных тел были примерно одинакового диа-
метра).
Но если такой влажный участок тела привести в соприкосновение с сухим
телом, капилляры которого имеют меньший радиус, то узкие капилляры будут
высасывать жидкость из широких. Следовательно, в этом случае движение жид-
кости будет происходить от участка с нулевым потенциалом (влажный участок
с равномерным заполнением капилляров) к участку с более низким, отрицатель-
ным потенциалом (сухое тело с узкими капиллярами). Это явление вполне ана-
логично передаче теплоты ог тела с нулевой температурой к телу с более низкой
отрицательной температурой.
Только в телах с резко выраженной лолидисперсной структурой возможно
примерно равномерное распределение жидкости по объему.
Если внутри пористого тела, частично заполненного жидкостью, происходит
ее испарение, го наблюдается движение жидкости по капиллярно-пористой си-
стеме в зону испаренйя. Это движение обусловлено действием различных причин.
В простейшем случае можно считать, что при испарении жидкости более узкие
капилляры впитывают жидкость из широких капилляров аналогично перемеще-
нию жидкости из широкого капилляра в узкий. Некоторые исследователи счи-
тают, что при испарении кривизна мениска увеличивается, в результате чего
жидкость перемещается в зону испарения.
По другим соображениям, движение жидкости в узкой части капилляра со-
провождается испарением и конденсацией пара в широкой его части. Согласно
этим представлениям единого потока жидкости в капиллярах не существует.
Жидкость, перемещаясь по узкой части капилляра, достигает широкой его части.
Здесь происходит испарение, сопровождаемое диффузией пара с последующей
его конденсацией на поверхности мениска узкой части капилляра. Как показы-
вают многочисленные опыты по сушке влажных материалов, пар, образующийся
яри испарении жидкости, диффундирует по капиллярно-пористой системе тела,
не конденсируясь в жидкость. Конденсация пара на поверхности мениска в мак-
рокапиллярах требует некоторого избытка пара, что -не может иметь места даже
при полном насыщении паровоздушной среды.
Таким образом, при движении жидкости по капиллярам, вызванном испа-
рением или конденсацией влаги, потенциал ф для отдельного капилляра (или
365
соединенных капилляров) определяется соотношением (5-7-52), При этом необхо.
димым условием движения является наличие неравенства
Если в качестве модели тела принять модель конического капилляра, изме-
нение радиуса которого по его длине определяется в соответствии с кривой рас..
пределения поверхностной пористости по радиусу fs (г), то на основании соотно-
шения (5-7-52) получим формулу, аналогичную (5-7-44) для потока влаги. При
этом зависимость между капиллярным потенциалом и радиусом пор будет опре-
делена Другим соотношением.
Перенос парообразной влаги в капиллярно-пористом теле
Обычно перенос пара во влажном теле при наличии испарения описывают
законом диффузии с поправкой на конвективный стефановский поток [см. фор-
мулу (3-1-103)]. Однако эго будет справедливо только для макрокапиллярной
трубки (г > 1О'& см). В микрокалиллярах поток парообразованной влаги опре-
деляется законом эффузии. Кроме того, при испарении влаги из пористого тела
могут иметь место и другие явления переноса.
В капиллярах при молекулярно-вязкостном режиме помимо диффузионного
и эффузионного переноса пара имеет место видимое (конвективное) движение,
обусловленное гидродинамическим тепловым и диффузионным скольжением. Если
положить общее давление постоянным (р ~ const), т. е, Кр (1 — РцО/Дг > I,'
то скорость конвективного переноса, как это следует из формулы (5-7-34), будет
равна:
к3. cMfl РюКт.сМх
кРм ] ₽1<l+Kp(i-p1«)v7-
Тогда суммарный поток пара, состоящий из молекулярного (диффузионного)
потока /1 д, конвективного потока pjV* и эффузионного потока /э, будет ранен:
BiPiaAfi (!	Кд.с\	РгоКг.с
RT(1 - р10) V,	. м Кр / к
Vk =
Давление пара рг является функцией’ влагосодержания
Pi (и< ТЪ поэтому можно написать;
(5.7-53)
(5-7-54)
температуры
и
VT.
Тогда формулу (5-7-54) можно написать так;
капРо^-^капРо77,’
(5-7-56)
где а1кап и аГкап — соответственно коэффициенты диффузии и термической диф.
фузии парообразной влаги в капиллярно-пористом теле,
а1КапРо= >—-----------
''RT (1 — рю)
(5-7-57)
т	/ М1р10Кдс \ / dPl \	/ dpJ^T ^РюКт.с
°mP,l= \	мкГЛ"аГ/в + Е1К’**	К '
(5-7-68)
Необходимо отметить, что в формуле (5-7-58) третий член имеет знак минус.
Это означает, что перенос парообразной влаги диффузией скольжения направлен
пр’отив потока теплоты. Поэтому если сумма первых двух членов в формуле
(5-7-58) меньше третьего члена, то коэффициент afKan будет отрицательным.
366
Суммарный поток влаги будет равен:
/ = /j + /9 = -	кагА	~ ЙХ кзпР.Л Г>
(5-7-59)
|Де °л1кап и °.-икап“ к0ЭФФии11ентЬ1 диффузии и термической диффузии влаги,
равные:
аткап'=а1кап~^а%к&П’ аткап~а1ткап~^'а^тк&п-	(5-7-60)
Перенос жидкости и газа под действием капиллярных сил рассматривается
и в теории фильтрации. Капиллярное давление определяется по формуле
2<jcqs6
J (W),
(5-7-61)

где к — коэффициент проницаемости; J (о) —функция Леверетта, Вид функции
Леверетта для пропитки (вытеснение менее смачивающей жидкости более сма-
чивающей) и осушки (вытеснение более смачивающей жидкости менее смачи-
вающей) приведен на рис. 5-37.
Рис. 5-38- Зависимость
относительной фазовоИ
проницаемости Ki’K от
насыщенности <у, %.
Рис. 5-37. Вид функции
Леверетта.
f — истощение; 2 — впитыва-
ние.
1 — газ; 2 — ясвдкость.
Если предположить, что каждая жидкость движется независимо от другой,
то можно написать:
/i = P|0| = --5^-vW, 1 = 1, 2,	(5-7-82)
где /<, (щ) называются фазовыми проницаемостями,
Отношение К, (<у)/д называется относительной фазовой проницаемостью.
Вид кривых фазовых пронипаемостей (рис. 5-38) может быть рассчитан по
кривым распределения пор [Л. 5-78)-
Основным недостатком этих теорий является принятие независимости дви-
жения отдельных фаз (каждая жидкость движется в занятой ею части капилляров
и пор так, как если бы все остальное пространство было скелетом тела).
Наиболее правильный подход к анализу явлений переноса в капиллярно-
пористом селе состоит в рассмотрении взаимного влияния фаз при переносе много-
фазной жидкости.
367
Влагоперенос в коллоидных капиллярно-пористых телах
Влажные материалы являются капиллярно-пористыми коллоидными телами
перенос влаги в которых определяется разными делениями, рассмотренными
выше при анализе переноса в коллоидных и пористых телах.
Если исключить из рассмотрения пористые тела монокапиллярной струк-
туры, а также пренебречь влиянием силы тяжести (типично капиллярно-пористые
коллоидные тела), то влагоперенос описывается градиентом влагосодержания и
температуры. Это происходит потому, что различные термодинамические силы
влагопереноса являются функциями и и Т, поэтому они могут быть выражены
через Vu и ГГ,
Таким образом, влагоперенос в коллоидных капиллярно-пористых телах
описывается следующей формулой:
=	(’“ + «’7').	(5-7-63)
где am и — соответственно коэффициенты диффузии и термодиффузии галаж-
/ aJ\
пых тел; 6 — относительный коэффициент термодиффузии (б = —).
ат /
Согласно формулам (5-7-60), (5-7-51) и (5-7-49) коэффициенты ат, и 6 равны
соответственно:
ат кап ^атк’ аткап ~^атк’ j
Й = ^K3i|gW кап 4~|	(5-7-64)
amk ~>Гат «ап	J
Коэффициенты ат и 6 являются функциями влатосодержания и температуры.
Характер изменения коэффициента ат при различных влагосодержациях
определяется формой связи влаги с телом и видом влагопереноса (перенос пара
или жидкости). Для типичных капиллярно-пористых тел с повышением влагр-
содержания коэффициент возрастает и при больших влагосодержаниях стано-
вится постоянным.
Непрерывное увеличение коэффициента ат с повышением влагосодержа-
ния типичных капиллярно-пористых тел характерно для переноса пара. Если
массоперепос происходит в виде жидкости, то коэффициент ат может возрастать
или оставаться постоянным с повышением влагосодержания в зависимости от
вида дифференциальной кривой распределения пор по радиусам.
Экспериментальные данные по коэффициенту диффузии ряда материалов
достаточно хорошо описываются эмпирической формулой’
-“-=1—Лрои,	(5-7-65)
ат
где ат0, А — постоянные коэффициенты, определяемые из опыта (табл. 5-9),
приближенно для капиллярно-пористых тел А = 0,035, а для коллоидных капил-
лярно-пористых тел А == 0,020. Коэффициент ат0 зависит от температуры:
я™ = а«>3	(5-7-66)
где постоянная приведена в табл. 5-9; приближенно для капиллярно-пористых
тел В = 10s; п — 20; для коллоидных капиллярно-пористых тел В = 1, п — 10.
По данным [J1. 5-79] коэффициент А приближенно равен:
Для капиллярно-пористых	тел...................................0,0032
Для коллоидных гел............................................  0,0008
Для капиллярно-пористых	коллоидных	тел........................0,0019
368
Коэффициент ar,l0 определяется по формуле [Л. 5-79]:
(5-7-67)
постоянные Ао и п приведены в табл, 5-10 и 5-1L
Таблица 5-10
Постоянные -4П-10-5 и п для некоторых влажных материалов
Наименование материала	Ро	Т, к	%	Ао.10-‘	п
Огнеупорный шамотный кирпич	1900	307—320	8—16	3,30	16,6
Пенобетон	450	295—318	10-10	3,86	1,0
Газобетон па смешанном вяжущем	712	293—313	10—30	27,9	20,0
Пенобетон на смешанном вяжущем	885	207—307	5—35	31,2	20,0
Диатомовая крошка	510	323—338	10—60	40,3	20,0
Керамика	1684	293—321	4-16	57,4	20,0
Таблица 5-11
Постоянные Ао, п и ат(1 для глины различных месторождений
Месторождение	Ро	т, к	и, %	и0, кг/кг	л0-ю-	ат0-10»	п
Принсвскос	1650	294—305	6—15	0.211	0,61	1,673	11,76
Осиневское	1820	280—308	6-15	0,264	1,20	0,833	8,35
Часов-Ярское	1850	308—338	10—2.5	0,320	1,50	0,666	6,85
Рендинекое	1650	296—308	10—25	0,279	1,65	0,606	9,00
Полынковское	1865	296—315	10-27	0,348	2,90	0,345	6,40
Васютииское	1750	293—315	10—25	0,300	4,40	0,227	11,10
Для ряда материалов кривая ат — f (и) имеет сложный вид. Тогда коэффи-
циент aw вычисляется по формуле

(5-7-68)
где —влэгосодержание, соответствующее максимуму кривой дгп=/:(н);
постоянная гтт0 определяется по формуле (5-7-67).
Например, для шерстяного сукна (0,05 < и < 0,15) 8 — 45' Ао = 5 95 X
X IG6; п= 15; им = 0,05,
В большинстве случаев коэффициент термодиффузии 6 увеличивается с повы-
шением влагосодержания, достигая наибольшего значения, а затем остается по-
стоянным или уменьшается.
Согласно экспериментальным исследованиям В, И. Дубницкого термогра-
диецтный коэффициент теплоизолирующих материалов практически не зависит
от температуры, он может быть подсчитан по эмпирической формуле
6= Аи2 ехр (— Ви),	(5-7-69)
где А и В — постоянные, при этом В — целое число. Например, для диатомовой
крошки А = 9,12; 8—9,
370
Конвективно-фильтрационный влагоперенос во влажных телах
При интенсивном нагреве влажного тела температура его быстро повы-
шается. При температуре тела выше 100°С парциальное давление насыщенного
пара pi становится больше барометрического давления воздуха в окружающей
среде (Pi > р)‘ В результате диффузионный перенос пара в пористом теле заме-
няется молярным. Такой механизм переноса парообразной влаги, происходящий
под действием градиента общего давления, мы называем конвективно-фильтра-
ционным или прорто фильтрационным переносом пара.
Следует подчеркнуть, что градиент общего давления (Vp) возникает не только
при температуре тела выше 100°С, Если нагрев тела происходит изнутри (напри-
мер, при сушке в поле токов высокой частоты), то градиент общего давления воз-
никает н при температуре ниже 100°С. Это объясняется молекулярным натека-
нием воздуха по микрокапиллярам и диффузией скольжения в микрокапиллярах.
Релаксация градиента общего давления происходит по системе открытых
макрокапилляров, по благодаря интенсивному парообразованию внутри тела и
наличию сопротивления в виде скелета влажного тела устанавливается некото-
рый градиент Vp, отличный от нуля. Это явление впервые было экспериментально
подтверждено Г.’А, Максимовым при сушке влажных тел с внутренними источ-
никами теплоты.
Наличие градиента общего давления Vp внутри капиллярно-пористого тела
вызывает молярный перенос парогазовой смеси (пара и воздуха) по типу фильт-
рации газа через пористые среды. Этот молярный перенос пара нс учитывается
законом массопереноса (5-7-59), поэтому в уравнение необходимо ввести допол-
нительный член, учитывающий поток конвективного переноса пара.
Фильтрационный поток влажного воздуха через пористое тело по закону
Дарси
/в = ри = — AVp,	(5-7-70)
где k — коэффициент воздухопроницаемости, кг/(м-ч-мм рт. ст.); р — плотность
влажного воздуха. Количество пара, переносимого этим фильтрационным пото-
ком воздуха,
/’1Ф =	~	(5-7-71)
где Рю == pi/p — относительная концентрация пара, равная отношению кон-
центрации пара к плотности влажного воздуха; kp — коэффициент молярного
переноса,
=	=	,	(5-7-72)
где d —влагосодержание воздуха,
Суммарный поток влаги при наличии градиента Vp будет равен:
/ = — 3тР(|5'“-атРо?7'-VP-	(5-7-73)
Соотношение (5-7-73) не учитывает переноса жидкости под действием силы
тяжести или градиента гидростатического давления (фильтрация жидкости через
пористые среды). Интенсивность такого молярною переноса жидкости во мною
раз больше влагопереноса под действием диффузионных и капиллярных сил.
Поэтому фильтрационное движение жидкости в дисперсных средах обычно рас-
сматривается независимо от влагопереноса.
Коэффициент воздухопроницаемости k является коэффициентом пропорцио-
нальности между потоком влажного воздуха и градиентом общего давления, т, е,
характеризует перенос парогазовой смеси (пара и сухого воздуха).
Относительное количество пара, переносимого таким фильтрационным дви-
жением влажного воздуха, по отношению ко всему потоку парогазовой смеси
равно отношению коэффициентов
371
Влагопроводность и термовлагопроводность влажных тел
Влагосодержание является аналогом теплосодержания и поэтому не мон,ег
служить потенциалом влагопереноса. Поэтому при применении формулы (5-7-73)
к системам, состоящим из нескольких соприкасающихся влажных тел, можно по-
лупить неправильные результаты, если не учитывать скачок влагосодержания
на границе их соприкосновения.
При изотермических условиях (ГТ — 0) при отсутствии градиента общего
давления (Гр = 0) согласно формуле (5-7-73) перенос влаги происходит из мест
с большим влагосодержанием к участкам с меньшим влагосодержанием. Это
справедливо только при неизменной массоемкости. При разных массоемкостях
(система тел) перенос влаги может осуществляться в обратном направлении
как показано на рис. 5-19. Кварцевый песок при влагосодержанни ОД кг/кг
(Ц?! — 10%) имеет потенциал массопереноса 6 — 600°М, а торф при влагосодер-
жанив 3 кг/кг (1Г2 — 300%) имеет потенциал 0 — 350°М. При соприкосновении
этих тел влага переходит от тела с высшим потенциалом, но меньшим влагоиодер-
жанием (песок) к телу с низшим потенциалом, но большим влагосодержанием
(торф). Аналогичная картина наблюдается при переходе теплоты от свинцовой
пластины, удельная энтальпия которой при температуре =- 200°С равна
6 ккал-’кг, к алюминиевой пластине, удельная энтальпия которой при t2 = 100Т
равна 20 ккал/кг.
Только для однородного влажного тела справедлива формула влагопереноса '
при изотермических условиях
1 = -“„Р0	(5-7-75)
Аналогично закон теплопроводности Фурье (q = —XVT) можно написать
в виде
ЬГТ = —йрРГй,	(5-7-76)
так как
(5-7-77)
dli	,
где dj' — Cp—удельная изобарная теплоемкость тела; h — удельная энтальпия
тела; ар — коэффициент температуропроводности или коэффициент диффузии
теплоты (для твердого тела ар — av -= а).
Следовательно, закон теплопроводности Фурье можно сформулировать так:
'плотность потока теплоты прямо пропорциональна градиенту удельного тепло-
содержания. Коэффициент диффузии теплоты характеризует перенос эюальпии
аналогично коэффициенту диффузии 'массы ат. Потенциал переноса влаги б ЯВ'
ляется функцией .влагосодержания и температуры: б (», Т). Градиент влагосо-
держапия (Г«)г может быть выражен через градиент потенциала б;
(V“)z = (|‘)rV0 = ^V0,	(5-7-78)
где ст — изотермическая удельная массоемкость или ’влагоемкость тела.
Соотношение (5-7-76) справедливо для однокомпоненгной системы или твер-
дого тела. Следовательно, закон изотермическое влагопереноса будет иметь
вид:
/ = — offip0cmV6 — —(5-7-79)
где Кт = атор()Сгл назовем коэффициентом массопроводности или влагопровод-
ности тела аналогично коэффициенту теплопроводности тела А = оср0.
Перенос влаги под действием потенциала ГО называем влагопроводкостью,
а соотношение (5-7-79)— законом влагопроводности.
При недзотермических условиях закон влагопереноса имеет вид:
j - - ).mV8 - Ш - kp4p ,	,	(5-7-80)
ст
372
так как
“Jpo = "mPo8 = -~- Ss + lA’
С,J
В формуле (5-7-80) все виды влагопереноса выражены через градиенты потен-
циалов влагопереноса (^6, уТ, ур). Следовательно. закон термодиффузии влаги
il = - W'7'”- Т2- №т = -	(5-7-81)
‘•и
можно называть законом термовлагопроводности. Тогда коэффициент
будет коэффициентом термовлагопроводности, а коэффициент
г= Ь&/ст —относительным коэффициентом термовлагопроводности.
Различное физическое обоснование некоторых физических величин довольно
часто встречается в физике, например, коэффициент поверхностного натяжения
определяется как сила поверхностного натяжения, действующая па единицу длины
произвольного контура, по линии разреза поверхности жидкости, дин,А-м (сило-
вая характеристика). С другой стороны, коэффициент поверхностного натяжения
численно равен свободной потенциальной энергии при образовании единицы пло-
щади поверхности жидкости, эрг/см2 (энергетическая характеристика).
Точно так же коэффициент температуропроводности а (а — К/ср0), с одной
стороны, является коэффициентом диффузии теплоты (см. выше), а с Другой сто-
роны, характеризует скорость распространения изогермы. Поэтому коэффициент
а, имеющий единицу измерения см2/с, называется коэффициентом температуропро-
водности. Величина, обратная коэффициенту температуропроводности, 1/а харак-
теризует инерционные свойства тела ею отношению к перемещению изотерм.
Так как температура тела является потенциалом переноса теплоты, то коэффи-
циент а можно назвать коэффициентом потеициалопроводпости переноса теплоты.
Аналогичные соотношения имеют место при влагопсреносе. Коэффициент диффу-
зии влаги ат (ат,—	можно назвать коэффициентом потенциалопровод-
ности переноса влаги, так как оп характеризует скорость распространения изо-
потенциальной поверхности тела при изотермических условиях. Следовательно,
величина Uam характеризует инерЦЕЮнные свойства тела по отношению к переме-
щению изопотенциальной поверхности 6 = const во влажном теле (ат — А^'о).
Единицы измерения коэффициентов а и ат одинаковы (смг/с), они соответственно
равны:	'
Полная аналогия имеет место и в единицах измерения коэффициентов тепло-
проводности Х-, кал/(М'Ч-°С), и влагопроводности Х_, кг((м-ч-°М), а также тепло-,
емкости с, ккал/(кг>°С), и массоемкости ст, кг/(кг'°С),
Влагоперенос в электромагнитном поле
Влажные капиллярно-пористые тела являются поляризованными системами,
в которых приложенные напряженности электрического и магнитных полей релак-
сируются, Следовательно, такие сеестсмы являются релаксационно-поляризо-
ванными.
Обозначим электрическую и магнитную поляризации соответственно через
лэ и лм, а напряженности электрического и магнитного полей через Е н В, тогда
градиент химического потенциала А-го компонента будет:
V|is_-SsVT + V#Vp-(V£)ns-(Vi).,„+	<3'7'83)
I = 1
где S — энтропия; V — удельный объем.
373
Таким образом, помимо термодинамических сил уи и уТ в неоднородном маг-
нитном поле будут действовать термодинамические силы
Хэ = (Г£)лэ; X4~(VS)nM.	(5-7-34)
Таким образом, в однородном электромагнитном поло перенос влаги обуслоа-
лен действием не только сил диффузии (v«) и термодиффузии 1уТ), но и действием
сил и Х„. Следовательно, в общем случае поток влаги будет в соответствии
с уравнением Онзагера
Т2]Х] Ь22Х24-£.23Х3	(5-7-85)
определяться соотношением
/=-0m₽ov“--OoO'f) ”,-“Х (’3)	(5-7-85) .
где первый член формулы (5-7-86) определяет величину диффузии влаги, второй
член — термодиффузии влаги, Третий член соответствует переносу влаги под дей-
ствием неоднородного электрического поля, Этот вид переноса можно назвать
электродиффузией влаги Поток влаги, обусловленный действием силы (V5)nMi
назовем магнитодиффузией влаги в неоднородном магнитном поле.
Коэффициенты а3т и а” будут коэффициентами электро- и магпитодиффузиН
влаги во влажном материале.
Если электромагнитное поле однородное, но переменное, то поток влаги
будет определяться не только действием термодинамических сил и по и дви-
жущей силой Е, где Е разность между напряженностью поля в равновесии Ее
и в данный момент Е (Ё = Ее — Е).
Относительно термодинамической силы в(в — Ве — В) надо отметить сле-
дующее: величина В является н общем случае тензором и в соответствии с принци-
пом Кюри не может быть совместима с векторами и Однако при некото-
рых условиях величина В будет влиять на перенос влаги. Таким образом, для
переменного электрическою поля будем иметь:
( = - “Л'’я-“.»Ро'’7’-“ХЗ’	(5-7-87)
где а3т~коэффициентэлектродиффуэии влаги в переменном электрическом поле.
Величина потока влаги, обусловленная элсктродиффузией, будет равна:
/,= -“mPo terad 3) “тР(Л	(5-7-88)
Аналогичные соотношения получим для случая переменного магнитного поля:
= - ат (Srad В) - ~<Р Д	(S'7’89)
где черта над величиной В означает некоторое усреднение и снижение ранга тен-
зора.
Соотношения (5-7-88) и (5-7-89) показывают влияние электромагнитного поля
на влагоперенос. Очевидно, те же термодинамические силы влияют и на перенос
теплоты.
Исследования по сушке влажных материалов в переменном магнитном поле
подтверждают влияние переменного магнитного поля на перенос влаги, Однако еще
не накоплено достаточного экспериментального материала, чтобы можно было рас-
считать коэффициенты электрической и магнитной диффузии.
1 Необходимо отличать диффузию влаги под действием электроосмотических
сил.
374
5*8. ПРИМЕНЕНИЕ КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛ
В КОСМИЧЕСКОЙ ТЕХНИКЕ
Обширная и крайне актуальная сфера применения капиллярно-пористых ма-
териалов открывается в связи с решением вопросов, возникающих при освоении
космического пространства. При этом наиболее существенными являются проб-
лемы, связанные с поддержанием оптимальных температурных условий функциони-
рования различных устройств и элементов космического корабля. По существу,
решение этих вопросов заключается в разработке способов отвода тепловой энер-
гии, генерируемой внутри корабля, и сброса ее в окружающее пространство.
Если в обычных земных условиях способы охлаждения путем вдува газов и испаре-
ния жидкости в известной мере равноценны, то в специфических условиях кос-
моса (глубокий вакуум, состояние невесомости, жесткие требования к системам
терморегулирования) испарительное охлаждение оказывается не только единст-
венным, но и оптимальным вариантом. При космических условиях наиболее полно
раскрываются достоинства испарительного охлаждения: высокая эффективность
охлаждения, связанная с интенсивным испарением в вакууме* высокая экономич-
ность благодаря сильному эндотермическому эффекту фазового перехода; нетребо-
вательность к предварительной температурной подготовке охладителя; отсутствие
необходимости в специальных системах подачи охладителя, так как в условиях
невесомости капиллярный потенциал подвода жидкого охладителя к охлаждаемой
поверхности теоретически неограничое!. Следует отметить универсальность испари-
тельного охлаждения: оно применимо как для внешней тепловой защиты и для
сброса внутренней тепловой энергии в отдельности, так и для комплексного охлаж-
дения. Кроме того, испарительное охлаждение легко поддастся автоматическому
управлению путем дозирования подачи охладителя.
Важнейшей проблемой космических полетов является обеспечение нормаль-
ной жизнедеятельности космонавтов. Эта задача, достаточно сложная, но в то же
время вполне разрешимая при охлаждении кабин корабля, представляет исключи-
тельную трудность применительно к космонавту, покинувшем}' корабль. Так как
конструкция космического скафандра отвечает в первую очередь требованиям гер-
метичности, радиационной и метеоритной защиты, но в целом далеко не соответ-
ствует требованиям теплового режима, то в этом случае необходимо не только за-
щитить космонавта от внешних тепловых нагрузок (особенно солнечной радиации),
но и обеспечить отвод теплоты, выделяемой человеческим телом. Требования к си-
стеме терморегулирования крайне жесткие: температура внутренней поверхности
скафандра должна быть ниже температуры тела, система должна быть независима
от корабля, должна быть компактной и легкой. Возможным вариантом системы
можег служить совокупность расположенных вблизи соответствующих участков
тела контактных теплообменников, представляющих собой капиллярно-пористое
тело, составляющее часть скафандра и сообщающееся с резервуаром (емкостью)
жидкого охладителя. Характеристики охладителя, а также структурнопористые
и капиллярные свойства пористого тела следует подбирать такими, чтобы теплооб-
менник работал в режиме двойного фазового перехода (подводимый жидкий охла-
дитель замерзает в силу интенсивного фазового перехода и затем сублимирует),
обеспечивая низкую температуру при достаточной экономичности расхода охла-
дителя; при этом зона фазового перехода должна располагаться внутри капилляр-
но-пористого тела.
Выполнение последнего требования приводит к любопытной ситуации: тепло-
проводность пористого теплообменника в направлении к телу космонавта оказы-
вается крайне низкой благодаря высокому термическому сопротивлению сухой
зоны, выступающей в качество теплоизоляции, в то же время теплопроводность
внутри тела через влажную зону достаточно высока.
Подобные диодные свойства капиллярно-пористых систем с заглубленным
фронтом фазового перехода оказываются исключительно нужными и ценными в наи-
более сложных случаях защиты от совместного воздействия внутренней и внешней
тепловой нагрузки.
' Не менее требовательна к температурному режиму работы измерительная
и управляющая аппаратура, астронавигационное оборудование и многие другие
375
точнейшие приборы, которыми оснащен космический корабль. Применение различ-
ных модификаций пористого испарения для поглощения теплоты, выделяемой
в измерительных и рабочих схемах, позволяет устранить тепловые помехи
подавить тепловой шум и поднять качество микрорадиоэлектрояной аппарату’
ры на новую ступень, Значение же миниатюризации радиоэлектроники неоце.
нимо не только для космических аппаратов, но и для столь важных в народном
хозяйстве систем программного управления, счетно-решающих и кибернетических
устройств.
Пористое испарение является надежным средством терморегулирования эле-
ментов тепловой системы, предотвращения перегрева баков с торючим с целью
уменьшения потерь криогенного ракетного топлива и соблюдения крайне важных
мер взрывобезопасности. При этом охладителем может служить как специальная
жидкость, так и криогенное топливо. В последнем случае легко добиться весьма
целесообразного самозамораживания топлива.
Проблема нейтрализации внутренних тепловыделений на космическом ко-
рабле тесно связана с необходимостью отвода теплоты на периферию корабля.
Идеальное решение вопроса транспорта теплоты может быть достигнуто с помощью
устройств типа тепловой трубы. Тепловая труба, представляющая собой герметич-
ный капиллярно-пористый фитиль, насыщенный легколетучей жидкостью, с по-
мощью испарительно-конденсационного механизма переноса теплоты позволяет
в десятки тысяч раз увеличить теплопроводность по сравнению с теплопровод,
цостью лучших естественных проводников теплоты (металлов). Тепловая трубка
по существу является своеобразным сверхпроводником теплоты, Действующим
автоматически. Именно космос благодаря невесомости снимает с тепловых труб
всякие геометрические и пространственные ограничения и делает их незамени-
мыми в конструктивном плане. В частности, применение тепловых труб позволяет
не только устранить недопустимые температурные деформации корпуса корабля
и снять температурные напряжения конструкции, вызнанные сильным прогревом
корабля с солнечной стороны и резким охлаждением с теневой стороны, но и обра-
тить эти в общем неблагоприятные условия на пользу.
Одним из процессов, составляющих рабочий никл тепловых труб, расположен-
ных полукольцами по диаметру корабля между горячей и холодной сторонами кор-
пуса, оказывается процесс капиллярной перегонки рабочей жидкости по пористому
фитилю от холодной конденсационной секции трубы к горячей испарительной.
При правильно подобранных характеристиках рабочей жидкости и пористого фи-
тиля это приводит к возникновению потенциала течения полярной жидкости в по-
ристой среде, и тепловая труба начинает работать в режиме теплоэлектрического
преобразователя, обеспечивая корабль «даровой» электроэнергией.
Однако капиллярно-пористые материалы перспективны не только для реше-
ния тепловых космических проблем, перечисленных здесь лишь вкратце. Эти мате-
риалы решают также серьёзную проблему транспорта жидкости в условиях не-
весомости ,
Как уже отмечалось выше, капиллярный потенциал переноса жидкости в отсут-
ствие поля массовых сил беспределен и способен обеспечить нормальное функ-
ционирование топливной системы космических кораблей.
При использовании капиллярно-пористых материалов криогенной откачки
оказывается возможным создание откачных устройств, работающих благодаря ка-
пиллярному отсосу сконденсированных газов длительное время в стационарных
условиях.
Капиллярно-пористые тела в слабых гравитационных полях обладают ря-
дом специфических свойств, К ним относятся:
1)	потенциал капиллярного впитывания, характеризующий процесс взаимо-
действия жидкости со стенками капилляров;
2)	проницаемость для газа или жидкости;
3)	изменение в широких пределах эффективных коэффициентов переноса (на-
пример, эффективной теплопроводности в зависимости от того, совпадают ля тем-
пературное поле и поле концентраций в теле). Эффективная теплопроводность
капиллярно-пористых тел может изменяться от 10“3 Вт/(М'СС) до 103 Вт/(М‘^-)>
т. е, на 6 порядков;
4)	высокая удельная поверхность;
376
5)	низкая плотность (по сравнению с монолитом,, из которого изготовлен пори
стый материал);
6)	электрокииетические эффекты при течении жидкостей по капиллярно-по
ристому телу (потенциал течения);
7)	свойства избирательности, т. е. проницаемость для одних жидкостей и не-
проницаемость для других, проницаемость для тепловых потоков в одном направле-
нии и непроницаемость в обратном;
8)	возможность осуществления в порах тела фазовых переходов, сопровождае-
мых выделением или поглощением энергии, и ряд других интересных свойств.
Эти характеристики позволяют использовать капиллярно-пористые тела, как
было указано выше, в качестве материала для различного рода теплообменников
в космосе (конденсаторы, испарители, сублиматоры): Для защиты от внешних теп-
ловых потоков, для теплосброса в вакуум (термостатирование емкостей с жидко-
стями, переохлаждение жидкостей, термостатирование различных аппаратов,
подверженных нагреву солнечным излучением), для перекачки жидкости, для
преобразования тепловой энергии в механическую или электрическую с высоким
к. п. д., для создания специальных теплопроводов типа тепловых труб, обладаю-
щих теплопроводностью, в сотни раз превышающей теплопроводность меди. Нако-
нец, использование пористых материалов в качестве сопл двигателей позволяет
получить в вакууме газовые струи очень однородной структуры с хорошо развитым
изоэнтропическим ядром. Наиболее эффективной теплоизоляцией в вакууме явля-
ется пористая теплоизоляция.
Рассмотрим некоторые примеры практического применения капиллярно-
пористых тел в космосе.
Транспорт жидкости с помощью капиллярных фитилей
Благодаря силам капиллярного впитывания пористые материалы могут вы-
полнять роль насосов для перекачки жидкости из одних сосудов в другие. В отсут-
ствие поля гравитации силами, противодействующими силам капиллярного впиты-
вания, являются силы инерции и трения.
Перепад давления Др на участке фитиля Дх равен капиллярному давлению
Лапласа:
\ 'I Г3 !
(5-8-1)
где г{ и Ад — радиусы мениска в порах на входе и выходе из элемента Дх.
Будем считать, что этот перепад давления уравновешен силами трения
Др = Дра.
Если применить закон фильтрации Дарси, то будем иметь:
Др _ гр   2g / 1 1 \
Дх” К Дх \ rf r'i J’
(5-8-2)
Полагая
О (г'->со) для объемного потока жидкости (см8/с), полу-
чаем следующее выражение:
а л-
6 = Av =-----7~~л~~ ,
ту; Дх ’
(5-8-3)
где А—поверхность капиллярно-пористого тела.
Таким образом, параметром капиллярного насоса является величина К/г{.
Радиус мениска г{, как будет показано ниже (§ 5-9), равен:
2g
РЙ^макс
(5-8-4)
где — ускорение силы тяжести на поверхности Земли; /макс — высота капилляр-
ного поднятия.
377
Отсюда получим:
е=['
P«W л
1] / \ Дх /
(5 8.5)
Величину 1тК можно рассматривать как параметр, характеризующий способ-
ность капиллярного насоса к переносу жидкости.
Рис. 5-39. Схема капиллярной систе-
мы подачи, основанной па поверхно-
стном натяжении жидкости.
а — смачивающая жидкость; б — несмачи-
вающая жидкость.
Рис. 5-40. Схема-разрез системы
подачи с пористыми дисками.
I — оболочка: 2 — подогреватель; 3 —
испаритель; 4 — пористые диски.
В настоящее время нашли применение пористые среды с коническими капил-
лярами. Так, например, исрольэуется оригинальная система иодачи жидкости
Рис. 5-41. Аппараты подачи с пористыми пластинами.
а — разрез резервуара с рабочим телом; б — общий вид; / — трубка
подачи; 2 — резервуар с рабочим телом; 3 — внутренний подогреватель;
4 — пористый металлический стержень; 5 — радиальные пластины; 6 —
клапан откачки; 7 — клапан для пара; 8 — испаритель
в ионных двигателях, не имеющая движущихся частей и пригодная для работы
в условиях невесомости (фирма «Электро оптикал», США). В этой системе поступлю
37#
ние жидкости из бака к нагретой поверхности испарителя обеспечивают силы по-
верхностного натяжения жидкости. Схема капиллярной системы подачи, основан-
ной на поверхностном натяжении жидкости, показана на рис. 5-39. Испарение про-
исходит в том месте нагретой поверхности трубы, где жидкость встречает барьер.
Для несмачивающей жидкости (ртути) таким барьером служит тончайшая метал-
лическая сетка.
Фирмой «Электро-оптикал» были разработаны две конструкции для подачи
цезия, основанные на поверхностном натяжении. В .одной из них резервуар запол-
нялся тонкими пористыми металлическими дисками, плотно прилегающими один
к другому. Чтобы получить необходимую конусность, подбирались диски с раз-
личными размерами пор, постепенно уменьшающимися по направлению к испа-
рителю (рис. 5-40).
В другой конструкции использованы сходящиеся пластины (рис. 5-41).
В центре устройства установлен пористый металлический стержень, который дей-
ствует как фитиль и подает жидкость (цезий) непосредственно к поверхности, где
происходит испарение.
Представляет интерес применение конусной пористой структуры для увели-
чения коэффициента теплопередачи как в условиях космоса, так и в условиях
невесомости.
Тепловые трубы
Сущность работы тепловой трубы состоит в следующем: испарение жидкости
происходит из капиллярно-пористого фитиля. Пар диффундирует в холодную
Испарение
Рис. 5-42. Аналогия между движением жидкости в коническом (а) и в цилиндри-
ческом (б) капиллярах при испарении, и конденсации.
зону, где и конденсируется. Конденсат возвращается тем же фитилем. Это проис-
ходит потому, что при испарении кривизна мениска увеличивается, а при конден-
сации — уменьшается. В результате жидкость перемещается под влиянием кацил-
Ркс. 5-43. Схема тепловой трубы.
лярного потенциала аналогично перемещению жидкости в коническом капилляре
(рис. 5-42), Поэтому для большей эффективности устройства применяются кониче-
ские капилляры, в которых движение жидкости ускоряется за счет искривления
мениска при испарении и конденсации. Такое устройство показано на рис. 5-43.
Теплообменники для сброса теплоты в космосе
Схема теплообменника для сброса теплоты в космосе приведена на рис. 5-44.
Слой 1 выполнен из гидрофобного материала с большой пористостью, обладающего
незначительным гидравлическим сопротивлением и низкой теплопроводностью,
379
ТеплоподИод
Рис. 5-44. Схема теплообменника
для сброса тепловой энергии в кос-
мос.
например из фторопласта с порами 0,1 —0,5 мм (теплопроводность такого тела ниже
теплопроводности жидкости).
Слой 2 выполнен из гидрофильного материала, хорошо впитывающего жид
кость и обладающего высокой теплопроводностью скелета (больше теплопровод'
ности жидкости). К внутренней поверхности теплообменника подводится теплота'
которую необходимо сбросигь в вакуум’
чтобы охладить жидкость.	’
На границе раздела двух пористых ма-
териалов и частично выше этой границы
происходит Испарение или сублимация
хладоагепта с поглощением теплоты. Бла-
годаря высокоразвитой поверхности испа-
рения с единицы площади пористого мате-
риала можно снимать большие тепловые
нагрузки.
Процесс испарения жидкости или
льда в вакууме происходит с достаточно
большой скоростью. Поэтому скорость испарения определяется не только ско-
ростью диффузии массы (в случае молекулярно-вязкостного режима) или скоростью
эффузии (молекулярный режим испарения), но и скоростью кинетики фазового
перехода.
Если испарение происходит на поверхности тела, то интенсивность испарения
(плотность потока массы) можно определить по формуле [Л.5-80]
/™=^,s(c«z-c„);	(м-б)
здесь С^и С-о — концентрации пара на поверхности тела и вдали от поверхности;
й — средняя тепловая скорость движения молекул пара; /С* — коэффициент
массопередачи:
Тс “ NuD Кп + “В ’	(5'8'7)
где В — коэффициент испарения, определяемый из соотношений молекулярно-
кинетической теории испарения; Nun и Кп—диффузионное число Нуссельта
и число Кнудсена.
Если испарение происходит внутри капиллярно-пористого тела, то сопротив-
ление массопереносу i/К* состоит из сопротивления, определяемого кинетикой
фазового перехода 1 /Вй, сопротивления диффузионного пограничного слоя 1/₽
и сопротивления диффузионно-фильтрационному движению пара через капилляры
тела g/Kc, т. е.
+ + (5-М)
где Р — коэффициент массообмена; £ — расстояние поверхности испарения от
поверхности тела; Кс — коэффициент диффузии пара в пористом теле, отнесенный
к разности концентраций.
Соотношения (5-8-7) и (5-8-8) определены при адиабатических условиях испа-
рения. При нсадиабатических условиях испарения (внутреннем теплоподводе)
создаются условия перенасыщения пограничного слоя, сопровождаемые эффектом
конденсации пара. Кроме того, при испарении в вакуум резко увеличивается объем
вещества (при давлении около 1 мм рт. ст. увеличение объема фаз при переходе
изольда в пар составляет примерно 106 раз). Этот эффект резкого увеличения объема
создает фронт уплотнения, т. е. волны разрежения (аналог образования ударных
волн). В этом случае давление пара у поверхности тела не равно давлению насы-
щенного лара при данной температуре [Л.5-81].
Рассмотренный выше теплообменник можно использовать в космосе для тепло-
отвода за счет испарения или сублимации от скафандра человека или другого
объекта с внутренним тепловыделением.
Этот принцип охлаждения применим также для термостатирования криоген-
ных жидкостей в космосе, например для переохлаждения жидкого водорода.
380
5-9. ЯВЛЕНИЯ ПЕРЕНОСА В УСЛОВИЯХ НЕВЕСОМОСТИ
Для анализа процессов переноса в аппаратах и пористых средах, находящихся
в космическом пространстве, необходимо в первую очередь определить поведение
жидкости в условиях невесомости. Большое значение имеют процессы теплооб-
мена а жидкостях в отсутствие гравитации.
В условиях невесомости основными силами, действующими в жидкостях, яв-
ляются силы молекулярного взаимодействия.
Гидростатика жидкости в большом объеме
при частичной и нулевой гравитации
При нормальной гравитации жидкость, налитая в сосуд, заполняет его и при-
нимает форму сосуда. Силы тяжести преобладают над силами межмолекулярного
взаимодействия молекул, находящихся на поверх-
ности жидкости (сила поверхностного натяжения),
и свободная поверхность жидкости устанавливает-
ся горизонтально (рис. 5-45).
В состоянии невесомости и па путях к этому со-
стоянию общая картина поведения жидкости совер-
шенно меняется из-за изменения соотношения меж-
ду силами поверхностного натяжения и инерцион-
ными силами. Поэтому необходима оценка этого со-
отношения [Л. 5-82].
Бенедикт [Л.5-83] оценил порядок капиллярных
сил (сил поверхностного натяжения), действующих
на жидкость в сосуде линейных размеров L, через
aL, а действующие на жидкость инерционные си-
лы — через ngpL3, где п — фактор нагрузки, g—
ускорение силы тяжести. Тогда безразмерное отно-
шение этих двух величин
Рис. 5-45. Равновесие
В°~ pngL*
(5-9-1)
является мерой относительного значения капилляр-
ных сил в ускоряемой жидкости и называется чис-
лом Бонда. Из этого соотношения следует, что силы
поверхностного натяжения начинают играть суще-
ственную роль при Во >• 1, т. е. в случае жидкостей,
соответствующему значениям «<п#, где
жидкости в прямоуголь-
ном сосуде под действием
силы тяжести и поверх-
ностного натяжения.
а — смачивающая жидкость;
б — несмачивающая жид-
кость.
подвергаемых ускорению,
S)
Чтобы подтвердить вышеизложенное, Бенедикт теоретически рассмотрел ста-
тическое поведение жидкости, помещенной в сосуд с поперечным прямоугольным
сечением (см. рис, 5-45) с вертикальными боковыми стенками, бесконечно протя-
женными в направлении, перпендикулярном этому поперечному сечению.
Рассчитанные формы менисков для воды (р= 1 г/см3, ст — 72,75 дин/см,
О — 14°С) и ртути (р— 13,546 г/см8, о = 513,0 дин/см, О — 40°С) приведены
на рис, 5-46.
Как видно из рис. 5-46, с уменьшением фактора нагрузки влияние сил поверх-
ностного натяжения возрастает и при п — 0 поверхность принимает сферическую
форму. Однако автор не приводит данных о влиянии фактора нагрузки на угол сма-
чивания.
Первые описанные в литературе эксперименты по наблюдению формы поверх-
ности жидкости при пониженной гравитации принадлежат Рейнольдсу [Л.5-82],
но они носят весьма качественный и предварительный характер. На основе этих
381
экспериментов было сделано заключение, что жидкости, смачивающие сосуд, будУт
расползаться по его стенкам, так что в центре сосуда образуется газовый мешок
Если же жидкости не смачивают стенок, то они быстро отступают от стенок, и
сохраняет контакт со стенками. Однако смачивающие жидкости не могут распол-
заться бесконечно: площадь поверхности жидкости ограничена величиной энер-
гии, которую можно затратить на ес растяжение, и поэтому смачивающая жидкость
может не покрыть полностью стенок сосуда. Точно так же несмачивающая жид-
кость может стремиться образовать более чем одну глобулу, Энергия, которая
может быть затрачена на отрыв от дна, может оказаться недостаточной, чтобы под.
нять центроид па высоту, необходимую для образования шара. В этом случае в ка-
честве конечной формы жидкости вероятны два или большее число шаров [Л.5-82].
Рис. 5-46, Мениски для воды (а) и для ртути (б) при различных
факторах нагрузки.
/ — п ==0; 2 — п = 0,05; 3 — п —0,5; 4 — п=1,0.
Статические формы мениска жидкости для случая нормальной гравитации
и невесомости в сферическом сосуде приведены в [Л.5-82], где показано, что в со-
стоянии невесомости поверхность жидкости обязательно сферическая, а радиус
этой сферы полностью определяется углом контакта на поверхности раздела, фор-
мой сосуда и количеством жидкости в нем, Угол встречи сферической поверхности
жидкости со стенкой сосуда должен равняться углу контакта 6, существующему
всегда вне зависимости от гравитационного поля. Принимая во внимание эти гра-
ничные условия, для конфигурации жидкости в сферическом сосуде можно полу-
чить только единственное решение, которое для различных случаев представлено
на рис. 5-47.
То, что угол смачивания жидкостью поверхности твердого тела не зависит от
условий гравитации, следует из работ В. В. Шулейкина [Л.5-84]. Автор рассматри-
вает изменение формы мениска воды в стеклянном стакане (радиусом R) при раз-
ных зидчепиях гравитации и в случае невесомости. Общее уравнение равновесия
поверхности воды с главными радиусами кривизны и г2 при наличии поверхност-
ного натяжения а берется в виде
Рлг=а	(5-9-3)
\. О г2 /
где & < g.
Положив
2	Г1	Г2
-ft=s' T = lh; т = |'2-
где h2 = 2а/рй, можно записать (5-9-3) в виде
2‘
(5-9-4)
382
Уравнение (5-9-4) справедливо и в наземных условиях (когда g, = g) и при
весьма малой, но конечной весомости, характеризуемой различными значениями
Из (5-9-4) можно получить дифференциальные уравнения поверхности вращения,
пограничной между водой и воздухом. Обозначив через х расстояние от некоторой
точки этой поверхности до координатной оси, служащей осью вращения контура,
а через <р — угол между этой осью и нормалью в той же точке поверхности, после
некоторых преобразований получим из (5-9-4) систему уравнений-.
ds . de	1	_ sin	n
^p.smcp; ^=PlcoS4>i; pi=2S--------------j-,	(-9-5)
где I = x'k.
Рис. 5-47, Система жидкость — пар при нормальной гравитации g = 1
и в состоянии невесомости g = 0.
I, 2,4,5 — смачивающая жидкость; 3,6 — песмачивающая жидкость.
Исходный профиль а (рис. 5-48) был получен интегрированием системы
уравнений (5-9-5) при следующих граничных условиях: стекло идеально смачи-
вается водой и Rih^ 1 при g) = g. Остальные кривые получены с помощью
приближенных методов интегрирования. Предельный профиль при полной не-
весомости был построен из условия постоянства давления во всех частях свобод-
ной поверхности воды при отсутствии внешних сил:
1	I
-----1------ const.
Pl	Рз
Этому уравнению удовлетворяет единственная поверхность, которая одновре-
менно удовлетворяет условию на границе со стеклом: сферическая поверхность
радиусом R, касающаяся цилиндра (кривая д, рис. 5-4о).
В [Л.5-84] рассчитаны Статические профили мениска капли воды, соприкасаю-
щейся с гидрофобной поверхностью сгеарита цинка (0 = 135°) в процессе уменьше-
383
ния весомости до нуля. Эти профили представлены на рис. 5-49. Кривая ж соот-
ветствует случаю g=0. Результаты были проверены экспериментально. Следует
отметить такой интересный факт: если некоторое количество жидкости (смачиваю-
о
30 -
Рис. 5-48. Статические профили по-
верхности воды, возникающие в ста-
кане диаметром ПО мм при переходе
в невесомость.
Рис. 5-49. Правые половины меридио-
нальных сечений поверхности воды на
стеарите цинка (кривые для невесо-
мости).
а—исходное положение; б — е —: при раз-
ных значениях ——...—	------ •
весомость [Л.6-84].
щей) находится в закрытом цилиндрическом сосуде (рис. 5-50), то поверхно?ть
сосуда, не соприкасающаяся с макроскопическими слоями жидкости, покрывается
микроскопической пленкой этой жидкости. Развитие пленки особенно облегчено
в условиях невесомости, т. е. при ng = 0.
В [Л.5-85] дано следующее выражение для толщины этой пленки:
(5-9-6)
где Го — радиус кривизны поверхности стенок сосуда; /4 — постоянная.
Чтобы представить порядок величины А, в этой работе рассчитана толщина
такой пленки для жидкого кислорода (/1 = —9,8 > Ю-20 дин/см2) при г0= 20 см:
A as 2-10-i см.
В условиях развитой гравитации пленка получается на порядок тоньше.
Рис. 5-50. Смачивающая жидкость в закры-
том цилиндрическом сосуде в условиях не-
весомости.
Оценка толщины А, проведенная в этой работе, по порядку величины соот-
ветствует оценке, найденной другим методом в работе [Л.5-86]. Авторы получили
для жидкого кислорода (90 К) и жидкого водорода (20 К) толщину микроскопи-
ческой пленки порядка 7,5-10~- см. Экспериментальных данных по измерению тол-
щины этой пленки не имеется, поскольку для проведения такого эксперимента
необходимо «термостатировать» бак с криогенной жидкостью с точностью Л10-8 К
для кислорода и с ючностью ДсЮ“* К для водорода [Л.5-86].
384
Гидродинамика поведения жидкости в большом объеме
при изменении гравитации до нуля
Выше были рассмотрены статические формы поверхности мениска жидкости.
Однако конфигурация поверхности жидкости, находящейся на борту космиче-
ского корабля или в топливном баке ракеты, в любой момент времени является
функцией многих величин, в том числе энергий поверхностей раздела, формы
бака, коэффициента заполнения, механических возмущений н т. д. Так, напри-
мер, если жидкость, находящаяся в некотором объеме, выведена из состояния рав-
новесия, то силы поверхностного натяжения будут стремиться привести жидкость
к равновесной пространственной конфигурации, однако равновесие конфигура-
ции не может установиться до тех пор, пока не израсходуется избыток свободной
энергии поверхности по сравнению с энергией в равновесном состоянии [Л.5-86].
В [Л. 5-82] описаны колебания поверхности жидкости при переходе в состоя-
ние невесомости. Период колебаний Т поверхности жидкости определяется со-
отношением
F 4 <т *
где ш — масса капли жидкости.
Эксперименты доказывают существование этих колебаний, хотя гидродина-
мика этого явления почти не исследована.
' В общем случае для гидродинамических систем существуют три безразмерных
критических параметра, определяющих, будет ли течение управляться в основном
силами гравитации, инерционными или капиллярными силами, т. е. поверхност-
ным натяжением. Этими тремя величинами, характеризующими различные гидро-
динамические режимы, являются число Рейнольдса Re, число Бонда Во и число
Вебера We. Еще одним важным параметром, который можно получить, комбини-
руя числа Во и We, является число Фруда Fr.
В соответствии со значениями чисел Re, Во и We возможны разные режимы
движения, когда господствующими являются: 1) силы инерции; 2) капиллярные
силы; 3) гравитационные силы (см. рис. 5-13).
Используя эти безразмерные параметры, сделаем краткий обзор некоторых
работ, в которых рассматривается динамика поведения жидкости при невесомости
и в поле пониженной гравитации. Так, например, в ]Л.5-87] теоретически рассмат-
ривается осесимметричная задача движения жидкости в коническом баке, образо-
ванном (рис. 5-51) круговым конусом с углом полураствора а и сферой единич-
ного радиуса; движение вызвано приложенным к баку осевым ускорением, харак-
теризуемым величиной перегрузки п (т).
Объем жидкости задавался ординатой h плоскости, соответствующей поверх-
ности жидкости при отсутствии поверхностного натяжения. Жидкость считалась
идеальной, а движение — безвихревым. Полученные профили поверхности жад-
ности показаны на рис. 5-52.
Автор приходит к выводу, что высота всплеска и скорость движения жидкости
увеличиваются при уменьшении числа Бонда, т. е. при большем искривлении на-
чальной поверхности. Соответствие экспериментальных и расчетных данных удов-
летворительное.
Более общая задача была решена в [Л. 5-88], в которой исследовалась форма
свободной поверхности жидкости в предположении, Что она является осесиммет-
ричной поверхностью тока с заданным осесимметричным распределением ско-
рости. Результаты решений в безразмерных величинах представлены графически
на рис. 5-53.
Авторы пришли к выводам, которые несколько распространяются и на резуль-
таты [Л.5-87]:
1)поверхностная скорость оказывает сильное влияние па форму свободной
поверхности жидкости и на высоту мениска;
2) относительное влияние числа We на высоту мениска уменьшается с увели-
чением числа Во, т. е. с увеличением гравитации относительное влияние скорости
на форму мениска уменьшается;
3) для выбранного распределения скорости высота мениска в большинстве
случаев увеличивается с увеличением We.
13 Лыков А. В.	385
Рис. 5-51. К расчету дви-
жения жидкости в кру-
говом конусе [Л. 5-87].
Рис. 5-52. Формы свобод-
ной поверхности жидкос-
ти в коническом сосуде
(а = 12°).
а — равновесное состояние,
V = 5°, при критерии Во от
О до 300; б — последователь-
ные формы; у —5°: Во= 1,
п =— 0,5 (отрицательная пе-
регрузка) при времени т =
= 0 4- 0,6; в — положительная
перегрузка {n = 1) при Во = 0
для времена t=b-~D3,
386.
Л/I I I I I t
Рис. 5-53. Распределение безразмерной высоты свободной поверхности жид»
кости при различных значениях Во, 0. Rm и числах Вебера (о>).
13*
387
Повеление жидкости в капиллярах при невесомости
Большой интерес представляет поведение жидкости в капиллярах при неве-
сомости, поскольку, как следует из соотношения (5-9-1), влияние поверхностных
сил увеличивается за счет одновременного уменьшения ng и №. Поэтому явления
наблюдаемые в капиллярах в условиях нормальной гравитации, должны уси!
литься в состоянии невесомости. Явления перекоса в капиллярах при g = о
по-видимому, можно описать, исключая гравитационный член из уравнений, опи-
сывающих процессы переноса в капиллярах в условиях нормальной гравитации.
В [Л.5-89] в предположении, что движение жидкости в капилляре ламинар-
ное, было получено следующее уравнение капиллярного впитывания жидкости;
d4 1 / dl \а , 8т) dt ,	. 2о sin & _
+7чГлг+^,па---------^-=0'	Р'9-7)
где I—длина столбика жидкости; а—угол наклона оси капилляра к гори-
зонту; г —радиус капилляра; р—плотность жидкости; т — время. Решение
этого уравнения затруднено. Поэтому, если считать, что первый и второй
члены бесконечно малы, получаем следующее выражение для скорости и капил-
лярного поднятия:
(5-9-8)
а для высоты максимального поднятия
,	,	 2а cos 9	„ „ „
^макс — ^макс sin а — ——•	(5-9-9)
Следовательно, для случая невесомости (g=0) будем иметь;
Лмахс = ео.	(5-9-11)
Решение уравнения (5-9-7) для невесомости было дано в [Л.5-90] при
начальных условиях'
т=0; (==Ао+^1=/о; -^=0	(5-9-12)
в виде
/ _ 8vT \
'’-1) + (4‘77‘те9)т+'г’	(5’943>
где Ло—глубина, на которую погружена в жидкость трубка (рис. 5-54); v —
кинематическая вязкость (v = i)/p).
Для больших промежутков времени можно написать:
Р’9’14)
(В [Л.5-91] были рассчитаны кривые капиллярного впитывания для невесо-
мости по формуле (5-9-13). Оказалось, что формула (5-9-13) дает завышенные ре-
зультаты, которые еще больше расходятся с экспериментальными данными для
труб большого диаметра (d > 2 см). Эксперименты проводились с капиллярами,
которые находились в условиях свободного падения (невесомости). На рис. 5-55
приведена фотография одного из опытов.
Чтобы согласовать расчетные данные с экспериментальными,-были учтены
потери во входной зоне трубы в результате изменения количества движения, необ-
ходимого для развития профиля скоростей.
Уравнение движения
&1 , 1,14 / dl \а , 8г) dl , go ! 2ccose , , \	Q
да+—Ы +7v>+T-(^r+'inW=° <5-9-15>
385
отличается от уравнения Порхаева [Л.5-89] только коэффициентом при (dl/di)'1.
Следовательно, можно считать, что решение для случая невесомости в виде (5-9-13)
справедливо и для уравнения (5-9-15).
Таким образом, расчеты по уравнению (5-9-15) также ие будут совпадать с эк-
спериментальными данными. Поэтому в [Л.5-91] была сделана попытка учесть влня-
Рис. 5-54. К выводу уравнений жид-
кости в капилляре.
Рис. 5-55. Поднятие жидкости по ка-
пиллярным трубкам в условиях нор-
мальной гравитации и при невесомо-
сти в зависимости от времени (с).
Диаметр тру«5ок 0,196, 0,317 и 0,750 дюйма.
ике турбулентности, ослабление поверхностного натяжения при неустацоаившемся
режиме и инерцию жидкости в резервуаре, В результате было получено уравнение
5/Шу Sv «
('-0'25-г;^~ПлУ -7ГЛ- +
+ ±	+ пг = 0,	(5-9.16)
I гр \	и-Ь / I
которое дает расчетные данные для капиллярного поднятия при невесомости»
совпадающие с экспериментом. Решение этого уравнения весьма затруднительно,
289
ио если пренебречь членами с (Plldx* и (dZ/dx)2, то для скорости капиллярного под.
нятия при невесомости получим следующую формулу:
	dl _ 2or® cos б
V~ dx ~~ 0,2г2осо5 94-8т)/г ’	(5-9-17)
В формуле (5-9-17) для скорости капиллярного впитывания учитывается
влияние ослабления поверхностного натяжения, что ие отражено в формуле (5-9-10).
Из формулы (5-9-13) получаем для скорости движения:
di or А .	— тг
v=7? = «Гcos 1~8	!•	<5'9-18)
Эти три формулы для скорости капиллярного впитывания отличаются друг
от друга незначительно, а для больших значений времени формулы (5-9-10) и
(5-9-18) дают один и тот же результат. Из анализа формул (5-9-10), (5-9-17) и
(5-9-18) следует, что
(^макс)й,-0 = °О.
Судить о реальной величине (ZMaKc)g-o трудно, поскольку в литературе совсем
мало экспериментальных Данных по капиллярному впитыванию при невесомости.
Теория дает такой результат, по-видимому, потому, что в уравнении движения
жидкости по капиллярам не учтены все диссипативные процессы, которые для
условий нормальной гравитации ие имеют значения по сравнению с интенсивно-
стью сил тяжести. Следует отмстить тот факт, что процессы капиллярного впиты-
вания для очень узких капилляров (до 0,1 мкм) в условиях нормальной гравитации
описываются уравнением [Л.5-92]
Это уравнение подвергалось многочисленным проверкам, показавшим его
применимость. Уравнение (5-9-19) аналогично уравнению (5-9-10). Следовательно,
процессы в узких капиллярах при невесомости и в условиях нормальной гравита-
ции будут происходить одинаково.
Поведение жидкости в капиллярно-пористых телах при нулевой и понижен-
ной гравитации будет, по-видимому, подобно поведению их в единичном капил-
ляре, т. е. скорости капиллярного поднятия значительно большие, чем в условиях
нормальной гравитации, а высота капиллярного поднятия стремится к оо. Поэтому
капиллярно-пористые тела, могут служить хорошим транспортным средством для
подвода жидкости в условиях невесомости.
Использование свойств жидкости в условиях невесомости
Поскольку поведение жидкости в условиях невесомости определяется силами
межмолекуляриого взаимодействия на поверхности, то можно обеспечить жела-
тельное поведение жидкости в невесомости. Одно простое решение этой задачи
связано с, применением конических сосудов.
Рассмотрим конический сосуд с жидкостью (рис. 5-56). В случае несмачиваю-
щей жидкости поверхностные силы заставляют жидкую массу перемещаться по
направлению к большему по сечеиию концу сосуда, а в случае смачивающей жид-
кости — в противоположном направлении.
Таким образом, можно любую жидкость перемещать и перекачивать в соот-
ветствии с необходимостью. Это явление утке нашло применение для подачи рабо-
чего вещества в иоппых ракетных двигателях, созданных фирмой «Электро-опти-
кал» и не имеющих движущихся частей. Они вполне пригодны для работы в не-
весомости.
390
Очевидно, это явление можно использовать для конструкции емкостей и тру-
бопроводов космического корабля. Например, в [Л.5-86] предлагается воспользо-
ваться сопловой конструкцией, составленной из конусов с общей вершиной в вы-
Рис. 5-57. Коллекторы для сбора
жидкости в условиях невесомости.
'Жидкость	Жидкость
«)	V
Рис. 5-56. Жидкость в состоянии неве-
сомости в капиллярном сосуде.
а — иесмачипающая; б — смачивающая.
ходном отверстии бака для сбора смачивающей жидкости, Это устройство будет
играть роль «фитиля» для жидкости. Жидкость будет со стенок бака собрана
к центру. Два таких устройства представлены на рис. 5-57.
Процессы теплообмена в жидкостях при невесомости
и на путях к этому состоянию
Отсутствие силы тяжести должно сказаться также на процессах теплообмена
при невесомости.
В имеющейся литературе большое внимание уделено процессам теплообмена
при кипений в условиях невесомости и при пониженной гравитации, а также ме-
ханизму самого кипения. Результаты исследований процессов кипения, получен-
ные в работе [Л,5-82, 5-93, 5-971, сводятся к следующему: при невесомости пе-
риод пузырькового кипения очень мал, а преобладает пленочное кипение. Крити-
ческий тепловой, поток пропорционален (St'S) 1,/4. Наиболее полные данные приве-
дены в [Л.5-95], в которой исследовался механизм теплообмена в баке с водоро-
дом при невесомости.
Были получены следующие результаты: при умеренных, но постоянных тепло-
вых потоках процесс теплообмена в не подверженной возмущениям кипящей жид-
кости при невесомости распадается на 5 фаз:
1)	вследствие теплопроводности около стенок возникает тонкий тепловой
слой, который развивается, в результате чего образуется пленка перегретой жид-
кости;
2)	под действием потока теплоты от стенок и тепловой диффузии в перегре-
той жидкости возникают и растут ядра парообразования, причем они распреде-
ляются более или менее равномерно;
3)	по мерс роста паровых пузырей удельная теплота испарения начинает
играть все более важную роль;
4)	в процессе роста пузыри начинают выступать за пределы теплового слоя
и вступают в контакт с холодной основной массой жидкости,-
5)	паровые пузыри деформируются вследствие расширения их в боковом на-
правлении и приобретают форму сферических сегментов. Затем они начинают сли-
ваться друг с другом, а частицы жидкости, находящиеся между ними, подпиты-
вают процесс испарения, в результате чего тепловое сопротивление прослойки
между стенкой (источником теплоты) и холодной массой жидкости с течением вре-
мени увеличивается.
Таким образом, в условиях невесомости теплообмен осуществляется двумя
путями; молекулярной теплопроводностью и испарением жидкости,
391
Установлено также, что при пузырьковом кипении в условиях невесомости
и пониженной гравитации уменьшается скорость подъема пузырей и увеличива-
ется их диаметр [Л.5-82, 5-93, 5-95].
Коэффициент теплообмена не меняется при развитом пузырьковом кипении
[Л.5-82] и уменьшается с течением времени при невесомости, т. е. при пленочном
кипений [Л.5-95].
При вынужденном движении жидкости влияние невесомости на возможность
возникновения кризиса кипения различно [Л. 5-94].
Интересные результаты были получены по конденсации пара при невесомости
однако они носят качественный характер. Например, при конденсации паров
ртути в условиях невесомости конденсат можно собрать в трубчатом конденсаторе
путем использования сил вязкости и давления пара [Л.5-82]. Поверхность раздела
жидкость — пар может поддерживаться устойчивой.
Возможно, что на процессы испарения со свободной поверхности жидкости
условия невесомости не оказывают влияния, как не влияет невесомость на про-
цессы испарения внутри жидкости при кипении [Л.5-86].
Естественной конвекции в жидкостях при невесомости наблюдаться не будет
но случайная конвекция может иметь место [Л.5-82].
Следует также Отметить, что с уменьшением гравитации увеличивается теп-
ловая устойчивость жидкости по отношению к малым возмущениям, и наоборот
5-10. ТЕПЛОВЫЕ ТРУБЫ
Рис. 5-58. Цилиндрическая тепловая труба.
1—капилляр-фитиль; 2 — внешняя оболочка.
Тепловая труба Гровера [Л.5-98] — автономная инженерная конструкция,
которая имеет теплопроводность, намного большую той, которую получают ис-
пользованием однородного куска любого известного металла, Это свойство дости-
гается испарением жидкости внутри замкнутой оболочки, переносом пара в другую
часть сосуда, конденсацией пара и возвращением конденсата в испаритель через
фильтр определенной конструкции.
Преимущества тепловых труб реализуются наилучшим образом, когда трубы
длинные и тонкие, т. е. берется длинный цилиндр или вытянутая тонкая плоская
структура. Для определенности рассмотрим круговой цилиндр с большим отно-
шением длины к диаметру Ход
анализа для других форм оче-
виден, хотя не всегда прост в
деталях. Как видно на рис. 5-58,
такая тепловая труба состоит
Из замкнутой трубы длиной I и
внешним радиусом гр и кольце-
вой капиллярной структуры,
пропитанной смачиваемой жид-
костью, с внешним радиусом rw и
паровым пространством радиу-
сом r.v.
Так как теплота подводятся
к тепловой трубе и отводится от
нее через стенку обычной тепло-
проводностью, то стенка должна
быть максимально тонкой, чтобы
свести до минимума радиальную разницу температур, но, естественно, должна
выдерживать разность внутреннего и внешнего'давлений. Тепловые трубы стано-
вятся эффективными при внутреннем давлении порядка сотой доли атмосферы,
и их эффективность улучшается с увеличением давления.
Детали фитиля допускают широкие изменения, Его не обязательно распола-
гать на внутренней поверхности сосуда, хотя это обычно лучшее место. Так как
испарение и конденсация имеют место на границе раздела жидкость—пар, то
такое расположение фитиля допускает необходимую радиальную теплопере-
дачу, которая происходят через среду более высокой тепловой проводимости
и таким образом позволяет свести к минимуму радиальную разницу температур»
392
Поэтому гидравлический диаметр парового пространства делают максимально
большим, чтобы свести к минимуму градиент давлений вдоль оси в текущем паре,
фитиль может быть сделан из переплетенной ткани, войлока, шлака и тому подоб-
ных материалов или даже выполнен просто в виде канавок или желобков оболочки.
Капиллярная структура характеризуется средним радиусом пор, проницаемо-
стью и объемом жидкой фракции. Рабочая жидкость должна смачивать материал
фитиля; желательно, чтобы она смачивала также стенки оболочки, так как это
улучшает теплопередачу. Допускается небольшой излишек жидкости сверх коли-
чества, требуемого для насыщения фитиля. Недостаток жидкости может умень-
шить максимум теплопередачи за счет уменьшения эффективного объема фитиля
в зоне испарения тепловой трубы.
Факторами, характеризующими
работу тепловой трубы и определяю-
щими ее эффективность, являются:
1)	перенос массы (жидкости) в ка-
пиллярно-пористом фитиле, т. е. ра-
бота капиллярного насоса;
2)	теплосъем путем испарения
жидкости из капиллярно-пористого
тела, т. е. действительный тепловой
поток в испарителе;
3)	гидродинамика процесса пере-
носа массы в паровой фазе от испа-
рителя к конденсатору;
4)	теплопередача при конденсации
пара на пористую поверхность и от-
вод теплоты теплопроводностью через
фитиль и стоику трубы.
Любой из вышеуказанных факто-
Йис. 5-59. Схема расчета цилиндриче-
ской тепловой трубы.
ров может оказаться лимитирующим,
однако в большинстве практических случаев наиболее узким местом в успешном
использовании тепловых труб являются первые два фактора.
В большинстве исследований по гидродинамике и теплообмену в тепловых
трубах задачи решаются приближенно, бея учета взаимосвязи теплопереноса
и массопереноса, между тем как тепловая труба является типичным теплопередаю-
щим аппаратом, где теплообмен взаимосвязан с маесообменом, поэтому задача
конвективного теплообмена является сопряженной задачей.
В условиях ламинарного течения несжимаемого пара внутри тепловой трубы
сопряженная задача математически формулируется так (рис. 5-59) [Л.5-99]:
а)	уравнения переноса в полости тепловой трубы
divn=0; pTo (V .?) = —	+
(5-10-1)
(5-10-2)
где индекс v обозначает пар;
б)	уравнение теплопереноса в капиллярно-пористой оболочке в случае пол-
ного заполнения пор конденсатом можно написать так:
cfpfW(4Tf=KWrft	(5-10-3)
где Wf — скорость движения жидкости (индекс f обозначает жидкость),
Систему уравнений (5-10-1) — (5-10-3) необходимо дополнить уравнением
теплопроводности в корпусе трубы и уравнением фильтрации теплоносителя
через капиллярную структуру, Толщина корпуса трубы (Я2 — RJ значительно
меньше толщины капиллярного фитиля (/?х — R), поэтому перераспределением
теплоты вдоль корпуса можно пренебречь. Зависимость между тепловыми пото-
ками наружной поверхности qSi и внутренней поверхности qsl будет иметь вид
(см. рис. 5-59):
<5-10-4;
393
В качестве приближения будем считать, что фильтрация пара и жидкости
(конденсата) происходит в разных направлениях. Например, для цилиндрической
трубы движение жидкости происходит только в направлении х, а пара — только
вдоль г, т. е.
(iv)x=(if)r=°;	' lr = (iv)r-	(З-Ю-5)
Тогда уравнения теплопереноса примут вид:
I ['	|+1 [Г'1~С (О = °'
При этом коэффициенты теплопроводности теплоносителя и материала кар-
каса фитиля предполагаются близкими и достаточно высокими, что связано с вве-
дением равенства температур каркаса и теплоносителя.
Необходимо различать зону испарения и зону конденсации, так как условия
сопряжения будут разные. Дело в том, что температура образовавшегося при ис-
парении пара отличается от температуры поверхности жидкости. Поэтому для
граничных условий необходимо два соотношения; одно для вкорости испарения
другое для связи между температурой жидкости и пара у поверхности испарения'.
Кроме того, необходимо учесть, что испарение жидкости в пористом фитиле
происходит только с поверхности менисков. Поэтому вводится поправочный
коэффициент с, равный отношению площади испарения ко всей площади фитиля,
через которую проходит пар.
С учетом этих замечаний граничные условия примут вид:
-	СТ(4Р(-1_^=К. (5-io-iD
При > 0
®Г_Л=°-	 <5-'°-12)
Пр» jR=o
Необходимые условия работы тепловой трубы: 1) предельное значение ка-
пиллярного давления рсмакс фитиля с цилиндрическими порами радиусом гс
должно быть равно:
2о cos 6^ о
Рсмаксв—~у.------ g »
(5-10-14)
2) сохранение компоненты импульса нормальной к поверхности испарения или
конденсации
₽о+Р^’=Р/ + Р/ш’+оК,	(5-10-15)
где К — кривизна поверхности.
Используя соотношение (5-10-15) для любых двух точек 1-й я 2-й зоны испа-
рения и конденсации, можно написать (рис. 5-59):
pVi—p-02 — (P/i-PfJ+PmVri —	— (рг,2Уг2-р/^г2)=О1/(1-'О2^2- (5-10-16)
394
Это соотношение определяет капиллярное давление, необходимое для реа-
лизации заданных режимов течения пара и жидкости. С другой стороны, в стацио-
нарных условиях капиллярное давление, определяемое формулой (5-10-16), не
должно превышать рсмакс. Поскольку соотношение (5-10-14) выполняется для лю-
бых Двух точек в зонах цспарения и конденсации, то оно должно иметь место и
там, где левая часть формулы (5-10-16) имеет максимум. Таким образом, условие
работы тепловой трубы принимает вид:
max {(Pvi — Риг) -(Pfl — Pfi) + Pvl^ 1 — Pf^rl — (p^rl—	Pc макс •
(5-10-17)
Это соотношение является наиболее общим условием, позволяющим рассчи-
тать тепловую трубу и найти предел ее теплопередающей способности. Расчет
сводится к следующему: 1) расчет движения жидкости через капиллярную струк-
туру; 2) расчет движения пара в полости тепловой трубы; 3) нахождение мак-
симума левой части формулы (5-10-16) как функции двух переменных — коор-
динат первой и вторых точек — и проверка условий (5-10-17). Расчет движения
пара сложный. В зависимости от тепловой нагрузки пар может быть несжимае-
мым или сжимаемым, а режим движения ламинарным или турбулентным. Дви-
жение сжимаемого пара сопровождается значительными перепадами давления.
Поэтому, как правило, стараются избегать таких условий работы. В литературе
нет данных по величине ReKp (критическое число Рейнольдса в трубе со вдувом
и отсосом). В качестве первого приближения для ReKp принимаем 1250 (ReKp =
= 1250). Определим числа Рейнольдса Re и Маха Л1 по средней скорости лара
в теплоэкранированной зоне по формулам
QR	Q	г—	 срг)
Re = .^^	т=л-,
где — универсальная газовая постоянная.
Тогда можно выделить области ламинарного и турбулентного течения (см.
рис. 5-59). В отличие от движения пара в расчете фильтрации должна быть уч-
тена сила тяжести. Для этого из давления жидкости pj надо вычесть pjgxsina,
где а угол наклона трубы к горизонту.
Для щелочных металлов Re/y>l, поэтому можно пренебречь конвектив-
ными членами в уравнении движения. Для расчета движения жидкости по капил-
лярной структуре можно воспользоваться формулой Дарси.
Давление жидкости вдоль капиллярной трубы может быть представлено
в виде
Р/М = Р/(°)-^'г J J	'	(510-19)
О о
где К — проницаемость; Г — коэффициент, определяемый структурой пористого
фитиля.
Капиллярное давление зависит от радиуса поры в месте нахождения ме-
ниска. Если пористый фитиль имеет капилляры разных размеров, то возможен
случай, когда крупные капилляры частично осушаются, а топкие подают жидкость
на поверхность фитиля. Вследствие этого при работе тепловой трубы в условиях
частичного осушения фитиля степень заполнения фитиля жидкостью изменяется
вдоль трубы, следовательно также изменяется и коэффициент проницаемости.
При частичном осушении теплообмен фитиля осуществляется при условии углуб-
ления поверхности испарения (см. гл. IV).-
Обычно принимают коэффициенты теплопроводности жидкости и материала
каркаса фитиля близкими, что оправдывает введение для них одной температуры.
Тогда можно написать:
dll. д / ,дТ\ ,	1 dri„ i д I дт\ аьъ
= °- (5'10’20)
395
где hv — энтальпия образующегося пара — берется при температуре
+ 4р (Г) (2-а) [« + ₽ (I - a)]L/r, V Т Г (' ’21>
Изменение потока пара вдоль оси г связан0 с испарением внутри
фитиля. Если через обозначить суммарную площадь свободной поверхности
жидкости в единице объема фитиля, то можно написать:
drjvr __ __ 2а -ж / И Р»_ Р (Л 1 гс
дг	2~а г 2лД*1_/7\ V Т J 1‘
Если обозначить пористость осушенных пор е” для сечения фитиля, нормаль-
ного к оси г, то
(5.1М2)
где fi — коэффициент, определяемый геометрией капилляров, т. е. их извили-
стостью и пористостью.
Уравнения (5-10-20)—(5-10-22) описывают распространение теплоты через
капиллярную структуру в областях ее частичного осушения. Фильтрация тепло-
носителя описывается уравнением Дарси
dpy Vf
(5-10-23)
Для определения давления жидкости вдоль фитиля необходимо задать его
значение в какой-либо точке. При осушении фитиля появляется избыток теплоно-
сителя, который потоком пара оттесняется в зону конденсации. Поэтому в точке
минимальной кривизны свободной поверхности жидкости хМИ1| имеет место соот-
ношение
(Pf)x мин == (Рv)x мин — к-,	(5-10-24)
л •
d г
а Хмин определяется из условия [p-в—P/Lr мии = 0-
Если в зоне конденсации нет корня уравнения, то хмин = I. На основе вы-
шеприведенных уравнений в работе [Л.5-98] был проведен численный расчет для
натриевой тепловой трубы. Исходные данные: радиус отверстий фитиля 0,1 мм,
пористость 0,5, коэффициенты конденсации и аккомодации а = 0,1; 3 = 0,1.
Результаты расчетов приведены на рис. 5-60 для трех значений температуры
при пропорциональном изменении каждой зоны (IJI = 0,36; lzH — 0,5; Rx =
— 1 см). При работе трубы в вертикальном положении (кривая 4) QMaKC увели-
чивается мало по сравнению с горизонтальным расположением трубы. Одновре-
менно с рассмотренным методом расчета сделаем упрощенный расчет тепловой
трубы. Теория расчета приведена в 1-м издании справочника. Рассмотрим ста-
ционарный режим работы тепловой трубы. Примем следующие допущения:
1) площадь конденсатора значительно больше площади испарителя; 2) тепловой
поток, температура жидкости и пара постоянны по всей длине хт конденсатора,
причем пар имеет постоянное давление р„; 3) пар конденсируется на поверхно-
сти конденсатора и имеет постоянную ^скорость оп, перпендикулярную к поверх-
ности; 4) пористый фитиль является изотропным и несжимаемым. Тогда получим
общее интегральное уравнение энергии (неразрывности) импульса в виде
R"(x = x _)	х	х„
f dR f Q П/ f
- \	\	\	1, nw .	(5-Ю-25)
R' (* —0)	0	0
где xm — длина конденсатора; й0 =	— hf, у/ — удельный вес k = К'1»
396
Чтобы проинтегрировать уравнение (5-10-25), нужно знать пределы инте-
грирования.
В зоне конденсации тепловой трубы радиус поверхности раздела жидкость—
пар достаточно большой, и его можно принять стремящимся к бесконечности
(£"-> оо). В зойе испарения жидкости величина R' должна иметь какое-то мини-
мальное значение. Ее можно оценить, как /?мин = rc sec 6, где гс — эквивалент-
ный радиус капилляров. На практике R' можно найти по формуле Жюреиа.
(Вт/м2) от длины трубы I
(теплоноситель — натрий,
— 1 см); а = 0.
вым потоком q для разных зна-
чений /мвКс/^(СМ?) ДЛЯ воды при
б =» 0,25 см и т = 350 К-
/- 117 К; 2— 1075 К; 3 — 973 К;
4 — 973 К; а=-g-л; 5 - 973 К.
I— *макс/*= 1.37 '	2~ *макс/* =
= 0,63- 10-*; <У —/макс/Л=0,13- 10-*.
При расчете трубы обычно приходится находить максимальную длину ее
при заданном тепловом потоке, или, наоборот, определять максимальный тепло-
вой поток при заданной длине.
Для расчета максимальной длины конденсатора хт положим, что
при х=0
при х~хт
/?’-* оо;
R' Ямин*
Используя эти пределы, мы можем проинтегрировать уравнение (5-10-25)
и решить его относительно хт:
’Р/М Г	46	1'| 1/2
.	L^-™ (l JJ
(5-10-26)
Из формулы (5-10-26) при некотором ее упрощения получаем формулу
для максимального теплового потока:
<2«.KC=2A'('“VA^-jfe).	(5-10-27)
\xmJ \go ° / \ « /
Следует указать на то, что в формуле (5-10-27) не учитывалось влияние гра-
витации. Если учесть влияние гравитации, то уравнение (5-10-27) будет иметь вид,-
&„С=Ы-)	Sin 9] .	(5-10-28)
L \хт/ \ga а / rt, go \1„акс/ J £
На рис. 5-61 показана зависимость между максимальной длиной трубы и
рассеиваемым потоком теплоты для разных значений параметра /маКс/£| постро-
енная по формуле (5-10-27),
397
В большинстве тепловых труб секции испарения по площади меньше сек-
ции конденсатора, они не оказывают влияния иа работу конденсатора, пока теп-
ловой поток не достигнет критической величины. Однако в устройствах, пред,
назначенных для передачи малых тепловых потоков, испаритель может быть зна-
чительно длиннее конденсатора,
В заключение можно отметить, что для успешного применения тепловых
труб в космосе необходимо учитывать два фактора, связанных с работой конден-
сатора:
1) тепловой поток, при котором в испарителе начинается кажущееся пле-
ночное кипение;
2) максимальный поток жидкости, который может перекачиваться капил-
лярно-пористым телом в испарителе.
Для оценки эффективности работы капиллярного насоса была проанали-
зирована упрощенная схема, согласно которой работа капиллярного насоса за-
висит от параметров lHiKZ/k, N'. Оба эти параметра должны иметь как можно боль-
шую величину, чтобы устройство успешно работало.
Параметром капиллярного насоса является отношение максимума капилляр-
ных сил к силам трения при движении жидкости по фитилю.
Постоянная /мвКС является величиной, характеризующей действия капилляр-
ных сил в пористом фитиле. С точки зрения физики явления, /макс является высо-
той, на которую жидкость может подняться по вертикально поставленному об-
разцу капиллярно-пористого тела.
Постоянная /г характеризует действие сил трения, возникающих при движе-
нии жидкости через капиллярно пористое тело, когда применим закон Дарси.
Эту константу можно получить, измеряя перепад давлений в пористом, мате-
риале, по которому движется жидкость.
Таким образом, для анализа эффективности работы устройства необходимо
раздельное экспериментальное исследование величин /м&ке и k.
РАЗДЕЛ ШЕСТОЙ
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФУЗИИ ТЕПЛОТЫ И МАССЫ
6-1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛОМАССОПЕРЕНОСА
В данном разделе приводятся результаты последних работ в области неста-
ционарного переноса теплоты и массы в капиллярно-пористых телах и пористых
средах. Полученные аналитические решения могут быть использованы для рас-
чета взаимосвязанного тепломассопереноса в других системах. Большой вклад
в разработку методики решения и получения самих решений системы дифферен-
циальных уравнений тепломассопереноса внесли Ю. А. Михайлов [Л.6-1] и
М. Д. Михайлов [Л.6-21, которые весьма успешно продолжают работать в этой
области.
Примем следующую систему обозначений: индекс 1 обозначает пар, 2 — жид-
кость (вода), 3—лед, 4 — сухой воздух с приведенной молекулярной массой
М = 29, 0 — скелет пористого тела.
На основе закона сохранения массы вещества локальная производная объ-
емной концентрации г-го связанного вещества по времени равна сумме диверген-
ции потоков массы и источника t-ro вещества, обусловленного фазовыми пере-
ходами, т. е.
= ~ div Ci даф+Й моль)-4-Jj,	(6-1-1)
где 7<диф и /моль ~ соответственно плотности диффузионного и молярного пото-
ков i-ro связанного вещества.
В соответствии с соотношением (5-7-10) уравнение (6-1-1) перепишем так:
^^=-div(f;„,t+npA£)+.//.	(6-1-2»
398
При этом необходимо иметь в виду, что Vi является скоростью конвективного
(молярного) переноса; она отлична по своей физической природе от линейной ско-
рости диффузионного переноса 7/Д|,ф = 7ЛИф/Рь
Источники i-ro вещества обусловлены фазовыми переходами, поэтому их
сумма равна нулю:
£/,=0.	(б-1-з)
Если пренебречь усадкой тела (р= р0 = const), то уравнение (6-1-2) можно
Переписать в виде
Ра 7^- = — div (Tlxiit + nplbivi) +J-I.	(6-1-4)
Дифференциальные уравнения переноса теплоты получаем из уравнения
переноса энергии: локальная производная объемной концентрации энергии равна
дивергенции плотности потока энергии, Обычно для твердого тела изохорную
теплоемкость cv принимают равной изобарной теплоемкости ср, т. е. ср = cv = с.
Следовательно, для капиллярно-пористого тела локальная производная от объем-
ной концентрация энтальпии по времени равна дивергенции плотности потока
энтальпии, включая перенос энтальпии за счет конвективного и диффузионного
(молекулярного) движения:
(ЛоРо + ^AipoU,-)=— div {j д 4~	hi (ii диф 4-	,	(6-1 -5)
Где у — плотность потока теплоты, передаваемой путем теплопроводности,
Г?=— XgradT = — ОТ;	(6-16.)
здесь — суммарный коэффициент теплопроводности, характеризующий моле-
кулярный перенос теплоты через скелет пористого тела и связанное с ним вещество.
Обозначим удельную теплоемкость через
dh,
C‘~dT '
(6-1-7)
Тогда будем иметь:
(«оРо +2 ^Ро«()	+ Р« У = div (WT) Cl ffi днф + П^Ьм) VT -
i	i	i
— div(/\ диф4-/7р;^0().	(6-1-8)
Если умножить все члены уравнения (6-1-4) на hi, просуммировать по всем£
(t-=0, 1, 2, 3, 4) и полученные соотношения использовать для замены вели-
чины Л;-ро соответствующим выражением, то получим:
£ро = div (Л.р7’)4“^^(А	(/I лиф 4"^Р^/у/)	,
(6-1-9)
где с—приведенная удельная теплоемкость тела, равная:
c=c<i+£<W
(6-1-10)
Уравнение (6-1-9) совместно с (6-1-4) составляет наиболее общую систему
дифференциальных уравнений массотеплопереноса в капиллярно-пористых телах.
399
Дифференциальные уравнения фильтрации
Из уравнения (6-1-4) как частный случай получаются уравнения движения
жидкостей в пористых средах.
Если положить po«j = /7fyp/ (отсутствие физико-химической связи вещества
со скелетом пористого тела), /,• = 0 (отсутствие источника вещества) и ДИф = о
(отсутствие диффузионного переноса), то из (6-1-4) получим уравнение фильт-
рации несмешивающихся жидкостей (i=l, 2, 3...) в пористой среде;
П д (рф) = _ djv-,(моль= _ div р, (ур _ pvA) pij _	(6-1-11)
Плотность фильтрационного потока у7моль определялась из соотношения
—	—	k>
!i моль= npibiVi =	~ (Ур—pVA),	(6-1-12)
где k — общая проницаемость; — относительная проницаемость t-й фазы.
Монокапиллярная структура тела
В монокапиллярно-пористом теле (с монокапиллярной структурой) перенос
жидкости происходит с некоторой конечной скоростью ^кап, обусловленной дей-
ствием капиллярных сил = и^кап)- В большинстве случаев перенос пара и
воздуха в порах тела происходит диффузионным путем (взаимная диффузия пара
и воздуха). Только при наличии градиента общего давления (grad р) внутри пори-
стого тела будет фильтрационный перенос пара и воздуха. Известно, что при
наличии испарения жидкости с поверхности мениска капилляров взаимная диф-
фузия пара к воздуха вызывает конвективный перенос влажного воздуха (сте-
фановский поток), однако этот вид переноса можно учитывать путем введения
множителя в формулу для диффузии пара в паровоздушной смеси, так как ли-
нейная скорость конвективного переноса Стефана прямо пропорциональна
градиенту концентрации пара или градиенту парциального давления пара. Ана-
логичным путем вносится поправка на диффузионное скольжение. Кроме того,
под влиянием теплового скольжения влажный воздух движется с некоторой
скоростью, которая прямо пропорциональна температурному градиенту. Поэтому
этот вид переноса учитывается в виде составляющей термодиффузионного пере-
носа.
Таким образом, полагаем /2дйф = 0 (отсутствие диффузии жидкости), тогда
система дифференциальных уравнений массопереноса будет иметь вид:
р» = —й1т(ЙДИф)+Л;	(6-1-13)
Ро^ = —div(/7p262O2Mn) + A; .	(6-1-14)
Ро^-= — divO. диф)Н-А'	(6-1-16)
Так как в инертном газе (сухом воздухе) химические превращения отсут-
ствуют, то Jt = 0; фазовые превращения в области температур выше 0°С соот-
ветствуют переходу жидкости в пар.
Из этого следует, что У2 = — Л- Поскольку содержание пара и воздуха («1 4-
4- и4) в порах тела ничтожно мало по сравнению с влагосодержанием жидкости
«2 (и = Ui 4-	4- u* ~ u2), то изменением концентрации влажного воздуха
в капиллярах тела пренебрегаем (p^dUi/dx — O; p^ajdx = 0).
400
^7ра — — div (/7р2&2??2 кап) — div jj диф!
(6-1-16)
А— —	— — div Д диф»
(6-1-17)
div /4 диф — О-
(6-1-18)
Тогда исходя из уравнений (6-1-16)—(6-1-18) можно написать:
Пра	—I” иа KanVfiaj--------- /7рай2 div иа аап— div /j диф*
(6-1-19)
Скорость капиллярного движения Е^кап зависит от среднего радиуса капил-
ляра г, поверхностного натяжения о и коэффициента вязкости г)2-
Скорость капиллярного движения определяется формулой (5-7-23). Поэтому
для одномерной задачи дифференциальное уравнение (6-1-19) можно написать
так:
4	и;.,.™
дт Г)а х дх}	2 »]а х2 ’	' f
где В — постоянный коэффициент. 
Таким образом, для макрокапиллярно-пористого тела с монокапиллярной
структурой div Сакаи не равна нулю.
Коллоидное капиллярно-пористое тело
Выше было установлено, что влагоперенос парообразной (i = 1) н жидко-
образной (i = 2) влаги описывается следующими соотношениями:
(=1.2,	(6-1.21)
а суммарный перенос пара и влаги равен;
7-71+71=-®„Po’“-em₽oV7’=-°™₽0 (VU + 6VT).	(6-1-22)
Следовательно, система дифференциальных уравнений массопереноса будет
иметь вид1:
₽»^=-<Wi + A;	(6-1-23)
д,^- = -<11у7а + /3.	(6-1-24)
Суммируя (6-1-23) и (6-1-24), получаем:
Ра|2- = —div7i —div72.	(6-1-25)
Подставив вместо и и /г соответствующие выражения, получим:
Р« % =	[«,’“ +°™Р»’Т]+ div [Wov“+a«»₽oT7’}	(6- i -26)
Дифференциальное уравнение переноса теплоты будет иметь вид:
сро ~ = div	(6-1-27)
1 В дальнейшем индекс «диф» у потока массы j опускаем.
401
Источник жидкости J2 = /i2 определяется из уравнения (6-1-23), для чего
полагаем dujJdr^O;
J.2= J12= — J1 = — div/f.	(6’1-28)
Следовательно, 
C₽“ W = diV (W7') + ria d,v (<,'»IP»v“+°XtPo''7')—2 c^T'	t6'1’®)
Для зональной системы расчета, когда для каждого интервала (зоны) и и Т
коэффициенты переноса A, aml, am2, а[гЛ, а„2 полагаем постоянными, система диф.
ференциальиых уравнений тепломассопереноса будет иметь вид:
= ат рти + №7];	(6-1-30)
=	+aml	V2«-[(Ciaral + cs«ra2) Ги +
+ (с1“™+с2“м)тг]Г7’/С.	(6-1-31)
Рассмотрим некоторые частные случаи,
Связанное вещество жидкость — лед (I = 2,3). Имеем систему пористое тело-
жидкость — лед; процессами испарения льда (сублимация) и конденсацией пара
непосредственно в лед (аблимация) пренебрегаем (/Э1 = —Jl3 = 0).
Дифференциальное уравнение массопереноса для твердой фазы (( = 3) свя-
занного вещества значительно упрощается, так как переноса льда не происходит
Po = — div/a4-7а;	(6-1-32)
Р»^- = 23.	(6-1-33)
где J2 = J32 = —723 = —J3 — источник жидкости, обусловленный таянием
льда. Следовательно, уравнение (6-1-32) можно написать так:
Р» = - div’A + p»^-.	' (6-1-34)
При этом предполагаем, что пористое тёло имеет поликапиллярную струк-
туру, в которой перенос жидкости происходит путем капиллярной и молекуляр-
ной диффузии.
Обычно при рассмотрении систем, содержащих лед, вводится коэффициент
льдистости в8, равный отношению массы льда к массе вс£й влаги т:
=	, -g-.....,	(6-1-35)
/И	-f-Ug -j- Uj-f- U4 u2 -f-
так как массосодсржание пара и воздуха ничтожно по сравнению с массосодержа-
нием жидкости и льда.
Если тело не содержит льда (и3 — 0), то коэффициент е3 = 0. Если вся вода
превращается в лед (^ = 0), то е3 = 1. В большинстве случаев е3 < 1 (0 < е3 <
Пользуясь соотношением (6-1-35), находим:
du = e3du3,	(6-1-36)
откуда
(6-1-37)
402
Тогда дифференциальные уравнения массотеплопереноса будут иметь вид:
^^2 ___	I /1 V^T4 ^3	1^И2 .	/с | оо \
— Я_,„ V ~т~о„,л V I ,	----.	(О -1-00)
дх 012	1 m2 1 _ Сз дх ’	*•	>
^ = аТ2Г+?(Г^^-+с’(“™2Т“ + “™Т7')^ ' (6-1-39)
где г^з — удельная теплота замерзания жидкости (плавления льда); с — удель-
ная теплоемкость, равная:
С = ^о4~ с2^2 4-C3W3.	(6-1-40)
Эту систему дифференциальных уравнений можно написать так:
'	(6-1-41)
т] ’’f+V« V Л+С2 (“«’“+“>) V7’/c- (б-1-42)
Связанное вещество пар — л*д (i = 1,3). Пользуясь рассмотренным методом
определения источника 7а1 и полагая е3= I, находим:
, ди3 ди .
J— Ро"^“ — Р° dx (и~из),
получаем систему дифференциальных уравнений массопереноса:
* =[a„Jv2«+aJ1V3T].	(6-1-43)
= (И+“Г “»1) + Т~ “»1Л + Т (“mv“ +“mivr)	te’’-44)
где гуз — удельная теплота сублимации льда; с—удрльпая теплоемкость,
равная:
с—Co-f-CjUj с3и3.	(6-1-45)
Поскольку фильтрационный перенос массы в пористом теле отсутствует,
то в дифференциальном уравнении теплопереноса членами	можно
пренебречь. Тогда система дифференциальных уравнений тепломассопереноса
будет иметь вид:
^- = 7<11Т!И+^12Т2Г;	(6.1-46)
^ = Кгг^Т+К^и,	(6-1-47)
при этом коэффициенты 7<1а и Т<21 не равны между собой.
Для системы 1=1, 2
=	K1:t = ^ = am6;	(6-1-48)
^3=“+<.V;	(б->-«)
Для системы i=2, 3
^““«('-'з):	(в-1-50)
ка,=а+(1-Ез)°мг?;	(6’‘’51>
403
Для системы f= 1, 3
KU“"W K,l=“»r	(6-1-52)
Kaa=°+“»/f:	С6'1'63)
Уравнения (6-1-46) и (6-1-47) справедливы не только для нестационарного
состояния, но и для стационарного (ди/дх^О или dT/dx = Q).
6-Х ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЛАГОТЕПЛОПЕРЕНОСА
В ПРОЦЕССЕ СУШКИ
В капиллярношористых влажных телах в процессе сутки конвективная
составляющая переноса теплоты в уравнении теплопереноса (6-1-29) мала
по сравнению с кондуктивной составляющей div (Х^7).
К этому результату можно прийти на основании следующего анализа. Из-
вестно, что при (GrPr) <£ 1 • 10s суммарный коэффициент теплопроводности в дис-
персных средах равен коэффициенту молекулярной теплопроводности, т. е.
перенос теплоты происходит при помощи теплопроводности. Величина GrPr =
= 1-Ю3 соответствует эквивалентному числу ₽еэ = 22. Сделаем оценку этой ве-
личины. Наибольшая интенсивность переноса влаги при сушке в конвективных
сушилках составляет примерно 40 кг/(м4-ч). В самом неблагоприятном случае
диаметр эквивалентного капилляра d3 составляет около 3 мм (пористость тела 70%).
Вязкость воды г]2 при температуре 30°С равна 2,88 кг/(м-ч). Тогда число
,'ad,	40.3-10-3
R ’~ V?	0,7.2,88	’
т. е. значительно меньше 22. Поэтому величиной S ctfcT по сравнению с div'(AvT’)
можно пренебречь. Тогда система дифференциальных уравнений диффузионного
влагопереноса при отсутствии градиента общего давления будет иметь вид:
g-KtM+KaW;
дТ
(6-2-1)
(6-2-2)
где коэффициенты	Кц, Кц определяются соотношениями (6-1-48) и
(6-1-49).
Система уравнений (6-2-1) и (6-2-2) является наиболее общей, она справед-
лива не только для процессов сушки влажных материалов, но и для любого вида
влаготеплопереноса.
Процесс сушки является типичным нестационарным процессом тепломассо-
переноса. Для него источник влаги /2 = —Л может быть выражен через локаль-
ную производную влагосодержания по времени (du/dx). Воспользуемся методом
расчета, впервые приведенным в [Л.6-3].
Общее изменение влагосодержания тела du равно изменению deu в резуль-
тате переноса влаги и изменению d-u за счет фазового превращения жидкости
в пар, т. е.
du = deu-\-diu.	(6-2-3)
При этом предполагается, что общее влагосодержанне тела равно удельному
содержанию жидкости (« = их «j = Uj), т. е. в рассматриваемой системе
i = 1,2, щ = 0.
Если процесс влагопереноса нестационарный (du 0), то отношение dtu/du
будет конечной величиной, характеризующей относительное изменение влагосо-
держаиия за счет испарения по отношению к общему изменению влагосодержа-
ния в данной точке тела, Эта величина называется критерием или коэффициент
404
том фазового превращения жидкости в пар и обозначается через
djti
du. ’
(6-24)
Если diU ~ 0, то коэффициент е = 0, т. е. изменение влагосодержания про-
исходит только за счет переноса жидкости; при отсутствии переноса жидкости
(deu ~ 0), когда изменение влагосодержания тела в любой его точке происходит
только за счет испарения, коэффициент е=1. Следовательно, в общем случае
коэффициент е изменяется от нуля до единицы (0 е 1) и система дифферен-
циальных уравнений влагопереноса будет иметь вид:
= <зтзГ2и Н-QjTjiSV2?1 -J-e ;	(6-2-5)
= = «W+8 ГЛ- д^-.	(6-2-6)
от 1 с дх	*•	'
Сравнивая уравнение (6-2-5), которое можно переписать в виде
- Ж = (Й)-172“ + ^П,	(6-2-7)
с уравнением
(6-2-8)
которое справедливо для самого общего случая, можно прийти к заключению,
что они будут тождественны при условии выполнения равенств
“«“««/О-е); 6 = 6,.	(6-2-9)
Отсюда следует, что коэффициент
е=—=	(6-2-10)
'	Oml + O/na ат
Системы уравнений влаготеплопереноса (6-2-5) и (6-2-6) или (6-2-6) и
(6-2-8) могут быть записаны в виде системы уравнений (6-2-1) и (6-2-2), но
при этом коэффициенты Д'у (с = 1,2; (=1,2) будут равны:
(6-2-11)	
Кя=а + 6 ® Y^=°+B ~ М:	
	(6-2-12)
^=er&=8rf	
Таким образом, источник парообразной влаги для нестационарного влаго-
теплопереноса в процессе сушки выражается через соотношение
А=-Л = ер»^.	(6-2-13)
Оно аналогично соотношению (6-1-37), только вместо коэффициента испаре-
ния е в него входит коэффициент льдистости е3.
Соотношение (6-2-13) дает возможность выразить коэффициент в через
абсолютные значения потока жидкости |Je| и потока пара |7f|. В самом деле,
ди
представим вместо р0 соответствующее выражение
P»5~ = -<Hv7i-dlv/J
и воспользуемся равенством
Ja = = 71S=-^ div*fa.
405
Тогда будем иметь:	"
^2^8po^- = -E(div7i4-div72) = — div/i,
откуда
с... _div7i -Л । div28 V
div7i4-div/j \ ' div7i
(6-2-14)
ч
(6-2-16)
Для одномерных задач, когда векторы 71 и7г направлены параллельно
или антипараллельно, имеем;
div7a _Adldx}ii
divT, (д/дх) ii'
(6-2-16)
Если положить e = const, то, очевидно, и отношение (6-2-16) должно быть
постоянным и равным )7V17il=const> а из формулы (6-2-15) получаем:
17x1
Ш+Ш ’
(6-2-17)
Для сушки влажных материалов соотношение (6-2-17) можно написать
так;
г _ gni(v^4-6iVan
ат(^и^^Т) •
(6-2-18)
Если в соответствии с формулой (6-2-9) положим б=61 — б2, тогда полу-
чим равенство е = ат1/ат, что уже было установлено выше.
Таким образом, введение коэффициента е как характеристики отношений
потока жидкости и пара при нестационарном влагоперсносе в процессе сушки тре-
бует соблюдения равенства (6-2-9) или (6-2-17). Эти равенства выполняются в об-
ласти гигроскопического состояния влажных материалов. Введение коэффи-
циента 8 при помощи отношения (6-2-4) нс требует выполнения ряда требований,
в том Числе и постоянства его относительно координат.
Можно было считать формулу (6-2-17) за основу при выводе дифференциаль-
ных уравнений влаготеплопереноса, как это было сделано в [Л.6-4],
Из соотношения (6-2-17) следует.
1/7| = ]-ГТ !	(6-2-19)
Имеем;
/1 = 1/ii I/х ];	/2=1лз1/з],	(6-2-20)
где U и Тл2 — единичные векторы, направленные вдоль векторов и 7г. Тогда
из дифференциального уравнения
Ро = — div71 — div 7а	(6-2-21)
получаем:
Ра = div'tm '7 | — div ~ div I^i-div7a.
Если положить 1л1=Тя2, а это означает, что векторы и /2 направлены
одинаково, то получим:
Р» 5(7 = - div -|~^г72 - div7s-	(6-2-22)
Далее, предполагая, что коэффициент 8 не зависит от координат (e=const),
из (6-2-22) получаем
Ро “ div 7а 4- еро ~,	(6-2-23)
406
откуда находим выражение для источника влаги:
А=вРо •	-	(6-2-24)
Предположение о равенстве векторов 1л1 = 1л2 применительно к процессу
сушки означает, что векторы
/1 = —ат\ (Уи-\-&1УТ) р0;	(6-2-25)
/а = — ат2 (Vu-J- Ро	(6-2-26)
должны быть одинаково направлены, для чего необходимо, чтобы 6i=62-
Требование соблюдения равенства 6i = da будет выполняться в гигроскопи-
ческой области.
Необходимо отметить, что выражение (6-2-24) для источников влаги
ди , Л
справедливо только для нестационарного влаготеплопереноса, когда О-
ди л ,, .,	diU
Для стационарного влаготеплопереноса = 0- Коэффициент в =	Так
так du=0. Поэтому величина источника J2~со-0 есть неопределенность.
Чтобы раскрыть эту неопределенность, воспользуемся уравнением (6-2-5),
из которого следует.-
^^-“т2^-атА^Т	(6-2-27)
При стационарном состоянии д«/дт = 0, следовательно,
= - ат ртв+в*г»Т)=1 dlv/a,	(6-2-28)
ОТ	ро
С другой стороны, из дифференциального уравнения при ди/дг — 0 полу-
чим:	_	—
div/a=— div /j.	(6-2-29)
Таким образом, для источника влаги при стационарном ее потоке получаем
выражение
/2 = еро |^ == div 7а = — div ft,	(6-2-30)
т. е. соотношение (6-2-15).
Следовательно, уравнение для источника влаги
/2=—div7i = div po(amiVu	(6-2-31)
является более общим, справедливым как для нестационарного, так и для
стационарного влаготеплопереноса во влажных телах.
Таким образом, система дифференциальных уравнений (6-2-1) и (6-2-2)
остается прежней, только коэффициент Кц определяется формулами (6-2-11) и
(6-2-12).
Отсюда следует также, что коэффициент е является характеристикой
нестационарного влаготеплопереноса, аналогичной карактеристике т для
нагревания или охлаждения тела в стадии регулярного режима.
Темп нагревания
—	(6’М2)
является конечной величиной:
т = -£-В(Ч>,	(6-2-33)
.	R&
где ф —неравномерность температурного поля, изменяющаяся от 0 до 1 (0^
«5ф^1); R—гидравлический радиус тела; Bi —число Био. В стационарном
-407
состоянии ЭТ/Эт=О, а величина у^=сс (Т ==7'с). Следовательно,
аналогично коэффициенту е темп нагревания т является характеристикой
нестационарного теплообмена. Однако это не означает, что пои нестационарном
теплообмене величина т будет переменной, изменяющейся отМ) до со.
Следует отметить, что для расчета нестационарных полей температуры и
влагосодержания тела в процессе сушки необходимо знать коэффициенты а,
ат< ат' R н термодинамические характеристики с и г.
Однако если воспользоваться более общим соотношением (6-2-30), то теп-
лофизическими характеристиками будут а, с, г, ат1, а?, ат, а^. Таким образом,
введение коэффициента 8 уменьшает количество параметров с 7 до 6. Во всех слу-
чаях система дифференциальных уравнений влаготеплолереноса (6-2-1) и (6-2-2)
остается одной и той же, только в решениях этой системы выражение коэффициен-
тов К if будет разное в зависимости от теплофизических характеристик.
Диффузионно-фильтрационным влаготеплоперенос
При высокоинтенсивном процессе сушки (сушка токами высокой частоты,
кондуктивная сушка и т. д.) внутри влажного материала возникает градиент
общего давления влажного воздуха. В результате возникает дополнительный
перенос влаги и теплоты ввиду наличия гидродинамического (фильтрационного)
движения пара и жидкости.
Градиент общего давления внутри тела возникает в результате испарения
жидкости и наличия сопротивления скелета тела при движении пара. Этому спо-
собствуют наличие микрокапилляров, через систему которых идет молекулярное
(эффузионное) натекание воздуха из окружающей среды, и диффузия скольже-
ния в системе макрокапилляров.
В этом случае система дифференциальных уравнений влаготеплопереноса
применительно к процессу сушки имеет вид (подробно см. [Л.6-1]);
;	(6-2-34)
дТ
= W2«4-.	(6-2-35)
дР
£ = KalV2u + KaaV*T4-K83V2P,	(6-2-36)
где коэффициент Ktf, ij — 1» 2, 3 равны:
ku=v	^iS=“»,6=(“L+“L).'	«13=«л/р0:	(6-2-37)
=	(6-2-38)
Ks, = -V!L6:	(6-2-39)
CP	cp	X	cp /
где kp—коэффициент фильтрационного переноса влаги, определяемый из урав-
нения /р= —fepVp; ^—относительный коэффициент фильтрационного потока
влаги, 6р = йр/а^р0;	коэффициент конвективной фильтрационной диффузии
[а =—£-); сп—коэффициент емкости влажного воздуха в пористом теле,
\ £рРо1
определяемый соотношением d (Ui-j-u4)=cpdp. Если учесть изменение (^ 4-Ц4)
в зависимости от температуры, то к коэффициентам K3i (t = l, 2, 3) надо доба-
вить соответственно
^ратЬр.	(6-2-40)
408
Однако в случае фильтрационного переноса в уравнение переноса теплоты
(6-2-35) необходимо добавить члены, характеризующие перенос теплоты
конвекцией,

(6-2-41)
которые в ряде случаев значительно больше, чем члены диффузионного пере-
носа теплоты.
Приведенные уравнения влагопереноса справедливы для однородного влаж-
ного тела. Для системы влажных тел они также справедливы, ко надо учитывать,
что на границе соприкосновения влажных тел существует скачок влагосодержа-
ния. Это обусловлено тем, что влагосодержание тела не является потенциалом
переноса влаги, оно аналогично энтальпии, а не температуре.
Скачок влагосодержания на границе соприкосновения тел определяется по
влагоемкости соприкасаемых тел ст. На границе соприкосновения влажных
тел имеет место равенство потенциала влагопереноса 0(/+ij и скачок вла-
госодержаний
(6-2-42)
ст +
Система уравнений (6-2-34)—(6-2-39) будет справедлива, если вместо влаго-
содержания и поставить потенциал влагопереноса 0. При этом значения коэффи-
циентов /С/у определяются аналогичными соотношениями, например коэффици-
ент б надо заменить на б/ст, а бр на &р!ст н т. д.
Рассмотрим предельные переходы.
1,	Пусть в процессе тепловлагопереноса температура влажного капилляр-
дТ л т
ио-пористого тела не изменяется с течением времени, т. е. ^- = 0. Тогда возможны
два случая:
1)	из уравнения (6-1 -47) следует, что v2T = 0 и v2u = 0. Это тривиальный
случай равновесного состояния (температура и влагосодержание не изменяются
не только с течением времени, но и не зависят от координат и = const и Т =
= const) или стационарного состояния (температура и влагосодержание •— линей-
ные функции координат);
2)	поскольку Т = Т (Xj, т) и и — и (Х(, т), то при ® 0 из (6-1*47) сле-
дует;
V2U=	0	}=/ ft),	(6-2-43)
Лг!	1	>
т. е. поля влагосодержания и температуры подобны (где и* и 7’* — соответст-
венно безразмерные влагосодержание и температура). Так как вид функции
распределения f (х{) не зависит от времени, то согласно уравнению (6-1-46) ло-
ди
калъиая скорость тоже не будет зависеть от времени,
В частном случае при
ди
дт =
const
(6-2-44)
распределение температуры и влагосодержания в одномерных задачах описы-
вается простой параболой. Такой случай имеет место в периоде постоянной скоро-
сти сушки. Влагосодержание в любой точке является линейной функцией вре*
меня {—= const), а распределение влагосодержания по толщине тела (неогра-
ниченные пластина и цилиндр, шар) описывается параболой. Температура в лю-
бой точке тела не изменяется с течением времени = 0^. Если в периоде по-
стоянной скорости сушки испарение происходит внутри тела (в =£ 0, ami =£ 0),
409
то и распределение температуры в-соответствии с равенством (6-2-43) описывается
в таких одномерных задачах параболическим законом, так как Ка1 0.
3)	В частном случае при отсутствии испарения влаги внутри тела в периоде
постоянной скорости (е = 0 или ат1 = 0) температура во всех точках тела будет
одинаковой и в первом приближении равна температуре мокрого термометра’ТЛ}
(Т — Тм = const, v2T=0). Это не противоречит соотношению (£-2-43), так
dT
как при v2T = 0 е = 0 и — 0, а К22	0, v2u 0. В самом деле, при =
= 0 из (6-1-47), которое можно написать в виде
=	+	(6-1.473)
следует, что при е == 0 v2T = 0, откуда из уравнения (6-1-46) получаем класси-
ческое уравнение диффузии
^ = KiiV2«,	(6-1-46а)
т. е. перенос влаги в периоде постоянной скорости сушки происходит при изо-
термических условиях.
При постоянной скорости сушки (dQ/dx = const) локальная скорость
также будет величиной постоянной. Тогда из (6-1-46а) следует:
фи = const при = const.
(6-2-43а)
Это наблюдается при сушке медленно сохнущих коллоидных тел, например
при сушке желатины.
Все описанные выше случаи распределения влагосодержания и температуры
наблюдаются в периоде постоянной скорости сушки капиллярно-пористых колло-
идных тел и в настоящее время являются экспериментальными факторами в ранге
экспериментальных законов.
2,	Пусть в процессе тепловлагопереноса влагосодержание тела не изме-
няется с течением времени (квазистационарное состояние при нагревании влаж-
ного тела), т. е. = 0.
’ дх
Тогда из (6-1-46) следует:
Vau =	V2^ ПРН 5F=0-	(6-2-45)
Если	и К1а = afn 0, то поле влагосодержания подобно
полю температуры. Однако при = 0 локальная скорость 0 в соответствии
с уравнением (6-2-35), т, е. профиль температуры внутри тела не изменяется с те-
чением времени, так как температура в любой точке тела изменяется от вре-
мени по одному и тому же закону. Такие случаи наблюдаются в эксперименталь-
ной теплофизике, например в методе квазистационарпого нагрева влажного тела
при определении термоградиентного коэффициента и коэффициентов температуро-
проводности и теплопроводности влажного тела. В этом методе влажное тело на-
гревают с постоянной скоростью (температура окружающей среды является ли-
нейной функцией времени). С некоторого момента времени температура в любой
точке тела является линейной функцией времени, а для одномерных симметрич-
ных задач распределение температуры описывается законом параболы [Л.6-49],
Параболическому распределению температуры соответствует параболическое
распределение влагосодержания. По перепадам температуры и влагосодержа-
ния определяют коэффициенты а и б, а если известен коэффициент теплообмена,
то можно определить и коэффициент теплопроводности. Вполне естественно,
410
что и во втором случае, т. е. при = 0, может иметь место тривиальный слу-
чай:	0 при vsu = 0 и vB?= 0 (стационарное или-равновесное состояние).
В заключение рассмотрим переход уравнений (6-2-34), (6-2-35) к уравнению
теплопроводности, так как переход к уравнению двффузии дан выше. В абсо-
лютно сухом теле отсутствует массоперенос (при и — 0,	= К1а = Кц~ 0),
тогда из (6-2-34), (6-2-35) получается классическое уравнение теплопроводности •
дТ
-d- == K2aVST = av2f.	(6-2-4Q)
Это же уравнение мы получим из (6-2-34), (6-2-35) для влажного тела с мак-
симально возможным влагосодержанием имаКС (влага набухания), Тогда при
небольших температурных перепадах перенос влаги отсутствует (при и = ииакс,
Кц= К|2 = Kai = 0), следовательно, ^=0ииз (6-2-34), (6-2-35) получаем
уравнение (6-2-46). В этом случае влажное тело нагревается аналогично сухому
телу без перераспределения и испарения влаги (влагосодержание в любой точке
тела постоянно и одинаково: и — амакс). Аналогичный анализ можно сделать и
для системы уравнений тепловлагопереноса при наличии градиента общего дав-
ления (уР 0). Полученные вывода останутся в силе. При этом необходимо
принять допущения о равенстве температуры влаги и скелета тела н справедли-
вости закона Дарси (конвективной диффузии). Остаются в силе и другие допуще-
ния о теплофизических характеристиках.
В заключение следует отметить, что только на основе анализа решений си-
стемы уравнений (6-2-34), (6-2-35) удалось не только выяснить детальный механизм
тепловлагопереноса при сушке разнообразных материалов, но и создать серию
скоростных методов экспериментального определения теплофизических характе-
ристик влажных капиллярно-пористых тел.
6-3. ОБОБЩЕННАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ТЕПЛОМАССОПЕРЕНОСА
Для высокоинтенсивных процессов тепломассопереноса потоки теплоты и
массы описываются не системой уравнений Онзагера
=	(6-3-1)
а обобщенной системой уравнений:
- (6-3-2)
i
Например, вместо уравнения теплопроводности Фурье q =—ЬуТ будет
иметь место обобщенное уравнение
iq = q = XvT— Xrq	(6-3-3)
Строго говоря, соотношение (6-3-3) справедливо только для одномерных
задач. Для многомерных задач соотношение (6-3-3) можно принять в качестве приб-
лижения, в котором период релаксации xrq теплового напряжения определяется
как некоторая экспериментальная постоянная,
Аналогичное соотношение имеет место и для диффузии влаги.
* Из равенства и = 0 не следует, что согласно уравнению (6-1-46)	= 0,
так как сомножитель = 0.
411
Члены соответствуют конечной скорости распространения соответ-
ствующей субстанции. Период релаксации Trk напряжения соответствующей суб-
станции k (массы, теплоты и т. д.) определяется соотношением
dh	—
(6’3-4)
где Vh — конечная скорость распространения субстанции fe; а* — коэффициент
диффузии субстанции k.
Используя законы сохранения энергии и массы, а также систему обобщен-
ных уравнений Онзагера для случая градиентной зависимости между термоди-
намическими силами и соответствующими потенциалами переноса, получаем
систему дифференциальных уравнений переноса:
п
+	(^- + ov8^ = div 2£«я1Уви+/» (*=1, 2..........и),
(6-3-5)
где т— время; сдро— объемная обобщенная емкость соответствующего по-
тенциала 6 у — макроскопическая скорость; J— источник или сток потенци-
ала; Lu— кинетические коэффициенты переноса, между которыми существует
соотношение взаимности Онзагера, £/д = Ltf, п.{ — коэффициент пропорциональ-
ности между силой и градиентом потенциала. Даже при наличии только двух
потенциалов и термодинамических сил (», k= 1, 2) система уравнений (6-2-34)_
(6-2-36) описывает тепломассоперенос в движущейся бинарной газовой смеси,
тепломассоперенос в молекулярных растворах, двухфазное ламинарное течение
несмешивающихся жидкостей в пористых средах, диффузно-электрические яв-
ления в растворах электролитов, сушку в капиллярно-пористых телах и другие
процессы.
В случае постоянства коэффициентов и характеристик переноса уравнение
(6-3-5) принимает вид системы уравнений:
п
+	= 2 Кы^+Пь (S=l, 2............«),	(6-3-6)
где Кд; — коэффициенты переноса при соответствующих потенциалах, Kki =г
=£ Kik* между которыми уже не существует соотношений взаимности Онзагера;
Пь = ^fe/CfePo — удельная мощность дополнительных источников. Применительно
к сушке капиллярно-пористых тел при умеренных температурах (A, i — 1, 2)
и при условии trii = 0 входящие в систему (5-3-6) величины имеют следующий
вид:
- е1 = Т; е2 = в; /71 = 772 = 0; у=0;
/ f 1	С г
/Qi = dq -{-атбег ; /Cis = ат-,
Cq	Cq
Kii = am&/Cm' K<& = Omi
(6-3-7)
где T — температура тела; 9 — потенциал массопереноса; aq н ат — коэффи-
циенты диффузии тепла и вещества; Cq и ст— соответственно приведенная удель-
ная теплоемкость материала и изотермическая массоемкость; г—удельная
теплота фазового перехода; 8 — критерий фазового превращения. При переходе
от влагосодержания к потенциалу 6 было использовано соотношение du — cmdf),
которое, строго говоря, справедливо только для изотермических условий. При
неизотермических условиях это соотношение является приближенным. Поэтому’
лучше в качестве потенциала влагопереноса для однородного влажного тела поль*
эоваться влагосодержанием, т. е. системой уравнений (6-2-34)—(6-2-36).
412
Применительно к высокотемпературной сушке (k,i — 1,2, 3) входящие в урав-
нение (6-3-6) параметры записываются соотношениями
(^Т; 08 = 0;	П1==П2 = П3 = 0; о=0; Kn = aq-!rambe,r— ;
сч
С	f	/I	г	i .	г
ат‘> Kis~	р— \ ^2i~am8/Cm‘l К^ = С1т> Kt3 = Qm$plCm‘,
cq	CQ
К^==-&^а'т8т< К^~^ат,
Кзз = ар —8~°rn^p;	6;
(6-3-8)
здесь Р — потенциал фильтрационного массопереноса; ар — коэффициент по-
тенциалопроводности фильтрационного движения парогазовой смеси; ср—ем-
кость капиллярно-пористого тела по отношению к влажному воздуху или пару
в процессе его молярного переноса.
6-4. КРИТЕРИИ ПОДОБИЯ ТЕПЛОМАССОПЕРЕНОСА
Из системы дифференциальных уравнений влаготеплопереноса получаем
ряд критериев подобия и обобщенных переменных.
I.	Числа гомохромности полей потенциалов переноса, называемые числами
Фурье:
СлТ	ОпХ
го? = ^:	Fop = -^-’	(64-‘)
где % — характерный размер. Между этими числами существует взаимосвязь,
осуществляемая при помощи чисел Лыкова Lu и Lup.
Массообменное релаксационное число Фурье
(6-4-2)
где все величины известны (ат, R, тгггЛ. Период релаксации концентрационного
напряжения массы примерно в 103—10° раз больше, чем период релаксации теп-
лового напряжения. Поэтому массообменное релаксационное число Фурье во
много раз больше теплообменного релаксационного числа Фурье:
For?=a(?Tr9/7?a.
2.	Критерий диффузии влаги по отношению к диффузии теплоты, или диф-
фузионный критерий влаготеплопереноса:
Grt»	OD
Lu = ——Lu0 = —.	(6-4-3)
aq ’ p aq	v '
Число Lu равно отношению коэффициента диффузии массы влаги к коэффи-
циенту диффузии теплоты. .
Число Lu„ равно отношению коэффициента конвективной диффузии к коэф-
фициенту диффузии теплоты. Можно дать и другое физическое толкование чис-
ла Lu.
Число Lu определяет скорость распространения изоконцентрационной
поверхности по отношению к скорости распространения изотермической поверх-
ности, т. е. характеризует инерцию поля температур-относительно поля влаго-
содержания (критерий инерционности тепловлагопереноса).
Фильтрационное число Lup характеризует интенсивность распространения
поля потенциала фильтрации (поля давления) по отношению к развитию поля тем-
ператур.
413
Для ряда влажных тел число Lu увеличивается с повышением влагосодержа-
ния по линейному закону. Если число Lu больше единицы, то распространение
потенциала массопереноса б опережает развитие поля температуры.
Фильтрационное число Lup значительно больше единицы (порядка 100—
1000), поэтому релаксация общего давления парогазовой смеси в капиллярно-
пористом теле происходит иа 2—3 порядка быстрее по сравнению с релаксацией
поля температур.
Используя числа Lu и Lup, находим связи между числами Фурье:
Fom = FoLu; Fop=FoLup;	(6-4-4)
где Fo = Fo? — теплообменное число Фурье.
3.	Число Коссовича, определяемое соотношением
.. гст Д.6 т Ди
	(в-4-5)
Число Ко дает зависимость между количествами теплоты, затраченными на
испарение жидкости (гДи) и на нагревание влажного тела (cq^t).
4.	Число Поснова для диффузионного и фильтрационного переноса:
= °£Ро АГ = Д£р„ ДГ .
Ди	роит Ди	\т Дб ’
&р Др kp Др
Д« ~ роа^Да *
(6-4-6)
Число Рл равно отношению интенсивности термодиффузионного переноса
влаги к диффузионному перекосу влаги или отношению термовлагоРроводности
к влагопроводности. Число Рпр равно отношению интенсивности фильтрацион-
ного переноса влаги к диффузионному переносу влаги.
5.	В аналитических решениях в качестве обобщенной переменной часто встре-
чается величина, равная произведению sPnKo, которую иногда называют числом
Федорова:
вбг
Fe = sKo Рп=-------.	(6-4-7)
Число Федорова не зависит от выбора потенциалов тепломассопереноса и
определяется только коэффициентами 8 и о и термодинамическими характеристи-
ками Г И Сд.
Если обозначить безразмерный температурный коэффициент сушки через В,
где
Ди <?(77ДТ)
, ДТ “ <?(й/Дй)
(6-4-8)
(здесь b — dTIdu), то отношение В/Ко дает новый критерий, названный нами чис-
лом Ребиндера (Rb):
В СрЪ
Число Ребиндерз входит в основное уравнение баланса теплоты.
В отличие от числа Поснова, температурный коэффициент сушки характе-
ризует изменение среднеинтегральной температуры Т и среднеинтегрального
значения влагосодержания й, т. е. является кинетической характеристикой инте-
гральных характеристик тепловлагоперекоса. Число Посиова относится к ха-
рактеристикам локальных изменений Т и и.
6.	Из дифференциального уравнения (6-2-36) получаем критерий
„	Ви_	(6-4-10)
стДв Ко ’	'	1
414
где Bu — число Булыгина, определяемое по соотношению
Ви= гс‘^ .	(6-4-11)
	Cq ЬТ
7.	Из граничных условий третьего рода получаем два числа Био:
теплообменное число Био
=	=	(6-4-12)
У-q &q
н массообменное число Био
Bim = 4^-=-M.,	(6-4-13)
Числа Био изменяются от нуля до бесконечности (0 < Bi < со). Если потоки
теплоты q (т) и массы вещества j (т) ие могут быть определены граничными усло-
виями третьего рода, то вместо чисел Big и Bi^ используются два числа Кир-
пичева:
Л LSI	AiO
Если потоки <?.(т) и / (т) определяются законами Ньютона, между этими
числами существе? простая взаимосвязь:
Kira=Bimti.	(6-4-15).
Величины ДТ, Ди, Дб и Др, входящие в критерии подобия тепломассопе-
реноса, выбираются в соответствии с условиями задачи,
6-5. РЕШЕНИЕ УРАВНЕНИИ ТЕПЛОМАССОПЕРЕНОСА
ПРИ ОБОБЩЕННЫХ КРАЕВЫХ УСЛОВИЯХ
Система уравнений тепло- и влагопереноса в безразмерном виде для одно-
мерных неподвижных тел или сред принимает вид:
'=*2- ••• "> t6-5-1)
l=z 1
Где efe—безразмерный потенциал переноса; Xki—безразмерный простой или
комплексный критерий, характеризующий перенос #-й взаимосвязанной субстан-
ции под действием движущей силы с индексом i; П% — безразмерный источник
(или сток) А-перепоса; Fofe = -^-число гомохролности; X — безразмерная
координата; Г —постоянная формы, равная для неограниченной пластины нулю,
для неограниченного цилиндра—единице и для шара — двум.
Для диффузионного тепломассопереноса во влажных телах (k, t = l,2) вхо-
дящие в уравнение (6-5-1) безразмерные параметры имеют вид:
е2=е;	/7*=/?* = 0;
х*1«= i -Н Ко Рп Lu; К12 = — е Ко Lu; )	’
.	>	(6-5-2)
—Lu Рп; K22 = Lu,	|
где Т=	—Г—безразмерные температура и потенциал массопе-
Тс—»* — Vp
реноса (индекс ’характеризует фиксированное начальное значение потенциала),
415
Для молярно-молекулярного тепломассопереноса (k, i = \, 2, 3) безраз-
мерные параметры и Kti принимают следующий вид:
61 = Г; 63=б; е3 = Р; ЯГ = 0 (t=l,2, 3);
Кп—14-sKoPnLu; Ki2 = —eKoLu; Ki3 = eBuLup;
K*i=-UPn; Ksa = Lu; Кгг = - Lup 
4	T e Ko Pn . e Ko T ,
Лз1=—Lu—; Кз’ = Ьи-; ^33 = Lup(i — e),	(6-5-3)
где P = -———безразмерный .потенциал фильтрационного массопереноса. Си-
Ро
стему уравнения (6-5-1) можно переписать так:
aux, Fo)_ а»мх, Fo) , гаанх, Fo) ад Fo).
д Fo	№	+ X дХ ' d Fo ‘
dSs(X, Fo) Г^(Х, Fo) Г^(Х, Fo)1
6 Fo -LUL SX‘ +X dX J
LuPnE52®1^’ F0) -1- Г d^(X- F°)l
UraL Ж2 + X dX J
Bu гачя(Х, Fo) , г des(X, fo)].	*	,,,r.
Lu" kJ I —№— + x —эг-] 	(6's'5)
aes(X, Fo) rMs(X, Fo) Г dts(X, Fo)] Ко’ (X, Fo) „ _ .
““JfJ	axi ‘ T dx—J-~bJ---------------JfJ~ • (6’5’6>
где Ko* = 8 Ko.
Краевые условия принимаем:
6fe(X,0) = 0, A=I 2,	'	(6-5-7)
т. e. равномерное начальное распределение.
Для симметричных полей температуры и влагосодержания
а6> (dXF0> = °'	в‘(0. Fo)y=co,	(6-5-8)
Граничные условия имеют вид:
АХ	<F°) +11 ~е) Lu Ki3(Fo) = 0;	(6-5-9)
<?62 (1, Fo) <?(?! (1, Fo)	Bu Lu„ dSa (1, Fo)
------6^+Рл......6^.....+ Kj^Fo)+k^-uT—<6-5-10>
Ml> Fq) = (p3(Fo).
В случае граничных условий третьего рода критерии Kij (Fo) и Ki3 (Fo)
имеют вид:
Kift (Fo) = Bift [e/fe (Fo)-6ft (1, Fo)].	(6-5-11)
В процессе сушки влажных тел граничное условие третьего рода для мае-
сообмека непригодно и оно заменяется интегральным соотношением
-^=К(П-Ир).
которое можно записать так:
Kij (Fo) = K 1 -(Г+1) j Хг6г (X, Fo) dX .	(6-5-12)
4	L о	J
Представляет интерес решить задачу при обобщенных граничных условиях:
КсА(1. Fo)+/GA(1, Fo) + Kt3 a61(Jj<F°> +Кы-*У^- +
1	I
Ч-К*»(ГЧ-1)5XrBr(X, Ро)Л+К»,(Г-Н)$ХгМХ,Го)<1г.=ф4(Ро), (6-5-13)
О	о
где ip* (Fo)—произвольные ограниченные интегрируемые функции времени.
416
Система уравнений (6-5-4) -(6-5-6) с граничными условиями ^6-5-7) — (6-5-13)
била решена М. Д. Михайловым при помощи интегрального преобразования
Лапласа. В решения входят характеристические числа:
у^24(1+к°,Рп+^ +
+(->)']/(1+к°’Рп+пг)2-тт]: ,=1-2>	(6'М4>
которые характеризуют взаимосвязь тепло- и массопереноса. Для анализа
решений необходимы следующие соотношения:
v|4-Vi = l4-Ko*Pn4--^; v*vl = -^-;
(l-V?)(l-vl) = -Ko* Pn;
1
Lu ’
v? — v| — (vf — vl) = (v^ — vf) (ко*Рп4-~
(6-5-15)
(6-5-16)
В табл. 6-1 приведены значения Lu v? в зависимости от Lu и Ко* Рп
в пределах изменения Lu от 0,01 до 1,0 и Ко*Рп — от 0,1 до 1,0.
Таблица 6-1
Значения Lu v? |Л.6-6|
			Ко	Рп		
	0,1	0.2	0.4	|	о,6	|	0,8	1,о
0,01	0,00999	0,00998	0,00996	0,00994	0,00992	0,00990
	1,00101	1,00202	1,00404	1,00606	1,00808	1,01010
0,05	0,04974	0,04948	0,04897	0,04847	0,04798	0,04751
	1,00526	1,01052	1,02103	1,03153	1,04202	1.05249
0,1	0,09890	0,09783	0,09576	0,09379	0,09190	0,09010
	1,0110	1,02217	1,04424	1,06621	1,08810	1,10990
о.2	0,19515	0,19058	0,18218	0,17461	0,16775	0,16148
	1,02485	1,04942	1,00782	1,14539	1,19225	1,23852
0,4	0,37591	0,35581	0,32349	0,29808	0,27725	0,25969
	1,06409	1,12419	1,23651	1,34192	1,44275	1,54031
О-6	0,53184	0,48637	0,42361	0,37967	0,34603	0,31898
	1,12816	1,23363	1,41639	1,58033	1,73397	1,88102
0,8	0,65086	0,57950	0,49114	0,43318	0.39030	0,35660
	1,22914	1,38050	1,62886	1,84682	2.04970	2,24340
1,0	0,72984	0,64174	0,53668	0,46934	0,42020	038197
	1,37016	1,55826	1,86332	2,13066	2,37980	2,61803
Введем обозначения:
vl—I	V?—1
—ко*~’	—Ко*~~
Yffe — K/5-Ко*
14 Лыкоэ Л. В.
(6-5-17)
(6-5-18)
417
Тогда решение системы уравнений тепломассоперейоеа будет иметь вид?
MX, FoWHok- 2 ^1и ( Х),ехр	]
|	Г^1 ’*пт'п I 421	422 (|1Л) I	j
+ Вц f ф,'(Fo —Fo*) d Fo* — У	’МЧ3И„Х)|
J	С22Ы Г
Fp
X Ф1' (Fo—Fo*)exp (— Fo*) d Fo* +
. znJp V 2 I 4n(M QiHM I . J ,
+<h(0)|Bu 2^|wr(V„X) »7Hv!F„-<)! :|!<~!t"F°)j +
+ B12 j ф2 (Fo — Fo*) d Fo* — У -^|~X
X	I S (Fo- Fo*) exp (- Fo*) <»Fo*. (6-5-19)
82 (X. Fo) =Ф1 (0)
I (v?- I) "MV/) ('’I- >) Wr (VA*) I FJ ,
I «2! Ы «22 (P„) [exp(-M„Fo)| +
Fo	co
+ B21 j ?;(Fo-F0’)dFo*-1A- 2 X
I (v;-i) vr (v1(..X) (v|-1) ГГ’(,ЛХ) i
I	Q21 (Мд) Q22 (Цл)	I
Fo
X J (pj (Fo —Fo*)exp (—Fo*)d Fo4-(f2 (0)X
v I о 1 V [ 4и (Нд) 412 (Нл) . I
Хр! Ко* ZiHW„lM-l)47r(v1(l„X)(vi-l)lt7r(v.1P„X)l
!Fo	о,
+ Р!2 j ф; (Fo-Fo*)d Fo*—А- 2 X
j	411 (нп) Qis (ря)	i
I W- 1) vr №X) «-!) Wr (v^X) I X
Fo
X (pg (Fo — Fo*)exp (— p* Fo*) d Fo,
(6®5-20)
где
4лг(^я)“ан^г (\^л)“вн^НпУг(^Нл)4-Т« (f-M) —(6>5-21)
Задавая вид функции ^(Fo), можно из общего решения получить част»
ные решения,
418
Для большинства задач средние потенциалы переноса не вводятся в гра-
ничные условия, т. е.
Ki6«Kie=Ka5=K26 = 0.	(6-5-22)
Тогда в решении задачи функции Qkl и В#/ примут вид:
I	vfe —1
—Ко*
Кй+-^
(6-5-23)
3,,= -,^ ,;	B21=-^S--;	(6-5.24)
Ku K12	ацЛи	ПК ix Kia
jKaiKsal I K31 K.22I	1K21 Kaa I
_ Mv* И I Ko* Kxx - KiaKis I ,	’
KO* Lu Ко* ^ах-КааКаМ
^Ko* Рп+Хй") Ku — РпКхзКй
^Ko* Рп-J--jrV) K21 — PnKaaKai
I
X®'r(v1m)R7r(vam)+TT|
Г (vi*S»)
Kit Кц
1 I ^21 К23
А',, Кй
Км Км
vr (у^п) +|
Ku Кха
К21 Км
Vifi/j	V2nn
x v* MW-va MV
1 Vim 8 vaprt
f I K12 + 0 — О Kl^Kja I __ I Kll K14 j ) I
I 1 K22 + 0"O КааКзз I 1 K21 Ka-i I J J
р,д—корни характеристического уравнения:
«’- VS) I	I vr Wr (VA) +
+'fv._v.) AIK" IL.W /'.(W
Lu I Каз «и I V1(i„ Vsfi„
I Mvl^.) yr(vA) +
_j^iKi3 Kia
Lu I К22 Км
14*
. На
+ ЪГ
; (6-5-25)
vim vam
МЛ) MW
JKhKuI
4k.ikJ у. м*^,,).
' vjm
у'' I Ko*^! —K12K13 I I
\|Ko*Kax — КгаКзз | I
Wrt	v2|xn
Кц 4- PnKiaKH
Ках + Рп/СааКм
07 г (V») Мй)
ЧП»

= 0.
(6-5-26)
4W
Решения (6-5-19) — (6-5-20) правильны только при условии
KuKlsUo.
I Кп кя!
Рассмотрим теперь решение при условии
I Кп Kia I __ Q
I К21 Каз !
Из характеристического уравнения (6-5-26) видно, что ц»0
ется корнем. Тогда решения (6-5-19), (6-5-20) имеют следующие
-Kz&p ;
Кц Kj2
1 Ko*
«п-гри- ^-2-(г^1) 1
Ко*Рл+-=^—Ко* 1
4.	1 Lu	I
Каг + ^КазКгг + ^Кад J
ЙЦ== р [— ^+2^+0
Kjl + '^Kig Км + Кц 1
+ Ко*Рп + ^~— ко* j
( „ РпКо*Рп+Д
<X2	Lu 4.
~K>iF+2-(r+i) I
BS1=P
K%L Kt2
K12
— Рп	1	(
Kai + ^KagKaa + S/Cai J
Кп
РпКо*рп +-1_
1 Lu
В38=р КнК +2]Г+Т)|Х2
| Ки+2К1зК12 4-2К14
+	— Рп 1
где
I Ко* Кп- КиКи+Рп Ки | . _11 Кп Ku I ’
| Ко* Кл — КазКгз+Рп Ks41 Luj/fai
С~2(Г+1)
Кц 4- KiaKit I . I KuKia 4- Кu ft
Kaj4-KasKa4i | КазКаа 4-Ка4 1/
П rt Км Кв I I Ku ки h 1 + Ко»Р11 + с5 d Ko- Ka •
Г4-3 tj K22 K231 I K21 K24 IJ Г4-З	Ц Ko* Kgi-
_ | Ku+Рп KiaKu 11	Ж. IKl‘ Ku
I Kai+Pn K22K24 [/	Г4*3	| Kai Kai
Полученное решение (6-5-28)—(6-5-33) верно при условии, ч
| Ко * Кп - К12К13 + Рп Ku I , ± I Кп Ku I . 0
|Ко*К21-К22Км+РпК24КЬи|К21 К«П ’
(6-5-27)
также явля-
постоянные:
(6-5-28)
(6-5-29)
(6-5-3G)
(6-5-31)
(6-5-32)
-K13K13I
-К2аКаз|“'
(6-5-33)
(6-5-34)
420
Условие (6-5-34) не выполняется, когда К11 = Ку2 = ^21 = /<23=0. Для
, этого случая решение примет вид [Л.6-2];
1 [ (
(Х' F0) = lA'ia Kifl ft (0) J(Г +1) LuFo ГКо * Кга +1Ко*Рп + Кг,
2 2-^Zm^ »p[-^Luv?F°])+
Fo
(ко-Рп,+

cp{ (Fo —Fo*) Fo* d Fo* —
Fo	co 2	’
jVI(Fo-Fo*)dFo*- 2 S!'X
0	n = 1 i = 1
Fo
x 2да'^~ f exP[- ^L“ VJ р0']ф1 (F°- Fo*) d Fo* -
- Фа (0) |(Г +1) Lu F [ко* Kia + (ko’Pu +	Ku] -
1 /Г4-1	\ V V i 2^r(M)	1
-tНз-хГ«- 1 2	-
n = 1 i — 1	i
Fo
— (Г + 1) Lu [ко* Kl3 + (ко*Рп + i) Ku] j ф; (Fo —Fo*) Fo* d Fo* +
0
1 /Г -I-1	\	(	VI VI i г (Ня^)
Mr^xaF‘h'(Fo-FoW+ 2 2
0	n =* I i = 1	' '
Fo	)
X $ Ф' (Fo - Fo*) exp [- H= Lu v? Fo*] d Fo*J; (6-5-35)
6a=(X, Fo)= м , l_ (0) I Lu [Kjj+Pj]ы_
I Кзз %2i I 1-	I
1 ir +1 v.\ V V <•! 2Г Г (l*»X)	Г F-» .11
^llr+3-xr=-PL v]Fo ]]’
Fo
-	_(Г+1)Щ[К38+РпК84] $ cpj (Fo —Fo*) Fo* d Fo*4-
+xr4(F°-F0‘> “Fo*+„2 2 Sf,StS x
I- °	Г S T
P	Р-Л
X j q>[(Fo— Fo*)exp| -	Fo*JdFo*-}-q>8(0K(r4-l)LuFo [tfw+Pn A'iJ—
421'

Г и- 1
+
Fo
+ (Г +1) Lu (Ku + Pn Ки) J (й (Fo —Fo*) Fo* </Fo«-
0
1 l Г +1	\ P	V Vl s 21Г r (|i-X)
-т(г+3-Х!М ^(FO-FO^FO*- 2
0	n = 1 i — 1	4 '
X j4>;(Fo-Fo*)exp£-^Fo*pFo*,	(6-5-36)
^•=-^г1к°,^з+('’?-1)К*4! (^=1.2):	(М-37)
а'=^М-')-р%) (*=‘.	2);	(6-5-38)
|in—корни характеристического уравнения
М^) = 0-	(6-5-39)
Усредненные безразмерные потенциалы переноса определяются по формуле
в» (Fo) = (Г +1) 5 Хгв4 (X, Fo) dX.	(6-5-40)
О
6-6. ГРАНИЧНЫЕ УСЛОВИЯ ВТОРОГО РОДА
Во многих высокотемпературных процессах удельные потоки теплоты и
вещества на поверхности тела находятся в сложцоЙ зависимости от потенциалов
переноса. Например, при радиационном облучении тела тепловой поток пропор-
ционален разности четвертых степеней абсолютных температур поверхностей,
участвующих в теплообмене. Получение замкнутых решений системы диффе-
ренциальных уравнений тепломассопереноса в этом случае связано с очень боль-
шими трудностями. Их можно избежать, если в граничных условиях задать соот-
ветствующим образом подобранные функциональные зависимости потоков только
от времени. В этом случае система уравнений решается при граничных условиях
второго рода, которые для одномерных тел имеют вид:
^‘м~0)=К|1(ро);	<м-‘>
-p„^!M^ + ^fo) = KMFo).	(6.6.2)
Если на поверхности тела наряду с источником теплоты имеется и его сток,
подобно тому, как это наблюдается при динамическом охлаждении различных
предметов, находящихся под облучением, или при радиационной сушке влажных
дисперсных сред, условие (6-6-1) следует обобщить к оно примет вид:
Fo) = Ki, (Fo) -(1 -8) Lu Ko Kis (Fo).	(6-6-3)
Если на поверхности тела не имеется стока (s = 1), то обобщенное условие
(6-6-3) превращается в условие (6-6-1).
Сравнение граничных-условий (6-6-2), (6-6-3) с обобщенными граничными
условиями (6-5-13) показывает, что совокупности критериев подобия К.^т имеют
423
следующие значения:
Kii = O, К12=0, К13=1, /(„ = 0, К1Б-0, К1в = 0;	|
#21 = 0, ^-0. /<23 = -Рл, ^4-1, №5= 0, №e = 0, /	(''J
а также
epi (Fo) = Kii (Fo) —(I — е) Lu Ко Ki2 (Fo);	(6-6-5)
ф2 (Fo) = Kk (Fo).	(6-6-6)
После выполнения необходимых алгебраических преобразований решения
(6-5-35), (6-5-36) принимают следующий вид [Л.6-2]:
61 (X, Fo) = (Г+1) [ф1 (0) - Lu Ко*ф2 (0)] Fo -
со 2
- -2 (гй- Н ч» (о> - 2 2 <—огх
(1 + Ко* Pn - V?) Ф1 (0) + Ко*ф2 (0) 2ГГ (g„X)
Х	v1-vi	I'SWr (!'„) Х
Fo
Хехр(— p*Luv’Fo) + (r-)-l) J [ф! (Fo — Fo*) — Lu Ko* ф£ (Fo — Fo*)]X
о
Fo
XFo*dFo*-^(P±L-№) j <p[(Fo —Fo*)4Fo* —
S, v Ж'/' (g„X)	“?
- 1
zi = 1 i= 1	0
Фа (Fo — Fo*)] exp (— p.3 Lu v?Fo*) d Fo*
x —--------------------------'----;	(6'6'7)
et (X, Fo) = (r+ 1) Lu <f3 (0) FO—i (£±1_ »)x
VI V 2Bv (M)
х[рпЧ>1(0)+(Р2(0)]- у У	;x
vJPncp (0) + (v?-l)(pa(0)	/ ps \
X1---------- V!2V| ----------exP Г F°,)
Fo
+ (Г+1) Lu ( (Fo—Fo*) Fo*</Fo*—У(£±|-№)х
Fo
X [Pncp' (Fo —Fo*)-[-(pg (Fo — Fo*)] d Fo* —
-	<!“«<*«-H
+ (v< -1) <Й (Fo - Fo’)l ex₽ (- Fo‘) d Fo", (6-6-8)
где —корки характеристического уравнения
Vf(]i)^0.	(6-6-9)
423
Если потоки теплоты и массы на поверхности постоянны, т.е. Kif = const
и Kia = const, то решения (6-6-7) и (6-6-8) перепишутся так:
«1 (X, Fo)= (Г+1) (Л,-Lu Ко* Ki.) Fo—Ь (-р±± - Х=) N-
х* Xi 21г г
- 2 2	c<exP(~^LuTiFo); (6‘6-10>
в.(Х, Fo)=(F-|-l)LuKi.Fo —l(£±L_ №^(PnAi + Kia)-
v 2ГГ((1„Х)
- 2 2 w77m c‘exp(-^Luv'Fo)- f6-6-11)
n = 11 = 1 n ' n'
где
N— Kif — (1— s) Lu Ko Ki2;
iy 0 + К°* Pn—v^ + Ko* Kia)
1	(vf-vf)
Pn N — (Lu vj — h KU
rs _ f_1 \2_______l 1	/	2
i * >	A,? — vh Lu
(6-6-12)
(6-6-13)
(6-6-14)
Значения коэффициентов С} и C| в зависимости от значений отдельных
критериев подобия приведены в монографии [Л. 6-1].
Если в материале отсутствует термоднффузионный перенос массы, т. е.
Рл = 0( то, учитывая, что v?=~ и v|==l, из решения (6-6-10) и (6-6-11)
получим;
в, (X, Fo)=(F+l) (Kii-Lu Ко* Kl.) F°~- ха) К'х-
V 2гг(|*лХ) („	,	, Ко* Lu Ki.
- 2 ТР'НЫ |KVxp(-|'A|-»)+ Lu_!2X
X [exp(— P^FO)— exp (— p,JLuFo)]J;	(6-6-15)
в. (X, Fo) = Ki,[(F+1) Lu Fo - у (-£±|- - X>^ -
V, 2ГГ (ц„Х)	1
-2	ex₽(~^LuF°) •	(6'6'16)
n = I ' •'	J
Решение (6-6-15) можно написать гак [Л. 6-2]:
8,(Х, Fo) = el(X, Fo) -f-в]1 (X, Го)-us'11 (X, Fo),
(6-6-17)
424
где
е* (X, Fo)=Kix|jr+l)Fo—*-(£±L-№)_
V 2Г,(р.„Х)	1
-2 нуг(к exp^Fo):	(6'Ы8)
ej1 (X, Fo) = — Ко* Lu Ki3 рг +1) Fo + XuJT X
21Гг(цпХ)	1
\2 ЖЫ₽('ЙРО,|;	,6'6'19)
1 VI ^^rfU-X)
eI"(X, Fo) = Ko*Lu Ki, Lu_j- 7,	cxp(-|7. LuFo) . (6-6-20)
Следовательно, при отсутствии в материале термодиффуэионного переноса
массы, температура в теле определяется суперпозицией трех температурных по-
лей. Первое поле характеризует прогрев материала без учета массообмена и фа-
зовых превращений. Второе поле учитывает влияние неподвижных стоков (или
источников) теплоты. Наконец, третье поле характеризует влияние подвижных
стоков теплоты, связанных с массопереносом.
Если дополнительно принять, что в теле отсутствуют фазовые превращения
(Ко * = 0), температурное поле описывается только формулой (6-6-18), которая
дает классическое решение уравнения теплопроводности при граничных условиях
второго рода и при отсутствии источников. Отметим, чю безразмерный потенциал
массопереноса, определяемый по формуле (6-6-16), описывается классическим
решением после подстановки Fom = LuFo.
6-7. ГРАНИЧНЫЕ УСЛОВИЯ ТРЕТЬЕГО РОДА
В качестве первого приближения конвективный теплообмен можно описать
законом Ньютона, т. е.
Kix^Bi,. (Fo) —(1, Fo)}j Ki3=KiB(Fo). (6-7-1)
Тогда безразмерные граничные условия запишутся так:
в, (1, Fo) +-Х- d'J1^.F0) = 61‘ (О - (1 -в)	Ki, (Fo); (6-7-2)
-Ki, (FO).	(6-7-3)
После выполнения необходимых алгебраических преобразований решения
(6-5-19) и (6-5-20) принимают следующий вид (Л. 6-2]:
MX, Fo)=<Pi(0)-4ko‘Lu(1+^—да)ч>,(0)+-52^-ф1(0) х
m — I i~ 1	п — 1
1 ] ф1 (0) <213 (рп) I .у, , Уч I I ^п) ф1 (0) 1 mr / уЛ v
х{IФ,I * (v^+k(Fn) Ф,(0)I
425
Го
Хехр(-н;ро)+j [ф;.(Р0-Р0’)—i Ко* Lu ^1+-2_-Х^ X
X<p;(Fo-Fo*)]dFo* + ^l|- 2 2 C^Wr(^,nX) j 4>S(Fo-FO«)x
m = ] i = 1	. о
co	Fo
Xexp(-WFo.-£^j{^
X	ЙфИГоЗро^	W’) «Fo*. (6-7-4)
Mx, Fo) — [(Г + 1) Lu Fo-(1 -|-Ko* Pn Lu) -Xs)] ф2 (0)-|-
+ Vg-vf фд <0) 2 2 C™‘(v*_Orr(v<H-mX)exp(-P-J,F°)-
m = 1 t = I
“k^ 2 '^{IS(0)fewl(v;~
n = 1
+1 <?af Й ifc (°) | (va“ ’) Гг (v!P»x)|exp (-|i= Fo) + J [(Г + 1) Lu Fo* -
- j (1 + Ko* Pn Lu) (£±4 -	<p- (Fo - Fo*) d Fo* +^r
co 2	Fo
x 2 2	,VP*(FO’"FO’,'’XP('^'"F(,:’)t; Fo’-^r
m = 1 i= 1	0
x2^ni^;:z^^!si<^wr(^x)+
+ l Q,” Ы Zs (Fo —Fo*) I	') ClM)} «!> (-PS F“*) d FO*.
Г	*'‘ = -v^n^FL{(1+W-)Vr(V1f‘”)Vr(V“F») +
+ B& <virF (V1^)	(W FГ (^р.„)>-
-ViWr (V1F„) rr (v2p„)};
Qu (M=w г Ы —§17 vi нл v г (v< ь);
1-vf
Qvi (Hn)= v|Lu~Ko* (viP-s);
здесь |im—корни характеристического уравнения
Кг(У1^) = 0; Mv) = 0,
(6-7-5)
(6-7-6)
(6-7-7)
(6-7-8)
(6-7-9)
426
а |1л —корни характеристического'уравнения
Wr (v2pA	ц
(1	0 -'Э -Л5ГТ-=М-^-вГ- (6-7-9а)
Если температура окружающей среды и поток массы постоянны, г. е.
6y(Fo)=l и Ki2 = const,
то решения (6-7-4) и (6-7-5) перепишутся в следующем виде:
в,(Х, Fo) = 1 - Ко^ЕЧ-4 Ко* Lu Kl2 f 1 +-4--Х3^ —
Z	\ Ы1 /
‘со 2
2 2 C^r^^expt-^FO)-
т = 1 i — 1
со 2	.	.
-X 2 C-«Fr(v.M)e’P(-l*iF0); -	(6-7-10)
rt = I <= 1
MX, Fo) = ^r + l)LuFo—l-(l+Ko«Pn Lu)	- X») -
co 2	-i
2 2	(-^Fo) к,-
m = ) i = l	J
co 2
“T^2 2	(6-7.11)
n = I 1=1
к‘“Цгки'>;	<«-7-12)
(6-7‘13)
C»i = (-1)'-~{Ki2<?V-(1-Ko*X1)Q3/}(^‘’ ' = *). (6-7-14)
После подстановки решения (6-7-Ю) и (6-7-11) в (6-5-40) получаем средние
безразмерные потенциалы:
61 (Fo)= 1 - Ко* Ki, — Ко* Lu Ki, fvTV +ттН ~
\ г -j- □ Dlj у
~- K°iiu7f- 2 2^exp(-^Fo)-2 .2, °„<ехр (—^Fo); <6-7-i5)
[co 2
(F-l-l)LuFo-У 2Dm<(v*-1)w‘P(-l*mFo) К1,-
m = I i = (	J
«	2
-k^2 2D’‘<-v‘~ 1)ex₽(~^Fo),	<6-7-16)
rt=J/=J
где
Omi = (7+l)Cmi-4-pE-; О„г = (Г + 1)Сл1-ПХг1_. (6-7-17)
427
Анализ полученных решений показывает, что бесконечные суммы достаточно
быстро сходятся. С уменьшением числа Фурье необходимое для расчета количе-
ство слагаемых растет. Значения первых шести корней характеристических
уравнений даны в монографии [Л.6-1]. Значения постоянных коэффициентов
Cnl для различных совокупностей критериев подобия также даны в [Л.6-1].
Еще быстрее сходится бесконечная сумма по индексу т; начиная со значения
числа Fo = 0,05 в расчетах ее вообще можно не учитывать.
Первые члены решения (6-7-10) и (6-7-11) дают стационарное распределе-
ние температуры и потенциала массопереноса, полученные в работе'Ф. М. По-
лонской [Л.6-5]. При стационарном режиме в материале устанавливается парабо-
лическое распределение безразмерных потенциалов переноса.
Рассмотрим случай, когда тепло- и массообменные числа Кирпичева равны:
(Fo) — (1, Fo)};
Kig = Bi2 {0y3 (Fo) — 0g (1, Fo)}.
s Безразмерные граничные условия (6-5-9) и (6-5-10) запишутся так:
6.(1, Fo)-К, Ко* Ml. F°) + j-- dS1 ^F0) = B/i (Fo) -JGKo’fy, (Fo); (6-7-18)
Bi, Ml. Fo) - Pn F°) +	(J^F°) = K|, (Fo).	(6-7-19)
Сравнение граничных условий (6-7-18) и (6-7-19) с обобщенными гранич-
ными условиями (6-5-13) показывает, что совокупности критериев подобия
имеют следующие значения:
Ku=l, «i6 = 0,	Ki, = -KiKo*, *„= Ki„ = 0;		(6-7-20)
K21=0,	K'22=B12,	= —Pn,	KM = 1,	
*»=<>, а также	Ки=0,		
	«PilFoJ-S/HFoJ-K, Ko* <p, (Fo) = BI2 S/2 (Fo);	(Fo); }	(6-7-21)
к, =-1—5. Lu-|Я.	(6-7-22)
После выполнения необходимых алгебраических преобразований решения
(6-7-10) и (6-7-11) принимают следующий вид [Л. 6-2];
61(Х, Fo) = e;i(Fo)-4>1(0) 2 tV|oS(T‘X) o7Y“X)|X
IQgi(pn) Q22 (p-n) I
VI 2 la7r(v.p.„X) "MwA I Г
xexpf-HjFo)-^ 0 и о M 4>l(Fo-Fo’)X
Ря тп I Qgi (цл) Ч22 (pn) I fl
X exp (—p.* Fo*) d Fo* — ф (0) V	^s(l*“) |x
V 2 IQ11 (Ц/i)	Q12 (pn) If , t, л
X exp(_p„Fo)-	I	<Fr(v,p.„X)'| ' Фя ’	’
X exp (— p» Fo4) d Fo*;
(6-7-23)
428
% (Л Го) — 0/3 (Го) ср/ (0)	ф X
I М-1) Я’гЛнЛ (V’- 1) (7, (v2p.„X) I
I ftift*») w.) I ( "
_ i у 2 IМ-') “М'Т'Л М-1)vг ftM) 1 х
к°»	ц’ч>„ I <г21(ц„)	q22((1„)	|
X J ?;(Fo-Fo«)cxp(-^Fo«)dFo*-4!.!(0)-j-L.	X
О	« = 1
I Qii (Hn)	Qfa (Р-«) I , а р . _
Х|«-1)^гМиЛ) (v»-l) fTr(v2p.„X) Г₽( 14 *
1 VI 2 I Qii (р-л) .	912 (Р-л)	1 у
“ко* Z 7J%7 (vi—0 &r(viM}
п= I
Fo
X 5 <p£(Fo —Fo*) exp (—р,’Fo*) d Fo*,	(6-7-24)
о
-4^- {(1+~5ТГ" + w - Ki Ko*Pn) v^r
- (тг +	Bi’)	Vr Ml*„) +
+ [t (vi -	Г (V1 %) V Г M Ы +
+V,	I'r МН») ]}:	(6-7-2S)
Qu (P-») = p +(!-VD Ktl vr Ml*„) —BiT^F.l'r MP-»); (6-7-26)
MM=^{t^M7A)-bis	I6-?-27)
здесь p„—корни характеристического уравнения
vV (1 -v|) + (l - Vi) [v? (1 — v|) Kt —1^-]} Wr (V) VГ (VjP) -
-v1(i {v> (1 - v?) + (1 - Vi) [vSU-v«) Ki—B^]}^r(v2p) MMH
= M-vl){Bi2»’r(v1P)»7r(v2F) + ^ v1v!Fr(v1p.)Fr(vap)}. (6-7-28)
429
Если потенциалы окружающей среды и поток массы постоянны, т. е.
fyi(Fo) = l 11 6/a(F°)=l. решения (6-7-23) и (6-7-24) перепишутся в следующем
виде:
в,(Х. Fo)=l-J 5 Cn,rr(viP.„X)exp(-p,«Fo); (6-7-29)
п=1i=l
со 2
6,(Х, Fo)=l-1-L- 2	(6-7-30)
n=li=l
где
-=^- <6’7’31>
га та	\l — J ~ I /
Анализ показывает, что бесконечные ряды (6-7-29) и (6-7-30) сходятся доста-
точно быстро. С ростом числа Фурье ошибка, вносимая пренебрежением членами
ряда с п= 2,3 и т. д., уменьшается. Начиная с определенного исходного зна-
чения Fo первые два члена суммы дают правильный результат с заранее заданной
степенью точности. Исходные значения Fo для упрощенных расчетов меняются
с изменением совокупности входящих в решения критериев. Наибольшее влия-
ние на исходное значение Fo оказывает значение числа Lu. С ростов Lu исходное
значение Fo уменьшается. Значительно слабее на упрощаемости сказывается вли-
яние критериев е и Ко*Рп. Влияние числа Blj особенно сильно сказывается на
безразмерном потенциале теплопереноса. Аналогично исходное значение Fo
для безразмерного потенциала массы особенно существенно зависит от числа Bi2.
В целом исходное значение Fo ниже для теплообменных показателей, чем для мас-
сообменных.
При отсутствии в материале термодиффузионного переноса массы характе-
ристическое уравнение (6-7-28) в результате Рп перехода (Рп == 0) принимает вид:
^г(Р-) Р- I
1-7 (W Ч/
(6-7-32)
т. е. старая единая форма корня рл, содержащаяся в решении полной системы
уравнений, приняла двойственную форму рл = р.р и рл//Ъи = р.?. Поэтому
бесконечные суммы решения необходимо повторить 2 раза, подставив вместо р,л
вначале |лл = |1р, а потом pn/'/Lu = р.9. Решения (6-7-29) и (6-7-30) принимают
вид:
MX, F0)=l-2 4/l+^)rr(bX)exp(-p.JFo)- '
Р=1	,
со	г е Lu	1
e = l
(6-7-33)
%(Х, Fo)=1-2 AJZ’,. (ц4Х) ехр (- р» Lu Fo), (6-7-34)
<?= I
430
где
xe Lu Bi;
cp = Ko <------
(.Lu—1
8
Q — —
Lu-
(6-7-35)
'fr-CTMiy+J1-'-йЪ“) iVMi*,);
%=4^ г /lu) - /ьГ / (/lu );
2	Bi*
₽ HPMb)
A -_______________________P18__________.
здесь j*p, p.9— корни характеристических уравнений
Wr (ь)	м,.	Mb)_ = jb_
Mb)	6i*’	Mb) В1/
(6-7-36)
(6-7-37)
(6-7-38)
(6-7-39)
(6-7-40)
Если в материале кроме термодиффузионпого переноса массы отсутствуют
также и фазовые превращения (е = 0), то решения сохраняют вид (6-7-33) и
(6-7-34), но вместо <рр и <р? следует писать соответственно «р* я (р*. Последние вы-
ражаются следующим образом:
ф£=ко-|МРМУг(у=-); <р?=МиМь)- (в-7-41)
Характеристические корни и коэффициенты Ар и Ад определяются уже
приведенными уравнениями.
При отсутствии массообмена (Ко == 0) написанные выше решения превра-
щаются в обычные классические решения.
В вышеприведенные решения при расчетах входят следующие коэффициенты.
p-м
=77 [(К - ° (тТм1) -1К -2) Рп] 	(6’7'43>
Числовые значения этих коэффициентов приведены в табл. 6-2—6-4 в за-
висимости от чисел Lu, Рп и Ко*Рп в пределах изменения от 0,1 до 1.
Таблица 6-2
Значения коэффициента /7П-== (?22 [Л-6-61
Lu	Ко’Рп					
	0.1	од-	0,4	О.6	0.8	1.0
0,01	0,0000	0,0000	0,0000	0,0001	00001	0,0001
0,05	0,0003	0,0005	0,0011	0,0016	0,0020	0,0025
0,1	0,0012	0,0023	0,0045	0,0064	0,0081	'0,0097
0,2	0,0058	0,0110	0,0195	0,0262	0,0315	0,0358
0,4	0,0350	0,0575	0,0838	0,0976	0,1053	0,1096
0,6	0,1143	0,1521	0,1777	0,1835	0,1830	0,1799
0,8	0,2579	0,2753	0,2715	0,2595	0,2469	0,2350
1,0	0,4219	0,3909	0,3492	0,3194	0,2959 J	0,2764
431
Таблица 6-3
Значения коэффициента <?п [Л.6-6]
Lu	Pn	Ко*Рп					
		o.t	0.2	|	0.4	о,6	0,8	1.0
o,ot_	0,1	0,0010	0,0010	0,0010	0,0010	0,0010	0 0010
	0,2	0,0020	0,0020	0,0020	0,0020	0,0020	0 009Г)
	0,4	0,0040	0,0040	0,0040	0,0040	0,0040	00040
	0,6	0.0060	0,0060	0,0060	0,0060	0,0060	0/060
	0,8	0,0081	0,0081	0,0080	0,0080	0,0080	О008П
0,05	1,0	0,0101	0,0101	0,0101	0,0100	0,0100	0,0100 0 0050
	0,1	00052	0,0052	0,0051	0,0051	0,0050	
	0,2	0,0 Ю5	0,0104	0,0103	0,0102	0,0101	0,0100
	0,4	0,0209	0,0208	0,0206	0,0203	0,0201	0'0J99
	0,6	0,0314	0,0312	0,0309	0,0305	0,0302	00298
	0,8	0,0419	0,0416	0,0411	0,0407	0,0402	0,0398
0,1	1,0	0,0523	0,0520	0,0514	0,0509	0,0503	00498
	0,1	o,ono	0,0108	0,0105	0,0103	0,0100	0 0098
	0,2	0,0219	0,0216	0,0211	0,0206	0,0201	00196
	0,4	0,0438	0,0433	0,0422	0,0411	0,0402	00392
	0,6	0,0658	0,0649	0.0633	0,0617	0,0602	0’0588
	0,8	0,0877	0,0865	0,0843	0,0823	0,0803	00784
0,2	1,0	01096	0,1082	0,1054	0,1028	0,0104	0’098l 0,0186 0 0371
	0,1	0,0241	0,0233	0,0218	0,0206	0,0195	
	0,2	0,0482	0,0466	0,0437	0,0412	0,0390	
	0,4	' 0,0964	0,0931	0,0874	0,0824	0,0781	~0 0743
	0,6	0,1446	0,1397	0,1311	0,1236	0,1171	01114
	0,8	0,1928	0,1863	0,1747	0,1648	0,1562	OI4R6
0,4	1,0	0,2410	0,2329 0,0521	0,2184	0,2060	0,1952	0,1857 0 0312
	о,1	0,0581		0,0438	0,0383	0,01343	
	0,2	0,1162	0,1041	0,0876	0,0766	0,0686	0/625
	0,4 0,6	0,2325	0,2082	0,1752	0,1533	0,1373	0 1249
		0,3487	0,3123	0,2629	0,2299	0,2059	0'1874 0 2499
	0,8	0,4650	0,4165	0,3505	0,3066	0,2746	
0,6	1,0	0,5812	0,5206	0,4381	0,3832	0,3432	0/123
	o,i	0,1006	0,08(J3	0,0604	0,0500	0,0432	0,0384
	0,2	0,2012	0,1606	0,1209	0,0999	0,0865	0,0768
	0,4	0,4025	0,3212	0,2417	0,1999	0,1729	0 1530
	0,6	0,6037	0,4818	0,3626	0,2998	0,2594	02305
	и/	0,8049	0,6423	0,4835	0,3998	0,345?	0,3073
	1,0	1,0062	0,8029	0,6044	0,4997	0,4323	0 3841
0,8	0,1	0,1383	0,0999	0,0703	0,0.566	0’0482	-0,0424
	0,2	0,2767	0,1998	0,1406	0,1132	0,0964	00848
	0,4	0,аэ34	0,3995	0,2813	0,2264	0,1928	0,1696
	0,6	0,8301	0,5992	0,4219	0,3395	0,2893	
	0,8	1,1067	0,7990	0,5625	0,4527	0,3857	0,3392
1,0	1,0 >	1,3834	0,9987	0,7032	0,5659	0,4821	0 4240
	0,1	0,1562	0,1091	0,0754	0,0602	0,05 Ю	0/447
	0,2	0,3123 0,6247	0,2182	0,1507	0,1204	0,1021	0/894
	0,4		0,4364	0,3015	0,2408	0,2041	0,1789
	0,6	0,9370	0,6546	0,4523	0,3612	0,3062	0,2683 0 3578
	0,8	1,2494	0,8729	0,6030	0,4815	0,4082	
	1,0	1,5617	1,0911	0,7538 		0,6019	0,5103	0/472
432
Значения коэффициента Н21 [Л-в-б]
Таблица 6-4
Ln	Pn	Ko*Pn					
		0J 1	0.2	0.4	0.6	0.8	1.0
0,01	0,1	0,0101	0,0202	0,0402	0,0602	0,0801	0,1000
	02	0,0050	0,0101	0,0201	0,0301	0,0401	0,0500
	04	0,0025	0,0050	0,0101	0,0151	0,0200	0,0250
	06	0,0017	0,0034	0,0067	0,0100	0,0134	0,0167
	0,8	0,0013	0,0025	0,0050	0,0075	0,0100	0,0125
	1,0	0,0010	0,0020	0,0040	0 0060	0,0080	0,0100
0,05	0,1	0,0523	0,1040	0,2057	0.3052	0,4024	0,4975
	0,2	0,0262	0,0520	0,1029	0,1520	0,2012	0,2488
	04	0,0131	0,0260	0,0514	0,0763	0,1006	0,1244
	06	0,0087	0,0173	0,0343	0.0509	0,0671	0,0829
	08	0,0065	0,0130	0,0257	0,0381	0,0503	0.0622
	10	0,0052	0,0104	0,0206	0,0305	0,0402	0,0498
0,1	0 1	0,1096	0,2164	0,4217	0,6170	0,8031	0,9806
	02	0,0548	0,1082	0,2109	0,3085	0,401s	0,4903
	04	0,0274	0,0541	0,1054	0,1642	0,2008	0,2451
	0,6	0,0183	0,0361	0,0703	0,1028	0,l338	0,1634
	0,8	0,0137	0,0270	0,0527	0,0771	0,1004	0,1220
	1,0	0,0110	0,0216	0,0422	0,0617	0,0803	0,0981
0,2	0 I	0,2411	0,4657	0,8737-	1,2361	1 5617	1,8570
	0,2	0,1205	0/329	0,4368	0,6181	0,7809	0,9283
	0,4	0,0603	0,1164	0,2184	0,3090	0,3904	0,4642
	06	0,0402	0,0776	0.1456	0,2060	0,2603	0,3095
	0,8	0,0301	0,0582	0,1092	0,1545	0,1952	0,2321
	1 0	0,0241	0,0466	0,0874	0,1236	0,1562	0,1857
04	0,1	0,5812	1,0412	1,7524	2,2992	2 7456	3J235
	0,2	0,2906	0,5206	0,8762	1,1496	1,3728	1,5617
	04	0,1453	0,2603	0,4381	0,5748	0,6864	0,7809
	06	0,0969	0,1735	0,2921	0,3832	0,4576	0,5206
	08	0,0726	0,1301	0,2190	0,2874	0,3432	0,3904
	1,0	0,0581	0,1041	0,1752	0,2299	0,2746	0,3123
0,6	0 1	1,0062	1,6059	2,4174	2.9983	3,4583	3,8411
	0,2	0/031	0,8020	1,2087	1,4002	1,7292	1,9200
	0,4	0,2315	04015	0,6044	0,7496	0,8646	0,9603
	06	0,1677	0,2676	0,4029	0,4997	0/764	0,6402
	0,8	0,1258	0,2007	0,3022	0,3748	0,4323	0,4801
	1,0	0,1006	0,1606	0,2417	0,2993	0,3458	0,3841
0,8	0 1	1,3834	1,9975	2,8126	3,3955	3,8568	4,2400
	0,2	0,6917	0,9988	1,4063	1,6977	1,9284	2/200
	0,4	0,3459	• 0,4994	0,7032	0,8489	0,9642	1,0600
	0,6	0,2306	X3320	0,4688	0,5659	0,6428	0,7067
	08	0,1729	0,2497	0,3516	0,4244	0,4821	0,5300
	1.0	0,1383	0,1998	0,2813	0,3395	0,3857	0,4240
1,0	0,1		2,1822	3,0151	3,6116	4 0825	4,4721
	0,2	0,7809	1,0911	1,5076	1,8058	2,0412	2.2361
	04	0,3904	0/455	0,7538	0,9029	1,0206	1,1180
	06	0,2603	0,3637	0,5025	0,6019	0,6804	0,7454
	0,8	0,1952	0.2728	0,3769	0,4514	0,5103	0,5590
	1,0	0,1562	0,2182	0,3015	0,3612	0,4082	0,4472
433
6-8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ
ЧЕРЕЗ ПОРИСТЫЕ СРЕДЫ
Выше (§ 6-1 — 6-7) были рассмотрены явления переноса в капиллярно-по-
ристых телах при фазовых превращениях. Перенос массы в таких телах был обу-
словлен процессами диффузии к термодиффузии. При этом под диффузией массы
понималась не только молекулярная диффузия пара, газа и жидкости, но и ка-
I пиллярное движение жидкости, лотя по своей физической сущности капиллярное
I движение жидкости относится к молярному движению, описываемому законами
гидродинамики, по условно, в силу поликалиллярной структуры тела, оно при-
I равнивается к хаотическому движению, называемому капиллярной диффузией.
* Однако для монокапиллярной структуры тела капиллярная диффузия вырож-
дается в обычное гидродинамическое течение по эквивалентной капиллярной
• трубке, которое может быть ламинарным и турбулентным.
Перенос пара и неконденсирующихся газов происходит не только путем
молекулярной диффузии (концентрационная и термическая диффузия), по и
по закону фильтрации Дарси. Этот вид фильтрационного движения по своей фи-
[ зической сущности также является гидродинамическим течением, однако в случае
/ фильтрации через капиллярно-пористые тела, где путь движения массы весьма
[ запутан и извилист, такая фильтрация также условно относится к фильтрацион-
ной диффузии. Таким образом, перенос массы происходит диффузионным путем,
I если под диффузией понимать хаотическое движение, включающее не только мо-
\ пекулярную, но и капиллярную и фильтрационную диффузию.
' В результате диффузионный перенос массы описывается системой дифферен-
циальных уравнении параболического типа, подробно рассмотренных выше.
Пористые среды представляют собой тела со сложной системой пор. Струк-
тура таких сред и перенос массы в них были рассмотрены в разд. 5.
В случае пористых сред течение жидкости и газа под влиянием перепада
давления (фильтрационное течение) нельзя рассматривать как фильтрационную
диффузию. Только в одном частном случае, так называемой напорной фильтрации,
такое течение можно свести к фильтрационной диффузии. Обычно такие задачи
рассматриваются в теории фильтрации в грунтах, и они достаточно хорошо опи-
саны и разработаны [Л.6-7].
Дифференциальное уравнение напорной фильтрации яляется частным слу-
чаем дифференциального уравнения переноса массы в капиллярно-пористых те-
лах. Если положить pi = р, bj= 1, то из уравнения (6-1-11) получим диффе-
ренциальное уравнение напорной фильтрации:
n^=Aiv [y1”1
(6-8-1)
Уравнение (6-8-1) описывает движение сжимаемой жидкости в изотермиче-
ской среде.
Коэффициент ka для газов равен:

(6-8-2)
Коэффициент изотермического	сжатия обозначим через Р, т. е,
	Т')	'	(б-8-З) . др jr р \др )т	1	1
Если коэффициент р для сжимаемой жидкости считать постоянным, то по-
лучим:
Р =Р» ехр [р (р—р„)],	(6-8-4)
W ро — значение плотности при давлении рп.
Тогда для изотермических условий из соотношений (6-8-4) получим:
Vp — PpVp.	(6-8-5)
434
Подстановка (6-8-5) в дифференциальное уравнение (6-8-1) дает»
n-^- = div('4-Vp+— W1).	(6-8-6)
Если гравитационное давление не изменяется (й =const), то
n>“divUv4	(б-8-7)
В случае фильтрации газов уравнение (6-8-7) может быть написано в ином
виде:
обозначим фактор сжимаемости газа через я, т. е.
Р=
pm
tiRT ’
где m — молекулярная масса. В общем
р и Т, т, е. л (р, Т).
С учетом эффекта Клинберга бу-
дем иметь:
пЖ)=МШ(р+
+ 0) 4+^™)]'
Если h — величина постоянная,
то получим:
(6-8-10)
Обозначим через	величину
р + а:
ffi=p-\-a, (6-8-П) -
тогда будем иметь:
(6-8-8)
44=44^4
(6-8-12)
Рие. 6-1. Зависимость безразмерного
давления р* [р* - (р — р0) / (рг —
— Ро)] от координаты x/L в неогра-
ниченной пластине для случая р1/р0=
= 5 (Л. 6-81.
П°
Если величины л, b и k постоянны, го
(ад-13)
Это уравнение можно переписать так:
(6-8-14)
ch:	/Zt]	v '
В качестве первого приближения можно величину kp принять постоянной,
положив kp яЛрт, тогда получим:
(6-8-15)
дт 11 х\	'
Для иллюстрации на рис. 6-1 приведены профили безразмерного давления
в неограниченной пластине толщиной L, полученные из решения дифференциаль-
ного уравнения (6-8-15) при граничных условиях первого рода (при х=0, р =
~ pl = const). Обзор решений фильтрационных задач приведен в [Л.6-7, 6-9];
их анализ не входит в нашу задачу.
435
6-9. ДИФФУЗИЯ ЧЕРЕЗ ПОРИСТЫЕ СРЕДЫ
I Л Ш IV
Рис. 6-2. Механизм миграции влаги в ка-
пиллярно-пористом материале.
Перенос массы в капиллярно-пористых телах, как уже было рассмотрено
выше, описывался системой дифференциальных уравнений параболического
типа. Движущейся термодинамиче-
ской силой переноса массы для
однородных тел поликапиллярной
структуры являются градиент кон-
центрации (vwf = povUi) и гра-
диент температуры (уТ)*
В простейшей модели мигра-
ция жидкости в капиллярно-по-
ристом теле [Л.6-52] происходит в
виде капиллярного движения жид-
кости, пленочного движения жид-
кости (рис. 6-2, период /). В про-
цессе капиллярного движения жид-
кости часть наружного воздуха по-
падает внутрь капилляра (рис. 6-2,
период //). Величина этого пузырь-
ка увеличивается, возникает меха-
низм миграции влаги в виде испарения-конденсации (рис. 6-2, период ///), и,
наконец, наступает диффузия пара через капилляр (рис. 6-2, период IV). Однако
наличие градиента температуры осложняет механизм миграции пара в капилля-
рах и порах тела.
На рис. 6-3 схематически представлена схема возможного механизма пере-
носа влаги в слое капиллярно-пористого тела, который нагревается (поток теп-
лоты направлен справа налево) [Л.6-51]. В боль
ших полостях (кавернах) может быть циркуля-
ция воздуха наподобие рассмотренных в гл.З
(см. рис. 3-41 и 3-42). Поток Стефана и поток
теплового скольжения направлены против пото-
ка теплоты. Помимо этих потоков имеют место
потоки гидродинамического и дифракционного
скольжения,
При интенсивном испарении и наличии эф-
фузионного натекания воздуха из окружающей
среды по микрокапиллярам в крупных порах,
которые сообщаются с микрокапиллярами, воз-
никает градиент общего давления. Под влиянием
этого градиента общего давления возникает дви-
жение пара и воздуха аналогично фильтрации.
В этом случае фильтрационный перепое парооб-
разной влаги является основным видом перено-
са, так что остальными видами переноса можно
Рис. 6-3. Схема движения влаги и теплоты в
поверхностном слое капиллярно-пористого тела.
I — поток скольжения; 2 — поток Стефана; q — поток
теплоты; / — поток влаги,
пренебречь. Поэтому представляет интерес подробно рассмотреть механизм
фильтрационного переноса.
Механизм переноса
При изотермических условиях можно представить следующие виды переноса
массы в пористых средах. Предположим, что через пористую среду проходит
436
жидкость с растворенным веществом или газовая смесь. Тогда могут иметь место
следующие механизмы массопереноса.
1.	Молекулярная диффузия, если масштабы времени велики; массопереиос
является результатом молекулярной диффузии.
2.	Вихри: если течение в отдельном канале пористой среды становится тур-
булентным, массоперенос возникает в результате миграции вихрей,
3.	Перемешивание, вызванное препятствиями: в пористой среде имеются
разнообразные извилистые каналы, поэтому два элемента жидкости А и В
(рис. 6-4), начинающие движение на определенном расстоянии друг от друга и
имеющие одинаковую скорость, спустя определенный промежуток времени не
Останутся на том же расстоянии; произойдет перемешивание.
4.	Наличие автокорреляции в потоке: массоперенос может быть результа-
том того, что не вес поры пористой среды доступны для элемента жидкости, т. е,
результатом несвязности среды (рис. 6-5).
5.	Рециркуляция, вызванная локальными участками пониженного давле-
ния. Массоперенос может\ быть вызван рециркуляцией, возникающей благо-
Рис. 6-4. Смешивание
потоков в результате
преград.
Рис. 6-5. Неполная свя-
зуемость потока.
а—вход жидкости; 1 —
л эту ветвь нет входажид-
кости из сетки 2.
Рис. 6-6. Рециркуляция жид-
кости за счет локальных об-
ластей уменьшенного давле-
ния.
Даря наличию сужений в каналах вдоль течения. Переход энергии давления в ки-
нетическую энергию создает локальные участки низкого давления. Если такой
участок доступен для жидкости, ранее прошедшей через него, то начинается ре-
циркуляция, как это имеет место в случае, представленном на рис. 6-6.
6.	Глухие поры; закрытые объемы вызывают массоперенос в нестационарном
течении (изменяющиеся профили концентрации), так как по мере прохождения
через фронт, богатый растворенным веществом, происходит молекулярная диф-
фузия. После прохождения фронта происходят обратная диффузия этого раство-
ренного вещества и массоперенос в системе. Объем пор вносит некоторую неоп-
ределенность при экспериментальном определении характеристик переноса, так
как он измеряется как пористость, но эта пористость не влияет на поперечное
сечение потока.
7.	Адсорбция: массоперенос путем адсорбции есть явление нестационарное.
Так же как и в случае глухих пор, адсорбция увеличивает или уменьшает коли-
чество растворенного вещества в потоке и поэтому стремится выровнять профили
концентрации в движущейся жидкости.
8.	Гидродинамический массоперенос: макроскопический перенос происхо-
дит в капилляре даже в отсутствие молекулярной диффузии из-за наличия ско-
ростного профиля, создаваемого прилипанием жидкости к стенке. Это заставляет
частицы жидкости при различных радикальных положениях перемещаться отно-
сительно друг Друга, так что по мере движения по капилляру происходит мас-
сообмен.
9.	Макроскопическая дисперсия, вызванная неидеальностями, изменяю-
щими общие линии тока.
10.	Молярное движение, вызванное переходом концентрации вблизи стенок
поры, называемое диффузией скольжения.
437
Все эти виды массопереноса можно условно назвать диффузией массы. В ан-
глийской и американской литературе такой суммарный массоперенос называется
дисперсией (dispersion), что, очевидно, означает хаотическое рассеивание массы
в пористой среде. Движущей силой такого массопереноса в изотермических ус-
ловиях является градиент объемной концентрации (v<o). Для одномерных задач
такой вид массопереноса описывается дифференциальным уравнением
да> д2со ди
Ж=° ~д&— '’'аР
(6-9-1)
где коэффициент D называют коэффициентом дисперсии (dispersion coefficient);
vx — скорость фильтрационного движения, определенного законом Дарси. Если
принять их за величину постоянную, то уравнение (6-9-1) можно написать так:
|£. = _4(_D^ + t>A	' (6-9-2)
дх дх \ дх х /	'	‘
Следовательно, поток массы
im= —	’ (6-9-3)
Формула (6-9-3) аналогична формуле для потока массы, состоящего из диффу-
зионного потока — D и конвективного потока (их(о). Поэтому, с нашей точки
зрения, более целесообразно называть суммарный массоперенос в пористой среде,
описываемой уравнением типа (6-9-1), диффузией, понимая под диффузией все
виды переноса, описанные выше. В этом случае коэффициент дисперсии D будет
являться коэффициентом диффузии в пористой среде. Это целесообразно и в том
отношении, что массоперенос в пористой среде будет аналогичен массолереносу в
капиллярно-пористых телах.
Если воспользоваться формулой Дарси, то можно написать так:
д® k др
,т дх т| дх ’
(6-9-4)
мы получили соотношение для массопереноса в капиллярно-пористом теле.
В некоторых работах, например [Л. 6-15], уравнение (6-9-1) сводится к обыч-
ному уравнению диффузии путем преобразования
Х1 = Х—(6-9-5)
Тогда уравнение (6-9-1) примет вид:
' (6-9-6)
дх —= дх?	1	•
Если пористую среду заменить некоторой эквивалентной капиллярной труб-
кой, то распространение растворенного вещества (жидкости) будет характери-
зовать механизм массопереноса. В этом случае коэффициент диффузии будет ра-
вен:
г,
192Dm’
(6-9-7)
где R — радиус трубки; — средняя скорость течения жидкости; Dm — коэф-
фициент молекулярной диффузии.
Числитель в формуле (6-9-7) есть мера осевой молярной диффузии, знаменатель
отражает не только молекулярное перемешивание, по и общий эффект поперечного
молекулярного и молярного перемешивания.
Следовательно, любой механизм, увеличивающий поперечное перемешивание,
например турбулентные потоки, снижает коэффициент диффузии D. Этот вывод
в качественном отношении подтверждается опытами по массопереносу в пористых
телах.
438
В [Л. 6-111 дано обобщенное выражение для коэффициентов диффузии:
Д = ^ + 19й£-	.	<6-М>
Эта формула называется формулой Тэйлора—Ариса.
Приравнивая пористую среду к некоторой эквивалентной капиллярной
трубке, ряд авторов [Л. 6-12] в качестве структурного параметра принимают эф-
фективный диаметр пор d9. Тогда коэффициент D считается пропорциональным
произведению структурного параметра на скорость жидкости в порах в степени п:
D^d3vn.	(6-9-9)
Показатель степени п колеблется от 1 до 2 и зависит от диаметра d9. Значение
п — 1 соответствует случаю, когда имеется достаточно времени для перемешивания
жидкости, при п>— 2 перемешивание полное.
В двумерных задачах диффузии коэффициент D разный для различных на-
правлений:
дсо „	„ д2<я дсо	, ,с „ 1Л.
= D, ~^-+DTz^ — vx-z-,	(6-9-10)
дт L dxi rd^ dx‘	'	'
где/?^ и DT — соответственно коэффициенты продольной и поперечной диффузии,
В силу сложности пористой среды такие упрощенные методы подхода себя
не оправдывают. Экспериментальные данные значительно отличаются от расчет-
ных.
Микроскопический подход к описанию явления движения жидкости в пори-
стой среде очень сложен. В принципе, имея информацию о системе, можно рассчи-
тать траекторию движения каждой частицы жидкости. Однако такой подход прак-
тически бесполезен по причине того, что опреде-
ление точной границы раздела твердое тело —
жидкость невозможно; кроме того, Траница,
если бы даже она была известна, настолько
сложна, что задача не поддавалась бы матема-
тической обработке. Если бы даже можно было
получить решение для траекторий отдельных
частиц жидкости, то оно не представляло бы
практической ценности, так как необходимы
макроскопические или интегральные характери-
стики.
Статистический метод
Более плодотворен статистический метод
описания пористой среды. Можно рассматривать
течение через пористую среду как хаотическое
движение, аналогичное турбулентному потоку,
используя для описания разработанный матема-
тический аппарат. Кроме того, моделируя про-
в статистической модели по-
ристой среды.
странство между пустотами в виде перемеши-
вающихся ячеек, можно воспользоваться математическими приемами статисти-
ческой термодинамики, включая понятия функции Гамильтона. Однако это не
исключает такого метода, при котором пористая среда моделируется систе-
мой капилляров, состоящих из подэлементов, соединенных между собой, или
системой, состоящей из последовательно соединенных капилляров.
Хотя в принципе рассмотренные процессы не являются марковскими, все же
обычно для простоты используется марковское допущение. Другими словами, мы
обычно ограничиваемся процессами, в которых вероятность перехода элемента
жидкости из одного состояния в другое остается постоянной, в частности, не зави-
сит от времени (например, набухающие среды не рассматриваются). В действи-
тельности не только делается марковское допущение, но и предполагается также,
что обычно полностью отсутствует автокорреляция, т. е. вероятность попадания
439
Таблица 6-5
Значения коэффициентов диффузии, см2/с,
рассчитанные по статистической модели при скорости ®m = 0,1 см/с
а	ь	а	6		DT-10‘	DUDT
2	2	0	0	1,77	4,83	3,66
2	2	— 1/2	—1/2	7,28	787	9,37
2	2	—1/2	1	33,2	16,8	19,8
2	2	2	4	4,82	6,54	7,40
2	2	9	2	3,78	5,87	6;42
2	2	4	2	2,43	4,89	4,96 .
9	. 2	1	1	4,54	6,32	7,18
2	4	2	4	3,96	5,15	7,70
4	2	9	4	4,30	5,98	7,20
2	4	Г	1	4,78	4,96	9,65
4	2	1	I	^95	11,60	6,85
2	4	4	2	2,02	4,00	5,05
4	2	4	2	4 26	8,95	4,76
1	1	4	2	1,98	4,28	4,68
1	1	2	4	3,54	5,75	6,16
жидкости в пору данного размера и расположения не зависит от размера и распо-
ложения поры, которую покинула жидкость. Это несправедливо для сред, которые
характеризуются каким-то пехаотичсским, например слоистым, механизмом.
Используя статистический метод, можно подсчитать капиллярное давление,
проницаемость, продольную и поперечную диффузию с помощью некоторых пара-
метров я, М и ₽. В этой модели применяется элементарная пора (рис. 6-7). Если
обозначить безразмерную длину поры через /* (/* = //£), где L — длина самой
длинной поры; г* =-= r/R — безразмерный радиус; R — радиус самой большой
поры, тогда функции распределения / (/*) и F (г*) будут иметь вид [Л. 6-13]:
/ (;*)=(я^+1)1 (;♦)(!p-e-ii)
F(r*)=(atipt~<'*)<*(l~'*>11'	(б'9-12»
Используя эти соотношения, можно вычислить все структурные параметры,
в том числе и коэффициенты продольной DL и поперечной диффузии D т (табл. 6-5):
DL = f(a, b, а, р).	(6-9-13)
В описываемой модели частицы жидкости движутся по наиболее вероятной
траектории со скоростью V:
й = у,	(6-9-14)
где 3— скорость движения, определяемая законом Дарси, а величина J равна:
т _ (^ + О (<% + 2) (^ + Р + 4)	+ Р +	Г6-0.Ш
(а 4-3) (а-|-4) (а 4- р 2) (а 4-р-|-3) ’
Метод турбулентности
Используя представления и математические приемы теории турбу-
лентного течения жидкости, можно рассчитать характеристики диффузионного
потока жидкости через пористые среды.
440
Большинство авторов, следуя этому методу, использует уравнение
d<o . dii> d /	' dio \
dTk)>
(6-9-16)
где Djk — тензор диффузии.
Аналогичное уравнение было получено в (Л. 6-14]. Если индикатор жидкости
движется со средней скоростью то относительная концентрация ю* описывается
решением дифференциального уравнения
з
до* V4 d_ / dii)*\
“diT- L dx^ \l dxj’
(6-9-17)
где D{ — аксиальный компонент тензора диффузии.
Коэффициент диффузии D является тензором второго ранга. Если считать,
что коэффициент О инвариантен относительно вращения к направлению средней
скорости и является зеркальным отражением относительно плоскостей, то
.	(6-9-18)
где и*- — составляющая флуктуации средней скорости; 6,-/ — единичный тензор;
А и В — постоянные.
Если движение жидкости происходит в соответствии с законом Дарси, то
коэффициент D будет пропорционален произведению осредненной скорости на
характерную длину. В общем характерная длина не является скалярной величи-
ной, а представляет собой тензор четвертого ранга; для изотропной среды он равен:
4-	(й-9-1
где Н2 = Н3 и
8=^(1]); А = 2Нг(у\).	(6-9-20)
Чтобы формула (6-9-18) была справедлива, необходимо выполнение равенства
О</=Ч'Ы^.	(6-9-21)
Величины А, В или Ht и 7/г зависят от механизма смешения в пористой среде,
В каждой точке пористой среды вектор средней скорости изменяется произвольно
по отношению к локальной скорости:
ui = ni}tij,	(6-9-22)
где 77// — локальный тензор пористой среды.
Для одномерного течения
Оп = О(Лп)И=М;	_ |	(М23)
—D33—D (/7J2) lu — X2u, /
D/y=O, если
Отсюда
Dn/D!2 = £i,	(6-9-24)
где Xt и — соответственно составляющие тензора диффузии изотропной и по-
ристой среды.
Величина / составляет около половины диаметра частиц в неуплотненных
средах и половину средней длины прямой, соединяющей поры, в уплотненных
средах.
441
Если предположить идентичность сред, за исключением I, то, составляющие
тензора Пц будут равны, ;	я следовательно, (б-9"25)
т. е. коэффициент диффузии пропорционален размеру частиц.
Аналогичные результаты были получены в (Л. 6-141.
Таблица 6-6
Отношение коэффициентов продольной диффузии DL к поперечной
диффузии Dr по данным разных авторов
Экспериментальные данные	dl 3 f	Источник
Статистическая модель	DL _ 4	Г27 (д+6+2)2 vT 1 DT 95 "1 (o+I)7	</) ]	[Л.6-13]
Сплошная среда, метод турбулентности То же То же То же	«- ,	'	a 55	~	a ।	-i - "	L	8 ii	ii	a -jl S, к] K,	I'	। Q Q Q Q -Jl 1	Q |Q 8 0	[Л.6'14] [Л.6-15, ' 6-16] [Л.6-17] [Л-6-18]
	а14-агН— dl 07-3	[Л.6-19]
Результаты исследований переноса жидкостей разными авторами приведены
в табл. 6-6. В этой таблице X и М являются инвариантами тензора LyM-t А^ц —
симметричные тензоры, которые являются функциями структуры пористой среды
и свойств жидкости. Постоянные 1, 2, 3) характеризуют конфигурацию
пористой структуры х.
Экспериментальные данные
Представляет интерес сравнение расчетных данных с экспериментальными.
В (Л. 6-20] получены такие данные для'песчаника с пористостью 20% (средний
диаметр зерен 180 мкм, а средний размер пор 15 мкм).
1 Подробно см. [Л. 6-13 — 6-19].
442
Неуплотняющей средой были пакеты стеклянных шариков одинакового диа-
метра. Для шариков диаметром 1,5; 0,25 и 0,074 мм пористость составляла соответ-
ственно 37,5, 41 и 38%. Результаты расчета, выполненные на основе статистиче-
ской модели [Л. 6-13), приведены на рис. 6-8 и 6-9, откуда видно, что эксперимен-
тальные данные хорошо совпадают с расчетными в области, где преобладает мо-
лярная диффузия. При малых скоростях v коэффициент диффузии D не зависит
от скорости, что указывает на преобладающее влияние молекулярной диффузии.
Рис. 6-8. Зависимость коэффициентов Рис. 6-9. Зависимость DL и D? от о
диффузии и D7, см2/с, от скоро-	ддЯ песчаника. Прямые соответствуют
сти фильтрации и, см/с для пористой	расчетам по формулам (Л. 6-131, точ-
среды из стеклянных шариков. ки — экспериментальные данные [Л.
Прямые соответствуют расчетам по форму-	®
лам [Л.6-131; точки — экспериментальные
данные [Л.6-20].
Из рис. 6-8, 6-9 следует, что коэффициент диффузии является линейной функ-
цией скорости фильтрации v.
В [Л. 6-13] были обработаны экспериментальные данные по диффузии в квар-
цевом песке, В результате были получены следующие экспериментальные формулы:
для песка
~ = S3 Re1’2;	(6-9-26)
для среды из стеклянных шаров
— = 54 Re1’2,	(6-9-27)
где Re	v — коэффициент кинематической вязкости; k — проницаемость.
Аналогичные формулы в виде
— =АИел,	(6-9-28)
где А и л — постоянные, были получены и другими исследователями. При этом
показатель степени у числа Re зависит от диаметра зерен пористой среды-
Конвективная диффузия в модельных капиллярных трубках
Для исследования структуры пористой среды широко применяется метод
исследования диффузии растворенного вещества, введенного в жидкость, текущую
цо капиллярной трубке. Такая капиллярная трубка моделирует пористую среду.
443
Эта методика обусловлена не только стремлением исследовать структуры пористых
сред, но и практической ценностью полученных результатов для гидромеханики
нефтедобывающей промышленности. Поэтому таких исследований очень много
и дать полный обзор этих работ очень трудно.
При изучении диффузии растворимого вещества в текущем потоке жидкости
пользуются уравнением (6-9-1) и (6-9-6). Если положить в основу дифференциаль-
ное уравнение (6-9-6), то из его решения для простейших граничных условий
первого рода (полупространство с постоянной концентрацией на открытой поверх-
ности) можно рассчитать коэффициенты диффузии D (коэффициент дисперсии).
В этой методике исследования вводится так называемая длина смешения L,
численно равная расстоянию вдоль оси трубки» на которой средняя концентрация
введенного вещества изменяется от 10 до 90% по отношению к ее значению на входе
в трубку.
Используя решение уравнения (6-9-6) для величины коэффициента D, полу-
чаем;
°=т(зда) '	(6-9-29)
Однако расчеты по решению уравнения Цб-9-6) не всегда дают удовлетвори-
тельные результаты. Поэтому в [Л, 6-6] предложен метод, суть которого состоит
в следующем. Расчеты коэффициента диффузии производятся на основе изменения
средней концентрации <пт введенного в жидкость вещества. В качестве такого
вещества может быть взята любая жидкость, не смешивающаяся с первой (основ-
ной).
Зависимость между локальной концентрацией о и средней ыт принимается
в виде
»=«>»,+ У /л (т, »)	,	(6-9-30)
дх дх,
п = 1	1
где fn (т, у) — так называемая дисперсная функция.
Формула (6-9-30) является разложением в ряд Тэйлора локальной концен-
трации по средней концентрации.
В этом случае уравнение (6-9-6) примет вид:
р.
&"+2 '
(6-9-31)
Коэффициент диффузии D определяется из первого члена разложения (6-9-30).
Три первых члена формулы (6-9-30) необходимы для хорошего согласования
расчета с экспериментальными данными в зоне смешения:
°-3<2^<0'7’
а члены высшего порядка вносят поправку для расчета в крайних участках зоны
перемешивания,
Необходимо отметить, что все расчеты, основанные на решении уравнения
диффузии, применимы только в том случае, если ламинарное течение жидкости
в трубке полностью развито. Это условие аналитически отображается так:
где R — радиус трубки.
Используя понятие безразмерной длины перемешивания
444
условия полностью развитого ламинарного течения можем записать как
t-=0.26	0,8.	(6.9-35)
Для малых значений т* (т* < 0,01) L* = 0,8т*-
Для малых чисел диффузионного критерия Пекле Ред (PeD=~^—^в[Л.6-21]
получены следующие соотношения:
L* =2,5Рер°’75т*0-55;
т* > 0,05;
. Ь* = 2,5Ре^°'75т*0-60;
т* < 0,05.
i
(6-9-36)
(6-9-37) ‘
Зная величину L*, можно рассчитать и коэффициент диффузии.
Одномерная модель нестационарной диффузии лучше применима к турбулент-
ному течению, чем к ламинарному, так как время, необходимое для установ-
ления такого течения, которое моделировало бы движение жидкости в пористой
среде, значительно меньше.
Вышеприведенные аналитические решения могут быть использованы для
анализа экспериментального материала по тепломассоперсносу в капиллярно-
пористых телах. При этом необходимо иметь экспериментальные данные по пере-
носным свойствам капиллярно-пористых тел, К сожалению, таких данных в на-
стоящее время очень мало, что затрудняет их обзор и анализ,
Кроме того, аналитические решения могут быть положены в основу для раз-
работки экспериментальных методов определения коэффициентов тепломассо-
переноса, в том числе и скорости переноса массы о>т-Наличие таких методов позво-
лит накопить необходимый экспериментальный материал по структуре капилляр-
но-пористых и пористых тел, что является весьма актуальной задачей в этой об-
ласти теории тепломассопереноса. Дело в том, что моделирование пористой среды
в виде капиллярной трубки, с точки зрения гидродинамики, будет возможно тогда,
когда характер движения жидкости будет примерно одинаков в обоих случаях.
Для выполнения этого условия необходим режим установившегося течения в мо-
дельной капиллярной трубке.
Теория Тэйлора — Ариса применима в том случае, когда безразмерное'время
т* будет не меньше, чем т*ин;
0,6РеЬ
мин^Ре£,-|-192 •
(6-9-38)
Такой режим быстрее достигается при турбулентном течении. В этом случае
коэффициент диффузии D определяется по формуле
<б-м9>
где flg — функция, определяемая из формулы (6-8-30) Функция fls получена
на основе решения дифференциального уравнения
z 5" = ° 5-»+_ГТ-	(6-9-40)
от '' дх \дх3 1 г dr ar j	'	’
с учетом подстановки (6-9-5), при этом коэффициент диффузии включает в себя
коэффициент турбулентной диффузии. Если коэффициент турбулентной диффузии
значительно больше коэффициента молекулярной диффузии, то приближенное
445
значение для коэффициента диффузии D (коэффициент дисперсии) будет:
D = 10,iRn*,	(6-9-41)
где о* скорость трения, определяемая по формуле
=	=	(6-9-42)
здесь Cf — коэффициент трения; аш — напряжение трения на стенке трубки.
Таким образом, для коэффициента диффузии D получим соотношение
O = 7,IIRo,„l''C,.	(6-9-43)
Точность расчетного коэффициента D сильно зависит от точности определения
скорости. При числах Re Э?4,2-10* полученные коэффициенты диффузии могут
отличаться от опытных на 50%.
Из формулы (6-9-43) следует, что коэффициент диффузии прямо пропорциона,
лен средней скорости ит.
На рис. 6-10 дана зависимость обратной величины критерия Пекле 1/ReooT
критерия Re (Re = 2vmR/v] на основе расчета
по формуле Тэйлора — Ариса [см. (6-9-8)] и
по данным экспериментов.
На рис. 6-10 видно, что в пределах 10® <
< Re < 103 имеем удовлетворительное совпаде-
ние расчетных и экспериментальных данных, а
затем резкое их расхождение. Это объясняется
тем, что при числах Re > 10s течение становит-
ся турбулентным, что вызывает резкое умень-
шение коэффициента диффузии за счет попе-
речного турбулентного перемешивания.
Более совершенным моделированием струк-
туры пористой среды является замена цилинд-
рической капиллярной трубки капиллярными
трубками различных конфигураций: прямой ка-
нал, прямая щель, соосная и концентрическая
щели, в которых можно изучить эффекты асим-
метрии профиля скорости, искривления канала
и трубы, сходящихся и расходящихся каналов
(рис. 6-11). В частности, модель смешивающей
ячейки используется для объяснения того фак-
та, что коэффициент диффузии для цилиндриче-
ской трубки прямо пропорционален квадрату
скорости, а в пористой среде коэффициент диф-
фузии прямо пропорционален первой степени
линейной скорости течения. Однако надо отме-
тить, что в ряде работ было получено иное соотношение между D и vm, в част-
ности, коэффициент диффузии D прямо пропорциЬнален и”, где показатель сте-
пени л > 1.
Приведем результаты некоторых работ. Для плоскопараллельного капала
в случае полностью развитого ламинарного течения (т*	1) коэффициент диффу-
зии равен:
8 умакс^а
П—П _1_____—. макс
10
Рев
5
Sc-1
Re
Эксперимен -
тамные данные
Уравнение Тэйлора
-Ариса______
500 103	5000
Рис. 6-10. Сравнение рас-
четных данных с экспери-
ментом в виде зависимости
l/PeD (<),&-—] 01 числа Рей-
Re=^;
нольдса
(6-9-44)
где Н — половина ширины канала; циакс ~~ скорость движения на осевой линии,
Концентрические и эксцентрические каналы есть обобщение прямого канала
и прямой трубы и отражают эффект асимметричного профиля скорости, Коэффи-
циент диффузии в этом случае есть функция отношения внешнего и внутреннего
радиусов (1/Д = Rq/R}}- Для малых значений 1//С (узкая щель), когда ^-^1,5(
446
была получена следующая зависимость:
D = Dm
, 8_
*945
№2(1~*2Л
L 4Om J'
(6-9-45)
где Ro — радиус внешнего цилиндра.
Из формулы (6-9-45) следует, что с увеличением 1//( коэффициент D увеличи-
вается. Таким образом, эффект асимметрии в профиле скорости должен привести
к увеличению коэффициента диффузии.
Когда -г,' ^JOO, коэффициент диффузии
л
D равен коэффициенту диффузии для
цилиндрической трубки.
В [Л. 6-10] было показано, что эф-
"фект кривизны приводит к уменьшению
коэффициента диффузии по сравнению
с коэффициентом диффузии для прямой
трубки при числе Шмидта, равном и
большем 0,124 (Sc 0,124). Затем было
показано, что Эффект поперечного сме-
шивания за счет вторичного потока и
асимметричной осевой скорости приво-
дит сначала к увеличению, а затем к
уменьшению коэффициента диффузии.
При этом значения коэффициентов диф-
фузии становятся еще меньше их зна-
чений при больших числах Re (см.
рис. 6-10).
Поток в сходящихся и расходя-
щихся щелевых каналах ускоряется
или замедляется за счет изменения пло-
щади поперечного сечения. Даже не-
большие углы расхождения значитель-
но влияют на коэффициент диффузии,
особенно' при больших числах Пекле
[Л. 6-22].
Существование застойных участ-
ков жидкостей в пористых средах за
счет глухих проходов вдоль пути те-
чения является следствием геометрии
пористой среды.
Влияние емкости системы вызы-
вает увеличение длины пути переме-
шивания. Исследований, в основу ко-
торых была положена эта модель, было
проведено много. Обзор этих исследова-
ний дан в [Л, 6-23—6-26].
На основе методов теории подо-
бия можно показать, что процесс диф-
фузии зависит от обобщенных перемен-
ных чисел Пекле Ре^, чисел Рейнольд-
Рис. 6-11. Модельные капиллярные
трубки с профилями скорости течения
жидкости.
I — прямой канал; 2 — концентрический
кольцевой канал; 3 — расширяющийся ка-
нал; 4 — эксцентрический кольцевой канал;
5 — искривленная трубка (о — внутренняя
линия тока; б — внешняя линия тока, в —
линия тока); 6 — искривленный каиал; 7—
суживающийся канал
са Re, Грасгофа Gr и Фруда Fr.
Исходя из формулы (6-9-8), справедливой для ламинарного течения в
капиллярной цилиндрической трубке., можно получить зависимость безразмер-
ного коэффициента диффузии D* от числа Пекле:
D* « ——— « —-l J_
Dm^b РеЬ	48 *
(6-9-46)
447
Было проведено много работ и по движению в пористых средах иесмешиваю-
щихся жидкостей, когда влиянием гравитационного поля пренебречь нельзя.
Обзор этих работ не входит в нашу задачу,
Таким образом, исследуя картину диффузии индикатора в потоке жидкости
через модельную капиллярную трубку, можно получить важную информацию
о влиянии структуры пористой среды на механизм диффузии в пей. Однако такое
моделирование возможно при условии, что поток в трубке является полностью
развитым,
В [Л. 6-27] показано, что критерий применимости модели эквивалентной
капиллярной трубки определяется неравенством
^>0,04 -i-,	(6-9-47)
где Lj.— длина трубки или системы в направлении основного потока.
Из анализа работ с использованием модели -капилляров с емкостями (глухие
поры) требуется значительно большее время, с тем чтобы модельная система
могла быть применима.
Подводя итоги, можно отметить, что в основу анализа механизма массопе-
реноса в пористой среде был положен закон диффузии, обусловленный действием
градиента концентрации, при этом гидродинамический массоперенос, характе-
ризуемый средней скоростью движения жидкости в порах vm, входил в качестве
основного параметра в соотношения для коэффициента диффузии (коэффициента
дисперсии). Физически Это означает, что в расчетах массопереноса косвенным
образом вводилась конечная скорость переноса vm, Необходимость такого расчета
коэффициента диффузии обусловлена тем обстоятельством, что в основе аналити-
ческой теории диффузии лежит гипотеза о бесконечной скорости распространения
массы.
Известно, что аналитическая теория теплопроводности и диффузии основана
на бесконечно большой скорости переноса теплоты и массы. Однако эта гипотеза
не соответствует физической сущности явлений тепломассопереноса.
Поэтому можно наметить и другой путь исследования нестационарных явле-
ний тепломассопереноса, в основе которого с самого начала заложен принцип
конечной скорости тепломассопереноса, Как видно из вышеприведенного обзора,
это особенно важно для процессов переноса массы.
Такой метод анализа массопереноса в капиллярнопористых телах и пористых
средах был предложен автором этой книги.
6-10. ГИПЕРБОЛИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ТЕПЛОМАССОПЕРЕНОСА И ИХ РЕШЕНИЯ
В феноменологической теории теплопроводности предполагается, что скорость
распространения теплоты Wq является бесконечно большой = со). Это пред-
положение подтверждается результатами расчета температурных полей в различ-
ных телах при обычных условиях, встречающихся на практике.
Однако при некоторых условиях теплообмена необходимо учитывать, что
теплота паспространяется с конечной скоростью. На это впервые обратил внима-
ние П. Верно [Л. 6-28]. Независимо от него автором данной книги была предло-
жена гипотеза о конечной скорости диффузии массы и теплоты. Развивая принцип
Пригожина [Л. 6-29], автор [Л. 6-31] предложил обобщенную систему линейных
уравнений Онзагера.
Если обозначить потоки через fo, а термодинамические движущие силы —
через то это обобщение системы имеет вид;
/’*-2(1,Л+чЛ)+	(б-10-1)
где Lik, Lik и Lkr — кинетические коэффициенты (£/*= точка означает
производную по времени.
448
Для процессов массотеплопсрсноса можно пренебречь действием силы
тогда, не учитывая действия налагающихся эффектов (термодиффузии и диффузи-
онной теплопроводности), можно написать:
+	(б-'о-з)
Для одномерных потоков теплоты и массы будем иметь:
дТ
ч=-к-^-х^	(6-|м)
Л = -Ор^-т™/4.	(6-Ю-4)
где xrq, xrm — соответственно периоды (времена) релаксации тепломассопереноса.
Они связаны с коэффициентами диффузии теплоты а (коэффициент температуропро-
водности) и диффузии массы D соотношениями
(6-10-5)
где Wg и wm — соответственно скорость распространения теплоты и массы.
В соответствии с (6-10-3) и (6-10-4) дифференциальные уравнения теплопро-
водности и диффузии будут иметь вид:
дх 5т3 а дх2 ‘
Фло , _	<^о _ п
дх rm бт2 “ dx® ‘
(6-10-6)
(6-10-7)
Эти уравнения называются гиперболическими уравнениями теплопроводно-
сти и диффузии; они отличаются от обычных параболических уравнений, тепло-
проводности добавочными членами xrt/ и xrm —, которые учитывают ко-
нечную скорость переноса теплоты и массы. При до оо и хг -> 0 дифференциаль-
ные уравнения (6-10-6), (6-10-7) переходят в обычные ди^еренциальные урав-
нения тепло- и массопереноса параболического типа.
В отличие от последних решения уравнений (6-10-6), (6-10-7) имеют очерчен-
ный фронт волны, перемещающийся с конечной скоростью до. Отметим, что урав-
нения переноса гиперболического-типа, в частности волновое уравнение, были
получены различными путями рядом исследователей при анализе процессов диф-
фузии, теплопроводности, турбулентной диффузии и т. д.
Следует отметить, что конечная скорость распространения возмущений может
быть получена из решения нелинейного уравнения параболического типа [Л. 6-39—
6-43]
(в-10-8)
в том случае, когда коэффициент температуропроводности а стремится к нулю.
Решение уравнения (6-10-3) для этого случая в виде так называемых температур-
ных волн приведено в [Л. 6-28—6-36].
В последнее время появились работы (например, [Л.6-38]), в которых по-
лучены более общие результаты, связанные с конечной скоростью переноса
субстанции (массы или теплоты), выведены интегродифференциальные уравне-
ния для трехмерного случая с учетом конечной скорости и сформулирована
общая нелинейная задача переноса.
15 Лыков А. В.	449
Гиперболические уравнения тепло- и массопереноса могут иметь и другой
физический смысл. Представим себе, что испарение- жидкости внутри тела
происходит на некоторой поверхности, которая перемещается внутрь тела
с постоянной скоростью и>ф. В этом случае = шт — и скорость переме-
щения поверхности фазовых превращений изменяет свой физический смысл
(см. § 1-11). Тогда потоки теплоты q и массы / определяются обычными фор-
.	* a d2T D
мулами Фурье и Фика, а — —- и — ~^тз приобретают физическим смысл
источников теплоты и массы:
Тогда система уравнений (6-10-6), (6-10-7) будет иметь вид:
дТ{ .2Т a&i d^Ti
= , i = 1’2’
ф
(6-10-ба)
did/ пт.,,„	D/61/ d2v)i
-gr = D‘^‘------
(6-10-7а)
где св—относительная концентрация (ю = р/0); 6ц — дельта-функння,' 6ц=1
при г—1 и 6ц = 0 при i = 2.
Для поля температур при x^xrq	t=l (зона испарения);
при т ;> t = 2 (зона влажности состояния). *
Для поля концентрации при x^xrm (т/.т = О//цу|)) 1=1; при т>тгт
Перенос теплоты в полуограниченном теле с конечной скоростью
В первую очередь выясним некоторые особенности переноса теплоты в твер-
дом теле с конечной скоростью. Для этого возьмем простейший случай нагрева-
ния полуограпичснного тела (полупространства) при граничных условиях первого
рода. В начальный момент времени (т = 0) открытая поверхность тела имеет тем-
пературу То, которая поддерживается постоянной при протекании всего процесса
нагревания. Отсчет температуры производится от начальной температуры, которая
считается постоянной на всей глубине тела (равномерное начальное" распределе-
ние температуры). Решение такой простейшей задачи приведено в (Л, 6-44], оно
имеет вид:
LexpN>
T = x/r0/O
z Г17Т8_^М’/21	—
x •" л+Ч~ /7] (6-1О-9)
! V а )
— для Кто/а;
Г	Т* (т)=0
— для т Ах Кто/С‘
В этом решении т0 — период релаксации; а — коэффициент температуропро-
водности; /1 (г) —модифицированная функция Бесселя первого рода.,
Из решения (6-10-9) следует, что при т = х^т0/а
Т* = е “т/2т°.	(6-10-10)
На рис. 6-12 показано распределение температуры в зависимости от рас-
стояния х, из которого видно, что иа некотором расстоянии Д кривая Г* (х)
обрывается,
т*
Рис. 6-12, Изохрона
полупространства.
находится в противорс-
Следовательно, при х>тУа/т0 повышения температуры не наблюдается
(фронт теплового потока или точка разрыва). В классической же теории
теплопроводности такого разрыва в кривой распреде-
ления температуры нет. Этот фронт проникновения
можно считать глубиной проникнования теплоты.
Обозначив ее через Д, получим*.
(6-10-11)
ИЛИ	____
Д = у'г7го /ат.	(6-10-12)
Скорость распространения (проникновения) теп-
лоты
и9=-^- = ^. Ь /оТго) =/Й7т\и (6-10-13)
т. е. скорость распространения зависит от коэффи-
циента температуропроводности и т0-
Например, для твердых тел (металлов) толД О-11 с,
отсюда для стали Wq-= 1800' м/с.	!
В классической теории теплопроводности имеет-
ся понятие о скорости распространения изотермы
для нашего случая ат=2 Уа/т. Следова-
тельно, при т-0 &?=££), а при т->со гд^=О, что
чин с понятием о физическом механизме распространения теплоты.
Плотность потока теплоты находится из уравнения баланса теплоты
на поверхности тела (х = 0)
”w=W. i6-iws>
При т=0 (начальный момент времени)
а,(0)=1^ё..	<6-10-16)
V То
Соответствующее значение из классической теории теплопроводности
?«т=(тЖ) =“	(б-ю-17)
' Унт
т. е. поток теплоты бесконечен, что также противоречит физическому механизму
теплопереноса.
Сравним решение (6-10-9) с классическим решением аналогичной задачи. Для
tSst0, используя асимптотическое разложение
получаем:
1
У2зш ’
/1(2)
(6-10-19)
16»
(6-10-18)
451
1 Л3
Положим —	=и?, тогда для малых значений т0 (т2>х*т0!а} можно опустить
член х2тй/а;
e^x-^dx=.
xVXq/O
du —
и
-7-=. \ е”-“5 du — crfc и,
(6-10-20)
что является решением обычного классического уравнения теплопроводности для
данных краевых условий Ч
Аналогичным путем можно показать, что при малых значениях т0 величина
4о (т) будет иметь вид:
а	J _^Хср
°	V яг/т0	V.тт ’
(6-10-21)
что совпадает с выражением потока теплоты для классической задачи. Следова-
тельно, решения, получаемые из гиперболического уравнения теплопроводности,
являются более общими, и из них как частный случаи получаются решения клас-
сической теории теплопроводности.
Введем следующие безразмерные величины:
Т х
£“77=; т*=т/т0.	(6-10-22)
7 о	^ата	7
Тогда решение для профиля температуры в полуограниченном теле можно
написать так:

dT*-}-e
(6-10-23)
Соответственно для потоков теплоты
(6-10-24)
2Т '«(у**).	(6-10-25)
где	_
’’ (т’> =aTv^'	(6’|0’26)
То У Хер
По формулам (6-10-24), (6-10-25) были проведены расчеты. Так, на ркс, 6-13
представлена зависимость q* (т*) от безразмерного временит*, из которой
видно, что при малых значениях т* (т*<0,5) кривые для потьков, подсчи-
танные по формулам (6-10-25) и (6-10-21), резко расходятся. При больших
значениях т* (т* > 8) кривые q0 (т*) практически совпадают.
1 При этом используется приближенное соотношение
452
1__по уравнению с учетом ко-
нечной скорости переноса тепла;
2__по классическому решению
[Л.6-44].
Рис. 6-14, Зависимость безразмерной
температуры 0 * от обобщенной коор-
динаты изохроны £ для различных
значений безразмерного времени т*
[Л. 6-44].
-----классическое решение;-------реше-
ние при Wgсо. / — т* = 1; 2 — t* =2.
Представляет интерес Сравнить кривые 0 (?) для решений с учетом конеч-
ной скорости переноса теплоты цуд#=со [см. решение (6-10-23)] н для щ? = со
(классическое решение), когда
и
=	(6-10-27)
у п J
Решение (6-10-23) для малых значений т* можно упростить. Положим, что
/j (z)=yz при 0<г< I. Тогда получим;
в=%С 2^-e 2'' ) + е 2 \	(6-10-28)
что справедливо, когда
-%• Ki — g2/T*a -----1 ИЛИ Т,а<4-На-	(6-10-29)
На рис. 6-14 представлено семейство изохрон для т*-0,25; 1,0 и 2,0.
Для т» = 2 обо кривые 0(E)	------------------------
дают примерно одно и тоже значе-
ние /отклонение 13%) до £=т* = 2	,г
(фронт теплового потока или точка
разрыва). Для т*=1 вточке £=1 прохо-
дит фронт теплового потока. В этой
точке разница между кривыми 6(g)
составляет примерно 20%. Для ма-
лых т* разница между изохронами
Рис. 6-15. Изохроны 6 (?) для полу-
ограниченного тела для различных
значений т“ [Л. 6-44].
--—— — классическое решение; — — ре-
шение при И>^г£сО.
0,75
0	2,5	5,0	7,5	10,0 12,5
453
fl (£) велика и кончается на кривой 0 = е 2 на фронте тепловом вол-
ны.
Тангенс угла наклона Кривых 0 (|) характеризует интенсивность изменения
температуры по направлению. Для классических изохрон эта величина стремится
к бесконечности при т* -+ 0, для изохрон с учетом конечной скорости переноса
тепла тангенс угла наклона всегда конечен и не превышает 0,5.
Рассмотрим изохроны для больших значений времени (т* > 2). Методом гра-
фического интегрирования решения (6-10-23) были рассчитаны изохроны 0 (£)
для значений т* и сравнены с классическими изохронами О (£), Эго сравнение
приведено на рис. 6-15, откуда видно, что изохроны 0 (s) практически совпадают
вплоть до фронта потока теплоты.
Более общая задача на полуограниченное тело была решена в [Л. 6-45J, Были
приняты следующие граничные условия:
0)=Ж Т(О, г)=х«; дт^’ т) =0; ^-=f^
Решение имеет вид:
В [Л. 6-45, 6-47J был решен ряд задач для тел классической формы (неогра-
ниченная пластина, шар. цилиндр) при граничных условиях первого и второго
рода, а также при граничных условиях четвертого рода (сложные тела). Эти реше-
ния могут быть с успехом использованы для исследования механизма массопере-
носа в пористых телах.
Тепломассоперенос в капиллярно-пористых телах
Система дифференциальных уравнений тепломассопереноса с учетом конеч-
ной скорости переноса массы (wm оог Wq = оо) при условии постоянства пере-
454
носных свойств тела в обобщенных переменных имеет вид (Л, 6-45J:
<6-10-30)
/°т+*-/^=Еи(™-Рп?!7’>-	<6-10-31)
д2 Г д п ... п гг ахгт аат
г?е v’=w+ Та4 г“0' ' 2; л=~^“7?фздесь “ и ^-С00Т-
ветсгвенно коэффициенты диффузии теплоты и массы; х — безразмерная коор-
дината,
Уравнение (6-10-30) — параболического типа. Это обусловлено тем обстоя-
тельством, что скорость распространения теплоты очень велика [время релак-
сации тг„ для металлов составляет около I0-11 с (для алюминия), для газов xr?a;
^10’8с].
По данным [Л. 6'48], скорость распространения оплоты равна скорости рас-
пространения звука, т. е. очень велика (и>9 »330 м/с).
Что же касается скорости распространения массы при диффузии в капилляр-
но-пористых телах, то она меньше, чем примерно в 10е—107 раз, поэтому в урав-
нениях массопереноса ее необходимо учитывать.
Решения системы (6-10-30), (6-10-,31) были получены методом интегральных
преобразований для несимметричной iieoiраничешюй пластины (Г = 0), цилиндра
(/ = j), щара (Г — 2) и полуограниченного тела:
при граничных условиях первого рода [Л, 6-45]
Т (0, Fo)=rft(Fo), 0(0, Fo)=(p^Fo);
T(l, Fo)=7i|4 (Fo), 0(1, Fo)=4>a(Fo),
обобщенных граничных условиях второго рода
- дТ ах Р°) +Ю71 ~e>lu KoKg<F°W;
_^)+P„^+4(FO).0;
+ Ч -7 LU КО Ki» (Fo)=0;
-	+ ₽“ ЭТм— ' + к‘™ >Fo>=0
и при произвольных начальных условиях
Т (X, 0) = F, (X); О (X, 0) = Fa (X);	= F, р
При этом по переменной X производилось конечное интегральное преобра-
зование
Fo)pJ-s'(X)K^(Krl, X)dX	(6-10-37)
с ядром Кр(р-Я, х) и весом р</'(X)/S — 1 берется в случае (6-10-32), (6-10-33),
S=2 — в случае (6-10-34), (6-10-35), после чего применялось интегральное
преобразование Лапласа по переменному Fo.
Обратное преобразование по X производилось по формуле
 4s’(X, А>)-4»(р„	Го)	X),
л = I
(6-10-38)
(6-10-32)
(6-10-33)
(6-10-34)
(6-10-35)
(6-10-36)
455
•титгд
где
’ W = [j Рг ’ (X) Кг Х)г dx] ’ ;
Fo
rfr (р.„, Fo) = TS (0, Fo) = j [Ki»' (Fo') - Kii" (Fo’)] d Fo’ + '
0
Ko* Lu j [Kim (Fo')—Kim (Fo')] ^exp —° J — 1 j d Fo'-K
о
+ pi(X)dX + KKo*	F3(X)dX; (6-10-39)
F о
<£>об (po, Fo)=fioo(0, Fo) = Lu J [Kim (Fo') —Kim (Fo')]x
exp
^^jpFo' + рз (X) dX +
4-Kp— expf— J Fa(X)dX;	(6-10-40)
/Fo
a>iBr (|i0- Fo) =2Toi (0, Fo) = 2H Ki? '(Fo') d Fo'
Fo
FKo* Lu у Kim (Fo') £exp^— - °~F° j— 1] d Fo' -j.
4-J Xa(X)tfX-f-KKo* jexpf-I^-il f f8(X)Xdx|; (6-Ю-41)
o'	о	J
{Fo
Lu у (Fo') 1 — exp — -° к-’-— d Fo'
+ j F.m^^+Kfl-exp^--^^ jFs(X)Xdx|J
!Fo ,
j Ki»' (Fo')dFo' +
0
Fo
4-Ko’Lu f Kim (Fo’)[ exp (- -F°~^F°'	«] d Fo'-f-
+ X- dX+KK.o’|exp(-^-l] j К,(Х)Х'</х1;
u	M	'
(6-1C-42)
(6-10-43)
456
[ Fo
W$(l4 Fo)=3Bh2 (0, Fo)=3(Lu J KinV (Fo')x
I 0
] .
x[l -exp	d Fo' + J F, (X) X‘ dX +
0
+Kp-cxp	j Fa(X)№dXl	(6-10-44)
o	)
[нижний индекс T относится к Т'2’ (X, Fo), а нижний идекс 0—к О'2’ (X, Fo)].
В табл. 6-7 приведены значения Кр , рр\ (н«)’ а также характе-
ристические уравнения для граничных условий первого и второго рода.
Решения (6-10-30), (6-10-31) для тел классической формы при граничных
условиях первого рода (6-10-32), (6-10-33) и второго рода (G-10-34), (G-10-35)
с учетом (6-10-37), (6-10-38) —(6-10-44) и табл. G-7 запишутся следующим
образом;	*
Т<Р>(Х, Р0) = т<Л(р.„, Fo)+ 2	Х)Х
rt = ]
X S [ЗКр?4-2₽i (I + (1 + Lu + Lu Pn Ko’)]-*x
1 = 1
Г	Fo
x((K₽?+p,4-1-11(1,’) ) ®jp(Fo')exp[p/(Fo— Fo'))rfFo’ —
(	&
Fo	)
— pi Ko* j (Fo2) exp[p; (Fo — Fo')] Fo' + Xr, exp [p( Fo]|; (6-10-45)
Op(X, Ро) = 45е?(|10, Fo)+2	О*
n = l
3
' X у [2Kpi4-2₽i (I4-|1?>K)14-1>” (14-Lu-f-LuPn Ko-jHx
1=1
(Fo') exp [p (Fo-Fo')]o'Fo,4-(p/4-p.3)x
Fo	'	\
X Ф£Р (Fo') exp [p^ (Fo — Fo')] d Fo'-|-Afncxp [p, Fo]}, (G-lo-46)
0	)
где Pi—некратные корни характеристического уравнения
Л (р) = кр3 -]~0 Р 4- Р 0 -]-Lu Lu Рп Ко ) 4'P,ZI Lu = 0;	(6-10- 47)
Nn== Тпг (Кр?4~Р4*я Lu) -f-finr Ко рл Lu —Pi Ко* /СОопГ;	(G-10-48)
Мп^Тпгрп Lu РптрпГ [кр? 4-pz (14-РиК) 4-pn (1 4-LuPn Ко*)]4-
-f-вонгК (р(4-Рп).;	(6-10-49)
Ф”>(Ро) = ц„ [<р, (Fd)4-(— О’+Ч, Fo];
(F°) = P„ L“ [ч>2 (Fo)4-(- 1)"+Ч (Fo)]-Lu Рп фв> (Fo);
ФЙ'Ро-Цпф^о)
457
8
Таблица 6-7
Ядра интегральных преобразований и характеристические уравнения
Посто- янная форма	Ядра интегральных преобразований		р(?’ <Л>		Н(г ’ (*„)		Характеристические уравнения		(Цо. FO)	
Г		«7 (р„. X)	р?1 m	!>; (X)	Н7(^п)	н’г <Л)	I рода	[I рода	СО/'	со'/)
0	sin ]хпХ	cos	1	1	2	2	sinp. = 0; = п = 0, 1, 2...	sin |i = 0; р,л =пл п = 0, 1, 2...	0	«оо (0, Fo)
1	(|4, X)	/ц (j-l/A)	X	X	2	• 2 Ч (4)	'.«=0	4(1*) =0 '	0	2uBt (0, Fo)
2	sin р.пХ X	sin цпХ X	Х2	Xs	2	sin2 р,ч	sin р —0: цл= пл п = 0, I, 2...	tg ц = |»	0	3u02 (0, Fo)

где
x/fl + Ko-Pn+^y-^ (7=1,2).
Корни уравнений (6-10-47) и (6-10-52), подсчитанные на ЭВМ для широ-
ких интервалов входящих в-пих критериев, имеются соответственно в (Л.6-1]
и [Л.6-47].
В случае полуограниченного тела решение (6-10-30), (6-10-31) при Г=0
получается методом интегрального преобразования Фурье no X
t/(,u, Fo)=ft/(X, Fo)K(ti, X)dX
(6-10-53)
и Лапласа no Fo. Обратное преобразование по X осуществляется по формуле
U (ц, Fo) К (р., X) dp,.
(6-10-54)
При этом к условиям (6-10-32) и (6-10-34) в пуле при граничных усло-
виях соответственно первого и второго рода добавляется условие на бесконеч-
ности
дТ (со, Fo) дв (со, Fo)
дХ	дХ “°’
(6-10-55)
Решения системы (6-10-30), (6-10-31) для полуограниченного тела с учетом
(6-10-53), (6-Ю-54) запишутся так:
Fo) = -^ 7'(S) (И. Fo)K<S)(H, *)<Ф =
о
со	3
=	( К® (11. X)dfi 2 [SKpi + apifl+K^ + ll’tl + Lu + LuPilKo*)]-1 X
О	I = t
X ^(№piH-p/+Luu2) J ф(3) (Fo') exp [р/(Fo—Fo')] dFo'—р;Ко*Х
Fo	)
X (	(Fo') exp [Pl-(Fo—Fo')] dFo'-{—V, exp [p/Fo]>;	(6-10-56)
0(S) (X, Fo) =-?- j 0(S| (p, Fo) Ms> (|i, Х)Иц = -1 X
0
oo	3
X SK(S,(1*.	2 [3Kp;’ + 2p«(>+^2) + F!(1 + Lu-J-LuPnKo,)r1 X
0	i= 1
( Fo	Fo
X {fi3LuPn J Ф'5) (Fo') exp [pj (Fo — Fo')]d Fo'4-(p/ + p2) J ®{f)(Fo')x
l о	o'
Xexp [p( (Fo —Fo')]	exp [p(- Fo]l,	(6-10-57)
460
где
Ф(1' (Fo) = |1ф1 (Fo); (Fo) = Lupups, (Fo) - ШРпфо ’ (Fo);
ФГ (Fo) =- [Kii” (Fo)-(l -e)'LuKoKta (Fo)];
Ф?’(Fo) = —LuKim (Fo);
Ni, M, определяются из (6-10-48), (6-10-49) заменой на р. Соответствующие
решения для обычной системы дифференциальных уравнений тепломассопере-
носа при К=0 имеют вид:
со	2
T{S>(X, Fo) = ^- f №S) (и, X)*2 Й5/+1Х2 (l + Lu + LuPnKo-)r X
0	f—1
{Fo
(p/4-Lup2) J (Fo') exp [p, (Fo-— Fo')] dFo' — p/Ko*x
Fo	]
X j Ф(о5) (Fo') exp[p/(Fo —Fo')]d Fo'+N; exp[py-Fo]l.
о	J ’
от	2
j<s> (X, Fo) ==Д- f №5)(Л Л’НИ S 2P/+P2(4-LU+LuPnKo*)]-i X
о	/ = 1
(Fo	Fo
paLuPn J <D(j5) (Fo') exp [p/(Fo—Fo')] dFo' + (p/+p2) J <D^S)(Fo') X
о	о
Xcxp [fy (Fo — Fo')] d Fo' + Mj exp \pj Fo]|
(Mj, Ni определяются из (6-10-48), (6-10-49) при К-?-О заменой на jx с уче-
том 0ОЛГ = 0).
В зависимости от физического понятия rrm (t£>m или йУф) определяется
число Ki/w- Для учета конечной скорости переноса массы в граничных усло-
виях массообмена число Ki« заменяется па Kim = К17п-]-т/.7ПК1рп а в началь-
ных условиях (6-10-36) функции F3(X) приравнивается нулю, т. е. F3(X) = 0.
СПИСОК ЛИТЕРАТУРЫ
РАЗДЕЛ ПЕРВЫЙ
Ы. Whitaker S. Introduction to fluid mechanics. Prectice-Hall, 1968. 457 p,
1-2. Лыков А. В. Тепломассобмен. Справочник. M., «Энергия», 1972 . 560 с.
1-3. Brodkey R. S, The phenomena of fluid motions Addison—Wesley, 1967.
737 p.
1-4. Slattery J. C. Momentum, energy and mass transfer in continua. N. Y.,
McGraw-Hill, 1972.	t
1-5. De Groot S. R., Mazur P. Nonequilibrium thermodynamics. Amsterdam,
North-Holland, 1962.
1-6. Gyarmati I. Nonequilibrium thermodynamics field theory and variational
principles. Berlin, Springer-Verlag, 1970.
1-7. Брук-Левинсон Э. T. Исследование по статистической теории молеку-
лярных систем с нецентральными взаимодействиями. Диссертация на соиск.
учен. степ. канд. физ.-мат. наук. Минск, 1971 (БГУ).
1-8. Truesdell С- Rational thermodynamics. N. Y., McGraw-Hiii, 1967 . 208 p.
1-9. Lulkov A, V., Bubnov V. A. Motion equations for a discrete structure fluid.—
«Warme- und Stoffiibertragung», 1972, Bd 5, S. 64—72.
1-10. Day W. A. The thermodynamics of simple materials with fading me-
mory. Berlin, Springer-Verlag, 1972.
bll. Bird R. B., Stewart W. E., Lightfoot E. N. Transport phenomena,
N. Y., John Wiley, I960.
1-12. Предводителев А. С. Об аэродинамике разреженных газов и задачах
теплообмена. — В кн.: Тепло- и массоперенос. Т. 111. М., Госэнергоиздат, 1963,
с. 54-65.
1-13. Maxwell J. С. On the dynamical theory of gas. — «The Sclent. Papers»,
1927, vol. 11.
1-14. Предводителев А. С. О молекулярно-кинетическом обосновании урав-
нений аэродинамики. Минск, Изд. ИТМО АН БССР, 1970.
1-15. Erlngen А. С. Theory о! thermomicrofluids. — «J. Math. Anal, and
Appl.», 1972, vol. 38, p. 480.
1-16. Аэро Э. Л-, Булыгин A- H., Кувшиискнй E. В. Асимметрическая гидро-
механика, — «Прикл, мат. и мех.», т, 29, 1964, с, 297—308.
462
1-17. Lulkov A. V. Idrodinamlca c transmi'ssione del calore in fluldo con ten-
sore degli storzi asimmetrico. — «L’aerotecnica Missilic Spazio», 1972, № 3,
p. 188.
1-18. Кастерин H. П. Обобщение основных уравнений аэродинамики и элек-
тродинамики. М., Изд-во АН СССР, 1937.
1-19. Бубнов В. А. Одно замечание к специальным решениям уравнений
гидродинамики. — ИФ/К, т. 19, № 1, 1970.
1-20. Миловнч А. Я. Теория динамического взаимодействия тел и жидко-
сти. М., Стройиздат, 1955.
1-21. Гольдштик М. А. Одно парадоксальное решение уравнений Навье—
Стокса. — «Прикл. мат. и мех.», т. 24, вып. 4, i960.
1-22. Reynolds О. On the dynamical theory of incompressible viscous fluids
and the determination of the criterion. —-«Phil. Trans. Roy. Soc.», 1895, A186,
p. 123.	,
1-23. Boussinesque J. Theorie de Vecoulement tourbillant. — «Mem. pres,
par. div. sovants a 1’Acad. Sci.», 1877, vol. 23, p. 46.
1-24. Prandtl L. Uber die ausgebildetc Turbulonz. — «Zs. Angew. Math. Meeh.»,
1925, Bd 5, S. 136.
1-25. Taylor G. The transport of vorticityand heat through fluids in turbulent
motion. — «Phil. Trans. Roy. Soc. London», 1915, vol. 215, p. 1.
1-26. Reichard H. Uber eine neue Theorie der streien Turbulenz. — «Zs. An-
gew. Math. Meeh.», 1941, Bd 21, S. 257.
1-27. Колмогоров A. H. «Изв. АН СССР», 1942, т. 6, № 1, 2, с. 56.
1-28. Prandtl L. Uber ein neues Formelsystem dec ausgebildeten Turbulenz.—
«Nachr. Ges. Wiss. Gottingen, Math. Phys.», 1945, Bd 1, S. 6.
1-29. Rotta J. Statistische Theorie nichthomogener Turbulenz. — «J. Phys.»,
1953, Bd 131, № L S. 351.
- 1-30. Keller L. B., Friedman A. A. Differentialglejchungen Гйг die turbulente
Bewegung einer kompressiblen Fliissigkeit. — «Proc. Int. Congr. Appl. Meeh.,
Dellt», 1924, p. 395.
1-31. Коловаидин Б. А. О расчете основных характеристик теплообмена
в турбулентных течениях со сдвигом. — В кн.: Тепло- и массоперенос. ’Т. 1,
М.. «Энергия», 1968. с. 154.
1-32. Некоторые вопросы ламинарной естественной конвекции в вертикаль-
ной щели при переменной температуре стенки. — В кн.: Тепло- и массоперенос.
Т. 1. М-, «Энергия», 1968. с. 664, Авт.: А. В. Лыков, О. Г. Мартыненко, Б, А.
Коловандин и др.
1-33. Коловандян Б, А., Ватутин И. A. On statistical theory of non-uniform
turbulence. Seminar on Heat and Mass Transfer in Separated Flows, Herceg Novi,
Yugoslavia, 1969.
1-34. Миллионщиков M. Д. К теории однородной изотропной турбулентности.
«Доклады АН СССР», 1941, т. 32, № 9, с. 611.
1-35. Meixner J., Reik Н. In: Handbuch der Physik, Berlin, Springer-Verlag,
1959, Bd 3(2).
1-36. J. Edmund Fitzgerald. Thermodynamic restrictions in nonlinear rate
type materials. — «Pure Appl. Chem.», 1970, vol. 22, № 3/4*.
1-37. Coleman В. I)., Mizel V, I. On thermodynamic conditions for the stabi-
lity pl evolving systems. — «Arch. Rat.» Meeh. Anal.», 1968, vol. 29, p, 105.
463
1-38. Самонил И. Рациональная термодинамика нереагирующей бинарной
линейной жидкости. — ИФЖ> 1973, т. 25, № 2, с. 271—285.
1-39. Лыков А. В., Колпащнков В. Л. Об эффектах анизотропии переноса
тепла в потоках жидкостей и газов. — ИФЖ, 1973, т. 25, № 4, с. 72.
1-40. Truesdell С., Toupin R. The classical field theories. In: Handbuch der
Physik. Berlin, Springer-Verlag, 1960, p. 491—529.
1-41. Шульман 3. П. Постановка задач конвективного переноса в погранич-
ном слое пслинейно-вязкопластичных текучих систем (рсодинамика и теплооб-
мен). — В кн.: Проблема тепло- и массопереноса. М-, «Энергия», 1970, с. 20—55.
1-42. Hohenemer К., Prager W. — «Zs. Angew. Math. Meeh.», 1932, Bd 12,
S. 216.
1-43. Schowalter W. R. The application of boundary-layer theory to power-
law pscudoplastic fluids: similar solutions. — «Aichcj», 1960, vol. 6. p? 24.
1-44. Oldroyd L. P. Two-dimentional plastic flow of a Bingham Solid. A pla-
stic boundary-layer theory for slow motion. — «Proc. Cambridge Phil. Soc.», 1947,
vol. 43, p. 384.
1-45. Астрахан И. M. Об уравнениях движения вязкопластичной жидкости
в пограничном слое на произвольной поверхности. — «Изв. АН СССР», ОТН,
Мех. и машин., 1960, № 2.
1-46. Skelland Н. Р. Non-newtonian flow and heat transfer. N. Y., 1967,
p. 469.
1-47. Предводителев А. С. Учение о теплоте и римановы многообразия. —
В кн.: Проблема тепло- и массопереноса. М., «Энергия», 1970, с. 151—192.
1-48. Nunziato 1. W. On beat conduction in materials with memory. — «Qu-
art. Appl. Math.», 1971, № 7, p. 187.
1-49. Curtin M. E., Pipkin A. C. A general theory of heat conduction with
finite wave speeds. — «Arch. Rat. Meeh. Annal.», 1968, vol. 31, p. 113.
1-50. Norwood F. R. Transient thermal waves in the general theory of heat
conduction with finite wave speeds. — «Trans. ASME. ser. Е», 1972, № 3, p. 35.
1-51. Spalding D. B., Launder В. E. Mathematical models of turbulence, lec-
tures. Imperial College of Science and Technology, 1971.
РАЗДЕЛ ВТОРОЙ
2-1. Тихонов A. H., Самарский А. А. Уравнения математической физики.
М., Гостехиздат, 1954. 659 с.
2-2. Курант Р., Гильберт Д. Методы математической физики, М.4 Изд-во
иностр, лит., 1951.
2-3. Петровский И. Г. Лекции об уравнениях с частными производными.
М., Физматгиз, 1961.
2-4. Положий Г. Н. Уравнения математической физики. М.» «Высшая шко-
ла», 1969.
2-5. Мочалин А. И. Применение 6-функции Дирака к решению дифферен-
циальных уравнений параболического типа. — В кн.: Тепло- и массообмен
в процессах испарения. М., Иэд-во АН СССР, 1958.
2-6. Соколов А. А. Дельта-функция и ее применение к решению некоторых
математических задач геофизики. М., Гостехиздат, 1946,
464
2’7. Смирнов В. И. Курс высшей математики. Т. IV. М., Физматгиз, 1958-
2-8. Арсенин В- Я. Математическая физика. М-, «Наука», 1966.
2-9. Вян*дер-Поль Б-, Бреммер X. Операционное исчисление на основе дву-
стороннего преобразования Лапласа. М., Изд-во иностр, лит., 1952.
2-10. Уфлянд Я. С. Интегральное преобразование в задачах теории упру-
гости. М., Изд-во АН СССР, 1963.
2-И. Трантер К- Дж- Интегральные преобразования в математической
физике. М-, Гостехиздат, 1956.
2-12. Снеддон И. Н. Преобразование Фурье. М-, Изд-во иностр, лит., 1955-
2-13. Деч Г. Руководство к практическому применению преобразования
Лапласа. М-, Физматгиз, 1960. 207 с.
2-14. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного
переменного. М., Физматгиз, 1958.
2-15. Кошляков Н. С. Основные дифференциальные уравнения математиче-
ской физики. М-, Гостехиздат, 1936.
2-16. Гринберг Г. А. Избранные вопросы математической теории электриче-
ских и магнитных явлений. М., Изд-во АН С^СР, 1948.
2-17. Mikhailov М. D. Several solution of the equation of finite regions. —
«Int. J. Heat Mass Transfer», 1972, vol. 10, p. 577.
2-18. Лыков А. В. Теория теплопроводности. M., «Высшая школа», 1967.
599 с.
2-19. Будак Б- M.f Самарский А. А-, Тихонов А. Н. Сборник задач по мате-
матической физике. М., Гостехиздат, 1956.
2-20. Петровский И. Г. Лекции по интегральным уравнениям. М.,- «Наука»,
1965.
2-21. Ozisik М. N. Boundary value problems of heat conduction. Int. Text-
book Co., 1968.
2-22. Карслоу Г., Егер Д. Теплопроводность твердых тел. М., «Наука»,
1964?
2-23. Диткин В. А., Прудников А. П. Интегральные преобразования и опе-
рационное исчисление. М., «Высшая школа», 1966.
2-24. Olcer N- Y. Note of the general solution of the heat equation. — «Quart.
Appl. Math.», 1967, vol. 24, p. 380.
2-25. Nunziato J. W. On heat conduction in materials with memory. —
«Quart. Appl. Math.», 1971, vol. 29. № 7, p. 187.
2-26. Морс M., Фешбах Г. Методы теоретической физики. Т. 1, 2. М-, Изд-во
иностр, лит., 1958.
2-27. Шнейдер П. Инженерные проблемы теплопроводности. М-, Изд-во
иностр, лит., 1960.
2-28. Apraci V. Conduction heat transfer. Addison Wesley, 1966. 550 p.
2-29. Langmuir L, Adams E., Meikle F. Flow of heat trough furnace walls. —
«Trans. Am. Electrochem. Soc.», 1913, vol. 24, № 53.
2-30. Фукс Б. A-, Шабат Б. В. Функции комплексного переменного и неко-
торые их приложения. М., Физматгиз, 1959.
2-31. Волковысскнй Л. И., Лунн Г. Л., Арашанович И. Г. Сборник задач по
теории функций комплексного переменного. М-, Физматгиз, 1960.
2-32. Михайлов М. Д. Нестационарный тепло- и массоперенос в одномерных
телах. Минск, ИТМО, 1969. 184 с.
465
2-33. Лыков А. В. Теплопроводность и диффузия. М., Гизлегпром, 1941.
196 с.
2«34. Weinbaum S., Wheller Н. Heat transfer in sweat-cooled porous metals. —
«J. Appl. Phys.», 1949, vol. 20, p. 113.
2-35. Лыков А. В. Некоторые аналитические методы решения задач неста-
ционарной теплопроводности. Методы решения нелинейных уравнений нестацио-
нарной теплопроводности. «Изв. АН СССР. Энергетика и транспорт», 1969, № 2,
с. 3—27; 1970. № 5, с. 109—150.
2-36. Nonvood F. R. Transient thermal waves in the general theory of heat
conduction with finite wave speeds. — «J. Heat Transfer. Trans. ASME», ser. E,
1972, № 3, p. 351.
РАЗДЕЛ ТРЕТИЙ
3-1. Schlichting H. Grentzschicht-Theorie, Verlag G. Braun,- Karlsruhe,
1965.	'
. 3-2,’Blasius H. Grenzschichten in Diissigkeiten mit kleiner Reibung.— «Z.
Math. Phys.», 1908, Bd 56, № 1, S. 1-37.
3-3. Howarth L. On the solution of the laminar boundary layer equations. — -
«Proc, Roy. Soc. Lonson», 1938^ vol. A919, № 164, p. 547— 579.
3 4. Эккерт Э. P-, Дрейк P. M. Теория тепло- и массообмена. М., Госэнерго-
издат, 1961. 680 с.
3 5. Evans Н. Mass transfer through laminar boundary layers. 7 Further simi-
lar solutions to the b—equation for the case B-O, — «Int. J, Heat Mass Transfer»,
1962, vol. 5, p- 35.
3-6, Merk H. J. Rapid calculations for boundary layer heat transfer using wedge
solutions and asymptotic expansions. — «J. Fluid Mcch.s, 1928, vol. 5, p. 460—
480.
3-7. Hartree D. R. On an equation occurring in Falkner and Skan's approxi-
mate Ireatment of the equations of the boundary layer. — «Proc. Camb. Phyl.
Soc,», 1937, vol. 33, № 11, p, 223.
3 8. Яламов Ю, И., Ивченко И. Н., Дерягин Б- В. Расчет скорости диффу-
зионного скольжения бинарной газовой смеси. — «Докл. АП СССР», 1968, т. 180,
№ 2, с. 330-333.
3-9, Лыков А. В. Явления переноса в капиллярнопористых телах. М,—Л.,
Гостехиздат, 1954, 296 с.
3-10. Nikuradse J. GesetzmaBigkeifen der turbulenten Strdmung in glatten
Rohren. — «VD1—Forschungshelt», 1932, S, 356.
3-11. Reichart J. —«КАСА ТМ», 1943, p. 1047.
3-12. Karman T. Compt. Rend., 1948, vol. 226, p. 2108.
3-13. Sisson L. E., pitts D. R. Elements of transport phenomena. McGraw-
Hill, 1972. 814 p.
3-14. Hartnett J. P., Eckert E. R. G. Mass transfer cooling in laminar boundary
layer with constant fluid properties. — In: Recent Advances in Heat and Mass
Transfer, McGvaw-HiU, 1961, p. 142—160,
3-15. Emmons H. W,, Leigh D. C. Tabulation Blasius function. Fluid Motion
Sub—Committee. Aeron. Res. Counc,, Rep. NFM № 1915, 1953,
466
3-16. Sasfri V. M. Км Hartnett J. P. Effect of an unheated solid starting length
on skin friction and heat transfer tn a transpired laminar boundary layer. — In:
Progress in Heat and Mass Transfer, Pergamon Press, 1969, vol. 2, p. 213—223.
3-17. Sparrow E. M., Star J. B. The transpiration cooled flat plate with va-
rious thermal and velocity boundary conditions. — «Int. J. Heat Mass Transfer».
1966, vol. 9, № 5, p. 508—510.
3-18. Lagenellf A., Ames W. F., Hartnett J. p. Transpiration cooling in a la-
minar boundary layer with solid wall upstream effects. — «A1AAJ», 1968, vol. 6. ’
№ 2, p. '193—197.
3-19. A review of binary boundary layer characteristics. — «Project RAND»
RM 2516, 1959. Auth.: J. G. Gross, J. P. Hartnett. D. J. Masson, C. Gazley.
3 20- Шульман 3. П. Исследование конвективного тепломассообмена на по-
верхности тела произвольной конфигурации при испарительном пористом охлаж-
дении. Автореф. на соиск. учен, степени капд. техн, наук, Минск, 1962
(ИТМО).
3-21. Johnson В. V., Hartnett J. Р. — «Trans. ASME», ser. Е, 1969, № 2.
3-22. Черненко Л. Е., Шалит С. Я., Красовская Г. И. Физико-химические
основы пищевых производств. М., Пищепромиздат. 1952.
3-23. Лыков А. В. Тепло- и массообмен в процессах испарения. — ИФЖ,
1962, № 11, с. 12—24.
3-24. Де Бур Я. Динамический характер'адсорбции. М., Изд-во иностр, лит.,
1962.
3-25. Федякин Н. Н. Смачивание адсорбционных слоев. — В кн.- Тепло-
и массообмен в капиллярнопористых телах. М.—Л., Госэнергоиздат, 1957.
3-26. Matmquist L., Meichsner Н. Ober den Warmeiibergang bei der konvek-
tiven Trocknung von Hols in Heissdampf. — «Holz als Roh- u. Werkstofb, 1964,
Bd 22, S. 96—106.
3-27- Лыков А. В. Теория .сушки. M., «Энергия», 1969- 471 с.
3-28. Лыков А. В., Васильева Г. В. Исследование тепло- и массообмена при
испарении жидкости из капиллярнопористого тела. —ИФЖ, 1968, т. 14, № 3,“
с. 395-406.
3-29. Крылов Б. С., Захаров В. М. Тепло- и массообмен при испарении воды
из пористой стенки. — «Изв. вузов. Энергетика», 1971, № 8, с. 92—97.
3-30. Васильева Г. В. Исследование процессов тепло- и массообмена при ис-
парении жидкостей в ламинарный пограничный слой из капиллярнопористого
тела при наличии зоны заглубления. Автореф, дис. на соиск. учен, степени
канд. техн. наук. Минск. 1969 (ИТМО).
3-31. Сполдинг Д. Б. Конвективный массоперенос. М.—Л., «Энергия». 1965.
384 с.	,
3-32. Нестеренко А. В. Тепло- и массообмен при испарении жидкости со сво-’
бодной поверхности. — ЖТФ, 1954, № 4.
3-33. Shah В. К., London В R. Thermal boundary conditions for laminar duct
flow forced convection heat transfer. — «Trans. ASME», ser. C, 1972.
3-34. Whitaker S. Forced convection heat transfer correlations for flow in pi-
pes, past flat plates, single cylinders, single spheres and in flow in packed beds and
tube budles. — «А1СНЕ Journ.», 1972, vol. 18, № 2, p. 361.
3-35. Spalding D. B., Patankar S. V. Heat and mass transfer in boundary layers.
London, Edward Arnolds, 1967,
467
3-36. Мотулевич В. П. Турбулентный тепло- и массообмен па пластине при
пористом отсосе п подаче различных газов. — ИФЖ, 1963, № 1, с. 3—13.
3-37. Крылов Б. С., Захаров В. М. Особый случай взаимодействия капилляр-
нопористого тела с газовым потоком. — «Изв. вузов. Энергетика», 1971, № 6,
с. 122—125.
3-38. Van Driest Е. R. Turbulent boundary layer in compressible fluids.—
In: Recent Advances in Heat and Mass Transfer, McGraw-Hill, 1961, p. 22—54.
3-39. Дорранс В., Дор Ф. Влияние подачи массы на поверхностное трение
и теплопередачу в сжимаемом турбулентном пограничном слое. — В кн.: Ме-
ханика (Сб. переводов). М., «Мир», 1955, № 3.
3-40. Лапин Ю. В. Трение и тепломассообмен в сжимаемом турбулентном
пограничном слое при наличии химических реакций, обусловленных вводом ино-
родного вещества. — Ж’ГФ, 1960, т. 30, № 8, с. 984; № 10, с. 1227.
3-41. Кутателадзе С. С., Леонтьев А. И. Законы сопротивления и теплооб-
мена в турбулентном потоке сжимаемого газа. — В кн.: Тепломассоперенос.
М., Госэнергоиздат, 1963, т. 3, с. 106—130.
3-42. Кутателадзе С. С., Леонтьев А. И. Турбулентный пограничный слой
сжимаемого газа. Новосибирск, Изд-во СО АН СССР, 1962.
3-43. Leadon В. М., Scott С. J. Transpiration cooling experiments in a turbu-
lent boundary layer at M-3. — «JAS», 1956, vol. 23, № 3, p. 798, 799.
3-44. Tewfic О. E. Some characteristics of the turbulent boundary layer with
eir injection. — «AIAAJ», 1963, vol. 1, № 6, p. 29.
3-45. Rubesin M. W. An analytical estimation of the effect of transpiration
cooling on the heat-transfer and skin-friction characteristics of a compressible, turbu-
lent boundary layer. — «NACA TN 3341», 1954,
3-46. Micley H. S., Davis R. S. Momentum transfer for flow over a flat plate
with blowing. — «NACA TN 4014», 1957, № 11.
3-47. Kutateladze S. S. Fundamentals of heat transfer. N. Y„ Edward Arnold,
1963.
3-48. Вайнберг P. Ш. Обобщения данных no конвективному теплообмену
с испарением в турбулентный пограничный слой. — ИФЖ, 1967, т. 13, № 4,
с. 510—513.
3-49. Кутателадзе С. С., Леонтьев А. И., Миронов Б. П. Турбулентный по-
граничный слой на проницаемой поверхности с продольным градиентом давле-
ния в области сильных вдувов и конечных чисел Рейнольдса, — В кн.: Тепло-
и массоперенос. Т. 1. М., «Энергия», 1968.
3-50. Motulevich V. Р. Gas flow w'th porous bodies under the conditions of
intensive injection. Int. Centre for Heat and Mass Transfer, Herceg-Novi, 1969.
3-51. Мугалев В. П. Некоторые вопросы воздействия вдувания на турбулент-
ный пограничный слой. Тезисы доклада на симпозиуме по проблемам турбулент-
ных течений, включая геофизические приложения. Киев, 1967.
3-52. Moroney R. N., Giedt W. Н. The effect of mass injection on heat transfer
from a partially dissociated gas stream. — «Trans, ASME», ser, C, 1967, № 3,
p. 10.
3-53. Смольскнй Б. M., файнгольд Л. А. Исследование локального тепло-
и массообмена при вдуве газов в турбулентный пограничный слой пористой пла-
стины. — В кн.: Тепломассоперенос, Минск, «Наука и техника», 1968, т, 10,
с. 23-34,
463
3-54. Knscher 0., Loos G. Beitrag zur Frage des Warme- und Stoffaustausches
bei er/.uringener Stromung an Korpern verschiedener Form. — «Chem. Ing. Techn.»,
1958, Bd 30, № 2, S. 31-74.
3-55. Ede A. Advances in Tree convection. — fm Advances in Heat Transfer,
N. Y., Academic Press, 1967, vol. 4.
3-56. Dropkin D., Somescales E. Heat transfer by natural convection in li-
quids confined by two parallel plates which are inclined at various angles with res-
pect to the horizontal. — «Trans. ASME», ser. C, 1965, vol. 87, №l,p. 77.
3-57. Schmidt E. Einfiihrung in technische Thermodynamik. Berlin, 1944.
3-58. Исаченко В. П., Осипова В. А.. Сукомел А. С. Теплопередача. Изд.
2-е. М., «Энергия». 1969.
3-59. Лыков А. В., Берковский Б. М., Фертман В. Е. Возбуждение конвек
ции нагревом сверху. — В кн. Progress in Heat and Mass Transfer. Pergarnon
Press, 1969. vol1. 2, p. 77—85.
3-60- Лыков А. В., Берковский Б. M., Фертман В. E. Экспериментальное
исследование в замкнутых осесимметричных объемах. — ИфЖ, 1969, т. 16,
№ 6, с. 679.
3-61. Романенко П. Н., Харченко В. Н., Семенов Ю. П. Влияние попереч-
ного потока массы на сопротивление теплообмена при турбулентном течении сжи-
маемого газа. — ИФЖ, 1963, № 2, с. 52—59. Влияние па теплообмен и трение
подачи охладителей н турбулентный слой. — ИФЖ, 1965, т. 9, № 6, с. 816—833.
3-62. Михеев М. А. Основы теплопередачи. М., «Энергия», 1977.
РАЗДЕЛ ЧЕТВЕРТЫЙ
4-1. Chapman D. R., Rubesln М. W. Temperature and velocity profiles in the
compressible, laminar boundary layer with arbitrary distribution of surface tempe-
rature.— «JAS», 1949, vol. 16, № 9.
4-2. Schlichtlng ’H. Der Warmeubergang an einer langsangestromten Platte
mit verlanderlicher Wandtemperatur. — «Forsch. auf dem Gebiete des Ingenjeur-
wesens», 1951, Bd 17, № 1.
4-3. Baxter D. C., Reynolds W. S. — «JAS», 1958, vol. 25, № 6.
4-4. Лыков А. В., Перельман T. Л. О нестационарном теплообмене между
телом и обтекающим его потоком жидкости. В кн.: Тепло- и массообмен с ок-
ружающей газовой средой. Минск, «Наука и техника», 1965, с. 3.
4-5. Перельман Т. Л. О сопряженных задачах теплообмена. В кн.: Тепло-
и массоперенос. Ачинск, «Наука и техника», 1963. т. 5, с. 74.
4-6. Остроумов Г. А. Свободная конвекция в условиях внутренней задачи.
М., Гостехиздат, 1952.
4-7. Померанцев А. А. Нагревание стенки сверхзвуковым потоком газа. —
ИФЖ, I960, № 8, с. 39—46.
4-8. Кумар И. Дж., Бартман А. Б. Сопряженная задача тепломассопереноса
в ламинарном пограничном слое сжимаемого газа с излучением. — В кн.: Тепло-
и массоперенос.-Минск, «Наука и техника», 1968, т. 9, с. 481.
4-9. Алексашенко В. А. Сопряженная стационарная задача теплообмена
в полубесконечной трубе с движущейся жидкостью с учетом диссипации механи-
ческой энергии. — ИФЖ, 1968, т. 14, № 1, с. 100.
469
4-10. Luikov A. V., Perelman T. L., Ryvkin V. B. On determination of the heat
transfer coefficient in simultaneous conductive heat transfer. — «Ргос. IV Int.
Heat Transfer Conf.», Chicago, 1966, p. 12.
4*11. Zargary A. Conjugated transient heat transfer in pipe flow (Thesis).
Nav. Postgraduate School, Monterey, Calif., 1972.
4-12. Марченко В. M. Температурные поля и напряжения в конструкции
летательных аппаратов, М., «Машиностроение», 1965.
4-13. Kelleher М. D., Kwang-Tsu- Yang. A steady conjugate heat transfer prob-
lem with conduction and free convection. —- «Appl. Sei. Res.», 1967, vol, 17, p, 249,
4-14. Zinnes A. E. Tlic coupling of conduction with laminar natural convec-
tion from a vertical flat plate with arbitrary surface heating. — «J. Heat Transfer
Trans. ASME», 1970, № 3, p. 220.
4-15. Heat transfer from a plate in a compressible gas flow. — «Int. J. Heat
Mass Transfer», 1970, vol. 13, №8, p, 1261 — 1970. Autli.: A. V. Luikov, T. L. Pe-
relman, R. S. Levitin, L. B. Gdalevich.
4-16. Luikov A. V., Aleksashenko V. A., Aleksashenko A. A. Analytical method
of solution of conjugated problems in convective heat transfer. — «Int. J. Heat
Mass Transfer», 1971, vol. 4, p. 1047—1056.
4-17. Лаувервер Г. C. —В кп.: Механика (Сб. переводов.) 1961, № 1, с. 3.
4-18, Sleicher С. A., Traibus М. — c.Trans. ASME'*, sei1. С, 1957, vol. 79, № 4.
4-19. Latzko H. - «ZAMM», 1921, Bd 1, S. 268.
4-20. Лыков А. В. Теория теплопроводности. M./«Высшая школа», 1967.
599 с.
4-2t. Алдошин Г. Т., Жук К- П., Шляхтина В. И. Сопряженная задача теп-
лообмена при течении жидкости в канале. — В кн,: Тепло- и массоперенос.
Т. 1. М., «Энергия», 1968, с, 577—589.
4-22. Жаворонков Н. М. Гидравлические основы скрубберного процесса и
теплопередача в скрубберах. М., Гостехиздат, 1944.
4-23. Жаворонков Н, М., Малюсов В. А. Исследование гидродинамики и
массопередачи в процессах абсорбции и ректификации. — ТОХТ, 1967, т. 1, № 5.
4-24. Лыков А. В., Алексашенко А. А., Алексашенко В. А. Сопряженные
задачи конвективного теплообмена. Минск, Изд-во Б ГУ, 1971. 346 с.
4-25, Zargary A., Brock J. Е. An integral equation describing conjugate tran-
stent heat transfer in fluid flow through conjugated pipes. — «Int. J. Heat Mass’
Transfer», 1973.
РАЗДЕЛ ПЯТЫЙ
5-1. Klenkenberg L. J. Drilling and production practices. API, 1941.
5-2. Keey R. B. Drying principles and practice. Pergamon Press, 1972. 358 p.
5-3. Флорин В. А. Уплотнение земляной среды и фильтрация при переменной
пористости с учетом влияния связанной воды. — «Изв. АН СССР», ОТН, № II,
1951.
5-4. Кельтов Б, Ф. Труды совещания по механике грунтов, основаниям
и фундаментам. М., Госстройиздат. 1956.
5-5. Шейдеггер А. Э. Физика течения жидкостей через пористые среды. М-,
Гостоптехиздат, 1960.
5-6. Whitaker S. Advances in theory of fluid motion in porous media. — «Ind.
Eng.Chem.», 1969, vol. 61, № 12.
470
F-7. Leverett M. C. «Trans. А1МЕ», 1941, vol. 142, p. 152,
5-8. Нерлин С. В., Чудновский А. Ф. Физика почвы. M., «Наука», 1967.
5-9. Belghith М. М., Le Fur В. — «Acad. Sci. Paris», 1969, vol. 268, p, 349.
5-10.' Лыков А. В. Явления переноса в капиллярпопористых телах. М..
Гостехиздат, 1954. 296 с.
5-11. Slattery J. Р. Momentum, energy and mass transfer in continua. McGraw-
Hill, 1972.
5-12. Лыков А. В. Теория сушки. M., «Энергия^ 1968. 471 с. •
5-13. Поснов Б. А. Обобщенное уравнение скорости процессов гепло- и
массообмена твердых тел различной формы в регулярном режиме. — ЖТФ.
1953, т. 23, с. 865-
5-14. Полонская Ф. М. Исследование температурного поля влажных мате-
риалов в процессе сушки (период постоянной скорости).—ЖТФ. 1953, т. 23.
с. 796.
5-15. Никитина Л. М. Таблицы равновесного удельного влагосодержания
и энергия связи влаги с материалом. М., Госэнергоиздат, 1963; Термодинами-
ческие параметры и коэффициенты массопереноса во влажных материалах. М.,
«Энергия», 1968.
5-16. Тепло- и массообмен в пищевых продуктах. — «Труда МТИПП»,
1956, вып, 6.
5-17. Коган М. Н., Макашев Н. К- О роли слоя Кнудсена в теории гетеро-
генных реакций и в течениях с реакциями на поверхности, — «Изв. АН СССР,
МЖГ», 1971, №6, с. 3—12.
5-18. Winterbotfoin W. L. Vapor-solid interactions and the effusion oven.—
«J. Chcm. Phys.», 1967, vol. 47, № 9, p. 3546-3556.
5-19. Ивановский А. И. Некоторые вопросы взаимодействия измерительной
полости, с потоком разреженного газа. — «Труды Центр, аэрологической обсер-
ватории», 1964, вып. 56, с. 49—96.
5-20. Стрикленд-Констэбл Р. Ф. Кинетика и механизм кристаллизации.
Л,, «Недра», 1971-
5-21. Berman R., Simon F. Е., F. R. S., Ziinan M. The thermal conductivity
of diamond at low temperatures, — «Proc. Roy. Soc.», 1953, vol. 220, № 1141,
p. 171-183.
5-22. Де Бур Я- Динамический характер адсорбции. М., Изд-во иностр,
лит., 1962.
5-23. Sears G. W. A note on the flow of gases through very-fine tubes. — «J,
Chcm. Phys.», 1954, vol. 22, Ns 7, p. 1252—1253.
5-24. Winterbottom W. L., Hirth J. P. Diffusional contribution to the total
flow from a Knudsen cell. — «J. Chem. Phys.», 1962, vol. 37, Ns 4, p. 784— 793;
5-25. Bates T. R., Forester A. T. Coupled molecular flow and surface diffu-
sion. Application to cesium transport. — «Appl, Phys.», 1967. vol. 38, № 4, p. 1956—
1968.
5-26. Ахматов А. С. Молекулярная физика граничного трения. М., Физмат-
гиз, 1963.
5-27. Ван-Дайк М. Методы возмущений в механике жидкости. М., «Мир»,
1967.
5-28. Девиен М- Течения и теплообмен разреженных газов, М.< Изд-во
иностр, лит., 1962.
471
5-29. Максвелл Д. К. Положения к кинетической теории газов. — В кн.:
Основатели кинетической теории материн. О11ТИ, 1937, с. 185—215.
5-30. Дерягин Б. В., Баканов Е. П. Теория течения газа в пористом теле
в околокнудсеповской области. — ЖТФ, 1957, т. 27. вып. 9, с. 2056—2070.
5-31. Mason Е. A., Mallnauskas А. Р., Evans R. В. Flow and diffusion in po-
rous media. — «J. Chem. Phys.», 1967, vol. 46, № 8, p. 3199—3216.
5-32. Present R. D. Kinetic theory of gases. McGraw-Hill, 1958.
5-33. Клаузиус P. Кинетическая теория газов. — В кн.: Основатели кине-
тической теории материи. ОНТИ. 1937, с. 39—163.
5-34. Sparrow Е. М., Cess R. D. Radiation heat transfer. Wadsworth Publi-
shing Co., 1966.
5-35- Maxwell J. С. A treatise on electricity and magnetism. 3d ed. Oxford
University Press, 1891.
5-36. Чудновский А. ф. Теплофизические характеристики дисперсных
материалов. М., Физматгиз. 1962.
5-37. Thermal conductivity of porous systems. — «Int. J. Heat Mass Trans-
fer», 1968, vol. 11, № 2, p. 117—140. Auth.: A. V. Luikov, A. G. Shashkov, L. L,
Vasiliev, Yu. E. Fraiman.
5-38. Никитин В. С., Забродский С. С., Антонишин Н. В. О теплопроводности
засыпок дисперсного материала при высоких температурах в вакууме. «Изв.
АН БССР. Сер. физ.-энерг. наук», 1968, № 1, с, 82.
5-39. Krischer О. — «Gesund. Ing.», 1934, Н. 33.
5-40. Богомолов В. 3., Чудновский А. Ф. — «Труды Агрофизического инсти-
тута», вып. 3, 1941.
5-41. Загромов Ю. А., Ляликов А. С. Свободно-конвективный теплообмен
в горизонтальной цилиндрической прослойке при разлитом положении тепловы-
деляющего элемента. — ИФЖ, 1966, т. 10, № 5, с. 577— 583.
5-42. Burgers Н. С. — «Phys. Zs.», 1919, Н. 20, S. 73—75.
5-43. Fricke Н. A mathematical treatment of the electric conductivity and
capacity of disperse systems. — «Phys. Rev.», 1924, vol. 24, p. 575—587. •
5-44. Eucken A. Materials 1st calculation based on the thermal conductivity
of the components. — «Ztschr. VD1 Forschungsheft», 1932, S. 353.
5-45. Bruggeman D. A G. Berechnung verschiedener physikalischer Konstan-
ten von heterogenen Suhstanzen. — «Ann. der Phys.», 1953, H. 24, S. 635.
5-46. De Vries D. A. The thermal conductivity of granular materials. Paris.
Inst. Int. Froid, 1955.
5-47. Оделевский В, И. Расчет обобщенной проводимости гетерогенных си-
стем. — ЖТФ, 1951, т. 21, № 6.
5-48. Loeb L. A theory of thermal conductivity of porous materials. — «Amer.
Ceram. Soc.», 1954, vol. 37, № 2.
5-49. Кауфман Б, H. Теплопроводность строительных материалов. M.,
Госстройиздат 1955.
5-50. Ляликов А. С. К вопросу о теплопроводности зернистого материала.
Автореф. дис. на соиск. учен, степени канд. техн. наук. Томск, 1956.
5-51- Серых Г. М. «Изв. Томского политехнического института», вып. 101,
1958.
5-52. Дульнев Г. Н., Сигалова 3. В. Теплопроводность зернистых систем. —
В кн.: Тепло- и массоперенос. Т. 7. М., «Энергия», 1966.
472
^5-53. Дульнев Г. Н., Сигалова 3. В. Эффективная теплопроводность зерни-
стых материалов. — ИФЖ- 1967. т. 13, .4° 5.
5-54. Харламов Д. Г. Теплопроводность засыпки керамической дроби. —
ИФЖ. 1965 т. 9. № 1, с. 48—53.
5-55. Никитин В. С. Исследование эффективной теплопроводности засыпок
дисперсного материала при повышенных температурах. Автореф. дне. на соиск.
учен, степени канд. техн, наук, Минск, 1969.
5-56. Расчеты на прочность о машиностроении. Т. 2. М., Машгиз, 1958.
5-57. Васильев Л. Л. Исследование теплофизических свойств строительных
материалов при низких температурах. — В кн,: Проблемы строительной тепло-
физики. Минск, «Вышэйш. школа», с. 408.
5-58. Васильев Л Л. Теплопроводность сухих пористых систем. — В кн.:
Исследования по теплопроводности. Минск, «Наука и техника», 1967, с. 262.
5-59. Васильев А. Л., Фрайман Ю. Е. Теплофизические свойства плохих
проводников тепла. Минск, «Наука и техника», 1967.
5-60. Argo W. В., Smith J. М. — «Chem. Eng. Progr.», 1953, vol. 49, p. 443.
5-61. Schofte N. Thermal conductivity of packed beds. — «A1CHEJ», 1960,
vol. 6, Л.2 3.
5-62. Bosworth R. L. Heat transfer phenomena. John Wiley and Sons, 1952.
5-63. Oren J. C-, Churchill S. W. Radiant heat transfer in packed beds. —
«AlCHEJ», 1963, vol. 9, № I.
5-64. Серебряный Г. Л., Зарудный Л. Б., Шорни С. Н. Исследование тепло-
переноса в дисперсных средах применительно к высокотемпературной изоля-
ции. — В кн.: Тепло- и массоперенос. Т. 5. Минск, «Наука и техника», 1968,
с, 344,
5-65, Прасолов Р. С. Обобщение уравнения теплопроводности газов. — «Изв.
вузов. Приборостроение», 1961, т. 4, № 6.
5-66. Бретшнайдер С. Свойства газов и жидкостей. М., «Химия», 1968.
5-67. Каганер М. Г. Тепловая изоляция в технике низких температур. М„
«Машиностроение», 1968.
5-68. Deissler R. G., Boegli J. S. An investigation of effective thermal conduc-
tivities of powders in various gases. — «Trans. ASME», 1958, vol. 80, № 7.
5-69. Smoluchowski M. — «Acad. Wiss. Wien», 1899, CVII.
5-70. Костылев В. M. Теплопроводность дисперсных тел при различной вели-
чине атмосферного давления. — «ТВТ», 1964, т. 2, № 1.
5-71. Дульнев Г, Н., Сигалова Э. В. Теплопроводность зернистых систем. —
ИФЖ, 1964, № 10, с. 49—55.
5-72. Фрайман Ю. Е. Разработки абсолютного метода комплексного опреде-
ления теплофизических характеристик материалов в широком диапазоне темпера-
тур. Автореф. дне. на соиск. учен, степени канд. техн, наук. Минск, 1966.
5-73. Дульнев Г. Н. Перенос тепла через твердые дисперсные системы, —
ИФЖ. 1965, т, 9, № 3,
5-74. Дубницкий В. И. Исследование влажности изоляиии подземных тепло-
проводов, — «Известия ВТИ», 1952, Кв 10.
5-75. Казанский М. Ф., Куландина А. И. Влияние форм связи влаги на теп-
лоперенос в типичных капилярнопористых телах. — ИФЖ 1959, № 5, с. 88—92.
5-76, Кришер О. Научные основы техники сушки, М„ Изд«во иностр, лит,,
1961.
473
5-77. Бан А., Басниев К. С., Николаевский В. Н. Об основных уравнениях
фильтрации в сжимаемых пористых средах. — ПМТФ, 1961, .№ 3, с. 52.
5-78. Вайнер М. И. 0 несвязной насыщенности при фильтрации газирован-
ной жидкости и фильтрации жидкости с фазовыми превращениями. — «Изв.
АН СССР», МЖГ, 1966, № 2; с. 123.
5-79. Горобцова Н. Е, Исследование диффузии влаги во влажных материа-
лах. — ИФЖ, 1968, т. 15, № 6, с. 1019—1026.
5-80. Лыков А. В., Васильев Л. Л. Тепло- и массообмен капиллярнопори-
стых тел при обдувании их потоком разреженного газа. — В кн,: Тепло- и мас-
сообмен при низких температурах. Минск, «Наука и техника», 1970.
5-81. Luikbv А. V., Perelman Т. L., Anisimov S. 1. Evaporation of a solid into
vacuum. — «Int. J, Heat Mass Transfer», 1971, vol. 14, № 2.
5-82. Невесомость. M., «Мир», 1964.
5-83. Benedickt E. T. —«Amer, Rocket. Soc. J.», 1959, vol. 29, p. 350.
5-84. Шулейкин В. В. Форма поверхности жидкости, теряющей невесомость.—
ДАН СССР, 1962, вып. 147, № 1 и 5. Наземные опыты с невесомыми жидкостя-
ми.—ДАН СССР, 1963, вып. 152, № 5. с. 1082;- 1963, вып. 153, №6,
с. 1299.
5-85. Беляева М. А., Мышкис М. А.» Тюпцов А. Д. Гидростатика в слабых
гравитационных полях. Равновесные формы поверхности жидкости. — «Изв.
АН СССР, Мех. и машиносгр.», 1964, № 5, с. 39.
5-86. Нью Гуд. Ракетная техника и космонавтика. 1963, № 4.
5-87. Шашин В. М. Динамика жидкости в коническом баке при переходе от
малой весомости к значительной. — «Изв. АН СССР», МЖГ, 1968, № 6.
5-88. Чин Д, Г., Галлахер Л. В. Влияние движения жидкости на форму сво-
бодной поверхности при уменьшении гравитационных сил, — «Ракетная тех-
ника и космонавтика», 1964, № 12, с. 217.
5-89. Порхаев А. П. Явления переноса в полуограпиченных пористых телах,
Дис. на соиск. учен, степени д-ра техн, наук, М., 1964 (МТИПП).
5-90. Bosanquet С. Н. On the flow of liquids into capillary tubes. — «Phyl,
Mag.», 1923, vol. 45, p. 525.
5-91. Siegel R. Transient capillary rise in reduced and zero-gravity fields,—
«J. Appl. Meeh.», June 1961.
5-92. Федякин H. H. О движении жидкости в микрокапиллярах. — ЖФХ,
1962, т. 36, Ns 7.
5-93. Исследования теплообмена при кипении в условиях имитации слабых
гравитационных полей. — ИФЖ. 1969, т. 17, № 2, с. 201—209. Авт.: Ю. А. Кир-
пиченко, А. И. Чаркин, И. В. Липатова, В. Л. Полунин.
5-94. Ульянов А. Ф., Аладьев И. Т. Экспериментальное исследование кри-
гических тепловых потоков при вынужденном движении жидкости в условиях
невесомости, — «Космические исследования», 1968, т. 6, вып. 2, 3.
5-95. Смит Д. А., Мэджорс Д. Исследования механизма теплообмена в баке
с водородом при невесомости. — «Вопросы ракетной техники», 1968, № II, с. 3,
5-96. Кшивобоки М У. Влияние гравитационного поля на тепловую неустой-
чивость. — «Труды Амер, об-ва ипж.-мсх.», сер. С, 1967 № 4, с. 88.
5-97. Померанц М. А, Пленочное кипение на горизонтальной трубе в усилен-
ных гравитационных полях. — «Труды Амер, об-ва инж-мсх,», сер, С, 1964,
№ 2,
474
5-98. Grover G. M., Cotter T. P., Erinkson G. F. Structures of very high tber»
mal conductance. — «J. AppL. Phys.», 1964, vol. 35, p. 1990.
5-99. Левитин M. M., Перельман T. Л. К теории тепловых труб, В кн.: Тспло-
и массоперенос. Т, 2. ИТМО АН БССР. Минск, 1972, с. 136.
РАЗДЕЛ ШЕСТОЙ
6-1. Лыков А. В., Михайлов Ю. А. Теория тепло- и массопереноса, М.—Л.,
Госэнергонздат, 1963. 535 с.
6-2. Михайлов М. Д. Нестационарный тепло- и массоперенос в одномерных
телах. Минск, «Наука и техника», 1969.
6-3. Лыков А. В. Тепло- и массообмен в процессах сушки. М.—Л., Госэнер-
гоиздат, 1956. 464 с.
6-4. Лыков А. В. Теоретические основы строительной теплофизики. Минск,
«Наука и техника», 1961. 519 с.
6-5. Полонская Ф. М. Исследование температурного поля влажных материа-
лов в процессе сушки (период постоянной скорости), ЖТФ. 1953, т. 13, с. 796—
805.
6-6. Михайлов М. Д. Обобщенные решения нестационарного тепло- и массо-
переноса. — ИФЖ, 1969, т. 16, № 2, с. 299—307.
6-7. Развитие исследования по теории фильтрации в СССР. М., «Наука»,
1969.
6-8. Aronofsky J. S., Jenkins R.xProc. U. S. Nat, Congr. Appl. Meeh. Inst. —
«ASME», N. Y., 1952.
6-9. Longwell P. A- Mechanics of fluid flow. N, Y. McGraw-Hill, 1966; 1954,
vol. A225, -p. 473.
6-10. Taylor G. 1. Dispersion of soluble malter in solvent flowing slowly through
a tube. — «Proc. Roy. Soc.», 1953, vol. A219, p. 186; 1954, vol. A223, p. 446.
6-11, Aris R. On the dispersion of a solute by diffusion, convection and ex-
change between phases.—«Proc. Roy. Soc.», 1959, vol. 11, p. 194.
6-12. Harleman D. R., Melborn P. T., Rumer R. R. —«J. Hydraul. Div.,
Proc, Am. Soc. Civil Eng.», 1963, vol. 67t № 3,
6-13. Haring R. E., Greenkorn R. A. A statistical model of a porous medium with
nonuniform pores.—«A1CHEJ», 1970, vol. 16, № 3.
6-14. Николаевский В. H. Конвективная диффузия в пористых средах. —
ПММ. 1959,'т. 23, с. 1042.
6-15. Bear J. Some experiments in dispersion, — «Groph, Res.», 1966, vol.
66, p. 2455-'
6-16. Scheidegger A. E. Statistical theory of flow trough porous media, —
«Trans. Soc. Rheol.», 1965, vol. 9, p. 313.
6-17. Bachmat Y., Bear J. The general equations of hydrodynamic dispersion
in homogeneous, isotropic, porous mediums.— «Geophys. Res.», 1964, vol. 69, p. 256].
6-18. Pereh M. The dispersivity tensor in isotropic and axisymmetric medi-
ums. — «Geophys. Res.», 1965, vol. 70, p. 3969,
6-19. Whitaker S. Diffusion and dispersion in porous media, — «A1CHEJ»,
1967, vol. 13, p. 420,
6-20. Grane F. E., Gardner G. H. Measurements of transverse dispersion in
granular media, — «J, Chem, Eng. Data», 1961, № 6, p, 283,
475
6-21. Ananthakrlshnan V., Gill W. N., Barduhn A. J. Laminar dispersion in
capillares: part I. Mathematical analysis. — «A1CHEJ»,. 1965, vol. I], p. 1063.
6-22. Gucerl 0. Dispersion in Jeffery-Hamel flows. M. S. Thesis, Clarkson
College of Technology, Potsdam, N. Y., 1968.
6-23. Coats К* H., Smith D. B. — «Soc. Petrol. Eng. J.», 1964, vol. 4, p, 73,
6-24. Deans H. A. — «Soc. Petrol. Eng. J.», 1963, vol. 3, p. 49.
6-25. Goodnight R. C., Klikoff W. A., Fatt J. Non-steady-state fluid flow
and diffusion in porous media containing dead-end pore volume. — «J. Phys. Chem,»,
1960, vol. 64, p. 1162.
6-26. Griffiths A. On the movement of a coloured index along a capillary tube
and its application to the measurement of the circulation of water in a closed cir-
cuit.— «Proc. Phys. Soc.», London, 1911, vol. 23, p. 190.
6-27. Bischoff К- B., Levenspiel 0. —«Chem. Eng. Sci.», vol. 17, p. 257.
6-28. Vernotte P. Les paradoxes de la theorie continue de 1’equation de la cha-.
leur. — «Compt. Rend.», 1958, vol. 246, № 22, p. 3154—3155.
6-29. Cattaneo G. £ur une forme de 1’equation de la chaleur eliminant 1c para-
doxc d’une propagation instantance.—«Compt. Rend.», 1958, vol. 247, № 4,
p. 481-433.
6-30. Chandrasekhar S, Stochastic problems in physics and astronomy. — «Rev,
Mod. Phys.», 1943, vol. 15, № 1.
6-31. Лыков А. В. Применение методов термодинамики необратимых процес-
сов к исследованию тепло- и массообмеиа.— ИФЖ, 1965, т, 9, № 3, с. 287—304,
6-32. Фок В. А. — «Труды ГОИ», 1926, т. 4, вып. 34.
6-33. Давыдов В. И. Уравнение диффузии с учетом молекулярной скоро-
сти. — «ДАН СССР», 1935, вып. 2, № 7.
6-34. Ляпин Е. С. О турбулентном перемешивании воздуха в атмосфере, —
«Метеорология и гидрология», 1948, № 5.
6-35. Ляпин Е. С. — «Труды ГГО», 1950, вып. 19/81.
6-36. Монин А. С. — «Изв. АН СССР. Геофизика», 1955 вып. 13, № 12.
6-37. Реннер М. Феноменологическая реология. Т. 1, М., Изд-во ицостр,
лит., 1962.
6-38. Толубинский Е. В. Исследования по теплопроводности. Минск, «Наука
и техника», 1967.
6-39. Зельдович Я- Б., Компанеец А. С. К теории распространения тепла при
теплопроводности, зависящей от температуры, — В кц,: К 70-летию А. Ф. Иоф-
фе. М., Изд-во АН СССР, 1950, с. 61—71.
6-40, Зельдович. Я- Б., Райзер Ю. П. Физика ударных волн и высокотемпе-
ратурных гидродинамических явлений, М., «Наука», 1966.
6-41. Баренблатт Г. И. О некоторых неустановившихся движениях жид-
кости и газа в пористой среде. —ПММ, 1952, т. 16, вып. 1.
6-42. Баренблатт Г. И., Вишик М. И. О конечной скорости распростране-
ния в задачах нестационарной фильтрации жидкости и газа.—ПММ, 1956,
т, 20, вып. 3.
6-43. Самарский А. А., Соболь И. М. Примеры численного расчета темпера-
турных волн.— «ЖУрн. вычислит, матем, иматемат. физики», 1963, т. 3, № 4, с. 702,
6-44. Gonieaux В. Lupoussee conductive» liberee de ses paradoxes. Nouveaux
calcules sur le regime variable faisant suite a un echelon de la temperature faciale
sur une paroi plane semiinfinitc, — «EPE§, 1967. vol, 3, № 3,
476
6-45. Алексашенко А. А. Аналитическое исследование тепло- и массопере-
носа с учетом конечной скорости переноса. Дис. на соиск. учел, степени канд.
физ.-мат. наук. Минск, 1968 (ИТМО).
6-46. Пригожин И. Введение в термодинамику необратимых процессов.
М., Изд-во иностр, лит., 1960.
6-47. Алексашенко А. А., Алексашенко В. А., Селезнев Н. В. Решение урав-
нений тепло- и массопереноса для тел классической формы с учетом конечной
скорости капиллярного движения. — В кн.: Строительная теплофизика. М.—Л.,
«Энергий», 1966, с. 270—280.
6-48. Mikic В. A model rate equation for transient thermal conduction. —‘
«Int. J. Heat Mass Transfer», 1967, vol. 10, p. 1899—1904.
6-49. Luikov A. V. Analytical heat diffusion theory. New York, Academic
Press, 1968.
6-50. Лыков А. В. Теория сушки. М.-Л., «Энергия», 1968.
6-51. Кееу R. В. Drying principles and practice. Pergamon Press, 1972.
6-52. Лыков А. В. Явления переноса в капиллярнопористых телах, М„
Гостехиздат, 1954. 296 с,
4
СОДЕРЖАНИЕ
Предисловие редактора....... ..............................    3
Предисловие автора к первому изданию . ,	.	4
Раздел первый
ЯВЛЕНИЯ КОНВЕКТИВНО-ДИФФУЗИОННОГО ПЕРЕНОСА ....	6
1-1.	Некоторые аналитические соотношения . » .'.............. 6
Г-2.	Дифференциальные уравнения переноса . ....................   13
1-3.	Термодинамика явлений переноса......................... 24
1-4.	Многокомпонентные смеси....................................  27
1-5.	Вывод уравнений переноса на основе кинетической теории	газов	35
1-6.	Уравнения переноса для асимметричной жидкости.......... 45
1-7.	Гидродинамика жидкости вихревой структуры	49
1-8.	Процессы переноса при неоднородной турбулентности........	55
1-9.	Основы нелинейной термомеханиьи сплошных сред.......... 72
1-10.	Некоторые особенности гидродинамики реологических жидкостей	79
1-11.	О гиперболических уравнениях тепломассопереноса .......	87
Раздел второй
ТЕПЛОПРОВОДНОСТЬ . ................................................ 93
2-1.	Дифференциальное уравнение теплопроводности	.............. 93
2-2, Краевые условия / . . .......  j.	............. .	95
2-3,	Методы расчета расхода теплоты ........................... 99
2-4,	Методы решения задач теплопроводности . , ..............  100
2-5-	Стационарное температурное поле ............ .....	116
2-6.	Решение стационарных задач методом конформных	отображений	123
2-7,	Одномерное нестационарное поле (пластина,	шар,	цилиндр)	128
2-8.	Температурные волны ..................................... 145
2-9.	Граничные условия четвертого рода ....................... 155
2’10.	Двух- и трехмерные задачи ....................... 161
Раздел третий
КОНВЕКТИВНЫЙ ПЕРЕНОС...........................................  179
3-1	Тепломассообмен при обтекании	плоской пластины	.......	179
3-2.	Взаимосвязанный тепломассообмен при ламинарном	обтекании
плоской пластины......................................  202
3-3. Тепломассообмен при течении в трубах и при обтекании сложных
тел................................................     221
3-4.	Взаимосвязанный турбулентный	тепломассообмен .	....... 224
3-5.	Свободная конвекция ................................... 239
3-6.	Термоконвективные волны	................ 249
478


Раздел четвертый
СОПРЯЖЕННЫЕ ЗАДАЧИ ТЕПЛООБМЕНА.................................. 256
•1 (. Физическое обоснование сопряженных задач теплообмена .... 256
4-2	Критерий сопряженности  ............................  .	261
4-3. Приближенные решения задачи ламинарною обтекания плас-
тины .....................................    ......... 263
4-4. Точные решения задачи теплообмена пластины в потоке сжима-
емого газа с источником теплоты . ....................  266
4-5 Несимметричная задача без источника теплоты............. 269
4-6 Внутренние сопряженные задачи .........................  275
4-7. Нестационарный теплообмен при ламинарном движении несжи-
маемой жидкости в плоской и круглой трубах ............ 278
4-8. Сопряженная задача теплообмена при турбулентном течении жид-
кости и газа.............,	, ............. . . , .......  •	287
Раздел пятый
ЯВЛЕНИЯ ПЕРЕНОСА В КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛАХ. ...	299
5-1 Структурные характеристики ........................    .	299
5-2 Термодинамика поверхностных явлений....................  290
5-3. Закономерности усреднения.............................  312
5-4. Термодинамические характеристики влагопереноса . ,..... 319
5-5- Молекулярно-кинетический метод . .....................  333
5-6. Теплопроводность капиллярно-пористых тел и дисперсных сред 344
5-7 Перенос влаги в пористых телах.......................... 357
5-8. Применение капиллярно-пористых тел в космической технике 375
5-9. Явления переноса в условиях невесомости...............  381
5-10. Тепловые трубы . . . <............................     392
Раздел шестой
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ДИФФУЗИИ ТЕПЛОТЫ И МАССЫ
6-1. Дифференциальные уравнения тепломассопереноса ........	398
6-2. Дифференциальные уравнения влаготеплопереноса в процессе
сушки ............................................    404
6-3. Обобщенная система Дифференциальных уравнений теяломассо-
переноса . ............................ ..................	411
6-4. Критерии подобия тепломассопереноса.................  413
6-5- Решение уравнений тепломассопереноса при обобщенных кра-
евых условиях......................................   415
6-6. Граничные условия второго рода .	,....... 422
6-7. Граничные условия третьего рода ..................... 425
6-8. Дифференциальные уравнения фильтрации через пористые
среды...........................................      434
6-9. Диффузия через пористые среды ....................... 436
6-10, Гиперболические дифференциальные уравнения гепломассопсре-
поса и их решения .................................   448
Список литературы	........... 462
Пр
Пр
Ра;
ЯВ
!
 i
АЛЕКСЕЙ ВАСИЛЬЕВИЧ ЛЫКОВ
ТЕПЛОМАССООБМЕН
(СПРАВОЧНИК)
Редактор В. В. Красников
Редактор издательства М. И. Кузнецова
Художественный редактор В. Ф. Горелов
Переплет художника Н. И, Л а ды гин а
Технический редактор Т. А. М а с л о в а
Корректор М. Г. Г у л и н а
ИВ № 981
Сдано в набор 02.09.77 г. Подписано к печати 16.02.78 г,
Т-05129. Формат 60Х90'/(в. Бумага типографская № 3. Гари,
шрифта литературная. Печать высокая. Усл. печ. л. So,O.
Уч.-изд. л. 40,64. Тираж 20 000 экз. Зак. 1496. Цена 2 р. 40 к.
Издательство «Энергия»,
Москва, М-114, Шлюзовая наб., 10
Ордена Октябрьской Революции, ордена Трудового Красного
Знамени Ленинградское производственно техническое объе-
динение «Печатный Двор» имени А. М. Горького Союзноли-
графпрома при Государственном комитете Совета Министров
СССР по делам издательств, полиграфии и книжной торгов-
ли. J9713Q, Ленинград, П-136, Гатчинская ул., 26.
Раздё
кон!
3|
3;
з!
3j
з