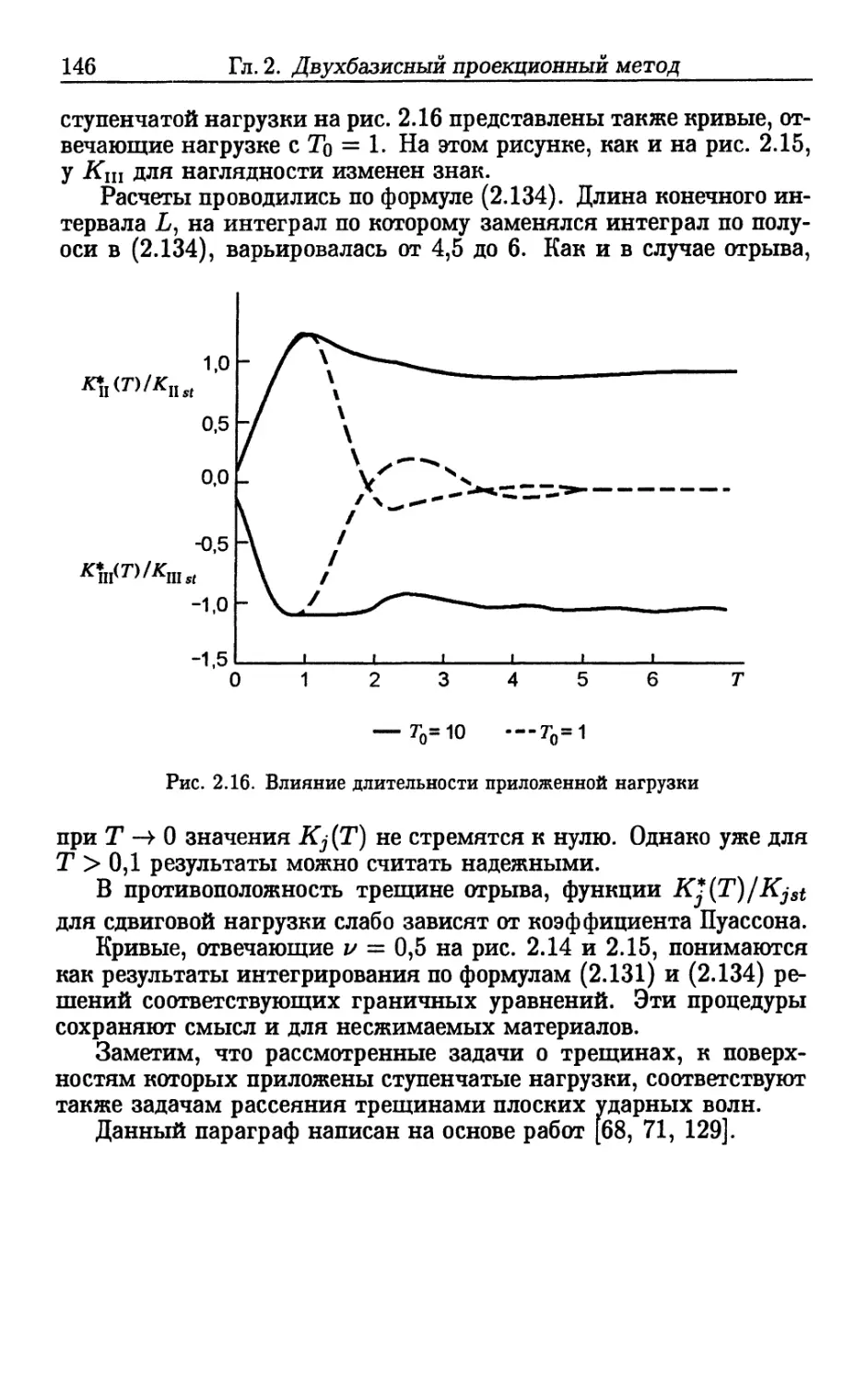
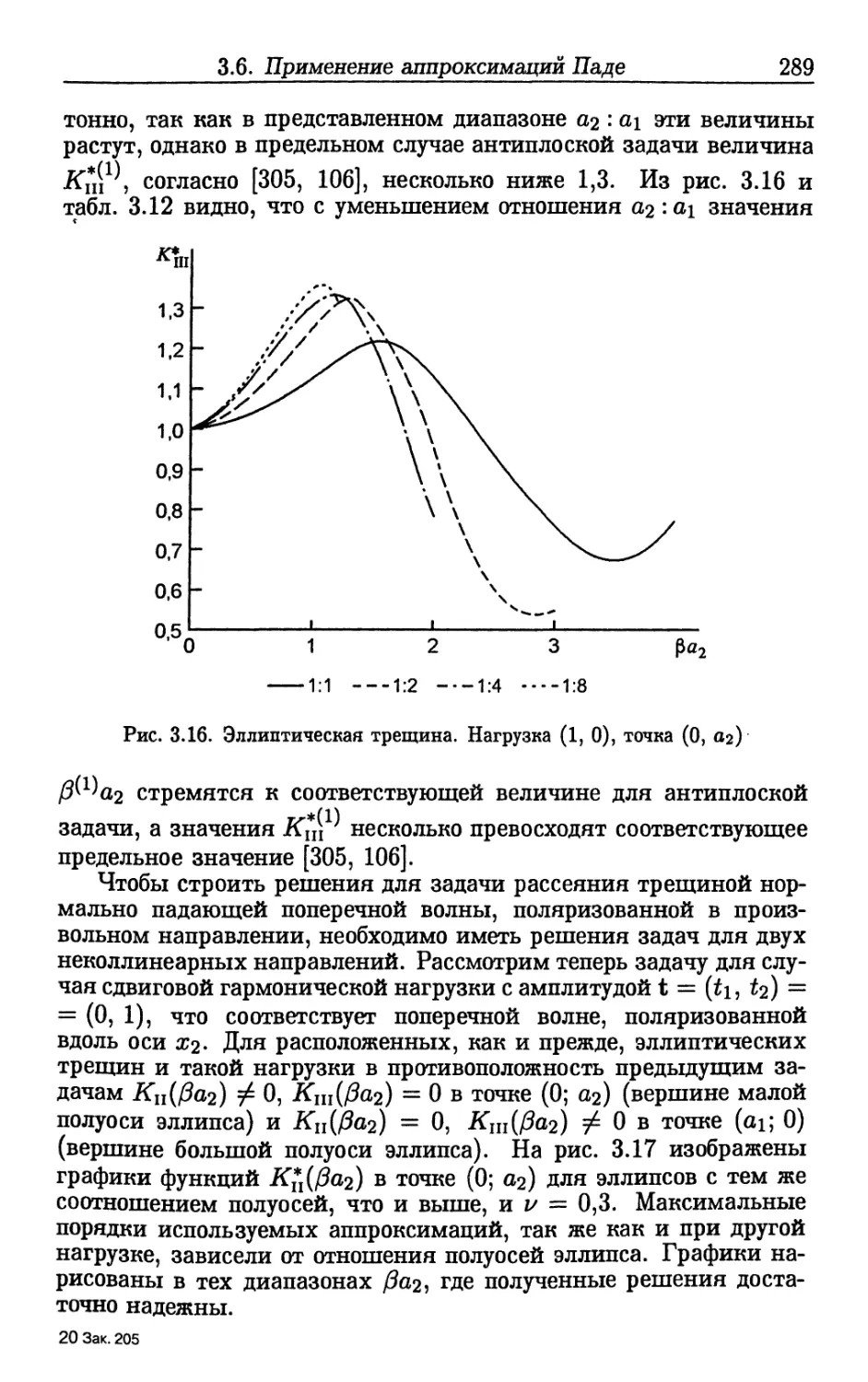
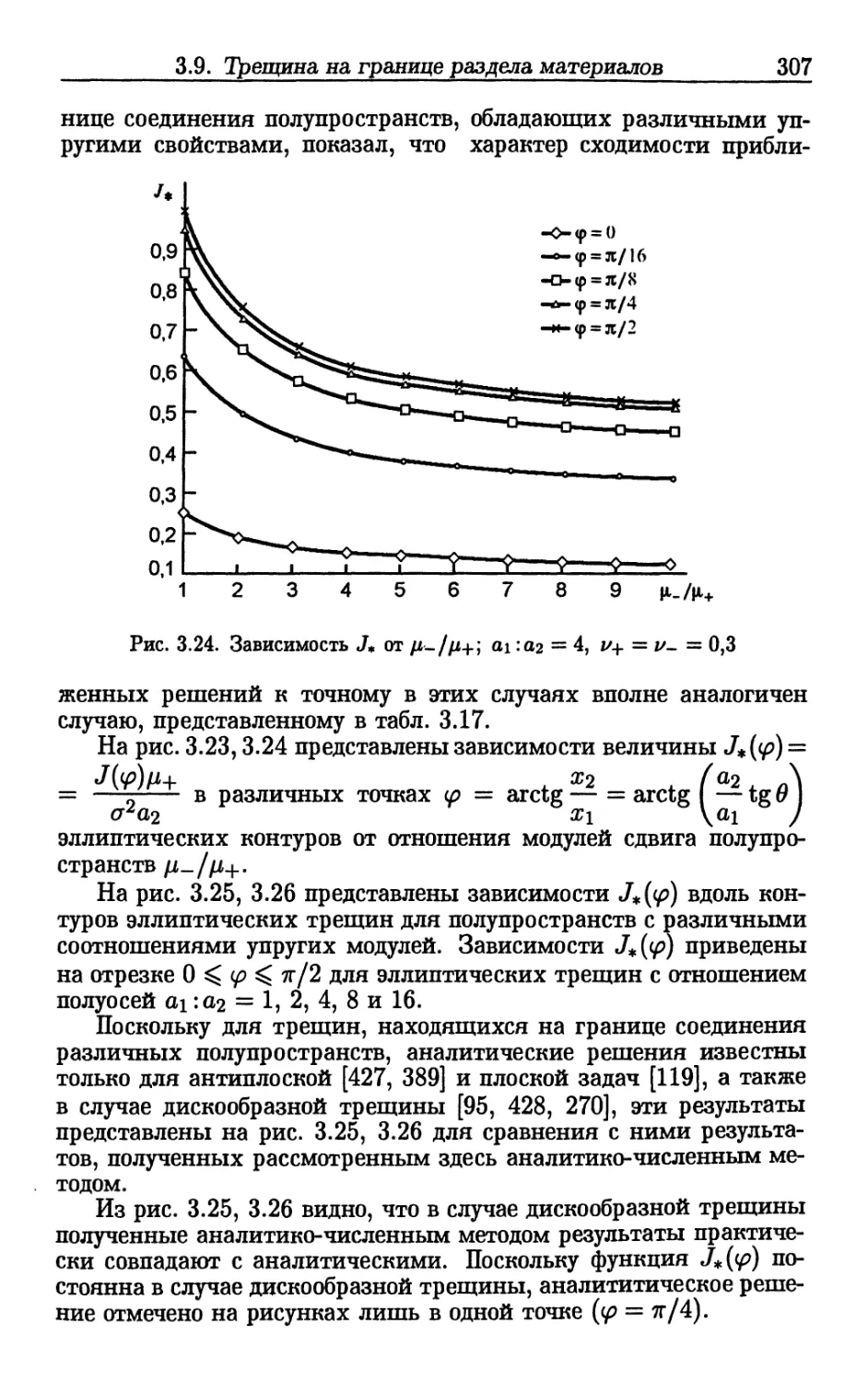
Author: Шифрин Е.И.
Tags: религия богословие физика механика физика твердого тела
ISBN: 5-94052-059-6
Year: 2002
Text
российская академия наук
институт проблем механики
Механика и ее приложения в технике и технологии
Серия основана в 2000 г.
Е.И.ШИФРИН
ПРОСТРАНСТВЕННЫЕ
ЗАДАЧИ
АИНЕЙНОЙ
МЕХАНИКИ
РАЗРУШЕНИЯ
Москва
Физматлит, 2002
ББК 22.311
Ш65
УДК 20.4.4
Редакционная коллегия серии:
Н. А. Анфимов, Д. Л. Быков, Н. А. Генералов,
Р. В. Гольдштейн (ученый секретарь), А. Ю. Ишлинский,
Д. М. Климов (председатель), С. В. Нестеров, Г. В. Новожилов, С. А. Шестериков
ШИФРИН Б. И. Пространственные задачи линейной механики разруше-
разрушения. — М: Издательство Физико-математической литературы, 2002. — 368 с. —
ISBN 5-94052-059-6.
Рассматриваются граничные псевдодифференциальные уравнения, отвечающие
статическим и динамическим задачам теории упругости для пространства, ослабленно-
ослабленного плоской трещиной. Представлены разработанные автором методы их численного и
аналитического решения. Приведены результаты расчетов. Исследованы качественные
свойства решений рассматриваемых уравнений.
Для научных работников, специализирующихся в области механики разрушения и
математической физики. Книга может быть полезна аспирантам и студентам указанных
специальностей.
Книга написана при частичной поддержке Федеральной Программы «Интеграция»,
Проект № А0083.
Научное издание
ШИФРИН Ефим Ильич
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
Редактор Л. А. Панюшкина
Компьютерная графика И. П. Казанский
Компьютерная верстка Г. М. Красникова
Оформление Ы. Н. Грицук
ИД № 01389 от 30.03.2000
Подписано в печать 25.08.2002. Формат 60x90/16.
Бумага офсетная № 1. Печать офсетная.
Усл. печ. л. 23,0. Уч.-изд. л. 25,3. Тираж 1000 экз. Зак. 205
Издательство Физико-математической литературы
119071 Москва, Ленинский пр-т, 15
Отпечатано с готовых диапозитивов в ГУП «Облиздат»
248640 Калуга, пл. Старый торг, 5.
ISBN 5-94052-059-6 О Е. И. Шифрин, 2002
ОГЛАВЛЕНИЕ
Предисловие 4
Введение 5
Глава 1. Граничные уравнения 32
1.1. Постановка задачи 32
1.2. Вывод граничных уравнений 33
1.3. Разрешимость граничных уравнений 42
Глава 2. Двухбазисный проекционный метод 58
2.1. Постановка задачи 58
2.2. Двухбазисный метод решения операторных уравнений 66
2.3. Статическая нормальная нагрузка 75
2.4. Гармоническая нормальная нагрузка 96
2.5. Гармоническая сдвиговая нагрузка 122
2.6. Ударная нагрузка 137
Глава 3. Аналитические методы 147
3.1. Постановка задачи 147
3.2. Нормальная полиномиальная нагрузка 153
3.3. Сдвиговая полиномиальная нагрузка 165
3.4. Гармоническая нормальная нагрузка 182
3.5. Гармоническая сдвиговая нагрузка 233
3.6. Применение аппроксимаций Паде 266
3.7. Ударное нагружение 294
3.8. Асимптотика решения для малых времен 298
3.9. Трещина на границе раздела материалов 301
Глава 4. Качественные методы 316
4.1. Постановка задачи 316
4.2. Теоремы сравнения 318
4.3. Изопериметрические оценки 322
4.4. Сходимость альтернирующего метода 331
4.5. Установившиеся колебания 340
Список литературы 344
ПРЕДИСЛОВИЕ
В монографии рассматриваются математические задачи ли-
линейной механики разрушения. Приведенные результаты по
приближенному решению граничных псевдодифференциальных
уравнений статической и динамической теории трещин, анали-
аналитическому решению задач для плоских трещин эллиптической
формы и оценкам решений задачи о трещине нормального раз-
разрыва получены, в основном, либо самим автором, либо в соавтор-
соавторстве с коллегами. Оригинальные результаты предваряет данный
во введении обзор, цель которого познакомить читателя с матема-
математическими проблемами, возникающими при решении простран-
пространственных задач теории трещин, многообразием имеющихся под-
подходов к их решению и выделить те проблемы, на решение которых
направлена данная книга. В силу указанных целей, приведенный
обзор не претендует на полноту.
Автор признателен А.В. Капцову, в соавторстве с которым полу-
получен ряд результатов, вошедших в книгу. Особую признательность
хотелось бы выразить Р.В. Гольдштейну, более двадцати лет на-
назад привлекшему внимание автора к задачам механики разруше-
разрушения. Без его ценных замечаний, сделанных в ходе обсуждений
практически всех результатов, вошедших в книгу, и постоянной
поддержки написание данной книги было бы невозможно.
ВВЕДЕНИЕ
В упругом теле, содержащем трещиноподобный дефект и на-
находящемся под действием внешних сил, вблизи границы дефе-
дефекта возникают области значительной концентрации напряжений.
Вследствие наличия перегруженных областей способность таких
тел сопротивляться действующим на них усилиям заметно сни-
снижается. Вместе с тем современные сложные конструкции и соору-
сооружения практически всегда содержат те или иные дефекты типа
трещин, возникающие либо в процессе эксплуатации, либо изна-
изначально присущие используемым материалам.
Поскольку разработанные для сплошных тел критерии прочно-
прочности оказываются неприменимыми к телам, содержащим трещины,
появилась необходимость в развитии методов прогнозирования
возможностей использования конструкций, в случае обнаружения
в них трещин. В результате были созданы различные, в зависи-
зависимости от свойств материала, теории разрушения тел с трещинами.
По механизму разрушения принципиально отличаются случаи, ко-
когда возникающие в окрестности края трещины зоны пластичности
и нелинейного деформирования материала малы по сравнению с
размерами трещины и расстояниями от края трещины до гра-
границы тела и когда указанные размеры сравнимы. Если размеры
пластической области остаются малыми практически вплоть до
разрушения, то такое разрушение называется квазихрупким. Так
как книга посвящена методам исследования и решения математи-
математических задач, отвечающих поведению квазихрупких тел с трещи-
трещинами, остановимся более подробно на наиболее существенных для
анализа напряженно-деформированного состояния характеристи-
характеристиках решения этих задач.
Основы механики хрупкого разрушения были заложены Гриф-
фитсом [222, 223]. По Гриффитсу, страгивание трещины происхо-
происходит тогда, когда приращение энергии деформации при прораста-
прорастании трещины достигает энергии, идущей на образование новой
свободной поверхности. Впоследствии этот критерий был обоб-
обобщен на квазихрупкий случай [248, 341], когда энергия расходу-
расходуется не только на образование новой свободной поверхности, но
и на образование новой малой пластической зоны у края тре-
6 Введение
щины. Были предложены также другие критерии, например си-
силовые (Г.И.Баренблатт [9-11], Дж.Ирвин [250], В.В.Новожилов
[100, 101]), основанные на анализе характеристик локального поля
напряжений, и деформационные, связанные с величиной раскры-
раскрытия трещины у ее кончика (М.Я.Леонов, В.В.Панасюк [84, 102],
Дагдейл [206], Уэлс [424]).
Эти подходы, отличающиеся описанием физических явлений,
влияющих на трещиностойкость и имеющие различные области
применимости, с математической точки зрения становятся экви-
эквивалентными при больших размерах трещин и малых зонах пла-
пластичности. Напомним теперь, как выглядит критерий прораста-
прорастания трещины в таком случае.
Как известно, решения задач линейной теории упругости для
тел с трещинами не являются вполне корректными и дают беско-
бесконечно большие значения деформаций и напряжений у края тре-
трещины. Однако в квазихрупком случае упругое решение близко к
точному вне малой пластической зоны. Вследствие этого условие
страгивания трещины может быть определено с помощью упру-
упругого решения. Главные члены компонент тензора напряжений
упругого решения у кончика трещины имеют особенность —0,5.
Коэффициенты при этих особенностях и определяют, будет ли раз-
развиваться трещина.
Связь между различными критериями прорастания трещины
проиллюстрируем на примере трещины нормального разрыва.
Пусть трещина расположена в плоскости х$ = 0, тогда напряже-
напряжение озз в плоскости трещины у ее края имеет вид 033 = Ns~~x/2 +
+ o(s~1/2), где s — расстояние по нормали до контура, ограничи-
ограничивающего трещину. Обозначим нормальное перемещение поверх-
поверхности трещины через щ. Из решения плоской задачи, отвечаю-
отвечающей сечению трещины плоскостью, нормальной к контуру в точке
его гладкости, получается, что вблизи ограничивающего трещину
контура г^з = 4A — v2)Nsll2/Е + o(s1^2). Здесь ?7, v — модуль
упругости и коэффициент Пуассона материала. В [141] соотноше-
соотношение такого типа между решением внутри области вблизи ее гра-
границы и правой частью вне области получено для класса псевдо-
псевдодифференциальных уравнений, включающего в себя и граничное
уравнение, связывающее нормальные смещения и напряжения в
плоскости трещины.
Изменение энергии деформации при прорастании трещины
определяется формулой Ирвина [249] (см. также [12, 96]) 8W =
= 2тгA - v2)E~lN28S, где SS — приращение площади, занимае-
занимаемой трещиной. Аналогичная формула также получена в [141] для
вариации энергетической характеристики решений класса псевдо-
псевдодифференциальных уравнений, включающего в себя как гранич-
граничное уравнение задачи о трещине в однородном линейно упругом
Введение 7
пространстве, так и уравнения задач о трещинах в пространстве
со специальным видом неоднородности.
Таким образом, локальное поле напряжений, раскрытие у края
трещины и приращение упругой энергии при вариации области
трещины в окрестности некоторой точки ее контура определяется
одним и тем же коэффициентом N. Согласно критериям линейной
механики разрушения рост трещины в окрестности рассматривае-
рассматриваемой точки контура начинается, когда коэффициент интенсивности
напряжений достигает критического значения N = NT. Обычно
используются другие величины, отличающиеся от указанной лишь
множителем: модуль сцепления К = 7rNT, по Г.И. Баренблатту,
и критический коэффициент интенсивности напряжений К1с ==
= iVT\/27r, по Дж. Ирвину. В дальнейших расчетах мы будем
пользоваться как величинами iV, так и величинами Кг = Ny/2n.
Если на тело, содержащее трещину, действует произвольная
система сил, то особенность вблизи ограничивающего трещину
контура возникает не только у сгзз, но и у других компонент тен-
тензора напряжений. Выделим компоненты а$п и сгзт? где п — напра-
направление внешней нормали к контуру, а г — касательной к контуру,
лежащих в плоскости трещины. Известно [117], что в плоскости
трещины вблизи ее края отмеченные компоненты тензора напря-
напряжений имеют вид
Kill , /
Здесь, как и выше, s — расстояние по нормали до контура тре-
трещины; КП} Кш — коэффициенты интенсивности напряжений.
Скачки смещений на поверхности трещины вблизи контура
также выражаются через Кп, Кт [117]:
= 2A - u)Kn /х-1 Л
V 7Г
[tin]
Здесь [г*п], [иТ] — скачки смещений на поверхности трещины в
направлениях нормальном и касательном к контуру в рассматри-
рассматриваемой точке, /j, — модуль сдвига.
При сложном нагружении рассматриваются различные крите-
критерии развития трещин. Как правило, эти критерии имеют вид
f(Ku KIU Km) = fcr [136, 103], где / — некоторая функция, зави-
зависящая от свойств материала. Достаточно подробный анализ раз-
различных критериев разрушения имеется в [135, 103]. В частности,
8 Введение
в [103] обсуждается следующий критерий:
где mi, Ш2, шз — константы материала; Klc, KUc, К
ческие значения коэффициентов интенсивности напряжений для
чистых отрыва, поперечного и продольного сдвигов соответственно.
Изменение энергии деформации при прорастании трещины
имеет вид [117, 136, 106]
SW = B/i) [A ¦- v) (К? + К*)+ К?п]SS = G*6S.
Поэтому рассматривается также критерий прорастания трещины
G* = С?с, где Gc — критическое значение скорости изменения
энергии деформации. В случае только нормального нагружения
Кц = Кщ = 0 и этот критерий переходит в записанный выше
критерий для трещины нормального разрыва.
В [274, 388] Си предложен критерий роста трещины, исполь-
использующий плотность энергии деформации на границе малой окрест-
окрестности края трещины. Этот критерий позволяет предсказать не
только момент страгивания трещины, но и направление ее ро-
роста. Поскольку плотность энергии деформации выражается через
коэффициенты интенсивности напряжений, этот критерий также
формулируется в терминах коэффициентов интенсивности напря-
напряжений. Некоторая модификация теории Си и обсуждение других
критериев представлены в [421].
Все пречисленные соотношения и критерии прочности отно-
относятся к линейно упругим квазихрупким телам с трещинами,
находящимся под действием статических нагрузок. При статиче-
статическом нагружении кроме коэффициентов интенсивности напряже-
напряжений интерес представляют и некоторые интегральные характери-
характеристики решения упругой задачи, например, энергия и компоненты
«объема». Компоненты «объема» (проинтегрированные по области
трещины скачки смещений) определяют главные члены возмуще-
возмущения, вносимого трещиной в дальнее поле напряжений, и потому
существенны при подсчете эффективных характеристик деформи-
деформирования среды с множеством трещин [120], а также важны при
анализе кинетики роста трещин в условиях, когда имеется при-
приток газа или жидкости в трещину [41].
Приведенные выше критерии роста трещины сформулированы
в предположении, что деформационные и прочностные свойства
материала не зависят от времени. Для некоторых материалов (по-
(полимеры, металлы при воздействии агрессивных сред и др.) это
предположение оказывается несправедливым и медленное подра-
подрастание трещины происходит даже при низких уровнях напряже-
напряжения. При таком квазистатическом росте трещины коэффициенты
Введение 9
интенсивности напряжений также являются важнейшими харак-
характеристиками решения, поскольку они определяют скорость про-
прорастания трещины. Подробное исследование законов кинетики
квазистатического роста трещин проведено в [13-16]. Согласно
[13-16] скорость прорастания трещины в направлении, перпенди-
перпендикулярном контуру трещины, при нормальном нагружении опреде-
определяется коэффициентом интенсивности напряжений Кх в данной
точке dr/dt = f(Kx). Здесь f{Ki) — некоторая функция, зави-
зависящая от свойств материала. Экспериментальные исследования,
направленные на определение вида функции / для конкретных
материалов, представлены, например, в [210, 27], см. также имею-
имеющиеся там ссылки.
Аналогичная картина имеет место и при усталостном разруше-
разрушении, когда рост трещины с увеличением числа циклов нагружения
определяется диапазоном изменения коэффициентов интенсивно-
интенсивности напряжений [345, 136, 66, 7, 135, 103].
Динамические задачи теории трещин можно разделить на два
типа: 1) быстро продвигающиеся трещины; 2) трещины стацио-
стационарны, а прикладываемые усилия зависят от времени. В данной
книге рассматривается только второй тип указанных динамиче-
динамических задач. При динамическом нагружении порядок особенности
напряжений у края трещины, вид асимптотики скачков смеще-
смещений вблизи контура трещины, а также связь асимптотики скачков
смещений с асимптотикой напряжений на продолжении трещины
остаются такими же, как и в статическом случае. Несмотря на то,
что критерии роста трещины при изменяющихся во времени уси-
усилиях менее изучены, чем при статическом нагружении, очевидно,
что и в этом случае возможность прорастания трещины определя-
определяется коэффициентами интенсивности напряжений. Согласно [114,
136, 31] трещина растет при достижении коэффициентом интен-
интенсивности напряжений критического значения, но вязкость разру-
разрушения зависит от скорости нагружения. Зависимость вязкости
разрушения от скорости и истории нагружения рассматривалась
в [263, 356, 278, 279, 198]. В работах [265, 264] предложен крите-
критерий, согласно которому для развития трещины необходимо, чтобы
коэффициент интенсивности напряжений превышал критическое
значение в течение некоторого инкубационного периода времени.
Инкубационное время считается константой материала.
Так как использование в практических целях критериев с кри-
критическими значениями параметров, зависящими от скорости и
истории нагружения, весьма неудобно, были разработаны крите-
критерии, свободные от этих недостатков. Упомянутый выше крите-
критерий, основанный на величинах плотности энергии деформации
на границе малой окрестности края трещины, было предложено
[274, 388] использовать и для случая динамических усилий. При
этом предполагалось, что критическое значение плотности энер-
1 Зак. 205
10 Введение
гии деформации не зависит от скорости нагружения. Однако дан-
данный критерий представляется недостаточно физически понятным
и обоснованным.
Критерий, обобщающий подход В.В. Новожилова на динамиче-
динамический случай, предложен в [91, ПО, 92]. Согласно [91, ПО, 92] тре-
трещина начинает развиваться, если величина напряжения, усред-
усредненная по характерному размеру материала и по некоторому
t a
t-r
где г и d — структурное время и структурный размер разрушения,
<7С — статическая прочность материала, <т(?, г) — максимальное
растягивающее напряжение у вершины трещины (г = 0). Если
на расстоянии d в течение времени т величина а(s, г) определя-
определяется главным членом асимптотики, то указанный критерий вы-
выражается через усредненное по времени значение коэффициента
интенсивности напряжений.
Кроме коэффициентов интенсивности напряжений в динами-
динамических задачах интерес представляют дальние поля смещений и
напряжений или выражающиеся через них различные характе-
характеристики решений (полное и дифференциальное сечения рассея-
рассеяния). Дальние поля используются в неразрушающих методах кон-
контроля для обнаружения трещиноподобных дефектов и определения
их местоположения, размеров и формы [406, 282, 362, 155, 361].
В [226] показано, что дальние поля выражаются через интегралы
от скачков смещений по области трещины.
Таким образом, как в статическом, так и в динамическом слу-
случае все важнейшие характеристики решений выражаются через
скачки смещений в области трещины. Поэтому при исследовании
задач механики разрушения необходимо тем или иным способом
определить скачки смещений, после чего можно вычислить лю-
любые интересующие величины. Задача отыскания скачков смеще-
смещений сводится к решению системы уравнений теории упругости
в области, занимаемой упругим телом, с разрезом, отвечающим
трещине.
Несмотря на достаточно четкую и простую математическую
формулировку, проблемы линейной механики разрушения оказы-
оказываются весьма сложными из-за математических трудностей, воз-
возникающих при исследовании и решении соответствующих уравне-
уравнений, особенно в пространственном случае. Прикладное значение
указанных проблем, а также глубина и разнообразие отвечающих
им математических задач привлекли внимание многих исследо-
исследователей. В течение нескольких последних десятилетий появилось
Введение 11
большое количество работ, посвященных решению задач линей-
линейной механики разрушения. Все эти работы по применяемым в них
методам можно разбить на три основных направления:
1. Численные методы решения. К этому направлению отно-
относится разработка и усовершенствование численных методов и ал-
алгоритмов и их компьютерная реализация.
2. Аналитические методы. К ним относятся: построение ана-
аналитических решений в случае канонических областей, занимае-
занимаемых трещиной и телом; асимптотические решения в некоторых
задачах, содержащих малые или большие параметры, а также
численно-аналитические решения, в которых аналитические вы-
вычисления сочетаются с расчетами на компьютере.
3. Качественные методы, в которых изучаются свойства реше-
решений и строятся гарантированные оценки тех или иных их харак-
характеристик, не прибегая к полному решению задачи.
Из перечисленных методов решения, безусловно, наиболее
универсальными, применимыми к широкому классу задач, явля-
являются численные. Однако при численном решении возникают про-
проблемы, связанные с надежностью и точностью получаемых резуль-
результатов. Кроме того, используя численный счет, сложно выявить
законы изменения решений при вариациях параметров задачи.
В связи с этим большое значение приобретают решения, полу-
получаемые аналитическим путем. Высокая точность таких решений
позволяет использовать их в качестве эталонных для проверки
численных методов и корректировки параметров численного счета.
Значительный интерес представляют также качественные ре-
результаты, поскольку они выявляют тенденции изменения реше-
решений или их характеристик при вариации параметров задачи и тем
самым позволяют судить о погрешностях, как вносимых вслед-
вследствие идеализации исходных данных, так и возникающих при
численном счете.
Среди методов численного решения пространственных задач
теории упругости для тел с трещинами различаются такие, при
которых решаются уравнения теории упругости во всем трехмер-
трехмерном теле (методы конечных разностей, прямых, конечных элемен-
элементов), и методы, в которых уравнения теории упругости предвари-
предварительно сводятся на границу тела и затем уже решаются граничные
уравнения.
Методы численного решения уравнений во всем трехмерном
теле являются достаточно универсальными, однако в силу высо-
высокой размерности задачи они приводят к системам линейных алге-
алгебраических уравнений высокого порядка. Это затрудняет решение
задачи и требует при программной реализации большого объема
памяти и значительных затрат машинного времени. Кроме того,
когда в решаемой задаче имеются области резкого изменения ве-
величин напряжений и смещений, как например, бывает в случаях
г
VI Введение
наличия трещин или других концентраторов напряжений, возни-
возникают серьезные проблемы с обеспечением удовлетворительной точ-
точности в указанных областях.
Метод прямых заключается в том, что делается конечно-раз-
конечно-разностное разбиение по двум переменным и решается система обык-
обыкновенных дифференциальных уравнений по третьей переменной.
Поэтому он находится как бы между численными и аналитиче-
аналитическими методами. В силу сложностей, связанных с определением
коэффициентов интенсивности напряжений особенно в случае кри-
криволинейного фронта трещины, этот метод к настоящему времени
не нашел широкого применения. Имеется лишь несколько работ,
в которых методом прямых решались пространственные статиче-
статические задачи о трещинах нормального разрыва. В [228], например,
решены некоторые задачи для цилиндра, трубы и прямоуголь-
прямоугольного параллелепипеда, содержащих внутренние и выходящие на
поверхность трещины. При этом почти во всех рассмотренных за-
задачах коэффициенты интенсивности напряжений не вычислены.
В [321] предложено усовершенствование метода, позволяющее по-
повысить точность решения, не прибегая к излишнему измельчению
сетки. Благодаря этому получены удовлетворительные результаты
при расчете коэффициентов интенсивности напряжений в задаче
о прямоугольной трещине, выходящей на границу пластины ко-
конечной толщины.
Метод конечных разностей также не очень часто применялся
для решения пространственных задач механики разрушения.
В [169] решались задачи для прямоугольных и полу эллиптиче-
эллиптических нормально нагруженных трещин, выходящих на границу
упруго-пластического параллелепипеда. Коэффициенты интенсив-
интенсивности напряжений для соответствующих упругих задач не вычи-
вычислены. Исторически так сложилось, что эффективные программы,
реализующие метод конечных разностей, были разработаны для
решения динамических задач и потому некоторые статические ре-
решения получены из динамических главным образом для иллю-
иллюстрации возможностей программы. Статическое решение в [385]
строилось методом динамической релаксации (введением дисси-
пативного члена в уравнение), а в [188] усреднением (по макси-
максимальному и минимальному значениям). В [385] решена задача о
сквозной прямоугольной трещине в слое при нормальном ударном
нагружении, однако коэффициенты интенсивности напряжений не
вычислены. В [188, 426, 388] представлены решения задач об
эллиптической внутренней и полуэллиптических поверхностных
трещинах в упругих параллелепипеде и трубе при нормальных к
поверхностям трещины ударных нагрузках. Получены зависимо-
зависимости Ki от времени. Применяемая в этих работах программа ис-
использует для сокращения машинного времени явную разностную
схему. Для вычисления Кг вблизи фронта трещины производи-
Введение 13
лось измельчение сетки. Сингулярное поведение решения у кон-
контура трещины в расчетной схеме не учитывалось. Используемая в
указанных работах программа требует больших объемов памяти
и значительного машинного времени и потому может быть реали-
реализована только на очень мощных компьютерах. Краткое описание
этой программы и некоторых полученных с ее помощью результа-
результатов приведено также в [106].
Наибольшее распространение получил метод конечных элемен-
элементов (МКЭ), который и в настоящее время продолжает интенсивно
развиваться. Этот метод обладает рядом достоинств. Прежде всего
к ним следует отнести слабую чувствительность к усложнению
геометрии упругого тела, поскольку МКЭ заключается в аппрок-
аппроксимации решений в локальных областях (конечных элементах) и
сшивании их на границах элементов. Кроме того, несмотря на
высокий порядок получающейся системы линейных алгебраиче-
алгебраических уравнений, матрица системы имеет ленточную структуру,
что упрощает процедуру ее обращения и позволяет снизить объем
необходимой памяти и машинного времени. Отметим также яс-
ясный механический смысл МКЭ.
Основные проблемы, осложняющие применение МКЭ, заключа-
заключаются в аккуратном вычислении коэффициентов интенсивности на-
напряжений (КИН), высоком порядке системы линейных алгебраи-
алгебраических уравнений и большом объеме информации, используемой
соответствующими программами в качестве исходных данных.
В целях разработки наиболее эффективных и экономичных
программ было испробовано множество вариантов МКЭ. Первона-
Первоначально применялись конечные элементы, отвечающие вариацион-
вариационной постановке задачи в перемещениях и не учитывающие особен-
особенности поведения решения вблизи фронта трещины. При этом КИН
вычислялись самым простым и естественным способом. Учиты-
Учитывая асимптотику решения вблизи контура трещины, соответствую-
соответствующее смещение в близкой к фронту трещины узловой точке дели-
делилось на s1/2 (s, как и выше, расстояние до контура трещины).
Такой подход был осуществлен в [187] при решении плоских за-
задач. Этот способ также подробно обсуждается в [242, 431]. Ясно,
что получающиеся таким образом значения КИН зависят от вы-
выбранного узла. Поэтому определяемые величины КИН недоста-
недостаточно точны, а для повышения точности требуется измельчение
элементов у фронта трещины и, следовательно, значительное уве-
увеличение числа степеней свободы получающейся системы. Поэтому
в дальнейшем для вычисления КИН были развиты более эффек-
эффективные методы.
Одним из путей повышения точности является использование
вблизи фронта трещины элементов, имеющих правильную асим-
асимптотику. Различные специальные элементы вблизи контура тре-
трещины, совместимые с остальными конечными элементами, пред-
14 Введение
лагались и исследовались в [413, 414, 178, 237, 179, 239-241, 172,
351, 180, 157]. Использование специальных элементов в ряде слу-
случаев позволяет достигнуть удовлетворительной точности опреде-
определения КИН при достаточно грубом разбиении тела на конечные
элементы.
Другой путь вычисления КИН связан с применением формулы
Ирвина. Различные методы, опирающиеся на эту формулу, полу-
получили название энергетических. К ним относятся:
1. Прямое вычисление изменения энергии деформации при ма-
малом расширении области трещины вблизи рассматриваемой точки
контура с дальнейшим учетом связи полученной величины с КИН.
В [346, 236] были получены формулы для вычисления изменения
энергии деформации непосредственно в терминах МКЭ. При этом
для повышения точности и сокращения времени счета в исходной
задаче и в задаче с возмущенной трещиной использованы одинако-
одинаковые разбиения на конечные элементы, за исключением окрестности
возмущенной части контура. В этой окрестности расширение тре-
трещины моделируется перемещением узловых точек. В результате
изменение энергии выражается через решение для невозмущен-
невозмущенной задачи и изменение матрицы жесткости, определяемое сме-
смещением узловых точек. Такой подход проверялся и использовался
при решении различных, весьма сложных трехмерных задач о
трещинах [238, 179, 319, 229]. В [202] была получена формула
для приращения энергии деформации при различных вариациях
формы трещины, не опирающаяся на конкретную численную реа-
реализацию задачи. В этой формуле изменение энергии выражается
через объемный интеграл по некоторой окрестности возмущенной
части контура. Возможность применения полученной формулы в
расчетах, проводимых МКЭ, рассматривалась в [203].
2. Расчет работы, требуемой для закрытия небольшой части
трещины, соседствующей с интересующей точкой контура. Для
этого ближайшие к рассматриваемой точке контура узлы нагру-
нагружаются силами, необходимыми для закрытия упомянутой выше
части трещины. В [365] представлено описание такой процедуры
для плоской задачи, содержащее несколько важных усовершен-
усовершенствований. Во-первых, в [365] рассмотрено несколько интегралов
закрытия трещины, что позволяет определять КИН не только для
трещин нормального, но и произвольного разрыва. Во-вторых,
там предложен приближенный способ определения догружающих
усилий, благодаря чему их можно вычислить из решения исходной
задачи и потому отпадает необходимость в многократном решении
задачи. Предложенный в [365] подход обобщен на трехмерный слу-
случай в [183].
3. К энергетическим относятся также методы, основанные на
вычислении трехмерных J-интегралов. В трехмерных задачах
с помощью J-интегралов можно оценить усредненные по охваты-
Введение 15
ваемой части фронта трещины значения КИН. Поскольку вели-
величина J-интеграла выражается через изменение энергии деформа-
деформации при прорастании трещины, способы вычисления изменения
энергии при расширении трещины, упомянутые выше, можно
одновременно рассматривать и как способы вычисления J-инте-
J-интеграла. На это было обращено внимание в [346, 236]. В [202, 380]
путем подсчета изменения энергии при вариации области трещины
получено выражение J-интегралов через объемные интегралы. Не-
Непосредственное вычисление J-интеграла, как интеграла по поверх-
поверхности, в конечноэлементных расчетах проведено в [326]. Здесь
также исследована устойчивость полученных результатов в зави-
зависимости от выбора поверхности. Поскольку результаты конечно-
элементных расчетов больше подходят для вычисления объемных
интегралов, интерес представляют методы, сводящие вычисление
J-интегралов к вычислению объемных интегралов. В [331, 99]
показано, как J-интегралы могут быть сведены к объемным инте-
интегралам и приведены примеры, иллюстрирующие эффективность
такого метода вычисления КИН для трещин произвольного раз-
разрыва.
Значительное развитие в решении задач механики разруше-
разрушения получили также гибридные МКЭ. В этих методах использу-
используются сингулярные элементы вблизи контура трещины и обыч-
обычные конечные элементы вне окрестности контура трещины. Связь
между сингулярными и обычными конечными элементами обеспе-
обеспечивается соответствующей гибридной вариационной формулиров-
формулировкой. В основном применяются два типа гибридных МКЭ. Один
из них основан на вариационной формулировке, являющейся мо-
модификацией принципа минимума потенциальной энергии, и на-
называется гибридным МКЭ в перемещениях. Другой тип основан
на модификации функционала дополнительной энергии. Он назы-
называется гибридным МКЭ в напряжениях. Среди работ, в которых
применялись гибридные МКЭ для решения трехмерных задач о
трещинах, отметим [165-168], где использовались гибридные эле-
элементы в перемещениях, и [288, 289], где использовались равновес-
равновесные гибридные элементы. Смешанные гибридные элементы были
предложены в [290].
Перечисленные выше усовершенствования позволили решить с
помощью МКЭ ряд важных как для теоретического анализа, так и
для приложений пространственных статических задач механики
разрушения. В частности, решены следующие задачи о трещи-
трещинах отрыва: полуэллиптическая трещина, выходящая на поверх-
поверхность пластины конечной толщины [351, 432]; полу эллиптические
трещины, выходящие на внутреннюю и внешнюю поверхности
цилиндрического сосуда давления [319, 165-168, 339, 353]; прямо-
прямоугольные поверхностные и сквозные трещины в пластинах конеч-
конечной толщины [414, 236, 180, 239, 288, 241, 325]; прямоугольная по-
16 Введение
верхностная трещина в балке, подвергаемой трехточечному изгибу
[416]; трещины, выходящие на поверхность цилиндрической по-
полости, расположенной в пластине [352]; поверхностные трещины,
лежащие в нормальном сечении трубы и цилиндра [167, 220, 221,
354]; угловые трещины в горловине цилиндрического сосуда да-
давления [238, 166, 167]; трещина, исходящая из цилиндрической
полости кругового сечения, расположенной в трубе [318]; пара вза-
взаимодействующих одинаковых полукруговых трещин, расположен-
расположенных в параллельных плоскостях и выходящих на поверхность
пластины конечной толщины [261].
Несмотря на то, что МКЭ является в настоящее время одним
из самых мощных вычислительных методов, сложности, возни-
возникающие при решении пространственных динамических задач о
трещинах, пока остаются для него непреодолимыми. Подавляю-
Подавляющее большинство решенных пространственных статических за-
задач являются задачами о трещинах нормального разрыва. По-
Попытки решения задач о трещинах произвольного разрыва до сих
пор были весьма редкими и, как правило, ограничивались реше-
решениями тестовых задач [331, 99]. Интересные обзоры, касающиеся
различных аспектов использования МКЭ при решении простран-
пространственных задач механики разрушения и имеющие обширные би-
библиографические ссылки, содержатся в [237, 412, 241, 280, 31, 296].
Обзор по применению сингулярных элементов при решении с по-
помощью МКЭ задач теории упругости в областях с нерегулярной
границей имеется в [8б|.
При решении задач для упругих тел с трещинами весьма ши-
широко применяются также методы, в которых уравнения теории
упругости сначала сводятся к интегральным или интегродиффе-
ренциальным уравнениям на границе тела, а затем полученные
граничные уравнения решаются тем или иным способом. Ос-
Основная идея этих методов — сократить размерность решаемой
задачи и тем самым понизить порядок системы линейных алге-
алгебраических уравнений, возникающих в процессе нахождения при-
приближенного решения.
Существует несколько способов построения граничных урав-
уравнений. Наиболее распространенным является метод, использую-
использующий тождество Сомильяна, в котором перемещения внутри тела
выражаются через перемещения и напряжения на границе. Осу-
Осуществляя переход к пределу при стремлении точки наблюдения к
границе, можно получить систему интегральных уравнений, свя-
связывающих перемещения и напряжения на поверхности тела.
В случае наличия в теле трещины (двухсторонней поверхно-
поверхности) получаемые таким образом уравнения вырождаются. Поэтому
при использовании граничных интегральных уравнений (ГИУ)
для решения задач о трещинах прибегают к одному из следую-
следующих специальных приемов:
Введение 17
1. Замена трещины тонким вырезом. Такой способ был пред-
предложен и применялся для решения пространственных задач в [196,
191]. Очевидно, что с помощью этого приема невозможно обеспе-
обеспечить высокую точность решения, в особенности вблизи контура
трещины, т. е. в наиболее важной для механики разрушения об-
области.
2. Использование симметрии задачи в тех случаях, когда та-
таковая имеется. При наличии симметрии рассматривается симме-
симметричная часть области, в границу которой входит только одна по-
поверхность трещины. Вся граница выбранной части тела состоит
из части границы исходного тела, поверхности трещины и поверх-
поверхности, проходящей внутри исходного тела. Граничные условия
для внутренней поверхности определяются из условий симметрии.
Использовать симметрию в задачах о трещине было предложено
в [192]. Этот подход с успехом применялся для решения многих
сложных пространственных задач (см., например, [194, 79, 197,
235, 407, 408, 164]).
3. В случае отсутствия симметрии можно воспользоваться прие-
приемом, предложенным в [291]. Этот прием заключается в том, что
упругое тело разбивается на несколько. В границу каждого из по-
полученных тел может входить лишь одна поверхность трещины.
ГИУ записываются для каждого из тел. На внешних границах и
поверхности трещины сохраняются исходные граничные условия,
а на внутренних поверхностях (т.е. на продолжении трещины)
принимаются условия сцепления между областями, заключающие-
заключающиеся в совпадении перемещений и противоположности усилий. Раз-
Разделение тела на подобласти применялось при решении статиче-
статических задач о трещинах в [195, 355, 259] и динамических задач с
гармонически зависящей от времени нагрузкой в [260].
4. Деление упругого тела на подобласти является достаточно
эффективным способом решения задач о трещинах. Однако в
процессе его эксплуатации выявились и некоторые негативные
моменты. К ним относятся: а) достаточно большой произвол в
способах разбиения тела на подобласти; б) увеличение количе-
количества неизвестных за счет добавления внутренних поверхностей;
в) необходимость использования специальных элементов, учиты-
учитывающих асимптотическое поведение решения вблизи контура тре-
трещины, не только для перемещений, но и для напряжений. Все
это может приводить к снижению точности получаемых прибли-
приближенных решений. Поэтому помимо данного способа значитель-
значительное развитие получил также иной метод построения граничных
уравнений. В тождестве Сомильяна можно провести дифферен-
дифференцирования и получить выражения напряжений внутри тела через
перемещения и напряжения на границе. Вновь, как и прежде, пе-
переходя к пределу при стремлении точки наблюдения к границе,
получим граничные уравнения, связывающие приложенные уси-
18 Введение
лия со скачками перемещений на поверхности трещины. Такие
уравнения в [349] названы граничными уравнениями в напря-
напряжениях.
Граничные уравнения в напряжениях для статической задачи
о трещине в безграничной среде были предложены в [186, 423].
Для динамической задачи при гармонической по времени нагрузке
они были выведены в [184]. Различные виды уравнений относи-
относительно скачков перемещений для динамических задач приведены
также в [255, 42, 393]. Уравнения статических задач для тре-
трещин, находящихся внутри ограниченного упругого тела, получены
в [36, 37].
Уравнения относительно скачков перемещений имеют то пре-
преимущество, что снижается количество неизвестных (неизвестны-
(неизвестными остаются только скачки перемещений в области трещины) и
исключается произвол, имеющий место при делении области тела
на подобласти. К недостаткам такого подхода следует отнести уве-
увеличение сингулярности ядер интегральных операторов за счет до-
дополнительного дифференцирования.
При таком дополнительном дифференцировании возможны не-
несколько способов записи получающихся уравнений: а) оставить
производные перед интегралами, которые являются интегралами
в смысле главного значения; б) перебросить производные на ска-
скачки смещений, стоящие под интегралами; в) продифференциро-
продифференцировать ядра интегральных операторов.
Численное решение уравнений, записанных в любом из ука-
указанных видов, как правило, осуществляется методом коллокации.
При этом возникают значительные проблемы, связанные с вы-
вычислением результата применения соответствующего оператора к
аппроксимирующим решение функциям. В случае а) помимо
сложностей вычислений интегралов в смысле главного значения
необходимо затем численно дифференцировать сами интегралы,
что приводит к существенным погрешностям, если только инте-
интегралы не вычисляются аналитически. Поэтому такой способ при-
применяется редко. В [262] для решения задач рассеяния предло-
предложено разбивать поверхность на конечные элементы, в каждом из
которых неизвестные функции аппроксимировать постоянными.
В этом случае интегралы вычисляются аналитически и возможно
их дифференцирование. Аналогичный подход при решении дина-
динамической задачи об эллиптической трещине отрыва осуществлен
в [185].
В случае б) проблемы возникают как при вычислении инте-
интегралов в смысле главного значения, так и за счет того, что при-
приходится дифференцировать неизвестные функции (скачки смеще-
смещений). Поэтому необходимо следить за гладкостью аппроксимаций
скачков смещений. Различным аспектам, связанным со способами
регуляризации и вычисления интегралов в смысле главного значе-
Введение 19
ния, а также их применению в статических и динамических зада-
задачах о трещинах, посвящены работы [411, 392, 393, 349, 292, 293].
В [349, 193] особое внимание уделяется сглаживанию аппроксима-
аппроксимации решения (скачков смещений) при использовании уравнений в
виде б), поскольку отмечено, что от точности дифференцирования
строящегося приближения самым существенным образом зависит
точность получаемого решения.
При использовании уравнений в виде в) исчезает необходи-
необходимость дифференцирования строящейся аппроксимации решения,
однако сами интегралы становятся расходящимися из-за сильной
особенности ядер интегральных операторов. Оказывается, что та-
такие интегралы можно понимать как конечные части расходящихся
интегралов, в связи с чем они называются конечночастными инте-
интегралами. Использовать конечночастные интегралы для решения
задачи о плоской трещине нормального разрыва в безграничной
среде было предложено в [245]. Развитию способов вычисления ко-
нечночастных интегралов и их применению в статических и дина-
динамических задачах о трещинах произвольного разрыва посвящены
работы [246, 85, 247, 297, 298, 333, 312, 313].
Использование конечночастных интегралов имеет то преиму-
преимущество, что уравнения получаются интегральными, а не интегро-
дифференциальными. Вместе с тем вычислить конечночастные
интегралы весьма непросто. Для этого проводится регуляризация
интеграла, в результате чего он представляется в виде суммы не-
нескольких интегралов, среди которых имеется и интеграл в смы-
смысле главного значения. Кроме того, регуляризация осуществля-
осуществляется путем вычитания и прибавления значений подынтегральной
функции в точке наблюдения. Чтобы после вычитания понизился
порядок особенности подынтегрального выражения, необходимо
потребовать дополнительной гладкости от искомой подынтеграль-
подынтегральной функции. На связь между порядком особенности ядра инте-
интегрального оператора и требованием к гладкости подынтегральной
функции обращено внимание в [312, 313].
Имеется существенно меньшее количество работ, где для ре-
решения граничных уравнений относительно скачков перемещений
применялся метод Бубнова-Галеркина. В этих работах для об-
облегчения вычислений в качестве базисных брались функции, для
которых часть интегралов можно вычислить аналитически. Одна-
Однако такие базисные функции не имеют правильной асимптотики у
контура трещины, что значительно снижает точность при вычи-
вычислении КИН. Метод Бубнова-Галеркина применялся в [44, 47, 26,
25] для решения статических и в [418, 419] для решения динами-
динамических задач о трещинах.
Несколько более подробно различные способы записи уравне-
уравнений относительно скачков смещений и методы их решения об-
обсуждаются в гл. 2 на примере трещины нормального разрыва в
20 Введение
безграничной среде. В этой же главе рассматривается развитый
автором метод решения таких уравнений, позволяющий избежать
вычисления нерегулярных интегралов, и показано, как он может
быть применен к статическим и динамическим задачам о трещи-
трещинах произвольного разрыва.
Эффективность применения ГИУ к задачам механики разру-
разрушения зависит не только от того, насколько в удачной форме за-
записано уравнение, но и от эффективности численных процедур его
решения и способов определения КИН. В подавляющем большин-
большинстве работ при решении ГИУ граница тела разбивается на конеч-
конечные элементы, а неизвестные постоянные определяются методом
коллокации. Разбиение поверхности тела на конечные элементы
роднит такой метод решения с МКЭ и потому называется методом
граничных элементов (МГЭ).
Первоначально с помощью ГИУ рассматривались только тела,
поверхность которых состояла из кусков плоскостей, а искомые
решения внутри каждого из конечных элементов аппроксимиро-
аппроксимировались постоянными [196, 191]. В [192] предложено внутри конеч-
конечных элементов неизвестные аппроксимировать линейными функ-
функциями, что позволяет существенно повысить точность получаемого
решения. Свое дальнейшее развитие методы уточнения описания
неизвестных функций и поверхности тела получили в [291], где
разработаны процедуры использования полиномов второго порядка
для аппроксимации кусков поверхности тела и полиномов второго
и третьего порядка для аппроксимации решения внутри конечных
элементов.
Способы определения КИН при использовании ГИУ остаются
практически теми же, что и в МКЭ.
Деление значений перемещений или умножение напряжений
вблизи фронта трещины на корень из расстояния до него с даль-
дальнейшей экстраполяцией полученных величин вплоть до контура
трещины применялось, например, в [191, 192, 194, 407, 408, 164]
и др. Возможность применения формулы Ирвина проверялась в
[194, 407, 408, 164]. Элементы, имеющие правильную асимпто-
асимптотику у контура трещины и тем самым позволяющие вычислять
КИН без какой-либо дополнительной процедуры, использовались
в [423, 301, 259, 260, 355].
Круг решенных с помощью ГИУ пространственных задач ме-
механики разрушения во многом совпадает с задачами, решенными
МКЭ. Так, например, путем численной реализации ГИУ, записан-
записанных в различных видах, решены следующие задачи о трещинах
отрыва: полукруговые и полуэллиптические трещины, выходящие
на границу полупространства или пластины конечной толщины
[190, 191, 79, 194, 407, 234, 323]; прямоугольные поверхностные и
сквозные трещины в пластинах конечной толщины [191, 192, 407];
угловая трещина в форме четверти эллипса [79, 194]; полуэлли-
Введение 21
птическая трещина, выходящая на поверхность полого цилиндра
[235, 407, 408, 301]; частично эллиптическая поверхностная тре-
трещина, расположенная в сечении, нормальном к оси цилиндра [164,
292]; взаимодействие двух круговых трещин, расположенных в
одной плоскости [301]; эллиптическая трещина, находящаяся
вблизи цилиндрической полости [148].
Следует отметить, что по сравнению с МКЭ в МГЭ удалось более
эффективно решать задачи для трещин произвольного разрыва
[195, 355, 292, 259, 260] и динамические задачи о трещинах [255,
256, 392, 297, 298, 97,185, 243, 244, 333, 332, 260, 89, 88]. Заметим,
что обычно рассматриваются два типа динамических задач — для
гармонической по времени и ударной нагрузок. Случай ударных
нагрузок может быть рассмотрен несколькими способами. Один
из них заключается в том, что сначала делается преобразование
Лапласа или Фурье по времени. Для преобразованного уравнения
записываются и решаются ГИУ. После этого производится обра-
обращение преобразования Лапласа или Фурье соответственно. Та-
Таким образом задачи решались, например, в [256, 392, 88]. Дру-
Другой путь — записать и решить ГИУ в пространственно-временной
области, как это сделано в [243, 244].
В литературе имеются сравнительные оценки МКЭ и МГЭ.
К достоинствам использования ГИУ и решения задач МГЭ от-
относят: снижение размерности задачи и, следовательно, снижение
порядка системы линейных алгебраических уравнений, к которой
после дискретизации сводится задача; существенное сокращение
необходимой для работы программы исходной информации, по-
поскольку дискретизируется только поверхность тела; более высо-
высокую точность получаемых решений главным образом в областях
с большими градиентами напряжений, в частности, вблизи кон-
контура трещины; меньшие требования к ресурсам компьютера при
произвольных статических и динамических нагружениях.
Преимущества МКЭ заключаются в слабой чувствительности
метода к усложнению геометрии и механических свойств тела, а
также, несмотря на высокий порядок системы линейных алгебраи-
алгебраических уравнений, в более простой матричной алгебре. В МКЭ
матрица имеет ленточную структуру, а в МГЭ матрица полностью
заполнена. Кроме того МКЭ основан на решении более простых
(дифференциальных) уравнений, в то время как метод ГИУ при-
приводит к сингулярным интегральным или интегродифференциаль-
ным уравнениям.
Поэтому, как отмечается в [195], сегодня МКЭ значительно
чаще применяется в инженерных приложениях. МГЭ главным
образом используется в исследовательских целях.
Для того, чтобы объединить достоинства каждого из методов
в [275, 163] разработан способ совместного использования МКЭ и
МГЭ. Для этого решение задачи об упругом теле с трещиной пред-
22 Введение
ставляется в виде суммы двух решений — задачи о трещине в
безграничной среде и задачи об упругом теле без трещины. По-
Поскольку метод ГИУ более точен в случае наличия концентраторов
напряжений, он используется в задаче о трещине в безгранич-
безграничной среде. Задача об упругом теле без трещины решается МКЭ,
что позволяет рассматривать тела сложной геометрии. В резуль-
результате дискретизации получается система линейных алгебраических
уравнений, включающая в себя уравнения МГЭ для трещины в
безграничной среде и уравнения МКЭ для тела без трещины. Для
замыкания этой системы к ней добавляются уравнения, учиты-
учитывающие, что сумма решений удовлетворяет заданным граничным
условиям.
Помимо применения формулы Сомилиана существует и иной
способ построения граничных уравнений, который основан на
использовании компенсирующих (фиктивных) нагрузок. Этот
способ был предложен в работах [1-3, 315]. Его основная идея
заключается в том, что вместо тела, имеющего границу, рас-
рассматривается безграничное пространство с объемными силами,
распределенными по поверхности тела. При этом ищется такая
плотность распределения объемных сил, которая обеспечивает вы-
выполнение заданных граничных условий. Таким путем, распреде-
распределяя усилия по обеим поверхностям разреза (используя распреде-
распределенные диполи), можно также прийти к граничным уравнениям в
случае тел с трещинами. Получающиеся с помощью метода ком-
компенсирующих нагрузок уравнения использовались для решения
задач о трещинах в ряде работ, см. например, [65, 4, 337, 327-
329, 338, 251-253, 294]. Круг решенных в этих работах задач
достаточно широк и во многом близок к тем задачам, которые ре-
решались рассмотренными выше методами. Большинство из решен-
решенных задач касалось трещин нормального разрыва. В [337] рассма-
рассматривались задачи об эллиптических трещинах, перпендикулярных
границе полупространства, и полуэллиптических трещинах, выхо-
выходящих на границу полупространства. Получены решения также
для двух одинаковых эллиптических трещин, расположенных в
безграничном пространстве и лежащих в одной плоскости. Вза-
Взаимодействие двух, вообще говоря, различных полу эллиптических
трещин, находящихся в одной плоскости и выходящих на границу
полупространства, рассмотрено в [328]. Распространение этих ре-
результатов на случай как взаимодействующих, так и не взаимодей-
взаимодействующих трещин произвольной формы, выходящих на границу
полупространства, представлено в [329]. Задачи об одной внешней
кольцевой трещине в цилиндре и периодической системе таких
трещин рассмотрены в [338]. В [252] получено решение задачи
об эллиптической трещине, перпендикулярной границам упругого
слоя, а в [253] рассмотрены полуэллиптические трещины, выхо-
выходящие на границу упругого слоя.
Введение 23
Были решены также некоторые задачи о трещинах произволь-
произвольного разрыва. В [251] рассмотрено взаимодействие двух эллипти-
эллиптических трещин, лежащих в параллельных плоскостях упругого
пространства. В [327] развивается способ решения задач для тре-
трещин произвольной формы, наклонно выходящих на поверхность
полупространства. В частности, приведены решения для наклон-
наклонных полуэллиптических, прямоугольных и треугольных трещин.
В [294] рассмотрены задачи об одной трещине и двух пересекаю-
пересекающихся трещинах, исходящих из точки приложения нормальной к
границе полупространства сосредоточенной силы.
Так же как и при численной реализации граничных уравне-
уравнений, получающихся с помощью формулы Сомильяна, основной
проблемой здесь остается эффективное вычисление сингулярных
интегралов. В [108, 109], см. также [107], было предложено рассма-
рассматривать значения интегралов в точках пространства вне плоскости
трещины вблизи от нее, т. е. там, где интегралы регулярны, а за-
затем провести экстраполяцию для вычисления интегралов в точках
области трещины. Поскольку при приближении точки к поверх-
поверхности трещины ядро интегрального оператора начинает быстро
расти, в [108, 109] предложено разбить область интегрирования на
малые элементы, а в элементах, находящихся вблизи от точки,
в которой вычисляется значение, произвести дополнительное раз-
разбиение. В качестве примера рассмотрена задача о дискообразной
трещине. Дальнейшего развития этот подход к вычислению син-
сингулярных интегралов не получил.
В случае эллиптических или полу эллиптических трещин в
[337] для вычисления сингулярных интегралов предложено при-
применять следующий прием. Эллипс специальным образом разбива-
разбивается на элементы. Предполагается, что интегралы по элементам,
не содержащим рассматриваемую точку, вычисляются достаточно
точно. Интеграл по элементу, содержащему особую точку, вычи-
вычисляется из известного аналитического решения задачи об эллипти-
эллиптической трещине под действием однородного давления. Для такой
задачи интеграл по элементу, содержащему особенность, можно
вычислить как разность между точным значением и суммой ин-
интегралов по элементам, не содержащим особенностей.
Динамические задачи о трещинах путем численной реализа-
реализации уравнений, отвечающих методу компенсирующих нагрузок, к
настоящему времени не решались.
Поскольку описанные выше методы численного решения до-
довольно трудны, их реализация на компьютере требует значитель-
значительного времени и не всегда обеспечивает достаточную точность, пред-
предпринимались попытки создания менее универсальных, но более
быстродействующих простых и надежных способов расчета. Та-
Такие способы иногда предназначаются для решения более узкого
класса задач, а в некоторых случаях — для решения конкретных
задач. Перечислим некоторые из них.
24 Введение
Метод разложения по собственным функциям использовался
для задач о трещинах в пластинах конечной толщины [230, 387].
В [8] предложены уравнения для задач о трещинах нормального
разрыва в безграничном пространстве, контур которых состоит из
отрезков прямых и дуг окружностей, при этом были использованы
известные точные решения задач о трещинах, имеющих форму
круга и полуплоскости. Эти уравнения применялись для реше-
решения задач о трещинах прямоугольной [127] и треугольной [128]
форм. В [317] решены задачи о трещинах нормального разрыва
различных форм. Разнообразными методами решались задачи
о трещинах отрыва и сдвига прямоугольной формы, см. напри-
например, [127, 423, 217, 268, 269]. Задача о прямоугольной трещине,
находящейся под действием гармонической по времени нагрузки,
рассмотрена в [255].
В [44] предложен вариационно-разностный метод решения ста-
статической задачи о трещине нормального разрыва в безграничной
среде. Усовершенствование этого метода и его применение к раз-
различным задачам о трещинах как отрыва, так и сдвига предста-
представлены в [37, 47, 26, 25]. Метод Бубнова-Галеркина со специально
выбранной системой базисных функций применялся для решения
задач о трещинах в случае гармонической по времени нагрузки в
[418, 419].
В [64] предложен метод решения статических задач о трещине
в безграничной среде, основанный на полученных в [62, 63] фор-
формулах, которые позволяют по известным решениям задачи о тре-
трещине заданной формы получить решение задачи для трещины со
слабо возмущенной границей. Таким образом, непрерывно пере-
переводя дискообразную трещину, для которой решение известно, в
трещину рассматриваемой формы можно построить приближен-
приближенное решение.
Пространственные задачи о трещинах, находящихся на гра-
границе соединения материалов с различными упругими свойствами,
гораздо более сложны, так как их решения обладают не только
корневой, но и осциллирующей особенностью вблизи фронта тре-
трещины. В связи с этим до настоящего времени не разработаны
эффективные методы выделения КИН из численных решений та-
таких задач.
Значительные усилия исследователей были направлены на по-
получение аналитических решений, поскольку такие решения, как
уже отмечалось выше, позволяют выяснить их качественную за-
зависимость от тех или иных параметров задачи, например, от вида
нагрузки или кривизны контура трещины, а также являются эта-
эталонами, на которых можно оценить и проверить численные про-
процедуры и выбрать наиболее подходящие параметры этих проце-
процедур. К настоящему времени аналитические решения построены
только для статических задач о трещинах канонической формы
Введение 25
(полуплоскость, круг, эллипс, внешность круга или эллипса) в без-
безграничной среде.
Решения задач о трещине в виде полуплоскости представлены
в [132, 121, 232], см. также [63]. Множество работ посвящено ре-
решению задач о дискообразной трещине. Случай однородной нор-
нормальной нагрузки рассмотрен в [82, 367, 400]. Решение задачи
для однородной сдвигающей нагрузки приведено в [368, 93, 425].
Различные осесимметричные нормальные нагрузки рассмотрены
в [400, 402, 274, 215, 208]. Осесимметричный радиальный сдвиг
изучался в [402, 274, 208]. Осесимметричные скручивающие на-
нагрузки рассматривались в [118, 402, 274]. Нагружение сосредото-
сосредоточенными объемными силами исследовалось в [189, 132, 403, 274].
Решения для произвольной нормальной нагрузки, приложенной
к поверхностям трещины, представлены в [102, 136, 227, 274].
Различные подходы к решению задач в случае произвольных как
нормальных, так и сдвиговых нагрузок применялись в [227, 274,
174, 284, 374, 134, 309, 399]. Разнообразные задачи о трещине,
занимающей внешнюю по отношению к кругу часть плоскости,
решались в [131, 132, 118, 300, 402, 274, 404].
Большое число работ посвящено также задачам об эллиптиче-
эллиптических трещинах. Здесь аналитические решения удалось построить
лишь для полиномиальных нагрузок. В [83, 219] получены реше-
решения для однородной нормальной нагрузки. Решение для однород-
однородного сдвига получено в [209, 271]. Линейная нормальная нагрузка
рассмотрена в [272]. В [373] приведены решения для линейной и
квадратичной нормальных нагрузок. В [274] рассмотрены различ-
различные нормальные нагрузки вплоть до полиномов шестого порядка,
однако не произвольного вида, а также скручивающая сдвиговая
нагрузка. В [370] представлена матрица системы линейных урав-
уравнений для решения задачи в случае нормальных полиномиальных
нагрузок до третьего порядка. В [397] сообщается о том, что ана-
аналогичная система уравнений получена для полиномиальных сдви-
сдвиговых нагрузок до третьего порядка, однако решение приведено
только для линейной нагрузки. Наконец, в [417, 335, 21, 310, 311]
разработаны конструктивные процедуры построения аналитиче-
аналитических решений для нормальных и сдвиговых полиномиальных на-
нагрузок произвольного порядка.
Некоторые задачи для трещин, занимающих внешнюю по от-
отношению к эллипсу часть плоскости, решались в [267, 273, 274].
Аналитический способ решения задачи для пары взаимодей-
взаимодействующих, расположенных в одной плоскости дискообразных тре-
трещин предложен в [130].
Некоторые осесимметричные задачи, например, задачи о коль-
кольцевых трещинах под действием растягивающих и скручивающих
нагрузок, хотя и не имеют аналитических решений, однако мо-
26 Введение
гут быть эффективно решены численно, поскольку они сводятся к
удобным для численных реализаций одномерным интегральным
уравнениям [61, 386, 316].
Во многих важных задачах, содержащих те или иные параме-
параметры, аналитические решения не могут быть построены, однако
в случаях, когда значение параметра задачи мало или велико,
удается построить асимптотические разложения решений. Асим-
Асимптотические решения весьма полезны, поскольку они достаточно
точны в определенных диапазонах изменения параметра, зача-
зачастую позволяют строить решения для таких значений параметра,
для которых численные процедуры плохо сходятся и, наконец, в
тех случаях, когда удается построить асимптотику как для малых,
так и для больших значений параметра, дают возможность путем
сращивания асимптотических разложений получить аппроксима-
аппроксимацию решения во всем диапазоне изменения параметра [177].
Асимптотические решения строились в самых разнообразных
пространственных задачах механики разрушения. Например, в
[123] получены асимптотические решения для задачи о кольцевой
трещине под действием растягивающей нагрузки в двух крайних
случаях — когда радиус одной окружности много меньше радиуса
другой и когда эти радиусы близки. Аналогичные асимптотиче-
асимптотические разложения получены в [266] для скручивающей нагрузки.
Задачи о вытянутых плоских трещинах асимптотически ре-
решены в [43] для нормальной и в [77] для сдвиговой нагрузок. Ре-
Решения задач о трещинах, полученных из дискообразной путем
малого возмущения ее контура, построены в [102, 94]. Более об-
общие результаты получены в [62, 63, 357, 211, 22-24], где развиты
методы построения решений для трещин, мало отличающихся от
таких, для которых решения известны.
В ряде случаев асимптотические методы позволяют учесть
влияние границы тела. Так, решены различные задачи о дис-
дискообразных трещинах, расположенных в срединной плоскости
достаточно толстого [122, 402] и тонкого [5] упругих слоев (см.
также [6]). В [402] и [274] приведены асимптотические решения
задач о дискообразной трещине, расположенной далеко от границ
тела, для тел в виде соосных цилиндра или шара, а также полу-
полупространства, граница которого параллельна плоскости трещины.
В [274] также решена задача о взаимодействии двух одинаковых
дискообразных трещин, расположенных в параллельных и уда-
удаленных друг от друга плоскостях. В [124] рассмотрена задача об
эллиптической трещине, нормальной к границе полупространства
и удаленной от его поверхности.
В [359, 200, 201, 433] разработан метод линейных пружин,
позволяющий решать пространственные задачи о вытянутых вну-
внутренних и поверхностных трещинах отрыва в пластинах и поло-
пологих оболочках конечной толщины путем сведения их к двум дву-
Введение 27
мерным задачам: задаче для пластинки или оболочки, в которой
трещина заменена сквозным разрезом с линейно упругими свя-
связями между берегами, и плоской задаче о трещине. В [45, 46] этот
подход распространен на случай трещин произвольного разрыва.
Одним из самых эффективных методов решения простран-
пространственных задач механики разрушения оказался численно-анали-
численно-аналитический альтернирующий метод. Этот метод применялся при
решении задач о дискообразных или эллиптических внутренних
трещинах и поверхностных трещинах, представляющих собой
часть круга или эллипса. Альтернирующий метод заключается
в том, что сначала решается задача о трещине в безграничном
пространстве с заданными усилиями на ее поверхностях и вы-
вычисляются отвечающие этой задаче усилия на поверхности тела.
В случае, когда поверхностная трещина представляет собой часть
эллипса, она достраивается до полного эллипса, причем нагрузки
на достроенной части доопределяются из соображений наиболь-
наибольшего удобства решения задачи о трещине в безграничном про-
пространстве. Вычисленные усилия на поверхности тела, очевидно,
не совпадают с приложенными. Поэтому затем решается задача
для упругого тела без трещины с такими усилиями на его по-
поверхности, которые снимают имеющуюся разницу. Однако в
результате этого на месте трещины возникают дополнительные
нагрузки. Следующим шагом является решение задачи о тре-
трещине в безграничном пространстве с усилиями на поверхности
трещины, снимающими появившуюся дополнительную нагрузку.
После этого все повторяется до тех пор, пока невязка не станет
малой по отношению к приложенным усилиям.
Альтернирующий метод применяется в случае круговых и эл-
эллиптических трещин, поскольку, как уже написано выше, только
для таких трещин в безграничном теле имеются аналитические
решения. Основное достоинство альтернирующего метода заклю-
заключается в том, что наименее аккуратный элемент численных про-
процедур —- вычисление КИН, здесь осуществляется аналитически.
Кроме этого, реализуемое численно решение задачи для тела с гра-
границей не требует специальных приемов, так как рассматривается
тело без трещины.
В развитии альтернирующего метода можно выделить несколь-
несколько этапов. Сначала решались задачи для трещин в полупростран-
полупространстве [394-396, 371, 372, 231, 281, 398], так как решение задачи для
полупространства без трещины можно выписать аналитически.
Решение задачи о поверхностной трещине в слое [415] также опи-
опиралось на возможность аналитического решения задачи об упру-
упругом полупространстве в совокупности с двумя альтернирующими
процессами.
Важным шагом вперед стало использование в альтернирую-
альтернирующей процедуре метода конечных элементов при решении задачи
28 Введение
для упругого тела без трещины. Это позволило рассмотреть за-
задачи для тел сложной формы, например, в виде пластины конечной
толщины с цилиндрическим отверстием, на поверхность которого
выходит частично эллиптическая трещина, при различных усло-
условиях нагружения [287, 286, 218].
Вместе с тем возможности по повышению точности альтерни-
альтернирующего метода оставались еще достаточно ограниченными, по-
поскольку к тому времени были известны аналитические решения
для эллиптических трещин в безграничной среде лишь для поли-
полиномиальных нагрузок не выше третьего порядка. В связи с этим
вычисленные дополнительные нагрузки на поверхностях трещи-
трещины приходилось аппроксимировать полиномами третьего порядка,
что в некоторых случаях оказывалось недостаточно. Решающим
шагом в развитии альтернирующего метода стали работы [417,
335], в которых были разработаны конструктивные процедуры по-
построения аналитических решений для полиномиальных нагрузок
произвольного порядка. В сочетании с МКЭ для решения задач
теории упругости в телах без трещин это позволило получить хо-
хорошие приближения решений сложных пространственных задач.
В частности, так решены задачи о внутренних и внешних про-
продольных полу эллиптических трещинах в цилиндрических сосудах
давления [334, 340], причем здесь рассматривались как одиночные,
так и взаимодействующие трещины. В [336] решена задача о
четверть-эллиптической трещине, выходящей на поверхность ци-
цилиндрической полости в пластине конечной толщины. В [335]
решались задачи о внутренних трещинах в цилиндре и парал-
параллелепипеде и о трещинах, выходящих на поверхность паралле-
параллелепипеда. В [350] рассмотрены задачи о поперечных трещинах,
представляющих собой часть эллипса, в полых цилиндрах.
Возможности аналитического, асимптотического и численно-
аналитического решения пространственных задач о трещинах
для гармонических по времени нагрузок значительно более огра-
ограничены, чем в статическом случае. Так, до настоящего времени
не было получено ни одного аналитического решения за исключе-
исключением задачи о трещине, имеющей форму полуплоскости [150]. До-
Достаточно аккуратные численные результаты имеются лишь для
дискообразных [304] и кольцевых [381, 383] трещин при растяги-
растягивающих и скручивающих осесимметричных нагрузках, поскольку
такие задачи, как и в статическом случае, сводятся к эффективно
решаемым численно одномерным интегральным уравнениям.
Большое число работ посвящено асимптотическому решению
задач для низких и высоких частот. Построению высокочастот-
высокочастотной асимптотики посвящены работы [342, 151-153, 212-214, 149,
154, 320, 277]. Заметим, однако, что эффективных способов вы-
вычисления асимптотики КИН для ограниченных трещин даже про-
простейших форм до сих пор не существует.
Введение 29
Низкочастотная асимптотика строилась в [360, 302, 303, 258,
199, 205, 409, 224, 225, 348, 429, 42, 363, 364] для дискообразных и
эллиптических трещин. Из перечисленных работ в [302, 303, 258,
42, 363, 364] вычислялась асимптотика КИН, а в остальных —
асимптотика характеристик дальнего поля. .
Более подробный обзор работ, касающихся асимптотического
решения задач для низкочастотных и высокочастотных нагрузок,
представлен в гл. 3. Здесь лишь отметим, что при построении низ-
низкочастотной асимптотики во всех работах ограничивались одной
или несколькими поправками к статическому решению.
В задачах о трещинах, расположенных на границе раздела ма-
материалов, аналитические решения получены лишь для дискообраз-
дискообразных трещин, находящихся под действием нагрузок простейшего
вида. В частности, в [95, 270] построено решение для однород-
однородной нормальной нагрузки, в [274] — для осесимметричных уси-
усилий радиального сдвига и скручивания, в [428] решение получено
для нагрузок достаточно общего вида, однако представлено оно в
довольно сложном виде в терминах преобразования Радона.
Подробные обзоры имеющихся численных, аналитических и
асимптотических решений пространственных задач о трещинах
представлены в [274, 388, 104, 280, 87, 31, 125].
По сравнению с численными и аналитическими методами, ка-
качественные методы исследования пространственных задач меха-
механики разрушения стали развиваться недавно. Первой работой в
этом направлении стала статья [38], в которой были установлены
теоремы сравнения в задаче о плоской трещине нормального раз-
разрыва в безграничном упругом пространстве. Теоремы сравнения
позволяют оценить скачки смещений и КИН для трещин сложной
формы путем вписывания в них и описывания вокруг них трещин
более простых форм, для которых решения известны. Результаты
в [38] получены применением принципа максимума к смешанной
краевой задаче для гармонической в полупространстве функции, к
которой сводится задача о трещине нормального разрыва. С помо-
помощью приблизительно той же техники теоремы сравнения распро-
распространены на более широкий класс механических задач в [39, 48,
138]. В [54] развита иная техника, позволившая доказать теоремы
сравнения для решений достаточно широкого класса псевдодиф-
псевдодифференциальных уравнений, включающего в себя граничные урав-
уравнения задач о трещинах отрыва в однородном линейно упругом
пространстве и в пространствах со степенной неоднородностью.
Кроме теорем сравнения, приводящих к локальным оценкам
решений, в уравнениях математической физики развиваются ме-
методы построения интегральных оценок, наиболее точными из ко-
которых являются изопериметрические. Типичным примером изо-
периметрической оценки является оценка интеграла от решения
задачи Дирихле для уравнения Пуассона в произвольной области
30 Введение
через соответствующий интеграл от решения аналогичной задачи
в шаре (круге) того же объема (площади). В механике деформируе-
деформируемого тела этот результат Полна приводит к изопериметрической
оценке жесткости при кручении стержня односвязного сечения че-
через жесткость при кручении стержня кругового сечения той же
площади.
В [39] было высказано предположение и приведены некоторые
подтверждающие его соображения о том, что аналогичное неравен-
неравенство имеет место и в задаче о трещине нормального разрыва при-
применительно к оценке объема трещины. Это предположение было
строго доказано в [50], причем доказательство опиралось на от-
отмеченную выше возможность сведения рассматриваемой задачи
к смешанной краевой задаче для гармонической в полупростран-
полупространстве функции. В [141] с помощью теории интерполяционных про-
пространств изопериметрические оценки доказаны для класса псев-
псевдодифференциальных уравнений, включающего в себя граничные
уравнения задач о трещинах отрыва как в однородном линейно
упругом пространстве, так и в пространстве со степенной неодно-
неоднородностью. В [141] получены также оценки минимального вдоль
контура трещины отрыва КИН сверху и максимального КИН снизу
через интегральные характеристики решения. Перечисленными
результатами по существу ограничиваются приложения качествен-
качественных методов к пространственным задачам механики разрушения.
Обзор имеющихся качественных результатов можно найти в [40].
Более подробно эти проблемы обсуждаются в гл. 4.
Как видно из представленного обзора, несмотря на интенсив-
интенсивные исследования пространственных задач о трещинах, прово-
проводимые уже более пяти десятилетий, в этой области остается еще
немало нерешенных проблем. Выделим здесь некоторые из них.
Достижение высокой точности, особенно в определении КИН,
при численном решении граничных псевдодифференциальных
уравнений в напряжениях. Основная трудность здесь заключена
в том, что при аппроксимации решения желательно использовать
функции, имеющие правильную асимптотику у контура трещины
и вместе с тем необходимо научиться эффективно вычислять воз-
возникающие при построении системы линейных алгебраических
уравнений сингулярные интегралы, включающие аппроксимирую-
аппроксимирующие функции. Для трещин произвольной формы такие функции,
которые бы удовлетворяли обоим указанным условиям, до сих пор
не найдены.
Построение, хотя бы для трещин простейших форм, анали-
аналитических или высокоточных численных решений динамических
задач, а также статических задач в случае, когда трещина нахо-
находится на границе соединения материалов.
Построение более эффективных оценок решений и их распро-
распространение на более широкий круг задач.
Введение 31
Основной целью данной книги является решение указанных
проблем.
Книга состоит из четырех глав. В гл. 1 приведен вывод гра-
граничных псевдодифференциальных уравнений относительно скач-
скачков смещений как для статических, так и для динамических задач
о плоских трещинах в упругом пространстве. Доказывается раз-
разрешимость полученных уравнений в пространствах Соболева.
Глава 2 посвящена обоснованию и приложениям разработан-
разработанного автором двухбазисного проекционного метода. Приведены
примеры применения этого методы к решению представленных
в гл. 1 граничных псевдодифференциальных уравнений.
В гл. 3 получены аналитические и аналитико-численные реше-
решения задач об эллиптических трещинах в условиях действия ста-
статических и гармонически зависящих от времени нагрузок. Рас-
Рассмотрены также статические задачи для эллиптических трещин
на границе соединения материалов.
Глава 4 посвящена построению оценок решений задач о тре-
трещинах нормального разрыва. Здесь приведены теоремы сравне-
сравнения и получены изопериметрические неравенства для некоторых
интегральных характеристик решений. Теоремы сравнения при-
применяются также для доказательства сходимости альтернирующего
метода в задаче о взаимодействии пары трещин, расположенных
в одной плоскости.
Глава 1
ГРАНИЧНЫЕ УРАВНЕНИЯ
1.1. Постановка задачи
Все рассмотренные ниже численные, аналитические и каче-
качественные методы применяются в данной книге к решению ста-
статических и динамических задач о плоских трещинах в безгра-
безграничной, линейно упругой среде. Эти задачи выбраны, поскольку
они представляют значительный самостоятельный интерес как
для теоретических, так и для прикладных исследований, на них
проще отработать и усовершенствовать предлагаемые методы, а
кроме того, как отмечалось во введении, решение таких задач мо-
может являться составной частью решения более сложных задач, в
которых учитывается влияние границы тела.
Во всех рассматриваемых задачах предполагается, что равные
по величине и противоположно направленные усилия действуют на
поверхности трещины. Это предположение не является ограничи-
ограничительным, поскольку, в силу линейности, решение любой задачи
с заданными усилиями на бесконечности и свободной от нагру-
нагрузок трещиной представляется в виде суммы двух решений. Одно
из этих решений соответствует задаче для пространства без тре-
трещины, а другое отвечает задаче о трещине в безграничной среде,
где усилия приложены только к поверхностям трещины и подо-
подобраны так, чтобы снять нагрузки, определяемые решением первой
задачи.
Всюду далее будем предполагать, что трещина занимает огра-
ограниченную плоскую область G в плоскости хз = 0. Рассматри-
Рассматривается случай, когда в процессе деформирования не происходит
налегания и взаимодействия поверхностей трещины. Для гар-
гармонической по времени нагрузки это означает, что либо имеется
некоторое начальное раскрытие трещины, либо рассматриваемые
динамические нагрузки накладываются на статические, раскры-
раскрывающие трещину усилия. Для исследования и решения исполь-
используются псевдодифференциальные уравнения относительно скачков
смещений в области трещины.
Сначала выводятся уравнения для динамической задачи об ус-
установившихся гармонических колебаниях однородного простран-
пространства, ослабленного плоской трещиной. Эти уравнения могут быть
также использованы для решения задач в случае ударных на-
1.2. Вывод граничных уравнений 33
грузок, так как решения последних получаются путем примене-
применения обратного преобразования Фурье к решениям задачи о гар-
гармонических колебаниях. Если для решения неустановившихся
динамических задач использовать преобразования Лапласа, то для
образов Лапласа система граничных псевдодифференциальных
уравнений получается из системы уравнений для амплитуд скач-
скачков смещений при гармонических колебаниях простой заменой и2
на —s2, где и — частота колебаний, as — параметр преобразова-
преобразования Лапласа.
Затем выводятся уравнения статических задач с помощью пре-
предельного перехода и -> 0 в уравнениях для установившихся гар-
гармонических колебаний.
В заключение выводятся уравнения для статических задач о
трещинах, находящихся на границе соединения материалов.
1.2. Вывод граничных уравнений
Пусть к поверхностям трещины приложены равные по вели-
величине и противоположно направленные усилия, гармонически за-
зависящие от времени. В частности, предположим, что к верх-
верхней поверхности трещины приложены усилия t(x) ехр (—го;т), где
х = (#1, Ж2), t(rr) = (ti(x), *2(#)? *з(#)) — вектор амплитуд при-
прикладываемых усилий, г — время. Тогда перемещения во всем
пространстве также гармонически зависят от времени и имеют
вид и(ж)ехр(—iur), где и(х) = (щ(х), U2(x), щ(х)) — вектор
амплитуд перемещений.
Уравнения Ламе, записанные для амплитуд, имеют вид
дв
цАщ + (А + /*)— = -QuPui {% = 1, 2, 3). A.1)
Здесь А, \х — упругие постоянные Ламе, Q = div u, A — оператор
Лапласа.
Для каждого % продифференцируем соответствующее из урав-
уравнений A.1) по Х{ и просуммируем полученные уравнения. В ре-
результате получим
(А + 2/Lt) Д0 + ои2в = 0.
Обозначим а = \Jq/{\ + 2/i)o;. С учетом этого обозначения
записанное уравнение принимает вид
Д0 + а20 = О. A.2)
Поделив уравнения A.1) на /i и обозначив C = yjqIv> ^, по-
получим
4 Зак. 205
34 Гл. 1. Граничные уравнения
Подействуем на эти уравнения оператором А+а2. Учитывая A.2),
придем к уравнениям
щ = 0. A.3)
Обозначим преобразование Фурье функции f(x) через /(?)>
( )
7@ = I/(x)e^'« dx, (х, 0 =
Применим преобразование Фурье по переменным (х\, х^) к
уравнениям A.3), получим ( см. [254])
где п? = {2 - а2, П?, = ?2-/?2, {2=tf+{f.
Для дальнейшего выберем ветви при извлечении корней для
щ и П2. Будем считать, что ^/i — положительное число при s > О
и ^/s = —г^/|^[ при 5 < 0.
Из A.4) следует, что образ Фурье любого решения уравнений
A.1) имеет вид
щ = А{ exp (-nixs)+Bi ехр (~П2Хз)+С{ ехр (пх#з)+А ехр ()
A.5)
Для того чтобы выделить из функций A.5) общий вид решений
уравнений A.1), выполним преобразование Фурье по переменным
(#ъ #2) системы A.1). Получим
^2# ^ =0 (j = 1, 2),
- п2щ - id* (ftSl + 6^) = 0. A.6)
Здесь производные по жз обозначены штрихом, d* = C2/а2 — 1.
Далее отдельно рассмотрим решения в верхнем и нижнем полу-
полупространствах. Все, что относится к верхнему полупространству,
пометим индексом +, а к нижнему — индексом —. На бесконеч-
бесконечности примем условия Зоммерфельда для задачи о гармонических
колебаниях и условия убывания для статической задачи.
Из A.5) и условий Зоммерфельда следует
uf = Af ехр (-щхз) + Bf ехр (-п2хг). A.7)
1.2. Вывод граничных уравнений 35
Подставив A.7) в исходную систему уравнений A.6) и при-
приравнивая коэффициенты при одинаковых экспонентах, получим
систему уравнений, связывающую коэффициенты Af', Bf\
. A.8)
1 пх 2 щ 3 п2
Из A.7), A.8) имеем
exP (~п1жз) + Bf exp {-п2х3) {j = 1, 2),
? }1. A.9)
С помощью A.9) вычислим напряжения в верхнем полупро-
полупространстве:
-i?jAj exp (-щжз) ^-^ ^ ехр (-п2ж3)
О" = 1, 2),
2? = 2т Лз+ ехр (~П1Жз) + i{UB* + 6Вз+) ехр ("П2Хз)>
В частности, в плоскости жз = 0 получим
2n2
Аналогично для нижнего полупространства из A.5) и условий
Зоммерфельда получим
??" = С7" ехр (П1Ж3) + D^ exp (п2^з). A-И)
После подстановки A.11) в A.6) и выражения С{~, С?", 1?^"
через G^~, Df, D^" получим
4*
j = -t^Cfn] ехр (п1Ж3) + ?>;" ехр (п2^з) 0' = 1, 2),
= <?з" ехР (П1^з) + <F^Г + ЬЩ)п21 ехр (п2ж3). A.12)
36 Гл. 1. Граничные уравнения
Далее, подсчитывая из A.12) напряжения в нижнем полупро-
полупространстве и рассматривая их в плоскости х$ = 0, получим
.^+
Из A.9) и A.12) запишем выражения для перемещений в плос-
плоскости #з = 0:
в; (j = i,2),
(U4)
Из A.10) и A.14) выразим А^, Bj**, В% через а^, З^, iEj" и
подставим в A.10) в выражение для 3^. В итоге получим
Af (flttf + N(O(^tz + 6SJ), A.16)
Аналогично из A.13) и A.15) выразим С3 , Z?x , ?>2 через <т13,
? ^з" и подставим в A.13) в выражение для 3^~3. Получим
Складывая A.16) и A.17) и учитывая, что в условиях рассма-
рассматриваемой задачи к поверхностям трещины приложены равные по
величине и противоположно направленные усилия, т. е. напряже-
напряжения ах и Ъ~ъ должны совпадать в плоскости х^ = 0
= 3^ =
1.2. Вывод граничных уравнений 37
г = 1, 2, 3), получим
^ ]. A.18)
Здесь и ниже квадратные скобки означают скачок соответствую-
соответствующей величины в плоскости х$ = 0 ([щ] = uf — uj', i = 1, 2, 3).
Аналогично выводу A.18) из A.10), A.14) выразим A3*, B+,
В% через uf, uf, 3^ и подставим в A.10) в выражения для
о+ (j = 1, 2). В результате получим
^ = л*@3й + ^к)г5" + г@^ 0" = 1,2), A.19)
где
l 2
_
2/32n2
Таким же образом из A.13), A.15) выразим С$, Df, Z>J через
ttj", uj, о$3 и подставим в A.13) в выражения для о~% (j = 1, 2).
В результате получим
ч (j = 1,2). A.20)
Складывая A.19) и A.20) с учетом равенств ст? = о^ при
= 0, получим
Усилия iz-, действующие на поверхность х$ = 0, ограничиваю-
ограничивающую верхнее полупространство, отличаются от сг^з на знак. Таким
образом, A.18), A.21) определяют систему псевдодифференциаль-
псевдодифференциальных уравнений, связывающих амплитуды скачков смещений в
плоскости жз = 0 с амплитудами действующих усилий
QM = ^ A-22)
Здесь [u] = ([^i], [г^], [щ]) и t = (*i, <2, <з) рассматриваются
как вектор-столбцы, Qp — матричный псевдодифференциальный
38 Гл. 1. Граничные уравнения
оператор с символом
Qflit) = *2l(O
V о о
где Кц{Ц) = -Sj{i) (j = 1, 2), ^зз(С) = -М@, K12(Q =
() ()
(?) (?)
Напомним, что согласно определению псевдодифференциаль-
псевдодифференциального оператора Q^[u(rr)] = F^Q/^fu^)], где F~l — обратное
] f]
преобразование Фурье ( F~ltp(?) = тт-т^ / <р(Ое~г^х'
R2
Из A.22) видно, что динамическая задача о произвольно на-
нагруженной плоской трещине в упругом пространстве распадается
на две независимые задачи — нормального отрыва и сдвига.
Исходя из A.22), краевая задача о плоской трещине, к поверх-
поверхностям которой приложены равные по величине и противоположно
направленные усилия, может быть сформулирована следующим
образом:
раОр[Ф)]=—> [u(s)]=0, x?G. A.23)
Здесь рс — сужение на область трещины G.
^-представление рассматриваемых здесь интегро-дифферен-
интегро-дифференциальных уравнений приведено в [184]. Уравнение для трещины
нормального разрыва в представленном здесь виде было записано в
[255]. Система псевдодифференциальных уравнений для трещины
сдвига приведена в [129].
Как уже отмечалось выше, уравнения статической задачи полу-
получаются из A.23) предельным переходом при ш ->• 0. В частности,
для трещины нормального разрыва получим краевую задачу
или
РсА[из(х)] = 2A - v)^lh{x)y [щ{х)] =0, х ? G. A.24)
Здесь Л — псевдодифференциальный оператор с символом |?| =
= (^ + ^lI^ v — коэффициент Пуассона.
Для статической задачи о трещине сдвига получим систему
уравнений
[2A - г/)]"W[u(*)] = ^, [и(х)] =0, х i G,
1.2. Вывод граничных уравнений 39
или
pGA[u{x)] = 2A - v)iTlt{x\ [u{x)] = О, х i G. A.25)
Здесь [u(x)] = {[ui{x)l [U2{x)])> t{x) = (h(x), t2(x)), A — ма-
матричный псевдодифференциальный оператор с символом
Уравнения A.24), A.25) совпадают с уравнениями, выведен-
выведенными в [36, 37], ^-представление этих уравнений было приведено
в [186, 423].
Выведем теперь граничные псевдодифференциальные уравне-
уравнения статической задачи о трещине, находящейся на границе сое-
соединения двух упругих полупространств, обладающих различными
упругими свойствами. В статическом случае и = 0 и, следова-
следовательно, a = /3 = 0. Устремляя и к нулю, получим что определен-
определенные выше функции М(?), iV(?), i?j(|), Sj(?), T(?) в статическом
случае равны
С учетом A.26) равенства A.16), A.19) примут вид
— №t - 7 v+
2/i+ 2A-1/+)'
2A-1/+)
40 Гл. 1. Граничные уравнения
Здесь /i+, v+ — модуль сдвига и коэффициент Пуассона верхнего
полупространства.
Аналогичным образом из A.17), A.20) и A.26) получим
<т~ 1 1 — 2z/_
21
2г/_ _ |^|
где /J,-, V- — модуль сдвига и коэффициент Пуассона нижнего
по лупр остр анства.
Из второго и третьего равенств A.27) имеем
A.29)
Из A.27), A.29) выразим перемещения через напряжения на
поверхности верхнего полупространства:
~+
Ч = -ТГ\~ [—2
A.30)
Аналогично, из второго и третьего равенств A.28) получим
+ Tfc&w . 1 — 2^_ _ 1^1 / - \
V Vd->-)'u+»
A.31)
1.2. Вывод граничных уравнений 41
Из A.28), A.31) выразим перемещения через напряжения на
поверхности нижнего полупространства:
Щ = 777
1 1 Г — /, 2ч~- Д-21/_ ~_
«2 = 177— I -V-Vim° + A > +
1 1 Г l-2i/_
«з = Т7Т— I 2—
A.32)
Вычитая A.32) из A.30) и учитывая, что на границе раздела
полупространств <т% = о~г = сг^з, получим выражения скачков
смещений через действующие напряжения:
= -777 1 Г" + ( — + —Ы *13-
1 f./l-2i/+ 1 — 2i/-\ , „
= "i?f г v~2^—2^-)imais+m<723)+
+ ± +
Введем для краткости следующие обозначения:
c= 1 , e=
3 Зак. 205
42 Гл.1. Граничные уравнения
Обращая равенства A.33), с учетом введенных обозначений по-
получим
^ ]} , A.34)
2Г
2Z7J2 {
Из A.34) следует, что задаче о трещине на границе соединения
материалов соответствует следующая система псевдодифференци-
псевдодифференциальных уравнений:
PGA* [u(x)] = t(a), [u(rc)] =0, о; ^ G. A.35)
Здесь Л* — матричный псевдодифференциальный оператор с сим-
символом
9
t(x) — вектор усилий, приложенных к верхней поверхности тре-
трещины (tj = —О^з).
Уравнения A.35) были получены в [428] (см. также [36]).
1.3. Разрешимость граничных уравнений
При доказательстве разрешимости уравнений статических за-
задач о трещинах мы будем опираться на следующую теорему функ-
функционального анализа.
Теорема 1.1. Пусть оператор А непрерывно отображает
сепарабельное гильбертово пространство Н в сопряженное
гильбертово пространство Н1\ причем удовлетворяет усло-
условию коэрцитивности
(Аи, и) ^ СИ* , С > 0 — const. A.36)
Здесь \\и\\н — норма в пространстве Н.
Тогда оператор А осуществляет взаимно однозначное ото-
отображение Н на Н\
Эта теорема, в более общей формулировке пригодной также для
нелинейного монотонного оператора, имеется, например, в [28].
1.3. Разрешимость граничных уравнений 43
Во всех рассматриваемых ниже задачах пространствами Н и
о
Н1 будут пространства Соболева-Слободецкого Н\/2 (G) и H_i/2(G)
соответственно, где G — ограниченная плоская область, занимае-
занимаемая трещиной. В задачах о трещинах нормального разрыва в од-
о
нородном пространстве под пространствами Н\/2 (G) и H_i/2(G)
будем понимать пространства скалярных функций, а в случае тре-
трещин произвольного разрыва или трещины на границе раздела
полупространств — пространства векторных функций. В силу
того, что операторы, отвечающие изучаемым статическим зада-
задачам, являются псевдодифференциальными, первого порядка, не-
о
прерывность осуществляемых ими отображений из Н\/2 (G) в
#_1/2(С?) очевидна. Таким образом, нам нужно только доказать
их коэрцитивность (выполнение условия A.36)).
о
Напомним, что пространство Н\/2 {G) определяется как попол-
пополнение пространства гладких функций, имеющих носитель в G, по
норме
я2
Сначала докажем однозначную разрешимость уравнения A.24),
отвечающего статической задаче о трещине нормального разрыва
в однородном пространстве. Поскольку
)] ы)])
в?
для доказательства коэрцитивности оператора Л достаточно дока-
доказать неравенство
2 A-37)
где || • || означает норму в пространстве 1^2, а С > О — посто-
постоянная.
Согласно [147]
1г A.38)
R2xR2
где С1 > 0 — постоянная.
Так как область G ограничена, существует круг с центром в
начале координат, содержащий область G. Обозначим радиус этого
44 Гл. 1. Граничные уравнения
крута через R. Поскольку носитель [мз(#)] принадлежит G, из
A.38) следует
], [«.(«>» >с / / №?±j&
a;€G|y|>2#
-с/ ^
Таким образом, коэрцитивность оператора Л доказана. Отсюда
следует, что \/?з(#) G H^i^iG) существует и единственное реше-
решение уравнения A.24) [^з(гг)] СНф {G).
Однозначная разрешимость уравнения A.24) была доказана в
[147] (см. также [50]).
Для доказательства коэрцитивности оператора А, отвечающего
статической задаче о трещине сдвига A.25), в силу неравенства
A.37), достаточно доказать неравенство
И?)[й(О], Р5(О1) > const K||[u(?)]|2. A.39)
Здесь (.,.) обозначает скалярное произведение в двумерном эрми-
эрмитовом пространстве.
Как нетрудно видеть,
= KI [A -
&] \\2], A-40)
где черта сверху означает комплексное сопряжение.
Из A.40) следует
1A [\ЫО]\2
и неравенство A.39) доказано для \v\ < 1. Этот диапазон включает
в себя все возможные значения коэффициента Пуассона. При до-
1.3, Разрешимость граничных уравнений 45
казательстве неравенства было учтено, что
(v2i+v22)[\[ui(O)\2 + \ЫО}\2] = |[2@]|2, A-41)
так как т/i + ^1 = 1.
Таким образом, однозначная разрешимость системы уравне-
уравнений A.25) доказана. Приведенное здесь доказательство было дано
в [51, 53].
Однозначную разрешимость уравнений A.35), отвечающих за-
задаче о трещине на границе соединения полупространств, докажем
аналогичным образом.
Здесь также для доказательства коэрцитивности оператора А*,
в силу A.37), нам достаточно доказать, что
\ A.42)
Из определения величин #, d, с, е следует
<?>2Н, g-c>2\d\. A.43)
Из этих неравенств получаем
^2g\d\-d*-g\d\-c\d\ Jd\{g-\d\-c) ^ d* >Q
' 9 + c g + c g + c
Из определения матрицы A*(?) имеем
+ dim ЫО] |«i@] +
(9 - erJ)\[u2(O]\2
-dim [Si@] Рз(О] - dim [«2@] 1«
Отсюда следует
Z^ {9\[Ш)]\2 -e(|f»ll|ui(O]| + \т\\Ы0]\)-
46
Гл. 1. Граничные уравнения
Используя вновь неравенство A.41), получим
+ Рз(Ш2) -
Из этого неравенства следует
Й*(?)[2@], [2@]) >
где ? = min{flf - y/2\d\, g-(e + \d\)}.
Согласно неравенствам A.43), A.44) q > 0 и коэрцитивность
оператора А* доказана.
Разрешимость уравнений A.35) была доказана представлен-
представленным здесь способом в [51, 53].
При доказательстве разрешимости уравнений, отвечающих
задаче о трещине, к поверхностям которой приложены гармони-
гармонические по времени усилия, мы будем опираться на следующую
теорему функционального анализа.
Теорема 1.2. Пусть ограниченные операторы В и С ото-
отображают гильбертово пространство Н в сопряженное про-
пространство й7, причем оператор В является обратимым, а
С — вполне непрерывным, тогда оператор D = В + С явля-
является фредгольмовым индекса ноль, т. е. имеет конечномерные
ядро и коядро, размерности которых совпадают.
Поскольку уравнения A.23) распадаются на независимые урав-
уравнения, соответствующие задачам о трещине нормального разрыва
и сдвига, рассмотрим эти уравнения отдельно.
Уравнение задачи о трещине нормального разрыва, согласно
A.22), имеет вид
Ы*)] = 0. * i G> A-45)
A.46)
где Qp — псевдодифференциальный оператор с символом
э-2
1.3. Разрешимость граничных уравнений
47
Символ оператора пр можно представить в виде
Таким образом, оператор пр может быть представлен в виде
суммы двух операторов, один из которых имеет символ -т- г,
2A — V)
а другой, назовем его Dp, имеет символ Dp{?). Первый оператор
лишь на множитель отличается от оператора статической задачи
о трещине нормального разрыва и, согласно доказанному выше,
о
изоморфно отображает пространство Hi/ziG) на H_i/2(G).
Оценим теперь символ оператора Dp при больших значениях
|?|. Пусть |?| > 2/?, запишем Dp{?) в виде
lei
2A-и)'
Для оценки Dp(?) нам понадобится следующее утверждение:
Лемма 1.1. Обозначим A+жO = l+jx+g(j, x). Предполо-
Предположим, что \х\ ^ 1/4. Тогда справедливы неравенства
I2
A.47)
И
6
Iff
2
A.48)
Доказательство. Ряд Тейлора для A + хI имеет вид
...+
'-хп + ... A.49)
Из A.49) следует
G-2)G-3)...G-п
48 Гл.1. Граничные уравнения
Отсюда для 7 = 1/2 имеем
г2 о Ы2 Ы2
, 8ll + m + W +...+ № +--^-8A.|я.|) ^ 6
и неравенство A.47) доказано.
При 7 = —1/2 получим
.12 |г|2
-...+ х "+...=
8A - \х\) " 2 •
Неравенство A.48) и, следовательно, лемма 1.1 полностью дока-
доказаны.
С учетом введенных обозначений имеем
Раскрывая скобки и проводя сокращения, придем к выражению
-Л Ли
2A-к) I,1 W51 2A-1») + |{| 4|?|»
Далее учтем, что 1 — а2//?2 = 1/BA — и)). В результате по-
получим
а2 - /?2/2 а2/?2
A.50)
1.3. Разрешимость граничных уравнений 49
Наконец, примем во внимание, что при |?| > 2/?, /32/|?|2 < 1/4
г а2/|?|2 < 1/4 и поэтому справедливы неравенства A.47), A.48).
1сходя из них можно записать оценку
¦
Оценка A.51) показывает, что оператор Dp имеет порядок не
*ыше —1-й степени и тем самым оператор pGDp является вполне
о
шпрерывным оператором, отображающим H\/2{G) B H-i/2(G)-
Таким образом, оператор PG^p представляется в виде сум-
о
ш обратимого и вполне непрерывного операторов из Н\/2 (G) в
^-1/2 (G)- Благодаря этому оператор pg^p является фредгольмо-
о
*ым индекса 0 из Н\/2 {G) в if_1/2(Gf).
Для тех значений /3, которые не принадлежат спектру, опе-
>атор PG^lp осуществляет изоморфизм между пространствами
о
9"i/2 (G) и H_i/2(G). Фредгольмовость оператора pg^/з была от-
отмечена в [69].
Теперь для доказательства однозначной разрешимости урав-
1ения A.45) достаточно доказать, что ядро оператора pg&p равно
хулю. Предварительно докажем вспомогательную лемму.
Лемма 1.2. Пусть v(x) — обобщенная функция, имеющая
компактный носитель. Предположим, что v(?) = 0 в окрест-
юсти некоторой произвольной точки, тогда v(x) = 0.
Доказательство. Так как v(x) имеет компактный носи-
носитель, то г;(?) — аналитическая функция по каждой из переменных
см. [34, 137]). Поскольку аналитическая функция равна нулю в
жрестности некоторой точки, то v(?) = 0. Отсюда следует, что
){х) = 0 и лемма доказана.
Теорема 1.3. Пусть [из(#)] €Hi/2(G) и рс^р[щ{х)] = 0,
погда \и%{х)\ = 0.
Доказательство. В силу условий теоремы
(ЩЫх)], [и3(х)]) = 0.
Следовательно,
])=0. A.52)
50 Гл. 1. Граничные уравнения
С учетом указанного выше правила выбора корней имеем
1
A.53)
Из A.52), A.53) следует, что [2з(О] = ° ПРИ If I < Р-
Таким образом, [г*з(#)] удовлетворяет условиям леммы 1.2,
вследствие чего [гдз(#)] = О- Теорема доказана.
Приведенное доказательство теоремы единственности близко к
доказательству единственности решений уравнений контактных
задач, представленных в [30].
Из того, что оператор рв&р является фредгольмовым индекса 0
и теоремы 1.3, следует, что уравнение A.45) однозначно разре-
разрешимо в указанных пространствах Соболева-Слободецкого.
Теперь докажем однозначную разрешимость системы уравне-
уравнений, отвечающих задаче о трещине, к поверхностям которой при-
приложены гармонические по времени сдвиговые усилия. Согласно
A.23), эти уравнения имеют вид
рсКр[и(х)] = t(x), [u(x)] =0, х ? СУ, A-54)
где Кр — матричный псевдодифференциальный оператор с сим-
символом
Выражения для Кц(?) приведены выше.
Сначала докажем, что оператор pgK@ является фредгольмовым
о
индекса 0 из Н\/2 (G) в H_i/2(G). Для этого представим оператор
К в виде
где А — оператор, отвечающий статической задаче о трещине
сдвига.
По доказанному выше оператор — tPgA отображает вза-
2A — V)
о
имно однозначно H\/2(G) на Я_1/2(С?). Покажем, что оператор
о
является вполне непрерывным из Н\/2 (G) в H^i
1.3. Разрешимость граничных уравнений 51
Обозначим через D\j псевдодифференциальные операторы, яв-
являющиеся элементами матричного псевдодифференциального опе-
оператора D*p, а через Dij(?, /3) их символы.
Согласно A.23), A.25)
Ш
2A-и)'
1 / Д2
/?) =
2A -
2A -Т)
Исследуем символы J3y(^, /3) при |?| > 2/?. Функцию
можно переписать в следующем виде:
Л,, (t R\ — J (At2 (&\\t\ I 1 ^ 1 O-
Используя разложения корней, в соответствии с введенными в
лемме 1.1 обозначениями, получим
(i+JL+J
?
52 Гл. 1. Граничные уравнения
Раскрывая скобки, имеем
щ
2,
Проводя сокращения и учитывая, что 2а2 — /З2 = — /?2 и
Г72 = 1 — 77?, получим
А.К, Я - - j^ {|| + («f И -
E. -jj
Из A.55) и оценок A.47), A.48) для функции #G? х) следует,
что при |?| > 2/3
|?>ii(?, /3)| < -jjr, Си > 0 — постоянная. A.56)
Аналогичным образом получается опенка
|-?>22(?> 0)\ < ттг» С22 > 0 — постоянная. A.57)
Символ оператора Df2 можно записать следующим образом:
-1/2
Л2 \ V^ л2 / о2 \
2A-1/)
1.3. Разрешимость грамичных уравнении 53
Используя разложение корней, получим
4KI (i - |j
Раскрывая скобки, получим
Проводя сокращения и учитывая, что 2а2 — /З2 = —
придем к выражению
Из A.58), оценок A.47), A.48) и неравенства |?i?2|
следует, что при |?| > 2/? справедлива оценка
§г, Ci2 > 0 — постоянная. A.59)
Из полученных оценок A.56), A.57), A.59) следует, что все опе-
операторы Djj' имеют порядок не выше — 1. В силу этого операторы
/Л\ О
PgD\j являются вполне непрерывными из Н1/2 (G) в Я_!/2(С),
о
а следовательно, и оператор pgD*@ вполне непрерывен из Н\/2 (G)
вЯ_1/2(С).
54
Гл, 1, Граничные уравнения
Таким образом, оператор pgK/з представлен в виде суммы обра-
обратимого и вполне непрерывного операторов и поэтому является
о
фредгольмовым индекса 0, действующим из Н\/2{@) в ff_1/2(G).
Теперь для доказательства однозначной разрешимости урав-
уравнений A.54) достаточно доказать, что ядро оператора рвКр равно
нулю.
Теорема 1.4. Пусь [n(x)] = (Ms)],
и(я)] = 0, тогда [и(х)] = 0.
Доказательство. В силу условий теоремы
Следовательно,
1т(К(,[п(х)Щх)])=0.
В силу равенства Парсеваля
я2
Подставляя выражения для <ЙГу(О> получим
6 Hi/2(G) u
A.60)
1.3. Разрешимость граничных уравнении
55
С учетом указанного выше правила выбора корней для мнимой
части записанного выражения имеем
/
0
-е)
\ш
- е (
<%+
Ifl^o
/
№
. A.61)
Здесь введены следующие обозначения:
/о = — -
I A-63)
56
Гл. 1. Граничные уравнения
Обозначим
ei[ffi@]+6pfe(fl]=g(fl. A-64)
Из A.63), A.64) следует, что выражение для I<i может быть
записано следующим образом:
Из A.65) следует неравенство
h < 0.
A.66)
Из A.62) и обозначения A.64) следует, что выражение для 1\
можно переписать в виде
Интеграл в A.67) разобьем в сумму двух интегралов:
A.68)
A-69)
Рассмотрим выражение
3/32 -
A.71)
Заметим, что в области (л/3/2)C < |?| имеет место неравенство
3/32-4^2<0. A.72)
1.3. Разрешимость граничных уравнений 57
Из A.70)-A.72) следует
/12 < -тЛга [ PWP2-e\[n(O)\2dt;^0. A.73)
Для оценки 1ц перепишем A.69) в виде
1 1
х г w2 - *е)\д(о\2 - рчр2 - е)Ш))\2 „ A74)
l€K(V5/2)/J
Из определения A.64) следует оценка
A-75)
Поскольку в области интегрирования З/?2 — 4^2 ^ 0, из A.74),
A.75) следует неравенство
г
J
BтгJ2/?2
Из A.60), A.61), A.67) и оценок A.66), A.73), A.76) следует
hi = In = /2 = 0.
Поскольку /i2 = 0, из A.73) следует, что в области (л/З/2)/? ^
^ |^| < /3 вектор [2@] = 0- Отсюда и из леммы 1.2 следует, что
[и(х)] = 0 и теорема 1.4 доказана.
Следовательно, \/t(x) E H_i/2(G) система уравнений A.54)
имеет и единственное решение [u(x)] E
Глава 2
ДВУХБАЗИСНЫЙ ПРОЕКЦИОННЫЙ МЕТОД
2.1. Постановка задачи
В этой главе излагается двухбазисный проекционный метод ре-
решения операторных уравнений, предложенный в [139, 140, 142], и
приводятся примеры его применения для численного решения ста-
статических и динамических задач о плоских трещинах произволь-
произвольного разрыва, расположенных в упругом пространстве. Двухба-
Двухбазисный проекционный метод предназначен главным образом для
решения краевых задач для псевдодифференциальных уравнений,
когда вычисления результатов применения оператора к базисным
функциям, необходимые в любом численном методе, встречают
серьезные затруднения.
Прежде чем переходить к строгому описанию предлагаемого
метода, коротко остановимся на основных традиционных мето-
методах приближенного решения операторных уравнений и тех труд-
трудностях, которые возникают при их численной реализации в случае
решения псевдодифференциальных уравнений.
Пусть требуется решить операторное уравнение
Ли = /, иеН, /ЕЯ'. B.1)
Здесь А — линейный оператор, отображающий сепарабельное
гильбертово пространство Я в сопряженное гильбертово простран-
пространство Н'.
При численном решении уравнения B.1) строится базис
ei, ..., е*;, ..., по которому раскладывается решение. Обозначим
подпространство, натянутое на ei, ..., еп, через Еп. Приближе-
п
ния решения ищутся в подпространствах Еп (в виде ип = J
ii
где с% — постоянные). Значения постоянных с% определяются из
решения системы линейных алгебраических уравнений. Способы
построения такой системы линейных уравнений могут быть раз-
различны.
Обозначим (.,.) — отношение двойственности между простран-
пространствами Н и Н1. Пусть, например, оператор А является симметрич-
симметричным и положительно определенным, т.е. ЗСь C<i > 0 такие, что
Cill^ll2 ^ (Аи, и) < СяНиЦ2, где ||.|| — норма в пространстве Н.
2.1. Постановка, задачи 59
В этом случае оператор А порождает новое скалярное произведение
{u, v} = (Ащ v), где и, v € Я, и отвечающую этому скалярному
произведению норму ||п||^ = (Аи, и).
Обозначим сепарабельное гильбертово пространство Я с вве-
введенным скалярным произведением {.,.} через НА. Пусть щ — ре-
решение уравнения B.1). Метод Ритца, заключающийся в миними-
минимизации функционала \\ип — щ\\\ на подпространстве Еп (ип Е Еп),
так же как и требование выполнения равенств
(Аип, ej) = (/, е,), j = 1, ..., n,
составляющее содержание метода Бубнова-Галеркина, пригодного
для более общего класса операторов А, приводят к следующей си-
системе линейных уравнений относительно с%\
п
, ej) = (/, ej), j = 1, ..., п. B.2)
Пусть оператор А изоморфно отображает Я на Я7. Предпо-
Предположим, что Hq — гильбертово пространство, причем Щ С Я;.
Через (., .)о обозначим Скалярное произведение в Щ. Предполо-
Предположим также, что / € Щ (где / — правая часть уравнения B.1))
и Ае{ Е Hq (i = 1, ..., п). Метод минимума квадратов заключа-
заключается в минимизации функционала \\Аип — /||q на подпространстве
Еп {ип € En)- Нетрудно видеть, что этот метод приводит к сле-
следующей системе уравнений относительно с%\
{, AejH = (/, Ае,H, j = 1, ..., п. B.3)
Упомянутые методы приближенного решения операторных урав-
уравнений подробно рассмотрены, например, в [90].
Если Н' — пространство функций, определенных в некото-
некоторой области евклидова пространства, то, приравнивая значения
Аип(х) и f(x) в специальным образом выбранных точках х\, к =
= 1, ..., п (метод коллокации), можно прийти к системе линейных
уравнений
D) =/D), к = 1,...,п. B.4)
t=l
Возможны и иные способы построения уравнений относитель-
относительно с», однако во всех случаях необходимо уметь вычислять значе-
значения Ае{. Если оператор А псевдодифференциальный, то вычисле-
вычисление Ае{ превращается в непростую задачу. Проиллюстрируем это
на примере статической задачи о трещине нормального разрыва.
60 Гл. 2. Двухбазисный проекционный метод
Граничное уравнение этой задачи, связывающее скачок нор-
нормального смещения [и(х)] в области трещины (здесь для про-
простоты записи мы опускаем индекс 3 у нормальных компонент сме-
смещений и нагрузок) с приложенными нормальными усилиями ?(#),
приведено в гл. 1 (формула A.24)). Оно может быть записано в
различных видах.
При использовании записи
1 (Ш = 2A - u)iTH{x) = /(*), xeG, B.5)
где F, как и выше, обратное преобразование Фурье, []
преобразование Фурье функции [и(х)], для вычисления Aei(x) не-
необходимо сначала вычислить преобразование Фурье от функции
б{(х) и затем, после умножения полученного образа Фурье на |?|,
выполнить обращение преобразования Фурье.
Как отмечалось во введении, для повышения точности опре-
определения КИН и снижения затрат машинного времени и памяти
за счет снижения количества базисных функций, необходимо учи-
учитывать в приближенном решении корневую особенность вблизи
гладкой части контура трещины, а в случае наличия угловых то-
точек у ограничивающего трещину контура и особенности в этих
точках. Вместе с тем, если в общем случае использовать базисные
функции, имеющие правильную асимптотику у контура трещины,
то как преобразование Фурье, так и его обращение придется вы-
выполнять численно, что понизит точность и увеличит время вычи-
вычислений.
При решении уравнения B.5) методом Ритца или Бубнова-
Галеркина входящие в B.2) скалярные произведения, которые для
уравнения B.5) имеют вид (Ле*, ej) (Л — псевдодифференциаль-
псевдодифференциальный оператор с символом |?|), можно вычислить ив образах Фурье:
B.6)
ej) =
я2
В этом случае также приходится выполнять численное интегри-
интегрирование на нескольких этапах — при вычислении образов Фу-
Фурье от функций ei(x) и при вычислении скалярных произведений
(Леь ej).
В связи с отмеченными трудностями в [44] было предложено
использовать базисные функции, для которых часть указанных
вычислений возможно выполнить аналитически. Этот метод был
назван вариационно-разностным. Более точно в [44] область тре-
трещины G аппроксимируется многоугольной областью, составлен-
составленной из квадратов со стороной Л. В качестве ei(x) берутся функции
2.1. Постановка задачи 61
фР1Р2{х, h), определяемые следующим образом:
¦фР1Р2(х, h) =
О,
где pi, р2 — целые числа, 9р^Р2 — квадрат со стороной 2ft и цен-
центром в точке (pift, P2^)-
Постоянные С{ определяются из уравнений Ритца~Бубнова-Га-
леркина B.2), имеющих в данном случае вид
При этом преобразования Фурье базисных функций фР1Р2 (ж, ft)
числяются аналитически
P2«2) sin2(/i6/2)sin2(/i{2/2)
а скалярные произведения
1 /*
= т—j I
2
я2
нужно вычислять численно лишь для случаев, когда расстояние
между точками (pi/i, P2^) и (gift, 92ft) невелико. В остальных
случаях для вычисления (AipPlp2, ^qiq2) можно пользоваться асим-
асимптотической формулой, полученной в [44]. Таким образом, пред-
предложенный в [44] метод позволяет существенно снизить объем вы-
выполняемых на компьютере вычислений, однако используемые
базисные функции не имеют правильной асимптотики у контура
трещины и КИН определяются делением значений скачка смеще-
смещений вблизи контура трещины на корень из расстояния до кон-
контура. Как отмечалось во введении, такой способ определения КИН
не является достаточно точным и эффективным. С целью повы-
повышения точности вычислений развитый в [44] метод был усовер-
усовершенствован в [47], где вблизи контура использовалась специальная
уточняющая сетка с шагом меньшим, чем шаг основной сетки.
Это позволило решить задачу для трещин различной формы и
даже проследить в некоторых случаях законы квазистатического
роста трещины, но всех проблем, связанных с отсутствием сингу-
сингулярных элементов, не сняло. Некоторая модификация и развитие
вариационно-разностного метода для решения задач о трещинах
сдвига представлены в [26, 25].
62 Гл. 2. Двухбазисный проекционный метод
Уравнение B.5) может быть записано и в другом виде [147], в
д> представлении:
Уг) d[u{y)] An
2n\J |Ж-у|3 дУ1 "»
XG G
B.7)
При использовании уравнения рассматриваемой задачи в виде
B.7) не нужно выполнять преобразование Фурье, однако для вычи-
вычисления Ае{(х) = Aei(x) приходится дифференцировать элементы
базиса и вычислять интегралы в смысле главного значения, за-
записанные в левой части B.7). Применять для решения задач о
трещинах уравнение B.7) и аналогичные уравнения для трещин
сдвига было предложено в [186, 423]. В частности, в [423] с по-
помощью этих уравнений решена задача о прямоугольной трещине,
причем рассмотрены случаи не только нормальной, но и сдвиговых
нагрузок. Разработанная численная процедура включала разбие-
разбиение прямоугольника на квадраты (конечные элементы). Внутри
области трещины использовалась кусочно-линейная аппроксима-
аппроксимация, а вблизи границы, за исключением угловых точек, учитыва-
учитывалась известная асимптотика решения. Для определения неизвест-
неизвестных постоянных применялись уравнения типа B.4).
Хотя, судя как по результатам расчетов, проведенных другими
численными методами (см., например, [217, 317, 127, 142, 143]),
так и по результатам асимптотического анализа [268, 269] полу-
полученные в [423] приближенные решения хорошо аппроксимируют
точные, в общем случае необходимость вычисления интегралов в
смысле главного значения и производных от приближенного ре-
решения может приводить к существенным погрешностям. В связи
с этим в дальнейшем в ряде работ исследовались и продолжают
исследоваться до сих пор различные способы регуляризации и вы-
вычисления интегралов в смысле главного значения, возникающих
при использовании в задачах о трещинах уравнений типа B.7)
(см., например, [349, 292, 293]).
В [349, 193] подчеркнуто, что точность дифференцирования ис-
искомого решения решающим образом сказывается на точности по-
получаемого приближенного решения. Поэтому в [349] разработана
достаточно сложная процедура сглаживания приближенного ре-
решения.
Уравнения относительно скачков смещений, содержащие ин-
интегралы в смысле главного значения и производные от искомых
скачков смещений, для динамических задач о трещинах пред-
предложены в [184]. Способы регуляризации этих уравнений и при-
примеры решения задач о круговой и эллиптической трещинах
при нормальном динамическом нагружении представлены в [393,
392,185].
2.1. Постановка задачи 63
Таким образом, основными источниками затруднений и по-
погрешностей при решении уравнений типа B.7) являются инте-
интегралы в смысле главного значения и производные от искомого ре-
решения. Для того чтобы избежать дифференцирования искомого
решения, было предложено записывать уравнения задач о тре-
трещинах в ином виде. Согласно [147] уравнение B.5) может быть
записано также в следующем виде:
*"/Wi *ea- B-8)
Здесь Ах — оператор Лапласа по переменным #i, #2-
Если точка х не принадлежит носителю функции [^(ж)], т. е.
х ? G, то лапласиан в левой части B.8) можно внести под знак
интеграла. В результате для х ? G имеем
Щ*у. B.9)
2тг У а?-у 2
G G
Правая часть равенства B.9) в противоположность записи B.7)
уже не содержит производных от подынтегральной функции [и(у)],
однако записанный интеграл имеет смысл только для х ф G. Если
формально воспользоваться записью правой части B.9) при х Е G,
то интеграл будет расходящимся из-за сильной особенности в ядре
интегрального оператора. Тем не менее такому интегралу можно
придать смысл. В [245] под интегралом / L dy (x € G)
J F-J/Г
G
понимается выражение
G\S0 So
So
где 5о — круг радиуса го с центром в точке я, принадлежащий G.
В правой части B.10) первый интеграл является обычным ре-
регулярным интегралом, второй интеграл существует в смысле глав-
главного значения, а третий интеграл по определению равен
2Ж B.11)
Sq So
64 Гл. 2. Двухбазисный проекционный метод
Понимаемый в соответствии с определением B.10), B.11)
интеграл называется конечночастным интегралом и обозначается
/¦р—-~ dy. Следовательно, уравнение B.5) помимо представле-
\х-у\6
G
ний B.7), B.8) может быть также записано в виде
= Дат). B.12)
Решение уравнения B.12) осуществляется следующим обра-
образом. Сначала область трещины разбивается на конечные эле-
элементы, в которых аппроксимируется решение. Затем результаты
применения оператора к приближенному решению в различных
точках вычисляются как значения конечночастного интеграла.
Наконец, для определения неизвестных постоянных используется
уравнение B.12). Такой подход к решению задачи о трещине
нормального разрыва был предложен в [245]. В [85] дано усовер-
усовершенствование методов вычислений конечночастных интегралов и
показано, как они могут быть использованы для решения статиче-
статических задач о трещине сдвига. В [298] конечночастные интегралы
применялись для решения динамических задач об эллиптических
трещинах отрыва и сдвига. Различным аспектам вычисления ко-
конечночастных интегралов и их применения к задачам о трещинах
посвящены работы [246, 247, 312, 313, 162, 161].
Несмотря на интенсивное и успешное развитие этого напра-
направления, многие проблемы, связанные с использованием конечно-
частных интегралов, еще не имеют достаточно эффективных ре-
решений. Во-первых, в результате регуляризации конечночастные
интегралы сводятся к нескольким интегралам, среди которых
имеются и интегралы в смысле главного значения. О трудно-
трудностях вычисления интегралов в смысле главного значения уже го-
говорилось выше. Во-вторых, как отмечено в [312, 313], более силь-
сильная сингулярность ядра интегрального оператора требует большей
гладкости от функции, к которой применяется этот оператор, т. е.
от искомого приближенного решения. Вследствие этого возникает
необходимость в применении различных процедур сглаживания.
Подытоживая краткий литературный обзор методов решения
интегродифференциальных уравнений относительно скачков сме-
смещений в области трещины, заметим, что усилия исследователей
главным образом были сосредоточены на разработке эффективных
способов регуляризации возникающих сингулярных интегралов.
Принципиально иной подход к решению таких уравнений, позво-
позволяющий вообще избежать вычисления нерегулярных интегралов и
вместе с тем учесть в приближенном решении все известные осо-
2.1. Постановка задачи 65
бенности точного решения, включая асимптотическое поведение
вблизи контура трещины, в том числе и вблизи угловых точек,
был предложен автором в [139, 140, 142].
Суть подхода заключается в следующем. Пусть А* — оператор,
сопряженный к А, и y>i, ..., од, ... — полная система элементов
пространства Н, для которой результаты применения оператора
A*од легко, например аналитически, вычисляются. Приближе-
Приближение решения уравнения B.1) ищем в подпространстве Еп (ип =
п
= Y1 Сг^г)- Подпространство Еп выбираем таким образом, чтобы
i=i
его элементы содержали известные особенности решения. Это по-
позволяет достичь хорошего приближения даже в подпространстве
невысокой размерности. Неизвестные с% будем определять из си-
системы уравнений
(Ann, од) = (/, од). B.13)
Поскольку {Аип, од) = (гхп, А*од), уравнения B.13) можно
переписать в виде
п
(tin, А*од) = ][>(«, А*<рк) = (/, од). B.14)
В уравнениях B.14) уже не нужно вычислять Ае^ а значения
А*од по предположению могут быть найдены в результате про-
простых вычислений или аналитически. Таким образом, для опреде-
определения коэффициентов линейной системы B.14) и правых частей
этих уравнений остается только вычислить скалярные произведе-
произведения (ei, А*од) и (/, од), что, как правило, бывает сделать доста-
достаточно просто.
Заметим также, что для построения полной системы уравне-
уравнений необходимо взять п элементов </?i, ..., <рп. Однако поскольку
базисы в{ и tpj никак не связаны между собой, этого может ока-
оказаться недостаточно для хорошей обусловленности системы урав-
уравнений B.14) и сходимости процесса. Поэтому приходится брать
большее, чем п, количество элементов од, а полученную пере-
переопределенную систему уравнений B.14) удовлетворять в смысле
минимума отклонения.
Несмотря на то, что A*<pj по предположению легко вычисля-
вычисляются, базис <pi, ..., од, ... не используется для аппроксимации
решения, поскольку он, в противоположность базису е*, может не
учитывать особенности точного решения.
Строгое обоснование предлагаемого метода приведено в следую-
следующем параграфе. Там же обсуждаются его связь с общими проек-
проекционными методами и различия между ними.
6 Зак. 205
66 Гл. 2. Двухбазисный проекционный метод
2.2. Двухбазисный метод решения
операторных уравнений
Рассмотрим уравнение B.1). Предположим сначала, что А —
положительно определенный, симметричный оператор, отобра-
отображающий Н на Н1. Предположим также, что <pi, ..., <рр, ... —
ортонормированный базис в НА (где НА — это пространство Н
со скалярным произведением {г*, г;} = (Аи, v), введенным выше).
Обозначим подпространство, натянутое на <р\9 ..., <pNi через HN.
Приближение решения уравнения B.1) ищем в подпространстве
п
Еп (ип = J2 <%•). Пусть щ — решение уравнения B.1). Обозна-
г=1
чим через S^(un) следующий функционал:
N N
Sl(un) = ? IK - «о
= Е 1^п' ^*)" (f> ^*)l2 = E Е^'^' ^*) - (Л
A;=l Aj=1 i=1
В качестве приближенного решения выберем элемент подпро-
подпространства Еп, доставляющий минимум функционалу 5^(tin). Обо-
Обозначим min Sjf(un) = ?>*N.
un?En
Формулируемая ниже теорема показывает, что минимум функ-
функционала Sjf(un) существует, причем, начиная с некоторого N,
достигается на единственном элементе из Еп.
Теорема 2.1. 1. 3JVb, что ViV ^ Щ существует и един-
единственный элемент unN G En, доставляющий минимум функцио-
функционалу S2N(un).
2. 3 lim unN = tinoo, причем на ипоо достигается минимум
N>oo
функционала \\ип - щ\\А, ип 6 Еп.
Доказательство. Поскольку ц>\,..., (pN — ортонормирован-
ортонормированный базис в HN, нетрудно видеть, что S%(un) = \\PnUti — -Рлг^оИл?
где PN — оператор ортогонального проектирования на HN. Обо-
Обозначим PNEn образ подпространства Еп при этом проектирова-
проектировании. Как известно, существует и единственный элемент vnN G
в PNEn такой, что \\vnN - PNu0\\A = inf \\v - PNuQ\\2A.
vENb
Следовательно, минимум функционала S^(un) всегда достига-
достигается и неединственность может быть только вследствие того, что
для некоторых и\, un G ЕП1 и\фи\, Pnu\ = Рци^. Однако так
2.2. Двухбазисныи метод решения операторных уравнении 67
как <pi, ..., <?р, ... — базис в #л, 3JVb, что ViV ^ JVo? следует
PNei ф PNej для г, j = 1, ..., n; i ^ 3-
Следовательно, при N ^ No оператор проектирования осуще-
осуществляет взаимно однозначное соответствие между Еп и PNEn и
п. 1 теоремы 2.1 доказан.
Для доказательства п. 2 обозначим inf ||г*п — г*о||д = ^поо-
uneEn
Заметим, что величины S%N не убывают с ростом N. Действи-
Действительно,
S2nN = \\PNunN - PNuQ\\2A ^ \\PNunN+l - PNu0\\
Кроме того, S2N < 5^, так как
Здесь, согласно введенному выше обозначению, unoo G En — эле-
элемент, доставляющий минимум функционалу ||izn —uo||^, un G En.
Поскольку последовательность S2N монотонно не убывает по N
и ограничена сверху, то существует lim S^N = D\. Покажем, что
N—юо
Dn = Snoo.
Из доказанных выше неравенств 5ПЛГ ^ 5пОо следует, что
-Dn ^ 'S'noo- Докажем теперь противоположное неравенство. По-
Поскольку \\PNunN - PNuo\\A < Dn, отсюда следует \\PNunN\\A <
^ Z?n + ||Pjvi*olU ^ Ai + H^olU ^ ^ = const. Таким образом,
множество PNunN ограничено по норме пространства Нл.
Поскольку (pi, ..., (ppj ... — ортонормированный базис вЯА,а
Еп — конечномерное подпространство, то VC > 0, 3iVo, M > О,
что из N ^ JVb, ||PjvtinlU ^ ^ следует ||un||A < М, т.е. из огра-
ограниченности проекции множества на HN следует ограниченность
самого множества.
Вследствие этого Уе > 0, 3Ni, VN > N\ имеют место нера-
неравенства IJ.1I0 - РлгЗДЦл < ?» Н^плг - Раг^плгНа < е-
Отсюда получим
Snoo ^ \\utiN -
Переходя к пределу при N -> сю, получим Snoo ^ Dn + 2e.
Поскольку это неравенство справедливо Ve > 0, имеем Snoo ^ ^п-
Из неравенств Dn < |5ПОО и 5noo ^ -Dn следует, что Dn = Snoo.
Отсюда вытекает, что unN -> unoo при N -)• сх>. Действительно,
6*
68 Гл. 2. Двухбайтный проекционный метод
предположим, что это неверно. Тогда в силу конечномерности Еп
и ограниченности множества unN следует, что существует подпо-
подпоследовательность unNt, сходящаяся при Nf —> оо к и* ф ипоо:
- щ\\А = Jjn^ ||tW " tlo|| = S
Snoo.
Таким образом, существует несколько элементов, принадлежа-
принадлежащих Еп (ипоо и и*), на которых реализуется минимум функцио-
функционала ||tin — tio|U» un G En, что невозможно. Теорема 2.1 доказана.
Поиск минимума функционала S%(un) сводится к решению
следующей системы линейных алгебраических уравнений отно-
относительно с*:
п N N
(/ )( A) j = 1, ..., n.
B.15)
Черта сверху в уравнениях B.15) означает комплексное сопря-
сопряжение для случая, когда рассматриваются комплексные гильбер-
гильбертовы пространства.
Теорема 2.1 показывает, что при iV, стремящемся к бесконеч-
бесконечности, приближения решения unN, получаемые по предложенному
методу, стремятся к приближению ипоо, получаемому в методах
Ритца и Бубнова-Галеркина при использовании базиса ei, ..., еп.
Для ряда операторов, для которых вычисление скалярных про-
произведений (Ае{^ е;), необходимых для реализации метода Бубнова-
Галеркина, затруднительно из-за сложностей, возникающих при
определений Ае^ оказывается возможным построить базис tpi, ...
..., ^?р, ... такой, что достаточно просто вычисляются Atpj, а с
ними и произведения (е*, Aipj), нужные для изложенного выше
метода. Заметим, что часто удается выбрать полную систему
функций ^i, ..., фр, ... такую, что Aij)j и (е^, Atpj) легко вычи-
вычисляются. Тогда ортонормированный базис <^i, ..., (рр, ... строится
с помощью процесса ортогонализации. Необходимые для ортого-
нализации скалярные произведения {ф^ ф^} = (Аф{, ф^) также
определяются без труда.
Во многих случаях более удобной оказывается несколько иная
разновидность построения приближенного решения. Пусть А, как
и прежде, оператор, изоморфно отображающий Н на Н1. Пред-
Предположим, что JR, Щ — гильбертовы пространства, причем R С
С Но С Н'. Через (.,.)о5 как и выше, обозначим скалярное про-
произведение в Щ. Считаем, что скалярное произведение в Но поро-
порождается некоторым оператором J5, так что для w G #o, v € Я,
(гу, v)o = (гу, Bv). Оператор В отображает ДвЯ.
Пусть пространство Еп таково, что АЕП С ifo, и пусть <^i, ...
..., <?р, ... — ортонормированный базис в Яо? причем щ G R.
2.2. Двухбазисный метод решения операторных уравнении 69
Для / € Яо на подпространстве En (un € Еп) введем новый
функционал, который по-прежнему будем обозначать ^
N N
N
- (/, ВЫ12 =? IK, л*?Ы - (/, ВЫ12 =
А:=1 fc=l
TV ' N
N n
A:=l t=l
Здесь, как и выше, А* — оператор, сопряженный к А.
Допустим, требуется найти решение уравнения B.1) при / G
€ Но. Приближение решения в Еп ищем, минимизируя S%(un).
Теорема 2.2. 1. 3iVb, что ViV ^ No существует и един-
единственный элемент unN G ??n, на котором достигается мини-
минимум Sl(un).
2. 3 \imunN = ипоо при N ~> оо, где на ипоо достигается
минимум функционала \\Аип — /||о, ип G Еп. Здесь \\ • ||о —
норма в пространстве Щ-
Доказательство теоремы 2.2 вполне аналогично доказа-
доказательству теоремы 2.1, однако для полноты изложения мы его все
же приведем.
Обозначим, как и выше, HN — подпространство, натянутое
на <^i, ..., <pN, PN — оператор ортогонального (в данном случае
в смысле скалярного произведения в Hq) проектирования на HN.
Из определения Sl(un) следует, что S%(un) = \\PNAun - PNf\\l-
Поскольку PNAEn — конечномерное подпространство, существует
и единственный элемент wnN € PNAEnj доставляющий минимум
функционалу ||ги — Рлг/Ио? w € PnAEu. Следовательно, неедин-
неединственность может быть только потому, что 3u^, u^ G Еп такие,
что PNAu], = PNAun, но и\ ф и„. Однако согласно условиям,
оператор А осуществляет взаимно однозначное соответствие, а
tpi, ..., <pN, ... — ортонормированный базис в #о. Поэтому 3N
ViV" ^ iVo из t«i, W2 G AEn, wi ф W2 следует PNw\ ф
Таким образом, п. 1 теоремы 2.2 доказан.
Для доказательства п. 2 обозначим inf \\Аип — /||q =
и€Е
70 Гл. 2. Двухбазисный проекционный метод
Величины S%N не убывают с ростом ЛГ, поскольку
SlN = \\PNAunN - PNf\\20 ^ \\PNAunN+1 - PNff0 ^
^ IKJV+I-A^njv+I ~~ -fW+l/Ho =
Последовательность 5^ ограничена сверху S%N ^ «S^qq, так как
SlN = ||P^AtiniV - P^/llJ < HP^iltlnoo - P^/llg <
\\Aunoo - f\\l = S
пост
Следовательно, существует lim S%N = D%. Нетрудно пока-
N+oo
зать, что Dn = 5noo-
Поскольку SnN ^ S^ooj то Dn < iSnoo- Докажем теперь проти-
противоположное неравенство. \\PNAunN — Р#/||о ^ I?n5 откуда
\\РмАип„\\0 ^Dn + \\PNf\\0 ^Dn + И/Ио < С = const.
Так как y>i, ..., у?р, ... — ортонормированный базис в Щ, а
?п — конечномерное подпространство, то VC > 0, 3iVo, М > 0
такие, что из N ^ iVo, ЦР^А^Цо ^ С следует ||Л?/П||о < М.
Вследствие этого Ve > 0, 3JVi, ViV ^ iNTi следует ||/-Р///||о <
< г, ||AttniV ~ Рлг^паг||о < е.
В результате
- PNAunN\\0 +
+ \\PNAunN - PNf \\o + \\PNf - /||o < SnN + 2e.
Переходя в этом неравенстве к пределу при N -» оо, получим
Snoo ^ Dn + 2e. Поскольку неравенство справедливо Ve, то Snoo ^
^ Dn. Следовательно, ^оо = Dn.
Отсюда получаем, что lim unN = unoo. Действительно, снача-
N?
ла покажем, что lim AunN = Aunoo в смысле Щ. Если это невер-
N->oo
но, то из конечномерности АЕП и ограниченности множества AunN
следует, что существует подпоследовательность AunNt, сходящаяся
к Аи* ф Aunoo. При этом ргг*-/||0 = lim \\AunN> - /||0 = Snoo.
ЛГ'-юо
Таким образом, существует несколько элементов, принадле-
принадлежащих АЕП, на которых реализуется минимум выражения
\\Aun — /||о, Aun G Л??п, что невозможно.
Из сходимости lim AunN = Aunoo в смысле Hq следует
7V>
lim txn;v = Unoo в смысле if, в силу непрерьюности обратного
JV-юо %
оператора. Теорема 2.2 доказана.
Заметим, что unoo приближение решения в Еп, получаемое по
методу минимума квадратов*при использовании базиса ei, ..., еп.
2.2. Двухбазисный метод решения операторных уравнений 71
Если подпространства АЕП таковы, что UAEn плотно в Щ, то
приближенные решения при п —> оо сходятся к точному.
Как отмечалось выше, метод минимума квадратов приводит к
системе уравнений B.3) и потому требует вычисления величин
(Aei, Aej)o и (/, Aej)o. Поиск минимума функционала Sjf(un)
сводится к решению следующей системы линейных уравнений от-
относительно С{\
Г N
г=1
A*Bipk)
lk=l
N
j = l,..,n. B.16)
Для построения системы уравнений B.16) необходимо уметь
вычислять A*Bipk и (ej, A*B(pk). В ряде случаев, когда вычи-
вычисление Ае{ затруднено, удается так подобрать <рк, что A*Bcpkl a
вследствие этого и (е^, Л*2?<^) достаточно просто вычисляются.
Если удается построить полную, линейно независимую систе-
систему фи ..., Vp, ... в #0, V>i € Л, такую, что А*Вфт, (е», -А*В^т)
и (^i, ^т)о легко вычисляются, то ортонормированный базис
(pi, ..., (fp, ... строится путем ортогонализации в if о системы
Фъ ..., ^р, ...
В заключение коротко обсудим взаимосвязь представленного
метода с известными общими проекционными методами. В 50-
60-х годах значительное развитие получили обобщения проек-
проекционных методов, для которых упомянутые выше методы Буб-
Бубнова-Га леркина, минимума квадратов и др. являются частными
случаями. В общем виде проекционные методы могут быть сфор-
сформулированы следующим образом. Рассмотрим уравнение
j4u = /, и?Нъ /6Я2, B.17)
где fii, i?2 — для определенности сепарабельные гильбертовы
пространства (можно рассматривать и банаховы пространства).
Пусть Еп — последовательность конечномерных подпро-
подпространств в Н\. Будем считаь, что ei, ..., е&, ... — базис в Н\
и подпространства Еп являются подпространствами, натянутыми
на ei, ..., еп. Обозначим через Пп оператор проектирования Н\
на Еп.
Обозначим через Fm последовательность подпространств в Яг.
Будем считать также, что <pi} ..., щ, ... — базис в i?2> подпро-
подпространства Fm натянуты на y>i, ..., y?m, a Pm — оператор проекти-
проектирования #2 на Fm.
Согласно общему проекционному методу [112, 113] (см. также
[78, 90, 28]), приближенным решением un = Unu e En уравнения
72 Гл. 2. Двухбазисный проекционный метод
B.17) называется решение следующего уравнения:
PnAun = Р„/. B.18)
Уравнение B.18) включает в себя все традиционные проекци-
проекционные методы. В частности:
1) если L — линейный оператор и щ = Le^ то проекционный
метод совпадает с методом моментов;
2) если в методе моментов оператор L совпадает с операто-
оператором А, то приходим к методу минимума квадратов;
3) если #2 = Н\ и (fi = е*, то получаем метод Бубнова-
Галеркина;
4) в случае, когда щ есть дельта-функции, сосредоточенные в
различных точках, получаем метод коллокации;
5) если (pi — некоторый базис, не строящийся одним из пе-
перечисленных выше способов, то такой приближенный метод для
ряда операторов А называется методом Галеркина-Петрова.
Если базис щ непосредственно не связан с базисом е^, то для
сходимости приближений все же нужно выполнение определенных
соотношений между пространствами Fn и пространствами АЕП,
являющимися образами подпространств Еп при отображениях А.
Условия сходимости были сформулированы и доказаны в [112, 113]
и получили название условий (А).
Для гильбертовых пространств #i, #2 условие (А) имеет сле-
следующий вид. Обозначим через vn произвольный элемент из АЕП.
Пусть тп = min ||Pnvn||. Условие (А) заключается в том,
vneAEn, |Ы|=1
что тп ф 0 для п ^ по и lim rn = т > 0.
п-»оо
Подробности, связанные с доказательствами достаточности и
необходимости условия (А), можно найти в [112, 113] и имею-
имеющихся там ссылках.
Поскольку проекционные методы в основном применялись для
решения дифференциальных и интегральных уравнений, т.е. в
случаях, когда вычисление результатов применения оператора к
любым функциям ei(x) не представляет труда, метод Галеркина-
Петрова или обобщенный проекционный метод использовались
либо тогда, когда i?2 Ф Н\ и #2 Ф Н[,в результате чего скалярные
произведения или отношение двойственности {Aei, e^), встречаю-
встречающиеся в методе Бубнова-Галеркина не определены, либо, для неко-
некоторых операторов А, с целью повышения точности приближенного
решения при сохранении количества элементов базиса [133]. Во
всех случаях для сходимости приближений, как уже отмечалось,
необходима все же некоторая связь между элементами базисов е^
и (pjj выраженная условием (А).
Рассмотренный здесь двухбазисный метод отличается от обоб-
обобщенного проекционного метода тем, что вместо одного прибли-
приближенного решения в En (un) рассматривается последовательность
2.2. Двухбазисный метод решения операторных уравнений 73
приближенных решений unN, N ^ п, которая строится из ус-
условий
\\PNAunN-PNf\\= inf \\PNAwn-PNfl B.19)
wneEn
В B.19) под || • || понимается норма в пространстве #2 или
каком-нибудь его подпространстве, в зависимости от свойств опе-
оператора А, пространств Hi, #2 и правой части уравнения B.17) /.
При таком построении приближенных решений уже не нужно тре-
требовать выполнения условия (А) и базисы е^ и (pj, вообще говоря,
могут быть совершенно не связаны.
Заметим, что при N = п условие B.19) переходит в уравнение
B.18). Таким образом, общий проекционный метод можно рассма-
рассматривать как частный случай рассмотренного здесь двухбазисного
проекционного метода.
Применение двухбазисного проекционного метода ко всем рас-
рассматриваемым ниже статическим и динамическим задачам о тре-
трещинах отрыва и сдвига осуществляется по одной и той же схеме.
Рассматриваются граничные псевдодифференциальные уравне-
уравнения, связывающие скачки смещений в области трещины G с
приложенными усилиями. Как доказано в гл. 1, эти уравнения
однозначно разрешимы в пространствах Соболева-Слободецкого
(прикладываемые усилия должны принадлежать пространству
о
H_i/2(G), а скачки смещений — Н\/2 (G)). Поскольку простран-
о
ство H_i/2{G) является сопряженным к Н\/2 {G), то в принятых в
о
общей схеме приближенного метода обозначениях Н\/2 (G) явля-
является пространством Я, a H_i/2{G) — Н1. Главным образом ис-
используется вторая из представленных выше разновидностей двух-
двухбазисного метода. При этом в качестве пространства Щ берется
пространство L/2(G).
Базис е; выбирается в виде ei = eo(x)gi(x), где функция ео(х)
имеет правильную асимптотику у контура трещины, а функции
(или вектор-функции) Qi{x) не имеют особенностей у фронта тре-
трещины и могут быть выбраны одним из следующих способов:
1) gi{x) — полная система гладких функций во всей области,
например, gi(x) — тригонометрические функции или полиномы;
2) применяется разбиение области G на конечные элементы, а
gi(x) — полиномиальные функции на конечных элементах.
Базис ipj строится путем ортогонализации специального вида
функций (или вектор-функций) фк с компактными носителями.
Носители функций фь имеют форму круга или эллипса. Резуль-
Результаты применения соответствующих операторов к таким функциям
удается вычислить аналитически. Полнота системы функций фь
5 Зак. 205
74 Гл. 2. Двухбазисный проекционный метод
достигается за счет изменения размеров и местоположения их но-
носителей. Поскольку функции y>j, а следовательно, и фь должны
о
принадлежать пространству Н\/2 (<?), носители функций ф^ дол-
должны принадлежать области G. В тех случаях, когда имеются труд-
трудности при вписывании окружности или эллипса в область G вблизи
контура трещины, можно использовать носители, выходящие за
область G, однако при этом следует рассматривать уравнения не
в области G, а в некоторой ее окрестности и в качестве нагру-
нагрузок вне области G использовать главные члены асимптотики, вы-
вычисляющиеся по асимптотике скачков смещений вблизи контура
трещины.
Во всех представленных ниже расчетах в качестве gi брались
гладкие функции во всей области G, ав качестве ф^ — функции
с носителями, принадлежащими области G. К преимуществам
такого выбора следует отнести очень низкий, не превышающий
несколько десятков, порядок получающейся системы линейных ал-
алгебраических уравнений и регулярность всех вычисляемых инте-
интегралов (е^, А*фк)- Среди недостатков можно отметить следующие:
1) трудности при использовании глобальной аппроксимации
решения в вытянутых областях и областях сложной формы;
2) необходимость интегрирования по всей области G при вы-
вычислении (е^, А*фк), даже в тех случаях, когда носитель фь мал
по отношению к G;
3) необходимость значительного измельчения носителей функ-
функций фь для их вписывания в область G при сложной форме контура
трещины;
4) произвол в выборе расположения и размеров носителей ф^,
причем из-за того, что здесь функции ег и ф^ совершенно не свя-
связаны, приходится, как будет видно ниже, брать сильно переопре-
переопределенные системы уравнений, т. е. брать количество функций ф^
в 2,5-3,5 раза превосходящее количество элементов базиса е^.
Использование разбиения G на конечные элементы для по-
построения базиса ei увеличивает порядок системы линейных урав-
уравнений, однако, может иметь и некоторые преимущества. К преи-
преимуществам следует отнести:
1) при вычислении (е$, А*фь) интегрирование производится
только по соответствующим конечным элементам;
2) возможно значительно снизить или вообще устранить про-
произвол в выборе фь, связав их носители с конечными элементами,
например, взяв круги или эллипсы, вписанные в эти элементы;
3) если связать выбор ф^ с конечными элементами, то можно
существенно снизить или исключить переопределенность системы
уравнений;
4) упрощается аппроксимация решения в областях сложной
геометрии.
2.3. Статическая нормальная нагрузка 75
Использование носителей фь, выходящих за пределы 67, упро-
упрощает построение ф^ с носителями вблизи контура трещины. Вме-
Вместе с тем при вычислении (/, ф^) в интеграле появляется особен-
особенность, так как вне G вблизи контура трещины нагрузка имеет
корневую особенность.
Более детально оценить достоинства и недостатки использова-
использования конечных элементов для построения в{ и носителей, выходя-
выходящих за пределы G, при построении фь можно будет в результате
реализации этих вариантов двухбазисного метода.
2.3. Статическая нормальная нагрузка
Для приближенного решения рассматриваемой задачи восполь-
воспользуемся уравнением A.24). Для удобства перепишем его снова:
pGA[u(x)] =/(ж), [u(x)]=0 при x<?G. B.20)
Здесь [и(х)] = [^з(я)] — скачок нормального смещения, f(x) =
= 2A — v)ix~ltz{x), ts{x) — нормальное усилие, действующее на
поверхность трещины.
По доказанному в гл. 1 уравнение B.20) однозначно разре-
разрешимо в пространствах Соболева-Слободецкого f(x) € -HL 1/2(^0?
[u(x)] G Hi/2(G)- Поскольку пространство H_i/2{G) является
о
сопряженным к пространству Н\/2 (<2)? в двухбазисном проекци-
о
онном методе можно взять Н\/2 (G) в качестве пространства Н
и H_i/2(G) в качестве пространства Я'. Для применения второй
разновидности двухбазисного метода введем пространство Щ =
= L2(Сг). В качестве пространства R также выберем ^(G), a
оператор В положим тождественным, т. е. Bv = v.
Для построения ортонормированного базиса <pi, ..., (ppi ...
можно взять, например, систему функций ^2(#ъ Х2) = Фа(х),
а = (аь а2, а3):
7, \х - ам\2 < а§,
п , 2 2
0, \х21
Здесь ам = (аь а2); |ж - ам|2 = (xi - aiJ + (x2 - а2J; аь а2,
аз — счетное множество, плотное среди чисел, удовлетворяющих
условиям: точки ам Е G, круг радиуса аз с центром в точке ам
принадлежит G; 7^1-
При изменении чисел щ и фиксированном 7 получаем счетное
множество функций, совокупность линейных комбинаций которых
5*
76 Гл. 2. Двухбазисныи проекционный метод
о
плотна в пространствах 1/2(С?) = Но и Н\/2 {G) = Н = Яд- Воз-
Возможно также использование функций с несколькими различными
значениями 7-
Таким образом, из системы функций ф2{х) можно построить
ортонормированный базис в L<i(G) или Н\. Скалярные произведе-
произведения (ег-, Аф2) вычисляются простым интегрированием, поскольку
выражения Кф^х) вычисляются аналитически.
Обозначим
0,
= Bтг) Л
в?
где г = |ж|, а Ф7(^) — образ Фурье функции
Для вычисления Ф7(?) перейдем в соответствующем выраже-
выражении к полярным координатам и воспользуемся известным пред-
представлением функции Бесселя с помощью определенного интеграла
(см., например, [60, с. 60] или [98, с. 175])
2тг
о
В результате получим
а 2тг
= /V(a?)ei(*'fl<to = /" /г(а2 - r2)^ e
0 0
1
JQ{l-Q2yjMt,\Q)dQ. B.22)
0 0
1
Интеграл, стоящий в правой части B.22), вычислен в [59]. Там
имеется следующая формула:
Jzx+1(l - z2yjx{bz)dz = 2TG + 1)Ь"G+1)Л+7+1(Ь) B.23)
при Ь > 0, Re Л > -1, Re7 > -1-
Здесь Г(^) — гамма-функция, Jv{s) — функция Бесселя.
2.3. Статическая нормальная нагрузка 77
Подставим выражение B.23) в B.22) с учетом того, что в нашем
случае А = 0 и b = a|?|. В результате получим
Далее подставим B.24) в выражение для ЛФ7, перейдем к поляр-
полярным координатам и воспользуемся формулой B.21). В результате
этого придем к выражению
АЪг(х) = B7г)~2 (|
я2
оо 2тг оо
= Bтг)-2 / f t4i{t)e-irtcos*dipdt = B7т)-1 ft2&(t)J0(rt)dt =
Интеграл, стоящий в правой части B.25), называется инте-
интегралом Сонина-Вебера-Шафхейтлина и вычисляется аналитиче-
аналитически (см., например, [59] или [126]). Согласно [59, 126]
00
Г J^{at)Jv
_ У Г((р + v - Л + 1)/2)
2А а""^1 Г(д/ + 1) Г((/х - I/ + А
Ь2\
, I/ + 1, ^J B.26)
при Re (^ + у - А + 1) > 0, Re А > -1, 0 < Ь < а и
00
[
У
00
Mat) Jv(bt) _ а» Г((А1 + и - А + 1)/2)
при Re (ц + v - А + 1) > 0, Re А > -1, 0 < а < 6.
Здесь 2-Р\(а> Ь\ с; z) — гипергеометрическая функция:
B.28)
78
Гл. 2. Двухбазисный проекционный метод
В B.28) (a)n означает символ Похгаммера
(о)„ = а(а + 1)...(о + п-1); (аH = 1.
Подставляя B.26), B.27) в B.25) с учетом того, что для нашего
случая в формулах B.26), B.27) следует принять fi = j+l, i/ = О,
А = 7 — 1 и ft = г, получим
== <
ГG +1/2)
в2(т+1)
3 1-27
) г < а,
г>а.
B.29)
При получении выражения B.29) после подстановки B.26),
B.27) в B.25) были проведены упрощения, учитывающие, что
= 1, ГC/2) = 7^/2/2, ГG + 2) = G-
Результаты применения оператора Л к функциям фа(х) полу-
получаются из B.29) простым сдвигом, а именно:
3 1-27
о;
2G+1)
C
/3 3
V2' 2''
;1;
а3
\х-ам\.
B.30)
К решению уравнения B.20), отвечающего статической задаче
о трещине отрыва, применимы обе разновидности двухбазисного
проекционного метода. Различие между ними заключается лишь в
том, что ортогонализация функций фа(х) для построения ортонор-
мированного базиса </?i, ..., </?р, ... проводится в пространствах с
различными скалярными произведениями. В первом случае функ-
функции фа(х) ортогонализируются в смысле скалярного произведения
в Яд- Для этого требуется вычисление величин (Афа(х), ф](х)).
Построенные затем приближения будут соответствовать реше-
решениям, получаемым по методу Бубнова-Галеркина. Во втором слу-
случае функции фа(х) ортогонализируются в смысле L2(G), для чего
требуется вычисление величин (ф%{х), ф](х)). Построенные та-
таким образом приближения будут соответствовать решениям, полу-
получаемым с помощью метода минимума квадратов.
2.3. Статическая нормальная нагрузка
79
Заметим, что ортогонализировать в L2(G) проще, чем в
поскольку, во-первых, при вычислении (^2(#), ф](х)), в проти-
противоположность вычислению (Афа(х), ф]{х))) не требуется опре-
определять значения гипергеометрических функций, а во-вторых, в
случае, когда носители функций ф1(х) и ф](х) не пересекаются
(фа{х), Ф]{х)) = 0, в то время как (Афа{х), ф](х)) Ф 0.
Кроме того, сходимость, получаемая во второй разновидности
двухбазисного метода, является более сильной, чем в первой. Дей-
Действительно, из сходимости рсА[ип] -> / в L,2(G) следует, что
о
[ип] -> [и] в #д = #1/2 №)• Вместе с тем из того, что [ип] -> [и]
в Яд? следует только сходимость рсА[ип] -> / в H^i/2{G).
В силу этого для решения конкретных задач всюду ниже ис-
используется вторая разновидность двухбазисного метода.
Помимо функций фа{х) для построения базиса cpj могут быть
использованы и функции, имеющие носители в форме эллипса.
Использование таких функций полезно при решении задач в вы-
вытянутых областях или при применении неравномерного разбиения
области трещины на конечные элементы для построения базиса е^.
Обозначим через (ра,а(я) следующие функции:
1
а\
при
при
(
I
(х2 -
(д?2 - QL2J
Л
1.
Л
¦«¦•
Здесь а = (oi, аг), а = (ai )
Покажем, что результат применения оператора Л к функциям
фа,а{х) (Л(/?а?а(ж)) вычисляется аналитически.
Обозначим через (р1(х) функции (plQ(x), т.е.
т? Г2\7 2 Т2
9 Of' 9^^9^'
а\ а\) а\ а\
0,
т2
а2
Очевидно, что нам достаточно вычислить функции Аср2(х), так
как после этого функции kipl,a{x) получаются сдвигом из A<pl(x).
80^ Гл. 2. Двухбаэисный проекционный метод
Для вычисления АсрЦх) предварительно вычислим образ Фурье
от функции (р2(х) и обозначим его $2(?)• Пусть Е1п — эллипс
{(#ъ Х2): x\la\ + #!/a2 ^ l}? тогда согласно определению
Сделаем в B.31) замену переменных x\ja\ = yi, ^2/^2 = У2-
В результате эллипс ?J/a перейдет в круг единичного радиуса К\.
Обозначим также a^i = Сь в2& = Сг, С = (Сь С2), Vo@ = *o(C)
и j/i + у2 = ^2. В итоге получим
>dy. B.32)
Ki
Перейдем в B.32) к полярным координатам и воспользуемся
формулой B.21). В результате получим
1 2тг
/ [Q(l-Q2)rrei^cosededQ =
о о
. B.33)
Вычисление интеграла, стоящего в правой части B.33), уже об-
обсуждалось выше (см. формулу B.23)). Подставляя B.23) в B.33),
получим
Формула B.34) с точностью до постоянного множителя и обо-
обозначений совпадает с B.24). Таким образом,
я2
% + % 1 Ф2(С) е~г(у'С) d(- B.35)
А2
2.3. Статическая нормальная нагрузка 81
Подставим в B.35) выражение B.34) вместо Фа (О- В резуль-
результате придем к следующей формуле:
J
R2
B.36)
В интеграле, стоящем в правой части B.36), перейдем к по-
полярным координатам как по переменной ?, так и по перемен-
переменной у (?i = icos A, ^2 = ?sinA, |C| = i, j/i = #cos0, j/2 =
При этом равенство B.36) преобразуется к следующему виду:
27Г 2\ • 2 \ \ 1/2
^ \ cm4 \ \ '
^G + 1) rfcos2
ж J \ a\
X sin2A
B.37)
Для вычисления интеграла, стоящего в B.37), следует разде-
разделить переменные t и А. С этой целью используем известное раз-
разложение плоской волны по Бесселевым функциям (см., например,
[60, с. 43])
00
e-idcos(s) = Jo(d) + 2 ?(-i)mJm(d) cos (ms). B.38)
m=l
В частности, заменяя в B.38) d на gt и s на Х-в, получим
-*) = Jo(^} + 2 g (_i)mJm(^} cos [m(A _ e)]. B.39)
m=l
Подставив B.39) в B.37), придем к равенству
7Г
(^ 22^I/2 j. B.40)
лов
82 Гл. 2. Двухбазисный проекционный метод
Таким образом, функция А(р2(х) разлагается в сумму ряда,
каждый элемент которого представляется произведением интегра-
. Интегралы по радиусу / 7+ _™—- dt являются интегра-
о
лами Сонина-Вебера-Шафхейтлина. Такие интегралы уже рас-
рассматривались выше. Выражения для них приведены в формулах
B.26), B.27).
2тг ,
Интегралы по углу /cos [m(A — в)] (cos2 A/a2 + sin2 А/а|) d\
о
вычисляются аналитически. Без ограничения общности здесь и
в дальнейшем будем предполагать, что а\ > п2- Для упрощения
записи введем обозначения:
/cos2 A sin2A\1/2
—— + -J-) =«
\ а1 а2
где к2 = 1 - a|/af = (a2 ~
о
Нетрудно видеть, что
2тг
= -/(l-A;2cos2AI/2dA =
а2 У v y «2
о
Здесь Е(к) — полный эллиптический интеграл второго рода.
2тг
[{ )]g() = ЛГ^ cos (тв) + A^ sin
Km = / cos [m(A — 1
B.42)
2тг 2тг
-^m = / cos (mty ?(^) d\] K^ = / sin (mA) q(X) dX.
о о
Величины K^ легко вычисляются. Сделаем замену перемен-
переменных А = S + тг. В результате выражение для if^ запишется в
2.3. Статическая нормальная нагрузка 83
виде
2тг тг
Kl= Г sin (гоЛ) q(X) dX = (-l)m Г sin (m5) q(S) dS. B.43)
О -тг
Поскольку функция q(S) четная, a sin (mS) — нечетная, интеграл
в B.43) равен нулю, т. е. К\ = 0. С учетом этого равенство B.42)
приобретает вид
^ B.44)
2тг 2тг
Кхт = [ cos (mA) g(A) rfA = a^1 f cos (mA) (l - k2 cos2 AI/2 rfA.
о о
B.45)
2тг .
Интеграл / cos (mA) (l - k2 cos2 A) / dX вычислен в [115, фор-
o
мула 2.5.19. 18]. Согласно [115]
2тг
f cos (mA) (I - k2 cos2 AI/2 dX =
о
О, т = 21 +1,
= { -ж(т-3)\\кт „(т-1 т-
(/L J
B.46)
Здесь I = 1, 2, 3, ..., Bn +1)!! = 1 • 3 • 5 •... • Bn +1) и (-1)!! = 1.
Подставив B.46) в B.45) и заменив т на 21 в случае, когда т
четно, получим
{0, m = 21 +1,
-7rBJ-3)!!
B.47)
Подставим B.47) в B.44). В результате получим
О, m = 21 + 1,
-тгB/ - 3)!! к21 cos B/0)
2'
B.48)
84 Гл. 2. Двухбазисный проекционный метод
Теперь все интегралы, необходимые для определения А(р2,(х),
вычислены. Подставим в B.40) вместо соответствующих интегра-
интегралов их выражения из B,26), B.27), B.41) и B.48). В результате,
после простейших преобразований, придем к следующим выраже-
выражениям. Внутри эллипса, т.е. при g < 1
Е(к) ./3 1 1 Л
7Г!/2ГG + 1/2)
,.2l.2/T,/, + 3/2)c0SBfg)
24' B/ - 1) (ЛJГG - Л-1/2)
B.49)
Иногда для представления k.<pl(ж) внутри эллипса вместо B.49)
удобнее пользоваться несколько видоизмененной формулой, в ко-
которой q21 cos B10) выражены через декартовы координаты ух, j/2-
Обозначим z = у\ + гуг = ?>еге. Тогда z21 = (yi + гугJ' =
= g2le2M. Отсюда имеем
^(^2'+I2'). B.50)
Здесь черта сверху означает комплексное сопряжение.
Раскрывая формулу B.50), получим
Е Bп).27-2„). ^^(l)
n=0 v 7 v y
Подставляя B.51) в B.49), окончательно имеем внутри эллипса
,
- / + 1/2) Bn)!B/- 2n)!
B.52)
2.3. Статическая нормальная нагрузка 85
Вне эллипса, т. е. при д > 1, получим
(-1)
Е (-d^^w^ ^ {l-hl+b2l+ь*2)cos
В случае круга a\ = a2 = a, A; = 0, i?@) = тг/2 и формулы
B.52), B.53) с точностью до постоянного множителя и обозначе-
обозначений совпадают с B.29).
Общие принципы построения базиса в{ были описаны выше.
Более детально их реализация рассматривается ниже на конкрет-
конкретных примерах. Здесь обратим внимание лишь на то, что при ис-
использовании второй разновидности двухбазисного метода следует
выбирать базис е^ таким образом, чтобы kei ЕЯои совокупность
линейных комбинаций Kei была плотна в Щ. Если в качестве
#о выбрать пространство Я_1/2(бг), то никаких проблем не воз-
возникает, поскольку оператор Л непрерывно и взаимно-однозначно
о
отображает Н\/2 (G) на H_i/2(G) и в качестве в{ можно выбирать
о
любой базис в Hi/2 (G). Если же в качестве Щ берется L2 (G), то
необходимо доказывать, что выбранный базис удовлетворяет сле-
следующим условиям: Ле* € L2(G) и совокупность линейных комби-
комбинаций Ав{ плотна в L/2{G).
Пусть элементы базиса ei, ..., еп, ... имеют вид е^х) =
= eo(x)gi(x). Здесь ео(#) —гладкая функция, положительная вну-
внутри G и имеющая правильную асимптотику у границы области G,
gi(x) — полная система гладких функций (это могут быть поли-
полиномы, тригонометрические функции или другие). Покажем, что
PGh(eo(x)gi(x)) e L,2(G) и система функций видароЛ(ео(ж)рп(х))
п
плотна в Ij2(G) = #о, где рп(х) = X) ci9i{x)-> ci = const.
г=1
о
Заметим, что ео(х) € Hi/2(G). Действительно, пусть область
трещины G ограничена, например, гладким контуром dG. Тогда
ео(х) имеет вблизи dG корневую асимптотику, а следовательно,
образ Фурье функции ео{х) убывает на бесконечности не медленнее,
чем |?|~3/2, и потому во (я) 6 Нф№). Так как ео(ж) €
86 Гл. 2. Двухбазисный проекционный метод
О
то и gi(x)eo(x) € Я1/2 (G), поскольку умножение на гладкую функ-
функцию является оператором нулевого порядка.
Покажем теперь, что ро&ео(х) Е L2(G). Обозначим w(x) ре-
решение уравнения B.20) в случае, когда f(x) — гладкая, положи-
положительная в замыкании G функция. В [38, 54, 138] (см. также гл. 4
настоящей книги) для решений класса уравнений, включающего
в себя уравнение B.20), доказаны следующие теоремы сравнения:
1. Если f(x) ^0 w w(x) — решение B.20) с правой частью
/(#), то w(x) ^ 0.
2. Если f(x) ^ 0 в области Gi, G\ С G2 и функции w\(x) и
{) являются решениями B.20) с правой частью f(x) в обла-
областях G\ и Сг2 соответственно, то w\(x) ^ W2(x).
Из сформулированных теорем сравнения следует, что вве-
введенная функция w(x) может быть представлена в виде w(x) =
= eo{x)g{x), где g(x) — гладкая, положительная в замыкании G
функция. Продолжим д(х) гладким образом на всю плоскость так,
чтобы ?2-норма д{х) была ограниченной:
pGA(ge0) =PGfifAe0 + pg[A, g]e0.
Функции PG^(deo) и pg[A, g]eo принадлежат L2(G), первая —
по условию, а вторая, поскольку коммутатор [Л, д] является опе-
оператором нулевого порядка и
, д]е0 е Hl/2(G) е
Следовательно, рвд^о ^ L2{G), а в связи с тем, что д(х) > 0
в G (G — замыкание G), то и рв^ео S ^(G). Отсюда очевидно
следует, что и рв^{д%^) € -MG), так как РвМшео) =PGpiAeo +
+ Pg[A, gi]e0.
Осталось показать, что с помощью линейных комбинаций
функций вида рвМ9гео) можно приблизить любую функцию в
Li2{G). Поскольку множество гладких функций плотно в ^(G)?
достаточно доказать, что по норме L2 (G) можно приблизить лю-
любую гладкую функцию. Пусть f(x) — гладкая функция и w(x) =
= д(х)ео(х) — решение уравнения B.20) с правой частью f(x).
Выберем рп(х) так, чтобы \\рп(х) - g(x)\\C4{G) < S, || • ||cfc(G) —
норма в пространстве Ck(G). Обозначим hn(x) = д(х) — рп(х).
Продолжим hn(x) на всю плоскость так, что ||Лп(гг)||с4(Д2) < CS
и !1^п(ж)|1я4(Л2) < С6, С — const:
- f(x)\\ = ||pGA(pneo) -рс
= \\pGhnAe0 +pg[A, hn]e0\\ < ||рс?ЛпАео|| + ||pg[A,
^ max|/in(x)|||pGAe0||
2.3. Статическая нормальная нагрузка 87
Пусть ИдеЛеоН < М, тогда ||р<?Л(/1пео)|| < 6M+\\pG[A, Лп]ео||.
Символ оператора [Л, hn] равен
B7Г)-2
Л2
-21 |f + ClUC)e-i(*'C) d( 1СК27Г)
= Bтг)-21 |f + ClUC)e-i(*'C) d( - 1СК27Г)
Я2 Я2
я2
Так как ||С + С| ~ ICI| ^ ICI? т0 можно оценить символ опера-
оператора [Л, hn]: |[А, Лп]| < Bтг) / |С||ЛП(С)ИС. В силу сделан-
я2
ных предположений |Лп(С)| ^ const • 6/A + |?| ). Следовательно,
|[Л, hn]\ ^ const-6. Из оценки символа оператора [Л, hn] и ограни-
ограниченности области G следует, что ||р<з[Л, /in]eo|| ^ const • S = М\8.
Таким образом,
||р<гЛ(рпео) - /(^)|| < SM + SMi <K5, K = const.
Следовательно, Ve > 0 можно подобрать J > 0 так, что Кб < е
и утверждение доказано. Из доказанного следует, что возможно ис-
использование базиса е;, удовлетворяющего указанным выше усло-
условиям, при решении задачи о трещине двухбазисным методом с
пространством L2(G), взятым в качестве Щ.
Рассмотрим теперь на примерах задач о трещинах различных
конфигураций конкретную реализацию общих принципов построе-
построения базисов е{ и cpj и проанализируем получающиеся результаты.
Представлены расчеты для трещин, имеющих в плане формы пря-
прямоугольника ((a?i, #2) : |si| < Q5 Nl < 1, Q = 1, 2, 4), равно-
равностороннего треугольника с вершинами в точках (—2, 0), A, Vo),
A, —л/3) и невыпуклой фигуры, занимающей область ((rci, X2) :
-тг - 3 ^ xi ^ тг + 3, \х2\ ^ F(xi)):
|a?i| < тг,
-тг.
Приведенные ниже результаты соответствуют случаю однород-
однородной нагрузки единичной интенсивности (*з(#ъ Х2) = !)•
Гл. 2. Двухбазисный проекционный метод
Для квадратной трещины было взято шесть и девять функций
базиса е{ вида е{ = е$д{. Функция ео выбрана так, чтобы учесть
особенности на границе квадрата, включая угловые точки, где,
согласно [173], порядок особенности равен г0)816 (близкие значения
порядка получены также в [324, 276, 216, 204]):
eo(ii, х2) = /A - х\){1 - х\) (п r2r3r4)-0'184,
т\ = (Х1 - IJ + (х2 - IJ, г2 = (Х1 - IJ + (х2 + IJ,
г2 = {хг + IJ + (Х2 + IJ, т\ = (Ж1 + IJ + (*2 - IJ.
В качестве gi{x\, Х2) брались функции двух типов:
1) gi — полиномы четных степеней не выше шестой, учиты-
учитывающие симметрию задачи (д\ = 1, 02 = %\ + ж2? 9з = %\ + х\,
#4 = х\х\, дь = х\ + х% д6 = х\х\ + х\х\)\
2) 5г — тригонометрические функции, учитывающие симме-
симметрию задачи (#1 = 1, дч = cos А + cos S, #3 = cos BA) + cos BB),
04 = cos A cos 2?, 05 = cos (ЗА) + cos C5), ge = cos BЛ) cos В +
+ cos Л cos BБ), 07 = cos DA) + cos DB), 08 = cos (ЗА) cos Б +
+ cosAcosC5), 09 = cosBA)cosBB), A = ttxi, 5 = 7ПГ2).
Расчеты проводились для шести и девяти функций этого базиса.
Количество элементов базиса (pi варьировалось от 10 до 18 в
случае шести элементов базиса е{ и доводилось до 22 в случае ба-
базиса ег-, состоящего из девяти элементов. Для построения базиса
cpi использовались функции ^2(х), описанные выше, которые за-
затем ортогонализировались в смысле L2{G). Очевидно, что каждая
из функций ^2 (х) может быть описана тройкой чисел (ai, #2, аз)?
соответствующих центру (ai, «2) и радиусу аз круга, в котором
функция Фа(х) отлична от нуля. Выбор функций фа(х) как в
этом примере, так и во всех остальных основывался на следую-
следующих принципах:
— круговые носители функций фа{х) должны заполнять как
можно большую часть области трещины;
— поскольку в рассматриваемых примерах использована гло-
глобальная аппроксимация решения базисом е^, выбираемые круги
(носители функций фа{х)) заметно отличаются друг от друга не
только расположением, но и радиусами;
— так как от решения задачи о трещине требуется повышен-
повышенная точность в окрестности ограничивающего ее контура, вблизи
контура берется больше кругов, чем в удаленной от него области;
— для сокращения времени счета, уходящего на ?2-ортогона-
лизацию, и уменьшения погрешностей вычислений выбираются
круги, имеющие не много взаимных пересечений;
2.3. Статическая нормальная нагрузка
89
— для снижения погрешностей также исключаются круги
слишком малого радиуса;
— количество функций фа(х) определяется устойчивостью
получаемых результатов, например, в рассматриваемых в этом
параграфе примерах их количество в 2 и более раз превышало
количество элементов базиса е*;
— при наличии симметрии в условиях задачи и базисе е*
можно ограничиться носителями фа{х) с центрами, находящи-
находящимися только в симметричной части области трещины.
С учетом указанных принципов 22 функции *ф%(х), выбранные
для построения базиса ipi с максимальным из использованных для
решения задачи о квадратной трещине количеством элементов,
имели в качестве носителей следующие круги: один крут радиуса 1
с центром в точке @; 0); три круга радиуса 0,5 с центрами в точках
@; 0), @,5; 0), @,5; 0,5); десять кругов радиуса 0,25 с центрами в
точках @,25г; 0) г = 0, 1, 2, 3, @,25(j + 1); 0,25) j = 0, 1, 2,
@,25(А; + 2); 0,5) к = 0, 1, @,75; 0,75); восемь кругов радиуса
0,125 с центрами в точках @,875; 0,125/) / = 0, ..., 7. Здесь было
принято во внимание, что согласно симметрии задачи и функций
ei = eoflff, центры круговых носителей ф^(х) можно брать в 1/8 ча-
части квадрата, ограниченной треугольником с вершинами в точках
@; 0), A; 1), A; 0).
Результаты расчетов (отношение объема трещины к объему
круговой трещины той же площади (V/VK) и коэффициенты ин-
интенсивности напряжений Ni в точках (хц, 1), i = 1, ..., 10,
хц = 0,1 (г — 1), обозначаемые Щ соответственно) приведены в
табл. 2.1.
Таблица 2.1
V/VK
0,951
0,946
0,952
ЛГ.1
0,551
0,514
0,536
N?
0,550
0,513
0,532
Л?
0,545
0,510
0,525
N?
0,536
0,503
0,514
N*
0,522
0,491
0,501
Л?
0,502
0,472
0,481
N1
0,473
0,447
0,455
Л?
0,435
0,415
0,422
N*
0,384
0,371
0,378
0,309
0,303
0,310
Первая строка в табл. 2.1 соответствует выбору gi в виде по-
полиномов, вторая — выбору gi в виде тригонометрических функ-
функций, количество которых равно шести, третья — девяти триго-
тригонометрическим функциям <#. Результаты в этих строках близки
между собой и удовлетворяют оценкам, следующим из упомяну-
упомянутых выше теорем сравнения при вписывании круга и описыва-
нии вокруг квадрата полосы. Действительно, как известно, для
круга радиуса 1 при однородной нагрузке единичной интенсивно-
интенсивности JVi = Nik = \/2/7г « 0,450, а для трещины в виде полосы,
имеющей ширину 2, значение NT равно Ni = Nis = l/\/2 « 0,707.
Как видно из табл. 2.1, NJK < N* < ЛГ15.
90 Гл. 2. Двухбазисныи проекционный метод
Максимальное значение коэффициента интенсивности напря-
напряжений (Nj1), представленное в первой строке, лучше соответствует
результату, полученному в [8], различие с которым не превосходит
0,9%. Данные первой строки табл. 2.1 лучше соответствуют пред-
представленным в графической форме результатам [127], но несколько
быстрее убывают при приближении к угловой точке. Различие
между ними практически отсутствует в средней части стороны
квадрата, составляя, например, в точках @; 1), @,2; 1) и @,4; 1)
всего 0,2, 1,5 и 0,2%, и увеличивается вблизи угловой точки, до-
достигая 5,8% в точке @,7; 1) и 14,6% в точке @,9; 1).
Вторая и третья строки табл. 2.1 ближе к результатам [423] и,
практически совпадающим с ними, [317], представленным там в
графической форме. Отличие коэффициентов интенсивности на-
напряжений, приведенных в третьей строке табл. 2.1 от данных [423]
в точках @; 1), @,2; 1), @,5; 1), @,7; 1) и @,9; 1) равно соответ-
соответственно 2,4, 4,4, 0,4, 1,2 и 2,6%.
Результаты, полученные в [217] и также удовлетворяющие оцен-
оценкам, следующим из теорем сравнения, несколько ниже, чем в
табл. 2.1 и указанных выше работах. Их отличие, например, от
данных третьей строки табл. 2.1 в точках @; 1) и @,5; 1) соста-
составляет 9,2 и 6,6%.
В [52, 53, 58] построены оценки и предложены приближенные
формулы для значений объема трещины и коэффициентов интен-
интенсивности напряжений. Данные табл. 2.1 хорошо согласуются с
этими оценками и приближенными значениями.
При решении задач о прямоугольных трещинах количество
элементов обоих базисов возрастало в зависимости от соотношения
между сторонами прямоугольника. Для прямоугольников ((xi, #2) •
|#i I ^ Q? |#2| ^ 1) в случае Q = 2 количество элементов базиса е\
было доведено до 20, а количество элементов базиса щ до 44, а в
случае Q = 4 было взято соответственно 32 элемента базиса е^ и
71 элемент базиса щ.
Функций е^, как и выше, имели вид ei(x) = eo(x)gi(x):
ео(х) =
Л = (XI - Q? + (Х2 - IJ, Т\ = (XI - Qf + (Х2 + IJ,
Л = (хг + QJ + (х2 + IJ, г\ = (хх + QJ + (х2 - IJ.
Очевидно, что функция ео(х) имеет правильную асимптотику
у границы прямоугольника, включая угловые точки. В качестве
gi(x) брались тригонометрические функции. Увеличение их коли-
количества при удлинении прямоугольника осуществлялось в основном
за счет функций, зависящих от координаты х\, изменяющейся
вдоль большей стороны прямоугольника. В случае Q = 2 двадцать
2.3. Статическая нормальная нагрузка 91
функций gi(x) были выбраны следующим образом: 1; cos (гЛ),
i = 1,...,8; cos(jf^)cos(S), j = 0,..., 4; cos(b4)cosBjB),
k = 0,1,2; cosCB); cos (A) cos CB); cosDB); A = ttxi/2,
J5 = 7ГЖ2.
Для Q = 4 тридцать две функции gi(x) имели вид: 1; cos (г\А),
г = 1,..., 16; cos (jA) cos (В), j = 0, ..., 8; cos (kA) cos BJ5),
k = 0, 1, 2; cos C5); cos {A) cos CB); cos DJ5); A = 7rrci/4, В =
= 7ГЖ2- Выбранные функции ^(я) учитывают симметрию реше-
решения относительно осей х\ ИЖ2.
Базисы щ строились путем ортогонализации функций Фа(х)
в смысле L2(G), которым соответствуют следующие круги. Для
Q = 2 сорок четыре круга состоят из двух кругов радиуса 1 с
центрами в точках @; 0) и A; 0); восьми кругов радиуса 0,5 с
центрами в точках @,5г; 0), % = 0,..., 3 и @,5j; 0,5), j = 0,..., 3;
одиннадцати кругов радиуса 0,25 с центрами в точках @,25г; 0,75),
i = 0, ..., 7 и A,75; 0,25,7'), j = 0, 1, 2; двадцати трех кругов
радиуса 0,125 с центрами в точках @,125г; 0,875), г = 0, ..., 15 и
A,875; 0,125;), j = 0,...,6.
Для Q = 4 семьдесят один круг состоит из четырех кругов
радиуса 1 с центрами в точах (г; 0), г = 0,..., 3; девяти кругов
радиуса 0,5 с центрами в точках @,5г; 0,5), i = 0, ..., 7 и C,5; 0);
девятнадцати кругов радиуса 0,25 с центрами в @,25г; 0,75), % =
= 0,..., 15 и C,75; 0,25j), j = 0, 1, 2 и тридцати девяти кругов
радиуса 0,125 с центрами в точках @,125г; 0,875), г = 0, ..., 31 и
C,875; 0,125j), j = 0,...,6.
Центры кругов, отвечающих функциям ^(#), с учетом симме-
симметрии задачи располагались в 1/4 части исходной прямоугольной
трещины, также являющейся прямоугольником с вершинами в
точках @; 0), @; 1), (Q; 1), (Q; 0).
Согласно расчету, отношение объема трещины к объему кру-
круговой трещины той же площади (V/VK) для прямоугольника с
Q = 2 составило 0,880, а в случае Q = 4 — 0,717. Значения ко-
коэффициентов интенсивности напряжений Nf в точках @,lQi; 1)
большей стороны прямоугольника и в точках (Q; 0,1г) — мень-
меньшей стороны прямоугольника (г = 0,..., 9) приведены в табл. 2.2.
Первая строка соответствует прямоугольнику с отношением сто-
сторон 1 : 2, вторая — прямоугольнику с отношением сторон 1 : 4.
Верхняя часть строк отвечает большей стороне прямоугольника, а
нижняя — меньшей.
Результаты табл. 2.1 и 2.2 удовлетворяют теоремам сравнения,
т. е. увеличение большей стороны прямоугольника влечет за собой
увеличение коэффициентов интенсивности напряжений на мень-
меньшей стороне. Отметим, что это увеличение КИН на малой сто-
стороне прямоугольника незначительно и величины КИН стремятся
92
Гл. 2. Двухбазисный проекционный метод
к предельным значениям. На большой стороне прямоугольника
теоремы сравнения также удовлетворяются, так например, КИН в
точке B; 1) для Q = 4 больше значения КИН в точке @; 1) для
Q = 2, а значение КИН в точке A; 1) для Q = 2 больше значения
КИН в точке @; 1) для квадрата.
Таблица 2.2
I/O
0,5
0,25
А?
0,638
0,564
0,694
0,571
Л?
0,637
0,561
0,695
0,568
JV?
0,636
0,554
0,697
0,561
0,630
0,544
0,693
0,549
0,622
0,530
0,683
0,534
Л?
0,608
0,508
0,673
0,512
0,581
0,479
0,660
0,483
Л?
0,546
0,444
0,638
0,449
Л?
0,487
0,400
0,590
0,405
JV,10
0,404
0,330
0,493
0,334
Величины объемов прямоугольной трещины, полученные чи-
численно, находятся в хорошем соответствии со значениями, вычи-
вычисляемыми по приближенным формулам [52, 53, 58].
Как и в случае квадратной трещины, результаты, представлен-
представленные в табл. 2.2, хорошо согласуются с данными работ [423, 127]
и несколько выше результатов, полученных в [217]. Отличие от
КИН, полученных в [217], составляет в точках @; 1), @,5Q; 1)
большой стороны прямоугольника соответственно 7,3, 9,2% для
Q = 2 и 7,8, 8,5% для Q = 4, а в точках (Q; 0), (Q; 0,5) малой
стороны прямоугольника 10, 6,6% для Q = 2 и 10,2, 6,8% для
Q = 4.
Некоторая немонотонность изменения КИН при движении от
центра большой стороны к вершине в случае Q = 4 вызвана тем,
что для длинных прямоугольников значения КИН в окрестности
середины большой стороны очень близки. Увеличение КИН по
сравнению со значением в середине большой стороны является
следствием погрешностей вычислений и не превосходит 0,5% по
данным табл. 2.2. Величина коэффициента интенсивности напря-
напряжений в середине большей стороны прямоугольника с отношением
сторон 1:4 меньше величины, отвечающей решению плоской за-
задачи на 1,8%.
В [143] помимо представленных здесь результатов вычислены
также КИН для прямоугольных трещин, поверхности которых
взаимодействуют по линейному закону.
При решении задачи о треугольной трещине было использо-
использовано семь элементов базиса е{ = ео5г> где д%{х) — полиномы, учи-
учитывающие симметрию задачи (#i = 1, 52 = s? 9s = *> 54 = s2?
9ъ = st, g6 = s3, g7 = t2, s = x\ + x\, t = x\- 3xix%).
Функция ео(х) выбрана с учетом симметрии и особенностей
в углах, которые согласно графическим данным [173] имеют для
2.3. Статическая нормальная нагрузка
93
углов тг/3 порядок « г0>912 (близкие значения порядка получаются
при интерполяции табличных данных [324] и в работах [276, 204]):
еоОп, х2) = ^/A - Х1) [(Х1 + 2J - 3*1] (г1Г2г3)-°>ш,
Г{ — расстояние до г-го угла, г\ = [х\ + 2J + х\, г2 = {х\ — IJ +
+ (Х2 ~ у/ЪJ, Г| = (Хх - IJ + (Х2 + Л/3J.
Количество элементов базиса щ доводилось до 22. Выбор кру-
кругов, отвечающих функциям ^2(ж), используемым при построении
базиса (pi, был основан на тех же соображениях, что и в случае пря-
прямоугольной области. Учитывалась симметрия задачи и базиса е^,
в результате чего центры всех кругов расположены в треугольнике
с вершинами @; 0), A; л/3)? A; 0). Круги выбирались так, чтобы
наиболее полно представить треугольную область. Более детально
представлена окрестность ограничивающего треугольник контура.
Для удобства описания 22 кругов, используемых при решении за-
задачи, обозначим (ai(i), с*2(г)) и с*з(^) координаты центра и радиус
г-го круга:
ai(t)= 0,2(t-l), aa(i)=0, as(i) = l-0,2(t-l),
1 = 1, ..., 5;
oi(i) = 0,2(t - 5), a2(i) = 0,2\/3(i - 5), a3(t) = 1 - ai(t),
i = 6, ...,9;
aiA0) = 0, a2A0) = 0, a3A0) = 0,5;
), aa(t) =0,l(t-ll), a3(«) = 0,2,
« = 11,...,15;
i - 15), a2(i) = ai(t), a3(i) = 0,3,
i = 16, 17, 18;
ai(<) = 0,84, a2(t) = B/3 + 0,16(г - 19))V3, a3(t) = 0,16,
г = 19, 20;
ai(t) = 0,7, a2(t) = 1 + 0,2(t - 21), a3(«) = 0,3, i = 21, 22.
Отношение объема трещины к объему круговой трещины той
же площади и значения КИН iV/ в точках A; Ж2г), г = 1,..., 10;
#2г = л/3(» — 1)/Ю приведены в табл. 2.3.
Таблица 2.3
v/vK
0,874
Л?
0,591
0,586
JVX3
0,573
Nf
0,553
0,526
Л?
0,495
N?
0,459
0,416
N?
0,362
JV,10
0,280
94 Гл. 2. Двухбазисный проекционный метод
Полученные результаты несколько ниже, чем в [128], и хо-
хорошо согласуются с оценками и результатами, следующими из
приближенных формул [52, 53, 58]. Отличие КИН, представлен-
представленных в табл. 2,3, от полученных в [128], в точках A; 0), A; 0,4\/3),
A; 0,7\/3) составляет соответственно 6,3, 12,2 и 19,5%. Отметим
также, что полученные результаты хорошо согласуются с резуль-
результатами [317], представленными там в графической форме.
Для решения задачи о трещине, занимающей невыпуклую об-
область, описанную выше, использовалось до пятнадцати функций:
ei(x) = eQ{x)gi{x), eo{x) = y/F2(xi) -x\, (gx = 1, g2 = cos (A),
Зз = cos (В), #4 = cosBA), <?5 = cosBB), дъ = cos (A) cos (jB),
<?7 = cos (ЗА), gs = cos CJB), gg = cos BA) cos (Б), дю = cos (A) x
xcosBJ3), 011 = cosDA), gu = cosEA), 0i3 = cosFA), gu =
= cos (ЗА) cos (J5), 0i5 = cos DA) cos (B), A = irxi/(n + 3), Б =
/)
/)
Здесь, как и в случае прямоугольной трещины, взято больше
функций 0г-, зависящих от координаты #i, вдоль которой вытянута
трещина. Все функции ег(ж) являются четными по координатам
х\ и ?2? что отвечает симметрии задачи.
Для построения базиса у>г использовалось до 36 функций ф^{х).
Этим функциям соответствовали круги со следующими значени-
значениями координат центра (ai(i), ct2(i)) и радиусов а^(г):
<*i@ = ^ , «2@ = 0, а3@ = 1, г = 1, ..., 6;
«!(г) = тг + г - 6, «2@ = 0, о?з@ = 15 » = 7, 8;
ai@ = ^ «2@ = 0,5A - 9), а3@ = 0,5, t = 9, ..., 14;
ai@ = 0,5(t - 15), a2@ = 0,5, a3@ = 0,5, г = 15, ..., 18;
ai(i) = 7r + 2,5cos(Ai), аг@ = 2,5 sin (Л<), аз@ =0,5,
где Xi = 0,1тг(г - 21), t = 21, ..., 25;
«i@ = тг + 2 cos (хг), a2{i) = 2sin(xi), «з@ = °?65»
где Xi = 0,l7r(i - 26), t = 26, ..., 30;
aiC1) - 0,75тг, a2C1) = 1, a3C1) = 0,25тг;
«i@ = n + l>5cos (^i), «2@ = 1,5 sin (^), az(i) = 0,6,
где ft = n(i - 32)/6, t = 32, 33, 34;
ai@ = тг/2 + 0,5(t - 34), a2@ = 1,5, «з@ = °?5? * = 35? 36-
Указанные круги выбирались из соображений, аналогичных тем,
которые применялись при других формах трещин.
2.3. Статическая нормальная нагрузка
95
Коэффициенты интенсивности напряжений ЛГ,1 рассчитаны
10 точках (хц, jF(#i;)), хц = 0,2тф* — 1), г = 1, ..., 6 и #н
«ь> v a \j ал. \кл .*&. 1 «л/ j т « л. 1 «л/ I Z / / ) tA>/ i Z v Ч *" #itv х г i v jl « • • • •
= тг + 0,75(г — 6), г = 7, ..., 10. Результаты приведены в табл. 2.4.
Таблица 2.4
v/v*
0,748
0,763
JV.1
0,926
1,126
0,995
1,188
Л?
0,998
1,154
Л?
0,859
0,935
0,753
0,777
Л?
0,733
0,742
N1
0,784
0,768
N?
0,767
0,774
Л?
0,689
0,810
0,750
0,793
В задаче о квадратной трещине при использовании 6 и 9 эле-
элементов базиса С{ были получены достаточно близкие результаты
(табл. 2.1). Однако для удлиненных трещин и трещин слож-
сложной формы малое количество элементов базиса е* может привести
к более существенным погрешностям. Для иллюстрации этого
в табл. 2.4 представлены результаты, отвечающие 10 элементам
базиса бг (первая строка) и 15 элементам этого базиса (вторая
строка).
Значения объемов трещин и коэффициентов интенсивности на-
напряжений, полученных при 10 и 15 элементах базиса е$, в целом до-
достаточно близки. Существенные различия, достигающие 13-18%,
обнаруживаются лишь в точках контура с координатой a?i, близ-
близкой к нулю (область невыпуклости контура), и координатой #i,
близкой к тг 4- 3 (отвечает вытянутости контура).
Контроль правильности представленного в табл. 2.4 реше-
решения, можно осуществить следующим образом. В рассматривае-
рассматриваемую область можно вписать достаточно длинный прямоугольник,
ширина которого равна 2 и середина большой стороны которого
касается контура в точке @; 1). Поэтому КИН в этой точке дол-
должен быть выше соответствующего решения плоской задачи, т.е.
выше 0,707. Вокруг области можно описать прямоугольник ши-
ширины б с отношением сторон 3/(тг + 3) « 1:2. Этот прямо-
прямоугольник будет расположен так, что середина малой стороны бу-
будет касаться контура в точке (тг + 3; 0), а большая сторона будет
касаться контура в точке (тг; 3), находящейся приблизительно в
центре между серединой стороны и углом. Отсюда и из данных
табл. 2.2 получим, что значение КИН в точке (тг + 3; 0) должно
быть меньше 0,564\/3 « 0,977, а значение в точке (тг; 3) меньше
0,608\/3« 1,053.
Кроме этого, учитывая, что удлинение прямоугольника мало
влияет на значения КИН на меньшей стороне, из аналогичных
соображений можно предположить, что КИН на части контура,
находящейся в области тг < х\ ^ тг+3, не очень сильно отличаются
от КИН для круговой области радиуса 3, который равен 0,780.
Результаты численного счета, представленного в табл. 2.4, удо-
удовлетворяют всем перечисленным требованиям.
96 Гл. 2. Двухбазисный проекционный метод
Напомним, что значения коэффициентов интенсивности на-
напряжений Къ употребляемых столь же часто, как и Nu получа-
получаются из приведенных в табл. 2.1-2.4 величин умножением на у/2ж.
Необходимость увеличения количества элементов базиса е* для
вытянутых трещин и трещин сложной формы указывает на то, что
в этих случаях более эффективным может оказаться упомянутый
выше гибридный метод, объединяющий идеи метода граничных
элементов при построении базиса е» с двухбазисным проекцион-
проекционным методом.
2.4. Гармоническая нормальная нагрузка
Напомним, что согласно A.45), A.46) задача о трещине, к по-
поверхностям которой приложены нормальные, гармонически изме-
изменяющиеся по времени усилия, сводится к псевдодифференциаль-
псевдодифференциальному уравнению
РаЩ[щ(х)]=^, [«з(а;)]=0, x?G, B.54)
где пр — псевдодифференциальный оператор с символом
) ¦ B-55)
В гл. 1 было доказано, что оператор pg^p изоморфно отображает
о
#1/2 (G) на H_i/2{G). Поэтому для численного решения уравне-
уравнения B.54) можно применить вторую разновидность двухбазисного
проекционного метода.
При применении двухбазисного метода, как и в случае стати-
статической задачи, выберем в качестве пространств Я, Н и #о Щ>о-
о
странства H\/2(G), H_i/2(G) и L2(G) соответственно. Заметим
также, что поскольку главный член оператора пр совпадает с опе-
оператором статической задачи, решение уравнения B.54) обладает
теми же особенностями, что и решение статической задачи, т. е.
например, имеет корневую асимптотику вблизи гладкой части кон-
контура. В связи с этим базис е{(х) можно строить таким же образом,
как и в статическом случае.
В предыдущем параграфе было показано, что при определенном
построении базиса е{(х) G Hi/2(G) функции рс&е{(х) ? L2(G).
Поскольку оператор Qp представляется в виде П^ = Л/BA — и)) +
+ Dp, причем ordD/? = -1, то PGDpei € H3/2{G) € Ьг(С) и
2.4. Гармоническая нормальная нагрузка 97
PGp^i принадлежит L2{G). Следовательно, если, как и в стати-
статическом случае, принять в качестве пространства R пространство
L2{G), а в качестве оператора В — тождественный, то останется
только построить базис <pj(x) такой, чтобы функции Щщ(х) легко
вычислялись. После этого можно будет представить решение в
п
виде [г1з(#)] « 2 с%е%{х)^ а неизвестные постоянные с», в данном
i=i
случае комплексные, определить из уравнений B.16).
Аналогично статической задаче, базис tpj будем строить пу-
путем ортогонализации в L2(G) функций ф1{х). Представим опе-
оператор Up в виде пр = Ар + iBp, где Ар и Вр — операторы с
вещественными символами. Поскольку операторы Ар и Вр ока-
оказываются симметричными, Щ = Ар — iBp. Таким образом, для
вычисления п*рф1 (х) нужно вычислить Арф2(х) и Врфа(%). Опе-
Оператор Щ, а также операторы Ар и Вр инвариантны относительно
сдвига и потому достаточно вычислить Арф% (х) и Врф$(х)у после
чего функции Арфа(х) и Врфа(х) получаются простым сдвигом.
Вычислим Арфц(х) = А/?Ф7(#) и BpW(x) в случае функции
Ф7(ж), имеющей круговой носитель радиуса а. Используя выра-
выражение B.24) для образа Фурье функции Ф7(#), получим
После перехода к полярным координатам имеем
B.56)
Здесь, как и выше, г = |х|, 9—угол между векторами х и ^.
8 Зак. 205
98 Гл. 2. Двухбазисный проекционный метод
Далее воспользуемся в B.56) формулой B.21) при интегриро-
интегрировании по углу. В результате получим
00
х f (
1)/Г2х
- /?2) V - «2
о
х J^i{ag)J0{rg)dg. B.57)
Из B.57) следует, что
{00
4 [д2-Цд2-/32)^2^+1(ад)х
0
00 ч
dg-J
B.58)
о
х JoM dg + J<ГW - /?2J(а2 - g2rl/2J^i(ag)MrQ) dg 1.
° B.59)
Из выражений B.58), B.59) видно, что для вычисления
1{х) и Bpsi1{x) достаточно уметь вычислять интегралы сле-
следующего вида:
d
I^{a, Ь, к, 0, d) = fxe~l{d2 - а;2I4 J,,(aa:) J^bx) dx, B.60)
о
00
¦M<*> ^ л» ^> ^) = f xB~l{x2 - d2)'' «Л/М J^te) dc. B.61)
Для сходимости Интеграла B.60) достаточно, чтобы выполня-
выполнялись условия: e + u + fi = 2a>0 (для сходимости в точке х = 0)
и ас > 0 (для сходимости в точке х = rf).
Сходимость интеграла B*61) обеспечивают условия /с > 0 (схо-
(сходимость в точке х = d) и 6>4-2к < 3 (сходимость на бесконечности).
2.4. Гармоническая нормальная нагрузка 99
Для интегралов, встречающихся в B.58), B.59), все эти усло-
условия выполняются в случае у > 3.
Чтобы вычислить интегралы B.60), B.61), воспользуемся
обобщением формулы Неймана, приведенным в [18, с. 57] и [116,
с. 207] и имеющим вид
nBaz)-/Bbz)~liJl/{az)Jli{bz) =
тг/2
= f ei<v~>l\cos{8)Y+li{\z)-v->iJu^{\z)ds, B.62)
где А = v/2cos (s) (a2eu + Ре-*').
Из B.62) получаем выражение для произведения функций Бес-
Бесселя
M*z)Mbz) = тг-1Bо)"BЬ)'хх
тг/2
х f eis("-'1)(cos(s))l'+''A-'/-''J1/+/4(Az)ds. B.63)
-тг/2
Для вычисления /„д(а, Ь, к, 9, d) подставим B.63) в B.60).
В результате получим
А
Ivfl(a, Ь, к, 9, d) = I xB~l{d2 - x^^Max^bx) dx =
о
d
= -K-x1v+»avb» fxe-\d2 - я2)"*
0
7Г/2
x f eis^-^(cos(s)Y+llX-l
-7Г/2
Переставляя порядок интегрирования, получим
ж/2
IvpL{a, b, к, в, d) = 7r-12"+"o'/^ / eie("-'J>(cos(s))'/+'iA-|'-'4x
-ж/2
d
х f xe~l(d2 - ж2)" Jv+(i(\x) dxds. B.64)
100 Гл. 2. Двухбаэисныи проекционный метод
В [116, с. 176] имеется следующая формула:
J х D х) Jt[
(ф???) (,65)
+ *>О, /е>0.
Здесь iF2(o; 6, с; z) — гипергеометрическая функция:
Подставим формулу B.65) во внутренний интеграл B.64). В ре-
результате формула B.64) приобретет вид
/„„(а, Ь, *, 0, d) п2"+»+1Г(к + @ +1/ + гл)/2)Г(и + ц + 1) "
У
V 2 2 4 )
Проводя сокращения и учитывая введенное выше обозначение
(в + v + /i)/2 = сг, получим
jt/2
х у е^""")(cos
B.66)
2.4. Гармоническая нормальная нагрузка 101
Для дальнейшего вычисления представим гипергеометриче-
гипергеометрическую функцию ii*2, входящую в B.66), в виде ряда. Это приведет
к следующему выражению:
«,
)=27rr(w+a)r(t/;;;1)
fИ-
EICT
4/ n!
f e**"-")(cos (в))^Аая <fa. B.67)
Далее подставим в B.67) вместо Л его выражение из B.62).
В результате получим
( )„( /)п V 4 У п!
1Г/2
х У e"(J/-'')(cosE))l/+''+n(o2e" + b2e-»8)nds. B.68)
-,г/2
Таким образом, для вычисления величины /^(а, Ь, к, d, d)
осталось вычислить интегралы вида
*/2
VI(a, /3, a, b, с) = / eiee (cos (8)f(a2eis + 62e-")cds. B.69)
Интегралы вида B.69) приведены в [19, с. 92], [59, с. 496] и
[115, с. 451], однако, поскольку во всех указанных литературных
источниках имеются опечатки (в [19] пропущен множитель, а в [59]
и [115] изменен знак у одного из аргументов гипергеометрической
функции), проведем вычисление таких интегралов.
102 Гл. 2. Двухбазисный проекционный метод
Предположим для определенности, что a < b, тогда
ж/2
VI(a, C, a, b, с) = Ь2с / e'as(cos(s)) Vic
-тг/2
т/2
(¦COSI
-тг/2
тг/2
= ^ / e'(-«=)* (c
00 ^ ^ /2\n
•П + 1)я /О^П / <{о
*/2
^+1)" ^ | cos ((a-c + 2n)s) (cos
-1Г/2
ж/2
c-n + l)n^\ Los((a_c
B.70)
Следовательно, осталось вычислить интеграл вида
/ cos (hs) (
cos (§)) as.
о
Такой интеграл имеется в [115, с. 402]. Согласно [115]
тг/2
/
/ cos (hs) (cos (s)) ds =
Подставив B.71) в B.70), получим
00 ( — -1-11 / 2
F/(a, /?, a, 6, с) = 2Ь2с2-Р~1пГ(р + 1) У^ — ;—— ( тт
1
2.4. Гармоническая нормальная нагрузка 103
Далее учтем, что T(z + п) = Y(z)(z)n- В результате получим
Заметим также, что Г(г — п) = Г(г)/(г — п)п. Воспользовав-
Воспользовавшись этим равенством, получим
a, Д о, 6, с) =
Г@8 + a - с)/2 + 1)Г((/3 - a + с)/2 + 1)
Наконец, учтем, что имеет место равенство (z — п + l)n = [~z)n x
х(—1)п. Из него следует
VI(a, /3, a, 6, с) =
a - с)/2 + 1)Г@9 - a + c)/2
(-c)B((a-/3-c)/2),/«»\»
Нетрудно заметить, что сумма в B.72) представляет собой ги-
гипергеометрическую функцию. Таким образом, окончательно имеем
VI(a, p, о, Ь, с) =
Г((/3 + a - с)/2 + 1)Г@9 - a + с)/2 + 1)
_ / a-P-c a + 0-c , a2\ /ft „.
х Л (-с, —j—; —j— +1; ^ J • B.73)
Еще раз заметим, что полученная формула B.73) отличается
от формулы, приведенной в [19], тем, что там пропущен множи-
множитель 62с, а от формул, имеющихся в [59] и [115], знаком второго
аргумента у гипергеометрической функции.
104 Гл. 2. Двухбазисный проекционный метод
Заменив интегралы в B.68) их выражениями из B.73), по-
получим
2тг Г(
^ (g)w 2"
. X у . v . ч I —— I "—7 X
7г2~|/~^*"пЬ2лГA/ + /i + п + 1)
X —
Выполнив сокращения и простейшие преобразования, оконча-
окончательно получим. В случае a < Ь
I (аЬкбЛ-
i^^o, о, к, с/, о;—
« + а)Г(и
B.74)
Очевидно, что при b < а имеет место равенство
/^(а, 6, к, 0, d) = VF, а, к, 0, rf). B.75)
Аналогично вычислению /^(а, 6, к, 0, с/) можно вычислить
интегралы ^^(а, 6, к, 0, d). Для этого прежде всего воспользу-
воспользуемся B.63) и подставим выражение для произведения функций
Бесселя в B.61). В результате имеем
00
Juli(a, Ъ, к, в, d) = />-V - d2)«-i
J
d
т/2
j г*»-*)(cos
оо
х| fxe-1{x2-d2)K-1Jl/+JXx)dx)ds. B.76)
(f в-1/ 2 л2чк-1
ч
2.4. Гармоническая нормальная нагрузка 105
Входящий в B.76) внутренний интеграл по х вычислен в [116,
с. 178]. Согласно [116]
с-1
Jt(cx)dx =
-к-
,де+2,с-3,2-0-2кГ(*-1 + @ + *)/2)
~'~ .ir-i-ft — в)/2)
При подстановке B.77) в B.76) получим
Лм(а, 6, ас, 0, d) = J^(a, Ь, «, 0, d) + J^{a, ft, «, 0, rf), B.78)
где
^(a, Ь, «, 0, d) = -
7Г/2
x / e«->(,
cos
(a, b, к, 9, d) =
B.79)
VW(k + (t-1)
тг/2
-«г/2
(dA\
1-«;2-к-о-, 2 + <7-/«-fl; — 1 ds. B.80)
Для вычисления J^(a» ^> K) ^» *Q и ^(a> ^» к> ^> *0 восполь-
воспользуемся тем же приемом, что и при вычислении IVfl(a,b,K,e,d), и
заменим в формулах B.79), B.80) гипергеометрические функции
7 Зак. 205
106 Гл. 2. Двухбазисный проекционный метод
1F2 их выражениями в виде ряда. После этого получим
^(а, Ь, к, 0, d) =
х
оо
-тг/2
к)ГA - к - а)
/
х /" e'^-ri (cos {s)Y+ll\2nds. B.81)
-тг/2
Подставив в B.81) вместо Л его выражение из B.62), получим
/„„(о, Ь, к, 0, rf) -
00
И,
/
/" e"('/-'i)(cos(s))l/+/'+n(o2eis + b2e-is)nds. B.82)
Интегралы, содержащиеся в B.82), уже вычислены выше
(см. формулу B.73)). Предположим для определенности, что
а < Ь, и подставим B.73) в B.82). В результате выражение для
J3/t(°) Ь) к) 0> d) примет вид
, fe, к,
х 2Fi [ -n, ~/i - n; v + 1; ^ J .
2.4. Гармоническая нормальная нагрузка 107
После сокращений и простейших преобразований окончательно
получим. При a < Ь
J4a b uO J)
jvli\ay о, к, и, а) - 2„
'^' "' "' v' "' 2"+/^+1ГA - a)V{y
00 / ч /
В случае а> b очевидным образом имеем
J*,(a, Ь, к, в, d) = Jl^(b, а, к, в, d). B.84)
Аналогично, J^a, b, к, в, d) можно представить в виде
а -
оо
п=о B ~ « - <т)« B + <т - « - ^)„
7Г/2
/ is(i/—fi) (
22tr+2«-3al'VtT(K + a-
тгГB - к + a - в)
•i)v
Z-^ (
n=0 v
/ ^2
2A—к—a) I ®
l\2\»
A 1 Л
-сР/4)п
\-а-к- в)пп\
v I pW^-M) /лло /о^|/+'* \2A-л-а+п) ^в /о qk\
Подставив в B.85) вместо Л его выражение из B.62), получим
A - к)п21-/с~<г+п (-d2/4)n
n/ х i ill Л L i— у
-*/2 B.86)
7*
108 Гл. 2. Двухбазисныи проекционный метод
Предположим, наконец, что о < Ь, и подставим в B.86) значе-
значения входящих в эту формулу интегралов из B.73). В результате
будем иметь
n\T(v + l)T{fi + 2-к-а + п)
x2Fi Iк + a-n-l, к + a-fi-n-l; u + 1; ^-J . B.87)
Делая в B.87) простейшие преобразования, в случае а < Ь
окончательно получим
а" 1 /2\в+2"~2
а 1 2
(a, Ь, K,9,d) = —- (j
X
00 /-
n=0 v
X
(« + о - п - 1, к + о - /х - п - 1; v + 1; -тх),
ИЛИ
0+2к-2
T(z/ + 1)Г(/х + 2 - к - сг)
^ B - к - а)„(/х + 2 - к - (т)„ п!
х 2^1 (к + <т - п - 1, к + <т - /г - п - 1; I/ + 1; ^-J . B.88)
В случае а> b справедливо равенство
J%{a, Ь, к, 0, d) = Jj,(b, а, к, 0, d). B.89)
2.4. Гармоническая нормальная нагрузка 109
Таким образом, интегралы /^(а, Ь, к, 0, d) и ^(а, Ь, к, 0, d)
вычислены.
ИзB.58) и определения B.61) следует, что
АеЧГЦх) = 2?" V+IrG + 1)/Г2{470,7+1 (г, а, |, 3 - 7, /?) -
-4Jo,7+i К. °' 2' 5 ~ 7) а) +4^2jo.7+i (r> °> 2' 3 ~7' а) ~
-/3*70,7+1 (г, а, i, 1 - 7,а)|. B.90)
Подставляя в B.90) вместо ^(а, 6, к, d, d) их вычисленные
выше значения из B.78), B.83), B.84) и B.88), B.89), получим
В случае г < а (т.е. внутри носителя функции
ГG
г2
"Х
4ГG + 3/2) ^ G + 3/2)nn!
V".4-T-n;l;^l. B.91)
Здесь »?2 = а2//?2 = A - 2i/)/B(l -1/)),
_ 2Bп+1) 2 Bп+1)Bп+3) 4
п + 1 V + (n + lKn + 2I7
В случае г > а (вне носителя функции
A/2)п„!
-n, ^-«57 + 2; ^J. B.92)
110 Гл. 2. Двухбазисный проекционный метод
Из B.59) и определения B.60) следует, что
BfiW{x) = -Я-^Цу + 1)/Г2{4/0O+1 (г, а, |, 3 - ъ
+4J0l7+i (г, а, -, 5 -7, а) - 4?2Jo,7+i (г, а, -, 3 - 7, ос) +
. B.93)
Подставим в B.93) вместо /^(a, b, к, 9, d) их вычисленные
выше значения из B.74), B.75). В результате получим. В случае
x 2FX (-n, -7 - 1 - n; 1; ^V B.94)
В случае г > о
4G + 1) ^ C/2)„п!
х 2^1 ( -n, -n; 7 + 2; ^ J . B.95)
Здесь
O/«« I 1\ Л?.(~* I 1 \ /«л I O\ T
o(fl-г 1; 2 lo^fl T" lj^fl H~ Zj 4 I
8(n +1)
Из формул B.91), B.92), B.94) и B.95) видно, что
разлагается в ряд по четным степеням /?, а Вр^!1{х) — по нечет-
нечетным степеням, начиная с третьей. При /? = 0 Вр^(х) обраща-
обращается в ноль, а Ар№(х) с точностью до постоянного множителя
совпадает с результатом применения к функции Ф7(ж) оператора
статической задачи (формула B.29)). Отличие на постоянный
множитель связано с несколько иной записью уравнения в дина-
динамическом случае.
Заметим, что первые два аргумента у гипергеометрических
функций, входящих в выражения для Л^Ф7(гг) и Вр^{х)) умень-
уменьшаются на единицу при переходе к следующему члену ряда. По-
2.4. Гармоническая нормальная нагрузка 111
этому в расчетах значения гипергеометрических функций можно
вычислить как непосредственно с помощью ряда B.28), так и с
использованием рекуррентных соотношений для гипергеометри-
гипергеометрических функций. Например, согласно [18]
2Fi(a - 1, 6 - 1; с; z) = р\ 2Fi{a, 6 - 1; с; z) + qi 2Fx{a, 6; с; z),
2Fi(a- 1, 6-2; с; z) = p22*i(a, 6- 1; с; z) + 922^1 (а, 6; с; г),
B.96)
где pi = (с - а - 6 + l)/(c - а); qx = F - 1)A - *)/(с - *);
р2 = [Р1(с - 26 + 2 + (Ь - ф) + qi(c - 6)]/(с -6+1); д2 =
( )/()
9( )/()
Таким образом, вычислив и запомнив значения для двух ги-
гипергеометрических функций 2Fi(a, b; с; z) и 2^1 (я> 6 — 1; с; г),
можно получать значения функций 2Р\ (а — п, 6 — п; с; z) для лю-
любого натурального п с помощью соотношений B.96).
После вычисления Щ^(х) имеются все необходимые анали-
аналитические результаты для разработки программы расчета динами-
динамической задачи о трещине отрыва двухбазисным проекционным
методом. Рассматрим примеры задач, решенных с помощью такой
программы.
Прежде всего рассмотрим задачу о круговой трещине и про-
проанализируем влияние коэффициента Пуассона v на решение за-
задачи. Для определенности при численном решении радиус круго-
круговой трещины брался равным единице. В случае, когда амплитуда
приложенной нагрузки однородна и равна единице (*з(#) = 1)?
первый базис е{(х) строился с учетом известной асимптотики ре-
решения у контура трещины и осевой симметрии задачи. В каче-
стве ео(х) была выбрана функция ео(х) = у/1 — \х\2 = \/1 — г2,
а в качестве д%{х) брались тригонометрические функции д%{х) =
= cos [(< — 1)тгг]. Рассматривались также д%(х), включающие как
тригонометрические функции, так и полиномы. Количество эле-
элементов первого базиса в зависимости от волнового числа /3 варьи-
варьировалось от четырех до семи.
Второй базис, как и в статическом случае, строился путем орто-
гонализации в Ь2{0) функций $*(#)• Количество элементов вто-
второго базиса доводилось до 19. При этом показатель у варьиро-
варьировался от двух до шести. Полученные результаты при различных
7 оказались близки между собой. Приведенные ниже результаты
соответствуют 7 = 3.
Так как осевая симметрия решения учтена в базисе е{(х) =
== ео(#Mг(ж), ПРИ построении базиса <pj достаточно пользоваться
функциями фа (#) с круговыми носителями, центры которых рас-
расположены вдоль какой-либо одной оси. Однако в выбранных функ-
функциях ф%(х) центры носителей брались не только на одной прямой
112
Гл. 2, Двухбазисный проекционный метод
для того, чтобы сократить количество пересечений носителей и
тем самым упростить ортогонализацию. В табл. 2.5 представлены
координаты центров (ai, аг) и радиусы аз круговых носителей,
отвечающих девятнадцати функциям фа(х), использованным в
расчетах.
Таблица 2.5
0
0
0,5
0
0,333
0
0,6
0
0
0
0
0
0
0
аз
1
0,5
0,5
0,333
0,333
ОД
0,2
он
0,667
0
0
0
0
0
а2
0
0
0,25
0,5
0,75
0,9
аз
0,333
0,25
0,25
0,25
0,25
ОД
ai
0,249
0,332
0,415
0,498
0,581
0,4
аг
0,249
0,332
0,415
0,498
0,581
0
а3
0,125
0,125
0,125
0,125
0,125
0,2
На рис. 2.1 представлены графики изменения отношения мо-
модуля амплитуды КИН к КЙН соответствующей статической задачи
(\Ni\/Ntst) в зависимости от /? при различных значениях коэффи-
v = 0,25 -о v = 0,4
0,5 -*-v = 0,25[304]
Рис. 2.1. Влияние коэффициента Пуассона
циента Пуассона. Сплошные линии отвечают полученным в расче-
расчетах результатам для коэффициентов Пуассона v = 0,25; 0,4; 0,49;
0,5 соответственно. Для сравнения на графике приведен также ре-
результат из [304], отвечающий v = 0,25 и изображенный штриховой
2.4. Гармоническая нормальная нагрузка
113
линией. Согласно полученным результатам, при v = 0,25 макси-
максимальное значение \Ni\/Nlst достигает 1,52, что несколько выше,
чем в [304] и в представленных в гл. 3 результатах аналитико-
численных расчетов. На рис. 2.1 не представлены также получен-
полученные в результате расчетов кривые, отвечающие v = 0,1 и^ = 0,3,
поскольку они совпадают с известными результатами (см., напри-
например, [388]) с такой же точностью, как и приведенные кривые для
v = 0,25.
Из рис. 2.1 видно, что максимальное значение \Ni\/Ni8t зави-
зависит от v. В табл. 2.6 приведены максимальные значения |М|/
обозначаемые |iVi|max/Ni5*, в зависимости от v.
V
0,1
1,51
0,25
1,52
0,4
1,69
0,45
1,84
Таблица 2.6
0,49
2,25
0,5
2,78
Согласно полученным результатам зависимость \Ni\max/Nist от
v не очень значительна до v = 0,4, где изменения происходят
в пределах от 1,5 до 1,7. В интервале 0,4 < у < 0,5 увеличение
щие i
от /3res
Рис. 2.2. Устойчивость результатов
становится существенным и достигает 2,78. Отвечаю-
Отвечаю/JV'ist значения f3 = /?res также зависят от v и меняются
1,5 при v = 0,25 до /?res ~ 1,9 при v = 0,5.
114
Гл. 2. Двухбазисный проекционный метод
Несмотря на то, что при v = 0,5 скорость распространения
продольной волны бесконечна, уравнение B.54) сохраняет смысл.
Поэтому на рис. 2.1 и в табл. 2.6 приведены результаты, отвечаю-
отвечающие предельному значению v.
Для иллюстрации устойчивости полученных численных ре-
результатов на рис. 2.2 приведены зависимости \Ni\/Nist от @ для
двух значений коэффициента Пуассона {у = 0,25 и и = 0,49) при
разных количествах первого и второго базисов. Коэффициенту
Пуассона v = 0,25 отвечают расчеты с пятью элементами первого
базиса и 15 второго (сплошная кривая) и шестью первого и 18
второго (штриховая кривая). Коэффициенту v = 0,49 отвечают
расчеты с пятью элементами первого и 17 второго (сплошная кри-
кривая) и пятью первого и 19 второго базисов (штриховая кривая).
Из рис. 2.2 видно, что кривые для разных базисов практически
совпадают.
Для анализа влияния неоднородности прикладываемой нагру-
нагрузки на зависимость КИН от волнового числа были проведены рас-
расчеты для случая нагрузок, амплитуды которых зависят от коор-
координат (<з = t(x))- Оказалось, что вид функции t(x) существенно
влияет на превышение амплитудой КИН статического значения.
На рис. 2.3 изображены зависимости \Ni\/Nf*8t от /?, отвечающие
0,5 1,0 1,5 2,0 2,5
-*-t-r2 -cw-1-r2
Рис. 2.3. Неоднородная амплитуда нагрузки
задаче о круговой трещине единичного радиуса при коэффици-
коэффициенте Пуассона и = 0,25 и нагрузках t(x) = г2 и t(x) = 1 — г2.
Здесь N®st — значение КИН, отвечающее статической задаче и
2.4. Гармоническая нормальная нагрузка
115
однородной нагрузке t{x) = 1. Значения \Ni@)\/N^sU вычислен-
вычисленные аналитически согласно [105], обозначены на рис. 2.3 штри-
штрихами и равны для нагрузок t(x) = г2 и t(х) = 1 — г2 2/3 и
1/3 соответственно. Если для t(x) = г2 максимальное значение
\Ni(/3)\/Ni@) равняется 1,3, что ниже, чем в случае t(x) = 1, ко-
когда max \Ni(C)\/Ni@) « 1,52, то при t(x) = 1 — г2 максимальное
значение \Ni(P)\/Ni@) достигает 2,1.
Влияние формы трещины на распределение КИН вдоль ее кон-
контура исследовалось на задачах о квадратной и эллиптических тре-
трещинах при однородной нагрузке.
На рис. 2.4 приведены зависимости \Ni(C)\ в двух точках A; 0)
и A; 0,6) стороны квадратной трещины. Расчеты проведены для
случая v = 0,2 и квадрата, длина стороны которого равна 2
Рис. 2.4. Квадратная трещина
(|| < 1, |#2| < 1)- Амплитуда нагрузки предполагается еди-
единичной (t(x) = 1). Штриховой линией проведена кривая, полу-
полученная в [255]. При решении задачи первый базис выбирался
аналогично статическому случаю. С учетом симметрии и осо-
особенностей в угловых точках в качестве функции ео(х) была
выбрана такая же функция, что и в §2.3, а именно: ео(х) =
= д/A-*?)A-*|) (ПГ2ГЗГ4)'184, где г? = (а* -1J + (а* -1J;
Т\ = (XI - IJ + (Х2 + IJ! Т\ = (X! + IJ + (Х2 + IJ! Л =
= (#i + IJ + (#2 — IJ- Функции д%{х) брались как в виде gi{x) =
= cos (kA) cos (mB) + cos (mi) cos (fcl?), A = irx\, В = тгжг, так
116
Гл. 2. Двухбазисный проекционный метод
и вместе с полиномиальными функциями. Количество элементов
первого базиса доводилось до семи. Количество элементов вто-
второго базиса доводилось до 18. Второй базис строился из функций
Фа(х). Значения c*i, с*2, с*з> отвечающие этим функциям, приве-
приведены в табл. 2.7.
Таблица 2.7
0
0
0,5
0,5
0
-0,25
а2
0
0
0
0,5
0
0
аз
1
0,5
0,5
0,5
0,25
0,25
«1
-0,5
-0,75
-0,75
-0,574
-0,398
0,277
С*2
0
0
-0,75
-0,574
-0,398
0,115
аз
0,25
0,25
0,25
0,25
0,25
0,25
ai
0,554
-0,875
-0,875
-0,875
-0,875
-0,875
а2
0,230
0
0,125
0,25
0,375
0,5
аз
0,25
0,125
0,125
0,125
0,125
0,125
Отметим, что для тех значений /?, до которых было доведено
решение в [255] @ ^ /? ^ 2,4), полученные там результаты (штри-
(штриховая кривая) хорошо совпадают с результатами, полученными с
помощью двухбазисного метода. В указанном диапазоне измене-
изменения /3 модуль амплитуды КИН достигает максимального значения
в серединах сторон квадрата. При дальнейшем увеличении C мак-
максимум модуля амплитуды КИН начинает смещаться от середины
стороны квадрата и достигается в 8 точках (по 2 точки на каждой
стороне, симметричные относительно середины этой стороны).
Расчеты для эллиптических трещин (rcf/af + x^/a^ ^ 1) про-
производились для эллипсов с отношениями полуосей а>2 :сц, равными
1:2 и 1:4. При этом в качестве ео(х) бралась функция ео(х) =
= A - х\/а\ - хЦа^I/2, а функции &(#)? с учетом симметрии
задачи, брались как в виде gi{x) = cos (kA) cos (mB) + cos (mA) x
x cos(fcB), A = nxi/ai, В = тгжг/аг, так и вместе с полиноми-
полиномиальными функциями. Количество элементов первого базиса дово-
доводилось до 15 (в определенных выше функциях д%{х) величины к
и га выбирались так, чтобы к + m ^ 15). Для эллипса с отноше-
отношением полуосей 1:2 количество элементов второго базиса доводи-
доводилось до 35, а для эллипса с отношением полуосей 1:4 — до 45.
Второй базис строился из функций Фа(х). Значения (ai, c*2, аз),
отвечающие функциям ф%{х), использованным при решении за-
задачи об эллиптической трещине с полуосями а\ = 2, a<i = 1,
приведены в табл. 2.8. Значения (ai, #2, аз)> отвечающие задаче
об эллиптической трещине с полуосями а\ = 4, a<i = 1, приведены
в табл. 2.9.
Кривые изменения нормированного значения модуля ампли-
амплитуды КИН \NI(/3a2)\/Ni@) от обезразмеренного волнового числа
2.4. Гармоническая нормальная нагрузка
117
/Зп2 для коэффициента Пуассона v = 0,25 и эллипсов с отношени-
отношениями п2 : ai, равными 1:1, 1:2 и 1:4 в вершинах малой полуоси
эллипсов @; аг), изображены на рис. 2.5 и в вершинах большой
полуоси (ai; 0) — на рис. 2.6. На рис. 2.5 помимо указанных кри-
кривых штриховой линией проведена также кривая, взятая из [305]
(см. также [391]), отвечающая решению плоской задачи для тре-
трещины длины 2а2.
Таблица 2.8
0
-0,5
1
0
0
-1,25
1,875
1,575
0,2
0,5
-0,5
-1,25
0
0
0
0
-0,75
0
0
0,475
0,87
0,843
-0,25
-0,25
1
0,5
0,816
0,25
0,25
0,25
0,125
0,117
0,125
0,124
0,25
0,25
ai
0
-1
-1
0
-0,75
1,775
0
0,3
0,6
-0,75
-0,5
0
0
0,5
-0,25
0
0
0,282
0,875
0,864
0,83
-0,25
-0,5
аз
0,5
0,5
0,35
0,25
0,25
0,25
0,12
0,125
0,125
0,123
0,25
0,25
<ы
0
-1,5
-1,5
0
-1
-1,75
1,675
-0,1
0,4
0,7
-1
«2
0,5
0
0,25
-0,5
0
0
0,393
0,874
0,855
0,812
-0,25
а3
0,5
0,5
0,341
0,25
0,25
0,25
0,118
0,125
0,124
0,123
0,25
Таблица 2.9
ai
0
1
-3,5
1,5
0,5
2
0
0,5
2
0,5
2
1
3,75
1
-3,875
OL2
0
0
0
0
0,5
0,5
-0,25
0
0
0,25
0,25
0,5
0
0,845
0
аз
1
0,966
0,428
0,5
0,492
0,362
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,123
0,125
ai
0
2
0,5
2
1
2,5
0
1
2,5
1
2,5
1,5
0
1,5
-3,675
OL2
0
0
0
0
0,5
0,5
-0,5
0
0
0,25
0,25
0,5
0,875
0,805
0,254
аз
0,5
0,856
0,5
0,5
0,467
0,275
0,25
0,25
0,25
0,25
0,25
0,25
0,125
0,121
0,12
ai
0
3
1
2,5
1,5
0
0
1,5
3
1,5
0,5
3,5
0,5
2
-0,347
OL2
0,5
0
0
0
0,5
0
-0,75
0
0
0,25
0,5
0,25
0,868
0,747
0,372
аз
0,5
0,632
0,5
0,5
0,425
0,25
0,25
0,25
0,25
0,25
0,25
0,211
0,125
0,118
0,112
118
Гл. 2. Двухбазисный проекционный метод
В табл. 2.10 приведены значения (/?a2)res? в которых функции
\Ni(C(i2)\/Ni(Q), рассматриваемые в вершине малой полуоси элли-
эллипса @; аг), достигают первого максимума и сами значения этих
Nl(pa2)\/Nl@)
1,4
1.2
1,03
0,8
0,6
i i i
0,0
0,5
1.0
1.5
-¦-1:1 -^-1:2 -ь-1:4 --м- [305]
Рис. 2,5. КИН в вершине малой полуоси эллипса
максимумов (|iVI(/9a2)|/iVI@))max. Для сравнения представлены
также соответствующие величины для решения плоской задачи.
-«-1:1 -—1:2 -4-1:4
Рис. 2.6. КИН в вершине большой полуоси эллипса
2.4. Гармоническая нормальная нагрузка
119
Из рис. 2.5, 2.6 и табл. 2.10 видно, что с увеличением отноше-
отношения а\ :п2 значения (/3a2)res? отвечающие точкам контура @; аг),
сходятся к величине (/3a2)res для плоской задачи. Сами же зна-
значения |iV/((/3a2)res)|/^4r@) в рассмотренном диапазоне изменения
а\: о>2 изменяются слабо, причем с увеличением a\: a<i ведут себя
немонотонно.
Таблица 2.10
а\ :п2
(/fo2)res
|W((/Ja2)«)|/M@)
1
1,5
1,52
2
1,15
1,55
4
0,95
1,52
00
0,8
1,3
Как уже отмечалось выше, задача о трещине, к поверхностям
которой приложены гармонически зависящие от времени усилия,
соответствует задаче рассеяния трещиной плоских упругих волн.
В частности, рассматриваемая здесь задача о трещине, поверхно-
поверхности которой нагружены равными по величине и противоположно
направленными, гармоническими по времени, нормальными к
поверхностям трещины усилиями, отвечает задаче рассеяния
трещиной нормально падающей продольной волны. Иными сло-
словами, это означает, что если в безграничном пространстве рас-
распространяется волна U\ = U2 = О, Щ = Aexp[—iu(r — xs)/cd]
(здесь U{ (i = 1, 2, 3) — компоненты вектора смещений, с<* =
= [(\+2ц)/д] — скорость распространения продольной волны)
и в плоскости #з = О имеется трещина, то решение задачи пред-
представляет собой сумму падающей и рассеянной волн. При этом
рассеянная волна определяется решением задачи о трещине, к по-
поверхностям которой приложены усилия ±te~luJT, t = (?1, ?2, *з)?
ti = <2 = 0, <з = Л(Х + 2fj,)iu/C(i. Эти нагрузки снимают усилия,
определяемые падающей волной.
Поэтому, когда рассматриваются задачи рассеяния, помимо
КИН интерес представляют и некоторые интегральные характе-
характеристики решения. К ним относится, например, полное сечение
рассеяния, используемое при обнаружении и идентификации де-
дефекта в неразрушающих методах контроля. Полное сечение рассе-
рассеяния характеризует эффективность рассеяния трещиной плоских
упругих волн. Согласно определению, полное сечение рассеяния
равно отношению усредненного по периоду колебаний потока энер-
энергии рассеянной волны, распространяемой во всех направлениях,
к так же усредненному потоку энергии падающей волны, прохо-
проходящей через единичную площадку, перпендикулярную направле-
направлению падения. В [171] показано, что рассматриваемая величина
выражается через главные члены асимптотики дальнего поля пе-
перемещений для рассеянной волны в направлении распростране-
120 Гл. 2. Двухбазисный проекционный метод
ния падающей волны. В [226] дано представление дальнего поля
перемещений через интегралы от скачков перемещений в плос-
плоскости трещины. Согласно [226] в направлении падающей волны
(в рассматриваемом здесь случае это направление @, 0, 1)) компо-
компоненты вектора перемещений рассеянной волны us = (u{, г^, г*§)
имеют вид
^, „.„ма^, ц«^ме-5 B97)
г г г
где г — расстояние от начала координат, расположенного в области
трещины, до точки наблюдения. Предполагается, что г велико по
сравнению с размерами трещины.
Из приведенных в [226] представлений для hj через скачки
перемещений в области трещины [u] = ([tii], [г^]? [^з]) следует
dx=i?
G G
dx=s /lW) "*¦
Поскольку здесь рассматривается падение продольной волны,
нормальное к плоскости трещины, то [щ] = [г^] = 0 и, следова-
следовательно, Л-i (/?) = /i2(/?) = 0. Полное сечение рассеяния для про-
продольной волны Ер, согласно [171], в случае, если перемещения
падающей волны имеют единичную амплитуду, представляется в
виде
Ер = — 1тЛ3(о), B.99)
a
где 1т обозначает мнимую часть числа.
Из B.98), B.99) следует, что
= Im I i / [г1з(жI dx I.
\l )
B.100)
Здесь [г*з(#)] — скачок нормального смещения в области тре-
трещины, отвечающий нормальной нагрузке *з = —г{\ + /
2.4. Гармоническая нормальная нагрузка
121
Таким образом, если обозначить скачок нормального смеще-
смещения, отвечающий нагрузке *з = А*? через [^(ж)], то из B.100)
получим следующее выражение для полного сечения рассеяния:
ЕР = ^ Am [ul{x)] dx, B.101)
где величина г) определена в B.91).
На рис. 2.7 представлены зависимости полного сечения рас-
рассеяния ЕР, нормированного на площадь S области, занимаемой
трещиной, от безразмерного волнового числа /За для случая кру-
-e-v-0,4 -o-v-0,45 — v-0,25
Рис. 2.7. Влияние коэффициента Пуассона на полное сечение рассеяния
говой трещины радиуса а и коэффициентов Пуассона v = 0,25,
i/ = 0,4 и i/ = 0,45. Расчеты проведены по формуле B.101), в
которой функция [г*з(#)] была определена из решения уравнения
B.54) двухбазисным проекционным методом.
Величины полного сечения рассеяния при рассеянии плоской,
нормально падающей продольной волны круговой трещиной были
вычислены в целочисленных точках /За = 1, 2, ..., 8 в [285] (см.
также [314]). Результаты, представленные на рис. 2.7, находятся
в хорошем согласии с результатами [285, 314].
Поскольку двухбазисный проекционный метод позволяет ре-
решать задачи для трещин произвольной формы, проанализируем
также влияние формы трещины на полное сечение рассеяния. На
122
Гл. 2. Двухбазисный проекционный метод
рис. 2.8 представлены зависимости Ер(^5го)/5Г для трещин тех же
форм, для которых выше были вычислены КИН, т.е. для ква-
квадрата, крута и эллипсов с отношением полуосей 1:2 и 1:4. Здесь
го — радиус круга, площадь которого равна 5. Всюду предполага-
предполагается, что коэффициент Пуассона v = 0,25.
Если обозначить через (/?ro)res значение, в котором HP(j3ro)/S
достигает первого максимума, то из рис. 2.8 видно, что с уве-
увеличением эксцентриситета эллипса значения ((Зго)те8 растут.
2,5
2,0
1,5
1,0
0,5
-•-круг -о-квадрат -*—эллипс 1:2 -*-эллипс 1:4
Рис. 2.8. Влияние формы трещины на полное сечение рассеяния
Среди рассмотренных форм трещин максимальное значение
ЕР ((/?ro)res) /S принимается на круговой трещине. Эти численные
результаты позволяют предположить, что имеет место следующее
изопериметрическое неравенство. ,
Среди всех трещин заданной площади максимальное значение
?P((/?ro)res) достигается на круговой трещине.
Представленные в данном параграфе результаты были полу-
получены в [67-70].
2.5. Гармоническая сдвиговая нагрузка
Система граничных псевдодифференциальных уравнений от-
относительно скачков смещений, отвечающая задаче о трещине
сдвига, нагруженной гармоническими по времени усилиями, при-
2.5. Гармоническая сдвиговая нагрузка 123
ведена в гл. 1 (формула A.54)). Она имеет вид
У& [u(s)]=0, x?G, B.102)
где [u(x)] = ([tii(ж)], [п2(ж)]) — вектор амплитуд скачков сме-
смещений, t(x) = (*i(#), t2{x)) — вектор амплитуд приложенных
усилий, Кр — матричный псевдодифференциальный оператор с
символом
(кп@
Выражения для функций Кц(?) (г = 1, 2; j = 1, 2) приведены в
гл. 1.
В гл. 1 было доказано, что оператор рвКр изоморфно отобра-
о
жает Н\/2 (G) на H_i/2(G). Поэтому для численного решения си-
системы уравнений B.102) можно применить вторую разновидность
двухбазисного проекционного метода.
При применении двухбазисного метода, как и в случае задачи
о трещине отрыва, выберем в качестве пространств Н, Н1 и Щ
о
пространства H\/2(G), H_i/2(G) и L2(G) соответственно. Заме-
Заметим также, что, поскольку главный член оператора Кр совпадает с
оператором статической задачи для трещины сдвига, решение си-
системы B.102) обладает теми же особенностями, что и решение ста-
статической задачи, в частности, имеет корневую асимптотику вблизи
гладкой части контура. В связи с этим базис ei(x) можно строить
аналогично случаю отрыва, т. е. приближать каждую из компонент
вектора скачков перемещений такими же базисными функциями,
которые были использованы при решении задач о трещине от-
отрыва.
Базис tpj будем строить путем ортогонализации в L2 {G) си-
системы вектор-функций, компонентами которых являются функции
^а(ж), использованные выше. Более точно, для построения <pj
используем вектор-функции фь = (фа (ж), 0) и фь = @, фа (ж)).
Для получения уравнений относительно коэффициентов разложе-
разложения решения по первому базису B.16) необходимо вычислить сле-
следующие вектор-функции:
124
Гл. 2. Двухбазисный проекционный метод
Из B.103) видно, что достаточно уметь вычислять
гласно определению
а- Со-
Сов?
B.104)
Поскольку вектор функции Кцф% для различных (ai, 0:2) от-
отличаются только на сдвиг, далее будем предполагать (ai, аг) =
= @, 0) и аз обозначать через а. Используя введенное выше
обозначение ф%(х) = Ф7(я), из B.104) и выражений для -К#(?),
приведенных в гл. 1, получим
. B.105)
Обозначим |а;| = yjx\ + х\ = г, |^| = i, подставим в B.105)
выражение B.24) для Ф7(?) и перейдем к полярным координатам.
Проинтегрировав по углу, получим
ОО \
+4^2 / \/*2-Р2Щъ а, г, t)dt\. B.106)
Здесь С = 2Т-1аТ+1ГG + 1); i?G, a, r, t) = rTJ7+1(ot)J0(r<);
j = 1, 2; а, /? — волновые числа.
Разделяя вещественную и мнимую части в операторах Kjj =
= Ajj + iBjj (j = 1, 2), из B.106), с учетом выбранных в гл. 1
2.5. Гармоническая сдвиговая нагрузка
125
ветвей при извлечении корней для ni(?) и П2(?)> получим
оо
' у, а, г, t)dt+
, a, г, t> *
00
3 P
==ldt+
, а, г, t) dt], B.107)
?
р
-р2 I i//32-t2DG, а, г,
о
д2 Г
—4 /
дхI
, а, г, t) dt—
Р(Ъ a, r, t)
dt-
-t2D(j,a,r,t)dt). B.108)
Аналогично,
f
. B.109)
Я2
Перейдя в B.109) к полярным координатам, заменив Ф7(?)
вьфажением B.24) и проинтегрировав по углу, получим
(Р dxi дх2
@0
4 f
00 ОО ч
/" В(Ъ a, r, t) dt _ 4 Г ^2_a2?,G) a> r> t)Л j. B.110)
У V<2-/32 / J
126
Гл. 2. Двухбазисный проекционный метод
Выделим в B.110) вещественную и мнимую части, учитывая
выбранные в гл. 1 ветви для квадратных корней при вычислении
ni(?) и П2(?)- В результате для вещественной и мнимой частей
оператора К и = Аи + гВи получим
BШ)
Из B.107), B.108), B.111), B.112) следует, чтоК^(х) выра-
выражаются через интегралы вида /^(а, 6, я, 0, d) и «/^(а, Ь, к, 0, d),
определенные в B.60), B.61), а также через вторые производные от
них. Вычисленные выражения для этих интегралов представлены
в формулах B.74), B,75), B.78), B.83), B.84), B.88) и B.89). Под-
Подставляя указанные выражения в B.107), B.108), B.111) и B.112),
получим
(-р2а2/4)пBп -
G + 1/2)„(п + 1)
при
2.5. Гармоническая сдвиговая нагрузка 127
Bп-1)(п-3/2J 1 (х
X
2 1 /-г2>
-". 2~п;7 + 4; г)]}
'-'1
п-1/2)(п + 1)! Bn3
E3 \
2 ~ п> 2 ~ 7 ~ П; 3; Z) При
2)г3
Bn-l)Bn-3),_ _ 1 _,_ 0^2п+2, / ^
n=0 ^
3 3 „ 1\ Bn-l)Bn-
1 /5 5
при z > 1,
128 Гл. 2. Двухбазисньш проекционный метод
+Bп + 1 + Vn+5) |2Fi(-n, -7 ~ n - 1; 2;
+nG + n + 1) ^2^(~п + 1, -7 - п; 3; z)\ \
При 2Г < 1,
+Bп
| (l + 2n^ J
2n2(n + 1) 1 ж?
-n,-n;7 + 3;i)
x 2F\ ( -n + 1, -n + 1; 7 + 4; - j > при z > 1,
(п + 1)(п + 2) / /32o2\w
+ 2)п V 4 j
E/2)„+2G
х 2-Fi(-rc, ~7 ~ n — 1; 3; 2:) при
2.5. Гармоническая сдвиговая нагрузка 129
Bп + 3 + 4т?2"+7)
E/2W2n! *
Здесь z = г2/а2) в соответствии с введенными выше обозначени-
обозначениями!/2 = A-2i/)/B(l-i/)); i = 1, 2.
В случае /3 = О формулы B.113) соответствуют результатам
применения элементов матричного оператора статической задачи
э трещине сдвига к функциям Ф7(#). Как видно из B.113), функ-
функции Ац^(х), отвечающие результатам применения веществен-
вещественных частей оператора Кр к базисным функциям, раскладываются
в ряд по четным степеням /?, а Б^Ф7(ж), отвечающие результа-
результатам применения мнимых частей оператора Кр, раскладываются в
ряд по нечетным степеням /?. Это вполне аналогично случаю опе-
оператора, соответствующего нормальному отрыву, рассмотренному в
предыдущем параграфе.
В результате применения двухбазисного проекционного метода
из уравнений B.16) определяются коэффициенты сг- разложения
решения по первому базису, что дает возможность найти прибли-
приближенные выражения для скачков смещений в области трещины [щ]
и [г42]. С помощью них можно вычислить все важнейшие харак-
характеристики решения исследуемой задачи. Как упоминалось во вве-
введении, согласно [117] КИЙ Кп и Кш определяются по скачкам
перемещений следующим образом:
К„ = Urn JЫ , ^, *1П = КшфЦ?, B.114)
1 в->6 2A-1/) у/з ' s-^o 2 yfs ' v ;
где [ttn], [ur] — скачки перемещений вблизи контура трещины
в нормальном и касательном к контуру трещины направлениях
соответственно. Значения [wn]5 [щ] берутся в точках области тре-
трещины G, лежащих на нормали к рассматриваемой точке контура
на расстоянии 5 от контура.
Сами скачки перемещений [nn], [ur] определяются с помощью
вычисляемых скачков [щ], [г^] по формулам
[ип] = [щ] cos в1 + [иг] sin в\ [ит] = — [iti] sin tf + [иг] cos
ЮЗак. 205
130 Гл. 2. Двухбаэисный проекционный метод
где О1 — угол между положительным направлением оси х\ и напра-
направлением внешней нормали к контуру трещины в рассматриваемой
точке.
Так же как и в случае отрыва, задача о трещине, к поверхно-
поверхностям которой приложены равные по величине и противоположно
направленные сдвиговые усилия, гармонически зависящие от вре-
времени, соответствует задаче рассеяния трещиной плоских упру-
упругих волн. В частности, если в безграничном упругом простран-
пространстве, ослабленном трещиной, занимающей область G в плоско-
плоскости #з = 0, распространяется плоская волна перемещений U\ =
= р1е-^(т-*з/с5)? и2 = р2е-{^т-х^\ щ = о (са = (/VeI/2 —
скорость распространения поперечной волны), то возникающие
перемещения представляются суммой перемещений, отвечающих
падающей и рассеянной волнам. При этом рассеянная волна опре-
определяется решением задачи о трещине, к поверхностям которой
приложены усилия ±te~lwr, ? = (ii, ?2, ^з)? h = цшР\/с8, t2 =
= fj,icvP2/cs, *з = 0. Эти усилия снимают напряжения, определяе-
определяемые падающей волной.
Для указанной задачи рассеяния полное сечение рассеяния Ss,
согласно [171], в случае, когда перемещения падающей волны име-
имеют единичную амплитуду, представляется в виде
Е* = jbn(b,h), B.H5)
где Im обозначает мнимую часть числа, b = Fi, Ьг? &з) — вектор
поляризации падающей волны, h = (/ii, h2, /13) — вектор, введен-
введенный в формуле B.97) и определяющий главный член асимптотики
поля перемещений рассеянной волны вдали от трещины в напра-
направлении распространения падающей волны @, 0, 1).
В случае, когда b = A, 0, 0) (т.е. Рх = 1, Р2 = 0), из B.115),
B.98) имеем
4тг f
25 = — Im/iiOS) =Imt / [ui]dx. B.116)
G
Обозначим вектор скачков перемещений, отвечающих нагрузке
t = (ti, i2, *з) = (^ 0, 0), через [u°] = ([u% [и§], 0). Выразив в
B.116) [щ] через [и% получим
Е3 = /3 flm[u\]dx. B.117)
G
В качестве примера рассмотрим задачи о круговой и квадрат-
квадратной трещинах. Во всех случаях будем предполагать, что ампли-
2.5. Гармоническая сдвиговая нагрузка Ш
туда приложенных к поверхностям трещины нагрузок имеет вид
t = (const, 0, 0).
При решении задачи о круговой трещине без ограничения
общности можно положить, что ее радиус равен единице. Пер-
Первый базис, как и прежде, будем строить в виде в{(х) = eo(x)gi(x),
где ео(х) = у/1 — г2, a gi{x) — полная система гладких вектор-
функций. При построении gi{x) удобно перейти к полярным ко-
координатам (г, 0), где в — полярный угол между радиусом векто-
вектором и осью х\. Разложим gi(x) в полярной системе координат в
ряд по тригонометрическим функциям и учтем, что для рассма-
рассматриваемой нагрузки решение обладает определенными свойствами
симметрии, а именно, [ui(rc)] является четной функцией по х\
и Ж2, a [w2(#)] является нечетной функцией по х\ и #2- В ре-
результате получим, что в качестве gi(x) можно выбрать следую-
следующую систему вектор-функций: gi(x) = (cos (jnr) cos Bтв), 0) и
gi(x) = (О, cos(&7rr)sinB/0)), где j, m, A;, / — целые неотрица-
неотрицательные числа.
Пусть для приближения решения использовалось п элементов
п
базиса в{. Обозначим ]? Cigi = [v] = ([vi], [t^]). Следовательно,
il
n
n
приближенное решение ?) сгег- представляется в виде ео(х) [v(x)].
г=1
Отсюда и из B.14) получаем выражения для Ки и Кт:
Ки' 2A-!/)' Кш~ 2 '
где [vn], [vr] — проекции вектора [v] на нормаль и касательную к
контуру трещины, а их значения берутся в рассматриваемой точке
контура.
Очевидно, что с ростом волнового числа /? для хорошего при-
приближения к решению нужно увеличивать количество используе-
используемых элементов базиса ег-(ж). Для значений /3 < 5,5 в расчетах
количество элементов этого базиса доводилось до 14. Количество
элементов второго базиса варьировалось от 50 до 70, для чего ис-
использовалось 25-35 функций вида ^(х). В функциях ipa(x) зна-
значение показателя 7 изменялось от 2 до 4. Полученные результаты
оказались близки друг к другу, т.е., как и в случае трещины от-
отрыва, значения 7 мало влияли на результаты численного счета.
Значения ai, c*2, аз, отвечающие использованным для построения
второго базиса функциям фа (ж)? приведены в табл. 2.11. В этой
таблице даны значения тридцати пяти троек чисел ai, c*2, аз,
для максимального количества функций ^2(#)? использованных
при решении задачи.
ю*
132
Гл. 2. Двухбазисныи проекционный метод
Таблица 2.11
0
0
0,25
0
0,75
0,74
0,5
0,77
0,62
0,13
0,31
0,5
0
0,5
0
0,25
0,25
0,5
0,74
0,37
0,13
0,62
0,81
0,25
аз
1
0,5
0,25
0,25
0,205
0,1
од
0,14
0,36
0,36
0,13
0,44
0
0,5
0,5
0,25
0
0
0,5
0,37
0,62
0,25
0,62
0,25
а2
0
0,5
0
0,25
0,5
0,75
0,5
0,77
0,37
0,25
0,62
0,5
аз
0,5
0,29
0,25
0,25
0,25
0,25
0,14
0,14
0,27
0,64
0,12
0,44
0,5
0
0,75
0,5
0,25
0,25
0,8
0,12
0,37
0,81
0,37
0
0
0
0,25
0,5
0,75
0,12
0,8
0,62
0,31
0,37
аз
0,5
0,25
0,25
0,25
0,25
0,205
0,19
0,19
0,27
0,13
0,2
Результаты расчетов представлены на рис. 2.9 и 2.10. На
рис. 2.9 изображены зависимости нормированных КИН Щг(Р) =
= \Ku(f3)\/Kn@) в точке контура 9 = 0 для коэффициентов Пуас-
1,3
1,2
1,1
1,0
0,9
0,8
0,7
0,6
0,5
0,4
1
5 р
v-0,1 v-0,3 ---v-0,5
Рис. 2.9. Влияние коэффициента Пуассона на Кп
сона v = ОД, v = 0,3 и v = 0,5. На рис. 2.10 изображены зави-
зависимости нормированных КИН K*u(l3) = \Km(P)\/Kul@) в точке
контура в = 7г/2 для тех же значений коэффициентов Пуассона.
В рассматриваемой задаче, так же как и в случае трещины от-
отрыва, несмотря на то, что при v = 0,5 скорость распространен
2.5, Гармоническая сдвиговая нагрузка
133
ния продольной волны бесконечна, граничное уравнение B.102)
сохраняет смысл. Поэтому на рис. 2.9, 2.10 приведены кривые,
отвечающие предельному значению и.
Полученные значения КИН для /3 = 0 отличаются от извест-
известных аналитических решений статической задачи не более, чем
Ч
1,3
1,2
1,1
1,0
0,9
0,8
0,7
0,6
0,5
-v-0,1
v-0,3 v-0,5
Рис. 2.10. Влияние коэффициента Пуассона на Кш
на 3%. Как видно из рис. 2.9, 2.10, в задаче о трещине сдвига уве-
увеличение v вплоть до 0,5 приводит к некоторому снижению КИН
в первом максимуме. В рассмотренной в предыдущем параграфе
задаче о трещине отрыва картина была противоположной и уве-
увеличение v до 0,5 приводило к существенному увеличению мак-
максимального значения КИН. В табл. 2.12 представлены значения
первого максимума на кривых К^/З) {Kflmax), а также значе-
значения первого максимума (if*IIniax) и первого минимума (-K"*IImin)
на кривых К*и(Р). Помимо этого, приведены соответствующие
значения /?, в которых указанные экстремальные значения КИН
достигаются.
Таблица 2.12
V
0,1
0,3
0,5
/з
1,71
1,85
2,05
ЛИтах
1,31
1,27
1,23
1,72
1,77
1,86
л III max
1,33
1,24
1Д7
Р
3,76
3,74
3,74
TV-*
лШтт
0,559
0,614
0,761
Кривые, представленные на рис. 2.9, 2.10, отвечающие и = 0,3,
хорошо согласуются с результатами расчетов [260], проведенных
134
Гл. 2. Двухбазисный проекционный метод
там для v = 0,25. Полученные результаты для v = ОД и v = 0,3
также согласуются с соответствующими результатами [97] вплоть
до первого максимума, а затем начинают несколько отличаться.
Различие возрастает с ростом /? и становится достаточно суще-
существенным в области второго максимума для К*и(C). Согласно
[97] второй максимум К?п(/3) для v = 0,3 превосходит первый.
В наших расчетах второй максимум функции К*п(C) существенно
ниже первого, что аналогично случаю падения продольной волны,
рассмотренному в § 2.4.
На рис. 2.11 приведены графики зависимости обезразмерен-
ного полного сечения рассеяния (Es/S, где S — площадь тре-
трещины) от волнового числа для тех же значений коэффициентов
Пуассона. Здесь кривая, отвечающая v = 0,5, понимается как
2S/S
2,0
1.5
1.0
0,5
0,0 0,5 1,0 1,5 2,0 2.5 3,0 3,5 4,0 4,5 5.0
— v-0,1 v-0,3 — --v-0,5
d v-0,1 [285] x v-0,3[285]
Рис. 2.11. Влияние коэффициента Пуассона на полное сечение рассеяния
результат расчетов по формуле B.117), которая сохраняет смысл
и для несжимаемых материалов. Для сравнения на графике от-
отмечены величины, полученные интерполяцией результатов [285].
Близкие к [285] результаты получены и в [314].
Из рис. 2.11 видно, что значения полного сечения рассеяния,
вычисленные с помощью двухбазисного метода, достаточно хо-
хорошо согласуются с известными результатами.
При решении задачи о трещине, имеющей форму квадрата
и занимающей область G {х : \х\\ < 1, \х2\ < 1}, для по-
построения приближенного решения использовалось до 12 вектор-
функций е((х) = eo(x)gi(x) (по шесть для аппроксимации каждой
2.5. Гармоническая сдвиговая нагрузка
135
из компонент скачков перемещений [щ] и [г^])- Расчеты проводи-
проводились для v = 0,25. В качестве ео(х) бралась функция, аналогичная
той, которая использовалась при решении статической и динами-
динамической задач о квадратной трещине отрыва:
ео(х) =
где т\ = [хх - IJ + (х2 - IJ, г2 = (Х1 - IJ + (х2 + IJ, г| =
= (XI + IJ + (х2 + IJ, Т\ = (XI + IJ + (Х2 - IJ-
Здесь отличие от трещины нормального разрыва заключается
лишь в степени, в которую возводится произведение Г1Г2Г3Г4. Это
различие вызвано тем, что согласно [344J (см. также [204]) особен-
особенности в угловых точках контура для трещин сдвига отличаются от
особенностей решений задач о трещинах отрыва при тех же ве-
величинах углов. В частности, в соответствии с [344] для угла тг/2
и v = 0,25 решение задачи о трещине сдвига имеет особенность
07492
С учетом того, что функция [i*i(a;)] должна быть четной по х\
и по ^2, а функция [г42(#)] — нечетной по х\ и #2, в силу симме-
симметрии задачи, для аппроксимации [i*i(a:)] были выбраны следую-
следующие вектор-функции gi(x): A; 0), (cos(tt#i); 0), (cosGr#2); 0),
(cos Btt^i); 0), (cos (ttxi) cos GПГ2); 0), (cos BтпЕ2); 0),
а для аппроксимации [^(я)] — вектор-функции gi(x), равные
@; sinGra;i)sinGra;2)), @; sin
@; sinGr#i)sinB7nr2)), @; si
@; sinB7T2;i)siiiB7rrc2)), @; s)
Количество элементов второго базиса в расчетах доводилось
до 66. Для этого использовалось до 33 функций фа(х)- Отвечаю-
Отвечающие им значения o?i, #2, аз приведены в табл. 2.13.
Таблица 2.13
0
0,5
0,5
0,5
0,75
0,875
0,875
0,875
0,25
0,625
0
0
0,5
0
0,25
0,5
0,125
0,5
0,875
0,875
0,875
0,75
а3
1
0,5
0,25
0,25
0,25
0,125
0,125
0,125
0,125
0,125
0,25
ai
0
0
0,75
0,75
0,75
0,875
0,875
0
0,375
0,75
0,25
а2
0
0
0
0,25
0,75
0,25
0,625
0,875
0,875
0,875
0,75
аз
0,5
0,25
0,25
0,25
0,25
0,125
0,125
0,125
0,125
0,125
0,25
Oil
0,5
0,25
0,25
0,5
0,875
0,875
0,875
0,125
0,5
0
0,5
а2
0
0
0,25
0,5
0
0,375
0,75
0,875
0,875
0,5
0,75
а3
0,5
0,25
0,25
0,25
0,125
0,125
0,125
0,125
0,125
0,5
0,25
136
Гл.2. Двухбазисныйпроекционный метод
На рис. 2.12 приведена зависимость нормированного значения
КИН от р (К*(р) = |#н(/?)|/#и@)) в точке контура A; 0), а на
рис. 2.13 представлен график функции К*и(/3) = \Ктф)\/Кш{$),
Ч
1.30
1,25
1,20
1,15
1,10
1,05
1,00
0,0 0,5 1,0
Рис. 2.12. Зависимость К
1,5 2,0 р
для квадратной трещины
вычисленный в точке @; 1). Величины Ки{C) и Km(f3) вычи-
вычислены из приближенного решения по формулам B.114). Приве-
Приведенные результаты соответствуют значению 7 = 3 для функций
1
1,30
1,25
1,20
1,15
1,10
1,05
1,00
0,0 0,5 1,0 1,5 2,0 р
Рис. 2.13. Зависимость KiU(l3) для квадратной трещины
Основная часть результатов, представленных в данном пара-
параграфе опубликована в [129].
2.6. Ударная нагрузка 137
2.6. Ударная нагрузка
Для анализа возможностей развития трещины, расположен-
расположенной в теле, находящемся под действием ударных нагрузок, не-
необходимо решать нестационарные уравнения Ламе, записанные
ниже в формуле B.118), с соответствующими граничными и на-
начальными условиями. К настоящему времени для решения таких
уравнений применялось несколько различных подходов. Один из
них заключается в том, что записываются граничные уравнения
в пространственно-временной области, которые затем решаются
численно. Такой подход был осуществлен в [243, 244] при ре-
решении задачи о круговой трещине, находящейся под действием
нормальной и скручивающей нагрузок. При этом подходе в гра-
граничных уравнениях увеличивается количество переменных, что
усложняет решение задачи.
Другой подход заключается в том, что по времени делается пре-
преобразование Лапласа. В результате для образов Лапласа получают-
получаются уравнения, аналогичные уравнениям для амплитуд перемеще-
перемещений, возникающим в случае гармонических по времени нагрузок.
При таком подходе приходится решать две задачи — решать урав-
уравнения для образов Лапласа при различных значениях параметра
преобразования и затем осуществлять численное обращение пре-
преобразования Лапласа.
Проще всего решать уравнения для образов при веществен-
вещественных значениях параметра преобразования Лапласа, так как в этом
случае уравнения получаются вещественнозначными и, следова-
следовательно, по сравнению с комплексными значениями параметров
вдвое сокращается порядок соответствующей вещественной си-
системы линейных уравнений. Благодаря такому упрощению ука-
указанный способ является достаточно привлекательным и неодно-
неоднократно использовался при решении различных нестационарных
пространственных задач о трещинах (см., например, [390, 388,
256, 257, 382, 384]). Основной проблемой здесь является эффек-
эффективное обращение преобразования Лапласа по значениям образа
на вещественной оси. Различные способы обращения предста-
представлены в [80, 81, 343, 322, 175, 176]. Критическая оценка имею-
имеющихся способов обращения преобразования Лапласа приведена в
[307, 330, 308]. Согласно этим работам известные процедуры обра-
обращения по значениям образа Лапласа на вещественной оси и, в
частности, один из наиболее распространенных способов [343]
являются неустойчивыми по отношению к параметрам процедуры
и погрешностям в определении образа. Вывод работ [307, 330, 308]
подтвердился и в наших расчетах, использовавших обращение с
помощью процедуры [343], вычисленной на вещественной оси ап-
аппроксимации образа Лапласа решения задачи о круговой трещине,
к поверхностям которой мгновенно прикладываются равные по ве-
величине и противоположно направленные однородные нормальные
9 Зак. 205
138 Гл. 2. Двухбазисный проекционный метод
усилия. Сама аппроксимация образа Лапласа находилась с помо-
помощью решения соответствующего граничного псевдодифференци-
псевдодифференциального уравнения двухбазисным проекционным методом. В силу
того, что результаты расчетов оказались существенно зависящими
от параметров процедуры [343], они здесь не приводятся.
В исследованиях [307, 330] пришли к заключению, что наи-
наиболее точные и устойчивые способы обращения имеют место при
обращениях, использующих значения образа на прямой, парал-
параллельной мнимой оси. В частности, самые хорошие результаты
показал метод обращения, предложенный в [207]. Этот метод ис-
использовался для решения нестационарных пространственных за-
задач о трещинах, например в [392]. Вместе с тем следует отметить,
что само определение требуемых для применения метода [207] зна-
значений образа Лапласа в различных точках прямой, параллельной
мнимой оси, в общем случае связано с преодолением значительных
вычислительных трудностей и может приводить к существенным
погрешностям.
Здесь мы покажем, что достаточно хорошие и устойчивые ре-
результаты получаются при обращении преобразования Лапласа по
значениям образа на мнимой оси, что совпадает с обращением
преобразования Фурье. При этом оказывается, что никаких до-
дополнительных расчетов делать не нужно, а достаточно восполь-
воспользоваться решениями, полученными выше для гармонической по
времени нагрузки, которые можно рассматривать как образы Фу-
Фурье решения нестационарной задачи. Разумеется, при простом
интегрировании образа Фурье с соответствующим ядром нельзя
получить хорошей аппроксимации решения в области малых вре-
времен, т.е. в окрестности момента приложения нагрузки, так как
известно, что асимптотика оригинала в нуле определяется асим-
асимптотикой образа на бесконечности. Построение асимптотики ре-
решения при больших значениях параметра преобразования Фурье
или Лапласа представляет собой отдельную достаточно трудную
задачу. Ссылки на работы по высокочастотной асимптотике реше-
решений приведены во введении. Один из способов получения главного
члена асимптотики решения вблизи нуля будет рассмотрен в гл. 3.
Несмотря на погрешности, возникающие вблизи нуля при обраще-
обращении преобразования Фурье путем простого интегрирования, по-
получаемые приближенные решения оказываются устойчивыми вне
малой окрестности начального момента времени и достаточно хо-
хорошо описывают точное решение в наиболее интересной области
(в окрестности его экстремального значения).
Уравнения Ламе нестационарной задачи теории упругости име-
имеют вид
/лАщ + (А + /х) Ujji = gui. B.118)
Здесь предполагается суммирование по повторяющимся индексам,
а точки сверху означают дифференцирование по времени.
2.6. Ударная нагрузка 13§
Чтобы сохранить полную аналогию с задачами о гармониче-
гармонических колебаниях, рассмотренными выше, где зависимости от
времени принимаются в виде e~UJTJ будем в этом параграфе под
преобразованием Фурье произвольной функции /(т) по времени
понимать функцию /(С)? определяемую следующим образом:
f(r)e-^Tdr. B.119)
-00
В случае определения преобразования Фурье по формуле B.119),
формула обращения будет иметь вид
оо
/(C)e*CrdC- B.120)
-00
Применим преобразование Фурье по времени к уравнениям
Ламе B.118). Относительно образов Фурье перемещений получим
систему уравнений
цАщ + (А + iA)ujji = -д{2щ. B.121)
Система уравнений B.121) с точностью до замены ? на и со-
совпадает с системой уравнений A.1) для амплитуд перемещений в
случае соответствующей гармонической по времени нагрузки.
Рассмотрим задачу о трещине, к поверхностям которой прило-
приложены равные по величине и противоположно направленные уси-
усилия, зависящие от времени. Обозначим эти усилия ±t(r, х) =
= ± (*i(r, ж), <2(т> #)> <з(г> я))- Сделаем преобразование Фурье
по времени приложенных усилий. Тогда для образов Фурье задача
сведется к решению уравнений B.121) с граничными условиями
в виде заданных на поверхностях трещины нагрузок ±t(C, %)-
Такая задача полностью аналогична рассмотренным выше за-
задачам о гармонических колебаниях (в случае, когда амплитуды
приложенных усилий ±?(С> #)) и для ее решения можно приме-
применять те же способы, например, сводить к граничным псевдодиф-
псевдодифференциальным уравнениям и решать их двухбазисным проек-
проекционным методом. Предположим, что в образах Фурье задача
оказалась решенной и вычислены наиболее важные характери-
характеристики решения, например КИН Kj(?) (j = I, II, III) в какой-либо
точке. Тогда функции Kj(r) могут быть вычислены с помощью
формулы B.120)
оо
Kj(t) = ± j kj{Qe*T <K. B.122)
-00
9*
140 Гл. 2. Двухбазисный проекционный метод
Формула B.122) упрощается, если учесть, что функции Kj(r)
вещественнозначные. В силу вещественнозначности Kj(t) и фор-
формулы для преобразования Фурье B.119), имеем равенство
B.123)
Здесь черта сверху означает комплексное сопряжение. Из B.123)
получаем равенство
Kj(-0 = J Kj(T)e-iT<dr. B.124)
-00
Сравнивая формулу B.124) и определение преобразования Фу-
Фурье B.119), получим Kj(-() = Kj(() или
Kj(-0 = Kj(O. B.125)
Используем равенство B.125) в B.122). В результате получим
00
Kj(r) = ~- / (Kj(QeiCT + 1
о
00
j(Q)e s ) aQ. (z.lzoj
Здесь Re означает вещественную часть числа.
Формулу B.126) можно записать в безразмерных переменных.
Пусть а — характерный размер трещины. Введем безразмерные
переменные Т = csr/a, A = Ca/Cs- Здесь cs, как и выше, —
скорость распространения поперечной волны. Обозначим также
Kj(t) = Kj(aT/cs) = Kj(T). Из введенных обозначений следует,
что (т = АГ. Кроме того, обозначим -К} (С) = Kj(Xcs/a) = ifj(A).
Подставляя это выражение в B.126) и переходя там к безразмер-
безразмерным переменным, получим
00
А„¦ A ) = I He [JXjyAje J ал. {Z.LZl)
о
Заметим, что при замене ( на о; величина А соответствует
введенной выше величине /За и, следовательно, Kj(А) являются
2.6. Ударная нагрузка 141
именно такими функциями, которые вычислялись в задачах о гар-
гармонических колебаниях.
Перейдем теперь к рассмотрению примеров. Пусть к поверхно-
поверхностям трещины приложены равные по величине и противоположно
направленные нормальные усилия ±$з(т). Обозначим через ^(С)
амплитуду КИН в какой-либо рассматриваемой точке контура тре-
трещины, отвечающую задаче о гармонических колебаниях с часто-
частотой С и приложенной нагрузкой, имеющей единичную амплитуду,
В таком случае ?,(С) = *з(С)Я?(О и ?,(А) = ?3(А)Я?(А), где
{l) () ?(С) ?(/) ?()
В результате формула B.127) записывается в виде
оо
К*(Т) = -^ /lie (h(X)KUX)eiXT) d\. B.128)
ж a J \ /
о
Пусть нагрузка tz(r) представляет собой ступенчатую функ-
функцию. Обозначим через Н(т) функцию Хевисайда
Н{т)
_fl, r>0,
~\0, т<0.
В качестве ts(r) возьмем функцию ts{r) = Н(т) — Н(т — то),
где то > 0. В этом случае функция *з(С) легко вычисляется:
то
о
Переходя к безразмерным переменным, получим
аA _ e-JATp)
B-129)
где То = с8т0/а.
Подставив B.129) в B.128), получим
B.L30)
Далее учтем, что 1 — е~гХт° = 1 - cos(ATo) + tsin(ATo) =
= 2 sin2 (АГо/2) +2» sin (АГ0/2) cos (АГ0/2) = 2г sin (AT0/2) e-iAr°/2.
Подставим это выражение в B.130) и в результате получим
оо
К*{Т) = 1
142 Гл. 2. Двухбазисный проекционный метод
В формуле B.131) функция -К^А) известна из решения за-
задачи об установившихся колебаниях пространства с трещиной.
Следовательно, имеется все необходимое для решения неустано-
неустановившейся задачи путем простого интегрирования.
Заметим, что решение К*(Т) не должно зависеть от То при
Г < То (т < го), причем в указанной области К*(Т) совпадает
с решением, отвечающим нагрузке в виде бесконечной ступеньки
Н(т) = Щт).
Выражения, аналогичные B.131), получаются для KUT) (j =
= II, III) при решении задачи о трещине сдвига. Пусть к по-
поверхностям трещины, имеющей характерный размер а, прило-
приложены равные по величине и противоположно направленные сдви-
сдвиговые усилия ±i(r) = (<i(t), 0). Обозначим через Щ(С) (j =
= II, III) амплитуды КИН в рассматриваемой точке контура, от-
отвечающие задаче о гармонических колебаниях с частотой С и при-
приложенными нагрузками, имеющими амплитуду t = A, 0). Ана-
Аналогично случаю нормальных усилий имеем Kj(Q = ii(()Kj(()
и Kj(X) = fi(A)^(A), где ii(C) — образ Фурье функции fi(r),
h(O = HXcs/a) = ti(A), #?(C) = KjiXcJa) = tfJ(A). В силу
этого формула B.127) приобретает вид
00
Щ{Т) = ^ [Re (ti(A)^(A)eiAr) d\. B.132)
о
Формула B.132) аналогична B.128). Если в качестве t\(r)
взять h(r) = Н(т) — Н(т — то), то с использованием явного вы-
выражения для h(X) формула B.132) примет вид
О ^ ^
B.133)
Преобразуя выражение B.133) аналогично тому, как преобра-
преобразовывалось B.130), получим
Ниже рассматриваются задачи, для которых функции К®(Х)
(j = I, II, III)) были вычислены в §2.4, 2.5. Напомним, что в тех
обозначениях величине А соответствует (За. В расчетах по форму-
2.6. Ударная нагрузка
143
лам B.131), B.134) полубесконечный интервал интегрирования
заменялся конечным. Его длина определялась максимальными
значениями А = /?а, для которых были проведены расчеты гармо-
гармонических по времени задач. Интегрирование по конечному
отрезку осуществлялось путем простого подсчета интегральных
сумм с измельчением разбиения отрезка. Величины К®(\) в
§ 2.4, 2.5 вычислялись с шагом 0,2-0,25 по А. Для получения ис-
используемых при интегрировании значений К®(\) в промежуточ-
промежуточных точках применялись кусочно-квадратичные и кусочно-куби-
кусочно-кубические интерполяции.
Рассмотрим задачу о круговой трещине радиуса а, к по-
поверхностям которой приложены нормальные усилия ±?з(т) =
= ± [Н(т) — Н(т — то)]. В качестве характерного размера выберем
радиус а. Обозначим Kist КИН для дискообразной трещины, нахо-
находящейся под действием статической нагрузки <з = 1- На рис. 2.14
-•-v-0,25 -o-v-0,45
-v-0,49
-v-0,5
Рис. 2.14. Круговая трещина. Нормальная ударная нагрузка
представлены зависимости K*(T)/Kist для различных коэффици-
коэффициентов Пуассона {у = 0,25, v = 0,45, v = 0,49 и и = 0,5).
Как и ожидалось, вблизи Т = 0 хорошей аппроксимации не
получилось (решения даже не стремятся к нулю]. Значение в
Т = 0 зависело от длины отрезка L, на интеграл по которому
заменялся интеграл по полубесконечной прямой в B.131). С уве-
увеличением L значение K*@)/Kist убывало. Для и = 0,25 зна-
значение L доводилось до 8, а для остальных и оно доводилось до
4-5. Вместе с тем вне малых окрестностей Т = 0 решения ведут
144 Гл. 2. Двухбазисный проекционный метод
себя устойчиво. Если обозначить через Tres(^) величины Т, в ко-
которых функции K*(T)/Kist достигают максимальных значений,
обозначаемых К^шъх{и)^ то для Т > TTes(u)/2 результаты расче-
расчетов слабо изменялись при вариациях L. Теоретически в области
Т <Tq решения не должны зависеть от То, однако для численных
результатов такая зависимость может существовать. В расчетах
рассматривались различные То от 10 до 20. В представленной на
рис. 2.14 области изменения Т (Т < 5,5) полученные численные
результаты практически не зависели от То, взятых в указанном
выше диапазоне.
Для всех значений v величины К*(Т) с увеличением Т (в обла-
области Т < То) выходят на соответствующие статические значения
(т. е. функция Kf(T)/Kist колеблется около 1 с убывающей ампли-
амплитудой). Сами значения максимумов K{*max(v) и соответствующие
им времена Tre8(u) зависят от i>, причем величины Kfmax{v)i как и
для гармонической нагрузки, растут с ростом z/, a Tre8(v) убывают.
Согласно расчетам для v = 0,25 Tres@,25) « 1,8, а 1^/^@,25) «
« 1,32. При росте v до 0,5 TTe8(u) убывает до Tres@,5) « 1,5,
а к?т*х(у) растет до #/^@,5) « 1,55.
Результаты расчетов для v = 0,25 можно сравнить с имеющи-
имеющимися в литературе. Рассматриваемая задача различными мето-
методами решалась в [392] и [244] для v = 0,25, в [388] для v = 0,29
и в [384] для v = 0,3. Поскольку как согласно [244], так и полу-
полученным нами результатам решения для i/, лежащих в интервале
0,25 < v ^ 0,3, очень мало отличаются друг от друга, можно срав-
сравнивать соответствующую кривую на рис. 2.14 с результатами всех
четырех работ. Так как в указанных работах результаты предста-
представлены лишь в графической форме, сравнение носит достаточно
приближенный характер. В области малых и средних времен
(Т ^ 2,6) из всех результатов заметно выпадает [392]. Величина
Tres@,25) согласно [392] меньше 1. По расчетам [388] и [384] вели-
величина Tres@,29) « 1,6. Согласно результатам [244] Tres@,25) « 1,8.
Сами величины К*тъ^ Для v — 0>25, v = 0,29 и v = 0,3 в расче-
расчетах указанных работ колеблются от #/^^@,29) « 1,23 в [388] до
*1Ятах@,3) « 1,37 в [384]. По графику [244] 1^@,25) » 1,28-
1,29. Таким образом, наши результаты ближе всего находятся
к результатам [244]. Существенное отличие результатов [392] от
остальных, вероятно, связано с погрешностями решения задачи
в образах Лапласа, поскольку и полученное в [392] решение за-
задачи для гармонической нагрузки заметно отличается от других
известных результатов.
Для больших времен (Т > 2,6) из отмеченных работ выпа-
выпадают результаты [388]. Это, по всей видимости, связано с тем, что
применяемый в [388] метод обращения преобразования Лапласа,
2.6. Ударная нагрузка
145
вляющийся модификацией метода [343], предложенной в [322],
о значениям образа на вещественной оси, как упоминалось выше
см. [307, 330]), недостаточно аккуратен для средних и больших
ремен.
Таким образом, можно сделать вывод, что применение обра-
цения преобразования Фурье к результатам решения гармониче-
кой по времени задачи путем простого интегрирования по фор-
формуле B.131) приводит к устойчивым и достаточно аккуратным
>езультатам вне малой окрестности Т = 0.
Рассмотрим задачу о круговой трещине радиуса а, находя-
цейся под действием ударной сдвиговой нагрузки (t(r) = (ti(r),0),
,li(t) = H(r) — Н(т — го)). Снова в качестве характерного размера
зыберем радиус а. На рис. 2.15 приведены результаты расчетов
нормированных КИН 1*Г*(Т)/1Гшг и К*п(Т)/КШ8^ вычисленных
з точках контура круговой трещины (а, 0) и @, а) соответственно
цля v = 0,1 и v = 0,5. Представленные на рис. 2.15 расчеты от-
отвечают нагрузке в виде бесконечной ступеньки, поскольку кривые
3 4 5 6 7
— v = 0,5
Рис. 2.15. Круговая трещина. Сдвиговая ударная нагрузка
изображены до Т = 7, а значения То выбирались ^ 10. При этом,
как и в случае отрыва, результаты от Го практически не зави-
зависели. Нормирующие значения КИН Kust и Kmst взяты в указан-
указанных точках из решения статической задачи, в которой величины
приложенных усилий равны ±? = ±A, 0). Для наглядности на
графиках у Кт изменен знак.
Аналогичные кривые для v = 0,3 приведены на рис. 2.16. По-
Помимо этого, для иллюстрации влияния длительности приложения
146
Гл. 2. Двухбазисный проекционный метод
ступенчатой нагрузки на рис. 2.16 представлены также кривые, от-
отвечающие нагрузке с Го = 1. На этом рисунке, как и на рис. 2.15,
у Кт для наглядности изменен знак.
Расчеты проводились по формуле B.134). Длина конечного ин-
интервала L, на интеграл по которому заменялся интеграл по полу-
полуоси в B.134), варьировалась от 4,5 до 6. Как и в случае отрыва,
1,0
st
0,5
0,0
-0,5
st
-1,0
-1,5
— го=ю — ro=i
Рис. 2.16. Влияние длительности приложенной нагрузки
при Г -> 0 значения Kj(T) не стремятся к нулю. Однако уже для
Т > 0,1 результаты можно считать надежными.
В противоположность трещине отрыва, функции Kj(T)/Kjst
для сдвиговой нагрузки слабо зависят от коэффициента Пуассона.
Кривые, отвечающие v = 0,5 на рис. 2.14 и 2.15, понимаются
как результаты интегрирования по формулам B.131) и B.134) ре-
решений соответствующих граничных уравнений. Эти процедуры
сохраняют смысл и для несжимаемых материалов.
Заметим, что рассмотренные задачи о трещинах, к поверх-
поверхностям которых приложены ступенчатые нагрузки, соответствуют
также задачам рассеяния трещинами плоских ударных волн.
Данный параграф написан на основе работ [68, 71, 129].
Глава 3
АНАЛИТИЧЕСКИЕ МЕТОДЫ
3.1. Постановка задачи
Хорошо известно, что результаты численных расчетов, осо-
особенно таких величин, как КИН, в значительной мере зависят от
параметров численных процедур. Поэтому, как подчеркивалось
в [280], не может быть полной уверенности в правильности полу-
получаемых численных результатов, даже если они подтверждаются
расчетами, проведенными разными авторами и использующими
различные численные методы.
В связи с этим особое значение приобретают найденные для
частных случаев аналитические или асимптотические решения.
Они служат эталонами для проверки и корректировки численных
процедур. Кроме того, как уже упоминалось во введении, аналити-
аналитические решения могут использоваться в качестве составной части
в общей схеме альтернирующего метода, позволяющего строить
решения гораздо более сложных задач.
К настоящему времени аналитические решения получены
лишь для весьма ограниченного класса пространственных задач о
трещинах, причем почти исключительно только в условиях стати-
статического нагружения. Ссылки на значительное количество работ,
в которых строятся аналитические решения, приведены во введе-
введении. Здесь мы подробнее остановимся на одной из самых важных
задач — задаче об эллиптической трещине в упругом простран-
пространстве.
Пусть трещина занимает область Е1а = {х: х\/а\+^/«2 ^ 1}
в плоскости жз = 0. В [369] доказано, что в случае, когда к
поверхностям трещины прикладываются нормальные усилия
±ts(x), причем ts(x) = Рпг(х) = -Рпз(#ъ Х2) — полином поряд-
порядка п, скачок нормального смещения [г*з(#)] имеет вид [мз(#)] =
= A — х\/а\ — Х2/а\I12Р^{х)^ где Р^{х) — полином порядка п.
В частном случае, когда полином Рпз(#) содержит только четные
степени как по rri, так и по а?2, это утверждение было доказано
в [272]. В [420] показано, что аналогичное утверждение имеет ме-
место и для трещины произвольного разрыва, т. е. если к поверхно-
поверхностям трещины приложены равные по величине и противоположно
направленные усилия ±t(x), t(x) = (<i(#), *2(#)> *з(#)M причем
148 Гл. 3. Аналитические методы
ti(x) = Pni(x) — полиномы порядка п (г = 1, 2, 3), то скачки
смещений имеют вид [^г(#)] =: A ~~ x\la\ ~~ ^l/0!I^2^^)» Где
Pni(x) — полиномы порядка п (i = 1, 2, 3).
Эти утверждения вполне аналогичны известной теореме Га-
Галина о виде функции давления под подошвой эллиптического в
плане штампа, поверхность которого описывается полиномиаль-
полиномиальной функцией [32], и в действительности могут быть легко из нее
выведены- Аналитическое решение задачи о штампе приведено
в [29].
Несмотря на то, что общий вид решения задачи об эллиптиче-
эллиптической трещине при полиномиальных нагрузках произвольного по-
порядка известен, конструктивно его построить оказывается весьма
непросто. Поэтому в течение достаточно длительного времени ре-
решения строились лишь для полиномов невысокого порядка. В [83]
и [219] получены решения для нагрузки в виде однородного да-
давления. Решение для однородного сдвига построено в [209, 271].
Детальное исследование полей напряжений, возникающих при од-
однородном сдвиге, проведено в [283]. Линейно изменяющаяся нор-
нормальная нагрузка рассмотрена в [272]. В [274] в качестве примера
рассмотрены различные нормальные нагрузки вплоть до полино-
полиномов шестого порядка, однако не произвольного вида, и крутящая
сдвиговая нагрузка. В [373] помимо теоремы об общем виде скачка
нормальных смещений, доказанной иным, чем в [369] способом,
рассмотрено несколько примеров для линейной и квадратичной
нормальных нагрузок. При этом показано, что в случае линей-
линейной нагрузки в решении [272] допущена погрешность. В [310]
в качестве примеров разбираются задачи для нормальных поли-
полиномиальных нагрузок до второго порядка и отмечается, что для
линейной нагрузки в результатах [272] имеется погрешность, а
в случае квадратичных нагрузок погрешности имеются в [274] и
[373]. Матрица системы линейных уравнений для решения за-
задачи в случае нормальных полиномиальных нагрузок до третьего
порядка приведена в [370]. В [397] сообщается о том, что такая
же система получена для полиномиальных сдвиговых нагрузок до
третьего порядка, однако решение приведено только для линей-
линейной нагрузки. В [311] приведены решения задач для однородной
и линейной сдвиговых нагрузок, результаты сравниваются с [274]
и [397], при этом отмечено, что другие виды сдвиговых нагрузок в
литературе подробно не рассматривались.
Для решения задачи об эллиптической трещине применялись
различные методы. Во многих работах было использовано то,
что задачи о трещинах сводятся к смешанным задачам для гар-
гармонических функций. Основываясь на этом, в [219, 272] было
предложено использовать потенциалы для эллиптического диска
3.1. Постановка задачи 149
где
, Х2, Х3) - J
А — эллипсоидальная координата, определяемая как положитель-
положительный корень уравнения w(s) = 0. В [369] помимо потенциалов
V'm'(a:i, Ж2, #з) для построения решений было предложено ис-
использовать и производные от них по a?i и ^2. Такие функции
применялись при построении решений в целом ряде работ [219,
271, 272, 274, 370, 397].
Учитывая связь задачи о трещине с некоторой задачей для
гармонических функций, оказалось также возможным получать
решения при помощи теоремы Дайсона [136]. В [373] решение
строится путем разделения переменных в эллипсоидальных ко-
координатах. В [401] на примере однородной нормальной нагрузки
показано, что задачу об эллиптической трещине можно решать,
используя граничное уравнение в образах Фурье.
В ходе дальнейшего развития некоторых из отмеченных ме-
методов были разработаны конструктивные процедуры построения
решения для полиномиальных нагрузок произвольного порядка.
В [417] и [335] конструктивная процедура развита на основе под-
подходящего выбора потенциалов V(m\x\, #2? #з) и производных от
них. В [21] для построения общего алгоритма использованы так
называемые потенциальные факторы для эллиптического диска и
теорема Дайсона. В [310, 311] конструктивный алгоритм развит на
основе подхода [401]. Этот подход состоит из следующих элемен-
элементов: использование граничных уравнений, связывающих скачки
смещений с приложенными нагрузками, в образах Фурье; раз-
разложение приложенных нагрузок и искомых скачков смещений в
ряд Фурье по угловой переменной; разложение каждой компоненты
ряда Фурье в ряд по ортогональным полиномам по нормированной
радиальной переменной.
Таким образом, существует ряд подходов к аналитическому ре-
решению целых классов статических задач о трещинах. Несмотря
на то, что все они приводят к весьма сложным и громоздким вы-
вычислениям, их все же можно, как видно из цитированной лите-
литературы, довести до окончательных результатов. В противополож-
противоположность этому для динамических нагрузок, за исключением случая,
когда трещина занимает полуплоскость (см. [150]), вообще отсут-
отсутствуют аналитические решения пространственных задач. Здесь
150 Гл. 3. Аналитические методы
в случае гармонических по времени нагрузок имеются лишь не-
некоторые асимптотические решения в области низких и высоких
частот.
Для низких частот решение задачи можно разложить в степен-
степенной ряд по частоте, при этом член при нулевой степени отвечает
статическому решению. В многочисленных работах, посвящен-
посвященных вычислению различного количества поправок к статическому
решению, исследовались как характеристики дальнего поля (ам-
(амплитуды перемещений, полное сечение рассеяния), так и КИН.
В частности, в [199] рассмотрена задача об упругом пространстве,
содержащем эллипсоидальное включение. Для амплитуд переме-
перемещений вдали от включения вычислена первая поправка к стати-
статическому решению. Поскольку включение может быть и полостью,
рассмотрен также случай эллиптической трещины как вырожден-
вырожденной эллипсоидальной полости. Развитая в [199] процедура построе-
построения асимптотики дальнего поля опиралась на уравнения теории
упругости, записанные для матрицы и включения в дифференци-
дифференциальной форме, и метод сращивания асимптотических разложений.
Тот же круг задач рассматривался в [205, 409, 224, 225]. В этих
работах для получения асимптотики дальнего поля использовалось
его интегральное представление с помощью формулы Сомильяна.
Эта формула позволяет выразить перемещения в матрице через
напряженно-деформированное состояние во включении. В случае
трещины перемещения вдали от нее выражаются через скачки
смещений. Сами скачки смещений для трещины или напряжения
и деформации для включения берутся из решения статической за-
задачи. Такой способ нахождения асимптотики назван в указанных
работах методом квазистатической аппроксимации.
В [360] получена асимптотика полного сечения рассеяния дис-
дискообразной трещиной нормально падающей продольной волны.
При получении асимптотического разложения использованы од-
одномерные интегральные уравнения, к которым с помощью прео-
преобразования Ханкеля сводится указанная задача. Результаты [360]
обобщены в [348], где получен главный член асимптотики полного
сечения рассеяния в случае косого падения плоской продольной
волны на дискообразную трещину. Дальнейшее развитие эти ре-
результаты получили в [429]. В [429] вычислены главные члены
асимптотики полного сечения рассеяния дискообразной трещиной
плоских наклонно падающих как продольных, так и поперечных
волн. Результаты для трещин получены в качестве частного слу-
случая рассеяния упругих волн на включениях. Для построения
асимптотического разложения использованы интегральные урав-
уравнения, отличные от применявшихся в [205, 409, 224, 225]. Здесь
уравнения построены для вспомогательных величин, названных
поляризованными напряжениями и поляризованным количеством
движения. Сам подход к построению уравнений назван поляри-
3.1. Постановка задачи 151
зационным. В [348] и [430] построенные асимптотические выра-
выражения для полного сечения рассеяния использованы для оценки
затухания волн в среде с большим числом далеко друг от друга
расположенных дефектов.
В [302] для задачи рассеяния дискообразной трещиной нор-
нормально падающей продольной волны получена первая, квадратич-
квадратичная по частоте, поправка к статическому значению коэффициента
интенсивности напряжений Кх. В [303] вычислены квадратич-
квадратичные по частоте поправки к статическим значениям величин Кп
и Кш в задаче о рассеянии дискообразной трещиной нормально
падающей волны сдвига. В [258] также рассмотрена задача о дис-
дискообразной трещине сдвига. В этой работе отмечено, что в [303]
при вычислении квадратичной поправки допущена ошибка. В дан-
данной статье отмеченная ошибка исправлена и сверх того вычислены
члены третьего и четвертого порядка по частоте. Помимо этого,
вычислены главные члены асимптотики полного сечения рассея-
рассеяния и амплитуды дальнего поля. В [42] вычислена квадратич-
квадратичная по частоте поправка для Кг в задаче рассеяния эллиптической
трещиной нормально падающей продольной волны. В [363] для
той же задачи вычислена еще кубическая поправка, что позволило
кроме К\ вычислить главный член асимптотики полного сечения
рассеяния. Развитие работы [363] представлено в [364], где для
скачков смещений получены члены разложения до третьего по-
порядка по частоте в случае сдвиговой нагрузки. В результате оказа-
оказалось возможно построить асимптотику полного сечения рассеяния
и КИН в задаче рассеяния эллиптической трещиной наклонно па-
падающих продольцых и поперечных волн. Во всех перечисленных
работах, в которых вычислялись КИН, при получении асимптоти-
асимптотического разложения исходили из записанных в различных видах
граничных уравнений.
Для получения асимптотики решения в области высоких ча-
частот главным образом использовался лучевой метод (геометриче-
(геометрическая теория дифракции). Этим методом решались задачи о тре-
трещинах, имеющих форму полуплоскости [151, 152, 212], круга [152,
153, 214, 149, 320, 212] и эллипса [156, 154]. Поскольку асимпто-
асимптотическое разложение решения вблизи контура трещины предста-
представляет значительные трудности, в указанных работах в основном
исследовались характеристики дальнего поля, такие как полное
сечение рассеяния [214] и амплитуды перемещений. В [212] для
задачи рассеяния дискообразной трещиной нормально падающей,
продольной, гармонической волны получены раскрытия трещины
вне окрестности ее контура. Значительно меньше имеется резуль-
результатов, касающихся асимптотики КИН. Подход к определению КИН
с помощью лучевого метода предложен в [152]. В этой работе по-
получены КИН для трещины в виде полуплоскости и дискообразной
трещины, находящейся под действием осесимметричных, скру-
152 Гл. 3. Аналитические методы
чивающих, гармонических усилий. Подробное изложение прило-
приложения геометрической теории дифракции к задачам о трещинах
представлено в [154]
Помимо лучевого метода имеются и другие подходы к построе-
построению высокочастотной асимптотики. В частности, исследуемые за-
задачи можно сводить к интегральным или интегродифференциаль-
ным уравнениям и затем пытаться решать их асимптотически.
Подобным образом были решены задачи рассеяния дискообраз-
дискообразной трещиной крутильных [342] и нормально падающей продоль-
продольной [277] гармонических волн. В [213] асимптотически решены
двумерные граничные уравнения задачи рассеяния нормально
падающих, плоских, продольных, гармонических волн в случае
дискообразной и эллиптических трещин. При использовании ин-
интегральных уравнений также оказывается трудно найти асимпто-
асимптотическое решение вблизи контура трещины. Поэтому и здесь КИН
вычислены только для дискообразной трещины и скручивающей
нагрузки.
Для наиболее интересного, включающего в себя максималь-
максимальные значения различных характеристик решения (КИН, полного
сечения рассеяния и др.) диапазона средних частот аналитиче-
аналитические и асимптотические решения отсутствуют. В этой области
имеются лишь численные решения. Среди них высокой точно-
точностью обладают главным образом решения, полученные численно-
аналитическими методами для круговых и кольцевых трещин и
осесимметричных нагрузок, когда оказывается возможным сведе-
сведение задачи к одномерным интегральным уравнениям (см., напри-
например, [304, 383]).
В этой главе представлен метод построения аналитических или
с высокой точностью их приближающих численно-аналитических
решений задач об эллиптических трещинах, находящихся под
действием как нормальных, так и сдвиговых нагрузок. Предлагае-
Предлагаемый метод тесно связан с двухбазисным проекционным методом,
изложенным в гл. 2, и аналогично ему опирается на возможность
аналитического вычисления результатов применения соответству-
соответствующих граничных операторов к функциям или вектор-функциям
специального вида. Для статических полиномиальных нагрузок
произвольного порядка метод дает новую, достаточно простую кон-
конструктивную процедуру построения аналитических решений. Па-
Параграфы 3.2 и 3.3, в которых излагается решение статической за-
задачи, написаны на основе статей [74, 75]. Для гармонических по
времени нагрузок разработанный метод позволяет получить лю-
любое количество членов при разложении решения в ряд Тейлора по
волновому числу. Таким образом, излагаемый ниже метод приво-
приводит к усилению перечисленных выше результатов, в которых для
низких частот были получены лишь несколько поправок к стати-
статическому решению. Однако наиболее существенным является то,
3.2, Нормальная полиномиальная нагрузка 153
что, имея достаточно большой отрезок ряда Тейлора, можно при-
применить аппроксимации Паде и получить исключительно хорошее
приближение к точному решению не только в области низких, но
и средних частот. Решения динамических задач, рассмотренные
в §3.4-3.7, написаны на основе публикаций [71-73, 145, 375-377,
146].
Развитый метод позволил также получить высокоточное чис-
численно-аналитическое решение статической задачи об эллиптиче-
эллиптической трещине на границе соединения различных упругих полу-
полупространств. Как указывалось во введении, ранее аналитические
решения были получены только для дискообразных трещин [95,
270, 274, 428, 366]. Решение задачи о трещине на границе соеди-
соединения материалов изложено в §3.9 на основе статей [378, 379].
3.2. Нормальная полиномиальная нагрузка
При разработке конструктивной процедуры построения анали-
аналитического решения для трещины, занимающей эллиптическую
область Ela = {х — (#i, X2) : x\/a\ + x\jo^ < 1} и нагружен-
нагруженной нормальной нагрузкой <з(#)? являющейся полиномом произ-
произвольного порядка, воспользуемся граничным псевдодифференци-
псевдодифференциальным уравнением B.20) и вычисленным в гл. 2 результатом
применения оператора Л к функциям (ра(х). Напомним, что
f / 9 9\7 9 9
М — ?l — ?2 1 ?i_i-~2
1,
а^
Значение функции A(fa(x) внутри области трещины Е1а при
а\ ^ п2 представлено в формуле B.52). При полуцелых значе-
значениях 7> т. е. 7 = т + 1/2? выражение B.52) принимает вид
,
24'-1B/-1)(ЛJГ(т-Л-1)Bп)!B/-2п)!
154 Гл. 3. Аналитические методы
где yi = Xi/ai (t = 1, 2), р2 = у\ + yl, k2 = {a\ - а1)/а\, внутрен-
внутренность эллипса соответствует р < 1.
Учитывая, что T(s) -* оо при s ->> О, —1, —2, ... и то, что
Г(М + 1) = М!, из C.1) получаем, что А(р™ ' (х) выражается
следующей конечной суммой:
m I
/=1 n=0
--,/ + -; 2/ +1; k2j 2Fi 11 + -, I - m; 21 + 1;
C.2)
Выражение в правой части C.2) можно упростить, приняв во
внимание, что для любого целого неотрицательного п имеет место
равенство
Напомним, что BL + 1)!! = 1 • 3 • 5 •... • BL + 1); (-1)!! = 1.
Подставляя C.3) в C.2), получим
- 2n)!
; И + 1; A) 2F! (l + l>l-m; 21
Рассмотрим некоторые из гипергеометрических функций, вхо-
входящих в C.4). Используя представление гипергеометрической
функции 2^*1C/2, —т; 1; р2) в виде ряда, получим
t—и
3.2. Нормальная полиномиальная нагрузка 155
Далее учтем, что A)^ = ?!, а (—m)t обращается в ноль при
t ^ т +1, так как соответствующее произведение будет содержать
нулевой сомножитель. Таким образом,
i=0 ^ "'
Аналогичные рассуждения приводят к заключению, что и ги-
гипергеометрические функции 2-Fi(?+3/2, l—m] 21+1] р2) при I ^ га
выражаются с помощью конечной суммы
3, -, , ,. Л y(l + 3/2),(l-m)l2t
С—U
Подставляя C.5), C.6) в C.4), окончательно получим
v
?^ 25'B/ 1)("J("» " QK2n)!BZ - 2n)!
Функции p2t являются полиномами
L* s\{t-s)\ ¦
Подставляя C.8) в C.7) и проведя сокращения, получим
_ Bm + 1)!! f E(fc) A C/2)t(-m)t Л ^
- 2mfl2 S m, Zjj t! ^
¦ \ t—U
+ТТ
1)\\itB1)\
- /)!Bn)!BZ - 2n)!
* OJ2n+2s4l2J+2t-2n-2s 1
156 Гл.З. Аналитические методы
Из формулы C.9) видно, что функция Atpa (x) является по-
полиномом степени 2га. Ясно, что линейными комбинациями функ-
функций вида А<р™+ ' (х) невозможно получить произвольный поли-
полином. Поэтому введем в рассмотрение функции Tpq(x) = y^yf^a^)?
где р, q — неотрицательные целые числа, и вычислим результат
1/2
применения оператора Л к Тщ (х).
Для этого нам нужно вывести соотношение, выражающее
функции Tpq(x) через производные от функций вида <ръ,(х).
Лемма 3.1. Имеет место равенство
Ш Ш
k\m\(p-2k)\(q-2m)\
1
C.10)
где Di = d/dyi (i = 1, 2), а квадратные скобки обозначают
целую часть числа.
Доказательство. Формула C.10) может быть доказана по
индукции. Для случаев, когда р) q равны 0 или 1, формула C.10)
проверяется непосредственно. Предположим, что C.10) имеет ме-
место для всех показателей степеней до р и q. Докажем ее для р +1,
д, т. е. покажем, что
1р+1 q\x> - (_2)р
[(р+1)/2] [q/2]
Е Е
?)P+1-2A:Z?|-2m(p2+p+1+'?~fc~m(x)
Х k\m\{p + l-2k)\{q-2m)\ ' ( '
Сначала заметим, что TJ+lq(x) — у\ТрЯ{х). Воспользовавшись
этим равенством и тем, что по предположению формула C.10)
3.2. Нормальная полиномиальная нагрузка 157
справедлива для Тщ(х), получим
[9/2] Dq-2m fo/2]
/a-?L C.12)
qkm) v y
Нетрудно видеть, что имеет место коммутационное соотно-
соотношение
yi?>i=?>iyi-/, C.13)
где / — тождественный оператор.
Применяя последовательно C.13), можно получить формулу
^Dlyi-rDl-K C.14)
Используем C.14) в равенстве C.12). В результате будем иметь
i(g _ 2m)!
+1 + р + я - к
(р - 2fc
C.15)
Поскольку Dnp^{x) = -2\ух{\ - у\ - yl)x~l и ?>2?>а(ж) =
— 2АугA — у\ — y2)A-1» имеют место соотношения
158 Гл.З. Аналитические методы
Воспользуемся первым из равенств C.16) в C.15). В результате
получим
A/ m!(g _ 2m)!
C.17)
Преобразуем сумму по fc, входящую в C.17):
Ь/2] j
^ А;!(р - 2А;)!ГG
• q — к — га)
Го/21 „ ou 1
+ ^ (-2)А;!(р-2А;)!ГG +
Поделим числители и знаменатели дробей, входящих во вто-
вторую сумму в правой части равенства, на р — 2к и заменим в этой
сумме к на г — 1. В результате получим
/о io\
Заметим, что суммирование во второй сумме в C.18) включает
только те значения г, при которых порядок производной р +1 — 2т
3.2. Нормальная полиномиальная нагрузка 159
неотрицателен (р + 1 - 2г > 0). Учитывая это, переобозначая во
второй сумме в C.18) г через к и приводя подобные, получим
Ь/2] х
?-; к\(р -
Ки
/ПР+1
4(-2)
2)G+p+l+g-fc-m)
Из C.17) и C.19) следует равенство C.11). Аналогично можно
доказать справедливость C.10) для Tpq+1(x). Таким образом,
Лемма 3.1 доказана.
1/2
Теперь можно перейти к вычислению функции ATPq (х). Из
C.10) следует, что
Далее воспользуемся формулой C.3) для вычисления гамма-
функций от полуцелых аргументов и перестановочностью операто-
операторов 2?}, Z>2 и Л. В результате будем иметь
p-2rng-2m
г!т!(р - 2r)\(q - 2т)!
Bр + 2q- 2r -2m +
Ь/2] [g/2] nP-2r ng-2m л p+g-r-m+1/2
V^ V^ Щ Щ A(P
^o t^o rlml(p ~ 2г№ "" 2m)!2r+mBP + 2g - 2r - 2m + 1)!!'
C.20)
160 Гл. 3. Аналитические методы
Теперь подставим в C.20) вместо Л</?? я-r-m / ^ вычислен-
вычисленные в C.9) выражения. В результате получим
_2r nq-2m
np_2r nq
l 2
-2q-2r-2m + l)\\ I E(k)
' Bp + 2q-2r -2m + l)!!2P+?-r-ma2 1 (p + q-r-m)\
l)\hBl)\
n)!B/ - 2n)!
! 2 / и W+1)*
]2n+2sni2l+2t-2n-2s
s\(t-s)l
5=0 V '
Проведя сокращения, окончательно будем иметь
[9/2] пР-2г n9-2m
l 2
f E(fc) ^;
|> + 9-r-m)! ^
^ ^0 r!m!(p - 2r)!(g - 2m)!
+) Л
+ E E
q-r-m- l)\Bl - l)Bn)\Bl - 2n)!
jlT2'
X
л \ p+q-r-m-l ,
l. O7 » 1. U2\ \T V
3.2. Нормальная полиномиальная нагрузка 161
Чтобы вычислить производные, стоящие в правой части C.21),
заметим, что для целых неотрицательных аи/?
О, 0<а,
1?Л 0 > а.
C.22)
Из C.21) и C.22) следует
Ь/2] [?/2] г f
*-j. ^-4 rlm\(p — 2r)\(q — 2m)! | (p + q — r — m)\
f=:0 171=0 \
x 2^ fi 2^s!(f_s)!x
p+q-r-m I
- r - m - l)\Bl- l)Bn)!B/ - 2n)!
^л Bn +2s)!B/ +2* -2n -J
^ s!(< - 5)!Bn + 2s + 2r - p)!B/ + 2t + 2m - 2n - 2s - q)\ f"
C.23)
Суммирование в C.23) производится только по тем сочетаниям
индексов, которые дают неотрицательные степени для у\ и j/2-
Для единообразия вычислений при определении ATPq (х) мож-
можно иметь ввиду, что полный эллиптический интеграл второго рода
-E?(fc), входящий в правую часть C.23), выражается через гипер-
12 3ак. 205
162 Гл. 3. Аналитические методы
геометрическую функцию
Обозначим АТрB{х) = Upq(y). Из C.23) видно, что Upq{y)
в области Ela является полиномом степени р + q. Рассмотрим
теперь уравнение B.20) в случае, когда нагрузка t$(x) является
полиномом произвольного порядка iV, т. е.
где Aij — постоянные, A*j = А^а\а32.
1/2
Заметим, что функции Tpq (х) принадлежат пространству Собо-
о
лева Н\/2 (Е1а) и являются линейно независимыми. Поскольку опе-
о
раторр^/аЛ, как показано в гл. 1, изоморфно отображает Hi/2 {Ela)
на H_i/2(Ela), то и полиномы Upq(y) линейно независимы. Так
как кроме этого количество функций Tpq (ж), а следовательно, и
С/рд(у), отвечающих условию р + q < JV, равно (N + 1)(N + 2)/2,
т.е. размерности пространства полиномов степени не выше N,
уравнение
BpqUpq(y) = 2A - v)»-1 ^ А^уУ» C.24)
где Bpq — постоянные, имеет и единственное решение.
Уравнение C.24) по существу является системой (N+l)(N+2)/2
линейных алгебраических уравнений относительно Bpq. Бели
ВРЯ — решение этой системы, то функция ^ BPqTpq (x) явля-
ется решением уравнения B.20), т.е. скачком нормального сме-
смещения.
После нахождения постоянных Bpq коэффициенты интенсив-
интенсивности напряжений вдоль контура трещины определяются без
труда. Уравнение контура эллиптической трещины записывается
в виде х\ = а\ cos в, Х2 = аг sin0 или у\ = cos в, 3/2 = sin0.
Точка, лежащая внутри эллипса на нормали к контуру, прове-
проведенной через точку с координатами (aicosfl, a2sin0), и находя-
находящаяся на расстоянии s от нее, имеет координаты х\ = а\ cos# —
X2 = о>2 sin0 — 5П2, где (ni, П2) — вектор единичной внеш-
3.2. Нормальная полиномиальная нагрузка 163
ней нормали. Следовательно, в этой точке
3-3
/ (ai cos в — sniJ (a2 sin 9 — 5П2J
= 4/1
a\
-H
cos @) п\ sin @) П2
а2
При малых 5 имеем
I 2
?V 2(х) ~ 5 у Va2 cos @) ni + ai sin @) n2. C.25)
Поскольку для эллиптического контура
Q2cos0 Qisin0
ni = , , n2 = у , C.26)
Ja\ sin2 0 + a2 cos2 0 Wa2 sin2 0 + a\ cos2 0
из C.25) и C.26) получим
~ ~ 2 2 л\ 1/^ /о от\
2 COS C7J . \д.П)
Как известно, величина коэффициента интенсивности напря-
напряжений Nj может быть определена из поведения скачка смещений
у контура трещины. Во введении приведена формула, согласно
которой
[и3] « 4A - v^Ntf1'2. C.28)
Поскольку в рассматриваемой задаче [мз(#)] = J2 BpqTVq (x),
отсюда, из C.27) и C.28) следует, что
2
x (aj sin2 0 + a2, cos2 ^Vjl - i/)~V- C.29)
12*
164 Гл. 3. Аналитические методы
В формуле C.29) при в = 0 и q = 0 или в = тг/2 и р = О,
в сомножителях sing б и cosp в соответственно, под величиной 0°
следует понимать 1.
Обозначим через B^q решение уравнения
т.е. 23 BpqUpqiv) является решением уравнения
Величина TVj через S^g выражается проще, чем в C.29), так
как из выражения исключаются упругие постоянные:
Напомним также, что Кх =
Замечание 3.1. Из формулы C.23) видно, что полином
11е)
ATpq (х) в случае, когда р — четное число, содержит yi только
в четных степенях. Если же р — нечетно, то полином ATPq (x)
содержит у\ только в нечетных степенях. Аналогичная ситуация
1 /9
имеет место и с четностями q и ATPq (x) как функции от j/2- По-
Поэтому вместо одной системы линейных уравнений C.24) порядка
(N + l)(N + 2)/2 можно решать четыре системы уравнений мень-
меньшего порядка. Для этого полином ^ AijUiVi следует разло-
жить в сумму четырех полиномов Р\{у\, j/г), Р2(уъ Уг), Ръ(у\, Ы
и P^iyi, 2/2M где Pi{yi, У2) представляет собой сумму одночленов
вида Cy2ky2rri, т. е. содержит только четные степени как по yi, так
и по у2; /^(yi? У2) является суммой одночленов вида Cy2ky2m+l\
-Рз(Уь Уг) представляется в виде суммы одночленов Cy^+Iy2m и
^4(Уь Уг) состоит из суммы одночленов вида Cylk+ly%m+1. После
этого вместо уравнения C.24) следует рассмотреть четыре ура-
3.3. Сдвиговая полиномиальная нагрузка 165
внения
B2k2mU2k2m(y) = 2A - v)lTlPi{Vu й),
B2k2m+lU2k2rn+l{y) = 2A - l/J/i^d/i, Ы>
= 2A - и)^1РЪ{уъ Itt),
) = 2A ~ 1/)/Е11
Из решений этих уравнений решение B.20) строится с помо-
помощью следующей суммы:
Е в^
3.3. Сдвиговая полиномиальная нагрузка
Построение аналитического решения задачи об эллиптической
трещине сдвига, находящейся под действием полиномиальных на-
нагрузок, осуществляется тем же путем, что и в случае отрыва. Для
этого используется граничное псевдодифференциальное уравнение
A.25) и находится результат применения соответствующего опе-
оператора к вектор-функциям специального вида. Уравнение A.25)
может быть записано в несколько ином виде:
166 Гл. 3. Аналитические методы
Э2
Здесь M{j — дифференциальные операторы Мц =
рр рр рр pp.
Ml2="d^'M22 = A - и)+
% щщ
псевдодифференциальный оператор с символом |?|el; G — область
трещины, которую в дальнейшем полагаем эллиптической и рав-
равной Ela\ [u(x)] = ([i*i(ж)], [^2(^)]) — вектор скачков смещений;
t(x) = (ii(x), *2(#)) — вектор приложенных усилий.
Прежде всего вычислим результат применения оператора Л"*1
к функциям (р1(х). Вычисление h~l(pl(x) проводится вполне ана-
аналогично вычислению Л<ра(ж), приведенному в §2.3 гл. 2. Вос-
Воспользовавшись формулой B.34) для образа Фурье функции ipl(x),
получим
= (СьС2), Сг = «^г (г = 1,2).
В интеграле, стоящем в правой части равенства C.31), часть
переменных записана через &, а часть через &. Перейдем от остав-
оставшихся переменных & к ?j, а от переменных Xj к yj = Xj/aj. В ре-
результате получим
В интеграле, входящем в C.32), перейдем к полярным коорди-
координатам ?i = tcosA, B = <sinA, j/i = gcosO, j/2 = ^sinfl. В новых
переменных будем иметь
Л
оо 2тг
// Т""'"- . . d\dt. C.33)
Для разделения переменных в интеграле в C.33) используем
разложение плоской волны по Бесселевым функциям, приведенное
3.3. Сдвиговая полиномиальная нагрузка 167
в формуле B.39). Подставив B.39) в C.3), получим
А-1 ,, v 2^-^G + 1)
}¦
А/о? + sin2 A/a|
C.34)
Следовательно, как и в случае оператора Л, функция A^VaC^)
разлагается в сумму ряда, каждый элемент которого представля-
представляется произведением интегралов. Интегралы по радиусу явля-
являются интегралами Сонина-Вебера-Шафхейтлина. Выражения для
этих интегралов приведены в B.26), B.27). Интегралы по углу
также могут быть вычислены аналитически. Как и в гл. 2, обо-
обозначим q(X) = л/cos2 \/a\ + sin2 X/a\ = а^лД -A;2 cos2 A, k2 =
= 1 — a2/a2. Через Sm обозначим интегралы
_ /
2тг
Sm
О
2тг *г/2
1 Г Л\
C.35)
Здесь i^(fc) — полный эллиптический интеграл первого рода.
Поскольку cos (m(A — в)) = cos (mA) cos (тв) + sin (mA) x
xsin(m0), интеграл Sm может быть представлен в виде суммы
двух интегралов
Sm = Sm cos (тв) + Sm sin (тв),
где
2тг 2тг
cos (mA) dA o2 f sin (mA) dA
о
168 Гл. 3. Аналитические методы
Так как sin(mA) и q(X) периодические функции с периодом
2тг, то
?2 _ fsm(mX)dX
-I
Учитывая, что q(X) — четная функция, a sin(mA) — нечетная,
заключаем, что S^ = 0. Таким образом, Sm = S^ cos (тв). Пере-
Перепишем интеграл S^ в виде
Интеграл C.36) вычислен в [115, формула 2.5.19.18 с. 426]. Со-
Согласно [115]
Sl^ ~ 0 ПРИ m = 2/ + 1,
при m = 2/, / = 1,2,... C.37)
Из C.34) и формул C.37) следует
/=1
" ОО
C.38)
Подставив в C.38) выражения B.26), B.27) для интегралов Сони-
на-Вебера-Шафхейтлина, получим
Л + I, г + I; 2/ + 1; fe2) cos B19) Я, 1. C.39)
3.3. Сдвиговая полиномиальная нагрузка 169
Здесь
0»ГA +1/2) .,,,.
При
(=1,2,...
Замечание 3.2. Поскольку граничное уравнение контакт-
контактной задачи о внедрении в полупространство, без трения, жесткого
штампа с острой кромкой имеет вид pchrlp{x) = v(#), p{x) €
о
ЕЯ-1/2 (G), v(x) € Hi/2{G), формула C.39) позволяет развить
двухбазисный проекционный метод на этот класс задач, причем
функции <pl(x) можно использовать для построения второго ба-
базиса.
Исследуем более детально выражение Л~ Va(s) внутри эллипса
(д < 1). Упростим выражение, стоящее справа в C.39), для д < 1,
приняв во внимание, что
{21 - 3)!! 1
В результате получим
VZM = ГG + 1)а2{^Л Q, -7 -1; 1;
A 1 1. Л
2' 2' ^ У
( ^^2Н. C.40)
Далее воспользуемся формулой B.51) для представления д21 х
х cos B19) в виде полинома и формулой C.3) для замены Г(/+1/2)
11 Зак. 205
170 Гл. 3. Аналитические методы
соответствующим выражением. В результате из C.40) получим
-ЙМ -ГG + В*[л*®тЛ Q, -7-1; li
В случае полуцелого 7 G == m + 1/2 ) формула C.41) приобре-
приобретает вид
X
+ 2)
Поскольку T(s) -> оо при s -> 0, —1, —2, ..., выражение C.42)
представляет собой конечную сумму
К(к)
х
ДГ(т + 2)
т+1 /о,
(m _, + 2)
ija + ljfc^aFi^ + i.Z-m-l^ + l
Упростим выражение C.43), заменив значения гамма-функции
от натурального аргумента соответствующими факториалами, а
значение Г(ш + 3/2) согласно формуле C.3). В результате будем
3.3. Сдвиговая полиномиальная нагрузка 171
иметь
- C-44)
Аналогично формулам C.5), C.6), рассматривавшимся для тре-
трещины нормального разрыва, покажем, что гипергеометрические
функции 2*1 A/2, -т-1; 1; д2) и 2F1(l +1/2, /-т-1; 2/ + 1; ?2),
входящие в C.44), являются полиномами. Действительно,
О--»-
t=0
~n/9W^T~1)Vt, C.45)
так как (l)t = t! и (—m — l)t = 0 при t ^ m + 2 . Аналогично,
-/ n, 19/ + 1
C.46)
Подставив C.45), C.46) в C.44), получим
t=0 ^ "^
2m+1 |^
У B/ - 1)!!у^
172 Гл. 3. Аналитические методы
t=0
Заменим в C.47) g2t его выражением в виде полинома C.8).
В результате будем иметь
t=O
. C.4S)
Замечание 3.3. Формула C.48) вместе с C.10) позволяет
вычислить аналитически функции ^^(ухУ^а (%)) = Vpqix)-
При этом функции Vpq(x) внутри эллипса оказываются полино-
полиномами степени р + q. Это дает возможность, аналогично случаю
трещины нормального разрыва, разработать конструктивную про-
процедуру построения аналитического решения задачи о внедрении в
полупространство жесткого штампа с острой кромкой, имеющего в
плане форму эллипса и ограниченного поверхностью, описываемой
полиномиальной функцией.
Для применения формулы C.48) при разработке конструктив-
конструктивной процедуры решения задачи о трещине сдвига введем предва-
предварительно в рассмотрение следующие вектор-функции:
3.3. Сдвиговая полиномиальная нагрузка 173
Из вида оператора C.30) следует
l2k-l<pl{x)\
А-1 7/ J-
22Л lipi{x)J
7 ( \ 1 (
2{l-v) \М22Л
Таким образом, согласно C.49), C.50), для вычисления
и К<?ав(#) нам достаточно вычислить MyA~V2(s). В свою оче-
очередь для вычисления МуА"х^а(^) нужно уметь вычислять функ-
функции
Поскольку
д2
д2 1 а2 1
функции Ф]Ах) можно переписать в виде
В случае, когда j = т + 1/2 и функции Л"^ ' (ж) являются
полиномами, функции Ф^+ ' (ж) можно вычислить из C.48) про-
простым дифференцированием по формуле C.22). В результате будем
174 Гл. 3. Аналитические методы
иметь
т+1/2 _ Bт + 1)!У^аЛ К (к)
^B/-1)Ну^B/)!А:2г / 1 1. Л
2, 2«(ЛJ(т + 1-012 Ч 2' 2' ' )
X
t=0
2s - 2)!Bn)!B/ - 2n)! J'
C.51)
/г , _ Bm + l)!!^f K(k)
22 И- |
д—77i — l)t ^-> Bi — 2s)\y^si
~t\ 2j( s!(t-s)!B<- 2s - 2)!
. ,. V^ \&ь-йау.ух у2
7 - Z^ oir*_ .eyr^-ae-^i"
t=l s=0
f- (-1)' ^_
C.52)
"Bf + 2< - 2n - 2^)!У;(П+Д)^('+<-"~s-1) 1
2n)!B/-2n)!B/ + 2<-2n-2s-2)! J'
3.3. Сдвиговая полиномиальная нагрузка 175
*m+i/2, x _ Bm + 1)I1Vt ) ВД
(-т - 1), Л
^ t\ ^sUt-s)U2s-l)\Bt-2s-l)\
S=l V ' Ч 7 Ч 7
i
ч (-l)"Bn + 2s)\Bl + 2t-2n- 2s)\
2n+2s-l 2i+2t-2n-2*-l
С помощью функций Ф^ ' (х) результат применения опера-
оператора К к вектор-функциям <р%?~ ' (х) и ц>™ъ ' (х) записывается
следующим образом:
C.54)
2A - „) ^A ^ф^^) + ф^%))
C.55)
Рассмотрим теперь вектор-функции ТРдн(ж) и ТРдВ(ж)
Здесь, как и выше, тЦ2(х) = Ух
Ц2(х) = УхУ&а
176 Гл. 3. Аналитические методы
Чтобы найти результат применения оператора К к вектор-функ-
вектор-функциям TpqB(x) и Tp'qH(x), нам достаточно уметь вычислять функции
ЩНх) 2= -—-—A~lTPq (x). В этом случае результаты приме-
иХ\ OX j
1 1<\ 1 ley
нения оператора N к вектор-функциям TPqH(x) и TpqB(x) прини-
принимают вид
()
иЩ(х)
" 2A - v) \A - u)R\\{x)
Воспользовавшись формулой C.10), выражающей функции тЦ (х)
через производные ох функций типа <р!(х), приходим к следую-
следующим соотношениям:
ПРЯ(х) =
!m!(p-2ifc)!(g-2т)!
Подставляя в C.58) выражения для Ф^- ' (ж) из C.51)—C.53),
и используя формулу C.22) для дифференцирования полиномов,
получим
Ь/2]|
^
r\m\{p — 2r)\(q — 2m)!
-г-m
2r - p - 2)!Bt + 2m - 2s - g)!
B/-l)!!BQ!fc2i
X
,
3.3. Сдвиговая полиномиальная нагрузка 177
t—U
B/
Bп + 2s Н- 2г -р - 2)!B/ + 2< + 2т - 2п - 2s - q)\
2n+2s+2r-p-2lt2l+2t+2m-2n-2s-q
1 У 2
\
C.59)
[р/2] [9/2]
^ ^ г\т\{р - 2r)\(q - 2m)!
=0 ra=0 ^ ' v^ '
q — r — m + 1)! -^rf *•
^ /o m/oj. о м 2s-\-2t—p 2t-\-2Tn—2s—q—2
^ч (zs)l(Zt — isy.y^ j/2
2r - p)!Bt + 2m - 2s - q - 2)!
t=0
Bn + 25 + 2r - p)!B/ + 2i + 2m - 2n - 25 - 9 - 2)!
s./j2n+2s4-2r-pflj2Z+2t+2m-2n-25-9-2
xJ/l У2
C.60)
178 Гл. 3. Аналитические методы
, |7г [Р/2Ш/2]
=
f^Q ?^0 r\m\(p - 2r)\{q - 2m)!
-r-
4f 5!(i - s)\{2s + 2r-p- l)!Bi + 2m - 2s - g- 1)!
B1-Щ21)\к*
P+g-r-m~'+1(/ + l/2)t
/, 1 , 1
x 2*1 N + -,/ + -;
t—0
¦2s|!B[+ 2f- 2n - 2s)!
Bn + 2s + 2r -p - 1)!B/ + 2t + 2m - 2n - 2s - q - 1)!
В формулах C.59)—C.61) суммирование производится только
по тем сочетаниям индексов, которые дают неотрицательные сте-
степени у\ и т/2- Для единообразия записи и вычислений можно иметь
ввиду, что
- f Л A, |;1;
Заметим также, что согласно C.59)—C.61) функции ЩНх)
являются полиномами степени р + q. Это дает возможность раз-
разработать конструктивную процедуру построения аналитического
решения уравнения C.30) в случае, когда приложенные нагрузки
*i(#)j *2(#) являются полиномами.
Пусть ?i(#), t2(x) — полиномы степени не выше N:
t2(x) =
3.3. Сдвиговая полиномиальная нагрузка 179
C30) в виде
Здесь А?/ = 4«Й, Щ = 4о14-
Решение уравнения C.30) ищем
где Bpq, Bpq — постоянные.
Применяя к вектор-функции [и(х)] = ([ui(a;)], [г*2(#)]) опера-
оператор Н, получим
= Е ^
Подставляя C.56), C.57) в C.62), будем иметь
if
' C>63)
Из C.30) и C.63) имеем систему линейных уравнений отно-
отно(
сительно B^g, B$q:
= м-х Е л&М-
C.64)
Уравнения C.64) представляют собой систему (N + 1)(N + 2)
линейных алгебраических уравнений относительно (N+l)(N+2)
неизвестных Bpq^ B^ p + q < N.
180 Гл. 3. Аналитические методы
1 /1 1 /2
Вектор-функции TPqB(x) и TpqH(x) являются линейно незави-
независимыми. Поскольку, как показано в гл. 1, оператор N осуществляет
взаимно однозначное соответствие между пространствами вектор-
о
функций Н\/2 {G) и H_i/2{G) (в данном случае область G = Ela),
вектор-функции #Тр'дв(х) и #TPqK(x) также линейно независимы.
Количество таких вектор-функций при условии р + q ^ N равно
(N + l)(N + 2), т.е. равно размерности пространства двумер-
двумерных векторов, каждая компонента которых является полиномом
степени не выше N. Благодаря этому система уравнений C.64)
имеет и единственное решение.
После определения постоянных J5^, B%q через них можно
выразить КИН на контуре трещины. КИН Кп и Кш выража-
выражаются через скачки смещений в нормальном и касательном к кон-
контуру трещины направлениях ([ип] и [ur] соответственно), согласно
приведенной выше формуле B.114). В точке контура, имеющей
координаты х\ = aicos0, Х2 = a2sin0, вектор единичной внеш-
внешней нормали п имеет координаты, записанные в C.26). Поэтому
скачки смещений [un], [ur] выражаются через скачки [iii(a;)],
[1*2B;)] следующим образом:
г 1 _ f^1 (ж)]а2 cos ^ + [U2 (х)]<*>1 sin в
Ы = (аЫп2в + а22со8Ч)^ '
C.65)
-[ui(x)]ai sing + [u2(x)]a cosg
[Url " (a? sin2 9 + a22 cos2
Скачки смещений [ui(#)], [гл2(ж)] могут быть записаны в виде
[«!(*)] = [п^хЫ^х), [u2(x)} = №{x)]<Af*(x), C.66)
где
Используя асимптотику функции сра (х) вблизи контура тре-
трещины C.25), из B.114) и C.65), C.66) получим
__ jjl I тг п2 cos в [и® (х)] + а\ sin в [г*2 (х)]
11 = ^
[л I тг — а\ sin в [«?(ж)] + О2 cos
Кш~2
3.3. Сдвиговая полиномиальная нагрузка 181
Здесь в соответствующих точках контура трещины
, [u°2{x)]= J] В^шР 0 smq 9.
p+q^N
C.67)
В формулах C.67) так же, как и в случае отрыва, для в = тг/2,
в = 37г/2 и р = 0 или 0 = 0, 0 = тгид = Ов сомножителях cosp 0
и smq6 соответственно, под величиной 0° следует понимать 1.
Замечание 3.4. Аналогично случаю нормального разрыва,
система линейных уравнений C.64), отвечающих трещине сдвига,
может быть разделена на четыре системы линейных уравнений
более низкого порядка. Действительно, согласно формулам C.59),
C.60) из четности р следует, что полиномы Щ\{х)^ Щ2(х) содер-
содержат только четные степени yi, если же р нечетно, то полиномы
jRji(ж), R22(x) содержат только нечетные степени у\. Аналогич-
Аналогичная связь существует между четностью q и четностью полиномов
Щ1(х)^ Щ^{х) п0 У2- В противоположность этому, согласно C.61),
из четности р (q) следует, что R{2{x) содержит только нечетные
степени у\ {у2) и из нечетности р (q) следует четность всех степе-
степеней у\ (у2) в полиноме В^{х). Разложим каждый из полиномов
А*1у\у2 и J2 AijUlvi B сумму четырех полиномов, как
это делалось и в случае нормального разрыва. Пусть
1=1
где к = 1, 2, Pfiyi, У2) — полиномы степени не выше N (I =
= 1, 2, 3, 4), причем полиномы P*(yi, 2/2) содержат только четные
степени j/i и j/2? ^(Уъ У2) содержат четные степени по у\ и нечет-
нечетные по г/2? Р${уъ Уг) содержат нечетные степени по у\ и четные
по уг и, наконец, Р%(уи 2/2) — нечетные степени как по j/i, так и
по J/2- Вместо уравнения C.30) рассмотрим четыре уравнения:
М ( 2^! ) , У = (Уь У2), [и1^)] € Я1/2
C.68)
К [u2(a;)] = /г (^А , [п2(х)] €Я1/2 (Ela), C.69)
\^з (У)/
182 Гл. 3. Аналитические методы
К[u3(a0] = „-1 (?|^) , [u3(a0] бЯ1/2 (Ela), C.70)
. C71)
Здесь [и*(ж)] = ([i*i(aj)], [^IC^)]) — вектор-функции. Решение
уравнения C.30) представляется суммой решений уравнений
C.68Н3.71) [и(*0] = ?[«*(*)]¦
Из отмеченных выше свойств полиномов ЩНх) следует, что
при решении уравнений C.68)—C.71) функции [г*х(ж)] и [4]
могут быть представлены в следующем виде:
№(*)]= Е
[ul(x)}=
= E
2A;+2m4
= E
2z+2j+l
= E
2k+2m+
= E
)]= E
Здесь Вг^ — постоянные.
3.4. Гармоническая нормальная нагрузка
Для построения разложения решения динамической задачи о
трещине нормального разрыва в ряд Тейлора по волновому числу
так же, как и в статическом случае, рассмотрим граничное псев-
3.4. Гармоническая нормальная нагрузка 183
додифференциальное уравнение и найдем результаты применения
1 /9
соответствующего оператора к функциям Tv'q (x). Граничное псев-
псевдодифференциальное уравнение, связывающее амплитуду скачка
нормального смещения с амплитудой приложенной нагрузки, пред-
представлено в B.54), B.55). Для удобства перепишем его здесь:
] = ^, ь(х) е я.1/2(О), Ых)] е H1/2(G).
C.72)
Символ псевдодифференциального оператора пр нам будет удобно
записать в виде, несколько отличном от B.55). Из B.55) сле-
следует, что
№ - ?№ - «2Г1/2} =
рче ~р2I/2 ~
<*2г1/2} = ~
Напомним обозначение, введенное в гл. 2 (а = 77/?), и подста-
подставим в полученное выражение. В результате будем иметь
- C.73)
Обозначим через От(с) псевдодифференциальный оператор с
символом (?2 — с2)т/2. Здесь с — постоянная, а под (?2 — с2I/2,
как и выше, подразумевается положительное значение корня, если
под корнем стоит положительное число, и положительное значе-
значение корня из модуля подкоренного выражения, умноженное на —г,
если под корнем отрицательное число. С учетом этого обозначения
184 Гл. 3. Аналитические методы
и формулы C.73) оператор пр может быть представлен в виде
+ 4/?2 [0@) - Brj2 - 1HG,/?)] -
C.74)
Прежде чем вычислять прТр( (ж), найдем, как и в статическом
случае, результат применения оператора пр к функциям (fa(x).
Из C.74) следует, что для этого достаточно уметь вычислять
O3(c)<pZ(x), 0(c)(p2(x) и 0~г{с)(р1(х). Начнем с вычисления
0(с)(р2,(х). С учетом формулы B.34) для образа Фурье функции
<Ра(х) функцию O(c)ipZ(x) можно записать в виде
R2
где О = flffi.
Переходя от оставшихся переменных & к &, получим
R?
Здесь, как и прежде, yi = Хг/щ.
Перейдем к полярным координатам ?i = icosA, C2 = isinA,
yi = gcosO, y2 = ?sin#. В результате будем иметь
s' Л/g? +
cos' Л/g? +iW Л/а^ ^.(«^(^
C.75)
3.4. Гармоническая нормальная нагрузка 185
Введем обозначение П(А) = cos2 А/а2 + sin2 A/a2. Выражение
C.75) тогда запишется следующим образом:
о о
тГ j
2тг
х J7+1(<)e-^C0S(A^ dtdX - i I (П(А))
1/2х
X
о
Далее используем разложение плоской волны по Бесселевым
функциям B.39). В результате получим
0{с)<р1{х) =^^х
x I JQ{gt) + 2^2 H)mJm(Qt) cos [m(A - в)]
m=l
с/(П(Л)I/2
0 0
+ 2 f^(-i)mJm(gt) cos [m(\-e)]\dtd\\. C.76)
m=l J J
В функции O(c)ip2l(x) можно выделить вещественную и мни-
мнимую части:
186 Гл. 3. Аналитические методы
В вещественную часть из первого интеграла в C.76) входят
члены суммы с га = 2/, а из второго интеграла члены суммы с
га = 2/ + 1. Собирая эти члены, получим
27~1ГG + 1)
КеО{с)(рЦх) = х
2тг оо
' / п
с/(П(Л)I/2
оо 27Г °°
+2^(-1)' /(П(А)I/2 /
ГТ J J
'-1 0 с/(Щ\)I/*
cos [2l(A -
2тг
00
О О
х Jn+i{eb)cosp + 1)(A - в)]dtdxl. C.77)
В lmO(c)(p2(x) из первого интеграла в C.76) входят слагаемые
с га = 2/ + 1, а из второго интеграла — cm = 21. Таким образом,
имеем
c/(n(A))V2
cos [B/
2тг КЩХ)I*2
'=1 О О
х J7+i (t) J2i (gt) cos [2Z(A - в)] dt dX >. C.78)
3.4. Гармоническая нормальная нагрузка 187
Будем рассматривать ReO(c)ipa(x) и 1тО(с)(р2(х) внутри эл-
эллипса, т.е. при д < 1. Сначала вычислим Re0(с)ipl(#)• Для этого
предварительно упростим выражение C.77). Если в каждом члене
последней суммы в C.77) в повторном интеграле взять интеграл
по радиусу ?, то мы придем к выражениям вида
2тг
[ f (П(A)) cos [B/ + 1) (А - 0)] dA,
о
где / — некоторые функции. Обозначим записанный интеграл
через L. Учитывая, что cos [B/ + 1)(А - в)) = cos [B/ + 1)А] х
х cos [B/ + 1H] + sin [B/ + 1)A] sin [B1 + 1)9], величину L можно
записать в виде
L = Lx cos [B/ + 1H] + L2 sin [B/ + 1H],
где
2тг
Li= f f(n(\))cos[Bl
о
2тг
L2= ff(U(\))sm[Bl
Заметим, что П(А) — четная периодическая функция с пери-
периодом 2тг, поэтому и /(П(А)) — четная периодическая функция с
периодом 2тг. Поскольку sin [B1 + 1) А] также периодическая функ-
функция, имеющая период 27Г, справедливо равенство
7Г
L2= f f (П(А)) sin [{21 + 1) A] dX.
Так как /(П(А)) — четная функция, a sin [B/+ 1)А] — не-
нечетная, под интегралом стоит нечетная функция. Следовательно,
Вычислим теперь L\. Поскольку и /(П(А)) и cos [B1 + 1)А] —
периодические функции, имеющие период 2тг, их произведение
также имеет период 2тг. Поэтому можно написать равенство
Зтг/2
Ьг = / /(П(А)) cos [B/ + 1)А] dX.
-тг/2
188 Гл. 3. Аналитические методы
Сделаем теперь в интеграле замену переменных А = s + тг/2.
В результате получим
Li = IS (П (я + |)) cos [B/ + 1)я + /7Г + |] ds =
Обозначим U(s + тг/2) = g(s). Из вида функции П(А) следует,
что g(s) также является четной функцией и потому /(g(s)) — чет-
четная функция. Так как sin [B/ + l)s] нечетная функция, под инте-
интегралом стоит нечетная функция и потому L\ = 0. Таким образом,
в итоге получаем
2тг
L = //(П(А)) cos [B/ + 1)(А - 0)]d\ = 0. C.79)
о
Из C.79) следует, что последняя сумма в C.77) пропадает и вы-
выражение для Re0(c)</?a(#) приобретает следующий вид:
17 Jy+i(t)Mot)dtd\+
с/(П(А)I/2
2тг оо
/
I.
х J7+1(<)J2/(^)cos[2/(A ~ 9)}dtd\ I. C.80)
В повторных интегралах, стоящих в C.80), вычислим инте-
интегралы по t. Эти интегралы имеют вид B.61) и они уже были вы-
вычислены в гл. 2 (см. формулы B.78), B.83), B.84), B.88), B.89)).
Подставив значения этих интегралов в C.80) и заменив возникаю-
возникающие при этом гамма-функции вида Г(п +1) на п! и вида Г(п +1/2)
3.4. Гармоническая нормальная нагрузка 189
на выражение из C.3), получим
т>п,\>г,\ 27ГG + !)( 2-У/2 ^ (-c2/4)?
?
(- 1
2*
р^о(-1/2-ОрA/2 + 7-
, i
2тг -
/*(П(А)) 1/2~р cos [2Z(A - в)] dX
X
о
Проводя сокращения, придем к соотношению
X
2тг
|-Р, \-7-р; 1; е2) J(Щ\)I/2-рd\+
fe 2'-1B/)!ГA/2 + 7-0
^(-l/2-0p(l/2 + 7-0rfrf'
п /3 ' 1 f
2тг ч
х /(П(Л)I/2"рсо8[2/(Л~0)]йл1. C.81)
190 Гл. 3. Аналитические методы
Теперь нам осталось только вычислить интегралы вида
2ir 2тг
V= f(E{X))~SdX и W= f(U(X))~Scos[2l{X-e)}d\.
о о
Для вычисления величин V и W нам потребуется следующий
интеграл:
_ 1
A-A;2cos2ж)" Х~2
. C-82)
Здесь к2 < 1, /х > -1/2, i/ > -1/2.
Докажем равенство C.82):
тг/2 тг/2
^ ^ Г sin/ia;cos'/a;(—1)
/ /
/sin^ ж cos^ х Г
(l-k4os*x)PdX= J
о
о
тг/2
/
= /
A - cos2 ж)^-1)/2 cos" ж (-1)
1 ~~Т^——^
у
о
A - fc2 cos2 я)
Сделаем замену переменных cos ж = s. В результате будем
иметь
• dx = —
l
¦/
l
(Л — q2\(p-
IJ. О I v
— ds.
о
Далее сделаем еще одну замену s2 = t. Это приведет к равен-
равенству
П/2 1 (Л -Л(^-1)/2^-1)/2
dt. C.83)
3.4. Гармоническая нормальная нагрузка 191
Используем также известное интегральное представление для
гипергеометрической функции (см. [98, с. 336])
Л(«, ft 7; ж) = г(а)г(^ tt)
C.84)
Интеграл, стоящий в правой части C.83), совпадает с интегра-
интегралом из C.84) с точностью до замены обозначений. Величина а из
C.84) соответствует (i/+l)/2 из C.83), 7 соответствует (//+^)/2+1,
/3 — pnz — k2. Из C.83) и C.84) следует равенство C.82).
Заметим теперь, что
n(A) = -^(l-fc2cos2A), C.85)
Ч
где, как и выше, к2 = (af — a2)/0?-
Из определения величины V и C.85) следует, что
2тг
V = <$ [{l-k2co82\)-sd\.
О
Поскольку функция, стоящая под интегралом, имеет период 2тг,
справедливо равенство
V = at* J A-к2 cos2 \ysd\.
—7Г
Из четности подынтегральной функции следует
7Г
K = 2af [(l-k2cos2\)-sd\.
о
Теперь обратим внимание на то, что подынтегральная функция
на самом деле является периодической с периодом тг и потому
V = 2af / A-й2со82А)-^А.
-7Г/2
Из четности подынтегральной функции получим
it/2
V = 4а2/ f(l-k2 cos2 A)"* d\. C.86)
192 Гл. 3. Аналитические методы
Интеграл, входящий в правую часть C.86), в точности совпа-
совпадает с левой частью равенства C.82) для /х = ^ = 0ир = 5. Таким
образом, из C.86) и C.82) имеем
2тг
V =J{U(X)ySdX = 2vaf2Fl Q, <*; 1; А;2) . C.87)
Поскольку cos [2/(А - в)] = cos B/Л) cos B/0)+sin B/Л) sin BW),
величину W можно записать в виде
W = W\ cos {2W) + W2 sin BW),
где
2тг 2тг
Wi = [ (Щ\))~5 cos B1X) dA, W2 = [{Щ\)У6 sin Bl\) dA.
о о
Функция (П(А))~ sinB/A) имеет период 2тг. Вследствие этого
7Г
W2= f(U(X))~5sinBlX)dX.
—7Г
Учитывая теперь, что (П(А))~ четная функция, a sinB/A) —
нечетная, получим W2 = 0.
Функция (П(А))~ cosB/A) также является 2тг-периодической
и потому
Wi= f(U(X))~Scos{2lX)dX.
Так как здесь под интегралом стоит четная функция, имеем
7Г
Wi = 2 [(ЩХ)У6 cos B/A) dA.
о
Заметим теперь, что и (П(А))~~ и cosBZA) имеют период тг.
Поэтому и в силу четности подынтегрального выражения получим
тг/2 тг/2
(П(А)) "J cos BfA) dA = 4 / (П(А)) "* cos B/A) dA.
3.4. Гармоническая нормальная нагрузка 193
Из формулы B.51) следует, что
cos BД)=g (ът%cos2s Xsin2l~2a А' C<88)
Подставляя правые части равенств C.85) и C.88) в выражение
для PFi, получим
dX
•^ ~ 4°2 JL Bs)\Bl - 2s)!
Таким образом, выражение для W\ свелось к интегралам типа
C.83). Подставляя C.83) в C.89) будем иметь
. „U+S AГ(ИIГA д + 1/2)Г(д + 1/2)
1- 2 S (аО!B12*)ш
+ i,E;/ + l;
Подставив теперь вместо гамма-функций выражения из C.3),
окончательно получим
!(И-- 2. - 1I1Bа - 1)!!
C.90)
Выражение C.90) можно упростить, приняв во внимание ра-
равенства
{21 - 2s - 1I1 _ 1 Bs - 1)!! __ 1
B1 - 2s)! ~ 2l~s(l - s)V Bs)\ "" 2ss\'
Отсюда и из C.90) имеем
I
W1 = тга2 / ^
5=0
14 Зак. 205
194 Гл. 3. Аналитические методы
Из C.91) окончательно получаем
2тг
W = f (П(А)) ~* cos [2/(А - в)] d\ = naf cos B/6) х
Подставив вычисленные интегралы C.87), C.92) в C.81), для
ReO(c)<p2,{x) получим
A B/ + l)!!g2' cos BW)
23//! pg И/2 - 0РГA/2 + 7 +P - l)p\
2Н.
Несколько более удобно записать это выражение в виде
| -p, i -7-p; 1;
^ B/ + l)!!g2< cos BW)
^o (-1/2 ~ 0РГA/2 + 7 + P - О?!
;e2) >• C.93)
3.4. Гармоническая нормальная нагрузка 195
В случае 7 = га + 1/2 выражение C.93) заметно упрощается.
Действительно, подставив 7 = тп + 1/2 в C.93), получим
A 1 \ /3 \
-,p--;l]k2JFi[--p,-m-p;l;Q ) +
L I J \& /
^^B1 + l)!!g2' cos BW) {-112)р(-<?аЦА)Р Л (-1)*
Далее учтем, что значения гамма-функций от целых неположи-
неположительных значений аргумента равны бесконечности. Кроме того,
заменим гамма-функции от натуральных значений аргумента со-
соответствующими факториалами, а от полуцелых значений аргу-
аргумента — выражением C.3). В результате будем иметь
)P
*2Fi^-,p--;l; J2 i\^-p,-m-p; ;
{-l/2)p{-(?allAY ^ B1 + Ще21 cos
p\ Z-j 23/-4!(-l/2 - lUm + p -1)\
p=0 r 1=1 x ' Fy
2Fi[- + l-p,l-m-p;2l + l;
Выше (см. формулы C.5), C.6)) было показано, что гипергео-
гипергеометрические функции в случае, когда один из двух первых аргу-
аргументов является целым неположительным числом, превращаются
14*
196 Гл. 3. Аналитические методы
в полиномы. Используя C.5), C.6), получим
m+p
A 1 \
2'"-2;lifc2)i; W
B/ + l)!!e2/cos
ip-i;
Из C.94) видно, что ReO(c)<p^ ' (x) разлагается в степен-
степенной ряд по четным степеням с. Преобразуем выражения для ко-
коэффициентов этого ряда, заменив g2t и g21 cos B10) на полиномы
с помощью равенств C.8) и B.51) соответственно. В результате
будем иметь
C/2 ~p)t(-m ~P)t
p!
( '
3.4. Гармоническая нормальная нагрузка 197
Из C.95) следует, что коэффициенты степенного ряда по с
являются полиномами от j/i, г/2? причем при с2р коэффициентом
является полином степени 2(т+р).
Аналогичным образом вычисляется 1тО(с)<ра(ж). Из C.78)
и C.79) следует, что в выражении для 1тО(с)(ра{х) пропадает
первая сумма, так как интегралы, содержащие в подынтегральных
выражениях множитель вида cos [B/ + 1)(А — 0)], обращаются в
ноль.
В результате 1тО(с)(р2,(х) представляется в виде
с/(П(Л)I/2
{c2/mt-t2I/2Jnl(t)J0(gt)dtd\+
О
2тг с/СПСЛ)I/2
: х
'=1 О О
xJi+i(t)J2t{gt) cos [2/(Л - в)] dtdX 1. C.96)
В повторных интегралах, входящих в C.96), возьмем инте-
интегралы по t. Эти интегралы имеют вид B.60). Они уже были
вычислены в гл. 2 (см. формулы B.74), B.75)). Подставив выра-
выражения из B.74), B.75) в C.96), в случае д < 1 (внутри эллипса)
получим
„, 2Т-1ГG + 1) f 7 (П(А))-гс3ГC/2)ГA) ^
Г 1
\ J
^ о
2)ГE/2)ГA)
'—1
+ 5/2)ГB/ + 1)ГG + 2)
198 Гл. 3. Аналитические методы
00
X
x 2*i(-P, -7 - Р - 1; 2Z + 1; Q2) d\ \.
После упрощений выражение для Im O(c)(pa(x) будет иметь вид
25Г
х
о
25Г
J{U(\))-p-1d\2Fl(-p, -7-р- 1; 1;
2тг
о
C.97)
Интегралы, входящие в C.97), были вычислены выше (см.
формулы C.87), C.92)). Подставив их значения в C.97), получим
\, р +1; 1; fc2j 2^1 (-Р, -7 -р -1; 1;
ff (l + l)p(ca2feos()
hh22p+3l{l+5/2)(+2)!BZ+3)!!
. C.98)
3.4. Гармоническая нормальная нагрузка 199
Преобразуем C.98) заменив переменную суммирования I на
переменную t = / + р. В результате получим
х 2^1 (-j, P + 1; 1; к2) 2Fi(-p, -7 -p - 1; 1;
~ «Zi (i _ p + 1)р(са2J{+3д2^-^ cos [2(i -
. C.99)
Заметим теперь, что гипергеометрические функции, завися-
зависящие от е2, имеют в качестве первого аргумента целое неполо-
неположительное число —р и потому являются полиномами от q2.
Подставим в C.99) вместо этих гипергеометрических функций
соответствующие полиномы. В результате получим
&
a (< - Р + 1)„^-р> cos p(i -
s 23i"p(i -
s=o
200 Гл. 3. Аналитические методы
Заменим теперь g2t и q2(x~p) cos [2(i — р)в] соответствующими
полиномами от у\, уг с помощью равенств C.8) и B.51) соответ-
соответственно. В результате придем к следующему равенству:
Ы0(сШх).
ОО t—I
^ Bn)!B« - 2р- 2n)! ^ sl(i-p-
n=0 v ' v e ' s=0 v ^
l2ti+2n# )
" J? ]CI00)
Из C.100) видно, что ImO(c)(pa(x) разлагается в степенной ряд
по нечетным степеням с, начиная с с3. При этом коэффициентами
при с2п+3 являются полиномы от yi, J/2 степени 2п.
В частном случае при j = m + 1/2 равенство C.100) приобре-
приобретает следующий вид:
1
(т + 3/2)о2
рт + 5/2)р
-р)Д-т - р - 3/2)f ' y?»
t=0 5=0 V
3.4. Гармоническая нормальная нагрузка 201
!Bг - 2р + 3)!!
2.
ttI(,_tt)I j-
C.101)
Таким образом, вычисление О(с)(ра (х) завершено.
Перейдем теперь к вычислению О~1(с)<ра(х). Оно проводится
совершенно аналогичным образом. Поэтому приведем лишь фор-
формулы, получающиеся после каждого этапа вычислений, без подроб-
подробных комментариев.
Используя выражение для образа Фурье функции ipj(ж), имеем
[ A+i(ICI)
я2
Переходя от переменных Х{ к гц и от оставшихся переменных
к &, получим
Л/2'
Переходя теперь к полярным координатам ?i = icosA, B
tsinA, j/i = ^cos^, 2/2 = ?sin0> получим
x f—i
XJ (П(А)
13 Зак. 205
202 Гл. 3. Аналитические методы
Используя разложение экспоненты по Бесселевым функциям и
разделяя вещественную и мнимую части, получим
J7+1«)JqH
У 1} У (П(Л)
. (ЩА)I/**
о
00
X
/
.. Г 1 ¦ /" Л+1(^)^-ц(е<)cos [B/ + 1)(Л -9))
Х/(П(А)I/2 У
/(())
7Г
~ 2тг
оо
х 7
cos [B1 + 1)(А - 0)]
О
v f—J— f
ХУ (H(A))V2 У
JT+i(t)M&) cos [2/(A - в)]
Поскольку интегралы, содержащие в качестве множителя в по-
подынтегральном выражении cos [B/ + 1)(Л - 0)], равны нулю, вы-
3.4. Гармоническая нормальная нагрузка 203
ражения для ReO~l(c)<p2,(x) и 1тО~1(с)(ра(х) упрощаются:
оо ^ 2тг
X
с/(П(Л)I/2
00
1г( 7 m
1/2 v " '—¦*¦-//
C.102)
т n
ImO
-U
7Г
с/спсл)I/2
X
о
2тг
J1+l{t)J2l{Qt)
C.103)
Рассматривая ReO-1(c)y>2(a;) внутри эллипса (д < 1), вычислим
в C.102) интегралы по t. В результате будем иметь
13*
204 Гл. 3. Аналитические методы
х
х
о
A/2)р(-с2/4)
р
U + | -Р, / - \ -Р-7; 2Л-1; Л х
2; 1
х / (П(А)) ~1/2"р cos [2/(A - в)] d\ \.
о '
о
После интегрирования по А, получим
ГG+1)агт'/г[
р=0
2
^0 A/2 -0/G + 3/2 +р -Op!
C.104)
Из C.104) следует, что ReO^)^^) также разлагается в
степенной ряд по четным степеням с. В случае, когда 7 = m +1/2,
гипергеометрические функции, зависящие от g2, превращаются в
3.4. Гармоническая нормальная нагрузка 205
полиномы. В результате равенство C.104) приобретает вид
шо-1(с)ч>™+112(х) = т^,;1'7Г°2<У^ rc Q2/.;t .х
¦ 1)!р!
l),?2'cosB/0)
:Х
l-l)\p\
5=0 V '
t=0
l)tt\
Заменив здесь g2t и д21 cos {219) на соответствующие полиномы
от 2/i, j/2> окончательно получим
^ {m+p +l)\p\
^ 4 J
((I +1),J
p+m+l-l + l _ __ ^ _ / (-1)^
x \ ^ A L t-hl tL ll \ Л i—?— ч> x
c=0 it—-0
206 Гл. 3. Аналитические методы
Из C.105) видно, что ИеО~г(сIр™+1'2(х) разлагается в сте-
степенной ряд по четным степеням с, коэффициентами этого ряда
являются полиномы от ух, J/2, причем при с2р стоит полином по-
порядка 2р + 2т + 2.
Для получения ImO~1(c)(p2(x) возьмем в C.103) интегралы
по ?. В результате будем иметь
т n-i
+ 3/2)B0!ГG + 2)
2тг
X
О
После вычисления интеграла по А и простейших преобразова-
преобразований, получим
|, р +1; 1; кЛ 2Fi(-p, -т -1 -р; 1;
(/+ 1)p(cq2Jp+2'+1
Гипергеометрические функции, зависящие от q2, имеют в
качестве первого аргумента неположительные целые числа —р и
потому представляются в виде полиномов. Благодаря этому
3.4. Гармоническая нормальная нагрузка 207
Im О" (с)(р2 (х) записывается в виде
т п
22p+1C/2)p(t
t=o
X
3=1
V
X
p-l)t.2t|
w I'
Заменим теперь индекс суммирования / на % = / +р. В резуль-
результате имеем
r^ (-"P)t(- -p-l)t 2t \-^y^ QK P)cos[2(г -pH]
p + 3/2)pG + 2)pp! ?j «!(• - p -
2^1 U +1, i +1; * -P +1;
«=o
208 Гл.З. Аналитические методы
Запишем g2t и #2(*~р) cos [2(г — р)в] в виде полиномов от j/i,
В результате получим
00 t—1
2г+1
X
)!!(i-p + 3/2)pG
2(«+n) 2(i+t-p-n-u) 1
Из C.106) следует, что ImO"^)^^) раскладывается в сте-
степенной ряд по нечетным степеням с, причем коэффициентами при
степенях с являются полиномы от j/i, j/2- Заметим, что коэффи-
коэффициентами при с2р+1 являются полиномы порядка 2р. В частном
случае при у = гп + 1/2 равенство C*106) приобретет вид
(~1)P(CO2JP+1 x
(да + 3/2) ^ 22p+iC/2)p(m + 5/2)р
х
x
+ Z. ^) Z. 2«-PBi-?p + l)I!(t-p + 3/2)p(m.
Bг-2р)! ^ (_!)•+-«
3.4. Гармоническая нормальная нагрузка 209
и=0
Вычисление О l(c)<pa{x) завершено.
Наконец, таким же путем вычислим O*(c)ipl(x). Из выраже-
выражения B.34) для образа Фурье функции (р2,(х) имеем
3 2тгГG +1)д1аа
о (сы(х) = ——2—
Переходя от переменных а^ к yi и от оставшихся переменных
& К ?г> ПОЛуЧИМ
я2
После перехода к полярным координатам имеем
&{с)<р1(х) = 27ГG + 1) /(П(Л)K
о о
^dtd\.
Здесь Ci = tcosA, C2 = tsinA, y\ = qcosO, j/2 = gsin0.
Разложим экспоненту в ряд по Бесселевым функциям и разде-
разделим вещественную и мнимую части. В результате будем иметь
00
х I
f
210 Гл. 3. Аналитические методы
2]Г(-1)'/(П(А)K/2со8[2/(А-ф
7 (t2 - с2/П(А)K/2
c/(n(A))V2
2w
3/2,
'=0 о
tT
7Г
bf^-l)'*1 /(П(А)K/2со8[BГ
0
00
X
с/(П(А)I/2
/(ЩА)K'2
о о
2тг
о
X
О
V (с2/п(А) - t*f2jy+1(t) Met) ШЛ
n /
3.4. Гармоническая нормальная нагрузка 2П
Учитывая, что интегралы, содержащие в подынтегральном вы-
выражении cos [B/ + 1)(А — 0)], обращаются в ноль, получим
{2~^^{x)K2
с/(П(А)I/2
{t2~^^{x)Kj1+l(t)Met)dtdx+
00
X
c/(II(A))V2
-1)< / (n(A)K/2cos[2/(A-0)]x
J Р-*™ГЫ*)Ш)ЛЛ C.108)
X (У
(Qt)
in
о
~ 2тг
х / ~—- dtd\>. C.109)
о >
Рассмотрим ReOs(c)ip2{x) внутри эллипса (д < 1). Вычислим
в C.108) интегралы по t. В результате будем иметь
212 Гл. 3. Аналитические методы
[
3/2-р ,д
г=1
х 2^1 И + | ~Р,1 + 3/2 - 7 ~р; 21 + 1; ^2J x
х / (П(А)K/2"Р cos [ЩХ - в)] dX
о
Подставляя значения интегралов по углу А, получим
а|
Г 6 ^ (са2JЧ-1)р ..
00 °° BZ + 3)!!e2icos(^)(co2Jp(-l)P(-3/2I,
-х
р=01=1 - .-,;+р-1-
X
5=0
C.110)
Из C.110) видно, что и Re O3(c)(p2(x) разлагается в ряд по чет-
четным степеням с. При у = т + 1/2 входящие в C.110) гипергеоме-
гипергеометрические функции, зависящие от g2, превращаются в полиномы.
3.4. Гармоническая нормальная нагрузка 213
В результате приходим к соотношению
т+р—1 /с /о ч
.. V^ E/2-Р)
*=0
1=1
5=0
t(l
(*0
л
-т-р)
2
BZ +
-Ч1(т+:
5)! \
/ j
t=0
Q т-
3)!!52'
' 2';
(/ + 5/
^ (са2Jр(-1)Р(-3/2)р
р=0
cos (Ив)
¦1)!Н-3/2)р
2,/ + l,*jx
-2-p)t(/+i-TO_p)t 2;
Заменим теперь g2t и д21 cos B10) на соответствующие поли-
полиномы от з/i, J/2- После этого выражение для ReO3(c)<#T (ж)
примет вид
- Bm+ 1I1* [А (са2Jр(-1)'
t=0
(са2J*(-1У(-3/2)%
У ( + )( + )! Л (-1)'-»
2 2«2M3/2U + Zl)!^B)!BZ2)!
i=i
214 Гл. 3. Аналитические методы
5=0
'l(l + b/2-p)t{
x
C.111)
Таким образом, согласно C.111), ReO3(c)<?™+ ' (x) разлага-
разлагается в ряд по четным степеням с. Коэффициентами этого ряда
являются полиномы от yi, у2) причем при с2р стоит полином по-
порядка 2р + 2га — 2.
Для получения ImО3(c)(pl{x) вычислим в C.109) интегралы
по t. С учетом того, что д < 1, получим
00
о '=1
00
X
. .-5)!!B0!(/ + 7/2),G-
2тг
1-"-1 cos [2/(А - в)] d\ iFri-p, -7 -p - 1; 2/ + 1; ^2) 1.
О
Интегрируя по А получим
1 С 00
х 2JF1 Q, p +1; 1; fc2j 2^1 (-P, -7 - p -1; l;
(ca2K(l + l)pecosBW)
(
М(' + 7/2),G-
s + ^, р +1 +1; / +1; fc2) 2*i(-p, -7 -Р-1; 2Л-1;
3.4. Гармоническая нормальная нагрузка 215
Так как у гипергеометрических функций, зависящих от д2,
первыми аргументами являются целые неположительные числа
—р, эти функции представляются в виде полиномов. В результате
выражение для ImО3(с)<ра{х) приобретает вид
J2t
1 Z^ Z^t 22P+*lBl
1=1 p=0
I
X
a
Заменим теперь g2t и д21 cos B/0) на соответствующие поли-
полиномы от у 1,2/2- В результате получим
hh22р+3|Bг
s=0
X
t=0
216 Гл. 3. Аналитические методы
Заменим индекс суммирования / на г = I + р. Получим выра-
выражение
hh 23i~p{2i ~2p+5)!!(i ~
?——Т) * 1 ^П
V"^ (""!) l^t — Zpfl v^ ( —lr
x X \ / v ^U X v
+ ,t + l
a (*-*+i)« i ^-)i г (ЗЛ12)
Из C.112) следует, что Im Ог(с)(р1(х) разлагается в ряд по не-
нечетным степеням с, начиная с пятой степени. Коэффициентами
при степенях с являются полиномы от j/i, $/2- При этом коэффи-
коэффициентом при с2р+5 служит полином степени 2р. В частном случае
7 = m + 1/2 из C.112) имеем
(-1ГцBг-2р)! ^ (-1)'
Bu)!Bi - 2р - 2u)! ^ «!(t -p -
3.4. Гармоническая нормальная нагрузка 217
р (_р),(_m - р _ з/2), « у^)^^--) ]
а (*-*+!)« i •!(«-«)! /• (ЗЛ13)
После вычисления О (с) <pl {х), О~1(с)^2(ж), О3(с)(^2(ж) можно
перейти к вычислению О^^2(а;)- Из вида оператора пр C.74) и
формул C.95), C.105) и C.111) следует
x
3
p=0 v
-1
h
f-f 23l-2(-l-Z/2)Jm + p-l-l)\^Bu)\Bl- - '¦
X
5=0
f
+
2 fB»2
1 • . , 9\ V~^ C/2 — Х?)+(—771 — о),
х oi^i ( -, р - г; 1; Дг 1 > ^^ ^-^^ ^х
218 Гл. 3. Аналитические методы
х
BЛ-1I!A +1), Л (-1)'
h
- о» h
' C/2 +1 - p)t (I - m - p)t f y;("-Hy2('+'
B/ + 1)* S u!(*-t>)!
Bm + 1)!!.
B1 + l)\\(l + 1),
-2 L—: is—, x
-0!
C/2 +1 _ p)t(< _ m - p)t
^0 B«)!B/ - 2u)! ^
v=O
m+p+l
A/2 - p)t(-m - p - l)t y^ yfV ;
t! ^J !(< )l
t! ^J «!(< - v)l
t=O v=O K '
.
+Р+1-1I
3.4. Гармоническая нормальная нагрузка 219
v=0
Учитывая, что в C.74) [O3(/3)-O3fo/?)],
и O~l(r)C) множатся на разные степени /?, проведем в C.114) сле-
следующие замены: в первых квадратных скобках р — 1 заменим
на п, во вторых квадратных скобках р на п и в третьих р + 1
на п. Вынеся к тому же общий множитель Bт + 1)!!тг/ Bm+102)
за скобки, получим
n=0
-r, "I. I- h2
v x C/2 - n)t(-m - n)t ^ Ух^2__,
t=o
Z. 23*-3(_г _ 3/2)„+1(ш + n - 7)! ^J Bu)!(M - 2u)
x E
t=o
B1 + l)t
t y2(u+v)y2(l+t-u-v) oo^
220 Гл. 3. Аналитические методы
n=0
г- (-1)'
Z^, 23l-4-l/2 - l)(m + n-f\\*-i aUl - .
I t л \J—ii
¦x
у C/2 + f - n)t(l -m-n)t* yf^yf
*=0
4
x^^ ^ ^L - - +
t=0 " v=0
B1 + 1I1A + 1),
t "f C/2 +1 -n)t(l -m-n)t
2(u+«) 2(l+t-u-v) 00
^ Е
Ы(^д)|
У C/2 - n)t(-m - n)t Л у?yf -«)
(-1)"+W"+2 - V» + r?^
4»(n -1)!
у (-1)'
- l)n.x{m + n-l)\^Q s\(l - e)l
3.4. Гармоническая нормальная нагрузка 221
Здесь i?(n) функция, которая при п = 0 равна нулю (# @) = 0) и
Н(п) = 1 при п > 0.
Собирая коэффициенты при одинаковых степенях /За,2, по-
получим
x I (-An - l)rJn+2 + 2(n + l)rJn + 2n - 1 + H{n)n{n + 1) x
X DV2n+2 - 4rj2n + Г?2")] 2fl Q, „ _ I; 1; fc2) X
C/2-n)f(-m-n)f^
A)A/2)и[Dп 1)^ + Bn 4-1)^2" + 2n - 1]
4»(+l)!
B/
x v
_ ^ 2«-iH-l/2)n(m + n-0!
m+n-l /, о /o ч /. v t
y v^ l' + ''/2-"M'--")t^i.i .. ,
^ 2^-1A/2 - 0n_!(m + n - 0! {
- 0! {? W ~
222 Гл. 3. Аналитические методы
1- \ 771-1-71—/ /I I о /гь \/т \
1 , ^ .21 v^ (/ +3/2-nU/ -ra-nh
2' 2' ' у ?jj BЛ-1L
/ , -ч»„„ t 2(u+v) 2(/+t-it-v) 1
^1 J/2 I
v!(t-t;)! J*
При выводе этого равенства было учтено, что B1 + 3)!! =
= B* + 1)"B/ + 3); (-3/2)п+1 = (-3/2)(-1/2)в; (-/- 3/2)п+1 =
= Н-3/2)Н-1/2)п.
Далее примем во внимание, что Н(п)п = п; A/2)п_1 = (—2) х
_ (-/ - 1/2)„ _ 2гB/ + 1)!!
" (-1-1/2) И( + h ~ 21 + 1 •
В результате будем иметь
п=о v ' '
х [(An2 - 1)т}2п+2 - 2Bп2 + п- 1)г72п + п(п + I)??2"-2 + 2п - l] x
. f 2Fi A/2, n - 1/2; 1; fc2) ^n C/2 -n)t(-m-n)t
I (^+«)! h tl
i H - l/2)B(m + n - /)!
S+2'n~2;
v=0
Таким образом, согласно C.115), Refi/з^ ' (x) разлагается
в ряд по четным степеням /Заг, причем коэффициентами при сте-
степенях /Зп2 служат полиномы от yi, j/2- Коэффициентом при (/Заг) п
является полином степени 2п + 2т.
3.4. Гармоническая нормальная нагрузка 223
„ I 1 /О
С помощью выражений для КеПр(ра ' (х) можно вычислить
и RetyjTp1/2^). Из C.10) имеем
Dp-2rDq-2m v+q-r-m+1/2,,
1 Z » ц У /
X
r=0 т=0
1
r(p + q-k-m + 3/2)
[р/2] [q/2] nP~2r п9-2т D+g-r-m-t-i/z / ч
\Г"^ V' "* 1 2 fd v /
2»-+mr!m!(p _ 2r)!(g - 2т)!Bр + 2q-2r-2m + 1)!!"
C.116)
Из C.115) и C.116) следует
[р/2] I?/2) r)P-2r rjg-2m
^!ЕЕ ор--л ¦х
г=0 т=0
(р - 2г)!(д - 2т)!а2 ^ 4»(п + 1)!
х [Dп2 - 1)»72п+2 - 2Bп2 + п - l)rfn + п(п + I)»;2" + 2п - l] x
х< — •—"*——х
I [р + q — г — тп + п)\
p+q-r-m+n C/2 -n)t(r + m-p-q-n)t
^ Н~ I "~ "~* I • i X
=0 /=1
5=0
" B/ + l)t
¦v) 2(i+t-w-v) n
«к*-»)! ;¦
224 Гл.З. Аналитические методы
Проводя дифференцирования согласно формуле C.22), оконча-
окончательно получим
.) = f
п=0
[Dп2 - 1)т]2п+2 - 2Bп2 + п - l)q2n + n(n + l)^2" + 2n -
4»(n + l)!
^ ~fQ r\m\{p - 2r)\(q - 2m)! | (p + g-r-ra + n)!
C/2-n)t(r + m-p-g-n Л
Bv + 2r-p)\ Bt + 2m-2v- q)
2
2tH-2r-p 2t+2m-2v-q
У
x
x h
X
^ v\(t - г;)! Bи + 2v + 2r - р)\ B1 + 2t + 2m-2u-2v- q)\'
У?
C.117)
Прежде всего заметим, что суммирование в C.117) ведется
только по тем индексам, которые дают неотрицательные степени
ух и у2- Из C.117) видно, что КепрТЦ2{х) разлагается в ряд по
четным степеням (/?аг). Коэффициентами при (/Заг) п являются
2
() ф
полиномы от ух, 2/2 степени 2п +р + д.
3.4. Гармоническая нормальная нагрузка 225
1/2
Аналогичным образом вычисляется и imQpTpq (х). Из вида
оператора Up C.74) и формул C.101), C.107) и C.113) следует
(-p).(-m-p-3/2), Л у
<=0 v=0 v ' г=1
X *~^
•X
• 1К-1У*1 /1 2\
3.2?H-iE/2)p(m + 6/2)p ^ U* /
xAf——ii ±<Ж^)\ +
9\Bi-2p + 3)"
(-l)<-"Bi - 2p)!
16 Зак. 205
226 Гл. 3. Аналитические методы
t 2(u+n) 2(t+t-p-n-«)
+ ^B^ 1)
«!(*-«)! J yy ' ' (m + 3/2)
X
*=0 3=0 v ' г=1
'Р
р=0- v-w -_)!!(г-р + 3/2)р(т
^0 Bn)!Bi
« у2(
Собирая члены с одинаковыми степенями /3 и меняя в связи с
этим обозначения индексов суммирования, получим
п=0
xr/2n+5-8(n +l)Bn +5)т/2п+3+Bп +5)Bn +3)r;2n+1+8(n +1)] х
2, п + 1; 1; fc2) ^ (-n)t(-m - п - 3/2), ^
(»-« + !).
(n - v + 7/2)v(m
3.4. Гармоническая нормальная нагрузка 227
^ Bn-2v)\ ^
Bп - 2v + 5)!! ^ Bj)!Bn - 2v - 2j)! ^ sl{n -v-s)\
НОЛ-"» ~ f ~ 3/2)f
(u+j) 2(n+t-v-j-u) )
^ . C.118)
u)! /
Из C.118), C.116) и C.22) следует
СЮ
п + l)(n + 2)V2n+5 - 8(n
n=0
xBn + 5)??2n+3 + Bn + 3)Bn + 5)?72n+1+8(n + 1)]
1
«2
Ь/2] [9/2]
^ ^0 2r+mr!m!(p - 2r)\{q - 2m)\Bp + 2q-2r-2rn + 3)!!
.. V^ (-n)t(r + m-p-q-n- 3/2)t.,
t=0
t
Bs)! B*-2s)! y2s+2r-py2t+2m-2S-g
2s-g)! s\(t - s)\
n-1 ,
(n — v-
_jj 23n-«(n _ „ + 7/2)> + 9 - г - m + 5/2)vv!
Bn-2«)!
Bn - 2v + 5)!! -^ Bj)!Bn - 2v - 2j)\ ^ s\(n -v-s)\
' u=0
16*
228 Гл. 3. Аналитические методы
{2n + 2t-2v-2j-2u)\
Х Bn + 2i + 2m - 2v - 2j -2u- q)\ *
Xy2u+2j+2r-py2n+2t+2m-2v-2j-2u-q 1
Из C.118) и C.119) видно, что1тпрр™+1/2(х) и1тп/зТ}{2(х)
разлагаются в ряд по нечетным степеням /?, причем в обоих слу-
случаях коэффициентами при (/За2) п+ являются полиномы степени
2п. Напомним также, что в C.119) суммирование ведется только
по тем сочетаниям индексов, которые дают неотрицательные сте-
степени yi и у2.
Заметим, что О^(с) — оператор третьего порядка и потому
O3(c)Tpq(x) g H_i/2{Ela), однако, поскольку в оператор пр вхо-
входит разность 03(/3) — О3(г/^б), которая уже является оператором
первого порядка, UpTpq(x) G H-i/2{Ela), что и видно из формул
C.117), C.119).
Вычислив ReUpTpq(x) и imupTpq (я), можно переходить к
конструктивной процедуре разложения решения уравнения C.72)
в ряд Тейлора по /За2. Для этого предварительно введем некоторые
обозначения. Согласно C.117)
00
КеПрТ^2(х) = Y,№arfnU(P> «' 2п> 2п+Р + Ь У)- C-12°)
п=0
Здесь функции U являются полиномами от у = (j/i, уг)- Первые
1/2
два аргумента функции U указывают, к какой функции TPq (x)
применялся оператор. Третий аргумент показывает, при какой
степени Ра2 наша функция U является коэффициентом. Наконец,
четвертый аргумент указывает, полиномом какого порядка явля-
является функция U.
Аналогичным образом, согласно C.119), можно записать
00
^) = ]Г (Ca2Jn+3V(p, g, 2n + 3, 2п, у). C.121)
71=0
Аргументы функции V имеют тот же смысл, что и аргументы
функции U. А именно: первые два аргумента указывают, к какой
функции тЦ2(х) применялся оператор, третий аргумент показы-
показывает, при какой степени /За2 эта функция является коэффициентом,
и четвертый аргумент говорит о том, что функция V является по-
полиномом от у степени 2п.
3.4. Гармоническая нормальная нагрузка 229
Из C.120), C.121) следует, что
ВД/(х) = f; (f3a2JnU(p, q, 2n, 2n +p + q, y)+
n=0
00
+i ? (^2Jn+V(p, q, In + 3, 2n, y). C.122)
n=0
Напомним, что в формулах C.120)—C.122) предполагается, что
рассматриваются значения функций внутри эллипса Ela.
Предположим, что амплитуда приложенной к поверхностям
трещины нагрузки ts(x) может быть представлена в виде
— = Ё (Pa2)N{PN(y)+iQN(y)), C.123)
^ N=0
где PN(y), Qn(v) — вещественные полиномы степени не выше
N + J (oxdPN(y) <. iV + J, ordQiV(y) ^ iV + J), J — некоторое
произвольное заданное натуральное число.
Заметим, что нормальные нагрузки, возникающие в задачах
рассеяния трещиной плоских продольных и поперечных волн,
распространяющихся вообще говоря наклонно к плоскости тре-
трещины, могут быть записаны в виде C.123).
Будем искать решение задачи C.72) в виде
( Br(p,q,m)T}l2(x)+
m=0 \
. C.124)
Здесь 5r(p, q, m), Bl(p, q, m) — вещественные постоянные.
Верхний индекс указывает на то, являются ли эти коэффи-
коэффициенты коэффициентами разложения вещественной или мнимой
части. Первые два аргумента указывают на то, перед какими функ-
функциями TPq (x) записанные константы являются коэффициентами.
Третий аргумент указывает, при какой степени /Зп2 данная кон-
константа является коэффициентом.
Подставляя C.124) и C.123) в C.72), получим
p+q^m+J ' N=Q C.125)
230 Гл. 3. Аналитические методы
лучим
оо
1/2
Подставив в C.125) выражения для upTpq (x) из C.122), по-
поm=0 yq^
х Е (Pa2JnU(p, q, 2n, 2n + p + g, y)+
00 -,
+i E (/?«2Jn+V(p, </, 2n + 3, 2n, y) +1 E 5^' 9, rn)x
[00 00
E (Pa2JnU(p, q, 2n, 2n
n=0 n=0
D
Г=О
Do
Преобразуем естественным образом полученное уравнение.
В результате будем иметь
ОО 00
E ^r(p,g,
m=0 n=0 pg<
-(/?а2J7г+т+3 ? В*(р, 9, m)F(p, g, 2n + 3, 2п,
p+q^m+J
оо оо
m=0 n=0
+(Pa2Jn+m Yl 5>' ?' ГО)^(Р» ?' 2n' 2n +p + 9, y)) =
oo
= Е'(^2Г(Р^(у)+^;у(у)). C.126)
N=0
oo
Для приведения левой части C.126) к виду ?) {Pa2)NCN^ где
лг=о
С^ — некоторые коэффициенты, сделаем замены. В суммах, со-
содержащих (/?a2Jn+m, заменим m на N = 2n + m, а в суммах,
содержащих (/?а2Jп+т+3, т заменим на N = 2п + т + 3. В ре-
3.4. Гармоническая нормальная нагрузка 231
зультате получим
оо е AN/2]
Е О**)"{ ( Е Е Br(p,Q,N-2n)x
N=0 I ^ n=0
хЩр, q, 2n, 2n + p + q, y) - W(N)x
9, q, 2n + 3,2n, i
n=0 p|9^
[JV/2J
, q, 2n + 3, 2n, y)+J2 J2 В*(Р> Ь N ~ 2n)x
n=0
xU(p, q, 2n, ) J
, y) J = J
C.127)
Здесь квадратные скобки обозначают целую часть числа, введен-
введенная функция W(N) определена на целочисленных неотрицатель-
неотрицательных значениях аргумента:
Приравнивая вещественные и мнимые части коэффициентов
при {Ea,2)N в C.127), получим систему уравнений
[N/2]
J2 Е Br(p,q,N-2n)U(p,q,2n,2n
п—О p+g^N+J-2n
[(JV-3)/2)
-W(N) ^
n=0
232 Гл. 3. Аналитические методы
[N/2]
]Г ? В'& 9>N~ 2n)U(P> Я, 2п, 2n+p +
п=0
E Br(p,Q,N-2n-3)
n=0
C.129)
Распишем более подробно процедуру решения системы C.129).
Перепишем C.129) в следующем виде:
Br(p, q, N)U(p, q,0,p + q, у) = PN(y)-
p+q^N+J
[Л/2]
- J3 Z) Br(p,q,N- 2n)U{p, q, 2n, 2n+p + q,
n=l p+g^Af+J-2n
[(ЛГ-3)/2]
E E ВЧр,<7,ЛГ-2п-3)х
n=0 p+g^JV+J-2n-3
xF(p, q, 2n + 3, 2n, y),
[N/2]
"E E B%q,N
n=l р+д<ЛГ+^-2п
[(ЛГ-3)/2]
-^) E E Br(p,q,N-2n-Z)x •
n=0 p+g^J\T+./-2n-3
xK(p, g, 2n + 3, 2n, y).
C.130)
Отметим, что в C.130), если при суммировании верхний пре-
предел оказывается меньше нижнего, то предполагается, что соответ-
соответствующая сумма пропадает.
Заметим также, что уравнения C.130) отвечают решению ста-
статической задачи при комплекснозначной полиномиальной нагру-
3.5. Гармоническая сдвиговая нагрузка 233
зке порядка N + J, причем правые части C.130) соответствуют
нагрузкам.
Решение C.130) осуществляется последовательно. Сначала за-
задается N = 0 и из C.130) находятся Br(p, g, 0) и 5*(р, д, 0),
Р+Я ^ J- Затем берется N = 1, 2 и т. д. При увеличении N реше-
решения, полученные на предыдущих шагах, попадают в правые части
уравнений C.130). Таким образом, мы можем найти i?r(p, g, N)
и S*(p, g, iV), вообще говоря, для сколь угодно большого N и тем
самым вычислить сколь угодно длинный отрезок ряда Тейлора.
Заметим, что в этом параграфе были вычислены результаты
применения оператора пр к функциям (pi {х) и TPq (x) внутри эл-
эллиптической области. Поскольку
и
где № — сопряженный к Ир оператор, а черта сверху означает
комплексное сопряжение, результаты применения сопряженного
оператора к функциям <ра(х) и Tv'q (x) внутри эллипса также явля-
являются вычисленными. В силу этого для использования в описан-
описанном в гл. 2 двухбазисном проекционном методе функций <ра(х) и
TPq (x) в качестве элементов второго базиса осталось вычислить
результаты применения к ним оператора Щ вне области эллипса.
Такие вычисления могут быть проведены вполне аналогично.
3.5. Гармоническая сдвиговая нагрузка
Задача об эллиптической трещине сдвига решается аналогично
случаю отрыва. Для ее решения используется граничное псев-
псевдодифференциальное уравнение. Это уравнение приведено выше
(см. B.102)). Оно имеет следующий вид:
t(x) е #_1/
C.131)
где [u(x)] = ([ui(#)], [^2B?)]) — вектор амплитуд скачков сме-
смещений, t(x) = (*i(a;), <2(#)) — вектор амплитуд приложенных
усилий, Кр — матричный псевдодифференциальный оператор с
символом
\ш к22@)
15 Зак. 205
234
Гл. 3. Аналитические методы
Выражения для
саны в виде
приведены в гл. 1 и могут быть запй-
* J = 1'2' C-132)
C.133)
Символам Kij(?) соответствуют псевдодифференциальные опе-
операторы К^, которые согласно C.132), C.133) и введенным в
§ 3.4 обозначениям принимают вид
J\ п 1* — лО
J = 1, 2, (З.Ш)
Вычислим результаты применения операторов К^ к функциям
<р™+1/2{х) и тЦ2(х). В силу C.134), C.135) и в связи с тем, что
результаты применения операторов О(с) и О (с) к указанным
функциям вычислены в § 3.4, осталось только найти производные
\dxm
Поскольку
a2 id2
C.136)
dx\ 8x2
3.5. Гармоническая сдвиговая нагрузка 235
из выражения для ReO(c)<p™ ' (х) C.95) и формул дифферен-
дифференцирования C.22) будем иметь
Re
(д2
—оО(с)ц>™+1/2(:
+ 1)!!тг[А (-c2aj/4)p /1 _ 1 ^ fc2\
00 /
Л (-1)'
Ы 23/-1/!(-1/2 - l)p(m + Р-1У.^О s\(l - «)!
)
14^}, C.137)
Re
Bm + l)!k(^ (c^/4) /1 l.i.
C/2-p)t(-m-p)t Л 1 B»)l
15*
236 Гл. 3. Аналитические методы
X-2*-ll°1-2,y-y
^(/ + р^р^ 1 Bu + 2v)\
Bl + l) ^\(t)\B 2l)\
t=o v n v=o
Bl + 2t-2u-2v)\
C.138)
Re
R
0/2 -P)t(-m -p)t
(-1/2)р(-с2О1/4)
1/4)р
p\
p=0 y
У (я+ 1I1 Л (-iy
(« + i)H f
-1/2-l)p{m + p-l)\f^Q
y
l)p(m + p-1I ^ ,!(/ - *)!
C/2 + f - p)t(f - TO - p) «
BZ + 2t - 2u - 2v)!
Bi 2f222
C.139)
3.5. Гармоническая сдвиговая нагрузка 237
Аналогичным образом для мнимой части функции
"(ж) из C.101), C.136) и C.22), имеем
р
Е(— p)i(—тп — р — 3/2)^ чг-л 1 Bs)!
7\ 2-, s4t-s)U2s-2VX
С/ • vail/ ^ I • V *<U « / ¦
V )+
Bг - 2р + 3)!! ^ Bп)!Bг - 2р - 2п)\ j^n s\(i-p- s)\
" (-p)t(-m-p-3/2)f.
/ey,U + 2n)\ ^2(ц+я-1). 2(t+»-p-n-u)
92
(m + 3/2)аю| \^J 3 ¦ 2*+>(S/2), (m + 5/2)
t=o
B* ~2s)! 2,-! 2t_2s-i
f-2S-l)!yi 2
frfl ^+3y (<P + i), 1 x
^ 23'"Р^ p + W (m + 5/2)P!Bi - 2p + 3)!!
238 Гл. 3. Аналитические методы
Bг-2р)!
( s + -, г + 1; г - р + 1; fc2J J]
Bt + 2i-2p-2n-2u)\
x x i '- Ь ?. L x
^ u\(t - u)\ Bu + 2n - 1)! Bi + 2% -2p-2n-2u- 1)!
1
f
г=1
1
Bг - 2рI
^ Bn)!Bt - 2р- 2n)! ^ s\(i-p- e)!
Bt + 2% - 2р - 2n - 2гг)!
г - 2р - 2п - 2ц - 2)! Х
-П-и-1)| C142)
3.5. Гармоническая сдвиговая нагрузка 239
Таким же образом вычислим производные от Re О" (с) х
х<Р?+1/2(х) и lmO^l{c)ipTl'2{x). Из C.105), C.136) и C.22)
имеем
dx\
v=0
5
t=0
\J-u
(-1)'-" y^ 1 Bu + 2v)\
i)!BZ - 2u)l ^ v\(t - v)\ Bu + 2v - 2)!
--Ч, C.143)
*! ^J «!(*-«)! B» - 1)!
240 Гл. 3. Аналитические методы
2Г2(^
B/
" B1 +
№¦
:!]
•2-)!
2t-
+D,]2 ^
S (^
Л 1 B«
^jj w!(t - v)\ Bu +
- 2u - 2«)! 2(«+t»:
2u_2u-l)!yi
^
«4
2v
п м
-1)!
У2
\
•
C.144)
Bт + 1IкГА (-c2oj/4)p /1 1 M
t=0 ' v=0
I
Bt-2v)l
p!
Л (-1)'-" Л 1 B1 + 2t - 2u - 2v)\
^ Bu)!BZ - 2u)! f^ »!(t - v)\ B1 + 2t-2u-2v- 2)!
xy2(u+v)y2{l+t-u-v-l
3.5. Гармоническая сдвиговая нагрузка 241
Производные от мнимой части 0~1{с)ф™+ ' (х) вычисляются
из C.107), C.136), C.22):
U=o
р=0
Р ( _л / - о/о\ * 1 /ол\|
Л Z-.s!(<_s)!Bs-2)!
00 t-1 /.• _ i 1 \
2(s-l) 2(t-s)
Vl У2 -
x 1 v< (K-JWi
(m + 5/2)^! ^ Bп)!Bг - 2p - 2n)! ^ <!(t -p - s)\
^ + _,, + 1;t_p + 1;
! BЦ + 2П)! 2(u+n-l) 2(
\(t-u)\Bu + 2n2)\yi У2
а2
771 I ¦—
7*^*1.1/7 1 lfH + n/7 1 Л
kp=0
p i -\ /
X
Й
00 i-1 ^_
1У2 S + X, (саг) t+ 22 23i~PBi -2p+ 1)!!
i=l p=0 v '
г-р
Bt-2p)!
i - p + 3/2)p(m + 5/2)^! ^ Bn)!Bi - 2p - 2n)!
242 Гл. 3. Аналитические методы
B« + 2n)! .,
( + p ) 2
Bi + 2i-2p-2n-2u-l)!yi
j + It — 2p — In — 2u)\ 2(«+n)-l 2(i+t-p-n-u)-l 1
*' У2 h
C.147)
(«-P+1L 1
" 2p + 1)!!(t" - P + 3/2)p (m
B»-2p)I ^
^ Bn)!Bt - 2p - 2n)! ^ «l(i -p -
Bг + 2< - 2p - 2n - 2ц)!
2n - 2« - 2)!X
-«-«-1)| C148)
3.5. Гармоническая сдвиговая нагрузка 243
Из вида оператора Кц C.134) и полученных формул C.137),
C.95) и C.143) следует
x[
Х > "" « ^V!(i-V)!BV-2)!X
t=0
) 2(t,) ,
У2 +
p=0
У (Д + 1)Н Л (-1)'
x h 23/1/!(i/2 o(+- о» s e!c - s)! x
2(t-v)
Уг +
p=o
(-1)'
^ 23'-4!(-l/2 - 0p(m +p - 01 ^ *K' "
чу 1? I « _J_ я^ . I _1_ 1 . ^ I \ v ' V
244 Гл. 3. Аналитические методы
v=0
2
У2
DJ2 f (-D
X
Л (-!)'-" Л 1 Bц + 2у)!
Х ^ B«)!B/ - 2и)\ ^ v\(t - v)l Bti + 2v - 2)! X
Собирая коэффициенты при одинаковых степенях (/Заг), по-
получим
m+n+1
X
A/2 — п)Д— m — n — 1L y-
t!
t=0 v=0
n=0
3.5. Гармоническая сдвиговая нагрузка 245
X
иг
fe 2*-Цт + п + 1-1IA/2 -l)n2-<os\(l-
~l (I + 1/2 - n)t(l - m - n - l)t,
Bц + 2v)\
^ ( + /)t()t
^ Bu)\Bl - 2u)! ^ »!(* " «)! B« + 2v- 2)!'
p2(n-H»-l)f2(t+t-tt-i;)l _,_ _L
„/1 ln ,.2\ y^" C/2 - n)t(-m - n)t
X2^i^2' n~2! ; ' ^^ ^ ^X
t=0
4"n!
{ti -t-1^;;
. , 2«-4!(-l/2-Z)n(ro + n-0!
m+n—/
X
C.149)
Таким образом, согласно C.149), Re Кц<Ра+ (х) разлагается
в степенной ряд по четным степеням /?аг, причем коэффициентами
при (/?аг) п являются полиномы от у\, уг порядка 2т + 2п.
246 Гл. 3. Аналитические методы
Из вида оператора Кц C.134) и полученных формул C.140),
C.101), C.146) для ImKU(p™+l/2(x) имеем
?j «*-.)! B.-2)!
Х> - */2i+3x«2i+3 E ^|
i=l р=0
(t -р +5/2)р(т +5/2)^1B^ -2р +3)!!^ Bn)!Bt -2p -2п)\
р
X
BЦ + 2П)! 2(«+n-l) 2(W-p-n-u)l ^
B« + 2n - 2)!У1 Уз J (m + 3/2)a2
х \ (~Р)г(-т-Р~/2)г у^ Уг8У2 * ,
*=0 5=0
оо г-1
+
^ 23^Р(^ " P + 5/2)p(m + 5/2)^!
Bt - 2p + 3)!! 2-* Bn)!Bi - 2p - 2n)! ^ e!(» - p - s)!
3.5. Гармоническая сдвиговая нагрузка 247
v=0
(го + 3/2)а?
t=0 8=0
00 *-l
+
«!(*-«)! B*-2)!"
"^2i - 2p + 1)!!(г - p + 3/2),
Bi-2p)! ^ ^
(m + 5/2)pp! ^ Bn)!Bi - 2p- 2n)! ^ «!(« -p-s)\
-p),(-m-p-3/2),,
xa4-, .--r^.-r^.-j'-r*»'» y^ Bi-2p+l)t
Л ( + ) 2(u+n-l) 2(i+t-p-n-u)]
^ y У J
Собирая члены при одинаковых степенях (/Заг) и принимая во
внимание, что в полученном выражении надо учитывать только
члены, содержащие положительные степени у\ и уг, получим
G'n+2;1;A2)g
x2F1(^n + 2;l;^)>:biziMz^^V2)lx
1 Bз)! ) , V2-
h
248 Гл. 3. Аналитические методы
х Bп + 1 + 4п2п+ь) V4 (n-v + 2)v
v=0
SJ
S—\J
) '
Bu
E/2)n
A (-n),(-m-n-3/2)t Л 1 2s 2(t-s)
xh t\ Lut)\yiy> +
t=0 ' s=0
00 П-1 /
n=l v=0
л n-v
Bn-
(n -» +5/2)„(т +5/2)ww!Bn -2« +3)!!^Bj)!Bn -2v -2j)\
X>]-17-J^ rra^i e + x, n + l;n-t7 + l;A:2 x
. C.150)
Из C.150) видно, что ImKnip™* ' (x) разлагается в ряд по
нечетным степеням /За2, начиная с 3. Коэффициентами при
(/?ei2Jn+3 служат полиномы от ух, j/2 степени не выше 2п.
3.5. Гармоническая сдвиговая нагрузка 249
Совершенно аналогично, из вида оператора К22 C.134) и полу-
полученных формул C.139), C.95) и C.145), будем иметь
1 I Л
h
n),(-m-n-l) ' 1
Bt-2v)\ *.**—
XBt-2v-2)\yiV2
v ' n=0
Br,2n+2+n-l)
(l + l/2-n)t(l-m-n-l)t
t=o v /l
1 B/ + 2t - 2u - 2v)\
^ »!(t - «)! B/ + 2t - 2u - 2v - 2)!
(-l)n ^
C/2 ~ n)t!"m"n)t
, n -11; ^ f!
2"(
А (^а2J"(-1/2)п(-1)" К (M + 1)!!
^ 2 • 4nn! ?^ 23'-4!(-l/2 - l)n{m + n-l)\
2u)\Bl - 2u)\
x ^ C/2 + 1-яу-т-п)<у:У| У2 , (злб1)
*=0
250 Гл. 3. Аналитические методы
Из C.134) и формул C.142), C.101), C.148) имеем
l о i 1л\ V^ (-*» ~ Ш-т - п - 5/2).
г»" + 2; 1; к21? * и±— i-^
1 B* - 2з)! 2. 2U-»
yi У2
2. Sl(t-s)\Bt-2s-2)\
«=0 v / v / п=0
4-1) V (п -1; + 2)„
+ 1) ^
1
Bп - 2и + 5)!! ^ B;)!Bп +2 - 2v - 2j)!
E ,l(n.t.l-i>-
t=0 e=0 V ' n=l
n—1 / , - \ -
^ 23«"v (n-v + 5/2)v(m + 5/2)vvlBn-2v + 3)!!'
Bn - 2v)\
)!Bn - 2v - 2j)\ 2- 5!(n - « -
3.5. Гармоническая сдвиговая нагрузка 251
+ »,П + 1;„_, + 1;
Таким же образом, подставляя в C.135) формулы C.138),
C.144), и собирая члены при одинаковых степенях (/Заг), по-
получим
X
^ Й
t=0 «=0
Bц)! B* - 2рI ^-,^-2,-!
B1)!B<21)!У1 У2
1 n=0
m+n+l Г/7 . 1\ I2
+ П-1)
X
5=
X
t=0
X f- Bu)!BJ - 2u)\ ^ V!(t - t;)! B/ + 2< - 2u - 2^ - 1)!
l 1
Согласно C.153), при разложении Re Ky^pS (x) в степенной
ряд по (Cci2) коэффициентами при (/Зп2Jп также являются поли-
полиномы от ух, у2 степени 2т + 2п, а члены, содержащие нечетные
степени Фа2), отсутствуют.
252 Гл. 3. Аналитические методы
Из C.135) с помощью формул C.141), C.147) получим
Й(-п-2),(-т-п-7/2),
^— '-Ь
2' ' ' ' ) ^ t\
К 1 Bs)! Bt-2s)! 2, 1 и о- 1
X
5=1 -V- "'
00
+ /^ vPa2 j 1^7/ + АП + Oj X
n=0
n+1 / _ оч
-(n-t; + 9/2)v(m + 5/2)^!X
n+2~v /o . .
Bn-2v + 7)!! f^ Bj)!Bn + 4-2v-2j)!
A ^w+5--7
^ e!fn + 2-t;-e:
{2t + 2n-2v-2u- 2j + 4)!
Bt + 2n-2v-2u-2j + 3)\
C.154)
Таким образом, 1та.К\2<ра+ (ж) разлагается в степенной ряд
но нечетным степеням (/Заг), начиная с 5. Коэффициентами при
(/?агJп+5 являются полиномы от j/i, 2/2 степени 2п + 2 или, как
и выше, коэффициентами при (/?О2Jп+3 являются полиномы сте-
степени 2п.
3.5. Гармоническая сдвиговая нагрузка 253
Из формул C.149)—C.154) и представления функций T$q{x) че-
через функции вида (рЦх) и их производные C.10) имеем
и <*> [р/2][д/2]
п=0 r=0 m=0
(? - 2m)! I a? I 4"+1(p + q-r-m + n+ l)!(n + 1)!
-.-lAi.fcA V^ tl/2 -n)t(r +m -p -q -n -l)t,
«=o r>
vI Bv + 2r~P- 2)! Bt + 2m-q- 2v)\
lv+2r-p-22t+2m-q-2v , (-1)" A/2)пBту2"+2 + П - 1
У +
p+g-r-m+n+l
x
-r—m+1—<
Л (-1)'-"
1r - p - 2)!
- 2u - 2v)\
2m-2u-2v-q)\
2u+2«+2r-p-2 2(/+t+m-u-w)-9] ,
[ 2^42' г'1'
t=0 v=0 v '
() ( ) 2v+2r-p 2t+2m-2v-q ,
Bv + 2r-p)\ B* + 2m - 2u - q)\Vl V<1
254 Гл. 3. Аналитические методы
4«n! j^ 2*1-1 (-1/2-l)n(p+q-r-m+n-l)\
p+q—r—m+n—l
B1 +1),
Bи + 2v)! B1 +
^ v\(t - v)\ [2u + 2v + 2r-p)\ B1 + 2t + 2m-2u-2v- q)\
Xy2u+2v+2r-Py2l+2t+2m-2u-2v-q\
[p/2] [g/2]
2r+mrjyn[
n=0 r=0 m=0
1 I O2
(p - 2r)\(q - 2m)!Bp + 2q-2r-2m + 3)!! 1 a\
A \ n+1 Z' /к,
' t=i
(—n — l)t(r + m — p — 5 — n — 5/2)t
t! X
^ 5!(t - 5)! B5 + 2r ~p - 2)! Bt + 2m -. 2s - g)!
(n - v + 2)v
v=0
1
(p + q-r-m + 5/2)vv\Bn -2v + 5)!!
?^ B.;)!Bп + 2-2г;-2.7)! ^ 3!(n + l-v-s)!
1 l2\
3.5. Гармоническая сдвиговая нагрузка 255
.. у (Ч(г + m-p-q-v-
Bt + 2n + 2 - 2v - 2j - 2ц)!
Bt + 2n + 2m + 2 - 2v - 2j - 2u - g)!
#2tt+2j+2r-p-2f/2(t+n+m+l-»-i-«)-g I j_ J_ [ (~^
a2
x 2u+2j+2rp2y2(j)q + }_\zDHl
t=0
Л 1
2г-р)!B«+2т-2з-9)!
fl—1 / .. . ч \
1
(n - v + 5/2)„(р + q - г - m + 5/2)vw!Bn - 2v + 3)!!
п~*Bп-2у)! 1
)! Bn - 2t; - 2j)! Jj e!(n - v - s)\
+ -,n + l\n-v + l; k2) x
Bn-2t, + l)t
Bu + 2j)! Bt + 2n-2v-2j-2u)!
+ 2r-p)\ Bt + 2n + 2m-2v-2j -2u-q)\
Xy2«+2i+2r-py2(t+n+m-«-i-«)-,
l \ ^ш)
256 Гл. 3. Аналитические методы
Здесь, как и выше, Н@) = 0, Н(п) = 1 при п > О.
n=0 r=0 m=0 ' *v
: 1: fc2)
4n+1(n + 1)! l[p + q-r-m + n + l)i
p+g-r-m+n+l /i /«* \ / , _ _ _ _Л*
t=0 v=0
1 - f (-1)"Bт?2"+2 + п - 1) ГаЛA/2, я + 1/2; 1; fc2)
(g-2m)![ 4Л+1(п + 1)! [(p + g-r-m + n +1)!
Bv + 2r- p)\ Bt + 2m-q-2v- 2)!
gr-r-m-fn+l
- 2v)\ 2v+2r-p 2t+2m-g-2v-2 ¦
q-2v-2)\yi Vi
• 1 \ p+^f—Г—77i
X
t/f I \
M + r-n)
\ 2 Л
*
^ Bu)!BZ - 2^)! ^-( v\(t - v)! Bu + 2v + 2r -p)!'
u=0 V—/-V— --'/• v=0
X
B/ + 2* + 2m - 2tt - 2« - g - 2)!yi
M+Hn,,^,!),,] Н"Ш1/2,П^1/2;1^2)
Bv + 2r-p)\ Bt + 2m-2v- q)l
2
+ , -. x ,- 1№
2v+2r-p 2t+2m-2v-g ,
l У*
V 2;B ?-
3.5. Гармоническая сдвиговая нагрузка 257
/
/
/
(-1)' ./
p+q—r—m+n—l
u!(i-u)!Bu4
C/2
*,+
•2v4
+ Z-n)t(/ + r
2w)! 1
-2r-p)!BZ +
+ m — p
B/ + 2t -
2i + 2m
(-1)'-
- 2u - 2v)\
-2u-2v-
\
utlj.
.]}.,
Ь/2][?/2]
n=0 r=0 m=0
(p - 2r)!(g - 2m)!Bp + 2g - 2r - 2m + 3)!! | B
, n + 2; l;fc2)
Я ~ r - m + 5/2)n+1
n+±(-n-l)t(r + m-p-q-n-5/2)t^ 1 ,
B^)! Bt - 2s)\ 2s+2r-p 2t+2m-2e-g-2 ,
Be + 2r-p)!Bf + 2m-2s-g-2)!yi V*
Bn + 2-2v)\
«!Bп~2» + 5)Н ^ Bj)!Bn + 2 - 2v - 2j)\
x
5=0
¦^ (~v)t(r + m-p-q-v- 3/2)t ^
Bn + 3 - 2v)t ^ n!(t - ti)!
t=o v 7t w=o v '
18 Зак. 205
258 Гл. 3. Аналитические методы
Bц + 2j)\ Bt + 2п + 2 - 2v - 2j - 2ц)!
Х Bц + 2j + 2г-р)\ Bt + 2n + 2m-2v- 2j - 2u -q)\
, n + l;l;fc2)
5/2)n3
t=Q
3
Bt - 2s)! 2s+2r-p 2t+2m-2s-0 „, , yi (n-P+1)
+2m-2s-9)!yi Уг ( ^ 2»»-
(n - u + 5/2)u(p + g - r - m + 5/2)vv!Bn - 2v + 3)!!
x
Х2^1 fs + -,n + l;n-u + l; A;2) x
? Bn-2v + l)t ^
Bц + 2j)! Bt + 2n - 2v - 2j - 2ц)!
Bц + 2j + 2r -p)\ Bt + 2n + 2m-2v- 2j -2u- q)\
\m\[p — 2r)\(q — 2m)!
V^ (W-n)t(r + m-p-q-n-l)t
3.5. Гармоническая сдвиговая нагрузка 259
X
Л i
Bt - 2v)\
Bt + 2m — q — 2v — 1
\ p+g-r—m+n+1
* ^ (—IM /
~ ^-^ s!(/ — s)\ z* L \
n+p-hg-r-m+l-i n л /о
i=O
1 / \l t
1 ^ Bu)!B/ - 2u)\ ^ «!(
B«)!
Bu "f" 2t* ™" jo
2v+2r—p—1
)!V' [((+
q-r-m+
B1 + 1
t - v)\ B« +
— 2u- 2v)\
2t+2m-q-2v-l ,
\
B« + 2v)\
2v + 2r-p-l)!"
B/ + 2t + 2m - 2u - 2v - q - 1)!
X
+ 2n + 3)x
1 n=0
Ь/2] [9/2]
~JQ ~?q 2r+mr!m!(p - 2r)\{q - 2m)!Bp + 2q-2r-2m + 3)!!
„f (-1)^A/2,п + 3;1;А:2)
-r-m + 5/2)n+2
x
t=i
Ba)! Bt-
X Bs + 2r -p- 1)! Bi + 2m - 2s - q - 1)! "
v=0
18*
260 Гл. 3. Аналитические методы
1
(п - v + 9/2)„(р + q - г - m + 5/2)v«!Bn - 2v + 7)!!
j=0
n+2-« /
-p-g-t;~3/2),
+ 52)
2n + 2m + 3 - 2v - 2j - 2u -
BtX + 2j)!
C.160)
Напомним, что в полученных выражениях C.155)—C.160) сум-
суммирование ведется только по тем сочетаниям индексов, которые
дают неотрицательные степени у\ и т/2-
Из формул C.155)-C.160) следует, что функции
разлагаются в степенные ряды по четным степеням (/Заг)- Коэф-
Коэффициентами при фп2Jп являются полиномы от yi, у2, степени
которых не превосходят 2n+p + q. Функции ImKijTpq (x) разла-
разлагаются в степенные ряды по нечетным степеням (^аг). При этом
разложение функций Im КjjTPq (x) начинается с членов порядка
(/ЗагK, а коэффициентами при (/?а2Jп+3 являются полиномы от
Уъ У2ч степени которых не превосходят 2п. Разложение функций
imKuTpq (х) начинается с членов порядка (/Заг) , а коэффициен-
коэффициентами при (/?а2Jп+5 являются полиномы от j/i, 2/2 степени не выше
2п + 2.
Формулы C.155)-C.160) позволяют развить конструктивную
процедуру получения коэффициентов разложения решения систе-
системы уравнений C.131) в ряд Тейлора по волновому числу. Пусть
приложенные нагрузки в области малых частот допускают следую-
следующее разложение:
? = Е @a2)N{PN№ + iQNj(y)), 3 = 1, 2. C.161)
3.5. Гармоническая сдвиговая нагрузка
261
Здесь у = (уь у2), Pnj(v) и QNj(y) — полиномы, ^)
< N + J, ordQNj(y) < N + J, где J — произвольное фиксирован-
фиксированное натуральное число.
В параграфе, посвященном трещине нормального разрыва, уже
отмечалось, что такое условие, налагаемое на приложенные на-
нагрузки, не является слишком ограничительным, так как ему, в
частности, удовлетворяют амплитуды сдвиговых нагрузок, отве-
отвечающих задачам рассеяния трещинами плоских, наклонно падаю-
падающих, продольных и поперечных волн.
В силу формул C.155)-C.160) можно ввести обозначения:
Ъ*КцТ%2{х) =
Щ(Р, Q, 2п, у),
C.162)
п=0
, q, 2n + 3, у),
n=0
00
= ]T (/?a2Jn+5K12(p, g, 2n + 5, y). C.163)
n=0
Здесь i = 1, 2; j = 1, 2; Е/#(р, g, 2n, у) — полиномы по у =
= (j/ь Уг) степени не выше 2n+p + g, Vjj(p, g, 2n + 3, у) — поли-
полиномы по у степени не выше 2п и Vi2(p, g, 2n + 5, у) — полиномы
по у степени не выше 2п + 2.
Формулы C.162), C.163) позволяют искать решение системы
уравнений C.131) в следующем виде:
m=0
C.164)
Здесь j' = 1, 2; В^(т) и BpJ(m) — вещественные константы.
Подставим C.164), C.161) в уравнения C.131) и учтем фор-
формулы C.162), C.163). В результате будем иметь
m=0
n=0
oo
\n=0
iflj}(ro))x
262
Гл. 3. Аналитические методы
2
n=0
00
\n=0
+ E
n=0
00
\n=0
n=0
00
\n=0
„ 1
- (ЗЛ65)
Собирая в левой части равенства C.165) члены при одинаковых
степенях (/?а2), получим
(W2)
HE E
ЛГ=0 I n=0
[
\Ul2(p,q,2n,y)
[(JV-5)/2]
E
n=0
+t
-2n)+iB&N -2n))x
(B}rq(N-2n-3)+
[Ar/2]
3.5. Гармоническая сдвиговая нагрузка 263
Е (Bp2J(JV-2n-5) + zBp2j(iV-
C.166)
В записи C.166) предполагается, что члены сумм по п, где
верхний индекс в знаке суммы отрицателен, отсутствуют.
Из C.166), разделяя вещественную и мнимую части и при-
приравнивая коэффициенты при одинаковых степенях (За,2, получим
систему уравнений
0
Е Е
n=0
C.167)
264 Гл. 3. Аналитические методы
[N/2]
Vu(p,q,2n + 3,y)\ 2 r(N_2n_
s
Перепишем систему уравнений C.167) в следующем виде:
Uu(p,
, q, О, у)\ дзг/дл fUuip, q, О, у)\
ф, q, 2П, у))
п=О pfl<
°
(N - 2п - 3)
C.168)
3.5. Гармоническая сдвиговая нагрузка 265
BU(N) (Un^ 9) °' УЛ +B2i(N)
Bpq\") \Ui2(p, q, О, у)) ^пт^>
[Л/2]
|(АГ-3)/2]
_ у^
п=О
- Е
S
В C.168), если в знаке суммы верхний предел оказывается
меньше нижнего, то предполагается, что соответствующая сумма
пропадает.
Уравнения C.168) представляют собой последовательность си-
систем линейных алгебраических уравнений относительно постоян-
постоянных B$q(m) и Вр\(т). Решение C.168) осуществляется последо-
последовательно. Сначала задается N = 0 и из C.168) находятся S^@)
и jB^(O) для j = 1, 2; р + q < J. Затем берутся N = 1, 2 и т. д.
При увеличении iV решения, полученные на предыдущих шагах,
попадают в правые части уравнений C.168). Заметим, что на
каждом шаге уравнения C.168) отвечают решению статической
задачи, причем правые части соответствуют комплекснозначным
полиномиальным нагрузкам. На iV-м шаге порядок полиномов,
отвечающих нагрузкам, не превосходит N + J. С помощью пред-
представленного алгоритма можно найти Bj>q(N) и Bplq(N), вообще го-
говоря, для сколь угодно больших N и тем самым вычислить сколь
угодно длинный отрезок разложения решения в ряд Тейлора.
Выражения для функций Кц<р™+ ' (х) внутри эллиптической
области, вычисленные в этом параграфе, если их еще дополнить
выражениями для функций Kijip™* ' (х) вне эллиптического но-
17 Зак. 205
266 Гл. 3. Аналитические методы
сителя, которые могут быть вычислены аналогично, дают возмож-
возможность использовать функции у™ ' (х) для построения второго
базиса в двухбазисном проекционном методе при решении задач о
трещинах произвольной формы.
3.6. Применение аппроксимаций Паде
Полученные в § 3.4, 3.5 разложения решений задач об устано-
установившихся колебаниях пространств с эллиптическими трещинами
в ряд Тейлора по волновому числу могут дать хорошую аппрок-
аппроксимацию точных решений лишь в небольшой окрестности /9 = 0,
т. е. вблизи статического решения. Действительно, решения как
функции от /3 не являются аналитическими и потому ряд Тей-
Тейлора сходится в круге, радиус которого равен расстоянию до пер-
первой особой точки. Однако имея достаточно длинный отрезок ряда
Тейлора, можно переразложить решение по другому базису, с по-
помощью чего построить высокоточную аппроксимацию решения в
более широкой области, включающей особые точки.
Представленные ниже решения различных задач получены с
помощью аппроксимаций Паде. Идея аппроксимаций Паде за-
заключается в переразложении функции, заданной рядом Тейлора,
по базису рациональных функций. Это позволяет хорошо аппрок-
аппроксимировать функцию в области, где ее ряд Тейлора уже не схо-
сходится, и кроме того исследовать поведение функции при комплекс-
комплексных значениях аргумента.
Подробное описание свойств аппроксимаций Паде, условий их
сходимости и приложений имеется в [17]. Здесь напомним лишь
основные формулы. Пусть для функции /(z), z € R1, известен ее
00
ряд Тейлора f(z) « ?) C{Zl. Аппроксимацией Паде порядка [L/M]
г=0
называется рациональная функция вида
разложение которой в ряд Тейлора (с центром в нуле) совпадает с
разложением функции f(z) с точностью до члена порядка L+M+1:
00
J2 Ciz1 = [L/M] + 0{zL+M+1). C.170)
t=0
Коэффициенты су, bk из C.169) определяются следующим обра-
образом. Умножим C.170) на знаменатель дроби [L/M]. В результате
3.6. Применение аппроксимаций Паде 267
М
? bkzK C.171)
k=0
Из C.171) следует, что коэффициенты, стоящие в левой части
равенства при степенях 2L+1, 2L+2, ..., zL+M, нужно приравнять
нулю. В результате будем иметь систему линейных алгебраиче-
алгебраических уравнений относительно 6&:
получим
00
i=0
м
к=0
bkzk
L
= y^
3=0
Сх-М+2 Сх-
М+2 Сх-М+3
C.172)
Здесь положено Cj = 0 для j < 0; кроме того, поскольку коэффици-
коэффициенты в [L/M] определены с точностью до постоянного множителя,
предполагается, что bo = 1.
После определения 6& из системы уравнений C.172) коэффи-
коэффициенты clj могут быть найдены из C.171) приравниванием коэф-
коэффициентов в левой и правой частях при одинаковых степенях z
для степеней от z° до zL. Из этого следуют соотношения
«о = со, a>i = с\ + bico, ... , aL=cL+ ]jP Ъ{Сь-{. C.173)
Уравнения C.172), C.173) называются уравнениями Паде. Они
позволяют достаточно просто по коэффициентам ряда Тейлора вы-
вычислить коэффициенты числителя и знаменателя аппроксимации
Паде [L/M]. Имеется ряд теорем, выясняющих условия сходимо-
сходимости последовательности аппроксимаций Паде [Lk/M^] к исходной
функции [17]. В отсутствие дополнительной информации о функ-
функции, подлежащей приближению с помощью аппроксимаций Паде,
наиболее целесообразно пользоваться диагональными [М^/Мь]
или парадиагональными [Mk ±//М^], М& -» оо последовательно-
последовательностями. Такие последовательности обеспечивают сходимость, на-
например, к мероморфным функциям. Отметим, что поскольку ап-
аппроксимации Паде приближают функцию в достаточно широкой
области по конечному числу коэффициентов разложения в одной
точке, коэффициенты ряда Тейлора должны быть вычислены до-
достаточно точно.
17*
268
Гл. 3. Аналитические методы
Ниже рассмотрены применения изложенного в этой главе ап-
аппарата как к динамическим задачам, решенным в гл. 2 двухба-
зисным проекционным методом или рассмотренным в других ра-
работах, так и к новым задачам. При вычислении тех или иных
характеристик решения сначала по ряду Тейлора для скачков сме-
смещений вычислялся ряд Тейлора для исследуемой характеристики,
а затем применялись аппроксимации Паде.
Сначала рассмотрим задачу рассеяния эллиптической трещи-
трещиной нормально падающей, плоской, продольной волны (этому
соответствует однородная амплитуда нормальной нагрузки). На
рис. 3.1 изображены зависимости нормированных коэффициентов
2,5
2,0
1,5
1,0
0,5
О 1 2 3 4 pa
v = 0,25 v=0,4 v = 0,45
v = 0,49 v = 0,5
Рис. З.1. Влияние коэффициента Пуассона
интенсивности напряжений от обезразмеренного волнового числа
(\Ni(l3a)\) /Nist) для задачи о круговой трещине при различных
значениях коэффициента Пуассона v = 0,25; 0,4; 0,45; 0,49; 0,5.
Здесь a — радиус трещины, а iVIsj, как и выше, — значение КИН
для соответствующей статической задачи. В расчетах использова-
использовались аппроксимации Паде вида [L/L], [L + 1/L], [L/L + 1]. Ве-
Величина L доводилась до 12. Результаты расчетов в представлен-
представленном диапазоне изменения /За оказались не зависящими от вида
аппроксимации, причем с увеличением L результаты быстро уста-
устанавливались.
Чтобы проиллюстрировать, насколько быстро устанавливают-
устанавливаются результаты, выберем, например, кривую, отвечающую и = 0,25,
и обозначим первый максимум на этой кривой через \Щ |/iVIS?,
3.6. Применение аппроксимации Паде
269
первый минимум через \Щ \/Nist и второй максимум через
\N{; |/i\fi5t. Значения обезразмеренных волновых чисел, при ко-
которых достигаются указанные экстремумы, обозначим соответ-
соответственно /З^а, /3B)а и /З^а.
Покажем, как величины \Ni \/Nlst и fi^a (г = 1, 2, 3) зависят
от порядка аппроксимаций Паде. Здесь и ниже эти экстремальные
величины определялись из дискретного набора значений, выдавае-
выдаваемых в расчетах с шагом Afia = 0,1. В табл. 3.1 приведены зави-
зависимости \Ni\/Nist и (З^а (г = 1, 2, 3) от L для аппроксимаций
Паде вида [L/L].
Таблица 3.1
[L/L]
|ЛР>|
Nut
\N™\
Nut
\N^\
Nut
[3/3]
1,4701
1,5
0,3274
5,2
-
-
[4/4]
1,4788
1,5
0,4071
3,0
0,6422
5,2
[5/5]
1,4791
1,5
0,3971
3,0
0,7570
5,5
[6/6]
1,4791
1,5
0,4023
3,0
0,6929
4,3
[7/7]
1,4791
1,5
0,3980
3,0
0,7876
4,3
[8/8]
1,4791
1,5
0,3975
3,0
0,8296
4,3
[9/9]
1,4791
1,5
0,3975
3,0
0,8358
4,3
Из табл. 3.1 видно, что значения /?^a, определяемые, как отме-
отмечалось выше, с точностью до 0,1, устанавливаются: для (З^а, уже
начиная с порядка аппроксимации Паде [3/3], для /З^а — с [4/4]
и для (З^а — с [6/6]. Для значений \Ni\/Nlst, уже начиная с по-
порядка аппроксимации [5/5], устанавливаются четыре знака после
запятой. Для \щ \/Nlst четыре знака после запятой устанавли-
устанавливаются, начиная с порядка [8/8], однако и для меньшего порядка
аппроксимаций погрешность оказывается небольшой. Так отли-
отличие значений, даваемых аппроксимацией [9/9] от [4/4] составляет
2,4%, от [5/5] — 0,1% и от [6/6] — 1,2%. Для величин \N^\/Nlst
в приведенном диапазоне изменения порядка аппроксимаций че-
четыре знака после запятой еще не устанавливаются, однако, раз-
различие результатов, даваемых аппроксимациями порядка [8/8] и
[9/9], составляет всего 0,74%.
270 Гл. 3. Аналитические методы
Аналогичная скорость сходимости и устойчивость получае-
получаемых результатов наблюдается и в случае использования парадиа-
гональных последовательностей аппроксимаций Паде, а также
для материалов с другими значениями коэффициентов Пуассона.
В табл. 3.2 в качестве примера для круговой трещины, расположен-
расположенной в упругом пространстве с v = 0,4, представлены зависимости
\Ni\/Nlst и Р^а от порядка аппроксимаций Паде при использо-
использовании аппроксимаций вида [L/L +1]. В табл. 3.2 результаты при-
приведены, начиная с такого порядка аппроксимаций, который при-
приблизительно соответствует установившимся результатам в случае
v = 0,25 (см. табл. 3.1).
Таблица 3.2
[L/L + 1]
Nut
\N™\
Nut
/?<2>а
WC)|
Nut
/9<8>a
[7/8]
1,5842
1,6
0,3621
ЗД
0,6288
4,4
[8/9]
1,5842
1,6
0,3617
3,1-3,2
0,6829
4,5
[9/10]
1,5842
1,6
0,3617
3,1
0,6692
4,4
[10/11]
1,5842
1,6
0,3617
3,1
0,6689
4,4
[11/12]
1,5842
1,6
0,3617
3,1
0,6695
4,4
[12/13]
1,5842
1,6
0,3617
ЗД
0,6695
4,4
В табл. 3.3 представлены зависимости значений \Щ%' \/Ni8t и
а от коэффициента Пуассона и.
Таблица 3.3
V
~Nu7
NUT
Nu7
/?<3>a
0,25
1,4791
1,5
0,3975
3,0
0,8358
4,3
0,4
1,5842
1,6
0,3617
3,1
0,6695
4,4
0,45
1,7269
1,6
0,3368
3,2
0,5660
4,4
0,49
2,1147
1,8
0,3369
3,4
0,4950
4,4
0,5
2,7373
1,9
0,3912
3,4
0,5614
4,3
3.6. Применение аппроксимаций Паде
271
Рисунок 2.1 и табл. 2.6 показывают, что полученные в гл. 2 с
помощью двухбазисного проекционного метода численные резуль-
результаты в целом неплохо соответствуют полученным здесь с помо-
помощью аппроксимаций Паде по существу аналитическим результа-
результатам. Для большей наглядности сравнения на рис. 3.2 приведены
1,4
1,2
1,0
0,8
0,6
0,4 _
0,2
У
//
/У
¦ /
-
\\
\\
\\
V,
\\
\\
V //^
\ V
i i i
1 2
—двухбазисный метод
3 4 р
—аппроксимации Паде
Рис. 3.2. Сравнение результатов
зависимости \Ni(f3a)\ /Nlst для случая v — 0,25, полученные в гл. 2
и здесь. Рисунок 3.2 показывает хорошее соответствие между чи-
численными результатами гл. 2 и численно-аналитическими резуль-
результатами гл. 3. Полученные с помощью аппроксимаций Паде резуль-
результаты для v = 0,25 хорошо согласуются и с известными результа-
результатами [304, 383].
Поскольку аппроксимации Паде, приближающие КИН, явля-
являются рациональными функциями, они имеют полюсы (нули зна-
знаменателя дроби), которые, вообще говоря, по мере увеличения
порядка аппроксимации должны сходиться к полюсам КИН, как
функции от комплексного волнового числа. Поэтому интересно
вычислить полюсы аппроксимаций Паде, выяснить, как они уста-
устанавливаются при росте порядка аппроксимации, и проанализиро-
проанализировать их влияние на поведение КИН как функции от вещественных
значений волнового числа.
Вычисления корней полиномов, являющихся знаменателями
аппроксимаций Паде, проводились с помощью стандартной под-
подпрограммы. Расчеты показали, что значения полюсов аппрокси-
аппроксимаций Паде расположены только в нижней полуплоскости, причем
вместе с полюсом /За = v + iw обязательно содержится и симме-
272 Гл. 3. Аналитические методы
тричный относительно мнимой оси полюс —/За = —г; + iw. Здесь
черта сверху означает комплексное сопряжение. В качестве ил-
иллюстрации того, насколько быстро устанавливаются полюсы по
мере увеличения порядка аппроксимаций Паде [L/L], в табл. 3.4
приведены зависимости первых трех полюсов ((Зау" = Vj + iwj
(j = 1, 2, 3) от величины L для рассмотренной задачи о круговой
трещине радиуса а в упругом пространстве с v = 0,25.
Здесь предполагается, что полюсы Vj + iwj и — Vj + iwj нуме-
нумеруются одним и тем же номером, и в табл. 3.4 из симметричной
относительно мнимой оси пары полюсов представлены только по-
полюсы с положительной вещественной частью.
Таблица 3.4
[L/L]
VI
Wi
V2
W2
V3
W3
[4/4]
1,638
-0,595
4,249
-2,332
-
-
[5/5]
1,639
-0,595
4,713
-2,239
-
-
[6/6]
1,639
-0,595
4,006
-0,989
2,851
-3,081
[7/7]
1,639
-0,595
4,249
-0,708
2,581
-4,293
[8/8]
1,639
-0,595
4,359
-0,771
2,440
-3,904
[9/9]
1,639
-0,595
4,351
-0,713
2,308
-3,850
Из табл. 3.4 видно, что при увеличении порядка аппроксима-
аппроксимации до [9/9] устанавливаются три первых полюса. Заметим, что
вещественные части двух первых полюсов 1,639 и 4,351 со срав-
сравнительно небольшими абсолютными величинами мнимых частей
приблизительно соответствуют координатам двух первых макси-
максимумов на кривой \Ni(l3a)\/Nist. Полученный результат достаточно
естествен, так как если бы полюс находился на вещественной
оси, то это привело бы к безграничному возрастанию функции
\Ni(/3a)\/Ni8t. В случае, когда полюс смещен, однако не слиш-
слишком значительно, в комплексную плоскость, это приводит к росту,
в данной ситуации ограниченному, рассматриваемой функции в
окрестности проекции полюса на вещественную ось.
Связь экстремумов функции \Ni(Pa)\/Nlst с полюсами в ком-
комплексной плоскости показьюает принципиальную невозможность
приблизить решение с помощью ряда Тейлора в окрестности мак-
максимума вне зависимости от того, какое количество членов ряда
Тейлора взято. Для иллюстрации этого на рис. 3.3 для той же
задачи приведены графики функций \Ni(/3a)\/Niatj вычисленных
по 9 членам ряда Тейлора (до порядка (/За)8 включительно) и по
построенным с их помощью аппроксимациям Паде порядка [4/4].
3.6. Применение аппроксимаций Паде
273
Рисунок 3.3 показывает, что ряд Тейлора и аппроксимации
Паде дают практически совпадающие результаты вплоть до малой
окрестности первого максимума. Однако в этой окрестности раз-
различия начинают расти, и если функция, построенная по отрезку
ряд Тейлора аппроксимации Паде
Рис. 3.3. Сравнение ряда Тейлора и аппроксимаций Паде
ряда Тейлора вообще не имеет максимума, то аппроксимации Паде
порядка [4/4] в представленном диапазоне изменения (За уже дают
результаты, почти совпадающие с точным решением.
На рис. 3.4, 3.5 представлены зависимости \Ni(f3a2)\/NiSt от
/Зп2 для эллиптических трещин с отношениями полуосей а,2 : сь\
равными 1:1, 1:2, 1:4 и 1:8. Результаты даны для случая v =
= 0,25. На рис. 3.4 приведены графики нормированных КИН в
точке @; аг) контура эллиптической трещины (вершине малой по-
полуоси), а на рис. 3.5 приведены аналогичные графики для точки
(oi; 0) (вершина большой полуоси). Нормирование производится
на значение КИН (Nist) в соответствующей статической задаче в
той же точке контура. В расчетах порядок аппроксимаций Паде до-
доводился до [9/9], так что приведенные результаты соответствуют
порядку [9/9].
Ограничение порядка аппроксимаций здесь вызвано тем, что
при увеличении эксцентриситета эллипса, при вычислении ма-
матрицы линейной системы для определения коэффициентов ряда
Тейлора, а также в процессе решения самой этой системы воз-
возникают погрешности. Эти погрешности определяются как, воз-
возможно, недостаточностью двойной точности, с которой проводи-
проводились все вычисления, так и усложнением, в случае возрастания
274
Гл. 3. Аналитические методы
эксцентриситета эллипса, вычислений гипергеометрических функ-
функций, требуемых для формирования матрицы системы.
1.4
1.2
1.0
0,8
0,6
0,4
0,2
1
2 3 4 Ра2
1:1 1:2 —1:4 -—1:8
Рис. 3.4. Эллиптическая трещина. Вершина малой полуоси
В результате при использовании более высоких порядков ап-
аппроксимаций Паде происходит потеря точности. Ухудшение сходи-
1,4
1,2
1,0
0,8
0,6
0,4
0.2
1
2 3 4 |
1:1 1:2 —1:4 —1:8
Рис. 3.5. Эллиптическая трещина. Вершина большой полуоси
мости аппроксимаций Паде с увеличением эксцентри
пса (при увеличении порядка аппроксимации до [9/9]
3.6. Применение аппроксимаций Паде
275
1:8 в точке @; аг) стабилизируется лишь первый максимум) свя-
связано и с тем, что в предельном случае плоской задачи разложение
скачков смещений в асимптотический ряд по волновому числу со-
содержит не только степенные, но и логарифмические члены [306].
Ухудшение сходимости с увеличением эксцентриситета эллипса
естественно проявляется и при анализе полюсов аппроксимаций
Паде. Так если при увеличении порядка аппроксимации до [9/9]
для круговой трещины установились три ближайшие нулю пары
полюсов (см. табл. 3.4), то для эллипса с отношением полуосей 1:8
установилась лишь одна пара полюсов.
Полученные здесь результаты подтверждают обнаруженный в
гл. 2 (с помощью численных расчетов, использующих двухбазис-
ный проекционный метод) немонотонный характер изменения ве-
величин \щ \/NiSt в точке @; аг) при росте эксцентриситета эл-
эллипса. Сравнение рис. 3.4 с результатами [305] показывает, что
с уменьшением отношения полуосей эллипса п2'-а\ до 1:8 график
функции \Ni(Ca2)\INist для точки контура @; аг), а вместе с ним и
величины C^0,2 и \Щ \/Nlst приближаются к соответствующим
графику и величинам для решения плоской задачи. Сравнения
рис. 3.4, 3.5 с рис. 2.5, 2.6 соответственно показывают хорошее
совпадение результатов расчетов, полученных численным методом
1.4
1.2
1.0
0,8
0,6
0,4
0,2
¦ -^
-
-
-
i
\\
\_
х
i i
0,0 0,5 1,0
1:2(гл.2) 1:4(гл.2) -
1,5 ^
-1:2(гл.З) 1:4(гл.З)
Рис. 3.6. Сравнение результатов в вершине малой полуоси
гл. 2 и представленным в этой главе численно-аналитическим ме-
методом. Для большей наглядности сравнения на рис. 3.6 приведены
кривые \Ni(/3(i2)\/NiSt для эллипсов с отношениями полуосей а2 :c&i
276
Гл. 3. Аналитические методы
равными 1:2 и 1:4 в точке контура @; аг), полученные в этой главе
(сплошные линии) и в гл. 2 (штриховые линии). Аналогичное
сравнение результатов в точке (а\; 0) представлено на рис. 3.7.
Имея разложение в ряд Тейлора по волновому числу скачка
нормального смещения при нормальной гармонической нагрузке с
однородной амплитудой *з = М> можно воспользоваться формулой
\Nl(pa2)\/Nlgt
0,0 0,5 1,0 1,5 ра2
1:2(гл.2) —- 1:4(гл.2) 1:2(гл.З) 1:4(гл.З)
Рис. 3.7. Сравнение результатов в вершине большой полуоси
B.101) для полного сечения рассеяния в случае нормального паде-
падения плоской продольной волны, почленно проинтегрировать ряд
и получить разложение в ряд Тейлора полного сечения рассеяния.
После этого уже возможно применение аппроксимаций Паде для
того, чтобы приблизить полное сечение рассеяния с высокой точ-
точностью. Из вида разложения скачка нормального смещения в ряд
Тейлора по волновому числу и формулы B.101) следует, что полное
сечение рассеяния разлагается в ряд только по четным степеням /3,
начиная с /З4. Поэтому при практической реализации указанного
способа расчета аппроксимации Паде применялись не для функ-
функции Ер (Ер — полное сечение рассеяния), а для функции Sp//34.
Кроме того, поскольку эта функция разлагается в ряд по четным
степеням /3, в качестве независимой переменной бралось /З2 и ап-
аппроксимации Паде производились по такой переменной. В резуль-
результате при использовании того же количества членов ряда Тейлора
для скачка нормального смещения, что и выше, порядок аппрок-
аппроксимаций Паде за счет деления на /З4 и введения новой переменной
был ниже, чем при вычислении КИН. В расчетах рассматривались
аппроксимации Паде вида [L/L + 1] и [L/L + 2].
3.6. Применение аппроксимаций Паде
277
На рис. 3.8 представлены отвечающие аппроксимациям порядка
[3/4] графики зависимости обезразмеренного полного сечения рас-
рассеяния Ер/5 (здесь S — площадь области трещины) от /?го, где
го — радиус круга, площадь которого равна 5, для эллипсов с от-
отношениями полуосей п2 : ai, равными 1:1, 1:2, 1:4 и v = 0,25.
2JS
круг эллипс 1:2 эллипс 1:4
Рис. 3.8. Полное сечение рассеяния
Графики из рис. 3.8 хорошо согласуются с полученными в гл. 2
численным методом графиками из рис. 2.8. Графики для элли-
эллипсов 1:2 и 1:4 доводятся на рис. 3.8 только до /Зго = 3, так как
до этой же величины были доведены графики численных расчетов
на рис. 2.8 и потому, что далее может оказаться недостаточным
используемый порядок аппроксимаций.
Перейдем теперь к задаче о гармонических колебаниях про-
пространства с эллиптической трещиной сдвига или соответствую-
соответствующей ей задаче рассеяния трещиной плоской, гармонической, нор-
нормально падающей поперечной волны. Рассмотрим сначала задачу
о дискообразной трещине (G = {(#ъ #2): х\ + х\ ^ а2}) и пред-
предположим, что вектор амплитуд приложенных к поверхностям
трещины усилий равен t = (?1, ?2) = A; 0). Такая нагрузка с точ-
точностью до постоянного множителя совпадает с нагрузкой, отвечаю-
отвечающей задаче рассеяния трещиной нормально падающей поперечной
волны, поляризованной вдоль оси х\. На рис. 3.9 представлены
зависимости нормированных КИН К*гA3а) = \Кц(/За)\/Ки@) в
точке контура (а; 0) для пространств с различными коэффици-
коэффициентами Пуассона и = 0,1, v = 0,3 и v = 0,5. Представленные
графики отвечают порядку аппроксимации Паде [9/9].
278
Гл. 3. Аналитические методы
Поскольку в диапазоне обезразмеренных волновых чисел /За ^
^ 6, у функций К*г(Ра) имеется лишь один максимум К*} , в
табл. 3.5 приведены значения этих максимумов и отвечающие им
волновые числа /З^а для тех же значений коэффициента Пуас-
Пуассона.
Таблица 3.5
V
од
1,2901
1,6
0,3
1,2650
1,7
0,5
1,2224
1,9
Сравнение графиков на рис. 3.9 и 2.9 показывает достаточно
хорошее совпадение результатов, полученных численным методом
в гл. 2 и численно-аналитическим методом в гл. 3. Хорошее совпа-
совпадение подтверждает и сравнение табл. 3.5 и 2.12. Значения К*}
1,2
1,1
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0 12 3 4 5 ^
v=0,1 v=0,3 v=0,5
Рис. З.9. Круговая трещина. Сдвиговая нагрузка
из табл. 3.5 с очень высокой точностью совпадают с соответствую-
соответствующими значениями из табл. 2.12, в то же время отвечающие им
резонансные значения волновых чисел, полученные численно (см.
табл. 2.12), несколько сдвинуты вправо по отношению к результа-
результатам из табл. 3.5.
3.6. Применение аппроксимации Паде
279
Для удобства сравнения приведем также графики функций
К^фа), отвечающие и = 0,3, полученные численно в гл. 2 и с
помощью численно-аналитического метода в гл. 3, на одном ри-
рисунке. На рис. 3.10 сплошной линией проведена кривая, получен-
1.2
1.1
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0 1 2 3 4 5 ра
аналитический численный
Рис. 3.10. Сравнение результатов
ная численно-аналитическим методом, а штриховой линией кри-
кривая, полученная с помощью двухбазисного проекционного метода.
Рисунок 3.10 также подтверждает хорошее соответствие резуль-
результатов.
В табл. 3.6 для случая и = 0,3 приведены данные, иллюстри-
иллюстрирующие скорость сходимости результатов по мере увеличения по-
порядка аппроксимаций Паде. В этой таблице представлены зависи-
зависимости величин К*г в точке экстремума /За = (З^а = 1,7, а также
в точках /За = 3,0; 4,0; 5,0 и 6,0 от порядка аппроксимаций Паде
вида [L/L].
Таблица 3.6
[L/L]
ра = 1,7
ра = 3,0
Ра = 4,0
ра = 5,0
Ра = 6,0
[3/3]
1,2706
0,94881
0,68159
0,53630
0,45368
[4/4]
1,2651
0,94886
0,74470
0,61029
0,51661
[5/5]
1,2650
0,95551
0,77286
0,61144
0,49059
[6/6]
1,2650
0,98035
0,71776
0,57844
0,50141
[7/7]
1,2650
0,96355
0,79526
0,51350
0,41241
[8/8]
1,2650
0,96327
0,80043
0,50091
0,40578
[9/9]
1,2650
0,96330
0,79936
0,50622
0,40306
280 Гл. 3. Аналитические методы
Как следует из табл. 3.6, значение первого максимума функ-
функции ^(/За), так же как и в случае нормального отрыва, уста-
устанавливается достаточно быстро. Уже начиная с аппроксимации
[4/4] значения K*i практически не отличаются, а начиная с ап-
аппроксимации [5/5] устанавливаются четыре знака после запятой.
Значения 1^C) также устанавливаются быстро. Все значения
iffjC), начиная с аппроксимации [3/3], отличаются от -К"пC) для
аппроксимации [9/9] не более чем на 1,77%. Начиная же с аппрок-
аппроксимации [7/7], значения К^C) вообще практически не меняются.
Разбросы в значениях К*гфа) при /За = 4,0; 5,0 и 6,0 по мере
увеличения порядка аппроксимаций Паде естественно становятся
больше. Однако и здесь, начиная с аппроксимаций [7/7], колеба-
колебания в значениях К*г не превосходят: для (За = 4,0 — 0,51%, для
/За = 5,0 — 1,42% и для /За = 6,0 — 2,32%. Таким образом, в
диапазоне изменения /За, представленном на рис. 3.9, имеющиеся
там графики, очевидно, практически совпадают с точными реше-
решениями.
На том же примере {у = 0,3) посмотрим теперь, как уста-
устанавливаются полюсы функции Щг{Cа) (корни знаменателя ап-
аппроксимаций Паде) с ростом порядка аппроксимации. Здесь, так
же как и в случае нормального разрыва, полюсы симметричны
относительно мнимой оси и расположены в нижней полуплоско-
полуплоскости. В табл. 3.7 приведены зависимости первых трех пар полюсов
(/3a)W = Vj + iwj ( j = 1, 2, 3) от величины L в аппроксима-
аппроксимациях Паде вида [L/L]. Как и выше, симметричная пара полюсов
имеет один номер и в табл. 3.7 даны представители пар, имеющие
неотрицательные вещественные части.
Таблица 3.7
[L/L]
VI
Wi
V2
W2
V3
IU3
[4/4]
1,898
-1,090
2,369
-2,075
-
-
[5/5]
1,923
-1,108
3,071
-1,852
0
-5,694
[6/6]
1,919
-1,118
3,284
-0,514
2,560
-2,710
[7/7]
1,922
-1,116
3,889
-1,213
1,375
-4,449
[8/8]
1,922
-1,116
3,968
-1,287
1,310
-3,367
[9/9]
1,922
-1,116
3,941
-1,266
1,031
-3,280
Из табл. 3.7 видно, что достаточно быстро устанавливается пер-
первый полюс. С определенной долей уверенности можно говорить о
том, что и второй полюс установился. О третьем же полюсе по
3.6. Применение аппроксимаций Паде
281
приведенным данным можно судить лишь весьма приближенно,
так как разница в значениях v$ даже между аппроксимациями
[8/8] и [9/9] составляет 27%. Как и в случае отрыва, точка дости-
достижения кривой К*г(/3а) первого максимума приближенно соответ-
соответствует вещественной части первого полюса. Хотя третий полюс
имеет меньшую вещественную часть, чем первый, но во-первых,
он еще не установился, в связи с чем о нем трудно делать окон-
окончательные выводы, а во-вторых, он расположен достаточно далеко
от вещественной оси (газ = —3,28) и поэтому не проявляется на
графике функции К^/За). Возможно его влиянием вызвано то,
что резонансное значение (З^а = 1,7 несколько сдвинуто влево
по отношению к вещественной части первого полюса {v\ = 1,922).
Сложное взаимодействие полюсов, вероятно, привело к тому, что
на кривой Ки(Cа) в диапазоне (За ^ 6 отсутствует второй макси-
максимум, т. е. не проявляет себя второй полюс.
Аналогично случаю отрыва, покажем на примере той же задачи
(у = 0,3), что рядом Тейлора (вне зависимости от того, сколько
взято его членов) невозможно приблизить функцию К^/За) даже
в окрестности первого максимума. На рис. 3.11 сплошной линией
05 1 0
-ряд Тейлора
1 5 20
аппроксимации Паде
Рис. 3.11. Сравнение ряда Тейлора и аппроксимаций Паде
изображен график функции К*г(ра)^ полученной с помощью ап-
аппроксимаций Паде порядка [8/8], а штриховой — график функции,
вычисленной с помощью отвечающего данной аппроксимации от-
отрезка ряда Тейлора, т. е. отрезка, содержащего 17 членов ряда. Из
рис. 3.11 видно, что графики практически совпадают до /За = 1,5.
282
Гл. 3. Аналитические методы
В интервале 1.5 ^ /За ^ 1,7 графики отличаются очень мало, но
далее функция К*г([3а), вычисленная по аппроксимациям Паде,
начинает убывать, а вычисленная с помощью ряда Тейлора, — бы-
быстро возрастает. Таким образом, хотя в точке максимума /За = 1,7,
различие очень мало, однако функция, вычисленная по ряду Тей-
Тейлора, не имеет максимума.
Для гармонической нагрузки с амплитудой t = A; 0) в рассма-
рассматриваемой точке окружности (а; 0) в силу симметрии Кш{Cа) =
= 0. Если рассмотреть на окружности точку @; а), то там, на-
наоборот, Кп(ра) = 0, а Кш(Ра) ф 0. Поэтому ниже для рассмо-
рассмотренных задач приведены данные, касающиеся Кш(Ра) в точке
@; а). На рис. 3.12 представлены зависимости нормированных
л
\\ч—
\\
/~ \
/ / \ \
/ / \ \
/ / /-ч \
/ / \ \
/ / \ ч
' / \ \
/ . V
1,3
1,2
1,1
1,0
0,9
0,8
0,7
0,6
05
1 0 1 2 3 4 5 ра
v=0,1 v=0,3 v=0,5
Рис. 3.12. Круговая трещина. Сдвиговая нагрузка
КИН К?и(/3а) = \KUi(Ca)\/Кш@) для пространств с коэффициен-
коэффициентами Пуассона v = 0,1, v = 0,3 и v = 0,5. Графики на рис. 3.12
отвечают порядку аппроксимации [9/9].
В представленном на рис. 3.12 интервале изменения /За у функ-
функций К*п(Ра) имеется два максимума и один минимум. Анало-
Аналогично случаю отрыва, обозначим первый максимум через К^
*C)
первый минимум через K*{i ' и второй максимум через К*п
Соответствующие им значения обезразмеренных волновых чисел
обозначим /З^а, (З^а и (З^а. В табл. 3.8 представлены значения
K*ii и (З^а (г = 1, 2, 3) для различных коэффициентов Пуассона.
3.6. Применение аппроксимаций Паде
283
V
0,1
0,3
0,5
pVa
1,6
1,6
1,6
¦*ми
1,3060
1,2252
1,1396
P^a
3,4
3,4
3,3
*и(г2)
0,5517
0,6587
0,7475
Таблица 3.8
4,6
4,7
4,8
0,8005
0,9606
1,1731
Если сравнить табл. 3.8 с табл. 2.12, где приведены некоторые
из тех же величин, полученных двухбазисным проекционным ме-
ме'
и
тодом, то можно убедиться, что различие в значениях
*B)
il П1 , полученных обоими методами, невелико. Так, для v = 0,1
разница в значениях Кп\ } и Кп\ , представленных в табл. 2.12
и 3.8, составляет соответственно 1,8% и 1,3%, для v = 0,3 — 1,2%
и 6,8%, а для v = 0,5 — 2,7% и 1,8%. Вместе с тем, так же как
было отмечено и для величин K*i в точке (а; 0), соответствую-
соответствующие значения /?Ма, полученные численным методом, несколько
сдвинуты вправо. На примере пространства с v = 0,3 покажем,
как устанавливаются значения К*^ и /З^а с ростом порядка ап-
аппроксимаций Паде вида [L/L]. В табл. 3.9 приведены зависимости
величин K*ii и Р^а (г = 1, 2, 3) от L.
Таблица 3.9
[L/L] [3/3]
К*^ 1,2229
/3A)а 1,6
к;™
[4/4]
1,2253
1,6
0,6872
3,2
0,8903
4,3
[5/5]
1,2252
1,6
0,6738
3,4
0,8508
4,8
[6/6]
1,2252
1,6
0,6655
3,4
0,8889
4,8
[7/7]
1,2252
1,6
0,6636
3,4
0,8999
4,8
[8/8]
1,2252
1,6
0,6587
3,4
0,9610
4,7
[9/9]
1,2252
1,6
0,6587
3,4
0,9606
4,7
Из табл. 3.9 видно, что первый максимум устанавливается до-
достаточно быстро. Величина /З^а определяется уже аппроксима-
аппроксимацией [3/3], а различие между величинами К*и для аппроксима-
аппроксимаций порядка [3/3] и [9/9] составляет всего 0,19%. Начиная же с
аппроксимации порядка [5/5], устанавливаются четыре знака по-
еле запятой. Значение минимума JKni устанавливается немного
284 Гл. 3. Аналитические методы
позже. Здесь величина /З^а устанавливается с аппроксимации по-
порядка [5/5]. Отличие в значениях К*и для аппроксимаций [5/5]
и [9/9] составляет 2,3%. Разница между значениями #ш Для
аппроксимаций [6/6] и [9/9] составляет уже 1,0%, а у величин,
определяемых аппроксимациями [8/8] и [9/9], совпадают четыре
знака после запятой. Полученные значения второго максимума не-
несколько менее надежны. Хотя различие между значениями ИГ*,} ,
определяемыми аппроксимациями [8/8] и [9/9], ничтожно (всего
0,04%), при переходе от аппроксимаций [7/7] к аппроксимациям
[8/8] имеется небольшой скачок как в значении /З^а, так и в зна-
значении K*ii •
Немонотонный характер сходимости при увеличении порядка
аппроксимаций Паде связан с тем, что с увеличением порядка
появляются новые полюсы и уточняется положение уже обнару-
обнаруженных полюсов. Это может приводить к маленьким скачкам в
решениях. Проследим за тем, как устанавливаются полюсы для
функции Kfn\fia) в рассматриваемой задаче. Полюсы функции
К*и(/3а) обладают теми же свойствами, что и полюсы рассмо-
рассмотренных выше функций \Ni(Ca)\/Nlst и К^/За)^ т.е. они сим-
симметричны относительно мнимой оси и расположены в нижней по-
полуплоскости. В табл. 3.10 приведены представители первых трех
пар полюсов и показана их зависимость от порядка аппроксима-
аппроксимаций Паде.
Таблица 3.10
[L/L]
VI
Wi
V2
W2
vz
[4/4]
1,923
-1,130
3,792
-1,029
-
-
[5/5]
1,923
-1,119
4,140
-1,578
0
-3,492
[6/6]
1,921
-1,116
4,308
-1,360
1,617
-2,402
[7/7]
1,921
-1,116
4,349
-1,304
1,820
-2,432
[8/8]
1,922
-1,116
4,570
-0,949
1,683
-3,362
[9/9]
1,922
-1,116
4,569
-0,951
1,695
-3,371
Из табл. 3.10 следует, что первый полюс устанавливается весь-
весьма надежно, а второй и третий устанавливаются приближенно.
Вещественные части первого и третьего полюсов приближенно со-
соответствуют первому максимуму на кривой К*и($а). Поскольку
третий полюс находится достаточно далеко от вещественной оси,
он, вероятно, не может определять максимум на кривой K*u{fia),
однако он способствует сдвигу этого максимума влево по отноше-
отношению к вещественной части первого полюса. Вещественная часть
3.6. Применение аппроксимаций Паде
285
второго полюса приближенно соответствует второму максимуму на
кривой K*u(Ca). При переходе от аппроксимации порядка [7/7] к
аппроксимации порядка [8/8] второй полюс существенно прибли-
приближается к вещественной оси. Это, как и предполагалось, является
причиной некоторого скачка в значении второго максимума К*^ '
и его местположении fi^a.
Интересно отметить, что первый полюс функции K*u(/3a) в
точке окружности @; а) (табл. 3.10) в точности совпадает с первым
полюсом функции Ku(/3a) в точке окружности (а; 0) (табл. 3.7).
Впрочем, это неудивительно, так как, несмотря на то, что век-
вектор скачков смещений [u] = ([ui]> [иг]) зависит как от координат
х = (#i, яг), так и от волнового числа /За и поэтому полюсы КИН
как функции от /?а могут зависеть от положения точки на кон-
контуре трещины, ясно, что полюсами могут являться собственные
значения задачи Дирихле для граничного матричного оператора
РвКр (уравнение C.131)), которые от координат не зависят. Та-
Таким образом, полюс v\ + iw\, очевидно, и является собственным
значением задачи Дирихле для оператора рвКр.
Возможности вычисления функции К?п(/3а) с помощью ряда
Тейлора, так же как и в случае функций Ni(J3a) и К^/За), ог-
ограничиваются интервалом изменения /За вплоть до первого резо-
резонансного значения (З^а. Для иллюстрации этого на рис. 3.13
05 10
-ряд Тейлора
15 20
— аппроксимации Паде
Рис. 3.13. Сравнение ряда Тейлора и аппроксимаций Паде
приведены отвечающие v = 0,3 графики функций К*п(Cа)^ вы-
вычисленные с помощью аппроксимаций Паде порядка [8/8] (сплош-
(сплошная линия) и с помощью соответствующего отрезка ряда Тейлора
286
Гл. 3. Аналитические методы
(штриховая линия). Здесь, как и в рассмотренных выше приме-
примерах, функция K*u(/3a)) рассчитанная по ряду Тейлора, не имеет
максимума и после /За = /З^'а начинает быстро расти.
Выше было проведено сравнение функций Kfu(j3a), вычислен-
вычисленных с помощью аппроксимаций Паде и численно в гл. 2, по двум
первым экстремальным значениям (табл. 3.8 и 2.12). Для более
полного сравнения на рис. 3.14 для v = 0,3 приведены графики
функций К?п(/3а), вычисленных в этой главе — сплошная линия
и в гл. 2 — штриховая линия.
Рисунок 3.14 показывает, что характер кривых, полученных
обоими способами, сохраняется. До первого максимума различие
между кривыми незначительно. Далее, несмотря на то, что от-
отличие в абсолютных значениях величин возрастает, кривые оста-
остаются похожими, просто кривая, полученная численным методом,
1,2
1,1
1.0
0,9
0,8
0,7
0,6
- /
-
-
-
\\
\\
\ \
\\
\\ />
\\ //
1 2 3
аналитический
4 5
численный
Рис. 3.14. Сравнение результатов
как бы несколько сдвинута вправо относительно кривой, полу-
полученной с помощью аппроксимаций Паде. Различие, вероятно,
объясняется тем, что для имеющего место здесь более сложного
характера поведения решения, количество базисных функций,
используемых для аппроксимации решения в численном методе,
становится недостаточным. Кроме того, при сложном поведении
решения предпочтительнее аппроксимировать его не с помощью
глобального базиса во всей области, как это делалось в гл. 2, а
локально, используя конечные элементы.
Проследим теперь за влиянием формы трещины на распреде-
распределение КИН вдоль ее контура при сдвиговых гармонических на-
нагрузках. Всюду далее будем предполагать, что v = 0,3. Сначала
3.6. Применение аппроксимаций Паде
287
по-прежнему рассмотрим нагрузку, амплитуда которой равна t =
— (*ъ Ы = A? 0). На рис. 3.15, 3.16 приведены графики функций
К*гфа2) в точке контура (аи 0) и К*п(Cа2) в точке контура @; аг)
соответственно для эллипсов с отношениями полуосей 1:1, 1:2, 1:4
и 1:8. Заметим, что если в случае отрыва ограничение порядка ап-
аппроксимаций было главным образом связано с потерей точности,
то в случае сдвига ограничения вызваны большим временем счета.
1.2
1,1
1.0
0,9
0,8
0,7
0,6
0,5
0,4
0,0 0,5 1,0 1,5 2,0 2,5 $а2
1:1 1:2 1:4 1:8
Рис. 3.15. Эллиптическая трещина. Нагрузка A, 0), точка (oi, 0)
Время счета быстро возрастает при увеличении порядка аппрокси-
аппроксимаций. Так, если в задаче о круговой трещине сдвига для ап-
аппроксимаций порядков [3/3], [4/4] и [5/5] время счета на IBM PC
AT 486 составляло секунды и минуты, то при увеличении порядка
аппроксимации до [9/9] время счета возросло приблизительно до
10 часов. Так как при вытягивании эллипса время счета, из-за
необходимости вычисления гипергеометрических функций, также
возрастает, то для эллипса с a<i: а\ = 1:2 пришлось ограничиться
аппроксимациями порядка не выше [8/8], для эллипса 1:4 — по-
порядка [7/7], а для эллипса 1:8 — [6/6]. В связи с этим по мере
вытягивания эллипса область надежных результатов по перемен-
переменной /Зп2 сужалась. Поэтому приведенные на рис. 3.15, 3.16 кривые
для различных эллипсов доведены до разных значений /?а2> т.е.
представлены только в тех областях где результаты надежны.
В табл. 3.11 представлена зависимость величины первого мак-
^ функции #*(/?а2) в точке контура (сц; 0) и соответ-
симума К
ствующего значения
от отношения полуосей эллипса
288 Гл. 3. Аналитические методы
В представленных в табл. 3.11 значениях К*} ' для круга и
эллипса с п2 : а\ = 1: 2 гарантированы все приведенные знаки.
В случае а>2: а\ = 1:4 возможно отличие К*} ' от точного значения
в третьем знаке после запятой, т.е. погрешность может соста-
составлять доли процента. Для эллипса 1:8 погрешность может соста-
составить величину порядка процента. По рис. 3.15 видно, что функция
К*г(/3а2) для эллипса с п2 : а\ = 1:8 на достаточно большом по
/Зп2 интервале слабо отличается от 1. Это аналогично поведению
функции К*фа,2) = Щ((Зп2) = \Ni(l3a2)\/Ni8t в вершине большой
полуоси вытянутого эллипса в случае отрыва (см. рис. 3.5). Из
табл. 3.11 также следует, что величины jKh ' и /З^аг монотонно
убывают при убывании отношения аг:а\.
O2:ai 1:1
KnA) 1,2650
P{1)a2 1,7
1:2
1,1838
1,4
Таблица 3.11
1:4
1,1454
1,1
1:8
1,038
0,6
В табл. 3.12 представлена зависимость величины первого мак-
максимума K*ii функции КщОЗсъ) в точке контура @; аг) и соответ-
соответствующего значения (За2 = C^A2 от отношения полуосей эллипса
Таблица 3.12
U2-CL1 1:1
K^ 1,2252
/?A)a2 1,6
1:2
1,3149
1,3
1:4
1,3297
1,2
1:8
1,3557
1,0-1,1
Для величин К*п ' в табл. 3.12 в случае эллипсов с а2: а\ = 1:1
и п2 : а\ = 1:2 гарантированы все приведенные знаки, а для эл-
эллипса 1:4 возможна погрешность порядка нескольких тысячных,
т< е. доли процента. В случае эллипса 1:8 дела обстоят хуже. Здесь
значение К*^ еще не установилось с такой высокой точностью
и возможна погрешность в несколько процентов» Для уточне-
уточнения следует просчитать аппроксимации более высокого порядка.
В табл. 3.12 даны два значения /3^п2 для эллипса 1:8, так как
для аппроксимаций [б/б] (максимального из просчитанных для
данного случая порядков) значения K*n(fia2) в точках /?аг = 1,0 и
/За,2 = 1,1 совпали. Заметим, что с уменьшением отношения п2'-а\
значения Р^а2 убывают, а величины jRThi ^ ведут себя немоно-
3.6. Применение аппроксимации Ладе
289
тонно, так как в представленном диапазоне п2 : а\ эти величины
растут, однако в предельном случае антиплоской задачи величина
K*ii\ согласно [305, 106], несколько ниже 1,3. Из рис. 3.16 и
табл. 3.12 видно, что с уменьшением отношения п2 :ai значения
1,3
1,2
1,1
1,0
0.9
0.8
0.7
0,6
п с:
- /^Ч
- 4'i/ \\
г \\
\
-
\
\
\ \ ,
\
N
\
'0 1 2 3 $а2
1:1 1:2 1:4 1:8
Рис. 3.16. Эллиптическая трещина. Нагрузка A, 0), точка @, аг)
стремятся к соответствующей величине для антиплоской
задачи, а значения К*п несколько превосходят соответствующее
предельное значение [305, 106].
Чтобы строить решения для задачи рассеяния трещиной нор-
нормально падающей поперечной волны, поляризованной в произ-
произвольном направлении, необходимо иметь решения задач для двух
неколлинеарных направлений. Рассмотрим теперь задачу для слу-
случая сдвиговой гармонической нагрузки с амплитудой t = (<i, *г) ==
= @, 1), что соответствует поперечной волне, поляризованной
вдоль оси Х2- Для расположенных, как и прежде, эллиптических
трещин и такой нагрузки в противоположность предыдущим за-
задачам Ки(рп2) ф 0, Кт(Cа>2) = 0 в точке @; 0,2) (вершине малой
полуоси эллипса) и Ки(/3а2) = 0, Кш(Cа2) ф 0 в точке (аи 0)
(вершине большой полуоси эллипса). На рис. 3.17 изображены
графики функций К*1($п2) в точке @; аг) для эллипсов с тем же
соотношением полуосей, что и выше, иг/ = 0,3. Максимальные
порядки используемых аппроксимаций, так же как и при другой
нагрузке, зависели от отношения полуосей эллипса. Графики на-
нарисованы в тех диапазонах /За2, где полученные решения доста-
достаточно надежны.
20 Зак. 205
290
Гл. 3. Аналитические методы
В табл. 3.13 приведены значения первых максимумов К*} ' и
соответствующих им величин (За,2 = /З^аг Для представленных
на рис. 3.17 кривых. Для эллипсов 1:1, 1:2, 1:4 при использо-
использованных порядках аппроксимаций установились все приведенные
1.2
1.1
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
12 3 4 5
1:1 ---1:2 ---1:4 ----1:8
Рис. 3.17. Эллиптическая трещина. Нагрузка @, 1), точка @, аг)
в табл. 3.13 знаки величин К*} \ В случае эллипса 1:8 данные
табл. 3.13 содержат погрешность порядка нескольких десятых про-
процента. Заметим, что с уменьшением отношения a<i: a\ величины
Р^п2 монотонно убывают, а величины К*} ' изменяются немоно-
немонотонно. Для эллипса с отношением полуосей а>2: о>\ = 1:8 соответ-
соответствующие график на рис. 3.17 и данные табл. 3.13 приближаются к
решению плоской гармонической по времени задачи для трещины
конечной длины при поперечном сдвиге [106].
Таблица 3.13
u2'-Q>i 1:1
K#l) 1,2650
Р{1)а2 1,7
1:2
1,2854
1,3
1
1:4
,2321
1Д
1
1:8
,1695
1,0
Зависимости Щп{^а2) в точке эллипса (oi; 0) для рассматри-
рассматриваемой задачи представлены на рис. 3.18, а в табл. 3.14 даны со-
соответствующие значения К*п ' и
3.6. Применение аппроксимаций Паде
291
Все знаки чисел K*{i ', приведенные в табл. 3.14, являются
установившимися. Заметим, что, как и в других примерах, с
уменьшением отношения п2 : а\ первые экстремальные значения
КИН и соответствующие им значения обезразмеренных волновых
1,2
1,1
1,0
0,9
0,8
0,7
0,6
1 2 3
-1:1 1:2 1:4 1:8
Рис. 3.18. Эллиптическая трещина. Нагрузка @, 1), точка (oi, 0)
чисел убывают. Для эллипса 1:8 величина К^ ' уже не является
столь важной, как для эллипсов с малым эксцентриситетом, так
как функция K*u(f3a2) на достаточно большом по (Зп2 интервале
слабо отличается от 1 и при таких малых колебаниях значения
следующих максимумов могут превосходить первый максимум.
Таблица 3.14
a2:ai
xVf jj 1
0A)a2
1:1
,2252
1,6
1:2
1,0975
1,0
1:4
1,0267
0,6
1:8
1,0061
0,3
Для иллюстрации того, как работает развитый метод и разра-
разработанная программа в случае гармонических по времени нагрузок,
имеющих неоднородную амплитуду, рассмотрим задачу об элли-
эллиптической трещине, находящейся под действием скручивающих
нагрузок. Пусть амплитуда нагрузок имеет вид t = (*i, ?2) =
= (—#2? a?i). Для круговой трещины при такой нагрузке отлична
от нуля только функция Кт(/3а2), а Кп(/3а2) = 0. Для элли-
эллиптических трещин функция Кц(/3а2), вообще говоря, отлична от
20*
292
Гл. 3. Аналитические методы
нуля, однако в точках контура (ai; 0) и @; аг) Ku(/3a2) = 0.
На рис. 3.19 и 3.20 представлены графики функций К*пфп2) =
1,4
1,3
1.2
1.1
1.0
0,9
1 2 3
1:1 1:2 1:4
Рис. 3.19. Скручивающая нагрузка, точка (ai, 0)
@) в точках контура (ai; 0) и @;
ственно для эллипсов с отношениями полуосей п2 :
соответ-
соответ= 1:1,
1.7
1,6
1.5
1.4
1,3
1.2
1.1
1.0
0,9
f
/1 \
/7 >
\
\
\
\
( \
\ \
\ \
0 12 3 $a2
1:1 1:2 1:4
Рис. 3.20. Скручивающая нагрузка, точка @, аг)
1 : 2 и 1 : 4. В расчетах аппроксимации Паде доводились до по-
порядка [7/7] для всех указанных эллипсов. Графики представлены
3.6. Применение аппроксимаций Паде 293
в интервалах, в которых решения уже установились. Все расчеты
проведены для случая v = 0,3.
В табл. 3.15 представлены значения первого максимума К*^
и соответствующих величин /3A'а,2 для кривых K*u(/3a2), отве-
отвечающих точке контура (сц; 0).
Таблица 3.15
CL2'.ai
/?A)а2
1:1
1,4847
зд
1
1:2
,1733
1J
1:4
1,0487
0,9-1,0
Все знаки представленных в табл. 3.15 величин К*^ уже уста-
установились. Для эллипса 1:4 приведены два значения (№а>2 — 0,9 и
1,0, так как в этих точках значения К*п(/3а2) совпали. Как видно
из рис. 3.19 и табл. 3.15, в вершине большой полуоси эллипса с
уменьшением а2 : а\ величины К*и и /З^аг убывают. Кривая,
отвечающая эллипсу с п2 : а\ = 1:4 на начальном участке, мало
отличается от 1.
Таблица 3.16
О2'.о\ 1:1
К^ 1,4847
/3A)а2 3,1
1
1:2
,7073
2,5
1:4
1,5351
1,9
Задача о круговой трещине при исследуемой здесь скручиваю-
скручивающей гармонической нагрузке рассматривалась прежде [106, 304].
Представленные результаты хорошо согласуются с результатами,
полученными в указанных работах. Заметим, что для круговой
трещины и скручивающей нагрузки величина /3A'а,2 = 3,1 зна-
значительно сдвинута вправо по отношению к аналогичным величи-
величинам в случае, когда амплитуда нагрузки однородна (напомним,
что там для функций ^(/Заг) и К?п(/3а2), вычисленных в соот-
соответствующих точках контура, величины /З^аг равнялись 1,7 и
1,6 соответственно). Если мы проанализируем полюсы функции
К*и(Cп2), то обнаружим, что первая пара полюсов расположена в
точках (/За2)A) = ±3,387 - гО,951. Таким образом, и при скру-
скручивающей нагрузке вещественная часть первого полюса прибли-
приблизительно соответствует первому резонансному значению волнового
числа. Из анализа результатов следует, что при скручивающей на-
нагрузке пропадает первая пара полюсов, отвечающих однородному
294 Гл. 3. Аналитические методы
сдвигу (/Зп2)^ = ±1,922 — г1,116. Таким образом, оказывается,
что полюсы зависят не только от формы трещины и координат
рассматриваемой точки контура, но и от вида приложенной на-
нагрузки.
В табл. 3.16 представлены значения первого максимума IT*,, '
и соответствующих величин /3^п2 для кривых К*и{^п2)ч отве-
отвечающих точке контура @; 02).
Как уже было отмечено выше, у значения К*}г ' для круга уста-
установились все приведенные в таблице знаки. Для эллипсов с отно-
отношениями полуосей 1:2 и 1:4 установились 2 знака после запятой,
т. е. погрешность возможна в третьем знаке после запятой и та-
таким образом она составляет доли процента. Аналогично рассмо-
рассмотренным выше задачам, с уменьшением отношения a<i: a\ отве-
отвечающие вершине малой полуоси эллипса значения C^п2 убывают,
а величины К*и изменяются немонотонно.
3.7. Ударное нагружение
В § 3.6 с помощью аппроксимаций Паде были получены хоро-
хорошие приближения к решениям задач об эллиптических трещинах
при гармонических нагрузках в достаточно широком диапазоне
изменения волновых чисел. Имея такие приближения и исполь-
используя методику, основанную на обращении преобразования Фурье,
которая была описана и использована для решения задач в § 2.6,
можно получать решения задач при нестационарных нагрузках.
Вместе с тем, поскольку аппроксимации Паде дают приближение
к решению не только для вещественных значений волновых чи-
чисел, но и в некотором круге в комплексной плоскости, открываются
дополнительные возможности для построения решения нестацио-
нестационарных задач.
Если к уравнениям динамической задачи теории упругости
B.118) применить преобразование Лапласа по времени (напомним,
что образ Лапласа функции /(г) определяется следующим образом:
00
Lf(s) = / f(r)e~ST dr), то для образов Лапласа перемещений при
о
условии, что в начальный момент времени перемещения и скоро-
скорости перемещений равны нулю, получим уравнения
+ (А + ij)Lujji = gs2Lui. C.174)
Уравнения C.174) совпадают с уравнениями для амплитуд пере-
перемещений в случае гармонических нагрузок при замене квадрата
частоты J2 на — s2. Отсюда следует, что и соответствует либо is,
либо — is. Для определения правильного соответствия между и и 5
3.7. Ударное нагружение 295
учтем, что для частотной задачи выбиралась такая ветвь квадрат-
квадратного корня, что для и) > О vcj2 = cj, у—tj2 = — iu. Принимая во
внимание, что для 5 > 0 vs2 = 5, и извлекая квадратный корень
из обеих частей равенства —о;2 = s2 (и > О, s > 0), получим,
что величине и соответствует is. Теперь остается только приме-
применить преобразование Лапласа к краевым условиям (приложенным
нагрузкам). Поскольку уравнения для образов Лапласа переме-
перемещений с краевыми условиями, являющимися образами Лапласа
нестационарных краевых условий, получаются из уравнений для
амплитуд перемещений в случае гармонических нагрузок заменой
ш на is при соответствующих краевых условиях, то и решения в
образах Лапласа получаются из соответствующих решений гармо-
гармонической задачи.
Таким образом, для эллиптических трещин при нестационар-
нестационарных нагрузках методами, развитыми в этой главе, можно получить
приближенные выражения для образов Лапласа скачков смещений
и КИН в виде рациональных функций от параметра преобразо-
преобразования Лапласа. Это позволяет пользоваться для построения ре-
решения во временной области всем многообразием способов обра-
обращения преобразования Лапласа, ссылки на которые были даны в
§ 2.6, в том числе и одним из наиболее эффективных методов [207].
Здесь мы покажем, что достаточно хорошее приближение к
решению можно получить и с помощью совсем простой проце-
процедуры явного обращения рациональной функции. В качестве при-
примера рассмотрим задачу о трещине нормального разрыва. Пред-
Предположим, что к поверхностям трещины прикладываются усилия
±?з(т), где h(r) = Н(т) — функция Хевисайда. Тогда образ Ла-
Лапласа приложенных усилий будет равен Lt$(s) = LH(s) = 1/s.
Пусть амплитуда КИН для рассмотренной в § 3.6 задачи об уста-
установившихся колебаниях пространства с эллиптической трещиной,
находящейся под действием нормальной гармонической нагруз-
нагрузки с однородной единичной амплитудой, описывается функцией
Kf(xf, о;), где х1 — точка на контуре трещины. Тогда образ Ла-
Лапласа КИН для рассматриваемой нестационарной задачи будет ра-
равен Щ(х', is)/s. Следовательно, зависимость КИН в заданной
точке контура от времени г выражается формулой
so+ioo
Kt{x', т) = -^т / Kf(x',is)s-leSTds. C.175)
2тгг J
so-ioo
В действительности в § 3.6 решения записывались не как функ-
функции от о;, а как функции от обезразмеренного волнового числа
/За5 т. е. вместо функции Щ(х\ и) строилась функция К*г(х\ (Зп2)
{xf, ш) = K*r(xf, Ca2), Ca2 = \/ф.иа<1 = ua2/Cs, Cs — ско-
296 Гл. 3. Аналитические методы
рость распространения поперечной волны в безграничной среде).
Если частоте ш соответствует параметр преобразования Лапласа $,
то величине /Заг соответствует параметр р, где р = su2/Cs. Таким
образом, равенство C.175) можно переписать в виде
50+1ОО
so-ioo
po+ioo
/
= K;(x',T). C.176)
PQ—ioo
Здесь Т — безразмерное время (Г = /)
Таким образом, K*(xfy T) есть обратное преобразование Ла-
Лапласа от от функции Kfr(xr, ip)/p. В §3.6 функции К*т{х', f5a*i)
были приближены рациональными функциями от /?а2. Будем те-
теперь под К\т{х\ ($0,2) понимать рациональное приближение. Пусть
Kfr(xf, Ca,2) является аппроксимацией Паде порядка [L/M] и пред-
предположим для простоты, что функция К*г(х\ (Зп2) имеет простые
полюсы (/Заг)^ {j = 1, ..., М), которые, очевидно, отличны от
нуля. В этом случае и функция K*(xr, ip)/p имеет простые по-
полюсы и потому может быть представлена в виде
р р j^p-Pj
Здесь
Из C.176), C.177) следует, что
м
К*, (х1, Г) = Ао + X) Ai <?jT- C-178)
Выше отмечалось, что в случае гармонической нагрузки по-
полюсы (/?O2)(J) расположены в нижней полуплоскости, причем для
каждого полюса имеется также полюс, симметричный относитель-
относительно мнимой оси. Поскольку pj = —iiPctyft', следовательно, полю-
полюсы pj расположены в левой полуплоскости и для каждого полюса
3.7. Ударное нагружение
297
имеется комплексно сопряженный к нему полюс. То, что все по-
полюсы расположены в левой полуплоскости, означает, что в формуле
C.178) нет растущих при Г —> оо экспонент. Результаты расчетов
задач об эллиптических трещинах с отношениями полуосей 1:1,
1:2, 1:4 и 1:8, которые расположены в пространствах с v = 0,25 и
находятся под действием указанной выше нормальной ступенча-
ступенчатой нагрузки, представлены на рис. 3.21, 3.22. На этих рисунках
0,2
0 12 3 4 Т
1:1 1:2 1:4 1:8
Рис. 3.21. Ударная нагрузка, точка @, аг)
приведены зависимости нормированных КИН К?(х', T)/Kist(xf)
от безразмерного времени Т. Здесь Kl8t(xf) = К*(х^ оо) — зна-
значение КИН в той же точке контура х' для статической задачи,
отвечающей единичной нормальной нагрузке. На рис. 3.21 приве-
приведены КИН для точки контура х1 = @; аг), а на рис. 3.22 — для
точки xf = (ai; 0).
Из рис. 3.21 видно, что максимумы функций K*(xl\ T)/Kist(xf)
в точке xf = @; аг) с уменьшением отношения п2 : сь\ изменяются
немонотонно. Решение задачи о круговой трещине хорошо согла-
согласуется с решением, полученным в §2.6 (см. рис. 2.14). Для элли-
эллипса с 0,2 : ai = 1:8 полученное решение приближается к решению
плоской задачи [410, 106]. В точке х' = (аи 0) при уменьшении
отношения п2 : ах максимумы функций К*(х\ T)/Kist(xf) моно-
монотонно убывают, стремясь к 1 (см. рис. 3.22).
В представленном здесь методе решения нестационарных за-
задач, так же как и в методе, рассмотренном в § 2.6, получаемые при-
приближенные решения хорошо аппроксимируют точные вне некото-
некоторой окрестности точки Г = 0. Это связано с тем, что используемая
19 Зак. 205
298
Гл. 3. Аналитические методы
рациональная аппроксимация образа Лапласа пригодна лишь для
ограниченной области изменения параметра преобразования Ла-
Лапласа, а поведение решения в нуле определяется поведением образа
К*г(Т)/Кы
1,0
0,6
0,2
-0,2
2 3 4
-1:1 1:2 1:4 1:8
Рис. 3.22. Ударная нагрузка, точка (<ц, 0)
Лапласа на бесконечности. Поэтому, как видно из рис. 3.21, 3.22,
при Г = 0 решения даже не обращаются в ноль.
Заметим, что помимо представленных в §3.6 и 3.7 приложе-
приложений резонансных частот, они могут также использоваться в за-
задачах обнаружения и идентификации трещиноподобных дефектов
[181]. Отличные от предложенного здесь подходы к вычислению
[>езонансных частот для некоторых форм трещин рассмотрены в
158, 35].
3.8. Асимптотика решения для малых времен
В § 2.6 и 3.7 рассматривались задачи о трещинах при ударном
нагружении. В обоих случаях, как при использовании обращения
преобразования Фурье, так и при обращении преобразования Ла-
Лапласа не удавалось получить хорошую аппроксимацию решения
в области малых времен. Как уже отмечалось выше, для получе-
получения асимптотики решения в нуле необходимо построить асимпто-
асимптотику образа Лапласа или Фурье на бесконечности. В §3.1 были
приведены ссылки на значительное количество работ, в которых
рассматривалась высокочастотная асимптотика решения задач о
трещинах. Однако в указанных работах главным образом строи-
строилась асимптотика дальних полей. Асимптотика КИЙ была полу-
получена только для круговой трещины при скручивающей нагрузке
[342, 152] и для трещины в виде полуплоскости [150, 152].
3.8. Асимптотика решения для малых времен 299
Здесь, на примере задачи о трещине нормального разрыва,
покажем, что главный член асимптотики может быть получен до-
достаточно простым способом, развитым в работе автора [143] при
решении статической задачи о трещине с берегами, взаимодей-
взаимодействующими по линейному закону.
Рассмотрим задачу о круговой трещине, к поверхностям ко-
которой приложены нормальные усилия ±*з(т), где t^(r) = Н(т).
Предположим, что радиус круговой трещины равен а. Как от-
отмечалось выше, граничное уравнение для образа Лапласа скачка
нормального смещения [Ьщ(х, s)] может быть получено из урав-
уравнения B.54) для амплитуды скачка смещений при гармонических
колебаниях заменой частоты ш на — is и амйлйтуды действующей
нагрузки ts(x) на 1/5. Таким образом, граничное уравнение для
образа Лапласа скачка нормального смещений приобретает вид
pKaU*s [Ьщ{х, а)] = —, [Lu3(x, а)]=0, х$ Ка. C.179)
flS
Здесь Ка — круг радиуса а, ?2* — псевдодифференциальный опе-
оператор с символом
+ V
(ЗЛ80)
где Cs — скорость распространения поперечной волны.
Разлагая в асимптотический ряд при 5 -> со выражение C.180)
для символа оператора Л*, получим, что главный член асимпто-
асимптотики Щ(?) при s -? оо равен
Из уравнения C.179) и асимптотики символа C.181) следует, что
асимптотика \Lu${x, s)] при s -> оо вне окрестности контура тре-
трещины имеет вид
[Ьщ(х, ,)] = Щ. C.182)
fJ,S
Поскольку асимптотика скачка нормального смещения C.182)
справедлива вне малой окрестности контура трещины, из нее
можно получить асимптотику энергии деформации тела с трещи-
трещиной, находящейся в заданном поле нагрузок:
W
19*
= 2 J 3(X' S) f 3(Ж' S)} W 2"^Г = "^з~- (ЗЛ83)
300 Гл. 3. Аналитические методы
Рассмотрим теперь ту же задачу для круговой трещины ра-
радиуса аA 4- е), где е > 0 — малое число. Из формулы C.183)
следует, что энергия деформации тела с такой трещиной прибли-
приближенно равна
и, следовательно, с точностью до малых более высокого порядка
приращение энергии деформации равно
. C.184)
С другой стороны, согласно формуле Ирвина [12, 96], 8W =
= тгA — v)n~~lN28S, где SS — приращение площади трещины.
Учитывая, что в данном случае 5S, с точностью до малых более
высокого порядка, равно SS = 2тга2?, получаем
6W = ^^JVJWg. C.185)
Приравнивая правые части соотношений C.184), C.185), полу-
получим выражение для коэффициента интенсивности напряжений Nx:
Заметим, что выражение C.186) для Ni не зависит от радиуса
трещины а. Учитывая, что при преобразовании Лапласа функция
rXk переходит в функцию r(Ajb + lM~(Afc) и, следовательно, s~3/2
является образом Лапласа функции г1/2/ГC/2) = 2т1/2/тг1/2, по-
получаем асимптотику Ni вблизи г = 0:
C.187)
Если перейти к безразмерному времени Т = тС8/а, то выра-
выражение для Nx C.187) примет вид
Поскольку для статической задачи о круговой трещине радиуса
а при действии единичной нагрузки величина КИН равна Nlst =
= \/2а/тг, нормированное значение КИН выражается следующей
формулой:
iVI ~~ лг "~ П1 "~ TS
3.9. Трещина на границе раздела материалов 301
3.9. Трещина на границе раздела материалов
Граничные псевдодифференциальные уравнения, отвечающие
задаче о трещине на границе соединения полупространств, были
приведены в A.35). Эти уравнения можно переписать в следую-
следующем виде:
д2 — сР
Здесь, как и выше, G — область трещины, Л и Л — псевдодиф-
псевдодифференциальные операторы с символами |?| и l^)" соответственно.
Предположим, что G — эллиптическая область:
4 4
где п2 ^ а\.
Предположим также, что приложенные нагрузки могут быть
разложены в степенные ряды:
4 Е Ы к = ii2'3- C-189)
Здесь Л*^ — постоянные и, в соответствии с принятыми выше
обозначениями, zjj = Xj/a,j, j = 1, 2.
В этом случае можно искать решение системы уравнений
C.188) в виде
[**(*)] = Е ВктТЦ2{х), к = 1, 2, 3, C.190)
где 5р9 — постоянные.
302 Гл. 3. Аналитические методы
Обозначим, как и выше,
d^ ЩХ)> •". 3 = 1, 2, C.191)
и кроме того, введем обозначения
^ ед. C.192)
Подставив C.189), C.190) в C.188) и воспользовавшись обозначе-
обозначениями C.191), C.192), придем к системе уравнений
{ f
Е В},и>Чх) + е f) 5Р
оо оо ^
-е J2-. ^Дй(«) - d J3 5p3gLf (х) =
J
¦1^{-е f; ^?k^)+5 f;
Q2
{ P,9=0 P,g=O
OO 00 ^ OO
P>Q=O
f;
oo ^ oo
+9 E Sp^P9(*) = E
J
C.193)
Заметим, что согласно C.23) и C.59)-C.61) Upq(x) и Д??(х) —
полиномы степени р +• д. Функции L^q(x) и ^29(ж) МОГУТ быть
3.9. Трещина на границе раздела материалов 303
разложены в степенной ряд. Действительно,
' (ЗЛ94)
Аналогичным образом получается и другое разложение
г) - — I V7-1V1 Г- -«
^2 )
n=0 ч /n k=0
1
Г
)
Подставив C.23), C.59)-C.61), C.194) и C.195) в C.193), убежда-
убеждаемся, что уравнения C.193) представляют собой равенства между
степенными рядами. Приравнивая коэффициенты при одинако-
одинаковых степенях, получим бесконечную систему линейных уравне-
уравнений относительно неизвестных постоянных В^г Для решения
этой системы следует рассмотреть усеченные конечные системы
линейных уравнений, в которых p + q^Nni+j^N.
После вычисления постоянных .0* можно вычислить скорость
высвобождения энергии деформации при продвижении трещи-
трещины J, как функцию, определенную на контуре трещины. Восполь-
Воспользуемся параметрическим заданием эллиптического контура тре-
трещины
х\ = a\ cos 0, Х2 = й
Обозначим проекции вектора перемещений ([tii(#)]? [г*2(^)]) на
направления внешней нормали и касательной к контуру трещины
в точке (aicos0, a,2sm6) через [г*п(ж)] и [wT(a;)] соответственно.
Выражения для [глп(ж)] и [мт(ж)] приведены в C.65). Как из-
известно, компоненты вектора скачков смещений вблизи контура
304 Гл. 3. Аналитические методы
трещины имеют следующую асимптотику (см. [358, 422]):
[«,(»)] « ^./И. C.197)
Здесь 5 — расстояние от ж до контура трещины, К = Кг +
+ t\Kn — комплексный коэффициент интенсивности напряжений,
е и /i* — постоянные, определяемые упругими постоянными верх-
верхнего и нижнего полупространств:
2тг
Аналогично C.66) введем обозначения:
), j = 1,2,3, C.198)
(„\] — \ifi(<r\\i/J-fo(<A (% 1QQ^
Из C.65), C.197), C.27) и C.199) следует, что величина К1п в
точке л, принадлежащей контуру трещины, выражается следую-
следующей формулой:
М, ПГ [- K(aQ] aisi [()] 2|
Хш-УУ^1 (f2^ i2^)i/4 J' C-
Из C.190), C.198) следует, что на контуре трещины
00
[и°к(х)] = ]Г B^qcospesmqe, к = 1, 2, 3. C.201)
Подставив C.201) в C.200), получим
2
00
х ]Г [#2ga2 cosp+1 ^ sin9 в - Blvqai cosp ^ sin9+1 ^]. C.202)
Р,9=0
3.9. Трещина на границе раздела, материалов 305
Из C.196), C.27), C.198) и C.199) получим
sin2 в + 4 cos2
u} + i[Ku-2eKl]}
~(l + 4e2)ch(,r?)
C.203)
Приравнивая модули левой и правой частей равенства C.203), по-
получим
2{^(a;)]2 + [<(z)]2}, C.204)
где ж — точка на контуре трещины.
Из C.201) следует, что на контуре трещины
00
C.205)
Аналогичное выражение для [^(ж)] получается из C.65), C.199)
и C.201).
Заметим, что согласно [119, 136, 422] скорость высвобождения
упругой энергии J при продвижении трещины выражается через
коэффициенты интенсивности напряжений следующим образом:
\ \ I 11/ с%.. ill v '
Таким образом, вычислив постоянные В* и воспользовавшись
формулами C.206), C.202), C.204) и C.205), можно вычислить
величину J.
Рассмотрим некоторые численные примеры.
Сначала предположим, что к поверхностям трещины прило-
приложены однородные нормальные усилия
t(х) = @,0, а).
Как отмечалось выше, для приближенного решения бесконечной
системы линейных уравнений C.193) следует решать усеченные
конечные системы уравнений, в которых р + q ^ N и %I + j ^ N.
Для иллюстрации того, насколько быстро устанавливается реше-
решение с ростом JV, в табл. 3.17 приведена зависимость безразмерной
306
Гл. 3. Аналитические методы
величины «7* =
a2a
от N для дискообразной трещины радиуса
а и материалов полупространств, коэффициенты Пуассона кото-
которых равны z/+ = V- = 0,3, а отношение модулей сдвига равно
/i+:/i_ = l:4.
Таблица 3.17
N
J*
N
J*
N
Л
ЛГ
Л
0
0,265579
6
0,271510
12
0,272141
18
0,272400
1
0,275671
7
0,274080
13
0,273735
19
0,273575
2
0,269958
8
0,271804
14
0,272248
20
0,272456
3
0,274720
9
0,273927
15
0,273670
21
0,273539
4
0,271015
10
0,272000
16
0,272332
5
0,274313
11
0,273817
17
0,273618
Результаты, представленные в табл. 3.17, показывают,. что
связь между нормальными и сдвиговыми скачками смещений,
определяемая системой уравнений C.188), весьма слабая. В связи
с этим достаточно хорошее приближение к точному решению мож-
можно получить даже при замене бесконечной системы линейных
1 23456
Рис. 3.23. Зависимость J* от /х_//г
89 |i_/|i+
:аг = 2, i/+ = i/_ = 0,3
уравнений конечной системой невысокого порядка. В то же время
уточнение приближенного решения с ростом N происходит до-
довольно медленно. Ряд расчетов, проведенных для эллиптических
трещин с различным отношением полуосей, находящихся на гра-
3.9. Трещина на границе раздела материалов
307
нице соединения полупространств, обладающих различными уп-
упругими свойствами, показал, что характер сходимости прибли-
Рис. 3.24. Зависимость J» от //-///+; oi :аг = 4, */+ = i/- = 0,3
женных решений к точному в этих случаях вполне аналогичен
случаю, представленному в табл. 3.17.
На рис. 3.23,3.24 представлены зависимости величины J*((p) =
{ Л
х Ж2 , {о>2 .
в различных точках у? = arctg — = arctg I — tg 0
эллиптических контуров от отношения модулей сдвига полупро-
полупространств /i_//i+.
На рис. 3.25, 3.26 представлены зависимости J*(y?) вдоль кон-
контуров эллиптических трещин для полупространств с различными
соотношениями упругих модулей. Зависимости J*(y?) приведены
на отрезке 0 < (р ^ тг/2 для эллиптических трещин с отношением
полуосей ai :а2 = 1, 2, 4, 8 и 16.
Поскольку для трещин, находящихся на границе соединения
различных полупространств, аналитические решения известны
только для антиплоской [427, 389] и плоской задач [119], а также
в случае дискообразной трещины [95, 428, 270], эти результаты
представлены на рис. 3.25, 3.26 для сравнения с ними результа-
результатов, полученных рассмотренным здесь аналитико-численным ме-
методом.
Из рис. 3.25, 3.26 видно, что в случае дискообразной трещины
полученные аналитико-численным методом результаты практиче-
практически совпадают с аналитическими. Поскольку функция J*((p) по-
постоянна в случае дискообразной трещины, аналититическое реше-
решение отмечено на рисунках лишь в одной точке (<р = тг/4).
308
Гл. 3. Аналитические методы
21 2i 2i
-*— 02*^1 = 1:8 -о-а^ч*! = 1:16 Округ
D плоская деформация
Рис. 3.25. График J*(<p)\ v+ = 0,2, i/_ = 0,4,
0.0
0,1
0,2
—о— аг:ах = 1:1 -о-а2:а1
-и—a2:fli = 1:8 -o-a2:ai
П плоская деформация
0,3
1:2
0,4
""^2^1 = 1'4
) круг
Рис. 3.26. График J*(
= 0,2, i/_ = 0,4, //+:^- =1:10
3.9. Трещина на границе раздела материалов
309
Из рис. 3.25, 3.26 видно, что значения J*{ix/2) для вытянутых
эллипсов {а\ :п2 = 16) лишь немного меньше, чем значения соот-
соответствующих величин, отвечающих решению задачи о трещине в
условиях плоской деформации.
Рассмотрим теперь случай однородной сдвиговой нагрузки вида
t(x) = (т, 0, 0). В данном случае величину скорости высвобожде-
высвобождения энергии деформации при продвижении трещины обезразме-
рим следующим образом:
C.207)
Характер сходимости численных результатов к точному решению
с ростом iV, представленный в случае нормальной нагрузки в
табл. 3.17, сохраняется и для сдвиговой нагрузки. Для иллюстра-
иллюстрации этого в табл. 3.18 даны зависимости приближенного значения
Мф) от N в трех различных точках контура <р = 0, (р = тг/4 и
<р = 7г/2. Результаты приведены для задачи о дискообразной тре-
трещине радиуса а и материалов полупространств с v+ = z/_ = 0,3 и
отношением модулей сдвига /i+:/i_ = 1:4.
Таблица 3.18
N
0
1
2
3
4
5
6
7
8
9
10
МО)
0,3766
0,3859
0,3798
0,3851
0,3808
0,3847
0,3813
0,3845
0,3816
0,3843
0,3819
Л(тг/4)
0,3186
0,3257
0,3217
0,3250
0,3224
0,3247
0,3228
0,3246
0,3230
0,3245
0,3231
Л(тг/2)
0,2605
0,2655
0,2635
0,2650
0,2640
0,2648
0,2642
0,2647
0,2643
0,2646
0,2644
N
11
12
13
14
15
16
17
18
19
20
21
МО)
0,3842
0,3820
0,3841
0,3821
0,3840
0,3822
0,3839
0,3823
0,3839
0,3824
0,3838
Л(тг/4)
0,3244
0,3232
0,3243
0,3233
0,3243
0,3234
0,3243
0,3234
0,3242
0,3234
0,3242
Л(тг/2)
0,2646
0,2644
0,2646
0,2644
0,2646
0,2645
0,2646
0,2645
0,2646
0,2645
0,2646
Сходимость результатов для других сдвиговых нагрузок, элли-
эллиптических трещин с различным отношением полуосей и материа-
материалов полупространств с различным отношением упругих постоян-
постоянных аналогична представленной в табл. 3.18.
На рис. 3.27, 3.28 приведены графики функций J*((f) для не-
неоднородного пространства с J/+ = i/_ = 0,3 и отношениями
/х+: //_ = 1:4 и 1:10 соответственно. Результаты представлены на
отрезке 0 < (р < 7г/2.
Для удлиненных эллипсов величины «7*(тг/2) должны стре-
стремиться к величине J*a скорости высвобождения энергии деформа-
деформации при продвижении трещины антиплоского сдвига длины 2
310
Гл. 3. Аналитические методы
0,2
0,0 0,1 0,2 0,3 0,4
= 2 -+-ai:a2=4
22=1б О/*«
П /2с 04с
Рис. 3.27. График Л(</?); v+ = 0,3, i/- = 0,3, fi+ifi- = 1:4
0,0
0,1
"п"/?
0,2 0,3
= 2
0.4
j^ =4
Рис. 3.28. График J.(y); "+ = 0,3, f- = 0,3, fi+.fi- = 1:10
3.9. Трещина на границе раздела материалов ЗИ
Согласно [427, 389]
7 -
2/х*
Величины J*a также представлены на рис. 3.27, 3.28. Из рисун-
рисунков видно, что величины «/*(тг/2) для эллиптических трещин с
а\ :п2 = 16 лишь немного ниже величин J*a.
В случае дискообразных трещин возможен следующий путь
сравнения полученных численных результатов с аналитическими.
Согласно [428] значения J*((p) заполняют отрезок
4?(i+?w^ Г,+ /
(E-е)тг?(И-е2) + с/J L V 9 + c
C.208)
где 0 < A < 1.
Из C.208) следует, что экстремальные значения Лс достига-
достигаются при Л = 0 и Л = 1. Эти значения равны
л =
соответственно.
Экстремальные значения J*c также представлены на рис. 3.27,
3.28. Из этих рисунков видно, что экстремальные значения, полу-
полученные аналитико-численным методом, практически совпадают с
соответствующими аналитическими величинами.
Помимо сравнения экстремальных значений, в случае диско-
дискообразных трещин можно также сравнить усредненные значения
J*(<p) вдоль контура трещины, полученные численно, с соответ-
соответствующими точными значениями. Обозначим энергию деформа-
деформации пространства, ослабленного трещиной через W. Нетрудно
видеть, что в случае дискообразной трещины радиуса а и одно-
однородных нагрузок, приложенных к поверхностям трещины, имеет
место следующая формула:
2тг
J Or
о
Определим среднее значение безразмерной скорости высвобо-
высвобождения упругой энергии при продвижении контура трещины еле-
312 Гл. 3. Аналитические методы
дующим образом:
2тг
C.210)
Из C.209), C.210) и аналитического выражения для W, приве-
приведенного в [428], следует
Значения J*, полученные с помощью аналитической формулы
C.211), и численным интегрированием функции J*(<^), получен-
полученной аналитико-численным методом, приведены в табл. 3.19. Дан-
Данные таблицы подтверждают хорошее совпадение аналитических и
численных результатов.
Таблица 3.19
i/+ = 0,3,
v+ = 0,3,
i/+ = 0,2,
v+ = 0,2,
i/+ = 0,4,
i/+ = 0,4,
V
V-
V-
V-
1/-
= 0,3
= 0,3
= 0,4
= 0,4
= 0,2
= 0,2
p+:/i_ = 1:4
/z+:/i- = 1:10
(л+ф- = 1:4
/i+:/i_ = l:10
/i+:/i_ = 1:4
ti+Ф- = 1:10
C.211)
0,3244
0,2830
0,3340
0,2955
0,3104
0,2665
Приближенные
0,3243
0,2827
0,3334
0,2946
0,3104
0,2665
Рассмотрим теперь однородную сдвигающую нагрузку, дей-
действующую в направлении малой оси эллипса,
t(x) = @, г, 0).
На рис. 3.29, 3.30 представлены графики функций J*(??), опреде-
определенных согласно C.207).
В случае нагрузок данного вида величина J* (тг/2) для вытяну-
вытянутых эллипсов должна приближаться к величине скорости высвобо-
высвобождения упругой энергии для трещины поперечного сдвига длины
2а2, которую мы обозначим J*{. Согласно [119]
Величины J*i представлены на рис. 3.29, 3.30. Из рисунков видно,
что величины J*(n/2) для эллиптических трещин с отношением
а\ :а>2 = 16 лишь немного меньше величин J*?.
3.9. Трещина на границе раздела материалов
313
0,0
0,1
0,2
0,3
0,4
-о— al:a2-1 -o-aj =2
-и— ax:a2 = 8 -o-ai:a2 = 16
О Jl О Ac
Рис. 3.29. График Л (у?); i/+ = 0,4, v~ = 0,2, /[i+:/i- = 1:4
0,0
Рис. 3.30. График
= 0,4, i/_ = 0,2,
314
Гл. 3. Аналитические методы
Для дискообразных трещин экстремальные и усредненные
значения скоростей высвобождения упругой энергии не зависят
от направления приложенных усилий. Величины J+c и J}c также
приведены на рис. 3.29, 3.30.
В качестве примера неоднородной нагрузки рассмотрим скру-
скручивающую нагрузку вида
C.212)
t(x) = (--S2, -
Графики функций Л (у?), определяемых формулой C.207) и от-
отвечающих скручивающей нагрузке, приведены на рис. 3.31, 3.32.
В случае скручивающей нагрузки аналитические решения извест-
КХХХХХХХХХХХХХХХХ><>О><ХХХХ>0<ХХХХХХХХХХХ>-
0,1
0,4
0,2 0,3
и fli:62 = B —*— 6i:fl2 = 16 D V/*/
Рис. 3.31. Нагрузка C.212); */+ = 0,3, i/_ = 0,3,
*/*
_ = 1:4
ны только для дискообразной трещины [389]. Согласно [389] обез-
размеренная величина скорости высвобождения упругой энергии
J*t для дискообразной трещины равна
«/** =
Поскольку величины «/** не зависят от угла <р, они представлены на
рис. 3.31, 3.32 только в одной точке. Величины J*t в точности со-
совпадают с результатами, полученными аналитико-численным ме-
методом.
3.9. Трещина на границе раздела материалов
315
Для скручивающей нагрузки диапазон изменения значений,
принимаемых функцией J*(y>), быстро растет с ростом эксцентри-
эксцентриситета эллипса. В связи с этим представить на одном рисунке
1//*
кхххххххххххххх^^
0,1
0,2
0,3 0,4
_ г2 = 16 ? 1//J
Рис. 3.32. Нагрузка C.212); v+ = 0,4, i/_ = 0,2, /x+:/xl = 1:10
графики функций J*((p) для эллипсов с различным соотношением
полуосей становится затруднительно. Поэтому на рис. 3.31, 3.32
приведены графики функций 1/Л {Ф)-
Глава 4
КАЧЕСТВЕННЫЕ МЕТОДЫ
4.1. Постановка задачи
Эта глава посвящена построению оценок различных характе-
характеристик решений некоторых задач о трещинах. Оценки строятся,
не прибегая к полному решению задачи, с помощью замены ис-
исходной задачи на другую, более простую. Такой подход к исследо-
исследованию сложных задач оказывается полезным в тех случаях, когда
не удается получить их аналитические или асимптотические ре-
решения, а построение достаточно аккуратных численных решений
также вызывает значительные затруднения. Кроме того, каче-
качественные исследования могут быть использованы при оценке кор-
корректности получаемых численных результатов.
Построение оценок наиболее важных характеристик решений
широко применяется в различных областях механики сплошных
сред, например, в теории упругости (задачи о кручении стержня
[111], контактные задачи[32]), в теории пластичности [33], в тео-
теории фильтрации жидкости в пористой среде [40] и др. Различным
вопросам, связанным с построением оценок и их приложениями,
посвящены работы [111, 347, 170, 40].
В механике разрушения качественные методы стали разви-
развиваться с появлением статьи [38]. В этой работе были установлены
теоремы сравнения в задаче о плоской трещине нормального раз-
разрыва в безграничном линейно упругом пространстве. Теоремы
сравнения позволяют оценивать скачки смещений и КИН для тре-
трещин сложной формы путем вписывания в них и описывания во-
вокруг них трещин более простых форм, для которых решения
известны. Результаты в [38] получены применением принципа
максимума к смешанной краевой задаче для гармонической в по-
полупространстве функции, к которой сводится с помощью предста-
представления Папковича-Нейбера рассматриваемая задача. В работах
[39, 48, 138] теоремы сравнения распространены на более слож-
сложные задачи. В частности, в [39] с помощью полученных резуль-
результатов для трещины в безграничном пространстве и метода по-
последовательных приближений теоремы сравнения доказаны для
трещины отрыва, расположенной в срединной плоскости доста-
достаточно толстого слоя. В [48] аналогичные результаты получены для
безграничной среды, но в случае, когда допускаются знакопере-
4.1. Постановка задачи 317
менные нормальные нагрузки, в результате чего могут произойти
налегания поверхностей трещины. В этой работе доказательство
опиралось на сравнение решений вариационных неравенств, полу-
полученное в [233]. В [138] теоремы сравнения доказаны для трещин,
берега которых взаимодействуют по линейному закону.
Несмотря на то, что в указанных статьях теоремы сравнения
распространены на более широкий, чем в [38], класс задач, во
всех этих работах для приведенных доказательств принципиально
важна была связь задачи о трещине в безграничной среде с некото-
некоторой краевой задачей для гармонической функции. Таким образом,
в идейном плане существенного продвижения по сравнению с [38]
достигнуто не было. Шагом вперед стали работы [54, 56, 57], в ко-
которых теоремы сравнения доказаны для целого класса псевдодиф-
псевдодифференциальных уравнений. Этот класс уравнений, в частности,
включает в себя граничные уравнения задач о трещинах отрыва
не только в однородном линейно упругом пространстве, но и в
неоднородном, со специальным (степенным) видом неоднородно-
неоднородности. Главное достижение работ [54, 56, 57] заключается в том, что
теоремы доказаны методом, который применим непосредственно к
псевдодифференциальным уравнениям и не предполагает наличия
связи между псевдодифференциальным уравнением и краевой за-
задачей для какого-либо дифференциального уравнения в полупро-
полупространстве. В §4.2 приведены результаты этих работ. В §4.5 с
помощью метода, развитого в укзанных работах, теоремы срав-
сравнения доказаны для уравнения, представляющего собой два пер-
первых члена асимптотического разложения граничного уравнения
задачи о трещине нормального разрыва в условиях гармониче-
гармонических низкочастотных колебаний. Параграф 4.5 написан на основе
работы [70].
Имея оценки раскрытия трещины через раскрытия вписанных
и описанных трещин, можно оценить и объем трещины нормаль-
нормального разрыва (проинтегрированный по области трещины скачок
нормального смещения). Однако такие оценки окажутся недо-
недостаточно точными. Более аккуратные оценки дают изопериме-
трические неравенства. Типичным примером такого неравенства
является известная оценка жесткости при кручении стержня че-
через жесткость при кручении стержня, имеющего круговое сечение
той же площади [111]. В [39] было высказано предположение, что
аналогичное неравенство имеет место и в задаче о трещине нор-
нормального разрыва. Более точно это предположение формулируется
следующим образом. В случае, когда к поверхностям трещины
приложено однородное давление, объем трещины не превосходит
объема круговой трещины той же площади. В работах [49, 50] ука-
указанное предположение было доказано. Доказательство здесь опи-
опиралось на возможность сведения задачи о трещине нормального
разрыва к смешанной краевой задаче для гармонической в полу-
318 Гл. 4. Качественные методы
пространстве функции. Результаты [49, 50] существенно обобщены
и усилены в [141], где изопериметрические неравенства доказаны
для решений того же класса псевдодифференциальных уравнений,
для которого в [54] были доказаны теоремы сравнения. Приве-
Приведенные в [141] доказательства опираются на теорию интерполяци-
интерполяционных пространств [20] и не предполагают возможности записи
псевдодифференциального уравнения как граничного уравнения,
отвечающего некоторой краевой задаче для дифференциального
уравнения в полупространстве.
Результаты [54, 141) показывают, что свойства решений рас-
рассматриваемого там класса уравнений вполне аналогичны свойст-
свойствам решений задачи Дирихле для уравнения Пуассона. На связь
между решениями псевдодифференциального уравнения, отвечаю-
отвечающего задаче о трещине отрыва, и уравнения Пуассона было обра-
обращено внимание также в [53, 58]. Вместе с тем, полученные в [111]
изопериметрические неравенства для решений уравнения Пуас-
Пуассона были значительно усилены в [405, 299, 159, 160]. Это дало
основание полагать, что усиленный вид неравенств справедлив и
для рассмотренного в [54, 141] класса псевдодифференциальных
уравнений. Данное предположение оказалось верным и его до-
доказательству посвящен §4.3. Из представленных в §4.3 результа-
результатов следует не только изопериметрическое неравенство для объема
трещины, но и для максимального раскрытия и Lp-норм. Пара-
Параграф 4.3 написан на основе работы [144].
Полученные оценки решений позволяют также обосновать не-
некоторые численные методы. В частности, в § 4.4 с помощью тео-
теорем сравнения доказана сходимость альтернирующего метода в
статической задаче о двух трещинах нормального разрыва, распо-
расположенных в одной плоскости на произвольном расстоянии друг от
друга.
4.2. Теоремы сравнения
Рассмотрим класс псевдодифференциальных уравнений, вклю-
включающий уравнение задачи о трещине нормального разрыва в од-
однородном пространстве:
и(х) е Нц/2(О), 0<ц<2.
Здесь Л*4 — псевдодифференциальный оператор с символом |?|^.
Все приводимые ниже утверждения справедливы не только для
двумерных областей, поэтому далее будем предполагать, что огра-
ограниченная область GcKn, где п ^ 2. Однозначная разрешимость
уравнения D.1) в указанных пространствах доказана в [147].
Для доказательства теорем сравнения нам понадобится нес-
несколько предварительных утверждений.
4.2. Теоремы сравнения 319
О
Лемма 4.1. Пусть и(х) ? Нф№) и и(х) ^ О, х € G, при-
причем и(х) ф О, тогда А**и(х) < 0 вне G, G — замыкание G.
Доказательство. Согласно [147] при — п< /3 < О
u(y)dy
- . - - I
где С = const > 0.
Заметим, что А^и = A2A/i"~2u, причем — п < /л—2 < 0 и потому
А/»«(Я) = 2/T@g + ")/2) /• «(у)^ СГ "(з
- -СД.Jf j—f+&> C-
D.2)
Здесь в обозначении Д^ подчеркивается, что оператор Лапласа
применяется по переменным х.
Если точка х ^ supp u(y) (supp u(y) — носитель функции
и(у)), то А**и(х) — гладкая функция в окрестности точки ж, при-
причем оператор Лапласа в D.2) можно внести под знак интеграла.
Обозначим n + /i — 2 = к>0:
-Д.(|* - 2/Г) = к(п - 2 - к)\х -
следовательно,
()
D.3)
В силу D.2) и D.3) получим А^и(х) < 0 при х ф G.
Заметим, что если и(х) < 0, х € G, причем г*(а;) ^ 0, то
> 0 при х ? G.
Лемма 4.2. Пусть и(х) —решение уравнения D.1), причем
f(x) ^ 0, f(x) ф 0. Тогда не может быть, чтобы и(х) < 0 во
всей области G.
Доказательство. Поскольку и(х) — решение уравнения
D.1), имеет место равенство
(А"«(«), «(»)) = (/(»),«(»)). D.4)
Так как f(x) ф 0, то и(х) ф 0 и, следовательно,
(A"u, «) = щ; I \тЯ0\2<%>0. D.5)
320 Гл.4. Качественные методы
Если и(х) ^ 0 в области G, то из условий леммы 4.2 следует
(f(x), u(x)) = j f(x)u(x) dx < 0. D.6)
G
Неравенства D.5), D.6) противеречат равенству D.4), что доказы-
доказывает лемму.
Теорема 4.1. Пусть f(x) ^ 0 в области G, тогда решение
уравнения D.1) и{х) ^ 0.
Доказательство. Пусть утверждение теоремы неверно, то-
тогда в G можно выделить две подобласти G+ и G- такие, что
<7+П<2- = 0, и(х) > 0 при х е G+, и{х) < 0 при х е G- и
и{х) = 0 при х в G\{G+\JG-).
Введем обозначения:
е НфЦВ+)> и.{х)
Из уравнения D.1) получим
Обозначим /(ж) -р<7_Л^гц-(#) = р(гс). Так как G+f)G- = 0,
то в силу леммы 4.1 р<з_Л/хМ4-(#) < 0 и потому д(х) > 0. Заметим,
что u-(x) является решением уравнения
что противоречит лемме 4.2. Теорема доказана.
Теорема 4.2. Если f(x) ^0w f(x) ф 0, то в условиях тео-
теоремы 4.1 можно утверждать, что и(х) > 0 внутри области G.
Доказательство. Рассмотрим произвольную точку хо € G.
Сначала предположим, что существует окрестность точки #о? О(жо),
в которой f(x) ^ S > 0. Возьмем функцию <?>(#) € Со°@(а;о))
такую, что (р{хо) > 0, у?(ж) ^ 0. Поскольку <р(х) € Со°@(жо)),
то А^ср(х) = д(ж) G C°°(lRn). Поэтому существует М = const > 0
такая, что \д(х)\ < М при х G 0(жо), 0(жо) — замыкание O(xq).
Выберем е > 0 так, что гМ < 5. Обозначим ф(х) = в<р(а;), ^(ж)
является в области G решением уравнения
= ед{х), <ф(х) €
4.2. Теоремы сравнения 321.
По построению в O(xq), ед(х) < S < /(ж). Вне O(xq), eg(x) <
< 0 в силу леммы 4.1 и потому ед{х) < /(ж), # € G. Из тео-
теоремы 4.1 следует и(х) ^ ф(х), но ^(#о) > 0 по построению, откуда
получаем и(хо) > 0. Если нельзя выбрать окрестность точки гго, в
которой f(x) отделена от нуля, то, поскольку f(x) ф 0, существует
точка х1 и ее окрестность O(xf) такая, что f(x) ^ Si > 0 при
х Е O(rc'), O(x') $ xq. Строим функцию ф(х) аналогично тому,
как это делалось выше, только на этот раз в окрестности О(хг).
Рассмотрим функцию v(x) = u(x) — ф(х):
pGhflv{x) = f(x) - ед(х).
Выше было отмечено, что f(x) — ед(х) ^ 0, следовательно, v(x) ^
^ 0. Поскольку ^(#о) = 0, то v(xq) = u(xq).
Из леммы 4.1 следует, что существует окрестность O(xq), где
ед(х) строго меньше нуля, вследствие чего f(x) — eg(x) строго
больше нуля в этой окрестности. Тогда по доказанному выше
v(xo) > 0, но v(xq) = u(xo), что доказывает теорему.
Теорема 4.3. Пусть f(x) определена и неотрицательна в
области G\ и пусть G С G\. Предположим также, что f(x) ф
ф 0 в G\. Рассмотрим уравнения
pG№uG{x) = f(x), uG(x)
о
pGl№uGl(х) = /(ж), uGl (х) е
Решения этих уравнений удовлетворяют неравенству uGl (x) >
> uG(x) в области G.
Доказательство. Согласно условиям теоремы uG(x)G
о о
€ ЯМ/2(С) и, следовательно, uG(x) G H^/2(Gi). Таким образом,
uG(x) можно рассматривать как решение уравнения
о
pGl№uG{x) = /i(x), uG{x) €
f , , Г f{x), xeG,
Jl[X) ~ \
В силу теоремы 4.1 uG(x) ^ 0 в G. Используя далее лемму 4.1,
получим, что pGl\G^fJ>uG(x) ^ 0 в Gi\G. Обозначим v(x) =
pGlA»v(x) = 5(ж) = f(x) - fi(x), v(x)
0, ^ G G,
22 Зак. 205
322 Гл. 4. Качественные методы
Следовательно, д(х) ^ 0, причем д(х) ф 0. Действительно,
если f(x) = 0 при х 6 G, то по условиям теоремы д(х) ^ 0,
д[х) = /(ж) ^ 0, х е G\\G. Если f(x) ф О в G, то согласно
теореме 4.2 iag(z) > 0? х Е G и Pg1\g^ug{^) < 0 в Gi\G.
Следовательно, д(х) ^ 0, #(#) ^ О, х € G\. Применяя далее
теорему 4.2, установим, что v(x) > 0 в G\ и потому ^^(ж) >
> uq{x) в G.
Замечание 4.1. Как видно из доказательства теоремы 4.3,
она остается справедливой и при более слабых условиях. Для того
чтобы имело место неравенство ugx(x) > uq(x) в области G, до-
достаточно потребовать выполнения условий uq(x) ^ 0; f(x) ^ 0,
xeGi\G.
Как известно [147], если f(x) — достаточно гладкая функция
и dG — гладкая граница области G, то решение уравнения D.1)
и(х) имеет вблизи dG асимптотику и(х) = N(xf)s^2 + O(W2+1),
где 5 — расстояние до dG по нормали, х' — соответствующая точка
на границе области. Из теоремы 4.3 получаем
Следствие 4.1. Пусть f(x) — гладкая функция, неотри-
неотрицательная в области Gi, область GcGi, причем dG касается
8G\ в точке М. Тогда, если точка х лежит на нормали к
dG и 9Gi, проведенной из точки М, то uq{x) = Ng(M)s^2 +
+ O(W2+1), uGl(x) = iVGl(M)W2 + O(W2+1) и справедливо
неравенство Nq{M) ^ Nq^M). В случае // = 1 уравнение D.1)
переходит в граничное уравнение задачи о трещине нормаль-
нормального разрыва, а данное неравенство переходит в неравенство
для коэффициентов интенсивности напряжений.
Замечание 4.2. Доказательства теорем сравнения, приве-
приведенные выше, без изменения переносятся на уравнения более об-
общего вида
где Ац — псевдодифференциальный оператор с символом
(S%j + ?#)&?; If I'4"» $ij — символ Кронекера, величины ец малы
по сравнению с единицей, 0 < /i < 2.
4.3. Изопериметрические оценки
Прежде чем переходить к формулировке и доказательству ре-
результатов, представленных в этом параграфе, напомним основные
определения и теоремы, используемые ниже.
Функции f(x) и д(х) называются равноизмеримыми, если
Va, Ъ fi{x: а < f(x) < 6} = /х{ж: а < д(х) < 6}. Здесь //{• • • } —
мера соответствующего множества.
4.3. Изопериметрические оценки 323
Говорят, что функции f(x) и д(х) имеют одинаковое направле-
направление роста, если Vz, у, (f(x) - /(у)) (д(х) - д(у)) ^ 0.
Пусть функция f(x) ^ 0. Скажем, что функция /*(#) получена
из f(x) путем симметризации Шварца, если /*(#) равноизмерима
с /(#), сферически-симметрична и не возрастает с ростом радиуса.
Пусть f(x) ^ 0, д(х) ^ 0. Предположим, что f+(x) равноиз-
равноизмерима с /(я), а д+{х) — с д(х), причем функции /+ (х) и д+ (х)
имеют одинаковое направление роста, тогда справедливо неравен-
неравенство [111]
f(x)g(x) dx^J U(x)g+(x) dx. D.7)
Пусть f(x) ^ 0, g{x) ^ 0, h(x) ^ 0, тогда [182, 295]
/ f(x)g(x - y)h{y) dxdy < / f*(x)g*(x - y)K{y) dxdy. D.8)
Основные методы построения изопериметрических неравенств для
решений дифференциальных уравнений были разработаны в [111].
В частности, в [111] доказана следующая оценка.
Пусть uG(x) — решение уравнения
-Аи(х) = 1, жЕ(?, G С Mn, u\qG = 0. D.9)
Тогда справедливо неравенство
I uG{x)dx < / uK{x)dx, D.10)
G к
где К — шар, объем которого равен объему области G.
Очевидным образом эта оценка обобщается на случай произ-
произвольной правой части в уравнении Пуассона. Пусть uG(f, x) —
решение уравнения
—Аи(х) = /(ж), f(x) ^0, a;GG, u\dG = 0- D-И)
Обозначим
= / uG(f} x)f(x)dx.
G
Имеет место оценка
WQ(S) < WK(fJ. D.12)
В [141] оценки типа D.10), D.12) доказаны для решений класса
псевдодифференциальных уравнений следующего вида:
V\si \ 1/iT*! I "h*1011 П*\ ~~ т( Т*1 г / 7* 1 ^^ II
Lffjlx. LLKJbj \Г v UiKJU) ~~ J \***) * J V у ^* J
xEG, u(x) € Ha/2(G), 0<a<2.
22*
324 Гл.4. Качественные методы
Здесь, как и выше, Ла — псевдодифференциальный оператор с
символом |?|а, рс — сужение на область G.
В работах [405, 299] неравенства D.10), D.12) для решений
уравнений D.9), D.11) были усилены. Усиленная оценка имеет вид
*)• D-14)
Для уравнений, содержащих младшие члены
-Аи(х) + t2u{x) = f{x), }{x) > 0, х € G, u\dG = 0,
в [299] доказано несколько менее сильное неравенство
/ (^g)*(/, x)dx^ I uK(f*, x) dx. D.15)
Kr Kr
Здесь Kr — шар с центром в начале координат и радиусом г, г —
произвольное число из интервала 0 < г ^ г (К), г (К) — радиус
шара К.
Из D.15), в частности, следуют также неравенства
тахгг<з(/, х) < тахг/к(/*, ж), D.16)
X X
, x)dx ^ JuK{U, x)dx. D.17)
G К
Ниже неравенства D.15)—D.17) доказаны для решений уравнений
D.13). Для простоты в дальнейшем будем полагать t = 0. Случай
? > 0 рассматривается без каких-либо изменений.
Будем теперь обозначать ид{/, х) — решение уравнения
PGAau{x) = f(x), xeG, f(x)?0,
о D.18)
u(x) € Ha/2 (G), 0 < a < 2.
Как известно [141], «<?(/, x) доставляет минимум функционалу
^^, u(x) e Ha/2(G), D.19)
причем I(G, f, uG(f, x)) = We\f).
Сначала иным способом докажем неравенства, полученные ра-
ранее в [141], и установим свойства решений.
о
Лемма 4.3. Пусть и(х) G Ha/2(G) ии(х) ^ 0, тогда имеет
место неравенство
(Л<4 и) > (Лаи„ и,). D.20)
4.3. Изопериметрические оценки 325
Доказательство. Согласно [147]
Обозначим Km(s) — функцию, определенную в области О
s < оо:
1 1
тп+а s<±
т
Имеем
{Aau,u) = Ca lim /li:m(|«-z|)|ti(«)-ti(x)|2da;<te= lim Jm(u),
Tn—?ooJ m—?oo
Jm(u) = Ca lY^fzJXmd^ - a:|) dxdz+
+ Ju2(x)Km(\z-x\)dxdz-2Sm(u,u)].
Здесь 5m(u, v) = Ju(z)v(x)Km(\z - ж
В интеграле Ju2(x)Km(\z — x\)dzdx возьмем сначала инте-
интеграл no z. В результате получим Ju2(x)Km(\z — х\) dzdx = С\ х
х f u2(x)dx, C\ > 0 — const. Аналогично, взяв сначала в инте-
интеграле /гА2(г)#т(|;гг — #|) cfeda; интеграл по ж, будем иметь
fu2{z)Km(\z-x\)dzdx = Ci fu2{z)dz = Ci fu2(x)dx.
Таким образом,
Jm(u) = Cmfu2{x) dx - 2Ca5m(u, ti),
где Cm = 2C\Ca — положительная постоянная.
Запишем аналогичное выражение для Jm{u*)
JmM = Сш I ul{x) dx - 2Ca5m(w+, ti*).
В выражениях для Jm(u) и Jm(u*) первые члены совпадают,
поскольку симметризация Шварца сохраняет Ьг-норму функции.
326 Гл. 4. Качественные методы
Для вторых членов справедливо неравенство 5m(u, w) ^ ?m(u*, и*)
в силу приведенного выше неравенства D.8). Таким образом, по-
получаем неравенство Jm{u) ^ <Лп(^*)- Переходя к пределу при
m -> oo, приходим к утверждению леммы D.20). Неравенство
D.20) было доказано в [141] при помощи теории интерполяцион-
интерполяционных пространств.
Из утверждения леммы 4.3 и D.19) следует оценка D.12). Дей-
Действительно, из теорем сравнения для решений уравнения D.18)
следует, что если f(x) ^ 0, то uo{f, х) ^ 0. Таким образом, для
функции uo(f, x) справедливо неравенство D.20), т.е.
{AauG(f, х), uG(f, х)) > (Л>СЫ/, х), (uGUf, x)).
Кроме того, функции /*(#) и (uc)*(f, x) имеют одинаковое напра-
направление роста и потому, в силу D.7)
/ f{x)uG{f, x)dx^ / f*{x){uG)*(f, x)dx.
Таким образом, имеем
(/, uG(f, x)) *
x)(«G),(/,x)) t
>w*v*>- D22)
Неравенство D.22) эквивалентно неравенству D.12). Заметим, что
из доказательства D.22) следует, что функция uK(f*, x) инвари-
инвариантна относительно симметризации Шварца, поскольку в против-
противном случае можно было бы к uK(f*, x) применить симметризацию
Шварца, уменьшив значение функционала D.19).
Перейдем теперь к доказательству неравенств D.15)-D.17) для
решений уравнений D.18).
о
Лемма 4.4. Пусть и(х), v(x) G Яа/2(^)? тогда
i°U, v)=Ca I У " "' L+a dxdV =
• D.23)
\z - x\n+a
Здесь черта сверху означает комплексное сопряжение.
4.3. Изопериметрические оценки 327
Доказательство соотношения D.23) проводится полно-
полностью аналогично тому, как выводится в [147] выражение для
(Ааи, и). Обозначим, как и выше, й(?) преобразование Фурье
функции и(х), й(?) = /и(х)ег(х& dx.
Из соотношения
и(х + у)- и(х) =
аналогичного равенства для v(x) и равенства Парсеваля следует
(и(х + у) - и(х)) (у(х + у) - v(x))
= (Sf/"K)"KW"« "" **¦ D24)
В интеграле, стоящем в правой части D.24), возьмем сначала
интеграл по у. Согласно [147]
\е-Ш) - Ц2
ы„+а Ф, = СЖ. D-25)
Здесь С'а>0 — постоянная.
Центральное место в доказательстве неравенств D.15)-D.17)
занимает следующая теорема.
о
Теорема 4.4. Пусть и(х) ^ 0, v(x) ^ 0 € На/2{@) — веще-
ственнозначные функции, которые имеют одинаковое напра-
направление роста, тогда справедливо неравенство
(Ааи, v) ^ (Аащ, v*). D.26)
Доказательство. Обозначим
и, v) = Са [ Km(\z - х\) (u(z) - и(х)) {v(z) - v(x)) dz dx,
где Кт — ядро, введенное выше.
Очевидно (Аащ v) = lim Rm{u, v). Выражение для Rm(u, v)
m—>oo
можно переписать в виде
v) = 2Ca ru{z)v(z)Km{\z-x\)dxdz-2CaSm{u, v),
где функционал 5m(u, v) был введен выше.
328 Гл. 4. Качественные методы
Проинтегрировав в выражении для Rm{u, v) первое слагаемое
по ж, получим
u, v) = Cmfu(z)v(z) dz - 2CaSm(u, v).
Поскольку функции u(x), v(x) имеют одинаковое направле-
направление роста по условию, а функции щ(х), v*(x) равноизмеримы с
ними и имеют одинаковое направление роста по построению, то
fu(z)v(z)dz = fu*(z)v*(z)dz. Кроме того, Sm(u, v) < Sm(u*, v*)
в силу неравенства D.8). Следовательно, Rm{u, v) ^ Д^гх*, v*).
Переходя здесь к пределу при m -* сю, приходим к D.26). Тео-
Теорема 4.4 доказана.
Теорема 4.5. Для решений уравнения D.18) справедливо
неравенство
{Ла(исШ х\ v.(x)) < (А°иж(Л, х), v.(x)). D.27)
Здесь v*(x) — произвольная неотрицательная, инвариантная
относительно симметризации Шварца функция из простран-
о
ства Н
Доказательство. Пусть функция v(x) равноизмерима с
v*(x) и имеет одинаковое направление роста с функцией ug(/, ж),
тогда, согласно D.26)
{AauG(f,x), v(x)) > {Aa(uG)*(f, x), v.(x)). D.28)
С другой стороны,
, х), v(x)) = (f{x), v(x)) < (Д(х), v.(x)) =
x),v.(x)). D.29)
Вывод неравенства D.29) опирался на то, что функции f(x) и
/¦(ж), а также v(x) и v*(x) равноизмеримы, причем /*(#) и v*(x)
имеют одинаковое направление роста. Из D.28), D.29) следует
D.27). Теорема 4.5 доказана.
В качестве следствия теоремы 4.5 получим неравенства D.15)-
D.17) для решений уравнения D.18).
Докажем справедливость D.15). Рассмотрим функцию г>*(ж),
являющуюся решением уравнения D.18) в шаре К с правой ча-
частью 5*(#)> равной единице в шаре Jfr, лежащем в if, и нулю
вне Кг. Поскольку такая функция д*(х) инвариантна относи-
относительно симметризации Шварца, таким же свойством, как указы-
4.3. Изопериметрические оценки 329
валось выше, обладает и v*(x). Поэтому, согласно D.27)
= / (tiG?)*(/» ж)<^ < (A°W(/*, ж), 17*(я:)) = /
Неравенство D.15), а следовательно, также неравенства D.16),
D.17) доказаны.
Заметим, что неравенство D.17) означает, что ||г*<7(/, x)||i ^
< ||wK(/*, ж)||i, где || • ||i — норма в пространстве L±. Неравенство
D.16)означает,что \\uG(f,x)\\c < \\uK(f*,x)\\c или ||иа(/,ж)||оо ^
^ ||^к(/*5 ж)||оо> гДе II • \\с — норма в пространстве С (непрерыв-
(непрерывных функций), а || • ||оо — норма в пространстве Д».
Покажем, что аналогичные неравенства имеют место и в нор-
нормах пространств Lp, Vp, I < р < оо. Это утверждение также легко
следует из неравенства D.27). Выберем в качестве функции v*(x)
решение уравнения
PKAav(x) = (иа)ГЧ/, ^), Ф) € На/2 (К). D.30)
Функция (г*о)*~ (Л х) инвариантна относительно симметризации
Шварца и потому функция г>*(#), являющаяся решением уравне-
уравнения D.30), также инвариантна относительно симметризации Шва-
Шварца. Поэтому имеет место неравенство D.27)
х), vm(x)). D.31)
Преобразуем левую часть неравенства D.31)
D-32)
Здесь || • ||p — норма в пространстве Lp.
Оценим теперь правую часть неравенства D.31)
аг), «.И)
= fuK{U,x){uGy-\f,x)dx. D.33)
21 Зак. 205
330 Гл. 4. Качественные методы
Применим к правой части равенства D.33) неравенство Гельдера
/ «*¦(/*, x)(uG)^~1(f, x)dx ^ \\uK{f*, x)\\p IKug)*!/» жI1р')
гдер'=р/(р-1);
= (/(«о)г(/, *)<ь) = и(«о).(/, «jiir1-
Таким образом, имеем
D.34)
/¦
Из D.31), D.32) и D.34) следует неравенство
ИЛИ
II(«g)*(/, ж)||р < \\uK(f*,
Так как функции и<з(/, ж) и (ис)*(/, х) равноизмеримы, то
U х)\\р = II(^g)*(/, ж)||р. Таким образом, получаем неравен-
неравенство
)Нр < Н«*(Л, ^I1р- D-35)
Напомним, что уравнения D.18) при п = 2 отвечают зада-
задачам о трещинах в однородном и неоднородном линейно упругих
пространствах. В частности, в случае a = 1 уравнение D.18)
совпадает с уравнением, отвечающим задаче о трещине нормаль-
нормального разрыва в однородном линейно упругом пространстве. При
0 < a < 1 уравнение D.18) соответствует задаче о трещине от-
отрыва в неоднородном пространстве, модуль Юнга которого сте-
степенным образом зависит от расстояния до плоскости трещины
xz = 0 (Е = Еа\хз\г~а, Еа = const, 0 < а < 1). Уравнения
D.13) соответствуют тем же задачам о трещинах в условиях, когда
между поверхностями трещины имеются линейные связи. Правые
части уравнений D.13), D.18) с точностью до постоянных множи-
множителей совпадают с прикладываемыми усилиями, а решения — с
раскрытиями трещины.
Таким образом, неравенства D.16), D.17) и D.35) дают оценки
максимального раскрытия трещины, ее объема и ?р-норм скачков
смещений через аналогичные характеристики задачи о круговой
трещине той же площади с нагрузками, получаемыми при помощи
симметризации Шварца из исходных нагрузок.
4.4. Сходимость альтернирующего метода 331
4.4. Сходимость альтернирующего метода
Во введении отмечалось, что одним из самых эффективных ме-
методов решения трехмерных задач о трещинах является альтерни-
альтернирующий. Большое количество разнообразных задач как для тре-
трещин, находящихся внутри тела, так и выходящих на поверхность,
было решено этим методом (см., например, [394-396, 371, 415, 231,
398, 334-336, 340, 350]). Вместе с тем в настоящее время практи-
практически отсутствуют строгие обоснования альтернирующего метода,
за исключением случаев, когда трещины, при их взаимодействии,
удалены друг от друга и от поверхности тела (см., например, [55]).
Ниже приводится доказательство сходимости альтернирую-
альтернирующего метода для статической задачи о двух трещинах нормаль-
нормального разрыва, расположенных в одной плоскости на произвольном
расстоянии друг от друга. Доказательство опирается на качествен-
качественные свойства решений соответствующего граничного пседодиффе-
ренциального уравнения, приведенные в § 4.2.
Как и выше, будем предполагать, что трещина занимает огра-
ограниченную область G в плоскости хз = 0 в безграничном упругом
теле. Предполагается также, что G = G1UG2, причем G\f\G2 = 0,
где G{ — замыкание области G{.
Напомним, что, согласно B.20), граничное уравнение рассма-
рассматриваемой задачи имеет вид
PGA[u(x)} = f(x), [«(*)] е Я1/2 (G), D.36)
где f(x) = 2A — v)ii~~H$(x)i t%(x) — приложенные к поверхно-
поверхностям трещины нормальные усилия, [и(х)] — скачок нормального
смещения.
Будем считать, что *з(#)> а следовательно, и f(x) достаточно
гладкие функции, причем *з(#) ^ 0, т.е. приложены раскрываю-
раскрывающие трещину усилия. Обозначим
.)]. .во,, We)]_{[-ML -g.
Очевидно, что уравнение D.36) эквивалентно системе уравне-
уравнений относительно [wi(#)] и [г*2(#)]:
/Gi), D.37)
PG2A[u2(x)] = f{x) -РОаА[«!(х)], [щ(х)] е tfi/2(G2). D.38)
21*
332 Гл. 4. Качественные методы
Альтернирующий метод применительно к решению уравнения
D.36) заключается в следующем. Сначала строятся первые при-
приближения к решению, определяемые следующим образом:
4% 41} Gi), D.39)
PGiK[4\x)} = f(x) -PG2A[UV(x)], [4%)] € H1/2(G2).
D.40)
Затем указанная процедура продолжается, так что на n-м шаге
приближения определяются с помощью решения уравнений
= № -л^] [] /
D.41)
/И -^2Л[и[п)(ж)], [*Р(х)] еH1/2(G2).
D.42)
Используя теоремы сравнения для решений уравнения D.36),
можно доказать следующую теорему.
Теорема 4.6. Полученные альтернирующим методом
функции образуют монотонно неубывающие последовательно-
последовательности непрерывных неотрицательных функций, ограниченные
сверху точным решением, т. е.
0 ^ [и^(х)] ^ ... ^ [«[п)
0 < [и21)(х)} < ^ [и2п)(х)]
Доказательство. Согласно [147], если /(х) — достаточно
гладкая функция, то и решение уравнения D.39) является гладкой
функцией внутри Gi, которая корневым образом стремится к нулю
при приближении к гладкой части контура. Поскольку f(x) ^ 0, из
уравнения D.39) и теоремы 4.1 следует, что [г^ (#)] ^ 0. Кроме
того, поскольку G\ С G, в силу теоремы 4.3 имеем [г^ (х)] ^
Так как [и[' (х)] < [t/i(rc)], из леммы 4.1 следует, что
[] < &[щ (х)] ПРИ х € G2- Из последнего неравенства
видно, что правая часть уравнения D.38) не меньше правой части
уравнения D.40), а следовательно, согласно теореме 4.1, получим
4%
4.4. Сходимость альтернирующего метода 333
Так как [и}1*(ж)] € #i/2(Gi) и [u^\x)] ^ 0, то из леммы 4.1
следует, что ро2А[и\ (х)] < 0. Учитывая, что f(x) ^ 0 по усло-
условию, отсюда заключаем, что правая часть уравнения D.40) нео-
неотрицательна. Отсюда и из теоремы 4.2 получим неравенство 0 ^
Таким образом, доказаны неравенства
0 < [и^(х)] < [щ(х)], 0
Доказательство теоремы 4.6 проведем по индукции. Предполо-
Предположим, что уже построено п приближений, причем
0 < [4%)] < • • • < [4%)]
Согласно принятой процедуре, [tx^ {x)] является решением
уравнения
^Нх)} = f(x) -PGlA[u^(x)}. D.43)
Из леммы 4.1 и принятого предположения, что [щ1 (х)]
< [г*2 (ж)], следует неравенствоpc?iЛ[г*2 (ж)] ^PGih[u2 " (#]
Учитывая это неравенство и сравнивая правые части уравнений
D.41) и D.43), приходим к заключению, что правая часть урав-
уравнения D.43) не меньше правой части уравнения D.41). Отсюда и
из теоремы 4.1 следует неравенство [mJl (#)] < [щ* (я?)].
Проводя аналогичные рассуждения, из сделанного предположе-
предположения [^2 (%)] ^ [^2(#)] и леммы 4.1 получим следующее нера-
неравенство: рсгА[и2(х)] ^ po1A[u2l\x)]. Согласно этому неравен-
неравенству правая часть уравнения D.43) не превосходит правой части
уравнения D.37). Отсюда и из теоремы 4.1 заключаем, что
4)
Таким образом, для [*4п+1^(ж)] требуемые неравенства дока-
доказаны. Аналогичным образом доказываются неравенства и для
[^2 (х)]- [U2 Vх)] является решением уравнения
[<4п+1)(*)]- D.44)
334 Гл. 4. Качественные методы
Согласно доказанному, [и^ (ж)] < [щ1 (#)]. Из этого нера-
неравенства и леммы 4.1 следует, что
Из последнего неравенства следует, что правая часть уравнения
D.42) не превосходит правой части уравнения D.44). Таким обра-
образом, принимая во внимание теорему 4.1, получим неравенство
Поскольку [«1 '(х)] < [«i(x)], из леммы 4.1 получим
Следовательно, правая часть уравнения D.44) не превосходит пра-
правую часть уравнения D.38). Воспользовавшись также теоре-
теоремой 4.1, отсюда получим неравенство [щ1 + (х)] ^ [г^Оя)].
Таким образом, неравенства для [щ1 (х)] доказаны и тео-
теорема 4.6 полностью доказана.
Пользуясь результатами теоремы 4.6, можно доказать теорему
сходимости.
Теорема 4.7. Последовательность функций [и^ (х)] схо-
сходится как по норме пространства C(Gi), так и по норме про-
пространства Соболева Hi/2(Gi) к функции [щ(х)]. Последова-
Последовательность функций [г4 (х)] сходится по нормам пространств
С(Ст2) и #1/2(^2) к [u2{x)]. При этом функции [щ(х)], [u2(x)]
являются решениями системы уравнений D.37), D.38) или, что
эквивалентно, функция [и(х)] = [^(ж)] + [^(ж)] является ре-
решением уравнения D.36). Здесь C(G\), C{G2) —пространства
непрерывных функций на компактах Gi, G2 соответственно.
Доказательство. Поскольку, согласно доказанной выше
теореме 4.6, [щ1 (#)], [щ* {х)] — монотонно неубывающие, рав-
равномерно ограниченные сверху последовательности функций, имеет
место поточечная сходимость [щ1 (х)] -> [uj(a;)], [1*2 (ж)] "->
-> [г/^ж)]. Далее нам потребуется следующая лемма.
Лемма 4.5. Обозначим щ' (х) = f(x)— рфА^г" \х)] пРи
х G G\ и цу2 (х) = f(x)~PG2&[ui (х)] пРи х € G2- Справедливо
следующее утверждение:
4.4. Сходимость альтернирующего метода 335
Последовательность непрерывных функций <pi(x) является
фундаментальной в пространстве C(G\), а следовательно, и
в H_i/2{Gi). Последовательность функций щ {х) является
фундаментальной в пространстве С(С?2) и соответственно в
Я_1/2(СУ2).
Доказательство. Доказательство леммы 4.5 проведем для
последовательности функций у>\ \х). Для последовательности
Ч>2 (х) доказательство проводится совершенно аналогично.
Из теоремы 4.6 следует, что Vn, [щ1 ~ (х)] ^ 0. Поэтому
в соответствии с леммой 4.1 получим рагА[и2 (х)] ^ 0 и
V (х) ^ 0. Из теоремы 4.6 следует также, что [и^1" (х)] ^
j, a; G (?2. Из этого неравенства и леммы 4.1 получим,
[)} ^ ро^Щ {х)], Vn. Следовательно, у?р(х) ^
^ f(x) —pGi&[u2(x)]. Таким образом, установлено, что щ '(х) —
равномерно ограниченная последовательность.
Поскольку [г4П~ \х)] ^ [W2 (ж)]' из леммы 4.1 следует, что
4) ^%^ S)
т.е. последовательность ip™'(x) монотонно не убывает.
Покажем, что множество функций щ (х) равностепенно не-
непрерывно, т.е. докажем, что Ve > 0, 38 > 0, Vn и Va/, x" G C?i,
|х; - ж"| < * следует irfV) ~ ^(^Ol < *•
Обозначим шах [^(ж)] = М2. Согласно [147],
где r(s) — гамма-функция, г — размерность пространства.
В частности, в плоском случае (г = 2) получим
\х-у\'
Если х не принадлежит носителю функции v(x), то лапласиан
можно внести под знак интеграла. Следовательно,
G2
336 Гл. 4. Качественные методы
Для (fi (х) получаем выражение
Поскольку функция f(x) непрерывна на компакте G, то она
Г>авномерно непрерьюна и потому 3 8\ > О, что Vx' х" E G,
х* - х"\ < ^следует \f{xf) з_/(/'I < е/2.
Так как G\ ПФг = 0 и Gi, G2 — компакты, то #(Gi, G2) =
== d > О, где #(Gi, G2) — расстояние между множествами G\ и G2.
Следовательно, функция |а; — у|~3 непрерывна на компакте G\ x G2
как функция переменных (я, у), где а; Е Gi, у G G2, и потому рав-
равномерно непрерывна. Поэтому Ve > 0 3#2 > 0, У(ж', у;), (х", ;/
таких, что д[(х\ у'), (ж'', у11)] < 82 следует
Здесь g[(a;', у;), (ж", у'')] — расстояние между точками (ж;, у') и
(rr7/, y/;); /i(G2) — мера множества G2.
Пусть задано е > 0. Выберем соответствующие^ и ^- Обо-
Обозначим 6 = min{$i, 82} > 0. Тогда Vn и V#', ж;/ G Gi имеем
к'-у|3
G2
е
^ 2~
) m)
G2 G2
Равностепенная непрерывность семейства функций щ1 '(х) дока-
доказана.
Следовательно, семейство непрерывных функций щ1 '{х) рав-
равномерно ограничено и равностепенно непрерывно в G\. Поэтому по
теореме Арцела (см., например, [76]) из последовательности функ-
функций (fi (х) можно выбрать фундаментальную подпоследователь-
подпоследовательность в смысле нормы пространства C(Gi). Так как последова-
последовательность {pY'(x) является монотонно неубывающей, то из того,
4.4. Сходимость альтернирующего метода 337
что из нее можно выбрать фундаментальную подпоследователь-
подпоследовательность, следует, что вся последовательность щ'(х) является фун-
фундаментальной и потому (р± (х) равномерно сходится к некоторой
непрерывной функции ip*{x).
В силу того, что 3 С > О, С — const, такая что Уф(х) Е C(G\)
справедлива оценка ||</>||-i/2 < C|Mlc(Gi)> где II' II—1/2 ~~ норма в
пространстве H_i/2{Gi), || • \\C(Gi) — норма в пространстве C(Gi),
последовательность функций щ (х) фундаментальна и по норме
пространства H^i^Gi). Лемма доказана.
Теперь можно завершить доказательство теоремы 4.7.
о
В связи с тем, что оператор ро& изоморфно отображает Н\/2 (G)
на #-1/2(<3) справедлива априорная оценка (см. [50] и §1.3) для
о
решения уравнения pcAv(х) = g(x), v(x) G НфЮ, д(х) G
е я.1/2(е)
11Ф)Н1/2< const \\g\U/2. D.45)
о
Здесь || • Цх/2 — норма в пространстве H\/2{G).
Рассмотрим уравнение D.41), которое в соответствии с приня-
принятыми обозначениями имеет вид
[«}в)(х)]=^">(х). D.46)
Поскольку доказано, что последовательность ср^ (х) фундамен-
фундаментальна по норме пространства -ff_1/2(Gfi), из априорной оценки
D.45) и линейности оператора рвх^ следует, что последователь-
последовательность функций [щ1 (х)] фундаментальна в пространстве Hi/2 (Gi)-
Следовательно, [щ1 (х)] сходится по норме пространства Н\/2 (Gi)
к некоторой функции. Вьппе было показано, что [щ1 (х)] сходится
к функции [гг*(ж)] поточечно. Следовательно, [щ1 {х)] сходится к
[г^(#)] и по норме пространства Hi/2{G\) и [г^|(ж)] € Hi/2(Gi)-
Пусть v\ (x) является решением уравнения
PGxAviix) = 1, ы{х) е Hi/2(Gi). D.47)
Функция vi(x) непрерывна в G\ и потому достигает своего мак-
максимума. Обозначим величину этого максимума через М\. Из тео-
теоремы сравнения 4.1 можно получить априорную оценку решения
338 Гл. 4. Качественные методы
уравнения D.46)
\Ып)Шс<!Вг) < У^Шс^Мг. D.48)
Из априорной оценки D.48), линейности оператора Pd^ и того,
что последовательность ip™'(х) фундаментальна в пространстве
C(Gi), следует, что последовательность [г/^ (#)] фундаментальна
в пространстве C{G\). Следовательно, [щ1 (х)] сходится к неко-
некоторой функции по норме C(Gi). Из доказанного выше заключаем,
что [^i(#)] ? C(G\) и [и^ (х)] ~> [^(ж)] по норме пространства
C(GX).
Аналогичным образом доказывается, что [щ1 (х)] -» [^(ж)]
о
как по норме пространства Н\/2 (G^)? так и по норме пространства
С{Щ.
Перейдем в уравнениях D.41), D.42) к пределу при п —> оо с
учетом доказанной сходимости. В результате получим
х)} = f(x) -PGlA[vZ(xj\, D.49)
] = f(x) -PG2A[ul(x)]. D.50)
Уравнения D.49), D.50) полностью совпадают с уравнениями
D.37), D.38) и в силу единственности их решения следует
Теорема 4.7 полностью доказана.
Из теорем 4.6 и 4.7 следует, что в задаче о взаимодействии
двух трещин отрыва, находящихся в одной плоскости, последо-
последовательность функций, получаемых альтернирующим методом,
монотонно сходится к решению снизу. Более того, нетрудно по-
показать, что имеет место сходимость не только приближений рас-
раскрытия трещины по различным нормам, но и равномерная сходи-
сходимость КИН.
Действительно, пусть v\(x) — решение уравнения D.47). Обо-
Обозначим через Kii(xf) — коэффициент интенсивности напряжений
в точке х1 € 9Gi, отвечающий нагрузке, соответствующей уравне-
уравнению D.47). Обозначим К* = max Kii(xf). Как было показано
x'QdG
выше, правая часть уравнения D.41) <Pi (х) равномерно сходится
на G\ к правой части уравнения D.37) <pl(x) = f(x)—p[]
4.4. Сходимость альтернирующего метода 339
Следовательно, [u^ix)] = [щ(х)] + [w{"\x)]. Здесь [w^ix)] —
решение уравнения
€ Нф (Gx). D.51)
Обозначим КИН, отвечающие раскрытиям трещины [и^1 (ж)],
[til(ж)] и Яп)(ж)], через #,(п)(а;')> ^i(^) и #fiV) соответствен-
соответственно (ж' е dGi). Покажем, что \/е > О, ЗМ, Vm > М и Vx' G dGi
следует |i^i (ж') — Ki(x')\ < е, т.е. нужно доказать, что \/тп> М
иУх'е dGi следует \K^\xf)\ < e.
Из равномерной сходимости (fi(x) к (р\{х) следует, что ЭМ,
Vm > М и Vrr G Gi =Ф l^frc) - Vi(«)l < е/Щ-
Из уравнения D.51), последнего неравенства и теоремы срав-
сравнения 4.1 следует, что \к[™\х')\ < К*е/К* = е, что и требовалось
доказать.
Таким образом, доказано, что на dG\ коэффициенты интенсив-
интенсивности напряжений, получаемые альтернирующим методом, равно-
равномерно сходятся к КИН, отвечающим точному решению задачи,
снизу. Аналогично доказывается равномерная сходимость КИН и
на 8G2-
Замечание 4.3. Предположим, что.для некоторой непре-
непрерывной функции [щ (#)], определенной на Gi, известно, что
[u[ {x)] ^ [ui(rc)]. После этого строится приближение [г^
как решение уравнения
Gi
D.52)
Дальнейшие приближения строятся согласно уравнениям D.41),
D.42).
Тогда на любом шаге получаемые приближения являются оцен-
оценками сверху точного решения.
Доказательство, [^(ж)] удовлетворяет уравнению D.38),
которое можно записать в ином виде:
D.53)
Gl
340 Гл. 4. Качественные методы
Из предположения [и[' (х)] ^ [щ (х)] следует, что правая часть
уравнения D.52) не меньше правой части уравнения D.53). Следо-
Следовательно, согласно теореме 4.1 приходим к неравенству [щ (х)] ^
^ [^2(ж)]. Далее, рассуждая при оценке решений уравнений D.41),
D.42) аналогично тому, как это делалось при доказательстве тео-
теоремы 4.6, придем к заключению, что Vn
4.5. Установившиеся колебания
Рассмотрим задачу о плоской трещине, находящейся под дей-
действием гармонических по времени нормальных нагрузок. Гра-
Граничное псевдодифференциальное уравнение, связывающее ампли-
амплитуду скачка нормального смещения с амплитудой приложенной
нагрузки представлено в B.54) и имеет вид
^М ] = 0, . * ф G. D.54)
Символ псевдодифференциального оператора пр представлен в
формуле B.55). В случае низких частот (малых /3) символ fy?(?)
можно разложить в асимптотический ряд по /3. В результате по-
получится выражение [42]
где хр(О имеет по E более высокий порядок малости, чем /З2.
Таким образом, с точностью до малых более высокого порядка,
оператор Clp может быть записан в виде
^-1. D.56)
Здесь С = G— 12и + 8и2)/A6A — иJ) — постоянная, причем, как
нетрудно видеть, С > 0.
При разложении решения уравнения D.54) в асимптотический
ряд по C амплитуда скачка смещения может быть представлена в
виде
[и3(х)) = [изоМ] + Р2 Ы(х)] + rfi(x). D.57)
Здесь функция гр(х) имеет более высокий, чем /?2, порядок мало-
малости по р.
4.5. Установившиеся колебания 341
Основываясь на результатах § 4.2, можно доказать следующую
теорему сравнения для коэффициентов разложения решения
[що(х)] и [@]
Теорема 4.8. Для коэффициентов разложения решения
D.57) уравнения D.54) при малых C справедливы оценки
1. Если правая часть уравнения D.54) неотрицательна, т. е.
h(x) ^0,тои [ни(ж)] > 0 (г = 0, 1).
2. Если ts(x) ^ 0 при х е &2, G\ С G2 и функции [щ)(х)]
отвечают разложению решения уравнения в области (?i, a
[U3i (х)] — в области С?2, то имеют место неравенства
4
Доказательство. Из уравнения D.54) и разложений опе-
оператора D.56) и решения D.57) следует, что коэффициенты разло-
разложения решения удовлетворяют следующим уравнениям:
57Г—чРсА[мзо(я?)] = —, hob)] =0, х $ G, D.58)
— гроЛ[t*3i(ж)] = Срс&~1 [изо 0е)], [ti3i(ж)] =0, ж g G.
D.59)
Пусть г$(х) G H_i/2(G) и ?з(#) ^ 0, тогда согласно результатам
§4.2 заключаем, что для решения уравнения D.58) справедливо
неравенство [глзо(#)] ^ 0. Поскольку обратное преобразование Фу-
Фурье на плоскости от функции l^l равно Bтт|д;|)~ (см. [147]),
правая часть уравнения D.59) может быть записана в виде
!у, х € G. D.60)
Выше уже было установлено, что [ггзо(#)] ^ 0. Отсюда и из
представления D.60) следует, что правая часть уравнения D.59)
неотрицательна. Кроме того, [изо(#)] € H\/2{G), Л — опе-
оператор порядка —1 и потому Л~1[гбзо(^)] € #3/2 (^2) и тем более
рс?Л[гАзо(ж)] € H_i/2(G). Таким образом, мы снова можем ис-
использовать результаты §4.2 и из уравнения D.59) заключить, что
[г/31 (#)] ^ 0. Следовательно, первое утверждение теоремы 4.8 до-
доказано.
342 Гл. 4. Качественные методы
Для доказательства второй части теоремы запишем уравнения
D.58), D.59) в областях Gi и G2 (Gi С G2, h{x) ^ О, х Е G2):
^ []/Gi), D.61)
D.62)
^ 6 JI1/2(G2), D.63)
2ji^ = CftbA-^iig^*)], [J$(x)] eH1/2(G2).
D.64)
Из теоремы сравнения 4.3 для решений уравнений D.61),
D.63) следуют неравенства
0 <[«$(*)] <[«8}(*)]. D-65)
Из неравенств D.65) и представления оператора СрсгЛ D.60)
следует Срс2&~1 [щ^(х)] ^ 0, причем в области х G G\
1 г fi\ n 1 r fO\ i
^CpGxA [що(х)\ ^ CpGxA [u\q{x)\. D.66)
Так как согласно первой части теоремы [щ± (х)] ^ 0 и, кроме
того, [г/31(х)] € Hi/2(Gi)i то в силу леммы 4.1 для х ? G\
B(l — i/))~ Л[г^з1(х)] ^0. Следовательно,
—\PG2\G1A\un Кх)\ ^ О- D-Ь7)
Таким образом, функцию [гг^ (ж)] можно рассматривать как
решение уравнения типа D.62) только не в области Gi, а в области
б?2 с соответствующей правой частью, т. е.
———pG2A[uy(x)] =g(x), [i4i(s)J ^^i/2(G2), D.68)
Z\L — V)
тлед(х) = CpciA-^uSfta;)], a; G
хА[4?(я?)] <0, xeG2\Gi.
4.5. Установившиеся колебания 343
Из неравенств D.67), D.66) следует, что правая часть уравне-
уравнения D.68) не превосходит правую часть уравнения D.64) и, следо-
следовательно, в силу первой части доказываемой теоремы, для реше-
решений уравнений D.64), D.68) справедливо неравенство [щг (х)] ^
^ [*4i (ж)]- Теорема 4.8 полностью доказана.
Таким образом, в случае низких частот из доказанной теоремы
следует:
1) при увеличении амплитуды прикладываемых усилий растут
амплитуды скачков смещений и КИН не только для главного члена
(статического решения), но и для первой поправки;
2) для положительных амплитуд прикладываемых нагрузок
при расширении области трещины на общей части контура ра-
растут как амплитуды КИН для главного члена, так и для первой
поправки;
3) при положительных амплитудах нагрузок увеличение ча-
частоты приводит к квадратичному по /3 росту амплитуд скачков
смещений и КИН.
СПИСОК ЛИТЕРАТУРЫ
1. Александров А.Я. Об одном приближенном методе решения плос-
плоских контактных задач теории упругости /Тр. НИИЖТ. Вып. 11.—
Трансжелдориздат. 1955. С. 5-28.
2. Александров А.Я. Решение основных трехмерных задач теории упру-
упругости для тел произвольной формы путем численной реализации метода
интегральных уравнений /Тр. НИИЖТ. 1972. Вып. 137. С. 5-10.
3. Александров А.Я. Решение основных задач теории упругости путем чи-
численной реализации метода интегральных уравнений.—В сб.: Успехи меха-
механики деформируемых сред.—М.: Наука, 1975. С. 3-24.
4. Александров А.Я., Зиновьев Б.М. Приближенный метод решения
плоских и пространственных задач теории упругости для тел с армирую-
армирующими элементами и разрезами.—В сб.: Механика деформируемых тел и
конструкций.—М.: Машиностроение, 1975. С. 15-25.
5. Александров В.М., Сметании Б.И. Равновесная трещина в слое ма-
малой толщины /Прикладная математика и механика (ПММ). 1965. Т. 29.
Вып. 4. С. 782-785.
6. Александров В.М., Сметанин Б.И., Соболь Б.В. Тонкие концен-
концентраторы напряжений в упругих телах.—М.: Наука, 1993. 222 с.
7. Андрейкив А.Е. Пространственные задачи теории трещин.—Киев: На-
укова думка, 1982. 346 с.
8. Андрейкив А.Б., Стадник М.М. Распространение плоской трещины
с кусочно-гладким контуром /Прикладная механика. 1974. Т. 10, X* 10.
С. 50-56.
9. Баренблатт Г.И. О равновесных трещинах, образующихся при хруп-
хрупком разрушении. Общие представления и гипотезы. Осесимметричные тре-
трещины /ПММ. 1959. Т. 23, № 3. С. 434-444.
10. Б а р е н б л а т т Г. И. О равновесных трещинах, образующихся при хрупком
разрушении. Прямолинейные трещины в плоских пластинках / ПММ. 1959.
Т. 23, ИР» 4. С. 706-721.
11. Баренблатт Г.И. О равновесных трещинах, образующихся при хруп-
хрупком разрушении. Устойчивость изолированных трещин. Связь с энергети-
энергетическими теориями /ПМТФ. 1959. Т. 23, № 5. С. 893-900.
12. Б а р е н б л а т т Г. И. Математическая теория равновесных трещин, образу-
образующихся при хрупком разрушении /ПМТФ. 1961. № 4. С. 3-56.
13. Баренблатт Г.И., Ентов В.М., Салганик Р. Л. О кинетике распро-
распространения трещин. Общие представления. Трещины, близкие к равновес-
равновесным / Инженерный журнал. Механика твердого тела. 1966. № 5. С. 82-92.
14. Баренблатт Г.И., Ентов В.М., Салганик Р. Л. О кинетике рас-
распространения трещин. Условие разрушения и длительная проч-
прочность /Инженерный журнал. Механика твердого тела. 1966. № 6. С. 76-80.
15. Баренблатт Г.И., Ентов В.М., Салганик Р. Л. О кинетике распро-
распространения трещин. Флуктуационное разрушение /Инженерный журнал.
Механика твердого тела. 1967. К* 1. С. 122-129.
16. Баренблатт Г.И., Ентов В.М., Салганик Р.Л. О кинетике рас-
распространения трещин. Замечание о правиле суммирования повреждаемо-
повреждаемостей / Инженерный журнал. Механика твердого тела. 1967. № 2. С. 148-150.
17. Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде.—М.: Мир,
1986. 502 с.
18. БейтменГ., ЭрдейиА. Высшие трансцендентные функции. Т. 2.—М.:
Наука, 1966. 295 с.
Список литературы 345
19. БейтменГ., ЭрдейиА. Высшие трансцендентные функции. Гипергео-
Гипергеометрическая функция. Функции Лежандра. Т. 1.—М.: Наука, 1973. 295 с.
20. Берг Й., Лефстрем Й. Интерполяционные пространства: Введение.—
М.: Мир, 1980. 264 с.
21. Бородачев А.Н. Определение коэффициентов интенсивности напря-
напряжений для плоской эллиптической трещины при произвольных граничных
условиях /Изв. АН СССР. Механика твердого тела. 1981. № 2. С. 63-69.
22. Б о р о д а ч е в Н. М. Об одном вариационном методе решения пространствен-
пространственной задачи теории упругости для тела с плоской трещиной /Прикладная
механика. 1986. Т. 22, К* 4. С. 71-76.
23. Бородачев Н.М. Метод возмущений для смешанных пространствен-
пространственных задач теории упругости со сложной линией раздела краевых усло-
условий /Прикладная математика и механика (ПММ). 1988. Т. 52. Вып. 4.
С. 628-634.
24. Бородачев Н.М. О решении интегрального уравнения для трещины,
близкой к круговой / Проблемы прочности. 1993. № 4. С. 50-56.
25. Брутян А.Р., Гольдштейн Р.В., Федоренко Р.П. Статика и кине-
кинетика пространственных трещин сдвига.—М.: Институт прикладной мате-
математики им. М.В.Келдыша АН СССР. Препринт № 88. 1985. 28с.
26. Брутян А.Р., Федоренко Р.П. Метод численного решения задач
о трещинах отрыва и сдвига.—М.: Институт прикладной математики
им. М.В.Келдыша АН СССР. Препринт № 107. 1984. 30с.
27. Вавакин А.С, Салганик Р.Л. К экспериментальному исследованию
скоростной зависимости трещиностойкости /Изв. АН СССР. Механика
твердого тела. 1975. № 5. С. 127-133.
28. В а й н б е р г М. М. Вариационный метод и метод монотонных операторов.—
М.: Наука, 1972. 415 с.
29. Ворович И.И., Александров В.М., Бабешко В.А. Неклассические
смешанные задачи теории упругости.—М.: Наука, 1974. 456 с.
30. Ворович И.И., Бабешко В. А. Динамические смешанные задачи тео-
теории упругости для неклассических областей.—М.: Наука, 1979. 319 с.
31. Вычислительные методы в механике разрушения / Под ред. С. Атлури.—М.:
Мир, 1990. 391с.
32. Галин Л. А. Контактные задачи теории упругости и вязкоупругости.—М.:
Наука, 1980. 304 с.
33. Гвоздев А.А. Расчет несущей способности конструкций по методу пре-
предельного равновесия.—М.: Стройиздат, 1949. 280 с.
34. Гельфанд И.М., Шилов Г.Е. Обобщенные функции. Вып. 2. Простран-
Пространства основных и обобщенных функций.—М.: Государственное издательство
физико-математической литературы, 1958. 307 с.
35. Глушков Е.В., Глушкова Н.В. Резонансные частоты рассеяния упру-
упругих волн пространственными трещинами /Прикладная математика и ме-
механика. 1998. Т. 62. Вып. 5. С. 866-870.
36. Гольдштейн Р.В. Плоская трещина произвольного разрыва в упругой
среде /Изв. АН СССР. Механика твердого тела. 1979. № 3. С. 111-126.
37. Гольдштейн Р.В. К пространственной задаче теории упругости для тел
с плоскими трещинами произвольного разрыва. Препринт.—М.: Институт
проблем механики АН СССР, 1979. 65 с.
38. Гольдштейн Р.В., Ентов В.М. Вариационные оценки для коэффици-
коэффициента интенсивности напряжений на контуре плоской трещины нормального
разрыва /Изв. АН СССР. Механика твердого тела. 1975. N* 3. С. 59-64.
346 Список литературы
39. Гольдштейн Р.В., Ентов В.М. Некоторые качественные методы в ме-
механике разрушения.—М.: Институт проблем механики АН СССР. Препринт
№76. 1976. 53 с.
40. Гольдштейн Р.В., Ентов В.М. Качественные методы в механике
сплошных сред.—М.: Наука, 1989. 224с.
41. Гольдштейн Р.В., Ентов В.М., Павловский Б.Р. Модель развития
водородных трещин в металле /ДАН СССР. 1977. Т. 237, № 4. С. 828-831.
42. Гольдштейн Р.В., Капцов А.В. О трещине нормального отрыва в
упругой среде под действием гармонической волны /Изв. АН СССР. Ме-
Механика твердого тела. 1984. № 6. С. 93-100.
43. Гольдштейн Р.В., Капцов А.В., Корелыптейн Л.Б. Асимптоти-
Асимптотическое решение пространственных задач теории упругости о вытянутых
плоских трещинах отрыва /Прикладная математика и механика (ПММ).
1984. Т. 48. Вып. 5. С. 854-863.
44. Гольдштейн Р.В., Клейн И.С, Эскин Г.И. Вариационно-разност-
Вариационно-разностный метод решения некоторых интегральных и интегродифференциальных
уравнений трехмерных задач теории упругости.—М.: Институт проблем
механики АН СССР. Препринт № 33. 1973. 55 с.
45. Гольдштейн Р.В., Корельштейн Л.Б. Метод асимптотического ин-
интегрирования и «метод пружинок» в задачах об упругих пластинах с вытя-
вытянутым вырезом /Прикладная математика и механика (ПММ). 1988. Т. 52.
Вып. 4. С. 666-674.
46. Гольдштейн Р.В., Корельштейн Л.Б. Асимптотический метод ре-
решения задач о несквозных вытянутых вырезах и трещинах в упругой пла-
пластине при произвольном нагружении.—М.: Институт проблем механики АН
СССР. Препринт № 319. 1988. 73 с.
47. Гольдштейн Р.В., Отрощенко И.В., Федоренко Р.П. Метод уточ-
уточняющих граничных сеток в пространственных задачах о трещинах в упру-
упругих телах.—М.: Институт проблем механики АН СССР. Препринт JV* 230.
1984. 69 с.
48. Гольдштейн Р.В., Спектор А. А. Вариационные оценки решений не-
некоторых смешанных пространственных задач теории упругости с неизвест-
неизвестной границей / Изв. АН СССР. Механика твердого тела. 1978. № 2. С. 82-94.
49. Гольдштейн Р.В., Шифрин Е.И. Оценки некоторых локальных и ин-
интегральных характеристик решения задач о плоских трещинах в трехмер-
трехмерных телах.—В кн.: Всесоюзная конференция по теории упругости (Ереван,
13-16 ноября 1979 г.). Тезисы докладов. 1979. С. 118-120.
50. Гольдштейн Р.В., Шифрин Е.И. Изопериметрические неравенства и
оценки некоторых интегральных характеристик решения пространствен-
пространственной задачи теории упругости для тела с плоскими трещинами нормального
разрыва /Изв. АН СССР. Механика твердого тела. 1980. № 2. С. 68-79.
51. Гольдштейн Р.В., Шифрин Е.И. Некоторые энергетические методы
построения оценок в пространственных задачах теории упругости о плоских
трещинах произвольного разрыва / Изв. АН СССР. Механика твердого тела.
1981. № 4. С. 61-76.
52. Гольдштейн Р.В., Шифрин Е.И. Некоторые оценки решений трех-
трехмерных задач теории упругости для тел с трещинами.—В кн.: Смешан-
Смешанные задачи механики деформируемого тела. II Всесоюзная научная кон-
конференция (Днепропетровск, 15-18 сентября 1981 г.). Тезисы докладов.—
Днепропетровск, 1981. С. 67, 68.
Список литературы 347
53. Гольдштейн Р.В., Шифрин Е.И. Пространственная задача теории
упругости для тел с трещинами. Препринт.—М.: Институт проблем меха-
механики АН СССР, 1981.66 с.
54. Гольдштейн Р.В., Шифрин Е.И. Теоремы сравнения для некоторого
класса псевдодифференциальных уравнений и их приложения / ДАН СССР.
1982. Т. 262, № 5. С. 1113-1116.
55. Гольдштейн Р.В., Шифрин Е.И. Плоская трещина произвольного
разрыва в ограниченном упругом теле /Прикладная математика и меха-
механика (ПММ). 1982. Т. 46, № 3. С. 472-481.
56. Гольдштейн Р.В., Шифрин Е.И. Оценки некоторых локальных ха-
характеристик решения задачи о плоской трещине нормального разрыва в
деформируемой среде в условиях установившейся ползучести.—В кн.: Все-
Всесоюзный симпозиум «Ползучесть в конструкциях» (Днепропетровск, 21-24
сентября, 1982 г.). Тезисы докладов.—Днепропетровск, 1982. С. 86, 87.
57. Гольдштейн Р. В., Шифрин Е. И. Об оценках решений задачи о плос-
плоской трещине отрыва в линейно упругом теле и материале со степенным
упрочнением.—В кн.: Школа-семинар «Теория упругости и вязкоупруго-
сти» (Цахкадзор, 22-25 ноября 1982 г.). Тезисы докладов.—Ереван, 1982.
С. 18, 19.
58. Гольдштейн Р.В., Шифрин Е.И. Оценки и приближенные формулы
в задаче теории упругости о плоской трещине нормального разрыва / Изв.
АН СССР. Механика твердого тела. 1983. № 1. С. 120-127.
59. Град штейн И. С, Рыжик И.М. Таблицы интегралов, сумм, рядов и
произведений.—М.: Физматгиз, 1962. 1100 с.
60. Грей Э., Мэтьюз Г.Б. Функции Бесселя и их приложения к физике и
механике.—М.: ИЛ, 1953. 371с.
61. Гринченко В.Т., Улитко А.Ф. Растяжение упругого пространства,
ослабленного кольцевой трещиной / Прикладная механика. 1965. Т. 1, JY* 10.
С. 61-64.
62. Захаревич И.С. О вариации решений интегродифференциальных
уравнений смешанных задач теории упругости при вариации обла-
области / Прикладная математика и механика. 1985. Т. 49. Вып. 6. С. 961-968.
63. Захаревич И.С. Интегродифференциальные уравнения: формулы вари-
вариации, законы сохранения, точные решения.—М.: Институт проблем меха-
механики АН СССР. Препринт № 325. 1988. 69 с.
64. Захаревич И.С. Метод прогонки для псевдодифференциальных уравне-
уравнений в расчете статики и кинетики трещин.—В кн.: Пластичность и раз-
разрушение твердых тел. Сер. Пластичность и вязкоупругопластичность / Под
ред. Р.В. Гольдштейна.—М.: Наука, 1988. С. 186-196.
65. Зиновьев Б.М. Один приближенный метод расчета тел с разрезами.—
В сб.: Механика деформируемого тела и расчет сооружений. Тр. НИИЖТ.
1972. Вып. 137. С. 105-125.
66. Ирвин Дж., Парис П. Основы теории роста трещин и разрушения.—
В кн.: Разрушение. Т. 3.—М: Мир, с. 17-66.
67. Капцов А.В., Шифрин Е.И. Решение некоторых пространственных
статических и динамических задач теории упругости о трещинах двух-
базисным проекционным методом / Смешанные задачи механики дефоор-
мируемого тела. III Всесоюзная конференция. Тезисы докладов.—Харьков,
1985. С. 143.
68. Капцов А.В., Шифрин Е.И. О решении некоторых динамических
задач теории упругости для пространства, ослабленного плоской трещи-
348 Список литературы
ной / Шестой Всесоюзный съезд по теоретической и прикладной механике.
Аннотации докладов.—Ташкент, 1986. С. 328.
69. Капцов А. В., Шифрин Е.И. О рассеянии плоской трещиной нормально
падающей продольной гармонической волны /Изв. АН СССР. Механика
твердого тела. 1986. № 6. С. 106-112.
70. Капцов А.В., Шифрин Е.И. Плоская трещина, к поверхностям кото-
которой приложены нормальные, гармонически изменяющиеся во времени уси-
усилия / Сб. научных трудов. Теория распространения волн в упругих и упру-
гопластических средах.—Новосибирск, 1987. С. 143-147.
71. Капцов А.В., Шифрин Е.И. О некоторых методах решения динамиче-
динамических задач теории упругости для пространства, ослабленного плоской тре-
трещиной /Тезисы докладов региональной конференции. Динамические за-
задачи механики сплошной среды. Ч. 1.—Краснодар, 1988. С. 67-68.
72. Капцов А.В., Шифрин Е.И. Применение аппроксимаций Паде к реше-
решению динамических задач теории упругости для пространства, ослабленного
плоской трещиной /ЖВМиМФ. 1990. Т. 30, № 11. С. 1757, 1758.
73. Капцов А.В., Шифрин Е.И. Решение динамических задач об элли-
эллиптической трещине в упругом пространстве с помощью аппроксимаций
Паде /Прикладная математика и механика (ПММ). 1991. Т. 55. Вып. 3.
С. 511-519.
74. Капцов А.В., Шифрин Е.И. Аналитическое решение задачи об элли-
эллиптической трещине в безграничном упругом пространстве. I. Статическая,
нормальная, полиномиальная нагрузка / Институт проблем механики РАН.
Препринт К* 554. 1995. 24с.
75. Капцов А.В., Шифрин Е.И. Аналитическое решение задачи об элли-
эллиптической трещине в безграничном упругом пространстве. И. Статическая,
сдвиговая, полиномиальная нагрузка /Институт проблем механики РАН.
Препринт JY* 559. 1996. 30 с.
76. Колмогоров А.Н., Фомин СВ. Элементы теории функций и функцио-
функционального анализа.—М.: Наука, 1972. 496с.
77. КорелыптейнЛ.Б. Асимптотическое решение пространственных задач
теории упругости о вытянутых плоских трещинах сдвига / Прикладная ма-
математика и механика (ПММ). 1986. Т. 50. Вып. 5. С. 835-843.
78. Красносельский М.А., Вайникко Г.М., Забрейко П.П., Ру-
тицкий Я.Б., Стеценко В.Я. Приближенное решение операторных
уравнений.—М.: Наука, 1969. 456 с.
79. Круз Т. Метод граничных интегральных уравнений в механике разру-
разрушения.—В кн.: Метод граничных интегральных уравнений.—М.: Мир,
1978. С. 46-67.
80. Крылов В.И., Скобля Н.С. Справочная книга по численному обраще-
обращению преобразования Лапласа.—Минск: Наука и техника, 1968. 296 с.
81. Крылов В. И., Скобля Н. С. Методы приближенного преобразования Фу-
Фурье и обращения преобразования Лапласа.—М.: Наука, 1974. 223 с.
82. Леонов М.Я. К теории расчета упругих оснований /Прикладная матема-
математика и механика. 1939. Т. 3, № 2. С. 53-78.
83. Леонов М.Я. Некоторые задачи и приложения теории потенциала /При-
/Прикладная математика и механика. 1940. № 5, 6. С. 73-86.
84. Леонов М.Я., Панасюк В.В. Розвиток найдр1бшших трщин в твердому
тип /Прикладна мехашка, АН УССР. 1959. Т. 5, № 4. С. 391-401.
85. Линьков A.M., Могилевская С.Г. Конечночастные интегралы в зада-
задачах о пространственных трещинах /Прикладная математика и механика
(ПММ). 1986. Т. 50. Вып. 5. С. 844-850.
Список литературы 349
86. Л у щи к 0. Н. Сингулярные конечные элементы: обзор и классифика-
классификация /Изв. РАН. Механика твердого тела. 2000. № 2. С. 103-114.
87. Механика разрушения и прочность материалов. Справочное пособие. Т. 2
/ М.П. Саврук. Коэффициенты интенсивности напряжений в телах с трещи-
трещинами. 1988. 620 с.
88. Михаськив В.В., Станкевич В.Э., Хай М.В. Граничные интеграль-
интегральные уравнения трехмерных задач об установившихся колебаниях полупро-
полупространства с плоскими трещинами /Изв. РАН. Механика твердого тела.
1993. К* 6. С. 44-53.
89. Михаськив В.В., Хай М.В. Взаимодействие в теле компланарных тре-
трещин при динамических ударных нагрузках / Физико-химическая механика
материалов. 1991. Т. 27, № 3. С. 50-55.
90. Мих лин С.Г. Вариационные методы в математической физике.—М.: На-
Наука, 1970. 380 с.
91. Морозов Н.Ф., Петров Ю.В. Динамическая вязкость разрушения в за-
задачах инициирования роста трещин /Изв. АН СССР. Механика твердого
тела. 1990. № б. С. 108-111.
92. Морозов Н.Ф., Петров Ю.В. О концепции структурного времени в тео-
теории динамического разрушения хрупких материалов /ДАН (Россия). 1992.
Т. 324, № 5. С. 964-967.
93. МоссаковскийВ.И. Первая основная задача теории упругости для про-
пространства с плоской круглой щелью /Прикладная математика и механика.
1955. Т. 19, № 4. С. 443-452.
94. Моссаковский В.И., Моссаковская Р.Л. Прочность упругого про-
пространства, ослабленного плоской трещиной, близкой к круговой /Гидро-
/Гидроаэромеханика и теория упругости. 1977. Вып. 22. С. 56-74.
95. Моссаковский В.И., Рыбка М.Т. Обобщение критерия Гриффитса-
Снеддона на случай неоднородного тела /Прикладная математика и меха-
механика. 1964. Т. 28. Вып. 6. С. 1061-1069.
96. МусхелишвилиН.И. Некоторые основные задачи математической тео-
теории упругости.—М.: Наука, 1966. 707с.
97. Мыхаськив В.В., Хай М.В. Прочность бесконечного тела с диско-
дискообразной трещиной, находящегося под действием циклических нагру-
нагрузок /Проблемы прочности. 1987. № 1. С. 13-16.
98. Никифоров А.Ф., Уваров В.Б. Специальные функции математической
физики.—М.: Наука, 1984. 344с.
99. Никишков Г.П. Расчет энергетического интеграла методом эквивалент-
эквивалентного объемного интегрирования.—В кн.: Вычислительные методы в меха-
механике разрушения /Под ред. С. Атлури.—М.: Мир, 1990. С. 365-382.
100. Новожилов В.В. О необходимом и достаточном критерии хрупкой проч-
прочности /ПММ. 1969. Т. 33, № 2. С. 212-222.
101. Новожилов В.В. К основам теории равновесных трещин в упругих те-
телах /ПММ. 1969. Т. 33, JY* 5. С. 797-812.
102. Панасюк В.В. Предельное равновесие хрупких тел с трещинами.—Киев:
Наукова думка, 1968. 246 с.
103. Панасюк В.В. Механика квазихрупкого разрушения материалов.—Киев:
Наукова думка, 1991. 415 с.
104. Панасюк В.В., Андрейкив А.Е., Стадник М.М. Пространственные
задачи теории трещин. (Обзор). Ч. 2. Упругое и предельное равновесие твер-
твердых тел с трещинами при силовом нагружении /Физико-химическая ме-
механика материалов. 1979. Т. 15, № 4. С. 39-55.
350 Список литературы
105. Парис П., Си Дж. Анализ напряженного состояния около трещин.—В кн.:
Прикладные вопросы вязкости разрушения.—М.: Мир, 1968. С. 64-142.
106. Партон В.З., Борисковский В.Г. Динамическая механика разруше-
разрушения.—М.: Машиностроение, 1985. 264с.
107. Партон В.3., Перлин П.И. Интегральные уравнения теории упруго-
упругости.—М.: Наука, 1977. 312 с.
108. Перлин П.И., Самаров В.Н. Применение теории обобщенного потенци-
потенциала к решению пространственных задач теории упругости для тел с раз-
разрезами и оценке хрупкого разрушения конструкций сложной формы / Изв.
АН Казахской ССР. Серия физико-математическая. 1974. № 5. С. 72, 73.
109. Перлин П.И., Самаров В.Н. Применение теории потенциала к ре-
решению пространственных задач теории упругости для тел с разреза-
разрезами /Прикладные проблемы прочности и пластичности. 1977. Вып. 6.
С. 42-46.
ПО. Петров Ю.В. О «квантовой» природе динамического разрушения хрупких
сред /ДАН СССР. 1991. Т. 321, № 1. С. 66-68.
111. Полна Г., Сеге Г. Изопериметрические неравенства в математической
физике.—М.: Физматгиз, 1962. 336с.
112. Польский Н. И. Об одной общей схеме применения приближенных мето-
методов /ДАН СССР. 1956. Т. 111, № 6. С. 1181-1184.
113. Польский Н.И. Проекционные методы в прикладной математике /ДАН
СССР. 1962. Т. 143, № 4. С. 787-790.
114. Прикладные вопросы вязкости разрушения.—М.: Мир, 1968. 552 с.
115. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и
ряды. Элементарные функции.—М.: Наука, 1981. 799 с.
116. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и
ряды. Специальные функции.—М.: Наука, 1983. 750 с.
117. Райе Дж. Математические методы в механике разрушения.—В кн.: Разру-
Разрушение. Т. 2. Математические основы теории разрушения.—М.: Мир, 1975.
С. 204-335.
118. Салганик Р.Л. Об осесимметричных трещинах продольного сдвига
/ПМТФ. 1962. № 3. С. 77-80.
119. Салганик Р. Л. О хрупком разрушении склеенных тел /Прикладная ма-
математика и механика. 1963. Т. 27. Вып. 3. С. 957-962.
120. Салганик Р. Л. Механика тел с большим числом трещин / Изв. АН СССР,
Механика твердого тела. 1973. JV* 4. С. 149-158.
121. Си Г., Либовиц Г. Математическая теория хрупкого разрушения.—В кн.:
Разрушение. Т. 2.—М.: Мир, 1975. С. 83-203.
122. Сметанин Б.И. Некоторые задачи о щелях в упругом клине и слое
/Инженерный журнал. Механика твердого тела. 1968. № 2. С. 115-122.
123. Сметанин Б.И. Задача о растяжении упругого пространства, содер-
содержащего плоскую кольцевую щель /Прикладная математика и механика
(ПММ). 1968. Т. 32. Вып. 3. С. 458-462.
124. Сметанин Б.И., Соболь Б.В. Растяжение упругого полупространства
с трещиной, расположенной перпендикулярно к его поверхности /При-
/Прикладная математика и механика (ПММ). 1981. Т. 45. Вып. 5. С. 940-943.
125. Справочник по коэффициентам интенсивности напряжений. Т. 2 / Под ред.
Ю. Мураками.—М.: Мир, 1990. 1013 с.
126. Справочник по специальным функциям / Под ред. М. Абрамовича, И. Сти-
гана.—М.: Наука, 1979. 830 с.
Список литературы 351
127. Ста дни к М. М., Горбачевский И. Я. Предельное равновесие хрупкого
тела с прямоугольной трещиной /Физико-химическая механика материа-
материалов. 1981. № 2. С. 66-70.
128. Стадник М.М., Горбачевский И.Я. Предельное равновесие тела с
плоской треугольной трещиной /Прикладная механика. 1981. Т. 17, № 7.
С. 101-105.
129. Старосельский А.В., Шифрин Е.И. Рассеяние плоской трещиной
нормально падающей поперечной волны /Изв. РАН. Механика твердого
тела. 1995. № 3. С. 87-103.
130. Улитко А.Ф. Растяжение упругого пространства, ослабленного двумя кру-
круговыми трещинами, расположенными в одной плоскости.—В кн.: Концен-
Концентрация напряжений.—Киев: Наукова думка, 1968. Вып. 2. С. 201-208.
131. Уфлянд Я.С. Упругое равновесие неограниченного тела, ослабленного
внешней круговой щелью /Прикладная математика и механика. 1959.
Т. 23, № 1. С. 101-108.
132. Уфлянд Я.С. Интегральные преобразования в задачах теории упру-
упругости.—Л.: Наука, 1967. 402 с.
133. Флетчер К. Численные методы на основе метода Галеркина.—М.: Мир,
1988. 352 с.
134. Хай М.В. Обращение системы интегральных уравнений одной трехмер-
трехмерной задачи математической теории трещин / ДАН УССР. Сер. А. Физико-
математические и технические науки. 1981. J№ 1. С. 50-53.
135. Хеллан К. Введение в механику разрушения.—М.: Мир, 1988. 364с.
136. Черепанов Г.П. Механика хрупкого разрушения.—М.: Наука, 1974. 640с.
137. Шилов Г.Е. Математический анализ. Второй специальный курс.—М.:
Изд-во Моск. ун-та, 1984. 207 с.
138. Шифрин Е. И. Плоская трещина нормального отрыва при наличии линей-
линейных связей между ее поверхностями /Изв. АН СССР. Механика твердого
тела. 1982. X* 3. С. 80-86.
139. Шифрин Е.И. Некоторые методы приближенного решения уравнений и
их применение к решению пространственных задач для тел с трещинами.
Институт проблем механики АН СССР. 1982. 21 с. (Деп. в ВИНИТИ 1 марта
1983 г., № 1082-83 Деп.).
140. Шифрин Е.И. Об одном подходе к приближенному решению простран-
пространственных задач о трещинах в упругих телах.—В кн.: Всесоюзная кон-
конференция. Численная реализация физико-механических задач прочности.
(Горький, 31 мая-2 июня 1983 г.). Тезисы докладов.—Горький, 1983. С. 131,
132.
141. Шифрин Е.И. Оценки решения задачи о плоской трещине нормального
разрыва в материале со степенным упрочнением / Изв. АН Арм. ССР. Ме-
Механика. 1984. Т. 37, № 4. С. 31-43.
142. Шифрин Е.И. О приближенном решении уравнений некоторых смешан-
смешанных задач теории упругости.—В кн.: Механика деформируемого
тела. Сер. Прочность, упруговязкопластичность. Сб. статей /Под ред.
А.Ю. Ишлинского.—М.: Наука, 1986. С. 154-164.
143. Шифрин Е.И. Плоская трещина нормального разрыва, берега которой
взаимодействуют по линейному закону / Изв. АН СССР. Механика твердого
тела. 1988. № 5. С. 94-100.
144. Шифрин Е.И. Изопериметрические оценки решений одного класса псев-
псевдодифференциальных уравнений и их приложение к задачам о трещи-
трещинах /Прикладная математика и механика (ПММ). 1989. Т. 53. Вып. 6.
С. 1044-1048.
352 Список литературы
145. Шифрин Е.И. Аналитический метод решения статических и динамиче-
динамических задач об эллиптических трещинах. 1-й Семинар. Неклассические про-
проблемы теории упругости и механики разрушения (Москва, 9-14 июля 1995).
Тезисы докладов.—М., 1995. С. 26, 27.
146. Шифрин Е.И. Аналитико-численное решение задачи об установившихся
колебаниях пространства, ослабленного эллиптической трещиной. IX Кон-
Конференция по прочности и пластичности (Москва, 22-26 января 1996). Труды
конференции. Т. 2.—М., 1996. С. 185-190.
147. Эскин Г. И. Краевые задачи для эллиптических псевдодифференциальных
уравнений.—М.: Наука, 1973. 232 с.
148. Abe H., Hay as hi К., Так ah as hi S. Stress intensity factors for an
embedded crack near a cylindrical cavity.—In: Advanced boundary ele-
element methods. IUTAM symposium / Ed. T.A. Cruse.—San Antonio, Texas:
Springer-Verlag, 1988. P. 1-8.
149. Achenbach J.D., Adler L., Lewis D.K., McMaken H. Diffraction
of the ultrasonic waves by penny-shaped cracks in metals: Theory and exper-
experiment /The journal of the Acoustical Society of America. 1979. V. 66, K* 6.
P. 1848-1856.
150. Achenbach J.D., Gautesen A. K. Elastodynamic stress — intensity fac-
factors for a semi-infinite crack under 3-d loading / Trans, of the ASME. Series
E. Journal of applied mechanics. 1977. V. 44, № 2. P. 243-249.
151. Achenbach J.D., Gautesen A.K. Geometrical theory of diffraction for
three-D elastodynamics / The journal of the Acoustical Society of America.
1977. V. 61, № 2. P. 413-421.
152. Achenbach J.D., Gautesen A.K.A ray theory for elastodynamic stress-
intensity factors / Trans, of the ASME. Series E. Journal of applied mechanics.
1978. V. 45, flb 1. P. 123-129.
153. Achenbach J.D., Gautesen A.K., McMaken H. Diffraction of point-
source signals by a circular crack / Bulletin of the seismological society of
America. 1978. V. 68, № 4. P. 889-905.
154. Achenbach J.D., Gautesen A.K., McMaken H. Ray methods for
waves in elastic solids.—Boston-London-Melbourne: Pitman Advanced Pub-
Publishing Program, 1982. 251 p.
155. Achenbach J.D., Norris A., Viswanathan K. Inversion of crack
scattering data in the high - frequency domain.—In: Acoustic, electro-
electromagnetic and elastic wave scattering-focus on the T-matrix approach /Eds
V.K. Varadan, V.V. Varadan.—USA: Pergamon Press, 1980. P. 591-604.
156. Adler L., Achenbach J.D. Elastic wave diffraction by elliptical cracks:
theory and experiment /Journal of nondestructive evaluation. 1980. V. 1,
№ 2. P. 87-99.
157. Akin J.E. Elements for the analysis of line singularities.—In: The math-
mathematics of finite elements and applications. III. MAFELAP 1978 /Ed.
J.R. Whiteman.—Academic Press, 1979. P. 65-75.
158. Alves С., На Duong T. Numerical experiments on the resonance poles as-
associated to acoustic and elastic scattering by a plane crack / Proc. 3-d Intern.
Conf. on Math, and Numer. Aspects of Wave Propagation / Ed. G. Cohen.—
Philadelphia: SIAM, 1995. P. 544-553.
159. Alvino A., Lions P.-L., Trombetti G. Comparison results for solutions
of parabolic and elliptic equations via symmetrization. The case of Schwarz
symmetrisation / Comptes rendus de l'Academie des Sciences. Serie I: math-
ematique. 1986. V. 303, № 19. P. 947-950.
Список литературы 353
160. Alvino A., Lions P.-L., Trombetti G. Comparison des solutions
d'equations paraboliques et elliptiques / Comptes rendus de PAcademie des
Sciences. Serie I: mathematique. 1986. V. 303, № 20. P. 975-978.
161. Andr a H. Integration of singular integrals for the Galerkin-type boundary
element method in 3D elasticity /Computer methods in applied mechanics
and engineering. 1998. V. 157. P. 239-249.
162. Andr a H., Schnack E. Integration of singular Galerkin-type boundary
element integrals for 3D elasticity problems / Numerische Mathematik. 1997.
V. 76. P. 143-165.
163. Annigeri B.S. Fracture mechanics research using the surface integral and
finite element hybrid methods.—In: Boundary element methods in applied
mechanics. Proceedings of the first joint Japan / US symposium on bound-
boundary element methods. Tokyo, Japan 3-6 October, 1988 /Eds M.Tanaka,
T.A. Cruse.—Pergamon Press, 1988. P. 191-202.
164. Athanassiadis A., Boissenot J.M., Brevet P., Francois D.,
Raharinaivo A. Linear elastic fracture mechanics computations of cracked
cylindrical tensioned bodies /International journal of fracture. 1981. V. 17,
№ 6. P. 553-566.
165. Atluri S.N., Kathiresan K. 3d analyses of surface flaws in thick-
walled reactor pressure-vessels using displacement-hybrid finite element
method /Nuclear engineering and design. 1979. V. 51, № 2. P. 163-176.
166. Atluri S.N., Kathiresan K. Influence of flaw shapes on stress intensity
factors for pressure vessel surface flaws and nozzle corner cracks /Trans, of
the ASME. Journal of pressure vessel tachnology. 1980. V. 102, № 3. P. 278-
286.
167. Atluri S.N., Kathiresan K. Stress intensity factor solutions for arbi-
arbitrarily shaped surface flaws in reactor pressure vessel nozzle corners /The
international journal of pressure vessels and piping. 1980. V. 8, JY* 4. P. 313—
322.
168. Atluri S.N., Nakagaki M., Kathiresan K. Hybrid-finite-element
analysis of some nonlinear and 3-dimensional problems of engineering frac-
fracture mechanics /Computers & Structures (an international journal). 1980.
V. 12, № 4. P. 511-520.
169. Ayres D.J. A numerical procedure for calculating stress and deformation
near a slit in a three dimensional elastic-plastic solid / Engineering fracture
mechanics. 1970. V. 2, JY* 2. P. 87-106.
170. В an die С Isoperimetric inequalities and applications.—Boston: Pitman
Publ. Inc., 1980. 227p.
171. Barrat P. J., Collins W.D. The scattering cross-section of an obstacle
in an elastic solid for plane harmonic waves / Proc. Camb. Phil. Soc. 1965.
V. 61. Pt. 4. P. 969-981.
172. В ar soum R. S. On the use of isoparametric finite elements in linear fracture
mechanics / International journal for numerical methods in engineering. 1976.
V. 10, № 1. P. 23-37.
173. Bazant Zdenek P. Three-dimensional harmonic functions near termi-
termination or intersection of gradient singularity lines: a general numerical
method /International journal of engineering science. 1974. V. 12, № 3.
P. 221-243.
174. Bell J.С Stresses from arbitrary loads on a circular crack /International
journal of fracture. 1979. V. 15, № 1. P. 85-104.
175. Bellman R.E., Kalaba R.E., Lockett J. A. Numerical inversion of the
Laplace transform.—Amsterdam: Elsevier, 1966. 249 p.
23 Зак. 205
354 Список литературы
176. Bellman R.E., Roth R.S. The Laplace transform.—Singapore: World
Scientific Publishing Co Pte Ltd, 1984. 158 p.
177. Benthem J.P., Koiter W.T. Asymptotic approximations to crack
problems.—In: Mechanics of fracture. V. 1. Methods of analysis and solutions
of crack problems /Ed. G.C.Sih.—Leyden: Noordhoff International Publish-
Publishing, 1973. P. 131-178.
178. Blackburn W. S. Calculation of stress intensity factors at crack tips using
special finite elements.—In: The mathematics of finite elements and applica-
applications/Ed J.R. Whiteman—London, N.Y.: Academic Press, 1973. P. 327-336.
179. Blackburn W. S., Hellen Т.К. Calculation of stress intensity factors in
three dimensions by finite element methods / International journal for numer-
numerical methods in engineering. 1977. V. 11, № 2. P. 211-229.
180. Bloom J.M., Van Fossen D.B. An evaluation of the 20-node quadratic
isoparametric singularity brick element /International journal of fracture.
1976. V. 12, № 1. P. 161-163.
181. Bollig G., Langenberg K.J. The singularity expansion method as ap-
applied to the elastodynamic scattering problem /Wave Motion. 1983. V. 5,
№ 4. P. 331-354.
182. Brascamp H. J., Lieb E.H., Luttinger J.M. A general rearrangement
inequality for multiple integrals / Journal of functional analysis. 1974. V. 17,
№ 2. P. 227-237.
183. Buchholz F.G., Grebner H., Dreyer K.H., Krome H. 2D-and 3D-
applications of the improved and generalized modified crack closure integral
method.—In: Computational Mechanics'88. Theory and applications. Proc.
of the Int. conference, 1988.—Atlanta, USA: Springer-Verlag, 1988. V. 1.
P. 1411-1414.
184. Budiansky В., Rice J.R. An integral equation for dynamic elastic re-
response of an isolated 3-d crack /Wave motion. 1979. V. 1, № 3. P. 187-191.
185. Budreck D.E., Achenbach J.D. Scattering from three-dimensional pla-
planar cracks by the boundary integral equation method / Trans, of the ASME.
Journal of applied mechanics. 1988. V. 55, № 2. P. 405-412.
186. Bui H.D. An integral equations method for solving the problem of a plane
crack of arbitrary shape /Journal of the mechanics and physics of solids.
1977. V. 25, № 1. P. 29-39.
187. Chan S.K., Tuba I.S., Wilson W.K. On the finite element method in
linear fracture mechanics /Engineering fracture mechanics. 1970. V. 2, X* 1.
P. 1-17.
188. Chen Y.M., Wilkins M.L. Stress analysis of crack problems with a three-
dimensional, time-dependent computer program /International journal of
fracture. 1976. V. 12, № 4. P. 607-617.
189. Collins W.D. Some axially symmetric stress distributions in elastic solids
containing penny-shaped cracks. I. Cracks in an infinite solid and a thick
plate /Proceedings of the Royal Society. Series A. 1962. V. 266, № 1326.
P. 359-386.
190. Cruse T. A. Numerical evaluation of elastic stress intensity factors by the
boundary-integral equation method.—In: The surface crack: physical prob-
problems and computational solutions /Ed. J.L.Swedlow.—N.Y.: ASME, 1972.
P. 153-170.
191. Cruse T. A. Application of the boundary-integral equation method to three
dimensional stress analysis /Computers and structures. 1973. V. 3, № 3.
P. 509-527.
Список литературы 355
192. Cruse Т. A. An improved boundary-integral equation method for three di-
dimensional elastic stress analysis / Computers and structures. 1974. V. 4, № 4.
P. 741-754.
193. Cruse T.A. Boundary element analysis in computational fracture
mechanics.—Kluwer Academic Publishers, 1988. 162 p.
194. Cruse T.A., Meyers G.J. Three-dimensional fracture mechanics anal-
analysis /Proceedings of the ASME. Journal of the structural division. 1977.
V. 103, № ST2. P. 309-320.
195. Cruse T.A., Rave en dr a S.T. Application of advanced BEM code
to three-dimensional stress analysis and fracture mechanics analysis.—In:
Boundary element methods in applied mechanics. Proceedings of the first
Japan/US symposium on boundary element methods. Tokyo, Japan, 3-6 Oc-
October 1988 /Eds M. Tanaka, T.A. Cruse.—Pergamon Press, 1988. P. 117-128.
196. Cruse T. A., Van Buren W. Three-dimensional elastic stress analysis of
fracture specimen with an edge crack /International journal of fracture. 1971.
V. 7, № 1. P. 1-15.
197. Cruse T.A., Wilson R.B. Advanced applications of boundary-integral
equation methods /Nuclear engineering and design. 1978. V. 46, № 1. P. 223-
234.
198. Dally J.W., Barker D.B. Dynamic measurements of initiation toughness
at high loading rates /Experimental mechanics. 1988. V. 28, № 3. P. 298-303.
199. Datta S.K. Diffraction of plane elastic waves by ellipsoidal inclusions /The
journal of the Acoustical Society of America. 1977. V. 61, № 6. P. 1432-1437.
200. Delale F., Erdogan F. Line-spring model for surface cracks in a Reiss-
ner plate /International journal of engineering science. 1981. V. 19, № 10.
P. 1331-1340.
201. Delale F., Erdogan F. Application of the line-spring model to a cylindri-
cylindrical shell containing a circumferential or axial part-through crack / Trans, of
the ASME. Series E. Journal of applied mechanics. 1982. V. 49, № 1. P. 97-
102.
202. deLorenzi H. G. On the energy release rate and the J-integral for 3-D crack
configurations /International journal of fracture. 1982. V. 19, № 3. P. 183-
193.
203. deLorenzi H.G. Energy release rate calculations by the finite element
method /Engineering fracture mechanics. 1985. V. 21, № 1. P. 129-143.
204. Dimitrov A., Andr a H., Schnack E. Efficient computation of corner
singularities in 3d-elasticity /International Journal for Numerical Methods
in Engineering. 2001. P. 1-23.
205. Domany E., Krumhansl J.A., Teitel S. Quasistatic approximation to
the scattering of elastic waves by a circular crack / Journal of applied physics.
1978. V. 49, X* 5. P. 2599-2604.
206. Dug dale D. S. Yielding of steel sheets containing slits /Journal of the me-
mechanics and physics of solids. 1960. V. 8, № 2. P. 100-104.
207. Durbin F. Numerical inversion of Laplace transforms: an efficient improve-
improvement to Dubner and Abate's method /The computer journal. 1974. V. 17,
№ 4. P. 371-376.
208. England A.H., Shail R. Orthogonal polynomial solutions to some mixed
boundary-value problems in elastisity II / The quarterly journal of mechanics
and applied mathematics. 1977. V. 30. Pt. 4. P. 397-414.
209. Eshelby J.D. The determination of the elastic field of an ellipsoidal in-
inclusion, and related problems / Proceedings of the Royal Society. London.
Series A. 1957. V. 241, W 1226. P. 376-396.
23*
356 Список литературы
210. Evans A.G. A simple method for evaluating slow crack growth in brittle
materials / International journal of fracture. 1973. V. 9, № 3. P. 267-275.
211. Gao H., Rice J.R. Shear stress intensity factors for a planar crack with
slightly curved front /Trans, of the ASME. Journal of applied mechanics.
1986. V. 53, № 4. P. 774-778.
212. Gautesen A.K. A geometrical theory of diflruction for crack-opening dis-
displacements /Wave motion. 1988. V. 10, № 5. P. 393-404.
213. Gautesen A.K. Asymptotic solution to the crack-opening displacement in-
integral equations for the scattering of plane waves by cracks: I. The symmetric
problem / The journal of the Acoustical Society of America. 1990. V. 87, № 3.
P. 937-942.
214. Gautesen A.K., Achenbach J.D., McMaken H. Surface-wave rays
in elastodynamic diffraction by cracks / The journal of the Acoustical Society
of America. 1978. V. 63, № 6. P. 1824-1831.
215. Glad well G.M.L., England A.H. Orthogonal polynomial solutions to
some mixed boundary-value problems in elasticity theory /The quarterly
journal of mechanics and applied methematics. 1977. V. 30. Pt. 2. P. 175-185.
216. Glushkov E., Glushkova N., Lapina O. 3-D elastic stress singularity
at polyhedral corner points / International Journal of Solids and Structures.
1999. V. 36. P. 1105-1128.
217. Goldstein R.V., Entov V.M., Zazovski A.F. Application of di-
direct variational method to the solution of mixed boundary value prob-
problems / International journal for numerical methods in engineering. 1978. V. 12,
№ 8. P. 1213-1239.
218. Grandt A.F., Kullgren Т.Е. Stress intensity factors for corner cracked
holes under general loading conditions / Trans, of the ASME. Journal of en-
engineering materials and technology. 1981. V. 103, N* 2. P. 171-176.
219. Green A.E., Sneddon I.N. The distribution of stress in the neighbour-
neighbourhood of a flat elliptical crack in an elastic solid / Proceedings of the Cambridge
Phylosophical Society. 1950. V. 46. P. 159-164.
220. Grebner H. Finite element calculation of stress intensity factors for com-
complete circumferential surface cracks at outer wall of a pipe /International
journal of fracture. 1985. V. 27, № 3, 4. P. R99-R102.
221. Grebner H., Strathmeier U. Stress intensity factors for circumferential
semielliptical surface cracks in a pipe under thermal loading /Engineering
fracture mechanics. 1985. V. 22, X* 1. P. 1-7.
222. Griffith A. A. The phenomena of rupture and flow in solids / Phylosophical
Transactions Royal Society of London, Series A. 1921. V. 221. P. 163-198.
223. Griffith A. A. The theory of rupture.—In: Proceedings of the First Inter-
International Congress for Applied Mechanics.—Delft, 1924. P. 55-63.
224. Gubernatis J.E. Long-wave approximations for the scattering of elastic
waves from flaws with applications to ellipsoidal voids and inclusions / Journal
of applied physics. 1979. V. 50, № 6. P. 4046-4058.
225. Gubernatis J.E., Domany E. Raileigh scattering of elastic waves from
cracks /Journal of applied physics. 1979. V. 50, K« 2. P. 818-824.
226. Gubernatis J.E., Domany E., Krumhansl J.A. Formal aspects
of the theory of the scattering of ultrasound by flaws in elastic materi-
materials /Journal of applied physics. 1977. V. 48, № 7. P. 2804-2811.
227. Guidera J.T., Lardner R.W. Penny-shaped cracks /Journal of elasti-
elasticity. 1975. V. 5, № 1. P. 59-73.
Список литературы 357
228. Gyekenyesi J.P., Mendelson A. Three-dimensional elastic stress and
displacement analysis of finite geometry solids containing cracks /Inter-
/International journal of fracture. 1975. V. 11, № 3. P. 409-429.
229. Hall C.A., Raymund M., Palusamy S. A macro element approach
to computing stress intensity factors for three dimensional structu-
structures /International journal of fracture. 1979. V. 15, № 3. P. 231-245.
230. Hartranft R.J., Sih G.C. The use of eigenfunction expansions in the
general solution of three-dimensional crack problems / Journal of mathema-
mathematics and mechanics. 1969. V. 19, Jf* 2. P. 123-138.
231. Hartranft R.J., Sih G. С Alternating method applied to edge and surface
crack problems.—In: Mechanics of fracture. V. 1. Methods of analysis and
solutions of crack problems /Ed. G.C. Sih.—Leyden, 1973. P. 179-238.
232. Hartranft R.J., Sih G.C. Three-dimensional growth characteristics of
a plane crack subjected to concentrated forces / Journal of applied mechanics.
1974. V. 41, N* 3. P. 808, 809.
233. Haugazeu M. Sur des inequations variationelles /Comptes Rendus Acad.
Sc. Paris. Series A. 1967. V. 265, № 3. P. 95-98.
234. Hayashi K., Abe H. Stress intensity factors for a semi-elliptical crack in
the surface of a semi-infinite solid / International journal of fracture. 1980.
V. 16, Л* 3. P. 275-285.
235. Heliot J., Labbens R. C., Pellissier-Tanon A. Semi-elliptical cracks
in a cylinder subjected to stress gradients.—In: Fracture mechanics. ASTM
STP 677 /Ed. C.W.Smith. 1979. P. 341-364.
236. H e 11 e n Т. К. On the method of virtual crack extensions / International jour-
journal for numerical methods in engineering. 1975. V. 9, № 1. P. 187-207.
237. Hellen Т.К., Blackburn W. S. The calculation of stress intensity factors
in two and three dimensions using finite elements.—In: Computational frac-
fracture mechanics /Eds E.F.Rybicki, S.E. Benzley—N.Y.: ASME, 1975. P. 103-
120.
238. Hellen Т.К., Dowling A.R. Three-dimensional crack analysis applied to
an LWR nozzle-cylinder intersection / The international journal of pressure
vessels and piping. 1975. V. 3, № 1. P. 57-74.
239. Hilton P.D. A specialized finite element approach for three-dimensional
crack problems.—In: Mechanics of fracture. V. 3. Plates and shells with
cracks /Ed. G.C.Sih.—Leyden: Noordhoff International Publishing, 1977.
P. 273-298.
240. Hilton P.D., Kiefer R. V. The enriched element for finite element analysis
of three-dimensional elastic crack problems / Trans, of the ASME. Journal of
pressure vessel technology. 1980. V. 102, JY* 4. P. 347-352.
241. Hilton P.D., Perice D. С The enriched element formulation for 3-D com-
combined mode elastic crack problems.—In: Computational fracture mechanics-
nonlinear and 3-D problems.—N.Y.: ASME, 1984. P. 65-76.
242. Hilton P.D., Sih G.C. Applications of the finite element method to
the calculation of stress intensity factors.—In: Mechanics of fracture. V. 1.
Methods of analysis and solutions of crack problems /Ed. G.C. Sih.—Leyden,
1973. P. 426-473.
243. Hirose S., Achenbach J.D. Application of BEM to transient analysis of
a 3-D crack.—In: Boundary element methods in applied mechanics. Proceed-
Proceedings of the first joint Japan / US symposium on boundary element methods.
Tokyo, Japan 3-6 October 1988 /Eds M.Tanaka, T.A.Cruse.—Pergamon
Press, 1988. P. 255-264.
358 Список литературы
244. Hirose S., Achenbach J.D. Time-domain boundary element analysis of
elastic wave interaction with a crack /International journal for numerical
methods in engineering. 1989. V. 28, № 3. P. 629-644.
245. Ioakimidis N. I. Application of finite-part integrals to the singular integral
equations of crack problems in plane and three-dimensional elasticity / Acta
Mechanica. 1982. V. 45, № 1, 2. P. 31-47.
246. IoakimidisN.I. A natural approach to the introduction of finite-part in-
integrals into crack problems of three-dimensional elasticity / Engiueering frac-
fracture mechanics. 1982. V. 16, № 5. P. 669-673.
247. Ioakimidis N.I. Validity of the hypersingular integral equation of crack
problems in three-dimensional elasticity along the crack boundaries /Engi-
/Engineering fracture mechanics. 1987. V. 26, № 5. P. 783-788.
248. Irwin G.R. Fracture dynamics.—In: Fracturing of metals.—Cleveland:
ASM, 1948. P. 147-166.
249. Irwin G.R. Analysis of stresses and strains near the end of a crack traversing
a plate /Journal of applied mechanics. 1957. V. 24, № 3. P. 361-364.
250. Irwin G.R., Kies J.A., Smith H.L. Fracture strength relative to onset
and arrest of crack propagation / Proceedings of the American Society for
Testing and Materials. 1959. 58. P. 640-657.
251. Isida M., Hirota K., Noguchi H., Yoshida T. Two parallel ellipti-
elliptical cracks in an infinite solid subjected to tension / International journal of
fracture. 1985. V. 27, № 1. P. 31-48.
252. Isida M., Noguchi H. Tension of a plate containing an embedded elliptical
crack /Engineering fracture mechanics. 1984. V. 20, № 3. P. 387-408.
253. Isida M., Noguchi H., Yoshida T. Tension and bending of finite thick-
thickness plates with a semi-elliptical surface crack / International journal of frac-
fracture. 1984. V. 26, № 3. P. 157-188.
254. Itou S. Three-dimensional wave propagation in a cracked elastic solid
/ Trans, of the ASME. Series E. Journal of applied mechanics. 1978. V. 45.
P. 807-811.
255. Itou S. Dynamic stress concentration around a rectangular crack in an infi-
infinite elastic medium /ZAMM. 1980. V. 60, № 8. P. 317-322.
256. Itou S. Transient analysis of stress waves around a rectangular crack under
impact load / Trans, of the ASME. Journal of applied mechanics. 1980. V. 47,
X* 4. P. 958, 959.
257. Itou S. Transient analysis of stress waves around two rectangular cracks
under impact load /Engineering fracture mechanics. 1981. V. 14, № 4. P. 685-
695.
258. Jain D. L., Kan wal R. P. Diffraction of a plane shear elastic wave by a cir-
circular rigid disc and a penny shaped crack / Quarterly of applied mathematics.
1972. V. 30, № 3. P. 283-297.
259. Jia Z.H., Shippy D.J., Rizzo F. J. Three-dimensional crack analysis us-
using singular boundary elements / International journal for numerical methods
in engineering. 1989. V. 28, № 10. P. 2257-2273.
260. Jia Z.H., Shippy D.J., Rizzo F.J. Boundary-element analysis of wave
scattering from cracks / Communications in applied numerical methods. 1990.
V. 6. P. 591-601.
261. Jiang Z.D., Petit J., Bezine G. Stress intensity factors of two parallel
3D surface cracks /Engineering fracture mechanics. 1991. V. 40, № 2. P. 345-
354.
Список литературы 359
262. Jones D.S. Boundary integrals in elastodynamics /IMA Journal of Applied
Mathematics. 1985. V. 34, № 1. P. 83-97.
263. К alt h off J. F. Time effects and their influences on test procedures for mea-
measuring dynamic material strength values.—In: Application of Fracture Me-
Mechanics to Materials and Structures /Eds G.C.Sih, E.Sommer, W.Dahl.—
Martinus Nijhoff Publishers, 1984. P. 107-136.
264. Kalthoff J.F. Fracture behavior under high rates of loading /Engineering
fracture mechanics. 1986. V. 23, № 1. P. 289-298.
265. Kalthoff J.F., Shockey D.A. Instability of cracks under impulse
loads /Journal of applied physics. 1977. V. 48, № 3. P. 986-993.
266. Kanwal R.P., Pasha M.L. Axially symmetric stress distributions in elas-
elastic solids containing ring-shaped cracks under torsion / Trans, of the ASME.
Series E. Journal of applied mechanics. 1974. V. 41,№ 2. P. 516, 517.
267. К assiг М.К. On the problem of an external elliptic crack in an infinite
solid / Trans, of the ASME. Series E. Journal of applied mechanics. 1968.
V. 35, № 2. P. 422-424.
268. Kassir M.K. Stress-intensity factor for a three-dimensional rectangular
crack /Trans, of the ASME. Journal of applied mechanics. 1981. V. 48, № 2.
P. 309-312.
269. Kassir M.K. A three-dimensional rectangular crack subjected to shear load-
loading / International journal of solids and structures. 1982. V. 18, № 12. P. 1075-
1082.
270. Kassir M.K., Bregman A.M. The stress intensity factor for a penny-
shaped crack between two dissimilar materials / Trans, of the ASME. Series E.
Journal of applied mechanics. 1972. V. 39, № 1. P. 308-310.
271. Kassir M.K., Sih G.C. Three-dimensional stress distribution around an
elliptical crack under arbitrary loadings / Trans, of the ASME. Series E. Jour-
Journal of applied mechanics. 1966. V. 33, № 3. P. 601-611.
272. Kassir M.K., Sih G.C. Geometric discontinuities inelastostatics / Journal
of mathematics and mechanics. 1967. V. 16, № 9. P. 927-948.
273. Kassir M.K., Sih G.C. External elliptic crack in elastic solid /Inter-
/International journal of fracture mechanics. 1968. V. 4, № 4. P. 347-356.
274. Kassir M.K., Sih G. С Three dimensional crack problems. V. 2. A new se-
selection of crack problems in three dimensional elasticity.—Ley den: Noordhoff,
1975. 452 c.
275. Keat W.D., Annigeri B.S., Cleary M.P. Surface integral and finite
element hybrid method for two- and three-dimensional fracture mechanics
analysis /International journal of fracture. 1988. V. 36, № 1. P. 35-53.
276. Keer L.M., Parihar K.S. A note on the singularity at the corner of a
wedge-shaped punch о crack / SIAM journal on applied mathematics. 1978.
V. 34, № 2. P. 297-302.
277. Keogh P. S. High-frequency scattering of a normally incident plane compres-
sional wave by a penny-shaped crack / The quarterly journal of mechanics and
applied mathematics. 1986. V. 39. Pt. 4. P. 535-566.
278. Knauss W. G. Fundamental problems in dynamic fracture.—In: Advances
in Fracture Research (Fracture 1984). V. 1. 6th International Conference on
Fracture.—New Delhi. India. 4-10 December 1984.—Pergamon Press, 1986.
P. 625-652.
279. Knauss W.G., Ravi-Chandar K. Fundamental considerations in dy-
dynamic fracture /Engineering fracture mechanics. 1986. V. 23, X4 1. P. 9-20.
360 Список литературы
280. Kobayashi A.S. Numerical analysis in fracture mechanics.—In: Appli-
Application of Fracture Mechanics to Materials and Structures /Eds G.C. Sih,
E. Sommer, W. Dahl.—Martinus Nijhoff Publishers, 1984. P. 27-56.
281. Kobayashi A.S., Enetanya A.N., Shah R.C. Stress intensity fac-
factors for elliptical cracks.—In: Prospects of fracture mechanics /Eds G.C. Sih,
H.C. Van Elst, D.Broek.—Noordhoff, 1974. P. 525-544.
282. Kogan V. G., Hsu D.K., Rose J. H. Characterization of flaws using the
zeroes of the real and imaginary parts of the ultrasonic scattering ampli-
amplitude /Journal of nondestructive evaluation. 1985. V. 5, № 2. P. 57-67.
283. Kostrov B.V., Das S. Evaluation of stress and displacement fields due to
an elliptical plane shear crack / Geophysical journal of the Royal Astronomical
Society. 1984. V. 78, № 1. P. 19-33.
284. Krenk S. A circular crack under asymmetric loads and some related integral
equations / Trans, of the ASME. Journal of applied mechanics. 1979. V. 46,
№ 4. P. 821-826.
285. Krenk S., Schmidt H. Elastic wave scattering by a circular crack /Phil.
Trans. R. Soc. London. 1982. V. A308, № 1502. P. 167-198.
286. Kullgren Т.Е., Smith F.W. Part-elliptical cracks emanating from open
and loaded holes in plates / Trans, of the ASME. Journal of engineering ma-
materials and technology. 1979. V. 101, № 1. P. 12-17.
287. Kullgren Т.Е., Smith F.W., Ganong G.P. Quarter elliptical cracks
emanating from holes in plates / Trans, of the ASME. Journal of engineering
materials and technology. 1978. V. 100, № 2. P. 144-149.
288. Кuna M. Three-dimensional elastic analysis of CT specimen with straight
and curved crack fronts / International journal of fracture. 1982. V. 19, № 3.
P. R63-R67.
289. К una M. Hybrid crack tip elements for three dimensional fracture pro-
problems.—In: Application of fracture mechanics to materials and structures.
Proceedings of the international conference. 1983 / Eds G.C. Sih, E. Sommer,
W. Dahl.—Freiburg: FRG, 1984. P. 607-617.
290. Кипа М., Zwicke M. A mixed hybrid finite element for three-dimensional
elastic crack analysis /International journal of fracture. 1990. V. 45, № 1.
P. 65-79.
291. Lachat J.C., Watson J.O. Effective numerical treatment of boundary
integral equations: a formulation for three-dimensional elastostatics /Inter-
/International journal for numerical methods in engineering. 1976. V. 10, № 5.
P. 991-1005.
292. Le Van A., Peseux B. Boundary element analysis of an integral equation
for three-dimensional crack problems /International journal for numerical
methods in engineering. 1988. V. 26, № 11. P. 2383-2402.
293. Le Van A., Royer J. A numerical procedure for regularized integral equa-
equations for elastostatic problems of flat cracks in opening mode / Engineering
fracture mechanics. 1991. V. 40, № 2. P. 237-250.
294. Li Yingzhi, Hills D.A. The analysis of three-dimensional cracks gener-
generated by sharp indentation / Journal of the mechanics and physics of solids.
1990. V. 38, № 2. P. 255-272.
295. L i e b E. H. Existence and uniqueness of the minimizing solution of Shoquard's
nonlinear equation /Studies in applied mathematics. 1977. V. 57, JY* 2. P. 93-
105.
296. Liebowitz H., Moyer E. T. Jr. Finite element methods in fracture me-
mechanics /Computers & Structures. 1989. V. 31, № 1. P. 1-9.
Список литературы 361
297. Lin W., Кеег L.M. Scattering by a horizontal subsurface penny-shaped
crack / Proceedings of the Royal society of London. Series A. Mathematical
and physical sciences. 1986. V. 408, № 1835. P. 277-294.
298. Lin W., Keer L.M. Scattering by a planar three-dimensional crack /Jour-
/Journal of the Acoustical Society of America. 1987. V. 82, № 4. P. 1442-1448.
299. Lions P.-L. Quelques remarques sur lasymetrisation de Schwartz.—In: Non-
Nonlinear partial differential equations and their applications. Research notes in
mathematics 53. College de France seminar. 1980. V. 1. P. 308-319.
300. Lowengrub M., Sneddon I.N. The distribution of stress in the vicin-
vicinity of an external crack in an infinite elastic solid / International journal of
engineering science. 1965. V. 3, № 4. P. 451-460.
301. Luchi M.L., Rizzuti S. Boundary elements for three-dimensional elastic
crack analysis / International journal for numerical methods in engineering.
1987. V. 24, № 12. P. 2253-2271.
302. Mai A. K. Dynamic stress intensity factor for an axisymmetric loading of the
penny shaped crack / International journal of engineering science. 1968. V. 6,
№ 11. P. 623-629.
303. Mai A. K. Dynamic stress intensity factor for a non-axisymmetric loading of
the penny shaped crack / International journal of engineering science. 1968.
V. 6, JY* 12. P. 725-733.
304. Mai A.K. Interaction of elastic waves with a penny-shaped crack /Inter-
/International journal of engineering science. 1970. V. 8, JY* 5. P. 381-388.
305. Mai A.K. Interaction of elastic waves with a Griffits crack /International
journal of engineering science. 1970. V. 8, № 9. P. 763-776.
306. Mai A.K. A note on the low-frequency diffraction of elastic waves by a
Griffith crack / International journal of engineering science. 1972. V. 10, № 7.
P. 609-612.
307. Manolis G.D., Beskos D.E. Dynamic stress concentration studies by
boundary integrals and Laplace transform / International journal for numer-
numerical methods in engineering. 1981. V. 17, № 4. P. 573-599.
308. Manolis G.D., Beskos D.E. Boundary element methods in elastodyna-
mics / Academic Division of Unwin Ну man Ltd. 1988. 282 p.
309. Martin P. A. The discontinuity in the elastostatic displacement vector across
a penny-shaped crack under arbitrary loads / Journal of elasticity. 1982. V. 12,
№ 2. P. 201-218.
310. Martin P.A. Orthogonal polynomial solutions for pressurised elliptical
cracks / The quarterly journal of mechanics and applied mathematics. 1986.
V. 39. Pt. 2. P. 269-287.
311. Martin P.A. Orthogonal polynomial solutions for elliptical cracks under
shear loadings / The quarterly journal of mechanics and applied mathematics.
1986. V. 39. Pt. 4. P. 519-534.
312. Martin P. A., Rizzo F. J. On boundary integral equations for crack prob-
problems /Proceedings of the Royal society of London. Series A. 1989. V. 421,
№ 1861. P. 341-355.
313. Martin P.A., Rizzo F.J., Gonsalves I. R. On hypersingular boundary
integral equations for certain problems in mechanics /Mechanics research
communications. 1989. V. 16, № 2. P. 65-71.
314. Martin P.A., Wickham G.R. Diffraction of elastic waves by a penny
shaped crack: analytical and numerical results /Proceedings of the Royal
Society of London. 1983. V. A390, № 1798. P. 91-129.
362 Список литературы
315. Massonet C.E. Numerical use of integral procedures.—In: Stress analy-
analysis. Recent developments in numerical and experimental methods /Eds
O.C. Zienkiewicz, G.S. Holister.—Wiley, 1965. P. 198-235.
316. Mastrojannis E.N. A note on the problem of an annular crack subjected
to an arbitrary normal pressure / International journal of engineering science.
1983. V. 21, № 9. P. 1129-1136.
317. Mastrojannis E.N., Keer L.M., Mura T. Stress-intensity factor for a
plane crack under normal pressure / International journal of fracture. 1979.
V. 15, № 3. P. 247-258.
318. Mattheck C, Morawietz P., Munz D. Calculation of the stress inten-
intensity factor of a circumferential crack in a tube originating from a hole under
axial tensile and bending loads / Engineering fracture mechanics. 1985. V. 22,
JY* 4. P. 645-650.
319. Me Go wan J. J., Raymund M. Stress intensity factor solutions for in-
internal longitudinal semi-elliptical surface flaws in a cylider under arbitrary
loadings.—In: Fracture mechanics. ASTM STP 677 /Ed. C.W. Smith.—
American Society for Testing and Materials, 1979. P. 365-380.
320. McMaken H. A uniform theory of diffraction for elastic solids / The journal
of the Acoustical Society of America. 1984. V. 75, № 5. P. 1352-1359.
321. Mendelson A., Alam J. The use of the method of lines in 3-D
fracture mechanics analyses with application to compact tension speci-
specimens /International journal of fracture. 1983. V. 22, JY* 2. P. 105-116.
322. Miller M.K., Guy W. T. Numerical inversion of the Laplace transform by
the use of Jacobi polynomials / SIAM journal of numerical analysis. 1966.
V. 3, № 4. P. 624-635.
323. Miyoshi Т., Shiratori M. 3D-BEM analysis of surface cracks by
supercomputer.—In: Boundary element methods in applied mechanics. Pro-
Proceedings of the first joint Japan /US symposium on boundary element
methods. Tokyo, Japan 3-6 October 1988 /Eds M.Tanaka, T. A. Cruse.—
Pergamon Press, 1988. P. 149-158.
324. Morrison J.A., Lewis J.A. Charge singularity at the corner of a flat
plate /SIAM journal on applied mathematics. 1976. V. 31, № 2. P. 233-249.
325. Moyer E.Т., Liebowitz H. Comparative study on three-dimensional
crack tip modeling methodology.—In: Application of fracture mechanics
to materials and structures. Proceedings of the International conference.
Freiburg, FRG, 1983 /Eds G.C.Sih, E.Sommer, W.Dahl. 1984. P. 595-606.
326. Murakami Т., Sato T. Three-dimensional J-integral calculations of part-
through surface crack problems /Computers & Structures. 1983. V. 17,
№ 5, 6. P. 731-736.
327. Murakami Y. Analysis of stress intensity factors of modes I, II and III for
inclined surface cracks of arbitrary shape / Engineering fracture mechanics.
1985. V. 22, № 1. P. 101-114.
328. Murakami Y., Nemat-Nasser S. Interacting dissimilar semi-elliptical
surface flaws under tension and bending /Engineering fracture mechanics.
1982. V. 16, № 3. P. 373-386.
329. Murakami Y., Nemat-Nasser S. Growth and stability of interacting
surface flaws of arbitrary shape / Engineering fracture mechanics. 1983. V. 17,
№ 3. P. 193-210.
330. Narayanan G.V., Beskos D.E. Numerical operational methods for time-
dependent linear problems / International journal for numerical methods in
engineering. 1982. V. 18, X* 12. P. 1829-1854.
Список литературы 363
331. Nikishkov G.P., Atluri S.N. Calculation of fracture mechanics param-
parameters for an arbitrary three-dimensional crack, by the 'equivalent domain in-
integral* method /International journal for numerical methods in engineering.
1987. V. 24, tf* 9. P. 1801-1821.
332. Nishimura N., Guo Q. С, К ob ay as hi S. Elastodynamic crack analysis
by BIEM.—In: Boundary element methods in applied mechanics. Proceed-
Proceedings of the first joint Japan / US symposium on boundary element methods.
Tokyo, Japan 3-6 October 1988 /Eds M.Tanaka, T.A.Cruse.—Pergamon
Press, 1988. P. 245-254.
333. Nishimura N., Kobayashi S. An improved boundary integral equa-
equation method for crack problems.—In: Advanced boundary element methods.
IUTAM symposium. San Antonio. Texas. 1987 /Ed. T.A.Cruse.—Springer-
Verlag, 1988. P. 279-286.
334. Nishioka Т., Atluri S.N. Analysis of surface flaw in pressure vessels by
a new 3-dimensional alternating method / Trans, of the ASME. Journal of
pressure vessel technology. 1982. V. 104, № 4. P. 299-307.
335. Nishioka Т., Atluri S.N. Analytical solution for embedded elliptical
cracks and finite element-alternating method for elliptical surface cracks sub-
subjected to arbitrary loading /Engineering fracture mechanics. 1983. V. 17,
№ 3. P. 247-268.
336. Nishioka Т., Atluri S.N. An alternating method for analysis of surface
flawed aircraft structural components /AIAA Journal. 1983. V. 21, JY* 5.
P. 749-757.
337. Nishitani H., Murakami Y. Stress intensity factors of an elliptical crack
or a semi-elliptical crack subject to tension / International journal of fracture.
1974. V. 10, № 3. P. 353-368.
338. Nisitani H., Noda N. Tension of a cylindrical bar having an infinite row
of circumferential cracks / Engineering fracture mechanics. 1984. V. 20, X* 4.
P. 675-686.
339. Newman J.C., Raju LS. Stress-intensity factors for internal surface cracks
in cylindrical pressure vessels / Trans, of the ASME. Journal of pressure vessel
technology. 1980. V. 102, № 4. P. 342-346.
340. O'Donoghue P.E., Nishioka Т., Atluri S. N. Analysis of interaction
behaviour of surface flaws in pressure vessels.—In: Computational Fracture
Mechanics-Nonlinear and 3-D Problems.—N.Y.: ASME, 1984. P. 77-92.
341. Or о wan E. Energy criteria of fracture /The welding journal. 1955. V. 34,
№ 3. P. 1576-1606.
342. Osborne A.D. Diffraction of high frequency torsion waves by a penny-
shaped crack /International journal of engineering science. 1974. V. 12, № 9.
P. 773-785.
343. Papoulis A. A new method of inversion of the Laplace transform /Quar-
/Quarterly of applied mathematics. 1957. V. 14, № 4. P. 405-414.
344. Parihar K.S., Keer L. M. Stress singularity at the corner of wedge-shaped
crack or inclusion /ASME Journal of applied mechanics. 1978. V. 45, J№ 4.
P. 791-796.
345. Paris P.C, Gomez M.P., Anderson W.E. A rational analytic theory
of fatigue /The Trend in Engineering. 1961. V. 13. P. 9-14.
346. Parks D.M. A stifness derivative finite element technique for determination
of crack tip stress intensity factors / International journal of fracture. 1974.
V. 10, № 4. P. 487-502.
347. Payne L.E. Isoperimetric inequalities and their applications /SIAM Re-
Review. 1967. V. 9, № 3. P. 453-488.
364 Список литературы
348. Р i аи М. Attenuation of a plane compressional wave by a random distribution
of thin circular cracks /International journal of engineering science. 1979.
V. 17, № 2. P. 151-167.
349. Polch E.Z., Cruse T.A., Huang C.-J. Traction BIE solutions for flat
cracks /Computational mechanics. 1987. V. 2, № 4. P. 253-267.
350. R a j и I. S., A11 и г i S. N. Finite-element — alternating method for analysis of
cracked three-dimensional solids.—In: Computational Mechanics'88. Theory
and Applications. International conference. 1988. Atlanta, USA. V. 1 /Eds
S.N.Atluri, G.Yagawa.—Springer-Verlag, 1988.
351. Raj и I. S., Newman J. C. Stress-intensity factors for a wide range of semi-
elliptical surface cracks in finite-thickness plates / Engineering fracture me-
mechanics. 1979. V. 11, № 4. P. 817-829.
352. Raj и I.S., Newman J.C. Stress-intensity factors for two symmetric cor-
corner cracks.—In: Fracture mechanics. ASTM STP 677 /Ed. C.W.Smith —
American Society for Testing and Materials, 1979. P. 411-430.
353. Raj и I. S., Newman J. С Stress-intensity factors for internal and external
surface cracks in cylindrical vessels / Trans, of the ASME. Journal of pressure
vessel technology. 1982. V. 104, № 4. P. 293-298.
354. Raj и I.S., Newman J.C. Stress-intensity factors for circumferential sur-
surface cracks in pipes and rods under tension and bending loads /Fracture
mechanics. Seventeenth volume. ASTM STP 905 /Eds J.H.Underwood, et
al.—Philadelphia, PA.: American Society for Testing and Materials, 1986.
P. 789-805.
355. Raveendra S.T., Cruse T.A. BEM analysis of problems of fracture
mechanics.—In: Developments in boundary element methods-5. Industrial
applications of boundary element methods /Eds P.K.Banerjee, R.B.Wilson.
1989. P. 187-204.
356. Ravi-Chandar K., Knauss W.G. An experimental investigation into
dynamic fracture: 1. Crack initiation and arrest /International journal of
fracture. 1984. V. 25, № 3. P. 247-262.
357. Rice J.R. First-order variation in elastic fields due to variation in location
of a planar crack front / Trans, of the ASME. Journal of applied mechanics.
1985. V. 52, № 3. P. 571-579.
358. Rice J. R. Elastic fracture mechanics concepts for interfacial cracks / Journal
of applied mechanics. 1988. V. 55, № 1. P. 98-103.
359. Rice J.R., Levy N. The part-through surface crack in an elastic
plate /Trans, of the ASME. Series E. Journal of applied mechanics. 1972.
V. 39, JY* 1. P. 185-194.
360. Robertson LA. Diffraction of a plane longitudunal wave by a penny-shaped
crack / Proceedings of the Cambridge Philosophical Society. 1967. V. 63. Pt. 1.
P. 229-238.
361. Rose J.H., Elsley R.K., Tittman В., Varadan V.V., Vara-
dan V.K. Inversion of ultrasonic scattering data.—In: Acoustic, electro-
electromagnetic and elastic wave scattering-focus on the T-matrix approach /Eds
V.K. Varadan, V.V. Varadan.—N.Y.: Pergamon Press, 1980. P. 605-614.
362. Rose J.H., Krumhansl J.A. Determination of flaw characteristics from
ultrasonic scattering data /Journal of applied physics. 1979. V. 50, № 4.
P. 2951, 2952.
363. R о у A. Diffraction of elastic waves by an elliptic crack / International journal
of engineering science. 1984. V. 22, № 6. P. 729-739.
364. Roy A. Diffraction of elastic waves by an elliptic crack-II /International
journal of engineering science. 1987. V. 25, № 2. P. 155-169.
Список литературы 365
365. Rybicki E.F., Kanninen M.F. A finite element calculation of stress
intensity factors by a modified crack closure integral /Engineering fracture
mechanics. 1977. V. 9, № 4. P. 931-938.
366. Schwarzer N., Richter F., Michel B. Penny shaped interface crack
under uniform pressure and shear loading.—In: Modeling and simulation
based engineering. V. II / Eds S.N. Atluri, P.E. Donoghue.—USA: Published
by Tech. Science Press, 1998. P. 1580-1585.
367. Sack R.A. Extension of Griffith theory of rupture to three dimen-
dimensions /Proc. Phys. Soc. 1946. V. 58. P. 729-736.
368. Segedin CM. Note on a penny-shaped crack under shear /Proc. of the
Cambridge Phylosophical Society. 1950. V. 47. P. 396-400.
369. Segedin CM. A note on geometric discontinuities in elastosta-
tics / International journal of engineering science. 1968. V. 6, № 5. P. 309-312.
370. Shah R. C, Kobayashi A. S. Stress intensity factor for an elliptical crack
under arbitrary normal loading /Engineering fracture mechanics. 1971. V. 3,
№ 1. P. 71-96.
371. Shah R.C, Kobayashi A.S. On the surface flaw problem.—In:
The surface crack: physical problems and computational solutions /Ed.
J.L.Swedlow.—N.Y.: ASME, 1972. P. 79-124.
372. Shah R. С, Kobayashi A.S. Stress intensity factors for an elliptical crack
approaching the surface of semiinfinite solid / International journal of frac-
fracture. 1973. V. 9, № 2. P. 133-146.
373. Shail R. Lame polynomial solutions to some elliptic crack and punch prob-
problems /International journal of engineering science. 1978. V. 16, № 8. P. 551-
563.
374. Shail R. Orthogonal polynomial solutions to some mixed boundary-value
problems in elasticity III / The quarterly journal of mechanics and applied
mathematics. 1980. V. 33. Pt. 2. P. 235-249.
375. Shifrin E.I. Semi-analytical solution of the problem of elastic wave scat-
scattering by elliptical cracks.—In: ICIAM 95. The Third International Congress
on Industrial and Applied Mathematics.—Hamburg: Book of Abstracts, 3-7
July, 1995. P. 438.
376. Shifrin E.I. Semi-analytical solution of the problem of elastic wave scat-
scattering by elliptical cracks /Zeitschrift fur Angewandte Mathematik und
Mechanik (ZAMM). 1996. V. 76 S5. P. 471, 472.
377. Shifrin E.I. Analytical solution of three-dimensional problem for elliptical
crack subjected to arbitrary time-harmonic loads /ESF 11-Mechanisms and
Mechanics of Damage and Failure. V. I / Ed. J. Petit. Co-editors J. de Fouqet,
G.Henaff. Printed by the CHAMELEON PRESS LTD.—London: UNITED
KINGDOM, 1996. P. 497-502.
378. Shifrin E.I., Brank B. On solution of elliptical interface crack prob-
problem /Fields Institute Communications. 2000. V. 25. P. 485-496.
379. Shifrin E.I., Brank В., Surace G. Analytical-numerical solution of
elliptical interface crack problem /International journal of fracture. 1998.
V. 94. P. 201-215.
380. Shih C.F., Moran В., Nakamura T. Energy release rate along a three-
dimensional crack front in a thermally stressed body / International journal
of fracture. 1986. V. 30, № 2. P. 79-102.
381. S h i n d о Y. Diffraction of torsional waves by a flat annular crack in an infinite
elastic medium / Trans, of the ASME. Series E. Journal of applied mechanics.
1979. V. 46, № 4. P. 827-831.
366 Список литературы
382. Shin do Y. Sudden twisting of a flat annular crack /International journal
of solids and structures. 1981. V. 17, № 11. P. 1103-1112.
383. Shin do Y. Normal compression waves scattering at a flat annular crack in
an infinite elastic solid /Quarterly of applied mathematics. 1981. V. 39, № 3.
P. 305-315.
384. S h i n d о Y. Axisymmetric elastodynamic response of a flat annular crack to
normal impact waves /Engineering fracture mechanics. 1984. V. 19, JV* 5.
P. 837-848.
385. Shmuely M., Alterman Z.S. A three dimensional numerical analysis of
stress distribution in the vicinity of a crack tip / Israel journal of technology.
1971. V. 9, № 5. P. 523-530.
386. Shoi L, Shield R.T. A note on a flat toroidal crack in an elastic isotropic
body / International journal of solids and structures. 1982. V. 18, № 6. P. 479-
486.
387. Sih G.C. A review of the three-dimensional stress problem for a cracked
plate /International journal of fracture. 1971. V. 7, № 1. P. 39-61.
388. Sih G.C. Ed. Mechanics of fracture. V. 4. Elastodynamic crack problems.—
Leyden: Noordhoff, 1977. 352 p.
389. Sih G.C., Chen E. P. Mechanics of fracture. Cracks in composite materials.
V. 6. Martinus Nijhoff Publishers. 1981.
390. Sih G.C., Embley G.T. Sudden twisting of a penny shaped crack/ASME
Journal of applied mechanics. 1972. V. 39, № 2. P. 395-399.
391. Sih G.C., Loeber J. F. Wave propagation in an elastic solid with a line of
discontinuity or finite crack / Quarterly of applied mathematics. 1969. V. 27,
№ 2. P. 193-213.
392. Sladek J., Sladek V. Dynamic stress intensity factors studied by
boundary integro-differential equations / International journal for numerical
methods in engineering. 1986. V. 23, № 5. P. 919-928.
393. Sladek V., Sladek J. Transient elastodynamic three-dimensional prob-
problems in cracked bodies /Applied mathematical modelling. 1984. V. 8, № 1.
P. 2-10.
394. Smith F. W. The elastic analysis of the part-circular surface flaw problem
by the alternating method.—In: The surface crack: physical problems and
computational solutions /Ed. J.L.Swedlow.—N.Y.: ASME, 1972. P. 125-152.
395. Smith F. W., Alavi M. J. Stress intensity factor for a penny-shaped crack
in a half space /Engineering fracture mechanics. 1971. V. 3, № 3. P. 241-254.
396. Smith F.W., Kobayashi A.S., Emery A.F. Stress intensity factors
for penny-shaped cracks: part I — infinite solid, part II — semi-infinite
solid / Trans, of the ASME. Series E. Journal of applied mechanics. 1967.
V. 34, № 4. P. 947-959.
397. Smith F. W., SorensenD.R. The elliptical crack subjected to nonuniform
shear loading / Trans, of the ASME. Series E. Journal of applied mechanics.
1974. V. 41, № 2. P. 502-509.
398. Smith F.W., Sorensen D.R. The semi-elliptical surface crack. A solution
by the alternating method / International journal of fracture. 1976. V. 12, JV* 1.
P. 47-57.
399. Smith R.N.L. Stresses from arbitrary loads on a penny-shaped
crack /International journal for numerical methods in engineering. 1984.
V. 20, № 11. P. 2093-2105.
400. Sneddon I. N. The distribution of stress in the neighbourhood of a crack in
an elastic solid / Proc. Roy. Soc. London. Series A. 1946. V. 187. P. 229-260.
Список литературы 367
401. Sneddon I. N. The stress intensity factor for a flat elliptical crack in an elas-
elastic solid under uniform tension / International journal of engineering science.
1979. V. 17, № 2. P. 185-191.
402. Sneddon I.N., Lowengrub M. Crack problems in the classical theory
elasticity.—N.Y.: John Wiley and Sons, Inc., 1969. 221 p.
403. Sneddon I.N., Tweed J. The stress intensity factor for a penny-
shaped crack in an elastic body under the action of symmetric body
forces / International journal of fracture mechanics. 1967. V. 3, № 4. P. 291-
299.
404. Stallybrass M.P. On the concentrated loading of certain elastic half-space
problems and related external crack problems. A new approach / International
journal of engineering science. 1981. V. 19, № 8. P. 1123-1144.
405. Talenti G. Elliptic equations and rearrangements /Ann. Scuola Norm.
Super. Pisa. Ser. 3. 1976. V. 30, № 4. P. 697-718.
406. Tarn К.С Two-dimensional inverse Born approximation in ultrasonic flaw
characterization /Journal of nondestructive evaluation. 1985. V. 5, № 2.
P. 95-106.
407. Tan C. L., Fenner R. T. Elastic fracture mechanics analysis by the bound-
boundary integral equation method /Proceedings of the Royal Society (London).
Series A. 1979. V. 369, № 1737. P. 243-260.
408. Tan C.L., Fenner R.T. Stress intensity factors for semi-elliptical sur-
surface cracks in pressurised cylinders using the boundary integral equation
method /International journal of fracture. 1980. V. 16, № 3. P. 233-245.
409. Teitel S. Determination of crack characteristics from the quasistatic ap-
approximation for the scattering of elastic waves /Journal of applied physics.
1978. V. 49, № 12. P. 5763-5767.
410. Thau S. A., Lu T.-H. Transient stress intensity factors for a finite crack in
an elastic solid caused by a dilatational wave / International journal of solids
and structures. 1971. V. 7, № 7. P. 731-750.
411. Theocaris P.S., Ioakimidis N.L, Kazantzakis J.G. On the nu-
numerical evaluation of two-dimensional principal value integrals / International
journal for numerical methods in engineering. 1980. V. 15, № 4. P. 629-634.
412. Tong P., Atluri S.N. On hybrid finite element technique for crack
analysis.—In: Fracture mechanics and technology. Proceedings of an interna-
international conference. Hon Kong, March 21-25, 1977 /Eds G.C.Sih, C.L.Chow.
V. II. Sijthoff & Noordhoff International Publishers. 1977. P. 1445-1466.
413. Trace у D.M. 3-D elastic singularity element for evaluation of К along an
arbitrary crack front / International journal of fracture. 1973. V. 9, № 3.
P. 340-343.
414. Tracey D.M. Finite elements for tree-dimensional elastic crack analy-
analysis /Nuclear engineering and design. 1974. V. 26, № 2. P. 282-290.
415. Tresher R.W., Smith F. W. Stress-intensity factors for a surface crack in
a finite solid / Trans, of the ASME. Series E. Journal of applied mechanics.
1972. V. 39, № 1. P. 195-200.
416. Tseng A. A. A three-dimensional finite element analysis of the three-point
bend specimen / Engineering fracture mechanics. 1980. V. 13, № 4. P. 939-
943.
417. Vijayakumar K., Atluri S. N. An embedded elliptical crack in an infinite
solid, subject to arbitrary crack-face tractions / Trans, of the ASME. Journal
of applied mehcanics. 1981. V. 48, X* 1. P. 88-96.
368 Список литературы
418. Visscher W.M. Theory of scattering of elastic waves from flat cracks of
arbitrary shape /Wave motion. 1983. V. 5, № 1. P. 15-32.
419. Visscher W.M. Elastic wave scattering by a surface-breaking or subsurface
planar crack II. Three-dimensional geometry / Journal of the applied physics.
1985. V. 57, № 5. P. 1538-1550.
420. Walpole L. J. Some elastostatic and potential problems for an elliptical
disc /Proceedings of the Cambridge philosophical society. 1970. V. 67. Pt. 1.
P. 225-235.
421. Wang M.-H. A modified S theory /Engineering fracture mechanics. 1985.
V. 22, № 4. P. 579-584.
422. Wang T.-C, Shih C.F., Suo Z. Crack extension and kinking in laminates
and bicristals / International journal of soUds and structures. 1992. V. 29, № 3.
P. 327-344.
423. Weaver J. Three-dimensional crack analysis / International journal of solids
and structures. 1977. V. 13, № 4. P. 321-330.
424. Wells A. A. Unstable crack propagation in metals-cleavage and fast frac-
fracture.—In: Proc. Crack propagation Symposium, Granfield. 1961. P. 210-230.
425. Westmann R. A. Asymmetric mixed boundary-value problems of the elastic
half-space / Trans, of the ASME. Series E. Journal of applied mechanics. 1965.
V. 35, № 2. P. 411-417.
426. Wilkins M.L. Fracture studies with two- and three-dimensional computer
simulation programs.—In: Fracture Mechanics and Technology. V. 2. Pro-
Proceedings of an International conference. Hon Kong. 21-25 March, 1977 /Eds
G.C. Sih, C.L. Chow.—Sijthoff & Noordhoff International Publishers, 1977.
P. 965-980.
427. Willis J.R. Fracture mechanics of interfacial cracks /Journal of the me-
mechanics and physics of solids. 1971. V. 19. P. 353-368.
428. Willis J.R. The penny-shaped crack on an interface /Quarterly Journal of
Mechanics and Applied Mathematics. 1972. V. 25. Pt. 3. P. 367-385.
429. Willis J.R. A polarization approach to the scattering of elastic waves —
I. Scattering by a single inclusion / Journal of the mechanics and physics of
solids. 1980. V. 28, № 5/6. P. 287-305.
430. Willis J.R. A polarization approach to the scattering of elastic waves —
II. Multiple scattering from inclusions / Journal of the mechanics and physics
of solids. 1980. V. 28, № 5/6. P. 307-327.
431. Wilson W. K. Finite element methods for elastic bodies containing cracks.—
In: Mechanics of fracture. V. 1. Methods of analysis and solutions of crack
problems /Ed. G.C.Sih.—Leyden, 1973. P. 484-515.
432. Wu X. R. Stress intensity factors for half-elliptical surface cracks subjected
to complex crack face loadings / Engineering fracture mechanics. 1984. V. 19,
№ 3. P. 387-405.
433. Yashi O. S., Erdogan F. A pressurized cylindrical shell with a fixed end
which contains an axial part-through crack / International journal of fracture.
1985. V. 28, № 3. P. 161-187.