/
Text
А. И. Колчин В. П. Демидов
РАСЧЕТ АВТОМОБИЛЬНЫХ И ТРАКТОРНЫХ ДВИГАТЕЛЕЙ
ВЫСШАЯ ШКОЛА
1980
ББК- Ждб-Кбо
УДК 621.43
Рецензент
Канд. техн, наук, доц. В. В. Лайок (Московский автомеханический институту
Колчин А. И., Демидов В. П.
К 60 Расчет автомобильных и тракторных двигателей: Учеб, пособие для вузов. —2-е изд., перераб. и доп.—М.: Высш, школа, 1980. — 400 с., ил.
В пер.: 1р. 10 к.
Книга содержит необходимые сведений и систематизированную методику расчетов автомобильных и тракторных двигателей. Взаимосвязь теплового расчета с динамическим, а также с расчетом деталей иа прочность и с расчетами систем показана на примерах комплексных расчетов карбюраторного двигателя и дизеля с наддувом.
Во втором издании (первое вышло в 1971 г.) дополнительно даны анализ теоретических циклов, методы борьбы с токсичными выбросами двигателей, расчеты агрегатов наддува, безударных кулачков и систем питания; расширены тепловые расчеты карбю-1 раториого двигателя и дизеля, описана возможность применения электронно-вычислительных машин при расчете теоретических циклов
П редназначается в качестве учебного пособия для студентов вузов, обучающихся по специальностям «Автомобильный транспорт», «Строительные и дорожные машины и оборудование», а также «Автомобили и тракторы». Может быть испо^зована инженерно-техничет ими работниками
31803—383 6П2.24
к 001(01)—80 78-80 3603000000 ББК 39.35
Альберт Иванович Колчин, Виктор Петрович Демидов
РАСЧЕТ АВТОМОБИЛЬНЫХ И ТРАКТОРНЫХ ДВИГАТЕЛЕЙ
Зав. редакцией Н. И. Хрусталева. Редактор И. Е, Якушина
Мл. редакторы Т. Ф. Артюхина, С. Ф. Шабарина. Художник Ю. С Шлепер.
Худож. редактор Т, А. Дурасова. Техн, редактор Н. А. Битюкова.
Корректор Р. К Косинова.
ИБ№ 2088
Изд. № СТ Д-323. Сдано в набор 16.04 80. Подп. в печать 28.08.80. Т-15038. Формат бОхЭО'/и- Бум, тип. № 2. Гарнитура литературная. Печать высокая. Объем 25 усл. печ. л.
Уч.-изд. л. 25,94 Тираж 30 000 экз. Зак. №370 Цена 1 р. 10 к.
Издательство «Высшая школа», Москва, К-51, Неглинная ул., д. 29/14.
Ярославский полнграфкомбинаТ Союзполнграфпрома прн Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. 150014. Ярославль, ул. Свободы, 97.
© Издательство «Высшая школа», 1980
ПРЕДИСЛОВИЕ
Решениями XXV съезда КПСС и последующих пленумов ЦК КПСС определены перспективы развития в нашей стране всех отраслей народного хозяйства, в том числе и перспектива развития двигателе-строения.
Прогресс в автомобильной и тракторной промышленности, дальнейшее увеличение грузооборота автомобильного транспорта, значительное расширение тракторного парка в сельском хозяйстве предусматривают не только количественный рост автотракторного парка, но и значительное улучшение использования имеющихся автомобилей и тракторов, повышение культуры их эксплуатации, увеличение межремонтных сроков.
В области развития и совершенствования автомобильных и тракторных двигателей основными задачами на современном этапе являются: расширение использования дизелей, снижение топливной экономичности и удельной массы двигателей, стоимости их производства и эксплуатации. На принципиально новый уровень ставится борьба с токсичными выбросами двигателей в атмосферу, а также задачи по снижению шума двигателей в процессе их эксплуатации. Значительно больше внимания уделяется использованию электронно-вычислительных машин при расчетах и испытаниях двигателей. Намечаются пути использования вычислительной техники непосредственно в конструкциях двигателей и в первую очередь в конструкциях дизелей.
Выполнение этих задач требует от специалистов, связанных с производством и эксплуатацией автомобильных и тракторных двигателей, глубоких знаний теории, конструкции и расчета двигателей внутреннего сгорания.
Курс «Теория, конструирование и расчет автомобильных и тракторных двигателей» является комплексным и состоит из четырех самостоятельных разделов: «Теория двигателей», «Питание двигателей», «Динамика двигателей», «Конструирование и расчет автомобильных и тракторных двигателей».
Книга содержит необходимые сведения и систематизированную методику расчетов автомобильных и тракторных двигателей.
Учебное пособие подготовлено в соответствии с утвержденной программой курса «Автомобильные двигатели» для специальности 1609 «Автомобильный транспорт». Оно преследует цель не только помочь студентам в усвоении материала, приобретении глубоких зна-"ний, но и в практическом применении этих знаний при проектировании и расчетах автомобильных-и тракторных двигателей.
В отличие от первого издания второе издание учебного пособия
з
дополнено и переработано. Введены: глава II, в которой дан анализ теоретических замкнутых и разомкнутых циклов; методы борьбы с токсичными выбросами двигателей; глава о наддуве двигателей и методика расчетов агрегатов наддува с пояснительными примерами, взаимосвязанными с общим комплексным расчетом дизеля; глава по расчету основных элементов систем питания карбюраторных двигателей и дизелей. Приведен тепловой расчет карбюраторного двигателя не для одной точки, а для четырех, что существенно расширяет его познавательность. Тепловой расчет дизеля проведен в двух вариантах — для дизеля с наддувом и без наддува. Описана возможность применения электронно-вычислительных машин при расчете теоретических разомкнутых циклов, даны программа и результаты расчетов на ЭВМ. При рассмотрении механизма газораспределения приведен материал о безударных кулачках, методе их профилирования и пример расчета безударного кулачка для легкового автомобиля.
Материал между авторами распределен следующим образом: А. И. Колчин — гл. I (§ 3, 4), гл. II—VI, VII (§ 27, 31—34), гл. IX, XIII, XV (§ 61—65), гл. XVII (§ 72—74); приложения I—IV; В. П. Демидов — гл. I (§ 1, 2), гл. VII (§ 28—30), гл. VIII, X— XII, XIV, XV (§ 66, 67), гл. XVI, XVII (§ 75), гл. XVIII, XIX, литература, приложение V.
Авторы будут признательны читателям, которые пришлют критические замечания по адресу: Москва, К-51, Неглинная, ул., д. 29/14, издательство «Высшая школа».
Авторы
Часть первая
РАБОЧИЕ ПРОЦЕССЫ И ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ
Главе I
ТОПЛИВО И ХИМИЧЕСКИЕ РЕАКЦИИ
§ 1. ОБЩИЕ СВЕДЕНИЯ
Физико-химические свойства топлив, применяемых в автотракторных двигателях, должны отвечать определенным требованиям, зависящим от типа двигателя, особенностей его конструкции, параметров рабочего процесса и условий эксплуатации. Для современных автомобильных карбюраторных двигателей в основном применяются бензины прямой перегонки и крекинг-процесса или их смеси. В табл.1 приведены в соответствии с ГОСТ 2084—67 основные показатели автомобильных бензинов.
Таблица 1
Нормы по маркам бензина
Показатели А-66 А-72 А-76 АИ-93 АИ-98
Детонационная стойкость: октановое число, определяемое по моторному методу, не не менее ........................
октановое число, определяемое по исследовательскому методу, не менее.............., ,
Содержание тетраэтилсвинца в г на 1 кг бензина, не более .........
66 72 76
Не нормируется
0,41
85
93
0,82
89
98
0,82
Автомобильные бензины, за исключением бензина марки АИ-98, подразделяют на виды:
а) летние — предназначены для применения во всех районах страны, кроме северных и северо-восточных, в период с 1 апреля по 1 октября; в южных районах допускается применение летних видов бензинов в течение всего года;
б) зимние — предназначены для применения в течение всех сезонов в северных и северо-восточных районах страны, в остальных районах с 1 октября по 1 апреля.
5
В период перехода с бензина летнего вида на зимний и наоборот допускается в течение одного месяца применять бензин как зимнего, так и летнего вида, а также их смеси.
Основным показателем автомобильных бензинов является октановое число, характеризующее способность бензина противостоять детонации и в основном определяющее максимально допустимую степень сжатия. Для карбюраторных двигателей без наддува ориентировочно можно принять следующую взаимосвязь допустимой степени сжатия и необходимого октанового числа топлива:
Степень сжатия .................. 5,5—7,0 7,0—7,5 7,5—8,5 8,5—10,5
Октановое число.................. 66—72 72—76 76—85 85—100
При использовании наддува необходимо применять топливо с повышенным октановым числом.
Для двигателей с воспламенением от сжатия применяют более тяжелые фракции нефти — дизельное топливо, получаемое прямой церегонкой или смешением продуктов прямой перегонки с каталитическим газойлем (не более 20% в составе смеси). В соответствии с ГОСТ 305—73 и ГОСТ 4749—73 дизельное автотракторное топливо выпускается следующих марок:
А — арктическое дизельное автотракторное топливо, рекомендуемое для дизелей, работающих при температуре —50° С и выше;
3 — зимнее дизельное автотракторное топливо, рекомендуемое для дизелей, работающих при температуре —30° С и выше;
Л — летнее дизельное автотракторное топливо, рекомендуемое для дизелей, работающих при температуре 0° С и выше;
С — специализированное дизельное топливо.
Дизельное топливо должно соответствовать требованиям, указанным в табл. 2.
Основным показателем дизельного, топлива является цетановое число, которое в первую очередь определяет способность топлива к самовоспламенению, что является необходимым условием работы
Таблица 2
Нормы по маркам топлива
Показатели
Л 3 Л ЗС ДА ДЗ
Цетановое число, не менее . .
Фракционный состав:
50% перегоняется при температуре, °C, не выше . . .
90% перегоняется при температуре, °C, не выше . . .
Фактические смолы на 100 мл топлира, мг, не более ..........
Сера, %, не более.............
Водорастворимые кислоты и щелочи ...........................
Механические прнмесн и вода .
45' 45
45 45
240 250
280 280
330 340
30 30
0,4 0,5
360 340
40 30
0,5 0,5
255 280
330 340
30 30
0,2 0,2
Отсутствуют »
дл
45
290
360
50
0,2
ДС
50
280
340
50
0,2
6
двигателя с воспламенением от сжатия. В некоторых случаях повышение цетанового числа топлива достигается добавлением в него специальных присадок (нитраты и различные перекиси) в количестве 0,5—3,0%.
Кроме указанных топлив для автомобильных и тракторных двигателей применяют различные виды природных и промышленных горючих газов. Газообразные топлива транспортируют в баллонах в сжатом или сжиженном состоянии, а подаются непосредственно в двигатель через подогреватель (или теплообменник-испаритель), редуктор и смеситель. Таким образом, независимо от агрегатного состояния транспортируемого газа в двигатель поступает газовоздушная смесь.
Все виды топлив, используемых в автомобильных и тракторных двигателях, представляют собой смесь различных углеводородов и отличаются элементарным составом.
Элементарный со^ав жидких топлив (бензин, дизельное топливо) обычно выражается в единицах массы (кг), а газообразных — в объемных единицах (м3 или моль).
Для жидких топлив
С + Н + 0 = 1, (1)
где С, Н и О — массовые доли углерода, водорода и кислорода в 1 кг топлива.
Для газообразных топлив
SCnHmOr + N2 =1, (2)
где CnHmOr — объемные доли каждого газа, входящего в 1 м3 или в 1 моль газообразного топлива; N2 — объемная доля азота.
Средний элементарный состав бензинов и дизельных топлив в массовых долях представлен в табл. 3, а газообразных топлив в объемных долях — в табл. 4.
Таблица 3
Жидкое топливо Содержание, кг
С н О
Бензин 0,855 0,145
Дизельное топливо 0,870 0,126 0,004
Таблица 4
Газообразное топливо Содержание, м3 нлн моль
Метан СН4 Этаи с,нв Пропан С3Н« Бутан с4н10 Тяже лые углеводороды нт Водород И, Окись углерода СО Углекислый газ СО2 Азот N,
Природный газ . 90,0 2,96 0,17 0,55 0,42 0,28 0,47 5,15
Синтезгаз . . . 52,0 — — — 3,4 9,0 I 11,0 — 24,6
Светильный газ 16,2 — — — 8,6 27,8 20,2 5,0 22,2
7
i 1 ХИМИЧЕСКИЕ РЕАКЦИИ ПРИ СГОРАНИИ ТОПЛИВА
Для полного сгорания массовой или объемной единицы топлива необходимо вполне определенное количество воздуха, которое называется теоретически необходимым и определяется по элементарному составу топлива.
Для жидких топлив
/0=—— (— С + 8Н — О) (3)
0 0,23 \ 3 /
где /о — теоретически необходимое количество воздуха в кг для сгорания 1 кг топлива, кг возд/кг топл; £0 — теоретически необходимое количество воздуха в кмоль для сгорания 1 кг топлива, кмоль возд/кг топл; 0,23 — массовое содержание кислорода в 1 кг воздуха; 0,208— объемное содержание кислорода в 1 кмоль воздуха.
Причем
^0 = (5)
где рв = 28,96 кг/кмоль — масса 1 кмоль воздуха.
Для газообразных топлив
<6)
где L'o — теоретически необходимое количество воздуха в моль или м3 для сгорания 1 моль или 1 м3 топлива (моль возд/моль топл или м3возд/м3 топл).
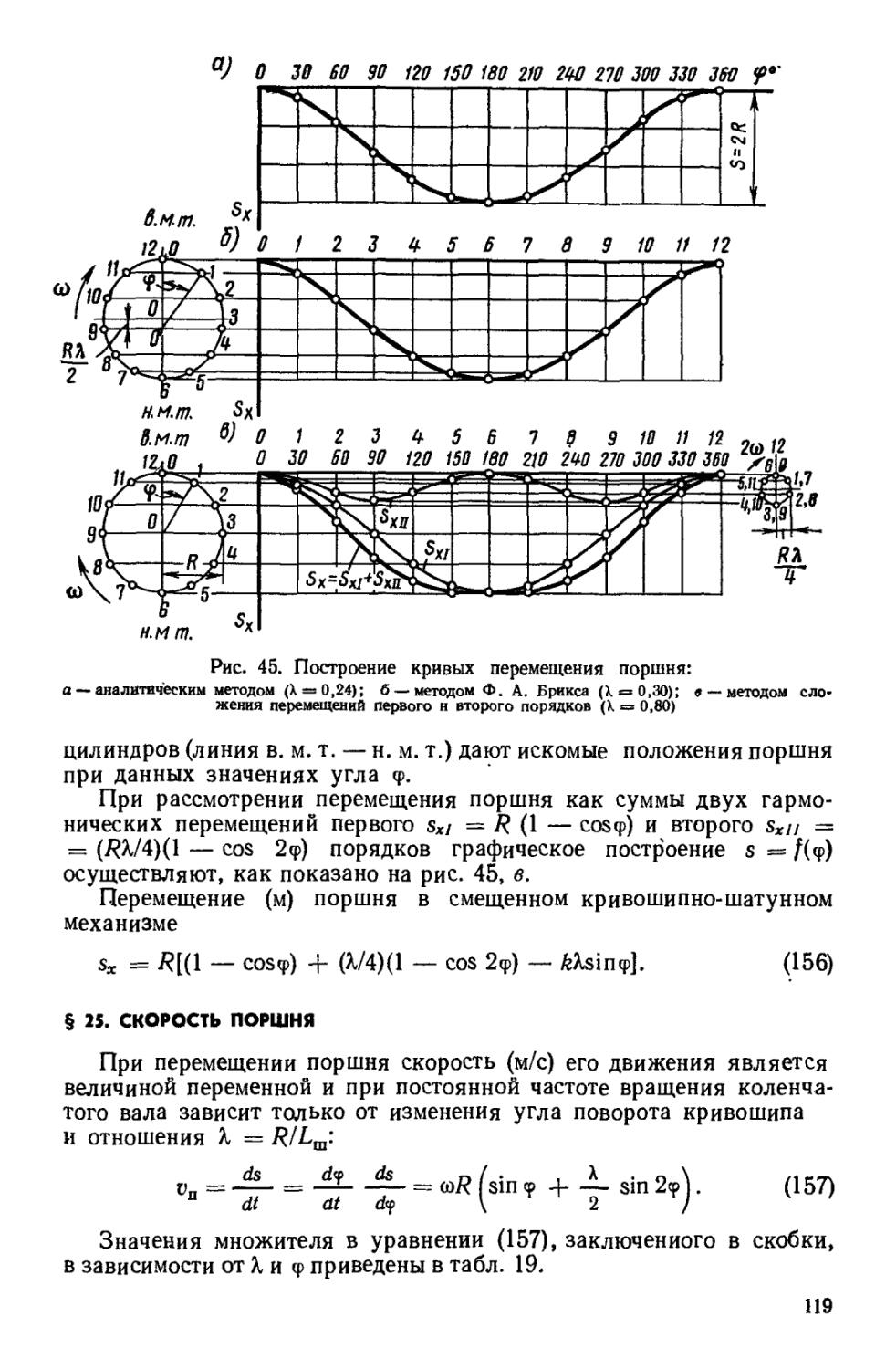
В зависимости от условий работы двигателя, способа регулирования мощности, типа смесеобразования и условий сгорания топлива на каждую массовую или объемную единицу топлива приходится количество воздуха, которое может быть больше, равно или меньше теоретически необходимого для полного сгорания топлива.
Отношение действительного количества воздуха I (или L), участвующего в сгорании 1 кг топлива, к теоретическй необходимому количеству воздуха /0 (или Lo) называется коэффициентом избытка воздуха:
а = l/l0 = L/Lo. (7)
Для различных двигателей при номинальной мощности принимаются следующие значения а:
Карбюраторные двигатели......................... 0,80—0,96
Двигатели с форкамерно-факельным зажиганием . . . 0,85—0,98
и выше
Дизели с неразделенными камерами и объемным смесеобразованием ................................. 1,50—1,70
Дизели с неразделенными камерами и пленочным смесеобразованием............................... 1,50—1,60
Вихрекамерные дизели ........................... 1,30—1,45
Предкамерные дизели............................. 1,40—1,50
Дизели с наддувом............................... 1,30—2,2
8
В двигателях с наддувом, когда осуществляется продувка цилиндров воздухом, используют суммарный коэффициент избытка воздуха а с = до, где <рп =1,0— 1,25 — коэффициент продувки четырехтактных двигателей.
Снижение а — один из эффективных путей форсировки рабочего процесса двигателя. Для заданной мощности двигателя уменьшение (до определенных пределов) коэффициента избытка воздуха приводит к меньшим размерам цилиндра. Однако с уменьшением величины а возникает неполнота сгорания топлива, ухудшается экономичность и увеличивается термическая напряженность двигателя. Практически полное сгорание топлива в двигателе возможно только при а > > 1, так как при а — 1 невозможно получить такую совершенную смесь топлива с воздухом, в которой каждая частица топлива была бы обеспечена необходимым количеством кислорода воздуха.
Горючая смесь (свежий заряд) в карбюраторных двигателях состоит из воздуха и испарившегося топлива и определяется величиной
Mi = а£о + 1/тт, (8)
где Mi — количество горючей смеси (кмоль гор.см/кг топл); тт — молекулярная масса паров топлива, кг/кмоль.
Для различных топлив принимаются следующие значения тт:
Для автомобильных бензинов ....... тт=110—120 кг/кмоль Для дизельных топлив тт=180—200 кг/кмоль
Величиной 1/тт при определении Afi для двигателей с воспламенением от сжатия пренебрегают, как относительно малой по сравнению с объемом воздуха. Поэтому для этих двигателей
Mi L aLo. (9)
Для газовых двигателей
/И1 =а£о, (Ю)
где М'1 — количество горючей смеси (моль гор.см/моль топл или м8 гор.см/м3 топл).
Для любого топлива масса горючей смеси
mi = а/0 + h (И)
где mi — массовое количество горючей смеси, кг гор.см/кг топл.
При полном сгорании топлива (а > 1) продукты сгорания состоят из углекислого газа СО2, водяного пара Н2О, избыточного кислорода Ог и азота N2.
Количество отдельны^ компонентов продуктов сгорания жидкого топлива при-а > 1:
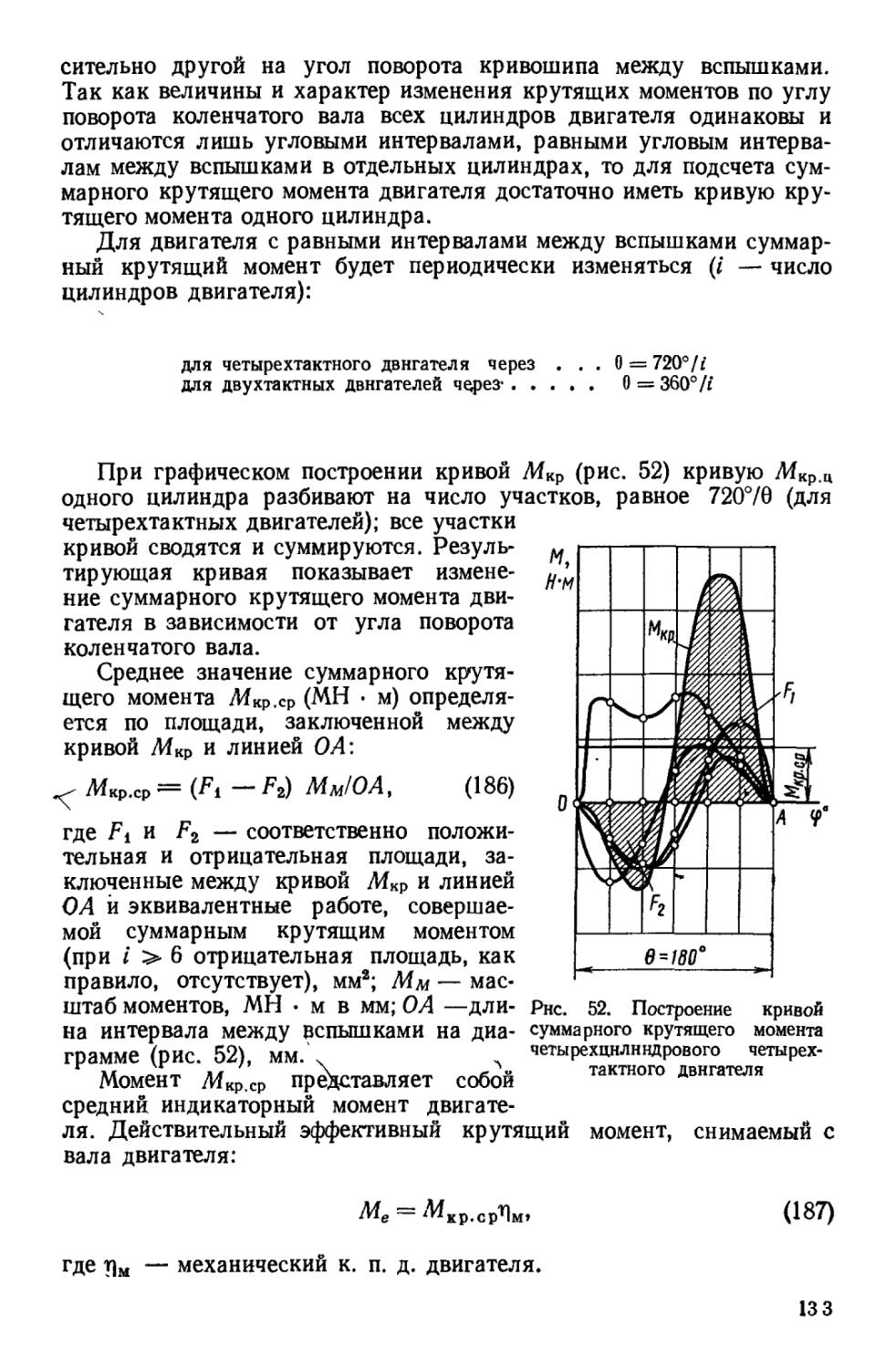
•а
углекислого газа (кмоль СОа/кг топл)
Мсо,=С/12;
водяного пара (кмоль Н2О/кг топл)
""•о-И/* (12)
кислорода (кмоль О^кг топл)
Afo, = 0,208(a —1)£о;
азота (кмоль N2/kt топл)
Mn, = O,792aLo.
Общее количество продуктов полного сгорания жидкого топлива (кмоль пр. сг/кг топл)
М2 = Мео, + Мн,о + Мо, 4- Мц, = C/12 Н/2 4- (а —0,208) Lo. (13)
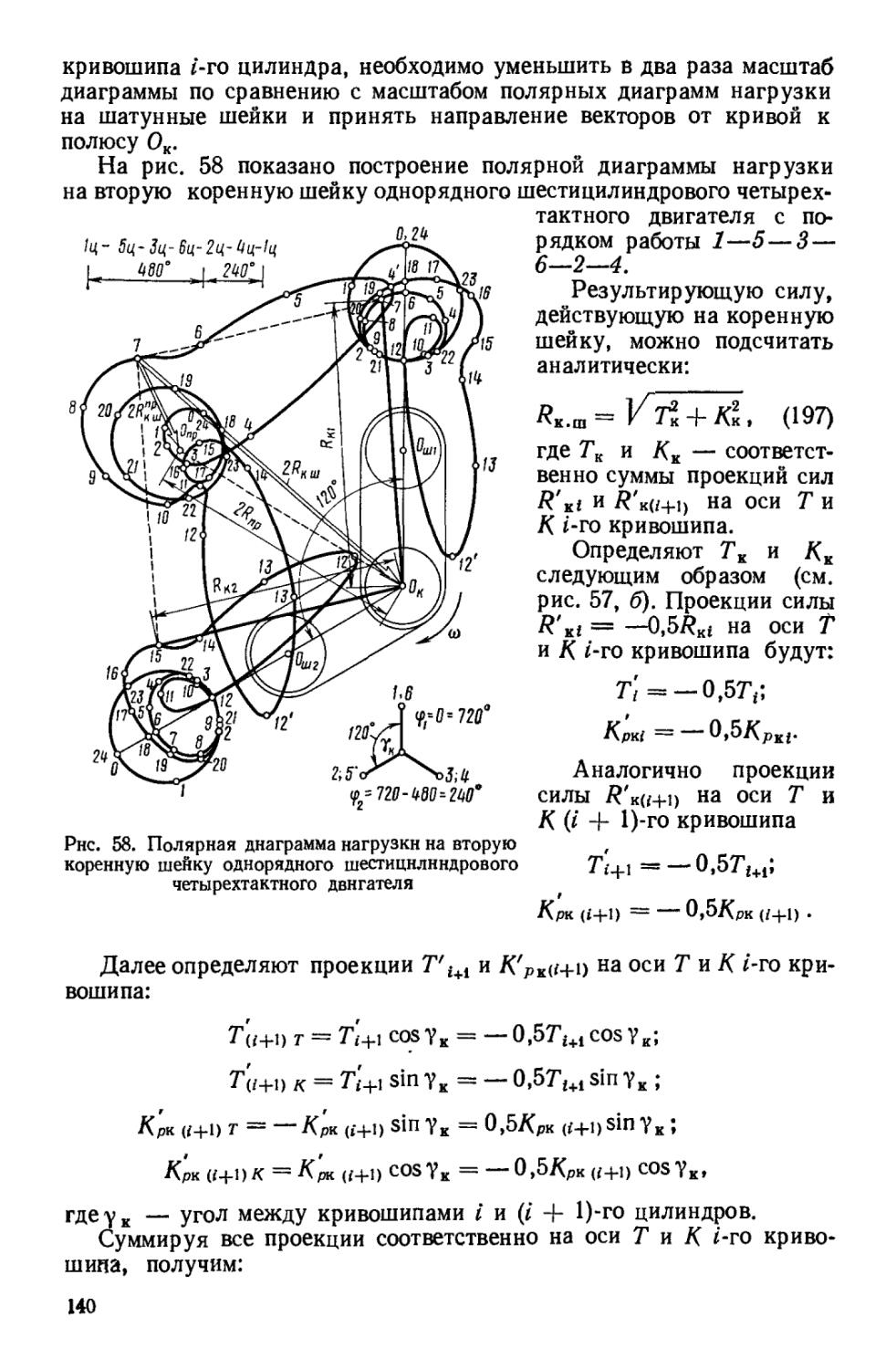
Количество отдельных компонентов продуктов сгорания газообразного топлива при а >• 1:
углекислого газа (моль СО2/моль топл) Moo, ='2«(CnHmO>)i ’ водяного пара (моль Н2О/моль топл)
Мн,о= J] y-(CnHmOr);
кислорода (моль О2/моль топл)
М'о, = 0,208 (a - l)Lo;
азота (моль N моль топл)
MNi = O,792aLo 4- N2,
(14)
где N2 — количество азота в топливе, моль.
Общее количество продуктов полного сгорания газообразного топлива (моль пр. сг/моль топл)
Л42 = Л4со, + Мщо + + ^ns •
(15)
При неполном сгорании топлива (а< 1) продукты сгорания представляют собой смесь окиси углерода СО, углекислого газа СО2, водяного пара НгО,свободного водорода Н2 и азота N2.
Количество отдельных компонентов продуктов неполного сгорания жидкого топлива:
10
углекислого газа (кмоль СОз/кг топл)
Мео, = ------2 -1^- 0.208L,;
’ 12 Ц-/С °’
окиси углерода (кмоль СО/кг топл)
Мео = 2 O,2O8Lo;
1 т* Л
водяного пара (кмоль Н2О/кг топл)
LT 1 /т (1 6)
Л4н,о = ~~2Х O,2O8Lo;
2 1 -f- Л
водорода (кмоль Нз/кг топл)
Mh, = 2K±=£O,2O8Lo;
1 4- А
азота (кмоль Ы2/кг топл)
Mn, = 0,792otL0,
где К — постоянная величина, зависящая от отношения количества водорода к окиси углерода, содержащихся в продуктах сгорания (для бензина К = 0,45 4- 0,50).
Общее количество продуктов неполного сгорания жидкого топлива кмоль пр. сг/кг топл)
М2 — Мео, + Мео + Мн,о + Мн, + Mn, = ~ + О,792а£о. (17)
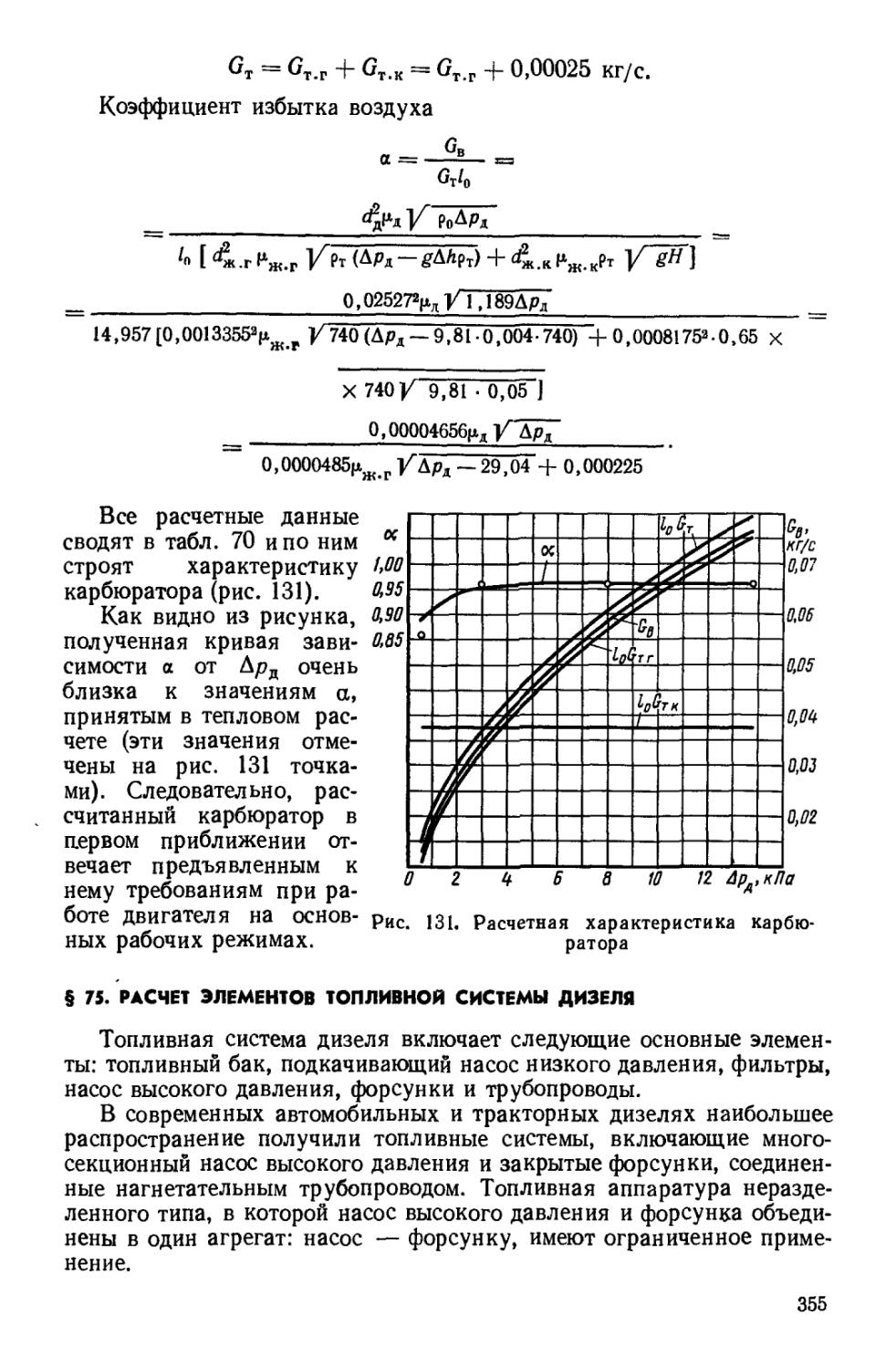
Зависимость количества горючей смеси (свежего заряда), продуктов сгорания и их составляющих от коэффициента избытка воздуха, в карбюраторном двигателе и в дизеле представлены на графиках (рис. 1 и 2).
Изменение количества молей рабочего тела при сгорании определяется как разность (кмоль см/кг топл):
ДЛ1 = М2 — Ml. (18)
Для жидкого топлива количество молей продуктов сгорания всегда больше, чем количество молей свежего заряда (горючей смеси). Приращение объема продуктов сгорания АЛ1 происходит вследствие увеличения суммарного количества молекул в результате химических реакций распада молекул топлива и образования новых молекул. Рост числа молей продуктов сгорания — положительный фактор, так как увеличивает объем продуктов сгорания и, следовательно, способствует некоторому возрастанию полезной работы газов при их расширении.
Изменение количества молей ДМ' в процессе сгорания газообразных топлив зависит от природы входящих в топливо углеводородов, их, количества, соотношения между количеством углеводородов, водорода, окиси углерода. Оно может быть как положительным, так й, отрицательным.
11
М^кмоль/кг топл
Рис. 1. Зависимость количества горючей смеси (свежего заряда), продуктов сгорания и их составляющих от коэффициента избытка воздуха в карбюраторном двигателе (mT = 110)
М1,кмоль/кгтопл
Рис. 2. Зависимость количества горючей смеси (свежего заряда), продуктов сгорания и их составляющих от коэффициента избытка воздуха в дизеле
Относительное изменение объема при сгорании характеризуется величиной химического коэффициента молекулярного изменения горючей смеси р0, который представляет собой отношение количества молей продуктов сгорания к количеству молей горючей смеси
Ро = Мг/Mt = 1 + ДЛ4/Л11.
(19)
Величина р0 для жидких топлив всегда больше единицы й возрастает с уменьшением коэффициента избытка воздуха (рис. 3). Излом кривой в точке, соответствующей а = 1, получается вследствие прекращения выделения окиси углерода СО и полного сгорания углерода топлива с образованием углекислого газа СО2.
В цилиндре реального
двигателя в сгорании участвует не горючая смесь, а так называемая рабочая смесь, которая состоит из свежего заряда (горючей смеси) Mt и остаточных газов МГ, т. е. части продуктов сгорания, не удаленной из цилиндра в процессе выпуска.
Относительное коли-
Рис. 3. Зависимость химического коэффициента молекулярного изменении горючей смеси от коэффициента избытка воздуха:
I — смесь Сеязина с воздухом; 2 — смесь днзельногб топлива с воздухом
честно остаточных газов характеризуется коэффициентом остаточных газов Тг = MTIMi. (20)
Изменение объема при сгорании рабочей смеси (горючая смесь + остаточные газы) учитывает действительный коэффициент молекулярного изменения рабочей смеси, который представляет собой отношение общего количества молей газов в цилиндре после сгорания (Л12 + Afr) к числу молей до сгорания М + мгу.
tb=(M2+Mr)/(M1 + Mr)= = (Po + Yr)/(b + U (21) Из выражения (21) следует, что действительный коэффициент молекулярного изменения рабочей смеси р зависит от коэффициента остаточных газов и химического коэффи-
Рис. 4. Зависимость коэффициента молекулярного изменения рабочей смеси от коэффициента остаточных газов, состава топлива и коэффициента избытка воздуха:
------бензин;----— дизельное топливо
циента молекулярного из-
менения горючей смеси р0. В свою очередь р0 зависит от состава топлива и коэффициента избытка воздуха а.
Наибольшее влияние на изменение величины р (рис. 4) оказывает именно коэффициент избытка воздуха а. С уменьшением а действительный коэффициент молекулярного изменения рабочей смеси растет и особенно интенсивно при обогащении смеси (а< 1).
Величина р изменяется в пределах:
Для карбюраторных двигателей .................... 1,02—1,12
Для дизелей...................................... 1,01—1,06
§ 3. ТЕПЛОТА СГОРАНИЯ ТОПЛИВА И ТОПЛИВОВОЗДУШНЫХ СМЕСЕЙ
Теплотой сгорания топлива называют то количество теплоты, которое выделяется при полном сгорании объемной или массовой еди ницы топлива.
Различают высшую HQ и низшую Ни теплоту сгорания топлйва. Под высшей теплотой сгорания понимается то количество теплоты, которое выделяется при полном сгорании топлива, включая теплоту конденсации водяных паров при охлаждении продуктов сгорания.
Под низшей теплотой сгорания понимается количество теплоты, которое выделяется при полном сгорании топлива, но^без учета теплоты конденсации водяного пара. Ни меньше высшей теплоты сгорания Но на величину скрытой теплоты парообразования
13
воды. Так как в двигателях внутреннего сгорания выпуск отработавших газов происходит при температуре выше температуры конденсации водяного пара, то для практической оценки тепловой ценности топлива обычно служит низшая теплота сгорания топлива.
Если известен элементарный состав жидкого топлива, то для приближенного определения его низшей теплоты сгорания (МДж/кг) обычно пользуются формулой Д. И. Менделеева
Ни = 33.91С + 125,60 Н — 10,89(0 — S) — 2,51(9 Н + W), (22)
где IF — количество водяных паров в продуктах сгорания массовой или объемной единицы топлива.
Для газообразного топлива его низшая теплота сгорания (МДж/м3)
Ни = 12,8(20 + 10,8На + 35,7Н4 + 56,0С2Н2 + бЭ.бОД + 63,ЗС2Нв +
+ 90,9СзН8 + 119,7С4Н10 + 146,2С5Н12. (23)
Примерные значения низшей теплоты сгорания автотракторных топлив Ни приведены ниже:
Топливо........ Бензин Дизельное Природный Пропан
газ
Ни.............44,0 МДж/кг 42,5 35,0 85,5
МДж/кг МДж/м3 МДж/м3
Бутан
112,0 МДж/м3
Для более полной характеристики тепловой оценки топлива не-
обходимо иметь не только теплоту сгорания самого топлива, но и теплоту сгорания топливовоздушных смесей. Отношение теплоты сгорания единицы топлива к общему количеству горючей смеси принято называть теплотой сгорания горючей смеси. При отношении
Рис. 5. Зависимость теплоты сгорания топливовоздушной смеси от коэффициента избытка воздуха:
/—•смесь воздуха с бензином, //^ = 44 МДж/кг;
2 — смесь воздуха с дизельным топливом, На *= = 42,5 МДж/кг
Ни к единице объема (кмоль) Ягор.см будет выражена в МДж/кмоль гор. см, а к единице массы — в МДж/кг гор. см.
Ягор.см = ИЛИ
^гор.см = (24)
В двигателях, работающих при а< 1, имеет место химическая неполнота сгорания топлива (МДж/кг) из-за недостатка кислорода
ДЯи = 119,95(1 — a)L0.
(25)
Следовательно, формула (24) при а< 1 примет вид
14
^гор-см — (#в и)!Mi ИЛИ Нгор-см в ЬНи)1Щ‘ (26)
На рис. 5 представлены зависимости теплоты сгорания топливовоздушных смесей от коэффициента избытка воздуха а. Необходимо отметить, что теплота сгорания горючей смеси не пропорциональна теплоте сгорания топлива. При одинаковых значениях а теплота сгорания смеси дизельного топлива с воздухом несколько выше теплоты
сгорания смеси бензина с воздухом. Это объясняется тем, что для полного сгорания единицы дизельного топлива требуется меньшее количество воздуха, чем для сгорания такого^же количества бензина. (Так как в процессе сгорания участвует не горючая смесь, а рабочая (горючая смесь + остаточные газы), то целесообразно теплоту сгорания топлива относить к общему количеству рабочей смеси (МДж/ кмоль раб. см):
при а > 1
Нраб .см == Н иКМл Мг) =
= Ни1\М1(\ +тг)], (27)
при а < 1
Рис. 6. Зависимости теплоты сгорания рабочей смеси от коэффициента избытка воздуха и коэффициента остаточных газов:
/ — смесь воздуха, остаточных газов и бензина, На =» в 44 МДж/кг; 2 — смесь воздуха, остаточных газов и дизельного топлива. Ни =» 42,5 МДж/кг
/Уралом = (Ни- ЬНи)!\М1 (1 + ?,)].
(28)
Из уравнений (27) и (28) следует, что теплота сгорания рабочей смеси меняется пропорционально изменению теплоты сгорания горючей смеси. При одинаковых значениях коэффициента избытка воздуха теплота сгорания рабочей смеси увеличивается при уменьшении коэффициента остаточных газов (рисб).) Это положение справедливо как для бензина, так и для дизельного топлива.
§ 4. ТЕПЛОЕМКОСТЬ ГАЗОВ
Средней теплоемкостью рабочего тела называется отношение количества теплоты, сообщаемой телу в заданном процессе, к изменению температуры при условии, что разность температур является конечной величиной. Величина теплоемкости зависит от температуры и давления тела, его физических свойств и характера процесса.
Для расчетов рабочих процессов двигателей обычно пользуются средними мольными теплоемкостями при постоянном объеме тсу
15
и при постоянном давлении тср [кДж/(кмоль-град)]. Между ними существует зависимость
тср — mcv = 8,315. (29)
Для определения средних мольных теплоемкостей различных газов в зависимости от температуры используют либо эмпирические формулы, либо справочные таблицы или графики*.
В табл. 5 даны значения средних мольных темплоемкостей некоторых газов при постоянном объеме**, а в табл. 6 приведены эмпирические формулы, полученные на основании анализа табличных данных. Отклонения значений средних мольных теплоемкостей, полученных по эмпирическим формулам, от табличных значений не превышают 1,8%.
Таблица 5
t, °C Средняя мольная теплоемкость отдельных газов при постоянном объеме, кДж/(кмоль-град)
Воздух О, 1 N« Н2 СО СО, Н2О
0 20,759 20,960 20,705 20,303 20,809 27,546 25,185
100 20,839 21,224 20,734 20,621 20,864 29,799 25,428
200 20,985 21,617 20,801 20,759 20,989 31,746 25,804
300 21,207 22,086 20,973 20,809 21,203 33,442 26,261
400 21,475 22,564 21,186 20,872 21,475 34,936 26,776
500 21,781 23,020 21,450 20,935 21,785 36,259 27,316
600 22,091 23,447 21,731 21,002 22,112 37,440 27,881
700 22,409 23,837 22,028 21,094 22,438 38,499 28,476
800 22,714 24,188 22,321 21,203 22,756 39,450 29,079
900 23,008 24,511 22,610 21,333 23,062 40,304 29,694
1000 23,284 24,804 22,882 21,475 23,351 41,079 30,306
1100 23,548 25,072 23,142 21,630 23,623 41,786 30,913
1200 23,795 25,319 23,393 21,793 23,878 42,427 31,511
1300 24,029 25,549 23,627 21,973 24,113 43,009 32,093
1400 24,251 25,763 23,849 22,153 24,339 43,545 32,663
1500 24,460 25,968 24,059 22,333 24,544 44,035 33,211
1600 24,653 26,160 24,251 22,518 24,737 44,487 33,743
1700 24,837 26,345 24,435 22,698 24,917 44,906 34,262
1800 25,005 26,520 24,603 22,878 25,089 45,291 34,756
1900 25,168 26,692 24,766 23,058 25,248 45,647 35,225
2000 25,327 26,855 24,917 23,234 25,394 45,977 35,682
2100 25,474 27,015 25,063 23,410 25,537 46,283 36,121
2200 25,612 27,169 25,202 23,577 25,666 46,568 36,540
2300 §6,746 27,320 25,327 23,744 25,792 46,832 36,942
24О0 25,871 27,471 25,449 23,908 25,909 47,079 37,331
2500 25,993 27,613 25,562 24,071 26,022 47,305 37,704
2600* 26,120 27,753 25,672 24,234 26,120 47,515 38,060
2700* 26,250 27,890 25,780 24,395 26,212 47,710 38,395
2800* 26,370 28,020 25,885 24,550 26,300 47,890 38,705
* Теплоемкость при 2600 , 2700 и 2800° С подсчитана методом интерполяции.
? В диапазоне давлений, используемых в автомобильных и тракторных двигателях, влиянием давления на средние мольные теплоемкости пренебрегают.
** Таблица рассчитана по данным учебника [9].
16
Наименование газа
Воздух .......................................
Кислород О2...................................
Азот Na.......................................
Водород На....................................
Окись углерода СО.............................
Углекислый газ СОа............................
Водяной пар НаО ..............................
Таблица 6
Формулы для определения средних мольных теплоемкостей отдельных газов при постоянном объеме, кДж/(кмоль-град), для температур
от 6 до 1500°С от 1501 до 2800°С
mcv = 20,600+0,0026381 mcv =22,387+0,001449 /
«^о =20,930+0,004641/ — — 0,00000084 й ««Vo, = 23,723+0,001550 /
тстг =20,398+ 0,002500 t • mcvti, =21,951+0,001457 /
«<+н= 20,684+ 0,000206 /+ +0,00Д0Р0Д88 /а «сИН!= 19,678+ 0,001758 /
«сУСО = 20,597+0,002670 / «сИсо =22,490+0,001430 /
™исо =27,941+0,019 /— — 0,000005487 /а ««too. = 39,123+0,003349 /
mcvn,o = 24,953+0,005359 / mcj,Hjo=26,670+ 0,004438/
GO
Таблица 7
Температура t,°c Средняя „мольная теплоемкость продуктов сгорания, кДж/ (кмоль- град), бензина при а i
0,70 0,75 0,80 0,85 0,90 0,95 1,00 1,05 1,10 1,15 1,20 1,25
0 21,683 21,786 21,880 21,966 22,046 22,119 22,187 22,123 22,065 22,011 21,962 21,916
100 21,902 22,031 22,149 22,257 22,356 22,448 22,533 22,457 22,388 22,325 22,266 22,216
200 22,140 22,292 22,431 22,559 22,676 22,784 22,885 22,796 22,722 22,650 22,584 22,523
300 22,445 22,618 22,776 22,921 23,055 23,973 23,293 23,200 23,115 23,036 22,964 22,898
400 22,777 22,968 23,143 23,303 23,450 23,586 23,712 23,613 23,521 23,437 23,360 23,289
500 23,138 23,345 23,534 23,707 23,867 24,014 24,150 24,045 23,948 23,859 23,777 23,702
600 23,507 23,727 23,929 24,113 24,284 24,440 24,586 24,475 24,373 24,280 24,193 24,114
700 23.882 24,115 24,328 24,523 24,868 25,021 24,905 24,798 24,700 24,610 24,527
800 24,249 24,493 24,715 24,919 J5JH7 >?280 25,441 25,319 25,208 25,106 25,012 24,925
900 24,608 24,861 25,092 25,304 25,500 OR КЯП 25,847 25,720 25,604 25,498 25,400 25,309
1000 24,949 25,211 25,449 25,668 25,870 1б?05б 26,229 26,098 25,977 25,867 25,766 25,672
1100 25,276 25,545 25,791 26,016 26,224 26,415 26,593 26,457 26,333 26,219 26,114 26,016
1200 25,590 25,866 26,118 26,349 26,562 26,758 26,940 26,800 26,672 26,554 26,446 26,345
1300 25,887 26,168 26,426 26,662 26,879 27,080 27,265 27,121 26,989 26,868 26,757 26,653
1400 26,099 26,456 26,719 26,959 27,180 27,385 27,574 27,426 27,291 27,166 27,051 26,945
1500 26,436 26,728 26,995 27,240 27,465 27,673 27,866 27,714 27,575 27,447 27,330 27,221
1600 26,685 26,982 27,253 27,501 27,729 27,941 28,136 27,981 27,836 27,708 27,588 27,477
1700 26,924 27,225 27,499 27,751 27,983 28,197 28,395 28,236 28,091 27,958 27,835 27,722
1800 27,147 27,451 27,728 27,983 28,218 28,434 28,634 28,473 28,324 28,188 28,063 27,948
1900 27,359 27,667 27,948 28,205 28,442 28,661 28,863 28,698 28,548 28,409 28,282 28,164
2000 27,559 27,870 28,153 28,413 28,652 28,873 29,078 28,910 28,757 28,616 28,487 28,367
2100 27,752 28,065 28,351 28,613 28,854 29,077 29,283 29,113 28,958 28,815 28,684 28,562
2200 27,935 28,251 28,539 28,803 29,046 29,270 29,478 29,306 29,148 29,004 28,870 28,747
2300 28,104 28,422 28,712 28,978 29,223 29,449 29,658 29,484 29,324 29,177 29,042 28,917
2400 28,268- 28,588 28,879 29,147 29,394 29,621 29,832 29,655 29,494 29,345 29,209 29,082
2500 28,422 28,744 29,037 29,305 29,553 29,782 29,993 29,815 29,652 29,502 . 29,364 29,236
2600 28,570 28,892 29,187 29,458 29,706 29,936 30,149 29,969 29,804 29,653 29,513 29,384
2700 28,711 20,036 29.332 29,604 29,854 30,085 30,298 30,116 29,950 29,797 29,657 29,527
2800 28,847 29,173 29*470 29,743 29,994 30,226 30,440 30,257 30,090 29,936 29,794 29,663
Таблица 8
Температу-ра г, °C Средняя мольная теплоемкость продуктов сгорания, кДж/(кмоль град}, дизельного топлива при а
1 1,1 1,2 1.3 1,4 1.5 1.6 1.8 2,0 2.2 2,4 2.6
0 22,184 22,061 ' 21,958 21,870 21,794 21,728 21,670 21,572 21,493 21,428 21,374 21,328
100 22,545 22,398 22,275 22,169 22,078 21,999 21,929 21,812 21,717 21,640 21,574 21,519
200 22,908 22,742 22,602 22,482 22,379 22,289 22,210 22,077 21,970 21,882 21,808 21,745
300 23,324 23,142 22,989 22,858 22,745 22,647 22,560 22,415 22,300 22,202 22,121 22,052
400 23,750 23,554 23,390 23,249 23,128 23,022 22,930 22,774 22,648 22,544 22,457' 22,384
500 24,192 23,985 23,811 23,662 23,533 23,421 23,322 23,157 23,023 22,914 22,822 22,743
600 24,631 24,413 24,229 24,073 23,937 23,819 23,716 23,541 23,401 23,285 23,188 23,106
700 25,069 24,840 24,648 24,484 24,342 24,218 24,109 23,927 23,780 23,659 23,557 23,471
800 25,490 25,251 25,050 24,879 24,731 24,602 24,488 24,298 24,144 24,018 23,912 23,822
9Q0 25,896 25,648 25,439 25,261 25,107 24,973 24,855 24,657 24,487 24,366 24,256 24,162
1000 26,278 26,021 25,804 25,620 25,460 25,321 25,199 24,993 2^,828 24,692 24,578 24,481
1100 26,641 26,375 26,151 25,960 25,795 25,652 25,525 25,313 25,142 25,001 24,883 24,783
1200 26,987 26,713 26,482 26,286 26,116 25,967 2г,837 25,618 25,442 25,296 25,175 25,071
1300 27,311 27,029 26,792 26,589 26,415 26,262 26,128 25,903 25.722 25,572 25,447 25,341
1400 27,618 27,328 27,085 26,877 26,698 26,541 26,404 26,173 25,986 25,833 25,705 25,596
1500 27,907 27,610 27,361 27,148 26,965 26,805 26,664 '26,427 26,237 26,080 25,948 25,836
1600 28,175 27,873 27,618 27,400 27,212 27,049 26,905 26,663 26,468 26,308 26,173 26,059
1700 28,432 28,123 27,863 27,641 27,449 27,282 27,135 26,888 26,690 26,526 26,389 26,272
1800 28,669 28,354 28,089 27,863 27,668 27,497 27,348 27,096 26,894 26,727 26,587 26,469
1900 28,895 28,575 28,305 28,076 27,877 27,704 27,552 27,296 27,090 26,921 26,781 26,658
2000 29,107 28,782 28,508 28,275 28,073 27,898 27,743 27,483 27,274 27,102 26,958 26,835
2100 29,310 28,980 28,703 28,466 28,262 28,083 27,926 27,663 27,451 27,276 27,130 27,005
2200 29,503 29,169 28,888 28,648 28,441 28,260 28,101 27,834 27,619 27,442 27,294 27,168
2300 29,680 29,342 29,057 28,815 28,605 28,422 28,261 27,991 27,774 27,595 27,444 27,317
2400 29,851 29,510 29,222 28,976 28,764 28,580 28,417 28,144 27,924 27,743 27,591 27,462
2500 30,011 29,666 29,375 29,127 28,913 28,726 28,562 28,286 28,064 27,881 , 27,728 27,598
2600 30,164 29,816 29,523 29,272 29,056 28,868 28,702 28,424 28,199 28,015 27,860 27,729
2700 30,311 29,960 29,664 29,412 29,194 29,004 28,837 28,557 28,331 28,144 27,988 27,856
2800 30,451 30,097 29,799 29,546 29,326 29,135 28,966 28,684 28,456 28,269 28,111 27,978
,При выполнении расчетов теплоемкость свежего заряда в карбюраторных двигателях и дизелях обычно принимается равной теплоемкости воздуха, т. е. без учета влияния паров топлива, а в газовых двигателях — без учета разности в теплоемкостях газообразного топлива и воздуха.
Среднюю мольную теплоемкость продуктов сгорания определяют как теплоемкость смеси газов [кДж/(кмоль- град)]:
(mc’v)to = ri (mcvl)t0, (30)
1=1
где гi = Mt/М2 — объемные доли каждого газа, входящего в данную смесь; (mcv i)k —средние мольные теплоемкости каждого *0
газй, входящего в данную смесь, при температуре смеси tx.
При полном сгорании топлива (а > 1) продукты сгорания состоят из смеси углекислого газа, водяных паров, азота, а при а> 1 и кислорода. При этом
{тсу}\г = -±- рИсо, (mcv со, У/ + МН10 (mcVti,o )\г /И2 L *о
+ /Hn2 (^i/n2)^ + Мо2 , (31)
где — температура, равная 0°С; iz — температура смеси в конце видимого сгорания.
При неполном сгорании топлива (а< 4) продукты сгорания состоят из смеси углекислого газа, окиси углерода, водяного пара, сво-'бодного водорода и азота. При этом
= ^-[Мсо, (mcv со,)!* + ^со (тсу со )£ +
+ Л4н,о (mfy Hj0)/* + Л4н, (тсу н; )<о ^N« (тси n,)<o]* (^2)
Значения средней мольной теплоемкости продуктов сгорания бензина (состав: С = 0,855; Н = 0,145) в зависимости от а даны в табл. 7, а значения средней мольной теплоемкости продуктов сгорания дизельного топлива (состав: С = 0,870; Н =0,126; О =0,004) — в табл. 8.
Глава II
ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
§ S. ОБЩИЕ СВЕДЕНИЯ
Теория двигателей внутреннего сгорания основана на использовании термодинамических зависимостей и приближении их к действительным условиям путем учета реальных факторов. Поэтому глубокое изучение теоретических (термодинамических) циклов, осно
20
ванное на знании термодинамики, является необходимым условием успешного изучения процессов, происходящих в цилиндрах реальных автомобильных и тракторных двигателей.
Замкнутые теоретические циклы в отличие от действительных процессов, происходящих в цилиндре двигателей, осуществляются в воображаемой тепловой машине и характеризуются следующими осо-бенностямц:
1. Преобразование теплоты в механическую энергию осуществляется в замкнутом объеме одним и тем же несменяемым количеством рабочего тела.
2. Состав и теплоемкость рабочего тела остаются постоянными.
3. Подвод теплоты производится от постороннего источника только при постоянном объеме и постоянном давлении.
4. Процессы сжатия и расширения протекают адиабатически, т. е. без теплообмена с окружающей средой, с одинаковыми и постоянными показателями адиабат.
5. В< теоретических циклах отсутствуют какие-либо потери теплоты (в том числе на трение, излучение, гидравлические потери ит.п.), кроме отвода теплоты холодному источнику. Эта потеря является единственной и обязательной для замкнутого теоретического цикла.
* Прототипами реальных рабочих циклов поршневых двигателей внутреннего сгорания без наддува являются теоретические циклы, приведенные на рис. 7: 1) цикл с подводом теплоты при постоянном объеме (рис. 7, а); 2) цикл с подводом теплоты при постоянном давлении (рис. 7, б) и 3) цикл со смешанным подводом теплоты при постоянном объеме и постоянном давлении (рис. 7, в).
Основные термодинамические соотношения показателей и параметров замкнутых теоретических циклов приведены в табл. 9.
Каждый теоретический цикл характеризуется двумя основными показателями: теплоиспользованием, которое определяется термическим коэффициентом полезного действия, и работоспособностью, которая определяется удельной работой цикла.
Термическим к. п. д. называется отношение количества теплоты, превращенной в полезную механическую работу, к общему количеству теплоты, подведенной к рабочему телу:
П f = (Qi - Q2)/Qi = 1 - Q2/Q1, (33)
где Qi — количество теплоты, подведенное к рабочему телу от постороннего источника; Q2 — количество теплоты, отведенное от рабочего тела холодному источнику.
Удельной работой цикла называется отношение количества теплоты, превращенной в механическую работу, к рабочему объему и выражается в Дж/м3:
Pt = (Qi - Q2)/(Va - Vc) = Lu/(Va - Vc), (34)
где Va — максимальный объем, занимаемый рабочим"телом в конце процесса расширения (н. м. т.), м3; Vc — минимальный объем, занимаемый рабочим телом в конце процесса сжатия (в. м. т.), м3; £ц =
Qi — Q2 — работа цикла, Дж (Н*м).
21
Таблица 9
Наименование и обозначение параметров Й показателей Основные определения Основные термодинамические соотношения теоретических циклов
со смешанным подводом теплоты при |Z = const и p=const с подводом теплоты при И—const с подводом теплоты при n==const
Степень сжатия е Отношение объемов в начале и конце сжатия e = Va/Vc = p8 В = Vaivc= 8 e=Va/Vc=P8
Показатель адиабат сжатия и расширения k Отношение теплоемкостей рабочего тела при р=const и V =-- const — cp!cv —(fy Н" R)/cv —1
Степень повышения давления в случае подвода теплоты при постоянном объеме X Отношение максимального давления цикла к давлению в конце сжатия X=pz/pc^7> ITc=rzl?Tc, ЛТое^(1+/гр-!г) X — Pz/Pc — TzlTc, . Q. (*-») , . RTaek~' + x = 1
Степень предварительного расширения в случае подвода теплоты при постоянном давлении р Отношение объемов в точках г и с P = VZIVC=^=TZ/\TC, Qi (fe—1) feX—X-J-1 P- RTaek-ikX 4 ЙХ P= 1 P = VZ/VC = S/B =TZ/TC, = Q, (fe-1) ₽ /?Tae*“l k
Степень последующего расширения б Отношение объемов в точках b и г 8 = VbIVz = VaIVz = e/p = = eX TCITZ 8 = VbIVz=VaIVc = e » = VbIVz^VaIVz = e/p =eTcITz
Общее кол и чество под веде иной теплоты Qi Qi— Д rae»-ip-i + + W(p-1)] 7 ' г ot Ьч ftr 1 •ад 1 СУ 7 г « (1) F-? OP 7 •ад II <7?
Количество отведенной теплоты Q2 Q2- bR, T’HXp*-!) я—I D Q2- . . Ta (X-l) я—1 p Qa- . . Ta(P*—1) я—1
Даиление рс и температура Тс в конце сжатия
Тг> тг, = ТаХе*-'
Тг тг = та\^р
Рг' рг, = раХе*
Рг Рг = Р0^*=рг,
Ть ть = W
pfe Рь = Р</Р*
Термический к. п. д. Отношение количества теплоты, превращен ной в полезную работу, к общему количеству подведенной теплоты Q1-Q2 , Q, хР*—1
Среднее давление цикла Pt Отношение количества теплоты, превращенной в работу, к рабочему объему Va-Vc k—l-f-feX (p—1) x fe-1
Pc = Pa*k И Tc = Task~l
— —
Гг = ТаХе*-1 тг = Тарв*->
— —
Рг = Ра^к = Рс
Tb = т> Ть=ТоРк
Pb = Рак РЬ = РаРк
__ Qi""Qa _ 1 * ' Q, е*"> Q1 Q2 Q, _ _ 1 pft—1 -1~ е*"’ й(р—1)
£Л ' e-1 X Р/ TZ Ра । X Va—Vc £—1 Л—1 х k_\ . 1-•ад i % 17 1 U) II «X £ II
Рис. 7. Диаграммы рУ и TV теоретических циклов (е =8; k — 1,4; ра = 0,1 МПа; Та = 300 К; Qi « 40 МДж/кмоль): а — с подводом теплоты при постоянном объеме (V = const); б — с подводом теплоты при постоянном давлении (р = const); в — со смешанным подводом теплоты прн постоянном объеме и постоянном давлении (V = const, Р ~ const, — Q* — 0,5Q, — 20 МДж/кмоль)
Удельная работа цикла (Дж/м8 = Н • м/м8 = Н/м2) численно равна среднему постоянному за цикл давлению (Па = Н/м2).
Рассмотрение и анализ теоретических циклов позволяет решить трн основные задачи: 1) оценить влияние термодинамических факторов на изменение термического' к. п. д. и среднего давления для данного цикла и на этой основе установить (если это возможно) оптимальные значения термодинамических факторов для получения наилучшей экономичности и максимальной удельной работы цикла; 2) провести сравнение различных теоретических циклов с точки зрения нх экономичности и работоспособности при однаковых условиях; 3) получить конкретные числовые значения термического к.п.д. и среднего давления цикла, которые могут являться критериями для оценки степени совершенства реальных двигателей по экономичности и удельной работе (мощности).
$ 6. ЗАМКНУТЫЕ ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ
Цикл с подводом теплоты при постоянном объеме. Для цикла с подводом теплоты при постоянном объеме термический к. п. д. и удельная работа (среднее давление цикла) соответственно определяются по формулам
T)t=l —1М’1; (35)
X — 1 ,ос.
— — ч>- (36)
Термический к. п. д. г] t зависит только от степени сжатия е и показателя адиабат сжатия и расширения k (рис. 8). Анализ формулы (35) и графика (рис. 8) показывает, что термический к. п. д.
постоянно растет при увеличении степени сжатия и показателя адиабаты. Однако возрастание заметно уменьшается при высоких степенях сжатия, начиная примерно с е = 12 4- 13. Изменение показателя адиабаты зависит от природы рабочего тела. Для расчета приняты три значения k, которые приближенно соответствуют рабочему телу, состоящему: 1) из двухатомных газов (воздух k = 1,4); 2) из смеси двух- и трех
атомных газов (продукты сгорания, k = 1,3); 3) из смеси воздуха и продуктов сгорания (k = 1,35).
Величина среднего давления цикла дополнительно зависит от начального давления ра и степени повышения давления А. Для двигателей, работающих без наддува,
Рис. 8. Зависимость термического к. п. д. цикла с подводом теплоты при постоянном объеме от степенй сжатия при различных показателях адиабаты
верхним предельным значением начального давления является атмосферное давление. Поэтому во всех расче
25
тах теоретических циклов давление ра принято равным атмосферному, т. е. ра =0,1 МПа. Изменение степени повышения давления обусловлено в первую очередь изменением количества подведенной к циклу теплоты Qi:
X = Q1(A-l)/(/?Tas^+l), (37)
где R =8315 Дж/кмоль- град— универсальная газовая постоянная; Та — начальная температура цикла, К.
На рис. 9 показана зависимость pt от степени повышения давления X при различных степенях сжатия е и двух значениях показателя адиабаты (k =1,4 — сплошные и k = 1,3 — штриховые линии). Такая зависимость pt при постоянных начальных условиях (ра = =0,1 МПа; Та = 350 К и Vfl = const) получается при увеличении количества подведенной к циклу теплоты от Qi = 0 при X = 1 до Qi = 120,6 МДж/кмоль при X = 6 и е = 20. Учитывая, что теплота сгорания бензовоздушных смесей при а = 1 не превышает 84 МДж/ кмоль, максимально возможное среднее давление теоретического цикла с подводом теплоты (Qi = 84 МДж/кмоль) при постоянном объеме не может быть выше 2,1 МПа при е = 20 и X = 4,5, а при е = = 8 и X =6 pt не превысит 1,85 МПа (см. кривую Qi = 84 МДж/ кмоль, пересекающую линии pt на рис. 9). Для получения более высоких значений X и pt необходимо подводить большее количество теплоты, т. е. иметь топливо с более высокой теплотой сгорания.
На рис. 10 представлены результаты расчета r| f, pt и X в зависимости от изменения степени сжатия при трех значениях количества подведенной теплоты (Qi = 80, 60 и 40 МДж/кмоль). Из приведенных данных видно, что среднее давление цикла возрастает прямо пропорционально росту количества теплоты, подведенной за цикл, но возрастание pt с увеличением е при одинаковом количестве подводимой теплоты протекает менее интенсивно, чем рост термического к. п. д. Так, при изменении е от 4 до 20 q t возрастает на 69%, a pt— только на 33%. Интенсивность возрастания pt при увеличении е не зависит от количества подведенной за цикл теплоты, т. е. при любом значении Qi (80, 60 или 40 МДж/кмоль) при изменении е от 4 до 20 среднее давление цикла увеличивается на 33%.
Уменьшение степени повышения давления с ростом степени сжатия при постоянном количестве подводимой теплоты соответствует обратно пропорциональной зависимости X от е*"1 [см. формулу (37)].
Из проведенного анализа термического к. п. д. и среднего давления замкнутого теоретического цикла с подводом теплоты при постоянном объеме можно сделать следующие выводы:
1. ^Минимальные потери теплоты в данном цикле получаются в случае использования в качестве рабочего Ъела воздуха и составляют не ниже 37% при е= 12 и не ниже 30,5% при е — 20 (см. рис. 8). Потери теплоты при использовании в качестве рабочего тела топливовоздушных смесей повышаются.
2. Максимальное значение среднего давления цикла при подведении теплоты Qi = 84 МДж/кмоль, приблизительно равной теплоте
26
сгорания бензовоздушной смеси, составляет не более 2,0 МПа при 8= 12 я не более 2,1 МПа при 8 = 20 (см. рис. 9).
3. По данному циклу целесообразно осуществлять рабочий процесс реального двигателя со степенями сжатия, не превышающими 8= 114- 12. Дальнейшее повышение степени сжатия дает увеличение удельной работы и к. п. д. цикла, но незначительно — в пределах 1—2% для r]t и 0,7 — 1,3% для pt при увеличении степени сжатия на одну единицу
Рис. 10. Зависимость термического к. п. д., среднего давления и степени повышения давления цикла с подводом теплоты при постоянном объеме от степени сжатия при различном количестве подведенной теплоты (ра — =0,1 МПа; Та = 350 К; k = 1,35; R =
—0,008315 МДж/(кмоль* град).
Индексы: 1 — при Q, = 80 МДж/кмоль; 2 — при Qi = 60 МДж/кмоль; 3 — при Qt = 40 МДж/кмоль
Рис. 9. Зависимость среднего давления цикла от степени повышения давления при различных степенях сжатия и показателях адиабаты:
------ k= 1,4;-----£=1,3
Цикл с подводом теплоты при постоянном давлении. Термический к. п. д. и среднее давление цикла с подводом теплоты при постоянном давлении определяются по формулам:
. ~ 1
* Мр-1) ’
k (р — 1) — ,|‘-
’it =1 —
1
- е — I
Ра
(38)
(39)
Термический к. п. д. данного цикла, так же как и цикла с подводом теплоты при постоянном объеме, растет с увеличением степени сжатия е и показателя адиабаты k. Однако при любых степенях сжатия 211 цикла с подводом теплоты при р ~ const меньше 211 цикла с
27
подводом тегглоты при V = const, так как множитель (pfe—1)/[£(р — — 1)] всегда больше единицы [см. (35) и (38)],
Термический к. п. д. цикла с подводом теплоты при р~ const зави*-сит также от степени предварительного расширения р,_т. е. отнагрузкиг + h (40)
С увеличением количества подведенной теплоты, т. е. с увеличе-. нием степени предварительного расширения, термический к. п. д.
падает. Это объясняется тем,
Рис. 11. Зависимость термического к. п. д. цикла с подводом теплоты при р = const от степени сжатия при различных значениях
что с увеличением р растет количество отведенной теплоты холодному источнику и, следовательно, уменьшается количество теплоты, превращенной в механическую работу. Таким образом максимальное значение термического к. п. д. достигается при минимальном количестве подведенной теплоты, что в реальных условиях наблюдается при холостом ходе двигателя.
На рис. 11 представлена зависимость термического к. п. д. цикла с подводом
степени предварительного расширения и показателя адиабаты (ра = 0,1 МПа; Та— =350 К, Va = const).
Индексы: 1 — при р = 2 и А = 1,4, 2 — при р — 3 и k= 1,4; 3 — при Qi = 80 МДж/кмоль и А= 1,4;
4 — при Qi = 80 МДж/кмоль и k = 1,3
теплоты при р = const от степени сжатия е при различных значениях степени предварительного расширения р и двух значениях показателя адиабаты (k — 1,4 — сплош-
ные, k— 1,3 —пунктирные линии). Две кривые рассчитаны и построены при р = 2 и р = 3 и, следовательно, при переменном количестве подводимой теплоты Qi для каждой величины степени
сжатия, а две кривые построены при одинаковом количестве подведенной теплоты (Qt = 80 МДж/кмоль) и, следовательно, переменных значениях степени предварительного расширения. Полученная при этом зависимость р от е также представлена на рис. 11.
Зависимость среднего давления цикла pt от степени сжатия е и показателя адиабаты k аналогична зависимости термического к. п. д.
от тех же параметров. Но цри увеличении количества подводимой теплоты $1, т. е. при увеличении степени предварительного расшире-
ния р, среднее давление цикла pt растет, несмотря на падение термического к. п. д. (рис. 12).
Из анализа формул и графиков изменения r]f и pt можно сделать
сл ед у ющи е вы воды:
1. Значения и pt цикла с подводом теплоты при р — const для небольших степеней сжатия значительно ниже соответствующих
28
Рис. 12. Зависимость термического к. п. д. и среднего давления цикла с подводом теплоты при постоянном давлении от количества подведенной теплоты при различных значениях степени сжатия
показателей цикла с подводом теплоты при постоянном объеме. Даже при £—10 потери теплоты составляют от 46% при р = 2 до 57% при р — 4,1 в воздушном цикле, а при k — 1,3 потери теплоты при е^=-Ю составляют 66%.
2. При малых степенях сжатия и значительном подводе теплоты цикл р ~ const вообще не существует, так как р не может превышать е. Например, при Qi — 80 МДж/кмоль (см. рис. 11) цикл может существовать только при 8 > 5.
3. Уменьшение величины показателя адиабаты с k — ~ 1,4 до k ~ 1,3 влечет за собой значительное уменьшение термического к. п. д. ц* и среднего давления цикла pt. Так, при 8 = 20 и Qi = 80 МДж/кмоль по расчетным данным потери теплоты возрастают с 41 до 52% (см. кривые г] *з и T]f4 на рис. 1*1), а среднее давление цикла уменьшается на 20%.
4. Использование цикла в качестве прототипа рабочих процессов в реальных двигателях целесообразно только при значительных степенях сжатия (более 10), при работе с неполной нагрузкой (уменьшение р) и при значительно обедненной смеси (приближение k к значению k воздушного цикла). Следует отметить, что данный цикл не используется в качестве прототипа для организации рабочего цикла в современных автомобильных и тракторных двигателях.
Цикл со смешанным подводом теплоты. В этом цикле подвод теплоты Qi осуществляется как при постоянном объеме Qi, так и при постоянном давлении Qi (см. рис. 7, в):
Qi = Qi + Qi = [X — 14- лх <p — 1)], (41)
где Qi = -—-Т^1^ — 1) — теплота, подведенная при постоянном Я 1
R
объеме; Q1 *= -—рТаеА’1^Х(р—1) — теплота, подведенная при постоянном давлении.
Соотношение между Qi и Qi может изменяться в' пределах от
Qi = Qi и Q'[ = 0 до Qi — 0 и Q'i — Qi. При Qi == Qi и Q'[ = 0
29
вся теплота подводится при постоянном объеме и, следовательно, данный цикл превращается в цикл с подводом теплоты при постоянном объеме. В этом случае степень предварительного расширения Р = 1 и формула (41) превращается в формулу для цикла с подводом теплрты при постоянном объеме (см. табл. 9).
При Q[ == 0 и Q[ = Qi вся теплота подводится при постоянном давлении, а цикл превращается в цикл с подводом теплоты при постоянном давлении, для которого степень повышения давления X = 1. В этом случае формула (41) превращается в формулу для цикла с подводом теплоты при постоянном давлении (см. табл. 9).
Рис. 13. Зависимость между степенью предварительного расширения (в = 16;
повышения давления и степенью Ql = Qf Qf = 80 МДж/кмоль)
I Г ft
I При всех промежуточных значениях Qi и Qi существует жесткая взаимосвязь между X и р для данного количества подведенной теплоты Qi и заданной степени сжатия е. На рис. 13, а представлена зависимость между степенью повышения давления X и степенью предварительного расширения р при Qi = 80 МДж/кмоль и 8 = 16, а по кривым на рис. 13, б определяется количество теплоты, подведенной при V = const и р = const в зависимости от выбранных значений X и р. Например, значениям Х= 3,5 и р = 1,25 (рис. 13, а) соответствует Qi = 55 МДж/кмоль —теплота, подведенная при V = const, и Q1 = 25 МДж/кмоль—теплота, подведенная при р = const (рис. 13, б). Вели же задано количество теплоты, подведенной при V = const и р = const, например Qi = Q” = 0,5 Qi = 40 МДж/кмоль, то по кривым, изображенным на рис. 13, б, определяются значения Х=2,8 и р=1,5.
Термический к. п. д. и среднее давление цикла со смешанным под-
водом теплоты:
T]i= 1
_1__________Хрй—1 .
е*-1 х — 1 + а (р — 1) ’
(42)
30
„ _ „ 8* x —i +&x(P-1)
Pt ~ Pa e _ [ b i
(43)
k— 1
Анализируя формулы (42) и (43) и аналитические зависимости двух других, уже рассмотренных циклов (см. табл. 9), можно сделать вывод, что при одинаковых начальных условиях й одинаковом количестве подведенной теплоты значения термического к. п. д. и среднего
Рис. 14. Зависимость термического к. п.д. и среднего давления теоретических циклов от степени сжатия при различных способах подвода теплоты (ра = 0,1 МПа; Та == 350 К; k = 1,4; Qi = 84 МДж/кмоль; Va ~ const).
Индексы: V — цикл с подводом теплоты при V = const, / — цикл со смешанным подводом теплоты при = Qt = 0.5Q! = 42 МДж/кмоль, 2 — цикл со смешанным подводом теплоты при А = 2 = const; 3 — цикл со смешанным подводом теплоты при р — 3,2 — const; р — цикл с подводом теплоты при р 5= const
давления цикла со смешанным подводом теплоты всегда меньше соответствующих значений и pt цикла с подводом теплоты при по-стоянном объеме и всегда больше соответствующих значений г|( и р( цикла с подводом теплоты при постоянном давлении. Это положение подтверждается и расчетными данными, представленными в виде графиков на рис. 14, а, б.
Расчет термического к. п. д. и среднего давления цикла со смешанным подводом теплоты приведен для трех различных условий подвода теплоты:
1) при всех значениях степени сжатия количество подведенной теплоты при постоянном объеме остается постоянным и равным количеству теплоты, подведенной при постоянном давлении, т. е. Qi = = Q1 = 0,5Qi = 42 МДж/кмоль. В этом- случае значения степени повышения давления X и степени предварительного расширения р
31
Рис. 15. Зависимость максимальных температур 7\, давлений pz и температур в конце расширения Ть от степени сжатия при различных способах подвода теплоты (ра =0,1 МПа; Та = 350 К; k = 1,4; Qi = 84 МДж/кмоль). Индексы. V — цикл с подводом теплоты при V » const; а — цикл со смешанным подводом теплоты при = Q* ® 0,5Qt = 42 МДж/кмоль, X — цикл со смешанным подводом теплоты при X ss 2 = const;
р — цикл с подводом теплоты при р » const
постоянно изменяются в зависимости от изменения степени сжатия е. Характер же изменения термического к, п. д. и среднего давления цикла примерно соответствует характеру изменения соответствующих параметров цикла с подводом теплоты при V — const (см. кривые с индексами 1 и V на рис. 14, а, б);
2) при всех значениях степени сжатия сохраняется постоянное значение степени повышения давления X — 2. В результате с увеличением степени сжатия количество подводимой теплоты при постоянном объеме возрастает, а при ” " постоянном давлении — сок-
ращается. Поэтому термический к. п. д. и среднее давление цикла с увеличением е возрастают более интенсивно, чем в первом случае, и на больших степенях сжатия (е= 17 — 20) их значения приближаются к значениям соответствующих показателей цикла с подводом теплоты при V = const (см. кривые с индексом 2);
3) при всех значениях степени сжатия сохраняется | постоянное значение степени предварительного расширения р = 3,2. В результате с
увеличением 8 количество подведенной теплоты при V= = const сокращается, а при р = const — возрастает. Рост термического к. п.д. и среднего давления цикла менее интенсивен, чем в первых двух случаях, а их значения приближаются к значениям r)z и pt цикла с подводом теплоты
прн р~ const (см. кривые с индексами 3 и р).
Для более полного анализа теоретических циклов необходимо
рассмотреть кроме изменения термического к. п. д. и среднего давления циклов изменения значений максимальных температур и давлений циклов, а также температур в конце расширения. В реальных условиях максимальные значения давлений ограничиваются условиями допустимой прочности деталей двигателя, а максимальные значения температур, кроме того, условиями бездетонацнонной работы двигателя на данном топливе и качеством смазки. Большое значение имеет и температура конца расширения, при которой в действительных циклах начинает вытекать рабочее тело из цилиндра. Надежная работа выпускных органов двигателя достигается за счет
82
установления определенных ограничений на температуру конца расширения.
На рис. 15 представлены кривые изменения максимальных значений температур и давлений, а также температур в конце расширения для вышерассмотренных циклов в зависимости от степени сжатия. Естественно, что абсолютные значения параметров теоретических циклов не отражают значений, которые получаются в действительных циклах, но соотношения рассматриваемых параметров теоретических циклов вполне определяют характер этих же соотношений в действительных циклах.
Как видно из графиков, приведенных на рис. 15, наибольшие значения максимальных температур и давлений получаются в цикле с подводом теплоты при V = const (см. кривые с индексом V), а наименьшие— в цикле с подводом теплоты при р = const (см. кривые с индексом р). Промежуточные значения Т z и р z получаются в цикле со смешанным подводом теплоты (см. кривые с индексами Q и X). Значительное повышение максимальных температур и давлений с увеличением степени сжатия в цикле с подводом теплоты при V = ~ const ограничивает применение данного цикла в реальных условиях прн повышенных е. Вместе с тем данный цикл по сравнению с другими имеет наименьшую температуру в конце расширения. Однако прн смешанном подводе теплоты и равном распределении подводимой теплоты при V = const и р = const (см. кривые с индексом •Q) максимальная температура цикла снижается почти на 600 К (или на 11%), а температура конца расширения увеличивается всего на 60—100 К (или на 3,3—4,7%).
На основе проведенного анализа можно сделать следующие выводы:
1. Значения основных термодинамических показателей цикла со смешанным подводом теплоты находятся между значениями соответствующих показателей циклов с подводом теплоты при V = const и р — const.
2. Циклы с подводом теплоты при V = const и р = const являются частными случаями цикла со смешанным подводом теплоты. Причем циклы с подводом теплоты при V = const и р ~ const являются предельными, при осуществлении которых получаются соответственно максимальные и минимальные значения т]ь Pt* Тz и pz прн одинаковых начальных условиях и одинаковом количестве подводимой теплоты.
3. В цикле со смешанным подводом теплоты при увеличении доли теплоты, подводимой прн V — const (увеличение X), н при уменьшении доли теплоты, подводимой при р — const (уменьшение р), повышаются значения термического к. п. д. и среднего давления цикла.
4. Цикл со смешанным подводом теплоты целесообразно применять при значительных степенях сжатия (больше 12) и с возможно большими значениями степени повышения давления. По данному циклу работают все быстроходные автомобильные и тракторные дизели без наддува.
2—370 33
Теоретические циклы двигателей с наддувом. Повышение давления в начале сжатия (см. точки а на рис. 7) с целью увеличения удельной работы (среднего давления) цикла называется наддувом. В автомобильных и тракторных двигателях наддув осуществляют за счет
предварительного сжатия воздуха или топливовоздушной смеси в компрессоре. Привод компрессора может быть механическим, не-
нлн газовым, от газовой турбины, работающей за счет энергии вы-
пускных газов поршневого двигателя. Кроме того, Повышение давления в начале сжатия возможно получить за счет использования скоростного напора, инерционных н волновых явлений во впускной системе двигателя, т. е. за счет так называемого инерционного наддува.
Прн инерционном наддуве и наддуве компрессором с механическим приводом характер протекания теоретических циклов (см. рнс. 7) не изменяется. Изменяются только конкретные значения термодинамических параметров, зависящие от изменения давления и температуры в конце впуска (см. формулы в табл.9). Необходимо также учитывать, что в реальном двигателе часть мощности затрачивается на привод компрессора.
При газотурбинном наддуве получается комбинированный
посредственно от вала двигателя,
Рис. 16. Теоретический цикл 'Комбинированного двигателя (дизель с турбокомпрессором и постоянным давлением перед турбиной)
двигатель, состоящий из поршневой части, газовой турбины и компрессора. В автомобильных и тракторных двигателях применяют турбокомпрессоры с постоянным давлением газов перед турбиной. Прототипом рабочего процесса комбинированного двигателя является теоретический цйкл; изображенный на рис. 16. Цикл асг'гЬа осуществляется в поршневой части двигателя, а цикл afgla — в турбокомпрессоре. Теплота QT, отводимая прн V = const в цикле поршневой части двигателя (линия Ьа), подводится прн постоянном давлении в турбокомпрессорном цикле (линия af). Далее в газовой турбине осуществляется продолженное расширение по адиабате (кривая fg), отвод теплоты Q2 ПРН постоянном давлении (линия gl) и адиабатическое сжатие в компрессоре (линия 1а).
Термический к. п. д. такого совмещенного цикла
х-1 +йХ(Р-1) ’
(44)
34
где е0 V i!Vc = eeft—общая степень сжатия комбинированного двигателя, равная произведению степеней сжатия поршневой части &—VaIVc и компрессора sk^=Vi/Va.
Среднее давление цикла, отнесенное к рабочему объему поршневой части двигателя:
$ 7. РАЗОМКНУТЫЕ ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ
Замкнутые теоретические циклы (см. § 6) дают наглядное представление о протекании процессов в реальных двигателях и о характере изменения их основных показателей и pt) в зависимости от различных термодинамических факторов. Однако количественные показатели замкнутых теоретических циклов далеки от реальных и прежде всего потому, что не учитывают трех основных процессов, протекающих в любом реальном двигателе.
Во-первых, это процесс газообмена (впуска и выпуска рабочего тбла), который в замкнутом цикле полностью исключен принятым допущением о постоянстве рабочего тела и его теплоемкости. В реальном двигателе каждый цикл осуществляется с участием вновь поступившей свежей смеси и после каждого цикла производится очистка цилиндра от отработавших газов. Кроме того, в действительном цикле теплоемкость рабочего тела зависит от температуры и от постоянно изменяющегося состава рабочего тела.
Во-вторых, процесс сгорания топлива, который в замкнутом теоретическом цикле заменен процессом сообщения теплоты от постороннего источника. В реальном двигателе процесс сгорания протекает во времени по сложному закону с интенсивным теплообменом.
В-третьих, дополнительные тепловые потери, связанные с наличием непрерывного теплообмена между рабочим телом и окружающей средой через стенки цилиндра, головку блока, днище поршня, а также с утечкой рабочего тела через неплотности между цилиндром и поршнем, с преодолением механических и гидравлических сопротивлений. Кроме того, потерн теплоты в реальном двигателе зависят от температуры (подогрева) остаточных газов и избыточного воздуха (прн а > 1) или от химической неполноты сгорания топлива (при «< 1).
Разомкнутые теоретические циклы по сравнению с замкнутыми (рис. J7), используя термодинамические соотношения, дополнительно учитывают:
1) процессы впуска н выпуска, но прн полном отсутствии сопротивлений и без изменения температуры и давления рабочего тела, а также без учета затрат энергии на газообмен;
2) изменение качества рабочего тела на протяжении одного цикла, т. е. учитывают изменения состава рабочего тела н зависимость его теплоемкости от температуры;
3) зависимость показателей адиабат сжатия и расширения от
2*
35
средней теплоемкости, но без учета теплопередачи и, следовательно, без учета тепловых потерь в процессах сжатия и расширения;
4) процесс сгорания топлива, точнее подвод теплоты, который зависит от теплоты сгорания рабочей смеси и учитывает изменение количества рабочего тела при сгорании (учет коэффициента молекулярного изменения);
Рис 17. Разомкнутые теоретические циклы (е = 8, Та «= 350 К; Ра = 0,1 МПа; а = 1):
« — со сгоранием бензина при V = const; б — со сгоранием дизельного топлива при р = const, в — со сгоранием дизельного топлива при V = const, р = const и Л = 2
5) потери теплоты, связанные с изменением температуры (подогревом) остаточных газов и избыточного воздуха (при а > 1) или с химической неполнотой сгорания топлива при недостатке кислорода воздуха (а < 1).
Таким образом, разомкнутые теоретические циклы значительно точнее отражают процессы, происходящие в реальных двигателях, а количественные показатели параметров этих циклов могут служить оценочными для соответствующих параметров действительных процессов.
Количественный анализ разомкнутых циклов во многом сложнее замкнутых, так как термодинамические соотношения в них значи
36
тельно усложнены. Однако использование современной вычислительной техники позволяет решить эту задачу достаточно просто.
Для проведенного ниже анализа разомкнутых теоретических циклов с подводом теплоты при V = const были разработаны алгоритм и программа расчета на электронно-вычислительной машине БЭСМ-6 (см. пр вложения II и III).
Изменение количественных показателей конкретного разомкнутого цикла при использовании определенного топлива зависит только от четырех независимых переменных: степени сжатия е, температуры Та и давления ра в начале сжатия и коэффициента избытка воздуха а. Причем из 28 параметров, достаточно полно характеризующих разомкнутый цикл, десять (Л^; Мео; Мео,; Мн,; Мн,о; Mn2; Mq,; М2; цо и Д#и) зависят только от а; коэффициент остаточных газов у г — только от е; пять параметров зависят от двух переменных: показатель адиабаты сжатия kh температура конца сжатия Тс и средняя мольная теплоемкость свежего заряда (воздуха) в конце сжатия (tncy)^ —от е и Tat а коэффициент молекулярного изменения ц и теплота сгорания //раб.см рабочей смеси —от е й а; давление в конце сжатия рс —от е, Та и ра; восемь параметров [(шсу)?с, (mc'vfy, {rw'vfa Tz, k2t К Tb и г)Л —от трех переменных—
*0 *0 *0
— е, Та и а; и только три параметра (pz, рь и pf) —от всех четырех переменных — е, Tai а и ра .
Разработанная программа позволяет одновременно получить для анализа количественные показатели указанных параметров для нескольких сот или даже тысяч разомкнутых циклов при различных значениях четырех независимых переменных (е; pQ; Та и а) и различном их сочетании.
Данный анализ может быть использован:
для получения количественных соотношений между исходными (заданными) и основными параметрами разомкнутых циклов;
для получения предельных значений любых из 28 параметров реального цикла, имеющего те же начальные параметры, что и разомкнутый цикл. Наличие предельных значений таких параметров, как температура и давление в характерных точках цикла (рс и Тс; pz и Т z\ Ръ и Ть), степень повышения давления, коэффициент молекулярного изменения, коэффициент остаточных газов и др., позволяет для любого двигателя определить направление его дальнейшего совершенствования или доводки.
Например, изменение величины термического к. п д. разомкнутого цикла хо сгоранием топлива при V— const зависит от изменения трех исходных параметров е, Та и а:
аТ g/oRe е 1
“ На е - 1
______1_
fej — 1
(46)
1
где RB—удельная газовая постоянная для воздуха.
На рис. 18 представлена эта зависимость, рассчитанная на ЭВМ по программе, распечатка которой приведена в приложении III.
37
линия на рис. 18 вышла за пределы графика).
Для более глубокого анализа разомкнутых циклов важно иметь не только
кнутого цикла со сгоранием топлива при V = =const от коэффициента избытка воздуха при различных значениях степени сжатия и при начальной температуре:
--------Та = 290 К,---------Та = 440 К
значения термического
к. п. д., но и значения других основных параметров, таких, как максимальные давления и температуры, давления и температуры на выпуске и т. п. Сравнительные показатели основных параметров замкнутых и разомкнутых теоретических циклов с подводом теплоты при V — const в зависимости от степени сжатия представлены на рис. 19. Прежде всего необходимо отметить, что максимальные значения температуры и давления разомкнутого цикла при всех значениях степени сжатия значительно ниже соответствующих параметров замкнутого цикла, что объясняется учетом переменной теплоемкости рабочего тела, возрастающей с повышением температуры. В результате уменьшаются значения температуры и давления в конце расширения (точка Ь) и особенно значительно при степенях сжатия, не превышающих е= 10-F 12.
Термический к. п. д. разомкнутого цикла со сгоранием топлива при V — const зависит [см. (46)] от изменения Tai е, a, ki и k2, а также от /0, Ни и RB, значения которых для данного топлива постоянны. Входящие в формулу показатели адиабат сжатия и расширения k2 в свою очередь зависят от степени сжатия е и начальной
38
Рис. 19. Зависимость основных параметров замкнутых (сплошные линии) и разомкнутых (штриховые линии) теоретических циклов с подводом теплоты при К ~ const от степени сжатия (ра = 0J МПа; Та = 350 К; «= 1; Уа 5=2 const)
температуры Та. Таким образом, при заданном топливе (например, бензине) термический к. п. д. зависит только от изменения параметров е, а и Та (рис. 20). Как видно из рисунка, начальная температура цикла незначительно влияет на величину термического к. п. д., так как при •изменении начальной температуры, при прочих равных условиях, почти пропорционально изменяется температура конца расширения. Основным фактором, кроме степени сжатия, влияющим на изменение т)ь является коэффициент избытка воздуха а. Рост термического к. п. д. с обеднением смеси объясняется относительным уменьшением содержания топлива в горючей смеси, а следовательно, относительным умен ыпе н и ем кол ичества продуктов сгорания, кото-
Рис. 20. Зависимость термического к. п. д разомкнутого цикла со сгоранием топлива при К == —const от степени сжатия и коэффициента избытка воздуха (Та — 350 К)
39
Рис. 21. Зависимость термического к. п. д. и
среднего давления разомкнутого цикла со сгоранием топлива при V = const от коэффициента избытка воздуха и степени сжатия (Та = 350 К
и ^ = 0,1 МПа)
рые обладают более высокой теплоемкостью. Естественно, что наибольшее значение термического к. п. д. будет иметь чисто «воздушный» цикл (а=оо). Следует отметить, что с увеличением а увеличивается прирост значений термического к. п. д. при изменении степени сжатия (кривая r|t при a =1,3 круче кривой гл прн а — 1 н значительно круче кривых Tjt при a =0,8 и а — =0,7).
Вместе с тем обеднение смеси (прн a > 1) уменьшает удельную работу (среднее давление) разомкнутого цикла (рис. 21): Pt=paHux]t/(aTal0RB). (47)
Среднее давление разомкнутого цикла достига
ет максимального значения при a = 1, т. е. *в период подвода максимального количества теплоты. Дальнейшее же обеднение смеси, несмотря на рост термического к. п. д., уменьшает pf. Изменение среднего давления цикла пропорционально изменению начального давления ра [см. формулу (47) и рис. 21]. В реальном двигателе превышение начального давления ра над атмосферным возможно
при наддуве.
Аналогичный анализ можно провести и для разомкнутых циклов с подводом теплоты при р = const н смешанным подводом теплоты при р — const и V = const.
Глава III
РАСЧЕТ ДЕЙСТВИТЕЛЬНОГО ЦИКЛА ДВИГАТЕЛЯ
$ 8. ПРОЦЕСС ВПУСКА
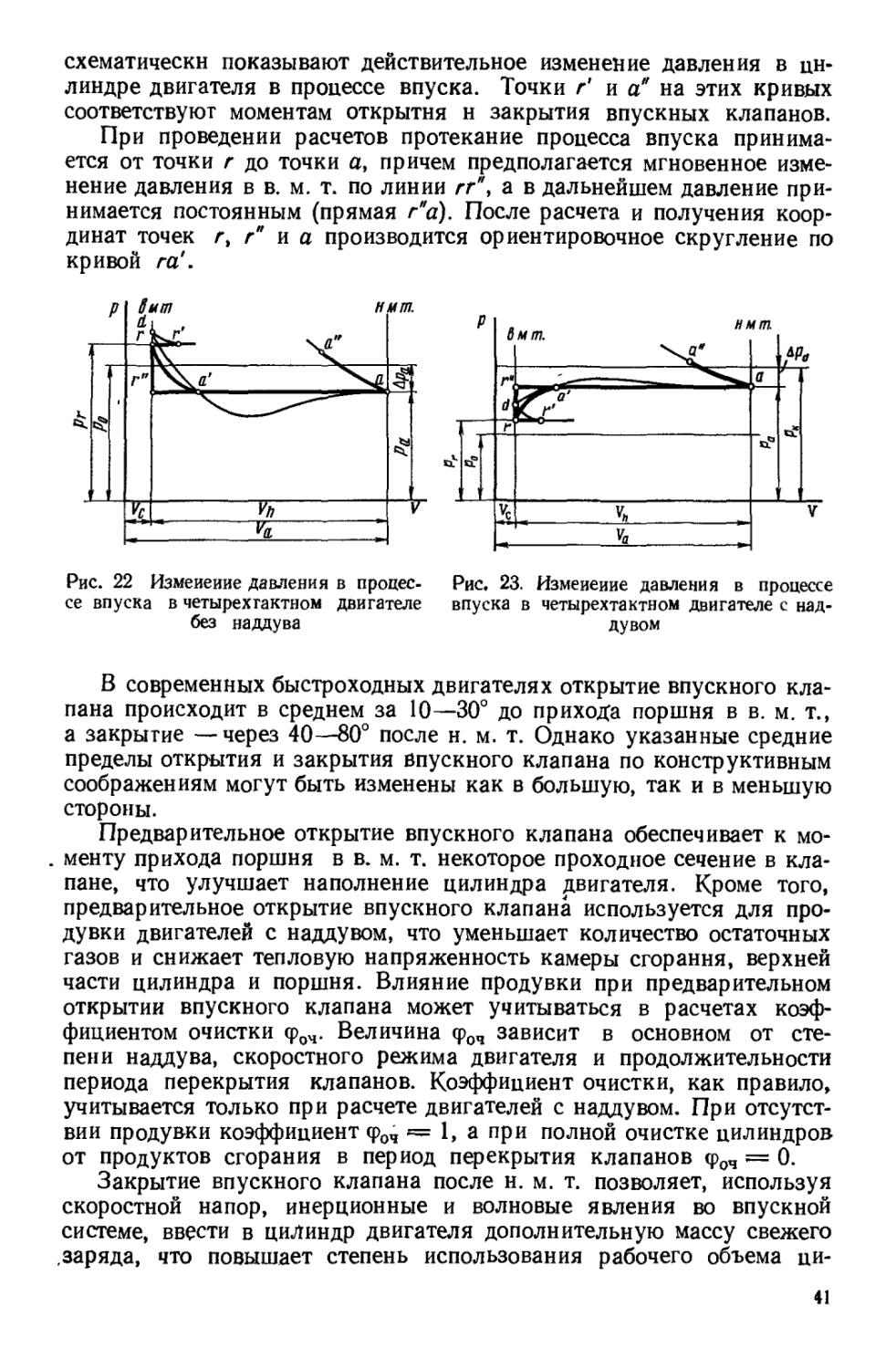
За период процесса впуска осуществляется наполнение цилиндра двигателя свежим зарядом. Изменение давления в процессе впуска в двигателе без наддува приведено на рис. 22, а в двигателе с наддувом — на рис. 23. Кривые r'da'aa", изображенные на этих рисунках, 40
схематически показывают действительное изменение давления в цилиндре двигателя в процессе впуска. Точки г' и а” на этих кривых соответствуют моментам открытия н закрытия впускных клапанов.
При проведении расчетов протекание процесса впуска принимается от точки г до точки а, причем предполагается мгновенное изменение давления в в. м. т. по линии гг\ а в дальнейшем давление принимается постоянным (прямая /Лг). После расчета и получения координат точек г, га и а производится ориентировочное скругление по кривой га‘.
Рис. 22 Изменение давления в пронес- Рис. 23. Изменение давления в процессе се впуска в четырехтактном двигателе впуска в четырехтактном двигателе с над-без наддува дувом
В современных быстроходных двигателях открытие впускного клапана происходит в среднем за 10—30° до прихода поршня в в. м. т., а закрытие —через 40—80° после н. м. т. Однако указанные средние пределы открытия и закрытия впускного клапана по конструктивным соображениям могут быть изменены как в большую, так и в меньшую стороны.
Предварительное открытие впускного клапана обеспечивает к моменту прихода поршня в в. м. т. некоторое проходное сечение в клапане, что улучшает наполнение цилиндра двигателя. Кроме того, предварительное открытие впускного клапана используется для продувки двигателей с наддувом, что уменьшает количество остаточных газов и снижает тепловую напряженность камеры сгорания, верхней части цилиндра и поршня. Влияние продувки при предварительном открытии впускного клапана может учитываться в расчетах коэффициентом очистки фоч. Величина сроч зависит в основном от степени наддува, скоростного режима двигателя и продолжительности периода перекрытия клапанов. Коэффициент очистки, как правило, учитывается только при расчете двигателей с наддувом. При отсутствии продувки коэффициент (роч ~ 1, а при полной очистке цилиндров от продуктов сгорания в период перекрытия клапанов <роч = 0.
Закрытие впускного клапана после н. м. т. позволяет, используя скоростной напор, инерционные и волновые явления во впускной системе, ввести в цилиндр двигателя дополнительную массу свежего .заряда, что повышает степень использования рабочего объема ци
41
линдра. Дополнительное наполнение цилиндра после прохода поршнем н. м. т. называется дозарядкой. Влияние дозарядки на параметры процесса впуска может быть учтено в расчете коэффициентом дозарядки <рдоз. Дозарядка рабочего объема цилиндра свежим зарядом в основном зависит от соответствующего подбора фаз газораспределения (прежде всего от величины угла опаздывания закрытия впускного клапана), длины впускного тракта и частоты вращения коленчатого вала. По данным проф. И. М. Ленина при удачно выбранных вышеуказанных параметрах дозарядка на номинальном режиме работы двигателя может достигать 12—15%, т. е. <рД03 = 1,12ч- 1,15. Однако при уменьшении частоты вращения коэффициент дозарядки уменьшается, а при минимальной частоте вращения вместо дозарядки наблюдается обратный выброс, достигающий 5—12%, т. е. фД03~ = 0,95 ч- 0,88.
Давление и температура окружающей среды. При работе двигателя без наддува в цилиндр поступает воздух из атмосферы. В этом случае при расчете рабочего цикла двигателя давление окружающей среды принимается равным р0 = 0,1 МПа, а температура—То = = 293 К.
При работе автомобильных и тракторных двигателей с наддувом воздух поступает в цилиндр из компрессора (нагнетателя), где он предварительно сжимается. В соответствии с этим давление и температура окружающей среды при расчете рабочего цикла двигателя с наддувом принимается равной давлению рх и температуре Тх воздуха на выходе из компрессора. При наличии промежуточного холодильника воздух из нагнетателя поступает в него, а затем в цилиндр двигателя. В этом случае за давление рк и температуру Тк окружающей среды принимается давление и температура воздуха за холодильником.
В зависимости от степени наддува принимаются следующие значения давления рл наддувочного воздуха:
При низком наддуве.............................. 1,5 рй
При среднем наддуве ............................ (1,5-=-2,2) р0
При высоком наддуве.............................(2,2-j-2,5) р0
Температура воздуха за компрессором
Гк-Т0(рк/р0)("1'~1)М«, (48)
где пк — показатель политропы сжатия воздуха в компрессоре (нагнетателе).
Из выражения (48) следует, что температура наддувочного воздуха зависит от степени повышения давления в нагнетателе и показателя пол итропы сжатия.
По опытным данным в зависимости от типа наддувочного агрегата и степени охлаждения величину пк принимают:
Для поршневых нагнетателей............................ 1,4—1,6
Для объемных нагнетателей............................. 1,55—1,75
Для осевых и центробежных нагнетателей................ 1,4—2,0
42
Температуру Тк можно определить также по выражению
т _ т Г1 (Рк/Ро)<й-1)/й-1 ’
1 к — 1 О 1-4----------------»
^ад.к
где Цад к ~ 0,66-г 0,80 —адиабатический к. п. д. компрессора.
Давление остаточных газов. В цилиндре двигателя перед началом процесса наполнения всегда содержится некоторое количество остаточных газов, находящихся в объеме Vc камеры сгорания (см. рис. 22 и 23). Величина давления остаточных газов устанавливается в зависимости от числа и расположения клапанов, сопротивлений впускного и выпускного трактов, фаз газораспределения, характера наддува, быстроходности двигателя, нагрузки, системы охлаждения и других факторов.
Для автомобильных и тракторных двигателей без наддува, а также с наддувом и выпуском в атмосферу давление остаточных газов (МПа)
Рг = (1>05-г 1,25) р0.
Большие значения рг принимаются для двигателей с высокой частотой вращения коленчатого вала.
Для двигателей с наддувом и наличием газовой турбины на выпуске
Рг ~ (0,75-г 0,98)рк.
Давление остаточных газов заметно снижается с уменьшением частоты вращения коленчатого вала. При необходимости определения рг на различных скоростных режимах двигателя и выбранном значении рг при номинальном режиме можно использовать приближенную формулу
рг = р0 (1,035 + Ар • 10’8 га2), (49)
где Ар = (prN —1,035 ро) • 1О8/(рогалг); ргн —давление остаточных газов на номинальном режиме, МПа; — частота вращения коленчатого вала на номинальном режиме,об/мин.
Температура остаточных газов. В зависимости от типа двигателя, степени сжатия, частоты вращения и коэффициента избытка воздуха устанавливается значение температуры Тг остаточных газов в пределах:
Для карбюраторных двигателей ......................... 900—1100 К
Для дизелей ........................................ 600—900 К
Для газовых двигателей.............................. 750—1000 К
При установлении величины Тг необходимо иметь в виду, что при увеличении степени сжатия и обогащении рабочей смеси температура остаточных газов снижается, а при увеличении частоты вращения — возрастает.
Температура подогрева свежего заряда. В процессе наполнения температура свежего заряда несколько увеличивается благодаря подогреву от нагретых деталей двигателя. Величина подогрева ДТ зависит от расположения и конструкции впускного трубопровода, си
43
стемы охлаждения, наличия специального устройства для подогрева, быстроходности двигателя и наддува. Повышение температуры улучшает процесс испарения топлива, но снижает плотность заряда и, таким образом, отрицательно влияет на наполнение двигателя. Эти два противоположных фактора, появляющиеся в результате повышения температуры подогрева, должны быть учтены при установлении величины Д7\
В зависимости от типа двигателя значения ДТ принимают:
Для карбюраторных двигателей............... О—20°
Для дизелей без наддува.................... 10—40°
Для двигателей с наддувом .................(—5)— (+10)°
В двигателях с наддувом величина подогрева свежего заряда снижается благодаря уменьшению температурного перепада между деталями двигателя и температурой наддувочного воздуха. При повышении температуры наддувочного воздуха возможны и отрицательные значения Д7\
Изменение величины АТ в зависимости от скоростного режима двигателя при ориентировочных расчетах может быть определено по формуле
ДТ = Лт (ПО — 0,0125п), (50)
где Лт = Д7\/(110—0,0125 и nN—соответственно
температура подогрева и частота вращения коленчатого вала при номинальном режиме работы двигателя.
Давление в конце впуска. Давление в конце впуска (МПа) — основной фактор, определяющий количество рабочего тела, поступающего в цилиндр двигателя:
Ра =Pk — &Ра ИЛИ ра = р0 — Дра. (51)
Потери давления Дра за счет сопротивления впускной системы и затухания скорости движения заряда в цилиндре при некотором допущении можно определить из уравнения Бернулли:
Арй = ф8 + 1вп) (<»«п/2) pft • 10-е, (52)
где Р — коэффициент затухания скорости движения заряда в рассматриваемом сечении цилиндра; |вп — коэффициент сопротивления впускной системы, отнесенный к наиболее узкому ее сечению; совп — средняя скорость движения заряда в наименьшем сечении впускной системы (как правило, в клапане или в продувочных окнах); pft и р0 — плотность заряда на впуске соответственно при наддуве и без него (при Рь =Ро И pft =р0).
По опытным данным в современных автомобильных двигателях на номинальном режиме (₽2 + Ввп) =2,5 4-4,0 и совп = 50 4-4- 130 м/с.
Гидравлические потери во впускной системе уменьшаются при увеличении проходных сечений, придании обтекаемой формы клапанам, обработке внутренних поверхностей впускной системы, правильном выборе фаз газораспределения и т. д.
44
Плотность заряда (кг/м3) на впуске
Pfc = Ph • или Ро = Рй • IWRbTo,
где RB — удельная газовая постоянная воздуха:
RB — R/pB = 8315/28,96 = 287 Дж/(кг- град), где R = 8315 Дж/(кмоль • град) — универсальная газовая ная.
Средняя скорость движения заряда в наименьшем сечении впускной системы
(53)
(54) постоя н-
®вп=»птах ~= — П V 1+ X2 • —-/ вп V вп
= п . /1 + = А„п, (55)
12<Увп Л ' '
где Fa — площадь поршня, м2; Дш — площадь наименьшего сечения впускной системы, м2; R и D — соответственно радиус кривошипа и диаметр поршня, м; 1 = R/Lm — отношение радиуса кривошипа к длине шатуна; п — частота вращения коленчатого вала, об/мин; Аа = (/?я2Р2ГПГ^)/12(увп.
Подставив (55) в формулу (52), получим
ДРа = (^ + Ввп) (^«2/ 2) Pfc • IO’®. (56)
У четырехтактных двигателей без наддува величина Дра колеблется в пределах:
Для карбюраторных двигателей Для дизелей без наддува . . .
(0,054-0,20) р0
(0,034-0,18) р0
Дизели по сравнению с карбюраторными двигателями при той же частоте вращения им^ют несколько пониженное значение Дра. Это объясняется снижением гидравлических сопротивлений благодаря отсутствию карбюратора и более упрощенной впускной системе.
При работе двигателя с наддувом (см. рис. 23) значение ра приближается к pk) однако абсолютные значения сопротивлений во впускных органах возрастают. Для четырехтактных двигателей с наддувом Дра = (0,03 -г 0,10) pk МПа.
Коэффициент остаточных газов. Величина коэффициента остаточных газов уг характеризует качество очистки цилиндра от продуктов сгорания. С увеличением уменьшается количество свежего заряда, поступающего в цилиндр двигателя в процессе впуска.
Коэффициент остаточных газов для четырехтактных двигателей: с учетом продувки и дозарядки цилиндра
Y . ЧочРг ,
Тг есРдозРа ТочРг без учета продувки и дозарядки (фоч = <рдоз 1) = + АГ . Рг
Tr zPa — Рг где в — степень сжатия.
(57)
(58)
45
В четырехтактных двигателях величина уг зависит от степени сжатия, параметров рабочего тела в конце впуска, частоты вращения и других факторов. С увеличением степени сжатия е и температуры остаточных газов Тг величина уг уменьшается, а при увеличении давления рт остаточных газов и частоты вращения п — возрастает.
Величина уг изменяется в пределах:
Для бензиновых и газовых двигателей без наддува . . 0,04—0,10
Для дизелей без наддува..........................0,02—0,05
При наддуве величина коэффициента остаточных газов снижается.
Температура в конце впуска. Эта температура (Та в К) с достаточной степенью точности определяется на основании уравнения баланса теплоты, составленного по линии впуска от точки г до точки а (см. рис. 22 и 23):
Mt (тср)% (Тк +ЬТ) + МГ (тс$'9 Tr = (М, + Mr) (mc'p)fra, (59) где М^тср)\к(Гк 4- АТ) — количество теплоты, внесенное свежим зарядом, с учетом подогрева заряда от стенок; Мг{тс^\г Тг — количество теплоты, заключающееся в остаточных газах; (Л4( 4- Mr) X х Та — количество теплоты, заключающееся в рабочей смеси.
Принимая в уравнении (59) (mcp)^ = (mc’p)/o ~ (тсР)<о * ПОЛУЧИМ Та = (Тк 4- АТ + угТг)/(1 4- ТЛ- (60)
Величина Та в основном зависит от температуры рабочего тела, коэффициента остаточных газов , степени подогрева заряда и в меньшей степени — от температуры остаточных газов.
У современных четырехтактных двигателей температура в конце впуска Та изменяется в пределах:
Для карбюраторных двигателей....................... 320—370 К
Для дизелей.......................................... 310—350 К
Для четырехтактных двигателей с наддувом........... 320—400 К
Коэффициент наполнения. Наиболее важной величиной, характеризующей процесс впуска, является коэффициент наполнения, представляющий собой отношение действительного количества свежего заряда, поступившего в цилиндр, к тому количеству, которое могло бы поместиться в рабочем объеме цилиндра при условии, что температура и давление в нем равны температуре и давлению среды, из которой поступает свежий заряд:
т)у = G„/Go = Уя/У0 = (61)
где Ga, Уд, Л4Д — действительное количество свежего заряда, поступившего в цилиндр двигателя в процессе впуска, соответственно в кг, м3, моль; Go, Vo, Мо — количество заряда, которое могло бы поместиться в рабочем объеме цилиндра при р0 и То (или рк и 7\), соответственно в кг, м3, моль.
46
Из уравнения (59) баланса теплоты по линии впуска устанавливается связь коэффициента наполнения с другими параметрами, характеризующими протекание процесса впуска.
Для четырехтактных двигателей с учетом продувки и дозарядки цилиндра
’Jy = г-7) Лт ' ‘ “ Чо'РЛ- (62)
+ ДГ £—1 pk
Для четырехтактных двигателей без учета продувки и дозарядки (Фоч ~ Фдоз ” О
= F~Tat • —Ч • ~ (63)
7\ + ДТ е —1 pk
Величина коэффициента наполнения в основном зависит от такт-ности двигателя, его быстроходности и совершенства системы газораспределения.
Из выражений (62) и (63) следует, что коэффициент наполнения возрастает с увеличением давления в конце впуска и понижается с увеличением давления выпуска и температуры подогрева рабочей смеси.
Значения коэффициента наполнения для различных типов автомобильных и тракторных двигателей при работе их с полной нагрузкой изменяются в пределах:
Для карбюраторных двигателей......................0,70—0,90
Для дизелей без наддува..........................0,80—0,94
Для дизелей с наддувом ........................., 0,80—0,97
§ 9. ПРОЦЕСС СЖАТИЯ
В период процесса сжатия в цилиндре двигателя повышаются температура и давление рабочего тела, что обеспечивает надежное воспламенение и эффективное сгорание топлива.
Изменение давления в процессе сжатия показано на рис. 24. В ре-
альных условиях сжатие происходит по сложному закону, практиче-
ски не подчиняющемуся термоди намическим соот-ношениям, так как на изменение температуры и давления в этом процессе влияют кроме изменения теплоемкости рабочего тела в зависимости от температуры: утечка газа через н еп л отности п ор шневых колец, дозарядка цилиндра до момента закрытия впускных клапанов, изменение направления и интенсивности теплообмена между рабочей смесью и
Рис. 24. Изменение давления в процессе сжатия
47
стенками цилиндра, испарение топлива (только в двигателях с искровым зажиганием), начало сгорания топлива в конце процесса сжатия.
Условно принимается, что процесс сжатия в действительном цикле происходит по политропе с переменным показателем nt (кривая adc на рис. М который в начальный период сжатия (участок ad) превышает показатель адиабаты (идет подвод теплоты от более нагре-
48
тых стенок цилиндра к рабочему телу), в какой-то момент времени точка d) принимает значение, равное значению (температуры стенок и рабочего тела выравнялись), а далее (участок de) имеет меньшее значение, чем kt (идет отвод теплоты от рабочего тела в стенки цилиндра).
В связи с трудностью определения переменной величины nt и усложнением расчетов обычно принимают, что процесс сжатия происходит по политропе с постоянным показателем nt (кривая аа"с'с), величина которого обеспечивает получение такой же работы на линии сжатия, как и при переменном показателе nt.
Расчет процесса сжатия сводится к определению среднего показателя политропы сжатия nt, параметров конца сжатия (р с и Те) и теплоемкости рабочего тела в конце сжатия (mcy)^ (te — температура смеси в конце сжатия, °C).
Величина nt уста швливается по опытным данным в зависимости от частоты вращения коленчатого вала двигателя, степени сжатия, размеров цилиндра, материала поршня и цилиндра, теплообмена и других факторов. Учитывая, что процесс сжатия протекает достаточно быстро (0,015 — 0,005 с на номинальном режиме), суммарный теплообмен между рабочим телом и стенками цилиндра за процесс сжатия получается незначительным и величину nt можно оценить по среднему показателю адиабаты kt. По номограмме, изображенной на рис. 25, для соответствующих значений е и Та определяется величина kt. Номограмма построена в результате совместного решения на электронно-вычислительной машине двух уравнений, связывающих kt с Та, Те, е и теплоемкостью воздуха (лгеу )к:
£, = 1+(lgTc-lgTa)/lge; (64)
ki = 1 + 8,315/(тс„)£, (65)
где
(mcv)^ = [(mcv)j‘ te — (rncv)‘t“ta]/(tG — ta). (66)
Более точно номограмму можно построить, если в формуле (65) теплоемкость воздуха (тсу )*« заменить теплоемкостью рабочей ' t 1а
смеси (mcv)y.
1а
Значения показателей политропы сжатия nt в зависимости от устанавливаются в следующих пределах:
’Для карбюраторных двигателей ........ (й,—0,00)4-(/г,—0,04)
Для дизелей ......................... (/г14-0,02)-е-(/г1—0,02)
При одинаковых значениях е и Та значение гг( для карбюраторных двигателей обычно ниже, чем для дизелей, так как в процессе сжатия топливовоздушной смеси происходит испарение топлива с поглощением теплоты. Кроме того, наличие паров топлива повышает теплоемкость смеси. Оба фактора снижают величину nt.
49
При определении значения «1 по соответствующему показателю' адиабаты необходимо учитывать, что с увеличением частоты вращения коленчатого вала двигателя, а также с уменьшением отношения поверхности охлаждения к объему цилиндра гц увеличивается. Повышение средней температуры процесса сжатия и увеличение интенсивности охлаждения двигателя уменьшают значение «ь В двигателях с воздушным охлаждением значение П\ при прочих равных условиях выше, чем в двигателях с жидкостным охлаждением. Перевод открытой жидкостной системы на закрытую также повышает значение П\.
Давление (МПа) и температура (К) в конце процесса сжатия определяются из уравнения политропы с постоянным показателем nt:
Рс = Ра^ (67)
те = ТЛел,_1 • (68)
В современных автомобильных и тракторных двигателях давление и температура в конце сжатия изменяются в пределах:
Для карбюраторных двигателей........ рс=0,9-=-2,0МПа и
7\=600—800 К
Для быстроходных дизелей без наддува . . . pt=3,5-r-5,50 МПа
и 7^—7004-900 К
Для дизелей с наддувом значения ре и Тс повышаются в зависимости от степени наддува.
Средняя мольная теплоемкость свежей смеси в конце сжатия принимается равной теплоемкости воздуха и определяется по табл. 5 или по формуле из табл. 6 в интервале температур 0—1500° С. Средняя мольная теплоемкость остаточных газов в конце сжатия (mcyfa [кДж/(кмоль • град)] может быть определена непосредст-*о
венно по табл. 7 для бензина или по табл. 8 для дизельного топлива.-При невозможности определить (пгсу)^ по этим таблицам (несоот-*о
ветствие элементарного состава топлива) средняя мольная теплоемкость остаточных газов определяется по уравнению
(тСу)*о ~ (mCV coAo ^С0 СО^ (mcv Hto)^ +
+ Мн,(тс’т^ + A4N, + МОг (mc;o « <69)
где средние мольные теплоемкости отдельных компонентов продуктов сгорания определяются по табл. 5 или по формулам табл. 6 в интервале температур 0—1500° С.
Средняя мольная теплоемкость рабочей смеси (свежая смесь + остаточные газы) определяется по уравнению
(*4)!:=гтг W:+• (70)
50
После расчета и определения параметров точки с производится ориентировочное исправление линии сжатия с целью учета начала сгорания. Положение точки с' (см. рис. 24) определяется величиной угла опережения зажигания (впрыска). Для современных быстроходных двигателей угол опережения зажигания при работе на номинальном режиме колеблется в пределах 30—40°, а угол опережения впрыска — в пределах 15—25°. Положение точки f (отрыв линии сгорания от линии сжатия) определяется периодом задержки воспламенения рабочей смеси. При этом давление в конце сжатия ориентировочно повышается до значения рс" =(1,15-4-1,25) рс (точка с").
§ 10. ПРОЦЕСС СГОРАНИЯ
Процесс сгорания — основной процесс рабочего цикла двигателя, в течение которого теплота, выделяющаяся вследствие сгорания топлива, идет на повышение внутренней энергии рабочего тела и на совершение механической работы.
Изменение давления в процессе сгорания топлива в карбюраторном двигателе с воспламенением от искры показано на рис. 26, а в дизеле — на рис. 27. Кривые crf(frz^ схематически показывают действительное изменение давления в цилиндрах двигателей в процессе сгорания. В реальных двигателях процесс сгорания, точнее — догорание топлива, продолжается и за точкой гд на линии расширения.
На характер протекания процесса сгорания оказывает влияние большое количество различных факторов: параметры процессов впуска и сжатия, качество распыливания топлива, частота вращения коленчатого вала двигателя и т. д. Зависимость параметров процесса сгорания от целого ряда факторов, а также физико-химическая сущность процесса сгорания моторных топлив пока что изучены недостаточно полно.
С целью упрощения термодинамических расчетов автомобильных и тракторных двигателей принимают, что процесс сгорания в двига-
Рис. 26. Изменение давления в процессе сгорания в карбюраторном двигателе
Рис. 27. Изменение давления в процессе сгорания в дизеле
51
телях с воспламенением от искры происходит при V — const, т. е. по изохоре (прямая cd'z на рис. 26), а в двигателях с воспламенением от сжатия — при V = const и р — const, т. е. по циклу со смешанным подводом теплоты (прямые cc"z' и г'г на рис. 27).
Целью расчета процесса сгорания является определение температуры и давления в конце видимого сгорания (точки z и гд), а для дизеля — и объема Уг.
Температура газа Tz в конце видимого сгорания определяется на основании первого закона термодинамики, согласно которому dQ = = dU + dL. Применительно к автомобильным и тракторным двигателям:
Ни — QnoT = (U г — Uc) + Lc z — сгорание при а > 1; (71) {Ни — ДЯи) — QnoT = Wz — Нс) + LCI — сгорание при а< 1, (72) где Ни — низшая теплота сгорания топлива, кДж; Qn0T — потери теплоты вследствие теплоотдачи, догорания топлива на линии расширения и диссоциации, кДж; U z — внутренняя энергия газов в конце видимого сгорания, кДж; Uс — внутренняя энергия рабочей смеси в конце сжатия, кДж; Lc z — теплота, идущая на работу расширения газов от точки с до точки z (для двигателей с воспламенениемрт искры Гсг =0), кДж.
Тепловой баланс на участках сг можно записать в более краткой форме:
ltHи =(Цг- Ue) + Lcz; (73)
5 АН и - ЬНи) = {UZ-Ue) + Lcz, (74)
где | г = [{Ни — ДДи) — QuotViHu — ЬНи) — коэффициент использования теплоты на участке видимого сгорания сг.
Коэффициент £z выражает долю низшей теплоты сгорания топлива, используемую на повышение внутренней энергии газа (U z — — U с) и на совершение работы Lcz.
Величина коэффициента использования теплоты принимается на основе экспериментальных данных в зависимости от конструкции двигателя, режима его работы, системы охлаждения, формы камеры сгорания, способа смесеобразования, коэффициента избытка воздуха и частоты вращения коленчатого вала.
По опытным данным величина £ z при работе двигателей с полной нагрузкой изменяется в пределах:
Для карбюраторных двигателей ...................... 0,80—0,95
Для быстроходных дизелей с неразделенными камерами сгорания.......................................... 0,70—0,88
Для дизелей с разделенными камерами сгорания . . . 0,65—0,80
Для газовых двигателей............................. 0,80—0,85
Меньшие значения коэффициента использования теплоты характерны для двигателей с несовершенным смесеобразованием. Величина £ г повышается за счет сокращения потерь теплоты от газов в стенки, выбора рациональной формы камеры сгорания, уменьшения догора-52
ния в процессе расширения и выбора коэффициента избытка воздуха, обеспечивающего увеличение скорости сгорания рабочей смеси. Величина коэффициента использования теплоты | z зависит также от скоростного и нагрузочного режимов работы двигателя и, как правило, уменьшается при снижении нагрузки и частоты вращения.
Расчетные уравнения сгорания для автомобильных и тракторных двигателей получаются путем преобразований уравнений теплового баланса (73) и (74) (см. участки сг на рис. 26 и 27).
Для двигателей, работающих по циклу с подводом теплоты при V — const, уравнение сгорания имеет вид:
|2//раб.см + (mc'v)ic0 4 = 1* (>”4)!* G. (75)
где //раб.см — теплота сгорания рабочей смеси, определяемая по (27) или (28); (тсу),е — средняя мольная теплоемкость рабочей смеси в конце процесса сжатия, определяемая по (70); (тсу)^ — *0 средняя мольная теплоемкость продуктов сгорания, определяемая по (32).
Для двигателей, работающих по циклу со смешанным подводом теплоты при V = const и р = const, уравнение сгорания имеет вид
М/р*.™ + [(тс;Й + 8’315х1 + 2270(X-ц) = и (тср^ tz, (76)
где X ~pjpc— степень повышения давления; 2270 = 8,315 • 273.
Величина степени повышения давления для дизелей устанавливается по опытным данным в основном в зависимости от количества топлива, подаваемого в цилиндр, формы камеры сгорания и способа смесеобразования. Кроме того, на величину X оказывает влияние период задержки воспламенения топлива, с увеличением которого степень повышения давления растет:
для дизелей с неразделенными камерами сгорания и объемным смесеобразованием X — 1,6 4 2,5;
для вихрекамерных и предкамерных дизелей, а также для дизелей с неразделенными камерами и пленочным смесеобразованием X — 1,2 4- 1,8;
для дизелей с наддувом величина 'X определяется допустимыми значениями температуры и давления в конце видимого процесса сгорания.
В уравнения сгорания (75) и (76) входят две неизвестные величины: температура в конце видимого сгорания 1z и теплоемкость продуктов сгорания при постоянном объеме (тсу)^ или постоянном давлении (tnCpYf при этой же температуре t г. Используя для определения *0
(ГпсуУ/ или (тСрУ/ табличные значения (см. табл. 5), уравнения V /о *о
сгорания решаются относительно t z методом последовательных приближений (подбором значений tz). При использовании для определения (rncvYf или (тср)\г приближенных формул (см. табл. 6), *0 *0 *
уравнения сгорания после подстановки в них числовых значений
53
всех известных параметров и последующих преобразований принимают вид уравнения второго порядка
At2z + Btz — C= О, (77)
где А, В и С—числовые значения известных величин.
Откуда
tz = (—В + VВ2 + 4АС )/(2А), °C и Tz = tz + 273 К.
Определение величины давления р г в конце сгорания зависит от характера осуществляемого цикла.
Для двигателей, работающих с подводом теплоты при V = const, давление (МПа)
Pz =PcliTz/Tc, (78)
а степень повышения давления
X — Р zlp f (79)
Для карбюраторных двигателей X = 3,2 ч-4,2, для газовых двигателей X =3-4-5.
Для двигателей, работающих по циклу со смешанным подводом теплоты при V = const и р = const:
Pz =^Рс, (80)
а степень предварительного расширения
Р = ^(pc/pz)(Tz/Te) = №)(TZ/TC). (81)
Для дизелей р = 1,2 -4- 1,7.
Объем, освобождаемый поршнем в процессе предварительного расширения:
Vz-Vc = Ve(p —- 1). (82)
После проведения расчета и получения координат точек гиг' производится ориентировочное приближение расчетных линий сгорания к действительным.
Для двигателей, работающих по циклу с подводом теплоты при V = const (см. рис. 26), р ад = 0,85р z. Положение точки f, зависящее от продолжительности периода задержки воспламенения, определяется величиной угла Д<рь изменяющегося в пределах 5—18° поворота коленчатого вала (п. к. в.). Положение точки гд по горизонтали определяется допустимой скоростью нарастания давления на каждый градус поворота коленчатого вала Др/ Д<р2, где Др = р 2Д — — рс«, а Дф2 Для карбюраторных двигателей находится в пределах 8—12° п. к. в. Для современных карбюраторных двигателей считается допустимой работа при Др/Дф2 = 0,1 -г 0,4 МПа/град. п. к. в. При Др/Д<р2<0,1 значительно увеличивается догорание на .Линии расширения, что ухудшает экономичность двигателя, а при Др/Д<рг > > 0,4 повышенная скорость нарастания давления увеличивает жесткость работы, что приводит к увеличению износа и даже поломкам деталей двигателя.
54
Для дизелей, работающих по циклу со смешанным подводом теплоты (см. рис. 27), р 2Д = pz. Положение точки Д зависящее от продолжительности периода задержки воспламенения (0,001 — 0,003 с), определяется величиной угла Дфь который для автомобильных и тракторных дизелей изменяется в пределах A<pi = 8 4-12° п. к. в. Положение точки гд по горизонтали, так же как и для двигателей с подводом теплоты при V = const, определяется величиной Др/Дф2 Для дизелей допустимая скорость нарастания давления Др/Д<р2 = = 0,2 4- 0,5 МПа/град. п. к. в. Для дизелей с объемным смесеобразованием максимальная скорость нарастания давления достигает Др/Дфг = 1,0 4- 1,2 МПа/град. п. к. в. при Д<р2 = 6 4- 10° п. к. в. после в. м. т.
Значения температуры и давления конца сгорания для современных автомобильных и тракторных двигателей при работе с полной нагрузкой изменяются в следующих пределах:
Для карбюраторных двигателей....... Tz=240042900 К,
pz=3,547,5 МПа, Ргд=3,04б,5 МПа Для дизелей ....................... Тг =180042300 К,
Pz”Pza=5,0412,0 МПа
Для газовых двигателей................ 7^=220042500 К,
pz=3,045,0 МПа, ргд=2,544,5 МПа
Более низкие температуры конца сгорания у дизелей по сравнению с карбюраторными и газовыми двигателями являются следствием большей величины коэффициента избытка воздуха а, а следовательно, и больших потерь теплоты на нагревание воздуха; меньшей величины коэффициента использования теплоты на участке видимого сгорания; различий в характере протекания процесса сгорания и догорания при ходе расширения; частичного использования теплоты на совершение работы в процессе предварительного расширения (участок z'z).
§ 11. ПРОЦЕСС РАСШИРЕНИЯ
В результате осуществления процесса расширения происходит преобразование тепловой энергии топлива в механическую работу.
Изменение давления в процессе расширения показано на рис. 28. Кривые Zpb'b" схематически показывают действительное изменение давления в цилиндрах двигателей в процессе расширения. В реальных двигателях расширение протекает по сложному закону, зависящему от теплообмена между газами и окружающими стенками, величины подвода теплоты в результате догорания топлива и восстановления продуктов диссоциации, утечки газов через неплотности, уменьшения теплоемкости продуктов сгорания вследствие понижения температуры при расширении, уменьшения количества газов в связи с началом выпуска (предварение открытия выпускного клапана).
Так же как и при рассмотрении процесса сжатия, условно считают, что процесс расширения в действительном цикле протекает по
55
политропе с переменным показателем, который в начальный период изменяется от 0 до 1 (идет настолько интенсивное догорание топлива, что температура газов повышается, несмотря на расширение), затем увеличивается и достигает значения показателя адиабаты (выделение теплоты вследствие догорания топлива и восстановления продуктов диссоциации уменьшается и становится равным отводу теплоты за счет теплообмена и утечки газов через неплотности) и, наконец, превышает показатель адиабаты (выделение теплоты меньше отвода теплоты). Для упрощения расчетов кривая процесса расширения обычно принимается за политропу с постоянным показателем п2 (кривые zb'b на рис. 28).
Рис. 28. Изменение давления в процессе расширения: а — карбюраторного двигателя; б — дизеля
Величина среднего показателя политропы расширения п2 устанавливается по опытным данным в зависимости от ряда факторов. Значение п2 возрастает с увеличением коэффициента использования теплоты, отношения хода поршня S к диаметру D цилиндра и интенсивности охлаждения. С ростом нагрузки и увеличением линейных размеров цилиндра (при S/D = const) средний показатель политропы расширения п2 уменьшается. При увеличении быстроходности двигателя величина п2, как правило, снижается, но не для всех типов двигателей и не на всех скоростных режимах.
Учитывая, что по опытным данным величина среднего показателя политропы расширения п2 незначительно отличается от показателя адиабаты &2и, как правило, в меньшую сторону, при предварительных расчетах новых двигателей величину п2 можно оценить по величине k2 Для соответствующих значений е (или 6), а и 7\. Показатель адиабаты расширения в этом случае определяется в результате совместного решения двух уравнений:
= 1 + (lg7\ — lg?\)/lge — Для карбюраторных двигателей (83) или k2 = 1 + (IgT z — Ig^/lgS — для дизелей (84)
И k2 == 1 + 8,315/{mcv^b, (85)
56
Рис. 29. Номограмма определения показателя адиабаты расширения &2 Для каР‘ бюраторного двигателя
где
(т4Й = [(mcv)%— (mcv)tb9 /(tz ~ Q- (86>
Решаются эти уравнения методом подбора величин kz и Ть довольно сложно и с различной степенью точности. Для упрощения расчетов по определению fe на основе системы уравнений (83) — (86) и формул (см. табл. 6) для определения средних мольных теплоемкостей продуктов сгорания построены номограммы (рис. 29 и 30).
Определение kz по номограммам производится следующим образом; по имеющимся значениям е (или о для дизеля) и Т г определяют точку, которой соответствует значение при а = 1. Для нахождения значения /?2 при заданном а необходимо полученную точку перенести по горизонтали на вертикаль, соответствующую а = 1, и далее параллельно вспомогательным кривым до вертикали, соответствую-
57
Рис. 30. Номограмма определения показателя адиабаты расширения для дизеля
щей заданному значению а. На рис. 29 и 30 показано определение k2 для рассчитываемых карбюраторного двигателя и дизеля.
Средние значения величины л2, полученные из анализа индикаторных диаграмм, для различных современных автомобильных и тракторных двигателей изменяются в пределах (для номинальной нагрузки):
Для карбюраторных двигателей............................ 1,23—1,30
Для дизелей......................................... 1,18-? 1,28
Для газовых двигателей ............................... 1,25-2-1,35
58
Значения давления (МПа) и температуры (К) в конце процесса расширения определяются по формулам политропического процесса. Для двигателей, работающих по циклам, с подводом теплоты при постоянном объеме
Ръ-Рг/^, (87)
Ть~Тг/^-1-, (88)
со смешанным подводом теплоты
= (89)
Ть = 7’г/8л’~1, (90)
где 6 = е/р — степень последующего расширения.
Примерные значения давления рь и температуры Ть для современных автомобильных и тракторных двигателей без наддува (на номинальном режиме) лежат в пределах:
Для карбюраторных двигателей . . р* = 0,35 -5- 0,60 МПа и Tb = 1200--1700 К Для дизелей................pf> = 0,20 — 0,50 МПа’ и Ть — 1000-5-1200 К
§ 12. ПРОЦЕСС ВЫПУСКА И МЕТОДЫ СНИЖЕНИЯ
ТОКСИЧНОСТИ ДВИГАТЕЛЕЙ ПРИ ИХ ЭКСПЛУАТАЦИИ
За период выпуска из цилиндра двигателя удаляются отработавшие газы.
Изменение давления в процессе выпуска в цилиндре четырехтактного двигателя без наддува показано на рис. 31, а в двигателе с наддувом — на рис. 32. Кривые b'b"r'da' схематически показывают действительное изменение давления в цилиндре двигателя в процессе выпуска. Точки Ь' и а' на этих кривых отмечают соответственно моменты открытия и закрытия выпускных клапанов. Прямые Ы и 1г являются расчетными прямыми процесса выпуска, которые после определения координат точек & и г ориентировочно заменяются кривыми b"r'r.
Открытие выпускного клапана до прихода поршня в н. м. т., снижая полезную работу расширения (площадь b'bb"b'), способствует качественной очистке цилиндра от продуктов сгорания и уменьшает работу, необходимую для выталкивания отработавших газов. В современных двигателях открытие выпускного клапана происходит за 40—80° до н. м. т. (точка Ь') и с этого момента начинается истече
Рис. 31. Изменение давления в процессе выпуска в двигателе без наддува
Рис. 32. Изменение давления в процессе выпуска в двигателе с наддувом
59
ние отработавших газов с критической скоростью 600—700 м/с. За этот период, заканчивающийся вблизи н. м. т. в двигателях без наддува и несколько позже при наддуве, удаляется 60—70% отработавших газов. При дальнейшем движении поршня к в. м. т. истечение газов происходит со скоростью 200—250 м/с и к концу выпуска не превышает 60—100 м/с. Средняя скорость истечения газов за период выпуска на номинальном режиме находится в пределах 60—150 м/с.
Закрытие выпускного клапана происходит через 10—50° после в. м. т., что повышает качество очистки цилиндра за счет эжекцион-ного свойства потока газа, выходящего из цилиндра с большой скоростью.
В начале расчета процесса впуска (см. § 8) задаются параметрами процесса выпуска (рг и Тг), а точность выбора величины давления и температуры остаточных газов проверяется по формуле
(91 >
При проектировании двигателя стремятся уменьшить величину рг, чтобы избежать возрастания насосных потерь и коэффициента остаточных газов. Кроме того, увеличение давления выпуска уменьшает коэффициент наполнения, ухудшает процесс сгорания и повышает температуру и количество остаточных газов. Увеличение давления в конце выпуска при газотурбинном наддуве, как правило, вполне компенсируется повышением давления на впуске (рис. 32).
Быстрый рост автомобильного и тракторного парков как & нашей стране, так и во всем мире за последние годы остро поставил проблему снижения токсичности двигателей при их эксплуатации. Основным источником загрязнения атмосферы в процессе эксплуатации двигателей являются продукты сгорания, в которых токсичными компонентами являются: окись углерода (СО), окислы азота (NOX) и углеводороды (CnHm). Кроме того, углеводороды попадают в атмосферу в виде паров топлива и масел из баков, топливных насосов, карбюраторов, картеров. По некоторым данным [2] один автомобильный двигатель в течение года выбрасывает в атмосферу примерно 600 кг окиси углерода и 40 кг окислов азота.
В настоящее время проблема снижения токсичности решается как создателями, так и эксплуатационниками двигателей. С точки зрения конструкции двигателей эта проблема решается по трем основным направлениям:
1. Совершенствование рабочего процесса существующих типов поршневых двигателей внутреннего сгорания с целью существенного сокращения выброса в атмосферу токсичных составляющих как с продуктами сгорания, так и с парами топлива и масел. Применение различных способов воздействия на процессы смесеобразования (например, системы питания с электронным управлением) и сгорания (например, совершенствование камер сгорания); дёфорсирование двигателей за счет уменьшения степени сжатия и частоты вращения коленчатого вала; вентиляция картера; подбор горючих смесей с меньшей токсичностью продуктов их сгорания и ряд других меро
60
приятий уже сейчас позволяют существенно снизить загрязнение атмосферы в процессе эксплуатации автомобильных и тракторных двигателей.
2. Разработка дополнительных устройств (нейтрализаторы, улавливатели, дожигатели и т. п.) и установка их на двигатели позволяет в большей или меньшей степени очистить продукты сгорания от токсичных составляющих.
3. Разработка принципиально новых двигателей (электрических, инерционных, аккумуляторных и др.), позволяющих кардинально решить проблему незагрязнения, окружающей среды в процессе эксплуатации автомобильных и тракторных двигателей, является направлением на длительную перспективу. Однако использование в таких крупных городах, как Москва или Ленинград, электромобилей для внутригородских перевозок уже в ближайшее время может значительно уменьшить загрязнение атмосферы токсичными компонентами.
С точки зрения эксплуатации автомобильных и тракторных двигателей данная проблема решается повышением требований к качеству регулировки топливоподающей аппаратуры, систем и устройств смесеобразования и сгорания; более широким применением газовых топлив, продукты сгорания которых обладают меньшей токсичностью, а также переводом бензиновых двигателей на газообразное топливо.
$ 13. ИНДИКАТОРНЫЕ ПАРАМЕТРЫ РАБОЧЕГО ЦИКЛА
Рабочий цикл двигателя внутреннего сгорания характеризуется средним индикаторным давлением, индикаторной мощностью и ин-
дикаторным к. п. д.
Среднее индикаторное давление. Изменение давления в течение всего рабочего цикла двигателя с искровым зажиганием и дизеля показано на расчетных индикаторных диаграммах (рис. 33 и 34). Площадь нескруглен-ных диаграмм (асгЬа) в определенном масштабе выражает теоретическую расчетную работу газов за один цикл двигателя. Эта работа, отнесенная к ходу поршня, является теоретическим средним индикаторным давлением р/.
При графическом определении pt' по индикаторной диаграмме (рис. 33 и 34) необходимо:
Рис. 33. Индикаторная диаграмма карбюраторного двигателя
61
а) определить площадь под кривой ас (работа, затраченная на сжатие рабочей смеси) и, отнеся ее к ходу поршня, получить величину среднего давления процесса сжатия Ра с»
б) определить площадь под кривой zb (рис. 33) или под кривой z'zb (рис. 34), которая выражает работу расширения. Отнеся эту площадь к ходу поршня, определить среднее давление процесса расширения ргь или рг-г*;
в) определить = p2ft — — Рас Для карбюраторного двигателя или p’t — p2,zb — — ра с Для дизеля;
г) сравнить площадь заштрихованного прямоугольника со сторонами p't и Vh и площадь индикаторной диаграммы ac(z')zba. При пра-и p't сравниваемые площади
вильном определении pec, pzb (pZ’d>) должны быть равны.
Для карбюраторного двигателя (рис. 33), работающего по циклу с подводом теплоты при V = const, теоретическое среднее индикаторное давление
(92)
Для дизеля, работающего по циклу со смешанным подводом теплоты (рис. 34):
Pi =
Рс Г ?-Р / ] _ 1 \
( — 1 L»2 — 1 \ 8я»-1 )
-гЧ(1--?Н+Х(|,-1)1-(93) “ Д у t у J
Среднее индикаторное давление действительного цикла отличается от значения на величину, пропорциональную уменьшению расчетной диаграммы за счет скругления в точках с, г, Ь.
Уменьшение теоретического среднего индикаторного давления вследствие отклонения действительного процесса от расчетного цикла оценивается коэффициентом полноты диаграммы <ри и величиной среднего давления насосных потерь Дрг.
Коэффициент полноты диаграммы <ри принимается равным:
Для карбюраторных двигателей
Для дизелей.................
0,94—0,97
0,92—0,95
Й2
Среднее давление насосных потерь (МПа) при процессах впуска и выпуска
&Pi — рг~ Ра- (94)
Для четырехтактных двигателей без наддува величина положительна. В двигателях с наддувом от приводного нагнетателя при ра > рг величина Др, отрицательна. При газотурбинном наддуве значение ра может быть как больше, так и меньше рГ) т. е. величина Дрг может быть как отрицательной, так и положительной.
При проведении расчетов потери на газообмен учитываются в работе, затрачиваемой на механические потери, так как при экспериментальном определении работы трения обычно пользуются методом прокрутки двигателя, и, естественно, в определяемых таким методом механических затратах на прокрутку двигателя учитываются и затраты на насосные ходы. В связи с этим принимают, что среднее индикаторное давление pt отличается от р/ только на коэффициент полноты диаграммы
р, = Фир; . (95)
При работе на полной нагрузке величина pt (МПа) достигает:
Для четырехтактных карбюраторных двигателей.....0,6—1,4
Для четырехтактных карбюраторных двигателей форсированных ............................................ до 1,6
Для четырехтактных дизелей без наддува..........0,7—1,1
Для четырехтактных дизелей с наддувом............до 2,2
Меньшие значения среднего индикаторного давления в дизелях без наддува, по сравнению с карбюраторными двигателями, объясняются тем, что дизели работают с большим коэффициентом избытка воздуха. Это вызывает неполное использование рабочего объема цилиндра и дополнительные потери теплоты на нагревание избыточного воздуха.
Индикаторная мощность. Индикаторная мощность двигателя
— работа, совершаемая газами внутри цилиндров в единицу времени.
Для многоцилиндрового двигателя (кВт)
^^=PiVAzn/(30r), (96)
где pi — среднее индикаторное давление, МПа; Vh — рабочий объем одного цилиндра, л (дм3); i —число цилиндров; п —частота вращения коленчатого вала7 об/мин; т —тактность двигателя.
Для четырехтактных двигателей
= ргУАт/120. (97)
Индикаторная мощность одного цилиндра
= Pi VAn/(30r). (98)
Индикаторный к. п. д. и удельный индикаторный расход топлива. Индикаторный к. п. д. т]г характеризует степень использования в дей
63
ствительном цикле теплоты топлива для получения полезной работы и представляет собой отношение теплоты, эквивалентной индикаторной работе цикла, ко всему количеству теплоты, внесенной в цилиндр с топливом.
Для 1 кг топлива
Ъ = Ц/Ни, (99)
где Ц —теплота, эквивалентная индикаторной * работе, МДж/кг; Ии —низшая теплота сгорания топлива, МДж/кг.
Таким образом, индикаторный к. п. д. учитывает все тепловые потери действительного цикла.
Для автомобильных и тракторных двигателей, работающих на жидком топливе:
rii = р&аЦН upftTlv ), (100)
где pt выражено в МПа; /0 — в кг/кг топл.; Ни — в МДж/кг топл; —в кг/м8.
Для автомобильных и тракторных двигателей, работающих на газообразном топливе:
т), = 371,2 • ^М'^рДНм), (101)
где Mi' —выражено в моль/моль топл; Тк —в К; р, и —в МПа; Ни —в МДж/м3.
В современных автомобильных и тракторных двигателях, работающих на номинальном режиме, величина индикаторного к. п. д. составляет:
Для карбюраторных двигателей . ....................0,26—0,35
Для дизелей..........................................0,38—0,50
Для газовых двигателей..............................0,28—0,34
При известной величине индикаторного к. п. д. индикаторный удельный расход [г/(кВт-ч) ] жидкого топлива
gi = 3600/(7)гЯи) или gt = 36OQpkfiv/(Piloa). (102)
Для двигателей, работающих на газообразном топливе, индикаторный удельный расход [м8/(кВт-ч)] газового топлива
п, = 3,6/^) или Vi = 9700717рА/(/И1'глрг), (103)
а удельный расход [МДж/(кВт-ч)] теплоты на единицу мощности
<7/ = vX « 9700^phH;/(M’,rkPi). (104)
В формулах (102) — (104) pi и pk выражены в МПа; рк — в кг/м8; Ии — в МДж/кг; Н'и — в МДж/м8; /0 — в кг/кг топл; AfJ — в моль/моль топл; Тк — в К.
Удельные расходы топлива на номинальном режиме:
Для карбюраторных двигателей . . . ^=235-5-320 г/(кВт-ч)
Для дизелей . . .s..............gi = 170-5-230 г/(кВт-ч)
Для газовых двигателей..........qi = 10,5-5- 13,5 МДж/(кВт-ч)
64
$ 14. ЭФФЕКТИВНЫЕ ПОКАЗАТЕЛИ ДВИГАТЕЛЯ
Параметры, характеризующие работу двигателя, отличаются от индикаторных наличием необходимых затрат полезной работы на преодоление различных механических сопротивлений (трение в кривошипно-шатунном механизме, приведение в действие вспомогательных механизмов и нагнетателя и др.) и на совершение процессов впуска и выпуска.
Механические потери. Потери на преодоление различных сопротивлений оценивают величиной мощности механических потерь или величиной работы, соответствующей мощности механических потерь, отнесенной к единице рабочего объема цилиндра.
При проведении предварительных расчетов двигателей механические потери, характеризуемые средним давлением рм, приближенно можно определять по линейным зависимостям от средней скорости поршня Оп.ср (выбор значений оп.сР приведен в гл. IV).
Ниже даны эмпирические формулы для определения величины рм (МПа) в двигателях различного типа:
для карбюраторных двигателей с числом цилиндров до шести и отношением S/D > 1
ры = 0,049 + 0,0152опср; (105)
для карбюраторных восьмицилиндровых двигателей с отношением S/£>< 1
рм= 0,039 + 0,0132оп.Ор; (106)
для карбюраторных двигателей с числом цилиндров до шести и отношением S/D < 1
рм = 0,034 +0,0113оп.ср; (107)
для четырехтактных дизелей с неразделенными камерами
рм = 0,089 +0,0118оп.ср; (108)
для предкамерных дизелей
рм = 0,103 + 0,0153оп.ср; (109)
для дизелей с вихревыми камерами
рм = 0,089 + 0,0135«п ср. (НО)
Среднее давление механических потерь рм подсчитывается по формулам (105) —(ПО) без учета качества применяемых масел, теплового состояния двигателя, качества поверхностного трения и наддува. Поэтому, прежде чем воспользоваться значениями р„, полученными по приведенным формулам, необходимо критически их оценить.
При использовании в качестве агрегата наддува приводного нагнетателя (механический наддув) потери в двигателе увеличиваются на величину затрат мощности на его привод.
3—370
65
Среднее эффективное давление. Среднее эффективное давление ре представляет собой отношение эффективной работы на валу двигателя к единице рабочего объема цилиндра. В расчетах двигателей ре определяется по среднему индикаторному давлению
Pe = Pi~ Рм- (Н1)
Для двигателей с механическим наддувом
Pe = Pi~ Рм— ря, (112)
где ря —потери давления на привод нагнетателя.
Значения среднего эффективного давления ре (МПа) при номинальной нагрузке изменяются в следующих пределах:
Для четырехтактных карбюраторных двигателей .... 0,6—1,1
Для четырехтактных карбюраторных двигателей форсированных .......................................... до 1,3
Для четырехтактных дизелей без наддува...........0,55—0,85
Для четырехтактных дизелей с наддувом ........... до 2,0
Для двухтактных быстроходных дизелей.............. 0,4—0,75
Для газовых двигателей........................... 0,5—0,75
С ростом среднего эффективного давления улучшаются условия использования рабочего объема цилиндра, что дает возможность создавать более легкие и компактные двигатели.
Длительное время при создании автомобильных и тракторных двигателей отмечалась тенденция к постоянному увеличению ре. Однако за последние 10—12 лет эта тенденция заметно изменилась в связи с постоянно растущими требованиями во всем мире по уменьшению токсичности двигателей в процессе их эксплуатации. Таким образом, для современных автомобильных и тракторных двигателей характерно сохранение или даже некоторое снижение ре при резком уменьшении токсичности за счет лучшей организации рабочего процесса, применения высокосортных топлив, совершенствования систем питания и использования наддува.
Механический к. п.д. Отношение среднего эффективного давления к индикаторному называется механическим к. п. д. двигателя:
Пм = PjPi или Г]м = 1 —Pulpt. (113)
С увеличением потерь в двигателе г]м уменьшается. При снижении нагрузки в карбюраторном двигателе значительно возрастает рм из-за увеличения потерь на газообмен. При холостом ходе рг = рм и Т]м = 0.
Величина механического к. п. д. возрастает с уменьшением потерь на трение и на привод вспомогательных механизмов, а также с увеличением нагрузки до определенных пределов.
По опытным данным механический к. п. д. т]м для различных двигателей, работающих на номинальном режиме, изменяется в следующих пределах:
Для карбюраторных двигателей....................... 0,7—0,9
Для четырехтактных дизелей без наддува............. 0,7—0,82
Для четырехтактных двигателей с наддувом (без учета потерь мощности на нагнетатель)....................... 0,8—0,9
66
Для двухтактных быстроходных дизелей................ 0,7—0,85
Для газовых двигателей .............................0,75—0,85
Эффективная мощность. Полезная работа, получаемая на валу двигателя в единицу времени, называется эффективной мощностью Ne. Величина Ne (кВт) может быть определена по индикаторной мощности через механический к. п. д.:
^e==^M = PKW(3(h), (114)
где ре —выражено в МПа; Vh —вл; п —в об/мин.
Связь между эффективной мощностью и основными параметрами двигателя выражается следующей зависимостью:
(115)
30т а/0
где Vh —выражено вл; п —в об/мин; Ни —в МДж/кг; —в кг/м3.
Из анализа выражения (115) следует, что эффективная мощность двигателя может быть повышена в общем случае за счет: а) увеличения рабочего объема цилиндра (увеличения линейных размеров диаметра цилиндра и хода поршня); б) увеличения количества цилиндров; в) увеличения частоты вращения коленчатого вала двигателя; г) перехода с четырехтактного на двухтактный цикл; д) повышения низшей теплоты сгорания топлива; е) повышения плотности заряда и коэффициента наполнения (например, путем наддува, а также за счет улучшения организации газообмена, снижения сопротивлений на впуске и выпуске, применения инерционного наддува для увеличения дозарядки и т. д.); ж) повышения индикаторного к. п. д. (за счет совершенствования процесса сгорания и сокращения потерь теплоты топлива в процессах сжатия и расширения); з) повышения механического к. п. д. двигателя (например, за счет использования высококачественных масел, уменьшения соприкасающихся поверхностей, сокращения насосных потерь и т. д.).
Эффективный к. п. д. и эффективный удельный расход топлива. Эффективный к. п. д. и эффективный удельный расход топлива ge характеризуют экономичность работы двигателя.
Отношение количества теплоты, эквивалентной полезной работе на валу двигателя, к общему количеству теплоты, внесенной в двигатель с топливом, называется эффективным к. п. дл
^LJHut (116)
где Le —теплота, эквивалентная эффективной работе, МДж/кг топл; Ни —низшая теплота сгорания топлива, МДж/кг топл.
Связь между эффективным и механическим к. п. д. определяется выражением:
Для двигателей, работающих на жидком топливе:
Pq CtZfQ 7L = -----— .
P*v на
двигателя
(117)
(118)
з*
67
Для двигателей, работающих на газообразном топливе:
= 371,2 • 10^рвТкМ[/(рк^Нги). (119)
Эффективный к. п. д. двигателя характеризует степень использования теплоты топлива в двигателе с учетом всех потерь —тепловых и механических.
Значения эффективного к. п. д. т]е на номинальном режиме приведены ниже:
Для карбюраторных двигателей.......................0,25—0,33
Для дизелей........................................0,35—0,40
Для газовых двигателей ............................0,23—0,30
Более высокие значения эффективного к. п. д. т]е у дизелей по сравнению с т]е карбюраторных двигателей являются, в основном, следствием повышенных значений у них коэффициентов избытка воздуха, а следовательно, и более полного сгорания топлива.
Эффективный удельный расход [г/(кВт-ч)] жидкого топлива
ge = 3600/(7/^) или ge = 3600?jjiv/(peloa). (120)
Для двигателей, работающих на газообразном топливе, эффективный удельный расход [м3/(кВт-ч)] газового топлива
пе = 3,6/(т)Х) или ve = 9700рлт]и/(Ре^1'Л). (121)
а удельный расход теплоты [МДж/(кВт-ч)] на единицу эффективной мощности
Че = veH'u = 9700р^Я;/(реЛ1;п). (122)
Для современных автомобильных и тракторных двигателей, эффективный удельный расход топлива при номинальной нагрузке имеет следующие значения:
Для карбюраторных двигателей ............ §^ = 2504-325 г/(кВт-ч) Для дизелей с неразделенными камерами.......ge = 2104-245 г/(кВт-ч)
Для вихрекамериых и предкамерных дизелей....ge = 2304-280 г/(кВт-ч)
Для газовых двигателей удельный расход теплоты ... qe~ 124- 17МДж(кВт-ч)
Основные размеры цилиндра двигателя. Если задана эффективная мощность двигателя и выбрана величина S/D (выбор S/D приведен в гл. IV), то основные конструктивные параметры двигателя (диаметр цилиндра и ход поршня) определяются следующим образом.
По эффективной мощности, частоте вращения коленчатого вала и эффективному давлению определяется литраж (л) двигателя
Ул = 3(HVe/(pen), (123)
где Ne выражена в кВт; ре —в МПа ил —в об/мин.
Рабочий объем одного цилиндра (л)
vh = Va/i. (124)
Диаметр цилиндра (мм)
D = 100 13/—• (125)
68
Ход поршня (mmJ
S = D • S/D. (126)
Полученные значения D и S округляют до целых чисел, нуля или пяти. По окончательно принятым значениям D и S определяют основные параметры и показатели двигателя:
литраж двигателя (л)
Гл ?=яР25//(4 • 10е); (127)
эффективную мощность (кВт)
Ne = peVan/(3Qr); (128)
эффективный крутящий момент (Н • м)
Ме = (3 • 10*/я)(ад; (129)
часовой расход топлива (кг/ч)
GT = Nege; (130)
среднюю скорость поршня (м/с)
Уп ср == Sn/(3 • 104). (131)
При расхождении между ранее принятой величиной Оп.ср и полученной по формуле (131) более 3—4% необходимо пересчитать эффективные параметры двигателя.
$ 15. ПОСТРОЕНИЕ ИНДИКАТОРНОЙ ДИАГРАММЫ
Индикаторная диаграмма двигателя внутреннего сгорания строится с использованием данных расчета рабочего процесса. При построении диаграммы ее масштабы рекомендуется выбирать с таким расчетом, чтобы получить высоту равной 1,2 — 1,7 ее основания. В начале построения (рис. 35 и 36) на оси абсцисс откладывается отрезок АВ, соответствующий рабочему объему цилиндра, а по величине равный ходу поршня в мас-
Рис. 35. Построение индикаторной диаграммы карбюраторного двигателя аналитическим методом
69
Рис. 36. Построение индикаторной диаграммы дизеля с наддувом графическим методом
штабе Ms, который в зависимости от величины хода поршня может быть принят 1:1, 1,5 : 1 или 2:1.
Отрезок О А (мм), соответствующий объему камеры сгорания:
ОА ~ АВ/(& —1). (132)
Отрезок z'z для дизелей, работающих по циклу со смешанным подводом теплоты (рис. 36):
z'z = 0A(p —1). (133)
При построении диаграммы рекомендуется выбирать масштабы давлений = 0,02; 0,025; 0,04; 0,05; 0,07 —0,10 МПа в мм.
Затем по данным теплового расчета на диаграмме откладывают в выбранном масштабе величины давлений, в характерных точках: а, с, z', г, 6, г.
Построение политроп сжатия и расширения мож-
но производить аналитическим или графическим методом. При аналитическом методе построения политроп сжатия и расширения (рис. 35) вычисляется ряд точек для промежуточных объемов, расположенных между Vс и Va и между Vz и Vb по уравнению политропы pVni = const.
Для политропы сжатия = раУа\ откуда
Px-Pa(Va/Vx)n\
(134)
где рх и Vx —давление и объем в искомой точке процесса сжатия.
Отношение Va/Vx изменяется в пределах 1 —е.
Аналогично для политропы расширения
Рх-Рь(Уь/Ух)П2. (135)
Для карбюраторных двигателей отношение Vb/Vx изменяется в интервале 1 —е, а для дизелей — 1 —8.
При аналитическом методе построения диаграммы определение ординат расчетных точек политроп сжатия и расширения удобно производить в табличной форме (см. ниже табл. 10).
Соединяя точки а и с плавной кривой, проходящей через вычисленные и нанесенные на поле диаграммы точки политропы сжатия, 70
а точки z и b — кривой, проходящей через точки политропы расширения, и соединяя точки с с z, a b с а прямыми линиями (при построении диаграммы дизеля точка с соединяется прямой линией с точкой г', аг’ —с z —см. рис. 36), получаем расчетную индикаторную диаграмму (без учета насосных ходов). Процессы выпуска и впуска принимаются протекающими при р = const и V = const (прямые bl, lr, гг" и г"a —см. рис. 33 и 34).
При графическом методе, по наиболее распространенному способу Брауэра политропы сжатия и расширения строят следующим образом (рис. 36).
Из начала координат проводят луч ОС под произвольным углом а к оси абсцисс (для получения достаточного количества точек на политропах рекомендуется брать а = 15°). Далее из начала координат проводят лучи 0D и ОЕ под определенными углами и к оси ординат. Эги углы определяют из соотношений
tg₽i = (1 + tga)"1- 1; tgp2 = (l + tgap- 1. (136)
Политропу сжатия строят с помощью лучей ОС и 0D. Из точки с проводят горизонталь до пересечения с осью ординат; из точки пересечения — линию под углом 45° к вертикали до пересечения с лучом 0D, а из этой точки — вторую горизонтальную линию, параллельную оси абсцисс. Затем из точки с проводят вертикальную линию до пересечения с лучом ОС'; из точки пересечения — под углом 45° к вертикали линию до пересечения с осью абсцисс, а из этой точки — вторую вертикальную линию, параллельную оси ординат, до пересечения со второй горизонтальной линией. Точка пересечения этих линий будет промежуточной точкой 1 политропы сжатия. Точка 2 находится аналогичным путем при выборе точки 1 за начало построения.
Политропу расширения строят с помощью лучей ОС и ОЕ, начиная от точки г, аналогично построению политропы сжатия.
Полученные диаграммы (рис. 35 и 36) являются расчетными индикаторными диаграммами, по которым можно определить
Р( = F'MP/AB, (137)
где F’ —площадь диаграммы ac(z')zba, мм2; Мр —масштаб давлений (МПа в мм); АВ — отрезок, мм.
Значение p't, полученное по формуле (137), должно быть равно значению p't, полученному в результате теплового расчета.
Действительная индикаторная диаграмма ac'c"znb'b"ra отличается от расчетной, так как в реальном двигателе за счет опережения зажигания или впрыска топлива (точка с') рабочая смесь воспламеняется до прихода поршня в в. м. т. (точка /) и повышает давление в конце процесса сжатия (точка с"). Процесс видимого сгорания происходит при изменяющемся объеме и протекает по кривой с"гд, а не по прямой cz, для карбюраторных двигателей (рис. 35) или по прямым сг' и z’z для дизеля (рис. 36); открытие выпускного клапана до прихода поршня в н. м. т. (точка Ь') снижает давление в конце расширения (точка Ь“, которая обычнр располагается между точками
71
b и а). Для правильного определения местоположения указанных точек необходимо установить взаимосвязь между углом ф поворота коленчатого вала и перемещением поршня sx. Эта связь устанавливается на основании выбора длины шатуна Lm и отношения радиуса кривошипа R к длине шатуна X = R/L^. Порядок выбора £ш, определения Хи установления взаимосвязи между <р и приведен в гл. VI.
По индикаторной диаграмме для проверки теплового расчета и правильности построения диаграммы acfcnzjb'b№a определяется
Pi = FMP/AB, (138)
где F —площадь диаграммы ac,c"zJIbfb"a.
Глава IV
ТЕПЛОВОЙ РАСЧЕТ И ТЕПЛОВОЙ БАЛАНС ДВИГАТЕЛЯ
§ 16. ОБЩИЕ СВЕДЕНИЯ
Тепловой расчет позволяет с достаточной степенью точности аналитическим путем определить основные параметры вновь проектируемого двигателя, а также проверить степень совершенства действительного цикла реально работающего двигателя,
В данном учебном пособии основное внимание уделено расчету вновь проектируемого двигателя. В связи с этим приводятся основные положения, необходимые для выбора исходных параметров, которые используются при выполнении как теплового, так и последующих расчетов двигателя.
Мощность и частота вращения коленчатого вала. ^При расчете двигателя величиной номинальной мощности обычно задаются или ее определяют с помощью тяговых расчетов. Номинальной мощностью Ne называют эффективную мощность, гарантируемую заводом-изготовителем для определенных условий работы. В автомобильных и тракторных двигателях номинальная мощность равна максимальной мощности при номинальной частоте вращения коленчатого вала. Выбор или задание номинальной мощности определяется прежде всего назначением двигателя (для легкового или грузового автомобилей, трактора); его типом (карбюраторный, газовый, дизель); условиями эксплуатации и т. д. Мощность современных автомобильных и тракторных двигателей колеблегся в очень широких пределах —15— 500 кВт.
Другим важнейшим показателем двигателя является частота вращения коленчатого вала, характеризующая тип двигателя и его динамические качества. На протяжении длительного времени существовала тенденция/ повышения частоты вращения коленчатого вала. Результатом этого являлось снижение основных размеров двигателя, его веса и габаритов. Однако с увеличением частоты вращения возрастают инерционные силы, ухудшается наполнение цилиндров, возрастает токсичность продуктов сгорания, повышается износ деталей и узлов двигателя, снижается его срок службы. В связи с этим за 72
последнее десятилетие частота вращения коленчатого вала двигателей практически стабилизировалась, а для отдельных типов автомобильных двигателей, особенно американских, снизилась.
В настоящее время частота вращения коленчатого вала двигателей легковых автомобилей колеблется в пределах 4000—6000 об/мин и только в отдельных моделях (например, у двигателей спортивных автомобилей) превышает 6000 об/мин. Двигатели, предназначенные для грузовых автомобилей и тракторов, в целях снижения инерционных нагрузок и повышения моторесурса значительно дефорсируются по частоте вращения коленчатого вала. Тем не менее в отдельных моделях двигателей грузовых автомобилей и тракторов частота вращения коленчатого вала достигает 3000—4000 об/мин( дизели) и 4000— 4500 об/мин (карбюраторные двигатели). Частота вращения коленчатых валов современных тракторных дизелей 1500—2500 об/мин.
Число и расположение цилиндров. Выбор числа цилиндров и их расположение зависят от мощностных, динамических и конструктивных факторов. Наибольшее распространение в европейских странах получили четырех- и шестицилиндровые автомобильные двигатели, а в Америке—восьмицилиндровые. При особо высоких требованиях к массе и габаритам число цилиндров автомобильных двигателей достигает 12 и крайне редко — 16. Тракторные двигатели обычно имеют четыре цилиндра, реже — бив отдельных случаях — 12. С увеличением числа цилиндров повышаются возможности форсировки двигателей по частоте вращения, улучшаются пусковые качества и проще решаются вопросы уравновешенности. Однако с увеличением числа цилиндров повышаются механические потери и ухудшаются экономические показатели.
Выбор количества цилиндров во многом зависит от литража двигателя. Так, литраж Ул четырехцилиндрового карбюраторного двигателя обычно составляет 0,7—2,2 л и лишь отдельные модели имеют Ил > 2,2 л. Литраж четырехцилиндровых дизелей значительно выше и в среднем составляет 4—8 л, отдельные модели тракторных дизелей имеют Ул>10л. Шестицилиндровые карбюраторные двигатели имеют Vх л ж 2,0—5,6 л, а дизельные —до Йл « 20 л.
Современные автомобильные и тракторные двигатели имеют рядное, V-образное и оппозитное расположение цилиндров. Наибольшее распространение получили четырехцилиндровые рядные двигатели, как наиболее простые в эксплуатации и более дешевые в производстве. В последние годы в автотракторостроении наметилась тенденция к применению двигателей с V-образным расположением цилиндров. По сравнению с рядными они имеют более высокий механический к. п. д., меньшие габариты и лучшие удельно-массовые показатели. Повышенная жесткость V-образных двигателей позволяет, кроме того, достигать более высоких частот вращения коленчатого вала.
В ряде стран созданы и эксплуатируются двигатели с горизонтальными оппозитно расположенными цилиндрами, отличающимися более удобным расположением их на используемых установках.
Размеры цилиндра и скорость поршня. Размеры цилиндра — диаметр и ход поршня —являются основными конструктивными пара-
73
метрами 'двигателя. Величина диаметра D (мм) цилиндра современных автомобильных и тракторных двигателей изменяется в достаточно узких пределах 60—150 мм и в основном зависит от типа и назначения двигателя. Величина D различных двигателей изменяется приблизительно в следующих пределах:
Для карбюраторных двигателей легковых автомобилей . . 60—100 Для карбюраторных двигателей грузовых автомобилей . . 70—ПО Для тракторных дизелей......................? . . . . 70—150
Для автомобильных дизелей............................. 80—130
Ход поршня обычно характеризуется относительной величиной S/Df непосредственно связанной со скоростью поршня. В зависимости от величины S/D различают двигатели короткоходные (S/D< 1) и длин-ноходные (S/D > 1). При переходе к короткоходным двигателям снижается высота двигателя и его масса, увеличивается индикаторный к. п. д. и коэффициент наполнения, уменьшается скорость поршня и износ деталей двигателя. В то же время снижение величины S/D приводит к более высокому давлению газов на поршень, ухудшению условий смесеобразования и увеличению габаритной длины двигателя.
Современные карбюраторные двигатели проектируются с невысоким отношением S/О. Обычно <$/£) = 0,7 — 1,0. Для автомобильных дизелей отношение хода поршня к диаметру цилиндра принимается близким к единице (S/D = 0,9 — 1,2). Большинство же дизелей имеют S/D > 1. Для тракторных дизелей S/D = 1,1 4- 1,3.
Скорость поршня ип ср является критерием быстроходности двигателя. В зависимости от величины ип ср двигатели подразделяют на тихоходные (ип.сР< 6,5 м/с) и быстроходные (ип.сР > 6,5 м/с). Все автомобильные и почти все тракторные двигатели являются быстроходными, так как имеют ип.сР > 6,5 м/с.
С увеличением скорости поршня возрастают механические потери, повышается тепловая напряженность деталей, сокращается срок службы двигателя. В связи с этим увеличение средней скорости поршня неразрывно связано с необходимостью повышения долговечности деталей, применения более совершенных материалов в двига-телестроении и улучшения качества применяемых масел.
В современных автомобильных и тракторных двигателях скорость Vn.cp (м/с) поршня обычно изменяется в пределах:
Для карбюраторных двигателей легковых автомобилей 7 . . 12—15
Для карбюраторных двигателей грузовых автомобилей . . . 9—12
Для автомобильных газовых двигателей . ..............7—11
Для автомобильных дизелей.............................6,5—12
Для тракторных дизелей................................5,5—10,5
Степень сжатие. Величина степени сжатия является одной из важнейших характеристик двигателя. Ее выбор в первую очередь зависит от способа смесеобразования и рода топлива. Кроме того, величину степени сжатия выбирают с учетом наличия или отсутствия 74
наддува, быстроходности двигателя, системы охлаждения и'других факторов.
Для карбюраторных двигателей выбор степени сжатия прежде всего определяется детонационной стойкостью применяемого топлива (см. § 1). При определенном сорте топлива возможно добиться повышения степени сжатия за счет: а) выбора рациональной формы камеры сгорания и расположения свечи (расположение свечи на приблизительно равном удалении от стенок камеры сгорания позволяет повысить е); б) размеров цилиндра (уменьшение диаметра цилиндра повышает е вследствие сокращения пути пламени и увеличения относительной поверхности охлаждения); в) повышения частоты вращения коленчатого вала двигателя (увеличение п повышает ев основном вследствие роста скорости сгорания); г) выбора материала поршня и головки цилиндра (поршень из алюминиевого сплава позволяет повышать е на 0,4—0,7, а применение головки цилиндров из алюминиевого сплава вместо чугунной дополнительно повышает значение е на 0,5—0,6); д) выбора системы охлаждения (жидкостная система охлаждения допускает более высокие значения е, чем воздушная); е) применения обогащенной (а<0,8) или обедненной (а>0,9) рабочей смеси.
В современных карбюраторных двигателях е=6~- 12. Двигатели грузовых автомобилей имеют значения е ближе к нижнему пределу, а у двигателей легковых автомобилей обычно е > 7 и только при воздушном охлаждении е иногда несколько ниже 7. Повышение степени сжатия для карбюраторных двигателей выше 12 ограничивается как возможностью самовоспламенения смеси, так и возникновением детонации в процессе сгорания. Кроме того, при повышении 12 относительное и абсолютное увеличение индикаторного к. п. д. незначительно (см. гл. II). В последние годы наметилась тенденция к некоторому понижению е, что позволяет снизить токсичность продуктов сгорания и продлить срок службы двигателей. Как правило, даже двигатели легковых автомобилей высокого класса имеют степень сжатия не более 9.
Минимальная степень сжатия для дизелей должна обеспечить в конце процесса сжатия получение минимальной температуры, необходимой для самовоспламенения впрыснутого топлива. Учитывая, что впрыск топлива осуществляется раньше полного завершения процесса сжатия и с повышением температуры сжатия сокращается период задержки воспламенения, в дизелях без наддува не применяются значения степени сжатия меньше 14, а в дизелях с наддувом —меньше 11.
Для современных автомобильных и тракторных двигателей с воспламенением от сжатия 8=14-^22. Увеличение степени сжатия более 22 нецелесообразно, так как приводит к высоким давлениям сгорания, падению механического к. п. д. и утяжелению конструкции двигателя.
Выбор степени сжатия для дизелей прежде всего определяется формой камеры сгорания и способом смесеобразования. В зависимости от этих параметров значения степени сжатия е дизелей находятся в пределах:
75
Для дизелей с неразделенными камерами сгорания н объем-
ным смесеобразованием ............................. 14—17
Для вихрекамерных дизелей .............................. 16—20
Для предкамерных дизелей ...........................*. 16,5—21
Для дизелей с наддувом .................................. 11—17
На основе установленных или заданных исходных данных (тип двигателя, мощность Ne, частота вращения коленчатого вала и, число i и расположение цилиндров, отношение S/D, степень сжатия е) проводят тепловой расчет двигателя, в результате которого определяют основные энергетические (ре, Л/л), экономические (get т]е) и конструктивные (D, S, Ул) параметры двигателя. По результатам теплового расчета строят индикаторную диаграмму. Параметры, полученные в тепловом расчете, используются при построении скоростной характеристики и являются исходными при проведении динамического и прочностных расчетов.
В данном учебном пособии приводятся примеры расчетов двух двигателей: карбюраторного и дизеля. С целью рассмотрения различных методов и приемов проведения тепловых, динамических и прочностных расчетов тепловой расчет карбюраторного двигателя проводится для четырех скоростных режимов, а тепловой расчет дизеля — для номинального скоростного режима, но в двух вариантах: а) для дизеля без наддува и б) для дизеля с наддувом. На базе теплового расчета для каждого двигателя построена внешняя скоростная характеристика, проведены динамический расчет и расчет основных деталей и систем двигателя. В связи с этим задание на расчет каждого двигателя приводится один раз перед выполнением теплового расчета.
$ 17. ТЕПЛОВОЙ РАСЧЕТ И ТЕПЛОВОЙ БАЛАНС КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
Произвести расчет четырехтактного карбюраторного двигателя, предназначенного для легкового автомобиля. Эффективная мощность двигателя Ne — 60 кВт при частоте вращения коленчатого вала п = 5600 об/мин. Двигатель четырехцилиндровый, i^= 4 с рядным расположением. Система охлаждения жидкостная закрытого типа. Степень сжатия е = 8,5.
Тепловой расчет
При проведении теплового расчета для нескольких скоростных режимов обычно выбирают 3—4 основных режима. Для карбюраторных двигателей такими режимами являются:
1) режим минимальной частоты вращения nmin=600 4- ЮООоб/мин, обеспечивающий устойчивую работу двигателя;
2) режим максимального крутящего момента при нлг=(0,4 4-4- 0,6)п#;
3) режим максимальной (номинальной) мощности при пдг;
4) режим максимальной скорости движения автомобиля при «max =(1,05 4-1,20)^.
76
С учетом приведенных рекомендаций и задания (пи = 5600 об/ мин) тепловой расчет последовательно проводится для п ~ 1000, 3200, 5600 и 6000 об/мин.
Топливо. В соответствии с заданной степенью сжатия е = 8,5 Можно использовать бензин марки АИ-93.
Средний элементарный состав и молекулярная масса топлива С =0,855; Н =0,145 и /ит =115 кг/кмоль.
Низшая теплота сгорания топлива
Яц = 33,91С + 125,60Н — 10,89 (О — S) — 2,51 X (9Н + Щ = = 33,91 • 0,855 + 125,6 • 0,145—2,51 • 9 • 0,145=43,93 МДж/кг= = 43 930 кДж/кг.
Параметры рабочего тела. Теоретически необходимое количество воздуха для сгорания 1 кг топлива
. _ 1 / С Н_________О_\ _ 1 /0,855 0,145 \ _
0 ~ 0,208 ( 12 + 4 32 J 0,208 ( 12 4 /
= 0,516 кмоль возд/кг топл;
L = — С + 8Н — О') = —— (— 0,855 + 8 • 0,145'
° 0,23 \ 3 / 0,23 \ 3 t
= 14,957 кг возд/кг топл.
Коэффициент избытка воздуха устанавливается на основании следующих соображений. На современных двигателях устанавливают многокамерные карбюраторы, обеспечивающие получение почти идеального состава смеси по скоростной характеристике. Возможность применения для рассчитываемого двигателя двухкамерного карбюратора с обогатительной системой и системой холостого хода позволяет получить при соответствующей регулировке ка1£ мощностной, так и экономичный состав смеси. Стремление получить двигатель достаточно экономичный и с меньшей токсичностью продуктов сгорания, которая достигается при а ~ 0,95 4- 0,98, позволяет принять а = = 0,96 на основных режимах, а на режиме минимальной частоты вращения а =0,86 (рис. 37).
Количество горючей смеси
М{ = а^о + 1/апт;
при п = 1000 об/мин = = 0,86 • 0,516 + 1/| 15 = 0,4525 кмоль гор. см/кг топл;
при п = 3200, 5600 и 6000 об/мин М{ =0,96- 0,516+1/115= = 0,5041 кмоль гор. см/кг топл.
Количество отдельных компонентов продуктов сгорания при К = 0,5 и принятых скоростных режимах:
а 1,0 0,3 0,8
0,95 0,90 0,85
0,80
1000 2000 3000 4000 5000 п, о5/мцн
Рис. 37. Исходные параметры для теплового расчета карбюраторного двигателя
77
при п = 1000 об/мин
Мс0 = —-------2 • O,2O8Lo =- — 2 1~0’-86 • 0,208 • 0,516 =
12 1 + К 0 12 1 + о,5 ’
— 0,0512 кмоль СО2/кг топл;
Мео == 2 O,2O8Lo = 2 -!~0,86 - 0,208 • 0,516 =
1 + К 1+0,5
= 0,0200 кмоль СО/кг топл;
Мн,о = • 0,208£о =
2 1 4" А 2
— 2-0,5 1 — . 0,208 • 0,516 = 0,0625 кмоль Н2О/кг топл;
1 +0,5
Мн, = 2% _Lz± . 0,208 • Lo = 2-0,5 - 1-0,86 - 0,208 • 0,516 =
1 + К ° 1+0,5
= 0,0100 кмоль Н2/кг топл;
Mn, = 0,792а£о = 0,792 - 0,86 • 0,516 = 0,3515 кмоль Ы2/кг топл; при п = 3200, 5600 и 6000 об/мин
Мео = ±^1 — 2 1-0,96 - 0,208-0,516 = 0,0655 кмоль СО2/кгтопл;
12 1+0,5 ’
Мео = 2 1 ~0’— • 0,208-0,516 = 0,0057 кмоль СО/кг топл;
1 + 0,5
Мн О = -^ — 2 - 0,5 -1 —’96 - 0,208 • 516 = 1 2 1 + 0,5
= 0,0696 кмоль Н2О/кг топл;
Мн, = 2 - 0,5 1 ~-°:96. . 0,208 - 0,516 = 0,0029 кмоль Н2/кг топл;
1 4- 0,5
Mn, = 0,792 • 0,96 • 0,516 = 0,3923 кмоль Мг/кг топл.
Общее количество продуктов сгорания
М2 = Мео, + Мео + Мн,о + Мн, + Mn, = С/12 + Н/2 + О,792а£о; при п = 1000 об/мин М2 = 0,0512 + 0,02+- 0,0625 + 0,01 + + 0,3515 = 0,4952 кмоль пр. сг/кг топл.
Проверка: М2 = 0,855/12 + 0,145/2 + 0,792 - 0,86 • 0,516 = = 0,4952 кмоль пр. сг/кг топл;
при и = 3200, 5600 и 6000 об/мин М2=0,0655 + 0,0057+0,0696+ + 0,0029 + 0,3923 = 0,5360 кмоль пр. сг/кг топл.
Проверка: М2 = 0,855/12 + 0,145/2 + 0,792 - 0,96 • 0,516 =
= 0,5360 кмоль пр. сг/кг топл. 78
Параметры окружающей среды и остаточные газы. Давление"» температура окружающей среды .при работе двигателя без наддува рк =р0 =0,1 МПа и Тк = То = 293 К.
Температура остаточных газов. Прн постоянном значении степени сжатия е = 8,5 температура остаточных газов практически линейно .возрастает с увеличением скоростного режима при а = const, но уменьшается при обогащении смеси. Учитывая, что при п = = 1000 об/мин а = 0,86, а на остальных режимах а = 0,96, принимается (рис 37):
п= 1000; 3200; 5600: 6000 об/мин;
Гг= 900, 1000, 1060, 1070 К.
Давление остаточных газов рг за счет расширения фаз газораспределения и- снижения сопротивлений при конструктивном оформлении выпускного тракта рассчитываемого двигателя можно получить на номинальном скоростном режиме
prN= 1,18р0 =#= 1,18- 0,1 = 0,118 МПа.
Тогда
Ар = (PrN~ Ро 1.035) 108/( = (0,118-
-0,1-1,035) 108/(^60(F • 0,1) = 0,4624;
рг = р0( 1,035 + Ар • 10-8п2) = 0,1 (1,035 + 0,4624 - Ю^п2) =
= 0,1035 + 0,4624- 10-®п2.
Отсюда получим:
п = 1000; 3200; 5600; 6000 об/мин;
рг = 0,1040; 0,1082; 0,1180; 0,1201 МПа.
Процесс впуска. Температура подогрева свежего заряда. С целью получения хорошего наполнения двигателя на номинальном скоростном режиме принимается Д7\ = 8°С. Тогда
Лт = Д Гу/( 110 — 0,0125 nw) = 8/(110 —0,0125 • 5600) = 0,2;
ДГ = Ат (110 — 0,0125 п) = 0,2 (110 - 0,0125 п) = 22 — 0,0025 п.
Далее получим:
п = 1000; 3200; 5600; 6000 об/мин;
Д7= 19,5; 14; 8; 7 °C.
Плотность заряда на впуске
Ро = р0 - 10«/(RB7o) = 0,1 • 10«/(287 - 293) = 1,189 кг/м3, где RB = 287 Дж/кг- град — удельная газовая постоянная для воздуха.
79
Потери давления на впуске. В соответствии со скоростным режи-мом двигателя (п = 5600 об/мин) и при условии качественной об-работки ’ внутренней поверхности впускной системы можно принять (З2 + £вп =2,8 и о>вп = 95 м/с. Тогда
Ап = ^вп/^дг = 95/5600= 0,01696;
&Ра = Ф2 +-&ш) Л2япЧ - 10-*/2.
Отсюда получим:
при п = 1000 об/мин &ра = 2,8 • 0.016962 - 10002 . 1,189 х х 10-в/2 = 0,0005 МПа;
при п =3200 об/мин Арв = 2,8 0.016962 - 32002 • 1,189 х х 10-8/2 = 0,0049 МПа;
при п = 5600 об/мин Дрв = 2,8 • 0.016962 • 56002 • 1,189 х X 10-8/2 = 0,0150 МПа;
при п = 6000 об/мин Дра = 2,8 • 0.016962 • 60002 - 1,189 х X 10-8/2 = 0,0172 МПа.
Давление в конце впуска
Ра =Ро— &Ра, п = 1000; 3200; 5600; 6000 об/мин;
ра = 0,0995 0,0951 0,0850 0,0828 МПа.
Коэффициент остаточных газов. При определении уг для двигателя без наддува принимается коэффициент очистки фоч = 1, а коэффициент дозарядки на номинальном скоростном режиме фдоз = 1,10, что вполне возможно получить при подборе угла опаздывания закрытия впускного клапана в пределах 30—60\ При этом на минимальном скоростном режиме (п = 1000 об/мин) возможен обратный выброс в пределах 5%, т. е. фдоз =0,95. На остальных режимах значения Фдоз можно получить, приняв линейную зависимость фдоз от скоростного режима (рис. 37). Тогда
у __ 4- Д7*<рочРг
При п — 1000 об/мин
= 0,0516;
при п = 3200 об/мин
= 0,0461;
при п = 5600 об/мин
= 0,0495;
при п = 6000 об/мин «= 0,0509.
*г ьфлозРа ФочРг
_ 293+ 19,5 _________0,104_________
т~ 900 ’ 8,5-0,95 0,0995 — 0,104
_ 293 + 14 ___________0,1082
г~ 1000 ' 8,5-1,025-0,0951 —0,1082
293 + 8 __________0,118____________
“ 1060 ’ 8,5 • 1,1 • 0,085 — 0,118 ~
293 + 7 __________0,1201___________
~ 1070 ’ 8,5-1,11-0,0828 — 0,1201
80
Температура в конце впуска
Та = (То + ДТ + ?гТг)/(1 +?г).
При п = ЮООоб/мин Т. = (293 + 19,5 + 0,0516 • 900/(1 +0,0516) = = 341 К;
при п = 3200 об/мин Та = (293 + 14 + 0,0461 • 1000)/(1 +0,0461)= = 338 К;
при п = 5600 об/мин Та = (293 + 8 + 0,0495 • 1060)/(1 +0,0495) = = 337 К;
при п = бОООоб/мин Та = (293 + 7 + 0,0509 • 1070)/( 1 +0,0509) = = 337 К.
Коэффициент наполнения
~ т , АТ I ~ (?доз®Ра ТочРг)' Т0+ДГ е —1 р0
При п = 1000 об/мин т) = .-----— ------------!----- — (0,95 X
и v 293 + 19,5 8,5— 1 0,1
X 8,5 • 0,0995 — 0,104) = 0,8744;
при п. = 3200 об/мин т = ——— --------------- • — (1,025 • 8,5 х
и 17 293 4- 14 8,5 — 1 0,1 '
х 0,0951 —0,1082) = 0,9167;
при п= 5600 об/мин •»]..= ———------------!--- . — (1 1 . 8,5 х
и v 293 4-8 8,5-1 0,1 4
X 0,085 — 0,118) = 0,8784;
при п = 6000 об/мин 7]„= ——— ----------------- — (1,11 • 8,5 х
н 17 293 4-7 8,5—1 0,1
х 0,0828 — 0,1201) = 0,8609.
Процесс сжатия. Средний по азатель адиабаты сжатия kt при 8 = 8,5 и рассчитанных значениях Та определяется по графику (см. рис. 25), а средний показатель политропы сжатия принимается несколько меньше kt. При выборе tii учитывается, что с уменьшением частоты вращения теплоотдача от газов в стенки цилиндра увеличивается , а гц уменьшается по сравнению с более значительно:
п — 1000; 3200; 5600; 6000 об/мин;
6, = 1,3767; 1,3771; 1,3772; 1,3772;
Та= 341, 338, 337, 337 К;
п,= 1,370; 1,376; 1,377; 1,377.
Давление в конце сжатия
Рс = Ра®"1 •
Дри п = 1000 об/мин рс = 0,0995 • 8,5'’37° = 1,8666 МПа;
при п = 3200 об/мин рс = 0,0951 • 8.51’376 = 1,8072 МПа;
81
при п = 5600 об/мин ре = 0.085 • 8.51'377 = 1,6184 МПа; при п = 6000 об/мин р0 = 0,0828 • 8,51,377 = 1,5765 МПа. Температура в конце сжатия
ф ___ф «1—1
* с 1 а®
При п = 1000 об/мин Тс = 341 . в.б1-370-1 = 753 К;
при п = 3200 об/мин Те = 338.8.51,376-1 = 756 К;
при п = 5600 об/мин Та = 337 • 8.51’377-1 = 755 К;
при п = 6000 об/мин Те = 337.8,5* 377-1 = 755 К.
Средняя мольная теплоемкость в конце сжатия: а' свежей смеси (воздуха)
== 20,6 + 2,638 • 10-\,
где tc = Тс - 273°С;
п = 1000; 3200; 5600; 6000 об/мин;
ta *= 480; 483; 482; 482 °C;
(tnCyfc = 21,866; 21,874; 21,872; 21,872 кДж/(кмоль-град);
б) остаточных газов
(mcj,)*' — определяется методом экстраполяции по табл. 7: при п — 1000 об/мин, а — 0,86 и te = 480°С
(mcvC = 23’303 + (23-450 — 23,303)0,01/0,05 =
= 23,332 кДж/(кмоль град), где 23,303 и 23,450 — значения теплоемкости продуктов сгорания при 400°С соответственно при а = 0,85 и а — 0,9, взятые по табл. 7; (/ис’у )^° = 23,707 + (23,867 — 23,707) 0,01 /0,05 =
= 23,739 кДж/(кмоль-град), где 23,707 и 23,867 — значения теплоемкости продуктов сгорания при 500°С соответственно при а = 0,85 и а = 0,9, взятые по табл. 7. Теплоемкость продуктов сгорания при tc = 480 °C (/ису)^ = 23,332 + (23,739 - 23,332) 80/100 =
= 23,658 кДж/(кмоль-град);
82
при п = 3200 об/мин, а = 0,96 и te = 483 °C определение производится аналогично методом экстраполяции с использованием данных табл. 7.
= 23,586 + (23,712 — 23,586)0,01/0,05 =
= 23,611 кДжДкмоль • град);
= 24,014 4- (24,150 — 24,014)0,01/0,05 =
= 24,041 кДж/(кмоль • град);
= 23,611 + (24,041 — 23,611) 83/100 =
= 23,968 кДжДкмоль-град);
при п = 5600 и 6000 об/мин, а = 0,96 и = 482 °C
(/пс^)!ос = 23,611 4- (24,041 — 23,611) 82/100 =
= 23,964 кДж/(кмоль-град);
в) рабочей смеси
При п = 1000 об/мин
(та )‘с =------!-----121,866 + 0,0516 • 23,658| =
' к"о 1+0.0516
= 21,954 кДж/(кмоль-град);
при п = 3200 об/мин (тс;\{.с =------5——- |21,874 4- 0,0461 х
F ' k"o 1 +0,0461
х 23,968] = 21,966 кДж/(кмоль-град);
при п = 5600 об/мин (mc’v = o~O495 121,872 4- 0,0495 х
х 23,964] = 21,971 кДж/(кмоль-град);
при п = 6000 об/мин (тс'и)1.с =-----5---- 121,872 4- 0,0509 х
н ' v,ta 1 +0,0509
х 23,964] =21,973 кДж/(кмоль-град).
Процесс сгорания. Коэффициент молекулярного изменения горючей р0 = и рабочей смеси р = (р0 4- уг)/(1 + Тг)-
При п = 1000 об/мин р0 = 0,4952/0,4525 = 1,0944; р = (1,0944 + + 0,0516)/(1 + 0,0516) = 1,0898;
при п =3200 об/мин р0 = 0,5360/0,5041 = 1,0633; р =(1,0633+ + 0,0461)7(1 + 0,0461) = 1,0605;
4*
83
при п =5600 об/мин р0 = 0,5360/0,5041 = 1,0633; р = = (1,0633 + 0,0495)/(1 4- 0,0495) = 1,0603;
при п = 6000 об/мин р0 = 0,5360/0,5041 = 1,0633; р = (1,0633+ + 0,0509)/(1 + 0,0509) = 1,0602.
Количество теплоты, потерянное вследствие химической неполноты сгорания топлива:
Д//и = 119950(1— a) Lo.
При п= ЮООоб/мин Д//и = 119 950 (1 —0,86)0,516 = 8665 кДж/кг;
при п = 3200, 5600 и 6000 об/мин ЬНи = 119 950(1 — 0,96) х х 0,516 = 2476 кДж/кг.
Теплота сгорания рабочей смеси
Нраб.см = (Н и — + ?г)].
При п = ЮООоб/мин Ираб.см==(43 930 — 8665)/[0,4525(1+0,0516)] = = 74 110 кДж/кмоль раб. см;
при п=3200 об/мин //раб.см=(43930 — 2476)/[0,5041 (1+0,0461)] = = 78 610 кДж/кмоль раб. см;
при п = 5600 об/мин //раб см = (43 930 — 2476)/]0,5041 (1 + + 0,0495)] = 78 355 кДж/кмоль раб. см;
при п = 6000 об/мин //раб.см = (43930 — 2476)/[0,5041 (1 +
+ 0,0509)1=78251 кДж/кмоль раб. см.
Средняя мольная теплоемкость продуктов сгорания
== [^со. (стсисо.Й + Мсо ("ЧсоЙ +
+ MHtO(mcv н>о )<* + Мн, (/иС; н> )£+ Мы, (mcv NJ*].
При n= 1000 об/мин (zn4)^ = (1/0,4952) 10,0512 (39,123 + + 0,003349/,) + 0,02 (22,49 + 0,00143;,) + 0,0625 • (26,67 + + 0,004438/г) + 0,01 (19,678 + 0,001758/,) + 0,3515 (21,951 + + 0,001457/,)j = 24,298 + 0,002033/, кДж/(кмоль-град);
при п = 3200, 5600 и 6000 об/мин = (1/0,536) [0,0655 х х (39,123 + 0,003349/,) + 0,0057(22,49 + 0,00143/,) + 0,0696(26,67 + + 0,004438/,) + 0,0029 х (19,678 + 0,001758/,) + 0,3923(21,951 + + 0,001457/,)! = 24,656 + 0,002077/, кДж/(кмоль«град). 84
Величина коэффициента использования теплоты £ , при п = 5600 и 6000 об/мин в результате значительного догорания топлива в процессе расширения снижается, а при п — 1000 об/мин £ г интенсивно уменьшается в связи с увеличением потерь тепла через стенки цилиндра и неплотности между поршнем и цилиндром. Поэтому при изменении скоростного режима £, ориентировочно принимается (рис. 37) в пределах, которые имеют место у работающих карбюраторных двигателей:
п — 1000; 3200; 5600; 6000 об/мин;
£, = 0,82; 0,92; 0,91; 0,89.
Температура в конце видимого процесса сгорания
БЛраб.см + (mc'v)tt4e = V-ifnc'vi’tz-
При п = 1000 об/мин 0,82 - 74110 + 21,954 - 480= 1,0898(24,298+ + 0,002033/,) /„ или 0,002216/1 + 26,480/г — 71 308 = 0, откуда
tz = (— 26,480 + ]/ 26,482 + 4.0,002216 - 71 308 )/(2 - 0,002216) = = 2264 °C;
?, = /,+ 273 = 2264 + 273 = 2537 К;
при п = 3200 об/мин 0,92 • 78 610 21,966 • 483 = 1,0605 X X (24,656 + 0,002077/,) /„ или 0,002203/1 + 26,148/, — 82 931 = 0, откуда
/г = (— 26,148 + /26.1482 + 4 • 0,002203.82931 )/(2-0,002203) =
= 2602 °C;
71, = /, + 273 = 2602 + 273 = 2875 К;
при п = 5600 об/мин 0,91 • 78355 + 21,971 . 482 = 1,0603 X х (24,656 + 0,002077/,)/„ или 0,002202/1 + 26,143/, —81 893 = 0, откуда
tz = (— 26,143 + V26.1432 + 4 • 0,002202 - 81 893)/(2 • 0,002202) = = 2575 °C;
Г, = /, + 273 = 2575 + 273 = 2848 К;
при п = 6000 об/мин 0,89-78 251 + 21,973 - 482 = 1,0602 X X (24,656 + 0,002077/,)/,, или 0,002202/1 + 26,140/z —80234 = 0, откуда
/г = (— 26,140 +]/ 26,142 + 4 - 0,002202 - 80234 )/(2 - 0,002202) =
= 2530 °C;
Tz = tz + 273 = 2530 + 273 = 2803 К.
85
Максимальное давление сгорания теоретическое.
Pt /^Л/Л-
при п = 1000 Об/мин pz = 1,8666 • 1,0898 • 2537/753 е= = 6,8537 МПа;
при п =3200 об/мин Рг ~ 1,8072 • 1,0605 • 2875/756 =
= 7,2884 МПа;
при п — 5600 об/мин Р z — 1,6184 • 1,0603 • 2848/755 = = 6,4730 МПа;
при п = 6000 об/мин Р z = 1,5765 - 1,0602 • 2803/755 =
= 6,2052 МПа.
Максимальное давление сгорания действительное
ргЛ = 0,85рг;
п = 1000; 3200; 5600; 6000 об/мин;
р2Д = 5,8256; 6,1951; 5,5021; 5,2744 МПа.
Степень повышения давления
= Рг/Ре,
п = 1000; 3200; 5600; 6000 об/мин;
к = 3,672; 4,033; 4,000; 3,936.
Процессы расширения и выпуска. Средний показатель адиабаты расширения k2 определяется по номограмме (см. рис. 29) при заданном 8 = 8,5 для соответствующих значений а и Т г, а средний показатель политропы расширения п2 оценивается по величине среднего показателя адиабаты:
п — 1000; 3600; 5600; 6000 об/мин;
а = 0,86; 0,96; 0,96; 0,96;
2537; 2875; 2848; 2803 К;
^2 “ 1,2605; 1,2515; 1,2518; 1,2522;
1.260; 1,251; 1,251; 1,252.
Давление и температура в конце процесса расширения
Рь = Рг^ и Т„ = Тг /ел,—’ .
При п. — 1000 об/мин
рь т 6,8537/8,5*,26 = 0,4622 МПа и Ть = 2537/8,5*,26-1 = 1455 К; при Л — 3200 об/мин
р6 = 7,2884/8,5*,251 = 0,5013 МПа и Ть = 2875/8,5* ,25*~* = 1680 К;
.86
при п = 5600 об/мин
рь = 6,4730/8,5*251 =0,4452 МПа и Ть = 2848/8,5*-251-* = 1665 К;
при п — 6000 об/мин
Рь = 6,2052/8,5*1252 = 0,4259 МПа и Ть = 2803/8,5*252-1 = 1634 К.
Проверка ранее принятой температуры остаточных газов:
Т ___ ь
* г 3 _____ •
/ Pt>/Pr
При /г = 1000 об/мин
Тт =-------1122---= 885 К; А = 100 (885 — 900)/900 = — 1,7%;
^'0,4622/0,104
при п = 3200 об/мин
Тт =-------—---------= 1008 К;
^0,5013/0,1082
А = 100(1008 — 1000)/1000 = + 0,8%;
при п — 5600 об/мин
Тг --------1225---= Ю70 К; А =100(1070— 1060)/1060 = +0,9%;
^0,4452/0,118
при п = 6000 об/мин
Тг = 1634/^0,4259/0,1201 = 1072 К;
Д = 100(1072— 1070)/1070 = + 0,2%, где Д — погрешность расчета.
На всех скоростных режимах температура остаточных газов принята в начале расчета достаточно удачно, так как ошибка не превышает 1,7%.
Индикаторные параметры рабочего цикла. Теоретическое среднее индикаторное давление
' Рс Г 1 1 1 \ Р‘ ~~ е — 1 п2 — 1 ( «2-1 ) Л При п = 1000 об/мин _ Ь8666 Г 3,672 / j 1 \ _ ~ 8,5— 1 1,26— 1 1 8 51.2б-1 = 1,1317 МПа; при п = 3200 об/мин ' 1,8072 Г 4,033 /. ‘ 8,5 — 1 1,251 — 1 1 !— Л !—V = 1,376— 1 1 8,5*'376-*/ _1_ Л !_ \ 1 - [1-Ц ея*-1 /] —Mi——1 1,370— 11 8 5*’37-* / 1 \ __ 8,5*-25’-*/ = 1,2546 МПа;
87
при п = 5600 об/мин
' 1,6184
Pi 8,5-1
4,000 Л _ 1
1,251 — 1 I 8 б1*261”1
1
1,377 - 1
1
8,5Ь377’"1
1,1120 МПа;
при п = 6000 об/мин
1,5765 Г 3,936 /|_ 1
8,5 — 1 1,252 —11 1 я .1.252-1
L \ о»**
—L—. А-------L_
1,377-1 I gs1- 377-1
= 1,0600 МПа.
Среднее индикаторное давление
Pi = <РиА = 0,96а , где коэффициент полноты диаграммы принят <ря = 0,96; п— 1000; 3200; 5600; 6000 об/мин;
Pt => 1,0864; 1,2044; 1,0675; 1,0176 МПа.
Индикаторный к. п. д. и индикаторный удельный расход топлива
’ll — Pi№(h*№v) и gt = 3600/(77 итц).
При п = 1000 об/мин t| t = 1,0864 - 14,957 • 0,86/(43,93 х X 1,189 • 0,8744)- = 0,3060; gi = 3600/(43,93 - 0,3060) = = 268 г/(кВт- ч);
при п = 3200 об/мин тр = 1,2044 • 14,957 . 0,96/(43,93 х X 1,189 • 0,9167) =0,3612; gt =3600/(43,93 - 0,3612) =227 г/ (кВт • ч);
при п =5600 об/мин т| i = 1,0675 • 14,957 • 0,96/(43,93 х X 1,189 • 0,8784) = 0,3341; gt =3600/(43,93 - 0,3341) = = 245 г/(кВт- ч);
при п =6000 об/мин ГН = 1,0176 • 14,957 - 0,96/(43,93 - 1,189 х X 0,8609) =0,3249; gt =3600/(43,93 - 0,3249) = 252 г/(кВт- ч).
Эффективные показатели двигателя. Среднее давление механических потерь для карбюраторного двигателя с числом цилиндров до шести и отношением S/D < 1
ры =0,034 + 0,0113 сь.ер.
Предварительно приняв ход поршня S равным 78 мм, получим ц, — = Sn/З 10* =78 п/3 • 10* = 0,0026л м/с, тогда ры = = 0,034 + 0,0113 • 0,0026 п МПа, а на различных скоростных режимах:
п = 1000; 3200; 5600; 6000 об/мин^
«пср= 2,6; 8,32; 14>5б; 15,6 м/с;
рм = 0,0634; 0,1280; 0,1985; 0,2103 МПа.
Среднее эффективное давление и механический к. п. д.
Рв = Pt — Рм и = Pa/Pt;
п,— 1000; 3200; 5600; 6000 об/мин;
pt = 1,0864; 1,2044; 1,0675; 1,0176 МПа;
рв = 1,0230; 1,0764; 0,8690; 0,8073 МПа;
•Им = 0,9416; 0,8937; 0,8141; 0,7933.
Эффективный к. п. д. и эффективный удельный расход топлива 11в = 'П^м и ge= 3600/77 „ту
п. = 1000; 3200; 5600; 6000 об/мин;
7)1 = 0,3060; 0,3612; 0,3341; 0,3249;
1% = 0,2881; 0,3228; 0,2720; 0,2577;
&,= 284; 254; 301; 318 г/(кВт-ч).
Основные параметры цилиндра и двигателя. Литраж двигателя
Ул = 30tN„/M = 30.4.60/(0,869 • 5600) = 1,4795 л.
Рабочий объем одного цилиндра
Vh = Vjl = 1,4795/4 = 0,3699 л.
Диаметр цилиндра. Так как ход поршня предварительно был принят S = 78 мм, то
D = 2 . 10s V Vft/(«S) = 2 • Ю3 /0,3699/(3,14-78) = 77,72 мм.
Окончательно принимается D = 78 мм И S = 78 мм.
Основные параметры и показатели двигателя определяются по окончательно принятым значениям D и S:
V„ = kD2Si/(4 • 10е) = 3,14 • 782 • 78 • 4/(4 • 10е) = 1,49 л;
Fn = vD*/4 = 3,14 • 782/4 = 4776 мм2 = 47,76 см2;
Ne = PeV„n/30x; Л1в = — GT = A^e.10-3,
71 п
п. = 1000; 3200; 5600; 6000 об/мин;
рв= 1,0230; 1,0764; 0,8690; 0,8073 МПа;
Ме = 12,70; 42,77; 60,42; 60,14 кВт;
Ме = 121,3; 127,7; 103,1; 95,8 Н-м;
GT= 3,607; 10,864; 18,186; 19,125 кг/ч.
Литровая мощность двигателя
Na = NJVa = 60,42/1,49 = 40,55 кВт/л.
89
Построение индикаторной диаграммы. Индикаторную диаграмму (см. рис. 35) строят для номинального режима работы двигателя, т. е. при Ne = 60,42 кВт и п = 5600 об/мин.
Масштабы диаграммы: масштаб хода поршня Ms = 1 мм в мм; масштаб давлений Мр — 0,05 МПа в мм.1
Приведенные величины, соответствующие рабочему объему цилиндра и объему камеры сгорания (рис. 35):
АВ = S/M3 = 78/1,0 = 78 мм; ОА = АВ1(г — 1) = 78/(8,5 —1) = 10,4 мм.
Максимальная высота диаграммы (точка z)
р t/Mp = 6,473/0,05 = 129,5 мм.
Ординаты характерных точек:
ра/Мр =0,085/0,05 = 1,7 мм; рс/Мр = 1,6184/0,05 = 32,4 мм;
pjMp =0,4452/0,05 =8,9 мм; Рг/Мр =0,118/0,05 =2,4 мм;
р0/Л4р = 0,1/0,05 = 2 мм.
Построение политроп сжатия и расширения аналитическим методом:
а) политропа сжатия рх = ра (Va/Vac)'tl. Отсюда
PxlMp=^pa/Mp){OBlOX)n' = 1,7 (88,4/ОХ)1,377 мм,
где ОВ = ОА + АВ = 10,4 + 78 = 88,4 мм;
б) политропа расширения рх = Рь(Уъ№Х* • Отсюда
рх/Мр = (рь1Мр)(0В10Х)п* = 8,9(88,4/ОХ)1’251 мм.
Результаты расчета точек политроп приведены в табл. 10. Расчетные точки политроп показаны на рис. 35 только для наглядности. При выполнении практических расчетов на диаграмме их не показывают.
Теоретическое среднее индикаторное давление
р\ = FJAP/AB = 1725 - 0,05/78 - 1,106 МПа,
где F' = 1725 мм2 — площадь диаграммы aczba на рис. 35.
Величина р/ = 1,106 МПа, полученная планиметрированием индикаторной диаграммы, очень близка к величине р/ = 1,112 МПа, полученной в тепловом расчете.
Скругление индикаторной диаграммы осуществляется на основании следующих соображений и расчетов. Так как рассчитываемый двигатель достаточно быстроходный (п = 5600 об/мин), то фазы газораспределения необходимо устанавливать с учетом получения хорошей очистки цилиндра от отработавших газов и обеспечения до-зарядки в пределал, принятых в расчете. В связи с этим начало от-
90
Таблица 10
№ точек ох, им о о Политропа сжатия Политропа расширения
/ОВХ1’377 Рх/Л/р,мм 'МПа /ОВ0.251 Рх/мр,^ Рх, МПа
1 10,4 8,5 19,04 32,4 1,62 (точка с) 14,55 129,5 6,47 (точка г)
2 11,0 8 17,52 29,8 1,49 13,48 120,0 6,00
3 12,6 7 14,57 24,8 1,24 ' 11,41 101,5 5,08
4 17,7 5 9,173 15,6 0,78 7,490 66,7 3,34
5 22,1 4 6,747 11,5 0,58 5,666 50,4 2,52
6 29,5 3 4,539 7,7 0,385 3,953 35,2 1,76
7 44,2 2 . 2,597 4,4 0,22 2,380 21,2 1,06
8 58,9 1,5 1,748 3,0 0,15 1,661 14,8 0,74
9 88,4 1 1 1,7 0,085 (точка а) 1 8,9 (точка Ь) 0,445
крытия впускного клапана (точка г') устанавливается за 18° до прихода поршня в в. мл., а закрытие (точка а") — через 60° после прохода поршнем н. м. т.; начало открытия выпускного клапана (точка Ь') принимается за 55° до прихода поршня в н. м. т., а закрытие (точка а') — через 25° после прохода поршнем в. м. т. Учитывая быстроходность двигателя, угол опережения зажигания 0 принимается равным 35°, а продолжительность периода задержки воспламенения Аф4 = 5°.
В соответствии с принятыми фазами газораспределения и углом опережения зажигания определяют положение точек г’, а', а", с', f и Ь' по формуле для перемещения поршня (см. гл. VI):
ЛХ = [(1 — cos ср) Н—~ (1 — cos 2ср)1,
где X — отношение радиуса кривошипа к длине шатуна.
Выбор величины X производится при проведении динамического расчета, а при построении индикаторной диаграммы предварительно принимается X =0,285.
Расчеты ординат точек г', а', а", c^fnb' сведены в табл. .11.
Таблица 11
Обозначение точек Положение точек (1—cos<p) + А- х 4 X (1 — cos 2 ср) Расстояние точек от в. м. т. (АХ), мм
г' 18° ДО В. М. Т. 18 0,0655 2,6
а‘ 25° после в. м. т. 25 0,1223 4,8
а" 60° после н. м. т. 120 1,6069 62,5
с' 35° до в. м. т. 35 0,2313 9,0
f 30° до в. м. т. 30 0,1697 6,6
b' 55° До н. м. т. 125 1,6667 65,0
91
Положение точки с" определяется из выражения
ре == (1,15 4-1,25) ре = 1,25 • 1,6184 = 2,023 МПа;
ре /Мр= 2,023/0,05 = 40,5 мм.
Действительное давление сгорания
Pza = о,85рг = 0,85 • 6,473 = 5,5021 МПа;
ргд/ЛГР= 5,5021/0,05 = 110 мм.
Нарастание давления от точки с" до гл составляет
5,5021 — 2,023 = 3,479 МПа или 3,479/12 = 0,29 МПа/град п. к. в., где 12° — положение точки гя по горизонтали (для упрощения дальнейших расчетов можно принять, что действительное максимальное давление сгорания ргл достигается через —10° после в. м. т., т. е. при повороте коленчатого вала на 370°).
Соединяя плавными кривыми точки г с а', с' с с" и далее с гд и кривой расширения, Ь' с Ь" (точка Ь" располагается обычно между точками Ь и а) и линией выпуска b"r'r, получим скругленную действительную индикаторную диаграмму га'ас'fс” гяЬ'Ь"г.
Тепловой баланс
Общее количество теплоты, введенной в двигатель с топливом:
Qo = HaGT/3,6 = 43930GT/3,6 = 12203 Gr;
n= 1000; 3200; 5600; 6000 об/мин;
GT= 3,607; 10,864; 18,186; 19,125 кг/ч;
Qo= 44020; 132 570; 221 920; 233 380 Дж/с.
Теплота, эквивалентная эффективной работе за 1 с:
Qe= 1000A/e,
п = 1000; 3200; 5600; 6000 об/мин;
Qe == 12 700; 42 770; 60 420; 60140 Дж/с.
Теплота, передаваемая охлаждающей среде:
QB = ciD™mnm {Ни - ДЯ а)/(а//а),
где с = 0,45 4- 0,53 — коэффициент пропорциональности для четырехтактных двигателей. В расчете принято с = 0,5; i — число цилиндров; D — диаметр цилиндра, см; п — частота вращения коленчатого вала двигателя, об/мин; пг = 0,6 4- 0,7 — показатель степени для четырехтактных двигателей. В расчете принято при п= 1000 об/мин т — 0,6, а на всех остальных скоростных режимах — т = 0,65.
При п = 1000 об/мин QB = 0,5 • 4 • 7,8,+2'0-6 • 1000п’6 X
х (43 930 — 8665)/(0,86 • 43930) = 10 810 Дж/с;
92
при п = 3200 об/мин QB = 0,5 • 4 • 7,81+2’0’65 - 32OO0’65 к X (43 930 — 2476)/(0,96 • 43930) = 42050 Дж/с;
при п = 5600 об/мин QB = 0,5 • 4 • 7,81+2’0’65 • 5600й’65 X
X (43930 —2476)/(0,96- 43930) = 60510 Дж/с;
при п = 6000 об/мин QB = 0,5 • 4 • 7,81+2'0’65 • 6ООО0’65 х
X (43930 — 2476)/(0,96 • 43 930) = 63 280 Дж/с.
Теплота, унесенная с отработанными газами:
Qr = (GT/3,6) { M2[(mcy)f' + 8,315] tr -M, [ (mev)“ + 8,315] /0}.
При п = 1000 об/мин Qr = (3,607/3,6) {0,4952 [24,197 + 8,315[ х х 612 — 0,4525 [20,775 + 8,315] 20} = 9610 Дж/с, где (/ису)^ = 24,197 кДж/(кмоль-град)— теплоемкость остаточных газов (определена по табл. 7 методом интерполяции при а = 0,86 и tr=Tr — 273 = 885 — 273 = 612°С); (/ncv^=20,775 кДж/(кмоль х X град) — теплоемкость свежего заряда определена по табл. 5 для воздуха методом интерполяции при /0 = То — 273 = 293 — 273=20 °C.
При п = 3200 об/мин Qr = (10,864/3,6) {0,536 [25,043 + 8,315] х х 735 — 0,5041 [20,775 + 8,315] 20} = 38770 Дж/с, где (тсуУ/ — 25,043 кДж/(кмоль • град) — теплоемкость ос-таточных газов (определена по табл. 7 методом интерполяции при а = 0,96 и = Tf — 273 = 1008 — 273 = 735° С);
при п = 5600 об/мин Qr = (18,186/3,6){0,536(25,300 + 8,315] х X 797 — 0,5041 [20,775 + 8,315] 20} = 71 0§0 Дж/с, где (тсуУ/ = 25,300 кДж/(кмоль-град) — теплоемкость оста-го
точных газов (определена по табл. 7 методом интерполяции при а = = 0,96 и tr = Тг — 273 = 1070 — 273 = 797° С);
при п. = 6000 об/мин Qr = (19,125/3,6) {0,536 [25,308 + 8,315] х X 799 — 0,5041 [20,775 + 8,315] 20} = 74 940 Дж/с,
где (тсуУ.г = 25,308 кДж/(кмоль- град)— теплоемкость оста-точных газов (определена по табл. 7 методом интерполяции при а — = 0,96 и tr = Тг — 273 - 1072 — 273 = 799° С).
Теплота, потерянная из-за химической неполноты сгорания топлива:
Qh.c = A/7uGT/3,6.
При п = 1000 об/мин QH с = 8665 • 3,607/3,6 == 8680 Дж/с;
при п = 3200 об/мин Qh.c == 2476 • 10,864/3,6 = 7470 Дж/с;
93
Рис. 38. Зависимость составляющих теплового баланса карбюраторного двигателя от частоты вращения коленчатого вала
при п = 5600 об/мин Qh.c = ==2476 18,186/3,6 = 12 510 Дж/с;
При п =6000 об/мин Que — = 2476 • 19,125/3,6= 13 150 Дж/с.
Неучтенные потери теплоты
QoCT = Qo - (Qe+QB + Qr +
При n = 1000 об/мин Q0CT = =44 020 —(12 700+10810+9610+ + 8680) = 2220 Дж/с;
при n = 3200 об/мин Q0CT = = 132 570 — (42 770 + 42 050 + + 38770 + 7470) = 1510 Дж/с;
при n = 5600 об/мин Qoct = = 221 920—(60 420 + 60 510+ +71060 + 12 510) = 17 420 Дж/с;
при n =6000 об/мин QoCT = = 233 380 — (60 140 + 63 280 + +74940 + 13 150) = 21 870 Дж/с.
Составляющие теплового баланса представлены в табл. 12 и на рис. 38.
Таблица 12
Составляющие теплового баланса Частота аращения двигателя об/мнн
юоо 3200 5600 6000
Д ж/с ч. % Д ж/с а. % Q. Д ж/с % Q, Д ж/с <?< %
Теплота, эквивалентная эффективной работе . . . 12 700 28,9 42 770 32,3 60 420 27,2 60 140 25,8
Теплота, передаваемая охлаждающей среде . . 10810 24,6 42 050 31,7 60 510 27,3 63 280 27.1
Теплота, унесенная с отработанными газами 9610 21,8 38 770 29,3 71 060 32,0 74 940 32,1
Теплота, потерянная из-за химической неполноты сгорания топлива . 8 680 19,7 7 470 5,6 12510 5,7 13 150 5.6
Неучтенные потери теплоты 2 220 5,0 1510 1,1 17 420 7,8 21 870 9,4
Общее количество теплоты, введенной в двигатель с топливом • « « . 44 020 100 132570 100 221920 100 233380 100
94
$ 18. ТЕПЛОВОЙ РАСЧЕТ И ТЕПЛОВОЙ БАЛАНС ДИЗЕЛЯ
Произвести расчет четырехтактного дизеля, предназначенного для грузового автомобиля. Дизель восьми цилиндровый (i = 8) с неразделенными камерами сгорания, объемным смесеобразованием, частотой вращения коленчатого вала при максимальной мощности п = 2600 об/мин и степенью сжата я|^^2, Расчет выполнить для двух вариантов двигателя: а) дизель без наддува с эффективной мощностью Ne =170 кВт; б) дизель с турбонаддувом рк =0,17 МПа (центробежный компрессор с охлаждаемым корпусом и лопаточным диффузором и радиальная турбина с постоянным давлением перед турбиной).
Тепловой расчет
Топливо. В соответствии с ГОСТ 305—73 для рассчитываемого двигателя принимаем дизельное топливо (для работы в летних условиях — марки Л и для работы в зимних условиях — марки 3). Цетановое число топлива — не менее 45.
Средний элементарный состав дизельного топлива
С =0,870; Н =0,126; О =0,004.
Низшая теплота сгорания топлива
Ни = 33,91 С + 125,60 Н — 10,89(0 — S) — 2,51 (9 Н + W) = = 33,91 • 0,87 + 125,60 • 0,126 — 10,89 • 0,004 — 2,51 . 9 0,126 = = 42,44 МДж/кг = 42 440 кДж/кг.
Параметры рабочего тела. Теоретически необходимое количество воздуха для сгорания 1 кг топлива
, _____1 /_С_ _Н_____О_\ = 1 / 0,87 0,126 _
0 0,208 \ 12 + 4 32 / 0,208 \ 12 + 4
—Т) в 0>500 кмоль возд/кг топл;
L = —— (—С + 8Н — О) = —— f— 0,87 + 8 • 0,126 —
0 0,23 \ 3 ’ 0,23 \ 3
— 0,004^ = 14,452 кг возд/кг топл.
Коэффициент избытка воздуха. Уменьшение коэффициента избытка'воздуха а до возможных пределов уменьшает размеры цилиндра и, следовательно, повышает литровую мощность дизеля, но одновременно с этим значительно возрастает теплонапряженность двигателя, особенно деталей поршневой группы, увеличивается дымность выпускных газов. Лучшие образцы современных дизелей без наддува со струйном смесеобразованием устойчиво работают на номинальном режиме без существенного перегрева при а == 1,4 4- 1,5, а с наддувом
95
при а = 1,6 4-1,8. В связи с этим можно принять: а =1,4 — для дизеля без наддува на = 1,7 — для дизеля с наддувом.
Количество свежего заряда:
при а = 1,4 /Mj = aL0 = 1,4 • 0,5 = 0,7 кмоль св. зар/кг топл;
при а = 1,7 Afj = aL0 = 1,7 • 0,5 = 0,85 кмоль св. зар/кг топл.
Количество отдельных компонентов продуктов сгорания
Л4со, = С/12 = 0,87/12 = 0,0725 кмоль СО2/кг топл;
/Ин,о = Н/2 = 0,126/2 = 0,063 кмоль Н2О/кг топл.
При а=1,4 /Ио, = 0,208(а—1)£0 = 0,208(1,4—1)0,5 = = 0,0416 кмоль О2/кг топл;
/Wn, = O,792aLo = 0,792 • 1,4 • 0,5 = 0,5544 кмоль N2/Kr топл;
при а = 1,7 Mo, = 0,208(а—1)LO = 0,208(1,7— 1)0,5 = = 0,0728 кмоль О2/кг топл;
A4n, = O,792aLo = 0,792 *1,7 - 0,5 = 0,6732 кмоль N2/Kr топл.
Общее количество продуктов сгорания
М2 = Л4со, + Л4н,о + Л4о, + Mn, .
При а = 1,4 /И2 = 0,0725 + 0,063 + 0,0416 4- 0 5544 = = 0,7315 кмоль пр. сг/кг топл;
при а = 1,7 /И2 = 0,0725 + 0,063 + 0,0728 + 0,6732 = = 0,8815 кмоль пр. сг/кг топл.
Параметры окружающей среды и остаточные газы. Атмосферные условия
р0 = 0,1 МПа; То = 293 К.
Давление окружающей среды для дизелей:
без наддува рк = р9 = 0,1 МПа;
с наддувом рк — 0,17 МПа — по заданию.
Температура окружающей среды для дизелей:
без наддува Тж = То = 293 К;
с наддувом Тк = Т0(рк/р0)(Пк~Г>/Пк= 293 (0,17/0,1)“’6S-I)/1,65 = = 361 К, где пк — показатель политропы сжатия (для центробежного нагнетателя с охлаждаемым корпусом принят пк = 1,65).
Температура и давление остаточных газов. Достаточно высокое значение е — 17 дизеля без наддува снижает температуру и давление остаточных газов, а повышенная частота вращения коленчатого вала несколько увеличивает значения Тт и рт. При наддуве температурный режим двигателя повышается и увеличивает значения Тт и рг. Поэтому можно принять для дизелей:
96
без наддува Тг = 750К, рт~ 1.05 • р0 = 1,05 • 0,1 = 0,105 МПа; с наддувом Тг = 800 К, рг — 0.95 рк = 0,95 • 0,17= 0,162 МПа. Процесс впуска. Температура подогрева свежего заряда. Рассчитываемый двигатель не имеет специального устройства для подогрева свежего заряда. Однако естественный подогрев заряда в дизеле без наддува может достигать « 15—20°С, а при наддуве за счет уменьшения температурного перепада между деталями двигателя и температурой наддувочного воздуха величина подогрева сокращается. Поэтому принимаем для дизелей:
без наддува Д Т = 20°С;
с наддувом ДТ = 10°С.
Плотность заряда на впуске
Рк= Рк 10®/(/?втк);
без наддува рк = 0,1 • 10®/(287 • 293) = 1,189 кг/м8;
с наддувом рк = 0,17 • 10*/(287 • 361) ~ 1,641 кг/м8.
Потери давления на впуске в двигателе:
без наддува Дра = (g2 4- £вп) ы2п • рк • 10"«/2 = 2,7- 702 • 1,189 х х КГ«/2 = 0,008 МПа;
с наддувом Ар0 = 2,7 • 702 • 1,641 • 10 °/2 = 0,011 МПа, где (В2 4- £вп) = 2,7 и швп = 70 м/с приняты ’в соответствии со скоростным режимом двигателей и с учетом небольших гидравлических сопротивлений во впускной системе дизеля с наддувом и без наддува.
Давление в конце впуска
Ра = Рк — ДРа!
без наддува ра = 0,1 —0,008 = 0,092 МПа; с наддувом ра ~ 0,17 —0,011 = 0,159 ЛЩа.
Коэффициент остаточных газов
у = Гк + АГ . Рг .
Тг *Ра — Рг
без наддува Тг = 293 4-20 0,105 = 0,030;
750 17-0,092 — 0,105
с наддувом Тг = 361 4- Ю 0,162 = 0,030.
800 17 • 0,159 — 0,162
Температура В конце впуска
Та = (Тж 4- ДТ 4- 7гТг)/(1 + 7г);
без наддува Та = (293 + 20 + 0,03 • 750)/(1 4- 0,03) = 326 К; с наддувом Та = (361 + Ю + 0,03 • 800)/(1 4- 0,03) = 384 К.
Коэффициент наполнения
t)v — Тк(&ра PrW\ 4* &Т) (в 1) рк];
без наддува nv = 293(17 • 0,092 — 0,105)/[(293 4- 20)(17— — 1) 0,1] = 0,854;
с наддувом rjv = 361(17 . 0,159 — 0,162)/[(361 + 10)(17 — — 1) 0,17] = 0,909.
Процесс сжатия. Средние показатели адиабаты и политропы сжатия. При работе дизеля на номинальном режиме можно с достаточной степенью точности принять показатель политропы сжатия приблизительно равным показателю адиабаты, который определяется по номограмме (см. рис. 25):
а) для дизеля без наддува при е ~ 17 и Та = 326 К
nl яз ki = 1,370;
б) для дизеля с наддувом при е = 17 и Та = 384 К
ki— 1,3615, аи(« 1,362.
Давление и температура в конце сжатия
= и TC = V1;
без наддува Рс = 0,092 • 171’37 = 4,462 МПа, Тс = 326-171,37"1 = = 930 К;
с наддувом рс = 0,159 • 1711362 = 7,538 АПа, Те = 384- 171,36г~’ == = 1071 К.
Средняя мольная теплоемкость в конце сжатия:
а) воздуха (mcv^ = 20,6 + 2,638 • 10’3/с:
для дизеля без наддува = 20,6 + 2,638 х 10-8 • 657 = = 22,333 кДж/(кмоль*град), где t с = Тс - 273 = 930 - 273 = 657°С;
для дизеля с наддувом (тс^ = 20,6 + 2,638 • 10-3 > 798 =
= 22,705 кДж/(кмоль-град),
где t с ~ Те — 273 — 1071 — 273 = 798°С;
б) остаточных газов (определяется по табл. 8 методом интерполяции);
для дизеля без наддува при а = 1,4 и tc — 657°С
(fnc’v)tC = 24,168 кДж/(кмоль-град);
для дизеля с наддувом при а = 1,7 и te = 798 °C
(mCyfy = 24,386 кДж/(кмоль-град);
в) рабочей смеси
(т<)!о = 11 /(1 + Тг)1 + М'ЧЙ;
для дизеля без наддува (mCy)fc = [l/(l + 0,03)] [22,333 + 0,03 х X 24,168] = 22,386 кДж/(кмоль-град);
для дизеля с наддувом (пгс^)^ = [1/(1 + 0,03)] х [22,705+0,ОЗх X 24,386] = 22,754 кДж/(кмоль• град).
98.
Процесс сгорания. Коэффициент молекулярного изменения свежей смеси в дизелях:
без наддува р0 == М21М\ — 0,7315/0,7 = 1,045;
с наддувом go = Ala/Ali = 0,8815/0,85 = 1,037.
Коэффициент молекулярного изменения рабочей смеси в дизелях: без наддува ц. = (р0 4- Yr)/(1 4- Yr) = (1,045 4- 0,03)/(1 4- 0,03) = == 1,044;
с наддувом ц = (ро + Yr)/(l + Yr) = (1,037 + 0,03)/(1 4- 0,03)= = 1,036.
Теплота сгорания рабочей смеси в дизелях:
без наддува Н^.см = + у г)] = 42 440/(0,7(1 + 0,03)]=
= 58 860 кДж/кмоль раб. см;
с наддувом Нраб.см = + Yr)) = 42 440/(0,85(1 4- 0,03)]=
= 48 480 кДж/кмоль раб. см.
Средняя мольная теплоемкость продуктов сгорания в дизелях:
(т<Й = O/MJ |Mco,(m<COi)^ + MH,o(m<,Hso)/o +
= Mo, (mcvo^a + MN, = (mcvfc 4- 8,315;
без наддува = (1/0,7315) (0,0725 (39,123 4- 0,003349/,)4-
4- 0,063(26,67 4- 0,004438/,) 4- 0,0416(23,723 4- 0,00155/,) +
4- 0,5544 (21,951 4- 0,001457/,)] = 24,160 4- 0,00191/,;
(тс'р)!’ = 24,160 4- 0,00191/, 4- 8,315 = 32,475 4- 0,00191/,;
с наддувом ==(1/0,8815) (0,0725 (39,123 4-0,003349/,)-4-
4- 0,063(26,67 4- 0,004438/,) 4- 0,0728(23,723 4- 0,00155/,) 4-
4- 0,6732(21,951 4- 0,001457/,)] = 23,847 4- 0,00183/,;
(тс'р)% = 23,847 4- 0,00183/, 4- 8,315 = 32,162 4- 0,00183/,.
Коэффициент использования теплоты для современных дизелей с неразделенными камерами сгорания и хорошо организованным струйным смесеобразованием можно принять для двигателя без наддува в 0,82, а при наддуве в связи с повышением теплонапряженности двигателя и созданием более благоприятных условий для протекания процесса сгорания — <р z = 0,86.
Степень повышения давления в дизеле, в основном, зависит от величины цикловой подачи топлива. С целью снижения газовых нагрузок на детали кривошипно-шатунного механизма целесообразно иметь максимальное давление сгорания не выше 11—12 МПа. В связи с этим целесообразно принять для дизеля без наддува X—2,0, а с наддувом к — 1,5.
Температура в конце видимого процесса сгорания
^раб.см 4- [(т<)£ 4- 8,315Х]/С 4- 2270 (к - р) = р(тс'р)&;
99
для дизеля без наддува 0,82 • 58 860 4- [22,386 4- 8,315 • 2J657 4-+ 2270(2,0 — 1,044) = 1,044(32,475 + 0,0019Uz)/z или 0.001994/2 4-4- 33,904 tz — 76 069 = 0, откуда
tz — (—33,904 + |/33,9042 + 4 • 0,001994 • 76069)/(2 • 0,001994) = = 2007° С;
Tz = t z 4- 273 = 2007 4- 273 = 2280 К;
для дизеля с наддувом 0,86 • 48 480 + [22,754 4- 8,315 • 1,5)7984-4- 2270 (1,5 — 1,036)= 1,036(32,162 4- 0,00183 tz}tz или 0,001896 4 + 33,320 /г — 70 860 = 0, откуда
tz = С— -33,32 4- /33,322 4- 4-0,001896 • 70 860)/(2 0,001896) = = 1919° С;
Tz = tz + 273= 1919 4- 273 = 2192 К.
Максимальное давление сгорания для дизелей: без наддува рг = Крс = 2,0 • 4,462 = 8,924 МПа; с наддувом pz — ‘kpc= 1,5 7,538= 11,307 МПа. Степень предварительного расширения для дизелей: без наддува р = р TZ/(XTC) = 1,044 • 2280/(2,0 • 930)= 1,28; с наддувом р = рТг/(кТс) = 1,036 • 2192/(1,5 • 1071) = 1,41. Процесс расширения. Степень последующего расширения для дизелей:
без наддува 8 = е/р = 17/1,28 = 13,28;
с наддувом 8 = е/р = 17/1,41 = 12,06.
Средние показатели адиабаты и политропы расширения для дизелей выбираются следующим образом. На номинальном режиме можно принять показатель политропы расширения, с учетом достаточно больших размеров цилиндра, несколько меньше показателя адиабаты расширения, который определяется по номограмме (см. рис. 30). Для дизелей:
без наддува при 8=13,28; Тг — 2280 и а =1,4 k2 = 1,2728, a п2 принимаем равным 1,260;
с наддувом при 8 = 12,06; Т г = 2192 Л и а = 1,7 k2 = 1,2792, а л2 принимаем равным 1,267.
Давление и температура в конце расширения для дизелей:
без наддува рь = рг/8"’ = 8,924/13,281-26 = 0,343 МПа; Ть = = Tz/8n’-1 = 2280/13,28*,26_| = 1164 К;
с наддувом pb = pz/^ = 11,307/12,Об1 267 = 0,482 МПа; Ть = = 7’z/8n’~I = 2192/12,Об1’267-1 = 1129 К-
Проверка ранее принятой температуры остаточных газов для дизелей:
без наддува Тг = Ть/рь/рг = Н64/0,343/0,105 = 784 К;
А = 100(784 —750)/784 = 4,3%, что допустимо;
100
с наддувом Tr = pb/pr = 1129 / j/ 0,482/0,162 = 786 К;
Д = 100(786 — 800)/786= 1,8%, что допустимо.
Индикаторные параметры рабочего цикла. Теоретическое среднее индикаторное давление
1
_______!_) !_Л !_ ) «! — 1 \ s"*-1
4-462 Г2(1,28-1)+'.^’. . ' 1,26—1
1
1 13,28* 1’2*-1
1,37 — 1
для дизеля с наддувом pt =
для дизеля без наддува pt
773W-)]- ‘.ОН МПа;
^[1,5(1,41 — 1) + -~5' 1,41
17 —1[ 1,267—1
1 \1 1 ОСС
12,06*'2б7—| / 1,362 —
|71,362—1
Среднее индикаторное давление для дизелей:
без наддува р( = <рнР/ = 0,95 • 1,011 = 0,960 МПа, где коэффициент полноты диаграммы принят <рн = 0,95;
с наддувом pt = <p„pt' = 0,95 • 1,266 = 1,203 МПа.
Индикаторный к. п. д. для дизелей
т)( = ptloa/.(Hupsi]v)-
без наддува = 0,96 • 14,452 1,4/(42,44 • 1,189 • 0,854) = = 0,450;
с наддувом я/ == 1,203 • 14, 452 1,7/(42,44 1,641 • 0,909) = = 0,467.
Индикаторный удельный расход топлива для дизелей:
без наддува gi = 3600/(Л/„т]/) = 3600^(42,44 • 0,45) = Я= 189 г/(кВт ч);
с наддувом gi = 3600/(A/ur]f) = 3600/(42,44 • 0,467) = = 182 г/(кВт • ч).
Эффективные показатели двигателя. Среднее давление механических потерь
рм = 0,089 + 0,0П8цп ср = 0,089 + 0,0118 • 10,2 = 0,212 МПа, где средняя скорость поршня предварительно принята ип.сР= 10,2 м/с.
Среднее эффективное давление и механический к. п. д. для дизелей: без наддува = pt —рм — 0,960 — 0,212 = 0,748 МПа; т]м = = Pe/Pl = 0,748/0,96 = 0,779;
с наддувом ре = pi—ри= 1,203 —0,212 = 0,991 МПа; т]м = = pe/Pi = 0,991/1,203 = 0,824.
Эффективный к. п. д. и эффективный удельный расход топлива для дизелей:
без наддува т,е = = 0,45 • 0,779 = 0,351;
g„ = 3600/(//вП,) = 3600/(42,44 • 0,351) = 242 г/(кВт-ч);
101
с наддувом т)в = “= 0,467 • 0,824 = 0,385;
.ge = 3600/(7/Л) = 3600/(42,44 • 0,385) = 220 г/(кВт-ч).
Основные параметры цилиндра и двигателя. Литраж двигателя
Ул = WzNjM = 30 • 4 • 170/(0,748 • 2600) = 10,49 л.
Рабочий объем цилиндра
|/А= Vali= 10,49/8= 1,311 л.
Диаметр и ход поршня дизеля, как правило, выполняются с отношением хода поршня к диаметру цилиндра S/D > 1. Однако уменьшение S/D для дизеля, так же как и для карбюраторного двигателя, снижает скорость поршня и повышает т]м. В связи с этим целесообразно принять S/D — 1:
D = 100 V 4Ул/(кЗ/О) = 100|/ 4 - 1,311/(3,14-1')=118,7 мм.
Окончательно принимаем D = S = 120 мм.
По окончательно принятым значениям D и S определяются основные параметры и показатели двигателя:
Ил = лО2Зг7(4 • 10е) = 3,14 • 1202 • 120 . 8/(4 • 10е) = 10,852 л;
Fa = nDW = 3,14 • I202/4 = JI 300 мм2 = 113 см2;
уп.ср = Sn/(3 • 10*) = 120 • 2600/(3 • 104) = 10,4 м/с, что достаточно близко (ошибка < 2%) к ранее принятому значению опср = = 10,2 м/с;
для дизеля без наддува.
Ne = рв7лп/(30с) = 0,748 • 10,852 • 2600/(30 • 4) = 175,9 кВт;
Мв = 3 • 104 • Nj&n) = 30 • 10» • 175,9/(3,14 2600) = 646,4 Нм;
GT = Nege = 175,9 • 0,242 = 42,57 кг/ч;
Мл = Ne/Va~ 175,9/10,852 = 16,21 кВт/дм8;
для дизеля с наддувом
Ne = рвИлп/(30т) = 0,991 • 10,852 • 2600/(30 • 4) = 233,0 кВт;
Ме = 3 • 10* • Ne/{m) = 3 • 10» • 233,0/(3,14 • 2600) = 856,2 Н-м;
Gt = Nege = 233,0 • 0,220 = 51,26 кг/ч;
Мл = 233,0/10,852 = 21,47 кВт/дм8.
Построение индикаторной диаграммы дизеля с наддувом. Масштабы диаграммы (см. рис. 36): масштаб хода поршня — Afs = 1,5 мм в мм; масштаб давлений — Мр = 0,08 МПа в мм.
Приведенные величины рабочего объема цилиндра и объема камеры сгорания соответственно:
102
4B = S/A4,= 120/1,5 = 80 мм; ОЛ = ЛВ/(е — 1) = 80/(17 — — 1) = 5 мм.
Максимальная высота диаграммы (точки г' и г) и положение точки г по оси абсцисс
рг1Мр = 11,307/0,08= 141,3 мм; г'г = ОЛ (р — 1) = 5(1,41— 1) = = 2,05 ~ 2 мм.
Ординаты характерных точек:
Ро/Мр = 0,1/6,08 = 1,3 мм; pJMp = 0,17/0,08 = 2,1 мм;
ptIMp = 0,162/0,08 = 2,025 мм; pJMv =* 0,159/0,08 = 1,988 мм;
pJMj, = 7,538/0,08 = 94,23 мм; рь1Мр = 0,482/0,08 = 6,02 мм.
Построение политроп сжатия и расширения проводится графическим методом (см. рис. 36):
а) для луча ОС принимаем угол а = 15°;
б) tgfr = (1 + tga)«* - 1 = (1 + tg 15°)>да - 1 = 0,381; fr = = 20°49';
в) используя лучи OD и ОС, строим политропу сжатия, начиная с точки с;
г) tg?2 = (1 + tga)«. -1= (1+tgl5°)'.267 __i = 0.350; = 19°14';
д) используя лучи ОЕ и ОС, строим политропу расширения, начиная с точки г.
Теоретическое среднее индикаторное давление
р/ = Г'МР/ЛВ = 1254 • 0,08/80 = 1,254 МПа,
что очень близко к величине р/ = 1,266 МПа, полученной в тепловом расчете (F' — площадь диаграммы acz'zba).
Скругление индикаторной диаграммы. Учитывая достаточную быстроходность рассчитываемого дизеля и величину наддува, ориентировочно устанавливаются следующие фазы газораспределения: впуск — начало (точка г’) за 25° до в. м. т. и окончание (точка а") —60° после н. М; т.; выпуск — начало (точка Ь’) за 60° до н. м. т. и окончание (точка а') — 25° после в. м. т.
С учетом быстроходности дизеля принимается угол опережения впрыска 20° (точка с') и продолжительность периода задержки воспламенения Дф1 = 8° (точка /).
В соответствии с принятыми фазами газораспределения и углом опережения впрыска определяется положение точек Ь', г', а', а", с' и f по формуле для перемещения поршня (см. гл. VI):
АХ = (ЛВ/2)[(1 — costp) + (X/4) (1 — cos 2<р)],
где X—отношение радиуса кривошипа к длине шатуна. Выбор величины X производится при проведении динамического расчета, а при построении индикаторной диаграммы ориентировочно устанавливаем К = 0,270:
103
Результаты расчета ординат точек Ь', г', а’, а", с' и f приведены в табл. 13.
Таблица 13
Обозначение точек Положение точек — cos у) 4- + — (1 — cos 2<Р) 4 Расстоянне АХ точек от в. м. т., мм
Ъ’ 60° ДО Н. м. Т. 120 1,601 64,0
г' 25° до в. м. т. 25 0,122 4,9
а' 25° после в. м. т. 25 0,122 4,9
а” 60° после н. м. т. 120 1,601 64,0
с’ 20° до в. м, т. 20 0,076 3,0
t (20—8°) до в. м. т. 12 0,038 1 >5
Положение точки с" определяют из выражения
рс. = (1,15ч-1,25) ре = 1,15.7,538 = 8,669 МПа;
рс, /Мр = 8,669/0,08 = 108,34 мм.
Точка гд лежит на линии г'г ориентировочно вблизи точки г.
Нарастание давления от точки с" до гд составляет 11,307 — 8,669= = 2,638 МПа или 2,638/10 = 0,264 МПа/град п. к. в., где 10 — положение точки гд по оси абсцисс, град.
Соединяя плавными кривыми точки г с а', е'с f и с" и далее с гд и кривой расширения,5' с Ь" (точка Ь" располагается между точками b и а) и далее с г' и г, получаем скругленную индикаторную диаграмму ra'oc'fc"zab*b"r.
Тепловой баланс
Общее количество теплоты, введенной в двигатель с топливом для дизелей:
без наддува Qo = Яибт/3,6 = 42 440 . 42,57/3,6 = 501 850 Дж/с; с наддувом Qo= 42 440 • 51,26/3,6 = 604 300 Дж/с.
Теплота, эквивалентная эффективной работе за 1 с, для дизелей: без наддува Qe = 1000 Ne — 1000 • 175,9= 175 900 Дж/с;
с наддувом Qe = 1000 Ne = 1000 • 233,0 = 233 000 Дж/с.
Теплота, передаваемая охлаждающей среде, для дизелей:
без наддува QB = С1Р™пт(У1л) = 0,48 • 8- 12,01*2’0'67 • 2600°-юх X (1/1,4) = 178460 Дж/с;
с наддувом QB = 0,53-8. 12,01+2 0>68 • 26OO0,68 • (1/1,7) = = 184520 Дж/с, где С — коэффициент пропорциональности (для четырехтактных двигателей С = 0,45 4- 0,53); i — число цилиндров; D — диаметр цилиндра, см; т — показатель степени (для четырехтактных двигателей т = 0,6 4- 0,7); п — частота вращения коленчатого вала двигателя, об/мин.
104
Теплота, унесенная с отработавшими газами (в дизеле с наддувом часть теплоты отработавших газов используется в газовой турбине), Qr = (GT/3,6) (М2 (me;)!; tT - (/№₽/#,];
для дизеля без наддува Qr = (42,57/3,6) (0,7315 -31,892 -511 — — 0,7 • 29,09.20] = 136150 Дж/с,
где (тс^ = (mcj,)£ + 8,315 = 23,577-+ 8,315 =
= 31,892 кДж/(кмоль-град); (mcv)/'=23,577 — определено по табл. 8 методом интерполяции при а = 1,4 и tr — Tr— 273 = 784 — 273 = = 511°С; (mcp)!» = (тс„)'“+ 8,315 = 20,775 + 8,315 =
= 29,090 кДж/(кмоль-град); (nwv)t” — 20,775 — определено по табл. 5 (графа «Воздух») при /к = Тл — 273 = 293 — 273 = 20°С;
для дизеля с наддувом Qr = (51,26/3,6) [0,8815 • 31,605 • 513 — — 0,85 • 29,144 • 88] = 164770 Дж/с,
где (тс'р)‘(' = (тсу)1(' + 8,315 = 23,290 + 8,315 =
= 31,605 кДж/(кмоль-град);
(mcv^tro — 23,290 — определено по табл. 8 методом интерполяции при а = 1,7 и tr = Тг — 273 = 786 — 273 = 513°С; (тср)‘* = (mcv)^ + + 8,315 = 20,829 + 8,315 = 29,144 кДж/(кмоль-град); =
= 20,829 — определено по табл. 5 (графа «Воздух») при /к = 7\— — 273 = 361 — 273 = 88°С.
Неучтенные потери теплоты
Qoct = Qo—(Qe+Qb+ Qr);
для дизеля без наддува Qoct — 501850 — (175900 + 178 460 + + 136 150) = 11 340 Дж/с;
для дизеля с наддувом Q0CT = 604 300 — (233 000 + 184 520 + + 164 770) = 22 010 Дж/с.
Составляющие теплового баланса представлены в табл. 14.
Таблица 14
Составляющие теплового баланса Дизель без наддува Дизель с наддувом
Q. Дж/с Q> % 0» Дж/с <7. %
Теплота, эквивалентная эффективной работе 175 900 35,1 233000 38,6
Теплота, передаваемая охлаждающей среде 178 460 35,6 184 520 30,5
Теплота, унесенная с отработавшими гезамв 136 150 27,1 164 770 27,3
Неучтенные потери теплоты 11 340 2,2 22010 3.6
Общее количество теплоты, введенной в двигатель с топливом 501 850 100,0 604 300 100,0
105
Глава V
СКОРОСТНЫЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ
§ 19. ОБЩИЕ СВЕДЕНИЯ
Для анализа работы автомобильных и тракторных двигателей
используются различные характеристики: скоростные, нагрузочные, регуляторные, регулировочные и специальные. Обычно все характеристики получают экспериментальным путем при испытаниях двигателей.
При проектировании нового двигателя отдельные характеристики (например, скоростная и нагрузочная) могут быть построены расчетным путем. В этом случае ряд параметров определяют по эмпирическим зависимостям, полученным на основании обработки большого
числа опытных данных.
Скоростная характеристика показывает изменение мощности, крутящего момента, расходов топлива и других параметров от частоты
вращения коленчатого вала.
В зависимости от положения органа, управляющего подачей топли-
ва, различают внешнюю и частичную скоростные характеристики.
Скоростная характеристика, полученная при полном дросселе (карбюраторный двигатель) или при положении рейки топливного насоса (дизель), соответствующем номинальной мощности, называется внешней. Внешняя ско
Рис. 39. Скоростная характеристика двигателя ВАЗ-2106
ростная характеристика позволяет провести анализ и дать оценку мощностных, экономических, динамических и эксплуатационных показателей при работе двигателя с полной нагрузкой.
Любая скоростная характеристика двигателя, полученная при неполном открытии дроссельной заслонки (карбюраторный двигатель) или при положении рейки топливного насоса (дизель), соответствующем частичной мощности, называется частичной скоростной характеристикой. Такие характеристики используют для выяснения влияния целого ряда факторов (угла one-
режения зажигания, состава смеси, минимально
106
устойчивых частот вращения и т. д.) на работу двигателя при частичных нагрузках и дают возможность наметить пути улучшения его мощностных и экономических показателей.
На рис. 39 представлена внешняя скоростная характеристика карбюраторного двигателя, а на рис. 40 —дизеля.
§ 20. ПОСТРОЕНИЕ ВНЕШНЕЙ СКОРОСТНОЙ ХАРАКТЕРИСТИКИ
При построении внешних скоростных характеристик вновь проектируемых двигателей иногда используют результаты теплового расчета, проведенного для нескольких режимов работы двигателя
с полной нагрузкой. Однако этот метод
расчета скоростных характеристик дает надежные результаты только при наличии достаточно полных экспериментальных данных по целому ряду параметров работы двигателя на частичных скоростных режимах (см. § 17).
С достаточной степенью точности внешнюю скоростную характеристику можно построить по результатам теплового расчета, проведенного для одного режима работы двигателя — режима максимальной мощности, и использования эмпирических зависимостей.
Построение кривых скоростной характеристики ведется в интервале: а) для карбюраторных двигателей от nmin = 600 — 1000 об/мин ДО «max ~ (1»05 -г 1,20) «л,; б) для дизелей бтпт|П = 350 4- 800 об/мин до nN, где пц —частота вращения коленчатого вала при номинальной мощности.
Максимальная частота вращения коленчатого вала ограничивается: условиями качественного протекания рабочего процесса, термическим напряжением деталей, допустимой величиной инерционных усилий и т. д.; минимальная — определяется условиями устойчивой работы двигателя при полной нагрузке.
Расчетные точки кривой эффективной мощности определяются по следующим эмпирическим зависимостям через каждые 500— 1000 об/мин:
для карбюраторных двигателей
107
для дизелей с неразделенными камерами
NeX=Ne -2^1’0,87 + 1,13-22-----
® ® nN L я* \ nN ) J ’
для дизелей с предкамерой
Nex=Ne [о,64-1,4 -22---------
вХ в nN L nN \nN ) J ’
для дизелей с вихревой камерой
(139)
(140)
(141)
= *’ ТГ [°’7 +1>3 тг - (тг)2] • (142)
В формулах (139)—(142) принято: Ne и —номинальная эффективная мощность (кВт) и частота вращения коленчатого вала (об/мин) при номинальной мощности; Nex и пх — эффективная мощность (кВт) и частота вращения коленчатого .вала (об/мин) в искомой точке скоростной характеристики двигателя.
По рассчитанным точкам в масштабе Mn строят кривую эффективной мощности.
Точки кривой эффективного крутящего момента (Н м) определяют по формуле
Меж = 3. 10*Увх/(«Пх). (143)
Кривая крутящего момента, построенная в масштабе Мм, выражает также изменение среднего эффективного давления, но в масштабе /Ир(МПа/мм):
Мр = /Ил^т/(1037л). (144)
Величину среднего эффективного давления рвх (МПа) для рассчитываемых точек можно определить по кривой Мех или из выражения
Рех=^вя30г/(|7л/гя). (145)
Точки кривой среднего индикаторного давления находят по формуле
Plx = Рех + Рмх, (146)
где рмх — среднее давление механических потерь (МПа) определяют в зависимости от типа и конструкции двигателя по уравнениям (105)— (ПО), приведенным в гл. III.
Кривая среднего индикаторного давления, построенная в масштабе Мр, выражает также изменение индикаторного крутящего момента, но в масштабе Мм (Н • м/мм):
Мм = Мр • 103Ил/(лт). (147)
Расчетные точки индикаторного крутящего момента можно onplh делить по кривой pix или из выражения
Mis = pisVa- 103/(лт). (148)
108
Удельный эффективный расход топлива, г/(кВт • ч), в искомой точке скоростной характеристики:
для карбюраторных двигателей
8ех = geN [1.2—\,2nJnN 4- (nx/nN)2]-, (149)
для дизелей с неразделенными камерами
ёех = geld 1.55 — 1,55nx/nN 4- (nx/nN)2], (150)
где geN — удельный эффективный расход топлива при номинальной мощности, г/(кВт • ч).
Часовой расход топлива, кг/ч
G"X = geXNeX' ЮЛ (151)
Для определения коэффициента наполнения необходимо задаться законом изменения а по частоте вращения. Для карбюраторных двигателей с достаточной степенью точности можно принять значения а постоянными на всех скоростных режимах, кроме минимального. При пх = nmin следует принимать смесь несколько более обогащенную, чем при пх == лд/, т. е. аЛгтНп< алл/.
В дизелях при работе по скоростной характеристике с увеличением частоты вращения значение а несколько увеличивается. Для четырехтактного дизеля с непосредственным впрыском можно принять линейное изменение а, причем anmin — (0,7-? 0,8)<хад.
При выбранном законе изменения коэффициент наполнения
= Рех^0%к^ех/(3600рк). (152)
По скоростной характеристике определяют коэффициент приспособляемости К, представляющий собой отношение максимального крутящего момента ЛТетах к крутящему моменту при номинальной мощности:
К = MemJMeN. (153)
Этот коэффициент служит для оценки приспособляемости двигателя к изменению внешней нагрузки и характеризует способность двигателя преодолевать кратковременные перегрузки. Для карбюраторных двигателей К= 1,20—1,35; у дизелей кривая крутящего момента протекает более полого и значения коэффициента приспособляемости находятся в пределах К — 1,05 ч- 1,20.
Кроме изложенного метода построения скоростных характеристик существует ряд других методов. Так, проф. И, М. Ленин для построения внешних скоростных характеристик двигателей рекомендовал пользоваться процентными соотношениями между мощностью, частотой вращения и удельным расходом топлива, полученными в результате построения относительйых скоростных характеристик.
Соотношения между параметрами относительной скоростной характеристики карбюраторного двигателя приведены ниже.
Частота вращения коленчатого вала л, %............... 20 40 60 80 100 120
Эффективная мощность Ntf, % 20 50 73 92 100 92
109
Удельный эффективный расход топлива ge %................ 115 100 97 95 100 115
Для четырехтактных дизелей процентные соотношения между параметрами относительной скоростной характеристики следующие:
Частота вращения коленчатого вала п, % 20 40 60 80 100
Коэффициент избытка воздуха а . . . 1,40 1,35 1,30 1,25 1,20
Эффективная мощность Ne, %......... 17 41 67 87 100
В приведенных данных за 100% приняты те значения мощности, частоты вращения Коленчатого вала и удельного расхода топлива, которые получены на основе теплового расчета.
§ 21. ПОСТРОЕНИЕ ВНЕШНЕЙ СКОРОСТНОЙ ХАРАКТЕРИСТИКИ КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
На основании теплового расчета, проведенного для четырех скоростных режимов работы карбюраторного двигателя (см. § 17), получены и сведены в табл. 15 необходимые величины параметров для построения внешней скоростной характеристики (рис. 41).
ПО
Таблица 15
Частота вращения коленчатого вала л, об/мин Параметры внешней скоростной характеристики
кВт ge, г/(кВг-ч) ме, Нм GT, кг/ч V а
1000 12,70 284 121,3 3,607 0,8744 0,86
3200 42,77 254 127,7 10,864 0,9167 0,96
5600 60,42 301 103,1 18,186 0,8784 0,96
6000 60,14 318 95,8 19,125 0,8609 0,96
Коэффициент приспособляемости по скоростной характеристике Л = = 128/103 = 1,24.
Для сравнения различных методов построения скоростных характеристик и проверки правильности выполнения теплового расчета (см. § 17) для нескольких скоростных режимов двигателя дополнительно приведен расчет изменения мощности и удельного расхода топлива на основе процентных соотношений между параметрами относительной скоростной характеристики.
Результаты расчета сведены в табл. 16, а на рис. 41 нанесены расчетные точки мощности и удельного расхода топлива.
Таблица 16
Частота вращения коленчатого вала, п Мощность, Удельный расход топлива, g&
% об/мин % кВт % 1 | г/(кВт-ч)
20 1120 20 12,08 115 346
40 2240 50 30,21 100 301
60 3360 73 44,11 97 292
80 4480 92 55,59 95 286
100 5600 100 60,42 100 301
120 6720 92 55,59 115 346
На основе сравнения полученных данных с кривыми Ne nge (рис.41), построенными по результатам теплового расчета, можно сделать следующие выводы:
1. Точки относительной характеристики практически полностью совпадают с внешней скоростной характеристикой мощности рассчитываемого двигателя.
2. Точки относительной характеристики удельного расхода топлива несколько отличаются от кривой ge, построенной по данным теплового расчета, в сторону увеличения и особенно при малых значениях частоты вращения коленчатого вала. Максимальное расхождение составляет при п == 1000 об/мин около 23% [350 и 284 г/(кВт • ч)]. Учитывая, что в последних моделях двигателей Волжского автомобильного завода удельный расход топлива при п = 1000 об/мин составляет
111
300—325 г/(кВт • ч), можно считать данные, полученные в тепловом расчете, достаточно близкими к реальным расходам топлива уже созданных и работающих двигателей.
$ 22. РАСЧЕТ ВНЕШНЕЙ СКОРОСТНОЙ ХАРАКТЕРИСТИКИ ДИЗЕЛЯ
На основании теплового расчета, проведенного для режима номинальной мощности (см. § 18), получены следующие параметры, необходимые для расчета и построения внешней скоростной характеристики дизеля:
а) без наддува — эффективная мощность ffe = 175,9 кВт; частота вращения коленчатого вала при максимальной мощности = = 2600 об/мин, тактность двигателя т = 4; литраж Ул = 10,852 л; ход поршня S = 120 мм; теоретически необходимое количество воздуха для сгорания 1 кг топлива /0 = 14,452 кг возд/кг топл; плотность заряда на впуске рк — 1,189 кг/м3; коэффициент избытка воздуха алг = 1,4; удельный эффективный расход топлива geJV = 242 г/(кВт-ч);
б) с наддувом — эффективная мощность Ne = 233,0 кВт; частота вращения коленчатого вала при максимальной мощности = = 2600 об/мин; тактность двигателя т = 4; литраж Ул = 10,852 л; ход поршня S = 120 мм; теоретически необходимое количество воздуха для сгорания 1 кг топлива /0 = 14,452 кг возд/кг топл; плотность заряда на впуске рк = 1,641 кг/м3; коэффициент избытка воздуха ajv — 1,7; удельный эффективный расход топлива = 220 г/(кВт-ч).
Расчетные точки скоростной характеристики. Принимаем: nmin = = 600 об/мин; пХ1 — 1000 об/мин; далее через каждые 500 об/мин и = 2600 об/мин.
Все расчетные данные заносятся в табл. 17.
Таблица 17
600 43,7 696 0,805 2,4 0,117 0,922 797 301 13,15 1,20 0,983
1000 78,3 748 0,867 4,0 0,136 1,003 867 267 20,91 1>,24 0,970
1500 120,7 769 0,890 6,0 0,160 1,050 907 239 28,85 1,29 0,927
2000 155,3 742 0,859 8,0 0,183 1,042 900 230 35,72 1,34 0,895
2500 174,5 669 0,772 10,0 0,207 0,979 846 238 41,53 1,39 0,863
2600 175,9 646 0,748 10,4 0,212 0,960 829 242 42,57 1,40 0,854
Дизель с наддувом
600 57,9 922 1,067 2,4 0,117 1,184 1023 274 15,86 1,25 0,895
1000 103,6 990 1,146 4,0 0,136 1,282 1108 242 25,07 1,34 0,910
1500 159,8 1018 1,178 6,0 0,160 1,338 1156 217 34,68 1,46 0/914
2000 205,6 982 1,137 8,0 0,183 1,320 1140 2Q9 42,92 1,57 0,914
2500 231,2 884 1,023 10,0 0,207 1,230 1063 217 50,17 1,68 0,914
2600 233,0 856 0,991 10,4 0,212 1,203 1039 220 51,26 1,70 0,909
112
Мощность в расчетных точках
Nex = (Nenx/nN) [0,874- 1 ,\3nx/nN — (nx/nN)2] кВт;
для дизеля без наддува NeX = (175,9 пж/2600)[0,87 4- 1,13пж/2600— — (пж/2600)2] кВт;
для дизеля с наддувом NeX = (233,0 пж/2600)[0,87 4- 1,13пх/2600— — (пж/2600)2] кВт.
Эффективный крутящий момент
МеХ =NeX- 3 • 104/(лПх) = 9554^/^ Н • м.
Среднее эффективное давление
Рех = Мех 30т/Рлпх = 30 • 4 • Nex/(\0,852nx) = 11,058Nex/nx МПа.
Средняя скорость поршня
рп ср = Snx/3 • 104 = 120/30000 = 0,Q04nx м/с.
Среднее давление механических потерь
рмх = 0,089 4- 0,0118 ип.ср МПа.
Среднее индикаторное давление
Ргх = Рех 4- Рмх МПа.
Индикаторный крутящий момент
Mix =pixVa 103/(лт) = 10,852 • 103pix/(3;14 • 4) = 864 pixH-M.
Рис. 42. Скоростные характеристики дизеля: а — без надцува; б — с наддувом
5—370 113
Удельный эффективный расход топлива для дизелей
=8eN [1,55—1,55/1^ 4- (Пх/плг)2];
без наддува geX =242 [1,55—1,55 n.;JnN 4- (Пх/«лг)2] г/(кВт • ч); с наддувом geX =220 [1,55—1,55 пх1пц 4- (Пх/«лг)2] г/(кВт • ч). Часовой расход топлива
Gtx = КГ/4*
Коэффициент избытка воздуха. Принимаем для дизелей:
без наддува ая тщ = 0,86aw — 0,86 • 1,4 я? 1,2;
с наддувом a„ min = 0,74aw = 0,74 • 1,7 = 1,25.
Соединяя точки anmin и o-n (рис. 42, а, б) прямой линией, получим значения ах Для всех расчетных точек дизелей без наддува и с наддувом.
Коэффициент наполнения
Г)ух ~ Рех4)®хйех/(5600р к) J
для дизеля без наддува г)ух = 14,452 peXOxgeX/(26Q0 • 1,189) = = o,oo338peXaxgex;
для дизеля с наддувом — 14,452режаж gex/(3600 • 1,641) = = 0,00245pexaxgex.
По расчетным данным, приведенным в табл. 17, строим внешние скоростные характеристики дизелей без наддува (рис. 42, а) и с наддувом (рис. 42, б).
Коэффициент приспособляемости для дизелей:
без наддува К = Memsa/MeN = 769/646 = 1,19;
с наддувом К = Memsa/MeN = 1018/856 = 1,19, где ЛГеШах определены по скоростным характеристикам.
Часть вторая КИНЕМАТИКА И ДИНАМИКА ДВИГАТЕЛЯ
Глааа VI КИНЕМАТИКА КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА
§ 23. ОБЩИЕ СВЕДЕНИЯ
В двигателях внутреннего сгорания возвратно-поступательное движение поршня преобразуется во вращательное движение коленчатого вала посредством кривошипно-шатунного механизма.
Кривошипно-шатунный механизм может быть центральным, когда оси коленчатого вала и цилиндров лежат в одной плоскости (рис. 43, а), или смещенным (дезаксиальным), когда оси коленчатого вала и цилиндров лежат в разных плоскостях (рис. 43, б). Дезаксиальный механизм может быть получен также и за счет смещения оси поршневого
пальца.
В настоящее время в автомобильных и тракторных двигателях
наибольшее распространение получил центральный кривошипно-шатунный механизм. На рис. 43, а приведены основные обозначения такого механизма: $ж — текущее перемещение поршня (точка А — ось
поршневого пальца); ф — угол поворота кривошипа (ОВ), отсчитываемый по оси цилиндра (Д'О) в направлении вращения коленчатого вала по часовой стрелке (точка О обозначает ось коленчатого вала; точка В — ось шатунной шейки; точка А'— в. м. т.); Р — угол отклонения оси шатуна (ДВ) от оси цилиндра; (о — угловая .скорость вращения коленчатого вала; R = О В — радиус кривошипа ; S = = 2R = А'А" — ход поршня (точка Д" обозначает н. м. т.); Lm = АВ— клина шатуна; X = /?/Lm — отношение радиуса криво-
Рис. 43. Схемы кривошипно-шатунных механизмов:
в — центрального; б — смещенного (дезаксиального)
шипа к длине шатуна;
5*
115
Рис. 44. Схема кривошипно-шатунного механизма для определения минимальной длины шатуна
R + = А'О — расстояние от оси ко-
ленчатого вала до в. м. т.
В смещенном кривошипно-шатунном механизме (рис. 43, б), в отличие от принятых обозначений для центрального механизма угол <р -поворота кривошипа отсчитывают от прямой СО, параллельной оси цилиндра A'D и проходящей через ось коленчатого вала, а 3 = А'А" Ф 2R. Дезаксиальный механизм характеризуется величиной относительного смещения k — —a!R = 0,05 4- 0,15, где а = OD— величина смещения оси цилиндра относительно оси коленчатого вала.
Величины инерционных усилий, действующих в двигателе, зависят от указанных выше размеров и их соотношений.
Установлено, что с уменьшением X = = RILm (за счет увеличения Lm) происходит снижение инерционных и нормальных сил, но при этом увеличивается высота двигателя и его масса. В связи с этим в
автомобильных и тракторных двигателях принимают X = 0,23 4- 0,30.
Конкретные значения X для некоторых автомобильных и тракторных двигателей следующие:
Марка двигателя... МеМЗ-965 МЗМА-412 ВАЗ-2106 ЗИЛ-130 Д-20 СМД-14 ЯМЗ-240 КамАЗ-740 А . . 0,237 0,265 0,295 0,257 0,280 0,280 0,264 0,267
Для двигателей с малым диаметром отношение 7?/Lm выбирают с таким расчетом, чтобы избежать задевания шатуна за нижнюю кромку цилиндра.
Минимальную длину шатуна и максимально допустимое значение X без задевания шатуна за кромку цилиндра определяют следующим образом (рис. 44): на вертикальной оси цилиндра наносят центр коленчатого вала О, из которого радиусом 7? = S/2 проводят окружность вращения центра шатунной шейки. Далее, пользуясь конструктивными размерами элементов коленчатого вала (см. табл. 56), из точки В (центр кривошипа, находящегося в н. м. т.) радиусом гш,ш проводят окружность шатунной шейки, из центра О радиусом — вторую окружность вращения крайней точки щеки или противовеса:
Для двигателей без противовесов <............ ,15-^1,25) ш
Для двигателей с противовесами .............. /’1=^+(1,3 4- 1,5) ш
Отступя на 6—8 мм вниз от точки С, проводят линию А — А перпендикулярно оси цилиндра, определяющую минимально допустимое приближение нижней кромки поршня к оси коленчатого вала.
116
Пользуясь конструктивными соотношениями размеров поршня (см. табл. 50), от линии А — А вверх наносят контур поршня, в том числе и центр поршневого пальца (точка 4"). Расстояние между точками А" и В — минимальная длина шатуна Lm min, по которой определяют \пах ~ min-
Во избежание задевания шатуна за стенки проверяют его траекторию при движении поршня от в. м. т. до н. м. т. Для этого вырезают из кальки контур шатуна и перемещают его по чертежу так, чтобы центр поршневой головки шатуна перемещался по оси цилиндра, а центр кривошипной головки — по окружности радиуса R. При этом шатун не должен задевать за нижнюю кромку цилиндра, которая может находиться на 10—15 мм выше нижней кромки поршня при его нахождении в н. м. т. (линия Е — Е). Если шатун при движении задевает за нижнюю кромку цилиндра, то длину шатуна увеличивают или делают прорези в стенках цилиндра для прохода шатуна. На этой же схеме наносят траекторию движения крайних точек кривошипной головки шатуна для определения габаритных размеров картера двигателя и размещения распределительного вала. Значение К, принятое предварительно при построении индикаторной диаграммы, сохраняют при условии X < Хшах.
Расчет кинематики кривошипно-шатунного механизма сводится к определению пути, скорости и ускорения поршня. При этом принимается, что коленчатый вал вращается с постоянной угловой скоростью со (в действительности за счет постоянно изменяющихся газовых нагрузок на поршень и деформации коленчатого вала <о =#= const). Это допущение позволяет рассматривать все кинематические величины в виде функциональной зависимости от угла поворота коленчатого вала <р, который при <о = const пропорционален времени.
§ 24. ПЕРЕМЕЩЕНИЕ ПОРШНЯ
Перемещение поршня (м) в зависимости от угла поворота кривошипа для двигателя с центральным кривошипно-шатунным механизмом
sx = Я^(1 — cos ф) + (1 — cos?)J. (154)
Для расчетов удобнее пользоваться выражением, в котором перемещение поршня является функцией только одного угла ф.
Для практических расчетов такое выражение получают с достаточной степенью точности при замене в формуле (154) значения
cos 8 = 1--— X2 sin2 ®---!— X4 sin4 ® — • • •
г 2 , 2 • 4 т
только первыми двумя членами, пренебрегая вследствие малой величины членами выше второго порядка:
s3C = 7?f(l—cos<p)H—— (1—cos2cp) . (155)
L 4
117
Таблица 18
<р° Значения (1— cos (?) + —~— (1—cos 2(?) прн X 4 <р°
0,24 0,25 0,26 0,27 0,28 0,29 0,30 о,31
0 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 360
10 0,0188 0,0190 0,0191 0,0193 0,0194 0,0196 0,0197 0,0199 350
20 0,0743 0,0749 0,0755 '0,0761 0,0767 0,0773 0,0779 0,0784 340
30 0,1640 0,1653 0,1665 0,1678 0,1690 0,1703 0,1715 0,1728 330
40 0,2836 0,2857 0,2877 0,2898 0,2918 0,2939 0,2960 0,2980 320
50 0,4276 0,4306 0,4335 0,4364 0,4394 0,4423 0,4452 0,4482 310
60 0,5900 0,5938 0,5975 0,6013 0,6050 0,6088 0,6125 0,6163 300
“ 70 0,7640 0,7684 0,7728 0,7772 0,7816 0,7860 0,7905 0,7949 290
80 0,9428 0,9476 0,9525 0,9573 0,9622 0,9670 0,9719 0,9767 280
90 1,1200 1,1250 1,1300 1,1355 1,1400 1,1450 1,1500 1,1550 270
100 1,2900 1,2948 1,2997 1,3045 1,3094 1,3142 1,3191 1,3239 260
ПО 1,4480 1,4524 1,4568 1,4612 1,4656 1,4700 1,4745 1,4789 250
120 1,5900 1,5938 1,5975 1,6013 1,6050 1,6088 1,6125 1,6163 240
130 1,7132 1,7162 1,7191 1,7220 1,7250 1,7279 1,7308 1,7338 230
140 1,8156 1,8177 1,8197 1,8218 1,8238 1,8259 1,8280 1,8300 220
150 1,8960. 1,8973 1,8985 1,8998 1,9010 1,9023 1,9035 1,9048 210
160 1,9537 1,9543 1,9549 1,9555 1,9561 1,9567 1,9573 1,9578 200
170 1,9884 1,9886 1,9887 1,9889 1,9890 1,9892 1,9893 1,9895 190
180 2,0000 2,0000 2,0000 2,0000 2,0000 2,0000 2,0000 2,0000 180
Из уравнения (155) следует, что при ф = 90° $эо° = Я(1 + + Х/2) м, а при ф == 180° $i8o° — 2R м. Значения множителя, заключенного в квадратные скобки, в зависимости от X и ф представлены в табл. 18.
Пользуясь выражением (155) и данными табл. 18, аналитическим путем определяют значения перемещения поршня от в. м. т. до н. м, т. для ряда промежуточных значений ф (в зависимости от необходимой точности через каждые 10, 15, 20 или 30°) и строят кривую s = /(ф) (рис. 45, а).
При повороте кривошипа от в. м. т. до н. м. т. движение поршня происходит под влиянием перемещения шатуна вдоль оси цилиндра и отклонения его от этой оси. Вследствие совпадения направлений перемещений шатуна при движении кривошипа по первой четверти окружности (0—90°) поршень проходит больше половины своего пути. Это следует и из уравнения (155). При движении кривошипа по второй четверти окружности (90—180°) направления перемещений шатуна не совпадают и поршень проходит меньший путь, чем за первую четверть. При графическом построении перемещения поршня указанную закономерность учитывают введением поправки Брикса 7?Х/2 —
=
Ца рис. 45, б показано графическое построение s — ^(ф) по методу Ф. А. Брикса. Центр окружности радиуса 7? смещают в сторону н.м.т. на величину 7?Х/2 и из нового центра через определенные значения ф (на рис. 45, б через каждые 30°) проводят радиус-вектор до пересечения с окружностью. Проекции точек пересечения (1, 2, 3, ...) на ось
118
а) О ЗВ SO 90 120 150 180 210 200 220 300 330 360 ?*'
Рис. 45. Построение кривых перемещения поршня:
а — аналитическим методом (X 0,24); б — методом Ф. А. Брикса (X s= 0,30); 9 — методом сложения перемещений первого н второго порядков (X •== 0,80)
цилиндров (линия в. м. т. — н. м. т.) дают искомые положения поршня при данных значениях угла ф.
При рассмотрении перемещения поршня как суммы двух гармонических перемещений первого sxi = 7? (1 — costp) и второго sx// = = (7?V4)(1 — cos 2<р) порядков графическое построение s = f(<p) осуществляют, как показано на рис. 45, в.
Перемещение (м) поршня в смещенном кривошипно-шатунном механизме
sx = 7?[(1 — costp) + (V4)(l — cos 2<р) — &Л^пф]. (156)
§ 25. СКОРОСТЬ ПОРШНЯ
При перемещении поршня скорость (м/с) его движения является величиной переменной и при постоянной частоте вращения коленчатого вала зависит только от изменения угла поворота кривошипа и отношения X = R/Lm:
— = co/?fsin<p + — sin2?Y (157) п dt at df \ T 2 / '
Значения множителя в уравнении (157), заключенного в скобки, в зависимости от % и <р приведены в табл. 19.
119
Таблица 19
т° Знак Значения ( sin ср + sin 2ср j при X Знак 9°
0,24 0,25 0,26 0,27 0,28 | 0,29 0,30 0,31
0 + 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 360
10 + 0,2146 0,2164 0,2181 0,2198 0,2215 0,2232 0,2249 0,2266 — 350
20 + 0,4191 0,4224 0,4256 0,4288 0,4320 0,4352 0,4384 0,4416 — 340
30 + 0,6039 0,6083 0,6-126 0,6169 0,6212 0,6256 0,6299 0,6342 — 330
40 + 0,7610 0,7659 0,7708 0,7757 0,7807 0,7856 0,7905 0,7954 — 320
50 + 0,8842 0,8891 0,8940 0,8989 0,9039 0,9088 0,9137 0,9186 — 310
60 + 0,9699 0,9743 0,9786 0,9829 0,9872 0,9916 0,9959 1,0002 — 300
70 + 1,0168 1,0201 1,0233 1,0265 1,0297 1,0329 1,0361 1,0393 —- 290
80 + 1,0258 1,0276 1,0293 1,0310 1,0327 1,0344 1,0361 1,0378 — 280
90 + 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 — 270
100 + 0,9438 0,9420 0,9403 0,9386 0,9369 0,9352 0,9335 0,9318 — 260
ПО + 0,8626 0,8593 0,8561 0,8529 0,8497 0,8465 0,8433 0,8401 — 250
120 + 0,7621 0,7577 0,7534 0,7491 0,7448 0,7404 0,7361 0,7318 — 240
130 +-Ч 0,6478 0,6429 0,6380 0,6331 0,6281 0,6232 0,6183 0,6134 — 230
140 + 0,5246 0,5197 0,5148 0,5099 0,5049 0,5000 0,4951 0,4902 — 220
150 + 0,3961 0,3917 0,3874 0,3831 0,3788 0,3744 0,3701 0,3658 210
160 + 0,2649 0,2616 0,2584 0,2552 0,2520 0,2488 0,2456 0,2424 — 200
170 + 0,1326 0,1308 0,1291 0,1274 0,1257 0,1240 0.1223 0,1206 — 190
180 И* 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 — 180
Из уравнения (157) следует, что скорость поршня в мертвых точках (<р = 0 и 180°) равна нулю. При ф = 90° уп = 7?со, а при ф = = 270° vn = —7?со, т. е. в этих точках абсолютные значения скорости поршня равны окружной скорости оси шатунной шейки коленчатого вала.
Максимальная скорость поршня зависит (при прочих равных условиях) от величины X, учитывающей конечную длину шатуна, и достигается при ф <90°(+ уп) и ф > 270°(—Уп). С увеличением X максимальные значения скорости поршня растут и сдвигаются в стороны мертвых точек:
t»n max « 0>R К 1 ~t~ Л2 1158)
На рис. 46, а представлена кривая изменения скорости поршня в зависимости от ф, рассчитанная аналитическим методом по формуле (157). Построение кривых скорости поршня графическими методами показано на рис. 46, б, в.
Для построения кривой скорости поршня на рис. 46, б использована схема кривошипно-шатунного механизма. Значения скорости поршня для каждого.угла ф определяют на оси, перпендикулярной оси цилиндров, по величинам отрезков (0Г, 02', 03', ...), отсекаемых осевой линией шатуна, и переносят на вертикали соответствующих углов ф. В этом случае
уп = соТ? sin (ф + P)/cos р. (159)
На рис. 46, в кривая скорости поршня построена сложением гармо-
120
Рис. 46. Построение кривых скорости поршня:
а — аналитическим методом (X =0,24); б — графическим методом по схеме крнвошнпно-шатунного механизма (X = 0,30); в — методом сложении скоростей первого и второго порядков (X = 0,80)
ник скорости первого v„i — co7?sin<p и второго vnll = ®/?(%/2)sin2q> порядков.
Для сравнения быстроходности двигателей в расчетах часто используют среднюю скорость (м/с) поршня
^п.ср = sn/зо = 2со/?/-гс,
где s и R выражены в м, п — в об/мин и со — в рад/с.
Отношение va шах к 1>п.срдля Х= 0,24 ч- 0,31 составляет 1,62—1,64:
Рп шах Ч.ср = (^/2)/1 +Х*.
Скорость поршня в смещенном кривошипно-шатунном механизме va = a>R fsin <р + sin 2<p — kk cos <p). (160)
121
б 26. УСКОРЕНИЕ ПОРШНЯ
Ускорение (м/с2) поршня
/ = •^7 (cos ? + Xcos2<p). (161)
at at dcp
Значения множителя в формуле (161), заключенногб в скобки, в зависимости от 1 и <р приведены в табл. 20.
Таблица 20
Знак Значения (cos <р 4- X cos 2 ср) прн X Знак <р°
0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31
0 + 1,2400 1,2500 1,2600 1,2700 1,2800 1,2900 1,3000 1,3100 + 360
10 + 1,2103 1,2197 1,2291 1,2385 1,2479 1,2573 1,2667 1,2761 + 350
20 + 1,1235 1,1312 1,1389 1,1465 1,1542 1,1618 1,1695 1,1772 + 340
30 + 0,9860 0,9910 0,9960 1,0010 Ц0060 1,0110 1,0160 1,0210 + 330
40 + 0,8077 0,8094 0,8111 0,8129 0,*8146 0,8163 0,8181 0,8198 + 320
50 + 0,6011 0,5994 0,5977 0,5959 0,5942 0,5925 0,5907 0,5890 + 310
60 + 0,3800 0,3750 0,3700 0,3650 0,3600 0,3550 0,3500 0,3450 + 300
70 + ' 0,1582 0,1505 0,1428 0,1352 0/1275 0,1199 0,1122 0,1045 + 290
80 0,0519 0.06J3 0,0707 0,0801 0,0895 0,0989 0,1083 0,1177 280
90 — 0,2400 0,2500 0,2600 0,2700 Д1,2800 0,2900 0,3000 0,3100 — 270
100 — 0,3991 0,4085 0,4179 0,4273 0,4367 0,4461 0,4555 0,4649 — 260
ПО — 0,5258 0,5335 0,5412 0,5488 0,5565 0,5641 0,5718 0,5795 — 250
120 — 0,6200 0,6250 0,6300 0,6350. 0,6400 0,6450 0,6500 0,6550 — 240
130 — 0,6845’ 0,6862 0,6879 0,6897 (Г, 6914 0,6931 0,6949 0,6966 — 230
140 — 0,7243 0,7226 0,7209 0,7191 0,7174 0,7157 0,7139 0,7122 — 220
150 — 0,7460 0,7410 0,7360 0,7310 0,7260 0,7210 0,7160 0,7110 — 210
160 — 0,7559 0,7482 0,7405 0,7329 0,7252 0,7176 0,7099 0,7022 — 200
170 — 0,7593 0,7499 0,7405 0,7311 0,7217 0,7123 0,7029 0,6935 — 190
180 — 0,7600 0,7500 0,7400 0,7300 0,7200 0,7100 0,7000 0,6900 — 180
Максимальное значение ускорения поршня достигается при <р=0°:
/тах=<»2₽(1 +Х). (162)
Минимальное значение ускорения поршня при:
а) Х<0,25 в точке <р = 180°; /min = — <в2/? (1 —X);
б) Х>0,25 в точке <p = arccos(—1/4Х); /min = = -<в2₽[Х+ 1/(8X)J.
(163)
Пользуясь уравнением (161) и данными табл. 20, аналитическим путем определяют значения ускорения поршня для ряда значений угла <р в интервале <р = 0 — 360° и строят кривую /=/(<р) (рис. 47, а). Графически кривую ускорения можно построить методом касательных или методом сложения гармоник первого и второго порядков.
При построении кривой ускорения по методу касательных (рис.47,6) сначала строят кривую / == f(sx), а затем перестраивают в кривую / = /(<р). На отрезке АВ = s в точках Ли В в определенном масштабе откладывают: вверх / = ю2/?(1 + X) и вниз / = —<в2Я(1 — X).
В2
Рис. 47. Построение кривых ускорения поршня:
а — аналитическим методом (К ® 0,24); б — методом касательных (X «= 0,30); в — методом сложения гармоник первого н второго порядков (X 0,60)
Полученные точки Е и С соединяют прямой. В точке D пересечения прямых ЕС и АВ перпендикулярно Л В вниз откладывают величину 3<о2/?Х. Полученную точку F соединяют прямыми с точками £ и С. Отрезки EF и CF делят на произвольное, но равное число частей. Одноименные точки (a, b, с, d) на отрезках EF и CF соединяют прямыми аа, ЬЬ, сс, dd. Огибающая кривая, касательная к этим прямым, является кривой ускорения / = f(sx) в зависимости от перемещения поршня. Перестроение / = f(sx) в / — /(<р) производится по методу Ф. А. Брикса (рис. 47, б). -
Построение кривой / =/(<р) (рис. 47, в) проведено сложением гармоник ускорения первого // = co2/?cos<p и второго ju = co2/?Xcos2q> порядков.
Ускорение поршня в смещенном кривошипно-шатунном механизме
/ — gFR. (cos <р + X cos 2<р + Ek sin <р). (164)
123
Глава VII
ДИНАМИКА КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА
§ 27. ОБЩИЕ СВЕДЕНИЯ
Динамический расчет кривошипно-шатунного механизма заключается в определении суммарных сил и моментов, возникающих от давления газов и сил инерции. По этим силам рассчитывают основные детали на прочность и износ, а также определяют неравномерность крутящего момента и степень неравномерности хода двигателя. Во время работы двигателя на детали кривошипно-шатунного механизма действуют силы давления газов в цилиндре, силы инерции возвратно-поступательно движущихся масс, центробежные силы, давление на поршень со стороны картера (приблизительно равное атмосферному давлению) и силы тяжести (силы тяжести в динамическом расчете обычно не учитывают).
Все действующие в двигателе силы воспринимаются полезным сопротивлением на коленчатом валу, силами трения и опорами двигателя.
В течение каждого рабочего цикла (720° для четырех- и 360° для двухтактного двигателя) силы, действующие в кривошипно-шатунном механизме, непрерывно изменяются по величине и направлению. Поэтому для определения характера изменения этих сил по углу поворота коленчатого вала их величины определяют для ряда отдельных положений вала обычно через каждые 10—30°. Результаты динамического расчета сводят в таблицы.
$ 28. СИЛЫ ДАВЛЕНИЯ ГАЗОВ
Силы давления газов, действующие на площадь поршня, для упрощения динамического расчета заменяют одной силой, направленной по оси цилиндра и приложенной к оси поршневого пальца. Ее определяют для каждого момента времени (угла <р) по действительной индикаторной диаграмме, снятой с двигателя, или по индикаторной диаграмме, построенной на основании теплового расчета (обычно для номинальной мощности и соответствующей ей частоты вращения коленчатого вала).
Перестроение индикаторной диаграммы в развернутую по углу поворота коленчатого вала обычно осуществляют по методу проф. Ф. А. Брикса. Для этого под индикаторной диаграммой строят вспомогательную полуокружность радиусом R = S/2 (рис. 48). Далее от центра полуокружности (точка 0) в сторону н. м. т. откладывают поправку Брикса, равную /?М2. Полуокружность делят лучами из центра 0 на несколько частей, а из центра Брикса (точка О') проводят линии, параллельные этим лучам. Точки, полученные на полуокружности, соответствуют определенным углам <р (на рис. 48 интервал между точками равен 30°). Из этих точек проводят вертикальные линии до пересечения с линиями индикаторной диаграммы и полученные величины давлений откладывают на вертикали соответствующих 124
Рис. 48. Перестроение (развертка) индикаторной диаграммы в координаты р — ф
углов ф. Развертку индикаторной диаграммы обычно начинают от в. м. т. в процессе хода впуска. При этом следует учесть, что на свернутой индикаторной диаграмме давление отсчитывают от абсолютного нуля, а на развернутой показывают избыточное давление над поршнем Дрг = рг— Ро-Следовательно, давления в цилиндре двигателя, меньшие атмосферных, на развернутой диаграмме будут отрицательными. Силы деления газов, направленные коси коленчатого вала, считаются положительными, а от коленчатого вала — отрицательными.
Сила давления (МН) на поршень
Рт = (Рг— Ро)(165)
где F&^~ площадь поршня, м2; рг и р0 — давление газов в любой момент времени и атмосферное давление, МПа.
Из уравнения (165) следует, что кривая сил давления газов по углу поворота коленчатого вала будет иметь тот же характер изменения, что и кривая давления газов Дрг.
Для определения газовых сил Рг по развернутой диаграмме давлений'Дрг необходимо пересчитать масштаб. Если кривая Дрг построена в масштабе М МПа в мм, то масштаб этой же кривой для Рг будет Мр = MpFn МН в мм.
§ 29. ПРИВЕДЕНИЕ МАСС ЧАСТЕЙ КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА
По характеру движения массы деталей кривошипно-шатунного механизма можно разделить на движущиеся возвратно-поступательно (поршневая группа и верхняя головка шатуна); совершающие вращательное движение (коленчатый вал и нижняя головка шатуна) и
125
Рис. 49. Система сосредоточенных масс, динамически эквивалентная кривошипно-шатунному механизму:
а — приведенная система кривошилно-шатунного механизма, б —приведение масс кривошипа
совершающие сложное плоскопараллельное движение (стержень шатуна).
Для упрощения динамического расчета действительный кривошипно-шатунный механизм заменяется динамически эквивалентной системой сосредоточенных масс.
Массу поршневой группы та считают сосредоточенной на оси поршневого пальца в точке А (рис. 49, а). Массу шатунной группы тш заменяют двумя массами, одна из которых сосредоточена на оси поршневого пальца в точке А, а другая (тш.к) — на оси кривошипа в точке В. Величины этих масс (кг)
^Ш.П = ^Ш.К = (166)
где Lm — длина шатуна; £ш.к — расстояние от центра кривошипной головки до центра тяжести шатуна; £ш.п — расстояние от центра поршневой головки до центра тяжести шатуна.
Для большинства существующих конструкций автомобильных и тракторных двигателей тш.п= (0,2 4- 0,3) т^, атш.к = (0,7 4- 0,8)тш. При расчетах можно принимать средние значения
/Пш.п = 0,275тш, /Ищ.к «0,725/Ищ. (167)
Массу кривошипа заменяют двумя массами, сосредоточенными на оси кривошипа в точке В (тк) и на оси коренной шейки в точке 0 (то) (рис. 49, б). Масса коренной шейки с частью щек, расположенных симметрично относительно оси вращения, является уравновешенной. Масса (кг), сосредоточенная в точке В:
= fftn.n 4- 2тщр/7?, (168)
где тщ.щ — масса шатунной шейки с прилегающими частями щек; /Пщ — масса средней части щеки по контуру abed, имеющей центр тяжести на радиусе р.
126
У современных короткоходных двигателей величина мала по сравнению с и ею можно в большинстве случаев пренебречь. При расчетах tn^,^ и в необходимых случаях /Ищ определяют исходя из размеров кривошипа и плотности материала коленчатого вала.
Таким образом, система сосредоточенных масс, динамически эквивалентная кривошипно-шатунному механизму, состоит из массы /И; = /пп + /Пш.п, сосредоточенной в точке А и имеющей возвратно-поступательное движение, и массы т% = /7^+ tnm.Ki сосредоточенной в точке В и имеющей вращательное движение. В V-образных двигателях со сдвоенным кривошипно-шатунным механизмом == = /Пк + 2/Пш.к.
При выполнении динамического расчета двигателя значения /пп и tnm принимают по данным прототипов или же подсчитывают по чертежам.
Для приближенного определения значений и /пк можно
использовать конструктивные массы tri = tn/Fn (кг/м2 или г/см2), приведенные в табл. 21.
Таблица 21
Элементы кривошипно-шатунного механизма Конструктивные массы, кг/м1
Карбюраторные двигатели (£>=;=60 4 100 мм) Дизели (£>=*80 4'120 мм)
Поршневая группа (mn=mn/Fn): поршень из алюминиевого сплава 80—150 150—300
чугунный поршень 150—250 250—400
Шатун (т^тщ/Гп) 100—200 250—400
Неуравновешенные части одного колена вала без противовесов (mK=mK/Fn): стальной кованый вал со сплошными шейками 150-200 200—400
чугунный литой вал с полыми шейками , . . 100—200 150—300
При определении масс по табл. 21 следует учитывать, что большие значения tri соответствуют двигателям с большим диаметром цилиндра. Уменьшение SJD снижает tn^ и т'к; V-образным двигателям с двумя шатунами на шейке соответствуют большие значения triк.
§ 30. СИЛЫ ИНЕРЦИИ
Силы инерции, действующие в кривошипно-шатунном механизме, в соответствии с характером движения приведенных масс подразделяют на силы инерции поступательно движущихся масс Р; и центробежные силы инерции вращающихся масс (рис. 50, а).
Сила инерции от возвратно-поступательно движущихся масс
Pj — — tnjj == — tnjRtf (cos ср + X cos 2cp). (169)
127
Аналогично ускорению поршня сила Pj может быть представлена в виде суммы сил инерции первого Рц и второго Рщ порядков:
Р} = P/j 4- Pj п == — (т}Ра? cos <р 4- mjRafr. cos 2<р). (170)
В уравнениях (169) и (170) знак минус показывает, что сила инерции направлена в сторону, противоположную ускорению. Силы инер-'
Рис. 50. Схема действия сил в кривошипношатунном механизме:
а — инерционных и газовых; б — суммарных
ции возвратно-поступательно движущихся масс действуют по оси цилйндра и как силы давления газов, являются положительными, если они направлены к оси коленчатого вала, и отрицательными, если они направлены от коленчатого вала.
Кривую силы инерции возвратно-поступательно движущихся масс строят аналогично кривой ускорения поршня (см. рис. 47).
Расчеты Р} должны производиться для тех же положений кривошипа (углов <р), для которых определялись Дрг и Рр.
Центробежная сила инерции вращающихся масс
Лв = — mRRa? (171)
постоянна по величине (при <» = const), действует по радиусу кривошипа и направлена от оси коленчатого вала.
Центробежная сила инерции Rr является результирующей двух сил:
силы инерции вращающихся масс шатуна
АНш=-'”ш.Л®2 (172)
и силы инерции вращающихся масс кривошипа
Кнк = — тк/?ш2. (173)
Для V-образных двигателей
= Rrk ~f~ Rr Ш. Л 4* R Я Ш*П == ~~~ 4* ^Ш. К. Л ~Ь" К.п) R^> (174)
где К^ш.л и Rnm.n — силы инерции вращающихся масс левого и правого шатунов.
Для V-образных двигателей, у которых два одинаковых шатуна расположены рядом на одной шейке:
Rrx = Rrk + 2^нш = — (mK 4- 2тш. к) Т?®8 = — /пнх£<»2. (175)
128
§ 31. СУММАРНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ В КРИВОШИПНО-ШАТУННОМ МЕХАНИЗМЕ
Суммарные силы (кН), действующие в кривошипно-шатунном механизме, определяют алгебраическим сложением сил давления газов и сил возвратно-поступательно движущихся масс:
Р = РР + ^- (176)
При проведении динамических расчетов двигателей целесообразно пользоваться неполными, а удельными силами, отнесенными к единице площади поршня. В этом случае удельные суммарные силы (МПа) определяют путем сложения избыточного давления над поршнем Дрг (МПа) и удельных сил инерции р7(МН/м2 = МПа):
р = ДрР4-ръ (177)
где
Pi = = — (т^а2/Рп) (cos <р 4- X cos 2<р). (178)
Графически кривую удельных суммарных сил р строят с помощью диаграмм Дрг = /(ср) и Pj = f(y) (см. рис. 48). При суммировании этих диаграмм, построенных в одном масштабе Мр, полученная диаграмма р будет в том же масштабе.
Суммарная сила Р, как и силы Рг и Pjt направлена по оси цилиндра и приложена к оси поршневого пальца (рис. 50, б). Воздействие от силы Р передается на стенки цилиндра перпендикулярно его оси и на шатун по направлению его оси.
Сила JV(kH), действующая перпендикулярно оси цилиндра, называется нормальной силой и воспринимается стенками цилиндра:
N = Ptgp. (179)
Нормальная сила N считается положительной, если создаваемый ею момент относительно оси коленчатого вала направлен противоположно направлению вращения вала двигателя.
Сила S (кН), действующая вдоль шатуна, воздействует на него и далее передается кривошипу. Она считается положительной, если сжимает шатун, и отрицательной, если его растягивает:
S = P(l/cosP). (180)
От действия силы S на шатунную шейку возникают две составляющие силы (рис. 50, б);
сила, направленная по радиусу кривошипа (кН):
Л = Р cos (ср + p)/cos?, (181)
и тангенциальная сила, направленная по касательной к окружности радиуса кривошипа (кН):
7 = Psin((p + ₽)/cosp. (182)
Сила К считается положительной, если она сжимает щеки колена.
129
Таблица 22
Знак Значения tg р при X Знак «Р°
0,24 0,25 0,26 0,27 | 0,28 0,29 0,30 0,31
0 0 0 0 0 0 0 0 0 360
10 0,042 0,043 0.045 0,047 0,049 0,050 0,052 0,054 _— 350
20 0,082 0,086 0,089 0,093 0,096 0,100 0,103 0,106 —. 340
30 0,121 0,126 0,131 0,136 0,141 0,146 0,151 0,156 — 330
40 0,156 0,162 0,169 0,176 0,182 0,189 0,196 0,202 — 320
50 0,186 0,194 0,202 0,210 0,218 0,226 0,234 0,243 310
60 0,211 0,220 0,230 0,239 0,248 0,257 0,267 0,276 300
70 0,230 0,240 0,250 0,260 0,270 0,280 0,291 *0,301 290
80 0,241 0,252 0,263 0,273 0,284 0,295 0,306 0,316 280
90 0,245 0,256 0,267 0,278 0,289 0,300 0,311 0,322 270
100 0,241 0,252 0,263 0,273 0,284 0,295 0,306 0,316 _— 260
110 0,230 0,240 0,250 0,260 0,270 0,280 0,291 0,301 __ 250
120 0,211 0,220 0,230 0,239 0,248 0,257 0,267 0,276 __ 240
130 0,186 0,194 0,202 0,210 0,218 0,226 0,234 0,243 — 230
140 0,156 0,162 0,169 0,176 0,182 0,189 0,196 0,202 220
150 0,121 0,126 0,131 0,136 0,141 0,146 0,151 0,156 210
160 0,082 0,086 0,089 0,093 0,096 0,100 0,103 0,106 200
170 0,042 0,043 0,045 0,047 0,049 0,050 0,052 0,054 190
180 0 0 0 0 0 0 0 0 — 180
Т а б лн ц а 23
ч° Знак Значения 1/cos 3 прн X Знак v°
0,24 0,25 0,26 0,27 0,28 0.29 0,30 0.31
0 1 1 1 1 1 1 1 1 360
10 1,001 1,001 1,001 1,001 1,001 1,001 1,001 1,001 350
20 1,003 1,004 1,004 1,004 1,005 1,005 1,005 1,006 340
30 1,007 1,008 1,009 1,009 1,010 1,011 1,011 1,012 330
40 1,012 1,013 1,014 1,015 1,016 1,018 1,019 1.020 320
50 1,017 1,019 1,020 1,022 1,024 1,025 1,027 1,029 310
60 1,022 1,024 1,026 1,028 1,030 1,032 1,035 1,037 300
70 1,026 1,028 1,031 1,033 1,036 1,039 1,041 1,044 290
80 1,029 1,031 1,034 1,037 1,040 1,043 1,046 1,049 280
90 1,030 1,032 1,035 1,038 1.041 1,044 1,047 1,050 270
100 1,029 1,031 1,034 1,037 1,040 1,043 1,046 1,049 260
ПО 1,026 1,028 1,031 1,033 1,036 1,039 1,041 1,044 250
120 1,022 1,024 1,026 1,028 1,030 1,032 1,035 1,037 240
130 1,017 1,019 1,020 1,022 1,024 1,025 1,027 1,029 230
140 1,012 1,013 1,014 1,015 1,016 1,018 1,019 1,020 220
150 1,007 1,008 1,009 1,009 1,010 1,011 1,011 1,012 210
160 - 1,003 1,004 1,004 1,004 1,005 1,005 1,005 1,006 200
170 1,001 1,001 1,001 1,001 1,001 I 1,001 1,001 1,001 190
180 + 1 1 1 1 1 1 1 1 180
130
Таблица 24
Знак Значения cos (H-3)/cos 3 при X Знак
0,24 0,25 0,26 0.27 0,28 0,29 0,30 0,31
0 J- 1 1 1 1 !i 1 1 1 + 360
10 .— 0,978 0,977 0,977 0,977 i0,976 : 0,976 0,975 0,975 + 350
20 0,912 0,910 0,909 0,908 SO,907 5 0,906 0,905 0,903 + 340
30 0,806 0,803 0,801 0,798 |0,795 0,793 0,790 0,788 330
40 1— — 0,666 0,662 0,657 0,653 10,649 0,645 0,640 0,636 + 320
50 1— — 0,500 0,494 0,488 0,482 *0,476 0,469 0,463 0,457 + 310
60 + 0,317 0,309 0,301 0,293 SO,285 0,277 0,269 0,261 + 300
70 + 0,126 0,117 0,107 0,098 ,0,088 . 0,078 0,069 0,059 + 290
80 — 0,064 0,075 0,085 0,095 0,106 0,117 0,127 0,138 280
90 — 0,245 0,256 0,267 0,278 ,0,289 0,300 0,311 0,322 — 270
100 — 0,411 0,422 0,432 0,443 0,453 0,464 0,475 0,485 — 260
ПО — 0,558 0,568 0,577 0,586 0,596 5 0,606 0,615 0,625 — 250
120 — 0,683 0,691 0,699 0,707 0,715 0,723 0,731 0,739 240
130 — 0,785 0,792 0,798 0,804 0,810 0,816 0,822 0,829 — 230
140 —— 0,866 0,870 0,875 0,879 0,883 ’ 0,887 0,892 0,896 — 220
150 — 0,926 0,929 0,931 0,934 0,937 0,939 0,942 0,944 — 210
160 — 0,968 0,969 0,970 0,971 0,973 0,974 0,975 0,976 — 200
170 — 0,992 0,992 0,993 0,993 0,993 0,994 0,994 0,994 — 190
180 — 1 1 1 1 1 1 1 1 — 180
Таблица 25
<р° Знак Значения sin (q>+₽)/cos3 при К - 1 Знак <Р°
0,24 0,25 0,26 0,27 0,28 0,29 0,30 0.31
0 + 0 0 0 0 0 0 0 0 360
10 + 0,215 0,216 0,218 0,220 0,221 0,223 0,225 0,227 — 350
20 + 0,419 0,423 0,426 0,429 0,432 0,436 0,439 0,442 — 340
30 + 0,605 0,609 0,613 0,618 0,622 0,627 0,631 0,636 — 330
40 + 0,762 0,767 0,772 0,777 0,782 0,788 0,793 0,798 — 320
50 + 0,886 0,891 0.896 0,901 0,906 0,912 0,917 0,922 — 310
60 + 0,972 0,976 0,981 0,985 0,990 0,995 0,999 1,004 — 300
70 + 1,018 1,022 1,025 1,029 1,032 1,035 1,039 1,043 — 290
80 + 1,027 1,029 1.030 1,032 1,034 1,036 1,038 1,040 — . 280
90 + 1 1 1 1 1 1 1 1 — 270
100 + 0,943 0,941 0,939 0,937 0,936 0,934 0,932 0,930 — 260
ПО + 0,861 0,858 0,854 0,851 0,847 ( 0,844 0,840 0,837 — 250
120 + 0,760 0,756 0,751 0,747 0,742 1 0,737 0,733 0,728 — 240
130 + 0,646 0,641 0,636 0,631 0,626 0,620 0,615 0,610 — 230
140 + 0,524 0,519 0,513 0,508 0,503 0,498 0,493 0,488 — 220
150 + 0,395 0,391 0,387 0,382 '0,378 0,373 0,369 0,364 — 210
160 0,265 0,261 0,258 0,255 0,252 0,248 0,245 0,242 — 200
170 + 0,133 0,131 0,129 0,127 0,126 0,124 0,122 0,121 — 190
180 + 0 0 0 0 0 0 0 0 — 180
131
Рнс. 51. Построение сил Р, /V, S, К н Т по углу поворота кривошипа
Сила Т принимается положительной, если направление создаваемого ею момента совпадает с направлением вращения коленчатого вала. ‘ Численные значения тригонометрических функций, входящих в уравнения (179) — (182), для различных X и <р приведены в табл. 22—25. По данным, полученным в результате решения этих уравнений, строят кривые изменения полных сил N, S, К яТ (рис. 51) или удельных сил рк, ps, рк и рт (см. рис. 74).
Графически 7\,р определяют по площади, заключенной под кривой Т:
ТС? = (Ы-
— Zf2)MP/OB, (183)
где SA и 2А—соответственно положительные и отрицательные площади, заключенные под кривой Т, мм8; Мр — масштаб полных сил, МН в мм; ОВ — длина основания диаграммы, мм (рис. 51).
Точность расчетов и построения кривой силы Т проверяют по уравнению
Т'ср — 2р/Гп/(тте),
(184) где Тср —среднее значение тангенциальной силы за цикл, МН; — среднее индикаторное
давление, МПа; Fn—площадь поршня, м8; т —тактность двигателя. По величине Т определяют крутящий момент одного цилиндра (МН • м):
Мкр.„ = п?. (185)
Кривая изменения силькТ в зависимости от <р является также и кривой изменения Мкр.ц, но в масштабе Мм MpR МН • м в мм.
Для построения кривой суммарного крутящего момента AfKp многоцилиндрового двигателя производят графическое суммирование кривых крутящих моментов каждого цилиндра, сдвигая одну кривую отно
132
сительно другой на угол поворота кривошипа между вспышками. Так как величины и характер изменения крутящих моментов по углу поворота коленчатого вала всех цилиндров двигателя одинаковы и отличаются лишь угловыми интервалами, равными угловым интервалам между вспышками в отдельных цилиндрах, то для подсчета суммарного крутящего момента двигателя достаточно иметь кривую крутящего момента одного цилиндра.
Для двигателя с равными интервалами между вспышками суммарный крутящий момент будет периодически изменяться (I — число цилиндров двигателя):
для четырехтактного двигателя через . . . О = 720°/4
для двухтактных двигателей через-......... О = 360°/i
При графическом построении кривой Л1кр (рис. 52) кривую 2Икр.ц одного цилиндра разбивают на число участков, равное 72070 (для
четырехтактных двигателей); все участки кривой сводятся и суммируются. Результирующая кривая показывает изменение суммарного крутящего момента двигателя в зависимости от угла поворота коленчатого вала.
Среднее значение суммарного крутящего момента Л1кр.сР (МН • м) определяется по площади, заключенной между кривой Л1кр и линией ОА:
Мкр.ср = (F1 — F2) Мм/ОА, (186) где Ft и F2 — соответственно положительная и отрицательная площади, заключенные между кривой Л1кр и линией ОА й эквивалентные работе, совершаемой суммарным крутящим моментом (при i > 6 отрицательная площадь, как правило, отсутствует), мм8; Мм — масштаб моментов, МН - м в мм; ОА —дли-
Рнс. 52. Построение кривой
суммарного крутящего момента четырехцнлнндрового четырехтактного двигателя
на интервала между вспышками на диаграмме (рис. 52), мм. . ч
Момент Л!кр.ср представляет собой средний индикаторный момент двигателя. Действительный эффективный крутящий момент, снимаемый с
вала двигателя:
Ме — Л^кр.срйм»
(187)
гДе Им — механический к. п. д. двигателя.
133
§ 32. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ КОЛЕНЧАТОГО ВАЛА
Силы, действующие на шатунные шейки рядных и V-образных двигателей, определяют аналитическим способом или графическим построением.
Рядные двигатели. Аналитически результирующая сила, действующая на шатунную шейку рядного двигателя (рис. 53, а):
(188)
где Рк = К 4- — сила, действующая на шатунную шейку по
кривошипу, Н.
Рис. 53. Силы действующие на: а — шатунную шейку вала; б — колено вала
Направление результирующей силы Рш.ш для различных положений коленчатого вала определяется углом ф, заключенным между вектором /?ш.ш и осью кривошипа. Угол ф находится из соотношения
1§ф = 77Рк, (189)
Результирующую силу /?шш, действующую на шатунную шейку, можно получить геометрическим сложением силы Рк, действующей по кривошипу, и тангенциальной силы Т либо геометрическим сложением суммарной силы S, действующей по шатуну, и центробежной силы Krw вращающихся масс шатуна (см. рис. 53, а).
Графическое построение силы /?ш.ш в зависимости от угла поворота кривошипа осуществляется в виде полярной диаграммы (рис. 54, б) с полюсом в точке Ош.
При рассмотрении силы /?ш.ш как суммы сил Т иРк построение полярной диаграммы производится следующим образом (рис. 54, а).
Из точки 0ш — полюса диаграммы — по оси абсцисс вправо, откладывают положительные силы Т, а по оси ординат вверх — отрицательные силы Рк. Результирующую силу Рш.ш для соответствующего угла поворота коленчатого вала определяют графически как геометри-
134
Рис, 54, Построение полярной диаграммы нагрузки на шатунную шейку:
а — построение Яш.ш как сумма Т и рк; б — полярная диаграмма; в — построение как суммы S и
ческую сумму сил Т и Рк. На рис. 54, а дано построение сил /?ш.ш для углов фо == 0> Ф1 = 30 и ф13 = 390°. Аналогично строят силы и для других положений коленчатого вала.
Для получения полярной диаграммы концы результирующих сил Rui.m последовательно в порядке нарастания углов соединяют плавной кривой.
На рис. 54, б, в полярная диаграмма нагрузки на шатунную шейку построена геометрическим сложением сил S и Кцш. Различие заключается в построении сил S. На рис. 54, б силы S определены геометрическим сложением сил Т и А, т. е. S = V Т* + № и показано построение силы Х1з, соответствующей углу ф13 = 390° поворота кривошипа. На рис. 54, в силы S, предварительно подсчитанные аналитически, непосредственно суммируются с силой АЛш.
Построение полярной диаграммы нагрузки на шатунную шейку (рис. 54, в) геометрическим сложением суммарной силы S, действующей по оси шатуна, с центробежной силой инерции действующей по кривошипу, осуществляется следующим образом.
Из точки О, представляющей собой центр условно неподвижной коренной шейки, радиусом, равным в принятом масштабе радиусу кривошипа, описывают окружность. Из точки О' — центра шатунной шейки в в. м. т. — проводят вторую окружность радиусом, равным в том же масштабе длине шатуна. Окружность с центром О делят на равное чисйо частей (обычно на 12 или 24). Через точки деления из центра О проводят лучи до пересечения с окружностью, проведенной из точки О'. Эти лучи представляют собой относительные положения оси условно вращающегося цилиндра двигателя. Принято, что цилиндр вращается с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости вращения коленчатого вала. Соединяя точку с концами проведенных лучей, получают отрезки 0'1", 0'2" и т. д. Эти отрезки — относительные положения оси шатуна при определенных углах поворота коленчатого вала. Из точки О' по направлениям оси шатуна откладывают в определенном масштабе Мр с учетом знаков векторы сил S (на рис. 54, в показаны силы S13, при ф13 = 390° и Хгз при ф23 = 690°) и концы их соединяют плавной линией. Полученная кривая называется полярной диаграммой сил S с полюсом в точке О'.
Для нахождения результирующей силы Дш.ш необходимо переместить полюс О' по вертикали на величину силы (АЛш постоянна по величине и направлению), взяв ее в том же масштабе Мр. Полученная точка Ош называется полюсом полярной диаграммы результирующих сил Дш.ш> действующих на шатунную шейку.
Чтобы геометрически сложить векторы сил S и для какого-либо положения кривошипа (например, 23), достаточно провести из полюса Ош вектор От23. Этот вектор, являющийся геометрической суммой векторов ОШО' = Крш и 0'23 = S23, по величине и направлению соответствует искомой силе Яш.шгз-
Таким образом, векторы, соединяющие начало координат (полюс Ош) с точками на контуре полярной диаграммы сил S, выражают по 136
величине и направлению силы, действующие на шатунную шейку при соответствующих углах поворота коленчатого вала.
Для получения результирующей силы >= Дш.ш + (см. рис. 53, б), действующей на колено вала и изгибающей шатунную шейку, необходимо полюс 0ш переместить по вертикали (см. рис. 54) на величину центробежной силы инерции вращающихся масс кривошипа К.цк — — mKR<f>2 в точку 0к. На рис. 54, б, в показано построе-
ЯшШ
О 2 4 68 10 J/2 /4 16 Iff 26 22
О 60 120 180 240 300 360 420 480 540 600 600 720 <f°
Рис. 55. Диаграмма нагрузки на шатунную шейку в прямоугольных координатах
ние результирующих сил Дк для углов <р13 = 390°. Аналитически сила (см. рис. 53, б)
R* = V Т2+ Арк, (190)
где КРК — Рк + Krk К + Кяш + Krk = К + Kr — сила, действующая на колено вала по кривошипу (на рис. 54, б показано построение силы RKJ при cpj = 30°).
Для определения средней результирующей силы за цикл /?ш.ш сР, а также ее максимального Rm.m тахи минимального Rm ш min значений полярную диаграмму перестраивают в прямоугольные координаты в функции угла поворота коленчатого вала (рис. 55). Для этого на оси абсцисс откладывают: для каждого положения коленчатого вала углы поворота кривошипа, а на оси ординат — значения результирующей силы Rm ш, взятые из полярной диаграммы. При построении диаграммы все значения Rm ш считаются положительными. Среднюю величину результирующей силы Rm.ш ср находят путем планиметрирования площади ПОД кривой Rm ш = /(ф).
V-образные двигатели. При определении результирующих сил, Действующих на шатунную шейку V-образного двигателя, необходимо учитывать конструктивное выполнение соединения шатунов с коленчатым валом.
Для V-образных двигателей с сочлененными шатунами (с шатунной шейкой соединен только один шатун) результирующую силу Rm.m е, действующую на шатунную шейку, определяют геометриче
137
ским сложением суммарных сил 7\ и Р^, передающихся от левого и правого шатунов (рис. 56):
Хш.шх = Ут1 + гЪ. (191)
Силы Тв и Ркв определяют табличным способом с учетом порядка работы двигателя
— Тл + Тц;
(192)
Рк2 = Рк л + Рк п =/Сл +/<НШ.Л + /<п + Хйш.п =^2 + Кйш* (193)
Углы поворота коленчатого вала в V-образных двигателях отсчитывают от положения первого кривошипа, соответствующего в. м. т.
в левом цилиндре от носка
при правом вращении коленчатого вала.
Если интервалы между рабочими ходами правых и левых цилиндров на различных кривошипах одинаковы, то суммарные силы, определенные для первого кривошипа, могут быть использованы и для других кривошипов.
Для V-образных двигателей с одинаковыми шатунами, расположенными рядом на одной шейке, результирующие силы Rm ш.л и дейст-
вующие на соответствующие участки шатунной
Рис. 56. Силы, действующие на шатунную шейку коленчатого вала V-образного двигателя
шейки, определяются раздельно так же, как и для однорядного двигателя. Однако для приближенного определения результирующей силы действующей на колено вала, подсчитывают условную силу ше> действующую на шатунную шейку сдвоенного кривошипного механизма. Силу &ц.ш s определяют без учета смещения шатунов аналогично определению этой же силы для двигателя с сочлененными шатунами. В этом случае
+ Krk-
(194)
Полярные диаграммы нагрузок на шатунную шейку и на колено вала V-образных двигателей строят так же, как и для рядных двигателей.
138
$ 33. СИЛЫ, ДЕЙСТВУЮЩИЕ НА КОРЕННЫЕ ШЕЙКИ КОЛЕНЧАТОГО ВАЛА
Результирующая сила RK.m, действующая на коренную шейку (рис. 57, а, б), определяется геометрическим сложением сил, равных, но противоположных по направлению силам, передающимся от двух смежных колен:
Ru.m = «к, + R* (<+1), (195)
где RK{ = — RKih/^ и Rk (,+d = ~ Rk (Н-1Л/Ь — соответственно усилия, передаваемые от I и (г + 1)-го колен на коренную шейку, заклю
Рис. 57. Коренная шейка: а — схема коленчатого вала; б — схема сил, действующих иа коренную шейку
ченную между ними; /± и /2 — расстояния по оси вала между центрами коренной и шатунной шеек; L — расстояние между центрами соседних коренных шеек.
При симметричных коленах ₽к/=—0,5/?кО /?к (Ж) =—0,5/?к(ж), тогда __
RK.m = -0,5(RKi + RKU+i))- (196)
Полярную диаграмму сил RK.m строят с помощью двух полярных диаграмм нагрузок на смежные шатунные шейки, полюса Ок которых совмещены в одной точке (рис. 58). Графически точки полярной диаграммы нагрузки на коренную шейку для соответствующих углов поворота вала определяют геометрическим сложением попарно векторов RK обеих диаграмм, одновременно действующих на колено вала в соответствии с порядком работы цилиндров. Каждый из полученных результирующих векторов представляет собой удвоенную силу RK.m с обратным знаком. Соединяя концы результирующих векторов плавной кривой в порядке возрастания углов поворота коленчатого вала, получают полярную диаграмму.
Для определения с помощью этой диаграммы результирующей силы RK.m, приложенной к коренной шейке приданном угле поворота
139
кривошипа г-го цилиндра, необходимо уменьшить в два раза масштаб диаграммы по сравнению с масштабом полярных диаграмм нагрузки на шатунные шейки и принять направление векторов от кривой к полюсу Ок.
На рис. 58 показано построение полярной диаграммы нагрузки на вторую коренную шейку однорядного шестицилиндрового четырех-
тактного двигателя с порядком работы 1—5—3 — 6—2—4.
Результирующую силу, действующую на коренную шейку, можно подсчитать аналитически:
Рнс. 58. Полярная диаграмма нагрузки на вторую коренную шейку однорядного шестицнлнндрового четырехтактного двигателя
+ (197)
где Тк и — соответственно суммы проекций сил ₽'к! И ₽'к(/+1) на оси Т и К i-ro кривошипа. Определяют Тк и Кк следующим образом (см. рис. 57, б). Проекции силы R'Kl = —G,5Rki на оси Т и К г-го кривошипа будут:
Т\ = —0,57\;
Крх! =
Аналогично проекции силы ₽'к(г+1) на оси Т и К (I + 1)-го кривошипа
П+1------0,5Тг+1;
Крк 04-1) = — 0,5Крк 04-1) .
Далее определяют проекции 7,'г+1 и К'Рко4-1) на оси Т и К i-ro кривошипа:
Т((+1) т — Tt+i cosyK = —0,57^ cosyK;
To+i) к = 7^4-1 sinyK = — 0,57\+1sin ук ;
Крк ((4-1) т — — Крк. ((4-1) sin ук = 0,5/Срк ((4-1) sin ук;
Крк 04-1) К = Крк ((4-1) COSук = — 0,5Крк ((4-1) COSУк,
гдеук — угол между кривошипами i и (г + 1)-го цилиндров.
Суммируя все проекции соответственно на оси Т и К i-ro кривошипа, получим:
140
TK~Ti + Т(q_i) т + Крк (f+n т = — 0>5 (7\+7\+1 cos Тк —' — Лрк а+п sin ?к);
7СК = 7СРк/ + Т(H_i) к + ТСрк (i+i) к — — 0,5 (/CpKi + + Тм sin YK + ЛрК (,+D cos ук).
(198)
При определении 71к и /<к для различных углов поворота коленчатого вала удобнее использовать табличную форму (табл. 26).
Табл. 26 составляют по углу поворота кривошипа первого цилиндра от начала цикла. Углы поворота ср^и ф^+1 и соответствующие им силы определяют с учетом углового смещения порядка работы цилиндров. При угле между кривошипами = 0; 90; 180° и т. д. таблица значительно упрощается (см. табл. 32).
По значениям 71к и /<к, взятым для различных углов поворота коленчатого вала, строят полярную диаграмму результирующих сил ₽к.ш, действующих на коренную шейку в координатах Т и К Z-го цилиндра. Диаграмма строится аналогично полярной диаграмме нагрузки на шатунную шейку.
Определение результирующих сил7?к действующих на коренные шейки V-образных двигателей, и построение для них полярных диаграмм осуществляют так же,' как и для рядных двигателей, но с учетом действия на каждое колено вала суммарных сил от двух цилиндров (см. § 32). Перестроение полярной диаграммы сил 7?к.ш (рис. 58) в прямоугольные координаты 7?к.ш —Ф (рис. 59, а) и определение по ней Як.ш.ср, Як.ш max и ₽к.ш min производится так же, как это делалось при перестроении диаграммы сил
141
a — без учета противовесов; б — вал с противовесами
$ 34. ДИАГРАММЫ ИЗНОСА ШЕЕК КОЛЕНЧАТОГО ВАЛА
На основании полярных диаграмм нагрузок на шейки коленчатого вала можно построить диаграммы износа шеек. Эти диаграммы дают возможность определить наиболее и наименее нагруженные участки шатунных и коренных шеек, что необходимо для правильного определения местоположения масляного отверстия. Кроме того, они дают наглядное представление о характере износа шейки по всей окруж-
ности в предположении, что износ пропорционален усилиям, действующим на шейку.
Диаграмму износа шатунной шейки (рис. 60) строят по полярной диаграмме, приведенной на рис. 54,6, следующим образом. Проводят окружность, изображающую в произвольном масштабе шатунную шейку; делят ее на равное количество участков лучами 0ш2, 0ш2 и т. д. (обычно на 12 или 18 участков).
Дальнейшее построение
Рис. 60. Диаграмма износа шатунной шейки
142
осуществляют в предположении, что действие каждого вектора силы Rm.iui распространяется на 60° по окружности шейки в обе стороны от точки приложения силы. Таким образом, для определения величины усилия (износа), действующего по каждому лучу (например, по лучу Ош//), необходимо:
а) перенести луч с диаграммы износа параллельно самому себе на полярную диаграмму;
б) определить по полярной диаграмме сектор на шатунной шейке (по 60° в каждую сторону от луча в котором действующие силы создают нагрузку (износ) по направлению луча Ош11;
в) определить величину каждой силы /?ш.шь действующей в секторе луча От11 (в секторе луча Ош11 действуют всего три силы:
и Яш.ш15)> и подсчитать результирующую величину
(/?ш.шХ{ == + 4- для луча ОШП;
г) отложить результирующую величину в выбранном
масштабе на диаграмме износа по лучу Ош11 от окружности к центру;
д) определить таким же образом результирующие величины сил, действующих в секторах каждого луча (например, в секторе луча
действуют все силы кроме одной 7?ш ш13, а в секторах лучей Ош4 и Ош5 нет ни одной действующей силы);
е) отложить на каждом луче отрезки, соответствующие в выбранном масштабе результирующим величинам сил а концы от-
резков соединить плавной кривой, характеризующей износ шейки;
ж) перенести на диаграмму износа ограничительные касательные к полярной диаграмме ОШЛ и ОШВ и, проведя от них лучи ОША' и ОтВ' под углом 60°, определить граничные точки (А" и В ") кривой износа шатунной шейки, между которыми обычно располагается ось масляного отверстия.
Для упрощения подсчета результирующих величин составляют таблицу (см. табл. 31), в которую заносят значения сил действующих по каждому лучу, и их сумму.
Диаграмму износа коренной шейки строят аналогично.
Глава VIII
УРАВНОВЕШИВАНИЕ ДВИГАТЕЛЕЙ
§ 35. ОБЩИЕ СВЕДЕНИЯ
Силы и моменты, действующие в кривошипно-шатунном механизме, непрерывно изменяются и, если они не уравновешены, вызывают сотрясение и вибрацию двигателя, передающиеся раме автомобиля или трактора.
К неуравновешенным силам и моментам относятся:
а) силы инерции возвратно-поступательно движущихся масс Pj—Pji+Piii* и центробежные силы инерции вращающихся масс KR;
* При уравновешивании двигателей обычно рассматривали силы инерции только первых двух порядков.
143
б) продольные моменты М)*=Мц 4- М]ц и Mr, возникающие в многоцилиндровых двигателях от неуравновешенных сил Р} и Kr отдельных цилиндров;
в) крутящий момент Мкр и равный ему, но противоположно направленный опрокидывающий момент Л4олр = —Мкр, воспринимаемый опорами- двигателя.
Двигатель считается полностью уравновешенным, если при установившемся режиме работы силы и моменты, действующие на его опоры, постоянны по величине и направлению.
Однако поршневые двигатели не могут быть полностью уравновешенными, так как крутящий момент Мкр всегда является периодической функцией угла поворота коленчатого вала и, следовательно, величина опрокидывающего момента Л40пр всегда переменна.
Условия уравновешенности двигателя с любым числом цилиндров (при соблюдении равенства масс движущихся частей и идентичности протекания рабочего процесса во всех цилиндрах, а также обеспечении статической и динамической уравновешенности коленчатого вала) принято записывать в следующем виде:
а) результирующие силы инерции первого порядка и их моменты равны нулю: S Pjj = 0 и S Мц = 0;
б) результирующие силы инерции второго порядка и их моменты равны нулю: 2Pju = 0 и SM/// = 0;
в) результирующие центробежные силы инерции и их моменты равны нулю: ZKr = 0 и S Mr = 0.
Таким образом, решение вопроса уравновешивания двигателей сводится к уравновешиванию лишь наиболее значительных сил и их моментов.
Уравновешивание сил инерции первого и второго порядков достигается подбором определенного числа цилиндров, их расположением и выбором соответствующей кривошипной схемы коленчатого вала. Так, например, в шести- и восьмицилиндровых рядных двигателях полностью уравновещены силы инерции первого и второго порядков и их моменты.
При невозможности подобрать для проектируемого двигателя соответствующего количества и расположения цилиндров для полного уравновешивания сил инерции они могут быть уравновешены противовесами, расположенными на дополнительных валах, имеющих механическую связь с коленчатым валом.
В рядных двигателях уравновесить силы инерции первого и второго порядков установкой противовесов на коленчатом валу невозможно. При соответствующем выборе массы противовеса можно частично перенести действие силы инерции первого порядка из одной плоскости в другую, тем самым уменьшив максимальную неуравновешенность в одной плоскости.
Центробежные силы инерции вращающихся масс практически можно уравновесить в двигателе с любым количеством цилиндров установкой противовесов на коленчатом валу.
В большинстве многоцилиндровых двигателей результирующие силы инерции уравновешиваются без установки противовесов за счет
144
соответствующего числа и расположения колен вала. Однако даже уравновешенные валы часто снабжают противовесами в целях уменьшения и более равномерного распределения нагрузки /?к.ш на коренные шейки и подшипники, а также для уменьшения моментов, изгибающих коленчатый вал.
При установке противовесов на продолжении щек коленчатого вала результирующая сила, действующая на коренную шейку:
Якрш = R* ,ш + Япр. (199)
где R„p — сила инерции противовеса.
Для получения полярной диаграммы силы /?кРш необходимо полюс 0к полярной диаграммы силы /?к.ш (см. рис. 58) переместить по биссектрисе угла при RnPi ~ ₽гтр(!+1) между кривошипами на величину Rnv= Rnpt + /?пр(«+1) в масштабе диаграммы. Полученная точка 0пр будет полюсом полярной диаграммы сйлы
Снижение средней нагрузки на коренную шейку при установке противовесов показано на развернутой диаграмме результирующих сил, действующих на коренную шейку (см. рис. 59, б).
§ 36. УРАВНОВЕШИВАНИЕ ДВИГАТЕЛЕЙ РАЗЛИЧНОГО ТИПА
Одноцилиндровый двигатель (типа УД-1, Д-20, УНД-5). В одноцилиндровом двигателе неуравновешенными силами являются Рц; Pjn и KR (рис. 61 и 62).
Неуравновешенных моментов нет, т. е. SA4// = 0; 2А4ш = 0 и S MR = 0.
Для уравновешивания центробежной силы инерции вращающихся масс Ar (рис. 61) на продолжении щек устанавливают два одинаковых противовеса, центры тяжести которых расположены на расстоянии р от оси коленчатого вала.
Рис. 61. Схема уравновешивания центробежных сил инерции в одноцилиндровом двигателе
Рис. 62. Схема переноса действия силы инерции первого порядка одноцилиндрового двигателя из вертикальной в горизонтальную плоскость
6—370
145
Полное уравновешивание силы Кц достигается при условии
2mnp R рсо2 = mR₽co2
за счет подбора и р.
По конструктивным соображениям в одноцилиндровых двигателях, как правило, не уравновешивают силу инерции второго порядка, а действие неуравновешенной силы инерции первого порядка частично (обычно 0,5 Pji) переносят из вертикальной плоскости в горизонталь
Рис. 63. Схема сил инерции, действующих в двухцилиндровом рядном двигателе с кривошипами, направленными в одну сторону
Рис. 64. Схема сил инерции, действующих в двухцилиндровом рядном двигателе с кривошипами под углом 180°
ную (рис. 62) установкой противовесов. Как видно из рисунка, вертикальная составляющая силы инерции противовеса /?npV уменьшает силу Р//, ио в двигателе возникает дополнительная горизонтальная Сила /?прй*
Масса противовесов (кг)
2mnp/ = 0,5mj/?/p. (200)
Таким образом, общая масса каждого противовеса в одноцилиндровом двигателе будет
/Япр — R Н" ^пр j ~ + 0,5/и^). (201)
Двухцилиндровые двигатели (типа Д-16, УД-2, УНД-7 и УНД-10). Двухцилиндровый рядный двигатель с кривошипами, направленными в одну сторону (рис. 63). Порядок работы двигателя 1—2. Промежутки между вспышками равны 360°. Коленчатый вал двигателя имеет кривошипы, направленные в одну сторону.
При принятой схеме расположения кривошипов для каждого цилиндра будут одинаковыми силы Рц, P/ц и Kr Равнодействующие 146
этих сил для первого и второго цилиндров соответственно:
Е Рц = 2Рц = 2mjRa>2 cos <р ; ЕР/П = 2Рщ = 2m}Re>zk cos 2<р;
Е/Сн = 2КН = 2/ПвРсо2.
Неуравновешенных моментов нет, так как действующие силы и плечи приложения этих сил одинаковы: SAf/j =0; =0 и
ЕЛЦ =0.
Уравновешивание двухцилиндрового двигателя осуществляете^ тем же способом, что и одноцилиндрового.
Двухцилиндровый двигатель с кривошипами под углом 180° (рис. 64). Порядок работы двигателя 1—2. Промежутки между вспышками чередуются через 180 и 540°.
При принятой схеме расположения кривошипов силы инерции первого порядка при любом положении коленчатого вала уравновешиваются: ЕР/, — 0.
В плоскости осей цилиндров эти силы создают неуравновешенную пару с моментом
2А4/1 = P/ifl, где а — расстояние между осями цилиндров.
С помощью противовесов, масса которых mnp j = nijRa/(pjb), можно перенести действие момента ЕМ// в горизонтальную плоскость (Ь — расстояние между противовесами).
Таким образом, установка противовесов не уравновешивает момента сил инерции первого порядка, а перемещает его из вертикальной плоскости в горизонтальную.
Силы инерции второго порядка Рщ для первого и второго цилиндров равны и одинаково направлены. Равнодействующая этих сил
2 Р) и = 2mjR<tfk cos 2<р.
Уравновешивания силы ЕР/;; можно добиться противовесами, установленными на дополнительных валах. Момент от сил инерции второго порядка равен нулю: ЕЛ4/П = 0. Центробежные силы инерции от первого и второго цилиндров взаимно уравновешиваются: SKR =0.
Возникающий от действия центробежных сил инерции свободный момент ЕЛЦ = Krcl- Уравновешивание этого момента осуществляется противовесами, масса которых
= mRRa/(pRb).
Четырехцилиндровый рядный двигатель с кривошипами, расположенными под углом 180°. Порядок работы двигателя 1—2—4—3 или 1—3—4—2. Промежутки между вспышками равны 180°. Коленчатый вал двигателя имеет кривошипы, расположенные под углом 180°. По такой схеме (рис. 65) выполнены двигатели: М-24, ВАЗ-2101,
6*
147
ВАЗ-2ЮЗ, МЗМА-412, МЗМА-407, Д-30, Д^35, Д-37, Д-48, Д-54, СМД-14, КДМ-46 и др.
Силы инерции первого порядка и их моменты при указанном расположении кривошипов взаимно уравновешиваются: SP// = 0 и = 0. Силы инерции второго порядка для всех цилиндров равны и направлены в одну сторону. Их равнодействующая
2 Pj п = 4Pj п = 4/n7Rco2X cos 2cp.
Силы инерции второго порядка можно уравновесить лишь с помощью дополнительных валов. Суммарный момент этих сил равен нулю:
SAljn =0. Центробежные
Рис. 65. Схема сил инерции, действующих в четырехцилиндровом ридном двигателе
силы инерции для всех цилиндров равны и направлены попарно в разные стороны. Равнодействующая этих сил и момент равны нулю: 'ЯК# = = 0 и =0.
Некоторые двигатели (например, МЗМА-407^ имеют коленчатые валы с противовесами для уменьшения центробежных сил, действующих на коренные подшипники.
Шестицилиндровые двигатели. Однорядный шестицилиндровы'й двигатель (рис. 66). По-
рядок работы двигателя: 1—5—3—б—2—4 или 1—4—2—6—3—5. Промежутки между вспышками равны 120°. Коленчатый вал имеет кривошипы, расположенные под углом 120°. По такой схеме выполнены двигатели: ЗИЛ-164, ЗИЛ 120, ЗАЗ-51, ЗАЗ-12, «Урал-5м», Д-6, 6КДМ-50.
Шестицилиндровый рядный двигатель уравновешен полностью:
Рис 66 Схема сил инерции, действующих в шестицилиндровом рядном двигателе
148
2 Pi i —о и
S и “ О и S и = O;
Kr = о и Мд = o.
1Пестицилиндровые рядные двигатели выполняют с семи- и четырехопорными коленчатыми валами.
На рис. 66 показана схема семиопорного коленчатого вала двигателя ЗИЛ-164 без противовесов. Некоторые двигатели (например,
Рис. 67. Схема сил инерции, действующих в шести цилиндровом V-образном двигателе
ЗИЛ-123Ф, ЗАЗ-51 и др.) имеют коленчатые валы с противовесами для разгрузки коренных подшипников от действия центробежных сил.
V-образный шестицилиндровый двигатель с углом развала цилиндров 90° итремя спаренными кривошипами под углом 120° (рис. 67). Порядок работы двигателя: 1л—1п—2л—2п—Зл—Зп. Вспышки чередуются через 90 и 150°. Коленчатый вал имеет кривошипы, расположенные под углом 120°. По такой схеме выполнены двигатели, ЯМЗ-236.
Для каждой секции двигателя, которая включает два цилиндра (левый и правый), равнодействующая сил инерции первого порядка является постоянной величиной и направлена всегда по радиусу кривошипа. Равнодействующая сил инерции первого порядка для всего двигателя равна нулю: SP//S = 0. Суммарный момент от сил инерций первого порядка действует во вращающейся плоскости, составляющей с плоскостью первого кривошипа угол 30°, и равен
SMi 1 а = КЗ Р/1 аЯ = 1,732т jRrfa.
Равнодействующие сил инерции второго порядка для каждой секции всегда направлены по горизонтали перпендикулярно оси коленчатого вала (см. рис. 67). Сумма этих равнодействующих сил равна нулю:
S Р/ п s = Pi п s + Р/ II 2 + Pj п s = 0.
Суммарный момент от сил инерций второго порядка действует в горизонтальной плоскости:
(и =1/2 nijRa^a (1,5 cos 2<р + 0,866 sin 2<р).
149
Центробежные силы инерции взаимно уравновешиваются: S/Cr =0.
Суммарный момент от центробежных сил действует в одной плоскости с моментом
SMrs = 1^3 K.Rsa = 1,732(ти 4- 2/пшк) Ra?a.
Уравновешивание моментов SAly/s и осуществляется
с помощью противовесов, устанавливаемых на продолжении щек коленчатого вала, а момента — установкой противовесов
на двух дополнительных валах.
V-o бразный шестицилиндровыйдвигатель с углом развала цилиндров 60° и шестью крив о-
Рис. 68. Схема шестицилиндрового V-образного двигателя с углом развала цилиндров 60°
шипами под углом 60° (рис. 68). Порядок работы двигателя: 1л—1п—2л—2п—Зл—Зп. Чередование вспышек равномерное через 120° По такой схеме выполнен двигатель ГАЗ-24-16.
Для каждой секции двигателя, которая включает два цилиндра (левый и правый), равнодействующие сил инерции первого и второго порядков постоянны по величине, а равнодействующие сил инерции дервого и второго порядков для всего двигателя равны нулю: SPZI = = 0 и SPy// = 0. Равнодействующая центробежных сил также равна нулю: =0.
Суммарный момент от сил инерции первого порядка действует во вращающейся плоскости, совпадающей с плоскостью первого левого и третьего правого кривошипов:
= 1,5mjR&a.
Суммарный момент от сил инерции второго порядка действует в плоскости, вращающейся с угловой скоростью 2о> в сторону, противоположную вращению коленчатого вала:
2Л1/ п — 1,5т
150
Суммарный момент от центробежных сил действует в одной плоскости с моментом SAI//:
2 MR = tnRR<& ((2а + b) + 1,732 (а — 6) J.
Уравновешивание моментов SAfp и SA1r осуществляется с помощью противовесов, устанавливаемых на продолжении двух крайних щек коленчатого вала, а момента SAf/n — путем постановки противовесов на дополнительном валу, вращающемся со скоростью 2со.
Рис. 69. Схема сил инерции, действующих в восьмипилиндро-вом рядном двигателе
Восьмицилиндровые двигатели. Восьмицилиндровый рядный двигатель (рис. 69). Порядок работы двигателя 1—6—2—5—8—3—7—4. Промежутки между вспышками равны 90°. Коленчатый вал имеет восемь кривошипов, которые расположены в двух взаимно перпендикулярных плоскостях. По такой схеме выполнены двигатели ЗИЛ-110.
Двигатель полностью уравновешен:
2 Р/1 = 0 и 2 Mj । = 0; 2 Р/ п = 0 и 2 М/ ц = 0;
2Ан — 0 и 2 Mr = 0-
Для разгрузки коленчатого вала от действия местных центробежных сил в некоторых двигателях применяют противовесы.
В ос ьми ци л и н д р овый V-образный двигатель. Порядок работы двигателя: 1л—1п—4л—2л—2п—Зл—Зп—4п. Промежутки между вспышками равны 90° Угол развала цилиндров у =90°. Коленчатый вал имеет кривошипы, расположенные в двух взаимно перпендикулярных плоскостях (рис.70). Потакой схеме выполнены двигатели ЯМЗ-238, ЗИЛ-111, ЗИЛ-130, ЗИЛ-375, ЗАЗ-13, ЗАЗ-41, ЗАЗ-66.
В. двигателях рассматриваемого типа силы инерции первого порядка взаимно уравновешиваются: SP// = 0. Суммарный момент
151
этих сил действует во вращающейся плоскости, составляющей с плоскостью первого кривошипа угол 18°26':
2 А1/1 — j/10 mjRoPa,
Равнодействующие сил инерции второго порядка для каждой секции двигателя всегда направлены по горизонтали перпендикулярно оси коленчатого вала (рис. 70). Сумма этих равнодействующих сил равна нулю: SP/// =0.
Суммарный момент сил инерции второго порядка также равен нулю: SM/// =0. Центробежные силы инерции для всех секций
Рис. 70. Схема сил инерции, действующих в восьмицилиндровом V-образ-ном двигателе
Левый впавый
равны и направлены попарно в разные стороны. Равнодействующая этих сил = 0.
Суммарный момент SA1R центробежных сил действует в той же плоскости, что и равнодействующий момент сил инерции первого порядка
S Мв = У10 Кпа = УТО (тк + 2тш, к) Rm2a.
Уравновешивание моментов SAf/z и осуществляется противовесами, устанавливаемыми на продолжении щек вала (рис. 70) или путем установки двух противовесов на концах коленчатого вала в плоскости-действия моментов, т. е. под углом 18°26' (см. рис. 87).
Очевидно, что
£Л1,- 1 + £Мн = (т} + тк + 2тш к).
Масса каждого общего противовеса, установленного на конце вала:
/ипр х = а/? УТО" (nij + тк + 2/пш к)/(р6), где р — расстояние от центра тяжести общего противовеса до оси коленчатого вала; b — расстояние между центрами тяжести противовесов.
152
§ 37. РАВНОМЕРНОСТЬ КРУТЯЩЕГО МОМЕНТА И РАВНОМЕРНОСТЬ ХОДА ДВИГАТЕЛЯ
Рис. 71. Кривые крутящих моментов четырехтактных двигателей с различным числом одинаковых цилиндров (двигатели имеют интервалы между вспышкамв 6 = 720/Z).
а — одноцилиндровый i = 1 i б — двухцилиндровый i да 2} в — четырехцилиидровый I = 4; г = шестицилицдровый t = 6; д — восьмицилиндровый I да 8
При определении суммарных сил, действующих в двигателе, было установлено, что крутящий момент Л1кр представляет собой периодическую функцию угла поворота коленчатого вала. Неравномерность изменения суммарного крутящего момента обусловливается особенностями протекания рабочего процесса двигателя и кинематическими свойствами его кривошипно-шатунного механизма.
Для оценки степени равномерности индикаторного крутящего момента дви гателя обычно испол ь-зуют коэффициент неравномерности крутящего момента:
— (Мкр max — — MKptnin)/MKp. ср, (202) Где ^кртах» ^^Kpmin И А1Кр.ср — соответственно максимальный, минимальный и средний индикаторные крутящие моменты двигателя.
Для одного и того же двигателя величина коэффициента р зависит от режима его работы. Поэтому Для сравнительной оценки различных двигателей значения коэффициента неравномерности крутящего момента оп редел яют для режима номинальной мощности.
Для двигателей с одно
размерными цилиндрами коэффициент р уменьшается с увеличением числа цилиндров. Это наглядно иллюстрируется кривыми Мкр = /(ф) (рис. 71).
Индикаторный крутящий момент двигателя Мкр (Н • м) в каждый момент времени уравновешивается суммарным моментом сопротивления МСопр и моментом сил инерции Jo всех движущихся масс двигателя» приведенных к оси коленчатого вала. Эта взаимосвязь выражается уравнением
Мжр = Л4сопр 4" (203)
153
где d<s>ldt — угловое ускорение коленчатого вала, рад/с2.
Для установившегося режима работы двигателя Л4СОпр = Мкр.ср-Графически это означает, что линия Л4кр.ср, построенная на диаграмме суммарного крутящего момента (рис. 72), определяет также значение
момента сопротивления. Из
Рис. 72. Изменение крутищего момента и угловой скорости вращении коленчатого вала при установившемси режиме работы двигатели
а видно, что Мкр.ср пересекает кривую крутящего момента, образуя положительные (Fj) и отрицательные (F2) площадки. Площадки, лежащие над линией момента сопротивления, пропорциональны избыточной работе крутящего момента, поглощаемой движущимися частями двигателя. Избыток работы идет на увеличение кинетической энергии и, следовательно, скорости движущихся масс. При недостатке работы происходит отдача энергии от движущихся частей, что вызывает замедление вращения коленчатого вала.
Величина избыточной работы ЛИЗб крутящего момента определяется графически по площади Ft:
^изб = F±Мм М^, (204)
где Fi — площадь над прямой Л4кр.ср, полученная планиметрированием или другим способом, мм2; Мм — масштаб момента, Н м в мм; М* = 4л/(«’ • ас) — масштаб угла поворота коленчатого вала, рад в мм (отрезок ас — в мм; i — число цилиндров).
Избыточная работа крутящего момента может быть получена аналитически из уравнения (203) в виде приращения кинетической энергии вращающихся масс, обусловленного изменением угловой скорости вала от сошах до comin:
Ьизб = ~~ (®тах —COtaiin) — Jo -Шах (©max— COmln)- (205)
Нетрудно видеть, что изменения угловой скорости коленчатого вала вызваны отклонением мгновенного значения Л4Кр от среднего значения крутящего момента Л4кр.ср = Л4СОпр. При Л4кр > Л4СОпр коленчатый вал имеет положительное угловое ускорение н узловая скорость его увеличивается. Если Л4кр<;Л1сопр> то, наоборот, угловая скорость коленчатого вала уменьшается. При Л1кр = Л1СОпр уравнение (203) примет вид:
Joda/dt = 0
154
В этом случае d^/dt — 0, а угловая скорость вала со = сотах или со = comjn.
Колебание угловой скорости при установившемся режиме работы двигателя вследствие неравномерности крутящего момента характеризуется коэффициентом неравномерности хода
8 = (<omax <omjn)/(ocp. (206)
Если принять, что средняя угловая скорость (рад/с)
wcP == О) = (о>тах 4" 0)min)/2, (207)
то уравнение (205) можно записать в виде
§ = 1изб/(Л<о2). (208)
Подставляя значение средней угловой скорости соср = со = лп/30 в уравнение (208)/получим
^900£изб/[/о(кп)2]. (209)
Коэффициент неравномерности хода 6:
Дли автомобильных двигателей..................0,01—0,02
Дли тракторных двигателей..................... 0,003—0,010
Из уравнения (209) следует, что при LH36 = const увеличение частоты вращения и момента инерции вращающихся масс приводит к уменьшению коэффициента неравномерности хода.
При определении коэффициента неравномерности хода предполагалось, что коленчатый вал является абсолютно жестким. В действительности коленчатый вал и соединенные с ним механизмы обладают упругими свойствами и подвержены действиям крутильных колебаний. В связи с этим расчетная величина коэффициента неравномерности хода будет несколько отличаться от действительной.
При расчете вновь проектируемогодвигателя, задаваясь величиной 6, можно определить из формулы^£08) момент инерции (кг • м2) движущихся масс двигателя:
Jo = LH36/(6®2). (210)
Конкретные значения величины момента инерции для некоторых атомобильных и тракторных двигателей следующие:
Марка дви-
гателя . . . МеМЗ-965 МЗМА-407 М-21 ЗИЛ-130 ЯМЗ-236 Д-35 Д-54
Момент инер-
ции Jo,
кг.м2 . . . 0,076 0,147 0,274 0,610 2,450 2,2602,260
§ 38. РАСЧЕТ МАХОВИКА
Основное назначение маховика — обеспечение равномерности хода двигателя и создание необходимых условий для трогания машины с места.
155
Для автомобильных двигателей, работающих обычно с большой недогрузкой, характерен облегченный разгон машины и поэтому маховик автомобильного двигателя, как правило, имеет минимальные размеры.
В тракторных двигателях кинетическая энергия маховика должна обеспечить трогание машины с места и преодоление кратковременных перегрузок, поэтому маховики тракторных двигателей по сравнению с автомобильными имеют большую массу и размеры.
Расчет маховика сводится к определению момента инерции JM маховика, махового момента mMD2cp , основных размеров и максимальной окружной скорости.
Для расчета можно принять, что момент инерции маховика со сцеплением автомобильного двигателя составляет 80—90% от момента инерции Jo двигателя, а тракторного — 75—90%.
Маховой момент (кг • м2)
^М^ср — Mt (211)
где тм — мйсса маховика, кг; Dcp — средний диаметр маховика, м.
По величине махового момента осуществляют подбор основных размеров маховика, руководствуясь в основном соображениями конструктивного характера. Так, диаметр маховика выбирают с учетом габаритов двигателя, возможности размещения механизма сцепления и т. д. Для приближенных расчетов можно принять Dop = (2 3)<S,
где <S — ход поршня, м.
По условиям прочности внешний диаметр DM маховика должен быть выбран с учетом обеспечения допустимых окружных скоростей.
Окружная скорость на внешнем ободе маховика
пм = itDMn/60, (212)
где п — частота вращения двигателя, об/мин.
Окружная скорость:
Для чугунных маховиков.................. ом < 25-т-ЗО м/с
Для стальных маховиков.................. ом < 404-45 м/с
Глава IX
РАСЧЕТ КИНЕМАТИКИ И ДИНАМИКИ ДВИГАТЕЛЯ
$ 39. РАСЧЕТ РЯДНОГО КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
Примеры расчетов кинематики и динамики, изложенные ниже, приведены для того же двигателя, для которого в гл. IV дан пример теплового расчета, а в гл. V — расчет скоростной характеристики. В связи с этим все исходные данные для расчетов кинематики и динамики рядного карбюраторного двигателя взяты соответственно из § 17 и 21.
156
Кинематика
Выбор к и длины Гш шатуна. В целях уменьшения высоты двигателя без значительного увеличения инерционных и нормальных сил величина отношения радиуса кривошипа к длине шатуна предварительно была принята в тепловом расчете X. = 0,285. При этих условиях = /?/Х = 39/0,285 = 136,8 мм.
Построив кинематическую схему кривошипно-шатунного механизма (см. рис. 44), устанавливаем, что ранее принятые значения Lm и к обеспечивают движение шатуна без задевания за нижнюю кромку цилиндра. Следовательно, перерасчета величин Ьш и X делать не требуется.
Перемещение поршня
sx = R ^(1 — cos <р) + (1 — cos 2<p)j = 39 ^(1 — cos ?) +
+ (1 — cos 2<р/| мм.
Расчет sx производится аналитически через каждые 10° угла поворота коленчатого вала. Значения для [(1 — cos<p) + 2^5. (1— — cos2<p)] при различных <р взяты из табл. 18 как средние между значениями при к= 0,28 и 0,29 и занесены в гр. 2 расчетной табл. 27 (для сокращения объема значения в таблице даны через 30°).
Таблица 27
f(l—cos <р)+ , °’285 м 4 (1—cos 2?)) 4 SX ’ мм (sin4-^- х » 2 X sin 2f) м/с (cos f + 4- 0,285 cos 2cp) /. м/с*
1 2 3 4 5 6 7
0 0,0000 0,0 0,0000 0,0 + 1,2850 +17209
30 +о, 1697 6,6 +0,6234 + 14,2 + 1,0085 + 13506
60 +0,6069 23,7 +0,9894 +22,6 +0,3575 + 4788
90 + 1,1425 44,6 +1,0000 + 22,9 —0,2850 -3817
120 + 1,6069 62,7 +0,7426 +17,0 —0,6425 —8605
150 +1,9017 74,2 +0,3766 +8,6 —0,7235 . -9689
180 +2,0000 78,0 0,0000 0,0 —0,7150 —9576
210 + 1,9017 74,2 —0.3766 —8,6 —0,7235 —9689
240 +1,6069 62,7 —0,7426 —17,0 —0,6425 —8605
270 + 1,1425 44,6 — 1,0000 —22,9 -0,2850 -3817
300 +0,6069 23,7 —0,9894 —22,6 +0,3575 +4788
330 +0,1697 6,6 —0,6234 —14,2 + 1,0085 + 13506
360 +0,0000 0,0 0,0000 0,0 +1,2850 + 17209
Угловая скорость вращения коленчатого вала со = 1ГЦ/30 = 3,14 • 5600/30 = 586 рад/с.
Скорость поршня
157
ип = cousin <p + y-sin 2q>) = 586 • 0,039 ^sin<p + —^85 sin 2уj м/с.
Значения для [sin<₽ + (0,285/2)sin2<p] взяты из табл. 19 и занесены в гр. 4, а рассчитанные значения ип — в гр. 5 табл. 27.
Ускорение поршня
/ = со2/? (cos <р + X cos 2<р) = 5862 • 0,039 (cos <р + 0,285 cos 2<р) м/с2.
Рис. 73. Путь, скорость и ускорение поршня карбюраторного двигателя
Поправка Брикса
Значения для (cos<₽ -4--f- 0,285 cos2<₽) взяты из табл. 20 и занесены в гр. 6, а расчетные значения / — в гр. 7.
По данным табл. 27 построены графики (рис. 73) sx в масштабе Ма — 2 мм в мм, оп — в масштабе Mv = 1 м/с в мм, / — в масштабе М} = 500 м/с2 в мм. Масштаб угла поворота коленчатого вала M.v = 3° в мм.
При / = 0 оп = ± ишах, а на кривой sx — это точка перегиба.
Динамика
Силы давления газов. Индикаторную диаграмму (см. рис. 35), полученную в тепловом расчете, развёртывают по углу поворота кривошипа (рис. 74, а) по методу Брикса.
/?Х/(2/Ив) = 39 • 0,285/(2 - 1) = 5,56 мм,
где /И, — масштаб хода поршня на индикаторной диаграмме.
Масштабы развернутой диаграммы: давлений и удельных сил /Ир = 0,05 МПа в мм; полных сил /И₽ = /HpFn = 0,05 • 0,004776 = = 0,000239 МН в мм, или МР = 239 Н в мм, угла поворота кривошипа /И? = 3° в мм, или
/И^ = кк/ОВ = 4 • 3,14/240 = 0,0523 рад в мм,
где ОВ — длина развернутой индикаторной диаграммы, мм
По развернутой диаграмме через каждые 10° угла поворота кривошипа определяют значения Дрг и заносят в гр. 2 сводной табл. 28
158
сл со Лрг ’ МПа м/с» МПа р, МПа tg ₽ PN » МПа
1 2 3 5 6 7
0 30 60 90 120 150 180 210 240 270 300 330 360 370 390 420 450 480 510 540 570 600 630 660 690 720 +0,018 —0,015 —0,015 —0,015 —0,015 —0,015 —0,015 —0,015 -0,015 +0,020 +0,150 +0,720 + 1,923 +5,402 +3,420 +1,350 +0,720 +0,450 +0,280 +0,150 +0,025 +0,018 +0,018 +0,018 +0,018 +0,018 + 17209 + 13506 +4788 —3817 —8605 —9689 —9576 —9689 —8605 —3817 +4788 + 13506 + 17209 J-16775 +13506 +4788 —3817 —8605 —9689 —9576 —9689 —8605 —3817 +4788 + 13506 + 17209 —2,426 —1,904 —0,675 +0,538 + 1,213 + 1,366 +1,350 +1,366 + 1,213 +0,538 —0,675 —1,904 —2,426 —2,365 -1,904 —0,675 +0,538 + 1,213 + 1,366 + 1,350 +1,366 + 1,213 +0,538 -0,675 —1,904 —2,426 —2,408 —1,919 —0,690 +0,523 + 1,198 + 1,351 +1,335 + 1,351 + 1,198 +0,558 —0,525 —1,184 —0,503 +3,037 +1,516 +0,675 +1,258 +1,663 + 1,646 + 1,500 + 1,391 + 1,231 +0,556 —0,657 —1,886 —2,408 0,000 +0,144 +0,253 +0,295 +0,253 +0,144 0,000 —0,144 —0,253 —0,295 —0,253 —0,144 0,000 +0,050 +0,144 +0,253 +0,295 +0,253 +0,144 0,000 —0,144 —0,253 —0,295 —0,253 —0,144 0,000 0,000 —0,276 —0,175 +0,154 +0,303 +0,195 0,000 -0,195 —0,303 —0,165 +0,133 +0,170 0,000 +0,929 +0,218 +0,171 +0,371 +0,421 +0,237 0,000 -0,200 —0,311 —0,164 +0,166 +0,272 0,000
Таблица 28
1 Ps . МПа cos(cp+3) Pk » МПа sin (?+3) pt , МПа Г, кН ^Kp. Ц, Нм
COS 3 cos 3 cos p
8 9 10 11 12 -13 14 15
1,000 —2,408 + 1 —2,408 0 0 0 0
1,010 —1,938 +0,794 —1,524 +0,625 —1,199 —5,726 —223,3
1,031 —0,711 +0,281 —0,194 +0,993 —0,685 —3,272 —127,6
1,043 +0,545 —0,295 —0,154 + 1 +0,523 +2,498 + 97,4
1,031 +1,235 —0,719 —0,861 +0,740 +0,887 +4,236 + 165,2
1,010 + 1,365 —0,938 —1,267 +0,376 +0,508 +2,426 + 94,6
1,000 + 1,335 —1 —1,335 0 0 0 0
1,010 + 1,365 —0,938 —1,267 —0,376 —0,508 —2,426 — 94,6
1,031 + 1,235 —0,719 —0,861 —0,740 —0,887 —4,236 —165,2
1,043 +0,582 —0,295 —0,165 —1 —0,558 —2,665 —103,9
1.031 —0,541 +0,281 —0,148 —0,993 +0,521 +2,488 + 97,0
1,010 —1,196 +0,794 —0,940 —0,625 +0,740 +3,534 +137,8
1,000 —0.503 +1 —0,503 0 0 0 0
1,001 +3,040 +0,976 +2,964 +0,222 +0,674 +3,219 +125,5
1,010 —1,531 +0,794 +1,204 +0,625 +0,948 +4,528 + 176,6
1 1,031 +0,696 +0,281 +0,190 --0,993 —0,670 +3,200 + 124,8
I 1,043 -1,312 —0,295 —0,371 --1 --1,258 +6,008 +234,3
1 1,031 + 1,715 —0,719 —1,196 +0,740 +1,231 +5,879 +229,3
1,010 +1,662 —0,938 —1,544 +0,376 +0,619 +2,956 + 115,3
1,000 -1,500 —1 —1,500 0 0 0 0
1,010 + 1,405 -0,938 —1.305 —0,376 -0,523 —2,498 —97,4
1,031 • + 1,269 - -0,719 —0,885 - -0,740 - -0,911 -4,351 —169,7
1,043 • +0,580 -0,295 —0,164 • -1 -0,556 —2,655 —103,5
1,031 - -0,677 . +0,281 - -0,185 - -0,993 - 4-0,652 • +3,114 +121,4
1,010 -1,905 - -0,794 - -1 ,497 - -0,625 - bl,179 - +-5,631 +219,6
1,0ОО - -2,408 - -1 -2,408 0 0 0 0
Рис. 74. Графики динамического расчета карбюраторного двигателя: а — развертка индикаторной диаграммы и построение кривых удельных сил pj и р\ б — построение кривых удельных сил р и р^; в — то же, удельных сил р^; г — то же, удельных сил р^; д — построение Л1Кр динамического расчета (в таблице значения даны через 30° и точка при <₽ — 370°).
Приведение масс частей кривошипно-шатунного механизма. По табл. 21 с учетом диаметра цилиндра, отношения S/D, рядного расположения цилиндров и достаточно высокого значения р г устанавливаются:
160
массй поршневой группы (для поршня из алюминиевого сплава принято пгп = 100 кг/м2)
та = 4Fn = 100 • 0,004776 = 0,478 кг;
масса шатуна (для стального кованого шатуна принято тш =150 кг/м2)
/пш = ЧЛ = 150.0,004776 = 0,716 кг;
масса неуравновешенных частей одного колена вала без противовесов (для литого чугунного вала принято т* = 140 кг/м2)
= tn’KFa = 140 • 0,004776 = 0,669 кг.
Масса шатуна, сосредоточенная на оси поршневого пальца;
тш.п = 0,275/пш = 0,275- 0,716 = 0,197 кг.
Масса шатуна, сосредоточенная на оси кривошипа:
/пш.к = 0,725/пш = 0,725 • 0,716 = 0,519 кг.
Массы, совершающие возвратно-поступательное движение:
т} ~ та + тш.п — 0,478 4- 0,197 = 0,675 кг.
Массы, совершающие вращательное движение:
/пн = /пк 4- тш.к = 0,669 + 0,519 = 1,188 кг.
Удельные и полные силы инерции. Из табл. 27 переносят значения j в гр. 3 табл. 28 и определяют значения удельной силы инерции возвратно-поступательно движущихся масс (гр. 4):
р} = — jnij/Fп = — j - 0,675 • 10-в/0,004776 = — j - 141 - 10’6 МПа.
Центробежная сила инерции вращающихся масс
KR = —1,188 - 0,039 - 5862 - Ю’8 = — 15,910 кН.
Центробежная сила инерции вращающихся масс шатуна
= —тш.к/?(о2 = —0,519 - 0,039 • 5862 - 10’3 =—6,950 кН.
Центробежная сила инерции вращающихся масс кривошипа
XRK = — = —0,669 -• 0,039 5862 - 10'8 = —8,960 кН.
Удельные суммарные силы. Удельная сила (МПа), сосредоточенная на оси поршневого пальца (гр. 5): р = Дрг 4- р}.
Удельная нормальная сила (МПа) pN = ptgp. Значения tg|J определяют для X = 0,285 по табл. 22 и заносят в гр. 6, а значения Pn — в гр. 7.
Удельная сила (МПа), действующая вдодь шатуна (гр. 9): ps = = p(l/cosp).
Удельйая сила (МПа), действующая по радиусу кривошипа (гр. 11): р« = pcos(<₽ 4- f3)/cosp.
161
Удельная (гр. 13) и полная (гр. 14) тангенциальны^ силы (МПа и кН):
рт = psin(cp + p)/cosp и Т = pTFn = рт - 0,004776 • 103.
По данным табл. 28 строят графики изменения удельных сил р^ р, Р$, Av, Ркъ рт& зависимости Ьт изменения угла поворота коленчатого вала ср (рис. 74).
Среднее значение тангенциальной силы за цикл: по данным теплового расчета
Тср = ——PlFa = 2 -*7-1.0675 • 0.004776 = 812 Н; F хт 3,14’4
по площади, заключенной между кривой рт и осью абсцисс (рис. 74, г):
1980—1160 лл- л,_.
рт — —-------==— Мр —-----------0,05 = 0,171 МПа, а
ср OS р 240
Тср = рт ср Fa = 0,171 • 0,004776 - 10« = 816 Н;
ошибка А = (812 — 816) 100/812 = 0,5%.
Крутящие моменты. Крутящий момент одного цилиндра (гр. 15)
Л4кр.ц = TR = T - 0,039 - 103 Н - м.
Период изменения крутящего момента четырехтактного двигателя с равными интервалами между вспышками
0 = 720/1 = 720/4 = 180°.
Суммирование значений крутящих моментов всех четырех цилиндров двигателя осуществляется табличным методом (табл. 29) через каждые 10° угла поворота коленчатого вала и по полученным данным строится кривая /Икр (рис. 74, д) в масштабе Мм = 10 Н • м в мм.
Средний крутящий момент двигателя: по данным теплового расчета
Мкр.ср = Я =/ИеЛ]м = 103,1/0,8141 = 126,6 Н - м;
по площади, заключенной под кривой /Икр (рис. 74, д):
.. Fi— 1370 — 606 ,л 1О7Ои
/Икр.ср = ~ Мм =------------- Ю = 127,3 Н-м;
(Лт, Ov
, . 126,6— 127,3 ,лл лс0/
ошибка А =------------1— 100 = 0,6%.
126,6
Максимальный и минимальный крутящие моменты (рис. 74, д) Мкр шах ~ 650 Н-MJ /Икр min = 360 Н-м.
Силы, действующие на шатунную шейку коленчатого вала. Для проведения расчета результирующей силы, действующей на шатунную 162
Таблица 29
<р° Цилиндры Мкр* Н м
1-й 2-й 3-й 4-й
,ЛО 9 Кривошипа ^Кр.Ц’ Нм 9° кривошипа МКр ц* Н м 9° кривошипа МКр. Ц’ Н м 9° кривошипа ^Kp, ц» Н м
0 0 0 180 0 360 0 540 0 0
10 10 —132,4 190 —28,0 370 + 125,5 550 -29,8 —64,7
20 20 —203,2 200 —65,2 380 + 161,3 560 -67,1 -174,2
30 30 —223,3 210 -94,6 390 + 176,6 570 —97,4 -238,7
40 40 —209,7 220 —123,0 400 + 156,6 580 — 126,8 -302,9
50 50 —174,3 230 -154,7 410 ++28,6 590 -155,7 -356,1
60 60 — 127,6 240 — 165,2 420 + 124,8 600 -169,7 -337,7
70 70 — 65,2 250 —159.4 430 + 142,6 610 -165,9 -247,9
80 80 + 19,6 260 — 139,8 440 + 185,5 620 -146,3 —81,0
90 90 + 97,4 270 — 103,9 450 +234,3 630 -103,5 1-124,3
100 100 + 140,7 280 —36,3 460 +248,9 640 -39,1 +314,2
ПО ПО + 160,3 290 + 32,6 470 +244,2 650 +61,5 -498,6
120 120 + 165,2 300 +97,0 480 +229,3 6С0 + 121,4 +612,9
130 130 + 152,9 310 + 123,0 490 + 190,1 670 + 183,6 -649,6
140 140 + 127,7 320 + 138,0 500 + 147,3 680 +208,8 1-621,8
150 150 +94,6 330 + 137,8 510 + 115,3 690 + 219,6 -567,3
160 160 + 63,4 340 + 120,2 520 + 76,4 700 +201,3 -461,3
170 170 +29,8 350 + 71,8 530 + 30,8 710 + 139,8 -272,2
180 180 0 360 0 540 0 720 0 0
шейку рядного двигателя, составляют табл. 30, в которую из табл. 28 переносят значения силы Т.
Суммарная сила, действующая на шатунную шейку по радиусу кривошипа:
Ря = К + = (К - 6,95) кН,
где К = РкРа ~ Ря • 0,004776 • 103 кН.
Результирующая сила Rm.m, действующая на шатунную шейку, подсчитывается графическим сложением векторов сил Т и Рк при построении полярной диаграммы (рис. 75, а). Масштаб сил на полярной диаграмме для суммарных сил Мр =0,1 кН в мм. Значения ш для различных ср заносят в табл. 30 и по ним строят диаграмму Rm.m В' прямоугольных координатах (рис. 75, б).
По развернутой диаграмме 7?ш.ш определяют
Рш. ш. СР = Р • Мр /ОВ = 26 640 • 0,1/240 = 11,100 кН;
Rm. штах = 18,451 кН; Rm. ш min = 0,645 кН,
где ОВ — длина диаграммы, мм; F — площадь под кривой R,B ш, мм2.
По полярной диаграмме (рис. 75, а) строят диаграмму износа шатунной шейки (рис. 76). Сумму сил Rw действующих по каждому лучу диаграммы износа (от 1 до 12), определяют с помощью табл. 31 (значения Rm ш/ в табл. 31 выражены в кН). По данным табл. 31 в
163
Таблица 30
т° Полные силы, кН
Т К . ш *к
0 0 —11,501 —18,451 18,451 —27,411 27,411
30 —5,726 — 7,279 —14,229 15,250 —23,189 23,820
60 —3,272 — 0,927 — 7,877 8,550 — 16,837 17,050
90 +2,498 — 0,736 — 7,686 8,050 —16,646 16,830
120 +4,236 — 4,112 —11,062 11,850 —20,022 20,490
150 +2,426 — 6,051 —13,001 13,240 —21 ,961 22,080
180 0 — 6,376 —13,326 13,326 —22,286 22,286
210 —2,426 — 6,051 —13,001 13,240 —21.961 22,080
240 —4,236 — 4,112 —11,062 11,820 —20,022 20,460
270 —2,665 — 0,788 - 7,738 8,180 —16,698 16,920
300 +2,488 — 0,707 — 7,657 8,040 — 16,617 16,860
330 +3,534 — 4,489 — 11,439 11,910 —20,399 20,610
360 0 — 2,402 — 9,352 9,352 —18,312 18,312
370 +3,219 + 14,156 + 7,206 0,645 - 1,754 3,660
390 +4,528 + 5,750 — 1,200 4,650 -10,160 11,140
420 +3,200 + 0,907 - 6,043 6,880 —15,003 15,370
450 +6,008 — 1,772 — 8,722 1(1,720 —17,682 18,710
480 +5,879 - 5,712 —12,662 ИЗ,890 —21,622 22,420
510 +2,956 — 7,374 — 14,324 14,590 —23,284 23,460
540 0 — 7,164 —14,114 14,114 -23,074 23,312
570 -2,498 — 6,233 —13,183 13,430 —22,143 22,230
600 —4,351 — 4,227 — 11,177 11,960 -20,137 20,560
630 —2,655 — 0,783 — 7,733 7,850 —16,693 16,880
660 +3,114 — 0,884 — 7,834 8,280 —16,794 17,090
690 +5,631 - 7,150 -14,100 15,350 —23,060 23,740
720 0 -11,501 —18,451 18,451 —27,411 27,411
Таблица 31
Значения «Ь i, для лучей
ш i 1 2 3 4 5 6 7 8 9 /0 // 12
. ш U 18,451 18,451 18,451 — — -и — — — — 18,451 18,451
^ш.шЗО 15,250 15,250 15,250 — — — — — — — — 15,250
^ш.шбО 8,550 8,550 8,550 — — — — — — — 8,550
^ш.ш90 8.050 8,050 — — — — — — —— — 8,050 8,050
^ш.ш 120 11,850 11,850 — — — — — — — — 11,850 11,850
^ш.ш 150 13,240 13,240 — — — — — — — — 13,240 13,240
^ш.ш!80 13,326 13,326 13,326 — — — — — — 13,326 13,326
210 13,240 13,240 13,240 — — — — — — — — 13,240
U1240 11,820 11,820 11,820 — — — — — — — — 11,820
ш270 8,180 8,180 8,180 — — — — — — — — 8,180
.шЗОО 8,040 8,040 — — — — — — — 8,040 8,040
шЗЗО 11,910 11,910 — — — — — — -—г — 11,910 11,910
^ш.шЗСО 9,352 9,352 9,352 — — — — — — — 9,352. 9,352
ш390 — — — — — — — — 4,650 4,650 4,650 4,650
^ш.ш420 6,880 6,880 — — — — — — — — 6,880 6,880
ш450 10,720 — — — — — — — — 10,720 10,720 10,720
.ш480 13,890 13,890 — — — — — — — — 13,890 13,890
ш510 14,590 14,590 — — — — — — — 14,590 14,590
ш540 14,114 14,114 14,114 — — — — — — — 14,114 14,114
ш570 13,430 13,430 13,430 — — — — — — — — 13,430
шбОО 11,960 11,960 11,960 — — — — — — — — 11,960
.шбЗО 7,850 7,850 7,850 — — — — — — — — 7,850
^ш.шббО 8,280 8,280 — — — — — — — — 8,280 8,280
^ш.шбЭО 15,350 15,350 — — — — — — — — 15,350 15,350
g} ^ш.ш/ 268,323 257,603 145,523 — — — — — 4,650 15,370 182,693 272,973
масштабе Мр — 50 кН в мм по каждому лучу откладывают величины суммарных сил 2Яш.ш/ от окружности к центру (рис. 76). По лучам 4 и 5 силы 2 ш! не действуют, а по лучам 6, 7 и 8 действуют силы только в интервале 360° < <р < 390°.
По диаграмме износа определяют расположение оси масляного отверстия (фм = 68°).
Силы, действующие на колено вала. Суммарная сила, действующая на колено вала по радиусу кривошипа:
Ярк = Рк + Янк = ^-8,960 кН.
Результирующая сила, действующая на колено вала, RK — R^.m + +- КРк определяется по диаграмме /?ш.ш (рис. 75, а). Векторы из полюса Ок до соответствую-
Рис. 76. Диаграмма износа шатунной шейки карбюраторного двигателя
щих точек на полярной диаграмме в масштабе Мр = 0,1 кН в мм выражают силы RKt значения которых для различных <р заносят в табл. 30.
Силы, действующие на коренные шейки. Коленчатый вал рассчитываемого двигателя полноопорный с кривошипами, расположенными под угломук= 180° (рис. 77, а). Порядок работы двигателя 1—3—4—2. Следовательно, когда первый кривошип повернут на угол q>i = 0°, третий кривошип будет находиться в положении <р3 = = 0(720)—180 = 540°, чет-
вертый — ф4 = 0 (720)—ЗСО = 360° и второй — <р2 = 0(720)—540 = = 180°.
Сила, действующая на первую коренную шейку: RK Ш1 =—0,5/?Ki (см. табл. 32, гр. 2 и 4). Изменение силы RK mi в зависимости от ср показывает полярная диаграмма RK (см. рис. 75, а), но повернутая на 180° и в масштабе Мр = 0,5Мр =* 0,5 • 0,1= 0,05 кН в мм. Перестроенная указанным способом полярная диаграмма RK mi приведена на рис. 77, б.
Сила, действующая на вторую коренную шейку:
^И.ш2 = ' 7к2 4"Кк2 ,
где Т к 2 = — 0,5(7'14- T^cos у к и—2) — Крхъ sin у к и—2>) = — 0,5 (7\ 4-4- T2cosl80—KpK2sinl80) = —0,5(7, —Тг);
Ritz— — 0,5 (/Срк14"72 sin у к (1—2) 4-КРк2 cos Yk <i—2>) = — 0,5 (KpKi~b
166
180°
V86
1-3-3-2-Т-3-3-2 j t 530°.
S)
320(60) 660(300) 350(90)
120(380.
380(120)
690(330)
150(510)
510(150)
-Кк
390 (30)
-Тк 370
330
(530)
(360)
720:0 +Кк
530
(180)
630(270)
60(320) 230(600) 600(230) 210(570) 30(390)
570(210)
360° 360'
В)
А 320
320 (60)
-Гц 350
(90)
300 (660)
120(380)4811
(120)
1390
(30)
600(230
530
550 (180) (190)
60(320) 570
(210)
90
(350)
660(300
510(150)
630(270)
0,720(360)
г)
390
(390)/ Ъ
270(630)
210(570)
360
720
10
1
90
350
230(600)
Рис. 77. Силы, действующие на коренные шейки коленчатого вала;
а —схема коленчатого вала и порядок работы двигателя, б —силы, действующие на 1 (5)-ю коренную шейку; в —силы, действующие на 2 (4)-ю коренную шейку; г — силы, действующие иа 3-ю коренную шейку
+ T2sin 180 + KpK2cos 180) = — 0,5(Крк1 —Крк2).
Расчет силы Т?к.ш2 приведен в табл. 32 (гр. 5—12).
Сила, действующая на третью коренную шейку:
#к.ш з — V ГкЗ + КкЗ .
где Тк3 = — 0,5 (Тг + Г3 cos ук (2-з) — Kps3 sin ук (2-з)) cos ук 0_2) = = — 0,5 (Т2 + Т3 cos 0 — KpHi sin 0) cos 180 = 0,5 (Тг + Т3)\ Кхз = = — 0,5 (Крк2 + Т3 sin ук (2—з) + КрКз cos ук (2-^) cos ук (i_2) = — 0,5 х X (Крк2 + r3sin 0 + Криз cos 0) cos 180 = 0,5(КрК2 + Крк3).
167
8
<р° 1-я коренная шейка 1-й кривошип 2-я коренная шейка
о *кь кН Ti, кН Крк!» кН гк2» кН /<к2> кН Як.ш2, кН о ь
Як.ш1, кН
1 2 3 4 5 6 7 8 9 10
0 13,706 0 27,411 0 —27,411 0 + 2,563 2,563 180
30 11,910 30 23,820 —5,726 —23,189 + 1,650 + 0,614 1,761 210
60 8,525 60 17,050 —3,272 —16,837 —0,482 — 1,593 1,664 240
90 8,415 90 16,830 +2,498 —16,646 —2,582 — 0,026 2,583 270
120 10,245 120 20,490 +4,236 —20,022 —0,874 + 1,703 1,914 300
150 11,040 150 20,080 --2,426 —21,961 +0,554 + 0,781 0,957 330
180 11,143 180 22,286 0 —22,286 0 + 1,987 1,987 360
190 11,110 190 22,220 —0,780 —22,260 +2,000 + 10,253 10,440 370
210 11,040 210 22,080 —2,426 — 21,961 +3,477 + 5,901 6,849 390
240 10,230 240 20,460 —4,236 —20,022 +3,718 + 2,510 4,485 420
270 8,460 270 16,920 —2,665 —16,698 +4,337 — 0,492 4,364 450
300 8,430 300 16,860 +2,488 —16,617 + 1,696 — 2,503 3,023 480
330 10,305 330 20,610 +3,534 -20,399 —0,289 — 1,443 1,708 510
360 9,156 360 18,312 0 —18,312 0 — 2,381 2,381 540
370 1,830 370 3,660 +3,219 — 1,754 —2,050 — 10,533 10,720 550
390 5,570 390 11,140 +4,528 —10,160 —3,513 — 5,992 6,947 570
420 7,685 420 15,370 +3,200 — 15,003 —3,776 — 2,567 4,567 600
450 9,355 450 18,710 +6,008 —17,682 —4,332 + 0,495 4,360 630
480 11,210 480 22,420 +5,879 —21,622 —1,340 + 2,414 2,761 660
510 11,730 510 23,460 +2,956 —23,284 + 1,338 + 0,112 1 ,343 690
540 11,656 540 23,312 0 —23,074 0 — 2,169 2,169 720
550 11,480 550 22,760 —0,880 —22,820 —0,720 — 2,030 2,154 10
570 11,115 570 22,230 —2,498 —22,143 —1,614 — 0,523 1,696 30
600 10,280 600 20,560 —4,351 —20,137 + 0,540 + 1,650 1,736 60
630 8,440 630 16,880 —2,655 —16,693 +2,577 + 0,024 2,577 90
660 8,545 660 17,090 +3,200 —16,794 +0,518 — 1,614 1,695 120
690 11,870 690 23,740 +5,631 —23,060 — 1,603 + 0,550 1,695 150
720 13,706 720 27,411 0 —27,411 0 + 2,563 2,563 180
Таблица 32
2-й кривошип 3-я коренная шейка 3-й кривошип
Г2, кН Тк3, кН «КЗ. «И <?3 Тв.кН КркЗ>
11 12 13 14 15 16 17 18
0 —22,286 0 —22,680 22,680 540 0 —23,074
—2,426 —21,961 —2,462 —22,052 22,190 570 —2,498 -22,143
—4,236 —20,022 —4,294 —20,080 20,530 600 —4,351 —20,137
—2,665 —16,698 —2,660 —16,696 16,900 630 —2,655 —16,693
4-2,488 — 16,617 +2,844 — 16,706 16,950 660 +3,200 —16,794
4-3,534 —20,399 +4,583 —21,730 22,200 690 +5,631 —23,060
' 0 —18,312 0 —22,862 22,862 720 0 —27,411
4-3,219 - 1,754 +0,450 — 14,317 14,330 10 —2,320 —26,880
4-4,528 —10,160 —0,599 —16,675 16,680 30 —5,726 —23,189
4-3,200 — 15,003 —0,036 — 15,920 15,925 60 —3,272 —16,837
4-6,008 — 17,682 +4,253 — 17,164 17,680 90 +2,498 —16,646
4-5,879 —21,622 +5,058 —20,822 21,484 120 +4,236 —20,022
4-2,956 —23,284 +2,691 —22,623 22,780 150 +2,426 —21,961
0 -23,074 0 —22,680 22,680 180 0 —22,286
—0,880 —22,820 —0,830 —22,540 22,558 190 —0,780 —22,260
—2,498 —22,143 -2,462 —22,052 22,190 210 —2,426 —21,961
—4,351 —20,137 —4,294 —20,080 20,530 240 —4,236 —20,022
—2,655 — 16,693 —2,660 —16,696 16,900 270 —2,665 — 16,698
4-3,200 —16,794 +2,844 —16,706 16,950 300 +2,488 —16,617
4-5,631 —23,060 +4,583 —21,730 22,200 330 +3,534 —20,399
0 —27,411 0 —22,862 22,862 360 0 —18,312
—2,320 —26,880 +0,450 —14,317 14,330 370 +3,219 — 1,754
—5,726 —23,189 —0,599 -16,675 16,680 390 +4,528 -10,160
—3,272 -16,837 —0,036 —15,920 15,925 420 +3,200 — 15,003
4-2,498 —16,646 +4,253 —17,164 17,680 450 +6,008 —17,682
4-4,236 —20,022 +5,058 —20,822 21,484 480 +5,879 —21,622
4-2,426 -21,961 +2,691 —22,623 22,780 510 +2,956 —23,284
0 —22,286 0 —22,680 22,680 540 0 —23,074
Рис. 78. Диаграммы нагрузок на коренные шейки карбюраторного двигателя в прямоугольных координатах
Расчет силы /?к.шз приведен в табл. 32 (гр. 11—18).
По данным табл. 32 строят полярные диаграммы нагрузки на вторую и третью коренные шейки (рис. 77, г) в масштабе Л4д —0,1 кН в мм.
Нагрузки на 4-ю и 5-ю коренные шейки в соответствии с порядком работы двигателя и расположением кривошипов равны нагрузкам, действующим на 2-ю и 1-ю шейки, но смещены на 360° (рис. 77, б, в с обозначением ср в скобках).
Диаграммы 7?к шь /?к.Ш2 и перестроенные в прямоугольные координаты, представлены на рис. 78. По этим диаграммам определяют: для 1 (5)-й коренной шейки
Як.ш icp = РМОВ 35 460 • 0,1/360 - 9,85 кН,
где/7! —площадь под кривоймм2, ОВ —длина диаграммы, мм;
1 max 13,706 кН; ш i min == 1 >83 кН;
для 2(4)-й коренной шейки
Як.шзер == Р^аЮВ = 10 800.0,1/360 = 3,0 кН,
где F2 — площадь под кривой RK ш2, мм2;
10,77 кН; /?к.ш2т1п — 0,90 кН;
169
1 1
Рис. 79. Диаграммы износа коренной шейки: а — без противовесов; б — с противовесами
Таблица 33
Значения £ <к ш 3, для лучей
.„О 1 ? 3 4 5 6 7 8 9 10 и 12
0 30 60 90 120 150 180 210 240 270 300 330 360 390 420 450 480 510 540 570 600 630 660 690 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78 22,68 22,19 20,53 16,90 22,86 16,68 15,93 22,68 22,19 20,53 16,90 22,86 16,68 15,93 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 | 1 1 1 । 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 к , 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 22,68 16,95 22,20 22,86 17,68 21,48 22,78 22,68 16,95 22,20 22,86 17,68 21,48 22,78 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78 22,68 22,19 20,53 16,90 16,95 22,20 22,86 16,68 15,93 17,68 21,48 22,78
^к.шЗ/ 477,72 477,72 275,54 — — — — — — — 293,26 477,72
170
для 3-й коренной шейки
Як.шзср = ^Л4в/ОВ - 70 380 * 0,1/360 = 19,55 кН,
где F3 — площадь под кривой RKpUI3, мм2;
Як.шзтах - 23,20 кН; /?к.шзтщ - 14,33 кН.
Из сравнения диаграмм RK шь RK ш2 и Як.ш3 видно, что максимально нагруженной является 3-я коренная шейка, а минимально нагруженными — 2-я и 4-я шейки.
По полярной диаграмме (см. рис. 77, г) строят диаграмму износа наиболее нагруженной 3-й шейки (рис. 79, а). Сумма сил 2/?к.шЗе, действующих по каждому лучу диаграммы износа (от 1-го до 12-го), определяется с помощью табл. 33 (значения 2 RK шз, в таблице выражены в кН). По данным этой таблицы в масштабе Мд = 50 кН в мм строят кривую износа.
Уравновешивание
Центробежные силы инерции рассчитываемого двигателя и их моменты полностью уравновешены: = 0; 2Л1д = 0.
Силы инерции первого порядка и их моменты также уравновешены: 2 Р//= 0; 2 Мр = 0.
Силы инерции второго порядка для всех цилиндров направлены в одну сторону:
У Pj и = 4Pj п = 4myRco2k cos 2<p.
Уравновешивание сил инерции второго порядка в рассчитываемом двигателе нецелесообразно, ибо применение двухвальной системы с противовесами для уравновешивания ЯРщ значительно усложнит конструкцию двигателя.
Моменты от сил инерции второго порядка в связи с зеркальным расположением цилиндров полностью уравновешены: 2Мр/ = 0.
В целях разгрузки 3-й коренной шейки от местных инерционных сил целесообразно установить противовесы на продолжении щек, прилегающих к ней. Расположение центра тяжести и величину массы противовесов можно определить из следующих соображений:
а) за счет силы инерции противовесов целесообразно переместить полюс Ок3 полярной диаграммы RKpln3 (см. рис. 77, г) в центр диаграммы. Следовательно, противовесы должны воздействовать на шейку силой
Рцрз = h3MR = —195 • 0,1 = —19,5 кН, где h3 — расстояние от полюса Окз диаграммы RK шз до центра Опрз диаграммы Япкршз, мм;
б) противовесы не должны увеличивать габаритов двигателя. Целесообразно принять р — 20 мм;
в) так как каждый противовес расположен только на одной щеке колена, для определения силы инерции и массы противовеса необходимо установить размеры кривошипа. Предварительно принимаем
171
I = 94 мм и /i = 70 мм (см. рис. 77, а). Тогда сила инерции одного противовеса
Рцр = — 0,5Pnp3///i - — 0,5 (— 19,5) 94/70 = 13,09 кН;
г) масса каждого противовеса
тпр = Лзр/И2) = 13,09 • 103/(0,02 • 5862) - 1,906 кг.
На рис. 79, б показана диаграмма износа 3-й коренной шейки после установления противовесов. Диаграмма износа построена по данным табл. 34 в масштабе Mr =10 кН в мм. По этой диаграмме определено направление оси масляного отверстия (<рм = 35°).
Для уравновешивания центробежных сил Рпр противовесов, расположенных на продолжении щек, прилегающих к 3-й коренной шейке, и для уменьшения нагрузки на 1-ю и 5-ю коренные шейки целесообразно на продолжении щек, прилегающих к 1-й и 5-й шейкам, также установить противовесы Рцр1 = Рп рэ — РПрЗ*
Смещение центров полярных диаграмм в связи с установкой противовесов на величину, пропорциональную реакции от противовесов, Рпр1(5)= 0,5/^ = —9,75, кН, показано на рис. 77, б (/ii(5) = 97, 5 мм).
Таблица 34
Значения Япр К I nS сН, для лучей
¥ / 2 3 4 5 6 7 6 4 ю // /2
0 3,20 3,20 3,20 3,20 3,20
30 5,55 5,55 5,55 5,55
60 — 4,35 4,35 4,35 4,35 — — — — — —
90 —. — — 3,90 3,90 3,90 3,90 — — — —
120 — — — — — — 4,00 4,00 4,00 4,00 —
150 5,05 5,05 5,05 5,05
180 3,35 3,35 3,35 — —. — — — — — 3,35 3,35
210 — — — — 2,90 2,90 2,90 2,90 — — —
240 — — — — 3,65 3,65 3,65 3,65 — — —
270 — — — — — — — 4,90 4,90 4,90 — —
300 5,20 5,20 5,20 5,20
330 4,05 4,05 4,05 4,05
360 3,20 3,20 3,20 — — — — — — — 3,20 3,20
390 5,55 5,55 5,55 5,55
420 — 4,35 4,35 4,35 4,35 — — — — — —
450 — — — 3,90 3,90 3,90 3,90 — — — — —
480 — — — — — — 4,00 4,00 4,00 4,00 —
510 5,05 5,05 5,05 5,05
540 3,35 3,35 3,35 — — — — — — — 3,35 3,35
570 — — — — 2,90 2,90 2,90 2,90 — — — —
600 — — И-' — 3,65 3,65 3,65 3,65 — — — —
630 — — — — — — — 4,90 4,90 4,90 —
660 5,20 5,20 5,20 5,20
•690 4,05 — 4,05 4,05 4,05
к.ш3 32,30 32,90 32,90 27,60 29,60 20,90 28,90 30,90 38,30 46,40 41,70 41,7»
172
^Развернутые диаграммы сил ЯкРшз = Рк.ш3 + Рпр3 и Р"рш i(6) = = Rk.ui Ц5) + Pnpi (5) представлены на рис. 78 и по ним определены: для 1 (5)-й коренной шейки
РПЛ1 (5) ср = F^Mr/OB = 8490 • 0,1/360 = 2,36 кН;
«ПЛ1 (5) max = 9,10 кН; ^рш1 (5) min = 0,15 кН;
для 3-й коренной шейки
/?к₽ш3ср = Fn3pMR/OB = 15010 • 0,1/360 = 4,17 кН;
Япкршз max = 5,60 кН; ₽пкрш3 min = 0,40 кН,
где FiP(5) и F3p— соответственно площади под кривыми РкРШ1 (5) и Рк?шЗ, ММ2.
Равномерность крутящего момента и равномерность хода двигателя
Равномерность крутящего момента
[1 = (Мкр max Мкр т1п)/МКр>Ср = [650 — (— 360)]/127,3 = 7,93.
Избыточная работа крутящего момента
Ьизб = FabcMMM? = 840 • 10 • 0,0523 = 439,3 Дж, где Fabc— площадь над прямой среднего крутящего момента (см. рис. 74, д), мм2; М' - 4к /(ЮА) = 4 • 3,14/(4 • 60) = 0,0523 рад в мм — масштаб угла поворота вала на диаграмме Мкр.
Равномерность хода двигателя принимаем 8 = 0,01.
Момент инерции движущихся масс двигателя, приведенных к оси коленчатого вала:
Jo = Ьизб /(Зю2) = 439,3/(0,01 • 5862) = 0,128 кг-м2.
§ 40. РАСЧЕТ V-ОБРАЗНОГО ЧЕТЫРЕХТАКТНОГО ДИЗЕЛЯ
Примеры расчетов кинематики и динамики, изложенные ниже, приведены для того же дизеля, для которого в гл. IV дан пример теплового расчета, а в гл. V — расчет Скоростной характеристики. В связи с этим все исходные данные для расчетов кинематики и динамики V-образного четырехтактного дизеля с наддувом взяты соответственно из § 18 и 22.
Кинематика
Выбор X и длины шатуна Ьш. В целях уменьшения высоты двигателя с учетом опыта отечественного дизелестроения оставляем значение Х = 0,270, как уже было принято предварительно в тепловом расчете, В соответствии с этим
= ЯД 60/0,270 = 222 мм.
173.
Рис. 80. Зависимости пути (а), скорости (б) и ускорения (в) поршня дизеля от угла поворота кривошипа
Перемещение поршня. Изменение хода поршня по углу поворота коленчатого вала строят графическим методом (рис. 80, а) в масштабе Ms = 2 мм в мм и Mf — 2° в мм через каждые 30°. Поправка Брикса
Rl = 60 • 0,270/(2 2) = 4,05 мм.
Угловая скорость вращения коленчатого вала со = кп/30 = 3,14 • 2600/30 = 272,1 рад/с.
Скорость поршня. Изменение скорости поршня по углу поворота коленчатого вала строят графическим методом (рис. 80, б) в масштабе Мо = 0,4 м/с в мм:
174
&R/MV = 272,1 • 0,06/0,4 = 40,8 мм;
co/?X/(/Wv2) = 272,1 • 0,06 • 0,270/(0,4 • 2) = 5,5 мм;
± On max « VT+T2 = 272,1 • 0,06 у1 4- 0,272 = 16,9 м/с.
Ускорение поршня. Изменение ускорения поршня по углу поворота коленчатого вала строят графическим методом (рис. 80, в) в масштабе Mj = ЮО м/с2 в мм:
aPR/Mj = 272,12 • 0,06/100 = 44,4 мм;
<о2/?Х/Л4; = 272,12 • 0,06 • 0,270/100 = 12,0 мм;
/max = <O2R(1 + X) = 272,12 • 0,06(1 + 0,27) = 5642 м/с2;
/min=- <o2r (х+4-)=272’12 • °-°6 (°>27+=3256 -m/c2-
Значения sx, ип и / в зависимости от q>, полученные на основании построенных графиков, заносят в табл. 35.
При / = 0 пп = ± оПтах == ± 16,9 м/с, а точки перегиба s соответствуют повороту кривошипа на 76 и 284°.
Таблица 35
<р° S, мм М/с /, М/С2 । S, мм %• м/с /. М/С2
0 0 0 +5640 210 113,9 -6,3 —3250
30 10,0 + 10,1 +4450 240 95,9 -12,2 —2820
60 35,9 + 16,0 + 1620 270 67,8 —16,3 —1200
90 67,8 + 16,3 —1200 300 35,9 -16,0 М620
120 95,9 + 12,2 —2820 330 10,0 — 10,1 +4450
150 113,9 +6,3 —3250 360 0 0 +5640
180 120,0 0 —3240
Динамика
Силы давления газов. Индикаторная диаграмма (см. рис. 36), полученная в тепловом расчете, развертывается по углу поворота кривошипа (рис. 81) по методу Брикса.
Масштабы развернутой диаграммы: хода поршня М3= 1,5 мм в мм, давлений Л4Р = 0,08 МПа в мм; сил Мр— MpFn = 0,08 • 0,0113 = = 0,0009 МН в мм или Мр = 0,9 кН в мм, угла поворота кривошипа Л49 = 3° в мм или
M'v = Ьк/ОВ = 4 • 3,14/240 == 0,0523 рад в мм,
где ОВ— длина развернутой индикаторной диаграммы, мм.
Поправка Брикса
/?Х/(2Л48) = 60 • 0,270/(2 • 1,5) = 5,4 мм.
175
Рис. 81. Развертка индикаторной диаграммы дизеля по углу поворота кривошипа и построение удельной суммарной силы р
По развернутой индикаторной диаграмме через каждые 30° угла поворота кривошипа определяют значения Дрг = рр —р0 и заносят в табл. 36.
Приведение масс частей кривошипно-шатунного механизма. По табл. 21 с учетом диаметра цилиндра, отношения S/D, V-образного расположения цилиндров и достаточно высокого значения pz устанавливаются:
масса поршневой группы (для поршня из алюминиевого сплава гл'п = 260 кг/м2)
тв = m'FB = 260 - 0,0113 = 2,94 кг;
Таблица 36
Дрг> МПа /, М/С Pjt МПа р, МПа Дрг, МПа 7, м/с Ру, МПа р, МПа
0 ' 0,062 +5640 —1,933 —1,871 380 7,880 +5040 —1,727 +6,153
30 0,05» +4450 —1,525 — 1,466 390 6,060 +4450 —1,525 +4,535
60 0,059 + 1620 —0,555 —0,496 420 2,030 + 1620 —0,555 + 1,475
90 0,059 —1200 +0,411 +0,470 450 0,930 —1200 +0,411 +1,341
120 0,059 —2820 +0,966 -И 1,025 480 0,560 —2820 +0,966 + 1,526
150 0,059 —3250 + 1,П4 + 1,173 510 0,390 —3250 + 1,114 + 1,504
180 0,059 —3240 + 1,Н0 + 1,169 540 0,220 —3240 + 1,110 + 1,330
210 0,080 —3250 + 1,114 + 1,194 570 0,140 —3250 + 1,114 + 1,254
240 0,130 —2820 +0,966 +1,096 600 0,062 —2820 4-0,966 + 1,028
270 0,240 —1200 +0,411 +0,651 630 0,062 —1200 +0,411 +0,473
300 0,690 + 1620 —0,555 +0,135 660 0,062 -1-1620 —0,555 —0,493
330 2,310 +4450 -1,525 +0,785 690 0,062 + 4450 — 1,525 —1,463
360 8,569 +5640 —1,933 +6,636 720 0,062 +5640 —1,933 —1,871
370 11,207 +5430 —1,861 +9,346
176
масса шатуна (т'ш — 300 кг/м2)
тш = т'шРп = 300-0,0113 = 3,39 кг;
масса неуравновешенных частей одного колена вала без противовесов (для стального кованого вала т'к = 320 кг/м2)
тк = /n'Fn = 320-0,0113 = 3,62 кг.
Масса шатуна, сосредоточенная на оси поршневого пальца:
«ш.п = 0,275/п^ = 0,275 - 3,39 = 0,932 кг.
Масса шатуна, сосредоточенная на оси кривошипа:
/пш.к = 0,725/Пщ = 0,725 3,39 = 2,458 кг.
Массы, совершающие возвратно-поступательное движение:
mj = тп + /пш.п = 2,94 + 0,932 = 3,872 кг.
Массы, совершающие вращательное движение:
тД2 — тк + 2/пш.к = 3,62 + 2 • 2,458 — 8,536 кг.
Полные и удельные силы инерции. Силы инерции возвратно-поступательно движущихся масс определяют по кривой ускорений (см. рис. 80, в и табл. 35):
полные силы Р} = — jm}-10~* = — / • 3,872 • 10'3 кН;
удельные силы pj — Рj/Fn = Pj • 10-8/0,0113 МПа.
Значения р, заносят в табл. 36.
Центробежная сила инерции вращающихся масс шатуна одного цилиндра
ЯВш = —/пш.кК<о2 • 10-3 = — 2,458 • 0,06 • 272,12 - 10-3 = —10,9 кН.
Центробежная сила инерции вращающихся масс кривошипа
ЛДк = -тЕ/?<о2-10-3 =-3,62-0,06-272,12- 10-3 = — 16,1 кН.
Центробежная сила инерции вращающихся масс, действующая на кривошип:
КД2 = Яйк + 2/(Дш = т- 16,1 + 2(- 10,9) = -37,9 кН.
Удельные суммарные силы. Удельная суммарная сила (МПа), сосредоточенная на оси поршневого пальца (рис. 81 и табл. 36):
р = ЬрТ + р3.
Удельные силы p/v, ps > рк и Рт определяют аналитическим методом. Расчет значений этих сил для различных <р сводят в табл. 37.
Графики изменения удельных сил ptf, ps, рк и Рт в зависимости отф представлены на рис. 82, где Л4Р = 0,08 МПа в мм и Mv = 3°в мм.
177
7—370
8ZT
si © © © © ©qi © 4* 4-4-сэ ©>© ©со eg to to to—— — * 8SliS3§3SSSSgSS^S3S3gSSSggo
111+++++++++++++++++++++111 н-н-ООн-н-н-н-^)-~АО)<0 0)0 0 0~~~~~С|0'--'-- QO 4^ 4^ 4^ © ND © © © CO 4^ © — CO © "О — © O'- — — О 4x 4». 4 00 -0©©-qt0©©©t04-<!©©4©©©©©©©-0t0-<!©©'0 -WWWQoboSO'-UiCnWOOOiUi'-O^OWUiOOO'- p, МПа
1 1 1 1 1 + + + + + + + 1 1 1 1 1 +++H—h OOOOOOOOOOOOOOOOOOO©©©©©©©© — NDtOND — - ND ND ND — Q © и-ЮЮЮ- - ND ND ND — co CO -<! CO CO co CO <! CO CO © 4- © CO -<! CO CO CO CO -<! CO CO ©©00©© © © 00 © © co -o ©©00©© ©©oo©© tg 3
++I11 +++++++ Mill +++II ©©©©©©©©©©©©©©©©e> © © © © © © © © © © ^-^L-tO — ND CO CO CO © ©4 *— © — ND — — tO —— — (D-W4>>4 © © -*q © — -q co © co oo cd © © 4 co — © Фоо-О- © © CO CO -q ND © ->) ND — ND ND ©© —©© pМПа N i
88*888 8888888 *8*8*8*88 88888 . © go oo oo © © © oo oo Ф — © oo oo oo © © oo oo oo © cos 3 —
11 t+++++++++++++++++++++111 — ^©©--и-1-и-^и-^^(0^оо©-'-'-'-'-ОС!^ — oo4©4ptoco©©co©© —co©-q — © — to — — 04©40o -q-q©©©©^ — ф©— -^l-q©CO©Cj?-*qtO©©©©©— -0'^1-‘'^и1000&ЮО)ОООСЛОЮС005-ЧСЛФ4-^ОООФ- p$ , МПа
+++ 1 1 1 1 1 1 1 +++-F+++ 1 1 1 1 1 1 1 -F+ + — ©ООО© —©©ОрООО— ОООО© — ©©©© O — \]~N3Nd\]© ©~-J ND ND SJ©© ^0NDND*-*0© ©~-<ГкЭКэ\| © ©-~q © CD CO©^J©©©^J OOSOW WOSOO D0W00S4 4 -q 00 co 00 00 -O 00 co 00 -q 4 4SOOQQQO cos 0 Q О (Л + "СО
1 1 1 1 1 1 1 111+++++++1 1 1 1 1 1 1 1 1 1 h-i-©©C>h-h-h-h-O©C0U1^O©©©©'-'--O©©-'- Q0~— —C04©C04©©- ©©© — -q—— ©-q — — H-.QO CO ND -О CO © ч-MW 00 WWM^ 00-*q-©©КЭС04-0-0 h-44-b“-q'-©UiCDWtOCO-q'-ООО -СЛСЛСЗОСЛ-СЛО*- рк, МПа
1111111111+++++++1111111111 ND — — - 00----^^^О'--ЧЧ© ЮО0-- - CO---M — СО» ’ - CO ©©ND- - О 00 ©4- * - - ND CO ND- • - W — - * ©4ND- - - - ND 00- - CO- ©4© SI- - - - 4 ©- - 00 ; К, кН
II 1 1 1 +++++~Ы“ lllll “1—F++ + ©©о — © ©©© ©—ppppoop —pp©p ©—© © © CD© *S|C0 CO SI OO^ ND *©© Sl’co CO S| ©CD 00 >Й. oo 00 4». 00-‘to ND —‘ 00 >Й- 00 00 4* 00 — 00 ел -0 to ND -O CD 00 © © QO CD -q ND ND -q СЯ0О cos 3 □ +
++1I1 +++++++ lllll +++1I OOOOOO О О~ — КЭ К w ooooopoop op о о © 4». 4ь -чд 4». © — CO 4»- 00 ф © 4k — ©00 4* 4»-^J 4* 4* © ©00-Ч©"0 Ч4>4СЛО^СЛ 00 CO СЛ — ел д^чооо 4-©CO oo© ©©—coco©© ©co—©© 00©©©© Pp , МПа
+ + 1 | | + + ++ + + + lllll + + + 1 1 ©—СЛСЛООСЯ©© — —— © to to© CD — -q©CD©CDOOCDCD — © ©- - - - - ND©©—©© - - - - - -.-«-© ’ Q?’ - - * - - 4. CD co to— ©©С0СЯ- to©»Soo— ©go-4. ©go nd oo©©©© ©©—co to to ©©N3-OCOCO 4^ T. кН i
++I11 +++++++0]1111 °...11 ° 5§8gg 833S838 8S£8© 88S82? o©© ©©©©© Мкр. ц, Н-м
Co ND — — ND ND ND ND ND ND — CO©©© ——NDNDtOtOND — — NDCO ND © CO CO — 4* © -q © — *0C0©©4.©©© — 4* 4». CO — © © © ND © — ~-q© ©\i© © 4*. © ©oo nd to — \i oo ©\ioo — ©© © oo — © Ящ.ш, кН
Таблица 37
Среднее значение уде^ной тангенциальной силы за цикл: по данным теплового расчета
рГср = 2Л/(1гт) = 2 • 1,203/(3,14 • 4) = 0,192 МПа;
по площади, заключенной под кривой Рт:
Prep = CS Л — 2 fа) Мр/ОВ = (1350 — 770) 0,08/240 =0,193 МПа;
ошибка Д = (0,193 — 0,192) 100/0,192 = 0,52%.
Крутящие моменты. Крутящий момент одного цилиндра
Л4вр.ц = TR = Т • 0,06 кН-м.
179
Рис. 83. Суммарный крутящий момент дизеля
Измец^ие крутящего момента цилиндра в зависимости от <р выражает кривая рт (рис. 82 и табл. 37), но в масштабе
Мм = MpFnR = 0,08 • 0,0113 X х0,06 • 103 = 0,0542 кН-м в мм, или Мм = 54,2 Н-м в мм.
Период изменения крутящего момента четырехтактного дизеля с равными интервалами между вспышками
0 = 720/f = 720/8 = 90°.
Таблица 38
<р° коленчатого вала Цилиндры
1-й 2-й 3-й 4-й
(р° Кривошипа ^кр и. п -м I кривошипа ^кр ц. Н-м й ° о.® 9-м а Ыкр’ “ Н-м н о о. Е э-м 3 Ц. Н*м
0 0 0 90 ИЗ 15 180 0 270 —440
10 10 -400 100 -445 190 — 105 280 —270
20 20 —560 ПО -525 200 —215 . 290 —190
30 30 —610 120 -520 210 —310 300 —90
40 40 —610 130 -450 220 —395 310 —150
50 50 —510 140 -360 230 —485 320 —275
60 60 —330 150 -300 240 —555 330 —330
70 70 -145 160 -175 250 —605 340 —320
80 80 + 110 170 -80 260 —580 350 —255
90 90 +315 180 0 270 —440 360 0
Продолжение табл. 38
Цилиндры
В* CQ 5? ч 5-й 6-й 7-й 8 й
<р° коле того ва и g s Е O.S 9-м 3 м н кр Ц. м кривошипа нкр “ Н «м Sg я Е о 0,5 э-м а ^кр.ц, Н-м И <0 X g о о.® э- м а ^кр .ц, Н м ^кр,^*м
0 360 0 450 (-910 540 0 630 -320 465
10 370 (-1390 460 -890 550 —120 640 -170 1660
20 380 -1790 470 -860 560 —260 650 (-100 2050
30 390 -1900 480 -770 570 —325 660 -330 2185
40 400 -1420 490 -680 580 —380 670 -480 1495
50 410 -ИЗО 500 -535 590 —450 680 -580 885
60 420 -985 510 -390 600 —520 690 -615 555
70 430 -890 520 -260 610 —515 700 -515 255
80 440 -880 530 (-110 620 —445 710 -270 170
90 450 -910 540 0 630 —320 720 0 465
180
Суммирование значений крутящих моментов всех восьми цилиндров двигателя производится табличным методом (табл. 38) через каждые 10° угла поворота коленчатого вала. По полученным данным строят кривую Мкр (рис. 83) в масштабе Мм— = 25 Н ’ м в мм и = 1° в мм.
Средний крутящий момент двигателя:
по данным теплового расчета
Л^кр.ср ~ = Ме (I/'IQm) =
= 856,2/0,824 = 1039 Н-м;
по площади Fm, заключенной под кривой Л4кР (рис. 83):
Л^кр.ср “ FмМм/ОА =
= 3745 -25/90 = 1040 Н м;
ошибка Д = (1040—1039) 100/ /1023 = 0,10%.
Максимальное и минимальное значения крутящего момента двигателя (рис. 83): Л4кр max = = 2200 Н-м; Мкр min *— 160Н-М.
Силы, действующие на шатунные шейки коленчатого вала от одного шатуна.
Полярную диаграмму силы S (рис. 84), действующей на шатунную шейку, строят графическим сложением векторов сил К и Т (см. табл. 37). Масштаб полярной диаграммы Мр *= — 0,5 кН в мм.
Диаграмма силы S с центром в точке 0ш(00ш^=^ш/М/з== = —10,9/0,5 = —21,8 мм) явля
ется полярной диаграммой нагрузки Дш.ш на шатунную .шейку от действия одного шатуна.
Значения силы /?ш.ш для различных <р, снятые с полярной
диаграммы (рис. 84), заносят в табл. 37 и по ним строят диаграмму в прямоугольных координатах (рис. 85). Масштабы развернутой диаграммы: W = 1 кН в мм и =35 в мм.
181
Рис. 85. Диаграмма нагрузки иа шатунную шейку дизеля в прямоугольных координатах
Рис. 86 Диаграмма износа шатунной шейки дизели
По развернутой диаграмме /?ш.ш определяют
Яш.ш.ср == MpF/OB = 1 . 5500/240 - 22,9 кН;
max ~ 95,2 кН; Лдрш min = 6,5 кН.
По полярной диаграмме (см. рис. 84) строят диаграмму износа шатунной шейки (рис. 86). Сумму сил действующих по каждому лучу диаграммы износа (от 1-го до 12-го), определяют с помощью табл. 39 (значения в таблице выражены в кН). По диаграмме износа (Mr = 40 кН в мм) определяют положение оси масляного отверстия (фл< = 90°).
Условные силы, действующие на шатунные шейки от двух смежных шатунов. Коленчатый вал рассчитываемого двигателя полноопорный с кривошипами, расположенными в вертикальной и горизонтальной плоскостях (рис. 87). Порядок работы двигателя: 1л—1п—4л—2л—2п—Зл—Зп— —4п. Чередование вспышек равномерное через 720/8 » 90°.
В соответствии с' порядком работы двигателя на 1,2 и 3-ю шатунные шейки одновременно действуют силы от левого и правого шатунов, смещенные одна относительно другой на 90°, а на 4-ю шейку действуют силы от левого и правого шатунов, смещенные на 450°.
Суммарные тангенциальные силы, действующие на шатун-
182
Таблица 39
Значения /?ШфЦИ, , кН, д ;ля лучей
?° 1 2 3 4 5 6 7 8 9 10 и 12
0 32,0 32,0 32,0 — — — 32,0 32,0
30 26,1 26,1 26,1 26,1
60 13,8 13,8 13,8 13,8
90 13,5 13,5 — 13,5 13,5
120 21,0 21,0 — 21,0 21,0
150 23,9 23,9 — 23,9 23,9
180 24,1 24,1 24,1 — — — —— — — 24,1 24,1
210 24,3 24,3 24,3 24,3
240 21,7 21,7 21,7 — S 21,7
270 15,0 15,0 15,0 15,0 —- — — — — 15,0
300 10,8 10,8 10,8 10,8
330 6,7 6,7 6,7 6,7
360 — — 64,1 — 64,1 64,1 64,1 64,1 64,1 —
390 — — — — — — 33,8 33,8 33,8 33,8
420 17,5 17,5 17,5 17,5
450 21,5 — 21,5 21,5 21,5
480 26,4 26,4 26,4 26,4
510 27,5 27,5 — 27,5 27,5
540 25,9 25,9 25,9 — — — —— — — —— 25,9 25,9
570 24,7 24,7 24,7 24,7
600 21,0 21,0 21,0 21,0
630 13,5 13,5 13,5 13,5
660 13,7 13,7 — 13,7 13,7
690 26,1 26,1 — 26,1 26,1
433,2 411,7 323,7 21,7 64,1 64,1 97,9 97,9 115,4 72,8 273,1 444,0
ные шейки от двух смежных шатунов:
Л = тл + тд.
Суммарные силы, действующие на шатунные шейки,по радиусу кривошипа от двух смежных шатунов:
*2 = *л + *П.
Рис. 87. Схема коленчатого вала V-образного дизеля
183
2
Левые цилиндры 1(2, 3)-й правый цилиндр
о *л Кл,кН Г-, кН л Ящ.ш.Л, кН э С 9- да ,lu)Z X •£ В Ящ.ш.пЬ кН
1_ 2 3 4 5 6 7 8
0 —21,1 0 32,0 630 —1,5 —5,3 13,5
30 —13,2 —10,2 26,1 660 —1,6 +5,5 13,7
60 —1,6 —5,5 13,8 690 —13,2 + Ю,2 26,1
90 —1,5 4-5,3 13,5 720 —21,1 0 32,0
100 —3,6 +7.7 16,6 10 —20,1 —6,3 31,6
110 —6,0 +8,7 19,0 20 —17,3 —9,9 29,9
120 —8,2 4-8,7 21,0 30 —13,2 —10,2 26,1
150 —12,4 +5,1 23,9 60 —1,6 —5,5 13,8
180 —13,2 0 24,1 90 —1,5 +5,3 13,5
210 —12,6 , 5 2 24,3 120 —8 2 +8,7 21,0
240 —8,8 —9’3 21,7 150 —12,4 +5,1 23,9
270 —2,1 —7,4 15,0 180 —13,2 0 24,1
300 4-0,5 —1,5 10,8 210 —12,6 —5,2 24,3
330 4-7,1 —5,5 6,7 240 $ g —9,3 21,7
360 4-75,0 0 64,1 270 —2*1 —7,4 .15,0
370 4-103,2 4-23,2 95,2 280 —0,7 —4,2 12,3
380 4-63,1 4-29,8 60,2 290 0 —2,4 11,2
390 4-40,9 4-31,7 33,8 300 +0,5 —1,5 10,8
420 4-4,9 4-16,4 17,5 330 +7,1 —5,5 6,7
450 —4,2 4-15,2 21,5 360 + 75,0 0 64,1
460 —5,8 4-15,0 22,4 370 + 103,2 +23,2 95,2
470 —9,8 4-13,5 25,0 380 +63,1 + 29,8 60,2
480 — 12,2 4-12,9 26,4 390 +40,9 +31,7 33,8
510 —15,9 4-6,5 27,5 420 +4,9 + 16,4 17,5
540 —15,0 0 25,9 450 —4,2 + 15,2 21,5
570 —13,2 —5,4 24,7 480 —12,2 + 12,9 26,4
600 —8,2 —8,7 21,0 510 —15,9 + 6,5 27,5
630 — 1,5 —5.3 13,5 540 —15,0 0 25,9
660 —1,6 +5,5 13,7 570 —13,2 —5,4 24,7
690 —13,2 +10,2 26,1 600 g 2^ —8,7 21,0
720 —21,1 0 32,0 630 —1’5 —й^З 13,5
Таблица 4U
1(2. 3)-я шатунная йЙейка 4-й правый цнлнндр 4- в шатунная шейка
со л 5 3
5 5 м а 5 5 ш 24 5 ш 24
о = м ах в в а •Л « * а
(% & Я- or к
9 10 11 12 13 14 15 16 17 18 19 20
0 —22,6 -5,3 44,7 270 —2,1 —7,4 15,0 0 —23,2 —7,4 45,5
30 —14,8 —4,7 36,8 300 + 0,5 —1,5 10,8 30 —12,7 —11,7 36,4
60 —14,8 +4,7 36,8 330 +7.1 —5,5 6,7 60 +5,5 —11,0 19,6
90 —22,6 +5,3 44,8 360 + 75,0 0 64,1 90 +73.5 +5,3 51,7
100 —23,7 + 1,4 45,5 370 + 103,2 +23,2 95,2 100 +99,6 +30,9 83,4
по —23,3 -1,2 45,1 380 +63,1 +29,8 60,2 ПО +57,1 +38,5 52,0
120 —21,4 —1,5 43,1 390 +40,9 +31,7 33,8 120 +32,7 +40,4 41,7
150 —14,0 —0,4 35,8 420 +4,9 + 16,4 17,5 150 —7,5 +21,5 36,4
180 —14,7 +5,3 36,8 450 *—4,2 + 15,2 21,5 180 —17,4 + 15,2 41,8
210 —20,8 + 3,5 42,8 480 —12,2 + 12,9 26,4 210 —24,8 +7,7 47,0
240 —21,2 —4,2 43,1 510 —15,9 +6,5 27,5 240 —24,7 —2,8 46,5
270 —15,3 —7,4 37,7 540 —15,0 0 25,9 270 —17,1 —7,4 39,5
300 —12,1 —6,7 34,5 570 —13,2 —5,4 24,7 300 —12,7 -. б g 35,0
330 —1,7 —14,8 27,9 600 —8,2 —8,7 21,0 330 —1,1 —14,2 26,9
360 +72,9 —7,4 51,5 630 —1,5 —5,3 13,5 360 +73,5 —5,3 51,7
370 + 102,5 + 19,0 82,8 640 —0,2 —2,5 11,4 370 + 103,0 +20,7 83,5
380 +63,1 +27,4 49,5 650 —0,2 +2,0 11,3 380 +62,9 +31,8 51,6
390 +41,4 +30,2 35,8 660 —1,6 +5,5 13,7 390 +39,3 +37,2 41,0
420 + 12,0 + 10,9 14,5 690 —13,2 + Ю,2 26,1 420 —8,3 +26,6 40,3
450 + 70,8 + 15,2 51,1 720 —21,1 0 32,0 450 —25,3 + 15,2 49,5
460 +97,4 +38,2 84,5 10 —20,1 —6,3 31,6 460 —25,9 +8,7 50,0
470 +53,3 +43,3 53,4 20 —17,3 —9,9 29,9 470 —27,1 +3,6 48,6
480 +28,7 +44,6 45,0 30 —13,2 —10,2 26,1 480 —25,4 +2,7 47,0
510 —11,0 +22,9 40,0 60 —1,6 —5,5 13,8 510 —17,5 + 1.0 39,0
540 —19,2 + 15,2 43,7 90 —1,5 +5,3 13,5 540 —16,5 +5,3 38,5
570 —25,4 + 7,5 47,6 120 —8,2 +8,7 21,0 570 —21,4 +3,3 43,1
600 —24,1 —2,2 46,0 150 —12,4 +5,1 23,9 600 —20,6 —3,6 42,4
630 —16,5 -5,3 38,5 180 —13,2 0 24,1 630 —14,7 —5,3 36,8
660 —14,8 +0,1 36,4 210 —12,6 -5,2 24,3 660 —14,2 +0,3 35,9
690 —21,4 + П5 43,0 240 —8,8 -9,3 21,7 690 —22,0 +0,9 43,6
720 —22,6 —5,3 44,7 270 —2,1 —7,4 15,0 720 —23,2 —7,4 45,5
Рис. 88. Условные полярные диаграммы нагрузки иа шатуииые шейки и ко* леиа вала V-образиого дизеля
Условные суммарные силы, действующие на шатунные шейки, строят при условии, что во всех левых цилиндрах отсчет углов начинается от0°. Силы Та и Ks рассчитывают табличным методом (табл. 40). По полученным данным строят условные полярные диаграммы суммарных сил S2 = S„ + Sn> действующих на 1 (2, 3)-ю (рис. 88, а) и 4-ю (рис. 88, б) шатунные шейки от каждой пары смежных шатунов. Масштаб диаграмм Мр*= 0,5 кН в мм.
Диаграммы сил & i <2. з> и с центрами в точках ОШ1 р, з> и Ош4 (01 е. з) ОШ1 (2.з)= 040ш4=2КВш/Мр = 2 (— 10,9)/0,5 = - 43,6 мм) являются соответственно полярными диаграммами условных нагрузок на 1,2 и 3-ю шатунные шейки — &ш.шШ(2.з> и на 4-ю шатунную' шейку — Рш.шЕ4-
Значения сил /?ш.шШ(2.з) и Для различных <р, снятые с полярных диаграмм (рис. 88), заносят в табл. 40 (гр. 12 и 16) и по иим строят диаграммы кш.шШ(2,з) н /?ш.ш24 в прямоугольных координатах
185
2-е колено ^15’0— О1 QOlQOWOOQLOOlOWQlOLOWlOinWOOWOWQOLOOOLOOOOOOLOO © —<(DOO^COCOON»-<С00100Ь-ФС*5оОЮ^ЮЬ-С^ОО^Ь-»-«Ь-СОч^Ь-иЗЬ-—«^© Гч-©>—«04—«b.CDU3CO—«СЧ~ —«©©О4О4О4О4©©©©О4СОО4—<04COCOt'-CO©COLQ.©t'“- 17777 и П++++11++1I1+++1I।I+++++177 I I
(6*zc — S3>/)s;o = = ^№•0 — ^©©©©©©©©©©©©©©©©©©©©lq©©©©©©©©©©©©©©© 4fb.b-cD’^©b-be©©C4©’4j*CO©C4COCOC4OO©COOCOCOb-CO©OO©OO©CO©b-0j4j* coaib-^f^oooo—Гг^со"сосрд?о"соосГоод>1п«эь.оо*д>дю10оь-оГсч—*о»«э — счг 1 О1счсчсоеососчсчс4«51«счс4соеосо51счс4с4сч5151с4с4—«—«со —«ц_—«—* +++1 1 1 1111 1 1 1 1 11 1 1 111 1 1 1 1 1 1 1 1 1 1++++1+
p»a> о о ©©©©©©©©©Q©©©©©©©©©©©©©©©©©©©©©©©©©©© © СО Г- 00 —«ч^©©Ь-ОсО<’$'©СО©04СОСО©©’—'О4©00©© —«^Ь-ОсОФЬ-®ФС1Ю —*—<—<—«—«—«04040404COC0COC0COC04fTf
2-я коренная шейка гк*у + 4—* _p Z3Mj 4- 4— а> NOXNLOLOOlO — XLOTf COOOlOWNOJON WOOOO(N(NLOlOO(NLOaJWOOLOaiN ©©С4ч^©аГоО*©©—«—«—^«—©ОиЗ©©С4©"^СООрЬ- —« —«*ООЬ-©С4«ЭОрОО —«ь- © 04 СО —« COCOCOCOTfTfTfTfTfTfTfCOCOOJCOLQTfTfCOCOLQLQLQTfTfTfTfCOCO—«—«0^04
со ©©©©©©©©©©©©©©©©©©©Q©©©©©©©©©©©©©©©©© СО—*00©©СО©СО©©© —« Tf СО 00 со —«ООО—«—«b-cOOOlOCQO^d—« b- 04 04 <х> С1ОЮ«^С1^ЮЮЬ-00фФф00СПЬ-Ь.ОС0СЧ-«С0ОС4ОС4ОСЧЮ00ОЬ-СЧ—« ^ Q4 04—« I 1 —« 040404040404СЧ040404СЧ04—«О4СО—« 1 —« —« СО —« 1 04 СО СО СО СО —« — — 04 04 ++++++++++++++++++1II1+111+++++++++++
гки</№’0 + 4- 1^29*0— ^я2 г- оюююороюооюоооююоююооюооюююооюоююоооо —«СО—« 04 00 04 —«000 00 004—«ЮЮООЮСОСОЬ-^^ОСОСОО^Г^-Г*-—« 04 <О Ь- Ь- —* о’со—« 04 О —«ОООООО)О)ХЬ-0СОХ^О^^-«С0*ь-*0—« —«чфдрооо^со—«со о — СО—« I 04СОС0СОС0С0С<01О40404СЧ04—«04т^ч^^СОСОт^10Ю«фС004—<О4СО—< _|_—« — +++11II 111 11111111IIII1111II11l++++l+
1-е колено l32S40— со iQOOOOinOQOpOQQOOOOOOQOOOQOOOOOOOlQOQUOOO СОсО^СОСООЬ-ФЬ-МООООЬ-—«b-CO^fb-LOb-—<TfOt>-OC04fcOt>-—«ооооь-о С4СОСОС4СЧСЧ000 0 04СОс7—«"o^COCObTcOOCOOlOr-Cl—«*04—«Ь*'со—«ОД—«*~о'о04 ++++1 I I+++iiii+++++177।177771•++++11 +
(6‘Z£ — ,гУ)5’0— = = i^s-o- 1Л ЮО10Ю1^1Л)ООЮЮООЮЮ U3*O QQOOQOUOlOOOOOOinpOOOlOlQUO C4C4'^*COCOC4QOoOOC004’4j*COOOOOOOOCOOb-0'^*b-b-cD'4fOci5oC40-4j*COOC4 o' 0 Г- Ф Ф О О О О Ю 0 N 00 gi 0 Ю (Ji N (N О?-<" (N Ю Л N 00 -« —« N Ю Ю Ю ф О COC4040404COCOC004040404Q404040404—<—«СО—« 1 —< —« 04 | |04СЧС0С0ОДСЧ04ОД04С0 ++++++++++++++++++1111+111+++++++++++
+ 4—* 4- isnrm^ =. 4— 4— ЧГ 040Ь-04С004—«<£>V0C004O00C0(X>OO,XiC0t'-CC>TfLQt'-O00t'-TfTf—«ЮОЬ-О—«Ь-О4 ^-OUQCOCO—« О1 —«С504СОЮЮС5С5^004ьОгОрОООЮОЮ1Л"Ф05т^04ЮСОСОСОстГ—« со ю из итйэ с©<©<©изизизизизизизизизт$*со<ососо04соь-т$*^иЬ1осооизизизизизо
'и4 о СО OOOOOOOOOOQOOOOOOOQOQOOOOOOOOOOOOOOOO —« 04 СО СО 05 О —ч(МизООФО — ’^t'-ocO<Ot'-QOO>04LQcOt'-00—«-rfb-pCOXflOCOOC^ <~-.04040404cOCOCOCOCOCOTfTfTfTF4frlLQ<OLQCO<0<OcO<0<Ot'-
—eIS 4— 4— ВМЦЭШ BBHHddOM К-1 сч OPU30U3QU30U3U30QQU30QU30U3U300U3U300U300U3U30UDPU3U30 ЗэизООСОСОСООООЬ-—«<0иЗфс000От$*С0С0С0С0040400ОС100 04Ь-©Счи300и5и30035 ©ФЬ-СОСО©—«©0><0С0Г'*Ь.О)О)Ь.|1хз—«b.cO00U3'4fC'-U3O4O4t'»-p)O4—«Ь-cDcOCOOiO С004С4С404СОСОС004СЧСЧСЧСЧ040404С404’— СО —< «— «— —«С004СЧСЧ04СОСОС4С4С40404СО
О<Ь вива OJQLBhHOirOM uxodoaou IfOJX — ©©©©©©©©©©©©Q©©©©©©©©©©©©©©©©©©©©©©©© © -иО4<?ЗСОС1©—«^иЗООС!©—чт**£"-©СОСОЬ.СО©«иЭСОЬ*.ОР—«ФЬ-©СО^*»5<О©С41 00 —04 04 04 04 55 «О СО СО СО СО Tf гГ Tf ©1Л© © СО СО СО © © Ъ- 'CS
Таблица 41
3-я коренная шейка З-е колено 4-я коренная шейка 4-е калено 5-я коренная шейка
1 ы я о “ в га". s?° + £ to ' 3 II Ьч CO10-яо * + + co till M t* + о *3 &- о* co 1 0 ra _ и "К 1 II CO M fe о + CO w S ж S fa и 3 CO +st* 1* + 3 Ifoc з S t« ii о М + ", в -St* fee + Л Тог 1О О 1 II S а У*
13 14 I5 16 17 18 19 20 21 22 23
+43,25 +55,80 +33,55 +20,4 —4,65 —46,05 —62,00 —43,35 —33,40 -18,05 -43,65 —56,35 -34,10 —21,75 —5,20 —1,70 +5,30 +4,65 —3,05 -4,20 —4,20 -3,30 +3,70 +3,95 + 1,85 —1,25 —3,00 —3,20 +3,45 +4,65 +6,15 +43,80 +59,50 +41,05 +31,10 + 16,60 +43,25 -11,30 —22,70 —25,15 —25,65 — 18,85 —11,30 +3,20 +8,70 + 11,35 +6,55 +10,25 +21,65 +22,65 +22,25 + 10,70 + 10,25 +6,10 —3,45 —5,30 —2,65 —0,40 +0,80 +0,95 -5,30 —6,60 —6,05 —4,10 +4,45 +6,35 +2,60 +7,20 +6,35 —6,50 —10,90 -13,35 —7,55 —11,30 44,8 60,2 42,0 32,6 19,3 47,5 62,1 44,2 35,2 19,3 44,8 60,1 41,0 31,0 11,9 10,3 9,5 5,8 6,0 5,0 4,0 3,2 3,9 6,5 7,0 6,5 5,0 5,4 7,3 5,5 9,5 44,4 59,8 42,4 33,8 15,8 44,8 270 280 290 300 330 360 370 380 390 420 450 460 470 480 510 540 570 600 630 640 650 660 690 720 10 20 30 60 90 120 150 180 190 200 210 240 270 J t-26,80 -26,05 -25,55 -25,00 hl9,80 -17,50 -32,30 -12,60 -1,75 h12,95 -16,45 -29,75 —7,70 +4,60 h24,45 -28,55 -31,65 -31,00 -27,20 -26,60 -26,40 -26,35 -29,65 -30,25 -29,20 -27,45 [-26,35 -26,35 -30,25 -29,65 -25,95 -26,30 -27,20 -28,45 -29,35 [-29,55 -26,80 —3,70 -3,60 -3,50 —3,35 —7,40 -3,70 +9,50 + 13,70 + 15,10 +5,45 +7,60 + 19,70 +21,65 +22,30 + 11,45 +7,60 +3,75 — 1,10 —2,65 —1,95 -1,00 +0,05 +0,75 —2,65 —3,60 -3,45 —2,35 +2,35 +2,65 —0,75 —0,20 +2,65 +3,00 +2,80 + 1,75 —2,10 —3,70 54,0 53,0 52,0 50,9 42,6 35,3 66,7 36,6 30,4 28,5 35,7 70,0 45,8 45,7 54,4 59,4 64,1 62,5 55,0 53,7 53,0 53,1 59,7 61,2 59,0 55,7 53,2 53,3 61,2 59,5 52,3 53,2 55,0 55,8 59,3 59,6 54,0 43,0 лз,о 43,0 43,0 41,3 36,0 37,4 18,0 13,1 28,3 29,9 35,5 14,1 3,5 19,8 40# 1 52,1 50,0 46,5 45,5 44,5 43,5 *42,0 40,6 39,5 38,0 36,4 26,1 34,4 48,4 46,0 44,8 44,4 43,2 43,3 42,9 43,0 540 550 560 570 600 630 640 650 660 690 720 10 20 30 60 90 120 150 180 190 200 210 240 270 280 290 300 330 360 390 420 450 460 470 480 510 540 55,2 57,0 59,0 60,0 59,0 53,4 ^51,4 51,0 52,5 60,3 61,9 59,0 56,5 52,4 34,5 35,3 40,8 50,7 57,8 60,5 62,0 63,7 63,1 56,0 54,5 53,2 51,5 42,0 35,3 37,3 54,0 65,5 67,0 66,8 63,8 55,9 55,2 27,60 28,50 29,50 30,00 29,50 26,70 25,70 25,00 26,25 30,15 30,95 29,50 28,25 26,20 17,25 17,65 20,40 25,35 28,90 30,25 31,00 31,85 31,55 28,00 27,25 26,60 25,75 21,00 17,65 18,65 27,00 32,75 33,50 33,40 31,90 27,95 27,60
187
кН
Рис. 89. Условные диаграммы нагрузки на шатунные шейки V-образного дизеля в прямоугольных координатах
(рис. 89). Масштабы развернутой диаграммы: Мр — 1 кН в мм и Mf = = 3° в мм.
По развернутым диаграммам определяют:
Яш.ш si (2. з)ср = (2. з) Мр/ОВ = 9390 • 1/240 = 39,1 кН;
/?ш.ш з 1 <2, з)шах = 84,5 кН; з 1 (2, з)т|П ~ 3,6 кН;
Яш.ш 3 4 == FiMp /ОВ = 9600 • 1 /240 = 40,0 кН; Ср
^ш,шЕ4 == 83,5 кН; 4min == 8,0 кН. max
Силы, действующие на колена вала. Суммарные силы, действующие на колена вала по радиусу кривошипа:
+ 2КДш + КДк = + 21,8 + 16,1 - (Кг + 37,9) кН.
Полярные диаграммы сил /?ш.шзн2,з) и с центрами в точках Ок1 (2, 3) И Ок4 (Ош1 (2, 3)О«| (2, 3) “ = Кпх/Мр = — 16,1 /0,5 =
= — 32,2 мм) являются соответственно полярными диаграммами нагрузок на колена вала /?ке i (2.3) и /?«S4 (см. рис. 88). Значения /?kei(2, з) и /?к 2 4 для различных <р заносят в табл. 41 (гр. 4, 19, 22).
Силы, действующие на коренные шейки. Силы, действующие на 1-ю и 5-ю коренные шейки:
~---О,5/?К3 1 И /?К.ШЕ5= —0,5/?к2 4.
Изменение сил и /?к.ше5 в зависимости от ф показывают соответственно полярные диаграммы /?kei и /?кЕ4 (см. рис. 88, а и б), но повернутые на 180° и в масштабе Mr = 0,25 кН в мм. Значения этих сил для различных ф сведены в табл. 41 (гр. 2 и 23).
Силы, действующие на 2-ю и 3-ю коренные шейки и ориентированные относительно первого кривошипа:
188
460
370
'Тк£
450
380
390
Ош?
20
420
660
640
330
90
690
510
630
I y^fO-1209
КГ
i 9^-720-270-450'
650
0:720
180
480
Рис. 90. Полярная диаграмма нагрузив на 2-ю коренную шейку дизеля
1л-1п'-4л~2л-2п~3л~3п-4п~1л 450° I
270
600
Rft.ni 22 — 1/ 22 “F Кк22 И Т?к.ш23
к 23
где Тк22— Тщ “И '^'ъ2т~^'рк^2т— 0,5 (Т21+Т22 cos 90 /CpK22sin90 )— == 0,5Т21 + 0,5/<рк22; Кк22 = Крк21 + ^рк22№== 0,5(/СдК21 +
+ Т22 sin 90° + К₽к22 cos 90°) = - 0,5RpK21 - 0,5Т22; . Тк23 = Т'2Г + ~1~ Кркх2г~^ + ^ркезг “ 0,5 (Т22 cos 90 R₽ks2 s*n 90 +
+ 7x3cos270 R₽K23s^n270 )=.0,5K₽k22 0,5R₽k23; Rk23 =RpkS2k +
~i~ ^22K + Кркхзк "I- ^2зк “ 0,5(K₽k22cos90 + 7\2 sin 90 + x
x cos270° + T23sin270°) - -0,57\2 г 0,5Г23; Kp^2 +KRs =
(Rxa 57,9) кН; R^kx3 = Rs3 “h Rrx = (Rs3 5 7,9) кН.
В соответствии с порядком работы двигателя силы, действующие на 2-й кривошип, смещены относительно сил, действующих на Ьй кривошип, на 270° угла поворота коленчатого вала, а силы, действующие на 3-й кривошип, — на 450°.
Расчет сил Т^, Ккгг» Ткез и /(кез приведен в табл. 41, а полярные диаграммы Т?к.шЕ2 и 7?к.Щ£з,- построенные геометрическим сложением соответствующих векторов 7\s и RKS, представлены на рис. 90 и 91. Масштаб диаграмм Mr ~ 0,5 кН в мм.
Сила, действующая на 4-ю коренную шейку:
^К.Ш24 ~ 0>5 (Rk23 + RKld) •
189
270°
450'
-/С
60
-1\
360
100
110
120
540
180
270
210
KZ
200
1л-1п-4л-2л-2п-3л-3п-4п
L 450
50
240
50
450
330 Ощг
0«з
30
20
0,720
640
420
300 00
660
690
650
630
1 180{9
4к=720~450=270° ()
^0=720^
02
4*^720-270=450'
Рис8 9L Полярная диаграмма
нагрузки на 3-ю коренную шейку дизеля
Рис. 92.
Построение полярной
диаграммы нагрузки на 4-ю коренную шейку дизеля
Полярная диаграмма нагрузки на 4-ю коренную шейку (рис. 92) построена графическим сложением полярных диаграмм /?каз и /?кЕ4, повернутых на 180°. Масштаб диаграммы /?к.шд4 — Л4д= 0,25 кН в мм.
Диаграммы 7^к.шя1, ^?к.шзз, и /?к.шз5, перестроен-
ные в прямоугольные координаты, представлены на рис. 93. Масштабы диаграмм Мн = 1 кН в мм и Mv = 3° в мм. По этим диаграммам определяют:
для 1-й коренной шейки
₽ж.ш21ор = FiMn/OB = 6320 - 1,0/240 = 26,3 кН;
=35,0 кН; ₽к.ш21 =2,6 кН;
KLnzlmax к •UIZ’mln
для 2-й корен ной шейки
Дж.ш12ср = F2Mr/OB = 8860 • 1,0/240 = 37,0 кН;
/?к.шз2так = 57,2 кН; ^K-msaniin = 4,7 кН;
191
Рис. 93. Диаграммы нагрузки на коренные шейки дизеля в прямоугольных координатах
а — 1-я шейка; б — 2-я шейка; в — 3-я шейка; е — 4-я шейка; д — 5-я шейка
для 3-й коренной шейки
Яж.ш23ср =ГзМв/ОВ = 4540 • 1,0/240= 18,9 кН;
^“•ш23тах ~ 62,1 ^К ШХЗШ111 = 2>9 К^;
для 4-й коренной шейки
Яж.ш24Ср = F^Mr/OB = 9000 • 1,0/240 = 37,5 кН;
^ж-ш24тах = 58,2 кН; пип = 3,5 кН;
192
для 5-й коренной шейки
Яж.ш»>сп ~ FMOB = 6340 • 1,0/240 = 26,4 кН; up
^ж-шИпгах — 34,1 кН; ^K.ni£5min —2,3 кН.
Из сравнения диаграмм ₽к.швь Як .шЕ2» Як .ШЕЗ> Як Ш24 И Я к. шЕ5 видно, что максимально нагруженной является 4-я коренная шейка, а минимально нагруженной — 3-я шейка.
Уравновешивание
Центробежные силы инерции рассчитываемого двигателя полностью уравновешены: 2Kr = 0.
Суммарный момент центробежных сил действует во вращающейся плоскости, составляющей с плоскостью первого кривошипа угол 18°2б' (см. рис. 87), величина его
2 Mr = KIO (m, 4- 2/пш. ж) Rate.
Силы инерции первого порядка взаимно уравновешены: 2 Рц = 0.
Суммарный момент сил инерции первого порядка действует в той же плоскости, где и равнодействующий момент центробежных сил (£м. рис. 87), величина его
2Л4/ / = УТО т}Я<п2а.
Силы инерции второго порядка и их моменты полностью уравновешены: = 0; 2Л4/п == 0.
Уравновешивание моментов 2Л4;у и 2Л4« осуществляется установкой двух противовесов на концах коленчатого вала в плоскости действия моментов, т. е. под углом 18°26' (см. рис. 87).
Суммарные моменты 2Л4// и 2Л4« действуют в одной плоскости, поэтому
^М,, + ^MR = аЯ&УТ0 (т} + тя + 2тш.ж).
Масса каждого противовеса определяется из условия равенства моментов
«гпр2Р®г6 = SA4/z + 2МВ.
Расстояние центра тяжести общего противовеса от оси коленчатого вала принимаем р = 125 мм.
Расстояние между центрами тяжести общих противовесов — Ь ₽= == 720 мм.
Расстояние между центрами шатунных шеек — а = 160 мм.
Масса общего противовеса
тпр 2 = аЯУТв (т} + тх + 2тш.ж)/(р6) =
= 160 • 60 • /ТО (3,872 + 3,62 + 2 • 2,458)/(125 • 720) = 4,185 кг.
193
Установка противовесов на концах коленчатого вала двигателя в целях уравновешивания суммарных моментов S/И/у и2/Й« приводит к возникновению дополнительных центробежных сил инерции масс противовесов, передающих свое усилие на 1-ю и 5-ю коренные шейки вала.
Определение результирующих сил, действующих на 1 (5)-ю коренную шейку, осуществляется построением полярной диаграммы способом, аналогичным тому, который был принят при определении нагрузки на 2,3 и 4-ю коренные шейки.
Равномерность крутящего момента и равномерность хода двигателя
Равномерность крутящего момента
Н = (Мкргаах— Л4кр т|П)/Л4кр.0р = (2200— 160)/1040 = 1,96.
Избыточная работа крутящего момента
£-азб = = 1175 • 25 • 0,0174 = 511 Дж,
где Fu — площадь над прямой среднего крутящего -момента (см. рис. 83), мм2; Л<; = ЬпЩОА) = 4 . 3,14/(8 . 90) = 0,0174 рад в мм— масштаб угла поворота вала'на диаграмме /Икр.
Равномерность хода двигателя принимаем 8 = 0,01.
Момент инерции движущихся масс двигателя, приведенных к оси коленчатого вала:
Jo = LH36/(8®2) = 511/(0,01 • 272,12)=0,69 кг м?.
Часть третья
РАСЧЕТ ОСНОВНЫХ ДЕТАЛЕЙ ДВИГАТЕЛЯ
Глава X
ПРЕДПОСЫЛКИ К РАСЧЕТУ И РАСЧЕТНЫЕ РЕЖИМЫ
§ 41. ОБЩИЕ СВЕДЕНИЯ
Расчет деталей с целью определения напряжений и деформаций, возникающих при работе двигателя, производится по формулам сопротивления материалов и деталей машин. До настоящего времени большинство из используемых расчетных выражений дают лишь приближенные значения напряжений.
Несоответствие расчетных и фактических данных объясняется различными причинами, основными из которых являются: отсутствие действительной картины распределения напряжений в материале рассчитываемой детали; использование приближенных расчетных схем действия сил и места их приложения; наличие трудно учитываемых знакопеременных нагрузок и невозможность определения их действительных значений; трудность определения условий работы многих деталей двигателя и их термических напряжений; влияние не поддающихся точному расчету упругих колебаний; невозможность точного определения влияния состояния поверхности, качества обработки (механической и термической), размеров детали и т. д. на величину возникающих напряжений.
В связи с этим применяемые методы расчета позволяют получить напряжения и деформации, являющиеся лишь условными величинами и характеризующие только сравнительную напряженность рассчитываемой детали.
Основными нагрузками, действующими на детали двигателя, являются силы давления газов в цилиндре и инерции поступательно и вращательно движущихся масс, а также усилия от упругих колебаний и тепловых нагрузок.
Нагрузка от давления газов непрерывно изменяется в течение рабочего цикла и имеет максимальное значение лишь на сравнительно небольшом участке хода поршня. Нагрузка от инерционных сил имеет периодический характер изменения и в быстроходных двигателях иногда достигает значений, превышающих нагрузку от давления газов. Указанные нагрузки являются источниками различных упругих колебаний, представляющих опасность при явлениях резонанса.
Усилия от температурных нагрузок, возникающие в результате выделения тепла при сгорании рабочей смеси и трения, снижают ме
195
ханическую прочность материалов и вызывают дополнительные напряжения в сопряженных деталях при их различном нагревании и различном линейном (или объемном) расширении.
$ 42. РАСЧЕТНЫЕ РЕЖИМЫ
Величина и характер изменения основных нагрузок, воздействующих на детали двигателя, зависят от эксплуатационного режима работы двигателя. Обычно рассчитывают детали для режимов, на которых они работают в наиболее тяжелых условиях.
Для карбюраторных двигателей (рис. 94, а) за основные расчетные принимают режимы:
Рис. 94. К выбору расчетных режимов работы двигателя: а — карбюраторный двигатель; б — дизель с наддувом
1) максимального крутящего момента Метах при частоте вращения Пм = (0,4-ь 0,6) /?л/, когда давление газов достигает наибольшего значения pzmax, а силы инерции сравнительно малы;
2) номинальнойлиощности NeN при частоте пх, когда все расчеты деталей производятся от совместного действия газовых и инерционных нагрузок;
3) максимальной частоты вращения при холостом ходе пх.хтаХ= (1,05-4 1,20)/?л/, когда силы инерции достигают наибольших значений, а давление газов незначительно или даже равно нулю*.
Для быстроходных дизелей (рис. 94, б) принимают расчетные режимы:
1) номинальной мощности N£n при частоте вращения когда давление достигает максимального значения pzmaLX, а детали рассчитывают от совместного действия газовых и инерционных нагрузок;
2) максимальной частоты вращения при холостом ходе nx.xmax =
* При работе двигателя с ограничителем частоты вращения или с упорным винтом регулировки частоты вращения на холостом ходу.
196
= (1,04-4- 1,07) Плг, при котором силы инерции достигают наибольших значений*.
При расчетах деталей карбюраторных двигателей максимальное давление газов р2тах определяют или по тепловому расчету, проведенному для режима максимального крутящего момента, или приближенно принимают равным расчетному (без учета скругления индикаторной диаграммы) максимальному давлениюpz сгорания, полученному по тепловому расчету для режима номинальной мощности. Инерционными силами при расчетах на режиме максимального крутящего момента пренебрегают.
При расчетах на режиме номинальной мощности условно принимают, что максимальная газовая сила Р z действует совместно с максимальной инерционной силой в в. м. т. Величину максимальной газовой силы определяют по тепловому расчету для режима номинальной мощности с учетом скругления индикаторной диаграммы.
При расчетах на режиме максимальной частоты вращения при холостом ходе давлением газов пренебрегают.
§ 43. РАСЧЕТ ДЕТАЛЕЙ С УЧЕТОМ ПЕРЕМЕННОЙ НАГРУЗКИ
Практически все детали автомобильных и тракторных двигателей даже на установившихся режимах работают в условиях переменных нагрузок. Влияние не только максимальных величин нагрузок, но и характера их изменения по времени на работоспособность деталей автомобильных и тракторных двигателей значительно увеличивается при повышении частоты вращения и степени сжатия. В связи с этим ряд ответственных деталей современных двигателей рассчитывают на статическую прочность от действия максимальной силы и на усталостную прочность от действия постоянно изменяющихся нагрузок.
Усталостная прочность деталей зависит от: характера изменения нагрузки, вызывающей симметричное, асимметричное или пульсирующее напряжение в рассчитываемой детали; пределов усталости °-i> CT-ip и т _t (соответственно при изгибе, растяжении-сжатии и кручении) и текучести от итт материала детали; от ее формы, размеров, механической и термической обработки, упрочнения поверхности детали.
В зависимости от характера изменения действующей нагрузки в детали возникают напряжения, которые изменяются по симметричному, асимметричному или пульсирующему циклам. Характеристиками каждого цикла являются: максимальное оП1ах и минимальное omin напряжения, среднее напряжение от, амплитуда цикла сга и коэффициент г асимметрии цикла. Соотношения между характеристиками для указанных циклов приведены в табл. 42.
При статических нагрузках за предельное напряжение принимают предел прочности ов или предел текучести от. Предел прочности используется при расчетах деталей, выполненных из хрупкого материа-
При работе двигателя с регулятором.
197
Таблица 42
Характеристики циклов Циклы
симметричный асимметричный пульсирующий однозначный
положительный знакопостоянный знакопеременный
Максимальное напряжение °тах=—°min== =аа>0 °tnax=aa4* стах==гоа_1" °max—gao+ —2o/nO>0
Минимальное напряжение °fnin=“cmax=: ——0 omln=<Tm— —эа>0 — gmin— 0
Среднее напряжение 0 qmax~l~qfnln 2 qmax4~qfnin 2 ° tn ax ’m°- 2
Амплитуда напряжения аа =отах— =—°min °max—gmin qmax gmtn qmax ’a0 ~ ~
2 °fl== 2
Коэффициент асимметрии °min . Г — — 1 °тах 0<r<l —l<r<0 r = ^mln_=0 amax
ла, а для пластичных материалов за опасное напряжение принимается предел текучести.
При переменных нагрузках за опасное напряжение принимается предел усталости ог (для симметричного цикла ог = для пульсирующего ог — о0) или предел текучести от. При расчете деталей соответствующий предел зависит от асимметрии цикла напряжений.
При возникновении в детали нормальных или касательных напряжений, удовлетворяющих условию
Оа/’т > (?> - )/(1 - ) ИЛИ та/тт> )/(1 - 0, ), (213)
расчет производится по пределу усталости.
При возникновении в детали напряжений, удовлетворяющих условию
°a/em<(^ — )/(1 — М ИЛИ ах)/(1— М, (214)
расчет производится по пределу текучести. Здесь и (i, — отношение предела усталости при изгибе или кручении к пределу текучести:
₽» и ₽г =^-1/^, (215)
а, и ах — соответственно коэффициенты приведения асимметричного цикла к равнооцасному симметричному при нормальных и касательных напряжениях.
198
Значения аа и ат для сталей с различными пределами прочности приведены в табл. 43. Для чугуна ао <= (0,3-? 0,7); at == (0,5 -4- 0,7).
При отсутствии данных для решения уравнений (213) и (214) запас прочности детали определяют или по пределу усталости или по пределу текучести. Из двух полученных значений прочность оценивают по меньшему коэффициенту.
Таблица 43
Предел прочности МПа Изгиб a Растяжение- сжатие a 9 Кручение a*
350—450 0,06—0,10 0,06—0,08 0
450—600 0,08—0,13 0,07—0,10 0
600—800 0,12—0,18 0,09—0,14 0—0,08
800—1000 JLLfi=£U2. - o.u-Q.n 0,06—0,10
1ГЯ50—1200 0,20—0,24 0,16—0,26
1200—1400 0,22—0,25 0,16—0,23 0,10—0,18
1400—1600 0,25—0,30 0,23—0,25 0,18—0,20
Для приближенной оценки пределов усталости при переменной нагрузке используют эмпирические зависимости:
для сталей o_t = 0,40ов; а_1р = 0,28ств; = 0,22 тв; o_ip =
= (0,7—0,8) o.bT.i == (0,4—0,7) О-ь
Таблица 44
Марка стали Механические свойства легированных сталей, МПа
°в °—1 °-1р ч t-1
20Х 650—850 400—600 310—380 230 360 230
ЗОХ 700—900 600—800 360 260 420 220
ЗОХМА 950 750 470
35Х 950 750
35ХМА 950 800 — —
38ХА 950 800 —
40Х 750-1050 650т=Э50 320^-480 240—340 210—260
40ХН 1000-1450 800—1300 460—600 320—420 390 240
45Х 850—1050 700—950 400—500
50ХН 1100 850 550 —
12ХНЗА 950—1400 700—1100 420—640 270—320 400 220—300
18ХН24А 1100 850'
‘18ХНВА 1150—1400 850—1200 540—620 360—400 550 300—360
25ХНМА 1150 — —
20ХНЗА 950—1450 850—1100 430—650 310 240—310
25ХНВА 1100—1150 950—1050 460—540 310—360 600 280—310
ЗОХГСА 1100 850 510—540 500—530 220—245
37XH3A 1150—1600 1000—1400 520—700 320—400
40ХНМА 1150—1700 850—1600 550—700 — 700 300—400
199
Таблица 45
Марка Механические свойства углеродистых сталей. МПа
стали а а 0
В т -1Р хт
10 320—420 180 160 120—150 140 80—120
15 350—450 200 170 120—160 140 85—130
20 400—500 240 170 -220 120—160 160 100—130
20Г 480—580 480 250 180 170 90
25 430—550 240 190 — ——
30 480—600 280 200—270 170—210 170 110—140
35 520—650 300 220—300 170—220 190 130—180
35Г2 680—830 370 260 190 240 160
40 570—700 310-400 230—320 180—240 140—190
40Г 640—760 360 250 180 210 150
45 600—750 340 250—340 190—250 220 150—200
45Г2 700—920 420 310—400 210 260 180—220
50 630—800 350 270—350 200—260 — 160—210
50Г 650-850 370 290—360 — «V* ——
60Г 670—870 340 250—320 210 250 170
65 750—1000 380 270—360 220—260 260 170—210
65Г 820—920 400 300 220 260 180
Таблица 46
Марка чугуна °в °вс °ви хв °—1 x-i % (условный)
Механические свойства । серых чугунов, МПа
СЧ15-32 150 650 320 240 70 50
СЧ21-40 210 750 400 280 100 80
СЧ24-44 240 850 440 300 120 100 —
СЧ28-48 280 1000 480 350 140 ПО
СЧ 32-52 320 1100 520 390 140 110 —
СЧ35-56 350 1200 560 400 150 115 Ml
СЧ38-60 380 1300 600 460 150 115 —-
Механические свойства высокопрочных чугунов, МПа
ВЧ45-0 450 — 700 — — —- 350
ВЧ45-5 450 — 700 —— м> 330
ВЧ40-10 400 — 700 М> — 300
ВЧ50-1.5 500 900 м. 380
ВЧ60-2 600 — 1100 — — 420
Механические свойства ковких чугунов, МПа
КЧЗО-6 300 — 490 — —. м» 190
КЧЗЗ-8 330 530 —- —. м> 210
КЧ35-10 350 — 570 — — — 220
КЧ37-12 370 ___ 580 м> —. м> 230
КЧ45-6 450 700 м> м. 280
КЧ50-4 50 800 м» м> м> 320
КЧ60-3 60 —* 950 — —- — 380
200
для чугуна о_! — (0,3—0,5) ов; о_1р (0,6—0,7) o_i; t_i = (0,7— —0,9) a.t, тт = (0,2—0,6) ов;
для цветных металлов g_i = (0,24 —0,50) ав.
Основные механические характеристики для сталей и чугуна приведены в табл- 44, 45 и 46.
Запас прочности без учета формы, размеров и обработки поверхности деталей определяется из выражений:
при расчете по пределу усталости
По = a_!/(aa 4- ae ат), (216)
IU = т_1/(та + at тго); (217)
при расчете по пределу текучести
Лг» = °т/(°а + am)> (218)
Пп = тт/(та 4- Тго). (219)
Влияние на усталостную прочность детали ее формы, размеров и качества обработки поверхности учитывают следующими величинами:
1) коэффициентами концентрации напряжений: теоретическим аю и эффективным fe, (kt), учитывающими местное повышение напряжений в связи с изменением формы детали (отверстия, выточки, галтели, резьбы ит. п.);
2) масштабным коэффициентом ем, учитывающим влияние абсолютных размеров тела на предел усталости;
3) коэффициентом поверхностной чувствительности еп, учитывающим влияние состояния поверхности детали на предел прочности.
Теоретическим коэффициентом концентрации напряжений назы-
Таблица 47
Вид концентратора напряжений
Полукруглая выточка при отношении радиуса к диаметру стержня:
0,1......................................................
0,5......................................................
1,0......................................................
2,0......................................................
Галтель при отношении радиуса галтели к диаметру стержня: 0,0625 ....................................................
0,125 ...................................................
0,25.....................................................
0,5......................................................
Переход под прямым углом...................................
Острая V-образная выточка (резьба).........................
Оаверстия при отношении диаметра отверстия к диаметру стержня от 0,1 до 0,33 ...........................................
Риски от резца на поверхности изделия . . . ...............
кз
2,0
1,6
1,2
1,1
1,75
1,50
1,20
1,10
2,0
3,0-4,5
2,0-3,0
1,2-1,4
201
вают отношение наибольшего местного напряжения к номинальному при статической нагрузке без учета эффекта концентрации
= отах/°ноМ" (220)
Значения акя для ряда наиболее распространенных концентраторов приведены в табл. 47.
Влияние на предел прочности не только геометрии концентратора, но и материала образца учитывают эффективным коэффициентом концентрации напряжений k„. При переменных напряжениях
кя = o.t/o-lt (221)
где о_1 и — предел усталости гладкого образца соответственно при симметричном цикле и с концентратором.
Связь между коэффициентами ак« и Л» выражается следующей приближенной зависимостью:
k, = 1 + <7(ако — 1), (222)
где q — коэффициент чувствительности материала к концентрации напряжений (изменяется в пределах 0 с q с 1).
Величина q зависит в основном от свойств материала:
Для серого чугуна.................................. 0
Для высокопрочных и ковких чугунов.................0,2—0,4
Для конструкционных сталей.........................0,6—0,8
Для высокопрочных легированных сталей .......
Кроме того, коэффициент q можно определить по соответствующим графикам, приведенным на рис. 95.
При отсутствии в рассчитываемой детали резких переходов и при качественной обработке поверхностей единственным фактором, вызы-
Рис. 95. Коэффициент чувствительности сталей к концентрации напряжений
вающим концентрации напряжений, является качество внутренней структуры материала. В этом случае эффективный коэффициент концентрации
кя = 1,2+ 1,8- 10-‘(ов — 400), (223)
где ов — предел прочности, МПа.
Связь между коэффициентами к, и kx можно выразить по опытным данным зависимостью
kt = (0,4 Ч- 0,6) k, . (224)
При проектировании деталей двигателя следует свести к минимуму влияние местных напряжений, чтобы увеличить, усталостную проч
202
ность. Это достигается увеличением радиусов закругления во внутренних углах детали, расположением отверстий в зонах пониженных напряжений и т. д.
Масштабным коэффициентом 8^ называют отношение предела усталости образца с диаметром d к пределу усталости стандартного образца (d„ = 10 мм). Значения коэффициента 8М для конструкционных сталей и высокопрочных чугунов приведены в табл. 48.
Таблица 48
Масштабные коэффициенты Размеры детали, мм
10* 10—15 15—20 20—30 30—40 40—50 50-100 100—201
£ма 1 I-0,95 0,95-0,90 0,90-0,85 0,85— 0,80 0,80— 0,75 0,75— 0,65 0,65-0,55
Емт 1 1— 0,94 0,94— 0,88 0,88— 0,83 0,83— 0,78 0,78— 0,72 0,72— 0,60 0,60— 0,50
♦ Для деталей размером меньше 10 мм значения емз и «мх могут достигать 1,1—1,2 —
это гм при растяжении-сжатии и изгибе, емт — это »м при кручении).
Коэффициентом поверхностной чувствительности еп называют отношение предела усталости образца с заданным состоянием поверхности к пределу усталости такого же образца, но с полированной поверхностью. Значения коэффициента еи, « епТ для различных состояний поверхности приведены в табл. 49.
Для повышения усталостной прочности рекомендуется высокая чистота поверхности, особенно вблизи концентраторов. Ответственные детали, работающие в тяжелых условиях циклических напряже-
Таблица 49
Вид обработки или поверхностного упрочнения епаИепх Вид обработки или поверхностного упрочнения 6 пег * ®пт
Полирование без поверхностного упрочнения . . . 1 Обдувка дробью . . 1,1—2,0
Шлифование без поверхностного упрочнения . . . 0,97—0,85 Обкатка роликом . . 1.1—2,2
Чистовое обтачивание без поверхностного упрочнения 0,94—0,80 Цементация .... 1,2—2,5
Грубое обтачивание без поверхностного упрочнения 0,88—0,60 Закалка 1,2—2,8
Без обработки и без поверхностного упрочнения . 0,76—0,50 Азотирование . . . 1,2—3,0
Примечание. При поверхностном упрочнении детали вид предварительной механической обработки не влияет на величины епо и гп. . С увеличением коэффициента концентраций напряжений ka и с уменьшением размеров детали значения епа и ent увеличиваются.
203
ний, обычно шлифуют и полируют, а в ряде случаев производят механическое или термическое упрочнение.
С учетом влияния концентрации напряжений, размера и качества обработки поверхности детали максимальное напряжение цикла (МПа)
Стах == /(емеп) 4" °т (225)
или
Ттах = ТсЛх / (емеп) 4" (226)
а запасы прочности:
при расчете по пределу усталости
П, = о_4/(аак + а3 ат), (227)
я* = ^-1/(так 4" ат тт); (228)
при расчете по пределу текучести
Лто = °т/(°ак 4" °т)» (229)
Лтх = тт/(так 4" тт)» (230)
где оак = / (£меп) и = xakx /(sMsn).
При сложном напряженном состоянии общий запас прочности детали при совместном действии на нее касательных и нормальных напряжений
п = п3 «а 4- Пт , (231)
где Лз и пх — частные коэффициенты запаса прочности.
Для определения минимального общего запаса прочности следует в формулу (23-1) подставить минимальные значения па и пх . Влияние температуры на усталостную прочность сказывается в том, что с ее повышением предел усталости обычно падает у гладких образцов и у образцов с концентраторами.
Величина допускаемого запаса прочности зависит от качества материала, вида деформаций, условий работы, конструкции, характера действующих нагрузок и других факторов. От правильного установления допускаемого напряжения зависит прочность и безопасность проектируемой конструкции, количество затрачиваемого материала.
Глава XI
РАСЧЕТ ПОРШНЕВОЙ ГРУППЫ
§ 44. ПОРШЕНЬ
Наиболее напряженным элементом поршневой группы является поршень (рис. 96), воспринимающий высокие газовые, инерционные и тепловые нагрузки, поэтому при его изготовлении к материалу предъявляются повышенные требования. Поршни автомобильных и тракторных двигателей изготовляют в основном из алюминиевых сплавов и реже из чугуна.
204
Основные конструктивные соотношения размеров элементов поршня (рис. 96) приведены в табл. 50. Величину верхней части поршня выбирают, исходя из обеспечения одинакового давления опорной по-
верхности поршня по высоте цилиндра и прочности бобышек, ослабленных отверстиями для пропуска масла. Это условие обеспечивается при
(Л4 —Лг)>^б/2, где йр — высота головки поршня.
Расстояние b между торцами бобышек зависит от способа крепления поршневого пальца и обычно принимается на 2— Змм больше длины верхней головки шатуна /ш. Конкретные значения конструктивных элементов поршня принимаются по прототипам с учетом соотношений, приведенных в табл. 50.
Поверочный расчет элементов поршня осуществляется без учета переменных нагрузок,
Рис. 96. Схема поршня
величина которых учитывается при установлении соответствующих
допускаемых напряжений. Рас-
считывают днище, стенку головки, верхнюю кольцевую перемычку, опорную поверхность и юбку поршня.
Днище поршня рассчитывается на изгиб от действия максимальных газовых усилий pzmax как равномерно нагруженная круглая плита, свободно опирающаяся на цилиндр. Для карбюраторных двигателей наибольшее давление газов достигается при работе на режиме максимального крутящего момента. Для дизелей максимальное давление газов обычно достигается при работе на режиме максимальной мощ-
ности.
Напряжение изгиба (МПа) в днище поршня °из “ Миз/^из "
(232)
где Мй3 = (1/3)ргтахгЗ — изгибающий момент, МН-м; №из = (l/3)rz82 — момент сопротивления изгибу плоского днища, м3; ргтах = pz — максимальное давление сгорания, МПа; = [D/2 — (s +1 + A/)J — внутренний радиус днища, м.
При отсутствии у днища ребер жесткости допустимые значения напряжений [оиз] (МПа) лежат в пределах:
-Для поршней из алюминиевых сплавов........... 20—25
Для чугунных поршней......................... 40—50
При наличии ребер жесткости [оИз] возрастают:
Для алюминиевых поршней........................до 50—150
Для чугунных.........................* • • . • 80—200
205
Таблица 50
Наименование
Карбюраторные двигатели
Дизелв
Толщина днища поршня 8..............
Высота поршня Н.........................
Высота верхней части поршня /ц..........
Высота юбки поршня Аю ..................
Диаметр бобышки dg .....................
Расстояние между торцами бобышек b . . .
Толщина стенки юбки поршня 8Ю, мм ... Толщина стенки головки поршня s.........
Расстояние до первой поршневой канавки е Толщина первой кольцевой перемычки Яп Радиальная толщина кольца /: компрессионного ........................
маслосъемного ........................
Высота кольца а, мм.....................
Разность между величинами зазоров замка кольца в свободном и рабочем состоянии Ло ,
Радиальный зазор кольца в канавке поршня Д/, мм: компрессионного ..........................
маслосъемного.........................
Внутренний диаметр поршня dj............
Число масляных отверстий в поршне пм . .
Диаметр масляного канала dM.............
Наружный диаметр пальца dn..............
Внутренний диаметр пальца dB ...........
Дяина пальца /п: закрепленного ..........................
плавающего............................
Длина втулки шатуна /ш: закрепление го пальца...................
плавающего пальца.....................
(0,054-0,10) D
(0,84-1,3) D
(0,454-0,75) D
(0,64-0,8) D
(0,34-0,5) D
(0,34-0,5) D
1,54-4,5
(0,054-0,10) D
(0,064-0,12) D
(0,034-0,05) D
(0,124-0,20) D (1,04-1,7) D (0,64-1,0) D (0,64-1,1) D
(0,34-0,5) D
(0,34-0,5) D 2,0—5,0
(0,054-0,10) D (0,114-0,20) D (0,044-0.07) D
(0,0404-0,045)D (0,0404-0,045) D (0,0384-0,043)0 (0,0384-0,043) D 2—4 3——5
(2,5—4,0) i (3,24-4,0) i
0,70—0,95 0,70—0,95
0,9—1,1 0,9—1,1
0—2 (s +1 + ДО
6—12 (0,34-0,5) ц (0,224-0,28) 0 (0,654-0,75) dn
(0,884-0,93) 0 (0,784-0,88) 0
(0,284-0,32) 0 (0,334-0,45) 0
6—12
(0,34-0,5) a (0,304-0,38) 0 (0,504-0,70) dn
(0,884-0,93) 0
(0,804-0,90) 0
(0,284-0,32) 0
(0,334-0,45) 0
Кроме напряжений от давления газов в днище поршня возникают тепловые напряжения из-за разности температур внутренней и наружной поверхностей. Тепловые напряжения (МПа) охлаждаемых чугун-ных поршней
сттеп = а£б?8/(200Хтеп), (233)
где а — Н - 10“® — коэффициент линейного расширения чугуна, 1/град; Е = (1,0 ч-1,2)10®—модуль упругости чугуна, МПа; q— удельная тепловая нагрузка, Вт/м2; 8 — толщина днища, см; Хтеп =58 — коэффициент теплопроводности чугуна. Вт/(м • К).
Для четырехтактных двигателей приближенно
q = 11 ,'63 (6000 + 26n) pt, (234)
где п — частота вращения, об/мин (для карбюраторных двигателей п = пы, а для дизелей п =пи); pt — среднее индикаторное давление, МПа (дая карбюраторных двигателей при пм, а для дизелей при пы ).
206
Суммарное напряжение (МПа) в охлаждаемом чугунном днище = °из Н” °теп = Рг max (г//8)2 -|- а£(/8/200Хтеп . (235)
Из уравнения (235) следует, что с уменьшением толщины днища поршня тепловые напряжения уменьшаются, а напряжения от газовых сил увеличиваются. Допустимые суммарные напряжения в чугунных днищах автомобильных и тракторных двигателей находятся в пределах [os I = 150 4- 250 МПа.
Тепловые напряжения охлаждаемых алюминиевых поршней обычно определяются термометрированием при экспериментальных исследованиях. Головка поршня в сечении х — х (рис. 96), ослабленная отверстиями для отвода масла, проверяется на сжатие и разрыв.
Напряжение сжатия (МПа)
°сж ~ Рг max / Fх-х, (236)
где Рг max = PzFn — максимальная сила давления газов на днище поршня, МН; Fx_x— площадь сечения х — х, м2:
Fx_x = («/4) (d2K — d?) — nMF'. (237)
Здесь dK=D— 2(/ + Д/) — диаметр поршня по дну канавок, м2; Р' = |(dK — dtf/2] dM — площадь продольного диаметрального сечения масляного канала, м2.
Допустимые напряжения на сжатие для поршней из алюминиевых сплавов [о0ж] = 30 -т- 40 МПа, а чугунных — [осж] = 60 ч- 80 МПа.
Напряжение разрыва (МПа) в сечении х — х
°р = Pj/Fx-X. (238)
Сила инерции возвратно-поступательно движущихся масс (МН) определяется для режима максимальной частоты вращения при холостом ходе двигателя
Р/ = /Па._аЛ?(Ох.х max (1 4" ^)> (239)
где тх_х — масса головки поршня с кольцами, расположенная выше сечения х — х (рис. 96), определяемая по геометрическим размерам или тх_х « (0,4 -г- 0,6) /Иц, кг; тп — масса поршневой группы, кг; R — радиус кривошипа, м; (ох.Хтах = лПх.хтах/30 максимальная угловая скорость холостого хода двигателя, рад/с;
I = R/Lm — отношение радиуса кривошипа к длине шатуна.
Допустимые напряжения на разрыв для поршней из алюминиевых сплавов [ор] = 4 -=- 10 МПа, а для чугунных — [ор] = 8 4- 20 МПа.
Толщина верхней кольцевой перемычки (йп на рис. 96) форсированных двигателей с высокойстепенью сжатия рассчитывается на срез и изгиб от действия максимальных газовых усилий ргшах. Перемычка рассчитывается как кольцевая пластина, защемленная по окружности основания канавки диаметром dK = D — 2(/ 4- Д/) и равномерно нагруженная по площади FK.n = л(О2 — сР)/4 силойРкя^ 0,9pZfnaxX
Напряжение среза кольцевой перемычки (МПа)
т = 0,0314ргтахП/йп, (240)
где D н hu — диаметр цилиндра и толщина верхней кольцевой перемычки, мм.
Напряжение изгиба кольцевой перемычки
аНз = 0,0045рг тах (О/Йп)2. (241)
Сложное напряжение по третьей теории прочности
аа = )/ 4з+ 4т2. (242)
Допускаемые напряжения os (МПа) в верхних кольцевых перемычках с учетом значительных температурных нагрузок находятся в пределах:
Для поршней из алюминиевых сплавов....... 30—40
Для чугунных поршней..................... 60—80
Максимальные удельные давления (МПа) юбки поршня йю и всей высоты Н поршня на стенку цилиндра определяются соответственно из уравнений:
91 = ^тах/(/1юО); (243)
92 = Afmax/(tf D), (244)
где Л^тах— наибольшая нормальная сила, действующая на стенку цилиндра при работе двигателя на режиме максимальной мощности и определяемая по данным динамического расчета.
Для современных автомобильных и тракторных двигателей = = 0,3 4- 1,0 и 9г = 0г2 4- 0,7 МПа.
В целях предотвращения заклинивания поршней при работе двигателя размеры диаметров головки Оги юбки Ою поршня определяют, исходя из наличия необходимых зазоров Дг и Дю между стенками цилиндра и поршня в холодном состоянии. По статистическим данным для алюминиевых поршней с неразрезными юбками Дг = (0,006 4-4- 0,008) D и Аю = (0,001 4- 0,002)D, а для чугунных поршней Дг = = (0,004 4- 0,006) D и Аю = (0,001 4- 0,002)D. Установив Др и Дю, определяют Dv = D — Дг и Ою = D — Дю.
Правильность установленных размеров Dv и Ою проверяют по формулам
A; = D[1 +ац(Тц-Т0)]-Ог[1 +ап(Тг-Т0)] (245)
И
Дю = D [I + ап (Ти - То)\ - Яю [1 + ап (Тю - То)], (246)
где Дг и Дю — диаметральные зазоры в горячем состоянии соответственно между стенкой цилиндра и головкой поршня и между стенкой цилиндра и юбкой поршня; мм; ац и ап — коэффициенты линейного расширения материалов цилиндра и поршня. Для чугуна ац = = ап = 11 • 10‘6 1/К; для алюминиевых сплавов ац = ап =22х
208
X 10"® 1/К; Тц, Тг и Тю — соответственно температура стенок цилиндра, головки и юбки поршня в рабочем состоянии. При водяном охлаждении Тц = 383 4- 388, ТР = 473 4- 723 и Тю = 403 4- 473 К, а при воздушном Тд =443 4-463, Тг = 573 4- 873 и Тю =483 4-613 К; То =293 К — начальная температура цилиндра и поршня.
При получении отрицательных значений Др или Д„ (натяг) поршень непригоден к работе. В этом случае необходимо увеличить Дг или Дю и соответственно уменьшить Dr или DK или предусмотреть разрез юбки поршня. При нормальной работе поршня Др = = (0,002 4- 0,0025)D и Д» = (0,0005 4- 0,0015) D.
Расчет поршня карбюраторного двигателя. На основании данных расчетов (теплового, скоростной характеристики и динамического) получили: диаметр цилиндра D = 78 мм, ход поршня S = 78 мм, действительное максимальное давление сгорания, рга =6,195 МПа при = 3200 об/мин, площадь поршня FB = 47,76см2, наибольшую нормальную силу Nmax — 0,0044 МН при <р = 370°, массу поршневой группы та = 0,478 кг, частоту вращения пх хтах = 6000 об/мин и X = 0,285.
В соответствии с существующими аналогичными двигателями и с учетом соотношений, приведенных в табл. 50, принимаем: толщину днища поршня 8 = 7,5 мм, высоту поршня Н = 88 мм; высоту юбки поршня Лю =58 мм, радиальную толщину кольца t =3,5 мм, радиальный зазор кольца в канавке поршня Д/ = 0,8 мм, толщину стенки головки поршня з = 5 мм, величину верхней кольцевой перемычки Лп = 3,5 мм, число и диаметр масляных каналов в поршне — Ю и dn = 1 мм (рис. 96). Материал поршня — алюминиевый сплав, ап = 22 10-® 1/К; материал гильзы цилиндра — чугун, Од = 11 • КГ® j/к.
Напряжение изгиба в днище поршня
анз = р2д (г£/8)2 = 6,195 (29,7/7,5)2 = 97,1 МПа,
где гг = D/2 — (s + t 4- At) — 78/2 — (5 4- 3,5 4- 0,8) = 29,7 мм. Днище поршня должно быть усилено ребрами жесткости. Напряжение сжатия в сечении х — х
осж = P2JFx_x = 0,0296/0,00096 = 30,8 МПа,
где Р2д = pz-FB = 6,195 47,76 • 10~4 = 0,0296 МН; Рж_х=(к/4)(г/2— — d?) — п>Д= ((3,14/4) (69,42 — 59,42) - 10-5] - 10"® = 0,00096 м2;
dK =D — 2 (f 4- At) = 78 — 2 (3,54-0,8) = 69,4 мм; F'=(dK — dt) dj2 = = (69,4 — 59,4)- 1/2 = 5 мм<
Напряжение разрыва в сечении х — х:
максимальная угловая скорость холостого хода
®х.хтах = ипх.хтах/30 = 3,14 - 6000/30 = 628 рад/с;
8—370 209
масса головки поршня с кольцами, расположенными выше сечения х — х:
тх_х = 0,5/Пц = 0,5 • 0,478 = 0,239 кг;
максимальная разрывающая сила
Р} = mx-Ж.хтахО + М = °-239 • 0,039 • 6282 (14-0,285). 10~в =
= 0,0047 МН;
напряжение разрыва
Ор = Pj/Fx_x = 0,0047/0,00096 = 4,9 МПа.
Напряжения в верхней кольцевой перемычке:
среза
т = 0,0314pZjD/An = 0,0314 • 6,195 • 78/3,5 = 4,34 МПа;
изгиба
оиз== 0,0045ргд(Д/Лп)2 = 0,0045 • 6,195(78/3,5)2 = 13,88 МПа;
сложное __________
а2 = V 4з4- 4г2 = V 13,882 4-4.4,342 = 16,4 МПа.
Удельное давление поршня на стенку цилиндра:
91 = ^шах/(ЛкД = 0,0044/(0,058 • 0,078) = 0,97 МПа;
92 = A/max/(/7D) = 0,0044/(0,088 • 0,078) = 0,64 МПа.
Диаметры головки и юбки поршня:
Dr=,D —Дг = 78 —0,55 = 77,45 мм;
D„ = D —Дю = 78 — 0,156 = 77,844 мм,
где Др = 0.007D = 0,007 • 78 = 0,55 мм; Дю = 0.002D = 0,002 - 78 = = 0,156 мм.
Диаметральные зазоры в горячем состоянии
д; = Э[1 4-ац(Тц-Т0])-Пг[1 +ап(Тр-Т0)] =
= 78[1 4- П • 10-6(383—293)| —77,45[1 4-22. 10-6(593 —
— 293)] = 0,116 мм;
Дю =О[1 4-ап(7’10-Т0)]-ОюГ1 4-ап(Т10-Т0)] =
= 78(1 4-11 • 10-6(383 —293)] —77,844] 1 4-22. 10-6(413 — 293)] =
= 0,035 мм,
где Тц == 383 К, Тг = 593 К, Тю ~ 413 К приняты с учетом водя* ного охлаждения двигателя.
210
Расчет поршня дизеля. На основании данных расчетов (теплового, скоростной характеристики и динамического) диаметр цилиндра D = 120 мм, ход поршня S = 120 мм, максимальное давление сгорания р z = 11,307 МПа при п.ц = 2600 об/мин, площадь поршня Fn = 113 см2, наибольшая нормальная сила Nmax = 0,00697 МН при <р = 390°, масса поршневой группы тп = 2,94 кг, частота вращения «х.хшах = 2700 об/мин, А = 0,270.
В соответствии с существующими аналогичными двигателями и с учетом соотношений, приведенных в табл. 50, принимаем: высоту поршня Н = 120 мм, высоту юбки поршня Лю = 80 мм, радиальную толщину кольца t = 5,2 мм, радиальный зазор кольца в канавке поршня М =0,8 мм, толщину’стенки головки поршня s = 12 мм, толщину верхней кольцевой перемычки Лп = 6 мм, число и диаметр масляных каналов в поршне пк = 10 и dM = 2' мм (рис. 96). Материал поршня — алюминиевый сплав, ап = 22 • 10"® 1/К; материал гильзы цилиндра — чугун, ац = 11 • 10"® 1/К.
Напряжение сжатия в сечении х — х:
площадь сечения х — х
Рх-х = (^/4) (d2K - d?) - п'и F' = [(3,14/4) (1082 - 842) -
— 10 - 20] • 10"® = 0,0034 м2,
где =D —2(/+ А/) = 120—2(5,2 +0,8) = 108 мм; dt = D — — 2(s +/ + 10=120—2(12 + 5,2 + 0,8) =84 мм; F'=dM(dK—d,/2= = 2(108—88)/2 = 20 мм2;
максимальная сжимающая сила
Pzmax = p2Fn = 11,307- 113- 10~4 = 0,128 МН;
напряжение сжатия
аож = Рг m^/Fx_x = 0,128/0,0034 = 37,6 МПа.
Напряжение разрыва в сечении х — х-. максимальная угловая скорость холостого хода
®x.jcmax = шах/30 = 3,14 • 2700/30 = 283 рад/с;
масса головки поршня с кольцами, расположенными выше сечения х — х:
тх_х = 0,6тп = 0,6 • 2,94 = 1,764 кг;
максимальная разрывающая сила
Pj = mx-xR<&.* max (1 + X) = 1,764 - 0,06 - 2832 - (1 + 0,27) - 10-® =
= 0,0108 МН;
напряжение разрыва
ар = P}/Fx_x = 0,0108/0,0034 = 3,18 МПа.
8*,
211
Напряжения в верхней кольцевой перемычке: среза
т = 0,0314pzD/hn = 0,0314 • 11,307 • 120/6 = 7,1 МПр;
изгиба
Онз = 0,0045рг (D//in)2 = 0,0045 • 11,307 (120/6)2 = 20,4 МПа;
сложное
<js = V а2нз4-4т2 = ]/ 20,42 4- 4- 7,12 = 24,9 МПа.
Удельные давления поршня на стенку цилиндра:
<?! = Л/тах/(/1юО) = 0,00697/(0,08 • 0,12) = 0,73 МПа;
<?2 = = 0,00697/(0,12 • 0,12) = 0,484 МПа.
Диаметры головки и юбки поршня:
DP = D —Дг = 120 — 0,72 = 119,28 мм;
D„ = D —Дю = 120-0,24= 119,76 мм,
где Дг = 0.006D = 0,006 • 120 = 0,72 мм; Дю = 0.002D = 0,002-120= = •0,24 мм,
Диаметральные зазоры в горячем состоянии:
Д'Р = D [1 + ац (Тц - То)] — Dr [1 + ап (Тг — То)] =
= 120(1 + 11 - 10-е (388 — 293)] — 119,28(1 4-
4-22 • IO'6(493 —296)] = 0,3 мм;
Дю = D [1 4- ац (Уц — Т’о)! — Цо П + ап (Т’ю — Т’о)! =
= 120(1 4- Н • 10-<>(388 — 293)] — 119,76(1 4-22-10-0(428—293)] = = 0,06 мм,
где Тц = 388, Тг = 493 и Тю = 428 К приняты с учетом водяного охлаждения двигателя.
$ 45. ПОРШНЕВЫЕ КОЛЬЦА
Поршневые кольца работают в условиях высоких температур и значительных переменных нагрузок. Изготовляют их из серого или легированного чугуна. Для форсированных двигателей компрессионные кольца изготовляют из легированных сталей.
Основными конструктивными параметрами поршневых колец являются: отношение диаметра цилиндра к радиальной толщине кольца D/t; отношение разности между величинами зазоров замка кольца в свободном и рабочем состояниях к толщине кольца Ao/t; высота кольца а. Значения конструктивных параметров поршневых колец карбюраторных двигателей и дизелей представлены в табл. 50.
212
Расчет колец заключается: а) в определении среднего давления кольца на стенку цилиндра, которое должно обеспечивать достаточную герметичность камеры сгорания и не должно резко увеличивать потери мощности двигателя на трение колец о стенки цилиндра; б) в построении эпюры давления кольца по окружности; в) в определении напряжений изгиба, возникающих в сечении, противоположном замку, при надевании кольца на поршень и в рабочем состоянии; г) в установлении монтажных зазоров в прямом замке кольца.
Среднее давление (МПа) кольца на стенку цилиндра
рср = 0,152Е-----, (247)
где Е — модуль упругости материала кольца (для серого чугуна Е — = 1 • 105 МПа, для легированного чугуна Е — 1,2 • 105 МПа, Для стали Е = (2 4- 2,3) 105 МПа).
Среднее радиальное давление рср (МПа) будет:
Для компрессионных колец...................0,11—0,37
Для маслосъемных колец .............«... 0,2—0,4
При снижении частоты вращения двигателя и увеличении диаметра цилиндра величина рср должна иметь значение ближе к нижнему пределу. Для обеспечения хорошей приработки кольца и надежного уплотнения давление р кольца на стенку цилиндра в различных точках окружности должно изменяться по эпюре (рис. 97), построенной по следующим данным, рекомендованным ГОСТом:
Угол ф, град........ 0 30 60 90 120 150 180
Отношение р/рср == jjtK 1,05 1,05 1,14 0,90 0,45 0,67 2,85
Значительное повышение давления у замка (рис. 97) способствует равномерному износу кольца по окружности.
Напряжения изгиба кольца (МПа): в рабочем состоянии
аиз1 = 2,61рср (D//— I)2; (248)
при надевании его на поршень
4£ (1 — 0,114Ло/0
m {DU- 1,4)(Z>/0 ’
(249)
где tn — коэффициент, зависящий от способа надевания кольца (при расчете принимается т = 1,57). Допустимые напряжения при изгибе кольца [оиз] = 220 450 МПа. Нижний пре-
дел относится к двигателям с большим диаметром цилиндра. Обычно аиз2 > аиз1 Ю—30%.
Рис. 97. Эпюра давлений компрессионного кольца карбюраторного двигателя
213
Монтажный зазор (мм) в прямом замке поршневого кольца в холодном состоянии
Дк = Д/ + [<Ч (Т* ~ То) - % (Тц - То)], (250)
где д; — минимально допустимый зазор в замке кольца во время работы двигателя (Дк = 0,06 4- 0,10 мм); ак и ац — коэффициенты линейного.расширения материала кольца и гильзы цилиндра; Тк, Ти и То— соответственно температура кольца, стенок цилиндра в рабочем состоянии и начальная температура То = 293 К; при водяном охлаждении Тц = 383 4- 388, Тк = 473 4- 573 К; при воздушном Тц = 443 4-4- 463, Тк = 523 4- 723 К.
Расчет поршневого кольца карбюраторного двигателя. Необходимые данные для расчета приведены в § 44. Материал кольца — серый чугун, Е = 1,0 • 105 МПа.
Среднее давление кольца на стенку цилиндра
рср = 0,152Е
AJt (D/t—l)3 (D/t)
= 0,152. 1 • 105 X
10,5/3,5
(78/3,5 — l)s (78/3,5)
= 0,212 МПа,
где Ло = 3/ = 3 • 3,5 = 10,5 мм.
Давление (МПа) кольца на стенку цилиндра в различных точках окружности
Р = PapV'K'
Значения рк для различных углов ф приведены выше.
Результаты расчета р, а также рк для различных углов ф приведены ниже:
ф, град . ............. 0 30 60 90 120 150 180
Рк..................... С05 1,05 1,14 0,90 0,45 0,67 2,85
р, МПа................. 0,223 0,223 0,242 0,191 0,0955 0,142 0,604
По этим данным построена эпюра давлений кольца на стенку цилиндра (рис. 97).
Напряжение изгиба кольца в рабочем состоянии
аиз, = 2,61pcp(D//— I)2 = 2,61 • 0,212(78/3,5— I)2 = 251 МПа.
Напряжение изгиба при надевании кольца на поршень
_ Ур-УШМ _ «1.10. (1—0.114-10,5/3,51 m (£)// — 1,4) (£///) 1,57(78/3,5 — 1,4) (78/3,5)
Монтажный зазор в замке поршневого кольца
Дк = Дк + nD [ак (Тк - То) - ац (Тц - То)] = = 0,08 + 3,14.78(11 • 10-6(493—293)— 11 10-6(383 — 293)] = = 0,352 мм,
где д; = 0,08 мм, Тц = 383, Тк = 493 и То = 293 К.
214
Расчет поршневого кольца дизеля. Необходимые данные для расчета приведены в § 44. Материал кольца — серый чугун, Е = = 1-105 мПа.
Среднее давление кольца на стенку цилиндра
= 0,1522?------------------= 0,152 - Ь 105 х
СР (£>//—I)3 (£>//)
X
15,6/5,2
(120/5,2— 1)3 (120/5,2)
= 0,186 МПа,
где Ло = 3/ = 3 • 5,2 = 15,6 мм.
Давление (МПа) кольца на стенку цилиндра в различных точках окружности
Р 3 РсрР-к.
Результаты расчета р, а также рк для различных углов ф приведены ниже:
ф, град............... 0 30 60 90 120 150 180
р.к................... 1,05 1,05 1,14 0,90 0,45 0,67 2,85
р, МПа................ 0,195 0,195 0,212 0,167 0,0837 0,125 0,53
По этим данным построена эпюра давлений кольца на стенку цилиндра (рис. 98).
Напряжение изгиба кольца в рабочем состоянии
°из1 = 2,61/?ср (D[t I)2 =
= 2,61 - 0,186(120/5,2 — I)2 -
« 235 МПа.
Напряжение изгиба при надевании кольца на поршень
4£(1 — о, 114Л0/0
Оно 9 = ‘ " 1 —
tn(D!t — 1,4) (D/t)
4-1 -105 (1— 0,114-15,6/5,2) = “ 1,57(120/5,2— 1,4) (120/5,2)
= 337 МПа.
Рис. 98. Эпюра давлений компрессионного кольца дизеля
Монтажный зазор в замке поршневого кольца
дк = Дк + KD к (Тк - То) — ац (Тц — то)] = 0,08 + + 3,14 . 120(11 • IO’6 (498 —293) —11 • 10“® (388 — 293)] = 0,536 мм, где Д' =. 0,08 мм, Тц = 388, Тк = 498 и То = 293 К.
215
§ 46. ПОРШНЕВОЙ ПАЛЕЦ
Во время работы двигателя поршневой палец подвергается воздействию переменных нагрузок, приводящих к возникновению напряжений изгиба, сдвига, смятия и овализании. В соответствии с указанными условями работы к материлам, применяемым для изготовления пальцев, предъявляются требования высокой прочности и вязкости. Этим требованиям удовлетворяют цементированные малоуглеродистые и легированные стали.
Основные конструктивные размеры поршневых пальцев (см. рис. 96) обычно принимаются по статистическим данным (см. табл. 50) или по данным прототипов с последующей проверкой расчетом.
Расчет поршневого пальца включает определение удельных давлений пальца на втулку верхней головки шатуна и на бобышки, а также напряжений от изгиба, среза и овализации.
Максимальные напряжения в пальцах карбюраторных двигателей возникают при работе на режиме максимального крутящего момента, а в пальцах дизелей — при работе на номинальном режиме.
Расчетная сила (МН), действующая на поршневой палец:
Р — Pzmax Fп + kPj. (251)
Для карбюраторных двигателей: /?гтах — максимальное давление газов на режиме максимального крутящего момента (МПа); k = 0,76 4- 0,86 — коэффициент, учитывающий массу поршневого пальца; Р; =—Ю"6 — сила инерции поршневой группы прим ==пд1,МН;
для дизелей: pz rnax— максимальное давление газов на номинальном режиме, МПа; k =0,68 — 0,81 — коэффициент, учитывающий массу поршневого пальца; Pj =—хппсо2/?(1 + К) • 10-6 — сила инерции поршневой группы при п = МН.
Удельное давление (МПа) пальца на втулку поршневой головки шатуна
(252) где dn — наружный диаметр пальца, м, — Длина опорной поверхности пальца в головке шатуна, м.
Удельное давление плавающего пальца на бобышки
q^PlWu-b}], (253)
где /п — общая длина пальца, м; Ь — расстояние между торцами бобышек, м; (Zn—Ь) — длина опорной поверхности пальца в бобышках, м.
Для современных автомобильных и тракторных двигателей ~ == 20 60 и ?б = 15-?-50 МПа. Нижние пределы относятся к трактор-
ным двигателям.
Напряжение изгиба пальца (МПа) при условии распределения нагрузки по длине пальца согласно эпюре, приведенной на рис. 96:
оиз = Р (/п + 2b - 1,5/ш)/[1,2 (1 - a*) rf3] > (254)
216
где а = d3/da — отношение внутреннего диаметра пальца к наружному.
Для автомобильных и тракторных двигателей [оиэ] = 1004-250 МПа.
Касательные напряжения (МПа) от среза пальца в сечениях, расположенных между бобышками и головкой шатуна:
т = 0.85Р (1 + а + «2)/[(1 — «*) 4] • (255>
Для автомобильных и тракторных двигателей [т] = 60 4- 250 МПа. Нижние пределы относятся к тракторным двигателям, а верхние — к пальцам, изготовленным из легированной стали.
Рис. 99. Расчетная схема поршневого пальца: а — распределение нагрузки; б — эпюры напряжений
Вследствие неравномерного распределения сил, приложенных к пальцу (принимается синусоидальное распределение нагрузки по поверхности пальца — рис. 99, а), при работе двигателя происходит деформация сечения пальца (овализация). Возникающие при этом напряжения имеют различные значения по длине пальца и его сечению.
Максимальная овализация пальца (наибольшее увеличение горизонтального диаметра Adnmax, мм) наблюдается в его средней, наиболее напряженной части:
Arfn max = Цтг- [°.1 - (« - 0,4)3L (256)
где Е — модуль упругости материала пальца (для стали £п = (2,0 4-4-2,3)105 МПа).
Значение Adnmax не должно быть больше 0,02—0,05 мм.
Напряжения, возникающие при овализации пальца на внешней и внутренней поверхностях (рис. 99, 6), определяют для горизонтальной (точки 1 и 2 при <|» = 0°) и вертикальной (точки 3 и 4 при <|» = 90°) плоскостей по следующим формулам:
217
на внешней поверхности пальца в горизонтальной плоскости (точки 1, ф =0°)
О„0б = _1!р.[о,19 (2 + °)(1+°)--!_][(),1 —(а—0,4)3] МПа;
L «-»> 1—.J (257)
на внешней поверхности пальца в вертикальной плоскости (точки 3, ф = 90е)
___ 15р [о 171 (2+ «)d + «) a. Q.'?36l х Мп L ’ (1-а)? 1-“J
X [0,1 — (а — 0,4)3] МПа; (258)
на внутренней поверхности пальца в горизонтальной плоскости (точки 2, ф = 0°)
°<о» —
__15Р_ Го19(1+.2*)(1-Н± + _J_1 х
Wn L (1—а)*а 1-aJ
х |0,1 — (а — 0,4)»] МПа; (259)
на внутренней поверхности пальца в вертикальной плоскости (точки 4, ф — 90°)
. = J5L. [0,17411+^1+^ - 2^1 х
i9° Мп L (1-а)аа 1—а]
X [0,1 — (а — 0,4)эJ МПа. (260)
Наибольшее напряжение овализации возникает на внутренней поверхности пальца в горизонтальной плоскости. Это напряжение, подсчитанное по формуле (259), не должно превышать 300—350 МПа.
Расчет поршневого пальца карбюраторного двигателя. Основные данные для расчета приведены в §44. Кроме того, принимаем: действительное максимальное давление сгорания рг max = ргд = 6,195 МПа при пм == 3200 об/мин (из расчета скоростной характеристики), наружный диаметр пальца dn = 22 мм, внутренний диаметр пальца с/д — 15 мм, длину пальца 1П = 68 мм, длину втулки шатуна 1т^= = 28 мм, расстояние между торцами бобышек b = 32 мм. Материал поршневого пальца — сталь 15Х, Ё — 2 • 105 МПа. Палец плавающего типа.
Расчетная сила, действующая на поршневой палец: газовая
Рг max = Датах = 6,195 • 47,76 • 10"‘ = 0,0296 MHj инерционная
Р, = — (1 + К) • 10~6 = — 0,478 • 335а • 0,039 (1 + 0,285) х
X IO”6 = — 0,00269 МН, где сом = ппм/30 — 3,14 • 3200/30 = 335 рад/с;
218
расчетная
Р = Рг max + kPj = 0,0296 — 0,82.0,00269 = 0,0274 МН.
Удельное давление пальца на втулку поршневой головки шатуна
р 0,0274 .. с »ЛГ,
ош ------- ------:-----= 44,5 МПа.
<Un 0,022 0,028
Удельное давление пальца на бобышки
dn(ln—b) 0,022(0,068 — 0,032)
Напряжение изгиба в среднем сечении пальца о Р(/п + 26-1,5/,„) из 1,2(1—a4) d®
__ 0,0274 (0,068 + 2 • 0,032 —1,5-0,028) = 24g j МПа 1,2- (1—0,682*) - 0,022s
где а = djdy, ₽= 15/22 — 0,682.
Касательные напряжения среза в сечениях между бобышками и головкой шатуна
х = 0,85Р(1 +« + «2) _ 0,85 - 0,0274 (1 + 0,682 + 0,682s) = МПа (1—«*)dg (1 —0.6824) • 0,022s
Наибольшее увеличение горизонтального диаметра пальца при овализации
., 1,35Р ( 1 + «\3ГЛ t Z Л
max — I ‘ I [0,1 — (в —0,4) ] —
. Ela \ 1 — а )
= 1,3 5.0.,02 7± /l + O^X3 |0)1_(0)682_,0,4)3]. ЮЗ = 2-10s-0,068 U—0,682/
= 0,0313 ММ.
Напряжения овализации на внешней поверхности пальца: в горизонтальной плоскости (точки 1, <|» = 0°)
= tF - rd'»-1 -
1,5 - 0,0274 Гф ig (2 + 0,682) (1 +0.682)___1 1
0,068 - 0,022 [ ’ (1—0,682)s 1—0,682 J*
X [0,1 — (0,682 — 0,4)3] = 114 МПа;
в вертикальной плоскости (точки 3, <|> = 90°)
°«90° =---7Т- [°,174 2~ (*+ 4 + ^1 [0,1 - (а - 0.4)3] =
‘n^n I U—а) 1—“J
219
15 - 0,0274 Г/л 17л (2 + 0,682) (1 +0,682) , -------------I и, 11ч----------------------+
0,068 - 0.022 |_\ (1 —0,682)8
+ 0,6ff 1 [0,1 — (0,682 — 0,4)3] = — 208,5 МПа. 1 -0,682]
Напряжения овализации на внутренней поверхности пальца: в горизонтальной плоскости (точки 2, ф ~ 0°)
Ci 0°
= 15Р Го 19(1+2а)(1+а) +
Zndn _ (1 а)2 а
—— [0,1—(а —0,4)31 =
1 —а
= *5*0,0274 Го 19 (1+ 2 > 0,682) (1 + 0,682)
0,068 • 0,022 |_ ’ (1 —0,682)2’0,682
+-----5---1 [0,1 — (0,682 — 0,4)3] = — 300 МПа;
в вертикальной плоскости (точки 4, ф = 90°)
О = [о,174 (.!+2а) (»+<*) _ +6361 [0д _ (а _ о 4)3] =
190 Wn L (1—а)2я 1 —а J v ’
15 0,0274 [q 171 (1 + 2 - 0,682) (1 +0,682) 0,068 • 0,022 [ ’ (1 — 0,682)2 • 0,682
----2^36_1 [0,1 —(0,682 —0,4)3] = 171 МПа.
1 —0,682]
Расчет поршневого пальца дизеля. Основные данные для расчета приведены в § 44. Кроме того, принимаем: наружный диаметр пальца dn — 45 мм, внутренний диаметр пальца dB = 27 мм, длину пальца /п = 100 мм, длину втулки шатуна /ш = 46 мм, расстояние между торцами бобышек Ь = 51 мм. Материал поршневого пальца — сталь 12ХНЗА, Е — 2,2 • 105 МПа. Палец плавающего типа.
Расчетная сила, действующая на поршневой палец: газовая
ИЗ. 10-‘ = 0,128 МН;
инерционная
Pj = — тп<огЯ(1 + К) = — 2,94 • 272г • 0,06(1 + 0,27) =—0,0166 МН, где со — лПл/730 = 3,14 • 2600/30 = 272 рад/с;
расчетная
Р = PZ max +kPj = 0,128 — 0,72.0,0166 = 0,116 МН.
Удельное давление пальца на втулку поршневой головки шатуна qm = Р/(с!п/ш) = 0,116/(0,045 • 0,046) = 56 МПа.
Удельное давление пальца на бобышки
Чб = P/[d„(la — />)] = 0,116/10,045(0,1 — 0,051)] = 52,6 МПа.
Напряжение изгиба в среднем сечении пальца
220
= Р (1П + 26 — 1,5/ш) = 0,116(0,1 + 2 • 0,051 — 1,5 — 0,046) _
0,13 1,2(1—1,2(1—0,64) • 0,0453 “
= 161 МПа,
где а — dB/dn = 27/45 — 0,6.
Касательные напряжения среза в сечениях между бобышками и головкой шатуна
_ 0,85Р (1 + а + а2) _ 0,85-0,116(1 +0,6 + 0,62) _ 1Па мп
(1 —0,6*) *0,0452
Наибольшее увеличение горизонтального диаметра пальца при овализации
Д^птах = -г— —— Г0-1 — (а~ 0,4)3] -Ып \ I —а )
= 1,35 -0,116 / l. + 0i6 y [0 j _ (о 6_0 4)3] 10з = Q 042 мм<
2,2 10s • 0,1 \ 1 —0,6 )
Напряжения овализации на внешней поверхности пальца:
в горизонтальной плоскости (точки 1, ф = 0°)
<3 = Го,19-£+аШ -----— 1 [0,1 — (а —0,4)3] =
“° 1пап L (1-«)2 1-«J
= 15-0,116 Го 19(2+0,6) (1 4-0,6) _ 1 1 0 J _
0,1-0,045 [’ (1 — 0,6)2 1—0,6 J ’
— (0,6 —ОД)3] = 87 МПа;
в вертикальной плоскости (точки 3, ф = 90°)
с =-------[0,174 .(2+a)(1+jL). 21^5.1 [Q1 — (а —ОД)3] =
а9° /А [ (1 — а)2 1 - а J 4 ’
15-0,116 Гп (2 + 0,6) (1 +0,6) 0,636 1
= 0,1-0,045 L ’ (1-0.6)2' + 1 -0,6 ] Х
X [0,1—(0,6 —0,4)3] =—218 МПа
Напряжения овализации на внутренней поверхности пальца: в горизонтальной плоскости (точки 2, ф = 0°)
о.0о =----— |о,19^ + 2а>-(1+-^+ —1 [ОД — (а —0,4)3] =
1 lada L (1 —а)ая 1 -a J ' 7
15-0,116 Го 19 (1+2-0,6) (1 + 0,6) 0,1 • 0,045 [ ’ (1 — 0,6)2 • 0,6
----?--1 [ОД — (0,6 — 0,4)3] = _ 337 МПа;
1—0,6 J ’
в вертикальной плоскости (точки 4, ф — 90°)
221
. = J5P- Г0,174(1+-2а) -+а) - [0,1 -(а-0,4)31
90 lndn L (1—а)?а 1—а]
= 15-0,116 rQ 171 (1 + 2 • 0,6) (1 +0.6) 0,1 • 0,045 [ ’ (1 — 0,6)2 . о,б
0,636
1—0,6
[0,1 — (0,6 —0,4)3] = 170,5 МПа.
Глава XII
РАСЧЕТ ШАТУННОЙ ГРУППЫ
б 47. ПОРШНЕВАЯ ГОЛОВКА
Конструкция шатунов, применяемых в автомобильных и тракторных двигателях, разнообразна и зависит в основном от типа двигателя и расположения цилиндров. Расчетными элементами шатунной группы являются: поршневая и кривошипная головки, стержень шатуна и шатунные болты. На рис. 100 приведена расчетная схема шатуна.
При работе двигателя шатун подвергается воздействию знакопеременных газовых и инерционных сил, а в отдельных случаях эти силы создают ударные нагрузки. Поэтому шатуны изготовляют из углеродистых или легированных сталей, обладающих высоким сопротивлением усталости. Шатуны карбюраторных двигателей изготовляют из стали марок 40, 45, 45Г2, а дизелей — из стали с более высокими пределами прочности и текучести 40Х, 18ХНВА, 49ХНМА. Механические характеристики сталей приведены в табл. 44 и 45. Для повышения усталостной прочности шатуны после штамповки подвергают механической и термической обработке — полированию, обдувке дробью, нормализации, закалке и отпуску.
Значения основных конструктивных параметров поршневой головки шатуна приведены в табл. 51.
Таблица 51
Величина Карбюраторные двигатели Дизели
Внутренний диаметр поршневой головки d: без втулки с втулкой ......... (1,104-1 ,25) da d^da (1,10-5-1,25) dn
Наружный диаметр головкн dv , . (1,25-5-1,65) dn (1,3-5-1,7) dn
Длина поршневой головки шату-на /щ! закрепленный палец » , « . . (0,28-5-0,32) D (0,28-5-0,32) D
плавающий палец (0,33-5-0,45) D (0,33-5-0,45) D
Минимальная радиальная толщина стенки головки йг (0,16-5-0,27) d„ (0,16-5-0,27) dn
Радиальная толщина стенки втулки Sb ..... . . . . , . . . (0,0554-0,085) da (0,070-r0,085) dv
222
Поршневая головка ша- 1щ,
туна (рис. 100) рассчитывается на:
а) усталостную прочность в сечении I —/от действия инерционных сил (без учета запрессованной втулки), достигающих максимальных значений при работе двигателя на режиме максимальной частоты вращения при холостом ходе;
б) напряжения, возникающие в головке от воздействия на нее запрессованной втулки;
в) усталостную прочность в сечении А — А (место перехода головки шатуна в стержень — заделка головки) от действия суммарных (газовых и инерционных) сил и запрессованной втулки. Расчет в этом случае производится для того режима работы
100. Расчетная схема шатунной группы
двигателя, при котором амплитуда
изменения суммарных сил максимальна.
Сечение / — I поршневой головки нагружается на режиме п ~ «= «х.х переменной силы инерции масс поршневой группы та и верхней части головки тв.г (выше сечения / — /)
Pj = — (та + /Ив.г) (Вх.х max R (COS <р + 1 COS 2ср). (261)
Величина тв.г определяется по геометрическим размерам- верхней части головки и удельной массе материала шатуна или ориентировочно принимается в пределах 6—9% массы шатуна.
Сила Pj создает в сечении /—/ максимальное сттах = (^п + + /Пв.г) «>х.хтах Р(1 + Х)/(2/гг/ш) и минимальное от1п = 0 напряжения, так как приР/ > 0 сила инерции направлена к оси коленчатого вала и не нагружает сечение / —/.Следовательно, напряжения в сечении / — / изменяются по закону пульсирующего цикла.
Запас прочности определяется по формулам, приведенным в § 43, и составляет для автомобильных и тракторных двигателей 2,5—5.
Напряжения в поршневой головке шатуна, возникающие от запрессовки в нее втулки и от различия коэффициентов расширения материалов втулки и головки, характеризуются суммарным натягом (мм)
Д2= Д + Af, (262)
223
где Д — натяг посадки бронзовой втулки (при расчете принимается наибольшая величина в соответствии с применяемой посадкой), мм; Д t — температурный натяг, мм:
A, = d(aB —аг)ДТ. (263)
Здесь d — внутренний диаметр головки, мм; ав = 1,8 • 10~51/К — термический коэффициент расширения бронзовой втулки; ар = 1,0х X 10~51/К — термический коэффициент расширения стальной головки; ДТ = 100-4- 120 К — средняя температура подогрева головки и втулки при работе двигателя.
Удельное давление (МПа) от суммарного натяга на поверхности соприкосновения втулки с головкой
___________________________________________, (264)
(<? + &)/( 4-<?) + ? (^ + ^)/(^-^,)-(Л
Еш + Е«
где dr, d и da — соответственно наружный и внутренний диаметры головки и внутренний диаметр втулки, мм; р =0,3 — коэффициент Пуассона; Еш = 2,2 • 10s — модуль упругости стального шатуна, МПа; Ев«1,15- 105 —модуль упругости бронзовой втулки, МПа.
Напряжения от суммарного натяга на внешней и внутренней поверхностях поршневой головки определяются по формуле Ляме:
, 2d2
% = (265)
d2T — d2
' 4 +
= P . (2C6)
d?T- d2
Значения o'o и a'i могут достигать 100—150 МПа. Следует отметить, что для плавающей втулки напряжения от суммарного натяга
Рис. 101. Рапределенне нагрузок на поршневую головку шатуна-
а — при растяжении; б — при сжатии
равны нулю.
Сечение А —А поршневой головки на режиме п — = пм или п = нагружается переменными суммарными силами Р = Рг Р- и постоянной силой от действия запрессованной втулки.
Суммарная сила, растягивающая головку, достигает максимального значения при положении поршня в в. м. т. во время начала впуска. Эта сила определяется без учета незначительной в этот момент величины газовых сил
P/n—'WO +*), (267)
224
где та —масса поршневой группы, кг; о — угловая скорость (<о = == лПдг/30 рад/с при расчете на режиме п = nN и ш = лп^/ЗО рад/с— на режиме п = пм).
На основании экспериментальных и расчетных данных принимают, что радиальное давление от силы распределяется равномерно по внутренней поверхности верхней половины головки (рис. 101, а).
В соответствии с расчетной схемой (рис. 101, а) принимается, что нижняя часть головки, опирающаяся на стержень большой жесткости, не деформируется, а действие отброшенной правой части головки заменяется нормальной силой N >0 (Н) и изгибающим моментом М>0 (Н* м). Приближенно
Nj о - - Pj п (0,572 - 0,0008?ш.3); (268)
Му о = -Р;пгср(О,ОООЗЗ?ш.3-0,0297), (269)
где <рш з — угол заделки, град; гср= + d)/^— средний радиус поршневой головки, м.
На участке 1, лежащем в интервале изменения угла от 0 до 90°:
Nji = Afjocos Тш — О^/пО — созсрш); (270)
Mji = M;o+ AVcp (1 “ cos <РШ) + 0,5Pjnrcp (1 — cos <рш). (271)
На участке 2, лежащем в интервале изменения угла <рш от 90° до угла заделки фш,3:
N it = N jo cos — 0,5 Pja (sin — cos <?ш); (272)
A4j2 ЛЪо + NjQ^Cp (1 cos ^ш) 4~ 0,5Pjnrcp(sin - cos ^ш). (273)
Для опасного сечения А —А при фш = фш.з значения нормальной силы и изгибающего момента подсчитывают по формулам (272) и (273).
По значениям Л^/срш.з и 7И/срщ.з определяют напряжения в головке на внешнем и на внутреннем волокнах.
Без учета запрессованной втулки напряжения (МПа) в сечении А —А головки шатуна:
на внешнем волокне
на внутреннем волокне
(274)
(275)
гдеЛг = (dp—d)/2 — толщина стенки головки, м; /ш —длина поршневой головки, м.
При наличии запрессованной втулки в головке шатуна происходит их совместная деформация. Вследствие этого на головку передается не вся нормальная сила ЛГ/^Ш з, а ее часть, пропорциональная коэффициенту К. Влиянием втулки на уменьшение изгибающего момента М/у>ш 3 пренебрегают.
225
Коэффициент
K = EMEaFP + EBFB), (276)
где Fr = (dr —й)1ш и FB — (d —— соответственно площадь сечения стенок головки и втулки.
С учетом коэффициента К напряжения
*2Л1/9 ш.з 6'ср + Лг пьз 10~8 (277)
”а1 — Лг(2гор + Лг) /шЙг
<hi = — 2М/9 ш 6гср + ^г 3 (2гср — Лг) - + Ш>3 ЦТ» /щ^Г (278)
Суммарная сила (Н), сжимающая головку, достигает максимального значения после в. м. т. (10—20° угла поворота кривошипа) в начале расширения
Feat — (P-z д ро) “Ь Р/п — (Ргд ^°)
— maRa>2 (cos <р + X cos 2<р),
(279)
где р z — максимальное давление сгорания, определяемое по скругленной индикаторной диаграмме; Pjn — сила инерции массы поршневой группы при значении ф, соответствующем значению угла кривошипа при р tR,
Пренебрегая смещением максимальной газовой силы относительно в. м. т., находим приближенно
Рек = (j% - Ро) Fn - (1 + X). (280)
Радиальное давление от сжимающей силы Рсж на внутреннюю поверхность нижней половины головки принимается косинусоидальным, как показано на расчетной схеме (рис. 101, б).
Для любого сечения на участках 1 и 2
^СЖ1 = р СК -^СО5ФШ; ^СЖ (281)
^СЖ1 " ^сж^ср ^СЖ 0 Р г L сж ср *1 + -^-(1-с05фш) ^сж ; (282)
sin?ni 2
СК 0
р
сж
ср ]
------— sin фш COS Ф, тс тс
^СЖ 2 Рек
^сж 2 ^ся/ср
о
Р г
сж ср
^(1-со3фш)-сж
sin ф ср 1
~~------------— sin фш — — COS фш
2 тс тс
(284)
226
В уравнениях (283) и (284) значения угла фш в отношение (рш/л подставляют в радианах, а значения Мож0/^аж и Мсжа/(Рсжгср) в зависимости от угла фщ.з заделки определяют по табл. 52.
Таблица 52
Параметры Угол заделки 3, град
100 105 110 115 120 125 130
сж Мсжо/(^сжгср) 0,0001 0 0,0005 0,00010 0,0009 0,00025 0,0018 0,00060 0,0030 0,00110 0,0060 0,00180 0,0085 0,00300
Таблица 53
Угол заделки <pIU 3> град
100 105 по 115 120 125 130
COS Фш.з —0,1736 —0,2588 —0,3420 —0,4226 —0,5000 —0,5736 —0,6428
1— СОЗсрщ.з 1,1736 1,2588 1,3420 1,4226 1,5000 1,5736 1,6428
sinVS-C0S<Pni.3 1,1584 1,2247 1,2817 1,3289 1,3660 1,3928 1,4088
8!п<рш,з 2 ~ 0,0011 0,0020 0,0047 0,0086 0,0130 0,0235 0,0304
— .Тш-3 sinx тс
Тш. 3 1 — COS срШв3 тс
Для облегчения вычислений изгибающего момента и нормальной силы в табл. 53 приведены значения тригонометрических зависимостей в функции угла фш.
Значения нормальной силы Л^сж<рш 3 и изгибающего момента МСЖу для опасного сечения А —А (фш — фш,3) определяются по формулам (283) и (284).
Напряжения от суммарной сжимающей силы в сечении А —А: на внешнем волокне
га сж — I 2МСЖ(р
Ш. 3
'6гср + Лг
_________+ ДОа, Аг(2гср+Ч
Ш .3
1 • 10~6 ттт *
(285)
на внутреннем волокне
сж
— 2Л4сжц>
6Г°р+—+ 7<Л'СЖ¥
11
ш-3 Аг(2гср-М
1 i i02 ’Ш-3
(286)
227
где К — коэффициент, учитывающий наличие запрессованной бронзовой втулки [см. формулу (276)].
Запас прочности поршневой головки шатуна в сечении А — А определяется по уравнениям, приведенным в §43. Суммарные напряжения, вызываемые в этом сечении газовыми и инерционными силами и запрессованной втулкой, изменяются по асимметричному циклу, а минимальным запасом прочности обладает наружное волокно, для которого
^max = (287)
amin = < + <»„ cat. (288)
Запас прочности поршневых головок изменяется в пределах 2,5— 5,0. Повышение запаса прочности и снижение напряжений внешнего волокна достигаются за счет уменьшения угла заделки до (рш.з = 90° и увеличения радиуса дуги сопряжения головки со стержнем.
Расчет поршневой головки шатуна карбюраторного двигателя. Из теплового и динамического расчетов имеем давление сгорания р Zr = 5,502 МПа на режиме п = nN ~ 5600 об/мин при tp = 370°, массу поршневой группы та = 0,478 кг; массу шатунной группы тт = 0,716 кг; максимальную частоту вращения при холостом ходе «х.хтах = 6000 об/мин; ход поршня S = 78 мм; площадь поршня Fn = 47,76 см2; X = 0,285. Из расчета поршневой группы имеем диаметр поршневого пальца da ~ 22 мм; длину поршневой головки шатуна /ш = 28 мм. По табл. 51 принимаем: наружный диаметр головки d? = 30,4 мм; внутренний диаметр головки d ~ 24,4 мм; радиальную толщину стенки головки hr—(dr—d)/2=(30,4—24,4)/2 = 3 мм; радиальную толщину стенки втулки sB = (d —dn)/2 = (24,4—22)/2 = = 1,2 мм.
Материал шатуна —углеродистая сталь 45Г2; Еш = 2,2 • 105МПа, аг = 1 • 10~51/К. Материал втулки —бронза; Ев~ 1,15 • 105 МПа, ав= 1,8 • 10-Ч/К.
По табл. 43 и 45 для углеродистой стали 45Г2:
предел прочности ив = 800 МПа;
пределы усталости при изгибе o_i = 350 МПа и растяжении - сжатии ст_1р = 210 МПа;
предел текучести пт = 420 МПа;
коэффициенты приведения цикла при изгибе аа =0,17 и растяжении - сжатии а„ = 0,12.
По формулам (213) —(215) определяем: при изгибе
В = — = 0,833 и -* ~а° = °’833-°>17 = 3,97; ат 420 1 —1—0,833
при растяжении-сжатии
р = = 0,5 и —° ~aj • = °’- ~°’12 .= о,76.
от 420 1 —1—0,5
Расчет сечения 1 —I (см. рис. 100):
228
максимальное напряжение пульсирующего цикла
(m„ + mBr)o)2xmax/?(l+X) tfmax — ~ ' —
t 2 • /ip/щ
(0,478 + 0,043) • 6282 - 0,039 (1 + 0,285) - Ю"6 СЛ П1 ><гт
= ---------------------------------------= ои,У1 МПа,
2-0,003-0,028
где Мы = 0,06/Ищ = 0,06 • 0,716 — 0,043 кг —масса части головки выше сечения I — /;
®х.хтах ~ 'ГСЯх.х тах/30 = 3,14 • 6000/30 = 628 рЗД/CJ
среднее напряжение и амплитуда напряжений
сг/по — % ~ атах/2 = 60,91/2 = 30,455 МПа;
аДКо = оаЛ / (£меп) = 30,455 • 1,272/(0,86 - 0,9) = 50 МПа, где ka = 1,2+ 1,8 - 10~4(ав — 400) = 1,2 + 1,8 - 10"4 (800 — 400) = = 1,272 — эффективный коэффициент концентрации напряжений (головка не имеет резких переходов и концентрация напряжений в основном зависит от качественной структуры материала); ем = 0,86 — масштабный коэффициент, определяется по табл. 48 (максимальный размер для сечения / — / составляет 28 мм); еп= 0,9 — коэффициент поверхностной чувствительности, определяется по табл. 49 (чистовое обтачивание внутренней поверхности головки);
так как = 50/30,455 = 1,64 > ( — «о)/( 1 - Ро) = 0,76,
то запас прочности в сечении / — / определяется по пределу усталости:
па = а_1р/Кк0 + % %) = 210/(50 + 0,12 - 30,455) = 3,9.
Напряжения от запрессованной втулки: суммарный натяг
д2 = Д + At = 0,04 + 0,0215 = 0,0615 мм,
где Д = 0,04 мм—натяг посадки бронзовой втулки; At = d(aB — — аг)АТ= 24,4(1,8 • 10'5—1,0 • 10’5) • 110 = 0,0215 мм—температурный натяг; ДТ = НО К — средний подогрев головки и втулки;
удельное давление на поверхности соприкосновения втулки с головкой
____________________^2________________________ _
(d* + d2)/(^-d2) + f* (<Р+<%)?(*-d*) - и '
£ш + Ев
__________________0,0615______________________________
Г(30,42+24,42)/(30,42 — 24,42)+0t3 , (24,42+222/(24,42 — 222)—0,3 24,4 ----------------------------+ ------------------------
’ L 2,2 • 105 1,15 • 10® J
- 24,2 МПа, где [х = 0,3 — коэффициент Пуассона;
229
напряжение от суммарного натяга на внутренней поверхности головки
и’ = р (& + d2)/( d2r — d2) = 24,2 (30,42 + 24,42)/(30,42 — 24Д2) = = 111,8 МПа;
напряжение от суммарного натяга на внешней поверхности головки о' = р2<?/( dr — d2) = 24,2 • 2 • 24,42 /(30,42 — 24,42) = 87,6 МПа. Расчет сечения А —А (см. рис. 100 и 101) на изгиб:
максимальная сила, растягивающая головку на режиме п = пы: Pjn = — maR(iP (1 + X) = — 0,478 • 0,039 • 5862 (1 + 0,285) =
= — 8230 Н,
где со — т.пN/30 = 3,14 • 5600/30 = 586 рад/с;
нормальная сила и изгибающий момент в сечении 0—0:
N}0 = — PJa (0,572 — 0,0008^.3) = — (— 8230) (0,572 — -0,0008- 105) = 4016 Н;
Mj0 = - Р^ср (0,00033Тш.3- 0,0297) = - (- 8230) X х 0,0137(0,00033 • 105 — 0,0297) = 0,56 Н-м, где ?ш.3 = 105° — угол заделки; гор = (dr + d)/4 = (30,4 4- 24,4)/4 = = 13,7 мм — средний радиус головки;
нормальная сила и изгибающий момент в расчетном сечении от растягивающей силы:
^ш.з = Ni° C°S Тш-3 ~ °’5Руп (3’П Тш-а “ C°S <Рш-8> =
= 4016 cos 105° — 0,5 • (— 8230) (sin 105° — cos 105°) = 4000 Н;
з ~ 4“ ^ЛГор 0 COS срш.з) + О.бРуцГдр X
х (sin <рш>3 —cos <рш-3) = 0,56 4-4016 • 0,0137(1 — cos 105°) + 4-0,5(—8230) • 0,0137(sin 105° — cos 105°) = 0,75 Н-м;
напряжение на внешнем волокне от растягивающей силы - +KN„ ]-!£--
1 ’ш-з hr (2гор + hr) ш-з /ШЛГ
= 2 • 0,75 Г---+ °’003-------------f_ 0,827 40001 --—------=
[ 0,003(2 - 0,0137 + 0,003) J 0,028 • 0,003
= 56,2 МПа,
230
где К = EmFr/(EmFr + EBFB) = 2,2 • IO5 • 168/(2,2.10’ - 168+1,15 х X 10s • 67,2) = 0,827; Fr = (dr —d)/m = (30,4 — 24,4) • 28 = 168 мм2; FB = (d — da) 1Ш = (24,4 — 22) • 28 = 67,2 мм2;
суммарная сила, сжимающая головку;
Раж = (Ргя — Ро) Ра — mnR(B2 (cos <Р + X cos 2<Р) =
= (5,502 — 0,1) • 0,004776 • 10е —0,478 • 0,039 • 5862(cos370° + + 0,285 cos 740°) = 17 780 Н;
изгибающий момент в расчетном сечении от
нормальная сила и сжимающей силы:
Раж
— cos <рш.л
^сжО [ fsinV3 ^ш-з „:п сж \
= 17 780 (0,0005 + 0,002) = 44,5 Н;
Г M
Л4сжср == PCH^Cp
Ш-3
1 N
р^о+с®о (1_со8<рпьз)_ “сж Гср сж
!!2lnb?_2sisincp -J-COSCP '
2 те тш-з те тш-з
= 17 780-0,0137 X
X (0,0001 + 0,0005 1,2588 — 0,002) =— 0,31 Нм,
где Л/ож0/Рс® = 0,0005 и Мсж0/(Рсжгср) = 0,0001 определены по табл. 52, а
sin ср q> 1
f (?ш.в) = —~ --------------— sin срш,3 — — cos ?ш.3 =
Z тс тс
= 0,002 и f (<рш.з) = 1 — cos срш>3 = 1,2588 — по табл. 53; напряжение на внешнем волокне от сжимающей силы
6г „ + Лг 1 10'6
ср-г—+кмсж? 4— =
ш*3 I СщПр
2Л4сж<р
ва сж
+ 0,827 • 44,5 X
Ш.з hr (2rop + ftp) 6 0,0137 + 0,003 0,003(2 - 0,0137 + 0,003)
х-----_ 6,45 МПа;
0,028 - 0,003
максимальное и минимальное напряжения асимметричного цикла: Отах = 4“ ^ai ~ 87,6 -f- 56,2 = 143,8 MTIaj
23Г
Omin = <*' + (Ja ож = 87,6 — 6,45 = 81,15 МПа;
среднее напряжение и амплитуды напряжения;
om = (CTmax + CTmin)/2 = (143,8 + 81,15)/2 = 112,48 МПа;
ао = (Птах-amtn)/2 = (143,8-81,15)/2 =31,33 МПа;
оая = аЛ /(емеп) = 31,33 • 1,272/(0,86 • 0,9) = 51,5-МПа.
Так как стак/от = 51,5/112,48 = 0,458< (Р„ — а, )/(1 — ра) = 3,97, то запас прочноси в сечении А —А определяется по пределу текучести:
п„ = «т/(авк + am) = 420/(51,5 + 112,48) = 2,56.
Расчет поршневой головки шатуна дизеля. Из теплового и динамического расчетов имеем: максимальное давление сгорания р ад = = 11,307 МПа на режиме«м =2600об/мин при q> = 370°; массу поршневой группы та — 2,94 кг; массу шатунной группы — 3,39 кг; максимальную частоту вращения при холостом ходе nx хтах= 2700 об/мин; ход поршня S = 120 мм; площадь поршня Fa = 113 см2; А = = 0,270. Из расчета поршневой группы имеем: диаметр поршневого пальца dn = 45 мм; длину поршневой головки шатуна /ш = 46 мм. По табл. 51 принимаем: наружный диаметр головки dr = 64 мм; внутренний диаметр головки d = 50 мм; радиальную толщину стенки головки 4Г = (dr —d)/2 = (64—50)/2 = 7 мм; радиальную толщину стенки втулки sB = (d — dn)/2 = (50—45)/2 = 2,5 мм. Материал шатуна—сталь 40Х; Еш — 2,2 • 10s МПа; а,,= 1 . 10~8 1/К. Материал втулки—бронза; Ев = 1,15 • 108 МПа; ав = 1,8 • 10‘8 1/К.
По табл. 43 и 45 для стали 40Х: предел прочности ов = 980 МПа; пределы усталости при изгибе о_4 = 350 МПа и растяжении-сжатии ст_1Р = 300 МПа; предел текучести от = 800 МПа; коэффициенты приведения цикла при изгибе аа = 0,21 и при растяжении-сжатии а, = 0,17.
По формулам (213)—(215): при изгибе
р, = o.j/e, = 350/800 = 0,438 и (р, — оц )/(1 — ) =
= (0,438— 0,21 )/(1 — 0,438) = 0,406;
при растяжении-сжатии
р, = ст_1Р/от = 300/800 = 0,375 и (р, — а, )/(1 — р,) = = (0,375 — 0,17)/(1 — 0,375) = 0,328.
Расчет сечения I —I (см. рис. 100): максимальное напряжение пульсирующего цикла
(Мп + mB.r) “х.х гаахЯ (1 + X) • Ю-» ^тах----------------—~~ —
2/гр/щ
= (2>94 + 0,27) 2832 • 0,06 • (1 + 0,27) • Ю~6 = 30 3 МПа 2 • 0,007 • 0,046 ’
832
где тъл == 0,8/тгш = 0,08 • 3,39 = 0,27 кг — масса части головки выше сечения / — /;
х тах/30 — 3,14 * 2700/30 -— 283 рЗД/CJ
среднее напряжение и амплитуда напряжений
~ °ао “ tfmax/2 = 30,3/2 =: 15,15 МПа;
(W = aaOk /(£м£п) = 15,15 • 1,3/(0,77 • 0,72) = 35,5 МПа,
где fe3 =1,2 + 1,8- 10"4 (ов — 400) = 1,2 + 1,8- 10-4 (980 — 400) =
= 1,3 — эффективный коэффициент концентрации напряжений (головка не имеет резких переходов); ем = 0,77 — масштабный коэффициент, определяется по табл. 48 (максимальный размер для сечения / — / составляет 46 мм); еп=0,72 —коэффициент поверхностной чувствительности, определяется по табл. 49 (грубое обтачивание);
так как оаКо/сГто = 35,5/15,15 ?= 2,34 — аа)/(1 —) =
= 0,328, то запас прочности в сечении I — I определяется по пределу усталости
Пз = (Х_1р/((1ак0 + а3 ат0) = 300/(35,5 + 0,17 • 15,15) = 7,9.
Напряжения от запрессованной втулки:
суммарный натяг
As = А + At = 0,04 + 0,044 = 0,084 мм,
где А = 0,04 мм — натяг посадки бронзовой втулки; At = d(aB — — аг)ДТ = 50(1,8 1СГ5—1,0 - 10‘5)110 = 0,044 мм; АТ= ПО К — средняя температура подогрева головки и втулки;
удельное давление на поверхности соприкосновения втулки с головкой
(d2+d2)/(d2r-d2) + |x (d*+ dj)!
Еш + Ев
0,084
50 Г(642-J-502)/(642 — 502) -|-0,3 (502 + 452)/(502 — 452) —0,3 L 2,2 • 105 + 1,15 • 10s = 16,73 МПа,
где [х = 0,3 — коэффициент Пуассона;
напряжение от суммарного натяга на внешней поверхности головки а'а = p2d2/( d2 — d2) = 16,73 • 2 • 502/(642 — 502) = 52,4 МПа;
напряжение от суммарного натяга на внутренней поверхности головки
а'. = р ( d2 + d2)/( d2 - d2) = 16,73 • (642 + 502)/(642 - 502) =
= 69,1 МПа.
233
Расчет сечения А —А (см. рис. 100, 101) на изгиб: максимальная сила, растягивающая головку на режиме п — п^:
Р}а = — тп/?®2 (1 + X) = — 2,94 • 0,06 • 2722 (1 + 0,27) = — 16 580 Н, где <в = ^/30 = 3,14 • 2600/30 = 272 рад/с;
нормальная сила и изгибающий момент в сечении 0—0: = - Pja (0,572 - 0,0008<рш.з) =
= — (— 16 580) (0,572 — 0,0008 -110) = 8025 Н;
Myo = - Pjarcv (0,00033?ш.3 - 0,0297) = -(-16 580) X х 0,0285(0,00033 • 110 — 0,0297) = 3,12 Нм, где <рш.8 И0° — угол заделки;
гср = (dr + d)/4 = (64 + 50)/4 — 28,5 мм;
нормальная сила и изгибающий момент в расчетном сечении от растягивающей силы:
= Ni0 COS ?ш.з — °»5Руп (sin <Рш.з — cos <Рш.з) =
= 8025 cos 110° — 0,5 (— 16 580) (sin 110° — cos 110°) = 7880 Hj
3 ~ Mjo + NJo^cp 0 COS 9Ш,a) + 0»5Р^пГСр X X (sin<pm.3 — cos<pm.3) = 3,12 + 8025 • 0,0285(1 — cos 110°) + + 0,5(—16580) • 0,0285 (sin 110°— cos 110°) = 7,12 Н м;
напряжение на внешнем волокне от растягивающей силы а . = [9М... - 6ГСР + hr
а) [ "Х-з Лг(2гср + Лг) ’ГЛЛ'л’ш.з] lmhr = [2 • 7,12 —6-0,0285 + 0,007------- 0,842-78801 ------—_____
L 0,007(2 0,0285 + 0,007) J 0,046 0,007
= 38,2 МПа,
где К = ЕШЕГ/(ЕШЕГ + EBFB) = 2,2 - 105 - 644/(2,2 X 105 . 644 + + 1,15- 10s • 230) = 0,842;
Fr = (dr — d) /ш = (64 — 50) 46 = 644 мм2, FB = (d — d„) /ш = (50 — 45) 46 = 230 мм2; суммарная сила, сжимающая головку:
Р<™ (Ргд — Ро) Ра ~ та№ (cos <р + X cos 2<р) =
= ( 11,307 — 0,1) 0,0113 • 10е — 2,94 0,06 - 2722 (cos 370° + + 0,27 cos 740°) = 110470 Н;
234
нормальная сила и изгибающий момент в расчетном сечении от сжимающей силы:
Л / sin <р ср
_ сжо I / * ущ.в _ _*nb3_ ч;п ф _____
__ ----- ын <рш,3
Рсж \
------ cos срш>3^1 = 110470(0,0009 + 0,0047) = 619 Н;
ТС /J
Мсжср = Р0жГ0р. (1 -СО8?ш.а)-
ш-3 L Рсжгср “сж
/ sin ® « . 1 У
- ------------------ Sin -------------C0S =
\ 2 тс тс 7
= 110470 • 0,0285(0,00025 + 0,0009- 1,342 — 0,0047)= —10,2 Н-м» где Nсж О/Рсж “ 0,0009 и Мсж $/(Рсж^ср) “ 0 ,00025 определяют по табл. 52, a f (<рш,3) = •>~ш'9-sin <рш-3 — -Lcos<рш,3 = 0,0047 и
f (?ш.з) = 1 — cos <РШ,3 = 1,342 — по табл. 53;
напряжение на внешнем волокне от сжимающей силы
^ср + ftr
аа сж = 2Мсж <р " <р X
L ш.з hT (2гср + Лг) ш.з J
X = [2 (— 10,2)--------------6-0,0285 + 0,007--- 0 842 . 6191 х
Mr L 0,007(2 - 0,0285 + 0,007)
щ-в
X---------------- — 23,5 МПа;
0,046 • 0,007
максимальное и минимальное напряжения асимметричного цикла:
Чшах == од + в 52,4 + 38,2 = 90,6 МПа;
Чт'ш = + са сж = 52,4 — 23,5 = 28,9 МПа;
среднее напряжение и амплитуда напряжений:
= (Отах + от1п)/2 = (90,6 + 28,9)/2 = 59,75 МПа;
За = (Отах — <Ып)/2 = (90,6 — 28,9)/2 = 30,85 МПа;
Оак = оЛ /(еме„) = 30,85 • 1,3/(0,77 • 0,72) = 72,3 МПа.
Так как оак/от = 72,3/59,75 = 1,21 > (ра — а, )/(1 — М == 0,406, то запас прочности в сечении А —А определяется по пределу усталости
Я» = в-1/(оак + ат) = 350/(72,3 + 0,21 . 59,75) = 4,12.
235
§ 48. КРИВОШИПНАЯ ГОЛОВКА
Основные конструктивные размеры кривошипной головки шатуна приведены в табл. 54.
Таблица 54
Размеры кривошипной головки Пределы изменения Размеры кривошипной головки Пределы изменения
Диаметр шатунной шейки 4Ш ш Толщина стенки вкладыша /в: тонкостенного толстостенного (0,564-0,75) D (0,03-0,05) ш 0.1 Расстояние между шатунными болтами сб Длина кривошипной головки /к . . (1,304-1,75) (0,45-0,95)
Точный расчет кривошипной головки весьма затруднен вследствие невозможности полного учета влияния конструктивных факторов. Приближенный расчет кривошипной головки шатуна сводится к определению напряжения изгиба в среднем сечении II — II крышки головки от инерционных сил Р]р (МН), имеющих максимальное значение в начале впуска (tp = 0°) при работе двигателя на режиме максимальной частоты вращения при холостом ходе:
Р]р = — ®х.х max # К/Иц + ^щ.п) U + *) + (/Иш.к — ^кр)1 Ю"’. (289) где тп — масса поршневой группы, кг; тш.п и /пш.к — соответственно массы шатунной группы, совершающие возвратно-поступательное и вращательное движения, кг; ткр « (0,20 н- 0,28) — масса крыш-
ки кривошипной головки, кг; тш — масса шатунной группы, кг.
Напряжение изгиба крышки (МПа) с учетом совместной деформации вкладышей
_ _ п Г 0,023сб 0,4'
И3 'Р L (1 + W №из + FT .
(290)
где св — расстояние между шатунными болтами, м; JB = == /к /в и J = /к (0,5сб — ri)3 — момент инерции расчетного сечения соответственно вкладыша и крышки, м4; №из = 1к(0,5сб — —
момент сопротивления расчетного сечения крышки без учета ребер жесткости, м3; rt — 0,5(dm.m + 2Q — внутренний радиус кривошипной головки, м; <1Ш.Ш — диаметр шатунной шейки, м; /в — толщина стенки вкладыша, м; F„ = /к • 0,5(сб —*1Ш.Ш) — суммарная площадь крышки и вкладыша в расчетном сечении, м2.
Значение а„з изменяется в пределах 100—300 МПа.
Расчет кривошипной головки шатуна карбюраторного двигателя.
Из динамического расчета и расчета поршневой головки шатуна имеем: радиус кривошипа R = 0,039 м; массу поршневой группы тп =
236
= 0,478 кг; массу шатунной группы /пш = /ищ.п+ тшх = 0,197 + + 0,519 = 0,716 кг; угловую частоту вращения <ox.xmax — 628 рад/с; Х= 0,285. По табл. 54 принимаем: диаметр шатунной шейки йш.ш = = 48 мм; толщину стенки вкладыша tB = 2 мм; расстояние между шатунными болтами сб = 62 мм; длину кривошипной головки /к = = 26 мм.
Максимальная сила инерции
Pjp = — <х max R + %п) 0 + Х) + (^ш-к “ >«кр)1 ’ Ю’® =
= — (628)2 • 0,039 [(0,478 + 0,197) (1 + 0,285) +
+ (0,519 — 0,179)] • IO"8 = — 0,0186 МН,
где /пкр = 0,25 • тш = 0,25 - 0,716 — 0,179 кг.
Момент сопротивления расчетного сечения
Гиз = /к(0,5сб — г^/б = 0,026(0,5 • 0,062 — 0,026)2/6 = 1,08-10"7 м8, где rt = 0,5(йш.ш + 2/в) = 0,5(48 + 2 • 2) = 26 мм — внутренний радиус кривошипной головки шатуна.
Моменты инерции вкладыша и крышки:
= lfB = 26 • 23 • IO’12 = 208 • 10'12 м4;
J = lK(P,5c6 — rJ9 • 10'12 = 26(0,5 • 62 —26)3 • 10“12 =
= 3250 • 1012 м4.
Напряжение изгиба крышки и вкладыша
_ D Г 0,023сб , 0,4 ' _
°ИЗ “ /₽ L (1 + 7В//) №из FT J ~
= 0,0186 Г-----------°’023.' Z1’062------ + —1 = 273 МПа,
L(1 + 208.10-12/3250 • КГ12) 1,08 • 10~7 0,000182 J
где Fr = /к0,5(сб— dm.m) = 26 • 0,5(62 — 48, • 10’® = 0,000182 м2.
Расчет кривошипной головки шатуна дизеля. Из динамического расчета и расчета поршневой головки шатуна имеем: радиус кривошипа R = 0,06 м; массу поршневой группы та — 2,94 кг; массу шатунной группы тш — 0,932 + 2,458 = 3,39 кг; (ox.xmax — 283 рад/с; X = 0,27. По табл. 54 принимаем: диаметр шатунной шейки ш = — 80 мм; толщина стенки вкладыша = 3,0 мм; расстояние между шатунными болтами сб = 106 мм; длина крйвошипной головки /к = = 33 мм.
Максимальная сила инерции
Pjp = — Ч.х max R 1Ип + /Пш.п) (1 + М + (^ш.к — ^кр)! • 10"® =
= — (283)2 • 0,06 [(2,49 + 0,932) (1 + 0,27) + (2,458 — 0,848)]• 10’® =
= —0,0286 МН, где ткр = 0,25/пш = 0,25 • 3,39 = 0,848 кг.
237
Момент сопротивления расчетного сечения
Гиз = /к(0,5сб— г^/б = 33(0,5 • 106 — 43)2 • 10'9/6=
= 5,50- 10'7 м8,
где =: 0,5(dm.m + 2/в) = 0,5(80 + 2 3) = 43 мм — внутренний радиус кривошипной головки шатуна.
Моменты инерции вкладыша и крышки
JB = lfa = 33 3s'. IO'12 = 891 - IO'12 м4;
J = lK (0.5c6 — rt)3 = 33 (0,5 -106 — 43)3 • 10~12 =
= 33000 • IO’12 m4.
Напряжение изгиба крышки и вкладыша
_ ____р Г 0,023сб
из F/pL (1 + /в//)Гю
+ -Ml = 0,0286 х J
____________°i°23_M°e_______________+ _М. .1 = iso Мпа.
(1 + 891 • 10-12/33 000 • 10'12) .5,50. 10~7 0,000429 J
где Fv = /к0,5 (сб — == 33.0,5 (106 — 80). Ю"6 = 0,000429 м2.
§ 49. СТЕРЖЕНЬ ШАТУНА
Основными конструктивными параметрами стержня шатуна кроме длины Ьш = /?/Х являются размеры его среднего сечения В — В (см. рис. 100). Значения этих параметров для отечественных автомобильных и тракторных двигателей приведены в табл. 55.
Таблица 55
Размеры сечения шатуна Карбюраторные двигатели Дизели
min (0,504-0,55) dr (0,504-0,55) dr
d.2-1,4) /1шга!п (1,24-1,4) ftratnin
Ьш (0,504-0,60) 1ш (0,554-0,75) 1ш
(2,54-4,0) (4,04-7,5)
Стержень шатуна рассчитывают на усталостную прочность в среднем сечении В —В от действия знакопеременных суммарных сил (газовых и инерционных), возникающих при работе двигателя на режимах п — или п = пм- Обычно расчет ведется для режима максимальной мощности. Запас прочности сечения определяется в плоскости качания шатуна и в перпендикулярной плоскости. Условием равнопрочности стержня шатуна в обеих плоскостях является пх = пу.
238
Сила, сжимающая шатун, достигает максимального значения в начале рабочего хода при р и определяется по результатам динамического расчета или по формуле
Рсж - Рг + - [Fn (р2д - До) - (cos ср + A cos2cp)] • 1О'*, (291)
где та + 0,275тш — масса возвратно движущихся частей кривошипно-шатунного механизма (условно предполагается, что среднее сечение В —В находится в центре тяжести шатуна).
Сила, растягивающая шатун, достигает максимального значения в начале впуска (в в. м. т.) и также определяется по результатам динамического расчета или по формуле
Рр =Pr + Pj-[prFn-^/?(o2(l +Х)1 • 10-е, (292)
где рг — давление остаточных газов.
От сжимающей силы Рсж в сечении В —В возникают максимальные напряжения сжатия и продольного изгиба (МПа):
в плоскости качания шатуна
^тах х = КХРсж/^ср> (293)
£2
где Кх ~ 1 + . т . р — коэффициент, учитывающий влия-
ет Л- СР
ние продольного изгиба шатуна в плоскости качания шатуна; ое = =ов— предел упругости материала шатуна, МПа; Lm = R/K— длина шатуна, м; Jx = [bmh^ — (bm ~ ош)(Лш — 2/ш)3]/12 — момент инерции сечения В — В относительно оси х—х, перпендикулярной плоскости качания шатуна, м4; FcP - hmbm — (bm — am)(hm — 2/ш) — площадь среднего сечения шатуна, м2;
в плоскости, перпендикулярной плоскости качания:
Отах у == AyFC)K/Fcp, (294)
g £2 * Fc
где УС = 1 +___— • -—-— коэффициент, учитывающий влия-
4/у
ние продольного изгиба шатуна в плоскости, перпендикулярной плоскости качания шатуна; Lj = Lm — (d + dJ/2 — длина стержня шатуна между поршневой и кривошипной головками, м; = [Лщ£>ш — — (^ш ~ 2/ш)(йш — аш)3]/12 — момент инерции сечения п — В относительно оси у — у, лежащей в плоскости качания шатуна, м4.
Для современных автомобильных и тракторных двигателей на-
пряжения Отах х и отах у (МПа) не должны превышать:
Для углеродистых сталей.......................... 160—250
Для легированных сталей.......................... 200—350
Минимальное напряжение, возникающее в сечении В — В от растягивающей силы Рр, определяется в плоскости качания шатуна и в перпендикулярной плоскости:
^min = Fp/F Ср. (295)
239
Запасы прочности стержня шатуна в- плоскости качания пх и в перпендикулярной плоскости пу определяются по уравнениям, приведенным в § 43. При определении пх и пу принимается, что коэффициенты концентрации напряжений &<, зависят только от материала шатуна. Для шатунов автомобильных и тракторных двигателей значения пх и пу не должны быть ниже 1,5.
Расчет стержня шатуна карбюраторного двигателя. Из динамического расчета имеем: РСж == Рг + Pj = 14 505 Н » 0,0145 МН при <Р = 370°; Рр =РГ+ Р, = —11 500 Н = —0,0115 МН при <р = 0°; £ш = 136,8 мм. По табл. 55 принимаем (см. рис. 100): = 23 мм;
= 16 мм; аш = 3,2 мм; — 3,4 мм. Из расчетов поршневой и кривошипной головок шатуна: d = 24,4 мм, dt — 52 мм; характеристики прочности материала шатуна (сталь 45Г2).
Площадь и моменты инерции расчетного сечения В — В:
^"ср = (Ьщ ^ш) (^Ш 2/щ) =
= 23 16 —(16 —3,2) (23 —2 • 3,4) = 160,6 мм2=160,6-10’» м2;
jx = [6шЛш - (Ьш - аш) (Лш - 2/ш)3]/12 =
= [16-233 — (16 — 3,2) (23 — 2 • 3,4)3]/12 =
= 11687 мм4 « 116,9 • 10-’» м4;
/у = [Мш-(/?ш-2и(5ш- аш)31/12 =
= [23-163 — (23 — 2-3,4)(16— 3,2)3]/12 = 5020 мм4 = 502• 10-11 м4.
Максимальное напряжение от сжимающей силы: в плоскости качания шатуна
W, ^KXPCJFCP = 1,095.0,0145/(160,0 • 10'6) = 99 МПа,
/2 где Kx = l+-^- .-HL.Fcp=l ТС с щ j х
800
3,142-2,2-106
136,88
11687
160,6=
= 1,095, ое = ав = 800 МПа;
в плоскости, перпендикулярной плоскости качания шатуна: зтахг/ = KyPC№/Fcp = 1,029 • 0,0145/(160,6 • 10'») = 93 МПа,
где К = 1 + • — • F = 1 н-----------------------х
у 1&ЕШ 4Jy ср 3,14J • 2,2 • 106 4-5020
X 160,6 = 1,029; Lt = Lm —(d + dJ/2 = 136,8—(24,4 + 52)/2 = — 98,6 мм.
Минимальное напряжение от растягивающей силы
Omin = Pp/Fcp = —0,0115/160,6- 10-е = — 71,6 МПа.
Средние напряжения и амплитуды цикла:
°тх = («тахх + <Jmtn)/2 = (99 - 71,6)/2 = 13,7 МПа;
= (°тах ц + 0min)/2 = (93 71,6)/2 = 10,7 МПа;
240
аах — (°max х — ®min)/2 — (99 4" 71 ,6)/2 = 85,3 МПа;
°ау = (°тах и ®min)/2 = (93 4* 71,6)/2 = 82,3 МПа;
®акх = °а*Ь> /(sMsn) = «5,3 • 1,272/(0,88-1,3) = 94,8 МПа;
®аку = »eyk./W = 82,3-1,272/(0,88-1,3) = 91,5 МПа, где ka = 1,2 4- 1,8-10-4 (ов —400) = 1,2 + 1,8-10"4 (800 —400) = 1,272; ем = 0,88 — определяется по табл. 48 (максимальный размер сечения стержня шатуна 23 мм); sn = 1,3 — определяется по табл. 49 с учетом поверхностного упрочнения стержня шатуна обдувкой дробью»
Так как —а— — = 0,76 (см. расчет поршневой
головки шатуна карбюраторного двигателя) и ааХу/ату = 91,5/10,7 > >0,76, то запасы прочности в сечении В—В определяются по пределу усталости:
п,х = а_1р/(®окх + а, атх) = 210/(94,80 4- 0,12 - 13,7) = 2,18;
п,и = W(*aKy + «» °ту) = 210/(91,5 + 0,12-10,7) = 2,26.
Расчет стержня шатуна дизеля. Из динамического расчета имеем: Рсж = Л + Pj = 105,6 кН = 0,1056 МН при <р = 370°; Р. = Рг 4-4- Pj= — 21,14 кН =—0,02114 МН при <р = 0°; длину шатуна Lm = = 222 мм. По табл. 55 принимаем (см. рис. 100): /гш = 40 мм; Ьш = =30 мм; аш = 7 мм; /ш= 7 мм. Из расчетов поршневой и кривошипной головок: d = 50 мм; dt = 86 мм; характеристика прочности материала шатуна (сталь 40Х).
Площадь и моменты инерции расчетного сечения В — В
Fср = ЬШЬШ - (Ьш - аш) (hm - 2/ш) = 40 • 30 - (30 -' 7) (40-2 - 7) = = 602 мм2 = 60,2 - 10’5 м2;
Jх ~ (Ьт аш) (Лш 2/ш)8]/12 =
= [30 • 403 — (30 — 7) (40 — 2 - 7)3]/12 = 123 800 мм4 « 124 -1 О’® м4;
= [Мш-(/1ш-2^ш)(&ш-аш)81/12 =
= [40-303—(40 — 2-7)(30 —7)3]/12 = 63 700 мм4 = 63,7 - Ю"9 м4.
Максимальные напряжения от сжимающей силы: в плоскости качания шатуна
°™xx=KxPcl«/Fcp = 1,108 • 0,1056/(60,2 • 10~5) = 194 МПа,
lx 1 I г- j . 980 2222 алп
где /С„ — 1 -р---- *-----* сп — i “Ь----------—— * -----* 602 “
л2£ш J* Р 3,142 • 2,2 • 10s 123800
= 1,108; ае = <?в = 980 МПа;
в плоскости, перпендикулярной плоскости качания шатуна:
9—370
241
amax # = КуРсж/Рсх> = 1,025 • 0,1056/(60,2 • 10-5) = 180 МПа,
„ i , ае 4 с if 980 1542 v,
где /(« = 14-------—--------гСп = 1 4-------------------------х
* тс2£ 4J ср 3,142 • 2,2 • 106 4-63700
ш у ’ ’
х 602 - 1,025; Lt = Lm — (d + 2 == 222 — (50 + 8б)/2 = 154 мм.
Минимальное напряжение от растягивающей силы
<jmln == Рр/Гср =—0,02114/(60,2 • 10-5) = —35 МПа.
Средние напряжения и амплитуды цикла:
°тх — faniaxx + °min)/2 = (194 35)/2 = 79,5 МПа;
°ту — (°тах у + <Jmin)/2 — (180 35)/2 = 72,5 МПа;
°ах («’тахх —<Jmin)/2 = (194 4~ 35)/2 = 114,5 МПа;
Qay = (<*тах у — °т1п)/2 = (180 + 35)/2 = 107,5 МПа;
= / (емеп) = 114,5 - 1,3/(0,8 -1,3) = 143 МПа;
°аку = /(ем£п) = 107,5 • 1,3/(0,8 *1,3) = 134 МПа,
где k, = 1,2+ 1,8- 10"4(дв — 400) = 1,2 + 1,8-10'4(980— 400) = 1,3; ем =0,8 определяется по табл. 48 (максимальный размер сечения стержня шатуна 40 мм); еп =1,3 определяется по табл. 49 с учетом поверхностного упрочнения стержня шатуна обдувкой дробью.
Так как qgK— = 143 - = 1,8 >-—-----— = 0,328 (см. расчет пор-
79,5 1-3. н и
шневой головки шатуна дизеля) и даКу/оту = 134/72,5 >0,328, то запасы прочности в сечении В — В определяются по пределу усталости:
п.х = «_1р/(оакх + а3 атх) = 300/(143+ 0,17 - 79,5) = 1,92;
п,у = °-ир/(°аку + а3 ату) = 300/(134 + 0,17 - 72,5) = 2,05.
§ 50. ШАТУННЫЕ БОЛТЫ
В четырехтактных двигателях болты, стягивающие половинки кривошипной головки шатуна, подвергаются растяжению от действия сил инерции поступательно движущихся масс поршня и шатуна и вращающихся масс, расположенных над плоскостью разъема кривошипной головки. Величину этих сил инерции определяют по формуле (289). Кроме того, болты испытывают растяжение от предварительной затяжки.
Шатунные болты должны обладать высокой механической прочностью и надежностью. Изготовляют их из стали 35Х, 40Х, 35ХМА, 37XH3A. При больших напряжениях затяжки болты изготовляют из легированной стали с более высокими пределами текучести — 18ХНВА, 20ХНЗА, 40ХН, 40ХНМА.
242
При работе двигателя силы инерции Р/р стремятся разорвать болты. В связи с этим они должны быть затянуты настолько, чтобы не была нарушена плотность соединения при действии этой силы.
Сила предварительной затяжки (МН)
Рпр-(2^3)Р^б, (296)
где i6 — число шатунных болтов.
Суммарная сила, растягивающая болт:
^б = Рпр + х^р/^ (297)
где х — коэффициент основной нагрузки резьбового соединения:
Х = Кш/(Кб + Кш). (298)
где /<ш — податливость стягиваемых частей шатуна; Кб — податливость болта.
По опытным данным коэффициент х изменяется в пределах 0,15— 0,25. С уменьшением диаметра шатунного болта значение х> как правило, также уменьшается.
Максимальные и минимальные напряжения, возникающие в болте, определяют в сечении по внутреннему диаметру резьбы:
«шах = 4P6/(ud2B), (299)
«mln = 4Рпр/(™/2), (300)
где dB =d— 1,4/ — внутренний диаметр резьбы болта, мм; d— номинальный диаметр болта, мм; t — шаг резьбы, мм.
Запасы прочности болта определяют по уравнениям, приведенным в § 43; коэффициент концентрации напряжения ka — по формуле (222) с учетом вида концентратора и свойств материала. Для шатунных болтов значения запаса прочности не должны быть ниже 2.
Расчет шатунного болта карбюраторного двигателя. Из расчета кривошипной головки шатуна имеем: максимальную силу инерции, разрывающую кривошипную головку и шатунные болты: =
— 0,0186 МН. Принимаем: номинальный диаметр болта d = 11 мм; шаг резьбы t = 1 мм; количество болтов i6 = 2. Материал — сталь 40Х.
По табл. 43 и 44 для легированной стали 40Х определяем:
пределы прочности <тв = 980 МПа; текучести от = 800 МПа и усталости при растяжении-сжатии o_ip — 300 МПа;
коэффициент приведения цикла при растяжении-сжатии аа = ==0,17.
По формулам (213)—(215):
= 300/800 = 0,375; (р, --= а3 )/(1 — ^ ) =
= (0,375 —0,17)/(1 —0,375) = 0,328.
Сила предварительной затяжки
Рпр = (2 4-3) Р/р//б = 2 • 0,0186/2 = 0,0186 МН. 9*
243
Суммарная сила, растягивающая болт:
Р6 = Рпр + хР/рЛе = 0.0186 + 0,2 • 0,0186/2 = 0,0205 МН, где х =0,2.
Максимальные и минимальные напряжения, возникающие в болте:
Отах = 4P6/(udi) = 4 • 0,0205/(3,14 • 0.00962) = 283 МПа;
°min = 4Рпр /(*£') = 4 • 0,0186/(3,14 • 0.00962) = 257 МПа,
где dB = d — 1,4/ = 11 — 1,4 • 1,0 == 9,6 мм = 0,0096 м.
Среднее напряжение и амплитуды цикла
От = (Отах + От1п)/2 = (283 + 257)/2 = 270 МПа;
О„ = (Отах — amin)/2 = (283 — 257)/2 = 13 МПа;
«ах = аЛ / (Ем£п) = 13-3,43/(0,99 0,82) = 54,9 МПа,
где k, = 1 + 9(«ка— 1) = 1 + 0,81 (4— 1) = 3,43; ако = 4,0 — определяется по табл. 47; q = 0,81 — определяется по рис. 95 при ств = = 980 МПа и аК(> = 4,0; ем = 0,99 — определяется по табл. 48 при d= 11 мм; еп = 0,82 определяется по табл. 49 (грубое обтачивание).
Так как = 0,203<—-------— = 0,328, то запас проч-
ат 270 1
ности болта определяется по пределу текучести:
= От/Кк + °т) = 800/(54,9 + 270) = 2,46.
Расчет шатунного болта дизеля. Из расчета кривошипной головки шатуна имеем: максимальную силу инерции, разрывающую кривошипную головку и шатунные болты, Р;р = 0,0286 МН. Принимаем: номинальный диаметр болта d = 14 мм; шаг резьбы t = 1,5 мм; количество болтов /б = 2. Материал — сталь 40ХН.
По табл. 43 и 44 для легированной стали 40ХН определяем: пределы прочности ов = 1300 МПа, текучести от = 1150 МПа и усталости при растяжении-сжатии <т_1р = 380 МПа;
коэффициент приведения цикла при растяжении-сжатии Оа = 0,2. По формулам (213) — (215) определяем
= о_1р/от = 380/1150 = 0,33; (₽» — ао )/(1 — ₽0) =
= (0,33 — 0,2)/(1 — 0,33) = 0,194.
Сила предварительной затяжки
Рпр = (2 4- 3) PJv/i6 = 2,5 • 0,0286/2 = 0,03575 МН.
Суммарная сила, растягивающая болт:
Р6 = Pav + xP/p/i6 = 0,03575 + 0,2 • 0,0286/2 = 0,0386 МН, гдех = 0,2.
Максимальные и минимальные напряжения, возникающие в болте:
244
«max = 4p6/(ud2B) = 4-0,0386/(3,14.0,01192) = 347 МПа;
°min - 4Pnp/(ud2B) = 4-0,03575/(3,14 • 0,01192) = 322 МПа,
где dB = d—1,4/= 14—1,4-1,5 = 11,9 мм = 0,0119 м.
Среднее напряжение и амплитуды цикла:
От = (Отах + <Мп)/2 = (347 + 322)/2 = 334,5 МПа;
«а = (отах-ОтйО/г = (347- 322)/2 = 12,5 МПа;
бок = ajb / (емеп) = 12,5 • 4,2/(0,96 • 0,82) = 66,7 МПа,
где k, = 1 + q (<хкз — 1) = 1 + 1 (4,2 — 1) = 4,2; акз = 4,2 определяется по табл. 47; q — 1 определяется по рис. 95 при ав= 1300 МПа и ако = 4,2; ем = 0,96 определяется по табл. 48 при d = 14 мм; еп = = 0,82 определяется по табл. 49 (грубое обтачивание).
Так как -— == 66,7. — 0,199> —------— =0,194, то запас прочат 334,5 1 -?,
ности болта определяется по пределу усталости
п, = o-ip/^K + а» от) = 380/(66,7 + 0,2 • 334,5) = 2,84.
Главе XIII
РАСЧЕТ КОЛЕНЧАТОГО ВАЛА
$ 51. ОБЩИЕ СВЕДЕНИЯ
Коленчатый вал — наиболее сложная в конструктивном отношении и наиболее напряженная деталь двигателя, воспринимающая периодические нагрузки от сил давления газов, сил инерции и их моментов. Действие этих сил и моментов приводит к возникновению в материале коленчатого вала значительных напряжений скручивания, изгиба и растяжения-сжатия. Кроме того, периодически изменяющиеся моменты вызывают крутильные колебания вала, которые создают дополнительные напряжения кручения.
Таким образом, из-за исключительно сложных и тяжелых условий работы коленчатого вала предъявляются высокие и разнообразные требования к механическим свойствам материалов, применяемых для изготовления коленчатых валов. Материал коленчатого вала должен обладать высокой прочностью и вязкостью, большой сопротивляемостью износу и усталостным напряжениям, сопротивлением действию ударных нагрузок и твердостью. Такими свойствами обладают правильно обработанные углеродистые и легированные стали, а также высококачественный чугун. Коленчатые валы отечественных автомобильных и тракторных двигателей изготовляют из сталей 40, 45, 45Г2, 50, специального чугуна, а для форсированных двигателей—из высоколегированных сталей 18ХНВА, 40ХНМА и др.
Сложная форма коленчатого вала, многообразие действующих на
245
Рис. 102. Расчетные схемы коленчатого вала: а, б—одно- и в, г — двухпролетного
него сил и моментов, характер изменения которых зависит от жесткости вала и его опор, а также ряд других причин не позволяют про-вести точный расчет коленчатого вала на прочность. В связи с этим используют различные приближенные методы расчета, позволяющие получить условные напряжения и запасы прочности в отдельных элементах коленчатого вала. Общепринятой расчетной схемой коленчатого вала является схема разрезной двухопорной балки с одним (рис. 102, а и б) или двумя (рис. 102, виг) пролетами между опорами.
При расчете коленчатого вала принимается, что: кривошип (один или два) свободно лежит на опорах; опоры и точки приложения сил проходят через средние плоскости шеек;
весь пролет (один или два) между опорами представляет собой абсолютно жесткую балку.
Коленчатый вал обычно рассчитывают для номинального режима (п = пц) с учетом одновременного действия следующих сил и моментов (рис. 102, б):
1) КРк = К + Kr = К + Клш 4- Krk — силы, действующие на колено вала по кривошипу, без учета противовесов, где (см. § 30— 32) К = Pcos(g> + p)/cosp — суммарная сила, направленная по радиусу кривошипа; K.R = —rirRo? — центробежная сила инерции вращающихся масс; = —тш,к R&2 — сила инерции вращаю-
246
щихся масс шатуна; Krk ——тк — сила инерции вращающих-
ся масс кривошипа;
2) Zs = Крк + 2Рнр — суммарной силы, действующей в плоскости кривошипа, где (см. гл. IX) РпР = + /ппРрсо2— центробежная сила инерции противовеса, расположенного на продолжении щеки;
3) Т — тангенциальной силы, действующей перпендикулярно плоскости кривошипа;
4) Zs = Крк + Рпр — реакции опоры от суммарных сил, действующих в плоскости кривошипа, где Крк = —0,5Крк и Рпр = —Рпр;
5) Tf = —0,5 Т — реакции опоры от тангенциальной силы, действующей в плоскости, перпендикулярной кривошипу;
6) Мк.ш/— набегающего крутящего момента, передаваемого расчетному колену со стороны передней части вала;
7) Мкр.ц = ТК — крутящего момента, создаваемого тангенциаль ной силой;
8) Мк.ш(Ж) =Мк.1ш + Мкр ц—сбегающего крутящего момента, передаваемого расчетным коленом следующему колену.
Основные конструктивные соотношения элементов коленчатого вала, необходимые для поверочного расчета, приведены в табл. 56.
Размеры коренных и шатунных шеек выбирают с учетом получения необходимой прочности, жесткости вала и допустимых значений удельных давлений на подшипники. Сокращение длины шеек и увеличение
Таблица 56
Двигатели //D . щ/& &к, 'к.ш/О**
Карбюраторные;
однорядные V-образные с последовательным расположением шатунов 1,20—1,28 0,60—0,70 0,45—0,65 0,60—0,80 0,45-0,60 0,74—0,84
на одной шейке 1,25—1,35 0,56—0,66 0,8—1,0 0,63—0,75 0,50—0,70 0,70—0,88
Дизели:
однорядные V-образные с последовательным расположением шатунов на 1,25—1,30 0,64—0,75 0,7-1,0 0,70—0,90 0,45—0,60 0,75—0,85
одной шейке 1,47—1,55 0,65-0,72 0,8—1,0 0,70—0,75 0,50—0,65 0,65—0,86
* D — диаметр цилиндра двигателя; /ш ш — полная длина шейки с учетом галтелей.
** Приведены данные для промежуточных и крайних (или средних) ш коренных шеек.
247
их диаметра повышает жесткость вала и уменьшает габариты и массу двигателя. Перекрытие шеек (4ц.ш+<4.ш > 2₽) также повышает жесткость вала и увеличивает прочность щек.
Радиус галтелей коленчатого вала во избежание возникновения больших концентраций напряжений не должен быть менее 2—3 мм, в практике расчетов его принимают в пределах 0,035—0 080 соответственно от диаметра коренной или шатунной шейки. Наибольшие концентрации напряжений возникают при расположении галтелей коренных ц шатунных шеек в одной плоскости.
Согласно статистическим данным ширина щек коленчатых валов автомобильных и тракторных двигателей изменяется в пределах (1,0—1,25)D для карбюраторных двигателей и (1,05—l,30)D — для дизелей, а толщина щек — в пределах соответственно (0,20—0,22)D и (0,24—0,27)D.
§ 52. ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ДАВЛЕНИЯ НА ПОВЕРХНОСТИ ШЕЕК
Величина удельного давления на рабочую поверхность шейки определяет условия работы подшипника и срок его службы. При работе подшипников стремятся не допускать выдавливания масляного слоя, разрушения антифрикционного материала и ускоренного износа шеек вала. Расчет шеек ведется от действия средних и максимальных результирующих всех сил, нагружающих шейки.
Максимальные (/?ш.штах и /?к.ш max) И Среднее (/?ш.щ ср и /?кш.ср) значения результирующих сил определяют из развернутых диаграмм нагрузки на шатунные и коренные шейки. Построение таких диаграмм было показано в § 32, 33, а с учетом разгружающего действия противовесов — в § 35.
Среднее удельное давление (МПа):
на шатунную шейку
Ш* ср ср/ (^ПЫП ); (зон
на коренную шейку
^К.Ш. ср = Я.Ш.Ср/(^К.ДГ^к‘1иХ ИЛИ ср = /?К.ш.ср/(^к.щ4 ш). (302)
где ор, ср—соответственно результирующие силы, дейст-
вующие на шатунную и коренную шейки, МН; /?кРш. ср — результирующая сила, действующая на коренную шейку при наличии противовесов, МН; б/к.ш—соответственно диаметр шатунной и
коренной шеек, м; /ш.ш, /к.ш — соответственно рабочая ширина шатунного и коренного вкладышей, м.
Величина среднего удельного давления достигает значений:
Для карбюраторных двигателей................ 4—12 МПа
Для дизелей................................. 6—16 МПа
Наибольшее давление на шейки определяется по аналогичным формулам ОТ деЙСТВИЯ МаКСИМалЬНЫХ результирующих СИЛ Яш.ш max, 248
ш max или /?к?ш max- Значения максимальных удельных давлений на шейки kma* (МПа) изменяются в пределах:
Для рядных карбюраторных двигателей............... 7—20
Для V-образных карбюраторных двигателей ...... 18—28
Для дизелей....................................... 20—42
§ 53. РАСЧЕТ КОРЕННЫХ И ШАТУННЫХ ШЕЕК
Расчет коренных шеек. Коренные шейки рассчитывают только на кручение. Максимальные и минимальные значения скручивающих моментов определяют с помощью построения диаграмм (см. рис. 105) или составления таблиц (табл. 57) набегающих моментов, последовательно подходящих к отдельным коренным шейкам. Для составления таблиц используют данные динамического расчета.
Таблица 57
<р° . пт?
0
10 (или 30)
И т. д.
Порядок определения набегающих моментов для рядного и V-об-разного двигателей показан на рис. 103, а и б.
Набегающие моменты и крутящие моменты отдельных цилиндров алгебраически суммируют с учетом порядка работы двигателя, начиная от первого цилиндра.
Максимальные и минимальные касательные напряжения (МПа) переменного цикла коренных шеек:
Ттах = /тах/й^тк. ш 1 (303)
^mln = ^4к.ш I тш / к.ш » (304)
Где W'tK.m — Лк.ш I 1 10 I кручению, м3; <2г.ш и 8к.т
I_j — момент сопротивления шейки \ ^к.ш/ _
— соответственно наружный и внутренний
диаметры коренной шейки, м.
По известным ттах и тпцп определяют запас прочности коренной шейки по формулам, приведенным в § 43. Эффективный коэффициент кон-
центрации напряжений при расчете принимают с учетом наличия в коренной шейке масляного отверстия. Для приближенных расчетов можно принять /(емхепх) = 2,5.
Запасы прочности коренных шеек имеют значения:
249
Рис. 103. Схемы определения набегающих моментов на коренные шейки коленчатого вала:
а — рядного двигателя; б — V-образного двигателя
Для карбюраторных двигателей.............................3—5
Для дизелей без наддува.................................. 4—5
Для дизелей с наддувом ................................... 2—4
Расчет шатунных шеек. Шатунные шейки рассчитывают на кручение и изгиб. Скручивание шатунной шейки происходит под действием набегающего момента Мщ.шь а изгиб — под действием изгибающих моментов в плоскости кривошипа М z и в перпендикулярной плоскости Мт. Так как максимальные значения скручивающего и изгибающих моментов не совпадают по времени, запасы прочности шейки от кручения и изгиба определяют независимо друг от друга, а затем их суммируют, определяя общий запас прочности.
Скручивающий момент, действующий на f-ю шатунную шейку: для однопролетного вала (см. рис. 102, а и б)
^ш.ш i i Т
для двухпролетного вала (см. рис. 102, виг)
-^иг»[п i i ””
Для определения максимально нагруженной шейки строят диаграмму (см. рис. 106) или составляют таблицу (табл. 58) набегающих моментов для каждой шатунной шейки.
Соответствующие значения Л4к.шг переносят в табл. 58 из табл. 57 набегающих моментов, а значения T't или Ты определяют по табл. 32 или 41 динамического расчета.
На основании данных табл. 58 определяют значения максимальных Мщ.шгтах И МИНИМЗЛЬНЫХ Мп.ш < mln СКруЧИВЗЮЩИХ МОМвНТОВ ДЛЯ
250
Таблица 58
<₽
1-я шатунная шейка
2-я шатунная шейка
l-я шатунная шейка
^Ш.Ш1 — = - 1\ R
.ш2
t'2r
^ш.ш2 — = ^к.ш2'
-t2r
Ti к
^ш.ш£ —
= ^K,£Ltf — Tj R
0
30 И т. д.
наиболее нагруженной шейки. Экстремальные значения касательных напряжений цикла (МПа):
^шах Л1ш.ш t max /W~ ш.ш > ^min = ЛТщ.ш i min/W^T ш. ш , 4П
— момент сопротивления кру-
(305)
(306)
те з Г / S
где 4ш.ш 1 -
16 L \ dm.m . _
чению шатунной шейки, м3; и Вш ш — соответственно наружный и внутренний диаметры шатунной шейки, м.
Запас прочности Пт определяется так же, как и для коренной шейки, с учетом наличия концентрации напряжений от масляного отверстия.
Моменты, изгибающие шатунную шейку, обычно определяют табличным методом (табл. 59).
Таблица 59
<р
мт sinn<
ZS
Mz
мг 005
м
'Рм
М,
о 30 и т. д.
Изгибающий момент (Н • м), действующий на шатунную шейку в плоскости, перпендикулярной плоскости кривошипа:
Мт = Г//2, (307)
+ 2А)— расстояние между серединами коренных
где I — (1К.Ш ^ш.ш шеек, м.
Изгибающий момент (Н • м), действующий на шатунную шейку в плоскости кривошипа:
Mz = Z'J/2 + Рпра,
где а = 0,‘5(/ш.ш + Л), м; Z'L = К'рк +Р'пр, Па.
(308}
251
Значения Т' и Крк. определяют по табл. 32 динамического расчета и заносят в табл. 59.
Суммарный изгибающий момент
Л4ИЗ = У М2т + М. (309)
Так как наибольшие напряжения в шатунной шейке возникают у краев масляного отверстия, то определяется обычно изгибающий момент, действующий в плоскости оси масляного отверстия:
= S*n — MZ COS <Рм’ (31 °)
где фм — угол между осью кривошипа и осью масляного отверстия, которое обычно выводится в центр наименее нагруженной поверхности шатунной шейки. Угол <рм обычно определяют по диаграммам износа.
Положительный момент Л4?м вызывает у краев отверстия сжатие, а отрицательный — растяжение.
Максимальное н минимальное значения М?м определяют по табл. 59 или графическим методом непосредственно по полярной диаграмме нагрузки на шатунную шейку (см. рис. 54, б) следующим образом. Из точки Ок проводят луч 0/7 параллельно оси масляного отверстия. Два перпендикуляра к лучу 0кС, касательные к крайним точкам а' и а" полярной диаграммы, отсекают отрезки 0KD и ОКЕ, которые в масштабе сил диаграммы равны экстремальным значениям проекций результирующих сил Rw и Rm’ на луч 0кС. Следовательно, 0xD — Та' sin <рм К.рка' COS <Ри= Rxar — Rk?m шах И OK£,=7'a’Sin <рм — Крка’ cos <рм = Rm- — Rk<?m шт, а моменты, изгибающие шатунную шейку без учета сил инерции противовесов:
_ I _ — Sin <рм +/Сркд, COS<pM / __
Л1?мтах- ~ ~ ~ 2 -
= Л4Гв'sin <рм — Мш'Созфм; (311)
Я л - sin Фм + К „ COS фм j
_____________ксрм min I __ д’ ™ ркд* ™ I 4>м min *”___2 2 2 2
== Мга" Sin фм — Мка" COS фм,
(312)
где Мта’ (а*) = Та' (а’)=-^-Z л
^а* (а") ТГ лл . __ iz ________
~ I и /Икд' (aff) —Дрка'(д")
^ркат (а")
2
При наличии противовесов необходимо момент М% сложить с моментом, возникающим от силы инерции противовеса РпР й от ее реакции Рпр.
По полученным значениям Л4^мтах и определяют экстре
252
мальные значения напряжений изгиба в шатунной шейке:
Cfrnax = Л4?м тах/^а ш.ш И От1п = mjn/W\ ш ш , (313)
где №аш.ш = 0,5 Ц7ТШ ш-
Запас прочности па по изгибу и общий запас прочности Пщ.ш шатунной шейки определяют по формулам, приведенным в § 43.
Запас прочности Пщ.ш:
Для автомобильных двигателей.................2,0—3,0
Для тракторных ..............................3,0—3,5
Методика расчета шатунной шейки V-образного двигателя с двумя шатунами, расположенными рядом на одной шейке (см, рис. 102, г), аналогична вышеприведенной, а расчет шатунной шейки в некоторых случаях производят для трех сечений: по масляным отверстиям и по среднему сечению шейки (см. § 56).
$ 54. РАСЧЕТ ЩЕК
Щеки коленчатого вала воспринимают сложные переменные напряжения: касательные от кручения и нормальные от изгиба и растяжения-сжатия. Наибольшие напряжения возникают в местах перехода шейки в щеку в галтелях (сечение А — А, рис. 102 б).
Касательные напряжения кручения вызываются скручивающим моментом
Мк.щ==Г.0,5((к.ш + й). (314)
Значения Тщах и Ттт определяют по табл. 59 или по кривой Т (см. рис. 51), а максимальные и минимальные касательные напряжения — по формулам
Тшах = А4и.щ шах/И^иц И Тт;п = Л4к.щ min/И^тщ» (315)
где = §bh2 — момент сопротивления кручению прямоугольного поперечного сечения щеки. Значение коэффициента & выбирают в зависимости от отношения ширины b расчетного сечения щеки к ее толщине h:
b/h . . . 1 1,5 1,75 2,0 2,5 3,0 4,0 5,0 10,0 оо
».... 0,208 0,231 0,239 0,246 0,258 0,267 0,282 0,292 0,312 0,333
Запас прочности /гх щеки при кручении и коэффициенты ем и «п определяют по формулам, приведенным в § 43. Для приближенных расчетов можно принимать для сечения А — А у галтелей kx /(емеп) «2.
Нормальные напряжения изгиба и сжатия-растяжения вызываются изгибающим моментом Л4и.щ, Н • м (без учета изгиба, создающего незначительные напряжения в плоскости, перпендикулярной плоскости кривошипа) и сжимающей или растягивающей силой Рщ, Н:
Ми.ш = 0,25 (К + Кв + 2₽пр) /к.ш; (316)
= 0,5 (К + Кв). (317)
253
Экстремальные значения К. определяют по таблицам динамического расчета (Kr и Рпр постоянны), а максимальные и минимальные нормальные напряжения — по уравнениям
<31»)
°s min == Ми.ш mln /^ощ 4“ Рщ min/Рщ> (319)
где = (Ла/6 — момент сопротивления щеки изгибу; рщ = bh — площадь расчетного сечения А — А щеки.
Рис. 104. Зависимость Ла/(еиеп) ОТ Ггял/h
При определении запаса прочности щеки от нормальных напряжений п, коэффициент концентрации в галтелях определяют по таблицам и графикам, приведенным в гл. X, или принимают в зависимости от отношения радиуса перехода шейки в щеку к толщине щеки. На рис. 104 приведена зависимость k, /(емеп) от ггал/й. Суммарный запас пщ прочности щеки определяют по формуле (231):
Для автомобильных двигателей ........ не менее 2,0—3,0
Для тракторных двигателей................... 3,0—3,5
$ 55. РАСЧЕТ КОЛЕНЧАТОГО ВАЛА РЯДНОГО ДВИГАТЕЛЯ
На основании данных динамического расчета имеем: коленчатый вал полноопорный (см. рис. 77, а) с симметричными коленами, но с асимметричным расположением противовесов (см. рис. 102, а); сила инерции противовеса, расположенного на продолжении щеки, РПр = = 13,09 кН; реакция на левой опоре от противовеса Рпр == —9,75 кН; центробежная сила инерции вращающихся масс = —15,91 кН; радиус кривошипа R = 39 мм. С учетом соотношений, приведенных в § 51, и анализа существующих двигателей принимаем следующие основные размеры колена вала (см. рис. 102, а и б): 1) коренная шейка — наружный диаметр dK,m = 50 мм, длина 1к.ш= 28 мм; 2) шатунная шейка — наружный диаметр </ш.ш = 48 мм, длина 1ш.ш = 28 мм; 3) расчетное сечение А — А щеки — ширина b — 76 мм, толщина h = 18 мм. Материал вала — чугун ВЧ 40-10.
По табл. 46 и соотношениям, приведенным в § 43, определяем: пределы прочности ов = 400 МПа и текучести (условные) ат == = 300 МПа ит7 =160 МПа;
пределы усталости (выносливости) при изгибе = 150 МПа,
растяжении-сжатии о_1р = 120 МПа и кручении = 115 МПа;
коэффициенты приведения цикла при изгибе = 0,4 и кручении От = 0,6.
По формулам (213)—(215) определяем:
при изгибе
254
при кручении
«, = iL = _ 0,719 я = °-719-»'6 _
Г тт 160 1—1—0.719
Удельное давление на поверхности шатунных шеек
= = 11 ЮО-10'в/(48-22-10-в) = 10,5 МПа;
йш.штах = ^ш.штаХ/(^ш.ш1ш.ш)== 18451-10-«/(48-22.10-e)=17,5 МПа, где ср = И ЮОН и ^щ.щтах = 18 451 Н — соответственно средняя и максимальная нагрузки на шатунную шейку (см. § 39);
— 2гГал=28 — 2-3 — 22 мм — рабочая ширина шатунного вкладыша; ггал — радиус галтели принят равным 3 мм;
коренных шеек
&.ШСР = ^к.ш.ср/(^к.ш/к.ш) = 4170 • 10-в/(50-22-1 О-в) = 3,8 МПа;
= Як.штаЛ<пЛ.ш) = 10 770 • 10~®/(50 • 22 • 1-О-в) = 9,8 МПа,
где 7?к.ш.ср = Яклпзср = 4170 Н — средняя нагрузка на 3-ю коренную шейку, которая являетя наибольшей (см. § 39); Яклтах =/?к.ш2шах= = 10770 Н — максимальная нагрузка на 2-ю коренную шейку, которая является наибольшей (см. § 39); — 2ггал = 28 — 2-3 =
= 22 мм — рабочая ширина коренного вкладыша.
Расчет коренной шейки. Набегающие моменты, скручивающие коренные шейки, рассчитаны графическим способом (рис. 105). Значения Мкр.Ц| взяты из табл. 28, а Мкр.ц{ — с учетом порядка работы двигателя 1—3—4—2.
Момент сопротивления коренной шейки кручению
W\K.m = ^.ш/16 = 3,14 50s • Ю-в/16 = 24,5 • 10~« м3.
Максимальное и минимальное касательные напряжения знакопеременного цикла для наиболее нагруженной 4-й коренной шейки (рис. 105), на которую воздействует крутящий момент, имеющий наибольший размах АМк.ш шах=
Ттах = мк.шт1а/№хк.ш = 527 • 10-в/(24,5 • Ю"6) = 21,5 МПа;
тш1п = Мк.ш mln / wx к.ш = — 485 • 10-в/(24,5 • 10'6) = — 19,8 МПа.
Среднее напряжение и амплитуды напряжений
тт = (Ттах + хт1„)/2 = (21,5 — 19,8)/2 = 0,85 МПа;
= (Ттах —-СтнО/г = (21,5 + 19,8)/2 = 20,65 МПа;
тал = =* 20,65 • 1,1/(0,72 • 1,2) = 26,3 МПа,
255
М,Н-м
MtfrM
300
too 0
-too
г
3001 _ MtH‘M
500
300
too
-100
-зоо
- A h. /М?
BWB
-555’
М,Нм
M* iu5~ * Mffp ~ ^«p
600
400
200
Z7<
-200
-400
0 60 120 180 240 300 360 420 4вГ~540 600 ~660 f'
*
£ I
- c 5
в 5
£
£
5
5Э
£
S
5?
Рис. 105. Кривые набегающих моментов на коренные шейки коленчатого вала карбюраторного двигателя
Рис, 106. Построение кривых набегающих моментов, скручивающих шатунные шейки коленчатого вала карбюраторного двигателя
где kx = 0,6[1 + q(aw — 1)] - 0,6[1 + 0,4(3,0 — 1)]== 1,1—коэффициент концентрации напряжений, определенный по формулам (222) и (224); q = 0,4 — коэффициент чувствительности материала к концентрации напряжений, принятый по данным § 43; аК7 = 3,0 — теоретический коэффициент концентрации напряжений, определенный по табл. 47 с учетом наличия в шейке масляного отверстия; емх = 0,72 — масштабный коэффициент, определенный по табл. 48 при dK и, — 50 мм; епт = 1,2 — коэффициент поверхностной чувствительности, определенный по табл. 49 с учетом закалки шеек токами высокой частоты на глубину 2—3 мм,
257
Так как = 30,9 > —--— = 0,42, то запас прочат 0,85 ’ 1-рх
ности коренной шейки определяют по пределу усталости:
Их = т_1/(так + ат тт) = 115/(26,3 + 0,6 • 0,85) = 4,3.
Расчет шатунной шейки. Набегающие моменты, скручивающие шатунные шейки, определены графическим способом (рис. 106). Значения /Ик.шг взяты по графикам (см. рис. 105), а —T'R == = 4-0,5 Мкр.ц; —для однопролетного симметричного вала.
Момент сопротивления кручению шатунной шейки
Гхш.о! = (^/16) dLm = (3,14/16)-48s-IO’9 = 21,7-IO’6 м3.
Максимальное и минимальное касательные напряжения знакопеременного цикла для наиболее нагруженной 4-й шатунной шейки (рис. 106):
Ттах = Мш.штах/ГС'хш.ш = 588 • 10"e/(21,7 - 10-®) = 27,1 МПа;
Тт1п = М1п.1пт1п/»,тш.ш = —420 - 10-в/(21,7. Ю’3) = — 19,4 МПа.
Среднее напряжение и амплитуды напряжений:
Тт = (Ттах + Tmin)/2 = (27,1 — 19,4)/2 = 3,85 МПа;
Та = (Ттах - Tmin)/2 = (27,1 + 19,4)/2 = 23,25 МПа;
хак = / (вм^) = 23,25-1,1 /(0,73 -1,2) = 29,2 МПа,
где = 1,1 и еПт=1>2 определены при расчете коренной шейки» sMt: — 0,73 — масштабный коэффициент, определенный по табл. 48 при dm.ui = 48 мм.
.р ТОК 29,2 *7 Г- ~~ Л лп
Так как ----- = —1— = 7,6 >------------= 0,42, то запас прочности
3,85 1 —
шатунной шейки от касательных напряжений определяют по предел)' усталости:
П. = т_!/(ток + Tm) = 115/(29,2 + 0,6 - 0,85) = 3,87.
Расчет моментов, изгибающих шатунную шейку, приведен в табл. 60, где значения /СрК1 =—0,5/(„к1 и Т\ ~ —0,57\ взяты из табл. 32:
Air = 7"iZ/2 = 7\ • 0,5 (/щ,ш /к.ш 4- 2й) =
= Тх 0,5(28 4- 28 4- 2 • 18) 10’3 = 0,04674 Н-м;
Тм = 68° (см. рис. 82); Z[ = Крк 4- Л.Р = — 9750 Н;
Mz = Zsl/2 4- Рпра = 0,046Zs 4- 13090 • 0,023 =
= 0,046Zs 4- 301 Н-м;
а = 0,5 (/ш.ш 4- h) = 0,5 (28 4- 18) 10’3 = 0,023 м;
Л4?м = /Иг sin <рм — Mz cos <f>M.
258
Таблица 60
9° н мТ , Н-м мт sin<pM’ Н-м 4к1 . Н , н 0,046 Zj, Н м мг Н м S 9- сл О N 3 1 X I М , Н-м
0 0 0 0 + 13 706 +3956 + 182,0 +483 —181 —181
30 +2863 + 131,7 + 122 + 11595 + 1845 + 84,9 +386 —145 — 23
60 +1636 + 75,3 + 70 + 8 419 —1331 — 61,2 +240 — 90 — 20
90 —1249 — 57,5 — 53 + 8323 —1427 — 65,6 +235 — 88 —141
120 —2118 - 97,4 — 90 +10 011 + 261 + 12,0 +313 —117 —207
150 —1213 — 55,8 — 52 + 10981 + 1231 + 56,6 +358 —134 —186
180 0 0 0 + 11 143 + 1393 + 64,1 +365 -137 —137
210 +390 + 17,9 + 17 + 10981 + 1231 + 56,6 +358 —134 —117
240 +2118 + 97,4 + 90 + 10011 + 261 + 12,0 +313 —117 — 27
270 + 1333 + 61,3 + 57 + 8 349 —1401 — 64,4 +237 - 89 — 32
300 —1244 - 57,2 — 53 + 8309 —1441 — 66,3 +235 — 88 —141
330 —1767 - 81,3 - 75 + 10 200 + 450 + 20,7 +322 —121 -196
360 0 0 0 + 9 156 — 594 . — 27,3 +274 —103 —103
390 —2264 —104,1 — 97 + 5 080 —4670 —214,8 + 86 — 32 —129
420 —1600 — 73,6 — 68 + 7 502 —2248 —103,4 + 198 — 74 —142
450 —3004 —138,2 —128 + 8841 — 909 — 41,8 +259 — 97 —225
480 —2940 —135,2 — 125 + 10811 +1061 + 48,8 +350 —131 —256
510 —1478 - 68,0 - 63 + 11 642 + 1892 + 87,0 +388 —145 —208
540 0 0 0 + 11 537 + 1787 + 82,2 +383 —143 -143
570 + 1249 + 57,5 + 53 + 11072 + 1322 + 60,8 +362 — 136 — 83
600 +2176 +100,1 + 93 + 10 069 + 319 + 14,7 +316 —118 — 25
630 + 1328 + 61,1 + 57 + 8 347 —1403 — 64,5 +237 — 89 — 22
660 —1600 — 73,6 - 68 + 8 397 —1353 — 62,2 +239 — 90 —158
690 —2816 —129,5 -120 + 11 530 + 1780 + 81,9 +383 —143 —263
720 0 0 0 + 13 706 +3956 + 182,0 +483 —181 —181
Максимальное и минимальное нормальные напряжения асимметричного цикла шатунной шейки:
«таХ = Мф /^ш.ш=-20.10-8/(10,85- 10-6) = —1,8 МПа;
emin = /Гяа1.ш = — 263 • 10-8/(10,85-10-8) = — 23,6 МПа, тм min /
где №яш.т = 0,5Гтш.т = 0,5-21,7 - 10"® = 10,85 • Ю'8 м3.
Среднее напряжение и амплитуда напряжений:
°т = (Отах + omin)/2 = (-1,8- 23,6)/2 = —12,7 МПа;
+ = (Отах - emIn)/2 = (-1,8 + 23,6)/2 = 10,9 МПа;
0 = 0 _Л_ = ю,9 1,8 - = 21,5 МПа,
4% 0,76-1,2
где ka = 1 + q (акя — 1) = 1 +0,4 (3,0 — 1) = 1,8; q = 0,4; акя = 3,0 и епя = еПТ=1,2— определены при расчете коренной шейки; емя =
259
= 0,76 — масштабный коэффициент, определенный по табл. 48 при ^ш.щ = 48 мм.
Запас прочности шатунной шейки от нормальных напряжений определяется по пределу усталости (при om<z 0):
п, =-----2=1---=---------—--------= 9,13.
®ок+ “<>’« 21,5+0,4 (—12,7)
Общий запас прочности шатунной шейки
«ш.ш = По Пх / V п2+п2 = 9,13.3,87/ /9,132 + 3,872 = 3,56.
Расчет щеки. Максимальный и минимальный моменты, скручивающие щеку:
Мк щтах = Т'тах • 0,5(/ж.ш + Л) = 2863 • 0,5(28 + 18) 10~3 = 65,8 Н-м;
Мклцт|п = T;in • 0,5 (/ж.ш + Л) = - 3004.0,5(28 + 18) 10"3 = = — 69,1 Нм,
где Т'тах — 2863 Н и Т^1П = — 3004 Н определены по табл. 60.
Максимальное и минимальное касательные напряжения знакопеременного цикла щеки:
тшах = Л4к щтах/ = 65,8 • 10-0/(6,99 • 10"6) = 9,41 МПа;
Tmin = Мк mmin / = —69,1 • 10-0/(6,99 • 10-0) = _9>89 МПа,
где П7Х1Д = рМ2 = 0,284 • 76 • 182 • 10Ч) = 6,99 • Ю"* м3 — момент сопротивления расчетного сечения А — А (см. рис. 102, б) щеки (р = = 0,284 определен при b/h = 76/18 = 4,2).
Среднее напряжение и амплитуды напряжений:
тт = (ттах + тт1п)/2 = (9,41 - 9,89)/2 = — 0,48 МПа;
т0 = (ттах - Tmin)/2 = (9,41 + 9,89)/2 = 9,65 МПа;
так = / (емхет) = 9,65 • 0,70/(0,64 • 0,75) = 14,1 МПа,
где k = 0,6[1 + </(аю — 1)] = 0,6[1 + 0,4(1,4 1)] = 0,70 — коэффициент концентрации напряжений, определенный по формулам (222) и (224); q = 0,4 — коэффициент чувствительности материала к концентрации напряжений, принятый по данным § 43; ак, =1,4 — теоретический коэффициент концентрации, определенный по табл. 47 с учетом наличия концентрации напряжений у галтели (радиус галтели принят 3 мм) при гРал/А =3/18 = 0 17; емх =0,64 — масштабный коэффициент, определенный по табл. 48 при b = 76 мм; епх = 0,75— коэффициент поверхностной чувствительности, определенный по табл. 49 для необработанной щеки.
Запас прочности щеки от касательных напряжений определяют по пределу усталости (при тт< 0):
Ъ =------2=1-------------11!------= 8,3.
14,1+0,6(—0,48)
260
Максимальное и минимальное нормальные напряжения щеки:
max — Л^и.щ max / ^щтах/^щ = 124 • 10 ®/(4,21 * 10~6) 4~
+ (— 877 • 10^/(1368 - IO’6) - 28,8 МПа;
min ~ Л^и.щ min / Н~ ^щтт /^щ (— 55,4 * 10 6)/(4,21 • 10-6) 4х + (— 13705 • 10’6)/(1368 • 10"6) = — 23,2 МПа,
где Ми.щтах = 0,25 [йпах + Лв + 2 (—Р;₽)],ш = 0,25 [14156 — — 15910+ 2 • 9750] • 28 • 10‘3 = 124 Н м; Рщтах = 0,5(Лтах +ЛВ) = = 0,5 (14 156 - 15 910) = - 877 Н; Ми.щ т1п = 0,25 [Лт1п + Лв + + 2(~^р)Рх.ш = 0,25 (—11501 — 15910 + 2 • 9750). 28- 10’3 = = — 55,4 Н • м; Рщ min = 0,5 (/(min + Кr) — 0,5 (— 11 501 — 15910) = = —13 705 Н; значения /Стах и Ктш взяты из табл. 30;
№ощ = ЬЛ2/6 = 76 -18а • 10-9/6 = 4,21 • 10-0 м3;
= bh = 76 • 18 • IO"6 = 1368 • 10-« м2.
Среднее напряжение и амплитуды напряжений:
=>т = (Зтах + Зтш)/2 = (28,8 -23,2)/2 = 2,8 МПа;
«0 = (этах-Зт1п)/2 = (28,8 + 23,2)/2 = 26,0 МПа;
Зак — (За^> /(емА1«) = 26,0 • 1,16/(0,7 • 0,75) = 57,4 МПа,
где k, =-1 + g(aKa— 1)= 1 + 0,4(1,4— 1) = 1,16; ак,= 1,4; д = 0,4 и еп, = ет = 0,75 определены при подсчете касательных напряжений; ема = 0,70 — по табл. 48 при b = 76 мм.
Так как = -57’4-- = 20,5 > —-------— = 0,2, то запас прочнос-
°т 2,8 1 Ра
ти щеки от нормальных напряжений определяют по пределу усталости:
= 3-1/(3ак + а» Зш) = 150/(57,4 + 0,4 • 2,8) = 2,56.
Суммарный запас прочности щеки
пш = п,Пг / К пГ+пГ = 2,56 • 8, з/у2,56а • 8,За = 2,45.
$ 56. РАСЧЕТ КОЛЕНЧАТОГО ВАЛА V-ОБРАЗНОГО ДВИГАТЕЛЯ
На основании данных динамического расчета имеем: коленчатый вал (см. рис. 87) с симметричными коленами (см. рис. 102, г) и с противовесами, расположенными только на концах вала; центробежную силу инерции вращающихся масс Дяв — ЛВк + 2Кдш =—16,1 + + 2(—10,9) = —37,9 кН; радиус кривошипа R =60,0 мм.
261
С учетом соотношений, приведенных в § 51, и анализа существующих двигателей принимаем следующие основные размеры колена вала (см. рис. 102, б и г): 1) коренная шейка — наружный диаметр dK-m — = 90 мм, длина /к.ш = 37 мм; 2) шатунная шейка — наружный диаметр б/ш ш =80 мм; внутренний диаметр 8Ш Ш = 30 мм, длина /ш.ш = 68 мм; 3) расчетное сечение А — А щеки — ширина Ь = 130 мм, толщина h = 26 мм; 4) радиус галтелей ггал = 4 мм. Материал вала — сталь 50Г.
По табл. 43 и 45 для углеродистой стали 50Г определяем:
пределы прочности ств ;= 800 МПа и текучести стт = 370 МПа и т т = 250 МПа;
пределы усталости (выносливости) при изгибе = 340 МПа, растяжении-сжатии ст_1р = 0,75o_i = 0,75 • 340 = 255 МПа и кручении т_1 = 0,53o_i = 0,53 • 340 = 180 МПа;
коэффициенты приведения цикла при изгибе Оа = 0,18, кручении а.х =0,08 и растяжении-сжатии а. —0,14.
По формулам (213)—(215) определяем:
при изгибе
В, = -^+- = — =0,919 и
и ат 370
Ра ~ Яа = 0,919—0,18 1—ft, 1—0,919
при растяжении-сжатии
255
370
= 0,689 и
0,689 — 0,14
1 —0,689
при кручении
« =2i = -^- = 0,72 и =2iL2-0.08 = тт 250 1 —ft, 1—0,72
Удельное давление на поверхности: шатунной шейки
^ш.ш.ср = Яш.ш. сР/(йш.ш/;.ш ) = 22,9 • 10-3/(80 -29-10~6) = 9,9 МПа;
&ш.штах = = 95,2-10 3/(80-29-10 ®) = 41,0 МПа,
где ср = 22,9 кН и /?ш.штах = 95,2 кН —соответственно средняя и максимальная нагрузки на шатунную шейку (см. § 40); Г т ж (1 /2) {/ш.ш — [2гГал + (2 4-3) мм]} = (1/2) [68 — (2 • 4 + 2)] = 29 мм — рабочая ширина одного шатунного вкладыша;
коренной шейки
/гк.ш. ср = Як.ш. ср/(^.ш/;.ш) = 37,5.10-3/(90-27. Ю’8) = 15,4 МПа;
^к.штах ’ /?к.ш max/(^/к.ш/к.ш) 58,2-10 3/(90-27-10 8) = 24,0 МПа,
ГДе ср == ^?к.ш 2 4 ср == 37,5 кН И /?к.ш max === ^?к.ш 2 4 max58,2 кН * соответственно средняя и максимальная нагрузки на 4-ю наиболее нагруженную шейку (см. § 40); — [2гГал + (2 4- 3) мм] =
— 37 — (2 • 4 + 2) = 27 мм — рабочая ширина коренного вкладыша.
262
Расчет коренной шейки. Набегающие моменты, скручивающие коренные шейки, приведены в табл. 61, где значения тангенциальной силы Т взяты из табл. 37 и рис. 82, Мк.ш1 = 0, значения Мкр.ц.л/ И Л4Кр.ц.п< приняты с учетом порядка работы двигателя 1л—1п — 4л— 2л — 2п—3jf—Зл — 4п, а Мк.ш/ = Мк.ш(/-1) + + Мкр.ц.л а—1) + Мкр.ц.п (/—1) •
Момент сопротивления коренной шейки кручению
Гтк.ш = = 3-14 • 9°3 ' 10‘9/16 = 143 • 10-« мз
Максимальное и минимальное касательные напряжения знакопеременного цикла для наиболее нагруженной 3-й коренной шейки (см. табл. 61):
ттах = Мк.штахЖк.ш = 2960 • 10-0/(143 • 10-«) = 20,7 МПа;
Tmin =Л4к.шшиЖк.ш = — 1180. 10-0/(143. 10-«) = —8,3 МПа.
Среднее напряжение и амплитуды напряжений:
Тт = (Ттах + тт!п)/2 = (20,7- 8,3)/2 = 6,2 МПа;
хо = (ттах-тт!п)/2 = (20,7 + 8,3)/2 = 14,5 МПа;
ток = /(емхЕпг) = 14,5 - 1,45/(0,62-1,2) = 28,3 МПа,
где kz = 0,6[1 + </(ак, — 1)] = 0,6[+ 0,71(3—1)] = 1,45 — коэффициент концентрации напряжений, определенный по формулам (222) и (224); q = 0,71 — коэффициент чувствительности материала к концентрации напряжений, определенный по графику (см. рис. 95) при ов = 800 МПа и ака =3; аКз = 3 — теоретический коэффициент концентрации напряжений, определенный по табл. 47 с учетом наличия масляного отверстия в шейке; 8МХ = 0,62 — масштабный коэффициент, определенный по табл. 48 при dK.m =90 мм; 8ПХ =1,2 — коэффициент поверхностной чувствительности, определенный по табл. 49 с учетом закалки шеек токами высокой частоты.
Так как —— = —:— = 4,6>---------------= 2,3, то запас прочности
Ъи 6,2 1—
коренной шейки определяют по пределу усталости:
= т_1/(таж + а, Тт) = 180/(28,3 + 0,08 • 6,2) = 6,25.
Расчет шатунной шейки. Набегающие моменты, скручивающие шатунные шейки, приведены в табл. 62, где значения Мк.ш/, Л4кр.ц.лг и/Икр.ц.ш взяты из табл. 61,аЛ4ш.ш/ == Л4к.ш/ Н- 0,5 (Л4кр.ц,л/-|“ + Мкр.ц.п/) Для двухпролетного симметричного вала.
Момент сопротивления кручению шатунной шейки
263
<е° 2-я коренная шейка З-я коренная шейка
*к.л! "’Н Vol Ч 4 &» ? я ьс г X о И S- ^кр.ц.л2' Н-м о » w-H со а ьс я з £
1 2 3 4' 5 6 7 8 9 10 11
0 0 0 630 —320 —320 450 +910 360 0 +590
10 10 —400 640 —170 —570 460 + 890 370 + 1390 + 1710
20 20 —560 650 + 100 —460 470 + 860 380 + 1790 +2190
30 30 —610 660- +330 —280 480 +770 390 + 1900 +2390
40 40 —610 670 +480 —130 490 + 680 400 + 1420 + 1970
50 50 —510 680 +580 +70 500 +535 410 + 1130 + 1735
60 60 —330 690 +615 +285 510 +390 420 +985 + 1660
70 70 —145 700 +515 +370 520 +260 430 +890 -г 1520
80 80 + 110 710 +270 +380 530 + 110 440 +880 + 1370
90 90 +315 720 0 +315 540 0 450 +910 + 1225
120 120 +520 30 —610 —90 570 —325 480 + 770 +355
150 150 4-300 60 -330 —30 600 -520 510 +390 — 160
180 180 0 90 +315 +315 630 —320 540 0 —5
210 210 —310 120 +520 +210 660 +330 570 —325 +215
240 240 —555 150 +300 —255 690 +615 600 —520 —160
270 270 —440 180 о —440 720 0 630 —320 —760
300 300 —90 210 —310 -400 30 —610 660 +330 —680
330 330 —330 240 —555 -885 60 —330 690 +615 —600
340 340 —320 250 —605 -985 70 —145 700 +515 —555
360 360 0 270 —440 —440 90 +315 720 0 —125
370 370 + 1390 280 —270 + 1120 100 +445 10 —400 + 1165
380 380 + 1790 290 -190 + 1600 НО +525 20 —560 +1565
390 390 + 1900 300 -90 + 1810 120 +520 30 —610 + 1720
420 420 +985 330 —330 +655 150 +300 60 —330 +625
450 450 +910 360 0 +910 180 0 90 +315 + 1225
470 470 +860 380 + 1790 +2650 200 —215 ПО +525 +2960
480 480 ' +770 390 + 1900 +2670 210 —310 120 +520 +2880
510 510 +390 420 +985 + 1375 240 —555 150 +300 + 1120
540 540 0 450 +910 +910 270 —440 180 0 +470
570 570 —325 480 +770 +445 300 -90 210 —310 +45
600 600 —520 510 +390 — 130 330 —330 240 —555 —1015
610 610 —515 520 +260 —255 340 —320 250 —605 -1180
630 630 —320 540 0 —320 360 0 270 —440 —760
660 660 +330 570 —325 +5 390 + 1900 300 —90 +1815
690 690 +615 600 —520 +95 420 +985 330 —330 +750
720 720 0 630 —320 —320 450 +910 360 0 +590
Максимальное и минимальное касательные напряжения знакопеременного цикла для наиболее нагруженной 3-й шатунной шейки (см. табл. 62):
ттах = Мш.ттах/^гш.ш = 2740 • 1(Г«/(98,5.Ю’®) = 27,8 МПа;
Ттш = мш.шт1п/^ш.ш = - 1165 • 10_в/(98,5 • 10-8) = — 11,8 МПа.
Среднее напряжение и амплитуды напряжений:
264
Таблица 61
4-я коренная шейка 5-я коренная шейка
СО ч о а &• ^кр.ц.лЗ-Н-м о ^кр.ц.пЗ* Н м а м ? 3 д ч о ЬС &• ^кр.ц.л4' Н м о ^кр.ц.п4' Н-м i ьс ? 5 ГЦ
12 13 14 15 16 17 18 19 20
270 —440 180 0 + 150 540 0 90 +315 +465
280 —270 190 —105 +1335 550 —120 106 +445 + 1660
290 —190 200 —215 + 1785 560 -260 НО +525 +2050
300 —90 210 —310 + 1990 570 —325 120 +520 +2185
310 -150 220 —395 + 1425 580 —380 130 +450 + 1495
320 —275 230 —485 +975 590 -450 140 +360 +885
330 —330 240 —555 +775 600 -520 150 +300 +555
340 —320 250 —605 +595 610 -515 160 + 175 +255
350 —255 260 —580 +535 620 —445 170 +80 +170
360 0 270 —440 +785 v630 —320 180 0 +465
390 +1900 300 -90 +2165 660 +330 210 —310 +2185
420 +985 330 —330 +495 690 +615 240 -555 +555
450 +910 360 0 +905 720 0 270 —440 +465
480 +770 390 + 1900 +2885 30 —610 300 -90 +2185
510 +390 420 +985 + 1215 60 —330 330 -330 +555
540 0 450 +910 + 150 90 +315 360 0 +465
570 -325 480 +770 —235 120 +520 390 + 1900 +2185
600 —520 510 +390 —730 150 +300 420 +985 +555
610 -515 520 +260 —810 160 + 175 430 +890 +255
630 —320 540 0 —445 180 0 450 +910 +465
640 —170 550 —120 +875 190 -105 460 +890 + 1660
650 + 100 560 —260 . + 1405 200 -215 470 +860 +2050
660 +330 570 —325 + 1725 210 —310 480 +770 +2185
690 +615 600 —520 +720 240 -555 510 +390 +555
720 0 630 —320 +905 270 —440 540 0 +465
20 —560 650 +100 +2500 290 -190 560 —260 +2050
30 —610 660 +330 +2600 300 -90 570 -325 +2185
60 —330 690 +615 + 1405 330 —330 600 —520 +555
90 +315 720 0 +785 360 0 630 —320 +465
120 +520 30 -610 —45 390 + 1900 660 +330 +2185
150 +300 60 —330 —1045 .420 +985 690 +615 +555
160 +175 70 —145 — 1150 430 +890 700 +515 +255
180 0 90 +315 —445 450 +910 720 0 -1-465
210 —310 120 +520 +2025 480 +770 30 —610 +2185
240 -555 150 +300 +495 510 +390 60 —330 +555
270 —440 180 0 + 150 540 0 90 +315 +465
тт = (Tmax + тт|п)/2 = (27,8 — 11,8)/2 = 8,0 МПа;
= (Tmax — tmtn)/2 = (27,8 + 11,8)/2 = 19,8 МПа;
тЛк = ’Л /(eMt8nt) = 19,8.1,45/(0,65-0,87) = 50,8 МПа,
где/г, =1,45 — определен при расчете коренной шейки; 8Mt = 0,65— масштабный коэффициент, определенный по табл. 48 при = 80 мм; ®пт = 0,87 — коэффициент поверхностной чувствительности материа-
265
Таблица 62
<р° 1 -я шатунная шейка 2-я шатунная шейка 3-я шатунная шейка 4-я шатунная шейка
я Х+х 1ГЭ - > 2* э < 5 Х + я X i и + _ х а ? о + X я X i а я X Л а X + si • 4 * х о. •s и я о + X я X СО а а я X ч* а X я-Н ' (fru*lrdH;v+ я X а а
0 —160 —320 +455 + 135 + 590 —220 +370 + 150 +158 +308
30 -140 —280 + 1335 + 1055 +2390 —200 +2190 + 1990 +98 +2078
60 + 143 +285 +688 +973 + 1660 —443 +1217 +775 —110 +665
90 +158 +315 +455 +770 +1225 —220 + 1005 +785 —160 +625
120 —45 —90 +223 +133 +355 +905 +1260 +2165 + 10 +2175
150 —15 —30 —65 —95 —160 +328 + 168 +495 +30 +525
180 +158 +315 —160 + 155 —5 +455 +450 +905 —220 +685
210 +105 +210 +3 +213 +215 +1335 + 1550 +2885 —350 +2535
240 —128 —255 +48 —207 —160 +688 +528 +1215 —330 +885
270 —220 —440 —160 —600 —760 +455 —305 +150 + 158 +308
зоо —200 —400 —140 —540 —680 +223 —457 —235 + 1210 +975
330 —443 —885 + 143 -742 —600 —65 —665 —730 +643 —87
360 -220 —440 + 158 -282 —125 -160 -285 —445 +455
370 +560 + 1120 +23 +1143 + 1165 —145 +1020 +875 +393 +1268
380 +800 +1600 —18 +1582 + 1565 —65 + 1500 + 1405 +323 + 1728
390 +905 + 1810 —45 + 1765 + 1720 +3 + 1723 + 1725 +230 + 1955
420 +328 +655 —15 +640 +625 +48 +673 +720 —83 +637
450 +455 +910 + 158 + 1068 + 1225 -160 + 1065 +905 —220 +685
470 + 1325 +2650 -г-155 +2805 +2960 —230 -Г 2730 +2500 —225 +2275
480 + 1335 +2670 + 105 +2775 +2880 —14Q +2740 +2600 —208 +2392
510 +688 +1375 —128 +1247 +1120 + 143 +1263 + 1405 —425 +980
540 +455 +910 —220 +690 +470 +158 +628 +785 —160 +625
570 +223 +445 -200 +225 +45 —45 0 —45 + 1115 +1070
600 —65 —130 —443 —573 -1015 —15 —1030 —1045 +800 —245
610 —128 —255 —463 —718 -1180 + 15 —1165 -1150 + 703 —447
630 -160 —320 —220 —540 —760 +158 —602 —445 +455 +ю
660 +3 +5 +905 +910 +1815 +105 + 1920 +2025 +80 +2105
690 +48 +95 +328 +423 + 750 —128 +622 +495 +30 +525
720 -160 —320 +455 + 135 +590 —220 +370 + 150 + 158 +308
ла к концентрации напряжений, определенный по табл. 49 для внутренней поверхности шейки (сверления), на которую выходит масляное отверстие.
Так как = -50’8- — 6,3> —---------— = 2,6, то запас прочности
8,0 1-рх
шатунной шейки от касательных напряжений определяют по пределу усталости:
тт) = 180/(50,8 + 0,08 • 8,0) = 3,50.
Моменты, изгибающие шатунную шейку двухпролетного коленчатого вала (см. рис. 102, г):
266
в плоскости, перпендикулярной плоскости колена, для сечения I — I по оси масляного отверстия
Мта-п = 7; (0,51 — с) = 7;(0,5 • 157 — 17) 10'3 = 7^-0,0615 Н-м;
для среднего сечения В — В
МГ(В-В) = к • 0,51 = т; • 0,5 - 157 - 10'3 = 0,07857^ Н-м,
/~ 0,51+с , 0,51 —с\ 0,5-157 + 17 .
где Та = — 7Л------+ Тп--------------------7, ——-----+
\ I * / \ ID/
+ та °’5'1g-17..) юз = _ (608Тл + 3927п) Н; I = 1К.Ш + 1Ш.Ш + + 2h = 37 + 68 + 2 • 26 = 157 мм; с = 1ш.ш/4 = 68/4 = 17 мм;
в плоскости колена для сечения / — I подсчет не производят, так как на основании анализа полярной диаграммы (см. рис. 84) и диаграммы износа (см. рис. 86) масляное отверстие на шатунной шейке целесообразно сделать в горизонтальной плоскости (<рм = 90°) и, следовательно, М<рм =
для среднего сечения В — В
МК(в—в) = МКр (в—в) + Мкт? (В—в), где Мкр (в-в) 0,51 = Д'; • 0,5 • 157- 10'3 = 0,0785/^ Н-м;
Л4К/? (в-в) = • 0,51 + /С?шс=18,95 • 0,5-157—10,9-17=1302 Н-м;
= — 0,5KR£ = — 0,5(— 37,9) = 18,95 кН;
расчет моментов М?м и Миз = ]ЛМг (в-в) + Мк <в-в> приведен в табл. 63, где значения Т„, Та, Кл и Кп взяты из табл. 40.
Максимальные и минимальные нормальные напряжения в шатунной шейке:
в сечении I — I
Отах = м?м тах /Ц7. ш.ш = 430 - 10-3/(49,2 • 10'3) = 8,7 МПа;
°mfn = М?мmin /№,ш.ш = — 1247-10-3/(49,2-10)-з = — 25,3 МПа,
где 1Г3ш ш = 0,51Гхш.ш = 0,5 • 98,5 - Ю"3 = 49,2 - 1О'в м3;
в сечении В — В
«тах = Мизтах/И7аш.ш = 3733 • 10'3/(49,2 - 10-3) = 75,9 МПа;
°min = Мизт>п/1Гаш.ш = Ю48 • 10'3/(49,2 - 10'«) = 21,3 МПа.
Среднее напряжение и амплитуды напряжений: для сечения I — I
°т = (°тах Н- °пип)/2 = (8,7 — 25,3)/2 = — 8,3 МПа;
=а = (°тах — =т,п)/2 = (8,7 + 25,3)/2 = 17,0 МПа;
°ак = / (®м«®па) = 17,0-2,42/(0,69-0,87) = 68,5 МПа,
267
Таблица 63
to
8
о &- X ьс >> т ° 1 л — т ,5Z4-c / л -608, Н нм * 11 « X !L+ Q - * S II
т о со = II
0 30 0 —10,2 0 -6202 —5,3 +5,5 — 2 078 + 2156 + 2 078 + 4 046 + 128 +249
60 —5,5 -3344 +10,2 + 3998 —654 —40
90 120 +5,3 +8,7 +3222 +5290 0 —10,2 0 -3 998 — 3 222 — 1 292 —198 —79
150 +5,1 +3101 —5,2 -2 156 - 945 —58
180 4 210 0 —5,2 0 -3162 +5,3 +8,7 + 2 078 + 3 410 —2 078 —248 —128 —15
240 —9,3 -5654 +5,1 + 1999 + 3 655 +225
270 300 330 1 1 1 Сл — СП U1 + —4499 —912 —3344 0 —5,2 —9,3 0 -2 038 -3 646 + 4 499 + 2 950 + 6 990 +277 + 181 +430
360 370 0 +23,2 + 0 14 ПО —7,4 —4,2 -2 901 -1 646 + 2 901 — 12 460 + 178 —766
380 390 420 +29,8 +31,7 +16,4 + + 18 120 19 270 И 9 971 —2,4 —1.5 -5,5 —941 —588 -2 156 — 17180 — 18 680 — 7 815 —1057 —1149 —481
450 460 +15,2 +15,0 -9242 -9120 0 +23,2 0 + 9 094 -9 242 — 18210 —568 —1120
470 +13,5 - 8 208 + 29,8 + 11 680 — 19 890 —1223
480 + 12,9 к 7 843 +31,7 + 12 430 — 20 270 —1247
510 +6,5 - 3 952 + 16,4 + 6 429 — 10 380 —638
540 0 0 + 15,2 + 5 958 — 5 958 —366
570 —5,4 -3 283 + 12,9 + 5 057 — 1 774 —109
600 —8,7 -5 290 +6,5 + 2 548 + 2 742 + 169
630 660 —5,3 +5,5 — 3 222 + 3 344 0 —5,4 0 -2117 + 3 222 — 1 227 + 198 -75
690 +Ю,2 + 6 202 —8,7 -3 410 — 2 792 —172
720 0 0 —5,3 -2 078 + 2 078 + 128
+ 163 —21,1
+318 —13,2
—51 —1,6
—253 —1,5
— 101 —8,2
—74 —12,4
—163 —13,2
— 19 —12,6
+287 —8,8
+353 —2,1
+232 +0,5
+549 +7,1
+204 +75,0
—978 +103,2
—1349 +63,1
—1467 +40,9
—613 +4,9
—725 —4,2
—1429 —5,8
—1561 —9,8
—1591 —12,2
— 815 —15,9
— 468 —15,0
— 139 —13,2
+215 —8,2
+253 —1,5
—96 —1,6
—219 —13,2
+ 163 —21,1
— 12830 —1,5
— 8 026 —1,6
—973 —13,2
—912 —21,1
— 4 986 —13,2
— 7 539 —1,6
— 8 026 —1,5
— 7 661 —8,2
— 5 350 — 12,4
— 1 277 — 13,2
+304 —12,6
+ 4317 —8,8
+ 45 600 —2,1
+ 62 750 —0,7
+ 38 360 0
+ 24 870 +0,5
+ 2 979 +7,1
— 2 554 +75,0
— 3 526 +103,2
— 5 958 +63,1
— 7418 +40,9
— 9 667 +4,9
— 9 120 —4,2
— 8 026 —12,2
— 4 986 —15,9
—912 —15,0
—973 —13,2
— 8 026 —8,2
— 12 830 —1,5
—588 + 13 420 +1053 1-2355
—627 + 8 653 +679 -1981
— 5174 + 6147 +483 -1785
— 8 271 + 9183 +721 -2023
— 5174 + 10 160 +798 -2100
—627 + 8 166 +641 -1943
—588 + 8614 +676 -1978
— 3 214 + 10 875 +854 -2156
— 4 861 + 10210 +801 -2103
— 5174 + 6 451 +506 -1808
— 4 939 + 4 635 +364 -1666
— 3 450 —867 —68 -1234
—823 — 44 780 —3515 -2213
—274 — 62 480 —4905 —3603
0 — 38 360 —ЗОН -1709
+ 196 — 25 070 —1968 —662
+ 2 783 — 5 762 —452 +850
+ 29 400 — 26 850 —2108 —806
+ 40 450 — 36 920 —2898 -1596
+ 2+740 — 18 780 —1474 —172
+ 16 030 — 8 612 —676 +626
+ 1 921 + 7 746 +608 1—1910
— 1 646 + 10 770 +845 -2147
— 4 782 + 12810 +1006 -2308
— 6 233 + 11 220 +881 -2183
— 5 880 + 6 792 +533 1-1835
— 5174 + 6147 +483 Н1785
— 3214 + 11 240 +882 -2184
—588 + 13 420 +1053 -2355
x
2360 2005 1786 2037 2102 1944 1984 2156 2122 1842 1682 1350 2223 3733
2177 1609 1048 1084 2142 1570 1710 2076 2197 2312 2193 1852 1787 2195
2360
где A, = 1 + <7(ака—1)=1 + 0,71(3— 1) = 2,42; значения q = 0,71 и акв = 3 определены при расчете коренной шейки; емз = 0,69 — масштабный коэффициент, определенный по табл. 48 при = 80 мм; епо = 0,87 — коэффициент поверхностной чувствительности, определенный по табл. 49 для внутренней поверхности шейки (сверление), на которую выходит масляное отверстие;
для сечения В — В
°т = (Отах + °min)/2 = (75,9 + 21,3)/2 = 48,6 МПа;
0о = (Отах - 0т1п)/2 = (75,9-21,3)/2 = 27,3 МПа;
оок = / (Wn,) = 27,3 • 2,42/(0,69 -1,2) = 79,8 МПа,
где k, = 2,42; 8MJ = 0,69 (как и для сечения I —-/); 8ПЗ = 1,2 (как и для коренной шейки).
Запас прочности шатунной шейки от нормальных напряжений определяется:
для сечения I — I — по пределу усталости (при стт< 0)
°ак + “3 °т 68,5+0,18 (—8,3) ’ ’
для сечения В — В — по пределу текучести, так как
lab = 22JL — 1,64 < ^э~°3 =9,1; °т 48,6 1-р9
Пта = от/(бок + сга) = 370/(79,8 + 48,6) = 2,88.
Общий минимальный запас прочности шатунной шейки для наиболее нагруженного среднего сечения В — В
«ш.ш = ПтаПг / У п*а + п\ = 2,88 • 3,50// 2,882 + 3,50“2 = 2,22.
Расчет щеки. Максимальный и минимальный моменты, скручивающие щеку:
Мк щтах = г;тах • 0,5(/к.ш + h) = 6990 • 0,5 (37 + 26) 10’3 = 220 Н-м;
Мк.Щт1п = г;т1п 0,5 (/к.ш + h) = -20 270 0,5(37 + 26) Ю’3 = = — 639 Н-м.
Максимальное и минимальное касательные напряжения знакопеременного цикла щеки
Ттах = Мк.щтах / = 220 10'0/(25,66 - 10‘«) = 8,6 МПа;
Тт1п = Мк.щ min / = — 639 • 10-0/(25,66 10'0) = — 24,9 МПа,
где №\щ = &Ыг2= 0,292 • 130 262 • 10'9= 25,66 • Ю'6—момент сопротивления щеки, м3; & = 0,292 определен по данным § 54 при ЫН = = 130/26 = 5,0.
Среднее напряжение и амплитуды напряжений
269
= (^max + тт1п)/2 = (8,6 — 24,9)/2 = — 8,15 МПа;
ta = (^max-Tmin)/2 = (8,6 + 24,9)/2 = 16,75 МПа;
хах — / (емтбт) = 16,75 • 0,75/(0,57 • 0,7) = 31,5 МПа,
где kz = 0,6[1 + <7(ака — 1)] = 0,6[1 + 0,6(1,4 — 1)] = 0,75 — коэффициент концентрации напряжений, определенный по формулам (222) и (224); q = 0,60 — коэффициент чувствительности материала к концентрации напряжений, определенный по графику (см. рис. 95) при ав =800 МПа и аКо = 1,4; ак<> — 1,4 — теоретический коэффициент концентрации, определенный по табл. 47 при rranlh = 4/26 =0,15; емт = 0,57 — масштабный коэффициент, определенный по табл. 48 при b = 130 мм; 8пг = 0,7 — коэффициент поверхностной чувствительности, определенный по табл. 49 для необработанной щеки в месте перехода к галтели.
Запас прочности щеки от касательных напряжений определяют по пределу усталости (при тт< 0);
T-i 180 к ол
1к =-----г-1----—-------------------— 5,84.
т<7к + агтт 31,54-0,08 (—8,15)
Максимальное и минимальное нормальные напряжения щеки
max = Мн.щтах/^ощ 4“ Рш тах/Т"щ ~
= 602 • 10-в/(14,6 • IO-6) + (32550 • 10-®)/(3380 • 10~6) = 50,9 МПа;
min = Мн.щ mln /1^ащ 4" Рщ mln /Рщ ~
= — 601 • 10-6/(14,6 10-6) + (— 32 500-10-6/(3380-1 О'6) = = — 50,8 МПа,
где Мн щ max = 0,25 (Kz тах + КД2) /к.ш = 0,25 (103 000 — 37 900) х X 37 - IO'8 = 602 Н-м; Мн.щт1п = 0,25 (Kzmm + КД2)/к.ш = 0,25 X X (—27100 —37900) • 37 • 10~3 = — 601 Н-М; Рщтах = 0,5(Kzmax4-+ КД2) = 0,5(103 000 - 37 900) = 32 550 Н; Рщт1п = 0,5(Kzmin + + КД2) = 0,5(— 27 100 —37 900) = — 32 500 Н; Kzmax = ЮЗ кН = = 103000Н и Kzт(п = —27,1 кН = — 27100 Н взяты из табл. 40J
= 6й2/6 = 130 • 262 • 10-9/6 = 14,6 -10’8 м3; Рщ= bh = 130 - 26 • 10~в= = 3380 • IO’6 м2.
Среднее напряжение и амплитуды напряжений:
Om = (°тах + °min)/2 = (50,9 — 50,8)/2 = 0,05 МПа;
о„ = (Отах — бтш)/2 = (50,9 + 50,8)/2 = 50<85 МПа;
°Ок = / (wm) = 50,85 • 1,24/(0,62 • 0,7) = 145 МПа,
«70
где йз = 1 + <7(аю—1)= 1+ 0,&(1,4—1) = 1,24; <? = 0,6; ака =
= 1,4 и eIM = ет ~ 0,7 определены "при подсчете касательных напряжений; еМа = 0,62 определен по табл. 48 при Ь = 130 мм.
Так как = 145- -= 2900 > —-------— =9,1, то запас прочнос-
0,05 1—₽о
ти щеки от нормальных напряжений определяют по пределу усталости
л, = о_1/(оак + aa am) = 340/(145 + 0,18 • 0,05) = 2,34.
Общий запас прочности щеки
лщ = лапт/]//и+^ = 2,34-5,84 //2,342 + 5,842 = 2,17.
Глава XIV
РАСЧЕТ КОРПУСА ДВИГАТЕЛЯ
§ 57. БЛОК-КАРТЕР
У большей части современных автомобильных и тракторных двигателей блок цилиндров выполнен заодно с верхней частью картера и называется блок-картером. Кблок-картеру крепят и в нем размещают различные механизмы и отдельные детали двигателя. При работе двигателя блок-картер воспринимает значительные динамические и тепловые нагрузки. Схема передачи сил давления газов через элементы блока определяет силовую схему блок-картера. В современных автомобильных и тракторных двигателях наибольшее распространение получили следующие силовые схемы: с несущим блоком цилиндров; с несущим блоком рубашек и с несущими силовыми шпильками.
При несущем блоке цилиндров силы давления газов передаются через- головку блока цилиндрам и рубашкам, представляющим собой единую отливку. Головку блока крепят к блок-картеру с помощью шпилек или болтов, ввертываемых в блок цилиндров.
При несущем блоке рубашек силы давления газов растягивают в осевом направлении только рубашку, а вставные гильзы цилиндров испытывают только радиальное давление от газовых сил. Головки блока крепят к блок-картеру шпильками, ввертываемыми в тело блока рубашек.
В схемах с несущими силовыми шпильками силы давления газов передаются силовым шпилькам, которые стягивают головку блока и цилиндр. Обычно длинные силовые шпильки проходят через головку и блок цилиндров и ввертываются в верхнюю часть картера.
В двигателях с воздушным охлаждением применяют в основном две силовые схемы соединения головки блока, цилиндра и картера: 1) с несущими силовыми шпильками и 2) с несущим цилиндром.
В первом случае длинные силовые шпильки стягивают головку блока и цилиндр и ввертывают в картер. Во втором случае с помощью коротких шпилек или болтов цилиндр крепят к картеру, а головку блока навертывают на цилиндр или присоединяют ее к нему с помощью коротких силовых шпилек.
271
Блок-картер должен обладать высокой прочностью и жесткостью. Увеличение жесткости блок-картера достигается за счет оребрения его перегородок, применения туннельного картера, расположения плоскости соединения нижней половины картера с верхней ниже плоскости разъема коренных подшипников, а также других конструктивных мероприятий.
Материалом для блок-картера обычно служит серый чугун СЧ44; СЧ40, СЧ15-32 и СЧ32, а также алюминиевые сплавы АСЛ4 и СЗ-26 (силумин).
Конструкция блок-картера и его габаритные размеры определяются назначением, условиями работы и мощностью двигателя. Толщина перегородок чугунного блока и стенок водяной рубашки обычно не превышает 4—7 мм, а толщина перегородок и стенок верхней половины картера — 5—8 мм. В алюминиевом блок-картере толщина стенок соответственно увеличивается на 1—3 мм.
Одним из наиболее важных конструктивных показателей блок-картера является отношение расстояния Lo между осями соседних цилиндров к диаметру D цилиндра. Величина LJD характеризует компактность двигателя по длине. Она зависит от схемы расположения, конструкции и длины коренных подшипников, размеров шатунных шеек, типа гильз и других конструктивных факторов. В табл. 64 (данные взяты из [1]) приведены отношения LJD для блок-картеров различных двигателей с жидкостным и воздушным охлаждением.
Таблица 64
Конструкция двигателя Карбюратор* ный двнГа тель Дизель
Однорядный с сухими гильзами, коренные подшипники скольжения расположены через два цилиндра (двухпролетный вал) 1,20—1,24
Однорядный с однопролетным коленчатым валом и с подшипниками скольжения . . 1,20—1,28 1,25—1,30
V-образный с последовательным расположением шатунов на шейке вала и с подшипниками скольжения 1,33 1,47—1,55
Двигатели с роликоподшипниками в качестве коренных опор 1,30 1,30
Двигатели с воздушным охлаждением 1,15—1,36 —
Расчет блок-картера на прочность представляет большие трудности в определении действующих усилий из-за сложности конфигурации и здесь не приводится.
§ 58. ГИЛЬЗА ЦИЛИНДРА
Гильзы цилиндров являются наиболее нагруженными деталями двигателя. Они испытывают напряжение от действия сил газов, бокового давления поршня и тепловых нагрузок. Тяжелые условия ра
272
боты гильз цилиндров приводят к необходимости использовать для их изготовления высококачественные легированные чугуны СЧ28-48 и СЧ35-56 или азотируемую сталь 38ХМЮА.
Основные конструктивные размеры гильз устанавливают с учетом получения необходимой прочности и жесткости, обеспечивающей отсутствие овализации цилиндра при сборке двигателя и во время его работы. Толщину 8Г чугунной стенки гильзы обычно принимают по экспериментальным данным.
Толщину стенки гильзы, выбранную конструктивно, проверяют по формуле, применяемой для расчета цилиндрических сосудов:
8г.р=0,5Г>(Ж + 0,4р2)/(Ог-1,Зр2) -1), (320)
где D — диаметр цилиндра, мм; ог — допустимое напряжение на растяжение (для чугунных втулок о 2 = 50—60, для стальных втулок о2 = 80—100 МПа); р z— дав-
ление газов в конце сгорания, МПа.
При расчете гильзы цилиндров на прочность определяют напряжения только от основных нагрузок: максимального давления газов, бокового давления поршня и перепада температур в стенке.
Наиболее опасной нагрузкой является максимальное давление сгорания p2max. вызывающее растягивающее напряжение по образующей
цилиндра и по его кольцевому сечению (рис. 107).
Растягивающее напряжение ор от действия сил газов определяют по приближенной зависимости, которая не учитывает неравномерности распределения напряжений по толщине гильзы:
Рис.
107. Расчетная схема гильзы цилиндра
°р — Pz max П/(28г),
(321)
где pZmax — максимальное давление газов, условно отнесенное к положению поршня в н. м. т., МПа; D —диаметр цилиндра, мм; 8Г — толщина стенки гильзы цилиндра, мм.
Допускаемые напряжения ор для гильз цилиндров, выполненных из чугуна, изменяются в пределах 30—60 МПа, а для стальных — 80— 120 МПа.
Растягивающее напряжение по кольцевому сечению гильзы
°р = Рг шах D/(48p). (322)
Величина ор определяется в основном для несущих гильз двигателей воздушного охлаждения, у которых разрыв по образующей цилиндра менее возможен за счет усиления стенок ребрами.
10—370
273
Напряжения от нормальной силы Nmax, действующей на несущую втулку (рис. 107), определяют обычно в двигателях с отдельными цилиндрами.
Изгибающий момент от силы Afmax, приложенной в середине поршневого пальца:
Л4из “ ЛГшах ub/(u Ь), (323)
где ЛГтах — максимальное значение нормальной силы, определяемое из динамического расчета, МН; а — расстояние от оси пальца до в. м. т., мм; Ь — расстояние от оси пальца до н. м. т., мм.
Напряжение изгиба
виз = Миз/IF, (324)
где № — момент сопротивления поперечного сечения гильзы, м3:
W = 0,1 (Di — D*)/Di, (325)
Di и D — наружный и внутренний диаметры гильзы, м.
Суммарное напряжение от растяжения и изгиба в стенках несущего цилиндра
02 = а'р + ^нз. (326)
Для чугунных гильз величина os не должна превышать 60 МПа, а для стальных — 110 МПа.
Во время работы двигателя между внутренней и наружной поверхностями гильзы возникает значительный перепад температур, вызывающий тепловые напряжения
°t = ЕацД77[2(1 — [*)], (327)
где Е — модуль упругости материала, МПа (для стали £=2,2 • 10s, а для чугуна Е = 1,0 • Ю5); ац — коэффициент линейного расширения (для чугуна ац = 11 • 10"в1/К); Д71 —перепад температур, К (по опытным данным для верхней части втулки ДТ = 100 ч- 150); ц — коэффициент Пуассона (для стали ц = 0,25 ч- 0,33, для чугуна ц = 0,23 ч- 0,27).
Напряжениям растяжения на наружной поверхности гильзы соответствует знак плюс, а напряжениям сжатия на внутренней поверхности — знак минус.
Суммарные напряжения от давления газов и перепада температур: на наружной поверхности гильзы цилиндра
= °р + °t> (328)
на внутренней поверхности
а" = ар — at. (329)
Суммарное напряжение в чугунной гильзе не должно превышать 100—130 МПа, а в стальной — 180—200 МПа.
274
Расчет гильзы цилиндра карбюраторного двигателя. На основании проведенного теплового расчета имеем: диаметр цилиндра D = 78 мм, максимальное давление сгорания р zmax = р 2Д = 6,195 МПа при п = пм = 3200 об/мин. Материал гильзы цилиндра — чугун: ац = = 11 . 10"61/К; Е ₽ 1,0 • 105 МПа и ц = 0,25.
Толщину стенки гильзы цилиндра выбирают конструктивно: 8Г = 6 мм.
Расчетная толщина стенки гильзы
8г.р = 0,5Dl(]/(az + 0,4pz)/(az-l,3pz) - 1] =
= 0,5 • 78 (К(60 + 0,4 • 6,195)/(60 -1,3 - 6,195) — 1 ] = 3,74 мм, где a z = 60 МПа — допустимое напряжение на растяжение для чугуна.
Толщину стенки гильзы выбирают с некоторым запасом прочности, так как 8Г > 8Г.Р.
Напряжение растяжения в гильзе от действия максимального давления газов
<зр = pzmax £>/(2§г) = 6,195.78/(2 • 6) = 40,3 МПа.
Температурные напряжения в гильзе
о* = (ЕацДГ)/[2 (1 — ц)] == (1,0 • 105- 11 • IO’6-120)/[2 (1—0,25)] = = 88 МПа,
где ДГ= 120 К — температурный перепад между внутренней и наружной поверхностью гильзы.
Суммарные напряжения в гильзе от давления газов и перепада температур:
на наружной поверхности
= Ор + af = 40,3 + 88 = 128,3 МПа;
на внутренней поверхности
а; = <jp — Of = 40,3 — 88 = — 477 МПа.
Расчет гильзы цилиндра дизеля. На основании проведенного теплового расчета имеем: диаметр цилиндра D — 120 мм; максимальное давление в конце сгорания pz = ргтах = 11,307 МПа при п = = пк ~ 2600 об/мин; материал гильзы цилиндра — чугун; ац = = 11 - 1О’в 1/К; Е— 1,0 • 105 МПа иц =0,25.
Толщину стенки гильзы цилиндра выбирают конструктивно: = = 14 мм.
Расчетная толщина стенки гильзы
8г.р = 0,5Dl/(Oz + 0,4pz)/(Oz-l,3pz) - 1] =
= 0,5 • 120 [/(60+ 0,4-П,307)/(60 - 1,3-11,307) — 1J = 11,4 мм, где ог=60 МПа—допустимое напряжение на растяжение для чугуна.
10*
275
Толщину стенки гильзы выбирают с некоторым запасом прочности, так как 8Г > 8Г>Р.
Напряжение растяжения в гильзе от действия максимального давления газов
% = рг max 0/(2^) = 11,307 - 120/(2 • 14) = 48,5 МПа.
Температурные напряжения в гильзе
at = (ЕодДЛ/12 (1 — tx)] = (1,0 • 105 11 • IO-6 • 1 Ю)/[2 (1 —0,25)] = = 80,7 МПа, где ДТ= ПО К —температурный перепад между внутренней и наружной поверхностью гильзы.
Суммарные напряжения в гильзе от давления газов и перепада температур:
на наружной поверхности
= Ср -]- С| в 48,5 -]- 80,7 = 129,2 МПа;
на внутренней поверхности
= « — 0. = 48,5 — 80,7 = — 32,2 МПа. 2i Р * ’ '
$ 59. ГОЛОВКА БЛОКА ЦИЛИНДРОВ
Головка блока цилиндров представляет собой деталь сложной конфигурации. Конструкция головки и ее основные размеры зависят от размеров впускных и выпускных клапанов, свечей, форсунок, цилиндров и формы камеры сгорания. В автомобильных и тракторных двигателях с жидкостным охлаждением головки цилиндров обычно изготовляют в виде общей отливки для одного ряда цилиндров, а в двигателях с воздушным охлаждением устанавливают индивидуальные головки или головки, объединяющие два соседних цилиндра.
Головки блока цилиндров работают в условиях воздействия на них больших знакопеременных нагрузок и высоких температур, вызывающих значительные напряжения. Вследствие сложности конструктивных форм, определяющихся влиянием различных факторов, а также невозможности точного учета всех действующих на головку сил, расчет ее на прочность является весьма условным. В связи с этим в практике двигателестроения при конструировании головок блока основные размеры их принимают по опытным данным.
Материал для изготовления головки блока должен обладать повышенной прочностью как в отношении механических, так и тепловых нагрузок. Этим требованиям в большей степени удовлетворяют алюминиевые сплавы АО5 и серые чугуны СЧ15-32, СЧ28-48 с легирующими присадками. В двигателях с воздушным охлаждением головки цилиндров изготовляют из сплавов АС9, АЛ5 и АК4.
Головка блока должна быть достаточно жесткой, чтобы не допустить коробления седел клапанов и других элементов головки при работе 276
двигателя. Жесткость конструкции головки обеспечивается за счет соответствующего выбора ее основных размеров.
Толщина Вгол нижней опорной стенки головки и толщина Вр стенок водяной рубашки для двигателей с диаметром цилиндра D = 8 ч--Н 150 мм могут быть определены по следующим приближенным зависимостям (данные взяты из [1]):
Для карбюраторных двигателей..........................
Для дизелей ..........................................
Для всех двигателей ..................................
5Гол=0,09 D мм йгол=и ,5+0 J09D)mm Вр—(2,2+0,03 D) мм
При использовании алюминиевых сплавов толщина стенок соответственно увеличивается на 2—3 мм.
В двигателях с воздушным охлаждением индивидуальные головки рассчитывают на разрыв по сечению х —х (рис. 108).
Напряжение разрыва
°р = Pz max / Fх—х » (330)
где Pz max = Рг max ^D\!4 — расчетное разрывное усилие, МН; Fx_x = = тс —Z>?)/4 — расчетное сечение, м2.
Напряжение разрыва ор изменяется в пределах 10—15 МПа. Низкие значения допускаемых напряжений связаны с появлением больших тепловых нагрузок при работе двигателя, которые не учитываются формулой (330).
§ 60. ШПИЛЬКИ ГОЛОВКИ БЛОКА
Силовые шпильки служат для соединения головки блока с блок-картером (рис. 109). Они работают в условиях воздействия на них сил от предварительной затяжки, давления газов и нагрузок, возникающих из-за неравенства температур и коэффициентов линейного расширения материалов головки блока, блок-картера и шпилек. Количество силовых шпилек, их конструктивные размеры и предва
Рис. 108. Расчетная схема голдвки блока двигателя с воздушным охлаждением
Рис. 109. Расчетная схема шпильки
277
рительная затяжка должны обеспечивать надежное уплотнение газового стыка на всех режимах работы двигателя.
Материалом для изготовления шпилек в карбюраторных двигателях Я дизелях служат углеродитые стали с высоким пределом упругости и высоколегированные стали (18ХНМА, 18ХНВА, 20ХНВА, 40ХНМА и др.). Использование материалов с высоким пределом упругости способствует уменьшению остаточных деформаций, возникающих при работе двигателя, что обеспечивает хорошую герметичность газового стыка.
При нерабочем состоянии и холодном двигателе силовые шпильки нагружены силой предварительной затяжки Рпр, которую по опытным данным принимают в виде следующей приближенной зависимости: pnp«m(i-z)p;m„, psi)
где т — коэффициент затяжки шпильки; у — коэффициент основной нагрузки резьбового соединения; Р zrnax сила давления газов при сгорании, приходящаяся на одну шпильку, МН.
Величина т изменяется в пределах 1,5—2,0, а в соединении с прокладками она повышается до 5 и более.
Коэффициент основной нагрузки резьбового соединения*
X ^Пр/С^пр + Кшп + Кгол)> (332)
где Дпр, Кшп и А'гол— податливость соответственно прокладки, шпильки и головки блока.
Для автомобильных и тракторных двигателей величина */ изменяется в пределах 0,15—0,25.
При работе двигателя кроме усилия затяжки на шпильки действует растягивающая сила давления газов, достигающая наибольшего значения в момент сгорания.
Сила давления газов при сгорании, приходящаяся на одну шпильку:
?z max = Pz max ^шп» (333)
где р2тах — максимальное давление сгорания, МПа; FK — проекция поверхности камеры сгорания на плоскость, перпендикулярную оси цилиндра, м2; ггап — число шпилек на один цилиндр.
При расположении клапанов: нижнем FK/Fn= 1,7 ч- 2,2; верхнем FK /Fn = 1,1 ч- 1,3, где Fn — площадь поршня.
Под действием силы предварительной затяжки происходит растягивание шпильки и сжатие соединяемых деталей. При работе двигателя сила давления газов при сгорании вызывает дополнительное растяжение шпильки и сжатие головки.
С учетом уменьшения силы давления ДР в стыке от сил давления газов при сгорании суммарная сила, растягивающая шпильку:
Рр max = Рпр АР + Р2 таХ * (334)
* Для силовых схем блок-картеров с несущим блоком цилиндров и с несущим блоком рубашек.
278
Используя значения податливости шпильки и соединяемых деталей, уравнение (334) можно привести к виду:
или
Рр max Рпр “Ь Х^\ max *
Рр max /Л (1 X) Pz max + Х^\ тах •
Минимальная сила, растягивающая шпильку:
Рр min — Рпр,
(335)
(336)
или
Ррт1п = /П(1 — хИгтах
При изготовлении головки и блок-картера из алюминиевых сплавов в стальных шпильках при работе двигателя появляются дополнительные тепловые нагрузки. Они возникают при повышении температуры из-за различия коэффициентов линейного расширения материалов шпилек и стягиваемых деталей. Тепловая деформация деталей увеличивает давление в стыке и нагрузку на шпильки.
Растягивающая шпильку сила
Pt ~ (агол^^гол^гол ашп^^шп^шп )/СК гол Н- Кшп)> (337)
где агол и ашп — коэффициенты линейного расширения материалов головки и шпильки; для стали ашп= 11 . 10‘6 1/К, для алюминиевых сплавов агол= 22 • 10-6 1/К; АТГОЛ и АТШП — повышение температуры головки и шпильки, К (при установившемся тепловом состоянии двигателя с жидкостным охлаждением можно принять А ТГОЛ~ А Тшп = = 70-? 80 К); /гол — высота головки, мм; /шп—расчетная длина шпильки (принимается равной расстоянию от нижнего торца гайки до последнего, ввернутого в блок витка резьбы), мм; Кгол и Кшп — податливость головки и шпильки.
Для шпильки с постоянной площадью поперечного сечения
Кшп ~ ^mn/(FF0) > (338)
где /шп — расчетная длина шпильки, мм; Е — модуль упругости материала шпильки (для стали Е = 2,2 • 105 МПа); Fo — площадь поперечного сечения стержня шпильки, мм2.
Для головки цилиндров соответственно
К гол ^го л/гол)’ (339)
где /гол — высота головки, мм; Е — модуль упругости материала головки (для алюминиевых сплавов Е = 7,3 • 104 МПа); Fr0JI—площадь поперечного сечения головки, приходящаяся на одну шпильку, мм2. Для рассматриваемого случая максимальная сила, растягивающая шпильку:
или
Fpmax — Fnp + /F2max + Pit
P p max = ГП (i X) P2 max + jPz max + Ff.
(340)
279
Минимальная растягивающая сила
ИЛИ
Рр min — ^пр "Ь Р]
Ppmin = m(l-x)^nMX+/’t-
(341)
Из-за сложности определения силы Pt в предварительных расчетах ею можно пренебречь.
Максимальные и минимальные напряжения в шпильке определяют по наименьшему сечению стержня и по внутреннему диаметру резьбы (МПа):
°max — Рр max/ Fq и °mln = F Р min/F0‘,
°тах : = Рртах /Fдр И Gmln — Рр min/Fдр,
где Fo — площадь минимального сечения стержня шпильки, м2;
Fop — площадь сечения шпильки по внутреннему диаметру резьбы, м2. Амплитуды и средние напряжения цикла (МПа):
% = ( <nax — °'min)/2 И °'т = ( °тах + °min)/2;
= (°niax °min)/2 И ат “ (^max °min)/2.
Запасы прочности шпильки определяют по уравнениям, приведенным в § 43; коэффициент концентрации напряжений ka — по формуле (222) с учетом вида концентратора и свойств материала. Допускаемые запасы прочности изменяются в пределах: па = 2,54-4,0 и лта = = 1,5ч- 2,5.
Расчет шпильки головки блока карбюраторного двигателя. На основании проведенного теплового расчета имеем: диаметр цилиндра D = 78 мм; площадь поршня Гп = 0,004776 м2; максимальное давление сгорания р zmax = р 2Д = 6,195 МПа при п = пм = 3200 об/мин. Количество шпилек на один цилиндр /шп = 4; номинальный диаметр шпильки d = 12 мм; шаг резьбы t = 1 мм; внутренний диаметр резьбы шпильки dB = d— 1,4/ — 12—1,4 • 1 = 10,6 мм. Материал шпильки — сталь ЗОХ.
По табл. 43 и 44 для легированной стали ЗОХ определяем: пределы прочности ов = 850 МПа, текучести от = 700 МПа и усталости при растяжении-сжатии о_1р =260 МПа;
коэффициент приведения цикла при растяжении-сжатии ао = 0,14.
По формулам (213)—(215) определяем.
₽а = = 260/700 = 0,372; --~°а = Р.’372-°>14 = о,369.
г ,р т . 1—ра 1—0,372
Проекция поверхности камеры сгорания на плоскость, перпендикулярную оси цилиндра при верхнем расположении клапанов;
FK = l,2Fn = 1,2- 0,004776 = 0,00573 м2.
Сила давления газов, приходящаяся на одну шпильку:
280
Р'гтах = /’zmax FK/imn = 6,195 • 0,00573/4 = 0,00887 MH.
Сила предварительной затяжки
Рпр = т (1 — х) р; тах = 3 (1 — 0,2) • 0,00887 = 0,0213 МН,
где т = 3 — коэффициент затяжки шпильки для соединений с прокладками; х = 0,2 — коэффициент основной нагрузки резьбового соединения.
Суммарная сила, растягивающая шпильку без учета силы Р(:
Рртах = Рпр + хР;тах = 0,0213 + 0,2 • 0,00887 = 0,02307 МН.
Минимальная сила, растягивающая шпильку:
Ppmin =Рпр= 0,0213 МН.
Максимальные и минимальные напряжения, возникающие в
шпильке:
р р max р Г р max 0,02307 — 9К1 МПл*
°max — — ZrUl 1*11 ш,
% 3,14-0,01062/4
р р min р 1 р min 0,0213 941 МПя
(7m in — Z,*xl 1*11 lu,
f0P nd2j4 3,14 0,01063/4
где Fop = tcdll4 — площадь сечения шпильки по внутреннему диаметру резьбы, м2.
Среднее напряжение и амплитуда цикла:
От = (Отах + ош1п)/2 = (261 + 241)/2 = 251 МПа;
оа = (Стах — omin)/2 = (261 — 241)/2 = 10 МПа.
Величина сак = aak„ /(е„еп) = 10 • 3,22/(0,98 - 0,82) = 40 МПа, где ka = 1 + q(aKa — 1) — 1 + 0,74(4,0 — 1) = 3,22; ако = 4,0 определяется по табл. 47; q = 0,74 — по рис. 95 при ств = 850 МПа и ака = 4,0; ем = 0,98 — по табл. 48 при d = 12 мм; еп = 0,82 — по табл. 49 (грубое обтачивание).
Так как = 0,159 —--------— = 0,369, то запас проч-
стт 251 1-₽а F
ности шпильки определяется по пределу текучести:
«та = oT/(oaIt + Сга) = 700/(40 + 251) = 2,4.
Расчет шпильки головки блока дизеля. На основании проведенного теплового расчета имеем: диаметр цилиндра D = 120 мм; площадь поршня Fn = 0,0113 м2; максимальное давление в конце сгорания рг = р zmax = 11,307 МПа при «лг = 2600 об/мин; количество шпилек на один цилиндр /шп = 4; номинальный диаметр шпильки d = 20 мм; шаг резьбы t = 1,5 мм; внутренний диаметр резьбы шпильки dB = —1,4/ = 20—1,4 • 1,5 = 17,9 мм; материал шпильки — сталь 18ХНВА.
281
По табл. 43 и 44 для легированной стали 18ХНВА определяем: пределы прочности ои= 1200 МПа, текучести ат == 1000 МПа, усталости при растяжении-сжатии ст_1р = 380 МПа;
коэффициент приведения цикла при растяжении-сжатии а„ = = 0,22.
По формулам (213)—(215) определяем:
= O-jp/’t = 380/1000 = 0,38; (р, - аа )/(1 — ₽,) =
= (0,38— 0,22)/(1 —0,38) = 0,258.
Проекция поверхности камеры сгорания на плоскость, перпендикулярную оси цилиндра при верхнем расположении клапанов:
FK = 1,25Fd= 1,25 • 0,0113 = 0,01413 м2.
Сила давления газов на одну шпильку
р,г^ = РгшахМшп = 11.307 • 0,01413/4 = 0,0399 МН.
Сила предварительной затяжки
Рпр = т (1 — z)P;max = 3,5(1—0,22) • 0,0399 = 0,109 МН, где т = 3,5 — коэффициент затяжки шпильки для соединений с прокладками; / = 0,22 — коэффициент основной нагрузки резьбового соединения.
Суммарная сила, растягивающая шпильку, без учета силы Pt
Рр max = Рпр + /р;тах = 0,109 + 0,22 • 0,0399 = 0,1178 МН.
Минимальная сила, растягивающая шпильки:
Ppmin- Pup = 0,109 МН.
Максимальные и минимальные напряжения, возникающие в шпильке:
--------------= 468,3 МПа;
3,140,01792/4
------------------ 433,3 МПа, 3,14-0,01792/4
° max “
Р Р
1 р max _ * р max
FOP 7И,»/4
_ Рр min Рр min
°min л ! л
Fop W4
где Fop = ™Р/4 — площадь сечения шпильки по внутреннему диаметру резьбы, м2.
Среднее напряжение и амплитуда цикла
= (^max + omin)/2 = (468,3 + 433,3)/2 = 450,8 МПа;
= (tfmax — *min)/2 = (468,3 — 433,3)/2 - 17,5 МПа.
Величина
°ак == /(£м£п) = 17,5 • 3,85/(0,9.0,82) = 91,3 МПа,
282
где ka = 1 + ^(«ка — 1) = 1 + 0,95(4,0— 1) = 3,85; aKe = 4,0 определяется по табл. 47; q = 0,95 — по рис 95 при ов = 1200 МПа и акз = 4,0; ем = 0,9 — по табл. 48 при d = 20 мм; еп = 0,82 — по табл. 49 (грубое обтачивание).
Так как аак/от = 91,3/450,8 = 0,2025 < (^ — )/(1 — ) = 0,258. то запас прочности шпильки определяется по пределу текучести
лтв = ат/(аак + от) = 1000/(91,3 + 450,8) - 1,84.
Главе XV
РАСЧЕТ МЕХАНИЗМА ГАЗОРАСПРЕДЕЛЕНИЯ
§ 61. ОБЩИЕ СВЕДЕНИЯ
Для газообмена в существующих автомобильных и тракторных двигателях применяются клапанные механизмы, выполненные в основном по двум конструктивным схемам: с верхним и нижним расположением клапанов. В настоящее время большинство двигателей имеет верхнее расположение клапанов.
При конструировании клапанного механизма необходимо стремиться к максимально возможному удовлетворению двух противоположных требований: 1) получению максимальных проходных сечений, обеспечивающих хорошее наполнение и очистку цилиндра, и 2) сокращению до минимума массы подвиж
ных деталей газораспределения для уменьшения инерционных нагрузок.
Проектирование механизма газораспределения начинают с определения проходных сечений в седле клапана Ркл и в горловине FroP (рис. ПО). Площадь проходного сечения в клапане определяют при условии неразрывности потока несжимаемого газа по условной средней скорости в сечении седла при максимальном подъеме клапана на режиме номинального числа оборотов:
^кл = ^п.ср Рп/(^*кл^вп)> (342)
где уп.ср — средняя скорость поршня, м/с; — площадь поршня, см2; /Кл — число одноименных клапанов; оувп — скорость газа в проходном сечении клапана (для впускного клапана должна быть равна или меньше скорости, принятой в тепловом расчете при определении потерь давления на впуске Дра), м/с.
Проходное сечение в горловине не должно ограничивать пропускную способность впускного (или выпускного) тракта. Учитывая, что через горловину проходит стебель клапана, ее площадь обычно принимают FroP = (1,1 1,2) Гкл. Диаметр горловины (мм)
283
= У 4Frop/« • Ю. (343)
Максимальный диаметр горловины ограничивается возможностью размещения клапанов в головке блока при заданных диаметре D цилиндра, конструктивной схеме газораспределения и типе камеры сгорания. В связи с этим значение droP впускного клапана, полученное по формуле (343), не должно быть больше:
droP = (0,384- 0,42) D —при нижнем расположении клапанов;
droP = (0,354- 0,52)0 — при верхнем расположении клапанов, в том числе:
droP = (0,354- 0,40) О — для вихрекамерных и предкамерных дизелей;
droP — (0,384- 0,42) О — для дизелей с непосредственным впрыском;
droP ~ (0,424- 0,46) О — для двигателей с клиновидной и плоскоовальной камерами сгорания;
droP== (0,464- 0,52) ZX — для двигателей с полусферическими камерами сгорания.
Диаметры горловин выпускных клапанов обычно принимают на 10—20% меньше drop впускных клапанов.
Проходное сечение клапана с коническим уплотнением (рис. ПО) при высоте подъёма клапана Лкл в рассматриваемый момент времени
^*кл ==: тсЛкл (^гор COS (X (X COS (X), (344)
где б40р ~ di — диаметр горловины, равный малому диаметру посадочного конуса клапана (при d^p > di площадь FKJl определяют по формулам для двух участков подъема клапана), см; а — угол фаски клапана (у современных двигателей а = 45° для выпускных клапанов, а » 45° и реже а = 30° для впускных клапанов);
FKa = 2,72dmphK]I + 1,18ЛкЛ см2 при а = 30°; (345)
FKJI = 2,22drop/iKJI + 1 .ПйклСм2 при а = 45°. (346)
Максимальную высоту подъема клапана (см) при известных значениях Гкл и а определяют из уравнений (345) и (346):
Лкл = К7.4rfrop + 4,72ГКЛ / 2,72 — drop при а = 30°; (347)
Лкл = 4,934оР + 4,44Fkji / 2,22 - drop при а = 45°. (348)
Максимальная высота подъема клапана в автомобильных двигателях изменяется в пределах max (0,184- 0,30) drop, а в тракторных — Лкл тах в (0,16 4- 0,24) drop. Для угла а = 45° величину ^кл max берут по верхнему пределу.
Окончательная проверка установленных значений диаметра горловины и высоты подъема клапана, а также выбранных в тепловом расчете фаз газораспределения проводится по условной скорости швп потока, определяемой по интегральной проходной площади в седле клапана.
284
tf
Так как интегральную площадь (время-сечение) | FK^U определяют по диаграмме подъема клапана Екл = F(0 за время его перемещения от в. м. т. (или н. м. т.) до н. м. т. (или в. м. т.), то а>вп находят после установления профиля кулачка и построения кривой подъема клапана.
$ 62. ПОСТРОЕНИЕ ПРОФИЛЯ КУЛАЧКА
Мгновенные открытие и закрытие клапана позволяют получить максимальное время-сечение, но даже при незначительных массах деталей механизма газораспределения приводят к возникновению больших сил инерции. В связи с этим при проектировании органов газораспределения подбирают такой профиль кулачка, который, обеспечивая достаточное наполнение цилиндра, вызывает допустимые по величине силы инерции.
Профиль кулачка обычно строят в соответствии с выбранным законом образования профиля, что обеспечивает получение относительно простых в изготовлении кулачков.
В современных автомобильных и тракторных двигателях применяют следующие виды кулачков: выпуклый, тангенциальный, вогнутый и безударный.
На рис. 111 представлены наиболее распространенные кулачки: выпуклый (рис. 111, а) — профиль образован дугами двух радиусов Г1Иг2и тангенциальный (рис. 111, б) — профиль образован с помощью двух прямых, касательных к начальной окружности г0 в точках Д и Д' и дуги радиусом г2.
Выпуклый профиль кулачка можно применять для подъема плоского, выпуклого и роликового толкателей, а тангенциальный — главным образом для роликовых толкателей.
Профиль кулачка строят от начальной окружности. Ее радиус Го выбирают из условия обеспечения достаточной жесткости механизма
Рис. 111. Построение профиля кулачка
285
газораспределения в пределах г0 “ (1,54- 2,5) Лкл max, а для двигателей с наддувом — до г0 = (3 4- 4) Лкл тах-
Величину угла <рР0 определяют в соответствии с выбранными фазами газораспределения. Для четырехтактных двигателей
?ро^(?др+18О°+?зп)/4, (349)
где фпР — угол предварения открытия клапана; <рзп — угол запаздывания закрытия клапана.
Точки А и А' являются точками начала открытия и конца закрытия клапана. Точку В находят по величине максимального подъема толкателя /iTmax- Без учета зазоров, при нижнем расположении клапанов Лттах = Лклтах, а при верхнем расположении и наличии рычага или коромысла ЛТтах ~ Лклтах/Т//кл, где 1Т и /кл— длина плеч коромысла, прилегающих соответственно к толкателю и клапану. Отношение /т//кл выбирается по конструктивным соображениям и изменяется в пределах 0,50—0,96.
Для построения профиля кулачка (рис. 111) по выбранным или заданным значениям Лгтах и г0 задаются величиной (или г2) и для обеспечения сопряжения дуг определяют значение г2 (или
Для тангенциального профиля кулачка — оо, а радиус (мм) при вершине кулачка
COS ср r2 = r0 - hr max --122— • (350)
‘-^'Рро
Для выпуклого профиля кулачка
+ “2 — 4 — 2го“ COS Ср_л
(351>
r _ r»b - °'5/tT max — (rl - fo) ('0 + hr max) COS <pp0
2 b — (ту — ra) cos <pp0 ’ ( '
где a = r0 4- hT max — г21 мм; b = rl — rQ — hT тах , мм.
При определении п значение r2 принимают по технологическим соображениям г2 > 1,5 мм, а при расчете г2 принимают = (84- 20) х Хаттах- Выбор слишком малого значения и может привести к получению по формуле (352) отрицательного значения г2. В этом случае необходимо повторить расчет, выбрав большее значение
Для обеспечения зазора в клапанном Механизме тыльную часть кулачка выполняют радиусом гк, меньшим радиуса г0 на величину зазора As: гк = г0 —As. ВеличинаД$ включает в себя температурный зазор и упругие деформации механизма газораспределения. Для впускных клапанов As — (0,254- 0,35) мм, а для выпускных — As = = (0,354- 0,50) мм. Сопряжение окружности радиусом гк с дугами радиусом или прямыми = оо) производится по параболе или по дугам определенных радиусов.
В зависимости от выбранного профиля кулачка и типа толкателя определяют подъемд скорость и ускорение толкателя и клапана. Для выпуклого кулачка с- плоским толкателем:
286
Лц = (ri — r0) (1 — cos <РР1);
“'т1 = (П’—'’о)®к8Ш<рр1;
/т1 = (П —'•o)<cos<ppl;
ftl2 = a cos <pp2 + r2 — r0;' ayT2 = <oKasin<pp2;
/т2------<o2acos<pp2,
(353)
где ftT1, ayTi и jT1 — соответственно подъем (м), скорость (м/с), ускорение (м/с2) толкателя при его движении по дуге радиуса от точки А до точки С; Лт2, и»т2 и /т2 —соответственно подъем (м), скорость (м/с) и ускорение (м/с2) толкателя при его движении по дуге радиуса г2 от точки С до точки В; a — г0 + Лттах — гг, м; сок — угловая скорость вращения распределительного вала, рад/с; <ppi и <рр2 — текущие значения углов при движении толкателя соответственно по дугам и г2.
Значение угла <jppt отсчитывают от радиуса О А, а угла <рр2 — от радиуса ОВ. Их максимальные значения определяют из условия, что в точке С подъем йт1 = йт2,
sin <рР1 max = a sin <рро/(Г1— г2); (354)
?р2 max = <?ро Tplmax (355)
Для тангенциального кулачка с роликовым толкателем:
Рис. 112. Схемы приводов клапанов: а —одноплечий рычаг, б — двуплечнй рычаг
287
hit = (r0 + r) (1 — cos ?pl)/cos <ppl;
Лта = a (cos <pp2 4- — ]/”1 — a? sin2 <рр2^ — (r0 4- r); \ “i 1
^ti = ('о 4- r) ®Ksin <ppl/cos2 <ppl;
шТ2 = ayKfl[sin <pp2 4- (af sin2<pp2) / (2 p41 — af sin2) ];
/т< = (r0 4- г) <в? (1 4- sin2 <?pl)/(cos2 <ppl);
/та = — ®ка [cos ?p« + (aicos 2<?p2 + aisin4 ?p2)/(i —
(356)
- a?sin2?p2)3/2],
где r — радиус ролика, м; == a/(r2 -4 r).
Максимальное значение угла <pP2max определяют по уравнению (355), фрtmax — из соотношения
tg ?pi max — а sin ?ро/(го 4- г). (357)
Рис. 113. Диаграммы подъема, скорости и ускорения толкателя; полное время-сечение клапана
Для кул ачков с симметричным профилем закон изменения Лт, wv и /т при подъеме и опускании остается неизменным.
Подъем, скорость и ускорение клапана для механизма газораспределения с нижним расположением клапанов определяют по уравнениям (353)—(356), так как йкл = Лт> ^кл = wT и /Кл= /т> а для механизма с подвесными клапанами и наличием коромысел или рычагов — по соотношениям (рис. 112, а и б) hKJI = = Ну1кд/1Т1 = ^т^кл^т» /кл = /т ^кд/^т*
На рис. 113 представлены диаграммы Лт> /т плоского толкателя при движении по выпуклому кулачку в зависимости от <рр. Эти же диаграммы, но в масштабе, измененном
288
на величину /кл//т, ускорения клапана.
являются диаграммами подъема, скорости и
$ 63. ПРОФИЛИРОВАНИЕ БЕЗУДАРНЫХ КУЛАЧКОВ
Профилирование применяющихся в настоящее время для быстроходных двигателей так называемых безударных кулачков в отличие от рассмотренных производят в соответствии с заранее вйбранным и рассчитанным законом движения клапана. Закон движения клапана
ний клапана при работе с безударными .кулачками
Рис. 115. Построение профиля безударного кулачка
выбирают с таким расчетом, чтобы при минимально возможных ускорениях получить максимально возможное время-сечение клапана. Обязательным условием получения безударного профиля кулачка является плавное и непрерывное изменение кривой ускорения клапана и толкателя (рис. 114).
В отличие от кулачков, спрофилированных по дугам окружностей (см. § 62), профилирование безударного кулачка начинают с построения диаграммы ускорений клапана. По выбранному закону изменения ускорений определяют законы изменения скорости и перемещения клапана. Для получения этих законов и построения диаграммы скорости и перемещения клапана и толкателя используют различные графо-аналитические методы, методы графического интегрирования и дифференцирования, а все расчеты, как правило, выполняют на электронно-вычислительных машинах.
Безударные кулачки проектируют примерно в такой последовательности:
1. Устанавливают фазы газораспределения фаР, <рзп и фро, максимальную высоту подъема клапана hK„ max и толкателя Лт тах.
289
2. Определяют закон изменения ускорения толкателя, обеспечивающий положительные ускорения, не превышающие 1500—3500, и отрицательные, не превышающие 500—1500 м/с2.
3. Вычерчивают начальную окружность (рис. 115) радиусом г0 и окружность тыльной части кулачка радиусом rK s= г0 — As, где As — зазор между клапаном и толкателем (рекомендации по установлению величин г0, гк и As даны в § 62).
4. Определяют положение точек начала открытия А и конца закрытия А' клапана в соответствии с принятым углом фро [см. формулу (349)].
5. Откладывают углы <рко, соответствующие выбору зазора на участках набегания и сбегания (участок сбега — Фо, рад):
Фо = t2As/(2 - 1 ЗОсо^к), (358)
где (оток = 0,008 ч- 0,022 —скорость толкателя в конце сбега (точки А или Л'), мм/град.
6. Проводят из центра 0 через 0,5° (или 1—2? в зависимости от точности построения) радиальные лучи 00, 01, 02 и т. д.).
7. Откладывают на проведенных лучах от окружности радиуса гк величины подъемов толкателя (с учетом выбора зазора As) aibi, 412^2* ^ibi, Hi+l^i+1,..- И Т. Д.
8. Восставляют перпендикуляры к радиальным лучам из точек bi, b2, .... bt, bi+i, ... в сторону оси симметрии кулачка.
9. Проводят к восставленным перпендикулярам огибающую, которая и будет искомым профилем безударного кулачка.
В зависимости от требований, предъявляемых к механизму газораспределения, безударные кулачки можно проектировать с учетом или без учета упругости деталей привода клапана. К числу кулачков, проектируемых без учета упругости деталей механизма газораспределения, относится кулачок, спроектированный на основе закона изменения ускорения, приведенного на рис. 116 (кулачок Курца). Графики ускорений этого кулачка состоят из четырех участков: 1) сбега Фо — косинусоида, 2) положительных ускорений Ф4 — половина волны синусоиды, 3) первого участка отрицательных ускорений Ф2 — четверть волны синусоиды, 4) второго участка отрицательных ускорений Ф3 — отрезок параболы.
Угловую протяженность Ф1( Ф2, и Ф3 различных участков ускорения толкателя рекомендуется выбирать из соотношений
Ф| + Ф2 + Ф3 = (77/180) ?р0; Ф2 = (0,10 4- 0,25) Ф3;
ф2 + ф3 = (1,5 ч- 3,0) ФР (359)
Чем короче участок положительных ускорений, тем больше площадь под кривой подъемов толкателя. При этом положительные ускорения возрастают, а отрицательные — уменьшаются.
Выражение для пути, скорости и ускорения толкателя при безударном кулачке для различных участков профиля кулачка приведены ниже
Участок сбега кулачка (0 < <рк = фко < Фо):
290
Рис. 116. Диаграмма подъема, скорости и ускорения толкателя; полное время-сечение клапана при работе с безударным кулачком
ft0 = As(l— cos -£-<Рко);
Участок положительных ускорений (0 с <рк = ?ki < ®i):
(360)
291
hi = As + CjiTki — c12 sin <pK1;
WT1~ ®к(Сц C12~C0ST~ ?k! \ <
(361)
• 2 Г / К \2 . 7C 1
Л1 = ®K |c12) Sln — ?K1] •
Первый участок отрицательных ускорений (0 с фк= фк2 Ф2):
й2 — Л1к 4“ <?21SPk2 “Ь ^22 sin (рК2,
hiK = As + сиФ1;
®12 = ®к (с2! + 4,2 cos ?ка) : (362)
. 2 Г / тс \2 . тс I
м = ®к[-<Ц—)sin— ?к2].
Второй участок отрицательных ускорений (0 <рк = <рк3 < Ф3):
Лз = ^2к “Ь С31 (Ф3 ?кз)4 С32 (Фз ?кз)2 + С33»
Л2К = As + спФ! 4- с21Ф2 + с22;
<*>тз = «К [— 4^31 (Ф3 — ?кз)3 + 2с32 (Фз — <Ркз)1;
/тз = <о2 [ 12с31 (Ф3 <ркз)2 2с32].
В формулах (360)—(363), на рис. 115, 116 и в дальнейших расчетах приняты следующие обозначения: <ок — угловая скорость вращения распределительного вала, рад/с; фк — текущее значение угла пово-рота кулачка, град; фКо, фкь фк2, фкз — текущие значения углов поворота кулачка от начала соответствующего участка профиля кулачка (фк/н = 0°) до конца участка (фк/к = Ф?); в (360)—(363) значения ф^, не находящиеся под знаком тригонометрических функций, выражены в радианах, а в остальных случаях — в градусах; Фо, Фь Ф2, Ф3 — угловые интервалы соответствующих участков ускорения толкателя (в формулах угловые интервалы выражены в радианах, а на рисунках— в градусах); ЛКл max И Лт тах — максимальные подъемы клапана и толкателя, мм; h = hT 4- As — перемещение толкателя с учетом выбора зазора, мм; Ло, Ль Л2, h3 — текущие перемещения толкателя на соответствующих участках профиля кулачка, мм; <отО, <oTi, ©т2, <отз — скорости толкателя на соответствующих участках, мм/с или м/с; <о"тОк скорость толкателя в конце участка сбега, мм/рад; /т0, /ть /т2, /тз—ускорения толкателя на соответствующих участках, мм/с2 или м/с2; hiHt ]TiH, фк/н — путь, скорость, ускорение толкателя и угол поворота кулачка в начале соответствующего участка; AfK, cotzk, /тгк, Фк1к — путь, скорость, ускорение толкателя и угол поворота кулачка в конце соответствующего участка; с12, c2j, с22» сзп сз2» сзз — коэффициенты закона движения толкателя, определяемые из равенства перемещений, скоростей и ускорений на границах участков по системе уравнений:
292
^Зк max 4“ As, £цФ1 4“ ^21^2 4“ ^22 4“ ^33 Ат max ж Oj
^зн = А2К, ^з1Фз сзгФз 4“ £*зз “ 6>
<ОТ1Н= <°ток; Си — V/Oi — <ок = 0;
^Т2Н“ ®т!к> Cf J 4“ С|2ТС/Ф| ^21 С22ТС'/2Ф2 = 0;
®тзн= ®т2к! c2i 4- 4с31Ф3 2с32Ф3 = 0;
/тзн = /т2ю с22 (тс/2Ф2)2 4“ 12с31Ф3 2с32 = 0.
(364)
Так как уравнений только шесть, а коэффициентов семь, добавляется еще одна зависимость, характеризующая фо^слу отрицательной части кривой ускорения:
/т2к//тЗк (365)
Для кулачка Курца рекомендуется Z — 5/8.
Принимая для сокращения записи обозначения
*,-ez(-by, ^=<±“ф3;1
\ • Г 6 4 з (366)
4“ ^2 4“ &3Ф2’» К2 = k3 4“ 47Ф2/тс,
получаем окончательную систему уравнений для определения семи коэффициентов закона движения толкателя
Сц = (^С1®т0к 4“ К* 2 Ат шах )/(2^4-W; 1
ci2 “ (си ®ток)Ф1/те; (367)
С32 ” (^Сц Сйт0к)/-^С2> ^21 55 С32^3» С22 =
с31 = с32 (1 . г)/(бФз); С33 = ^32^2-
По формулам (365) — (367) подсчитывают с точностью до шесто-го-седьмого знака значения всех коэффициентов, а затем по формулам (364) проверяют полученные результаты. Несовпадения величин перемещений и скоростей в точках перехода одного участка в другой не должны превышать 0,0001, а ускорений — 0,001.
После вычисления коэффициентов рассчитывают по формулам (360)—(363) перемещения, скорости и ускорения, а также характерные для кинематики толкателя и профиля кулачка величины.
Максимальная скорость толкателя (мм/с)
®ттах (Сц 4“ ^12^/Ф1) (^21 4“ ^22^/^Фг) = ®к^2^32' (368)
Максимальное и минимальное ускорение толкателя (мм/с2)
/т max = ^£12 (ТСФ1)2» (369)
/т min ~ ^2с32. (370)
Минимальный радиус кривизны (мм) вершины профиля кулачка при плоском толкателе
293^
Pmin — 4~ 2c3a. (371)
Максимальный радиус кривизны (мм) профиля кулачка при плоском толкателе
Ртах = Гк + As + СпФ,/2 + с12 [(г/ФО2 - 1 ]. (372)
Значения pmin и ртах используют при определении контактных напряжений между кулачком и толкателем, а по величине ртах ориентировочно определяют форму бокового участка профиля кулачка.
На рис. 116 представлены диаграммы подъема (перемещения), скорости и ускорения плоского толкателя при движении по безударному кулачку в зависимости от угла поворота распределительного вала. Эти же диаграммы, но в масштабе, измененном на величину /к /1т, являются диаграммами подъема, скорости и ускорения клапана.
$ 64. ВРЕМЯ-СЕЧЕНИЕ КЛАПАНА
По диаграмме подъема клапана (рис. 113 и 116) графически опре-деляют время-сечение клапана С (мм2 • с) и среднюю площадь Ркл.ср (мм2) его проходного сечения за такт впуска:
j ^кл^ — М.^Мр F abed ;
?, кл MiMpF^d = 'MF ^2 ^1 ladMf I ad
(3-73)
(374)
где Mt = М^р/бпр — масштаб времени по оси абсцисс на диаграмме подъема клапана, с/мм; Mw —^масштаб угла поворота распределительного вала, град/мм; пр — частота вращения распределительного' вала, об/мин; Мр= Mht:drOpCOsa — масштаб площади проходного сечения клапана по оси ординат, мм2/мм; Mh — масштаб подъема клапана, мм/мм; drop — диаметр горловины, мм; а — угол фаски посадочного конуса клапана (Мр= A4A2,72drop при а = 30°, MF «= = AiA2,22drop при а = 45°)Г FalfCd — площадь под кривой подъема клапана за такт впуска, мм2; lad — продолжительность такта впуска по диаграмме, мм.
Полное время-сечение клапана с момента открытия до его закрытия
*зп
J FKBdt = MtMFFBB, ^пр
где /пР и /зп — время открытия и закрытия впускного клапана, с; FBn = МрРдьсвНав —площадь под вбей кривой подъема клапана, мм2.
294
Время-сечение и среднюю площадь проходного сечения выпускного клапана за такт выпуска определяют аналогично по кривой подъема выпускного клапана.
Средняя скорость потока в седле клапана
®вп = VcpW.cp • (375)
Для карбюраторных двигателей Ювп = 90ч- 150 м/с, а для дизелей — Ивп = 80-? 120 м/с.
$ 65. РАСЧЕТ ГАЗОРАСПРЕДЕЛЕНИЯ КАРБЮРАТОРНОГО ДВИГАТЕЛЯ
Из теплового расчета имеем: диаметр цилиндра D = 78 мм, площадь поршня Fn = 47,76 см2; частоту вращения при номинальной мощности «№ 5600 об/мин; угловую скорость вращения коленчатого вала и = 586 рад/с; среднюю скорость поршня оп.сР= 14,56 м/с; скорость смеси в проходном сечении седла при максимальном подъеме впускного клапана <овп = 95 м/с; угол предварения открытия впускного клапана <рпР = 18°; угол запаздывания закрытия впускного клапана <Рзп = 60е. Механизм газораспределения верхнеклапанный с верхним расположением распределительного вала.
Расчет проведен для двух типов кулачков: выпуклого, профиль которого образован дугами окружностей и безударного '(кулачок Курна), имеющего симметричный профиль.
1. Основные размеры проходных сечений в горловине и в клапане:
площадь проходного сечения клапана при максимальном подъеме
^кл = Уп.ср Fn/<oBn = 14,56 • 47,76/95 = 7,32 см2;
диаметр горловины клапана
drop = /4Ггор /г. = У 4 • 8,20/3,14 = 3,23 см,
где Frop = 1,12ГКЛ = 1,12 • 7,32 = 8,20 см2.
Из условия возможного размещения клапанов в головке при верхнем их расположении (камера сгорания клиновидная или плоскоовальная) диаметр горловины может достигать tfroP = 0.45D = 0,45 • 78 = = 35 мм. Принимаем droP = 32,5 мм;
максимальная высота подъема клапана при угле фаски клапана a s= 45°.
/1клтах= P^4,93drop + 4,44FKJJ / 2,22 t/гор =
= У 4,93 • 32,52+ 4,44-732 /2,22 — 32,5 = 8,92 мм.
2. Основные размеры в п у с-к, н о г о кулачка: радиус начальной окружности
ГО= (1,3 ч- 2,0) /1кл max = (1,34-2,0) • 8,92 = (11,6 ч- 17,8) мм; принимаем г о ~ 15 мм;
295
максимальный подъем толкателя
Лттах — ^клтах/т//кл = 8,92 • 33,5/52,6 = 5,68 ММ,
где /т — 33,5 мм н = 52,6 мм — расстояния от опоры (см. рис. 112, а) до кулачка и клапана (в данном механизме роль толкателя выполняет качающийся рычаг, находящийся в непосредственном контакте с кулачком), принятые по конструктивным соображениям.
3. Профилирование выпуклого кулачка с плоским толкателем. Радиус дуг выпуклого профиля кулачка г2 > 1,5 мм, принимаем г2 = 8,5 мм, тогда
_ °а + Гр — — 2аГ(| cos <рр0 _
Г1 “ 2 (r0 — г2 — a cos !рр0) ~
12,182+ 152 — 8,52 — 2 • 12,18 • 15cos64°30' _» п
*= • • • Of .2 мм*
2 (15 — 8,5 — 12,18 cos 64°30')
где а= г0 + Лттах — г2 = 15 4- 5,68— 8,5 = 12,18 мм; <?ро = (?пр4-4- 180° + ?зп)/4 = (18 + 180 + 60)/4 = 64°30'.
Максимальный угол при подъеме толкателя по дуге радиусом г4
. asin<Ppo 12,18sin 64°30' nQOfi loonoz
Sin <ppl max---------- — ZTT-----— — 0,226, max — 13 03 .
Гi — /*2 ui — 8,u
Максимальный угол при подъеме толкателя по дуге радиусом га
?р2 max = ?ро — ?pl max — 64°30/ — 1 3°03/ ==51 °27/«
Подъем толкателя по углу поворота распределительного вала
Лц = (П — Л>) (1 — cos <рр1) = (57,2 — 15) (1 — cos <f>pl) «
= 42,7 (1 — cos <рр1) мм;
Лт2 = a cos <рр2 4- г2 — г0 = 12,18 cos fpa 4- 8,5 — 15 =
= (12,18cos<pp2 — 6,5) мм.
Скорость и ускорение толкателя
шт1 == (rf — г0) sin <рр1 = (57,2 — 15) 10-3 • 293 sin ?р1 =«
= 12,36 sin <рр1 м/с;
щт2 = <oKasin <рр2 — 293 • 12,18 • 10~3sin <рр2 = 3,57sin <рр2 м/с;
/т1 = (П “ го) ®к cos ?р1 = (57,2 — 15) 10“3 • 293® cos ?р1 ==
= 3623 cos <рр1 м/с2;
/т2 = — <o£acos<pp2 = —2932 • 12,18 • 10-3cos<pp2 = = — 1046 cos <рр2 м/с2,
где ик = О,5со = 0,5 • 586 = 293 рад/с — угловая скорость вращения распределительного вала.
296
Таблица 65
Фазы газо-распределия Параметры
9°, п. к. в. ОЗ о а _* 9- О. Я о fpl о м cos (Ppi и cos <РР2 1——cos Vpi И a cos <рр2 sin <рр1 и sin (рр2 hT , мм <от , м/с jT , м/с* SF^dt
<Рпр = 18° J 702 351 0 1 0 0 0 0 +3623 0
1 712 356 5 0,9962 0,0038 0,0872 0,162 +1,078 +3609 0,002
В. м. т. 0 0 9 — 0,9877 0,0123 0,1564 0,525 +1,933 +3578 0,011
Г13°03' 0,9744 0,0256 0,2258 1,093 -4-2,791 +3530 0,032
о Ub 4 03 Л 51°27' 0,6234 7,5930 0,7820 1,093 +2,791 —652 0,032
31 15°30' — 40 0,7660 9,3300 0,6428 2,830 +2,295 —801 0,180
51 25°30' — 30 0,8660 10,5479 0,5000 4,048 +1,785 —906 0,408
Такт впуска 71 35°30' — 20 0,9397 11,4455 0,3420 4,946 + 1,221 —983 0,712
(180°) 91 45°30' 10 0,9848 11,9949 0,1736 5,495 +0,620 —1030 1,064
111 55°30' — 0 1 12,1800 0 5,680 0 —1046 1,439
131 65°30' — 10 0,9848 11,9949 0,1736 5,495 —0,620 —1030 1,814
151 75°30' — 20 0,9397 11,4455 0,3420 4,946 —1,221 —983 2,166
171 85°30' — 30 0,8660 10,5479 0,5000 4,048 —1,785 —906 2,470
Н. м. т. 180 90 — 34°30' 0,8241 10,0375 0,5664 3,538 —2,022 —862 2,581
' 191 95°30' 40 0,7660 9,3300 0,6428 2,830 —2,295 —801 2,698
— 51°27' ' 0,6234 7,5930 0,7820 1,093 —2,791 —652 2,845
213°54' 106°57'
?зл=60° 222 111 13°03' 0,9744 0,0256 0,2258 1,093 —2,791 +3530 2,845
230 115 9 — 0,9877 0,0123 0,1564 0,525 —1,933 +3578 2,867
840 120 5 — 0,9962 0,0038 0,0872 0,162 —1,078 +3609 2,876
0 1 0 0 0 0 +3623 2,878
Значения Лт, ют и /т, подсчитанные по приведенным формулам, в зависимости от угла поворота распределительного (и коленчатого) вала приведены в табл. 65.
По данным табл. 65 на рис. 113 представлены диаграммы подъема, скорости и ускорения толкателя.
4. Профилирование безударного кулачка с плоскимтолкателем. Зазор между клапаном и толкателем принимаем As = 0,25 мм, а затем определяем радиус окружности тыльной части кулачка (см. рис. 115)
гк = г0 — As = 15 — 0,25 = 14,75 мм.
Протяженность участка сбега
ф =------------= 3,14159*-0,25 = 0,342694 рад« 19с38',
° 2-180^ 2.180-0.02
где ю'ток = 0,02 мм/0 — скорость толкателя в конце сбега, принята в пределах, рекомендованных для безударных кулачков (см. § 63).
Протяженность других участков ускорения толкателя Ф1 = 23°30' = 0,410152 рад; Ф2 = 4°= 0,069813 рад; Ф3 ;= 37° = 0,645771 рад удовлетворяет рекомендуемым соотношениям (359):
Oj + Ф2 + Ф3 = я?р0/180; ф, + ф2 + ф3 — я?рО/180 = 0;
0,410152 + 0,069813 + 0,645771 — 3,14159 • 64,5/180 = 0;
ф2 = (0,14- 0,25) Ф3; Ф2/Ф3 = 0,1 4- 0,25;
0,069813/0,645771 = 0,108;
Ф2 + Ф3 = (1,5 4- 3,0) Ф,; (Ф2 + Ф3)/Ф1 = (1,5 4- 3,0);
(0,069813 +0,645771)/0,410152 = 1,745.
Вспомогательные величины [см. (366)] и коэффициенты закона движения толкателя [см. (367)]:
kt = 8z(-Ь-У = 8 — ( °’069813 У = 0,002469;
\ я / 8 \ 3,14159 J
fe, = Ф3 = 5 + 5/8 0,6457712 = 0,390956;
6 6
k3 = 4 + 2Z ф3 = 4-+2'5/8 0,645771 = 1,130099;
3 3
Ki = ki + k2 + &3Ф2 = 0,002469 + 0,390956 + 1,130099-0,069813 =
= 0,472321;
К2 = fe3 + 4Z -^ = 1,130099 + 4 — • 0,069813 = 1,185654,
2 3 л 8 3,14159
где Z = 5/8 — принято по рекомендациям для кулачка Курца (см. §63);
298
^1“тОк + A max 0,472321 • 1,145917+ 1,185654 • 5,68 - no.cn_
си =------------------ = ---------------------1-------— = 5,084597,
11 2К1 + К2.Ф! 2-0,472321 + 1,185654 . 0,410152
где ®ток — скорость толкателя в конце сбега, мм/рад: = ®ток • 18°/д = °.02 ' 180/3,14159 == 1,145917;
С12 = (с11 — <0к)Ф1/= (5,084597— 1,145917) - 0,410152/3,14159 = = 0,514217;
с32 = (2сн — <ок)/К2 = (2-5,084597— 1,145917)/1,185654=7,610380,
с21 = c32k3 = 7,610380 • 1,130099 = 8,600483;
с22 = c32ki = 7,610380 • 0,002469 = 0,018790;
с3. = с32 —- = 7,610380 - = 1,140589;
31 32 6Ф2 6-0,6457712
с33 = c32fe2 = 7,610380 • 0,390956 = 2,975324.
Проверка вычисленных значений коэффициентов по формулам (364): СцФ2 4~ с2|Ф2 Н- с22 с33— h-т max = 5,084597-0,410152 +
+ 8,600483 - 0,069813 + 0,018790 -t- 2,975324 — 5,68 = = — 0,000002 « 0;
с3,Фз —с32ф| + сз3 = 1,140589 • 0,6457714 —7,610380-0,64577Р + + 2,975324 = — 0,000003 « 0;
Си —С12^/Ф1 — ю;0к = 5,084597 — 0,514217 • 3,14159/0,410152 — — 1,145917 = — 0,000004 « 0;
Си + С121Г/Ф1 — с21 — С221С/(2Ф2) = 5,084597 + + 0,514217 - 3,14159/0,410152 — 8,600483 — -0,018790-3,14159/2-0,069813 = 0,000022 « 0;
с21 + 4с31Фз — 2с32Ф3= 8,600483 + 4-1,140589-0,645771 — — 2 - 7,610380 • 0,645771 = — 0,000002 « 0;
с22 (У + 12с31Фз — 2с32 = 0,018790 ( 3’1415—? + 22\2Ф2/ 31 32 \ 2-0,069813 /
+ 12 • 1,140589 • 0,6457712 — 2-7,610380 = — 0,000508 «0.
Полученные результаты находятся в допустимых пределах, так как несовпадение величин перемещений и скоростей в точках перехода одного участка в другой меньше 0,0001, а ускорений —меньше 0,001.
299
Подъем (перемещение) толкателя по углу поворота кулачка фк (распределительного вала фр):
ho = As (1 — cos <рк0'); <рк0 = 0° — 19°38';
ho = 0,25 (1 - cos 2 .Y342697 <Fk0) = 0,25 ° ~ 008 4>583666<?ко);
Af = As + Сц?к1 c12 s*n
¥Гфк‘:
<pK1 = 0°— 23°30';
hi = 0,25 + 5,084597<pK1 —0,514217sin ?K1 =
= 0,25 + 5,084597<pK1 — 0,514217 sin 7,659575<pK1;
при <pK1 = <pK1K = 23°30' = 23,5° = 0,410152 рад
Л1К = 0,25 + 5,084597 • 0,410152 —0,514217sin 7,659575-23,5 =
= 2,335458 мм;
+ с21Фк2 + C22 sin фк2; ф^ = 0° — 4°;
h. = 2,335458 + 8,600483фк2 + 0,018790 sin -3’1-1-59 фк2=
2 кг 2-0,069813 “
= 2,335458 + 8,600483фк2 + 0,018790 sin 22,500036фк2;
при Фка ~ Фкгк = 4° = 0,069813 рад
Л2К = 2,335458 + 8,600483 • 0,069813 + 0,018790 sin 22,500036-4 =
= 2,954674 мм;
Лз — hoK + См (Ф3 Фкз)4 с32 (Ф3 Фкз)2 + Сз3; фк3 = 0° 37°;
= 2,954674 + 1,140589(0,645771 —фй)4 — 7,610380(0,645771 —
-Фкз)2+ 2,975324;
при Фкз = ФКЗк = 37° = 0,645771 рад
Л3 = 2,954674+ 1,140589(0,645771 —0,645771 )4 — 7,610380 X
X (0,645771 — 0.645771)2 + 2,975324 =
= 5,929998 « 5,93 мм = hj max + As.
Величины перемещений толкателя по участкам Фо, Ф1 и Ф3 рассчитывают через 1°, а по участку Ф2 — через 30' ₽= 0,5° и сводят в таблицу. В целях сокращения объема в табл. 66 приведены значения ho, hu Л2 и Л3 через большие интервалы.
Скорость толкателя
®т0 = <ок • 10’3As —— sin фи,; Фко = 0° — 19°38';
т0 к 2Ф0 2Ф0 к0
300
о
Участок сбега при опускании <,09= = “«di 1 E » || ^ s Такт впуска (180°) ? —° H 7* о II Участок сбега при подъеме — Фазы газораспределения
to to to to to -J CM СЛ 4ь rfa. ФФФФО о о о о CM CM CM CM tptotototo^-^-^-^— •^coto^-ococooopopooo OOtOOOCOCOcOCnCnO QO-sJO^rf^tO^^-CO-sJCMrf^COCOCOtOtOtO^-ОСЛСЛСЛСЛ*— ^--J-J-J-J-J-jCOcO<OtOtOO te^o о to to см см см см О СО 00 см to to to to to ° tf^3 Tf^ to (р° п. ,к.в
со со to to to to CO о 0 о о о co co co co 00 00 00 00 " О * to^-^-OOcOcOcpcOcOcO ОСЛн- слосмсм*&ююо О О О О О со со со со со о о о о о " " " " о сООООО“^СМСЛСЛ4ьСОЬрЬО'— *— *— •— Т* 0“'JtOtOtOCMCMOOOOOOOOQOQOCM4b4b1— о о о оооо с о о о о о о о CJS Q сососососососососососососососо ООООООООООООООО ’чЧ'4*'4*4*4*'*'*'4*4*'*'4* co co co CM СЛ СЛ о CM — co co co co co ел co co — CM — CM — о о о о to to to to to to to to 00 -е TJ О Я . р В
Фо—19°38' Ф1=23°30' Ф2=4 е II СО е со II СО 1 и =23°30' Ф0=19р38'
О СЛ О CM CO о co 00 - * ' •— to to о СЛ СО ел о со о to-f^ to о О ° со со о о •— to со со со со to •— to to •— tOCMOOO-'J-'JOOOCMOrf^tOOCOOCMcO о о со со о о CO СЛ О CO СЛ О СЛ О о со 00 СЛ рота ку чка -osou НЛ о □
-6 к о -6 -6 к к ►* ы> -6 -6 -6 -6 к о La м м п &> S
о о о о о о о to to СО СЛ о о со о ooo^-^-tototototoco to СО cnL-\j со со см со io со CM-JCM^-cOCOC04bCMCMtO ОСЛСОСЛСОСЛСЛСОСЛСЛ^- С0С04ьелСЛСЛСЛСЛСЛ4ьС0ЮЮЮЮЮ^-^-О СО см То То 00 со io OOtOtOC7>COCO<7>COCO^J^-CM ЬОСМсОСМ1—COCO>— СМЮСМСЛСЛ+хСОСОСО'—CM ^--j^jco-^joo-jcp-j-^слслсослслсослсо ООО СЛ CO to CM ел co СЛ о оооо ioi-oo о СЛ СО to о со см о о h=hT мм + As, п Е
1 1 1 1 1 ooo^-tototototoco о СО оо Ъ1 О О 00 Vj kj о (О'— O^noOOOOO^ елсоелсослслсослсл^- сосо+ьслслслслслсл+ьсоьоьоьоьоьо1—оо О+• о о ел см СМ СЛ О О 4ь\] Vj 00 О О ел 00 со -sJ^-^^-CM00 00CM^-4b^-OOcO00 00 4b^-i— --J -*J СО —J О О —J СО —J --J СЛ СЛ СО СЛ СЛ СО СЛ СО о о coi— о to со сл 1 1 1 1 1 /1т , мм
-0,3358 —0,3129 —0,2408 —0,1307 0 1 1 1 1 1 1 1 1 1 1 1 о о •— to to to to to to to СО СЛ OOUlO) см см "ел ел со COQO-J-sJ^-^^O^-^-CO СЛ СЛ СО СО СО --J СО СО СО ОО^-сОСМООООООСЛсОсОСЛ 1 1 1 1 1 ++++Ч-+++++++ toto^-^oooo^-^-tototototototo^-1--СО io io io yi Сл io ip io ел ел см см см СЛ io о СОСлООО*^ CO -J — 00 to tOOO'-^-'JcOcO-'JCOCOcOCMrf^ СЛ co “-J CO 4^СО-^СОСОСОСЛООООООСМСО +0,3358 +0,5841 + 1,0749 0 +0,1307 +0,2408 +0,3129 +0,3358 00 <ОТ , м/с
1 11 । ++++I11111 •— to to О СМ 4ь СО о о сл 00 00 Q0 о *— CM “'j •— •— 00 СЛ “-J со 00 — I 1 1 I I I I I I 1 J_ _J L 1 0 +1605 +2417
'T-г 1 г 4ь СО |_— ел •— •— см о •— ел 4** со 1 1 iiii ++t OOCOpbOtOCOCOtObOOCOOOOOCMOO^-COrf*. оо^^оаюоаю^^1-1-^ см *₽*• •— ^-OMWc£)“s]“s]OCOCMO^^^ 00 CO -J Ч—1—1—ь о СО rfb 4b о >— ел СО 4ь СЛ •— СО /т , м/с2
1 1 1 1 1 tototototototototototo CM CM CM CM СП Ц1 СЛ СЛ 4* 4ь 4ь CMCMCMCOcO^^COcOcOrf* СЛЬОСМЮ^-ОООО — — tototo^^-^-^-^-ooooooooooo ел co io со ел co w ok) w io k- L- L- L- о о о ehoocMOncoo3copocO"^JCMg>co^-^--jcoo A^j^-^ootOtOChOOQOtOOOOPCOOOQOCO^-^J 0,006 0,003 0,007 1 1 1 1 1 о {х *пр мм2* с
Таблица 66
onQ in-з лос 3,14159 . 3,14159
о 0 = 293 -10 3 • 0,25---’------sin-----------Фко —
T0 2 • 0,342694 2 > 0,342694
= 0,3357548^4,5836664)^ м/с;
<oT1 = coK10’3 tai —cos-^- <pta; <pKi =0° —23°30';
coT1 = 293 • 10-3 (5,084597 — 0,514217 3,14159 cos 3’141--<pta =
T1 \ 0,410152 0,410152 K1/
= 1,489787—1,154034 cos 7,659575<pK1 м/с;
при <рк1 =фк1к = 23°30'=23,5°=0,410152рад coTl = <йт)к=±<Огшах;
<oTmax = 1,489787— 1,154034 cos 7,659575-23,5 = 2,643821 м/с;
<от2 = <oK 1 O’3 (c2i + c22 cos <ркД <pK2 = 0° — 4°;
<0r2 = 293 • 10‘3 ( 8,600483 + 0,018790 3,14159 cos 3,14159 =
r2 \ 2 • 0,069813 2 • 0,069813 K2/
= 2,519942 + 0,123873cos22,500036<pK2 м/с;
шгз = шк Ю 3 [2сз2 (Ф3 — Фкз) 4с31 (Ф3 фкз)3]; Фкз = 0° — 37°;
шт3 = 293 • 10’3 [2 • 7,610380 (0,645771 — фк3) — 4 • 1,140589 X
X (0,645771 — ф3>3] = 4,459683(0,645771 — фк3) —
— 1,336770(0,645771 — Фк3)3 м/с.
Значения <от0, соц, сот2 и сотз, подсчитанные по приведенным формулам, в зависимости от углов поворота кулачка (распределительного вала) заносят в табл. 66.
Ускорение толкателя
/т0 = • 10-3Дз (-1- Y cos фк0; фк0 = 0° - 19°38';
опо2 m-з л лк ( 3,14159 \2 3,14159
/тП = 2932 • 10 3 • 0,25 ----------1 cos----:------Фко=
/т0 \ 2 • 0,342694 / 2 • 0,342694
= 450,921838 cos 4.583666ФК0 м/с2;
/Т1 = • Ю-Зс12 (sin фк1; фк1 = 0° - 23°30';
• опой 1 л-3 л С1ЛО17 / 3,14159 . 3,14159
/гр1 = 2932 • 10 3 • 0,514217 —----- sin---------фК1=
iTi ' \ 0,410152/ 0,410152 *K1
= 2589,947827 sin 7,659575фк1 м/с2;
при фк1 = фк1к = 23°30' = 23,5° = 0,410152 рад /Т1 = /т1к;
/Т1к = 2589,947827 sin 7,659575 • 23,5 = 0;
302
in = — • 10-3c22 (^-)2 sin — Фк2; <рк2 = 0° — 4°;
/т2 = — 2932 • 10’8 • 0,018790 ( 3’14159- У sin -I’14-1- Фк2 =
1 \ 2-0,069813 ) 2-0,069813 т 2
= — 816,635846 sin 22,500036(рк2 м/с2;
/тз = <в? - 10’3 [ 12см (Ф3- Фкз)2 - 2сзг]; Фкз = 0° - 37°;
/т3 = 2932 • 10~3 [12 - 1,140589(0,645771 — Фк3)2 — 2 • 7,610380] =
= 1175,021101 (0,645771 — фкз)2 — 1306,687025 м/с2;
ПрИ Фк3 — ФкЗк = 87 — 0,645771 рЗД /т3 = /т3к = JT mini /т min — = 1175,021101 (0,645771—0.645771)2—1305,687025=—1306,687025 м/с2.
Значения /т0, /т1, /т2 и /т3, подсчитанные по приведенным формулам, в зависимости от углов поворота кулачка (распределительного вала) заносят в табл. 66.
По данным табл. 66 на рис. 116 построены графики перемещения (подъема), скорости и ускорения толкателя.
Минимальный и максимальный радиусы кривизны профиля безударного кулачка при плоском толкателе:
Pmin = rK + Л — 2с32 = 14,75 + 5,93 — 2 • 7,610380 = 5,45924 мм,
где h = /iTmax + As = 5,68 + 0,25 = 5,93 мм;
ртах = Гк + As + сиФ4/2 + с12 [(^/ФО* - 1 ] = 14,75 + 0,25 +
+ 5,084597 - 0,410152/2 + 0,514217 [(3,14159/0,410152)2 — 1 ] =
= 45,697155 мм.
5. Врем я-с ечение клапана. Диаграммы подъема толкателя (см. рис. 113 и 116), построенные в масштабе по оси абсцисс Л4?р?= 17мм, по оси ординат /ИЛТ — 0,1 мм/мм, являются диаграммами подъема клапана, если изменить масштаб по оси ординат на
МЛКЛ — Ак\тахЛ4йг/ Аттах = 8,92 • 0,1/5,68 = 0,157 мм/мм.
Время-сечение клапана
J FKadt = MtMFFabcd,
А
где Mt = М?р/(6пр) = 1/(6-2800) = 5,952 • Ю'5 с/мм; MF =MltKa х
X 2,22drop = 0,157 • 2,22 • 32,5 = 11,3 мм2/мм;
для выпуклого кулачка
( FKadt = 5,952 • 10-3 • 11,3 • 3820 = 2,569 мм2-с,
303
где Fabcd ?= 3820 мм2 — площадь под кривой подъема толкателя (см. рис. 113) за такт впуска;
для безударного кулачка
t,
[ FMdt = 5,952 • IO"5 • 11,3 • 3600 = 2,421 мм2-с, t,
где Fabcd — 3600 мм2 — площадь под кривой подъема толкателя (см. рис. 116) за такт впуска без учета площади, соответствующей выбору зазора As.
Средняя площадь проходного сечения клапана
Ркл. ср — FKndt/(/2 — Fabcd/lad,
t,
где lad — 90 мм — продолжительность такта впуска по диграммам (см. рис. 113 и 116):
для выпуклого кулачка
FKn.cp = П.З • 3820/90 = 480 мм2 = 4,80 см2;
для безударного кулачка
Гкл.ср = 11,3- 3600/90 = 452 мм2 = 4,52 см2.
Средняя скорость потока смеси в седле клапана:
юВп= ^п.ср Fa/FKn.cp;
для выпуклого кулачка
ш'вп = 14,56 • 47,76/4,80 = 145 м/с;
для безударного кулачка
й>;п = 14,56 • 47,76/4,52 = 154 м/с.
Полное время-сечение клапана
G j FKlldt = MtMPFx, *пр
где /пР — момент начала открытия впускного клапана; tx и Fx — текущие значения времени и площади под кривой подъема толкателя (см. рис. 113 и 116).
Зависимости полного времени-сечения клапана от углов поворота кулачка (распределительного и коленчатого валов) представлены на рис. 113 для выпуклого и на рис. 116 для безударного кулачков, а численные значения подсчитаны и занесены соответственно в табл. 65 и 66.
Сравнивая основные показатели газораспределения с выпуклым и безударным кулачками, можно сделать следующие выводы:
304
1. При одинаковых начальных условиях (wK> rKi Шах, Лттах, <pp0, й)вп) максимальные положительные ускорения, а следовательно, и максимальные инерционные нагрузки при безударном кулачке уменьшились на 33,3% (2417 против 3623 м/с8), отрицательные уско' рения несколько возросли (с 1046 до 1307 м/с2).
2. Время-сечение клапана при безударном кулачке уменьшилось на 5,8% (с 2,569 до 2,421 мм2 • с), что повлекло за собой увеличение средней скорости потока смеси в седле клапана от 145 до 154 м/с.
3. При переходе с выпуклых кулачков на безударные необходимо для сохранения и тем более улучшения основных расчетных показа-
телей газораспределения (I FKndtt Ркл.ср, о>вп) увеличивать проходное сечение клапана за счет расширения фаз газораспределения и увеличения максимальной высоты подъема клапана.
§ 66. РАСЧЕТ ПРУЖИНЫ КЛАПАНА
Пружина клапана должна обеспечивать при всех скоростных режимах двигателя: 1) плотную посадку клапана в седле и удержание его в закрытом положении в течение всего периода движения толкателя по начальной окружности г0; 2) постоянную кинематическую связь между клапаном, толкателем и кулачком во время движения толкателя с отрицательным ускорением.
Плотная посадка клапанов обеспечивается:
для выпускного клапана при
Р пр min Z> F гар[рг — Pa)t (376)
где РПр min — минимальное усилие пружины при закрытом клапане, Н; Ргор — площадь горловины, м2; р/ и ра — давление газов соответственно в выпускном трубопроводе и в цилиндре при впуске, МПа. В карбюраторных двигателях разность давлений (рг' — ра) достигает Д05—0,07 МПа, а в дизелях — 0,02—0,03 МПа;
для впускного клапана в двигателях без наддува практически при любом минимальном усилии пружины, а в двигателях с наддувом при
Рпр min Prop (Рк Рг)» (377)
где рк и рг — давление газов соответственно во впускном трубопроводе (давление наддува) и в цилиндре при выпуске, МПа.
Кинематическая связь между деталями клапанного механизма обеспечивается при
РдР " ДР/ кл 2 > (378)
где К — коэффициент запаса (для дизелей при наличии механических центробежных регуляторов Д = 1,28 ч- 1,52, для карбюраторных двигателей Д = 1,33 ч- 1,66); Р/КЛ2—приведенная к клапану сила инерции механизма при движении толкателя с отрицательным ускорением, Н.
11—370
305
Расчет пружины клапана сводится к : 1) определению силы упругости пружины Р/кла; 2) подбору по силе Р/клг с учетом коэффициента запаса К. характеристики пружины: 3) проверке ее минимального усилия при закрытом клапане; 4) выбору размеров пружины и 5) определению запаса прочности и числа собственных колебаний пружины.
Сила инерции, приведенная к оси клапана, при движении толкателя с отрицательным ускорением
Pj кл2 — — Мкл/кл2 — ~~ Л4кл/та/кл/^т’ (379)
где Мкл — суммарная масса клапанного механизма, приведенная к клапану, кг.
При нижнем расположении клапанов
Мкл = ткл + /Ппр/3 + тт, (380)
где ткл — масса комплекта клапана (клапан, тарелка пружины, замок); /пвр — масса пружины (пружин); /пт — масса толкателя.
При верхнем расположении клапанов
Мкл = ткл + /Ппр/3 + (тт + тШТ)(1Т/1кл)3 + т', (381)
где лгшт — масса штанги;' = JK //L ~ т* (/кл + /т)2/12/£л — масса коромысла, приведенная к оси клапана, при двуплечем рычаге с опорной стойкой в виде шпильки; т* — JK П1л «/«к /^/(3/^) — масса коромысла, приведенная к оси клапана, при одноплечем рычаге с опорной стойкой в виде болта (см. рис. 112); JK и тк — соответственно момент инерции коромысла относительно оси качания и его масса.
При расчетах вновь проектируемых двигателей массы ткл, ягпр,-/пт, ттт и Шк принимаются по конструктивным размерам и статистическим данным аналогичных клапанных механизмов. Конструктивные массы А4м == Мкл/^гор Для впускных клапанов при различном их расположении и приводе имеют следующие значения (кг/м2):
При нижнем расположении клапанов ................... 220—250
При верхнем расположении клапанов с нижним расположением распределительного вала ...................... 230—300
При верхнем расположении клапанов с верхним расположением распределительного вала..................... 180—230
На рис. 117 представлена кривая силы инерции Р^г поступательно движущихся масс, приведенных к оси клапана. По этой кривой при выбранном значении К строят кривую abc необходимых сил упругости пружины Рпр = КР/клг при движении толкателя с отрицательным ускорением. С помощью диаграммы подъема /гкл клапана кривую Рпр г= /(<рр) перестраивают в координаты /пр —Рпр (деформация пружины — сила упругости пружины), как показано на рис. 117. Полученная кривая а"Ь"с'' представляет собой зависимость необходимой силы упругости пружины от высоты подъема клапана, т. е. необходимую характеристику пружины (для выпуклого кулачка с плоским 306
толкателем кривая aVc" — прямая линия. Заменяя кривую а"Ь"с' прямой а“с“ и продолжая ее до пересечения с вертикальной осью (точка О"), получают возможную характеристику реальной пружины.
Отрезок, отсекаемый прямой а "О" на горизонтальной оси (Лкл= 0), соответствует минимальной силе упругости пружины при закрытом клапане, т. е. силе Рир min предварительной затяжки пружины. Если полученное значение Рпр тш не обеспечивает выполнения неравенств (376) или (377), необходимо увеличить силу Рпр тш за счет увеличения К ИЛИ /max-
По характеристике пружины, построенной графическим способом, определяют: предварительную деформацию./тш, полную деформацию /тах = /ттЧ- ^кл max И ЖвСТКОСТЬ ПруЖИНЫ С <= Рпр max//max.
Для выпуклого кулачка с плоским толкателем характеристику пружины можно подобрать непосредственно по параметрам кулачка: максимальная сила упругости пружины
Рпр max — Aftoj-ffaZ кл
минимальная сила упругости пружины
Рпр min = МклЯ (^о — 7j) ^кл®^/^5
11* 307
жесткость пружины
с = /ИклКсо2;
предварительная деформация пружины
fmln — Рпр min / С = (Zp Га) 1кп/ !
полная деформация пружины
/max = fmin“b Лклтах = Ц^кл/^т-
Основными конструктивными размерами пружины являются: средний диаметр пружины DnP, диаметр проволоки 8пр, число витков /, шаг витка t и полная длина £св свободной пружины.
Средний диаметр пружины обычно принимают по конструктивным соображениям в зависимости от диаметра горловины клапана Dap~ = (0,7 ч- 0,9) drop, а диаметр проволоки 8пр= (3,5 ч- 6,0) мм. При наличии двух пружин на одном клапане диаметр проволоки внутренней пружины 8пр — 2,2 ч- 4,5 мм.
По принятым значениям ОпР и подобранной характеристике пружины определяются:
число рабочих витков пружины
t’p = б8пр/тах/( 8Рпр max Г>пР), (382)
где б = 8,0 ч- 8,3— модуль упругости второго рода,.МН/см2; Рпртах— сила упругости пружины, МН; Dnp и /тах — соответственно средний диаметр и полная деформация пружины, см; 8пР — диаметр проволоки, см;
полное число витков пружины ia^= ip + 2;
шаг витка свободной пружины
t — ^пр 4* /тах//р 4~ Amin >
где Amin = 0,3 — наименьший зазор между витками пружины при полностью открытом клапане, мм;
длина пружины при полностью открытом клапане
/-mln == Ai^np 4“ /pAmin» (383)
длина пружины при закрытом клапане
Z-0 = /'min + hKn щах i (384)
длина свободной пружины
/-св = /“min 4” /max- (385)
Максимальное касательное напряжение, возникающее в пружине:
"Чпах = 8Рпртах /^np/f’^np) , (386)
где k' — коэффициент, учитывающий неравномерное распределение напряжений по поперечному сечению витка пружины и зависящий от отношений’Дцр/Вцр. Значения коэффициента k' приведены ниже:
308
Onp/»np .3 4 5 6 7 8 9 ю 11 12
k' . . . . 1,5 1,38 1,3 1,23 1,2 1,17 1,15 1,13 1,11 1,1
Максимальное напряжение в быстроходных двигателях тшах= = 450-4- 650 МПа.
Минимальное напряжение в пружине при закрытом клапане
Tmiti = k ^Рпр min Onp/fwSnp) . (387)
Запас прочности п, пружины определяется по формулам, приведенным в §43. Для пружин автотракторных двигателей /ц >1,2-4--4-1,4, а предел усталости при кручении для пружинных сталей в расчетах т_4 = (340 -4- 400) МПа.
При больших силах инерции на каждый клапан устанавливают по две пружины (наружная и внутренняя). В этом случае рассчитывается каждая пружина аналогичным способом, но с соблюдением УСЛОВИЙ. РПр max ~ Рпр.н шах 4* Рпр.в max и Рдр min — Рпр.н min~h Рпр.в mln-Усилия между пружинами распределяются по конструктивным соображениям в пределах Рпр.в = (0,35 -4- 0,45)Рпр.
Для обеспечения нормальных радиальных зазоров между направляющей втулкой и внутренней пружиной, а также между пружинами размеры пружин (мм) должны удовлетворять требованиям:
Опр.в 4- 8др.в 4- 2; ОПр.и Опр.в 4- ^пр.в 4- 8прн 4- 2,
где^вТ — диаметр втулки клапана; Опр.в иОпрв —средние диаметры соответственно внутренней и наружной пружин; 8пР в и 8прн — диаметры проволоки соответственно внутренней и наружной пружин.
Во избежание появления резонанса — совпадения частоты собственных колебаний пружины с вынужденными — определяется число свободных колебаний клапанной пружины
пс = 2,17 • 1078np/(zpZ>nP). (388)
Отношение числа собственных свободных колебаний пс пружины к частоте вращения пр распределительного вала не должно равняться целому числу (особенно опасно nc/np = 1), а при наличии двух пружин, кроме того, должно соблюдаться неравенство nCtli/np Ф п^.в/п^.
Расчет клапанной пружины карбюраторного двигателя. Из расчета газораспределения (см. § 65) имеем: частоту пр = 0,5 n/v = 2800 об/мин и угловую скорость вращения сок = 293 рад/с распределительного вала; максимальную высоту подъема впускного клапана /гклтах = = 8,92 мм; диаметр горловины впускного клапана drop = 32,5 мм; размеры кулачка с выпуклым профилем: rQ = 15 мм, = 57,2 мм, г2 = 8,5 мм; hT max = 5,68 мм, а = rQ + /гт тах— г2 = 12,18 мм; размеры коромысла: /кл = 52,6 мм, /т = 33,5 мм; диаграммы подъема, скорости и ускорения толкателя (см. рис. 113 и табл. 65). Расположение клапанов верхнее с приводом от распределительного вала, размещенного в головке блока. Усилие от кулачка передается непосредственно на коромысло, имеющее плоскую поверхность соприкоснове
309
ний с кулачком. Материал пружин — пружинная сталь, == = 350 МПа, ов = 1500 МПа.
Максимальная сила упругости пружин
Рпртах = КЛ4жла/жл®«//, = 180 • 1,4 • 12,18 • 52,6-293® • 10«/33,5 =
= 414 Н,
где К. = 1,4 — коэффициент запаса; Л4ЖЛ = /пжл 4- — /ппр 4- (лгт 4-3
4- /пшт) (—*-^4- т'к ~ 1154- —75 4- 40 = 180 г— суммарная масса клапанного механизма, приведенная к клапану; тяа = 115 г, тпр = = /«пр. н 4- /иПр.в = 55 4- 20 = 75 г — массы соответственно клапана и пружин (наружной и внутренней), принятые по конструктивным соображениям; т'к = /пж/£л/(3/£л) = 120 • 52,6®(3 • 52,6®) = 40 г — масса коромысла, приведенная к оси клапана; тк = 120 г — масса коромысла.
Минимальная сила упругости пружин
Рпр mln = КМкл (/"о ~ /”а) ^кл®®Дт =
= 180-1,4(15—8,5)-52,6-293®-10-в/33,5 = 221 Н.
Жесткость пружин
с = Мкл^ = 180 • 1,4 - 293® - 10-е = 21,6 кН/м.
Деформация пружин:
предварительная
fmin = (/"о“/"а) ^кл/^т = (15 —— 8,5) • 52,6/33,5 = 10,2 мм;
полная
Алах = Anin 4" кклтах — 10,2 4“ 8,92 = 19,12 MM.
Распределение усилий между наружной и внутренней пружинами: внутренняя пружина
Рпр.в max = 0,35Рпртах = 0,35 • 414 = 145 Н;
Рпр.в min = 0,35РПрт1п = 0,35 • 221 = 77,4 Н;
наружная пружина
Рпр.в max = Рпр max Рпр.в max = 414 — 145 = 269 Н;
Рпр.в mln = Рпр mln ““ Рпр.в mln = 221 — 77,4= 143,6 Н.
Жесткость наружной и внутренней пружин
/-пр.в = Рпр.в max/fmax = 269 • 10 ®/(19,12 • 10 ®) = 14,06 кН/MJ
й,р.. = Рпр.в max/fmax = 145 • 10-®/(19,12 - Ю’») = 7,58 кН/м;
с = Спр.в 4“ /-пр. в = 14,06 4- 7,58 = 21,64 кН/м.
310
Рис. 118. Характеристика совместно работающих двух пружин
По найденным значениям
Рпр max — Рпр. в max. + Рпр. н max *
Рпр min = Рпр в min "l” ^пр.н min строится характеристика клапанных пружин (рис. 118).
Размеры пружин (приняты по конструктивным соображениям): диаметр проволоки 8прн = = 3,6 мм; 8пр.в = 2,4 мм;
средний диаметр пружин ^пр-н = 28 мм; £>вр.в = 19 мм;
dBT + ^пр.в + 2 = 14-|- 2,4 -|- 2 = 18,4 мм<£>пр.в = 19 мм; ^пр.в + 8Пр.в + ^пр.н + 2 = 19 + 2,4 + 3,6 + 2 = 27,0 MM<;Dnp>H =
= 28 мм (где диаметр втулки клапана dBT = 14 мм).
Число рабочих витков пружин
^пр.н ^тах 8,3-0,364• 1,912 г с
tp н — ~~ — 1 — О,OJ
₽ 8Р D3 8-269-10~6-2,83
'пр.н max'-пр.н *
Gftnp.B ^тах 8,3 • 0,244-1,912 с с
Р 8Р D3 8-145-10“6-1,93 'пр. в max пр в
где G =8,3 — модуль упругости второго рода, МН/см2; полное число витков пружин
«п.н = *р.н + 2 = 5,6 + 2 = 7,6; 1П.В = /р.в + 2 - 6,6 + 2 = 8,6; длина пружин при полностью открытом клапане
Lh min ~ Gx-н^пр.н + гр.н^тш = 7,6 • 3,6 + 5,6 • 0,3 = 29,1 мм;
Lemin = ^п.Лхр.в “И ^p.B^min = 8,6-2,4+ 6,6 0,3 = 22,6 мм;
Lmin = Lamin 29,1 ММ; длина пружин при закрытом клапане
Lq = Lmin + ^клтах 29,1 + 8,92 = 38,02 мм;
ЗП
длина свободных пружин
£н.св = £нт1п 4- /тах = 29,1 + 19,Г2 = 48,22 мм;
^«в.св = /«в mln 4" /тах = 22,6 4" 19,12 = 41,72 ММ.
Максимальные и минимальные напряжения в пружинах: внутренняя пружина
х.„ - - 1,17 ' = 595 МПа;
«»» З.Ц.2.Р-1<П
пр. в
тт1п = k'B ^р в^пр.3 = 1,17 8‘?7?4' 191°-‘ =318 МПа, "»3„р.в 3,14.2,4».10-»
где Ав =1,17 определен при = 19/2,4 = 7,9;
наружная пружина
Ттах = k'a = , 18 .8-_ 269.28.10-» =
^пр.н 3,14.3,63.10-»
_ £ ^,mnAp.« = , 18 8:.НЗ,6.28.1о-» =
3,14.3,63-10~»
где k'„ =1,18 определен при £>Пр.и^пр.н= 28/3,6 = 7,8.
Средние напряжения и амплитуды напряжений: внутренняя пружина
= (^ш« + тт1п)/2 = (595 + 318)/2 = 456,5 МПа;
та = (tmax — тт1п)/2 = (595 — 318)/2 = 138,5 МПа.
Так как концентрация напряжений в витках пружины учитывает* ся коэффициентом k', a k, /(емеп) « 1, то
так = /(®меп) = 138,5 • 1 =138,5 МПа;
наружная пружина
= (Ттах + Tmin)/2 = (485 + 259)/2 = 372 МПа;
То = (Ттах — тга)п)/2 = (485 — 259)/2 = 113 МПа;
'сак = ха= ПЗ МПа.
Запасы прочности пружин: внутренняя пружина
п* = x_tf(xaK + а, тт) = 350/(138,5 + 0,2 • 456,5) = 1,52, где ск = 0,2 определяется по табл. 43;
наружная пружина
Пг = т_1/(уак + а, хт) = 350/(113 + 0,2 • 372) = 1,87.
312
Расчет пружин на резонанс:
п0.в =2,17 • 1078np.B/(jp.B^np.B) = 2,17 • 107 • 2,4/(6,6 • 102) = 21 850;
«с.в/Яр = 21 850/2800 = 7,8 =?*= 1,2, 3...;
п0.и = 2,17 • 1078пР.н/(1р.н^р.н) = 2,17 107• 3,6/(5,6-282) = 17790;
«св/Яр = 17 790/2800 = 6,35 =^1,2,3...;
Яс.в/Яр “ 7,8 я0.и/пр = 6,35.
$ 67. РАСЧЕТ РАСПРЕДЕЛИТЕЛЬНОГО ВАЛА
Распределительные валы изготовляют из углеродистых (40, 45) или легированных (15Х, 12ХНЗА) сталей и легированных чугунов. При работе двигателя на распределительный вал со стороны клапанного привода действуют: сила упругости пружины Рпр.т, сила инерции деталей клапанного механизма Рут и сила давления газов Рг.т, приведенные к толкателю. Суммарная сила, действующая на кулачок со стороны клапанного привода:
Рт = Рпр.т + Р/т + Рг.т = (Рпр + рг) + М (389)
*т
Наибольшая сила Рт тах передается на кулачок от выпускного клапана в начальный период его открытия (чч = 0). Для выпуклого кулачка
Рт max
Рпр max 4----- (рг — Рг)
4 J
•у2- + МТ<£(Г'— Г0), (390) •т
где Рпр mm — сила упругости пружины при закрытом клапане, Н; dB — наружный диаметр тарелки выпускного клапана, м; рг— давление в цилиндре в момент начала открытия выпускного клапана (точка д'на рис. 35) для расчетного режима, Па; р/ — давление в выпускном трубопроводе (при выпуске в атмосферу р/« р0), Па; 1КЛ и /т — плечи коромысла, мм; сок — угловая скорость вращения распределительного вала, рад/с; rQ я г1 — соответственно радиусы начальной окружности и первого участка профиля кулачка, м;
Л4Т = Я1пр/3) (/
кл/^т )2 + тт + /гашт 4- т'к
— масса движущихся деталей механизма распределения, приведенная к толкателю, кг; ткл, тпр, тТ, и ml — соответственно массы клапана, пружин, толкателя, штанги и коромысла, кг; тк & тк (1КЛ 4-4- /т)2/(12/т2) — масса коромысла, приведенная к оси толкателя, при двуплечем рычаге с опорной стойкой в виде шпильки; ml « тк ^л/ /(3/?) — масса коромысла, приведенная к оси толкателя, при одноплечем рычаге с опорной стойкой в виде болта (см. рис. 112).
Основным расчетом распределительного вала является расчет на жесткость, который заключается в определении стрелы прогиба у под действием суммарной силы РттВх. Расчетная схема вала представ-
313
ляег собой свободно лежащую на опорах двухопорную разрезную балку; нагруженную в месте действия толкателя (рис. 119).
Стрела прогиба, мм
у = 0,8РТШах а^/[Е1(а4р — Зр)],
(391)
где а и b — расстояния от опор до точки приложения силы РттаХ> мм; I — расстояние между опорами вала, мм; dp и 8р — наружный и внутренний диаметры рас
пределительного вала, мм; Е — модуль упругости первого рода, МПа.
Величина прогиба у не должна превышать 0,02— 0,05 мм. Напряжения смятия, возникающие в местах контакта рабочих поверхностей
Рис, lift Расчетная схема распределительного вала
кулачка и толкателя, определяют для плоского и роликового толкателей:
асм х= 0,418 ]/PTmax£/(Vi) . (392)
асм = 0.418У(РТ „„£/(,,) (1Л + I/'i)> (393)
где Ьк — ширина кулачка, м; г — радиус ролика толкателя, м. Допускаемые напряжения смятия [осм] =400— 1200 МПа.
Кроме определения стрелы прогиба и напряжений смятия иногда определяют суммарные напряжения возникающие в распределительном вале от совместного действия изгибающего и скручивающего моментов. Напряжение изгиба
®из = Л4НЗ тах/^из = шах&« • 32/ (1 - 8£/ d«) I ]. (394)
Скручивающий момент от каждого кулачка обычно достигает максимальной величины в конце первого периода подъема толкателя, когда его точка касания с кулачком наиболее удалена от оси толкателя.
Для кулачка с выпуклым профилем и плоским толкателем
Мкр i max — (395)
Tpi max
ГДе (Рт)« = Рпр .т 4“ Р/т! ПрИ фр1 — фр max J /И — ” “ (Го -|-
т pl max Г1 — Г2
+ Аттах —G) Sin фр.
Для определения максимального скручивающего момента Мкртах от одновременного действия всех кулачков необходимо построить кривые набегающих моментов.
Напряжения скручивания и суммарное
<*тах = Мкртах/^7кр> (396)
314
eE — j/” Онз И- 4ттах > (397)
где Гкр = 0,5ГИз— момент сопротивления кручению расчетного сечения.
Величина ох не должна превышать 100 4- 150 МПа.
Расчет распределительного вала. Из расчета клапанной пружины (§66) и газораспределения (§65) имеем: массы подвижных деталей механизма газораспределения /икл = 115 г, тпр = 75 г, тТ — 0, =
= 0 и тк = 120 г; размеры кулачка г0 = 15 мм, rj = 57,2 мм, гг = = 8,5 мм, ЛттаХ = 5,68 мм; размеры коромысла /кл == 52,6 мм, =а = 33,5 мм; угловую скорость вращения распределительного вала (ок = 293 рад/с; минимальную силу упругости пружины Рлр mm = = 221 Н; диаметр горловины впускного клапана dTOP = 32,5 мм.
Максимальная сила от выпускного клапана, действующая на кулачок:
т max —
D
* пр гшп“1“ '
•~(рг —Рг) =
4 /т к
= [221 + ' °’0-332 (0,445 — 0,1) • 10*1 • + 444-293® (57,2 —
[4 J 33,5
— 15) • 10“® = 2417 Н,
/ 1 \ 35
где dB = I ——— I dB„ = = 33 мм — диаметр тарелки выпуск-
ного клапана; dBn = (1,06 4-1,12) drop = 1,076 • 32,5 = 35 мм — диаметр тарелки впускного клапана; рг = 0,445 МПа определяется по индикаторной диаграмме (точка Ь' на рис. 35); р'»ро=О,1 МПа;
М, = (/пкл + тпр/3) • (/кл//т)2 + тТ + тшт + тк =
= (115 + 75/3) • (52,6/33,5)2 + 99 = 444 г; тк = ткРкл/(3^) = = 120 • 52,6а/(3 • 33,52) = 99 г.
Стрела прогиба распределительного вала
= 0 8 Ртшах^Ь2 = 0 8 2417 • 262 • б92
у ’ El(d*p-^) ’ 2,2 • 106 95 (32< - 10«)
= 0,00029 мм,
где Е = 2,2 • 105 МПа — модуль упругости стали; I =а + Ь = = 26 + 69 = 95 мм — длина пролета распределительного вала (рис. 119), принята по конструктивным соображениям; dp = 2г0 + + 2 =2 • 15 + 2 = 32 мм — наружный диаметр вала; 8р = 10 мм— внутренний диаметр вала, принятый с учетом использования его для подвода смазки к кулачкам и сохранения достаточной жесткости.
Напряжение смятия
°см — 0,418P-tmax £/(6^1) —
= 0,418 /0,002417 • 2,2 • 105/(0,025 • 0,0572) = 255 МПа, где Ьк = 25 мм — ширина кулачка.
Часть четвертая СИСТЕМЫ ДВИГАТЕЛЕЙ
Глава XVI
НАДДУВ ДВИГАТЕЛЕЙ
§ ба. ОБЩИЕ СВЕДЕНИЯ
Анализ формулы эффективной мощности двигателя
Ав = Нр 2n W р (398)
показывает, что если принять неизмененными рабочий объем цилиндров и состав смеси, то величина Ne при п = const будет определяться отношением значением w и параметрами воздуха, поступающего в двигатель.
Так как массовый заряд воздуха GB( кг), остающегося в цилиндрах двигателя:
G* = Vnw, (399)
то выражение (398) можно записать в виде:
Ав = ' 2 —— GB. (400)
ZoflE t
Из уравнений (398)—(400) следует, что при увеличении плотности воздуха (наддува), поступившего в двигатель, эффективная мощность Ne значительно повышается.
Имеются и другие возможности повышения мощности N& однако по сравнению с наддувом они менее эффективны. Например, повышение мощности N9 за счет увеличения рабочего объема и числа цилиндров ухудшает массо-габаритные показатели двигателя. Увеличение же частоты вращения двигателя возможно только в случае сохранения качественного протекания рабочего процесса при высоких значениях коэффициента наполнения щу и механического к. п. д. т)м, что на практике осуществить чрезвычайно трудно.
Увеличение эффективной мощности двигателей путем наддува позволяет повысить массовое наполнение цилиндров двигателя и, следовательно, сжигать в двигателе большее количество топлива. Эффективный к. п. д. двигателя при наддуве также несколько повышается за счет увеличения давления цикла и уменьшения удельных потерь в результате использования части энергии выпускных газов двигателя в агрегатах наддува.
316
В соответствии с применяемой классификацией наддува различают двигатели: 1) с низким наддувом (мощность увеличивается менее чем на 30%);
2) со средним наддувом (мощность повышается от 30 до 45%);
3) с высоким наддувом (мощность повышается свыше 45%).
В настоящее время низкий, средний и высокий наддувы широко применяются в автомобильных и тракторных двигателях внутреннего сгорания как за рубежом, так и в Советском Союзе, обеспечивая этим самым необходимую форсировку двигателей.
$ 69. АГРЕГАТЫ И СИСТЕМЫ НАДДУВА
Форсирование двигателей по эффективному давлению за счет увеличения давления наддува предъявляет ряд требований к агрегатам, обеспечивающим дизель воздухом. Особенно важное значение имеет правильный выбор принципиальной схемы агрегата наддува и его конструктивное решение.
В настоящее время в транспортных ДВС применяют следующие системы наддува: инерционный; с механическим приводом нагнетателя; газотурбинный и комбинированный. При любой системе наддува общими условиями организации рабочего процесса в двигателе является достижение надежности и наивыгоднейших показателей работы.
Наиболее простой системой наддува является инерционная. Она позволяет использовать волновые процессы путем подбора соответствующих длин впускных и выпускных трубопроводов двигателя для увеличения количества воздуха, поступающего в цилиндры. В настоящее время инерционный наддув применяется редко, так как требуется сложная настройка впускной и выпускной систем.
Более часто используется система с механическим приводом нагнетателя (рис. 120, а). При этой системе наддува воздух подается нагнетателем, приводимым во вращение от коленчатого вала двигателя. В качестве наддувочного агрегата можно использовать центробежные, поршневые и роторно-шестеренчатые нагнетатели.
Рис. 120. Схемы наддува
317
Наддув по этой системе увеличивает мощность двигателя. Это происходит в том случае, когда прирост мощности от нагнетателя превышает мощность, потребляемую приводом. Следует отметить, что этот избыток мощности снижается по мере уменьшения нагрузки двигателя вследствие увеличения относительной работы, затрачиваемой на привод нагнетателя. Из-за расхода части полезной работы двигателя на привод нагнетателя его экономичность снижается. В качестве наддувочных агрегатов обычно используют нагнетатели объемного типа и центробежные компрессоры. Центробежные компрессоры компактны вследствие их большой быстроходности. Однако ненадежность механического привода центробежного компрессора и повышенная шумность агрегата при работе снижают его достоинства. Как правило, приводные центробежные компрессоры используют для наддува четырехтактных двигателей. В двухтактных двигателях наибольшее распространение имеют объемные нагнетатели типа Рут.
Некоторые недостатки, присущие системе с приводными нагнетателями не обнаруживаются в агрегатах с газотурбинным наддувом (рис. 120, б), объединяющих газовую турбину и компрессор (турбокомпрессор). В настоящее время этот способ наддува наиболее широко применяется в автомобильных и тракторных двигателях внутреннего сгорания.
Газовая турбина работает на выпускных газах двигателя, энергия которых используется турбиной для привода компрессора. Газовая связь турбины с двигателем обеспечивает наиболее приемлемую компоновку всего наддувочного агрегата и простоту его конструктивного выполнения.
Комбинированный наддув предусматривает наличие механического привода нагнетателя от двигателя и газовой связи с ним. Например, в схеме, приведенной на рис. 120, а, турбокомпрессор, выполняющий роль первой ступени наддува, механически не связан с двигателем, а вторая ступень компрессора является приводной от коленчатого вала двигателя.
В схеме, приведенной на рис. 120, а, вал турбокомпрессора механически связан с коленчатым валом двигателя. Такая компоновка позволяет при избытке мощности газовой турбины отдавать ее на коленчатый вал двигателя, а при недостатке — отбирать от двигателя. Если мощность газовой турбины и компрессора равна, то энергия не перераспределяется.
В настоящее время комбинированный наддув применяется в основном в двигателях большой мощности (судовые, тепловозные и др.).
В агрегатах турбонаддува применяют радиальные и осевые турбины и компрессоры. Осевые компрессоры не нашли широкого распространения при наддуве автомобильных и тракторных дизелей. Это объясняется в основном тем, что в малорасходных осевых компрессорах потери энергии значительны из-за малых высот сопловых и рабочих лопаток и относительно больших радиальных зазоров. Кроме того, в ступени осевого компрессора степень повышения давления лк < 1,3. Поэтому при более высоких значениях л «осевой компрессор должен быть многоступенчатым.
318
Таблица 67
Основные параметры и размеры Типоразмеры
ТКР-7 ТКР-8,5 ТКР-11 ТКР-14 TKP-18 ТКР-23
Номинальный базовый диаметр колеса компрессора, мм . . Степень повышения давления 70 1,3- 85 -1,9 по 1,3— 140 -2,5 180 1.3- 230 -3,5
Температура газов перед турбиной прв длительной работе, °C, не более .... 650
Максимальная температура газов перед турбиной, допускаемая в течение 1 ч, °C, не более 700
К. п. д. компрессо-сора на заданном режиме, не менее: с лопаточным диффузором .... с безлопаточным диффузором . . К. п. д. турбины, не менее Приме диффузо! 0,66 0,70 некие л оз за не реко 0,68 0,72 паточного мен дуется 0,70 0,74 0,75 0,72 0,74 0,76 0,72 0,76 0,78 0,74 0,76
Степень повышения давления в центробежных компрессорах значительно выше. В компрессорах высокофорсированных двигателей величина лк = 3,0 ч- 3,5. Возможно в одной ступени получить и более высокую степень повышения давления — 4,5—5,0.
Газовые турбины, как и компрессоры, могут быть радиальными и осевыми. В агрегатах газотурбинного наддува применяют оба типа турбин. Однако в большинстве случаев используют радиальные турбины, имеющие некоторые преимущества по сравнению с турбинами осевого типа.
В соответствии с ГОСТ 9658—66 в Советском Союзе турбокомпрессоры (ТК) выпускают двух типов— с осевой ТК (рис. 121, а) и центростремительной ТКР (рис. 121, б) турбинами. Для дизелей с эффективной мощностью 100—800 кВт применяют центробежные компрессоры и центростремительные турбины с наружным диаметром колес 70— 230 мм.
В табл. 67 приведены основные параметры и габаритные размеры турбокомпрессоров по ГОСТ 9658—66. Их выполняют с турбинами и
319
компрессорами при консольном расположении колес относительно опор (рис. 121) и используют в основном для наддува высокооборотных дизелей.
Одной из главных задач при внедрении газотурбинного наддува является создание оптимальных условий для более полного использования энергии выпускных газов.
В современных автомобильных и тракторных двигателях применяют следующие системы наддува: 1) импульсные — с переменным давлением газов в выпускном коллекторе; 2) изобарны е—
5)
.Входной патрубок турбины
3
4
Выходной SOOK ны
Вход Воздуха
1 7 6
Выход газа к Вход газа
Выходной патрубок турбины
1
5 Б
Рнс. 121. Схемы турбокомпрессоров:
а — с осевой турбиной (ТК); б — с радиальной центростремительной турбиной (ТКР); I — корпус ТК; 2 — центробежный компрессор; 3 — направляющий аппарат турбины;
4 — рабочие лопатки турбины; 5 — диск турбины; 6 — подшипники; 7 — ротор ТК
с постоянным давлением газов в выпускном коллекторе; 3) к о м б и -нированные — с разделенным выпускным коллектором и общим (изобарным) корпусом турбины.
При относительно малом уровне форсировки по наддуву более эффективна импульсная система.
Эффективность импульсной системы наддува можно повысить, например, за счет уменьшения объема трубопроводов, идущих от цилиндров к турбине. Это позволяет повысить эффективную мощность дизеля и его экономичность на большую величину, чем при наддуве с постоянным давлением газов.
Для обеспечения высокой степени использования энергии импульсов входной аппарат турбины проектируют многосекционным (два, четыре и т. д.) и выпуск газов производят в многосекционный коллектор с учетом чередования вспышек в цилиндрах. При такой системе наддува уменьшается давление в конце такта выпуска и снижается величина насосных потерь.
Таким образом, применение импульсной системы при относительно малом объеме трубопроводов и умеренном наддуве несколько улучшает мощностные и экономические характеристики двигателей по сравнению с системой наддува при постоянном давлении. Однако использование системы наддува при постоянном давлении значительно упро
320
щает конструкцию выпускной системы. Поэтому для каждого конкретного случая выбор системы осуществляют с обязательным учетом ее преимуществ и недостатков.
§ 70. ОСНОВЫ РАСЧЕТА ТУРБОКОМПРЕССОРА
Технико-экономические показатели дизелей с наддувом в большой степени зависят от выбора геометрических и конструктивных параметров элементов проточной части турбокомпрессоров. Определение геометрических размеров элементов турбины и компрессора и их параметров, обеспечивающих требуемую производительность и напор при заданной эффективности, и является целью проведения газодинамического расчета.
Компрессор
В настоящее время наиболее распространенным типом центробежного компрессора, применяемого для турбокомпрессоров, является радиально-осевой компрессор полуоткрытого типа с радиальным расположением лопаток на выходе из рабочего колеса.
На рис. 122 представлена схема проточной части центробежного компрессора с лопаточным диффузором. Основными конструктивными элементами компрессора (рис. 122) являются входное устройство 1, рабочее колесо 2, диффузор 3 и воздухосборник 4.
На рис. 122 буквой с обозначена абсолютная, w — относительная, и — окружность скорости. Сечение авх—авхсоответствует параметрам потока на входе в подводящий патрубок, I — I — перед входны
Рнс. 122. Схема проточной части центробежного компрессора с лопаточным диффузором
321
ми кромками лопаток, 11 — 11 за выходными кромками на диаметре £)2, Hl — HI на выходе из безлопаточного диффузора, IV — /V на выходе из лопаточного диффузора и V — V на выходе из воздухосборника. Окружные составляющие абсолютной скорости имеют индекс и, радиальные — г, осевые — а.
Компрессор рассчитывают для одного режима — или номинального или максимального крутящего момента.
Основными параметрами, характеризующими работу центробежной ступени, являются степень повышения давления в компрессоре и массовый расход воздуха (?в.
Эффективность ступени оценивается изоэнтропическим (адиабатическим) к. п.д. 7)ад.к — отношением работы адиабатического сжатия к действительной работе сжатия. При проектировании компрессора надо исходить из требований ГОСТ 9658—66, устанавливающего значения к. п. д. в зависимости от наружного диаметра D2 колеса компрессора (см. табл. 67).
Производительность компрессора (массовый расход воздуха через двигатель), кг/с, определяют по данным теплового расчета.
Объемный расход духа (нм3/с)
Qb — GB/pe, где ро — плотность духа, кг/м3.
Для расчета компрессора сначала задаются параметрами окружающей среды (см. § 8, гл. III).
Входное устройство и рабочее колесо. Температуры потока на выходе и входе патрубка компрессора (сечение I — / и аВх — аВ1, рис. 122) принимают равными, т. е. Тав1 = Т0К. Это условие выполняется, если пренебречь теплообменом с окружающей средой при движении воздуха от входного сечения патрубка к выходному.
Давление потока в сечении авт — апг Од ИХ
Ровх = Ро ^Рвс’ где Дрвс = 0,002 -j- 0,006 — потери давления на преодо
Рис. 123. Расходные характеристики турбокомпрессоров типов ТК (а) и ТКР (б) по ГОСТ 9658—66
ВОЗ-
(401) воз-
322
ление сопротивлений на всасывании в компрессор, МПа. Величина Арвс зависит в основном от сопротивления воздушного фильтра и трубопроводов.
С целью снижения потерь энергии во входном устройстве ему придают форму конфузора, обеспечивающего непрерывное ускорение потока вдоль оси входного патрубка. Для осевого и коленообразного патрубков отношение между площадями входного и выходного сечений = 1.3-т-2,0, а для радиально-кругового FaBX/Ft = 2,0 ч- 3, 5.
Для определения степени повышения давления лк в компрессоре кроме давления равх необходимо знать величину давления воздуха рк на выходе из него: «к = рн/ рОвх.
По значениям QB и л к (рис. 123) определяют типоразмер турбокомпрессора, а по табл. 67 — номинальный базовый диаметр колеса компрессора Е>2.
Для оценки напорных качеств компрессора используют коэффициент напора Над.к, характеризующий эффективность использования окружной скорости колеса для совершения адиабатической работы сжатия и представляющий отношение адиабатической работы сжатия Z-ад.к (Дж/кг) к квадрату окружной скорости и2(м/с) на наружном диаметре колеса: _
Ндд.к — Ьад.к I ^2 > (402)'
где
Ьад.к = RBTa ( я/'* - 1) . (403>
й — 1 вх \ у
__ Для полуоткрытых осерадиальных колес коэффициент напора Яад.к = 0,56 — 0,64 и зависит от наружного диаметра колеса D2, окружной скорости U2 и качества профилирования проточной части* компрессора. Меньшие значения Яад к принимают для колес с О2 = ~ 70 4- ПО мм, более высокие — с D2 > ПО мм. В компрессорных ступенях с лопаточным диффузором величина Яад.к выше на 0,02—0,04, чем при безлопаточном диффузоре.
Окружная скорость и% на наружном диаметре рабочего колеса определяется из уравнения (402)
^2 ‘' ^ад.к'^ад.к •
Величина окружной скорости колеса зависит от степени повышения' давления воздуха в компрессоре л к. В высоконапорных компрессорах ц2 = 250—500 м/с. Частота вращения компрессора пк = 60 u2/(nD2) об/мин.
Параметры воздуха в выходном сечении / — / (рис. 122) патрубка можно определить, если задаться абсолютной скоростью Ci потока в этом сечении. Величина абсолютной скорости Cf потока перед колесом, может изменяться в широких пределах (ci = 604- 150 м/с). Б6льшие> значения абсолютной скорости а принимают для компрессоров с высокими окружными скоростями («2 = 3004- 500 м/с). При осевом? входе потока осевая составляющая абсолютной скорости с1а перед колесом принимается равной абсолютной скорости т. е. с1а — ъ.
323’
Температура воздуха на входе в колесо (сечение I — /)
—k—w
гдеcp —теплоемкость воздуха при постоянном давлении, Дж/(кг • К).
Относительные потери в воздухоподводящем патрубке компрессора оценивают коэффициентом потерь 5ВХ. Для патрубков с осевым входом = 0,03-е-0,05, для коленообразных патрубков £Вх = 0,10 ч-Ч- 0,15. Задавшись величиной определяют потери в воздухоподводящем патрубке компрессора (Дж/кг):
LrM = М/2. (405)
Показатель политропы пвх на участке входа воздуха в компрессор определяют из выражения
_Д»1_ = ----------------- (406)
«вх-1 Л-1 Лв^-Тв,,)
Давление воздуха перед колесом компрессора
Площадь Fi (м2) поперечного сечения входа в рабочее колесо при известном-значении pj определяют по расходу воздуха GB и абсолютной скорости ci потока в сечении / — /:
Fi = GB/(c1P1).
Диаметр рабочего колеса (м) на входе в компрессор
£>! = ]/---------------------,
У 0,785 [1 - (Do/D^q
где Do — диаметр втулки рабочего колеса, м.
Величина D0IDi в выполненных конструкциях изменяется в пределах 0,25—0,60.
Диаметр О0 втулки колеса
Dq —
Одним из основных конструктивных параметров компрессора является отношение Di/Dz, называемое относительным диаметром колеса на входе. Для большинства созданных конструкций центробежных компрессоров £>1/02 = 0,5 ч- 0,7. Отношение Di/D2 выбирают предельно наибольшим для уменьшения габаритных размеров компрессора.
По известным значениям Di и Do определяют средний диаметр на входе в колесо
D10p = / (Di + Di)/2
324
и относительный средний диаметр входного сечения колеса
^1ср ^1ср/^2*
Работа, затрачиваемая на сжатие воздуха в компрессоре, его к. п.д. и напор зависят от числа лопаток колеса. Строгих и однозначных рекомендаций по выбору числа лопаток нет. В выполненных конструкциях компрессоров для иаддува автомобильных и тракторных двигателей гк—12-4 16, для колес малых диаметров (£>2 = 70-4 ~ 100 мм) принимают меньшие значения гк.
При бесконечном числе лопаток работа сжатия (Дж/кг) без закрутки потока на входе в колесо
Хп = ^2 •
При конечном числе лопаток работа сжатия Ln отличается от работы Ьл. Это отличие оценивают коэффициентом мощности
4 — LjLn = ^2u/^2* (407)
Коэффициент мощности р для осерадиальных колес в области расчетных режимов можно определить с достаточной точностью по формуле П. К. Казанджана
Р =-----——‘--------j-----. (408)
i+— -----------!-----
3 гк ’-PlcpW
Из выражения (407) следует, что окружная составляющая абсолютной скорости на выходе из колеса с2и ~ Радиальная скорость с2т определяется из заданного соотношения с2т!и2. В выполненных компрессорах с2г — (0,25-4 0,40)и2 м/с. Абсолютная скорость (м/с) воздуха на выходе из колеса находится из треугольника скоростей (рис. 122): с2 = у clu + Обычно с2 = (0,90-4 0,97) и2 м/с.
Температуру воздуха (К) на выходе из рабочего колеса можно определить из уравнения
Т2 - Л + (!л + az - |л2/2) н|/ср, (409)
где — коэффициент дисковых потерь (для полуоткрытых колес az;= 0,04-4 0,08).
При определений давления р2 воздушного потока на выходе из колеса величину показателя политропы сжатия воздуха ик определяют по эмпирическим зависимостям или принимают по опытным данным. В выполненных конструкциях компрессоров ик — 1,4-4 1,6.
Давление воздуха за колесом
ра = Р1(Л/Л)Пк/(Лк-,). (410)
По значениям р2 и Т"2 можно определить величину плотности р2 воздушного потока и найти ширину (м) рабочих лопаток колеса на диаметре D2 (см. рис. 122):
325
bt — GB/(irZ)jCjrpj). (411)
Относительная ширина лопаток b2 *= b2/D2. Максимальный к.п.д, компрессора обычно обеспечивается при Ь2;= 0,04-;- 0,07.
Существующие малоразмерные компрессоры выполняют с относительной шириной колеса В B/D2 = 0,25-? 0,35. Ширина колеса В зависит в основном от технологии изготовления и геометрических размеров колеса. Чем меньше D2, тем труднее обеспечить плавный поворот потока в меридиональном сечении, тем шире должно быть колесо. Ориентировочно можно принять В 0,3 при D2 > 110 мм и В >0,3 при D2 с 110 мм. Однако увеличение В свыше 0,35 не приводит к заметному повышению к. п. д. компрессора.
Диффузоры и воздухосборник. Воздушный поток на выходе из колеса имеет высокую кинетическую энергию. В диффузоре кинетическая энергия преобразуется в потенциальную за счет торможения потока.
Ширина Ь3 безлопаточной части диффузора принимается по известному значению высоты Ь2 лопаток компрессора на выходе, т. е. Ь3 ^= = (0,90-г- 1,0) Ь2. Если за безлопаточным диффузором следует лопаточный, то принимают Ь8 ~ Ь2.
Наружный диаметр D3 безлопаточного диффузора D8s==(l,05-? -? 1,20) D2. При отсутствии лопаточного диффузора D3 — 1,4-? 1,8.
Абсолютная скорость (м/с) на выходе из безлопаточного диффузора в первом приближении
„ _ С2 Ь2
С3 — ~ •
D3 6з
(412)
В компрессорах, в которых за безлопаточным следует лопаточный диффузор, отношение с2/с3 = 1,08 —1,25. При одном безлопаточном диффузоре с2/с3 — 1,65 4- 2,2.
При газодинамическом расчете лопаточного диффузора по принятым конструктивным размерам определяют температуру, давление и скорость движения воздушного потока в межлопаточных каналах.
Применение лопаточного диффузора позволяет повысить максимальное значение к. п. д. и коэффициента напора компрессора по сравнению с безлопаточным диффузором за счет уменьшения потерь.
Наружный диаметр D4 лопаточного диффузора определяют в зависимости от величины D2, т. е. О4 = (1,35 4- 1,70) D2. Ширину 64 лопаточного диффузора на выходе принимают равной Ь3 или несколько большей, т. е. 64 > Ь3. Если велики потери на трение, желательно выполнять диффузор со стенками, расходящимися под углом v = = 54- 6°.
Ширина (м) лопаточного диффузора на выходе
b4 = b3 + (Dt — D3) tg v/2. (413)
Давление за лопаточным диффузором
Р4 ~ Ра вхкк*
326
Для определения температуры Т* необходимо определить величину показателя политропы сжатия пд в диффузоре. В щелевом и лопаточном диффузорах лд = 1,6-г- 1,8.
Температура (К) за диффузором
Л = Л(Р4/Р2)(Пд"1)/Пд.
Скорость воздушного потока (м/с) на выходе из лопаточного диффузора определяют из уравнения энергии:
с4 = /с1-(Л-Т2) • 2ср . (414)
Из лопаточного диффузора центробежного компрессора воздух поступает в воздухосборник, позволяющий подвести поток к впускному трубопроводу с минимальными потерями энергии.
Из применяемых воздухосборников наибольший к. п. д. имеет воздухосборник, выполненный в виде несимметричной улитки.
Площадь поперечного сечения воздухосборника в выходном сечении иногда принимают такой, чтобы скорость воздуха была равна или близка его скорости на выходе из лопаточного диффузора, т. е. с4 « cs.
Потери напора £гУЛ (Дж/кг) в улитке (воздухосборнике)
ЬГУЛ = и4/2, (415)
где 5ул==0,14- 0,3 — коэффициент потерь в улитке.
Имея в виду, что с6 « с4, температуру Т5 на выходе из улитки с известным приближением можно принять равной температуре Т4 на выходе из лопаточного диффузора, т. е. Тл « 7\.
Давление (МПа) на выходе из улитки
=
^гул
k__I \ £/(£—1)
k)
(416)
Скорость потока в улитке можно понизить, выполнив выходной патрубок воздухосборника диффузорным (рис. 124). В этом случае
несколько повышается давление р5.
Основные параметры компрессора. Давление р5 на выходе из улитки компрессора соответствует давлению рк наддувочного воздуха перед входом во впускной трубопровод двигателя, т. е. принимают Рь = рк.
Полученное давление р5 на выходе из компрессора не должно отличаться от принятого в тепловом расчете двигателя давления рк более чем на 2—4%. В противном случае необходимо произвести повторный расчет компрессора, изменив па
Рис. 124. Схема улитки
раметры, определяющие его напор.
327
Действительная степень повышения давления в компрессоре 7ГК = рй/РавХ = Рк/РавХ •
Адиабатическая работа (Дж/кг), определенная по действительной степени повышения давления:
Адиабатический к. п. д. компрессора
Лад.к = то ( - 1 )/(Т8 - то). (417)
Полученное значение к. п. д. компрессора должно удовлетворять требованиям ГОСТ 9658—66 (табл. 67) для нагнетателей данного типоразмера.
Коэффициент напора
7/ад.к == Z-ад .к / ^2 •
Величина //ад.к не должна отличаться от принятого в расчете Яад.к более чем на 2—4%.
Мощность (кВт), затрачиваемая на привод компрессора:
к = ^ад.к 0в/(1000т|ад.к)’ (418}
Газовая турбина
В комбинированных двигателях внутреннего сгорания применяют осевые и радиальные турбины. В автомобильных и тракторных двигателях в основном используют малоразмерные одноступенчатые радиальные турбины. При небольших расходах газа и высоких окружных скоростях радиальные турбины имеют более высокий к. п. д., чем осевые. Поэтому в соответствии с ГОСТ 9658—66 радиальные турбины применяют для турбокомпрессоров ТКР - 7 — ТКР-23 (см. табл. 67). Осевые турбины применяют при диаметрах колес турбокомпрессоров 180 мм и выше.
Входной направляющий аппарат малоразмерных турбин для автомобильных и тракторных двигателей может быть лопаточным или без-лопаточным. При безлопаточном направляющем аппарате расчетные параметры газового потока на входе в рабочее колесо обеспечиваются специальным профилированием улиточной части корпуса турбины.
Рабочие колеса газовых турбин выполняются обычно осерадиальными (рис. 125). Такая конструкция колеса обеспечивает наиболее полное срабатывание энергии выпускных газов.
На рис. 125 буквой с обозначены абсолютные скорости, w — относительные, и — окружные. Сечение 0 —0 относится к параметрам газа перед турбиной, / — / — на выходе газа из направляющего аппарата (перед входными кромками рабочих лопаток), II — II — к параметрам газа за турбиной. Окружные составляющие абсолютной скорости имеют индекс и, радиальные — г и осевые — а.
328
Вид A
Рис. 125. Схема проточной части радиальной турбины
При газодинамическом расчете турбины исходными данными являются результаты предыдущих расчетов (теплового расчета двигателя и компрессора).
В свободном турбокомпрессоре совместная работа газовой турбины и компрессора обеспечивается:
при соответствии частоты вращения ротора турбины частоте вращения ротора компрессора:
= ик,
при равенстве мощностей турбины и компрессора:
N, = лгк;
при наличии определенной зависимости между расходами газа через турбину Gr, воздуха через компрессор GB и воздуха и топлива через двигатель:
Gr=GB(l +-------7—), (419)
где Gr — количество выпускных газов, поступающих на турбину от двигателя, кг/с.
Температуру газов перед турбиной можно определить по данным теплового расчета двигателя из уравнения теплового баланса по температуре выпускных газов Тр. Величина Тр зависит в основном от параметров газа в конце процесса расширения, от коэффициента избытка воздуха а, давления в ресивере, теплообмена в выпускном тракте и Других факторов. Точно определить температуру Тр газа трудно, поэтому ее находят по приближенной зависимости без учета работы газов в цилиндре во время выпуска и гидравлических потерь в выпускных органах:
329
j Г p 1
Tp== m 41+Jr(W-1)l’ (420)
где 1,3— 1,5 — средний показатель политропы расширения газов в цилиндре во время выпуска; рр — давление газа в выпускном патрубке, МПа.
Температуру выпускных газов /р, состоящих из смеси отработавших газов с продувочным воздухом, определяют методом последовательных приближений из выражения
' ' __НоСр *р + ср(<рп—1)/к СпГр ------- —--------- ,
+ Тп — *
где ср, ср, ср — мольные теплоемкости соответственно продуктов сгорания при температуре /р, воздуха при температуре /к и смеси продуктов сгорания с воздухом при температуре /р.
Температуру 7\ газа перед турбиной с известным приближением можно принять равной температуре выпускных газов Тр, т. е. 7\ == = Тр. Необходимо иметь в виду, что температура газа перед турбиной при длительной работе двигателя не должна превосходить допустимых значений, указанных в табл. 67.
Противодавление р2 за турбиной обычно принимают на основании опытных данных. Величина р2 зависит в основном от длины и конфигурации отводящего трубопровода и гидравлических сопротивлений глушителя.
Для оценки к. п. д. турбины т]т можно воспользоваться рекомендациями ГОСТ 9658—66 (табл. 67) в соответствии с принятым типоразмером турбокомпрессора (см. расчет компрессора). Общий к. п. д. т|т турбины включает все механические потери в турбокомпрессоре.
Эффективность турбокомпрессора оценивают коэффициентом полезного действия, представляющим собой произведение к. п. д. турбины и компрессора.
Таким образом, к. п. д. турбокомпрессора
'’Qtk = ^тЛад.к • (421)
Для современных турбокомпрессоров т]тк = 0,48 4- 0,62.
Давление рт газа перед турбиной определяют из баланса мощности на валу турбокомпрессора (AfK = /V т)-
-------------, (422) fer-i L„!A yr/(*r-i) ’
^т^ад к /
где т]т — общий к. п. д. турбины (принимается ориентировочно).
Направляющий аппарат. В направляющем аппарате турбин автомобильных и тракторных двигателей обычно срабатывается лишь часть подводимой энергии газа. Поэтому они являются реактивными. Перераспределение теплоперепада в ступени турбины характеризуется степенью реактивности рт, которая представляет отношение теплопе-
330
репада, срабатываемого в рабочем колесе, к общему теплоперепаду. Для радиально-осевых турбин оптимальная степень реактивности Рт = 0,454- 0,55.
Полная адиабатическая работа расширения газа (Дж/кг) в турбине
£ад.т = Ьад.к GB/(TQTTQaA.K Gr). (423)
Адиабатическая работа расширения в направляющем аппарате
Lc = (1 Рт) Lax,? .
Абсолютная скорость (м/с) газа перед рабочим колесом
ct = 4>cV2re, (424)
где <рс — коэффициент скорости, учитывающий потери в направляющем аппарате. Для радиально-осевых турбин с диаметром колес 80—180 мм <рс = 0,92-г- 0,96.
После нахождения абсолютной скорости Сх определяют температуру 1\ газа на выходе из направляющего аппарата (сопла):
7^ — у1_________fl_____
1 Т 2Мг/(*г “ 1)
Характер течения газа в проточной части направляющего аппарата турбины определяется числом Маха:
/И1 = cja, = Oi/Vk^Ti, (425)
где ах — скорость звука, м/с.
Если /И1< 1, то поток газа —дозвуковой и сопло турбины должно быть конфузорного типа (суживающееся).
Для определения радиальной с1г и окружной ciu составляющих абсолютной скорости сх необходимо задаться величиной угла выхода газового потока из направляющего аппарата. Величина угла сц изменяется в широких пределах (сц= 124- 27°) и принимается исходя из условия получения максимального значения к. п. д. турбины.
Радиальная и окружная составляющие абсолютной скорости газа (м/с) перед рабочим колесом (рис. 125)
с1г “ ci s*n а11 с1и = Ci cos а1*
Окружной скоростью их на наружном диаметре колеса обычно задаются, стремясь обеспечить оптимальную величину параметра быстроходности турбины:
X = Ui/Сад, (426)
где сад = 'К2£ад.к — условная адиабатическая скорость истечения газа, м/с.
Значение х должно находиться в диапазоне 0,65 —0,70. Величину их обычно принимают несколько большей скорости tzlu, чтобы повысить
331
к. п. д. турбины. При этом условии угол входа потока на лопатки рабочего колеса будет больше 90°:
Pi = 90°-f-arctg ~ С1“ .
С1Г
Значение Pi должно находиться в интервале 75—110°. Если 110°< < 75°, то необходимо скорректировать <xt и р,.
Относительная скорость потока (м/с)
Wi = clr /sin Pi.
Наружный диаметр (м) рабочего колеса
Di = 60ui/(itnT).
Входной диаметр направляющего аппарата определяется величиной D0/Di, которая в выполненных конструкциях турбин изменяется в пределах 1,3—1,5:
= Di (Dq/Dj).
В рассматриваемых типах турбин число направляющих лопаток ti < 20.
Потери энергии в направляющем аппарате (Дж/кг) зависят от Ci и <рс:
AL0 = (1/<р?-1) с?/2. (427)
Установив величину потерь ALC, можно найти отношение
_!к_ = _Л_ ----------4^---- (428)
пс-\ fer-l /?r(TT-Ti) V ’
и, следовательно, определить давление газа на выходе из направляющего аппарата
Р1 = рт(7,1/7’т)Пе/(Пе-,), где пе — показатель политропы расширения в направляющем аппарате.
Плотность газового потока (кг/м8) на выходе из направляющего аппарата
Pi = Pi • 10»ВД-
Ширина лопаток (м) направляющего аппарата определяется из уравнения неразрывности:
Ь{ = Gr/(irDiPiCi sin aj. (429)
Рабочее колесо. В межлопаточных каналах одноступенчатого рабочего колеса процесс преобразования потенциальной энергии газового потока в кинетическую заканчивается.
Величина адиабатической работы расширения газа в колесе турбины определяется степенью ее реактивности:
/-Рк = Рт^ад.т1 (^30)
332
Конструктивные параметры рабочего колеса приведены в табл. 68.
Таблица 68
Наименование
Формула
Пределы изменения
Внутренний диаметр
Втулочный диаметр
Среднеквадратичный диаметр колеса на выходе
Ширина лопаток колеса на входе
Ширина колеса
= 0,24-0,3
В — = 0,304-0,35
Для радиально-осевых колес с диаметром Dt = 704- 140 мм число лопаток составляет z2 = 104-18. Рекомендуется колеса с наружным диаметром 01 = 704-85 мм проектировать с числом лопаток г2 = = 104-12, ас диаметром Dt = НО 4- 140 мм —с числом лопаток г2= 134- 18.
Относительная средняя скорость газа на выходе из рабочего колеса
а>2 = V wl + 2Lpx — u? (1 — ^ср) , (431)
где ф — коэффициент скорости, учитывающий потери в рабочем колесе турбины (для осерадиальных турбин ф = 0,80-4- 0,85); D2cp — = D^IDi —относительный среднеквадратичный диаметр колеса на выходе.
Величина окружной скорости колеса (м/с)
^2Ср ^1^2ср/^Г
Считая выход потока газа осевым (с2 = с2а), из треугольника скоростей (см. рис. 125) находят величину абсолютной скорости (м/с) на выходе из колеса
с2 = ]/ ^2 — и2ср.
Температура газа (К) на выходе из колеса
(432)
где =б,04-т-0,08 —коэффициент дисковых потерь.
333
Адиабатический к. п. д. турбины без учета потерь с выходной скоростью
Т1ад'т = т и _Г(р /р/V-DMr]' * (433)
Если учесть потери с выходной скоростью, то
Лад.т = Лад.т с|/(21»ад.т)-
Доля потери с выходной скоростью при отсутствии диффузора и больших углах <4 может быть весьма значительной.
Общий к. п. д. турбины определяется с учетом всех гидравлических и механических потерь:
“Пт ~ Лад.т 'Птк.мех »
где г]тк.мех — механический к. п. д. турбокомпрессора (для автомобильных и тракторных турбокомпрессоров г]тК .мех — 0,92 4- 0,96).
Расчетное значение величины г]т не должно отличаться более чем на 2—4% от ранее принятого значения при определении адиабатической работы газа в турбине [см. формулу (422)]. В противном случае требуется повторить расчет, изменив газодинамические и конструктивные параметры турбины.
Мощность, развиваемая турбиной (кВт):
Л/т = 1ад.тСг'*!т/1000 (434)
должна соответствовать мощности NKt потребляемой компрессором, т. е. NT != NK.
§ 71. ПРИБЛИЖЕННЫЙ РАСЧЕТ КОМПРЕССОРА И ТУРБИНЫ
Выбрать основные параметры и рассчитать турбокомпрессор для четырехтактного дизеля мощностью Ne s= 233 кВт при частоте вращения п «= 2600 об/мин. Тепловой расчет двигателя приведен в гл. IV. §18.
Расчет компрессора. Параметры окружающей среды и физические константы для воздуха приняты по данным теплового расчета (см. гл. III, §8). Компрессор радиально-осевой с лопаточным диффузором, одноступенчатый.
Массовый расход воздуха через двигатель
G = ^nl0Nege = 1,7-1,0-14,452-233-220 = Q „ в 36 • 10s 36-106 ’